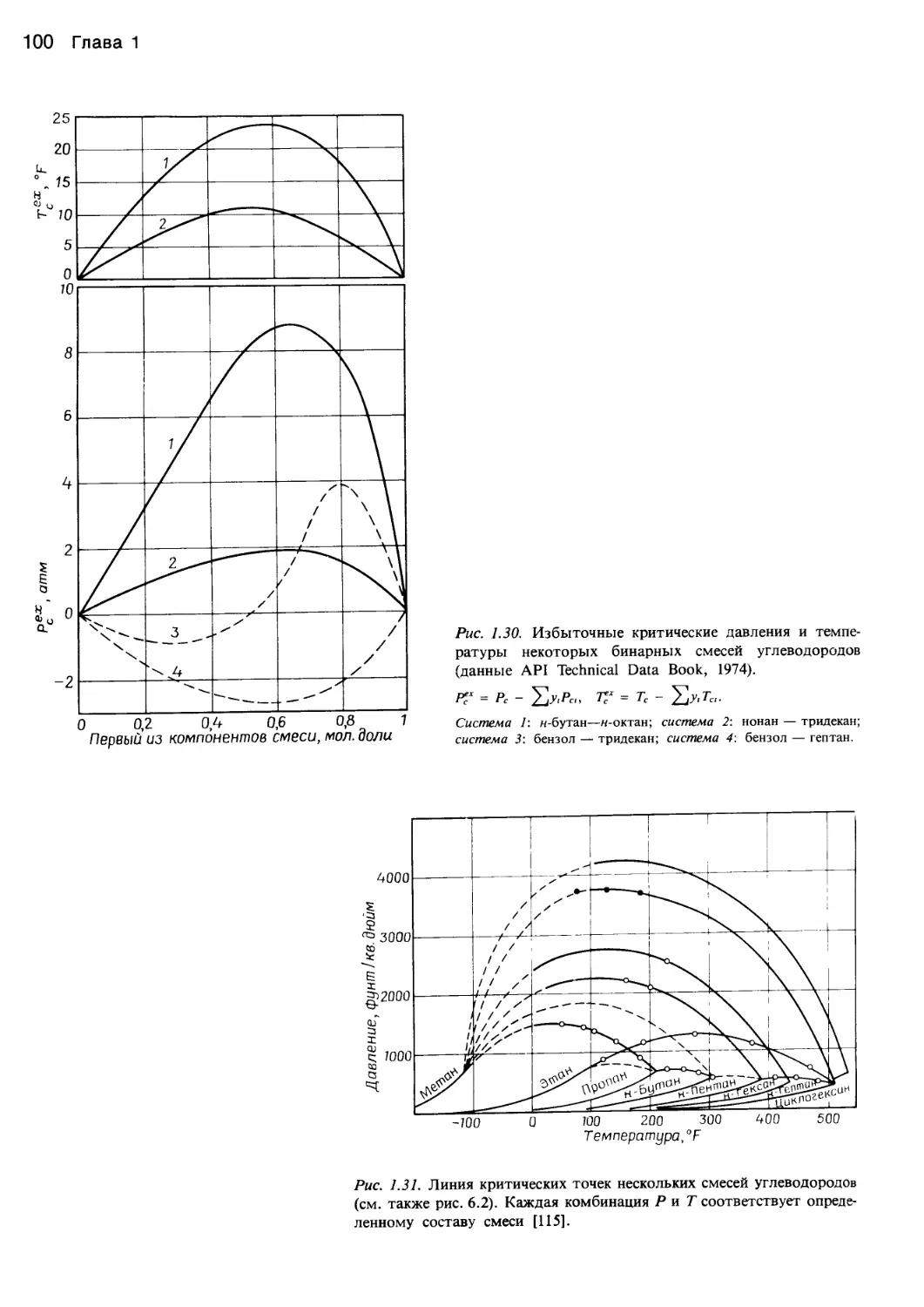
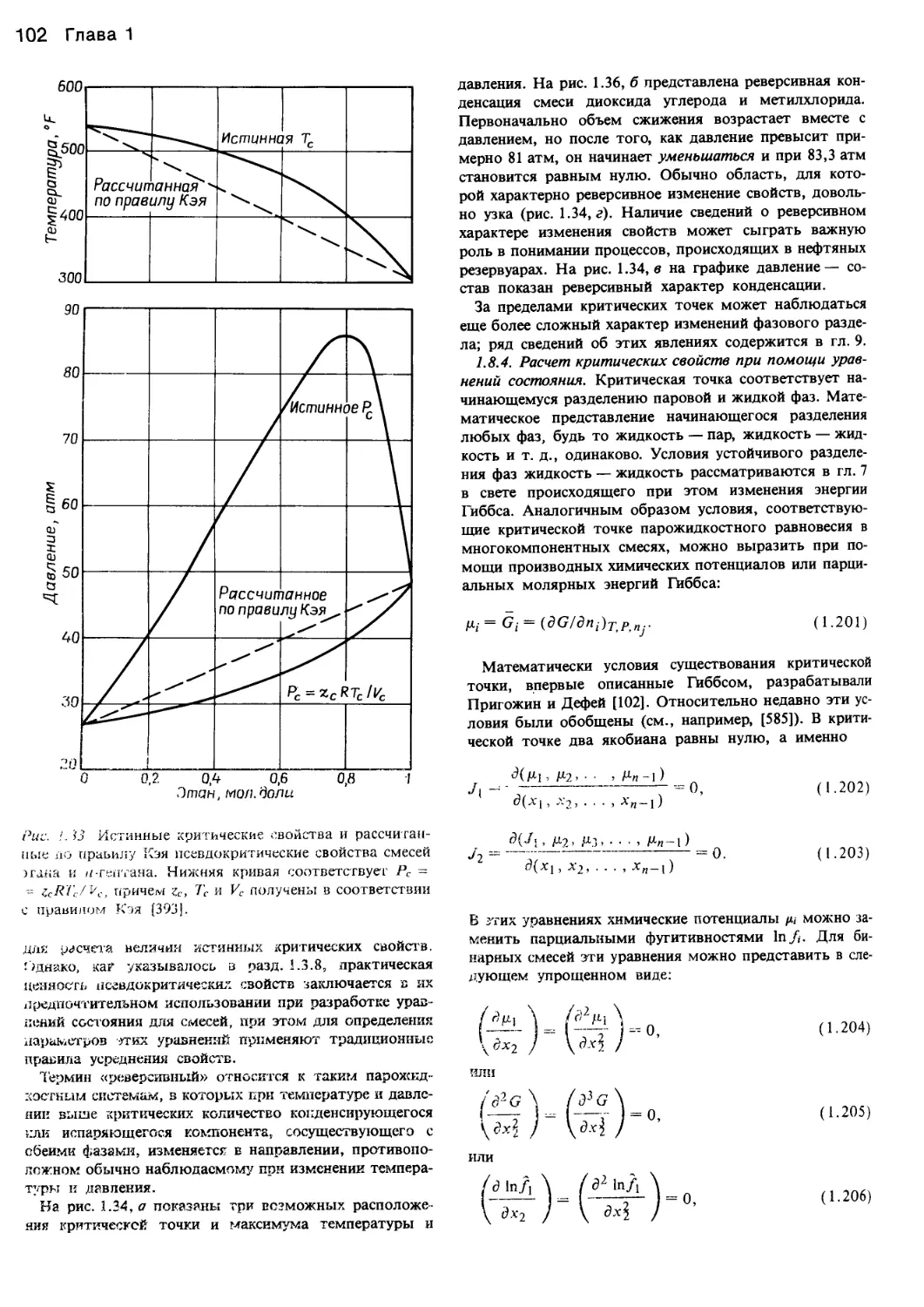
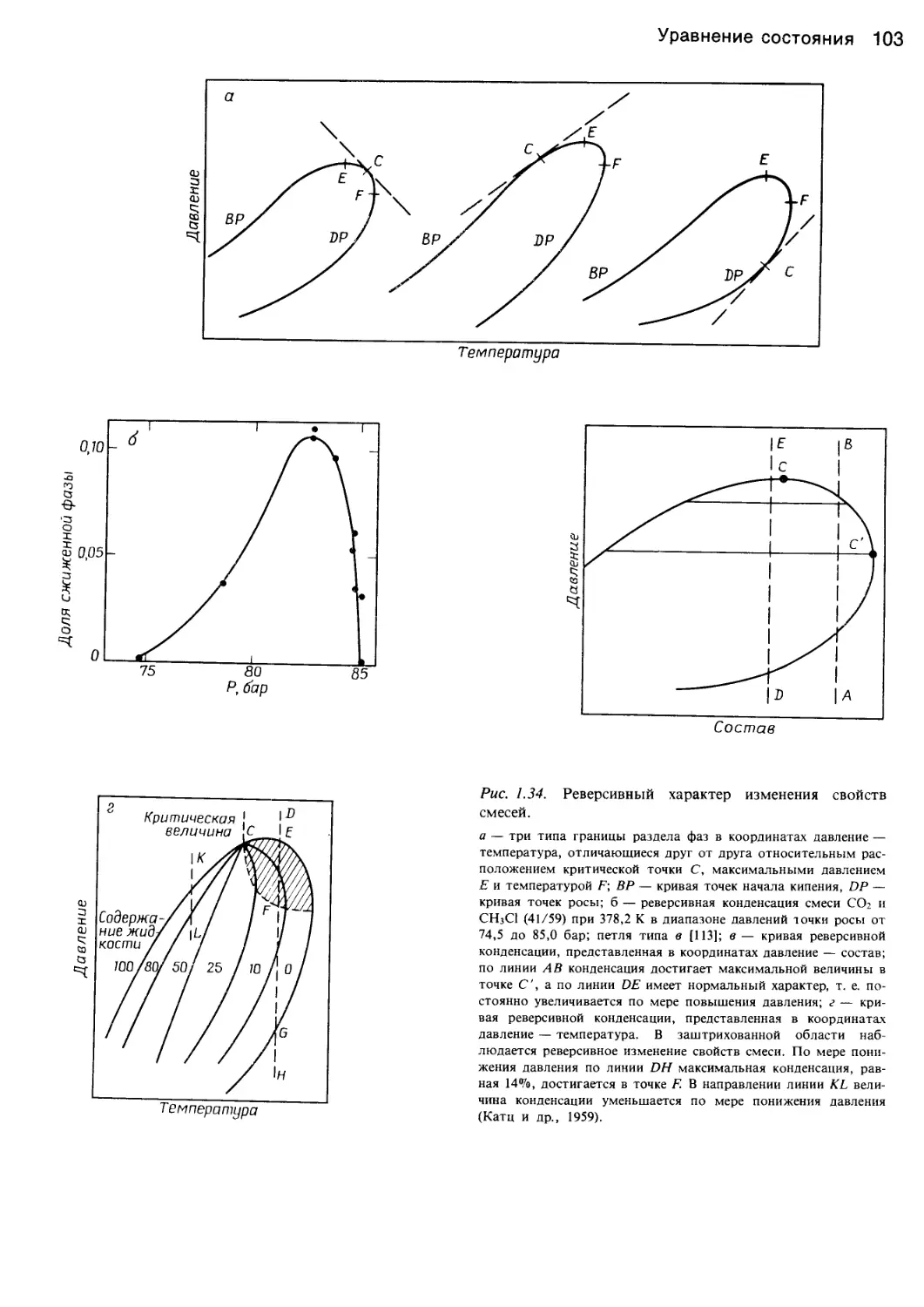
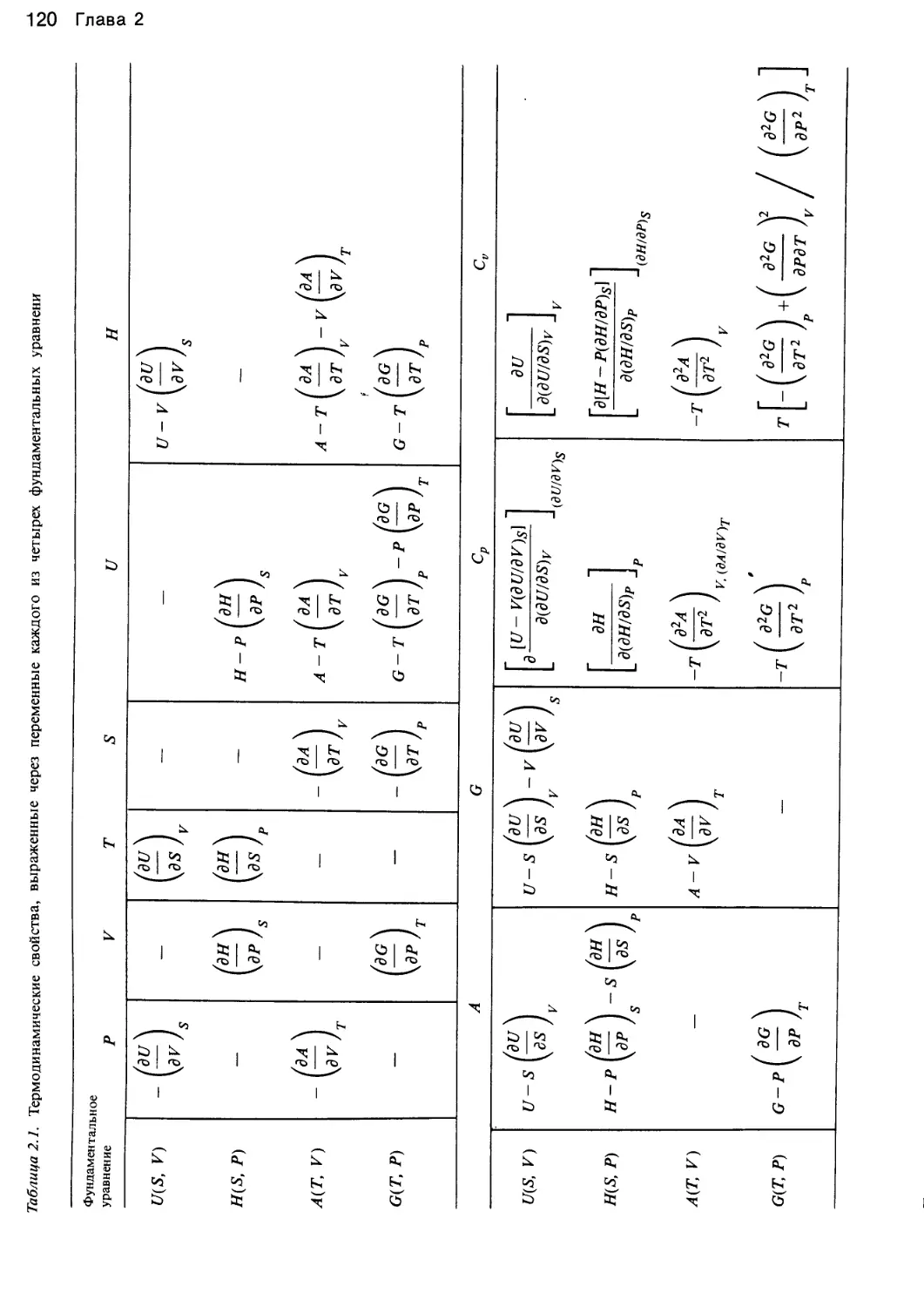
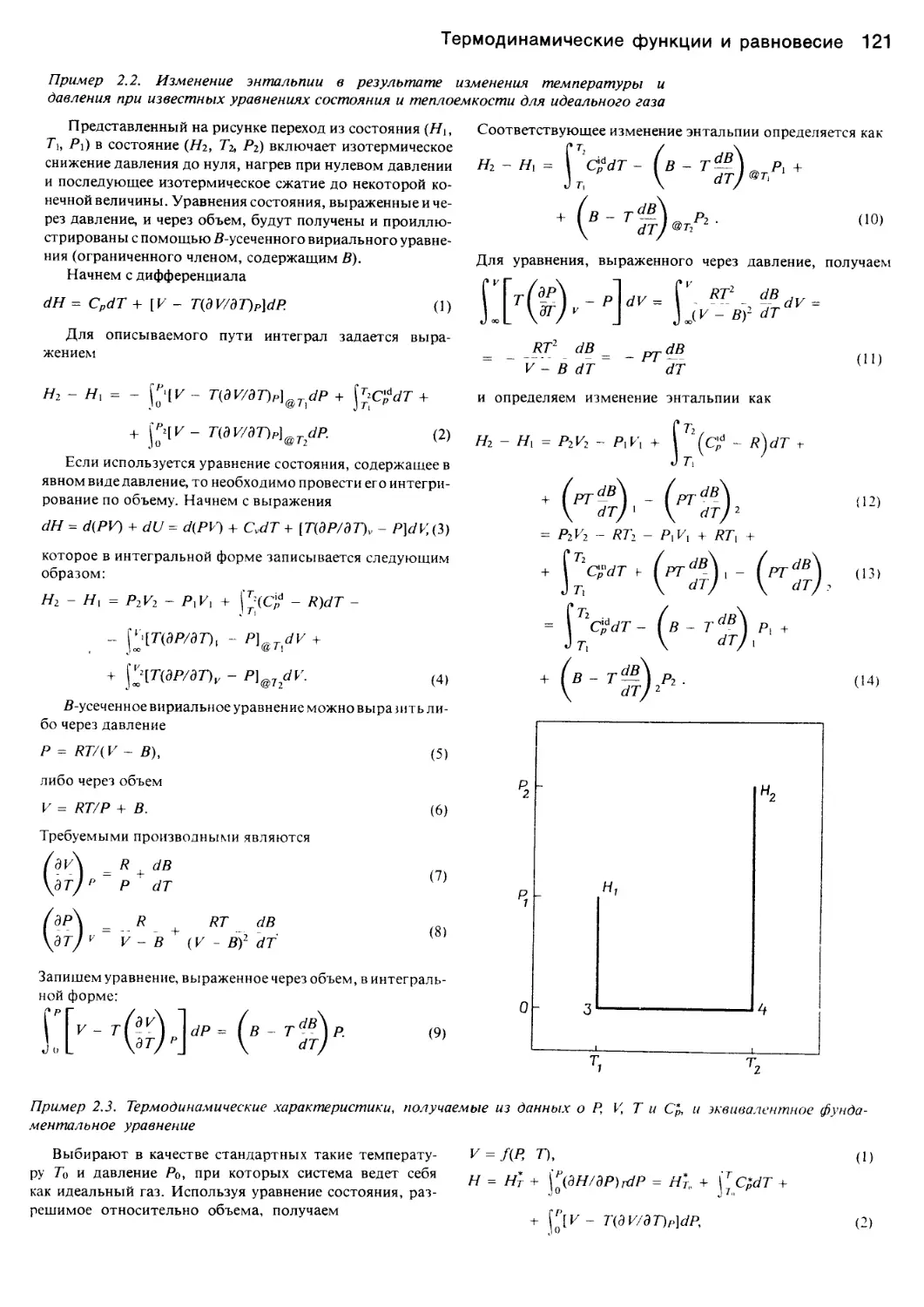
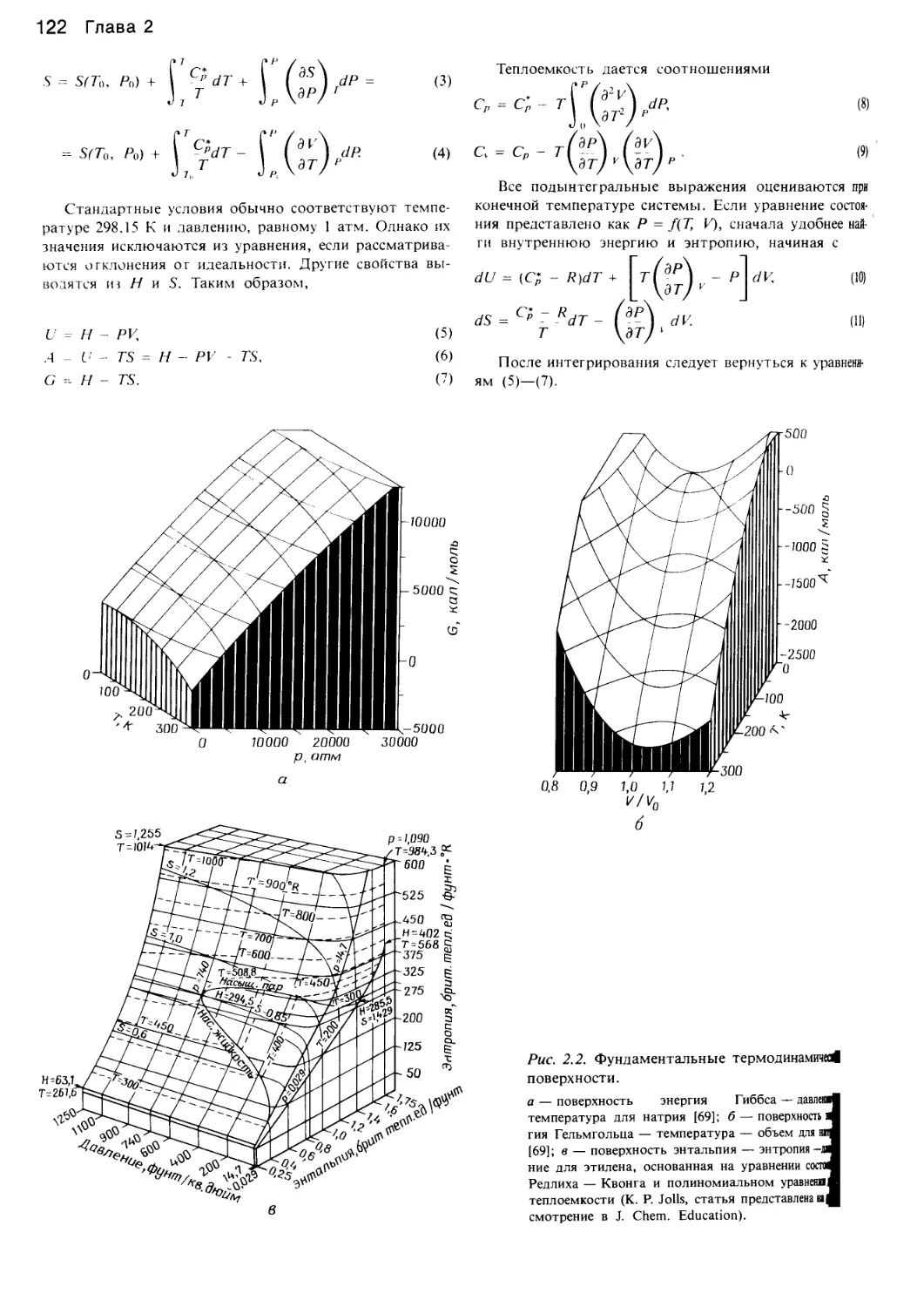
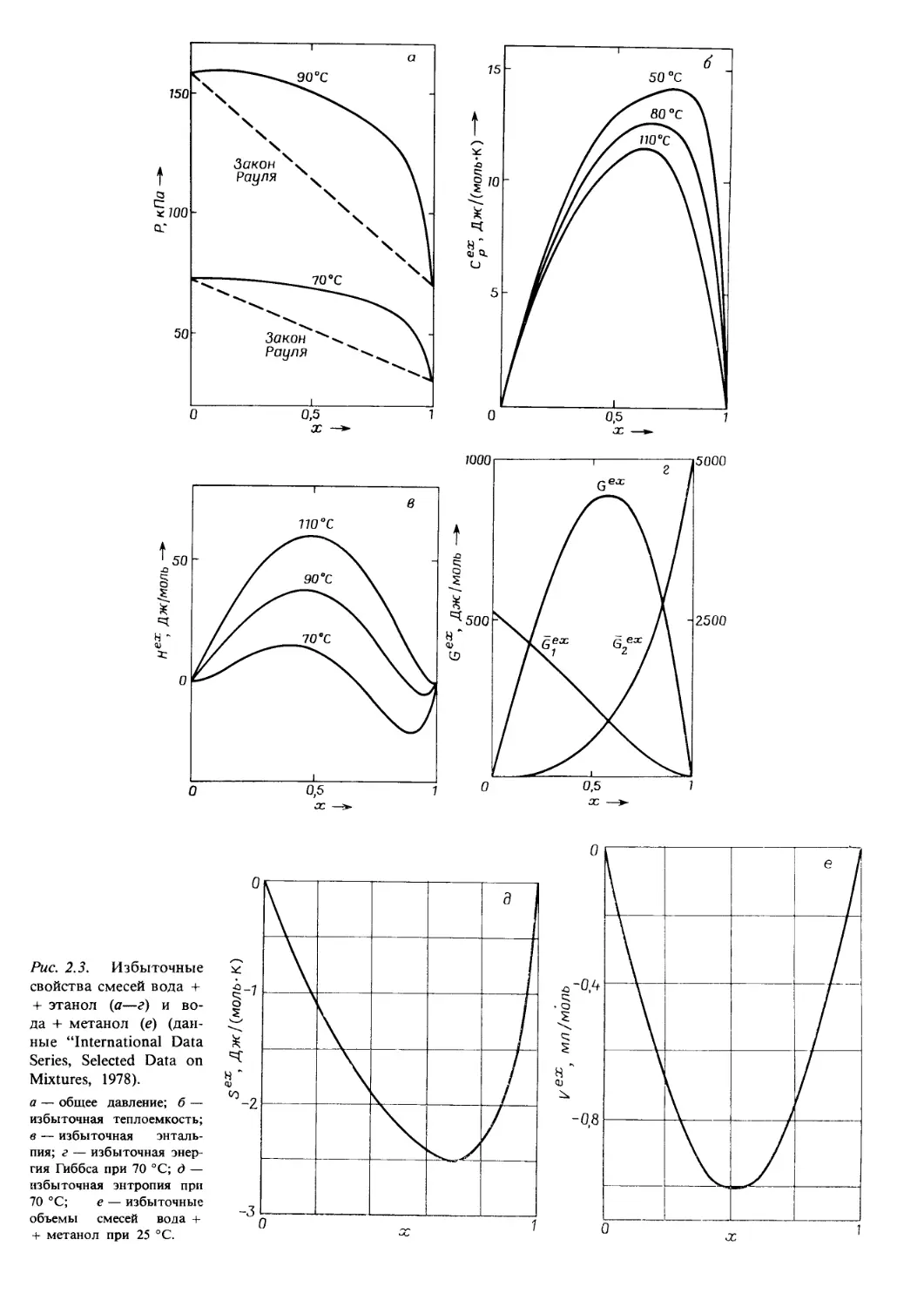
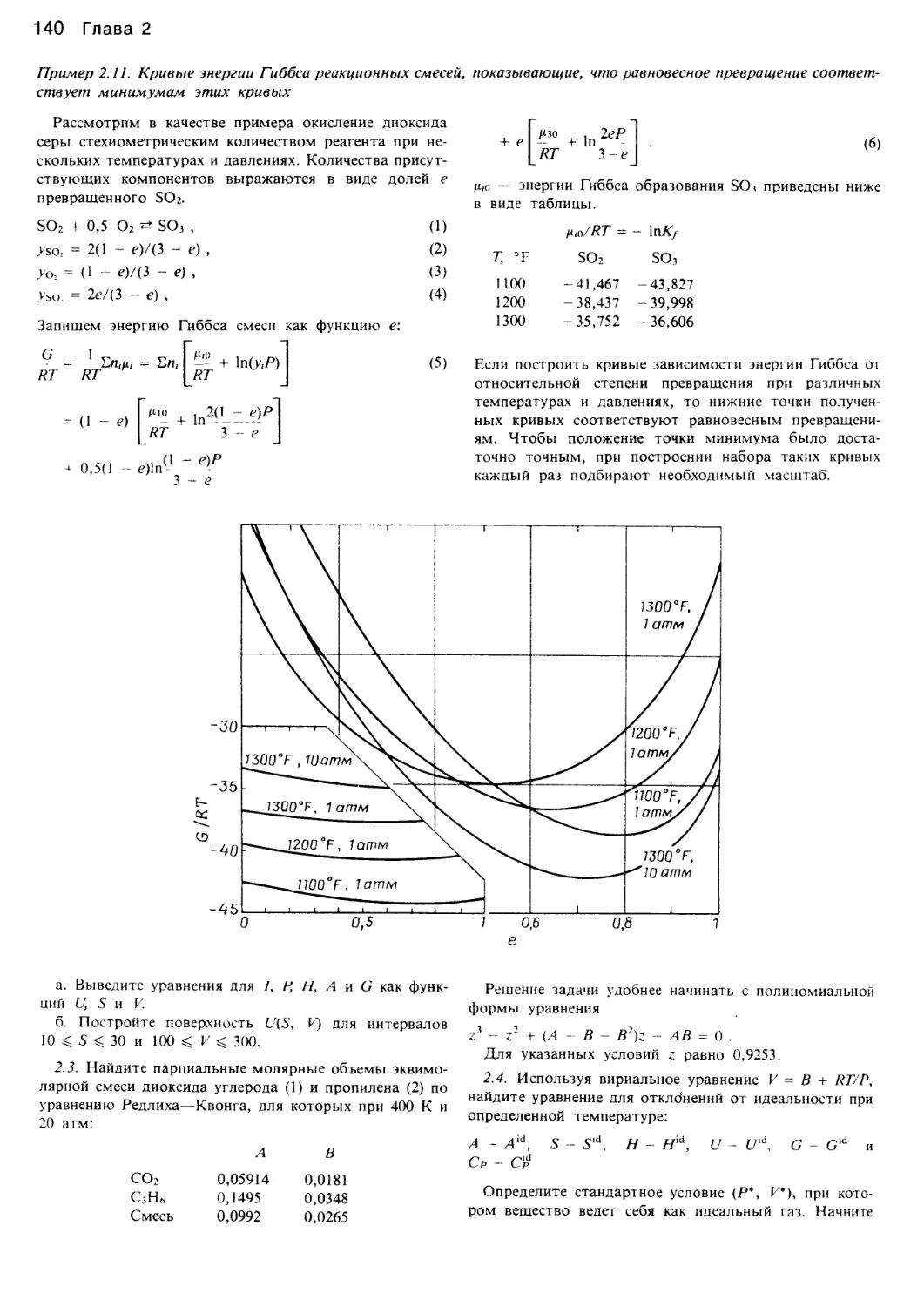
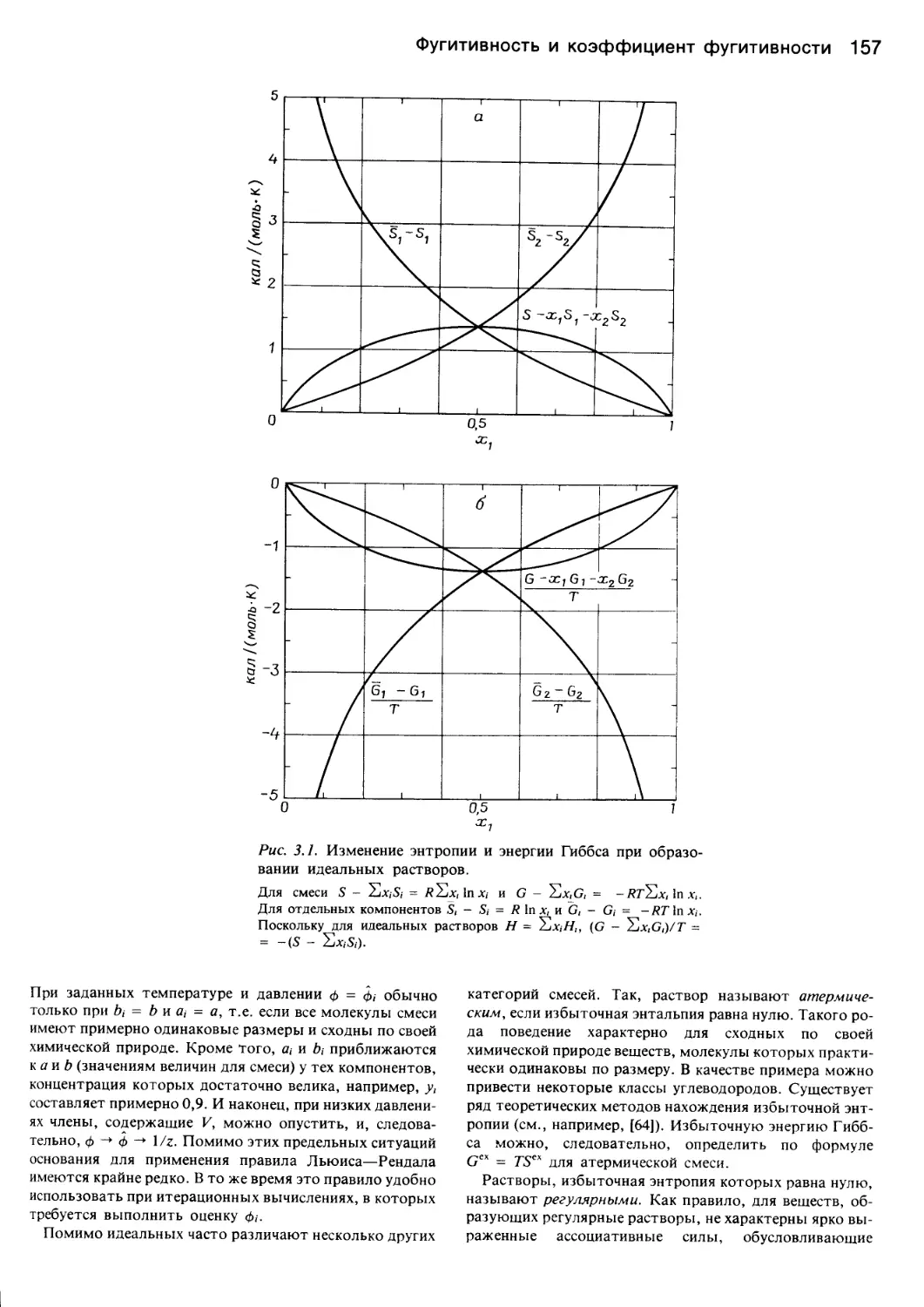
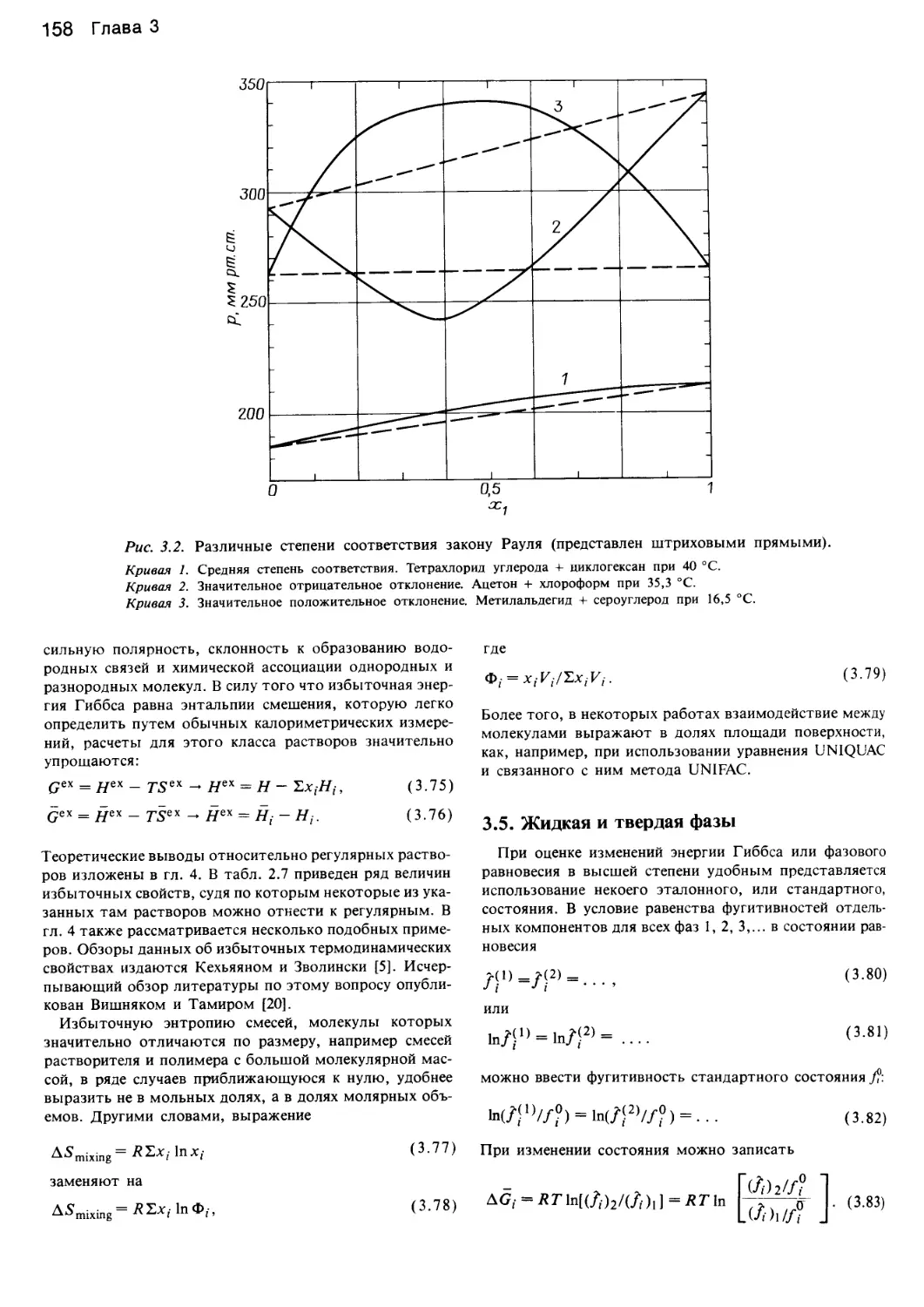
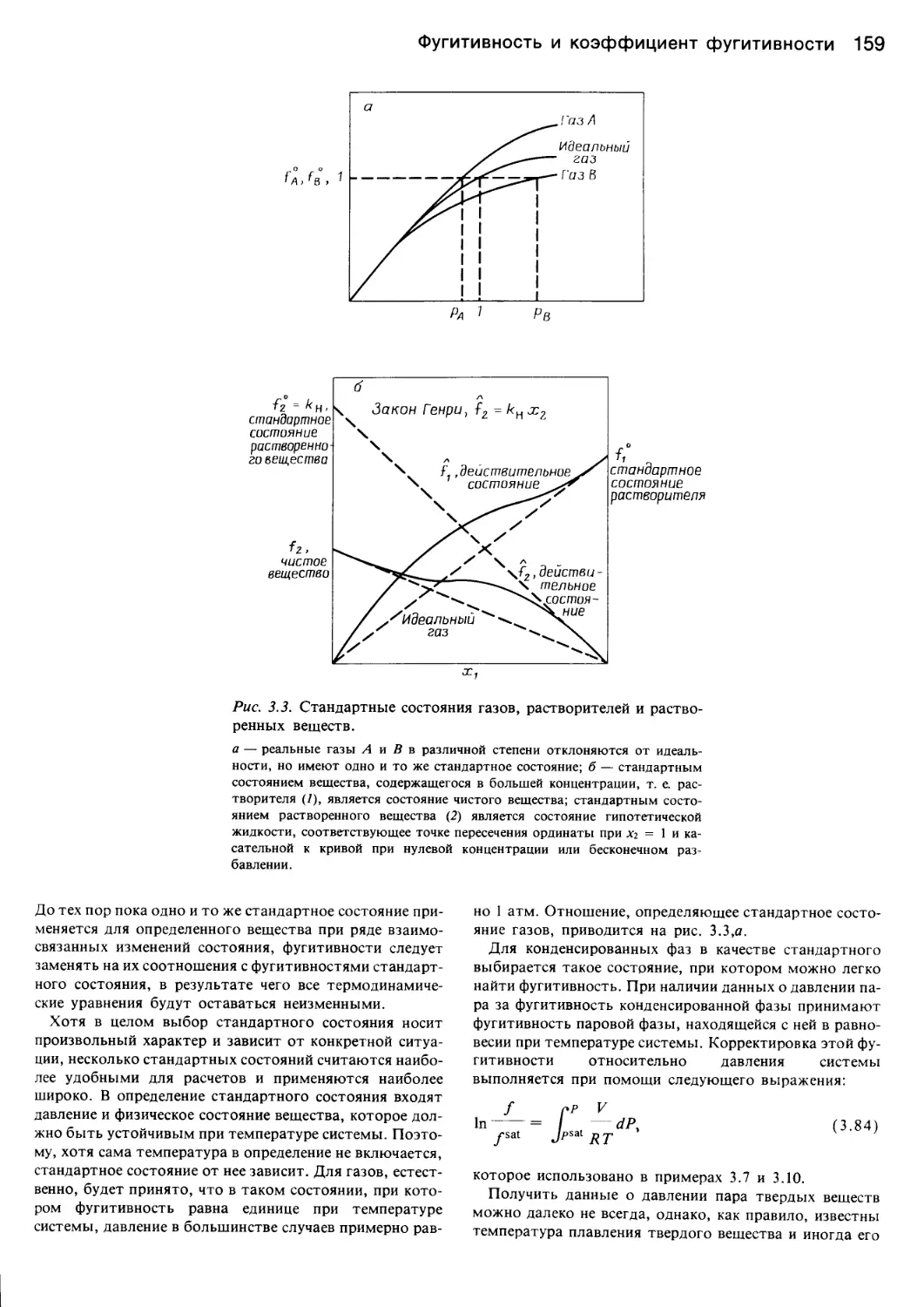
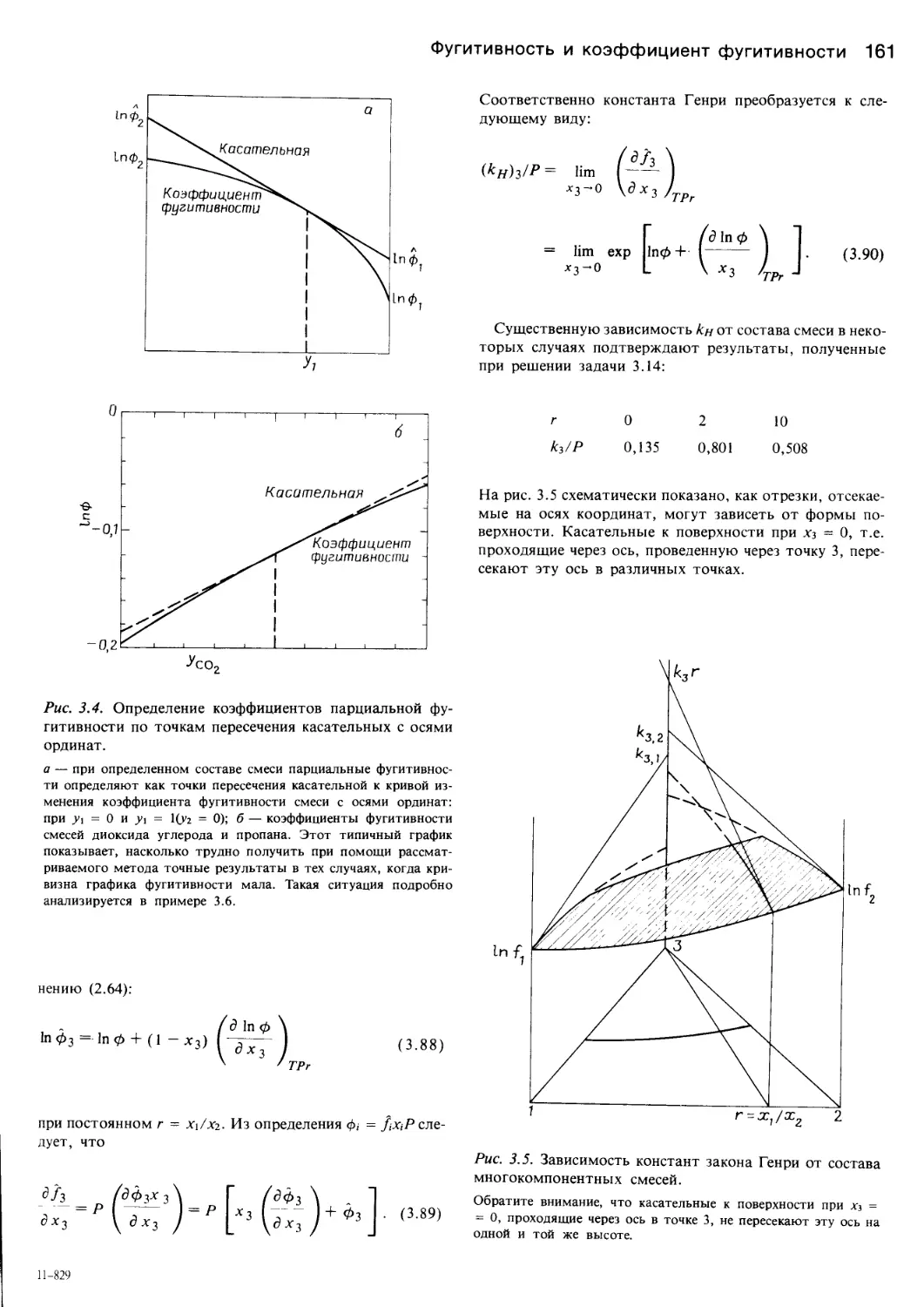
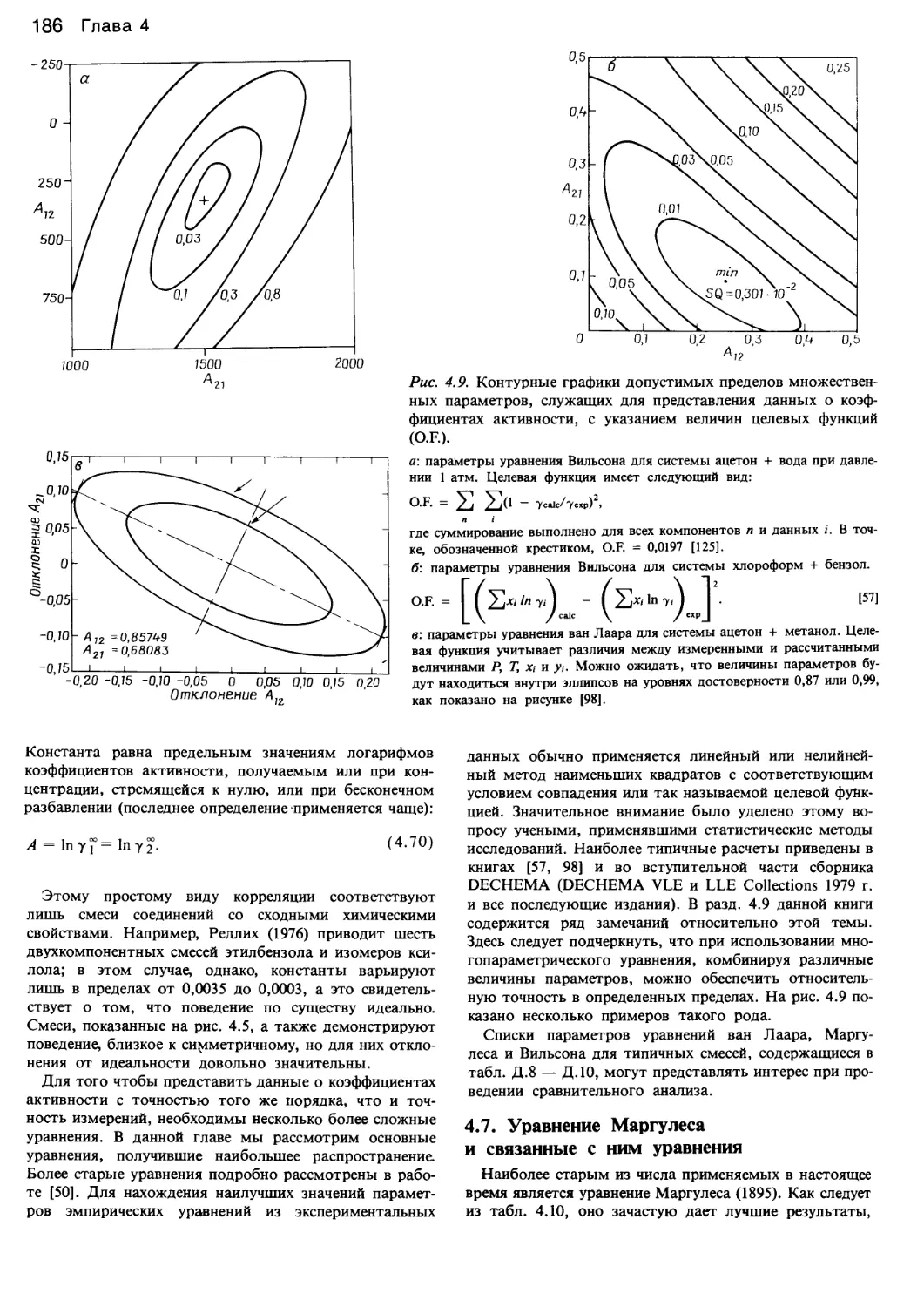
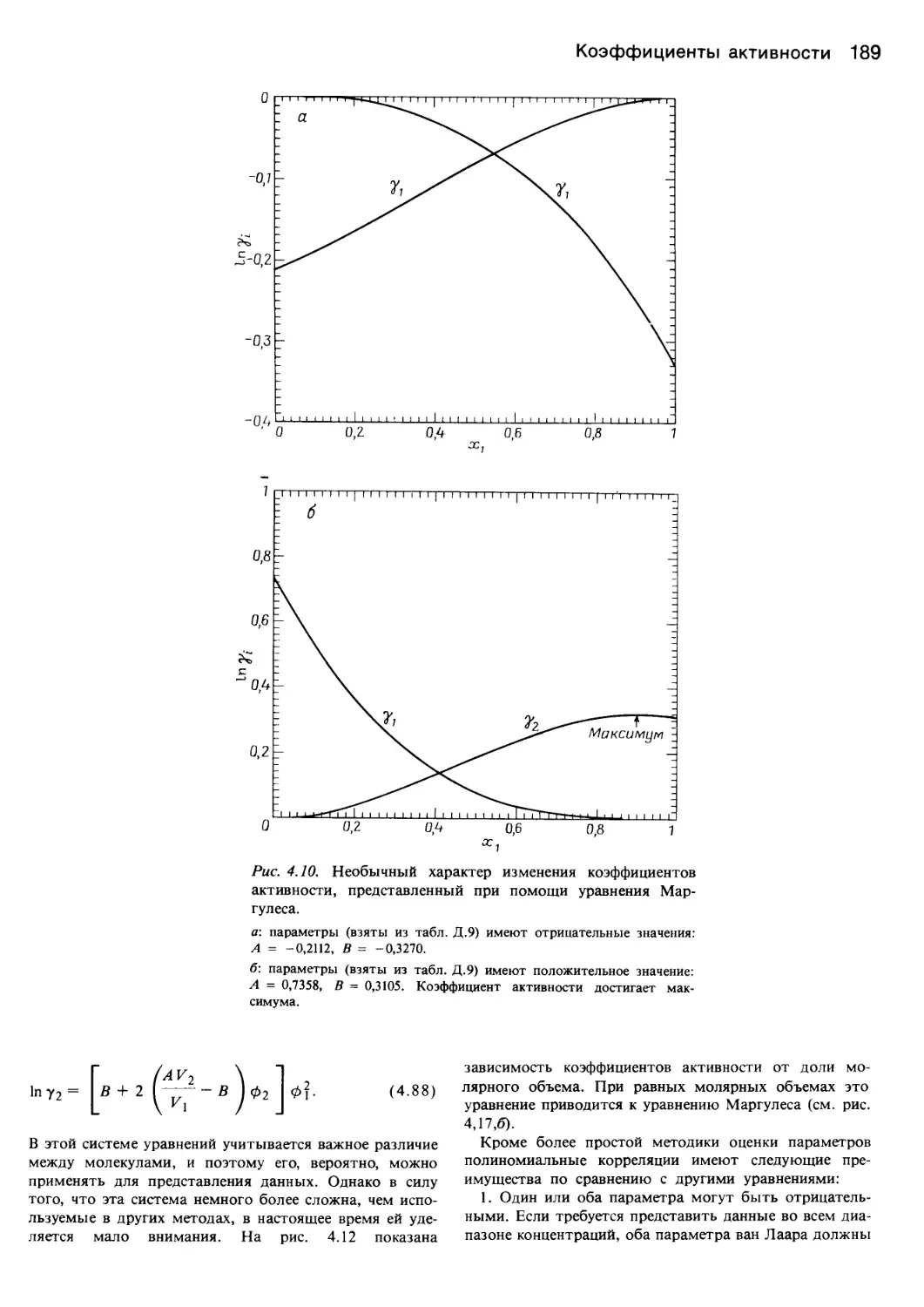
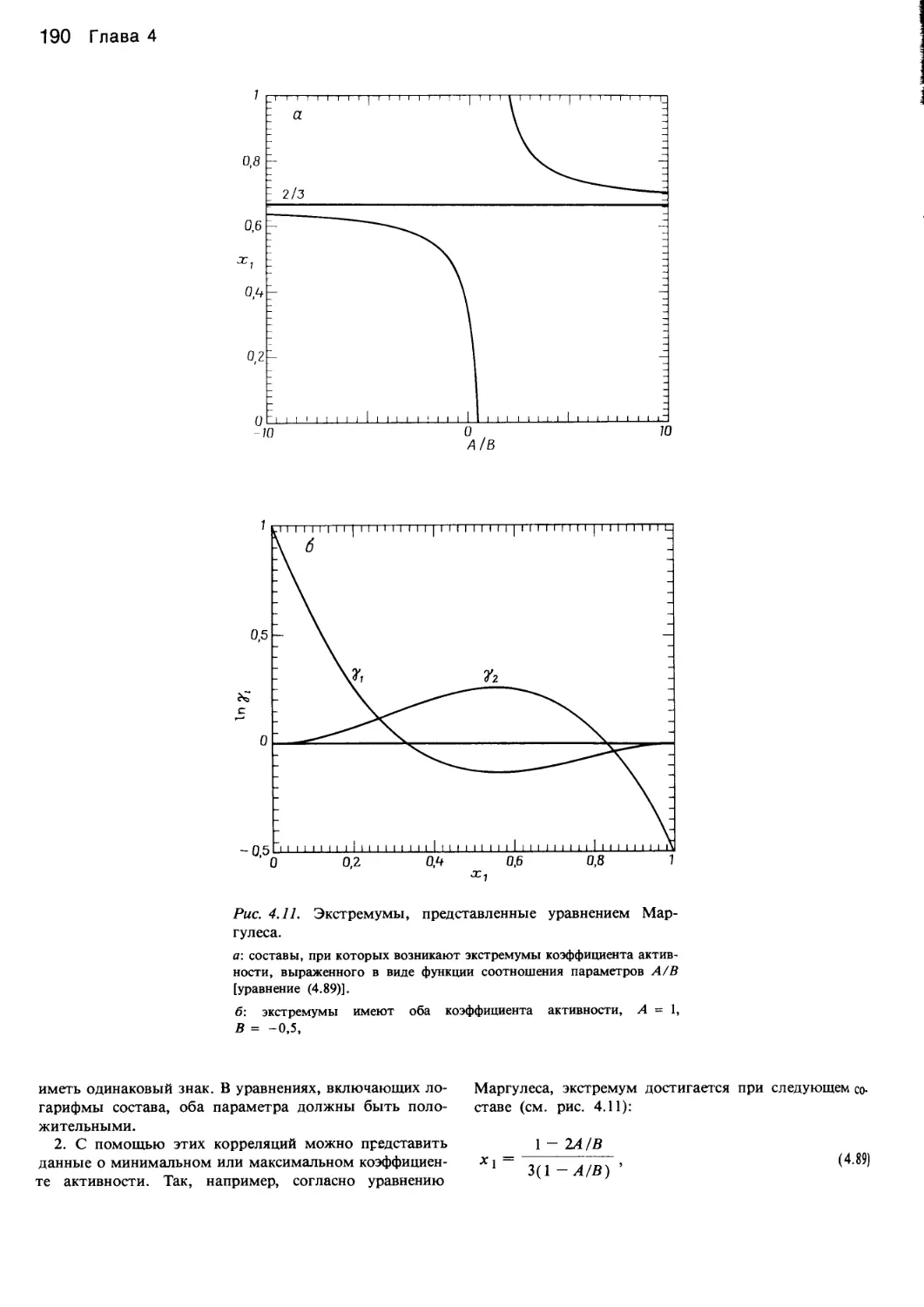
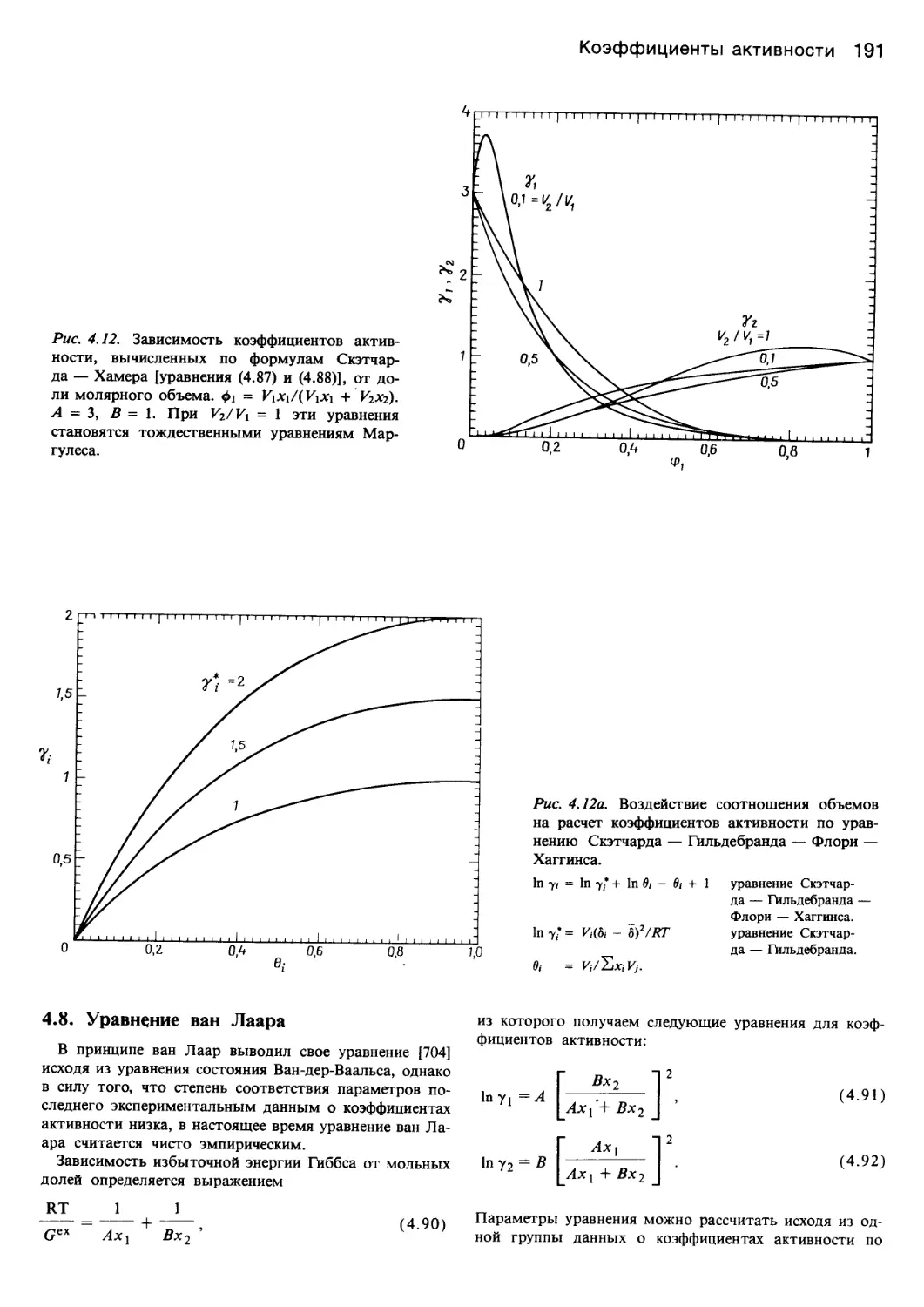
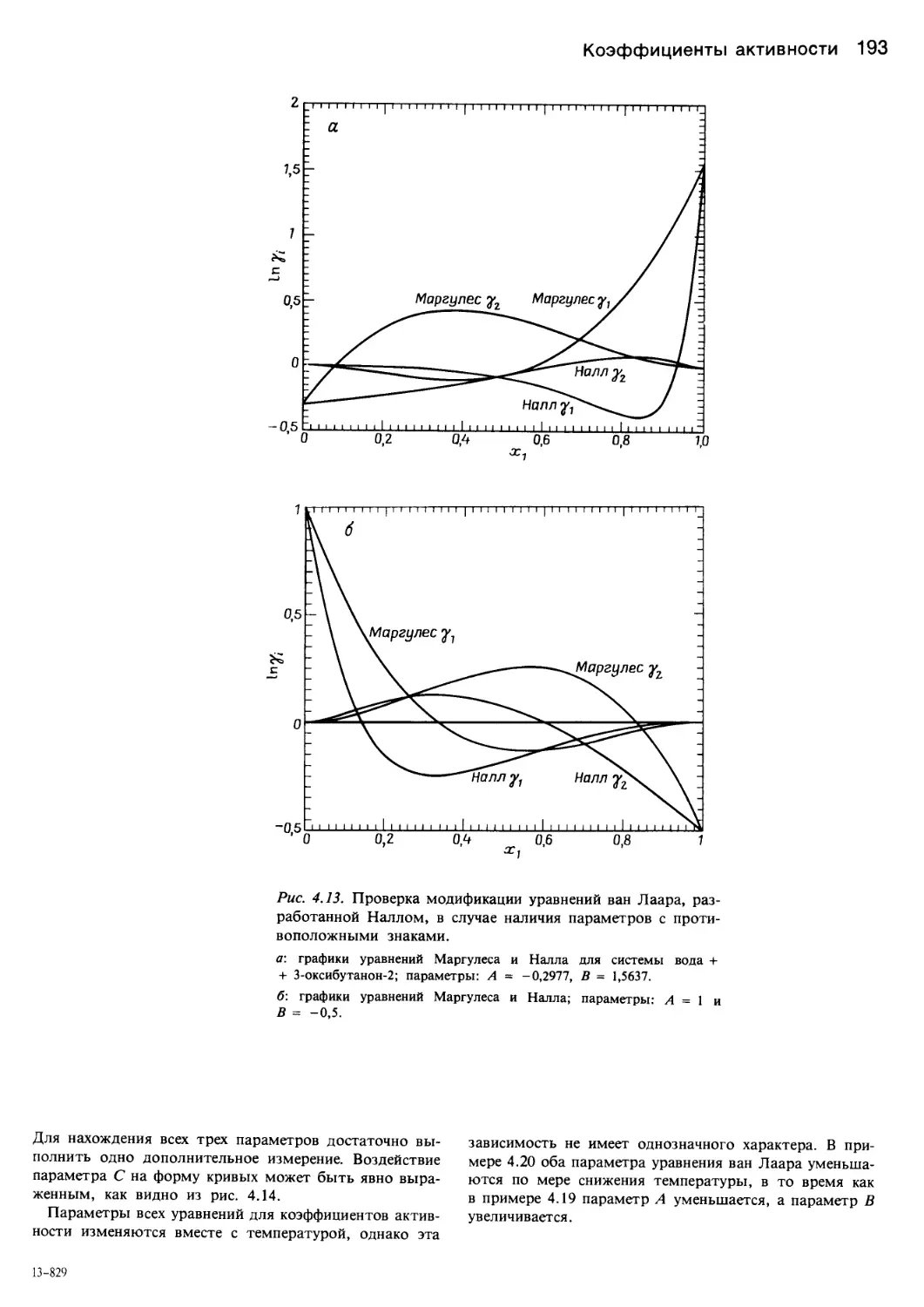
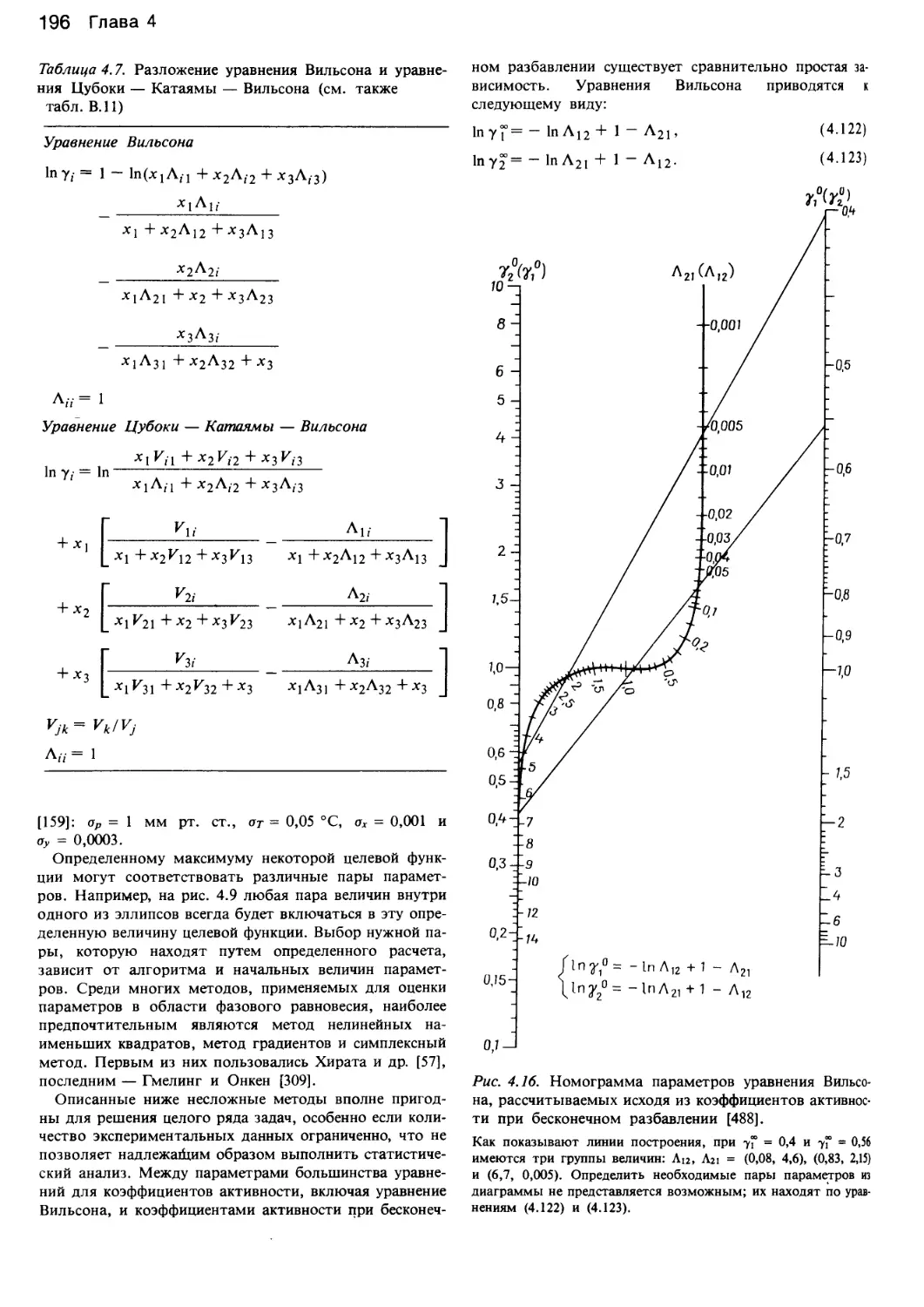
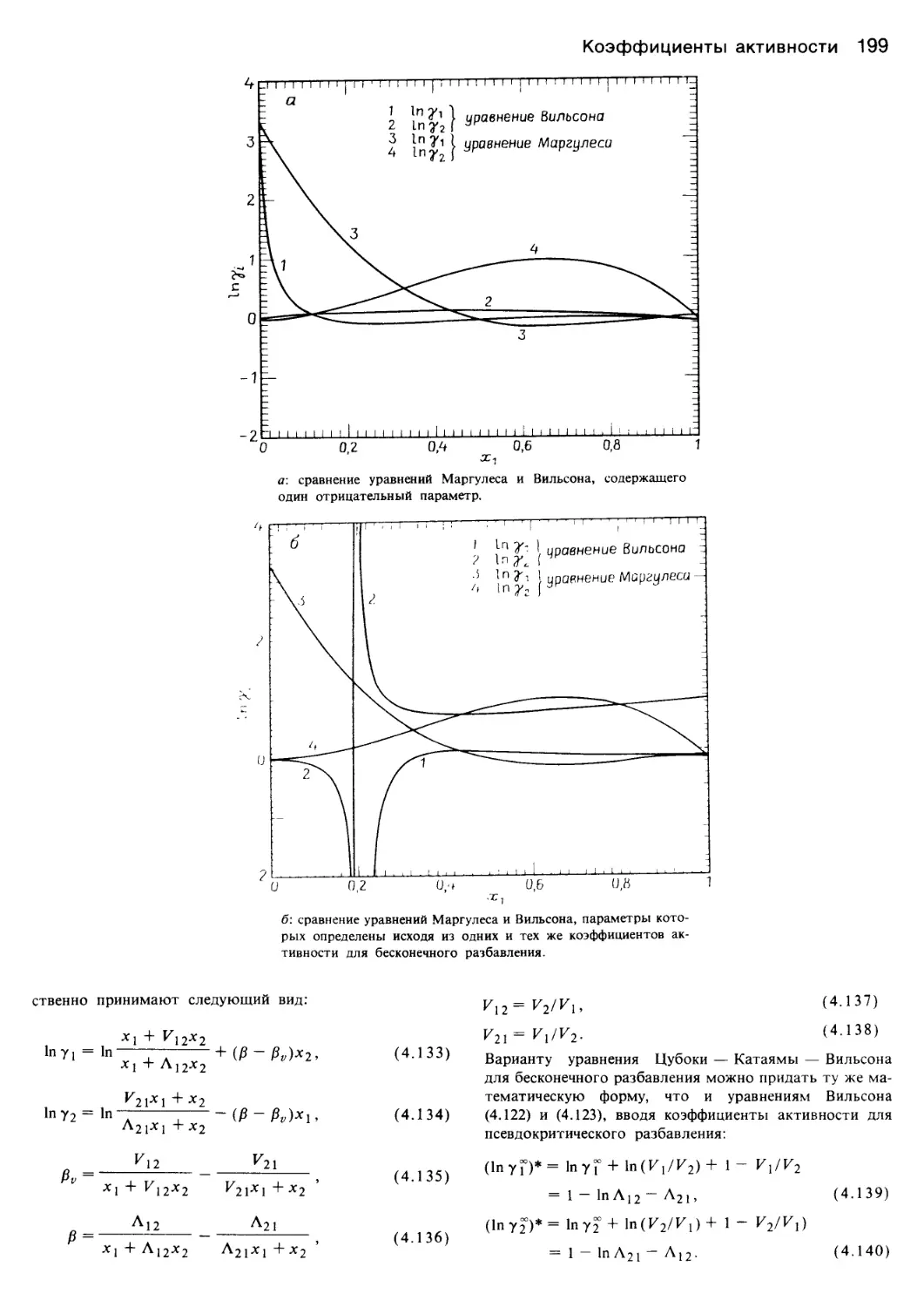
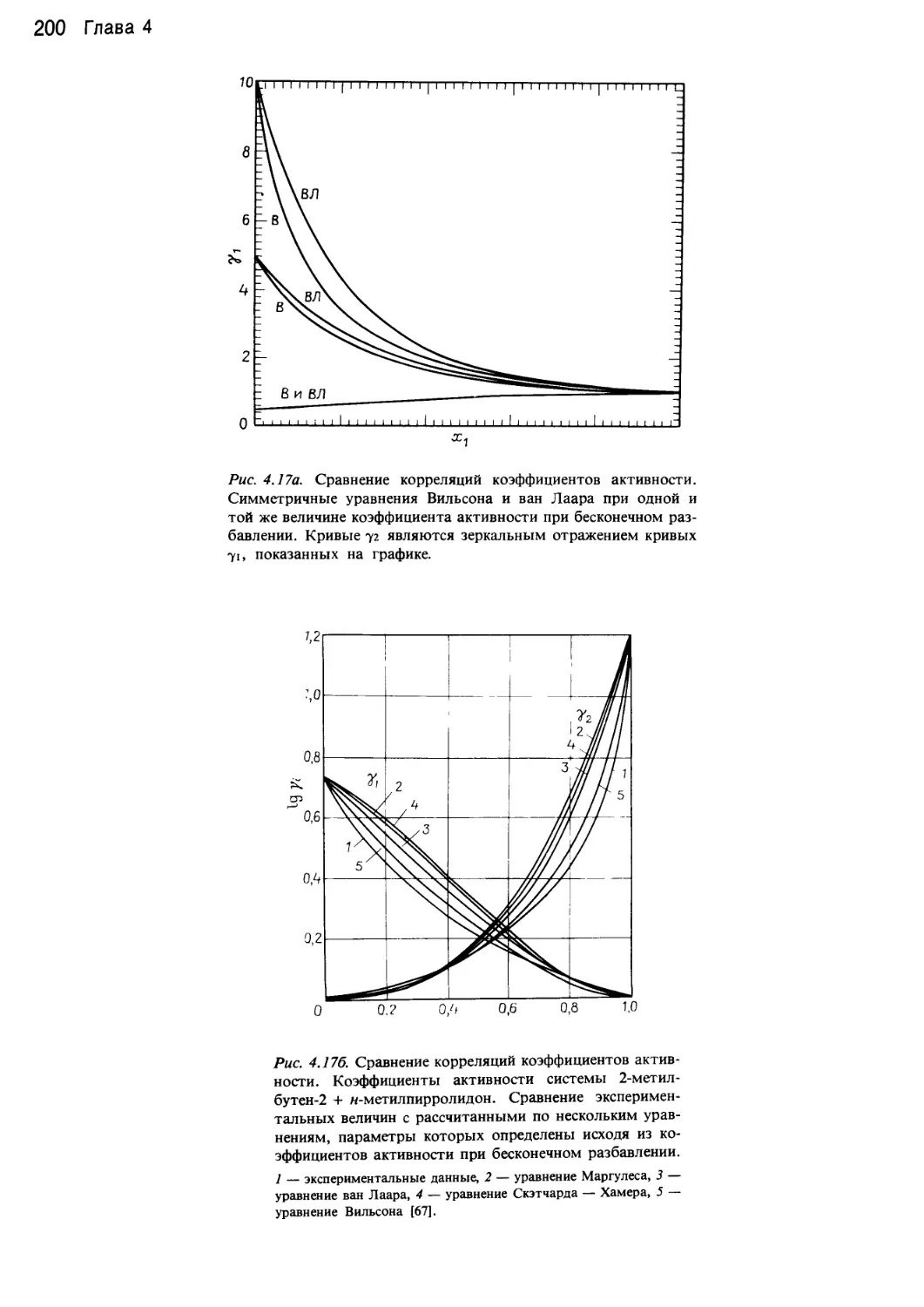
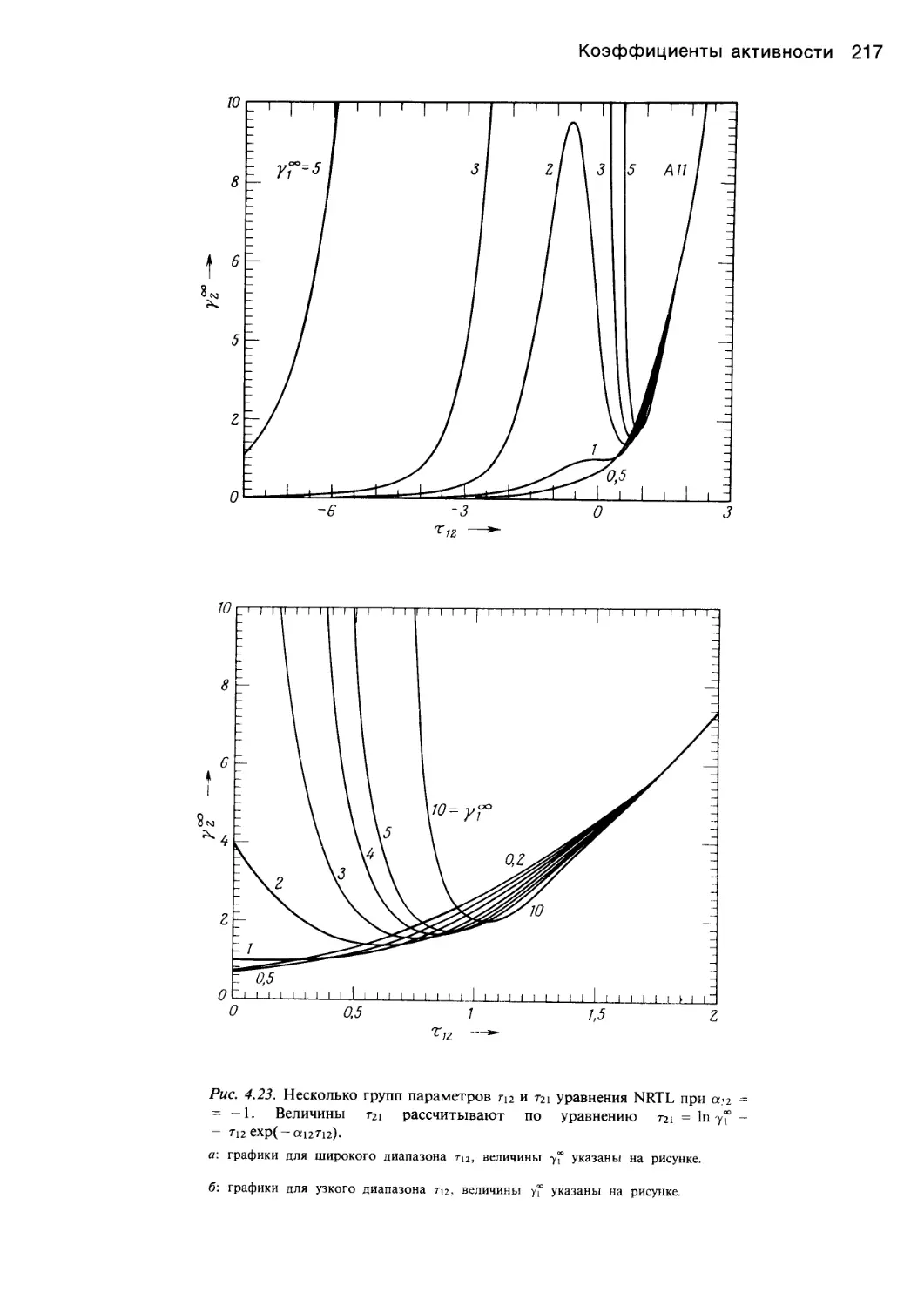
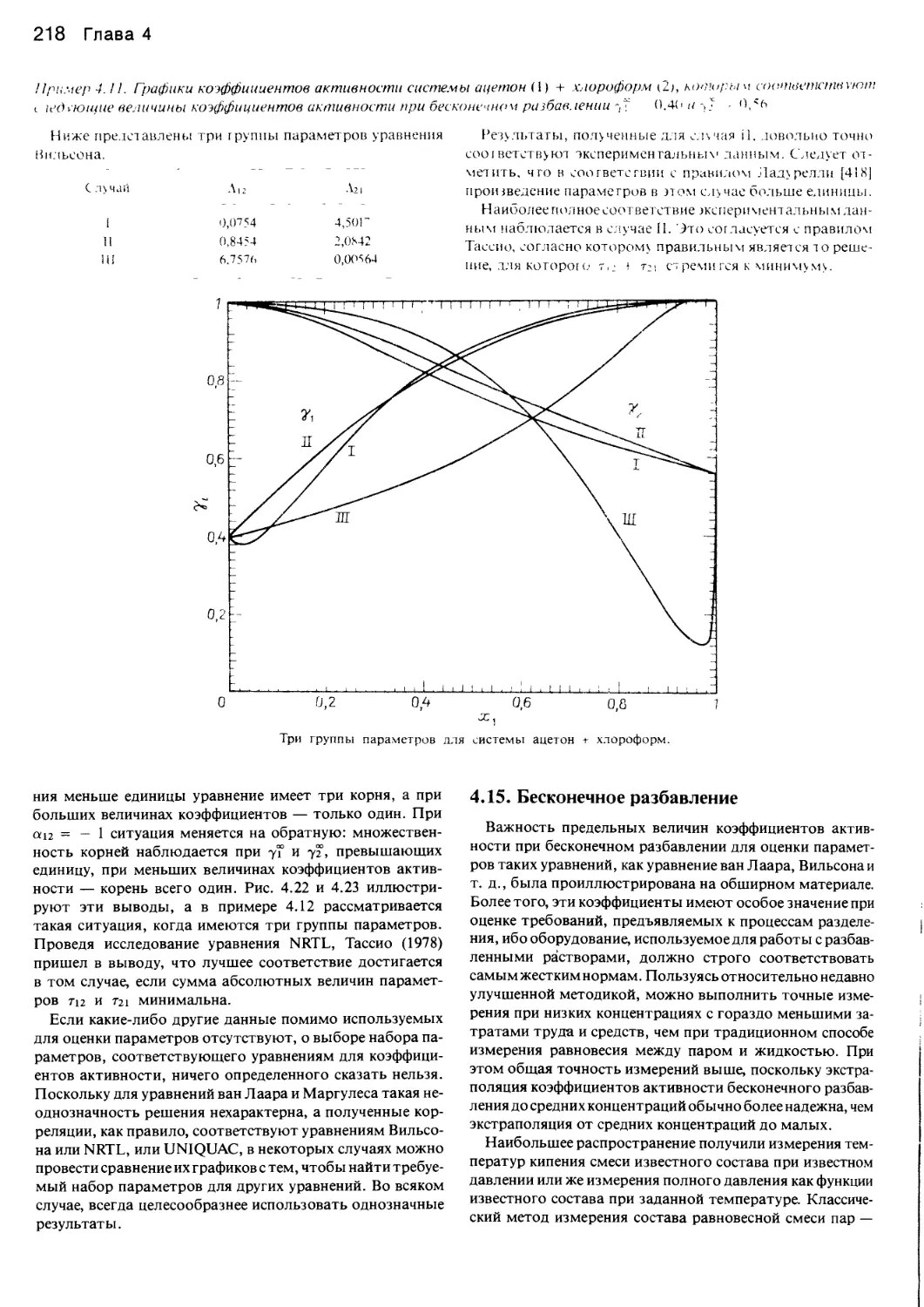
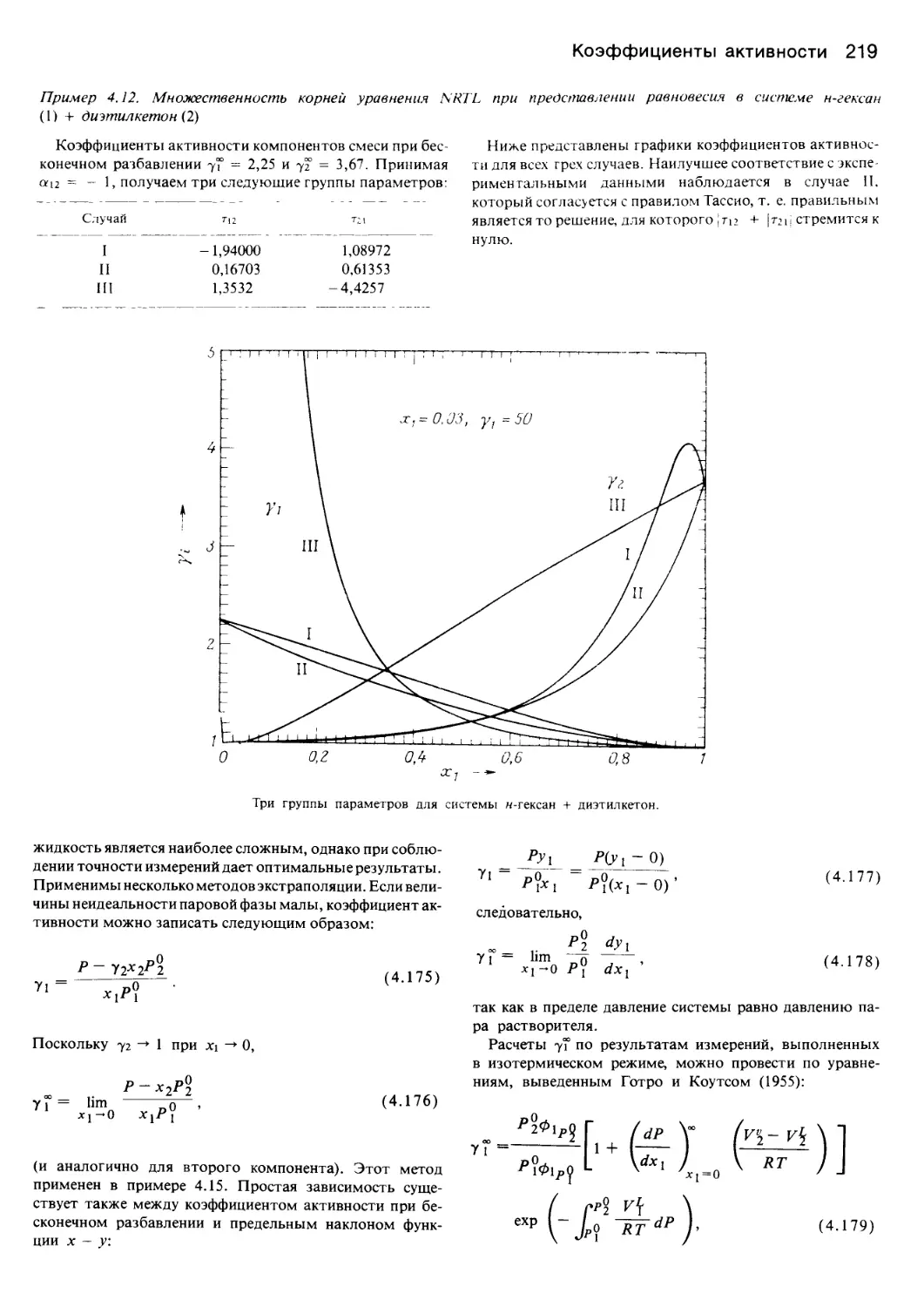
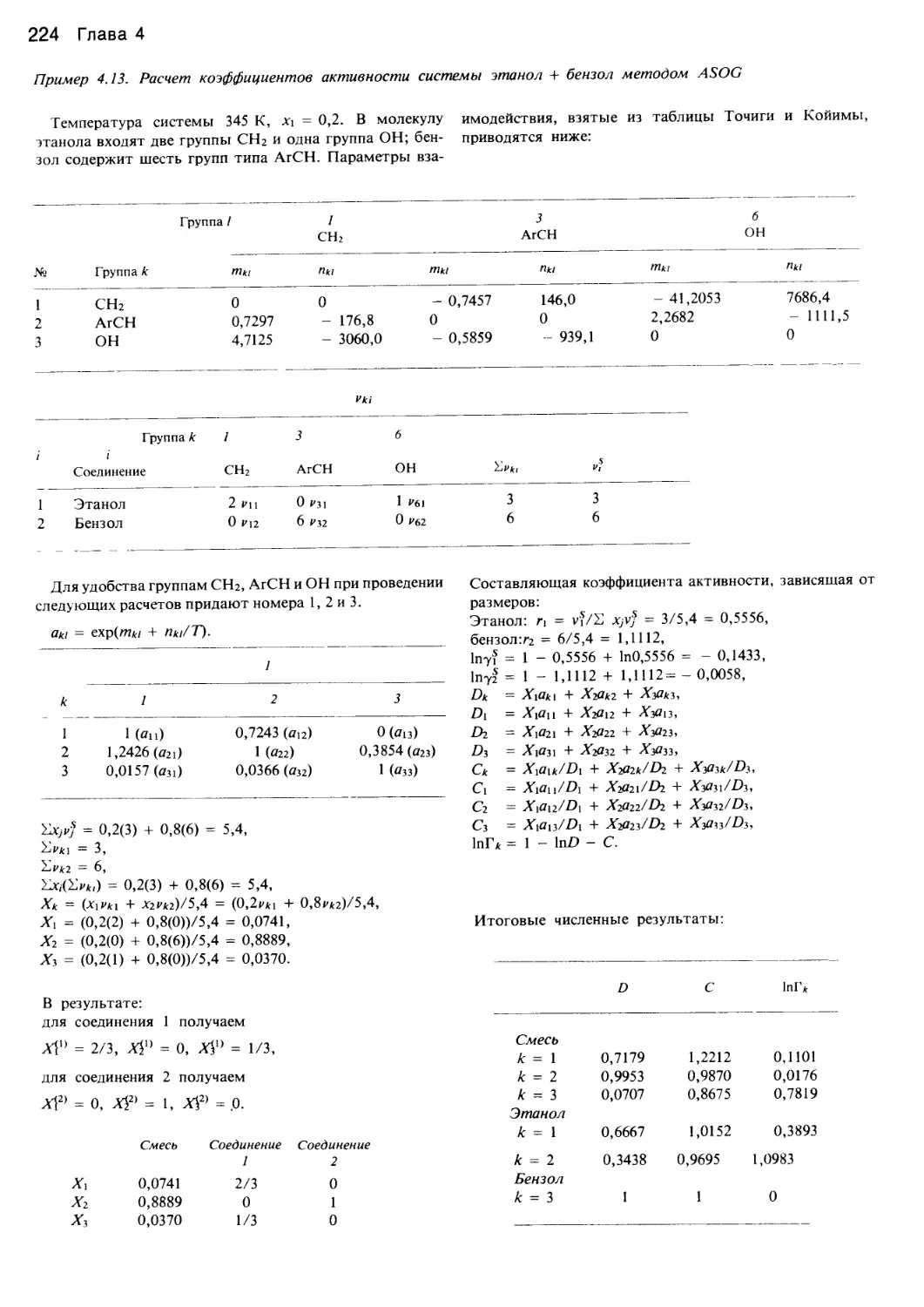
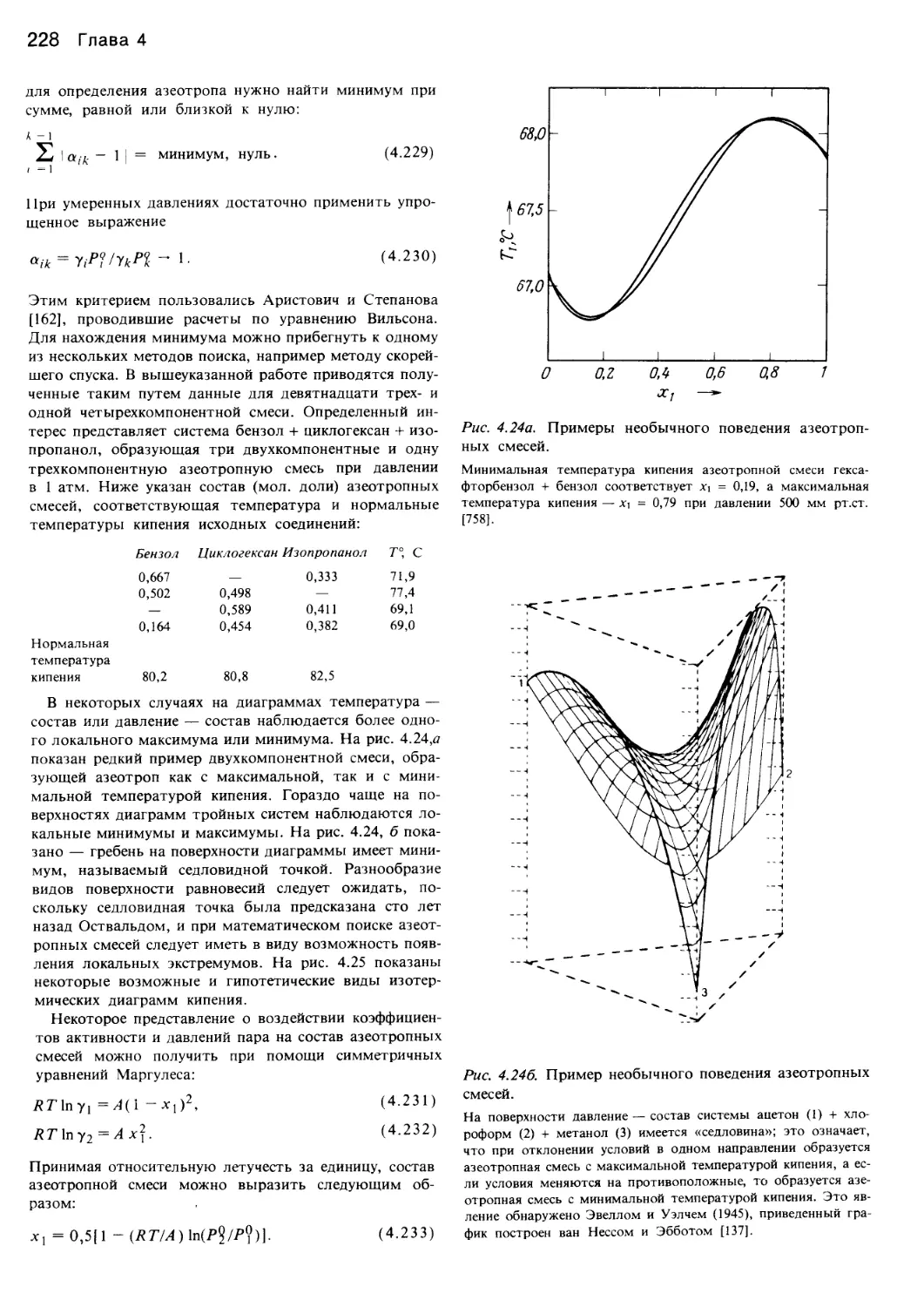
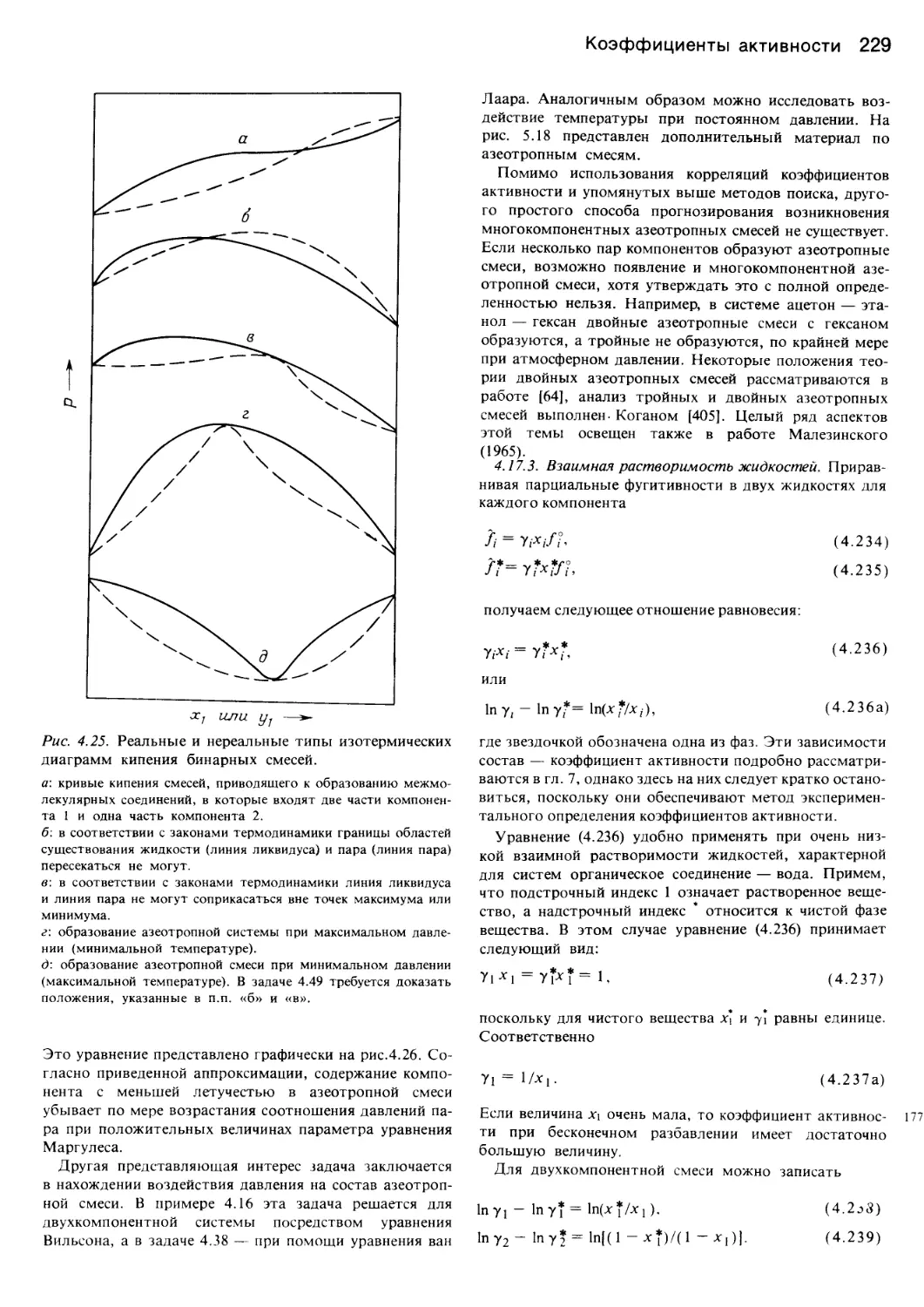
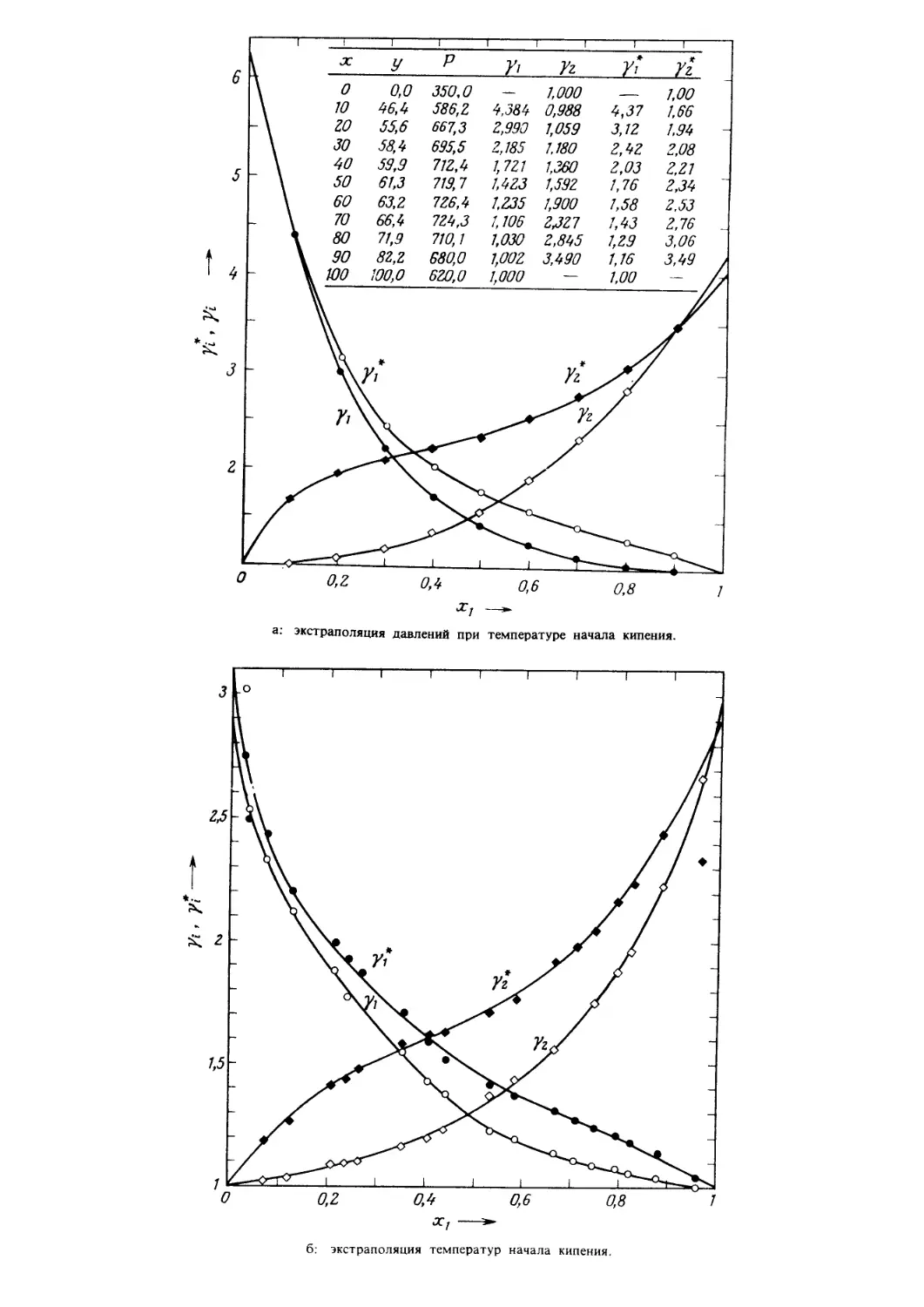
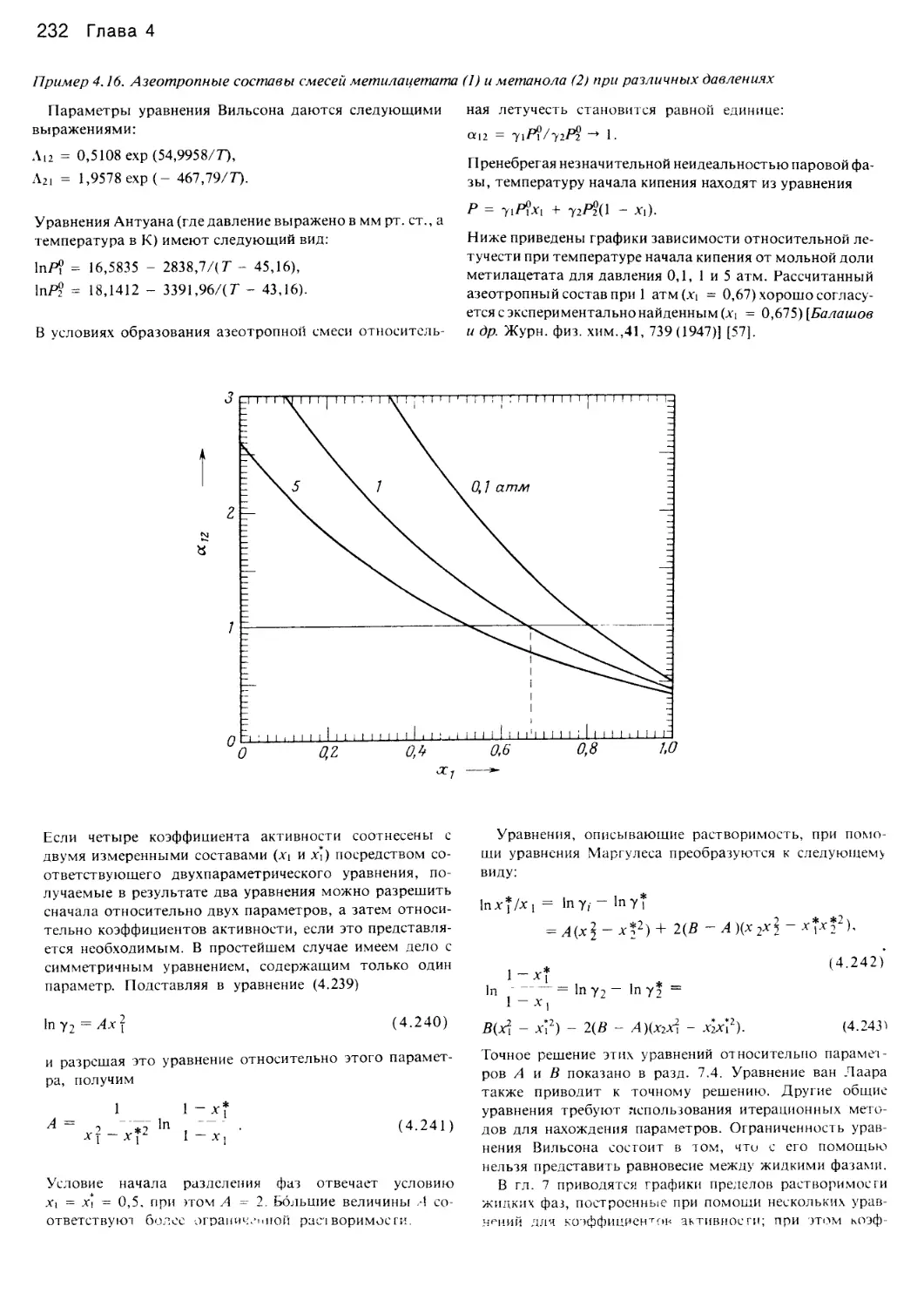
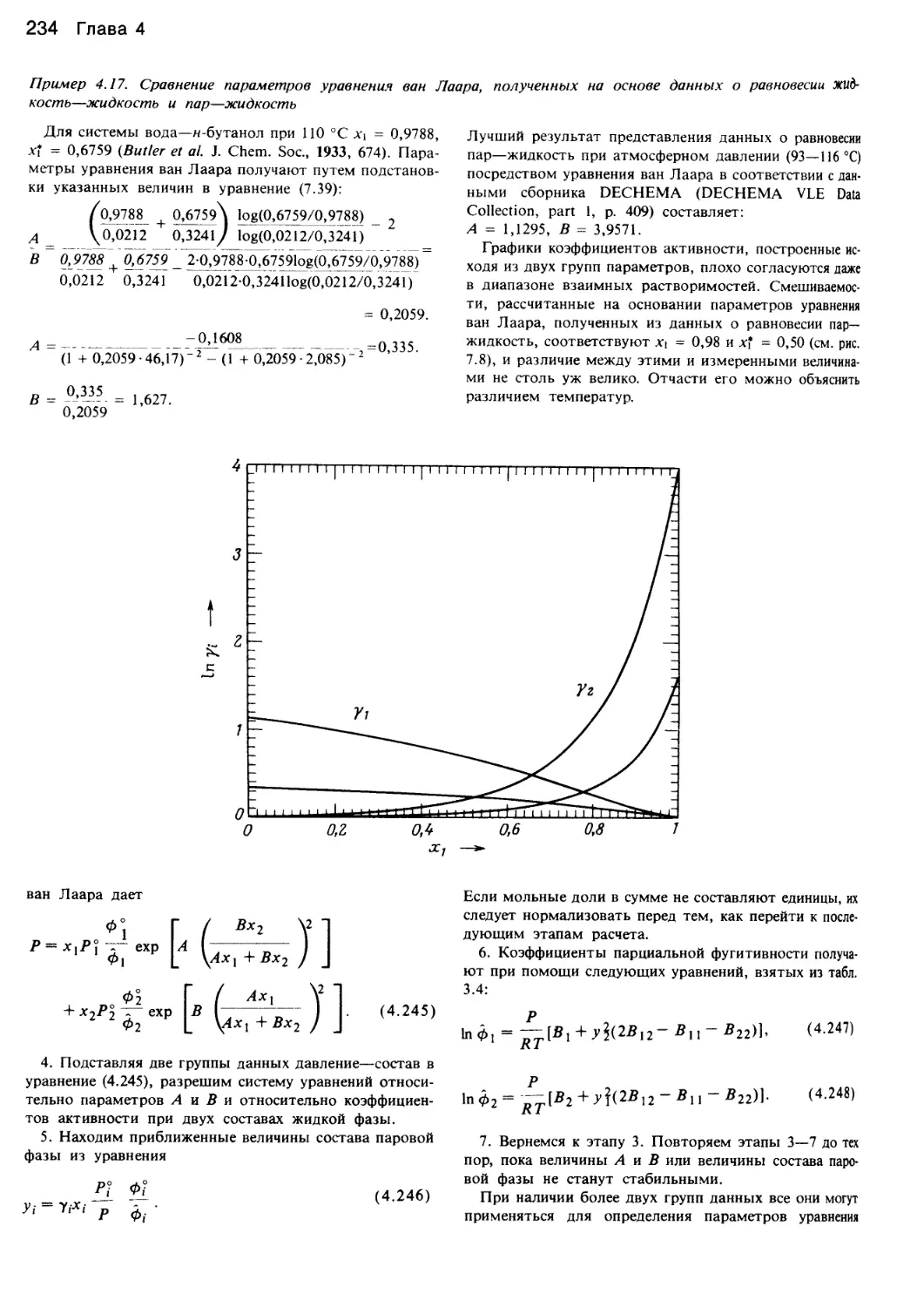
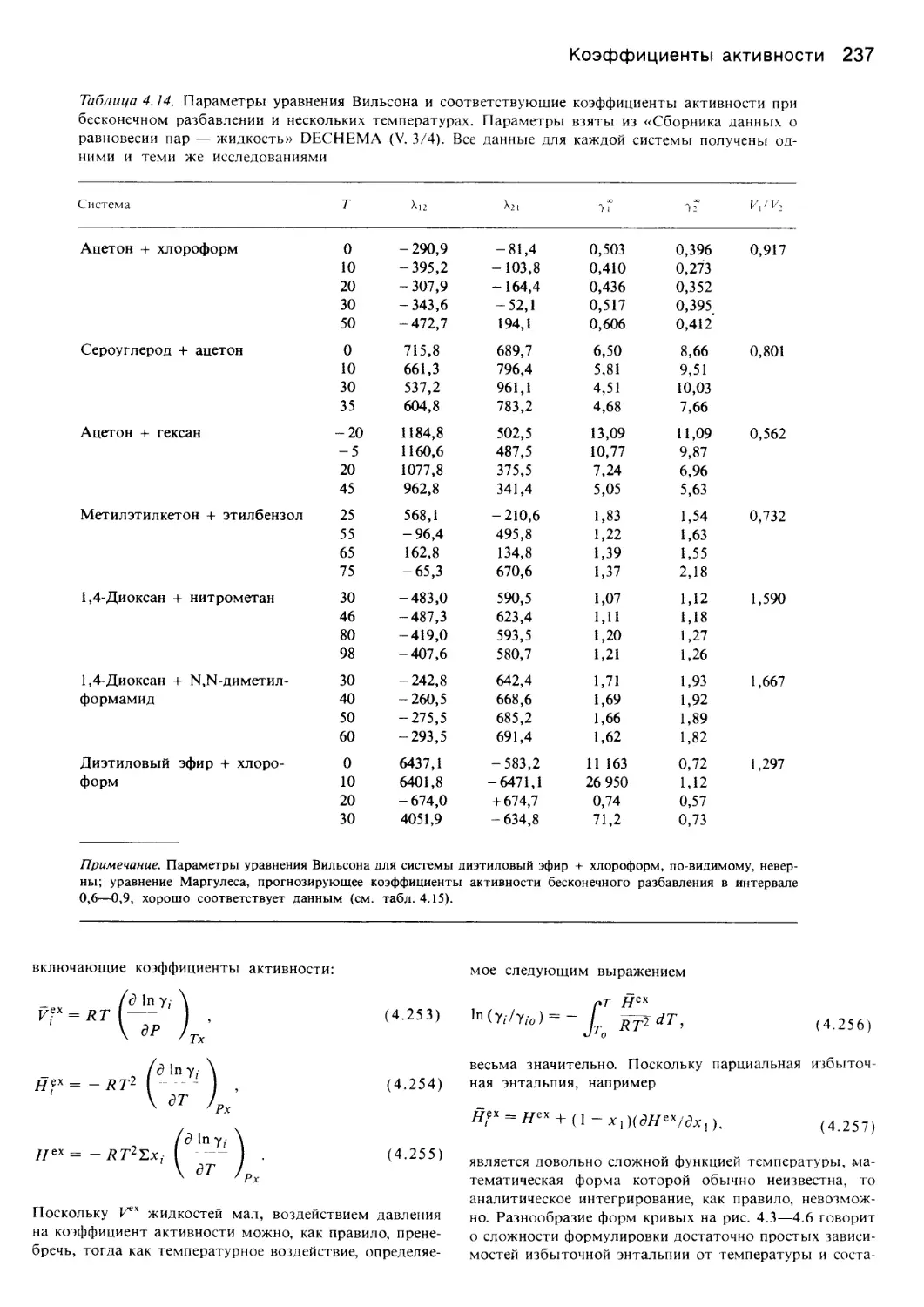
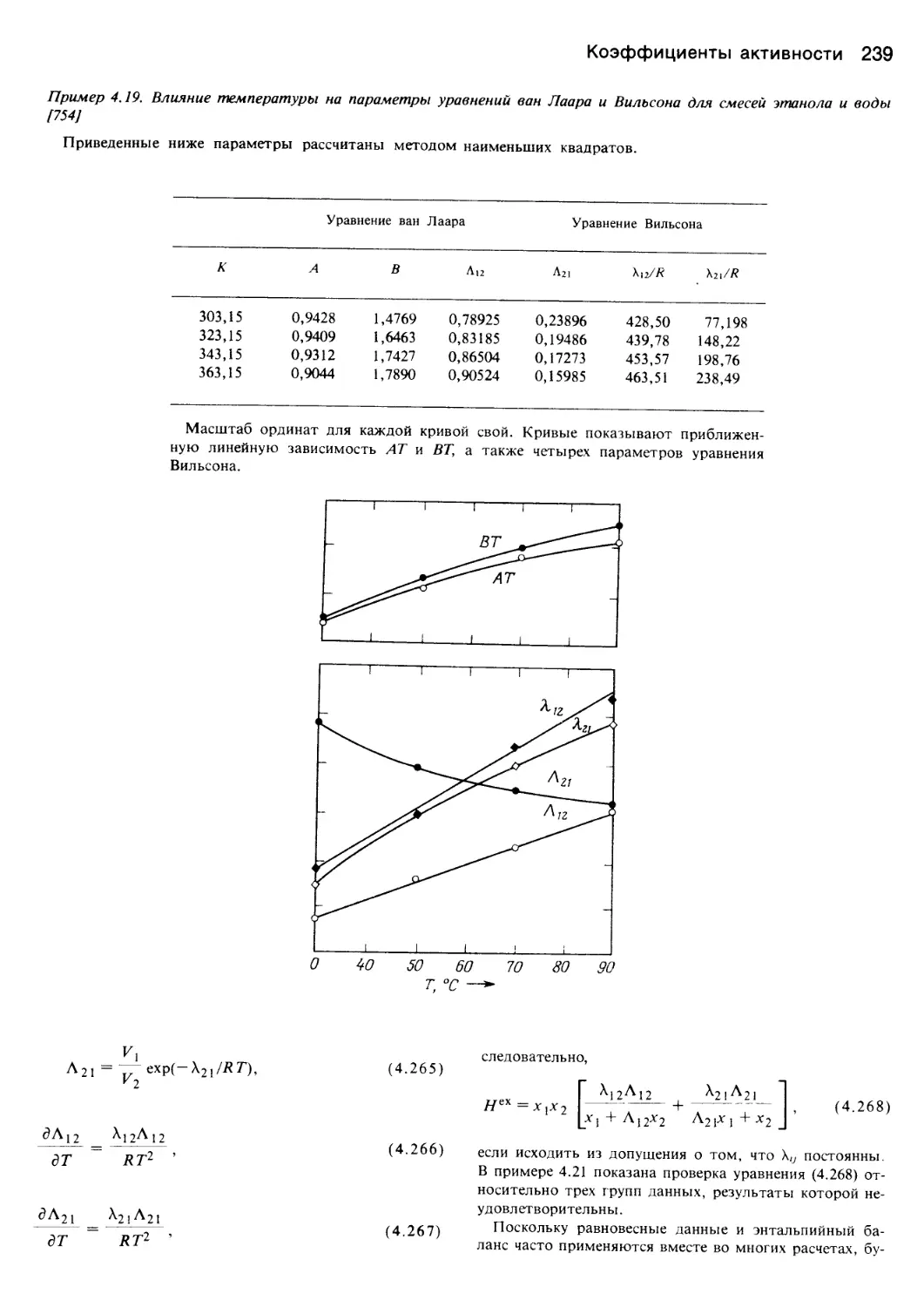
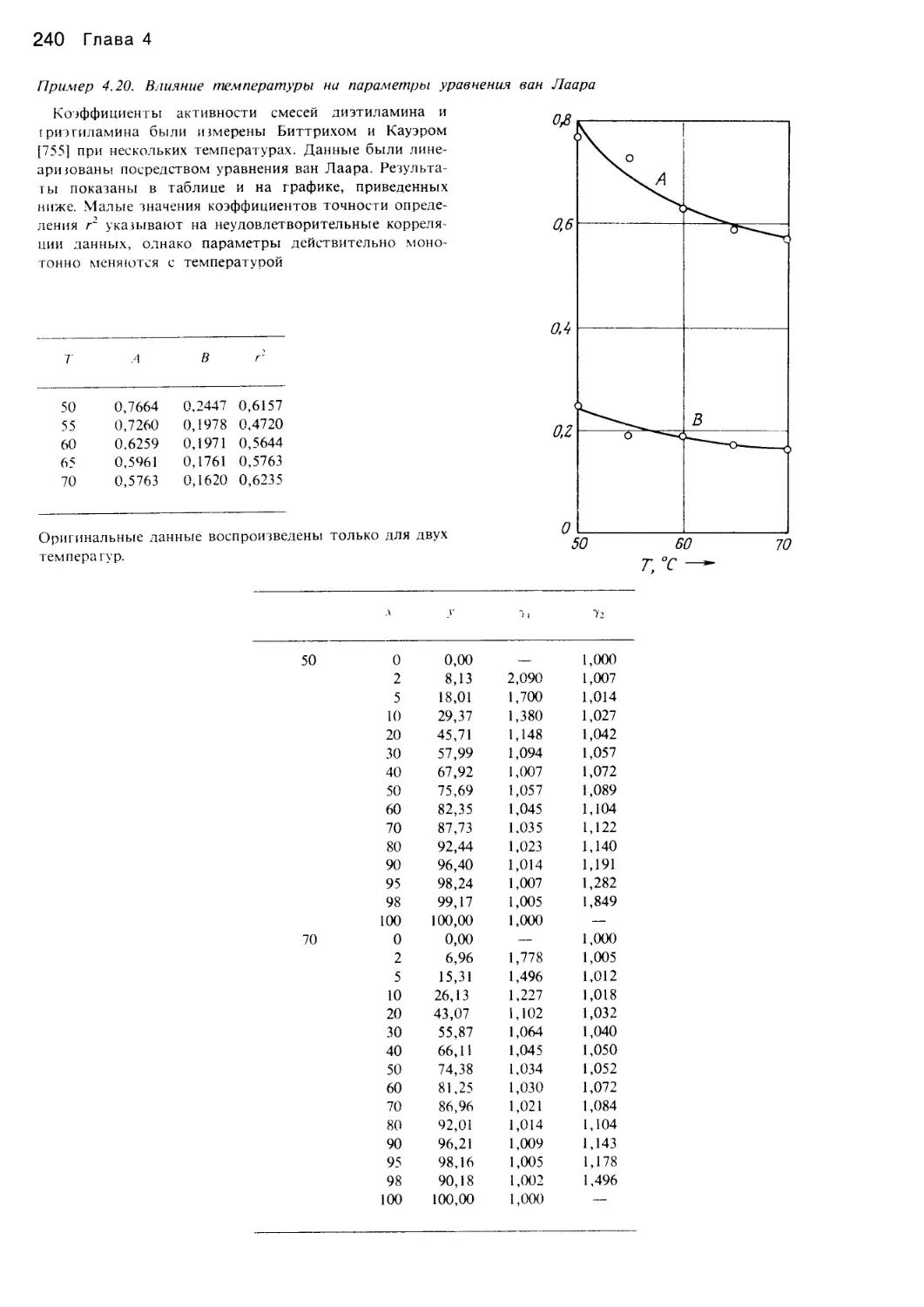
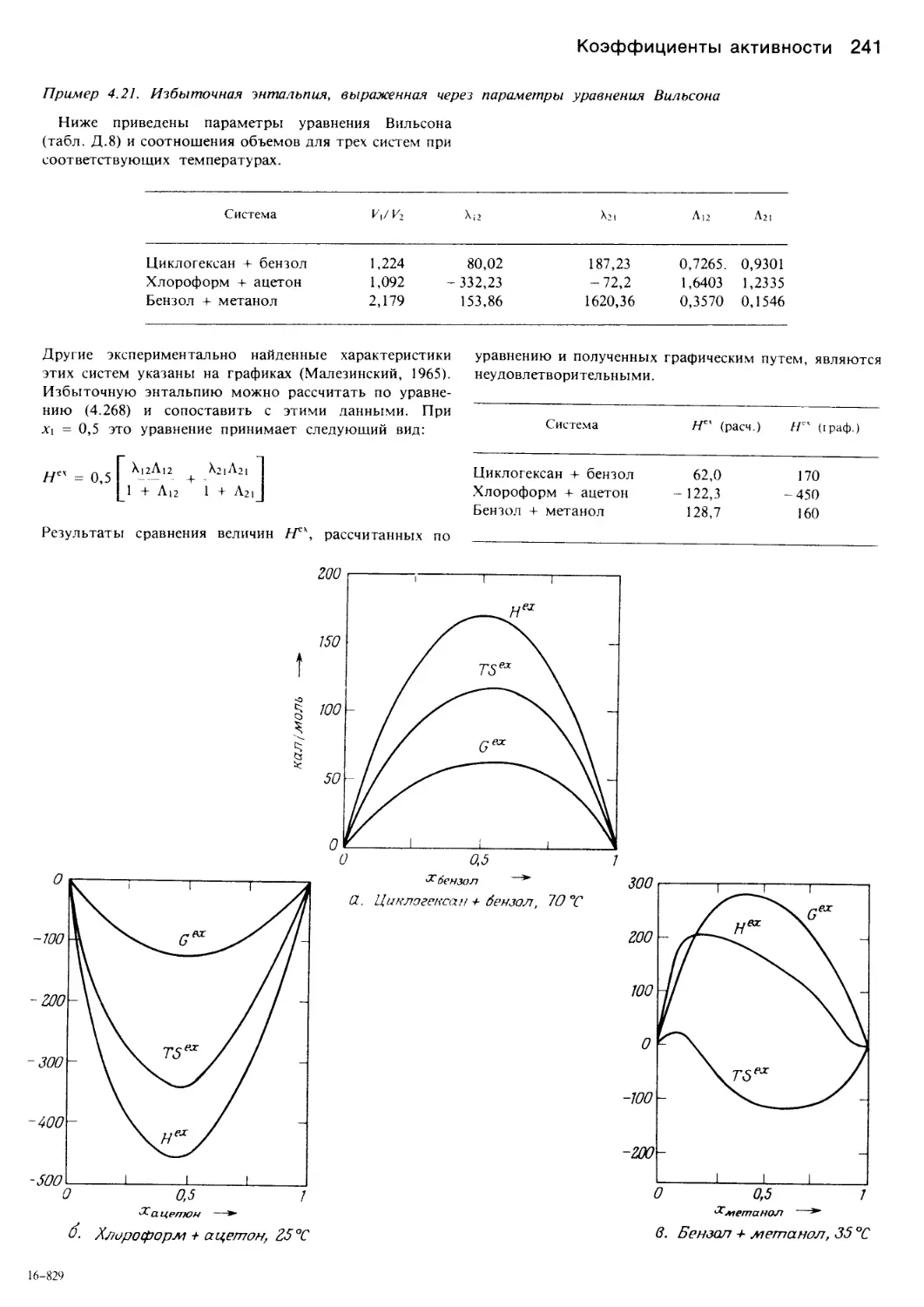
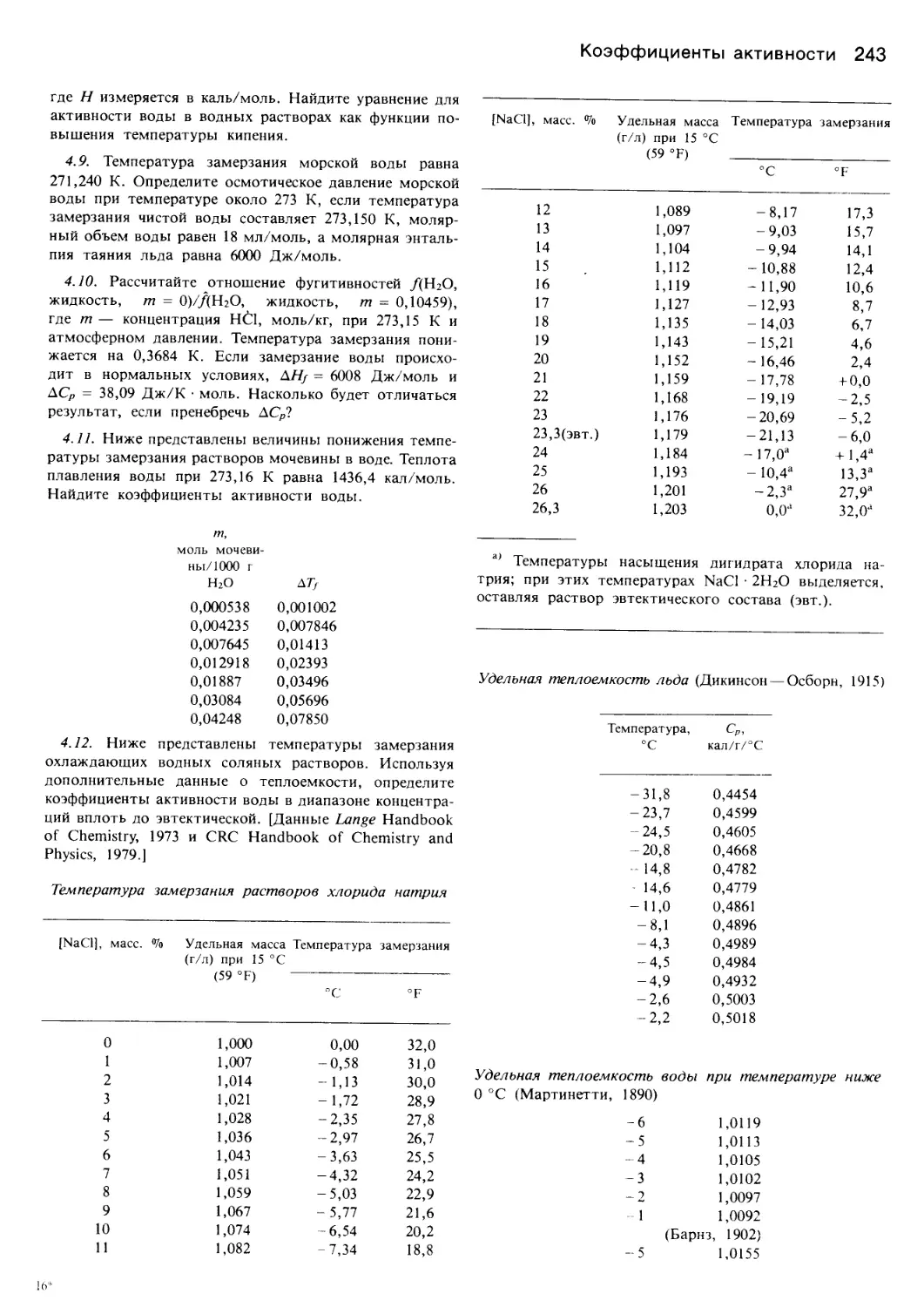
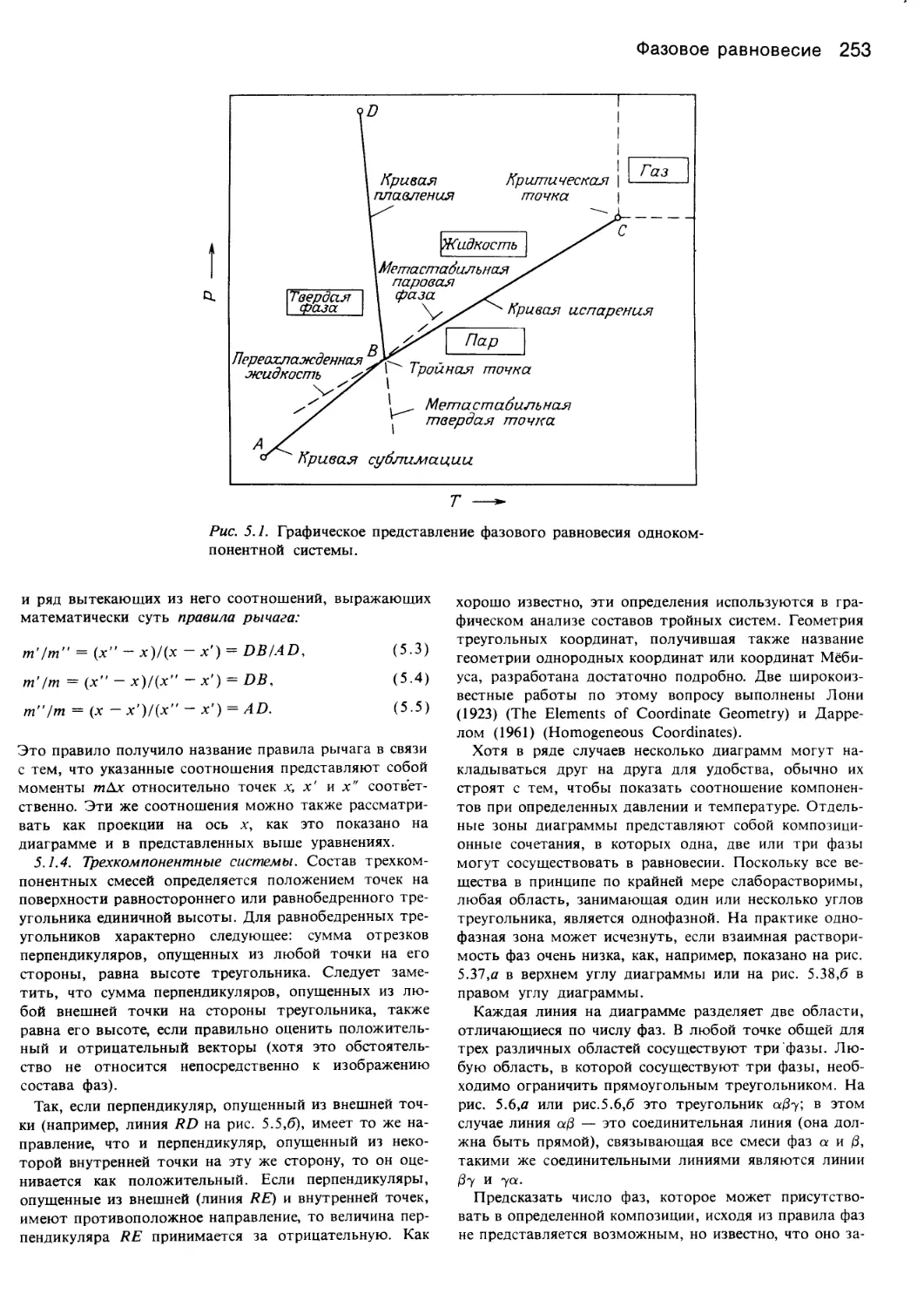
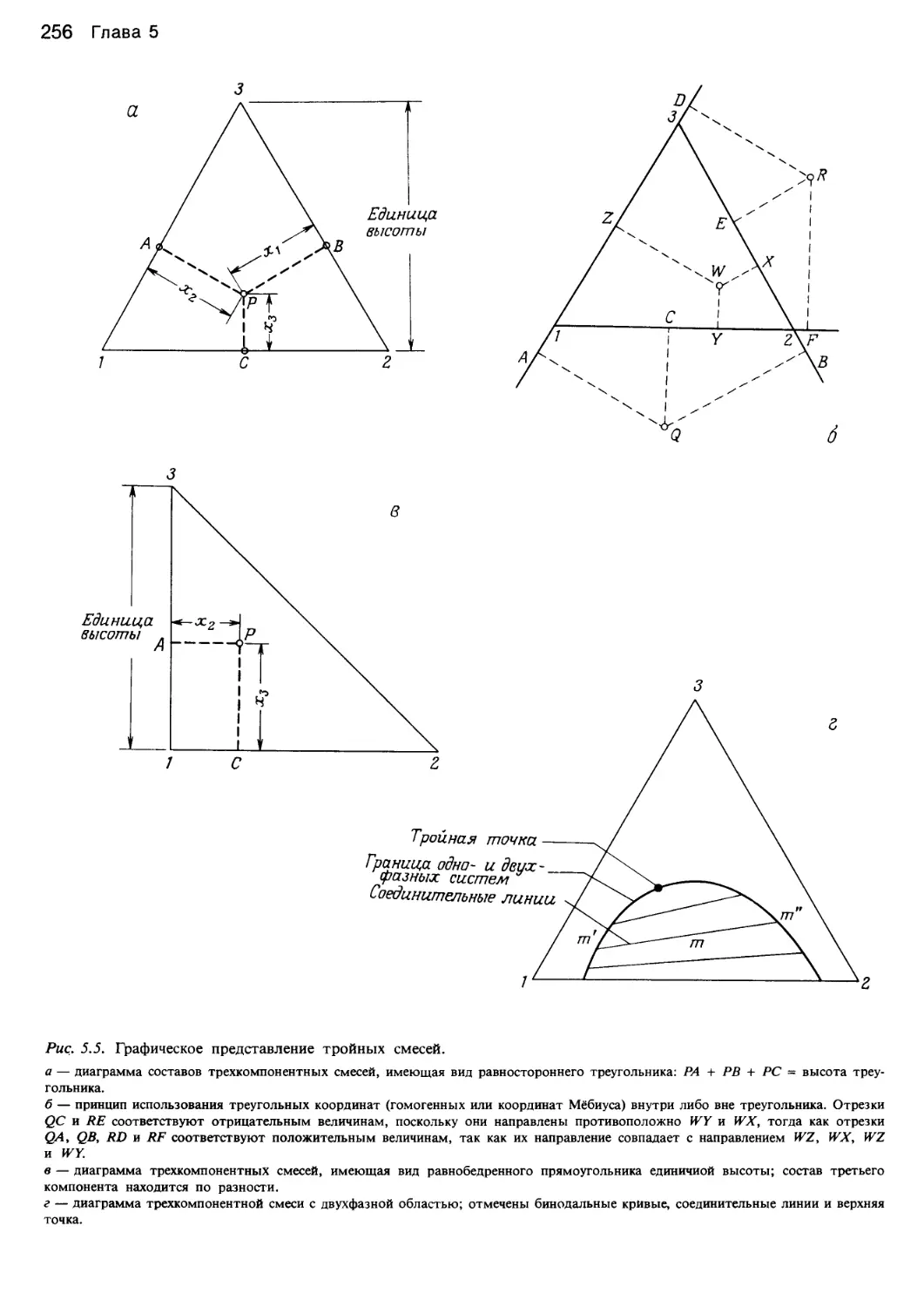
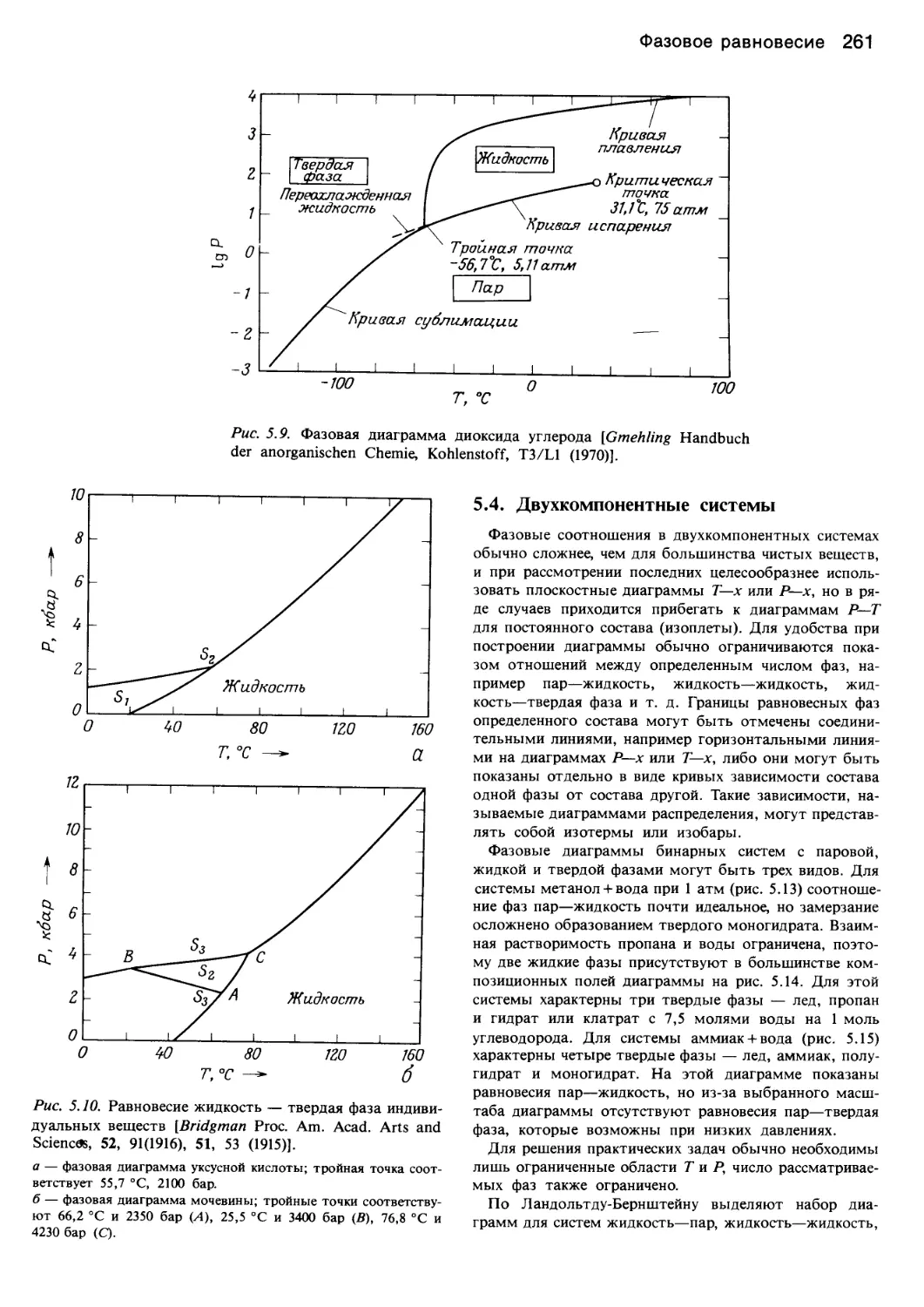
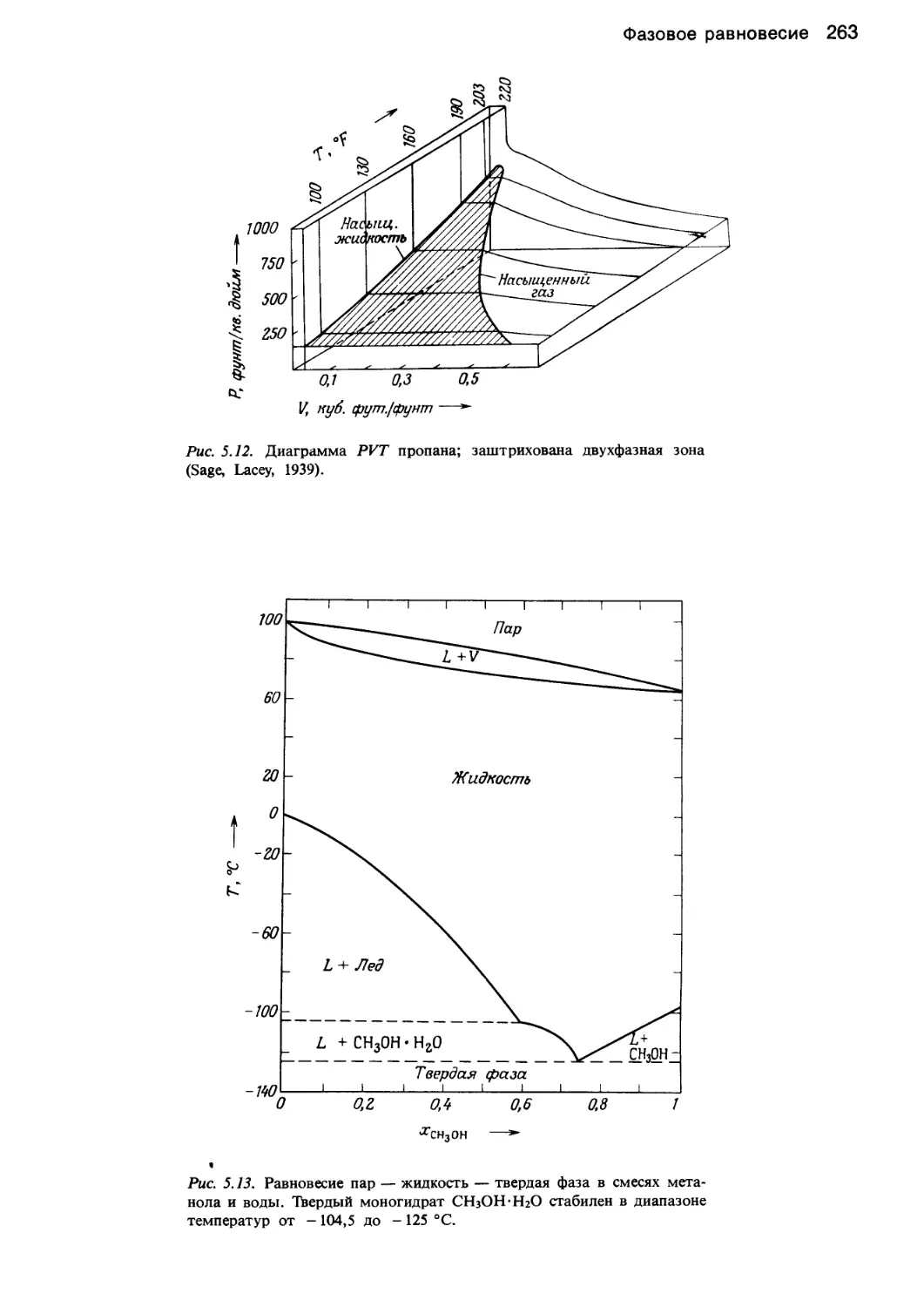
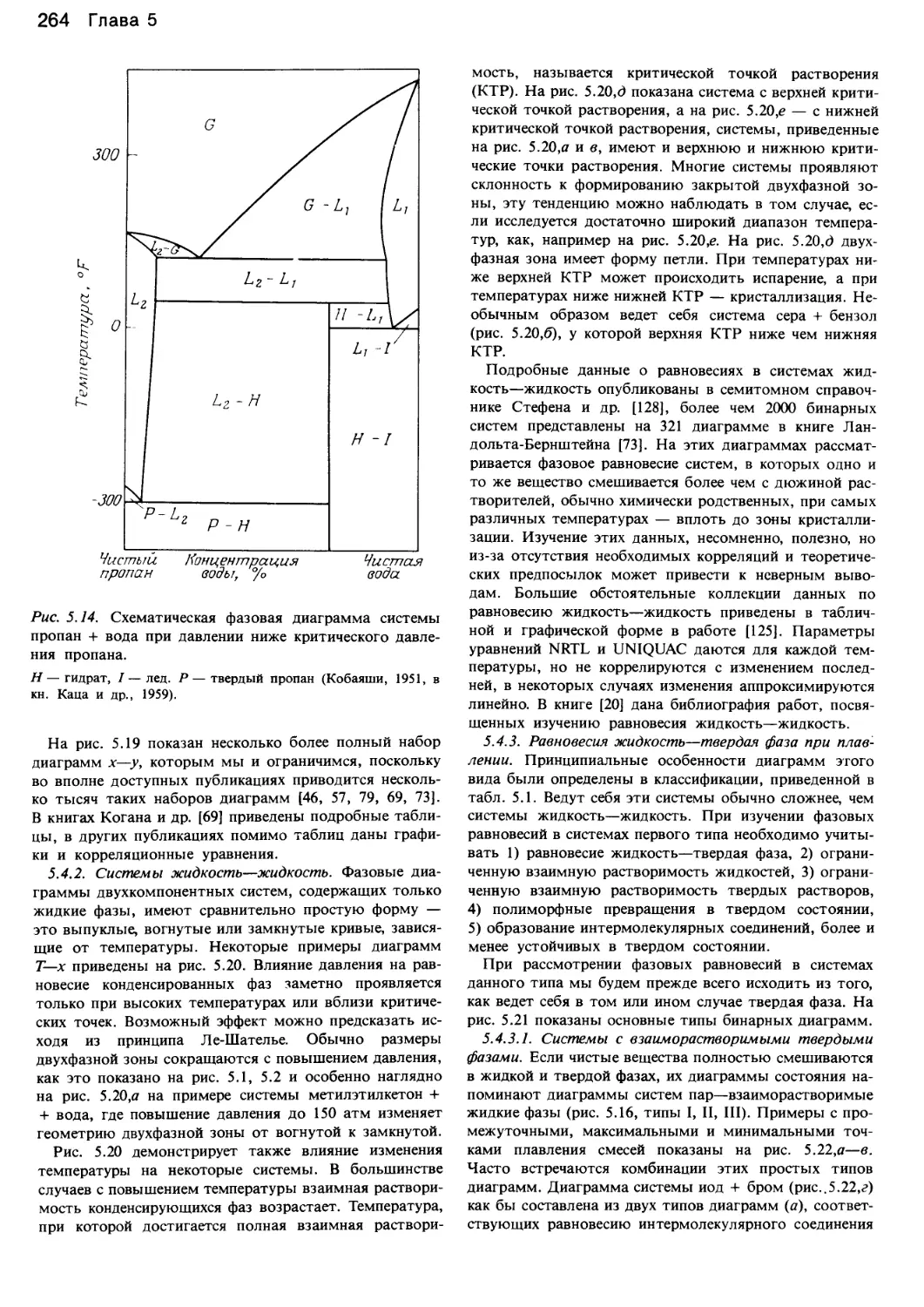
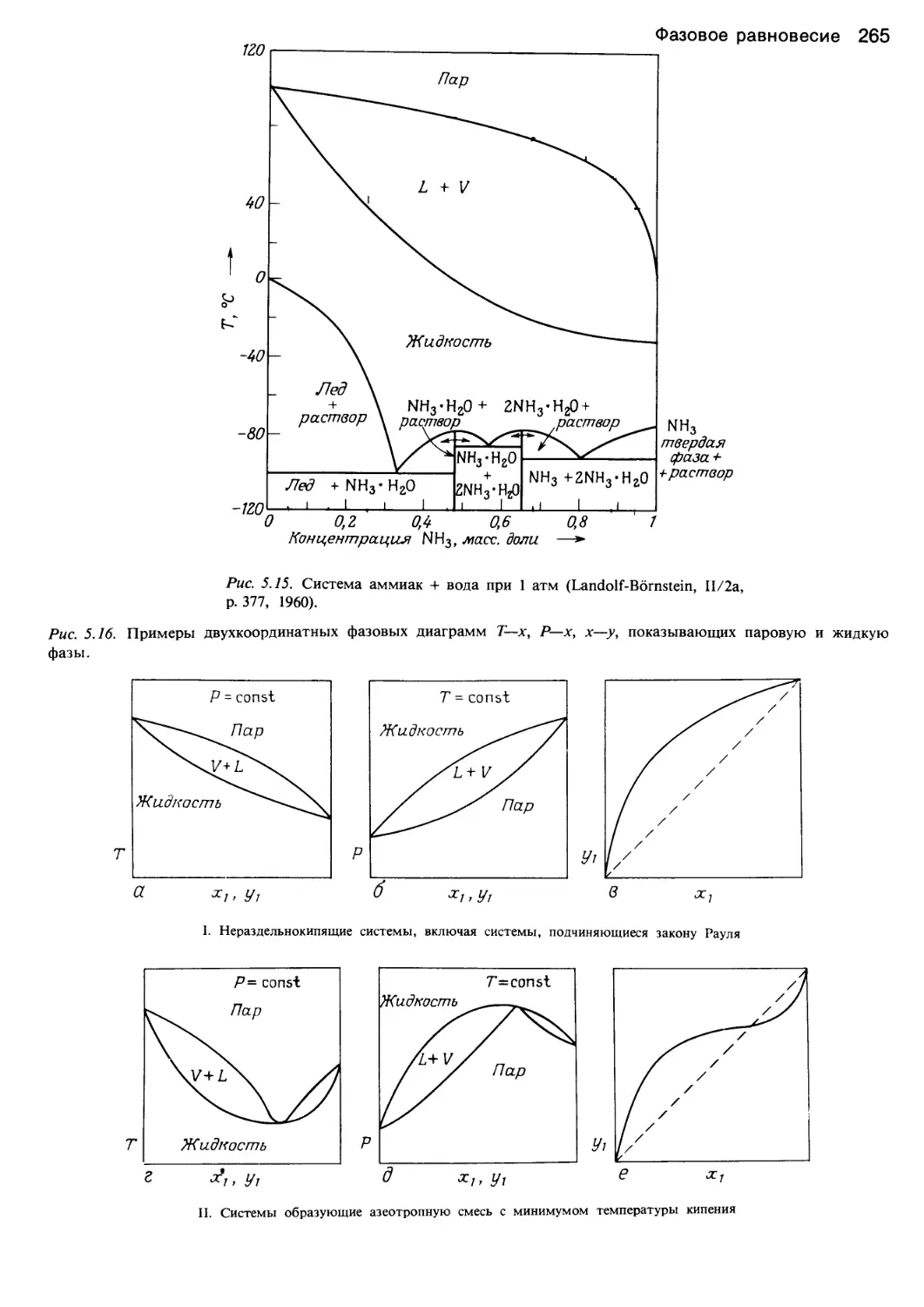
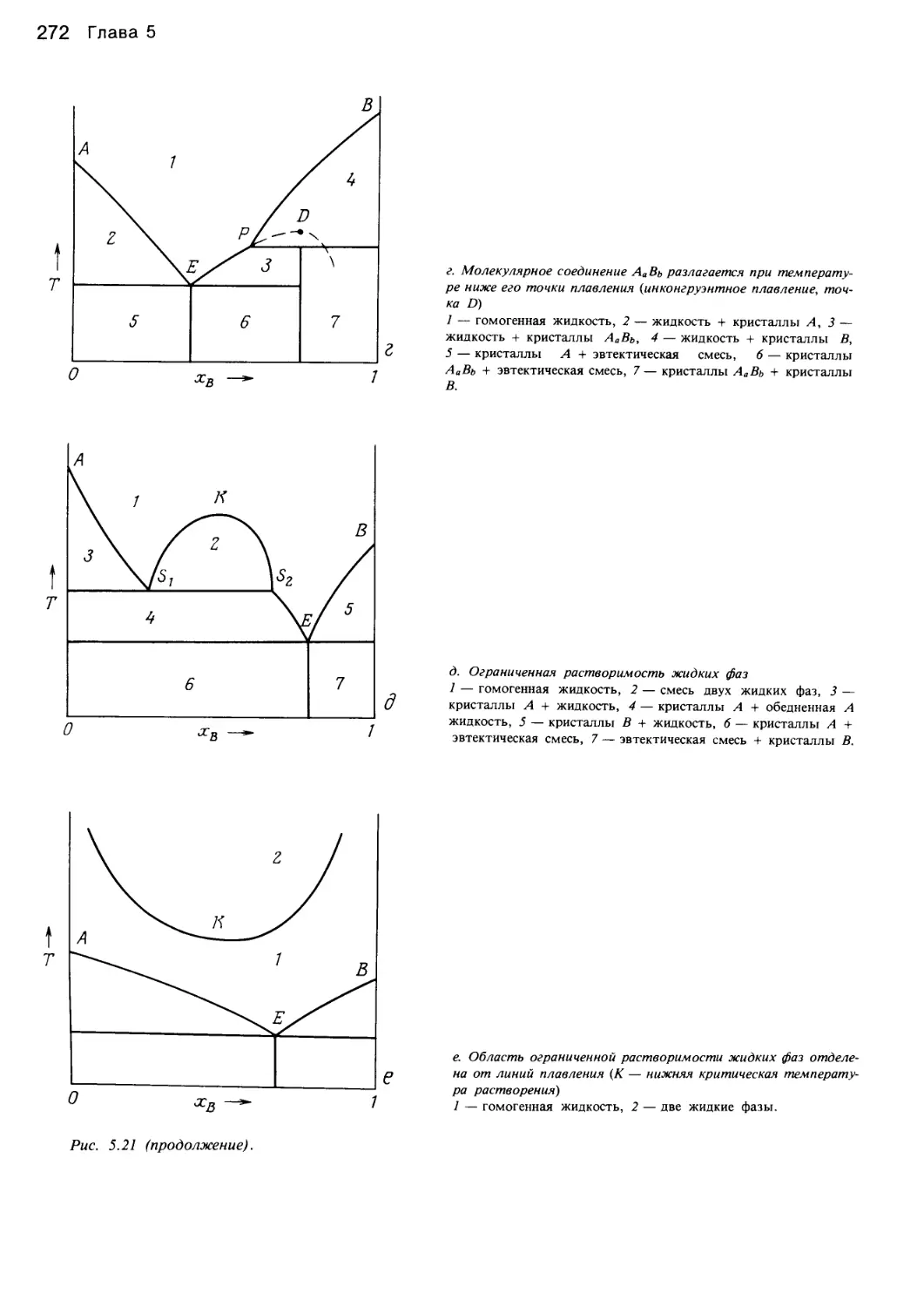
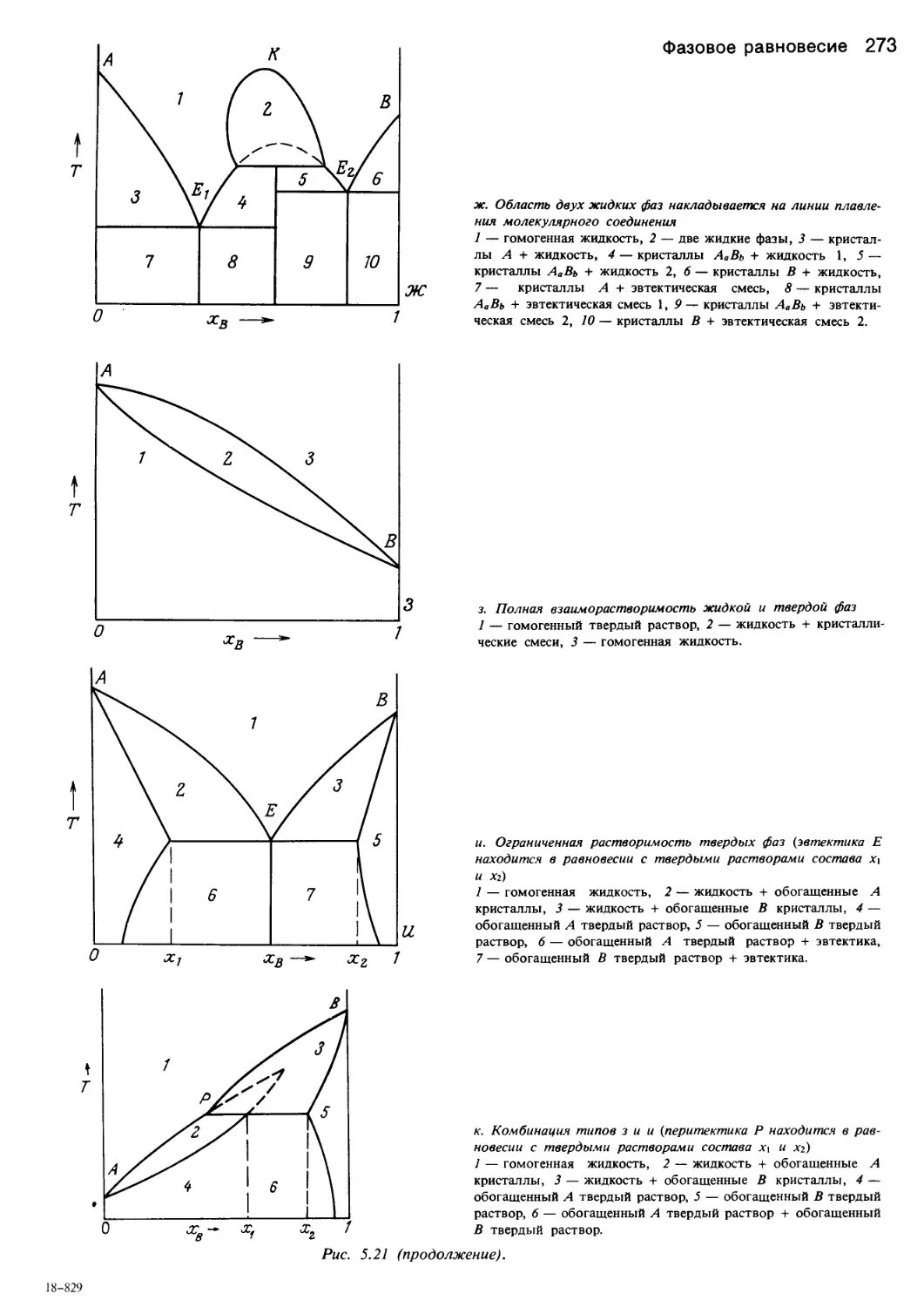
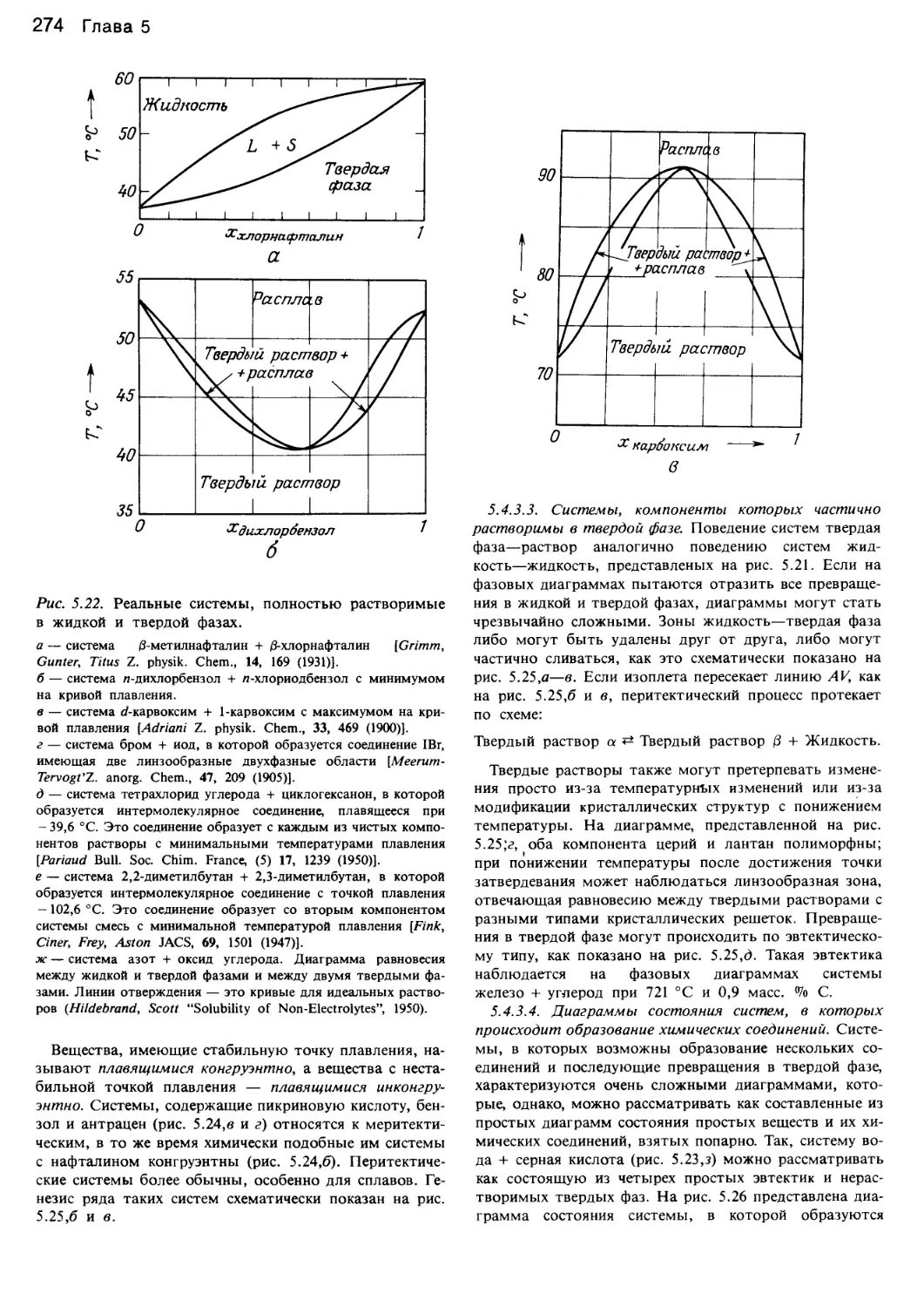
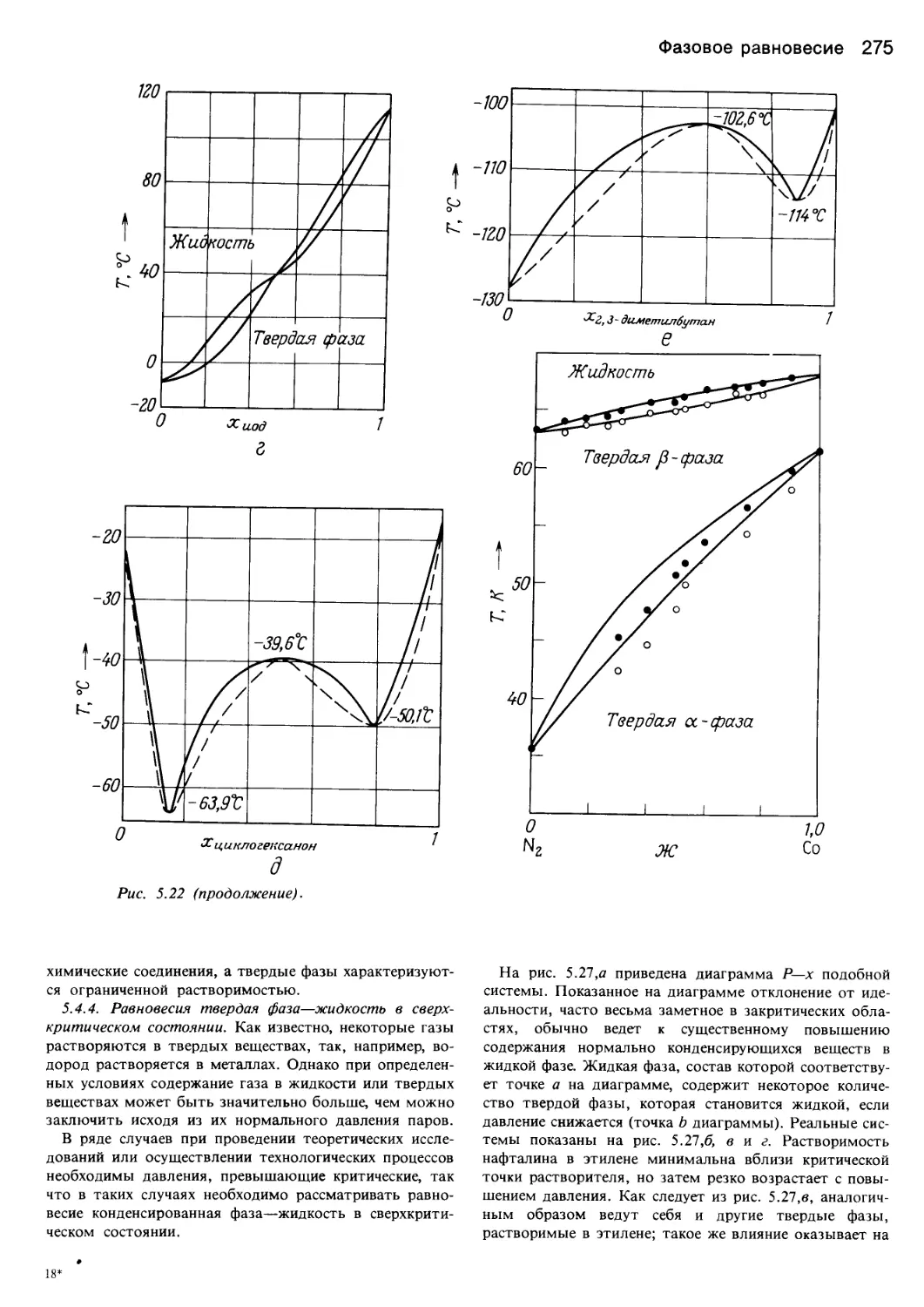
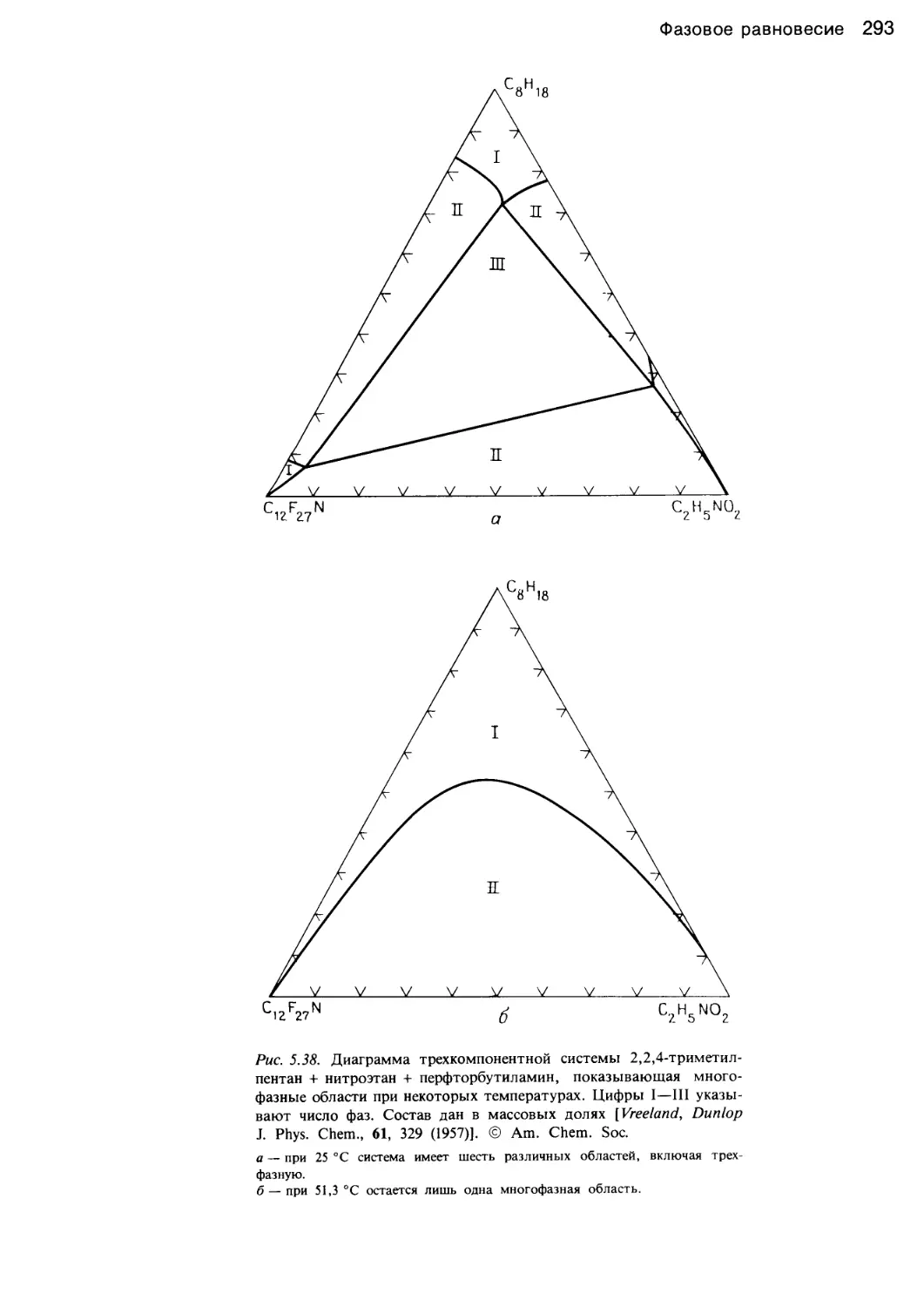
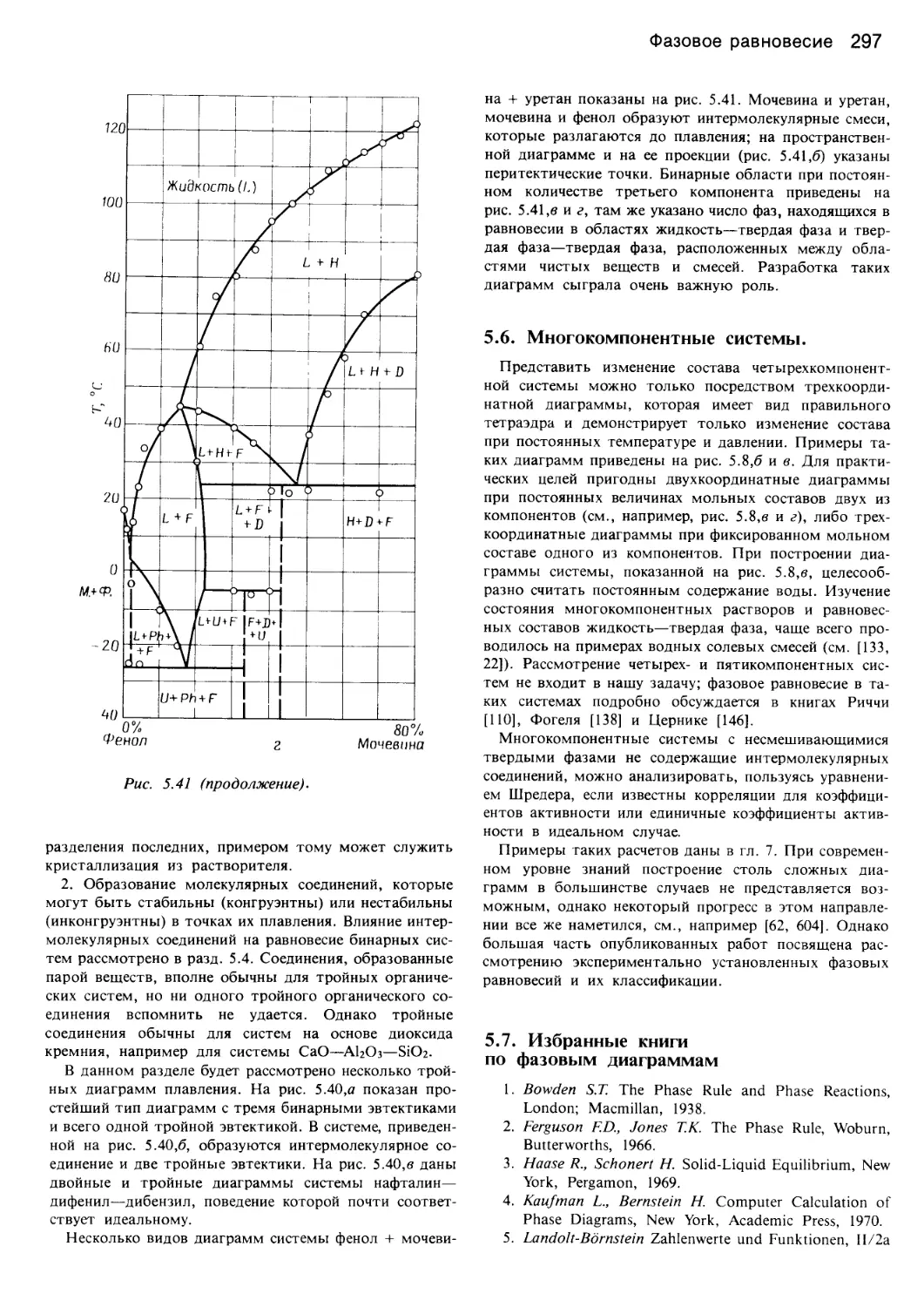
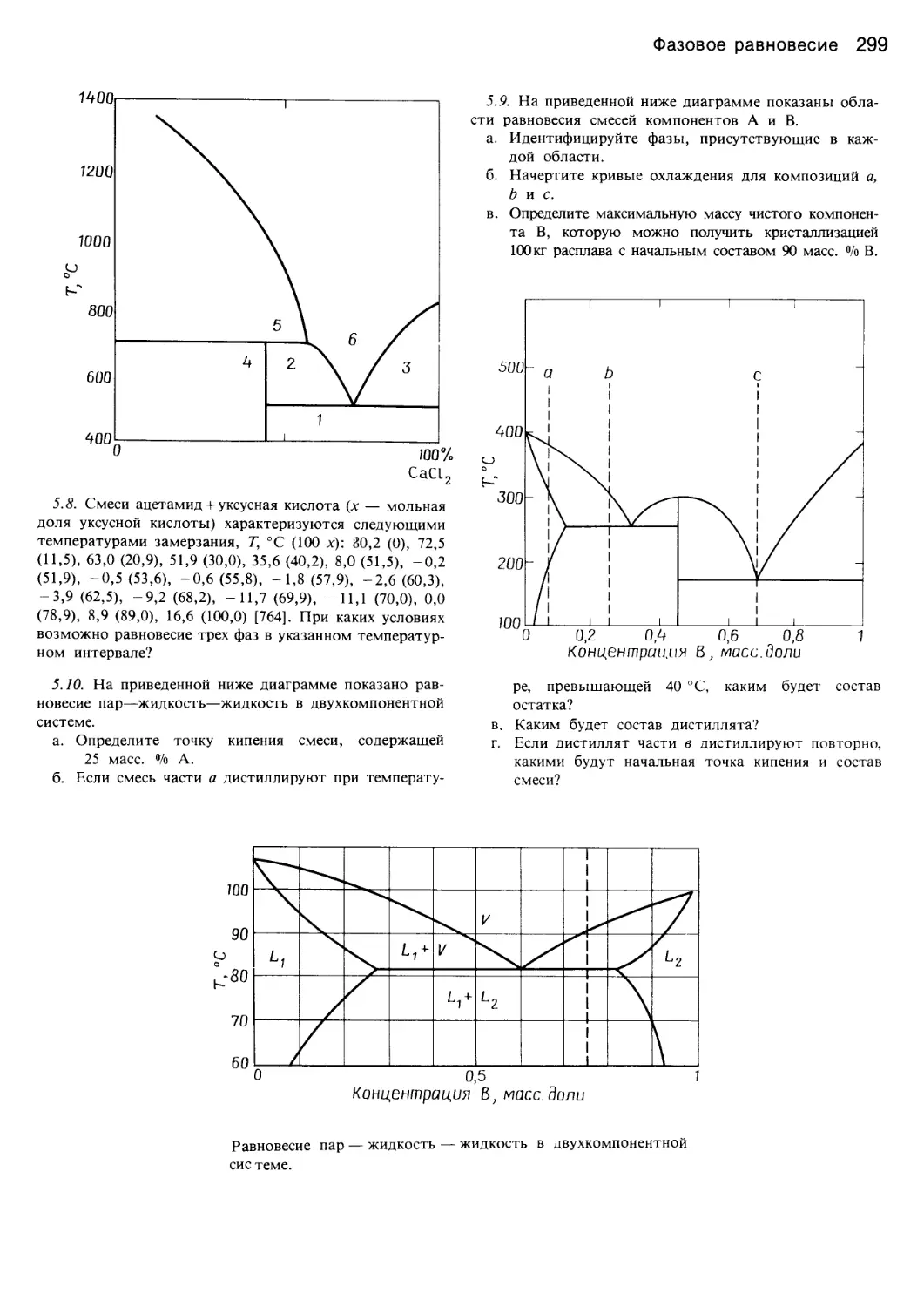
Author: Уэйлес С.
Tags: химия основные процессы и аппараты химической технологии химическая технология
ISBN: 5—03—001106—4
Year: 1989
Similar
Text
С.Уэйлес ФАЗОВЫЕ
РАВНОВЕСИЯ
В ХИМИЧЕСКОЙ
ТЕХНОЛОГИИ
1
ИЗДАТЕЛЬСТВО «МИР»
PHASE EQUILIBRIA IN
CHEMICAL ENGINEERING
Stanley M. Walas
Department of Chemical and Petroleum
Engineering
University of Kansas
and
The C.W. Nofsinger Company
BUTTERWORTH PUBLISHERS
Boston. London
Sydney. Wellington. Durban. Toronto
С. Уэйлес
ФАЗОВЫЕ
РАВНОВЕСИЯ
В ХИМИЧЕСКОЙ
ТЕХНОЛОГИИ
В 2-х частях
1
Перевод с английского
канд. техн, наук А.В. Беспалова,
канд. техн, наук А.П. Жукова и В.В. Паукова
под редакцией
д-ра техн, наук., проф. В.С. Бескова
МОСКВА «МИР»
1989
ББК 35.114
У97
УДК 541
Уэйлес С.
У97 Фазовые равновесия в химической технологии: В 2-х
ч. Ч. 1. Пер. с англ. — М.: Мир, 1989. — 304 с., ил.
ISBN 5—03—001106—4
Издание (автор проф. Канзасского университета, США, С.Уэйлес), в котором со-
браны и систематизированы все практические методы расчета равновесий для широ-
кого круга систем (пар (газ) — жидкость; жидкость — жидкость; жидкость — твер-
дое тело). Отличительная особенность книги — энциклопедическая широта охвата
обсуждаемых проблем. Формульный, графический и цифровой справочный материа-
лы, включая алгоритмы расчета на ЭВМ, удачно дополняют друг друга.
В русском издании выходит в 2-х частях. Вч. 1 рассматриваются уравнения состо-
яния, термодинамические функции, фугитивность и коэффициенты фугитивности, ко-
эффициенты активности, фазовые диаграммы.
Для исследователей, инженеров-практиков, использующих существующие раз-
работки и методы при создании новых технологий и обеспечивающего их инженерно-
го оборудования, а также для студентов химико-технологических вузов.
2801000000-159 147 89
041(01)-89
ББК 35.114
Редакция литературы по химии
ISBN 5—03—001106—4(русск.)
ISBN 5—03—001105—6
ISBN 0—409—95162—5 (англ.)
© 1985 by Butterworth
Publishers. All rights reserved.
© перевод на русский язык,
«Мир», 1989
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
Предлагаемая вниманию читателей книга «Фазовые
равновесия в химической технологии» написана профес-
сором Канзасского университета (США) Стенли М.
Уэйлесом, известным специалистом в этой области,
представляющим отдел инженерной химии и нефтехи-
мии вышеназванного университета и C.W. Nofsinger
Company.
Это своего рода энциклопедическая сводка по фазо-
вым равновесиям и термодинамике гомогенных и гете-
рогенных равновесий органических систем, играющих
столь важную роль в изучении и понимании процессов
химической технологии. В книге достаточно подробно
с привлечением большого числа примеров рассматрива-
ются общетеоретические вопросы, на высоком уровне
представлены современные научные достижения в этой
области.
В целом же четко прослеживается практическая на-
правленность книги. Как указывает сам автор, его труд
предназначен не столько тем, кто занят развитием тео-
рии фазовых равновесий, сколько практикам, использу-
ющим существующие разработки и методы для созда-
ния новых технологий и обеспечивающего их инженер-
ного оборудования. Автор обстоятельно и последова-
тельно излагает все существенные вопросы фазовых
равновесий. Он подробно рассматривает методы расче-
та свойств и параметров реальных газов и жидкостей
и их смесей. Отдельная глава посвящена такому прак-
тически важному вопросу, как графическое представле-
ние фазовых равновесий во всем их разнообразии и
интерпретация диаграмм.
Обсуждаются равновесия в системах пар—жидкость,
жидкость—жидкость, жидкость—твердая фаза. Освеще-
ны также такие вопросы, как равновесия в системах, со-
держащих электролиты, полимеры, жидкие кристаллы
и т. д. В книге описаны (правда, весьма кратко) экспе-
риментальные методы измерения фазовых равновесий.
Очень полезны приложения, в которых дана сводка
термодинамических формул, описаны численные мето-
ды расчета, приведены многочисленные программы для
ЭВМ, таблицы для расчета свойств компонентов и их
смесей.
Список цитированной литературы включает более
800 наименований, так что это издание может служить
ценным библиографическим справочником.
Все это позволяет надеяться, что книга Уэйлеса ока-
жется полезной самому широкому кругу читателей —
химикам-технологам, специализирующимся в области
процессов разделения и переработки смесей органиче-
ских веществ, инженерам-конструкторам, создающим
соответствующее оборудование, научным работникам,
занимающимся вопросами термодинамики растворов и
диаграмм состояния, а также преподавателям, аспиран-
там и студентам, изучающим курсы физической химии
и химической технологии.
И в заключение несколько слов собственно о перево-
де. Прежде всего о названии книги. Ее английское
название — «Phase equilibria in chemical engineering».
Понятие «chemical engineering» включает такие разделы
химической технологии, как процессы и аппараты хими-
ческой технологии, математическое моделирование хи-
мических процессов и реакторов, химическая гидроди-
намика, а также прикладные вопросы некоторых разде-
лов физической химии, физики, механики и математики.
Поэтому его было бы правильнее перевести как «хими-
ческая инженерия», но, к сожалению, в нашей литерату-
ре такой термин не используется. Далее, в книге часто
встречаются и внесистемные, и устаревшие единицы из-
мерения. Объясняется это следующим. Уэйлес подробно
излагает историю развития представлений о состоянии
газов и жидкостей и межфазных равновесий, начиная с
первых работ Бойля, Ван-дер-Ваальса, Клаузиуса, Боль-
цмана, Менделеева, и приводит множество графиков и
диаграмм, заимствованных из первоисточников. Имен-
но поэтому мы сочли возможным придерживаться тре-
бований СИ не столь уж строго. В конце книги при-
веден список всех внесистемных единиц и их современ-
ных эквивалентов. И последнее, некоторые из использу-
емых Уэйлесом терминов не имеют строго определен-
ных эквивалентов в нашей литературе, и поэтому, если
читатели сочтут необходимым предложить нам более
удачные варианты, мы с благодарностью примем их
предложения.
В. Бесков
ПРЕДИСЛОВИЕ
Все окружающие нас вещества находятся в состоянии
фазового равновесия или стремятся к нему. Большин-
ство технологических процессов проводится в условиях,
близких к равновесным, и если для каких-то процессов
предусмотрен другой режим, то все же в такой ситуа-
ции необходимо знать, к чему может привести наступ-
ление равновесия. К числу наиболее важных химико-
технологических процессов относятся смешение, конвер-
сия и разделение газов, жидкостей и твердых тел. На-
стоящая книга посвящена термодинамическим основам
и практическим аспектам расчетов условий равновесия
многофазных систем, характерных для вышеперечис-
ленных процессов.
В настоящее время теория и практика расчета процес-
сов, основанных на фазовом равновесии, постоянно из-
меняется и развивается. Однозначного решения задач
здесь не существует, и редко какой-либо определенный
метод заведомо превосходит все остальные. В связи с
этим автор поставил перед собой задачу — помочь осу-
ществить выбор правильных теоретических положений
и практических методов, не предлагая при этом каких-
либо универсальных решений, что обусловлено положе-
нием дел в данной области. Непосредственно после пре-
дисловия приводятся краткие рекомендации.
Поскольку автор специализируется главным образом
в области расчетов промышленных процессов, непо-
средственно предшествующих этапу конструирования
оборудования, настоящая книга предназначена в боль-
шей степени специалистам, применяющим теорию и
корреляции фазового равновесия на практике, а не зани-
мающимся теоретическими разработками. Основные
теоретические выводы и закономерности иллюстриру-
ются на материале включенных в текст числовых при-
меров или задач. Для решения этих задач достаточно
программируемого калькулятора или портативного
компьютера, в то же время, многие задачи можно рас-
ширить таким образом, что для их решения потребуют-
ся компьютеры модели 32 К и даже большей мощ-
ности. Расчет многостадийных равновесных процессов
в данной книге не рассматривается, поскольку этот во-
прос достаточно полно освещается в других источниках.
Несмотря на то что в книге используется множество
положений классической и статистической термодина-
мики, особенно при описании смесей, сами эти теории
сколько-нибудь подробно не рассматриваются. Автор
стремился создать своего рода практическое руковод-
ство, связав материал с конкретными примерами, тем
самым позволив читателям опираться на свой собствен-
ный опыт, если таковой имеется.
В очень многих случаях автор ссылается на перво-
источники, что позволяет при желании изучить исход-
ный материал. В каждом конкретном случае автор не-
пременно отмечает как достоинства, так и ограничения
рассматриваемых методов и подходов.
Оглавление показывает, как построена книга. Начина-
ется она с исторического обзора, который, будучи инте-
ресен сам по себе, одновременно подчеркивает значи-
мость современного уровня знаний и перспективы его раз-
вития в ближайшем будущем. Поскольку развитие тер-
модинамики теснейшим образом связано с разработкой
уравнений состояния, то первая глава книги посвящена
именно этой теме. Вслед за материалом об основах тер-
модинамики и отклонениях от идеальности, выражен-
ных через фугитивности и активности, следуют главы,
освещающие равновесие преимущественно между пара-
ми фаз. Ряд тем, не относящихся к этим вопросам и
не разработанных в количественном отношении, вклю-
чен в отдельную главу. Особый интерес представляет
глава, в которой рассматривается химическое равнове-
сие, поскольку в ходе многих процессов наблюдается
одновременное химическое и фазовое равновесия.
В двух завершающих книгу главах рассматриваются
оценка изменений энтальпии и энтропии неидеальных
веществ и смесей, которая обязательно входит в любую
методику расчета фазового равновесия, и эксперимен-
тальные методы определения фазового равновесия. По-
следняя глава включена в книгу ввиду того, что многие
читатели интересуются, каким образом были получены
используемые ими данные. В принципе эксперименталь-
ные методы определения фазового равновесия весьма
разнообразны и в ряде случаев очень сложны, так что
представленный в книге материал дает лишь приблизи-
тельное представление.
Настоящая книга может использоваться как справоч-
ник и как учебное пособие при изучении курса фазового
равновесия или смежных тем в рамках программы хи-
мико-технологических учебных заведений. Она может
быть также полезна для инженеров, специализирую-
щихся в области технологии процессов разделения и их
аппаратного обеспечения. В силу важности данного
предмета для многих отраслей химической технологии
в недалеком будущем, по-видимому, появятся более
Предисловие 7
полные курсы теории фазового равновесия как теорети-
ческого, так и справочного плана.
Интерес к данной теме возник у автора вследствие
того, что ему неоднократно приходилось участвовать в
решении производственных вопросов, и именно это об-
стоятельство позволило ему осознать, насколько важна
такая подборка материала. Стимулом для написания
этой книги также послужила экспериментальная рабо-
та, выполняемая в лаборатории низких температур
Канзасского университета под руководством проф.
Г.В. Свифта.
Многие из приведенных в книге рисунков выполнены
Г. Бушнеллом (C.W. Nofsinger Company). Программы для
ЭВМ подготовлены студентами-выпускниками Ч.-Г. Ху-
ангом, К. Роча, Л. Шелингом и Ш. Негабаном (его сле-
дует отметить особо), который также принимал
участие в написании гл. 7.
Профессор Дж.О. Кон (Нотр-Дамский университет)
рецензировал первый вариант рукописи; в соответствии
с его замечаниями текст был существенным образом
переработан. Позднее значительную помощь в работе
над материалом, изложенным в первых шести главах,
оказали проф. К. Джонстон (Техасский университет),
проф. А. Майерс (Пенсильванский университет) и проф.
Дж.П. О’Коннел (Университет шт. Флорида). Автор
выражает глубокую признательность всем научным ра-
ботникам и специалистам-практикам, а также Г. Френ-
клину и К. Бенн за помощь при редактировании ру-
кописи.
РЕКОМЕНДАЦИИ ПО ИСПОЛЬЗОВАНИЮ УРАВНЕНИЙ
Как специалистам в области фазового равновесия,
так и тем, кто только приступает к изучению данного
вопроса, очевидным является многообразие принципов
и методов оценки различных аспектов фазового равно-
весия. Лишь в очень редких случаях какой-либо один
метод во всех отношениях превосходит другие. Это во
многом затрудняет решение конкретных вопросов, но
таково положение дел, из которого следует исходить.
Тем не менее мы сочли возможным привести ряд реко-
мендаций, руководствуясь которыми можно, как прави-
ло, получить такие результаты, точность которых
достаточна по крайней мере для начального этапа ис-
следований.
1. Для нахождения уравнений PVT жидкостей и газов
следует использовать уравнение Соава или уравнение
Пенга — Робинсона. При известных параметрах и воз-
можности применять ЭВМ можно прибегнуть к уравне-
нию Бенедикта — Уэбба — Старлинга.
2. Для определения фугитивностей следует применять
уравнение Соава или уравнение Пенга — Робинсона.
Для определения фугитивностей пара приемлемы либо
В-усеченное вириальное уравнение, либо корреляция Цо-
нопулоса.
3. Для нахождения коэффициентов равновесия испаре-
ния углеводородов и сопутствующих неорганических га-
зов следует использовать уравнение Соава или Пен-
га — Робинсона, а в некоторых случаях — модифици-
рованное уравнение Чао — Сидера. Проверку по от-
дельным точкам следует проводить графическими мето-
дами NGPSA или API.
4. Для определения плотностей жидкостей в широких
диапазонах Т и Р рекомендуется метод Томсона, Бробс-
та и Ханкинсона; в тех случаях, если требуется согласо-
ванность со свойствами пара, например при расчетах
процессов дистилляции, вполне пригодно уравнение
Пенга — Робинсона.
5. Для осуществления корреляции коэффициентов ак-
тивности двух- и многокомпонентных смесей следует
прибегнуть к уравнениям Вильсона.
6. Для нахождения коэффициентов активности по ме-
тоду групповых вкладов наиболее разработанным явля-
ется метод UNIFAC, а при наличии данных для обоих
методов ему практически эквивалентен метод ASOG.
Метод параметра растворимости имеет лишь ограни-
ченную применимость.
7. Для описания равновесия жидкость — жидкость,
как правило, вполне пригодно уравнение NRTL при
«и = 0,2, даже если известны лишь параметры бинар-
ного взаимодействия; результаты его использования не-
сколько улучшаются, если имеются некоторые данные
о многокомпонентной смеси, позволяющие оценить па-
раметры уравнения.
8. Для описания равновесия жидкость — расплав сле-
дует применять уравнение Шредера, лучше модифици-
рованное путем введения коэффициентов активности,
либо полученных экспериментально, либо выведенных
исходя из структуры вещества.
9. Для описания химического равновесия вполне при-
годен релаксационный метод, если число стехиометри-
ческих уравнений не превышает шести или около того.
При решении более сложных задач для минимизации
энергии Гиббса необходима ЭВМ.
10. Отклонение энтальпии и энтропии от идеальности
лучше всего можно описать при помощи метода Ли —
Кеслера, однако, как правило, вполне допустимо ис-
пользование более простых уравнений Соава или Пен-
га — Робинсона.
Рекомендации для представления равновесия
пар — жидкость
Метод Чао — Сидера — Грейсона — Стрида. Этот
метод пригоден для представления систем, насыщенных
водородом, например при проектировании установок для
гидроочистки и риформинг-установок. Он дает удовлет-
ворительные результаты при проектировании оборудо-
вания для химической переработки легких и тяжелых
нефтяных фракций и, как выяснилось, эффективен при
расчетах систем синтетического топлива. Диапазон до-
пустимых температур составляет от - 20 до 450 °C при
давлении не выше 200 атм.
Уравнения Соава и Пенга — Робинсона. Чтобы точ-
ность результатов была максимальной, желательно рас-
полагать параметрами бинарного взаимодействия. В
этом случае использование уравнений обеспечивает
удовлетворительные результаты при проектировании
установок по переработке газов, как не содержащих ак-
тивных соединений серы, так и содержащих до 25%
H2S (высокосернистых). При помощи этих уравнений
можно прогнозировать фазовое поведение в критиче-
ской области, хотя для самой критической точки расче-
ты несколько нестабильны. Результаты описания сме-
Рекомендации по использованию уравнений 9
сей водорода и насыщенных углеводородов отличаются
высокой точностью, при представлении ароматических
соединений точность несколько снижается, но ее можно
улучшить путем введения соответствующих параметров
бинарного взаимодействия. Прогнозы сжимаемости
жидкостей достаточно точны для расчетов фугитивно-
стей, чего нельзя сказать о расчетах плотностей жидко-
стей; так, уравнение Соава может дать результат на
10—20% ниже действительного, уравнение Пенга — Ро-
бинсона является чуть более точным. Эти методы эф-
фективны при проведении расчетов режимов охлажде-
ния, очистных смесей и фазовых равновесий при
давлениях вплоть до 350 атм.
Уравнение Бенедикта — Уэбба — Рубина и уравнение
Бенедикта — Уэбба — Рубина — Старлинга. Для срав-
нительно небольшого числа таких веществ, для кото-
рых определены параметры, эти уравнения можно
рассматривать как стандартные. Будучи более сложны-
ми они, однако, не менее полезны, чем уравнение Соава
или уравнение Пенга — Робинсона, в тех случаях, когда
методика расчета предусматривает проведение много-
численных итерационных процедур.
Уравнение Ли — Кеслера и Ли — Кеслера — Плеке-
ра. Преимущество этих методов по сравнению с преды-
дущими состоит в универсальности параметров, однако
они неудобны при частом повторении расчетов.
Рекомендации по определению
коэффициентов активности жидкой фазы
В данных целях используются уравнения Вильсона,
Цубоки — Катаямы — Вильсона, NRTL, UNIQUAC,
Маргулеса и ван Лаара. Последние два непригодны для
представления многокомпонентных смесей при наличии
только параметров бинарного взаимодействия, а урав-
нение Вильсона нельзя применять для представления
равновесия жидкость — жидкость. Все модели пример-
но одинаково хорошо могут представлять равновесие
двухкомпонентных систем углеводородов. Системы, в
состав которых входят спирты с малой молекулярной
массой, лучше всего описываются уравнением Вильсо-
на, однако, если число атомов углерода превышает три,
преимущество этого менее ощутимо. Для водных сис-
тем самые лучшие результаты чаще всего дают уравне-
ния NRTL, хотя во многих случаях вполне пригодны и
уравнение Вильсона, и уравнение Маргулеса. Смеси ве-
ществ, образующих водородные связи, можно предста-
вить посредством уравнения Маргулеса (наилучший
вариант) и уравнения Вильсона (несколько худший вари-
ант). Решение уравнения Маргулеса и уравнения ван Ла-
ара не усложнено множественностью корней.
Даже применяя уравнения, в состав которых входит
температура, влияние последней лучше рассматривать
отдельно. Одна из используемых для этого корреляций
имеет следующий вид:
Iny, = At + ВУ Т + СУ Т\
Равновесие двухкомпонентных систем жидкость —жид-
кость можно моделировать при помощи всех перечис-
ленных выше уравнений, за исключением уравнения
Вильсона. DECHEMA рекомендует представлять равно-
весие в системе жидкость — жидкость посредством
уравнений UNIQUAC и NRTL при ст = 0,2, поскольку
эти уравнения пригодны для описания многокомпонент-
ных систем, по крайней мере в первом приближении,
при наличии только лишь данных о бинарном взаимо-
действии. Использование уравнения UNIQUAC может
быть предпочтительным для смесей, компоненты кото-
рых значительно различаются по размерам.
1. УРАВНЕНИЕ СОСТОЯНИЯ
Механическое состояние вещества в отличие от тер-
мического или термодинамического можно описать при
наличии известных величин давления, температуры и
объема. Поскольку эти три параметра связаны между
собой посредством так называемого уравнения состоя-
ния f(P, V, Г) = 0, только два из них независимы.
Основные уравнения термодинамики также представ-
ляют собой соотношения определенных трех парамет-
ров, например f(U, S, V) = 0, на основе которых
можно найти все прочие термодинамические свойства,
включая соотношение PVT. И напротив, как будет пока-
зано в гл. 2, данные о соотношении PVT в сочетании
с известной теплоемкостью идеального газа как функци-
ей температуры также составляют одно из основных
уравнений термодинамики.
Само же уравнение состояния соответствующего вида
может применяться для оценки многих важных свойств
чистых веществ и их смесей, например для оценки
1) плотности жидкой и паровой фаз, 2) давления пара,
3) критических свойств смесей, 4) равновесных отноше-
ний между паром и жидкостью, 5) отклонения энталь-
пии от идеального состояния, 6) отклонения энтропии
от идеального состояния.
В настоящее время не существует такого уравнения
состояния, которое было бы в равной степени примени-
мо для оценки всех этих свойств какой-либо обширной
группы веществ. В то же время работа в этом направ-
лении дала множество положительных результатов,
имеющих ограниченную сферу приложимости, о чем бу-
дет рассказано позднее. В данной же главе будет пред-
ставлено описание ряда уравнений состояния. Некото-
рые из этих уравнений представляют только исторический
интерес, однако большинство из них имеет как теорети-
ческую, так и практическую ценность.
1.1. Историческая справка
В табл. 1.1. представлены некоторые ключевые даты
в истории изучения количественных отношений между
давлением, объемом и температурой. Начало исследо-
ваниям в этой области было положено экспериментами
Бойля (1662), в результате которых он пришел к выво-
ду, что при данной температуре объем газа обратно
пропорционален его давлению, т. е. PV = const. Коли-
чественное выражение температурного воздействия бы-
ло установлено Шарлем и Гей-Люссаком (1802), кото-
рые обнаружили линейный характер этого отношения:
V = Ко(1 + кТ). В 1834 г. Клапейрон, основываясь на
двух вышеупомянутых уравнениях, впервые сформули-
ровал закон идеальных газов: PV = R(T + 267). Как
показали последующие исследования, в тех случаях,
когда температура выражена в градусах Цельсия, это
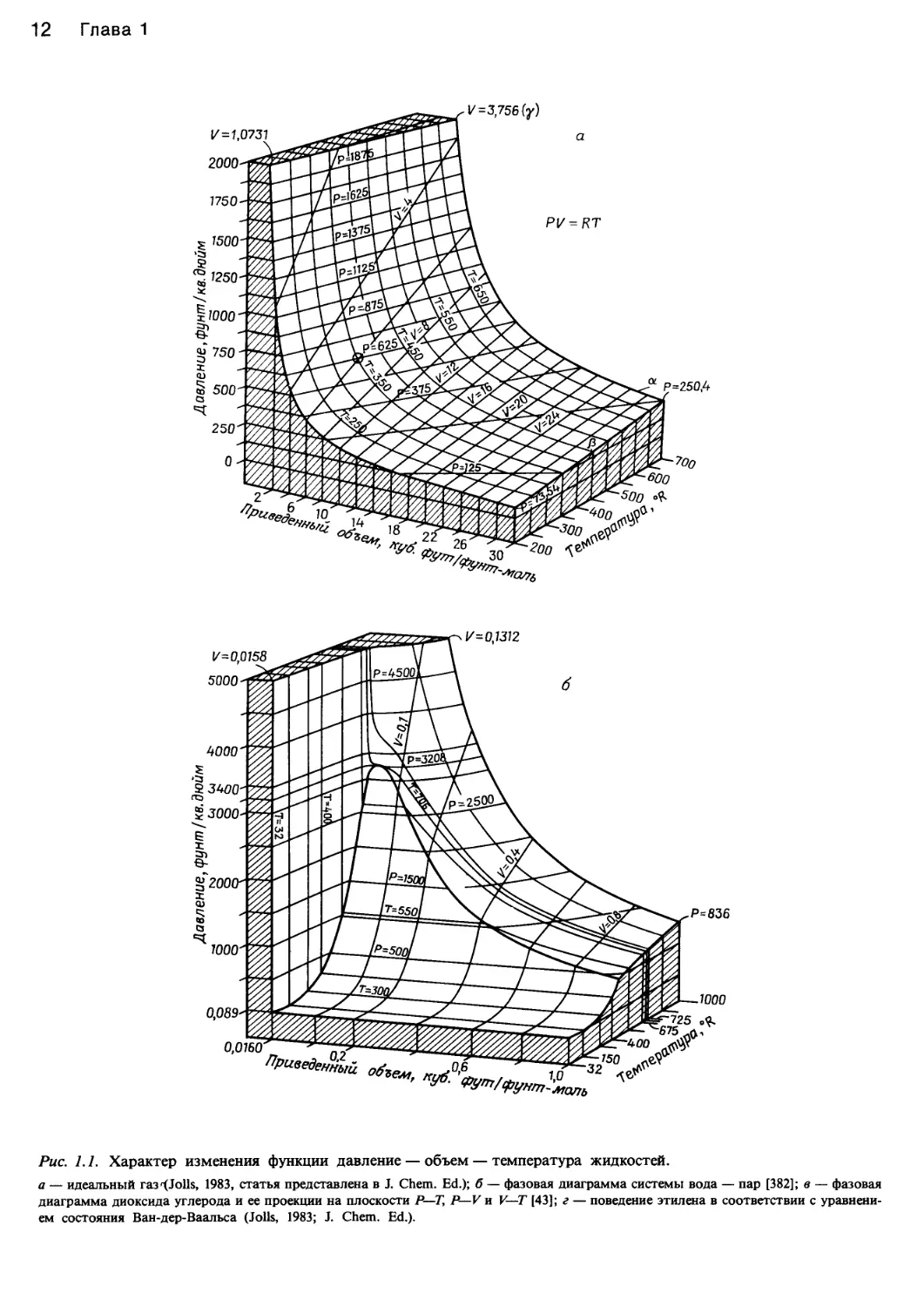
число равно 273,2. На рис. 1.1 показан трехмерный гра-
фик уравнения состояния идеального газа. Для сравне-
ния там же приводится такой же график подобного
типа для усовершенствованного уравнения состояния,
предложенного Ван-дер-Ваальсом, и для уравнения со-
стояния реального вещества (воды). Эти уравнения со-
стояния описывают условия существования жидкой фа-
зы при определенных значениях температуры и давле-
ния, что невозможно сделать при помощи уравнения
идеального газа.
Исследование смесей газов привело Дальтона к от-
крытию закона парциальных давлений (1801), согласно
которому в смеси каждый газ ведет себя так, как если
бы он занимал весь объем. Закон, открытый Амагатом
(1880), гласит, что объем смеси представляет собой сум-
му объемов компонентов, каждый из которых находит-
ся при температуре и давлении смеси. Чистые газы или
их смеси, для которых справедливы отношения
PV = RT и аддитивность парциальных объемов и дав-
лений, получили название идеальных, или совершен-
ных, газов. Прочие свойства, такие, как независимость
давления от внутренней энергии и энтальпии, вытекают
из этих основных законов.
Вопросам фазовых переходов жидкость — газ много
внимания уделял Фарадей, хотя еще примерно за 200
лет до него было установлено (например, ван Гельмон-
том), что при понижении температуры некоторые газы
могут конденсироваться. При определенных значениях
температуры и давления, характерных для каждого ин-
дивидуального вещества, свойства жидкостей и газов
становятся одинаковыми, а по мере приближения к
этим условиям некоторые свойства претерпевают значи-
тельные изменения. Это состояние, названное критиче-
ским, было впервые обнаружено Каньяром де ла Туром
(1822). Критические состояния чистых веществ и смесей
были всесторонне изучены Эндрюзом (1863), работа в
этом направлении продолжается и в наше время. На
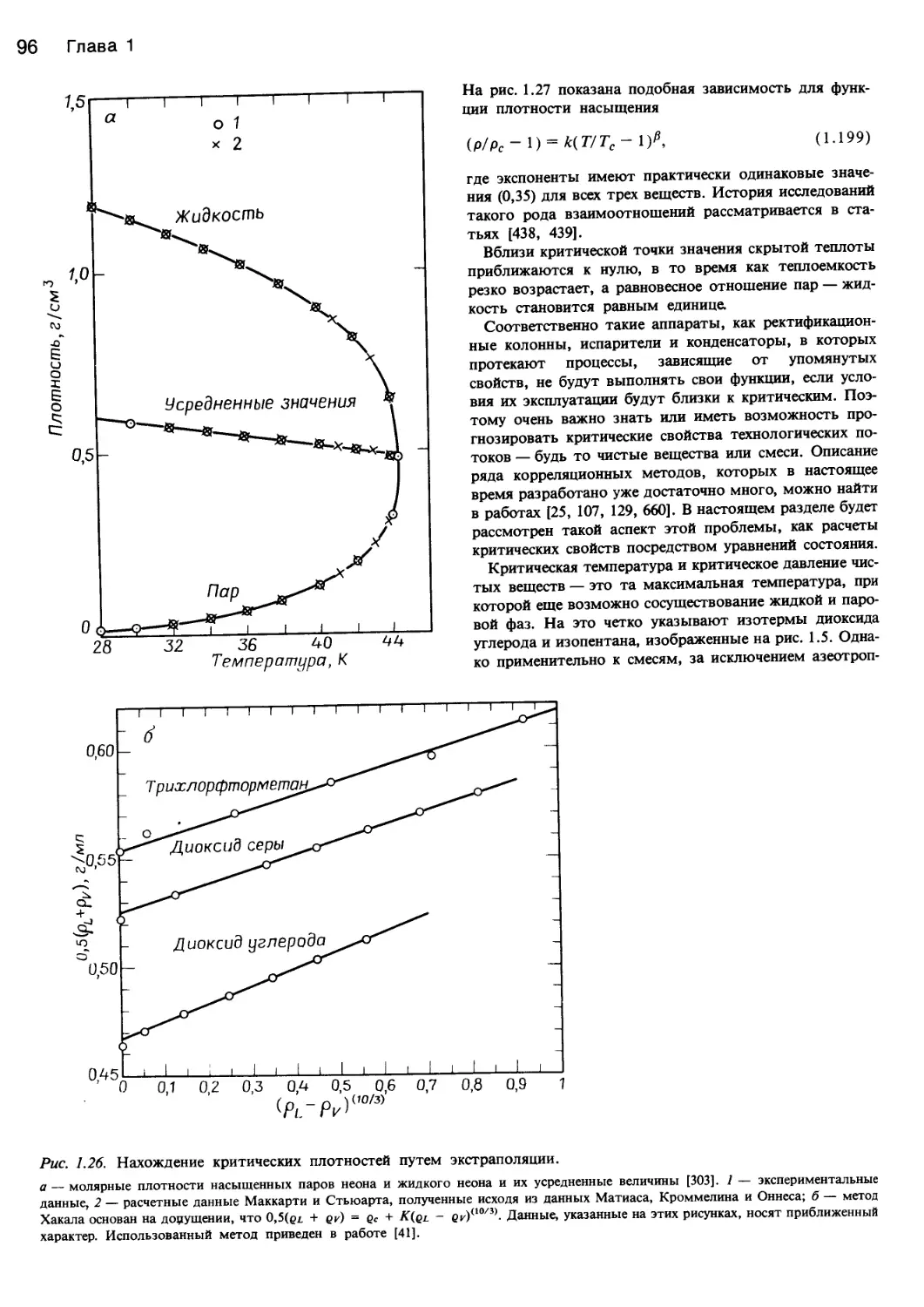
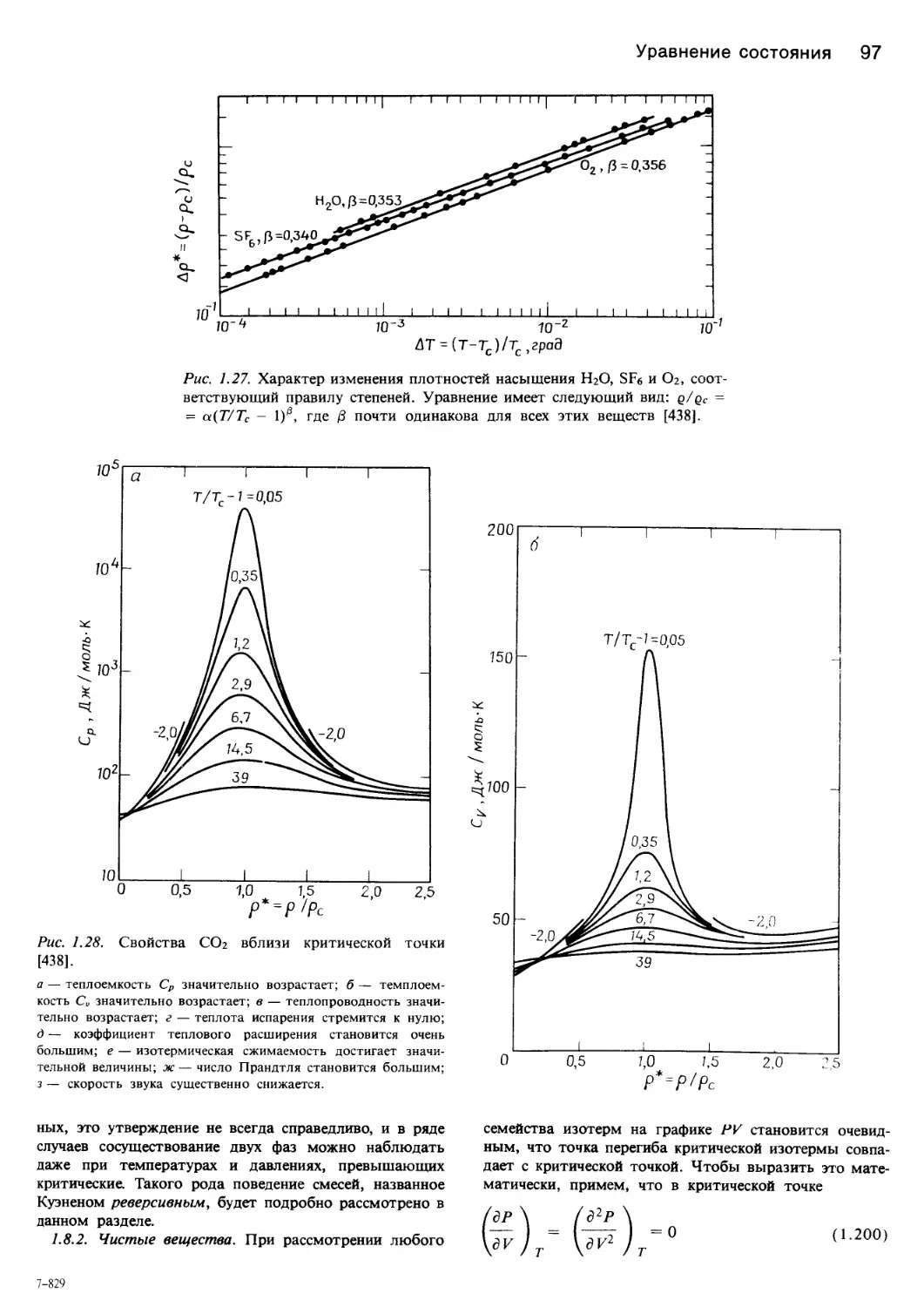
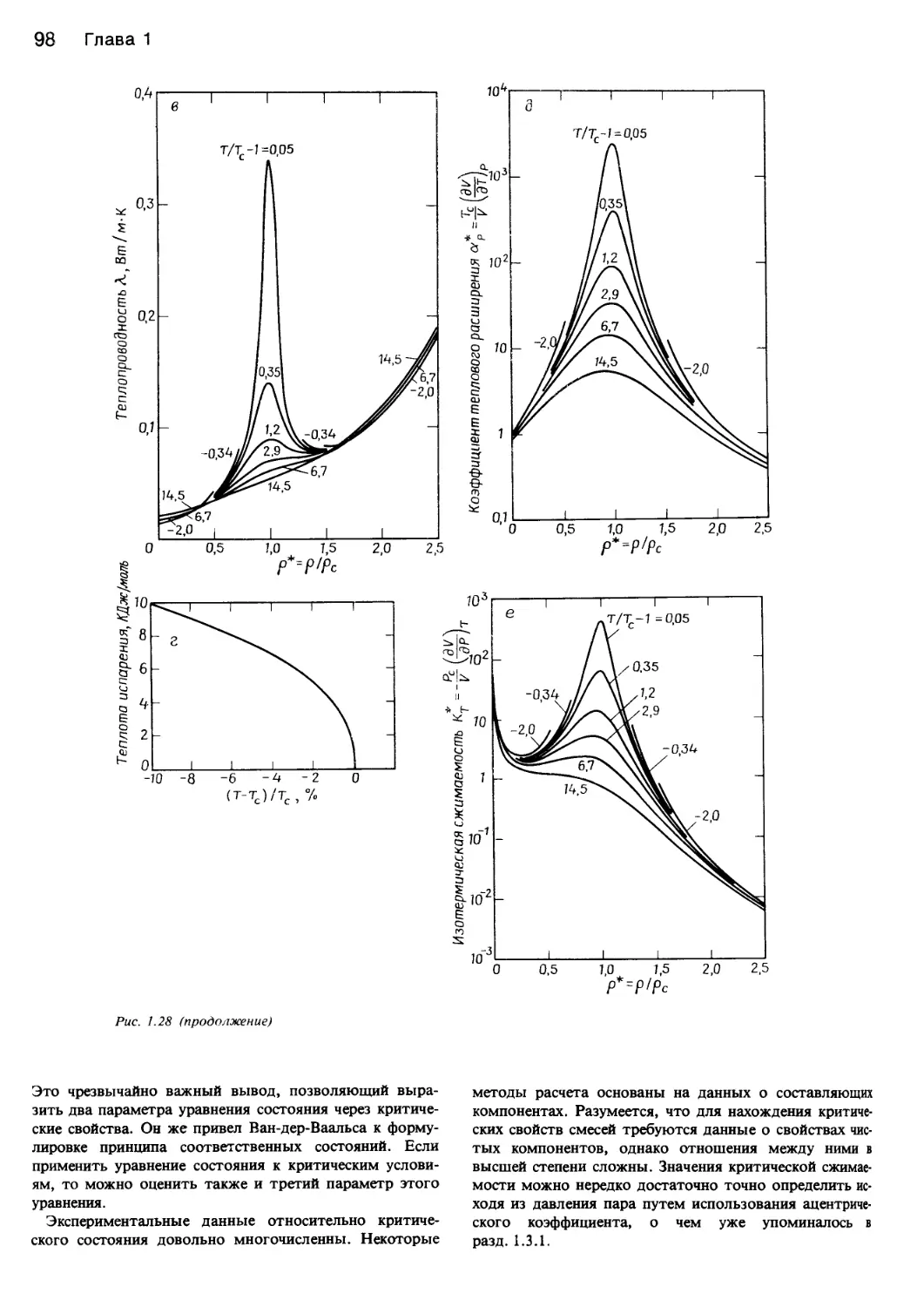
рис. 1.28 показан аномальный характер изменения неко-
Уравнение состояния 11
Таблица 1.1. Историческая справка о законах, описывающих поведение газов
1662 Закон Бойля: PV = const при постоянной температуре и массе
1787 Закон Шарля: ДК пропорциональна ДГ при постоянном давлении
1801 Закон парциальных давлений Дальтона. В смеси каждый газ ведет себя так, как если бы он один
занимал весь объем сосуда
1802 Гей-Люссак: подтверждение закона Шарля
1822 Каньяр де ла Тур: открытие явления критического состояния
1834 Клапейрон: объединение законов Бойля и Шарля РИ = R(t + 267)
1863 Эндрюз: всестороннее исследование критического состояния
1873 Ван-дер-Ваальс: научный труд о непрерывности газового и жидкого состояний. Уравнение состояния
и принцип соответственных состояний
1880 Закон Амагата: объем смеси газов равняется сумме объемов компонентов, каждый из которых нахо-
дится при температуре и давлении смеси
1901 Оннес: разработка вириального уравнения, имеющего эмпирический характер
1901 Льюис Г. Н.: введение понятия фугитивности
1927 Урселл: разработка вириального уравнения с использованием методов статистической механики
1937 Майер: дальнейшая теоретическая разработка вириального уравнения
1940 Бенедикт, Уэбб и Рубин: уравнение состояния
1949 Редлих и Квонг: улучшенное двухпараметрическое уравнение состояния
1955 Питцер: ацентрический коэффициент для параметров соответственных состояний
торых свойств диоксида углерода в состоянии, близком-
к критическому.
Еще на первоначальном этапе исследований было об-
наружено, что закон идеальных газов зачастую может
дать лишь очень приблизительное описание реального
газа. Эти отклонения объяснялись тем, что молекулы
имеют конечный объем, и влиянием межмолекулярных
сил отталкивания и притяжения. Ван-дер-Ваальс (1873)
предложил уравнение, в котором количественно учтены
оба этих фактора, и впоследствии оно было положено
в основу целого ряда уравнений состояния, широко при-
меняемых в наши дни. Это уравнение количественно
определяет условия одновременного существования
жидкой и паровой фаз и критическое состояние систе-
мы. В этой же работе Ван-дер-Ваальс выдвинул очень
важный принцип соответственных состояний (см.
разд. 1.3).
Для описания характера изменения функции PVTдля га-
зов предложены сотни уравнений, некоторые еще до появ-
ления уравнения Ван-дер-Ваальса, но подавляющее
большинство позднее. В разработке таких уравнений при-
нимали участие такие известные ученые, как Рэнкин, Клау-
зиус, Больцман, Планк и др. В табл. 1.2 показана
представляющая исторический интерес подборка уравне-
ний состояния, предложенных более чем пятьдесят лет
назад.
В результате исследования сил межмолекулярного взаи-
модействия Урселл (1927) вывел, используя методы стати-
стической механики, вириальное уравнение состояния,
фактически предложенное задолго до негоТизеном (1885),
который пришел к нему чисто эмпирическим путем, и раз-
витое впоследствии Оннесом (1901). Одним из преиму-
ществ такого способа вывода уравнения является создание
теоретических основ для соотнесения поведения смеси с ее
составом и свойствами чистых компонентов. Битти и
Бриджмен (1927), а впоследствии Бенедикт, Уэбб и Рубин
[181] разработали уравнение, связанное с вириальным
уравнением состояния; ряд модификаций первого широко
используется в настоящее время для легких углеводородов
и неорганических газов, жидких и паровых фаз, а также для
смесей. Некоторые из вариантов вириального уравнения
состояния включают до тридцати констант, поэтому при-
менять их, не располагая ЭВМ, практически невозможно.
Среди многочисленных модификаций уравнения Ван-
дер-Ваальса наиболее точными являются уравнение Ре-
длиха и Квонга [58] и более современные модификации,
предложенные Соавом [651], а также Пенгом и Робинсо-
ном [546]. Это кубические уравнения, в которые входят в
основном параметры, характеризующие критическое со-
стояние, но существуют и такие их модификации, в кото-
рые входят температура и такие параметры, как,
например, критическая сжимаемость или ацентрический
коэффициент (см. разд. 1.3.1).
Большинство модификаций этих уравнений эмпириче-
ские, их параметры можно подогнать к определенному ви-
ду экспериментальных данных, таких, как давление пара,
плотность или энтальпия. В последнее время, однако, ве-
дется работа по применению теории статистической меха-
ники в целях усовершенствования кубических уравнений
состояния. Сравнительно простые результаты получены
авторами работы [213], а более сложные — авторами ра-
боты [255]. Предпринята попытка распространить это
уравнение на полярные вещества [739].
Количественных данных, характеризующих поведение
жидкостей, получено гораздо меньше, чем для газов, хотя
в этом направлении в настоящее время ведутся обширные
исследования как теоретического, так и коррелятивного ха-
рактера. Типичным примером может служить работа [331]
о корреляции плотностей насыщенных жидкостей. Многие
уравнения состояния, как сложные, например уравнение
Бенедикта — Уэбба — Рубина [181], так и более простые,
например уравнение Пенга — Робинсона [545], а также
уравнения Харменса — Кнаппа [334], разработаны специ-
ально для представления плотностей жидкостей. Как осо-
бо значительное достижение в данной области следует
отметить появление методов ASOG и UNIFAC (см. гл. 4),
12 Глава 1
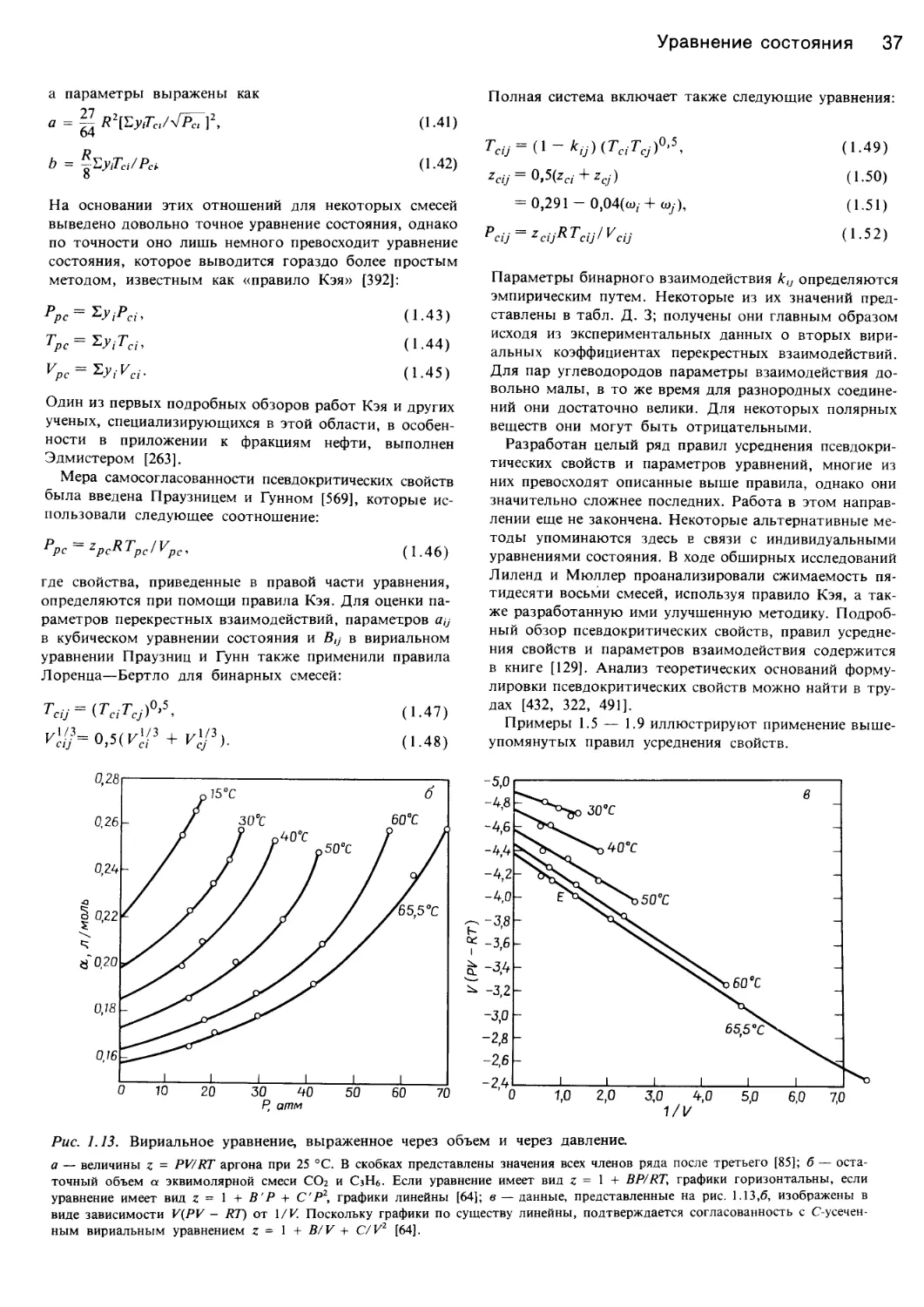
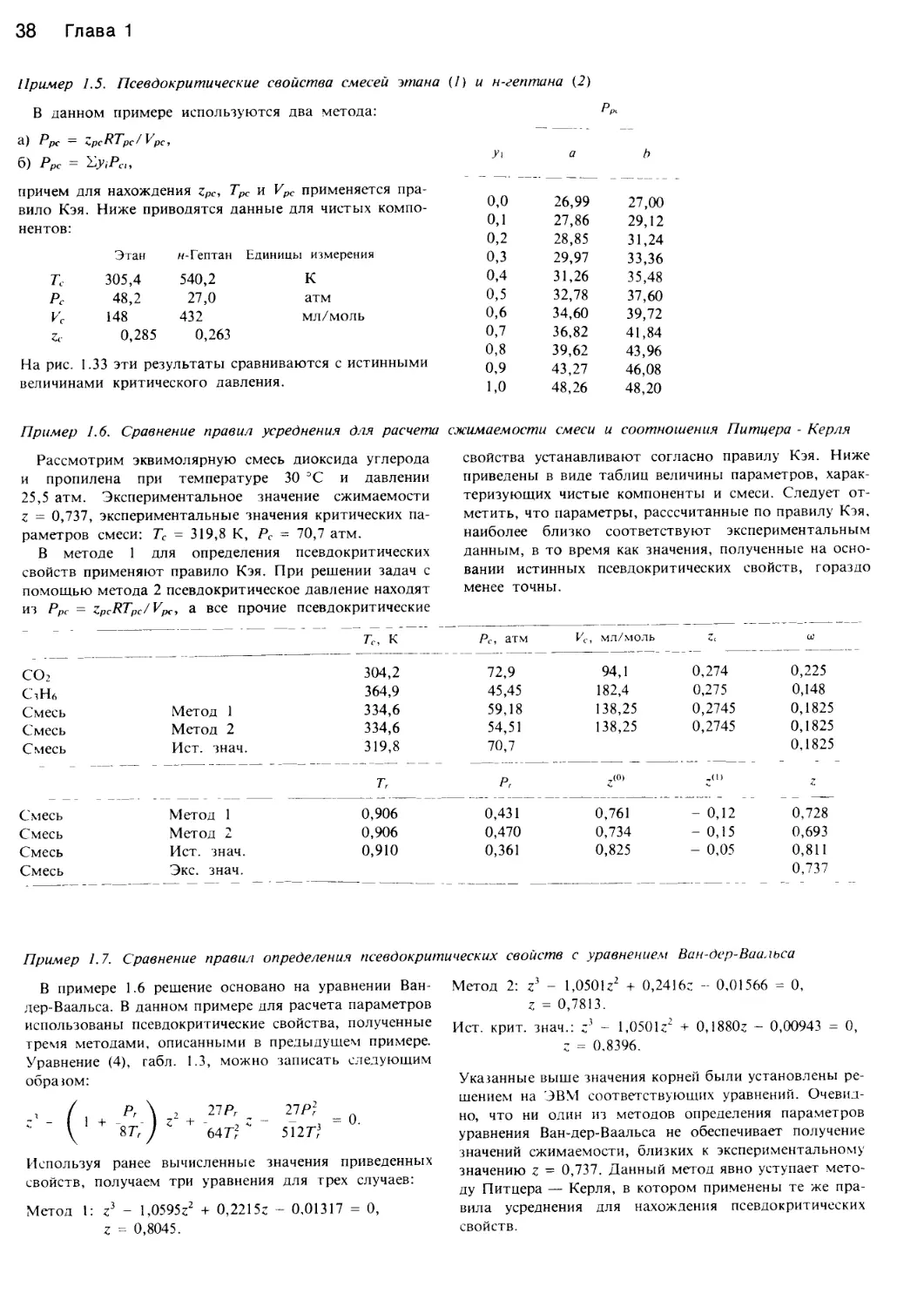
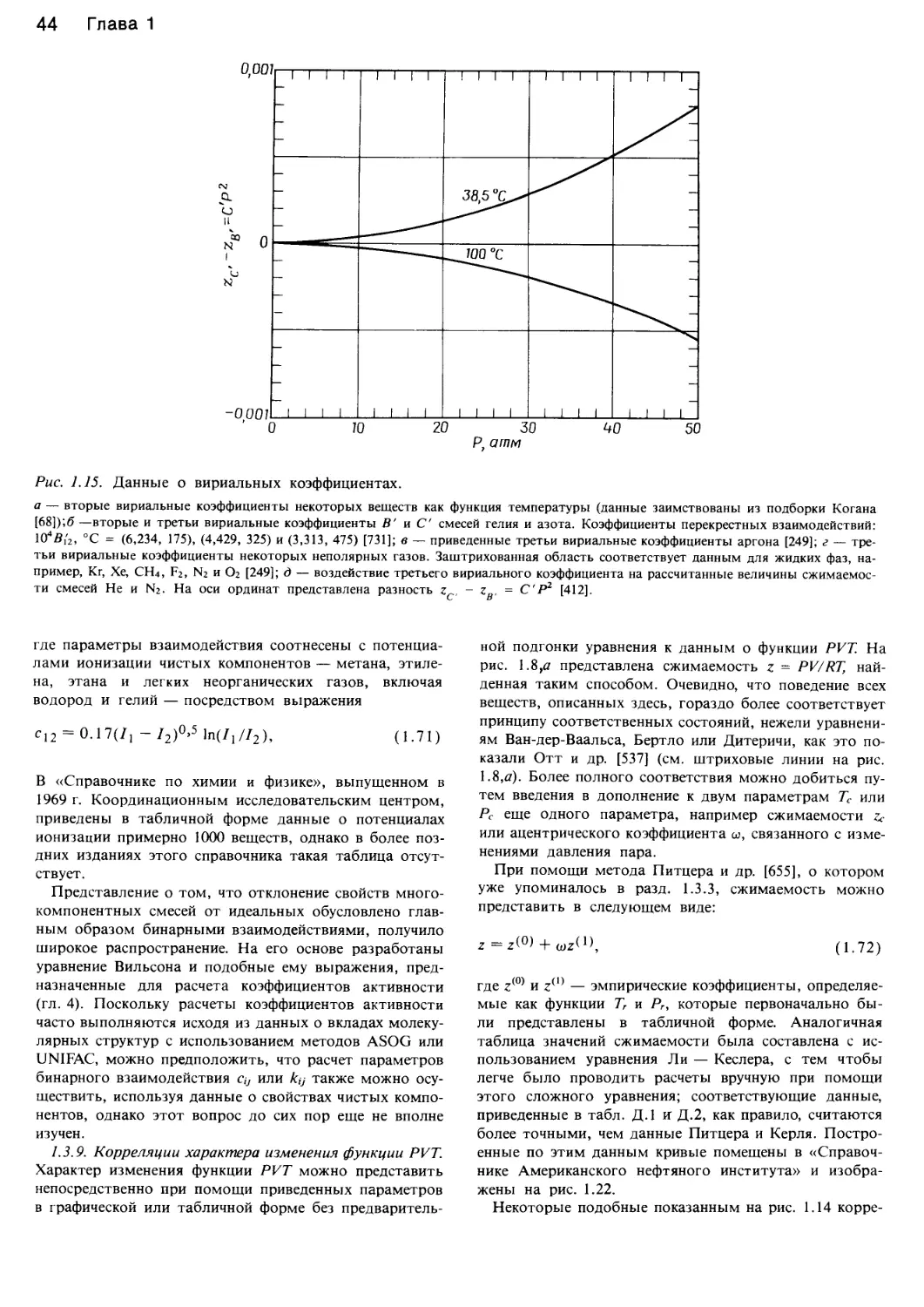
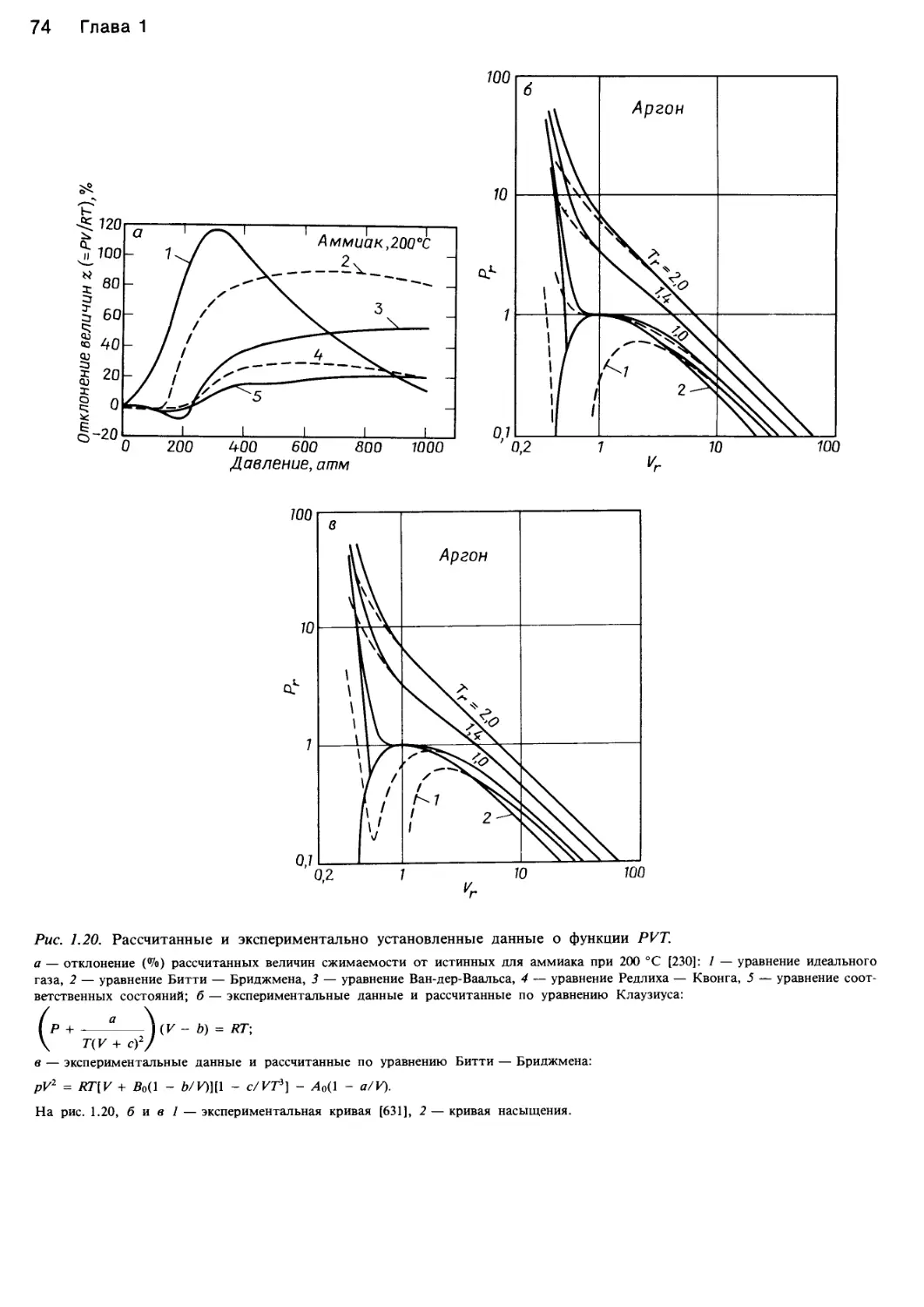
Рис. 1.1. Характер изменения функции давление — объем — температура жидкостей.
а — идеальный газ <XJoils, 1983, статья представлена в J. Chem. Ed.); б — фазовая диаграмма системы вода — пар [382]; в — фазовая
диаграмма диоксида углерода и ее проекции на плоскости Р—Т, P—V и V—T [43]; г — поведение этилена в соответствии с уравнени-
ем состояния Ван-дер-Ваальса (Jolls, 1983; J. Chem. Ed.).
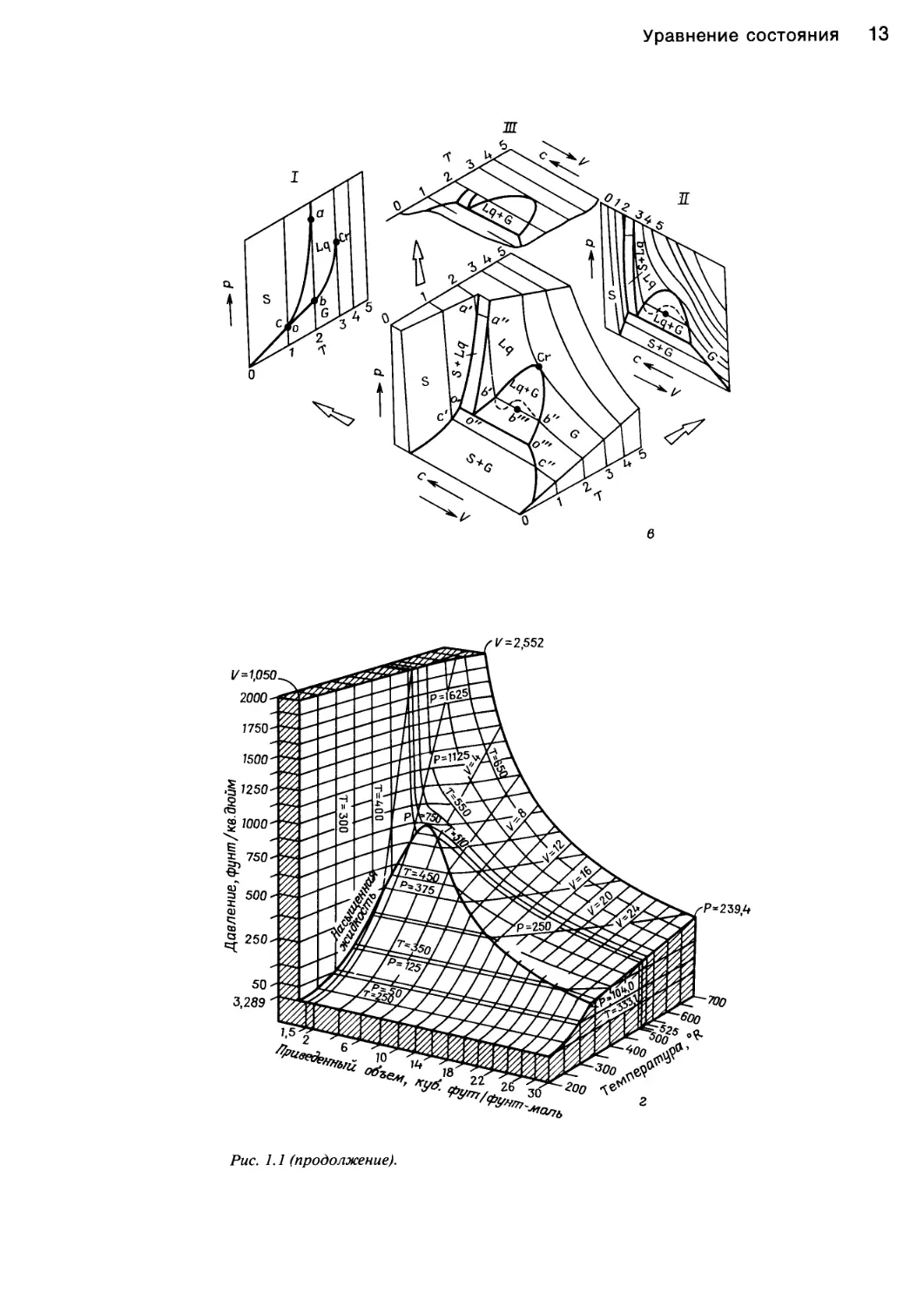
Уравнение состояния 13
Рис. 1.1 (продолжение).
14 Глава 1
Таблица 1.2. Некоторые из первых уравнений состояния3 [92]
1. pv = RT Бойль, Гей- (Boyle, Gay
где R — константа Люссак Lussac)6
2. pv = RT — a/Tv Рэнкин (Rankine) Phil. Trans., 144, 336
(1854)
где а — константа
3. pv = RT + ар/Т 2 Джоуль, (Joule, Phil. Trans., 152, 579
где а — константа Томсон Thomson) (1862)
. AT f(T) 4. Р = + -5- Дюпре (Dupre) Ann. Chim. et Phys., 4,
и + с и 426 (1865) или Bull. Acad.
где с — «совместный объем», А — константа ГОу gejg щ (1887)
5. (р + a)(v - b ) = RT Хирн (Hirn) Ann. Chim. et Phys., 11, 5
где а — «сумма внутренних действий» (1867); cp. de Heen
(«внутреннее давление») и b — сумма объ-
емов молекул
6. pv = RT(l — b/v) Рекнагель (Recknagel) Ann. phys. Ergbd., p. 563
где b = f(T) (1871)
Over de Continuiteit van
den Gas en Vloeistoftoe-
stand, Leyden, 1873; cp.
Jiiptner
7 \P+ 2)(L — b) = RT Ван-дер- (van der Zeit. phys. Chem., 63, 579
У и / Ваальс Waals) (1908); 73, 343 (1910)
где а, b и R константы
Ann. Phys., 9, 337 (1880);
14, 279 (1881); cp
„ ( а 8- ( Р + TV ) (и - b) = RT Клаузиус (Clausius) Sarrau Chem. Rev., 101,
\ Г(и + С)2 941, 994, 1145 (1885)
где а, Ь, с и R — константы
„ RT 9. р = - — 1 _ (ЛТ~Я - В')(у - 6)~ Клаузиус (Clausius) Ann. Phys., 14, 692 (1881)
(и - Ь) (и + с)2
где А, Ь, В , С , R и п — константы
/ а \ 10. ( р + — 1 и у и2 / = RT (1 + - ) \ V / Лоренц (Lorentz) Ann. Phys., 12, 127 (1881)
где а, b и А • константы
11. (р + f(T)ve~ = RT Уолтер (Walter) Ann. Phys., 16, 500 (1882) I
где е — основание натурального логарифма и
ь =Г(Т)
12. p(v - а) = f(v) ’т M(v - а) Амагат (Amagat) Chem. Rev., 94, 847 (1882);
L vm + av”-1 + ... + k_ 118, 566 (1894)
где а — атомный объем; т, к, а и т д. —
константы
_ КГ 13. р - Ke~r Cappay (Sarrau) Chem. Rev., 110, 880
(v - а) ( v + З)2 (1890)
где R, а, 0, К и £ — константы; ср. c yp.
(8)
14. pv = RT ( 1 + Г1 т2 \ 7 + 7+J Тизен (Thiesen) Ann. Phys., 24, 467 (1885)
где Тг, Т2 и т. д. — функции Т
Уравнение состояния 15
Продолжение табл. 1.2
15. pv = RT(1 + ai + аг + а3 + ... + bi + Ьг +
+ b3 + . ..)
где аз, аг, ... являютя функциями Т в зави-
симости от природы газа, a b\, Ь2, ... —ин-
Натансон (Natanson)
Kin. Theor. unvolk. Gase,
Dorpat, 1887; Ann. Phys.,
33, 683 (1888); Arch, de
Geneve, 28, 112 (1892)
тегралы
16.
17.
19.
1 -| г 2к ~
р 4----------v = RT I 1 -I-----------
и(и + к) [_ и + к
Сазерленд (Sutherland)
Phil. Mag., 24, 113 (1887),
35, 211 (1893)
Данное уравнение тождественно уравнению
(8) при f(T) = 1 - ct и F(T) = Ь/Фг.
Уравнение было выведено для СОг
аТ (г/Ь)2
b 1 - (г/Ь)3
Лагранж (Lagrange)
Bull. Acad. roy. Belg., 16,
171 (1888)
где а — константа, независимая от газа, г —
радиус атомов газа и 2d — среднее расстоя-
ние между их центрами, А — константа, за-
висящая от молекулярного притяжения
р + 0,000004568Л/37йр---------—
13596/7 .
-------------------------------- (v - b) =
2{(v - d)(l + at)}2 = RT
Виоли (Violi)
Rend R. Acc. dei Lincei, 4,
285, 316, 462, 513 (1888)
где n — число атомов в
pv = f(v)lA + Т - >/р]
где А п В — константы
молекуле
Антуан (Antoine)
20. p(v b) - RT + v — c v — Ct Тэйт (Tait)
где A, b, c, d, E — константы
21. В высшей степени сложное уравнение; выве- дено для диссоциирующих газов Суорт (Swart)
22. (р + (v — уТ) = RT у T(v + /3)7 Шиллер (Schiller)
где X, д, /3, 7 — константы, зависящие от
газа
23. / а\ / d\4 ,у,, 3 I р -1 I ( и ) = RTv3 \ v2J \ У Егер (Jager)
где а и b — константы
24. RT ml~* - пГ Бателли (Battelli)
Р , и — a (v + /З)2
25. АВС р = + + - v — a v — /3 v — 7 Бриллуин (Brillouin)
26. В высшей степени сложное уравнение Уэнстейн (Weinstein)
27. , с \ av Роуз Иннес (Rose Innes)
\ v + к - gv 2J v + к
где R, с, к, g, а — константы
28. (р+ + = КГ \ V2/ \ 32 v / Больцман (Boltzmann)
Chem. Rev., 108, 896
(1889); 110, 131, 1122
(1890); 112, 284 (1892)
Proc. Roy. Soc. Edin., 16,
65 (1889); 18, 265 (1891);
Trans. Roy. Soc. Edin., 36,
257 (1892)
Diss. Amsterdam, 1890;
Beib., 15, 339 (1891)
Ann. Phys., 40, 149 (1890)
Wien, Ber., 99, 1028, 1892
(1891); 101, 1675 (1892);
105, 15, 97 (1896)
Ann. Chim. et Phys., 25,
38 (1892)
Journ. de Phys., 2, 113
(1893)
Ann. Phys., 54, 544 (1895)
Phil. Mag., 44, 76 (1897);
45, 102 (1898)
Gastheorie, II, 153 (1898)
16 Глава 1
Продолжение табл. 1.2
или
(₽ +?)("?) = ет(
2 b
з 7
7 Ь2
24 V2
где a, b, R — константы
29.
с
V2 + С?
= RT
v - Т[а + m(v - b) + с(и - Ь) !]
Аги2,85 - а + nV(-0)2 + d2
Уравнение выведено для СОг; а, Ь, с, т, п,
к, d, а, & — константы
31. (р + ^\(v - bec/T) = RT
\ и/
где 0 = f(T), b, С, R — константы
32. (р + — ](v - b) = RT
\ и5/3 /
где a, b, R — константы
33. р(у - b) = RTe~c/RTv
где Ь, с, R — константы
34. P + A Tv3/2(vl/2 + ?)_ (u - b) = RT
35. P + Tv2/ b) = RT
36. P + 2 \ > U \ 1 ь2 V (v ~ b) = RT
\J4V2^/_
37. То же, что и уравнение (7), но
38. р = CRTe~Q/RT
39. (р +------](v-b) = RT
\ (и - а)2/
(а \
р +------I (у _ £0 + ьхр} = rt
(и - а)2/
уравнение для СОг
41. ( р + ае2 + -----------------------] (у - Ь) =
\ А + Bq + Cq2 + D^J — Ry
где q — плотность
42.
п (А + B/v)(v/k - 1)
pv = Kl —
43.
v2 - s
где А, В, к, s = f(T)
(уравнение для изопентана)
1/2(у - к)
и(и — X)
(уравнение для эфира)
pv = а(Т -
Больцман и Max (Boltzmann, Mache) Ann. Phys., 68, 350 (1899)
Амагат (Amagat) Chem. Rev., 128, 538, 649 (1899)
Рейнганум (Reinganum) Diss. Gottingen, 1899; Arch. Neerl., 5, 574 (1900); Ann. Phys., 6, 533 (1901)
Дитеричи (Dieterici) Ann. Phys., 69, 685 (1899); 5, 51 (1901)
Дитеричи (Dieterici) Ann. Phys., 66, 826 (1898)
Стаквезер (Starkweather) Am. J. Sci., 7, 129 (1899)
Бертло (Berthelot) Arch. Neerl., 5, 417 (1900)
Тамлирц (TUmlirz) Wien. Ber., 108, 1058
(1899); 111, 524 (1902)
Ван-дер- (van der
Ваальс Waals)
Май (Mie)
Zeit. phys. Chem., 38, 257
(1901)
Ann. Phys., 11, 657 (1903)
Гебель (Goebel) Zeit. phys. Chem., 47, 471 (1904); 49, 129 (1906)
Гебель (Goebel) Boltzmann Festschrift., Leipzig, p. 626, 1904
Смолу- (Smolu- Boltzmann Festschrift.,
ховский chowski) Leipzig, p. 626, 1904
Бащински
Бащински
(Batschinski) Ann. Phys., 19, 310 (1906);
21, 1001 (1906)
(Batschinski) Ann. Phys., 19, 310 (1906);
21, 1001 (1906).
Уравнение состояния 17
Продолжение табл. 1.2
44. КГ / 1 --1 - — ч и/ и2 - константы Планк (Planck) Preuss. Akad. Wiss., 633, 1908
Р = - — log (
/3 \
где а, к и /3 —
45. Р»2 =fi(T) - Tf2(T) Ледюк (Leduc) Chem. Rev., 148, 1670 (1909)
46. , В С D Е F pv — А 4- — 4- — 4- — 4- — 4- — V V2 v4 V6 и8 или в приведенном виде *ф~ы 1 + ^ + т (0 +J 0) + +е &+’ (О’] где к = RTc/PcVc и 0 = bi 4- bi/в 4- Ьз/03 4- 4- ь4/в4 + ь5/е5 Оннес (Onnes) Konink. Akad. Wetens, p. 273, 1912; cp. Jeans Dyn. Theory of Gases, p. 164, 1916
47. pv = Аеар + Ьр2 + где А, а, Ь, с ср3 + ... — константы Пежальски (Peczalski) Chem. Rev., 156, 1884 (1913)
48. ( е'~*\ ( тг 4- 3 1 (Зф — 1) = 8(9 \ Ф2 / Дальтон (Dalton) "Лапе. Roy. Soc. S. Africa, pt. 2, 123, 1914
49. / 2а > 1 Р + , \ О' + Ь)2) 1 _ V Кэм (Kam) Phil. Mag., 37, 65 (1919)
50. \Р + - -М (v-b) = RT \ Tv(v - b) T2v3/ Воль (Wohl) Zeit. phys. Chem., 87, 1 (1914)
51. Р log 2о и где b — константа (ср. с уравнением (44)) Шаха, Басу; Чепмен, Эплби (Shaha, Basu; Chapman, Appleby) Phil. Mag., 36, 199 (1918) Phil. Mag., 40, 197 (1920)
52. RT с кр2 v = - - 4- — 4- Ь р Т Т где с, к, R и b — константы Шрибер (Schrieber) Phys. Zeit., 21, 430 (1920)
53. т g £(-а/ф - Ь/ф2 - с/ф1) ф - 1/4 где тг — приведенное давление, 0 — приведен- ная температура, 0 — приведенный объем, а, Ь, с — константы Портер (Porter) Phil. Mag., 44, 1020 (1922)
54. (р 4- a/v2)(y - b) = RT(1 4- ф2/Т2)~3 где 0 — характеристическая температура Бойнтон, Брэмли (Boynton, Bramley) Phys. Rev., 20, 46 (1922)
55. , 0 Р + , (и 4- П)2_ где 0 = /(7), г выведено для (v - b) = RT 1, b — константы; уравнение воздуха Фуше (Fouche) Chem. Rev., 169, 1089 (1919)
56. р = 2,92855 Т/(ъ - <5) - 1623,63/(У + 0,2954)2 Смит, Тей- (Smith, J. Am. Chem. Soc., 45,
где 5 = 0,18683 того азота) - 0,3113/и (уравнение для чис- лор (для чистого азота Thylor) 2107 (1923)
а Аналогичная подборка приведена Отто [538], а более подробная приведена Вукаловичем и Новиковым в 1948 г.
[759].
6 Историю этого уравнения см. в книге Партингтона [92].
2-829
18 Глава 1
Таблица 1.2а. Некоторые из первых и современных формул определения давления
пара
1. In Р = (£j + кг Т) In Т
2. In Р = к\ In (кг + к3Т)
3. 1пР = к,Т/(Т + кг)
4.1пР = кх - к2/Т - к3Т2
5.1пР = ку - к2/(Т + к3)
6. In (Рс/Р) = к(Тс/Т - 1), к = 3
1.Pr(Vg - VL) = RT(\ - РГ)
8. In Pr = (1 - l/TVXAj - to In Tr)
9. InP = kx + кг/Т + k3T + k4T2
10. In P = k(Tc/T - 1) + (Tc/T) In Pc
11. In P = ki + k2/T + k3 In T + k4P/T2
12. InP = kx + кг/Т + k3T + k4T3
13. Pr In Pr = k\7 + ^2T1,5 + k373 + k476
7=1- T/Tc
Шмидт (1797)
Янг (1807)
Реде (1841)
Рэнкин (1849); Кирхгоф (1858)
Антуан (1888)
Ван-дер-Ваальс (1899)
Нернст (1906)
Карбонелли (1919)
Крэгоу (1928)
(Int. Crit. Tables III, p. 228)
Полл ара (1942)
Фрост и Калкварф (1953)
Парлахер и Браун (1970)
Райд, Праузниц и Шервуд (1977,
р. 188)
Миллер (1964)
Вагнер (1973);
Эмброуз (1978)
применяемых для прогнозирования поведения неидеаль-
ных жидких смесей на основе их молекулярных структур.
Интенсивная исследовательская работа в области разра-
ботки новых уравнений состояния ведется главным обра-
зом по следующим трем направлениям:
1. Разработка уравнений высокой степени точности, со-
держащих несколько постоянных, для таких важных чис-
тых веществ и смесей, как вода, воздух, аммиак, диоксид
углерода, легкие углеводороды, криогенные жидкости.
2. Разработка сложных уравнений и алгоритмов для та-
ких смесей, с которыми приходится работать в газо- и неф-
теперерабатывающей промышленности.
3. Разработка более простых уравнений типа кубиче-
ских, пригодных для выполнения многократных расче-
тов фазового равновесия и функций отклонения при
проектировании многостадийных процессов разделения
смесей с ограниченным использованием ЭВМ.
При создании уравнений состояния большое внима-
ние уделяют их применению для описания электроли-
тов, полимеров, каменноугольных жидкостей, а также
полярных веществ, для которых до сих пор не разрабо-
тано адекватное уравнение состояния.
1.2. Неидеальные газы
Важность понятия «идеальный газ» как основы для
сравнения трудно переоценить, поскольку все газы при
низких давлениях приближаются к идеальному состоя-
нию. Более того, для расчетов свойств идеальных газов
вполне применимы методы статистической механики,
причем результаты подобных расчетов зачастую пре-
восходят результаты экспериментов, проведенных на
газах, свойства которых приближаются к идеальным.
Дополнительную информацию по этим вопросам мож-
но получить в книге [112].
1.2.1. Отклонения от идеальности. Многие свойства
реальных веществ, чтобы упростить расчеты, можно
характеризовать по степени их отклонения от свойств
идеальных газов. Например, остаточный объем
ДИ = V - RT/Р может служить мерой неидеальности,
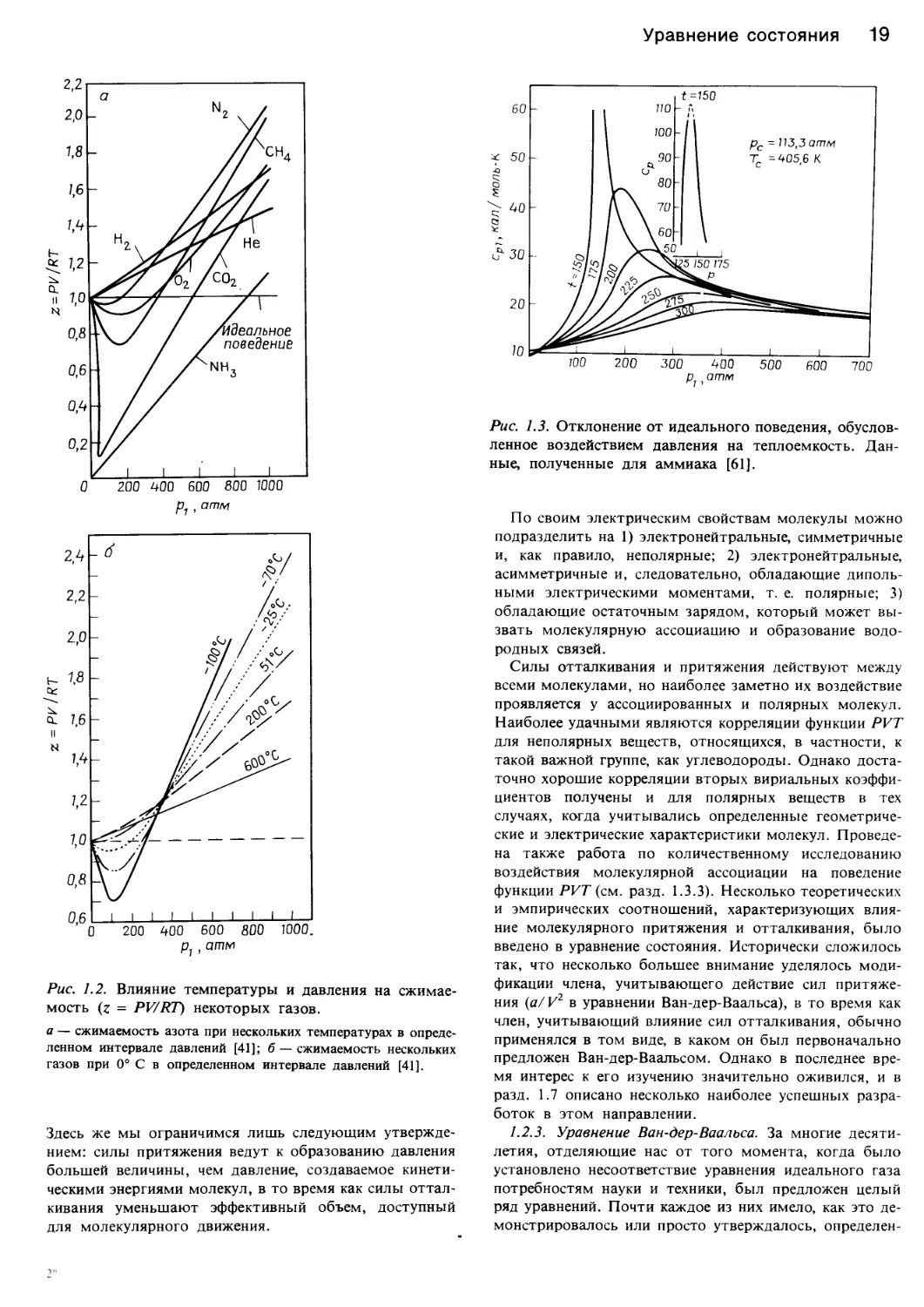
или сжимаемости, z - PV/RT. Как показывает рис. 1.2,
у некоторых веществ величина сжимаемости значитель-
но отклоняется от единицы. Графики сжимаемости
представлены также на рис. 1.8. Ниже будут описаны
некоторые корреляции этого свойства веществ. Изотер-
мы идеального газа в прямоугольной системе коорди-
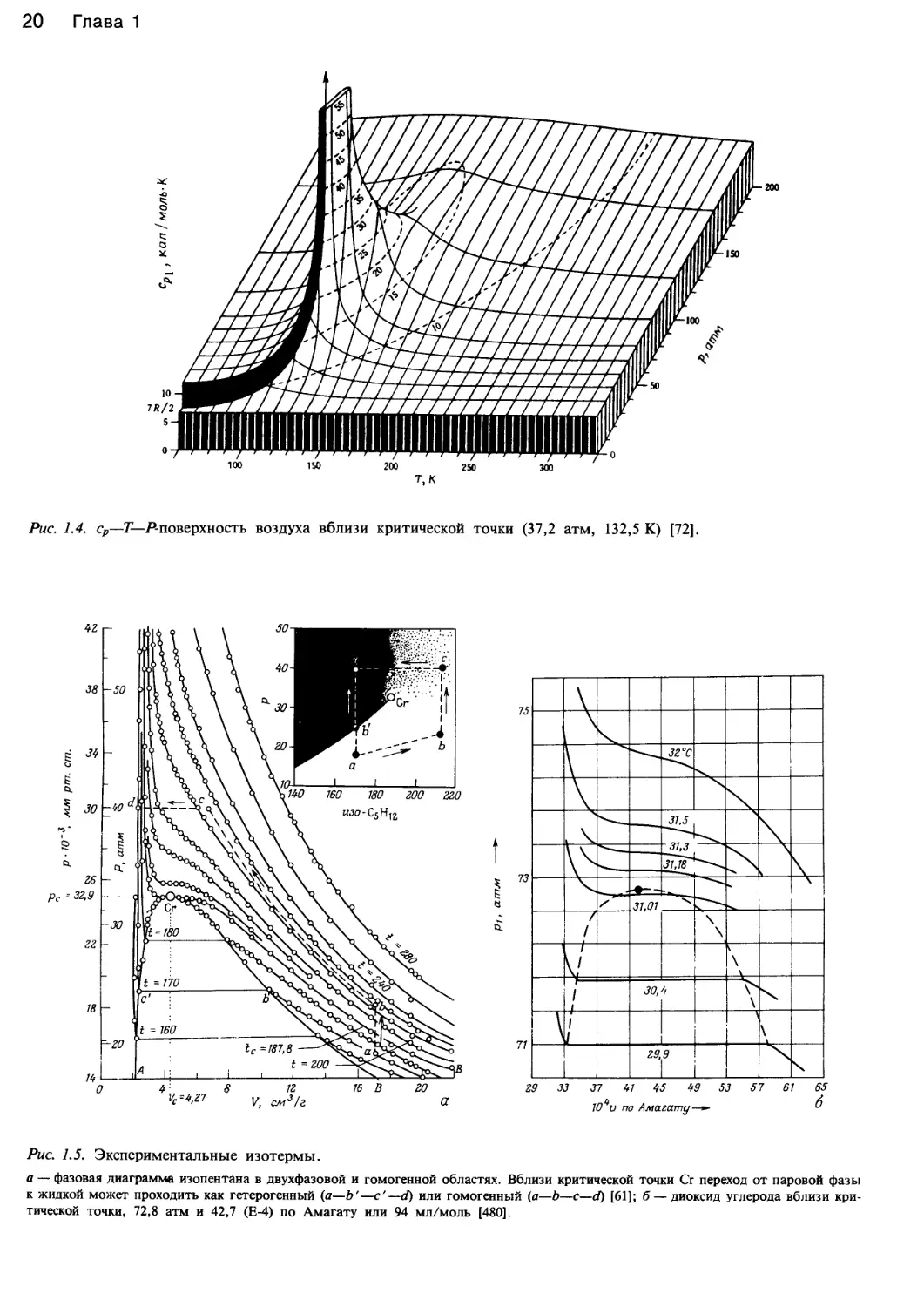
нат представляют собой гиперболы, однако изотермы
диоксида углерода и изопентана (рис. 1.5, а, б) сущест-
венно отличаются по форме от гиперболы, особенно в
области критической температуры.
Реальные газы отличаются от идеальных также ха-
рактером изменения их теплофизических свойств. Теп-
лоемкость идеальных газов не зависит от давления, но
на реальные газы это правило (рис. 1.3 и 1.4) не распро-
страняется. Кроме того, вблизи критического состояния
у реальных веществ в отличие от идеальных газов на-
блюдается аномальное изменение многих других их
свойств. Типичный пример такого аномального измене-
ния свойств диоксида углерода показан на рис. 1.28.
1.2.2. Силы межмолекулярного взаимодействия. Си-
лы, действующие между молекулами, а следовательно,
и характер изменения функции PVT определяются раз-
мерами, формой и структурой отдельных молекул. Си-
лы притияжения стремятся удержать молекулы вместе,
в то время как силы отталкивания препятствуют их вза-
имному уничтожению. Действие сил притяжения прояв-
ляется сильнее с увеличением расстояния между
молекулами, действие сил отталкивания — с его умень-
шением. Силы межмолекулярного взаимодействия
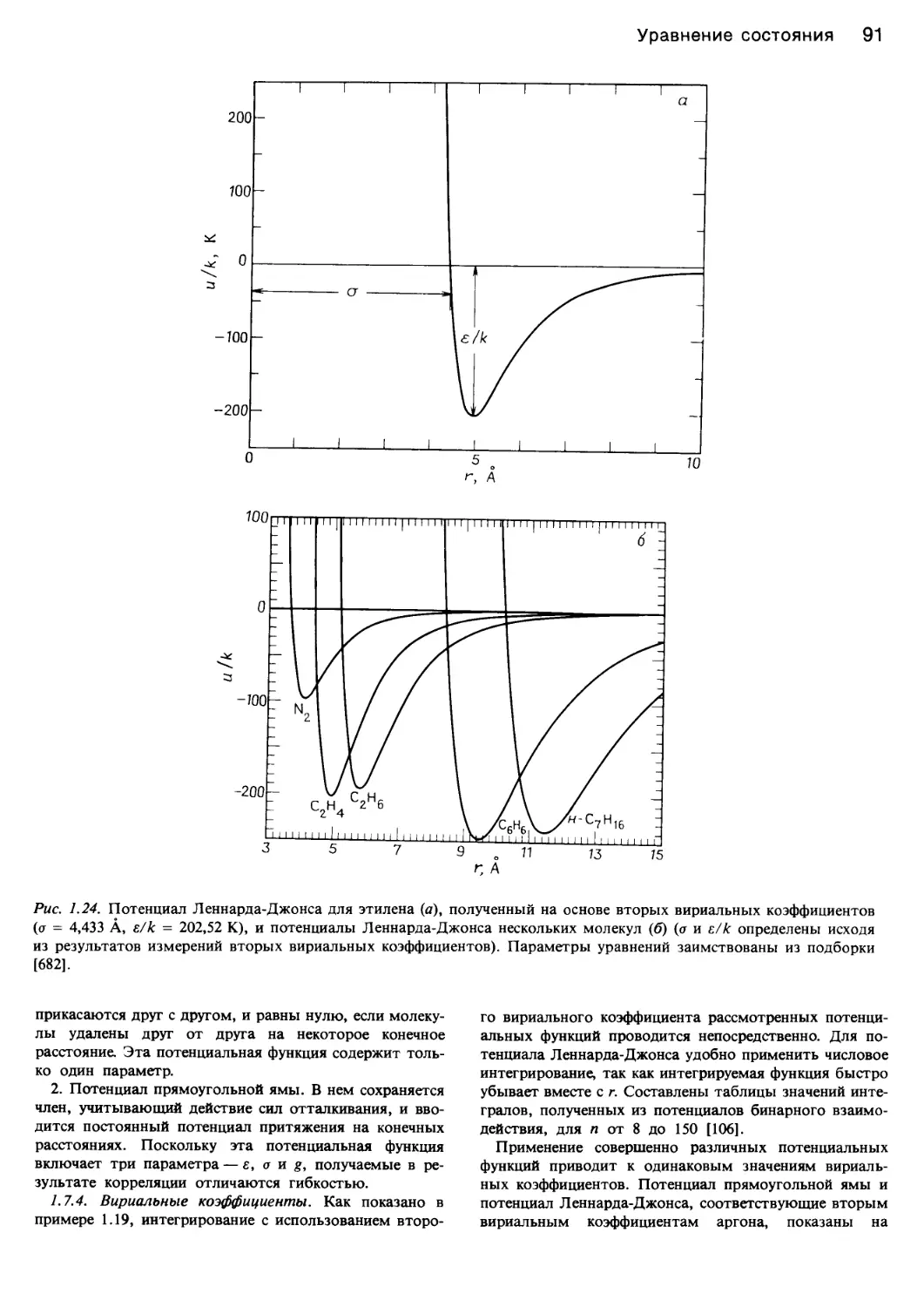
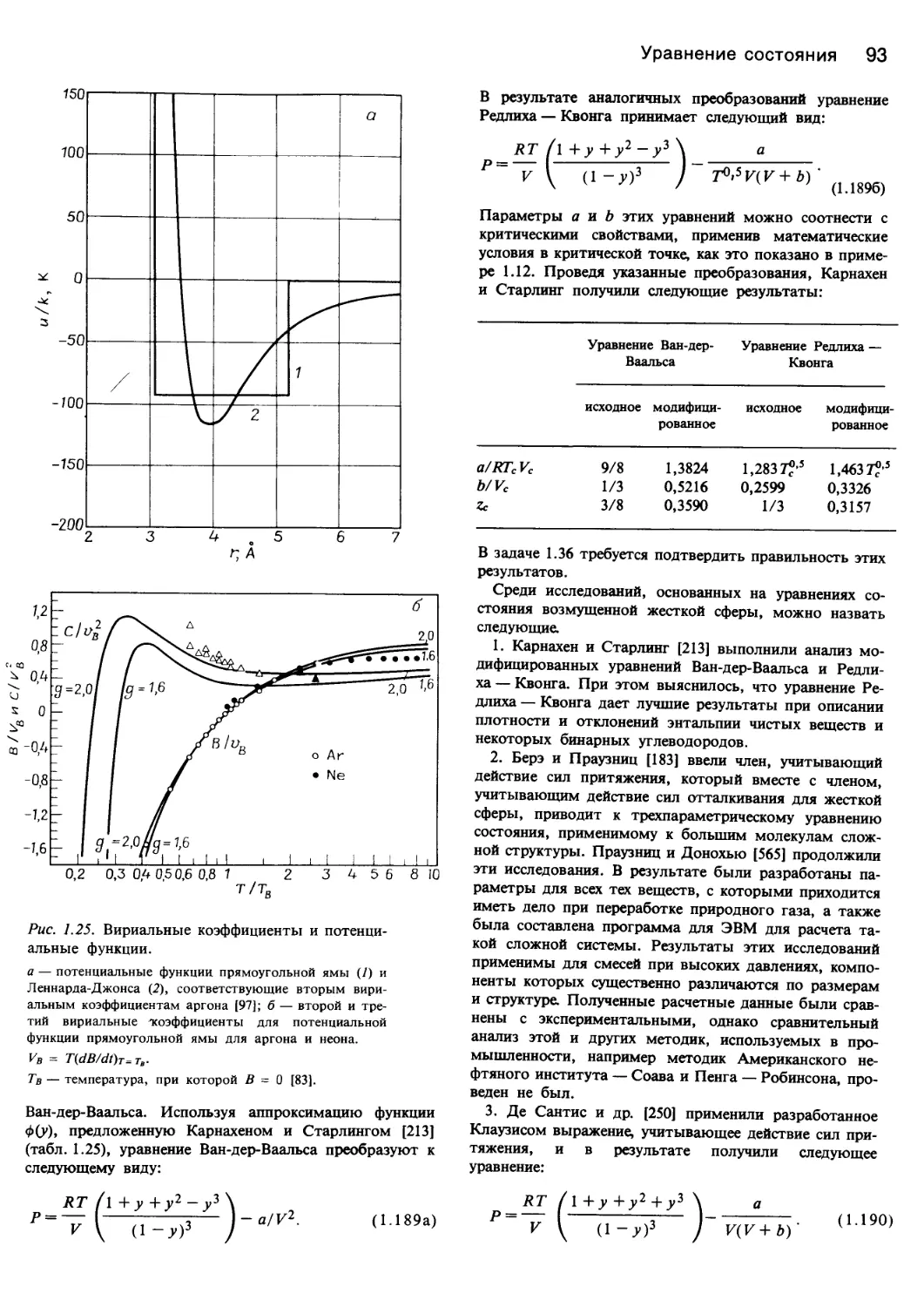
можно выразить через потенциалы, градиенты которых
определяют силы взаимодействия. На рис. 1.24 и в
табл. 1.23 показана зависимость потенциалов от рассто-
яния между молекулами. Некоторые количественные
аспекты этих вопросов рассматриваются в разд. 1.7.
Уравнение состояния 19
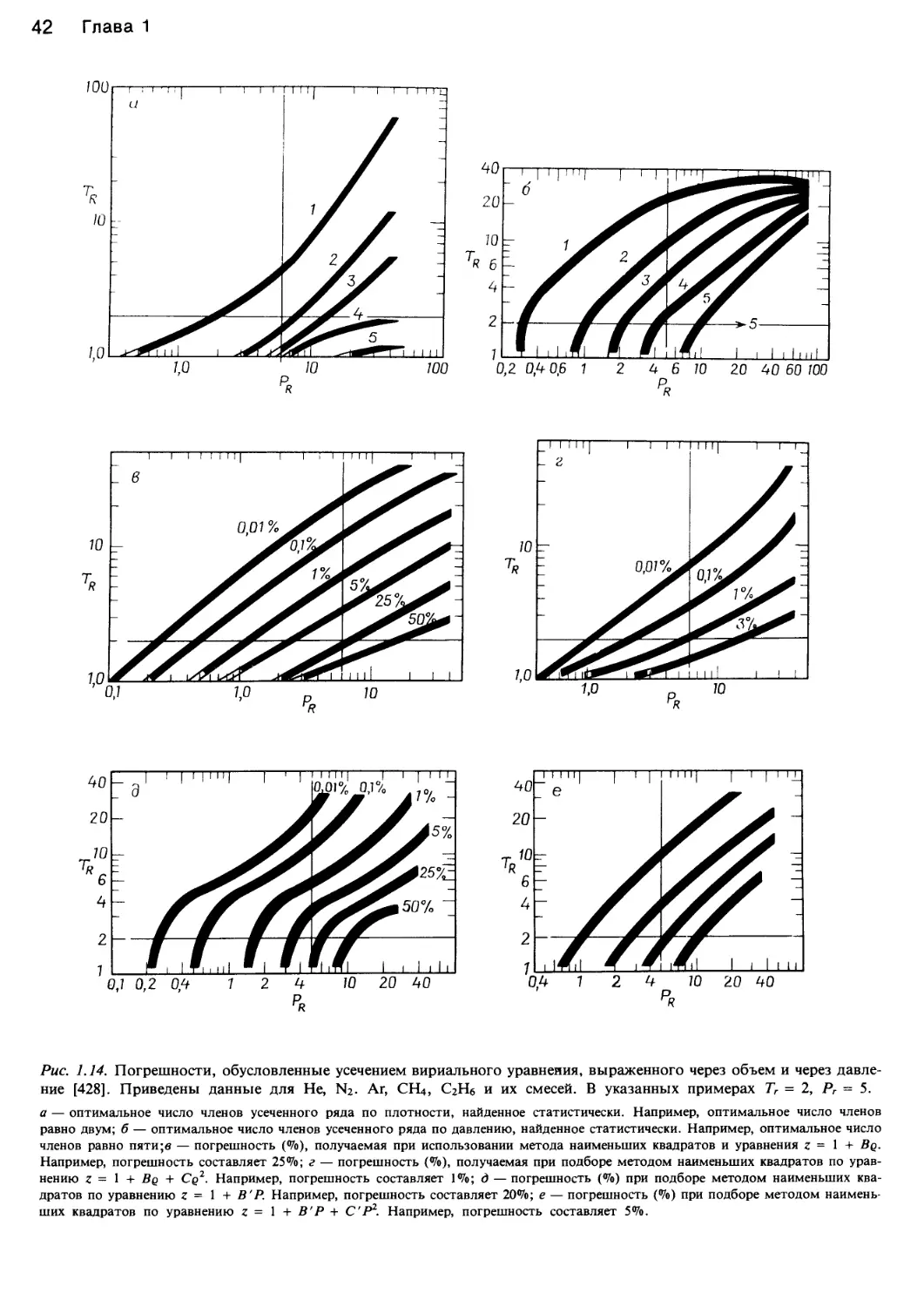
Рис. 1.2. Влияние температуры и давления на сжимае-
мость (z = PV/RT) некоторых газов.
а — сжимаемость азота при нескольких температурах в опреде-
ленном интервале давлений [41]; б — сжимаемость нескольких
газов при 0° С в определенном интервале давлений [41].
Здесь же мы ограничимся лишь следующим утвержде-
нием: силы притяжения ведут к образованию давления
большей величины, чем давление, создаваемое кинети-
ческими энергиями молекул, в то время как силы оттал-
кивания уменьшают эффективный объем, доступный
для молекулярного движения.
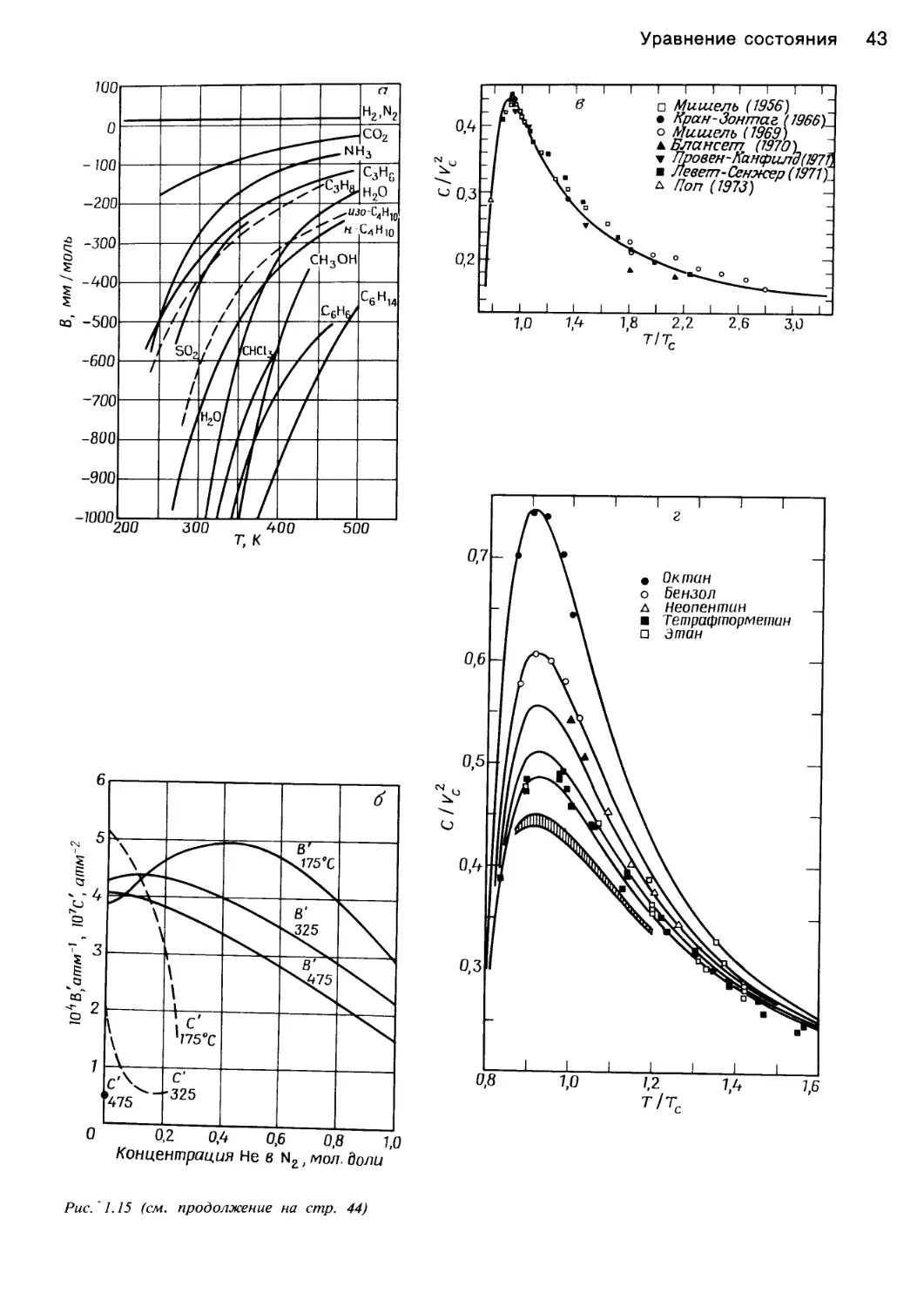
Рис. 1.3. Отклонение от идеального поведения, обуслов-
ленное воздействием давления на теплоемкость. Дан-
ные, полученные для аммиака [61].
По своим электрическим свойствам молекулы можно
подразделить на 1) электронейтральные, симметричные
и, как правило, неполярные; 2) электронейтральные,
асимметричные и, следовательно, обладающие диполь-
ными электрическими моментами, т. е. полярные; 3)
обладающие остаточным зарядом, который может вы-
звать молекулярную ассоциацию и образование водо-
родных связей.
Силы отталкивания и притяжения действуют между
всеми молекулами, но наиболее заметно их воздействие
проявляется у ассоциированных и полярных молекул.
Наиболее удачными являются корреляции функции PVT
для неполярных веществ, относящихся, в частности, к
такой важной группе, как углеводороды. Однако доста-
точно хорошие корреляции вторых вириальных коэффи-
циентов получены и для полярных веществ в тех
случаях, когда учитывались определенные геометриче-
ские и электрические характеристики молекул. Проведе-
на также работа по количественному исследованию
воздействия молекулярной ассоциации на поведение
функции PVT (см. разд. 1.3.3). Несколько теоретических
и эмпирических соотношений, характеризующих влия-
ние молекулярного притяжения и отталкивания, было
введено в уравнение состояния. Исторически сложилось
так, что несколько большее внимание уделялось моди-
фикации члена, учитывающего действие сил притяже-
ния (а/ V2 в уравнении Ван-дер-Ваальса), в то время как
член, учитывающий влияние сил отталкивания, обычно
применялся в том виде, в каком он был первоначально
предложен Ван-дер-Ваальсом. Однако в последнее вре-
мя интерес к его изучению значительно оживился, и в
разд. 1.7 описано несколько наиболее успешных разра-
боток в этом направлении.
1.2.3. Уравнение Ван-дер-Ваальса. За многие десяти-
летия, отделяющие нас от того момента, когда было
установлено несоответствие уравнения идеального газа
потребностям науки и техники, был предложен целый
ряд уравнений. Почти каждое из них имело, как это де-
монстрировалось или просто утверждалось, определен-
20 Глава 1
Рис. 1.4.
т, к
ср—Т— P-поверхность воздуха вблизи критической
точки (37,2 атм, 132,5 К) [72].
Рис. 1.5. Экспериментальные изотермы.
а — фазовая диаграмма изопентана в двухфазовой и гомогенной областях. Вблизи критической точки Сг переход от паровой фазы
к жидкой может проходить как гетерогенный (а—Ь'—с'—d) или гомогенный (а—b—с—d) [61]; б — диоксид углерода вблизи кри-
тической точки, 72,8 атм и 42,7 (Е-4) по Амагату или 94 мл/моль [480].
Уравнение состояния 21
ные преимущества по сравнению с предложенным
ранее, — теоретическая обоснованность, большая при-
менимость к определенному диапазону температур или
давлений или к определенной группе веществ, пригод-
ность для оценки каких-либо термодинамических
свойств или же простота использования, а в ряде случа-
ев разработка такого уравнения являлась следствием
интереса автора к данной области. Большинство этих
уравнений не получили распространения, так как они в
чем-то уступали предыдущим или не имели каких-либо
заметных преимуществ.
Наиболее известным и эффективным является уравне-
ние состояния, сформулиройанное в 1873 г. Ван-дер-Ва-
альсом в его диссертации «О непрерывности газообраз-
ных и жидких состояний». Впоследствии Ван-дер-Ва-
альс написал более ста трудов, главным образом по те-
ории жидкостей и смесей. В статье Раулинсона [603],
посвященной столетию создания этого уравнения состо-
яния, показано, сколь много из наследия Ван-дер-Вааль-
са нашло воплощение в достижениях современной тео-
рии. В уравнении Ван-дер-Ваальса
а — параметр, учитывающий действие сил притяжения,
b — параметр, учитывающий действие сил отталкива-
ния. Последний параметр, называемый эффективным
молекулярным объемом, согласно теоретическим расче-
там Ван-дер-Ваальса, должен в четыре раза превышать
действительный объем молекул. Рассуждения, которые
привели к созданию этого уравнения, и способ его вы-
вода можно найти в книге [92], где также представлены
и другие исторические материалы. Трехмерное пред-
ставление уравнения показано на рис. 1.1, г. Некоторые
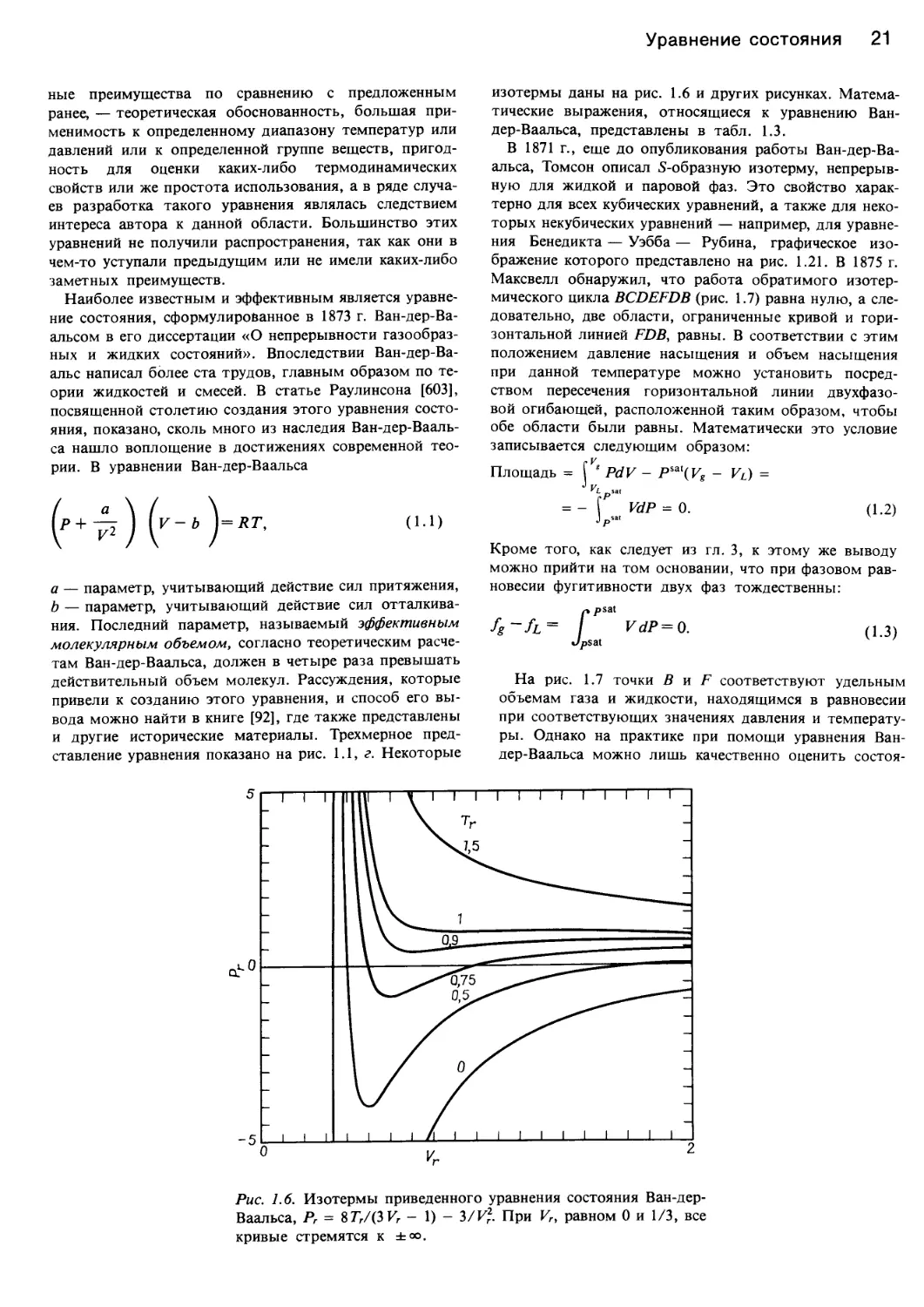
изотермы даны на рис. 1.6 и других рисунках. Матема-
тические выражения, относящиеся к уравнению Ван-
дер-Ваальса, представлены в табл. 1.3.
В 1871 г., еще до опубликования работы Ван-дер-Ва-
альса, Томсон описал 5-образную изотерму, непрерыв-
ную для жидкой и паровой фаз. Это свойство харак-
терно для всех кубических уравнений, а также для неко-
торых некубических уравнений — например, для уравне-
ния Бенедикта — Уэбба — Рубина, графическое изо-
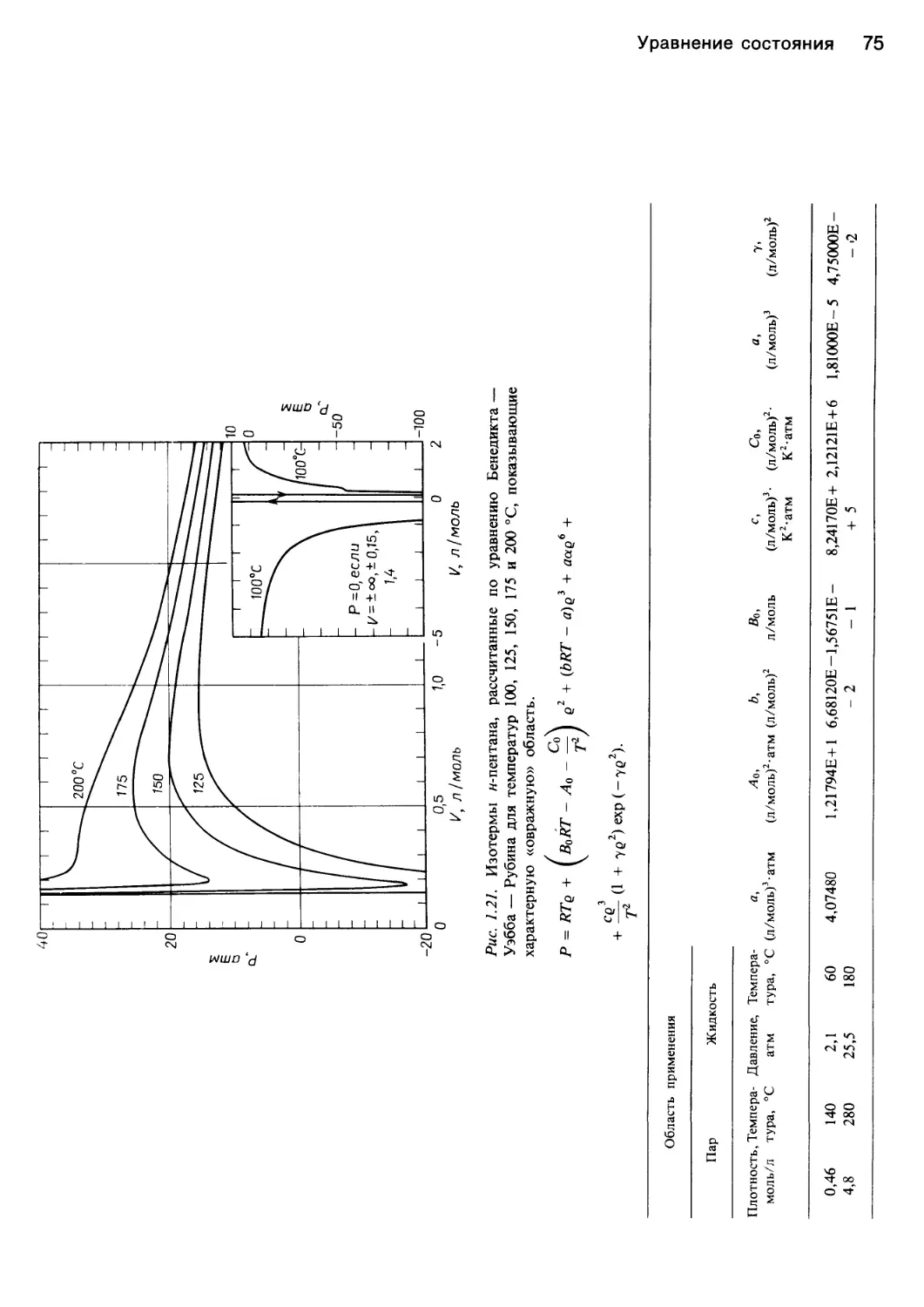
бражение которого представлено на рис. 1.21. В 1875 г.
Максвелл обнаружил, что работа обратимого изотер-
мического цикла BCDEFDB (рис. 1.7) равна нулю, а сле-
довательно, две области, ограниченные кривой и гори-
зонтальной линией FDB, равны. В соответствии с этим
положением давление насыщения и объем насыщения
при данной температуре можно установить посред-
ством пересечения горизонтальной линии двухфазо-
вой огибающей, расположенной таким образом, чтобы
обе области были равны. Математически это условие
записывается следующим образом:
Площадь = Г8 PdV - Psat(Kg - VL) =
>-
= -J^rap = o. (i.2)
Кроме того, как следует из гл. 3, к этому же выводу
можно прийти на том основании, что при фазовом рав-
новесии фугитивности двух фаз тождественны:
р psat
fg~fb= I VdP=Q. (1.3)
Jpsat
На рис. 1.7 точки В и F соответствуют удельным
объемам газа и жидкости, находящимся в равновесии
при соответствующих значениях давления и температу-
ры. Однако на практике при помощи уравнения Ван-
дер-Ваальса можно лишь качественно оценить состоя-
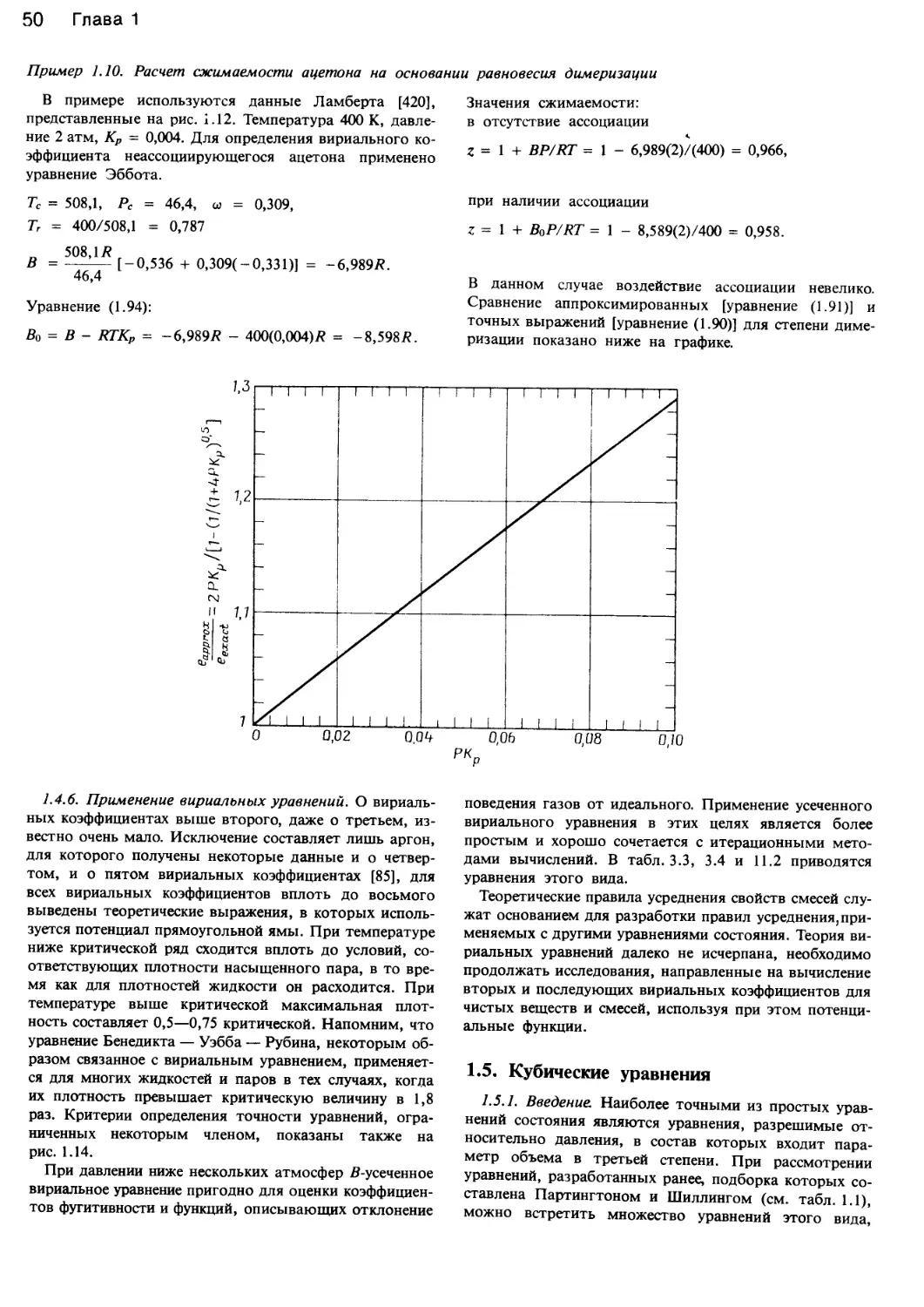
Рис. 1.6. Изотермы приведенного уравнения состояния Ван-дер-
Ваальса, Рг = 8 77/(3 К - 1) - 3/К?. При Vr, равном 0 и 1/3, все
кривые стремятся к ±оо.
22 Глава 1
Таблица 1.3. Уравнение состояния Ван-дер-Ваальса
Стандартный вид уравнения: изводные относительно V при постоянной Т равны ну-
(Р + а/У2)(У - b) = RT, (1) z = PV/RT = У/(У - b) - a/RTV. (2) лю. Выполнив дифференцирование, получаем 6^) = " 2 + ~3 = 0’ (11)
Уравнение в виде полинома: \дУ/т (Ус - Ь)2 У3
к3 - (ь + —у2 + а V - — = 0, (3) \ Р J Р Р / д2р\ 2RTC 6а п ( 1 = — - — = 0. (12) \дУ2/т (Ус - Ь)3 У?
3 (ЬР \ 2 аР аЬР2 г. \RT / (RT)2 (RT)3 Также ( Рс + ~ ) (Ус - b) = RTc. (13)
Вириальный вид уравнения: \
Z = 1 + (b - А) 1 + (^\ + + ... . (5) у rtJ у \у/ \у) Уравнения (11)—(13) решают одновременно, чтобы по- лучить результаты, приведенные в строках 7—9. Метод 2. В критической точке три корня полинома (3)
Приведенный вид уравнения: равны.
( Pr + -J(3Kr - 1) = 8ТГ. (6) у vj (У - ус)3 = у3 - з ус у2 + з у2У - У3 = 0. (14) Сравнение коэффициентов, имеющих одинаковую сте-
Параметры, выраженные через критические свойства: пень, уравнений (3) и (14) дает те же результаты, что и метод 1.
а = ЗРСУ2 = 21R2T2/MPc, (7) Ъ = Ус/3 = RTC/8PC, (8) R = 8РСУС/ЗТС, (9) Zc = 0,375. (Ю) Если рассматриваются смеси, параметры выража- ют через параметры чистых компонентов, используя правило аддитивности: / \2 а = ( (15)
Величина R, получаемая по уравнению (9), отличается от истинной газовой постоянной, 8,314 Дж/моль’К; ис- тинную величину следует использовать для оценки па- раметров а и Ь по уравнениям (7) и (8). Вывод формул для определения параметров а и Ь: b = ^ytbi (16) Уравнения фугитивности приведены в табл. 3.3 и 3.4, уравнения для определения остаточных свойств — в
Метод 1. В критических условиях первая и вторая про- табл.11.3
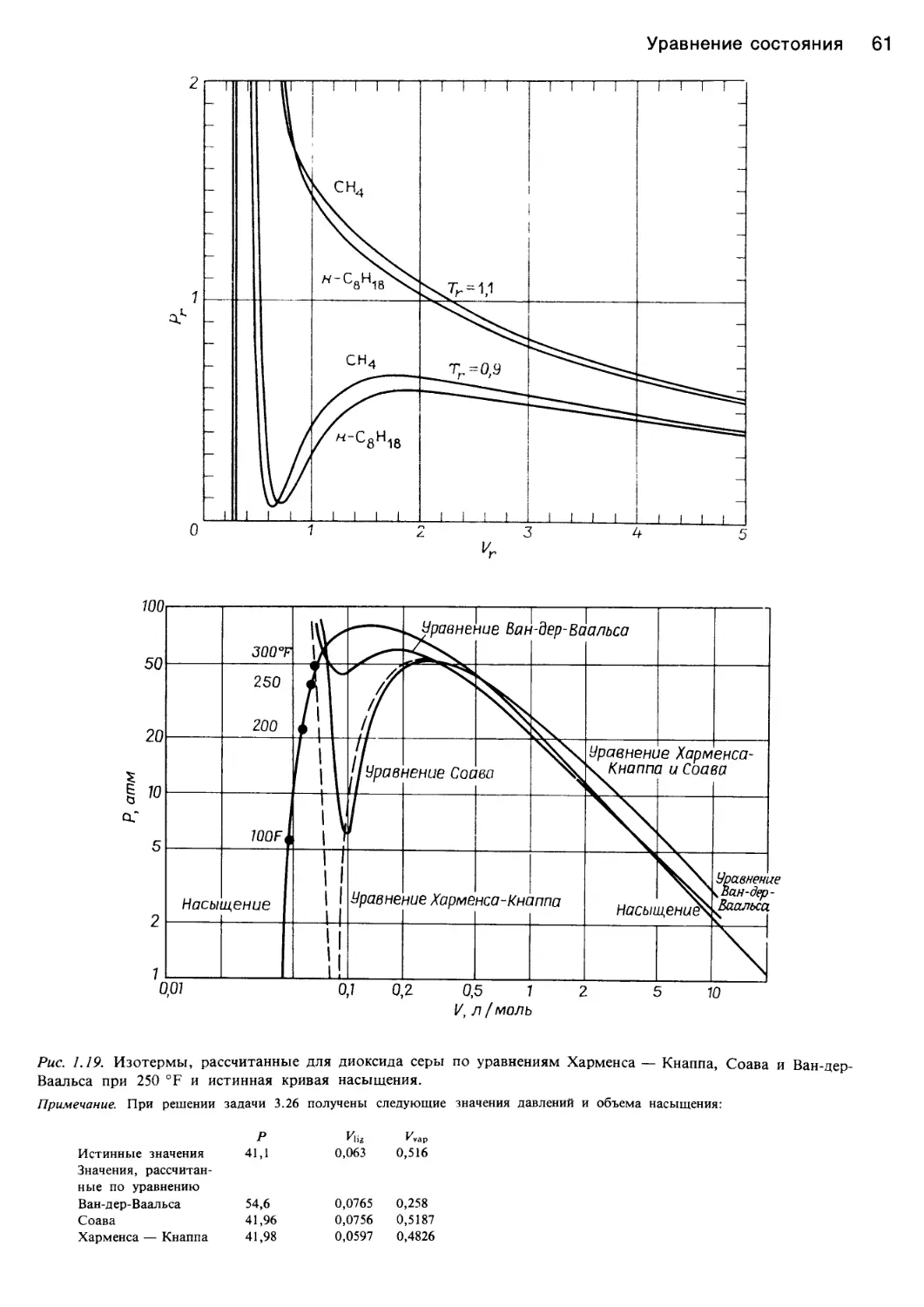
ние насыщения, доказательством чего являются
рис. 1.17 и 1.19, а также пример 1.2. В задаче 1.2 для
описания состояния насыщения требуется применить
уравнение Клаузиуса, сходное по форме с уравнением
Ван-дер-Ваальса. Для более точного представления на-
сыщения разработаны некоторые другие кубические
уравнения (см., например, задачу 3.26). Участки ВС и
FE кривой на рис. 1.7 соответствуют метастабильным
состояниям фаз, достигаемым экспериментально, а уча-
сток EDC — области, физически неосуществимой для
чистого вещества, так как соответствует изменениям
давления и объема в одном и том же направлении при
постоянной температуре.
Значительное внимание уделяется вопросам истолко-
вания значения 5-образной изотермы при отрицатель-
ном давлении. Обзор современных исследований в этой
области содержится в книге [134], авторы которой скло-
няются к мысли, что в подобных условиях жидкость
определенно находится в напряженном состоянии; в
частности, ими измерена прочность на разрыв воды
при температуре 10 °C и давлении 277 атм.
Поскольку уравнение Ван-дер-Ваальса является урав-
нением третьего порядка по объему, любая изотерма в
докритических условиях будет иметь три положитель-
ных корня, в то время как сверхкритические изотермы
имеют лишь один действительный корень. При наличии
трех действительных корней наименьший из них прини-
мается за удельный объем жидкой фазы, наиболь-
ший — за удельный объем паровой фазы, а средний же
физического толкования не имеет. Метод Кардано пред-
ставляет собой наиболее простой способ нахождения
действительных корней кубических уравнений; суще-
ствует ряд более простых методов их поиска, которые
предусматривают использование ЭВМ. Графические ме-
тоды решения кубических уравнений в настоящее время
практического значения не имеют; читателям, для кото-
рых они представляют интерес, следует обратиться к
трудам [76, 229], а также большой числовой таблице,
составленной автором монографии [116].
Приведенная форма уравнения. При рассмотрении
приведенных в данной главе критических изотерм ста-
новится очевидным, что точка перегиба изотермы прак-
тически совпадает с критической точкой. Математичес-
ки точку перегиба можно найти, приравняв первую и
вторую производные нулю при критическом объеме,
т. е.
(др\ (д2р\
\аг / р \аг2 / т °’ <1,4)
Уравнение состояния 23
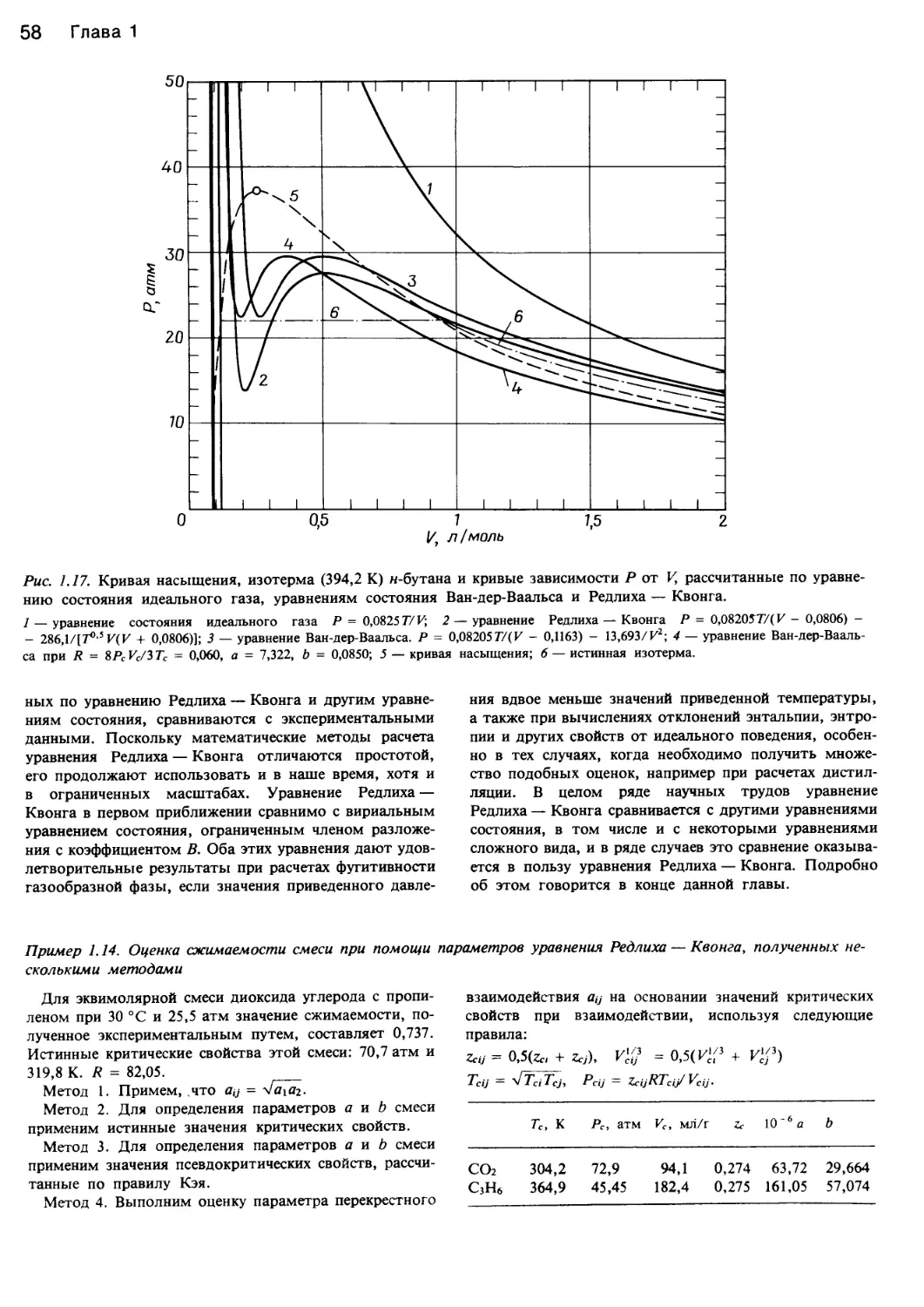
Рис. 1.7. Диаграмма кубического уравнения состояния в
двухфазовой области.
На диаграмме показаны метастабильные области и соедини-
тельная линия, связывающая объемы жидкой и паровой фаз в
состоянии равновесия. Площади FEDF и DCBD равны (принцип
Максвелла). Для чистого вещества область EDC физически не-
осуществима.
Таблица 1.4. Некоторые величины критической
сжимаемости (Ze), а также ее значения, рассчитанные
с использованием ряда уравнений состояния
Уравнение
Для идеального газа 1
Ван-дер-Ваальса 0,375
Редлиха — Квонга 0,333
Соава 0,333
Вириальное третьего порядка 0,333
Пенга — Робинсона 0,307
Бертло 0,281
Дитеричи 0,271
Вещество
Не
Н2
СО2
SO2
С12
изо-С5Н12
СбНб
СбН5Р
(С2Н5)2О
С2Н5ОН
Н2О
0,3141
0,3049
0,2869
0,2774
0,2755
0,2678
0,2663
0,2634
0,2430
0,2243
0,229
Преобразовав подобным образом уравнение Ван-дер-
Ваальса, можно найти параметры а и Ь, выразив их че-
рез критические свойства. Полученные при этом резуль-
таты представлены в табл. 1.3. К такому же заклю-
чению можно прийти, исходя из равенства трех корней,
сопоставляя коэффициенты разложения в ряд выраже-
ния (V - Ус)3 = 0 с коэффициентами полиномиальной
формы уравнения состояния в критической точке.
Выразив параметры а и Ь уравнения Ван-дер-Ваальса
через критические параметры, мы получаем математи-
ческое выражение чрезвычайно важного принципа соот-
ветственных состояний'.
(РГ + 3/Г2)(ЗГГ-1) = 8ТГ. (1.5)
Отношения вида Рг = Р/Рс называют приведенными
свойствами вещества, а само уравнение — приведен-
ным уравнением состояния, которое в принципе приме-
нимо для любых веществ. Однако по этому уравнению
рассчитать реальные параметры можно лишь при нали-
чии данных о значениях параметров каждого отдельно-
го вещества в критическом состоянии. Считается, что
вещества, имеющие одинаковые приведенные свойства,
находятся в соответственных состояниях. Из этого за-
кона вытекает целый ряд следствий, которые будут рас-
смотрены в разд. 1.3.
Исходя из уравнения Ван-дер-Ваальса, газовую посто-
янную RVdw можно выразить через критические свойства
следующим образом:
^ = 8РСИС/ЗТС,
т. е. для разных веществ она имеет различные значе-
ния. Лишь в некоторых случаях она чисто случай-
но равна универсальной газовой постоянной R =
= 8,314 Дж/моль • К. Поскольку желательно, чтобы
уравнение состояния можно было привести к уравнению
идеального газа при низком давлении, для оценки пара-
метров а и b всегда используют универсальное значение
R. Величины параметров, приведенные в табл. 1.4, бы-
ли получены именно таким путем. Поскольку уравнение
Ван-дер-Ваальса обычно не вполне соответствует экспе-
риментальным данным, Rvdw можно рассматривать как
параметр, имеющий различные значения для различных
веществ, т. е. подобный параметрам а и Ь. В некоторых
случаях при помощи уравнения (Р + а/У2)(У - Ь) =
= RvdwT можно описать опытные данные по крайней
мере так же точно, как и при помощи выражения
(Р + a/V2)(V - b) - RT. Даже модификация парамет-
ров а и Ь может привести к усовершенствованию урав-
нения состояния. Соответствующие примеры будут
приведены позднее. Сравнение параметров а и Ь, най-
денных экспериментальным путем и рассчитанных на
основании значений критических свойств, выполнено в
задаче 1.2.
Результаты расчетов, проводимых с использованием
уравнения Ван-дер-Ваальса, отличаются низкой сте-
пенью точности и лишь в редких случаях превышают
средний уровень. В связи с этим была проведена значи-
тельная работа в целях усовершенствования этого урав-
нения путем установления соотношения его параметров
24 Глава 1
с некоторыми другими параметрами помимо парамет-
ров критического состояния, а именно с точкой кипе-
ния, плотностью или коэффициентом термического
расширения. Результаты ряда первых работ в этой об-
ласти обобщены в монографии [92]. Параметры других
уравнений состояния, подобных по форме уравнению
Ван-дер-Ваальса, иногда представляют в виде зависимо-
стей от температуры и ацентрического коэффициента
или критической сжимаемости (см. рис. 1.8), о чем бу-
дет говориться ниже.
Смеси. Практическая ценность уравнений состояния
существенно возрастает, если их можно применять для
смесей. В этих случаях параметры смеси часто выража-
ют через состав и параметры чистых компонентов. Ло-
ренц (1881) и Бертло (1898) предложили следующие
правила аддитивности параметров уравнения Ван-дер-
Ваальса:
Va — Хур/а~ (1-6)
b = Zyibi, (1.7)
называемое правилом Лоренца — Бертло. Их примене-
ние в статистической механике смесей рассмотрено в
книге [113]. Существует и другой подход к решению
этой проблемы, заключающийся в оценке параметров
смеси на основании значений критических свойств при
помощи тех же уравнений, которые применяют к чис-
тым веществам. Поскольку критические свойства про-
извольных смесей редко можно найти эксперименталь-
ным путем и трудно измерить, разработана более удач-
ная методика, основанная на специально вводимых
псевдокритических свойствах Мрс. Наиболее простыми
из них являются средневзвешенные суммы мольных до-
лей соответствующих свойств компонентов смеси, т. е.
Ррс = S7|Pc/, Tpc = T.yiTci, Vpc = T.yiVci. (1.8)
Другие правила усреднения свойств будут рассмотрены
ниже. Непосредственное комбинирование параметров
индивидуальных веществ, составляющих смесь, для
многих уравнений состояния обычно более предпочти-
тельно, нежели использование псевдокритических
свойств, однако обе методики имеют своих привержен-
цев. Как показано в примере 1.8, несмотря на то, что
при помощи одного метода можно предсказать докри-
тическое состояние смеси (три действительных корня
уравнения состояния), а при помощи другого — сверх-
критическое (один действительный корень), полученные
значения сжимаемости для данной смеси в обоих случа-
ях практически одинаковы. Поскольку уравнений состо-
яния сравнительно немного, если не учитывать исполь-
зуемые для описания смесей, поэтому основные усилия
были направлены на то, чтобы сформулировать эффек-
тивные правила усреднения для расчета псевдокритиче-
ских свойств и параметров смеси, исходя из аналогич-
ных свойств компонентов с учетом бинарных взаимо-
действий (см. табл. 1.5). Рассмотрение этого вопроса
будет продолжено в разд. 1.3.7.
Современное состояние уравнения Ван-дер-Ваальса. В
недалеком прошлом изучению уравнения Ван-дер-Ва-
альса уделялось много внимания. В 1925 г. Пикеринг
[95] выполнил исчерпывающее сравнение этого уравне-
ния с экспериментальными данными и двумя другими
уравнениями, принятыми в то время (уравнениями
Бертло и Дитеричи) для девяти газов при давлении до
1000 атм. В этой главе также приводится несколько по-
добных сравнений. Несмотря на то что в современных
исследованиях можно все еще встретить ссылки на это
знаменитое уравнение, оно уже устарело, и его можно
рассматривать лишь как один из примеров простой мо-
дели, включающей некоторые поправки к закону иде-
альных газов, которые позволяют учитывать силы
межмолекулярного притяжения и отталкивания. В на-
стоящее время существует ряд значительно превосходя-
щих его уравнений состояния, не намного отличающих-
ся по сложности. Параметры уравнения Ван-дер-Вааль-
са и ряда других уравнений состояния для нескольких
веществ показаны в табл. 1.6.
Таблица 1.5. Некоторые правила усреднения псевдокритических свойств
П севд окритическое свойство Кэй [393] Праузниц и Ганн [570] Правила типа правил Лоренца — Бертло (ЛБ)
т 1 с ZyiTci ^У1Тс, {\-к^Тс^
zyivci (УсР + П/3)3/8
zc 0,5(zcl- + zcj) = 0,291 - 0,080w
ш 0,5 (ш,- + wy)
Рс Wei zcRTc/Vc zcRTc/Vc
Примечание. Параметры бинарного взаимодействия кц ряда веществ см. в
табл. Д.З. Правила расчета Тс и Vc, показанные в последнем столбце, называют
правилами Лоренца — Бертло. Они справедливы только для пар веществ и при-
меняются для нахождения параметров перекрестных взаимодействий ац кубиче-
ских уравнений или Вц вириального уравнения.
Уравнение состояния 25
Таблица 1.6. Константы некоторых уравнений состояния для ряда веществ
Уравнение Ван-дер-Ваальса: (Р + a/V2)(V — b) = RT, а = 277?2Т2/64РС, b = RTC/%PC
Уравнение Бертло: (Р + a/TV2)(V - b) = RT, а = 21R2T3C/64PC, b = 9RTC/128PC
Уравнение Дитеричи: Р(К - b) = RTexp (-a/RTV), а = 4R2T2/Pce2, е - 2,718
Уравнение Битти — Бриджмена: Р = RT/V + /3/И2 + 7/И3 + 6/ V4,
& = RTB0 - До - Rc/T2,
7 = RTBob + Ада — RcBg/T2,
5 = RB0bc/T2.
Используемые единицы: Р, атм; V, л/моль; Т, К, R = 0,08206.
Уравнение Ван-дер-Ваальса Уравнение Бертло Уравнение Дитеричи
Газ тс Рс а b а b а b
н2 33,2 12,8 0,24463 0,02661 8,1217 0,01497 0,3139 0,02881
Не 5,19 2,24 0,034161 0,023766 0,1773 0,013369 0,04383 0,025731
Аг 150,8 48,1 1,3431 0,032159 202,54 0,018089 1,7235 0,034818
n2 126,2 33,5 1,3506 0,03864 170,45 0,02174 1,7331 0,04184
о2 154,6 49,8 1,3634 0,03184 210,78 0,01791 1,7496 0,03448
со2 304,2 72,8 3,6111 0,04286 1098,5 0,02411 4,6337 0,04641
СН4 190,6 45,4 2,2732 0,04306 433,27 0,02422 2,9169 0,04662
С2Н5ОН 516,2 63,0 12,016 0,08405 6202,7 0,04728 15,418 0,09100
СбНб 562,1 48,3 18,583 0,11937 10 446,0 0,06715 23,845 0,12924
Уравнение Битти — Бриджмена
Газ ^4 о а Во b 10’4 с
Не 0,0216 0,05984 0,01400 0 0,004
Ne 0,2125 0,2196 0,02060 0 0,101
Аг 1,2907 0,02328 0,03931 0 5,99
Н2 0,1975 -0,00506 0,02096 -0,04359 0,050
n2 1,3445 0,02617 0,05046 -0,00691 4,20
о2 1,4911 0,02562 0,04624 0,004208 4,80
Воздух 1,3012 0,01931 0,04611 -0,01101 4,34
со2 5,0065 0,07132 0,10476 0,07235 66,00
СН4 2,2769 0,01855 0,05587 -0,01587 12,83
(С2Н5)2О 31,278 0,12426 0,45446 0,11954 33,33
1.3. Соответственные состояния
Когда Ван-дер-Ваальс записал уравнение состояния
при помощи приведенных свойств:
(Рг+3/И2)(ЗКГ- 1)= 8ТГ, (1.9)
он впервые сформулировал принцип соответственных
состояний (ПСС), согласно которому вещества, имею-
щие одинаковые приведенные давление и температуру,
имеют одинаковый приведенный объем. В приведенном
виде можно также записать и другие двупараметриче-
ские уравнения состояния, например вириальное уравне-
ние (табл. 1.8), уравнение Редлиха — Квонга (табл. 1.9)
и уравнение Клаузиуса (задача 1.4). Хотя приведенные
уравнения в принципе применимы для всех веществ, их
точность, конечно, не выше, чем у исходных уравнений.
Различные приведенные уравнения состояния могут зна-
чительно отличаться друг от друга, как это показано в
качестве примера на рис. 1.18. По-видимому, одна из
трудностей состоит в том, что при их выводе прихо-
дится опускать несколько важных переменных. Однако,
как установлено, экспериментальные данные зачастую
гораздо больше соответствуют принципу соответствен-
ных состояний, чем специальным уравнениям состоя-
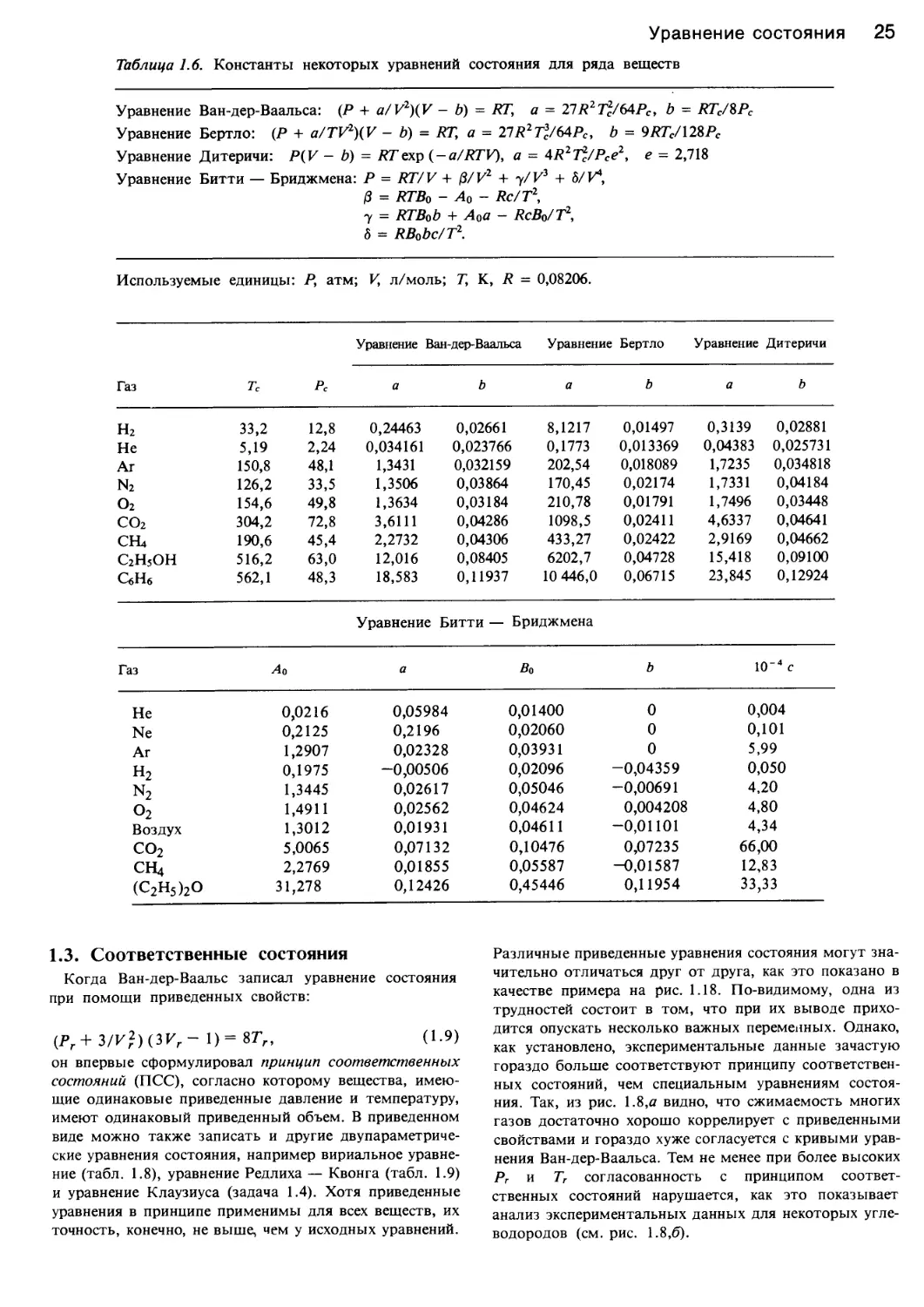
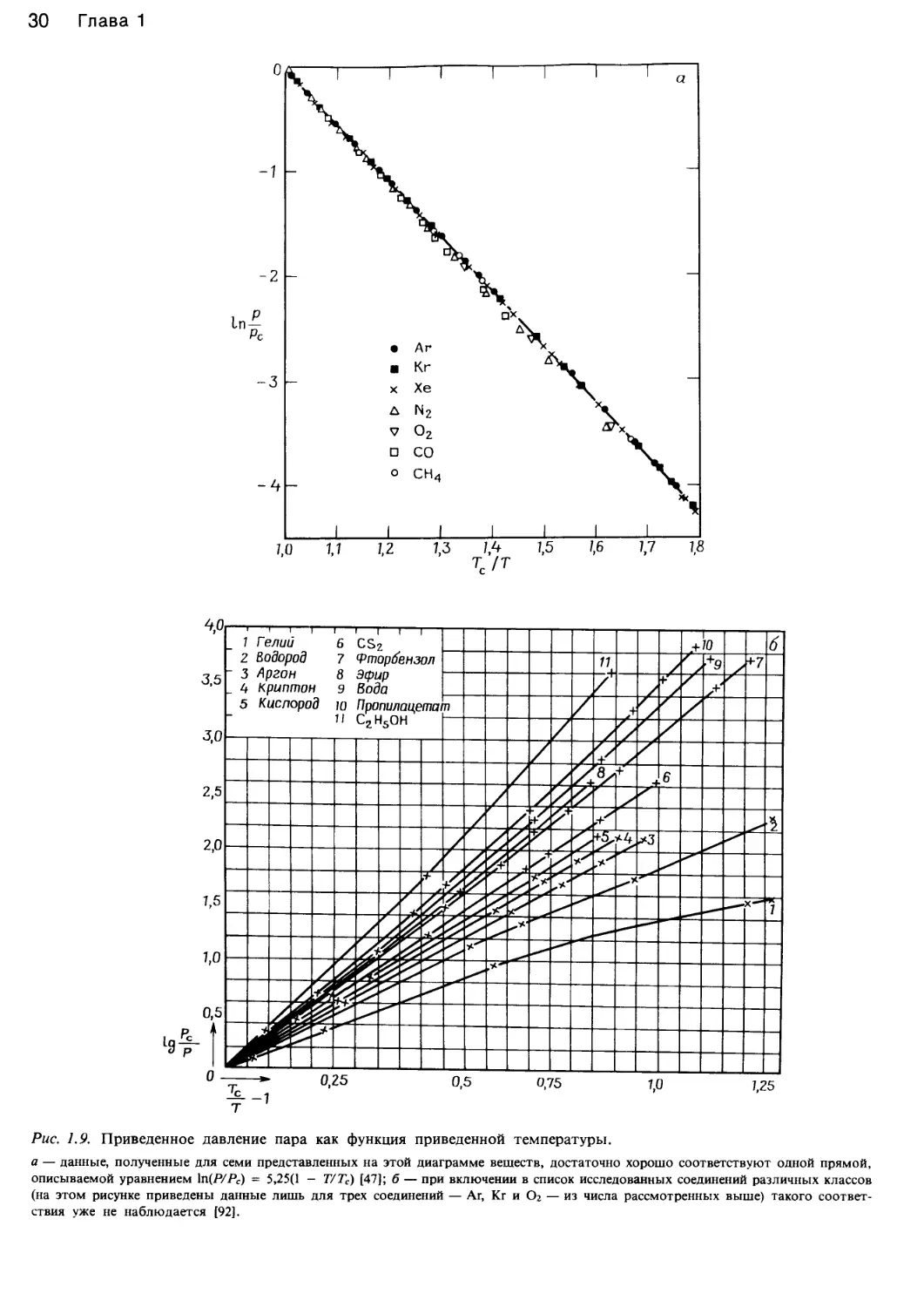
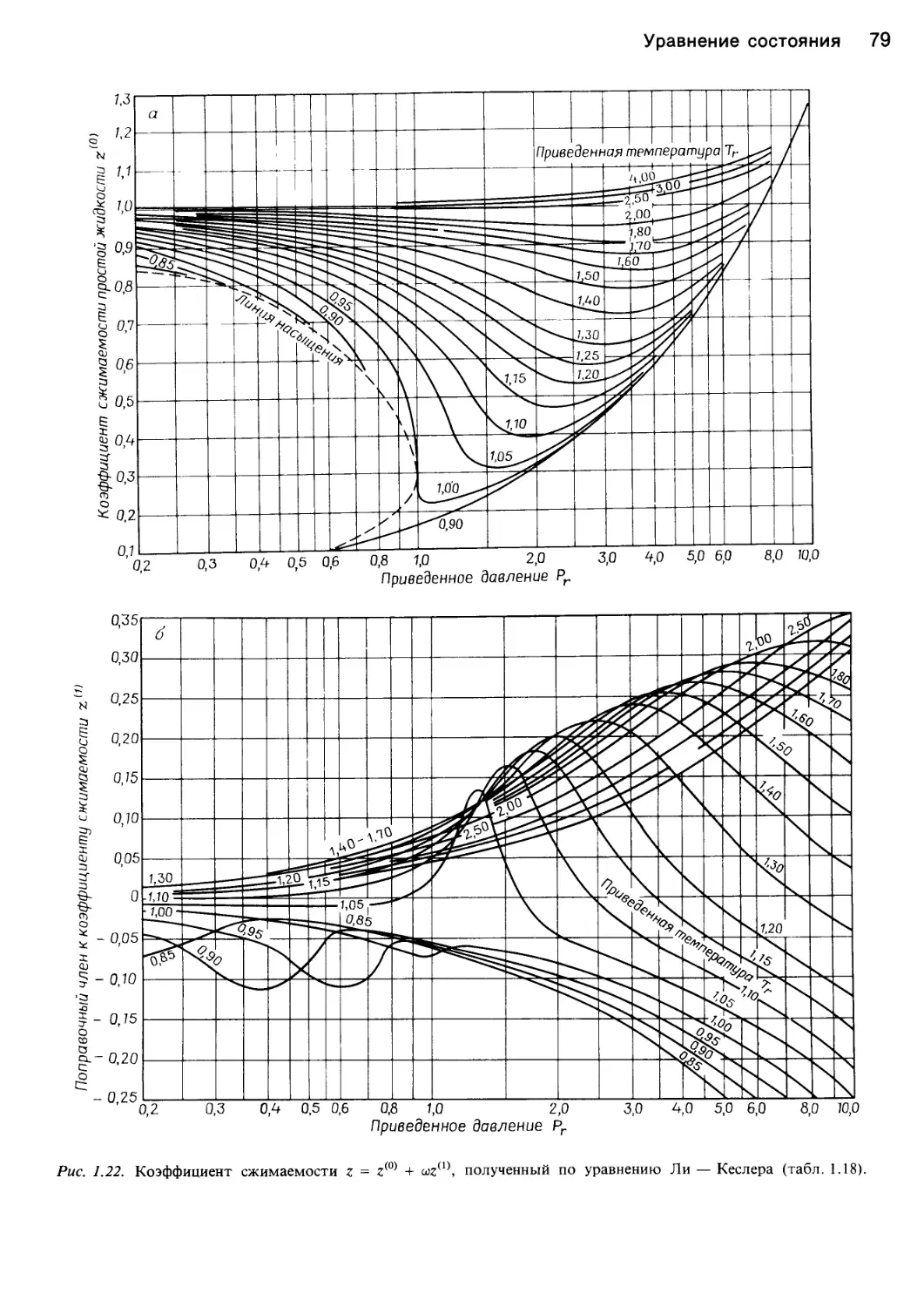
ния. Так, из рис. 1.8,а видно, что сжимаемость многих
газов достаточно хорошо коррелирует с приведенными
свойствами и гораздо хуже согласуется с кривыми урав-
нения Ван-дер-Ваальса. Тем не менее при более высоких
Рг и Тг согласованность с принципом соответ-
ственных состояний нарушается, как это показывает
анализ экспериментальных данных для некоторых угле-
водородов (см. рис. 1.8,6).
^>>4 тг = 1 5 ^5 б
сз Н8 СН^ сз68
У Д’
= 0,9 \ о ^0/^4
ч 'г ~ 1
5_ С5Ни
3. ~ 1~ сн4 —
С1 ^4 Но
Cs Г18 Н12
0,2 0,4 0,6 0,8 1,0 7,2 /,4 1,6 7,8 2 0 2 2 24 26 28 30
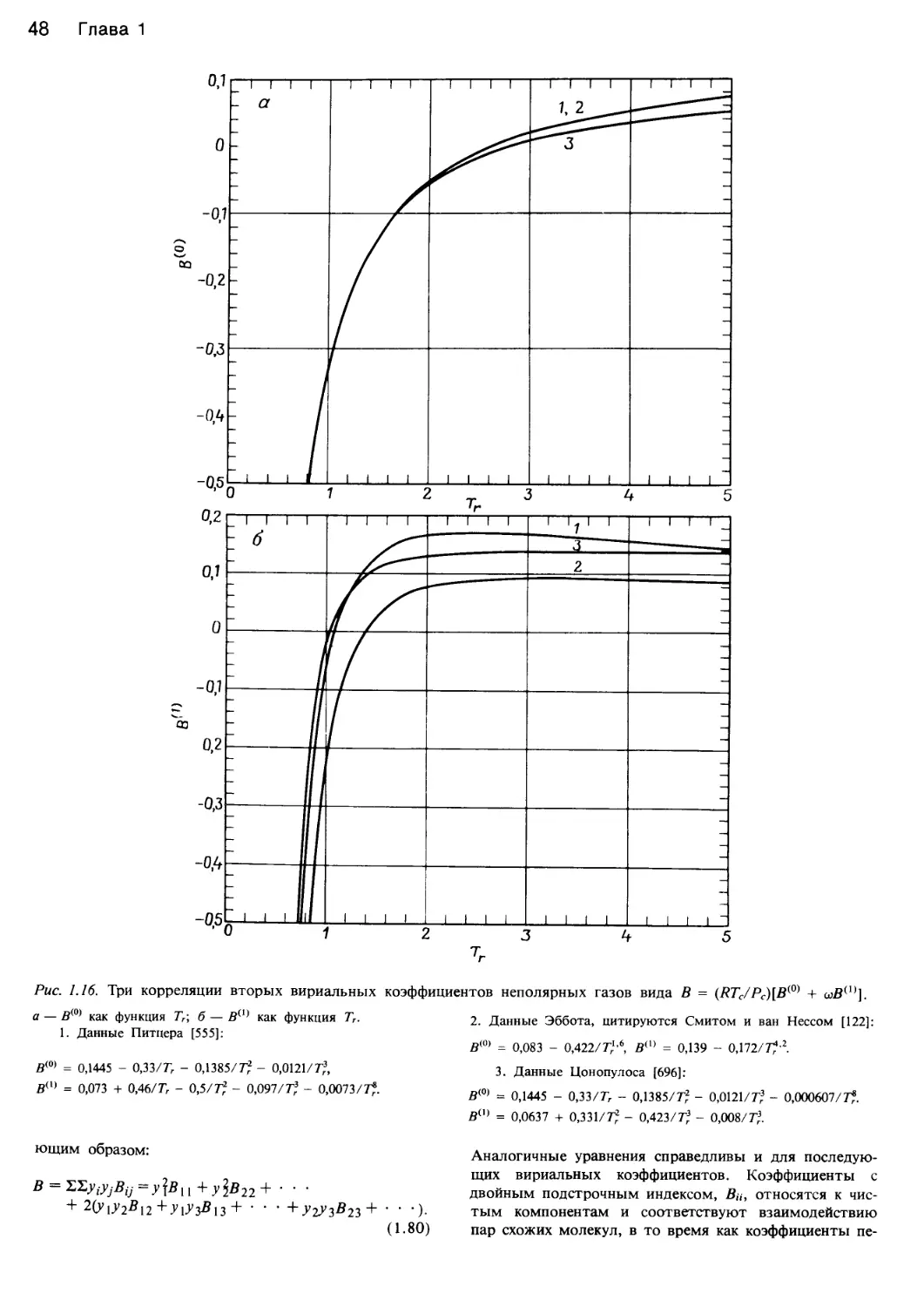
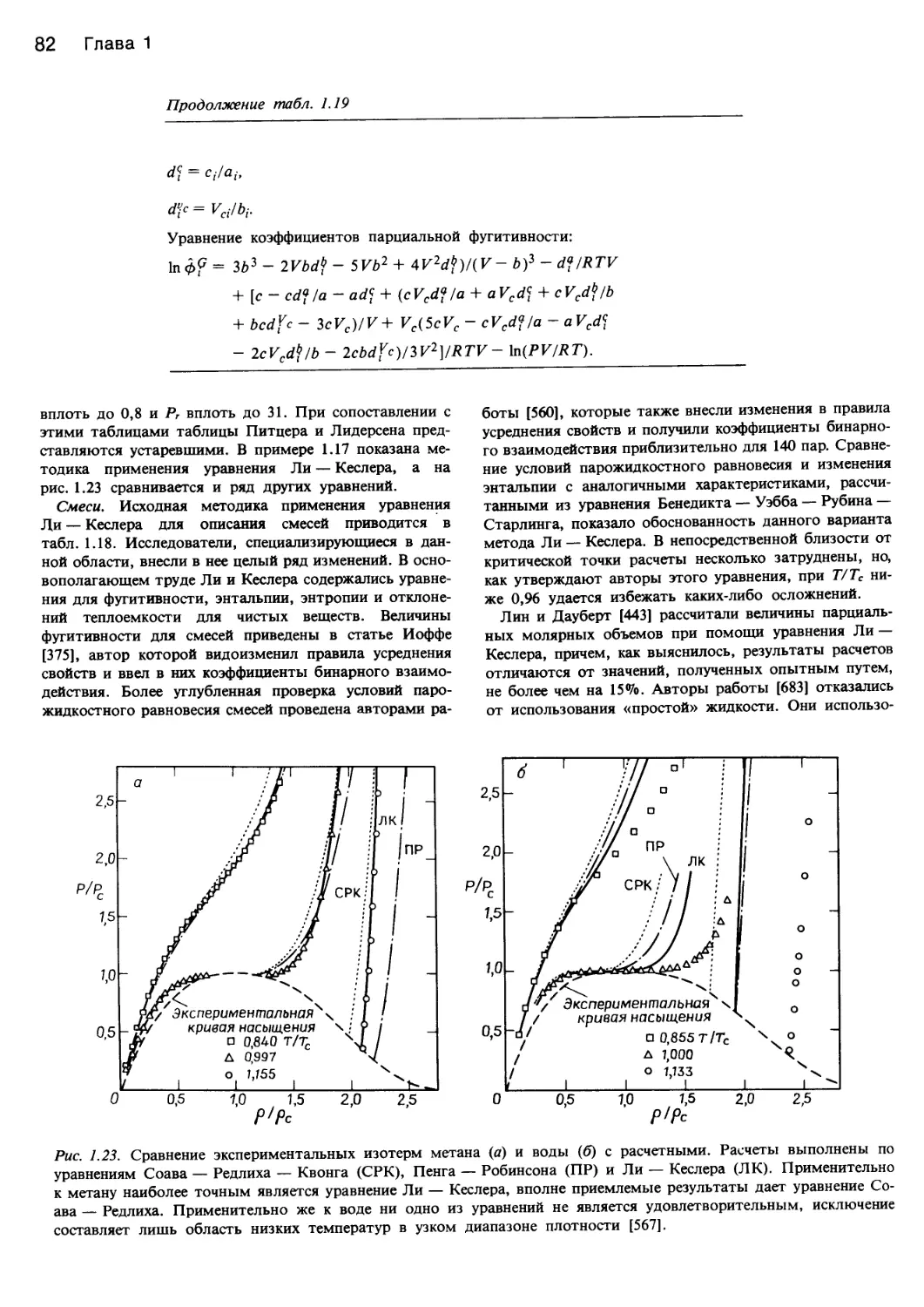
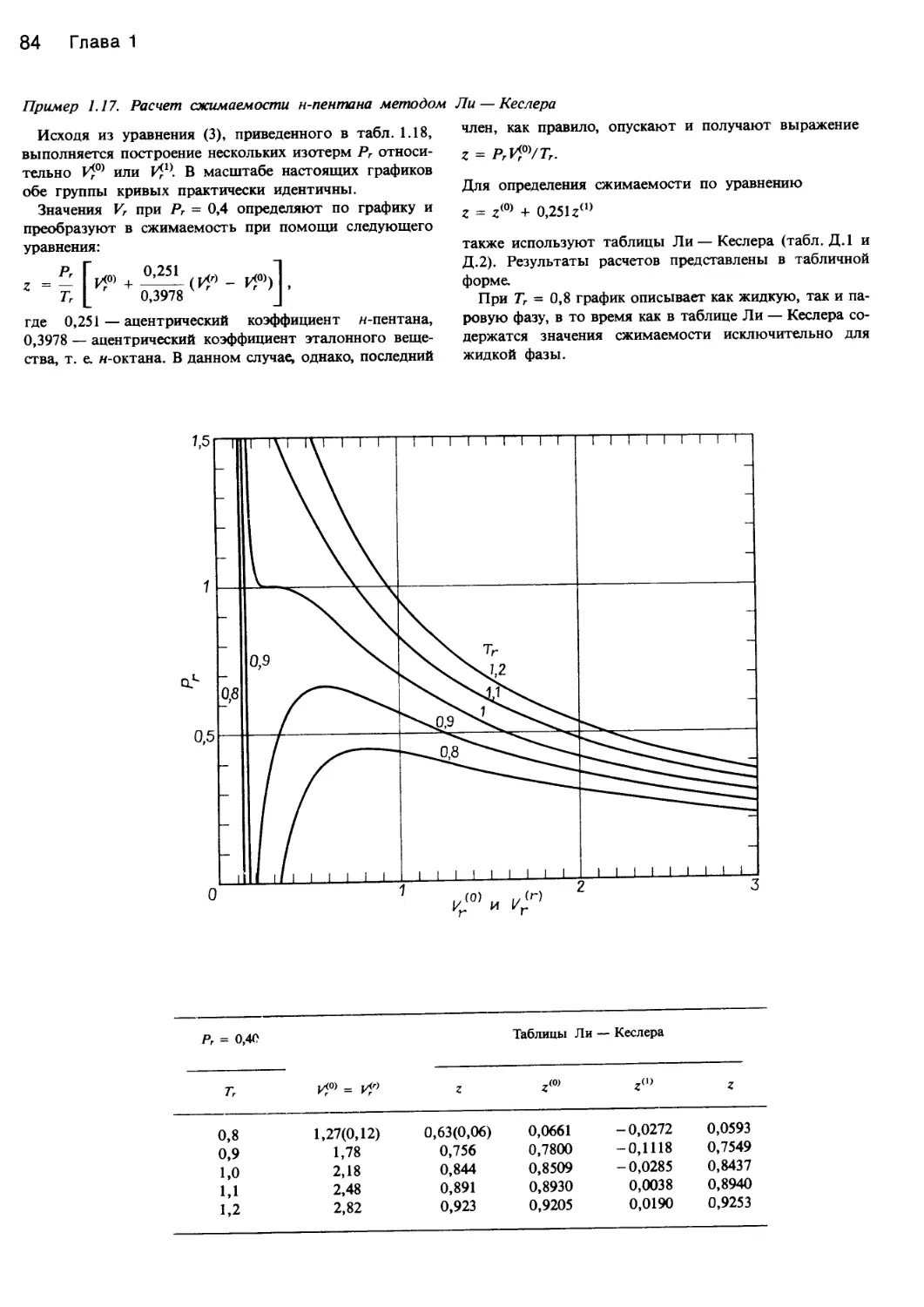
Рис. 1.8. Соответственные состояния.
а — корреляция сжимаемостей (z = PV/RT) обычных газов. Штриховые линии соответствуют уравнению Ван-дер-Ваальса, в = Т/Тс
[666] (© Am. Chem. Soc.); б — сжимаемость метана, пропана и пентана, не согласующаяся с принципом соответственных состояний
во всем диапазоне условий [204] (© Am. Chem. Soc.).
Уравнение состояния 27
Пример 1.1. Расчет объемов насыщения при помощи уравнения Ван-дер-Ваальса
При температуре 322 К давление паров метилхлорида
составляет 10,49 атм, удельный объем паров равен
0,0416 м3/кг, а удельный объем жидкости 0,0115 м3/кг.
Сравним эти экспериментальные данные с рассчитанны-
ми по уравнению Ван-дер-Ваальса.
Поскольку Рс = 65,9 атм, Тс = 416,3 К и R = 0,08206,
константы уравнения имеют следующие значения:
« = 2L = 7,4709,
64 Рс
b = RTc/ZPc = 0,0648.
Полиномиальное уравнение
И3 - (b + RT/P)V2 + — V - = 0
Р Р
преобразуется в уравнение следующего вида: И3 -
- 2.5837И2 + 0.7122И - 0,0461 = 0 с корнями V, рав-
ными 2,2802, 0,2047 и 0,0988 л/моль. Максимальная и
минимальная величины этих корней соответствуют сле-
дующим значениям удельного объема: Vg - 0,0448 и
Vl - 0,0195 м3/кг. Рассчитанный удельный объем газа
на 8 % отличается от экспериментально найденного, для
жидкости же степень соответствия опытным данным
крайне низка.
1.3.1. Подобие размерностей. В соответствии с пра-
вилом подобия размерностей любое отношение меж-
ду физическими переменными можно выразить в ви-
де отношения между ограниченным числом безразмер-
ных параметров. Таким образом, уравнение состояния
/1(Р, V, Т, Рс, Vc, Тс) = 0 эквивалентно некоторому дру-
гому уравнению fi{Pr, Vr, Tr) = 0. Адекватность отно-
шения, используемого для описания какого-либо явле-
ния, зависит от того, насколько полно определены тре-
буемые переменные. Несмотря на безусловную необхо-
димость использования приведенных переменных в
уравнениях состояния, применение только их представ-
ляется недостаточным. Как на характер изменения
функции PVT, так и на химическую активность могут
оказывать воздействие, например, различия в размерах
и форме молекул, момент инерции или радиус враще-
ния, а также электростатические параметры полярных
молекул и другие факторы. Во многих случаях попытки
улучшить уравнение состояния сводились к нахождению
легкоопределяемых параметров at, и в результате такой
модификации общее уравнение состояния приобретало
следующий вид:
Pr=f(Tr, Vr, ai, а2, . . .) = 0. (1.10)
В работе [129] перечислены следующие характеристики,
которыми должны обладать дополнительные па-
раметры.
1. Эти параметры должны соотноситься с молекуляр-
ной структурой и электростатическими свойствами мо-
лекулы .
2. Их можно определить при минимальном количе-
стве экспериментальных данных.
3. Критические свойства не должны оказывать непо-
средственное воздействие на их значения.
4. При оценке этих параметров надо избегать исполь-
зования данных о PVT, так как в противном случае те-
ряется смысл приведенного уравнения.
5. Дополнительные параметры должны быть функци-
ей температуры, предпочтительно приведенной.
Среди наиболее простых применяемых дополнитель-
ных параметров можно назвать критическую сжимае-
мость и наклон кривой давления пара в критической
точке. Еще одним параметром, измерение которого от-
личается чрезвычайной простотой, является ацентриче-
ский коэффициент. Он наиболее подходит для выше-
упомянутых целей и поэтому будет описан более под-
робно. Корреляцию поведения функции PVT для смесей
можно улучшить путем использования эксперименталь-
но обоснованных параметров бинарного взаимодейст-
вия, о чем будет сказано далее в связи с рассмотрением
правил усреднения свойств.
Пример 1.2. Расчет давления пара и объема насыщения
по уравнению Ван-дер-Ваальса
Необходимо определить давление пара и объем насы-
щения метилхлорида при 322 К и сравнить полученные
величины с указанными в примере 1.1.
Применяем принцип Максвелла:
- j VdP = \PdV - A(PV) = 0, (1)
f / RT a \
I I---------- ~ I dV - Psa,( Vg - VL) = 0, (2)
L \ V - b V2 1
V * L \ '
26,421n b, + a ) - PsaI(Vg -
r L b \ ' g УL J
- VL) = 0.
(3)
Значения параметров а и b взяты из примера 1.1. При
любом заданном давлении величину объема находят из
следующего кубического уравнения:
И3 - ( 0,0648 + ) V2 + ZilZP9 v _ 0,4841 = 4
У Р у Р Р
Корни и левую часть уравнения (3) находят при не-
скольких величинах давления. Результаты в последней
строке получены интерполяцией. Кроме того, все ре-
зультаты представлены графически. Степень соответ-
ствия данным, указанным в примере 1.1, очень низка.
р V V V Левая часть уравнения (3)
10,49 2,2802 0,2047 0,0988 15,13
20 1,0528 0,2352 0,0977 1,413
25 0,7634 0,2611 0,0972 -2,596
21,8 0,949 0,0975 0
28 Глава 1
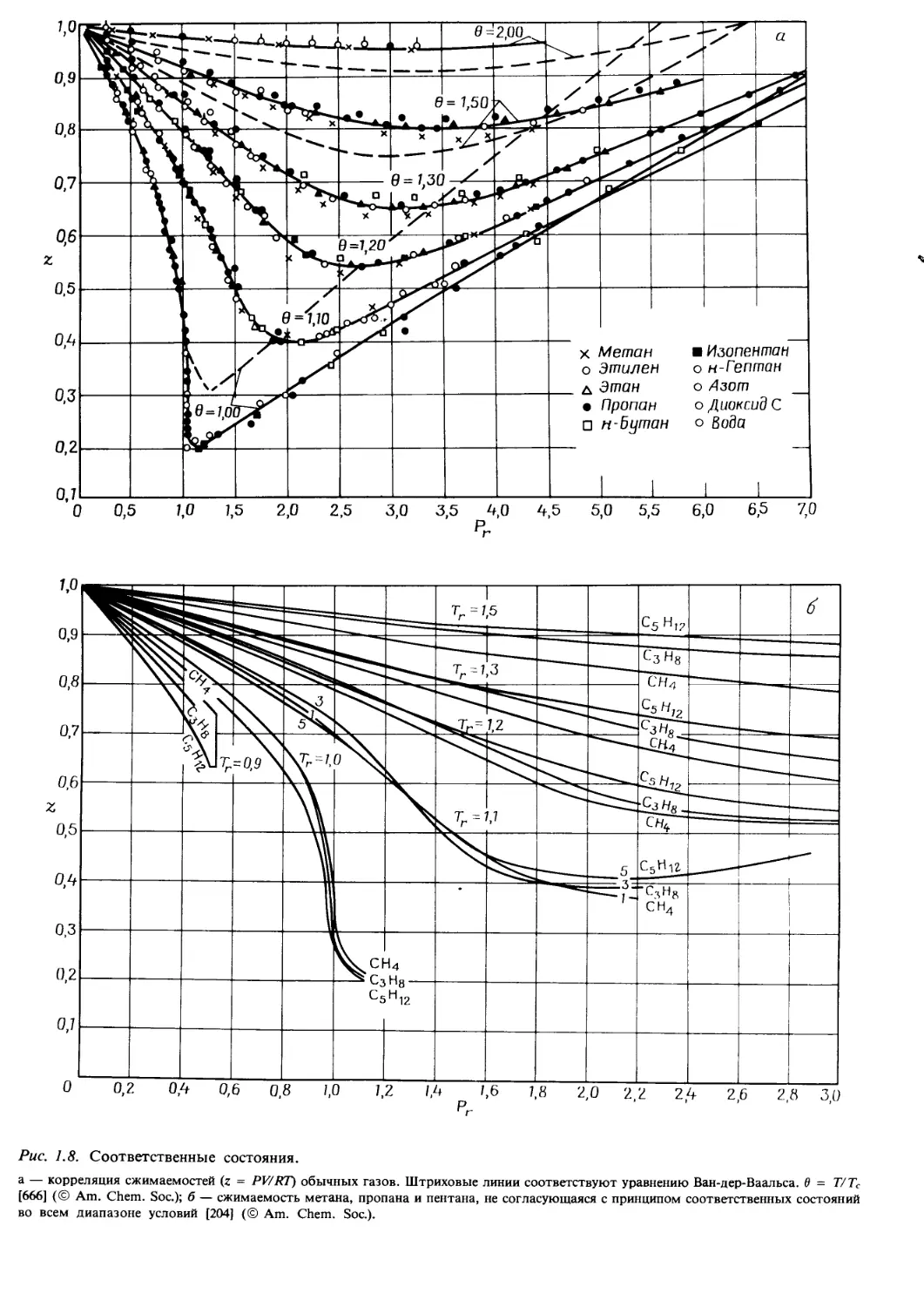
Пример 1.3. Численное решение кубических уравнений
При помощи метода Кардано можно найти как дей-
ствительные, так и комплексные корни кубических урав-
нений. При решении уравнений состояния требуется
вычислить только действительные корни, а для этого
вполне пригоден метод Ньютона — Рафсона. Ниже
приводится программа на языке Бейсик, посредством
которой определяют значения сжимаемости. Такой вид
уравнения состояния удобен для расчетов, поскольку
оценки между 1 и 0 обычно ведут к быстрому достиже-
нию сходимости. Здесь приводятся решения уравнений
с одним и тремя действительными корнями как в чис-
ленном, так и в графическом виде.
10 ’ Реальные корни кубического уравнения, Z л 3 +
+ AZ л 2 + BZ + С = 0. При наличии одного ре-
ального корня Zv = Z1.
Уравнение состояния 29
20 INPUT А, В, С
30 Z = 1! Trial value
40 GOSUB 210
50 Н = F/(3*Z л 2 + 2*A*Z + В)
60 IF ABS(H/Z) < = . 0001 THEN 90
70 Z = Z - H
80 GOTO 40
90 Z1 = Z
100 Z = .01 ! Second root trial
110 GOSUB 210
120 H = F/(3*Z л 2 + 2*A*Z + B)
130 IF ABS(H/Z) < = .0001 THEN 160
140 Z = Z - H
150 GOTO 110
160 Z2 = Z
170 Z3 = - A - Zl - Z2
180 PRINT USING 190; Zl, Z2, Z3,
190 IMAGE «Zv =» D.DDDD, 2X, «Zl =» D.
DDDD, 2X, «Zx =» D. DDDD
200 END
210 F = Z л 3 + A*Z л 2 + B*Z + C
220 RETURN
При наличии трех действительных корней: А = -1,
В = 0,089, С = -0,0013, Zv = 0,9030, Zl = 0,0183,
Zx = 0,0787.
При наличии одного действительного корня:
А = - 1, В = 0,4224, С = -0,0608, Zv = 0,2697,
Zl = 0,2697, Zx = 0,4606.
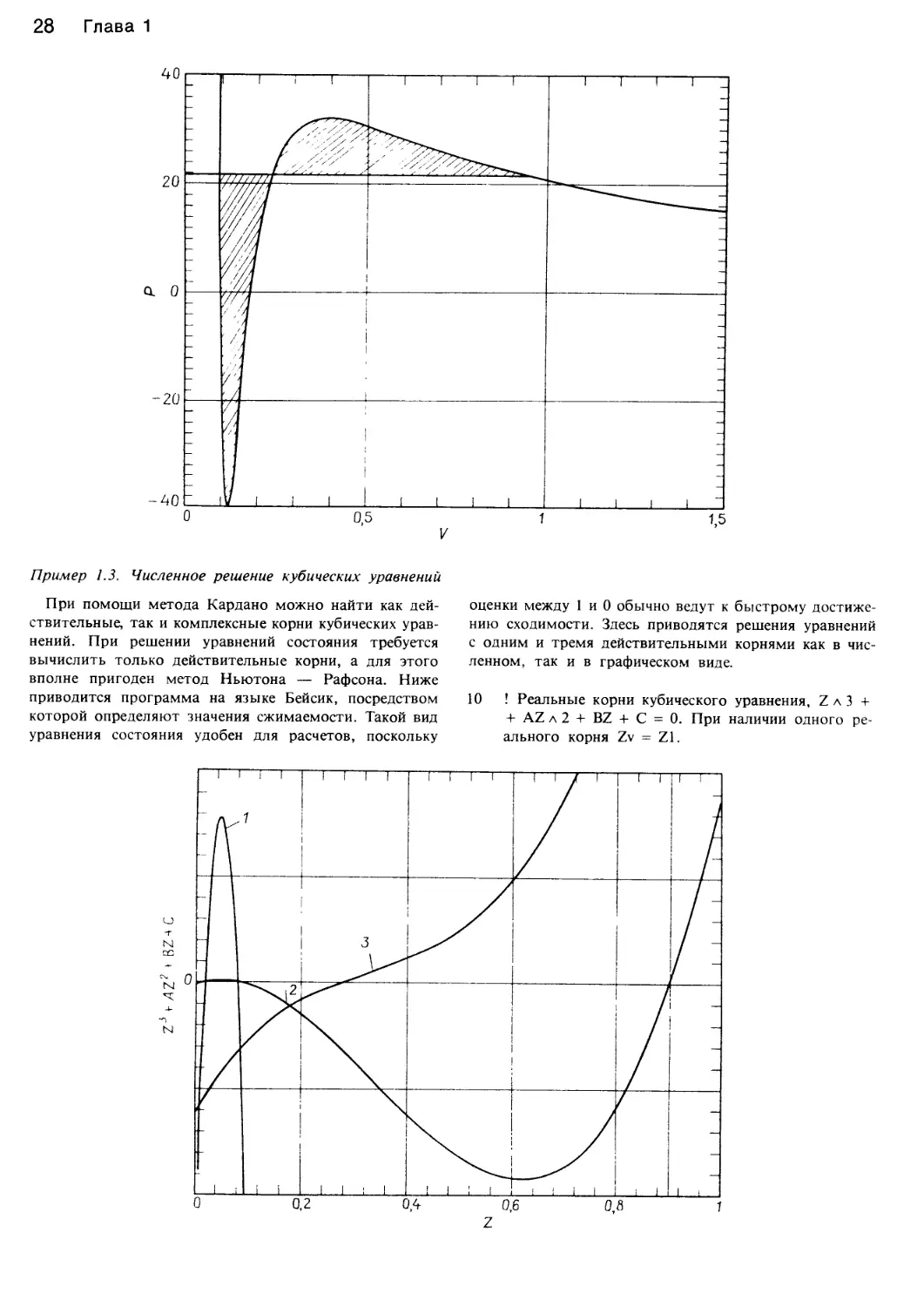
В последнем случае линия 170 не соответствует Zx.
Кривая 1 тождественна кривой 2, однако имеет рас-
ширенную ординату. Кривая 2 — это зависимость
z3 - z2 + 0,089z - 0,0013, имеющая три действитель-
ных корня. Кривая 3 — зависимость z3 - z2 + 0,4224г -
- 0,0608 = 0.
1.3.2. Вещество сравнения. Одним из методов, при-
меняемых для нормализации или приведения уравне-
ний, является соотнесение свойств рассматриваемого
вещества со свойствами вещества сравнения, которые
хорошо известны. Так, в ходе многолетней работы От-
мер [536] разработал линейную зависимость между ря-
дом свойств и некоторым другим свойством, например
давлением паров воды при постоянной температуре.
Питцер и др. [555] определили коэффициент сжимаемос-
ти как отклонение от значения коэффициента сжимае-
мости такой жидкости сравнения, как аргон. Ли и
Кеслер [425] соотносят свойства со свойствами двух хо-
рошо изученных жидкостей — «простой» жидкости и
«-октана. Авторы работы [684] в некоторых случаях
применяют в качестве жидкостей сравнения метан и
н-октан.
Одно из обобщений этого метода описано авторами
работ [491, 479]. Они разработали модельные формы
для температуры и объема, которые представляют со-
бой отношение приведенных значений этих величин:
0г=7*/7$, (1.11)
ву=У^/У§, (Ы2)
где индексом а обозначено неизвестное вещество, а под-
строчным индексом 0 — вещество сравнения (в качестве
такового автором работы [497] выбран метан). Если в
уравнение состояния вещества сравнения подставить
= т&/ет и = v&/ev, полученный результат будет
верен для вещества а. Ниже приводятся эмпирические
виды зависимостей:
0Г = 1 + (ша - шо)[О,О892 - 0,8493 In (Т*)
+ (0,3063 - 0,4506/Тд )(Кд — 0,5)], (1.13)
0у = {1+ (шв - <ио)[О,39ОЗ(Г*- 1,0177)
Zc
- 0,9462(Г^- 0,7663)1п(Т^)]}^7 (1.14)
z0
где и, - ацентрические коэффициенты, Zc, — критиче-
ские сжимаемости.
Принцип соответственных состояний как с использова-
нием дополнительных параметров, так и без них лежит
в основе многих количественных положений термодина-
мики, включая уравнения состояния. Уравнение Ван-дер-
Ваальса имеет чрезвычайно большое значение В послед-
нее время принцип соответственных состояний получил
надежное теоретическое обоснование методами статисти-
ческой термодинамики, о чем подробно говорится в тру-
дах [113, 432]. В последующих главах книги рассматри-
вается применение этого принципа к фазовому равнове-
сию. Анализ следствий принципа соответственных со-
стояний также содержится в книгах [25, 107, 129].
1.3.3. Давление пара и ацентрический коэффициент.
Применение принципа соответственных состояний для
описания давления пара не приводит к одинаковым со-
отношениям для всех веществ. Таким образом, как сле-
дует из рис. 1.9, представленные вещества действи-
тельно имеют практически одинаковые значения приве-
денного давления пара, в целом же графики имеют фор-
му прямых или почти прямых линий. В соответствии
с уравнением Клапейрона
d InP&rat/dTr = AHV/RTcbzT}, (1.15)
и его приближенной интегральной формой
lnP«at= к -
ЬНу \ 1
RTcbz J Тг ’
(1-16)
наклоны этих зависимостей должны различаться. Коэф-
фициент при 1/77 зависит от ряда свойств индивидуаль-
ных веществ, и поэтому нельзя предположить, что он
будет одинаковым для всех веществ. Питцер и др. [555]
приняли приведенное давление при определенной приве-
денной температуре 7777 = 0,7 в качестве характери-
стики вещества. При этих температурах приведенное
давление инертных газов, которые были выбраны в ка-
честве простого вещества, составит примерно 0,1. На
основании этого наблюдения было сформулировано
определение нового параметра — ацентрического коэф-
фициента ш, описывающего отклонение значения приве-
денного давления пара для определенного вещества от
приведенного давления вещества сравнения, в следую-
30 Глава 1
Рис. 1.9. Приведенное давление пара как функция приведенной температуры.
а — данные, полученные для семи представленных на этой диаграмме веществ, достаточно хорошо соответствуют одной прямой,
описываемой уравнением 1п(Р/Рс) = 5,25(1 - Т/Тс) [47]; б — при включении в список исследованных соединений различных классов
(на этом рисунке приведены данные лишь для трех соединений — Аг, Кг и Ог — из числа рассмотренных выше) такого соответ-
ствия уже не наблюдается [92].
Уравнение состояния 31
щем виде:
<д = (logPc/10Psat) @ Тг= 0.7. (1.17)
По определению Питцера [556] этот коэффициент явля-
ется «мерой отклонения функций межмолекулярного
потенциала от функций межмолекулярного потенциала
сферических молекул вещества сравнения». Уравнения
для приведенного давления пара представляют в виде
ряда по ш:
logPrat = (logPr/°) + (nllogP,/+ w2(logP,/2) + ... ,
(1.18)
который, как правило, ограничивают линейным чле-
ном. Обе величины с надстрочным индексом установле-
ны на основе экспериментальных данных и представ-
лены в оригинальных публикациях в табличной форме
как функции приведенной температуры.
Прочие свойства можно представить в таком же обо-
бщенном виде:
М = 11 + ш 2Л/121 + . . . . (1.19)
Уравнение для сжимаемости также обычно имеет ли-
нейную форму:
z = z(°) + wz( 1 )_
(1.20)
Таблицы, содержащие величины с надстрочными индек-
сами как функции приведенной температуры и давле-
ния, включены в оригинальные публикации. Они
приводяться также в работах Льюиса, Рэндала и др. и
представлены в графической форме в [265]. Обобщен-
ные данные Ли и Кеслера [425] приведены в табл. Д.1
и Д.2, а также даны в виде графика на рис. 1.22. Эмпи-
рические уравнения для второго вириального коэффици-
ента и некоторых других свойств, выраженные в форме,
предложенной Питцером, изображены на рис. 1.10.
Сжимаемость можно найти из уравнения для второго
вириального коэффициента следующим образом:
z= 1 + (Pr/Tr)(BPc/RTc),
(1-21)
однако при этом наблюдается неточность результата
для всего диапазона табличных значений z<0> и z(1>.
В 1977 г. вышла в свет книга Питцера [556], в кото-
рой он дает более современную формулировку понятия
ацентрического коэффициента, подвергшуюся частично-
му пересмотру. Предложено несколько направлений
дальнейшей разработки этого параметра, но они не бы-
ли достаточно хорошо изучены. Например, как указано
в работе [664], исходное определение применимо для не-
полярных и малополярных веществ при Тг > 0,7, а для
полярных веществ при низких температурах приведен-
ное давление пара предлагается выразить следующим
образом:
logpsat = (logP,/0) + ^(logP,)*1’ + w2(logPr)(2\ (1.22)
где
w2 = 1,552 + 1.7<o + (logP*at) @ Tr = 0.6, (1.23)
а также аналогичные члены для квадруполярных ве-
ществ, таких, как диоксид углерода. Эти предложения
не были распространены на сжимаемость, фугитив-
ность и избыточные свойства.
Предложено несколько обобщенных уравнений для
давления пара, содержащих ацентрический коэффици-
ент. Ли и Кеслер [425] разработали следующее уравне-
ние, применимое главным образом для углеводородов:
1пР*= 5,92714 - 6,09648/Т, - 1,28862 !п Тг
+ 0,169347 Т* + w(15,2518 - 15,6875/7,
- 13,4721 In Г,+ 0,43577 7^). (1.24)
Применив это уравнение при нормальной температуре
кипения Ть, получаем обобщенное уравнение для расче-
та ацентрического коэффициента, выразив Ты = Ть/Тс
и Р1 = Р^/Рс:
а> =
In Psbr-5,92714+6,09648/7),,+ 1,28862 In Tbr~0,169347 T$r
15,2518 - 15,6875/7),,— 13,4721 In 7),, + 0,43577 T'g,
(1.25)
Кеслер и др. [397] разработали уравнение, применимое
также для расчета давлений паров углеводородов, кото-
рые легко разлагаются при температуре ниже критиче-
ской точки. При использовании этого уравнения ошибка
вдвое меньше, чем в предыдущем случае. Нат и др.
[512] определили соотношения для приведенного давле-
ния паров некоторых высокополярных веществ, а также
углеводородов следующим образом:
2А logP, = -В + [В2 - 4А(Т~Х - С)]1/2, (1.26)
где
А = 0,0094- 0,0144 ш2, (1.27)
В = 0,4506- 0,4371<о + 0,2127ш2 (1.28)
и
С = 0,9827+ 0,0736(о - 0,0210ш2. (1.29)
В задаче 1.17 требуется сравнить это уравнение с урав-
нением Антуана для пиридина, дипольный момент ко-
торого составляет 2,3 Д. Это сравнение дает резуль-
таты достаточно полезные в практическом отношении,
оно также является более точным при низких темпера-
турах, чем уравнение Ли — Кеслера, которое, однако,
не предназначено для приложения к полярным ве-
ществам.
Если известны только нормальная температура кипе-
ния, критические давление и температура, ацентриче-
ский коэффициент можно рассчитать при помощи
уравнения Эдмистера [265]
3 Ть , .
- —-------=- logPc - 1
7 Тс - Ть
(1.30)
где Рс измеряется в атмосферах. Приблизительное соот-
ношение, также взятое из уравнения Эдмистера, между
критической сжимаемостью и ацентрическим коэффи-
32 Глава 1
Рис. 1.10. Корреляции, включающие ацентрический коэффициент [555] (цитируется по работе Льюиса и Рэндала
(1961)).
а — второй вириальный коэффициент представлен уравнением
BPc/RTc = (0,1445 + 0,073w) - (0,330 - ОЛб^Т)’1 -
- (0,1385 + 0,50ш)Т/2 - (0,0121 +
+ 0,097ш)773 - 0,0073 ш 778;
б — коэффициент фугитивности представлен уравнением
1g 0 = Рг/2,303[(0,1445 + 0,07 Зш) 77' -
- (0,330 - 0,46ш)772 - (0,1385 + 0,50ш)7/3 -
- (0,0121 + 0,097ш)774 - 0,0073 ш 77 9];
в — остаточная энтальпия представлена уравнением
(И - H'd)/RTC = Л[(0,1445 + 0,073ш) -
- (0,660 - 0,92ш)7Г' - (0,4155 + 1,50ш)772 -
- (0,0484 + 0,388ш)7/3 - 0,0657^778];
г — остаточная энтропия представлена уравнением
(S - S'd)/R = -1пР + Л[-(0,330 - 0,46ш)7)‘2 -
- (0,2770 + 1,00ш)7/3 - (0,0363 +
+ 0,29ш)7;’4 - 0,058477’].
Уравнение состояния 33
Рис. 1.10 {продолжение)
циентом
zc = 0,291 - 0.080<о,
(1.31)
часто подставляют в уравнения, чтобы определить Zc,
так как обычно величина ш известна более точно.
Помимо представленных здесь соотношений, предна-
значенных для определения давления пара, известно
множество других корреляций; более шестидесяти таких
соотношений включены в книгу {92]. Ряд других соот-
ношений цитируется Эмброузом [156]. Хронологический
список некоторых из них представлен в табл. 1.2А; наи-
более распространены уравнения (5), (9). (11) — (13). В
ряде случаев параметры соотносят с другими характе-
ристиками, которые в большей или меньшей степени
поддаются определению, например критическими свой-
ствами, нормальными температурами кипения, радиу-
сами вращения и т. д. В коммерческой моделирующей
системе CONCEPT применяется особо интересная фор-
мула, основанная на полиноме Чебышева,
Т\пР = £0 + кхх + к2(2х2 - 1) + &3(4х3 - 3),
(1.32а)
где
2Т — (Т + Т 1
V max 1 1 min/
Т — Т
1 max 2 min
(1.326)
3-829
34 Глава 1
Ттах и Tmin — температуры, определяющие диапазон
измеренных давлений пара, а к, — характеристики ин-
дивидуальных веществ [157, 429].
1.3.4. Полярность. Дипольный момент возникает в том
случае, если электрический центр связи не совпадает с
центром масс. Полярность определяют как величину
дипольного момента, выраженную в дебаях. Однако на
практике к полярным относят лишь те молекулы, ди-
польный момент которых превышает 1 Д, поскольку
некоторые характерные особенности полярных соедине-
ний при более низких величинах дипольного момента не
проявляются. Данные о дипольных моментах некото-
рых веществ представлены в табл. 1.7 и приложении Г.
У симметричных молекул дипольный момент равен
нулю, однако если составляющие элементы диполя уда-
лены друг от друга, молекула проявляет свойства, ха-
рактерные для полярных соединений. Это также
относится к симметричным молекулам, имеющим не-
сколько пар противоположных диполей. В качестве при-
мера можно привести диоксид углерода, обладающий
двумя противоположными диполями, которые называ-
ют квадруполями, и отличающийся ярко выраженными
полярными характеристиками. Полярные молекулы ха-
рактеризуются большей вязкостью и более высокими
температурами кипения и плавления по сравнению с не-
полярными молекулами примерно того же размера. На-
пример, у толуола СбНбСНз ц = 0,4 Д и Ть = 383,8 К,
а у анилина C6H5NH2 м = 1,6 Д и Ть = 457,5 К. Кроме
того, полярные молекулы лучше растворяются в воде,
у которой ц = 1,84 Д, и лишь ограниченно растворяют-
ся в неполярных веществах. Особое значение имеет
большее изменение термодинамических свойств, прояв-
ляемое полярными смесями.
Полярность связи возрастает с увеличением разделе-
ния в электроотрицательных рядах Н<С<О<С1<
< Br < I. Группы атомов вида -ОН, -CN, -NH2,
-СООН и -NO также усиливают полярность, в то
время как алкильные группы, например, обладают не-
полярными характеристиками. Несимметричные моле-
кулы, содержащие полярные атомы, имеют ярко
выраженные дипольные моменты; например, у CH3CI
дипольный момент равен 1,9 Д, в то время как у сим-
метричных молекул ССЦ он равен нулю. Примером
симметричной молекулы с нулевым дипольным момен-
том, но в то же время обладающей полярными свойст-
вами благодаря значительному разделению полюсов,
может служить л-дихлорбензол. Несмотря на то что
дипольный момент последнего равен нулю, его точка
кипения примерно равна точке кипения л«е/ш-изомера,
у которого ц = 1,4, а также орпго-изомера, у которого
ц. = 2,3. Однако точки плавления этих веществ в значи-
тельной степени различаются.
Таблица 1.7. Дипольные моменты некоторых веществ
Вещество у, Д
Фталевый ангидрид 5,3
Малеиновый ангидрид 4,0
Пропионитрил 3,7
Ацетонитрил 3,5
Метилэтилкетон 3,3
Нитрометан 3,1
Уксусный ангидрид 3,0
Глицерин 3,0
Гидразин 3,0
Ацетон 2,9
о-Дихлорбензол 2,3
л<-Дихлорбензол 1,4
я-Дихлорбензол 0
Формальдегид 2,3
1-Хлорбутан 2,0
Этилацетат 1,9
Вода 1,8
Этанол 1,7
Диоксид серы 1,6
Триоксид серы 0
Винилхлорид 1,5
Аммиак 1,5
Уксусная кислота 1,3
Изобутилен 0,5
Бутадиен-1,2 0,4
Бутадиен-1,3 0
Моноксид углерода 0,1
Диоксид углерода 0
Молекулярное взаимодействие можно описать при
помощи функций потенциалов, например функций по-
тенциалов Леннарда-Джонса 6-12 (см. разд. 1.7)
м(г) = 4е[(о-/г)12 - (сг/г)6]
(1.33)
где м(г) — потенциал, г — расстояние между центрами
молекул, а — диаметр молекулы, г/к — характеристи-
ческая энергия, К, £ — постоянная Больцмана. Безраз-
мерное соотношение е/кТ представляет собой энергети-
ческий параметр, который применяют для количествен-
ных расчетов поведения жидкостей, а также дипольного
момента, ионизационного потенциала и других электро-
статических и механических свойств молекул.
Пример 1.4. Расчет ацентрического коэффициента.
Рассчитаем ацентрический коэффициент метилхлорида
несколькими методами. Согласно данным табл. Г. 2,
этот коэффициент равен 0,156, в то время как в работе
[52] указано, что он равен 0,1530. Физические свойства
вещества: Рс = 65,9 атм, Тс = 416,3 К, Ть = 248,9 К,
ц = 1,9 Д, А = 16,1052, В = 2077,97, С = - 29,55. По-
следние три цифры — коэффициенты уравнения Антуа-
на, в котором давление пара выражено в мм рт. ст.
а. Если давление пара рассчитывается по уравнению
logPsal = А + В/ Т для температуры кипения при нор-
мальных условиях и критической температуре кипения,
Уравнение состояния 35
то это уравнение принимает следующий вид:
пара, получаем
logPsa*
ТЬТС
Ть
lOgPe
а) = 0,4343
@0,77;
Подставляя его в определение ш, получаем уравнение
Эдмистера [265]:
= 0,4343
In (0,1Рс)
3
7
Ть
Тс - Ть
10gPc =
= 0,4343 1п[О,1(76О)(65,9)] -
- 16,1052 +
2077,97
0,7(416,3) - 29,55
= 0,152.
1 (-----------------) log65,9 = 0,159.
7 I 416,3 - 248,9 )
в. Уравнение Ли и Кеслера (см. разд. 1.3.3) дает
Ты = Ть/Те = 248,9/416,3 = 0,5979.
б. Применяя уравнение Антуана для расчета давления
При подстановке в уравнение (1.25) получаем ш = 0,146.
1.3.5. Ассоциация молекул и образование водородных
связей. Поскольку атомы водорода ведут себя так, как
будто обладают избыточным зарядом, молекулы по-
лярных веществ стремятся к образованию ассоциаций
за счет так называемых водородных связей. Тенденция
к образованию таких ассоциаций снижается по мере
уменьшения электроотрицательности составляющих
атомов. Ионы фтора обладают наиболее сильным от-
рицательным зарядом, поэтому, например, фтороводо-
род образует прочные ассоциативные связи как в жид-
кой, так и в паровой фазах. Формула газообразного
фтороводорода при нормальных условиях (HF)e. Пары
уксусной и муравьиной кислот при температуре, немно-
го превышающей их точку кипения при атмосферном
давлении, бимолекулярны. Степень ассоциации молекул
можно определить спектроскопически. Константы хи-
мического равновесия для димеризации установлены од-
нозначно. Данные о них представлены в задаче 1.11.
Наиболее ярко тенденция к димеризации проявляется у
карбоновых кислот; в то же время спирты, эфиры, аль-
дегиды и другие вещества при нормальных давлении и
температуре также стремятся к ассоциации в значитель-
ной степени. Снижение этой тенденции наблюдается
при уменьшении давления и концентрации, а также при
повышении температуры. Классификация молекул, ко-
торые стремятся к ассоциации путем образования водо-
родных связей, выполнена Эвеллом и др. [278].
Для жидких фаз ассоциация вполне обычна. Аномаль-
ное поведение воды, учитывая ее низкую молекулярную
массу, объясняется главным образом образованием
олигомеров, а отклонение параметров растворов поляр-
ных веществ от идеальных значений часто является ре-
зультатом ассоциации. Несколько примеров ассоциации
в жидкой фазе показаны на рис. 1.11. На рис. 1.11 ,а по-
казано достижение полной димеризации при повышении
концентрации, а на рис. 1.11, б — несколько примеров
образования высших олигомеров, которые показывают,
что природа растворителя во многом определяет сте-
пень ассоциации. Приведенные кривые демонстрируют
также сильное влияние температуры на ассоциацию мо-
лекул фенола, растворенного в тетрахлориде углерода.
Подобные явления в той или иной степени характерны
и для химических реакций вообще. На рис. 1.12 показа-
5
5
с, моль!кг
Рис. 1.11. Молекулярная ассоциация в жидкой фазе.
а — относительная молекулярная масса нескольких веществ в
растворе бензола. М/Мо — отношение молекулярной массы,
полученной опытным путем, к формульной массе [45]; б — сте-
пени ассоциации различных спиртов и фенолов в различных
растворителях при различных температурах [474]. 1, 4, 6, 7 —
растворы фенола в ССЦ при - 24 °C (7) и 20 °C (4), в хлорбен-
золе (6) и бензоле (7) при 20 °C; 2 — раствор метанола в ССЦ
при 20 °C; 3 — раствор этанола в ССЦ при 20 °C; 5 — раствор
л-хлорфенола в ССЦ при 20 °C.
3
36 Глава 1
Рис. 1.12. Некоторые константы равновесия димериза-
ции Кр = /^dimer/^monomer [420].
ны некоторые данные по равновесию димеризации.
Еще много лет назад были изучены и описаны отно-
шение второго вириального коэффициента и константы
химического равновесия при слабой димеризации. В ра-
боте Нотнагеля и др. (1973) разработаны вопросы прак-
тического применения этого отношения, о чем будет
рассказано в разд. 1.4.
Отклонение поведения некоторых веществ от поведе-
ния идеального газа можно отчасти объяснить умень-
шением количества присутствующих молекул, вызван-
ным образованием соединений, которое сопровождает-
ся увеличением сжимаемости исходного вещества. На-
пример, если молекула вступает в реакцию лА «=* А„ при
степени превращения £, кажущаяся сжимаемость опре-
деляется следующим соотношением:
_ число молекул в равновесном состоянии _
число молекул исходного вещества
= 1 - £ + е/п, (1-34)
где £ — величина, определяемая константой равновесия
полимеризации,
£
«(1 - £)
1 — £( 1 — 1/п) п 1
Р(1 - £)
(1-35)
Аналогичные отношения можно вывести для условий,
допускающих одновременное существование димеров,
тримеров и т. д., а также межмолекулярных соедине-
ний, хотя данные о такого рода равновесии получить
трудно. Приведем в качества примера следующий рас-
чет: если К = 0,05, /5 = 2ил = 3, toe равно 0,3117,
a z равно 0,7925.
Если величина z превышает 1, это можно объяснить
диссоциацией, однако в большинстве случаев доказа-
тельства протекания этого процесса отсутствуют, и,
следовательно, причины роста сжимаемости следует ис-
кать в другом направлении.
Описано множество примеров ассоциации одинако-
вых и разнородных молекул, ссылки на последние рабо-
ты такого рода можно найти в книге Кноблера [402].
Праузниц и др. [98] подготовили таблицы данных о
константах равновесия, полученных главным образом
исходя из вторых вириальных коэффициентов для мно-
гих веществ и смесей.
Описание изменений PVT многокомпонентных систем
при помощи равновесия ассоциации представляется ис-
ключительно сложным, тем более что опытные данные
малодоступны. Поэтому для решения подобных задач
обычно применяют эмпирические уравнения состояния,
не учитывающие химическое равновесие, за исключени-
ем нескольких случаев димеризации кислородсодержа-
щих органических веществ, константы равновесия
которых достаточно точно установлены.
1.3.6. Псевдокритические свойства. Вероятно, можно
полагать, что принцип соответственных состояний при-
меним для смесей в той же мере, что и для чистых ве-
ществ. И как выяснилось, с учетом ряда ограничений
данный принцип вполне приложим к смесям. Несмотря
на то что приведенные уравнения состояния считаются
неверными, если они основаны на реальных значениях
свойств смесей в критическом состоянии, тем не менее
было признано допустимым выражать псевдокритиче-
ские свойства через состав и критические свойства чис-
тых компонентов. Как показано, например, на рис. 1.33,
величины таких псевдокритических параметров обычно
значительно отличаются от истинных величин соответ-
ствующих параметров. В действительности истинные
значения критических свойств смесей часто можно оце-
нивать, используя уравнения состояния, основанные на
псевдокритических свойствах, как описано в разд. 1.8.4.
При разработке определения псевдокритических
свойств используют правила усреднения для уравнения
Ван-дер-Ваальса, т. е.
va"= Ер, v а,, (1.36)
= (1.37)
Поскольку а = 3PCV2 = ~R2T2/PC, (1.38)
64
b = Ие/3 = 7?Те/8Я, (Е39)
то уравнения для псевдокритических свойств могут
быть записаны следующим образом:
Vpc = Xy.Ve,, (1.40)
Трс/^Рр^ = Еу,(Тс,/7яГ), (1.40а)
Трс/Ррс = Sy,(Tc,/Pc,), (1.406)
Уравнение состояния 37
а параметры выражены как
а = ~ Р2[^у[Гс,/^Р^]2,
о4
Ь = ^y.Tci/Pc>
о
(1.41)
(1-42)
На основании этих отношений для некоторых смесей
выведено довольно точное уравнение состояния, однако
по точности оно лишь немного превосходит уравнение
состояния, которое выводится гораздо более простым
методом, известным как «правило Кэя» [392]:
Ррс ^У iPci-> (1-43)
Tpc~^yiTci, (1.44)
("рс ^У ci- (1-45)
Один из первых подробных обзоров работ Кэя и других
ученых, специализирующихся в этой области, в особен-
ности в приложении к фракциям нефти, выполнен
Эд мистером [263].
Мера самосогласованное™ псевдокритических свойств
была введена Праузницем и Гунном [569], которые ис-
пользовали следующее соотношение:
Рре ~ ^pcRTpc/Vpc. (1.46)
где свойства, приведенные в правой части уравнения,
определяются при помощи правила Кэя. Для оценки па-
раметров перекрестных взаимодействий, параметров
в кубическом уравнении состояния и В,, в вириальном
уравнении Праузниц и Гунн также применили правила
Лоренца—Бертло для бинарных смесей:
Tcij=(TciTcj)Q>5, (1.47)
К*/3=О,5(Г’,/3 + KJ/3). (1.48)
Полная система включает также следующие уравнения:
Tcij = (1 - ^)(ГС;ТС7)0-5, (1.49)
zcij + zcj) (1 -50)
= 0,291 - 0,04(w; + a>7), (1.51)
Pczy — z CjjR Tcjj IVсц (1.52)
Параметры бинарного взаимодействия ки определяются
эмпирическим путем. Некоторые из их значений пред-
ставлены в табл. Д. 3; получены они главным образом
исходя из экспериментальных данных о вторых вири-
альных коэффициентах перекрестных взаимодействий.
Для пар углеводородов параметры взаимодействия до-
вольно малы, в то же время для разнородных соедине-
ний они достаточно велики. Для некоторых полярных
веществ они могут быть отрицательными.
Разработан целый ряд правил усреднения псевдокри-
тических свойств и параметров уравнений, многие из
них превосходят описанные выше правила, однако они
значительно сложнее последних. Работа в этом направ-
лении еще не закончена. Некоторые альтернативные ме-
тоды упоминаются здесь в связи с индивидуальными
уравнениями состояния. В ходе обширных исследований
Лиленд и Мюллер проанализировали сжимаемость пя-
тидесяти восьми смесей, используя правило Кэя, а так-
же разработанную ими улучшенную методику. Подроб-
ный обзор псевдокритических свойств, правил усредне-
ния свойств и параметров взаимодействия содержится
в книге [129]. Анализ теоретических оснований форму-
лировки псевдокритических свойств можно найти в тру-
дах [432, 322, 491].
Примеры 1.5 — 1.9 иллюстрируют применение выше-
упомянутых правил усреднения свойств.
Рис. 1.13. Вириальное уравнение, выраженное через объем и через давление.
а — величины z = PV/RT аргона при 25 °C. В скобках представлены значения всех членов ряда после третьего [85]; б — оста-
точный объем а эквимолярной смеси СО2 и СзН6. Если уравнение имеет вид z = 1 + BP/RT, графики горизонтальны, если
уравнение имеет вид z — 1 + В'Р + СР2, графики линейны [64]; в — данные, представленные на рис. 1.13,6, изображены в
виде зависимости V(PV - RT) от 1/К Поскольку графики по существу линейны, подтверждается согласованность с С-усечен-
ным вириальным уравнением z = 1 + В/V + C/V2 [64].
38 Глава 1
Пример 1.5. Псевдокритические свойства смесей этана
(1) и н-гептана (2)
В данном примере используются два метода:
а) Рpc — ZpcRTpc/ VpC,
б) Ррс = У1 а b
причем для нахождения zpc, Трс и Урс применяется пра- А А
вило Кэя . Ниже приводятся данные для чистых компо- и,и 26,99 27,00
нентов: о,1 27,86 29,12
0,2 28,85 31,24
Этан н-Гептан Единицы измерения 0,3 29,97 33,36
С 305,4 540,2 К 0,4 31,26 35,48
Рс 48,2 27,0 атм 0,5 32,78 37,60
Ус 148 432 мл/моль 0,6 34,60 39,72
Zc 0,285 0,263 0,7 36,82 41,84
0,8 39,62 43,96
На рис. 1 .33 эти результаты сравниваются с истинными 0,9 43,27 46,08
величинами критического давления. 1,0 48,26 48,20
Пример 1.6.
Сравнение правил усреднения для расчета
сжимаемости смеси
и соотношения Питцера - Керля
Рассмотрим эквимолярную смесь диоксида углерода
и пропилена при температуре 30 ЭС и давлении
25,5 атм. Экспериментальное значение сжимаемости
Z = 0,737, экспериментальные значения критических па-
раметров смеси: Тс - 319,8 К, Рс = 70,7 атм.
В методе 1 для определения псевдокритических
свойств применяют правило Кэя. При решении задач с
помощью метода 2 псевдокритическое давление находят
из Ррс = ZpcRTpc/Урс, а все прочие псевдокритические
свойства устанавливают согласно правилу Кэя. Ниже
приведены в виде таблиц величины параметров, харак-
теризующих чистые компоненты и смеси. Следует от-
метить, что параметры, расссчитанные по правилу Кэя,
наиболее близко соответствуют экспериментальным
данным, в то время как значения, полученные на осно-
вании истинных псевдокритических свойств, гораздо
менее точны.
Тс, к Рс, атм Ус, мл/моль г,
СО2 304,2 72,9 94,1 0,274 0,225
СзН6 364,9 45,45 182,4 0,275 0,148
Смесь Метод 1 334,6 59,18 138,25 0,2745 0,1825
Смесь Метод 2 334,6 54,51 138,25 0,2745 0,1825
Смесь Ист. знач. 319,8 70,7 0,1825
Тг Рг ?(0) г*1’ z
Смесь Метод 1 0,906 0,431 0,761 - 0,12 0,728
Смесь Метод 2 0,906 0,470 0,734 - 0,15 0,693
Смесь Ист. знач. 0,910 0,361 0,825 - 0,05 0,811
Смесь Экс. знач. 0,737
Сравнение правил определения псевдокритических свойств с уравнением Ван-дер-Ваальса
Пример 1.7.
В примере 1.6 решение основано на уравнении Ван-
дер-Ваальса. В данном примере для расчета параметров
использованы псевдокритические свойства, полученные
тремя методами, описанными в предыдущем примере.
Уравнение (4), габл. 1.3, можно записать следующим
обраюм:
/ Рг \ 2 2~ Р, _ _ 27/С
" - \ 1 + STr) z + 647? " 5?27?
Используя ранее вычисленные значения приведенных
свойств, получаем три уравнения для трех случаев:
Метод 1: ? - l,O595z2 + 0,2215z - 0,01317 = 0,
z = 0,8045.
Метод 2: z3 - l,0501z2 + 0,2416c - 0,01566 = 0,
z = 0,7813.
Ист. крит. знач.: д' - 1,0501<2 + 0,1880z - 0,00943 = 0,
z = 0.8396.
Указанные выше значения корней были установлены ре-
шением на ЭВМ соответствующих уравнений. Очевид-
но, что ни один из методов определения параметров
уравнения Ван-дер-Ваальса не обеспечивает получение
значений сжимаемости, близких к экспериментальному
значению z = 0,737. Данный метод явно уступает мето-
ду Питцера — Керля, в котором применены те же пра-
вила усреднения для нахождения псевдокритических
свойств.
Уравнение состояния 39
Пример 1.8. Сжимаемость трехкомпонентной, смеси
Определим сжимаемость чистых компонентов и трех-
компонентной смеси метилхлорида (1), хлороформа (2)
и тетрахлорида углерода (3) при давлении 10 атм и тем-
пературе 450 К, а также при yt = 0,2 и уг = 0,3. Вос-
пользуемся для этого уравнением Ван-дер-Ваальса.
Постоянные взяты из «Химического справочника»
Ланга (1973)
у а b z Т, Рс
СН3С1 0,2 7,471 0,06483 0,9617 416,3 65,9
СНСЬ 0,3 15,17 0,1022 0,9091 536,4 54,0
ecu 0,5 20,39 0,1383 0,8738 556,4 45,0
Смесь 15,784 0,1128 0,9073 522,38 51,88
Сначала параметры смеси оценивают в соответствии
с правилами Лоренца — Бертло, а именно:
а = (Xy,V<z( )2 = 15,784,
Ь = ХуД = 0,1128.
Таким образом, уравнение Ван-дер-Ваальса в полиноми-
альной форме принимает следующий вид:
г3 - 1,03055? + 0,11575г - 0,003536 = 0
и корни (г) его равны 0,9073, 0,0616 ± 0,0095у. Сжимае-
мость чистых компонентов находят аналогичным обра-
зом, ее значения показаны в таблице выше.
Согласно закону Амагата,
г = Уу,г< = 0,9020,
что примерно на 6% выше величины, определяемой при
помощи правил Лоренца — Бертло.
Применив правило Кэя для оценки псевдокритических
свойств, а следовательно, и параметров уравнения, по-
лучаем следующие результаты:
Л = ^yiPci = 51,88 атм,
Тс = 'Су.Те, = 522,38 К,
а = 21R2T2/64PC = 14,9351,
b = RTc/ZPc = 0,1033.
Уравнение принимает следующий вид:
г3 - 1,0280г2 + 0,10958г - 0,003066 = 0,
корни которого равны 0,9115, 0,0639, 0,0527. Наиболь-
ший из этих корней достаточно точно соответствует
значению, полученному при оценке параметров смеси
непосредственно на основании параметров чистых ком-
понентов, которые приведены в начале примера 1.8.
Различие между этими двумя методами состоит в том,
что один из них позволяет найти лишь один действи-
тельный корень, а другой — три действительных корня,
причем наибольший из них примерно равен корню, по-
лучаемому посредством прочих методов.
Пример 1.9. Сравнение нескольких правил усреднения свойств, предусматривающих использование вириального
уравнения Эббота
Удельный объем смеси 1/3 этана + 2/3 н-гептана при
температуре 400 К и давлении 20 атм можно опреде-
лить при помощи вириального уравнения, используя
корреляции Эббота для второго вириального коэффици-
ента. При этом можно воспользоваться тремя правила-
ми усреднения, указанными в табл. 1.5. В соответствии
с правилом Кэя Мс = 'Су.М^ для всех критических
свойств. Правила Праузнипа — Гунна аналогичны пра-
вилам Кэя, лишь Рс = ZcRTc/Vc- Результаты расчетов
суммированы в приведенной ниже таблице. Между рас-
четными значениями удельного объема смеси, опреде-
ляемыми тремя методами, наблюдаются значительные
различия. Экспериментальные данные, с которыми
можно было бы сравнить расчетные величины, отсут-
ствуют, и поскольку правила Лоренца — Бертло имею:
некоторое теоретическое обоснование, им отдается
предпочтение. Удельный объем находят, решая квадра-
тичное уравнение
2 _ RT BRT = 0
Р Р
U т, - Р,
- - — — _ _. - - - - -
11 305,4 148 0,285 0,098 48,2
22 469,6 363 0,262 0,251 33,3
12 Кэй 414,9 291 0,270 0,200 31,5
12 Праузниц — Гунн 414,9 240 0,270 0,200 35,5
12 Лоренц — Бертло 378,7 240 0,274 0,175 38,3
40 Глава 1
Л|2
В.2
В V, мл/моль
Этан 1,3098 - 95,1 1731,1
Пентан 0,8518 - 592,8 2103,4
Смесь Кэй 0,9642 - 335,0 1926,4
Смесь Праузниц — Гунн 0,9642 - 406,9 1978,5
Смесь Лоренц — Бертло 1,0562 - 304,8 - 409,5 1980,3
1.3. 7. Правила усреднения свойств. Правила усреднения
свойств служат для представления какого-либо свойства
смеси посредством ее состава и свойств чистых компоне-
нтов. В зависимости от типа рассматриваемого свойства
состав может быть выражен в мольных, объемных или
массовых долях. Для некоторых правил усреднения разра-
ботаны теоретические основы, однако подавляющее их
большинство имеет чисто эмпирический характер. Расчет
какого-либо свойства может быть значительно улучшен
путем введения ограниченного числа экспериментальных
данных о всей смеси или бинарных смесях ее компонентов,
так как бинарное взаимодействие оказывает решающее
влияние на характеристики смеси. Обоснованность даль-
нейшей разработки правил усреднения свойств зависит от
требуемой степени точности. Параметры бинарного взаи-
модействия рассматриваются в разд. 1.3.8.
При изучении уравнений состояния основной интерес
представляют правила усреднения псевдокритических
свойств (разд. 1.3.6), а также правила, предназначенные
для непосредственной оценки параметров. Эти правила
указываются для каждого уравнения, упоминаемого в на-
стоящей главе, тем не менее необходимо сделать несколько
замечаний общего характера. Теоретические основы разра-
ботаны лишь для правил, применяемых для коэффициен-
тов вириального уравнения, например, второй вириаль-
ный коэффициент можно представить следующим
образом:
(1.53)
В некоторых случаях при i # j параметры перекрестного
взаимодействия Ву могут быть аппроксимированы выра-
жением
ви ~ (*/Л/)0’5,
(1.54)
что позволяет упростить уравнение (1.53):
5°.5 = ^yjB^>5.
(1.55)
Наиболее простые правила усреднения, используемые
для усреднения параметров уравнения состояния Ван-дер-
Ваальса, уже упоминались выше, а именно указывалось,
что
b = ЕуД.
(1.56)
(1-57)
В подобных кубических уравнениях, таких, как уравнение
Редлиха — Квонга и его многочисленные модификации,
\Tataj заменяют параметром перекрестного взаимодей-
ствия ау, кроме того таким же образом, как и в уравнение
Соава, можно ввести параметры бинарного взаимодейст-
вия к,/.
аи = (I - к и) \ a flj . (1.58)
Основы правил усреднения для уравнения Ван-дер-Ва-
альса вытекают из теоретических правил усреднения вто-
рых вириальных коэффициентов. Поскольку
В = lim V(z — 1)
J/ —‘ОС
(1.59)
отношение вириального коэффициента и параметров дру-
гих уравнений состояния принимает следующий вид:
B = b- a/RT
(1.60)
Для уравнения Ван-дер-Ваальса
и В = b - a/RT''5 (1.60а)
для уравнения Редлиха — Квонга.
Рассмотрим уравнение состояния Ван-дер-Ваальса. Ви-
риальный коэффициент смеси определяется выражением
В = Ви
= a~b/RT= XXyiyjbij - (1 /RT) аф
(1-61)
поэтому правила усреднения можно записать следующим
образом:
а = (1.61а)
b = ЪЪу^Ьц. (1.61b)
Однако экспериментально установлено, что уравнение
(1.57) дает лучшие результаты, чем уравнение (1.615).
Гурон и Видал [366] предложили системы уравнений
для определения параметров некоторых кубических
уравнений состояния, в которых они соотнесли пара-
метры с избыточной энергией Гиббса. Их метод преду-
сматривает использование экспериментальных данных о
коэффициентах активности и разработан только для би-
нарных смесей, а потому выполняет коррелятивную
функцию, а не прогнозирующую.
В сложных уравнениях состояния, в большей части
эмпирических, применяют довольно произвольные пра-
Уравнение состояния 41
вила усреднения, имеющие, однако, экспериментальное
обоснование. Восемь коэффициентов уравнения Бене-
дикта — Уэбба — Рубина (табл. 1.16), применяемого к
смесям, получают, пользуясь следующими правилами:
(1.62)
где т = 1, 2 или 3 в зависимости от коэффициента.
При разработке модификации уравнения состояния
Старлинга — Хана, содержащей 11 констант, применя-
ются аналогичные правила, а также параметры взаимо-
действия для четырех параметров уравнения вида
(1 - кп)т, где т = 5.
1.3.8. Параметры бинарного взаимодействия. Харак-
тер поведения смесей, естественно, зависит от взаимо-
действия разнородных молекул, особенно если среди
них имеются полярные. Тройное взаимодействие и взаи-
модействие комбинаций более высокого порядка обыч-
но оказывают гораздо меньшее влияние, чем взаимо-
действие пар компонентов. Некоторые сведения о срав-
нительном эффекте бинарного и тройного взаимодейст-
вия можно получить при рассмотрении вириальных
уравнений, второй и третий вириальный коэффициенты
которых учитывают влияние подобного взаимодействия
между разнородными молекулами. При умеренном дав-
лении и температуре немного ниже критической эффект
третьего вириального коэффициента может быть очень
незначительным. Приведем в качестве примера некото-
рые данные, заимствованные из рис. 1.14,в и г:
Максимальная погрешность
в определении z, %
Тг РГ При наличии В При наличии В и С
2 1 1 0,01
2 5 У0 1
При решении многих задач погрешность в определе-
нии z в 1 % считается приемлемой, так что при Тг = 2
и Рг = 1 — 2 для веществ, указанных на рис. 1.14, вкла-
дом третьего вириального коэффициента можно прене-
бречь. На рис. 1.15,0 сравниваются уравнения вида
z - 1 = ВС + СР* 2 для смесей гелия и азота. Влияние
третьего вириального коэффициента представляется не-
существенным даже при 50 атм, если СР2/ВР равно
0,030 для верхней кривой и -0,022 для нижней.
Взаимодействия высшего порядка часто являются не-
существенными и в значительной степени маскируются
допущениями, принимаемыми в уравнениях состояния,
так что введение в уравнения данных о бинарных взаи-
модействиях в дополнение к данным о чистых компо-
нентах приводит к максимально возможному повыше-
нию точности уравнения состояния. Так, для «-компо-
нентной смеси существует «(« - 1)/2 возможных пара-
метров бинарного взаимодействия.
Эти параметры обычно вводятся при помощи какого-
либо одного из следующих методов:
1. Посредством корректировки какого-либо псевдо-
критического свойства пары веществ. Так, для уравне-
ния Редлиха — Квонга Чуэ и Праузниц [223] использу-
ют следующие выражения:
Tcij = (1 - кц) и (1.63)
аи= 0,42748(1 - ки)К\Тс1Тс^IPcij. (1.64)
Величина ку, как правило, находится в интервале от 0
до 0,2 или около этого. Значения величин указаны в
табл. Д. 3. Такие перекрестные псевдокритические вели-
чины температуры также используют для оценки вто-
рого вириального коэффициента перекрестных взаимо-
действий, примером чему могут служить уравнения
Эббота и Цонопулоса. Данные о ку для углеводородов
с 8—30 атомами углерода и для таких неполяр-
ных веществ, как вода и низшие кислородсодержащие
органические соединения, приводятся Цонопулосом
[696, 697].
2. Посредством введения поправок непосредственно в
некоторые параметры уравнения состояния, например в
параметры перекрестных взаимодействий в уравнении
Редлиха — Квонга или уравнении Соава:
aij = (1 ~ Cjj) Са^. (1.65)
Этот способ был предложен Зудкевичем и Иоффе [753].
Числовые данные для варианта уравнения Соава, разра-
ботанного Американским нефтяным институтом, пред-
ставлены в табл. 1.12. Параметры взаимодействия пар
углеводородов при такой корреляции равны нулю, в то
время как для смесей углеводородов с H2S, СО2 и N2
они соотнесены с параметрами растворимости каждого
из этих газов. Каких-либо корреляций более общего ха-
рактера разработано не было. В 1982 г. Изекве [279] по-
лучил усовершенствованное корреляционное уравнение
для смеси СОг с углеводородами:
logk:(y= -0,8849 - 0,2145 ш131- 3j\. (1.66)
В некоторые из одиннадцати параметров уравнения Бе-
недикта — Уэбба — Рубина — Старлинга введены по-
правки на бинарное взаимодействие, так как в этой
системе взаимодействия пар углеводородов также до-
статочно ощутимы.
Авторы работы [279] указывают, что два вида пара-
метров, входящих в уравнение Редлиха — Квонга, свя-
заны между собой следующим образом:
сц
Rz cij
где Zcu = 0,5(Zd + Zcj),
= O,5(K‘e,3 + V^h.
(1-67)
(1.68)
(1.69)
Эти исследователи выполнили оценку ку для нескольких
систем и обнаружили лишь несущественное воздействие
температур, превышающих 100 °C. Однако, если равно-
весная система содержит водную фазу, параметры би-
нарного взаимодействия воды с СО2 и H2S определен-
ным образом зависят от температуры [549].
Авторы работы [349] получили вириальные коэффи-
циенты перекрестного взаимодействия из уравнения
~ (1 С12) ' -®152’
(1.70)
42 Глава 1
Рис. 1.14. Погрешности, обусловленные усечением вириального уравнения, выраженного через объем и через давле-
ние [428]. Приведены данные для Не, Nj. Аг, СН4, СгНб и их смесей. В указанных примерах Тг = 2, Рг = 5.
а — оптимальное число членов усеченного ряда по плотности, найденное статистически. Например, оптимальное число членов
равно двум; б — оптимальное число членов усеченного ряда по давлению, найденное статистически. Например, оптимальное число
членов равно пяти;в — погрешность (%), получаемая при использовании метода наименьших квадратов и уравнения z = 1 + Bq.
Например, погрешность составляет 25%; г — погрешность (%), получаемая при подборе методом наименьших квадратов по урав-
нению z — 1 + Bq + Cq2. Например, погрешность составляет 1%; д — погрешность (%) при подборе методом наименьших ква-
дратов по уравнению Z = 1 + В'Р. Например, погрешность составляет 20%; е — погрешность (%) при подборе методом наимень-
ших квадратов по уравнению z = 1 + В'Р + С'Р2. Например, погрешность составляет 5%.
Уравнение состояния 43
мм I моль
со
700
0
- 100
-200
-300
-МО
-500
-600
-700
-800
-900
500
1000200 300 400
Т, К
Рис.'1.15 (см. продолжение на стр. 44)
44 Глава 1
Рис. 1.15. Данные о вириальных коэффициентах.
а — вторые вириальные коэффициенты некоторых веществ как функция температуры (данные заимствованы из подборки Когана
[68]);б —вторые и третьи вириальные коэффициенты В' иС смесей гелия и азота. Коэффициенты перекрестных взаимодействий:
104В12, °C = (6,234, 175), (4,429, 325) и (3,313, 475) [731]; в — приведенные третьи вириальные коэффициенты аргона [249]; г — тре-
тьи вириальные коэффициенты некоторых неполярных газов. Заштрихованная область соответствует данным для жидких фаз, на-
пример, Кг, Хе, СН4, F2, N2 и Ог [249]; д — воздействие третьего вириального коэффициента на рассчитанные величины сжимаемос-
ти смесей Не и N2. На оси ординат представлена разность zc, - zg, = С'Р2 [412].
где параметры взаимодействия соотнесены с потенциа-
лами ионизации чистых компонентов — метана, этиле-
на, этана и легких неорганических газов, включая
водород и гелий — посредством выражения
с12 = 0.17(7! - /2)°>5 ln(/j//2), (1.71)
В «Справочнике по химии и физике», выпущенном в
1969 г. Координационным исследовательским центром,
приведены в табличной форме данные о потенциалах
ионизации примерно 1000 веществ, однако в более поз-
дних изданиях этого справочника такая таблица отсут-
ствует.
Представление о том, что отклонение свойств много-
компонентных смесей от идеальных обусловлено глав-
ным образом бинарными взаимодействиями, получило
широкое распространение. На его основе разработаны
уравнение Вильсона и подобные ему выражения, пред-
назначенные для расчета коэффициентов активности
(гл. 4). Поскольку расчеты коэффициентов активности
часто выполняются исходя из данных о вкладах молеку-
лярных структур с использованием методов ASOG или
UNIFAC, можно предположить, что расчет параметров
бинарного взаимодействия с,, или ktJ также можно осу-
ществить, используя данные о свойствах чистых компо-
нентов, однако этот вопрос до сих пор еще не вполне
изучен.
1.3.9. Корреляции характера изменения функции PVT.
Характер изменения функции PVT можно представить
непосредственно при помощи приведенных параметров
в графической или табличной форме без предваритель-
ной подгонки уравнения к данным о функции PVT. На
рис. 1.8,я представлена сжимаемость z = PV/RT, най-
денная таким способом. Очевидно, что поведение всех
веществ, описанных здесь, гораздо более соответствует
принципу соответственных состояний, нежели уравнени-
ям Ван-дер-Ваальса, Бертло или Дитеричи, как это по-
казали Отт и др. [537] (см. штриховые линии на рис.
1.8,я). Более полного соответствия можно добиться пу-
тем введения в дополнение к двум параметрам Тс или
Рс еще одного параметра, например сжимаемости Zc
или ацентрического коэффициента ш, связанного с изме-
нениями давления пара.
При помощи метода Питцера и др. [655], о котором
уже упоминалось в разд. 1.3.3, сжимаемость можно
представить в следующем виде:
z = z<°) + (1.72)
где z(0) и z(1) — эмпирические коэффициенты, определяе-
мые как функции ТГ и РГ, которые первоначально бы-
ли представлены в табличной форме. Аналогичная
таблица значений сжимаемости была составлена с ис-
пользованием уравнения Ли — Кеслера, с тем чтобы
легче было проводить расчеты вручную при помощи
этого сложного уравнения; соответствующие данные,
приведенные в табл. Д.1 и Д.2, как правило, считаются
более точными, чем данные Питцера и Керля. Постро-
енные по этим данным кривые помещены в «Справоч-
нике Американского нефтяного института» и изобра-
жены на рис. 1.22.
Некоторые подобные показанным на рис. 1.14 корре-
Уравнение состояния 45
ляции второго вириального коэффициента можно ис-
пользовать для определения сжимаемости из уравнения
z = 1 + BP/RT.
(1-73)
Лидерсен и др. [451] приняли значение сжимаемости
в критическом состоянии Zc в качестве третьего корре-
ляционного параметра. Основываясь на эксперимен-
тальных данных о 82 соединениях, они составили
таблицы, при помощи которых можно получить сжи-
маемость при определенных величинах Рг, Тг и zc- Эти
таблицы были воспроизведены в монографии [59], там
же приведены данные о плотностях жидкостей и других
важных термодинамических характеристиках. Однако
ввиду сложности экспериментального определения точ-
ных значений Zc в качестве третьего корреляционного
параметра был практически повсеместно принят ацент-
рический коэффициент. Лидерсен и соавторы получили
следующее соотношение:
zc = 1/( 3,41 + 1,28ш),
(1.74)
а Эдмистер [265] установил отношение между этими
двумя коэффициентами:
zc = 0,291 - 0,080 ш.
(1-75)
Сравнение рассчитанных по этим уравнениям данных с
экспериментально найденными (см. приведенную ниже
таблицу) показывает, что ни одно из них не является
достаточно точным, чтобы им можно было воспользо-
ваться для расчета значений сжимаемости на основании
ацентрических коэффициентов. Исключение составляют
лишь углеводороды, для которых пригодны оба
уравнения.
Расчетное значение Zc
Вещество СО Zc Лидерсен Эдмистер
Ацетон 0,309 0,232 0,263 0,266
Аммиак 0,250 0,242 0,268 0,271
Этанол 0,635 0,248 0,237 0,240
Бензол 0,212 0,271 0,272 0,274
Гексан 0,296 0,260 0,264 0,267
Сероводород 0,100 0,284 0,283 0,283
Метан 0,008 0,288 0,292 0,290
1.4. Вириальное уравнение состояния
Три взаимосвязанные формы степенных рядов для
расчета коэффициента сжимаемости можно записать
следующим образом:
z = PV/RT = 1 + B/V+ C/V2 + . . . = (1.76)
= 1 + Bp + Ср2 + . . . = (1.77)
= 1 + В'Р + СР2 + . . . . (1.78)
Это так называемые V-, р- и P-формы вириального
уравнения. Отношения между коэффициентами двух
приведенных форм уравнений даны в табл. 1.8.
Первоначально это уравнение было предложено Тизе-
ном (табл. 1.2) как чисто эмпирическое, затем его разра-
боткой много занимался Оннес (табл. 1.2). Позднее, как
и следовало ожидать, в его основу были положены
принципы статистической механики для сил межмолеку-
лярного взаимодействия. Зачинателем исследований в
этом направлении был Урселл (1927). Используя раз-
личные формы математических выражений для потен-
циалов межмолекулярного взаимодействия (разд. 1.7),
можно получить теоретические выражения для некото-
рых коэффициентов. Коэффициент В отвечает взаимо-
действию между парами молекул, С — взаимодействию
между триплетами и т. д. Члены В, С, не помеченные
штрихами, называют вторым, третьим и т. д. вириаль-
ными коэффициентами. Теоретически для данного веще-
ства они зависят лишь от температуры. Теория вири-
альных уравнений применима не только для РКГфунк-
ции. Те же коэффициенты используют для описания
других свойств газов, в том числе вязкости, скорости
распространения звука и теплоемкости. Одним из на-
иболее важных следствий, вытекающих из теории вири-
альных уравнений, является установление точных отно-
шений между коэффициентами смеси и соответствую-
щими коэффициентами чистых компонентов и составом
смеси (см. табл. 1.8). Краткое изложение данной теории
дано в монографии [85].
Как следует из рис. 1.18, изотермы вириального урав-
нения не имеют S-образной формы, присущей изотер-
мам уравнения Ван-дер-Ваальса и подобных ему уравне-
ний, следовательно, даже при наличии большого коли-
чества членов оно не может описывать жидкую фазу,
а также систему жидкость — пар (см. задачу 1.23). При
больших величинах плотности бесконечный ряд в вири-
альном уравнении расходится [85].
1.4.1. Линейная зависимость. Поскольку использо-
вать для расчетов бесконечный ряд не представляется
возможным, уравнения обычно усекают на члене В или
С. Для данного ограничения разложение в ряд по плот-
ности более точно, чем разложение в ряд по давлению.
Это утверждение вполне справедливо для смеси СОг и
пропилена (рис. 1.13), а также для аргона, если только
давление не достигает 1000 атм. При таких условиях
оба ряда дают неточное представление.
Данные для Нг, Nj, Аг, СНд, СгНб и их смесей пока-
заны на рис. 1.14. Для определения оптимального числа
параметров вириальных уравнений разработан специ-
альный статистический критерий в виде функции приве-
денных температуры и давления. Использование р-фор-
мы дает более точные результаты. Например, как сле-
дует из рис. 1.14, г и е, при Рг = 5 и Тг = 2 ожидаемая
погрешность составляет примерно 1% при использова-
нии q-формы и 5% при использовании Р-формы.
1.4.2. Вириалъные коэффициенты. Исчерпывающая
подборка экспериментальных данных о втором и треть-
ем вириальных коэффициентах приведена в работе [36],
а краткие таблицы значений этих коэффициентов даны
в монографиях [67, 78]. Некоторые данные о чистых ве-
ществах представлены на рис. 1.15, а аналогичные дан-
ные о смесях — в задачах 1.6 и 1.12. Теоретические ме-
46 Глава 1
Таблица 1.8. Вириальное уравнение
Три основных вида уравнения:
Z = PV/RT = 1 + B/V + C/V2 + D/V3 + ... (1)
= 1 + Bq + Cq2 + Dq3 + . .. (2)
= 1 + В'Р + С’Р2 + D'P3 + . .. . (3)
Обычно применяемое линейное уравнение:
Z = 1 + В/V = 1 + В'Р = 1 + BP/RT. (4)
Согласно Праузницу [510] его можно заменить уравнением
Р 0,5Т I (^У.Тс^ (5)
Отношения между коэффициентами имеют следующий вид:
В = RTB', (6)
С = (RT)2(C + В'2} или С = (С - B2}/(RT)2, (7)
D = (RT)3(D' + ЗВ'С + В'3} или D' = (D - ЗВС + 2B3)/(RT)3, (8)
Е = (RT)4(E' + 4£>'В' + 6СВ’2 + 2С'2 + В'4) (9)
или Е' = (Е - 4DB - 2С2 + 10СВ2 - 5B4)/(RT)4. (10)
Расчет коэффициентов по предельным величинам функции PVT'.
В = lim (PV/RT - 1)К (Н)
i/и—о
С = lim [(PV/RT - 1)V- В] V (12)
I/И —О
D = lim [(PV/RT - 1)V2 - BV - CJV. (13)
l/K->0
Другие уравнения состояния, представляемые в виде вириальных уравнений:
уравнение Ван-дер-Ваальса: (Р - a/V2)(V - b) - RT, (14)
его вириальный вариант: z = 1 + (b - a/RT)Q + b2Q2 + b3Q3 + ... . (15)
Уравнение Битти — Бриджмена: z = (1 - c/VT2)(V + Во - bBo/V)/V -
- Ло(1 - а/ V), (16)
его вириальный вариант: z = 1 + (Во - Ao/RT - c/T3)q + (-Bob + aA0/RT -
- Boc/T3)q2 + (Bobc/T3)Q3. (17)
Уравнение Бенедикта — Уэбба — Рубина:
Z = 1 + (Во - Ao/RT - Co/RT3)q + (b - a/RT)Q2 + (aa/RT)e5 +
+ (c/RT3)(\ + 7e2)e2 exp (-7e2) (18)
(последний член, содержащий экспоненциальную функцию, включает все опу-
щенные члены вириального разложения).
Приведенное уравнение, усеченное по С:
ЛК, = 377(1 - l/Vr + 1/3V?). (19)
Параметры выражают через критические свойства, приравняв первую и вторую
производную Р относительно V при постоянной температуре нулю в критиче-
ском состоянии. Полученные в результате уравнения имеют следующий вид:
В = -Vc, (20)
С = У2/3, (21)
R = 3PcVc/Tc, (22)
Zc = 1/3. (23)
Правила усреднения свойств смесей имеют следующий вид:
в = ^^У^В. = У1Ви + У2В22 + 2У1У2В12, (24)
С = У^ У^ УвШУкСук = У1С111 + У2С222 + 3(У1У2Си2 + У1У2.С122)- (25)
Разложение в ряд показано для двух компонентов.
Уравнение состояния 47
Продолжение табл. 1.8
Корреляции вириальных коэффициентов. Данные о вторых вириальных ко-
эффициентах более обширны; разработано несколько корреляций главным об-
разом для неполярных газов.
Уравнение Питцера — Керла:
Ви = (BTci/PcU)(B^ + шВ«>), (26)
где члены с надстрочными индексами выражены через приведенную температу-
ру. Некоторые из имеющихся корреляций показаны на рис. 1.10, а и 1.16. Псев-
докритические свойства для оценки параметров перекрестных взаимодействий
(By) находят по модифицированным правилам Лоренца — Бертло (см. послед-
ний столбец табл. 1.5). Корреляции для третьих вириальных коэффициентов не-
полярных газов были выполнены в соответствии с моделью Питцера (Орби,
Вера, 1983):
С = (RTc/Pc)2(Cm + wC(1)), (27)
С(0) = 0,01407 + 0,02432(7?'8 - О,ОО313/7>10-5, (28)
С(1) = -0,02676 + 0,01770/Тг'8 + 0,040/7?'° - 0,003/7?’° - 0,00228/7?°’5. (29)
Использованные правила усреднения свойств смесей и параметры бинарного
взаимодействия заимствованы из табл. 1.5 и Д.З.
Уравнения фугитивностей содержатся в табл. 3.3 и 3.4; уравнения, приме-
няемые для определения для остаточных свойств, — в табл. 11.2.
тоды оценки вириальных коэффициентов, особенно вто-
рого вириального коэффициента, на основе потенци-
альных функций рассмотрены в разд. 1.7. Потенциаль-
ная функция прямоугольной ямы была применена авто-
рами работы [217] для получения вторых вириальных
коэффициентов при низких температурах. Эти авторы
выразили коэффициенты потенциальной функции через
ацентрический коэффициент и рассчитали данные для
девятнадцати веществ. Авторы работы [304] провели
расчеты с применением более сложных потенциальных
функций [304]; полученные ими результаты достаточно
хорошо совпадают с экспериментальными данными для
полярных веществ, включая воду. Методика экспери-
ментов по определению вириальных коэффициентов для
Не и СОг описана в работе [355].
На рис. 1.15 представлен ряд кривых изменения вто-
рого и третьего вириальных коэффициентов. Точность
определения третьего вириального коэффициента, как
правило, низка (рис. 1.15, в и г). Разброс данных гово-
рит о несовершенстве экспериментальной методики, а
также указывает на то, что для корреляции могут по-
требоваться какие-то другие переменные вместо приве-
денных свойств. В условиях, показанных на рис. 1.15, д,
третий вириальный коэффициент влияет на сжимае-
мость лишь незначительно.
Несколько корреляций вторых вириальных коэффици-
ентов неполярных газов были выражены в соответст-
вии с методом Питцера и соавторов следующим
образом:
В = (RTC/PC)(BW + (1.79)
Члены с надстрочными индексами выражены через при-
веденную температуру. На рис. 1.16 сравниваются три
корреляции этого вида. Предпринимались попытки при-
менить вириальные уравнения после введения в них до-
полнительных параметров для описания полярных
веществ.
1. В детально разработанной методике определения
вторых вириальных коэффициентов и констант равнове-
сия димеризации авторы работы [335] использовали ди-
польные моменты и радиусы вращения. Этот же под-
ход был распространен и на смеси аминов с метанолом
[662].
2. В работе [675] во второй вириальный коэффициент
введены радиус вращения и коэффициент полярности
при Тг = 0,6; там же приводятся данные для 100 раз-
личных веществ.
3. Авторы работы [381] получили вириальные коэф-
фициенты некоторых больших молекул углеводородов,
часто присутствующих в незначительных количествах в
газовых потоках при высоких давлениях.
4. Экспериментальные данные для перфторгексанов
получены в [681].
Возможные корреляции третьего вириального коэф-
фициента изучены гораздо меньше, что, по-видимому,
отчасти объясняется ограниченностью и недостаточной
точностью опытных данных. Так, в работе [129] приво-
дится уравнение для третьего вириального коэффициен-
та без экспериментального подтверждения. Авторы ра-
боты [249] разработали относительно простую корреля-
цию, включающую приведенную температуру, ацен-
трический коэффициент, молекулярный объем и диполь-
ную поляризуемость, и проверили некоторые данные на
смесях. Еще одно уравнение, аналогичное корреляциям
Питцера и Керля, предложено Орби и Вира (1983) (см.
табл. 1.8).
1.4.3. Смеси. Теоретически вторые вириальные коэф-
фициенты смесей соотносятся с составом смесей следу-
48 Глава 1
Рис. 1.16. Три корреляции вторых вириальных коэффициентов неполярных газов вида В = (RTC/Рс)\В{0} + шВ(1)1.
а — В<0) как функция 77; б — как функция Тг.
1. Данные Питцера [555]:
В<°) = о,1445 - 0,33/77 - 0,1385/7? - 0,0121/7?,
В<1) = 0,073 + 0,46/77 - 0,5/7? - 0,097/7? - 0,0073/7?.
ющим образом:
в = ^yiyjBij =у]Вц+у \В22 + • • '
+ 2(У[У2В12 + у1У3В13 + • • • +Т2Тз-®23 + ' ' ‘ )•
(1.80)
2. Данные Эббота, цитируются Смитом и ван Нессом [122]:
В<0) = 0,083 - 0,422/7?'6, В(1> = 0,139 - 0,172/7?’2
3. Данные Цонопулоса [696]:
д«» = 0,1445 - 0,33/77 - 0,1385/7? - 0,0121/7? - 0,000607/7?.
В(1) = 0,0637 + 0,331/7? - 0,423/7? - 0,008/7?.
Аналогичные уравнения справедливы и для последую-
щих вириальных коэффициентов. Коэффициенты с
двойным подстрочным индексом, В„, относятся к чис-
тым компонентам и соответствуют взаимодействию
пар схожих молекул, в то время как коэффициенты пе-
Уравнение состояния 49
рекрестных взаимодействий соответствуют взаимо-
действию пар разнородных молекул. В принципе мето-
ды изучения взаимодействия разнородных молекул не
должны быть сложнее методов исследования взаимо-
действия схожих молекул, и корреляции, разработанные
для этих двух видов взаимодействия, сходны по форме,
однако во многих случаях они содержат параметры, ха-
рактеризующие как псевдокритические свойства, так и
бинарное взаимодействие. Коэффициент перекрестных
взаимодействий определяется выражением
&ij ~ (К Tcij/Рcij) (В (j + (1.81)
в котором члены с надстрочными индексами рассчиты-
ваются из тех же соотношений, что и для чистых ве-
ществ, но через псевдокритические параметры. В насто-
ящее время общепринятыми считают следующие
уравнения:
<о,у= 0.5(ш, +ш,), (1.82)
zc,y = 0.5(2,-+ zy), (1.83)
^=O.5(kJ/3 + Kj/3), (1.84)
Tcij= (1 ~ kjj) (TciTcj)°-5, (1.85)
^cij zcijR TcijIVcij- (1.86)
Наиболее несовершенным является расчет Тсц- Много
усилий было затрачено на разработку корреляций пара-
метров бинарного взаимодействия кц, однако единого
общего уравнения создать так и не удалось. Некоторые
из этих вопросов рассматриваются в разд. 1.3.8. Обзор
современных исследований в этой области выполнен
Цонопулосом [697].
Для двухкомпонентной смеси парафинов разработано
уравнение средней точности:
kij =1-8 VVc,-Kc//(KJ/3 + kJ/3)3. (1.87)
Цонопулос также предложил отдельные корреляции для
смесей углеводородов с метаном, этиленом, этаном и
неорганическими газами, включающие такой параметр,
как число атомов углеводорода. Так, например, для
смеси метана с углеводородами предложено следующее
уравнение:
ки = 0.0279(ln nCj)2. (1.88)
Корреляции, предложенные для двойных смесей, содер-
жащих полярные и неполярные компоненты, менее
удачны, однако в статье Цонопулоса их довольно мно-
го. В разд. 1.3.8 уже упоминалось о корреляции, осно-
ванной на использовании ионизационного потенциала
[349].
1.4.4. Прочие уравнения состояния в вириальной фор-
ме. Несколько широко известных уравнений состояния
можно представить в вириальной форме (см. табл. 1.8,
пример 1.11 и задачу 1.22). При помощи подобных
уравнений можно прогнозировать особые виды воз-
действия температуры на коэффициенты, вследствие че-
го они зачастую отличаются более высокой степенью
точности по сравнению с вириальными уравнениями,
ограниченными членами с коэффициентами В или С. В
уравнении Ван-дер-Ваальса, выраженном в вириальной
форме, третий и все последующие коэффициенты не за-
висят от температуры, чем можно отчасти объяснить
его неточность в сравнении с другими кубическими
уравнениями. Для вириальных коэффициентов применя-
ются приведенные в табл. 1.8 уравнения (11)—(13), ко-
торые будут использованы в примере 1.11.
1.4.5. Димеризация. Отрицательное отклонение ха-
рактера изменения функции PVT от идеального иногда
объясняют процессами молекулярной ассоциации, на-
иболее распространенным из которых является димери-
зация. Установлено довольно простое отношение между
вторым вириальным коэффициентом и константой рав-
новесия димеризации. Для реакции 2А & Л 2 константа
равновесия при давлении Р определяется выражением
е / е \ /
Кр =Ра2/Ра = ~ I 1 “ ~ ~ е)2Р, (1.89)
где е — степень димеризации А. Это уравнение можно
разрешить относительно е:
е = 1 - У1/(1 + 4РХ/,). (1.90)
При невысокой степени ассоциации квадратные члены
можно не учитывать и е можно приблизительно вычис-
лить по уравнению
е=2РКр. (1.91)
Второй вириальный коэффициент получаем следующим
образом:
z = nt(l+ BP/RT) = (1 - е/2)(1 + BP/RT). (1.92)
При небольших значениях е это уравнение преобразует-
ся к виду
z = 1 - е/2 + BP/RT = 1 - РКр + BP/RT
= 1 + (В- RTKp)P/RT= 1+ BqP/RT, (1.93)
где наблюдаемый вириальный коэффициент Во и дей-
ствительный вириальный коэффициент В связаны соот-
ношением
B0 = B-RTKp. (1.94)
Если В получают исходя из соотношений, найденных
для неассоциирующихся молекул, второй вириальный
коэффициент ассоциирующейся системы можно опреде-
лить, если известна константа равновесия. Некоторые
измеренные значения Кр показаны на рис. 1.12 [420]. В
примере 1.10 проиллюстрировано применение этих дан-
ных. Для получения констант равновесия можно ис-
пользовать коррелятивный метод, разработанный авто-
рами работы [335]. Подробный список полученных та-
ким образом результатов приведен в работе [567].
Среди соединений с высокой степенью ассоциации важ-
ное место занимают кислородсодержащие органические
вещества. И в заключение следует отметить, что не все
отрицательные отклонения от идеальности обусловле-
ны процессами ассоциации, так же как и положитель-
ные отклонения не всегда вызваны диссоциацией
молекул.
4-829
50 Глава 1
Пример 1.10. Расчет сжимаемости ацетона на основании равновесия димеризации
В примере используются данные Ламберта [420],
представленные на рис. 1.12. Температура 400 К, давле-
ние 2 атм, Кр - 0,004. Для определения вириального ко-
эффициента неассоциирующегося ацетона применено
уравнение Эббота.
Тс = 508,1, Рс = 46,4, ы = 0,309,
Тг = 400/508,1 = 0,787
В = -?8,1^ [-0,536 + 0,309(-0,331)] = -6,989/?.
46,4
Уравнение (1.94):
Во = В - ВТКР = — 6,989/? - 400(0,004)/? = —8,598/?.
Значения сжимаемости:
в отсутствие ассоциации
Z = 1 + BP/RT = 1 - 6,989(2)/(400) = 0,966,
при наличии ассоциации
Z = 1 + BoP/RT = 1 - 8,589(2)/400 = 0,958.
В данном случае воздействие ассоциации невелико.
Сравнение аппроксимированных [уравнение (1.91)] и
точных выражений [уравнение (1.90)] для степени диме-
ризации показано ниже на графике.
1.4.6. Применение вириальных уравнений. О вириаль-
ных коэффициентах выше второго, даже о третьем, из-
вестно очень мало. Исключение составляет лишь аргон,
для которого получены некоторые данные и о четвер-
том, и о пятом вириальных коэффициентах [85], для
всех вириальных коэффициентов вплоть до восьмого
выведены теоретические выражения, в которых исполь-
зуется потенциал прямоугольной ямы. При температуре
ниже критической ряд сходится вплоть до условий, со-
ответствующих плотности насыщенного пара, в то вре-
мя как для плотностей жидкости он расходится. При
температуре выше критической максимальная плот-
ность составляет 0,5—0,75 критической. Напомним, что
уравнение Бенедикта — Уэбба — Рубина, некоторым об-
разом связанное с вириальным уравнением, применяет-
ся для многих жидкостей и паров в тех случаях, когда
их плотность превышает критическую величину в 1,8
раз. Критерии определения точности уравнений, огра-
ниченных некоторым членом, показаны также на
рис. 1.14.
При давлении ниже нескольких атмосфер В-усеченное
вириальное уравнение пригодно для оценки коэффициен-
тов фугитивности и функций, описывающих отклонение
поведения газов от идеального. Применение усеченного
вириального уравнения в этих целях является более
простым и хорошо сочетается с итерационными мето-
дами вычислений. В табл. 3.3, 3.4 и 11.2 приводятся
уравнения этого вида.
Теоретические правила усреднения свойств смесей слу-
жат основанием для разработки правил усреднения, при-
меняемых с другими уравнениями состояния. Теория ви-
риальных уравнений далеко не исчерпана, необходимо
продолжать исследования, направленные на вычисление
вторых и последующих вириальных коэффициентов для
чистых веществ и смесей, используя при этом потенци-
альные функции.
1.5. Кубические уравнения
1.5.1. Введение. Наиболее точными из простых урав-
нений состояния являются уравнения, разрешимые от-
носительно давления, в состав которых входит пара-
метр объема в третьей степени. При рассмотрении
уравнений, разработанных ранее, подборка которых со-
ставлена Партингтоном и Шиллингом (см. табл. 1.1),
можно встретить множество уравнений этого вида,
Уравнение состояния 51
включая знаменитое уравнение Ван-дер-Ваальса. За по-
следние 50 лет был разработан и предложен целый ряд
подобных уравнений. Они разрешимы аналитическим
путем относительно объема, однако численные методы
их решения часто являются наиболее удобными. Нали-
чие нескольких корней обычно не представляется серьез-
ным затруднением.
1.5.2. Оценка параметров. Для полного соответствия
условиям критического состояния, а также для пред-
ставления жидкой и паровой фаз требуется уравнение
как минимум третьей степени:
(дР \ ( д2Р \
)- )т-° (1-95>
Способы численного решения кубических уравнений по-
казаны в примере 1.3. Наибольший корень соответству-
ет паровой фазе, наименьший — жидкой, средний не
имеет физического толкования. В критической точке все
три корня равны.
Условия критического состояния, а также исходное
уравнение в приложении к критической точке дают воз-
можность оценить три независимых параметра, выра-
зив их через критические свойства. Параметры уравне-
ния Ван-дер-Ваальса определяют следующим образом:
а = 21R2T2/64PC = ClaR2T2/Pc, (1.96)
b = RTc/8Pc= ClbRTc/Pc. (1.97)
Третий параметр — R. К сожалению, во многих случаях
невозможно точно определить параметры уравнения со-
стояния, выразив их через критические свойства. Не-
сколько более точные результаты часто можно полу-
чить путем введения поправок в численные коэффициен-
ты 0а и О/, при переходе от одного вещества к другому,
однако при этом, разумеется, теряется универсальный
характер уравнения.
Поскольку уравнения состояния могут применяться
для определения плотностей жидкой и паровой фаз,
давления паров, фугитивности и отклонений теплофизи-
ческих свойств от идеальных, их параметры можно из-
менять так, чтобы они соответствовали данным о неко-
торых, а не всех вышеперечисленных типах свойств.
Подобная задача значительно упрощается, если в урав-
нение входит большое число параметров. Например, ку-
бические уравнения можно видоизменить так, чтобы
они точно отражали характер изменения давления пара,
однако при этом невозможно одновременно правильно
описать отклонение энтальпии.
Несколько важных кубических уравнений состояния,
например уравнение Редлиха — Квонга, Соава и Пен-
га — Робинсона, содержат только два основных пара-
метра. Другие уравнения, содержащие три и более па-
раметров, разработаны для того, чтобы можно было
лучше представить определенные группы эксперимен-
тальных данных. Одно из этих уравнений, основанное
на таком параметре, как критическая сжимаемость, яв-
ляется, по утверждению его авторов [359] , особо точ-
ным для области насыщения полярных и нормальных
веществ. Одна из модификаций трехпараметрического
уравнения Клаузиуса (1880) разработана автором рабо-
ты [234]; параметры уравнения выражены в виде функ-
ций температуры и соотнесены с данными об объеме
насыщения с учетом условия, что фугитивности двух
фаз в состоянии равновесия равны.
1.5.3. Общий вид кубических уравнений. В ряде опуб-
ликованных в последнее время статей проведен анализ
обобщенных форм кубических уравнений состояния,
предназначенных как для широкого использования, так
и для решения специальных задач. Мартин [466] начал
с уравнения
RT a(T) — 8(T)/V
V ~ (К+/3)(И+у)
(1-98)
и пришел к выводу, что наилучшей формой уравнения
является, по-видимому, следующая:
RT а
V-b (К+с)2
(1.99)
или если используются приведенные свойства, то
0,4219
----------------------т . (1.100)
Tnr(zcVr + 0,125 - В)2
Рассмотрим два параметра В и п, входящих в эти урав-
нения. Параметр В соотнесен с критической сжимаемос-
тью. При его выборе руководствуются необходимостью
обеспечения соответствия экспериментальным данным
в требуемом диапазоне плотности. Если плотность в 2
раза превышает критическую, то
В = O,857zc — 0,1674.
(1.101)
Если же плотность превышает критическую в 1,5 раза,
то
В = 0,752zc - 0,1520.
(1.102)
Постоянная п должна быть выбрана таким образом,
чтобы она хорошо соответствовала наклону кривой
приведенного давления пара в критической точке. Кри-
вую приведенного давления пара можно достаточно
точно оценить исходя из нормальной точки кипения.
Методика подобных расчетов описана Мартином. Неко-
торые типичные величины представлены ниже.
Вещество Zc В п
Аргон 0,291 0,082 0,55
Этилен 0,281 0,074 0,62
Перфторциклобутан 0,278 0,071 1,20
Трифторметан 0,259 0,055 1,00
Изопентан 0,270 0,064 1,10
Аммиак 0,242 0,040 1,10
При помощи уравнения Мартина, как правило, дости-
гается более точное соответствие данным о функции
PVT, чем при использовании уравнений Соава и других
двухпараметрических уравнений, что объясняется при-
менением в первом случае для оценки параметров боль-
шего числа данных. Как установил Иоффе [373], это
уравнение вполне применимо для некоторых двухкомпо-
нентных смесей, но не смесей вообще.
4-
52 Глава 1
Изучение пятипараметрического уравнения было вы-
полнено Эбботом [148]. Этот автор начал со следующе-
го уравнения:
RT(V2 + aV+ fi)
Р = :-------—г---------, (1.103)
К3 + ХК2 + мК+ v
и преобразовал его к виду
RT 0 (V — т))
Р =--------------------z--------- (1.104)
v-b (V-b)(V2 + 8V+ е)
где 0 — функция температуры и, вероятно, ацентриче-
ского коэффициента, член V— b включен для описания
постепенного уменьшения плотности жидкости. Путем
правильного подбора пяти параметров можно получить
большинство кубических уравнений обычного вида, и
эти уравнения рассмотрены в статье Эббота. Некото-
рые характеристики и ограничения кубических уравне-
ний проявляются при изучении критических изотерм.
Исследованием некоторых трехпараметрических урав-
нений занимались Харменс и Кнапп [334], а также
Шмидт и Венцель ]616]. Харменс и Кнапп использовали
критические параметры
RT а
Р =-------- - , (1.105)
V-b V2 + bcV+ b2(c - 1)
включая критическую сжимаемость и ацентрический ко-
эффициент, уравнения для расчета которых представле-
ны в табл. 1.14. Как показало сопоставление с экспери-
ментальными данными, полученными для 831 чистого
вещества, погрешность результатов, рассчитанных по
уравнениям Редлиха — Квонга (P-К) и Шмидта — Вен-
целя (Ш-В), вдвое меньше по сравнению с погрешнос-
тью расчетов, получаемых по уравнению, которое раз-
работал Американский нефтяной институт, и уравне-
нию Соава. Обе группы исследователей в настоящее
время занимаются вопросами приложения своих уравне-
ний к смесям.
Все упоминаемые здесь кубические уравнения содер-
жат член уравнения Ван-дер-Ваальса RT/(V - b), учи-
тывающий межмолекулярное отталкивание, однако
действие сил притяжения учитывается в них другим
членом, соответствующим члену а/V2 уравнения Ван-
дер-Ваальса. В последнее время особое внимание уделя-
ется преобразованиям противоположного характера:
член, учитывающий действие сил притяжения, в уравне-
нии оставляют в первоначальном виде, а член RT7
(V-b) заменяют членом, который находят при помо-
щи модели «возмущенной твердой сферы». Параметры
получаемого в результате уравнения состояния в основ-
ном выражают через критические свойства. К этим ис-
следованиям мы еще вернемся в разд. 1.7.5.
1.5.4. Корни кубических уравнений. Если кубическое
уравнение состояния, выраженное через z или V, имеет
три положительных действительных корня, наиболь-
ший из них соответствует паровой фазе, наименьший —
жидкой, а средний физического смысла не имеет. В ряде
расчетов, например при решении задач, связанных с
дистилляцией, необходимо быстро решить, какой фазе
соответствует найденный корень. Для этого можно ис-
пользовать разработанный авторами работы [561] эм-
пирический критерий, выраженный через коэффициент
изотермической сжимаемости. Например, для
уравнения
P = RT/(V~ b)~ a/VT V(V+Ь), (1.106)
этот коэффициент составляет
2 / dV \
" V /
\ /т
V(V2 - b2)2
RTV2(V+b)2-a(2V + b)(V-b)2/VT ' (1107)
Если давление выражено в атмосферах, критерии По-
линга, определяющие, к жидкой или паровой фазе отно-
сится рассчитанная величина объема насыщения,
составляют /3 < 0,005/атм для жидкой фазы и
0,9/Р < /3 < 3/Р для паровой фазы. Хотя эти правила
не отличаются жестким характером, считается, что они
верны для широкого диапазона температур и давлений.
Результаты расчетов, приведенных в примере 1.13 и за-
даче 1.24, подтверждают справедливость этих правил;
исключение составляет лишь одна точка, близкая к кри-
тическому состоянию.
1.5.5. Уравнение Редлиха — Квонга. Разработка урав-
нения состояния Редлиха — Квонга [581] в'свое время
явилась значительным шагом вперед по сравнению с
применяемыми тогда уравнениями относительно прос-
того вида. В течение последующих трех десятилетий
это уравнение в значительной степени сохранило свою
популярность и стало основой для ряда модификаций.
Очевидно, что уравнение Редлиха — Квонга
а \
(1.108)
построено по образцу уравнения Ван-дер-Ваальса (1873)
или уравнения Клаузиуса (1880), хотя и было разработа-
но спустя 70 лет. В своей книге, опубликованной в
1976 г., Редлих [580] пишет, что разрабатывая это урав-
нение состояния, они не руководствовались какими-
либо определенными теоретическими обоснованиями,
поэтому его можно рассматривать как произвольную,
но удачную эмпирическую модификацию предшествую-
щих уравнений. Вскоре после опубликования уравнения
Ван-дер-Ваальса выяснилось, что параметр а заметно
зависит от температуры, так что для введения члена
7ю’5 имелись определенные посылки. Еще до появления
уравнения Редлиха — Квонга предлагалось ввести ква-
дратичную зависимости от объема в знаменателе члена
уравнения, описывающего силы притяжения, однако
они имели несколько другой вид, чем в уравнении Ре-
длиха — Квонга. Несколько уравнений такого рода
сравниваются на рис. 1.7 и 1.8.
Параметры. В табл. 1.9 приведены различные виды
уравнения Редлиха — Квонга и связанные с ним величи-
ны. Применяя условия критического состояния, можно
найти параметры а и Ь, выразив их через критические
Уравнение состояния 53
Таблица 1.9. Уравнение состояния Редлиха — Квонга
Стандартный вид уравнения:
RT a
р = (1)
V - ь JTV(V + b)
Параметры (см. пример 1.12):
а = ilaR2T2’5/Pc = 0,42748R2T2C'5/PC, (2)
b = QbRTc/Pc = GM6URTC/PC, (3)
A = aP/R2T2,5 = 0,42748Pr/P3’5, (4)
В = ЬР/RT = 0,08664Pr/77. (5)
Уравнение в виде полинома:
, RT , 1 ( a , \ ab
V3 V2 + - 1 — - bRT - Pb2\ V - = 0, (6)
p p \VT / pVT
Z3 - z2 + (A - В - B2)Z - AB = 0, (7)
, , pr 0,42748 Pr P^r
z3 - z + — 0,08664 - 0,007506 — z - 0,03704 = 0.(8)
Tr yl ,5 у ^3,5
Приведенное уравнение:
3 77 9ЙО
Рг =------------------.
К--ЗЙ6 7?’5К(К + Зй6)
Уравнения для определения сжимаемости:
b ЬР 0,08664PTc 0.08664Л
h = — =-=---------=------,
V zRT VPc zTr
_1_д/а\_1_ 4,934 / h
1 - h bRT1’5 \1 + А/ 1 - А Т}’5 \1 + А
- V - а
V - b RI*'\V + b) '
(9)
(Ю)
(П)
(12)
Смеси:
а = ^^yiyjaij = yjan + у$а22 + ... + 2(yiy2ai2 + У1Узац + ...
• • + J2j3ff23 + . . .) (13)
b = Yjibi, (14)
Л = SSwA d5)
в = YjiBi. (16)
Параметры перекрестных взаимодействий:
aij = VaiOj (исходное правило Редлиха — Квонга) (17)
аи: = (1 - dj)^ [753] (18)
ЙОР(К*Р + K*/3)3[(l - kijl'/TeiTej]1’5
atj = -----J1------[99] (19)
8 [0,291 - 0,04(од + «/)]
свойства, как это показано в примере 1.12.
а = SlaR2T25/Pc,
b = Q.bRTc/Pc,
Па = 1/9(21/3 - 1) = 0,427480,
(1.109)
(1.110)
(1.111)
Пд = (21/3 - 1)/3 = 0,086640. (1.И2)
Как правило, степень соответствия уравнения состоя-
ния экспериментальным данным повышают путем
варьирования коэффициентов Йо и Йь в зависимости от
типа вещества. В примере 1.15А показано, как меняется
уравнение при изменении этих коэффициентов.
54 Глава 1
В последнее время были разработаны корреляции
этих коэффициентов с приведенной температурой и
ацентрическим коэффициентом. Наиболее широкое рас-
пространение получил способ корреляции, предложен-
ный Соавом, который рассмотрен в следующем разде-
ле. Авторы других работ [252, 253] оценивают вторые
вириальные коэффициенты некоторых полярных ве-
ществ по уравнению Редлиха — Квонга, модифициро-
ванному вышеописанным путем. В работе [327] Йо и Йь
представлены при помощи приведенных температур с
использованием уравнения, в которое входят четыре
константы, причем для каждого из 13 изученных ве-
ществ применяется свой набор констант. В работе [387]
предложены несколько более простые уравнения, одна-
ко и в этом случае для каждого вещества необходимы
свои константы.
Как указывают авторы работы [478], влияние темпе-
ратуры на йь значительно превосходит ее влияние на
коэффициент йо. Соответственно авторы оставили по-
следнюю константу Йо, а Йй выразили в виде функции
ацентрического коэффициента и приведенной темпера-
туры; однако, поскольку количество рассматриваемых
экспериментальных данных было крайне ограничен-
ным, широкое применение результатов этого исследова-
ния не представляется возможным. Автор работы [576]
применил другой подход к этой проблеме. Член уравне-
ния Редлиха — Квонга
А = SlaPr/T^s = a PIR1T1t (1.113)
он записал как
А = <*Парг/Т$ (1.114)
и выразил а как функцию приведенной температуры и
ацентрического коэффициента. Тем же принципом руко-
водствовался и Соав. Аналогичный подход привел Си-
моне и Бехара [639] к уравнению, при помощи которого
можно представить данные для углеводородов при дав-
лении до 700 атм в диапазоне приведенной температуры
от 0,5 до 1,5. Интересно отметить, что Редлих [580] су-
щественно сократил свое первоначальное уравнение и
ввел в обобщенное кубическое уравнение критическую
сжимаемость
Pzc=T/(V-b) - Q(T)/(V2 + jV + g). (1.115)
В этой же статье Редлих привел полученные им соотно-
шения между b, f, g и Q.
Как следует из всего вышесказанного, уравнению Ре-
длиха — Квонга уделялось значительное внимание. Од-
нако в настоящее время общепризнан тот факт, что
дальнейшая разработка вариантов этого уравнения бес-
перспективна и в целях совершенствования уравнений
состояния необходимо развитие новых направлений ис-
следований. В обзоре литературы, посвященной уравне-
нию Редлиха — Квонга [358], указано 112 публикаций,
и значительное число таких работ появилось уже после
издания данного обзора. Несколько скорректированных
параметров уравнения Редлиха — Квонга, о которых со-
общалось в литературе, приводится в табл. 1.10.
В результате рассмотрения всех изменений, внесенных
в это уравнение за годы его существования, возникает
вопрос, как следует называть данное уравнение — мо-
дифицированным уравнением Редлиха — Квонга или
модифицированным уравнением Ван-дер-Ваальса — или
же следует использовать какое-либо другое наименова-
ние. В настоящее время термином модифицированное
уравнение Редлиха — Квонга называют уравнения, в ко-
торых присутствует член, учитывающий силы межмо-
лекулярного притяжения и имеющий следующий вид:
а(Тг, ы, .. ,)/V(V + b). Поскольку этот вопрос не игра-
ет важной роли и поскольку самолюбие Редлиха задето
уже не будет (в 1978 г. он умер), мы будем использо-
вать различные наименования данного уравнения в за-
висимости от характера проведенной модификации.
Виды уравнения. Помимо уравнений, разрешимых
относительно давления, в табл. 1.9 приводятся также
полиномиальные уравнения, разрешимые относительно
объема и критической сжимаемости. Уравнения приве-
денного вида удобны тем, что их можно сравнивать с
другими уравнениями. Способ нахождения корней поли-
номиальных уравнений проиллюстрирован в примере
1.3. Конкретный вид уравнения зависит от выбора па-
ры трех переменных. Уравнения (9) и (10) (см. табл. 1.9)
для h и z предложены Редлихом и Квонгом; для реше-
ния этих уравнений практически всегда применима пря-
мая итерация; для ускорения сходимости можно прибег-
нуть к методу Вегштейна. Корни полиномиальных
уравнений легко находят методом Ньютона — Рафсона,
приравнивая вначале сжимаемость пара к единице, а
сжимаемость жидкости — к нулю. Кроме того, все три
корня можно установить методом Кардана. Для ЭВМ
фирмы Hewlett-Packard разработана программа нахож-
дения действительных и комплексных корней полиноми-
альных уравнений. В примере 1.13 показано применение
этой программы для определения корней уравнения для
пропилена в определенном интервале давлений на-
сыщения.
Используя уравнение Редлиха — Квонга, Эдмистер
[267] разработал ряд диаграмм для коэффициента сжи-
маемости и остаточных свойств, которые удобны при
проверке по отдельным точкам.
Смеси. Исходные правила усреднения свойств для па-
раметров уравнения Редлиха — Квонга для смесей со-
впадают с правилами усреднения свойств для уравнения
Ван-дер-Ваальса:
а = Ивд, (1.116)
b = 'Lyibi, (1.116а)
где за параметр перекрестных взаимодействий при-
нимают
aij = (а,а})°>5. (1.И7)
Позднее в эти правила были введены два важных изме-
нения: в их состав были включены псевдокритические
параметры перекрестных взаимодействий типа пара-
метров Лоренца — Бертл о для оценки ац, а также пара-
метры бинарного взаимодействия (см. разд. 1.3.7 и
1.3.8). Таким образом, Ду оценивается исходя из опреде-
ления ai по следующей схеме:
zciJ=0.5(zci + zcJ), Vc}p = 0.5 (Кс/3 + kJ/3),
Уравнение состояния 55
Tcij (1 к у) \/TcjTCj, Рсу zcijRTcijlVcy,
aij ~ Tcij /Pcij • (1.118)
Значения кц приблизительно для 100 пар веществ при-
ведены в табл. Д.З. Прочие данные перечислены в
разд. 1.3.8. В примере 1.15 показано применение такого
рода данных.
В примере 1.14 выполнен анализ нескольких методов
получения параметров двухкомпонентных смесей, в ре-
зультате которого можно заключить, что истинные
критические характеристики непригодны для оценки по-
Таблица 1.10. Предлагаемые корректировки параметров уравнения Редлиха — Квонга при Тг < 1
[724в]
Автор Корректируемые параметры Условия корректировки Опускаемые величины Примечания
Вильсон [726] а /calc = /ехр yG, VL йь = 0,0876; /£р находят из гра- фиков обобщенных фугитивно- стей; а обобщают
Соав [651] а /calc /calc 03 yL Йь = 0,08664; а = а/ Т0'5 обоб- щают
Праузниц, Чуэ [99] flj, й£ й£ о? VL1 = VL r calc r exp 03 = И5 ' calc ' exp /calc ~ /calc Независимые от температуры па- раметры оптимизируют для пло- тностей насыщенных жидкостей между нормальной температурой кипения и критической точкой
Зудкевич, Иоффе [753] Од г Оь yL, = vL r calc r exp fcalc = fexp v° /fxp получают из обобщенных таблиц
Иоффе и др. [379] Чанг, Лу (1970) Йо, Йь VL, = VL r calc r exp ./calc ~ /calc yG
Хирата и др. (1975) Харменс (1975) Хемам и др. [327] Од 0& VL, = VL * calc v exp ./calc ~ /calc yG Коэффициенты й обобщены
Като, Чунг и Лу [387] Од, Оь VL. = VL * calc r exp /calc ./calc yG Корректировка кажущихся крити- ческих свойств
Шодрон и др. (1973) Йв, Йь Оптимизация всей изотермы 0?, yL Высокая степень обобщения
Вогл и Холл (1970) Йв/Й^‘ Йь/Йь"‘ To же Vе, VL Приведенные параметры обоб- щены
Симон и др. (1976)
Джорджевич и др. [252] Йв, Йь 99 99 yG VL Скорректированные Й никоим об- разом не соотносятся с приведен- ной температурой
Хедерер и др. (1976) А, В, а Hale = /calc — /calc = дад yG А, Ь, а — функции нормальной температуры кипения, не завися- щие от температуры; корректи- ровка от произвольных величин двух точек давления пара и плот- ности жидкости
Венцель, Петер (1971) a, b Kfaic = /calc = /calc yG Параметры корректируют от ве- личины плотности жидкости и давления пара при температуре системы
56 Глава 1
ведения данной смеси, что подтверждает давно извест-
ное и справедливое практически для всех смесей по-
ложение.
Ярборо [736] подробно изучил методику применения
уравнения Редлиха — Квонга для жидкостей в резервуа-
рах. Он использовал в значительной степени видоизме-
ненное уравнение, в состав которого входили коэффици-
енты Йо и Qb (в качестве функций приведенной темпера-
туры и ш),а также параметры бинарного взаимодейст-
вия, разработанные для конкретных случаев.
Применение уравнения Редлиха — Квонга. Различные
модификации уравнения Редлиха — Квонга до сих пор
представляют определенный интерес, тем не менее в не-
которых областях их в значительной степени вытеснили
другие уравнения подобного типа, например уравнения
Соава или Пенга — Робинсона, хотя для достижения
высокой степени точности при применении указанных
уравнений требуется существенно больший объем
Пример 1.11. Вириальная форма кубического уравнения состояния Р = RT/(V - b) - а/(У2 4- сУ + d)
Установим соотношения между вириальными коэф-
фициентами и параметрами а, Ь, с и d данного уравне-
ния. Уравнение преобразуем к следующему виду:
b аУ
z - 1 =-----------------------.
V - b RT(V2 + сУ + d)
В табл. 1.8 приведены некоторые предельные выраже-
ния для вириальных коэффициентов В, С, D ... Таким
образом,
ЬУ аУ2
В = hm (z - 1) У = hm------------------------=
г-ос' V - b RT(V2 + eV + d)
= Ь - — .
RT
Аналогично
ас
С = lim Г(2 - 1)У - В]У - b‘ г — ,
, RT
и
D = lim [(z - 1)И2 - ВУ - С] У = Ь3 + -
И ос RT
Поскольку в уравнении Ван-дер-Ваальса с = d = 0, то
В = b - а/RT, С = Ь2 и D = d3, и т. д.
Соответственно получаем эквивалентное вириальное
уравнение
V- b RT(V2 + eV + d)
и эквивалентное уравнение Ван-дер-Ваальса
V - b RTV
Пример 1.12. Вывод уравнений для получения параметров уравнения Редлиха — Квонга при помощи критических
параметров
Уравнение Редлиха — Квонга можно записать в виде
полинома
С - V*
р
а— - bRT - b2} V - = 0. (1)
Г05 Р / РТ03
Отношения между параметрами и критическими
свойствами находим путем сравнения коэффициентов
этого уравнения в критической точке, причем уравнение
выводим, основываясь на допущении о равенстве в кри-
тической точке трех корней, а именно:
(И - j/c)3 = У3 - ЗУСУ2 + ЗУ2У - У3 = 0 (2)
Исходя из уравнений (4) и (5), опускаем а и получаем
Ь3 + 3 УСЬ2 + ЗУ2Ь - У3 = 0 • (6)
Корни этого уравнения находим при помощи стандарт-
ной методики, заимствованной из “The CRC Handbook
of Mathematical Sciences”. Между этой системой изобра-
жения величин и той, которая применяется в уравнении
(6), существуют следующие соотношения
b = у, (7)
р = ЗУс, (8)
Я = ЗУ2, (9)
г = -У3. (10)
Таким образом,
рст?- b
(3)
(4)
(5)
Соответственно
а = (9У2 - 9И2)/3 = 0,
/? = -!- [2(3 Ус)3 - 9(3 Ус)(3 У2) + 27(- У3)) = -2У3.
А = (У3 +
В = 0.
27
?)1/3 = 2
(И)
(12)
(13)
(14)
(15)
Уравнение состояния 57
Следовательно,
D ЗИс
Ь=х-—=А + В----------= (21/3 - 1)ИГ =
3 3
ВТс ВТс
= (21/3 - 1) — = 0,086640 -. (16)
ЗРс Рс
Чтобы найти а исходя их уравнений (3) и (5) исключаем
Vc, затем проводим подстановку выражения для Ь из
уравнения (16).
Для того чтобы решить уравнение, запишем
тогда значения х получим из
х = А + В,
А + В А - В
-----+-----
РсТ?-!
b
, Prf/' RTC
И3 -
b ЗРс
А + В _ А - В
2 ” 2
r2t2-! R2Tp5
- ---------- _ = 0,427480 -------.
9(2' 3 - 1)Л рс
(17)
Кубические уравнения. Кубическое уравнение у3 + ру2 1
+ qy + г = 0 можно привести к виду
х3 + ах + /3 = 0,
подставив вместо у величину х - р/3. Это дает
а = ~ (3q - р2) и /3 = (2р3 - 9pq + 27г).
Если р, q и г являются действительными числами, то:
/З2 а3 „
при + — >0 получим один действительным корень
4 27
&2 а3
и два сопряженных комплексных корня; при - + =
= 0 получим три действительных корня, их которых по
крайней мере два равны между собой; при @ + а < 0
4 27
получим три действительных корня, имеющих разные
значения.
[Тример 1.13.
Расчет сжимаемости пропилена на кривой насыщения из уравнения Редлиха - Квонга
Несмотря на то что уравнение Антуана не является
абсолютно точным для всего диапазона значений, для
наглядности мы воспользуемся им. Уравнение для рас-
чета давления пара:
Р = ~ ехр [15,7027 - 1807,53/(7' - 26,15)].
Поскольку Тс - 365 К и Л- = 46,5 атм, параметры урав-
нения Редлиха — Квонга равны
А = 0,42748(Р/46,5)(365/7)2’5 = 23398,9Р/7'2’5',
В = 0,08664(7746,5)(365 'Г) = 0,6801/77:
Коэффициенты и соответствующие корни полинома
уравнения Редлиха — Квонга z3 - Z2 + (А В B2)z
- АВ = 0 сведены в таблицу. Истинное значение давле-
ния пара при температуре 360 К составляет 41,5 атм по
сравнению с расчетной величиной 38,68. Другими слова-
ми в соответствии с теоретическими расчетами веще-
ство будет находиться в перегретом состоянии, для ко-
торого, как видно из таблицы, сжимаемость паров не-
возможно определить. Можно применить более точные
уравнения для расчета давления пара, отличающиеся
большей сложностью по сравнению с данным урав-
нением.
Г, К Р, атм А - В - В2 АВ г, Zl
300 11,81 0.14978 0,00475 0,08255 0,1304 0,044!
320 18,51 0,19553 0,00930 0,7583 0,1692 0,0725
340 27,39 0,24288 0,01647 0,6773 0,2027 0,1200
350 32,72 0,26645 0,02124 0,6312 0,2034 0,1655
360 38,68 0,28962 0,02690 0,5814 [0,2093 ± 0,0494/]
370 45,27 0,31212 0,03347 0,5307 [0,2346 ± 0,0895/]
информации о компонентах смеси, в частности, необхо-
димы данные об ацентрическом коэффициенте и пара-
метрах бинарного взаимодействия. Поскольку результа-
ты применения уравнения Редлиха — Квонга для описа-
ния жидкой фазы нельзя назвать удовлетворительными,
само по себе оно непригодно для расчета равновесия
между жидкостью и паром. Однако в сочетании с раз-
личными уравнениями для жидкой фазы уравнение Ред-
лиха — Квонга включено в высокоэффективную методи-
ку Чао — Сидера, служащую для оценки равновесия
между жидкостью и паром (гл. 6).
На рис. 1.17—1.20, а результаты расчетов, проведен-
58 Глава 1
Рис. 1.17. Кривая насыщения, изотерма (394,2 К) н-бутана и кривые зависимости Р от V, рассчитанные по уравне-
нию состояния идеального газа, уравнениям состояния Ван-дер-Ваальса и Редлиха — Квонга.
1 — уравнение состояния идеального газа Р = 0,0825 Т/ И; 2 — уравнение Редлиха — Квонга Р = 0,0820577) И - 0,0806) -
- 286,1/[7°'5V(V + 0,0806)]; 3 — уравнение Ван-дер-Ваальса. Р = 0,08205 77( И - 0,1163) - 13,693/И2; 4 — уравнение Ван-дер-Вааль-
са при R = 8РС Рс/3 Тс = 0,060, а = 7,322, b = 0,0850; 5 — кривая насыщения; 6 — истинная изотерма.
ных по уравнению Редлиха — Квонга и другим уравне-
ниям состояния, сравниваются с экспериментальными
данными. Поскольку математические методы расчета
уравнения Редлиха — Квонга отличаются простотой,
его продолжают использовать и в наше время, хотя и
в ограниченных масштабах. Уравнение Редлиха —
Квонга в первом приближении сравнимо с вириальным
уравнением состояния, ограниченным членом разложе-
ния с коэффициентом В. Оба этих уравнения дают удов-
летворительные результаты при расчетах фугитивности
газообразной фазы, если значения приведенного давле-
ния вдвое меньше значений приведенной температуры,
а также при вычислениях отклонений энтальпии, энтро-
пии и других свойств от идеального поведения, особен-
но в тех случаях, когда необходимо получить множе-
ство подобных оценок, например при расчетах дистил-
ляции. В целом ряде научных трудов уравнение
Редлиха — Квонга сравнивается с другими уравнениями
состояния, в том числе и с некоторыми уравнениями
сложного вида, и в ряде случаев это сравнение оказыва-
ется в пользу уравнения Редлиха — Квонга. Подробно
об этом говорится в конце данной главы.
Пример 1.14. Оценка сжимаемости смеси при помощи параметров уравнения Редлиха — Квонга, полученных не-
сколькими методами
Для эквимолярной смеси диоксида углерода с пропи-
леном при 30 °C и 25,5 атм значение сжимаемости, по-
лученное экспериментальным путем, составляет 0,737.
Истинные критические свойства этой смеси: 70,7 атм и
319,8 К. К = 82,05.
Метод 1. Примем, лто ау = у/агйг.
Метод 2. Для определения параметров а и b смеси
применим истинные значения критических свойств.
Метод 3. Для определения параметров а и Ь смеси
применим значения псевдокритических свойств, рассчи-
танные по правилу Кэя.
Метод 4. Выполним оценку параметра перекрестного
взаимодействия ау на основании значений критических
свойств при взаимодействии, используя следующие
правила:
Zcij = 0,5(Zc. + Zcj), = О,5(Г*,/3 + Г"3)
Tcij — у/ Tci Tcj, PciJ — ZcijKTcij/ Vcij.
Тс, к Pc, атм Vc, мл/г Zc IO6 a b
co2 304,2 72,9 94,1 0,274 63,72 29,664
СзНб 364,9 45,45 182,4 0,275 161,05 57,074
Уравнение состояния 59
Величину z рассчитывают по уравнениям (10) и (11),
приведенным в табл. 1.9. Очевидно, что использование
истинных значений критических свойств не дает удов-
летворительных результатов; в то же время при расчете
параметров перекрестного взаимодействия с помощью
правил, аналогичных правилам Лоренца — Берт л о (ме-
тод 4) достигается довольно высокая степень соответ-
ствия опытным данным.
Метод Тс смеси ИЛИ (Тсц) Рс смеси ИЛИ {Pcij) IO"6 a.j 10~6 а b Z
1 — — 101,3 106,84 43,36 0,7425
2 319,8 70,7 — 74,47 32,16 0,8388
3 334,55 59,18 — 99,58 40,19 0,7646
4 Экспе- римент: (333,17) (56,24) 103,7 108,04 43,36 0,73746 0,737
Пример 1.15. Воздействие параметра бинарного взаимодействия на рассчитанную величину сжимаемости экви -
молярной смеси СОг и СзН$
Расчеты выполнены для условий, описанных в приме- ре 1.14. В соответствии с данными, приведенными в табл. Д.З, kij = 0,1. Применяемые правила усреднения свойств даны в табл. 1.5. Метод 3 _ ' = 0,7588, z - 0,0449 1 + 22,251г что вполне соответствует величине 0,737, полученной экспериментально (см. пример 1.14).
Tc,j = (1 - kij){Tc,Tcj)°’5 = 0,9(333,17) = 299,85. Метод 4 Поправку на бинарное взаимодействие применим непо-
Соответственно средственно к параметру
Рс0 = 0,9(56,24) = 50,62 a.j = (1 - киУаа^ = 96,16(Е + 6).
и Qij = 88,54(Е + 6), а = 100,46(Е + 6), Следовательно, а = 104,27(Е + 6) Ь = 43,36, как ранее,
b = 43,36, как показано выше. Уравнения (10) и (И) (см. табл. 1.9) преобразуются к виду Z 5,4384 /104,27\ Z = ( 1 = z - 0,0449 1 + 22,251г \100,46/ г 5,6447
43,36(25,5) 0,0449 А = = , 82,05(299,85)z z = 0,7421, г - 0,0449 1 + 22,251г что гораздо более точно соответствует величине 0,737,
1 - 100,46(Е + 6) h = 1-й 43,36(82,05)(299,85)*5 1 + h полученной экспериментально. Преимущество метода 4 по сравнению с методом 3 так явно, как в данном случае, проявляется не всегда.
1.5.6. Уравнение Соава. В данном уравнении вместо члена а/ЧТуравнения Редлиха — Квонга, зависимого от температуры, введена функция а(Т, и>), включающая температуру и ацентрический коэффициент (см. табл. 1.11 и 1.12), в результате чего уравнение состоя- ния приобретает следующий вид: где а0-5 = 1 + (1 - 7?’5)(0,480 + 1,574ы - 0,176а>2). (1.121) Позднее Грабоски и Дауберт [315, 1] модифицировали этот член:
P=RT/(V~ b)-а(Т, м)/К(И + Ь). (1.119) Параметр а(Т, о>) первоначально был введен в уравне- ние для того, чтобы обеспечить соответствие уравнения экспериментальным данным о давлении паров углево- дородов, и имел следующий вид: а0.5 =! + (!- 7-0.548508 + 1.55171м - О.15613ш2). (1.122) Для водорода [315, 3] они предложили следующее уравнение:
а(Т, м) = аа = 0.4214S(R2T?/Pc)a, (1.120) а0-5 = 1.096 ехр( —0.15114 Тг). (1.123)
60 Глава 1
Рис. 1.18. Графики приведенных уравнений состояния Ван-дер-Ваальса, вириального уравнения и Редлиха —Квонга:
а) Тг = 0,8; уравнение Ван-дер-Ваальса: Р, = 8ГГ/(ЗК - 1) - 3/И?; вириальное уравнение: Рг = 377(1/К - 1/К? + 1/3 И’); уравне-
ние Редлиха — Квонга:
ЗТг 1
Рг ----------------------------------------;
Vr - 0,2599 0,25997?’5 К,(К- + 0,2599)
б) Тг = 0,9, 1,0 и 1,2;
Л 5, 9 — уравнение Редлиха — Квонга; 2, 6, 8 — уравнение Ван-дер-Ваальса; 3,4, 7 — вириальное уравнение состояния.
Пример 1.15А. Влияние на уравнение Редлиха — Квонга величин коэффициентов и 0&.
Ниже приведены наибольшее и
коэффициентов, перечисленных в
наименьшее значение
книге [99].
0а Пь
Метан 0,4278 0,0867
н-Октан 0,4760 0,0968
Расчетная величина 0,42748 0,08664
Графики для приведенного уравнения [уравнение (9) в
табл. 1.9] построены для двух веществ при приведенных
температурах 0,9 и 1,1. Расчетная кривая совпадает с
экспериментально найденной кривой для метана в
масштабе данного чертежа, в то же время между ре-
зультатами, полученными для двух углеводородов, су-
ществуют значительные различия.
Уравнение состояния 61
Рис. 1.19. Изотермы, рассчитанные для диоксида серы по уравнениям Харменса — Кнаппа, Соава и Ван-дер-
Ваальса при 250 °F и истинная кривая насыщения.
Примечание. При решении задачи 3.26 получены следующие значения давлений и объема насыщения:
Р Fvap
Истинные значения 41,1 0,063 0,516
Значения, рассчитан-
ные по уравнению
Ван-дер-Ваальса 54,6 0,0765 0,258
Соава 41,96 0,0756 0,5187
Харменса — Кнаппа 41,98 0,0597 0,4826
62 Глава 1
Таблица 1.11. Уравнение Соава (коэффициенты Грабоски и Дауберта)
Стандартная форма уравнения: 3 77 Рг = ~ о _ RT аа /)ч Vr - 0,2599 3,8473 a (10)
Vr(Vr + 0,2599) ’
V- b У(У +Ь)' и/ Смеси:
Параметры: аа = ^£1У1У](аа\ i, (11)
а = 0,42747 R2T3/PC, (2)
b = Gfi^MRTc/Pc, (3) b = ^y.bt, (12)
а = [1 + (0,48508 + 1,55171 ш - 0,15613 ш2)(1 _ (4) А = ^^yiyjAij, (13)
а = 1,202 ехр (-0,302887» для водорода [315], (5)
А = aaP/R2T2 = 0,42747 аРг/ Т2, (6) В = ^ytBi. (14)
В = ЬР/RT = Wf>fAPr/Tr, (7)
Параметры перекрестных взаимодействии:
Уравнение в виде полинома: (aa)ij = (1 - ки)V(aa),(aa)7, (15)
И3 - — V2 + Uaa - bRT - Pb2)V - — = 0, (8) параметры к и даны в табл. 1.12. (16)
Р Р Р ktj = 0 для пар углеводородов и водорода. (17)
Z3 - Z2 + (Л - В - B2)z - АВ - 0. (9) Коэффициенты фугитивности приведены в табл.3.3 и
Частично приведенное уравнение (см. пример 1.16): 3.4. Уравнения для остаточных свойств — в табл. 11.3.
В примере 1.16 показано воздействие ацентрического
коэффициента на форму приведенных изотерм и прове-
дено сравнение данного уравнения с уравнением Редли-
ха— Квонга, а на рис. 1.19 уравнение Соава сравнива-
ется с другими уравнениями состояния.
Для некоторых смесей правила усреднения совпадают
с правилами усреднения для уравнения Редлиха —
Квонга, причем параметр перекрестных взаимодействий
имеет следующий вид:
ац = (1 - М (1-124)
Для веществ с ярко выраженной полярностью, таких,
как вода, спирты и т. д., Соав [653] предложил следую-
щую модификацию уравнения:
а= 1 + (1 - Тг)(т +пТг), (1.125)
где m и п — параметры, которые следует вычислять ис-
ходя из экспериментальных данных о давлении паров
каждого чистого вещества. Упрощенная методика оцен-
ки этих параметров описана Соавом [653, 654]. Чтобы
это можно было применить к смесям, необходимы два
параметра бинарного взаимодействия:
нового двухпараметрического уравнения состояния,
включающего параметр объема в третьей степени (см.
табл. 1.13), Пенг и Робинсон [545] ставили перед собой
следующие задачи.
1. Выразить параметры через Тс, Рс и ацентрический
коэффициент.
2. Повысить точность уравнения для области вблизи
критической точки, особенно при расчетах Zc и плотно-
стей жидкости.
3. Вводить в правила усреднения свойств не более од-
ного параметра бинарного взаимодействия, который не
должен зависеть от температуры, давления и состава
смеси.
4. Обеспечить пригодность уравнения для любых рас-
четов жидкостных характеристик при переработке при-
родного газа.
Пенг и Робинсон предложили уравнение следующего
вида:
RT а(Т)
V-b V(V + b) + b(V - b)
RT a(T)
atj = 0,5(а(- + а;)( 1 - С,у),
= 0,5(6,- + bj)(l — Dy),
а = SSy,-_yyazay,
b = 'L'Lyiyjbibj.
(1.126)
(1.127)
(1.128)
(1.129)
v-b V2 + 2bV~b2'
(1.130)
В настоящей работе отсутствует обобщение этих пара-
метров взаимодействия. Однако авторами работы [277]
получены некоторые величины для высокосернистого
природного газа.
1.5.7. Уравнение Пенга — Робинсона. При разработке
В критической точке
a(Tc) = 0.45724Я2Т2/Рс,
6(ТС) = 0.07780ЯТс/Рс,
zc = 0,307.
(1.131)
(1.132)
(1.133)
При других значениях температуры параметр а (7) из-
меняют следующим образом:
а(Т) = а(Тс)а(Тг, ш),
(1.134)
Уравнение состояния 63
Таблица 1.12. Параметры бинарного взаимодействия
для уравнения Соава [315]
1. Корреляции, выраженные через абсолютные раз-
ности параметров растворимости углеводородов, 6нс и
неорганических газов
Газ ку
H2S 0,0178 + 0,024416нс - 8,801
СО2 0,1294 - 0,029216нс - 7,121 - 0,022216нс - 7,1212
N2 - 0,0836 + 0,1055 16нс - 4,441 - 0,0100 16нс - 4,4412
Для СО2 и углеводородов в работе [279] найдено:
log ки = -0,8849 - 0,2145 wHc 16нс - 7,121.
2. Непосредственный расчет величин из результа-
тов, полученных при измерении парожидкостного рав-
новесия
H2S СО2 n2 со
H2S — 0,102 0,140
со2 0,102 — -0,022 -0,064
n2 0,140 -0,022 — 0,046
со — -0,064 0,046 —
Метан 0,0850 0,0973 0,0319 0,03
Этан 0,0829 0,1346 0,0388 0,00
н-Пропан 0,0831 0,1018 0,0807 0,02
2-Метилпропан 0,0523 0,1358 0,1357 —
н-Бутан 0,0609 0,1474 0,1007 —
2-Метилбутан — 0,1262 — —
н-Пентан 0,0697 0,1278 — —
н-Гексан — — 0,1444 —
н-Гептан 0,0737 0,1136 — —
н-Октан — — — 0,10
н-Нонан 0,0542 — — —
н-Декан 0,0464 0,1377 0,1293 —
Пропилен — 0,0914 — —
Циклогексан — 0,1087 — —
Изопропилциклогексан 0,0562 — — 0,01
Бензол — 0,0810 0,2131 —
1,3,5 -Триметил бенз ол 0,0282 — — —
подобно тому, как это делают при решении уравнения
Соава. При соотнесении с кривой давления пара вплоть
до критической точки получают следующее выражение:
а0’5 = 1 + (1 - ТО>5)(0,37464 + 1,5422а> - 0,26992аР).
(1.135)
Робинсон и др. [594] определили возможную область
применения этого уравнения состояния. В примере 1.16
сравниваются изотермы данного уравнения и уравнения
Соава вблизи критической точки. Критическая сжимае-
мость по уравнению Пенга — Робинсона составляет
Zc = 0,307. Как следует из табл. 1.4, это значение для
многих веществ, особенно неполярных, ближе к реаль-
ному значению данного параметра, чем величины Zc,
вычисленные по некоторым другим двухпараметриче-
ским уравнениям состояния. Этим отчасти объясняется
тот факт, что на основании уравнения Пенга — Робин-
сона можно прогнозировать плотность жидкости более
точно, чем при помощи уравнения Соава, которое во
многих других случаях дает аналогичные результаты.
Большая точность определения плотности жидкостей
достигается также при использовании уравнения Фулле-
ра [294], в котором параметры а и Ь уравнения Соава
выражены в виде функций температуры и для их оценки
применимы критические объемы и парахоры. Уравне-
ние Фуллера вполне пригодно даже для описания таких
полярных молекул, как молекулы воды и аммиака. Ме-
тодики расчета плотности жидкостей по уравнениям
Соава и Фуллера рассматриваются в работе [225].
Правила аддитивности для системы Пенга — Робин-
сона, предназначенные для смесей, не отличаются от
обычно используемых в кубических уравнениях, однако
для определения параметра перекрестных взаимодейст-
вий в высшей степени существенным считается йсполь-
зование параметров бинарного взаимодействия:
aij ~ (1 ~ kjj) \aflr
(1.136)
Эти параметры устанавливают путем оптимизации дав-
лений точки начала кипения для соответствующих ин-
тервалов давления и температуры. Величины этих пара-
метров для смесей воды с СО2 и H2S зависят от темпе-
ратуры. В настоящее время в открытой литературе
отсутствует сколько-нибудь полная подборка парамет-
ров взаимодействия. Для смеси диоксида углерода и н-
бутана приводится значение 0,13, величины параметров
для смесей воды с углеводородами колеблются от 0,38
для смеси с бутеном-1 до 0,50 для смеси с метаном и
этаном. Прочие данные о параметрах взаимодействия
представлены в табл. 1.13.
Точность коэффициентов фугитивности обеих фаз,
установленных авторами работы [444] при помощи
уравнений Соава и Пенга — Робинсона, одинакова.
Пенг и Робинсон использовали предложенное ими урав-
нение для описания трехфазных смесей, содержащих во-
ду, и изложили методику всех необходимых расчетов.
Эти же ученые воспользовались разработанным ими
уравнением для расчетов равновесия в многофазовых
системах [549], например в смесях твердого и жидкого
диоксида углерода и смесях воды с углеводородами.
Методика экспериментов с фракциями тяжелых углево-
дородов описана Робинсоном и др. [597]. Первая под-
робная программа расчета параметров критического со-
стояния, входящих в уравнение состояния, была разра-
ботана для уравнения Пенга — Робинсона его авторами
[547].
Поставщиком программ ЭВМ для разного рода рас-
четов, выполняемых при помощи этого уравнения, яв-
ляется Ассоциация производителей газов, США, шт.
Оклахома, Талса. Разрабатываемые этой ассоциацией
программы содержат методику расчетов соотношений
равновесия испарения, образования гидратов, трехфаз-
ных систем, содержащих воду, параметров критическо-
го состояния, а также анализа фракций тяжелых углево-
дородов.
Уравнение Пенга — Робинсона опубликовано относи-
64 Глава 1
Таблица 1.13. Уравнение состояния Пенга — Робинсона [545]
Стандартная форма уравнения:
V - b V2 + 2bV - b2 '
Параметры:
а = 0,457247? 2 Т2/Рс, (2)
b = 0,07780Т?Тс/Рс, (3)
А = aaP/R2T2 = 0,45724аРг/ Т2, (5)
а = [1 + (0,37464 + 1,54226ш - 0,26992w2)(l - Т?’5)]2, (4)
В = ЬР/РТ = 0,0П80Рг/Тг. (6)
Уравнение в виде полинома:
Z3 - (1 - B)z2 + (А - ЗВ2 - 2B)z - (АВ -В2 - В3) = 0. (7)
Смеси:
аа = SS^(ea)u, (8)
ь = (9)
(aa)ij = (1 - kij)y/(aa)i(aa)j, (Ю)
А = ^^ytyjAtj, (Н)
В = ^y.Bt. (12)
Ац = (1 - ^)(Л,Л)0’5, (13)
kij = 0. (14)
Данные [389]:
азот + НС kij = 0,12
СО2 + НС 0,15
этан + НС 0,01
пропан + НС 0,01
этан 0
пропан 0
н-Сл 0,02
h-Cs 0,02
н-Сб 0,025
н-С1 0,025
метан + х н-С» 0,035
Н-Сд 0,035
H-Cio 0,035
н-Сго 0,054
бензол 0,06
циклогексан 0,03
тельно недавно, и, как сообщают Дауберт и др. [31], ко-
митет Американского нефтяного института не успел
выполнить его подробный анализ. Хотя уравнения Со-
ава и Пенга — Робинсона считаются в равной степени
более или менее пригодными для расчета соотношений
равновесия испарения, в основу стандартного метода
расчета фазового равновесия было положено уравнение
Соава с незначительно измененными коэффициентами и
множеством параметров бинарного взаимодействия,
специально для него разработанных (они приводятся в
табл. 1.12). Для описания свойств веществ при криоген-
ных температурах предпочтительным является уравне-
ние Бенедикта — Уэбба — Рубина — Старлинга, а для
представления отклонений энтальпии оптимальным
считается уравнение Ли — Кеслера. Однако в програм-
мах ЭВМ, где требуется многократная оценка свойств,
чаще всего используют уравнения Соава и Пенга — Ро-
бинсона, поскольку они относительно просты и точ-
ность получаемых результатов вполне приемлема.
Уравнение состояния 65
Пример 1.16. Изотермы приведенных уравнений состояния Редлиха — Квонга, Соава и Пенга — Робинсона
Приведенное уравнение Редлиха — Квонга (см.
табл. 1.9) имеет следующий вид:
ЗТГ 3,8473
Рг =---------------------------------- (1)
Vr - 0,2599 7?’5 Vr( Vr + 0,2599)
Для уравнения Соава при подстановке
а = ПаК2Т2/Рс, (2)
b = QbRTc/Pc, (3)
а = [1 + (1 - 7?15)(0,48508 + 1,55171 ш - 0,15613а,'2)]2 (4)
в следующее выражение
RT аа
р = ---- _ -------
V - b V(V + b)
(5)
получаем
ЗТг 3,8473а
Рг = ------------ ---------------. (6)
Vr - 0,2599 Vr(Vr + 0,2599)
Это уравнение нельзя назвать полностью приведен-
ным. так как а зависит от ацентрического коэффициен-
та. При Тг = 1 изотерма не зависит от ш, но другие изо-
термы в значительной степени связаны с этим коэффи-
циентом, особенно при температурах ниже
критической. При ш = 0 уравнения Соава и Пенга —
Робинсона практически совпадают в масштабе пред-
ставленного здесь графика.
Аналогичные преобразования уравнения Пенга — Ро-
бинсона дают следующее выражение:
3,2573 Тг 4,8514а
Рг =------------_-----------------------. (7)
Vr - 0,2534 V2 + 0,5068 Vr - 0,0642
На графиках наглядно видны существенные различия
между уравнениями Пенга — Робинсона и Соава вблизи
критической точки.
Пример 1.16, а. Сравнение уравнений Соава и Редлиха — Квонга при нескольких значениях приведенной темпера-
туры и ацентрического коэффициента
2
Cl'
1
0
0 12 3^5
5-829
66 Глава 1
Пример 1.16, б. Сравнение уравнений. Соава и Пенга — Робинсона при Тг = 0,9 и нескольких значениях ацентриче-
ского коэффициента
Пример 1.16, в. Сравнение уравнений Соава и Пенга — Робинсона при Тг = 1,2 и нескольких значениях ацентриче-
ского коэффициента
Уравнение состояния 67
1.5.8. Прочие кубические уравнения состояния. В
этом разделе рассматривается несколько уравнений со-
стояния, представляющих исторический интерес, а так-
же ряд кубических уравнений, разработанных в послед-
нее время.
Бертло (табл. 1.2) принял параметр с уравнения Клау-
зиуса (табл. 1.2)
(Р + a/T{V + с)2)(Г-b) = RT, (1.137)
равным нулю и, выполнив несколько аппроксимаций,
пришел к выводу, что
PV/RT= 1 + (b - a/RT2)(P/RT). (1.138)
Применение условий критического состояния дало сле-
дующие результаты:
а = ПаРсИ2Гс,
Р = ПЛРСКС/ТС.
(1.139)
(1.140)
(1-141)
Обычный подбор коэффициентов О,- приводит к доста-
точно точному соответствию данным при средних дав-
лениях и комнатной температуре. Ниже представлены
значения коэффициентов, полученные теоретическим пу-
тем и при корректировке по методу Бертло.
Величины коэффициентов
теоретические полученные при коррек-
тировке
0о 3 16/3
Оь 1/3 1/4
Or 8/3 32/9
В результате корректировки коэффициентов было по-
лучено приведенное уравнение
(Рг+ 16/ЗТгК2)(Гг- 1/4) = 32Тг/9 = РГ/РСКС.
(1-142)
Удобно также представить уравнение следующим
образом:
9 Рг ,
z = 1 +----------(1 - 6/Т2).
128 Тг
(1.143)
В старых изданиях иногда можно встретить приведен-
ные ниже уравнения для расчета теплоемкости и изме-
нений энтропии в зависимости от давления, выведенные
из уравнения Бертло, которые применимы при умерен-
ных давлениях и температуре, близкой к комнатной
[92]:
Ср~ CV^R(1 + 21РГ/16Т3Г). (1.144)
/55
VP
27
1 + ^Л/тз
(1.145)
Согласно Партингтону [92], при разработке двух ука-
занных ниже уравнений Дитеричи (табл. 1.2) использо-
вал полуэмпирический подход. Первое из этих уравне-
ний имеет следующий вид:
(Р+ д/И5/3)(И-6) = RT. (1.146)
При разложении уравнения
К8/3 - (ЬР + RT/P)V5/3 + (a/P)V - ab/P = 0
(1.147)
для К1/3 можно получить только три действительных
корня.
Поскольку Дитеричи (табл. 1.2) учитывал изменение
потенциальной энергии у стенок сосудов, предложенное
им уравнение имеет несколько необычный вид:
RT
Р=— ~ ехр(-в/7?ГИ)- (1.148)
V — ь
При низких давлениях или малых величинах экспоненты
уравнение преобразуется в
При использовании приведенных переменных уравнение
принимает следующий вид:
тг
Pr = j ехр[2(! ~ MTrVr)]. (1.1486)
Ниже представлены производные, полезные для расчета
изменения функций
дР \ Р
~ J =7^7(1 ~ a(V - b)/RTV2], (1.149)
дР \ Р
— =~(l + a/RTV), (1.150)
су у у Т
8V \ R Г 1 + a/RTV \
--- 1 = — 7 )ехр(—a/RTV).
дТ )р Р [1- в(К - b)/RTV2 )
(1-151)
Пикеринг [95] сравнивает результаты расчетов, прове-
денных по уравнениям Бертло и Дитеричи, с экспери-
ментальными данными и результатами расчетов по
уравнению Ван-дер-Ваальса при давлениях до 1000 атм.
При комнатной или близкой к ней температуре уравне-
ние Бертло в общем случае дает более точные результа-
ты в интервале давлений от 0 до 200 атм, исключение
составляют лишь этилен и диоксид углерода, для кото-
рых более пригодно уравнение Дитеричи. При более
высоких давлениях лучшие результаты дают уравнения
Ван-дер-Ваальса и Дитеричи. Для описания газов, кри-
тические температуры которых превышают 300 К, эти
три уравнения применимы в равной степени. В задаче
1.45 требуется провести сравнение приведенных форм
двух уравнений; как показывают полученные результа-
5:
68 Глава 1
Таблица 1.14. Трехпараметрическое кубическое уравнение состоя-
ния Харменса — Кнаппа [334]
Стандартная форма уравнения:
Р ят (1)
V-b и2 + bcV - b2(c - 1)
Параметры: /3 = 0,10770 + 0,76405С - l,24282f2 + 0.96210Г3, (2)
С = 0,3211 - 0,080а) + 0,0384о)2 (3)
Йо = 1 - ЗС + ЗС2 + 0f(3 - 6f + /ЗС) (4)
Пь = W (5)
а(7» = 1 + Л(1 - v'7» - В (1 - — Н (6)
при ш 0,2, А = 0,50 + 0,27767а) + 2,17225о)2 (7)
В = -0,022 + О,338о) - 0,845о)2 при ш > 0,2, (8)
А = 0,41311 + 1,14657а) (9)
В = 0,0118 (Ю)
при Тг > 1,0, а(Тг) = 1,0 - (0,6258 + 1,5227о))1п 7) + (0,1533 + 0,41о))(1п 7))2 (И)
R2T2 а - «(Г,)!!,, Рс (12)
RTC b = йь Ре (13)
, i - зг с = 1 н К (14)
Уравнения коэффициентов фугитивности и остаточных свойств:
. , . RT а т In ф = z - 1 + In L P(V - b) RT (15)
Н - Hid = PV - RT + [Т-- a] L \ dT / (16)
S - S'd = L — - R In -- (S,d — энтропия идеального газа
V ~ b при давлении 1 атм) (17)
К = \!с2 + 4с - 4
1 2V + Ь(с + К)
КЬ П 2V + Ь(С - К)
(18)
(19)
ты, расчетные параметры, соответствующие критиче-
ской точке, не совпадают с экспериментальными, и осо-
бенно сильное расхождение наблюдается для уравнения
Дитеричи.
Примером довольно сложного кубического уравнения
состояния может служить предложенное относительно
недавно уравнение Харменса и Кнаппа [334], которое
рассматривается в табл. 1.14. Это уравнение
_ RT _ а
Р v-b V2 + bcV - b\c - 1) (1.152)
при определенных величинах параметра с приводится к
нескольким обычным кубическим уравнениям состоя-
Уравнение состояния 69
ния. Оно имеет следующие полиномиальные формы:
a bcRT
-+ 42(1 -2с)------—
V
или
И3 + ЛИ2 + BV + С = 0
АР
z3 +--z2 + В
RT
b2(c- \)RT
+ b3(c - 1) + ----------
z + С
(1.153)
(1.154)
(1.155)
Дополнительные параметры /3 - b/Vc и f = (Pc/RTc)Vc.
Они описаны через ацентрические коэффициенты и при-
веденную температуру на основе данных о критических
изотермах и о давлении паров 20 веществ — от аргона
до н-декана. По сравнению с уравнениями Соава и Пен-
га-Робинсона новое уравнение отличается большей
точностью при расчете объемов на основе данных о
критических изотермах, температур кипения и объемов
насыщенной жидкости. Как следует из кривых, приве-
денных на рис. 1.19 для диоксида серы при 250 °F, урав-
нение Харменса — Кнаппа позволяет наиболее точно
рассчитать давление насыщения и объем насыщенной
жидкости.
Хотя это уравнение несколько сложнее, чем другие ку-
бические уравнения, оно дает более точные результаты.
Вопросы применения данного уравнения для описания
смесей и равновесия в системе пар — жидкость будут
освещены в последующих публикациях его авторов.
1.6. Сложные уравнения состояния
1.6.1. Введение. Для каждого из ранее предложенных
уравнений состояния имеется ряд более или менее серь-
езных ограничений относительно типов веществ, диапа-
зона допустимых условий или фаз. Одни уравнения бо-
лее приемлемы для описания функции PVT, другие —
для описания фазового равновесия, третьи — для пред-
ставления отклонений энтальпии или энтропии. Вероят-
ность создания некоего универсального уравнения со-
стояния средней степени сложности весьма мала.
Увеличение числа констант в уравнении часто, но да-
леко не всегда приводит к расширению области его при-
менения. В некоторых случаях двухпараметрические
уравнения превосходят уравнения, содержащие восемь и
более параметров. Однако это является исключением из
общего правила, и в настоящее время уравнения с боль-
шим числом параметров получили широкое распростра-
нение, в частности, благодаря интенсивному внедрению
ЭВМ.
Представив данные в графическом или табличном ви-
де, можно избежать необходимости подгонки уравнения
к результатам экспериментов. Например, при определе-
нии сжимаемости по Питцеру — Керлю z = Z<0) +
члены с надстрочными индексами выступают в качестве
функций приведенных свойств. Однако при многократ-
ных расчетах указанный подход невозможен ввиду тру-
доемкости таких операций, как поиск и интерполяция.
Уравнения состояния можно отнести к четырем
основным видам.
1. Уравнения, предназначенные для описания отдель-
ных веществ, таких, как вода, или определенных сме-
сей, таких, как воздух. Эти уравнения должны обеспе-
чивать высокую степень точности результатов в широ-
ком диапазоне условий, и поэтому они содержат много
постоянных.
2. Уравнения особого вида с различными числовыми
коэффициентами для разных веществ. Обычно, исполь-
зуя правила аддитивности и исходя из констант для чис-
тых компонентов, эти уравнения распространяют на
смеси.
3. Уравнения с универсальными параметрами, опре-
деляемыми через уже известные свойства отдельных
чистых веществ.
4. Уравнения двух предыдущих типов, применяемые
к смесям и содержащие параметры бинарного взаимо-
действия, полученные из экспериментальных данных о
двухкомпонентных смесях.
Кубические и прочие относительно простые уравне-
ния состояния можно аналогичным образом подразде-
лить на такие же группы. Здесь будут рассмотрены
примеры уравнений, относящихся ко всем перечислен-
ным типам. Не следует забывать, что, исходя из прак-
тических соображений, не всегда уже имеющееся урав-
нение следует заменять более новым и более совершен-
ным. Для ранее предложенного уравнения может быть
уже разработана универсальная программа для ЭВМ,
так что замена уравнения потребует слишком большого
изменения в программе и, следовательно, окажется не-
осуществимой. Многие части программы для ЭВМ мо-
гут быть взаимозависимы, и поэтому изменение одной
части повлечет за собой изменение другой.
1.6.2. Уравнение Бенедикта—Уэбба — Рубина. Зна-
менитое уравнение Бенедикта — Уэбба — Рубина [187,8,
181,10, 182] было разработано ими в процессе усовер-
шенствования уравнения Битти — Бриджмена. Некото-
рые этапы совершенствования этих уравнений показаны
в табл. 1.15. Подробное описание уравнения Бенеди-
кта — Уэбба — Рубина и дополнительный материал
приведены в табл. 1.16, значения параметров даны в
табл. Д.5. На рис. 1.20, а и в уравнение Битти — Брид-
жмена сравнивается с другими уравнениями, а также с
экспериментальными данными.
В этом уравнении давление (или сжимаемость) пред-
ставлено в виде полинома от плотности с коэффициен-
тами, зависимыми от температуры^ которые также со-
держат экспоненциальный член, введенный для компен-
сации членов более высокого порядка вириального
уравнения. Недостаток уравнения Битти — Бриджмена,
который разработчики уравнения Бенедикта — Уэб-
ба — Рубина намеревались устранить, заключается в
его непригодности для описания поведения жидкостей и
газов при плотности выше критической.
Для оценки восьми параметров использовались дан-
ные о характере изменения функции PVT для газов,
критических свойствах и давлении пара. Для достиже-
70 Глава 1
Таблица 1.15. Этапы разработки уравнения состояния Бенедикта — Уэбба —
Рубина
Вириальное уравнение (1885—1901):
Р = RTq(\ + Bq + Cq2 + 4- ...)
Уравнение Битти — Бриджмена (1927):
/ /?Л > /
Р = RTq + ( B0RT - Ao - — ) e + I -BobRT + Aoa -
\ T / \
RBoc\ ,
~^)e +
RBobc
---Q •
T2
Уравнение Бенедикта — Уэбба — Рубина (1940):
Р = RTq + (b0RT - Ao - Q2 + (bRT - a)e3 + cap6 +
+ ~ e3U + 762)exp(-7p2).
T2
Уравнение Старлинга (1970):
P = RTq +
(bRT -
d\ з
a---I q +
77
d\
+ — I
V
Q6 + e3(l + 7e2)exp(-7e2).
T2
Уравнение Нишиуми (1980) [520, 521]:
+ ~ + y(Pr)) e2(i + 7*e^-7’^.
Tr /
Пятнадцать коэффициентов, отмеченных звездочками, являются функциями
ацентрического коэффициента. Величины 0е и у(Тг) выражают воздействие
полярности на свойства паров и жидкостей соответственно.
ния большей точности для каждого конкретного веще-
ства требуется использование своих собственных пара-
метров, в то же время было проведено некоторое обоб-
щение параметров уравнений свойств чистых компо-
нентов. Наибольшее внимание было уделено легким
углеводородам и обычно сопутствующим им неоргани-
ческим газам.
Из-за высокой нелинейности уравнение Бенедикта —
Уэбба — Рубина использовать сложнее, чем кубические
уравнения, которые можно аналитически разрешить от-
носительно объема или сжимаемости. Метод Ньюто-
на — Рафсона, как правило, дает удовлетворительные
результаты. Процедура проведения расчетов по этому
методу подробно описана в работе [380]. Еще один ме-
тод, который всегда, хотя и медленно, приводит к схо-
димости, предложен Тангом [674].
На рис. 1.21 показаны изотермы, рассчитанные по
этому уравнению для н-пентана. Они имеют традицион-
ную 5-образную форму. Очевидной является возмож-
ность наличия трех действительных положительных
корней. В работе [235] выполнен тщательный анализ
уравнения при различных давлениях, температурах и
составах, а также проведено сравнение его с уравнением
Редлиха — Квонга. Усовершенствованный алгоритм для
оценки плотности был получен авторами работы [484].
Параметры. Существует целый ряд оценок парамет-
ров уравнений как обобщенных, так и используемых
для чистых веществ. Приведем несколько примеров.
1. В первой статье Бенедикта — Уэбба — Рубина,
опубликованной в 1951 г., даны постоянные для двенад-
цати углеводородов — от метана до н-гептана.
2. В работе [231] даны пятьдесят две группы парамет-
Уравнение состояния 71
ров для тридцами восьми веществ. Авторами этой ра-
боты выполнено обобщение приведенного уравнения
путем выражения параметров в виде линейной функции
ацентрического коэффициента для шестнадцати по-
стоянных.
3. В работе [186] содержится оценка коэффициентов
для шестнадцати веществ, представляющих интерес для
газовой промышленности.
4. Тридцать восемь групп данных для тридцати двух
соединений собраны и проанализированы Новаком и
др. [1972]. Материал этот также приводится в работе
[58]. Это единственный перечень, в котором помещены
параметры для водорода, ацетилена, бутадиена и ряда
других углеводородов. Они представлены в табл. Д.5.
5. Параметры для этанола получены авторами рабо-
ты [311], ими выполнена оценка параметров для ацето-
на [312].
6. Параметры для двадцати веществ при криогенных
температурах получены авторами работы [532].
7. В работе [656] установлена зависимость параметра
Со от температуры.
8. Разработка обобщенных форм уравнения, выпол-
ненная авторами работ [186, 520], позволила получить
параметры для углеводородов, следующих за н-
деканом.
9. По утверждению Хопке [357], как уравнение Бене-
дикта — Уэбба — Рубина, так и уравнение Бенедик-
та — Уэбба — Рубина — Старлинга не дают возмож-
ность получить достаточно точные параметры для во-
ды (см. следующий пункт).
10. Параметры для полярных веществ, включая воду,
получены авторами работы [521]. В этой работе приве-
дены данные для 92 веществ, для каждого из которых
необходимы три соответствующих параметра.
Различные выражения, связанные с уравнением Бене-
дикта— Уэбба — Рубина, приведены в табл. 1.16. Под-
робное описание методики применения этого уравнения,
включая методику определения коэффициентов по экс-
периментальным данным и оценку термодинамических
свойств, выполнено авторами работы [91].
Смеси. Важным положительным моментом, характе-
ризующим уравнение Бенедикта — Уэбба — Рубина, яв-
ляется его применимость для описания смесей. Правила
усреднения, первоначально предложенные для парамет-
ров М, имеют следующий вид:
М = (Ly,Ml/r)r, (1.156)
где г = 1 для Во, г = 2 для Ао, Со и 7 и г = 3 для дру-
гих четырех параметров. Параметры бинарного взаи-
модействия введены для четырех параметров Бишным
и Робинсоном [187], этими же авторами определены
значения kj для двенадцати веществ [188]. Правила ус-
реднения и числовые значения представлены в
табл. 1.16.
В работе [417] приведены корреляции параметров вза-
имодействия кц с общим числом атомов углерода, глав-
ным образом н-алканов. Авторами работы [523] прове-
дена более подробная корреляция с соотношениями
критических объемов, ими же проверены данные о рав-
новесии между паром и жидкостью для 125 двухкомпо-
нентных систем.
Модификации уравнения и их применение О двух мо-
дификациях уравнения уже упоминалось выше. В пер-
вом случае параметр Со представлен в виде функции
температуры. Во втором параметры обобщены как ли-
нейные функции ацентрического коэффициента, что при-
дает им универсальный характер и обеспечивает приме-
нимость ко всем веществам, для которых известны
ацентрические коэффициенты и критические свойства.
В уравнение был также внесен ряд более серьезных
изменений. Так, обобщенное уравнение, содержащее 16
параметров и 44 коэффициента [734], дает довольно
точные результаты при значениях приведенной плот-
ности вплоть до 2,8. Проверена применимость такого
модифицированного уравнения к смесям. В статье [452]
описан вариант уравнения Бенедикта — Уэбба — Ру-
бина, включающий 33 константы, специально для мета-
на. К тяжелым углеводородам от Сю до С20 применимо
уравнение с 15 коэффициентами, каждый из которых
выражен через Тс, Vc и о> [520].
Наибольшее распространение получила модификация
уравнения, предложенная Старлингом [127 и более ран-
ние издания], которая в свою очередь была подвергнута
значительным изменениям (см. табл. 1.17). В целях усо-
вершенствования зависимости от температуры коэффи-
циентов q2, q3 и q6 были введены три дополнительных
параметра Do, Ео и d. К четырем из одиннадцати пара-
метров относятся параметры бинарного взаимодейст-
вия. В книге Старлинга представлены значения пара-
метров для 18 веществ. Считается, что с помощью этих
уравнений можно рассчитать свойства при приведенной
температуре не ниже 0,3 и приведенной плотности до
3,0, т. е. в диапазоне криогенных температур. Обобщен-
ное уравнение, в которое входят свойства чистых ве-
ществ, известно под названием уравнения Хана —
Старлинга. В упомянутой выше книге полностью при-
водятся таблицы и термодинамические диаграммы для
пятнадцати веществ, а также программы для ЭВМ.
Уравнение Бенедикта — Уэбба — Рубина — Старлин-
га было распространено Лином и Хопке [445] на смеси
азота с метаном, этаном и пропаном. При определении
значений параметров они использовали 21 000 экспери-
ментальных данных о плотности, энтальпии, давлении
пара и равновесии пар — жидкость для этих веществ.
Лин и Хопке также приводят краткое описание регрес-
сионной методики.
Применение уравнений состояния этого вида. Как
указано в работах [154, 357], уравнения Бенедикта —
Уэбба — Рубина и Бенедикта — Рубина — Старлинга
нашли широкое применение в практической деятельнос-
ти. Они более эффективны, чем кубические, например,
для любых термодинамических расчетов, особенно для
криогенных систем. Соперничать с ними по степени
точности расчетов могут разве что уравнения Ли —
Кеслера и подобные им. В то же время усложненность
формы затрудняет их использование при расчетах дис-
тилляционных процессов в тех случаях, когда необходи-
мо выполнить многократную оценку величин фугитив-
ности, объема и энтальпии, поэтому в перечисленных
случаях часто применяют кубические уравнения. Однако
ряд ученых не придает большого значения этому огра-
ничению.
1.6.3. Принцип соответственных состояний и урав-
нение Ли — Кеслера. Один из наиболее результативных
Таблица 1.16. Уравнение состояния Бенедикта — Уэбба — Рубина
Стандартные формы уравнения:
Р= RTp + (B0RT- Ао - С0Т~2)р2 + (bRT-a)p3 + аар6 + cT~2p\l + ур2) еХр(-ур2),
Глава 1
(^о О) \ I а । act с
В°~^Т~ RT3 )Р + \b~~RT )Р +~RTp5 ^RT3 p2(1 + YP2) exP(~YP2).
Параметры: численные величины параметров даны в табл. Д.5. При температуре ниже нормальной Со часто выражают как функцию темпе-
ратуры; ссылки на целый ряд работ по этому вопросу содержатся в книге [585]
Смеси: исходные правила усреднения свойств имеют следующий вид:
Во = Sj^/Bo,-
Ао = [£,х((Л0/)1/2]2
Co = [Spc,(COl)1/2l2
b = [Ерс,(^)1/3]3
a = [S,xI-(aI)1/3]3
с = [S(x,(c,)1/3]3
У = [Е(*ХУ1)1/2]2
а = [S,xXa()1/3]3
Параметры бинарного взаимодействия были введены в правила усреднения свойств Бишнои и Робинсоном [187, 188], которые пришли к
выводу, что
в0 = п Е 1=1 п Е 7=1 п xixj B0ij > где До(у -y/BQjBQj
Ао = Е /=1 п Е 7=1 п xixJ^Oij, где A)iJ = v^i^o/U —кц)
Со = Е Е 7=1 xixJ » где ^OiJ Q)i O>7 (1 k-ij)
ь = п Е 1=1 п Е 7=1 E XiXjXkibijbjk bik)l/3, где btj — y/bibj
а = п Е i=i Е 7 = 1 п *E^ XiXjxk (au ajk aik)y3> n /1 где ац =\/ащ(1 -кц)
с = Е 1=1 п Е 7=1 п xixjxk (Cjj Cjk Cik) j n где сц =VciCj(l ~kij)3
а = Е 1=1 п Е 7 = 1 п ^E] XiXjxk (ttij ajk aiky/3, где <*ij =
У = Е 1=1 Е 7 = 1 xixj7ij , где 7ij = Vy,7j
Величины kij
со2 H2S n2 СН4 c2H6 С3Н8 «30-С4Н10 Н-С4Н10 «зо-С5Н12 н-С5Н12 н-СбНм H-C7H14
СО2 0 0,057* * 0,03* 0,03** 0,08** 0,11** 0,14 0,11** 0,166 0,166 0,188* 0,209*
Н2У 0 0,068* 0,09 ±0.01* 0,085** 0,076* 0,09 0,09 0,102 0,102 0,116* 0,129*
0 0,03 0,06* 0,09 0,113* 0,113* 0,14* 0,14* 0,166* 0,193*
n2 0 0,01 0,022 0,034* 0,03* 0,047* 0,05* 0,06* 0,072*
СН4 0 0 0 0 0,01 0,01 0,02 0,03
С2Н6 0 0 0 0,006* 0,006 0,014 0,021
СзНв 0 0 0 0 0,006* 0,012*
ИЗО-С4Н10 Н-С4Н1П 0 0 0 0,006* 0,012*
Н-С7Н14
Уравнения фугитивности и остаточной энтальпии и энтропии получают из соответствующих уравнений, основанных на уравнении Бене-
дикта — Уэбба — Рубина — Старлинга (см. табл. 1.17), принимая, что Do = Ео - d = 0.
* Величина дана в соответствии с оценками. ** Получено из вторых вириальных коэффициентов.
Уравнение состояния
74 Глава 1
Рис. 1.20. Рассчитанные и экспериментально установленные данные о функции PVT.
а — отклонение (%) рассчитанных величин сжимаемости от истинных для аммиака при 200 °C [230]: 1 — уравнение идеального
газа, 2 — уравнение Битти — Бриджмена, 3 — уравнение Ван-дер-Ваальса, 4 — уравнение Редлиха — Квонга, 5 — уравнение соот-
ветственных состояний; б — экспериментальные данные и рассчитанные по уравнению Клаузиуса:
(Р + ------ ) (И - b) = RT,
T(V + с)2/
в — экспериментальные данные и рассчитанные по уравнению Битти — Бриджмена:
pV2 = PT[V + Во(1 - Ь/И][1 - с/ИГ3] - Ло(1 - a/V).
На рис. 1.20, бив/ — экспериментальная кривая [631], 2 — кривая насыщения.
Область применения
Пар
Жидкость
Рис. 1.21. Изотермы н-пентана, рассчитанные по уравнению Бенедикта —
Уэбба — Рубина для температур 100, 125, 150, 175 и 200 °C, показывающие
характерную «овражную» область.
/ Со \
Р = RTq + ( BqRT — Ao — —- ) q2 + {bRT — o)q3 + actQ6 +
\ t2 /
+ —7 (1 + 762) exP (“ 762)-
T2
Плотность, Темпера- Давление, Темпера- а,
моль/л тура, °C атм тура, °C (л/моль)3-атм
Ао, Ь,
(л/моль)2-атм (л/моль)2
Во,
л/моль
с, Со,
(л/моль)3- (л/моль)2-
К2-атм К2-атм
а,
(л/моль)'
(л/моль)2
0,46 140 2,1 60 4,07480 1,21794Е+1 6,68120Е —1.56751Е - 8.24170Е+ 2Д2121Е + 6 1,81ОООЕ-5 4,75000Е-
4,8 280 25,5 180 - 2 - 1 + 5 - -2
Уравнение состояния
СП
76 Глава 1
Таблица 1.17. Уравнение состояния Бенедикта — Уэбба — Рубина —
Старлинга
Стандартная форма уравнения:
/ Cq Do Еп \ / d \
P = pRT+ +-2__2 }р2+ ЬйГ-„-— Ез
(d \ ср3
а + т IP6 + (1 + УР2) ехр(—ур2).
Параметры: в книге [127] даны величины одиннадцати параметров для пят-
надцати веществ.
Смеси: правила усреднения свойств включают параметры бинарного взаимо-
действия, которые приведены в этой же книге.
Бо — £ XiBQi
i
л о = S S xiXj Арр А q/2 (1 - kij)
Со = S S XiXj Cq-2 Cqj2 (1 - kjj)3
I J
D0 = Z Z XiXj Dq2 Dy2 (1 -
i j
[I3
T.Xidi/3
Eo = Z Z xiXj E^2 E^2 (1 - kij)5
Обобщенное уравнение Хана — Старлинга: корреляции параметров выраже-
ны через критические свойства и ацентрический коэффициент:
PciB0i - Л j + BjOij
PciA0i
------= Л
RTci
+
PciC()i _
ят3 _ 3
+ В3Ш1
Pci7i =A4 + B4a>i
Уравнение состояния 77
Продолжение табл. 1.17
p2jbi =A5 + B5<i)i
2
Pci<4 . . „
Dv = л6 + B^i
ci
Pciai = A1 + В1Ш1
2
PliCi
DT3 ~А»+В»Ш1
л-< ci
Pci^Oi
RT*, -^ + ^1
Pcidi
КТ2 ~ Л10 + В10ш{
л 1 ci
PciBOi rt5 -Лц + Бпа>,- ехр( —3.8 а>,)
Надстрочный индекс параметра j Величина параметра
AJ
1 0,443690 0,115449
2 1,28438 -0,920731
3 0,356306 1,70871
4 0,544979 -0,270896
5 0,528629 0,349261
6 0,484011 0,754130
7 0,0705233 -0,044448
8 0,504087 1,32245
9 0,0307452 0,179433
10 0,0732828 0,463492
11 0,006450 -0,022143
Парциальные фугитивности: решение для уравнения Бенедикта — Уэбба —
Рубина получают при помощи следующего уравнения, принимая, что Do =
= Ео = d = О
КТ\п(/{/х{) = RT\n(pRT) + p(BQ + BQi)RT
п
+ 2p X X;
; = i J
,,, rc0yc0l)1/2
(Л0уЛ0,)1/2(1 - kij) --------------
(1
- kij)3
(DQjDGi)x/3 (£qA)/)1/2
fi t1 kij)
' p
('-V +v
3(h2h,)1/3/?T- З(а2о()1/3
З(с?2с?,)1/3
T
<*p5 Г О 1/, 3(й?2с?,)1/3
+ З(а2а()1/3 +---------------
Зр5
5
(а2 а,)1/3
78 Глава 1
Продолжение табл. 1.17
З(с2с,)1/3р2 Г1 - ехр(~ ур2) ехр(-ур2) 1
т2 L ур2 2 J
1
1 + УР2 + ~ y2p4
1 - exp ( — yp2)
2с / у; \ 1/2
УТ2 \ У /
Уравнения для определения остаточной энтальпии и энтропии.*
Н - я0 = P(BqRT- Ао - 4С0/Т2 + 5DO/T3 - 6EQ/T*)
+ \/2p2(2bRT~ За - 4d/T) - 1/5р5а(6а + ld/T)
+ с/уТ2(3 — (3 + 1/2ур2 — у2р4) ехр( — ур2)),
S- S° = - 'LjXjRXn (RTpXj) - p(BqR + 2C0/T3 - 3Dq/T*
+ 4£0/Г5) - l/2p2 (bR + d/T2)
+ 1 /5p5 ad/T2 + 2с/yT2 (1 — [1 + l/2p2y] exp[ — yp2]),
видов уравнений, описывающих отношения между па-
раметрами PVT, разработан на основе корреляций от-
клонений этих свойств от свойств определенных эталон-
ных веществ. Начало разработки современных схем
этого типа было положено предложенными Питцером
и др. [555] корреляциями по сжимаемости в виде поли-
нома от ацентрического коэффициента:
Z = Z(0) + wZ(1) + W2z(2) + . . . .
На практике такое уравнение обычно прерывают на ли-
нейном члене. Член z(0) характеризует сжимаемость
«простой» жидкости, например аргона, а прочие члены
представляют собой поправки на отклонение от поведе-
ния «простой» жидкости. Первоначально члены z(0) и
Z(1) были представлены в табличной форме в виде функ-
ций приведенных температуры и давления, соответ-
ствующие графики были построены Эдмистером [265],
а их современная трактовка дана на рис. 1.22.
Лидерсен и др. [451] приняли критическую сжимае-
мость за корреляционный параметр. Значения сжимае-
мости, плотности жидкостей, коэффициентов фугитив-
ности и отклонений от энтальпии и энтропии были све-
дены в таблицы. Однако эти таблицы, как и таблицы
Питцера, применимы только при величинах приведен-
ной температуры выше 0,7; помимо этого, табличная
или графическая форма подачи материала затрудняет
использование компьютера. В любом случае таблицы и
уравнения Ли и Кеслера, о которых говорится ниже, во
многом превосходят их.
Разработан ряд корреляций z(0) и z(1), имеющих вид
уравнения. В этих целях Ли и Кеслер [425] использовали
уравнения, подобные уравнению Бенедикта — Уэбба —
Рубина. Они соотносили свойства всех веществ с двумя
жидкостями — простой и эталонной. При составлении
корреляций для z(0) были преимущественно использова-
ны данные о метане, аргоне и криптоне, а в качестве
эталонной жидкости был выбран н-октан — наиболее
тяжелый и достаточно хорошо изученный углеводород.
Было предложено следующее определение сжима-
емости:
z =z<°) + (ш/0,3978)(z(f) -z(0)) = z(0) + (OZ*1),
(1.157)
где 0,3978 — ацентрический коэффициент н-октана. Оче-
видно, что, согласно Питцеру, z(1) определяется следую-
щим выражением:
z(l) = (z(r)_z(O))/o,3978. (1.158)
Оба параметра сжимаемости представлены уравнения-
ми одного-и того же вида, имеющими, однако, разные
числовые коэффициенты. Вышеупомянутые и связанные
с ними уравнения приводятся в табл. 1.18.
Способ решения при известных величинах Тг и Рг со-
стоит в нахождении р4°) и p4D
методом подбора из
уравнения (3), приведенного в табл. 1.18, затем z(<)) и z(1>
и последующем определении на основе их значений па-
раметра сжимаемости. Наиболее удобный для практи-
ческого решения вид уравнения можно получить путем
подстановки 1/Vr = Pr/zTr, поскольку диапазон величин
Z обычно невелик — приблизительно от 1 до 0,05. Сле-
дует отметить, что в то время, как Рг и Тг являются
приведенными параметрами, Vr нельзя считать приве-
денным объемом, поскольку
Vr = PcV/RTc.
Уравнения для фугитивности и функций отклонения
имеют аналогичный вид, и их можно решить после на-
хождения Vr или z. Результаты решения уравнения бы-
ли представлены в табличной форме для интервалов
0,3 Тг С 4 и 0,01 Рг 10, чтобы облегчить прове-
дение расчетов. Была проведена проверка величин Тг
Уравнение состояния 79
Рис. 1.22. Коэффициент сжимаемости z = z(0) + сог(1), полученный по уравнению Ли — Кеслера (табл. 1.18).
80 Глава 1
Таблица 1.18. Уравнение состояния Ли — Кеслера
Z = Z<°) + (Z^ - Z(°)) = Z(°) + 0>Z(1). (1)
= 0,3978 (2)
(PrVr \ BCD C4 / у \ / у \
Jr ) Vr V2 V5r T2V2 у V2 ) P \ y2 у
\ 5 )
B = bx- b2/Tr~b3/T2- b4/T?. (4)
C = Cl - c2ITr + c3/T*. (5)
D — d 1 + d2/Tr.
(6)
Константы Простые жидкости Эталонные жидкости
bi 0,1181193 0,2026579
b2 0,265728 0,331511
b3 0,154790 0,027655
b4 0,030323 0,203488
Cl 0,0236744 0,0313385
c2 0,0186984 0,0503618
c3 0,0 0,016901
c4 0,042724 0,041577
dx X 104 0,155488 0,48736
d2 X 104 0,623689 0,0740336
P 0,65392 1,226
7 0,060167 0,03754
Уравнение коэффициента фугитивности:
(f\ BCD
In ( _ ) — Z — 1 — In (Z) + + — +-7 + E, (1\
\P) Vr 2V2 5^5 ’
где
E 2T’r{P+1 (* + 1 + vl )exp -^2 ) }
Уравнение отклонения энтальпии от идеальности:
Я- Н*
RTf
b2 + 2Ь3/ТГ + Ы4/Т2
С2 - Зсс/Т2
С?2
2TrV2
5ТГУ? + ЗЕ
(9)
Уравнение отклонения энтропии от идеальности:
s-s* (р \ bx + b3/T2+ 2bJT*
+ - )-.n(Z)---------------------
ct - 2с3/Т* _ dx
2V2 5Vsr
+ 2Е,
(10)
Уравнение состояния
81
Продолжение табл. 1.18
где Р* = 1 атм для данных проекта 445* Американского нефтяного институ-
та (API Research Project 445* data)
Псевдокритические свойства:
Vci = ZciRTci/Pci. (П)
Zci = 0.2905 - 0.085w;. (12)
^=7 E EW(rV3 + kJ/3)3. (13)
о j к i
Tc = — E E х}хк(У1с{3 + vcy3)3 ^T^T~ck. (14)
8KC j к
<O= Exy(Oy. (15)
Pc = Z(R.TC/VC = (0,2905 - 0,085(o)RTc/Kc. (16)
Уравнение ацентрического коэффициента:
lnPir - 5,92714 + 6,09648/7аг + 1,28862 In Tbr - 0,169347 Лг
<а =-----------------------------------------------------—------- (i 7)
15,2518- 15,6815/Tbr- 13,4721 In Tbr + 0,43577 v 7
Таблица 1.19. Трехпараметрическое уравнение состояния [351, 248]
P = RT(V3 + V2b + Vb2 ~ b3)/V(V - b)3 ~ a/V2 - c(V - Ис)2/Г4,
a = R2T2(a i + a2Tr + a3/Tr)/Pc,
b^RTJbi +b2Tr + b3/Tr)/Pc,
c = R2T2(ci + c2Tr)/Pc,
где
й! = - 0.45307 + 5.8405w,
a2 = 0.42448 - 3.5365(0,
a3 = 0.49780- 2.3553(0,
bi = - 0.07788 + 0.60629(o,
b2 = 0.05548 - 0.35642(o,
b3 = 0.06603 - 0.25554(o,
ct = 0.20570 + 0.38928(o,
c2 = - 0.15299 - 0.28783(o.
Параметры смесей
a = ZZy^jajj,
b = ZZy^bij,
C = oSj/Cf/O/,
Vc = b^yiVcilbit
aij = (an^-)1/2,
Z>iy=(Z>V3 + 6V3)3/8.
d’ = 2Ew,
d^l'Lyjbij,
j
6-829
82 Глава 1
Продолжение табл. 1.19
dcj = с;/а(,
d’ic=Vci/bi.
Уравнение коэффициентов парциальной фугитивности:
1П0С = 3d3 — IVbd1}- 5Vb2 + 4V2d^/{V- d)3 - df /RTV
+ [c — cd1} /a — ad1; + (cVcd^ /a + aVcd4 + cVcd^ /b
+ bcdYc - 3c Vc)/V+ Vc(5cVc - cVcda{ I a - a Vcd<;
- 2cVcd^/b - 2cbdYc)/3V2]/RTV - \a{PV/RT).
вплоть до 0,8 и Pr вплоть до 31. При сопоставлении с
этими таблицами таблицы Питцера и Лидерсена пред-
ставляются устаревшими. В примере 1.17 показана ме-
тодика применения уравнения Ли — Кеслера, а на
рис. 1.23 сравнивается и ряд других уравнений.
Смеси. Исходная методика применения уравнения
Ли — Кеслера для описания смесей приводится в
табл. 1.18. Исследователи, специализирующиеся в дан-
ной области, внесли в нее целый ряд изменений. В осно-
вополагающем труде Ли и Кеслера содержались уравне-
ния для фугитивности, энтальпии, энтропии и отклоне-
ний теплоемкости для чистых веществ. Величины
фугитивности для смесей приведены в статье Иоффе
(375], автор которой видоизменил правила усреднения
свойств и ввел в них коэффициенты бинарного взаимо-
действия. Более углубленная проверка условий паро-
жидкостного равновесия смесей проведена авторами ра-
боты [560], которые также внесли изменения в правила
усреднения свойств и получили коэффициенты бинарно-
го взаимодействия приблизительно для 140 пар. Сравне-
ние условий парожидкостного равновесия и изменения
энтальпии с аналогичными характеристиками, рассчи-
танными из уравнения Бенедикта — Уэбба — Рубина —
Старлинга, показало обоснованность данного варианта
метода Ли — Кеслера. В непосредственной близости от
критической точки расчеты несколько затруднены, но,
как утверждают авторы этого уравнения, при Т/Тс ни-
же 0,96 удается избежать каких-либо осложнений.
Лин и Дауберт [443] рассчитали величины парциаль-
ных молярных объемов при помощи уравнения Ли —
Кеслера, причем, как выяснилось, результаты расчетов
отличаются от значений, полученных опытным путем,
не более чем на 15%. Авторы работы [683] отказались
от использования «простой» жидкости. Они использо-
Рис. 1.23. Сравнение экспериментальных изотерм метана (а) и воды (б) с расчетными. Расчеты выполнены по
уравнениям Соава — Редлиха — Квонга (СРК), Пенга — Робинсона (ПР) и Ли — Кеслера (ЛК). Применительно
к метану наиболее точным является уравнение Ли — Кеслера, вполне приемлемые результаты дает уравнение Со-
ава — Редлиха. Применительно же к воде ни одно из уравнений не является удовлетворительным, исключение
составляет лишь область низких температур в узком диапазоне плотности [567].
Уравнение состояния 83
вали две эталонные жидкости, которые меняли в зави-
симости от конкретных обстоятельств, в результате че-
го были устранены ограничения на использование урав-
нения состояния. Посредством этой методики при
помощи одного из вариантов уравнения состояния Ре-
длиха — Квонга были рассчитаны значения плотности
жидких углеводородов, причем эталонными жидкостя-
ми служили этан и декан. В настоящее время авторы
указанной методики продолжают исследования в этом
направлении [683].
Выводы. Метод соответственных состояний Ли —
Кеслера в форме, предложенной Плекером и др. [560],
представляется наиболее точным методом общего ха-
рактера, пригодным для описания неполярных веществ
и смесей. Его можно распространить на полярные со-
единения, применяя вариант уравнения Бенедикта —
Уэбба — Рубина — Старлинга, содержащий коэффици-
ент полярности [520]. Плекер и др. [560] разработали
программы для ЭВМ для расчета величин сжимаемос-
ти, фугитивности и функций отклонения.
1.6.4. Другие обобщенные уравнения. В последнее
время значительное внимание уделяется члену уравне-
ния Ван-дер-Ваальса RT/(V — b), соответствующему си-
лам межмолекулярного отталкивания, описание кото-
рых приводится в разд. 1.7.5. В ходе исследований [351]
коэффициент сжимаемости рассматривался как состоя-
щий из трех составляющих — сил отталкивания жест-
ких сфер, сил межмолекулярного притяжения, выражен-
ных членом уравнения Ван-дер-Ваальса a/V2, и незначи-
тельной поправки, для определения которой предло-
жено несколько эмпирических выражений. Исходя из
этого, авторы работы [258] разработали следующее
уравнение:
V3 + bV2 + b2V a c(V~Vc)2
=---------------- - - --------------- , (1.159)
(V-b)3 V2 V3 v ’
параметры которого приводятся в табл. 1.19. Данное
уравнение применимо только для паровой фазы. Как
показало сопоставление расчетных величин с более чем
тысячей экспериментальных данных, погрешность опре-
деления плотности паровой фазы в среднем составляла
1,7%. При расчете равновесных состояний жидкость —
пар в условиях высокого давления это уравнение ис-
пользуют для представления паровой фазы. В целях
описания жидкой фазы его употребляют в сочетании с
вариантом уравнения, в состав которого введен пара-
метр растворимости. Данная методика, очевидно, явля-
ется значительно более эффективной по сравнению с
другими, гораздо более сложными методами исследова-
ния. Для смесей разработаны и применены на практике
правила усреднения, составлены также уравнения для
расчета величин фугитивности и изменений энтальпии.
Однако, чтобы данная методика могла соперничать с
методами, основанными на уравнении Бенедикта —
Уэбба — Рубина — Старлинга и уравнении Ли — Кесле
ра, необходимы дополнительные испытания.
Разработана еще одна комбинация членов новых ти-
пов, учитывающих межмолекулярные силы отталкива-
ния и притяжения, получившая название БАЧК по име-
нам ее создателей — Бублика (Boublik), Адлера (Adler),
Чена (Chen) и Креглевски (Kreglewski). Ее описанием и
применением для расчетов фазового равновесия занима-
лись Симник и др. [638]. Кудчакер [413] представил тер-
модинамические свойства азеотропной смеси CH3CI2 и
CCI2F2 при помощи уравнения БАЧК. Это уравнение
хорошо согласуется со структурой функции PVT для
многих веществ, а его параметры зависят только от
свойств чистых веществ. Анализ уравнений состояния,
в основе которых лежит .теория отталкивания жестких
сфер, был недавно выполнен Лилендом [431]. Описание
теоретических основ статистической механики содер-
жится в работе [192].
1.6.5. Жидкости. Для уравнений состояния Соава,
Пенга — Робинсона, Ли — Кеслера и им подобных, как
правило, характерна низкая степень точности представ-
ления плотности жидкостей. Специально для решения
этой задачи предложено множество уравнений. Уравне-
ние соответственных состояний для расчета значений
плотности насыщенных жидкостей (как чистых ве-
ществ, так и смесей) разработано Ханкинсом и Томсо-
ном [391, 329]. Величины, рассчитанные по этому урав-
нению, были сравнены с 6500 экспериментальными дан-
ными, и результаты сравнения оказались положи-
тельными. Значения удельного насыщенного объема
Kat определяют следующим образом:
VSIV*=V^(\-^V^), (1.160)
где V* — «характеристический объем», полученный для
нескольких сотен веществ и соотнесенный с ацентриче-
ским коэффициентом для ряда других веществ; —
характеристика сферических молекул; V$ — поправоч-
ный коэффициент; оба этих параметра соотнесены с
приведенной температурой. В табл. 1.20 даны некото-
рые значения плотности.
Томсон [686], используя уравнения Тейта, соотнес
плотности сжатых жидкостей и плотности насыщенных
жидкостей при помощи следующего выражения:
В + Р
V/Vs = 1 - С In П (1.160а)
В + Ps
Параметр С является линейной функцией ацентрическо-
го коэффициента, В — более сложной функцией ацент-
рического коэффициента и приведенной температуры
(см. также табл. 1.20). Вышеупомянутое уравнение
можно распространить и на смеси, применив соответ-
ствующую методику.
Еще одна методика расчета поправок к плотности
была разработана Ри и др. [579]. В соответствии с этой
методикой
И/Ид =/Сд/ТС (1.161)
где К — полином третьей степени от Тг, коэффициенты
которого являются полиномом четвертой степени от Рг;
Kr — та же функция, рассчитываемая при таких величи-
нах температуры и давления, для которых известен эта-
лонный удельный объем Vr. Двадцать числовых коэф-
фициентов, указанных в табл. 1.21, были найдены на
основе анализа 2600 экспериментальных данных.
6*
84 Глава 1
Пример 1.17. Расчет сжимаемости н-пентана методом
Исходя из уравнения (3), приведенного в табл. 1.18,
выполняется построение нескольких изотерм Рг относи-
тельно или В масштабе настоящих графиков
обе группы кривых практически идентичны.
Значения Vr при Рг = 0,4 определяют по графику и
преобразуют в сжимаемость при помощи следующего
уравнения:
z = _ |И0) + -°^251-(И') - И0)) ,
Тг [_ 0,3978
где 0,251 — ацентрический коэффициент н-пентана,
0,3978 — ацентрический коэффициент эталонного веще-
ства, т. е. н-октана. В данном случае, однако, последний
Ли — Кеслера
член, как правило, опускают и получают выражение
z = РЛб0)/Тг.
Для определения сжимаемости по уравнению
Z = z(0) + 0,251 z(1)
также используют таблицы Ли — Кеслера (табл. Д.1 и
Д.2). Результаты расчетов представлены в табличной
форме.
При Тг = 0,8 график описывает как жидкую, так и па-
ровую фазу, в то время как в таблице Ли — Кеслера со-
держатся значения сжимаемости исключительно для
жидкой фазы.
рг = 0,40 Таблицы Ли — Кеслера
Тг Z ?0) zm Z
0,8 1,27(0,12) 0,63(0,06) 0,0661 -0,0272 0,0593
0,9 1,78 0,756 0,7800 -0,1118 0,7549
1,0 2,18 0,844 0,8509 -0,0285 0,8437
1,1 2,48 0,891 0,8930 0,0038 0,8940
1,2 2,82 0,923 0,9205 0,0190 0,9253
Уравнение состояния 85
Таблица 1.20. Плотности насыщенных и сжатых жидкостей и смесей [331, 329, 686]
Плотность насыщенных жидкостей представлена в интервале 0,25 < Тг < 0,95 следующими урав-
нениями:
V
-^= К<г0)[1 - <оСРК а = -1,52816
У Ь= 1,43907
с = -0,81446
Г^0) = 1 + а(1 - ТЛ)1/3 + 6(1 - ТЛ)2/3 d = 0,190454
е = -0,296123
+ с(1 - ТЛ) + </(1 - ТЛ)4/3, /= 0,386914
g =-0,0427258
= [e+fTR +gT%+ hTR]/(TR - 1,00001), h = -0,0480645
В оригинальной литературе даны величины характеристического объема V* для нескольких сотен ве-
ществ, для этих же величин также имеются выраженные через ацентрический коэффициент корреляции
для девяти групп веществ:
в которых константы этих девяти групп равны:
Парафины Олефины и диолефины Циклопарафины Ароматические соединения Все углеводо- роды
а 0,2905331 0,3070619 0,6564296 0,2717636 0,2851686
b -0,08057958 -0,2368581 -3,391715 -0,05759377 -0,6379110
с 0,02276965 0,2834693 7,442388 0,05527757 0,01379173
Средняя абсолют- ная погрешность, % 1,23 1,43 1,00 0,58 1,89
Серусодержащие соединения Фторуглероды Криогенные жидкости Конденсирующиеся газы
а 0,3053426 0,5218098 0,2960998 0,2828447
b -0,1703247 -2,346916 -0,05468500 -0,1183987
с 0,1753972 5,407302 -0,1901563 0,1050570
Средняя абсолют- ная погрешность, % 1,98 0,82 0,85 3,65
V= vs
Ацентрический коэффициент «дсрк определяют достаточно точно по уравнению Ли — Кеслера [425], где
РЬг = 1/Рс и Ты - Ть/Тс — это приведенная атмосферная температура кипения (Рс выражено в атм):
\nPsbr - 5,92714 + 6,09648/7),, + 1,28862 In Tbr - 0,169347 7^
СО = ------------------------------------------------------
15,2518 - 15,6875/Тй, - 13,4721 In Tbr + 0,435777^
Отношение удельных объемов сжатой и насыщенной жидкости выражено через давление, давление
насыщенной жидкости Ps, ацентрический коэффициент и приведенную температуру с помощью группы
уравнений и параметров:
В + Р \
B + Ps )’
В/Рс = -1 + а(1 - Тл)1/3 + 6(1 — Тл)2/3 + d(l - TR) + е( 1 - Тл)4/3,
е= exp(/4-g wCPK + h ш2СРК), В
С - j + кысрк
а = -9,070217, g = 0,250047,
Ь = 62,45326, h = 1,14188,
d = -135,1102, j= 0,0861488,
f= 4,79594, = 0,0344483.
В оригинальных публикациях представлены правила усреднения свойств, позволяющие применять
данные корреляции к смесям.
86 Глава 1
Пример 1.18. Расчет псевдокритических свойств методом
В этом примере рассматривается использование доволь-
но сложных правил оценки псевдокритических свойств
смесей при помощи системы уравнений Ли — Кеслера.
В табличной форме представлены требуемые свойства
чистых компонентов и результаты, полученные для
смеси. Ниже приведены уравнения (11)—(16), помещен-
ные в табл. 1.18.
Zci = 0,2905 - 0,085 од,
ы = 2х,од,
Zc = 0,2905 - 0,085 Sx,од,
Vcl= S2,05 ZciTc/Pci.
Ис = x?Kci + xlVc2 + xlVd + 0,25[Х1Х2(Ис13 + K^3)3 +
+ Х1Хз(И№ + И^3)3 + х2Хз(И^3 + НИ3)3] =
Ли — Кеслера
= 0,04(269,29) + 0,09(175,38) + 0,25(157,21) 4-
+ 0,25(0,06(6,4576 + 5.5975)3 + 0,1(6,4576 +
+ 5.3971)3 + 0,15(5,5975 + 5.3971)3] = 183,63,
Ис Тс — XjRclTci + XjKclTcl + ХзН-зТсЗ +
+ 0,25[x,x2(TciTc2f-\V^ + Ис23)3 +
+ XiX3(TciTc3)0-5(K№ + И^3)3 +
+ Х2Хз(Тс2Тсз)0’5(И^3 + И^3)3] = 87,162,
Тс = 87,162/183,63 = 474,67,
Рс = ZcKTc/Vc = 0,2514(82,05)(474,67)/183,63 = 53,32.
Полученные в результате расчетов величины, как и сле-
довало ожидать, немного отличаются от аналогичных
характеристик чистых компонентов.
/ х тс Рс О) Zc к Ис1/3
1 0,2 600 50 0,2 0,2735 269,29 6,4576
2 0,3 500 60 0,4 0,2565 175,38 5,5975
3 0,5 400 50 0,6 0,2395 157,21 5,3971
Смесь 474,67 53,32 0,46 0,2514 183,63
Таблица 1.21. Корректировка известной плотности жидкости относительно
температуры и давления [579]
QT = (Кт/K^Qr-
Кг определяют из данного уравнения при таких температуре и давлении, для
которых известна плотность Qr. Кт определяют из того же уравнения для тре-
буемой температуры и давления:
К = Ао + А1ТГ + А2Т* + ЛзГ3,
где
Ai = Bo,i + BijPr + В2, iPf + B2'iP^. + B^.iP^
i B0,i Вц B2,i B3,i B4,i
0 1,6368 -0,04615 2,1138(10~3) —0,7845(10-5) —0,6923(10-6)
1 -1,9693 0,21874 — 8,0028(10-3) — 8,2823(10~5) 5,2604(10-6)
2 2,4638 -0,36461 12,8763(1О-3) 14,805 9(10-5) —8,6895(10-6)
3 -1,5841 0,25136 — 11,38О5(1О-3) 9,5 672(10-5) 2,1812(10“ 6)
Авторы работы [735] предложили относительно прос-
тую группу отношений:
Г41+(1-Гг)2/7)ехр(-(1 - т;)2/7),
(1.161а)
zc = 0,29056 — 0,08775 <о. (1.1616)
Критическую сжимаемость обычно выражают через
ацентрический коэффициент, поскольку точные экспери-
ментальные данные для критической сжимаемости не
всегда можно получить. V и Г/— значения удельного
объема и приведенной температуры. Спенсер и Дэннер
[660] изучили несколько правил усреднения свойств для
смесей. Одно из наиболее точных уравнений для удель-
ного насыщенного объема приводится ниже.
Vs = RCLxiTci/Pci)z,i.1+^-Tr'>2,1\ (1.161b)
zc = ’Lxizci. (1.161г)
Совершенно другой подход к решению задачи соотне-
сения плотностей насыщенных жидкостей предложен в
работе [685]. Суть метода соответственных состояний,
предложенного авторами работы [684], излагается в
разд. 1.6.3.
Уравнение состояния 87
Относительно простой метод, который можно приме-
нить и не располагая ЭВМ, позволяет соотнести плот-
ности при двух температурах Т и Г:
Де = ql - qv = (Де)*
тс - т*
Согласно данным работы [283], к имеет следующие
значения: 0,25 для спиртов и воды, 0,29 для углеводоро-
дов и эфиров, 0,31 для прочих органических соединений
и 0,33 для неорганических соединений. Авторы работы
[633] предложили выражение, посредством которого
осуществляется корреляция плотностей жидкостей, име-
ющая менее общий характер:
6 =А:1/А:2(’-ПТс)2/7
(1.162)
Величины констант приведены для 62 жидкостей.
При помощи уравнения Тэйта следующего вида мож-
но также соотнести плотности жидкостей при различ-
ных давлениях и плотности в состоянии насыщения
V/Vs = 1 - кх ln( 1 + Р/к2).
(1.163)
При этом для каждого вещества имеется своя собствен-
ная константа. В этих же целях можно прибегнуть к
аналогичному уравнению (1.160а), константы которого
носят более обобщенный характер. Множество данных
относительно сжимаемости содержится в разного рода
справочной литературе, например в “American Institute
of Physics Handbook” (П>ей, 1972) или “Handbook of
Tables for Applied Engineering Science” (Больц и Тьюв,
1973). Некоторые более ранние исследования плотности
жидкостей описаны Бретцнайдером [25], Райдом и др.
[107] и Стербекером и др. [129]. Партингтон [92] приво-
дит несколько представляющих исторический интерес
корреляций относительно величин термического расши-
рения и сжимаемости жидкостей, например:
К = Ио/( 1 — кТ) (Менделеев, 1860),
V= к\ — 1П(ГС — Т) (Авенариус, 1876),
(8V \
) = к 1 1п( 1 + к2Р>) (Тэйт> 1888).
(1.164)
(1.165)
(1.166)
Приведенное выше уравнение применяют при давлениях
до 25 000 атм.
дУ \
— 1 = кх/(к2 + к3С + Р), (Тэйт, 1888), (1.167)
где С — концентрация раствора соли. Еще много лет
назад было установлено: введение инородных молекул
в жидкость оказывает на ее плотность такое воздейст-
вие, которое в количественном отношени сходно с по-
вышением давления.
И= V*(kTb - T*)/(kTb - Т) (Гийе и Джордан, 1896),
(1.168)
где Ть — точка кипения при атмосферном давлении.
V = кг + к2/(1 + к3Р) (Тумлирц, 1909), (1.169)
1/V~ \/Vc = k^T-Тс)к2 (Герц, 1919), (1.170а)
V = к( 1 - Т/Тс)к2 (Герц, 1932). (1.1706)
1.6.6. Уравнения состояния для отдельных веществ.
Большое значение, придаваемое определенным вещест-
вам или смесям, обусловливает повышенный уровень
требований к точности, который недостижим при
использовании уравнений общего характера. Для целого
ряда веществ разработаны эффективные уравнения осо-
бого вида. В качестве такового примера в первую оче-
редь следует привести основное уравнение состояния
для воды, в котором энергия Гельмгольца выражена че-
рез плотность и температуру. Это уравнение приведено
в табл. 1.22. Как указывают Кинан и др. [63], это урав-
нение содержит 58 числовых коэффициентов и пригодно
для получения всех данных о паре, приведенных в таб-
лице. В той же табл. 1.22 представлен ряд уравнений,
выведенных из этого основного уравнения, которые
описывают другие свойства.
Параметры уравнений Бенедикта — Уэбба — Рубина
и других связанных с ними уравнений могут быть исполь-
зованы и как специфические, и как обобщенные. Неко-
торые наиболее точные модификации уравнения Бене-
дикта — Уэбба — Рубина были распространены [180] на
этилен и пропилен, как жидкий, так и газообразный, а
для описания ряда других веществ были применены
аналогичные уравнения. В работе [303] приведены экс-
периментальные данные и осуществлен критический
разбор уравнений состояния для неона при очень низких
температурах. В разд. 1.4 содержатся многочисленные
данные о втором и более высокого порядка вириальных
коэффициентах. Воксменом и Девисом (1979) выполне-
ны точные измерения вириального коэффициента для
этилена при низких температурах, а Гудвином (1979)
разработано сходное по структуре с уравнением Бит-
ти — Бриджмена уравнение состояния, параметры кото-
рого приложимы к пропану.
В статье [256] помещен детальный обзор работ, по-
священных экспериментальным исследованиям и корре-
лятивным разработкам, осуществленным для многих
чистых веществ, в том числе диоксида углерода, инерт-
ных газов, воздуха, аммиака, воды, водорода, легких
углеводородов, а также для некоторых смесей. В статье
приведен обширный перечень литературы, освещающей
экспериментальные исследования смесей и их классифи-
кацию на основе тринадцати термодинамических
свойств. В работе [200] приведен список почти двухсот
«наиболее важных работ» по изучению параметров
PVT, указаны исследованные диапазоны давлений и
температур, степень точности результатов и необходи-
мое для экспериментов оборудование.
88 Глава 1
Таблица 1.22. Фундаментальное уравнение для воды и
выводимые из него термодинамические функции [63]
Энергия Гельмгольца определяется как
Ф = ^0(7) + /?Т[1п е + qQ(q, т)],
где
6
фо = 2 С‘/т‘~ 1 + с71П т + С81п Т/7
i= 1
(1)
(2)
В уравнениях (1)—(3) Т — температура в кельвинах,
т — 1000/Г, q — плотность, г/см3, R = 4,6151 бар-см3/
/г-К или 0,46151 Дж/г-К, тс = 1000/Tcrit = 1,544912,
Е = 4,8 и
1.7. Силы межмолекулярного
взаимодействия
и уравнения состояния
В конечном итоге объемные свойства веществ
определяются свойствами составляющих их молекул и
особенностями взаимодействия последних. Рассмотре-
нием свойств веществ с таких позиций занимается ста-
тистическая термодинамика, и в данном разделе обсуж-
даются некоторые результаты этих исследований, име-
ющие отношение к уравнениям состояния.
1.7.1. Соотношения различных видов энергии. Един-
ственная форма энергии, которой обладают идеальные
газы, — это энергия поступательного движения состав-
ляющих молекул. Реальные вещества в соответствии с
расположением атомов в молекуле обладают также
вращательной, колебательной и потенциальной энерги-
ей. Обозначив эти виды энергии £,, мы получим так
называемую функцию молекулярного распределения:
Q = Zgi ехр(~Е{/кТ)
Ту = Tc(j = 1) = 2,5(/ > 1), Qaj = 0,634(/ = 1) = 1,0(/ > 1)
Коэффициенты
(Дж/г):
Ci = 1857,065
С2 = 3229,12
С3 = -419,465
для фо имеют
С4 = 36,6649
С5 = -20,5516
С6 = 4,85233
следующие значения
С7 = 46
С8 = -1011,249
Величины 50 числовых коэффициентов Ац приведены в
таблицах Кинана и соавт. [63]. Производные характери-
стики определяются
Давление:
р = qRT 1 + qQ +
следующим образом:
где £( — квантованная энергия любого из перечисленных
выше видов; gi — число квантованных состояний, име-
ющих одинаковую или почти одинаковую энергию;
к = постоянная Больцмана, 1,38О5(£-16) эрг/К.
Энергии молекул ансамбля колеблются в широких
пределах значений, описываемых распределением Макс-
велла — Больцмана:
gIexp(-EI/^T) g(exp( — е(7& Г)
Pi = NJN =---------------- =---------------,
' 1 Zgiexp(-£i/kT) Q
Внутренняя энергия:
/dQ\
и = RTqt ( — I +
у Эту е
Энтропия:
5 = -R In q + qQ
Энтальпия:
h = RT
d^or)
dr
ет
д(фот)
dr
- QT
дфо
~df
(4)
(5)
(6)
(7)
где Pi — доля молекул с квантованной энергией £,. Мо-
лекулярная энергия слагается главным образом из энер-
гии поступательного, вращательного и колебательного
движения, величины которых можно достаточно точно
определить методом спектрального анализа. Величины
потенциальной энергии, зависящие от расстояний меж-
ду атомами в молекулах, также довольно значительны,
однако эти теоретические положения проверены глав-
ным образом на молекулах с более простой структурой.
Основные термодинамические свойства можно выра-
зить при помощи функции распределения Q. Таким об-
разом, внутренняя энергия ансамбля является суммой
энергетических уровней всех молекул или
7VTE,£(exp( — Е{/к Т)
U Zgiexp(-Ei/kT)
(1-172)
Второй вириальный коэффициент:
в = Г p^/e^l 1 =Qe=0 (8)
V ^6 TJq=0
Фугитивность:
ф - Фо V
In (f/P) =----+ In — - In z + z - 1 (9)
RT Ko
N fdlnQ \
= ~ ^‘£igiexp( — £i/kT) = RT2 I I .
6 \ дТ /v
(1.173)
Другая, наиважнейшая характеристика такого ансам-
бля — энтропия — определяется следующим выра-
жением:
Сжимаемость:
z = P/qRT
(10)
d InQ
дТ
(1-174)
S = R
Т
Уравнение состояния 89
Из этих двух выражений путем проведения обычных
термодинамических преобразований можно получить
выражения, определяющие все прочие характеристики
системы
А = U- TS = - RTinQ,
(1.175)
(1.176)
Н =U+PV=RT
Т
/д \nQ \ /д \nQ \
\ дТ )v \ dv JT]
(1.177)
V
- In<2
(1.178)
(1.179)
(1.180)
(1.181)
1.7.2. Реальные вещества. Силы межмолекулярного
притяжения удерживают молекулы на своих местах, си-
лы отталкивания предотвращают их взаимное уничто-
жение. Математически эти виды взаимодействия можно
удобно выразить через потенциальные функции, гради-
енты которых соотносятся с межмолекулярными сила-
ми. Данные функции являются функциями расстояний
между молекулами. Для одномерного движения иско-
мое отношение записывают следующим образом:
dF
(1.182)
Изменения энергии находят путем интегрирования по
расстояниям.
Считается, что молекулы вступают во взаимодейст-
вие парами, триплетами и т. д. Это взаимодействие
приводит к отклонениям от идеального состояния, ко-
торые можно описать последовательностью вириаль-
ных коэффициентов в уравнениях состояния.
Z — 1 + Bq + + Dqз 4" ...
(1.183)
Известны и уравнения, предназначенные для определе-
ния коэффициентов через потенциальную функцию. Так,
второй вириальный коэффициент определяется следую-
щим уравнением:
В = 2-nNa
(1 - exp(~w/кТУ)гЧг,
(1.184)
где Na — число Авогадро. Вывод этого уравнения дает-
ся, например, в работе [178]. Уравнения для высших ви-
риальных коэффициентов гораздо более сложны, но
также основаны на потенциальной функции. Соответ-
ственно все термодинамические свойства, которые вы-
водятся из уравнения состояния, можно также получить
из потенциальной функции.
1.7.3. Потенциальные функции. Потенциальные
функции имеют эмпирический характер (табл. 1.23).
Они соответствуют силам притяжения и отталкивания.
Согласно одной из теорий, создателем которой являет-
ся Лондон, потенциалы притяжения обратно пропорци-
ональны межмолекулярным расстояниям в шестой сте-
пени, в то время как потенциалы отталкивания зависят
от межмолекулярных расстояний в какой-то более вы-
сокой, но не столь определенной степени. Автором од-
ной из получивших широкое распространение функций,
учитывающих приведенные выше рассуждения, являет-
ся Май (1903). Эту функцию
и = ar~n -Ьг~6. (1.185)
называют потенциалом бинарного взаимодействия.
Используя различные значения п—т для потенциаль-
ной функции, можно получить бесконечное число реше-
ний для вириальных коэффициентов. Широкое распро-
странение получил потенциал Леннарда-Джонса при
п = 12. На рис. 1.24, а приводится график потенциаль-
ной функции для этилена.
Помимо вириальных коэффициентов для нахождения
параметров потенциальных функций можно использо-
вать данные о таких свойствах веществ, как, например,
вязкость и рассеяние молекулярного пучка. Хиршфель-
дер и др. (1964) провели сравнительный анализ пара-
метров, рассчитанных по вириальным коэффициентам и
по данным о вязкости. На рис. 1.24, б приведены потен-
циалы Леннарда-Джонса, полученные исходя из вири-
альных коэффициентов для нескольких молекул. По-
скольку потенциал Леннарда-Джонса отвечает принципу
соответственных состояний, его параметры можно вы-
разить через константы критического состояния. Если
же более точные данные отсутствуют, параметры мож-
но оценить при помощи следующих приближенных
уравнений:
е/к = 0,775Тс, (1.185а)
ст3 = О,983А:ТС/РС. (1.1856)
Исследователи используют и многие другие потенци-
альные функции; наиболее простые из них помещены в
табл. 1.23. Ряд таких функций имеет теоретическое обо-
снование; другие, ведущие к интегрируемым уравнени-
ям, пригодным для теоретических исследований, имеют
лишь частичное обоснование. Потенциальные функции,
приведенные в табл. 1.23, имеют 0, 1, 2 или 3 парамет-
ра, которые можно подобрать в соответствии с экспе-
риментальными данными. Кроме потенциала Леннар-
да-Джонса существуют еще два вида потенциалов,
особо эффективных при теоретических изысканиях.
1. Потенциал жесткой сферы, основанный на следую-
щих допущениях: силы притяжения отсутствуют, а си-
лы отталкивания бесконечно велики, если молекулы со-
Таблица 1.23. Некоторые наиболее распространенные потенциальные
функции (см. также [85])
а. Идеальный газ, межмолекулярные
силы отсутствуют:
и = О
б. Точка отталкивания находится у
центров молекул:
и = аг~а
в. Потенциал жесткой сферы. Точка
отталкивания находится на поверхно-
стях молекул:
г < а
г > о
г. Потенциал прямоугольной ямы.
Точка отталкивания находится на по-
верхности, на ограниченном расстоя-
нии действует постоянная сила при-
тяжения:
go
д. Потенциал Сазерленда. Точка от-
талкивания находится на поверхнос-
ти, сила притяжения изменяется в за-
висимости от расстояния:
е. Потенциал бинарной системы, осо-
бым случаем которого является по-
тенциал Леннарда-Джонса:
ж. Потенциал Кихары. Точка оттал-
кивания находится в центре диаметра
d, длина которого меньше молеку-
лярного диаметра а:
г <
d
Уравнение состояния 91
Рис. 1.24. Потенциал Леннарда-Джонса для этилена (а), полученный на основе вторых вириальных коэффициентов
(а = 4,433 А, е/к = 202,52 К), и потенциалы Леннарда-Джонса нескольких молекул (б) (а и г/к определены исходя
из результатов измерений вторых вириальных коэффициентов). Параметры уравнений заимствованы из подборки
[682].
прикасаются друг с другом, и равны нулю, если молеку-
лы удалены друг от друга на некоторое конечное
расстояние. Эта потенциальная функция содержит толь-
ко один параметр.
2. Потенциал прямоугольной ямы. В нем сохраняется
член, учитывающий действие сил отталкивания, и вво-
дится постоянный потенциал притяжения на конечных
расстояниях. Поскольку эта потенциальная функция
включает три параметра — е, а и g, получаемые в ре-
зультате корреляции отличаются гибкостью.
1.7.4. Вириальные коэффициенты. Как показано в
примере 1.19, интегрирование с использованием второ-
го вириального коэффициента рассмотренных потенци-
альных функций проводится непосредственно. Для по-
тенциала Леннарда-Джонса удобно применить числовое
интегрирование, так как интегрируемая функция быстро
убывает вместе с г. Составлены таблицы значений инте-
гралов, полученных из потенциалов бинарного взаимо-
действия, для п от 8 до 150 [106].
Применение совершенно различных потенциальных
функций приводит к одинаковым значениям вириаль-
ных коэффициентов. Потенциал прямоугольной ямы и
потенциал Леннарда-Джонса, соответствующие вторым
вириальным коэффициентам аргона, показаны на
92 Глава 1
Таблица 1.24. Уравнение вириальных коэффициентов,
основанные на потенциале жесткой сферы [85]
В =(2тгУ0/3)ст3 = Ьо,
С/Ь% = 5/8 = 0,625,
, 1283 3 r73v/2+(81)(17)(arctany/2-7T/4) '
D/bk = +
0 8960 2 [_ (32)(35я)
= 0,286949,
E/b^ = 0,11040 ± 0,00006,
F/bl = 0,0386 ± 0,0004,
G/b^ =0,0138 ±0,0004,
H/bl ~ 0,005.
рис. 1.25, а. Из рис. 1.25, б очевидно, насколько близко
вторые вириальные коэффициенты соответствуют зна-
чительной части корреляции потенциала прямоугольной
ямы.
Третий и последующие вириальные коэффициенты
были оценены, исходя из нескольких потенциальных
функций. Библиографические данные о таких расчетах
содержатся в работе [106]. Потенциал жесткой сферы
был применен для расчета вириальных коэффициентов
вплоть до седьмого, результаты этих расчетов помеще-
ны в табл. 1.24. «Точное» вириальное уравнение, выве-
денное из потенциала жесткой сферы, приведено в пер-
вой строке табл. 1.25, в которой также показаны сте-
пенные разложения и полиномиальные эквиваленты.
1.7.5. Уравнение состояния возмущенной жесткой
сферы. Включение в рассмотрение сил отталкивания,
действующих между жесткими сферами, приводит к ви-
риальному уравнению, разрешимому относительно дав-
ления отталкивания Pr [583]:
R Т
PR= — (\ + 4у + 10у2 + 18,36у3 + 28,Зу4 + . . . )
RT
=—Ф(у\
где у = b/4 V,
(1.186)
(1.187)
b — мера объема, занимаемого молекулами, которую
также можно рассматривать как эмпирический пара-
метр. Предложено несколько аппроксимаций бесконеч-
ного ряда в конечной форме, приведенных в табл. 1.25.
У реальных газов давление складывается под воз-
действием как сил притяжения, так и сил отталкивания.
Например, второй член правой части уравнения Ван-
дер-Ваальса
р = ±±_в/К2 (1.188)
v-ь
рассматривается как член, учитывающий действие сил
притяжения, а член RT/(V — b), входящий в состав всех
традиционных кубических уравнений состояния, — как
член, учитывающий действие сил отталкивания, кото-
рый можно заменить Pr. Такая подстановка дает более
точное уравнение по сравнению с исходным уравнением
Таблица 1.25. «Точные» и приближенные формы коэффициента сжимаемости, основанные на потенциале жесткой
сферы, полученные несколькими исследователями [625]
(PV/RT)hs = ф(у)
у = b/4V
Ф(У) Разложение по степеням у
Точная форма 1+4у+10у2 + 18,365у3 + 28,24у4 + 39,5у5 + 56,5у6 + • • •
1(Ван-дер-Ваальс) 1/(1 - 4у) 1 + 4у + 1 бу 2 + 64у3 + 256у4 + 1024у5 + 4096у6 + • • •
П(РУ-давление) (1 + 2у + Зу2)/(1 - у)2 1 + 4у + 10у2 + 16у3 + 22у4 + 28у5 + 34у6 + • • •
ПЦотслоенная частица) (PY-сжима- емость) (1 + у + у2)/(1 - У)3 1 + 4у + 10у2 + 19у3 + 31у4 + 46у5 + 64у6 +•••
1У(Гугенгейм) 1/(1 - у)4 1 + 4у + 10у2 + 20у3 + 35у4 + 56у5 + 84у6 +•••
У(1 + 2у)/(1 - 2у) 1 + 4у + 8у2 + 16у3 + 32у4 + 64у5 + 128у6 +•••
VI(1 + Зу + 4у2)/(1 - 2у)(1 + у) УП(Флори)1/(1 - у1/3) 1 + 4у + 10у2 + 18у3 + 38у4 + 74у5 + 150у6 +•••
VIII Карнэхэн и Старлинг 1 + у + у2 - у3 (1 - у)3 1 + 4у+1Qv2+18у3 + 28у4 + 4Qv5 + 54у6 +••• = 1 + £ (л2 +п — 2)у”-1. 2
Уравнение состояния 93
Рис. 1.25. Вириальные коэффициенты и потенци-
альные функции.
а — потенциальные функции прямоугольной ямы (Г) и
Леннарда-Джонса (2), соответствующие вторым вири-
альным коэффициентам аргона [97]; б — второй и тре-
тий вириальные коэффициенты для потенциальной
функции прямоугольной ямы для аргона и неона.
Ив = T(dB/dt)T=TB-
Тв — температура, при которой В = 0 [83].
Ван-дер-Ваальса. Используя аппроксимацию функции
ф(у), предложенную Карнахеном и Старлингом [213]
(табл. 1.25), уравнение Ван-дер-Ваальса преобразуют к
следующему виду:
RT
1 + j + j* 1 2 - j
(1 -у)3 *
- a/V2.
(1.189а)
В результате аналогичных преобразований уравнение
Редлиха — Квонга принимает следующий вид:
RT
\ + у + у2 — у
(1 -У?
а
Параметры а и b этих уравнений можно соотнести с
критическими свойствами, применив математические
условия в критической точке, как это показано в приме-
ре 1.12. Проведя указанные преобразования, Карнахен
и Старлинг получили следующие результаты:
Уравнение Ван-дер-
Ваальса
Уравнение Редлиха —
Квонга
исходное модифици- рованное исходное модифици- рованное
a/RTcVc 9/8 1,3824 1,283 7?’5 1,463 Т°с'5
b/Vc 1/3 0,5216 0,2599 0,3326
Zc 3/8 0,3590 1/3 0,3157
В задаче 1.36 требуется подтвердить правильность этих
результатов.
Среди исследований, основанных на уравнениях со-
стояния возмущенной жесткой сферы, можно назвать
следующие.
1. Карнахен и Старлинг [213] выполнили анализ мо-
дифицированных уравнений Ван-дер-Ваальса и Редли-
ха — Квонга. При этом выяснилось, что уравнение Ре-
длиха — Квонга дает лучшие результаты при описании
плотности и отклонений энтальпии чистых веществ и
некоторых бинарных углеводородов.
2. Берэ и Праузниц [183] ввели член, учитывающий
действие сил притяжения, который вместе с членом,
учитывающим действие сил отталкивания для жесткой
сферы, приводит к трехпараметрическому уравнению
состояния, применимому к большим молекулам слож-
ной структуры. Праузниц и Донохью [565] продолжили
эти исследования. В результате были разработаны па-
раметры для всех тех веществ, с которыми приходится
иметь дело при переработке природного газа, а также
была составлена программа для ЭВМ для расчета та-
кой сложной системы. Результаты этих исследований
применимы для смесей при высоких давлениях, компо-
ненты которых существенно различаются по размерам
и структуре. Полученные расчетные данные были срав-
нены с экспериментальными, однако сравнительный
анализ этой и других методик, используемых в про-
мышленности, например методик Американского не-
фтяного института — Соава и Пенга — Робинсона, про-
веден не был.
3. Де Сантис и др. [250] применили разработанное
Клаузисом выражение, учитывающее действие сил при-
тяжения, и в результате получили следующее
уравнение:
RT (l+y+y2+y3 \ а
р-~У ( (1Л90)
94 Глава 1
Параметры а и b были рассчитаны как линейные функ-
ции температуры для 21 вещества.
4. Нагата и Ясуда [508] распространили уравнение
Карнахена — Старлинга — Квонга на насыщенные
пары.
5. Накамура, Бридвельд и Праузниц [509] вывели
уравнение для потенциала жесткой сферы, имеющее
следующий вид:
RT 1 + у + у2 + у3
V (1-у)3
(1.191)
где
а = а + Р/Т
1 ( 1 \
у = ехр I---------- I .
4И V \у + 8Т )
а
К( V + с) ’
(1.192)
(1.193)
Параметр с не зависит от температуры, но является ха-
рактеристикой вещества. Он равен нулю для неполяр-
ных веществ и имеет небольшую положительную вели-
чину для нескольких рассмотренных полярных веществ.
Для оценки as смесей необходимы параметры бинарно-
го взаимодействия. В работе [509] приведены констан-
ты для четырнадцати веществ.
6. Ишивака, Чанг и Лу [369] предложили более прос-
той, чем в уравнении потенциала жесткой сферы, член,
учитывающий действие сил отталкивания. Разработан-
ное ими уравнение записывается следующим образом:
RT 2V + b
Р =—-----
V 2V-b
а
OTV(V+b) ’
где а = ClaR2T2>5/Pc,
b = ObRTc/Pc
(1.194)
(1-195)
(1.196)
Числовые коэффициенты 0а и О* были определены ис-
ходя из давления пара и плотности насыщенных жидко-
стей для 22 веществ. Как считают сами авторы работы
[369], предложенное ими уравнение дает лучшие резуль-
таты, чем уравнения Соава и Пенга — Робинсона.
Для решения уравнений состояния на основе соотно-
шений статистической механики, кратко рассмотренных
в данной главе, необходимо гораздо больше сведений о
конкретных веществах — ограничиться критическими
свойствами и ацентрическим коэффициентом в этом
случае нельзя, а следовательно, и больше машинного
времени. Эти уравнения изучены и проверены не столь
подробно, как уравнения Бенедикта — Уэбба — Рубина
и Соава, которые были соотнесены с тысячами экспери-
ментальных данных. Более того, они не всегда имеют
теоретические обоснования, так как потенциалам жест-
кой сферы и прямоугольной ямы присущ исключитель-
но эмпирический характер и они, вероятно, нередко не-
реалистичны. Однако новые тенденции в оценке роли
члена, характеризующего действие сил отталкивания,
могут в недалеком будущем привести к ценным от-
крытиям.
Пример 1.19. Определение вторых вириальных козффь
функций
В литературе до статистической термодинамике отме-
чается, что второй зириальный коэффициент связан
потенциальной функцией и(г) следующим, выражением:
В - 2/rAci г2(1 -- ехр( - u/kT})dr, (1)
о
где No — число Авогадро, к — постоянная Больцмана.
Как правило, для решения уравнения прибегают к чис
ловому интегрированию, однако потенциал Леннарда-
Джонса
и = 4е[(аА-)12 - (о/г)6] (2)
имеет аналитическое решение
Этг пл + 0,5 <\
В = - — Noa3S ----------(£+А7)°'5', + 0'25Г ( 1 1 . (3)
3 4л! \ 4 J
Таблицы численных решений этого уравнения включе-
ны, например, в книгу [106] [(приложение Ж)], которая
также содержит список литературы по вопросам расче-
тов вириальных коэффициентов на основе различных
потенциальных функций. Применяя потенциал жесткой
сферы
получаем:
а
В = 2xNo\ Г2dr = (2r/3)2Voa3. (5)
Jo
'.'центов посредством нескольким виоов потенциальных
Уравнение состояния 95
Исходя из потенциала прямоугольной ямы
выражение
(6)
получаем
В = 2xN0
Г" > г*”
г dr + | (1 - exg>(p/RT)r2dr
Jo Jo
= (2x/3)Noa3[l + (g3 - 1)(1 - ехр(е/£Т))].
(7)
Выше приводятся графики вириальных коэффициен-
тов, рассчитанных по этим уравнениям для нескольких
значений парамегров. Путем правильного подбора па-
раметров a, s и g по крайней мере для некоторого ин-
тервала температур можно добиться довольно точного
соответствия любым экспериментальным данным о ви-
риальном коэффициенте
Для кривых 1—3, 5 значения а3 одинаковы, для кри-
вой 4 оно в 5/3 больше.
1 — прямоугольная яма, g = 1,5, о = ol/, 2 — прямо-
угольная яма, g - 2, д = аи; 3 — прямоугольная яма,
g - 2,5, а = aL;; 4 — потенциал Леннарда-Джонса, о =
~ olj', 5 — прямоугольная яма, g = 1,5, ст3 = 1,66а37
Пример 1.20. Расчет параметров потенциала прямоугольной ямы на основании данных о вторых вириальных
коэффициентах
Экспериментальные данные о вторых вириальных ко-
эффициентах:
Т, К 360 450 540
106 В, м3/моль -25,45 -17,68 - 12,96
Уравнение (7), заимствованное из примера 1Л9,
2
В = — к No а 3
3
можно для краткости записать следующим образом:
Решим уравнения относительно у:
Bt/Bi - 1
У =-------------------------- _
1 - ехр(?/7';) - [1 - ехри/72)}В-,/В2
В-л В3 - 1
=------------------- -- _ —
1 - exp(c'Ti) - [1 - exotz Гд\Bi,'Вз
После подстановки данных решаем путем подборки по-
следнее уравнение относительно z -- г/к, после чего не-
посредственно определяем параметры g и а.
В - х[1 4- XI - exp(z/T))]. (2)
Используем два значения В, чтобы исключить х.
Z - е/к = 200,25 К; у = 7,0097;
g = (1 ь vf'3 - 2,0008; .г - 6,0365(11 - Ъ,г
В<
1 + [у(1 - ехр(</1 J)} -- --- (1 з- у(1 - exp(z/r2))] (3)
В~,
2тг(6,02)(Е23), 3
-= i.685(F. - 10>м: 1,682 А);
в,
= - [Iх V(1 - exp(z/7n)]. (4)
Вз
Результаты подобных расчетов покапаны на пщ. 1.2», а
и б.
1.8. Критическое состояние
и критические свойства
1.8.1. Введение. Первые наблюдения над изменениями
характеристик веществ в критическом состоянии были
проведены при нагревании жидкостей в запаянных сте-
кляных трубках. При соответствующей величине сред-
ней плотности жидкости в трубке граница раздела сосу-
ществующих жидкой и паровой фаз в критическом со-
стоянии исчезает. Вблизи критической точки изотерма
(см. рис. 1.5) становится плоской, и для успешного про-
ведения такого эксперимента необязательно распола-
гать точными данными о плотности веществ. Феррелл
[281] приводит фотографии, иллюстрирующие поведе-
ние смеси анилина и циклогексана в процессе снижения
температуры этой смеси ниже критической. Другой гра-
фический материал и ряд сведений по истории вопроса
можно найти в работе [629]. Подробное описание и об-
ширная библиография исследований в этой области
включены в книгу [92].
По мере приближения к критическому состоянию все
характеристики двух фаз становятся тождественными,
причем многие из них претерпевают резкие изменения,
вплоть до нескольких их порядков. На рис. 1.28 пред-
ставлен ряд свойств диоксида углерода, изменение кото-
рых приобретает аномальный характер вблизи критиче-
ской точки. Традиционная методика определения крити-
ческого состояния заключается в проведении серии
измерений плотности двух фаз. На рис. 1.26 показано
два способа графического изображения эксперименталь-
ных данных с целью нахождения критической пло-
тности.
Аномальное или асимптотическое изменение физиче-
ских свойств вблизи критической точки можно доволь-
но точно представить посредством степенных зависимо-
стей, для чего имеются как теоретические, так и экспе-
риментальные основания. Иными словами, между
логарифмами двух свойств, например М и N, существу-
ет линейная зависимость:
log М = log к + р log N, (1.197)
или
M=kNP. (1.198)
96 Глава 1
На рис. 1.27 показана подобная зависимость для функ-
ции плотности насыщения
(р/рс- 1) = к{Т/Тс- 1/, (1.199)
где экспоненты имеют практически одинаковые значе-
ния (0,35) для всех трех веществ. История исследований
такого рода взаимоотношений рассматривается в ста-
тьях [438, 439].
Вблизи критической точки значения скрытой теплоты
приближаются к нулю, в то время как теплоемкость
резко возрастает, а равновесное отношение пар — жид-
кость становится равным единице.
Соответственно такие аппараты, как ректификацион-
ные колонны, испарители и конденсаторы, в которых
протекают процессы, зависящие от упомянутых
свойств, не будут выполнять свои функции, если усло-
вия их эксплуатации будут близки к критическим. Поэ-
тому очень важно знать или иметь возможность про-
гнозировать критические свойства технологических по-
токов — будь то чистые вещества или смеси. Описание
ряда корреляционных методов, которых в настоящее
время разработано уже достаточно много, можно найти
в работах [25, 107, 129, 660]. В настоящем разделе будет
рассмотрен такой аспект этой проблемы, как расчеты
критических свойств посредством уравнений состояния.
Критическая температура и критическое давление чис-
тых веществ — это та максимальная температура, при
которой еще возможно сосуществование жидкой и паро-
вой фаз. На это четко указывают изотермы диоксида
углерода и изопентана, изображенные на рис. 1.5. Одна-
ко применительно к смесям, за исключением азеотроп-
Рис. 1.26. Нахождение критических плотностей путем экстраполяции.
а — молярные плотности насыщенных паров неона и жидкого неона и их усредненные величины [303]. 1 — экспериментальные
данные, 2 — расчетные данные Маккарти и Стьюарта, полученные исходя из данных Матиаса, Кроммелина и Оннеса; б — метод
Хакала основан на допущении, что 0,5(gz. + = Qc + K(ql — er)<I0/3). Данные, указанные на этих рисунках, носят приближенный
характер. Использованный метод приведен в работе [41].
Уравнение состояния 97
Рис. 1.27. Характер изменения плотностей насыщения Н2О, SFe и Ог, соот-
ветствующий правилу степеней. Уравнение имеет следующий вид: q/qc =
= а{Т/Тс - I)*3, где /3 почти одинакова для всех этих веществ [438].
[438].
а — теплоемкость Ср значительно возрастает; б — темплоем-
кость Cv значительно возрастает; в — теплопроводность значи-
тельно возрастает; г — теплота испарения стремится к нулю;
д — коэффициент теплового расширения становится очень
большим; е — изотермическая сжимаемость достигает значи-
тельной величины; ж — число Прандтля становится большим;
з — скорость звука существенно снижается.
ных, это утверждение не всегда справедливо, и в ряде
случаев сосуществование двух фаз можно наблюдать
даже при температурах и давлениях, превышающих
критические. Такого рода поведение смесей, названное
Куэненом реверсивным, будет подробно рассмотрено в
данном разделе.
1.8.2. Чистые вещества. При рассмотрении любого
семейства изотерм на графике PV становится очевид-
ным, что точка перегиба критической изотермы совпа-
дает с критической точкой. Чтобы выразить это мате-
матически, примем, что в критической точке
(дР\
/ Т
(1.200)
7-829
98 Глава 1
Рис. 1.28 (продолжение)
Это чрезвычайно важный вывод, позволяющий выра-
зить два параметра уравнения состояния через критиче-
ские свойства. Он же привел Ван-дер-Ваальса к форму-
лировке принципа соответственных состояний. Если
применить уравнение состояния к критическим услови-
ям, то можно оценить также и третий параметр этого
уравнения.
Экспериментальные данные относительно критиче-
ского состояния довольно многочисленны. Некоторые
методы расчета основаны на данных о составляющих
компонентах. Разумеется, что для нахождения критиче-
ских свойств смесей требуются данные о свойствах чис-
тых компонентов, однако отношения между ними в
высшей степени сложны. Значения критической сжимае-
мости можно нередко достаточно точно определить ис-
ходя из давления пара путем использования ацентриче-
ского коэффициента, о чем уже упоминалось в
разд. 1.3.1.
Уравнение состояния 99
2000
U 1000
<С5
g 500
СО
СО
Е
О-
g 200
100
2,0
2,5
0 0,5
1,0 1,5
Р*=Р/Рс
Рис. 1.29. Изотермы и линии критических давлений и
критических температур смесей пропана и ацетона
[313].
7‘
100 Глава 1
Рис. 1.30. Избыточные критические давления и темпе-
ратуры некоторых бинарных смесей углеводородов
(данные API Technical Data Book, 1974).
PV = Pc - TV = Tc - ^y,Tcl.
Система 1: «-бутан—«-октан; система 2: нонан — тридекан;
система 3: бензол — тридекан; система 4'. бензол — гептан.
Рис. 1.31. Линия критических точек нескольких смесей углеводородов
(см. также рис. 6.2). Каждая комбинация Р и Т соответствует опреде-
ленному составу смеси [115].
Уравнение состояния 101
Рис. 1.32. Критические свойства тройных смесей: метан — н-бутан — декан (д) и метан — пропан — пентан (б)
(данные [115] приведены Катцем и др., 1959).
1.8.3. Смеси. Критическое состояние смесей, как и
чистых веществ, определяют как совокупность условий,
при которых свойства сосуществующих жидкой и паро-
вой фаз становятся тождественными. На рис. 1.29—1.33
показан характер изменения параметров PVT и состава
нескольких групп двухкомпонентных смесей вблизи кри-
тической точки. У смесей пропана с ацетоном в отличие
от смесей этана с гептаном зависимость критической
температуры от состава носит линейный характер. И
напротив, для обеих смесей наблюдается нелинейная за-
висимость значений критического давления от состава.
Очевидно, что для смеси этана с гептаном имеются
температуры и давления, превышающие критическую
величину, при которых продолжают сосуществовать две
фазы. Кривые 3 и 4 (рис. 1.30) наглядно демонстрируют
существенные отличия в характере изменения критиче-
ского давления смесей различных веществ. Как видно
из рис. 1.31, чем сильнее различаются критические дав-
ления чистых компонентов, тем больше величина избы-
точного критического давления смеси. Это положение
справедливо также и для трехкомпонентных смесей (см.
рис. 1.32).
На рис. 1.33 сравниваются два вида псевдокритиче-
ского давления с истинным критическим давлением для
двухкомпонентных смесей. Очевидно, что и правило
Кэя, и другое примененное здесь уравнение непригодны
102 Глава 1
Рис. !. 13 Истинные критические свойства и рассчитан-
ные но правилу Кэя псевдокритические свойства смесей
эгана и а-гептана. Нижняя кривая соответствует Рс -
- ZcR'l'c/ ^e, причем Zc, Тс и Vc получены в соответствии
с правилом Кэя [393].
для расчета величин истинных критических свойств.
Однако, кат указывалось в разд. 1.3.8, практическая
ценность псевдокритических свойств заключается в их
предпочтительном использовании при разработке урав-
нений состояния для смесей, при этом для определения
параметров этих уравнений применяют традиционные
правила усреднения свойств.
Термин «реверсивный» относится к таким парожид-
костным системам, в которых при температуре и давле-
нии выше критических количество конденсирующегося
или испаряющегося компонента, сосуществующего с
обеими фазами, изменяется в направлении, противопо-
ложном обычно наблюдаемому при изменении темпера-
туры к давления.
На рис. 1.34, а показаны три возможных расположе-
ния критической точки и максимума температуры и
давления. На рис. 1.36, б представлена реверсивная кон-
денсация смеси диоксида углерода и метилхлорида.
Первоначально объем сжижения возрастает вместе с
давлением, но после того, как давление превысит при-
мерно 81 атм, он начинает уменьшаться и при 83,3 атм
становится равным нулю. Обычно область, для кото-
рой характерно реверсивное изменение свойств, доволь-
но узка (рис. 1.34, г). Наличие сведений о реверсивном
характере изменения свойств может сыграть важную
роль в понимании процессов, происходящих в нефтяных
резервуарах. На рис. 1.34, в на графике давление— со-
став показан реверсивный характер конденсации.
За пределами критических точек может наблюдаться
еще более сложный характер изменений фазового разде-
ла; ряд сведений об этих явлениях содержится в гл. 9.
1.8.4. Расчет критических свойств при помощи урав-
нений состояния. Критическая точка соответствует на-
чинающемуся разделению паровой и жидкой фаз. Мате-
матическое представление начинающегося разделения
любых фаз, будь то жидкость — пар, жидкость — жид-
кость и т. д., одинаково. Условия устойчивого разделе-
ния фаз жидкость — жидкость рассматриваются в гл. 7
в свете происходящего при этом изменения энергии
Гиббса. Аналогичным образом условия, соответствую-
щие критической точке парожидкостного равновесия в
многокомпонентных смесях, можно выразить при по-
мощи производных химических потенциалов или парци-
альных молярных энергий Гиббса:
М,= Gi = (дС/дп{)Тр
(1.201)
Математически условия существования критической
точки, впервые описанные Гиббсом, разрабатывали
Пригожин и Дефей [102]. Относительно недавно эти ус-
ловия были обобщены (см., например, [585]). В крити-
ческой точке два якобиана равны нулю, а именно
Э(дь /л2, , Ми-1)
-----------------------„ (
<?(*!> Л?, . . . ,
д(Л, М?.. Мз. • • , Ми-1)
д(х{, х2, . . . , •¥„-!)
(1.202)
(1.203)
В стих уравнениях химические потенциалы щ можно за-
менить парциальными фугитивностями Inf,. Для би-
нарных смесей эти уравнения можно представить в сле-
дующем упрощенном виде:
(1.204)
(1.205)
(1.206)
Уравнение состояния 103
Температура
Доля сжиженной фазы
Рис. 1.34. Реверсивный характер изменения свойств
смесей.
а — три типа границы раздела фаз в координатах давление —
температура, отличающиеся друг от друга относительным рас-
положением критической точки С, максимальными давлением
Е и температурой F; ВР — кривая точек начала кипения, DP —
кривая точек росы; б — реверсивная конденсация смеси СОг и
СНзС1 (41/59) при 378,2 К в диапазоне давлений точки росы от
74,5 до 85,0 бар; петля типа в [113]; в— кривая реверсивной
конденсации, представленная в координатах давление — состав;
по линии А В конденсация достигает максимальной величины в
точке С, а по линии DE имеет нормальный характер, т. е. по-
стоянно увеличивается по мере повышения давления; г — кри-
вая реверсивной конденсации, представленная в координатах
давление — температура. В заштрихованной области наб-
людается реверсивное изменение свойств смеси. По мере пони-
жения давления по линии DH максимальная конденсация, рав-
ная 14%, достигается в точке Е В направлении линии KL вели-
чина конденсации уменьшается по мере понижения давления
(Катц и др., 1959).
104 Глава 1
или
д In ф]
дх2
(1.207)
Получив производные фугитивностей из соответствую-
щего уравнения состояния, можно найти критическую
температуру и давление или объем путем одновремен-
ного решения пары уравнений при определенном соста-
ве Xi. Поскольку уравнения нелинейны, для их решения
необходимо прибегать к ЭВМ даже при наличии всего
лишь двух компонентов. В примере 1.21 показано, как
вывести уравнение для бинарной смеси из уравнения Ре-
длиха — Квонга.
Для тройной смеси якобианы имеет следующий вид:
Разложение второго якобиана дает
d2G \ (d2G \ / B2G \2
— I (--------2 I +2 ---------- I
&х2 /Т,Р,х3\дхЗ /Т,Р,х2 \^Х2^Х3/Т,Р-
(1.210)
Читателям, желающим проверить алгебраические опе-
рации, следует обратиться к статье [254], где данные
уравнения записаны при помощи уравнения Редлиха —
Квонга.
Можно указать еще ряд более современных методов
использования указанных условий для определения кри-
тических свойств смесей. Так, авторы [378] применили
уравнение Редлиха — Квонга при изучении ряда бинар-
ных смесей и обнаружили, что для обеспечения высокой
степени точности расчета критических свойств необхо-
димо включать параметры бинарного взаимодействия.
Спиэр и др. [658] также применили скорректированное
уравнение Редлиха — Квонга для описания бинарных
смесей и провели соответствующие расчеты на ЭВМ. В
работе [609] в этих же целях применено уравнение Бене-
дикта — Уэбба — Рубина, а в работе [364] — уравнение
состояния Соава.
Изучением тройных систем занимались Спиэр и др.
[659], а также Домнина и Захаров [254]. Обе группы ис-
следователей пользовались уравнением Редлиха —
Квонга, в которое введены параметры взаимодействия.
Пенг и Робинсон [648] при помощи ранее разработан-
ного ими уравнения состояния получили данные о кри-
тическом состоянии многокомпонентных смесей, содер-
жащих вплоть до 12 компонентов. Эта же задача была
поставлена Хайдеманом и Халилом [343], применивши-
ми уравнение Соава. Последние авторы разработали
такую методику расчетов, которая позволила значи-
тельно сократить требуемое машинное время.
В результате перечисленных выше, а также ряда дру-
гих работ проблема определения критического состоя-
ния была в основном решена для большинства наиболее
часто встречаемых ситуаций. В работе [317] содержится
описание ряда сложных технологических задач, связан-
ных с вопросами фазового равновесия вблизи критиче-
ской точки.
1.9. Сравнение уравнении состояния
и предварительные
рекомендации
1.9.1. Введение. Появление в последнее время множе-
ства обзорных статей, посвященных уравнениям состоя-
ния и фазовому равновесию, свидетельствует, вероятно,
о существовании в этой области науки целого ряда не-
решенных проблем. Единым общим уравнением состоя-
ния пока мы не располагаем и вряд ли будем распола-
гать в ближайшее время. Даже уравнения, содержащие
по 30—40 констант и предназначенные для расчетов при
помощи ЭВМ, имеют значительные ограничения. По-
пытки выполнить обобщение уравнений, с тем чтобы
они охватывали более широкий круг веществ, обычно
ведут к снижению степени точности в конкретных слу-
чаях. Например, уравнение Хана — Старлинга, имею-
щее обобщенные коэффициенты, отличается гораздо
меньшей степенью точности по сравнению с соответ-
ствующим уравнением Бенедикта — Уэбба — Рубина,
коэффициенты которого меняются в зависимости от
конкретного вещества.
К уравнению состояния предъявляется целый ряд тре-
бований. Помимо традиционного расчета характера из-
менения параметров PVT при помощи уравнения состо-
яния рассчитывают давление пара, плотность жидко-
стей, фугитивности, соотношение фазового равновесия
паров, жидкости и твердого тела, а также отклонения
Уравнение состояния 105
Пример 1.21. Вывод уравнений для расчета критиче ских свойств
бинарной смеси из уравнения состояния Редлиха—
Квонга
Условие расчета выражено уравнением (1.207)
db
dy2
= -bx + b2 .
(9)
Производная ln0i
Э1пф1 _ д21пф1 _ q
дуг дуг
(1, 2)
Из табд. 3.4 уравнение для расчета коэффициента фуги-
тивности имеет следующий вид
dln0i _ bx dz _ (z - 1) db
dy2 b dy2 b dy2
dz + ____1 db
z dy2 V-b dy2
1пф, = (г - 1) - In
D
—Ц“51 ПГ “ 2-/aat
дЯТ15 b
(3)
v-b RTl5(V+b)'
2
b2
(10)
а = (1 - J2)2<7i + 72472 + 2у2(1 - J2)(<7i<72)° 5 , (5)
b = (1 - уг)&1 + УгЬг . (6)
Промежуточные производные равны
dz = И_________db
dzi (К- b)2 dyi
При помощи дополнительных расчетов можно также
вывести вторую производную. Неизвестные Т и V в
двух полученных уравнениях и будут критическими
свойствами. В табл. 1.9 величины а, b и z выражены
через Тс и Рс. Оба уравнения можно переписать, испо-
льзуя неизвестные Тс и Рс и сократив Vc, которое выра-
жают исходя из уравнения Редлиха—Квонга.
_______1_ _
RT1 5( V + Ь)2
(V+ Ь)
da , db
dy2 dy2
RTC
ЗРС ’
(Н)
~а = 2( - 2у,Д1 + у2а2 + (1 - г^^аг)0 5 ,
dy2
Полученную в результате нелинейную пару уравнений
можно решить односильно Рс и Тс.
энтальпии и энтропии от идеального состояния. Более
того, уравнения состояния можно применять для расче-
та свойств в криогенной и критической области. При
ограниченной доступности перечисленных выше данных
их можно использовать для расчетов противоположно-
го характера, а именно для разработки обобщенного
уравнения состояния. В связи с этим возникает такая
проблема, как недостаточный объем данных. Наиболь-
шее количество информации накоплено о легких углево-
дородах с числом атомов углерода, меньшим чем у н-
нонана, инертных и прочих газах, некоторых из бинар-
ных смесей этих газов и нескольких тройных и более
сложных смесях. С полярными веществами дело обсто-
ит еще хуже, только для воды и метанола получены
данные, необходимые для вывода уравнений, отличаю-
щихся широкой приложимостью.
Вместе с тем следует отметить, что разработки в
этой области продвинулись вперед значительно дальше
законов идеальных газов и исследований Рауля и Генри,
и целый ряд проблем, возникающих при разработке
технологического процесса, можно решить с высокой
степенью точности. В настоящем разделе будет рас-
смотрено использование для решения задач практиче-
ского характера пяти основных категорий уравнений со-
стояния. Рекомендуемые уравнения приводятся в
табл.1.26.
1.9.2. Рекомендации. К числу основных классов урав-
нений состояния, имеющих практическое применение,
относятся вириальные уравнения, кубические (по объ-
ему или сжимаемости), сложные уравнения типа урав-
нений Бенедикта — Уэбба — Рубина, уравнения соответ-
ственных состояний, выведенные по методу Питцера, а
также наиболее современные уравнения, рабработанные
на основе члена отталкивания потенциальной функции
жесткой сферы. Перспективная методика «групповых
вкладов», предложенная Вильсоном (727], в настоящее
время разработана еще недостаточно.
106 Глава 1
Таблица 1.26. Уравнения, рекомендуемые для выполнения оценки сжимаемости и фугитивности газовой фазы
для нескольких типов систем в определенном диапазоне параметров PVT* [677]
Тип системы Субкритическая температу- ра вне пределов области критического состояния6 Область критического состояния Сверхкритическая температура вне пределов области критического состояния
Чистые соединения: неполярные, РК, ЧРК, ИБА, РК, ЧРК, ИБА РК, ЧРК, вириальное
слабополярные сильнополярные вириальное вириальное РК вириальное, РК
Смеси: только неполярных и слабо- РК, ЧРК, ИБА, РК, ЧРК РК, ЧРК, вириальное,
полярных компонентов содержащие один вириальное РК, вириальное РК НБП РК, вириальное,
высокополярный компонент содержащие несколько вириальное РК НБП РК, вириальное, НБП
полярных компонентов Смеси вода — газ: вода и углеводород, РК, вириальное ДРК, РК НБП, ДРК, вириальное
вода и диоксид углерода Системы, содержащие аммиак ГРК, ГРК ГРК, РК
и воду Смеси с природным газом ИБА, ГРК, РК ИБА, ЧРК, РК
а В области критического состояния, как правило, велики по1решности при определении плотности, существенными могут
также быть погрешности определения коэффициентов фугитивности. Применяя вириальное уравнение следует учитывать, что
существует некоторая верхняя граница давления, за пределами которой результаты использования двухчленного вириального
уравнения либо неудовлетворительны, либо абсолютно неверны. Для большинства систем за этот предел можно принять Рг <
< (Тг - 0,65) при 77 < 1; Рг < (1,0577 - 0,35) при 77 > 1, где Pr = Р/Иу,Рс,-, Tr = T/'ZiyiTcl. Эти величины пределов были
установлены путем построения большого количества графиков для отклонения коэффициентов сжимаемости, полученных рас-
четным путем, а затем выявления той области, в которой отклонение не превышало 2% для чистых компонентов, 3% для
неполярных или слабополярных смесей и 5% для сильнополярных смесей.
6 РК:Редлих — Квонг, ЧРК:Чуэ — Редлих — Квонг, ИБА:Иоффе — Барнер — Адлер, СРКгСоав — Редлих — Квонг,
НБП:Накамура — Бридвельт — Праузниц, ДПК:Де Сантис — Редлих — Квонг, ГРК:Геррери — Редлих — Квонг.
Вириальное уравнение. Простота формы, доступность
большого количества данных (в частности, вторых ви-
риальных коэффициентов) и рациональный метод опи-
сания смесей обусловливают большую практическую
значимость вириальных уравнений даже по сравнению
с гораздо более сложными уравнениями. При значениях
давления, соответствующих Р/Рс 0,5(77Тс) или
q/qc 0,75, для нахождения фугитивности паровой фа-
зы, как правило, пригодно вириальное S-усеченное урав-
нение. Данный тип уравнения неприменим к сильно
сжатым газам или жидкостям.
Кубические уравнения. В качестве стандартных куби-
ческих уравнений в настоящее время общеприняты
уравнения API — Соава и Пенга — Робинсона, хотя в
литературе до сих пор периодически появляются опи-
сания новых разработок в этой области, оба вида куби-
ческих уравнений имеют сильных сторонников и посто-
янно применяются на практике. В оба уравнения вхо-
дят параметры бинарного взаимодействия, которые
можно найти в открытой литературе только для урав-
нения Соава. Организованное API тщательное изучение
.этих уравнений и других систем при расчете парожид-
костного равновесия показало [31], что оба они одина-
ково пригодны для решения вышеупомянутой задачи и
что, как правило, они дают лучшие результаты, чем па-
раллельно исследованные более сложные уравнения.
Уравнение Пенга — Робинсона более эффективно для
представления данных о PVT вблизи критической точ-
ки. В то же время эти уравнения дают менее точные
результаты, чем уравнение Ли — Кеслера при расчете
отклонений энтальпии. Кубические уравнения API —
Соава и Пенга — Робинсона довольно просто можно
ввести в компьютерные программы для расчета дистил-
ляции, они требуют в пять ряз меньше машинного вре-
мени, чем уравнения Бенедикта — Уэбба — Рубина —
Старлинга и им подобные. На рис. 1.23 сравниваются
экспериментальные изотермы для метана и воды и со-
ответствующие изотермы, рассчитаны е по уравнениям
Соава и Пенга — Робинсона, с тем чтобы читатель по-
лучил некоторое представление о применимости этих
уравнений.
Уравнения типа уравнений Бенедикта — Уэбба —
Рубина. Применение данного уравнения ограничивает
то обстоятельство, что его коэффициенты известны ме-
Уравнение состояния 107
нее чем для 50 веществ, главным образом углеводоро-
дов. При решении практических задач в качестве стан-
дартного принята модификация Старлинга — уравнение
Бенедикта — Уэбба — Рубина — Старлинга, однако чис-
ло известных наборов коэффициентов в этом случае еще
меньше, а параметры бинарного взаимодействия до-
ступны только для таких веществ, которые применяют-
ся при производстве и переработке легких углеводоро-
дов. Предложенный Ямадой [734] обобщенный вариант
данного уравнения, в состав которого входят 44 кон-
станты, применим при значениях приведенной плотнос-
ти до 2,8. В то же время обобщенные варианты уравне-
ния Бенедикта — Уэбба — Рубина, разработанные Ха-
ном — Старлингом, Ямадой и Нишиуми, далеко не
всегда дают более точные по сравнению с кубическими
уравнениями результаты. Модификация уравнения,
предложенная Барнером — Адлером, предназначена для
определения величин энтальпии жидкостей и равновесия
систем природного газа при криогенных температурах.
Применимость уравнения Нишиуми, распространенного
на полярные соединения, ограничена следующими зна-
чениями приведенной температуры 1 Tr С 1.3 и дав-
ления 1 Рг С 3.
Уравнения соответственных состояний. Типичным
примером уравнения соответственных состояний явля-
ется уравнение Ли — Кеслера, особенно в том виде, к
которому его приводят путем использования правил ус-
реднения свойств Плекера и др. Данный вид уравнения,
получивший название уравнения Ли — Кеслера — Плеке-
ра, или Л—К—П, можно считать наиболее точным из
всех имеющихся на настоящий момент обобщенных
уравнений, пригодным для расчета коэффициента рав-
новесия испарения, величин энтальпии и других термо-
динамических характеристик. Все сказанное не распро-
страняется только на полярные вещества. Использова-
ние данной системы уравнений полностью компью-
теризовано. Уравнение Ли — Кеслера считается спра-
ведливым для интервалов 0,3 С Тг 4 и 0 С Рг С Ю,
но, как отмечают Плекер и др., в диапазоне
0,93 Тг 1 или около того возникает ряд затрудне-
ний. Для расчетов без использования ЭВМ можно при-
менять таблицы значений сжимаемости и других
свойств как функций приведенной температуры и давле-
ния, разработанные Ли и Кеслером, а также графики,
приведенные в «Справочнике Американского нефтяного
института».
Уравнения возмущенной жесткой сферы. Разработки
в этой области, начатые относительно недавно, счита-
ются в высшей степени перспективными. Всесторонний
обзор теоретических основ этого направления исследо-
ваний был выполнен Бубликом [192], а также Роулинсо-
ном и Свинтоном [113]. Результаты изысканий, прове-
денных по инициативе Ассоциации производителей газа
(Gas Producers Associaton) и описанных Донохью и
Прузницем [255], являются достаточно надежными и
пригодными для использования. Методика, основанная
на применении данных уравнений, дает возможность
рассчитывать свойства большинства смесей, с которы-
ми приходится иметь дело при переработке нефти и
природного газа, включая смеси, компоненты которых
значительно различаются по размеру, форме и распре-
делению потенциальной энергии. Ассоциация произво-
дителей газа располагает необходимыми программами
для ЭВМ. В ходе исследований было проведено сравне-
ние расчетных и экспериментальных данных, однако
сравнения результатов, полученных этим и другими ши-
роко распространенными методами, осуществлено не
было.
1.9.3. Обзорные публикации. Поток литерутары по
вопросам уравнений состояния и фазового равновесия
привел к появлению множества обзоров, цель кото-
рых — помочь читателю разобраться в изданиях по ин-
тересующим его проблемам. Ниже приводится краткое
изложение нескольких обзорных статей, опубликован-
ных в разное время. Ввиду их значительного объема
полностью осветить содержание не представляется воз-
можным. Однако упоминание основных моментов бу-
дет в любом случае более информативным, чем простое
перечисление названий.
1. Отто [538]. Подробно рассмотрены эксперимен-
тальные методы и результаты расчетов изменения па-
раметров PVT газов. В книгу включен список, содержа-
щий 56 уравнений состояния, опубликованных до
1927 г., некоторые из них в табл. 1.2 отсутствуют. Осо-
бое внимание уделено нескольким уравнениям, и в пер-
вую очередь разработке Оннесом непосредственного и
приведенного видов вириального уравнения, коэффици-
енты которого соотнесены со значениями приведенной
температуры.
2. Партингтон [92]. В разд. 7, на который приходит-
ся около 300 страниц книги, рассматриваются свойства
газов, причем большое внимание уделяется истории во-
проса и экспериментальным методикам. В книге пред-
ставлено описание критических явлений, отношений па-
раметров PVT и уравнений, значений плотности, удель-
ной теплоемкости, вязкости, проводимости и диффузии.
Среди характеристических уравнений центральное место
занимает уравнение Ван-дер-Ваальса в его первоначаль-
ном виде. Помимо этого кратко рассматриваются не-
сколько десятков уравнений, включая вириальное урав-
нение состояния и уравнение Битти — Бриджмена. В
этой книге содержится исключительно важный справоч-
ный материал по данному вопросу.
2а. Вукалович и Новиков [136]. Примечательная осо-
бенность этой книги — подборка из 150 уравнений со-
стояния, последнее из которых датировано 1944 г. В со-
здании книги принимали участие несколько ученых из
европейских социалистических стран. Это издание по-
священо главным образом уравнению Ван-дер-Ваальса
и вириальным уравнениям, а также ассоциативной тео-
рии отклонения от идеального состояния изменения
PVT.
3. Эббот [148]. Как показано в этой книге, многие
широко распространенные уравнения состояния, приме-
няемые в особых ситуациях, представляют собой част-
ный случай обобщенного уравнения, т. е. кубического
уравнения относительно объема. Автором рассмотрены
предпосылки создания и ограничения, присущие уравне-
ниям Редлиха — Квонга, Соава и Пенга — Робинсона.
Эти уравнения достаточно хорошо сочетают точность,
простоту и общий характер.
4. Адлер и др. [154]. В статье рассмотрена возмож-
ность применения в промышленной практике ряда урав-
нений состояния. Для тех веществ, для которых извест-
108 Глава 1
ны константы, наиболее предпочтительно для практи-
ческого использования уравнение Бенедикта — Уэбба —
Рубина — Старлинга, несмотря на то, что оно требует
в пять раз больше машинного времени, чем уравнение
API — Соава. Уравнение Бенедикта — Уэбба — Руби-
на — Старлинга особенно эффективно при криогенных
температурах. В этой обширной статье приведено не-
сколько конкретных примеров, иллюстрирующих ис-
пользование двух указанных уравнений и метода
Чао — Сидера для расчета точек кипения, мгновенного
испарения Сг—С5 при давлении (0,070 кг/см2) и раство-
римости твердых веществ. Применению существующих
уравнений состояния препятствуют специфический ха-
рактер параметров бинарного взаимодействия и их ма-
лая пригодность для описания полярных веществ, не-
фтяных фракций и других сложных смесей, которые не-
просто описать при помощи криогенных свойств.
5. Бублик [192]. В статье этого ученого освещены на-
иболее современные разработки в области описания
систем посредством методов статистической термоди-
намики. Приводится изложение теории возмущения,
разработанной применительно как к чистым жидко-
стям, так и к смесям, причем основное внимание уделя-
ется выражениям, определяющим термодинамические
свойства. Исследования несферических и полярных мо-
лекул хотя и ведутся с большой интенсивностью, но
еще не закончены. В статье сравниваются некоторые
экспериментальные и расчетные данные. В списке лите-
ратуры, содержащем 200 или около того наименований,
преобладают издания, вышедшие в свет после 1970 г.
6. Кауэд и др. [235]. В статье приводятся численные
примеры, демонстрирующие влияние давления, темпе-
ратуры и состава на поведение уравнений Редлиха —
Квонга и Бенедикта — Уэбба — Рубина. Расчеты вы-
полнены для бинарных смесей метана с пропаном. Ана-
лизу подвергнуты фазовые огибающие и такие явления,
как реверсивное изменение свойств смесей. Наибольшее
внимание уделено нахождению правильного значения
корня при его выборе из трех возможных значений.
7. Кокс и Лоуренсон [237]. В статье упомянуто не-
сколько уравнений состояния, однако отсутствуют срав-
нительный анализ их достоинств и степень точности по-
лучаемых результатов. Практическую ценность пред-
ставляют включенные в данный обзор описания
методик измерения параметров PVT, в которых приве-
дены также ссылки на опубликованные ранее аналогич-
ные работы. Рассмотрен также принцип соответствен-
ных состояний, вторые вириальные коэфффициенты и
механизм ассоциации в паровой фазе. Кокс и Лоуренсон
обратили внимание на замечание Робертсона и Бэбба
(1969) о том, что им не известно ни одно уравнение, до-
статочно точно описывающее результаты их прецизион-
ных измерений.
8. Дауберт и др. [236]. 273 страницы данной статьи
посвящены главным образом проверке эксперименталь-
ных данных о равновесии пар — жидкость чистых и
смешанных жидкостей, осуществляемой при помощи
нескольких графических методов и девяти уравнений со-
стояния. В работе приводится несколько тысяч данных.
В результате удалось уточнить коэффициенты уравне-
ния Соава, распространить уравнение на водородсодер-
жащие смеси, а также описать данные о параметрах би-
нарного взаимодействия путем корректировки членов
уравнения, содержащих ацентрические коэффициенты.
Как правило, наилучшие результаты дают уравнения
Соава и Пенга — Робинсона, но Американский нефтя-
ной институт рекомендует пользоваться первым, так
как оно несколько проще. Для расчета отклонений эн-
тальпии наиболее пригодным считается уравнение
Ли — Кеслера. Как отмечают Дауберт и соавторы, что-
бы доказать предпочтительность какого-либо из урав-
нений для описания фазового равновесия или другие его
преимущества, в настоящее время необходимо проана-
лизировать огромный объем данных.
9. Дуслин [256]. В этой работе дан обзор современной
научной литературы, посвященной изучению критиче-
ских явлений, потенциалов межмолекулярного взаимо-
действия, вириальных коэффициентов, функции PVT,
термодинамических свойств и давления пара для мно-
гих веществ. Основное внимание уделено эксперимен-
тальным исследованиям. Дуслин систематизировал по
типу веществ и полученным данным и свел в таблицы
результаты ряда исследовательских работ, включая, по-
священные избыточным свойствам, функции PVT и
уравнениям состояния.
10. Фреденслунд и др. [291]. В статье рассмотрены
последние публикации, в том числе посвященные урав-
нениям возмущенной жесткой сферы, полярным соеди-
нениям, а также таким уравнениям, параметры кото-
рых можно получить при помощи метода групповых
вкладов. Данный метод считается перспективным для
описания таких смесей, как, например, продукты ожи-
жения углей, критические свойства которых не пред-
ставляется возможным определить.
11. Гиббонз и др. [303—305]. В статье дан анализ,
основанный на 2500 экспериментально найденных значе-
ниях констант равновесия уравнений Соава, Пенга —
Робинсона, Бенедикта — Уэбба — Рубина — Старлинга,
а также разработанного Маккарти уравнения, основан-
ного на принципе соответственных состояний (МПСС),
включающего 33 константы. Проведен сравнительный
анализ значений плотности пара и жидкости, констант
равновесия и точек росы. Как установлено, для расчета
плотности жидкостей уравнение соответственных состо-
яний Маккарти и уравнение Бенедикта — Уэбба — Руби-
на — Старлинга несомненно более приемлемы, чем дру-
гие более простые уравнения, однако при прогнозирова-
нии прочих перечисленных свойств преимущество этих
уравнений не так явно выражено.
12. Г})эй [316]. В статье анализируются достоинства
и недостатки модификации уравнения Редлиха — Кво-
нга, предложенной Иоффе и Зудкевичем, результаты
применения которого аналогичны полученным при ис-
следовании уравнений Соава и Пенга — Робинсона. Как
отмечает Грэй, эти уравнения вопреки ожиданиям поз-
воляют достаточно точно представить поведение сис-
тем вода — углеводород и диоксид углерода — углево-
дород. В то же время описание смесей, молекулы кото-
рых существенно различаются по размеру, гораздо
меньше соответствует экспериментальным результатам.
Широкая экстраполяция этих уравнений не представля-
ется возможной. Параметры их могут быть подогнаны
для различных интервалов величин. Завершается статья
перечнем рекомендаций (восемь пунктов), кдторые еле-
Уравнение состояния 109
дует учесть при разработке новых уравнений состояния.
13. Гренье и Кабр [757]. В статье представлено общее
описание программ для расчета дистилляции и мгновен-
ного испарения, а также термодинамических и физиче-
ских свойств с использованием одного из вариантов
уравнения Редлиха — Квонга (наименование варианта
отсутствует). Предложенные программы обеспечивают
получение достаточно хороших результатов для таких
газов, как водород, азот, кислород, монооксид углеро-
да, углеводороды.
14. Хорват [358]. Данная статья представляет собой
обзор литературы, освещающей исследования исходно-
го немодифицированного уравнения Редлиха — Квонга.
Автор приводит ссылку на 112 публикаций. Особо от-
мечены те работы, в которых результаты расчетов
сравниваются с экспериментальными данными или дан-
ными, полученными при помощи других уравнений со-
стояния. В приложении помещены уравнения для расче-
та фугитивности, отклонений энтальпии и прочих ха-
рактеристик чистых жидкостей и их смесей, разрабо-
танные на основе уравнения Редлиха — Квонга.
75. Кноблер [402]. В главе, подготовленной данным
автором для книги, посвященной преимущественно экс-
перментальным аспектам химической термодинамики,
рассмотрен ряд исследований объемных свойств газо-
вых смесей. Приводится также описание исследователь-
ских работ в области вириального уравнения состояния,
экспериментальной методики определения вириальных
коэффициентов, расчета перекрестных вириальных ко-
эффициентов, механизма ассоциации паровой фазы,
третьих вириальных коэффициентов и избыточных
функций. Цитируемая в данной главе' литература может
служить дополнением к библиографии, помещенной в
книге [85].
16. Кроликовски [409]. В этой статье приведены про-
граммы ЭВМ для расчета перегонки многокомпонент-
ных смесей и моделирования производственных процес-
сов. В описываемых программах применено десять
уравнений состояния — от уравнения идеального газа,
уравнения Соава и вириального уравнения Хэйдена —
О’Коннела до уравнения Бенедикта — Уэбба — Руби-
на — Старлинга. Как отмечает автор, несмотря на то,
что в литературе систематически публикуются разра-
ботки новых моделей, от старых моделей, как правило,
не отказываются. Если какой-либо технологический про-
цесс удается правильно рассчитать при помощи опреде-
ленной модели, эту же модель принято использовать
для прогнозирования прочих аналогичных процессов,
так как изменение старой модели в подобной ситуации
экономически необоснованно. В статье приводится при-
мер моделирования поведения смеси водорода, легких
углеводородов и нескольких кислородсодержащих орга-
нических веществ. Для моделирования паровой фазы
этой смеси применяется вариант уравнения Редлиха —
Квонга, а для жидкой фазы — уравнение Вильсона. По-
скольку в центре внимания автора производственные
процессы химической, а не нефтеперерабатывающей
промышленности, к моделям предъявляется целый ряд
требований — применимость к самым разнообразным
соединениям в широких интервалах температур и давле-
ний, а также простота и высокая скорость сходимости,
т. е. своего рода универсальный характер.
17. Лиленд [431]. В работе этого автора рассмотрены
возможные области применения уравнения Ван-дер-Ва-
альса и уравнения типа уравнения Бенедикта — Уэб-
ба — Рубина — Старлинга, а также правила усреднения
свойств смесей. Наиболее перспективными представля-
ются уравнения, включающие член, учитывающий
действие сил отталкивания, типа соответствующего
члена в потенциальной функции жесткой сферы. Приме-
ром тому может, в частности, служить уравнение Кар-
нахэна — Старлинга. В статье содержится ряд ссылок.
Для смесей предпочтение отдается модели соответ-
ственных состояний, предложенной Маккарти, в состав
которой входят члены, учитывающие действие сил от-
талкивания. Упомянут также ряд разработок в области
полярных смесей, не давших, однако, положительных
результатов.
18. Луна и Кастро [450]. В статье проведено сравне-
ние нескольких модификаций уравнения Редлиха — Кво-
нга и уравнений Хана — Старлинга и Чао — Сидера,
применяемых для расчета термодинамических свойств.
Результаты описания смесей компонентов природного
газа при помощи уравнения Соава отличаются высокой
точностью.
19. Мартин [466]. Это последняя из многочисленных
работ данного автора, занимающегося изучением урав-
нений состояния более двадцати лет. В ней сформули-
рован обобщенный вид кубических уравнений, многие
из традиционно применяемых уравнений можно рас-
сматривать как его частные случаи. Определенное вни-
мание уделено проблеме выбора оптимального вида ку-
бических уравнений, а также приведено четырехпара-
метрическое уравнение, позволяющее получить
достаточно точные результаты. Позднее Иоффе (1980)
ввел в уравнение Мартина функцию температуры, по-
добную той, которую включил в свое уравнение Соав,
чем обеспечил более высокую точность полученного в
результате уравнения по сравнению с уравнением Соава
при расчете плотности жидкой и паровой фаз, что,
однако, не сказалось на результатах прогнозирования
равновесия пар — жидкость.
20. Опфел и др. [91]. Данный труд посвящен преиму-
щественно уравнению Бенедикта — Уэбба — Рубина.
Некоторое внимание уделено уравнению Битти — Бри-
джмена, являющемуся его непосредственным предшест-
венником. В книгу включен список литературы об урав-
нениях состояния, в которой представлены 102 издания.
21. Отт и др. [537]. В этой небольшой статье выпол-
нено сравнение приведенных видов классических уравне-
ний состояния Ван-дер-Ваальса, Бертло и Дитеричи с
графиком соответственных состояний значений сжимае-
мости, полученных экспериментальным путем. Однако
результаты проведенного сравнения в настоящее время
считаются неудовлетворительными.
22. Отто [758]. В данной работе проведено сопостав-
ление результатов расчетов с применением девяти урав-
нений состояния, начиная от уравнения Ван-дер-Ваальса
и кончая уравнением Бенедикта — Уэбба — Рубина, с
данными, полученными экспериментальным путем для
таких веществ, как аргон и бутан. В некоторых случаях
результаты применения уравнений сравнивают между
собой. Приведено также тринадцать графиков, разрабо-
танных Шахом и Тодосом [631]. В работе помещены
110 Глава 1
таблицы констант уравнений Битти — Бриджмена и Бе-
недикта — Уэбба — Рубина, а также обширная таблица
коэффициентов фугитивности, найденных в ходе экспе-
риментальных исследований.
23. Пикеринг [95]. Этот обширный сравнительный
анализ уравнений Ван-дер-Ваальса, Бертло и Дитеричи
при давлениях до 1000 атм представляет значительный
интерес с исторической точки зрения, так как его автор
приводит подборку экспериментальных данных и би-
блиографию ранее издававшейся литературы. На
стр. 34 помещен список легких газов и диапазонов дав-
лений, в котором каждое из уравнений дает наиболее
удовлетворительные результаты.
24. Прузниц [565]. Как в этой, так и в следующей ра-
боте Праузница, который считается новатором в обла-
сти изучения фазового равновесия, освещено множество
проблем. Среди них условия, при которых можно рас-
считать коэффициент равновесия испарения или значе-
ния фугитивности паров. Выполнен ряд сравнений урав-
нения состояния с экспериментальными данными. И хо-
тя этот анализ показывает, что каждое из уравнений
имеет свои плюсы и минусы, содержащиеся в работе
конкретные примеры могут помочь определить их сте-
пень надежности. Значительное место отводится в рабо-
те рассмотрению коэффициентов активности жидкой
фазы.
25. Праузниц [567]. Тематика данной и указанной вы-
ше работ во многом совпадает, хотя более поздняя ра-
бота носит менее подробный характер. Праузниц приво-
дит ряд примеров применения уравнений Соава, Пен-
га — Робинсона и Ли — Кеслера, демонстрирующих
достаточную точность этих уранений при средних вели-
чинах давления. Для усовершенствования уравнений со-
стояния автор считает перспективным приложение тео-
рии возмущения и равновесия ассоциации. Он также
привлекает внимание к необходимости дальнейшей раз-
работки правил усреднения свойств смесей и изучения
воздействия различий в размерах молекул.
26. Шах и Тодос [631]. В статье выполнено сравнение
результатов применения уравнения состояния Редли-
ха — Квонга и одиннадцати других уравнений с данны-
ми, полученными экспериментальным путем для арго-
на, а также сопоставлены результаты расчетов по урав-
нениям Редлиха — Квонга, Битти — Бриджмена и
Бенедикта — Уэбба — Рубина с экспериментальными
данными для н-бутана. В уравнении Бенедикта — Уэб-
ба — Рубина отсутствовали константы для аргона. Как
было установлено, уравнение Редлиха — Квонга в об-
щем случае является не менее точным, чем уравнения
Битти — Бриджмена и Бенедикта — Уэбба — Рубина, и
более точным, чем уравнение Бенедикта — Уэбба — Ру-
бина, при описании свойств веществ вблизи критиче-
ской точки и гораздо более эффективным по сравнению
со всеми прочими из числа подвергнутых анализу урав-
нений. Среди упомянутых выше одиннадцати уравнений
состояния были уравнения Ван-дер-Ваальса, Бертло,
Клаузиуса, Дитеричи, Воля и шесть других уравнений,
разработанных для использования в данном исследова-
нии. Однако в 1968 г. Барнер и Адлер [172] выдвинули
ряд возражений против той негативной оценки, которая
была дана Шахом и Тодосом уравнению Бенедикта —
Уэбба — Рубина, и доказали ошибочность их расчетов.
27. Таракад и др. [677]. В статье рассмотрено восемь
уравнений состояния, а именно: вириальное уравнение,
исходное уравнение Редлиха — Квонга и его два вариан-
та, уравнение Соава, а также два других уравнения.
Уравнение Бенедикта — Уэбба — Рубина не было под-
вергнуто анализу, так как оно, как правило, считается
достаточно надежным, если известны значения соответ-
ствующих констант и параметров взаимодействия. Ав-
торы описывают методику применения данных уравне-
ний для расчета характеристик чистых компонентов,
смесей и неполярных систем, включая смеси вода — газ.
Как было установлено, при расчете сжимаемости газа
исходное уравнение Редлиха — Квонга дает не менее
точные результаты, чем его модифицированные вариан-
ты; исключение составляет лишь система диоксид угле-
рода — пропан. В интервале давлений от низких до
средних неполярные системы можно довольно точно
представить при помощи вириального уравнения. При
высоком давлении ни одно из вышеупомянутых уравне-
ний не отличается надежностью. В табл. 1.26 приводят-
ся рекомендации по использованию уравнений для рас-
четов свойств нескольких типов систем при различных
условиях.
28. Цонопулос и Праузниц [698]. Данная работа по-
священа главным образом тем уравнениям, которые
применимы при криогенных температурах. В общем,
случае для описания систем, плотность которых в 0,75
раз превышает критическую, можно применять вири-
альное уравнение, усеченное по члену С. Цонопулос и
Праузниц рассматривают несколько уравнений, пригод-
ных для расчета плотности жидкостей. Уравнение Бит-
ти — Бриджмена пригодно для описания систем, плот-
ность которых приблизительно равна критической, а
уравнение Бенедикта — Уэбба — Рубина — для пред-
ставления систем при плотностях, превышающих кри-
тическое значение не более чем в 1,8 раз. Вариант урав-
нения Бенедикта — Уэбба — Рубина, разработанный
Стропбриджем, был применен для описания жидкости,
плотность которой втрое больше критической. Вариант
уравнения Ван-дер-Ваальса, в состав которого включена
двадцать одна константа, можно использовать для рас-
чета свойств жидкостей, плотность которых вдвое пре-
вышает критическую. Для расчетов величин энтальпии
и коэффициентов равновесия испарения в интервале
криогенных температур пригодны, как установлено, не-
сколько вариантов уравнения Редлиха — Квонга, вклю-
чающих параметры бинарного взаимодействия. После
опубликования этой статьи для описания криогенных
жидкостей были применены уравнения типа Бенедик-
та — Уэбба — Рубина, в которые входит тридцать —
сорок констант, разработанных Бендером и ГУдвином,
а также предложенное Маккарти уравнение соответ-
ственных состояний, в состав которого входит множе-
ство констант.
29. Вихтперле [724]. Четвертая из работ этой серии
посвящена рассмотрению уравнений состояния, приме-
няемых для расчета коэффициентов равновесия испаре-
ния. Среди описываемых уравнений — несколько вари-
антов уравнения Редлиха — Квонга. Выполнен анализ
модификации правил усреднения и параметров бинарно-
го взаимодействия. Уравнение Бенедикта — Уэбба —
Рубина рекомендуется применять для расчета плотно-
Уравнение состояния 111
стей жидкостей в тех случаях, если оценка параметров
проводится на основе значений плотностей (как это де-
лают, например, при использовании уравнения Пен-
га — Робинсона). Это же уравнение дает хорошие ре-
зультаты при описании полярных соединений, не обра-
зующих сильных водородных связей, и азеотропных
систем. В обзоре литературы, посвященной уравнению
Бенедикта — Уэбба — Рубина, приведено с полдюжины
или около того модификаций этого уравнения. По-
скольку уравнения типа уравнений Редлиха — Квонга и
Бенедикта — Уэбба — Рубина дают вполне удовлетво-
рительные результаты, помимо них в статье упомина-
ется лишь несколько уравнений другого типа, главным
образом трехпараметрических. Автор дает положитель-
ную оценку методу соответственных состояний, в част-
ности уравнению Ли — Кеслера — Плекера, а также ме-
тоду сталкивающихся возмущенных жестких сфер, раз-
работанному Донохью и Праузницем.
1.4. Получите приведенные формы уравнения Лорен-
ца (1881) и два варианта уравнения Клаузиуса (1880):
Лоренц: (Р + a/V2)V = RT(\ + b/V).
Клаузис 1: [(Р + a/T(V + &)2] (И - b) = RT,
Клаузис 2: [(P + a/T(V + с)2] (V - b) = RT.
Примечание. В последнем случае можно получить лишь
частично приведенное уравнение. При V* = (V + с)/
(Рс + с) приводим уравнение к окончательному виду:
(Pr + 3/TrV*r2)(3V*r - 1) = 877 •
7.5. Найдите удельный объем эквимолярной трой-
ной смеси при давлении 40 атм и температуре 450 К,
используя уравнение Соава без учета параметров бинар-
ного взаимодействия. Ниже приведены характеристики
чистых компонентов:
1.10 Задачи
Рс, атм Тс, К
Метанол 79,9 512,6
Этанол 63,0 516,2
Ацетон 46,4 508,1
Vc, МЛ/МОЛЬ Zc ш
118 0,224 0,559
167 0,248 0,635
209 0,232 0,309
1.6. Используя три перечисленных ниже метода,
1.1. Используя уравнение состояния Клаузиуса (1880)
следующего вида:
сравните значения сжимаемости для смесей гелия и азо-
та при температуре 30 °C. Процентное содержание ге-
11 000
7\V + 0,14)2
[jz - 0,14] = 0,08206Г,
определите давление насыщения и удельные объемы
жидкой и паровой фаз в равновесном состоянии при
температуре 350 К. Примените правило Максвелла о
равенстве областей, лежащих выше и ниже давления на-
сыщения Ps в S-образной части графика Р—V, что
можно записать таким образом:
лия в смеси указано ниже.
а. Примените данные о вириальных коэффициентах,
приведенные в справочнике Ландольта—Бернштейна
II/I (1970, стр. 260), а именно:
А—В
Не—N3
А, мол. % В'-106,атм 1 С АО6, атм 2
21,608 2,099 1,505
50,747 5,066 0,597
80,349 5,590 0,141
VdP = Ps(Vg- И)- J^gPdy=0.
Предлагается, что Ps соответствует примерно 8 атм
(см. рис. 1.7).
1.2. При двух различных величинах температуры и дав-
ления плотность насыщенных паров метанола состав-
ляет
б. Примените усеченное вириальное уравнение, в ко-
тором член В определяется по уравнению Эббота, и
правила усреднения Лоренца—Бертло (см. табл. 1.5).
в. Примените усеченное вириальное уравнение, в ко-
тором член В определяется по формуле Цонопулоса, и
правила усреднения Лоренца—Бертло (см. табл. 1.5).
7.7. В справочнике Ландольта—Бернштейна, II/I
(стр. 265) приводятся следующие данные о вторых ви-
риальных коэффициентах для эквимолярной смеси про-
пана, бутана и метилбромида:
Т, °C Р, атм Q, г/мл
140 10,84 0,01216
230 68,04 0,1187
В, см3/моль
Исходя из этих данных, найдите численные значения
констант Ван-дер-Ваальса и сравните полученные значе-
ния с результатами расчета, основанного на следующих
значениях критических свойств:
Тс = 512,6 К, Рс = 79,9 атм, Ус = 118 мл/моль.
1.3. Сравните коэффициенты сжимаемости насыщен-
ных паров этилена при температуре 4,4 °C (40 °F) и
давлении 45,7 кг/см2 (654,56 фунт/кв.дюйм), используя
а) уравнение Редлиха—Квонга; б) вириальное уравне-
ние, усеченное до члена ряда, содержащего В, который
определяют по формуле Питцера—Керля; в) таблицы
Лидерсена.
Результаты сравните с экспериментально получен-
ным значением удельного объема 0,087 м3/кг (0,139 куб.
фут/фунт).
пропан бутан метилбромид
244,0 -610 - 1230 - 1040
273,0 -477 -932 -718
297,0 -394 -758 -567
321,0 -340 -635 -451
Т, К В[2, см3/моль
СзНз—СНзВг С4Ню- СНзВг
244,0 -617 -915
273,0 -474 -661
297,0 -411 -546
321,0 -356 -459
112 Глава 1
Сравните эти данные с результатами расчетов по фор-
мулам Эббота и Цонопулоса, используя правила усред-
нения Лоренца—Бертло (см. табл. 1.5).
1.8. Определите ацентрический коэффициент при по-
мощи констант уравнений давления пара (Антуан и Ваг-
нер, 1973) и критических констант:
Антуан: logP0 = А - В/(Т + С) и logP0 = А - В/Т.
Вагнер: log Р°/Рс = [(Л(1 - Тг) + В(1 - Г,.)1’5
+ С(1 - Тг)3 + Р(1 — Tr/)]/Tr.
1.9. Исследуемая смесь состоит на 2/3 из пропилена
и на 1/3 из диоксида серы, температура равна 425 К,
давление 60 атм. Определите плотность данной смеси
по уравнению Ван-дер-Ваальса при R = 0,08205
л-атм/моль-К.
1.10. Эквимолярная смесь метанола и азота при дав-
лении 100 атм и температуре 600 К расширяется в изо-
термической турбине со скоростью 1 моль/с. Применив
уравнение Соава, определите получаемую работу. Дав-
ление на выходе из турбины составляет 5 атм.
7.77. В работе [46] приведены константы равновесия
димеризации карбоновых кислот.
log К = log (Pdimer/P monomer) = А + В/Т,
где
Кислота А В
Муравьиная - 10,743 3083
Масляная - 10,100 3040
Уксусная - 10,421 3166
Пропионовая - 10,843 3316
а. Допуская, что отклонение от идеального состоя-
ния целиком обусловлено димеризацией, найдите значе-
ния сжимаемости при температуре 323, 373 и 423 К и
давлении 1, 5 и 10 атм для всех четырех кислот.
б. Сравните значения сжимаемости уксусной кисло-
ты, полученные при помощи уравнения Редлиха—
Квонга без учета димеризации и конденсации, с найден-
ными ранее значениями этой характеристики.
7.72. Проверьте приведенные ниже эксперименталь-
ные данные [385] о вторых вириальных коэффициентах
ацетона (1) и бутана (2), используя формулы Эббота,
Питцера—Керля, а также Цонопулоса и правила Ло-
ренца—Бертло.
Т, К -Ви - В22 -В12, мл/моль
282,3 2733 862 805
297,0 2268 758 656
312,0 1876 674 569
321,0 1680 635 504
7.73. Начертите изотермы приведенного уравнения
Соава для Тг = 0,9, 1,0 и 1,2 при ы = —0,2, 0 и 0,5.
7.14. Для определения третьего вириального коэффи-
циента Де Сантис и Гранд [249] применили следующие
уравнения:
С
— = Cq(Tr) + dC'(TR) + d2C”(TR),
V г
0,1961
С° =--------
„1/4
1 R
0,3972
T5r
4 °,5428 \ >
0,066847R - ~ j ехр(- TR),
< Т R /
64,5
[1 - 2,085 ехр(— Tj/)],
801,7
Используя эти уравнения, а также уравнения Цонопуло-
са для расчета вторых вириальных коэффициентов, вы-
числите сжимаемость бензола при давлении 24,15 атм и
приведенных температурах от 0,8 до 2,5. Параметр d -
= 0,0069, Тс ~ 562,1 К, Рс = 48,3 атм, Vc - 259 мл/моль,
ш = 0,215.
7.75. Покажите, что второй вириальный коэффици-
ент дается следующим выражением:
В' = lim
Р-0
Далее выразите второй вириальный коэффициент через
параметры уравнений состояния Ван-дер-Ваальса и Ре-
длиха—Квонга.
7.76. Применив соответствующие правила усредне-
ния свойств для эквимолярной смеси пропана (1), диок-
сида серы (2) и диоксида углерода (3), найдите па-
раметры
а) уравнения Ван-дер-Ваальса, принимая во внима-
ние следующие данные:
i а Ь
1 8,664 0,08445
2 6,714 0,05636
3 3,592 0,04267
б) уравнения Редлиха—Квонга с учетом следующих
данных:
и Рс Тс
И 41,9 369,8
22 77,8 430,8
33 72,8 304,2
12 56,54 399,1
13 53,97 335,4
23 74,99 362,0
в) уравнения Бенедикта — Уэбба — Рубина, исполь-
зуя данные, приведенные в этой главе.
7.77. Постройте график давления пара пиридина,
пользуясь для расчета уравнением Антуана
In/» = 16,091 - 3095,13/(7’ — 61,15),
Значения давления пара можно также вычислить по
формуле, разработанной Натом и соавторами, и при
Уравнение состояния 113
помощи уравнения Ли — Кеслера (см. разд. 1.3.3) для
интервала 1пРг(0, -40), 1/77(1,5). ш = 0,245, Тс = 620 К,
Рс = 55,6 атм. 7*" измеряются в мм рт. ст., Т — в
кельвинах.
1.18. Для газа в точке Бойля производная (д(РУ)/
дР)т = 0. Составьте уравнение, соотносящее температу-
ру либо с объемом, либо с давлением при заданных ус-
ловиях при помощи уравнения 1) Ван-дер-Ваальса и
2) Редлиха—Квонга. Данные о точке Бойля, предложен-
ные Амагатом для этилена, составляют 164 атм при
100 °C и 105 атм при 40 °C (см. [92]). Сравните эти ве-
личины с полученными в результате расчетов. Для
уравнения Ван-дер-Ваальса
а = 4,5574, b = 0,0583,
а для уравнения Редлиха — Квонга
а = 77,6030, b = 0,0404,
В качестве единиц измерения приняты атм, л/моль и
кельвины.
1.19. Составьте уравнения для следующих выраже-
ний при помощи уравнения Ван-дер-Ваальса:
1 / дУ
Коэффициент термического расширения: pl —
., 1 (Зг\
Изотермическая сжимаемость: . I .
V\aP 1 т
(^Г 1
nr, I •
дР I н
v , / дн\
Коэффициент давления энтальпии: I —- I .
\ дР / т
1.20. В «Справочнике Американского нефтяного инс-
титута» величины энтропии идеальных газов представ-
лены как функции температуры 5 = f(T). Найдите от-
ношение для функции разделения InQ, затем составьте
уравнение для расчета внутренней энергии U, выразив
ее через подобные функции температуры.
1.21. Найдите параметры Леннарда-Джонса £ и ст
для вещества, второй вириальный коэффициент для ко-
торого равен 25(10 6) м3/моль при 360 К и 11,9 (10-6)
м3/моль при температуре 540 К. Некоторые интегралы
В/No3 имеют следующие значения (см. [106])
Тк/Е -B/N<r
0,3 27,89
0,4 13,79
0,45 10,76
0,5 8,720
0,6 6,198
0,75 4,176
0,9 2,775
1 2,538
1,5 1,200
2 0,628
3 0,115
1.22. Используя результаты, полученные в примере
1.11, найдите вириальную форму уравнения Редлиха—
Квонга Р = ВТ/(У - b) - a/'/TViV + b) и уравнения
Пенга—Робинсона Р = ВТ/(У - b) - а/[К(К + Ь) +
+ b(K - Z?)].
1.23. К приведенному усеченному вириальному
уравнению
уравнению
V3r ~ 3(Tr/Pr)Vl + 3(Tr/Pr)Vr - Tr/Pr = 0,
примените метод решения кубических уравнений Карда-
на и покажите, что это уравнение имеет только один
реальный корень (см., например, CRC Handbook of Ma-
thematical Science, 1978, p. 40).
1.24. Примените критерии Полинга и др., изложен-
ные в разд. 1.5.4, для определения фазы жидкость/пар,
к которой относятся корни уравнения, найденные в при-
мере 1.13.
1.25. Тейлором и Ридом (AIChE Journal, 16, 738—
741) определены вириальные коэффициенты и критиче-
ские характеристики H-CeFu (и прочих перфторгекса-
нов). Ниже приводятся некоторые из этих величин.
т, К В, л/моль С, (л/моль)2
395,56 -1,051 0,25
415,48 - 0,920 0,23
432,68 -0,818 0,21
451,55 -0,725 0,20
Рс = 18,1 атм, Тс = 451 К, Ус = 0,555 л/моль,
ш = 0,483.
а) Определите величины сжимаемости, принимая во
внимание оба коэффициента (В и С).
б) Определите величины сжимаемости, принимая во
внимание только один коэффициент В.
в) Найдите вторые вириальные коэффициенты и со-
ответствующие значения сжимаемости, используя урав-
нение Цонопулоса. Давление составляет 10 атм.
1.26. Исходя из уравнения состояния Ван-дер-
Ваальса, составьте уравнения для
а) эффекта Джоуля: (дТ/дУ)у,
б) разности теплоемкостей: Ср - Cv.
1.27. Получите уравнение, описывающее зависи-
мость между Т и V для обратимого адиабатического
процесса в вандерваальсовом газе. Прежде всего следу-
ет найти (3773 V)s как функцию Т и V.
1.28. При помощи приведенного уравнения Ван-дер-
Ваальеа определите цСр/Ус как функцию Рг и Тг для
возможных переменных величин.
1.29. Точкой инверсии Джоуля—Томсона называют
температуру, соответствующую началу перехода от на-
гревания к охлаждению при дросселировании. Миллер
[483] предложил следующее уравнение, соотносящее экс-
периментально полученные данные:
Рг = 24,21 - 18,54/7/ - 0,825 Т*.
Эти данные показаны на приведенном ниже рисунке.
В заданном интервале условий определите соотно-
шения (Рг, Тг) для точки инверсии, исходя из а) вири-
ального уравнения, усеченного по коэффициенту С;
б) уравнения Редлиха—Квонга; в) уравнения Соава,
ацентрический коэффициент которого равен 0,5; можно
принимать во внимание любые другие величины, кото-
рые могут представлять интерес.
8-829
114 Глава 1
1.30. В ходе экспериментальных исследований дрос-
селирования при давлении 20 атм и двух различных
температурах были получены следующие значения ко-
эффициентов Джоуля—Томсона:
Г, К К л/моль jiCp
600 2,11 0,98
700 2,60 0,72
Допуская, что поведение газа соответствует уравнению
Ван-дер-Ваальса, найдите константы а и b для данного
вещества.
1.31. Вириальное уравнение, усеченное по коэффици-
енту В, записывают как z ~ 1 + BP/RT. Проведите под-
становку V - zRT/P в стандартное уравнение z = 1 +
+ В/V и сравните полученные значения z с рассчитан-
ными на основе первого уравнения. Величины BP/RT
варьируют в интервале от -0,25 до 0,25.
1.32. Плотность этана при температуре 25 °C и раз-
личных величинах давления составляет
Р, атм 10 20 30 40
е,
моль/л 0,4447 0,9893 1,7227 3,0817
Найдите второй и третий вириальные коэффициенты.
1.33. В уравнении Гугенгейма второй вириальный ко-
эффициент выражен в виде функции температуры:
BIVC = 1,51 - 1,60 ехр(0,936Тс/Л-
Для этана Ус ~ 142 мл/моль, а Тс = 305,7 К. Определи-
те температуру, при которой удельный объем этана при
давлении 100 атм будет вдвое меньше, чем при давле-
нии 75 атм и температуре 400 К.
1.34. Используя уравнение Соава, ацентрические ко-
эффициенты которого равны 0, 0,5 и 1,0, найдите вели-
чину работы, требуемой для сжатия газа от Рг = 0,2 до
Рг - 10 при Тг = 1,2. Запишите результаты в виде отно-
шения W/PCVC. Наиболее точным для решения этой за-
дачи будет уравнение Соава, формулировка которого
приводится в примере 1.16.
7.35. Уравнение состояния, предложенное Волем
[732]
RT а с
Р~ У-b ~ ТУ(У-b) + Т4/3У3 ’
можно записать как следующий полином:
Г4- (b + RT/P)V3+ аУ2/РТ — cV/PT^/3+ bc/PT^3= 0.
Выведите приводимые ниже отношения для парамет-
ров, выраженных через критические свойства
a =6V^PCTC- b = Vc/4 = RTC/15PC;
с — 4У3РСТ^3- RTC/PCVC= 15/4 = 3,75
и запишите данное уравнение состояния в приведенном
виде.
1.36. Уравнение Ван-дер-Ваальса, в которое введен
член потенциальной функции возмущенной жесткой сфе-
ры, учитывающий действие сил отталкивания, имеет
следующий вид:
RT
fl +у +у2- у3 \
(1-П3 /
а/У2,
где у = Ь/4У. Покажите, что при помощи следующих
формул можно правильно выразить параметры через
критические свойства:
a/RTcy(.= 1,38(9/8),
Ь/Ус = 0,5216(1/3),
zc = 0,359(3/8).
Числа в скобках приведены для сравнения, они соответ-
ствуют значениям параметров исходного уравнения со-
стояния Ван-дер-Ваальса.
1.37. В монографии [127] Старлинг приводит сле-
дующие данные:
Р, атм
У, л/моль
Т, К
40,82
0,2583
355,4
27,21
0,5864
456,4
Найдите а) параметры уравнения Ван-дер-Ваальса,
б) параметры уравнения Ван-дер-Ваальса, в которое
введен член потенциальной функции возмущенной жест-
кой сферы, учитывающий действие сил отталкивания
(см. задача 1.36).
1.38. Фтороводород в газовой фазе образует ди-,
гекса- и октамеры. Константы равновесия Кр составля-
ют [620]’
К2 = ехр(6429,73/Т- 24,171),
К6 = ехр(21011,97/7’— 69,7327),
Ks = ехр(25225,72/7’— 83,4731).
Определите величину сжимаемости исходного вещества
при давлении 20 атм и температуре 400 К.
Уравнение состояния 115
1.39. В работе Когана (1967) приводятся следующие
уравнения для расчета вторых вириальных коэффициен-
тов для пропилена (1) и диоксида углерода (2), выра-
женные в мл/моль:
38 360 2,3184(E9)logT
11 р •j'l
для интервала температур 315—345 К. Определите па-
раметры функций Леннарда-Джонса и потенциала пря-
моугольной ямы, которые как можно более точно соот-
ветствуют вириальным коэффициентам, полученным
экспериментальным путем (см. пример 1.19).
1.43. В работе Кейеса и Беркса (1927) помещены сле-
дующие экспериментальные данные, йолученные для
метана:
/-291,61 + 102,87 logr
522 = 1,000 ----------------------
V, мл/моль 320 320 320 640 640 640
Т, °C 0 100 200 0 100 200
Р, атм 60,13 92,24 121,81 32,297 46,474 60,486
4 810 1,393(Е7)
12 гр + pi
Параметры уравнения Ван-дер-Ваальса, выраженные в
атм, л/моль, К, составляют а\ = 8,379, аг = 3,592,
Ъ\ = 0,08272, Ьг = 0,04267. Используя вириальное урав-
нение состояния и уравнение Ван-дер-Ваальса, найдите
значения сжимаемости при давлении 20 атм и темпера-
туре 400 и 600 К для смесей, у которых Xi = 0, 0,5 и 1,0.
1.40. В работе [385] даны значения вторых вириаль-
ных коэффициентов для пропана, бутана и метилброми-
да. Определите величины сжимаемости при нескольких
различных температурах для эквимолярных смесей.
Т, К В, см3/моль
С3Н8 СШю СНзВг
244,0 -610 -1230 -1040
273,0 -477 -932 -718
297,0 -394 -758 -567
321,0 -340 -635 -451
Т,- К В\2, см3/моль
СзН8—СНзВг СдНю—СНзВг
244,0 -617 -915
273,0 -474 -661
297,0 -411 -546
321,0 -356 -459
1.41. Второй вириальный коэффициент (мл/моль)
тетрахлорида углерода определяется по уравнению
В = 575 - 2Е8/Т2
для интервала температур 315—345 К (Коган, 1967, стр.
400). Найдите параметры потенциала прямоугольной
ямы, которые как можно более точно соответствуют
этим данным (см. пример 1.19).
1.42. Второй вириальный коэффициент (мл/моль)
для нитрометана определяется при помощи следующего
эмпирического уравнения:
в = 100 - 4,19(Е5)/Т- 1,91(Е23)/Г2
Найдите оптимальные величины констант уравнений
Ван-дер-Ваальса и Редлиха—Квонга и сравните их с ве-
личинами, полученными при расчете на основе критиче-
ских свойств.
1.44. Как следует из рис. 1.19, на изотермах вириаль-
ного уравнения, усеченного на члене с коэффициентов
С, отсутствуют точки минимума. Покажите, что, если
dPr/dVr = 0, Vr = 1 и Рг = Тг и что данная точка явля-
ется точкой перегиба, а не минимакса.
1.45. Постройте изотермы приведенных уравнений
состояния Бертло и Дитеричи при Тг, равном 0,9, 1,0
и 1,2.
32Гг 16
Pr~ 9(Кг-0,25) 3TrVj ’
Тг Г ( 1
Интервал для Рг составляет от -2 до +4, для Vr —
от 0 до 2. Объясните специфику изменений графиков
вблизи критической точки.
1.46. Установите области метастабильного состоя-
ния по рис. 1.7. Уравнение Ван-дер-Ваальса, описываю-
щее свойства уксусной кислоты при температуре 500 К,
имеет следующий вид:
(Р+ 17,59/И2)(К- 0,1068) = 0,08205Г.
При помощи этого уравнения найдите пределы области
метастабильного состояния. Обратите внимание на то,
что в соответствии с решением (дР/дУ)т = 0 существу-
ют три точки минимакса, одна из которых физически
неосуществима. Постройте полную изотерму, на кото-
рой находились бы все точки минимакса.
1.47. Газообразная смесь четырех веществ имеет сле-
дующий состав: 60% А, 20% В и по 10% С и D. Допу-
стим, что константы равновесия димеризации аналогич-
ны константам равновесия кислот, которые приведены
в задаче 1.11 в том же порядке. Найдите значение сжи-
маемости z, исходя из того, что отклонение от идеаль-
ного состояния полностью зависит от процесса димери-
зации. Решите задачу при давлении, равном 0,5 атм, и
температуре 300 и 325 К.
8*
116 Глава 1
1.48. В «Chemical Engineer’s Handbook» (1973) приво-
дятся величины удельного объема изобутана при не-
скольких значениях давления и температуре 104,4 °C
(220 °F):
Р, фунт/
кв.дюйм: 50 100 150 200 250 300
V, куб. фут/
фунт: 2,379 1,1278 0,7091 0,4977 0,3649 0,2696
Сравните эти величины и значения, рассчитанные по
а) уравнению Редлиха—Квонга (а и b взяты из табл.
1.9); б) уравнению (1.1896), где а = 1,463 RT{C'S Vc,
b = 0,3326 Vc, Vc = 0,263 л/моль; в) уравнению (1.1896)
(см. п. «б») при Vc = 0,3157 RTc/Pc', г) уравнению Со-
ава. Выразите результаты в виде соотношения расчет-
ных и истинных величин давления для каждого значе-
ния объема.
2. ТЕРМОДИНАМИЧЕСКИЕ ФУНКЦИИ И РАВНОВЕСИЕ
В данной главе рассмотрены термодинамические
функции, используемые при изучении фазового и хими-
ческого равновесия, причем основное внимание уделено
тем из них, которые важны для определения равновес-
ного состояния и оценки изменения энергии, сопровож-
дающего переход из одного равновесного состояния в
другое. Однако детального описания всех уравнений, ко-
торые могут быть полезными при решении указанных
задач, мы приводить не будем. Основные соотношения
для наглядности сведены в таблицах, ряд таких таблиц
помещен в приложении А.
2.1 Термодинамические функции
Величины изменений функций сохранения энергии
определяются собственно теплотой, работой и перено-
сом массы. Основная характеристика такого вида —
это внутренняя энергия U, которая связана с другими
характеристиками в объединенной формулировке перво-
го и второго законов термодинамики:
dU= d(nU) = dQ — dW+^dy/dn^n dni (2.1)
= TdS ~ Pdy + 'Luidni, (2.2)
где щ — изменение внутренней энергии системы на
моль вещества i, происходящее при постоянных энтро-
пии и объеме. Другие эквиваленты будут даны позднее.
Внутренняя энергия является функцией независимых пе-
ременных 5, И Ль П2 ..., и ее можно записать в виде
следующего выражения:
U= U(S, V, п j, п2, . . . ). (2.3)
Путем преобразования уравнения (2.2) можно получить
несколько важных результатов. Так, подставляя в него
Ц = nU, S_- nS, V = nV и nt = пх,, получаем
d(nU) - Td(nS) + Pd(nV) - SMzd(nxz)
= (dU - TdS + PdV - Z^dx^n
вательно,
dU = TdS — PdV + ZjU.zt/xz,
U — TS - PV+Zxifii.
(2.5)
(2.6)
Если состав рассматриваемой системы не меняется,
уравнение (2.5) приводится к известному виду
dU = TdS-PdV. (2.7)
После дифференцирования уравнение (2.6) можно пре-
образовать следующим образом:
dU- TdS + PdV- 'LiLidxi— (SdT- VdP + Sxz^) = 0.
(2.8)
С учетом уравнения (2.5) приведенное в скобках выра-
жение также равно нулю, и, следовательно, уравнение
(2.8) можно записать как
= - SdT + VdP = (dG/dT)PdT+ (дв/дР^Р
(2.9)
Это соотношение, представляющее собой одну из форм
уравнения Гйббса—Дюгема, получило широкое распро-
странение.
Другие полезные термодинамические функции — эн-
тальпия (Н), энергия Гельмгольца (А) и энергия Гиббса
(G) — характеризуют внутреннюю энергию системы;
они приведены в табл. А.З и более подробно будут
освещены позднее. Можно показать, что в определен-
ных условиях эти различные термодинамические функ-
ции связаны с совершаемой работой довольно просто.
Энергетический баланс замкнутой и проточной откры-
той систем описывается следующими соотношениями:
dU = dQ- dW = TdS-PdV, (2.10)
dH = dQ ~dWs = TdS + VdP. (2.11)
Соответственно работа обратимых процессов в изотер-
мических или адиабатических условиях может быть
описана и систематизирована так:
+ (U~ TS + PV - Xxi/i^dn = 0. (2.4)
Поскольку n и dn выбираются произвольно, каждое
выражение в скобках в отдельности равно нулю, следо-
Тип системы Режим Работа процесса
Закрытая Адиабатический -dU (2.12)
Закрытая Изотермический -dA (2.13)
Открытая Адиабатический -dH (2.14)
Открытая Изотермический -dG (2.15)
118 Глава 2
Пример 2.1. Открытая система
Указанную систему проще анализировать, исходя из
уравнения для внутренней энергии
dU_ = d(nU) = ndU + Udn
— dQ — + EHinditin ~~ EHoutdnout (1)
а не уравнения (2.2). В уравнении (1) энергия, отнесен-
ная к молю вещества т, пересекающего границу систе-
мы, совершает работу потока Р/И, и складывается с его
внутренней энергией, что в сумме дает его энтальпию,
Н,. Если только один поток пересекает границу и если
он направлен внутрь системы, уравнение принимает вид
ndU = dQ - dW + (Нт - U)dn.
Вводя
dU = CvdT,
dH = CPdT,
получаем
T T
H - и = РоИо + Г CpdT - J CvdT,
Ta To
(3)
(4)
(5)
где индекс 0 относится к произвольно выбранному
стандартному состоянию. Прежде чем интегрировать
уравнение (2), на уравнение энергетического баланса на-
кладывают некоторые условия, например взаимосвязь
между пи Г. Задача 2.18 является таким специфическим
примером.
С этими уравнениями работы связаны некоторые тер-
мины, использовавшиеся в прошлом, например термин
«максимальная работа» (А), «свободная энергия» (кото-
рая может превращаться в работу G), но все эти термо-
динамические функции имеют множество применений,
не будучи связанными непосредственно с совершенной
работой и передачей тепла.
Интегральные и дифференциальные формы Н, А и
Рис. 2.1. Энергия Гиббса метилхлорида как функция
температуры и давления.
Точки на поверхности представляют равновесные состояния.
Одна из показанных при Р = 50 фунт/кв. дюйм и Т = 560 °R
свободных точек при G = +10 брит. тепл. ед./фунт соответ-
ствует неравновесному состоянию, а другая при G =
= -ПОбрит. тепл. ед./фунт физически невозможна; равновес-
ное значение G равна - 24,93 брит. тепл. ед./фунт (данные
Chemical Engineers Handbook, 1973).
G получаются из уравнений (2.5) и (2.6) подстановкой
Н = U + PV, А = U - TS и G = U + PV - TS:
Н = TS + ZXiPi, (2.16)
А = - PV+ZXjPi, (2.17)
G = SxZMz, (2.18)
dH = TdS + VdP + 'Lp.idXi, (2.19)
dA = — SdT — PdV +'Lp./dXj, (2.20)
dG = - SdT + VdP + Zp-idxi. (2.21)
Эти термодинамические соотношения тесно взаи-
мосвязаны, и их можно использовать для количествен-
ной оценки параметров, трудно поддающихся измере-
нию. В табл. А.4 приведены величины некоторых из
легкоизмеряемых параметров, а именно сжимаемости,
теплоемкости, коэффициента Джоуля—Томсона, и урав-
нения, используемые для расчета их величин, а также,
чтобы картина была более полной, указаны давление,
температура, объем и состав систем.
Хотя на практике лишь считанные вещества ведут
себя как идеальный газ, их поведение представляет ин-
терес как предельный случай. Основные термодинами-
ческие характеристики идеальных газов представлены в
табл. А.5, а табл. А.6 суммирует изменения их характе-
ристик в некоторых обычных процессах. Другие пре-
дельные соотношения преимущественно для смесей, на-
пример законы Генри, Рауля и Льюиса — Рэндалла, ис-
пользуются в последующих главах. В табл. А.2
представлено несколько именных термодинамических
уравнений.
2.2. Фундаментальные уравнения
Функциональное соотношение для системы постоян-
ного состава
U = U(S, V),
(2.22)
известно как фундаментальное уравнение, поскольку вся
термодинамическая информация о такой системе выво-
дится из этого соотношения, как вскоре это будет пока-
зано. Математического выражения такого уравнения не
Термодинамические функции и равновесие 119
существует, и его следует разрабатывать эмпирически;
такая работа выполнена для очень немногих веществ.
Используя методы статистической механики (см., на-
пример, разд. 1.7), можно прийти к теоретическим
уравнениям, выраженным через функции распределения.
Естественно, что такой процесс разработки фундамен-
тальных уравнений нельзя рассматривать как ординар-
ный рабочий этап. Тем не менее концепция фундамен-
тальных уравнений является обнадеживающей. Отноше-
ния между другими группами переменных записывают-
ся следующим образом:
H=H{S, Р),
А=А(Т, V),
G=G(T, Р).
(2.23)
(2.24)
(2.25)
Эти зависимости развивались естественным путем,
однако математически они выводятся из исходного фун-
даментального уравнения (2.22) с помощью преобразо-
вания Лежандра [86]. Другая группа переменных, из ко-
торых получают все другие термодинамические данные,
f(P, V, Т, Ср1) = О, (2.26)
включает уравнение состояния PVT и теплоемкость при
давлении, равном нулю, или в состоянии идеального га-
за. Поскольку переменные уравнения (2.26) относятся к
числу наиболее легко измеряемых, эта зависимость ис-
пользуется очень широко и обычно не как единственное
уравнение, а в виде ряда соотношений между указанны-
ми переменными.
Из табл. 2.1 действительно видно, что все термоди-
намические свойства можно представить каждой из че-
тырех групп соотношений (по три переменных в каж-
дой): (U, S, V), (Н, S, Р), (А, Т, V) или (G, Т, Р), хотя
это и не является формальным доказательством выше-
сказанного.
Так, например, в таблице записано
G=U-S(dU/dS)v~V(dU/dV)s (2.27)
= Н - S(dH/dS)p (2.28)
= A-V(dA/dV)T (2.29)
= G(T, P). (2.30)
Эти же соотношения можно также представить через
(Р, V, Т, Ср). Так, в примере 2.2 развивается представле-
ние о Н - РГй, в то время как в примере 2.3 выводятся
выражения для Н - FTd и S - Sld и показывается, ка-
ким образом можно получить из них другие характе-
ристики.
Хотя переменные Р и V связаны между собой по-
средством уравнения состояния, в зависимости от слож-
ности решения того или иного вида этого уравнения
одна из переменных может оказаться более предпочти-
тельной для представления изменений термодинамиче-
ских характеристик.
Этот вопрос рассматривается в разд. 2.7. В примере
2.2 конкретное уравнение состояния можно разрешить
и относительно Р, и относительно V Никаких преиму-
ществ использование той или иной переменной в дан-
ном случае не дает, однако во многих других ситуациях
выбор переменной играет важную роль.
Наиболее легко получить соотношения между тер-
модинамическими характеристиками, включающие пе-
ременные Р, V и Т. Если уравнение (2.26) выполняется
при всех условиях, все производные могут быть выра-
жены через указанные переменные и теплоемкость иде-
ального газа. В настоящее время разработано несколько
методов для таких переходов, самым простым и наибо-
лее известным из них является метод Бриджмена [26].
Как показано в табл. А.7, все производные включают
переменные 7] Р и 5 и наиболее легко поддающиеся из-
мерению производные (dV/dT)p, (дУ/дР)т и Ср =
(дН/дТ)р. Метод Бриджмена включает также определе-
ние вторых производных. Другой, возможно более об-
щий, подход разработан Шоу [634]. Этот подход был
позднее обоснован Шервудом [119] и упрощен Кэрро-
лом [215]. Метод, предложенный Моделлом и Рейдом
[86], включает сжимаемость z = PV/RT и удобен для
использования с соответствующими корреляциями со-
стояния или уравнениями состояния с г в явном виде.
Так, например, схему Бриджмена можно применять
для нахождения производных U и Н по 5 при постоян-
ной температуре. Производные такого типа представлен
ны в табл. А.7.
dU ]
JS Jr (dS)T
Полезность этой таблицы при нахождении необычных
комбинаций переменных иллюстрируется задачами,
приведенными в конце этой главы. Несколько «правил
частного дифференцирования», представленных в при-
ложении Б, могут быть также полезны при разработке
соотношений между производными.
Таблица 2.1. Термодинамические свойства, выраженные через переменные каждого из четырех фундаментальных уравнени
Фундаментальное
20 Глава 2
Термодинамические функции и равновесие 121
Пример 2.2. Изменение энтальпии в результате изменения температуры и
давления при известных уравнениях состояния и теплоемкости для идеального газа
Представленный на рисунке переход из состояния (Hi,
Ti, Pi) в состояние (Н2, Тъ Р2) включает изотермическое
снижение давления до нуля, нагрев при нулевом давлении
и последующее изотермическое сжатие до некоторой ко-
нечной величины. Уравнения состояния, выраженные и че-
рез давление, и через объем, будут получены и проиллю-
стрированы с помощью В-усеченного вириального уравне-
ния (ограниченного членом, содержащим В).
Начнем с дифференциала
dH = CpdT + [V - T(dV/dT)P]dP (1)
Для описываемого пути интеграл задается выра-
жением
Н2- Hl = - - T(dV/dT)p]@TdP + \Tr-c'ddT +
+ (Чи- T(dV/dT)p]@TdP. (2)
Если используется уравнение состояния, содержащее в
явном виде давление, то необходимо провести его интегри-
рование по объему. Начнем с выражения
dH = d(PV) + dU = d(PV) + CvdT + [T(dP/dT)v - P]dV,(3)
которое в интегральной форме записывается следующим
образом:
Н2- Hi = P2V2 - P1V1 + J£(C’d - R)dT -
- [ЧТ(ЭР/ЭГ)( - P\@Tdv +
+ ^{T(dP/dT)v - P]@1dV. (4)
В-усеченное вириальное уравнение можно выра игг ь ли-
бо через давление
Р - RT/(V - В), (5)
либо через объем
V = RT/P + В. (6)
Требуемыми производными являются
(= R + dB (7)
\дт) р р + dT
(др\ R RT dB ,0,
\дт) р V - В (V - В)2 dT
Запишем уравнение, выраженное через объем, в интеграль-
ной форме:
Соответствующее изменение энтальпии определяется как
ъ - Hl = j zcpddT - @TPi +
+ (в - Td~]^p2 . (10)
\ dT/ ®T1-
Для уравнения, выраженного через давление, получаем
RT2 dB = ^dB
V - В dT dT
и определяем изменение энтальпии как
Н2 - Hi = P2V2 ~ Pi И + I - R\dT г
J 7i
Пример 2.3. Термодинамические характеристики, получаемые из данных о Р, V, Т и Ср, и эквивалентное фунда-
ментальное уравнение
Выбирают в качестве стандартных такие температу-
ру ТЬ и давление Ро, при которых система ведет себя
как идеальный газ. Используя уравнение состояния, раз-
решимое относительно объема, получаем
V = f(P, Т), (1)
Н = Нт + \^(dH/dP)rdP = Нт„ + ^c'dT +
+ [° [И - T(dV/dT)P]dP, (2)
122 Глава 2
S -= S(T0, Р») +
Cp dT +
T
dP =
(3)
= S(T0, P0) + [ c^dT - [ (aiA dR (4)
I I I \ о / /
<4 J p, \ /
Теплоемкость дается соотношениями
Все подынтегральные выражения оцениваются при
конечной температуре системы. Если уравнение состоя-
ния представлено как Р = f(T, К), сначала удобнее най-
Стандартные условия обычно соответствуют темпе-
ратуре 298,15 К и давлению, равному 1 атм. Однако их
значения исключаются из уравнения, если рассматрива-
ются отклонения от идеальности. Другие свойства вы-
водятся из Н и S. Таким образом,
ти внутреннюю энергию и энтропию, начиная с
G = Н - РК (5)
А - U TS = Н - РК - TS. (6)
G =-- Н - TS. (7)
dU = (Q - R)dT +
dS = Ср - RdT -
Т
др\
дт)
dK.
dK
(Ю)
(И)
После интегрирования следует вернуться к уравнени-
ям (5)—(7).
Рис. 2.2. Фундаментальные термодинамичесй
поверхности.
а — поверхность энергия Гиббса — давлеи
температура для натрия [69]; б—поверхности
гия Гельмгольца — температура — объем для ни
[69]; в — поверхность энтальпия — энтропия—л
ние для этилена, основанная на уравнении состя
Редлиха — Квонга и полиномиальном уравнении
теплоемкости (К. Р. Jolls, статья представлена на)
смотрение в J. Chem. Education).
Термодинамические функции и равновесие 123
2.3. Общие и специфические свойства
Если рассматриваемые процессы сопровождаются
изменением массы или состава системы или входящих
в нее отдельных фаз, то необходимо проводить разли-
чие между общим (М) и удельным свойством системы,
отнесенным к единице ее массы (Л/). Об этом различии
уже упоминалось в разд. 2.1, а теперь оно будет рас-
смотрено подробнее.
Общее свойство системы обычно обозначают бук-
вой, подчеркнутой снизу. Для чистого вещества
рактеристик системы:
М = пМ,
(2.31)
В дифференциальной форме это выражение записывают
так:
с?М = п dM + М dn.
(2.32)
Если М является функцией двух переменных X и У, а
также числа молей нескольких веществ, то
М = М(Х У, п j, п 2, . . . ),
и
(2.33)
dM = d(nM)
d(nM)
dY
d(nM)
dn.
(2.34)
Производные термодинамических функций U, Н, А и G
по числу молей, обозначаемые специальными сим-
волами,
(2.35)
получили название химических потенциалов. Их можно
также рассматривать как парциальные молярные свой-
ства, если независимыми переменными X и Y являются
Т и Р. Частные формы уравнения (2.34), соответствую-
щие четырем фундаментальным уравнениям, записыва-
ются следующим образом:
dU = TdS ~ PdN_ + Zpidnt, (2.36)
dH = TdS + VdP + Zmdnt, (2.37)
dA = ~ SdT - PdN + ZfjLjdni, (2.38)
dG=~ SdT + NdP + 'Lpidnj. (2.39)
(2.40)
Вследствие важности Т и Р как независимых пере-
менных химический потенциал обычно рассматривают
как производную энергии Гиббса по числу молей, кото-
рая также является парциальной молярной энергией
Гиббса. Названия и Символы взаимозаменяемы.
Pi = Gi = (dG/dni)TPnj. (2.41)
Уравнения (2.9) и (2.21) выражают важные соотноше-
ния, связывающие энергию Гиббса и химические по-
тенциалы.
Анализ уравнения (2.36) вскрывает простую интер-
претацию физического смысла производных по числу
молей. Для систем постоянного состава передача энер-
гии посредством обратимых процессов идентифициру-
ется как
dW = PdV = - dU (при dQ = dn = 0), (2.42)
dQ = TdS = dU (при dlP= dn = 0), (2.43)
dU=p.dn (при dQ = dW=Q). (2.44)
Поскольку давление — это движущая сила при со-
вершении работы, а температура — это движущая сила
при передаче тепла, Р можно рассматривать как движу-
щую силу передачи внутренней энергии, сопровождаю-
щую перенос массы через границу системы.
2.4. Парциальные молярные свойства
Поскольку Т и Р представляют собой важные харак-
теристики системы, которые легко поддаются измере-
нию и контролю, фундаментальное уравнение энергии
Гиббса считается наиболее полезным.
G — G(T, Р, п j, п 2, ... )
(2.45)
В дифференциальной форме оно записывается следу-
ющим образом:
dG =
дG \ / dG \
— I + S -= dnj
Tn \dnj /ТРп.
(2.45а)
= - SdT+NdP + ZGidnt.
(2.46)
Если эти уравнения не выражают через п, они становят-
ся идентичны уравнениям (2.5) и (2.19)—(2.21).
Химический потенциал можно выразить через лю-
бую из четырех основных групп термодинамических ха-
Как следует из последнего уравнения, частная производ-
ная по числу молей данного вещества при постоянных
Т и Р обозначается специальным символом G,, полу-
124 Глава 2
чившим название парциальной молярной энергии Гиб-
бса. Это также химический потенциал /и, входящий в
уравнение (2.40). С учетом этого символа уравнения
(2.18) и (2.21) принимают следующий вид:
dG = ZGldxl
(2.47)
(2.48)
И как следует из этих уравнений, энергия Гиббса смеси
аддитивна парциальным молярным энергиям Гиббса.
Другие молярные производные при постоянных
температуре и давлении также получили название пар-
циальных молярных свойств системы. Согласно обще-
му определению,
М,=
д(пМ)
dni
(2.49)
К числу важных свойств такого рода относят
S, V, z, U, Н, A, G, Ср, Cv, 1п/ и 1пф.
Все эти свойства, за исключением связанных с фуги-
тивностью, соответствуют соотношению
M^'LxiMi. (2.50)
Для фугитивности парциальная молярная зависи-
мость записывается следующим образом:
1п(ЛА/) = (д(п \nf)/dni)TP„j, (2-51)
и это выражение входит в уравнение (3.15). Логарифми-
ческие формы записи относят к этой группе в силу
простой связи фугитивности с энергией Гиббса
dG = RTinf+ Л(Т, Х1,х2, . . .), (3.8)
dGj = RTlnfi + Х(Т), (3.9)
как это будет объяснено в разд. 3.1. Применяя уравне-
ние (2.50), получаем
1п/= ЕхДп^/хД, (2.51а)
или
/= n&i/xrfi. (2.516)
Выражения для М и Mt аналогичны. Любое из соот-
ношений между состояниями системы может быть пе-
реписано в соотношение такого же вида путем замены
характеристик состояния на соответствующие им пар-
циальные молярные свойства. Например,
G = H-TS и Gj^Hi-TSf,
dG = VdP и dGi = V{dP.
Почти полный список таких характеристик представлен
в табл. 2.2.
Дифференцирование парциальной молярной сжимае-
мости выполнено в примере 2.4.
Пример 2.4. Парциальные молярные свойства многокомпонентных смесей (свойство смеси выражается через
мольные доли)
Рассматриваемое свойство представлено уравнением Требуются шесть производных:
М = axj + bxi + схз + <7xiX2 + extxj + /Х2Х3. (1)
Переписывают это уравнение трижды, каждый раз ис- ключая одну из мольных долей путем замены .г, - 1 - Д, = ,х7; в результате получают \ЭХ1 у 1 ( — ) = (2о - </)Х1 + (d - 26)Х2 + (е - /)хз, (9) \dxjy
М = о(1 - х2 - Хз)2 + bxi + СХз + <7(1 - х2 - Хз)Х2 + + е(1 - х2 - х3)хз + /хрсз (2) = axj + 6(1 - Xi - хз)2 + схз + (dxi + /хз)(1 - Xi - хз) + вХ1Хз (3) = 0X1 + 6X2 + С(1 - X] - Х2)2 + (exi + /х2)(1 - Xi - х2) + dxixi. (4) (д— ) = (d - с)х> + (26 - f)xi + (J - 2с)хз, (10) \<?Х2У л- /ЭЛА = _ 2o)xi + (26 - d)x2 + (f - е)хз, (11) \дх2 у х'
Уравнения, необходимые для определения трех парци- альных молярных свойств системы, находят по уравне- нию (2.56): ( ) = (е - (7)xi + (/ - 26)х2 + (2с - /)хз, (12) \<ЭхзУ ( ] = (с - 2o)Xi + (f - d)x2 + (2с - с)хз. (13)
. . . . (дм\ (дМ\ \Эх2у *• удхзу 12 \Эх3у Уравнения (8)—(13) подставляют в уравнения (5)—(7),
.v (дм\ (дм\ уЭХ1 у п \ЭхзУ *' чтобы получить требуемые парциальные молярные свойства. Подобным образом оценивают в примере 3.5 парциальные молярные фугитивности. Для решения ра-
(дм\ (дм\ Мз = М - Xi 1 — I ~ х21 1 (7) \ЭХ1/Л- \ЭХ2/х' зобранной задачи можно также применить уравненм (2.56г) — (2.56е); в этом случае мольная доля Xi не бу- дет включена.
Термодинамические функции и равновесие 125
Таблица 2.2. Аналогии между парциальными молярными и соответствующими
исходными свойствами
Свойство Прациальное молярное свойство
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. М = ZMiXj Ui Si Н=U + PV А = U -TS G = U + PV-TS Р z~ V RT dU= TdS- PdV dH = TdS + VdP dA = — SdT — PdV dG = ~ SdT + VdP /dG\ — = v \dPjT (dG \ — = ~ 5 \dTjp /d(G/T)\ H \ dT Jp T2 / d In f \ V _ /dnM \ \ dn: / X /TPnJ Ui Si Hi = Ui + PVi A, = Ui - TSi Gi = Ui + PVi - TSi p _ Zi~ RTyi dUi = TdS/ - PdVi dHj = TdS/ + V/dP dAi= - SidT- PdVi dGi = - SidT + VidP / dGi \ — = П \ dP (dGi \ “ S‘ \ /_ x ' Pn (d{Gj/T) \ = _Hi_ \ dT )D T2 /d In Cfi/Xi) \ id In fi \ 1 Vi
15. \ dP )T RT ( d In f \ H — Hid \ dP L \ dP ) x ' Tx x ' /d 1п(Л/*|) \ (d In fi \ T RT Tx Hi - Htd
16. 17. 18. 19. 20. 21. V dT )p RT2 /d In ф \ V- Kid \ dP )T RT /d\n<(>\ H — Hid \ dT )p RT2 G = RT\n f+ A(T) lim (f/P) = 1 P-0 V dT )D \ dT ) / d In 0,- \ Vi - V‘-d \ dP Д RT / a in 0, \ Hi - Hxd \ T )D RT2 /d In Ti \ Hi ~ H'}6 \ dT J RT2 x ' Px Gi = RT\nfi + X(T, x) lim (f/XiP) = 1 P-0 D RT2 Px
126 Глава 2
Иногда необходимы производные (взятые по «,) других
свойств из числа не указанных выше перед уравнением
(2.49); однако для удобства их не называют парциаль-
ными молярными свойствами, если они «взяты» не при
постоянных Р и Т. Так, в ряде случаев (см., например,
задачу 2.19 и пример 3.4) определяют (dP/dni)TVn .
Часто удобнее иметь дело с составами, выраженны-
ми в мольных долях, а не в молях каждого присут-
ствующего компонента. Этот вопрос рассмотрен в
разд. 2.5, где упоминаются также методы оценки пар-
циальных молярных свойств на основе эксперименталь-
ных данных.
2.5. Дифференцирование по мольным долям
Если составы смесей представлены в мольных до-
лях, можно непосредственно дифференцировать по
мольным долям. Однако, если речь идет о формулиро-
вании парциальных молярных свойств системы, напри-
мер, при выражении таких производных через число
молей отдельных компонентов, необходима некоторая
осторожность. Число молей отдельных компонентов
может быть независимым, однако число мольных до-
лей ограничено Ex, = 1, так что при взятии частной
производной по крайней мере две мольные доли долж-
ны изменяться одновременно.
Заметим, что для бинарной смеси
п1 = пхх = (п j + n2)xi (2.52)
и
ndxl
dn j = ndx j + x^dn j = ~ (2.53)
1 - Xj
так что
M\ = (дпМ/дП1)трП2 = M + n(dM/dni)
= M + (1 — Xi)(dM/dxi)TP. (2.54)
Аналогично
M2 = M + Xi(dM/dx 2)TP = M — Xi(dM/dxi)rp.
(2.55)
В общем случае парциальное молярное свойство опре-
деляется следующим выражением:
Mi=M~ ^хк(дМ/дхк)Тр (2.56)
Поэтому проще всего использовать такой подход,
который позволяет при выполнении операции диффе-
ренцирования менять х в любой момент времени.
С этой целью
1) при получении М, сначала исключают х, из опреде-
ляющего уравнения путем подстановки х1> = 1 - Е7 х/,
2) выполняют эту операцию для каждого М,, кото-
рое необходимо найти.
В примере 2.4 эта процедура применяется к трехком-
понентной смеси, а в примере 3.5 — к четырехкомпо-
нентной смеси с целью определения парциальных
фугитивностей.
Уравнение (2.56) выведено, например, в работе [122],
а в работе [86] дан вывод эквивалентного уравнения.
Простое дифференцирование эквивалентного уравнения
основано на исключении мольной доли Xi в пользу об-
щего числа молей п. В результате соотношение прини-
мает следующий вид:
М = М(п j, п 2, . . . , пг)~ пМ(п, х 2, х з, . . . , хг)
Берем производную
Поскольку
(дМ/дп)„к = О,
(дп/дп,)Пк - 1
и
ij
П
1, если i=j
О, если i # j
то получаем
- [дпМ\ '
М'=Г^7) =м+ £ №/-*,>
х 7 пк
(2.566)
(2.56в)
Для трехкомпонентной смеси уравнение записывает-
ся так:
/ дМ \ / дМ \
Мх=М-х2 I ---- ) -х3 I ; • (2-56г)
\ дх2 / \ дх3 /Х2
/ дМ \ / дМ
М2 = М + (1 — х2) I ) — Лз I
\ дх2 / \ дх3
*3
(2.56д)
(2.56е)
Даже те относительно скудные данные о многоком-
понентных (тройных и т. д.) смесях, которыми мы I
настоящее время располагаем, позволяют избежать час-
того повторения рассмотренной выше процедуры. Осо-
бую группу тройных смесей представляют собой такие
a
Рис. 2.3. Избыточные
свойства смесей вода +
+ этанол (а—г) и во-
да + метанол (е) (дан-
ные “International Data
Series, Selected Data on
Mixtures, 1978).
a — общее давление; б —
избыточная теплоемкость;
в — избыточная энталь-
пия; г — избыточная энер-
гия Гиббса при 70 °C; д —
избыточная энтропия при
70 °C; е — избыточные
объемы смесей вода +
+ метанол при 25 °C.
128 Глава 2
смеси, которые получают добавлением различных коли-
честв третьего компонента к двум другим компоне-
нтам, чье соотношение фиксировано. Математически
такие системы эквивалентны двухкомпонентным систе-
мам. Представим соотношение двух мольных долей че-
рез г:
Г = Х1/Х2 (2.57)
и отметим, что
Х1 + х2 + lx3 = L (2.58)
Проведем дифференцирование по М:
dM = M\dxi + M2dx2+ M3dx3, (2.59)
запишем полученное дифференциальное уравнение сле-
дующим образом:
дМ _ dX[ _ дх2
—----= — + М2 — h Af3
дх з дх з дх з
(2.60)
или
М = Ml Xj + М2х2 + М3х3. (2.61)
Преобразуя эти уравнения, получим
-г -Xj
dxi = —7~ dx3 = —~Tdx3 (2-62)
г + 1 1*3
и
1 х2
dx2 = ~ rfx3 = - dx3. (2.63)
z r+1 1 — x3
Объединяя эти отношения, получаем в результате
следующее выражение:
М3 = М + (1 - Хт^дМ/дх^тр,- (2.64)
которое имеет такой же вид, что и уравнение (2.54).
Бинарные уравнения пригодны для графической
оценки парциальных молярных свойств, если заведомо
известно, что свойства смеси являются функциями
мольных долей; этот метод, получивший название «ме-
тода отрезков, отсекаемых касательной», демонстриру-
ется на рис. 3.4 (гл. 3). На такой диаграмме
парциальные молярные количества при определенной
мольной доле Xi представлены подкасательными при
составе с ординатами 0 и 1. Однако точность графиче-
ских методов низка, поэтому вышеописанный подход
может дать более точные результаты и оказаться более
удобным, если предварительно будут проведены опера-
ции численного дифференцирования (как в примере 2.6).
Парциальные молярные объемы в примерах 2.5 и 2.7
находят аналитическим дифференцированием уравнений
состояния. В примере 2.4 показано, как можно найти
парциальные молярные свойства, если состав выражен
в мольных долях.
Если абсолютные значения V, z, Ср, Cv и 1пф можно
измерять непосредственно, то, имея дело с Н, A, G, U
и 5, экспериментатор вынужден ограничиться лишь из-
мерением их изменения, например Д/7 = Н - х\Н\ - Х2Н2,
которое определяется калориметрически. Тем не менее
уравнение (2.54) может быть приведено к парциальной
молярной ДА/, например, следующим образом:
AHj = ДЯ + (1 -х1)(адя/ах1)гр, (2.65)
поскольку в принципе оперировать с приращениями не
сложнее, чем с абсолютными значениями. Смешанные
и избыточные свойства будут подробно рассмотрены в
следующем разделе.
2.6. Однородные функции
Термодинамические свойства, величины которых
пропорциональны массе, зависящие от общих парамет-
ров состояния, исключая z, Т и Р, математически клас-
сифицируются как однородные функции первой степени.
Функциональная взаимосвязь дается следующим выра-
жением:
М = М(а, Ь, . . . , пХ, п Y, nZ, . . . ) = пМ(а, Ь, ... ,
X, Y, Z, . . . ), (2.66)
где М, X, Y и Z — переменные, пропорциональные мас-
се, а а, b не зависят от массы. Теорема Эйлера связыва-
ет такую функцию и ее производные следующим
образом:
М = X(dM/dX)Yz + Y(dM/dY)xz + Z(dM/dZ)XY +...
(2.67)
в это выражение включены только производные по
свойствам, пропорциональным массе.
Рассмотрим в качестве примера энтальпию: Н =
= H(S . Р, пъ пг ...). Входящие в эту функцию S и л,
являются экстенсивными переменными, однако Р к та-
ковым не относится. Соответственно получаем хорошо
известное выражение:
н = s(dH/dS)Pn + Елдан/ал,)^ = rs + Хл,^-,
7 (2.68)
Используя этот подход, можно получить похожие ре-
зультаты и для других термодинамических функций.
Переменные, относящиеся к различным уравнениям ви-
да (2.67), представлены ниже:
Функция а Ь X Y Z
U(S,V, л) — — S у л
H(S, Р, п) — Р S — л
А(Т, V, л) Т — — у л
G(T, Р.п) Т Р — — л
Такие же результаты дает и теорема Эйлера:
U = TS + PV + Ъхцх, 9 (2.6)
H=TS+ ZXjiJLi, (2.16)
А — — PV + Sx/ju,, (2.17)
<7 = Sx;M;-. (2.18)
Термодинамические функции и равновесие 129
Пример 2.5. Парциальная молярная сжимаемость бинарной смеси газов и В-усеченное уравнение состояния
Запишем выражения, определяющие соответственно
сжимаемость:
2
= — (yiBi + У2В12 — В),
п
z = PV/RT = 1 + BP/RT
(1)
и парциальную молярную сжимаемость бинарной смеси
газов:
Подстановка уравнения (6)
2 2
— —I—- (П1В1 + П2В12) (5)
п п2
(6)
в уравнение (2) дает
Р (дпУ\
RT\dni) ТРп>
Р
RT
V + п
(2)
Z1 - —
RT
+ В + п
Р
Поскольку
V = RT/P + В (3)
И В — У\В\ + У2В2 + 2yiy2B\2
= ~(п2В\ + П2В2 + 2/11П2В12), (4)
п2
— 1 + —— (2y\Bi + 2у2Ви — В).
кГ
Аналогично
(7)
Z2 = 1 + ^_(2у2В2 + 2У1В12 - В). (8)
К1
С целью проверки из уравнений (7) и (8) получаем
производная записывается следующим образом:
z = yiZi + y2Z2 = 1 + BP/RT.
(9)
Пример 2.6. Парциальные молярные объемы смесей этилиодида (1) и этилацетата (2)
Результаты измерения удельных объемов этих смесей
даны Льюисом и Рендаллом. Часть этих данных пере-
ведена в необходимые единицы и представлена в пер-
вых трех колонках нижеследующей таблицы.
V иолид V V - Lx,К, д V/dXi И
0,0000 102,0895 0,0000 - 14,9730 87,12 102,09
0,1176 100,2749 0,3550 - 15,8880 86,26 102,14
0,2333 98,3846 0,6006 - 16,7880 85,51 102,30
0,3565 96,2870 0,7776 - 17,7310 84,88 102,61
0,4560 94,5025 0,8289 - 18,1380 84,64 102,77
0,5516 92,7498 0,8401 - 18,5290 84,44 102,97
0,6235 91,3477 0,7654 - 18,8900 84,24 103,13
0,7310 89,2606 0,6625 - 19,9400 83,90 103,84
0,8219 87,4077 0,4864 - 20,8280 83,70 104,53
0,9143 85,4777 0,2615 - 21,2110 83,66 104,87
1,0000 83,6342 0,0000 - 21,8110 83,63 105,45
Производные по мольным долям вычислены с по-
мощью формул дифференцирования Лагранжа (прило-
жение Б) и даны в четвертой колонке. В последних двух
колонках представлены парциальные молярные объ-
емы, рассчитанные по уравнениям
И = V + (1 - х{(дУ/дх}),
V2= V - Х1(ЭИ/ах1).
Предельные значения при бесконечном разбавлении из-
быточных молярных объемов равны Pjx = 3,49 и
РТ = 3,36 мл/моль. Дифференцирование можно вести
на ЭВМ по программе, составленной на языке Бейсик.
10 3-point Lagrange differentiation
20 Input X0, XI, X2, Y0, Yl, Y2
30 Input X
40 A = (2*X - XI - X2)*Y0/(X0 - Х1)/(Х0 - X2)
50 В = (2*X - X0 - X2)*Y1/(X1 - X0)/(XI - X2)
60 С = (2*X - X0 - X1)*Y2/(X2 - X0)/(X2 - XI)
70 D = A + В + C
80 Print using 90; X, D
90 Image D.DDDD, 3X, DDD.DDDD
100 GOTO 30
110 End
Пример 2.7. Парциальные молярные объемы бинарной смеси, представленные при помощи уравнения
Редлиха—Квонга
Рассматриваются смеси диоксида углерода (У) и про-
пилена (2) при 400 К и 20 атм. Значения параметров:
А, = 0,0592, А2 = 0,1491, 5, = 0,0181, В2 = 0,0347.
Уравнение для определения сжимаемости берется из
табл. 1.9. Исходя из уравнения
V = Z.RT/P,
записываем производную
/ = rt( эА
\Э.У1/ Р
(1)
(2)
Z - У1
(4)
Требуемые производные находят следующим образом:
А — y2Ai + (1 — yi)2A2 + 2yi(l — yi)\A{A2 , (5)
В — У1В1 + (1 — yi)B2,
(6)
) = 2УИ, - 2(1 - у/)Аг + 2(1 - 2уА'/А.А2 , (7)
dVi /
и уравнения для парциальных молярных объемов:
И, = RT
Р
(3)
(8)
9-829
130 Глава 2
z’ - z2 + (А - В - B2)Z - АВ = 0,
0,70 0,940 1,543 1,577 1,464
0,75 0,944 1,549 1,576 1,467
0,80 0.947 1,554 1,575 1,470
0.85 0,950 1,559 1,574 1,473
0,90 0,953 1,564 1,574 1,477
0,95 0,956 1,569 1,573 1,480
LOO 0,959 1,573 1,573 1,484
Следовательно,
(10)
/
\<3v,
{В - z)
Искомое уравнение получают путем подстановки урав-
нений (11), (7) и (8) в уравнения (3) и (4), которая вы-
полняется по приведенной ниже программе, составлен-
ной на языке Бейсик. Результаты расчетов даны в виде
таблицы и графиков. Отсутствие экспериментальных
данных не позволяет проверить выполненные расчеты.
Ho. Z V 1 < o. F< ,n6
0,00 0,878 1,441 1,624 1,441
0,05 0,883 1,450 1,618 1,441
0,10 0,889 1,458 1,613 1,441
0,15 0,894 1,467 1,608 1,442
0.20 0,899 1,475 1,604 1,443
0,25 0,904 1,483 1,599 1,444
0,30 0,908 1,491 1,596 1,445
0,35 0,913 1,498 1,592 1,447
0,40 0,917 1,505 1,589 1,449
0,45 0,921 1,512 1,586 1,451
0,50 0,925 1,519 1,584 1,453
0,55 0,929 1,525 1,582 1,456
0,60 0,933 1,531 1,580 1,458
0,65 0,937 1,537 1,578 1,461
10 ! PARTIAL MOLAL VOLUMES OF СО2 and
С,Н6 FROM THE R-K EQN AT 400 К and 20
ATM
20 READ Al, Bl, A2, B2, R, Г, P
30 DATA 0,0592, 0,0181, 0,1491, 0,0347, 0,08206, 400,
20
35 Z = 1
40 Y = 0
50 A = Y 2*A1 + (1 - Y) ' 2*A2 + 2*Y*(1 - Y)*
(A1*A2) 0,5
60 В = Y*B1 + (1 - Y)*B2
70 A3 = 2*Y*A1 - 2*(1 - Y)*A2 + 2*(1 - 2*Y)*
(A1*A2) 0,5
80 B3 = Bl - B2
100 GOSUB 300
110 Fl = F
120 Z = l,001*Z
130 GOSUB 300
140 F2 = F
150 H = 0,001*Z*Fl/(F2 - Fl)
160 Z = Z/1,001 - H
170 IF ABS(H/Z) <= 0,001 THEN 190
180 GOTO 100
190 Zl = ((B - Z)*A3 + (A + Z + 2*B*Z)*B3)/
(3*z‘ 2 - 2*Z + A - В - B* 2)
200 Ml = R*T/P*(Z + (I - Y)*Z1)
210 М2 = R*T/P*(Z - Y*Z1)
220 V = Z*R*T/P
230 PRINT USING 240; Y, Z, V, Ml, М2
240 IMAGE D.DD, 2X, D.DDD, 2X, D.DDD, 2X
D.DDD, 2X, D.DDD
250 IF Y< = 0,95 THEN 260 ELSE 280
260 Y = Y + 0,05
270 GOTO 50
280 END
300 F = Z'3-Z‘2 + (A-B-B‘ 2)*Z - A*B
310 RETURN
Термодинамические функции и равновесие 131
При постоянном составе суммы в этих выражениях за-
меняются на р, например
G = ц.
Некоторые из этих соотношений были получены в разд.
2.1 другим способом, но следует заметить, что все они
подчиняются общей закономерности. В примере 2.8 рас-
смотрены другие менее известные результаты, получен-
ные с использованием этой же теоремы.
2.7. Зависимость свойств от температуры
и давления
Влияние температуры и давления (или объема) на
различные термодинамические свойства детально рас-
сматривается в гл. 11, здесь же мы ограничимся обсуж-
дением основных зависимостей.
Поскольку теплоемкости обычно известны только
при низких (нулевых) давлениях, т. е. в состоянии иде-
ального газа, другие свойства соответственно относятся
к нулевому давлению как к стандартному. Чтобы найти
изменение свойства при переходе от состояния в
состояние (РгЛ), применяют трехступенчатый процесс
(как это показано на диаграмме для энтальпии в приме-
ре 2.2).
1. Снижают давление системы от Pi до нуля при тем-
пературе Т\ (изотермический режим).
2. Определяют изменение температуры от Л до Тг,
используя теплоемкости идеального газа.
3. Повышают давление до Рг при температуре Тг
(изотермический режим).
Разность между значениями показателя свойства в ре-
альном и идеальном состоянии называется отклонением
от идеального состояния. Записывают его следующим
образом:
^.M = M — Mid. (2.69)
Поскольку внутренняя энергия и энтальпия идеального
газа не зависят от давления, их отклонения от идеаль-
ного состояния можно записать так:
^и= и-Uid= и-и0 (2.70)
АН = Н — Hid = Н — Но (2.71)
где индекс 0 относится к нулевому давлению. Так как
энтропия и, следовательно, энергия Гельмгольца и
Гиббса идеальных газов зависят от давления, разности
5 - S,d, А — A'd, G - Gld будут совпадать с отклонени-
ями от идеального состояния, но при заданном давле-
нии-, как будет показано, они также включают интегри-
рование от 0 до Р более точных выражений.
Для удобства разности Н - 7Pd = Н - Но и S - Sld
часто оценивают исходя из нескольких корреляций PVT
и представляют в виде таблиц или графиков, охватыва-
ющих тот интервал пониженных температур и давле-
ний, который представляет практический интерес. Ряд
таких примеров приведен в гл. 11. Такая информация
используется для оценки изменений Н и S при переходе
от Р1Т1 к РгТг в соответствии с описанным ранее трех-
ступенчатым процессом. Процедура изменения энталь-
пии и энтропии представлена в примере 2.2 и
уравнениях (2.72а) — (2.72г).
Д$! = -(5 - 5id)p1Z1 - Я ^(Po/Pi), (2.72а)
Д52 = £2 (Cid/T)dT + ДЯ./Г,, (2.726)
Д53 - (5 - Sid)p2r2 - Я 1п(Р2/Р0).
(2.72в)
Суммарное уравнение имеет следующий вид:
S2 - Sj = (S - Sid)p2T2 — (5 — Sid)p1Z1 - Я ln(P2/P!)
+ (C«*/ T)dT + ДЯ./Т,. (2.72г)
где AHV — энтальпия фазового изменения при темпера-
туре Tv, находящейся в интервале Ti—Тг. Стандартное
давление Ро в пределе достигает нулевого значения, но
оно исключается из уравнения (2.72, г).
В табл. 11.1 даны выражения, позволяющие оценить
М - исходя из уравнений состояния, в которых
давление или объем представлены в явном виде. Запи-
шем основные соотношения для энтальпии и энтропии:
dH = (dH/dT)PdT 4- (dH/dP)TdP = CpdT
- (V- T(dV/dT)p)dP, (2.73)
dH = d(PV) + dU = d(PV) 4- (dU/dT)ydT
4- (dU/SV)TdV (2.74)
= d(PV) + CvdT+ (T(dP/dT)y- P)dV, (2.75)
и для энтропии:
dS = (dS/dT)PdT+ (dS/dP)TdP
— (Cp/T)dT — (dV/dT)PdP. (2.76)
dS= (dS/dT)vdT+ (dS/dVjpdV
= (Cv/T)dT+(dP/dT)vdV. (2.77)
Если же изменяется только давление,
d(S-Sid)=(R/P-(dV/dT)P)dP (2.78)
= ((дР/дТ)у- R/V)dV. (2.79)
Обратите внимание, что S - Sld = 0 при Р = 0.
2*
132 Глава 2
Пример 2.8. Применение теоремы однородных функций
а. Функция объема, в которой только гц являются экс-
тенсивными свойствами:
(л V \
— ) (1)
Деление на п дает известное соотношение
V = Ел,-И, .
б. Функция Масьё:
в. Функция Планка:
Ф. = G/T = Ф.(Г, Д ль Л2, ...) = Ел, ( ] (5)
у Эл,- у ТРгь
1 V
= Ел,71, .
Т
г. Внутренняя энергия смеси:
и (Г, V, л>, л2 = J +Ел, ( Э—) .(6)
\ Э V / Тл \ ди, J 7Xj>j
Например, первая из этих производных легкообрати-
ма в известные функции с помощью таблицы Бридж-
мена. Однако производные типа (Э_и/3л,)тулу не явля-
ются химическими потенциалами; к таковым относится
(3U/3n,)sv„„ а простого способа, позволяющего оце-
нить их через другие свойства, не существует.
Если состав смесей остается постоянным, то исполь-
зуются уравнения, приведенные выше. Для смесей пере-
менного состава соотношения между парциальными
молярными величинами аналогичны рассмотренным.
Например, для парциальной молярной энтальпии эти
соотношения таковы:
2. «Избыточность»
Мех = м- Mld
(2.83)
dS/ =
д2У
дп,дТ
I dP,
р
(2.80)
dSf =
представляет собой разность между свойством реаль-
ной смеси и свойством, которую бы смесь имела в тех
же самых условиях, если бы была идеальной. Согласно
этому определению, свойства идеальной смеси опреде-
ляются как аддитивные свойства чистых компонентов:
M'd = ЕХ|М;- + Ехрп, = Ех;-(Л/| + /иг). (2.84)
Для всех свойств /л, = 0 исключение составляют
лишь энтропия и определяемые через нее свойства. При
определении последних принимается во внимание изме-
нение энтропии, сопровождающее образование идеаль-
ного раствора.
д2Р
дп(дТ
(2.81)
После проведения суммирования dS = ExidS, получают
уравнения (2.76) и (2.77).
2.8. «Смешанные» и избыточные функции
Многие данные более информативны, и с ними легче
оперировать, если они выражены относительно некото-
рого вида идеального поведения. Наглядным примером
тому может служить разность между объемом реально-
го газа и объемом газа, подчиняющегося закону идеаль-
ных газов при тех же самых Р и Т. Для описания смесей
широко используются отклонения от идеального состо-
яния двух видов.
1. «Отклонение смеси»
Mmix=M_Zx.M. (2.82)
— это разность Между свойством смеси и средневзве-
шенной суммой свойств ее компонентов, определенных
в одних и тех же условиях.
ASld = — PZXj 1пхг.
(2.85)
В примере 2.9 это уравнение продифференцировано. Со-
ответственно значения лг, различных свойств могут
быть просуммированы:
Экстенсивное свойство т. М'й
Н, U, V, Ср, Cv 0 ExiM, (2.86)
S - 7?1пх, Ex,(Si - Alnx,) (2.87)
А ДЛпх, Ex, (Л, + Д71пх,) (2.88)
G Д71пх, Ex,(G, + RTlnxd (2.89)
A/RT = 14 1пх, EXi(At/RT + lux,) (2.90)
G/RT = Ф 1пх, Y,xl(Gi/RT + Inx,) (2.91)
Эти соотношения аналогичны по форме соответствую-
щим соотношениям, описывающим исходные, избыточ-
ные и избыточные молярные свойства. Некоторые из
них представлены в табл. 2.4. Аналогичные по форме
выражения для производных по свойствам смесей и ин-
тегралам даны в табл. 2.5. Их номенклатура представ-
лена в табл. 2.3.
Термодинамические функции и равновесие 133
Таблица 2.3. Перечень свойств смесей
М— некое общее свойство смеси: U, Н, V, Ср, Cv, S,
A, G
= ^XiMi
Mi — свойство вещества /
М- — свойство идеального газа i
Mld — свойство идеального раствора
= У]х< (Mi + mi)
mt - 0, кроме S, A, G,
Si = -R In Xi
at = RTlnXi
gi = RT In Xi
Mi — парциальное молярное свойство
_ /длЛ/\
\ дгц J TPnj
все свойства, перечисленные при М плюс In (fi/xi),
In ф,, In (Oi/xi), In у,
2sM' — отклонение от идеальности = (свойство компо-
нентов в состоянии идеального газа) — (истин-
ное свойство). Иногда используется следующая
запись: ДЛ/' = M'd - М
M"“ = разность между свойствами смеси и средневзве-
шенной суммой свойств ее компонентов
= ДМ (в некоторых книгах)
= М - ^XiMi = 2х,(М, ~ М)
= Л/ех + У^х/ли,
ЛГХ — разность между свойствами реальной и идеаль-
ной смесей
= М - Mid = У]х((М - Mi - mi)
= - ^Ximi
mt определяется в разд. 2.8 для различных свойств. Для
свойств с mi = 0 для газообразного состояния
ДМ' = -Мех
С учетом введенных понятий некое свойство М опре-
деляется следующим образом:
M = Mex + Mid = Mex +Sx,-(M,- + m() (2.92)
= Sx,-(M?x + Mi + mt), (2.93)
в которое включено отношение
Мех = Sx,-M-X.
(2.94)
Энергии Гиббса было уделено особое внимание
G=Ge* + Gid = Ex,(G?x + (7,+ЛПпх,), (2.95)
и для описания характера ее изменения предложены спе-
циальные термины. Детально они описаны в гл. 3 и 4,
но могут упоминаться и в данной главе. Термины, о ко-
торых идет речь, — это коэффициенты относительной
фугитивности и активности, фугитивность и актив-
ность.
При постоянной температуре для идеального газа
rfGid = VdP = RT d InP. (2.96)
Фугитивность f определяется как
dG = RTd\nf. (2.96а)
Интегрируя от нижнего значения Р = 0, при котором
G = Gid и f/P = 1, получаем
f
(}е*= G-Gld = RTln~ = RTlntp. (2.97)
Аналогично избыточность парциальной энергии Гиббса
определяется выражением
Gex = Gj - Gld = RT Ш/х,) -RT In P = RT \пЦ)/Х;Р)
= РТ1пф{. (2.98)
Конденсированные фазы, естественно, нельзя отнести
к состоянию идеального газа, но их можно отнести к
чистому веществу. Соответственно
Gex = G~ GTe{, (2.99)
Пример 2.9. Вывод уравнения для изменения энтропии смешения идеальных газов при постоянных Т и Р
Два газа помещены в закрытый сосуд, разделенный
перегородкой (см. рисунок). Число молей первого и
второго газов равно па и пь соответственно, давление
одинаково и равно Р. Когда перегородка извлекается,
газы смешиваются и их парциальные давления прини-
мают следующие значения: pt = ytP. Поскольку при по-
стоянной температуре
dS = - (V/T)dP = - Rd\nP, (1)
изменение общей энтропии для данного процесса со-
ставит
(па + /?/,)Д5 = - /?[ла1п(/?а/Р) + nbln(pb/P)] (2)
или Д5 =- /ф-а1п(1/уа) + ybln(I/yb)] . (3)
Ясно, что этот результат можно перенести на идеаль-
ные растворы с любым числом компонентов
Д.8 = /?Ех,1п(1/х,) , (4)
что аналогично уравнению (2.85).
"> 1 "ь Р, т па , пь
р 1 1 L Р Ра > Рь
134 Глава 2
Таблица 2.4. Аналогичные соотношения избыточных свойств и парциальных моляр-
ных избыточных свойств
Свойство Избыточное свойство Парциальное молярное избыточное свойство
V j/ex _ Г - Ех,-Г,- ^1 —-Л X II З1 1 (1)
и [/ex = и-^х.и. й?х = Uj - Ui (2)
Н~U+PV №х = цех + руех Я«х = tz?x + pvfx (3)
А = U- TS Лех = Uex - TSex = цех _ т$ех (4)
G = H~TS G&x = Нех - TSex &.х = я,ех - TS? (5)
G/T= Н/Т-S Gex/T = нех/т- sex д^х/т= н&х/т- sfx (6)
а Vi может быть опускают. записан как F7'f, a Ui — как C,rcf, но обычно для удобства верхние индексы
Таблица 2.5. Сопоставление избыточных свойств и парциальных молярных избыточных
свойств в дифференциальной и интегральной формах
Избыточное свойство
Парциальное молярное
избыточное свойство
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
Gex = G - Sx((G, + ЛГ1пх()
= RTT.Xj in у,-
j/ex = JZ- Ex.JZ.
( dGn \
dP /„
' Tx
d(G*x/T) \
№x = (---------
\ a(i/T) /
p ( d(Vex/T) \
------------ dP
* \ dT /_
' ' Px
11. = (Hex - Gex)/T
12.
13.
Gfx= Gf- (Gi + RTlnXi)
= RTln у,-
= / Vfx dP
Jp*
Йх = Vi- Vi
(dGf \
\ dP L
' 'Tx
fd(Gfx/T) \
Hfx= ----------
\d(l/T)
d(Vfx/T)
dT
= (Hfx - Gfx)/T
Примечание: P* — низкое давление, при котором поведение газа становится идеальным; если берутся при-
ращения, то Р исключается.
Термодинамические функции и равновесие 135
G-x = Gi - Gref = RTW&i/Xi) - RT\nf= RT\n(fi/Xif)
= RT\n-fi, (2.100)
где у; — коэффициент активности,
li^Ti/Xif. (2.101)
Избыточная энергия Гиббса определяется как
Gex = Sx,G-x = RTZxi Iny,-, (2.102)
по фазовому равновесию, которые позволяют непосред-
ственно оценить коэффициенты активности или фуги-
тивности. Избыточные энтропии рассчитывают из
выражения Sex = (№х - Gn)/T. Химические потенциа-
лы известны, если известны коэффициенты активности.
Другие парциальные молярные свойства получают пу-
тем дифференцирования исходных свойств. Все экспери-
ментальные методики подробно излагаются в послед-
них выпусках Journal of Chemical Thermodynamics и дру-
гих периодических изданиях. В изданной по инициативе
ИЮПАК монографии [7] приведен наиболее полный на
сегодняшний день список работ, а в книге Макглешана
[8] особое внимание уделено эксперименту.
и это выражение является одной из фундаментальных
зависимостей в термодинамике растворов. Коэффициен-
ты фугитивности и активности определяются экспери-
ментально, они зависят от состава системы, температу-
ры и давления. Некоторые экспериментальные данные
по избыточной функции приведены на рис. 2.3, а боль-
шая их часть дана в гл. 4. Литература по этому вопросу
довольно обширна [20]. Подробный обзор литературы
по теплотам смешения представлен в монографии [28].
Экспериментальная техника и литературные данные По
смешению объемов двух жидкостей приведены в обзоре
Ханда и Бенсона [328]. Чтобы подчеркнуть, что данная
тема продолжает интересовать исследователей и в на-
стоящее время, рассмотрим в качестве примера не-
сколько относительно недавних публикаций. Для изме-
рения объемов сжиженных природных газов Миллер и
др. [485] используют низкотемпературную методику.
Краткая статья Наканиши и др. [510] посвящена влия-
нию кольцевой структуры и степени ароматизации на
избыточные функции.
Бинарные избыточные функции, как известно, стре-
мятся к нулю при X] = 0 и Х2 = 0. Соответственно если
требуется выразить уравнение через состав, то ему при-
дают такой вид:
Afex = xix2/(xi, х2). (2.103)
Зависимость /(хь хг) эмпирическая, и такого рода функ-
ций используется очень много, особенно если они связа-
ны с энергией Гйббса. В IDS Selected Data on Mixtures
[5], как правило, применяется следующая зависимость:
п
Ме* =xj(l-Xi) Еаг(1 - 2хг)', (2.104)
0
где суммирование обычно распространяется на четыре
или пять членов. Для анализа состояния принята схема,
основанная на более сложном, но гибком методе поли-
номов Лежандра. (DECHEMA. Сборник данных по рав-
новесию пар-жидкость [1].)
Выбор того или иного метода для определения «сме-
шанных» и избыточных свойств зависит от требуемой
точности, природы системы, диапазона давления и тем-
пературы. Избыточные объемы жидкостей измеряются
различного рода дилатометрами. Для определения из-
быточных энтальпий используются калориметрические
методы различной степени сложности. Избыточные
энергии Гиббса обычно определяют исходя из данных
2.9. Уравнение Гиббса—Дюгема
и термодинамическое состояние
В разд. 2.1 дифференциал экстенсивной внутренней
энергии
U = U(S, V, «1, п2,. . .)
преобразован как уравнение (2.4):
(dU - TdS + PdV- bp.idXi) n
+ (U-TS + PV-'Lxitxi)dn = G. (2.105)
Используем теорему однородной функции, чтобы видо-
изменить подход к анализу, приведенному здесь. Со-
гласно этой теореме,
У = (dU/dS)VnS_ + (dU/dV)SnV + (2.106)
= T5-Pr+S/4In,-, (2.107)
или
U- TS + PV- ^х(= 0. (2.108)
Соответственно первая часть уравнения (2.105) равна
нулю, т. е.
dU-TdS + PdV — T^dx^ 0. (2.109)
В свою очередь дифференциал уравнения (2.108) имеет
следующий вид:
dU - TdS - SdT + PdV + VdP - ^dx, - Xx^ = 0.
(2.110)
Решая совместно уравнения (2.109) и (2.110), получаем
-SdT + VdP - l.Xidp.i = 0, (2.111)
или
(dG/dT)PxdT + (dG/dP)TxdP -T.xidGi = 0. (2.112)
Аналогичные уравнения могут быть записаны для
любой термодинамической функции, для которой исход-
ным является следующее уравнение:
(dM/dT)PxdT+ (SM/dP)TxdP = Т.х^{дпМ/дп,)ТРп..
(2.113)
136 Глава 2
Таблица 2.6. Некоторые формы уравнения Гиббса — Дюгема
Свойство Уравнение Гиббса — Дюгема
м / дМ \ /дМ \ /д (пМ) \ \аг J dT+\dP ) д ) \ / Рх X / Тх \ J / трп. (1)
= ZXidMf
М mix = М — 1.x ,М, (дмт™ _ /амт‘х \
1 1 dT + 1 I dP — 'LxidiMj — М,\ \ дт )Рх \дР )ТХ (2)
G - SdT + VdP = ZxidGi = Ъх^щ (3)
G/RT H V ~l^dT + ~RTdP = 2х^(М,/ЛГ) (4)
ДС7' G-Gid f ffex yex ~ dT + dp = ln Cfi/Xi)
RT — In RT Р (5)
= Ex,d In/} (6)
= Ex,d In ф, (7)
Gex RT G - Gref RT /Vх yex ~~RT2dT + ~RTdP== ZXid 1П (8)
= f In TV /ref — "Lxjd In y(- (9)
= Хг^1п (fi/ff) (10)
— Т.х$ In a,- (И)
а Следует отметить, что ДН' = H - H’ = Я" = H - H'd, так как H' = H'd.
дифференциальной
Общая форма уравнения Гиббса—Дюгема связывает
любое свойство, которое можно рассматривать как
функцию Т, Р, и состав с химическими потенциалами.
Поскольку G = G(T, Р) — это фундаментальное уравне-
ние, уравнение Гиббса—Дюгема наиболее широко при-
меняется с функциями, тесно связанными с энергией
Гиббса. Основная форма уравнения Гйббса—Дюгема за-
писывается следующим образом:
d м2 = ~ xxdfxx/( 1 - X])
или интегральной форме
М2 =
Xi X]
1 -Xj
(2.116)
(2.117)
-SdT+ VdP= ZxidGi = ZxidiJLi.
(2.И4)
В табл. 2.6 приведены различные модификации уравне-
ния Гиббса—Дюгема, выраженные через функцию
Планка Ф = G/RT и через смешанные и избыточные
свойства. Использование этих уравнений будет рассмот-
рено в последующих главах.
При постоянных Т и Р уравнение (2.114) упрощается:
Ех,- d/jLj = 0.
(2.115)
Это особенно полезно при рассмотрении двухкомпо-
нентных смесей. Используя упрощенное уравнение в
можно получить или химический потенциал, или парци-
альное молярное свойство одного из двух веществ, если
для другого вещества это свойство известно как функ-
ция состава. Уравнение (2.116) используется также в
следующей форме:
, + *2 д
дх । дх ]
(2.118)
Для проверки соответствия экспериментальных дан-
ных термодинамическим законам можно использовать
три вывода, которые вытекают из уравнения (2.118).
1. Согласно уравнению, наклоны dpt/dx\ для двух
Термодинамические функции и равновесие 137
компонентов одной смеси имеют противоположные
знаки.
2. Тангенс угла наклона щ равен нулю при %i = 1, и
тангенс угла наклона цг равен нулю при Х] = 0.
3. Оценка величины площади, как это показано в при-
мере 2.10, должна удовлетворять уравнению; причина
расхождений — колебания температуры и давления, хо-
тя следует заметить, что на конденсированные фазы ко-
лебания температуры не оказывают существенного вли-
яния, если давление нормальное.
В литературе уделено большое внимание термодина-
мической оценке данных. Оценка площади — это необ-
ходимое, но недостаточное условие, поскольку отдель-
ные данные могут оказывать противоположное влияние
и тем самым компенсировать неточности. В гл. 4 при-
ведены методики оценки данных по схеме «точка за
точкой».
Хотя этот метод трудоемок и требует множества дан-
ных, его применяют для оценки данных, полученных
для многокомпонентных смесей (трех и более); см., на-
пример, работу [338].
2.10. Условия равновесия
Термодинамика рассматривает главным образом свя-
зи между свойствами систем в состоянии равновесия и
различиями между этими свойствами в различных рав-
новесных состояниях. Например, уравнение состояния
PVT дает равновесное давление идеального газа при
определенных Т и V, хотя на практике возможно крат-
ковременное повышение или понижение давления, а в
метастабильных условиях значение давления вообще
может быть неопределенным. Все уравнения, приведен-
ные в этой книге, справедливы только для состояния
равновесия. Скорость достижения равновесия имеет
важное практическое значение, но этого вопроса мы ка-
саться не будем.
Состояние чистого вещества в единственной фазе под-
дается определению, если известны его две термодина-
мические характеристики. Как указано в разд. 2.2, пол-
ную информацию о такой системе содержит фундамен-
тальное уравнение состояния. Равновесное состояние ха-
рактеризуется максимумом энтропии или минимумом
энергетической функции при определенных значениях
двух других параметров используемого фундаменталь-
ного уравнения. Возможные в равновесных условиях
экстремумы перечислены ниже.
Независимые переменные Свойство
максимум минимум
и. V S —
S, V — и
Р н S —
Р, S — н
т, V — А
Р, т — G
Равновесное и другие состояния могут быть найдены
на пространственных диаграммах, подобных приведен-
ным на рис. 2.1 и 2.2. На диаграмме для метилхлорида,
например, при Р = 50 и Т = 560 равновесная энергия
Гиббса равна - 24,93 (это наименьшее возможное значе-
ние). Физически возможны только состояния, располо-
женные выше соответствующей поверхности; таким
образом, точка при G = -110 и названных Т и Р недо-
стижима, в то время как тойка при G = 10 достижима,
хотя и отвечает неустойчивому состоянию. На диаграм-
ме Гельмгольца для натрия достижимы только точки,
находящиеся над поверхностью. На диаграмме для эти-
лена в направлении оси энтропии достижимы только
точки, расположенные на поверхности и перед нею, в
то время как в направлении оси энтальпии достижимы
только точки, находящиеся на поверхности и выше ее.
2.10.1. Смеси. Число молей индивидуальных веществ
в фундаментальном уравнении смеси также представля-
ет собой переменную:
G = G(T, Р, Л], л2> • • • )’ (2.1 19)
и
dG = -SdT+ NdP + ZiL'dri,. (2.120)
Таким образом, кроме Т и Р для определения равновес-
ного состояния необходимы также химические потенци-
алы. При расчете фазового и химического равновесия
следует учитывать некоторые их особенности, которые
будут рассмотрены ниже.
2.10.2. Фазовое равновесие. Для температурного рав-
новесия контактирующих фаз требуется равенство их
температур, а для гидростатического равновесия — ра-
венство давлений. Диффузионное равновесие предпола-
гает равенство химических потенциалов. В осмотичес-
ких процессах, где межфазовая поверхность проницаема
для одного из веществ, для сохранения диффузионного
равновесия в условиях различной концентрации диффун-
дирующего вещества в обеих фазах необходима раз-
ность давлений. Чтобы избежать изменения концентра-
ции или химического потенциала, гидростатическим
равновесием в этом случае пренебрегают.
При передаче dru молей вещества между двумя фаза-
ми при одних и тех же Р и Т изменение энергии Гиббса
составит
dG = (g$2) - (2.121)
Поскольку G в условиях равновесия достигает мини-
мума, ее производная равна нулю:
(dG/dn^'pp^. = 0, (2.122)
так что из уравнения (2.121) следует, что
= (2-123)
Если число передаваемых веществ, равно как и число
контактирующих фаз, превышает два, равенство хими-
ческих потенциалов распространяется на все эти фазы
и все вещества:
м0) = м(2) = ... =М(Ю; (=1, 2,..., п. (2.124)
138 Глава 2
Пример 2.10. Уравнение Гиббса—Дюгема — проверка бинарной смеси при постоянных температуре и давлении
Дифференциал свойства
вило Симпсона, получаем следующие интегралы:
М — Х\М\ + Л'гЛ/г — Х\М\ +• (1 — Х\)М2 (1)
равен
dM = {хДМ\ + x2dM2} + {Midxi - M2dx{) . (2)
При использовании уравнения Гиббса—Дюгема первая
группа членов в скобках равна нулю, в результате по-
лучаем
dM = (Мх - M2)dxx. (3)
Предельные условия: М = М\, если лд = 1, и М = М2,
если ,Yt = 0. Запишем интеграл уравнения (3):
' dM = Л7-, - ЛГ = [(‘(Мх - M2)dxi , (4)
который может иметь также следующий вид:
1'(Л7. - A/Jt/Ai - Ц(ЛГ - M2)dx, - 0 (5)
или
^(ЛЛХ - M2)dx, = 0.
(6)
3ia теорема проверяется путем использования данных
о молярных энергиях Гиббса для смесей вода — этанол
яри температуре 343,15 К (см. рис. 2.3). Применяя пра-
Условие равновесия можно найти или непосредствен-
ной минимизацией энергии Гиббса, или используя прин-
цип равенства химических потенциалов. Для парожид-
костного равновесия, например, условие минимума
энергии Гиббса может быть записано в следующем
виде:
G/RT=Zli[G^) + 1пх,]+ Ь/,[(7$) + 1пу(]
-» минимум (2.125)
где I, и Vi — число молей индивидуальных компонентов
в жидкой и паровой фазах. Для данных общих коли-
честв индивидуальных веществ число независимых /,
или Vi равно числу присутствующих веществ, так что
нахождение минимума энергии Гйббса как функции рас-
пределения между фазами требует весьма трудоемких
расчетов. Однако, если исходить из принципа равенства
химических потенциалов в обеих фазах или, что равно-
сильно, равенства фугитивностей (см. гл. 6), задача
упрощается.
Для двухкомпонентных жидкофазных систем осу-
ществима прямая минимизация; несколько примеров,
иллюстрирующих изложенное, приведено в гл. 7.
2.10.3. Химическое равновесие. Для химической реак-
ции между веществами, определяемой с помощью Mi и
стехиометрических коэффициентов Vi,
v,M, = 0, (2.126)
=1179,57-1180,33= -0.76. (7)
Такой способ проверки равновесных состояний считает-
ся одним из лучших. Ряд других способов проверки по-
казан на рис. 4.7.
/' г. Дж/моль д‘|', Дж/моль ц Дж/моль
0,000 0,0 2640 0
0,050 128,5 2499 4
0,100 249,9 2375 14
0,150 364,2 2238 34
0,200 469,9 2086 66
0,250 565,8 1926 112
0,300 651,0 1766 173
0,350 724,9 1607 250
0,400 786,5 1448 345
0,450 834,8 1289 463
0,500 868,5 1129 608
0,550 886.5 972 782
0,600 887,1 819 989
0.650 868,9 672 1235
0,700 830,1 531 1528
0,750 768,3 397 1881
0.800 680,6 273 2310
0,850 563,3 163 2829
0,900 412,7 76 3445
0.950 225,5 19 4146
1,000 0,0 0 4920
а общая энергия Гиббса
G = £л((<7(0 + RT inхД.
(2.127)
Если имеет место единственная реакция, количества
всех присутствующих веществ связаны посредством сте-
хиометрического уравнения, так что имеется только
одна независимая переменная — скажем, превращение,
выраженное в долях одного из компонентов. Таким об-
разом, нахождение минимума энергии Гиббса и, следо-
вательно, равновесной степени превращения осущест-
вить проще, чем распределение фаз в равновесных усло-
виях. Например, химическое равновесие окисления диок-
сида серы при нескольких температурах и давлениях
находится как минимум на графиках энергии Гиббса
(см. пример 2.11). Для сложных многокомпонентных
реакций иногда проще применять численные методы,
чем прямую минимизацию энергии Гйббса (см. гл. 10).
2.10.4. Оценка химических потенциалов. Поскольку
химические потенциалы играют решающую роль в
определении равновесных состояний, в практической ра-
боте необходимо располагать их численными значения-
ми. Химические потенциалы являются функциями Т и
Р, а также состава. Их оценка из измеренных избыточ-
ных свойств, например Gex, ТГХ, Vе*, упрощается при
дифференцировании этих данных. Избыточную энергию
Гиббса, например, обычно находят из парожидкостных
и других данных о фазовом равновесии (см. гл. 4). Хи-
Термодинамические функции и равновесие 139
Таблица 2.7. Избыточные свойства некоторых эквимолярных бинарных
смесей®
Смесь Г, °C $ех
Пропанон + декан 65 1000 1980 -2,90
Метилацетат + циклогексан 30 959 1770 -2,68
Диоксан + гептан 40 838 1639 -2,56
Диоксан + гептан 45 838 1632 -2,50
Бутанон-2 + додекан 25 934 1647 -2,39
Бензол + гептан 50 297 867 -1,77
Бутанон-2 + гептан 25 860 1338 -1,60
Бутанон-2 + гексан 25 830 1252 -1,42
Циклогексан + диоксан 25 1069 1445 -1,24
Ацетон + гексан -5 1167 1385 -0,81
Тетрахлорид углерода + фуран 30 190 323 -0,44
Метилацетат + бензол 25 237 317 -0,27
Циклогексан + 2,3-диметилбутан 25 87 156 -0,23
Циклогептан + 2,3-диметилбутан 25 135 163 -0,09
Дихлорметан + фуран 30 -6,7 16,9 -0,08
Циклогептан + циклопентан 25 -4,5 3,9 -0,03
Циклогептан + циклогексан 25 8,6 6,0 0,01
Циклогептан + циклооктан 45 2,7 -2,0 0,02
Циклопентан + 2,3-диметилбутан 25 12,7 -1,8 0,05
1,2-Дихлорэтан + метанол 45 1114 957 0,49
Тетрахлорид углерода + циклопентан 25 34 80 0,15
Тетрагидрофуран + циклопентан 25 226 369 0,48
Дихлорэтан + метанол 45 1114 957 0,49
Дихлорметан + ацетон 30 -404 -887 1,59
Пропанол-1 + гептан 30 1291 660 2,08
Диметилсульфоксид + дибромметан 35 -208 -889 2,21
25 -157 -959 2,69
Вода + этанол 50 821 -121 2,92
90 901 378 1,44
а Данные взяты из Selected Data on Mixtures: International Data Series, Gn и ЛГ*
выражены в Дж/моль, S" — Дж/моль-К. Некоторые данные интерполированы.
мический потенциал определяется следующим выра-
жением:
^-С( = {дпС^/дп1)ТРп.. (2.128)
Для двухкомпонентных систем он равен
мГ= 6ех + (1 -х^дв^/дх^тр, (2.129)
как это объяснялось в разд. 2.5. Чтобы упростить пред-
ставление Gex, предложены специальные функции — фу-
гитивность и активность (см. гл. 3 и 4).
Химические потенциалы также часто связывают с
другими парциальными молярными свойстами, на-
пример
{дщ/дР)Тп.= Vh (2.130)
(д(щ/Т)/дТ)Рп.= -Н'/Т2. (2.131)
Эти соотношения включают дифференцирование по со-
ставам в широких пределах температуры и давления и
последующее интегрирование и поэтому используются
нечасто. Определить параметры парожидкостного рав-
новесия в системе и получить из них коэффициенты ак-
тивности и химические потенциалы гораздо проще, чем
провести с той же степенью точности калориметриче-
ские измерения.
2.11. Задачи
2.1. Постройте термодинамическую диаграмму для
фреона 22, используя данные Больца и Тува [771]. На
оси ординат отложите значения энтропии S и внутрен-
ней энергии U, а на оси абсцисс — логарифм удельного
объема.
2.2. Дано фундаментальное уравнение для некоторого
вещества в следующем виде:
U = 200 + 50S - 0,3 И + 0,8S2 - 0,004 V2 - 0,035И .
140 Глава 2
Пример 2.11. Кривые энергии Гиббса реакционных смесей, показывающие, что равновесное превращение соответ-
ствует минимумам этих кривых
Рассмотрим в качестве примера окисление диоксида
серы стехиометрическим количеством реагента при не-
скольких температурах и давлениях. Количества присут-
ствующих компонентов выражаются в виде долей е
превращенного SO2.
4- e
M30
RT
4- In
2eP
3 -e
(6)
SO2 + 0,5 О2 SO3 , (1)
yso2 = 2(1 - е)/(3 - е) , (2)
уо, = (1 - е)/(3 - е) , (3)
Уьо. = 2е/(3 - е) , (4)
Запишем энергию Гиббса смеси как функцию е:
g,o — энергии Гиббса образования SO я приведены ниже
в виде таблицы.
Hio/RT — — 1пЛ/
Т °F SO2 SO3
1100 -41,467 -43,827
1200 -38,437 -39,998
1300 -35,752 -36,606
G 1 v- v
- = LUM = Ln,
RT RT
-- + ln(y,P)
RT
^10 + ln2(I 3 -e)-P
RT 3 -- e
+ 0,5(1 - e)ln(1
3 - e
Если построить кривые зависимости энергии Гиббса от
относительной степени превращения при различных
температурах и давлениях, то нижние точки получен-
ных кривых соответствуют равновесным превращени-
ям. Чтобы положение точки минимума было доста-
точно точным, при построении набора таких кривых
каждый раз подбирают необходимый масштаб.
а. Выведите уравнения для 1, Р, Н, А и G как функ-
ций U, S и V.
б. Постройте поверхность U(S, Г) для интервалов
10 S 30 и 100 V 300.
2.3. Найдите парциальные молярные объемы эквимо-
лярной смеси диоксида углерода (1) и пропилена (2) по
уравнению Редлиха—Квонга, для которых при 400 К и
20 атм:
А В
СО2
С3Н6
Смесь
0,05914
0,1495
0,0992
0,0181
0,0348
0,0265
Решение задачи удобнее
формы уравнения
начинать с полиномиальной
г3 - Г 4- (А - В - B2)z - АВ = 0 .
Для указанных условий г равно 0,9253.
2.4. Используя вириальное уравнение V = В 4- RT/P,
найдите уравнение для отклонений от идеальности при
определенной температуре:
А - Hid, S - S'd, Н - Hid, U - U'd, G - G'd и
Ср - Ср
Определите стандартное условие (Р*, Г*), при кото-
ром вещество ведет себя как идеальный газ. Начните
Термодинамические функции и равновесие 141
с выражений
-(А - Aid) = Г PdV
J JZ*
!V / \ р V
( п RT\ , I RT >TZ
IP- — I dv + 1 —dV
\ V 1 V
пл \ r / -I 17* r
а Ь
СО2 3,592 0,04267
С3Нб 8,379 0,08272
Использованные единицы: атм, К и л/моль.
C _ oid = _ (д(А - Hid)\
\ dT ) v
2.5. Найдите уравнения для парциальных молярных
объемов бинарной смеси в терминах вириального урав-
нения и уравнения Ван-дер-Ваальса, начиная с полино-
миальной формы уравнения
И3 - (b + —V2 + —V - ~ = О
\ Р/ Р Р
2.6. Дано фундаментальное уравнение А = А(Т, V)
или = ф(Т, Р) для воды [63]. Проверьте справедли-
вость уравнений, в которых Р, U, S, Н и G выражены
через переменные фундаментального уравнения (см.
табл. 1.22).
2.7. Найдите эквиваленты следующих производных
(dU/дУ)н, (дТ/дР)н и (дС/дТ)н при постоянной энталь-
пии, выразив их через PVTCp.
2.8. Найдите связь между коэффициентом Джоуля—
Томсона (дТ/дР)н, теплоемкостью при постоянном дав-
лении и производной (дН/дРУг-
2.9. Преобразуйте (дН/дР)т в группы производных, в
которых две независимые производные выбираются в
свою очередь из группы переменных Р, V, Т и S’. В дан-
ном случае удобно воспользоваться методом Шоу [634],
рассмотренным, например, Шервудом и Ридом [120].
2.10. Некоторое количество вещества dne, обладаю-
щее свойствами ие, Ре, ve и Те, поступает в резервуар,
уже содержащий какое-то количество п того же веще-
ства со свойствами U и Т. Переданная теплота и совер-
шенная работа равны dQ и dW соответственно.
а. Покажите, что энергетический баланс может быть
записан следующим образом:
d(nU) = ndU + Udn = dQ - dW + (ue + peVe)dne .
б. Проинтегрируйте уравнение при следующих допу-
щениях: U = CVT, Н — СрТ, теплоемкости и (dQ — dW)/
/dn = а постоянны. Это даст связь между температу-
рой и количеством вещества п в резервуаре.
2.11. Дано фундаментальное уравнение
U = aSV + bS2 + eV2.
Найдите G и Си, выражая их через переменные
уравнения.
2.12. Составьте таблицу или изобразите графически
парциальные молярные объемы смесей диоксида угле-
рода (1) и пропилена при 400 К и 20 атм, исходя из
уравнения Ван-дер-Ваальса. Параметры а и b имеют
следующие значения:
2.13. Найдите коэффициент Джоуля т) = (дТ/дУ)ц из
уравнения Ван-дер-Ваальса при помощи таблицы
Бриджмена.
2.14. Выразите производную (дС/дТ)н через (дН/дР)т,
Ср и PVT.
2.15. Найдите (ди/дУ)н для а) идеального газа и б)
газа, уравнение состояния которого имеет следующий
вид: P(V - Ь) - RT.
2.16. Найдите производную (дС/дР)н из эксперимента
Джоуля—Томсона, используя уравнение Ван-дер-
Ваальса.
2.17. Примените рассмотренную в примере 2.2 мето-
дику решения с использованием В-усеченного вириаль-
ного точного уравнения
В = (1 + B/V)RT/V
или V = (RT/2P)(1 + 44BP/RT)
и приближенного уравнения
V = (Л77Р)(1 + BP/RT)
2.18. Дополните решение, рассмотренное в примере
2.1, следующим случаем: поток направлен наружу,
(dQ - dW)/dn - const, состояние газа принимается иде-
альным, а теплоемкости — постоянными.
2.19. Покажите, что для уравнения состояния
V - yibi - yzbz
производная определяется следующим выражением:
( др\ _P2(bl-bz)v
удЛ] / тил2 nRT
2.20. Покажите, что для U(S, V) в соответствии с при-
веденным в приложении Б правилом «изменение пере-
менных, поддерживаемых постоянными», дает
+
и
Используя таблицу Бриджмена, убедитесь, что данное
выражение корректно. Найдите также (dG/dT)s обоими
способами.
2.21. На приведенном ниже графике показаны данные
по избыточному свойству смесей метанола и пипериди-
на при 298,15 J< [510].
а. Найдите Gfx, FF7 и Г5ТХ при Хсн,он = 0,4.
б. Используя полученные значения, проверьте Gex =
= Ex,G/x и другие свойства. __
в. Сравните Н? - G" со значениями TSfx, вычислен-
ными ранее.
142 Глава 2
нением
= XiX2(ao + oi(l - 2xi))
коэффициенты которого зависят от температуры:
Т, °C 20 30 40 50
ао 517,7 379,9 254,1 140,3
Ch 44,0 35,0 26,0 17,0
Найдите изменение избыточной энергии Гйббса при
изменении температуры от 20 до 50 °C при Xi = 0,25.
2.25. Ниже указаны избыточные свойства (Дж/моль)
смеси, содержащей 25% воды + этанол
; °с Gn Нп
30 497,5 -211,0
50 536,2 -48,3
70 565,8 111,7
90 584,0 289,7
2.22. Ниже приведены данные по избыточным объ-
емам смесей вода — метанол (мл/моль при 25 °C). По-
лучите из этих данных полином второй степени от
(1 - 2xi) (IDS Selected Data on Mixtures).
Х1 |ЛХ |ЛХ 1 - 2xi
Х1Х2
0,0970 -324 -3699 0,8060
0,1843 -573 -3812 0,6314
0,3952 -939 -3929 0,2096
0,4706 -1004 -4030 0,0588
0,6260 -947 -4045 -0,2520
0,6938 -854 -4020 -0,3876
0,7279 -799 -4034 -0,4558
0,7670 -706 -3951 -0,5340
0,8092 -600 -3886 -0,6184
0,8464 -492 -3749 -0,6892
0,8892 -348 -3532 -0,7784
0,9146 -262 -3354 -0,8292
0,9526 -137 -3034 -0,9052
0,9623 -107 -2949 -0,9246
0,9714 -68 -2448 0,9428
2.23. Избыточная энергия Гиббса смесей этанола (1)
и н-гептана (2) представлена уравнением
G^/RT = - xiln(xi + Ах2) - х21п(ВХ1 + х2),
где
А = 1,8857 ехр (- 1055,11/Т) (данные табл. Д.7),
В = 0,5303 ехр ( — 310,57/7).
Избыточные энтальпии эквимолярных смесей (IDS
Selected Data on Mixtures) имеют следующие значения:
7, К 283 318 333 348
/Гх, Дж/моль 1450 1250 850 450
Оцените избыточные энтальпии из данного уравнения
для Gex и сравните с приведенными значениями.
2.24. Данные по избыточным энтальпиям (Дж/моль)
смесей н-гексана и н-гексадекана представлены урав-
Удовлетворяют ли эти данные уравнению Гиббса-
Гельмгольца
T(dGe*/dT) + №х = G" .
2.26. Даны коэффициент Джоуля—Томсона ^(К/атм),
теплоемкость Ср (кал/моль-К) и второй вириальный ко-
эффициент В (мл/моль) для азота.
а. Получите зависимость цСр = - d(B/T)/d(\/T).
б. Допуская, что значения В при 273 К корректны,
найдите значения вириального коэффициента при дру-
гих температурах из данных о ц и Ср.
Т к сР В
273 0,2655 6,596 -10,3
298 0,2216 6,958
323 0,1854 6,960 - 0,3
348 0,1555 6,966
373 0,1291 6,974 6,1
398 0,1069 6,986
423 0,0868 7,000 11,5
2.2 7. Результаты точных измерений удельных объ-
емов V (мл/г) водного раствора Н2О2 при 25 °C аппрок-
симируются уравнением
V = 0,0030 (1 - w) + 0,6935w - 0,0360w (1 - w),
где w — массовая доля Н2О2. Найдите парциальные мо-
лярные объемы для всего диапазона изменения кон-
центраций.
2.28. Даны энтальпии смешения тетрахлорида углеро-
да и циклогексана при 25 °C. Предполагается, что рас-
творы регулярные, и поэтому их мбжно описать
симметричным уравнением
Д77т,х = кХ]Х2.
Насколько это близко к действительности? Предложите
наилучший вид кривой, соответствующей приведенным
ниже данным:
х, 0,8529 0,7213 0,5955
Д/Г", Дж/моль
76,6 118,6 141,6
Термодинамические функции и равновесие 143
Х1 0,4745 0,3495 0,2335 0,0657
ДЯт, Дж/моль 146,7 134,9 107,9 37,8
2.29. Найдите интегральное соотношение, связываю-
щее температуру и объем при адиабатическом расшире-
нии газа, которое представлено вириальным уравнени-
ем V = RT/Р + ВсВ = а + ЬТ и Ср = с + dT.
2.30. Молярные объемы бинарной смеси коррелиру-
ются при помощи уравнения
V = 3 + 2(xi - х2) + (Xi - х2)2.
Найдите парциальные молярные избыточные объемы.
2.31. Энергия Гйббса смеси представлена уравнением
G = XilnviXi + Х21П72Х2
с 1п71 = 0,5x2 и 1п72 = 3,0X1. Определите равновесный
состав смеси.
2.32. Избыточная энтальпия (Дж/моль) смесей воды
(1) и этандиола (2) определяется уравнением
Н™ = xix2[ - 2431,9 + 1925(xi - х2) - 1467,6(Xi - х2)2 +
+ 385,9(xi - х2)3]
при 25 °C. Выведите уравнения для парциальных мо-
лярных энтальпий. (IDS Series В, No. 67, 1978.)
3. ФУГИТИВНОСТЬ И КОЭФФИЦИЕНТ ФУГИТИВНОСТИ
3.1. Определения и основные формулы
К понятию фугитивности можно прийти путем ана-
лиза изменений энергии Гиббса, обусловленных измене-
нием давления и температуры, т. е. путем анализа
выражения
dG = ~SdT+VdP. (3.1)
Для идеального газа при постоянной температуре
dG = VdP = RTd InP, (3.2)
а для компонента i идеальной смеси, парциальное дав-
ление которой составляет Р, = х>Р,
dG{ = RTd\nPi = RTd]nPxi= Й, dP. (3.3)
Подобного рода простые соотношения можно распро-
странить и на прочие вещества и смеси путем введения
понятий фугитивность и парциальная фугитивность,
которые при постоянной температуре определяются как
dG = RTd ln/= VdP при Г; (3.4)
dGi = RTd\nfi= VidP при T. (3.5)
Фугитивность и парциальная фугитивность приближа-
ются к давлению и парциальному давлению при малых
величинах, как это следует из приводимых ниже допол-
нительных условий.
lim//P= lim 0=1, (3.6)
Р-0 Р-0
lim //х,Р= lim 0, = 1. (3.7)
Р-0 Р-0
Отношения ф = f/P и ф, = fi/xtP называют коэффициен-
тами фугитивности и парциальной фугитивности.
Выполняя интегрирование при постоянной температу-
ре, получаем константы интегрирования, которые пред-
ставляют собой функции температуры:
G = RT\nf+ Л(Т), (3.8)
Gj = RT\nfi + Xi(T). (3.9)
В том случае, если требуется описать только изменения
энергии Гиббса, константы интегрирования опускают.
Тем не менее между этими константами существует
определенная зависимость, которую математически
определяют следующим образом.
Поскольку
6=гхД, (31°)
при подстановке фугитивности получаем
RT\nf+ Л(Т) = Ех,[ЯТ1п/; + Х,(Т)]. (3.11)
При малых величинах давления, т. е. в условиях, необ-
ходимых для существования идеального газа, последнее
уравнение можно записать как
RT\nP* + Л(Т) = РТ£х{ 1пх,Р* + гхД(Т). (3.12)
Сократив давление, получаем интересующее нас соот-
ношение
Л(Т) = ЛГХх,-Inx,• +Sx,X,(T), (ЗДЗ)
используя которое, находим простое уравнение, выража-
ющее отношение между фугитивностью смеси f и пар-
циальными фугитивностями, а именно:
RTlnf+ RTZXi 1пх,- + ЕхДДТ)
= R Т Zxz In/ + Zx,X,( T), (3.14)
или
ln/= Zx,-ln(/-/x,). (3.15)
Аналогичным образом получаем
In 0 = Zx(-In 0,-. (3.16)
Исходя из этого выражения, можно прийти к следую-
щим важным выводам:
/= П(//х,)^, (3.15а)
0=П(0,У<'. (3.16а)
Коэффициенты парциальной фугитивности в каждом
конкретном случае находят, используя методику опреде-
ления парциальных молярных величин (см. разд. 2.5).
Фугитивность и коэффициент фугитивности 145
Таблица 3.1. Фугитивность и коэффициенты фугитивности чистых веществ
Фугитивность
Коэффициент фугитивности
16. <t>=f/P
2а. dG — RTd }nf= VdP
рр2 ру2 (дР\
За. ЛПп/г/Л = / VdP = И1------
>1 \dV/
26. d(G - Gid) = RTd\n ф =
f Н- Hid \ V
6a. dlnf=- ——— МГ + — dP
\ RT2 у RT
(d In ф \ H~Hid
46. ---- =----------
\ dT )p RT2
(d In ф \ V - Kid
56. ---- =----------
\ dP )T RT
/ H~H{d \ (v- Kid \
66. d In 0 — — I \dT + I ~~ It/P
~ Id t2 I \ DT I
Например, для двойных смесей можно записать:
In ф j = In ф + (1 — х j )
(3.17)
Так как ф = 1 при Р = 0, то можно определить и абсо-
лютную величину коэффициента фугитивности. Так,
(3.18)
/ 1 рр ( RT
1П 0 = 1П— = / К —
Р PTJ0 \ Р
(3.23)
In 02 = In 0 — Xj
(3.19)
1п(Л/х i)= ln/+ u ~ *i)
(3.20)
Из сказанного выше вполне очевидно, что интегрируе-
мая функция представляет собой отклонения от поведе-
ния идеального газа и при Р = 0 стремится к нулю.
Более удобный способ преобразования уравнений со-
стояния, содержащих давление в явной форме, заключа-
ется в замене члена VdP его эквивалентом.
ln(/2/x2) = In/ - Xj
(3.21)
rPvdP= rd(PV)- {VPdv
Ipq Jpo Jyo
Прочие уравнения, включающие фугитивности и коэф-
фициенты фугитивности, приведены в табл. 3.1 и 3.2.
=PV-PoVo~
(3.24)
3.2. Чистые вещества
В тех случаях, когда величина объема либо известна
как функция давления, либо получена в результате непо-
средственного измерения или расчета, проведенного при
помощи какого-либо уравнения состояния, изменение
фугитивности можно установить путем интегрирова-
ния, т. е.
Соответственно коэффициент фугитивности можно оце-
нить следующим образом:
pv Р
ЯГ1п0= PV-RT- / PdV-RTln-----
Л Р0
(3.25)
/2 1 Г р2
lnf^==RTjPl VdP-
(3.22)
pv f RT \
=PV—RT— / IP------ ]dV
Jv0 \ V )
10-829
146 Глава 3
RT \ Р
— ]dV-RT\n— ,
V / Ро
(3.26)
или
1 р v [ RT \
In 0 = z — 1 — Inz — I I Р — jdV, (3.27)
если нижний предел давления равен нулю.
Способы интегрирования ряда наиболее распростра-
ненных уравнений состояния показаны в табл. 3.3 и 3.4,
способы интегрирования всех прочих уравнений — в
гл. 1 непосредственно после соответствующих уравне-
ний. Эдмистер [267] построил кривую изменения коэф-
фициента фугитивности, полученного из уравнения Ред-
лиха—Квонга, выбрав в качестве координат параметры
уравнения. Предложено также несколько корреляций, в
которых используются приведенные свойства и ацент-
рический коэффициент. Графическое изображение корре-
ляции, предложенной Питцером и Керлем, представле-
но на рис. 1.10, б. Усовершенствованная корреляция Ли
и Кеслера имеет следующий вид:
log(//P) = (log(//P))(0) + o>(log(//P))(l), (3.28)
где логарифмические члены в скобках — функции приве-
денной температуры и давления; некоторые величины
даны в табл. Д.6 и Д.7. В примере 3.1 сравниваются
фугитивности, полученные из экспериментальных дан-
ных о сжимаемости и аналогичных данных, рассчитан-
ных при помощи некоторых уравнений состояния. В
примере 3.2 коэффициенты фугитивности выводят из
двух видов В-усеченного вириального уравнения.
Таблица 3.2. Фугитивность и коэффициенты фугитивности смесей
Фугитивность
Коэффициент фугитивности
16. d>i=fi/yiP
2а. dGi = RTd\nfi = V{dP
26. dGfx = RTd\n<pi = K?x dP
За. PT In (/2//-j) = Gi2 ~Gix =
36. PT(ln 0,- - In 0,) = Gfx =
46.
PV
dV~ In-
RT
5a. ln/ = Zyz In (fi/yi)
6a. ln(//yz) = In/- E yk
k^i
(dlnf
\дУк
fdinfj \ Hf-Н{
la. ------ = ------------= -----
\ dT /D RT2 RT2
v 'Py
(d In/ \ К,-
8a. —— =-
\ dP / RT
' 'Ту
(d\n (fi/yi) \ ( d In 0Z \
9a. I---------- I = P I -------- I
' дУк 'TPyj^i,k ' дУк 'TPyj*ik
Hfx Й,
10a. d In/- = --- dT + — dP
1 RT2 RT
Па. Уравнение Гиббса — Дюгема
Яех V
^d^—^dT^-dP
12а. Уравнение Гйббса — Дюгема
при постоянных Т, Р
Ъу{ d 1п/ = 0
56. In 0 = Lyz In 0,-
66. In 0,- = In 0 — E k*i /d In ф Ук у дУк 'yj^i.k
fd In 0, \ 76. \ dT /_ x 'Py Hi - Hi
RT2 RT2
86. /d In 0,- \ dp \ Vi - Kjd ky~ RT JZ?x RT
/d In 0Z- \ d Г p p vfx 1
96. 1 _ L —dp
' дУк 'TPyj*i,k дУк L*, 0 RT J TPyjidi'k
Hfx K.ex
106. d In 0,- = - —-r dT +----dP
1 RT2 RT
116. Уравнение Гйббса — Дюгема.
^ex у ex
Т,У{ d In 0,- = — 9 dT + _ _ dP
‘ 1 RT2 RT
126. Уравнение Гйббса — Дюгема
при постоянных Т, Р
Eyz d In 0,- = 0
Таблица 3.3. Коэффициенты фугитивности чистых веществ, выведенные из некоторых уравнений состояния
Уравнение Ван-дер-Ваальса (табл. 1.3)
RT а
Р =------
v-b V2
а
In 0 = z — 1 — —— — In
RTV
2а
----— In
RTV
Вириальное уравнение (табл.1.8)
В С
2=1+ + 2"
V V2
2В 1.5С
In 0 = + -2— — In Z
v V V2
/Р \ /Р\2
‘ = 1 +в 7^ +(С-в2) — +...
( Р\ (С - В1) / Р \ 2 (D - ЗВС + 2В3) / Р \ 3
In 0 = В I I + I I + I I
\RT I 2 \RT / 3 \RT I
Уравнение Редлиха — Квонга (табл. 1.9)
RT а
Р~ V-b VTV( V+ b)
In 0 = Z — 1 — In
a
bRT1 5
A B
= z - 1 - ln(z - B) - - In I 1 + -
Уравнение Соава (табл.1.11)
RT aa
p =-----------
v-b V(V + b)
aa
bRT
A B
= z — 1 — ln(z — B) — ~ In I 1 + —
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(12)
(13)
Уравнение Пенга — Робинсона (табл. 1.13)
RT aa
P~ V-b V2 + 2bV-b2 (14)
A /z +2,4145 \
In 0 = z - 1 - ln(z - B) - —i~ In I--------- I (15)
7 2^2B \z- 0,4145 ) V ’
Примечание. Способы выведения коэффициентов фугитивности из уравнений Бенедикта — Уэбба — Рубина, Бенедикта — Уэб-
ба — Рубина — Старлинга и Ли — Кеслера показаны в табл. 1.16—1.18.
10*
148 Глава 2
Таблица 3.4. Коэффициенты парциальной фугитивности, выведенные из некоторых уравнений состояния
Уравнение Ван-дер-Ваальса (табл. 1.3):
RT а
(»
а = (Еу/х/а])2 (2)
b = ^yibi (3)
bj [ b \ 2 у/~аа~
1п ф: — ~ — In z I 1 — — I — (4)
v~b L \ vJ J RTV
Вириальное уравнение (табл. 1.8):
В С
z=1+^ + ^i <5)
. 2 1 ’5
1пф,- = - LykBki + —у 2L 2^укухСки - Inz
V к V к 1
(6)
ВР
RT
(7)
1П0,- =
RT
Bjj+0.5 Z Xyjy^j-Sjk)
_ J k
В =
bji = ZBji — Bjj - ВИ
8jk = 2Bjk - Bjj - Bkk
Уравнение для двух компонентов:
In 01 - RT^B\ + 3’2(25 12 - В\ - 52)]
(8)
(9)
(Ю)
(12)
ln02 = 7^^2 + 3’(?(2512-B1 -B2)] (13)
lx 1
Уравнение Редлиха — Квонга (табл. 1.9):
RT а
Р~ V - b y/TV(V + b)
а и b — параметры смеси [см. уравнения (2) и (3)]:
А = (£у;л/Л)2
bi
ln0Z = — (z - 1) - In
b
a bj
-~-2Vaai
In
(14)
(15)
(16)
(17)
В =
/ b \ 1 1
\1 ~ и/ + bRT'5
b
Bi A / Bj Aj \ B\
In 0Z = -y (z - 1) - ln(z - В) + I ~ 2 hj- 1 In I 1 + - ) (18)
Если вместо уравнения (2) применяется правило усреднения свойств а = в уравнении (17) следует вместо
\aai подставить
a ai - ^ykaik= ухац + y2ai2 +Уз«/з + • • • (19)
Уравнение Соава (табл. 1.11):
(aa)jj = (1 - kjj) у/(аа)ц(аа^-
(20)
Фугитивность и коэффициент фугитивности 149
Продолжение табл. 3.4
ки = О
aa =
b = 'Lyibi
А = (aa)P/(PT)2
В = bP/RT
Bi = biP/RT
bi
In 0,- = (Z — 1 ) — In
b-
aa
bRT
Bi A В{
= — (Z - 1)- In (z -5) + - —
В В В
2
aa
(21)
(22)
(23)
(24)
(25)
(26)
(27)
(28)
Уравнение Пенга — Робинсона (табл. 1.13):
Символы те же, что и в уравнении Соава,
численные коэффициенты в а несколько отличны.
In 0,-
В{ А
---(z — 1) — ln(z — В) 4-
В 4,828В
z 4- 2,414В
z - 0,414В
(29)
Примечание. Коэффициенты фугитивности, выведенные из уравнений Бенедикта — Уэбба — Рубина, Бенедикта — Уэбба — Руби-
на— Старлинга и Ли — Кеслера, представлены в табл. 1.16—1.19.
Для получения производных следует обратиться к
уравнению (3.8), содержащему определение
G = RT\nf + Л(Т),
(3.29)
и уравнению Гиббса—Гельмгольца (табл. А.З).
d(G/T) \ 1 td(G/T) \ Н
< дт /р т2 \<Э(1/т) )р т2 ’
(3.30)
Постоянную интегрирования Л(7) исключают, вычисляя
разность между состоянием реального и идеального
газа:
In/- InР = G/RT— G[,i/RT.
(3.31)
Поскольку при получении производных по температуре
давление считается постоянным, конечные результаты
идентичны и для фугитивности, и для коэффициента фу-
гитивности.
\ дР )т RT
и
/а Ш0 \ _ /а in (//Р) \ = _ 1 = XzJdl
\ ар )' \ ар / rt р rt
Х т 1 (3.34)
Воздействие изменений давления и температуры пред-
ставлено следующими уравнениями:
V H-Hld
d\nf = — dP- —dT,
J RT RT2
v- Kid н-н[й
<1\пф = ““ dP — dT.
RT RT2
(3.35)
(3.36)
Например, результаты подобных преобразований мож-
но применить к 5-усеченному вириальному уравнению
V = RT/P + В:
'д In А (д In (//Р) X /а 1п0
ч дТ )р \ дТ )р \ дТ
н-н1д
RT2
(3.32)
Производная по давлению является результатом преоб-
разования уравнения (3.4):
(3.37)
(3.38)
150 Глава 3
Уравнение (3.38) получают либо путем подстановки
V = RT/Р в уравнение (3.34), либо путем непосредствен-
ного дифференцирования уравнения (3.37). Для нахож-
дения производной по температуре правую часть
уравнения (3.32) можно определить, используя следую-
щее выражение:
(3.39)
Решая это уравнение совместно с уравнением (3.32), по-
лучаем
(3.39а)
3.3. Смеси
Фугитивность определенного компонента гомшенной
смеси при постоянной температуре определяют по урав-
нениям (3.5) и (3.7); дополнительные формулы приведе-
ны в табл. 3.2. Изменение парциальной фугитивности,
обусловленное изменением давления, можно найти ин-
тегрированием парциального молярного объема при по-
стоянном составе смеси:
1 Гр2 -
1п (fil/}! 1) = JiT JPi dp-
(3.40)
Абсолютные величины коэффициента парциальной фу-
гитивности получают, исходя из уравнения (3.7), соглас-
но которому 1п</>, = 0 при Р = 0. Интегралы давления
имеют несколько важных эквивалентов, которые удоб-
но применять при расчетах:
1 р р /_ RT \ 1 р р -
1пф‘ = 1ГтЬ [^-^)dp = ^J0 ^dP
(3.41)
(3.42)
При Р = 0 все интегрируемые функции стремятся к
нулю.
При наличии данных об объеме или сжимаемости
смеси парциальные молярные величины V, и zT можно
рассчитать по уравнению (2.56). Для двойной смеси
Пример 3.1. Расчет фугитивности аммиака по экспериментальным данным в сопоставлении с результатами приме-
нения ряда корреляций для вычисления фугитивности
Экспериментальные данные Тс = 405,6 К, Рс = Поскольку в данном случае требуется двойная интерпо-
= 111,5 атм, и = 0,25. ляция, определить можно всего несколько величин.
Величины сжимаемости при 100 и 200°С и определен-
ном интервале давлений указаны в Handbuch der anor-
ganischen Chemie, 4 ,426 (1935). Используется следующее
уравнение:
Уравнение Питцера и Керля, в которое входят члены Тг,
Рг и и, приведены вместе с рис. 1.10, б.
Анализ данных Ли—Кеслера (табл. Д.6 и Д.7) приво-
дит к выражению
log ф = (log ф)(0) + w(log ф)(1).
В табл. 3.3 приводится корреляция Редлиха—Квонга
для ф, численные значения которого найдены при помо-
щи ЭВМ.
Ниже представлены величины фугитивности, рассчи-
танные из экспериментально найденных значений z по
уравнениям Питцера—Керля, Ли—Кеслера и Редлиха—
Квонга. Как показывает сравнение результатов расчетов
сжимаемости, степень точности уравнений Редлиха—
Квонга и Ли—Кеслера примерно одинакова, в то время
как уравнение Питцера—Керля дает весьма неудовлетво-
рительные результаты, особенно при давлениях выше
400 атм.
Экспериментально найденные и рассчитанные по уравнениям Питцера—Керля (ПК), Ли—Кеслера (ЛК) и Редли-
ха—Квонга (РК) коэффициенты фугитивности ф при различных давлениях и температуре 100 и 200°С
100°С
200°С
р эксперимент ПК ЛК РК эксперимент ПК ЛК РК
100 0,5464 0,6560 0,5268 0,8322 0,8157
200 0,2896 0,4298 0,3126 0,6676 0,6926 0,6538
300 0,2124 0,2818 0,2106 0,2392 0,5466 0,5764 0,5595 0,5402
400 0,1756 0,1847 0,2057 0,4081 0,4797 0,4760
600 0,1426 0,0794 0,1508 0,1781 0,3888 0,3322 0,4237 0,4166
800 0,1299 0,0341 0,1713 0,3547 0,2301 0,3980
1000 0,1254 0,0147 0,1441 0,1742 0,3404 0,1593 0,3997 0,3985
Фугитивность и коэффициент фугитивности 151
Экспериментально найденные величины сжимаемости аммиака и рассчитанные коэффициенты фугитивности как
функция давления при температуре 100 и 200°С (некоторые из этих данных заимствованы из предыдущей таблицы)
100°С 200°С
Р, атм Z - l(f(z - 1) Ф Р, атм Z -l(f(z - 1) Ф
Р Р
0 1 (0) 1 0 1 (0) 1
1,374 0,9928 52 0,9964 1,747 0,9964 21 0,9982
3,573 0,9830 48 0,9857 4,519 0,9913 19 0,9929
5,832 0,9728 47 7,489 0,9856 19
8,632 0,9599 46 11,153 0,9786 19
11,352 0,9468 47 14,766 0,9716 19
14,567 0,9315 47 0,9362 19,098 0,9635 19
19,109 0,9085 48 25,361 0,9513 19 0,9544
22,84 0,8890 49 30,64 0,9409 19
26,12 0,8714 49 35,40 0,9318 19
30,47 0,8471 50 0,8660 41,89 0,9188 19
33,21 0,8310 51 46,12 0,9104 19
36,47 0,8111 52 51,29 0,9000 19 0,9085
40,41 0,7864 53 57,74 0,8865 20
45,19 0,7538 54 0,8016 66,05 0,8693 20
51,09 0,7102 57 77,13 0,8460 20
58,28 0,6481 60 0,7440 92,57 0,8122 20 0,8365
100 0,1158 88 0,5464 100
200 0,2221 39 0,2896 200 0,5506 22 0,6676
300 0,3202 23 0,2124 300 0,4615 18 0,5466
400 0,4145 15 0,1756 400 0,4949 13 0,4681
500 0,5060 10,0 0,1550 500 0,5567 8,9 0,4195
600 0,5955 6,7 0,1426 600 0,6211 6,3 0,3888
700 0,6828 4,5 0,1348 700 0,6826 4,5 0,3684
800 0,7684 2,9 0,1299 800 0,7546 3,1 0,3547
900 0,8507 1,7 0,1269 900 0,8235 2,0 0,3457
1000 0,9333 0,7 0,1254 1000 0,8915 1,1 0,3404
1100 1,0140 -0,1 0,1251 1100 0,9590 0,4 0,3379
можно, например, применить следующие уравнения:
(3.43)
(3.44)
Их используют в примере 2.5, а для решения задачи
3.20 следует прибегнуть к уравнению (2.56).
Парциальные фугитивности и коэффициенты фуги-
тивности отдельных веществ можно получить, исходя
из парциальных фугитивностей и коэффициентов фуги-
тивности смеси при помощи правил, обычно применяе-
мых для расчета парциальных молярных величин:
(дп In ф \
“ ) . (3.46)
dn,- /
Для некоторых уравнений состояния представляется бо-
лее удобным прежде всего найти выражение коэффици-
ента фугитивности смеси, а затем определить коэффи-
циенты парциальной фугитивности, применив уравне-
ния (3.45) или (3.46).
Поскольку среди уравнений состояния чаще всего
встречаются уравнения, выраженные через давление, ко-
эффициенты парциальной фугитивности можно полу-
чить при помощи следующего уравнения:
RT
V
dV~RT\nz,
(3.47)
fi
In
д п \nf \
дп; I
'TPnj^i
(3.45)
способ выведения которого показан в примере 3.3. Это
же отношение применяется в сочетании с уравнением
Редлиха—Квонга (см. пример 3.4).
152 Глава 3
Пример 3.2. Расчет коэффициентов полной и парциальной фугитивности для двухкомпонентных смесей при помо-
щи двух видов В-усеченного вириального уравнения
Используются следующие два вида вириального урав- нения: Учитывая зависимость второго вириального коэффици- ента от состава смеси
z = PV/RT = 1 + BP/RT = (1) = 1 + B/V (2) В = УиВц + У1Ви -I- У1У2О12, (9) 612 = 2В12 — В\\ — В22, (10)
Из уравнения (1) следует In ф = -1 f dP = ~Р • (3) RT Jo P RT находят коэффициенты парциальной фугитивности а) по уравнению (1): 1пф1 = rt (Ди 4- Яб12), (П)
Преобразования уравнения (2) начинают следующим об- разом: In Ф2 = Р (В22 + У1612); (Па) RT
RTdlnf = VdP = d(PV) - PdV. (4)
Из обеих частей уравнения вычитают RT d In Р и прово- дят перегруппировку: б) по уравнению (2): 2 In Ф1 = - O1B11 + У2В12) - In z, (12)
d In ф = dz Р dV - <7 In P. (5) RT V 2 In Ф2 = - O1B12 + У2В22) - In z. (12a)
После выполнения подстановки
P/RT = 1/V + B/V1 (6) Ниже показаны графики уравнений (11) и (12), которые при высоких давлениях существенно отличаются друг от
и интегрирования в пределах между Р и 0 получаем друга. Параметры уравнений, изображенных на графи-
In ф = z - 1 — In z + B/V = 2B/V - ln(l + B/V) = = 2(Z - 1) - In z (7) ках, имеют следующие значения: Вц = 0,5, В22 = 0,1, В\2 = 0,4. Применение данных результатов к многоком- понентным смесям показано в табл. 3.3 и 3.4. Эмпириче-
Коэффициенты парциальной фугитивности можно выве- сти из уравнений (3) и (7). ские корреляции вторых вириальных коэффициентов В обычно основаны на Я-усеченном вириальном уравнении,
In ф< = In ф + (1 - Vi) ( -д 1° , i = 1, 2 (8) \ ду, / т.е. уравнении (1), поэтому для расчета коэффициентов фугитивности предпочтительным является уравнение (П).
>7
Фугитивность и коэффициент фугитивности 153
Если состав выражается в мольных долях, для расче-
та фугитивности и коэффициентов фугитивности урав-
нение (2.56) преобразуют к виду
fi X? ( I
In = In/- 2^хк I I
X,- к \ иХк /
' ' 'TPxj^
~ /а in ф \
In 0Z = In 0 — 2ш1 Хк I I
к \ дХк /
T?xj^i, к
(3.48)
(3.49)
При расчете свойств компонента i подстановка х, =
= 1 - 'Ex.:*j, выполняемая перед получением производ-
ных, значительно облегчает ход вычислений. Данный
прием используется в примере 3.5.
Применение уравнений (3.48) и (3.49) для описания
двойных смесей дает
д In 0 \
“Г I = In 0i — In 02-
OX 1 /
(3.50)
Способ графического решения этого уравнения извес-
тен под названием метода отрезков, отсекаемых каса-
тельной (см. рис. 3.4). При условии точного построе-
ния касательной этот метод дает возможность легко
определить коэффициенты фугитивности отдельных ве-
ществ по коэффициенту фугитивности смеси.
3.3.1. Производные. Уравнения для расчета производ-
ных парциальной фугитивности и коэффициентов фуги-
тивности по температуре и давлению аналогичны
уравнениям (3.23)—(3.24). Таким образом,
Гораздо сложнее вывести формулу явной производной
уравнения Редлиха—Квонга. Так, в примере 3.4 [уравне-
ние (14)] следует учитывать изменения z и V, связанные
с изменением состава. В то же время численные произ-
водные получить достаточно легко. Так, например, при
решении задачи 3.14 получаем:
№н, 0NH, 1Об(д01/ду1)
0,4 0,845856 -14,72
0,5 0,845877 443,11
0,6 0,845942 880,94
Формально влияние изменения температуры, давления
и состава на некое общее свойство М можно представить
как
d(nM) = n(--\ dT+n(^^\ dP + ^Midm. (3.56)
\^)Рп \*р)Тп
Совместное преобразование таких двух уравнений дает
ZmdMi = п(^\ dT п( дМ\ dP (3.58)
\*Т)Рп \Ьр)Тп
или
ExirfM = f-^Л dT + dP, (3.59)
\dTJPn \wJTn
т.е. уравнение Гиббса—Дюгема. При подстановке урав-
нений (3.51)—(3.54) получаем
Нех V
ZXid ln(//xz) = - —+ ~_dP (3.60)
KI Jx 1
1п/ \ _ Н{ - Н,
< дТ )рх RT2
In 0Z \ НГ
< дТ /рх RT2 ’
In/- \ __П
к дР L RT’
^ln0z \ v^_
< дР )Тх RT ’
(3.51)
(3.52)
(3.53)
(3.54)
TLx^d In 0Z
№x
f/ex
- —7 dT +------dP.
RT2 RT
(3.61)
При постоянных температуре и давлении приведенные
выше уравнения принимают следующий вид:
Sxz d ln(/z/xz) = 0,
"Lxj d In 0Z — 0,
(3.62)
(3.63)
благодаря чему их широко применяют на практике для
расчета одного из коэффициентов фугитивности для би-
нарных систем, если другой коэффициент определяется
как функция состава:
Величина интеграла в уравнении (3.42) неявно зависит
от состава, так же как и от температуры и давления, сле-
довательно, изменения коэффициента фугитивности,
обусловленные изменениями состава, можно найти пу-
тем дифференцирования результата интегрирования. Ре-
зультат интегрирования вириального уравнения
представлен в примере 3.2 [уравнение (11)]. Соответ-
ствующую производную можно записать следующим
образом:
In 02 ~ In 02
d In 0i.
(3.64)
(д In 0i \ р
дуг / 2^2512лг-
(3.55)
3.3.2. Экспериментальные данные. Одной из основных
областей применения уравнений состояния является рас-
чет фугитивностей, именно поэтому во многих случаях
для оценки этих уравнений используют эксперименталь-
ные данные о фугитивности. Ниже перечислено несколь-
ко работ такого направления, опубликованных относи-
тельно недавно. Так, например, авторы работы [160]
провели измерение фугитивности смесей водорода, ам-
миака и пропана при помощи полупроницаемой мембра-
ны. Из числа рассмотренных этими авторами уравнений
состояния приблизительно одинаковую степень точности
154 Глава 3
Пример 3.3. Способ вывода уравнения (3.47) для расчета коэффициента парциальной фугитивности путем интегри-
рования уравнения состояния относительно объема
В определении парциальной фугитивности Интегрирование уравнения (5) дает
RTd In /, = VdP = ( ) dP (1) \ &п‘ / ЯГ1п [ (—- - ~- \d(nV) - ЯГ1п --- . (7) У, J Д dn, nV J RT
дифференциал давления можно исключить, используя по- следовательность частных производных (приложение Б), И наконец, после вычитания RT In P из обеих частей урав- нения получаем
= _ 1, (2) \ дп, ) \ дР J \dnVj ЯГ In ф,. = RT In X = У,Р
откуда = f ( ~ - -~}d(nV) - ЯГ In z. (8)
dP = VidP = - ЛхЛоГ(лЕ). (3) у дп, у у дп, у JA^ nV J
Выполнив подстановку в уравнение (1) и прибавив RTd\n(V/RT) к обеим частям уравнения, получим Исходя из того, что Р = zPT/V и / дР \ _ Р / d(nz) \
f.V I V RTd In - -- = - I °-]d(nV) + ЯШ In -- = (4) RT \ dm J RT \ дП‘ / Т.п К. п, \ дП‘ / Т.п Т.п,
= - (-P-\ + d(nV). (5) у dm у nV можно вывести уравнение для расчета коэффициента фу- гитивности путем подстановки вышеупомянутого выра- жения в уравнение (8) и последующей перегруппировки
Необходимо учесть, что In ф, = f fXX-A-X-inz. (10)
f у f lim In —— = lim In = In y,. (6) и-.» ЯГ P J Л / V Уравнение (8) применено в примере 3.4.
Пример 3.4. Расчет коэффициентов парциальной фугитивности по уравнению Редлиха—Квонга
В данном примере применено уравнение (8) из примера
3.3:
(1)
Если уравнение Редлиха—Квонга выразить через полный
объем V_= nV, то получим
nRT _ п2а_________
J/- nb vf_E(J/+ nb)
- _1_ in (X±J±\ д^а) _ ln z (4)
пЬФТ \ Y_ / дп,
В верхнем пределе интеграл равен нулю. Применим сле-
дующие правила усреднения свойств:
а = (Ey,VG,)2 = X (E/?,VgT)2, (5)
п
b = Ly,bi = - Ln,bi. (6)
п
Далее находим необходимую производную
ЭР \ = RT + nRT д(пЬ) _
дт / Tvnj X-nb (X- nb)2 дп,
_______________д(п2а) +_________п2а________д(пЬ)
+ nb) дп, <TV_(V_ + nb)2 дп, ' ( '
Поскольку производные по правой части уравнения (3) не
зависят от V , можно приступать к непосредственному
интегрированию уравнения (1):
Производные будут иметь следующий вид:
XLа- = 2-Jm Lm\ai = 2п\аа, , (7)
дп,
^’ b,. (8)
дт
Заменив производные в уравнении (4) их эквивалентами
и сократив п, получим
RTlnfr = - ЯГ In X—пЬ +
V
__nRT_____па
V_ — nb b>/T( V + nb)
+ ° in Y-+ nb д(пЬ)
ЬЧТ V дт
V - Ь
ЯГ In ф, = - ЯГ In —--
а , а i„ V +
bJt(V + Ь) ьЧт V
2\аа, . V + b
Ь\/Т V
V-b
bi -
(9)
Фугитивность и коэффициент фугитивности 155
Путем подстановки
V-b KT'\V + b)
(Ю)
Итак, коэффициент фугитивности определяется выраже-
нием
In ф, =
bi
Ь
(z - 1) +
и перегруппировки получаем
1
bRT" 5
(14)
(И)
При atj \la,aj правило усреднения [уравнение (5)] при-
нимает следующий вид:
При выводе уравнения для расчета коэффициента фуги-
тивности чистого вещества следует принять, что b, - b
и а, - а:
а = \ 'E'Enlnjalj. (12)
п1
Производную можно определить как
(15)
(13)
Пример 3.5. Уравнения для расчета парциальных фугитивностей четырехкомпонентной смеси, выведенные из урав-
нения для расчета полной фугитивности как функции состава
В примере применена методика, изложенная в разд.
2.6. Чтобы оценить/, исключают из уравнения для рас-
чета f мольную долю х, и после этого проводят диффе-
ренцирование
X, = 1 - 2 Xj.
Предполагаемое уравнение для расчета фугитивности
смеси и его необходимые в данном случае эквиваленты
будут иметь следующий вид:
In/ = axi + bxi + схз -I- <7х2 =
= о(1 - Х2 - Хз - Х4)2 + bxi + схз + dxl =
= axi + b(l - Xi - хз - x»)2 + схз + dxi =
= ох2 + bxi + с(1 - Xi - хг - X4)2 + <7x4 =
= OXi + bxi -I- СХз + <7(1 - Xi - X2 - X3)2.
Уравнения для расчета парциальных фугитивностей
можно записать следующим образом:
, /1 , , / df \ ( df\
In — = In/ - Х2 I -- - I - Хз I - 7 I
Xi \ dx2 / x \ дхз /
x> ( J = In/ - 2хг(-оХ1 + Ьхз) -
\ дхз /
\ /
- 2X;( ~ OX I + CX3) - 2x4(-OXi + <7x4),
7
In --2- = In/ - 2xi(ox1 ~ bxz) - 2хз(~Ьхг + схз) -
X2
- 2xi( - bxi -I- <7x»).
r
In - = In f - 2xi(0x1 - cxi) - 2xi( - Ьхг + CX3) -
Хз
- 2х4(-схз + (/хз).
In = In / - 2xi(oxi - <7x4) - 2x2( bx2 + dx*) -
x4
- 2хз(сх3 -I- (7xi).
(в пределах 2—3%) показали уравнение Бенедикта—
Уэбба—Рубина, вириальные уравнения третьего порядка
и уравнение Редлиха—Квонга. В результате анализа
большого количества экспериментальных данных для
углеводородов, выполненного авторами работы [442],
выяснилось, что в общем случае для расчета фугитивнос-
ти наиболее предпочтительны уравнения Соава и Ли—
Кеслера. Результаты расчетов, проведенных при испо-
льзовании этих уравнений, совпадают с эксперименталь-
ными данными в пределах 1—2%. Данному вопросу по-
священо множество публикаций, многие из которых ци-
тируются в гл. 1 и 6.
3.4. Идеальные смеси
Идеальной называют такую смесь, свойства которой
можно определить исходя из свойств чистых компонен-
тов, так же как свойства смеси идеальных газов находят
исходя из свойств отдельных компонентов. Однако это
не означает, что данные компоненты идеальной смеси
должны быть в обязательном порядке идеальными газа-
ми, ведь жидкие смеси и твердые растворы также могут
иметь «идеальные» характеристики, если вкладывать в
этот термин тот же смысл, что и здесь. Основываясь на
понятии «избыточные свойства» (см. разд. 2.9), идеаль-
156 Глава 3
Пример 3.6. Расчет коэффициентов фугитивности смесей диоксида углерода и пропана
Температура смеси: 37,8°С (100°F), давление: 14 кг/см2
(200 фунт/кв.дюйм), вириальные коэффициенты: Ви =
= —1,8, Bn = - 5,87, В12 = - 3,36. В примере исполь-
зуются уравнения, приведенные в табл. 3.3 и 3.4.
612 — 2512 — 5ц — 5гг = 0,95,
5 = - l,8yi - 5,87^2 + 0,95_У1_У2,
P/RT = 200/10,73(559,6) = 0,0333,
In ф = BP/RT = 0,03335,
1П ф[ =------(5ц + У2612),
RT
In Ф2 =------(В22 -I- .V1512).
Результаты расчетов сведены в таблицу. Полученные ко-
эффициенты в значительной степени зависят от состава
смеси, и, следовательно, в данном случае правило Льюи-
са—Рендала ф,/ф, = 1 неприменимо.
А о- ф О< о- Ос,ыч
0,0 0,8224 0,6958 0,8224
0,1 0,8360 0,7234 0,8496
10 0,2 0,8493 0,7506 0,8760 0,3 0,8623 0,7773 0,9015 0,4 0,8749 0,8035 0,9260 0,5 0,8871 0,8290 0,9493 0,6 0,8989 0,8536 0,9714 0,7 0,9103 0,8774 0,9921 0,8 0,9213 0,9001 1,0113 0,9 0,9318 0,9216 1,0290 1,0 0,9418 0,9418 1,0449 FOR Y - О ТО 1 STEP .1
20 В- -1.8*Y A2-6.72*Y*(1-Y)-5.87*(1 -Y)a2
30 Bl = - 2*(1.8*Y+3.36*(1 -2*Y)-5.87*(1 -Y))
40 F = EXP(.O333*B)
50 Fl = EXP(.O333*(B - (1 -Y)*B1))
60 F2 = EXP(.O333*(B+Y*B1))
70 PRINT USING 80; Y,F,Fl,F2
80 IMAGE D.D,2X,D.DDDD,2X,D.DDDD,2X,
D.DDDD
90 NEXT Y
100 END
ную смесь можно рассматривать как смесь, избыточные
свойства которой равны нулю. Соотношения, определя-
ющие объем и энтальнию идеальной смеси, записывают-
ся следующим образом:
j/ex= v_ Zx.v. = 2х.(кг- - Kz) = 0, (3.65)
Й-=П-, (3.66)
Яех = Я-2х1Я1 = Ех1-(Яг-Я1) = 0, (3.67)
= (3.68)
а идеальную энтропию и связанные с нею величины, как
показано в разд. 2.8, рассчитывают по уравнениям
5ех = 5-Ех;-5;+5Ех,1пх1 = 0, (3.69)
S, = Si + R lnxz, (3.70)
(7ех = (7-Ехг(7г-5Г2х;1пхг = 0, (3.71)
Gf = Gf - RT\nxf. (3.72)
На рис. 3.1 представлены кривые изменения энтропии
и энергии Гиббса в зависимости от состава идеальной
смеси. Избыточные свойства реальных смесей нередко
значительно отличаются от нуля и могут иметь как поло-
жительную, так и отрицательную величину в зависимос-
ти от диапазона концентрации и химической природы
смеси. В гл. 4 приводится несколько примеров, демон-
стрирующих сказанное. Идеальный характер изменения
парциального давления описывается законом Рауля. Ряд
возможных отклонений от этого закона показан на рис.
3.2.
Из уравнения (3.66) и соответствующих определений
[уравнений (3.4) и (3.5)] следует, что для идеальных
смесей
ф/ = ф/. (3.73)
и
Л = х/Л. (3-74)
Эти отношения называют правилом Льюиса—Рендала,
согласно которому парциальная фугитивность соотно-
сится с парциальной фугитивностью чистого компонента
так же, как парциальное давление соотносится с давлени-
ем пара. Поскольку фугитивность чистого компонента
рассчитать проще, чем парциальную фугитивность, пра-
вило Льюиса—Рендала нашло широкое применение.
Если в качестве условия принято, что ф, = фи значи-
тельные погрешности возможны даже при средних дав-
лениях. Например, как видно из примера 3.6, для смеси
СОг — пропан погрешность достигает примерно 25%.
Однако ничего более определенного о вероятных погреш-
ностях расчетов сказать нельзя. Условия, соответствую-
щие идеальному состоянию, можно хотя бы отчасти
объяснить исходя из уравнения Ван-дер-Ваальса. В табл.
3.3 и 3.4 представлены коэффициенты фугитивности, вы-
веденные по этому уравнению:
b 2а / Ь \
|пф=7ЛГ^“|п [г v)
(3.74а)
bj 2 \Гаа\ / b \
1п0г-7_£~ RTV ~ ln z у)
(3.746)
Фугитивность и коэффициент фугитивности 157
Рис. 3.1. Изменение энтропии и энергии Гиббса при образо-
вании идеальных растворов.
Для смеси S - SxjS, = Inx, и G — Xx,G, = — RT^Lxl In х,.
Для отдельных компонентов S, - S, = R 1пх, и G, - G, = -ЛПпх,.
Поскольку для идеальных растворов Н = HxtH,, (G - Tjx,Gt)/T =
= -(S - Sx,S,).
При заданных температуре и давлении ф = ф, обычно
только при bi = b и at = а, т.е. если все молекулы смеси
имеют примерно одинаковые размеры и сходны по своей
химической природе. Кроме того, о( и Ь, приближаются
к а и b (значениям величин для смеси) у тех компонентов,
концентрация которых достаточно велика, например, у,
составляет примерно 0,9. И наконец, при низких давлени-
ях члены, содержащие И, можно опустить, и, следова-
тельно, ф -> ф -> 1/z. Помимо этих предельных ситуаций
основания для применения правила Льюиса—Рендала
имеются крайне редко. В то же время это правило удобно
использовать при итерационных вычислениях, в которых
требуется выполнить оценку ф,.
Помимо идеальных часто различают несколько других
категорий смесей. Так, раствор называют атермиче-
ским, если избыточная энтальпия равна нулю. Такого ро-
да поведение характерно для сходных по своей
химической природе веществ, молекулы которых практи-
чески одинаковы по размеру. В качестве примера можно
привести некоторые классы углеводородов. Существует
ряд теоретических методов нахождения избыточной энт-
ропии (см., например, [64]). Избыточную энергию Гибб-
са можно, следовательно, определить по формуле
Gex = Г$ех для атермической смеси.
Растворы, избыточная энтропия которых равна нулю,
называют регулярными. Как правило, для веществ, об-
разующих регулярные растворы, не характерны ярко вы-
раженные ассоциативные силы, обусловливающие
158 Глава 3
Рис. 3.2. Различные степени соответствия закону Рауля (представлен штриховыми прямыми).
Кривая 1. Средняя степень соответствия. Тетрахлорид углерода 4- циклогексан при 40 °C.
Кривая 2. Значительное отрицательное отклонение. Ацетон + хлороформ при 35,3 °C.
Кривая 3. Значительное положительное отклонение. Метилальдегид + сероуглерод при 16,5 °C.
сильную полярность, склонность к образованию водо-
родных связей и химической ассоциации однородных и
разнородных молекул. В силу того что избыточная энер-
гия Гиббса равна энтальпии смешения, которую легко
определить путем обычных калориметрических измере-
ний, расчеты для этого класса растворов значительно
упрощаются:
(?ех =яех - TSex - Нех = Н- ZxfHj, (3.75)
Gex = Нех - TSex Нех = Н, - Mj. (3.76)
Теоретические выводы относительно регулярных раство-
ров изложены в гл. 4. В табл. 2.7 приведен ряд величин
избыточных свойств, судя по которым некоторые из ука-
занных там растворов можно отнести к регулярным. В
гл. 4 также рассматривается несколько подобных приме-
ров. Обзоры данных об избыточных термодинамических
свойствах издаются Кехьяяном и Зволински [5]. Исчер-
пывающий обзор литературы по этому вопросу опубли-
кован Вишняком и Тамиром [20].
Избыточную энтропию смесей, молекулы которых
значительно отличаются по размеру, например смесей
растворителя и полимера с большой молекулярной мас-
сой, в ряде случаев приближающуюся к нулю, удобнее
выразить не в мольных долях, а в долях молярных объ-
емов. Другими словами, выражение
ASmixing = /?Sxzlnxz (3.77)
заменяют на
Д$п™=^1пФ/, (3.78)
где
0z = xzKz/SxzKz.
(3.79)
Более того, в некоторых работах взаимодействие между
молекулами выражают в долях площади поверхности,
как, например, при использовании уравнения UNIQUAC
и связанного с ним метода UNIFAC.
3.5. Жидкая и твердая фазы
При оценке изменений энергии Гиббса или фазового
равновесия в высшей степени удобным представляется
использование некоего эталонного, или стандартного,
состояния. В условие равенства фугитивностей отдель-
ных компонентов для всех фаз 1, 2, 3,... в состоянии рав-
новесия
j.(l) =у(2) = , (3.80)
или
.... (3-81)
можно ввести фугитивность стандартного состояния У?:
Ь(7Р/Л°) = 1п(^2У/-°) = ... (3.82)
При изменении состояния можно записать
AGZ = RТ 1п[(Л)2/(Л )i ] = R Т In
~(Л)2/л° ’
(3.83)
Фугитивность и коэффициент фугитивности 159
Рис. 3.3. Стандартные состояния газов, растворителей и раство-
ренных веществ.
а — реальные газы Л и fl в различной степени отклоняются от идеаль-
ности, но имеют одно и то же стандартное состояние; б — стандартным
состоянием вещества, содержащегося в большей концентрации, т. е. рас-
творителя (2), является состояние чистого вещества; стандартным состо-
янием растворенного вещества (2) является состояние гипотетической
жидкости, соответствующее точке пересечения ординаты при Хг = 1 и ка-
сательной к кривой при нулевой концентрации или бесконечном раз-
бавлении.
До тех пор пока одно и то же стандартное состояние при-
меняется для определенного вещества при ряде взаимо-
связанных изменений состояния, фугитивности следует
заменять на их соотношения с фугитивностями стандарт-
ного состояния, в результате чего все термодинамиче-
ские уравнения будут оставаться неизменными.
Хотя в целом выбор стандартного состояния носит
произвольный характер и зависит от конкретной ситуа-
ции, несколько стандартных состояний считаются наибо-
лее удобными для расчетов и применяются наиболее
широко. В определение стандартного состояния входят
давление и физическое состояние вещества, которое дол-
жно быть устойчивым при температуре системы. Поэто-
му, хотя сама температура в определение не включается,
стандартное состояние от нее зависит. Для газов, естест-
венно, будет принято, что в таком состоянии, при кото-
ром фугитивность равна единице при температуре
системы, давление в большинстве случаев примерно рав-
но 1 атм. Отношение, определяющее стандартное состо-
яние газов, приводится на рис. 3.3,а.
Для конденсированных фаз в качестве стандартного
выбирается такое состояние, при котором можно легко
найти фугитивность. При наличии данных о давлении па-
ра за фугитивность конденсированной фазы принимают
фугитивность паровой фазы, находящейся с ней в равно-
весии при температуре системы. Корректировка этой фу-
гитивности относительно давления системы
выполняется при помощи следующего выражения:
In------=
/sat
/ — dP.
Jpsat
(3.84)
которое использовано в примерах 3.7 и 3.10.
Получить данные о давлении пара твердых веществ
можно далеко не всегда, однако, как правило, известны
температура плавления твердого вещества и иногда его
160 Глава 3
Таблица 3.5. Тройные точки и точки плавления некоторых органических
веществ3
Вещество
Температура
плавления, °C
Тройная точка
Т, °C Р, мм рт.ст.
Нафталин 80,2 80 7,4
Тетрахлорид углерода - 22,96 -22,6 7,9
Уксусная кислота 16,6 16,7 9,7
Бензол6 5,5 5,47 36,1
Аммиак -77,74 -77,7 43,4
Метан - 182,5 -183,2 70
Оксид углерода -207 -205,2 115,1
Камфора 179,5 175 354
Циан -27 -27,92 555
Ацетилен -81,5 -81 950
Диоксид углерода -56 -56,4 3906
а Данные о тройных точках заимствованы из работы [146], а данные о точках плавле-
ния — из “Handbook of Chemistry” (Lange, 1973); следует, однако, отметить, что они
не всегда совпадают.
6 Температура плавления бензола 32,5 °C при 1000 бар , 114,6 °C при 5000 бар и
190,5 °C при 10 000 бар (Бриджмен).
тройная точка, которые практически равны. Тройные
точки и температуры плавления ряда органических ве-
ществ представлены в табл. 3.5. В этих условиях за дав-
ление можно принять давление пара, которое находят
путем экстраполяции ниже точки замерзания уравнения
для расчета давления пара. Последующая корректировка
фугитивности твердого вещества относительно давления
и температуры системы выполняется в соответствии со
следующим уравнением:
f ГР V гт H'd — Н
1П4 = JPrpJiTdP+ JrrP ^T2 dT- (3-85)
Разность №d - Н можно рассматривать как теплоту
сублимации при умеренных давлениях. Если же данные
о теплоте сублимации отсутствуют, ее можно заменить
суммой теплоты плавления и теплоты испарения или же
рассчитать, исходя из данных о давлении пара твердого
вещества по уравнению Клаузиуса—Клапейрона. Табли-
ца констант Антуана многих твердых веществ, используя
которые можно выполнить подобный расчет, содержит-
ся, например, в CRC Handbook of Chemistry and Physics
(pp. C722—3, 1979). В примере 3.8 показана методика
определения фугитивности жидкости в определенном ин-
тервале температур. Пример 3.9 иллюстрирует примене-
ние уравнения (3.85).
3.5.1. Жидкие и твердые растворы. При проведении
термодинамических расчетов за стандартное чаще всего
принимают два следующих состояния.
1. За стандартное принимается состояние чистого жид-
кого или твердого компонента при температуре и давле-
нии системы либо при давлении, равном 1 атм или
равном давлению пара чистого компонента.
2. Необходимо разграничить растворитель (компо-
нент, присутствующий в смеси в большем количестве) и
растворенное вещество (компонент, присутствующий в
смеси в меньшем количестве). Стандартное состояние
растворителя — это состояние чистого компонента, со-
ответствующее п. 1, в то время как стандартное состоя-
ние растворенного вещества определяется по одной из
модификаций закона Генри:
= (3.86)
Константа уравнения представляет собой величину тан-
генса угла наклона касательной к кривой зависимости f
от Xi при концентрации, стремящейся к нулю, следова-
тельно, фугитивность в стандартном состоянии численно
равна константе Генри:
/ау; \
Л = кН = • (3.87)
х(=0
Эти условия, отвечающие стандартному состоянию, по-
казаны на рис. 3.3,6.
В двухкомпонентных системах смысл кн вполне опре-
делен, и при наличии соответствующих данных бесконеч-
ное разбавление представляется достаточно удобным
для практического применения в качестве стандартного
состояния. Если же растворитель является смесью, такое
понятие стандартного состояния становится менее опре-
деленным, поскольку кн зависит от состава. Однако по-
добное представление можно получить для некоторых
тройных смесей, представляющих собой растворы раз-
личной концентрации одного из компонентов в двухком-
понентном растворителе постоянного состава. Коэффи-
циент парциальной фугитивности определяется по урав-
Фугитивность и коэффициент фугитивности 161
Соответственно константа Генри преобразуется к сле-
дующему виду:
lim
х3-0
= lim exp
х3-0
(3.90)
Существенную зависимость кн от состава смеси в неко-
торых случаях подтверждают результаты, полученные
при решении задачи 3.14:
г 0 2 10
к3/Р 0,135 0,801 0,508
На рис. 3.5 схематически показано, как отрезки, отсекае-
мые на осях координат, могут зависеть от формы по-
верхности. Касательные к поверхности при хз - 0, т.е.
проходящие через ось, проведенную через точку 3, пере-
секают эту ось в различных точках.
Рис. 3.4. Определение коэффициентов парциальной фу-
гитивности по точкам пересечения касательных с осями
ординат.
а — при определенном составе смеси парциальные фугитивнос-
ти определяют как точки пересечения касательной к кривой из-
менения коэффициента фугитивности смеси с осями ординат:
при yi = 0 и yi = 1(У2 = 0); б — коэффициенты фугитивности
смесей диоксида углерода и пропана. Этот типичный график
показывает, насколько трудно получить при помощи рассмат-
риваемого метода точные результаты в тех случаях, когда кри-
визна графика фугитивности мала. Такая ситуация подробно
анализируется в примере 3.6.
нению (2.64):
In 03 — In 0 + ( 1 — Х3)
(3.88)
при постоянном г = Х\/хг. Из определения ф, = fiXtP сле-
дует, что
д/3 /дф3х3\
V = Р / = Р
дх3 V дх3 /
11-829
/<503 \
Х3 Lr ) + 03
у*3 /
(3.89)
Рис. 3.5. Зависимость констант закона Генри от состава
многокомпонентных смесей.
Обратите внимание, что касательные к поверхности при хз =
= 0, проходящие через ось в точке 3, не пересекают эту ось на
одной и той же высоте.
162 Глава 3
Пример 3.7. Зависимость фугитивности жидкого хлороформа от давления
При 20°С и 1 атм удельный объем хлороформа состав-
ляет 80,17 мл/моль, давление пара 0,079 атм. Влияние
давления на удельный объем определяется следующим
выражением (Ланге, 1973):
V = 80,17[1 - 94,9(Е - 6)(Р - 1)].
При 20°С можно принять, что фугитивность равна дав-
лению пара т.е. 0,079 атм. При прочих давлениях
Основываясь на допущении о несжимаемости жидкости,
рассчитывают фугитивность по данному уравнению и
представляют полученные значения в табличной форме.
Результаты проведенных расчетов показывают, что да-
же при небольших величинах давления, вплоть до 10 атм,
его воздействие на фугитивность является сущест-
венным.
f = Psa" exp Г (V/RTylP =
nn_o f 80,17
= 0,079 exp {----------------
82,05(293,16)
- 47,45(E - 6)P2] I
J 0,079
[0,99991P -
Р, атм f y/psa. f/P^' (несжим
0,079 0,079 1 1
1 0,0792 1,0031 1,0031
10 0,0817 1,0336 1,0336
100 0,1100 1,3929 1,3952
Пример 3.8. Коэффициент фугитивности насыщенного жидкого бензола в интервале от температуры плавления
до критической
Следует учесть, что фугитивность насыщенной жид-
кости равна фугитивности насыщенного пара. В примере
используются В-усеченное вириальное уравнение и фор-
мулы Эббота.
В = [0,083 - 0,422/Г,1’6 + ы(0,139 - 0,172/Т?’2)].
Рс
Критические свойства: Тс = 562,1 К, Рс = 48,3 атм,
ы = 0,212. Давление пара рассчитывают по следующей
формуле:
In (760Р) = 15,9008 - 2788,51/(7 - 52,36).
В соответствии с данным уравнением при критической
температуре получают 44,6 атм вместо 48,3 атм, однако
в данном случае этой неточностью можно пренебречь.
Коэффициент фугитивности находят по выражению
ф = ехр(ВР/РТ).
Ниже показаны кривые зависимости Р и ф от температу-
ры в интервале от точки плавления до критической тем-
пературы 562,1 К. В этом интервале величина ф
претерпевает значительные изменения.
Фугитивность и коэффициент фугитивности 163
Пример 3.9. Фугитивность твердого бензола при -30°С и 10 атм
В этом примере рассмотрены способы решения трех
следующих задач.
1. Определение фугитивности твердого вещества по
данным о давлении пара твердого вещества.
2. Определение фугитивности твердого вещества путем
корректировки фугитивности в тройной точке относи-
тельно давления и температуры.
3. Определение соотношения фугитивности твердого
вещества и переохлажденной жидкости.
Данные. Точка плавления 5,5°C принимается равной
тройной точке. При этой температуре давление пара со-
ставляет 35,7 мм рт.ст. При - ЗО°С давление пара твер-
дого вещества равно 1,96 мм рт.ст., а давление пара пере-
охлажденной жидкости составляет 3,62 мм рт.ст. Удель-
ный объем жидкого и твердого вещества одинаков и ра-
вен 87мл/моль. Теплота сублимации 10 566 кал/моль,
теплота плавления 2378 кал/моль.
1. При температуре -30°С поднимают давление от
1,96 мм рт.ст. до 10 атм. При низком давлении (т.е.
1,96 мм рт.ст.) фугитивность равна давлению:
Г 1 О£ Г (1А 1,96 \
/soi = 1,96 exp ----------- I 10 - —-— I =
|_ 82,05(243,2) \ 760 /
= 2,047 мм рт.ст.
2. Корректируют фугитивность, равную 35,7 мм рт.ст.
в тройной точке, относительно давления и температуры
(10 атм и -30°С):
In = - f -Affs"b dT +
35-7 J 278,7
+________87_____ ( ю - =
82,05(243,3) \ 760 )
10566 / 1____________1 \
1,987 \ 243,2 278,7 )
+ 0,0434.
/soi — 35,7 ехр( —2,7417) = 2,30 мм рт. ст.
3. Поскольку молярные объемы двух фаз приблизи-
тельно равны, уравнение (3.92) приводят к виду
/sol
/iq
A7/fUs (1 _ 1 \
R \Т Ttp J
2378 7 1 1
1,987 \ 243,2 278,7
0,6136.
= exp(-0,6136) = 0,5414.
/iq
Интересно отметить, что 0,5414 также представляет со-
бой соотношение давления пара твердого вещества и экс-
траполированной величины давления пара жидкости:
1,96/3,62 = 0,5414.
В данном случае экстраполяция в интервале от 5,5 до
-30°С дает достаточно точные результаты.
Пример 3.10. Воздействие температуры на давление разложения СаСОз, демонстрирующее влияние давления на
фугитивности твердых фаз
Константа равновесия реакции СаСОз СОг + СаО
заимствована из работы [59].
4G° = - RT\n(Ka) = 45037 - 58,14Т + 2,83Г1п(7Э -
- 0,7415(10 ~3)Т2 + 0,4125(10~б)Г3 - 99800/Г, (1)
где Дб° дана в кал/моль. Вириальный коэффициент при-
веден в работе Хайзелдена и др. [Proc. Roy Soc., А240,
№1220, 1 (1957)] для интервала температур от 273 до
873 К, но в данном примере его значение получают путем
экстраполяции:
В = (-291,61 + 44,67 In 7Э(1ООО/7Э мл/моль. (2)
Удельные объемы СаСОз и СаО составляют 36,93 и 21,4
мл/моль:
Ка = ДсОзАСао/ДСаСО,, (3)
аСо: = / = РФ = Р ехр(ВР/82,05Т), (4)
Дсао = ехр(ИСао(Р - 1)/82,057Э, (5)
осасо, = ехр(ИСаСО,(Р - 1)/82,О57'). (6)
В этих уравнениях за стандартное принимается такое со-
стояние газа, при котором фугитивность равна единице,
а в качестве стандартного состояния твердых веществ
выбирается состояние чистого вещества при давлении
1 атм. Постоянная равновесия преобразуется к следую-
щему виду:
Ка = ехр(-ДС°/1,9877) =
= Рехр[[ВР + (Р - 1)(Исао - Исасо,)]/82,0571. (7)
Данное уравнение следует решить относительно Р при
определенных значениях Т. В примере рассмотрено четы-
ре случая, анализ которых показал как суммарное, так
и индивидуальное воздействие на соотношение фугитив-
ностей твердых фаз таких факторов, как неидеальность
СОг и давление. Однако, поскольку при экстремальных
значениях рассмотренных здесь Р и Т степень точности
вириального уравнения низка, результаты не всегда под-
даются количественному определению.
Р, атм
к 1 2 3 4
1169 1,00 1,00 1,00 1,00
1200 1,58 1,58 1,58 1,58
1400 18,1 18,1 18,0 18,0
1600 106,9 108,1 104,8 106,1
1800 406,3 423,5 381,8 397,1
2000 1130,2 1263,9 979,5 1069,7
1954 — 1000 — —
1973 1000 — — —
1985 — — — 1000
2005 — — 1000 —
Случай 1. Идеальный газ, поправка на Рне учитывается.
Случай 2. Идеальный газ, поправка на Р учитывается.
Случай 3. Вириальный газ, поправка на Р не учиты-
вается.
Случай 4. Вириальный газ, поправка на Р учитывается.
И*
164 Глава 3
3.5.2. Выбор в качестве стандартного жидкого и пере-
охлажденного состояния. На рис. 5.3 показаны области
температуры и давления для переохлажденного жидкого
состояния. Выбор переохлажденного жидкого состояния
в качестве стандартного особенно удобен в том случае,
если требуется рассчитать растворимость твердых ве-
ществ в жидких. Применяя уравнения (3.33) к каждой из
двух фаз в отдельности и объединяя затем результаты,
получаем
d In
./solid
fliquid
-VL HS-HL .
dP - - - , dT.
RT RT2
(3.91)
Исходя из допущения о том, что изменения объема и эн-
тальпии при плавлении являются постоянными, и учиты-
вая, что соотношение фугитивности в тройной точке
равно единице, выполняем интегрирование от тройной
точки и получаем
RT l^/soijdZ/iiqujd) = А И(и5|Оп(Р~Р[р) ~AHfuslon(l T/Ttp).
(3.92)
Более того, если две фазы находятся в состоянии равно-
весия, фугитивность твердой фазы равна парциальной
фугитивности растворенного вещества:
г =?=vrfr j (3.93)
Ji, solid Ji УЛЛ,liquid, v
где 7/ — эмпирический коэффициент активности (гл. 4),
который часто приближается к единице. Объединяя два
последних уравнения, можно сократить стандартную фу-
гитивность чистой переохлажденной жидкости и найти
растворимость твердого вещества х, непосредственно по
формуле
R Т 1п(у;х,) = А Vfusion^ ~ — A77fusion( 1 T/Ttp).
(3.94)
Рассмотрение стандартных состояний будет продолжено
в гл. 4.
3.6. Область применения
Поскольку многие термодинамические функции связа-
ны между собой, фугитивность входит в выражения, ис-
пользуемые для определения целого ряда термодинами-
ческих параметров, наиболее важные из которых пере-
числены ниже.
1. Изменение энергии Гиббса служит мерой работы
изотермического потока. Таким образом,
-dWs = dG = RTd\nf (3.95)
и
-ws = PTln(/2//1) = Prin(02P2/01P1). (3.96)
2. Давление пара можно определить по изотермам за-
висимости PV в области выше критической. В состоянии
насыщения фугитивности жидкой и паровой фаз равны,
в результате чего
t t Г ^vapor
«7’ln(/v.p„r/7ii,„id) = 0 = JVdP-P» V“- PdV.
•'^liquid (3.97)
Эти отношения представлены в графическом виде на рис.
1.7. В примере 3.11 применен принцип, на котором осно-
вано уравнение (3.97).
3. Наиболее общий случай состояния фазового равно-
весия определяется равенством парциальных фугитивно-
стей каждого отдельного компонента во всех фазах:
у-(а) = /(ь) = .... в фазах а, Ь, с.... (3.98)
В настоящей книге фугитивность применяется главным
образом для решения этой задачи.
4. Химическое равновесие можно выразить через изме-
нение энергии Гиббса в условиях стандартного состояния
и активность, определяемую как а, = j\/fl, тле fl— фуги-
тивность в стандартном состоянии. Для реакции, проте-
кающей в соответствии со следующим стехиометриче-
ским уравнением:
аА + ЬВ + . . . rR + sS + . . . , (3.99)
Пример 3.11. Давление насыщения н-пентана при температуре 100°С, рассчитанное по уравнениям Редлиха—Квонга
и Соава
При давлении насыщения фугитивности обеих фаз рав-
ны. Данные для н-пентана: Тс = 469,7 К, Рс = 33,25 атм,
ш = 0,251. Экспериментально найденное значение давле-
ния пара: 5,86 атм. Уравнение Редлиха—Квонга приведе-
но в табл. 1.9, уравнение Соава — в табл. 1.11, уравнения
для расчета фугитивности — в табл. 3.3.
Расчет по уравнению Редлиха—Квонга
Z3 - Z2 + (А - В - B2)z - АВ = 0,
Z3 - Z2 + Р(0,01957 - 10,76(Е - 6)P]z -
- 74,95(Е - 6JP2 = 0.
In/ = z - 1 - In -г-—— - ~ In (1 + =
Р В \ zj
А = 0,42747
В = 0,08664
_ „ . , z - 0,00328Р
— z 1 in —~—~~———
р
- 6,967 In (1 + 0,00328Р\
Фугитивность и коэффициент фугитивности 165
Значения сжимаемости и фугитивности сведены в таб-
лицу. Прогнозируемая величина давления, найденная пу-
тем интерполяции, составляет 7,79 атм.
р Z f Соотношение
пар ЖИДКОСТЬ пар жидкость
4 0,9162 0,0206 3,9300 6,4823
5 0,8931 0,0259 4,5148 6,5155
6 0,8689 0,0310 5,3019 6,5493
7 0.8434 0,0361 6,0502 6,5832 0,9190
8 0,8162 0,0412 6,7596 6,6172 1,0215
7,79 (интерполяция) 1,0000
Расчет по уравнению Соава
Тс
а=[1 + (1-х/т7)(0,48508+1,55171ш-0,15163ш2)]2=1,1968,
' ч Г- -1 2
= 0,024377/
А = 0,42747а
= 0,00328/,
Z3 - г2 + /’[0,021097 - 10,76(Е - 6)/]z -
- 79,957(Е - 6)/2 = 0.
константа равновесия определяется выражением
ка = (aR)r(as)s • /(ал)а(ав)Ь • • =KjlKfQy
(3.100)
а изменение энергии Гиббса можно записать как
А<7° = ~RT\nKa .
(3.101)
Особые виды этого уравнения рассматриваются в гл. 10.
3.7. Задачи
3.1. Определите коэффициент фугитивности по уравне-
нию состояния Бертло PV = RT + (b - a/RT2)P.
3.2. Составьте уравнение для коэффициента фугитив-
ности вещества, исходя из уравнения состояния Ди-
теричи
3.3. Ниже приведены данные для водорода при темпе-
ратуре 0°С. Найдите коэффициент фугитивности при 500
и 1000 атм.
Pv Pv
Р RT Р RT
100 1,069 600 1,431
200 1,138 700 1,504
300 1,209 800 1,577
400 1,283 900 1,649
500 1,356 1000 1,720
, , Z - В А , (. В
In f = z - 1 - In---------- - In ( 1 + -
p B X
. , z - 0,00328/
= z - 1 - In------------------
P
- 7,43238 in Л + о^згв/А
В следующей таблице приведена величина давления пара,
полученная путем интерполяции (6,01), которая больше
соответствует экспериментальной величине (5,86 атм),
чем рассчитанное по уравнению Редлиха—Квонга. Урав-
нение Соава является более пригодным для описания
данных для жидкостей.
Р / Соотношение
пар жидкость пар жидкость
4 0,8943 0,0184 3,6650 5,1960
5 0,8637 0,0229 4,4774 5,2287 0,8563
6 0,8310 0,0275 5,2482 5,2512 0,9994
7 0,7955 0,03210 5,9775 5,2807 1,1320
6.01 (интерполяция) 1,0000
3.4. Сжимаемость газа можно представить как
PV/RT = А+ВР + СР2 + DP3,
где А, В, С, D — функции температуры. Исходя из этого
уравнения, составьте выражение для фугитивности как
функции давления при заданной температуре. Для азота
при 0°С А = 1,000, В = -5,314-Ю'4, С = 4, 276-Ю'6 и
D = - 3,292-10'9 при Р не выше 400 атм [Bartlett, J. Am.
Chem, Soc., 49, 687 (1927)]. Определите фугитивность газа
при давлении, равном 300 атм.
3.5. Найдите перечисленные ниже производные через
переменные, приведенные в таблице Бриджмена (табл.
А.7):
а) (8 ln//ar)s, б) (8 1п//85)ц, в) (8 In f/dS}H.
3.6. Исходя из данных о коэффициентах фугитивности,
соотнесенных с давлением при температуре 0°С, найдите
энергию, необходимую для изотермического сжатия газа
от 200 до 800 атм со скоростью 1 моль/с.
Р Ф Р ф
200 1,1219 600 1,4873
300 1,2030 700 1,5984
400 1,2898 800 •1,7177
500 1,3851
3.7. В уравнении (3.23) замените дифференциал dP вы-
ражением (dP/dV)jdV. Примените полученное уравнение
дР \
R Т In ф =
для определения коэффициента фугитивности из а) урав-
нения состояния P(V - Ь) = RT, б) уравнения Ван-дер-
Ваальса.
3.8. Найдите коэффициент фугитивности, исходя из
следующих двух видов /-усеченного вириального урав-
166 Глава 3
нения:
a. z = PV/RT — 1 + B/V = 1 + BP/zRT,
б. z = 1 + BP/RT,
Сравните две полученные величины ф и соответствую-
щие значения сжимаемости в интервале значений BP/RT
от -0,25 до 0,5.
3.9. В работе [639] приведены данные об избыточном
объеме смесей воды и тетрагидрофурана. Величины, взя-
тые из графика, представлены ниже в виде таблицы.
Объем чистых компонентов составляет 0,018 л/моль для
воды и 0,06403 л/моль для тетрагидрофурана. Найдите
значения парциального молярного объема при концент-
рации 10, 20, 40, 60 и 80% и соотнесите их с соотношени-
ем фугитивностей:
хТГФ 0,1 0,2 0,4 0,6 0,8
- Vе*, мл/моль 0,50 0,77 0,89 0,75 0,45
3.10. Молярные объемы компонентов А и В некоторой
смеси равны соответственно Уа = 25 + Зхв и Уь ~
= 15 мл/моль. Эквимолярную смесь загружают в изо-
термических условиях со скоростью 2 моль/мин в сосуд
объемом 1 л, в котором уже находится 10 моль компо-
нента В. Сколько времени потребуется для заполнения
сосуда?
3.11. Ниже приведены молярные объемы У\ и Уг (мл)
чистого водорода и чистого азота соответственно_при
различных давлениях Р и температуре 0°С. И и Уг —
парциальные молярные объемы смеси, в которой на каж-
дые 0,6 моль водорода приходится 0,4 моль азота; в этом
случае Р — полное давление. Vi Уг
Р Vi Уг
50 атм 464,1 441,1 мл 466,4 447,5 мл
100 239,5 220,6 241,3 226,7
200 127,8 116,4 129,1 120,3
300 90,5 85,0 91,1 86,9
400 72,0 70,5 72,5 71,8
Определите графическим путем фугитивность азота в
данной смеси при различных величинах полного давления
и сравните результаты со значениями, полученными для
чистых газов, т.е. проверьте применимость правила
Льюиса—Рендала к фугитивности газа в смеси [Merz,
Whittaker, J. Am. Chem. Soc., 50, 1522 (1928)].
3.12. Фугитивность смеси дается следующим выраже-
нием: In ф = 0,2xi + 0,5x1. Постройте кривые зависимос-
ти 0! и фг ОТ Х1.
3.13. Фугитивность тройной смеси рассчитывают по
формуле
In ф = 0,2х^ + 0,5х^ + 0,6х^.
Используя результаты, указанные в разд. 2.6, постройте
зависимости In фз от хз при величинах г = Xi/хг = 0, 0,2,
2, оо. Не упустите из вида, что если г приблизительно ра-
вен 2, In фз имеет максимальную величину при любом
данном значении хз.
3.14. Для тройной смеси, в которой поддерживается
постоянное соотношение концентраций двух компонен-
тов, xi/xz = г, найдите константу закона Генри
к з = lim
х3-0
lim
х3^0
Р
^303
< <?*3
в виде функции г. Найдите численные значения кз/Р в
подходящем интервале г, если коэффициент фугитивнос-
ти смеси представлен следующим уравнением:
In 0 =XjX2X3 + xi+x2+x3.
3.15. Составьте уравнения для 1п(/г//2) исходя из следу-
ющих двух отношений для ln/i: a) In/i = Ayl, б) In fi =
= Ayl +Byl + Cyiy2.
3.16. Пользуясь методикой, описанной в примере 3.4,
найдите коэффициенты парциальной фугитивности по
уравнению Ван-дер-Ваальса.
3.17. Молярные объемы (л/моль) двойной газовой сме-
си представлены уравнением V = RT/P + 0,2 +
+ 0,lyi - 0,2yi. Температура смеси 300 К, давление 25
атм. Определите коэффициенты парциальной фугитив-
ности эквимолярной смеси.
3.18. Ниже приведены величины парциального моляр-
ного объема азота в смеси азота (40%) с водородом при
0°С.
Р, атм 50 100 150 200
Уг, мл/моль 447,5 226,7 154,9 120,3
а. Найдите коэффициенты парциальной фугитивности
азота при 100 и 200 атм.
б. Найдите изменение парциальной молярной энергии
Гиббса азота при сжатии смеси от 100 до 200 атм.
3.19. Коэффициент парциальной фугитивности компо-
нента 1 двойной смеси определяется по уравнению
In 0) = 0,18(1 — 2хх )•
Коэффициент фугитивности чистого компонента 2 ф2 =
= ехр(-0,1). Составьте уравнение для коэффициента фу-
гитивности фт смеси как функции состава.
3.20. Коэффициент фугитивности некоторой тройной
смеси определяется в соответствии со следующим урав-
нением:
In0m = 0,2x^2 - O,3xjX3 + 0,15х2х3.
Найдите все коэффициенты парциальной фугитивности
эквимолярной смеси.
3.21. Определите коэффициент фугитивности и коэф-
фициенты парциальной фугитивности эквимолярной сме-
си этилена и аммиака при 350 К и 30 атм, используя урав-
нения, основанные на уравнениях состояния а) Ван-дер-
Ваальса, б) Редлиха—Квонга, в) Соава, г) вириальном
Фугитивность и коэффициент фугитивности 167
уравнении Цонопулоса. Данные для этилена: Тс =
= 282,4 К, Рс = 49,7 атм, а> = 0,085; данные для аммиа-
ка: Тс = 405,6 К, Рс = 111,3 атм, а> = 0,25.
3.22. Избыточная энтальпия чистого вандерваальсово-
го газа (гл. И) определяется следующим уравнением:
Яех = Я-Яи = ~[2alV-bRT/(v-b)}.
Найдите соотношение коэффициентов фугитивности ам-
миака при 30 атм и 350 и 450 К.
3.23. Найдите значения 0nh, в смесях, содержащих
этилен, при 350 К, 30 атм и xNh3 = 0,4; 0,5; 0,6. Далее
определите величины производных 50nh3/3xnh3 при трех
различных составах. Используйте уравнение Ван-дер-
Ваальса.
3.24. Реактор для синтеза аммиака функционирует при
давлении 150 атм. Состав сырья и коэффициенты парци-
альной фугитивности указаны ниже:
3.26. В приведенной ниже таблице представлены дан-
ные о функции TVP насыщенного диоксида серы.
а. Постройте диаграмму фазовых состояний в коорди-
натах Р - V.
б. Постройте изотермы при 250°F вблизи кривой насы-
щения для уравнений состояния Ван-дер-Ваальса, Соава,
Хармента—Кнаппа.
в. Используя каждое из этих уравнений, найдите вели-
чины давления пара и плотности насыщения и сопоставь-
те их с числами, соответствующими точкам пересечения
изотерм с двухфазовой огибающей.
Данные для Диоксида серы: Рс = 77,8 атм, Тс =
= 430,8 К, Vc = 0,122 л/моль, Zc = 0,268, ы = 0,251. Вы-
ше (см. предыдущую задачу) приведены примеры изо-
терм, используемых для определения корней уравнений.
(Возле кривых проставлены инициалы разработчиков со-
ответствующих уравнений.)
xi Ф/ Объем, куб. фут/фунт
н2 0,72 1,05 Температура, °F Абс. давление, жидкость пар
n2 0,24 0,95 фунт/кв.дюйм
NH3 0,01 0,50
СН4 0,03 0^80
Константа равновесия К/ = /nh3//n2/h2 = 22,7-10 6
Определите степень превращения.
3.25. Применяя уравнение Соава — Редлиха — Квонга,
найдите давление насыщения и удельные объемы паро-
образного и жидкого н-пентана при 100°С. Данные для н-
пентана: Рс - 33,25 атм, Тс = 469,7 К, ы = 0,251. Ниже
приведены некоторые корни уравнения в z-форме:
Р, атм ZG Zx Zl
4 0,8943 0,0873 0,0184
5 0,8637 0,1134 0,0229
6 0,8310 0,1415 0,0275
7 0,7955 0,1725 0,0320
Экспериментальные данные по давлению насыщенных
газов при общем давлении 5,86 атм. С — уравнение Со-
ава, ВдВ — уравнение Ван-дер-Ваальса, ХК — уравнение
Харменса—Кнаппа.
-100
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
90
100
ПО
120
130
140
150
160
170
180
190
0,294 0,009856 204,7
0,465 0,009954 132,9
0,710 0,010054 89,3
1,056 0,01015 61,0
1,550 0,01025 42,6
2,225 0,01034 30,4
3,12 0,01044 22,2
4,33 0,01053 16,5
5,88 0,01062 12,5
7,83 0,01072 9,48
10,26 0,01082 7,35
13,3 0,01092 5,77
16,9 0,01103 4,59
21,3 0,01114 3,70
26,6 0,01125 3,02
32,9 0,01137 2,48
40,3 0,01149 2,05
49,1 0,01162 1,70
59,3 0,01175 1,42
71,0 0,01189 1,20
84,1 0,01204 1,02
99,1 0,01219 0,868
116,3 0,01235 0,746
135,8 0,01251 0,646
157,7 0,01269 0,554
182 0,01288 0,481
209 0,01309 0,418
238 0,01330 0,364
272 0,01350 0,319
307 0,01371 0,281
168 Глава 3
Температура, °F Абс. давление, Объем, куб. фут/фунт
ЖИДКОСТЬ пар
фунт/кв.дюйм
200 347 0,01396 0,246
210 390 0,01422 0,217
220 437 0,01453 0,191
230 487 0,01487 0,168
240 543 0,01527 0,147
250 604 0,01574 0,129
260 669 0,01628 0,113
270 739 0,01690 0,0987
280 816 0,01767 0,0848
290 898 0,01861 0,0723
300 987 0,02002 0,0599
315,4 1143 0,03070 0,0307
3.29. Фугитивность некоторого вещества можно выра-
зить при помощи уравнения f = а + ЬР + cP2.
а. Найдите уравнение состояния, соответствующее
данному результату.
б. Найдите уравнения для Н - Н'л и V - Eld, соответ-
ствующие данному результату.
3.30. Ниже указаны значения растворимости иодида
олова(1У) в сероуглероде при нескопьких температурах.
Определите точку плавления и теплоту плавления этого
соединения.
Т, °C 10
SnH, г/100 г раствора 49,01
25
58,53
40
67,56
Экспериментально найденные величины
143,4°С и 4330 кал/моль.
составляют
3.31. Избыточная энергия Гиббса тройной смеси опре-
деляется следующим выражением:
3.27. Нафталин образует в бензоле идеальный раствор.
Его точка плавления 80°С, теплота плавления
35,6 кал/моль.
а. Определите растворимость при 25°C.
б. Установите температуру, при которой растворимость
равна 85 моль/моль бензола.
3.28. Покажите, что равенство dG = Ex/dGi =
= RT"Lxtd In f также можно записать следующим обра-
зом: dG = RTZxd ln(fi/xi), и с этой целью докажите, что
Ех,</ In Xi = 0. При этом следует учесть, что логарифмы
парциальных молярых фугитивностей являются парци-
альными молярными величинами, т.е.
In <pj =
дп In ф
дп^
ТРп;
Gex/RT = А12ххх2+ А13хух3 + А23х2х3.
Покажите, что для определения коэффициентов актив-
ности можно воспользоваться следующим уравнением:
ЯГ In ?! =Я12Х2 +Л13*3 + (^ 12 + 13 -^23)x2X3,
RTlny2=Al2x2+A23x2 + (Л12 + Л23 - Л13)х1х3,
ЯГ In у3 = Л 13Xj + Л 23х2 + М и + А23 - А12)хгх2.
3.32. Найдите коэффициент фугитивности по уравне-
нию состояния z = 1 + В/V и уравнению (3.27), а также
по уравнению состояния z = 1 + BP/RT и уравнению
(3.23). Определите диапазон изменения z, в котором по-
грешность уравнений не превышает 10%.
4. КОЭФФИЦИЕНТЫ АКТИВНОСТИ
Рассматриваемые нами процессы характеризуются из-
менениями термодинамических функций, например AS,
Д/7, AG, Д1п/ и т. д. На основе третьего закона термо-
динамики можно определить абсолютные величины
этих функций, по крайней мере для чистых кристалличе-
ских веществ при абсолютном нуле, однако, как прави-
ло, в этом нет необходимости. Пользоваться абсолют-
ными значениями термодинамических функций доста-
точно удобно, если исходить из понятия стандартного
состояния вещества, которое может оставаться одним
и тем же при решении самых различных проблем.
4.1. Активность
и коэффициенты активности
При проведении исследований и решении практиче-
ских задач удобно оперировать эталонными, или стан-
дартными, состояниями, выбор которых осуществля-
ется в соответствии с определенными требованиями. В
данной главе будут рассмотрены такие стандартные со-
стояния, которые входят в определение «фугитив-
ность», что особенно важно в силу того, что фугитив-
ность непосредственно связана с энергией Гиббса. Если
в результате какого-то процесса система переходит из
состояния 1 в состояние 2, то
A G = Gi ~ G] — ЯТ(1п fi — In f\)
= /?TAln/=/?Tln(/2//1). (4.1)
Вводя понятие стандартного состояния (обозначено
надстрочным индексом 0), получаем:
G = G° + ЯТ1п(///°) (4.2)
для чистого вещества,
Gi = G? + RTln(fj/f?) = С? + КТ1па( (4.3)
для компонента смеси,
где
«г=Л/Л° (4.4)
это так называемая относительная фугитивность, или
активность. Величина, получившая название «коэффи-
циент активности»,
yi=fi/xifi (4.5)
аналогична коэффициенту фугитивности
0/ = ~fi/X{P. (4.6)
Будучи преобразованным к следующиму виду
Z = (4-7)
определение становится подобным уже знакомым нам
выражениям, характеризующим некоторые предельные
или идеальные условия. При 7, = 1
fi = Xifi, (4.8)
что соответствует закону Рауля Р, = xtP^, а при кон-
центрации, близкой к нулю (или бесконечном разбавле-
нии), получаем выражение
fi = y'ixif(i=kHxi, (4.9)
аналогичное закону Генри. Как следует из приведенных
выше соотношений, фугитивность в некотором отноше-
нии можно рассматривать как кажущееся давление.
4.2. Стандартные состояния
Стандартные, или эталонные, состояния уже рассмат-
ривались в гл. 3, однако ввиду особой важности этой
темы применительно к жидким фазам (анализу которых
главным образом и посвящена данная глава) в ней бу-
дут повторены и несколько развиты основные ее по-
ложения.
Газы. За стандартное всегда принимается такое со-
стояние, в котором фугитивность равна единице,
вследствие чего активность численно равна фугитивнос-
ти, т. е. для газов
ai=fiiV)/ff=f(iV). (4.10)
Жидкости. Для того чтобы воспользоваться услови-
ем равенства фугитивностей отдельных компонентов во
170 Глава 4
всех фазах, находящихся в равновесном состоянии, стан-
дартные состояния конденсированной и паровой фаз до-
лжны согласовываться. В качестве фактора, определя-
ющего такое состояние, обычно используют давление
пара, при котором фугитивности паровой и конденсиро-
ванной фаз равны; таким образом, для жидкостей
/7at= 05atp?at.
(4.11)
Стандартное состояние определяют как состояние чис-
того вещества при температуре и давлении системы.
Чтобы получить уравнение фугитивности в стандарт-
ном состоянии, берут давление пара при температуре
системы и подставляют выражение (4.11) для фугитив-
ности в уравнение (3.32), определяющее давление в
системе
/О =ysat ехр
(4.12)
= 0?atP«at(PF)z, (4.13)
где
(PF)j = ехр
(4.14)
Рис. 4.1. Экстраполяция кривых давления пара в обла-
сти перегрева (а) и переохлаждения (Л).
Состояние компонента 1 соответствует точке, расположенной
выше критической, состояние компонента 2 — точке, располо-
женной между тройной и критической точками, а состояние
компонента 3 — точке, расположенной ниже своей тройной
точки.
Экспоненциальный член уравнения (4.14) называется ко-
эффициентом Пойнтинга. При умеренных давлениях он,
как правило, немного отклоняется от единицы.
Здесь и везде далее в этой главе соотношение между
коэффициентом активности и другими свойствами вы-
ражается уравнением
У Л Jv}Р = xi7i 0 ;sat Р •at (PF)i, (4.15)
основанным на следующем соотношении в равновесии:
7!И=//£)- (4-16)
Коэффициенты фугитивности и ф,?а' получают из
того же самого соотношения или из уравнения состоя-
ния. Коэффициенты активности рассчитывают или не-
посредственно по уравнению (4.15) из эксперименталь-
ных данных о равновесии, или используя данные о
структуре вещества, как будет показано ниже в данной
главе.
Твердые вещества и газы в сверхкритической обла-
сти. Как показано на рис. 4.1, кривые давления пара
этих веществ можно экстраполировать в область инте-
ресующих температур системы. Будучи приведенными
к давлению системы (путем использования коэффициен-
та Пойнтинга), получаемые в результате гипотетиче-
ские состояния жидкости вполне удовлетворительно
выполняют роль стандартных состояний. В некоторых
случаях, например при описании растворимости газов
и твердых веществ в жидкостях (см. другие разделы
данной книги), представляется более удобным приме-
нить другие стандартные состояния. Подробное описа-
ние этих стандартных состояний содержится в работах
[137, 567].
Стандартные состояния растворов рассматриваются
в разд. 3.5.
4.3. Термодинамические уравнения,
содержащие коэффициенты активности
Коэффициенты активности самым тесным образом
связаны с различными избыточными свойствами, мно-
гие из которых представлены на рис. 4.2—4.6. Выраже-
ния, отражающие эту взаимосвязь, можно записать,
практически взяв за образец соответствующие уравне-
ния для коэффициентов фугитивности, собранные в
табл. 3.2, начиная с определений
G = RT\n fi + X^T) (3.9,4.17)
и
(4.18)
Соответственно, поскольку Х,(7) сокращается,
Gf х = Gi ~ G‘d = R TIn fi - RT In xz/f = RT ln( az/xz)
= /?Tlnyz. (4.19)
Для смеси в целом можно записать
Gex = RTY.Xi In yz.
(4.20)
Следовательно, Inyj, парциальное молярное свойство,
можно представить при помощи уравнения (2.56) следу-
ющим образом:
RT 1пу, = Gex - S
k^i
dGex
dxk
(4.21)
TPxj^ik
Для компонента 1 бинарной смеси можно записать
/ асех
/? Г In У1 = Gex + (1 — Xj) —--
\ ох 1
(4.22)
Коэффициенты активности 171
Рис. 4.2. Избыточные свойства смеси этанол + вода
при нескольких температурах [102].
Это линейное дифференциальное уравнение разрешимо
относительно избыточной энергии Гиббса:
Gex = (l-Xi)/ -------~dx\-
. 0 М — Y. V
(4.23)
Например, при РЛпу! = д(1 - хД" решение находим
следующим образом:
Gex= 7ГТХ2(1-хГ1)-
(4.24)
Однако на практике принято измерять оба коэффициен-
та активности и рассчитывать по ним избыточную
энергию Гйббса, а не наоборот — находить коэффици-
енты активности из величин избыточной энергии Гиб-
бса, пользуясь уравнением (4.22).
Очевидно, что коэффициенты активности зависят от
Т, Р и состава. Эти зависимости можно выразить при
помощи следующих уравнений (табл. 2.6):
(d(G**/T)/dT)P = - Н™/Т2,
(4.25)
(dG*x/dP)T = Vex,
(4.26)
из которых получаем трубуемые уравнения, а именно:
Поскольку коэффициенты активности обычно измеря-
ются как функции состава, производные можно полу-
чить непосредственно из этих данных, так что к
выражению через избыточный объем прибегают крайне
редко.
Уравнение, в котором коэффициент активности выра-
жен через Т и Р, имеет следующий вид:
//ex j/ex
d In у,- = — 7 dT + dP,
RT2 RT
а для всех компонентов в сумме получаем
7/ех j/ex
Zxz d In уz = - -7 dT +-----dP.
1 RT2 RT
(4.30)
(4.31)
Уравнение (4.31) — это одна из форм уравнения Гиб-
бса — Дюгема, ряд других форм которого приведен в
табл. 2.7. Применительно к бинарным смесям это урав-
нение записывается следующим образом:
7/ех рлех
*1 dlnyj +x2dlny2 = 2dT + —— dP, (4.32)
К / KI
а специальная форма для постоянных Г и Р имеет та-
кой вид:
Xi d Inyj + х2 d In y2 = 0. (4.33)
Она положена в основу широко используемой методики
проверки достоверности экспериментальных данных,
проводимой следующим образом. В уравнении диффе-
ренциала энергии Гиббса
d(Gex/PT) = d(xj Inyj +x2lny2)
= (xj d InУ! +x2dlny2)
+ In У! dxx - In yj dXi (4.34)
выражение в скобках, согласно уравнению (4.33), равно
нулю. Поскольку избыточная энергия Гйббса в пределе
стремится к нулю, интегрирование оставшейся части
172 Глава 4
Рис. 4.3. Экспериментальные величины избыточных энергий Гиббса, избыточных энтальпий и избыточных энтро-
пий. На оси абсцисс отложены мольные доли первого из компонентов смеси (приведенные данные собраны Роу-
линсоном, издание 1969 г.).
а: метанол + тетрахлорид углерода, 35 °C; б: метанол + бензол, 35 °C; в: этанол + изооктан, 25 °C; г: этанол + бензол, 45 °C;
д: вода + диоксан, 25 °C; е: ацетонитрил + тетрахлорид углерода, 25 °C; ж: вода + пиридин, 80 °C; з: вода + пероксид водорода,
25 °C.
уравнения (4.34) дает
том [137]. С учетом
влияния Т и Р получаем
d(Ga/RT) = Г ln(yj/у2) dxx = 0.
dxj
(4.35)
•Tj Яех ppi Гех
—у dT + / ----dP = 0.
о RT2 Jp0 RT
Пример 4.2 иллюстрирует применение этого уравнения;
несколько других примеров проверки показано на рис.
4.7. Подробный анализ методики проверки согласован-
ности данных выполнен, например, ван Нессом и Эббо-
(4.36)
Однако, как правило, достаточно учитывать только
температурное воздействие. Для тех случаев, когда дан-
Рис. 4.3 (продолжение)
Рис. 4.4. Избыточные энергии Габбса, энтальпии и ко-
эффициенты активности четырех систем [757].
А: А(1) + О2(2), 86 К; Б: н-СбН,4(1) + h-Ci2H26(2), 25 °C;
В-. С6Н6(1) + С2Н5ОН(2), 45 °C; Г. С4Н8О (диоксан) (1) +
+ Н2О(2), 25 °C.
174 Глава 4
Рис. 4.5. Три системы, для которых характерно практи-
чески симметричное изменение коэффициентов ак-
тивности.
а: этанол + метилциклогексан (Редлих, 1976); б: 2-бутанон +
+ н-гексан [394]; в: 3-пентанон + н-гептан [394].
^иош/ж'п'\эц 'Зэ)
Рис. 4.6. Избыточные энтальпии смесей вода + этанол при нескольких температурах [75].
Коэффициенты активности 175
Пример 4.1. Расчет избыточных свойств по результатам измерения коэффициентов активности и избыточных
объемов
В п. 1—3 приведены данные, из которых можно рас-
считать величины прочих свойств. Условия протекания
процесса: 300 К, 25 атм, Xi = 0,3, R = 1,987 кал/моль-К
(82,07 мл • атм/молъ • К).
1. 1п71 = 0,4Г°-2(1 - X,)2 = 0,6133.
2. 1п72 = 0,4 = 0,1126.
= (1 - х0(-2 + l,2xi - 2,4х?)(5О/26)0,02 =
= - 1,3163 мл/моль.
9. 1П71 = 0,000409/ К.
оГ Т
3. Г" = 25X1X2(1 + 0,2x1) \-~
= 5,4149 мл/моль.
^0,02
10. = ~~ 1П72 = 0,000075/К.
01 1
4. 6“ = /?Т(ЕхДп7,) = 0,4/гТ1 ^!Х2 = 156,68 кал/моль.
(\ 0,02
= 0,4381.
11. нг = - RT2 / 31П71 у дТ 1 =73,12 кал/моль.
12. нг = - RT2\ ( ain72 1 аг ) = 13,42 кал/моль.
13. нп = TxiHF = 31,33 кал/моль.
14. Н = Н'Л + 1ГХ = XiHi + xiH2 + 31,33.
15. = HVRT = 5,7216/(ЗОО)(1,987) = 0,00023/атм.
Г = Г’ + (1 - хО)-^—) =
\ оХ1 1
= 5,4149 + О,7(О,4324)(5О/26)0'02 = 5,7216 мл/моль.
16.
Э1П71
8x1
I
ЯГ
Рагг
1 8X1
Jo
dP =
/ аг’
Х1 ( ——
\ дХ1
= 5,4149 - О,3(О,4324)(5О/26)0’02 = 5,2835 мл/моль.
5р / \ 0,02
/ 50 \ .
\ Р + 1 /
О X /
1,2992(5О)0,02 Г26о.^ _ п
ЗОО(О,98)(82,О7) ' ’
0,0014.
Пример 4.2. Проверка термодинамической достоверности данных о парожидкостном равновесии для смеси воды
и тиазола при 90°С (Metzger, Disteldorf J. Chim. Phys., 50, №3 (1953); [405])
В соответствии с уравнением Гйббса — Дюгема необ-
51
lg(7i/72)dxi = 0. Интегрируя по пра-
о
вилу Симпсона, получаем:
площадь над кривой 71/72 = I равна 0,1917,
площадь под кривой 71/72 = 1 равна 0,1987.
Разность/сумма = 0,0070/0,3904 = 0,018, т. е. рас-
хождение находится в пределах 2%, что подтверждает
хорошую степень точности.
ные об энтальпии смешения отсутствуют, предложен
ряд аппроксимаций [338], применение которых дает луч-
шие результаты, чем пренебрежение воздействием тем-
пературы. В настоящей главе рассматриваются также
методы проверки достоверности измерений равновесия
многокомпонентных смесей. Усовершенствованная ме-
тодика проверки достоверности данных предусматрива-
ет поочередный анализ каждого замера, что предотвра-
щает возможность взаимной компенсации отдельных
погрешностей.
176 Глава 4
нижения давления пара. Активность растворов электро-
литов также можно определить по результатам
измерения мольного эквивалента гальванических ячеек,
однако этот вопрос выходит за пределы темы данной
книги. Для оценки коэффициентов активности непосред-
ственно применимы уравнения (4.15), (4.27) и (4.28).
4.4.1. Осмотическое давление. На рис. 4.8 представ-
лены физические условия возникновения осмоса. Чис-
тый растворитель А при некоторых Т и Р и раствор
концентрации Ха при той же температуре и первона-
чально при том же давлении разделены перегородкой,
проницаемой только для растворителя. Давление со
стороны раствора повышается на величину APOsm, до-
статочную для установления равновесного состояния по
обе стороны перегородки. В этот момент равновесие
химических потенциалов определяется выражением
Р(Т,Р,ха= 1) = м(Г, Р+ APosm,xfl). (4.37)
Изменение химического потенциала растворителя, вы-
званное повышением давления со стороны раствора,
Рис. 4.7. Проверка согласованности коэффициентов ак-
тивности (Редлих, 1976).
а: этанол + метилциклогексан (данные термодинамически со-
гласованы); б: ацетон + бензол (термодинамически согласована
только четвертая группа данных).
4.4. Определение коэффициентов активности
Коэффициенты активности определяют главным об-
разом по данным измерений фазового равновесия,
обычно равновесия между паром и жидкостью или
жидкостью и жидкостью. Методики таких определений
описаны ниже в данной главе, здесь же мы кратко обсу-
дим ряд других методик, имеющих ограниченные обла-
сти применения, к которым прибегают лишь в особых
случаях, например при рассмотрении растворов нелету-
чих веществ. В этих методиках используются результа-
ты измерения 1) осмотического давления, 2) понижения
точки замерзания, 3) повышения точки кипения, 4) по-
Чистый
раство- —
ритель
Р)+^Р
__/ osm
Раствор
(сса - моль доля
растворителя)
___Мембрана,проницаемая
только для раство-
рителя
Рис. 4.8. Активности и изменение коллигативных
свойств растворов, зависящих главным образом от чис-
ла молекул, а не от их природы.
а: поведение растворов при осмосе. APOsm — избыточное давле-
ние, необходимое для прекращения перетекания растворителя
через полупроницаемую мембрану.
б: поведение растворов при замерзании (или испарении) и пове-
дение чистых жидкостей в одних и тех же условиях, в — это
либо понижение температуры замерзания, либо повышение
температуры кипения в сравнении с этими же характеристиками
чистой жидкости.
Коэффициенты активности 177
Таблица 4.1. Уравнения, используемые для определения коэффициентов активности
1- Y/= fj/Xifi = aJXi.
2. ЛТ1пТ) = Gfx = Gj - (Gf + ЯГ lnx;).
3. RT In уjXj = Gi - Gj.
4. RT Хх{\пу{ = Gtx = G- Gid = G - + RT Inx,).
5. RT Их, In yjXj = G — ZXjGi.
(d In у • \ Hi - Hfx
6. ------ = -------------= -----.
\ dT o RT2 RT2
/a in yz \ Vi - vt vfx
7 I------ I =--------- _ ----
\ ар К RT RT
/ainy,\ 1 /d Gf* \ 1 rp/dVfx\
8. ------ =------ ------- =----- / ---- dP.
\ dxk /Tp RT \ dxf, / RT \ dXfr /
H<}* yv*
’ d,n-''=-TTdT+TFdp-
f/ex у ex
10. Уравнение Гиббса — Дюгема: у,- = —-у dT +--dP.
R T R T
11. Уравнение Гйббса — Дюгема при постоянных Т и Р Ex-dlny( = 0.
12. Уравнение для двухкомпонентной смеси: In у2 = — Г * -'—d Jn У]
Л1=° 1 -х,
равно
Г, которая ниже температуры замерзания Го чистого рас-
АМ = М (Т,Р + APosm, ха) - р(Т,Р,ха)
творителя. В точке замерзания растворителя
^1(Го, жидкость, Ха = 1) -= Ц2<То, чистое твердое вещес-
osm —
K,dP
тво А), (4.40)
RT
= М(Г, P,xe=l)-M(T, P,xe)
= ЯГ (In /Рцге - In fa) = -Я T In аа = —Я Г In уаха.
(4.38)
И в итоге
1 r^o + ^^osm —
\r\aa = \nyaxa = -RTJp Va dP. (4.39)
Из последнего выражения можно найти коэффициент
активности, если известны концентрация растворителя
и осмотическое давление, а также изменение давления
парциального молярного_ объема растворителя. Для
разбавленных растворов V можно принять постоянным
и равным удельному объему чистого растворителя.
4.4.2. Понижение температуры замерзания. Данный
процесс состоит в переходе растворителя из раствора кон-
центрацией ха в чистое твердое состояние при температуре
в то время как в точке замерзания раствора
цз(Т, жидкость, Ха) = уАТ, твердое вещество А). (4.41)
Соответственно разность химических потенциалов за-
мерзших и чистых жидких растворителей при темпера-
туре Г составит
Д/4 = Д4( Г, твердое вещество А) - /х5( Г, чистая жидкость) =
= уз(Т, ЖИДКОСТЬ, Ха) - fis(T, чистая жидкость) = RTlnaa =
= (и - м) - 0.2- м) = - Г ВДжилкосгь) dT +
JTo 1
Я(твердое вещество)
То Т
(4.42)
что можно переписать как
рт Mlf
RTd\naa= I------dT,
JTo T
(4.43)
12-829
178 Глава 4
или
In а а = In Уаха
>Т AHf
-j^ptdT.
(4.44)
Интегрирование этого уравнения можно выполнить,
исходя из нескольких допущений.
1. Если AHf практически постоянна и равна энталь-
пии замерзания Хо чистой жидкости, а понижение точки
замерзания составляет 0 = То — Т, получаем следую-
щее выражение:
lnae = - Xoe/RTo(To- 0).
(4.45)
2. Разложение Д/7/в усеченный ряд Тейлора
АЯу= Хо + (dAHf/dT)(T ~ TQ)
= Xq + (Cpfliquid)- Cp(solid))(7’— To), (4.46)
и интегрирование результата дает следующее выражение:
(Хо- гоаср)0 дср т0-е
а RT0(T0-в) + r 1п е ’ (4’47)
которое при ДС’Р = 0, как и предполагалось, приводится к
уравнению (4.45).
3. При аналогичном разложении подынтегральной
функции ДЛу/Г2
AHf Хр 1 ( 2Хр \
= 72 + (АС, - —- (Т-То) (4.48)
1 1 О 1 О \ 7 0 /
и последующем интегрировании получаем
xog(To + в) аср 2
а RT% + 2RT2q ° ’
(4.49)
В случае необходимости уравнение (4.49) проще раз-
решить относительно в, чем уравнение (4.47), однако
при Ср = 0 оно не приводится к уравнению (4.45). Если
же тем не менее это имеет место, соотношение правых
частей уравнений (4.45) и (4.49) составит 1/[1 - (0/7Ь)2],
что менее чем на 1 °7о отличается от единицы при
в/То < 0,1. Например, для воды такая ситуация наблю-
дается в том случае, если понижение точки замерзания
составляет меньше 27 К.
Интегрирование этого уравнения выполняется доста-
точно просто, если известна энтальпия кристаллизации
в виде полинома, содержащего Т. Подобное уравнение
для энтальпии испарения приводится в задаче 4.8.
4.4.3. Повышение точки кипения. Если растворенное
вещество нелетуче, повышение точки кипения
0 = Т - То обусловлено теми же причинами, что и по-
нижение температуры замерзания. Таким образом,
от Hv - HL
In аа = In уаха = - / ——-— dT
JTQ RT2
FTq+0 АНУаро{а1Л^оп
/ ------ о------dT
lrQ RT2
При постоянной величине AHV = Хо это уравнение пре-
образуется к следующему виду:
lnafl = — Xo0/RTq(Tq + 0),
(4.51)
а при разложении АН? в ряд Тейлора получаем
In а,
1 (Хо-ТоАСр)0 т0 + в
R _ „ + ДСП In L Т0(Т0 +0) р То
(4.52)
Коэффициенты активности сильно разбавленных рас-
творов по существу равны единице, в силу этого усло-
вия активность идентична мольной доле Ха. В такого
рода случаях при помощи уравнений, перечисленных в
этом разделе, непосредственно соотносят мольную
фракцию растворенного вещества 1 - ха с осмотиче-
ским давлением, понижением точки замерзания и повы-
шением точки кипения. Если коэффициенты активности
поддаются определению каким-то независимым спосо-
бом, то воздействие состава на эти три свойства можно
определить даже для концентрированных растворов.
4.4.4. Понижение давления пара нелетучими раство-
ренными веществами. Перегруппировка уравнения
(4.15) приводит к выражению
y,$i Р Р
^\PF)t х.Р^ x,PfM ’
(4.53)
где у, равна единице, если растворенное вещество неле-
туче. Более того, при давлениях, достаточно близких к
атмосферному, вся группа в квадратных скобках также
по существу равна единице. Следовательно, коэффици-
ент активности можно установить, исходя из результа-
тов измерения давления Р, мольной доли растворителя
Xi и давления пара чистого растворителя.
4.5. Коэффициент активности
и уравнения состояния
Коэффициенты активности можно рассчитать по
уравнению (4.59), используя уравнения состояния, при-
менимые как для жидкой, так и для паровой фазы.
Однако в настоящее время подобные уравнения состоя-
ния охватывают лишь немногие группы веществ; так,
уравнение Соава и уравнения, аналогичные уравнению
Бенедикта — Уэбба — Рубина, разработаны для класса
легких углеводородов и нескольких других газов. Коэф-
фициент фазового распределения К, = yt/x, можно вы-
разить в виде отношений коэффициентов парциальной
фугитивности
К{ = (4.54)
или частично через коэффициенты активности
Р}‘Чф^Р. (4.54а)
Если смесь содержит такие вещества, которые нельзя
представить при помощи уравнения состояния для жид-
кой и паровой фаз, все коэффициенты активности следу-
ет находить по результатам измерения фазового
равновесия.
(4.50)
Коэффициенты активности 179
Пример 4.3. Расчет коэффициентов активности и давления пара водных растворов глицерина на основе данных
о понижении точки замерзания
Ниже представлены мольные доли глицерина, тем-
пература замерзания (°C) и давление пара чистой
воды (мм рт.ст.). Энтальпия плавления составляет
1,436 кал/моль. Давление пара глицерина практически
равно нулю.
Применив уравнение (4.45) для нахождения коэффици-
ента активности, получаем
. 1436(1,918) ПЛ1С7
lnywxw = —------------------—----------------= — 0,0187.
у 1,987(273,15,)(273,15 - 1,918)
= ехр( - 0,0187) =
1 - 0,0176
Уравнение (4.53) дает
Р = 7и,х„Па* = 0,9991(1 - 0,0176)(3,98) = 3,906 мм рт.ст.
Ниже представлены величины у» и Р, полученные для
трех составов:
'^глицерин Tf, °C na< Уи- P
0,0176 - 1,918 3,98 0,9991 3,906
0,0346 -3,932 3,43 0,9966 3,302
0,0822 - 10,58 2,14 0,9795 1,924
Пример 4.4. Расчет коэффициентов активности при
помощи уравнения Соава
В результате измерений парожидкостного равновесия
в системе изобутен (1) + изопрен (2), выполненных
Мервартом [Coll. Czech. Chem. Communications, 24,
№ 12, 4034 (1959)], были получены следующие результа-
ты: Xi = 0,288, yi = 0,555, Т = 72°С, Р = 5 атм. При-
меняя уравнение Соава, требуется рассчитать коэффи-
циенты активности обеих фаз, исходя из коэффициентов
парциальной фугитивности 1) жидкой и 2) паровой
фазы.
Чистый компонент 1:
Z1 - Z1 + O.1552Z1 - 0,004869 = 0
Zi = 0,0425, 0,1400, 0,8174
Чистый компонент 2:
Z2 - Zi + 0,07606^2 - 0,000865 = 0
Z2 = 0,0139, 0,0679, 0,9182
Изобутен Изопрен Жидкая смесь Паровая смесь
Tc 417,9 484
Pc 39,5 38,0
w 0,190 0,164
A 15,7528 15,8548
В 2125,75 2467,4
C -33,15 -39,64
P° 10,04 3,14
Tr 0,8259 0,7131
p? 0,2542 0,0826
m 0,7743 0,7354
aa 14,588 22,037 19,735 17,714
b 0,0752 0,0906 0,0862 0,0821
A 0,1826 0,0863 0,1230 0,1104
В 0,0267 0,0100 0,0152 0,0145
й|/Ь(жидк.) 0,8724 1,0510
Ь,/й(пар) 0,9160 1,1035
Для паровой фазы yi = 0,555
Zm„ - Zn,v + 0,0957zmv - 0,001601 = 0
Zm\ = 0,0214, 0,0835, 0,8951
ln</>iat = 0,08174 - 1 - ln(0,8174 - 0,0267) -
0,1826 . Л 0,0267 \
0,0267 у + 0,8174 у
dta' = 0,8457
M)at = 0,9182 - 1 - ln(0,9182 - 0,01) -
_ °>0863 i Л . o.oi \
0,010 у 0,9182 у
</dat = 0,9240
МУ = 0,9160(0,8951 - 1) - ln(0,8951 - 0,0145) +
°’1104 noiAA 2(0,555(14,588) + 0,445(17,93)]
0,0145 ’ j 17,714
x In ( 1 +
0,0145
0,8951
ф\ = 0,9241
аа = (0,288)2(14,588) + (0,712)2(22,037) +
+ (0,288)(0,712) 744388(22^37)" = 19,735
b = Hxibi
А = aP/R2T2
В = bP/RT
Жидкая смесь, Хг = 0,288:
dn - d+ 0,1076zm - 0,001871 = 0
zm = 0,0217, 0,0982, 0,8802
ln02 = 1,1035(0,8951 - 1) - ln(0,8951 - 0,10145) +
0,1104 2(0,555(17,93) + 0,445(22,04)]
0,0145 ’ " 17,714
x In
0,0145
0,8951
Ф2 = 0,8812
ln<5f = 0,8724(0,0217 - 1) - ln(0,0217 - 0,0152) +
12*
180 Глава 4
0,1230 А Q__ . 2(0,288(14,588) + 0,712(17,93)]
<WTГ 2: lv,7„ -----------
Коэффициенты активности рассчитывают по следую-
щим двум уравнениям:
х In
=
[i и. °>0152
0,0217
1,7214
1пф| = 1,0510(0,0217 - 1) - ln(0,0217 - 0,0152) +
0,1230
0,0152
„ 2(0,288(17,93) + 0,712(22,037)]
’ “ " 19,735
0,0152
0,0217
Компонент У
ур(1) УР(2) Мерварт
Изобутен 1,0309 1,0665 1,17
Изопрен 0,9811 0,9429 1,06
= 0,5732
, 94,46(5 - 10,04) „
,PF>‘ = “P 82,06(345,16> = °’’ЮЗ
,D„ 100,03(5 - 3,14) .
(pF)2 = exp - = 1,0066
Величины, рассчитанные исходя из данных для жид-
кой и паровой фаз, приближенно сопоставимы. Метод
расчета и данные о давлении пара, полученные Мервар-
том, проверены не были, однако степень их соответ-
ствия результатам настоящих вычислений невелика.
Условие равенства парциальных фугитивностей в со-
стоянии равновесия можно выразить несколькими спо-
собами:
(4.55)
л.ф(К)р=х.ф(2.)р, (4.56)
Лф(Пр= у.х.у0 (4.57)
= yzxz0?atP?at(PF)z. (4.58)
Соответственно коэффициент активности выражается
через свойства жидкой фазы следующим образом:
ф(Ь }Р
у. =------'-----, (4.59)
0fatP?at(PF)z
где коэффициенты фугитивности определяют из универ-
сального уравнения состояния.
Сопоставление коэффициентов активности, рассчи-
танных по уравнению (4.54) и уравнению Соава, с экс-
периментальными данными в примере 4.4 показывает
их весьма посредственное совпадение, хотя наблюдае-
мые расхождения и не выходят за некоторые пределы.
Во многих других случаях совпадение было намного
лучшим; уравнение Соава вообще малопригодно для не-
насыщенных веществ, например, таких, как изопрен.
4.6. Корреляция данных
Для корреляции коэффициентов активности с соста-
вом смеси и до некоторой степени с температурой пред-
ложено много уравнений состояния. Некоторые из них
имеют более или менее разработанное теоретическое
обоснование, другие являются чисто эмпирическими.
Обычно состав выражают в мольных долях х(, однако,
если молекулы значительно различаются по размерам
и химической природе, лучше пользоваться объемными
долями ф, или долями молекулярной поверхности.
В настоящее время наиболее широко применяется
шесть более или менее различных видов корреляций ко-
эффициентов активности, и основное внимание в дан-
ной главе мы уделим именно им. Поскольку
преимущества какого-либо одного метода не всегда яв-
но выражены, на практике следует исходить из имею-
щегося опыта и аналогий. Наиболее подробно эти пять
методов рассмотрены в сборниках DECHEMA (DECHE-
МА Vapor-Liquid Data Collection), издаваемых начиная
с 1979 г. В них для каждого случая указаны формулы,
наилучшим образом соответствующие эксперименталь-
ным данным. В итоговой табл. 4.10 представлены 3563
двухкомпонентные системы, что, по-видимому, состав-
ляет более половины данных, которые следует полу-
чить. Как показывает этот чисто статистический
анализ, наилучшие результаты дает уравнение Вильсо-
на, наименее результативны уравнения Ван Лаара и
UNIQUAC. Однако для определенных классов веществ
эффективность последних уравнений может быть су-
щественно выше; так, уравнение NRTL наиболее эффек-
тивно применительно к водным системам.
В табл. 4.4 приведены уравнения для двойных смесей,
а в табл. 4.5 — более простые по форме уравнения,
применяемые при бесконечном разбавлении. Все они со-
держат по два параметра; исключение составляют лишь
симметричное однопараметрическое уравнение Маргу-
леса и трехпараметрическое уравнение NRTL. Четыре
их этих уравнений применимы к многокомпонентным
смесям, при этом в них не нужно включать другие па-
раметры помимо параметров бинарного взаимодейст-
вия. Многокомпонентные уравнения перечислены в
табл. 4.6.
В принципе коэффициенты активности получают из
избыточных энергий Гйббса, однако на практике испо-
льзуют обратную процедуру: G” определяют из коэф-
фициентов активности. Ниже приведены основные
уравнения:
G&K/RT = In у,, (4.60)
Коэффициенты активности 181
Таблица 4.2. Избыточные энергии Гиббса двухкомпонентных смесей (обозначения даны в табл. 4.4)
Уравнение
Gn/RT
Симметричное Лхрс2
Маргулеса Х]Х2(Л21Х] +Л12х2)
Ван Лаара 1/(1/Л12Х] + 1М21х2)
Вильсона —X] 1п(Х] + Л12х2) — х2 1п(Л21Х] + х2)
Цубоки — Катаямы — Вильсона Xi + И2х2/И1 Xi In + Х2 In X] + Л12х2 A21xj +x2
r21G21 r12^12
WIL X]X2 t _xj + G21x2 Gi2Xj + x2
UNIQUAC *1 Ir 01 tfi* + In X] 2 0i — ~ q\ in(^j + 02t21) 01 J
+ x. 02 42z In + x2 2 02 In — q2 ln(0 02 lr12 + 02)
Скэтчарда —
Гильдебранда
(<$! - а2)2
Таблица 4.3. Избыточные энергии Гиббса многокомпонентных смесей (обозначения даны в табл. 4.4.)
Уравнение
Gex/RT
Вильсона
Цубоки — Катаямы
— Вильсона
NRTL
UNIQUAC
S Xj ln-^- + т S QiXj ln-^7 - S QjXi In
i z I 't'l t
Скэтчарда —
Гильдебранда
^Lx,r((5(-5)2
и
GeK /d(GeK/RT)\
In у,- = I ; I , (4.61)
RT \ dxk 1 ’
1 rAj^=ik
Gex
—— = Х1 In У1 + х2 1пу2,
а также для двухкомпонентных смесей
Корреляции избыточных энергий Гиббса имеют чисто
эмпирический характер или же частичное теоретическое
обоснование. Для двухкомпонентных смесей эффектив-
ны следующие основные типы формул:
T?Tlny2 = Gex - X!
(4.62)
(4.63)
(4.64)
182 Глава 4
Таблица 4.4. Уравнения, используемые для определения коэффициентов активности
двухкомпонентных смесей
Уравнение Параметры 1П71 И 1П72
Симметричное А Лх^ (1) Лх? (2)
Скэтчарда — Гильдебранда 51, 82 01 = ^/(^Xj + У2Х2 Ki — (1-01)2(51-52)2 (3) Л\ 1 К2 , — Ф?(51~52)2 (4) jKI ) (5)
Маргулеса А12 А2\ М12 + 2(Л21 — Л12)х]1 х\ (6) М21 +2(Л12-Л21)х2]х? (7)
Ван Лаара А12 А2\ ( А2\х2 Y Л12 , (8) V12xl + ^21х2 / ( А12х1 Y ^21 ( Л । Л ) (9) \Л12Х! +Л21х2 /
Вильсона ^21 - ^22 - ( ^12 Л21 \ -ln(xj +A12x2) +х2 1 - I (10) \Х! +Л12х2 Л21Х! +х2 / ( Л12 Л21 \ — 1п(х2 + A21x0 ~ X! 1 - 1 (11) \X1+A12X2 Л21Х!+х2 /
Л12 pf - У2 / = -^-р - молярный с \2 \ ' RT у бьем чистого л ( Л21 - exp 1- жидкого компонента i. ^21 \ RT у (12, 13)
Цубоки — Катаямы — Вильсона а\2 ~ а11 а21 ~ а22 = ^12 = ^21 хх + У2х2/Ух In 1 л + (Д ~ Pv)x2 хх + Л12х2 (14)
ИХ1/Г2 +х2 In -(Д-Д0*1 Л21^1 +х2 (15)
к2/и _ Ух/Уг Л12 _ Л21
*1 + ^2/И И*1/Г2 +*2 ’ Х1 + Л12х2 A21jq + х2
Ап и Л21 находят так же, как и в уравнении
Вильсона.
NRTL £12 — £22 £21 - £11 х$ ( 621 У+ / t12G12 (17)
*21 \*! + х2<?21 / "и \ (х2 +xjG12)2
®12 Х1 ( 6712 У+ / т21&21
И2 \х2 + Х!<?12 / \ (*1 +*2<?21)2 (18)
Коэффициенты активности 183
Продолжение табл. 4.4
Уравнение Параметры In-yi И 1П72
gij — параметр взаимодействия между компонентами ajj — параметр непроизвольности; ay = ctj. i и у; giJ = gjj
gl2 ~ё22
Tl2 - RT
g21 ~gll
RT
(19, 20)
UNIQUAC
G12 = exp(-ai2ri2) Gzi = exp(~ a2iT21) (21, 22)
“12 “ “22 “21 — “11 In yj = In yf+ In yf r <Pl z / q In у । = In +т?1 In +<P2 1/1 - /2 *1 2 \ r2 » ....... 1 r21 In yf + In yf3 In yf + In yf П2 \ (23) (24) (25) (26) (27) (28) (29)
П ‘U'"1 2l> U242 \^+^21 «М12+02 ) In y2 = lnyf+ Inyf c (?2 z ^2 1 r2 \ In уf = In + — q2 In +<?! l/2- /1 x2 2 % \ И /
lny£=-g2ln(>Vi2 + fl2) + >M2 ГТ “ a , 2q ) (30)
\04tj2+t*2 /
h= j to-<?,)-to-1) 2 = 10 (31)
gi — параметр площади компонента i
п — параметр объема компонента i
иц — параметр взаимодействия между компонентами i и J; и у = Uji
z — координационное число
yf — комбинаторная часть коэффициента активности компонента i
у? — остаточная часть коэффициента активности компонента i
о
и, = ------ доля площади компонента i
'EigJXj
riXi
4>i =------ объемная доля компонента i
HrjXj
/ Uy - Uii\
rij = exp I---------J
\ RT J
(32)
(33)
(34)
184 Глава 4
Таблица 4.5. Корреляции коэффициентов активности двухкомпонентных смесей
при бесконечном разбавлении
Ван Лаар и Маргулес
Л12 = Inyf (1)
Л21 = In у 2 (2)
Скэтчард — Гильдебранд
Vi
lnn - RT(si ~ (3)
И2
1пУ2 = ~ S2)2 (4)
Скэтчард — Гильдебранд — Флори — Хаггинс
И , Ki Vi
1пуГ = „т(^1 ~ $2)2 + In + 1 - Jx i И 2 У 2 (5)
и2 и2 v2
iny? = (^i ~ ^2) + in + 1 — 12 RT 1 27 Vi Vi (6)
Вильсон
In Л 12 -l" Л 21 = 1 — In У Т ~ кл (7)
Л12 + lnA2i = 1 ~ 1ПУ2 ~ к2 (8)
Л12 = exp(£j - ехр(£2 ~ Л12)) (9)
Л21 = ехр(&2 - Л12) (10)
Цубока — Катаяма — Вильсон
И, Vi
1пЛ12 + Л21 - In „ 00 +/=*3 (H)
И, И2
Л12 + 1пЛ21 = In ,, ,х. + = кл (12)
И2У2 V\
Л12 = exp[fc3 - ехр(&4 - Л]2)] (13)
Л21 = ехр(&4 - Л ]2) (14)
NRTL
т12ехр(—< »12г12) + Г21 = In-и - к5 (15)
г12 + ^21 ехр( —a j 2Г21) = *п У 2 = kf> (16)
Г21 = к5 ' - г12ехр(-а12т12) (17)
г12 = к6 ’ - r2iexp(-a12T2i) (18)
UNIQUAC
1 Г] ЩГ2 Г]12
= — In — In у j + 5qi In — + qi + 11 + 1 (19)
Ч\ r2 q^ri r2 J
1 Г2 ?2rl r21]
кг = In — In у 2 + 5>q2 In — + q2 + 12 + 1 (20)
42 [_ rl ЯЛ2 И J
т12 = ехр[&8 - exp(fc7 - Т12)] (21)
т21 = exp(fc7 - Иг) (22)
Коэффициенты активности 185
Таблица 4.6. Уравнения коэффициентов активности многокомпонентных смесей
(обозначения даны в табл. 4.4)
Уравнение
Параметры
In Ji
Скэтчарда — Гильдебранда <5/ Г 'V xJVJSi I2 — 8i - Z— J RT L > J
Вильсона С Ч \ А,-,- = exp 1 1 — In Kf \ RT / = А// = 1 / V* \ V xk^ki 1 Zu X.A, •• 1 + 1 - Zu m V =1 7 7 / k =i V J =! Xj^kj
NRTL (gji -gji) Tji = RT Gji = exp (-ajitji) тц = Tjj = 0 Gii = Gjj = 1 m m TjjGj^Xj m XjGjj / xnrnjGnj \ m "i" /5] m (m ) /S GijXi S GijXi GijXi
UNIQUAC Л"* -Г* ~ii ~ii 1 M N g «q - II 1 - ‘1 4 S’ kF 7 * ~ ’i । — 5* 5* я •4o ~-r> ~-r> II II + я S’ i ~ । -* 1 + S“ I N >-Q 11 SZ? в- O -«Hi, кд X -e IIM3 ~ 1 1
Цубоки — Катаямы — Вильсона ^ij, / 'r, \ V* xk^ki — In 1 Zu X.A,, 1 — Zu m V- / к^^х^- / чр \ у? / Vk \ + In 1 2u x;V;IVi 1+ L xj 1 1 b " > \T.v^vJ j_
в которых состав выражен в мольных и объемных до-
лях соответственно.
Функциональные зависимости либо могут базиро-
ваться на каком-то теоретически обоснованном способе
межмолекулярного взаимодействия, либо могут быть
чисто эмпирическими. Как, например, показано в рабо-
те [492], традиционно применяемые уравнения имеют
общее статистическо-механическое обоснование. Мно-
жители Х1Х2 или 0102 в выражении для Gex должны
стремиться к нулю для чистых веществ. На рис. 4.4 по-
казаны графики зависимостей коэффициентов активнос-
ти и соответствующих Gex.
Если функцию /(xi) принимают постоянной, получае-
мое в результате уравнение называют симметричным
уравнением или симметричным уравнением Маргулеса:
Gex
(4.67)
Применяя уравнение (4.22), находят коэффициенты ак-
тивности следующего вида:
In у] = AxjX 2 + Л( 1 —Xj)(l — 2х ]) — Ах %, (4.68)
lny2 = Axj.
(4.69)
186 Глава 4
Рис. 4.9. Контурные графики допустимых пределов множествен-
ных параметров, служащих для представления данных о коэф-
фициентах активности, с указанием величин целевых функций
(О.Е).
д: параметры уравнения Вильсона для системы ацетон + вода при давле-
нии 1 атм. Целевая функция имеет следующий вид:
O.F. = j ](1 — Tcalc/Texp)2i
п i
где суммирование выполнено для всех компонентов п и данных i. В точ-
ке, обозначенной крестиком, О.Е = 0,0197 [125].
б: параметры уравнения Вильсона для системы хлороформ + бензол.
в: параметры уравнения ван Лаара для системы ацетон + метанол. Целе-
вая функция учитывает различия между измеренными и рассчитанными
величинами Р, Т, х, и у,. Можно ожидать, что величины параметров бу-
дут находиться внутри эллипсов на уровнях достоверности 0,87 или 0,99,
как показано на рисунке [98].
Константа равна предельным значениям логарифмов
коэффициентов активности, получаемым или при кон-
центрации, стремящейся к нулю, или при бесконечном
разбавлении (последнее определение применяется чаще):
Л = 1пу^=1пу2- (4.70)
Этому простому виду корреляции соответствуют
лишь смеси соединений со сходными химическими
свойствами. Например, Редлих (1976) приводит шесть
двухкомпонентных смесей этилбензола и изомеров кси-
лола; в этом случае, однако, константы варьируют
лишь в пределах от 0,0035 до 0,0003, а это свидетель-
ствует о том, что поведение по существу идеально.
Смеси, показанные на рис. 4.5, а также демонстрируют
поведение, близкое к симметричному, но для них откло-
нения от идеальности довольно значительны.
Для того чтобы представить данные о коэффициентах
активности с точностью того же порядка, что и точ-
ность измерений, необходимы несколько более сложные
уравнения. В данной главе мы рассмотрим основные
уравнения, получившие наибольшее распространение.
Более старые уравнения подробно рассмотрены в рабо-
те [50]. Для нахождения наилучших значений парамет-
ров эмпирических уравнений из экспериментальных
данных обычно применяется линейный или нелийней-
ный метод наименьших квадратов с соответствующим
условием совпадения или так называемой целевой функ-
цией. Значительное внимание было уделено этому во-
просу учеными, применявшими статистические методы
исследований. Наиболее типичные расчеты приведены в
книгах [57, 98] и во вступительной части сборника
DECHEMA (DECHEMA VLE и LLE Collections 1979 г.
и все последующие издания). В разд. 4.9 данной книги
содержится ряд замечаний относительно этой темы.
Здесь следует подчеркнуть, что при использовании мно-
гопараметрического уравнения, комбинируя различные
величины параметров, можно обеспечить относитель-
ную точность в определенных пределах. На рис. 4.9 по-
казано несколько примеров такого рода.
Списки параметров уравнений ван Лаара, Маргу-
леса и Вильсона для типичных смесей, содержащиеся в
табл. Д.8 — Д.10, могут представлять интерес при про-
ведении сравнительного анализа.
4.7. Уравнение Маргулеса
и связанные с ним уравнения
Наиболее старым из числа применяемых в настоящее
время является уравнение Маргулеса (1895). Как следует
из табл. 4.10, оно зачастую дает лучшие результаты,
Коэффициенты активности 187
чем другие уравнения, и это может привести в замеша-
тельство тех, кто твердо верит в прогресс. Исследова-
ния Маргулеса были выполнены еще до того, как были
сформулированы такие понятия, как фугитивность и ко-
эффициенты активности, однако в сущности его предло-
жения сводятся к представлению 1П71 и 1П72 в виде
степенных рядов по составу:
In У! = 01X2 + *1Х2 + • • • >
In 72 = а2х1 + *2Х1 + • • •
(4.71)
(4.72)
для двухкомпонентных смесей. Как правило, применя-
ют линейные перегруппировки этих рядов, предложен-
ные Карлсоном и Кольборном [209]:
1п71 = (А + 2(В - А)Х1)Х2, (4.73)
In72 = (В + 2(А -B)x2)xi, (4.74)
в которых существует простая зависимость между пара-
метрами и коэффициентами активности при бесконеч-
ном разбавлении:
А = In у J0,
В = 1пу2.
(4.75)
(4.76)
Избыточная энергия Гиббса, соответствующая этим
уравнениям, составляет
Gc*/R Т = х}х2(Ах2 + Вх\). (4.77)
Х1 ~ х2 2 In 7j
В = х2 1П Y2 +
х 1 х2
(4.80)
Эти параметры можно определить исходя из одной
группы коэффициентов активности. В то же время при
наличии большего количества данных можно использо-
вать линейную форму уравнения:
1 / In 7!
RT \ 1 - X]
In 72 \
+ ------ I = А + (В - А) х j.
Х1 /
(4.81)
Это уравнение применяется в примере 4.5.
Разложение в ряд, сходное по форме с уравнением
(4.78), предложенное Редлихом и Кистером (1948):
Ge*/RT = х{х2[В + C(Xi ~х2) + D(x{ - х2)2 + . . . ],
(4.82)
позволяет получить трехпараметрические уравнения для
коэффициентов активности:
In7! = х2[В + С(3х7 - х2) + П(Х) - Х2)(5Х] - х2)]
(4.83)
In 72 = х2[2? + С(х ] - Зх2) + D(x j - х2)(х, - 5х2)].
(4.84)
Как показано в примере 4.6, параметры можно легко
определить из экспериментальных данных.
В уравнении, предложенном Скэтчардом и Хамером
[614], состав выражен в объемных долях, т. е.
Распространение также получили несколько уравнений
более общего характера с большим числом параметров,
например
Ф, = П-Ху/^ИуХу.
(4.85)
Вывод начинают со следующего уравнения:
Gn/RT= Х}Х2(Ах2 + Вх 1 + CxiX2 + . . . ) (4.78)
Gex/RT — 0i02(° 4- Ьф\ + сф2),
(4.86)
Параметры уравнений (4.73), (4.74) выводят следую-
щим образом:
х2~ хх 2 In у2
А = j ln Y1 + ’ (4.79)
х2 Х1
из которого находят следующие коэффициенты ак-
тивности:
In у*! =
(4.87)
Пример 4.5. Линейные графики уравнений Маргулеса и
Данные о смеси воды и этанола при 30°С взяты из
книги [544].
Уравнение Маргулеса. Данные представлены в виде
зависимости Gcx/xwXo от хо и аппроксимированы пря-
мой линией:
Ge'/xHxu - 3652,5 - 1353,0х«. (1)
Сравнение со стандартной формой
Ge'/RTxwxa = В + (А - В}ха (2)
дает следующие величины параметров: А = 0,9146.
В = 1,4514.
ван Лаара
Уравнение ван Лаара. Аппроксимирующую прямую
\Лп7„ - 0,968 - 0,795 с 1п7а (3)
запишем в следующем виде:
\ 1пу„ = - У А,В \ 1пу„ (4)
и получим значения параметров: А = 0,937, В = 1,4826.
Экстраполяция экспериментальных данных до бесконеч-
ного разбавления при помощи трехточечного уравнения
Лагранжа дает
ln>w = 0,906 и 1пу“ = 1,407,
что сравнительно хорошо соответствует величинам па-
раметров уравнений Маргулеса и ван Лаара.
88 Глава 4
Хи Уи р, кПа б/>, кПа 1П7„ ln>a G' , Дж/моль
0,00435 0,0412 4,413 0,001 0,00004 1,391 15,4
0,01524 0,1280 4,803 0,003 0,00039 1,355 53,0
0.02727 0,2043 5,203 0,002 0,00113 1,320 93,5
0,04633 0,2975 5,781 -0,007 0,00295 1,273 155,7
0,06783 0,3753 6,386 0,003 0,00608 1,221 223,0
0,10991 0,4743 7,329 0,001 0,01709 1,109 345,6
0,17111 0,5479 8,189 0,002 0,04813 0,9205 497,5
0,24688 0,5907 8,723 -0,007 0,1082 0,6926 636,4
0,32385 0,6194 9,085 0,011 0,1820 0,5069 723,9
0,38655 0,6406 9,303 0,003 0,2471 0,3885 760,5
0,41758 0,6508 9,403 -0,005 0,2811 0,3378 768,2
0,50492 0,6797 9,663 0,001 0,3835 0,2179 755,8
0,58087 0,7087 9,869 0,005 0,4758 0,1398 707,4
0,63434 0,7329 9,999 - 0,001 0,5391 0,09889 655,0
0,72455 0,7810 10,199 - 0,003 0,6437 0,04932 537,0
0,80840 0,8337 10,341 0,001 0,7447 0,01844 397,2
0,85785 0,8705 10,394 -0,003 0,7987 0,00754 302,5
0,89064 0,8979 10,427 0,003 0,8255 0,00365 235,7
0,89934 0,9056 10,435 0,004 0,8309 0,00301 217,6
0,92444 0,9284 10,445 - 0,001 0,8432 0,00181 164,8
0,95370 0,9556 10,457 -0,004 0,8554 0,00103 102,3
0,97315 0,9739 10,467 - 0,002 0,8691 0,00052 60,1
0,98153 0,9819 10,473 0,003 0,8788 0,00030 41,6
Коэффициенты активности 189
Рис. 4.10. Необычный характер изменения коэффициентов
активности, представленный при помощи уравнения Мар-
гулеса.
а: параметры (взяты из табл. Д.9) имеют отрицательные значения:
А = -0,2112, В = -0,3270.
б: параметры (взяты из табл. Д.9) имеют положительное значение:
А = 0,7358, В = 0,3105. Коэффициент активности достигает мак-
симума.
1пу2 =
(4.88)
В этой системе уравнений учитывается важное различие
между молекулами, и поэтому его, вероятно, можно
применять для представления данных. Однако в силу
того, что эта система немного более сложна, чем испо-
льзуемые в других методах, в настоящее время ей уде-
ляется мало внимания. На рис. 4.12 показана
зависимость коэффициентов активности от доли мо-
лярного объема. При равных молярных объемах это
уравнение приводится к уравнению Маргулеса (см. рис.
4,17,6).
Кроме более простой методики оценки параметров
полиномиальные корреляции имеют следующие пре-
имущества по сравнению с другими уравнениями:
1. Один или оба параметра могут быть отрицатель-
ными. Если требуется представить данные во всем диа-
пазоне концентраций, оба параметра ван Лаара должны
190 Глава 4
Рис. 4.11. Экстремумы, представленные уравнением Мар-
гулеса.
а-, составы, при которых возникают экстремумы коэффициента актив-
ности, выраженного в виде функции соотношения параметров А/В
[уравнение (4.89)].
б: экстремумы имеют оба коэффициента активности, А = 1,
В = -0,5,
иметь одинаковый знак. В уравнениях, включающих ло-
гарифмы состава, оба параметра должны быть поло-
жительными.
2. С помощью этих корреляций можно представить
данные о минимальном или максимальном коэффициен-
те активности. Так, например, согласно уравнению
Маргулеса, экстремум достигается при следующем со-
ставе (см. рис. 4.11):
1 - 2А/В
3(1 - А/В) ’
(4.89)
Коэффициенты активности 191
Рис. 4.12. Зависимость коэффициентов актив-
ности, вычисленных по формулам Скэтчар-
да — Хамера [уравнения (4.87) и (4.88)], от до-
ли молярного объема. = ViXi/(ViXi + V2X2).
А = 3, В = 1. При К2/К1 = 1 эти уравнения
становятся тождественными уравнениям Мар-
гулеса.
Рис. 4.12а. Воздействие соотношения объемов
на расчет коэффициентов активности по урав-
нению Скэтчарда — Гильдебранда — Флори —
Хаггинса.
In 7, = In 7* + In 6i — 9i + 1
In 7; = Vi(Si - l)2/RT
9i = Vi/'LxiVj.
уравнение Скэтчар-
да — Гильдебранда —
Флори — Хаггинса.
уравнение Скэтчар-
да — Гйльдебранда.
4.8. Уравнение ван Лаара
В принципе ван Лаар выводил свое уравнение [704]
исходя из уравнения состояния Ван-дер-Ваальса, однако
в силу того, что степень соответствия параметров по-
следнего экспериментальным данным о коэффициентах
активности низка, в настоящее время уравнение ван Ла-
ара считается чисто эмпирическим.
Зависимость избыточной энергии Гиббса от мольных
долей определяется выражением
из которого получаем следующие уравнения для коэф-
фициентов активности:
In У! = А
In у2 = В
Вх2
АХ1’+ Вх2
Axt
Ахг+ Вх2
(4.91)
(4.92)
RT 1 1
Gex Ах\ Вх2
(4.90)
Параметры уравнения можно рассчитать исходя из од-
ной группы данных о коэффициентах активности по
192 Глава 4
Пример 4.6. Нахождение констант уравнения Редлиха
— Кистера для системы вода +- тиазол
Вычитая из уравнения (4.83) уравнение (4.84), по-
лучаем
1071/72 = Л(Х2 ~ V1) + С(6Л'1Л'2 - 1) +
+- D(x? - х>)(1 - 8x1X2)- (D
Для определенных величин состава этот результат при-
нимает особо простую форму. Эти результаты приведе-
ны ниже в виде таблицы; соответствующие величи-
ны 1пу 1/72 найдены из графика, иллюстрирующего при-
мер 4.2.
именно:
Сех 1 1
+
Ахх Вх2
(4.96)
Следовательно, если параметры имеют противополож-
ные знаки, уравнения для коэффициентов активности
преобразуются к следующему виду:
1пу1=Л(1 -Z)2[l + 2Z(AB/\AB\ - 1)], (4.97)
lny2 = BZ2[l + 2(1 -Z(AB/\AB \ - 1)], (4.98)
Условие
1П71/72
Xi = Х2 0,5 0,3365
х,х2 = 1/6 0,2113, 0,7887 1,0438
Х1Х2 - 1/8 0,1464, 0,8536 0,9555
где
z = _____И IX1
|Л|Х1+ |B|x2
(4.99)
Выполняя подстановки в уравнение (1):
0,3365 = [6(0,25) - 1]С, (2)
1,0438 = (0,7887 - 0,2113)[В + (1 - 8/6)Р], (3)
0,9555 = (0,8536 - 0,1464)[В + (6/8)£>]. (4)
получаем следующие значения парамегров: В = 2,1732,
С - 0,6730, D - 1,0960.
уравнениям (4.93) и (4.94):
А = In у = In У!
х2 In у2
1 +----------
Xi In У1
В = In у 2 = 1пу2
Х1 In У]
1 +
*2 In у2
(4.93)
(4.94)
Одна из линейных форм уравнения ван Лаара предло-
жена Блэком [187]:
У1п
(4.95)
В поддержку предлагаемых уравнений не было предло-
жено никаких доказательств. Сравнение (рис. 4.13) это-
го уравнения с уравнением Маргулеса, допускающим
наличие параметров с противоположными знаками,
определенно свидетельствует не в пользу уравнений
Налла.
На рис. 4.13 рассматривается система вода + 3-окси-
бутанон-2, для которой в сборнике DECHEMA
[DECHEMA VLE Collection (1/1, 401)] приведены пара-
метры уравнения Маргулеса А = -0,2997, В = 1,5637.
Эти величины наилучшим образом соответствуют экс-
периментальным данным. Если принять те же значения
для коэффициентов активности при бесконечном разбав-
лении, эти величины параметров будут справедливы и
для уравнения ван Лаара. Сопоставление графиков
уравнений (4.96)—(4.98) с графиками уравнений Маргу-
леса отчетливо демонстрирует их существенное расхож-
дение, следовательно, уравнение Налла в данном случае
неприменимо. Пример, показанный на рис. 4.13,6, где
А = 1 иВ = -0,5, является чисто теоретическим и так-
же со всей очевидностью свидетельствует о существен-
ных расхождениях между уравнениями Маргулеса и
Налла.
Позднее было предложено несколько трехпараметри-
ческих модификаций уравнения ван Лаара с несколько
улучшенной точностью представления. Так, Блэк [189]
прибавил еще один член к первоначальному определе-
нию избыточной энергии Гиббса, что дало
В примере 4.5 сравниваются результаты расчетов, про-
веденных с применением уравнений ван Лаара и Маргу-
леса в линейных формах, и соответствующие экспери-
ментальные данные. Степень их соответствия можно
расценить как относительно хорошую.
При помощи уравнений ван Лаара невозможно пред-
ставить экстремумы коэффициентов активности, и если
требуется представить данные для всего диапазона кон-
центраций, оба параметра должны иметь одинаковый
знак. Налл [88] попытался устранить эту трудность и
предложил уравнение, в которое входят абсолютные ве-
личины параметров и которое приводится к стандарт-
ной форме, если параметры имеют одинаковый знак, а
G™/RT= \/{\/Ахх - 1/Вх2) + Сххх2(хх -х2)2.
(4.100)
Соответствующие выражения для коэффициентов ак-
тивности приводятся в задаче 4.46. Параметры связаны
с коэффициентами активности бесконечного разбавле-
ния следующим образом:
1пуГ=Л + С, (4-101)
1пу2 = В + С. (4.102)
Коэффициенты активности 193
Рис. 4.13. Проверка модификации уравнений ван Лаара, раз-
работанной Наллом, в случае наличия параметров с проти-
воположными знаками.
а\ графики уравнений Маргулеса и Налла для системы вода +
+ З-оксибутанон-2; параметры: А = -0,2977, В = 1,5637.
б: графики уравнений Маргулеса и Налла; параметры: Л = 1 и
В = -0,5.
Для нахождения всех трех параметров достаточно вы-
полнить одно дополнительное измерение. Воздействие
параметра С на форму кривых может быть явно выра-
женным, как видно из рис. 4.14.
Параметры всех уравнений для коэффициентов актив-
ности изменяются вместе с температурой, однако эта
зависимость не имеет однозначного характера. В при-
мере 4.20 оба параметра уравнения ван Лаара уменьша-
ются по мере снижения температуры, в то время как
в примере 4.19 параметр А уменьшается, а параметр В
увеличивается.
13-829
194 Глава 4
Рис. 4.14. Эффект включения третьего параметра С в моди-
фикацию уравнения ван Лаара [уравнение (4.100)].
Уравнения для коэффициентов активности приводятся в задаче 4.46.
Графики построены для = 3 и у" = 2.
G^/RT = l/(lZ4x, + 1/йх2) + Cxix2(xi - х2)2.
4.9. Уравнение Вильсона и его модификации
При разработке уравнения Вильсон [726] исходил из
того, что межмолекулярные взаимодействия зависят в
первую очередь от «локальных концентраций», которые
он выражал в объемных долях. Эти концентрации вхо-
дят в вероятностные члены энергетического распределе-
ния Больцмана. На рис. 4.15 представлена двухкомпо-
нентная смесь, состоящая из смеси молекул типа 1 и 2.
Вблизи молекулы типа 1 вероятность нахождения дру-
гих молекул того же типа равна Рц, а вероятность на-
хождения молекул другого типа составляет рц. Соот-
ветственно соотношение этих двух вероятностей опре-
деляется как
Рп Х!ехр(- an/RT)
р2Х х2ехр(~ a2i/RT)
Р\2 Х!ехр(~ а12//?Т)
Р22 х2ехр(- а22/ЯТ)
Объемные доли, выраженные через эти вероятности,
равны
рцУ\ ______________________!_____________
Р11У1 + /’21^2 X2V2
1 + —~ ехр[-(а21 - ац)/ЯТ]
xtZi
(4.105)
-----—------. (4.106)
X] + Л12х2
_______________[_____________________*2
22 Х1К1 г _ А21х1+х2’
1+ ехр[-(а12 - a22)/RT\
Х2У2
(4.107)
где Vi — молярный объем,
v2 У2
Л12 = ехр[-(а21 - ац)/ЛГ] - ехр(-Х12//?Т),
г 1 к 1
(4.108)
(4.103)
(4.104)
У\ У1
Л21 = — ехр[-(а12 - a22)/RT] = v2 — ехр(-Х21/ЛТ), v2
(4.109)
М2 = a2i — ai 1, (4.110)
Ml = а12 ~ а22» (4.1И)
°12 = °21 • (4.П2)
Если принять, что энергия Гиббса зависит от Inz, так
же, как идеальная величина G'd зависит от 1пх,, то из-
быточную энергию Гиббса можно представить следую-
щим образом:
G^/RT= (G - Gid)/RT = Zx; ln(z,/x,). (4.113)
Подстановка вместо z, дает
G&X/RT = — X] ln(xj + Ai2x2) — x2 1п(Л21Х] + x2).
(4.1 14)
Коэффициенты активности 195
Рис. 4.15. Два типа молекулярных кластеров в двухком-
понентных жидкофазных системах (в соответствии с те-
орией Скотта). Считается, что каждая молекула типа 1
или 2 окружена молекулами обоих типов в пропорции,
определяемой энергиями взаимодействия Гиббса, ука-
занными на рисунке.
а: в центре кластера молекула типа 1. б: в центре кластера мо-
лекула типа 2.
Применяя уравнение (4.21), находят коэффициенты ак-
тивности:
In Yi = - ln(xt + Л12х2) + 0*2 (4.115)
1пу2 = - ln(A2iXi + х2) - 0X1, (4.116)
= Л12 _л21 4 117
Х1 + А12* 2 A2iXi +х2
Обобщение этих результатов для любого числа ком-
понентов показано в табл. 4.6, из которой следует, что
для представления многокомпонентных смесей требу-
ются только параметры бинарного взаимодействия, и
в этом состоит преимущество уравнения Вильсона над
уравнениями, ранее рассмотренными в данной главе.
Еще одна положительная особенность уравнения Виль-
сона состоит в том, что в нем заранее учтен темпера-
турный эффект [уравнения (4.108) и (4.109)]. Параметры
Ху независимы от температуры как минимум до первой
аппроксимации. В большинстве подборок параметров
уравнения Вильсона приводят именно параметры Ху.
Было предпринято несколько попыток придать выво-
ду уравнения Вильсона более строгое теоретическое
обоснование и в некотором отношении улучшить его.
Так, Моулрап [492] вывел это и ряд других уравнений,
используя одну из модификаций уравнения Ван-дер-Ва-
альса, в которой учитывается локальный состав, при
этом он исходил в каждом случае из различных допуще-
ний. Нитта и Катаяма [524] рассматривают уравнение
Вильсона как вывод теории ассоциированных раство-
ров. Цубока и Катаяма [699] считают его частным слу-
чаем (предполагающим равенство молярных объемов
компонентов) своих выкладок. Некоторые модифика-
ции уравнения Вильсона будут рассмотрены в последу-
ющих разделах данной главы.
4.9.1. Оценка параметров. Уравнения Вильсона пред-
ставляют собой пару трансцендентных уравнений, раз-
решимых только численно относительно параметров
при наличии экспериментальных данных о коэффици-
ентах активности. В случае наличия нескольких изме-
рений выбор наиболее надежных величин параметров
представляется затруднительным. Для проверки точ-
ности расчетов необходимо определить некоторый кри-
терий, называемый целевой функцией и обозначаемый
О.Е (objective function). Целевая функция меньше, чем
отклонение величины некой прогнозируемой характери-
стики от ее измеренной величины. Выбор надлежащей
целевой функции зависит от вида имеющихся данных,
которые могут быть получены либо измерением Т, Р,
х или у, либо путем расчета, например, Gn/RT =
= 2х,1п7,-.
Целевая функция, использованная при составлении
подборки данных, опубликованной Хирата [57], равна
O.F. = Е[(<7ех//?Пса1с - (Сех/Яг)ехр] < eg, (4.118)
в то время как при подготовке сборника DECHEMA
Гмелинг и Онкен [309] использовали либо
O.F. - 2(1 - Уса1с/уехр)2 < еу
либо
O-F- ~ E^calc ~ ?ехр)2 — еР-
(4.119)
(4.120)
Если представляется возможным выполнить оценку
стандартных отклонений нескольких измеренных
свойств, Праузниц и др. [567] рекомендуют применять
Г\ Е? X ’(АР)2 (ST)2 (Ах)2 (Ду)2
О.Г . — 7 . 2 + 2 + 2 + 2
L °р аТ °х ау
— е,
(4.121)
где Д — разность расчетных и экспериментальных вели-
чин. Приведем наиболее типичные значения стандарт-
ных отклонений, найденные Андерсоном и Праузницем
196 Глава 4
Таблица 4.7. Разложение уравнения Вильсона и уравне-
ния Цубоки — Катаямы — Вильсона (см. также
табл. В. 11)
Уравнение Вильсона
1пуг- = 1 — + х2Лг-2 + х3Лг-3)
__________XlAlz______
xi +х2Л12 +х3Л13
__________^2^2/______
Х1Л21 + х2 + х3Л23
__________*3Л3/______
Х1Л31 + х2Л32 + х3
Л,7 = 1
Уравнение Цубоки — Катаямы — Вильсона
Х1К1 + x2Vi2 + Х3Г/3
In у, — In
xiA,i + х2Л,-2 + х3Л,-3
Ум Л1(-
+ X 1 —
|_Xi+х2Г12 + х3Г13 Xi+х2Л12 + х3Л13 _
Уц ^2i
' Х2 ' —
Х!Г21 +х2 + х3Г23 Х]Л21+х2+ х3Л23
Уз.' Л3,-
+ Х3 —
Х1Г31 + х2Г32 + х3 xjA31+х2Л32+х3
vjk = Vk/Vj
Л и = 1
[159]: ор = 1 мм рт. ст., от - 0,05 °C, ох = 0,001 и
ау = 0,0003.
Определенному максимуму некоторой целевой функ-
ции могут соответствовать различные пары парамет-
ров. Например, на рис. 4.9 любая пара величин внутри
одного из эллипсов всегда будет включаться в эту опре-
деленную величину целевой функции. Выбор нужной па-
ры, которую находят путем определенного расчета,
зависит от алгоритма и начальных величин парамет-
ров. Среди многих методов, применяемых для оценки
параметров в области фазового равновесия, наиболее
предпочтительным являются метод нелинейных на-
именьших квадратов, метод градиентов и симплексный
метод. Первым из них пользовались Хирата и др. [57],
последним — Гмелинг и Онкен [309].
Описанные ниже несложные методы вполне пригод-
ны для решения целого ряда задач, особенно если коли-
чество экспериментальных данных ограниченно, что не
позволяет надлежащим образом выполнить статистиче-
ский анализ. Между параметрами большинства уравне-
ний для коэффициентов активности, включая уравнение
Вильсона, и коэффициентами активности при бесконеч-
ном разбавлении существует сравнительно простая за-
висимость. Уравнения Вильсона приводятся к
следующему виду:
In у |°= — In Aj2 + 1 — Л21, (4.122)
Рис. 4.16. Номограмма параметров уравнения Вильсо-
на, рассчитываемых исходя из коэффициентов активнос-
ти при бесконечном разбавлении [488].
Как показывают линии построения, при 7]° = 0,4 и 7" = 0,56
имеются три группы величин: Ли, Л21 = (0,08, 4,6), (0,83, 2,15)
и (6,7, 0,005). Определить необходимые пары параметров из
диаграммы не представляется возможным; их находят по урав-
нениям (4.122) и (4.123).
Коэффициенты активности 197
Эти уравнения можно привести к уравнению с одной
переменной, относительно которой оно легкоразреши-
мо, а именно:
1 1
Л12 = “ехр 1 - — ехр(1 - Л12)
Y1 L Y2
Следовательно,
Л21 — 1 ln(Aj2yf).
(4.124)
(4.125)
Начальную величину для решения уравнения (4.124) ме-
тодом проб и ошибок можно определить по номограм-
ме, приведенной на рис. 4.16. Диапазон параметров
уравнения Вильсона в действительности довольно ши-
рок. В табл. Д.8, где представлены данные для 90 сис-
тем, параметр Ху варьирует от -500 до 3 500, что при-
близительно соответствует диапазону параметра Лу от
2,5 до 0,005. Как видно из номограммы, если коэф-
фициенты активности при бесконечном разбавлении
меньше единицы, математически возможно наличие не-
скольких групп параметров. То же самое допустимо и
для других уравнений для коэффициентов активности; в
этой главе будет уделено некоторое внимание множест-
венности корней уравнений.
Еще один достаточно простой метод нахождения па-
раметров разработан для эквимолярных смесей; в
этом случае уравнения также приводят к одному урав-
нению с одной переменной. Сначала определяют пере-
менные 3 и Лгь
2Л12 _ 2Л21
1 + л12 " 1 + л21 ’
4
= ---------------- 1,
Y1Y2U + Л12)
(4.126)
(4.127)
которые затем подставляют в следующее уравнение:
Л12 = — 1 + 2 ехр(0.5Д — In Y1 )•
(4.128)
Уравнение (4.128) содержит только одно неизвестное, и
его легко решить методом проб и ошибок.
При использовании любой другой пары у, для нахож-
дения параметров требуется решить систему нелиней-
ных уравнений. В примере 4.7 для этого применяется
метод Ньютона — Рафсона. Следует напомнить, что
если при нахождении параметров приходится ограничи-
ваться одной парой у,, необходимо принять во внима-
ние, что при этом можно получить отрицательные
величины, что, естественно, является недопустимым в
том случае, если требуется представить данные во всем
диапазоне концентраций. Например, yi = 1,5 и уг = 2
при Xi = 0,5; в этом случае Лц = - 0,0485 и
Л21 = 0,4013. Однако, как следует из уравнений (4.124)
и (4.125), при использовании коэффициентов активности
бесконечного разбавления получение отрицательных ве-
личин исключено, поскольку
0< у,”Л(7 < 2.303.
(4.129)
В разд. 4.15 представлен ряд других аргументов в по-
льзу применения коэффициентов активности бесконеч-
ного разбавления.
4.9.2. Преимущества и недостатки уравнений Виль-
сона. Важными достоинствами уравнений Вильсона яв-
ляются обычно наблюдаемые точность результатов при
представлении поведения коэффициентов активности
полярных и неполярных смесей и способность пред-
ставлять поведение многокомпонентных смесей на осно-
вании параметров бинарного взаимодействия. В то же
время для этих уравнений характерен ряд недостатков.
1. Множественность корней при у, < 1 обусловливает
необходимость выбора, который непросто ввести в ав-
томатическую компьютерную программу.
2. Отрицательные величины параметров недопусти-
мы в том случае, если требуется представить данные во
всем диапазоне концентрации.
3. Эти уравнения неприменимы для представления не-
смешиваемости жидкостей. Равновесие в системе жид-
кость — жидкость рассматривается в гл. 7, однако,
поскольку ряд модификаций уравнения Вильсона, разра-
ботанных главным рбразом в целях рашения этой зада-
чи, применим и для других видов равновесия, ниже мы
кратко обсудим этот вопрос.
4.9.3. Модификации уравнения. Простое введение
множителя Си в выражение
In Yi = С12[— 1п(Х] + Л12х2) + /Зх21 (4.1 30)
дает возможность представить равновесие в системе
жидкость — жидкость, однако остается неясным, мож-
но ли такой подход распространить на многокомпо-
нентные смеси. Введение члена с третьим параметром
обосновано теоретически более надежно. Хиранума
[347, 348] разработал довольно сложное уравнение, тре-
тий параметр которого имеет теоретическое обоснова-
ние. Эта работа была продолжена Шулте и др. [623].
Нагата и др. [502] предлагают прибавить к избыточной
энергии Гиббса член
(tfi - 52)2Ф1Ф2(ПХ1 + (4.131)
где 3, — параметры растворимости, ф, — объемные до-
ли, а К — молярные объемы. Поскольку параметры
растворимости — это характеристики чистых веществ,
уравнения, предложенные Нагатой, относятся к двупа-
раметрическим.
Предложенную Цубокой и Катаямой [699] модифика-
цию уравнения Вильсона, по-видимому, можно считать
наиболее простым из числа удачных вариантов. В дан-
ной книге она фигурирует как уравнение Цубоки — Ка-
таямы — Вильсона. Для расчетов избыточной энергии
Гиббса эти авторы используют следующее выражение:
<?ех *1+И12х2 И21х!+х2
~^7 = х11п +х21п * . >(4.132)
RT Х1 + Л12х2 Л21х1+х2 V
где ly(= Vj/И,) — соотношения молярных объемов, и
если эти соотношения равны единице, то мы вновь по-
лучаем уравнение Вильсона. Уравнения для определения
коэффициентов активности бинарных смесей соответ-
198 Глава 4
Пример 4.7. Определение параметров Вильсона методом Ньютона — Рафсона
В примере будут найдены параметры уравнений
Вильсона для смеси метил ацетата (1) и метанола (2).
При этом предполагается, что при 5907 мм рт. ст. и
Xi = 0,736 коэффициенты активности имеют следующие
значения: 71 = 1,0224 и 72 - 1,3983. Уравнения Вильсо-
на записывают следующим образом:
(A R \
--------ТТЛ- “ R-1- ) = °’
Х1 + Ах2 Вх\ + Х2 1
g = 1П72 + 1п(ВХ1 + х2) + Х1 (-— - D------) = 0. (2)
\ Х1 + Ах2 BX1+X2I
Запишем производные:
У = л ( Х2
дА \ Xi + Ах2
df
дВ
dg = / Xi \
дА у Xi + Ах2 J
dg_ = в( *1
дВ \ Вх\ + Х2
(3)
(4)
(5)
(6)
Запишем уравнения Ньютона — Рафсона с учетом по-
правок й и к к первоначальным величинам А и В:
+ =°’ (7) у У 0 у У 0
= °- (8) \ дА 1 о \ дВ 1 0
Начиная с первого приближения Ао = Во = 0,5, при
требуемой точности до 0,0001 последовательные итера-
ции составят
А
0,5
0,57151
0,31395
0,29528
0,29236
В
0,5
0,83994
1,1717
1,2602
1,2671
Программа для ЭВМ приводится в приложении В.5.
Аналогичным образом определим параметры уравне-
ния Вильсона, модифицированного Цубокой и Катая-
мой. Соотношение объемов IV И2 равно 0,5107.
Уравнения, используемые для определения f и g, отли-
чаются друг от друга, а их производные тождественны:
Х1 + АХ2 Вх\ + Х2 ’
Xi/0,5107 + Х2 Xi + 0,5107x2 '
Для решения требуется шесть итераций:
А В
0,5 0,5
0,72203 0,85748
0,36679 1,291
0,33135 1,4531
0,32109 1,4782
0,32104 1,4785
Пример 4.7А. Отрицательные величины параметров
уравнений Вильсона
При использовании одной группы данных для опреде-
ления параметров уравнений Вильсона можно получить
для них отрицательные величины. Так, измерение рав-
новесия в системе н-гептан (1) + толуол (2) привело к
следующим результатам: Xi = 0,45, yi = 0,54, 71 =
= 1,0914, 72 = 2,0893. Применяя программу, приведен-
ную в табл. В.5, получаем следующие параметры урав-
нений Вильсона: Ли = -0,2475 и Л21 = 1,3331, в то
время как в соответствии с уравнениями (4.79) и (4.80)
параметры уравнения Маргулеса имеют следующие зна-
чения: Ии = 3,3037 и Л21 = -0,0458. Параметры урав-
нений Вильсона, соответствующие коэффициентам
активности бесконечного разбавления уравнения Маргу-
леса, равны: Ли = 0,0059 и Л21 = 2,8289.
На приведенных ниже рисунках сравниваются коэффи-
циенты активности, полученные с использованием обе-
их групп параметров Вильсона, и коэффициенты ак-
тивности, найденные по уравнению Маргулеса. При от-
рицательной величине Ли (xi + Л12Х12) достигает нуля
при xi = 0,1984. Если состав исследуемой смеси не-
сколько отличается от указанного выше, коэффициенты
активности Вильсона и Маргулеса приблизительно рав-
ны; следовательно, коэффициенты активности уравне-
ний Вильсона, очевидно, можно использовать для
расчетов в этом интервале составов. В то же время до-
пущение о том, что даже приблизительно верные вели-
чины всегда будут иметь отрицательные параметры, не
является надежным, поэтому такими параметрами
обычно пользоваться не следует. Надежность парамет-
ров, получаемых исходя из коэффициентов активности
бесконечного разбавления уравнений Маргулеса, необхо-
димо проверять в каждом отдельном случае. Правомер-
ность оценки параметров уравнений Вильсона по
значениям уравнения Маргулеса основана на том, что
первые применимы для представления равновесных со-
стояний многокомпонентных систем, чего нельзя ска-
зать о параметрах уравнений Маргулеса.
Коэффициенты активности 199
а: сравнение уравнений Маргулеса и Вильсона, содержащего
один отрицательный параметр.
б: сравнение уравнений Маргулеса и Вильсона, параметры кото-
рых определены исходя из одних и тех же коэффициентов ак-
тивности для бесконечного разбавления.
ственно принимают следующий вид:
In у ] = In Х1 + ^12х2 Х1 + Л]2Х2 + (Д-^)Х2
Г21х1 + х2
In у2 — In ~ (Р~ ^)х1
A2ixi +х2
И12 ^21
+ ^12х2 И21х1 +х2
а Л12 Л21
Х1 + Л12х2 Л2 1х 1 + х2
И12=И2/И1, (4.137)
И21 = И1/Г2. (4.138)
(4.133) Варианту уравнения Цубоки — Катаямы — Вильсона
для бесконечного разбавления можно придать ту же ма-
тематическую форму, что и уравнениям Вильсона
(4.134) (4.122) и (4.123), вводя коэффициенты активности для
псевдокритического разбавления:
(4.135) (1птГ)*=1птГ + 1п(И1/И2)+ 1-
= 1 - 1пЛ12 - Л21, (4.139)
(4 136) (1п‘>'2)*= 1пГ2 + ln(K2/Ki) 4- 1 - И2/И])
= 1 1пЛ21 А12 • (4.140)
200 Г лава 4
Рис. 4.17а. Сравнение корреляций коэффициентов активности.
Симметричные уравнения Вильсона и ван Лаара при одной и
той же величине коэффициента активности при бесконечном раз-
бавлении. Кривые 72 являются зеркальным отражением кривых
7ь показанных на графике.
Рис. 4.176. Сравнение корреляций коэффициентов актив-
ности. Коэффициенты активности системы 2-метил-
бутен-2 + н-метилпирролидон. Сравнение эксперимен-
тальных величин с рассчитанными по нескольким урав-
нениям, параметры которых определены исходя из ко-
эффициентов активности при бесконечном разбавлении.
1 — экспериментальные данные, 2 — уравнение Маргулеса, 3 —
уравнение ван Лаара, 4 — уравнение Скэтчарда — Хамера, 5 —
уравнение Вильсона [67].
Коэффициенты активности 201
Рис. 4.17в. Корреляции коэффициентов активности, найденные
исходя из величин для бесконечного разбавления. Система н-гек-
сан (1) + диэтилкетон (2), 65 °C. у? = 2,25, у” = 3,67, V\/Vz =
= 1,236.
Рис. 4.18. Зависимость коэффициентов активности, определяемых по
уравнению NRTL, от параметра ад при у” = 5 и у” = 2. Числа у кри-
вых — величины этого параметра.
Несмотря на то что записано всего лишь несколько
наборов параметров уравнения Цубоки — Катаямы —
Вильсона, для их нахождения можно обратиться к
обширным подборкам параметров уравнений Виль-
сона, содержащихся в работах [354, 57] и сборнике
DECHEMA (1979 и все последующие издания). Целесо-
образность такой методики обусловлена в первую оче-
редь тем, что уравнение Цубоки — Катаямы — Виль-
сона применимо для представления равновесия жид-
кость — жидкость, в то время как уравнение Вильсона
для этой задачи непригодно. Один из способов нахож-
дения параметров уравнения Цубоки — Катаямы —
202 Глава 4
Рис. 4.19. Сравнение коэффициентов активности, полученных по
уравнению Вильсона (В), параметры которого указаны в
табл. Д.8, уравнению Скэтчарда — Гильдебранда (СГ), парамет-
ры растворимости для которого приведены в приложении Г, и
по уравнению Скэтчарда — Гильдебранда — Флори — Хаггинса
(СГФХ). См. также табл. 4.12.
Вильсона предусматривает следующие операции: опре-
деление коэффициентов активности бесконечного раз-
бавления исходя из параметров уравнения Вильсона,
подстановка этих величин в уравнения (4.139) и (4.140)
и в заключение в уравнения (4.124) и (4.125).
Полученные таким образом параметры уравнения
Цубоки — Катаямы — Вильсона дают вполне удовлет-
ворительные аппроксимации при анализе таких процес-
сов, в которых возможно установление равновесия
пар — жидкость и жидкость — жидкость. Равновесие
между жидкостью и жидкостью весьма чувствительно
к значениям параметров; даже те параметры, оценка
которых выполнена для всего диапазона коэффициентов
активности, основанных на данных о равновесии между
паром и жидкостью, не являются достаточно точными.
Этот вопрос будет рассмотрен в гл.7.
Коэффициенты активности 203
На рис. 4.17, в сравнивается несколько уравнений, па-
раметры которых получены при одном и том же значе-
нии 7/°; уравнения Вильсона и Цубоки — Катаямы —
Вильсона в этом масштабе дают практически идентич-
ные кривые, вероятно, в силу того, что соотношение
объемов (1,236) не намного отклоняется от единицы.
Как следует из рис. 4.17 и 4.19, расхождение между раз-
личными уравнениями гораздо более значительно.
204 Глава 4
4.10. Уравнение NRTL (Ренона)
Уравнение NRTL (nonrandom two-liquid) для избыточ-
ной энергии Гиббса выводят, основываясь на теории,
согласно которой жидкость в двухкомпонентной смеси
имеет ячеистую структуру, причем эти ячейки (класте-
ры) состоят из молекул типа 1 и 2, каждая из которых
окружена такими же молекулами, которые в свою оче-
редь имеют аналогичное окружение, и т. д. (рис. 4.15).
Гиббсовы энергии взаимодействий между молекулами
обозначают символом gy, где подстрочным индексом j
указывают центральную молекулу; таким же образом
обозначают и мольные доли в окружающих зонах хц.
Гиббсовы энергии двух типов кластеров определяются
как
£(1) = + х21£21, (4.141)
£(2) =*12£12+ *22£22, (4.142)
где gn и g22 — энергии Гиббса чистых веществ, при
этом предполагается, что gi2 = g2i. Следовательно, из-
быточная энергия Гиббса для множества кластеров бу-
дет иметь следующий вид:
^ех =Х1Х21(^21 - £11) + -^2^12(^12 — £22>- (4.143)
41 = (£12 ~gu)/RT, (4.152)
^12= ехр(-а12г12), (4.153)
G21 = exp(-a12r21). (4.154)
Коэффициенты активности получают дифференциро-
ванием:
Г ( g2‘ ¥
'П1'1 ~Х} р1 (z,+z2G21 ) +
42<42
(х2 + XjG^j)2
(4.155)
1пу2
41<41
Ч(Х! +x2G21)2
(4.156)
Локальные мольные доли х,у определяются по уравне-
ниям, аналогичным уравнениям Вильсона (4.102) и
(4.103):
*21 х2 ехр(-а12^21/ЛГ)
---- =--------------------, (4.144)
ХЦ xj ехр(-а12^и//гГ)
Xi2 Xj ехр(-а12^12/ЛГ) /Л1..Ч
---- = , (4.145)
х22-х2 ехр(-а12^22/ЛГ)
где «и — константа, принимаемая за характеристику
заданности смеси. Поскольку
*21 + *11 — 1’
*12 + *22 = 1,
(4.146)
(4.147)
локальные мольные доли можно вычислить следующим
образом:
_ *2 exp(-ai2(g2i -gn)/RT)
X2i *1 + *2 ехр(~а12(#21 ~gn)/RT) ’ (4.148)
_ Xj ехр(~а12(^12-^22)//?Г)
*12 x2 + xj exp(-a12te12~g22)/RT) ’ (4149)
Подставляя эти выражения в уравнение (4.143), получа-
ем следующее итоговое уравнение для избыточной
энергии Гиббса:
Эти уравнения содержат три независимых параметра:
«12, 712 и 72ь В табл. 4.6 показаны их обобщенные вы-
ражения для многокомпонентных смесей. Подобно
уравнениям Вильсона, многокомпонентные уравнения
NRTL можно полностью выразить при помощи пара-
метров бинарного взаимодействия.
4.10.1. Оценка параметров. Несмотря на то что Ре-
нон и Праузниц [587] установили приближенную зависи-
мость третьего параметра ап от обратной величины
координационного числа, т. е. числа молекул, соприка-
сающихся с центральной молекулой, диапазон экспери-
ментально полученных численных величин
свидетельствует о том, что данный параметр является
чисто эмпирическим и что между его величиной и ка-
ким-либо механизмом, по-видимому, не существует
сколько-нибудь определенной зависимости. Авторы
оригинальной публикации предлагают пользоваться
диапазоном величин от 0,2 до 0,47 в зависимости от хи-
мической природы составляющих компонентов. Однако,
как выяснилось [464], при ац = -1 обеспечивается вы-
сокая точность представления как смешивающихся, так
и частично несмешивающихся бинарных систем.
В том случае, если возможна удовлетворительная
оценка параметра ац, два других параметра можно по
таблицам Ренона и Праузница [588] вычислить в виде
коэффициентов активности бесконечного разбавления.
Подробный анализ уравнения NRTL выполнен Реноном
и др. [109], эти же авторы приводят программы для
ЭВМ для нахождения параметров с использованием ме-
тода наименьших квадратов Ньютона — Рафсона, а
также программы расчетов процессов дистилляции и
экстракции.
При бесконечном разбавлении и при условии, что ве-
личина параметра «12 поддается определению, уравне-
ния для коэффициентов активности можно привести к
уравнению с одной переменной, которое легкоразреши-
мо методом проб и ошибок. Если T2i из уравнения
41 = 1п?Г - 42 ехр(-а12т12) (4.157)
Gex r21G21 42<?12
RT — *1*2 xx+x2G2x Gi2xx + x2
подставить в
42 = 1пу2 - т21 ехр(-а12т21),
(4.158)
42 — (£12 — £22)/^^’
(4.151)
получим требуемое уравнение с одной переменной.
Коэффициенты активности 205
Таблица 4.8. Разложение уравнения NRTL и уравнения UNIQUAC
Уравнение NRTL
In у,- =
Г1,-(71,Х1 + T2iG2ix2 + ?3iG3ix3
G\ix\ + G2ix2 + G3ix3
x16|i
*1 + 612*2 + 613Х3 хг6|2 41
— — ri2
(712*1 + *2 + 632х3
хз6,-3
613*1 + 623*2 + *з 43
x2^21G2i + x3^31G31
*1 + x2G2l + x3G3l
Х1Г12^12 + Х3Г32^32
*j612 + X2 + X3G32
X1T13G13 + x2r23^23
613*1 + 623*2 + *3
4l — 0
Gii= 1
Уравнение UNIQUAC
In у। = In — + 5qt In— + Ц - — (xjZj + x2l2 + x3l3) + q,[ 1 - + 62T2i + 03r3,)]
_ ________________________°2^i2 _________________0343
01 + 02*21 + 0341 0142 + 02 + 03r32 01*13 + 02*23 + 03
*n = 1 *
rixi
0i= 7 7
rpci + r2x2 + r3x3
Qixi
e =----------------------
91*1 + <12x2 + ?3X3
/, = 5(r,- - q,) - r; + 1
4.10.2 . Численные величины ап. Рис. 4.18 показывает
относительно малую зависимость коэффициентов ак-
тивности от величин ап в диапазоне 0,1 — 0,5. Из это-
го рисунка также видно, что при оцг = - 1 и ап = 0,3
коэффициенты активности имеют близкие значения.
Приведенные в издаваемом DECHEMA (1979) «Сборни-
ке данных о равновесии между паром и жидкостью» ве-
личины о(12, полученные путем корреляции эксперимен-
тальных данных, соответствуют широкому диапазону
их положительных величин — от 0,01 до 100 и более;
предположительно симплексный метод программиро-
вался таким образом, чтобы получить лучшие положи-
тельные величины. Данные сборника DECHEMA были
подвергнуты тщательному анализу, с тем чтобы сфор-
мировать некоторые основные правила оценки ап при-
менительно к определенным классам смесей, что
привело, однако, к выводам весьма неопределенного ха-
рактера.
Часть 6А. Смеси углеводородов С4—Сб с углеводо-
родами и другими органическими веществами, кроме
кислородсодержащих. Для 588 групп данных средняя
величина ан равна 0,336 при среднеквадратичном от-
клонении 0,096; однако 16 групп данных были исключе-
ны из анализа, поскольку полученные для них резуль-
таты далеко выходили за границы допустимого диапа-
зона и лежали в пределах от 0,0167 до 3,53.
Часть 6В. Смеси углеводородов С7—Cis с углеводо-
родами и другими органическими веществами, кроме
кислородсодержащих. Для 419 групп данных средняя
величина оцг равна 0,316 при среднеквадратичном от-
клонении 0,063; однако 34 группы данных были исклю-
чены из анализа, поскольку для них а 12 изменялась в
пределах от 0,0207 до 125,57, в большинстве случаев
превышая 1,0.
Части 3 + 4. Альдегиды, кетоны и эфиры. Для 478
групп данных среднее значение ац равно 0,310 при
среднеквадратичном отклонении 0,056. Данные, рас-
сматриваемые в качестве средних, находились в диапа-
зоне 0,1—0,8; 40 групп данных не были включены в это
число, поскольку полученные значения лежали в преде-
лах 0,008—7,86. Для многих смесей, у которых величи-
ны параметров значительно отличались от среднего
206 Глава 4
Таблица 4.9. Частота наилучшего соответствия пяти корреляций для коэффициентов активности, содержащихся
в «Сборнике данных о равновесии жидкость — пар» (DECHEMA)
Часть сборника Количество данных Маргулеса Ван Лаара Вильсона NRTL UNIQUAC
1 Водные органические вещества 504 0,143 0,071 0,240 0,403* 0,143
2А Спирты 574 0,166 0,085 0,395* 0,223 0,131
2В Спирты и фенолы 480 0,213 0,119 0,342 0,225 0,102
3/4Спирты, кетоны, эфиры 490 0,280* 0,167 0,243 0,155 0,155
6А Углеводороды С4—Сб 587 0,172 0,133 0,365* 0,232 0,099
6В Углеводороды С?—Си 435 0,225 0,170 0,260* 0,209 0,136
7 Ароматические соединения 493 0,260* 0,187 0,225 0,160 0,172
Всего в семи частях 3563 0,206 0,131 0,300* 0,230 0,133
* Наиболее часто встречающееся лучшее соответствие в каждой категории.
значения, были все же получены такие величины пара-
метров, которые близки к среднему значению. Напри-
мер, для смеси ацетон + гептан получены следующие
величины параметров: 0,0724, 0,2892, 0,2911, 0,2924,
0,2943, для смеси диэтиловый эфир + хлороформ:
0,2988, 0,3089, 0,3140, 1,9233, для смеси хлороформ +
+ дипропиловый эфир: 0,3054, 0,3027, 0,3156, 2,5188,
2,5550.
Часть1. Водные органические системы. Для 456 сис-
тем средняя величина аи равна 0,388 при среднеквадра-
тичном отклонении 0,136. У примерно половины
систем значения параметров находились вблизи 0,3 и у
половины лежали в пределах от 0,56 до 0,6. Для 48 сис-
тем ап < 0,1 или >0,9, в силу чего эти системы были
исключены из группы, имеющей средние значения. Кро-
ме того, у ряда систем некоторые величины параметров
значительно выходили за пределы указанного диапазо-
на, а некоторые были близки к среднему значению. Из
42 групп данных для смеси вода + этанол в 32 группах
средняя величина ап составила 0,296 при среднеквадра-
тичном отклонении 0,004, в то время как в остальных
10 группах величина параметра колебалась в пределах
от 0,0204 до 1,1614. Для системы вода + 2,3-метилбу-
тандиол были получены такие величины параметров:
0,0050, 0,2926, 0,3154, 0,3225 и 0,5553, для уксусного
альдегида — 12 групп данных в пределах от 0,0154 до
0,9817, а для этилендиамина — 14 групп данных в пре-
делах от 0,3764 до 4,4456.
В заключение следует сказать, что, проводя оценку
параметра ап, следует иметь в виду, что для неводных
смесей он должен быть близок к 0,3, а для водных
органических смесей — к 0,4. Вероятно, можно найти
объяснение значительным отклонениям от этих средних
величин в 5—6% случаев, однако этот вопрос изучен не
Пример 4.8. Определение трех параметров уравнения NRTL по ко эффициентам активности, полученным экспери-
ментальным путем
Ниже приведены данные для смеси сероуглерод + аце-
тонитрил [507]. Мы определим параметры уравнения
NRTL исходя из следующих величин: у? = 8,9,
у? = 19,5, у] = 2,019 при Xi = 0,475.
Сначала необходимо выбрать требуемую величину
параметра ап, далее вычислить ш и rzi по уравнениям
(4.157) и (4.158) и в заключение определить по уравне-
нию (4.155) 71 при Xi = 0,475. Полученные в итоге пара-
метры имеют следующие значения (см. таблицу):
а12 = 0,30, 712 - 2,913, 721 = 0,9704.
CS2-C2H3N
Of 12 712 72! yt при Xi = 0,475 х у / Р 71 T2
0,10 3,0339 -0,0541 2,219 0,0 0,0 20,5 70,6 8,9 1,000
0,15 2,8412 0,3307 2,169 12,8 79,4 318,0 6,508 1,064
0,20 2,8590 0,5720 2,146 17.5 81,7 355,2 5,470 1,115
0,25 2,8889 0,7829 2,094 47,5 81,7 355,2 2,019 1,753
0,30 2,9130 0,9704 2,019 71,6 81,7 355,0 1,336 3,241
0,35 2,9296 1,1353 1,930 73,6 81,7 356,0 1,300 3,487
0,40 2,9407 1,2791 1,837 87,1 81,7 355,2 1,099 7,136
0,45 2,9480 1,4038 1,745 100,0 100,0 303,0 1,000 19,50
0,50 2,9530 1,5115 1,657
Коэффициенты активности 207
Пример 4.9. Определение влияния температуры на коэффициенты активности в соответствии с уравнением
NRTL
В работе [109] параметры уравнения NTRL для смеси
н-гексан + ацетон представлены в виде функции темпе-
ратуры:
ап = 0,4539 + 0,001937(7^ - 273,15),
Д£12 = 758 - 2,67(7 - 273,15),
Ag2i = 754 - 0,66(7 - 273,15),
где Agy измеряется в кал/моль.
Рассматривается диапазон температур от 183,15 до
373,15 К. Коэффициенты активности определены при
температурах 300 и 350 К и представлены графически.
Полученные кривые свидетельствуют о существенном
влиянии температуры в указанном диапазоне.
был. Для водных органических систем вполне можно
ожидать несколько более широкого диапазона измене-
ния величин, так как поведение воды часто не соответ-
ствует прогнозам. Как следует из данных, приведенных
в табл. 4.9, третий параметр уравнения NRTL действи-
тельно улучшает корреляцию данных для водных сис-
тем по сравнению с четырьмя двухпараметричес-
кими уравнениями, проанализированными в сборнике
DECHEMA. Все приведенные в этом сборнике данные
(1978—1979) коррелируются с «и = 0,2.
4.10.3 . Преимущества и недостатки уравнения
NRTL. При помощи трехпараметрического уравнения
NRTL можно, как правило, достаточно хорошо предста-
вить данные о равновесии в бинарных системах. Пре-
имущество этого уравнения по сравнению с уравнени-
ями Маргулеса и ван Лаара состоит в том, что его
можно применять к многокомпонентным смесям, осно-
вываясь только на бинарных параметрах, а по срав-
нению с уравнениями Вильсона — в том, что его мож-
но использовать для представления равновесия жид-
кость — жидкость, хотя уравнение Цубоки — Катая-
мы — Вильсона также применимо в этих целях. В неко-
торых случаях какое-либо одно из уравнений дает луч-
шие результаты при описании равновесия пар — жид-
кость, но поскольку уравнение NRTL трехпараметриче-
ское, оно обычно предпочтительнее, чем уравнение
Вильсона или UNIQUAC. Однако при наличии данных
в двух точках и программы для ЭВМ это его преимуще-
ство становится незначительным. Уравнения Вильсона
и UNIQUAC используются для расчетов коэффициентов
активности методом групповых вкладов; уравнение
Вильсона положено в основу метода ASOG, уравнение
UNIQUAC — в основу метода UNIFAC. Однако, пользу-
ясь данными, полученными при проведении на ЭВМ
расчетов, базирующихся на этих уравнениях, можно по-
добрать параметры и для уравнения NRTL.
4.10.4 . Влияние температуры. Этот эффект отчасти
описывается уравнениями (4.151) и (4.152), поскольку в
некоторых случаях можно допустить, что не зави-
сит от температуры. В то же время в работе [109] «12,
Agi2 и Д§21 представлены в виде линейных функций тем-
пературы и там же приведено шесть констант для 82
смесей. Влияние температуры, рассмотренное в приме-
ре 4.9, достаточно заметно.
4.11. Уравнение UNIQUAC (universal quasi-
chemical - универсальное псевдохимическое)
При выводе этого уравнения, носившем полутеорети-
ческий характер, Абрамс и Праузниц [152] исходили из
модели двух жидкостей и концепции локального соста-
ва. Используемая ими модель предполагает, что избы-
точная энергия Гиббса обусловлена, во-первых, разли-
чием размеров и форм молекул (конфигурационная или
208 Глава 4
комбинаторная составляющие) и, во-вторых, энергией
взаимодействия молекул (вторая составляющая избы-
точной энергии Гиббса).
Уравнения UNIQUAC для двухкомпонентных систем
даны в табл. 4.4, в виде обобщенного варианта для
многокомпонентных смесей — в табл. 4.6, а в табл. 4.5
приведены варианты этого уравнения для бесконечного
разбавления. Параметры объема и поверхности г, и q,
получают главным образом путем кристаллографиче-
ских измерений. Значения этих коэффициентов для мно-
гих веществ указаны в работе [98] и в сборнике
DECHEMA (1979 и все последующие издания в прило-
жении к каждому из томов). Эти параметры можно по-
лучить также методом групповых вкладов — см.,
например, [107 , 40, 641, 745]. Некоторые данные содер-
жатся в табл. Д.11, Д.13. Для воды и спиртов Андер-
сон и Праузниц [159] предлагают пользоваться
особыми коэффициентами.
Маурер и Праузниц [470] предложили более простой
способ вывода этого уравнения, они же разработали
трехпараметрическую модификацию уравнения, кото-
рую, однако, невозможно распространить на многоком-
понентные смеси. Нагата и Като [501] предложили
уравнение, подобное уравнению UNIQUAC; эти авторы
пришли к выводу, что для точного представления рав-
новесия жидкость — жидкость в тройных смесях необ-
ходим третий общий параметр. Модификация комбина-
торной части уравнения UNIQUAC [399] позволила
улучшить корреляцию поведения алифатических углево-
дородов. Как указано в работе [152], если придать пара-
метрам г, и qt необходимые значения, то уравнения
Маргулеса, ван Лаара, Вильсона и NRTL можно рас-
сматривать как частные случаи уравнения UNIQUAC.
Аналогичную взаимосвязь уравнений показали Цубока
и Катаяма [699], включившие в эту группу уравнений
и свою модификацию уравнения Вильсона.
Как уравнения Вильсона и NRTL, в условиях беско-
нечного разбавления уравнения UNIQUAC можно пре-
образовать таким образом, чтобы их можно было
разрешить относительно одного параметра:
т12 = exp[fc8 - exp(fc7 - т12)], (4.159)
Г21 = кЪ ~~ 1пг12> (4.160)
где kj и кг — константы, определения которых даны в
табл. 4.5. Параметры Auu и Auzi перечислены в сбор-
нике DECHEMA; как следует из табл. 4.4, между ними
и тц существует простая зависимость.
4. 11.1. Влияние температуры. Первоначально все ко-
эффициенты в уравнении UNIQUAC принимались неза-
висимыми от температуры. Введение [642] зависимых
от температуры параметров взаимодействия иу привело
к некоторым улучшениям одновременного представле-
ния избыточных энергий Гиббса и энтальпий. Выраже-
ние координационного числа z в виде функции
температуры привело к более заметным улучшениям:
z = 35,2 - 0,1272Г + 0,00014Г2. (4.161)
Координационное число — это число наиболее близко
расположенных молекул, касающихся какой-либо опре-
деленной молекулы. Для многих жидкостей при нор-
мальных условиях z равно 10. Решение предыдущего
уравнения дает следующие величины координационного
числа: 9,6 при 300 К и 6,7 при 400 К. Несмотря на то
что величину z = 10 можно считать в большей или
меньшей степени общепринятой, в ряде случаев (см.,
например, работу [411]) координационное число z, рав-
ное шести, обеспечивает более точную корреляцию.
4. 11.2. Однопараметрическая форма уравнения
UNIQUAC. Однопараметрическую форму уравнения
UNIQUAC получают путем подстановки
Un = - Auiap/<7i, (4.162)
U22 = - Ди2ар/<?2, (4.163)
где Ди)ар — изменение внутренней энергии испарения
компонента /, которое предположительно известно.
Следующее допущение
м12 = М21 ~ С1 — с12) '/м11м22 (4.164)
ведет к такой формулировке уравнения, в котором экс-
периментальным путем необходимо определить всего
один параметр с 12. Эта форма уравнения эффективна в
том случае, если в наличии имеется очень ограниченный
объем данных, например всего один коэффициент ак-
тивности при бесконечном разбавлении, найденный ме-
тодом хроматографии или дифференциальной эбуллио-
скопии. В последнее время к этим экспериментальным
методам проявляется значительный интерес (см., на-
пример, [260, 608, 678]). Авторы работы [411] попыта-
лись сравнить несколько однопараметрических уравне-
ний, однако наиболее удачное из них выявить не
удалось.
4. 11.3. Преимущества и недостатки уравнения
UNIQUAC. Для уравнения UNIQUAC характерно сле-
дующее.
1. Применимость к многокомпонентным смесям с ис-
пользованием только бинарных параметров.
2. Применимость для представления равновесия жид-
кость — жидкость.
3. Учет влияния температуры по крайней мере для
среднего диапазона.
4. Возможность более точного представления смесей,
молекулы которых значительно различаются по
размеру.
5. Это уравнение положено в основу метода группо-
вых вкладов, применяемого для получения коэффициен-
тов активности, т. е. метода UNIFAC, основанного на
свойствах чистых компонентов. В этом направлении ве-
дется большая работа.
Основные недостатки уравнения UNIQUAC — это, ве-
роятно, его несколько большая алгебраическая слож-
ность, а также часто более низкая по сравнению с
некоторыми менее сложными уравнениями степень точ-
ности представления данных (см. табл. 4.10). На рис.
4.18 сравниваются графики коэффициентов активности,
полученные при помощи нескольких уравнений исходя
из данных о бесконечном разбавлении.
4.12. Многокомпонентные смеси
С увеличением числа компонентов смеси до трех и
более проведение эксперимента резко осложняется, и
поэтому сколько-нибудь полные исследования смесей,
Коэффициенты активности 209
Пример 4.10. Параметры уравнения UNIQUAC Оля
После подстановки
ехр(1 - к») и 72 -»ехр(1 - к2),
где к2 и к» находят по табл. 4.5, используя методи-
ку, показанную для уравнения Вильсона в разд. 4.9, оп-
ределяют параметры уравнения. Находят три группы
корней.
смесей ацетона (11 и хлороформа (21
Используя методику, примененную для уравнения
Вильсона, находят параметры уравнения UNIQUAC,
сначала выполнив подстановку
71° -> ехр(1 - kg) = 0,7759 и у2 - ехр(1 - к2) = 0,6725.
Полученные три группы параметров представлены
ниже.
Ацетон
Хлороформ
0,40 2,57 2,34
0,56 2,70 2,34
и/г2 = 0,9519, qi/q2 =1, Л = - 0,4200, /2 = 0,1000,
к, = 1,3968, к» = 1,2537.
Случай 712 721
I 0,08581 3,7097
II 1,8203 0,6549
III 2,5757 0,3076
_ _ _ _
содержащих более трех компонентов, вообще редко осу-
ществляются. В некоторых случаях правомерно допу-
стить, что избыточная энергия Гиббса смеси
представляет собой сумму избыточных энергий Гиббса
всех пар компонентов плюс дополнительные члены,
учитывающие взаимодействие триплетов и других ком-
бинаций молекул. Одно из более простых выражений
этого типа для избыточной энергии Гиббса тройной
смеси имеет следующий вид:
Gex = G\\ + G Гз + G е2хз
+ (С0 + QX! + С2х2 + С3х3)х1х2х3, (4.165)
где С, — тройные параметры. В некоторых работах,
например в работе [50], приводится несколько более
старых уравнений, содержащих только один параметр
тройного взаимодействия, два из которых представле-
ны ниже.
Симметричное уравнение:
Ge*/RT = х1х2(х1 + х2)Л12
+ Х1Х3(Х1 + х3)Л13
+ х2х3(х2 + *з)л23
+ х]Х2х3(Я12 +Аз + ^23 - О- (4.166)
Уравнение Маргулеса:
Ga/RT = Х]Х2(Л21Х] + Л12х2)
+ х\Х3(А31Ху + А13х3)
+ х2х3(А32х2 + А23х3)
+ XjX2x3(/l2i +Л[3 + Л32 — С). (4.167)
Параметры тройного взаимодействия можно иногда
аппроксимировать; так, Колборн [228] применил вы-
ражение
С = 0,5 (Л21 + A j 3 + Л32 — Л31 — А23). (4.168)
Как установили авторы работы [147], ни
С = 0,
ни
С= 0,5ЕЕЛ,у
(4.168а)
(4.1686)
не позволяют точно описать экспериментальные данные,
но при использовании полного уравнения (4.168) результа-
ты описания данных не выходят за пределы ошибок экспе-
римента. Обычно при использовании уравнений Маргуле-
са, ван Лаара и других более старых у равнений помимо дан-
ных о бинарных смесях требуется ряд других эксперимен-
тальных данных.
Значительный прогресс в области представления избы-
точных энергий Гиббса многокомпонентных смесей был
достигнут после разработки уравнения Вильсона, которое
теоретически применимо при наличии только параметров
бинарного взаимодействия. Это уравнение
Gn/RT= - Z х, In I ZxyA,y
(4.169)
не является простой суммой избыточных энергий Гибб-
са всех пар, но оно выражено через параметры бинар-
ного взаимодействия. В одной из ранних статей Шрай-
бера и Эккерта [621] справедливость этого уравнения
была проверена на примере многих систем. Корреляции
для ряда трехкомпонентных систем содержатся в сбор-
нике DECHEMA (DECHEMA VLE Data Collection).
Аналогичным образом к многокомпонентным систе-
мам можно применить уравнение NRTL; оно было прове-
рено на семнадцати трехкомпонентных системах пар —
жидкость и нескольких трехкомпонентных системах жид-
кость — жидкость [109].
Андерсон и Праузниц [159] проверили применимость
уравнения UNIQUAC на девяти трехкомпонентных систе-
мах пар — жидкость, а также десяти трех- и одной четы-
рехкомпонентной системе жидкость — жидкость. Как
выяснилось, корреляции, описывающие равновесие в
трехкомпонентных системах жидкость — жидкость,
можно значительно улучшить, если при оценке пара-
14-824
210 Глава 4
метров использовать хотя бы одну кривую из диаграм-
мы равновесия трехкомпонентной системы. Этот вы-
вод несомненно справедлив как для уравнения NRTL,
так и для уравнения Цубоки — Катаямы — Вильсона.
Предложенная Цубокой и Катаямой [699] модифика-
ция уравнения Вильсона, названная нами уравнением
Цубоки — Катаямы — Вильсона, была подвергнута
проверке с использованием семи систем пар — жид-
кость и четырех равновесных систем жидкость — жид-
кость; для четырех последних систем степень точности
прогнозирования оказалась более высокой, чем при ис-
пользовании уравнения NRTL.
Степень точности данных о равновесии жидкость —
жидкость, полученных авторами работы [40] для пяти-
десяти тройных систем, оказалась различной. Результа-
ты использования уравнения UNIQUAC для представ-
ления данных о равновесии жидкость — жидкость в
трех- и четырехкомпонентных системах обсуждаются в
работе [289]. Наиболее обширная подборка данных о
равновесии жидкость — жидкость, найденных экспери-
ментально и определенных по уравнениям NRTL и
UNIQUAC, опубликована Соренсеном и Арлтом [125]
(DECHEMA LLE Data Collection). В сборнике данных
о равновесии пар — жидкость (DECHEMA VLE Data
Collection) приведены параметры уравнений Вильсона,
NRTL и UNIQUAC для равновесия пар — жидкость в
трехкомпонентных системах.
Несмотря на то что теоретически для представления
данных о многокомпонентных системах достаточно
применить параметры бинарного взаимодействия, в ря-
де случаев, используя параметры, основанные на дан-
ных о многокомпонентном равновесии, можно повы-
сить точность расчетов. В сборнике DECHEMA неодно-
кратно сравниваются результаты представления равно-
весия в тройных системах с помощью параметров
бинарного взаимодействия и шести параметров, подо-
Габлица 4.10. Некоторые величины параметров
бранных к данным о трехкомпонентном взаимодейст-
вии. Однако в этом сборнике не показано, что в четы-
рехкомпонентных смесях и смесях с большим числом
компонентов равновесие лучше представлять при помо-
щи параметров бинарного взаимодействия, найденных
по данным о тройном взаимодействии, нежели при по-
мощи параметров, определяемых по измерениям бинар-
ного взаимодействия.
4.13. Сравнение уравнений
Итак, мы рассмотрели достоинства отдельных мето-
дов корреляций коэффициентов активности и сравнили
их (табл. 4.9). Сделаем теперь ряд выводов:
1. Уравнения Маргулеса, ван Лаара и связанные с ни-
ми алгебраические выражения характеризуются относи-
тельной простотой математического аппарата, легкос-
тью оценки параметров по данным о коэффициентах ак-
тивности и во многих случаях возможностью адекват-
ного представления двухкомпонентных смесей, до-
вольно значительно отклоняющихся от идеальных,
включая частично растворимые жидкие системы. Эти
уравнения неприменимы к многокомпонентным систе-
мам, если отсутствуют параметры взаимодействия
между тремя и более компонентами.
2. Уравнение Вильсона позволяет точно представить
равновесие пар — жидкость в двух- и многокомпонент-
ных смесях е использованием только параметров бинар-
ного взаимодействия. В силу большей простоты этого
уравнения его использование может быть предпочти-
тельным для решения указанной задачи, чем примене-
ние уравнений NRTL и UNIQUAC. Уравнение Вильсона
нельзя непосредственно применить для представления
равновесия жидкость — жидкость; использование в
этих целях его столь же простой модификации, уравне-
ния Цубоки — Катаямы — Вильсона, дает удовлетво-
Вещества Т, °C Р, мм рт.ст. V? У 2 Уравнение Вильсона
Х72
1-Гексан + толуол 30 1,27 1,34 -78,07 236,02
Ацетонитрил + вода 300 8,22 14,39 142,91 1961,72
Ацетонитрил + вода 760 32,50 6,06 1391,96 1356,93
Вода + диацетоновый спирт 100 3,14 11,23 1684,67 -3,88
Вода + пиридин 760 2,20 29,19 1020,97 1486,51
1-Октен + этилбензол 760 1,28 1,09 532,50 -211,19
Октан + бутиронитрил 90 2,78 4,10 -157,95 1299,67
Гептан + пиридин 67,8 7,94 3,58 747,06 717,91
Гептан + диметилформамид 5,0 28,71 37,36 1188,98 2426,56
Изопрен + ацетонитрил 760 4,86 8,14 163,51 1226,52
Гексан + октан 149,2 0,68 0,82 -464,70 301,61
Перфторгексан + гексан 35 15,71 8,18 1133,06 1051,54
Гексан + гептан 92,3 0,93 1,43 -514,84 1244,18
Этанол + вода 10 3,36 2,89 — 189,77 959,16
Этанол + вода 70 7,24 2,62 471,04 883,75
Примечания.
т“ и т” даны для уравнения, которое наилучшим образом соответствует экспериментальным
данным.
Коэффициенты активности 211
рительные результаты, хотя последнее не было
подвергнуто такой тщательной экспериментальной про-
верке, как другие уравнения. Уравнение Вильсона поло-
жено в основу метода групповых вкладов ASOG,
используемого для получения коэффициентов ак-
тивности.
3. При помощи уравнения NRTL можно достаточно
верно представить равновесие пар — жидкость и жид-
кость — жидкость в двух- и многокомпонентных систе-
мах, а применительно к водным системам оно часто
превосходит другие уравнения. Это уравнение проще по
форме, чем уравнение UNIQUAC, однако его недостаток
состоит в том, что для каждой пары составляющих не-
обходимы три параметра. Величину третьего парамет-
ра «и часто можно получить исходя из химической
природы компонентов; распространено также мнение
об универсальности величины аи = - 1. В сборнике
DECHEMA (DECHEMA LLE Data Collection) принято,
что для всех смесей «и = 0,2.
4. Уравнение UNIQUAC — наиболее сложное в алге-
браическом отношении, хотя в нем используется только
по два параметра для каждой пары компонентов. В
уравнении учитываются сведения о площадях поверх-
ности и объемах молекул чистых компонентов, которые
можно определить по данным о структуре, в силу чего
этот метод представляется особенно эффективным при-
менительно к смесям, молекулы которых значительно
различаются по размеру. Уравнение UNIQUAC приме-
нимо для представления равновесия пар — жидкость и
жидкость — жидкость в многокомпонентных смесях
при использовании только параметров бинарного взаи-
модействия и данных о чистых компонентах. Уравнение
UNIQUAC положено в основу метода групповых вкла-
дов UNIFAC, предназначенного для определения коэф-
фициентов активности по данным о структуре, и имеет
множество приверженцев среди ученых.
В табл. 4.9 представлены результаты анализа часто-
ты наиболее полного соответствия данным, приведен-
ным в сборнике DECHEMA, различных уравнений. В
табл. 4.10 показаны наиболее типичные величины пара-
метров. Табл. 4.11 представляет собой страницу из
сборника DECHEMA. Сравнение уравнений Вильсона и
Скэтчарда — Гильдебранда, как видно из табл. 4.12, го-
ворит о значительном расхождении между ними. Обла-
сти применения уравнений Вильсона, NRTL и UNIQUAC
рассмотрены в работе [261].
4.14. Множественность корней уравнений
Нетрудно видеть, что уравнения той же степени
сложности, что и применяемые для расчета коэффици-
ентов активности, могут включать несколько наборов
значений параметров, соответствующих определенным
значениям коэффициентов активности либо при беско-
нечном разбавлении, либо во всем диапазоне концент-
раций. Наиболее изученным в этом отношении является
уравнение Вильсона. Для бесконечного разбавления оно
записывается следующим образом:
1/1 \
л12= =Г ехр 1 1 - — ехр(1-Д12) I. (4.170)
V] \ 72 /
Зависимость
Л21 = 1 - 1п(уГ Д12) (4.171)
представлена графически на рис. 4.20. Очевидно, что,
если уТ и в том и в другом выражении превышает еди-
ницу, можно получить только один набор параметров;
если же в одном или в обоих выражениях у? меньше
единицы, можно получить до трех наборов значений
Уравнение NRTL Уравнение UNIQUAC Уравнение Маргулеса Уравнение ван Лаара
^g/2 ^g21 «/2 Д«72 Au27 A12 A21 A12 А21
171,21 -13,78 0,3001 235,06 -175,58 0,2378 0,2604 0,2377 0,2613
1301,23 1000,06 0,5352 1088,43 -124,55 2,0094 2,3275 1,9868 2,3643
1259,00 2085,68 0,5960 -1,76 852,83 2,5858 1,6373 2,9128 1,5513
1214,83 691,22 0,6205 -364,57 1245,78 1,1210 2,2439 1,2119 2,3600
2273,97 10,91 0,4855 -448,24 434,50 -0,1893 2,6832 0,7014 3,1029
-512,93 817,96 0,3382 -322,41 423,29 0,2072 0,0728 0,2499 0,0917
914,60 137,07 0,2982 758,50 -289,27 1,0224 1,4104 1,0526 1,4399
85,43 1200,21 0,2886 385,03 -28,85 1,7562 1,1417 1,9010 1,1691
1302,97 737,97 0,0693 714,48 38,71 3,3358 3,5318 3,3363 3,5321
929,99 695,80 0,6034 771,15 -76,82 1,4987 1,7361 1,4973 1,7588
901,90 -348,10 1,8262 688,45 -503,33 -0,2503 -0,8665 -0,4106 -0,9466
764,85 1237,73 0,4269 293,04 9,12 2,5122 1,8896 2,5666 1,8980
1224,51 -723,33 0,3160 668,92 -420,24 -0,1619 0,1246 -0,1587 —0,0102
223,43 488,82 0,2978 580,53 -242,22 1,2103 1,0529 1,2132 1,0596
-121,27 1337,86 0,2974 -30,19 337,00 1,6346 0,8563 1,7966 0,9238
Параметры уравнений Вильсона, UNIQUAC и NRTL выражены в кал/моль.
Данные заимствованы из «Сборника данных о равновесии между паром и жидкостью»
(DECHEMA VLE Data Collection).
14’
Таблица 4.11. Образец страницы из «Сборника данных о равновесии пар — жидкость» DECHEMA (1979, том 1/3 и 4, стр. 228)
(1) АЦЕТОН
СЗН60
(2) ГЕКСАН
С6Н14
***** ANTOINE CONSTANTS ОБЛАСТЬ ***** СОГЛАСОВАННОСТЬ
(1) 7.11714 1210.595 229.664 -13- 55 С МЕТОД 1 *
(2) 6.91058 1189.640 226.280 -30- 170 С МЕТОД 2 *
ТЕМПЕРАТУРА = 20.00 DEGREE С
ЛИТЕРАТУРА; BALL W., SCHAEFER К., Z. ELECTROCHEM., 63, 1019(1959)
КОНСТАНТЫ: А12 А21 АЛЬФА 12
МАРГУЛЕС 1,7448 1,8012
ВАН ЛААР 1,7416 1,8044
ВИЛЬСОН 1077,8013 375,5248
NRTL 632,4249 583,8331 0,2913
INIQUAC -41,9959 512,3937
212 Глава 4
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ МАРГУЛЕС ВАН ЛААР ВИЛЬСОН NRTL UNIQUAC
Р, мм , рт.ст. ,Х1 YI ОТКЛ. Р ОТКЛ. YI ОТКЛ. Р ОТКЛ. YI ОТКЛ. Р ОТКЛ. YI ОТКЛ. Р ОТКЛ. YI ОТКЛ. Р ОТКЛ YI
119.60 0.0 0.0 -0.67 0.0 -0.67 0.0 -0.67 0.0 -0.67 0.0 -0.67 0.0
187.20 0.0913 0.3966 4.24 0.0024 4.35 0.0028 -1.26 -0.0110 2.90 -0.0011 3.60 0.0008
226.70 0.2563 0.5421 -0.19 -0.0166 -0.13 -0.0166 1.52 -0.0023 0.07 -0.0137 -0.01 -0.0151
232.30 0.3019 0.5595 0.85 -0.0161 0.89 -0.0162 3.13 -0.0007 1.28 -0.0128 1.10 -0.0144
232.40 0.3543 0.5737 -2.36 -0.0154 -2.33 -0.0155 -0.02 -0.0009 -1.89 -0.0121 -2.09 -0.0137
237.00 0.4035 0.5827 0.37 -0.0153 0.38 -0.0155 2.40 -0.0032 0.76 -0.0125 0.58 -0.0139
238.80 0.5325 0.6092 -0.02 -0.0043 -о.оз -0.0046 0.92 -0.0020 0.10 -0.0039 0.04 -0.0043
237.70 0.6609 0.6362 -1.47 0.0045 -1.49 0.0042 -0.89 -0.0028 -1.44 0.0027 -1.46 О.ООЗЗ
239.30 0.7309 0.6564 1.22 0.0065 1.20 0.0063 1.76 -О.ООЗЗ 1.24 0.0042 1.22 0.0052
237.90 0.7679 0.6722 1.21 0.0081 1.19 0.0080 1.62 -0.0017 1.20 0.0060 1.19 0.0069
234.30 0.7862 0.6825 -1.38 0.0097 -1.41 0.0097 -1.10 0.0004 -1.43 0.0078 -1.43 0.0086
234.10 0.8219 0.6975 1.18 0.0038 1.14 0.0038 1.08 -0.0037 1.02 0.0024 1.07 0.0030
230.30 0.8528 0.7202 0.88 0.0028 0.83 0.0028 0.29 -0.0021 0.60 0.0021 0.70 0.0024
220.60 0.9105 0.7778 1.70 -0.0051 1.64 -0.0049 -0.07 -0.0026 1.18 -0.0041 1.38 -0.0044
202.90 0.9619 0.8739 -0.14 -0.0071 -0.18 -0.0069 -2.24 0.0009 -0.66 -0.0050 -0.44 -0.0059
181.50 1.0000 1.0000 -3.96 0.0 -3.96 0.0 -3.96 0.0 -3.96 0.0 -3.96 0.0
СРЕДНЕЕ ОТКЛОНЕНИЕ:
МАКСИМАЛЬНОЕ 1.23 0.0084 1.23 0.0084 1.31 0.0027 1.13 0.0064 1.17 0.0073
ОТКЛОНЕНИЕ: 4.24 0.0166 4.35 0.0166 3.13 0.0110 2.90 0.0137 3.60 0.0151
Коэффициенты активности 213
параметров. Рассмотрим в качестве примера систему
ацетон + хлороформ, для которой у? = 0,4 и 72 = 0,5.
Три набора параметров и соответствующие графики ко-
эффициентов активности показаны в примере 4.11.
Только один из этих наборов параметров достаточно
точно соответствует экспериментальным данным.
На приведенной на рис. 4.16 номограмме четко пока-
заны диапазоны коэффициентов, в которых возможна
множественность корней уравнения Вильсона для беско-
нечного разбавления.
При других составах помимо бесконечного разбав-
ления в некоторых диапазонах коэффициентов активно-
сти также возможна множественность корней Л12
(рис. 4.21).
Если какие-либо дополнительные данные помимо тех
немногих, которые использовались для определения па-
раметров, отсутствуют, физически верный выбор одно-
го набора параметров представляет собой сложную
задачу. Кривыми коэффициентов активности с ярко вы-
раженными точками максимума и минимума, подобны-
ми приведенным в данном разделе, можно пренебречь.
В соответствии с правилом, предложенным Ладурелли
и др. [418] для смесей молекул различных форм и раз-
меров, правильным решением, вероятно, будет то, при
котором произведение Л12Л21 > 1; это правило справед-
ливо для упомянутой выше системы ацетон —
хлороформ. Силвермен и Тассио изучив восемь приме-
ров множественности корней, представили параметры в
экспоненциальной форме:
X^RTln^ijVj/Vj). (4.172)
Во всех рассмотренных ими примерах наилучшее соот-
ветствие состава пара достигалось при минимальной
сумме абсолютных величин |Х1г| + IX21). Далее в этой
работе исследуется влияние множественности корней на
расчеты равновесия пар — жидкость в многокомпо-
нентных системах.
Параметры уравнения UNIQUAC определяют тем же
методом, что и параметры уравнения Вильсона, заме-
няя коэффициенты активности в условиях бесконечного
разбавления в уравнении Вильсона на
1пу7 - 1 - к3, (4.173)
In У2 1 — ^7’ (4.174)
(определение параметров ку и к% представлено в
табл. 4.5). Если разности (1 - к-,) и (1 - Лг8) меньше
единицы, в принципе можно получить несколько групп
параметров пг и Т21. Эта задача ставится в примере
4.10.
В силу наличия третьего параметра ап вопрос о мно-
жественности корней уравнения NRTL является более
сложным. При положительных величинах ai2 и значе-
ниях коэффициентов активности бесконечного разбавле-
Таблица 4.12. Сравнение коэффициентов активности при бесконечном разбавлении, полученных в соответствии
с параметрами уравнения Вильсона (табл. Д.8) и коэффициентов активности, полученных по уравнению Скэт-
чарда — Гильдебранда с использованием параметров растворимости Хоя [360], Хансена [333], а также Хенли
и Сидера [52]
Вещество Ван Винкль Хой Хансен Хенли и Сидер
У/ 72 у 7 72 У/ 72 У/ 72
1-Бутанол 2,398 3,887 1,984 2,185 1,797 1,944 1,824 1,975
Тетрахлорид углерода 1,084 1,121 1,049 1,053 1,016 1,017 1,004 1,004
Хлороформ 0,846 0,884 1,000 1,000 1,006 1,005 1,001 1,001
Циклогексан 1,401 1,459 1,127 1,157 1,097 1,120 1,124 1,153
Циклопентан 1,464 1,383 1,170 1,164 1,000 1,000 1,198 1,190
Этанол 3,935 6,599 5,355 2,997 7,061 3,575 6,061 3,221
н-Гептан 1,264 1,610 1,396 1,786 1,340 1,663 1,612 2,205
н-Гептан 1,281 1,724 1,428 1,800 1,367 1,674 1,664 2,229
н-Гексан 1,400 1,631 1,600 1,956 1,500 1,783 1,597 1,949
Метанол 6,035 8,699 44,649 5,247 50,118 5,509 45,126 5,152
Метилацетат 1,355 1,250 1,012 1,010 1,001 1,001 1,003 1,002
Метилциклогексан 1,242 1,542 1,000 1,000 1,203 1,325 1,236 1,381
Метилциклопентан 1,367 1,454 1,251 1,319 1,000 1,000 1,250 1,319
1-Пропанол 2,470 6,371 3,029 2,660 2,866 2,534 2,766 2,430
1-Пропанол 2,906 6,235 3,251 2,695 3,065 2,565 2,951 2,459
2-Пропанол 3,008 4,964 1,931 1,770 2,133 1,926 2,092 1,887
2-Пропанол 3,697 6,369 1,970 1,809 2,182 1,975 2,138 1,933
214 Глава 4
Рис, 4.20а. Графики уравнения Вильсона для бесконечного раз-
бавления, на которых показана область присутствия множест-
венных корней. Другой параметр рассчитывают по уравнению
Л21 = 1 - 1П(Л21У1°)-
Рис. 4.206. То же, что на и рис. 4.20а, масштаб на оси абсцисс
увеличен.
Рис. 4.21. Графики преобразования уравнения Вильсона, показывающие наличие множественных корней в некоторых интервалах значений
коэффициентов активности. Уравнение Вильсона приводится к этому виду при помощи формулы Сильвермена и Тассио [636]:
(tiO( Х/Х2)
1
Х1
+ —
Х2
^1п(71/) - 1 -
t = Xi + Л12Х2.
Как видно из графиков, при Xi = 0,5, 71 = 0,5 и 72 = 0,3 возможны две величины t: 0,22 и 1,70, а соответствующие величины параметра
Л12 равны -0,56 и 2,40.
a: Xi = 0,5, величины 71 указаны на рисунке;
б: 71 = 0,5 величины Xi указаны на рисунке.
Коэффициенты активности 215
216 Глава 4
Рис. 4.22. Несколько групп параметров т\г и 721 уравнения NRTL при поло-
жительных величинах ап. Величины 721 рассчитываются по уравнению
721 = 1П у” - 712 exp (-OI12T12).
a: ai2 = 0,2, величины у” указаны на рисунке;
б: ап = 0,5, величины у” указаны на рисунке.
Коэффициенты активности 217
Рис. 4.23. Несколько групп параметров т и т2\ уравнения NRTL при ап -
= -1. Величины 721 рассчитывают по уравнению 721 = In уГ -
— 712 еХр( — О!12Т12).
«: графики для широкого диапазона тц, величины у" указаны на рисунке.
б: графики для узкого диапазона та, величины у“ указаны на рисунке.
218 Глава 4
Пример 4. /1. Графики коэффициентов активности системы ацетон (1) + хлороформ Г2р которы ч соответствуют
с 1ссПющие величины коэффициентов активности при бесконечном разбавлении 0.41' а э? - 0,чб
Ниже представлены три группы параметров уравнения
Вильсона.
С ns чай
1 0,0754
11 0,8454
Ш 6.7576
Л21
4,501”
2,0842
0,01'564
Результаты, полученные для слччая И. довольно точно
соответствую! экспериментальным данным. Следует от-
метить. чго в соответствии с правилом Ладу реяли [418]
произведение параметров в этом случае больше единицы.
Наиболее полное соответствие экспериментальным дан-
ным наблюдается в случае II. Это согласуется с правилом
Тассио, согласно которому правильным является то реше-
ние, для которого у,: г стреми гея к минимуму.
ния меньше единицы уравнение имеет три корня, а при
больших величинах коэффициентов — только один. При
ai2 = - 1 ситуация меняется на обратную: множествен-
ность корней наблюдается при уТ и у?, превышающих
единицу, при меньших величинах коэффициентов актив-
ности — корень всего один. Рис. 4.22 и 4.23 иллюстри-
руют эти выводы, а в примере 4.12 рассматривается
такая ситуация, когда имеются три группы параметров.
Проведя исследование уравнения NRTL, Тассио (1978)
пришел в выводу, что лучшее соответствие достигается
в том случае, если сумма абсолютных величин парамет-
ров 712 и 721 минимальна.
Если какие-либо другие данные помимо используемых
для оценки параметров отсутствуют, о выборе набора па-
раметров, соответствующего уравнениям для коэффици-
ентов активности, ничего определенного сказать нельзя.
Поскольку для уравнений ван Лаара и Маргулеса такая не-
однозначность решения нехарактерна, а полученные кор-
реляции, как правило, соответствуют уравнениям Вильсо-
на или NRTL, или UNIQUAC, в некоторых случаях можно
провести сравнение их графиков с тем, чтобы найти требуе-
мый набор параметров для других уравнений. Во всяком
случае, всегда целесообразнее использовать однозначные
результаты.
4.15. Бесконечное разбавление
Важность предельных величин коэффициентов актив-
ности при бесконечном разбавлении для оценки парамет-
ров таких уравнений, как уравнение ван Лаара, Вильсона и
т. д., была проиллюстрирована на обширном материале.
Более того, эти коэффициенты имеют особое значение при
оценке требований, предъявляемых к процессам разделе-
ния, ибо оборудование, используемое для работы с разбав-
ленными растворами, должно строго соответствовать
самым жестким нормам. Пользуясь относительно недавно
улучшенной методикой, можно выполнить точные изме-
рения при низких концентрациях с гораздо меньшими за-
тратами труда и средств, чем при традиционном способе
измерения равновесия между паром и жидкостью. При
этом общая точность измерений выше, поскольку экстра-
поляция коэффициентов активности бесконечного разбав-
ления до средних концентраций обычно более надежна, чем
экстраполяция от средних концентраций до малых.
Наибольшее распространение получили измерения тем-
ператур кипения смеси известного состава при известном
давлении или же измерения полного давления как функции
известного состава при заданной температуре. Классиче-
ский метод измерения состава равновесной смеси пар —
Коэффициенты активности 219
Пример 4.12. Множественность корней уравнения NRTL при представлении равновесия в системе н-гексан
(1) + диэтилкетон (2)
Коэффициенты активности компонентов смеси при бес-
конечном разбавлении у? = 2,25 и у” = 3,67. Принимая
«12= - 1, получаем три следующие группы параметров:
Случай
I -1,94000 1,08972
II 0,16703 0,61353
Ш 1,3532 -4,4257
Ниже представлены графики коэффициентов активнос-
ти для всех грех случаев. Наилучшее соответствие с экспе-
риментальными данными наблюдается в случае II,
который согласуется с правилом Тассио, т. е. правильным
является то решение, для которого jTi2 + |т?ц стремится к
нулю.
Три группы параметров для системы н-гексан + диэтилкетон.
жидкость является наиболее сложным, однако при соблю-
дении точности измерений дает оптимальные результаты.
Применимы несколько методов экстраполяции. Если вели-
чины неидсальности паровой фазы малы, коэффициент ак-
тивности можно записать следующим образом:
У1 =
Р ~ У2*2Р2
г Р®
X 1
(4.175)
РУ1
Y1 — о0 —
Р1Х1
следовательно,
Р2
у Г = lim ту -------,
т,-о Р? dXl
Р(У1 ~ 0)
P?(xi-0)’
(4.177)
(4.178)
Поскольку 72 “► 1 при XI -► 0,
у Г = lim
xj—0
Р-Х1Р1
хн 1
(4.176)
(и аналогично для второго компонента). Этот метод
применен в примере 4.15. Простая зависимость суще-
ствует также между коэффициентом активности при бе-
сконечном разбавлении и предельным наклоном функ-
ции х — у:
так как в пределе давление системы равно давлению па-
ра растворителя.
Расчеты уТ по результатам измерений, выполненных
в изотермическом режиме, можно провести по уравне-
ниям, выведенным Готро и Коутсом (1955):
Г /dP
--------- 1 + ------
р0. Л----\dxi
Р1Ф1Р<) L ' 1
/ рр% rf
еХР \ JP°i RT dP
(4.179)
220 Глава 4
72 =
Р?02рО
Р202р^
ехр \ Jp® RT dP
(4.180)
Решающее значение имеет величина наклона (dP/
dxi)Xl = o и (dP/dx\)x, = i, которую можно определить с
большей степенью надежности, используя дополнитель-
ную функцию, выведенную авторами работы [272]:
(4.181)
Эта функция удобна тем, что в нее входят важные пре-
дельные свойства:
lim
xj-0
0
0
lim
xj-0
dP/dx\
1 — 2х i
(4.182)
lim
х2-0
(4.183)
Следовательно,
что устраняет необходимость численного дифференци-
рования или графического определения наклона. Со-
гласно авторам работы [458], Pd/x^Xi с изменением Xi
во многих случаях меняется линейно.
Сложность состоит в том, чтобы выполнить точные
измерения в диапазоне низких концентраций, поскольку
в этом случае необходима лишь ограниченная экстрапо-
ляция до нуля. Эккерт и др. [260, 262] смогли провести
точные эбуллиоскопические измерения при низких кон-
центрациях путем использования дифференциальной ме-
тодики. Они измеряли разность температур кипения
чистого растворителя и разбавленного раствора такими
приборами, которые позволяют фиксировать разность
температур b 0,001 К. При этом можно точно найти
концентрации намного ниже 0,005 мол. доли. Точный
эбуллиометр был также применен авторами работы
[688] для измерения концентраций ниже 3% в их про-
грамме по быстрому определению групповых вкладов
в коэффициенты активности по методу ASOG, кото-
рый был подробно разработан этими же авторами.
Еще в 1952 г. было предложено использовать для на-
хождения коэффициентов активности газовую хромато-
графию — один из наиболее распространенных спосо-
бов измерения низких концентраций. Однако необходи-
мая методика, позволяющая проводить быстрые и точ-
ные определения, была отработана лишь недавно. Чаще
всего для определения коэффициентов активности
пользуются двумя следующими подходами.
В первом случае через хроматографическую колонку,
заполненную инертным носителем (стеклянные шари-
ки), на который нанесен слой неподвижной жидкой фа-
зы, пропускают ток газа-носителя (гелия), в который
вводят примерно 0,001 мл исследуемого вещества, и
определяют время удерживания последнего, которое
математически связано с его коэффициентом актив-
ности.
Во втором случае в аналогичную колонку вводят при-
мерно 0,01 мл исследуемого вещества, растворенного в
20 мл растворителя, и, пропуская через колонку ток га-
за-носителя (гелия), регистрируют изменение концент-
рации растворенного вещества в выходящем из колонки
токе газа (элюате) при помощи детектора по теплопро-
водности или пламенно-ионизационного детектора (в
зависимости от летучести растворителя).
Тассио [678] применил хроматографию с целью срав-
нительной оценки растворителей для экстрактивной
дистилляции. В колонку, предварительно заполненную
инертным носителем с нанесенной неподвижной жидкой
фазой, вводили пары растворенных веществ в равных
объемных пропорциях и пропускали через нее ток газа-
носителя. Проведенные измерения позволили опреде-
лить относительные летучести пар веществ со сходны-
ми температурами кипения в присутствии нескольких i
растворителей, применяемых в экстрактивной дис-
тилляции.
Авторы работы [608] провели проверку хроматогра-
фического метода на шести углеводородах, растворен-
ных в феноле, фурфуроле и диметилформамиде, — рас-
творителях, получивших широкое распространение в
экстрактивной дистилляции. И как показали проведен-
ные ими исследования, в зависимости от выбранного
подхода расхождение в результатах может достигать
Ю°7о. Однако позднее Эккерт и др. [260] улучшили мето-
дику определения, что дало возможность измерять ко-
эффициенты активности даже в таких растворителях,
летучесть которых лишь незначительно выше летучести
растворенных веществ. Состояние равновесия достига-
лось достаточно быстро, что позволило выполнять по
нескольку десятков измерений в день. Указанными ав-
торами опубликованы данные более чем о десяти со-
единениях, растворенных в таких растворителях, как
бензол, 1,2-дихлорэтан и этанол. Результаты хромато-
графического определения достаточно хорошо согласу-
ются с некоторыми данными, полученными при изме-
рении равновесия между паром и жидкостью, и данны-
ми дифференциальной эбуллиоскопии. ;
Подробный анализ применения хроматографических
методов для измерения равновесия пар — жидкость вы- j
полнен авторами работы [437]. Серьезный недостатои
этих методов состоит в том, что с их помощью обычно
нельзя измерить оба коэффициента активности двух-
компонентной смеси при бесконечном разбавлении, из-
мерению поддается только коэффициент активносп
компонента с большей летучестью. Этой информации
Коэффициенты активности 221
достаточно для определения единственного параметра
однопараметрических вариантов уравнений Маргулеса,
Вильсона и UNIQUAC. Перечисленные уравнения могут
представлять интерес при проведении некоторых иссле-
довательских работ. Хроматографические методы в
основном используются, вероятно, для оценки относи-
тельных летучестей смесей, в которых присутствует
растворитель с меньшей летучестью, как, например,
при процессах экстрактивной дистилляции. Подобные
данные можно также получить при помощи уравнения
Гиббса — Дюгема или уравнения (4.23).
В то же время дифференциальная эбуллиоскопия не
имеет указанных ограничений и является в высшей сте-
пени перспективной методикой даже несмотря на то,
что экстраполяция до средних концентраций в некото-
рых случаях подвержена серьезным погрешностям. Тот
факт, что смеси могут иметь практически одинаковые
коэффициенты активности при бесконечном разбавле-
нии, еще не гарантирует такого же совпадения проме-
жуточных величин коэффициентов (см., например, рис.
4.17 и 4.18). При оценке азеотропности и расслаивания
жидкой фазы желательно располагать точными величи-
нами промежуточных активностей.
4.16. Оценка коэффициентов активности
на основании свойств чистых компонентов
Если точность измерений достаточна, то лучше всего
определять коэффициенты активности из свойств инди-
видуальных компонентов, не прибегая к экспериментам
со смесями. Второй наиболее распространенный ме-
тод — это метод расчета коэффициентов активности по
результатам измерений, проведенных только с двухком-
понентными смесями при помощи соответствующих
уравнений, например уравнений Вильсона, NRTL,
UNIQUAC. Разработано три способа применения мето-
да, основанного на свойствах чистых компонентов; ни-
же приводится их описание.
4.16.1. Регулярные растворы и параметр раствори-
мости. Регулярными называют растворы, в которых
отсутствуют межмолекулярные взаимодействия, такие,
как дипольное, ассоциативное или химическое. У ре-
гулярных растворов избыточная энтропия 5ех равна ну-
лю. Если же, кроме того, и избыточный объем равен
нулю, то для них справедливо следующее уравнение:
(?ех =Яех = (уех =RTZXj In у,-. (4.186)
Некоторые данные приведены в табл. 2.7.
В рамках изложенного представления о регулярных
растворах предполагается, что летучесть и смешивае-
мость жидких смесей зависят от относительной легкос-
ти, с которой молекулы отделяются одна от другой.
Вполне вероятно, что этот эффект измеряется энергией
испарения в расчете на единицу объема. По ряду при-
чин, которые будут изложены ниже, этот вид энергии
обозначается специальным знаком:
82 = \U/V, (4.187)
где 6 — параметр растворимости. Как установлено, чем
ближе значения параметров растворимости двух ве-
ществ, тем лучше их смешиваемость. Приняв ряд дру-
гих допущений, Скэтчард (1931) и Гильдебранд (1933)
провели количественное определение избыточной энер-
гии Гиббса и, следовательно, коэффициентов активнос-
ти. Более подробно эта теория изложена Гильдебран-
дом и др. [53] и Праузницем [97].
Прежде всего Скэтчард и Гильдебранд допускают,
что правила усреднения по объемным долям для второ-
го вириального коэффициента можно применить к соот-
ношению внутренняя энергия/объем:
^-=[Ъф^и/У)?’5\2, (4-188)
или д2 = (ЕфД)2, (4.189)
где ф, = х.У/^Уу. (4.190)
Дальнейшие допущения о том, что избыточный объем
и энтропия равны нулю, а также что
512 = (<Мг)0’5 (4.191)
приводят в итоге к формулировке следующих уравнений
для двухкомпонентных смесей:
У,
ln Y1 = ~ Ф1)2(^1 “ ^2)2’ (4.192)
К2
1ПУ2= (4193)
1\ 1
и
(51 з2)2-
(4.194)
Для компонента / многокомпонентной смеси
In у, = 1 (8i - 5)2,
К 1
(4.195)
где средневзвешенная величина параметра средней рас-
творимости смеси равна
Zx,K,.
(4.196)
Уравнение (4.195) называют уравнением Скэтчарда —
Гильдебранда или уравнением коэффициента активнос-
ти регулярных растворов, сокращенно СГ. С его по-
мощью прогнозируются величины коэффициента актив-
ности, превышающие единицу. Модификацию этого
уравнения, предложенную Флори и Хаггинсом, называ-
ют расширенным урвнением СГ или уравнением СГФХ:
1пу, = К,(5; -5)2/АГ+ 1п0; + 1 - О., (4.197)
где
01^У1-/Хх,-У1-=ф//х1-
(4.197а)
222 Глава 4
— отношение молярного объема компонента i к средне-
взвешенному молярному объему смеси. Как следует из
приведенной на рис. 4.12 зависимости коэффициента ак-
тивности от в,, под влиянием последнего величина коэф-
фициента активности, получаемая из исходного урав-
нения Скэтчарда — Гильдебранда, всегда снижается.
Точность подхода, основанного на использовании па-
раметра растворимости, часто довольно низка. Напри-
мер, сравнение (табл. 4.14) коэффициентов активности
при бесконечном разбавлении, рассчитанных по пара-
метрам уравнения Вильсона [354] и коэффициентов ак-
тивности, вычисленных исходя из трех различных групп
параметров растворимости, взятых из литературы, по-
казывает довольно плохое их соответствие даже для
пар углеводородов. Было предпринято несколько попы-
ток исправить положение. Чао и Сидер [218] (см. также
гл. 6) сохранили форму уравнения (4.195), но произволь-
но видоизменили некоторые параметры растворимости,
с тем чтобы обеспечить более точное соответствие
уравнения экспериментальным данным о равновесии.
Маффиоло и др. [455] использовали некоторые аспекты
метода Чао — Сидера и применили уравнение Скэтчар-
да — Гильдебранда — Флори — Хаггинса. В результате
обстоятельных исследований, выполненных Даубертом
и др. [31], выяснилось, что такой подход дает лучшие
результаты, чем исходное уравнение, при исследовании
смесей нафтенов и ароматических углеводородов, а так-
же тяжелых углеводородов при низких давлениях.
В результате проведенной работы Дауберт и сотр.
пришли к выводу, что параметр растворимости удобен
для корреляции коэффициентов бинарного взаимодейст-
вия в уравнении Соава (табл. 1.12). Эти же авторы вы-
вели ряд соотношений, связывающих параметр
растворимости с другими характеристиками, например
параметрами уравнения Ван-дер-Ваальса, поверхност-
ным натяжением, показателем преломления и вязкос-
тью. В книге Бартона [176] приводится литература по
этому вопросу, а также обширная подборка величин 5.
Этот подход был распространен на неполярные сме-
си, которые в целом не соответствуют теории регуляр-
ных смесей. При этом было сделано следующее
допущение: параметр растворимости включает несколь-
ко составляющих, каждое из которых определяется не-
зависимо от других. Если энергию испарения записать
как
\U= \Unp + \Up + &UH, (4.198)
то параметр растворимости принимает следующий вид:
8 = У 82р + 52 + 5^, (4.199)
где индексами обозначены неполярный (пр) и полярный
(р) компоненты и компонент, характеризующий образо-
вание водородных связей (77). За неполярный компо-
нент принимается компонент углеводорода приблизи-
тельно того же размера, формы и структуры, называе-
мый гомоморфом рассматриваемой полярной молеку-
лы. Методы нахождения других компонентов описаны,
например, в работах [333] и [176], где, кроме того, пока-
зано, что эти компоненты можно определить методом
групповых вкладов. В указанных статьях приведены ве-
личины параметров растворимости для примерно 200
веществ; более обширная подборка, основанная на дан-
ных о давлении пара, дана в работе [360]. Типичным
примером применения рассматриваемого метода явля-
ется выбор растворителей для растворенного вещества
с известными компонентами 6,. Подходящие раствори-
тели — это жидкости, компоненты которых находятся
в пределах эллипсоида, оси которого соответствуют
6^, др и дн растворенного вещества. Специфический
пример использования данного метода описан Барто-
ном [176]. Параметры растворимости только с одним
или двумя компонентами удобны также для описания
растворяющей способности растворителя и ряда других
его свойств.
4.16.2. Влияние температуры. Температура зачастую
оказывает лишь очень незначительное влияние на раз-
ность параметров растворимости двух веществ, поэто-
му обычно выражение И,(5; - о)2 оценивают при 25°C
и принимают независимым от температуры. Однако в
действительности отдельные параметры заметно меня-
ются с изменением температуры. Так, например, Гиль-
дебранд [53] скоррелировал функцию b/Pc's с приведен-
ной температурой и ацентрическим коэффициентом.
Корреляции с температурой, записанные Хансеном,
приводятся в задаче 4.50.
4.16.3. Применение. Теория регулярных растворов
применяется для расчета коэффициентов активности,
растворимости газов и взаимной растворимости жидко-
стей. Последней теме посвящено наибольшее число ра-
бот, авторы которых исходили из того, что смешива-
емость зависит от степени совпадения величин парамет-
ров растворимости компонентов смеси. Смешиваемость
жидкостей рассматривается также в гл. 7, а раствори-
мость газов — в гл. 6.
Выше уже говорилось, что Чао и Сидер [218] испо-
льзовали уравнение (4.195) для описания относительно-
го состава фаз в парожидкостном равновесии.
Найденные ими параметры растворимости даны в
табл. 6.2. Бартон и др. [177] исследовали парожидкост-
ное равновесие углеводородов Сз — Cs, используя пара-
метры растворимости этих соединений; стремясь повы-
сить точность расчетов, эти авторы также применили
«кажущиеся» параметры растворимости. На рис. 4.19
сравниваются коэффициенты активности, вычисленные
по уравнению Вильсона, которые можно рассматривать
в качестве наиболее точных в данном случае, с коэффи-
циентами активности, рассчитанными по уравнениям
Скэтчарда — Гильдебранда и Скэтчарда — Гильдебран-
да — Флори — Хаггинса. Во всех случаях величины,
вычисленные-по последнему уравнению, более точно со-
гласуются с полученными по уравнению Вильсона, хотя
степень соответствия довольно низка (исключение со-
ставляет лишь система бензол — гептан).
Довольно точная корреляция коэффициентов актив-
ности бесконечного разбавления была предложена Хел-
пинштилем и ван Винклем [337], включившими в нее
двухкомпонентный параметр растворимости
Д(7/И=Л2 + т2, (4.200)
где X — параметр растворимости гомоморфа, т —
вклад неполярного компонента. Для коэффициента ак-
Коэффициенты активности 223
тивности они вывели следующее выражение:
куле j, т. е.
ЛТ1пу2 = RT
Ут.
In---+ 1
Ух
Ут
Ух
(4.203)
+ Г2[(Х1 -Х2)2 + (Г] -г2)2(1 ~^)],
(4.201)
где s'
\ 0,798 насыщенные углеводороды ± 11,6%
к = j 0,776 ненасыщенные углево-
/ дороды ± 8,5%
V 0,894 ароматические углево-
дороды ±13,5
Диапазон температур составляет от 0 до 125°C. Указан-
ные величины процентов представляют собой степень
согласованности с экспериментальными данными.
До сих пор не опубликовано подробного исследова-
ния определения коэффициентов активности по пара-
метрам растворимости, а результаты, представленные
в табл. 4.14, нельзя назвать обнадеживающими. Основ-
ное внимание уделялось методам ASOG и UNIFAC —
методам оценки коэффициентов активности исходя из
свойств чистых компонентов. Недостаток уравнения
(4.195) заключается в том, что оно позволяет представ-
лять только коэффициенты активности, превышающие
единицу; преимущество же состоит в том, что оно учи-
тывает влияние температуры, особенно если во внима-
ние принимается также воздействие температуры на
параметры растворимости. Обратная зависимость Т и
1пу, также является весьма удобной аппроксимацией при
использовании уравнений ван Лаара и Маргулеса.
4.16.4. Влияние структуры: модель ASOG. Многие
свойства сложных молекул можно оценить хотя бы
приближенно, исходя из того, что меньшая группа ато-
мов в молекуле определенным образом воздействует на
это свойство независимо от природы других групп ато-
мов, которые могут в ней присутствовать. Ленгмюр
[425] назвал это положение принципом независимого
действия. Применимость этого принципа для нахожде-
ния теплоемкостей, энтальпий образования и других
термодинамических функций четко установлена. Основ-
ные направления современных методов расчета коэффи-
циентов активности этим способом намечены
Вильсоном и Дилом [729], Дером и Дилом (1969), а
Койима и Точиги [70] разработали на основе этих прин-
ципов рабочую методику. Данный метод состоит из
нескольких этапов и включает несколько особых кон-
цепций.
1. Предполагается, что коэффициент активности —
величина аддитивная и что одна из его составляющих
обусловлена различием в размерах молекул, а дру-
гая — взаимодействием отдельных групп атомов, со-
ставляющих молекулу. Следовательно, для молекулы.
где Xj — мольная доля молекулы j, суммирование про-
водится по всем типам молекул, находящихся в смеси.
Первая составляющая коэффициента активности, зави-
сящая от размеров, для вещества i представляет собой
член уравнений Флори — Хаггинса:
In у f = 1 + In г,- — г,-.
(4.204)
3. При вычислении составляющей коэффициента ак-
тивности, обусловленной взаимодействием групп ато-
мов, состав системы выражают не через мольные доли
компонентов, а через группы атомов. При этом исполь-
зуются следующие члены: г*-, — число атомов, кроме
атомов Н, в группе к молекулы z с учетом следующих
величин: ^н2о = 1,6, ^сн = 0,8, vc = 0,5.
= Х|(У| 1 + v21 + v3) + . . . )
+ х2О12 + г22 + у32 + . . . )
+ . . . + Х,(У1/ + v2; + г3; +...). (4.205)
Если группы Н2О, СН и С отсутствуют, г, = Y.vk,. Доля
группы L в смеси равна
1 1
XL = 5 *iVLi= s(xxvLl + x2vL2 + x3vL3 + ...).
(4.206)
Долю группы L в отдельной молекуле i определяют,
принимая х, = 1 в уравнении (4.206), что дает
Х(р= vLi/ Tlvki =----------------------. (4.207)
L i V1Z + v2i + v3i + . . . ’
4. Взаимодействия групп атомов к и L в смеси пред-
ставляют при помощи эмпирических параметров щд,
которые в соответствии с приведенным ниже уравнени-
ем являются функциями температуры:
akL = exP(mkL + nkL/T).
(4.208)
Следует отметить, что Щг А ai.k и акк = 1. В более поз-
дней статье Точиги [690] предлагается улучшенная фор-
ма температурной зависимости, но коэффициенты
указываются не для всех групп атомов. Необходимы
два вида сумм, включающих эти параметры. Для груп-
пы к
In у,- = In у f + In у
(4.202)
Dk = Х{ак} + Х2ак2 + Х3ак3 + ... ,
(4.209)
2. Первая составляющая коэффициента активности
определяется через состав, выраженный числом vj ато-
мов, кроме атомов водорода, присутствующих в моле-
и
Q “ Хха\k/D 1 + Х2а 2k/D2 + Х3а 3k/D3 + . . . ,
(4.210)
224 Г лава 4
Пример 4.13. Расчет коэффициентов активности системы этанол + бензол методом ASOG
Температура системы 345 К, *i = 0,2. В молекулу имодействия, взятые из таблицы Точиги и Койимы,
этанола входят две группы СН2 и одна группа ОН; бен- приводятся ниже:
зол содержит шесть групп типа АгСН. Параметры вза-
Группа / 1 3 6 СН2 АгСН ОН
№ Группа к mki nki ты tiki nki
1 СН2 0 0 - 0,7457 146,0 - 41,2053 7686,4
2 АгСН 0,7297 - 176,8 0 0 2,2682 - 1111,5
3 ОН 4,7125 - 3060,0 - 0,5859 -- 939,1 0 0
Группа к 1 3 6
Соединение СН2 АгСН ОН Ху*, vf
1 Этанол 2 i'll 0 р31 2 Бензол 0 иг 6 р32 1 P6i 3 3 0 F62 6 6
Для удобства группам СН2, АгСН и ОН при проведении
следующих расчетов придают номера 1, 2 и 3.
вы = exp(mki + riki/T).
Составляющая коэффициента активности, зависящая от
размеров:
Этанол: п = vf/Д XjVj = 3/5,4 = 0,5556,
1
к 1 2 3
1 1 (Он) 0,7243 (ди) 0 (щ3)
2 1,2426 (a2i) 1 (022) 0,3854 (д23)
3 0,0157 (д31) 0,0366 (д32) 1 (о33)
XXjFj = 0,2(3) + 0,8(6) = 5,4,
^I'ki = 3,
= 6,
2k,(2>*,) = 0,2(3) + 0,8(6) = 5,4,
At = (xn>ki + х2г*2)/5,4 = (0,2f*i + 0,8г*2)/5,4,
Ai = (0,2(2) + 0,8(0))/5,4 = 0,0741,
X2 = (0,2(0) + 0,8(6))/5,4 = 0,8889,
A3 = (0,2(1) + 0,8(0))/5,4 = 0,0370.
бензол:г2 = 6/5,4 = 1,1112, In-yf = 1 - 0,5556 + 1пО,5556 = = - 0,1433
ln7f = 1 - 1,1112 + 1,1112= - - 0,0058,
Бк = XiOkl + X-^kl + ХзйкЗ, Di = Xian + Ajfln + Хзв1з, D2 = А1Д21 + АтДгг + Азй23, D3 = АдД31 + Х&зг + Азя33, Ск = Xiaik/Di + X2a2k/D2 + ХзАзк/Dj,
Ci = Xian/Di + X2a2\/D2 + Хзаз1/D3,
C2 = Xiai2/Di + Х'гРгг/Бг + ХзРзг/D3,
Сз — Xiavs/Di + АгД^ЛОг + 1пГ* = 1 - InD - С. Хз/азз/D3,
Итоговые численные результаты:
В результате:
для соединения 1 получаем
А?’ = 2/3, Al1’ = 0, Al1’ = 1/3,
для соединения 2 получаем
Al2’ = 0, А12’ = 1, Al2’ = .0.
Смесь Соединение 1 Соединение 2
Xi 0,0741 2/3 0
х2 0,8889 0 1
Х3 0,0370 1/3 0
D С 1пГ*
Смесь
к = 1 0,7179 1,2212 0,1101
к = 2 0,9953 0,9870 0,0176
к = 3 0,0707 0,8675 0,7819
Этанол
к = 1 0,6667 1,0152 0,3893
к = 2 0,3438 0,9695 1,0983
Бензол
к = 3 1 1 0
Коэффициенты активности 225
ln7f = 2(0,1101 - 0,3893 - 0) + 1(2,7819 - 0 - 1,0983) =
= 1,1252,
ln7? = 6(0,0176) = 0,1056,
ln7i = 1,1252 - 0,1433 = 0,9819,
yi = 2,6695,
1п72 = 0,1056 - 0,0058 = 0,0998,
72 = 1,1049.
Для всего диапазона концентраций (программа для
ЭВМ дана в приложении В.7) получены следующие ре-
шения:
Х1 71 72
0 7,4666 1
0,2 2,6626 1,1059
0,4 1,6234 1,3600
0,6 1,2258 1,7691
0,8 1,0518 2,5644
1 1 4,0501
где суммы рассчитываются для всех групп. Соответ-
ствующие выражения для чистых компонентов и
С1'* получают из предыдущих уравнений, заменяя Х'к на
Хк(,\
5. Составляющая коэффициента активности, завися-
щая от группы к, определяется по уравнению типа
уравнения Вильсона
In Г* = 1 — lnZ>£ — Ск.
(4.211)
Аналогичным образом составляющая коэффициента ак-
тивности, обусловленная наличием группы к, в каждом
чистом веществе равна
Inг£° = 1 - InOjt0- С^.
(4.212)
Если в молекуле присутствует группа атомов только од-
ного вида, то 1пГ£° = 0.
Суммарный вклад в коэффициент активности молеку-
лы i определяется выражением
нии метода ASOG, однако вместо члена, учитывающего
взаимодействие akL, уравнение (4.208), применяют следую-
щий член:
4>тп = ехр(~атп/Т), (4.215)
Долю группы L в смеси XL определяют по уравнениям
(4.206) и (4.207). Доля площади поверхности группы ато-
мов равна
em=XmQm/HxnQn. (4.216)
н
Средневзвешенный параметр взаимодействия группы к
составляет
Ек = ^101* + #202£ + вз^зк + • • • , (4.217)
а дополнительная функция Fk определяется следующим
образом:
In yf = SvH(ln Г* - In Г£'}).
к
(4.213)
Подставляя в уравнение (4.202) уравнения (4.204) и
(4.214), получаем коэффициент активности компонента
i в смеси. Этот метод применяется в примере 4.13. В
приложении В дана программа на языке Бейсик для ме-
тода ASOG; параметры ак/ являются частью програм-
мы от команды 270 по 3080.
4.16.15. Метод UNIFAC (функциональные групповые
коэффициенты активности UNIQUAC) [40]. В данном ме-
тоде составляющие коэффициента активности, обуслов-
ленные различием в размерах молекул и наличием
различных групп атомов, называют конфигурационной
(С) и остаточной (R) составляющими:
In у(' = Inyf + Inyf. (4.214)
Обе части коэффициента основаны на уравнении
UNIQUAC. Помимо параметров взаимодействия групп
атп и апт в данном методе учитываются параметры груп-
пового объема Rk и параметры поверхности Qk. Конфигу-
рационная составляющая тождественна аналогичной
составляющей уравнения UNIQUAC (табл. 4.4). Остаточ-
ную составляющую находят так же, как при использова-
Величины f)k, Ek и Fk оцениваются как для смеси, так и для
чистых компонентов. Для смеси получаем
1пГ\ = Qk(\ - ln£> - Fk), (4.219)
а для чистого компонента /
1пГ^ = 6^(1 ~ InM0-(4.220)
Если в молекуле присутствуют группы атомов только 171
одного вида, то 1пГ^’ = 0. Остаточная составляющая
коэффициента активности принимает следующий вид:
In у? = - InrV'b, (4.221)
k
а полное выражение для коэффициента активности
компонента i —
lny; = Inyf + SCHlnr*- InrV»). (4.222)
k
Этот метод применяется в примере 4.14 для решения
той же задачи, что и в примере 4.13, где она решается
методом ASOG.
И-Х29
226 Глава 4
Пример 4.14. Расчет коэффициентов активности системы этанол т бензол методом UNIFAC
Температура системы 345 К, Xi = 0,2. Распределение
по группам немного отличается от принятого в методе
ASOG. Этанол содержит одну группу типа СНз, одну
группу типа СНг и одну группу типа ОН, в то время
как бензол содержит шесть групп типа АгСН. Данные
о параметрах взяты из табл. Д.11 и Д.12.
этанол бензол Rk Qk
СНз 1 0 0,9011 0,848
СН2 1 0 0,6744 0,540
ОН 1 0 1,0000 1,2000
АгСН 0 6 0,5313 0,4000
<712 = 0 <721 = 0
Г?23 = <713 = 986,5 <732 = <731 = 156,4
<724 = <714 = 61,13 <742 = Й41 = - 11,12
<734 = 89,60 043 = 63 6,1
^12 = 1 1^21 ~ 1
фгз = '/'и = 0,0573 ^32 = фз1 = 0,6355
^24 - ^14 = 0,8376 1^42 = 1^41 = 1,0328
<Дз4 = 0,7713 1^43 = 0,15 82
1 = 2,5755
от XmQm XmQm = 11,4513
0,037(0,848 + 0,54 + 1,2) +-0,8889(0,4)
Смесь Этанол Бензол
0,0695 0,3277 —
02 0,0443 0,2087 —
0з 0,0984 0,4637 —
04 0,7879 — 1
Ек - 01&1к -1" 02<i>2k + бз'фзк + 04^4к
Смесь Этанол
Бензол
0,9901 0,8311 0
£2 0,9901 0,8311 0
Ез 0,2296 0,4944 0
е4 0,9591 — 1
г, = 0,9011 + 0,6744 +
Г2 = 6(0,5313) - 3,1878
<71 = 0,848 + 0,540 + 1,200 = 2,588
<72 = 6(0,4) = 2,4
0,2(2,5755)______ = 80
* 0,2(2,5755) + 0,8(3,1878)
<t>2 = 0,8320
_ = 0,2123
0,2(2,588) + 0,8(2,4)
02 = 0,7877
Ol^kl 02^k2 03^k3 04фк4
~Ei + Е2 + Ез + ~~Ё4~
Смесь
Этанол
Бензо 7
Е 0,8276 0,6992 —
f2 0,8276 0,6992 -
F3 1,1352 1,3481 —
f4 1,0158 — 1
/1 = 5(2,5755 - 2,588) + 1 - 2,5755 = - 1,6380
/2 = 5(3.1878 - 2,4) + 1 - 3,1878 = + 1,7512
1 s 1 0,168 cqq\i 0,2123 1п7, =!” + 5(2,588)ln-w +
+ 0,832 ( - 1,638 - AZ^h2512)Л = 0,3141
’ у 3,1878 у
. ,s , 0,832 , ... 0,7877 , 1п72 In - 0 8 - + 5(2, ) п 0,832 -
+ 0,168 fl,7512 - 3,1878( - 1,638) \ =ОО175
\ 2,5755 /
т
0,2^’' + ОМ?
0,2(3) + 0,8(6)
1пГ/с = Qk(l - \пЕк - Fk)
Смесь Этанол Бензол
1пГ| 0,1546 0,4120
1пГ2 0,0985 0,2623
1пГ3 1,6035 0,4276
1пГ4 0,0104 —
Смесь Этанол Бензол
СНз Ал 0,037 1/3 0
СН2 А’г 0,037 1/3 0
ОН Хз 0,037 1/3 0
АгСН х4 0,8889 0 1
In-yi = 0,3141 + 1(0,1546 - 0,4120) +
+ 1(0,0985 0,2623) + 1(1,6035 - 0,42761 =
= 1,0688
71 = 2,9119
1п72 = 0,0175 + 6(0,0104) = 0,0799-
72 = 1,0832
Соответствие результатам, полученным по методу
ASOG, 7i = 2,67 и 72 — 1.10, достаточно хорошее.
Коэффициенты активности 227
4.16.6. Сравнение методов ASOG и UNIFAC. Оба ме-
тода были подвергнуты многократной проверке (см.,
например, книги Точиги и Койимы [688] и Фреденслун-
да и др. [286]). Из двух описанных выше примеров (4.13
и 4.14) следует, что решение таких задач желательно
проводить на ЭВМ.
В книгах Точиги и Койима, а также Фреденслунда и
соавторов приведены соответствующие программы на
языке Фортран. Хотя данные о подробном сравнитель-
ном анализе методов ASOG. и UNIFAC в литературе от-
сутствуют, считается, что они в равной степени надеж-
ны. Последнему методу было уделено несколько боль-
ше внимания, и, в частности, был проанализирован
вклад большего числа групп. Одна из последних подбо-
рок данных опубликована Гмелингом и др. [308] (табл.
Д.11, Д.12). Для расчета равновесия жидкость — жид-
кость разработана специальная группа параметров [456]
(табл. Д.13, Д.14). Обе вышеупомянутые подборки
основаны на данных, приведенных в обстоятельнейших
сборниках DECHEMA о равновесии фаз.
4.17. Расчет коэффициентов
активности по результатам
измерения равновесия
4.17.1. Основные положения. Результаты тщательно
проведенных экспериментов, как правило, более предпо-
чтительны, нежели результаты расчетов, осуществлен-
ных, например, по уравнениям состояния или группо-
вым вкладам. В любом случае область применения и
справедливость этих методов и коррелирующих уравне-
ний можно определить только путем эксперименталь-
ных исследований. В данном разделе мы рассмотрим
различные виды данных и различные методы расчета,
которые пригодны для достижения этих целей и, следо-
вательно, для выполнения интерполяции и экстраполя-
ции ограниченного количества данных.
В наиболее общем случае задача нахождения парамет-
ров уравнений сводится к нелинейной регрессии, в этих
целях часто можно воспользоваться методом Нью-
тона — Рафсона (он представлен в виде программы В. 6
в приложении, а также рассмотрен в работе [57]).
DECHEMA применяет в этих случаях симплексный ме-
тод [154]. Вопроса о соответствующих целевых функци-
ях мы касались в разд. 4.9. Теоретически, чтобы можно
было определить параметры уравнения, необходимо
располагать таким числом данных, которое равно числу
этих параметров. Используемая в такой ситуации мето-
дика была проанализирована в разделе, посвященном
коэффициентам активности при бесконечном разбавле-
нии, однако, если следовать законам статистики, то, ко-
нечно, желательно располагать большим количеством
данных во всем диапазоне концентраций.
Равенство парциальных фугитивностей отдельных
компонентов во всех контактирующих фазах — основ-
ное условие фазового равновесия. Для вещества i в жид-
кой и паровой фазах
(4.223)
или
( С Р VL
Ф,РУ1 = У Iх (Л = ГМФГ'Р}* exp I J ^?at -^fdP
(4.224)
откуда
0,- Р
7i~ 0fat Pfat (Р1^‘ Xj
(4.225)
При давлении всего лишь в несколько атмосфер коэф-
фициент Пойнтинга мало отличается от единицы, и он,
как правило, не учитывается. Аналогично при умерен-
ном давлении соотношение коэффициентов фугитивнос-
ти может приближаться к единице, поэтому часто
достаточно применить следующее простое выражение
для коэффициента активности:
0/ ' Р У! Р У{
У; - —~7 -----7 --- ~-----7 --- (4.226)
У' 0fat P?at х,- P*at х.
Поскольку параметры бинарного взаимодействия совре-
менных уравнений обычно применимы для описания
равновесия между паром и жидкостью многокомпо-
нентных систем, а также с несколько меньшей степенью
точности для представления равновесия между жидкос-
тью и жидкостью, здесь будут главным образом рас-
смотрены бинарные смеси. Неидеальность паровых
фаз, представленная соотношением коэффициентов фу-
гитивности ф,7ф’а‘, учитываться не будет. Примеры то-
го, как проводятся расчеты в тех случаях, когда
неидеальностью пренебречь нельзя, содержатся в гл.6.
4.17.2. Азеотропия. Для многих двух-, а также неко-
торых трех- и многокомпонентных систем единствен-
ными известными данными о фазовом равновесии яв-
ляются данные об их азеотропных составах, температу-
ре и давлении, которые относительно легко найти. В
книгах Лека (1949) и Хорсли (1952—1973) приводится
несколько тысяч таких данных. Поскольку xi = yi, по
определению при этом условии коэффициент активнос-
ти принимает следующий вид:
У/ = 0|P/0?atPpat, (4.22
или
У( p/pw. (4.228)
если отношение фугитивностей близко к единице. Вы-
полнив оценку этих коэффициентов активности, можно
сразу найти параметры двухпараметрического уравне-
ния, как было показано для нескольких распространен-
ных уравнений в предыдущих разделах.
Обратный процесс нахождения условий образования
азеотропной смеси, когда известна корреляция коэффи-
циента активности, представляет особый интерес, в
частности, применительно к многокомпонентным сис
темам, так как проведение с ними экспериментов зани-
мает много времени. В точке азеотропы каждая
относительная летучесть равна единице, следовательно,
15“
228 Глава 4
для определения азеотропа нужно найти минимум при
сумме, равной или близкой к нулю:
А - 1
' aik ~ 1 I =
i = 1
минимум, нуль.
(4.229)
11ри умеренных давлениях достаточно применить упро-
щенное выражение
(4.230)
= - 1-
Этим критерием пользовались Аристович и Степанова
[162], проводившие расчеты по уравнению Вильсона.
Для нахождения минимума можно прибегнуть к одному
из нескольких методов поиска, например методу скорей-
шего спуска. В вышеуказанной работе приводятся полу-
ченные таким путем данные для девятнадцати трех- и
одной четырехкомпонентной смеси. Определенный ин-
терес представляет система бензол + циклогексан + изо-
пропанол, образующая три двухкомпонентные и одну
трехкомпонентную азеотропную смесь при давлении
в 1 атм. Ниже указан состав (мол. доли) азеотропных
смесей, соответствующая температура и нормальные
температуры кипения исходных соединений:
Бензол Циклогексан Изопропанол т° С
0,667 — 0,333 71,9
0,502 0,498 — 77,4
— 0,589 0,411 69,1
0,164 0,454 0,382 69,0
Нормальная
температура
кипения 80,2 80,8 82,5
В некоторых случаях на диаграммах температура —
состав или давление — состав наблюдается более одно-
го локального максимума или минимума. На рис. 4.24,я
показан редкий пример двухкомпонентной смеси, обра-
зующей азеотроп как с максимальной, так и с мини-
мальной температурой кипения. Гораздо чаще на по-
верхностях диаграмм тройных систем наблюдаются ло-
кальные минимумы и максимумы. На рис. 4.24, б пока-
зано — гребень на поверхности диаграммы имеет мини-
мум, называемый седловидной точкой. Разнообразие
видов поверхности равновесий следует ожидать, по-
скольку седловидная точка была предсказана сто лет
назад Оствальдом, и при математическом поиске азеот-
ропных смесей следует иметь в виду возможность появ-
ления локальных экстремумов. На рис. 4.25 показаны
некоторые возможные и гипотетические виды изотер-
мических диаграмм кипения.
Некоторое представление о воздействии коэффициен-
тов активности и давлений пара на состав азеотропных
смесей можно получить при помощи симметричных
уравнений Маргулеса:
ЯПпу! = Л(1-xj2, (4.231)
/?Г1пу2=Лх?. (4.232)
Принимая относительную летучесть за единицу, состав
азеотропной смеси можно выразить следующим об-
разом:
X! = 0,5(1 - (ЯГМ)1п(Р9/Р?)]. (4.233)
Рис. 4.24а. Примеры необычного поведения азеотроп-
ных смесей.
Минимальная температура кипения азеотропной смеси гекса-
фторбензол + бензол соответствует xi = 0,19, а максимальная
температура кипения — Xi = 0,79 при давлении 500 мм рт.ст.
[758].
Рис. 4.246. Пример необычного поведения азеотропных
смесей.
На поверхности давление — состав системы ацетон (1) + хло-
роформ (2) + метанол (3) имеется «седловина»; это означает,
что при отклонении условий в одном направлении образуется
азеотропная смесь с максимальной температурой кипения, а ес-
ли условия меняются на противоположные, то образуется азе-
отропная смесь с минимальной температурой кипения. Это яв-
ление обнаружено Эвеллом и Уэлчем (1945), приведенный гра-
фик построен ван Нессом и Эбботом [137].
Коэффициенты активности 229
Рис. 4.25. Реальные и нереальные типы изотермических
диаграмм кипения бинарных смесей.
о: кривые кипения смесей, приводящего к образованию межмо-
лекулярных соединений, в которые входят две части компонен-
та 1 и одна часть компонента 2.
6: в соответствии с законами термодинамики границы областей
существования жидкости (линия ликвидуса) и пара (линия пара)
пересекаться не могут.
в: в соответствии с законами термодинамики линия ликвидуса
и линия пара не могут соприкасаться вне точек максимума или
минимума.
г: образование азеотропной системы при максимальном давле-
нии (минимальной температуре).
д: образование азеотропной смеси при минимальном давлении
(максимальной температуре). В задаче 4.49 требуется доказать
положения, указанные в п.п. «б» и «в».
Это уравнение представлено графически на рис.4.26. Со-
гласно приведенной аппроксимации, содержание компо-
нента с меньшей летучестью в азеотропной смеси
убывает по мере возрастания соотношения давлений па-
ра при положительных величинах параметра уравнения
Маргулеса.
Другая представляющая интерес задача заключается
в нахождении воздействия давления на состав азеотроп-
ной смеси. В примере 4.16 эта задача решается для
двухкомпонентной системы посредством уравнения
Вильсона, а в задаче 4.38 — при помощи уравнения ван
Лаара. Аналогичным образом можно исследовать воз-
действие температуры при постоянном давлении. На
рис. 5.18 представлен дополнительный материал по
азеотропным смесям.
Помимо использования корреляций коэффициентов
активности и упомянутых выше методов поиска, друго-
го простого способа прогнозирования возникновения
многокомпонентных азеотропных смесей не существует.
Если несколько пар компонентов образуют азеотропные
смеси, возможно появление и многокомпонентной азе-
отропной смеси, хотя утверждать это с полной опреде-
ленностью нельзя. Например, в системе ацетон — эта-
нол — гексан двойные азеотропные смеси с гексаном
образуются, а тройные не образуются, по крайней мере
при атмосферном давлении. Некоторые положения тео-
рии двойных азеотропных смесей рассматриваются в
работе [64], анализ тройных и двойных азеотропных
смесей выполнен - Коганом [405]. Целый ряд аспектов
этой темы освещен также в работе Малезинского
(1965).
4.17.3. Взаимная растворимость жидкостей. Прирав-
нивая парциальные фугитивности в двух жидкостях для
каждого компонента
(4.234)
Л*=У,%П (4.235)
получаем следующее отношение равновесия:
у,х, = у,Ч* (4.236)
или
In у, — In у*= 1п(х */хг), (4.236а)
где звездочкой обозначена одна из фаз. Эти зависимости
состав — коэффициент активности подробно рассматри-
ваются в гл. 7, однако здесь на них следует кратко остано-
виться, поскольку они обеспечивают метод эксперимен-
тального определения коэффициентов активности.
Уравнение (4.236) удобно применять при очень низ-
кой взаимной растворимости жидкостей, характерной
для систем органическое соединение — вода. Примем,
что подстрочный индекс 1 означает растворенное веще-
ство, а надстрочный индекс * относится к чистой фазе
вещества. В этом случае уравнение (4.236) принимает
следующий вид:
У1Х1 = У*** = 1, (4.237)
поскольку для чистого вещества х? и у* равны единице.
Соответственно
У1 = 1/х!. (4.237а)
Если величина Xi очень мала, то коэффициент активное- 177
ти при бесконечном разбавлении имеет достаточно
большую величину.
Для двухкомпонентной смеси можно записать
In у । — In у * = ln(x */х j). (4.2л8)
lny2- lny?= ln[(l - xf)/( 1 -Х1)]. (4.239)
230 Г лава 4
Пример 4.15. Экстраполяция изобарических и изотермических данных о температуре начала кипения для
дения коэффициентов активности при бесконечном разбавлении
Известны параметры системы метанол + этилацетат
при 1 атм и системы метанол + дихлорэтан при 60° С.
Перегруппировка уравнения
Р = ЦХ1Р? + 72Х2Р2 (1)
дает следующие уравнения для коэффициентов ак-
тивности:
71 = (Р ~ 72Х2Р2)/Х1Р?, (2)
72 = (Р - 71Х1Р?)/Х2^. (3)
Коэффициенты активности при бесконечном разбавле-
нии — это предельные значения «кажущихся» коэффи-
циентов активности при концентрации компонентов,
стремящейся к нулю:
71 = (Р - ХгР^/х.Р?, (4)
72 = (Р - Х1Р?)/Х2К (5)
7“ = Нт у*, х,=0 (6)
72 = lim 72. х2 = 0 (7)
Ниже показаны графики экспериментальных и «кажу-
щихся» коэффициентов активности. Очевидно, что экс-
траполяции к нулевым концентрациям согласуются.
Коэффициенты активности при бесконечном разбавле-
нии, определенные по этим графикам, для двух рас-
сматриваемых смесей имеют следующие значения:
нахож-
метанол + этилацетат: = 3,05, у* = 2,9,
метанол + дихлорэтан: уГ = 6,3, у” = 3,9.
Состав паровой фазы для этих двух систем известен,
что позволяет рассчитать для них коэффициенты актив-
ности, однако для построения графиков «кажущихся»
коэффициентов активности эта информация не требует-
ся, и, пользуясь этими графиками, можно соответствен-
но найти коэффициенты активности при бесконечном
разбавлении по данным только о составе жидкой фазы
и либо полного давления при постоянной температуре,
либо температуры начала кипения при постоянном
давлении.
а. Экстраполяция данных о давлении начала кипения
жидкостей известного состава для нахождения коэффи-
циентов активности при бесконечном разбавлении
Данные для системы метанол + дихлорэтан при 60°С
взяты из статьи Мак-Кетта и Каца [IEC, 40, 853 (1948)].
Кажущиеся коэффициенты активности (см. разд. 4.15)
экстраполируют до бесконечного разбавления. Для этой
системы известны истинные коэффициенты активности,
представленные на рис. а для сравнения.
б. Экстраполяция температур начала кипения жид-
костей известного состава для нахождения коэффици-
ентов активности при бесконечном разбавлении
Данные для системы метанол + этилацетат при
1 атм взяты из статьи Миллера и Блисса {IEC, 32, 123
(1940)]. Для этой системы известны истинные коэффи-
циенты активности; они представлены на рис. б для
сравнения.
Х1 У1 t 71 72 РГ Р?' 71 72
2,8 12,0 74,4 3,020 1,002 1108,4 694,0 2,75 1,08
3,7 13,3 74,0 2,533 0,997 1092,1 684,8 2,49 1,09
7,3 22,0 71,5 2,329 1,016 994,8 629,9 2,43 1,18
12,3 31,0 69,3 2,115 1,028 915,2 584,4 2,20 1,26
21,1 42,0 66,4 1,867 1,086 818,4 528,6 1,99 1,41
23,6 44,2 66,0 1,784 1,076 805,7 521,2 1,90 1,43
23,9 44,0 65,8 1,767 1,092 799,4 517,6 1,92 1,44
26,5 46,8 65,3 1,729 1,094 783,9 508,6 1,86 1,48
35,2 52,6 64,0 1,539 1,157 744,8 485,7 1,70 1,58
40,8 55,8 63,7 1,425 1,193 736,0 480,5 1,58 1,62
44,0 57,3 63,6 1,363 1,222 733,1 478,8 1,52 1,63
53,3 62,0 63,1 1,221 1,363 718,7 .470,3 1,41 1,72
58,5 64,7 62,9 1,189 1,432 713,0 466,9 1,36 1,77
66,4 68,7 62,4 1,135 1,560 698,9 458,6 1,31 1,92
70,8 71,1 62,4 1,102 1,658 698,9 458,6 1,27 1,98
74,8 73,7 62,4 1,081 1,748 698,9 458,6 1,23 2,05
79,3 76,8 62,4 1,062 1,877 698,9 458,6 1,20 2,17
82,2 79,0 62,5 1,050 1,969 701,7 460,3 1,18 2,'24
88,3 84,2 62,8 1,030 2,230 710,2 465,3 1,13 2,44
96,1 93,4 64,0 1,001 2,667 744,8 485,7 1,04 2,43
б: экстраполяция температур начала кипения.
232 Глава 4
Пример 4.16. Азеотропные составы смесей метилацетата (1) и метанола (2) при различных давлениях
Параметры уравнения Вильсона даются следующими
выражениями:
Л12 = 0,5108 ехр (54,9958/Т),
Л21 = 1,9578 ехр (- 467,79/Т)-
Уравнения Антуана (где давление выражено в мм рт. ст., а
температура в К) имеют следующий вид:
1пР? = 16,5835 - 2838,7/(7 - 45,16),
1пР? = 18,1412 - 3391,96/(7' - 43,16).
В условиях образования азеотропной смеси относитель-
ная летучесть становится равной единице:
«12 = yiPl/yiP^ 1.
Пренебрегая незначительной неидеальностью паровой фа-
зы, температуру начала кипения находят из уравнения
Р = 71Р?Х1 + 72/^(1 - X,).
Ниже приведены графики зависимости относительной ле-
тучести при температуре начала кипения от мольной доли
метилацетата для давления 0,1, 1 и 5 атм. Рассчитанный
азеотропный состав при 1 атм(х, = 0,67) хорошо согласу-
ется с экспериментально найденными, = 0,675) [Балашов
и др. Журн. физ. хим.,41, 739(1947)] [57].
Если четыре коэффициента активности соотнесены с
двумя измеренными составами (х, их,) посредством со-
ответствующего двухпараметрического уравнения, по-
лучаемые в результате два уравнения можно разрешить
сначала относительно двух параметров, а затем относи-
тельно коэффициентов активности, если это представля-
ется необходимым. В простейшем случае имеем дело с
симметричным уравнением, содержащим только один
параметр. Подставляя в уравнение (4.239)
In у2 = Ах\ (4.240)
и разрешая это уравнение относительно этого парамет-
ра, получим
1 1 - xf
А= y2 _~v*1 ln , • (4.241)
х! х1 1 X ]
Условие начала разделения фаз отвечает условию
х, = х, = 0,5, при этом А = 2. Большие величины ,4 со-
ответствуют более ограниченной растворимости.
Уравнения, описывающие растворимость, при помо-
щи уравнения Маргулеса преобразуются к следующему
виду:
Inxf/Xj = In у, - In 7*
= А(х$ — х*2) + 2(В ~ А )(х 2*2 ~ х Iх 22)'
В(х\ - х*2) - 2(В - Д)(х2х? - э&б2).
(4.242)
(4.243^
Точное решение этих уравнений относительно парамет-
ров А и В показано в разд. 7.4. Уравнение ван Лаара
также приводит к точному решению. Другие общие
уравнения требуют использования итерационных мето-
дов для нахождения параметров. Ограниченность урав-
нения Вильсона состоит в том, что с его помощью
нельзя представить равновесие между жидкими фазами.
В гл. 7 приводятся графики пределов растворимости
жидких фаз, построенные при помощи нескольких урав-
нений для коэффициентов активности; при этом коэф-
Коэффициенты активности 233
Рис. 4.26. Составы азеотропных смесей, рассчитанные по симметричным
уравнениям Маргулеса. Уравнение (4.233). Xi = 0,5[1 - RT/A 1п(Рга‘/f^dt).
фициенты активности бесконечного разбавления ис-
пользуются как параметры. В пределах (х, х*) определя-
ют значения у?, которые впоследствии можно приме-
нить для нахождения обычных параметров уравнений
(Аи, A2i), (ti2, 721) и т. д. Как следует из указанных
графиков, прогнозы относительно расслоения жидких
фаз, полученные исходя их этих нескольких уравнений,
не однозначны. Прогнозы относительно равновесия
между паром и жидкостью, основанные на тех же коэф-
фициентах активности при бесконечном разбавлении,
также не совпадают, но в меньшей степени. Опыт рабо-
ты с конкретными системами может помочь в выборе
определенного уравнения в конкретной ситуации. Одна-
ко, как правило, предпочтение отдается уравнению
NRTL при ап = 0,2 и уравнению UNIQUAC, так как
они легкоприменимы и для многокомпонентных смесей.
Обычно при помощи коэффициентов активности, по-
добранных к данным о равновесии жидкость — жид-
кость, равновесие пар — жидкость можно представить
лишь довольно условно, то же самое следует сказать и
о представлении равновесия жидкость — жидкость по-
средством уравнений для равновесия пар — жидкость
(см. пример 4.17). Более подробно эта тема рассмотре-
на в гл. 7.
4.17.4. Данные «давление—состав» и «температу-
ра—состав». Экстраполяция данных о составе жидких
смесей и давлении или температуре начала кипения в
целях нахождения коэффициентов активности при беско-
нечном разбавлении была рассмотрена в разд. 4.14.
Аналогичным образом эти данные можно использовать
для непосредственного определения параметров уравне-
ний для коэффициентов активности и, следовательно,
самих коэффициентов активности во всем диапазоне
концентраций. Этот способ позволяет избежать трудно-
стей, связанных с проведением экспериментальных ис-
следований (с отбором проб и анализом паровых фаз),
однако необходимо принять справедливость определен-
ных форм уравнений состояния паровой фазы и метода
корреляции коэффициентов активности жидкой фазы.
Хотя любое количество данных можно описать регрес-
сионным уравнением, в данной главе методика экстра-
поляции будег объяснена на примере только двух групп
данных для двухкомпонентной смеси с использованием
В-усеченного вириального уравнения и уравнения ван
Лаара.
В начале записывают выражение для полного давле-
ния; если коэффициентом Пойнтинга можно прене-
бречь, оно приобретает следующий вид:
Р= У\Х{Р\ф\/фх + У2Х2Р2Ф2/Ф2- (4.244)
Если известны две группы изотермических дан-
ных, дальнейшая методика распадается на следующие
этапы.
1. Поскольку известны температура и давление паров
Р°, коэффициенты фугитивности чистого компонента </>,°
находят по вириальному уравнению.
2. Поскольку состав пара неизвестен, в качестве пер-
вой попытки принимают каждый коэффициент парци-
альной фугитивности ф, или соотношение ф,7ф, равны-
ми единице. Установив пробную величину состава пара,
вычисляют коэффициенты парциальной фугитивности
по вириальному уравнению.
3. Замена коэффициентов активности в уравнении для
полного давления их эквивалентами из уравнения
234 Глава 4
Пример 4.17. Сравнение параметров уравнения ван Лаара, полученных на основе данных о равновесии жид-
кость—жидкость и пар—жидкость
Для системы вода—н-бутанол при НО °C x'i = 0,9788,
х* = 0,6759 (Butler et al. J. Chem. Soc., 1933 , 674). Пара-
метры уравнения ван Лаара получают путем подстанов-
ки указанных величин в уравнение (7.39):
/0,9788 + 0,6759^ log(0,6759/0,9788) _ 2
А _ \ 0,0212 0,3241/ log(0,0212/0,3241)
В 0,9788 0,6759 ~Т0,9Ж 0,67591^(0^759/6,9788) ”
0,0212 0,3241 0,0212-0,32411og(0,0212/0,3241)
= 0,2059.
-0,1608
А =-------------------------------------------=0,335.
(1 + 0,2059-46,17)" 2 - (1 + 0,2059-2,085)" 2
В = = 1,627.
0,2059
Лучший результат представления данных о равновесии
пар—жидкость при атмосферном давлении (93—116 °C)
посредством уравнения ван Лаара в соответствии с дан-
ными сборника DECHEMA (DECHEMA VLE Data
Collection, part 1, p. 409) составляет:
A = 1,1295, В = 3,9571.
Графики коэффициентов активности, построенные ис-
ходя из двух групп параметров, плохо согласуются даже
в диапазоне взаимных растворимостей. Смешиваемос-
ти, рассчитанные на основании параметров уравнения
ван Лаара, полученных из данных о равновесии пар-
жидкость, соответствуют Xi = 0,98 и х* = 0,50 (см. рис.
7.8), и различие между этими и измеренными величина-
ми не столь уж велико. Отчасти его можно объяснить
различием температур.
ван Лаара дает
0°1
Р = XjPj “ ехр
01
Ф°2
+ x2P2j- ехр
02
' Вх2
Axt 4- Вх2
' Ахх
Ах{ 4- Вх2
(4.245)
4. Подставляя две группы данных давление—состав в
уравнение (4.245), разрешим систему уравнений относи-
тельно параметров А и В и относительно коэффициен-
тов активности при двух составах жидкой фазы.
5. Находим приближенные величины состава паровой
фазы из уравнения
Р,? 0,?
= Р 0,-
(4.246)
Если мольные доли в сумме не составляют единицы, их
следует нормализовать перед тем, как перейти к после-
дующим этапам расчета.
6. Коэффициенты парциальной фугитивности получа-
ют при помощи следующих уравнений, взятых из табл.
3.4:
In 0! = “[Bi 4- j!(2Pi2“ Ви - В22)], (4.247)
Г\ 1
In 02 = “~[В2 4-j?(2B12 - Вц - В22)]. (4.248)
К 1
7. Вернемся к этапу 3. Повторяем этапы 3—7 до тех
пор, пока величины А а В или величины состава паро-
вой фазы не станут стабильными.
При наличии более двух групп данных все они могут
применяться для определения параметров уравнения
Коэффициенты активности 235
Пример 4.18. Расчет коэффициентов активности по данным о Т—х при помощи симметричного уравнения и
уравнения Маргулеса
Рассмотрим систему метилацетат + метанол при
5907 мм рт. ст. Ниже приведены характеристики этой
системы.
Х| Т, °C Р° Р?
0,294 123,5 4951,9 5145,4
0,736 125,6 5195,2 5445,4
Примем, что ф,/ф° = 1 и что коэффициенты активности
не зависят от температуры. Симметричные уравнения
имеют следующий вид:
yi = ехрАхг, 72 = expHxi
Используя первую группу данных, получаем
Р = 71-^1 Pia' + yzXiP^',
5907 = 0,294(4951,9)ехр[Л(1 - 0,294)2] +
+ 0,706(5145,4)ехр[Л(0,294)2].
Методом проб получаем
А = 0,688 и 7, = 1,41, 72 = 1,06.
Использование второй группы данных дает
0,6473ехр(0,0697Л) + 0,2434ехр(0,5417Л) -1=0,
откуда
А = 0,548 и 71 = 1,04, 72 = 1,35.
Поскольку полученные величины А существенно разли-
чаются, очевидно, что при помощи симметричного
уравнения нельзя достаточно хорошо представить эти
данные. При использовании полных уравнений Маргу-
леса следует решить уравнения (1) и (2):
0,2456ехр[(Л + 2{В - A)xi)X2] +
+ 0,6150ехр[(В + 2(А - B)x2)xj] -1=0, (1)
0,6473ехр[(Л + 2(В - Л)Х1)Лг] +
+ 0,2434ехр[(В + 2(А - В)х^)] -1=0. (2)
Подставим в уравнения величины мольных долей:
0,2465ехр[0,4984(Л + О,588(В - Л))] +
+ 0,6150ехр[0,0864(В + 0,1412(Л - В))] -1=0.
0,6473ехр[0,0697(Л + 0,1472(В - Л))] +
+ 0,2434ехр[0,5417(В + 0,5280(Л - В))] -1=0.
Последние два уравнения можно решить методом Нью-
тона—Рафсона, как в примере 4.7, однако здесь они ре-
шены графически. Графики строят последовательно
точка за точкой, задаваясь значениями Л и находя соот-
ветствующие величины В, используя метод Ньютона—
Рафсона для одной переменной. Точка пересечения кри-
вых соответствует Л = 0,83 и В = 0,42. Как видно из
приведенной ниже таблицы, степень соответствия меж-
ду рассчитанными и экспериментально найденными со-
ставами паровой фазы вполне удовлетворительна.
Х| 7! 72 У1
расч. эксп.
0,294 1,34 1,09 0,330 0,336
0,736 1,02 1,42 0,660 0,678
236 Глава 4
ван Лаара методом наименьших квадратов, т. е. путем
решения пары уравнений
д
- [L(P,- - RHS;)2] = 0, (4.249)
[L(P,- RHSj)2] = 0. (4.250)
Аналогичная методика применяется для обработки
изобарических данных, но при очень широком диапазо-
не температур следует использовать уравнение для ко-
эффициентов активности, учитывающее воздействие
температур, например уравнение Вильсона.
В принципе этот метод нахождения коэффициентов
активности был предложен Баркером [171], применив-
шим вириальное уравнение для описания паровой фазы
и уравнение Скэтчарда—Рэймонда (см. [614]) для опре-
деления коэффициентов активности. Свифт и сотрудни-
ки использовали уравнения Барнера—Адлера, Вильсона
и Цубоки—Катаямы—Вильсона. При умеренных давле-
ниях, т. е. если псевдоприведенные давления составля-
ют менее половины псевдоприведенных температур,
вириальное уравнение вполне пригодно для решения
этой задачи, и использовать его особенно легко, потому
что оно не усложнено множественными корнями в от-
личие от кубических уравнений состояния. Праузниц и
др. [98] приняли в качестве стандартных В-усеченное ви-
риальное уравнение и уравнение UNIQUAC. Содержа-
щиеся в сборнике DECHEMA корреляции, включающие
данные вплоть до давления 15 бар, не учитывают не-
идеальность паровой фазы; исключение составляют
лишь корреляции, приведенные для монокарбоновых
кислот, для которых характерна сильная ассоциация.
4.18. Влияние температуры
и избыточной энтальпии
Хотя в ряде уравнений из числа широко применяемых
для определения коэффициентов активности учитыва-
ется зависимость последних от температуры, это лишь
отчасти компенсирует температурное воздействие, и
степень соответствия данных обычно улучшается, если
параметры зависят от температуры. В табл. 4.13 об-
суждается влияние температуры на параметры ряда
специальных уравнений, а в табл. 4.14 и 4.15 представ-
лены соответствующие экспериментальные данные для
параметров уравнений Вильсона и Маргулеса. Эти дан-
ные включают все системы из цитируемого источника,
для которых имелись соответствующие значения пара-
метров по крайней мере при четырех температурах. Ис-
ходя из этих результатов, трудно определить общую
закономерность зависимости параметров уравнения
Вильсона от температуры, в то же время очевидно, что
изменение коэффициентов активности бесконечного раз-
бавления, вычисленных по данным параметрам уравне-
ния Вильсона, в зависимости от температуры является
более регулярным. Это заключение связано с тем, что
пары, обладающие совершенно различными параметра-
ми, могут представлять определенные данные с одина-
ковой степенью точности (разд. 4.9, рис. 4.9). Для
тщательно собранных данных о системе этанол + вода
действительно очевидна простая зависимость от темпе-
ратуры (пример 4.19). Для данных, использованных в
примере 4.20, характерно более беспорядочное поведе-
ние, однако общее направление вполне очевидно.
Помимо коэффициента активности и связанной с ним
избыточной энергии Гиббса легче всего поддаются из-
мерению такие избыточные характеристики, как избы-
точный объем и избыточная энтальпия. Краткое опи-
сание дилатометрических и калориметрических мето-
дов, используемых в этих целях, содержится, например,
в книге [81]. Кроме основных определений, выражен-
ных через избыточную энергию Гиббса,
Gfx = 7?7’1пу;-, (4.251)
Gex = RTXXj In у, , (4.252)
очень эффективны термодинамические соотношения,
Таблица 4.13. Температурная зависимость параметров уравнений коэффициентов активности
Уравнение Параме,р Коммент арии
Скэтчарда — In у, = (о, - З)2 Разность 3, - 3 часто лишь в очень незначительной степе-
Гильдебранда RT ни зависит от температуры. Отдельные 3, являются функ- циями ы, Р( и 77.
Вильсона А„ - (1 ’/ Г) ехр ( - K//RT) Х„ часто принимают независимым от температуры, одна- ко следует обратиться к табл. 4.14.
NRII т(/ = C„/RT C,j и од даны в виде линейных функций температуры в
С ч = ехр (- a,j книге [109, р. 168].
UNIQUAC Тч = ехр ( - &u,,/RT) Дну обычно принимают независимым от температуры. В
Z = 35,2 - 0,12727" + 0,00014 Г2 работе [642] координационное число z выражено в виде функции температуры
Маргулеса и ван Лаара Л|2, Л?! Параметры можно приближенно считать линейными функциями 1/7", в некоторых случаях возрастающими, в других убывающими, иногда в одном и том же направле- нии, иногда в противоположных. См. табл. 4.15.
Коэффициенты активности 237
Таблица 4.14. Параметры уравнения Вильсона и соответствующие коэффициенты активности при
бесконечном разбавлении и нескольких температурах. Параметры взяты из «Сборника данных о
равновесии пар — жидкость» DECHEMA (V. 3/4). Все данные для каждой системы получены од-
ними и теми же исследованиями
Система т /12 /21 7 1 7 2° IVIA
Ацетон + хлороформ 0 -290,9 -81,4 0,503 0,396 0,917
10 -395,2 -103,8 0,410 0,273
20 - 307,9 -164,4 0,436 0,352
30 -343,6 -52,1 0,517 0,395
50 -472,7 194,1 0,606 0,412
Сероуглерод + ацетон 0 715,8 689,7 6,50 8,66 0,801
10 661,3 796,4 5,81 9,51
30 537,2 961,1 4,51 10,03
35 604,8 783,2 4,68 7,66
Ацетон + гексан -20 1184,8 502,5 13,09 11,09 0,562
-5 1160,6 487,5 10,77 9,87
20 1077,8 375,5 7,24 6,96
45 962,8 341,4 5,05 5,63
Метилэтилкетон + этилбензол 25 568,1 -210,6 1,83 1,54 0,732
55 -96,4 495,8 1,22 1,63
65 162,8 134,8 1,39 1,55
75 -65,3 670,6 1,37 2,18
1,4-Диоксан + нитрометан 30 -483,0 590,5 1,07 1,12 1,590
46 -487,3 623,4 1,11 1,18
80 -419,0 593,5 1,20 1,27
98 -407,6 580,7 1,21 1,26
1,4-Диоксан + N.N-диметил- 30 -242,8 642,4 1,71 1,93 1,667
формамид 40 -260,5 668,6 1,69 1,92
50 -275,5 685,2 1,66 1,89
60 -293,5 691,4 1,62 1,82
Диэтиловый эфир + хлоро- 0 6437,1 -583,2 11 163 0,72 1,297
форм 10 6401,8 -6471,1 26 950 1,12
20 - 674,0 + 674,7 0,74 0,57
30 4051,9 -634,8 71,2 0,73
Примечание. Параметры уравнения Вильсона для системы диэтиловый эфир + хлороформ, по-видимому, невер-
ны; уравнение Маргулеса, прогнозирующее коэффициенты активности бесконечного разбавления в интервале
0,6—0,9, хорошо соответствует данным (см. табл. 4.15).
включающие коэффициенты активности:
мое следующим выражением
И,ех = RT
<Мпу,-
др
HfK = - RT2
d In у,-
Не* =
RT2Xx(
(4.253)
(4.254)
(4.255)
ln(y,7yzo) =
Яех
RT2 dT>
(4.256)
весьма значительно. Поскольку парциальная избыточ-
ная энтальпия, например
Я₽х = Яех + (1 _ Х1)(аЯех/аХ] (4 25
Поскольку Сх жидкостей мал, воздействием давления
на коэффициент активности можно, как правило, прене-
бречь, тогда как температурное воздействие, определяе-
является довольно сложной функцией температуры, ма-
тематическая форма которой обычно неизвестна, то
аналитическое интегрирование, как правило, невозмож-
но. Разнообразие форм кривых на рис. 4.3—4.6 говорит
о сложности формулировки достаточно простых зависи-
мостей избыточной энтальпии от температуры и соста-
238 Глава 4
Таблица 4.15. Параметры уравнения Маргулеса при несколь-
ких температурах (рассматриваются те же системы, что и в
табл. 4.14.)
Система Т 412 421
Ацетон + хлороформ 0 -0,6632 -0,9089
10 -0,8380 -1,2639
20 -0,8050 -1,0303
30 -0,5948 -0,9382
50 -0,3922 -0,8919
Сероуглерод + ацетон 0 1,7119 1,8948
10 1,6133 1,9497
30 1,3842 1,9494
35 1,4354 1,8091
Ацетон + гексан -20 2,1671 2,1376
-5 2,0155 2,1024
20 1,7448 1,8012
45 1,5061 1,6352
Метилэтилкетон + этил- 25 0,5482 0,4348
бензол 55 0,1121 0,4893
65 0,3242 0,4370
75 0,3069 0,6176
1,4-Диоксан + нитрометан 30 0,0509 0,1288
46 0,0899 0,1687
80 0,1815 0,2372
98 0,1837 0,2314
1,4-Диоксан + Ы,1Ч-диметил- 30 0,2755 0,5793
формамид 40 0,2701 0,5554
50 0,2596 0,5351
60 0,2271 0,5058
Диэтиловый эфир +
+ хлороформ 0 -0,0556 -0,5893
10 -0,2485 -0,6292
20 -0,2429 -0,5252
30 -0,3380 -0,5353
ва. Общая форма уравнения
Н'*=хххгДТ,хх)
(4.258)
удовлетворяет требованиям при предельных величинах
состава. В некоторых диапазонах концентрации, часто
при соотношениях компонентов, близких к эквимоляр-
ным, зависимость от состава незначительна, и если
влияние температуры также можно считать неболь-
шим, интеграл с симметричной избыточной энтальпией
и в некоторых случаях экстраполяция коэффициентов
активности в малых диапазонах температур, если из-
вестны величины коэффициентов для двух температур,
может дать вполне удовлетворительные результаты.
Определенный интерес может также представлять об-
ратный процесс нахождения избыточных энтальпий по
данным о коэффициентах активности как функциях тем-
пературы. В этом случае требуемое уравнение выводят,
используя уравнение Вильсона, например, при помощи
следующей последовательности формул:
Яех = Анххх2,
Н^ = Ан(\-хх)2
(4.259)
(4.260)
Яех = _ RT1
fd(Gn/RT)
, дТ
(4.262)
будет довольно простым:
Ge*/RT= - ln(xi + Л12х2) ~*2 ln(A2i*i +х2),
Ан(1
In У1/(У1)о= д
1 1
Го ~т
(4.261)
л12= ехр(-Х12/ЛГ),
(4.263)
(4.264)
Коэффициенты активности 239
Пример 4.19. Влияние температуры на параметры уравнений ван Лаара и Вильсона для смесей этанола и воды
[754]
Приведенные ниже параметры рассчитаны методом наименьших квадратов.
Уравнение ван Лаара Уравнение Вильсона
К А В Л12 Л21 х12//? х21//г
303,15 0,9428 1,4769 0,78925 0,23896 428,50 77,198
323,15 0,9409 1,6463 0,83185 0,19486 439,78 148,22
343,15 0,9312 1,7427 0,86504 0,17273 453,57 198,76
363,15 0,9044 1,7890 0,90524 0,15985 463,51 238,49
Масштаб ординат для каждой кривой свой. Кривые показывают приближен-
ную линейную зависимость АТ и ВТ, а также четырех параметров уравнения
Вильсона.
дЛ12 М 2Л 1 2
дТ RT2
дЛ21 ^21Л21
дТ RT2
(4.265)
следовательно,
Яех
^12^12 ^21^21__
Х\ + А\2Х2 Л21Х1+х2
(4.268)
(4.266) если исходить из допущения о том, что Х,7 постоянны.
В примере 4.21 показана проверка уравнения (4.268) от-
носительно трех групп данных, результаты которой не-
удовлетворительны .
(4 267) Поскольку равновесные данные и энтальпийный ба-
ланс часто применяются вместе во многих расчетах, бу-
Х|Х2
240 Глава 4
Пример 4.20. Влияние температуры на параметры уравнения ван Лаара
Коэффициенты активности смесей диэтиламина и
триэгиламина были измерены Биттрихом и Кауэром
[755] при нескольких температурах. Данные были лине-
аризованы посредством уравнения ван Лаара. Результа-
ты показаны в таблице и на графике, приведенных
ниже. Малые значения коэффициентов точности опреде-
ления г2 указывают на неудовлетворительные корреля-
ции данных, однако параметры действительно моно-
тонно меняются с температурой
т А В г~
50 0,7664 0,2447 0,6157
55 0,7260 0,1978 0,4720
60 0,6259 0,1971 0,5644
65 0,5961 0,1761 0,5763
70 0,5763 0,1620 0,6235
Оригинальные данные воспроизведены только для двух
температур.
Т, °C
50 0 2 0,00 8,13 2,090 1,000 1,007
5 18,01 1,700 1,014
10 29,37 1,380 1,027
20 45,71 1,148 1,042
30 57,99 1,094 1,057
40 67,92 1,007 1,072
50 75,69 1,057 1,089
60 82,35 1,045 1,104
70 87,73 1.035 1,122
80 92,44 1,023 1,140
90 96,40 1,014 1,191
95 98,24 1,007 1,282
98 99,17 1,005 1,849
100 100,00 1,000 —
70 0 0,00 — 1,000
2 6,96 1,778 1,005
5 15,31 1,496 1,012
10 26,13 1,227 1,018
20 43,07 1,102 1,032
30 55,87 1,064 1,040
40 66,11 1,045 1,050
50 74,38 1,034 1,052
60 81,25 1,030 1,072
70 86,96 1,021 1,084
80 92,01 1,014 1,104
90 96,21 1,009 1,143
95 98,16 1,005 1,178
98 90,18 1,002 1,496
100 100,00 1,000 —
Коэффициенты активности 241
Пример 4.21. Избыточная энтальпия, выраженная через параметры уравнения Вильсона
Ниже приведены параметры уравнения Вильсона
(табл. Д.8) и соотношения объемов для трех систем при
соответствующих температурах.
Система И/ Из Х12 Хз । Л12 Л2,
Циклогексан + бензол 1,224 80,02 187,23 0,7265. 0,9301
Хлороформ + ацетон 1,092 - 332,23 -72,2 1,6403 1,2335
Бензол + метанол 2,179 153,86 1620,36 0,3570 0,1546
Другие экспериментально найденные характеристики
этих систем указаны на графиках (Малезинский, 1965).
Избыточную энтальпию можно рассчитать по уравне-
нию (4.268) и сопоставить с этими данными. При
Xi = 0,5 это уравнение принимает следующий вид:
Я" = 0,5
Х12Л12 Х21Л21
---- Ц- _
1 + Л12 1 + Л21
уравнению и полученных графическим путем, являются
неудовлетворительными.
рассчитанных по
Система Нс' (расч.) 1Г' (граф.)
Циклогексан + бензол 62,0 170
Хлороформ + ацетон - 122,3 -450
Бензол + метанол 128,7 160
Результаты сравнения величин /Дх,
16-829
242 Глава 4
дет удобно выразить их через одни и те же параметры.
К сожалению, по крайней мере при использовании мо-
делей локального состава (уравнения Вильсона, NRTL,
UNIQUAC) одновременная корреляция равновесия жид-
кость — пар и ВТ* обычно ведет к ухудшению соответ-
ствия как минимум одному типу данных. Установление
зависимости параметров от температуры часто улучша-
ет результаты, однако число параметров при этом по
крайней мере удваивается, что серьезно затрудняет опи-
сание многокомпонентных систем. Определенный успех
в этом направлении был достигнут Скьёлдом-Йоргенсе-
ном и др. [642], которые выразили координационное
число z в уравнении UNIQUAC как общую функцию
температуры (см. табл. 4.13). При использовании этой
функции параметры уравнений UNIQUAC/UNIFAC по-
лучают через регрессионное уравнение, описывающее
данные о равновесии пар — жидкость и о РР*. Однако
общая группа параметров UNIFAC такого рода пока не
разработана, и, вероятно, необходима более тщатель-
ная проверка такой корреляции температуры.
Пока же в большинстве случаев следует полагаться
на корреляции энтальпии, независимые от корреляций
коэффициентов активности.
4.19. Задачи
4.1. Объем двухкомпонентной жидкой смеси пред-
ставлен уравнением
К= Л(7’/Р)°>1(1 +х32).
Получите уравнения для 1/СХ, V2, 7, и 72.
4.2. Избыточная энтальпия двухкомпонентной смеси
выражена в виде функции состава и температуры (К)
посредством уравнения
Нех = H-Hid=x1x2(l 200+ 200.x, + 1,5х,Г),
где FTX выражена в кал/моль. При 300 К коэффициенты
активности при бесконечном разбавлении имеют сле-
дующие значения: 7Г = 6,00, 7? = 4,4. При 400 К
= 4008 и Pi = 2643 мм рт. ст.
Определите для эквимолярной смеси
а) парциальные молярные энтальпии РР? и Рр? как
функции 7°;
б) коэффициенты активности как функции Т, допу-
ская, что уравнение ван Лаара справедливо при 300 К;
в) давление начала кипения при 400 К при условии,
что коэффициенты парциальной фугитивности пара рав-
ны = 0,95, а коэффициенты парциальной фугитив-
ности чистых жидкостей при давлениях их паров
</>? = 0,98.
Избыточный объем жидкой фазы практически равен
нутю.
4.3. Ниже приведены результаты измерений, выпол-
ненных для двухкомпонентной смеси при 350 °C:
X, Н Т! T’
0 500 15,00 1
0,2 1500 5,66 2
0,4 2500 2,65 3
0,6 4000 1,54 5
0,8 2000 1,11 12
1,0 0 1,00 30
Найдите избыточную энтальпию как функцию состава.
4.4. Осмотическое давление водного раствора, содер-
жащего 1,00 г антипирина (СцН12^О) в 100 мл, при
0 °C равно 1,18 атм. Рассчитайте, исходя из этих дан-
ных, молекулярную массу и сравните ее с формульной
массой.
4.5. Среднее осмотическое давление человеческой кро-
ви равно 7,7 атм при 40 °C. а) Какова мольная доля
различных растворенных веществ в крови? б) Какова
точка замерзания крови?
4.6. Осмотическое давление водного раствора, содер-
жащего 0,001 мол. доли растворенного вещества В, рав-
но 0,139 МПа при 300 К, если растворитель А
находится под давлением в 0,100 МПа. Принимая, что
Va = 0,018 л/моль и не зависит от давления, рассчитай-
те величину g (А, 300 К, 0,1 МПа, Хь = 0,001) — ц (А,
300 К, 0,1 МПа, хь - 0).
4.7. Постройте изотермы коэффициентов активности
воды относительно мольной доли сахарозы, исходя из
приведенных ниже величин осмотического давления
водных растворов сахарозы. Для этой системы избы-
точный объем практически равен нулю во всем диапазо-
не концентраций.
Осмотическое давление, атм
моль/1000 г Н2О 0 °с 20 "С 40 °C 60 °C 80 °C
0,100 2,46 2,59 2,66 2,72
0,200 4,72 5,06 5,16 5,44
0,300 7,09 7,61 7,84 8,14
0,400 9,44 10,14 10,60 10,87
0,500 11,90 12,75 13,36 13,67
0,600 14,38 15,39 16,15 16,54
0,700 16,89 18,13 18,93 19,40
0,800 19,48 20,91 21,80 22,33 23,06
0,900 22,12 23,72 24,74 25,27 25,92
1,000 24,83 26,64 27,70 28,37 28,00
4.8. Энтальпия испарения воды рассчитывается по
следующему уравнению:
\HV = 13 425 - 9,917^ + 7,5(£ - 5)Г2
+ 4,46(£ - 7)Г3 ,
Коэффициенты активности 243
где Н измеряется в каль/моль. Найдите уравнение для
активности воды в водных растворах как функции по-
вышения температуры кипения.
4.9. Температура замерзания морской воды равна
271,240 К. Определите осмотическое давление морской
воды при температуре около 273 К, если температура
замерзания чистой воды составляет 273,150 К, моляр-
ный объем воды равен 18 мл/моль, а молярная энталь-
пия таяния льда равна 6000 Дж/моль.
4.10. Рассчитайте отношение фугитивностей /(Н2О,
жидкость, т = 0)//(Н2О, жидкость, т = 0,10459),
где т — концентрация H(jl, моль/кг, при 273,15 К и
атмосферном давлении. Температура замерзания пони-
жается на 0,3684 К. Если замерзание воды происхо-
дит в нормальных условиях, AHf = 6008 Дж/моль и
ДСР = 38,09 Дж/К моль. Насколько будет отличаться
результат, если пренебречь УС pl
4.11. Ниже представлены величины понижения темпе-
ратуры замерзания растворов мочевины в воде. Теплота
плавления воды при 273,16 К равна 1436,4 кал/моль.
Найдите коэффициенты активности воды.
[NaCl], масс. % Удельная масса (г/л) при 15 °C (59 °F) Температура замерзания
°C °F
12 1,089 -8,17 17,3
13 1,097 -9,03 15,7
14 1,104 -9,94 14,1
15 1,112 - 10,88 12,4
16 1,119 -11,90 10,6
17 1,127 -12,93 8,7
18 1,135 - 14,03 6,7
19 1,143 - 15,21 4,6
20 1,152 - 16,46 2,4
21 1,159 - 17,78 + 0,0
22 1,168 - 19,19 -2,5
23 1,176 -20,69 -5,2
23,3(эвт.) 1,179 -21,13 -6,0
24 1,184 - 17,0а + 1,4а
25 1,193 - 10,4а 13,За
26 1,201 -2,За 27,9а
26,3 1,203 о,оа 32,0а
моль мочеви-
ны/1000 г
Н2О 477
0,000538 0,001002
0,004235 0,007846
0,007645 0,01413
0,012918 0,02393
0,01887 0,03496
0,03084 0,05696
0,04248 0,07850
4.12. Ниже представлены температуры замерзания
охлаждающих водных соляных растворов. Используя
дополнительные данные о теплоемкости, определите
коэффициенты активности воды в диапазоне концентра-
ций вплоть до эвтектической. [Данные Lange Handbook
of Chemistry, 1973 и CRC Handbook of Chemistry and
Physics, 1979.]
Температура замерзания растворов хлорида натрия
[NaCl], масс. % Удельная масса Температура (г/л) при 15 °C замерзания
(59 °F) °C °F
0 1 1,000 1,007 0,00 -0,58 32,0 31,0
2 1,014 -1,13 30,0
3 1,021 - 1,72 28,9
4 1,028 -2,35 27,8
5 1,036 -2,97 26,7
6 1,043 -3,63 25,5
7 1,051 -4,32 24,2
8 1,059 -5,03 22,9
9 1,067 -5,77 21,6
10 1,074 -6,54 20,2
11 1,082 -7,34 18,8
а) Температуры насыщения дигидрата хлорида на-
трия; при этих температурах NaCl 2Н2О выделяется,
оставляя раствор эвтектического состава (эвт.).
Удельная теплоемкость льда (Дикинсон — Осборн, 1915)
Температура, °C СР, кал/г/°С
-31,8 0,4454
-23,7 0,4599
-24,5 0,4605
-20,8 0,4668
- 14,8 0,4782
- 14,6 0,4779
- 11,0 0,4861
-8,1 0,4896
-4,3 0,4989
-4,5 0,4984
-4,9 0,4932
-2,6 0,5003
-2,2 0,5018
Удельная теплоемкость воды при температуре ниже
0 °C (Мартинетти, 1890)
-6 1,0119
-5 1,0113
-4 1,0105
-3 1,0102
- э 1,0097
1 1,0092
(Барнз, 1902)
-5 1,0155
16*
244 Глава 4
4.13. Температуры кипения водных растворов NaOH
при атмосферном давлении равны
[NaOH], масс. % 20 30 40 50 60 Метанол + хлороформ 12 1703,68 -373,30
Температура ки- Метанол + этилацетат 13 985,69 -200,36
пения, °F 221 233 249 288 305 Хлороформ + этилацетат 23 -367,50 -92,50
В этом температурном интервале энтальпию воды
можно принять независимой от давления. Определите
коэффициенты активности воды при различных темпе-
ратурах.
4.14. Ниже указана взаимная растворимость (масс.
%) фурфурола (А) и воды (В) при различных темпера-
турах [663].
А в Г, °C А В т, °C А В Г, °C
7,9 92,1 10 14,8 85,2 80 91,4 8,6 60
8,3 91,7 20 16,6 83,4 90 92,4 7,6 50
8,8 91,2 30 18,4 81,6 97,9 93,3 6,7 40
9,5 90,5 40 84,1 15,9 97,9 94,2 5,8 30
10,4 89,6 50 86,7 13,3 90 95,2 4,8 20
11,7 88,3 60 88,7 11,3 80 96,1 3,9 10
13,2 86,8 70 90,3 9,7 70
а) Определите коэффициенты активности для каждого
условия равновесия.
б) Подберите эмпирические уравнения к кривым, ха-
рактеризующим зависимость параметров уравнения ван
Лаара от температуры.
4.15. Ниже указано давление пара водного раствора
КНСОз при 100 °C в виде функции мольной доли соли
(х).
xsalt PS, атм xsalt атм
0,0089 0,9847 0,0822 0,8263
0,0176 0,9689 0,0970 0,7895
0,0346 0,9224 0,1253 0,7237
0,0510 0,8979 0,1519 0,6392
0,0668 0,8629
а) Определите коэффициент активности воды при не-
скольких концентрациях.
б) Найдите отношение 7/7” для соли как функцию
температуры, используя метод экстраполяции к нулевой
концентрации, описанный Левисом и Рэнделлом (1961).
4.16. Параметры уравнения ван Лаара для смесей
этанол + вода имеют следующие значения: А = 0,7292,
5 = 0,4104. Аппроксимируйте осмотическое давление
как функцию мольной доли этанола в растворе.
4.17. Найдите избыточные энтальпии всех эквимоляр-
ных двухкомпонентных и эквимолярной тройной смесей
при 300 К, используя приведенные ниже параметры
уравнения Вильсона (кал/моль).
4.18. Вещество А следует выделить из раствора в ве-
ществе В путем диффузии через полупроницаемую мем-
брану. Чистота слоя растворителя С, находящегося по
одну сторону мембраны, поддерживается посредством
протока. По другую сторону мембраны = 5,7 атм,
хао = 0,9, 7оо = уьп = 1,25. Применив уравнение ван Ла-
ара, найдите концентрацию ха, при которой скорость
массопередачи через мембрану составит 10% исходной
величины.
4.19. Ниже приведены данные о парциальных давле-
ниях (мм рт. ст.) толуола и уксусной кислоты при
69,94 °C (International Critical Tables, Volume III, pp. 217,
223 и 288). Для решения этой задачи допустим, что пар-
циальное давление каждого компонента тождественно
его фугитивности.
М (толуол) Ni (уксусная кислота) Р\ (толуол) Pi (уксусная кислота)
0,0000 1,0000 0 136
0,1250 0,8750 54,8 120,5
0,2310 0,7690 84,8 110,8
0,3121 0,6879 101,9 103,0
0,4019 0,5981 117,8 95,7
0,4860 0,5140 130,7 88,2
0,5349 0,4651 137,6 83,7
0,5912 0,4088 145,2 78,2
0,6620 0,3380 155,7 69,3
0,7597 0,2403 167,3 57,8
0,8289 0,1711 176,2 46,5
0,9058 0,0942 186,1 30,5
0,9565 0,0435 193,5 17,2
1,0000 0,0000 ^02 0
а) Постройте кривую зависимости от М. Покажите
(штриховой линией) на графике зависимость, описывае-
мую законом Рауля.
б) Постройте кривую зависимости /2 от Nz. Покажите
(штриховыми линиями) на графике зависимости, опи-
сываемые законами Рауля и Генри.
в) Найдите константу закона Генри для уксусной кис-
лоты в растворах толуола путем экстраполяции зависи-
мости fz/Nz от Nz до бесконечного разбавления.
г) Рассчитайте активности и коэффициенты активнос-
ти уксусной кислоты, исходя из величин /2, найденных
из закона Генри. Постройте графики зависимости этих
величин от N2.
д) Рассчитайте активности и коэффициенты активнос-
ти уксусной кислоты, исходя из величин /2' найденных
Коэффициенты активности 245
из закона Генри. Нанесите эти данные на график, по-
строенный согласно требованиям п. «г».
е) Рассчитайте активности и коэффициенты активнос-
ти толуола, являющегося растворителем в этих рас-
творах.
4.20. Активность компонента двухкомпонентной сме-
си определяется по уравнению Ы71 = а/(1 + bxi/x2)2.
Составьте уравнение для определения избыточной энер-
гии Гиббса, используя уравнение (4.22).
4.21. Данные о равновесии были получены в рецирку-
ляционном перегонном аппарате для системы тетрахло-
рид углерода + хлороформ при 40 °C. Известны сос-
тав, давление пара, полное давление, вторые вириаль-
ные коэффициенты и молярные объемы жидкости. Оп-
ределите коэффициенты активности и избыточную энер-
гию Гиббса. х2 = 0,5242, у2 = 0,6456, Р]м = 28,443 кПа,
Р2М = 48,064, Р = 40,242, Вц = - 1465 мл/моль,
В22 = - 1040, би = 0, rf = 99 мл/моль, Г2' = 82.
4.22. Ниже указаны температуры кипения системы
этанол + бензол при 750 мм рт. ст. Путем экстраполя-
ции графиков «кажущихся коэффициентов активности»
У* = (Р - х2РЬ/х\р<1 ,
у* = (p_X1P'J)/x2P^
определите коэффициенты активности при бесконечном
разбавлении. Сравните графики кажущихся коэффициен-
тов активности с графиками коэффициентов активнос-
ти, рассчитанных по уравнению ван Лаара, исходя из
этих же vT и у2.
*1 T psat psat
0,0 79,7 804 750
0,04 75,2 671 648
0,11 70,8 560 562
0,28 68,3 507 518
0,43 67,8 497 509
0,61 68,3 507 518
0,80 70,1 545 549
0,89 72,4 598 592
0,94 74,4 650 632
1,00 78,1 750 711
4.23. Полное давление смеси СбН6(7) и CCI2FCCIF2
(2) при 25 °C и X] = 0,26 равно 291,9 мм рт. ст.
Компонент С, мл/моль Psal
1 89 95,2
2 120 333,1
а) Найдите разность параметров растворимости
51 — 5г.
б) Определите состав пара.
4.24. Формулы для определения влияния температу-
ры на параметры растворимости, приведенные в работе
[333], включают коэффициент термического расширения
а. Эти формулы имеют следующий вид:
d\n8D/dT = -1,25а,
d\r\8P/dT = —0,5а,
din 8H/dT = -(0,00122 + 0,5а).
Для этанола при температуре 298,2 К 5о = 7,7, 5р =
= 4,3, 5н = 9,5 и а = 0,0011. Определите параметр рас-
творимости при 75 °C.
4.25. Определите коэффициенты активности при бес-
конечном разбавлении по уравнению Вильсона и с ис-
пользованием параметров растворимости Гоя для не-
скольких смесей из числа приведенных в табл. Д.8.
4.26. Ниже приведены данные о равновесии и давлении
пара смеси метилацетат + метанол при 5907 мм рт. ст.
X У T°C P? P5
0,294 0,336 123,5 4 951,9 5 145,4
0,471 0,471 123,2 4 917,8 5 103,6
0,736 0,678 125,6 5 195,2 5 445,4
Принимая, что </>!а1/ф, = 1, найдите коэффициенты ак-
тивности и параметры уравнений Маргулеса и ван
Лаара.
4.27. Ниже указаны составы равновесных смесей
ацетон + гексан и их полные давления при - 5 °C.
X У P
0,2618 0,5688 70,29
0,6039 0,6161 73,26
0,8535 0,6850 70,87
Давления пара равны Р? = 53,54 и Р? = 34,23 мм
рт. ст. Определите коэффициенты активности и пара-
метры уравнений Маргулеса и ван Лаара. Регрессия
полных данных для этой системы дана в сб. DECHEMA
(DECHEMA VLE Data Collection part 3—4, 227); для
уравнения Маргулеса A = 2,016, В = 2,102; для уравне-
ния ван Лаара А = 2,012, В = 2,106.
4.28. Используя уравнения Эллиса и Джона (разд.
4.15), найдите коэффициенты активности при бесконеч-
ном разбавлении по данным задачи 4.35 для системы
метанол + дихлорэтан при 40 °C. Примите поведение
газа за идеальное и исходите из допущения о том, что
удельные объемы жидкости пренебрежимо малы по
сравнению с удельными объемами паров.
4.29 Найти избыточные энтальпии эквимолярных
смесей этанол + вода при 25, 50 и 75 °C. Согласно рис.
4.2,
Т, °C 25 50 75
Яех, кал/моль -100 -10 50
Параметры уравнений Вильсона, известные для 50 °C, мо-
гут считаться постоянными (DECHEMA VLE Data Collec-
tion, Part 1, p. 191): Xi2 = 101,81, X21 = 916,49 кал/моль,
Kj/Kz = 0,308.
246 Глава 4
Примечание. Степень соответствия может быть доволь-
но низкой.
4.30. Для некоторой двухкомпонентной смеси извест-
ны следующие данные: In «Г = 3, Iny* = 2, И/Иг = 2,5,
NRTL an = 0,3, UNIQUAC kj = - 2,2, к» = - 0,8 (табл.
4.5). Найдите следующие параметры уравнений для ко-
эффициентов активности: уравнение Вильсона Х12, Л21;
уравнение Цубоки — Катаямы — Вильсона Л12, Л21;
уравнение NRTL 712, 721; уравнение UNIQUAC 712, 721.
Постройте графики при помощи уравнений Вильсона и
NRTL.
4.31. Температура плавления о равна 1808 К, энталь-
пия плавления составляет 1,536 • 104 Дж/моль. Теплоем-
кость железа в жидком состоянии превышает его
теплоемкость в кристаллическом состоянии примерно
на 1,3 Дж/К • моль. Покажите, что разность свободной
энергии жидкого и кристаллического железа как функ-
ция температуры при постоянном давлении, выражен-
ная в Дж/моль, составит
Д<7°= 1,3 X 104— 1,ЗГ1пГ+ 2,6Г.
При 1673 К жидкая смесь железа и сульфида железа,
содержащая 0,870 мол. доли железа, находится в состо-
янии равновесия с почти чистым кристаллическим <5-же-
лезом. Определите коэффициент активности железа в
данном жидком расплаве.
4.32. Сравните величины коэффициентов активности,
рассчитанные по уравнению Скэтчарда — Гильдебранда
и уравнению Скэтчарда — Гильдебранда — Флори —
Хаггинса, включающего поправку на энтропию, и экспе-
риментальные данные для смеси бензол (/) + цикло-
пентан (2) при 35 °C, полученные Герменсеном и Прауз-
ницем (1963).
Х1 71 72
0,0 1,5541 1,0000
0,1 1,4218 1,0047
0,2 1,3150 1,0186
0,3 1,2294 1,0416
0,4 1,1611 1,0742
0,5 1,1075 1,1165
0,6 1,0664 1,1693
0,7 1,0362 1,2333
0,8 1,0157 1,3096
0,9 1,0038 1,3993
1,0 1,0000 1,5044
4.33. Ниже приведены данные о равновесии между
двумя жидкими и одной паровой фазой системы
бутан + вода, состав которой указан в мольных про-
центах бутана [405].
Х1 V* Х1 У1 °C Р psat psat
0,0044 99,909 98,57 37,9 3,550 3,78 0,065
0,0059 99,662 96,49 71,1 8,493 8,63 0,323
0,0105 99,075 94,70 104,6 17,741 16,90 1,178
0,0186 97,20 92,49 137,8 33,429 29,24 3,355
Найдите коэффициенты активности бутана и воды в
двух жидких фазах:
а) исходя из взаимной растворимости компонентов
системы и используя уравнение ван Лаара;
б) исходя из данных о равновесии между паром и
жидкостью и используя указанные давления пара;
в) исходя из простого правила, согласно которому
для малорастворимых соединений 7, = 1/х.
4.34. Исходя из разложения в ряд, предложенного
Редлихом и Кистером для определения избыточной
энергии Гиббса,
Сех/В7’ = х1х2[Л + В(хх ~х2) + С(Х] -х2)2
+ D(X1 -х2)3 + . ..],
выведите следующие уравнения для коэффииентов ак-
тивности:
In у ] = а*1 Ьс + М1 Ьс + с*1 Ьс 2 + </( 1 Ьс + . . . ,
Iny2 = a(2)xj + b^x2 + c(2)xf + + . . . ,
где
а<»=А + ЗВ + 5С + 1D, а<2> = А — ЗВ + 5С — 1D,
М1) = —4(В + 4С + 9D), М2) = 4(В - 4С + 9D),
с*1’ = 12(С + 5D) с<2> = 12(С - 5£>),
d^^~32D d^ = 32D.
4.35. Для следующих четырех групп коэффициентов
активности найдите параметры уравнений Редлиха —
Кистера второй, третьей, четвертой и пятой степени.
Применив статистический критерий F, определите целе-
сообразность использования этих сложных уравнений
для указанных данных (взяты из работы [69]).
Азотная кислота + вода (Р = 760 мм рт. ст.)
X У t Р 71 72
6,1 0,36 104,0 760 0,0324 0,9288
9,6 0,95 106,4 0,0188 0,8884
И,7 1,50 107,8 0,0633 0,8592
13,9 2,11 109,4 0,0703 0,8420
17,5 4,23 111,8 0,1046 0,8065
18,3 5,10 112,3 0,1212 0,7525
22,5 8,95 114,8 0,1588 0,7080
26,6 13,60 116,8 0,1955 0,6937
27,7 15,99 117,5 0,2151 0,6447
34,1 25,90 119,4 0,2660 0,5919
37,4 36,50 119,9 0,3430 0,5408
38,3 37,45 120,0 0,3420 0,5372
48,5 73,00 116,1 0,5720 0,3110
52,1 81,08 113,4 0,6393 0,2517
54,7 85,00 110,8 0,7063 0,2316
65,1 94,20 102,9 0,8434 0,1501
71,9 97,20 96,1 0,9425 0,1153
76,5 98,75 92,0 — —
81,6 99,30 88,4 — —
100,0 100,00 83,4 — —
Коэффициенты активности 247
Гептан + фурфурол (Р = 760 мм рт. ст.)
X У t Р 71 72
10 78,4 114,0 760 5,262 1,019
20 86,8 102,3 3,960 1,082
30 88,6 98,7 2,939 1,201
40 89,1 98,3 2,236 1,393
50 88,8 98,7 1,762 1,690
60 88,5 99,2 1,445 2,158
70 88,4 99,2 1,235 2,897
80 89,2 98,9 1,100 4,103
90 92,1 98,4 1,024 6,152
Метилэтилкетон + циклогексан (Р = 760 мм рт. ст.)
X У t Р 71 72
6,0 16,4 77,0 760 2,9678 0,9947
13,1 25,3 74,7 2,2586 1,0326
17,5 29,9 73,7 2,0644 1,0532
24,7 35,6 72,6 1,8055 1,0976
36,9 42,0 71,8 1,4640 1,2101
48,0 46,5 71,5 1,2585 1,3675
64,5 57,4 72,1 1,1334 1,5647
73,6 63,4 73,0 1,0650 1,7568
80,4 69,8 74,0 1,0387 1,8919
87,6 77,7 75,3 1,0173 2,1202
Метанол + дихлорэтан (t = 40 °C)
X У t Р 71 72
0 0,0 40 150,0 — 1,000
10 47,9 265,4 4,800 1,024
20 56,9 303,5 3,261 1,093
30 59,2 319,9 2,380 1,239
40 60,3 325,0 1,848 1,435
50 60,5 326,8 1,493 1,720
60 61,4 327,9 1,278 2,110
70 64,0 327,4 1,130 2,619
80 69,7 320,4 1,053 3,241
90 81,0 301,7 1,012 4,020
100 100,0 265,0 1,000 —
4.36. Рассмотрите смесь н-гексан + диэтилкетон, ха-
рактеристики которой даны в задаче 4.50. Используя
только один из коэффициентов активности при беско-
нечном разбавлении, найдите за один прием С|2 однопа-
раметрического уравнения UNIQUAC и соответственно
712 и 721, отвечающие каждому из этих уТ. Величины
внутренней энергии испарения рассчитывают исходя из
скрытых энтальпий испарения по уравнению Питцера
(см. пример 4.7а), что дает
Дм jaP = 6161 кал/моль,
Д«2ар = 7,222 кал/моль.
4.37. Коэффициенты активности при бесконечном
разбавлении системы ацетон (1) + хлороформ (2) при
1 атм равны 0,37 и 0,46 соответственно. При Л] = 0,345
и 64,5 °C образуется азеотропная смесь. Определите ко-
эффициенты активности при равном 0,25, 0,50 и
0,75, исходя из обеих групп данных при помощи а)
уравнения Маргулеса, б) уравнения Вильсона, в) уравне-
ния NRTL при ai2 = 0,30.
4.38. Согласно данным, приведенным в табл. Д.10,
параметры уравнения ван Лаара системы метилацетат
(1) + метанол (2) имеют следующие значения: А =
= 0,4262 и В = 0,4394 [Бушмакин, Киш Журн. прикл.
хим., 30, 200 (1957)]. Определите азеотропный состав
при давлении 1 атм и сравните его с полученным в при-
мере 4.16 на основании других экспериментальных дан-
ных. Параметры даны для давления 1 атм.
4.39. Коэффициенты активности компонентов некото-
рых двухкомпонентных смесей определяют при помощи
следующих уравнений:
7?71n-yi = ах?.,
RTlnyi = axl.
где а — функция только давления. Получите выраже-
ния для изменения функции Гиббса и энтальпии при
смешении чистых компонентов при постоянных темпе-
ратуре и давлении.
В процессе смешения, которое ведется при постоян-
ной скорости подачи потока, эквимолярная смесь с
а =- 418 Дж/моль, разделяется на чистые компоненты
путем дистилляции. Впуск и выпуск осуществляются
при 20 °C и 1 атм. Единственным источником энергии
является термостат, в котором поддерживается посто-
янная температура 100 °C. Рассчитайте, какое количе-
ство теплоты (на моль дистиллируемой смеси) следует
отвести охлаждающей водой при 20 °C, если энергия
используется с максимальной эффективностью (Den-
bigh).
4.40. При атмосферном давлении этилацетат и этило-
вый спирт образуют азеотропную смесь, содержащую
53,9 мол. % этилацетата, с температурой кипения
71,8 °C.
Определите а) величины констант А и В в эмпириче-
ских уравнениях ван Лаара:
1пу1
1пу2 =
и б) состав азеотропной смеси и соответствующее пол-
ное давление при кипении при температуре 56,3 °C, ес-
ли А и В не меняются.
Давление пара (мм рт. ст.) чистых жидкостей:
71,8 °C 56,3 °C
Этанол
Этилацетат
587 298
636 360
248 Глава 4
4.41. Проверьте возможность существования экстре-
мумов на кривых коэффициентов активности, построен-
ных по а) уравнению ван Лаара и б) уравнению
Вильсона.
4.42. Рассмотрите величины параметров уравнения
Вильсона, обусловливающих появление экстремумов на
графиках зависимости Ы71 от х(. Рассмотрите тот осо-
бый случай, для которого Л12 = 0, и найдите величины.
Л21, определяющие появление экстремумов в интервале
значений х( от 0,1 до 0,9.
4.43. Избыточные энергии Гиббса смесей метан +
пропан описываются уравнением
Ge = (1 — х)х S а.( 1 — 2х)‘-
i =0
т, к Ge\ Дж/моль
а0 а/ «2
90 756,8 277,4 19,8
95 755,1 287,0 40,0
100 759,6 297,7 45,8
105 766,8 308,7 43,5
110 774,2 318,9 54,0
где х — мольная доля пропана (Selected Data on
Nonelectrolyte Mixtures, 1973).
а) Найдите соответствующие уравнения для коэффи-
циентов активности; б) проверьте справедливость допу-
щения того, что ТЛп7, = const.
4.44. Для смеси с 7“ = 3 и 7" = 2 постройте графики
уравнения Вильсона и уравнения Маргулеса. Парамет-
ры уравнения Вильсона: Л12 = 0,3465, Л21 = 0,9612.
4.45. Для интеграла j*'ln(7i/72)dxi, применяемого
для оценки термодинамической согласованности, найди-
те только ту величину, которая превышает 71/72 = 1.
Используйте для этого а) симметричное уравнение, для
которого Gex/RT = ДХ1Х2; б) уравнения ван Лаара.
4.46. Покажите, что функция избыточной энергии
Гиббса Ge*/RT =-----1----+ Cxix2(xt - х2)2 приводит
--„ -----
Axi Вхг
к формулировке следующего уравнения Блэка [189]:
1п71 = А (— ВХ---) + Cxi(2x2 — 1)(6х2 — 5),
+ BxzJ
(Л у, \ ~
— — ) + Cxi(2xi - 1)(6х, - 5).
Axi + Вхг/
Найдите величины параметров при условии, что 1П7Г =
= 3, 1П72 = 2 и 1п7| = 0,6 при Xi = 0,5.
4.47. Для системы ацетон + гексан определите состав
равновесной паровой фазы при 55 °C и х(, равном
0,1846 и 0,8021, используя уравнения Маргулеса, Виль-
сона и NRTL. Давления пара составляют 731,5 и 483,0
мм рт. ст., соотношение удельных объемов V\/Vz =
= 0,562. Параметры уравнений имеют следующие зна-
чения: уравнение Маргулеса А = 1,4449, В = 1,6488;
уравнение Вильсона Х32 = 921,52 кал/моль, X2i = 420,36;
уравнение NRTL /?7т12 = 746,25 кал/моль, RTT21 =
= 424,42, O!i2 = 0,292. Экспериментальные величины со-
ставляют: yi = 0,476, У2 = 0,700 (DECHEMA VLE Data
Collection part 3/4, p. 224).
4.48. Ниже приведены экспериментальные данные и
параметры уравнения Вильсона для равновесия пар—
жидкость тройной смеси. Для данного состава жидкос-
ти сравните рассчитанный состав паровой фазы с экспе-
риментально найденным.
х у Psat, атм
Ацетон 1 0,3130 0,5240 1,190
Тетрахлорметан 2 0,2440 0,2100 0,666
Бензол 3 0,596
Х12 = 744,085 X2i = - 74,704 кал/моль
Х13 = 442,011 Xi3 = - 152,877 кал/моль
Х23 = - 26,5 25 х32 = 142,519 кал/моль
Т = 64,2 °C
4.49. При помощи уравнения Гиббса—Дюгема, запи-
санного в следующей форме:
яех dT уех dp (/1пу1 d in у2
RT2 dx] RT dxi dx\ dx.
покажите, что в условиях, соответствующих образова-
нию азеотропной смеси,
а) при постоянной температуре dP/dxx = dP/dy\ = 0,
б) при постоянном давлении dT/dxx = dT/dy\ = 0,
т. е., другими словами, что линия ликвидуса и линия
пара на диаграммах Р — Xi или Т — Xi (см. рис. 4.25)
не могут ни пересекаться, ни соприкасаться нигде, кро-
ме экстремумов.
4.50. Согласно данным, полученным Марипури и Рэт-
клифом [J. Appl. Chem. Biotechnol., 22, № 899 (1972)],
коэффициенты активности при бесконечном разбавле-
нии н-гексана (1) и диэтилкетона (2) равны 7“ = 2,25 и
У2 = 3,67. Данные о давлении пара представлены сле-
дующими уравнениями:
Р? = ехр[15,8366 - 2 607,55/(7’ — 48,78)],
Р° = ехр[16,8138 - 3 410,51/(7’ — 40,15)],
где Р измеряется в мм рт. ст., а Т — в кельвинах.
Удельная масса составляет соответственно 0,659 и
0,814.
а. Найдите параметры следующих корреляционных
уравнений, используемых для определения коэффициен-
тов активности: 1) уравнения ван Лаара, 2) уравнения
Вильсона, 3) уравнения Цубоки—Катаямы—Вильсона,
4) уравнения UNIQUAC, 5) уравнения NRTL при
«12 = - 1.
б. При помощи каждой из этих корреляций, а также
уравнения для идеальных смесей определите число тео-
ретических тарелок, необходимое для разделения экви-
Коэффициенты активности 249
молярной смеси на верхний погон (yi = 0,95) и кубовый
остаток (xi = 0,02) при условии, что поток флегмы на
20<% превышает минимальную величину. Молярный пе-
реток при дистилляции можно считать постоянным, за
сырье можно принять насыщенную жидкость. Давление
равно 1 атм.
4.51. Покажите, что уравнения Маргулеса (4.73) и
(4.74) согласуются со следующей формой уравнения
Гиббса—Дюгема:
X] d In у j + х2*/1пУ2~0-
Покажите также, что А должен равняться В при Inyi =
= Axl и 1пу2 = Вх\.
4.52. При помощи программы, приведенной в табл.
В.11, определите состав пара, находящегося в равнове-
сии с жидкой фазой следующего состава: метанол 0,1,
этанол 0,1, изопропанол 0,18, вода 0,62. Давление пара
равно 3,50, 2,23, 1,11 и 1,00 соответственно. Параметры
уравнения Вильсона даны в таблице
J
i 1 2 3 4
1 1 2,3357 2,7385 0,4180
2 0,1924 1 1,6500 0,1108
3 0,2419 0,5343 1 0,0465
4 0,9699 0,9560 0,7795 1
4.53. Составьте программу для решения на ЭВМ
уравнения NRTL, аналогичную программе для решения
уравнения Вильсона, приведенной в табл. В.11.
4.54. Для смесей метилацетата (1) и метанола (2) при
40 °C Хирата и др. [57] приводят следующие парамет-
ры уравнения Вильсона: Ai2 = 0,45159 и Л21 = 0,57116.
Постройте а) диаграмму х—у при давлении 760 мм рт.
ст., б) графики зависимости 6ех, /7ех и T'S" от xi при
40 °C.
5. ФАЗОВОЕ РАВНОВЕСИЕ
В данной главе мы поставили себе целью рассмот-
реть классификацию некоторых типов равновесия и об-
судить характерные примеры таких равновесий глав-
ным образом из органической химии. Количественные
корреляции и расчеты фазовых превращений, и их при-
менений анализируются в последующих главах.
Фазовая диаграмма описывает влияние температуры,
давления и состава на вид и число фаз, которые могут
сосуществовать. Число фаз определяется согласно пра-
вилу фаз Гиббса рядом переменных (разд. 5.2). Вид фаз,
которые могут сосуществовать в каких-то конкретных
условиях, зависит от химической природы компонен-
тов. Графическое представление фазового равновесия
более удобно, чем составление числовых таблиц, по-
скольку позволяет охватить взаимные связи между все-
ми переменными, провести интерполяцию или экстра-
поляцию. Использование нескольких видов диаграмм
полезно потому, что позволяет подчеркнуть зависи-
мость от нескольких переменных. Проще всего строить
двухкоординатные диаграммы, но они, конечно, огра-
ничены изменением только двух переменных. Для того
чтобы показать влияние других переменных, необходи-
мо построить серию таких диаграмм при постоянных
значениях одной или более переменных, например в ви-
де изобар, изотерм или изоплет (исходная смесь посто-
янного состава). Во многих случаях целесообразно
пользоваться пространственными трехмерными фазо-
выми диаграммами. Известным исследователем Рузебу-
мом [138] — пионером систематизации данных по
фазовым равновесиям — построено несколько про-
странственных моделей диаграмм. Прекрасные стерео-
скопические диаграммы (восемьдесят образцов)
сделаны Тамасом и Палом [132].
Очевидно, что число многофазных систем весьма ве-
лико. Однако более сложные диаграммы, как правило,
можно рассматривать как комбинацию более простых
диаграмм, так что кажущееся разнообразие не беспре-
дельно. В табл. 5.1 показана практическая классифика-
ция многофазных систем [89]. Подобные классификации
даны в обстоятельных книгах Риччи [НО] и Фогеля
[139] (см. также разд. 5.7). Различные типы фазовых
диаграмм представлены также на рис. 5.16 и 5.21.
Первичная классификация соответствует числу компо-
нентов, затем типу и числу фаз. Учитывается также
возможность межмолекулярных взаимодействий и по-
лиморфных превращений в твердых средах. Число воз-
можных комбинаций резко возрастает с увеличением
числа компонентов, поэтому экспериментальных иссле-
дований систем более чем с тремя компонентами край-
не мало. В некоторых областях фазовые превращения
в многокомпонентных системах могут быть оценены из
данных для небольшого числа простых систем, включа-
ющих отдельные компоненты.
Не все комбинации переменных встречаются часто
или представляют практический интерес. Наиболее рас-
пространены двух- или трехкомпонентные системы, со-
держащие только паровую и газовую фазы, либо две
или три жидкие фазы, либо жидкую и твердую фазы.
Данные об одном виде равновесных систем, например
пар — жидкость, для одной группы компонентов мож-
но в определенных пределах распространить и на дру-
гие системы, например жидкость — жидкость или
твердая фаза — жидкость; общая концепция такой
оценки основана на понятиях парциальной фугитивнос-
ти или химических потенциалов.
Помимо состава систем наибольшее внимание при их
изучении уделяется влиянию температуры и давления
(особенно для парожидкостных систем) или только
температуры (для конденсированных систем). В боль-
шей части работ, посвященных изучению фазовых рав-
новесий конденсированных систем, рассматриваются
соединения кремния, металлы и водные растворы со-
лей. Однако аналогичным образом могут себя вести и
органические системы, которым уделено основное вни-
мание в данной главе. Подробная библиография работ,
посвященных этой теме, опубликована авторами обзо-
ра [20], более старые работы рассмотрены в обзоре
[73]. Ряд источников указан в соответствующих главах
Изучение фазового равновесия в многокомпонентных
системах, например подобных тем, с которыми прихо-
дится иметь дело в металлургии, потребовало много-
летнего труда многих исследователей. Специфические
сложные органические системы редко имеют столь же
важное промышленное значение, поэтому фазовому рав-
новесию таких систем уделено значительно меньше вни-
мания. Поведение органических систем иногда описыва-
ется адекватно поведению идеальных систем или только
в рамках бинарных систем, которые можно объединять
в несколько типовых систем для определения поведения
многокомпонентных систем, составленных из отдель-
ных пар. Краткий обзор экспериментальных методов
исследования фазовых равновесий представлен в гл. 12.
Фазовое равновесие 251
Таблица 5.1. Классификация систем твердая фаза — жидкость [89]
Число компонентов Класс Группа Свойства
1 I а Единственная модификация Тройная точка ниже атмосферного давления
b Тройная точка выше атмосферного давления
II а Несколько модификаций Все модификации стабильны
b Одна из модификаций нестабильна
2 I а ai Компоненты в твердой фазе нерастворимы Компоненты не образуют стехиометрических со- единений Компоненты в жидкой фазе полностью растворимы
а2 Компоненты в жидкой фазе частично растворимы
а3 Компоненты в жидкой фазе нерастворимы
b bi Компоненты образуют стехиометрические соединения Соединение стабильно вплоть до температуры
плавления
b2 Соединение нестабильно при температуре плавления
II а ai Компоненты в твердой фазе полностью растворимы Компоненты не образуют твердых соединений Кривая температур плавления не имеет максимумов или минимумов
а2 Кривая температур плавления имеет максимум или минимум
b Компоненты образуют твердое соединение
III а Компоненты в твердой фазе частично растворимы Температуры плавления компонентов близки
b Температуры плавления компонентов значительно различаются
3 I а Компоненты в твердой фазе нерастворимы Компоненты не образуют стехиометрических со- единений
b bi Компоненты образуют стехиометрическое соединение Образуются бинарные соединения
b2 Образуются тройные соединения
II а Компоненты в твердой фазе взаиморастворимы Компоненты твердой фазы полностью растворимы
b Компоненты в твердой фазе частично растворимы
4 I Четыре различных компонента
II Попарные соляные системы
252 Глава 5
Таблица 5.2. Важнейшие характеристики, используемые
для идентификации или описания фазового равновесия
I. Однокомпонентные системы, для которых спра-
ведливо следующее правило фаз: Ph - 3 - F
1. Равновесие пар — твердое вещество
2. Равновесие пар — жидкость
3. Равновесие жидкость — твердое вещество
4. Полиморфизм кристаллического состояния
5. Критические и тройные точки
II. Бинарные системы, Ph = 4 - F
1. Система пар — жидкость, зависимости Т— х и
Р— х
а. Одна жидкая фаза
1. Монотонное изменение давления паров
2. Изменение давления паров характеризу-
ется минимаксом
2. Система жидкость — твердое вещество, зависи-
мости Т— х
а. Чистые твердые фазы
б. Твердые растворы
в. Наличие минимума (эвтектика) или максиму-
ма на кривой плавления
г. Перитектика (два твердых раствора и одна
жидкая фаза)
3. Интермолекулярные соединения в твердой фазе
а. Конгруэнтное плавление (без разложения)
б. Инконгруэнтное плавление (с разложением)
III. Тройные системы, Ph - 5 - F
1. Пар и одна жидкая фаза
2. Множество жидких фаз
3. Жидкая и твердая фазы
а. Чистые твердые фазы
б. Твердые растворы
4. Интермолекулярные соединения в твердой фазе
IV. Системы четвертого и высших порядков, Ph = 2 +
+ С - F.
5.1. Графическое представление
При построении фазовой диаграммы системы из п ве-
ществ необходимы следующие переменные: Т, Р и
п - 1 мольных фракций. Взаимозависимость трех пере-
менных можно отразить лишь посредством простран-
ственных диаграмм, однако возможен и альтернатив-
ный подход, позволяющий упростить построение: мож-
но использовать серию плоскостных диаграмм при
определенных фиксированных значениях третьей пере-
менной, либо контурами показывать значения третьей
переменной на одной диаграмме. Мольный состав трой-
ных систем представляется на плоской треугольной диа-
грамме, а мольный состав четырехкомпонентных сис-
тем — на пространственной диаграмме в виде правиль-
ного тетраэдра. Различные области фазовой диаграм-
мы могут иметь различное смысловое значение,
поскольку число фаз в них неодинаково, и может зави-
сеть от числа компонентов в системе. Связь между чис-
лом компонентов, числом фаз и рядом переменных,
определяющих состояние системы, обсуждаются в сле-
дующем разделе.
5.1.1. Однокомпонентные системы. На фазовой диа-
грамме однокомпонентной смеси типа изображенной на
рис. 5.1 каждая из фаз представлена в виде открытой
зоны, твердая фаза — в зоне выше линий АВ и левее
линии BD. Вдоль линии типа АВ две фазы находятся
в равновесии, в данном случае это твердая и газовая
фазы. В точке пересечения трех линий, точка В, три фа-
зы находятся в равновесии; это наибольшее число фаз,
способных сосуществовать в равновесии в однокомпо-
нентных системах. Как будет показано позднее, чистые
твердые фазы могут иметь несколько стабильных кри-
сталлических форм, поэтому зона твердой фазы ABD
может быть представлена несколькими областями. По-
скольку некоторые классы веществ могут образовывать
жидкие кристаллы, зона DBC также может состоять из
нескольких областей. Точка С — критическая точка диа-
граммы, по достижении которой исчезают различия
между свойствами жидкости и газа. Критические точки,
соответствующие другим парам фаз, отсутствуют.
Штриховыми линиями показаны границы зон метаста-
бильной переохлажденной жидкости и перегретого
пара.
5.1.2. Двухкомпонентные системы. Совместное влия-
ние Т и Р на состав двухкомпонентных смесей представ-
лено на пространственных диаграммах (рис. 5.2,а,
5.2,6). Необходимо заметить, что та же самая инфор-
мация представлена на этих диаграммах в более удоб-
ной форме в виде изобарических (или в отдельных
случаях изотермических) сечений или в виде проекций
на основание (рис. 5.2,6). Двухфазные зоны заштрихо-
ваны. На рис. 5.3 показаны три общих типа двухфаз-
ных систем при постоянном давлении, демонстриру-
ющие впияние температуры и общего состава смеси на
состояние фаз системы. Области однофазных сис-
тем различного состава ограничены отрезками ха—хь,
хс—Xd, хе—Xf изотермы af (рис. 5.3,в). В других обла-
стях существуют двухфазные смеси с различным соот-
ношением количеств фаз состава хь и хс или Xd и хе. В
двухфазных областях состав фаз фиксирован, но их от-
носительные количества меняются в соответствии с об-
щим составом смеси и не влияют на условия
равновесия.
При снижении температуры вдоль изоплеты, напри-
мер g—к, пересечение ею любой линии указывает на ка-
кое-то изменение фазового состояния. Между точками
h и i образуются две фазы различного состава, соотно-
шение которых также может быть различным, тогда
как в зоне между точками I и j существует единичная
твердая фаза, а после точки j существуют смеси двух
твердых фаз фиксированного состава.
5.1.3. Правило рычага. Количество и состав каждой
из двух фаз равновесной двухфазной системы определя-
ются общим составом смеси, и их можно рассчитать,
исходя из уравнения материального баланса.
Запишем уравнение материального баланса для двух
фаз (обозначенных на рис. 5.4 одним и двумя штрихами
соответственно)
тх = т'х' + т"х"
= т'х' + (т — т')х",
(5.1)
(5.2)
Фазовое равновесие 253
Рис. 5.1. Графическое представление фазового равновесия одноком-
понентной системы.
и ряд вытекающих из него соотношений, выражающих
математически суть правила рычага:
т' /т" = (х” — х)/(х — х') = DB/AD, (5.3)
т' /т = (х" — х)/(х" — х') = DB, (5.4)
т" /т — (х — х')/(х” — х') = AD. (5.5)
Это правило получило название правила рычага в связи
с тем, что указанные соотношения представляют собой
моменты тДх относительно точек х, х' их" соответ-
ственно. Эти же соотношения можно также рассматри-
вать как проекции на ось х, как это показано на
диаграмме и в представленных выше уравнениях.
5.1.4. Трехкомпонентные системы. Состав трехком-
понентных смесей определяется положением точек на
поверхности равностороннего или равнобедренного тре-
угольника единичной высоты. Для равнобедренных тре-
угольников характерно следующее: сумма отрезков
перпендикуляров, опущенных из любой точки на его
стороны, равна высоте треугольника. Следует заме-
тить, что сумма перпендикуляров, опущенных из лю-
бой внешней точки на стороны треугольника, также
равна его высоте, если правильно оценить положитель-
ный и отрицательный векторы (хотя это обстоятель-
ство не относится непосредственно к изображению
состава фаз).
Так, если перпендикуляр, опущенный из внешней точ-
ки (например, линия RD на рис. 5.5,6), имеет то же на-
правление, что и перпендикуляр, опущенный из неко-
торой внутренней точки на эту же сторону, то он оце-
нивается как положительный. Если перпендикуляры,
опущенные из внешней (линия RE) и внутренней точек,
имеют противоположное направление, то величина пер-
пендикуляра RE принимается за отрицательную. Как
хорошо известно, эти определения используются в гра-
фическом анализе составов тройных систем. Геометрия
треугольных координат, получившая также название
геометрии однородных координат или координат Мёби-
уса, разработана достаточно подробно. Две широкоиз-
вестные работы по этому вопросу выполнены Лони
(1923) (The Elements of Coordinate Geometry) и Дарре-
лом (1961) (Homogeneous Coordinates).
Хотя в ряде случаев несколько диаграмм могут на-
кладываться друг на друга для удобства, обычно их
строят с тем, чтобы показать соотношение компонен-
тов при определенных давлении и температуре. Отдель-
ные зоны диаграммы представляют собой композици-
онные сочетания, в которых одна, две или три фазы
могут сосуществовать в равновесии. Поскольку все ве-
щества в принципе по крайней мере слаборастворимы,
любая область, занимающая один или несколько углов
треугольника, является однофазной. На практике одно-
фазная зона может исчезнуть, если взаимная раствори-
мость фаз очень низка, как, например, показано на рис.
5.37,<z в верхнем углу диаграммы или на рис. 5.38,6 в
правом углу диаграммы.
Каждая линия на диаграмме разделяет две области,
отличающиеся по числу фаз. В любой точке общей для
трех различных областей сосуществуют три фазы. Лю-
бую область, в которой сосуществуют три фазы, необ-
ходимо ограничить прямоугольным треугольником. На
рис. 5.6,а или рис.5.6,б это треугольник а(3у, в этом
случае линия а/3 — это соединительная линия (она дол-
жна быть прямой), связывающая все смеси фаз а и (3,
такими же соединительными линиями являются линии
(Зу и уа.
Предсказать число фаз, которое может присутство-
вать в определенной композиции, исходя из правила фаз
не представляется возможным, но известно, что оно за-
254 Глава 5
Рис. 5.2. Пространственная и соответствующая плоскостная диа-
Pi
граммы, показывающие влияние температуры и давления на смеси.
а — диаграмма состав — температура — давление двухкомпонентной смеси с
сечениями по изобаре, заштрихованы двухфазные области:
б — влияние температуры и давления на область взаиморастворимости;
в —плоскостная диаграмма показывает изобары, отмеченные на пространст-
венной диаграмме.
висит от химической природы присутствующих в ней
веществ. Так, на рис. 5.39,« показаны три трехфазные
области. Каждая из них соответствует смеси с различ-
ным соотношением фаз определенного состава, но для
каждой из трехфазных областей эти составы различны.
Однако, согласно правилу фаз, при постоянных темпе-
ратуре и давлении составы фаз в трехфазной области
фиксированы, хотя какими они должны быть, правило
не указывает. В таких системах, как показанная на рис.
5.39, возможно также образование одно- и двухфазных
областей, существование которых в очень большой сте-
пени зависит от изменения температуры.
Значения составов фаз, находящихся в равновесии, об-
разуют на диаграмме линии, называемыми коннодаля-
ми. По этим линиям можно установить все возможные
равновесные составы фаз. Относительные количества
двух фаз определяют исходя из уравнений материально-
го баланса индивидуальных компонентов. Если состав
действительно соответствует показанному соединитель-
ной линией, например т'тт" на рис. 5.5,г, относи-
тельные количества двух фаз связаны с мольной долей
отдельных компонентов, как и в двухкомпонентных
смесях, по уравнениям (5.1)—(5.5), например:
т'/т = (х,- - xj')/(x;- - x'i'), (5.6)
где подстрочный индекс i равен 1, 2 или 3.
В трехфазной области (например области, ограничен-
ной треугольником afiy на рис. 5.6,<7 или рис. 5.6,6)
мольный состав ф, = пц/т трех имеющихся в наличии
фаз, если общий состав смеси соответствует точке Ь, да-
Фазовое равновесие 255
Рис. 5.3. Графические представления фазового равнове-
сия двухкомпонентных систем при фиксированном
давлении.
а — влияние температуры на равновесие пар — жидкость в
двухкомпонентной системе.
б — частичная взаиморастворимость двух жидких фаз, зависи-
мость состава от температуры; ха и хь — составы фаз при рав-
новесии при указанной температуре.
в — равновесие жидкость — твердая фаза, точки А и В показы-
вают пределы взаиморастворимости твердой фазы. В эвтекти-
ческой точке Е жидкость находится в равновесии с твердыми
растворами состава ха и хв-
Рис. 5.4. Иллюстрация правила рычага.
Если х— общий состав смеси, доля фазы состава х' показана
отрезком DB, а доля фазы состава х" — отрезком Л О; т —
массы фаз.
ется следующими уравнениями материального баланса:
(х1а ~ х1у)0а + (х1д ~ х 1 у)фд = х15 ~х1у, (5.7)
(х2а - х2у)Фа + (*2/3 ~ х2у)Ф/3 = х28 ~ х2у, (5-8)
фу = 1 - фа~фр. (5.9)
Систему приведенных линейных уравнений легко разре-
шить относительно ф1 с помощью детерминантов.
Возможен и другой подход. Фазовый состав можно
найти, измеряя отрезки на фазовой диаграмме. Так, для
диаграммы, приведенной на рис. 5.6,6,
ФУ 1 _____
, 4- = Т1 = 8е/У8’ (5.Ю)
фа+ фр
и
Фр/Фа =
в результате получаем
(5.И)
(5.12)
(5.13)
(5.9)
Уравнения, описывающие соединительные линии,
подробно обсуждаются в других главах. Для бинарных
смесей пригодно следующее простое соотношение:
х1' ~ ^1* 1 >
(5.14)
256 Глава 5
Рис. 5.5. Графическое представление тройных смесей.
а — диаграмма составов трехкомпонентных смесей, имеющая вид равностороннего треугольника: РА + РВ + РС = высота треу-
гольника.
б — принцип использования треугольных координат (гомогенных или координат Мёбиуса) внутри либо вне треугольника. Отрезки
QC и RE соответствуют отрицательным величинам, поскольку они направлены противоположно WY и WX, тогда как отрезки
QA, QB, RD и RF соответствуют положительным величинам, так как их направление совпадает с направлением WZ, WX, WZ
и РТУ.
в — диаграмма трехкомпонентных смесей, имеющая вид равнобедренного прямоугольника единичной высоты; состав третьего
компонента находится по разности.
г — диаграмма трехкомпонентной смеси с двухфазной областью; отмечены бинодальные кривые, соединительные линии и верхняя
точка.
Фазовое равновесие 257
Рис. 5.6. Диаграммы трехкомпонентной смеси с много-
фазными зонами.
а — трехкомпонентная смесь с одной трехфазной (III), тремя
двухфазными (II) и тремя однофазными (I) зонами.
б — диаграмма, предназначенная для определения относитель-
ных количеств трех фаз. (В разд. 5.1 дан вывод формул, в кото-
рых используются величины отрезков ас, £/3, уб и Зе.)
которое справедливо в ограниченном диапазоне соста-
вов при постоянной величине коэффициента распределе-
ния К\; однако обычно сильное влияние оказывает
температура. Отношения между составом паровой и
жидкой фаз аппроксимируются законами Генри и Рауля,
а более точные соотношения рассчитываются с исполь-
зованием коэффициентов активности и фугитивности,
как это всюду указывается в тексте.
Влияние температуры (или давления) может быть по-
казано на диаграмме в виде трехгранной призмы. На
рис. 5.7,а представлена фазовая диаграмма тройной
системы, на которой показаны изотермические сечения,
демонстрирующие ограниченную растворимость жид-
кости, а на рис. 5.7,6 представлена система, содержа-
щая жидкую и твердые фазы. На обеих диаграммах
даны контуры проекций изотерм на основание.
5.1.5. Многокомпонентные системы. Состав четы-
рехкомпонентных систем может быть показан точками,
находящимися внутри правильного тетраэдра, см., на-
пример рис. 5.8. Одна такая диаграмма необходима для
иллюстрации влияния каждой пары значений Т и Р.
Данный тетраэдр характеризуется следующей особен-
ностью: сумма перпендикуляров из внешней точки тет-
раэдра на каждую сторону равна высоте. Однако
удобнее пользоваться тетраэдром, у которого за едини-
цу измерения принято ребро, а не высота. Так, состав
системы, указанной на рис. 5.8,«, можно легко опреде-
лить, проведя параллельные к нескольким ребрам (как
это показано на рисунке).
Поскольку пространственные диаграммы сложно и
строить и использовать, для получения информации о
твердых моделях, предложено применять соответ-
ствующие виды плоскостных проекций: некоторые из
таких проекций описаны в работах [ПО, 138]. Одна из
наиболее наглядных схем предполагает использование
треугольных диаграмм, изображающих смеси только
трех компонентов А, В и С при нескольких концентра-
циях компонента D в виде либо ряда таких диаграмм,
либо одной диаграммы с горизонталями, соответству-
ющим разным концентрациям D.
Четырехкомпонентных систем органических веществ
исследовано лишь несколько. Два простых типа таких
систем, включающих только жидкие фазы, представле-
ны на рис. 5.8,6 и в в несколько упрощенном виде. Со-
отношения фаз в многокомпонентных системах можно
аппроксимировать, принимая их поведение за поведение
идеальных растворов. Более точные четырехкомпонент-
ные диаграммы можно получить в том случае, если из-
вестны бинарные коэффициенты активности или, что
еще лучше, известны непосредственно трехкомпонент-
ные диаграммы. Методика, основанная на использова-
нии коэффициентов активности, пригодна для любого
числа компонентов и фаз, если исключена вероятность
образования интермолекулярных соединений, но поль-
зуются ею редко (исключения составляют равновесия
жидкость—жидкость или пар—жидкость).
5.2. Правило фаз
Правило фаз Гиббса устанавливает связь между чис-
лом фаз (Ph), находящихся в равновесии, числом компо-
нентов (Q при определенном составе, температуре и
давлении. Гравитационные, электрические и им подоб-
ные характеристики учитываться нами не будут. Состав
фаз можно выразить значением С - 1 мольных или
массовых долей в каждой фазе. Поэтому вместе с тем-
пературой и давлением общее число переменных, опре-
деляющих все фазы системы, равно Ph(C - 1) + 2. По-
скольку химический потенциал или каждого ком-
понента i одинаков для каждой фазы j в условиях рав-
новесия, то число независимых величин, характеризу-
ющих систему, равно (Ph - 1)С. Разность между чис-
лом независимых условий и числом химических потен-
циалов называется вариацией или числом степеней сво-
боды, F, системы и выражается следующим урав-
нением:
F = Ph(C - 1)4- 2- (Ph - 1)С = С + 2 - Ph.
Если используются плоскостные диаграммы, выраже-
ние правила фаз упрощается. Поскольку для бинарных
17-829
258 Глава 5
Рис. 5.7. Пространственные и соответствующие плоскостные диаграммы, показывающие влияние температуры и
давления на трехкомпонентные смеси.
а' — влияние температуры на зону взаиморастворимости при постоянном давлении; а" — плоскостная диаграмма, показывающая
изотермы, приведенные на пространственной диаграмме.
б', б" —диаграммы смесей висмут + свинец + олово, имеющих двойную и тройную эвтектику £4, в которой жидкий расплав
и три твердые фазы находятся в равновесии при 97 °C и следующем составе (мол. доли): 0,51 Bi, 0,33 Pb, 0,16 Sn. Проекция на
основание показывает также эвтектики и изотермы.
систем возможны диаграммы типа Т—х или Р—х, пра-
вило фаз выражается уравнением Ph = 3 - Fnet, в кото-
ром Fnet не может превышать 2, допустим, Xi и либо
Р, либо Т. В том случае, если плоскостная диаграмма
трехкомпонентной системы изображена при постоян-
ных Т и Р, правило фаз также определяется уравнением
Ph = 3 - Fnet, где максимальное значение Fnet вновь
равно 2 (две из трех мольных фракций). Эти результа-
ты приведены в табл. 5.3.
С — это минимальное число химических частиц, не-
обходимых для определения химической природы систе-
мы. Если эти химические частицы инертны, С —
просто их число; например, для смеси кислорода и азо-
та при атмосферном давлении С = 2. Однако, если ве-
щества реакционноспособны, каждая независимая
реакция уменьшает на единицу число независимых ком-
понентов. Как определить число независимых реакций
объяснено в гл. 10. Для реакционноспособных систем,
таким образом, число компонентов определяется выра-
жением:
С = Се - Ср + С/,
где Се — число химических элементов, присутствующих
в системе; Ср — число реакций, приводящих к образова-
нию интермолекулярных соединений или изомеров, или
полимеров, в каждой из которых химические элементы
Фазовое равновесие 259
Рис. 5.8. Диаграмма четырехкомпонентной смеси, име-
ющая вид тетраэдра.
а — композиционный тетраэдр с ребром единичной длины.
Чтобы определить положение точки Р(хв, хь, хс, Xd), проводим
линию Da = хв, штриховую линию ab = хь, параллельную ре-
бру BD, и штриховую линию ЬР = хс, параллельную ребру DC.
б — диаграмма системы лигроин(Л) + фурфурол (В) + изобу-
тан(С) + бутадиен(£>) при 20 °F ( — 6,67 °C); КК' — локус кри-
тических точек растворения. [Smith A. S., Braum Т. В. Ind. Eng.
Chem., 37, 1047 (1945)]. © Am. Chem. Soc.
e — диаграмма системы ацетон + вода + хлороформ + уксус-
ная кислота при 25 °C [194]. © Am. Chem. Soc.
присутствуют в одних и тех же пропорциях и в левой
и в правой части стехиометрического уравнения; С; —
число реакций, ингибируемых при достижении рав-
новесия.
Рассмотрим несколько конкретных примеров. Так,
для димеризации бутадиена
2 С4Н6 ~ (С4Н6)2,
с= 2- 1 + 0= 1.
Если Нг и N2 реагируют с образованием аммиака
С=2~0+0 = 2,
но если взаимодействие Н2 и N2 затруднено из-за низ-
ких температур в отсутствие специальных катали-
заторов,
С= 2- 0+ 1 = 3.
Для системы, в которой пропан образует гидрат:
С3Н8+ п Н2О ~ С3Н8 • (Н2О)„,
С= 3 - 1 + 0 = 2.
Особого внимания заслуживает влияние интермолеку-
лярных соединений на число компонентов, так как эти
соединения часто встречаются на диаграммах состоя-
ния. Хотя при образовании таких соединений число хи-
мических частиц в системе меняется, стехиометрические
отношения для каждого случая дают значение 1, и чис-
тое влияние этого явления на «число компонентов» в
правиле фаз равно нулю.
По числу компонентов системы делят на одно-, двух-,
трехкомпонентные и т. д., а по числу степеней свободы
различают системы инвариантные, моновариантные и
т. д. Такая классификация систем показана в табл. 5.3.
Как следует из таблицы фазовых состояний, в трехком-
понентной системе при определенных температуре, дав-
лении и составе, т. е. при F = 0, возможно наличие
пяти фаз. Однако на треугольных диаграммах состоя-
ния трехкомпонентных систем при фиксированных зна-
чениях Р и Т могут быть показаны максимум три
фазы. На пространственных диаграммах (типа приве-
денной на рис. 5.7) возможное сосуществование четырех
фаз (трех фаз твердых и одной жидкой) идентифициру-
ется как тройная эвтектика £4. Согласно правилу фаз,
17’
260 Глава 5
Таблица 5.3. Компоненты (Q фазы (Ph) и число степеней свободы (F) при фазовом
равновесии
Порядок системы Тип системы С Ph Независимые переменные
Общее число F = С + 2 - Ph При постоянном Р F = С + 1 - Ph При посто- янных Т и Р F = С - Ph
Одноком- Двухвариантная 1 1 Т и Р Т Нет
понентная Одновариантная 1 2 Т или Р Нет —
Инвариантная 1 3 Нет — —
Двухком- Трехвариантная 2 1 Т Р, х Т или х X
понентная Двухвариантная 2 2 Любые 2 X Нет
Одновариантная 2 3 Любая 1 Нет —
Инвариантная 2 4 Нет — —
Трехком- Четырехвари- 3 1 Т, Р, Xi, х2 Т, xi, х2 Х1, х2
понентная антная
Трехвариантная 3 2 Любые 3 Х1, х2 Х1
Двухвариантная 3 3 Любые 2 Х1 Нет
Одновариантная 3 4 Любая 1 Нет —
Инвариантная 3 5 Нет — —
такая точка моновариантна, но поскольку давление ока-
зывает весьма малое влияние на конденсированные сис-
темы, тройная эвтектика по существу инвариантна.
Однако при очень низких давлениях может образовы-
ваться паровая фаза, которая сосуществует с тремя
твердыми и одной жидкой фазой тройной эвтектики,
образуя тем самым систему с пятью фазами, что и сле-
дует из правила фаз.
При фиксированных значениях температуры и давле-
ния, а именно для таких условий и получено большин-
ство данных о фазовых равновесиях в многокомпо-
нентных системах, максимальное возможное число фаз
равно числу компонентов. В задаче 5.15 рассматривает-
ся шестикомпонентная система с шестью жидкими фа-
зами при атмосферном давлении.
5.3. Однокомпонентные системы
Для однокомпонентных систем Ph = 3 - F, следова-
тельно, в условиях равновесия в таких системах могут
присутствовать одна, две или три фазы. Показанная на
рис. 5.9 фазовая диаграмма диоксида углерода является
типичной. Характерные ее особенности — это зоны, в
которых существуют однофазные системы, линии,
вдоль которых возможно сосуществование двух фаз,
критическая точка, в которой свойства жидкой и паро-
вой фазы становятся идентичными, и тройная точка, в
которой три фазы сосуществуют в равновесии. Однако
на диаграмме отсутствуют соответствующие точки для
других возможных пар фаз.
При повышенных давлениях многие твердые веще-
ства проявляют полиморфизм, т. е. способность суще-
ствовать в двух или нескольких кристаллических струк-
турах. Примеры полиморфизма фосфора, серы, олова,
воды часто обсуждаются в химической литературе. На
рис. 5.10, <z и б приводятся примеры такого поведения.
Так, уксусная кислота может существовать в двух кри-
сталлических модификациях, а уретан — в трех. Воз-
можны более сложные примеры полиморфизма органи-
ческих веществ, так, камфора имеет одиннадцать кри-
сталлических модификаций.
Особый интерес представляют водные конденсиро-
ванные фазы, в которых идентифицировано девять
твердых фаз. На рис. 5.11 представлены диаграммы
Р—Т, сведения о тройной точке и пространственная диа-
грамма Р—Т. Лед IV, по-видимому, является метаста-
бильной фазой. На этой диаграмме отмечены другие
метастабильные фазы и указан ряд неопределенностей.
Представляют интерес модификации льда, способные
находиться в равновесии с жидкостью при температуре
плавления, значение которой возрастает с повышением
давления. Исключение составляет обычная модифика-
ция — лед I. При давлении 40 000 кг/см2 лед плавится
при 200 °C, следовательно, такая модификация льда
имеет большую плотность чем жидкость. Заметим, что
хотя история исследования этих диаграмм насчитывает
около 60 лет, ряд моментов до сих пор не выяснен.
Переход точки кристаллизации наблюдается при не-
скольких тысячах атмосфер, что необычно для боль-
шинства химических процессов.
На рис. 5.12 показана диаграмма Р—Т пропана, а рис.
5.14 демонстрирует, что твердый пропан существует
при температуре ниже -162,2 °C (300 °F).
Фазовое равновесие 261
4
3
г
1
о
-7
-г
-з
-100
100
Рис. 5.9. Фазовая диаграмма диоксида углерода [Gmehling Handbuch
der anorganischen Chemie, Kohlenstoff, T3/L1 (1970)].
Рис. 5.10. Равновесие жидкость — твердая фаза индиви-
дуальных веществ [Bridgman Proc. Am. Acad. Arts and
Sciences, 52, 91(1916), 51, 53 (1915)].
a — фазовая диаграмма уксусной кислоты; тройная точка соот-
ветствует 55,7 °C, 2100 бар.
б — фазовая диаграмма мочевины; тройные точки соответству-
ют 66,2 °C и 2350 бар (А), 25,5 °C и 3400 бар (В), 76,8 °C и
4230 бар (0.
5.4. Двухкомпонентные системы
Фазовые соотношения в двухкомпонентных системах
обычно сложнее, чем для большинства чистых веществ,
и при рассмотрении последних целесообразнее исполь-
зовать плоскостные диаграммы Т—х или Р—х, но в ря-
де случаев приходится прибегать к диаграммам Р—Т
для постоянного состава (изоплеты). Для удобства при
построении диаграммы обычно ограничиваются пока-
зом отношений между определенным числом фаз, на-
пример пар—жидкость, жидкость—жидкость, жид-
кость—твердая фаза и т. д. Границы равновесных фаз
определенного состава могут быть отмечены соедини-
тельными линиями, например горизонтальными линия-
ми на диаграммах Р—х или Т—х, либо они могут быть
показаны отдельно в виде кривых зависимости состава
одной фазы от состава другой. Такие зависимости, на-
зываемые диаграммами распределения, могут представ-
лять собой изотермы или изобары.
Фазовые диаграммы бинарных систем с паровой,
жидкой и твердой фазами могут быть трех видов. Для
системы метанол + вода при 1 атм (рис. 5.13) соотноше-
ние фаз пар—жидкость почти идеальное, но замерзание
осложнено образованием твердого моногидрата. Взаим-
ная растворимость пропана и воды ограничена, поэто-
му две жидкие фазы присутствуют в большинстве ком-
позиционных полей диаграммы на рис. 5.14. Для этой
системы характерны три твердые фазы — лед, пропан
и гидрат или клатрат с 7,5 молями воды на 1 моль
углеводорода. Для системы аммиак + вода (рис. 5.15)
характерны четыре твердые фазы — лед, аммиак, полу-
гидрат и моногидрат. На этой диаграмме показаны
равновесия пар—жидкость, но из-за выбранного масш-
таба диаграммы отсутствуют равновесия пар—твердая
фаза, которые возможны при низких давлениях.
Для решения практических задач обычно необходимы
лишь ограниченные области Т и Р, число рассматривае-
мых фаз также ограничено.
По Ландольтду-Бернштейну выделяют набор диа-
грамм для систем жидкость—пар, жидкость—жидкость,
262 Глава 5
Рис. 5.11. Равновесие вода — отдельные кристалличе-
ские фазы воды.
а — диаграмма PVT при 10 000 атм [44].
б — фрагменты диаграммы температуры — давление (Gmeh-
ling, Handbuch).
жидкость—твердая фаза, но все три типа диа1 рамм для
одних и тех же пар веществ, известны не всегда.
5.4.1. Равновесие пар—жидкость. Основные типы фа-
зовых диаграмм таких систем суммированы на рис.
5.16. Распространены диаграммы типа Т—х, Р—х, х—у.
В такой классификации для типа I (рис. 5.16) характер-
но плавное изменение температур кипения растворов в
диапазоне между температурами кипения чистых жид-
костей, включая системы, подчиняющиеся закону Рау-
ля. В рассматриваемых системах возможно образование
азеотропных смесей, для которых характерно равенство
состава жидкой и паровой фаз, температур кипения и
состава паровой фазы или постоянство диапазона со-
ставов. На диаграммах х—у кривая для азеотропных
систем пересекает диагональ (45°). Типы II и III — это
гомогенные азеотропы. Азеотропные смеси с миниму-
мом на кривой температур кипения распространены до-
статочно широко, более редки смеси с максимумом на
кривой температур кипения. Система с двумя азеотро-
пами показана на рис. 4.24,а. Типы IV и V включают
соответственно частично смешивающиеся или несмеши-
вающиеся жидкие фазы, т. е. гетерогенные азеотропы.
В не столь распространенных системах типа VI несме-
шивающиеся жидкие фазы существуют в температур-
ном интервале, ограниченном температурами конденса-
ции чистых веществ; в этих системах составы фаз жид-
кость—жидкость остаются постоянными в широком
диапазоне составов паровых фаз. Если бинарные систе-
мы образуют интермолекулярные соединения, стабиль-
ные при температуре кипения, их фазовые диаграммы
6 Р, кбар —
должны выглядеть как диаграммы типа VII. Подо-
брать характерные примеры довольно трудно, но по-
добные диаграммы для систем жидкость—твердая фаза
даны на одном из фрагментов рис. 5.22.
Заметные изменения в виде фазовых диаграмм часто
вызваны изменениями температуры и давления. Рис.
5.17 иллюстрирует это положение на примере смесей
этана и «-гептана. Изоплета (рис. 5.17,я) показывает
критические точки, а также максимумы температуры и
давления для двухфазных огибающих. Диапазон обла-
стей, в которых возможно существование двух фаз, ре-
зко сужается с повышением давления в системе.
Давление оказывает значительное влияние на состав
азеотропных систем. Для системы вода + этанол, на-
пример, соответствующие давления-(Р, мм рт. ст.) и со-
ставы азеотропов (Н2О, масс. %) меняются с повыше-
нием давления следующим образом: 94,9 и 0,5, 200 и
2,7, 760 и 4,4, 1500 и 4,87. Во многих случаях, как и
в приведенном выше примере, азеотропную смесь мож-
но разрушить, понизив давление. Подобный эффект
проявляется на диаграммах х—у системы метилаце-
тат + метанол, состоящих из нескольких изобар и изо-
терм (рис. 5.18). Эти кривые получены на основе урав-
нения Вильсона, но они хорошо согласуются с
экспериментальными данными.
Фазовое равновесие 263
Рис. 5.12. Диаграмма PVT пропана; заштрихована двухфазная зона
(Sage, Lacey, 1939).
Рис. 5.13. Равновесие пар — жидкость — твердая фаза в смесях мета-
нола и воды. Твердый моногидрат СНзОН-НгО стабилен в диапазоне
температур от -104,5 до -125 °C.
264 Глава 5
Рис. 5.14. Схематическая фазовая диаграмма системы
пропан + вода при давлении ниже критического давле-
ния пропана.
Н—гидрат, I—лед. Р—твердый пропан (Кобаяши, 1951, в
кн. Каца и др., 1959).
На рис. 5.19 показан несколько более полный набор
диаграмм х—у, которым мы и ограничимся, поскольку
во вполне доступных публикациях приводится несколь-
ко тысяч таких наборов диаграмм [46, 57, 79, 69, 73].
В книгах Когана и др. [69] приведены подробные табли-
цы, в других публикациях помимо таблиц даны графи-
ки и корреляционные уравнения.
5.4.2. Системы жидкость—жидкость. Фазовые диа-
граммы двухкомпонентных систем, содержащих только
жидкие фазы, имеют сравнительно простую форму —
это выпуклые, вогнутые или замкнутые кривые, завися-
щие от температуры. Некоторые примеры диаграмм
Т—х приведены на рис. 5.20. Влияние давления на рав-
новесие конденсированных фаз заметно проявляется
только при высоких температурах или вблизи критиче-
ских точек. Возможный эффект можно предсказать ис-
ходя из принципа Ле-Шателье. Обычно размеры
двухфазной зоны сокращаются с повышением давления,
как это показано на рис. 5.1, 5.2 и особенно наглядно
на рис. 5.20,я на примере системы метилэтилкетон +
+ вода, где повышение давления до 150 атм изменяет
геометрию двухфазной зоны от вогнутой к замкнутой.
Рис. 5.20 демонстрирует также влияние изменения
температуры на некоторые системы. В большинстве
случаев с повышением температуры взаимная раствори-
мость конденсирующихся фаз возрастает. Температура,
при которой достигается полная взаимная раствори-
мость, называется критической точкой растворения
(КТР). На рис. 5.20,0 показана система с верхней крити-
ческой точкой растворения, а на рис. 5.20,е — с нижней
критической точкой растворения, системы, приведенные
на рис. 5.20,а и в, имеют и верхнюю и нижнюю крити-
ческие точки растворения. Многие системы проявляют
склонность к формированию закрытой двухфазной зо-
ны, эту тенденцию можно наблюдать в том случае, ес-
ли исследуется достаточно широкий диапазон темпера-
тур, как, например на рис. 5.20,е. На рис. 5.20,0 двух-
фазная зона имеет форму петли. При температурах ни-
же верхней КТР может происходить испарение, а при
температурах ниже нижней КТР — кристаллизация. Не-
обычным образом ведет себя система сера + бензол
(рис. 5.20,6), у которой верхняя КТР ниже чем нижняя
КТР.
Подробные данные о равновесиях в системах жид-
кость—жидкость опубликованы в семитомном справоч-
нике Стефена и др. [128], более чем 2000 бинарных
систем представлены на 321 диаграмме в книге Лан-
дольта-Бернштейна [73]. На этих диаграммах рассмат-
ривается фазовое равновесие систем, в которых одно и
то же вещество смешивается более чем с дюжиной рас-
творителей, обычно химически родственных, при самых
различных температурах — вплоть до зоны кристалли-
зации. Изучение этих данных, несомненно, полезно, но
из-за отсутствия необходимых корреляций и теоретиче-
ских предпосылок может привести к неверным выво-
дам. Большие обстоятельные коллекции данных по
равновесию жидкость—жидкость приведены в таблич-
ной и графической форме в работе [125]. Параметры
уравнений NRTL и UNIQUAC даются для каждой тем-
пературы, но не коррелируются с изменением послед-
ней, в некоторых случаях изменения аппроксимируются
линейно. В книге [20] дана библиография работ, посвя-
щенных изучению равновесия жидкость—жидкость.
5.4.3. Равновесия жидкость—твердая фаза при плав-
лении. Принципиальные особенности диаграмм этого
вида были определены в классификации, приведенной в
табл. 5.1. Ведут себя эти системы обычно сложнее, чем
системы жидкость—жидкость. При изучении фазовых
равновесий в системах первого типа необходимо учиты-
вать 1) равновесие жидкость—твердая фаза, 2) ограни-
ченную взаимную растворимость жидкостей, 3) ограни-
ченную взаимную растворимость твердых растворов,
4) полиморфные превращения в твердом состоянии,
5) образование интермолекулярных соединений, более и
менее устойчивых в твердом состоянии.
При рассмотрении фазовых равновесий в системах
данного типа мы будем прежде всего исходить из того,
как ведет себя в том или ином случае твердая фаза. На
рис. 5.21 показаны основные типы бинарных диаграмм.
5.4.3.1. Системы с взаиморастворимыми твердыми
фазами. Если чистые вещества полностью смешиваются
в жидкой и твердой фазах, их диаграммы состояния на-
поминают диаграммы систем пар—взаиморастворимые
жидкие фазы (рис. 5.16, типы I, II, III). Примеры с про-
межуточными, максимальными и минимальными точ-
ками плавления смесей показаны на рис. 5.22,77—в.
Часто встречаются комбинации этих простых типов
диаграмм. Диаграмма системы иод + бром (рис..5.22,г)
как бы составлена из двух типов диаграмм (т?), соответ-
ствующих равновесию интермолекулярного соединения
Фазовое равновесие 265
120
Концентрация NH3, масс. доли —*
Рис. 5.15. Система аммиак + вода при 1 атм (Landolf-Bornstein, П/2а,
р. 377, 1960).
Рис. 5.16. Примеры двухкоординатных фазовых диаграмм Т— х, Р—х, х—у, показывающих паровую и жидкую
фазы.
II. Системы образующие азеотропную смесь с минимумом температуры кипения
266 Глава 5
III. Системы, образующие азеотропную смесь с максимумом температуры кипения
IV. Системы с взаимонерастворимыми жидкими фазами
частично взаимонерастворимыми жидкими фазами
VI. Системы с взаимонерастворимыми жидкими фазами в интервале температур, ограниченном точками конденсации чистых
веществ
Фазовое равновесие 267
VII. Системы, образующие интермолекулярные соединения с температурами кипения, лежащими в интервале, ограниченном точка-
ми кипения чистых компонентов.
Рис. 5.16 (продолжение).
Рис. 5.17. Система этан + н-гептан. Влияние давления и температуры на составы смеси (Кэй, 1938, заимствовано
из кн. Hougen et al. “Thermodynamics”, 1959). © Am. Chem. Soc.
a — кривые давление — температура для некоторых составов смеси; С, — критические точки, Е, и F,- — максимальные температура
и давление для данного состава.
б — кривые температура — состав при различных давлениях.
(1:1) с каждым из элементов. На диаграммах систем
тетрахлорид углерода + циклогексан (1:1) даны мини-
мальные температуры плавления подсистем чистое ве-
щество— интермолекулярное соединение (рис. 5.22,6), в
то время как интермолекулярное соединение (2:3) дает
стандартную диаграмму с 2,3-диметилбутаном и диа-
грамму с минимумом по температуре плавления с 2,3-
диэтилбутаном (рис. 5.22,е). Азот и моноксид углерода
(рис. 5.22,ж) образует равновесные взаиморастворимые
системы как в жидкой, так и в твердой фазе.
5.4.3.2. Диаграмма с нерастворимыми твердыми фа-
зами. Основные виды диаграмм состояния систем с ча-
стично растворимыми или полностью нерастворимы-
ми твердыми фазами представлены на рис. 5.23. Для
бинарных систем такого типа характерно следующее:
добавка каждого из составляющих снижает температу-
ру плавления другого. На диаграмме Т— х две кривые
плавления или затвердевания встречаются в точке ми-
нимума, именуемой эвтектической. Некоторые характе-
ристики таких систем показаны на рис. 5.23,а. Несколь-
ко необычно поведение системы пиридин + формамид
(рис. 5.23,6). Возможно большинство известных органи-
ческих веществ кристаллизуются из расплавов как чис-
тые вещества, но для металлических систем частичная
растворимость вполне обычна. Эвтектика представляет
собой смесь мелких кристаллов, в то время как при
температурах выше эвтектической образуются крупные
кристаллы. Бинарная эвтектика — это двухфазная сис-
268 Глава 5
Рис. 5.18. Диаграммы х—у системы метилацетат + метанол при постоянных давлении и температуре (Hirata et
al., 1976).
а — парожидкостное равновесие при постоянном давлении.
б — парожидкостное равновесие при постоянной температуре.
Жидкость
Рис. 5.19. Диаграммы некоторых парожидкостных композиций главным образом при атмосферном давлении. Со-
ставы даны по массовой доле первого компонента. (Это одна из четырех аналогичных диаграмм, приведенных
в кн. Kirschbaum “Destillier and Rektifiziertechnik”, 1969.)
Фазовое равновесие 269
тема даже при самом тщательном перемешивании ком-
понентов системы.
Для таких систем характерно образование интермоле-
кулярных соединений, устойчивых в твердом состоянии.
На рис. 5.23,в показана диаграмма системы (1:1)
н-толуидин + фенол, в которой наблюдается тенденция
к образованию простых эвтектик с каждым из чистых
веществ. При затвердевании частично смешивающихся
жидкостей фенол + вода образуются две эвтектики
(рис. 5.23,г).
На рис. 5.23,е представлена менее распространенная
ситуация: каждый из компонентов рассматриваемой
системы в жидком состоянии может находиться в двух
различных формах — аморфной и оптически изотроп-
ной в виде так называемых жидких a-кристаллов. Неко-
торые особенности таких веществ описаны в гл. 9. В
этом примере (рис. 5.23,е) равновесие между жидкими
фазами представлено общей линзообразной диаграм-
мой, тогда как линия солидуса жидких кристаллов име-
ет простую эвтектику.
Некоторые диаграммы плавкости обнаруживают пет-
лю на ветви диаграммы, как например, в точке D рис.
5.24,а. Такие петли соответствуют изменениям, проис-
ходящим при постоянной температуре, и могут быть
отнесены либо к химическим превращениям, либо к из-
менениям кристаллической решетки. Штриховая линия
Концентрация серы, масс, доли
б
Рис. 5.20. Примеры равновесий двухкомпонентных систем жидкость — жидкость.
а — вода + метилэтилкетон при 1 и 150 атм.
б — система сера + бензол; редкий тип диаграммы, в котором нижняя критическая температура растворения больше верхней.
в — система глицерин + бензилэтиламин; на данной диаграмме имеются как верхняя, так и нижняя критические температуры рас-
творения (DECHEMA LLE Data Collection, V/1, 1079).
г — система 4-метил-З-этйлпиридин + вода; в рассматриваемом примере достижению верхней критической температуры растворе-
ния препятствует парообразование (DECHEMA LLE Data Collection, V/1, 1979).
d — система 2-бутанон + вода; в данном случае достижению нижней критической температуры растворения препятствует кристал-
лизация (DECHEMA LLE Data Collection, V/1, (1979).
270 Глава 5
Рис. 5.20 (продолжение).
DCE — это гипотетическая линия кристаллизации при
наличии веществ, которые распадаются при температу-
ре более низкой, чем предполагаемая, или метастабиль-
ная, точка плавления; скрытый максимум, точка С —
это метастабильная точка плавления. Системы, у кото-
рых кривая плавления прерывается из-за химических
превращений в твердой фазе, называются меритектиче-
скими (частично плавящимися [24]), а в целом процесс,
включающий оба превращения — химическое и алло-
тропическое — в твердой фазе, называют перитектиче-
ским. Такой процесс записывается следующим урав-
нением:
Жидкость + Твердая фаза А «=* Твердая фаза В,
где А и В могут быть химически идентичны.
Фазовое равновесие 271
а. Система с простой эвтектикой
1 — гомогенная жидкость, 2 — жидкость + кристаллы А, 3 —
жидкость + кристаллы В, 4 — кристаллы А + эвтектическая
смесь, 5 — эвтектическая смесь + кристаллы В.
б — А имеет две кристаллические формы. Линия плавления
А " UE' Е" нестабильна
1 — гомогенная жидкость, 2 — жидкость + кристаллы А 3 —
жидкость + кристаллы А ", 4 — жидкость + кристаллы В, 5 —
кристаллы А " + эвтектическая смесь, 6 — эвтектическая
смесь + кристаллы В.
в. Молекулярный состав АаВь обозначен точкой D
1 — гомогенная жидкость, 2 — жидкость + кристаллы Л; 3 —
жидкость + кристаллы АаВь, 4 — жидкость + кристаллы
АаВь, 5 — кристаллы В + жидкость, 6 — кристаллы А + эв-
тектическая смесь, 7 — эвтектическая смесь + кристаллы D,
8 — эвтектика Ег + кристаллы D, 9 — эвтектика Ег + кристал-
лы В.
Рис. 5.21. Различные типы диаграмм состояния двух-
компонентных систем жидкость — твердое вещество.
А и В — компоненты системы, Е — эвтектика, D — химическое
соединение АаВь, Р — перитектика, S — предел растворимости,
К — критическая точка растворения (Mauser, in Ullmann Enzyk-
lopadie der technischen Chemie, II/l, 638—664, 1972).
272 Глава 5
г. Молекулярное соединение АаВь разлагается при температу-
ре ниже его точки плавления (инконгруэнтное плавление, точ-
ка D)
1 — гомогенная жидкость, 2 — жидкость + кристаллы А, 3 —
жидкость + кристаллы АаВь, 4 — жидкость + кристаллы В,
5 — кристаллы А + эвтектическая смесь, 6 — кристаллы
АаВь + эвтектическая смесь, 7 — кристаллы АаВь + кристаллы
В.
д. Ограниченная растворимость жидких фаз
1 — гомогенная жидкость, 2 — смесь двух жидких фаз, 3 —
кристаллы А + жидкость, 4 — кристаллы А + обедненная А
жидкость, 5 — кристаллы В + жидкость, 6 — кристаллы А +
эвтектическая смесь, 7 — эвтектическая смесь + кристаллы В.
Рис. 5.21 (продолжение).
е. Область ограниченной растворимости жидких фаз отделе-
на от линий плавления (К — нижняя критическая температу-
ра растворения)
1 — гомогенная жидкость, 2 — две жидкие фазы.
Фазовое равновесие 273
ж. Область двух жидких фаз накладывается на линии плавле-
ния молекулярного соединения
1 — гомогенная жидкость, 2 — две жидкие фазы, 3 — кристал-
лы А + жидкость, 4 — кристаллы АаВь + жидкость 1, 5 —
кристаллы АаВь + жидкость 2, б — кристаллы В + жидкость,
7 — кристаллы А + эвтектическая смесь, 8 — кристаллы
АаВь + эвтектическая смесь 1, 9 — кристаллы АаВь + эвтекти-
ческая смесь 2, 10 — кристаллы В + эвтектическая смесь 2.
з. Полная взаиморастворимость жидкой и твердой фаз
1 — гомогенный твердый раствор, 2 — жидкость + кристалли-
ческие смеси, 3 — гомогенная жидкость.
и. Ограниченная растворимость твердых фаз (эвтектика Е
находится в равновесии с твердыми растворами состава Xi
и хг)
1 — гомогенная жидкость, 2 — жидкость + обогащенные А
кристаллы, 3 — жидкость + обогащенные В кристаллы, 4 —
обогащенный А твердый раствор, 5 — обогащенный В твердый
раствор, 6 — обогащенный А твердый раствор + эвтектика,
7 — обогащенный В твердый раствор + эвтектика.
к. Комбинация типов з и и (перитектика Р находится в рав-
новесии с твердыми растворами состава Xi и xi)
1 — гомогенная жидкость, 2 — жидкость + обогащенные А
кристаллы, 3 — жидкость + обогащенные В кристаллы, 4 —
обогащенный А твердый раствор, 5 — обогащенный В твердый
раствор, 6 — обогащенный А твердый раствор + обогащенный
В твердый раствор.
Рис. 5.21 (продолжение).
18-829
274 Глава 5
Рис. 5.22. Реальные системы, полностью растворимые
в жидкой и твердой фазах.
а — система /3-метилнафталин + /3-хлорнафталин [Grimm,
Gunter, Titus Z. physik. Chem., 14, 169 (1931)].
6 — система n-дихлорбензол + л-хлориодбензол с минимумом
на кривой плавления.
в — система rf-карвоксим + 1-карвоксим с максимумом на кри-
вой плавления [Adriani Z. physik. Chem., 33, 469 (1900)].
г — система бром + иод, в которой образуется соединение IBr,
имеющая две линзообразные двухфазные области [Меегит-
Tervogt'Z. anorg. Chem., 47, 209 (1905)].
д — система тетрахлорид углерода + циклогексанон, в которой
образуется интермолекулярное соединение, плавящееся при
- 39,6 °C. Это соединение образует с каждым из чистых компо-
нентов растворы с минимальными температурами плавления
[Pariaud Bull. Soc. Chim. France, (5) 17, 1239 (1950)].
e — система 2,2-диметилбутан + 2,3-диметилбутан, в которой
образуется интермолекулярное соединение с точкой плавления
—102,6 °C. Это соединение образует со вторым компонентом
системы смесь с минимальной температурой плавления [Fink,
Ciner, Frey, Aston JACS, 69, 1501 (1947)].
ж — система азот + оксид углерода. Диаграмма равновесия
между жидкой и твердой фазами и между двумя твердыми фа-
зами. Линии отверждения — это кривые для идеальных раство-
ров (Hildebrand, Scott “Solubility of Non-Electrolytes”, 1950).
Вещества, имеющие стабильную точку плавления, на-
зывают плавящимися конгруэнтно, а вещества с неста-
бильной точкой плавления — плавящимися инконгру-
энтно. Системы, содержащие пикриновую кислоту, бен-
зол и антрацен (рис. 5.24,в и г) относятся к меритекти-
ческим, в то же время химически подобные им системы
с нафталином конгруэнтны (рис. 5.24,6). Перитектиче-
ские системы более обычны, особенно для сплавов. Ге-
незис ряда таких систем схематически показан на рис.
5.25,6 и в.
5.4.3.3. Системы, компоненты которых частично
растворимы в твердой фазе. Поведение систем твердая
фаза—раствор аналогично поведению систем жид-
кость—жидкость, представленых на рис. 5.21. Если на
фазовых диаграммах пытаются отразить все превраще-
ния в жидкой и твердой фазах, диаграммы могут стать
чрезвычайно сложными. Зоны жидкость—твердая фаза
либо могут быть удалены друг от друга, либо могут
частично сливаться, как это схематически показано на
рис. 5.25,а—в. Если изоплета пересекает линию AV, как
на рис. 5.25,6 и в, перитектический процесс протекает
по схеме:
Твердый раствор а ** Твердый раствор /3 + Жидкость.
Твердые растворы также могут претерпевать измене-
ния просто из-за температурных изменений или из-за
модификации кристаллических структур с понижением
температуры. На диаграмме, представленной на рис.
5.25,'г, оба компонента церий и лантан полиморфны;
при понижении температуры после достижения точки
затвердевания может наблюдаться линзообразная зона,
отвечающая равновесию между твердыми растворами с
разными типами кристаллических решеток. Превраще-
ния в твердой фазе могут происходить по эвтектическо-
му типу, как показано на рис. 5.25,6. Такая эвтектика
наблюдается на фазовых диаграммах системы
железо + углерод при 721 °C и 0,9 масс. % С.
5.4.3.4. Диаграммы состояния систем, в которых
происходит образование химических соединений. Систе-
мы, в которых возможны образование нескольких со-
единений и последующие превращения в твердой фазе,
характеризуются очень сложными диаграммами, кото-
рые, однако, можно рассматривать как составленные из
простых диаграмм состояния простых веществ и их хи-
мических соединений, взятых попарно. Так, систему во-
да + серная кислота (рис. 5.23,з) можно рассматривать
как состоящую из четырех простых эвтектик и нерас-
творимых твердых фаз. На рис. 5.26 представлена диа-
грамма состояния системы, в которой образуются
Фазовое равновесие 275
Рис. 5.22 (продолжение).
химические соединения, а твердые фазы характеризуют-
ся ограниченной растворимостью.
5.4.4. Равновесия твердая фаза—жидкость в сверх-
критическом состоянии. Как известно, некоторые газы
растворяются в твердых веществах, так, например, во-
дород растворяется в металлах. Однако при определен-
ных условиях содержание газа в жидкости или твердых
веществах может быть значительно больше, чем можно
заключить исходя из их нормального давления паров.
В ряде случаев при проведении теоретических иссле-
дований или осуществлении технологических процессов
необходимы давления, превышающие критические, так
что в таких случаях необходимо рассматривать равно-
весие конденсированная фаза—жидкость в сверхкрити-
ческом состоянии.
На рис. 5.27,а приведена диаграмма Р—х подобной
системы. Показанное на диаграмме отклонение от иде-
альности, часто весьма заметное в закритических обла-
стях, обычно ведет к существенному повышению
содержания нормально конденсирующихся веществ в
жидкой фазе. Жидкая фаза, состав которой соответству-
ет точке а на диаграмме, содержит некоторое количе-
ство твердой фазы, которая становится жидкой, если
давление снижается (точка b диаграммы). Реальные сис-
темы показаны на рис. 5.27,6, в и г. Растворимость
нафталина в этилене минимальна вблизи критической
точки растворителя, но затем резко возрастает с повы-
шением давления. Как следует из рис. 5.27,в, аналогич-
ным образом ведут себя и другие твердые фазы,
растворимые в этилене; такое же влияние оказывает на
18*
276 Глава 5
Рис. 5.23. Равновесия жидкость — твердая фаза с нерастворяющимися твердыми фазами.
а — пример системы, образующей простую эвтектику. В точке g изоплеты fj смесь начинает затвердевать и полностью затвердева-
ет в точке й. В точке с количество жидкой фазы и твердой фазы А определяется соотношением отрезков ас и cd; состав жидкой
фазы соответствует точке d. Та, Тв — температуры плавления веществ, Те — температура плавления эвтектики.
б — система пиридин + формамид. При -56,7 °C образуется простая эвтектика с 32,3 мол.% формамида [Stephanou, Vanderwerf,
Sisler JACS, 70, 264 (1948)]. © Am. Chem. Soc.
в — система л-толуидин (A) + фенол (В). Образуется интермолекулярное состояние (1:1), которое дает простые эвтектики с каж-
дым из компонентов.
г — система фенол + вода. Образуются частично растворимые жидкие фазы и взаимонерастворимые лед и твердый фенол.
д — система трифенилметан + м-фенилендиамин. Образуются взаимонерастворимые жидкие фазы и интермолекулярное соедине-
ние (1:1), которое распадается при температуре ниже точки плавления.
е — система л,л'-азоксифенетол + метоксикоричная кислота. Характерно равновесие между жидкими кристаллами и аморфной
жидкостью и затвердевание жидких кристаллов {Prins Z. physik. Chem., 67, 718 (1909)].
ж — система нитрат калия + нитрат таллия. Образуется эвтектика из двух твердых растворов. Точка К — гипотетическая крити-
ческая температура растворения твердых растворов Si и Si (Bowden, “The Phase Rule and Phase Reactions”, 1938).
3 — система вода (И7) + серная кислота (S). Образуются интермолекулярные соединения, моно-(ЛТ), ди-(27) и тригидраты (Т) с
точками плавления +7, -40 и —25 °C соответственно.
них и изменение температуры. На рис. 5.27,г сравнива-
ется реальное и идеальное поведение бензойной кисло-
ты в диоксиде углерода при повышенных давлениях и
различных температурах. Влияние давления хорошо
предсказывается уравнениями Соава и Пенга—Робинсо-
на. О промышленном применении экстракции газов
сверхкритических параметров говорится в гл. 9. Отно-
сительно недавно опубликована обстоятельная серия
статей по этой проблеме [15].
5.4.5. Влияние давления на равновесие жидкость—
твердая фаза при плавлении. Непосредственное влияние
давления на плавление или растворение твердых ве-
ществ можно предсказать исходя из принципа Ле-Ша-
телье. Обычно увеличение давления повышает точку
плавления и увеличивает растворимость. Примером то-
му могут служить жидкие фазы, показанные на рис.
5.20,а, взаимная растворимость которых значительно
меняется с изменением давления. На рис. 5.28 показано
несколько примеров влияния давления на равновесие
жидкость—твердая фаза при плавлении; на рис. 5.28,а
форма двухфазной зоны меняется незначительно, хотя
сама зона сдвигается. На диаграммах, показанных на
рис. 5.28,6 и г, эвтектические температуры несколько
возрастают, однако состав эвтектических композиций
Фазовое равновесие 277
Одна жидкость
~63аС
/ Две \
'жидкости \
1,3 °с
О
-1,3
Жидкость + фенол
L + W „ 3
Лед + фенол
ОС фенол
дг,5°с
Концентрация п,^-азокси-
фенетола, мол. доли
е
Рис. 5.23 (продолжение).
278 Глава 5
6 Концентрация пикриновой кислоты,
мол. доли
Концентрация пикриновой кислоты,
о мол. доли
и
Концентрация пикриновой кислоты,
? мол. доли
Рис. 5.24. Образование интермолекулярных соединений в системах с пикриновой кислотой (Миндович, 1956).
а — упрощенная диаграмма системы, образующей интермолекулярное соединение V, которое распадается (в точке D) до достиже-
ния температуры плавления. Точка С — нестабильная точка плавления, DCE — гипотетическая кривая отверждения с И в качестве
твердой фазы.
б — система пикриновая кислота + нафталин. Образуется интермолекулярное (1:1) соединение, стабильное при температуре плавле-
ния (148 °C), которое дает две эктектики, содержащие около 5 и 90% пикриновой кислоты.
в — система пикриновая кислота + бензол. Образуется интермолекулярное соединение, которое легко распадается при температуре
ниже его стабильной точки плавления. Штриховая линия VA — нестабильная часть кривой отверждения.
г — система пикриновая кислота + антрацен. Образуется интермолекулярное соединение, которое быстро распадается при темпера-
туре ниже предполагаемой точки плавления. Левая часть кривой плавления (часть Ь) почти горизонтальна.
Фазовое равновесие 279
Рис. 5.25. Системы с ограниченно растворимыми твердыми фазами и с превращениями в твердых фазах
(на ординатах указана температура, на абсциссах — состав).
а — генезис эвтектики системы твердых растворов, приводящий к расширению и перекрыванию простых двухфазных областей.
В ограниченных пределах такие превращения могут быть обусловлены изменением давления, но обычно различие в виде диаграмм
связывают с различием в химической природе компонентов.
б — генезис системы перитектического (с нестабильной точкой плавления) типа, приводящий к расширению и перекрыванию прос-
тейших двухфазных областей, V — перитектическая точка. О линии VA см. в разд. 5.4.3.3.
в — генезис перитектической системы с минимумом в точке плавления. О линии AV см. в разд. 5.4.3.3.
г — церий и лантан проявляют в твердом состоянии полиморфизм.
д — пример системы, в которой твердый раствор имеет ограниченную растворимость в твердых фазах чистых компонентов и
образует твердофазную эвтектику с ними. Системы железо + углерод образуют такую эвтектику при 721 °C и 0,9 масс. % С.
е — система азооксибензол + азобензол. Образуются твердые растворы [Hildebrand, Scott “Solubility of Non-Electrolytes, 1964).
ж — система л-хлориодбензол + л-дииодбензол. Образуются твердые растворы, наблюдается перитектическая точка (Hildebrand,
Scott, Solubility of Non-Electrolytes, 1964).
з — циклогексан + метилциклопентан. Циклогексан имеет две стабильные кристаллические формы в этом температурном интерва-
ле [Dale Encyclopedia of Chemical Processing and Design, 13, 471 (1981)].
280 Г лава 5
-144,72 “С
Концентрация циклогексана, мол. %
Рис. 5.25 (продолжение).
Фазовое равновесие 281
Рис. 5.26. Пример сложной диаграммы. Ее можно рас-
сматривать как выполненную из двух простых диа-
грамм: вещество А + интермолекулярное соединение С
и интермолекулярное соединение С + вещество В. Все
вещества ограниченно растворимы в твердой фазе. Не-
которые из приведенных выше простых диаграмм так-
же можно объединять.
Р, бар
Рис. 5.27. Бинарное (твердое вещество — жидкость) равновесие, сжиженная фаза находится в сверхкритических
условиях. Подобная информация приведена также на рис. 8.16 и в гл. 9.
а — равновесие между твердой (S) и сжиженной (F) фазами вблизи их критической точки. При понижении давления ниже значения,
соответствующего точке с раствор (точка а) разлагается с образованием раствора (точка Ь) и чистого вещества (d).
б — растворимость нафталина в этилене при 25 °C и повышенном давлении. Например, при давлении ~ 100 бар нафталин присут-
ствует в сжиженной фазе в количествах, достигающих х = 0,01; растворимость минимальна (х = 10-5) при давлении 40 бар и
достигает 4 • 10'5 при атмосферном давлении [Цекановская и др. Журн. физ. хим., 38, 2166 (1964)].
в — растворимость 2,3-диметилнафталина в этилене при повышенных давлениях. Кривые рассчитаны по уравнению Пенга —
Робинсона (Kurnik, Holla, Reid, 1981) © Am. Chem. Soc.
г — растворимость бензойной кислоты в диоксиде углерода при повышенных давлениях. Линии отверждения рассчитаны по урав-
нению Пенга — Робинсона (Kurnik, Holla, Reid, 1981). © Am. Chem. Soc.
282 Глава 5
Рис. 5.27 (продолжение).
меняется незначительно, а на диаграмме, приведенной
на рис. 5.28,в, значительно меняются и температура и
состав эвтектики. В этих и нескольких других работах
такого же типа изучалось также влияние давления; в
обычных исследованиях конденсирующихся фаз это не
практикуется, хотя полученная информация может
представлять определенный интерес.
5.4.6. Равновесие и реальные условия. Фазовые диа-
граммы показывают условия равновесия. Для ряда пре-
вращений, происходящих в твердой фазе при низких
температурах, характерны очень малые скорости, и ес-
ли нет возможности ускорить достижение равновесия,
то проводимые в таких условиях исследования могут не
иметь практического смысла. На рис. 5.25,г и д показа-
ны два из немногих примеров исследования твердофаз-
ных равновесий. Соответствующие исследования
необходимо проводить при предельно высокой темпера-
туре, и кроме того, время его проведения не должно
быть ограничено. Например, твердый раствор, содер-
жащий 25% нитрата таллия (рис. 5.23,е), нельзя приго-
товить простым смешиванием ингредиентов в
соответствующих пропорциях при комнатной темпера-
туре. Так что исследователю необходимо набраться тер-
пения, расплавить смесь при 300 °C и затем медленно'
охладить до температуры ниже 285 °C. При температу-
рах ниже эвтектической такие приемы, к сожалению, не
применимы. Следует также заметить, что поскольку
скорость превращений в твердой фазе преимущественно
контролируется стадией диффузии, маловероятно, что
она может катализироваться микропримесями посто-
ронних материалов. Таким образом, контролировать
превращения можно только путем изменения времени и
температуры.
5.5. Трехкомпонентные системы
Плоскостные диаграммы состояния трехкомпонент-
ных систем при постоянных значениях Р и Т — это диа-
граммы состава, показывающие зоны, линии и точки,
в которых возможно существование различных фаз. Со-
став равновесных фаз может быть очерчен соединитель-
ными линиями (коннодалями), но в целях упрощения
интерполяции и устранения нечеткостей на небольших
диаграммах предпочтительны определенные виды не-
прерывных корреляционных соединительных линий. На
рис. 5.29,а штриховая соединительная кривая — это
геометрическое место точек пересечения горизонталей,
проведенных через правую часть соединительной линии,
и вертикалей, проведенных через левую часть соедини-
тельной линии, хотя в принципе пригодна любая после-
довательность направлений линий, проходящих через
Фазовое равновесие 283
Рис. 5.28. Влияние давления на отдельные бинарные (жидкость — твердая фаза) равновесия.
а — система 1,4-Дихлорбензол + 1,4-Дибромбензол при давлении 1 и 500 атм. [Deffet Bull. Soc. Chim. Belgique, 47, 461 (1938)].
6 — система фенол + анилин при давлении 1, 600 и 1000 атм. Наблюдается образование интермолекулярного соединения и двух
эвтектик [Deffet Bull. Soc. Chim. Belgique, 47, 461 (1938)].
в — система бензол + этилуретан при давлении 1 и 2550 атм. Наблюдается значительное влияние давления на состав эвтектики
[Пущин Журн. физ. хим., 118, 447 (125)].
г — влияние давления на кривую замерзания водных растворов гидрохлорида гидроксиламина. Наблюдается лишь незначительное
смещение эвтектической точки [Marthieu Bull. Soc. Chim. Belgique, 58, 112 (1949)].
соединительную линию. Отдельная диаграмма распре-
деления может быть построена, как показано на рис.
5.29,6. В этом случае хса — доля компонента С в А-
обогащенной (левая сторона) фазе и хсв — доля того
же компонента в В-обогащенной (правая сторона) фазе.
Как будет показано позднее, диаграммы распределения
также удобны для представления трехфазных компози-
ций. Некоторые приемы построения зависимостей дают
в определенных ситуациях линейные зависимости, удоб-
ные для экстраполяции и интерполяции (см. также
гл. 7).
Полное графическое представление влияния Т, Р и со-
става в трехкомпонентных системах не всегда просто
выполнимо. Для систем жидкость—пар и жидкость—
жидкость—пар более удобной может оказаться алгебра-
ическая форма представления указанного влияния с при-
менением коэффициентов активности и фугитивности и
данных о давлении пара; такое представление, как пра-
284 Глава 5
Рис. 5.29. Изображение равновесных составов двух фаз трехкомпонентной смеси.
а — штриховая линия представляет собой соотношение соединительных линий; она строится как локус пересечения горизонталей,
проведенных с правой стороны окончаний соединительных линий, с вертикалями, проведенными от левосторонних окончаний
этих же соединительных линий.
б — распределительная кривая, построенная как локус пересечений отражения проекции горизонтали, проведенной из правосторон-
него окончания соединительных линий на прямую (образующую угол 45° с осью абсцисс), с горизонталью, проведенной из левосто-
роннего окончания соединительной линии.
вило, адекватно, если поведение системы не осложнено,
например образованием химических соединений. Для
некоторых классов соединений, в частности, кислород-
содержащих органических производных, влияние обра-
зования химических соединений на фазовое равновесие
можно учесть, поскольку константы равновесия из-
вестны.
Ниже перечислены некоторые условия, определяющие
число фаз, способных находиться в равновесии в трех-
компонентных системах.
1. Две фазы могут находиться в равновесии во всем
диапазоне составов при фиксированных Т и Р.
2. Три фазы имеют один и тот же состав при опреде-
ленных Т и Р, но если определены лишь Т или Р,
состав может меняться. Соотношение трех фаз опре-
деляется из общего состава.
3. Четыре фазы однородны, если определена лишь тем-
пература (давление). Если в системе присутствуют
только конденсированные фазы, влияние давления
обычно незначительно, так что оно не рассматрива-
ется как соответствующая переменная, и условия су-
ществования четырех фаз инвариантны.
4. Условия существования пяти фаз инвариантны,
если давление оказывает влияние на поведение си-
стемы.
Последующее обсуждение трехкомпонентных систем
проводится в соответствии с числом или типом содер-
жащихся в них фаз с привлечением в качестве примеров
органических систем. Поскольку системы, состоящие
только из твердых фаз применительно к органическим
соединениям не представляют особого интереса, а поэ-
тому и слабоизучены, равновесию газ—твердая фаза
здесь будет уделено мало внимания (см., однако, гл. 9).
Некоторые свойства треугольных диаграмм, описываю-
щих трехкомпонентные композиции, иллюстрируют
рис. 5.5 и 5.6.
5.5.1. Системы пар—жидкость. На рис. 5.30 приведе-
ны некоторые характерные типы диаграмм системы
ацетон + метанол + вода, показывающие а) зависи-
мость состава жидкой фазы при 100 °C от величины
давления, соответствующего началу кипения (например,
смесь, содержащая по 30% воды и ацетона, начинает
кипеть при давлении 3,46 атм); б) зависимость состава
системы от температуры начала кипения при давлении
1 атм (например, та же смесь при 1 атм начинает ки-
петь при температуре 61,7 °C); в) зависимость состава
паровой фазы при равновесии от состава жидкой фазы
(например, та же жидкая смесь находится в равновесии
с парами, содержащими 10% воды и 57% ацетона).
Рис. 5.30, г и д характеризуют систему водород +
+ азот + монооксид углерода при фиксированных зна-
чениях Т и Р; составы равновесных фаз представлены
линиями. Например, жидкость, содержащая 10% Н2 и
43% СО, находится в равновесии с парами, содержащи-
ми 10% СО и 3% N2, при -195 °C и 150 атм. Паро-
жидкостные композиции для системы метан + н-бу-
тан + декан при трех давлениях показаны на рис. 5.3О,е.
На рис. 5.31 на примере системы ацетон + хлоро-
форм + 4-метилпентанон демонстрируется другой спо-
соб изображения парожидкостного равновесия. И, нако-
нец, температуры кипения можно также изображать на
треугольных диаграммах, но в таких масштабах велика
вероятность недоразумений, и поэтому предпочтитель-
нее раздельные диаграммы.
Фазовое равновесие 285
Рис. 5.30. Изотермы, изобары и равновесные парожидкостные со-
ставы некоторых треххомпоиентных систем.
а — изобары смесей вода + метанол + ацетон при 100 °C. Диаграмма пока-
зывает, что давление смеси, содержащей по 30% воды и ацетона, составляет
3,45 атм [Griswold, Wong СЕР Symposium Series, 3, 18 (1952)].
б — изотермы смесей вода + метанол + ацетон при 1 атм. Диаграмма пока-
зывает, что у смеси, содержащей по 30% воды и ацетона, при 1 атм темпера-
тура насыщения равна 61,5 °C [Griswold, Wong СЕР Symposium Series, 3, 18
(1952)].
286 Глава 5
Рис. 5.30 (продолжение).
в — равновесные парожидкостные составы смесей вода(1) + метанол(2) +
ацетон(З) при 1 атм. Сплошные линии соответствуют у\, штриховые — у3.
Диаграмма показывает, что жидкая фаза, содержащая по 30% воды и ацето-
на, находится в равновесии с паровой фазой (yi = 0,1 и у3 = 0,57) [Griswold,
Wong СЕР Symposium Series, 3, 18 (1952)].
г — равновесные парожидкостные составы водород + азот + оксид углерода
при 150 атм и -195 °C. Состав паровых фаз показан штриховыми линиями
[Руеман, Цинн Журн. физ. хим., 12, 389 (1937)].
Фазовое равновесие 287
Рис. 5.30 (продолжение)
0 — та же система, что и выше, но при 150 атм и -185 °C. Наблюдается
резкое изменение формы двухфазной области.
е — составы сосуществующих фаз в системе метан + н -бутан + декан при
280 °F (137,78 °C) и различных давлениях. Нижние концы соединительных ли-
ний соответствуют жидким фазам, верхние — паровым [Riemer, Sage, Lacey
Ind. Eng. Chem., 43, 1436 (1951)]. © Am. Chem. Soc.
288 Глава 5
Рис. 5.31. Трехкоординатная диаграмма х—у и двухкоординатные диаграммы Т—х—у системы 2-метилпента-
нон-4(1) + хлороформ(2) + ацетон(З) при 1 атм.
На трехкоординатной диаграмме штриховые линии показывают величины уг, а сплошные — величины у3. Например, эквимолярная
жидкость находится в равновесии с паровой фазой состава у2 = 0,35 и у3 = 0,57 [Landolt-Bornstein, П/2а, 527, 608, 609, 756].
5.5.2. Системы пар и две жидкие фазы. Ряд возмож-
ных путей представления составов трех равновесных
фаз показан на рис. 5.32. На рис. 5.32,а равновесные
составы системы жидкость—жидкость показаны пря-
мыми соединительными линиями, тогда как линия со-
става пара представлена штриховой линией с числами,
указанными также на соединительных линиях.
На кривых распределения, приведенных на рис. 5.32,6,
на абсциссе указан мольный состав ацетона в обогащен-
ной водой фазе, на ординате указаны мольные доли аце-
тона и хлороформа в паровой фазе, а распределительная
кривая равновесия жидкость—жидкость построена как
на рис. 5.29. Отдельные линии х—у, характеризующие
однородное состояние жидкости (рис. 5.33), определя-
ются линиями, соединяющими соответствующие соста-
вы (пар—жидкость); эту диаграмму (рис. 5.30) можно
использовать в таких целях при наличии достаточного
количества данных для его построения.
5.5.3. Жидкие фазы. Трехкомпонентные системы при
заданных температуре и давлении могут образовывать
множество однофазных, двухфазных и трехфазных об-
ластей, большинство исследованных систем подобного
рода имеет по одной—две одно- и двухфазной области.
Формы этих областей могут значительно различаться,
причем они часто подвержены влиянию температуры.
Пространственная диаграмма, приведенная на рис. 5.34,
иллюстрирует один из видов температурного влияния,
для которого характерно наличие как верхней, так и
нижней критической температуры растворимости. Наи-
более часто встречающийся тип поведения — это увели-
чение области растворимости с повышением темпера-
туры. На рис. 5.35 показано влияние роста температу-
ры на изменение верхней критической точки раствори-
мости в тройных композициях. Рис. 5.7 демонстрирует
тройную систему, которая имеет бинарную критиче-
скую точку растворимости. На ряде других рисунков
этого раздела показаны другие возможные варианты
влияния температуры.
Один из простых принципов классификации диаграмм
предусматривает их деление на группы в соответствии
Фазовое равновесие 289
Рис. 5.32. Система ацетон + хлороформ + вода при 1 атм.
а — показаны линии равновесных фаз жидкость — жидкость. Штриховая линия показывает состав пара, находящегося в равновесии
со смесями жидкость — жидкость (соединительные линии с тем же номером).
б— распределительные кривые: хи — мольная доля ацетона (3) в обогащенной водой фазе (1), х32 — мольная доля ацетона (3)
в обогащенной хлороформом фазе (2); уг и уз мольные доли хлороформа и ацетона в паровой фазе [Landolt-Bornstein, II/2, 727].
Рис. 5.33. Диаграмма, показывающая равновесия жидкость — жидкость и
пар — жидкость в гомогенных жидких областях системы вода + эта-
нол + этилацетат при 70 °C.
Незачернеиный кружок — состав паров, зачерненный — состав жидкой фазы на той
же самой соединительной линии [Mertl Coll. Czech. Chem. Common, 37, 366 (1972)].
19-829
290 Глава 5
Рис. 5.34. Влияние температуры на размер и форму
двухфазной области трехкомпонентной системы. Пока-
зана система с верхней и нижней критическими темпера-
турами растворения (см. также рис. 5.2, а и б).
с числом одно-, двух- и трехфазных областей, присут-
ствующих в системе. Отдельные простейшие примеры
даны на рис. 5.36. Наиболее распространены диаграм-
мы с одиночными двухфазными областями (рис. 5.36,а
или б). На рис. 5.36,а также имеется одна однофазная
область. На рис. 5.36,в показаны две двухфазные обла-
сти, которые могут расширяться и даже сливаться, в
результате чего однофазная область делится на две ча-
сти (см. рис. 5.36,6). Три гетерогенные области, пока-
занные на рис. 5.36,<? также могут расширяться до
соприкосновения или слияния. Если они лишь коснутся
друг друга, возможно образование трехфазной зоны
(заштрихована квадратной сеткой), подобной показан-
ной на рис. 5.6 и ряде других рисунков этого раздела.
Принимая во внимание доступность ряда обширных
коллекций фазовых диаграмм, в частности коллекции
Ландольта-Бернштейна, можно ограничиться рассмот-
рением лишь некоторых из них. Одна из наиболее на-
глядных серий из 464 тройных диаграмм с диоксидом
углерода как одним из компонентов, опубликованная в
работе [284], демонстрирует, насколько сильно может
различаться поведение систем. Три серии диаграмм,
приведенные на рис. 5.37 — 5.39, показывают в основ-
ном влияние температуры. Так, например, в системе
вода—триэтиламин—фенол с повышением температу-
ры растворимость фенола увеличивается, но смешивае-
мость воды и триэтил амина уменьшается. На рис. 5.38
при температуре 25 °C зарегистрировано шесть зон, а
при более высоких температурах только две. Повыше-
ние температуры всего на 10 °C достаточно для исклю-
чения трех трехфазных зон из системы (рис. 5.39) и
снижения числа возможных зон в системе с двенадцати
до четырех. Мицеллярные системы отличаются особен-
но сложным поведением (см. рис. 9.12).
Эти немногие рассмотренные примеры могут вну-
шить серьезные сомнения относительно теоретических
методов корреляции или прогнозирования поведения
Рис. 5.35. Влияние температуры на двухфазную область системы аце-
тон + вода + фенол. Верхняя критическая температура растворения 92 °C.
Волнистая линия — локус критических точек [Schreinemakers Z. physik.
Chem., 33, 75 (1900)].
Фазовое равновесие 291
19*
Рис. 5.36. Обобщенные примеры трехкомпонентных диаграмм с однофазными и двухфазными областями. Показа-
ны соединительные линии, связывающие равновесные составы фаз.
а — одна однофазная и одна двухфазная области.
б — бинодальные кривые образуют полосу, ограниченную двумя однофазными областями.
в — две двухфазные области.
г — три двухфазные области.
д — двухфазная зона с двумя лишь компонентами в каждой фазе.
е — распределительная кривая для предыдущей диаграммы, построенная как на рис. 5.29.
292 Глава 5
Фенол
Фенол
Рис. 5.37. Система вода + триэтиламин + фенол. Состав указан
в массовых долях \Meerburg Ъ. phisik. Chem., 40, 642 (1902)].
а — при 10 °C система имеет две двухфазные области.
б — при 75 °C две пары компонентов смешиваются полностью, а во-
да + триэтиламин — лишь частично.
Фазовое равновесие 293
Рис. 5.38. Диаграмма трехкомпонентной системы 2,2,4-триметил-
пентан + нитроэтан + перфторбутиламин, показывающая много-
фазные области при некоторых температурах. Цифры I—III указы-
вают число фаз. Состав дан в массовых долях [Vreeland, Dunlop
J. Phys. Chem., 61, 329 (1957)]. © Am. Chem. Soc.
a — при 25 °C система имеет шесть различных областей, включая трех-
фазную.
б — при 51,3 °C остается лишь одна многофазная область.
294 Глава 5
Рис. 5.39. Диаграмма системы гликоль + додеканол + 1-
нитроэтан, для которой характерно образование при опреде-
ленных температурах множества гомогенных и гетерогенных
областей.
а: 14 °C, 1 атм, б: 24 °C, 1 атм. Состав указан в массовых долях.
I — одна жидкая фаза; II — две жидкие фазы; III — три жидкие фа-
зы; IV — одна жидкая и одна твердая фазы; V — две жидкие фазы
и одна твердая фаза (Francis, 1956). © Am. Chem. Soc.
Фазовое равновесие 295
Рис. 5.40. Диаграмма равновесия при плавлении некото-
рых тройных систем.
а — система нитрат аммония + нитрат лития + нитрат гуани-
дина образует простую бинарную и тройную эвтектику. Со-
став указан в масс. % [Clark et al. J. Phys and Colloid Chem.,
53, 225 (1949)].
6 — система дифенил + бензофенон + дифениламин. Послед-
ние два компонента образуют химическое соединение (1:1).
Тройные эвтектики наблюдаются при 18,8 °C (0,205 мол. долей
бензофенона, 0,49 мол. долей дифениламина) и при 16,5 °C
(0,52 мол. долей бензофенона, 0,18 мол. долей дифениламина.
[Lee, Warner JACS, 4474 (1933)]. © Am. Chem. Soc.
в — система нафталин + дифенил + дибензил. Тройная эвтек-
тика наблюдается при 17,4 °C (0,27 нафталина, 0,338 дифенила,
0,392 дибензила). Состав указан в мольных долях [Lee, Warner
JACS, 57, 318 (1935)]. © Am. Chem. Soc.
многокомпонентных систем. До сих пор корреляции на
базе методик NRTL и UNIQUAC применялись главным
образом для двухфазных систем, что практически важ-
но, и лишь иногда для трехфазных систем. Использова-
ние этих методов для характеристики бинарных систем
теоретически неограничено, но на практике ситуация
осложняется из-за возможности взаимодействия выс-
ших порядков и влияния температуры, которое не сис-
тематизировано.
5.5.4. Равновесия жидкость—твердая фаза при плав-
лении. Представить себе удовлетворительным образом
полную картину фазовых превращений можно только
посредством трехмерных диаграмм (рис. 5.7 или 5.8)
или стереоскопических изображений подобных выпол-
ненным в работе [132]. К сожалению, многие публикуе-
мые пространственные диаграммы перегружены линия-
ми, а нанесенная на них штриховка или затемнения не-
адекватны, так что вполне понятны они только авто-
рам. Читателю следует изыскать возможность и
ознакомиться со стереодиаграммами Тамаша и Пала
[132], из которых особенно наглядны следующие:
№ 14. Система H2S2O7 + HSO3CI + H2SO4, показываю-
щая две бинарные композиции.
№ 18. Система с конгруэнтной тройной композицией.
№ 20. Система с перитектической тройной композицией.
№ 37. Кривая равновесия при кристаллизации.
№ 38. Система СбНдСЬ + СбНдВгг + СбН4С1Вг.
№ 59. Система с несмешивающимися жидкостями.
№ 11. Система дифенил+бензофенон + дифениламин с
конгруэнтным бинарным соединением.
По ряду причин, которые будут указаны, равновесия
при плавлении часто более сложны, чем равновесия ти-
па жидкость—жидкость или пар—жидкость. К
счастью, на конденсированные системы давление ока-
зывает лишь незначительное влияние, что часто позво-
ляет представлять систему серией изотермических
диаграмм, добавляя в случае необходимости изоплеты.
Приведем ряд факторов усложняющих диаграммы
тройных систем.
1. Образование твердых растворов веществ различ-
ной степени растворимости — в пределах от нуля до
полной растворимости. Такие растворы образуют ве-
щества, имеющие одинаковую кристаллическую струк-
туру и близкие значения молекулярных объемов.
Образование твердых растворов весьма характерно для
органических веществ и может быть использовано для
296 Глава 5
Уретан
Рис. 5.41. Пространственная диаграмма системы фе-
нол + мочевина + уретан. Образуются два интермоле-
кулярных соединения, которые распадаются до дости-
жения точки плавления [Hrynakowski, Sztnit Z. physik.
Chem., 175A, 83 (1933)].
a — пространственная модель системы. Ai и Аг — перитекти-
ки, Pi — тройная эвтектика, включающая два метастабильных
соединения.
б — проекции трех- и двухкомпонентных систем. Ai и Аг — пе-
ритектические точки. Наблюдаются три тройные эвтектики при
23,2, -3,5 и -24 °C.
в — вертикальное сечение при 30 масс. % фенола. D — соедине-
ние мочевины и уретана, F — соединение мочевины и фенола,
Н — мочевина, L — жидкость, Ph — фенол, I/ — уретан.
г — вертикальное сечение при 20 масс. % уретана. Обозначения
те же.
Фазовое равновесие 297
Рис. 5.41 (продолжение).
разделения последних, примером тому может служить
кристаллизация из растворителя.
2. Образование молекулярных соединений, которые
могут быть стабильны (конгруэнтны) или нестабильны
(инконгруэнтны) в точках их плавления. Влияние интер-
молекулярных соединений на равновесие бинарных сис-
тем рассмотрено в разд. 5.4. Соединения, образованные
парой веществ, вполне обычны для тройных органиче-
ских систем, но ни одного тройного органического со-
единения вспомнить не удается. Однако тройные
соединения обычны для систем на основе диоксида
кремния, например для системы СаО—АЬОз—S1O2.
В данном разделе будет рассмотрено несколько трой-
ных диаграмм плавления. На рис. 5.40,а показан про-
стейший тип диаграмм с тремя бинарными эвтектиками
и всего одной тройной эвтектикой. В системе, приведен-
ной на рис. 5.40,6, образуются интермолекулярное со-
единение и две тройные эвтектики. На рис. 5.40,в даны
двойные и тройные диаграммы системы нафталин—
дифенил—дибензил, поведение которой почти соответ-
ствует идеальному.
Несколько видов диаграмм системы фенол + мочеви-
на + уретан показаны на рис. 5.41. Мочевина и уретан,
мочевина и фенол образуют интермолекулярные смеси,
которые разлагаются до плавления; на пространствен-
ной диаграмме и на ее проекции (рис. 5.41,6) указаны
перитектические точки. Бинарные области при постоян-
ном количестве третьего компонента приведены на
рис. 5.41,в и г, там же указано число фаз, находящихся в
равновесии в областях жидкость—твердая фаза и твер-
дая фаза—твердая фаза, расположенных между обла-
стями чистых веществ и смесей. Разработка таких
диаграмм сыграла очень важную роль.
5.6. Многокомпонентные системы.
Представить изменение состава четырехкомпонент-
ной системы можно только посредством трехкоорди-
натной диаграммы, которая имеет вид правильного
тетраэдра и демонстрирует только изменение состава
при постоянных температуре и давлении. Примеры та-
ких диаграмм приведены на рис. 5.8,6 и в. Для практи-
ческих целей пригодны двухкоординатные диаграммы
при постоянных величинах мольных составов двух из
компонентов (см., например, рис. 5.8,в и г), либо трех-
координатные диаграммы при фиксированном мольном
составе одного из компонентов. При построении диа-
граммы системы, показанной на рис. 5.8,в, целесооб-
разно считать постоянным содержание воды. Изучение
состояния многокомпонентных растворов и равновес-
ных составов жидкость—твердая фаза, чаще всего про-
водилось на примерах водных солевых смесей (см. [133,
22]). Рассмотрение четырех- и пятикомпонентных сис-
тем не входит в нашу задачу; фазовое равновесие в та-
ких системах подробно обсуждается в книгах Риччи
[НО], Фогеля [138] и Цернике [146].
Многокомпонентные системы с несмешивающимися
твердыми фазами не содержащие интермолекулярных
соединений, можно анализировать, пользуясь уравнени-
ем Шредера, если известны корреляции для коэффици-
ентов активности или единичные коэффициенты актив-
ности в идеальном случае.
Примеры таких расчетов даны в гл. 7. При современ-
ном уровне знаний построение столь сложных диа-
грамм в большинстве случаев не представляется воз-
можным, однако некоторый прогресс в этом направле-
нии все же наметился, см., например [62, 604]. Однако
большая часть опубликованных работ посвящена рас-
смотрению экспериментально установленных фазовых
равновесий и их классификации.
5.7. Избранные книги
по фазовым диаграммам
1. Bowden S.T The Phase Rule and Phase Reactions,
London; Macmillan, 1938.
2. Ferguson F.D., Jones T.K. The Phase Rule, Woburn,
Butterworths, 1966.
3. Haase R., Schonert H. Solid-Liquid Equilibrium, New
York, Pergamon, 1969.
4. Kaufman L., Bernstein H. Computer Calculation of
Phase Diagrams, New York, Academic Press, 1970.
5. Landolt-Bornstein Zahlenwerte und Funktionen, II/2a
298 Глава 5
(I960), II/2b (1962), II/2c (1964), П/3 (1956), IV/3,
New York, Springer, 1975.
6. Nyvlt J. Solid-Liquid Phase Equilibrium, New York,
Elsevier, 1977.
7. Prince A. Alloy Phase Equilibria, N. Y., Else., 1966.
8. Reisman A. Phase Equilibrium, N. Y„ Acad., 1970.
9. Ricci J. The Phase Rule and Heterogeneous Equilibri-
um, New York, Van Nostrand, 1951.
10. Tamas F., Pal I. Phase Equilibrium Spatial Diagrams,
Woburn, MA, Butterworths, 1970.
11. Treybal R. Liquid Extraction, New York, McGraw-
Hill, 1963.
12. Vogel R. Die Heterogenen Gleichgewichte, Leipzig,
Akademische, 1959.
13. West D.R.F. Ternary Equilibrium Diagrams, London,
Chapman and Hall, 1982.
14. Zernike J. Chemical Phase Theory, Deventer, Kluwer,
1955.
5.8. Задачи
5.1. Ниже указаны мольные доли пропионовой кисло-
ты в водной (х„) и октановой (хо) фазах:
xw 0,030 0,081 0,167 0,274
х0 0,057 0,124 0,181 0,252
Подберите уравнение для определения коэффициентов
распределения как функции концентрации пропионовой
кислоты в одной из фаз.
5.2. Ниже приведены координаты трехфазных точек
(в массовых долях) при 25 °C для системы, показанной
на рис. 5.38:
g2 0,042 0,712 0,159
g3 0,075 0,269 0,722
Определите относительные количества этих трех фаз
для смеси, имеющей одинаковый общий массовый
состав.
5.3. Система гексадекан (1) + анилин(2) + бензол(З)
находится в равновесии при 25 °C и 1 атм при следую-
щем соотношении компонентов:
Фаза, обедненная CsHvN Фаза, обогащенная CsH7N
х2 хз х2 хз
0,141 0,000 0,990 0,000
0,144 0,147 0,896 0,095
0,147 0,180 0,879 0,111
0,152 0,227 0,852 0,137
0,162 0,303 0,804 0,183
0,165 0,323 — —
0,181 0,370 0,744 0,237
— — 0,742 0,239
0,194 0,396 — —
— — 0,671 0,299
0,249 0,449 — —
— — 0,562 0,378
0,340 0,456 — —
— — 0,453 0,426
Постройте соединительные коррелирующие кривые и
определите путем экстраполяции точку полного смеше-
ния [760]. Траектория средних точек аппроксимируется
прямыми.
5.4. а. Для системы SO3 + Н2О характерны конгруэнт-
ные точки плавления при составе смеси 68,96, 81,63 и
89,89 масс. % SO3. Назовите формулы этих соединений.
5.4.6. У системы «-гептан + 2,2,4-триметилпентан су-
ществует простая эвтектическая точка при -114,4 °C,
соответствующая 24 мол. % «-гептана [761]. Определи-
те аналитически максимальное количество (мол. %) н-
гептана, которое можно выделить кристаллизацией из
двухкомпонентных смесей, содержащих соответственно
80, 90 и 95 мол. % «-гептана.
5.5 Постройте фазовую диаграмму системы
HF + KF исходя из следующих данных [762].
а. Температура фазового перехода a-KHF2 в /3-KHF2
равна 195 °C.
б. a-KHF2, /3-KHF3 и жидкий HF находятся в равно-
весии при 195 °C, если общее содержание HF рав-
но 53,82 мол. %.
в. Соединения имеют следующие точки плавления:
KF 880 °C, /3-KF-HF 239 °C, KF•2HF 71,7 °C,
2KF 5HF 64,3 °C, KF • 3HF 65,8 °C, KF • 4HF
72,0 °C, HF -83,7 °C.
г. Эвтектические температуры и содержание HF
(мол. %) соответственно равны: -97 °C при
93,11%, 63,6 °C при 77,1%, 62,4 °C при 72,7%,
61,8 °C при 69,69%, 68,3 °C при 64,9%, 229,5 °C
при 48,6%.
Опишите, что будет происходить при постепенном до-
бавлении KF при 65 °C в жидкий HF до образования
смесей с преимущественным содержанием KF.
5.6. Постройте диаграмму состояния системы
СС14(А) + диоксан-1,4(B) по следующим температурам
плавления [772]:
*В 0,000 0,035 0,049 0,060 0,090
Т(°С) -22,7 -24,0 -24,6 -24,2 -23,0
хв 0,312 0,331 0,349 0,370 0,411
Т(°С) -18,4 -18,3 -18,3 -18,4 -18,8
0,645 0,713 0,755 0,802 0,846
л °C) -7,3 -3,7 -1,6 +0,9 + 3,4
*В 0,109 0,141 0,205 0,250 0,284
Л °C) -22,4 -21,2 -19,2 -18,6 -18,4
*в 0,472 0,489 0,514 0,556 0,604
Л °C) -19,8 -20,0 -17,6 -13,1 -9,9
*в 0,912 0,967 1,000
Л °C) +7,0 + 10,1 + 11,8
Определите химический состав и температуры плавле-
ния всех эвтектик и всех химических соединений.
5.7. На диаграмме, полученной Плато [763] представ-
лена система СаС12 + СаГг При 737 °C происходит рас-
пад интермолекулярного соединения (1:1). Определите
составляющие для каждой области. Опишите измене-
ния, происходящие при медленном нагревании систе-
мы с 50—55 % СаС12.
Фазовое равновесие 299
5.8. Смеси ацетамид + уксусная кислота (х — мольная
доля уксусной кислоты) характеризуются следующими
температурами замерзания, Т, °C (100 х); 80,2 (0), 72,5
(11,5), 63,0 (20,9), 51,9 (30,0), 35,6 (40,2), 8,0 (51,5), -0,2
(51,9), -0,5 (53,6), -0,6 (55,8), - 1,8 (57,9), -2,6 (60,3),
-3,9 (62,5), -9,2 (68,2), -11,7 (69,9), -11,1 (70,0), 0,0
(78,9), 8,9 (89,0), 16,6 (100,0) [764]. При каких условиях
возможно равновесие трех фаз в указанном температур-
ном интервале?
5.9. На приведенной ниже диаграмме показаны обла-
сти равновесия смесей компонентов А и В.
а. Идентифицируйте фазы, присутствующие в каж-
дой области.
б. Начертите кривые охлаждения для композиций а,
b и с.
в. Определите максимальную массу чистого компонен-
та В, которую можно получить кристаллизацией
100 кг расплава с начальным составом 90 масс. % В.
5.10. На приведенной ниже диаграмме показано рав-
новесие пар—жидкость—жидкость в двухкомпонентной
системе.
а. Определите точку кипения смеси, содержащей
25 масс. % А.
б. Если смесь части а дистиллируют при температу-
ре, превышающей 40 °C, каким будет состав
остатка?
в. Каким будет состав дистиллята?
г. Если дистиллят части в дистиллируют повторно,
какими будут начальная точка кипения и состав
смеси?
Равновесие пар — жидкость — жидкость в двухкомпонентной
сис теме.
300 Глава 5
5.11. Хадсон [773] провел исследование фазового рав-
новесия в системе никотин + вода в жидкой области и
получил следующие данные.
Никотин, масс. % Температура появ- Температура, при пения второй фазы, которой система
°C вновь становится гомогенной, °C
6,8 94 95
7,8 89 155
10 75 —
14,8 65 200
32,2 61 210
49,0 64 205
66,8 72 190
80,2 87 170
82,0 129 130
Постройте фазовую диаграмму состав—температура
для этой системы. Обозначьте все зоны и определите
состав (составы) каждой (всех) фазы (фаз), находящейся
в равновесном состоянии при следующих условиях:
Содержание никотина, масс. % Г, оС
а 20 45
б 20 120
в 20 220
г 90 120
5.12. Для системы о-динитробензол + н-динитробен-
зол получены следующие данные [765]:
Динитробензол, мол. % Температура плавления, °C
100 173,5
90 167,7
80 161,2
70 154,5
60 146,1
50 136,6
40 125,2
30 111,7
20 104,0
10 110,6
0 116,9
Постройте диаграмму температура—состав для систе-
мы и определите по ней эвтектическую температуру и
состав эвтектики.
Определите максимальное количество (%) н-динитро-
бензола, которое можно получить кристаллизацией из
двухкомпонентной смеси, содержащей первоначально
95, 75 и 45°7о «црд-изомера.
5.13. Определите число компонентов в каждой из сле-
дующих систем.
a. NH4C1(c), NH4+(a<y), СГ(<цу), Н2О(//^), Н3О + (бц?),
H2O(g), NH3(g), ОН“(д<7), NH4OH(a<7).
б. NH4C1(c), NH3(g), HCl(g), в которой парциальное
давление NH3 всегда равно парциальному давле-
нию НС1, как в том случае, если весь газ образует-
ся в результате сублимации NH4CI(c).
в. NH4C1(c), NH3(g), HCl(g), в которой парциальное
давление NH3 не обязательно равно парциальному
давлению НС1.
г. CH3COONH4(c), CH3COO~(a<7), NH4+(az?),
Н3О + (а<у), NH3(a^), ОНДщу), СН3СООН(д^),
Н2О(//<у), H2O(g), учитывая возможность гид-
ролиза,
д. NaCl(c), КВг(с), К + (д<?), Na + (a<7), СГ(д<7),
Вг“(д<7), Н2О(//<7), H2O(g).
е. NaCl(c), КС1(с), Na + (flg), СГ(я<7), Н2О(//<7),
H2O(g).
ж. СаС12 • 6Н2О(с), Са2 + (д<7), СГ(а^), Н2О(//?),
H2O(g).
з. СаСО3(с), СаО(с), CO2(g), в которой СаО и СО2
образуются в результате разложения СаСО3(с)
[766].
5.14. Определите для каждой из следующих систем
число компонентов С (предполагая соответствующий
ряд компонентов), возможные внутренние изменения и
число F степеней свободы (предположите приемлемый
ряд независимых внутренних изменений) [767].
1. а) СаСО3, находящийся в равновесии с СаО и СО2;
б) NiO и Ni, находящиеся в равновесии с Н2О, Н2, СО2
и СО.
2. а) Водород и кислород в газовой фазе и растворен-
ные в воде при 25 °C; б) водяной пар, нагретый до
2000 °C и содержащий при этой же температуре Н2, О2,
ОН, О, Н; в) произвольная смесь водорода и кислорода,
нагретая до 2000 °C, содержащая образующиеся при
этой температуре Н2О, ОН и др.
3. а) Жидкий N2O4, находящийся в равновесии с га-
зом, содержащим NO, N2O3, NO2 и N2O4; б) смесь N2,
О2 и NO при 25 °C; в результате реакции между NO и
О2 образуются NO2 и другие оксиды азота; в) смесь,
указанная в п. «в», нагретая до 3000 °C.
4. а) Смесь твердых NaCl, КО, NaNO3 и KNO3, нахо-
дящаяся в равновесии с водой; б) смесь NaCl и KNO3,
находящаяся в равновесии с водой; в) водные растворы,
содержащие а различных катионов, b различных анио-
нов и с различных их соединений (например, Na +, Н +,
К + , Hg2 + , 8ОГ, СГ, HSO4“, HgSO4, HgCl + , HgCl2).
Фазовое равновесие 301
5. 15. Сосуд, имеющий форму усеченного конуса (диа-
метром 1 и 3,5 см), содержит равные массы шести не-
смешивающихся жидких фаз, упомянутых в «Правиле
фаз» Боудена: гексан (q = 0,65), вода (q = 0,99), анилин
(б = 1,02), фосфор (е = 1,83), галлий (q = 6,1) и ртуть
(q = 13,6). Эта смесь уравновешивается соляным ра-
створом (@ = 1,15), помещенным в колонку. Какова от-
носительная высота столба соляного раствора?
5. 16. На рис. 5.6,6 показаны системы, состоящие из
трех фаз а (0,5, 0,2, 0,3), 3 (0,1, 0,7, 0,2), у (0,2, 0,1,
0,7). Определите соотношение всех трех фаз как функ-
цию Xi при Хз = 0,35.
ОГЛАВЛЕНИЕ
Предисловие редактора перевода................ 5
Предисловие .................................. 6
Рекомендации по использованию уравнений ...... 8
Рекомендации для представления равновесия
пар—жидкость ............................... 8
Рекомендации по определению коэффициентов
активности жидкой фазы...................... 9
1. Уравнение состояния...................... 10
1.1. Историческая справка.................. 10
1.2. Неидеальные газы ..................... 18
1.3. Соответственные состояния............. 25
1.4. Вириальное уравнение состояния........ 45
1.5. Кубические уравнения................ 50
1.6. Сложные уравнения состояния........... 69
1.7. Силы межмолекулярного взаимодействия
и уравнения состояния................. 88
1.8. Критическое состояние и критические
свойства ............................. 95
1.9. Сравнение уравнений состояния и пред-
варительные рекомендации 104
1.10. Задачи ............................. 111
2. Термодинамические функции и равновесие.. 117
2.1. Термодинамические функции ........... 117
2.2. Фундаментальные уравнения ........... 118
2.3. Общие и специфические свойства....... 123
2.4. Парциальные молярные свойства........ 123
2.5. Дифференцирование по мольным долям . 126
2.6. Однородные функции................... 128
2.7. Зависимость свойств от температуры и
давления ............................ 131
2.8. «Смешанные» и избыточные функции .... 132
2.9. Уравнение Гиббса—Дюгема и термоди-
намическое состояние..................... 135
2.10. Условия равновесия.................. 137
2.11. Задачи ............................. 139
3. Фугитивность и коэффициент фугитивности ... 144
3.1. Определения и основные формулы ...... 144
3.2. Чистые вещества...................... 145
3.3. Смеси ............................... 150
3.4. Идеальные смеси ...................... 155
3.5. Жидкая и твердая фазы ................ 158
3.6. Область применения ................... 164
3.7. Задачи ............................... 165
4. Коэффициенты активности .................. 169
4.1. Активность и коэффициенты активности 169
4.2. Стандартные состояния................. 169
4.3. Термодинамические уравнения, содержа-
щие коэффициенты активности ............. 170
4.4. Определение коэффициентов активности . 176
4.5. Коэффициенты активности и уравнения
состояния ............................... 178
4.6. Корреляции данных..................... 180
4.7. Уравнение Маргулеса и связанные с ним
уравнения ............................... 186
4.8. Уравнение ван Лаара................... 191
4.9. Уравнение Вильсона и его модификации 194
4.10. Уравнение NRTL (Ренона) ............. 204
4.11. Уравнение UNIQUAC (universal quasi-che-
mical — универсальное псевдохимическое) 207
4.12. Многокомпонентные смеси ............. 208
4.13. Сравнение уравнений.................. 210
4.14. Множественность корней уравнений .... 211
4.15. Бесконечное разбавление.............. 218
4.16. Оценка коэффициентов активности на
основании свойств чистых компонентов . 221
4.17. Расчет коэффициентов активности по ре-
зультатам измерения равновесия ..... 227
4.18. Влияние температуры и избыточной эн-
тальпии .................................. 236
4.19. Задачи ............................. 242
5. Фазовое равновесие...................... 250
5.1. Графическое представление............ 252
5.2. Правило фаз ......................... 257
5.3. Однокомпонентные системы ............ 260
5.4. Двухкомпонентные системы ............ 261
5.5. Трехкомпонентные системы ............ 282
5.6. Многокомпонентные системы ........... 297
5.7. Избранные книги по фазовым
диаграммам........................... 297
5.8. Задачи .............................. 298
УВАЖАЕМЫЙ ЧИТАТЕЛЬ!
Ваши замечания о содержании книги, ее оформлении,
качестве перевода и другие просим присылать по
адресу: 129820, Москва И-110, ГСП, 1-й Рижский пер.,
д. 2, издательство «Мир».
Научное издание
Стенли М. Уэйлес
ФАЗОВЫЕ РАВНОВЕСИЯ В ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
В 2-х частях
1
Заведующий редакцией академик О.А. Реутов.
Зам. зав. редакцией З.Ф. Ходецкая. Старший научный редактор Р.И. Краснова.
Младший редактор И.С. Ермилова. Мл. научный редактор И.И. Землячева. Художник
Ю.С. Урманчеев. Художественный редактор М.Н. Кузьмина. Технический редактор
Н.И. Борисова. Корректоры В.А. Валуева, Р.Л. Вибке.
ИБ № 6583
Подписано к печати 22.12.88.
Формат 84 х 108 Ив- Бумага офсетная № 1.
Гарнитура тайме. Печать офсетная, (фотоофсет).
Объем 9,50 бум. л. Усл. печ. л. 31,92.
Усл. кр.-отт. 60,48. Уч.-изд. л. 31,97.
Изд. № 3/5746. Тираж 3200 экз. Зак.829.
Цена 6 р. 60 к.
Издательство «Мир» В/О «Совэкспорткнига» Государственного комитета СССР
по делам издательств, полиграфии и книжной торговли.
129820, ГСП, Москва И-110, 1-й Рижский пер., 2.
Набрано в Межиздательском фотонаборном центре издательства «Мир»
Можайский полиграфкомбинат В/О «Совэкспорткнига»
Государственного комитета СССР по делам издательств,
полиграфии и книжной торговли.
143200, Можайск, ул. Мира, 93.