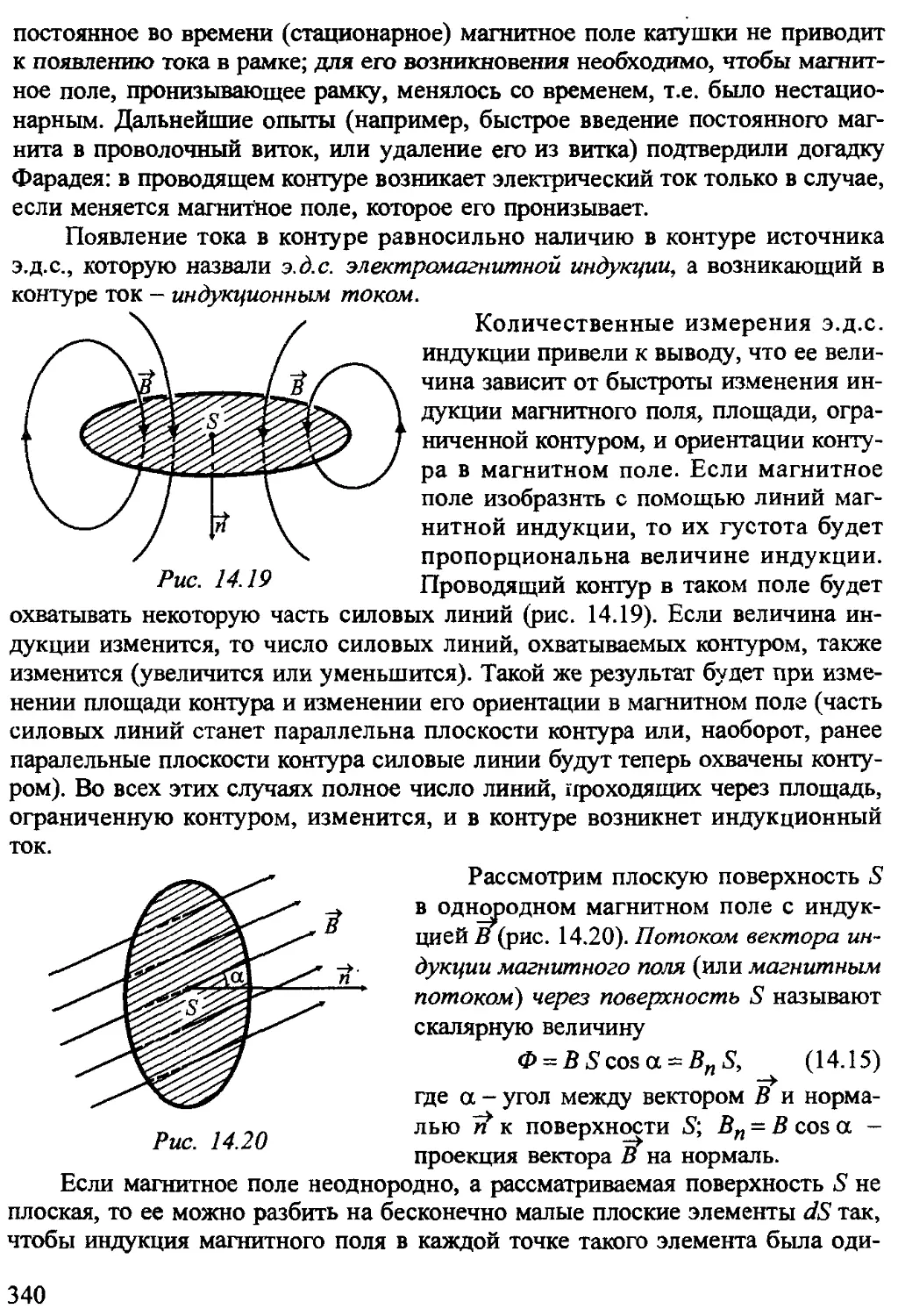
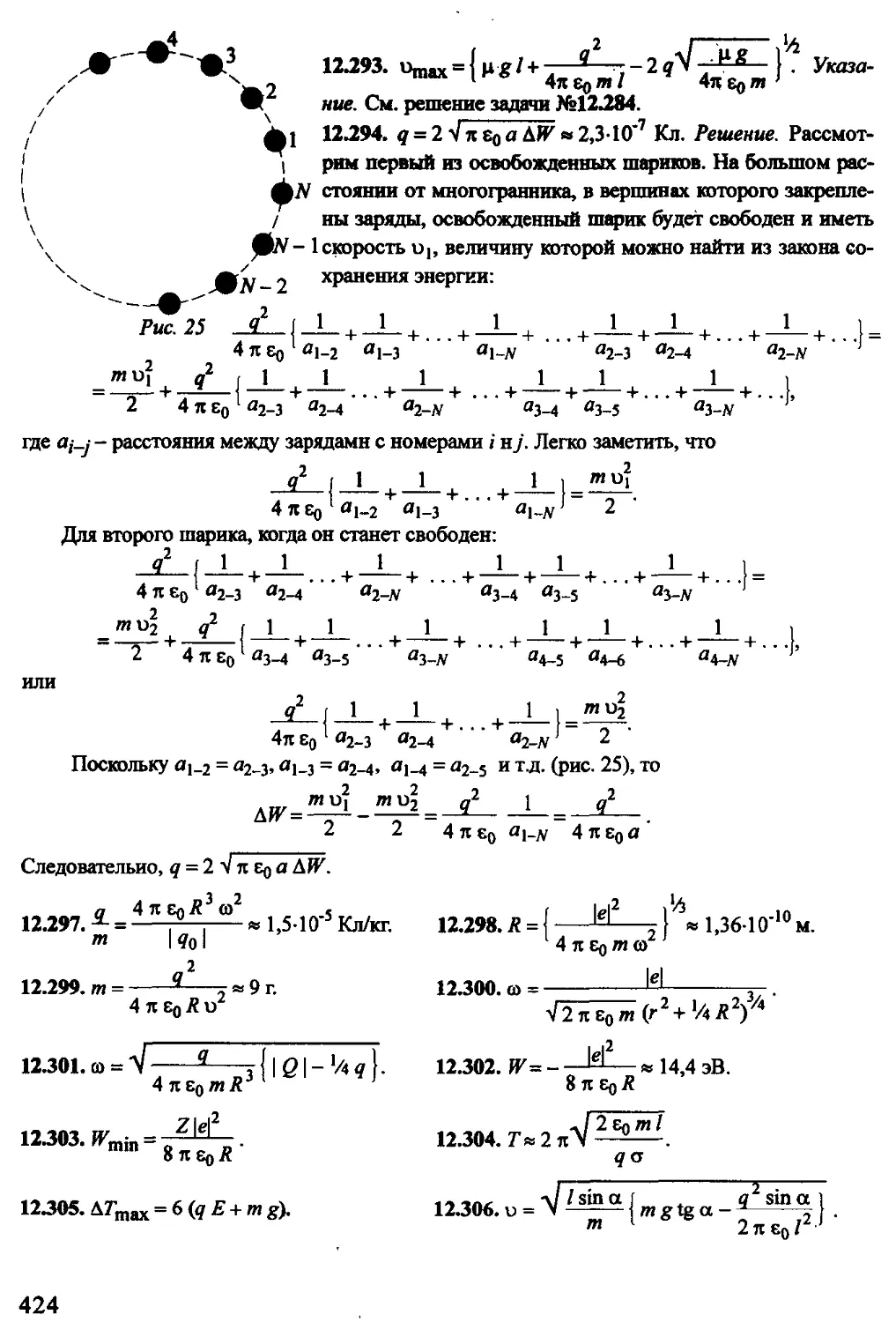
Text
В.П.Демков, О.Н.Третьякова
В ПОМОЩЬ ПОСТУПАЮЩИМ В ВУЗЫ. ФИЗИКА.
МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ. ЭЛЕКТРИЧЕСТВО
И МАГНЕТИЗМ
М.: Изд-во МАИ, 1999. 440 с.
В пособии помещены задачи, большая часть которых предлагалась на
вступительных экзаменах по физике в Московском государственном авиационном
институте (техническом университете). Пособие состоит из трех частей, первая из
которых - «Механика» - была издана в 1995 г. и 1996 г., а вторая - «Молекулярная
физика. Тепловые явления. Электричество и магнетизм» - содержится в данной
книге. Каждому разделу предшествует теоретическая часть, содержащая
основные сведения и формулы, используемые при решении задач. Все задачи
снабжены ответами, а типовые и наиболее трудные - решениями и указаниями.
Для слушателей подготовительных отделений вузов, учащихся и
преподавателей средней школы, учащихся физико-математических школ, а также
лиц, занимающихся самообразованием.
Оглавление
Предисловие 4
Глава II. Молекулярная физика. Тепловые явления 5
§9 . Основы молекулярно-кинетической теории газов. Уравнение состояния 9
идеального газа
§10 . Теплота и работа. Физические основы термодинамики 61
§11 . Уравнение теплового баланса. Изменение агрегатного состояния 104
вещества. Влажность
Глава III. Электричество и магнетизм 137
§12 . Электростатика 138
§13 . Постоянный ток 251
§14 . Магнетизм 329
Ответы и указания 397
Предисловие к первому изданию
Предлагаемое пособие является второй частью трехтомного издания и
содержит главы «Молекулярная физика. Тепловые явления», «Электричество
и магнетизм».
Пособие содержит достаточно подробную теоретическую часть и общие
рекомендации по решению задач каждого из разделов. В пособии преимуще-
ственно представлены задачи, предлагавшиеся в течение ряда лет на вступи-
тельных экзаменах по физике в Московском авиационном институте. Задачи
сгруппированы по темам и располагаются в порядке возрастания сложности.
Большая часть задач снабжена подробными решениями. Ко всем задачам
даны ответы как в общем виде, так и в числовом выражении; для сложных
задач обычно излагается краткий алгоритм решения.
Пособие не может служить основным учебником по физике, поскольку
уровень изложения теории и методы решения задач предполагают достаточно
свободное владение материалом курса физики и математики в рамках обще-
образовательной школы. Наиболее полезным оно может быть слушателям
подготовительных отделений и курсов вузов, учащимся и преподавателям фи-
зико-математических школ, студентам младших курсов вузов, а также лицам,
желающим самостоятельно повысить уровень знаний по физике. Пособие в
первую очередь предназначено в помощь школьникам при подготовке к сдаче
выпускных экзаменов в школе и вступительных экзаменов в ВУЗ.
Авторы выражают глубокую благодарность доцентам кафедры физики
МАИ С.Н. Бреусу и Г.Э. Солохиной за существенный вклад в работу по под-
готовке предварительного варианта рукописи.
Авторы с благодарностью примут замечания и пожелания читателей, на-
правленные на улучшение содержания рукописи, которые будут учтены в пос-
ледующих изданиях пособия. По всем вопросам, касающимся содержания или
распространения книги, обращаться по адресу: 125871, Москва, Издательство
МАИ, или по телефону (095) 158-86-98.
Авторы
4
ГЛАВА II
МОЛЕКУЛЯРНАЯ ФИЗИКА.
ТЕПЛОВЫЕ ЯВЛЕНИЯ
Любое вещество состоит из огромного числа мельчайших частиц, сохра-
няющих все химические свойства данного вещества. Эти мельчайшие части-
цы называются молекулами. Сами молекулы могут состоять из более простых
частиц - атомов. Например, молекула воды Н2О состоит из трех атомов:
одного атома кислорода и двух атомов водорода. Если различного вида мо-
лекул известно огромное число (миллионы), то различных атомов совсем не-
много. В настоящее время известно 105 различных видов атомов, причем в
природе их встречается 88, а 17 получено искусственным путем. Это атомы
так называемых химических элементов. Размеры молекул и составляющих их
атомов чрезвычайно малы: если представить их в виде шариков, то их радиус
имеет численное значение порядка 10'10 м. Зато число частиц в веществе не-
обычайно велико. В одном грамме воды, например, содержится 3,3-Ю22 мо-
лекул.
Массы атомов и молекул тоже малы, поэтому их удобнее измерять не в
килограммах, а в специальных единицах. Эта единица называется атомной
единицей массы [а.е.м.]. По определению
1 а.е.м. = тиед [кг] = i/i2 (масса атома изотопа углерода 6С12). (П.1)
Согласно современным измерениям
1 а.е.м. = тед = 1,66-10'27 кг. (П.2)
Масса атома, выраженная в [а.е.м.], называется относительной атомной
массой А. Относительные атомные массы химических элементов приведены
в таблице Менделеева. Так, например, для водорода Ан= 1,0079, для кисло-
рода Ао = 15,9994, а для атома изотопа углерода 6С12 относительная атомная
масса равна точно 12. Масса молекулы, выраженная в [а.е.м], называется от-
носительной молекулярной массой ц', которая, очевидно, равна сумме отно-
сительных атомных масс атомов, составляющих данную молекулу. Так, на-
пример, относительная молекулярная масса молекулы воды равна
ц'н 0 = 2 -Ан + Ао ® 2-1 + 16=18 а.е.м.
Для нахождения массы молекулы т0 в килограммах нужно ее относи-
тельную молекулярную массу ц' умножить на тед= 1,66-10‘27 кг, то есть
то = М' тед- (П-3)
В молекулярной физике удобно использовать понятие количества веще-
ства. Единица количества вещества называется молем. По определению моль
любого вещества — это такое количество вещества, которое содержит столько
же молекул (или атомов, если вещество состоит из одноатомных молекул),
5
сколько их содержится в 0,012 кг углерода бС12 Из определения моля следует,
что моль любого вещества состоит из одинакового числа молекул. Это число
называется числом Авогадро Nk и равно
хг 0,012 [кг]
лА =--------L—х
m 12
где mri2 = ц'г12 т.„ -масса атома в килограммах, a ц'г12 =12 а.е.м. Следо-
вательно, 6 6
А0Ц= 101=^10^= 023 [-L-J.
12тзд т№ 1,66-10’27 lMonbJ
10“3
(П.4)
Масса одного моля вещества называется его молярной массой ц [кг/моль].
Ясно, что
М = то na-
Используя (П.З) и (П.4), получим
H = H'mM^ = p'mM^-=10-3n'[-^-]. (П.5)
''•ед миль
Например, молярная масса воды цн^0 = Ю'3^'^ = 0,018 кг/моль, а молярная
масса углерода 0,012 кг/моль. Если какое-либо тело имеет массу т [кг], то го-
ворят, что в этом теле находится v = m/\i количества вещества. Число молекул
в т [кг] вещества
tf=vlVA = ^lVA. (П.6)
С помощью (П.6) легко проверить более раннее утверждение о количе-
стве молекул в одном грамме воды.
Между молекулами вещества существуют силы взаимодействия: на боль-
ших расстояниях друг от друга молекулы притягиваются, а при сближении
они отталкиваются. Эти силы, несмотря на то, что каждая молекула электри-
чески нейтральна, имеют в основном электрическое происхождение. Само су-
ществование трех различных агрегатных состояний вещества - твердого,
жидкого и газообразного - указывает на существование межмолекулярных
сил. В твердом и жидком состояниях молекулы притягиваются друг к другу
настолько, что тела сохраняют свой объем, а в случае твердого тела - еще и
форму. В газообразном состоянии силы взаимодействия значительно меньше,
так что газ заполняет весь предоставленный ему объем. Этот последний факт
указывает еще на одну очень важную особенность частиц любого вещества:
молекулы вещества находятся в постоянном движении. Характерной особен-
ностью этих движений является их полная беспорядочность, хаотичность. Это
хаотическое движение молекул носит название теплового движения. В твер-
дых телах молекулы тоже совершают хаотическое тепловое движение, состо-
ящее из непрерывных беспорядочных колебаний молекул около своих поло-
6
жений равновесия, образующих в твердых телах правильную кристалличес-
кую решетку. В хаотическом тепловом движении молекул заключена природа
теплоты и тепловых явлений.
Если привести в соприкосновение два тела, то молекулы этих тел, стал-
киваясь между собой, будут передавать друг другу энергию. Тело, которое
при этом теряет энергию, называют более нагретым, а тело, к которому энер-
гия переходит, - менее нагретым. Как показывает опыт, такой переход энер-
гии продолжается до тех пор, пока не установится некоторое состояние, в
котором тела могут находиться сколь угодно долго. Это состояние называют
состоянием теплового равновесия.
Для характеристики степени нагретости тел служит понятие температу-
ры. В физике в качестве температурной шкалы пользуются так называемой
абсолютной шкалой (шкалой Кельвина), глубоко связанной с наиболее общи-
ми тепловыми свойствами всех тел.
Ясно, что физическое определение температуры должно основываться на
такой физической величине, которая становится одинаковой для двух любых
тел, находящихся в состоянии теплового равновесия друг с другом. Оказы-
вается, что этим замечательным свойством обладает средняя кинетическая
энергия поступательного движения частиц (молекул или атомов) тела. По
этой причине средняя кинетическая энергия поступательного движения час-
тиц внутри любого тела - ,
mou _ 1 v
1 N
= — У
2 Nt=\ 2
(где т0 - масса частицы, и, - скорость i - ой частицы и N- число частиц в
теле) может быть выбрана для определения величины температуры. По оп-
ределению абсолютная температура Т в кельвинах:
2
2^2
Т=~------~к--- [К], (П.7)
где к= 1,38-10'23 Дж/К - коэффициент, переводящий энергию в джоулях [Дж]
в кельвины [К], называется постоянной Больцмана.
Из (II.7) следует, что в состоянии теплового равновесия при температуре
Т средняя энергия поступательного движения молекулы вещества
. тп и2 . з
<-^-> = рГ (П.8)
Следует отметить, что формула (II.8) справедлива не только для молекул
вещества, но и для частиц больших, макроскопических масштабов, например,
мелких пылинок, взвешенных в жидкости, которые можно наблюдать через
микроскоп (так называемое броуновское движение).
Для характеристики скорости теплового движения частиц можно вос-
пользоваться квадратным корнем из входящей в определение температуры
7
величины < v2>; его обычно называют тепловой ит или среднеквадратичной
(средней квадратичной) Uq, ю скоростью частицы вещества:
ит = °сркв = ^<и2> = • (П.9)
т ср.кв. 7
Для среднеквадратичной скорости молекул (II.9) можно получить более
удобное выражение, умножив под корнем числитель и знаменатель на число
Авогадро Nk. Учитывая, что тй Nk = ц (молярная масса вещества), а
*Уа= 1,38-10’23-6,02-1023 = 8,31 Г ]=А- (П.10)
Кмоль
универсальная газовая постоянная, получим
у1 3 RT ,тт _..
«ср.кв. = N —- • (П.11)
м
В технике и быту часто используется не шкала Кельвина, а шкала Цель-
сия. Температура t [°C] по этой шкале связана с абсолютной температурой
Т [К] соотношением:
/= Г-273,16. (П.12)
Благодаря тепловому движению своих молекул газ (или жидкость) оказы-
вает давление на стенки заключающего его сосуда. Молекулы газа, сталкива-
ясь со стенкой, передают ей часть своего импульса. Изменение же импульса
тела в единицу времени определяет действующую на него силу. Если отнести
силу AF„, действующую со стороны газа (или жидкости) в направлении, нор-
мальном к участку поверхности стенки AS, к величине AS, то мы получим
давление на этом участке:
Р = [Н/м2 = Па]. (11.13)
Свойства тел, рассматриваемых в целом, не вдаваясь в детали их молеку-
лярной структуры (с которой эти свойства в действительности связаны), назы-
ваются макроскопическими свойствами. Температура и давление являются
важнейшими величинами, характеризующими макроскопическое состояние
тела. К числу этих величин относится также и объем тела V. Однако эти три
величины не являются независимыми. Уравнение, связывающее эти три вели-
чины, называется уравнением состояния данного тела и является одним из
наиболее важных соотношений, характеризующих его тепловые свойства. По-
лучить же теоретически уравнение состояния можно лишь в случае самых
простых тел (например, для идеального газа).
Следует теперь уточнить, введенное выше понятие теплового равновесия,
как состояния, в котором температуры двух соприкасающихся тел выравни-
ваются. Вообще состоянием теплового равновесия системы тел называют
такое состояние, при котором в системе не происходит никаких самопроиз-
вольных тепловых процессов и все части системы покоятся друг относительно
8
друга, не совершая никаких макроскопических движений. Следовательно, в
состоянии равновесия выравниваются не только температуры частей системы,
но и давления, иначе эти части пришли бы в движение.
§9. Основы молекулярно-кинетической теории газов.
Уравнение состояния идеального газа
Идеальным газом называется такой газ, в котором силами взаимодействия
молекул можно пренебречь. Время от времени молекулы сталкиваются между
собой, но столкновения происходят настолько редко, что большую часть вре-
мени молекулы газа движутся равномерно и прямолинейно. Чем более раз-
режен реальный газ, тем ближе его свойства к свойствам идеального. Для
такого газа оказывается возможным получить зависимость между его макро-
скопическими параметрами р, V и Т, рассматривая движение одной молеку-
лы, а затем усредняя это движение по огромному числу составляющих этот
газ молекул (при обычных условиях в 1 см3 газа содержится 2,7-1019 молекул).
Если в сосуде объемом V содержится N одинаковых молекул идеального
газа массой т0 каждая, движущихся хаотически, то эти молекулы, сталкива-
ясь со стенками сосуда и передавая им часть своего импульса, оказывают на
них давление
р = 2Л и < епост >, (9.1)
где и = У / И - концентрация газа, < епост > = < Vi т0 и2 > - кинетическая энер-
гия поступательного движения молекулы, усредненная по всем У молекулам
газа, и - скорость поступательного движения молекулы. Уравнение (9.1) на-
зывается основным уравнением кинетической теории идеального газа.
Если воспользоваться определением абсолютной температуры (II.7), со-
гласно которому
то уравнение (9.1) можно записать в виде
р = пкТ. (9.2)
Это и есть уравнение состояния идеального газа, причем оно записано в
такой форме, которая не содержит никаких специфических свойств того или
иного конкретного газа. Так, из (9.2) следует, что при заданных давлении р и
температуре Т, концентрации молекул любого газа одинаковы и равны
р/к Т.
Если в сосуде содержится смесь из г различных идеальных газов, то пол-
ное число молекул в сосуде равно
N=iNt, (9.3)
где Nj - число молекул i -го сорта.
9
Подставляя (9.3) в (9.2) и учитывая, что все газы находятся в равновесии
(т.е. обладают одинаковой температурой Т), получим
кт r r N- г
p = ^LNi = kT'L1y = kT'Lni, (9.4)
К i=i ' /=1К i=i ' '
где n^Nj/V- концентрация молекул г-го сорта.
Соотношение (9.4) можно записать в виде
Р = (9-5)
где Р' = п, к Т- так называемое парциальное давление i -го компонента смеси,
т.е. давление, которое производил бы этот компонент смеси, если бы он один
занимал весь объем сосуда. Уравнение (9.5) является математической записью
закона Дальтона для смеси идеальных газов, который гласит, что давление
смеси газов равно сумме парциальных давлений компонентов смеси.
Вернемся к уравнению состояния (9.2) для идеального газа, состоящего
из N одинаковых молекул массой тй каждая. Число молекул газа массой т
и молярной массой ц равно (см.(П.б))
У=^Уа = уУа,
где v = т /ц - число молей газа. Подставляя это выражение для N в (9.2) и
учитывая, что kNA = R (см.(П.Ю)), получим уравнение, которое называется
уравнением Менделеева-Клапейрона'.
pV= — RT=vRT. (9.6) И
Это уравнение, в отличие от (9.2), содержит специфическое свойство кон-
кретного газа - его молярную массу. Разделив (9.6) на объем газа V и введя
плотность газа Р = у, (9.7)
получим p = ^RT. (9.8)
Из уравнения (9.8) следует, что плотность газа не постоянна, а опреде-
ляется его давлением и температурой.
Для смеси различных газов, находящихся в равновесии, уравнение (9.6)
можно записать в виде рК= — RT, (9.9)
или М-СМ
(9.Ю)
p = -S-RT,
Рем
10
где р = S/1 ] pt - давление смеси, ти = S, = । т,- - полная масса смеси (т,- - масса
z-го компонента смеси), р = m/V = j m//V = Ei=I р/- плотность смеси га-
зов (р; - плотность i -го компонента смеси) и
Мем
£ т.
1
£ т/т
'=' М,
(9.11)
средняя молярная масса смеси. Здесь т/т - относительное содержание (по массе)
/—го компонента смеси. Например, молярная масса воздуха, состоящего из
азота N2 (® 78%), кислорода О2 (~ 21%) и небольшого количества аргона,
водорода и других газов, равна 0,029 кг/моль. Используя это значение и урав-
нение (9.10), можно, например, найти плотность воздуха при нормальных ус-
ловиях, т.е. при давлениир0 = 1,013-105 Па и температуре То = 273,16 К (или при
/=0°С):
_ Ро Мем
р°_ ят0
1,013-105-0,029
8,31-273,15
® 1,29 (кг/м3).
Обратимся еще раз к уравнению Менделеева-Клапейрона (9.6), описы-
вающему связь между макроскопическими параметрами газа р, V и Т (будем
считать, что количество вещества в газе v = m/p = const). При изменении сос-
тояния газа меняются, вообще говоря, все три параметра газа, связанные урав-
нением (9.6). Если бы мы попытались изобразить графически эти изменения,
то мы бы получили некоторую поверхность (при постоянном числе молей
v) в трехмерной системе координат, на осях которой откладывались величи-
ны р, V и Т. Поскольку, однако, пространственное построение на практике
неудобно, ограничиваются обычно построением плоских графиков, изображая
на них кривые, представляющие собой сечения поверхности плоскостями, пер-
пендикулярными той или иной координатной оси. Так, пересекая поверхность
плоскостями, перпендикулярными оси температур Т (при этом Т = const), мы
получим семейство кривых, изображающих зависимость давления р от объе-
ма V при различных заданных значениях температуры Т; такие кривые назы-
ваются изотермами. Для идеального газа при Т = const (см. (9.6))
pV= const. (9.12)
Соотношение (9.12) выражает за-
кон Бойля-Mapuomma. Семейство изо- Р .
терм, как видно из (9.12), представляет \ \
собой семейство гипербол (рис. 9.1, a), 2> Т>Т
расстояние до которых от начала коор- 3 2
динат увеличивается при увеличении
температуры. Изотермический процесс v
можно изобразить и на диаграммах зави-
симости р от Т и V от Т (рис. 9.1, б, в). Рис. 9.1, а
И
Рис. 9.2, б
Аналогичным образом можно по-
строить семейство изобар - кривых,
изображающих зависимость V от Т при
заданных значениях давления р. Для
идеального газа при р = const из (9.6)
следует соотношение
Рис. 9.2, в V/T= const, (9.13)
которое выражает закон Гей-Люссака. Изобары на диаграмме V -Т представ-
ляют собой семейство прямых, проходящих через начало координат, угол на-
клона которых к оси температур Т уменьшается с увеличением давления
(рис. 9.2, в). Изобарический процесс можно также изобразить на диаграммах
р - V (рис. 9.2, а) и р - Т (рис. 9.2, б).
Пересекая поверхность, описывающую зависимость давления р от объе-
ма К и температуры Т, плоскостями, перпендикулярными оси объемов V, по-
лучим семейство изохор - кривых зависимости давления р от температуры
Т при заданных значениях объема, занимаемого газом. Для идеального газа
из (9.6) при V = const получим соотношение
12
р/Т = const, (9.14) и
которое выражает закон Шарля. Семей- у___________________________.
ство изохор на диаграммер-Т- семей- 3
ство прямых, проходящих через начало к2
координат, угол наклона которых к оси____________________________
температур Т уменьшается с увеличени- 1
ем объема V (рис. 9.3, б). На рис. 9.3, а, в —--------------------------‘т
изохорический процесс изображен на Рис. 9.3, в
диаграммах р - V и V-T.
Рекомендации по решению задач
Хотя в данном параграфе разговор идет о идеальном газе, необходимо твердо уяс-
нить, что такие понятия, как моль, молярная масса, число Авогадро, температура, средняя
кинетическая энергия движения молекул, тепловая скорость, относятся как к газам, так и
любому другому агрегатному состоянию вещества. Отметим те основные положения мо-
лекулярно-кинетической теории, которые можно считать основными:
- вещество имеет «зернистую» структуру: оно состоит из молекул (атомов). В одном моле
вещества содержится одинаковое число молекул независимо от его агрегатного состояния
равное числу Авогадро;
- молекулы вещества находятся в непрерывном тепловом движении;
- характер теплового движения зависит от степени взаимодействия молекул друг с другом
и изменяется при переходе вещества из одного агрегатного состояния в другое;
- интенсивность теплового движения молекул зависит от степени нагретости вещества,
характеризуемой абсолютной температурой.
В случае идеального газа предполагают, что средняя кинетическая энергия молекул
< е > много больше потенциальной энергии их взаимодействия 1/вз: < е > » ию. Это ус-
ловие достигается при достаточно высоких температурах н при достаточно сильном раз-
режении газа. Иными словами, газ можно считать идеальным, если он достаточно нагрет
и разрежен. Все уравнения и законы, содержащиеся в §9, относятся именно к таким газам.
При решении задач на общие положения молекулярно-кинетической теории вещест-
ва, достаточно ясного понимания основ теории.
При решении задач на идеальные газы обязательно используется уравнение состоя-
ния (9.2) или уравнение Менделеева-Клапейрона (9.6), которое в случаях, если какой-либо
параметр состояния остается неизменным (при постоянной массе газа), автоматически
переходит в одно из трех уравнений: закон Бойля-Мариотта (9.12), Гей-Люссака (9.13)
илн Шарля (9.14).
Рассмотрим более подробно уравнение Менделеева-Клапейрона:
pV=vRT,
полагая число молей газа неизменным. Очевидно, что изменение одного из параметров
(р, V, Т) обязательно приведет к изменению других. Рассмотрим два различных состояния
некоторого идеального газа с начальными параметрами (рь Г,) н конечными - (р2,
V2, Т2). Из уравнений Менделеева-Клапейрона:
р1К1 = уЛ7’|, P2^2 = v^^2
можно получить связь между параметрами начального н конечного состояний:
Р| И _Р2 *2
Л Т2 '
Это соотношение, записанное в виде
р V
= const,
13
называют объединенным газовым законом; при постоянном одном из параметров состоя-
ния (р, V, или Г) газа из него следуют законы изопроцессов (Гей-Люссака, Шарля или
Бойля-Мариотта соответственно).
Основную группу задач этого параграфа составляют задачи, где заданы несколько
состояний одного и того же газа, в которых применимо уравнение объединенного газового
закона (или его частные случаи). Последовательность решения таких задач может быть
следующей:
а) прочитав условие задачи, нужно ясно представить, в скольких различных процессах уча-
ствует данный газ при переходе из начального состояния в конечное. Если газ последо-
вательно участвует в нескольких процессах, то удобно сделать схематический чертеж, на
котором изобразить все процессы и отметить состояния газа в начале и в конце каждого
из них;
б) для каждого процесса написать уравнения, связывающие начальные и конечные пара-
метры состояния газа в процессе: либо уравнения Менделеева-Клапейрона для начального
и конечного состояний газа в процессе, либо уравнение объединенного газового закона
(в частности, изопроцесса);
в) записать все вспомогательные условия, связывающие параметры (р, V, Т, т) в различных
состояниях;
г) при необходимости дополнить полученные уравнения развернутым значением парамет-
ров, выразив их через известные величины, заданные в условии задачи. Решить получен-
ную систему уравнении.
Другую группу задач составляют задачи, в которых рассматриваются смеси различ-
ных газов. Если имеется смесь газов и рассматриваются процессы, связанные с изменением
ее состояния, то все действия, указанные для первой группы задач, нужно проделать для
каждого компонента смеси отдельно, а результирующее давление смеси определить с по-
мощью закона Дальтона (9.5). Если рассматриваются процессы образования смеси (напри-
мер, при соединении нескольких сосудов, содержащих разные газы, или при диссоциации),
то последовательность решения задач может быть такой:
а) записать уравнение состояния для каждого газа до образования смеси;
б) выяснить, какие компоненты образуются в результате возникновения смеси и записать
уравнение состояния для каждого компонента смеси;
в) записать закон Дальтона для смеси;
г) записать все вспомогательные условия и решить систему уравнений.
Часто встречаются задачи, в которых требуется умение вычислять давление газа в
том или ином конкретном состоянии. К этим задачам отнесем задачи на расчет параметров
газа, заключенного в сосуде под тяжелым поршнем, в прямой и U-образной трубке, где
объем, занимаемый газом, ограничен столбиком жидкости и т.п. Здесь для нахождения
давления следует использовать закон Паскаля: выбрать нулевой уровень, отделяющий газ
от поршня или жидкости, и записать уравнение равновесия поршня или столба жидкости.
В остальном этн задачи решаются аналогично задачам первой группы.
В комбинированных задачах, где рассматривается движение сосуда с газом (например, воз-
душного шара), уравнения состояния газа дополняются уравнениями механики.
Наконец, встречаются задачи, в которых задан закон изменения параметров состояния
газа, отличный от изопроцессов. Здесь также можно использовать схему решения задач первой
группы, а в качестве вспомогательных условий использовать уравнение процесса (т.е. зависи-
мость между параметрами состояния в данном процессе), записав его в начальном и конечном
состояниях газа Если в задаче закон изменения параметров состояния задан графически (в
любых переменных), необходимо представить его в виде математического уравнения, которое
также использовать в качестве дополнительного условия (это может быть уравнение прямой,
параболы н т.п. в переменных р - V, р -Т или V- Г). Если при этом требуется в таком урав-
нении перейти от одних параметров состояния к другим, то нужно воспользоваться уравне-
нием Менделеева-Клапейрона н исключить «лишний» параметр. Это часто используют, если
14
требуется графически изобразить на рисунках некоторый процесс в различных перемен-
ных.
Задачи
9.1. Найти концентрацию молекул углекислого газа СО2, если его плот-
ность р = 1 кг/м3.
• Решение. Относительная атомная масса, выраженная в атомных единицах массы, из таб-
лицы Менделеева для углерода равна Ас = 12 а.е.м., для кислорода - Ао » 16 а.е.м. Следо-
вательно, молярные массы углерода цс = 12-10’3 кг/моль, кислорода Цо» 16-10"3 кг/моль,
углекислого газа ц = 1-цс + 2-цо = 44-10'3 кг/моль.
По определению, концентрация - это число молекул в единице объема:
n = N/V.
Количество молекул в одном моле численно равно числу Авогадро NA. Число моле-
кул N, содержащихся в v молях газа, равно
#=v#A = — Na,
где т/у, - число молей газа.
По определению плотности: р = m/V. Следовательно,
>»1Уа Р^а , ,п25 -3
п =-----=----® 1,36-10 м .
Гц ц
• Ответ', п = р#А/ц® 1,36-Ю25 м’3.
9.2. Определить число молекул в объеме V= 1 см3 воды. Плотность воды
р = 103 кг/м3, молярная масса ц= 18-10’3 кг/моль.
9.3. Оценить концентрацию свободных электронов в натрии, пола-
гая, что на один атом приходится один свободный электрон. Плотность
натрия р = 970 кг/м3, молярнаи масса ц = 23-10'3 кг/моль.
9.4. Подсчитать число молекул в т = 100 г углекислого газа. Найти массу
молекулы и концентрацию молекул, если плотность газа р= 1,98 кг/м3, мо-
лярная масса ц = 44-10'3 кг/моль.
9.5. Радоновые ванны содержат N= 1,8-106 атомов радона на V= 1 дм3
воды. На сколько молекул воды приходится один атом радона? Плотность
воды р = 103 кг/м3, молярная масса воды ц = 18-10’3 кг/моль.
9.6. Где больше молекул: в стакане воды или в стакане ртути? Плотность
воды р] = 103 кг/м3, плотность ртути р2 = 13,6-103 кг/м3, молярная масса воды
Р] = 0,018 кг/моль, молярная масса ртути ц2 = 0,2 кг/моль.
9.7. Если пометить все молекулы в одном стакане воды и вылить эту
воду в мировой океан, а потом вновь зачерпнуть стакан воды, то сколько в
нем будет меченных молекул? Объем воды мирового океана V} = 1,3-1018 м3,
объем стакана Г2 = 200 см3, плотность воды р= 103 кг/м3, молярная масса
ц = 18-10"3 кг/моль.
9.8. Сколько молекул воды приходится на одну молекулу углекислого
газа СО2 в бутылке с лимонадом объемом V = 0,5 л, если в ней растворено
т = 2,2 мг этого газа? Плотность воды р= 103 кг/м3, молярная масса воды
Р] = 18-10'3 кг/моль, молярная масса углекислого газа ц2 = 44-10’3 кг/моль.
15
9.9. В комнате объемом V= 60 м3 испарили капельку духов, содержащую
т = Ю"4 г ароматического вещества с относительной молекулярной массой
А = 50 а.е.м. Сколько молекул этого вещества попадает в легкие человека при
каждом вдохе? Объем легких принять равным Ко = 2,2 л.
9.10. В сосуде объемом V= 8 л находится т = 8 г гелия при давлении
р = 1 агм. Определить количество молекул гелия в сосуде и их полную кинети-
ческую энергию. Молярная масса гелия ц = 4-10"3 кг/моль.
• Решение. В газе молекулы находятся на таких больших расстояниях друг от друга, что
их можно считать практически невзаимодействующими. Каждая из молекул движется не-
зависимо от других молекул, испытывая относительно редкие столкновения. При этом
каждая молекула участвует в трех типах движения: поступательном, вращательном и ко-
лебательном (атомы внутри молекулы колеблются друг относительно друга). Если моле-
кула одноатомная, например, молекула гелия, то имеет место только поступательное дви-
жение.
Кинетическая энергия поступательного движения одной молекулы гелия, усреднен-
ная по всем N молекулам газа, равна
<Ei> = 3/ikT.
Следовательно, энергия всех N молекул будет равна произведению < Е| > на полное
число молекул газа:
<e> = 3/iNkT,
где N=(m/p.)NAa 1,2-1024 молекул.
Запишем уравнение Менделеева-Клапейрона для гелия при заданных параметрах со-
стояния р н V:
pV= — RT.
М
Теперь кинетическую энергию молекул с учетом уравнения состояния можно запи-
сать в виде
<е> = |-#ААТ=|-ЛТ=|рК=1,2 кДж,
2 ц 2 ц 2
где учтено, что N^k = R.
• Ответ’. N = ~1,2-1024 молекул; < е > = К= 1,2 кДж.
9.11. Во сколько раз изменилась температура аргона, если средняя кине-
тическая энергия его атома увеличилась на п = 50%?
9.12. На сколько изменилась температура аргона, если средняя кинети-
ческая энергия его атома уменьшилась в п = 1,2 раза? Начальная температура
аргона То = 400 К.
9.13. Чему равна средняя кинетическая энергия поступательного движе-
ния атома аргона, если v = 2 моля этого газа в баллоне объемом И= 10 л
создают давление р = 106 Па?
9.14. Определить среднюю кинетическую энергию N= 105 молекул гелия
при температуре t = 47°С.
9.15. Определить количество молей одноатомного идеального газа, если
средняя кинетическая энергия всех атомов при температуре Т= 500 К равна
< е > = 800 Дж.
16
9.16. Под каким давлением находится в баллоне кислород, если емкость
баллона У= 5 л, а средняя кинетическая энергия поступательного движения
всех молекул кислорода < е > = 6 кДж?
9.17. Одноатомный газ при давлениир = 5’ 102 Па занимает объем V= 4 л.
Найти суммарную кинетическую энергию движения молекул.
9.18. В сосуде объемом V= 20 см3 при температуре t = 27°С и давлении
р = 104 Па находится одноатомный идеальный газ. Определить число атомов
газа в сосуде и их суммарную кинетическую энергию.
9.19. Найти концентрацию молекул идеального газа, если при температу-
ре Т= 300 К плотность газа равна р = 1,2 кг/м3, а средняя квадратичная ско-
рость молекул исркв = 500 м/с.
• Решение. Концентрация молекул идеального газа может быть выражена через его плот-
ность р и молярную массу ц (см. решение задачи №9.1):
Р^А
п =---.
Ц
Поскольку средняя квадратичная скорость движения молекул вещества связана с мо-
лярной массой соотношением
J3RT
°ср.кв. - ’ ,
н
°ср.кв.
Следовательно, 2
Р /^А °ср.кв. „ , . „23 -з
и =---—»2,410 м .
Р ^А °ср.кв. - . ,„23 -3
• Ответ: п =--— » 2,4-10 м .
Зл 1
9.20. Определить среднюю квадратичную скорость молекул водорода при
температуре t = 100°С. Молярная масса водорода ц = 2-10'3 кг/моль.
9.21. Определить молярную массу идеального газа, если при температуре
Т= 350 К средняя квадратичная скорость его молекул равна иСр.кв. = 522 м/с.
9.22. В воздухе взвешена пылинка массой т = 1,242-10'20 кг. Определить
среднюю квадратичную скорость пылинки, если температура воздуха Т = 300 К.
9.23. Какова средняя квадратичная скорость капельки воды, взвешенной
во влажном воздухе, находящемся при температуре Т = 290 К? Радиус капель-
ки г = 10"6 см, плотность воды р = 103 кг/м3.
9.24. Найти среднее значение импульса молекулы азота, движущейся со
средней квадратичной скоростью при температуре Т - 300 К. Молярная масса
азота ц = 28-10'3 кг/моль.
9.25. Молекула кислорода движется со средней квадратичной скоростью,
соответствующей температуре t= 17°С. Определите максимально возможное
изменение импульса молекулы при ее упругом ударе о стенку. Молярная
масса кислорода ц = 32-10'3 кг/моль.
17
9.26. При какой температуре средняя квадратичная скорость молекул
азота равна второй космической скорости Земли? Радиус Земли равен
R = 6400 км, молярная масса азота ц = 28-10'3 кг/моль.
9.27. Один из сосудов заполнен гелием, а другой - кислородом. Вначале
температуры газов одинаковы и равны 7\ = 300 К. На сколько следует уве-
личить температуру одного из газов, чтобы средние квадратичные скорости
молекул гелия и кислорода стали равными? Молярные массы гелия и кисло-
рода равны = 4-10'3 кг/моль и = 32-10'3 кг/моль соответственно.
• Решение. Так как средняя квадратичная скорость движения молекул связана с темпера-
турой и молярной массой газа соотношением
хГзяТ
иср.кв. — ’ >
то получим
~3RT\ л/ЗЯ Т2
> иср.кв. 2— ’ > °ср.кв. 1 - иср.кв. 2'
Ml М2
Следовательно,
Mi М2
Так как ц, < ц2> то необходимо нагреть газ с большей молярной массой, т.е. кисло-
род, до температуры
М? - Mi
ДТ = Т2 -Ti = Ti 2 =2100 К.
-
• Ответ: ДТ=Т.И2 И1=2100К.
Ml
9.28. Во сколько раз отличаются молярные массы двух идеальных газов,
если отношение средних квадратичных скоростей их молекул при одной и
той же температуре равно и= 1,5 раза?
9.29. При некоторой температуре молекулы кислорода имеют среднюю
квадратичную скорость исркв] = 460 м/с. Какова при этой температуре сред-
няя квадратичная скорость исркв,2 молекул азота? Молярная масса кислорода
ц1 = 32-10'3 кг/моль, азота - = 28-10’3 кг/моль.
930. Каково давление идеального газа, если его плотность равна
р = 3 кг/м3, а средняя квадратичная скорость его молекул иср кв. = 100 м/с?
• Решение. Состояние идеального газа описывается уравнением Менделеева-Клапейрона:
pV= — RT, или p = e-RT.
М М
Из выражения для средней квадратичной скорости молекул газа
лГзяТ
иср.кв. — ’
получим
Т М °ср.кв.
ЗЯ
18
Следовательно, 2 2
р R М иср.кв. Р иср.кв. , Л4 _
P = --------3-----10 Па- .
2
• Ответ: р = к ю4 ["ia
9.31. Средняя квадратичная скорость молекул газа равна = 400 м/с.
Определить объем, который занимает т = 1 кг газа при давлении р = 105 Па.
932. В сосуде объемом V= 10 л при давлении р = 105 Па находится иде-
альный газ массой т = 300 г. Определить среднюю квадратичную скорость
молекул этого газа.
9.33. В сосуде объемом V= 1 л находится т = 3 г кислорода. Определить
давление кислорода, если средняя квадратичная скорость его молекул
^ср.кв. = 420 м/с.
9.34. В баллоне емкостью V= 50 л находится v = 0,12 кмоля водорода при
давлении р = 6 МПа. Определить среднюю квадратичную скорость движения
молекул газа. Молярная масса водорода ц = 2-10'3 кг/моль.
9.35. Средняя квадратичная скорость молекул некоторого газа при темпе-
ратуре Т=296 К равна исркв = 480 м/с. Сколько молекул содержится в
т = 10 г этого газа?
9.36. Найти концентрацию молекул водорода при давлении р= 105 Па,
если средняя квадратичная скорость его молекул равна иср = 1000 м/с. Мо-
лярная масса водорода ц = 2-10’3 кг/моль.
9.37. Определить среднюю квадратичную скорость молекул идеального
газа, если в т = 5 г газа при нормальных условиях (t = 0°С, р0 = 105 Па) содер-
жится N = 9,7-1022 молекул.
9.38. Выразить среднюю квадратичную скорость молекул газа исркв.
через давление газа р и его плотность р.
9.39. При давлении р= 105 Па плотность воздуха равна р= 1,29 кг/м3.
Найти среднюю квадратичную скорость его молекул.
9.40. Баллон массой т= 1 кг, объемом V= 1 л заполнен азотом так, что
при температуре t = 20°С давление в баллоне р = 1 атм. С какой скоростью
стал бы двигаться баллон, если бы удалось упорядочить хаотическое тепловое
движение так, что все молекулы азота двигались бы в одну сторону. Молярная
масса азота ц = 28-10'3 кг/моль.
9.41. Альпинист при каждом вдохе поглощает т = 5-10’3 кг воздуха.
Какой объем воздуха должен вдыхать альпинист в горах, где давление возду-
ха составляет р = 8-104 Па при температуре t = - 13°С? Сколько молекул он
вдыхает за один раз? Какова их концентрация? Молярная масса воздуха
ц = 29-10'3 кг/моль.
• Решение. Так как для нормального дыхания альпинист при каждом вдохе должен пото-
щать одинаковое количество молекул воздуха, то из уравнения Менделеева-Клапейрона
19
pV= — RT
M
получим
Г=-^^»4,7-10’3м3.
MP
Число молекул воздуха, содержащихся в этом объеме, равно
N=vNa = — УАя> 1,04-М)23 молекул,
а их концентрация
п = -р = -А;»2,2 1025 м’3,
г к 1
Где учтено, что R = к NA.
• Ответ: V=™ 4,7-Ю'3 м3, #=— NA« 1.04-1023 молекул, и = -/?=»2,21025 м’3.
цр р кТ
v 9.42. На рис. 9.4 точки 1 и 2 изобра-
.2 жают термодинамическое состояние одной
и той же массы газа. В каком из указанных
• 1 состояний больше давление, объем и тем-
т пература газа?
9.43. Может ли человек поднять груз,
равный массе воздуха, заключенного в за-
ле размерами 20*30*5 м3? Воздух находится при нормальных условиях
(Zo = 0°С, р0 = 105 Па). Молярная масса воздуха ц = 29-10"3 кг/моль.
9.44. Идеальный газ в количестве v = 0,15 кмоль при давлении р = 900 мм
рт.ст. имеет температуру t = 40°С. Определить объем, занимаемый газом.
9.45. Какое количество молей идеального газа находится в объеме V= 1 л
при температуре Т= 120 К и давлении р = 2 МПа?
9.46. Сколько молекул воздуха будет находиться в сосуде объемом V = 1 см3
при температуре t = 10°С, если давление воздуха в сосуде р = 4 мкПа?
9.47. Полученный в лабораторных условиях глубокий вакуум достигает
величины р= 1,31 10^ Па. Сколько молекул при этом находится в объеме
V = 1 м3? Температура газа t = 20°С.
9.48. Определить температуру N= 1,8-Ю24 молекул идеального газа, на-
ходящегося в сосуде емкостью V= 15 л при давлении р= 0,5 МПа.
9.49. При каком давлении находится идеальный газ в баллоне емкостью
У= 10 см3, если при температуре t = 300°С в баллоне находится N = 3- 1О20 мо-
лекул?
9.50. Определить плотность идеального газа, если концентрация его
молекул при некоторых условиях равна и = 5 1 024м’3, а молярная масса
ц = 40-10'3 кг/моль.
9.51. Температура идеального газа плотностью р = 0,54 кг/м3 при давле-
нии р = 3-105Па равна Т=273 К. Найти массу его молекулы.
20
9.52. Определить плотность кислорода при температуре / = 47°С и дав-
лении р = 0,831-105 Н/м2. Молярная масса кислорода ц = 32-10'3 кг/моль.
9.53. На высоте h = 10 км давление воздуха равно р - 3,04-104 Па, а тем-
пература - t = - 43°С. Найти плотность воздуха на этой высоте. Молярная
масса воздуха ц = 29-10‘3 кг/моль.
9.54. До какой температуры надо нагреть кислород, чтобы его плотность
стала равной плотности водорода при том же давлении и температуре
Г =200 К? Молярная масса кислорода щ = 32-10‘3 кг/моль, водорода -
Р2 = 2-10‘3 кг/моль.
9.55. Вода полностью заполняет сосуд при температуре t = 27°С. Чему
стало бы равно давление внутри сосуда, если бы исчезли силы взаимодей-
ствия между молекулами воды? Молярная масса воды ц = 18-10’3 кг/моль,
плотность воды р= 103 кг/м3.
9.56. В сосуде находится v = 1 моль некоторого газа. Из опытов найдено
р/Т = 371 Па/К. Определить концентрацию молекул и объем сосуда.
9.57. Для некоторого идеального газа из опытов найдено р/Т = 371 Па/К.
Найти массу молекулы, если плотность газа р = 0,18 кг/м3.
9.58. Один литр газа при температуре t = 0°С и давлении р = 1 атм имеет
массу m = 0,0894 г. Какой это газ?
• Решение. Единственной специфической характеристикой конкретного газа в молекуляр-
но-кинетической теории является его молярная масса. Из уравнения Менделеева-Клапей-
рона, записанного для газа при заданных параметрах состояния р, V и Т,
pV=-RT,
М
получим
mRT
ц pv
Подставляя числовые значения, найдем молярную массу газа:
8,94-10-5-8,31-273 „ ,п.3 ,
ц = —-----——------«210 кг/моль.
105-10~3
Единственный газ, который может иметь такую молярную массу - это водород Н2.
• Ответ ', водород Н2.
9.59. Газ плотностью р = 5,95 кг/м3 находится при температуре Z = O°C.
Найти давление газа, если масса молекулы равна т0 = 7,3-10"26 кг. Какой это
газ?
9.60. Масса т = 716 г пара органического соединения углерода ^С, во-
дорода |Н и кислорода 'g О с формулой (CjH^O),, занимает при температуре
t = 200°С и давлении р = 105 Па объем V = 242,6 см3. Найти число п.
9.61. При температуре t = 27°С и давлении р = 4,155-105 Па плотность газа
равна р = 2,833 кг/м3. Известно, что молекулы этого газа представляют собой
соединение азота 14N с водородом ]Н. Определить молекулярную формулу
этого соединения.
21
9.62. Газ массой т = 15 г, молекулы которого состоят из атомов водорода
и углерода, содержит N= 5,64-1023 молекул. Определить массу атомов угле-
рода и водорода, входящих в состав этого газа.
9.63. Сосуд объемом Vx = 4 л, заполненный идеальным газом при давле-
нии р} = 1,2-105 Па, соединяют с пустым сосудом объемом V2 = 2 л. Опреде-
лить установившееся давление газа, считая его температуру неизменной.
• Решение. Соединение сосудов приведет к расширению газа, содержащегося в объеме
V\, до объема (И| + К2). При этом установится новое давление р2. Так как процесс протекал
изотермически, то из закона Бойля-Мариотта получим
Pl Vl=Pl<.Vl + V2>-
Следовательно,
р2 = P,V' = 8-Ю4 Па.
Р2 К1 + К2
Р\ И 4
• Ответ'. р2 =----= 8-104 Па.
К1 + Г2
9.64. Стеклянная лампа наполнена азотом при давлении рх = 600 мм
рт.ст. Емкость лампы V = 500 см3. Какая масса воды войдет в лампу, если в
ней сделать небольшое отверстие под водой при давлении р2 = 760 мм рт.ст.?
Плотность воды р = 103 кг/м3. Температуру азота считать постоянной.
9.65. При нагревании идеального газа на АТ = 3 К при постоянном объеме
его давление увеличилось на а = 1% от первоначального давления. Опреде-
лить начальную температуру газа.
• Решение. Изохорическое нагревание газа постоянной массы подчиняется закону Шарля:
ТГ Т2 '
Так как первоначальное давление рх газа увеличилось на а процентов (т.е. на
Др = ар], где а = 0,01), то конечное давление
р2=рх + Др = (1 +а)р,.
Следовательно, температура Т2 в
Тг Pi ,
— = — =1 +а
Т\ Pi
раз стала больше начальной Тх.
Используя данные условия задачи
Т2 - Т, = АТ
получим
7\ (1 + а) - Тх = АТ,
или
Т, = — = 300 К.
АТ а
• Ответ: Т\ - — = 300 К.
а
22
9.66. На сколько изменилось давление воздуха в шине автомобиля при
повышении температуры на АТ = 30 К, если первоначально при Tt = 270 К
давление было равно р} = 1,8 атм? Изменением объема шины пренебречь.
9.67. Средняя квадратичная скорость молекул идеального газа в закры-
том сосуде увеличилась в п= 1,5 раза. На сколько процентов увеличилось
давление газа?
• Решение. Так как средняя квадратичная скорость молекул газа связана с его температу-
рой соотношением
J3RT
°ср.кв. — ’ >
Г*
то ее увеличение, очевидно, было обусловлено нагреванием газа.
Записав закон Шарля для двух состояний газа
£1_£2
Л ’ Т2 ’
получим
11
Р2-Р1Т{-
Следовательно, при нагревании давление газа увеличилось на
Ю0% = Р2 Pi
Pi Pi
100% = -т 1 . 100% = Ur - 1 • 100%
71 J
процентов.
Согласно условию задачи
Л/^37? Г] Л/ 3 7? Г2 иср.кв. 2 \/ ^2
иср.кв. 1 “ ’ > иср.кв.2— ’ » и— — ’ т •
Ц Ц иср.кв. 1
Поэтому
2
ц = {°°р кв-2 - 1} • 100% = (л2 - 1)100% = 125%.
иср.кв. 1
• Ответ-, на г] = (л2 - 1)100% = 125%.
9.68. В закрытом сосуде находится идеальный газ. Во сколько раз нужно
увеличить температуру газа, чтобы средняя квадратичная скорость молекул
увеличилась в п = 1,2 раза?
9.69. Идеальный газ нагревают в закрытом сосуде так, что средняя квад-
ратичная скорость его молекул увеличивается вдвое. Во сколько раз увели-
чивается давление газа /»?
9.70. В закрытом сосуде находится идеальный газ. На сколько процентов
изменится его давление, если средняя квадратичная скорость его молекул уве-
личится на 20%?
9.71. Давление идеального газа после его нагревания в закрытом сосуде
увеличилось в п= 16 раз. Во сколько раз изменилась средняя квадратичная
скорость его молекул?
23
9.72. Во сколько раз возрастет средняя квадратичная скорость теплового
движения молекул газа, помещенного в закрытый сосуд, движущийся со ско-
ростью и = 2иср кв , при его резкой остановке? Во сколько раз изменится тем-
пература газа? Массой оболочки сосуда пренебречь.
9.73. При повышении температуры на ДГ= 3 К объем газа увеличился
на а = 1%. Какова была первоначальная температура, если процесс протекал
изобарически?
• Решение. Изобарическое нагревание газа постоянной массы подчиняется закону Гей-
Люссака:
Т\ т2-
Так как начальный объем Vy газа увеличился на а процентов (т.е. на ДИ = a Vy, где
а = 0,01), то конечный объем
И2 = И1+ДИ=(1+а)И|.
Следовательно, температура Т2 в
Ту Vy 1 “
раз стала больше начальной Ту.
Используя данные условия задачи
Т2 - Ту = ДТ
получим
Т] (1+а)-7] =ДТ,
или
?,= — = 300 К.
ДГ “
• Ответ: Ту= — = 300 К.
а
9.74. При изобарическом нагревании идеального газа его объем увели-
чился в п = 4 раза. Во сколько раз изменилась средняя квадратичная скорость
его молекул?
9.75. В вентиляционную трубу жилого дома поступает наружный воздух
при температуре q = - 10°С. Какой объем займет каждый кубический метр
наружного воздуха, когда он поступит в комнату и нагреется до t2 = 20°С?
Давление воздуха постоянно.
9.76. При сгорании топлива в цилиндре дизельного двигателя во время
предварительного расширения объем газа увеличился в п = 2,2 раза при по-
стоянном давлении. Определить изменение температуры газа, если начальная
температура Т = 1650 К.
9.77. До какой температуры следует изобарически нагреть газ, чтобы его
плотность уменьшилась в и = 2 раза по сравнению с плотностью при ?0 = 0°С?
9.78. Воздушный шар внесли с улицы, где температура воздуха была
?! = -13°С, в комнату с температурой ?2 = 17°С. На сколько процентов увели-
чился объем шара? Натяжением резины пренебречь.
24
9.79. Газовый термометр состоит из шара с припаянной к нему гори-
зонтальной стеклянной трубкой. Капелька ртути, помещенная в трубку, от-
деляет объем шара от внешнего пространства. Площадь поперечного сече-
ния трубки S = 0,1 см2. При температуре 7} = 273 К капелька находилась на
расстоянии /] = 30 см от поверхности шара, при Т2 = 278 К - на /2 = 50 см.
Найти объем шара.
9.80. Тонкостенный полый шар объемом V = 5 см3 имеет небольшое не-
сквозное отверстие. Шар нагревают до температуры = 400°С и опускают
отверстием на поверхность ртути. Какая масса ртути войдет в шар при его
охлаждении до температуры t2 = 16°С? Плотность ртути р= 13,6-103 кг/м3.
Расширением шара пренебречь.
9.81. Баллон, содержащий = 1,45 кг азота, при испытании лопнул при
температуре tt = 427°С. Какую массу кислорода т2 можно хранить в таком
же баллоне при температуре ?2 = 17°С, имея четырехкратный запас проч-
ности (т.е. давление в баллоне не должно превышать одной четвертой зна-
чения давления, при котором баллон разрушается)? Молярная масса азота
Pj = 0,028 кг/моль, кислорода - И2 = 0,032 кг/моль.
9.82. Посередине запаянной сверху тонкой баро-
метрической трубки имеется столбик воздуха а у за-
паянного конца - столбик жидкости (рис. 9.5). При
температуре t0 = 0°С длина столбика воздуха равна
/0 = 10 см. Какой станет длина столбика воздуха при
Г=20°С?
Рис. 9.5
9.83. Баллон содержит сжатый идеальный газ при температуре tx = 27°С
и давлении pt = 0,2 МПа. Каким будет давление р2 в баллоне, когда из него
будет выпущено а = 0,7 массы газа, а температура понизится до t2 = 0°С?
• Решение. Так как масса газа в сосуде изменилась, непосредственно использовать закон
Шарля для изохорического процесса нельзя. Запишем уравнение Менделеева-Клапейрона
для начального и конечного состояний газа:
Pl mi V=-lRTi , m? p2V= — RT2.
Й Ц
Откуда получим Pl mi Tt m2 T2
Pz = ~-3=-, 7И2 *2 P^T^i
где т2 - масса газа, оставшегося в сосуде:
т2 = mt - a mt = (1 - а) mt.
Следовательно, давление в баллоне станет равно
Т2
р2 =р, (1 - а) уг « 5,46-104 Па.
• Ответ-. р2= рх(\ - а) Т2/Т\ « 5,46-104 Па.
25
9.84. В баллоне емкостью V = 0,5 м3 находится идеальный газ при тем-
пературе t= 27°С. Вследствие утечки давление снизилось на Др = 103 Па. Ка-
кое количество молекул вышло из баллона, если температура газа не изме-
нилась?
9.85. В закрытом сосуде находится идеальный газ под давлением
р0 = 0,5 МПа. Какое давление установится в сосуде, если после открытия кра-
на а = 4/5 массы газа выйдет из сосуда? Температура газа не менялась.
9.86. Из баллона выпустили Аги = 2 г идеального газа, в результате чего
давление уменьшилось на и = 10%. Определить объем баллона, если в начале
плотность газа была равна р = 2-1 О'4 г/см3. Температура газа не менялась.
9.87. В баллоне объемом К= 10 л содержится водород при температуре
Г=20°С и давлении р= 10 атм. Какое количество водорода было выпущено
из баллона, если при полном сгорании оставшегося образовалось т = 50 г
воды? Молярная масса водорода и кислорода равны р.^2-10’3 кг/моль и
ц2 = 32-10‘3 кг/моль соответственно.
9.88. Какую часть газа выпустили из баллона, если давление в нем упало
втрое, а абсолютная температура вдвое по отношению к первоначальным
значениям?
9.89. В баллоне объемом V= 10 л находится гелий под давлением р, = 106 Па
и при температуре = 27°С. После того, как из баллона было взято А»г = 10 г
гелия, температура в баллоне понизилась до t2 = 17°С. Определить давление
р2 гелия, оставшегося в баллоне. Молярная масса гелия ц = 4-10‘3 кг/моль.
9.90. Стеклянная колба с воздухом при давлении окружающего прост-
ранства р0 = 105 Па закрыта пробкой и взвешена при температуре = 15°С. Вы-
нув пробку, колбу нагрели до t2 = 80°С. При последующем взвешивании колба
оказалась на Дт = 0,25 г легче. Чему равен объем колбы V? Молярная масса
воздуха ц = 29-10’3 кг/моль.
• Решение. Первоначально в колбе находился воздух массой Ш| при температуре и дав-
лении окружающего пространства. После открывания колбы и нагревания ее до темпера-
туры t2 из сосуда выйдет некоторая масса газа Аги, при этом давление в колбе останется
прежним.
Запишем уравнение Менделеева-Клапейрона для первого и второго состояния воз-
духа в колбе, учитывая, что объем сосуда и давление воздуха не менялись:
, т, пъ
p0V=-^RT2.
и второго уравнений массы газа mt, т2 и вычитая их, получим
. НРо v ( 1 1 I
tM = mi -m2 = —g~i у-
Выражая из первого
Откуда находим
&jnTtT2R
Ответ: K=-----‘
РРо (Тг ~ Tj)
Am Ti Т2 R , ,
V=-------——» 1,1-Ю-3 м3.
Ц/>0(72-Г1)
1,110'3 м3.
26
9.91. После того, как в комнате протопили печь, температура поднялась
с = 15°С до ?2 = 27°С. На сколько процентов уменьшилось число молекул в
этой комнате?
9.92. При аэродинамическом торможении в атмосфере планеты темпера-
тура внутри автоматического спускаемого аппарата увеличилась с ?j = 20°С
до t2 = 80°С. Какую часть воздуха необходимо выпустить, чтобы давление
внутри аппарата не изменилось?
9.93. Баллон емкостью К= 10 л содержит сжатый водород при темпера-
туре ?! = 7°С и давлении р = 5 МПа. Вследствие неисправности вентиля часть
газа вытекает. Какая масса водорода вышла из баллона, если при температуре
?2 = 17°С давление оказалось равным первоначальному? Молярная масса во-
дорода р. = 2-10'3 кг/моль.
9.94. Аэростат наполнен водородом при нормальном атмосферном дав-
лении р0 = 105 Па и температуре ?0 = 15°С. В солнечный день температура
водорода поднялась до ? = 37°С. Чтобы давление в оболочке аэростата не из-
менилось, Лт = 6 кг водорода было выпущено через клапаны. Определить
объем аэростата. Молярная масса водорода р. = 2-10‘3 кг/моль.
9.95. Баллон объемом V= 103 м3 с предохранительным клапаном содер-
жит водород при температуре ?, = 15°С и давлении р = 105 Па. При нагревании
баллона до температуры ?2 = 37°С через клапан выходит часть водорода,
вследствие чего давление не изменяется. Определить массу выпущенного во-
дорода. Молярная масса водорода р. = 2-10'3 кг/моль.
9.96. В стальном резервуаре находится сжатый воздух при температуре
?! = -23°С. На резервуаре имеется предохранительный клапан. Клапан откры-
вается, если давление в резервуаре увеличивается на Др = 2 атм. При нагре-
вании резервуара до ?2 = 27°С из него вышло т| = 10% массы газа. Какое дав-
ление было первоначально в резервуаре?
9.97. Сосуд объемом Vx = 50 л соединен с помощью короткой тонкой
трубки с сосудом объемом V2 = 15 л. В трубке имеется клапан давления, по-
зволяющий газу просачиваться из большего сосуда в меньший, если давление
в большем сосуде превышает давление в меньшем на Др = 1,2 атм. При тем-
пературе ?! = 17°С больший сосуд содержит идеальный газ при давлении
р0 = 1 атм, а меньший сосуд вакуумирован. Какое давление будет в меньшем
сосуде, если оба сосуда нагреть до ?2 = 200°С?
9.98. Когда объем, занимаемый идеальным газом, уменьшили на а= 10%,
а температуру увеличили на Д?=16°С, его давление возросло на 0 = 20%.
Какова начальная температура газа?
• Решение. Запишем уравнение Мендлеева-Клапейрона для начального и конечного со-
стояний газа:
р|К|=У|ЛТ|, p2V2 = v2RT2. (1)
27
По условию
V|=V2, /?2 = 1,2/?,, Г2 = 0,9Г,, Т2 = Т,+ДГ.
(2)
Подставив (2) в уравнения (1), после несложных преобразований получим
PiVt 1,2/?; 0,9 F,
Т, Т|+ДГ ’
Г' = (Щ = 200К-
Откуда находим
• Ответ: Тх = = 200 К.
U,Uo
9.99. Температуру некоторого газа увеличили вдвое, а объем уменьшили
втрое. Во сколько раз увеличилось давление газа?
9.100. Топочные газы при выходе из дымовой трубы в атмосферу имеют
температуру Т, = 400 К, причем их первоначальный объем увеличивается в
п = 2 раза. Определить начальную температуру газа, если давление газа при
прохождении в трубе изменяется в к = 0,25 раза.
9.101. В дизельном двигателе в начале такта сжатия температура горючей
смеси равна = 40°С, а давление рх = 78,4 кПа. Во время сжатия объем умень-
шается в п = 15 раз, а давление возрастает до р2 = 3,5 МПа. Определить тем-
пературу рабочей смеси в конце такта сжатия.
9.102. Идеальный газ при температуре tf = - 50°С и давлении pt = 196 кПа
занимает объем Vl = 4 л. При каком давлении этот газ займет объем = 16 л
после нагревания до температуры t2 = 20°С?
9.103. Определить на сколько процентов изменилось количество газа в со-
суде, если объем сосуда увеличился на а = 20%, давление возросло на р = 10%,
а температура увеличилась на у = 40%.
9.104. В сосуде объемом Vx = 4-10'3 м3 при давлении р} = 1 атм находится
т = 2 г водорода. Газ сжали. При этом давление газа стало равным р2 = 4 атм,
а объем уменьшился на ЛИ=2-10‘3 м3. На сколько градусов изменилась тем-
пература газа? Молярная масса водорода ц = 210‘3 кг/моль.
9.105. Перед стартом при нормальных условиях (р0 = 105 Па, t0 = 0°С)
объем аэростата с эластичной оболочкой был равен = 4000 м3. Аэростат
поднимается на высоту, где давление составляет р = 5-104 Па, а температура
понижается до t = - 17°С. На сколько изменился объем аэростата? Натяжени-
ем материала оболочки пренебречь.
9.106. Эластичная оболочка метеозонда, заполненная гелием массой
т = 1 кг при температуре Т= 300 К, была пробита метеоритом. Сечение от-
верстия 5= 10 мм2. Через какое время нз оболочки вытечет а = 50% газа,
если скорость истечения гелия через пробоину постоянна равна и = 5 м/с, а
объем оболочки меняется так, что плотность газа остается все время посто-
янной? Молярная масса гелия д. = 4-10'3 кг/моль, атмосферное давление
р0= 105Па. Температуру гелия считать постоянной. Натяжением материала
оболочки пренебречь.
28
• Решение. Так как плотность газа внутри метеозонда остается постоянной, то за время
t через пробоину вытечет масса
тВЫ1=р5и1
гелия, которая по условии задачи равна:
7Ициг ОС /И.
Следовательно,
„ . . ат
а т = р S и t, или t =--------.
pSv
Записав уравнение Менделеева-Клапейрона в виде
p = ^RT,
Ц
получим
рр атНТ
р = ^Р^., или 1 =----—« 17,3 часа.
л/ ppSv
„ am RT ,
• Ответ -. t =--—® 17,3 часа.
\ipS-o
9.107. «Свисток» тепловоза выпускает пар, имеющий температуру
Т = 500 К, со скоростью и = 5 м/с. Определить массу пара, выпускаемого в
атмосферу за t = 1 мин, если поперечное сечение отверстия в «свистке» равно
5=1 см2, а давление пара р = 3 атм. Молярная масса пара ц = 18-10'3 кг/моль.
9.108. По цилиндрической дымовой трубе поднимаются топочные газы.
В нижней части трубы их температура равна Т\ = 1073 К, а скорость -
и = 6 м/с. Определить их скорость в верхней части трубы, где они остывают
до температуры Т2 = 423 К. Изменением давления в трубе пренебречь.
9.109. По трубе сечением 5= 51 О’4 м2 течет углекислый газ под давле-
нием р = 3,92-105 Па при температуре Г =280 К. Найти среднюю скорость
протекания газа по трубе, если через поперечное сечение за t= 10 минут про-
ходит m = 20 кг газа. Молярная масса углекислого газа ц = 44-10"3 кг/моль.
9.110. Аэростат объемом V= 300 м3 заполнен водородом при температуре
t = 20°С и давлении р = 95 кПа. Сколько времени производилось наполнение,
если в аэростат каждую секунду поступало А»г = 2,5 г водорода? Молярная
масса водорода ц = 2-10'3 кг/моль.
9.111. Сколько ходов должен сделать поршень компрессора, чтобы уве-
личить давление в баллоне объемом V от атмосферного р0 до р, если объем
рабочего цилиндра компрессора равен Го? Забор воздуха производится из ат-
мосферы. Изменение температуры не учитывать.
• Решение. После п ходов поршня компрессора нз атмосферы будет «забран» объем воз-
духа V„ = п Рд при давлении р0. Эта масса воздуха будет введена в объем баллона, создав
в нем парциальное давление р'п. Так как по условию задачи изменением температуры сле-
дует пренебречь, то справедлив закон Бойля-Мариотта:
р'пУ=роп Уд.
Откуда имеем
29
, » Го
Pn~P0 jz
Давление в баллоне через л ходов станет равным
- 11 1
Рл=/’О+/’л=/’о(1 +лу)-
Следовательно, для достижения необходимого давление рп=р поршень компрессора
должен сделать
V\_p_ il
n = ~tri ~1
Г() 1 Ро 1
ходов.
„ v[_p_ il
• Ответ-, п = уг-1 — If.
Г0 1 Ро 1
9.112. В камеру футбольного мяча объемом V= 2,5 л накачивают воздух
насосом, забирающим при каждом качании Ио = 0,15 л атмосферного воздуха
при давлении р0 = 105 Па. Каково будет давление в камере мяча после и = 50
качаний, если камера вначале была пустой? Изменением температуры прене-
бречь.
9.113. На сколько изменится давление в резервуаре пневматического тор-
моза трамвайного вагона после п = 250 качаний насоса, если объем резервуара
равен V= 30 л, а насос за одно качание подает Ко = 600 см3 воздуха при нор-
мальном атмосферном давлении р0 = 105 Па? Изменением температуры пре-
небречь.
9.114. Автомобильную камеру емкостью V= 10 л нужно накачать до дав-
ления р = 2 атм. Найти, сколько качаний следует сделать насосом, забираю-
щим при каждом качании Ио = 500 см3 воздуха из атмосферы, если камера
вначале была заполнена воздухом при нормальном атмосферном давлении
р0 = 105 Па. Изменением температуры пренебречь.
9.115. Давление воздуха в резервуаре компрессора равно атмосферному
давлению (р0 = Ю5 Па). Объем цилиндра компрессора в к= 40 раз меньше
объема резервуара. Сколько качаний должен сделать поршень компрессора,
чтобы давление в резервуаре стало р = 4 атм? Изменением температуры пре-
небречь.
9.116. Сколько ходов должен сделать поршневой насос с объемом рабо-
чего цилиндра Ио, чтобы откачать воздух из баллона емкостью V от давле-
ния рй до давления р2 Изменением температуры пренебречь.
• Решение. Если в начале первого рабочего хода воздух в баллоне занимал объем V прн
давлении р0, то к концу первого хода та же масса воздуха займет объем (F+ Ио) прн дав-
лении р\. Так как температура воздуха не меняется, то по закону Бойля-Мариотта получим
Ро Г=Р1 (Г+ Го).
Откуда
Pl =Ро V+ Ео '
30
В начале второго хода поршня объем и давление воздуха в баллоне равны соответ-
ственно V и pt, а в конце хода - (V+ и р2. Поэтому
Pi V=P2(V+Vo)
или
V [ V I2
Рг Piv+v0 Ро‘Г+Го'’
Продолжая аналогичные рассуждения, находим, что к концу п -то рабочего хода дав-
ление в баллоне станет равным
f V ]п
Рп ~Ро I Г+ j/0 1 '
Следовательно, число ходов насоса для достижения требуемого давления рп=р
будет равным
1g (Р/Ро) _ 1g (Рс/Р)
1g [К/(Г+ Ко)] " 1g [(Г+ Ко)/К]
„ 1g (Р(/Р)
• Ответ : п = -—------- .
1g [(И+ Vo)/V]
9.117. После одного хода откачивающего поршневого насоса, объем ра-
бочей камеры которого в два раза меньше объема откачиваемого сосуда, дав-
ление воздуха в сосуде упало до р= 16 кПа. Определить начальное давление
газа в сосуде. Температуру считать постоянной.
9.118. Поршневым воздушным насосом откачивают воздух из сосуда. За
один ход поршня откачивается а = 1/10 объема воздуха в сосуде. Во сколько
раз уменьшится давление воздуха в сосуде после двух ходов поршня? Тем-
пературу считать неизменной.
9.119. Давление воздуха в сосуде было равно р0 = 105 Па. После трех
ходов откачивающего поршневого насоса давление воздуха упало до
р = 2 кПа. Определить отношение объема сосуда к объему цилиндра порш-
невого насоса. Температуру считать постоянной.
9.120. После и = 6 ходов поршня откачивающего насоса давление в со-
суде стало равным р = 35 мм рт.ст. Каким было первоначальное давление газа
в сосуде, если объем сосуда равен V = 300 см3, а объем цилиндра насоса
Vo = 200 см3? Температуру считать постоянной.
9.121. Сначала давление в сосуде увеличили в а = 8 раз, а затем выпус-
тили Р = 0,25 массы газа, находящегося в сосуде. Во сколько раз изменилась
концентрация молекул газа, если температура не изменилась?
• Решение. Газ последовательно участвует в двух процессах. Рассмотрим первый процесс -
процесс изотермического сжатия газа. Так как в этом процессе масса газа и температура
не меняются, то, очевидно, увеличение давления происходит за счет уменьшения объема,
занимаемого газом, от И| до У2. Из закона Бойля-Марнотта
Р\ У\ =Рг
находим
31
a
P1 = Kl
Pl *2
Второй процесс - уменьшение массы газа в сосуде.
Первоначально в сосуде находилось Nj = N2 = V| = v2 молекул, а осталось
W3 = v3 Na молекул, где vb v2, v3 - число молей газа; NK - число Авогадро.
По условию задачи
v3 т3 т2- &т
v2 ” т2 ~ т2 ~ 1 Р’
где Am - масса выпущенного газа.
По определению концентрации:
М ^2
"|_7Г’ "2"К’ ”3-^'
Откуда
и2 К| и3 W3 v3
И| V2' п2 N2 v2
Следовательно,
— = а, —=1-Р, — = а(1-р) = 6.
Пу п2 Г И| ' "
• Ответ', концентрация увеличилась в а (1 - Р) = 6 раз.
9.122. Идеальный газ, занимающий объем Vx при давлении рх и темпера-
туре Г] = 300 К, расширился изотермически до объема V2 = 2 л. Затем давление
газа было уменьшено изохорически в два раза. Далее газ расширился при по-
стоянном давлении до объема И4 = 4 л. Определить температуру Г4 газа в ко-
• Решение. Так как газ последовательно про-
ходит несколько состояний, участвуя в трех
различных процессах, то для удобства реше-
ния задачи изобразим на рисунке графики
процессов, например, в переменных р - V
(см. рнс. 9.6).
Запишем уравнения изотермического,
изохорического и изобарического процес-
сов, согласно обозначениям, принятым на
рисунке:
- изотермический процесс: />1 К| = р2 У2,
- изохорический процесс:
- изобарический процесс:
Pi Рз
т2-т3’’
Тз IV
Решая полученную систему уравнений с учетом, что Т2 = Ту и р2/р2 = 2, найдем ко-
нечную температуру газа:
32
7’-=гзк=7’2йй4г^=3(х)к-
1 V1
• Ответ: Т4 = Т, = 300 К.
2 т2
9.123. Идеальный газ сначала изотермически сжимают в п = 4 раза, а
затем изобарически расширяют в т = 2 раза. Построить этот процесс на
р-Т и V—T —диаграммах.
9.124. Давление идеального газа сначала изохорически уменьшают в
п = 4 раза, а затем изотермически увеличивают в т = 2 раза. Построить этот
процесс нар-Г и V-Т- диаграммах.
9.125. Начальное состояние идеального газа определяется объемом Ио,
температурой То и давлением р0. Газ подвергли сначала изобарическому рас-
ширению до объема после чего нагрели при постоянном объеме до дав-
ления р2. Чему равна температура Т2 газа в конечном состоянии?
9.126. Идеальный газ сначала изохорически нагрели до абсолютной тем-
пературы в два раза больше первоначальной, а затем изобарически темпе-
ратуру увеличили еще в два раза. Во сколько раз конечный объем газа
больше первоначального?
9.127. Идеальный газ, находящийся при температуре = 127°С и давлении
/>! = 4-105 Па, занимает первоначально объем = 2 л. Этот газ изотермически
сжимают, затем изохорически охлаждают до температуры t3 = - 73°С и далее
изотермически доводят его объем до Г4 = 1 л. Определить установившееся дав-
ление р4 газа.
9.128. Во сколько раз изменится среднее расстояние между молекулами
идеального газа, если выпустить из сосуда а = 1/4 часть газа при постоянных
температуре и объеме, а затем в сосуде увеличить температуру в 0 = 6 раз,
поддерживая давление постоянным?
9.129. Приближенно воздух можно считать смесью азота (а1 = 80% по
массе) и кислорода (о^ = 20% по массе). Найти молярную массу воздуха. Мо-
лярная масса азота p-j = 28-10’3 кг/моль, кислорода - = 32-10’3 кг/моль.
• Решение. Число молекул в некотором объеме смеси двух газов равно
^=^l+^2.
Количество молекул Nlt N2 каждого из газов, содержащихся в выбранном объеме,
можно выразить через их массы т^ т2 и молярные массы р(, ц2:
mi т2
N2 = -+Nh.
Pl Р2
Следовательно,
т mt т2
Рвозд. Р1 Р2
Откуда получим молярную массу воздуха:
33
'"М1Н2
Мвозд. ~
т1 М2 + т2 Ml
----—---------« 28,7-10’3 кг/моль.
«1 ц2 + а2ц,
• Ответ: Цвозд =-----~---» 28,7-10’3 кг/моль.
а! М2 + «2 Ml
9.130. Смесь содержит а, = 70% кислорода и а2 = 30% гелия. Определить
молярную массу смесн. Молярная масса кислорода Ц]=32-10'3 кг/моль,
гелия - Ц2 = 410'3 кг/моль.
9.131. Определить молярную массу смеси кислорода массой т1 = 25 г и
азота массой т2 - 75-Ю"3 кг. Молярная масса кислорода ц, = 32-Ю"3 кг/моль,
азота - Р2 = 28-10'J кг/моль.
9.132. В кислороде имеется примесь азота, массовая доля которого равна
a = 2% массовой доли кислорода. Определить парциальное давление азота,
если смесь газов находится при давлении рп = 105 Па. Молярная масса азота
ц, = 28-10'3 кг/моль, кислорода - = 32-Ю"3 кг/моль.
9.133. Полагая, что воздух состоит в основном из кислорода и азота,
определить процентное содержание масс этих газов в атмосфере. Молярная
масса воздуха ц = 29-10‘3 кг/моль, кислорода - Ц] =32-10’3 кг/моль, азота -
Р2 = 28-10’3 кг/моль.
9.134. При некоторых температуре и давлении один газ имеет плотность
р] = 0,4 кг/м3, а другой - р2 = 0,6 кг/м3. Какую плотность будет иметь при
тех же условиях смесь газов, если их массы одинаковы?
9.135. Плотность смеси водорода и азота при температуре t = 47°С и дав-
лении р = 2 атм равна р = 0,3 г/л. Чему равна концентрация молекул водорода
в смеси? Молярная масса водорода щ = 2 г/моль, азота - = 28 г/моль.
• Решение. Для смеси газов справедлив закон Дальтона:
р=Р1+р2> (1)
где р{, р2 - парциальные давления водорода и азота, которые могут быть определены из
уравнений состояния:
Pi=»ik Т, р2 = п2к Т,
где п1; п2- концентрации соответствующих газов.
Складывая уравнения (2) с учетом закона Дальтона, получим
р = (П] + пг) к Т.
Плотность смеси газов равна
m mx+m2
P~V~ V ’
где mlt т2 - массы водорода и азота в данной смеси.
Учитывая, что концентрация любого газа, содержащегося в объеме К,
N т
п~ V’
выразим массы газов через их концентрации:
Hi ”1 V Н2 ”2 К
т'=^Г' т2=~^Г'
(2)
(3)
(4)
(5)
34
Подставляя соотношения (5) в выражение (4), получим
Ml "1 + М2 ”2
Р уА • (6)
Система уравнений (3), (6) позволяет найти концентрацию молекул водорода в смеси:
ЛГА(рц2/ЯГ-р) 22 -з
П|=---------------» 4,18-10 м ,
М2 "Ml
где учтено, что к NA = R.
NA(p u.2/RT- р) „ ,
• Ответ: nt =--------------»4,1810и м'3.
Н2-Н1
9.136. В колбе емкостью V= 1 л находится водород массой тя1 = 1 г и
углекислый газ массой т2 = 1 г при температуре t = 27°С. Определить давле-
ние смеси газов. Молярная масса водорода ц, =2-10'3 кг/моль, углекислого
газа Ц2 = 44-10'3 кг/моль.
9.137. В сосуде объемом V= 1 л содержится кислород массой т1 = 10 г
и гелий массой т2 = 5 г. Определить температуру этой смеси газов, если дав-
ление смеси равно р = 4 МПа. Молярная масса кислорода ц, = 32-10’3 кг/моль,
гелия - ц2 = 4-10"3 кг/моль.
9.138. В закрытом сосуде объемом V= 100 л при температуре Т = 300 К
находится водород массой mi= 4 г и гелий массой т2 = 4 г. Найти давление
н сосуде после того, как в него поместили W= З-Ю23 молекул азота. Молярная
масса водорода ц1 = 2-10'3 кг/моль, гелия - Ц2 = 4-10'3 кг/моль. Температуру
считать постоянной.
9.139. В сосуде объемом V= 10 л содержится смесь водорода и кислорода
в равных массовых количествах (масса каждого т = 2г). Весь кислород, со-
единяясь с частью водорода, образует воду. Каким будет давление оставше-
гося водорода при t = 17°С? Молярная масса водорода щ = 2-10'3 кг/моль, кис-
лорода - Н2 = 32-10‘3 кг/моль.
9.140. Определить плотность смеси mt = 4 г водорода и т2 = 32 г кисло-
рода при температуре t = 7°С и давлении р = 700 мм рт.ст. Молярная масса
водорода ц, = 2-10'3 кг/моль, кислорода - р? = 32-10'3 кг/моль.
9.141. Концентрация атомов гелия в смеси гелия и азота при нормальных
условиях и = 1,6-1025 м'3. Определить плотность смеси. Молярная масса гелия
щ = 4-10‘3 кг/моль, азота - |12 = 28-10‘3 кг/моль.
9.142. В баллонах объемами V} = 20-10’3 м3 и К2 = 44-10'3 м3 содержится
одинаковый идеальный газ. Давление в первом баллоне р} = 2,4-106 Па, во
втором р2 = 1,6-106 Па. Определить общее давление после соединения балло-
нов, если температура газов не изменилась.
• Решение. После соединения баллонов общее давление р' газов можно найти по закону
Дальтона:
Р' =Pl+P2>
35
где р\,Рг - парциальные давления газов, первоначально находившихся в сосудах объемом
К] и V2 соответственно. Уравнения состояния каждого из газов после соединения баллонов
,Pl’(H + ^ = Vi/fT, p2’(K1 + K2) = v2j?r
позволяют записать закон Дальтона в виде
V[ + v2
И + И2
RT.
Число молей V, и v2 легко можно определить из уравнений Менделеева-Клапейрона,
записанных до соединения баллонов:
Pi V = vt R Т, р2 И2 — v2 R Т.
Следовательно,
, Pl Vl + Р2 V2 . о,
р = ————— » 1,85 МПа.
И + ”2
Л , Pl И +Р2 V2 , m
Ответ: р = ————— » 1,85 МПа.
9.143. Какое давление р} воздуха должно быть в сосуде объемом
Vi = 10 л, чтобы при соединении его с сосудом объемом V2 = 30 л, в котором
находится воздух при давлении р2 = 1 атм, установилось давление р = 2 атм?
Температуру считать постоянной.
9.144. В двух сосудах находится одинаковый идеальный газ. Сосуды со-
единены трубкой с краном. В первом сосуде масса газа тх = 1 кг при давлении
Pi = 105 Па, во втором - т2 = 2 кг при давлении р2 = 4-105 Па. Какое устано-
вится давление в сосудах, если открыть кран? Температуру считать постоян-
ной.
9.145. Два сосуда, содержащие некоторые газы, соединены трубкой с кра-
ном. Давления в сосудах равны р} и р2, а число молекул Nt и N2 соответст-
венно. Каким будет давление, если открыть кран соединительной трубки?
Температура газов не изменяется.
9.146. Лазерные трубки объемом Vo = 60 см3 заполняются смесью гелия
и неона в молярном отношении 5:1 при давлении р0 = 5 мм рт.ст. Имеются
баллоны этих газов, каждый объемом V= 2 л. Давление в баллоне с гели-
ем pi = 50 мм рт.ст., с неоном - р2 = 20 мм рт.ст. Какое количество трубок
можно заполнить?
9.147. На гладком горизонтальном столе лежит цилиндрический сосуд
длиной Z, разделенный пополам герметической перегородкой. В одной части
сосуда находится под некоторым давлением азот, а в другой - углекислый
газ под вдвое большим давлением. В некоторый момент перегородка теряет
герметичность. На сколько и в каком направлении окажется смещенным
сосуд после того, как газы перемешаются? Температуры газов не меняются.
Массой сосуда пренебречь. Молярная масса азота ц, =28-10‘3 кг/моль, угле-
кислого газа - Цз = 44-10'3 кг/моль.
36
9.148. В сосуде объемом V= 1 дм3 находится т = 0,28 г азота. Газ нагре-
вают до температуры t= 1500°С, при которой а = 30% молекул азота диссо-
циировало на атомы. Определить давление в сосуде. Молярная масса азота
р = 2810'3 кг/моль.
• Решение. После того, как часть молекул азота распалась на атомы, газ в сосуде можно
считать состоящим их двух компонентов: молекулярного азота с молярной массой ц и ато-
марного азота с молярной массой ц/2. Запишем уравнение Менделеева-Клапейрона для
того и другого компонента:
7И|
PiV= — RT, (1)
И
т2
P2V=-+RT, (2)
ц/2
где pi, р2 - парциальные давления компонентов газа.
Давление всей смеси по закону Дальтона равно
RTlmi 2и21 ...
Р=Р1+Р2 = -Г|- + —(3)
Если массы компонентов представить в виде
т, = (1 - а) т, т2 = а т,
то уравнение (3) упростится:
р = ~^(]. + а)« 1,910s Па.
Гц
• Ответ: р = (1 + а) » 1,9-105 Па.
Гц
9.149. Некоторое количество водорода находится при температуре
7\ = 200 К и давлении р{ = 400 Па. Газ нагревают до температуры Т2 = 104 К,
при которой молекулы водорода полностью распадаются на атомы. Опреде-
лить давление газа р2, если его объем и масса не изменились. Молярная масса
водорода ц = 2-10'3 кг/моль.
9.150. В сосуде находится озон (О3) при температуре tt = 527°С. Через
некоторое время он полностью превратился в кислород (О2), а температура
упала до t2 = 127°С. На сколько процентов изменилось давление в сосуде?
9.151. В сосуде находится идеальный двухатомный газ. При увеличении
температуры в и = 3 раза давление газа увеличилось в т = 3,15 раза. Сколько
процентов молекул от их начального количества распалось на атомы?
9.152. В колбе находится двухатомный газ. Под действием ультрафиоле-
тового излучения распалось на атомы а = 12% молекул. При этом в колбе
установилось давление р = 93 кПа. Найти первоначальное давление газа.
9.153. В сосуде емкостью V= 0,5 л находится т = 1 г парообразного йода
J2. При температуре Т = 300 К давление оказалось равным р = 200 мм рт.ст.
Какова доля молекул, распавшихся на атомы в этих условиях? Молярная
масса йода J2 равна ц = 0,254 кг/моль.
9.154. При комнатной температуре t0 = 20°С четырехокись азота N2O4
частично диссоциирует, превращаясь в двуокись NO2. В откачанный сосуд
объемом К=250 см3 вводят т = 0,92 г жидкости N2O4 при температуре
t = 0°С. При температуре /j = 27°С жидкость целиком испаряется и давление
становится равным />=128 кПа. Определить долю четырехокиси азота, ко-
торая диссоциировала. Молярная масса четырехокиси азота N2O4 равна
ц = 92-10"3 кг/моль.
9.155. В закрытом сосуде < .'ъемом V = 22,4' 10"3 м3 при нормальных усло-
виях (t = 0°С, р0 = 1 атм) находится кислород и т = 5-Ю'3 кг углерода. После
того, как часть углерода сгорела с образованием углекислого газа СО2, тем-
пература в сосуде повысилась на ДГ= 100 К. Определить конечное давле-
ние в сосуде. Молярная масса кислорода щ = 32-10'3 кг/моль, углерода -
Из = 12-10'3 кг/моль.
9.156. Сосуд емкостью К разделен пополам полупроницаемой перегород-
кой. В одну половину сосуда введен водород массой т1 и азот массой т2, а в
другой половине вакуум. Через перегородку может диффундировать только
водород. Какие давления установятся в обеих частях сосуда, если температура
постоянна и равнаТ? Малярная масса водорода Ц], азота - ц2.
• Решение. При заполнении одной половины сосуда смесью газов молекулы водорода
будут диффундировать через перегородку в другую половину до тех пор, пока давления
водорода по обе стороны от перегородки не сравняются. Так как перегородка делит сосуд
на равные части и температуры в них одинаковы, то во вторую половину сосуда продиф-
фундирует ровно половина начального количества водорода. После этого в одной части
сосуда окажется смесь азота с водородом, а в другой - продиффундировавший водород.
Уравнения состояния водорода и азота в первой половине сосуда
у т, у т->
рЛ = —^КТ, p2^ = — RT
2 2 щ 2 ц2
и закон Дальтона
Р=Р\ +Р2
позволяют найти полное давление смеси:
( ">1 ">2 ) 2 Я Г
V
Из уравнения состояния, записанного для продиффундировавшего водорода,
у »>i
P'y=z-L*:r
2 2 щ
найдем давление в другой половине сосуда:
mi RT
Р = Ml К '
„ т,ц2 + 2т2ц1 rt т{ Rp
• Ответ", р =-------------тт- ; р =---тг.
Ц1Ц2 V Ml Г
38
9.157. Сосуд разделен пополам полупроницаемой перегородкой. Объем
каждой части равен V= 1 л. В первую половину введены т1 = 2 г водорода
и т2 = 28 г азота. В другой половине сосуда вакуум. Какие давления устано-
вятся в обеих частях сосуда, если перегородка пропускает только водород, а
температура остается постоянной и равной 7”= 373 К? Молярная масса водо-
рода ц, = 2-10'3 кг/моль, азота - = 28-Ю"3 кг/моль.
9.158. Одинаковые по массе количества водорода и гелия поместили в
сосуд объемом К,, который отделен от пустого сосуда объемом V2 полупро-
ницаемой перегородкой, свободно пропускающей молекулы водорода и не
пропускающей гелий. После установления равновесия давление в первом со-
суде упало в два раза. Определить отношение объемов V2/Vv Температуру
считать постоянной. Молярная масса водорода m = 2-10’3 кг/моль, гелия -
ц2 = 4-10‘3 кг/моль.
9.159. В вертикальном сосуде под поршнем находится т = 1 г азота. Пло-
щадь поршня S = 10 см2, масса М= 1 кг. Азот нагревают на А7’= 10 К. На
сколько при этом поднимется поршень? Давление над поршнем нормальное.
Молярная масса азота ц = 2810'3 кг/моль. Трением пренебречь.
• Решение. В положении равновесия на поршень действуют три силы: сила тяжести порш-
ня М^и силы давления над поршнем poS и под поршнем pS, где ро и р - внешнее дав-
ление и давление под поршнем сечением S соответственно. При этом указанные силы
уравновешивают друг друга:
Mg+p0S=pS.
Следовательно, давление под поршнем равно
Mg
Р = ~^+Ро
и зависит только от массы, сечения поршня (сосуда) и давления над ним, т.е. не зависит
от параметров газа под поршнем. Поэтому можно заключить, что процесс нагревания азота
протекает изобарически. В этом случае справедлив закон Гей-Люссака:
Т, Т2’ ““ К, Г,’
где К] = 5 й], К2 = S ^2 _ объемы, занимаемые азотом до и после нагревания. Так как пере-
мещение поршня равно
&h - h2 - h\,
то получим
, К2-И KlfK2 .1_И(72 .1 Лгт Т'-Ллг
S S I К] 1J S'-Ti 1 J STi^2 Ti) S Ti
Используя уравнение начального состояния азота
р Pi=^RTi
в виде
( Mg 1 т „ „
+р0 (И1= — RTi, или
'о ц
^1 _ mR
Ti p(Mg/S+p0)’
39
окончательно имеем
т RAT mRAT
An =---------=----------и 2,7 см.
H(Mg/S+p0)S n(Mg+p0S)
• Ответ: Ah =—mRAT 27 см.
(Mg+poS)
9.160. В вертикальном открытом сверху цилиндрическом сосуде, имею-
щем площадь поперечного сечения S, на высоте h от дна находится поршень
массой М, поддерживаемый сжатым идеальным газом с молярной массой
ц. Температура газа Т, атмосферное давление р0. Пренебрегая трением, опре-
делить массу газа в сосуде.
9.161. В вертикальном открытом сверху цилиндрическом сосуде по-
перечным сечением S= 100 см2 под тяжелым поршнем находится т= 10 г
кислорода. После увеличения температуры кислорода на АТ = 50 К поршень
поднялся на высоту h = 12 см. Определить массу поршня, если над поршнем
давление рй = 105 Па. Трением поршня о стенки цилиндра пренебречь. Мо-
лярная масса кислорода ц = 32-10'3 кг/моль.
9.162. В вертикальном открытом сверху цилиндрическом сосуде попереч-
ным сечением S = 40 см2 на высоте h = 40 см от дна находится в равновесии
поршень массой т = 2 кг, поддерживаемый столбом воздуха. На сколько опус-
тится поршень, если на него поставить гирю массой М= 10 кг? Атмосферное
давление рй= 105 Па. Трения нет, температуру воздуха считать постоянной.
9.163. Газ, находящийся в вертикальном открытом сверху цилиндре под
поршнем, нагрели при постоянном давлении так, что его объем увеличился
в и = 1,5 раза. Затем поршень закрепили и нагрели газ так, что его давление
возросло в т = 2 раза. Найти отношение конечной температуры газа к началь-
ной.
9.164. Чтобы изотермически уменьшить объем газа в открытом сверху
цилиндре с поршнем в и раз, на поршень поместили груз массой т. Какой
массы груз нужно добавить, чтобы объем газа изотермически уменьшить еще
в к раз?
9.165. В вертикальном открытом сверху
цилиндре под поршнем находится воздух. Пор-
шень имеет форму, показанную на рис. 9.7.
Сила тяжести поршня Рх = 60 Н, площадь сече-
ния цилиндра S = 20 см2, атмосферное давле-
ние р0 = 1 атм. Какого веса груз нужно поло-
жить на поршень, чтобы объем воздуха умень-
шился в два раза? Температуру считать посто-
„ „ „ янной, трения нет.
Рис. 9.7 ’ г
40
9.166. В гладкой, открытой с обоих торцов
вертикальной трубе, имеющей два разных сече-
ния, находятся в равновесии два поршня, соеди-
ненные невесомой нерастяжимой нитью, а меж-
ду поршнями v = 1 моль идеального газа (рис.
9.8). Площадь сечения верхнего поршня на
S = 10 см2 больше, чем нижнего. Общая масса
поршней т = 5 кг. Давление наружного воздуха
р0 = 1 атм. На сколько градусов надо нагреть газ
Рис. 9.8
между поршнями, чтобы они переместились на расстояние AZ = 5 см?
9.167. В вертикальном открытом цилиндре над закрепленным снизу
поршнем находится газ, закрытый сверху другим поршнем. Расстояние
между поршнями равно h0. На верхний поршень до самого верха цилиндра
налит слой жидкости плотностью р высотой h0. На какое расстояние надо
поднять нижний поршень, чтобы над верхним остался слой жидкости вы-
сотой h < h0? Атмосферное давление р0. Массой поршней пренебречь, тем-
пературу считать постоянной.
• Решение. Так как до и после перемеще-
ния поршней система находится в равнове-
сии, то это означает, что давления над и
под поршнем В одинаковы (рис. 9.9). Сле-
довательно,
Pi=Po + Pgfto, P2=Po + Pgh> (О
где Pi, Р2~ давления газа, заключенного в
объеме между поршнями до и после пере-
мещения поршня А соответственно. Ис-
пользуя уравнения состояния газа в начале
и в конце процесса сжатия
PihoS^uRT, p2(2hQ-х - h) S - ]х R Т
(где х - величина перемещения поршня Л), получим
Piho=P2<2ho-x-h).
Теперь уравнения (1) можно переписать в виде
т- (2Ло-х-й)=ро + Р^Ло.
«о
Р2=Р0 + Р^Л,
ИЛИ
Po + Pgh ... ,
-------- (2h0-x-h)=p0 + pgh0.
Окончательно получаем
х = 2йд —й —
Ответ: х = 2й0
A) + pgA0
-й---------- кд.
Po + Pgh
Po+Pghp
Po + Pgh
ho.
41
9.168. В открытом вертикальном цилиндрическом сосуде, заполненном
воздухом, находятся в равновесии два одинаковых тонких тяжелых поршня.
Расстояние между поршнями и расстояние от нижнего поршня до дна сосуда
одинаковы и равны I. Давление между поршнями равно удвоенному атмо-
сферному давлению р - 2р0. На верхний поршень давят таким образом, что
он перемещается на место нижнего. На каком расстоянии от дна будет нахо-
диться нижний поршень? Трения нет, температуру считать постоянной.
9.169. Вертикальный герметически закрытый цилиндрический сосуд вы-
сотой 21 разделен посередине тонким невесомым подвижным поршнем. В
поршне имеется отверстие, закрытое пробкой. По обе стороны от поршня
находится одинаковое количество воздуха при давлении р. На какое рассто-
яние нужно сдвинуть поршень, чтобы пробка вылетела, если она вылетает
при перепаде давления Др? Трения нет, температуру считать постоянной.
9.170. В закрытом цилиндрическом сосуде находится в равновесии тя-
желый поршень. Над поршнем и под ним находятся одинаковые массы иде-
ального газа при одинаковой температуре. Отношение верхнего объема к
нижнему равно трем. Каким будет отношение объемов, если температуру газа
и в верхней части и в нижней увеличить в два раза?
9.171. В закрытом вертикальном цилиндрическом сосуде высотой 2h = 60 см
и сечением S = 10'2 м2 находится в равновесии тонкий поршень массой т = 0,3 кг,
делящий объем сосуда на равные части. Над поршнем находится гелий при дав-
лении р= 100 Па, а под поршнем - кислород. В некоторый момент поршень
становится проницаем для гелия, но непроницаем для кислорода и через боль-
шой промежуток времени занимает новое равновесное положение. Найти сме-
щение поршня. Каким стало давление гелия под поршнем? Трения нет. Тем-
пературу считать постоянной.
9.172. Тонкий подвижный поршень массой М разделяет объем вертикаль-
ного цилиндрического сосуда длиной / на две равные части. В сосуде по обе
стороны от поршня находится идеальный газ при температуре Т. Период
малых колебаниях поршня равен т. Найти количество газа в сосуде. Темпе-
ратуру считать постоянной. Трением пренебречь.
9.173. Три одинаковых шара
А, Б, В (рис. 9.10) соединены труб-
ками одинаковой длины и одинако-
вого сечения. Внутри трубок нахо-
дятся капельки ртути, которые в.
исходном положении (при темпе-
ратуре Tj) расположены таким образом, что объем воздуха в каждом шаре и
части трубки до капельки ртути равен Vx. Куда и на сколько передвинутся
капельки, если шар Б нагреть на АГ, а шар В - на 2Д7? Поперечное сечение
трубок равно S. Считать, что ДГ« Тх.
42
• Решение. Ввиду относительной малости изменений температуры и объема газа слагаемые
типа ЬТ-ЬУ во всех встречающихся при решении задачи соотношениях будем отбрасывать
как величины второго порядка малости.
Будем полагать, что в результате нагревания шаров Би В объем газа, заключенного
в шаре А, уменьшится на некоторую величину ДИ,, а объем газа в шаре В увеличится на
величину ДК2. Тогда объем газа в шаре Б возрастет на величину ДК, - ДК2.
Так как по условию задачи неизменными остаются лишь массы газа, заключенного
в сосудах, будем использовать условие, что прн всех протекающих процессах для каждого
из сосудов справедливо у
= const.
С учетом условий задачи и сделанных предположений, можно записать, что газ в
сосуде А был в начальном состоянии при параметрах ру Vy Ту а в конечном - при р2,
V\ - ДГ|, Ту Поэтому можно записать, что
Р1 И Р2(И-ДИ1)
Г, Г| .
Аналогично, параметры состояния газа в шаре Б: начальные - ру К,, Ту конечные -
Р2, И + ДК, - ДК2, Ti + ДГ. Следовательно,
Pi И^рдСИ + ДИ-ДКг)
Ti Т1 + ДТ ’ ’
Параметры состояния газа в шаре В: начальные - ру Vy Tt; конечные - р2,
V\ + ДГ2, Т[ + 2 ДТ. Следовательно,
Р.К. ргСИ + ДКг)
г, т^+гдт ’ u
Используя соотношения (1)—(2) и (2)-(3), запишем:
(И - ДГ,) (Л + ДТ) = (И + ДК, - ДКг) Ту
(И + ДИ - ДИ) (Г, + 2 ДТ) = (И + ДИ) (Т, + ДТ).
Раскрывая скобки и отбрасывая слагаемые вида ДТ ДИ получаем
2 ДИ Т1= И ДТ+ДПЛ,
2 ДК2 Т, = И ДГ+ Д^1 Л-
Решая полученную систему двух уравнений, находим
ди=ди = иу:. или Д/1 = Д/2=И#-
11 д 11 f Kj АГ
• Ответ', каждая капелька ртути передвинется влево иа одну и ту же величину А/ = с .
О 71
9.174. Внутри закрытого с обоих торцов горизонтального цилиндра нахо-
дится в равновесии тонкий поршень. С одной стороны поршня находится
Ш] = 2 г водорода, с другой - ги2 = 14 г азота. Какую часть объема цилиндра
занимает азот, если температуры газов одинаковы? Молярная масса водорода
Ц] = 2-Ю'3 кг/моль, азота - = 28-10"3 кг/моль.
9.175. Цилиндрический закрытый с обоих торцов горизонтальный со-
суд длиной 10 = 40 см разделен на две части легким тонким поршнем, сколь-
зящим без трения. Поршень находится на расстоянии I = 26,7 см от одного из
торцов цилиндра. С одной стороны поршня находится водород (молярная
масса р-! = 2-10’3 кг/моль), а с другой - идеальный газ с неизвестной молярной
массой Р2- Чему равна газа, если его масса равна массе водорода, а темпе-
ратуры газов одинаковы?
43
9.176. В открытом вертикальном цилиндрическом сосуде, заполненном
воздухом, находятся в равновесии два одинаковых тонких тяжелых поршня.
Расстояние от края сосуда до верхнего поршня равно 2Z, расстояние между
поршнями и расстояние от нижнего поршня до дна сосуда одинаковы н равны
I. Давление между поршнями равно удвоенному атмосферному давлению
р = 2р0. Сосуд герметически закрывают и переводят в горизонтальное положе-
ние. Определить расстояния AZj и Л/2, на которые сместятся верхний и нижний
поршни соответственно. Трения нет, температуру считать постоянной.
9.177. Закрытый с обоих торцов горизонтальный цилиндрический сосуд
содержит идеальный газ при температуре t = 0°С. Внутри сосуд перегорожен
поршнем радиусом г = 2 см, не проводящим тепло, на две части объемами
Kj = 10 см3 и У2 = 50 см3. Поршень находится в равновесии. На какое рассто-
яние ДА переместится поршень, если газ, заключенный в большем объеме,
нагреть на ДТ = 30 К?
9.178. Закрытый с обоих торцов горизонтальный цилиндрический сосуд
разделен подвижным поршнем, не проводящим тепло, на две части объемами
К, =200 см3 и У2 = 100 см3. Поршень находится в равновесии. Сначала тем-
пература идеального газа в сосуде 1\ = 300 К, а его давление рх = 105 Па.
Затем меньший объем охладили льдом до температуры Т2 = 273 К, а больший
нагрели паром до Т3 = 373 К. Какое давление установится в сосуде?
9.179. Вертикальный цилиндрический сосуд, открытый сверху, разделен
тонким поршнем массой m так, что объемы воздуха в верхней и нижней час-
тях одинаковы. Высота сосуда 21, площадь поперечного сечения S. Давление
в верхней части равно атмосферному р0. Сосуд герметически закрывают и
переворачивают вверх дном. На сколько сместится поршень? Треиия нет, тем-
пературу считать постоянной.
9.180. Закрытый с обоих торцов горизонтально расположенный цилинд-
рический сосуд разделен подвижным поршнем на две части, объемы которых
относятся как один к двум. Температура газа в обеих частях одинакова и
равна То = 300 К. До какой температуры нужно нагреть газ в сосуде меньшего
объема, чтобы отношение объемов изменилось на обратное?
9.181. Два расположенных гори-
зонтально цилиндрических сосуда пере-
крыты поршнями, соединенными не-
сжимаемым стержнем (рис. 9.11). Меж-
ду поршнями и вие них находится воз-
дух при атмосферном давлении р0. Пло-
щади поршней равны 5, и S2. Первона-
чальный объем воздуха между поршня-
ми равен Уо. На сколько сместятся поршни, если давление в камере А повы-
сить до значения р? Трения нет, температуру считать постоянной.
31
A': . \ ~ .Ро
ро; ;рр>о ' .|
44
9.182. В цилиндрический сосуд, лежащий на горизонтальной поверхнос-
ти, начинают медленно вдвигать с открытого конца гладкий поршень. Найти
давление воздуха в сосуде в тот момент, когда сосуд сдвинется с места. Масса
сосуда вместе с поршнем т = 2 кг, площадь поршня 5=6 см2, атмосферное
давление р0 = 105 Па. Коэффициент трения между горизонтальной поверхнос-
тью и сосудом ц = 0,3.
, 1 < 1 .
' • ’ воздух ’ • •
==~ -жидкость-"^
Рис. 9.12
TOWWWWWWWWWWW
Рис. 9.13
9.183. В прямоугольном закрытом с обоих торцов горизонтальном сосуде
длиной 21 находится с одной стороны жидкость, отделенная подвижным тон-
ким поршнем от воздуха в другой части сосуда (рис. 9.12). В начальный мо-
мент поршень находится в равновесии и делит объем сосуда на равные части.
На сколько сместится поршень, если температуру воздуха уменьшить в три
раза? Трения нет.
9.184. На гладком столе лежит прямоугольный сосуд длиной I = 1 м.
Внутри сосуда находится тонкий поршень, делящий объем сосуда на равные
части (рис. 9.13), в каждой из которых содержится воздух при температу-
ре t = 27°С. На сколько переместится сосуд, если воздух в одной части сосуда
нагреть на АТ = 60 К, а в другой - охладить на АТ = 60 К? Трения между
поршнем и сосудом нет. Массой сосуда и поршня пренебречь.
9.185. Цилиндрический сосуд,
наполненный газом, лежит на глад-
кой горизонтальной поверхности.
Длина сосуда / = 1 м. Внутри сосуда
на расстоянии !Д I от одного из его
торцов находится тонкая перегород-
ка (рис. 9.14), отделяющая такой же
газ, но прн давлении большем, чем в
3/4 I
‘/4 I
Рис. 9.14
остальной части сосуда. В результате повреждения перегородка лопнула. Оп-
ределить, во сколько раз изменилось давление внутри сосуда, если он смес-
тился на расстояние b = 0,3 м. Массой сосуда и перегородки пренебречь. Тем-
пературу газа считать постоянной.
9.186. Найти период малых колебаний поршня массой т, разделяющего
горизонтальный закрытый с обоих торцов цилиндрический сосуд сечением 5
45
на две равные части длиной I каждая. По обе стороны от поршня находится
воздух при давлении р0. Трения нет. Температуру считать неизменной.
9.187. На какой глубине h радиус пузырька воздуха вдвое меньше, чем
у поверхности воды? Атмосферное давление р0 = 105 Па, температуру воды
считать неизменной, плотность воды р = 103 кг/м3.
• Решение. Пренебрегая силами поверхностного натяжения, можно считать, что давления
воздуха в пузырьке на глубине h и у поверхности воды равны соответственно
Pi=Po + Pgh, Р2=Ро-
Так как по условию задачи температура воздуха в пузырьке не менялась, то спра-
ведлив закон Бойля-Мариотта:
Р1 И=Р2 *2,
или с учетом выражений для объемов: V\ = 4/з л г3, V2 = 4/з л г23:
(Po + pg/i)r3 =РОГ23.
Следовательно,
h = — [(г2/г,)3 - 1 ] = —— = 71,4 м.
Pg Pg
7 pn
• Ответ: h = ——==71,4 м.
Pg
9.188. Пузырек воздуха находится под водой на глубине h = 1 м. Темпера-
тура воды t = 17°С, давление над поверхностью воды р0= 1 атм. Определить
плотность воздуха в пузырьке. Молярная масса воздуха ц = 29-10‘3 кг/моль,
плотность воды р = 103 кг/м3.
9.189. Воздушный пузырек всплывает со дна водоема на его поверхность.
Во сколько раз увеличивается при этом радиус пузырька? Глубина водоема
h = 10 м, атмосферное давление р0 = 105 Па. Температуру воды считать неиз-
менной, плотность воды р = 103 кг/м3.
9.190. При температуре = 27°С и давлении рх - 105 Па объем воздуш-
ного шара, заполненного гелием, равен Vt = 500 м3. Каким станет объем этого
шара, если при подъеме в верхние слои атмосферы температура понизится
до t2 = - 33°С, а давление станет равным р2 = 5-104 Па?
9.191. Тонкостенный резиновый шарик радиусом г, = 3 см наполнен воз-
духом при температуре = 27°С и нормальном атмосферном давлении
р0 = 105 Па. Каким станет радиус шарика, если его опустить в воду при тем-
пературе t2 = 7°С на глубину h = 30 м? Натяжением резины пренебречь. Плот-
ность воды р = 103 кг/м3.
9.192. Аквалангист, находясь на глубине h= 15 м от поверхности воды,
вдохнул воздух, заполнивший объем легких V = 5,5 л. До какого объема рас-
ширятся его легкие, если аквалангист быстро вынырнет на поверхность?
Плотность воды р = 103 кг/м3, атмосферное давление р0 = 105 Па.
9.193. Баллон объемом У= 100 л наполнили воздухом при температуре
Г] = 27°С до давления р} = 10 МПа. Какой объем Уо воды можно вытеснить из
46
цистерны подводной лодки воздухом этого баллона, если вытеснение произ-
водится на глубине й = 40 м? Температура воздуха после расширения
Г2 = 3°С, атмосферное давление р0 = 105 Па.
9.194. Стеклянная трубка длиной 10 наполовину погружена в ртуть. Ее
закрывают пальцем и вынимают. При этом часть ртути вытекает. Какова
длина I столбика ртути, оставшегося в трубке? Атмосферное давление равно
pQ = Н мм рт.ст.
• Решение. Полагая температуру неизменной,
воспользуемся законом Бойля-Мариотта для
изотермического процесса:
Pi К]=р2К2,
где р\, Р2, К2 - давление н объем газа, за-
ключенного между пальцем и ртутью в начале
и в конце процесса.
До того, как трубка была закрыта, давле-
ние газа было равным атмосферному:
Pi —Ро-
(1)
Когда трубку вынули из ртути давление газа стало равным
P2=Po~PSl> (2)
где I- длина столбика ртути, оставшегося в трубке (рис. 9.15, б), р - плотность ртути.
Объемы, которые занимал газ в начале и в конце процесса
Vi = l/zSl0,
V2 = S(l0-l\
где S- площадь поперечного сечения трубки.
Следовательно,
(3)
(4)
Откуда
x/iPoSlo = (Po-pgl)S{la-l).
jl _ Pp + Pglp J + Po k _ 0
pg 2pg
Если учесть связь единиц измерения давления в [Па] и в [мм рт.ст.]
(5)
(6)
Po=PgH,
то уравнение (6) можно записать в виде
, Hip
l2-(H+lo)l + ^ = O,
решая которое, получим
Н + 10±^Н2+12
______ 2
яцЛяМ
Значение I ----------- не удовлетворяет очевидному физическому условию:
I = 0 прн 0. Поэтому
_______ 2
• Ответ'. I = !ф {Н+10 - "V № + /g}.
47
9.195. В большой сосуд с водой опрокинут цилиндрический сосуд. Уровни
воды внутри и вне цилиндрического сосуда находятся на одинаковой высоте.
Расстояние от уровня воды до дна опрокинутого сосуда I = 40 см. На какую
высоту ДА поднимется вода в цилиндрическом сосуде при понижении темпера-
туры от Т\ = 310 К до Т2 = 273 К, если сосуды закреплены? Атмосферное дав-
ление нормальное. Плотность воды р = 103 кг/м3.
9.196. Тонкая вертикальная трубка длиной / запаяна с верхнего конца, а
нижним концом касается поверхности жидкости плотностью р. Во сколько
раз нужно изменить температуру воздуха в трубке, чтобы жидкость поднялась
в ней на высоту 'Л /? Начальное давление в трубке равно давлению окружа-
ющего воздуха р0.
9.197. Тонкая пробирка длиной / = 50 см расположена вертикально вверх
дном так, что открытый конец касается поверхности ртути. При этом жид-
кость заполняет половину объема пробирки. Во сколько раз нужно изменить
температуру воздуха в пробирке, чтобы ртуть поднялась до трех четвертых
ее объема? Атмосферное давление рй = Н мм рт.ст., где Н= 760 мм.
9.198. Трубка, запаянная с одного конца, имеющая длину / = 45 см, опу-
щена открытым концом в ртуть на глубину Л = 40 см. Какова будет высота
Ао столбика ртути в трубке? Атмосферное давление pQ= 105 Па, плотность
ртути р= 13,6-103 кг/м3.
9.199. В пробирке, расположенной горизонтально, находится капля ртути
массой m = 16 г. Между дном пробирки и ртутью имеется пузырек воздуха.
Когда пробирка ставится вертикально открытым концом вверх, объем пузырь-
ка уменьшается втрое. Чему равно атмосферное давление, если диаметр про-
бирки d= 1 мм?
9.200. В запаянной с одного конца стеклянной трубке длиной /0 = 90 см
находится столбик воздуха, ограниченный сверху столбиком ртути высотой
h = 30 см. Ртуть доходит до верхнего края трубки. Трубку осторожно повора-
чивают открытым концом вниз, при этом часть ртути выливается. Какова вы-
сота / оставшегося столбика ртути, если атмосферное давление р0 = 1 атм?
Плотность ртути р= 13,6-103 кг/м3.
9.201. В стеклянной трубке находится столбик воздуха, закрытый столбиком
ртути длиной h = 8 см. Если держать трубку открытым концом вверх, то длина
воздушного столбика 1Х = 4 см, если открытым концом вниз - /2 = 5 см. Каково
атмосферное давление р0? Плотность ртути р = 13,6-103 кг/м3.
9.202. В сосуд с ртутью погружена в вертикальном положении трубка с
поршнем. Если поршень находится на расстоянии /0 = 1 см от поверхности
ртути в сосуде, то уровни ртути в сосуде и в трубке одинаковы. Найтн дав-
ление воздуха в трубке после подъема поршня над уровнем ртути в сосуде
до высоты Z = 75 см. Атмосферное давление р0 = 0,1 МПа, плотность ртути
р= 13.6-103 кг/м3.
48
9.203. В длинной узкой пробирке с воздухом, расположенной горизон-
тально, капелька ртути находится на расстоянии от дна. Если пробирку пе-
ревернуть вверх отверстием, то капелька окажется на расстоянии 12 от дна.
На каком расстоянии от дна окажется капелька, если перевернуть пробирку
вверх дном? Температуру считать постоянной.
9.204. В вертикальной запаянной снизу тонкой трубке длиной 2h в верх-
ней половине находится столбик ртути, а в нижней - воздух при температуре
То. До какой минимальной температуры нужно нагреть воздух, чтобы он вы-
теснил всю ртуть? Внешнее давление равно pa = h мм рт. ст.
9.205. Вертикальный цилиндрический сосуд сечением S и высотой h за-
полнен жидкостью плотностью р и запаян при атмосферном давлении р0.
При этом высота столба воздуха в сосуде равна hQ. Какое количество жид-
кости вытечет из сосуда, если в его нижней части сделать небольшое отверс-
тие? Температуру считать постоянной. г
• Решение. Так как сосуд с жидкостью запаян прн ат-
мосферном давлении р0, то если в его ннжней части сде-
лать отверстие, давление на уровне отверстия изнутри
сосуда будет больше атмосферного н жидкость начнет ,
вытекать. Прн этом воздух в сосуде будет расширяться
н его давление уменьшаться. В некоторый момент вре-
мени давление воздуха уменьшится на столько, что
жидкость перестанет вытекать. Тогда давление, дейст-
вующее на уровне отверстия (рис. 9.16), станет равным
атмосферному:
р + р£(й-йо-Дй)=р0, (1)
где Дй - высота слоя жидкости, которая вытечет нз сосуда.
Используя уравнения состояния воздуха в начале и в конце процесса расширения
PnhnS = ц RT, p(ho + ЛИ) S = ц R Т,
получим
р0Л0=р(йо-ДЛ)- (2)
Следовательно, уравнение (1) с учетом (2) примет вид
Рп fin
-r—r + Pgfh -h0-M)=p0.
flQ + АЛ
Приведя это выражение к общему знаменателю, получим квадратное уравнение:
ДА2 + (2й0 - й +Р(/Р g) ДА - й0 (й - й0) = 0,
решая которое относительно величины Дй, получим
ДйЛ| — + 2й0-й+\{^- + 2й0-й}2+4й0(й-й0)к
2 1 pg pg ' '
Следовательно, из сосуда вытечет жидкость массой
Дт = р S Дй = р S | — + 2й0 - й + V I — + 2й0 - й f + 4й0 (й - й0)}.
2 Р g Pg'
• Ответ: &т = р S | — + 2й0 - й + ’ | — + 2й0 - й I + 4й0 (й - й0) I.
2 'pg lpg > i
49
9.206. В цилиндрический сосуд
высотой h через крышку вертикально
вставлена немного не доходящая до
дна сосуда тонкостенная трубка дли-
ной I (рис. 9.17). В сосуд через трубку
наливают жидкость плотностью р.
Найти высоту уровня жидкости от
дна сосуда, когда трубка полностью
заполнится жидкостью. Атмосферное
давление р0. Соединение крышки со-
суда с трубкой герметичное.
• Решение. Так как трубка лишь немного не доходит до дна сосуда, то жидкость создаст
«пробку» н воздух, заполняющий сосуд, не сможет выходить наружу. Поэтому, по мере
заполнения сосуда жидкостью, воздух в сосуде будет сжиматься, а его давление будет воз-
растать. В некоторый момент времени давление воздуха станет достаточно большим н
жидкость достигнет верхнего края трубки. Тогда давление, действующее на поверхность
жидкости (на уровне АВ), станет равным давлению воздуха в сосуде:
P=Po + P£(!-&h), (1)
где ДА - высота слоя жидкости в сосуде.
Используя уравнения состояния воздуха в сосуде в начале и в конце процесса сжатия
pohS=pRT, pQi- tJi) S=pRT,
получим
р0А=р(А-ДА). (2)
Следовательно, уравнение (1) с учетом (2) примет вид
pnh
^Pg + pg^-M).
Приведя это выражение к общему знаменателю, получим квадратное уравнение:
pg&h2-(po + pgl+pgh)&h + pghl = O,
решая которое относительно искомой величины ДА, находим
ДА = Н +1 + h - "Vl —+ Z + a|2-4AZ|.
2 1 pg I pg > I
• Ответ: ДА = ^{— + l + h- У {— + Z + A i -4A Zi.
2>pg >pg I )
9.207. Открытая сверху вертикальная цилиндрическая трубка высотой 2h
поровну разделена горизонтальной перегородкой. Над перегородкой находит-
ся жидкость плотностью р, а под ней - воздух при атмосферном давлении
р0. В перегородке открывается небольшое отверстие, и жидкость начинает
перетекать под перегородку. Какой толщины будет слой жидкости в нижней
части трубки в момент, когда воздух начнет проходить через отверстие вверх?
Температуру считать постоянной.
50
Рис.
6)
9.18
9.208. Цилиндрический стакан массой М, высотой h и сечением 5 пла-
вает верх дном в жидкости плотностью р. При температуре Т\ глубина по-
гружения стакана равна hy. До какой величины надо понизить температуру
воздуха в стакане, чтобы глубина погружения стала равной Л2?
• Решение. Так как до и после изменения температуры воздуха стакан находится в рав-
новесии, то это означает, что давления на произвольном горизонтальном уровне, прохо-
дящем через жидкость, одинаковы. В частности, например, на уровнях АВ (рис. 9.18, а, б):
Ро + Р£А1=Р1 + Р£*ь Ро + Р£а2=.Р2 + Р£*2> 0)
где рь р2 - давления воздуха в стакане при температуре и Т2 соответственно. Используя
уравнения состояния газа при начальной Г, н конечной Т2 температурах
р1(й-х1)5=цЛГ1, p2(h-x^S=pRT2,
получим
Р2(Л-Х2)_Г2
Р1(Л-Х!) Tt- W
Из условия равновесия стакана
Mg + p0S=pyS, Mg + p0S=p2S (3)
следует:
Pi =Р2-
Теперь уравнение (2) можно переписать в виде
h - х2 Т2
h-xy Ту'
или с учетом (1), (3):
т _h~xiT _PgS(,h-h^ + mg
2 h-xi 1 pgS(h-hy) + mg *'
Ответ-. T2 =
pgS(h-h£ + mg
pgS(h-hy) + mg
Л-
9.209. На поверхности жидкости плотностью р плавает цилиндрический
тонкостенный стакан, наполовину погруженный в жидкость. На сколько по-
грузится стакан в жидкость, если его поставить иа поверхность жидкости
дном вверх? Высота стакана h, атмосферное давление р0.
51
9.210. Цилиндрический стакан плавает в воде так, что его края находятся
у поверхности, когда он наполовину заполнен водой. Вынув стакан и вылив
из него воду, его хотят погрузить вверх дном на такую глубину h, где он
будет находиться в равновесии. Определить глубину h, отсчитывая ее от верх-
него уровня воды в стакане. Плотность воды р = 103 кг/м3, атмосферное дав-
ление р0 = 105 Па. Толщину дна и стенок стакана не учитывать. Температуру
считать постоянной.
9.211. Цилиндрический стакан высотой Н= 10 см плавает вверх дном в
воде так, что его дно находится у поверхности, когда он наполовину заполнен
водой. На какую глубину h, отсчитывая ее от верхнего уровня воды в стакане,
нужно погрузить стакан, чтобы он стал заполнен водой на три четверти объема?
Толщину дна и стенок стакана не учитывать. Плотность воды р — 103 кг/м3,
атмосферное давление р0= 105 Па. Температуру считать постоянной.
9.212. В U-образной трубке высота столба воздуха /0 = 300 мм, а высота
столба ртути h0 = 110 мм (рис. 9.19, а). В правое колено долили столько ртути,
что ее уровень поднялся на АЛ = 40 мм. На сколько поднялся уровень ртути
в левом колене? Атмосферное давление р0 = Н мм рт.ст., где Н= 760 мм.
• Решение. Рассмотрим воздух, за-
ключенный между ртутью и запа-
янным концом трубки. При доли-
вании ртути в правое колено, вы-
сота столба ртути в левом колене
увеличится на Д/ (рис. 9.19, б) и
объем газа уменьшится. Считая
процесс сжатия изотермическим,
запишем закон Бойля-Мариотта
для двух состояний газа:
Р\ И =Р2 *2-
где Vi = l0S, V2 = (l0-&T)S, (S -
сечение трубки); р, =/>о + р£Йо,
/’2=Ро + Р^(Ло + АЛ-Д/) (р-
плотность ртути). Следовательно,
Рис. 9.19
(Po + pgho)loS=\pQ + pg(ho + ^h-M')] (!0-bP) S.
Учитывая связь единиц измерения давления в [Па] и в [мм рт.ст.]
p0 = pgH,
получим уравнение
(Я+ Йо) /0 = (Я + й0 + Дй - Д/) (Zo- AZ),
которое можно записать в виде
Д/2 -Д/(/0 + й0 + Дй + Я) +дл/0 = о.
Решая последнее уравнение относительно Д/, получим
Д/ = Ч> (10 + й0 + Дй + Я) - "V ‘/4 (/0 + й0 + Дй + Я)5-Дй Zo = 10’2 м,
где знак «+» перед радикалом отброшен в силу физических условий (Д7 < 10).
• Ответ: Д/ = х/1 (10 + й0 + Дй + Я) - V 1/4 (/0 + й0 + Дй + Я)2- Дй /0 ® 10‘2 м.
52
9.213. В U-образйый манометр налита ртуть
(рис. 9.20). Открытое колено манометра соединено
с окружающим пространством при нормальном ат-
мосферном давлении pQ = 105 и ртуть в открытом ко-
лене стоит выше на ДА = 10 см, чем в закрытом. При
этом свободная от ртути часть закрытого колена
имеет длину 10 = 20 см. Когда открытое колено при-
соединили к баллону с воздухом, разность уровней
ртути увеличилась и достигла значения ДА, = 26 см.
Найти давление воздуха в баллоне. Плотность ртути
р= 13,6-Ю3 кг/м3.
9.214. В пространство над ртутным столбиком в трубке барометра попало
немного воздуха. Когда барометр показывал давление р, = 748 мм рт.ст.,
длина части трубки, занятой воздухом, была / = 60 мм. Трубку выдвинули из
сосуда со ртутью еще на ДА = 21 мм, после чего барометр стал показывать
давление р2 = 751 мм рт.ст. Считая температуру по- -г
стоянной, определить атмосферное давление. Ответ |
выразить в [мм рт.ст.]. А
9.215. В U-образной стеклянной трубке находит-
ся ртуть (рис. 9.21). Высота столбика воздуха над
ртутью в закрытом колене А = 20 см, а давление
р0 = 76 мм рт.ст. Пользуясь краном К, часть ртути
выливают. На сколько понизится уровень ртути в за-
крытом колене, если в открытом он понизился на
ДА = 60 см?
9.216. Два одинаковых сообщающихся цилиндрических сосуда с порш-
нями частично заполнены жидкостью плотностью р. Расстояния от поршней
до поверхностей жидкости одинаковы и равны А. Один из поршней закрепили,
а второй поднимают на высоту Ао. При какой высоте Aq разность уровней
жидкости в сосудах будет равна А? Начальное давление воздуха в сосудах
равно р. Температура постоянна.
9.217. Два одинаковых сообщающихся цилиндрических сосуда сечением
S заполнены частично жидкостью плотностью р при атмосферном давлении
р0. Один из сосудов запаяли. При этом высота столба воздуха в нем Ао. Найти
установившееся значение разности уровней исходной жидкости, если в от-
крытый сосуд налить несмешивающуюся с ней жидкость массой т и плот-
ностью, меньшей р. Температура постоянна.
9.218. Два одинаковых сообщающихся цилиндрических сосуда сечением
S заполнены частично жидкостью плотностью р при атмосферном давлении
р0. Один из сосудов запаяли. При этом высота столба воздуха в нем h0. К
53
другому сосуду присоединили баллон объемом И, содержащий воздух при
некотором давлении. После этого уровни жидкости в сосудах установились
на высоте Дй друг относительно друга. Найти первоначальное давление воз-
духа в баллоне. Температура постоянна.
9.219. Два одинаковых сообщающихся цилиндрических сосуда сечением
S заполнены частично жидкостью плотностью р при атмосферном давлении
р0. Один из сосудов запаяли. При этом высота столба воздуха в нем й0. Найти
установившееся давление в закрытом сосуде, если в открытый сосуд помес-
тить тело массой т и плотностью pt > р. Температура постоянна.
9.220. В воздушном шаре с эластичной тонкой оболочкой находится газ
объемом Ио = 1500 м3 при температуре /0 = 0°С. На сколько изменится подъ-
емная сила воздушного шара, если газ в нем нагреть на Д/ = 20°С? Давление
и температура воздуха в атмосфере равны р0 = 105 Па, Го = 273 К соответст-
венно. Молярная масса воздуха ц = 29-10'3 кг/моль.
• Решение. На воздушный шар действуют три силы
(рис. 9.22): сила тяжести оболочки шара M~g, сила тя-
жести газа m g и выталкивающая сила со стороны воз-
духа, равная ГА = р g V, где V- объем шара, р - плот-
ность окружающего шар воздуха. Подъемная сила шара
будет равна разности этих сил:
Г’П = Р? V-(Mg + mg).
При изменении температуры газа изменяется толь-
ко объем шара, т.к. оболочка эластична (р = const) и не-
проницаема (m = const).
Следовательно,
AFn = pgAK
изобарных условиях, то справедлив закон Гей-Люссака:
Г0 + ДГ_И0
Г0 + ДГ Го ’
Так
как газ расширяется
в
откуда
Следовательно,
ЛГ’п = р?И0^?.
Определяя плотность воздуха из уравнения Менделеева-Клапейрона, записанного
при заданных условиях
т. т п „ т РоР
Ро^-ХГ», или Р = ? = ^г,
получим
11 й) Ко g АГ q
= и ио os— Ю ! 38.10з н
п ЯГ02
ц ра Vo g ЛГ 1
• Ответ: ДГП= „ 1,38-Ю3 Н.
ЯГ02
54
9.221. На дне сосуда, заполненного воздухом, лежит полый стальной
шарик радиусом г = 2 см и массой т = 5 г. До какого давления нужно сжать
воздух в сосуде, чтобы шарик поднялся вверх? Температура постоянна и
равна t = 20°С. Молярная масса воздуха ц = 28-10"3 кг/моль.
9.222. Сможет ли воздушный шар, наполненный гелием, поднять груз
массой М= 150 кг, если его объем И =500 м3, а масса оболочки ш = 8 кг?
Давление и температура гелия и окружающего воздуха одинаковы и равны
р0= 105 Па и t = 15°С. Молярная масса гелия щ =410’3 кг/моль, воздуха -
|12 = 29-10‘3 кг/моль.
9.223. Чтобы не стать помехой движению самолетов, аэростат, наполнен-
ный гелием у поверхности земли при давлении р0 = 1 атм и температуре
То = 300 К, должен подняться на высоту h = 1,5 км, где плотность воздуха на
а = 20% меньше, чем у поверхности земли. Найти массу оболочки аэростата,
если его объем V = 500 м3. Оболочка нерастяжима и герметична. Молярная
масса гелия щ = 4-10'3 кг/моль, воздуха - = 29-10'3 кг/моль.
9.224. Полый шар с жесткой оболочкой, масса которой т = 10 г, наполнен
водородом. Объем шара V= 10 л. Температура водорода и окружающего шар
воздуха t = 0°С. Найти давление водорода в шаре, если подъемная сила шара
равна нулю. Атмосферное давление ро=1О5 Па. Молярная масса водорода
Ц] = 2-10‘3 кг/моль, воздуха — = 29-10'3 кг/моль.
9.225. Воздушный шар объемом V заполнен подогретым воздухом. Тем-
пература окружающего пространства Т, давление р. Температура воздуха
внутри шара 7\. Найти подъемную силу F. Молярную массу воздуха принять
равной ц. Весом оболочки шара пренебречь. Примечание: излишек воздуха
может свободно выходить из отверстия внизу шара, через которое осущест-
вляется подогрев.
9.226. В воздушном шаре наполняющий его водород заменили гелием.
Во сколько раз изменилась при этом подъемная сила шара? Весом оболочки
шара пренебречь. Молярная масса водорода ц1=2-10’3 кг/моль, гелия -
Р2 = 4-10’3 кг/моль, воздуха - ц3 = 29-10"3 кг/моль.
9.227. Оболочка стратостата открыта снизу и заполнена частично водо-
родом и частично воздухом. Масса водорода т. Какова подъемная сила стра-
тостата? Весом оболочки пренебречь. Молярная масса водорода ц15 воз-
духа - |12.
9.228. Во время сжатия идеального газа его давление р и объем V изме-
няются по закону р V -1 = const. Температура газа уменьшилась при этом в
п = 4 раза. Каково было начальное давление р} газа, если после сжатия
р2= 105 Па?
• Решение. Запишем уравнение состояния газа до и после сжатия:
Р] К] = Г], р2У2 = у^Т2-
55
Разделим эти уравнения друг на друга:
Pl?! Г,
P2V2 тг-
Используя уравнение процесса в виде
Pi Р2
V, = V2 ’
(1)
(2)
получаем
И Р1
V2~ Р2
или с учетом соотношения (1):
A~T* *
Следовательно, искомое давление
р, =p2Vr1/7’2=21O5 Па.
• Отвепг. pt = р2 Т\/Т2 = 24 О5 Па.
9.229. Определите, уменьшается или увеличивается давление идеального
газа, нагревающегося по закону И2/ Т = const. Ответ обосновать.
9.230. Состояние данной массы m идеального газа изменяется в соответ-
ствии с законом: р2/Г = а, где а - известная константа. Определить зависи-
мость давления р газа от его объема V в этом процессе. Молярная масса газа
равна ц.
9.231. Процесс в идеальном газе сначала идет так, что давление и объем
связаны равенством р V 1/2= Ь. Когда температура газа достигает некоторого
значения Т, процесс продолжается при другом характере зависимости давле-
ния от объема: р И2 = d. Найти значение температуры Т, считая константы b и
d, а также количество молей v газа известными.
9.232. Идеальный газ расширяется по закону р И2 = const и его объем уве-
личивается в три раза. Найти первоначальную температуру газа Tt, если после
расширения его температура равна Т2 = 100 К.
9.233. Гелий массой m = 20 г бесконеч-
но медленно переводят из состояния 1, ко-
торому соответствует объем V\ = 32-10'3 м3
Гтах и Давление р{ = 4,1-105 Па, в состояние 2,
где И2 = 9-10’3 м3ир2 = 15,5-Ю5 Па. Какой
У наибольшей температуры достигает газ в
V2 Ио этом процессе, если зависимость давления
Рис 9 23 от °®ъема изобразится прямой линией? Мо-
лярная масса гелия ц = 4-Ю'3 кг/моль.
• Решение. Каждой точке иа графике зависимости давления газа от занимаемого им объема
(рис. 9.23) соответствует определенное значение температуры. Графически состояние, в
56
котором температура гелия максимальна, можно определить, построив семейство изотерм.
Прн этом изотерма, соответствующая наибольшей температуре (очевидно, что прямая за-
висимости давления от объема должна быть касательная к ней), определит значения дав-
ления ро и объема Ко, при которых температура максимальна.
Аналитически значения р0 и Ко легко найти, исследовав на экстремум зависимость
температуры от давления или от объема.
Так как давление зависит от объема линейно, т.е.
p = aV+b, (1)
то, решая систему уравнений
Pi = a Kj + Ь, р2 = а К2 + Ъ
с двумя неизвестными, найдем, что
а = Р' ~Рг = - 5-Ю7 Па/м3, Ь=Рг V' ~Pl = 2106 Па.
И - и2 И - v2
Подставляя зависимость (1) в уравнение состояния идеального газа
pV=-RT,
И
получим
(2)
т л
Значение объема Ко, при котором температура газа максимальна, находим из условия
dT/dV=0. Следовательно, дифференцируя зависимость (2) температуры от объема газа,
получим
2aVo + b = 0.
Откуда
Ко = -^ = 21О-2м3. (3)
С учетом (3) из выражения (1) следует:
роЦ=1О6Па.
Подставив значения р0 и Ко в уравнение состояния, получим
Решение можно упростить, если заметить, что зависимость (2) температуры от объе-
ма имеет вид параболы, координата вершины которой совпадает с (3).
• Ответ: Гтах = 481 К.
9.234. v молей идеального газа бесконечно медленно переводят из состо-
яния 1 в состояние 2 по закону: р = - а И2+ р, где а и р - некоторые извест-
ные положительные постоянные. Какой наибольшей температуры может до-
стичь газ в таком процессе?
9.235. Один моль идеального газа бесконечно медленно переводят из со-
стояния 1 в состояние 2 по закону: а2р2+ р2К2 = у2, где а, р, у- некоторые
известные постоянные. Какой наибольшей температуры может достичь газ в
таком процессе?
57
р 1 J 9.236. Один моль идеального газа
'ч совершает процесс, который нар - V диа-
f грамме представляет собой дугу окруж-
7 \ ности радиусом а (рис. 9.24). Какова наи-
/___________ у гм31 большая температура газа в этом процес-
1 3 се? Чему равны давление и объем газа в
Рис. 9.24 состоянии с наибольшей температурой?
9.237. Определить наименьший объем одного моля идеального газа в
процессе, протекающем по закону Т= Тй + ар3, где Го и а - положительные
постоянные. Каковы температура н давление газа в состоянии с наименьшим
объемом?
9.238. Определить наименьшее давление идеального газа в процессе, про-
текающем по закону Т= То + а И,2 где То и а - положительные постоянные.
Каковы температура и объем одного моля газа при этом давлении?
9.239. На р - И диаграмме, изобра-
женной на рис. 9.25, а, представлен цик-
лический процесс, проведенный с иде-
альным газом. Участки 1-2 и 3—4 лежат
на прямых, проходящих через начало ко-
ординат, участки 4-1 и 2-3 - изотермы.
Найти объем И3, если известны объемы
V и и известно, что объемы И, и V.
1 г2 к4 гз равны. Изобразить этот циклический про-
вис. 9.25, а цесс на V-T диаграмме.
• Решение. Так как процессы 1-2 и 3-4 изображаются линейной зависимостью давления
от объема, то справедливо, что
Р±_Р2 Рз Р4
VX~V2 и и3-и4'
По условию задачи кривые 2-3 и 4-1 изотермы, поэтому
р2^2=Рз^ и pxVx=p^.
(1)
(2)
С учетом, что V2 = К4, из системы уравнений (1)-(2) получим
И3=К4 —=И4 ^-^=к4
4 Л Р4 Уз 4
Р1 у22 К,____И24
Р1ИЧ~И12И3’
Следовательно,
и3 = и22/иь
В переменных У- Т процессы 1-2 н 3-4 будут иметь вид парабол, ветви которых
будут вытянуты вдоль оси температур. В этом легко убедиться, записав уравнение прямой:
р = а V
и уравнение Менделеева-Клапейрона:
pV'=vRT.
58
Откуда получим
а V1 = v R Т, или V = 'ivR Т/а .
Так как прямой 1-2 иа графике в перемен-
ных р - V соответствует большее значение ко-
эффициента а, чем прямой 3-4, то иа V-Т диа-
грамме график процесса 1-2 будет расположен
ближе к оси температур, чем график процесса
3-4 (рис. 9.25, 6).
• Ответ'. = И22/ Vx = 29-10'3 кг/моль.
9.240. На рис. 9.26 приведен процесс
изменения состояния идеального газа.
Когда газ занимал объем Vx, его темпера-
тура равнялась Т}. Какова будет темпера-
тура газа Т2, когда он займет объем И2?
9.241. Один моль идеального газа
расширяется так, что его давление в за-
висимости от объема изменяется по закону р = а V, где а = 2-107 Па/м3. По-
строить графики этого процесса на р-V, р-Т и V-Т- диаграммах, если
температура газа изменилась от Г, = 200 К до Т2 = 500 К.
9.242. Один моль идеального газа расширяется так, что его давление в
зависимости от температуры изменяется по закону р = а/Т, где а = 2-Ю7 Па К.
Построить графики этого процесса нар -V, р-Т и V-Т- диаграммах, если
объем газа изменился от = 10 л до V2 = 30 л.
9.243. Один моль идеального газа сжимают так, что его объем в зависи-
мости от температуры изменяется по закону И=а Г2 где а= I.S-IO'V/K2.
Построить графики этого процесса нар - 7, р-Т и V-Т- диаграммах, если
давление газа изменилось от рх = 100 кПа до р2 - 300 кПа.
9.244. С идеальным газом осуществляется цикл, представленный на рис.
9.27 в виде зависимости объема V от температуры Т. Изобразить этот же цикл
на графике зависимости давления р от объема V.
9.245. Решить задачу №9.244 для цикла, представленного на рис. 9.28.
59
Рис. 9.30
9.246. Решить задачу №9.244 для цикла, представленного на рис. 9.29.
9.247. С идеальным газом осуществляется цикл, представленный на рис.
9.30 в виде зависимости давления р от температуры Т. Изобразить этот же
цикл на графике зависимости давления р от объема V.
9.248. Решить задачу №9.247 для цикла, представленного на рис. 9.31.
9.249. Изобразить на р - Г и V-Т- диаграммах процессы, приведенные
на рис. 9.32. Вещество - идеальный газ.
Рис. 9.33 Рис. 9.34
9.250. Изобразить цикл 1-2-3, показанный на рис. 9.33 (участок 2-3 -
изотерма) в координатах р - Г, где р - плотность газа.
9.251. Идеальный газ совершает циклический процесс, представленный
на рис. 9.34. Температуры газа в состояниях 1 и 3 равны Г, = 300 К и Г3 = 400 К
соответственно. Найти температуру газа в состоянии 2.
9.252. С идеальным газом происходит процесс 1-2-3—4—1, представлен-
ный на рис. 9.35. В состоянии 3 на отрезке диаграммы 2-3-4 давление такое
60
же, как и в состоянии 1. Определить объем И3 газа в состоянии 3, если из-
вестно, что К] = 1 м3, И2 = 4 м3, Г] = 100 К, Г4 = 300 К.
9.253. С одним киломолем идеального газа совершается цикл, представ-
ленный на рис. 9.36 в виде зависимости давления р от температуры Т. Каковы
минимальный Kmjn и максимальный Ктах объемы газа при таком цикле?
Параметры рь р2, Т\, Т2 известны.
§10. Теплота и работа.
Физические основы термодинамики
Обратимся теперь к энергетической стороне процесса изменения состо-
яния какого-либо тела.
Любое тело (твердое, жидкое, газообразное), находящееся в состоянии
теплового равновесия (см. §9), которое характеризуется его макроскопичес-
кими параметрами р, V и Т, обладает определенным запасом внутренней энер-
гии U. Внутренняя энергия тела складывается из кинетической энергии дви-
жения молекул, кинетической энергии движения атомов внутри молекулы
(если молекула не одноатомная), потенциальной энергии взаимодействия
между атомами внутри молекулы и потенциальной энергии взаимодействия
молекул между собой. В нее, однако, не входит кинетическая энергия дви-
жения тела как целого - 1/2 т и2 (где т - масса тела и и - скорость его центра
масс), и потенциальная энергия внешних сил, действующих на тело.
Внутренняя энергия тела обладает тем замечательным свойством, что при
переходе тела из какого-то первоначального состояния 1 (р1г Т\) в конечное
состояние 2 (р2, V2, Т2) изменение внутренней энергии &UX_2 не зависит от
того, с помощью какого процесса произошел этот переход, и
Д1/1_2=1/2-1/1, (10.1)
где Ui - внутренняя энергия тела в начальном и U2 - в конечном состояниях.
Если над телом совершается циклический процесс, то изменение внутренней
энергии при этом АЦ_2 = 0, так как U2 = Ux (в результате циклического про-
цесса тело возвращается в исходное состояние). Поэтому говорят, что внут;
ренняя энергия тела является функцией состояния.
61
Внутреннюю энергию тела можно изменить двумя способами:
1) если теплоизолировать тело и совершить над ним механическую рабо-
ту т4]_2 или предоставить ему возможность совершить механическую работу
т4]_2 над окружающими телами. В первом случае работа А}_2 считается отри-
цательной, а во втором - положительной. Ясно, что в этом случае изменение
внутренней энергии
At/^2 = — Я]_2; (Ю-2)
2) привести тело в контакт с более нагретым или менее нагретым телом. При
этом наше тело может получать (или отдавать) энергию путем ее непосред-
ственного перехода от других тел (к другим телам), без совершения при этом
механической работы. Такой процесс называют теплопередачей, а получае-
мую (или отдаваемую) телом энергию - количеством тепла Q{_2, причем
01-2 > 0, если тело получает энергию и Qt_2 < 0, если оно энергию отдает. В
этом случае
д^-2=а-2- (ю-з)
Если тело может совершать механическую работу ^1-2 и получать энер-
гию 0j_2 от других тел, то полное изменение внутренней энергии равно
А{7[_2 = U2 - Ul = 01-2 ~-^i-2-
Это соотношение обычно записывают в виде
01-2 = At^i-2+Л1_2- (Ю-4)
Уравнение (10.4) выражает закон сохранения энергии при тепловых про-
цессах и представляет собой содержание первого начала (закона) термоди-
намики: количество тепла, сообщенное телу, идет на приращение внутрен-
ней энергии тела и на совершение этих телом работы над другими телами.
Необходимо подчеркнуть, что работа А }_2 и количество тепла Q\_2 зави-
сят в отличие от &UX_2 не только от начального и конечного состояний тела,
но и от процесса, с помощью которого происходило изменение состояния.
По этой причине ни в коем случае нельзя говорить о «количестве тепла, за-
ключенном в теле» и считать, что 01-2 = 02 - 0Р Бессмысленность такого
утверждения особенно наглядно проявляется при циклическом процессе,
когда тело возвращается в исходное состояние, между тем как общее коли-
чество поглощенного (или выделенного) тепла 0 отнюдь не равно нулю, а
равно полной механической работе тела за цикл А:
Q=A. (10.5)
Рассмотрим теперь каждое из слагаемых, входящих в первое начало тер-
модинамики (10.4). Начнем с работы Ах_2.
При расширении тело перемещает окружающие его тела, т.е. производит
над ними механическую работу. Если объем тела увеличивается на бесконеч-
но малую величину dV (при этом давление тела р можно считать неизмен-
ным), то тело совершает бесконечно малую, или элементарную, работу
62
V
dV V2
Рис. 10.1
(Ю.7)
Рис. 10.2
dA=pdV. (10.6)
Работа dA > 0 при расширении тела (dV > 0), когда тело производит ра-
боту над окружающими телами, и dA < 0 при сжатии тела (dV < 0), когда ра-
бота производится над телом окружающими телами. Если объем тела не ме-
няется (dV = 0), то работа dA = 0.
Пусть тело с помощью какого-либо
процесса переходит из состояния 1 (рх,
Г]) в состояние 2 (р2, И2, Т2). Произведен-
ная при этом работа тела Ах_2 допускает
наглядную геометрическую интерпрета-
цию, если изобразить процесс графически
на диаграмме р - V (рис. 10.1). При увели-
чении объема на dV при произвольном дав-
лении р совершаемая телом работа равна
р dV, т.е. площади бесконечно узкого заштрихованного прямоугольника. Поэ-
тому полная работа тела Ах_2 при его расширении от объема V\ до объема
И2, складываясь из элементарных работ dA, изобразится площадью криволи-
нейной трапеции \-2-V2-Vx, заключенной под кривой между двумя крайними
вертикальными линиями. Математически это можно записать в виде
Л[_2= [dA = jpdV.
и,
Если тело вернуть из состояния 2 в состояние 1 с помощью такого же
процесса, то оно совершит такую же, но отрицательную работу А2_х =~А}_2,
поскольку тело при этом сжимается.
При изобарическом процессе (р = const) площадь трапеции 1-2-^-^
равна р (И2 - И]) и работа тела
^=p{V2-Vx).
При циклическом процессе тело воз-
вращается из состояния 2 в состояние 1 по
другому пути (рис. 10.2). На участке
1-а-2 тело расширяется и совершает поло-
жительную работу, равную площади под
кривой 1-а-2. На участке 2-b-i тело сжи-
мается и производит отрицательную рабо-
ту, равную площади под кривой 2-6-1.
Суммарная работа тела за цикл равна, сле-
довательно, разности этих двух площадей,
т.е. изображается заштрихованной на рис. 10.2 площадью, заключенной внут-
ри замкнутой кривой. Если бы тело переходило из состояния 1 в состояние
(10.8)
63
2 по пути 1-6-2, а возвращалось бы в исходное состояние по пути 2-о-1, то
работа тела за цикл оказалась бы отрицательной. Итак, работа тела за цикл
численно равна площади цикла на диаграмме р - V и положительна, если со-
стояние тела изменяется в цикле по часовой стрелке. При изменении состо-
яния тела в цикле против часовой стрелки, работа тела за цикл отрицательна.
Следует помнить, что и в том и в другом случаях работа за цикл А = Q (см.
выражение (10.5)).
Пусть тело при контакте с другими телами получает элементарное ко-
личество тепла dQ, причем на основании первого начала термодинамики
(Ю.4)
dQ = dU+dA, (Ю.9)
где dA - элементарная работа и dU - элементарное (бесконечно малое) изме-
нение внутренней энергии тела. При этом температура тела увеличивается на
бесконечно малую величину dT. Теплоемкостью тела Стела называется отно-
шение
Стела = ^- (Ю.Ю)
Теплоемкость одного килограмма вещества называется удельной тепло-
емкостью с, а теплоемкость одного моля вещества - молярной теплоемкос-
тью С. Ясно, что
Стела = т с = v с> (10.11)
где т - масса тела и v = т/ц - количество молей в теле.
Такое определение теплоемкости (10.10) само по себе еще недостаточно,
так как требуемое для изменения температуры на dT количество тепла dQ за-
висит не только от температуры, но и от других условий, в которых произ-
водится нагревание тела; необходимо еще указать какой именно процесс со-
вершается над телом. В связи с этой неоднозначностью возможны и различ-
ные определения теплоемкости.
Наиболее часто используемы в физике так называемые теплоемкость
при постоянном объеме (Стела)у и теплоемкость при постоянном давлении
(Стела)р, определяющие количества тепла (dQ)v и (dQ)p при нагревании тела
в условиях, когда поддерживаются неизменными соответственно его объем
V (изохорический процесс) или давление р (изобарический процесс). На ос-
новании (10.10)
(rZ0)v=(CTCJia)v^, (10.12)
И2)р= (1-тела)р dT. (10.13)
При переходе тела из состояния 1 (р}, Т}) в состояние 2 (р2, V2, ТУ
количества полученного тепла {dQx_^)N и (</Qi_2)p равны:
64
*2
(01-2)у=1(Стела)у<Я; (10.14)
Г,
г2
(01-2)р= 1(Стела)р^ (Ю.15)
' । т>
Во многих процессах важной характеристикой тела является отношение
его теплоемкостей (Стела)у и (С,тела)р, обычно обозначаемое у,
_ (^тела)р _ ср
(^тела)у cv
Ср
Су
(10.16)
и называемое показателем адиабаты.
Из определения теплоемкости (10.10) следует, что при изотермическом про-
цессе (7 = const и dT = 0) теплоемкость тела (C^mX--» оо, что, однако, не озна-
чает, что количество тепла (<ф)т = (Cj^y^dT, полученного телом при посто-
янной температуре, является бесконечно большой величиной.
Применим полученные выше соотношения к идеальному газу, т.е. газу,
взаимодействием молекул которого между собой можно пренебречь. Начнем
с его внутренней энергии U.
Внутренняя энергия газа складывается из кинетической энергии посту-
пательного движения молекул газа, кинетической энергии движения атомов,
входящих в состав молекулы, и потенциальной энергии взаимодействия ато-
мов молекулы между собой. Энергией взаимодействия молекул можно пре-
небречь, так как газ считается идеальным. Если газ одноатомный, то внут-
ренняя энергия такого газа, состоящего из N молекул
U=N<l/zm0\32>, (10.17)
где < 'Л т0 и2> - средняя кинетическая энергия поступательного движения
одной молекулы, которая согласно определению абсолютной температуры
(П.7) равна % k Т. Следовательно, для одноатомного газа (см. (П.8))
U=N^kT=-NAkT=-^RT. (10.18)
2 ц 2 ц 2
Прежде чем находить внутреннюю энергию двухатомного газа, уточним
определение абсолютной температуры тела Т. В статистической физике до-
казывается, что в состоянии теплового равновесия при температуре Т кине-
тическая энергия распределяется поровну между всеми степенями свободы
системы, причем на одну степень свободы приходится средней кинетической
энергии
< е1 кин > — ^ikT.
(10.19)
65
Напомним, что число степеней свободы системы (см. гл. I, §1) равно
минимальному числу независимых координат, с помощью которых можно
однозначно задать положение системы в пространстве. Если система состоит
из N невзаимодействующих материальных точек (одноатомный газ), то у
каждой материальной точки имеются i = 3 степени свободы (три ее декартовы
координаты в какой-либо системе отсчета). Эти три степени свободы соот-
ветствуют поступательному движению молекулы. Вся система обладает 3N
поступательными степенями свободы, поэтому ее внутренняя энергия
U=3/zNkT, (10.20)
что совпадает с (10.18).
Если молекула идеального газа состоит из двух атомов, расстояние
между которыми не изменяется (жесткая двухатомная молекула), что, как пра-
вило, выполняется при не слишком высоких температурах, то такая молекула
имеет i = 5 степеней свободы, из которых три (координаты центра масс мо-
лекулы) соответствуют поступательному движению молекулы и две - враща-
тельному движению молекулы вокруг двух взаимно перпендикулярных осей,
лежащих в плоскости, перпендикулярной линии, соединяющей атомы, и про-
ходящей через центр масс молекулы. Для газа, состоящего из N жестких двух-
атомных молекул, внутренняя энергия равна
U=5/zNkT. (10.21)
Объединяя (10.20) и (10.21), можно написать выражение для внутренней
энергии идеального газа:
U=^NkT=~-RT, (10.22)
2 2 ц
где число степеней свободы: i = 3 - для одноатомного газа и i = 5 - для газа,
состоящего из жестких двухатомных молекул.
Используя уравнение Менделеева-Клапейрона (9.6), выражение (10.22)
можно записать в виде
U=^pV. (10.23)
Из (10.22) следует, что внутренняя энергия идеального газа определяется
только его температурой. При переходе тела из состояния 1 в состояние 2
изменение внутренней энергии
Д17= I У* ДТ= I Л ДТ= i Л (Т2 - Г,) = i (Р2 к2 -Р1 И), (10.24)
а элементарное изменение внутренней энергии
dU~NkdT=^-RdT. (10.25)
2 2ц
66
Из (10.24) видно, что изменение внутренней энергии Д17=0, если газ
изменяет свое состояние при постоянной температуре Т = const (изотермичес-
кий процесс). При этом (0i-2)t = (^i-2)t-
Если газ изменяет свое состояние при постоянном объеме V = const, то ра-
бота газа dA =р dV= 0 и элементарное количество тепла (</0Х,= dU. Поэтому
теплоемкость идеального газа при постоянном объеме (см. (10.10), (10.25)):
(Cwa\=^ = ^k=^R, (10.26)
CN = ^Nkk=^R. (10.27)
Используя первое начало термодинамики, можно показать, что теплоем-
кость идеального газа при изобарическом процессе
. W2)p . ... х „ * + 2 in i + 2 m в
(^тела)р- — (^"тела)y + Nk — (CTena)v + R — 2 Nk— Л, (10.28)
Cp = Cv + NAk=Cv + R = ^R. (10.29)
Показатель адиабаты у для идеального одноатомного газа равен
(^тела)р ^р _ i + 2 _ 5
(^тела)у
а для газа, состоящего из жестких двухатомных молекул,
(^тела)р ^р _ i + 2 _ 7
(^тела)у 1 5
(10.30)
(10.31)
Если идеальный газ переходит из начального состояния 1 в конечное
состояние 2 изохорически или изобарически, то количества полученного га-
зом тепла (0i-2)v или (С?1-г)р определяются выражениями (10.14), (10.15). По-
скольку теплоемкости идеального газа (Стела)у и (Стела)р не зависят от тем-
пературы (см. (10.26), (10.28)), их можно вынести в (10.14) и (10.15) за знак
интеграла и получить:
(0i-2)v = (C™i)v ЛГ = ^Л(Т2-Г1), (10.32)
(ei-2)p = (Стела)р ДГ= л (Г2 - Ъ). (10.33)
Отметим, что
(01-2)р = (Стела)р ДГ= у (Стела)у ДГ= у (Q^. (10.34)
Помимо изохорического (И = const), изобарического (р = const) и изотер-
мического (Г= const) процессов в термодинамике важную роль играет тепло-
67
вой процесс, который называется адиабатическим. Этот процесс состоит в
расширении или сжатии газа при условии, что в течение всего процесса газ
остается теплоизолированным от внешней среды, т.е. никуда не отдает и ни-
откуда не получает тепла. При адиабатическом процессе dQ = 0 и газ совер-
шает при расширении работу (или при сжатии над ним совершается работа)
за счет уменьшения (или увеличения) его внутренней энергии. При этом (см.
(Ю.4))
Л,_2 = - Д17ь, = Ц - U2 = - (Г, - Т£. (10.35)
z И
Из (10.35) видно, что при адиабатическом расширении температура иде-
ального газа понижается, т.к. А ,_2 > 0, а при его адиабатическом сжатии -
повышается.
Используя уравнение Менделеева-Клапейрона, можно показать, что при
адиабатическом переходе из начального состояния 1 (ру Т\) в конечное
состояние 2 (р2, К2,
Pl У' = Р2 ^2’ (10-36)
где У= (Стела)р/(Стела)у- показатель адиабаты газа.
Поскольку у> 1, из (10.36) следует, что кривая зависимости р от V на
диаграмме р - V для адиабатического процесса (адиабата) идет круче изотер-
мы (рис. 10.3-10.4).
Обратимся теперь к проблеме, послужившей, собственно, в свое время
(начало XIX века) причиной возникновения термодинамики как науки - про-
блеме превращения теплоты в механическую работу, или, говоря иначе, про-
блеме теплового двигателя.
Изобретение методов получения механической работы за счет теплоты
явилось началом новой эпохи в истории цивилизации. Дело в том, что меха-
ническую энергию всегда можно полностью превратить в тепловую (напри-
мер, за счет трения), а полное превращение тепловой энергии в механическую
без каких-либо изменений в окружающих телах, как оказалось, невозможно.
Последнее утверждение называется вторым началам термодинамики.
68
Любая тепловая машина, превращающая теплоту в работу (паровые ма-
шины, двигатели внутреннего сгорания и т.д.), действует циклически, т.е. в
ней процессы передачи тепла и преобразование его в работу периодически
повторяются. Для этого нужно, чтобы тело, совершающее работу (рабочее
тело), после получения теплоты Qt от источника (нагревателя), находяще-
гося при температуре 7\, вернулось в исходное состояние, чтобы снова начать
такой же процесс. Другими словами, рабочее тело должно совершать цикли-
ческий процесс. Но мы знаем, что для того, чтобы суммарная работа тела за
цикл А оказалась положительной, тело должно вернуться в исходное состоя-
ние на диаграмме р - К по более «низкой» кривой (кривая 2-Ъ-\ на рис. 10.2).
Однако более «низкой» кривой на диаграмме р - V соответствует более низ-
кая температура. Поэтому перед сжатием рабочее тело должно быть охлаж-
дено, т.е. от него нужно отнять некоторое количество тепла Q2 и передать
его еще одному (третьему) телу - холодильнику, температура которого Г2 ни-
же температуры нагревателя Т\. Вот почему никакая циклическая тепловая
машина не может обойтись только источником тепла и рабочим телом. Если
бы можно было обойтись только рабочим телом и нагревателем, то для по-
лучения механической работы можно было бы воспользоваться такими ис-
точниками тепла, как вода морей и океанов, от которых можно заимствовать
практически неограниченное количество тепловой энергии. Такая машина на-
зывается «вечным двигателем» второго рода, в отличие от «вечного двигате-
ля» первого рода, который совершает механическую работу, не тратя при
этом никакой энергии, существование которого запрещается законом сохра-
нения энергии (первым началом термодинамики). «Вечный двигатель» вто-
рого рода не запрещен законом сохранения энергии, т.к. в таком двигателе
работа совершается за счет теплоты. Но опыт показывает, что такая машина
не может быть построена.
Итак, для работы циклической машины, кроме
нагревателя и рабочего тела, необходимо наличие
третьего тела - холодильника, температура кото-
рого ниже температуры источника тепла. В реаль-
ных тепловых машинах в качестве холодильника
служит окружающая среда. Структурно тепловая
машина представлена на рис. 10.5.
Полная механическая работа, совершаемая ра-
бочим телом за один цикл (см. выражение (10.5)),
А = 21-б2- (Ю.37)
Эту работу легко найти, если изобразить циклический процесс на диа-
грамме р - V и найти площадь петли. Эта площадь, как мы знаем, численно
равна работе А.
69
Коэффициентом полезного действия (к.п.д.) Т] тепловой машины назы-
вается отношение
л-е1’
(10.38)
где Q, > 0 - количество тепла, полученного рабочим телом за цикл.
Как практически найти Qlt если
циклический процесс, изображен на
диаграмме р - V и рабочее тело - иде-
альный газ? Обычно весь процесс на
диаграмме р - V состоит из нескольких
отрезков непрерывных кривых или
прямых линий, соответствующих про-
цессам перехода рабочего тела из i - го
начального состояния в (i + 1) - ое ко-
нечное состояние. Один такой произвольный участок цикла изображен на
рис. 10.6. Если процесс i —> i + 1 адиабатический, то Qt , +1 = 0; если процесс
изотермический (Г; = Г1+ ] или pt Кг =р,+ [ Vi+l), то Qt i+ j > 0 (тело получает
тепло) при расширении рабочего тела (И; +1 > Г)); если процесс i -> i + 1 изо-
хорический (К,- = Vj + [), то Qi j +1 > 0 при увеличении давления (Pj+i>р[); и,
наконец, если процесс изобарический (pt=pt+\), то g, /+1 >0 при расшире-
нии тела (Vj+l> Vj). Полное количество тепла, полученное рабочим телом за
цикл,
ei=Sft,i + b (10.39)
где суммируется лишь тепло Q, ;-+1 на тех отрезках цикла, где это тепло по-
ложительно.
Для нахождения полученного телом тепла 2i, i+i при изохорическом н
изобарическом процессах нужно использовать соотношения (10.32)-(10.33) н
уравнение состояния идеального газа.
Можно доказать, что из всех возможных циклических тепловых машин
максимальным к.п.д. обладает машина, работающая по циклу, схематически
представленному на рис. 10.7, который называется циклом Карно. На участке
1-2 рабочее тело, находясь в контакте
с нагревателем при температуре Г1;
изотермически (Т{ = const) расширяется
и совершает положительную механи-
ческую работу А{_2 за счет тепла 2г
отнятого у нагревателя. При этом рабо-
та Л]_2 = 2i> так как при постоянной
температуре внутренняя энергия тела
не изменяется (U2 = U}). На участке 2-3
70
рабочее тело теплоизолировано от нагревателя и адиабатически (02-з= 0) Рас“
ширяется, совершая положительную механическую работу Л2_3 за счет убыли
его внутренней энергии: Л2_3 - С/2 - и3. При этом температура рабочего тела
уменьшается до температуры холодильника Т2. Па участке 3—4 рабочее тело
приводят в контакт с холодильником и изотермически (Т2 = const) сжимают.
При этом С74 = U3 и газ совершает отрицательную работу Л3_4 = - Q2, где
Q2 - тепло, отданное рабочим телом холодильнику. И, наконец, на участке
4-1 рабочее тело изолируют от холодильника и адиабатически сжимают до
тех пор, пока его температура не станет равной температуре нагревателя Т{.
В результате рабочее тело возвращается в исходное состояние и далее цикл
повторяется. При адиабатическом сжатии Q4_\ = 0 и тело совершает отрица-
тельную работу А4_^ = U4~ U{. Полная работа тела за цикл, как и следовало
ожидать,
Л = Л]_2 +Л2_3 + Я3_4+Я4_1 = Qi + U2- U3- Q2+ U4- Ul = Ql- Q2, (10.40)
где учтено, что U2=UX и U3 = U4.
Так как 01 =Л]_2 (работа при Г] = const) и 02 = -Л3^, (работа при
Г2 = const), можно показать, что для цикла Карно
Qi Qi
Ti~T2-
Тогда к.п.д. цикла Карно
А 01 ~ 02 . 02 . ^2
'ТТ’Т’Т
(10.41)
(10.42)
В термодинамике доказывается, что любая тепловая машина, работаю-
щая при заданных значениях температур нагревателя Т\ и холодильника Т2,
имеет к.п.д. меньший, чем машина, работающая по циклу Карно при тех же
значениях температур нагревателя и холодильника. При этом ее к.п.д. не за-
висит от природы рабочего тела.
В заключение заметим, что разновидностью
тепловых машин является, так называемая, холо-
дильная машина. Для ее работы необходимо осу-
ществить «обратный» цикл: расширение рабочего
тела следует производить по более «низкой» кри-
вой 1-6-2 (рис. 10.2), а сжатие по кривой 2-а-1.
Совершая расширение 1-6-2 машина будет заим-
ствовать у холодильника тепло Q2, при сжатии
она передаст нагревателю тепло Q{ > Q2. При этом
над машиной будет произведена положительная
работа A' =Qx-Q2. Структурная схема холодиль-
ной машины представлена на рис. 10.8.
Рис. 10.8
71
Рекомендации по решению задач
В отличие от молекулярно-кинетической теории, термодинамика изучает процессы
обмена энергией между телами с общих позиций, не опираясь ни на какие модельные
представления о атомно-молекулярной структуре вещества.
Одной из самых важных величин, характеризующих произвольную систему тел, яв-
ляется ее энергия. Как показывает опыт, изменить энергию системы (не изменяя саму сис-
тему, например, добавляя к ней или удаляя из нее частицы) можно двумя способами:
- совершая работу над системой или предоставляя ей возможность совершить работу;
- вследствие передачи теплоты от окружающих тел системе или, наоборот, отбирая теп-
лоту от системы к телам.
Полная энергия системы состоит из механической энергии и внутренней. В термо-
динамике обычно рассматривают покоящиеся тела, механическая энергия которых ие ме-
няется. В этом случае первое начало термодинамики удобно сформулировать в виде: из-
менение внутренней энергии системы за время ее перехода из одного состояния в другое
равно сумме совершенной над системой работы внешними телами и полученного системой
тепла в результате теплообмена с другими телами. Работа и процессы теплообмена - это
различные способы изменения и передачи энергии от одного тела к другому. В то время
как энергия характеризует состояние рассматриваемой системы, теплообмен н работа ха-
рактеризуют изменение состояния, т.е. происходящие в системе процессы.
Задачи данного параграфа можно разделить на две основные группы. К первой груп-
пе отнесем задачи, в которых требуется рассчитать те или иные характеристики иде-
ального газа (или смеси газов) прн переходе системы из одного состояния в другое.
Решение таких задач основано на непосредственном применении первого начала тер-
модинамики в виде
ДС/=± Й±Л,
где знаки «плюс» относятся к случаям, когда газ приобретает энергию, а знаки «минус» -
когда газ отдает энергию окружающим телам.
Прежде чем приступить к обсуждению методов решения задач, отметим, что:
1. Внутренняя энергия U системы является функцией состояния н ее изменение &U опре-
деляется лишь начальным и конечным состояниями системы, т.е. не зависит каким образом
система перешла из одного состояния в другое:
U=~vRT, &U=^vR6T=^(p2lr2-pllrl),
где i - число степеней свободы (1 = 3 для одноатомного газа н i = 5 для двухатомного, со-
стоящего из жестких молекул); р1( р2, V\, V2 - давления и объемы газа в начальном и ко-
нечном состояниях соответственно;
2. Работа, совершаемая при переходе нз одного состояния в другое, зависит не только от
начального и конечного состояний, но н от вида процесса, с помощью которого про-
исходило изменение состояния. Однако, независимо от процесса, совершаемая газом
работа положительна, если в процессе происходит расширение газа, и отрицательна в
противном случае;
3. Количество теплоты, поглощаемой или выделяемой системой при переходе из одного
состояния в другое, так же, как и работа, зависит от вида процесса.
Рассмотрим более подробно известные процессы, совершаемые идеальным газом,
число молей которого остается неизменным.
1. Изотермический процесс (Т = const):
а) изменение внутренней энергии AU = 0;
б) работа, совершаемая газом при переходе из состояния с параметрами (рь И], Т) в со-
стояние - (р2, V2, Г), определяется интегралом
72
A = jpdV,
п
или с учетом уравнения Менделеева-Клапейрона в виде p = v RT//:
. f2v RT . ^2 „ _ . Pi
A = I dV=vRTln-^- = vRTla —.
V P2
При расширении газа A > 0; при сжатии А < 0;
в) количество теплоты Q = A: при изотермическом расширении газ получает извне тепло
Q и такое же количество энергии в виде работы возвращает в окружающую среду.
2. Изохорический процесс (К = const):
а) изменение внутренней энергии равно ДС/= v Cv ДГ = Ух v R ДГ = Ух V fyr,
б) работа в процессе А = 0;
в) количество теплоты Q = Д U: при изохорическом нагревании газ получает извне теплоту
Q, которая полностью переходит во внутреннюю энергию газа.
3. Изобарический процесс (р = const):
а) изменение внутренней энергии равно ДС/ = v Cv l\T = '/xv R &Т=Ухр ДГ;
б) работа в процессе А =р ДГ;
в) количество теплоты Q = ЛИ + А = v Ср ДГ= ('/> + 1) v R &Т= (Ух + Г)р ДГ при изобари-
ческом расширении газ получает извне теплоту Q и часть полученной энергии идет на
совершение работы А, а другая часть - на приращение внутренней энергии.
4. Адиабатический процесс (Q = 0):
а) изменение внутренней энергии &U = v Cv ДТ = Ух v R ДТ;
б) работа в процессе А = —Д17; при адиабатическом расширении работа совершается за счет
внутренней энергии газа;
в) количество теплоты Q = 0.
При решении задач удобно пользоваться таблицей:
Процесс Изменение внутренней энергии Работа в процессе Количество теплоты
изотермический ьи=о И? в. Л=уЯТ1п -^=vRTln^- У1 Р1 Q=A
изохорический bU=±V&p А = 0 Q = tJJ
изобарический bU=±pbV A=pKV Q=&U+A
адиабатический bU=±vR6T A=-bU 6 = 0
Прн решении задач первой группы можно придерживаться следующей последова-
тельности:
а) прочитав условие задачи, нужно ясно представить, в скольких различных процессах уча-
ствует данный газ при переходе из начального состояния в конечное. Если газ последо-
вательно участвует в нескольких процессах, то удобно сделать схематический чертеж, на
котором изобразить все процессы и отметить состояния газа в начале и в конце каждого
из них;
73
б) для каждого процесса написать выражения для изменения внутренней энергии Д(7, ра-
боты А и количества теплоты Q в соответствии с таблицей; ДЙ, А и Q при переходе из
начального состояния в конечное найти как алгебраическую сумму ДЦ-, А/ и Qj для всех
рассматриваемых процессов;
в) при необходимости для того или иного процесса (или для всех) записать уравнение объ-
единенного газового закона (или его частный случай), связывающее начальное и конечное
состояния газа в данном процессе. Дополнить полученные уравнения развернутыми зна-
чениями параметров, выразив их через известные или искомые величины. Если рассмат-
ривается смесь газов, то записать закон Дальтона для установления результирующего дав-
ления компонентов;
г) записать все вспомогательные условия, связывающие параметры р, V, Т газа в различных
состояниях. Если рассматриваются комбинированные задачи, связанные с механическим
движением системы, то уравнения дополнить законами механики;
д) решить полученную систему уравнений.
Во вторую группу выделим задачи, в которых рассматриваются циклические про-
цессы. Эту группу задач можно разбить на две части; первая из которых включает задачи
на произвольные циклы, а вторая - на цикл Карно.
При решении задач на определение количества тепла, полученного или отданного
рабочим телом за цикл, работы за цикл или к.п.д. цикла, удобно придерживаться следую-
щей последовательности:
а) внимательно рассмотрев циклический процесс, ясно представить в каких процессах уча-
ствует рабочее тело. Часто удобно изобразить цикл графически на р - V диаграмме; если
по условию задачи цикл уже задан графически, но в переменных р-Т или V- Т, то пере-
строить его нар - V диаграмму, отметив параметры состояния в начале и в конце каждого
процесса;
б) используя схему решения задач первой группы, найти работу совершаемую рабочим
телом (или над ним), и количество тепла Qj, полученное (или отданное) им, для всех рас-
сматриваемых процессов, составляющих цикл;
в) проанализировав условие задачи, установить, на каких участках цикла рабочее тело от-
давало тепло, а на каких получало. Сумма количеств теплоты на участках, где Qj > 0 будет
равна количеству теплоты, полученной рабочим телом за цикл, т.е. теплу, полученному
от нагревателя: Qt = I Qj. Сумма количеств теплоты в процессах, где Qj < 0 будет равна
теплоте, отданной за цикл холодильнику: Q2 = S | Qj |;
г) работу А за цикл вычислить как алгебраическую сумму работ на каждом из его участ-
ков. Если график цикла в переменных р - V представляет собой простую геометрическую
фигуру (треугольник, квадрат, трапеция и т.п.), то работу можно определить как площадь
фигуры, ограниченной петлей цикла; при этом работа положительна, если состояние ра-
бочего тела изменяется в цикле по часовой стрелке, в противном случае - отрицательна;
д) к.п.д. цикла вычислить по одной из формул:
_ Л _ . _ 02 _ 01 ~02
П"0Г 01" 01
Если тепловая машина работает по циклу Карно, то схема решения задач такая же
хак для произвольного цикла, за исключением, что к.п.д. такой машины можно также вы-
числить через температуры нагревателя Т\ и холодильника Т2 по формуле
, Т2 Tj-T2
П" Т, ?! •
Следует также помнить, что машина Карно получает тепло лишь на участке изотер-
мического расширения, а отдает - на участке изотермического сжатия. При этом количе-
74
ство полученного или отданного тепла за цикл равно работе соответствующего изотерми-
ческого процесса.
Если рассматривается холодильная машина, решение задан ничем не отличается от
решения в случае тепловой, кроме того, что для таких машин Qt < 0, > 0 и над машиной
будет произведена работа А > 0.
Задачи
10.1. При сообщении идеальному газу количества теплоты Q газ совер-
шает работу А. Какой была внутренняя энергия газа Ux, если его температура
возросла в п раз?
• Решение. Воспользуемся первым началом термодинамики: количество теплоты, сообщае-
мое газу, идет на увеличение его внутренней энергии и на работу, совершаемую газом
при его расширении:
е=да+л.
Внутренняя энергия газа в начальном и конечном состояниях равна
U' = vCvT\, U2 = vCvT2, (2)
где Cv - молярная теплоемкость данного газа при постоянном объеме, Тр Т2 - начальная
и конечная температуры. По условию задачи Т2/Т\ = п, поэтому, используя (2), найдем:
Н1_п
их~п-
(1)
(3)
Из (1) следует, что
u2-u} = q-a.
Откуда с учетом соотношения (3) получим
Q-A
• Ответ : Ut .
п — 1
10.2. Газу сообщено количество тепла 0 = 51О5 Дж. Какая часть тепла
пошла на увеличение внутренней энергии газа, если работа расширения газа
в этом процессе равна А = 2105 Дж?
10.3. т] = 20% сообщаемого газу количества тепла идет на увеличение его
внутренней энергии, которое равно ДС/=4 кДж. Определить работу газа в
процессе.
10.4. Определить внутреннюю энергию гелия массой т = 1 кг при тем-
пературе Т = 300 К. Молярная масса гелия ц = 4-Ю'3 кг/моль.
10.5. Аргон находится в вертикальном цилиндре под поршнем массой
т = 1 кг и площадью 5=10 см2. Какова внутренняя энергия газа, если объем
газа V= 4 л? Атмосферное давление р0 = 105 Па.
10.6. Воздух, занимавший объем = 1 л при давлении = 0,8 МПа,
изотермически расширился до V2 = 10 л. Определить изменение его внутрен-
ней энергии и работу, совершенную газом. Какое количество тепла было со-
общено газу в процессе расширения?
• Решение. При изотермическом расширении температура воздуха не меняется, а, следо-
вательно, не меняется и его внутренняя энергия, т.е.
75
MJ=O. (1)
При расширении v молей газа от объема И до V2 при постоянной температуре
Т будет совершена положительная работа
Г,
A = vRT\n.y.
Так как число молей газа и его температура неизвестны, то, воспользовавшись урав-
нением Менделеева-Клапейрона, записанным для начального состояния воздуха:
Pi Vi=vRT,
работу расширения найдем как
Г,
A=pi V\ In jr * 2,6 кДж. (2)
Количество тепла, сообщенного газу, найдем из первого начала термодинамики:
£) = Д£7+Л,
или с учетом выражений (1)-(2):
V2
Q =pi F] In у-« 2,6 кДж.
К '
• Ответ-. &U = О, A =pt К] In jp» 2,6 кДж, Q=P\ V\ In -у» 2,6 кДж.
10.7. Одноатомный идеальный газ изотермически расширился из состо-
яния с давлением рх = 106 Па и объемом = 1 л до вдвое большего объема.
Найти внутреннюю энергию газа в конечном состоянии.
10.8. Идеальный одноатомный газ в количестве v = 2 кмоля переводят из
одного состояния в другое. При этом температура газа в обоих состояниях
одинакова и равна t = 27°С. Определить внутреннюю энергию газа в обоих
состояниях, ее изменение MJ и работу А, совершенную газом при этом пере-
ходе, если известно, что в процессе было затрачено количество теплоты
0=10 кДж.
10.9. Один моль идеального газа изотермически сжимают от давления
Р] = 1 атм дор2 = 2 атм. Определить количество теплоты, необходимой для про-
цесса сжатия, если температура газа равна Т = 300 К.
10.10. Идеальный одноатомный газ, находящийся в закрытом сосуде объ-
емом К= 2 л, изохорически охлаждают. Найти количество выделившейся теп-
лоты, если давление газа изменилось от = 2 атм до р2 = 1 атм.
• Решение. При охлаждении газа происходит изменение его внутренней энергии на вели-
чину
AU= v Cv (Т2 - ГО,
где Cv - молярная теплоемкость газа при постоянном объеме (в нашем случае одноатом-
ного газа Cv = А), Т\, Т2 - температура газа в начальном и конечном состояниях.
По условию задачи известен объем газа и изменение его давления. Воспользовавшись
уравнением Менделеева-Клапейрона, записанным для начального и конечного состояний
газа
PxV=vRT\, p2V=vRT2,
получим
76
vR^-T^fa-p^.
Теперь выражение для AU можно представить в виде
AU=34V(p2-Pi).
Так как р2<Р\, то ДС/ < 0. Это означает, что внутренняя энергия газа уменьшится,
а так как при изохорном процессе работа не совершается, то это изменение энергии газа
будет выделено в виде тепла:
е = 3ЛГ(р1-р2) = ЗОО Дж.
• Ответ-. Q = 3Д ^(Pi -Рз) = 300 Дж.
10.11. Идеальный одноатомный газ совершает процесс при постоянном
объеме так, что его давление увеличилось от рх = 105 Па до р2 = 5-105 Па. При
этом внутренняя энергия газа изменилась на ДС/ = 5-1O3 Дж. Определить
объем, занимаемый газом.
10.12. В закрытом сосуде находится v = 3 моля гелия при температуре
t = 27°С. На сколько процентов увеличится давление в сосуде, если газу со-
общить количество теплоты Q = 3 Дж?
10.13. Температура аргона, содержащегося в сосуде объемом V= Юл, при
изохорическом процессе уменьшилась в и = 2,5 раза. Определить изменение
внутренней энергии газа, если начальное давление в сосуде было равно
р0= 10s Па.
10.14. Баллон содержит v = 4 моля одноатомного идеального газа при
температуре Т = 300 К. При нагревании баллона средняя квадратичная ско-
рость молекул газа увеличилась в п - 1,3 раза. Какое количество теплоты со-
общили газу?
10.15. Одни киломоль гелия расширяется изобарически. Температура газа
при этом увеличивается на Д/ = 20°С. Определить изменение внутренней энер-
гии газа, совершенную газом работу и количество теплоты, сообщенной газу.
• Решение. При изобарическом нагревании гелия часть теплоты, сообщенной газу, идет
на увеличение его внутренней энергии, а часть - на совершение работы при расширении
газа.
Если v молей гелия нагреть на АТ градусов, то внутренняя энергия газа увеличиться на
AU=vCNAT,
где Cv - молярная теплоемкость гелия при постоянном объеме, в случае одноатомного газа
равная Cv = 3Л R Т. Следовательно,
ДС=3ЛуА АТ=>2,5105 Дж.
Работа, совершаемая газом прн изобарическом процессе,
A=p(V2-Vx),
где F], V2 - объемы, занимаемые гелием в начальном и конечном состояниях. Восполь-
зовавшись уравнением Менделеева-Клапейрона, записанным для двух состояний газа
pV]=-vRT\, pV2 = vRT2,
выражение для работы запишем в виде
А = v R (Т2 - ТО = v R АТ » 1,7-105 Дж.
77
Количество теплоты, сообщенной газу, найдем, используя уравнение первого начала
термодинамики:
Q = AU+A = ’4уЛ ДГ»4,240s Дж.
• Ответ: &U= 3Л v Я ДТ» 2,540s Дж, А « v R Ь.Т*> 1,740s Дж, Q = 5Л v R ДТ1» 4,240s Дж.
10.16. Сколько процентов от сообщенного идеальному одноатомному
газу тепла идет на работу при изобарическом расширении?
10.17. В эластичный сосуд помещено v молей гелия. Газ нагревают от
температуры tx до температуры t2- Найти работу, совершенную газом, и из-
менение его внутренней энергии. Натяжением материала сосуда пренебречь.
10.18. В процессе изобарического расширения одноатомного идеального
газа было затрачено Q = 1200 Дж тепла. Определить работу А, совершенную
газом, и теплоемкость Ср одного киломоля газа в этом процессе.
10.19. Азот массой т = 280 г нагревают при постоянном давлении, сооб-
щив газу 2 = 600 Дж тепла. Найти изменение температуры азота, если его
удельная теплоемкость при постоянном объеме равна cv = 745 Дж/кг-К. Мо-
лярная масса азота ц = 2840'3 кг/моль.
10.20. Кислород изобарически сжали до объема в и = 5 раз меньше пер-
воначального. Определить работу, совершенную над газом, если масса кис-
лорода т = 160 г, молярная масса ц = 324 О’3 кг/моль, а начальная температура
1 = 27°С.
10.21. Неон массой т = 1,5 кг сжимают при постоянном давлении
р = 2 10s Па, совершая работу А = 105 Дж. Определить конечный объем, за-
нимаемый газом, если его начальная температура Т\ = 300 К. Молярная масса
неона ц = 20 10'3 кг/моль.
10.22. Для того, чтобы изобарически уменьшить объем гелия была со-
вершена работа А = 20 кДж. При этом температура газа уменьшилась в
и = 3 раза. Найти начальный объем гелия, если давление равно р = 105 Па.
10.23. v = 5 молей аргона расширяются при постоянном давлении так,
что объем газа увеличивается в и = 5 раз, а изменение внутренней энергии
равно ДС7 = 60 кДж. Определить начальную температуру аргона.
10.24. Найти работу, совершаемую двумя молями идеального одноатом-
ного газа при изобарическом расширении, если концентрация молекул газа в
конечном состоянии вдвое меньше, чем в начальном при температуре
Т\ = 300 К.
10.25. В цилиндре под поршнем массой m = 50 кг с площадью основания
S = 50 см2 находится воздух при температуре 1\ - 300 К. Подвижный поршень
первоначально расположен на высоте h = 50 см от основания цилиндра.
Какую работу совершит газ при расширении, если его нагреть на ДТ = 30 К?
Атмосферное давление р0 = 105 Па.
78
• Решение. Как было показано в задаче №9.159, процесс нагревания туза, заключенного
под подвижным поршнем, будет протекать изобарически. Работа газа при изобарическом
процессе
A=p(V2-Vl).
Давление газа р складывается из атмосферного давления рд и дополнительного дав-
ления, обусловленного силой тяжести поршня:
p=p0 + mg/S. (1)
Из закона Гей-Люссака для изобарического процесса
и условий задачи
Vx=hS, &T=T2-Tt
следует:
A=p^rhS. (2)
Подставляя в (2) вместо давления р выражение (1), получаем
Л = + Дж.
1 О 1 1 |
• Ответ-. А=1рд + 1 й S « 49,5 Дж.
1 О i 11
10.26. т = 10 г водорода находятся в цилиндре, закрытом тяжелым порш-
нем. Температуру газа увеличивают на А/= 100°С. Какую работу совершит
газ при расширении? Молярная масса водорода ц = 210’3 кг/моль.
10.27. Какое количество водорода находится под поршнем в цилиндри-
ческом сосуде, если при нагревании его от Т\ до Т2 при постоянном давлении
на поршень газ произвел работу А?
10.28. На сколько градусов нужно нагреть И= 4 м3 воздуха, находивше-
гося в цилиндре при температуре I = 0°С, чтобы при поднятии поршня была
совершена работа А = 105 Дж? Воздух под поршнем находится под давлением
р= 0,15 МПа.
10.29. В вертикальном цилиндрическом сосуде под легким поршнем на-
ходится m = 0,15 кг гелия. На поршне стоит груз массой М = 74 кг. На сколько
нужно нагреть гелий и какое количество тепла подвести, чтобы груз поднялся
на высоту й = 0,6 м. Процесс считать изобарным, теплоемкостью сосуда и
внешним давлением пренебречь. Молярная масса гелия ц = 4-103 кг/моль.
10.30. В сосуде под поршнем массой М= 1 кг и площадью S= 10 см2
находится m = 1 г неона. Какое количество теплоты нужно затратить, чтобы
нагреть газ на Д/ = 10°С? На сколько при этом поднимется поршень? Атмо-
сферное давление pQ = 105 Па. Молярная масса неона ц = 210'2 кг/моль.
10.31. Азот содержится в цилиндре под поршнем, находящемся на высоте
й] - 50 см, при температуре t, = 27°С. До какой температуры нужно нагреть
газ, чтобы поршень поднялся до /12 = 80 см?
79
1032. Один моль гелия находится при температуре Г, = 300 К в верти-
кальном теплоизолированном цилиндре, закрытом поршнем массой т = 2 кг и
диаметром d= 10 см. Когда на поршень поставили гирю массой М= 3 кг, он
опустился на h = 5 см. Определить установившуюся температуру газа и изме-
нение его внутренней энергии, если атмосферное давление р0 = 105 Па.
1033. Один моль кислорода, находившийся при температуре Т\ = 290 К,
адиабатически сжат так, что его давление возросло в и = 10 раз. Найти темпе-
ратуру газа после сжатия и работу, которая была совершена над газом.
• Решение. Адиабатический процесс протекает при условии, что в течение всего процесса
газ остается теплоизолированным от внешней среды, т.е. никуда не отдает и ниоткуда не
получает тепло. В таком процессе Q = 0 и при сжатии работа А', совершаемая над газом,
идет на увеличения его внутренней энергии:
J' = -^=At7=vCv(7’2-7’1), (1)
где Cv - молярная теплоемкость газа при постоянном объеме (в нашем случае двухатом-
ного газа Cv = R), А - работа газа, Т2 - конечная температура газа.
Для определения температуры Т2 воспользуемся уравнением Менделеева-Клапейро-
на, записанным для двух состояний
pxVx=vRTx, p2V2 = vRT2, (2)
и уравнением адиабатического процесса
Г,Т=Л У2\ (3)
где у = 7/s - показатель адиабаты для двухатомного газа.
Из уравнений (2)—<3) легко получить, что
T2~T}PiVx’ ^,i=p2'
ИЛИ
т2 = Ti — {—} Т{ {— )* Тх п<У ” 1)/У= Т] « 560 К.
Используя полученное выражение для температуры, работу (1) найдем как
А' =5Л у R Тх (п^- 1)» 5,6 кДж.
• Ответ: Т2=Тхп^ « 560 К, А' = 5Л vR Тх (п^ - 1)»5,6 кДж.
1034. При адиабатическом сжатии одного киломоля двухатомного газа
была совершена работа А = 146 кДж. На сколько увеличилась температура
газа при сжатии?
1035. При адиабатическом расширении m = 1 кг азота газом была совер-
шена работав = 300 Дж. Найти изменение внутренней энергии и температуры
газа. Удельная теплоемкость азота при постоянном объеме cv = 745 Дж/кг-К.
1036. Кислород, занимавший объем V} = 10 л при давлении р} = 100 кПа,
был адиабатически сжат до объема V2 = 1 л. Найти давление кислорода после
сжатия.
80
1037. Из баллона, содержащего водород при давлении р, = 1 МПа и тем-
пературе Ту = 300 К, выпустили половину, находившегося в нем количества
газа. Определить конечную температуру и давление газа, считая процесс адиа-
батическим.
Р Р
Рис. 10.9 Рис. 10.10
1038. Некоторый идеальный газ расширяется от объема И, = 1 л до объе-
ма = 11 л. Давление при этом изменяется по закону р = а V, где а = 4 Па/м3.
Определить работу, совершаемую газом.
• Решение. По условию задачи газ расширяется по закону, при котором давление изме-
няется в зависимости от объема как р = а V. Работа расширения в этом случае может быть
определены одним из трех способов:
I) через определенный интеграл:
Уг ?г
А = J pdV = Ja VdV = а (Г22 - Vy2) = 2,4- Ю’4 Дж;
И И
2) как площадь трапеции, ограниченной графиком функции р(У) и вертикальными линия-
ми У=Уу и У=У2 (рис. 10.9):
А = {/г (ру +р£ (У2 - К,) = 'Л (a V2 + а Уу) (У2 - У,) = ’/2 а (У22 - Уу2);
3) как произведение среднего значения функции р(У) на изменение объема ЛУ= У2 - Уу:
А = <р(У)> ДГ= < а У> (У2 - У,) = ’Л (а У2 + а Уу) (У2 - У,) = '/> а (У22 - Уу2).
• Ответ: А-'Ла (У2 - Уу2) = 2,4-1 О'4 Дж.
1039 . Определить изменение внутренней энергии идеального одноатом-
ного газа в процессе, представленном на рис. 10.10, где р0 = 0,1 МПа, Уо = 2 л.
10.40. Газ расширяется от давления Ру = 2 кПа до давления р2 = 1 кПа по
закону р = a - р V, где a = const, р = 0,5 Па/м3. Определить работу, совершае-
мую газом при таком расширении.
10.41. Определить работу, совершаемую идеальным газом при расшире-
нии от объема Vy = 1 м3 до объема К2 = 10 м3, и количество теплоты, подве-
денной к газу, если давление в процессе изменяется по закону р = a V, где
a = 1 Па/м3.
10.42. Один моль идеального одноатомного газа, находившегося при нор-
мальных условиях (р0 = 10s Па, t0 = 0°С), нагрели так, что его объем увели-
81
чился в п = 3 раза. Найти количество тепла, сообщенного газу при нагревании,
если давление газа возрастало прямо пропорционально его объему.
10.43. Один киломоль идеального одноатомного газа сжимается так, что
его объем уменьшается вдвое. Сжатие происходит по закону pV2= const. На-
чальная температура газа Т\ = 200 К. Найти изменение внутренней энергии
газа.
10.44. Определить работу v молей идеального одноатомного газа при
расширении от объема до объема V2 в процессе, при котором температура
изменяется по закону Т= а V 2 где а - положительная постоянная.
10.45. Один киломоль идеального газа расширился по закону р = а/У 2
где а = 2R (R- универсальная газовая постоянная). При этом начальный
объем газа Vx ~ 5 л увеличился в два раза. Какую работу совершил газ при
расширении, если молярная теплоемкость газа в процессе С = Cv - R, где
Cv - молярная теплоемкость газа при постоянном объеме?
• Решение. Газ расширяется по закону, при котором давление изменяется в зависимости
от объема как р = а/У2 Аналогично задаче №10.38 работа расширения в этом случае
может быть определена через определенный интеграл:
.Г2 ^/-Р“ лг-“- “ “(^2-И) <х(2Г,-Г,) а 2Я
i2dv V2 V^V1 2Г[И 2Г] 2К]
И п
«1,66 кДж.
Второй н третий способы решения из задачи №10.38 здесь использовать нельзя, так
как трапеция, ограниченная графиком функции р(У) и вертикальными линиями
К=И] и V=V2, будет криволинейной, а среднее значение нелинейной функции
р = a/V2 не известно как определить.
Определим работу газа, исходя из первого начала термодинамики:
Л = б-ДС/,
где количество сообщенного газу тепла и изменение внутренней энергии газа
e = vCAT, AC/=vCvA7’.
Следовательно,
А = v С AT- v Cv ДТ= v (Cv - Л) ДТ- v Cv ДТ= - v R Л.Т.
Записав уравнение Менделеева-Клапейрона для начального и конечного состояний
газа
Pi Vt=vRT\,
и уравнение процесса
р^а/1/Л
р2 = v Л Тъ
получим
„ а а а а « (Ki - ИД
vR&T=p2y2-P\ у2Г2~ V2~ VXV2
Тогда работа расширения:
Я- “(^2-^) аРИ-И) g 2R ,,, „
Л vR&T- - 2Г] 2Ki 2Vi*‘X’
82
Хотя второе решение гораздо длиннее первого, оно проще, так как не связано с ин-
тегрированием нелинейной функции.
• Ответ: А = R/Vi и 1,66 кДж.
10.46. Один киломоль идеального газа расширился по закону р= а V, где
а = 0,17? (R - универсальная газовая постоянная). При этом начальный объем
газа Kj = 20 л увеличился в три раза. Какую работу совершил газ при расши-
рении, если молярная теплоемкость газа в процессе С = Cv + где Cv - мо-
лярная теплоемкость газа при постоянном объеме?
10.47. Один киломоль идеального газа расширился по закону р = а V2
где a = R/9 (У? - универсальная газовая постоянная). При этом начальный
объем газа = 3 л увеличился в два раза. Какую работу совершил газ при
расширении, если молярная теплоемкость газа в процессе С = Су + lAR, где
Cv - молярная теплоемкость газа при постоянном объеме?
10.48. Один киломоль идеального газа сжимают так, что давление и тем-
пература изменяются по закону р = а Т2 где a -R/2 (R - универсальная га-
зовая постоянная). При этом начальный объем газа Vx = 3 л уменьшается в
два раза. Какую работу совершил газ при сжатии, если молярная теплоем-
кость газа в процессе С = Cv + 27?, где Cv - молярная теплоемкость газа при
постоянном объеме?
10.49. Одни киломоль идеального газа расширяется по закону р = а/7)
где а = 47? (7? - универсальная газовая постоянная). При этом начальный
объем газа Vx = 0,5 л увеличивается в четыре раза. Какую работу совершил
газ в процессе расширения, если молярная теплоемкость газа в процессе
С = Cv + 37?, где Cv - молярная теплоемкость газа при постоянном объеме?
10.50. Один киломоль идеального газа сжимают так, что давление и тем-
пература изменяются по закону р = а/Т2 где а = 0,17? (7? - универсальная га-
зовая постоянная). При этом конечное давление газа по сравнению с началь-
ным р} = 0,01 МПа возрастает в восемь раз. Какую работу совершил газ при
сжатии, если молярная теплоемкость газа в процессе С = Cv + '/У?, где
Cv - молярная теплоемкость газа при постоянном объеме?
10.51. Моль идеального газа, имевший вначале температуру 7\ = 290 К,
расширяется изобарически до тех пор, пока его объем не увеличится в и = 2
раза. Затем газ охлаждается изохорически до первоначальной температуры
7). Найти изменение внутренней энергии ДС7 газа, работу А, совершенную
газом, и количество тепла Q, полученное газом.
• Решение. Газ последовательно участвует в двух процессах. Рассмотрим первый процесс -
изобарное расширение газа от объема К] до НРИ постоянном давлении р\ (рис. 10.11).
В этом процессе, количество тепла 21-г> сообщенного газу, идет на приращение его внут-
ренней энергии и совершение работы расширения:
83
/>1 =Р2
Рз
1 2
1 3
_ ----ф — - — 1 L——.
К1 к2=г3
Рис. 10.11
V
61-2“ Д^Л-2 +Л1-2,
гае Л1-2=Р1 (V2 - f'l)-
Используя условие задачи (У2/У} = ")>
выражение для работы Л\_2 можно предста-
вить в виде
^1-2=/’1(”И-И)=р1 И ("-!)•
Далее, воспользовавшись уравнением
Менделеева-Клапейрона для начального со-
стояния газа
Pi Vi=vRTiy
получим
Л|_2 = vR Г] (и - 1).
Во втором процессе - процессе изохорического охлаждения, как следует из решения
задачи №10.10, работа совершаться не будет, а внутренняя энергия газа увеличится, за
счет чего будет выделено количество теплоты 6т-з> равное
62-3 = д^2-з-
Так как по условию задачи температуры газа в начальном и конечном состояниях
равны, а внутренняя энергия является функцией состояния газа н может быть представлена
в виде
At/= = v Cv AT,
то за весь процесс 1-2-3 ДТ= 0 и Д(7 = 0.
Работа за процесс 1-2-3 будет равна работе Я|_2, так как Л2-з=
Л=Л1_2 = уЛГ|(п~1).
Количество теплоты, полученной газом за процесс 1-2-3, равно сумме количеств теп-
лоты, полученных газом в процессах 1-2 и 2-3:
Q = 61-2 + 62-3 = Д^1-2 +-^1-2 + Д^2-3-
Так как Д(7|_2 + Дб^-з= д^1-з = 0> то
6 = ^i-2 = v/?T1(n-l).
Следовательно,
Д(7=0, е = Л = уЛГ1(и-1) = 2,41 кДж.
• Ответ-. ДС/ = 0, Q = А = v R Т| (и - 1) = 2,41 кДж.
10.52. При нагревании т = 1 кг идеального газа на ДТ= 1 К при посто-
янном давлении требуется Qp = 909 Дж тепла, а при нагревании при посто-
янном объеме - Qv = 649 Дж. Какой это газ?
10.53. Чтобы нагреть идеальный газ массой т = 5 кг на At = 2°С при по-
стоянном давлении потребовалось на AQ = 4,155-Ю4 Дж больше теплоты, чем
при нагревании при постоянном объеме. Найти молярную массу газа.
10.54. Во сколько раз больше теплоты необходимо для нагревания иде-
ального одноатомного газа до одной и той же температуры в сосуде, прикры-
том поршнем, если: а) поршень движется без трения; б) поршень не переме-
щается?
R4
10.55. Идеальный газ в количестве v = 5 молей сначала нагревают при
постоянном объеме так, что абсолютная температура возрастает в и = 3 раза,
а затем сжимают при постоянном давлении, доводя температуру газа до пер-
воначального значения Т= 100 К. Какая работа была совершена при сжатии?
10.56. Один киломоль идеального газа, находящегося при температуре
Т= 300 К, охлаждается изохорически, в результате чего его давление умень-
шается в и = 2 раза. Затем газ изобарически расширяется так, что в конечном
состоянии его температура равна первоначальной. Определить изменение
внутренней энергии Д17, работу А, произведенную газом, и количество под-
веденного к газу тепла Q.
10.57. Идеальный газ переводят из состояния 1 с давлением рх = 0,4 МПа
и объемом = 3 м3 в состояние 2 с давлением р2 = 0,2 МПа и объемом
К2 = 1 м3 различными путями. Один раз переход совершался сначала по изо-
баре, а затем по изохоре, а второй раз - сначала по изохоре, а затем по изо-
баре. В каком случае выделяется больше тепла? Определить разницу в теп-
Рис. 10.12
10.58. Один моль идеального одноатомного газа участвует в процессе,
представленном на рис. 10.12. Параметры рх, р2, Vb V3 заданы. Найти коли-
чество теплоты, полученное системой при переходе из состояния 1 в состо-
яние 3.
10.59. Некоторое количество азота сжали в и = 5 раз один раз адиабати-
чески, другой - изотермически. Начальные состояния газа в обоих случаях
одинаковы. Найти отношение соответствующих работ, затраченных на сжа-
тие.
10.60. Газ, занимавший объем К] = 2 л при давлении р} =0,1 МПа, рас-
ширили изотермически до К2 = 4 л. После этого, охлаждая изохорически,
его давление уменьшили в два раза. Далее газ изобарически расширился
до К4 = 4 л. Найти работу, совершенную газом.
• Решение. В координатах р - V графики процессов, в которых участвует газ, представле-
ны на рнс. 10.13.
85
Рассмотрим последовательно все процессы, записав для каждого из них выражения
для работы и уравнения процессов согласно обозначениям, принятым на рисунке:
- изотермический процесс: Л]_2 = v R Tt In (V2/Vi), р\ Vx =р2 V2, 7\ = 7’2;
- изохорический процесс: Л2_3 = 0, Рт/Т2 = р3/Т3, 1 V2 = К3;
- изобарический процесс: Лн = р3 (К4 - К2), К3/Т3 = К4/Т4, р3 = р4.
Работу за весь процесс найдем как алгебраическую сумму работ на каждом из участ-
ков:
Л = Л,_2 + Л2_3 + = V R Г, In (К2/К,) +р3 (К4 - К3).
Если воспользоваться уравнениями процессов и условием задачи (pi/p$ = 2), то легко
получить, что
v R Л =р, И, р3 (К4 - К3) = 'ЛPi и, (Т4/К2 - 1).
Следовательно,
А =Р1 И [ In (К2/%) + 'Л (К4/К2 - 1)] «238,6 Дж.
• Ответ: А =рх К| [ In (К2/К|) + ‘Л (К4/И2 - 1)] « 238,6 Дж.
10.61. Идеальный газ сжимают поршнем и одновременно подогревают.
Как изменилась его внутренняя энергия, если объем газа уменьшился в
и = 5 раз, а давление возросло в т = 7 раз?
10.62. Три моля идеального газа, находящегося при температуре
То = 273 К, изотермически расширили в и = 5 раз, а затем изохорически на-
грели так, что его давление стало равным первоначальному. За весь процесс
газу сообщили количество тепла Q = 80 кДж. Найти показатель адиабаты для
этого газа.
10.63. В сосуде объемом Vx находится идеальный одноатомный газ при
давлении рх и температуре Т\, а в сосуде объемом V2- идеальный одноатом-
ный газ при давлении р2 и температуре Т2. Какое давление р и температу-
ра Т установятся в сосудах при их соединении? Теплообменом с окружающей
средой и стенками сосуда пренебречь.
• Решение. Запишем уравнения состояния одного и другого газа до соединения сосудов:
PiVi=viRTi, (1)
p2V2 = v2RT2 (2)
и уравнение состояния смеси:
p(K1 + K2) = (v1+v2)^T, (3)
где р,Т- давление и температура, которые установятся в сосудах при их соединении.
Откуда получим
. . R Т ...
р = (V, + v2) —. (4)
Так как система теплоизолирована, то внутренняя энергия смеси газов будет равна
сумме внутренних энергий компонентов:
Ui + U2=U. (5)
С учетом того, что оба газа одноатомные (Cv । = Cv 2), можно записать:
86
Vj Су R Tj + v2 Cv R Г2 = (vj + v2) Cy R 71 (6)
Следовательно, используя уравнения (l)-(2), получим
Pi K1+p2K2=p(K1 + K2), (7)
откуда находим давление, которое установится в сосудах:
Pl И +Р2
Р~ У1 + У2
Тогда из (4) с учетом полученного выражения для давления н уравнений (1)-(2):
Т=Т т
‘ 2Pi V1T2+P2V2T1 '
„ Pl У\ +Р2 У2 „ „ „ Pl У\ +Р1 Уг
Ответ : р = ————— ; Т= Т\ г2 ——-----т, _ .
К| + К2 р\ К, Г2 +р2 к2 тх
10.64. Найти внутреннюю энергию смеси газов, состоящей из m j = 20 г
гелия и m 2 = 10 г неона при температуре Т= 300 К. Молярная масса гелия
ц , = 410'3 кг/моль, неона - ц 2 = 20-10'3 кг/моль.
10.65. Сосуд содержит тх = 42 г криптона и т2 = 20 г аргона. Найти из-
менение внутренней энергии смеси при ее нагревании на Л/ = 50°С. Молярная
масса криптона ц1 = 84-10’3 кг/моль, аргона - = 4-10'2 кг/моль.
10.66. Сосуд постоянного объема заполнен смесью газов, состоящей из
неона, масса которого тх = 4 г, и аргона, масса которого т2 = 1 г. Считая газы
идеальными, определить удельную теплоемкость этой смеси газов. Молярная
масса неона = 2-10'2 кг/моль, аргона - pj = 4-10'2 кг/моль.
10.67. В вертикальном открытом сверху цилиндре под поршнем находит-
ся смесь трех газов, содержащая по одному молю каждого компонента.
Смесь нагревают, и поршень перемещается на АА = 0,1 м. Какую работу со-
вершила смесь газов? Начальный объем под поршнем И= 100 л, температура
Т = 400 К. Площадь поперечного сечения поршня 5= 100 см2. Трения нет.
10.68. В двух одинаковых теплоизолированных сосудах, соединенных
тонкой трубкой с краном, находятся одноатомные газы при одинаковых тем-
пературах То = 300 К, но разных давлениях. В момент, когда после открытия
крана давления сравнялись, температура газа в одном из сосудов стала равна
Т, = 350 К. Найти температуру газа в этот момент во втором сосуде.
10.69. В длинном вертикальном открытом
сверху цилиндрическом теплоизолированном со-
суде на высоте h от дна на нити висит поршень
массой tn, под которым находится моль одно-
атомного газа при давлении окружающего про-
странства и температуре То (рис. 10.14). Какое ко-
личество тепла нужно сообщить газу, чтобы пор-
шень поднялся до высоты 2/г? Трения нет.
• /и .
Г
h РО’То
1I I
Рис. 10.14
87
• Решение. Так как первоначально давление под поршнем равно давлению окружающего
пространства (т.е. давлению газа над поршнем), то это означает, что нить ие натянута и
поршень на газ ие давит. Поэтому, для того, чтобы поршень поднялся на высоту 2й, газ
сначала необходимо нагреть до температуры Г2, сообщив некоторое количество тепла
Qx при постоянном объеме
e^AC/^vCv^-To),
а затем - до температуры Г3 при постоянном давлении (напомним, что расширение газа
под незакрепленным поршнем при отсутствии трения происходит изобарически):
02 = Д(/2+Л2 = уСр(Г3-Т2),
где СУ = 3ЛЯ, Ср = 5ЛЯ - молярные теплоемкости одноатомного газа при постоянном
объеме и постоянном давлении соответственно.
Следовательно,
Q = Ql + Q1 = V R (Т2 - Та) + 5Л V R (Т3 - ту.
Запишем уравнение Менделеева-Клапейрона для трех состояний газа:
pohS = v RT0, phS = vRT2, p2hS = vRT3,
где p0 - атмосферное давление, p=p0 + m g/S - давление под поршнем при расширении
газа, S - поперечное сечение поршня. Откуда получим
Т’2=Т0{1+^|}, 7’3 = 27’o{l+f^},
а количество тепла, сообщенного газу:
!2 = 3ЛуТ?{7’о{1+^}-7’о} + 5ЛуТ?{27’о{1+^}-7’о{1+^)} =
Ро ь Ро* роъ “
, 4m g v R Тп ,
= 56vRT0 +---- с ° = 5Л v R 7Ь + 4m g h.
РоЪ
• Ответ: Q=5/iv RT0 + 4m gh.
10.70. В вертикальном открытом сверху цилиндрическом теплоизолиро-
ванном сосуде сечением 5= 120 см2 под невесомым поршнем находится одно-
атомный газ при давлении окружающего пространства р0 = 105 Па и темпе-
ратуре То = 300 К. Сосуд внутри разделен на две равные части горизонтальной
перегородкой с небольшим отверстием. После того как на поршень положили
груз массой т = 0,36 кг, он переместился до перегородки. Найти установив-
шуюся температуру газа.
10.71. В вертикальном теплоизолированном цилиндре под поршнем
имеется v = 1 моль идеального одноатомного газа. Вначале поршень удер-
живают и газ занимает объем Ко = 10 л при температуре Го = ЗОО К. Затем
поршень освободили, и после нескольких колебаний он пришел в состояние
покоя. Пренебрегая трением, найти температуру и объем газа в новом по-
ложении. Масса поршня М= 10 кг, площадь 5= 10 см 2. Атмосферное дав-
ление р0 = 1 атм.
10.72. В длинном горизонтальном цилиндрическом теплоизолированном
сосуде находится поршень, удерживаемый ограничителем на некотором рас-
88
стоянии от закрытого торца сосуда (рис. 10.15). Поршень отделяет от внеш-
него пространства моль одноатомного газа при давлении в два раза меньшем
атмосферного и температуре То Какое количество тепла нужно сообщить
газу, чтобы его объем увеличился в два раза? Треиия нет.
Рис. 10.15 Рис. 10.16
10.73. В горизонтальном цилиндрическом теплоизолированном сосуде
сечением S и длиной 21 удерживается тонкий поршень, делящий объем сосу-
да на две равные части. Одну половину занимает одноатомный газ при тем-
пературе То и давлении р0, а в другой половине - вакуум. Поршень соединен
с торцом вакуумированной части сосуда пружиной жесткостью к и длиной в
недеформированном состоянии 21 (рис. 10.16). Пренебрегая трением, найти
установившуюся температуру газа после того, как поршень отпустили.
10.74. Закрытый с торцов горизонтальный теплоизолированный цилинд-
рический сосуд массой m перегорожен подвижным поршнем массой М» т.
С обеих сторон от поршня находится по одному молю идеального одноатом-
ного газа. Коротким ударом сосуду сообщают скорость и, направленную
вдоль оси сосуда. На сколько изменится температура газа после затухания
колебаний поршня? Трением между поршнем и стенками сосуда, а также теп-
лоемкостью поршня пренебречь. Масса газа тт« т.
• Решение. После удара сосуд придет в движение, что приведет к сжатию газа в одной
части сосуда и расширению в другой. Возникшая разность давлений с разных сторон от
поршня заставит последний двигаться в сторону объема с меньшим давлением. При дви-
жении поршня сила результирующего давления постепенно будет уменьшаться до нуля,
но так как поршень массивен, то он пройдет по инерции положение равновесия и сожмет
газ в той части сосуда, где он первоначально был разрежен. Возникшая разность давлений
заставит двигаться поршень в другую сторону и т.д. Такое движение поршня будет про-
исходить до тех пор, пока колебания не затухнут.
Так как в направлении движения сосуда система «сосуд-поршень-газ» замкнута, то
по закону сохранения импульса можно записать:
т и = (т + М + тг) и,
где тг - масса газа в сосуде, и - скорость движения системы после прекращения колеба-
ний поршня.
Разность кинетических энергий системы в начале движения сосуда и в конце, когда
колебания поршня затухнут, равна энергии, отданной газу:
т и2 - (т + М + mr) м2 = ДЕ.
Учитывая, что масса газа в сосуде тг « М и масса сосуда т « М, получим
89
т . _ т(М-т) и2
U = VM’ AE= 2M
Так как после затухания колебаний поршня система будет двигаться с постоянной
скоростью, то в обеих частях сосуда давления будут одинаковыми, а так как массы газа
по обе стороны от поршня равны, то это приведет к тому, что поршень опять разделит
сосуд на равные части, т.е. будет находиться в том же положении, что и до движения
сосуда. Поэтому суммарная работа будет равна нулю, а энергия ДЕ, отданная газу, пол-
ностью уйдет на увеличение его внутренней энергии:
ДЕ = Д(/= 2v Cv ДТ,
где Cv - молярная теплоемкость газа при постоянном объеме: Су = R.
Следовательно,
_ _ т (М-т) о2 _ т (М-т) и2 т и2
4мМСу " 6v MR ~6vR
т и2
®----- , где v = 1 моль.
OVA
m, т2
— fр0; и0.-. \—2-
2
Ответ : ДГ = °-
Ро’ :u :-’ \ 'М ’; Ро.
Рис. 10.17
Рис. 10.18
10.75. Поршень массой М, замыкающий объем Ио одноатомного газа при
температуре То и давлении р0, однократным толчком приводят в движение с
начальной скоростью и (рис. 10.17). Найти температуру газа при максималь-
ном сжатии. Система теплоизолирована, теплоемкостями поршня и сосуда
пренебречь. Сосуд закреплен. Трения нет.
10.76. В длинной пустой горизонтальной теплоизолированной трубе на-
ходятся два поршня массами т1 и т2, между которыми в объеме Ко при дав-
лении pg находится одноатомный газ (рис. 10.18). Поршни отпускают. Опре-
делить их максимальные скорости Dj и и2, если масса газа много меньше
массы любого из поршней. Трения нет.
10.77. В длинной горизонтальной теплоизолированной трубе между
двумя одинаковыми поршнями массой т каждый находится один моль одно-
атомного газа при температуре То. В начальный момент скорости поршней
направлены в одну сторону (вдогонку друг другу) и равны и и Зи. До какой
максимальной температуры нагреется газ? Массой газа и теплоемкостью
поршней пренебречь.
10.78. В длинном горизонтальном закрепленном цилиндрическом тепло-
изолированном сосуде находится поршень массой т, отделяющий от внеш-
него пространства моль одноатомного газа. Газ нагревают и одновременно
90
отпускают поршень, который, двигаясь равноускоренно, приобретает ско-
рость и. Найти количество тепла, сообщенного газу. Трения нет. Внешнее
давление не учитывать.
Р
Рз = 1Ро
Р\ = 2Ро
Р2=Р0
Рис. 10.19 Рис. 10.20
10.79. Определить работу, которую совершает идеальный одноатомный
газ в цикле 1-2-3-1, представленном на рис. 10.19, где р0 = 105 Па, Ко = 1 м3.
• Решение. Так как циклический процесс 1-2-3-1 нар - V- диаграмме представляет собой
простую геометрическую фигуру - треугольник, то площадь, ограниченная петлей цикла,
может быть легко определена. Численно она будет равна работе, совершенной газом за
цикл:
Л='4(й-р2)(К2-К1) =
= И (Зр0 -Ро) (4И0 - К0) = Зр0 Ко = 3-105 Дж.
• Ответ: А - Зр0 Ко = ЗЮ5 Дж.
10.80. Цикл, в котором в качестве рабочего вещества используется одно-
атомный идеальный газ, состоит из двух изохор и двух изобар (рис. 10.20).
Найти совершаемую газом работу за один цикл. Известно, что максимальные
значения объема и давления газа в два раза больше минимальных значений,
равных р0 = 105 Па, Ро = 0,5 м3.
10.81. Идеальный газ совершает работу, изменяя свое состояние по зам-
кнутому циклу, состоящему из двух изохор и двух изобар (рис. 10.20). В
состоянии 1, температура газа равна Т\, в состоянии 2 - Т2. Определить ра-
боту, совершаемую газом за один цикл, если масса газа равна т, молярная
масса ц и в состоянии 4 температура Г4 = Г2.
10.82. Один моль идеального одноатомного газа участвует в процессе,
график которого, состоящий из двух изохор и двух изобар, представлен иа
рис. 10.20. Температуры в состояниях 1 и 3 равны Т\ и Т3 соответственно.
Определить работу, совершаемую газом за цикл, если точки 2 и 4 лежат на
одной изотерме.
10.83. С идеальным газом, взятым в количестве v = 3 моля, проводят зам-
кнутый процесс, состоящий из двух изохор и двух изобар. Отношение дав-
лений на изобарах а = 5/4, отношение объемов на изохорах Р = 6/5. Разность
максимальной и минимальной температур в процессе ДТ = 100 К. Определить
работу, совершаемую газом за один цикл.
91
р
Pl
Pl
Pl
Pl
P
Pi
Puc. 10.22
V
10.84. С идеальным одноатомным газом проводят циклический процесс
1-2-3-4-1 (рис. 10.21). Определить количество теплоты, полученное газом
2], и отданное газом Q2. Давление в цикле меняется от р} до р2, а объем -
от Vx до V2.
10.85. Найти работу идеального газа в циклическом процессе, изобра-
женном на рис. 10.22, если р5 -р2 =p2-pl=p, - V5 - Vs - К, = V. На каких
участках цикла газ получает тепло и на каких отдает?
10.86. Один моль идеального одноатомного газа совершает процесс сжа-
тия 3-1 (рис. 10.23) без теплообмена с окружающими телами, при этом его
объем уменьшается в и = 3 раза. Температура газа в состоянии 1 задана и
равна Тх. Определить работу газа при сжатии, если известно, что работа в
циклическом процессе 1—2—3—4—1 равна Ао.
10.87. Определить работу, которую совершает идеальный одноатомный
газ в цикле 1—4—3—2—1, представленном на рис. 10.24, где = 10 л, V2 = 20 л,
Р] = 105 Па, р0 = З Ю5 Па, р2 = 4-105 Па.
10.88. Идеальный газ совершает
циклический процесс 1-2-3-4-1, гра-
фик которого нар - К - диаграмме изо-
бражается квадратом, диагонали кото-
рого параллельны координатным осям
ГДм3] (рис. 10.25). Давление газа в сос- тоя-
У ниях 1 и 3 равно р = 5 кПа. Минималь-
ные. 10.25 ная температура газа в состоянии 4 в
92
и = 3 раза меньше максимальной температуры в цикле. Найти работу, совер-
шаемую газом за цикл.
10.89. Идеальный газ совершает циклический процесс 1-2-3-4-1, график
которого на р - V - диаграмме изображается квадратом, диагонали которого
параллельны координатным осям (рис. 10.25). Объем газа в состояниях 2 и
4 равен V= 3 м3. Максимальная температура газа в состоянии Зв и = 2 раза
больше минимальной температуры в цикле. Найти работу, совершаемую
газом за цикл.
10.90. Максимальная температура
в цикле 1—2—3—4—1 (рис. 10.26), совер-
шаемом одним молем идеального газа,
равна Ттях = 320 К. Участки 2-3 и 1—4
на р- V - диаграмме изображаются
дугами окружностей, радиусы которых
отличаются в два раза. Отрезки 1-2 и
Рис. 10.26
3—4 принадлежат прямым, которые делят прямой угол на р - V - диаграмме
на три равные части. Определить работу, совершаемую газом за цикл.
Рис. 10.27
Рис. 10.28
10.91. v = 2 моля идеального одноатомного газа участвуют в циклическом
процессе 1—2—3—4—1, представленном на рис. 10.27. Температуры газа в со-
стояниях 1 и 2 равны Г| = 300 К и Т2 = 400К соответственно. Найти работу,
совершенную газом за цикл, если на участке 3-4 газу сообщили Q = 2000 Дж
тепла.
• Решение. Из рнс. 10.27. видно, что процесс 1-2 - изохорический, 2-3 и 4-1 - изобари-
ческие, а 3—4 - изотермический. Изобразим наш процесс на графике зависимости давления
от объема (рис. 10.28).
Работа газа за весь процесс будет равна алгебраической сумме работ на соответст-
вующих участках:
4 = Л1-2 + 42-3 +43_4 +Л4-|.
Из графика на р - V- диаграмме видно, что
1) 41_2 = так как объем газа не меняется;
2) 42-з = Pi (Уз - И|) как площадь под графиком процесса 2-3;
3) 4з_д = 2з_4 - ДС/з_4 = Q, так как в изотермическом процессе Аб'з-.д = 0;
93
4) Лд_| = р\ (Vi - K4) как площадь под графиком процесса 4-1, причем работа отри-
цательна, так как объем газа уменьшается.
Следовательно,
^=р2(Кз-К1) + е+Р1 (К,-К4),
или
•4 =pi V3 ~Р2 V\ + Q +Pi V{ -pi K4.
Используя уравнение Менделеева-Клапейрона, записанное для каждого нз состояний
газа
PiVi=vRTb p2Vi=vRT2, p2V3 = vRT3, ptV4 = vRT4,
с учетом, что Г3 = Г4, получим
Л=Р1 Vl-p2Vl +Q = v R Tf-v R Т2 +Q = v R(TI-T^ +Дж.
• Ответ: А = v R (Т{ - Tj) + Q ~ 339 Дж.
10.92. Определить работу, которую совершают v = 2 моля идеального
одноатомного газа в цикле 1-2-3—4-1, представленном на рис. 10.29, где
= 100 К.
10.93. v = 5 молей идеального одноатомного газа участвуют в цикличес-
ком процессе 1—2—3—4—1, представленном на рис. 10.30. Температуры газа в
состояниях 1 и 4 равны Г, = 300 К и Т4 = 450 К соответственно. Найти работу,
совершенную газом за цикл, если на участке 2-3 газу сообщили Q = 8000 Дж
10.94. С одним киломолем идеального газа осуществляется цикл, изобра-
женный на рис. 10.31. Газ последовательно проходит состояния 1—2—3—4—1.
Известна температура Г4 газа в состоянии 4. Найти работу, совершаемую
газом за один цикл, если известно, что р3 = 1р3.
10.95. Идеальный газ массой тп = 20 г и молярной массой ц = 28 г/моль
совершает циклический процесс, изображенный на рис. 10.32. Найти работу
94
за один цикл, если температуры равны 7\ = 300 К, Т2 = 496 К, а при расши-
рении на участке 2-3 объем газа увеличивается в два раза.
10.96. v = 1,5 моля идеального одноатомного газа участвуют в цикличес-
ком процессе 1—2—3—4-1, представленном на рис. 10.33. Температуры газа в
состояниях 3 и 4 равны Г3 = 600 К и Г4 = 300 К соответственно. Найти работу,
совершенную газом за цикл, если на участке 1-2 у газа забирают Q = 2740 Дж
тепла.
10.97. Найти отношение работ, совершаемых идеальным одноатомным
газом в циклических процессах 1—2—3—4—1 и 4—3-5-6—4, представленных на
рис. 10.34. Температуры газа в состояниях 2 и 4 и в состояниях 3 и 6 оди-
наковы. Температуры в состояниях 1 и 5 отличаются в и = 8 раз.
10.98. v = 1 моль идеального одноатомного газа участвует в циклическом
процессе 1-2-3-1, представленном на рис. 10.35. На участке 3-1 давление
изменяется в зависимости от температуры по закону р = a 'J Т, где а - поло-
жительная постоянная. Температуры газа в состояниях 1 и 2 равны 1\ - 400 К
и Г2= 500 К соответственно. Найти работу, совершенную газом за цикл.
• Решение. Из рис. 10.35 видно, что процесс 1-2 - изохорический, 2-3 - изобарический.
Изобразим наш процесс на графике зависимости давления от объема. Для этого найдем
зависимость р от V в процессе 3-1, выразив температуру из уравнения процесса
Т=р2/а2,
и подставив ее в уравнение Менделеева-Клапейрона:
pV=vRT, pV=vRp2/a2, V=vRp/a2.
Следовательно, на р - V - диаграмме процесс 3-1 изобразится прямой линией (см.
рис. 10.36).
95
Так как иа графике зависимости давления от объема циклический процесс представ-
ляет собой треугольник, то работу за цикл можно найти как площадь, ограниченную сто-
ронами фигуры:
Л = 1Л(р2 ~Р\) (К3 - К,) = '/> (р2 V3-Р2 V, -Pi V3 +Pi И).
Используя уравнение Менделеева-Клапейрона, записанное для каждого из состояний
Р1 И, - v R Ту, p2Vy=v RT2, p2V3=v RT3,
с учетом уравнения процесса 3-1
P1 = aVn, p2 = aV^,
получим
т3 = т22 /Ту, V3 = Г, Т2/Ту.
Следовательно, 2
Л = (V R Т3 - V R Т2 - V R Т2 + V R 7\) = 1Л v Я « 104 Дж.
11
10.99. v = 1 моль идеального одноатомного газа из начального состояния
1 с температурой Ту = 100 К адиабатически переводят в состояние 2. Затем
газ сжимают так, что давление изменяется прямо пропорционально объему,
и, наконец, изохорически переводят в начальное состояние 1 (рис. 10.37)
Найти работу, совершенную газом при расширении 1-2, если в процессах
2-3-1 газу было сообщено Q = 72 Дж тепла, а точки 2 и 3 принадлежат одной
изотерме.
10.100. v = 1 моль идеального одноатомного газа участвует в цикличес-
ком процессе 1-2-3-1, представленном на рис. 10.38. На участке 3-1 объем
газа изменяется в зависимости от температуры по закону V= а Г, где
a - положительная постоянная. Температуры газа в состояниях 1 и 2 равны
Ту = 400 К и Т2 = 500 К соответственно. Найти работу, совершенную газом за
цикл.
10.101. Один моль идеального газа, занимающего объем К, = 1 л при дав-
лении ру = 10 атм, расширился изотермически до давления р2 = 5 атм и объема
V2 = 2 л по загону р = a - р V, где аир- известные постоянные. Затем при
этом объеме давление газа было уменьшено и = 2 раза. В дальнейшем газ
расширялся при постоянном давлении до объема И4 = 4 л. Начертить график
96
зависимости давления р от объема V и, используя его, установить, при каком
из перечисленных процессов газ совершил наибольшую работу. Определить
значение температуры Т в конце каждого из процессов.
10.102. Зная к.п.д. цикла 1-2-3-1
Ц] = 1/13 (рис. 10.39), найти к.п.д. цикла 1-
3-4-1. Рабочее тело - идеальный газ.
• Решение. По определению к.п.д. цикла равен
81 ~Q1 А ,
(1)
где 2, - тепло, подведенное за цикл от нагревателя; g2 - тепло, переданное холодильнику;
А - работа, совершаемая рабочим телом за цикл.
В замкнутом процессе 1-2-3-1 тепло к системе подводится иа участках 1-2 и 2-3,
для цикла 1-3^1-1 - на участке 1-3. Следовательно, так как работа в том и другом циклах
одинакова (площади, ограниченные кривыми 1-2-3-1 и 1-3-4-1, равны):
А А
У1-2 + Ql-З У1-3
21-2 + 02-3
Так как за цикл изменение внутренней энергии рабочего тела равно нулю, то из пер-
вого начала термодинамики следует, что тепло, полученное рабочим телом за цикл (тепло
от нагревателя «минус» тепло, отданное холодильникам), равно работе, совершаемой за
Откуда находим
цикл:
2|-2 + Ql-3 -Q3-1 ~ А-
(2)
(3)
Количество теплоты, отведенное в цикле 1-2-3-1, равно количеству теплоты, под-
веденному в цикле 1-3-4-1: £2з_, =Si-3- Следовательно, с учетом (3) к.п.д.
А + бз-i А + 2|_3
•П2 = И1 ~7)-= ’ll ~7)---= ’ll (П2 + *)•
У1-3 У1-3
Окончательно получим Т|| j
п ’ll 1 П2-1-’ll - 12 '
• Ответ: т|2 = ---= 'гг •
1-П1 12
10.103. Коэффициент полезного действия цикла 1—2—3—4—1, представлен-
ного на рис. 10.39, равен t)j =40%. Определить к.п.д. цикла 1-3-4-1.
10.104. Известно, что к.п.д. цикла 1-2-3-4-1 т)1=40% (рис. 10.39).
Найти: 1) к.п.д. т]2 цикла 1-2-3-1; 2) во сколько раз количество теплоты Q3
подводимое рабочему газу в цикле 1-
3—4-1, больше совершаемой им за
этот цикл работы А3. Рабочее тело -
идеальный газ.
10.105. Во сколько раз к.п.д. гц
цикла 1-2—4-1 (рис. 10.40) больше
к.п.д. т)2 цикла 2-3-5-2? Рабочее тело
- идеальный одноатомный газ.
97
10.106. На рис. 10.41 нар - V - диаграмме представлены графики циклов
1-2-3-1 и 1-4-2-1, проводимых с идеальным одноатомным газом. Участок
1-2 соответствует изобарическому, а участки 1-3 и 4-2 - изохорическому
процессам. Отрезки 1-4 и 3-2 принадлежат прямым, проходящим через на-
чало координат. К.п.д. какого из этих циклов больше? Ответ обосновать.
10.107. Идеальный газ участвует в цикле 1-2-3-1 (рис. 10.42). Известно,
что работа, совершаемая газом в цикле, в и = 9 раз меньше количества теп-
лоты, отдаваемого газом на участке 3-1. Определить к.п.д. цикла.
10.108. К.п.д. цикла 1-2-3—4-1 (рис. 10.43) равен т] = 1/9. Определить
давление газа в состоянии 4, если давление газа в состоянии 2 равно
р = 4 МПа. Известно, что давления газа в состояниях 1 и 3 одинаковы, участ-
ки 4-1 и 2-3 соответствует изохорическим процессам, а участки 1-2 и 3-4
принадлежат прямым, проходящим через начало координат. Газ одноатом-
ный. Количество газа v = 1 моль.
10.109. Найти к.п.д. цикла, представленного на рис. 10.44, где т, п> 1.
Рабочее тело - идеальный одноатомный газ.
• Решение. По определению к.п.д.
(1)
где А - работа газа в цикле, Q - подведенное тепло.
Работа за один цикл равна площади, ограниченной кривыми процессов 1-2-3-1 на
р- V - диаграмме:
Л = 'Л(т-1)(П-1)р0И0. (2)
К соотношению (2) можно также прийти, последовательно вычислив работу на участ-
ках 1-2, 2-3, 3-1.
98
Для нахождения подведенного к рабочему телу в цикле тепла, рассмотрим последо-
вательно его участки. Очевидно, что температуры Т3 > Т2 > Т\. Значит, тепло подводилось
на участках 1-2 и 2-3.
На участке 1-2 объем газа ие меняется, следовательно (см. решение задачи №10.10),
Qx-г = ДЦ_2 = v Cv (Т2 - Т() = 3Л Др Ко = 3Л (т - 1)р0 Ко. (3)
На участке 2-3 процесс протекал изобарически, поэтому (см. решение задачи
№10.15)
й2-з = &U + Л2_3 = 3Лр2 &V+P2 ДК= 5Лр2 ДК= 5Л mрй&V = 5Л (и - 1) mрй Ко. (4)
На участке 3-1 тепло отводилось и нас не интересует.
Следовательно, подведенное в цикле количество теплоты равно
Q = £21-2 + £?2-3- (5)
Из (1)—(5) получим
Ответ', ц =
Р
(m-l)(n-l)
3 (т - 1) + 5 т (и - 1) '
(ш-1)(И-1)
3 (т - 1) + 5 т (п - 1)
Р2
Р1
6
3
4
Рис. 10.45
Рис. 10.46
10.110. Один моль азота совершает циклический процесс 1-2-3—4—1 (рис.
10.45) . Найти к.п.д. цикла, если = 2 атм, р2 = 4 атм, V\ = 10 л, V2 = 20 л.
10.111. Найти отношение к.п.д. циклов 1-2-3—4-1 и 1-5-6-4-1 (рис.
10.46) , если температуры газа в состояниях 2 и 4 одинаковы. Рабочее тело -
идеальный одноатомный газ.
Рис. 10.47
Рис. 10.48
10.112. Найти к.п.д. цикла 1-2-3—4-1, представленного на рис. 10.47. Ра-
бочее тело - идеальный одноатомный газ.
10.113. На р - U - диаграмме (U- внутренняя энергия газа) представле-
ны циклические процессы 1-2-3-1 и 2—4-3-2, проводимые с идеальным одно-
атомным газом (рис. 10.48). Внутренняя энергия в состояниях 1 и 4 отлича-
99
ется в и = 9 раз. Найти к.п.д. цикла 1-2-3-1, если к.п.д. цикла 2-4-3-2
равен т)2. Изобразить процесс на р - V - диаграмме.
Рис. 10.50
10.114. Изобразить приведенный на рис. 10.49 циклический процесс на
р - V - диаграмме. Найти к.п.д. цикла. Рабочее тело - идеальный одноатом-
ный газ.
10.115. Один моль идеального одноатомного газа совершает циклический
процесс, состоящий из изобарного расширения, изохорного охлаждения и изо-
термического сжатия. К.п.д. цикла г) = 25%. Определить количество тепла,
отданного газом при изотермическом сжатии, если работа газа за цикл равна
А = 1 кДж.
10.116. Идеальный одноатомный газ совершает цикл, показанный на рис.
10.50. Найти к.п.д. цикла, если p2 = 2pj и К2 = ЗКГ
10.117. При каком значении а к.п.д. цикла 1-2-3-1 (рис. 10.51) равен
г) = */б? Какая часть подводимого к рабочему телу тепла отдается им внешним
телам? Рабочее тело - идеальный одноатомный газ.
10.118. Показать, что к.п.д. изобра-
женного на рис. 10.52 цикла не превы-
шает 20%. Рабочее тело - идеальный
одноатомный газ.
10.119. Определить к.п.д. цикла 1-
У 2-3—4-1, представленном на рис. 10.53.
Рабочее тело - идеальный одноатомный
газ.
100
10.120. Известно, что к.п.д. т]; цикла 1-2-3-1 и к.п.д. т]2 цикла 3-2—4-3
связаны соотношением т)2 = 0,75 гц (рис. 10.54). Найти, во сколько раз дав-
ление в изобарическом процессе 2-4 превышает давление в изобарическом
процессе 3-1. Рабочее тело - идеальный одноатомный газ.
10.121. Определить к.п.д. цикла 1-2-3-1 (рис. 10.55), если температуры
в состояниях 1 и 2 одинаковы. Рабочее тело - идеальный одноатомный газ.
• Решение. Для определения к.п.д. цикла воспользуемся формулой
r\=A/Q,
где А - работа газа за цикл, Q - количество теплоты, получаемой от нагревателя за цикл.
Так как работа А численно равна площади фигуры, ограниченной кривыми цикла в
переменных р - V, то, как следует из рисунка:
Л = Vi (И2 - И3) (р! -рг) = 3^Ро И)-
Рассмотрим процесс 1-2. Из уравнения Менделеева-Клапейрона, записанного для со-
стояний 1 и 2:
2Ро V\ = vRTb Ap<xVt> = vRT2,
с учетом, что Тх = Т2 , следует
Н=2И0.
Газ получает тепло на участках 3-1 и 1-2. На участке 3-1
бз-1 = АС/з-1 + Лз-1 = V Cv (Г, - Т3) + 'Л (р, +р3) (И - И3) = 3Л v й (7) - Г3) + 3/2р0 И)>
где учтено, что молярная теплоемкость одноатомного газа равна Cv = 3/з й, а работа на
участке 3-1 численно равна площади трапеции Л-3-1-В.
Используя уравнение Менделеева-Клапейрона, записанное для состояний 1 и 3:
4ро И0 = уйГ|, р0И0 = УЙГз,
получим
2з-1 = 3Л (4р0 Ио —р0 Ио) + 3/2р0 Ио = 6р0 Ио.
Аналогично на участке 1—2:
Si-2 = ДЦ-2 + 41_2 = v Cv (Г2- Г,) + '/2 (pi +Рг) (И2 - И0 = 3Лро 2 Ио = Зр0 Ио.
Следовательно,
Q = £?з—1 + S1-2 = 9 ро Ио и п = '/б.
• Ответ: ц = !/б.
10.122. Найти к.п.д. цикла, изображенного на рис. 10.56. Рабочее тело -
идеальный одноатомный газ.
101
Рис. 10.57
10.123. Определить к.п.д. цикла 1-
2-3-4-1, представленного на рис. 10.57,
если температуры в состояниях 2 и 3
одинаковы. Рабочее тело - идеальный
одноатомный газ.
10.124. Определить к.п.д. цикла 1-
2-3-1, представленного на рис. 10.58,
если температуры в состояниях 1 и 2
одинаковы. Рабочее тело - идеальный
одноатомный газ.
10.125. Мощность идеальной тепловой машины Карно /7 = 104 Вт. Тем-
пература нагревателя Т\ = 500 К, холодильника - Т2 - 300 К. Определить теп-
ловую мощность Nit получаемую от нагревателя, и количество теплоты Q2,
отдаваемое холодильнику за т = 10 с работы машины.
• Решение. К.п.д. тепловой машины, работающей по циклу Карно, можно вычислить по
формуле
п- г ,
или
Si ” S2
Л = ~вГ’
где Г2 ~ температуры нагревателя и холодильника, Qt, Q2 - количества тепла, получа-
емого от нагревателя и отдаваемого холодильнику за один цикл работы машины.
Следовательно,
\-T2/Tx = \-Q2/Qv
Orvsypp. находим
S2 = S1
Так как за время т была совершена работа Л == W т, то на основании закона сохране-
ния энергии получим
Sl-S2=^-
Следовательно,
S2 = (S2+^) Ti/Ti,
или
JVtT, ,
52 = ^^-=1ЛЮ5Дж,
а мощность, получаемая от нагревателя,
102
1 т гТ2 Тх-т2
NxT2 5 NT, d
. Ответ: Q2 = —^= 1,510s Дж, Nx =—^ = 2,5 IO4 Вт.
Л - ‘2 “ l2
10.126. В каком случае к.п.д. тепловой машины Карно увеличится боль-
ше: при увеличении температуры нагревателя на АГ или при таком же по-
нижении температуры холодильника?
10.127. Определить к.п.д. идеальной тепловой машины, если температуры
нагревателя и холодильника равны tt = 200°С и t2 = 11°С. На сколько нужно
повысить температуру нагревателя, чтобы к.п.д. цикла увеличился в и = 2
раза?
10.128. Тепловая машина Карно а = 70% тепла, получаемого от нагрева-
теля, отдает холодильнику. Определить температуру нагревателя, если тем-
пература холодильника t2 = 49°С.
10.129. Тепловая машина Карно а = 80% тепла, получаемого от нагрева-
теля, отдает холодильнику. Найти к.п.д. машины и работу, совершаемую за
цикл, если машина получает от нагревателя за цикл Qt = 6,28 кДж тепла.
10.130. Идеальная тепловая машина совершает за один цикл работу
А = 73,5 кДж. Температура нагревателя = 100°С, температура холодильника
t2 = 0°С. Найти к.п.д. цикла и количество тепла, отдаваемого за один цикл
холодильнику.
10.131. Идеальная тепловая машина получает за один цикл от нагрева-
теля Q, = 1 кДж теплоты. Температура нагревателя Гг=600 К, температура
холодильника Г2 = 300 К. Какую работу совершает машина за один цикл?
Какое количество теплоты отдается за цикл холодильнику?
10.132. Тепловая машина, которая работает по циклу Карно, имеет полез-
ную мощность А = 73,5 кВт и работает в интервале температур от Г, = 373 К
до Г2 = 273 К. Определить энергию, получаемую машиной от нагревателя, а
также энергию, отдаваемую холодильнику за т = 1 час работы.
10.133. Найти работу на участке изотермического расширения рабочего
тела теплового двигателя, работающего по циклу Карно, если коэффициент
полезного действия равен т] = 80%, а количество тепла, отдаваемого за цикл,
6 = 2 Дж.
10.134. Тепловая машина работает по циклу Карно. Температура нагре-
вателя Г1 = 600 К, температура холодильника Г2 = 300 К. Найти к.п.д. цикла
и количество тепла, отдаваемого за один цикл холодильнику, если работа на
участке изотермического расширения рабочего тела равна А = 200 кДж.
10.135. Циклический процесс 1-2-3—4-5-6-7-1 (рис. 10.59) состоит из
трех изотерм 1-2, 3—4, 5-6-7, соответствующих температурам = 227°С,
103
Рис. 10.60
t2 = 127°С, f3 = 27°C и трех адиабат 2-3, 4-5, 7-1. Определить к.п.д. цикла
1-2-3-4—5-6-7-1, если работа, совершаемая рабочим телом в цикле 1—2—3—
6-7-1 в два раза больше работы, совершаемой в цикле 3—4-5-6-3.
10.136. Циклический процесс 1-2-3-4—5-6-7-1 (рис. 10.60) состоит из
трех изотерм 1-2-3, 4-5, 6-7 и трех адиабат 3-4, 5-6, 7-1. Определить к.п.д.
цикла 1-2-3-4—5-6-7-1, если к.п.д. цикла 1-2-6-7-1 г|1=40%, к.п.д. цикла
2-3-4—5-6-2 г|2 = 60% и работа, совершаемая над рабочим телом при изотер-
мическом сжатии 6-7 в три раза больше работы, совершаемой над рабочим
телом при изотермическом сжатии 4-5.
10.137. Тепловая машина совершает
циклический процесс 1-2-3-1, представ-
ленный на рис. 10.61. Рабочее тело -
идеальный газ. Определить максимально
возможный к.п.д. тепловой машины, ра-
ботающей в том же диапазоне темпера-
тур.
§11. Уравнение теплового баланса.
Изменение агрегатного состояния вещества. Влажность
Плавление твердого тела, затвердевание или испарение жидкости, кон-
денсация пара в жидкость относятся к явлениям, которые в физике называ-
ются фазовыми переходами. Состояния вещества, между которыми осущест-
вляется фазовый переход, называются его фазами. Так, например, лед, вода
и пар - фазы воды.
Переход из одной фазы в другую всегда происходит (при заданном дав-
лении) при строго определенной температуре. Лед, например, начинает пла-
виться (при атмосферном давлении) при 0°С и при дальнейшем нагревании
температура остается постоянной и равной температуре плавления, пока весь
лед не превратится в воду. Такое поведение льда при плавлении является
частным случаем общего правила: при температуре фазового перехода обе
104
фазы находятся в состоянии теплового равновесия, и при отсутствии подвода
внешнего тепла они могут существовать неограниченно долго. При темпера-
турах же выше или ниже точки перехода может существовать только одна
из двух фаз.
При изменении давления меняется и
температура фазового перехода. Эту зави-
симость можно изобразить графически в
виде кривой на так называемой фазовой
диаграмме, на осях которой откладывают-
ся давление р и температура Т. На рис.
11.1 представлена кривая испарения, даю-
щая значения давления и температуры, при которых жидкость и ее пар могут
существовать в равновесии друг с другом. Справа от кривой вещество может
находиться только в газообразном состоянии, а слева - только в жидком.
Переход вещества из одной фазы 1 в другую 2 всегда связан с выделе-
нием или поглощением некоторого количества тепла £2]_2 - так называемой
скрытой теплоты, или теплоты перехода. В случае перехода твердого тела
в жидкость говорят о теплоте плавления, в случае перехода жидкости в газ -
о теплоте парообразования. Ясно, что
0.-2 =-02-1. (Н.1)
т.е., если при некотором фазовом переходе теплота поглощается (при плав-
лении твердого тела и при испарении жидкости) Ql-2 > 0, то обратный пере-
ход сопровождается выделением такого же количества тепла 02-. = _ 0.-2
(при затвердевании жидкости и при конденсации пара). Теплота перехода,
отнесенная к единице массы вещества, называется удельной теплотой пере-
хода. Так, для плавления т [кг] вещества требуется количество тепла
0i_2 = Xw, (11.2)
где X - удельная теплота плавления, а для испарения т [кг] жидкости -
Qx-2 = rm, (11.3)
где г - удельная теплота парообразования.
Представим теперь, что в какой-либо теплоизолированный сосуд помес-
тили несколько тел с различными температурами, например жидкость, кусок
льда, металлическое тело и т.д. Между телами происходит теплообмен, в ре-
зультате которого более нагретые тела охлаждаются, а менее нагретые - на-
греваются. При этом лед может частично или полностью растаять, а жидкость
замерзнуть. Эти процессы могут происходить до тех пор, пока в системе не
установится тепловое равновесие, когда температуры всех тел выровняются
и все фазовые переходы прекратятся. Поскольку наша система теплоизоли-
рована, алгебраическая сумма всех количеств теплоты (поглощенных и вы-
деленных) в системе должна равняться нулю:
105
(п-4)
‘j
Напомним, что при нагревании (охлаждении) т [кг] вещества от темпе-
ратуры Г] до температуры Т2 поглощается (выделяется) тепло
0I_2=WC(7’2-7’I), (11.5)
где с — удельная теплоемкость вещества.
Уравнение (11.4) называется уравнением теплового баланса.
Если сосуд не теплоизолирован, то уравнение (11.4) нужно записать в
виде
^QH = Q, (П.6)
i,j
где Q - количество тепла, полученное (отданное) системой. Например, тепло
может подводиться к системе за счет сгорания топлива; при полном сгорании
топлива массой т [кг] выделяется энергия равная
0 = (11.7)
где q - удельная теплота сгорания.
Рассмотрим теперь более подробно фазовый переход: жидкость - пар.
Возьмем герметичный сосуд, частично заполненный жидкостью, и допустим,
что первоначально над жидкостью воздух был удален. В этом случае наиболее
быстрые молекулы будут испаряться в пространство над жидкостью (процесс
парообразования), а так как они движутся вблизи жидкости, то некоторые из
них будут сталкиваться с ней и возвращаться в жидкое состояние (процесс
конденсации). Число молекул пара возрастает до тех пор, пока не будут до-
стигнуты такие условия, когда число покидающих жидкость молекул за оп-
ределенный промежуток времени не станет равным числу возвращающихся
в нее. Между жидкостью и паром установится подвижное равновесие и оно
будет существовать до тех пор, пока не изменится температура или объем
системы. Пар, находящийся в равновесии со своей жидкостью, называется
насыщенным, а о его давлении говорят как об упругости насыщенного пара.
Д авление насыщенного пара не зависит от объема пространства над жид-
костью. Если увеличить объем сосуда, то плотность пара уменьшится. При
этом число молекул, испаряющихся с поверхности жидкости, превысит число
молекул, возвращающихся в нее: возникнет дополнительный поток молекул
из жидкости, и этот процесс будет продолжаться до тех пор, пока пар и жид-
кость снова не придут в равновесное состояние. Разумеется, это справедливо,
если в сосуде жидкости достаточное количество для достижения насыщения.
В противном случае вся жидкость испарится и пар будет ненасыщенным. Если
объем пространства над жидкостью не меняется, а температура возрастает,
то упругость насыщенного пара будет увеличиваться, так как при более вы-
соких температурах больше молекул имеют энергию, достаточную для пере-
хода из жидкого состояния в газообразное. Следовательно, состояние равно-
106
весия будет достигнуто при более высоком давлении. Поэтому кривую рав-
новесия жидкость - пар (см. рис. 11.1) можно рассматривать и как кривую
зависимости упругости насыщенного пара от температуры.
Следует отметить, что насыщенный пар не является идеальным газом.
Поэтому законы идеального газа для изопроцессов можно применять к нена-
сыщенным парам только в случае, если пар далек от насыщения. Для насы-
щенного пара использование этих законов приводит к абсурду. Однако урав-
нение Менделеева-Клапейрона можно применять для нахождения массы или
плотности насыщенных паров, если известна их упругость и, наоборот, зная
массу или плотность насыщенного пара, можно найти его упругость. Таким
образом уравнение Менделеева-Клапейрона:
pV=-RT, или p^RT (11.8)
Н Ц
справедливо для конкретной температуры и конкретного объема пара и не
выражает зависимость давления от температуры при постоянном объеме и
давления от объема при постоянной температуре, так как при этом меняется
масса насыщенных паров и их плотность.
Другим видом парообразования является кипение. Кипением называется
парообразование, которое происходит в объеме всей жидкости и при посто-
янной температуре.
Выясним особенности процесса кипения жидкости. При нагревании жид-
кости на дне и на стенках сосуда образуются пузырьки растворенного в жид-
кости воздуха, содержащие также пары жидкости. В момент образования пу-
зырька суммарное давление воздуха и пара в нем равно внешнему давлению
P=Po + Pgh,
где р0 - атмосферное давление, р g h - гидростатическое давление вышеле-
жащих слоев жидкости (при записи выражения для давления мы пренебрегли
так называемым лапласовским давлением, связанным с кривизной поверхнос-
ти пузырька).
При нагревании жидкости давление насыщенных паров в пузырьках воз-
растает, поэтому увеличивается объем пузырьков. При достаточно большом
объеме пузырька действующая на него сила Архимеда отрывает его от по-
верхности сосуда и поднимает вверх. Если нагрев жидкости осуществляется
снизу, то при подъеме пузырька, вследствие того, что верхние слои жидкости
холоднее нижних, насыщенный пар в нем конденсируется и объем пузырька
уменьшается. Поэтому многие из пузырьков, не достигнув поверхности жид-
кости, схлопываются.
Когда температура всей жидкости выравнивается, объем пузырьков при
подъеме будет уже возрастать, так как давление насыщенного пара внутри
пузырька не меняется, а гидростатическое давление уменьшается. При росте
107
размеров пузырька все пространство внутри него заполняется насыщенным
паром. Когда такой пузырек достигнет поверхности, то давление насыщенно-
го пара в нем практически станет равным атмосферному давлению на поверх-
ности жидкости, поскольку давление воздуха в пузырьке в этот момент мало
и им можно пренебречь. На поверхности жидкости пузырек лопается, а на-
ходящийся в нем насыщенный пар выходит в окружающую среду. Это и есть
кипение. Таким образом, кипение жидкости происходит при одинаковой тем-
пературе всей жидкости, когда давление насыщенного пара этой жидкости
равно внешнему давлению.
Опыт показывает, что температура кипящей жидкости и температура
пара над ее поверхностью одинаковы. Поэтому температурой кипения жид-
кости называется такая температура, при которой давление насыщенных
паров этой жидкости равно внешнему давлению на ее поверхности. При
уменьшении внешнего давления температура кипения уменьшается, а при
увеличении давления - увеличивается. Температура кипения жидкости при
нормальном атмосферном давлении называется точкой кипения. Например,
вода закипает при Г= 100°С при атмосферном давлении р= 105 Па.
Процесс кипения тесно связан с наличием растворенного газа, а также
примесей в жидкости. Если из жидкости удалить растворенный в ней газ,
например, предварительным продолжительным кипячением, то можно нагре-
вать эту жидкость до температуры, превышающей температуру ее кипения.
Такую жидкость называют перегретой.
Обратимся снова к фазовой диаграмме р - Т на рис. 11.1. По мере по-
вышения температуры Т давление (упругость) насыщенного пара рп быстро
возрастает, что приводит к увеличению плотности насыщенного пара, которая
приближается к плотности жидкости. При некоторой температуре эти плот-
ности выравниваются и пар становится неотличимым от жидкости, т.е. кривая
равновесия жидкости и газа на фазовой диаграмме р-Т заканчивается в не-
которой точке (точка К на рис. 11.1). Эта точка называется критической. Ее
координаты определяют критическую температуру Гк и критическое давле-
ние рк вещества. Так, для воды Гк = 647 К (или 374°С) и рк = 218 атм. Если
газ находится при температуре Т < Тк, то, увеличивая давление, его можно
перевести в жидкое состояние. Если же температура газа Т > Тк, то ни при
каком давлении его нельзя превратить в жидкость. Часто проводят различие
между терминами «газ» и «пар»: вещество находящееся в газообразном со-
стоянии при температуре Т < Тк, называется паром; если же Т> Тк, то оно
называется газом.
Влажность
Когда мы говорим о погоде, что она сухая или влажная, то мы имеем в
виду содержание паров воды в воздухе. Величина, характеризующая содер-
жание водяных паров в атмосфере Земли, называется влажностью.
108
На практике различают абсолютную и относительную влажность.
Абсолютной влажностью воздуха называют плотность водяного пара,
находящегося в воздухе
/=Р=7> (И-9)
где V, т - объем сосуда, в котором находится воздух, и масса водяных паров
в этом объеме соответственно.
Относительная влажность воздуха определяется как отношение парци-
ального давления р паров воды, содержащихся в воздухе, к давлению рп на-
сыщенного пара при данной температуре. Обычно она выражается в процен-
тах:
<р = 7?--100%. (11.10)
Рн
Относительную влажность можно определить и через плотность водяных
паров, так как при постоянной температуре плотность водяного пара пропор-
циональна давлению (см. формулу (11.8)):
Ф = -е--100%, (11.11)
Рн
где р - плотность водяных паров, т.е. абсолютная влажность.
Поскольку р = m/V и рн = mH/V, то для вычисления относительной влаж-
ности можно использовать также формулу
Ф = —-100%. (11.12)
тн
Из формул (11.10)—(11.12) видно, что относительная влажность опреде-
ляется не только абсолютной влажностью, но и температурой воздуха (так
как давление и плотность насыщенного пара зависят от температуры). Сле-
дует отметить, что рн и рн являются табличными величинами.
При относительной влажности 100% парциальное давление р воды в воз-
духе равно упругости рн насыщенного пара при данной температуре. Иногда
в воздухе содержится такое количество воды, что парциальное давление пара
превышает упругость насыщенного пара при данной температуре. Такой пар
называется пересыщенным. Такая ситуация может возникнуть при внезапном
понижении температуры. Для превращения пара в жидкость нужны центры
конденсации, которыми в обычном воздухе служат пылинки. В абсолютно
чистом воздухе пар может быть пересыщенным сколь угодно долго, но если
появляются центры конденсации, то избыток воды сконденсируется и выпа
дет в виде росы, а давление пара станет равным давлению насыщенного пара
при данной температуре, т.е. при понижении температуры относительная
влажность воздуха повышается и пар, находящийся в воздухе, из ненасыщен-
ного может превратиться в насыщенный. Температура, при которой водяной
пар, находящийся в воздухе, становится насыщенным, называется точкой
109
росы для воздуха заданной влажности. При понижении температуры ниже
точки росы часть пара конденсируется.
Рекомендации по решению задач
Решение основной части задач этого параграфа основано на применении закона со-
хранения энергии в форме уравнения теплового баланса (11.6), которое более удобно ис-
пользовать в виде
^*Спол = ^*ботд>
где 20пол> ^ботд _ суммарные количества теплоты, полученной н отданной телами сис-
темы в процессе теплообмена.
К сожалению, при решении подобных задач на составление уравнения теплового ба-
ланса часто необходимо проводить промежуточные вычисления, так как конечное состо-
яние системы определяется конкретными начальными значениями температур тел н их фи-
зическими свойствами. Если по условию задачи непосредственно неясно, в каких фазах
будут находиться тела, составляющие систему, после завершения теплообмена, то в таких
задачах особое внимание следует обратить на возможность наличия агрегатных превра-
щений. Так как любое вещество после теплообмена при установившейся температуре
одновре - що может находиться в двух фазах, то для решения задачи нужно иметь ясное
представление о том, будет ли конкретное вещество находиться в одном или сразу в двух
агрегатных состояниях. Например, если вещество находится в газообразной (жидкой) фазе
и участвует в теплообмене с более холодными телами, находящимися прн температуре
ниже температуры конденсации (отвердевания) данного вещества, то при установившейся
температуре в системе оно может или оставаться в первоначальной фазе, но прн более
низкой температуре, или частично перейти в новую фазу (т.е. сразу находиться в двух
фазах), или полностью перейти в новую фазу. В таких случаях необходимо сделать чис-
ловой расчет и определить, сколько тепла Qt нужно для нагревания более холодных тел
до температуры соответствующего фазового перехода (плавления или кипения данного ве-
щества), и сколько тепла Q2 может выделить данное более горячее тело прн остывании
до температуры перехода и при самом переходе (отвердевании или конденсации). Если
окажется, что > Q2, то после теплопередачи получится одна фаза вещества, а если
Q\ < 02> т0 ПРИ установившейся температуре будут находиться две фазы при температуре
фазового перехода.
Порядок решения таких задач следующий:
а) внимательно прочитав условие задачи, нужно установить, у каких тел, участвующих в
теплообмене, энергия уменьшается, а у каких увеличивается;
б) если прн теплообмене возможны фазовые переходы, то следует провести числовые рас-
четы и выяснить, в каких фазах будут находиться тела системы при установившейся тем-
пературе;
в) определить суммарное количество теплоты, полученное более холодными телами сис-
темы при их нагревании и фазовых переходах (плавлении и парообразовании);
г) определить суммарное количество теплоты, отданное более горячими телами системы
при их охлаждении и фазовых переходах (конденсации и кристаллизации). Прн записи
выражения для количества теплоты, отданного телом, в форме с т (l2 - <i), всюду нужно
вычитать из большей температуры меньшую;
д) составить уравнение теплового баланса и решить его относительно искомой величины.
При решении некоторых задач на фазовые переходы и уравнение теплового баланса
необходимо дополнительно привлекать уравнения и законы механики.
Решение задач на влажность принципиально не отличается от задач на идеальные
газы. Основные затруднения здесь обычно связаны с неумением пользоваться уравне-
110
ниями, выражающими газовые законы, и попытками с их помощью описать процессы, про-
исходящие с насыщенными парами. Следует помнить, что законы идеального газа для изо-
процессов можно применять лишь к парам, далеким от насыщения. Для насыщенного пара
необдуманное использование этих законов может привести к грубым ошибкам. Поскольку
уравнение Менделеева-Клапейрона в случае насыщенного пара справедливо для конкрет-
ной температуры и конкретного объема пара и не выражает зависимость давления от тем-
пературы при постоянном объеме и зависимость давления от объема при постоянной тем-
пературе (так как при изменении объема или температуры меняется также масса насы-
щенного пара), то данное уравнение можно применять в каждом конкретном состоянии,
т.е. по известной плотности насыщенного пара можно определить его давление (упру-
гость): ра = рн R Т/р (где р - молярная масса пара) н, наоборот, зная давление насыщен-
ного пара, можно найти его плотность. Следует также помнить, что, если задана темпе-
ратура насыщенного пара, то его давление и плотность при этой температуре можно найти
в таблицах, если же известны температура и давление (плотность) насыщенного пара, то
его плотность (давление) можно определить нз уравнения Менделеева-Клапейрона. Если
известна температура ненасыщенного па- ра Г и его точка росы Гр, то с помощью таблиц
можно определить абсолютную и относительную влажность при температуре Г, так как
при температуре Гр пар станет насыщенным.
Порядок решения задач на алажность может быть таким:
а) установить, какой газ рассматривается в задаче: чистый пар жидкости илн его смесь с
сухим воздухом;
б) выяснить, в скольких разных состояниях будет последовательно находится пар по ус-
ловию задачи. Для каждого состояния пара записать уравнение Менделеева-Клапейрона,
формулу абсолютной или относительной влажности в любой нз форм (через давления, или
через плотности, или через массы пара). Если в объеме находится не только пар, но и
некоторый газ (например, воздух), то для смеси газа и пара (а также для смеси паров,
если рассматривается такая смесь) записать закон Дальтона;
в) если рассматривается насыщенный пар, используя таблицы, определить упругость и
плотность пара при заданной температуре. Записать дополнительные условия, связываю-
щие величины, входящие в составленные уравнения, и решить полученную систему.
Задачи
Уравнение теплового баланса. Изменение агрегатного состояния вещества
11.1. Латунный калориметр массой тх = 0,1 кг содержит т2 = 0,2 кг воды
при температуре = 7°С. В калориметр с водой опускают брусок массой
т3 = 0,1 кг при температуре t3 = 127°С, после чего в калориметре устанав-
ливается температура 0 = 27°С. Определить удельную теплоемкость с3 ма-
териала, из которого изготовлен предмет. Удельная теплоемкость латуни
С[ = 380 Дж/(кг-К), воды - с2 = 4200 Дж/(кг-К).
• Решение. Примем систему «калориметр-вода-брусок» как теплоизолированную и будем
считать, что с окружающей средой ее теплообмен ничтожно мал н им можно пренебречь.
В такой системе полная внутренняя энергия остается неизменной.
Основным уравнением, описывающим процесс теплового взаимодействия между те-
лами системы, является уравнение теплового баланса. Поскольку температура калориметра
н воды Г| меньше температуры бруска t3, то при взаимодействии тел брусок остынет, отдав
количество тепла, равное
G1 = с3 т3 (13 ~ 6)>
а вода и калориметр получат такое же тепло:
111
2г = Cl (9 - h) + c2 »12 (0 - Z|),
в результате чего в системе установится температура 9.
Записав уравнение теплового баланса Qt - Q2 в виде
с3 /и3 (/3 - 0) = (С] mt + с2 mi) (0 - (,),
найдем удельную теплоемкость материала бруска:
сз =------“ 1756 Дж/(кг К).
т3 V3 - 9)
(ci т, + с-> тт) (0 - Л) ____
• Ответ: с^ =-----------------» 1756 Дж/(кг-К).
т3 (13 - 0)
11.2. Чтобы довести до кипения воду в кастрюле, потребовалось ей со-
общить Q = 600 кДж тепла. Определить объем воды в кастрюле. Начальная
температура воды t = 22°С, плотность воды р = 103 кг/м3, удельная теплоем-
кость с = 4200 Дж/(кг-К).
11.3. В воду массой тх = 5 кг при температуре Т} = 353 К добавили
т2 = 2 кг холодной воды. При этом начальная температура снизилась на
п = 5%. Определить начальную температуру холодной воды.
11.4. В каком отношении следует смешать две массы воды, взятые при
температурах = 55°С и t2 = 0°С, чтобы температура смеси стала равной
0 = 21°С?
11.5. В воду объемом V = 20 л при температуре tx = 27°С налили некото-
рое количество кипятка, в результате чего температура воды стала равна
t2 = 60°С. Сколько добавили кипятка? Плотность воды р = 103 кг/м3.
11.6. В теплоизолированном сосуде имеются две жидкости с удельными
теплоемкостями с{ и с2, разделенные теплонепроницаемой перегородкой. Тем-
пературы жидкостей различны. Перегородку убирают. После установления
теплового равновесия разность между начальной температурой одной из жид-
костей и установившейся в сосуде температурой оказывается в два раза мень-
ше разности начальных температур жидкостей. Найти отношение масс первой
и второй жидкостей.
11.7. В стеклянный стакан массой т1 = 120 г при температуре = 15°С
наливают т2 = 200 г воды при t2 = 80°С. Какое количество теплоты будет
передано стакану? Удельная теплоемкость стекла с{ = 840 Дж/(кг-К), воды
с2 = 4200 Дж/(кг-К).
11.8. Для измерения температуры воды в нее погрузили термометр, ко-
торый показал температуру t{ = 32,4°С. Какова действительная температура
воды, если теплоемкость термометра С= 1,9 Дж/К и перед погружением в
воду он показывал температуру t2 = 17,8°С? Масса воды т = 66 г, удельная
теплоемкость с = 4200 Дж/(кг-К).
11.9. В калориметр налили V= 1 л воды при температуре = 27°С. Затем
в воду опустили металлический брусок массой т = 0,25 кг, нагретый до тем-
112
пературы t2 = 127°С. В результате температура воды поднялась до 0 = 34°С.
Пренебрегая теплоемкостью калориметра, определить удельную теплоемкость
металла, из которого изготовлен брусок. Удельная теплоемкость воды
С] = 4200 Дж/(кг-К), плотность воды р = 103 кг/м3.
11.10. В алюминиевом калориметре массой Л/=500 г находится
/И] = 250 г воды при температуре tt = 19°С. Если в калориметр опустить ме-
таллический цилиндр массой т2 = 180 г, состоящий из двух частей - алюми-
ниевой и медной, то температура воды поднимется до 0 = 27°С. Определить
массу алюминия тк и меди ты в цилиндре, если его начальная темпера-
тура t2 = 127°С. Удельные теплоемкости алюминия, меди и воды равны
С] = 900 Дж/(кг-К), с2 = 400 Дж/(кг-К) и с3 = 4200 Дж/(кг-К) соответственно.
11.11. В калориметр, заполненный Г= 2 л воды при температуре = 25°С,
опустили лед, находящийся при t2 = -10°С, а затем алюминиевый брусок мас-
сой т3 = 100 г, нагретый до t3 = 200°С. Какую массу льда опустили в калори-
метр, если брусок охладился до температуры 0 = 20°С? Удельная теплоем-
кость воды cf=4200 Дж/(кг-К), льда - с2 = 2100 Дж/(кгК), алюминия -
с3 = 900 Дж/(кг-К). Удельная теплота плавления льда X = 0,33 МДж/кг, плот-
ность воды р= 103 кг/м3. Теплоемкостью калориметра пренебречь.
• Решение. Будем считать систему «вода-лед-брусок» теплоизолированной, Полагая, что
внутренняя энергия системы остается неизменной.
Поскольку конечная температура системы равна 0 - 20°С, то, очевидно, в калори-
метре при установившейся температуре будут находиться вода и брусок (т.е. весь лед
растает).
При тепловом взаимодействии «горячие» тела - вода и брусок - остынут до темпе-
ратуры 0, отдав более холодному телу - льду - количество теплоты
Qb = С] mi 01 - 0) = с, р Г(т, - 6)> <2бр = сз тз 03 - е)
соответственно. В результате внутренняя энергия более горячих тел уменьшится на вели-
чину
Qi = QB + Q6p = c\ Р и(/, -0) + с3/из(г3-0).
Эта энергия перейдет ко льду: часть на нагревание льда от температуры t2 до тем-
пературы плавления 1^ = 0°С:
Qn = с2 т10пл —
часть на плавление льда:
&1Л ~ А. т2
и часть иа нагревание образовавшейся воды от /пд до конечной температуры системы 0:
Qh = С1 т2 (9 _ 'пл)-
Следовательно, в результате теплообмена лед получит количество тепла
Qi ~ Qn + £2пл + Qh ~ т21С2 0пл — + А. + С] (0 — /пл)].
Записав уравнение теплового баланса в виде
Qi = Q2>
или
113
P v с, (Г, - 0) + т3 с3 Оз - 0) = т2 [с2 (?пл - '2) + X + «л (0 -
найдем искомую массу льда:
рКс|(/|-0) + т3с3(/з-0)
т, = — --------—-----—------- и 134 г.
с2 Опп _ + X + С1 (0 _ ^пл)
Ответ: т2 =
Р Ус\ (?t-0)+ т3 с3 (?3 - 0)
с2 (?пл — ^г) + X + С1 (® ~ 01л)
»134 г.
11.12. Какое минимальное количество тепла нужно сообщить т = 1 кг
льда при температуре Т = 263 К, чтобы расплавить его? Удельная теплоем-
кость льда с = 2100 Дж/(кг-К), удельная теплота плавления X = 0,33 МДж/кг.
11.13. Какая масса льда нужна, чтобы охладить воду в ванной от темпе-
ратуры ?j= 17°С до /2 = 7°С? Объем воды V= 100 л, удельная теплоемкость
воды с = 4200 Дж/(кг-К), плотность воды р = 103 кг/м3. Температура льда
?3 = 0°С, удельная теплота плавления X = 0,33 МДж/кг.
11.14. Какую массу льда можно расплавить при подводе к нему такого
же количества тепла, какое необходимо, чтобы довести до кипения V= 3 л
воды, взятой при температуре ? = 20°С? Удельная теплоемкость воды
с = 4200 Дж/(кг-К), плотность воды р = 103 кг/м3, удельная теплота плавления
льда X = 0,33 МДж/кг. Начальная температура льда t0 = 0°С.
11.15. В медный теплоизолированный сосуд, нагретый до температуры
?! = 350°С, положили т2 = 600 г льда при температуре /2 = -10°С. В результате
в сосуде оказалось т3 = 550 г льда, смешанного с водой. Найтн массу сосуда.
Удельная теплоемкость меди Cj = 420 Дж/(кгК), льда - с2 = 2100 Дж/(кг К),
удельная теплота плавления льда X = 0,33 МДж/кг.
11.16. В большом куске льда, находящегося при температуре = 0°С,
сделано углубление, объем которого Ко= 160 см3. В это углубление налили
тв = 60 г воды, температура которой ?2 = 5°С. Какой объем будет иметь сво-
бодное от воды углубление, когда вода остынет? Удельная теплоемкость воды
с = 4200 Дж/(кг-К), удельная теплота плавления льда X = 0,33 МДж/кг, плот-
ность льда рл = 900 кг/м3, плотность воды рв = 103 кг/м3.
11.17. В большом куске льда сделана лунка объемом Vo = 100 см3, в ко-
торую налили т = 1 кг расплавленного свинца при температуре плавления
?! = 327°С. Найти объем лунки свободной от воды и свинца после достижения
теплового равновесия. Удельная теплоемкость свинца С\ = 125 Дж/(кг-К),
удельная теплота плавления свинца X! = 23 кДж/кг, плотность свинца
Р! = 11-103 кг/м3, удельная теплота плавления льда Х2 = 0,33 МДж/кг, плот-
ность льда р2 = 900 кг/м3, плотность воды р = 103 кг/м3.
11.18. Кусок льда массой т = 100 г при температуре ?= 0°С заключен в
теплонепроницаемую оболочку и подвергнут сжатию до давления
р = 1200 атм. Найти массу Дги растаявшей части льда, если понижение тем-
пературы плавления происходит прямо пропорционально давлению и при уве-
114
личении давления на Др = 138 атм температура плавления понижается на
Д/= 1°С. Удельная теплота плавления льда Х = 340 кДж/кг, удельная тепло-
емкость льда с = 2100 Дж/(кг К). Атмосферное давление р0 = 103 Па.
11.19. В теплоизолированный сосуд, содержащий К, = 0,5 л воды при тем-
пературе tt = 6°С, помещают mt = 0,9 кг льда, имеющего температуру
/л = - 25°С. После достижения теплового равновесия половину воды из этого
сосуда перелили в другой такой же сосуд, содержащий Г2 = 2 л воды при
температуре /2 = 18°С, добавив в него т2 = 0,45 кг льда при температуре
г* = 0°С. Найти температуру, которая установится во втором сосуде. Плот-
ность воды р = 103 кг/м3, удельная теплоемкость воды св = 4200 Дж/(кг-К),
льда - сл = 2100 Дж/(кг-К), удельная теплота плавления льда X = 0,33 МДж/кг.
Теплоемкости сосудов не учитывать.
• Решение. Чтобы определить установившуюся температуру во втором сосуде, необходимо
знать, какие вещества и прикаких температурах будут в этот сосуд помещены. Для этого
найдем массу воды Ат, которую перелили из первого сосуда во второй, и ее температу-
ру t.
Так как в первом сосуде первоначально находилась вода массой тв 1 = РИ при тем-
пературе Г] = 6°С н лед массой при температуре Гл = - 25°С, то непосредственно не видно,
что будет в сосуде (вода, лед или обе фазы одновременно) при установившейся темпера-
туре t. Для понимания происходящих в сосуде процессов проведем предварительные рас-
четы.
Определим, какое количество тепла необходимо льду для нагревания до температуры
плавления ГШ1 = 0°С:
ОлаГР = сл т1 Опл ~ 61) = 47,25 кДж.
Вода прн этом должна остыть до такой же температуры, отдавая тепло, равное
Ов — св тв 1 Ci “ бы) = (:в Р И (6 — 6in) ~ 12,6 кДж.
Поскольку 2лагР > то это означает, что лед, получив тепло за счет осты-
вания воды, не нагреется до Гщ,.
Найдем количество тепла Q$mcr, которое может быть передано льду при замерзании
воды:
gKPHCT = mB1X= р ^1=165 кДж.
Сравнивая (?лагР с + <2£РИСТ, видим, что (?лагР < + бвРист. Следовательно,
для нагревания льда до температуры (щ, вода в первом сосуде должна остыть и часть ее
превратиться в лед прн
Записав уравнение теплового баланса в виде
енаП> = еосг + тв'1Х,
найдем массу mBI замерзшей воды:
"»в 1 =----------- «0,1 кг.
Следовательно, во второй сосуд перелили
Ат = х/г (тъ ] - mB i) = 'Л (р К] - тв ]) » 0,2 кг
воды при температуре Г = 0°С.
115
Рассмотрим теперь содержимое второго сосуда: в нем находится вода массой
тв2 = рК2 при температуре t2 = 18°С, вода массой Д/n при температуре г = 0°С и лед мас-
сой т2 при температуре гл = 0°С.
Так как лед находится при температуре плавления !л = Гщ, = 0°С, то, чтобы его рас-
плавить, необходимо сообщить ему количество тепла, равное
^}лавл = т2Х= 148,5 кДж.
Это тепло может быть получено за счет остывания воды массой тв 2 до температуры
^пл = 0°С:
= св mB2 (t2 — Тдд) = св р К2 (t2 — Тдд) = 151,2 кДж.
Так как ^ллавл < бв”, то весь леД 80 втором сосуде растает, а образовавшаяся вода
нагреется до температуры 0, которую найдем, записав уравнение теплового баланса в виде
05лавл + св т2 (0 - Гпд) + св &т (9 - Г) = св р Г2 (Г2 - 0).
Откуда получаем
9 _ вр 2 2 ил------и Од 1()с
СВ (т2 + А™ + Р Pj)
• Ответ: 0 и 0,11°С.
11.20. Имеются два теплоизолированных сосуда. В первом из них нахо-
дится К] = 5 л воды при температуре tx = 60°С, во втором К2 = 1 л воды при
температуре /2 = 20°С. Вначале часть воды перелили из первого сосуда во
второй. Затем, после установления во втором сосуде теплового равновесия,
из него в первый сосуд отлили столько воды, чтобы ее объемы в сосудах
стали равны первоначальным. После этого температура в первом сосуде стала
равна t* = 59°С. Сколько воды переливали из первого сосуда во второй?
11.21. Два одинаковых цилиндрических калориметра высотой h - 75 см
заполнены на треть своих объемов. Первый - льдом, образовавшемся в ре-
зультате замерзания налитой в него воды, второй - водой при температуре
t= 10°С. Воду из второго калориметра переливают в первый, в результате
чего он оказывается заполненным на две трети. После того как температура
в первом калориметре установилась, уровень заполнения его увеличился на
ДЛ = 0,5 см. Найти начальную температуру льда в первом калориметре. От-
ношение плотностей льда и воды рл/рв = 0,9. Удельная теплота плавления
льда А = 0,33 МДж/кг, удельная теплоемкость льда сл = 2100 Дж/(кг-К), во-
ды - св = 4200 Дж/(кг-К).
11.22. В теплоизолированном сосуде находится вода при температуре
t = 0°С. Из сосуда откачивают воздух, в результате чего вода замерзает за
счет охлаждения ее при испарении. Определить, какая часть воды при этом
испарится, если известно, что удельная теплота парообразования воды при
t = 0°С г = 2,54 МДж/кг, а удельная теплота плавления льда А = 0,33 МДж/кг.
• Решение. Прн испарении воды вылетают наиболее быстрые молекулы, вследствие чего
суммарная энергия оставшихся молекул уменьшается и температура воды понижается.
Если теплообмен с окружающей средой отсутствует, то, откачивая пары воды, энергию
116
молекул, оставшихся в сосуде, можно уменьшить настолько, что они образуют твердую
фазу воды - лед.
Для образования пара массой тп необходима энергия, равная
Qi = г тп,
которая будет получена за счет образования льда массой тл:
Й = ил = (т ’ ип) Ъ
где т - первоначальная масса воды в сосуде.
На основании уравнения теплового баланса
Q\ = Q2, или rmn = (m- X,
получим т .
^п=_Ь 0,115.
тп х т г + X
• Ответ: — =----0,115.
т г + Х
11.23. Какое количество воды, взятой при температуре / = 30°С, можно
испарить, затратив энергию Q=IQQ Дж? Удельная теплоемкость воды
с = 4200 Дж/(кг К), удельная теплота парообразования г = 2,26 МДж/кг.
11.24. На сколько градусов можно нагреть воду массой тъ = 3 кг, взятой
при температуре t = 0°С, за счет тепла, выделяющегося при конденсации пара
массой тп = 0,2 кг? Удельная теплоемкость воды с = 4200 Дж/(кг-К), удель-
ная теплота парообразования г = 2,26 МДж/кг.
11.25. Какую массу льда, взятого при температуре /=0°С, можно рас-
плавить при сообщении ему такого же количества тепла, которое необходимо
для испарения V= 2 л воды? Плотность воды р = 103 кг/м3, удельная теплота
плавления льда А = 0,33 МДж/кг, удельная теплота парообразования воды
г = 2,26 МДж/кг.
11.26. Какое минимальное количество теплоты надо сообщить т = 2 кг
льда, взятого при температуре =- 10°С, чтобы превратить его в пар при
температуре t2 = 100°С? Удельная теплоемкость воды св = 4200 Дж/(кг-К),
льда - сл = 2100 Дж/(кг-К), удельная теплота плавления льда А = 0,33 МДж/кг,
удельная теплота парообразования воды г = 2,26 МДж/кг.
11.27. Из колбы, в которой находилось т = 800 г воды при г = 0°С, от-
качивают воздух и водяные пары, благодаря чему вода в колбе замерзает.
Определить массу образовавшегося льда. Удельная теплота парообразова-
ния воды при t = 0°С равна г = 2,54 МДж/кг, удельная теплота плавления
льда А = 0,33 МДж/кг.
11.28. В калориметр поместили тл = 0,5 кг льда при температуре
/л = -15°С, тв = 0,25 кг воды при температуре /в = 0°С и тип = 0,25 кг пара при
температуре /п = 100°С. Определить, сколько воды окажется в калориметре
после установления теплового равновесия. Удельная теплоемкость воды
св = 4200 Дж/(кг-К), льда - сл = 1/гсв, удельная теплота плавления льда
А = 0,33 МДж/кг, удельная теплота парообразования воды г = 2,26 МДж/кг.
Теплоемкостью калориметра пренебречь.
117
• Решение. Исходя из условия задачи непосредственно не видно, будет ли при установив-
шейся температуре в сосуде находиться вода в одной или двух фазах и в каких именно.
Для ясности понимания процессов, происходящих в калориметре, и составления уравнения
теплового баланса (считая, что система «лед-вода-пар» теплоизолирована) проведем пред-
варительный числовой анализ.
1. Количество теплоты, которое необходимо льду для нагревания от температуры (л до
температуры плавления (пл = 0°С и его плавления равно
ел = Сл'»л(^пл~^л) + ^'”л «1>8 Ю Дж. (1)
2. Количество теплоты, которое может отдать пар, если он весь сконденсируется равно
Qn = гтп и 5,615-105 Дж. (2)
Поскольку Qn > 2л> то эт0 означает, что весь лед расплавится и при установившейся
температуре в системе может находиться только вода и пар или только вода.
3. Поскольку конечная температура системы не задана, определим, какое наибольшее ко-
личество теплоты может поглотить вода (это будет в том случае, если вода и растаявший
лед нагреются до температуры tn = 100°С):
(?в = ((^в + (Ид) (1п ~ ^пл) « 3,15-10 Дж. (3)
Из выражений (1) и (3) определим количество теплоты, необходимое для плавления
льда н нагревания всей воды в системе то температуры tn:
ел + 0в« 4,95-105 Дж. (4)
Сравнивая (Qn + Qb) с Q„, можно сделать вывод о направлении процесса: поскольку
(6л + 6в) < £?п> то конечная температура смеси будет равна (п = 100°С и сконденсируется
только часть пара массой т0, которую найдем из уравнения теплового баланса:
гт0 = 6л + 6в-
Откуда получим
вл + вв „ „„
т0 =-------я 0,22 кг.
Следовательно, в калориметре будет масса воды, равная
m = тв + тл + т0 и 0,97 кг.
• Ответ: т » 0,97 кг.
11.29. В калориметр поместили = 2 кг воды при температуре = 5°С
и т2 = 5 кг льда при температуре t2 = - 40°С. Определить установившуюся
температуру в калориметре. Удельная теплоемкость воды св = 4,2 Дж/(г-К),
льда - сл = 2,1 Дж/(г-К), удельная теплота плавления льда X = 333 Дж/г, плот-
ность воды рв = 103 кг/м3, льда - рл = 900 кг/м3. Теплоемкостью калориметра
пренебречь.
1130. Теплоизолированный сосуд содержит mi =2 кг льда и т2= 10 кг
воды при общей температуре tt = 0°С. В сосуд подают водяной пар при тем-
пературе t2 = 100°С. Какая масса воды окажется в сосуде, когда там устано-
вится температура = 80°С? Удельная теплоемкость воды с = 4,2 кДж/(кг-К),
удельная теплота плавления льда X = 0,33 МДж/кг, удельная теплота парооб-
разования воды г = 2,26 МДж/кг. Теплоемкостью сосуда пренебречь.
118
11.31. В теплоизолированный сосуд, содержащий т1 = 50 г водяных паров
при температуре = 100°С, поместили кусочек льда массой т2 = 100 г при
температуре t2 = - 5°С. Какая температура установится в сосуде? Удельная
теплота плавления льда X = 333 Дж/г, удельная теплота парообразования воды
г = 2260 Дж/г, удельная теплоемкость воды св = 4,2 Дж/(г-К), удельная тепло-
емкость льда сл = 2,1 Дж/(г-К). Теплоемкостью сосуда пренебречь.
1132. В теплоизолированном латунном сосуде массой тх = 200 г нахо-
дится т2 = 1 кг льда при температуре tx = -10°С. В сосуд помещают т2 = 200 г
пара при температуре t2= 110°С. Какая температура установится в сосуде?
Удельная теплоемкость латуни с} = 400 Дж/(кг-К), воды - с - 4200 Дж/(кг-К),
льда - с2 = 2100 Дж/(кг-К), удельная теплоемкость пара в интервале темпера-
тур [100°С-г 110°С] с3 = 1670 Дж/(кг-К), удельная теплота плавления льда
Х = 0,33 МДж/кг, удельная теплота парообразования воды г = 2,26 МДж/кг.
11.33. В электрический чайник мощностью N= 1 кВт наливают V= 2 л
воды при температуре t = 18°С и включают в сеть. Через какое время вся вода
испарится? К.п.д. нагревателя т| = 50%. Удельная теплоемкость воды
с = 4,2 кДж/(кг-К), удельная теплота парообразования воды г = 2,26 МДж/кг,
плотность воды р = 103 кг/м3.
• Решение. К.п.д. чайника определяется как отношение суммарного количества теплоты,
которое идет на нагревание воды до температуры кипения гк = 100°С
61 = с m (Гк - О
и парообразование
62 = г т,
к количеству энергии, получаемой нагревателем чайника от сети:
E = xN,
где т - время, за которое вода закипит, т.е.
61 + 62 с т ('к “ О + г т
ИЛИ Л=-----------------
Следовательно,
рК[с(Гк-0 +г]
т =--------------я 3 часа.
п N
Р V [с (tK -t) + г]
• Ответ', т =-------------® 3 часа.
т| N
11.34. В электрическом чайнике мощностью У =800 Вт можно вскипя-
тить V= 1,5 л воды, имевшей начальную температуру / = 20°С, за т = 20 мин.
Найти к.п.д. чайника. Удельная теплоемкость воды с = 4,2 кДж/(кг-К), плот-
ность воды р = 103 кг/м3.
11.35. Сосуд с тх = 100 г воды при температуре tx = 0°С был подвешен
посередине комнаты. Через промежуток времени Tj = 15 мин температура
воды поднялась до t2 = 2°С. Когда же в сосуде изначально при той же тем-
пературе находилось т2 = 100 г льда, то он растаял за время т2= 10 часов.
119
Оценить удельную теплоту плавления льда, если удельная теплоемкость
воды с = 4200 Дж/(кг-К).
11.36. Кусок льда с начальной температурой / = -20°С и массой
т = 0,8 кг растопили на электроплитке мощностью У = 1 кВт. Полученную
воду довели до кипения и кипятили до тех пор, пока четвертая часть ее ис-
парилась. Время всего процесса т = 40 минут. Определить к.п.д. плитки.
Удельная теплоемкость льда сл = 2,1 кДж/(кг-К), воды св = 4,2 кДж/(кг-К),
удельная теплота плавления льда А = 330 кДж/кг, удельная теплота парообра-
зования воды г = 2,26 МДж/кг.
11.37. При изготовлении льда в бытовом холодильнике температура воды
за Т] = 5 мин понизилась с Ч = 16°С до t2 = 12°С, и еще через т2 = 1 час 55 мин
вода превратилась в лед. Найти удельную теплоту А плавления льда, если
удельная теплоемкость воды с = 4200 Дж/(кг-К). Мощность, потребляемая хо-
лодильником, постоянна.
11.38. За время т = 2 часа в холодильнике превращается в лед при тем-
пературе = 0°С масса воды т = 7,2 кг, имевшая начальную температуру
tQ = 20°С. Какая мощность потребляется холодильником от электросети, если
он отдает в окружающее пространство в единицу времени количество тепло-
ты No = 700 Дж/с? Удельная теплоемкость воды с = 4200 Дж/(кг-К), удельная
теплота плавления льда А = 0,33 МДж/кг.
11.39. Для нахождения удельной теплоемкости воды определяли вре-
мя, затраченное на образование льда в бытовом холодильнике. В одном из
опытов получили, что для охлаждения воды, взятой при температуре = 4°С, до
температуры /2 = 0°С потребовалось Tj = 5 мин. Еще т2= 107,5 мин понадо-
билось для превращения охлажденной воды в лед с температурой = - 12°С.
Используя данные опыта, найти удельную теплоемкость воды. Удельная теп-
лоемкость льда с = 2100 Дж/(кг-К), удельная теплота плавления льда
А = 0,33 МДж/кг.
11.40. При нагревании некоторой массы воды от t0 = 0°С до температуры
кипения t= 100°С на электрическом нагревателе понадобилось Tj = 15 мин.
После этого потребовалось т2 = 80 мин для превращения этой воды в пар.
Определить удельную теплоту парообразования. Удельная теплоемкость воды
с = 4200 Дж/(кг-К).
11.41. В чайник налили воду при температуре /0 = 10°С и поставили на
электроплитку. Через = 10 мин вода закипела. Через какое время вода пол-
ностью выкипит? Удельная теплоемкость воды с = 4200 Дж/(кг-К), удельная
теплота парообразования г = 2,26 МДж/кг.
Теплота сгорания топлива
11.42. На реактивном авиалайнере установлено п = 4 двигателя, каждый
из которых при полной нагрузке развивает силу тяги FT = 40 кН. Оценить
120
количество топлива, необходимое самолету для преодоления расстояния
5 = 103 км, если удельная теплота сгорания топлива q = 40 МДж/кг, а к.п.д.
двигателя Г) = 40%.
• Решение. Из количество теплоты Q, которое выделяется при сгорании топлива
6 = 9 (1)
на полезную работу А идет
A = i\Q. (2)
С другой стороны, работа силы тяги п двигателей на пути S равна
А = п FT S. (3)
Приравнивая правые части выражений (2) и (3) с учетом (1), получим
д q т = п FT S.
Откуда находим
nFTS . 14
• Ответ: т =---~ 10* кг.
П Ч
11.43. Пуля массой М= 9 г вылетает из ствола винтовки со скоростью
о = 900 м/с. Определить к.п.д. выстрела, если масса порохового заряда т = 4 г,
а его удельная теплота сгорания q = 300 МДж/кг.
11.44. Мощность двигателя автомобиля N= 100 кВт. Сколько бензина
расходует автомобиль за т = 1 час работы, если к.п.д. двигателя т] = 30%,
а удельная теплота сгорания бензина q = 46 МДж/кг?
11.45. Судно развивает мощность N= 1500 кВт при к.п.д. двигателя
т] = 30%. Найти расход топлива на один километр пути при скорости дви-
жения о = 72 км/час. Удельная теплота сгорания топлива q = 50 МДж/кг.
11.46. Реактивный самолет пролетает со скоростью о = 900 км/час
расстояние 5= 1800 км, затрачивая массу топлива т = 4 т. Мощность
двигателя самолета У =5900 кВт, к.п.д. т]=23%. Какова удельная теп-
лота сгорания топлива, применяемого на самолете?
11.47. На сколько километров пути хватит одной заправки автомобиля
(объем бака К =40 л) при средней скорости движения о = 60 км/час, если
к.п.д. двигателя равен т| = 50%, а развиваемая автомобилем мощность
N= 40 кВт? Плотность бензина р = 700 кг/м3, удельная теплота сгорания
q = 46,1 МДж/кг.
11.48. Двигатель представляет собой идеальную тепловую машину с
максимально возможным к.п.д., у которого Т\ и Т2 - температуры нагре-
вателя и холодильника соответственно. Сколько топлива расходует двига-
тель за время т = 1 с, если его мощность N, а удельная теплота сгорания
топлива q?
11.49. Для нагревания на спиртовке М = 300 г воды в железном сосуде
теплоемкостью С = 42 Дж/К от температуры fj = 18°C до температуры
121
Z2 = 68°C было израсходовано т = 1 г спирта. Найти к.п.д. спиртовки, если
удельная теплоемкость воды с = 4,2 кДж/(кг-К), удельная теплота сгорания
спирта q = 29,3 МДж/кг.
11.50. Газовая нагревательная колонка потребляет Ко = 1,8 м3 метана СН4
в час. Найти температуру воды, подогреваемой этой колонкой, если вытекаю-
щая струя воды имеет скорость и = 50 см/с. Диаметр струи <7=1 см, начальная
температура воды /= 11°С. К.п.д. нагревателя Т| = 60%. Метан находится под
давлением р = 105 Па. Удельная теплоемкость воды с = 4,2 кДж/(кг-К), плот-
ность воды р= 103 кг/м3, удельная теплота сгорания метана q = 54,4 МДж/кг,
молярная масса метана ц = 16-10'3 кг/моль.
11.51. Какое количество природного газа надо сжечь, чтобы т = 4 кг
льда, взятого при температуре tx = -20°С, превратить в пар с температурой
/2=100°С? К.п.д. нагревателя т| = 60%. Удельная теплоемкость воды
= 4,2 кДж/(кг-К), удельная теплоемкость льда с2 = 2,1 кДж/(кг-К), удельная
теплота плавления льда X = 0,33 МДж/кг, удельная теплота парообразования
г = 2,26 МДж/кг, удельная теплота сгорания газа q = 34 МДж/кг.
Превращение механической энергии в тепловую
11.52. С какой минимальной скоростью свинцовая пуля должна ударить
в подвижный экран, чтобы расплавиться? Считать, что удар абсолютно не-
упругий, а на нагрев и плавление пули идет ц = 60% энергии деформации.
Масса пули т = 10 г, масса экрана М = 1 кг. Удельная теплоемкость свинца
с= 130 Дж/(кг-К), удельная теплота плавления свинца А. = 25 кДж/кг, темпе-
ратура плавления свинца = 600 К. К моменту удара пуля имела темпера-
туру/0= 100°С.
• Решение. Так как удар пули об экран абсолютно неупругий, то часть механический
энергии системы «пуля-экран» перейдет в тепло. Считая систему в направлении ее дви-
жения замкнутой, из законов сохранения импульса и энергии
т и = (М+ т) и, m и2 = '/г (Л/+ т) и2 + Q
найдем скорость и системы после соударения и количество теплоты Q, выделившейся
при ударе:
_ т u ci - т А/°2
М + т ’ 2 (Л/+т)
По условию задачи на нагрев и плавлении пули идет энергия, равная
С другой стороны, на нагрев пули от начальной температуры 10 до температуры
плавления = 337°С и на плавление свинца необходимо количество теплоты
Q1 = с т ((„л - Го) + X т.
Следовательно, на основании уравнения теплового баланса, получим
„ п mA/о2 г
Qi=,Qi, или ц -т = т[с(Гпл-Г()) + Х].
Z \М + ТП)
122
Откуда находим
л/2(Л/+т)[с((пл-<0) + Х] _ ,
о = ’----------—---------» 420 м/с.
q М
„ л/2(Л/+т)[с(Гпл-/0) + 1] _ ,
Ответ-, о = ’---------—--------» 420 м/с.
г| м
11.53. С какой высоты должна упасть капля воды, чтобы при ударе о
землю она нагрелась на Д/=1°С? Сопротивлением воздуха пренебречь.
Удельная теплоемкость воды с = 4200 Дж/(кг-К). Ускорение свободного паде-
ния считать постоянным.
11.54. С какой наименьшей высоты должна упасть льдинка, чтобы при
ударе о землю она растаяла? Сопротивлением воздуха пренебречь. Началь-
ная температура льдинки /=0°С. Удельная теплота плавления льда
А = 0,33 МДж/кг. Считать, что при ударе т| = 80% энергии идет на плавление
льдинки. Ускорение свободного падения считать постоянным.
11.55. На сколько возрастает температура воды у подножия 50-метрового
водопада? Удельная теплоемкость воды с = 4200 Дж/(кг-К).
11.56. С какой наименьшей высоты должны были бы свободно падать
дождевые капли, чтобы при ударе о землю от них не осталось мокрого места?
Начальная температура капель /0 = 20°С. Удельная теплоемкость воды
с = 4200 Дж/(кг-К), удельная теплота парообразования г = 2,26 МДж/кг. Со-
противление воздуха не учитывать. Ускорение свободного падения считать
постоянным.
11.57. Бензовоз, двигавшийся со скоростью и = 36 км/час, резко затормо-
зил. Определить, на сколько градусов поднялась температура перевозимого в
цистерне бензина. Удельная теплоемкость бензина с = 2200 Дж/(кг-К).
11.58. Стальной шар, падая свободно, достиг скорости и = 41 м/с и, уда-
рившись о землю, подскочил на высоту h = 1,6 м. Определить изменение тем-
пературы шара, считая, что т] = 50% выделившейся при ударе теплоты идет
на увеличение внутренней энергии шара. Удельная теплоемкость стали
с = 460 Дж/(кг-К). Сопротивление воздуха не учитывать.
11.59. Стальной шарик падает с высоты hY = 10 м на гладкую горизон-
тальную поверхность. После удара он поднимается на высоту /^ = 1 м. На
сколько поднимется температура шарика после удара, если он получает
г| = 60% выделившегося при ударе количества теплоты? Удельная теплоем-
кость стали с = 460 Дж/(кг-К). Сопротивление воздуха не учитывать.
11.60. Свинцовая пуля, летевшая со скоростью и, =420 м/с, попадает в
закрепленную стальную плиту и отскакивает от нее со скоростью
и2 = 310 м/с. Какая часть пули расплавится, если температура пули в мо-
мент удара была равна tl = 107°С, а на нагревание и плавление идет
Т| = 75% выделившейся при ударе энергии? Удельная теплоемкость свинца
123
с = 130 Дж/(кг-К), температура плавления Гщ, = 600 К, удельная теплота плав-
ления X = 25 кДж/кг.
11.61. При выстреле вертикально вверх свинцовая пуля ударилась о
неупругую преграду и расплавилась. На какой высоте произошло это
столкновение, если начальная скорость пули и0 = 350 м/с, а на нагревание
и плавление пули ушло т| = 50% выделившегося количества теплоты? Тем-
пература пули в момент соударения fo=lOO°C, температура плавления
свинца Т= 600 К, удельная теплоемкость свинца с= 120 Дж/(кг-К), удель-
ная теплота плавления X = 2 кДж/кг. Сопротивление воздуха не учитывать.
11.62. С какой минимальной скоростью относительно поверхности кос-
мического корабля должен двигаться небольшой железный метеорит,
чтобы расплавиться в результате удара? Считать, что удар абсолютно не-
упругий и до столкновения температура метеорита равна То= 100 К, а на
плавление и нагревание идет т] = 25% выделившейся при ударе энергии.
Удельная теплоемкость железа с = 460 Дж/(кг-К), температура плавления
железа tnjI= 1535°С, удельная теплота плавления Х = 270 кДж/кг.
11.63. Свинцовая дробинка, летящая со скоростью и = 100 м/с, попа-
ла в закрепленную доску и застряла в ней. На сколько градусов измени-
лась температура дробинки, если т] = 52% выделевшегося при ударе коли-
чества теплоты пошло на ее нагревание? Удельная теплоемкость свинца
с = 130 Дж/(кг-К).
11.64. Свинцовая пуля, летящая горизонтально со скоростью и = 100 м/с,
пробила брусок, лежащий на гладком горизонтальном столе, и вылетела
из него, потеряв половину своей первоначальной скорости. На сколько из-
менилась температура пули, если т] = 26% выделившегося при ударе коли-
чества теплоты пошло на ее нагревание? Масса бруска в п = 10 раз больше
массы пули. Удельная теплоемкость свинца с= 130 Дж/(кг-К).
11.65. Два одинаковых кусочка льда летят навстречу друг другу с рав-
ными скоростями и при ударе обращаются в пар. Оценить минимально
возможные скорости льдинок перед ударом, если их температуры равны
f = -12°C. Удельная теплоемкость льда <^ = 2,1-Ю3 Дж/(кг-К), воды -
с2 = 4,2103Дж/(кг-К), удельная теплота плавления льда Х = 3,3-105 Дж/кг,
удельная теплота парообразования воды г = 2,3-106 Дж/К.
Насыщенные и ненасыщенные пары
11.66. В цилиндрическом сосуде под поршнем при температуре t = 100°С
находится насыщенный водяной пар. При изотермическом вдвигании порш-
ня выделилось количество теплоты 0= 180 Дж. Найти совершенную при
этом работу А. Удельная теплота испарения воды г = 2,26 МДж/кг. Моляр-
ная масса воды р. = 0,018 кг/моль.
124
• Решение. Так как пар насыщенный, то при вдвигании поршня будет происходить его
конденсация и давление пара меняться не будет. Следовательно, работа может быть оп-
ределена как
Л =Рц ДК,
где рИ - упругость насыщенных водяных паров при данной температуре, ДК= - К2 - из-
менение объема, занимаемого паром.
Записав уравнение состояния пара до и после вдвигания поршня
т, _ т2 _
p„V2 = -±RT,
г* Н
(где т2 - начальная и конечная массы пара под поршнем соответственно), выражение
для работы можно переписать в виде
tjnRT
А =------------=--------.
Н И
Тепло, выделившееся при вдвигании поршня и конденсации Дги [кг] пара, равно
Q = r tun.
Следовательно,
A = QJLLX 13>7
Г ц
• Ответ: А = ж 13,7 Дж.
ГЦ
11.67. В вертикальном теплоизолированном цилиндре под легким порш-
нем площадью 5= 100 см2 находится тп= 1,8 г насыщенного водяного пара
при температуре Гп = 100°С. В цилиндр впрыскивают тв = 1,8 г воды при тем-
пературе tB = 0°С. Куда и на сколько переместится поршень? Атмосферное
давление р0 = 105 Па. Удельная теплоемкость воды с = 4,2 кДж/(кг-К), удель-
ная теплота парообразования г = 2,26 МДж/кг. Теплоемкостью цилиндра и
поршня пренебречь. Молярная масса воды ц = 0,018 кг/моль, плотность воды
р = 103 кг/м3.
• Решение. Очевидно, что после впрыскивания воды пар в сосуде будет конденсироваться,
отдавая энергию на нагрев воды. Однако, исходя из условия задачи неизвестно, весь пар
при этом сконденсируется, или только его часть. Для установления этого проведем пред-
варительный числовой анализ.
1. Количество теплоты, которое может отдать пар при конденсации, равно
01 = г тп * 4068 Дж.
2. Количество теплоты, необходимое для нагревания воды до температуры кипения /п:
02 = с тв 0п ~ 'в) ~ 756 Дж-
Сравнивая Q\ и Q2, видим, что для нагревания воды до температуры Гп нужно мень-
ше тепла, чем может дать пар при полной конденсации. Это означает, что сконденсируется
только часть пара массой т0, которую найдем из уравнения теплового баланса:
г т0 = с тв (/п - /в).
Откуда находим
ств(/п-/в)
«о =-------» 0,334 г.
125
Следовательно, объем смеси «вода-пар» под поршнем станет равен
Р^в+Гп,
где Кв = (mB + т0)/р - объем, занимаемый водой; Гп - объем, занимаемый паром, который
найдем, используя уравнение Менделеева-Клапейрона:
mn-m0
Ро?п =—~—RT>
где ро = 105 Па - давление пара под поршнем (равное атмосферному давлению, так как
поршень невесомый), а Т= 373 К - температура пара. С учетом этого
тя + тп тп- тп ,
К= -5----2 + -°-s R Т~ 0,0023 м3.
Р РРо
Так как объем, занимаемый паром до впрыскивания воды, был равен
Го = — Л7’~ 0,0031 м3,
РРо
то поршень переместится вниз на величину
., ЛК ,
Wl =: ——- = « 6 СМ.
о о
• Ответ: поршень переместится вниз на АЛ к 6 см.
11.68. Удельная теплота парообразования воды при температуре t = 100°С
равна г - 2,26 МДж/кг. Какая часть теплоты парообразования идет на увели-
чение внутренней энергии системы? Молярная масса воды ц = 0,018 кг/моль.
11.69. В сосуд с поршнем налит слой воды толщиной h = 1 мм при тем-
пературе t = 20°С. На какую наименьшую высоту неодходимо поднять пор-
шень, чтобы вся вода испарилась? Плотность воды р= 103 кг/м3, молярная
масса ц = 0,018 кг/моль. Упругость насыщенных водяных паров при 20°С
равна рн = 2,33 кПа. Температура постоянна. Воздуха под поршнем нет.
11.70. В цилиндрическом сосуде под поршнем при температуре Т = 350 К
находится насыщенный водяной пар. При изотермическом вдвигании поршня
была совершена работа А = 2 кДж. Определить массу сконденсировавшегося
пара. Молярная масса воды ц = 0,018 кг/моль.
11.71. В цилиндрическом сосуде под легким поршнем площадью
S = 510'3 м2 находится т = 300 г воды при температуре t = 20°С. Воде сооб-
щили количество теплоты Q = 101,7 кДж. На какую высоту поднимется пор-
шень? Атмосферное давление р0 = 105 Па. Удельная теплоемкость воды
с = 4200 Дж/(кг-К), удельная теплота парообразования г = 2,26 МДж/кг. Мо-
лярная масса воды ц = 0,018 кг/моль. Воздуха под поршнем нет.
11.72. Пробирка погружена вертикально в широкий сосуд с водой запа-
янным концом вверх так, что расстояние от поверхности воды до запаянного
конца равно I = 2 м. При температуре = 20°С уровень воды в пробирке со-
впадает с уровнем воды в сосуде. На сколько опустится уровень воды в пробир-
ке, если температуру системы увеличить до t2 = 75°С? Упругость насыщенных
126
водяных паров при 75°С равна рн = 40 кПа, плотность воды р = 103 кг/м3, атмо-
сферное давление р0 = 105 Па. Упругостью насыщенных паров при 20°С пре-
небречь.
• Решение. Первоначально в пробирке находился
только воздух при давлении а после нагревания
системы - воздух н насыщенный водяной пар при дав-
лении р2. Давление смеси р2 будет равно сумме пар-
циальных давлений (закон Дальтона):
Р2 -Рн +Р{>
где р{ - парциальное давление воздуха.
С другой стороны очевидно, что (см. рис. 11.2)
Pl =Р0’ P2=Po + Pgx-
Рис. 11.2
Следовательно,
Рн+Р{ = P0 + pgx,
или
или
р{ =po-Ph+ps*- (1)
Из уравнения Менделеева-Клапейрона для воздуха при начальной температуре и
смеси воздуха и водяного пара при температуре 12
p0lS = vBR7\,
р{ (l + x)S = vBRT2,
pH(l + х) S = vn RT2
(где vB,vn-число молей воздуха и пара в пробирке соответственно) и выражения (1)
получим Р01Т2
^^=Р0~Рн + Р8Х’
pgPlx2 + Tl(po-pH + pgl)x-l[po(r2-Tl)+pHTI] = O.
Откуда находим
- <Ро ~Рн + Р g I) + ^(Ро-Рн + Pgl)2 +4pglTi [Ро(Т1-Т\)+рнТ\]
=-------------------------------------------------------» 1,27 м.
2pg7)
„ - (Ро -Рн+ Р gО + (Ро -Рн + Рg О* +4р g Z Л [р0 (Г2 - ГО +рн Т]]
•Ответ: х---------------------------------------------------— м.
2pgTi
11.73. Пробирка погружена вертикально в широкий сосуд с водой от-
крытым концом вниз на глубину, равную половине ее длины. При темпе-
ратуре t] = 0°С уровень воды в пробирке совпадает с уровнем воды в сосуде.
При какой максимальной длине пробирки воздух из нее начнет выходить,
если температуру системы довести до t2= 100°С? Атмосферное давление
р0 = 105 Па, плотность воды р = 103 кг/м3. Упругостью насыщенных паров при
0°С пренебречь.
11.74. Пробирка погружена вертикально в широкий сосуд с водой запа-
янным концом вверх так, что расстояние от поверхности воды до запаянного
127
конца равно 1 = 3 м. При температуре t = 85°С уровень воды в пробирке со-
впадает с уровнем воды в сосуде. Куда и на сколько сместится уровень воды
в пробирке, если ее опустить на h = 1,8 м? Упругость насыщенных водяных
паров при 85°С равна рн = 60 кПа, плотность воды р = 103 кг/м3, атмосферное
давление р0 = 105 Па.
11.75. Пробирка погружена вертикально в широкий сосуд с водой запа-
янным концом вверх так, что расстояние от поверхности воды до запаян-
ного конца равно Z = 2 м. При температуре t = 75°С уровень воды в пробирке
на некоторую величину х выше уровня воды в сосуде. Когда пробирку смес-
тили вниз на h = 1,2 м, то уровни воды в пробирке и сосуде сравнялись. Оп-
ределить величину х. Упругость насыщенных водяных паров при 75°С равна
рн = 40 кПа, плотность воды р = 103 кг/м3, атмосферное давление р0= 105 Па.
11.76. Пробирка ногружена вертикально в широкий сосуд с водой запа-
янным концом вверх так, что расстояние от поверхности воды до запаянного
конца равно I = 2,5 м. При температуре = 100°С уровень воды в пробирке
на некоторую величину х ниже уровня воды в сосуде. При охлаждении сис-
темы до /2 = Ю°С уровень воды в пробирке стал выше уровня воды в сосуде
на такую же величину х. Найти значение х. Плотность воды р = 103 кг/м3,
атмосферное давление р0 = 105 Па. Упругостью насыщенных паров при 10°С
пренебречь.
11.77. В трубке, которая погружена вертикально в широкий сосуд с водой
запаянным юнцом вверх, над поверхностью воды находится смесь гелия
и насыщенного водяного пара при температуре t = 17°С и занимает объем
К=30 см3. При этом уровень воды в трубке находится на х= 10 см выше
уровня воды в сосуде. Найти массы гелия и водяных паров в трубке. Моляр-
ная масса воды ц, = 18-10'3 кг/моль, гелия - ц2 = 4-10'3 кг/моль, плотность
воды р=103 кг/м3. Упругость насыщенных паров воды при 17°С равна
рн= 1,94 кПа, атмосферное давление р0 = 105 Па.
• Решение. Так как в трубке одновременно находятся гелий и насыщенный водяной пар,
то давление смесн будет равно сумме парциальных давлений (закон Дальтона):
Р=Р\ +Ръ
где Pi =рн- давление паров воды, р2 - давление гелия. С другой стороны, давление смесн
равно
P=Po~pgx-
Следовательно,
Рн+/’2=Ро-Р?Л>
или
Р2= Ро~ Рн~ Р g Х‘ О)
Из уравнения Менделеева-Клапейрона для водяного пара и гелия
рнК= —ЙГ, p2V=~RT
Hl Н2
128
и выражения (1) получим
,„,„.7 Р2?Р2 (Ро-Рн-Pg^V^
т' = ЯТ'* 4,310 кг’ 2 = ~R~f~~------R~f-------“4,9-10 кг.
„ PhV^i (Po-PH-Pgx)^ll2 Л„,„л
• Ответ: тх = — -» 4,3-10 'кг, т2 =-------------» 4,9-Ю41 кг.
К 1 К 1
11.78. В сосуде объемом V= 1 м3 находится смесь воздуха с парами эфира
при температуре Т = 303 К и давлении р = 107 кПа. Найти массы воздуха и
эфира в сосуде, если конденсация паров эфира начинается при Т0 = 273 К.
Упругость насыщенных паров эфира при температуре 273 К равна
рн = 24,4 кПа. Молярная масса эфира ц, = 74-10'3 кг/моль, молярная масса воз-
духа - Иг = 29-10"3 кг/моль.
Точка росы. Влажность
11.79. В запаянной трубке объемом К= 0,4 л находится водяной пар под
давлением р = 8,5-103 Па при температуре Тх =423 К. Какое количество Аги
росы выпадет на стенки трубки при охлаждении ее до Т2 = 295 К? Упругость
насыщенных водяных паров при температуре Т2 = 295 К равна рн = 2,64 кПа,
молярная масса воды р.= 18-Ю’3 кг/моль.
• Решение. В задаче рассматриваются два состояния пара в трубке - до и после охлаж-
дения. Независимо от того, каким был пар в начальном состоянии (насыщенным или не-
насыщенным), при конечной температуре Т2 = 295 К пар будет насыщенным. В этом легко
убедиться, записав уравнение Менделеева-Клапейрона для пара при температуре Т2, по-
лагая пар ненасыщенным:
m> и,
/>2^ = — RT2, или й = —И2,
р Ц V
где - масса пара в начале процесса охлаждения.
Используя уравнение состояния пара при температуре Тх
т, _
pV=-±RTb (1)
получим
р2=р Т2/Т\ « 5,93-Ю3 Па.
Как видим, давление пара массой т( при конечной температуре Т2 должно превы-
шать давление насыщенного пара рн = 2,64 103 Па. Но, так как рн-это максимальное
давление пара при данной температуре, то это означает, что, начиная с некоторой темпе-
ратуры (точки росы), пар начнет конденсироваться.
Из уравнения состояния (1) для пара в начале процесса охлаждения и уравнения
состояния насыщенного пара при конечной температуре
рнК=^ЯТ2
Н
(где т2 - масса пара в конце процесса), найдем массу росы, выпавшей на стенках трубки:
Дл1 = т, -т2 = ^у-{^--ф^ }»9,65-10’6 кг.
• Ответ: Лт = » 9,65-ИГ6 кг.
л *• 11 12 '
129
и.
р V= — RT,
Н
Откуда получим
11.80. Чему равна абсолютная и относительная влажность воздуха, за-
полняющего баллон емкостью V = 700 л при температуре t = 24°С, если до
полного насыщения пара понадобилось испарить в этот объем воду массой
т = 6,2 г? Упругость насыщенных водяных паров при этой температуре равна
ри = 3 кПа, молярная масса воды р.= 18-Ю"3 кг/моль.
• Решение. Массу воды, которую необходимо испарить в баллоне для полного насыщения
пара, можно представить как разность между массой пара mb который был первоначально
в баллоне, и массой пара т2, которая будет в баллоне после испарения воды:
m = m2-mt.
Запишем уравнение Менделеева-Клапейрона для пара до и после испарения воды:
т2 „
рнУ= — ПТ.
И
рУ, ,
т = т2-т]=^у(рн-р).
Следовательно, первоначальное давление пара н его масса равны
mRT ррУ РРн’''
Р = Рн~~^’ m^RT='RT-~m-
По определению абсолютной р и относительной <р влажности, получим
р = ^ = ^ " 13 г/м3, <₽ = -£-• 100% = { 1 -100%~60%.
V RT V рн ( ЦДН V J
• Ответ', р = » 13 г/м3, <р = I 1 - m I • 100% * 60%.
Л / И Црн И
11.81. Абсолютная влажность воздуха при температуре Т = 300 К равна
р = 10 г/м3. Чему равна относительная влажность воздуха, если плотность на-
сыщенных паров воды при этой температуре равна рн = 25,8 г/м3?
11.82. Найти абсолютную влажность воздуха при температуре t = 50°С,
если давление водяных паров равно р = 8 кПа. Молярная масса воды равна
ц = 18-10'3 кг/моль.
11.83. Найти давление паров воды в воздухе с относительной влажностью
Ф = 80%, если упругость насыщенных паров воды при этой температуре равна
рп = 12,3 кПа.
11.84. В комнате объемом У= 150 м3 поддерживается постоянная темпе-
ратура Тх = 293 К, а точка росы равна Г2 = 283 К. Определить относительную
влажность воздуха и массу водяных паров в комнате. Упругость насыщенных
паров при Т\ =293 К равна рн1 =2,3-103 Па, при температуре Г2 = 283 К -
ри2 = 1.2-103 Па, молярная масса воды ц= 18-10'3 кг/моль.
11.85. В сосуде находится воздух и насыщенный водяной пар при тем-
пературе t0 = 100°С и давлении р = Зр0, где р0 = 105 Па - атмосферное давле-
ние. Каким будет давление в сосуде при понижении температуры до t = 10°С?
Давлением насыщенных паров при t= 10°С пренебречь.
11.86. На некоторой высоте над поверхностью Земли слой воздуха объ-
емом V= 106 м3 имеет температуру =20°С при относительной влажности
130
<р = 70%. Воздух охладился до t2 = 10°С. Найти массу выпавшего дождя. Плот-
ность насыщенного водяного пара при температурах t2 равна соответст-
венно рн ] = 17,3 г/м3 и ри 2 = 9,4 г/м3.
11.87. Воздух имеет температуру = 60°С при абсолютной влажности
Pi = 50 г/м3. Какой будет абсолютная влажность р2 этого воздуха, если тем-
пература понизится до t2 = 10°С? Упругость насыщенных паров воды при
10°С равна ря = 1230 Па. Молярная масса воды р. = 18-10’3 кг/моль.
11.88. В цилиндре под легким поршнем в пространстве объемом
И, = 1,5 л находится воздух и насыщенный водяной пар при температуре
= 20°С. Какова будет относительная влажность воздуха в цилиндре, если
объем уменьшить до V2 = 0,1 л, а температуру повысить до t2 = 100°С? Упру-
гость насыщенных водяных паров при 20°С равна рн = 2,2-103 Н/м2. Атмосфер-
ное давление р0 = 1 атм.
11.89. Плотность насыщенного водяного пара при 1 = 25°С равна
рн = 23 10'3 кг/м3. Найти абсолютную влажность воздуха при этой темпера-
туре, если его относительная влажность <р = 50%.
11.90. Когда и во сколько раз больше абсолютная влажность воздуха: в
ноябре при температуре Т] = 0°С и влажности <р,=95% или в июле при
t2 = 35°С и влажности <р2 = 40%, если упругость насыщенных водяных паров
при 0°С равна рх = 600 Па, а при 35°С равна р2 = 5,5 кПа?
11.91. Определить относительную влажность воздуха, взятого при тем-
пературе Т = 363 К и давлении р = 105 Па, если отношение массы пара к массе
влажного воздуха в некотором объеме равно wn//nB = 0,25. Отношение мо-
лярных масс воды и сухого воздуха Цд/Цв - 0,6. Упругость насыщенных во-
дяных паров при этой температуре равна ри = 70 кПа.
11.92. Плотность влажного воздуха при температуре t = 27°С и давлении
р= 105 Па равна рв= 1,19 кг/м3. Определить абсолютную и относительную
влажность воздуха, если при температуре 27°С плотность насыщенных паров
равна рн = 0,027 кг/м3. Молярная масса воды щ = 18-Ю'3 кг/моль, молярная
масса воздуха Ц2 = 29-10'3 кг/моль.
11.93. Влажный воздух массой m = 1 г находится при температуре t = 25°,
давлении р = 745 мм рт. ст. и имеет относительную влажность <р = 40%. Найти
объем, занимаемый этим воздухом. Упругость насыщенных водяных паров
при 25°С равна рн = 23,3 мм рт. ст., плотность ртути р= 13,6103 кг/м3, мо-
лярная масса сухого воздуха ц1=29Ю"3 кг/моль, молярная масса воды
Р2 = 18-10’3 кг/моль.
11.94. В помещении объемом К=30 м3 при температуре 1 = 20°С отно-
сительная влажность воздуха равна <р = 60%. Определить упругость насы-
щенных водяных паров при этой температуре, если масса испарившейся в
помещении воды т = 31 г. Молярная масса воды равна |г= 18-10'3 кг/моль.
131
11.95. В герметически закрытый котел объемом И=5 м3 накачали
тв = 20 кг воды и затем котел нагрели до температуры t = 180°С. Найти массу
водяного пара и его давление в котле, если известно, что плотность насы-
щенных водяных паров при температуре 180°С равна рн = 5,05 кг/м3, моляр-
ная масса воды ц= 18-10'3 кг/моль.
11.96. В сосуде объемом V= 5 м3 при температуре t = 20°С находится
воздух с относительной влажностью ф0 = 20%. В сосуд ввели некоторое ко-
личество воды при температуре t, = 0°С. Найти относительную влажность воз-
духа в сосуде после полного испарения воды, если температуру сосуда
поддерживают равной 20°С, а в процессе установления равновесия сосуду
сообщено количество тепла £)=58,4-103 Дж. Упругость насыщенных водя-
ных паров при 20°С равна рн = 2,3-103 Па. Удельная теплоемкость воды
с = 4,2 кДж/(кг-К), удельная теплота парообразования г = 2,26 МДж/кг. Мо-
лярная масса воды |л= 18-10-3 кг/моль.
11.97. В сосуд объемом У= 10 дм3 поставили блюдце, содержащее т = 1 г
воды. После этого сосуд герметически закрыли и оставили при температуре
t = 20°С, при которой упругость насыщенных паров воды равна рн = 2,3 кПа.
Какая часть воды испарится? Объемом блюдца пренебречь. Молярная масса
воды |л= 18-10"3 кг/моль.
11.98. Сухой воздух заполняет закрытый сосуд объемом К=25 л при
давлении рх = 105 Па и температуре tt = -23°С. В сосуд кладут кусок льда
массой т = 9 г и нагревают сосуд до температуры t2 = 127°С. Определить дав-
ление влажного воздуха в сосуде. Упругость насыщенных водяных паров при
127°С равнаръ = 2,5-Ю5 Па. Молярная масса воды ц= 18-10'3 кг/моль.
11.99. В сосуде объемом К= 1 м3 при температуре t = 20°С находится
воздух с относительной влажностью ф, = 30%. Чему станет равной относи-
тельная влажность после добавления в сосуд /и = 20 г воды? Температура
поддерживается постоянной. Упругость насыщенных водяных паров при
20°С равна рн = 2,2-103 Па. Молярная масса воды ц = 18-10‘3 кг/моль.
11.100. В помещении объемом 60 м3 температура воздуха повыси-
лась с Zj = 17°С до t2 = 21°С, при этом влажность увеличилась с q>j = 40% до
Ф2 = 60%. Какая масса воды испарилась в воздух? Упругость насыщенных
водяных паров при температуре 17°С равна рн1 = 1,94-103 Па, а при 21 °C
ри2 = 2,49 кПа. Молярная масса воды ц= 18-10"3 кг/моль.
11.101. В комнате объемом V = 40 м3 воздух имеет температуру t = 20°С
и относительную влажность <Pj = 20%. Сколько нужно испарить воды в этой
комнате, чтобы относительная влажность ф2 достигла 50%? Упругость насы-
щенных паров воды при 20°С равна рн = 2,33-103 Па. Молярная масса воды
ц = 18-10'3 кг/моль.
132
11.102. Относительная влажность воздуха, заполняющего сосуд объемом
V = 0,7 м3, при температуре t = 24°С равна ф = 60%. Какую массу воды нужно
испарить в этот объем до полного насыщения пара? Упругость насыщенных
водяных паров при этой температуре равна рн = 3 кПа. Молярная масса воды
ц = 18-Ю"3 кг/моль.
11.103. Сосуд разделен перегородкой на две части так, что объем одной
части в два раза больше другой. В первой части находится воздух с относи-
тельной влажностью <р j = 30%, во второй - с относительной влажностью ф2 = 90%.
Какова будет относительная влажность в сосуде, если, не изменяя темпера-
туру, убрать перегородку?
• Решение. По определению относительной влажности
Р\ Рг
Ч>1 - , Ч>2 - „ >
Рн Рн
где Р\, Ру- начальное давление пара в одной н другой частях сосуда.
Когда перегородку убрали, то пар нз одного объема изотермически расширился,
заняв весь объем сосуда V= К| + К2. Его давление стало равным р\. Следовательно,
Р\ К] =Р\ (К, + Кг).
Аналогично для другой части:
Рт. ^2 = Pi (К + Кг).
По закону Дальтона
Р' =Р\ +Р2-
Искомая относительная влажность равна
Ф1 = £-.
Рн
Решая полученную систему уравнений, находим
<р- = X [ -P1ZL- + КЪ. 1 = + = 50%.
Рн\^ + Рг K, + K2J K,/K2+l
Ф1 К|/К2 + <р2
• Ответ', ф = —-----:— = 50%.
И Vx/V2 + 1
11.104. Смешали К] = 1 м3 воздуха с относительной влажностью ф] = 20%
и К2 = 2 м3 воздуха с относительной влажностью ф2 = 30%. При этом обе пор-
ции были взяты при одинаковых температурах. Смесь занимает объем
К= 3 м3. Определить ее относительную влажность.
11.105. В герметический сосуд объемом К = 0,8 м3, наполненный возду-
хом при температуре = 25°С с относительной влажностью ф] = 40%, помес-
тили блюдце с водой, масса которой т0 = 2 г. Затем температуру системы
понизили до t2 = 8°С. Какая масса воды будет в сосуде по истечении большого
промежутка времени? Упругость насыщенных паров воды при температуре
25°С равна рн 1 = 3,17 кПа, а при температуре 8°С -рн 2 = 1,07 кПа. Молярная
масса воды ц = 18-10‘3 кг/моль. Объемом блюдца пренебречь.
133
• Решение. Так как в начале пар был ненасыщенным, то при внесении блюдца с водой
вода может испаряться, увеличивая содержание паров в сосуде. При этом парциальное
давление паров прн заданной температуре будет расти, но не может превысить их упру-
ГОСТИ Рц 1 *
Если бы температура в системе не изменялась, то вода однозначно испарялась бы.
Однако при понижении температуры пар, первоначально содержащийся в сосуде, может
стать насыщенным н даже частично сконденсироваться. Определим, каким стало бы дав-
ление паров в сосуде прн понижении температуры системы от /| до t2. Для этого запишем
уравнение Менделеева-Клапейрона для первоначальной массы т пара в сосуде при тем-
пературах /| и t2:
PlV= — RTj, p2V= — RT2. (1)
р. ц
Следовательно, если бы пар не конденсировался, то он создал бы давление в сосуде
11
Р2 Pi р •
Используя определение относительной влажности
(2)
Рн 1
получим
Т2
Р2 = Ф1Рн1^« 1579 Па.
Так как р2>рн2= 1,07 кПа, то это означает, что прн новой температуре t2 пар в
сосуде станет насыщенным и часть его сконденсируется (см. решение задачи №11.79).
Массу Am сконденсировавшегося пара найдем из уравнения состояния
т. т - Ат _ _
Рн2 V=—-—RT2
с учетом уравнений (1)-(2):
Ph2kH Ф1Рн1^Ц Рнг^Ц
Am = m~~RTT = ~RTi RtT’
Следовательно, в сосуде окажется масса воды
.. . Кц/Ф1Рн| Рн2 1
Л/= Ат + т0 = —£1 —=---— + т0 и 2,77 г.
л k 11 ±2 ’
„ ,, . Уц [Ф1Рн1 Рн2) .
• Ответ: м = Дт + т0 = j —7----г + т0 « 2,77 г.
к Л 7 2
11.106. Стакан с водой объемом V\ = 0,2 л накрыли герметичным колпа-
ком, объем которого V= 2 м3. Начальная температура воздуха tx = 20°С, от-
носительная влажность <р = 80%.Затем температуру системы повысили до
t2 = 50°С. Какой объем воды останется в стакане по истечении большого про-
межутка времени? Упругость насыщенных паров воды при температуре 20°С
равна рИ! = 2,6 кПа, а при температуре 50°С-рн2 = 12,3 кПа. Молярная масса
воды ц= 18-10'3 кг/моль, плотность воды р= 103 кг/м3.
134
11.107. Герметичный сосуд объемом И= 0,5 л заполнен воздухом при
температуре Z, = 10°С и относительной влажности cpj = 60%. Когда в сосуд
поместили тонкостенный стакан с водой, а температуру системы повысили
до t2 = 30°С, то влажность воздуха стала <р2 = 80%. Какая масса воды была в
стакане? Упругость насыщенных водянных паров при температуре 10°С равна
рд1 = 1,26 кПа, а при температуре 30°С - рн2 = 4,23 кПа. Молярная масса
воды ц = 18-10'3 кг/моль.
11.108. Герметичный сосуд объемом И=4,5 л заполнен воздухом при
температуре = 10°С и относительной влажности ф] = 60%. Какую массу воды
нужно дополнительно испарить в сосуд, чтобы при повышении температуры
системы до 12 = 20°С относительная влажность стала равной <р2 = 70%? Плот-
ность насыщенных паров воды при температуре 10°С равна рн , = 9,38 г/м3, а
при температуре 20°С - рн2 = 17,21 г/м3.
11.109. В герметичный сосуд объемом /0 = 0,4 м3, наполненный воздухом
при температуре Г] = 30°С с относительной влажностью <Р] = 20%, поместили
массу воды объемом V= 1,5 см3, а затем температуру системы понизили до
t2 = 10°С. Какой объем воды останется в сосуде по истечении большого про-
межутка времени? Плотность насыщенных паров воды при температуре 30°С
равна рн1=30,2 г/м3, а при температуре 10°С -рн2 = 9,38 г/м3, плотность
воды р = 103 кг/м3.
11.110. Определить отношение плотностей сухого воздуха и воздуха с
относительной влажностью ф = 50%. Обе порции взяты при атмосферном дав-
лении pQ- 105 Па и температуре / = 20°С. Упругость насыщенных водяных
паров при этой температуре равна рв = 23 гПа. Отношение молярных масс
воды и сухого воздуха Цд/Нв = 0,6.
• Решение. Для сухого воздуха уравнение состояния
р0 V= — RT
Цв
позволяет найти его плотность:
т Ро Цв
Рсух- у- RT •
Влажный воздух представляет собой смесь воздуха без пара и водяного пара.
Давление влажного воздуха по закону Дальтона равно сумме парциальных давлений
воздуха без пара и водяного пара р2:
Po=Pi + Р2-
Давление водяных паров найдем из выражения для относительной влажности
Ф=Р2/Рн> Р2 = <? Рн-
Из закона Дальтона давление воздуха без пара будет равно
Pi =Ро ~Р2 ~Ро ~ ФРн •
Плотность влажного воздуха
135
т} + т2 mt т2
Рвл = у— = ~у + ~у = Р1 + Р2»
где р|, р2 - плотность воздуха без водяных паров и плотность пара соответственно.
Используя уравнение Менделеева-Клапейрона, записанное для воздуха без пара и
насыщенного пара в виде
P\=~RT, pH = — RT,
Ив Рп
получим
Цв-Pi М-вРо Ф Нв-Рн _ _ ФРн М-п
RT ~ RT ~ RT ’ Р2— Ф Рн — RT
Откуда находим плотность влажного воздуха
Рв(Ро- ФРн) ФРпРн
Рвл RT + RT
и отношение плотностей сухого и влажного воздуха
« 1,0046.
Рвл Ро-ФРн(1 "Pi/Pb)
• Ответ: -----------—--------« 1,0046.
Рвл Ро"ФРн(1 -Рп/Рв)
11.111. Отношение плотностей сухого и влажного воздуха, взятых при
температуре t = 30°С и давлении р = 104 Па, равно рсух /рдд = 1,09. Найти от-
носительную влажность воздуха. Упругость насыщенных водяных паров при
30°С равна рп = 4,24 кПа, отношение молярных масс воды и сухого воздуха
Рп/Рв = 0,6.
11.112. При температуре Г=20°С и давлении р=105 Па воздух имеет
относительную влажность ф = 100%. На сколько процентов он легче сухого
воздуха той же температуры и с тем же давлением? Упругость насыщенных
паров воды при 20°С равна рн = 2,33 кПа, молярная масса сухого воздуха
Р] = 29-10'3 кг/моль, молярная масса воды Рз = 18-10"3 кг/моль.
11.113. Определить отношение плотностей влажного (относительная
влажность ф = 90%) и сухого воздуха при давлении р0 = 105 Па и температуре
Г = 27°С. Плотность насыщенных паров при этой температуре равна
рн - 0,027 кг/м3. Молярная масса сухого воздуха Pj = 29-10'3 кг/моль, моляр-
ная масса воды Pj = 18-10'3 кг/моль.
136
ГЛАВА III
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
Как известно, в природе существует четыре вида взаимодействий: грави-
тационное, электрическое (или электромагнитное), ядерное (или сильное) и
слабое. Каждое из них характеризует взаимодействие разных материальных
объектов и проявляется в различных пространственных масштабах.
Гравитационное притяжение заметно между телами астрономических
масштабов (по крайней мере одно из тел должно быть очень массивным, на-
пример, планета или звезда). Ядерные силы отвечают за взаимодействие прото-
нов и нейтронов, входящих в состав атомного ядра. Слабое - возникает при
взаимном превращении определенных сортов частиц и характеризует силы,
возникающие при радиоактивном (J-распаде. При этом расстояния, на которых
обнаруживаются сильные и слабые взаимодействия, чрезвычайно малы (поряд-
ка 10'16 м -г 10'12 м). Электромагнитные взаимодействия проявляются в тех про-
странственных масштабах, в которых протекает наша повседневная жизнь. На-
пример, благодаря им мы видим книгу, которую сейчас читаем.
Каждый вид взаимодействия связан с определенной характеристикой час-
тиц. Например, гравитационное взаимодействие зависит от масс частиц (см.
книгу «Механика» §5), электромагнитное - от электрических зарядов.
Электрический заряд - это скалярная физическая величина, которая явля-
ется одной из основных характеристик частиц. Единицей измерения величины
заряда в системе СИ служит кулон [Кл].
Существует два вида электрических зарядов. Принято одни заряды назы-
вать положительными, другие - отрицательными. Заряд всех элементарных
частиц (если он не равен нулю) одинаков по абсолютной величине и равен
1,6-10'19 Кл. Его называют элементарным зарядом и обозначают буквой е. К
числу элементарных частиц принадлежат, в частности, электрон (отрицатель-
ный элементарный заряд -е), протон (положительный элементарный заряд +е),
нейтрон (заряд равен нулю). Из этих частиц состоят атомы и молекулы любо-
го вещества, поэтому элементарные заряды входят в состав всех тел. Обычно
частицы, несущие заряды разных знаков, присутствуют в теле в равных коли-
чествах и распределены с одинаковой плотностью. При этом алгебраичес-
кая сумма зарядов в любом элементарном объеме тела равна нулю, и каждый
такой объем (и тело в целом) будет нейтральным. Если каким-либо образом со-
здать в теле избыток зарядов одного знака, тело окажется заряженным. По-
скольку заряд q тела образуется совокупностью элементарных зарядов, то он
всегда будет кратным е:
q = ±N е.
137
Экспериментально установлено, что величина заряда, измеренная в раз-
личных системах отсчета, одинакова. Это означает, что величина заряда не за-
висит от того, движется этот заряд или покоится.
Электрические заряды могут исчезать и появлятся вновь. Однако всегда
исчезают или появляются два элементарных заряда противоположных знаков.
Например, электрон и позитрон (частица массой, равной массе электрона и за-
рядом +е) при взаимодействии исчезают (говорят, аннигилируют), превраща-
ясь в два нейтральных так называемых у-кванта. В ходе процесса, называемо-
го рождением пары, у-квант вблизи атомного ядра превращается в пару час-
тиц - электрон и позитрон. При этом возникают заряды -е и +е. Таким образом
суммарный электрический заряд не изменяется. Опыт показывает, что это
справедливо для любых процессов взаимодействия частиц, в которых изменя-
ется их состав: суммарный заряд электрически изолированной системы (т.е.
такой системы, в которой через поверхность ее ограничивающую не переносят-
ся электрические заряды) со временем не изменяется, какие бы процессы не
протекали в системе. Это утверждение называют законам сохранения заряда.
§12. Электростатика
Электрические заряды наделяют окружающее их пространство особыми
физическими свойствами - создают электрическое поле. Основным его свойст-
вом является то, что на находящуюся в нем заряженную частицу действует не-
которая сила. Раздел физики - электростатика - изучает постоянное во вре-
мени электрическое поле, создаваемое неподвижными зарядами.
Закон Кулона
Тот факт, что тело имеет электрический заряд, может быть обнаружен,
если к этому телу поднести другое заряженное тело. Опыт показывает, что
тела, обладающие зарядами одного знака (одноименно заряженные), отталки-
ваются друг от другу, а тела, обладающие зарядами разных знаков (разноимен-
но заряженные) - притягиваются друг к другу. Впервые количественное значе-
Рис. 12.1
ние силы взаимодействия заряженных
тел было получено Кулоном для то-
чечных зарядов. При этом под точеч-
ным зарядом понимают заряженное
тело, размеры которого малы по срав-
нению с расстояниями до других заря-
женных тел.
Рассмотрим два одноименных то-
чечных заряда и q2, положение ко-
торых в пространстве определяется ра-
диус-векторами Ту и (рис. 12.1).
138
Пусть Т^_2- сила, с которой заряд q2 действует на заряд q{, а - сила,
действующая на заряд q2 со стороны заряда qt. Тщательные измерения, прове-
денные Кулоном, Ампером и другими исследователями, показали, что сипа
взаимодействия точечных зарядов пропорциональна величине этих зарядов,
обратно пропорциональна квадрату расстояния между ними и направлена
вдоль прямой, соединяющей заряды. Этот закон называют законом Кулона.
Математически в системе СИ он может быть записан в виде:
F* _ 4l'42 j? 42'41 .Э' , 42'41 л? п
(12Л)
где R = r2-r^ - вектор, проведенный от заряда qt к заряду q2; R - его модуль,
т.е. расстояние между зарядами; е0 = 8,85-Ю'12 юЛНГ'-м’ - электрическая
постоянная.
Легко заметить, что соотноше-
ния (12.1) справедливы для любых
знаков зарядов q , и q2.
Рассмотрим теперь систему, со-
стоящую из N точечных зарядов q,
(где i= 1, 2, 3, . . . , N), положение
каждого из которых в пространстве
задано радиус-вектором rf (рис.
12.2). Опыт показывает, что сила, с
которой заряд q, действует на неко-
торый точечный заряд q, не зависит
от присутствия других зарядов:
где Rj = r-rj - вектор, соединяющий заряд qf с зарядом q, Я, - его модуль.
Очевидно, что результирующая сила F, с которой система зарядов qt дей-
ствует на заряд q, равна векторной сумме сил F], действующих на этот заряд
со стороны каждого из зарядов системы:
(12.3)
Это утверждение называют принципом суперпозиции сил. Свойство су-
перпозиции используется в электростатике при рассмотрении взаимодействия
заряженных тел, которые нельзя считать точечными.
Электрическое поле
При исследовании взаимодействия электрических зарядов, закономерно
возникают вопросы, почему появляются силы, действующие на заряды, и как
они передаются от одного заряда к другому? В процессе развития физики су-
139
ществовало два подхода к ответу на эти вопросы. Первоначально предполага-
лось, что заряженным телам присуще свойство действовать на другие заряды
на расстоянии без участия промежуточных тел или среды, и при наличии толь-
ко одного заряда никаких изменений в окружающем пространстве не происхо-
дит (теория дальнодействия). Несколько позже появилась вторая точка зре-
ния - силовые взаимодействия между разобщенными телами могут переда-
ваться только при наличии некоторой среды, окружающей эти тела, последова-
тельно от одной части этой среды к другой, и с конечной скоростью; наличие
даже одного заряда в окружающем пространстве приводит к определенным его
изменениям (теория близкодействия).
В настоящее время физика сохраняет только теорию близкодействия. При
этом для понимания происхождения и передачи силового взаимодействия не-
обходимо допустить наличие некоторой среды, создаваемой зарядами в окру-
жающем пространстве. Такой средой является особый вид материи - электри-
ческое поле. Электрическое поле является неизменным спутником каждого
электрического заряда. Судить о существовании электрического поля в данной
точке пространства можно только по наличию силы, с которой поле действует
на помещенный в эту точку электрический заряд.
Напряженность электрического поля
Поместим точечный заряд q в нача-
ло системы координат и рассмотрим си-
лы, действующие на заряды qt (где i = 1,2,
3,...), которые поочередно будем поме-
щать в некоторую точку с координатами х,
у, z (рис. 12.3).
Из (12.1) следует, что при измене-
нии заряда qt сила
-> Qi'Q
Fj= — .R (12.4)
1 4ле0Я3 v ’
также будет меняться.
Поскольку правая часть отношения
5 =---2---1
4л е0 R3
(12.5)
не зависит от величины заряда qjt а определяется лишь зарядом q и радиус-
вектором R, проведенным в данную точку пространства, то можно сделать
вывод, что отношение ifyqj характеризует электрическое поле, которое суще-
ствует в точке с координатами х, у, z, безотносительно к заряду qt.
Вектор, равный отношению силы М с которой заряд q действует на точеч-
ный малый положительный заряд q0 (так называеый пробный заряд), помещен-
ный в некоторую точку пространства,
140
Чо
(12.6)
называют напряженностью электрического поля, создаваемого зарядом q в
данной точке. С другой стороны, если напряженность электрического поля в
данной точке известна, то сила, действующая на произвольный заряд q, по-
мещенный в эту точку, равна
I?=ql?. (12.7)
Используя понятие электрического поля, можно перейти к другому спо-
собу описания взаимодействия зарядов. Вместо того, чтобы говорить о том,
что на некоторый заряд q^ действует заряд q с силой I? можно сказать, что
заряд q создает электрическое поле напряженностью и на заряд qit нахо-
дящийся в этом поле, действует сила F= q, I?. Такой способ описания взаи-
модействия очень удобен, так как формула (12.7), в отличие от закона Кулона,
справедлива для электрических полей, создаваемых любой системой зарядов.
Из соотношений (12.6) и (12.7) следует, что напряженность электричес-
кого поля точечного заряда q на расстоянии R от него равна
Ё*=—тХ Е =-------------(12.8)
4тг е0 R3 4тг е0 R2
Рассмотрим систему N неподвижных зарядов <?г- (где i = 1, 2, 3, . . . , N)
и вычислим результирующую силу, действующую на пробный заряд q0, по-
мещенный в некоторую точку пространства. Согласно (12.3) она будет равна
векторной сумме сил, действующих на этот заряд со стороны каждого из
зарядов системы. Разделив обе части соотношения (12.3) на qQ, получим
у pt
= (12.9)
. Чо ,'=Чо
Поскольку отношение Fj/q0 есть напряженность электрического поля
Ё* создаваемого зарядом q, в точке, где расположен заряд q0, то напряжен-
ность электрического поля Ё= j?/q0 системы зарядов в данной точке равна
Ё^.^Ё*, (12.10)
т.е. векторы напряженности электрического поля подчиняются, как и векторы
Рис. 12.4
сил, принципу суперпозиции.
Для описания электрического поля нужно задать векторы напряженности
в каждой точке поля. Это можно сделать аналитически, в виде зависимостей
наряженности поля от координат. Для
наглядности такую зависимость можно
представить и графически с помощью
силовых линий (рис. 12.4). Силовой ли-
нией называют такую линию, касатель-
ная к которой в каждой точке совпадает
141
с направлением вектора напряженности поля в этой точке. Поскольку каса-
тельная может иметь два взаимно противоположных направления, то силовым
линиям приписывают определенное направление, отмечая его на чертеже
стрелкой в направлении вектора напряженности. При этом силовые линии
нигде не пересекаются. В противном случае в точках пересечения вектор на-
пряженности поля имел бы одновременно разные направления.
Рис. 12.5
Рис. 12.6
Рис. 12.8
Рис. 12.9
Расмотрим положительный точечный заряд q. Перемещая в поле заряда q
пробный заряд qQ, можно легко построить векторы напряженности в каждой
его точке. Сила, с которой заряд q действует на пробный заряд q§, направлена
вдоль линий, соединяющих заряды, к заряду qQ. Точно также будут направлены
и векторы напряженности поля заряда q. Поэтому картина силовых линий для
положительного заряда будет иметь вид, представленный на рис. 12.5. Анало-
гично можно построить силовые линии для отрицательного заряда (рис. 12.6) и,
например, двух точечных зарядов разных знаков (рис. 12.7). В случае заряжен-
ных тел сложной формы картину силовых линий можно получить на опыте. Не
вникая в подробности таких экспериментов, приведем картины силовых линий
двух разноименно заряженных шариков (рис. 12.8) и двух разноименно заря-
женных пластин (рис. 12.9).
Обратим внимание на то, что вблизи зарядов, где напряженность электри-
ческого поля больше, силовые линии расположены гуще. Этот факт дает общее
правило изображения силовых линий: число силовых линий, пересекающих
единичную площадку, перпендикулярную направлению Е, должно быть про-
порционально величине напряженности поля в данном месте.
142
Кроме этого, из определения силовой линии следует, что они начинаются
только на положительных зарядах и заканчиваются на отрицательных (или
«уходят» на бесконечность от положительного заряда; или «приходят» из бес-
конечности к отрицательному заряду).
Наконец, обратим внимание на картину силовых линий поля, созданного
двумя разноименно заряженными параллельными пластинами (рис. 12.9): си-
ловые линии между пластинами параллельны и расположены на равных рас-
стояниях друг от друга, исключая области вблизи краев. Таким образом в цент-
ральной части напряженность электрического поля во всех точках одинакова.
Такие электрические поля называют однородными.
Электрический потенциал
Рассмотрим электрическое поле, создан-
ное положительным точечным зарядом q. В
любой точке этого поля на пробный заряд q0
действует сила
4ТГ Eq Г
Вычислим работу сил электрического
поля при перемещении заряда q0 из точки 1 в
точку 2 по произвольной траектории (рис.
12.10). Эта работа равна (см. книгу «Механи-
ка», формула (3.27))
gp-g
4тг е0 1
где а - угол между направлением радиус-вектора г*и бееконечно малым пере-
мещением dl. Из рисунка видно, что произведение dl cos а равно величине
приращения dr = радиус-вектора г*в данной точке траектории.
Следовательно, г
. Чо'Ч ?dr Чо'Ч г 1 14 Чо'Ч Чо'Ч
Л]_2 = “;-- | =-----1 ” I г =------------------• (12.12)
4тсе0/1г2 4ле01 г 4тг е0 п 4л е0 г2
Таким образом, работа сил электрического поля по перемещению точеч-
ного заряда в поле другого точечного заряда не зависит от формы траектории,
а определяется лишь начальным и конечным положениями зарядов. Как из-
вестно, такие силовые поля называются консервативными. Это означает, что в
электрическом поле можно ввести понятие потенциальной энергии одного за-
ряда в силовом поле другого.
Поскольку работа консервативной силы равна убыли потенциальной энер-
гии (см. книгу «Механика», формула (3.40))
Л1.2 = W{-W2, (12.13)
2 2 'з
143
(в электростатике энергию принято обозначать буквой ffQ, то из (12.12) сле-
дует:
Однако отношение
QrcQ Qb’Q
w = + const, = _чоч_ +
4л So Г] 4л So г2
Легко сообразить, что если нулевой уровень потенциальной энергии вы-
брать на бесконечности, то const = 0 и потенциальная энергия заряда q0, нахо-
дящегося на расстоянии г от заряда q, будет равна
qoq
(12.14)
4л So г
Если вместо заряда q0 в данную точку поля заряда q поместить другой
заряд qj, то его энергия станет равной
q,-q
4л е0 г
д
9i 4л е0 г
не зависит от значения qjt а определяется лишь зарядом q и расстоянием г
от него до данной точки пространства. Поэтому отношение Wj/q,, наряду с
напряженностью поля, является его характеристикой.
Скалярная величина, равная отношению потенциальной энергии пробно-
го заряда q0 в электрическом поле заряда q к величине этого заряда
W
<? = у, (12.15)
чо
называется потенциалом электрического поля заряда q в данной точке.
Из определения потенциала следует, что потенциал точечного заряда q на
расстоянии г от него равен
<P = -rJZ~ (12.16)
4л еог
Рассмотрим поле, создаваемое системой N точечных зарядов qj (где i = 1,
2, 3, ... , N), расстояние от каждого из которых до некоторой точки поля
равно rj. Работа, совершаемая силами этого поля при перемещении заряда q0
из точки 1 в точку 2, будет равна алгебраической сумме работ сил, обуслов-
ленных каждым из зарядов в отдельности:
N
Согласно (12.12) каждая из работ Aj равна
А _ 4o-<li Чо-Ч,
' 4л е0 ri,i 4п So г/>2 ’
где г-, ,, г12 - расстояния от заряда qj до начального и конечного положений
заряда q0 соответственно. Следовательно,
144
9o'9i
' /-i4nSor/3 <=14леог,-,'
Сопоставив это выражение с соотношением (12.13), получим для потенци-
альной энергии заряда q0 в поле системы зарядов выражение
у at
W=q0 S
° <=14л бог,-
из которого следует, что потенциал поля системы зарядов в данной точке
Л 4i
Ф = Х ------------------------------------
' = 1 4л е0 г,
равен алгебраической сумме потенциалов, создаваемых каждым из зарядов в
отдельности: N
Ф^.Фг (12.17)
Часто соотношение (12.17) называют принципом суперпозиции потенциала.
Используя определение потенциала (12.15), выражение для работы
(12.12) можно переписать в виде
^1-2 = Чо (Ф1 — Фз)- (12.18)
Поскольку потенциал точечного заряда убывает обратно пропорциональ-
но расстоянию от него до рассматриваемой точки поля, то на бесконечности
Фи, = 0. Поэтому работа сил поля по перемещению единичного положитель-
ного заряда из данной точки на бесконечность численно равна потенциалу в
этой точке: .
ф»о = у- (12.19)
Часто за «ноль» потенциала принимают его значение не на бесконечнос-
ти, а значение потенциала Земли. Это не существенно в тех задачах, в кото-
рых нужно найти разность потенциалов между точками поля, а не абсолютное
значение потенциалов в этих точках.
Формулу (12.19) можно использовать для установления единиц измере-
ния потенциала. За единицу потенциала в системе СИ, называемую воль-
том [В], принимают потенциал в такой точке поля, для перемещения в ко-
торую из бесконечности положительного заряда, равного 1 Кл, внешним
силам необходимо совершить работу в 1 Дж.
Потенциал можно использовать, подобно ли-
ниям напряженности, для графического изображе-
ния электрического поля. Объединяя в электричес-
ком поле точки, обладающие одинаковым потен-
циалом, получают некоторые поверхности, назы-
ваемые поверхностями равного потенциала или
эквипотенциальными поверхностями. Очевидно,
что для уединенных точечных зарядов эквипотен-
циальные поверхности представляют собой сово-
купность сфер с общим центром, расположенном
на заряде (рис. 12.11).
Фз <<р2
Рис. 12.11
Ф2<Ф1
145
1
% I А/ 2
Рис. 12.12
Связь между потенциалом и напряженностью электрического поля
Рассмотрим однородное электрическое
поле напряженностью Е, созданное некото-
рой системой неподвижных зарядов. Помес-
тим в точку 1 (рис. 12.12) заряд q и пере-
несем его в точку 2 вдоль вектора Д/. Рабо-
ту сил электрического поля при этом перемещении можно выразить, во-пер-
вых, через напряженность поля
А\_2 = q q Е cos а Д/ = qEj Д/
(где Ei - проекция вектора Ё* на направление перемещения, Д/ - величина
перемещения), во-вторых, через разность потенциалов точек 1 и 2:
A i-2 = Ч (ф 1 - Ф2) = ~ Ч (Фг - Ф1) = “ Ч ДФ-
Приравнивая оба выражения для работы, получаем
= (12-20)
В общем случае неоднородного поля точки 1 и 2 нужно выбирать до-
статочно близко друг от друга (строго говоря, бесконечно близко), чтобы на-
пряженность поля на перемещении Д/ можно было считать постоянной.
Переходя к пределу при Д/—> 0, из (12.20) получим
= (12.21)
Производная, стоящая в правой части выражения (12.21), характеризует
быстроту изменения потенциала в данном направлении. Следовательно, про-
екция Ei вектора напряженности на данное направление равна скорости убы-
вания потенциала в этом направлении.
Соотношения (12.20)-( 12.21) можно использовать для определения еди-
ницы измерения напряженности электрического поля. В системе СИ такой
единицей является вольт на метр [В/м] - это напряженность однородного
электрического поля, создаваемая разностью потенциалов в 1 В между точ-
ками, находящимися на расстоянии 1 м на линии напряженности.
Рассмотрим две эквипотенциальные
поверхности ф] и фт<Ф1 (рис. 12.13). Век-
тор напряженности Е электрического поля в
произвольной точке эквипотенциальной по-
<₽2<<Р1 верхности направлен перпендикулярно каса-
тельной к ней в данной точке. В этом легко
убедиться, если допустить наличие каса-
векгора например, на эквипотенциальной по-
Рис. 12.13
тельной составляющей £^асат
верхности фр тогда работа, совершаемая силами электрического поля по
146
перемещению заряда q вдоль эквипотенциальной поверхности на расстояние
Д/, имела бы, с одной стороны, значение А = q EKiCat AZ * 0, а с другой —
Я = q (ср( - ф|) = 0. Следовательно, ^асаг = 0- Поэтому силовые линии поля
всегда перпендикулярны эквипотенциальным поверхностям и направлены от
поверхности с большим потенциалом <pj к поверхности с потенциалом
Ф2<Ф1-
Теорема Гаусса
Рис. 12.14
£
Рис. 12.15
Вычисление величины напряженности электрического поля во многих
случаях сильно упрощается, если воспользоваться теоремой, излагаемой
ниже.
Прежде всего введем понятие потока вектора напряженности электри-
ческого поля.
Рассмотрим пощадку S, которую прозыва-
ют силовые линии однородного электрического
поля напряженностью Е, составляющие угол а
с нормалью ri площадке (рис. 12.14). Величину
ФЕ = Е$соза = Еп$ (12.22)
(где Еп = Е cos а - проекция вектора Е? на на-
правление нормали) называют потоком вектора
напряженности электрического поля через по-
верхность 5.
Если поле неоднородно и поверхность S, через которую ищут поток,
не является плоскостью, то эту поверхность можно разбить на бесконечно
малые элементы dS и каждый элемент считать плоским, а поле, его про-
низывающее - однородным. Элементарный поток через такую площадку
равен <1ФЕ = EdS cos а = Еп dS, а полный поток ФЕ через всю поверхность S—
их алгебраической сумме. Можно показать, что величина суммарного потока
ФЕ не зависит от формы поверхности S.
Из определения потока видно, что он может
быть положительным (если направление вектора
^составляет острый угол с нормалью), отрицатель-
ным (если направление вектора ^составляет тупой
угол с нормалью) и равным нулю (если вектор Ё
перпендикулярен нормали).
Рассмотрим картину силовых линий электри-
ческого поля неподвижного точечного заряда q > 0
(рис. 12.15).
Окружим заряд воображаемой сферой радиуса R с центром в точке рас-
положения заряда. Площадь поверхности сферы равна S = 4л Я2.
147
Поскольку векторы напряженности электрического поля во всех точках на
поверхности рассматриваемой сферы направлены по радиусу (т.е. по нормали
к поверхности сферы) и одинаковы по величине, то поток вектора напряжен-
ности электрического поля точечного заряда q через поверхность £ будет равен
Фе = Еп8=Еп 4л Л2.
Поскольку в точках на поверхности сферы (см. формулу (12.8))
£„ = £ =---
4л е0 Л2
ТО и
ФЕ=1-
Легко видеть, что поток вектора Е через поверхность сферы другого радиуса
также будет равен <?/е0. Можно показать, что этот результат справедлив для
любой замкнутой поверхности £0 (см. рис. 12.15) и для произвольного рас-
положения заряда (или зарядов) внутри этой поверхности. В этом суть тео-
ремы Гаусса', поток вектора напряженности электрического поля через про-
извольную замкнутую поверхность равен алгебраической сумме зарядов, за-
ключенных внутри этой поверхности, деленной на е0:
ФЕ = -Ъ<Ц. (12.23)
ео 1
Продемонстрируем возможности теоремы Гаусса на трех полезных для ре-
шения задач примерах. Прежде чем приступить к рассмотрению этих приме-
ров, введем понятия поверхностной и объемной плотностей заряда.
Если заряд сосредоточен в тонком поверхностном слое тела, то распреде-
ление заряда можно характеризовать с помощью поверхностной плотности
заряда о, которая определяется как величина заряда, приходящаяся на единицу
площади поверхности тела, несущего заряд. Если заряд распределен по объему
тела, то используется объемная плотность заряда р - заряд, находящийся
в единице объема тела. В случаях равномерного распределения заряда q по по-
верхности площадью £ тела или по его объему V
о = | или р =
соответственно.
1. Вычислим напряженность электрического поля, создаваемого равно-
мерно заряженной бесконечной плоскостью. Пусть для определенности по-
верхностная плотность заряда на плоскости о > 0. Из соображений симметрии
вытекает, что векторы напряженности поля в любой точке направлены перпен-
дикулярно плоскости. Также очевидно, что в симметрично удаленных от плос-
сости точках векторы напряженности одинаковы по величине и противополож-
ны по направлению.
Представим себе мысленно цилиндрическую поверхность с образующи-
ми, перпендикулярными к плоскости, и основаниями площадью S (рис. 12.16).
148
В chjiv симметрии£( =£2 =£ и
£^ = Ег перпендикулярны основа-
ниям цилиндра. Поскольку векто-
ры напряженности поля параллель-
ны боковой поверхности, то поток
вектора напряженности через всю
поверхность цилиндра будет равен
потоку через его основания:
ФЕ = £| «У + £2 = 2£ S.
С другой стороны, по теореме
Гаусса £2! *”2
ф£ = ^> Рис. 12.16
Ео
где q - заряд, заключенный внутри поверхности цилиндра, равный
q = о S.
Следовательно,
£ = ^-. (12.24)
2е0
Полученный результат свидетельствует о том, что величина напряжен-
ности поля бесконечной заряженной плоскости на любых расстояниях от нее
одинакова.
Для плоскости, заряженной отрицательно, результат будет таким же,
лишь направление вектора £ изменится на противоположное.
2. Вычислим напряженность электрического поля, создаваемого равно-
мерно заряженной сферой радиуса Л.
Поле, создаваемое сферической поверхностью, заряженной равномерно,
будет, очевидно, центрально-симметричным, т.е. в любой точке векторы на-
пряженности поля будут направлены вдоль радиусов сферы.
Вообразим концентрическую с заряженной
сферой поверхность радиуса r> R (рис. 12.17). Во
всех точках этой поверхности величина проек-
ции вектора £*на нормаль будет одинакова. Поэ- \
тому суммарный поток вектора напряженности , [ , j . j - r
поля через выбранную поверхность будет равен /2-^1
ФЕ(г> R) = EQnr2. \ /
С другой стороны, весь заряд сферы нахо-
дится внутри этой поверхности. Поэтому ' ------'
ф£(г>Л) = ^_ рис 1217
Следовательно,
£(r>£) = —5-3, (12.25)
4л Ео г
т.е. электрическое поле вне заряженной сферы тождественно полю точечно-
го заряда, помещенного в центр сферы.
149
Поверхность радиуса г < R не будет содержать зарядов. Поэтому внутри
заряженной сферы
E(r<R~) = 0. (12.26)
Очевидно, что для сферы, заряженной отрицательно, формулы (12.25)-
(12.26) остаются справедливыми, только векторы напряженности будут на-
правлены в противоположную стороны (к центру сферы).
Поскольку поле, создаваемое точечным зарядом, такое же, как поле вне за-
ряженной сферы, то потенциал сферы при r>R может быть вычислен по фор-
муле (12.16):
ф(г>Я) = —. (12.27)
4л Eq Г
Внутри сферы поле отсутствует, поэтому при перемещении заряда из
точки, расположенной на расстоянии г < Л от центра сферы, на ее поверхность
силы поля работы не совершают. Это означает, что работа сил поля при пере-
мещении заряда из этой точки на бесконечность равна работе при его переме-
щении с поверхности сферы на бесконечность. Поэтому потенциал внутри
сферы одинаков и равен потенциалу на ее поверхности:
ф(г<Л) = ф(г = Л) = —-2—. (12.28)
4тс 8q л
3. Вычислим напряженность электрического поля, создаваемого шаром
радиуса R, равномерно заряженным по объему с плотностью заряда р.
Поле, создаваемое таким шаром, будет
центрально-симметричным. Легко понять, что
вне шара для поля получится такой же резуль-
тат, что и для поля вне сферы.
Найдем поле внутри шара. Для этого выбе-
рем концентрическую с шаром сферическую
поверхность радиуса г <R (рис. 12.18). Очевид-
но поток через поверхность этой сферы равен
ФЕ(г < Л) = Е 4л г2.
где
С другой стороны, по теореме Гаусса:
Ф£(г<Л) = ^,
Ев
q' = р 4Л л г = Л---у = -
4Л л R3 R3
заряд, заключенный в сфере радиуса г. Следовательно,
Е(г<к) = —£~. (12-29)
4л eQR
Таким образом, внутри равномерно заряженного шара напряженность
поля растет линейно с расстоянием от его центра.
150
Проводники в электрическом поле
В проводниках имеется большая доля зарядов, которые могут свободно пе-
ремещаться внутри вещества. К проводникам относятся все металлы в жидком
и твердом состояниях, водные растворы солей н кислот и многие другие веще-
ства. Здесь же под проводником будем понимать твердое металлическое тело.
Рассмотрим проводник во внешнем
электрическом поле (на рис. 12.19 его си-
ловые линии показаны пунктиром). Под
действием поля свободные заряды в про-
воднике придут в движение. В результа-
те у границ проводника возникнут заря-
ды противоположных знаков, называе-
мые индуцированными. Электрическое
поле этих зарядов направлено противо-
положно внешнему. Следовательно, по- ?ис'
явление индуцированных зарядов приводит к ослаблению поля в проводнике.
За ничтожно малое время свободные заряды перераспределятся так, что напря-
женность электрического поля внутри проводника станет равной нулю (в
противном случае свободные заряды продолжали бы двигаться), а силовые
линии вне проводника вблизи его поверхности будут направлены перпендику-
лярно к ней (на рис. 12.19 они показаны сплошными линиями). Действительно,
если бы существовала касательная составляющая поля, то заряды перемеща-
лись бы вдоль поверхности проводника, что противоречит опыту.
Если проводнику сообщить некоторый избыточный заряд q, то в нем воз-
никнет электрическое поле и заряды придут в движение. Они будут переме-
щаться до тех пор, пока электрическое поле внутри проводника не станет рав-
ным нулю. При этом поток вектора напряженности электрического поля через
произвольную замкнутую поверхность внутри проводника будет равен нулю.
Это может означать только одно - избыточных зарядов внутри этой поверхнос-
ти нет, т.е. избыточные заряды внутри проводника отсутствуют, а распреде-
ляются по его поверхности.
Отмеченные условия означают, что потенциалы во всех точках поверх-
ности проводника (и внутри него) одинаковы, т.е. поверхность проводника
эквипотенциальна. Поэтому соединение заряженного проводника с другим
проводником приведет к тому, что заряды между проводниками перераспре-
делятся так, чтобы потенциалы тел выровнялись. В этом состоит принцип
«заземления», т.е.-соединения проводника с Землей: потенциал заземленного
проводника будет равен потенциалу Земли.
Рассмотрим проводник, внутри которого имеется полость (рис. 12.20). Со-
общим ему некоторый заряд и поместим проводник во внешнее электрическое
поле.
151
Вычислим работу сил электрического
а поля> совершаемую ими при перемещении не-
которого точечного заряда q по замкнутой
Л^ектории l-o-2-fr-l, часть которой прохо-
Дит через полость, а часть - через проводник.
Поскольку электрическое поле консерва-
тивно, то = 0. С другой стороны
Ai_a_2_b-i =^\-а-2 + ^2-6-1- Тах как поле внут-
Рис. 12.20 ри проводника отсутствует, то= 0. Сле-
довательно, А1_а_2 = Таким образом, независимо от траектории перемещения
заряда внутри полости, работа сил поля будет равна нулю. Это может быть
только в случае, если поле внутри полости отсутствует.
Если полый проводник находится во внешнем электрическом поле, то на
нем появятся индуцированные заряды. Эти заряды будут сосредоточены на по-
верхности проводника, а электрическое поле внутри проводника и в полости
будет равно нулю. Поэтому полый проводник экранирует электрическое поле
всех внешних зарядов. На этом свойстве основана элетростатическая защита:
для того, чтобы оградить чувствительные электрические приборы от воздейст-
вия внешних электрических полей, их заключают в замкнутые металлические
оболочки. При этом поля по обе стороны оболочки полностью не зависят друг
от друга.
Отметим, что полый проводник экранирует только поле внешних зарядов.
Если электрические заряды находятся внутри полости, индуцированные заря-
ды возникнут не только на внешней поверхности проводника, но и на внутрен-
ней. При этом распределение зарядов будет таким, чтобы результирующее
поле зарядов внутри полости и индуцированных зарядов в любой точке в толще
проводника было равно нулю. Однако внутри полости поле не будет равным
нулю.
Теперь представим себе, что вблизи некоторого проводника расположен
точечный заряд. Как индуцированный заряд распределится по поверхности
проводника, чтобы поле в его толще было равным нулю, а поверхность эквипо-
тенциальна, в общем случае выяснить чрезвычайно сложно. Не менее сложно
вычислить силу, с которой будет действовать поле индуцированных зарядов на
точечный заряд и наоборот. Рассмотрим один весьма интересный способ реше-
ния такой задачи в наиболее простом случае: определим силу взаимодействия
большой проводящей заземленной пластины с точечным зарядом q, располо-
женным вблизи ее поверхности.
Предварительно рассмотрим картину поля двух разноименных точечных
зарядов +q. Построим для них систему силовых линий и эквипотенциальных
поверхностей (см. рис. 12.21. а). Рассмотрим некоторую эквипотенциальную
поверхность А с потенциалом <рА. Предположим, что мы изогнули тонкий
152
металлический лист так, что он в точности совпал с частью поверхности А.
Если на нем к тому же установить потенциал <рА, то от появления листа в
картине поля ничего не изменится. Если этот же лист замкнуть по всей по-
верхности А, то он разделит пространство на две части: одна будет внутри,
другая - снаружи листа. Как указывалось выше, поля в этих областях не
зависят друг от друга. Поэтому независимо от того, каково поле внутри зам-
кнутого проводника, снаружи поле всег-
да одно и тоже (конечно, при условии,
что на поверхности проводника поддер-
живается потенциал фА). Можно даже
заполнить внутренную область металлом
(рис. 12.21, б). Следовательно, картина
силовых линий и эквипотенциальных
поверхностей точечного заряда (+<?) н
проводника будет такой же как у заряда
(+q) и у заряда (~q\ расположенного в
определенном месте пространства. Прн
этом заряд (~q) называют зарядом - изо-
бражением. ?ис 12.22
Легко сообразить, что потенциал поверхности В, расположенной посере-
дине между зарядами, равен нулю. Поэтому, если, например, левую часть
пространства от поверхности В заполнить металлом (рис. 12.22) и соединить
с Землей, то в правой части поле не изменится. Следовательно, поле двух
точечных зарядов ±q, расположенных на расстоянии 2h, друг от друга, тож-
дественно полю заземленной проводящей пластины и точечного заряда, рас-
положенного на расстоянии h от нее. Естественно, справедливо и обратное
утверждение: электрическое поле между заземленной пластиной и точечным
зарядом совпадает с полем, создаваемым этим зарядом и его зеркальным
изображением в этой пластине. При этом сила взаимодействия точечного
153
заряда с зарядом индуцированным на пластине будет равна силе взаимодей-
ствия двух разноименных точечных зарядов:
F=-----.
4л Eq (2й)2
Диэлектрики в электрическом поле
В отличие от проводников в диэлектриках свободных электронов крайне
мало. Заряды, входящие в состав молекул диэлектрика, называют связанными.
Под действием электрического поля заряды могут лишь немного смещаться из
своих положений равновесия; покинуть пределы молекулы, в состав которой
они входят, связанные заряды не могут. Примерами диэлектриков могут слу-
жить стекло, эбонит, различные пластмассы и все газы в нормальных условиях.
Всякая молекула представляет собой систему с суммарным зарядом, рав-
ным нулю. Однако распределение положительного и отрицательного заряда
внутри различных молекул может быть разным. Если центры масс положитель-
ных и отрицательных зарядов совпадают, то молекулу называют неполярной.
Рис. 12.23
Рассмотрим схематически молекулу такого вещества. Каждый атом такой
молекулы имеет положительно заряженное ядро, окруженное электронами, ко-
торые распределены вокруг ядра равномерно (рис. 12.23, а). В электрическом
поле ядро сместится вдоль силовых линий по полю, а электроны - противопо-
ложно (рис. 12.23, б). При этом центры масс ядра и электронов уже не будут со-
впадать. Этот процесс называют поляризацией вещества. В отличие от рассмот-
ренной молекулы, в природе существуют молекулы, у которых центры масс по-
ложительного и отрицательного зарядов не совпадают даже при отсутствии
внешнего поля. Такие молекулы называют полярными. Поэтому, независимо от
вида молекулы, в электрическом поле молекулу схематически можно предста-
вить в виде так называемого электрического диполя, сумарный заряд которого
равен нулю, а положительные (+ q) и отрицательные (- q) заряды смещены
друг относительно друга на малое расстояние I (рис. 12.23, в).
154
Если диполь поместить в однородное электрическое поле напряженнос-
тью Е, то на образующие его заряды (+ q) и (- q) будут действовать равные
по величине, но противоположные по направлению силы |F) | = [Fy = q Е. В
общем случае эти силы создадут момент сил, который стремится развернуть
диполь вдоль силовых линий поля. Например, в положении диполя, показан-
ном на рис. 12.23, в, относительно оси OZ, перпендикулярной плоскости ри-
сунка, на диполь действует момент сил
Mz = Fj 'Л I sin а + F2 I sin а = q ЕI sin а,
который при а = л/2 максимален
Мпах = ?£/ (12.30)
и обращается в ноль при а = 0 или а = л (в первом случае диполь будет на-
ходится в положении устойчивого равновесия, во втором - в положении не-
устойчивого равновесия).
Величина
Pe = ql (12.31)
называется электрическим моментом диполя. Его принято записывать в виде
вектора
p*e = qt (12.32)
где I - вектор, направленный от заряда (- q) диполя к заряду (+ q).
С учетом (12.31) выражение для момента сил, действующего на диполь
в электрическом поле (называемого механическим моментом), можно пред-
ставить в виде
M,=pe£sina, A/max=peE. (12.33)
Механический момент стремится повернуть диполь так, чтобы его элект-
рический момент р% установился по направлению поля Е.
Рассмотрим диэлектрическую
пластину во внешнем электрическом
поле напряженностью Ео. Со сторо-
ны поля на молекулы будут действо-
вать моменты сил таким образом,
чтобы развернуть их вдоль линий
поля (рнс. 12.24). При этом в толще
диэлектрика количество положи-
тельных и отрицательных зарядов
будет по-прежнему одинаково, а на поверхностях диэлектрика возникнут
нескомпенсированные заряды разных знаков, которые называют поляриза-
ционными. Поляризационные заряды создадут собственное поле Е\ направ-
ленное противоположно внешнему. Результирующее поле внутри диэлект-
рика, равное
Й=Ёд + Й\ Е = Е0-Е',
будет меньше внешнего Ед. Можно показать, что для однородного диэлект-
рика отношение е = Ед/Е есть величина постоянная, определяющая диэлект-
АЛ □ 0? /+\ /+\
Рис. 12.24
155
рические свойства материала. Ее называют диэлектрической проницаемостью
вещества: она показывает, во сколько раз величина напряженности электри-
ческого поля внутри однородного диэлектрика меньше величины напряжен-
ности внешнего поля:
Ел
£ = -^. (12.34)
Следует отметить, что понятие диэлектрической проницаемости для про-
извольных сред вводится гораздо сложнее и соотношение (12.34) в них не
выполняется.
Поляризацией объясняются многие явления, наблюдаемые в повседнев-
ной жизни. Например, наэлектризованная расческа притягивает маленькие ку-
сочки диэлектрика - бумаги (а ведь они нейтральны!). Дело в том, что на
кусочке бумаги возникают поляризационные заряды обоих знаков, притяги-
ваемые и отталкиваемые расческой. Однако бумага притягивается, потому
что поле вблизи расчески сильнее, чем вдали от нее. Если же этот кусочек
бумаги поместить в однородное электрическое поле, то он останется непо-
движен.
Электроем кость
Напомним, что сообщенный уединенному проводнику заряд распределит-
ся по его поверхности так, чтобы напряженность поля внутри проводника была
равна нулю. При этом проводник приобретет некоторый потенциал ф. Если
проводнику сообщить дополнительный заряд, то он также перераспределится
по его поверхности, и потенциал проводника изменится. Опыт показывает, что
потенциал проводника пропорционален находящемуся на нем заряду:
? = Сф, (12.35)
где коэффициент пропорциональности С называют электроемкостью (или
просто емкостью) проводника. В системе СИ электроемкость измеряется в
фарадах [Ф = Кл/В].
Конденсаторы
Если к заряженному проводнику подне-
сти какое-либо проводящее незаряженное
тело, то на этом теле появится индуцирован-
ный заряд; причем, заряды, противоположные
по знаку заряду проводника, расположатся
ближе к проводнику, чем одноименные с ним
(рис. 12.25). При этом, очевидно, потенциал
заряженного проводника уменьшится. Со-
гласно (12.35) это означает увеличение емкости проводника. Поэтому, при из-
готовлении систем, обладающих большой емкостью, используют два провод-
ника, расположенные близко друг от друга. Такие системы называют конденса-
торами, проводники - его обкладками, расстояние между ними - зазором.
156
Чтобы внешние тела не оказывали влияния на емкость конденсатора, об-
кладкам придают такую форму и так располагают их друг относительно друга,
чтобы поле, создаваемое зарядами обкладок, было сосредоточено между ними.
Ноиболее простая система, удовлетворяющая этим условиям, представляет
собой две параллельные металлические пластины, расположенные на малом
расстоянии друг от друга, на которых находятся разноименные равные по вели-
чине заряды. Такой конденсатор называют плоским.
Основной характеристикой конденсатора является его емкость, под кото-
рой понимают величину, пропорциональную величине заряда на одной из об-
кладок и обратно пропорциональную разности потенциалов между обкладка-
ми:
С = ~3~, (12.36)
Дф
при этом разность потенциалов Дф часто называют напряжением и обозна-
чают буквой U. Из определения (12.35)
измеряется в фарадах.
Рассмотрим плоский конденсатор
с пластинами площадью S каждая и +?
толщиной зазора d, полностью запол-
ненного однородным диэлектриком
проницаемостью е. Поместим на об-
кладки заряды +q. Заряды каждой об- ~Ч
кладки создадут в окружающем про-
странстве электрическое поле (если
зазор между обкладками по сравне-
нию с их размерами мал, то вблизи пластин поле приближенно можно считать
однородным): силовые линии (рис. 12.26) положительно заряженной об-
кладки будут направленны от нее перпендикулярно поверхности пластины, а
отрицательно заряженной — к пластине, причем по величине (см. формулу
(12-24))
Е+ = Е_ = — ,
+ 2е0
где с = q/S - поверхностная плотность зарядов на пластине.
Очевидно, что вне зазора конденсатора
£вне = £+- £_ = О, (12.37).
а внутри
Е.+Е_ а
^внутри = ” = (J > (12.38)
О О &Q 1Э
где учтено, что внутри диэлектрика поле ослаблено в е раз.
Используя связь (12.20) величины напряженности однородного поля с раз-
ностью потенциалов, получим напряжение между на обкладках конденсатора
157
и его емкость
U = Дф = Гнутой d =
v внутри е£о5
„ <7 <7 SEpS
U Дф d
(12.39)
(12.40)
Из (12.40) видно, что емкость плоского конденсатора тем больше, чем
больше размеры обкладок и чем меньше зазор между ними.
Последовательное и параллельное соединение конденсаторов
Изготовить конденсаторы с емкостями «на все случаи жизни» практичес-
ки невозможно. Поэтому, если требуется получить систему с заданной емкос-
тью, имеющиеся конденсаторы соединяют в батареи.
<9а
С1
F2 Ч>2,3??ФЗ,4 *РУ-1Л l
Рис. 12.27
Рис. 12.28
На рис. 12.27 и рис. 12.28 показано последовательное и параллельное со-
единения конденсаторов. Рассмотрим каждое из них.
При последовательном соединении заряды на всех конденсаторах одина-
ковы. Это легко понять, если рассмотреть соседние обкладки любых двух кон-
денсаторов (на рис. 12.27 они заключены в прямоугольник). Если заряд на по-
ложительно заряженной обкладке конденсатора емкостью С\ равен (+<?,), то на
второй обкладке он будет (-<?,) Выделенные на рисунке обкладки конденсато-
ров С] и С2 изолированы от внешней цепи: их суммарный заряд равен нулю.
Поэтому, заряд положительно заряженной обкладки конденсатора емкостью
С2 также равен (+<?,) и т.д. Следовательно, заряд батареи будет равен заряду
любого из конденсаторов:
Я = 91 = ?2 = ?з ~ • • • = In-
Разность потенциалов Дф = <рА - фв на концах батареи равна сумме разнос-
тей потенциалов на каждом из конденсаторов:
N
Дф^Дф/,
в чем легко убедиться, введя потенциалы ф^- точек между конденсаторами
емкостями С,- и Q:
Дф = (рА - фв = (<рл - ф1>2) + (ф^ - ф2 3) + (ф2 з - Фз 4) +... (фу_1Л - Фв).
Следовательно,
158
1 Дф Аф; + Дф; + Дфз + .., + Acpjy
Огосл. 9 9
или
1 Аф] Дф2 Дф3 Афдг 111. 1 ^1
^посл. Я Я Я Я С2 С3 CN t=iCf
При параллельном соединении конденсаторов заряд всей батареи будет
равен сумме зарядов на всех конденсаторах:
N
? = ?]?(>
где q, - заряд ('-го конденсатора, равный
4i= С/ Афр
Поскольку разность потенциалов Дф = фл - фв на концах батареи равна на-
пряжению на каждом конденсаторе
Дф = Дф] = Дф2 = Дфз = ... = Дфу,
то N
q = С] Дф + С2 Дф + С3 Дф +... + CN Дф = Дф 2^ Q,
а емкость батареи конденсаторов, соединенных параллельно:
С --У--£ С
паР~Дф'=1 г
Энергия электрического поля
Энергия взаимодействия зарядов
Выражение (12.14) можно рассматривать как взаимную потенциальную
энергию зарядов q и q0. Обозначив заряды как <?] и q2, а расстояние между ними
Г] 2, получим выражение для энергии взаимодействия двух точечных зарядов:
^U=7g'~ • (12.41)
М 4Л Е0 Г] 2
Если воспользоваться выражением (12.16) для потенциала точечного заря-
да, то формулу (12.41) можно переписать по-другому:
= «1Ф1 = ?2 Ч>2 = 2 ,?i4i (12-42)
где ф] - потенциал поля в точке расположения заряда <?], <р2 - в точке распо-
ложения заряда q2.
Рассмотрим систему, состоящую из N точечных зарядов q^ (где (=1,2,3,.
.., N), расстояние между любой парой которых равно гц. Энергия взаимодей-
ствия такой системы равна сумме энергий взаимодействия зарядов, взятых по-
парке,: „ ,
В формуле (12.43) суммирование производится по индексам i и j, при этом
оба индекса «пробегают» все значения от 1 до N, причем слагаемые, которым
соответствуют одинаковые значения индексов i и J, не учитываются.
(12.43)
159
С учетом формулы (12.42) для энергии взаимодействия двух точечных за-
рядов выражению (12.43) можно придать вид
(12.44)
где ф,- - потенциал, создаваемый всеми зарядами, кроме q„ в точке, где рас-
положен этот заряд.
Энергия проводника
Заряд q, находящийся на проводнике, можно рассматривать как систему
точечных зарядов Дд(-, энергия взаимодействия которых равна
где ф,- - потенциал, создаваемый всеми зарядами, кроме Дд,-, в точке на по-
верхности проводника, где расположен этот заряд. Поскольку поверхность
проводника эквипотенциальна, то
1 N 1
’Г=2<Р/?1Л9;= 29Ф’
или с учетом (12.35):
W=^=2C = ^- (12Л5)
Энергия конденсатора
Каждая из обкладок конденсатора представляет собой заряженный про-
водник. Если заряд (+q) находится на обкладке с потенциалом ф], а заряд (-q) -
на обкладке с потенциалом ф2, то энергия такой системы равна
W = | {(+<?) <Р1 + (гЯ) Фг} = | Я (Ф1 - Фг) = | Я ДФ>
или с учетом (12.36):
= = (12.46)
Энергия электрического поля
Применим формулу (12.46) к расчету энергии плоского конденсатора, об-
кладки которого имеют площадь S, а зазор шириной d полностью заполнен ди-
электриком с проницаемостью е:
С Д<о2 1 е е0 S . ,
^=С^Ф_ = ^
где использовано выражение для емкости конденсатора (12.40), а разность
потенциалов записана в виде Дф = Е d.
Запишем соотношение (12.47) по-другому:
е en Е2 е Ел Е2
W= ° Sd= ° V=wV, (12.48)
где V=Sd - объем, занимаемый полем (напомним, что у конденсатора поле
сосредоточено только между обкладками).
Величина
160
W ee0£2
w = y = —2—’ (12.49)
равная энергии поля, сосредоточенной в единице объема, называется объем-
ной плотностью энергии электрического поля.
В общем случае неоднородного поля выражение для объемной плотнос-
ти энергии электрического поля совпадает с (12.49). Энергию, заключенную
в некотором объеме V, можно найти, вычислив интеграл
(12.50)
v
Рекомендации по решению задач
Часть задач электростатики основана на применении закона Кулона к точечным за-
рядам и системам, сводящимся к ним (например, заряженную нить или кольцо можно
представить в виде бесконечно большого числа точечных зарядов, расположенных непре-
рывно), находящимся в равновесии. При решении таких задач следует:
1. Сделать схематический чертеж, на котором указать все силы, действующие на заряды.
Если в задаче рассматриваются только два заряда, то сила Кулона будет направлена вдоль
линии, соединяющей заряды; при этом следует помнить, что одноименные заряды оттал-
киваются, а разноименные - притягиваются. Если система содержит N > 2 точечных заря-
дов, то на каждый нз зарядов будет действовать У - 1 сила Кулона. Направления этих сил
для выбранного заряда нужно проставить, рассмотрев поочередно взаимодействие этого
заряда с каждым нз остальных. При этом может оказаться, что силы, действующие на заряд
(силы Кулона, сила тяжести, силы реакции опоры и натяжения нити и т.п.), не лежат в
одной плоскости. Замена всех сил Кулона их равнодействующей (на основании принципа
суперпозиции) в таких задачах, как правило, позволяет уйти от необходимости простран-
ственного рассмотрения условий равновесия и свести систему сил в одну плоскость. Сле-
дует иметь в виду, что при рассмотрении систем зарядов, на каждый нз которых действуют
одинаковые силы (например, одинаковые заряды расположены в вершинах треугольника,
квадрата или любой другой правильной геометрической фигуры), нет необходимости рас-
сматривать отдельно каждый заряд: достаточно рассмотреть любой нз них.
2. Выбрать систему координат, расположив ее осн в плоскости действия сил, и записать
условия равновесия для зарядов, составляющих систему. При этом для каждого из зарядов
удобно выбирать свою систему координат. Условия равновесия обычно записывают в виде
равенства нулю суммы проекций сил на осн:
£Fx = 0, £Fy = 0.
Если находящееся в равновесии тело имеет закрепленную ось вращения, исключающую
всякое поступательное движение тела, то в качестве условия равновесия удобно исполь-
зовать уравнение равенства нулю моментов сил относительно этой осн (см. книгу «Ме-
ханика» §6).
3. Записать развернутые выражения для всех сил, действующих на каждое из тел, и решить
полученную систему уравнений.
Другая большая часть задач связана с расчетами напряженности и потенциала элект-
рического поля, создаваемого системами точечных зарядов, заряженными плоскостями и
телами сферической формы.
В задачах на вычисление напряженности электрического поля особое внимание
нужно обратить на векторный характер Е-.
- векторы напряженности электрического поля уединенного точечного заряда направлены
от заряда, если он положителен, и к заряду, если он отрицателен;
- поле заряженной плоскости однородно; векторы Е поля плоскости направлены перпен-
дикулярно ее поверхности от плоскости, если ее заряд положителен, н к плоскости, если
заряд отрицателен;
161
- для электрического поля заряженной сферы в точках, расположенных за ее пределами,
векторы напряженности направлены так же, как у точечного заряда, находящего в центре
сферы; внутри сферы электрическое поле равно нулю;
- для поля шара, заряженного равномерно по объему, в точках, расположенных за его
пределами, векторы напряженности, направлены также, как у сферы; внутри - как у то-
чечного заряда, помещенного в центр шара (совпадают только направления, а не величи-
ны!); если шар проводящий, то нескомпенсированные заряды расположатся на его поверх-
ности, что с точки зрения электростатики эквивалеитио заряженной сфере;
- электрическое поле внутри полости проводника отсутствует (это справедливо независи-
мо от наличия у проводника заряда и внешнего электрического поля);
- направление вектора напряженности поля системы точечных зарядов в произвольной
точке определяется на основании принципа суперпозиции-строятся векторы Е, в данной
точке для каждого из зарядов q,, а результирующий вектор Е определяют как их векторную
сумму; направление вектора напряженности системы точечных зарядов и плоскости,
сферы или шара, или при любой другой комбинации заряженных тел, определяется ана-
логично.
Прн решении задач на расчет потенциала следует иметь в виду, что потенциал ска-
лярная функция, и его знак определяется знаком заряда, создающего поле. Потенциал то-
чечного заряда определяется формулой (12.16), сферы и шара в точках, расположенных
за их пределами, - формулой (12.27), внутри сферы или проводящего шара - он равен
потенциалу на поверхности и его значение можно найти по формуле (12.28). Потенциал
поля любой комбинации указанных тел будет равен алгебраической сумме потенциалов,
создаваемых каждым из них в отдельности. Потенциал электрического поля, создаваемого
заряженной плоскостью, вычислить нельзя; так как поле плоскости на любых расстояниях
от ее поверхности одинаково (см. формулу (12.24)), то работа сил поля по перемещению
положительного заряда из произвольной точки на бесконечность будет стремиться к бес-
конечности. Это значит, что потенциал также будет стремиться к бесконечности. Однако
в практических расчетах важно знать не потенциал в некоторой точке, а разность потен-
циалов между точками поля, которую можно найти из связи потенциала с напряженностью
(см. формулы (12.20), (12.21)). Так для двух точек поля, расположенных на расстояниях
Х| и х2 от плоскости (с одной стороны)
Дф|_2 = фг ~ ф| = Е А*,
где Дх = х2-Х|.
Определение потенциалов поля более сложных систем зарядов - достаточно трудо-
емкая задача, требующая навыков интегрирования.
Достаточно часто встречаются задачи, в которых происходит перераспределение за-
рядов между телами, например, прн соприкосновении тел друг с другом или соединении
их проводником. Следует помнить, что заряды перераспределятся таким образом, чтобы
потенциалы тел стали равными, а суммарный заряд сохранился. Очевидно, что если тела
одинаковы, то заряды распределятся между ними поровну. Сюда же относятся задачи, в
которых одним из тел является Земля (ее потенциал прн любых процессах считают неиз-
менным н равным нулю). Часто прн этом делают ошибку, полагая, что с заземлемленного
тела все заряды стекут на Землю. На самом деле заземление приводит лишь к тому, что
потенциал тела станет равным потенциалу Земли, а тело отдаст Земле или возьмет у нее
необходимый для этого заряд любого знака.
Прн графическом изображении поля следует иметь в виду, что силовые линии стро-
ятся так, чтобы векторы напряженности в любой точке были направлены по касательным
к ним, а сами силовые линии должны быть перпендикулярны эквипотенциальным поверх-
ностям и направлены в сторону убывания потенциала. Если задача состоит в построении
зависимостей значений величины напряженности поля или его потенциала от координат,
то следует помнить, что любая проводящая поверхность является эквипотенциальной и
162
«разрывает» силовые линии. При этом напряженность поля может измениться скачком, а
потенциал будет непрерывен (вспомните, он пропорционален работе сил поля, а она не
может меняться скачками). На рнс. 12.29 н рнс. 12.30 в качестве примера построены за-
висимости напряженности поля и потенциала сферы радиуса R, заряженной равномерно
положительным зарядом q (см. формулы (12.26), (12.25), (12.28) и (12.27)).
Следующая часть задач связана с расчетом параметров конденсаторов н образован-
ных из них цепей. Следует иметь в виду, что две близко расположенные заряженные плас-
тины представляют собой плоский конденсатор только в том случае, если на них находятся
равные по величине разноименные заряды. В противном случае, это всего лишь набор за-
ряженных проводников, создающих в окружающем пространстве однородное электричес-
кое поле.
Если требуется рассчитать емкость системы, составленной из набора проводящих
пластин, то можно пойти по такому пути:
- пластинам, соединенным с точками входа н выхода (назовем их крайними), сообщить
одинаковые разноименные заряды;
- рассчитать напряженность электрического поля во всем пространстве между этими плас-
тинами (это поле однородно);
- используя связь (12.20) между разностью потенциалов и напряженностью поля, опреде-
лить напряжение между крайними пластинами;
- по формуле (12.36) определить емкость системы.
Если между крайними пластинами находится толстая проводящая незаряженная
пластина, то на ее поверхностях появятся индуцированные заряды, которые не внесут ни-
каких изменений в картину поля; при этом саму пластину можно убрать н учесть ее,
уменьшив расстояние между крайними пластинами на величину, равную толщине этой
пластины. Если же между проводящими пластинами находится пластина из диэлектрика
с проницаемостью е, то на ее границах появятся поляризационные заряды, что приведет
к уменьшению поля внутри диэлектрика в е раз.
Если одна из крайних пластин соединена с каким-либо телом, например, с третьей
пластиной, то прн расчете параметров поля следует учесть тот факт, что, сообщенный этой
пластине заряд перераспределится между ней н третьей пластиной так, чтобы их потен-
циалы стали одинаковыми.
Прн расчете батарей конденсаторов прежде всего нужно выяснить тип соединений
(для этого, возможно, нужно будет нарисовать схему по-другому); понять, какие из кон-
денсаторов соединены между собой последовательно, а какие - параллельно. Далее, пос-
ледовательно заменяя два (или более) конденсатора одним с эквивалентной емкостью, цепь
постепенно упрощают, пока не будет найдена общая емкость. Если же соединение кон-
денсаторов не относится ни к последовательному, ни к параллельному, то общую емкость
такого соединения методами школьного курса физики можно найти сравнительно просто
только в тех случаях, если в схеме имеются точки с одинаковым потенциалом: такие точки
можно соединять н разъединять, при этом заряды на конденсаторах н емкость батареи не
изменятся. Соединяя и разъединяя точки с равным потенциалом, можно сложное соеди-
163
некие конденсаторов свести с комбинации
последовательных и параллельных соеди-
нений. Точки с одинаковым потенциалом
есть всегда в соединениях, обладающих
осью или плоскостью симметрии относи-
тельно точек входа и выхода. При этом,
если точки входа н выхода лежат на плос-
кости симметрии, то точки одного потен-
циала находятся на концах конденсаторов,
которые «перечеркиваются» этой плоскос-
Рис. 12.31
тью. Если плоскость симметрии перпендикулярна линии, на которой лежат точки входа
и выхода, то равные потенциалы имеют все точки пересечения этой плоскости с провод-
никами. Например, в известной схеме - мост емкостей, представленной на рис. 12.31, если
С] = С2 и С3 = С4, то плоскостью симметрии является плоскость, проходящая перпенди-
кулярно рисунку через точки входа А н выхода В. При этом потенциалы в точках а и b
будут одинаковы. Это означает, что конденсатор емкостью С5 не заряжен и в накоплении
зарядов участия не принимает: его можно не учитывать, удалив из цепи, или соединив
между собой точки а н Ь. Если С, = С3 и С2 = С4, то плоскость симметрии проходит через
точки а и Ь, которые будут иметь равные потенциалы. Очевидно, что рассмотренные слу-
чаи можно объединить: если С, С4 = С2С3, то точки а и b имеют равные потенциалы.
Такой мост называют уравновешенным или сбалансированным.
При расчете батарей конденсаторов следует помнить, что:
- при последовательном соединении заряды на всех конденсаторах одинаковы и равны заря-
ду батареи; разность потенциалов на концах батареи равна сумме разностей потенциалов на
каждом конденсаторе; емкость батареи будет меньше емкости конденсатора с наименьшей
емкостью;
- при параллельном соединении конденсаторов заряд батареи равен сумме зарядов всех кон-
денсаторов; напряжения на всех конденсаторах одинаковы и равны напряжению на концах
батареи; емкость батареи будет больше емкости конденсатора с наибольшей емкостью;
- алгебраическая сумма зарядов любой системы обкладок, изолированных от источника,
равна нулю (например, на рнс. 12.31 такие системы обкладок заключены в прямоугольни-
ки);
- если батарея конденсаторов подключена к источнику напряжения, то при изменении ем-
кости системы (вследствие изменения расстояния между обкладками, внесение или удале-
ние диэлектрика из зазора и т.п.) напряжение на концах батареи меняться не будет, а заряд
изменится;
- если батарею конденсаторов зарядить, а затем отключить от источника зарядов, то при из-
менении емкости системы заряд батареи меняться не будет, а напряжение на концах изме-
нится.
Вычисление энергии системы зарядов, проводника, конденсатора или электрическо-
го поля особых затруднений не вызывает. Эти величины могут быть найдены по формулам
(12.44), (12.45), (12.46), (12.48) или (12.50). Работа, совершаемая полем иад точечным за-
рядом, будет равна разности энергий заряда в конечной и начальной точках траектории
и не зависит от ее формы. Если же энергия системы по каким-либо причинам уменьши-
лась, то это означает, что часть энергии поля перешла в механическую энергию или сто-
ронние силы совершили отрицательную работу и часть энергии поля перешла в тепло.
Наконец, существенную часть задач представляют комбинированные задачи, сочн-
тающие электростатику с элементами механики. При решении таких задач можно исполь-
зовать рекомендации, предложенные для решения соответствующих задач механики в
книге «Механика». Единственное, что стоит отметить, это тот факт, что в случае иеодно-
164
родных полей (поле точечного заряда или системы, сферы, шара, или их комбинации) на-
пряженность будет меняться от точки к точке. При этом также будет меняться сила, дей-
ствующая на движущиеся заряды (см. формулу (12.7)). Поэтому движение заряженных тел
в таких полях следует описывать через законы сохранения, поскольку использование вто-
рого закона Ньютона приводит к дифференциальным уравнениям.
Задачи
Электрический заряд. Закон Кулона
12.1. С какой силой будут взаимодействовать два одинаковых свинцовых
шарика радиусом R - 1 см, расположенные в вакууме на расстоянии г = 1 м
друг от друга, если у каждого атома одного шарика «отнять» по одному элек-
трону и все их перенести на второй шарик? Относительная атомная масса свин-
ца равна А = 207 а.е.м., плотность свинца р = 11,3 г/см3. Заряд электрона
|е| = 1,610"19 Кл. Гравитационным взаимодействием шариков пренебречь.
• Решение. Если у N атомов одного шарика отнять по одному электрону и все их помес-
тить на другой, то первый шарик приобретет положительный заряд q\, а второй - отри-
цательный qi, причем |</j| = |</2| =lV|e|. При этом между шариками возникнет сила притя-
жения
P_j?lH92L_Jvi[el2
* — 2 — 2 ’
4 л е0 г 4л Со г
Число атомов, находящихся в каждом из шариков, равно
кг т кг
n=-na,
где т = “Ил Л3р - масса шарика, ц =А-10'3 кг/моль - молярная масса свинца (см. §9).
Следовательно, сила притяжения шариков будет равна
4л#А2 |е|2р2Лб .. '
Г =----- / , , « 4,36-10 8 Н.
9-1О“6еоЛ2г2
4лДГА2Н2р2Яб
Ответ'. F =-----у:---4,36-10 8 Н.
12.2. Какой заряд приобрел бы медный шар радиусом R = 1 см, если бы
удалось из него удалить все свободные электроны? Плотность меди равна
р = 8,9-103 кг/м3, относительная атомная масса А = 64 а.е.м. Считать, что на
каждый атом меди приходится один свободный электрон. Заряд электрона
|е| = 1,6-10’19 Кл.р = 8,9 г/см3, относительная атомная масса А = 64 а.е.м. Счи-
тать, что на каждый атом меди приходится один электрон проводимости. Заряд
электрона |е| = 1,6-10’19 Кл.
12.3. Медная монета массой т = 5 г обладает положительным зарядом
q = 0,8 мкКл. Какую долю своих электронов потеряла монета? Относительная
атомная масса меди А = 64 а.е.м. Заряд электрона |е| = 1,6-10"19 Кл. Заряд ядра
атома меди Z = 29-|е|.
12.4. Предположим, что 1 см3 воды разделили на элементарные заряды и
суммарные заряды противоположного знака разнесли на расстояние г = 100 км.
165
С какой силой взаимодействовали бы заряды? Заряд ядра атома водорода
Zx = |е|, заряд ядра атома кислорода Zj = 8-|е|, где |е| = 1,6-10’19 Кл - заряд элек-
трона. Молярная масса воды ц = 18-Ю'3 кг/моль, плотность воды р = 103 кг/м3.
12.5. Во сколько раз сила электростатического взаимодействия между
электроном и протоном больше силы их гравитационного взаимодействия?
Массы электрона и протона равны т = 9,1-Ю'31 кг и М= 1,67-Ю"27кг соответ-
ственно. Заряд электрона |е| = 1,6-10'19 Кл.
12.6. На двух одинаковых капельках воды находится по одному «лишне-
му» электрону, причем сила электростатического отталкивания капелек урав-
новешивает силу их гравитационного притяжения. Каковы радиусы капелек?
Заряд электрона |е| = 1,6-10"19 Кл, плотность воды р = 1 г/см3.
12.7. На двух одинаковых каплях масла радиусом г = 8,22-10'5 м находят-
ся одноименные равные по величине заряды. Определить величину этих заря-
дов, если сила кулоновского отталкивания уравновешивает силу гравитацион-
ного притяжения капель. Плотность масла р = 0,9-103 кг/м3.
12.8. Два заряженных шарика, находящиеся в вакууме на расстоянии
г = 2 м друг от друга, отталкиваются с силой F= 1 Н. Суммарный заряд шари-
ков |0|= 5-Ю'5 Кл. Определить величину заряда на каждом из шариков.
• Решение. Два заряженных шарика, расположенные в вакууме на расстоянии г друг от
друга, будут взаимодействовать с силой
„ Itfil-tal
F =-------2 ’
iiii 4ле0г
гае tel, tel - величины зарядов шариков.
Так как по условию задачи шарики отталкиваются, то это означает, что на шариках
находятся одноименные заряды. Поэтому суммарный заряд шариков равен
101= l?i + ?21 = l“?il + Iftl-
Откуда получаем
l«2l = 10 I" 1911-
Следовательно,
г_10|-|?1|~1?112
или е0 л-2
1?1|2 _ 1С1'1?11+4 я ео r2F= 0.
Решая полученное квадратное уравнение относительно находим
|91| = 'Л{| Q|±Л/02-16лео/2/’}, |?2| = |Q|-19|| = '4{1С1+Л/С2- 16л eor2^}.
Следовательно,
|?1Д| = 11QI ± С2- 16л е0 л-2 Г}; |9|| = 3,84-10’5 Кл, |?2| = 1,16-10’5 Кл.
• Ответ-. |91>2| = ’4{10|±^02-^Ео^г}; |91| = 3,84-10'5 Кл,* tel = 1Д6-10'5 Кл.
12.9. Два одинаковых точечных заряда взаимодействуют в вакууме на
расстоянии г = 1 м с силой F = 1 Н. Найти величину каждого заряда.
12.10. Определить расстояние rt между двумя одинаковыми электричес-
кими зарядами, находящимися в масле, £сли сила взаимодействия между
166
ними такая же, как и в вакууме на расстоянии г2 = 30 см. Диэлектрическая
проницаемость масла е = 3.
12.11. Три одинаковых заряда величиной q = ПТ* Кл каждый расположены
в вершинах равностороннего треугольника. Где и какой заряд Q нужно помес-
тить, чтобы вся система находилась в равновесии?
• Решение. Так как по условию задачи все заряды находятся на равных расстояниях друг
от друга и величины зарядов равны между собой, то между любыми двумя из них будет
действовать сила отталкивания
q*
42''
—Я"
a
q*
Puc. 12.32
г = 2 ’
4яе0<г
где а - расстояние между двумя произвольны-
ми зарядами (рис. 12.32).
Рассмотрим один из зарядов. Со сторо-
ны соседних зарядов иа него будут действо-
вать две равные по величине силы
2 „2
^1 = 7^ и F* = T^'
4 л е0 а 4 л so (Г
результирующая которых равна
F3 = 2 —2-—г cos а,
, 4 л е0 сг
где а = 30° Сида F3 будет направлена по диагонали параллелограмма, построенного на
векторах F\ и F2. Такие же по величине силы будут действовать и иа остальные два за-
ряда Поэтому, очевидно, что для равновесия системы в геометрическом центре треуголь-
ника (в случае равностороннего треугольника - это точка пересечения биссектрис, медиан
или высот) необходимо поместить отрицательный заряд Q, который будет притягивать
каждый из зарядов q с силой
2
F4 = F3 = - glg+
4л ео г2
где г = а/(2 cos а) - расстояние между зарядами q и Q.
Следовательно,
<7 cos g <?|g|cos2a
2л So а2 л Eq а2
ИЛИ
« -5,8-10'6 7 Кл.
6 = -^—
7 2 cos а
Ответ: заряд Q ® -5,8-10 Кл нужно поместить в геометрическом центре треугольника.
12.12. На расстоянии г = 3 м друг от друга расположены два точечных за-
ряда qx = -3-10'9 Кл и 92 = -12-10'9 Кл. Когда в некоторой точке поместили по-
ложительный заряд q0, то все три заряда оказались в равновеснн. Определить
величину заряда q0 и расстояние I между зарядами qx и q0.
12.13. На концах горизонтальной непроводящей трубы длиной I закрепле-
ны положительные заряды qx и q2. Найти положение равновесия шарика с по-
ложительным зарядом q, который помещен внутрь трубы. Трения нет.
12.14. Какая сила действует на заряд q, помещенный в центре квадрата со
стороной а, в вершинах которого расположены заряды qx, q2, q3, q4 одного
знака с q?
167
12.15. В центр квадрата, в вершинах которого находятся одинаковые заря-
ды q, помещен отрицательный заряд Q. Какова должна быть величина этого за-
ряда, чтобы система находилась в равновесии?
12.16. Внутри гладкой диэлектрической сферы радиусом R находится ма-
ленький шарик массой т и зарядом q. Какой величины заряд Q нужно помес-
тить в нижней точке сферы, чтобы шарик был в положении устойчивого равно-
весия в верхней точке?
а) б)
Рис. 12.33
12.17. Четыре положительных заряда q, Q, q, Q связаны пятью невесомы-
ми нерастяжимыми нитями, как показано на рис. 12.33, а. Длина каждой нити
I. Определить силы натяжения всех нитей.
• Решение. Рассмотрим два заряда q и Q, выделенные на рис. 12.33, б.
На заряд q действуют четыре силы: силы , F^' со стороны соседних с ним заря-
дов Q, сила Fj со стороны наиболее удаленного заряда q и силы натяжения нитей 7^,
7^’. Причем
Л=f; = г , f2=------------£-------2,
4 л е0 г 4л е0 (2/ cos 'Vi)
где а = 60°. Результирующая этих сил й будет направлена вдоль диагонали ромба, по-
строенного на вектах и /V, и равна:
Fi = 2 Fi cos % + F2 = —% &: cos % +--------— .
2л eo Г 16л eo Г cos2
Так как система зарядов находится в равновесии, то это означает, что вектор, равный
сумме сил натяжения нитей 7^ и 7^', будет лежать на указанной диагонали ромба и на-
правлен в сторону противоположную F^. Это возможно только в случае, если Т\ = Tj.
Следовательно, условие равновесия рассматриваемого заряда q
% + ?i + ?i = 0
в проекции на ось ОХ можно записать в виде
2 T’j cos > cos ?---5—.
2л е0/ 16л ео Г cos
168
Откуда получим
Г,-Г1 ~ 4л ео/2^ + 8 cos3 4яе0/2^+3^^
Аналогично для выделенного заряда Q.
На заряд Q действуют четыре силы: силы со стороны соседних зарядов q,
сила Лз со стороны заряда Q н силы натяжения нитей 7^ , ?2 и • Причем равнодейст-
вующая сил ,
Fl = g g а , fi'=Fi= g%, f3 = 2
4я e0 Г 4я e0 г 4л e011
будет направлена вдоль нити, соединяющей заряды Q и Q-.
F$ = 2Fi cos а + F3 = —g cos а + —.
2л ео Г 4я со г
С другой стороны, результирующая сил натяжения нитей также направлена вдоль
этой нити, но в противоположную сторону, и равна по величине силе F5. Очевидно, это
означает, что Ту = Т3 (рис. 12.33, б). Условие равновесия заряда Q можно записать в виде
<7 (2 cos a Q1
2 Tj cos а + Г, = -т- + —“—г .
2л ео Г 4л ео Г
Откуда, с учетом выражения для силы натяжения Ту и значения угла а, получим
Сила натяжения Т4 нити, соединяющей заряды q и Q, очевидно, равна Ту = Ту = Т3.
12.18. Шарик массой m = 50 мг подвешен на непроводящей нити и имеет
заряд q = 10‘8 Кл. На расстоянии I = 32 см от него снизу подносится другой ма-
ленький шарик. Каким должен быть заряд этого шарика, чтобы натяжение нити
увеличилось в и = 2 раза?
g
m О q
m • q
Puc. 12.34
12.19. Два маленьких одинаковых шарика массой т = 50 г каждый заряже-
ны одинаковыми электрическими зарядами и подвешены на длинных невесо-
мых нерастяжимых нитях так, как показано на рис. 12.34. Какой заряд должен
иметь каждый шарик, чтобы обе нити испытывали одинаковое натяжение? Рас-
стояние между шариками I = 20 см.
169
12.20. Три положительных заряда qlt q2, Чз расположены на одной прямой
и связаны невесомыми нерастяжимыми нитями длиной I каждая. Найти силы
натяжения нитей.
12.21. Четыре положительных заряда q, Q, q, Q связаны четырьмя невесо-
мыми нерастяжимыми нитями, как показано на рис. 12.35. Длина каждой
нити I. Определить углы между нитями.
12.22. Семь одинаковых зарядов величиной q каждый связаны друг с дру-
гом невесомыми нерастяжнмыми нитями, как показано на рис. 12.36. Длина
каждой нити I. Найти силу натяжения каждой нити.
12.23. У основания гладкой наклонной плоскости с углом наклона к гори-
зонту а = 30° закреплен заряженный шарик. Второй шарик, одноименно заря-
женный с первым, находится в равновесии на плоскости. Во сколько раз изме-
нится расстояние между шариками, если угол наклона плоскости увеличить в
два раза?
12.24. Три одинаковых шарика, расположенные на одной горизонтальной
прямой, соединены двумя одинаковыми невесомыми и непроводящими пружи-
нами жесткостью к каждая. Расстояние между крайними шариками равно /0.
Всем шарикам были сообщены одинаковые по величине и по знаку заряды, при
этом расстояние между крайними шариками стало равно I. Определить величи-
ну каждого заряда.
к к
а)
-уЛ
б)
Рис. 12.37
• Решение. Так как крайние шарики распо-
ложены симметрично относительно сред-
него и соединены с ним одинаковыми пру-
жинами, то для решения задачи достаточ-
но рассмотреть одни из иих, например,
шарик выделенный иа рис. 12.37, а.
После сообщения шарикам одинако-
вых зарядов q между ними возникнут си-
лы отталкивания: Ft - между средним н
крайними шариками, - между крайни-
ми шариками. В результате действия этих
сил каждая пружина будет растягиваться
до тех пор, пока силы, действующие на шарики, не уравновесят друг друга. В положении
равновесия каждая пружина растянется иа величину (Z -1^/2. При этом в пружине возник-
нет сила упругости Тут,, равная
F -к^
гупр-л 2 *
а силы электрического отталкивания примут значения
2 „2
Fi=-----2---у и Г2 = —2—Ч.
4ле0(//2)2 Длео/2
В положении равновесия иа рассматриваемый шарик будут действовать силы F\ , F2
и , направленные так, как показано на рис. 12.37, б. Условие равновесия запишем в
виде
170
F^F,.F^ ™
Откуда получаем
q = l'i2Ane0k(l-l0).
• Ответ: q = l я eo Jt(Z-/0).
12.25. Два одинаковых шарика, соединенные непроводящей невесомой
пружиной жесткостью к, лежат на гладком горизонтальном столе. При сооб-
щении шарикам одинаковых по величине разноименных зарядов q пружина
сжалась на величину Дх. Найти длину недеформированной пружины.
12.26. Каркас в форме квадрата со сторо-
ной а составлен из четырех одинаковых неве-
сомых непроводящих пружин жесткостью к
каждая. Пружины соединены между собой по-
парно небольшими шариками, как показано на
рнс. 12.38. Когда шарикам были сообщены
одинаковые заряды, площадь, ограниченная
каркасом, увеличилась в два раза. Найти заряд
каждого шарика.
Рис. 12.38
Рис. 12.39
12.27. Два одинаковых проводящих шарика, один из которых закреплен,
а второй подвешен на невесомой нерастяжимой нити, находятся в соприкос-
новении (рис. 12.39, а). Длина нити 1 = 20 см, масса каждого шарика т = 15 г.
Шарики заряжают одинаковыми зарядами, вследствие чего подвижный шарик
отклоняет нить на угол а = 60°. Найти заряд каждого шарика.
• Решение. После сообщения шарикам одинаковых зарядов между ними возникнет сила
отталкивания, в результате чего подвижный шарик будет отклоняться то тех пор, пока
все силы, действующие на него, ие уравновесят друг друга. В положении равновесия сила
электрического взаимодействия встанет равна
F= .. <?
4я БоГ2 ’
где г - расстояние между шариками в положении равновесия (рис. 12.39, б):
171
г = 21 sin %
На подвижный шарик будут действовать три силы: сила тяжести т g, сила натяжения
нити 7^и сила Запишем условие равенства нулю моментов всех сил, действующих на рас-
сматриваемый шарик, относительно осн OZ, проходящей через точку подвеса:
SA/z = mgZsina-FZcos% = 0.
Следовательно, используя равенство sin a = 2 sin % cos %, получаем
2
2 m g sin % =----.
16л Ear sin %
Откуда находим величину заряда q:
q = 4 I sin % з/ 2л eo m g sin % « 8,1-10'7 Кл.
Условия равновесия подвижного шарика можно было записать, например, через ра-
венство нулю проекций сил, действующих на шарик, на оси ОХ и OY системы координат:
"S.FX = F cos - Т sin а = О,
SFy = Fsin % + Т cos a - mg = 0.
Решение этой системы уравнений также приводит к ответу.
• Ответ- q = 4 I siny2ne0mg sin % » 8,1 • 10’7Кл.
12.28. Два маленьких шарика, заряженные равными разноименными заря-
дами, закреплены в горизонтальной плоскости на расстоянии I друг от друга.
Третий заряженный шарик подвешен над ними. Точку подвеса один раз поме-
щают так, что этот шарик в состоянии равновесия (когда шарики не заряжены)
находится точно над первым закрепленным шариком на расстоянии I от него, а
другой раз - так же над вторым шариком. Найти углы а! и а2 отклонения нити
от вертикали в двух указанных положениях, если над первым шариком угол от-
клонения нити в два раза больше, чем над вторым.
12.29. Чтобы измерить ускорение свободного падения в данном месте,
можно поступить следующим образом. В одной и той же точке на нитях одина-
ковой длины I подвешивают два одинаковых маленьких шарика массой т каж-
дый. Шарикам сообщают такие одинаковые заряды q, чтобы угол между нитя-
ми стал прямым. Определить величину ускорения свободного падения, если
при / = 1 м, т = 4,5-Ю"4 кг шарикам необходимо сообщить заряд равный
<7=10'6Кл.
12.30. Три маленьких шарика массой т = 10 г каждый подвешены в одной
точке на невесомых нерастяжимых нитях длиной I = 1 м. Шарики одинаково
заряжены и располагаются в вершинах равностороннего треугольника со сто-
роной a = 0,1 м. Каков заряд каждого шарика?
12.31. Два одинаковых заряженных маленьких шарика, подвешенные на
невесомых нерастяжимых нитях одинаковой длины, находятся в керосине. Ка-
кова должна быть плотность р шариков, чтобы угол расхождения нитей в воз-
духе и в керосине был один и тот же? Плотность керосина рк = 800 кг/м3, отно-
сительная диэлектрическая проницаемость е = 2.
172
12.32. Маленький шарик, заряженный
до величины q = 10"8 Кл, находится на рас-
стоянии / = 3 см от большой заземленной
металлической пластины. С какой силой они
взаимодействуют?
• Решение. Как указывалось в теоретическом введе-
нии к данному параграфу, сила взаимодействия
между точечным зарядом н большой заземленной
металлической плоскостью равна силе взаимодей-
ствия двух точечных зарядов q и (-?), расположен-
ных зеркально относительно плоскости (рис. 12.40).
Следовательно, 2
F =----2---у = —2—у « 2,5-10"4 Н.
2 4ле0(2/)2 16л е0Г
• Ответ: F = —2—у « 2,5-10‘4 Н.
16Л Eq Г
Q
я
-я
Рис. 12.40
Рис. 12.41
12.33. Два точечных заряда q = 2-10'8 Кл и Q = 4-10"8 Кл находятся вблизи
большой заземленной металлической пластины на расстояниях а = 10 см и
b = 20 см от ее поверхности соответственно. Причем оба заряда находятся на
одном перпендикуляре к поверхности пластины (рис. 12.41). Определить силу,
действующую на заряд q.
12.34. Маленький шарик подвешен на легкой пружине жесткостью к вбли-
зи большой металлической заземленной пластины (рис. 12.42). Если шарик не
заряжен, то он находится на расстоянии h от пластины. При сообщении шарику
некоторого заряда, расстояние уменьшается на величину Дй. Найти заряд, со-
общенный шарику.
12.35. Маленький шарик массой т = 1 г
подвешен на невесомой нерастяжимой нити
длиной I- 10 см вблизи большой металличес-
кой заземленной пластины (рис. 12.43). Точка
подвеса находится на расстоянии а = 10 см от
пластины. При сообщении шарику некоторого
заряда нить отклоняется от вертикали на угол
а = 30°. Найти заряд шарика.
173
12.36. Металлическое кольцо радиусом R несет на себе электрический
заряд q, при котором натяжение проволоки, из которой сделано кольцо, равно
Т. Какой заряд Q нужно поместить в центр кольца, чтобы оно разорвалось?
Проволока выдерживает максимальное натяжение То.
* Решение. Рассмотрим бесконечно малый элемент кольца длиной А/.
Полагая, что электрический заряд кольца q распределен по всей его длине равномерно,
найдем заряд А^ на выделенном элементе кольца. Так как на единицу длины приходится
заряд Адед = q/2n R, то на элементе кольца длиной А/ будет находиться заряд
Дд = Лдея Д1 = <1 А1/2л R.
Если длину А/ выразить через радиус кольца R и угол а (рис. 12.44, а), т.е. А/ = 2 R а,
то получим
&q=n-
Ha заряд Дд со стороны остальных зарядов кольца будет действовать кулоновская
сила X направленная по радиусу и стремящаяся разорвать кольцо. Кроме силы Ё^на эле-
мент AZ кольца будут действовать со стороны соседних участков силы натяжения Очевид-
но, что при этом выполняется равенство
F= 2 Т sin а.
Если в центр кольца поместить заряд Q, то на выделенный элемент кольца будет дей-
ствовать кулоновская сила Р^= ]?+ (рис. 12.44, б), где
АГ=-^Ц ,
4ЯЕОЛ2
и силы натяжения 7g. При этом, для того, чтобы кольцо разорвалось, должно выполняться
неравенство
2 То sin а < F,'
где
F'=F + , или F ’= 2 Т sin а + —.
4 л eo IT ^£qR1
Так как угол а мал, то можно положить, что sin а » а. Следовательно, с учетом выра-
жения для А?,
2Т0а<2Та +
4л2е0Я2
174
Откуда окончательно получаем
8т? Ер (Гр-Г) Я2
У> Ч
„ ^2^{T0-T)R2
• Ответ-. О >-----------.
Ч
12.37. Металлическое кольцо несет на себе электрический заряд q, прн
этом натяжение проволоки, из которой сделано кольцо, равно Т. В центр коль-
ца помещают заряд Q, при котором сила натяжения в кольце увеличивается
вдвое. Определить радиус R кольца.
12.38. В центр металлического кольца радиусом R, на которое нанесен
заряд Q, помещают точечный заряд q. На сколько при этом изменилась сила на-
тяжения кольца?
12.39. Металлическое заряженное кольцо разорвалось кулоновскими сила-
ми, когда заряд кольца был равен q0. Оценить, какой заряд q разорвет такое же
кольцо, если оно в два раза прочнее.
Напряженность электрического поля
12.40. Какой угол с вертикалью составит невесомая непроводящая нить, на
которой внеит шарик массой т = 25 мг, если поместить шарик в горизонталь-
ное однородное электрическое поле с напряженностью Е = 35 В/м, сообщив
ему заряд q = l мкКл?
• Решение. На заряженный шарик, помещенный в
электрическое поле напряженностью будут дейст-
вовать три силы: сила тяжести т g^ сила натяжения
нити 7^ и сила Мл, обусловленная наличием посто-
янного электрического поля, причем, так как заряд
шарика q > 0, то Мл будет направлена вдоль сило-
вых линий поля (рис. 12.45).
Под действием этих трех сил шарик будет от-
клонять нить от вертикального положения до тех пор,
пока все силы не уравновесят друг друга. Запишем
условие равновесия шарика, например, через равенство нулю моментов сил, действующих
на него относительно оси OZ, проходящей через точку подвеса О перпендикулярно плоскос-
ти рисунка:
ZA/z = mg/sina- I cos a = 0,
где I - длина нити, сила Fan = q E.
Следовательно,
т g sin а = q Е cos а.
Откуда получаем
дЕ ж qE „г0
tga = J—, или a = arctg — = 45 .
6 mg 6 mg
• Ответ: а = arctg = 45°.
mg
175
12.41. В однородном электрическом поле находится пылинка массой
т = 410"7 г, обладающая зарядом q = -1,6-Ю’11 Кл. Какой должна быть по мо-
дулю и направлению напряженность поля, чтобы пылинка оставалась в покое?
12.42. В однородном электрическом поле напряженностью Е = 1 МВ/м,
силовые линии которого направлены вертикально вниз, висит на невесомой не-
проводящей нити шарик массой т = 2 г, обладающий зарядом q = 10 нКл. Чему
равна сила натяжения нити?
12.43. В однородном электрическом поле, векторы напряженности которо-
го направлены горизонтально, висит на невесомой непроводящей нити шарик
массой т = 2 г, имеющий заряд q = 10 нКл. Найти силу натяжения нити, если
напряженность электрического поля равна Е = 106 В/м.
12.44. Заряженный шарик, подвешенный на невесомой диэлектрической
нити, находится во внешнем электрическом поле, силовые линии которого гори-
зонтальны. При этом нить образует угол а = 45° с вертикалью. На сколько изме-
нится угол отклонения нити прн уменьшении заряда шарика на т) = 10%?
12.45. Шарик, подвешенный на невесомой непроводящей пружине жест-
костью к, помещен в однородное электрическое поле, векторы напряженнос-
ти Е которого направлены вертикально вверх. На сколько изменится длина
пружины, если шарику сообщить положительный заряд ql
12.46. Шарик, несущий положительный
заряд q, положили на непроводящую невесо-
мую пластинку, прикрепленную к столу с по-
мощью пружины жесткостью £(рис. 12.46).
При включении однородного электрического
поля, векторы напряженности которого направ-
лены вертикально вниз, длина пружины изме-
нилась на величину Лх. Определить величину
напряженности электрического поля.
12.47. Шарик радиусом г, несущий положительный заряд q, висит на неве-
сомой непроводящей пружине. Если этот шарик поместить в жидкость плот-
ностью р и одновременно включить однородное электрическое поле, векторы
напряженности которого направлены вертикально вниз, то длина пружины не
изменится. Определить величину напряженности электрического поля.
12.48. Шарик радиусом г, несущий положительный заряд q, равномерно
опускается в жидкости, где создано однородное электрическое поле, векторы
напряженности которого направлены вертикально вверх. Плотности шарика и
жидкости равны р и р0 соответственно, причем р > р0. Определить величину
напряженности электрического поля. Трением о жидкость пренебречь.
12.49. Два одинаковых точечных заряда q расположены на расстоянии 2а
друг от друга. Определить максимальное значение величины напряженности
Рис. 12.46
176
электрического поля этой системы зарядов на прямой, перпендикулярной
линии, соединяющей заряды и проходящей через ее середину.
• Решение. Рассмотрим произвольную точку О
на прямой, перпендикулярной линии, соединяю-
щей заряды и проходящей через ее середину
(рис. 12.47).
Согласно принципу суперпозиции электри-
ческих полей каждый заряд создает поле незави-
симо от присутствия в пространстве других заря-
дов. Напряженность ^электрического поля в дан-
ной точке может быть найдена как геометричес-
кая сумма напряженностей и Ё^ полей, созда-
Рис. 12.47
ваемых каждым зарядом в отдельности:
Напряженности и Ё^ полей, создаваемых первым и вторым зарядом, будут равны
по величине
£,=£2 = -^,
4 л е0 г
где г - расстояние от каждого из зарядов то точки О.
Векторы Ё] и Ё^ направлены вдоль прямых, соединяющих заряды с точкой О, ат заря-
дов, если q > 0, и к зарядам, если д < 0. Рассмотрим случай д > 0.
В силу симметрии расположения зарядов относительно прямой 00, абсолютное зна-
чение вектора Сбудет равно
_ _ _ о cos а
Е = 2 £[ cos а = -3-j.
2 л еог
Обозначим расстояние 00 через х. Тогда расстояние г и значение cos а можно пред-
ставить в виде
.ГТ"—I х х
г = Ух + а, cos а = - = , , , .
„ r yir+7
Следовательно,
£ = £« =-------Тзл-
2ле0(х2 + д2)'4
Так как числитель функции Е = Е (х) линеен относительно х, а знаменатель растет как
х2, то это означает, что при небольших значениях х функция Е (х) растет, достигая макси-
мального значения при некотором х0. При х > х0 функция Е (х) убывает. Следовательно, в
некоторой точке на прямой ОО' функция Е (х) принимает максимальное значение.
Исследуем функцию £ = £ (х) на экстремум:
dE _ д (х2 + д2)3^ - 3Л х (х2 + д2)^ 2 х _ _
2 л Ео (х2 + д2)3
Откуда получим значение расстояния xq, при котором напряженность электрического
поля в точке О будет наибольшей:
(х2 + д2) - 3 Xq = 0, ИЛИ Х0 = a/'ll.
Следовательно, максимальное значение напряженности электрического поля на рас-
сматриваемой прямой равно
177
£max - E (xq) - -j .
3 N 3 Я Eotr
Если величина каждого заряда q < 0, то решение задачи ничем не отличается от рас-
смотренного выше и приводит к тому же результату. Читатель может убедиться в этом,
самостоятельно решив задачу для случая q < 0.
• Ответ: £тах = —=^--j.
3 V 3 7t 6q и
12.50. Какой заряд приобрел бы шарик объемом V= 1 см3, изготовленный
из железа 26Fe56, если бы удалось убрать т| = 1% его электронов? Найти напря-
женность электрического поля на расстоянии г = 1 м от центра шарика. Плот-
ность железа р = 7,8 г/см3.
12.51. Напряженность электрического поля в точке, удаленной от точеч-
ного заряда на расстояние = 5 см, равна Е = 150 кВ/м. Определить величи-
ну этого заряда и напряженность электрического поля в точке, удаленной на
расстояние г2 = 10 см от заряда.
12.52. Точечный заряд создает в
q*А С В точке А (рис. 12.48) напряженность элект-
рического поля £| = 36 В/м, а в точке В -
Рис. 12.48 £2 = 9 В/м. Найти напряженность поля в
точке С, находящейся посередине между точками А и В. Заряд и все три
точки А, В, С находятся на одной прямой.
12.53. Найти напряженность электрического поля в точке, лежащей по-
середине между зарядами qx = 8 нКл и q2 = - 6 нКл, расстояние между кото-
рыми равно /= 10 см.
12.54. Расстояние между двумя точечными положительными зарядами
q। = 9q и q2 = q равно I = 8 см. На каком расстоянии от первого заряда находит-
ся точка, в которой напряженность электрического поля равна нулю?
12.55. Диполь образован двумя разноименными зарядами величиной
q = 10'9 Кл каждый. Расстояние между зарядами / = 12 см. Найти напряжен-
ность электрического поля в точке, находящейся на перпендикуляре к сере-
дине отрезка, соединяющего заряды, на расстоянии г = 8 см от него.
12.56. Два точечных заряда qx и q2 находятся на расстоянии а друг от
друга. Определить напряженность электрического поля в точке, равноудален-
ной от обоих зарядов на расстояния, равные а.
а 12.57. Два одинаковых по величине разноименных
I заряда расположены на расстоянии / друг от друга.
1/2 При этом напряженность электрического поля в неко-
_______________торой точке А на прямой, перпендикулярной линии со-
единяющей заряды, равна (рис. 12.49). Если один
1/2____________из зарядов убрать, то в той же точке А напряженность
| электрического поля будет равна £2. Найти расстояние
р 17 ло от точки А Д° линии, соединяющей заряды.
178
12.58. Два одинаковых по величине разноименных заряда величиной
q = 18 нКл каждый расположены в вершинах равностороннего треугольника со
стороной а = 2 м. Определить напряженность электрического поля в третьей
вершине треугольника.
12.59. Три одинаковых заряда величиной q = 10’9 Кл каждый расположены
в вершинах прямоугольного треугольника с катетами а ~ 40 см и b = 30 см.
Найти напряженность электрического поля в точке пересечения гипотенузы
треугольника с перпендикуляром, опущенным на нее из вершины прямого
угла.
12.60. В вершинах квадрата со стороной а = 10 см расположены четыре за-
ряда: два величиной q = 10’9 Кл и два - q* = -10’9 Кл. Определить напряжен-
ность электрического поля в точке пересечения диагоналей квадрата.
12.61. В углах квадрата со стороной а расположены четыре одинаковых
точечных заряда q. Определить максимальное значение величины напряжен-
ности электрического поля £тах на оси, проходящей через середину квадрата
перпендикулярно его плоскости.
12.62. На тонком кольце радиусом R равномерно распределен заряд Q. Оп-
ределить силу, действующую на точечный заряд q, находящийся на оси кольца
на расстоянии h от его центра. Чему равна напряженность электрического поля
• Решение. Для определения величины напряженности электрического поля, создаваемого
заряженным кольцом, воспользуемся принципом суперпозиции электрических полей.
Разобьем кольцо на элементы Д/, каждый из которых будет иметь заряд AQ, рассмат-
риваемый как точечный. Тогда на оси кольца на расстоянии h от его центра такой заряд со-
здаст электрическое поле напряженностью
Д£ = ^Ц,
4л ео г
где г = R2+h2 - расстояние от заряда AQ до рассматриваемой точки О ( рис. 12.50, а).
Заряд др = др, расположенный на одном диаметре с зарядом др, в точке О создаст такое
же по величине поле, причем суммарное поле обоих зарядов будет направлено по оси
OZ.
179
Векторы напряженности Диэлектрических полей, создаваемых всеми зарядами AQ в
точке О, будут расположены по боковой поверхности конуса (рис. 12.50, б). При этом
суммы проекций векторов ДЁ^иа оси ОХ и OY будут равны нулю, на ось OZ -
Е AEZ = Е ДЕ cos а = Е —.
г 4пеог2'-
Следовательно, напряженность электрического поля в точке О будет равна
£ _ £_______________________h________S ДО =_____2-^_____
4 л £0 (Л2+h2)3/i 4 л е0 (Л2+h2)3/i 4 л е0(й2+й2)3/2
На заряд q, помещенный в рассматриваемую точку О, будет действовать сила
F = qE =-------------5- .
4л ео (Л2+ й2)21
Ответ: F =-----_-3- ; Е =---------—-г- .
4ле0(Е2+й2)/! 4ле0(й2+й2)22
12.63. Три одинаковых заряда q расположены на окружности радиусом R
на равных расстояниях один от другого. Найти напряженность электрического
поля на оси окружности на расстоянии Л от ее центра.
12.64. N точечных зарядов величиной q каждый равномерно распределены
по окружности радиусом R. Найти напряженность электрического поля на оси
окружности на расстоянии Л от ее центра.
12.65. Металлический шар радиусом
Я| = 10 см помещен в центр толстостен-
ной металлической сферы с внутренним
радиусом R2 = 20 см и наружным радиу-
сом Л3= 30 см (рис. 12.51). Заряд шара
qt = 1О'|оКл, заряд Сферы <?2 =-2-1O'10 Кл.
Найти и графически изобразить зависи-
мость величины напряженности электри-
ческого поля Е от расстояния г до центра
шара.
• Решение. Электрическое поле заряда q\ приведет к появлению индуцированных зарядов
q' и q" на внутренней и внешней поверхностях сферической оболочки, причем, как сле-
дует из закона сохранения заряда, q' + q"= 0.
Сферическая симметрия всех тел системы позволяет предполагать равномерное рас-
пределение зарядов на соответствующих поверхностях и строгую радиальность силовых
линий.
Так как силовые линии напряженности электрического поля терпят разрыв на любой
проводящей поверхности, то найдем величины напряженности поля в четырех разных об-
ластях - в точках, где расстояние г от центра шара ограничено соответствующими радиуса-
ми окружностей: 0 S г < R3, < г < R2, R2 < г < R3 и г > R3.
В области 0 2 г < электрическое поле равно нулю, так как шар радиусом R! изготов-
лен из металла:
180
£(О^г<Л|) = О. (1)
В области Л| < г < R2 результирующее электрическое поле будет равно полю, созда-
ваемому только зарядом q\, находящимся на шаре, так как внутри сферы электрическое
поле, создаваемое зарядами, находящимися на ее поверхности, равно нулю:
£(й1<г<Л2) = —(2)
4ле0Г
В области R2 < г < R3 электрическое поле равно нулю, так как сфера также изготов-
лена из металла:
Е (R2 < г < Л3) = 0. (3)
В области r>R3 результирующее поле будет создано всеми зарядами системы. В
силу симметрии векторы напряженности полей всех зарядов в любой точке будут колли-
неарны, т.е. лежат на одной прямой. Поэтому, следуя принципу суперпозиции электри-
ческих полей, получим
V — 2 , 2 , J. л 2 ’
4л е0 г 4л е0 г 4л е0 г 4л е0 г
или, учитывая закон сохранения заряда (q' + q " = 0):
E(r> R3) =
91 + 92
4 ЛЕоГ2
(4)
Вблизи границ областей (при г -> 7^
мул (2) и (4):
Е (г = Я,) = —г ® 90 В/м,
4л£07г12
E(r = R2) = —у « 22,5 В/м,
4л е0 /?22
а. + q2
E(r = R3) = « -10 В/м.
4л е0 Л32
График зависимости Е (г) будет иметь
вид, представленный на рис. 12.52: в пер-
вой и третьей из рассматриваемых облас-
тей, электрическое поле равно нулю, а во
второй и четвертой - уменьшается по аб-
солютной величине обратно пропорцио-
нально квадрату расстояния от центра
шара.
-> л2> г *з) значения полей найдем нз фор-
• Omeem-.E(0<r<Ri) = 0; E(Rl<r<R2) = —E(R2 < г < R3) = 0; E(r > R3) = —+?2 ;
4л Eo г 4л Eo r
E(r = Я,) = —^—7 « 90 В/м, E(r = R2) = —у « 22,5 В/м,
4л Eq Л] 4л во R2
Q\ + Q2
E(r = R3) = « -10 В/м.
4л e0 R 2
12.66. Напряженность электрического поля вблизи поверхности заряжен-
ного шара равна Е = 200 кВ/м. С какой силой это поле будет действовать на
электрон, помещенный вблизи шара? Заряд электрона |е| = 1,610’19 Кл.
181
12.67. Пусть в шарике диаметром d = 1 см, изготовленном из угля, на каж-
дый миллион атомов приходится один свободный электрон. Какова напряжен-
ность электрического поля вблизи поверхности шарика? Плотность угля
р = 1,7 г/см3. Считать, что уголь состоит из углерода 6С12. Заряд электрона
|е| = 1,6-10’19 Кл.
12.68. Известно, что у поверхности Земли имеется однородное электроста-
тическое поле напряженностью Е = 100 В/м. Каков полный заряд Земли? Ради-
ус Земли R = 6400 км.
12.69. Поверхностная плотность заряда на проводящем шаре равна
ст = 320 нКл/м2. Определить напряженность электрического поля в точке, уда-
ленной от поверхности шара на расстояние, равное утроенному радиусу.
12.70. Проводящая сфера равномерно заряжена с поверхностной плотнос-
тью ст= 1,Ь10'7 Кл/м2. Определить напряженность электрического поля: а) в
центре сферы; б) на расстоянии от центра сферы, равном половине ее радиуса;
в) вблизи поверхности сферы.
12.71. Подсчитать среднюю плотность электрических зарядов в атмосфе-
ре, если известно, что напряженность электрического поля вблизи поверхности
Земли равна Ео = 100 В/м, а на высоте h = 1,5 км - Е = 25 В/м. Радиус Земли
R»h.
12.72. Поверхность сферы радиусом R равномерно заряжена зарядом Q. В
сфере высверлили небольшое отверстие (радиус отверстия много меньше ра-
диуса сферы). Определить напряженность электрического поля в отверстии.
12.73. Заряд Q равномерно распределен по объему шара радиусом R из не-
проводящего материала. Найти напряженность электрического поля Е на рас-
стоянии г от его центра. Построить график зависимости Е от г. Диэлектричес-
кая проницаемость материала шара е = 1.
12.74. Имеются две полубесконечные плоскости, разделенные тонким ди-
электриком. Левая полуплоскость равномерно заряжена положительным заря-
дом, правая полуплоскость - отрицательным с той же поверхностной плотнос-
тью заряда. В некоторой точке А, лежащей у края полуплоскостей (рис.
12.53, а), напряженность электрического поля равна Et. Если убрать заряды на
одной из полуплоскостей, то напряженность в точке А станет равной Е2- Опре-
делить величину поверхностной плотности заряда.
• Решение. Для использования известной формулы напряженности электрического поля,
создаваемого бесконечной заряженной плоскостью, заменим, например, отрицательный
заряд на правой полуплоскости положительным зарядом с такой же поверхностной плот-
ностью а. В результате получим равномерно заряженную бесконечную плоскость. Напря-
женность электрического поля для такой системы зарядов не будет зависеть от расстояния
до плоскости и равна в любой точке (значит и в точке А)
182
Рис. 12.53
Так как левая н правая положительно заряженные полуплоскости абсолютно одинако-
вы, то расположенные на них заряды вносят одинаковый вклад в величину вектора напря-
женности Ё^.
По условию задачи одна полуплоскость в точке А создает электрическое поле напря-
женностью Ё2 .Тогда, очевидно, что поле Ё^ , создаваемое второй полуплоскостью, по вели-
чине также будет равно Е2. Согласно принципу суперпозиции электрических полей
?Л=?2+С
а так как |Ёз | = |Ёз | = Е2 н вектор Ёд направлен перпендикулярно заряженной плоскости,
то векторы Ej и Ез будут располагаться симметрично относительно вектора Ед (рис.
12.53, б).
Если теперь вернуться к условию задачи и поместить на правую полуплоскость отри-
цательный заряд, то это приведет к тому, что вектор Ё^ , оставаясь неизменным по величине,
изменит свое направление на противоположное, т.е. напряженность электрического поля,
создаваемого правой отрицательно заряженной полуплоскостью, будет равна Ё^ = - Ё^
(рис. 12.53, в).
Векторы Ё2 и Ёд в сумме дадут вектор Ё^ , который будет направлен вдоль диагонали
ромба, построенного на векторах 2^ и Ё^. Очевидно, что Е] будет направлен параллельно
заряженной плоскости.
Рассмотрим треугольник АВС. Так как i?A перпендикулярен плоскости, а Ё^ ей парал-
лелен, то ЛАВС прямоугольный, причем его стороны равны: АС = Е1, АВ = ЕА. Очевидно,
что BD = DC = Е2, а ВС = 2 Е2.
По теореме Пифагора получаем: (ВС)2= (ЛВ)2+ (ЛС)2, или
4Е22=Еа2+Е,2.
Используя выражение для Еа, последнее равенство запишем в виде
4Е22=^ + Е12
4 Со
Откуда найдем величину поверхностной плотности заряда:
а = 2 е0 4 Е22-Е2.
• Ответ', а = 2 £q V 4 Е22 -Е2.
12.75. Две пластины площадью S = 1 м2 каждая, заряженные одинаковыми
по величине разноименными зарядами, расположены параллельно друг другу
на расстоянии много меньшем линейных размеров пластин. Какой минималь-
ный заряд может находиться на пластинах, если «пробой» для воздуха наступа-
ет прн напряженности электрического поля Е = 30 кВ/см?
183
12.76. Две большие пластины расположены горизонтально на небольшом
расстоянии друг от друга, причем верхняя пластина положительно заряжена,
а на нижней (диэлектрической) находится маленький шарик с зарядом
q = 20 мкКл. На сколько изменится вес шарика, если пространство между
пластинами заполнить жидкостью плотностью р = 800 кг/м3 и диэлектричес-
кой проницаемостью е = 2? Объем шарика V= 1 см3, напряженность электри-
ческого поля, создаваемого верхней пластиной, равна Е = 100 В/м.
12.77. Около вертикальной равномерно заряженной плоскости на невесо-
мой нерастяжимой нити висит маленький шарик, заряженный с плоскостью
одноименно. При заполнении всего окружающего пространства диэлектричес-
кой жидкостью с плотностью р0 и проницаемостью е положение шарика отно-
сительно плоскости не изменилось. Найти плотность материала шарика.
12.78. К гладкой бесконечной плоскости, расположенной вертикально в
поле тяжести Земли и имеющей поверхностную плотность заряда а, прикреп-
лен на нити одноименно с ней заряженный шарик массой т и зарядом q.
Найти силу натяжения нити и угол отклонения нити от вертикали.
12.79. На горизонтальной плоскости вертикально установлена легкая ди-
электрическая пружина, на верхнем конце которой закреплен шарик массой
т = 10 г с зарядом q = 10'6 Кл. С какой поверхностной плотностью нужно за-
рядить пластину, чтобы энергия пружины увеличилась вдвое? Электрическое
поле пластины считать однородным.
12.80. Бесконечные проводящие плос-
кости 1 и 2 расположены параллельно друг
.А другу и заряжены разноименными заряда-
ми с одинаковой плотностью а = 10 нКл/м2.
----------------------- Найти силу, действующую на положитель-
ный заряд q = 2 нКл, помещенный в точку А
Рис. 12.54 (рис. 12.54), лежащую между плоскостями.
1?
О2 I в
“---------------------- U
г
Si 1А_________________ I
.С j
Рис. 12.55 Рис. 12.56
12.81. Равномерно заряженные тонкие бесконечно большие пластины на-
ходятся на небольшом расстоянии друг от друга (рис. 12.55). Найти поверх-
ностные плотности их зарядов а, и а2> если напряженность поля в точке А
равна Ех = 3000 В/м, а в точке В - Е2= 1000 В/м.
184
3g
2q
12.82. Две параллельные полубесконечные плоскости заряжены равномер-
но с одинаковой плотностью заряда, причем одна из полуплоскостей заряжена
положительно, другая - отрицательно. В некоторой точке А у края плоскостей
напряженность электрического поля равна £] и вектор £j направлен под углом
а к плоскостям (рис. 12.56). Определить напряженность поля в точке В, лежа-
щей у края плоскостей посередине между ними, а также в точке С, лежащей да-
леко от края плоскостей.
12.83. Три тонкие металли- q
ческие пластины, имеющие за-
ряды q, 3q и 2q, расположены
параллельно друг другу так, как
показано на рис. 12.57, а. Пло-
щадь каждой пластины S. Найти
силу, действующую на сред-
нюю пластину. Электрическое
поле, создаваемое каждой плас-
тиной, считать однородным.
• Решение. Сила, действующая на среднюю пластину с зарядом 3g, может быть определена
по формуле
a)
б)
Рис. 12.57
где напряженность электрического поля в месте расположения данной пластины, созда-
ваемого крайними пластинами.
Если q > 0, т.е. крайние пластины заряжены положительно, то векторы напряженнос-
ти электрических полей, создаваемых ими, будут направлены так, как показано иа
рис. 12.57, б. По условию задачи эти поля можно считать однородными, поэтому
г 01 <? г 2g
2 Ед 2 5 Bg 2 Bq 2 S Bq
Следовательно, средняя пластина будет находиться в электрическом поле напряжен-
ностью
Е = Е2-Е1 = -*~-
и на нее будет действовать сила z ° ко
4 2S&0'
Если q <0, то векторы и будут направлены так, как показано иа рис. 12.57,
б штриховыми линиями. При этом величина результирующего поля и искомая сила F не
изменятся. 2
• Ответ: F = .
2 Sbq
12.84. Заряженная пластина помешена в однородное электрическое поле,
вектор напряженности которого перпендикулярен ее поверхности. Напряжен-
ности полей слева и справа от пластины равны Е} и Е2 соответственно (рис.
12.58). Найти силу, действующую на пластину, если ее заряд равен q. Поле, со-
здаваемое пластиной, считать однородным.
185
=> -> «л
, Д1 9--------------------------------------------------------
•В
М___________^2_______ 2q-----------------------------------
" * .С
Рис. 12.58 Рис. 12.59
12.85. Две тонкие металлические пластины, имеющие заряды q и 2q, рас-
положены параллельно друг другу. Сила взаимодействия пластин друг с дру-
гом равна F. Найти напряженность электрического поля в точках А, В тлС (рис.
12.59). Поле, создаваемое каждой из пластин, считать однородным.
12.86. Две разноименно заряженные металлические пластины, располо-
женные параллельно друг другу, взаимодействуют между собой с силой F. На
сколько изменится величина силы, действующей на отрицательно заряженную
пластину, если ее поместить между двумя положительно заряженными пласти-
нами с прежними по величине зарядами? Поле, создаваемое каждой из плас-
тин, считать однородным.
12.87. Три металлические положительно за-
q
ряженные пластины расположены параллельно
друг другу, как показано на рис. 12.60. Заряд левой
пластины равен q. Известно, что сила, действую-
щая на среднюю пластину, равна Fx. Если правую
пластину убрать, то сила, действующая на сред-
нюю пластину, станет равной F2. Найти заряды
средней и правой пластин. Площадь каждой из
Рис 12 60 пластин равна S. Поле, создаваемое каждой плас-
тиной, считать однородным.
12.88. Две бесконечные, расположенные параллельно, проводящие плиты
заряжены так, что поверхностная плотность заряда обеих поверхностей первой
плиты равна а,, а второй - а2- Найти плотность заряда каждой поверхности
обеих плит.
• Решение. Как было отмечено в теоретическом введении, необходимым условием электро-
статического равновесия проводника является равенство нулю напряженности электричес-
кого поля внутри него. Это условие приводит к тому, что нескомпенсированные заряды
могут располагаться только на поверхности проводника.
Введем поверхностные плотности зарядов на внешних и внутренних поверхностях
плит а'р a'], aj, <з'2 соответственно (рис. 12.61, а), и заменим плиты четырьмя бесконечными
проводящими заряженными пластинами (рис. 12.61, б). При этом напряженность электри-
ческого поля меЖду пластинами 1 - 1 и 2 - 2 равна нулю.
Пусть для определенности заряды на пластинах 1 и 2 положительны, а на пластинах
1 и 2 - отрицательны.
186
Так как напряженность электрического поля в точках 1 и 2 равна нулю, а с другой сто-
роны
Ki = Е2 + Е\ + Е\ — Е2 = —%---------2=0,
1 2 е0
Е2 = Е2 + Е2 + £, -El = -2-----2----1---L = 0,
-z z -z ' “1 -> -'
1 s0
то складывая и вычитая эти равенства, получим
2o2 + 2aJ = 0, или <r2 = -<Tf (1)
2 а'| - 2 <т2 = 0, или <т',' = а2. (2)
Записав закон сохранения заряда иа каждой из плит в виде
О! = о'| + a'i, (3)
<т2 = а'2 + <т2, (4)
и решив систему уравнений (1)-(4) относительно aj, a'i, а2, <т2, получим
, , СТ] — СТ2 н и + &2
<т|=-а2 = - , (т1=(т2= - .
! t СТ] — CTj " " СТ] + ^2
• Ответ', aj = - а2 = —— > СТ1 = а2 = —2—
12.89. В однородное электрическое
поле с напряженностью Е внесли тонкую
металлическую пластину площадью S
(рис. 12.62). Какой заряд индуцируется
на каждой стороне пластины?
12.90. Две параллельные металли-
ческие пластины расположены на не-
большом расстоянии друг от друга.
Какие заряды будут индуцированы на по-
верхностях одной пластины, если другой
пластине сообщить заряд QI
Рис. 12.62
187
•А
•В
92 .с 2
Чз ,D 3
Ча .F Рис. 12.63 4
пластины равна S = 1 м2. Размеры
12.91. Четыре параллельно распо-
ложенные металлические пластины не-
сут заряды: первая q{ = -5 мкКл, вторая
q2 = 3 мкКл, третья q3 = 4 мкКл, четвер-
тая д4 = -1 мкКл (рис. 12.65). После
того как соединили первую пластину со
второй, а третью с четвертой, опреде-
лить напряженность электрического по-
ля в точках А, В, С, D, F, лежащих дале-
ко от краев пластин. Площадь каждой
истин значительно больше расстояний
между любыми попарно взятыми точками.
12.92. Равномерно заряженный проводник согнут в форме кольца некото-
рого радиуса. Если из проводника вырезать и убрать кусок длиной, равной
четверти длины кольца, то напряженность электрического поля в центре
(точке О, рис. 12.64, а) будет равна £0. Чему будет равна напряженность поля
в этой точке, если: а) вырезать и убрать еще одну четверть проводника, сосед-
нюю с первой вырезанной; б) вырезать и убрать еще две четверти проводни-
ка? Считать, что удаление части проводника не приводит к перераспределе-
нию заряда.
а) б) в)
Рис. 12.64
• Решение. Не нарушая общности постановки задачи, будем полагать, что проводник за-
ряжен положительно.
Разобьем проводник на элементарные заряды 6q, каждый из которых будем считать
точечным. Каждый такой заряд в точке О создаст электрическое поле напряженностью
В силу симметрии расположения зарядов относительно точки О, все векторы 6J? будут
направлены вдоль радиусов кольца. Так как дуга AD (рис. 12.64, а) кольца вырезана, то кар-
тина силовых линий будет иметь вид, представленный иа рис. 12.64, б, где векторы Д£* рас-
положенные между точками 1 и 2, созданы зарядами дуги CD, векторы между точками 2
и 3 - зарядами дуги ВС, векторы А^между точками 3 и 4 - зарядами дуги АВ. Очевидно, что
векторы дМ созданные зарядами на противоположных дугах АВ и CD, будут в сумме равны
188
нулю. Это означает, что поле напряженностью Ео будет создано лишь зарядами, находящи-
мися на дуге ВС, и вектор будет направлен вдоль оси симметрии кольца с вырезом (рис.
12.64, а).
Следовательно, вектор напряженности электрического поля, создаваемого любой чет-
вертью проводника, равен по величине Eq и направлен вдоль линии симметрии соответст-
вующей дуги.
Если вырезать и убрать четверть проводника, например дугу CD, то заряды на дугах
АВ и ВС создадут в точке О поля, векторы напряженности которых будут равны Ео и на-
правлены так, как показано на рис. 12.64, в. Следовательно, напряженность поля в точке О,
создаваемого зарядами полукольца ЛВС, равна
Е} = ^ Eq2 + Eq2 =Е0<2.
Если вырезать и убрать еще одну четверть кольца, то оставшаяся заряженная четверть
создаст в точке О поле напряженностью
12.93. Два тонких равномерно заряженных одинаковым зарядом стержня
составлены под прямым углом друг к другу так, как показано на рис. 12.65. При
этом напряженность электрического поля в точке А равна Ео. Чему станет рав-
ной напряженность поля в этой же точке, если один из стержней убрать?
12.94. Равномерно заряженный проводник согнут в форме правильного
шестиугольника. Если из проводника вырезать и убрать одно звено, то напря-
женность электрического поля в геометрическом центре (точке О, рис. 12.66)
будет равна Ей. Чему будет равна напряженность поля в этой точке, если: а) вы-
резать и убрать еще одно звено проводника, соседнее с первым вырезанным;
б) вырезать и убрать еще два звена, соседние с первым вырезанным? Считать,
что удаление части проводника не приводит к перераспределению заряда.
12.95. Равномерно заряженный стержень АВ создает в точке Офис. 12.67)
электрическое поле напряженностью Ео. Какой станет напряженность поля в
точке О, если в плоскости АОВ поместить еще один такой же и также заряжен-
ный стержень А В', причем АО = ВО = А'О = В'О и А'В' перпендикулярен АВ?
12.96. Точечный заряд q помещен в однородный безграничный диэлектрик
с диэлектрической проницаемостью е. Найти поляризационный заряд, возни-
кающий вблизи точечного заряда.
189
Рис. 12.68
• Решение. Точечный заряд q, помещенный в
вакуум, создаст вокруг себя радиально сим-
метричное электрическое поле напряженнос-
тью £q , которое в некоторой точке Л (рис.
12.68) на расстоянии г от заряда ра^но
Ео ~ ~ 2
4л еаг
Если пространство заполнено однород-
ным безграничным диэлектриком, то элект-
рическое поле заряда q приведет к появлению
у молекул дипольного момента, под действием которого диэлектрик будет поляризован и
вблизи заряда q возникнет поляризационный заряд qp. Электрическое поле Ев той же
точке А пространства теперь можно определить как сумарное поле зарядов q и qp:
Е-^—2+~^Ч-
4л с0 г 4л е0 Р
С другой стороны, известно, что электрическое поле внутри диэлектрика проницае-
мостью е ослабляется в е раз, т.е.
Е = — .
Следовательно, Е
q 9р q е -1
--- —2 +--- 2^ =-- --2 > или ?р = - 9-----
4л е0 г 4л е0 г 4л е е0 Р-----------------е
_ е - 1
• Ответ: 90 = -q--
И е
12.97. Два точечных заряда q, находящиеся на некотором расстоянии друг
от друга, помещены в однородный безграничный диэлектрик с диэлектричес-
кой проницаемостью е. Найти поляризационные заряды, возникающие вблизи
точечных зарядов.
12.98. Два точечных заряда q и -q, находящиеся на некотором расстоянии
друг от друга, помещены в однородный безграничный диэлектрик с диэлектри-
ческой проницаемостью е. Найти поляризационные заряды, возникающие
вблизи точечных зарядов.
12.99. Бесконечная равномерно заряженная пластина помещена в одно-
родный безграничный диэлектрик с диэлектрической проницаемостью е.
Найти поверхностную плотность поляризационных зарядов, возникающих с
каждой стороны пластины, если поверхностная плотность заряда пластины
равна а.
12.100. Две бесконечные параллельные одинаково заряженные пластины
помещены в однородный безграничный диэлектрик с диэлектрической прони-
цаемостью в. Найти поверхностные плотности поляризационных зарядов, воз-
никающих вблизи поверхностей пластин, если поверхностная плотность заряда
каждой пластины равна а.
12.101. Пространство между обкладками плоского конденсатора заполне-
но диэлектриком с диэлектрической проницаемостью в. Найти поляризацион-
ные заряды, возникающие вблизи поверхностей пластин, если заряд конденса-
тора равен q.
190
Электрический потенциал
12.102. В вершинах квадрата со стороной I находятся четыре заряда вели-
чиной q каждый. Чему равен потенциал электрического поля в центре квадра-
та? • Решение. Исходя из принципа суперпозиции потенциала электрического поля, потенциал в точке О (рис. 12.69) будет равен алгебраической сумме потенциалов полей, со- здаваемых каждым из зарядов в отдельности: Ч* 1 *4 1 \ / 1 1 \ / 1 l\ |z 1 z \ 1
ф = ф, +ф2 + ф3 + ф4. Так как заряды gt = д2 = д} = д4 = он расстояния от каждого из них до точки О равны г = 1/у2, то д Т2д Ф1=Ф2=Ф3=Ф4=4д<4лЕу Ч^ 1 Рис. 12.69
Следовательно, потенциал поля в центре квадрата равен
А Ч
Ф = = П /•
• Ответ : ф =--х .
я е01
12.103. Заряд qx = 0,1 нКл удален от заряда q2 = 0,2н Кл на расстояние
/ = 2 м. Чему равен потенциал электрического поля в точке, находящейся на
середине отрезка, соединяющего заряды?
12.104. Шесть точечных зарядов qx = 100 нКл, q2 = 10 нКл, <?3 = 1 нКл,
<у4 = -10 нКл, <у5 = — 1 нКл, д6 = -10 нКл находятся в вершинах правильного
шестиугольника со стороной I = 2 см. Чему равен потенциал электрического
поля этой системы зарядов в геометрическом центре шестиугольника?
12.105. Четыре заряда величиной q = 10'9 Кл каждый находятся в углах
квадрата со стороной / = 10 см. Найти разность потенциалов в поле этих заря-
дов между центром квадрата и серединой одной из его сторон.
12.106. Точка А находится на расстоянии г, = 2 м, а точка В - на r2 = 1 м
от точечного заряда q = 10'6 Кл. Чему равна разность потенциалов между точ-
ками Ли В?
12.107. Два электрических заряда qt = q и q2 = -2q расположены друг от
друга на расстоянии I = 6а. На плоскости, в которой находятся эти заряды,
найти геометрическое место точек, в которых потенциал электрического поля
равен нулю.
12.108. Сплошной металлический цилиндр радиусом R вращается вокруг
своей оси с постоянной угловой скоростью со. Найти зависимость напряжен-
ности электрического поля Е от расстояния г до оси цилиндра и разность по-
тенциалов Дер между поверхностью цилиндра и его осью. Масса электрона т,
заряд |е|.
12.109. Сфера равномерно заряжена. Потенциал в центре сферы равен
<р0 = 100 В, а на расстоянии 1 = 30 см от ее поверхности - <р = 50 В. Чему равен
радиус сферы?
191
@« Решение. Потенциал внутри сферы, включая и
I______________________________ ее центр, равен потенциалу на поверхности:
--------------Л = , (1)
гае q - заряд сферы, R - ее радиус.
Вне сферы потенциал изменяется по закону
Рис. 12.70 ф = _А_>
т 4л Ео г ’
гае г - расстояние от центра сферы до данной точки. Так как r = R + l (рис. 12.70), то в
точке А потенциал равен
Ф =-----2----. (2)
4л е0 (R + /)
Разделив уравнение (1) на уравиеиие (2), получим
Фо _ Д + /
Ф R
Откуда найдем радиус сферы:
R фо = R ф +1 <р, или R = I —®— = 30 см.
• Ответ: R = l—®— = 30 см. ’’’°
Фо-Ф
12.110. Чему равен потенциал в центре сферы радиусом R с зарядом 0?
12.111. До какого потенциала можно зарядить сферу радиусом R = 1 м, на-
ходящуюся в воздухе, если воздух выдерживает без пробоя напряженность
электрического поля Е = 30 кВ/м? Сколько электронов нужно удалить с по-
верхности сферы, чтобы довести ее до этого потенциала? Заряд электрона
|е| = 1,6-10'19 Кл.
12.112. Определить потенциал находящегося в вакууме металлического
шара радиусом R = 10 см, если на расстоянии I = 1 м от его поверхности потен-
циал равен <р0 = 20 В. Какой заряд сообщен шару?
12.113. На расстоянии а = 5 см от поверхности шара потенциал равен
<Р! - 1,2 кВ, а на расстоянии b = 10 см - <р2 = 900 В. Определить радиус шара,
его заряд и потенциал на поверхности.
12.114. Имеется п = 8 заряженных водяных капель. Радиус каждой капли
г = 10’3 м, а заряд q = -10"10 Кл. Капли сливаются в одну большую каплю.
Найти потенциал на поверхности получившейся
капли.
12.115. Две концентрические металлические
сферы радиусами 2?1 = 15 см и R2 ~ 30 см распо-
ложены в воздухе (рис. 12.71). На внутренней
сфере распределен заряд qt =-2-10‘8 Кл, а на
внешней - q2 = 4-10'8 Кл. Вычислить потенциал
электрического поля в точках, удаленных от
центра сфер на расстояния = 10 см, 12 = 20 см и
/3 = 40 см. Изобразить графически зависимость
потенциала от расстояния до центра сфер.
192
• Решение. Потенциал, так же, как и напряженность электрического поля, подчиняется
принципу суперпозиции, т.е. потенциал поля системы зарядов в данной точке может быть
найден как алгебраическая сумма потенциалов полей, создаваемых каждым зарядом в от-
дельности.
Так как в нашем случае система зарядов обладает сферической симметрией, то по-
тенциал в любой точке на равных расстояниях от центра сфер будет одинаков.
Потенциал поля, создаваемого равномерно заряженной сферой радиусом R и зарядом
б, внутри нее равен
Ф =—
Y 4л
а вие, иа расстоянии г от ее центра
2_
епй’
(1)
В области 0<г<й[ потенциал будет равен алгебраической сумме потенциалов
полей, создаваемых обеими сферами во внутренних областях. Используя формулу (1), по-
лучаем
tfi От
Ф(0^г<Л1) = —. (3)
4л8()Л| 4л BqR2
В области Л] < f < R2 потенциал поля внутренней сферы будет изменяться по закону
(2), а внешней - (1):
4>(Rl<r<R2) = -^— + —. (4)
4л £(, г 4л е0 R2
В области г > R2 потенциалы полей обеих сфер будут изменяться по закону (2):
, . „, 91 9г 91 + 9г
ф (г > ад = --+ -л----« -----. (5)
4lt Eq Г 4lt Eq Г 4п Eq Г
На границах областей (при r = Ri и г = R2) значение потенциала можно найти, на-
пример, по формулам (4)—(5), положив г = R^ и r = R2 соответственно:
, „, 91 9г „ 91 + 9г „
Ф (г = R.) = ———— + -— = 0, ф (г = Лт) = --— « 600 В.
4л£0Я1 4K€q^2 4л £q R2
Точки 1, 2 и 3 лежат в областях 0 < г < Ru Rt < г < R2, г > R2 соответственно. Поэтому
для точки, удаленной от центра сфер иа расстояние 1\, из формулы (3) получим
, , ч 91 92 л
ч’(г=/1) = 5^+^Г^=0-
В точке, соответствующей рассто-
янию от центра сфер равном 12, потен-
циал найдем по формуле (4), положив
г = 12:
ф (г=У = , —1 + ,~г „ “ 300 В.
4л £д 12 4л R2
Наконец, в точке иа расстоянии
/3 от центра сфер, потенциал определим
по формуле (5), положив г = 12:
91 + 92
ф(г = У = ^-^-«450В.
График зависимости ф(т) пред-
ставлен на рис. 12.72.
• Отеет: ф(г = /,) = + = 0; Ф(г = У = + 300В;
<р (г =/3) = ”7-—“ 450 В
4п £о *3
193
12.116. Заряд q = -Ю"6 Кл находится в центре металлической сферы ради-
усом R = 1 м. Заряд на поверхности сферы равен Q = 1,5-КГ6 Кл. Определить
напряженность электрического поля на расстоянии г = 1 м от поверхности
сферы и потенциал сферы.
12.117. Проводящий шар радиусом Rt =2 см и зарядом qt = 1,3310’8Кл
окружен тонкой концентрической оболочкой радиусом R2 = 5 см, заряд кото-
рой равен q2 = -210’8 Кл. Определить напряженность и потенциал электричес-
кого поля на расстояниях Z] = 1 см, 12 = 4 см и 13 = 6 см от центра шара.
12.118. Внутри сферы радиусом R находится концентрическая с ней сфера
радиусом г. Внешней сфере сообщают положительный заряд Q, а внутрен-
ней - отрицательный заряд q. Определить потенциалы на поверхностях сфер.
12.119. Потенциал внутренней сферы радиуса г равен нулю. Потенциал
внешней сферы радиуса 2г равен <р. Определить заряды сфер. Центры сфер со-
впадают.
12.120. Три проводящие концентрические сферы радиусами г, 2г и Зг
имеют заряды соответственно q, 2q и -3q. Определить потенциал каждой
сферы.
12.121. Два шара, находящиеся на большом расстоянии, один диаметром
dl = 10 см и зарядом q, = 6-10'10 Кл, другой - d2 = 30 см и q2 = -2-10’9 Кл, соеди-
няются длинным тонким проводником. Какой заряд переместится по нему?
• Решение. Так как по условию задачи шары находятся далеко друг от друга, то будем пола-
гать, что до соединения их проводником они не взаимодействуют друг с другом, а после со-
единения - заряды на поверхностях каждого из шаров распределятся равномерно.
После соединения шаров проводником заряды qx и q2 перераспределятся между
ними таким образом, чтобы потенциалы шаров стали одинаковыми.
Потенциал на поверхности шара радиусом R с зарядом Q равен
4 ЛЕоЯ
Следовательно, потенциалы шаров радиусами Я| - d\/2 и R2 = d2/2 после их соеди-
нения
, 2 41' , 2 42 , ,
Ф1=4^< ф2 = 4^’ ф|=ф2'
где qj, q2 - заряды, которые будут находиться на шарах после их соединения.
На основании закона сохранения заряда
<71 + <72 = 41+ Чг
получим
92 = 41 +Ч2~Ч\-
Следовательно,
2 91 _1(Я\+д2-Ч\)
4я So d\ 4я sq 4г
Тогда заряд qj, который окажется на шаре радиусом Rt, будет равен
194
Если первоначально на этом шаре был заряд а стал q\, то это означает, что по
проводнику переместился заряд
или
(?! +?2>^1
</| + 42
А? = q~~' = 9,5- Ю'10 Кл.
«I + «2
• Ответ: bq = 4x ‘j- Ч}- = 9,51О~10 Кл.
“I +“2
12.122. Два одинаковых шарика, обладающие зарядами qxvi q2, находятся
на расстоянии г друг от друга. Шарики приводят в соприкосновение и разносят
на некоторое расстояние, при этом сила взаимодействия шариков равна перво-
начальной. На какое расстояние удалены шарики после соединения?
12.123. Два одинаковых заряженных шарика, находящиеся на расстоянии
г = 0,2 м друг от друга, притягиваются с силой Fx = 4 мН. После того как шари-
ки были приведены в соприкосновение и затем разведены на прежнее расстоя-
ние, они стали отталкиваться с силой F2 = 2,25 мН. Определить первоначаль-
ные заряды шариков.
12.124. Два одинаковых шарика подвешены на длинных непроводящих
нитях к одному крючку. Шарики заряжены одинаковыми зарядами и находятся
на расстоянии а = 5 см друг от друга. Один из шариков разрядили. Каким стало
расстояние между шариками?
12.125. Два одинаковых шарика, заряженных разноименно, притягивают-
ся друг к другу с некоторой силой. Шарики привели в соприкосновение и раз-
несли на расстояние в п = 2 раза большее, чем прежде. При этом сила взаимо-
действия уменьшилась в т = 32 раза. Найти величину заряда первого шарика
до соприкосновения, если второй имел заряд qx = 1,6-10'19 Кл.
12.126. Два одинаковых проводящих шарика с зарядами qx = 8-Ю'9 Кл и
д2 = 52-10’9 Кл находятся в воздухе на некотором расстоянии друг от друга.
Затем шарики на некоторое время соединили и поместили в среду с диэлектри-
ческой проницаемостью е на прежнем расстоянии друг от друга. Сила взаимо-
действия между шариками при этом не изменилась. Определить диэлектричес-
кую проницаемость среды.
12.127. Металлический шар радиусом Rx, заряженный до потенциала <р0,
окружают сферической проводящей незаряженной оболочкой радиусом R2. На
сколько изменится потенциал шара после того как он будет на короткое время
соединен проводником с оболочкой?
12.128. Заряженный до потенциала <р = 1000 В шар радиусом Rx = 20 см
соединяют с незаряженным шаром длинным проводником. После соединения
потенциалы шаров стали равны <р0 = 300 В. Каков радиус второго шара?
12.129. Два металлических шара радиусами Л, и R2 расположены так, что
расстояние между ними во много раз больше радиуса большего из шаров. На
195
шар радиусом Rt помещен заряд Q. Какими будут заряды qx и q2 на шарах
после соединения их проводником, если второй шар не был заряжен?
„ „ 12.130. Из трех концентрических тонких
Ж металлических сфер радиусами Rlt R2 и R3
крайние заземлены (рис. 12.73), а средней со-
общен заряд q. Найти зависимость потенциа-
ла электрического поля от расстояния до
центра сфер. Сферы находятся в вакууме.
• Решение. При сообщении средней сфере заряда q
на поверхностях внутренней и внешней сфер будут
индуцированы заряды qt и q3.
Заземление любой поверхности приводит к
—тому, что на ней устанавливается потенциал, равный
Рис. 12.73 нулю.
На поверхности сферы радиусом Я] потенциал будет равен
91 д 9з п
4я е0 Л| 4я е0 Я2 4я ео Я3
а на поверхности сферы радиусом Я3:
91 д 9з п
4п GqR3 4neQ R3 4л gQ R3
илн
—+ + —= 0 —+ -3- + —= 0
7?1 R3 ’ R3 Rj R3
Решая эту систему уравнений относительно q} и д3, получаем
^(Дг-Дз) _ <з№ ~ *г)
91 q Я2(Я3-Я,)’ 92 9 я2(я3-я,)'
Учитывая, что потенциал внутри сферы постоянен и равен потенциалу на ее поверх-
ности, а вне сферы изменяется так же, как у точечного заряда, помещенного в центр сферы,
найдем потенциалы электрических полей во всех точках пространства:
а) при 0 £ г <Rf.
,п . _ D ч 91 , д 9з п
Ф(0^г<Л1) =--------+ —3-----+-------= 0;
4я Во 4л е0 Я2 4л во Я3
б) при Я] г < R2:
91 д 9з 9(г-Л1)(Л3-Л2)
4ясог 4яв0Я2 4ясоЯ3 4я во Я2 (Я3 - Я]) г
в) при Я2 г < Я3:
91 д 9з 9(Л3-г)(Я2-Я,)
Ф (Я, < г < Я3) =--+ —— +-----------=----------------;
4яв0г 4яе0г 4яе0Я3 4л воЯ2 (Я3 -Я0 г
г) при г^Я3 :
Ф (г > Я3) == 0.
4я е0 г 4я во г 4я Во г
q(r-Ri)(R3-R-2)
• Ответ-, ф (О^г < R}) = 0; (Ri г < R2) =
4я Во Я2 (Я3 - Я|) г
р \ 9 (-®3 — г) (-®2 —-®1) , п
ф(я2^<я3)=4яЕо/г2(/г;_/г|)г- ф(^з)=о.
196
12.131. Точечный заряд q находится на расстоянии I от центра изолирован-
ного металлического шара радиусом R «I. Полный заряд шара равен нулю.
Чему равен потенциал шара?
12.132. Определить заряд заземленного металлического шара радиусом г,
если на расстоянии I от его центра находится точечный заряд д.
12.133. Металлический шар радиусом Rt, заряженный до потенциала <р0,
окружают концентрической сферической оболочкой радиусом R?. Чему станет
равен потенциал шара, если заземлить внешнюю оболочку?
12.134. Внутри металлической сферы радиусом Л = 20 см концентрически
с ней помещен металлический шар радиусом г = 10 см. Шар через отверстие в
сфере соединен с Землей с помощью тонкого проводника. На внешнюю сферу
помещают заряд Q= 10’8 Кл. Определить потенциал этой сферы.
12.135. Заряженный металлический шарик окружают незаряженной ме-
таллической сферой, центр которой совпадает с центром шарика. Радиус шари-
ка/?), сферы - R2. Определить зависимость напряженности электрического
поля Е и потенциала <р от расстояния до центра шарика в случае, когда сфера
заземлена. Заряд шарика q.
Электроемкость. Конденсаторы
12.136. Определить силу, с которой притягиваются друг к другу пластины
плоского заряженного конденсатора. Разность потенциалов между пластинами
Aq> = 1 кВ, площадь каждой пластины S = 100 см2, расстояние между ними
d = 1 мм.
• Решение. Используя выражение для емкости произвольного конденсатора
Рис. 12.74
Дф
и формулу емкости плоского воздушного конденсатора
r eos
d ’
найдем заряд на обкладках нашего конденсатора, если разность потенциалов между ними
равна Д<р:
<7 = ДФ^-.
Так как заряды q на обкладках не точечные, то
непосредственно применять закон Кулона для опреде-
ления силы взаимодействия этих зарядов нельзя. В
плоском конденсаторе одну пластину можно рассмат-
ривать как тело с зарядом q, помещенное в электри-
ческое поле напряженностью Е, созданное другой
пластиной (рис. 12.74). При этом со стороны одной
пластины на другую будет действовать сила
a a F=4E>
где Е = -— = —— - напряженность поля, создаваемого одной пластиной. Следовательно,
2ео 2Де0 2 г г.2 2 . 2С„
Л Дф О Дф О 6л 9
F= « 4,4-Ю’2 Н.
2Se° 2W 2d2
.Ответ- F=M^«4,W2H.
2d2
197
:s: f®:
Рис. 12.75
12ЛЗП. Два электропроводящих
поршня площадью S каждый образуют в
непроводящей трубе плоский конденса-
тор, заполненный воздухом при атмо-
сферном давлениир0 (рис. 12.75). Во
сколько раз изменится расстояние между
поршнями, если их зарядить разноимен-
ными зарядами ±q? Температура воздуха постоянна, трения в системе нет. На-
чальное расстояние между поршнями много меньше размеров поршней.
12.138. Две одинаковые параллельно расположенные пластины находятся
друг от друга на малом расстоянии по сравнению с их линейными размерами.
На одной из пластин находится заряд q, на другой заряд 4g. Определить раз-
ность потенциалов между пластинами. Площадь каждой пластины S, расстоя-
ние между ними d.
• Решение. Так как пластины находятся на малом расстоянии друг от друга по сравнению
с их размерами, то электрическое поле между ними можно считать однородным.
Напряженность электрического поля вблизи пластины с зарядом q равна по вели-
1---
1_£__
Рис. 12.76
Е1 = —- = —‘,
2 е0 2 S ед
где ai = q/S - поверхностная плотность заряда на данной пластине.
Напряженность электрического поля £2 вблизи пластины с зарядом 4q равна
2 е0 2 S е0
где аг = bq/S - поверхностная плотность заряда на этой пластине.
Так как пластины заряжены одноименно, то
Ч поля£^ и/2 между пластинами будут направле-
ны в противоположные стороны (рис. 12.76). Поэ-
тому, исходя из принципа суперпозиции электри-
^Ч ческих полей, напряженность результирующего
поля найдем как
Следовательно, поле £между пластинами будет однородным. Это означает, что иско-
мая разность потенциалов будет равна
, . Д<р = Еd = Ч^
• Ответ: Дф = —— . 2 S Ед
2 S Ед
12.139. Две параллельные разноименно заряженные металлические
пластины находятся друг от друга на расстоянии d=5 см, много меньшем
размеров пластин. Поверхностная плотность зарядов на каждой пластине
равна g = 1О’10 Кл/см2. Определить разность потенциалов между пластинами.
12.140. В незаряженный плоский воздушный конденсатор параллельно его
обкладкам вносят тонкую металлическую пластину с зарядом q. Площади об-
198
d
Ф1 О.
(d-x)
Ф2 Xl
Рис. 12.77
ч
£
Ф
кладок конденсатора и внесенной пластины равны S, расстояние между об-
кладками конденсатора d. Как зависит разность потенциалов на обкладках кон-
денсатора от расстояния х между одной из обкладок и металлической пласти-
ной?
• Решение. Электрическое поле, создаваемое вблизи заряженной плоской пластины, будет
однородным и равным по величине
£ = J5_ = _2_>
2 So 2 S Sq
где a = q/S - поверхностная плотность заряда на пластине.
Тонкая пластина с зарядом q создаст по
обе стороны от поверхностей однородные
поляЁ^ и (рис. 12.77), причем
£,=£2 = 2S^’
что приведет к появлению индуцированных
зарядов на обкладках конденсатора. Однако
в силу закона сохранения заряда, суммарный
заряд каждой пластины останется равным нулю, а значит, результирующее поле, созда-
ваемое индуцированными зарядами, также будет равным нулю. Таким образом, между
обкладками конденсатора будет только поле, создаваемое внесенной пластиной.
Если потенциал одной из обкладок обозначить через <р ।, а другой - через ф2, то разнос-
ти потенциалов между каждой из них и внесенной пластиной будут равны
г, qx г- zj ч l(d-x)
Ф-Ф1 =£1Х=г5—, ф-ф2=^2(^~х)=^-\, ' ,
I i s0 2 о So
где <р - потенциал пластины, х и (<7- х) - расстояния между пластиной и обкладками кон-
денсатора.
Вычитая друг из друга два последних соотношения, получаем
. q(d-x) qx д . .
Дф = Ф1-ф2 = ^Т—= (d-2x\
2 о 2 о Eq 2 о
Очевидно, что в случае х = 0, т.е. когда пластина располагается на одной из обкладок,
мы приходим к известной формуле:
Лф = 25Т = 2^</=£</’
Z О Sq 2 So
выражающей разность потенциалов между двумя произвольными точками, находящимися
на расстоянии d в однородном электрическом поле напряженностью М создаваемом заря-
женной пластиной с поверхностной плотностью заряда a = q/S.
• Ответ: Дф = —?— (d-2 х).
2Sso
12.141. Чему равна разность потенциалов между крайними пластинами в
системе, состоящей из трех параллельных бесконечных пластин, заряженных
одноименными зарядами с поверхностной плотностью сть ст2, ст3? Средняя
пластина находится на расстоянии hl от первой и на расстоянии А2 от третьей
пластины.
12.142. Разность потенциалов между пластинами плоского конденсатора,
одна из которых заземлена, равна Д<р = 100 В. В воздушный зазор шириной
199
d = 4 см между пластинами вдвигается незаряженная металлическая пластина
на расстоянии I = 3 см от заземленной пластины. Определить потенциал внут-
ренней пластины и напряженность электрического поля по обе стороны от нее.
12.143. Найти напряженность электрического поля между тремя бесконеч-
но большими параллельными пластинами в случае, если средняя пластина за-
землена. Расстояния между средней пластиной и крайними равны а и Ь. Потен-
циалы крайних пластин равны ср.
12.144. Между двумя заземленными металлическими пластинами нахо-
дится одинаковая с ними по размерам тонкая пластина с поверхностной плот-
ностью заряда ст. Расстояния от нее до двух других пластин равны а и b и много
меньше линейных размеров пластин. Найти напряженность электрического
поля в зазоре между пластинами и поверхностную плотность зарядов, индуци-
руемых на них.
12.145. Между соединенными проводником обкладками плоского незаря-
женного конденсатора помещена металлическая пластина, делящая расстояние
между обкладками в отношении 1:3. Какой величины заряд протечет по про-
воднику, если на внутреннюю пластину поместить заряд ff!
• Решение. Заряд Q пластины создаст по обе стороны от нее электрическое поле напря-
женностью £* Так как рассматривается плоский конденсатор, то расстояние между двумя
любыми попарно взятыми пластинами будет много меньше их линейных размеров, поэ-
тому поля между ними можно считать однородными.
Электрическое поле ^приведет к появлению на обкладках конденсатора индуциро-
ванных зарядов, причем, как следует из закона сохранения электрического заряда, суммар-
ный заряд на обеих обкладках конденсатора не изменится, т.е. останется равным нулю. Как
следует из решения задачи №12.140, в случае, если обкладки конденсатора не соединены
1 м 2 А |<С> 1? 3
d 1 j2 Ml Е" % 42 Ч>2
Рис. 12.78
проводником, то наличие заряженной пласти-
ны приведет к возникновению разности потен-
циалов между ними. Так как в нашем случае
обкладки закорочены, то заряды будут переме-
щаться с одной обкладки на другую до тех пор,
пока потенциалы на них не станут равными. В
результате чего на обкладках возникнут заря-
ды <?] и q2 (рис. 12.78), причем qt + q2 = 0.
Пусть для определенности Q > 0, qt = q > 0, q2 = - q. Тогда векторы напряженности
электрического поля ft создаваемого зарядами средней пластины, векторы £^ поля, созда-
ваемого обкладкой с зарядом qx, и векторы £j поля обкладки с зарядом q2, будут направле-
ны перпендикулярно пластинам так, как показано на рис. 12.78. Следовательно, напряжен-
ность электрического поля между пластиной и обкладкой, находящейся на расстоянии
<7] = 'A d (где d - расстояние между обкладками конденсатора) от нее, будет равна
El = E-Ei-Е2, '
где Е = Q/(2 Sео), £1 = £2 = q/(2 Seo) - значения напряженностей электрических полей,
создаваемых средней и крайними пластинами соответственно; S- площадь пластины и
каждой из обкладок. Следовательно,
200
El = Q-i~4 = Q-li
1 2Se0 2Sso ’
Разность потенциалов между рассматриваемыми пластинами равна
г л Q~^4d (Q-2q)d
^=E'd'=T^4=^T’
где <pi, <р - потенциалы обкладки с зарядом q и пластины соответственно.
Аналогично для области между пластиной и второй обкладкой конденсатора с зарядом q2:
Ea = E+Et +е2 = ^±^ = ^Л,
11 1 2 2Se0 2Sso
<p - <p2 = £п J2 =
g + 2?3</ 3(Q + 2q)d
2Seo 4 8Se0
Так как обкладки соединены проводником, то ф| = ф2. Следовательно,
= ™ Q-U~-3^2q}.
о d Sq О d Eq
Откуда получим величину заряда, наведенного на каждой из обкладок:
q = q\=-qi = -'/*Q-
Если первоначально на обкладках заряда не было, а после того, как между ними была
помещена заряженная пластина, на каждой из них возникли разноименные заряды ± q, то
это означает, что заряд, равный \ q |, перетек по проводнику с одной обкладки на другую.
При этом обкладка, расположенная ближе к пластине, приобрела заряд противоположный
по знаку заряду пластины.
• Ответ -. | q | = lA Q.
12.146. Плоский конденсатор находится во внешнем электрическом поле
напряженностью Е, перпендикулярном пластинам. Площадь пластин S. Какой
заряд окажется на каждой из пластин, если конденсатор замкнуть проводником
накоротко?
12.147. Три одинаковые парад- т—j-------------------------
лельные друг другу пластины находят- ®д
ся на малых по сравнению с их линей- J
ными размерами расстояниях одна от I
другой. Крайние пластины закорочены I
проводником и на них помещен некото-
рый заряд. Средней пластине сообщен ^ис- ??
заряд Q. Чему равна разность потенциалов между пластинами А и В (рис.
12.79)? Расстояния a, d известны, площадь каждой пластины равна S.
12.148. Обкладки плоского воздушного конденсатора соединены провод-
ником. Между обкладками находится тонкая пластина такого же размера, что и
обкладки конденсатора. Зазор между обкладками d делится пластиной в отно-
шении 1:3. Определить разность потенциалов между пластиной и обкладками
конденсатора, если на пластину поместить заряд Q. Площадь каждой пласти-
ны S.
201
'Ad
в
M>i d Г
-f I a
d Дфг
Рис. 12.80 Рис. 12.81
12.149. В незаряженный плоский конденсатор с площадью пластин S
вставляют такой же конденсатор, у которого обкладки соединены между собой
проводником. Зазор между обкладками незаряженного конденсатора d при
этом делится одной из пластин закороченного конденсатора в отношении 1 ;3
(рис. 12.80). Определить разность потенциалов, возникающую между обклад-
ками незаряженного конденсатора, если пластинам закороченого конденсатора
сообщен заряд Q.
12.150. Четыре параллельные пластины расположены так, как показано на
рис. 12.81. Найти разность потенциалов между внутренними пластинами. Раз-
меры a, d и разности потенциалов Acpj, Дф2 заданы. Расстояния а и d много
меньше линейных размеров пластин.
12.151. Две одинаковые параллельно расположенные и закороченные про-
водником пластины находятся друг от друга на расстоянии d. малом по сравне-
нию с их линейными размерами. Такая же пластина с зарядом Q находится
между ними на расстоянии а от одной из них. Какой заряд протечет по закора-
чивающему проводнику, если заряженную пластину вынуть?
12.152. Между пластинами замкнутого плоского конденсатора находится
заряженная пластина такого же размера, что и обкладки конденсатора. Рассто-
яние между обкладками конденсатора равно d. Первоначально заряженная
пластина находится на расстоянии <1/3 от одной из обкладок. Какой заряд про-
течет по проводник}', замыкающему пластины конденсатора, при перемещении
заряженной пластины в новое положение на расстояние <ИЗ от другой из обкла-
док? Заряд пластины равен Q.
12.153. Расстояние между обкладка-
ми плоского закороченного заземлен-
ным проводником конденсатора равно d
(рис. 12.82). Между обкладками нахо-
дится параллельная им и такая же по раз-
мерам пластина с зарядом Q. Какой за-
— ряд протечет по проводнику, если плас-
„ тину переместить параллельно самой се-
Рис. 12.о2 g * ю
бе на расстояние AZ?
12.154. Расстояние между обкладками плоского закороченного проводни-
ком конденсатора равно d. Между обкладками помещают металлическую пло-
в
d id
202
скопараллельную пластину толщи-
ной b и зарядом Q на расстоянии а
от одной из обкладок. Определить
заряды на каждой из сторон пласти-
ны.
• Решение. Заряд Q пластины создаст по
обе стороны от нее электрическое поле
напряженностью М которое приведет к
появлению индуцированных зарядов
</! и q2 на обкладках конденсатора, причем qi=-q2 (см. решение задачи №12.145).
Пусть Q > 0, q\ = q > 0, q2 = - q. Тогда напряженность электрического поля в зазоре
шириной а (рнс. 12.83) равна
Ei = E-Ej-Е2=О^-,
2 Se0
а в зазоре шириной [</- (а + 6)] -
Ец = Е + Ех + Е2 = ^
2. о Ел
Так как потенциалы <р ( и <р2 равны между собой (обкладки закорочены), то разности
потенциалов между пластиной и обкладками также равны друг другу:
ф - ф| = ф - ф2,
или
а = Ец [d - (а + i)].
Следовательно,
(Q-2q)a = (Q + 2q)[d-(a + b)].
Откуда получим
Внутри металлической пластины напряженность Eq электрического поля равна нулю.
С другой стороны, можно записать, что она равна
£% = ?'+ +
где - напряженности полей, создаваемых зарядами Q'h Q" находящимися на про-
тивоположных поверхностях пластины, причем g'+ Q"= Q.
Напряженности ^’создаются одноименными зарядами (в нашем предположении -
положительными), поэтому направлены навстречу друг другу. Следовательно,
Eq = 0 = E-E"+Ei +Е2> или 0 = ^—8 +..£±Я
„ 2Sao
Решая систему уравнений
Q+Q"=Q, в'-в"+29 = 0,
получаем
q"=q_q-=q^,
£ а — и а — о
• Ответ: Q'=Q——-—— Q"=Q—-—.
* * d-b * * d-Ъ
12.155. Расстояние между обкладками плоского закороченного проводни-
ком конденсатора равно d. Между обкладками на расстоянии а от одной из них
203
Рис. 12.84
кладками на расстоянии а от одной из
металлическая пластина толщиной b с
течет по проводнику, если указанную
совместить с пластиной?
находится плоская параллельная им ме-
таллическая пластина толщиной b с за-
рядом Q (рис. 12.84). Какой заряд проте-
чет по проводнику, если заряд на плас-
тине увеличить вдвое?
12.156. Расстояние между обклад-
ками плоского закороченного провод-
ником конденсатора равно d. Между об-
них находится плоская параллельная им
зарядом Q (рис. 12.84). Какой заряд про-
обкладку переместить на расстояние а и
12.157. Между обкладками плоского воздушного конденсатора параллель-
но его пластинам помещается металлическая пластинка толщиной а. Размеры
пластинки совпадают с размерами обкладок, площадь которых равна S, а рас-
стояние между ними - d. Определить емкость получившегося конденсатора.
Рис. 12.85
• Решение. Для определения емкости получив-
шегося конденсатора, поместим на его обклад-
ки равные по величине разноименные заряды
q и (-q), как показано на рнс. 12.85, н емкость
определим по формуле
С = ^~,
Дф
где Дф = ф2 - ф] - разность потенциалов между
обкладками.
Заряды на обкладках конденсатора будут
индуцировать на сторонах незаряженной метал-
лической пластинки заряды Q и Qпротивопо-
ложные по знаку и равные по величине.
Пусть пластинка помещена на произвольном расстоянии х от одной нз обкладок, тогда
расстояние до другой обкладки будет равно [d - (а + х)].
Напряженность электрического поля в воздушном зазоре шириной х будет равна гео-
метрической сумме напряженностей (?(</), f?(-q) полей, создаваемых зарядами q и (-q), н
полей, создаваемых индуцированными зарядами Q н Q
= ?(</) + ?(-q) + /(0 + /(б’).
Так как Q - - Qто (?(б) = - ^(б )> поэтому
=/(?) +/(-$).
Векторы напряженностей (?(</) и (?(-?) между обкладками конденсатора направлены в
одну сторону. Следовательно,
2 So S' 2 sq S Pq S
Так как электрическое поле внутри конденсатора однородно, то разность потенциалов
между обкладкой с зарядом q и пластиной будет равна
204
Ф]-Ф = £]Х = ^, (1)
где ф - потенциал пластины.
Аналогично, для воздушного зазора шириной [</ - (а + х)]:
^2 = Д?) + ^(-9) + ^(2) + ^(2') = ^(я) + ^(-?)>
или
Е2 = Е (о) + Е (-а) = —3— + —3— = -3- .
2 w 1 4 2s0S 2eoS s0S
Разность потенциалов между обкладкой с зарядом (-q) и пластиной равна
q>-4>2 = K2[rf-(a + x)] = i^^l. (2)
So О
Складывая выражения (1) и (2), найдем разность потенциалов между обкладками кон-
денсатора:
Дф = ф ] - ф2 = [d - (а + х) + х] = .
So о Ео о
Следовательно, емкость получившегося конденсатора равна
п Sq 5
С=л • Р)
Дф а-а
Как видим, емкость получившегося конденсатора не зависит от места расположения
внесенной пластины и поэтому для определения емкости системы пластину можно распола-
гать на каком угодно расстоянии х. Если ее расположить непосредственно на одной из об-
кладок, то получим новый конденсатор с расстоянием между обкладками равном (d-а) и
емкостью (3).
Рассмотрим систему, состоящую из двух последовательно соединенных конденсато-
ров с одинаковыми пластинами площадью S н расстояниями между обкладками х и
[rf - (а + х)] соответственно. Их емкости, очевидно, равны
С _ с S°S
1 х ’ 1 d - (а + х) ’
а емкость системы
С] С2 е0 S
' С । + С2 d - а
Следовательно, можно сделать еще один вывод: если между обкладками конденсатора
поместить металлическую пластину, то образовавшуюся систему можно рассматривать как
два последовательно соединенных конденсатора. Это, очевидно, справедливо также для слу-
чаев, когда внутри конденсатора находится несколько пластин.
Еп
• Ответ: С = —--.
d-a
12.158. Плоский конденсатор имеет емкость С = 50 пФ. Какова разность
потенциалов между его обкладками, если конденсатору сообщен заряд
q = 2,5 мкКл?
12.159. Какой минимальный заряд может находиться на обкладках плос-
кого воздушного конденсатора, если «пробой» для воздуха наступает при на-
пряженности электрического поля 5 = 30 кВ/см? Площадь каждой обкладки
.$= 1 см2.
205
12.160. Во сколько раз и как изменится емкость плоского воздушного кон-
денсатора, если площадь его пластин увеличить в п = 3 раза, а расстояние
между ними увеличить в т = 5 раз?
12.161. На сколько надо изменить расстояние между пластинами плоского
воздушного конденсатора, чтобы его емкость увеличилась в п - 4 раза? Началь-
ное расстояние между пластинами равно d = 2 мм.
12.162. Плоский конденсатор имеет расстояние между пластинами d и
емкость Со. В пространство между обкладками вставлена металлическая плас-
тина толщиной а (а< d). Определить емкость получившегося конденсатора в
двух случаях: а) пластина вдвигается посередине; б) пластина вдвигается
вплотную к одной из обкладок.
12.163. Между обкладками плоского воздушного конденсатора параллель-
но им расположены две металлические пластины толщиной а каждая. Опреде-
лить емкость получившегося конденсатора, если площади пластин равны S и
их размеры совпадают с размерами обкладок. Расстояние между обкладками
конденсатора равно d.
Рис. 12.86
12.164. Конденсатор составлен из трех проводящих пластин площадью
S каждая. Расстояния между соседними пластинами dt и d2 много меньше
линейных размеров пластин (рис. 12.86, а). Крайние пластины соединены про-
водником. Определить емкость конденсатора между пластинами А и В.
• Решение. При решении задачи воспользуемся тем же приемом, что н в задаче №12.157,
т.е. поместив на пластины А и В разноименные одинаковые по величине заряды ± q, най-
дем разность потенциалов Дф между ними, а емкость определим по формуле
Пусть на пластину В помещен положительный заряд q > 0, а на пластину А - отрица-
тельный q' = - q. Так как пластины А и D соединены проводником, то заряды с пластины А
могут перемещаться на пластину D и наоборот. Пусть заряд пластины А перераспределяется
таким образом, что на пластине А будет заряд qj, а на пластине D - заряд q2, причем, как
следует из закона сохранения заряда,
(1)
<?! + 41 - _ ч-
Заряды ?[, q2 и q пластин A, D, В соответственно создадут электрические поля, векто-
ры напряженности которых будут направлены так, как показано на рис. 12.86, б. Напряжен-
206
ностн электрического поля в воздушных зазорах на основании принципа суперпозиции
будут равны
Ei = E(q) + E(q})-E(qd, Ea = E(q) + E^-E(qi)
между пластинами А, В и В, D соответственно.
По условию задачи размеры пластин велики по сравнению с расстояниями между
ними, поэтому поля Е (q), Е (q<) и Е (д2) можно считать однородными:
Е^-^-
Следовательно,
Е _ д 41 42 _g + ?i-<?2 г _ 4 4i _4 + 42~41
’ 2Ss0 +2Ss0 2,Se0 2SS0 ’ ~n 2Sc0+2Se0 2Ss0 '' 2Se0
Разности потенциалов между средней пластиной В и крайними пластинами А и D
равны
г , 4 + 41-42 . - , 4 + 42-41 ,
q>-<p1=£|d|= —di, <р - <р2 = Ец d2 = ——-—а2,
2 О Eq Z О Ь0
а так как пластины А и D соединены проводником, то
<Р1 = Ф2’
или
(.4 + 41- 41) <11 =(4 + 42~ 41) d2. (2)
Выразив нз уравнения (1) величину заряда д2
42 = ~4~4i,
и подставив в выражение (2)
(4 + 4t + 4 + 41) di = (д - д - 4t~4i)d2,
получим
«2
^1 , ^2 = -^-^1 = “^•
С*] + С*2 t*| + ^*2
Следовательно, разность потенциалов между пластинами А и В равна
t/j : tZ] С^2 I Я ^2
а емкость конденсатора
JL _ *$' Ео + dj)
Дф df d2
Эту задачу можно решить проще, если заметить, какую систему конденсаторов обра-
зуют пластины. Пластина В является общей обкладкой для двух конденсаторов: верхняя по-
верхность пластины образует конденсатор с пластиной А емкостью
г ^Е°
1" di ’
а нижняя - конденсатор с пластиной D емкостью
С1= d2
При этом систему пластин можно рассматривать как
два параллельно соединенных конденсатора (рис. 12.87). Ем-
кость такой системы равна
„ SeoCrfi+ty
• Ответ: С =----т—-----.
“I “2
С = С| + С2
5 Eq (di +1/2)
di d2
207
Рис. 12.88 Рис. 12.89
12.165. Четыре одинаковые металлические пластины расположены на рас-
стоянии d = 1 мм друг от друга. Площадь каждой пластины S - 220 см2. Найти
емкость системы между точками А и В, если пластины соединены так, как по-
казано на рис. 12.88.
12.166. Решить задачу аналогичную №12.165 для соединения пластин, по-
казанном на рис. 12.89.
12.167. Как изменится емкость плоского воздушного конденсатора, если
его поместить в изолированную металлическую коробку? Просвет между стен-
ками коробки и пластинами вдвое меньше, чем расстояние между пластинами.
12.168. Между обкладками плоского воздушного конденсатора параллель-
но его пластинам помещается диэлектрическая пластинка толщиной а и прони-
цаемостью е (рис. 12.90). Размеры пластинки совпадают с размерами обкладок,
площадь которых равна S, а расстояние между ними - d. Определить емкость
получившегося конденсатора.
• Решение. Для определения емкости конден-
сатора поступим таким же образом, как в слу-
чае задачи №12.157. Поместим на обкладки
конденсатора равные по величине разноимен-
ные заряды + q, как показано на рис. 12.90. На-
личие на обкладках этих зарядов приведет к
появлению в воздушном зазоре электрического
поля напряженностью
/=/(?) + /(-<?),
или в проекции на направление от положитель-
но заряженной пластины к отрицательно заря-
женной:
Е = Е (9) + Е (-а) = —Я— + —2— = -Я-.
v-ч, 2 560 2Ss0 Ss0
Внутри диэлектрика проницаемостью s поле £*будет ослаблено в s раз:
Е'=- = -Я—.
е See0
Так как поля Ё^и ^'созданы заряженными пластинами, расстояние между которыми
много меньше линейных размеров пластин, то их можно считать однородными, а разность
потенциалов между обкладками определить как
208
Дф = ф| - ф2 = (ф! - Фз) + (Фз - ф4) + (ф4 - Фг),
где ф] - фз = £ х, Фз - ф4 = £ 'а, ф4 - фз = £ [rf - (а + х)]. Следовательно,
. _ £ , ,, _[ 8 (х + d-a-x) + а 1 q [ . 1
Дф = £ х + — а + £ [d - (а + х)] = £ I —L-1- = — I е (d - а) + а .
8 1 8 8 8 8q 1 ’
Емкость конденсатора найдем как отношение заряда иа обкладках конденсатора к
разности потенциалов между ними:
_ <? _sspS
Дф s (d - а) + а '
Как и в случае конденсатора с внесенной между его обкладками металлической плас-
тиной, в нашем случае емкость конденсатора не зависит от места расположения диэлект-
рической пластины, а определяется лишь ее проницаемостью е и толщиной а. Поэтому
при определении емкости конденсатора пластину можно расположить на произвольном
расстоянии х. Расположив ее на поверхности одной из обкладок, получим систему двух
последовательно соединенных конденсаторов емкостями
e0S е SpS
Ci = — , с? = ,
1 d-a а
где С[ - емкость конденсатора с воздушным зазором шириной (d - а); Сг - емкость конден-
сатора, заполненного диэлектриком проницаемостью е и шириной а. Следовательно,
QQ _ espS
С| + С2 s (d— л) + а
Мы доказали, что конденсатор с внесенным между его обкладками диэлектриком,
можно рассматривать как систему двух последовательно соединенных конденсаторов.
Этот вывод можно обобщить также иа случай, если в конденсатор внесено несколько пло-
скопараллельных диэлектрических пластин.
880 5
• Ответ: С =--;--------.
е (а- а) + а
12.169. На сколько изменится емкость плоского воздушного конденсато-
ра, если пространство между пластинами заполнить керосином с диэлектричес-
кой проницаемостью е = 2? Расстояние между пластинами равно d = 4 мм, пло-
щадь каждой пластины 5=10 см2.
12.170. Во сколько раз и как изменится емкость плоского воздушного кон-
денсатора, если расстояние между его пластинами увеличить в и = 5 раз и
между ними вплотную вдвинуть лист слюды с диэлектрической проницаемос-
тью е = 7?
12.171. Емкость плоского конденсатора при заполнении пространства
между его пластинами керосином с диэлектрической проницаемостью е = 2
увеличилась на ц = 40 %. Во сколько раз и как при этом изменили расстояние
между пластинами?
12.172. Конденсатор зарядили и отключили от источника электрических
зарядов. Когда из конденсатора удалили имевшийся между его обкладками ди-
электрик, то разность потенциалов между обкладками возросла от Аф, = 100 В
до Афг = 600 В. Определить диэлектрическую проницаемость диэлектрика,
если он заполнял все пространство между обкладками.
209
12.173. Плоский воздушный конденсатор заряжен до разности потенциа-
лов Д<р0 = 60 В и отключен от источника электрических зарядов. После этого
внутрь конденсатора параллельно обкладкам вводится плоскопараллельная
пластинка из диэлектрика с проницаемостью 6 = 2. Толщина пластинки в два
раза меньше зазора между обкладками конденсатора. Чему равна разность по-
тенциалов между обкладками конденсатора после введения диэлектрика?
а) б)
Рис. 12.91
12.174. Зазор между обкладками плоского конденсатора заполнен двумя
плоскими слоями диэлектриков проницаемостями 62 и толщинами du d2 со-
ответственно (рис. 12.91, а). Найти емкость этого конденсатора, если площадь
каждой обкладки S.
• Решение. Воспользуемся результатами решения задачи №12.167 и будем рассматривать
конденсатор с двухслойным диэлектриком как два последовательно соединенных конден-
сатора (рис. 12.91, б). Тогда емкость такой системы будет равна
с_ QC2
Ci + C2’
где С[ = S| s0 S/dl - емкость конденсатора с диэлектриком проницаемостью S] и толщиной
rf|j С2 = s2 s0 S/d2 - емкость конденсатора с диэлектриком проницаемостью s2 и толщи-
ной dj.
Следовательно,
S|S2e05
, л. е,82 s0 S' eld2 + e2dl
• Ответ: С = — ----— .
8] d2 + S2 Я]
12.175 . Пространство между обкладками плоского конденсатора заполне-
но двумя слоями диэлектриков: стекла-толщиной dt = 1 см и парафина - тол-
щиной d2 = 2 см. Разность потенциалов между обкладками Дф = 3000 В. Опре-
делить напряженность электрического поля и падение потенциала в каждом из
слоев. Диэлектрическая проницаемость стекла Sj = 7,парафина -е2= 2
12.176 . Пространство между обкладками плоского конденсатора полнос-
тью заполнено двумя диэлектрическими слоями проницаемостями е, и %. При
каком соотношении между толщинами слоев диэлектриков падение потенциа-
210
ла и каждом слое будет равно половине разности патенциалов, приложенной к
конденсатору?
12.177 . Конденсатор состоит из трех полосок станиоли площадью
5 = 6 см2 каждая, разделенных двумя слоями слюды толщиной d= 0,1 мм.
Крайние полоски станиоли соединены между собой. Какова емкость такого
конденсатора? Диэлектрическая проницаемость слюды 6=7.
12.178 . Зазор между обкладками плоского конденсатора заполнен изо-
тропным диэлектриком, проницаемость которого изменяется в направлении
перпендикулярном обкладкам по линейному закону от £[ до 62, причем е2 >
Площадь каждой пластины S, расстояние между ними d. Найти емкость кон-
денсатора.
12.179 . Плоский воздушный конденсатор имеет емкость Со. Определить
емкость того же конденсатора, когда он наполовину погружен в трансформа-
торное масло так, что пластины перпендикулярны поверхности масла. Относи-
тельная диэлектрическая проницаемость масла е.
12.180 . В плоский воздушный конденсатор с I
обкладками площадью S каждая и расстоянием .—I-------------------
между ними d внесена плоская параллельная им |
пластина из диэлектрика проницаемостью 6 = 3 d
так, как показано на рис. 12.92. Во сколько раз из-
менилась емкость конденсатора после внесения
пластины? Площадь пластины и ее толщина в два
раза меньше соответствующих размеров конден- ^ис- 12-92
сатора.
12.181 . Найти емкость шарового проводника радиусом г, окруженного
прилегающим концентрическом слоем диэлектрика с внешним радиусом R и
диэлектрической проницаемостью е.
• Решение. Поместим на проводник заряд q. Тогда снаружи проводника возникнет элект-
рическое поле, напряженность которого в зависимости от расстояния р до центра провод-
ника внутри диэлектрика будет изменяться по закону
и вне диэлектрика - по закону
4 л s0 р2
Потенциал на поверхности проводника определим как работу по перемещению еди-
ничного положительного заряда с поверхности проводника на бесконечность:
J) R оо
Е dp = If] rfp + Je2 dp,
где учтено, что поле в диэлектрике и воздухе меняется по разным законам.
Следовательно,
211
ф = —9— f«£ + _2_ f = }Л
4л в е0 г р2 4л в^ р2 4лв01в1 р'г 1 1
_ Ч 11 Д-r 1 _ <? (R - г)+ е г
4л Sq ’ в г Д Д 1 4л ед в г Д
Тогда емкость проводника определим как отношение заряда, сообщенного провод-
нику, к потенциалу на его поверхности:
д 4л 8 Sq г Д
Дф г (в - 1) + Д
р 'я
„ 4л £ ёп г R
• Ответ: С = ———- - -.
г (в - 1) + R
12.182 . Определить электроемкость уединенного проводящего шарика
диаметром d= 3 см, находящегося в воздухе.
12.183 . При сообщении проводящему шару заряда q = 3-10"8 Кл его потен-
циал становится равным ф = 6-103 В. Определить электроемкость шара и его
радиус.
12.184 . Найти емкость сферического конденсатора, радиусы обкладок ко-
торого равны а и Ь, причем а < Ь, если пространство между обкладками запол-
нено однородным диэлектриком с проницаемостью е.
Параллельное и последовательное соединение конденсаторов
12.185. Определить емкость батареи конденсаторов, изображенной на рис.
12.93, а, где С, = 6 мкФ, С2 = 9 мкФ, С3 = 3 мкФ, С4 = 1 мкФ.
а) б) в)
Рис. 12.93
• Решение. Воспользуемся формулами для определения емкости системы параллельно н
последовательно соединенных конденсаторов:
спар = С| + Q+ - + Сп, =4" + ^- +• • • +
спосл С1 сп
где С|, С2, .... Сп- емкости конденсаторов, из которых составлена батарея.
В батарее, представленной на рис. 12.93, а, конденсаторы С2 и С3 соединены парал-
лельно. Их общая емкость
С2_3 = С2 + Су
Заменив два конденсатора С2 и С3 одним С2_3, получим новую батарею (рис. 12.93,6),
в которой конденсаторы С] и С2_3 соединены последовательно. Их общая емкость
1 _ 1 1 r _ G с2-) _ ci (Q + С3)
Q-2-з С] С2_3 ’ 1-2-3 С| + С2_3 С] + С2 + С3
212
Теперь батарею можно представить в виде двух параллельно соединенных конден-
саторов - С|_2-з и С4 (рис. 12.93, в). Следовательно, емкость батареи
С1(С2 + С3)
С| + с2 + с3
^-общ ~ ^1-2-3 ^4 » ИЛИ Сфбщ —
С, (С2 + С3)
• Ответ: Собщ = + С4 = 5 мкФ.
, С] + с2 + с3
+ С4 = 5 мкФ.
Рис. 12.94 Рис. 12.95
12.186. Определить емкость батареи конденсаторов, изображенной на рис.
12.94, где С[ = 2 мкФ, С2 = 5 мкФ, С3 = 8 мкФ.
12.187. Определить емкость батареи конденсаторов, изображенной на рис.
12.95, где С, = 5 мкФ, С2 = 10 мкФ, С3 = 15 мкФ.
Рис. 12.96 Рис. 12.97
12.188. Определить емкость батареи конденсаторов, изображенной на рис.
12.96, где С] = 4 мкФ, С2 = 10 мкФ, С3 = 2 мкФ.
12.189. Определить емкость батареи конденсаторов, изображенной на рис.
12.97, где Cj = 3 мкФ, С2 = 2 мкФ, С3 = 6 мкФ.
12.190. п одинаковых параллельно соединенных конденсаторов заполнены
жидким диэлектриком с диэлектрической проницаемостью е и заряжены до
разности потенциалов Д<р. Как изменится разность потенциалов, если из одного
конденсатора вытечет диэлектрик? Решить задачу, если конденсаторы соеди-
нены последовательно.
• Решение. 1). Емкость батареи п конденсаторов, соединенных параллельно, равна
Сдбщ ~ Oj + С2 + . . . + Сд = С + С+ ... + С = пС,
где С - емкость одного конденсатора.
Если из одного конденсатора вытечет диэлектрик, то его емкость уменьшится в в
раз. Тогда емкость батареи станет равной
^-общ ~(в - 1) С + С ,
где С = С/е - емкость конденсатора, из которого вытек диэлектрик.
213
Так как батарея конденсаторов была заряжена до разности потенциалов Дф и отклю-
чена от источника, то ее заряд останется неизменным н равным
Ч = ^-общ Дф-
После того как из одного конденсатора вытек диэлектрик величину заряда батареи
можно представить в виде
, Ч ~ О>бщ Дф >
где Д<р - разность потенциалов, которая установится между обкладками конденсаторов.
Следовательно,
Ч ~ ^-общ ^Ф ~ ^-общ Аф >
или
. - . О>бщ . пС . пе
Дф - Дф —-= - Дф------------= Дф----------.
Общ с (л - 1) + С/г 8 (п - 1) + 1
Изменение разности потенциалов, произошедшее в результате вытекания диэлектри-
ка из одного конденсатора, будет равно
Дфпар = Дф'- Дф = Дф - Дф = Дф ) П
2) . При рассмотрении батареи последовательно соединенных конденсаторов, вос-
пользуемся теми же обозначениями, что и при параллельном соединении. Емкость батареи
п конденсаторов, соединенных последовательно, равна
1 _ 1 1 J_________1 1 I n
Собщ Ci + C2 + '" + Cn С + С + " + С С'
или Собщ С/п.
После того как вытечет диэлектрик из одного конденсатора, емкость батареи станет
ранной
1 «-Il «— 1 6 ’
> " **' t f-' "1” Л'* ’ НЛИ ^обтц
Собщ С С С С
Так как заряд батареи останется неизменным, то
Я “ О)бщ “ ^общ Дф
Откуда получим
Дф' = Дф ^-_д
Собщ
Следовательно, разность потенциалов изменится иа величину
. . ' . . 8 + П - 1 . £ - 1
Дфпосл = Дф - Дф = Дф-~п------Дф = Дф
А К Е - 1 А А £ “ 1
• Ответ: ДфПар ~ Дф { ~ ,>. , '> Афпосл “ Дф
ъ (fl 1 I Т *
12.191. Разность потенциалов на обкладках заряженного и отсоединенно-
го от батареи плоского конденсатора удвоилась, когда вытек наполнявший его
диэлектрик. Определить диэлектрическую проницаемость этого диэлектрика.
12.192. Конденсатор емкостью С присоединен к источнику, который под-
держивает на обкладках конденсатора разность потенциалов Дф. Какой заряд
пройдет через источник при заполнении пространства между обкладками жид-
костью с диэлектрической проницаемостью е?
214
12.193. Два одинаковых плоских воздушных конденсатора соединены пос-
ледовательно и подключены к источнику постоянного напряжения. Внутрь
одного из них вносят диэлектрик с проницаемостью е, который заполняет все
пространство между обкладками. Во сколько раз изменится напряженность
электрического поля в этом конденсаторе?
12.194. Два одинаковых конденсатора соединены последовательно и под-
ключены к источнику постоянного напряжения. Во сколько раз изменится раз-
ность потенциалов на одном из конденсаторов, если другой погрузить в жид-
кость с диэлектрической проницаемостью е = 2?
12.195. Решить задачу №12.190, если диэлектрик вытечет из k< п конден-
саторов.
12.196. Обкладки конденсатора с неизвестной емкостью С], заряженного
до разности потенциалов Дф] = 80 В, соединяют с обкладками конденсатора
емкостью С2 = 60 мкФ, заряженного до разности потенциалов Дф2 = 16 В. Оп-
ределить емкость С], если разность потенциалов на конденсаторах после их со-
единения равна Дф 20 В, а конденсаторы соединяются обкладками, имеющи-
ми: а) одноименные заряды; б) разноименные заряды.
• Решение. Емкость конденсатора, заряженного зарядом а до разности потенциалов Дф,
равна
Дф
Следовательно, конденсаторы б.', и С2 имеют на обкладках заряды
q\ ~ С\ Дф| и <?2 = С2 Дф2
соответственно.
После соединения конденсаторов обкладками, имеющими одноименные заряды,
общий заряд батареи параллельно соединенных конденсаторов будет равен
+?2 = С| Дф! + С2 Дф2,
а емкость батареи
нон
Собщ-бц + Q.
Следовательно, разность потенциалов между точками а и Ь (рис. 12.98, а) станет рав-
Дф = — —-------------
б'общ С] + С2
Откуда получим
С] Дф + С2 Дф = С[ Дф[ + С2 Дф2,
С2 (Дф - Дфг)
Ci =------------= 4 мкФ.
— Дф
Если заряженные конденсаторы соединить обкладками,
имеющими разноименные заряды (рис. 12.98, б), то заряд ба-
тареи станет равным
или
Поэтому
9 = l?i -?2l = l G ДФ1 -C2<pj|.
Дф собщ
Откуда получим
Рис. 12.98
215
С| Дф + С2 Дф = | С| Дф] - С2 Дф21>
„ „ С2(Дф-Дф2) , „
• Ответ: С, =---------= 4 мкФ; С] =
Дф] — Дф
„ С2(Д<₽2 + Дф)
или С] =—----------------
Дф] - Дф
С2 (дФг + дф)
—------------= 36 мкФ.
Дф] - Дф
= 36 мкФ.
12.197. Два одинаковых плоских конденсатора соединены параллельно и
заряжены до разности потенциалов Дф0 = 150 В. Определить разность потен-
циалов на конденсаторах, если после отключения их от источника постоян-
ного напряжения у одного конденсатора уменьшили расстояние между плас-
тинами в два раза.
12.198. Два конденсатора емкостями С, и С2 независимо заряжают заря-
дами qt и q2, а затем соединяют разноименно заряженными обкладками. Оп-
ределить заряды, которые установятся на обкладках конденсаторов после со-
единения.
12.199. Конденсатор, заряженный до разности потенциалов Дф] = 100 В,
соединяют с конденсатором такой же емкости, но заряженным до Дф2 = 200 В:
один раз одноименно заряженными обкладками, другой - разноименно заря-
женными обкладками. Какие разности потенциалов установятся между об-
кладками в обоих случаях?
12.200. Два конденсатора емкостями С] = 1О'10 Ф и С2 = 2-Ю'10 Ф соеди-
нены последовательно и заряжены разностью потенциалов Дф - 600 В. Кон-
денсаторы, не разряжая, разъединяют и соединяют параллельно. Определить
разность потенциалов между обкладками, которая при этом установится, а
также заряды на каждом конденсаторе.
12.201. Незаряженный плоский конденсатор заполнен диэлектриком, ди-
электрическая проницаемость е которого изменяется в зависимости от раз-
ности потенциалов Дф на конденсаторе по закону е = аДф, где а = 0,1 В’1.
Параллельно ему подключают такой же конденсатор, но без диэлектрика, за-
ряженный до разности потенциалов Дф0 = 60 В. Какая разность потенциалов
установится на конденсаторах?
Рис. 12.99
менен). В рассматриваемой задаче участки ц
сованные тонкими линиями (рис. 12.100, а
любых процессах, происходящих в остальной
12.202. Найти емкость батареи
конденсаторов, показанной на рис.
12.99, между точками А кВ.
• Решение. Соединение конденсаторов в ба-
тарею, предложенную для расчета, называ-
ют мостом емкостей. Такое соединение ни-
какими перестроениями упростить нельзя.
При решении задачи воспользуемся
законом сохранения электрического заряда
(заряд изолированного участка цепи неиз-
епи, заключенные в прямоугольники, нари-
I, являются изолированными, поэтому при
цепи, суммарные заряды здесь остаются рав-
ными нулю.
216
Рис. 12.100
Для определения емкости батареи конденсаторов, присоединим к точкам Л и В ис-
точник, поддерживающий разность потенциалов Дф.
В схеме четыре участка цепи имеют разные потенциалы: фл, фв, <рм, фм. Если по-
тенциал точки А условно принять равным нулю, то потенциал точки В будет равен
фв = Дф. Обозначим потенциалы точек М и W через х и у соответственно, т.е. фм = х,
<^=У-
Используя закон сохранения заряда, можно утверждать, что суммарные заряды кон-
денсаторов С|, С3 и С; на обкладках, соединенных с точкой М, равны нулю. Пусть по-
тенциал фм > <pN, т.е. на обкладке конденсатора С5, присоединенной к точке М, будет на-
ходиться положительный заряд. Тогда
91 - 9з + 45 = °- (О
Аналогично, для зарядов на обкладках конденсаторов С2, С4, С;, присоединенных к
точке N'.
92 - 94 - 45 = °- (2)
где q\, ?з> ?4, Я$ ~ заряды на соответствующих конденсаторах.
Используя связь между зарядом на обкладках конденсатора и разностью потенциалов
между ними
q = С Дф,
заряды Яз> ?4» Я 5 можно представить в виде
91 = С) (4>м-Ф.О = Ci ж, 92 = С2(Фн-Фл) = С2>’> 9з = Q (Фв~ Фм) = g (дФ ~х)>
94 = с4 (Фв - Фи) = С4 (дф-У), 4s = с5 (Фм “ Фн) = Q (х-у).
Теперь выражения (1)-(2) можно записать по-другому:
g х - g (Дф-х) + С5 (х-у) = О, С2у-С4 (Дф-у) - С5 (х-у) = 0. (3)
Решив систему уравнений (3) относительно х и у, получим
. Q (С2 + С4 + С5) + С4 С;
X = Фм = Дф----------------------------> >
(С1 + С3 + С5) (С2 + С4 + С;) - С5
С4 (С, + С3 + С5) + с3 g
(С1+С3 + С5)(С2 + С4 + С5)-С52
Легко заметить, что в случаях, если g С4 = С2С3, потенциалы фм = фм, т.е. заряд
конденсатора емкостью С; будет равен нулю. Это означает, что конденсатор С; в накоп-
лении зарядов участия не принимает и его можно не учитывать при вычислении емкость
такой схемы. В этом случае говорят, что мост емкостей сбалансирован. Емкость такой
схемы будет, очевидно, равна (рис. 12.100, б):
г (g+c2)(g + c4)
общ g+c2 + g + g '
217
Вернемся к нашей задаче.
Если известны потенциалы в точках М и N, то полный заряд д иа батарее конден-
саторов (он равен суммарному заряду иа обкладках конденсаторов Ct и С2, присоединен-
ных к точке А, или заряду на обкладках конденсаторов С3 и С4> присоединенных к
точке В) может быть найден как
9 = 9з + 94 = С3 (фв - фм) + С4 (Фв - Фц) = С3 (Д<р-х) + С4 (Дф-у) =
. „ С32(С2 + С4 + С5) + С42(С1+Сз + С5) + 2С3С4С51
— Дф 1 С?+ С л---------------------------------о г.
1 (Cl+C3 + C5)(C2 + C4 + C5)-C52 J
Следовательно, емкость схемы между точками А и В равна
С3 (С2 + С4 + С5) + С42 (С, + С3 + С5) + 2 С3 С4 С5
о6щ Дф 2 4 (С1+Сз + С5)(С2 + С4 + С5)-С52
Используя значения емкостей конденсаторов (С] = С4 = С5 = С, С2 = С3 = Со), после
преобразований получаем
С(ЗСо + С)
(-общ - , г,
С(ЗС0 + С) зс + с0
• Ответ-- = -с +^ .
С2
В
Рис. 12.101
в
Рис. 12.102
12.203. Найти емкость батареи конденсаторов между точками АиВ, кото-
рая показана на рис. 12.101.
12.204. Найти емкость батареи конденсаторов между точками А и В, кото-
рая показана на рис. 12.102.
Рис. 12.104
С1 С2
Рис. 12.103
12.205. Найти емкость батареи конденсаторов между точками А и В, кото-
рая показана на рис. 12.103.
12.206. Найти емкость батареи конденсаторов между точками АиВ, кото-
рая показана на рис. 12.104.
12.207. Найти емкость батареи конденсаторов между точками АиВ, кото-
рая показана на рис. 12.105.
218
12.208. Определить емкость беско-
нечно длинной системы одинаковых
конденсаторов емкостью С, соединен-
ных друг с другом, как показано на рис.
12.106.
12.209. Найти емкость батареи кон-
денсаторов между точками А и В, кото-
рая показана на рис. 12.107.
Рис. 12.107
Рис. 12.106
12.210. Между каждой парой из п данных точек включен конденсатор ем-
костью С. Определить емкость системы между двумя произвольными точками.
Работа и энергия в электростатическом поле
12.211. Какую минимальную работу нужно совершить для того, чтобы
переместить заряд д0 из точки С в точку В в поле двух точечных зарядов и д2
(рис. 12.108). Расстояния a, d, I известны.
• Решение. Так как электрическое поле иепо- q\ q2 В С
движных зарядов потенциально, то работа по •- ---•------------1-----------•
перемещению заряда д0 из точки С в точку В |,_j ,, ; |____а_____J
не будет зависеть от формы траектории, по
которой перемещают частицу, и равна раз- . 7
ности энергий заряда qa в конечной и началь- rue.
ной точках пути:
A = W3-WC.
Энергия заряда q0 в поле двух точечных зарядов равна
W= q0 (<Pi + Фг),
где <р j, q>2 ~ потенциалы электрического поля зарядов q^ и соответственно в точке распо-
ложения заряда до.
Так как потенциал точечного заряда q в произвольной точке определяется как
0>=-2-,
4леог
то энергия заряда q^ в точке С будет равна
w [ 91 92 ]
с 0'4л Во (</ +1 + а) 4л е0 (Z + а) г
где первое слагаемое соответствует потенциалу электрического поля, создаваемого заря-
дом g|, а второе - зарядом q2.
219
Аналогично, для точки В:
IV - I 91 . 92 1
в ' 4л е0 (</ + Z) 4л е01
Следовательно, искомая работа равна
_ Чо | 91 92 _ 91_____92 1 _ Чоа 1______91______+ 92 1
4ле0'</+/+ I d + 1 + а l + а' 4л е0 ' (d + l) (d + l + d)+ I (I + d) '
„ . 4oa ( 91 92 1
• Ответ: A —---- --------------+ —-----1.
4л Bq 1 (d +1) (d +1 + a) 1(1 + a) 1
12.212. Вычислить работу сил электростатического поля при перемеще-
нии заряда q = 210'8 Кл из бесконечности в точку, находящуюся на расстоя-
нии d = 1 м от поверхности шара радиусом г = 1 см, равномерно заряженного
с поверхностной плотностью о = 10'9 Кл/см2?
12.213. Найти разность потенциалов между двумя точками электрическо-
го поля, если при перемещении частицы зарядом q = 5 мкКл из первой точки
во вторую силы поля совершили работу А = 35 мДж.
Рис. 12.109 Рис. 12.110
12.214. Два точечных заряда qx = 2 мкКл и q2 = 5 мкКл расположены на
расстоянии г = 40 см друг от друга в точках А нВ (рис. 12.109). Вдоль прямой
CD, параллельной АВ и расположенной на расстоянии I = 30 см от нее, пере-
мещают точечный заряд q0 = 100 мкКл. Найти работу по перемещению этого
заряда из точки С в точку D.
12.215. Точечные заряды qx =- 1,710’8 Кл и <?2 = 2-10’8 Кл находятся от
точечного заряда qQ = 3-10'8 Кл на расстояниях 1Х = 2 см и Z2 = 5 см соответст-
венно. Какую минимальную работу нужно совершить, чтобы поменять места-
ми заряды q} п q2?
12.216. Закрепленные точечные заряды qx = 3-10'6Кл и q2 = 5-10‘6Кл рас-
положены в соседних вершинах квадрата со стороной а = 0,9 м (рис. 12.110).
Найти работу, которую совершат электрические силы над зарядом q = 10~8 Кл
при перемещении его из вершины С в вершину D.
12.217. Два шарика с одинаковыми зарядами q = 10’7 Кл, лежащие на
гладкой горизонтальной плоскости, прикрепили к концам неидеальной пру-
жины длиной в недеформированном состоянии Zo = 8 см и отпустили. Какое
количество энергии перешло в тепло при затухании колебаний, если расстоя-
ние между шариками после прекращения колебаний стало равным 1= 10 см?
220
Рис. 12.111
-I ''X „
3i---------------------ь,2
12.218. Два параллельных тонких кольца, радиусы которых одинаковы и
равны R, имеют общую ось. Расстояние между их центрами равно d. На первом
кольце равномерно распределен заряд q} < 0, на втором - д2 > 0. Какую мини-
мальную работу необходимо совершить для перемещения заряда q > 0 из цент-
ра первого кольца в центр второго?
12.219. Докажите, что с помощью системы неподвижных зарядов нельзя
создать электрическое поле, векторы напряженности которого параллельны
друг другу, но от точки к точке в направлении, перпендикулярном силовым ли-
ниям, меняются по величине по определенному закону.
12.220. Точечный заряд д = 2-10'5 Кл рас-
положен вблизи бесконечной равномерно за-
ряженной пластины с поверхностной плотнос-
тью заряда а = -50 нКл/м2. Заряд перемещают
из точки 1 в точку 2 под углом а = 60° к плас-
тине (рис. 12.111). Определить минимальную
работу, которую необходимо совершить при
таком перемещении. Расстояние между точка-
ми 1 и 2 равно I = 5 м.
• Решение. Так как по условию задачи необходимо определить минимальную работу, то
заряд q будем перемещать без ускорения. Для этого приложим к нему силу F, равную по ве-
личине сиде F3n притяжения заряда шюскостью и противоположную ей по направлению,
т.е. F= - Fjn . Прн этом работа А силы F по модулю будет равна работе Лэл силы F3n .
Электростатическое поле является потенциальным, поэтому работа Аэл не зависит от
траектории перемещения заряда q. Выберем в качестве траектории перемещения ломан-
ную 1—3—2 (рис. 12.111). Тогда работа Яэл будет равна алгебраической сумме работ Л|_3
и Л3_2 на участках 1-3 и 3-2 соответственно.
Так как векторы напряженности электрического поля бесконечной пластины направ-
лены перпендикулярно ее поверхности, то на участке 1-3 работа совершаться не будет.
Это связано с тем, что направление перемещения из точки 1 в точку 3 перпендикулярно
вектору Е, а значит перпендикулярно силе F3n . На участке 3-2 заряд q будем перемещать
вдоль силовых линий электрического поля, причем направление перемещения противопо-
ложно направлению вектора напряженности. Следовательно,
•^3-2 = - Рэл $3-2 =-qES3_2,
где S3_2 = Z sin а - величина перемещения из точки 3 в точку 2; Е = |а|/2еп - напряженность
электрического поля, создаваемого заряженной пластиной.
Следовательно,
А = - Аэл = - Л-2 = Ч / sin а = 0,24 Дж.
_ . q |а| Z sin а „ _. „ ®°
• Ответ: А = J--------= 0,24 Дж.
2е° я
12.221. Точечный заряд д = 3-10 Кл расположен вблизи бесконечной рав-
номерно заряженной пластины с поверхностной плотностью заряда
о = 2 нКл/м2. Заряд перемещают из точки 1 в точку 2 под углом а = 30° к плас-
тине (рис. 12.112). Определить минимальную работу, которую необходимо совер-
шить при таком перемещении. Расстояние между точками 1 и 2 равно Z = 2 м.
2 Е0
221
Рис. 12.113
12.222. Точечный заряд q = -7-10'8 Кл расположен между обкладками
плоского конденсатора в точке 1 (рис. 12.113) вблизи положительно заряжен-
ной пластины. Заряд q перемещают из точки 1 в точку 3, расположенную вбли-
зи другой пластины, по ломанной 1-2-3. Определить минимальную работу, ко-
торую необходимо совершить при таком перемещении. Емкость конденсатора
равна С = 10"’° Ф, заряд 2= 5-Ю"4 Кл.
12.223. Три заряда q, q, -q находятся в точках с декартовыми координата-
ми (а, а, 0), (0, а, 0) и (0, а, -а) соответственно. Найти энергию этой системы за-
• Решение. Энергия системы N неподвиж-
ных зарядов равна
1 N
где ф, - потенциал электрического поля в
точке расположения заряда qi9 создаваемый
всеми (N - 1) зарядами за исключением за-
ряда
В нашем случае трех точечных заря-
дов энергия системы будет равна
*К=!Л(91Ф1+?2Ч>2 + ‘7зФз)>
где Фь q>2, Фз - потенциалы в точках 1,2 и 3 расположения зарядов qt = q, q2 = 9,9з= С0‘
ответственно (рис. 12.114):
ф1 -----□----------а.---; -----ч----------1; -----а----+-----ч----,
4л<ро/1-2 ^Фо-Ч-з 4nq>oz2-3 4*ф0/1-з 4лф0/2_3
где Zj_2 = Zj-3 = а- h-з - уГ2а ~ расстояния между зарядами, расположенными в точках 1-2,
2-3 н 1-3 соответственно. Следовательно,
Ф1 = —®------2_.— > ~ _ о, ц>. =-2-=— ч-2— ;
4л фо а 4л ф0 V 2 а 4л ф0 у 2 а 4л ф0 а
а энергия системы зарядов 2
У= ‘Л q (ф1 - ф3) = ~
q Z v Z Л
• Ответ’. Ж= - —----------.
2 х 2 я е0 а
12.224. На сколько увеличится энергия электрического поля двух точеч-
ных зарядов Q, первоначально удаленных друг от друга на большое расстоя-
ние, при сближении их на расстояние Z?
222
12.225. Точечные заряды q{, q2, q2 расположены в вершинах правильного
треугольника со стороной равной I. Определить энергию этой системы зарядов.
12.226. Два удаленных изолированных металлических шара радиусами
и R2 были заряжены до потенциалов <р. и <р2 соответственно. Чему будет равно
изменение энергии системы, если шары соединить длинным проводником?
12.227. Из заряженного не замкнутого иа внешнюю цепь конденсатора вы-
нули диэлектрик проницаемостью е. Во сколько раз при этом изменилась энер-
гия конденсатора? Какой будет результат, если конденсатор подключен к ис-
точнику постоянного напряжения?
• Решение. Энергия плоского конденсатора может быть вычислена по одной из формул
_______________________________________
2 2С 2 ’
Если конденсатор заряжен и отключен от источника, то заряд на его обкладках ме-
няться не будет. Поэтому здесь для вычисления энергии конденсатора удобно использо-
вать формулу 2
W=2C-
Если энергия конденсатора емкостью С с диэлектриком была равна
2
= 2 С ’
то после того, как диэлектрик вынули, она стала равной
2
172 = -2-,,
2С
где С = С/г - емкость конденсатора без диэлектрика. Следовательно,
Wx е’
т.е. энергия конденсатора возросла в с раз.
Если конденсатор подключен к источнику (разность потенциалов Д<р между обклад-
ками постоянна) и его энергия была равна
2 ,
то после того, как диэлектрик вынули, она стала равной
т.е. энергия конденсатора уменьшилась в е раз.
• Ответ', в первом случае энергия конденсатора увеличится в е раз; во втором случае энер-
гия конденсатора уменьшится в е раз.
12.228. Плоский конденсатор с пластинами площадью 5 = 200 см2, распо-
ложенными на расстоянии d = 1 мм друг от друга, заряжают до разности потен-
циалов Д<р= 1200 В. Не отключая конденсатор от источника, пространство
между пластинами заливают керосином. На сколько изменится энергия кон-
денсатора? Диэлектрическая проницаемость керосина е = 2.
где С '= С/г. Следовательно,
223
12.229. Отключенный от источника воздушный конденсатор емкостью С
имеет на обкладках заряд q. Какое количество теплоты выделится в конденса-
торе, если его заполнить веществом с диэлектрической проницаемостью е?
12.230. Конденсатор емкостью Cj = 3 мкФ, заряженный до разности по-
тенциалов Дф! = 300 В, и другой, емкостью С2 = 2 мкФ, заряженный до
Дф2 = 200 В, соединили одноименными полюсами. Какое количество теплоты
выделится при этом?
12.231. Конденсатор емкостью С] = Ю'4 Ф заряжен до разности потенциа-
лов Дф! = 100 В. Его соединяют параллельно с незаряженным конденсатором
емкостью С2 = 4-1 О'4 Ф. В момент соединения конденсаторов образуется искра.
Какое количество энергии расходуется на образование искры?
12.232. Расстояние между пластинами плоского конденсатора емкостью
С = 1 мкФ увеличивают в и = 2 раза, не отключая от источника, поддерживаю-
щего на между пластинами разность потенциалов Дф = 1000 В. Какая при этом
совершается механическая работа?
12.233. Плоский воздушный конденсатор с площадью пластин S и рассто-
янием между ними d заряжен до разности потенциалов Дф и отключен от ис-
точника напряжения. Определить работу, которую нужно затратить, чтобы раз-
двинуть пластины на величину Д/.
12.234. В однородном электрическом поле напряженностью £0 перпенди-
кулярно его направлению расположен заряженный плоский конденсатор, на-
пряженность поля между обкладками которого была равна Е (рис. 12.115, а).
Какую минимальную работу нужно совершить, чтобы расположить пластины
конденсатора параллельно внешнему полю? Площадь каждой обкладки кон-
денсатора равна S, расстояние между ними d.
а)
б)
Рис. 12.115
• Решение. При решении этой задачи необходимо помнить, что электрическое поле, созда-
ваемое зарядами на обкладках конденсатора, полностью сосредоточено между обкладками,
и заряженный конденсатор не вносит никаких изменений в окружающее пространство. Поэ-
тому при любом расположении конденсатора во внешнем поле Ео энергия окружающего
пространства не меняется. Однако в зависимости от того как расположен конденсатор во
внешнем поле энергия, сосредоточенная в объеме, ограниченном пластинами конденсатора,
будет разной. Искомую работу в данном случае можно определить как разность энергий
конденсатора до и после его разворота.
224
а энергия
Если конденсатор расположен так, что силовые линии поля Ё* направлены противо-
положно Eq (рис. 12.115, а), то объемная плотность энергии между пластинами конден-
СЭТОраравна е^-Е)’
И'1 = ” =---2-----’
е0(Е0-Е)2
= ----Sd,
где E1=Eq-E- напряженность результирующего поля в конденсаторе в первом случае;
V=Sd- объем, заключенный между пластинами.
Если конденсатор расположен так, что его обкладки параллельны внешнему полю
(рнс. 12.115, б), то энергия внутри конденсатора будет равна
епК,2 £q(Eq+E2)
W2 = W2r=^V = ^^---------'Sd,
2 z 2 2
где Е2 = Eq + Е2 ~ напряженность результирующего поля в конденсаторе во втором слу-
чае.
Следовательно,
A = W2-W,= {Е2+ Eq - (Eq - Е)2} = во S dEE0.
Ответ: А = в0 S d Е Eq.
12.235. Определить объемную плотность энергии электрического поля
внутри плоского воздушного конденсатора, полностью погруженного в непро-
водящую жидкость с относительной диэлектрической проницаемостью
е = 2. Напряженность электрического поля между пластинами Е = 5-106 В/м.
12.236. В однородном электрическом поле напряженностью Eq перпенди-
кулярно его направлению расположена металлическая пластина толщиной h и
площадью S. Какую минимальную работу нужно совершить, чтобы вынести
пластину из поля?
12.237. В однородном электрическом поле на- g + g ~ g
пряженностью Ео перпендикулярно его направле- " ---------1 ----►
нию расположен заряженный плоский конденса- +
тор, напряженность поля между обкладками кото- + ------►
рого была равна Е (рис. 12.116). Какую минималь- +
ную работу нужно совершить, чтобы развернуть
конденсатор на 180°? Площадь каждой обкладки +
конденсатора равна S, расстояние между ними d. ?иа
12.238. В однородном электрическом поле напряженностью Ео перпенди-
кулярно его направлению расположен заряженный плоский конденсатор, на-
пряженность поля между обкладками которого была равнаЕ (рис. 12.116).
Какую минимальную работу нужно совершить, чтобы сложить пластины кон-
денсатора вместе? Площадь каждой обкладки конденсатора равна S, расстоя-
ние между ними d.
12.239. В однородном электрическом поле напряженностью Ео перпенди-
кулярно его направлению расположен заряженный плоский конденсатор, пло-
225
Рис. 12.117
щадь обкладок которого равна 5, а расстояние
между ними d. Зазор между обкладками запол-
нен диэлектриком с проницаемостью е. До поме-
щения во внешнее поле напряженность электри-
ческого поля между обкладками была равна Е
(рис. 12.117). Какую минимальную работу
нужно совершить, чтобы вынуть диэлектрик из
конденсатора?
‘/W
Рис. 12.118
Рис. 12.119
12.240. Два одинаковых конденсатора емкостью С заряжены зарядом q
каждый и отсоединены от источника. Затем конденсаторы вставляют друг в
друга так, как показано на рис. 12.118. Определить, затраченную при этом рабо-
ту. Считать расстояние между любой парой пластин намного меньшим линей-
ных размеров пластин.
12.241. Какую минимальную работу нужно совершить, чтобы вставить
одну систему разноименно заряженных пластин в другую так, как показано на
рис. 12.119? Поверхностная плотность зарядов на пластинах ±о, площадь каж-
дой пластины 5, расстояние между ними h много меньше линейных размеров
пластин.
12.242. Два параллельно соединенных конденсатора емкостью С = 1 мкФ
каждый имеют на обкладках общий заряд q = 10’5 Кл. Какую минимальную ра-
боту необходимо совершить, чтобы развести обкладки одного конденсатора на
большое расстояние?
12.243. Два плоских воздушных
конденсатора с обкладками одинаковой
площади 5= 10 см 2 имеют равные заря-
ды q = 2-10'6 Кл и вставлены друг в друга
так, как показано на рис. 12.120. Рассто-
яние между обкладками первого конден-
сатора d = 10 мм вдвое больше, чем у
второго. На сколько изменится энергия
системы, если обкладки внутреннего
конденсатора сложить вместе?
226
12.244. Два плоских воздушных конденсатора с обкладками одинаковой
площади S = 5 см 2 имеют равные заряды q = 10'7 Кл. Расстояние между обклад-
ками первого конденсатора d = 4 мм вдвое больше, чем у второго. Какое мини-
мальное количество тепла выделится, если вставить второй конденсатор
внутрь первого так, как показано на рис. 12.120?
‘/W
'/id
'/id
Рис. 12.121
Рис. 12.122
12.245. Два плоских воздушных конденсатора с обкладками одинаковой
площади имеют равные заряды. Расстояние между обкладками первого кон-
денсатора вдвое больше, чем у второго. Как изменится энергия электрического
поля системы, если второй конденсатор вставить между обкладками первого
так, как показано на рис. 12.121? Ответ обосновать.
12.246. Два плоских воздушных конденсатора с обкладками одинаковой
площади S = 8 см 2 имеют равные заряды q = 4-1 О’6 Кл и вставлены друг в друга
так, как показано на рис. 12.121. Расстояние между обкладками первого кон-
денсатора d = 12 мм вдвое больше, чем у второго. Какое количество теплоты
выделится, если обкладки внутреннего конденсатора закоротить?
12.247. Два одинаковых плоских воздушных конденсатора с обкладками
площадью S = 10 см 2 и расстоянием между ними d = 10 мм имеют равные заря-
ды q = 2-10’6 Кл. Какую минимальную работу нужно совершить, чтобы вста-
вить конденсаторы друг в друга так, как
12.248. Два одинаковых плоских
воздушных конденсатора с обкладками
площадью 5= 15 см 2 и расстоянием
между ними d= 10 мм имеют равные
заряды q = 3-10’6 Кл и вставлены друг в
друга так, как показано на рис. 12.123.
Какую минимальную работу нужно со-
вершить, чтобы вынуть один конденса-
показано на рис. 12.122?
тор из другого?
12.249. Какую минимальную работу против сил электрического поля
нужно совершить, чтобы уменьшить в два раза радиус заряженной металличес-
кой сферы? Первоначальный радиус сферы равен R, его заряд Q.
• Решение. Работу здесь найдем как разность энергий системы в конечном и начальном со-
стояниях.
227
Энергия заряженного проводника равна
где С - электроемкость проводника.
Поскольку потенциал сферы радиуса R, обладающей зарядом Q, равен
4л e0R ’
то ее емкость .
С = & = 4neoR.
ф
Следовательно, первоначально сфера обладала энергией
w q2
1 8л Eq R
После уменьшения радиуса сферы до г = Vi Л ее емкость стала равной
С '= 4л в0 г = 2л Eq R,
а энергия:
W2 =—.
4л е0 Л
Работа, затраченная на уменьшение размеров сферы, равна разности энергий W2 и IK,:
О2
a = w2-w,=—.
8л Eq R
О2
• Ответ: А = „ с .
8лбоЛ
12.250. Металлическому шару радиусом Л = 10 см был сообщен заряд
</=10 мкКл. Какую минимальную энергию надо затратить, чтобы увеличить
заряд шара на 10%?
12.251. Какую минимальную работу против сил электрического поля
нужно совершить, чтобы собрать каплю ртути радиусом R и зарядом Q из N
одинаковых заряженных капель?
12.252. Заряженную проводящую сферу сжали так, что ее радиус умень-
шился в п раз. Во сколько раз увеличилась энергия электрического поля этой
сферы?
12.253. Для того, чтобы сложить вместе две одинаковые пластины с рав-
ными зарядами, которые были удалены друг от друга на большое расстояние,
необходимо совершить работу А. Какую работу необходимо совершить, чтобы
сложить вместе три такие пластины? п пластин?
Движение заряженных частиц в электрическом поле
12.254. Точечный заряд q = 10’7 Кл и массой т = 3-Ю"6 кг удерживается в
точке 1 вблизи равномерно заряженной бесконечной плоскости с поверхност-
ной плотностью заряда о = 5- 1О’10 Кл/м2. Какова будет скорость заряда в точке
2 (рис. 12.124), находящейся на расстоянии 1= 1 м от точки 1, если заряд осво-
бодить?
• Решение. Электрическое поле напряженностью I?бесконечной равномерно заряженной
плоскости будет действовать на точечный положительный заряд q с силой в на-
правлении силовых линий поля.
228
Запишем уравнение, выражающее второй закон
Ньютона, в проекции на ось ОХ:
max = F,
где т- масса заряда.
Так как напряженность электрического поля плос-
кости по величине равна
Рис. 12.124
и не завнснт от расстояния до плоскости, то при движе-
нии заряда нз точки 1 в точку 2 сила, а значит и ускоре-
ние, будут оставаться постоянными. Следовательно, справедливы законы равнопеременно-
го движения:
'ох = ах1.
В точке 2 координата заряда будет равна х = / и уравнение движения примет вид
1= И ах т2.
Откуда найдем время т движения заряда из точки 1 в точку 2:
т = V 2 1/а^.
Следовательно, скорость о частицы в конечной точке будет равна
о = ах т = V2 а, /.
Учитывая выражение для ускорения
F qts
ах = — = 7Г--•
т 2 теп
окончательно получаем _____u
О = а 1,37 М/с.
те0
При решении задачи можно воспользоваться теоремой о кинетической энергии: из-
менение кинетический энергии частицы при ее перемещении из точки 1 в точку 2 будет
равно работе силы г на этом пути, т.е.
т о2 . ,,, т о2 а а ,
——-0 = F/, или
2 2 2 ео
Откуда получаем искомую скорость.
Работу сил поля можно так же найти, как
А = q Дф,
где Дф = ЕI - разность потенциалов между точками 2 н 1 в однородном электрическом поле
напряженностью Е = */2 a/s(i.
• Ответ: о = Р- ж 1,37 м/с.
те0
12.255. Первоначально неподвижный электрон ускоряется электрическим
полем и приобретает энергию W= 100 эВ. Найти разность потенциалов между
начальной и конечной точками его пути в электрическом поле. Заряд элек-
трона |е| = 1,6-10’19 Кл.
12.256. Электрон, ускоренный электрическим полем, приобрел скорость,
при которой его полная энергия стала равна удвоенной энергии покоя. Чему
равна разность потенциалов, пройденная электроном? Заряд электрона
|е| = 1,6-10‘19 Кл, масса электрона т - 9,1-10'31 кг.
12.257. Электрон, имеющий начальную скорость ио = 2-1О4 м/с, влетает
в однородное электрическое поле напряженностью Е= 3-10’3 В/м и движется
229
по направлению силовых линий. Чему будет равна скорость электрона, если
он пройдет 1= 10 см пути? Через какое время скорость электрона станет рав-
ной нулю? Масса электрона т = 9,1 -10’31 кг, его заряд |е| = 1,6-10’19 Кл.
Рис. 12.125 Рис. 12.126 Рис. 12.127
12.258. Точечный заряд q~ 10’6 Кл массой /и = 210'9 кг движется пер-
пендикулярно к равномерно заряженной бесконечной плоскости с поверх-
ностной плотностью заряда с = -10'7 Кл/м“. В точке 1 скорость заряда равна
и, = 103 м/с (рис. 12.125). Какой будет скорость заряда в точке 2, находящейся
на расстоянии I = 10 см от точки 1?
12.259. Точечный заряд q - -10'6 Кл массой т = 9-10'8 кг закреплен меж-
ду пластинами плоского воздушного конденсатора вблизи его отрицательно
заряженной пластины (рис. 12.126). Емкость конденсатора С= 1 нФ, заряд на
пластинах Q= 10’3 Кл. Какова будет скорость заряда вблизи положительно
заряженной пластины, если заряд освободить?
12.260. Электрон влетает в плоский конденсатор через очень малое от-
верстие в положительно заряженной пластине. Вектор скорости электрона
перпендикулярен плоскости пластин и равен по величине и = 104 км/с. Какова
должна быть наименьшая разность потенциалов между пластинами, чтобы
электрон вылетел обратно из конденсатора? Поле между обкладками конден-
сатора считать однородным. Масса электрона т = 9,1 10'3! кг, заряд электрона
Н = 1,6-К)'19 Кл. Силой тяжести пренебречь.
12.261. Две заряженные частицы находятся в однородном внешнем элект-
рическом поле, напряженность которого равна Е. Частица массой т имеет от-
рицательный заряд (-q), частица массой М - положительный заряд Q (рис.
12.127). На каком расстоянии друг от друга должны находиться частицы, чтобы
при движении их взаимное расположение не изменилось?
12.262. /Два одинаковых маленьких шарика, заряженные одинаковыми по
величине и знаку зарядами q, соединены непроводящей невесомой нитью дли-
ной I. Система помещена в однородное электрическое поле, направленное
вдоль линии, соединяющей шарики. Определить силу натяжения нити.
12.263. При колебаниях двух заряженных шариков, связанных пружиной,
длина пружины меняется от Zt до 12. Длина недеформированной пружины /0,
заряд каждого шарика q. Определить жесткость пружины. Силой тяжести пре-
небречь.
230
12.264. Силовые линии электростатического поля представляют собой па-
раллельные прямые. Вдоль силовых линий напряженность поля возрастает по
закону Е = а-х, где а = 105 В/м2. Какую энергию приобретет частица с зарядом
q = 2-10'10 Кл, пройдя из начала координат вдоль силовой линии расстояние
/= 1 м?
• Решение. Для решения данной задачи можно воспользоваться одним из способов, рассмот-
ренных в задаче №12.254. Однако, мы убедились, что решение будет гораздо короче и
проще, если использовать теорему о кинетической энергии частицы.
При движении заряда в элеирическом поле его энергия будет меняться за счет со-
вершения над ним работы силой
F=qE. (1)
При бесконечно малом перемещении dx электрическое поле совершит элементарную
работу
dA = Fs dx,
где Fs - проекция силы, действующей на заряд при данном перемещении, на направление
движения:
Fs = q Е = q ах.
Так как напряженность электрического поля изменяется в зависимости от координа-
ты по линейному закону, то работа, совершаемая силой (1) на конечном перемещении
/, будет равна .
. „ , ~ , а •’max+ а ’чшп , а I .
A = <F> l = <q Е> l = <qax>l = q-------2------(2)
Изменение кинетической энергии частицы при ее перемещении в электрическом поле
Д1Г= w2 - = w
(где W\ = О, W2 = W-энергия частицы в начальной и конечной точках пути) будет равно ра-
боте (2). Следовательно, 2
2 W=q~ =!0'5Дж.
• Ответ: W=q = 10‘5 Дж.
Рис. 12.128 Рис. 12.129
12.265. Электрон, двигаясь со скоростью о, переходит из области электри-
ческого поля с потенциалом <р, в область поля с потенциалом ф2, причем
ф2 > Ф] (рис. 12.128). Под каким углом р к цранице раздела областей будет дви-
гаться электрон, если он подлетел к ней под углом а? Масса и заряд электрона
равны т и |е! соответственно.
12.266. Электрон, движущийся с некоторой скоростью вдоль оси ОХ, вле-
тает в область поля, потенциал которого изображен на рис. 12.129. При какой
231
минимальной скорости и„иП электрон сможет пройти эту область? Заряд элек-
трона |е|, масса электрона т.
12.267. Электрон влетает в точке х = 0 в тормозящее однородное электри-
ческое поле, направленное вдоль по оси ОХ, и движется вдоль силовых линий
поля. Начальная скорость электрона равна и = 104 м/с. Напряженность поля
возрастает пропорционально пройденному электроном расстоянию х, т.е. изме-
няется по закону Е = а х, где а = 9,1 • 10'3 В/м2. Найти максимальную величину
расстояния, на которое электрон может проникнуть в поле. Заряд электрона
|е| = 1,6-10’19 Кл, его масса т = 9,МО’31 кг.
12.268. Электрон, пройдя ускоряющую разность потенциалов Дер, влетает
в плоский воздушный конденсатор параллельно пластинам длиной I и вылетает
из него. В тот момент, когда электрон влетает в конденсатор, в последнем воз-
никает электрическое поле, напряженность которого меняется со временем по
закону Е = a t, где а - положительная постоянная. Вектор Е перпендикулярен
плоскости пластин. Определить, с какой скоростью электрон вылетает из кон-
денсатора. Заряд электрона |е|, масса электрона т.
12.269. Шарик массой т, имеющий заряд q, удерживается на одной верти-
кали под закрепленным зарядом (- q) на расстоянии I от него. Какую мини-
мальную скорость, направленную вниз, надо сообщить шарику, чтобы он упал
на Землю? Расстояние до Земли велико, движение происходит в поле тяжести
Земли, ускорение свободного падения считать постоянным.
12.270. Электрон, имеющий кинетическую энергию W, влетает в плоский
конденсатор, между пластинами которого поддерживается разность потенциа-
лов Дф. Расстояние между пластинами d, их длина I. На расстоянии h от кон-
денсатора находится экран (рис. 12.130). Начальная скорость электрона на-
правлена параллельно пластинам. Найти смещение электрона иа экране. Заряд
электрона |е|. Силой тяжести пренебречь.
• Решение. Решение задач о дви-
жении заряженных частиц в
электрическом поле конденсатора
илн заряженной плоскости сходно
с решением задач иа движение
тела, брошенного под углом к го-
ризонту вблизи поверхности
земли. Отличие состоит лишь в
том, что движение частиц в одно-
родном электрическом поле про-
_ исходит с некоторым ускорени-
ем а, отличным от ускорения свободного падения £ Действие силы тяжести в подобных за-
дачах обычно не учитывается, так как гравитационные силы ничтожно малы по сравнению
с электрическими.
Если электрон влетает в электрическое поле заряженного конденсатора со скоростью
и0, то под действием силы F поля он будет отклоняться от своего начального направления
движения и вылетит из конденсатора под некоторым углом к этому направлению.
232
По условию задачи электрон влетает конденсатор параллельно его обкладкам. Оче-
видно, что под действием силы F в поле конденсатора электрон будет двигаться по пара-
боле. Выберем осн системы координат XOY так, как показано на рис. 12.130. Тогда урав-
нение, выражающее второй закон Ньютона, в проекции на эти осн, можно записать в виде
ОХ: т ах = 0,
OY: т ау = F,
где т - масса частицы.
Так как сила F, действующая на электрон в электрическом поле, равна
F=|e|£, (1)
то движение частицы вдоль осн ОХ будет происходить с постоянной скоростью, а вдоль оси
OY - равноускоренно. Следовательно, уравнения движения электрона можно записать
таким образом:
х = ъ0I, у = Оу I2, (2)
где - скорость электрона при влете в конденсатор, ау - проекция ускорения электрона на
ось OY, равная
Если длина конденсатора равна Z, то уравнения движения (2) электрона в момент вы-
лета из конденсатора примут вид
/ = ъот, (ху^/ШуХ2, (4)
где т - время движения электрона в конденсаторе, Ayt - смещение электрона по оси OYза
этот промежуток времени.
Следовательно, „ ,2 , , „
avl eEt
Для определения смещения Д.у2 при движении электрона в области от края конден-
сатора до экрана, достаточно определить угол а, который будет составлять вектор его ско-
рости г?с пластинами, так как здесь электрон будет двигаться равномерно и прямолинейно.
С этой целью определим проекции вектора 5*на оси системы координат в момент вылета
электрона из конденсатора: lei Е/
v>x = ъ0, uv = av т = —.
y y mt>o
Следовательно,
л ь. .«у \e\Elh ...
Ay2 = Atga = A-t = 1J—5“ • (6)
4r mu0
Наконец, определим начальную скорость электрона при влете в конденсатор и вели-
чину напряженности поля между его обкладками.
Кинетическая энергии частицы равна
откуда получаем
= (7)
Так как между обкладками конденсатора поддерживается постоянная разность по-
тенциалов Д<р, то напряженность электрического поля в зазоре конденсатора будет равна:
£ = ^. (8)
Окончательно смещение электрона на экране найдем как сумму смещений Ду] н
Дуг с учетом выражений (7) и (8) для и Е:
-Отеет; Ду = ^(/ + 2Й).
4dW
233
12.271. Тело массой т с зарядом q (q >0) брошено под а углом к горизонту
с начальной скоростью и0. Движение тела происходит одновременное поле тя-
готения и однородном электростатическом поле напряженностью Е, силовые
линии которого направлены вертикально вниз. Определить время полета, даль-
ность полета и максимальную высоту подъема тела над линией горизонта.
т, q
Рис. 12.132
12.272. Электрон влетает в точке А в область однородного электрического
поля напряженностью Е = 200 В/м со скоростью и = 107 м/с (рис. 12.131). На
каком расстоянии от точки А электрон вылетит из поля, если он влетает под
углом а = 45° к направлению силовых линий? Заряд электрона |е| = 1,6-10’19 Кл,
масса электрона т = 9,1 -10"31 кг. Силой тяжести пренебречь.
12.273. Две параллельные проволочные сетки, находящиеся на небольшом
расстоянии друг от друга, подключены к источнику, поддерживающему между
сетками разность потенциалов Д<р. В эту область под острым углом а к направ-
лению силовых линий влетает электрон. При какой начальной скорости и0
электрон сможет преодолеть эту область? Заряд электрона |е|, масса электрона
т. Силой тяжести пренебречь.
12.274. Частица массой т и зарядом q > 0 влетает в плоский конденсатор,
обкладками которого являются металлические сетки (рис. 12.132). Напряжен-
ность поля в конденсаторе равна Е, расстояние между сетками d. Начальная
скорость частицы и0 составляет угол а с плоскостью первой сетки. С какой ско-
ростью и под каким углом к плоскости второй сетки частица вылетит из кон-
денсатора? Силой тяжести пренебречь.
12.275. Заряженная частица с зарядом q влетает в плоский конденсатор
длиной I под углом а к плоскости пластин, а вылетает под углом р. Опреде-
лить первоначальную кинетическую энергию частицы, если напряженность
поля внутри конденсатора равна Е. Силой тяжести пренебречь.
12.276. В плоский конденсатор длиной I = 5 см влетает электрон под углом
а = 15° к пластинам. Электрон обладает энергией W= 1500 эВ. Расстояние
между пластинами конденсатора d = 1 см. Определить разность потенциалов
между пластинами конденсатора, при которой электрон на выходе из него
будет двигаться параллельно пластинам. Заряд электрона |е| = 1,6-10’|9Кл.
Силой тяжести пренебречь.
234
12.277. Электрон влетает в плоский воздушный конденсатор параллельно
его пластинам со скоростью и = 4-107 м/с. Расстояние между пластинами
d = 1 см, их длина I = 5 см, разность потенциалов между ними Дф = 400 В.
Найти величину отклонения электрона от первоначального направления дви-
жения при вылете из конденсатора. Заряд электрона |е| = 1,610"19 Кл, масса
электрона т = 9,1-Ю'31 кг. Силой тяжести пренебречь.
12.278. Частица, имеющая заряд q, разгоняется до энергии W и влетает па-
раллельно пластинам в воздушный конденсатор емкостью С. Заряд на пласти-
нах конденсатора Q, расстояние между пластинами d. Первоначально частица
находится на одинаковом расстоянии от пластин. Какой должна быть длина
пластины, чтобы частица не упала на ее поверхность? Силу тяжести не учиты-
вать.’
12.279. Электрон влетает в плоский
заряженный конденсатор со скоростью и0,
направленной первоначально вдоль сред-
ней плоскости АВ конденсатора (рис.
12.133). Через какое время нужно изме-
нить направление электрического поля в
конденсаторе на противоположное, не из- ис'
меняя по абсолютной величине, чтобы на вылете из конденсатора электрон
пересек плоскость АВ в точке В? Длина пластин конденсатора /. Силу тяжести
не учитывать.
12.280. Электрон, пройдя ускоряющую разность потенциалов Дф, влетает
в плоский воздушный конденсатор параллельно пластинам длиной I и вылетает
из него. В тот момент, когда электрон влетает в конденсатор, в последнем воз-
никает электрическое поле, напряженность которого изменяется со временем
по закону Е = a t, где а - положительная постоянная. Вектор Е перпендикуля-
рен пластинам. Определить скорость электрона, вылетевшего из конденсатора.
Заряд электрона |е|, масса электрона т. Силой тяжести пренебречь.
12.281. Пылинка массой т = 10‘12 кг взвешена между горизонтальными
пластинами плоского конденсатора. Пылинка освещается ультрафиолетовым
светом и, теряя заряд, выходит из равновесия. Какой заряд потеряла пылинка,
если первоначально между обкладками конденсатора была разность потенциа-
лов Дф = 200 В, а затем, чтобы опять уравновесить пылинку, ее пришлось уве-
личить на Дф0 = 50 В? Расстояние между пластинами конденсатора d = 1,6 см.
12.282. Посередине между горизонтальными пластинами плоского кон-
денсатора висит капелька ртути. Расстояние между пластинами d= 5 см, раз-
ность потенциалов на пластинах Дф[ = 1000 В. В нижней пластине под каплей
имеется отверстие, сквозь которое она может свободно пройти. Внезапно раз-
ность потенциалов на пластинах падает до значения Дф2 = 995 В. Определить
235
СТ1
Q
а2
-------1-----
Рис. 12.134
путь, который пройдет капля за время t = 1,1 с. Сопротивлением воздуха и не-
однородностью электрического поля вблизи отверстия пренебречь.
г ц. 12.283. Две бесконечные парал-
лельно расположенные горизонталь-
ные пластины равномерно заряжены с
поверхностными плотностями зарядов
и а2. Расстояние между пластинами
I = 5 см. Посередине между ними рас-
положен точечный заряд Q. В верхней
пластине, непосредственно над точеч-
ным зарядом, просверлено отверстие
радиусом г = 1 мм (рис. 12.134). На сколько процентов должны отличаться по-
верхностные плотности зарядов на пластинах, чтобы точечный заряд находил-
ся в равновесии? Считать г «I. Силой тяжести пренебречь.
12.284. На горизонтальной плоскости на расстоянии d друг от друга удер-
живают два одинаковых тела массой т каждое, имеющие равные заряды q.
Какое расстояние пройдет каждое из тел, если их освободить? Какую макси-
мальную скорость итах приобретут тела в процессе движения? Коэффициент
• Решение. На каждое из тел будут
действовать четыре силы: сила тя-
жести mg; сила реакции опоры ft,
сила трения и сила электричес-
кого взаимодействия ^зл, направ-
ленные так, как показано на рис.
12.135. Если сила F3Si в начальном
положении превышает максималь-
ное значение силы трения покоя
трения тел о плоскость равен ц.
Рис. 12.135
^тр'пок = ЦМ то после освобождения тел они придут в движение.
Расстояние, которое пройдет каждое из тел, и их максимальную скорость в процессе
движения можно найти, записав уравнения динамики поступательного движения и урав-
нения кинематики. Однако так как при изменении расстояния между телами сила
Гэл будет изменятся обратно пропорционально квадрату расстояния между ними, то по-
добное решение задачи будет достаточно сложным. Гораздо проще здесь воспользоваться
теоремой о изменении полной механической энергии системы: изменение энергии будет
равно работе сторонних сил, действующих на тела системы, при данном перемещении.
В начальной и конечной точках пути полная энергия системы тел будет равна энер-
гии их взаимодействия, т.к. кинетическая и потенциальная энергии будут равны нулю.
Поэтому изменение энергии можно представить в виде
2 2
Д1Р= - W, =---------2----------2—,
4л Eq (d + 2 S) 4 л eod
где первое слагаемое соответствует энергии взаимодействия между телами в конечном по-
ложении, второе - в начальном.
Сторонней силой, Действующей на каждое из тел в процессе движения, будет явля-
ется сила трения, работа которой
236
A = —2 Fip S,
где Ftp = ц N = p m g, S - путь, пройденный каждым из тел до остановки; знак «-» связан с
тем, что сила трения и перемещение направлены в противоположные стороны. Следователь-
но,
а2 а2
Откуда получаем
q2d-q2(d + 2 S) =- 8л е0 dSp. mg(d + 2 S),
или
q2S = 4я 60 dS ц т g (d+ 2 S).
Окончательно находим расстояние S:
8neodnmg 2
Таким же образом можно найти максимальную скорость тел в процессе движения. Для
этого нужно мысленно представить, как двигались тела. Очевидно, что если в начальный
момент F3Jl > Fjp, то тела будут ускоряться до тех пор, пока Кэл не станет равной Fjp. После
этого тела будут двигаться замедленно до остановки. Следовательно, скорости тел будут
максимальны в момент движения, при котором F3n = F^, т.е.
_____д2
-----2--у = ц т g,
4л б0 (d + 2 х)2
где х - расстояние, которое пройдет каждое из тел из начального положения в точку, где
^эл = ^тр-
Записав теорему о изменении полной механической энергии системы в виде
-------------------q2 ,3т utnax д2 ~
___________________-----+ 2 —---------2— = - 2 ц т g х,
4 л е0 (d + 2 х) 2 4л е0 d
получим
J д2 .................................. дГ
тах 4л Eq т d 4 л е0 т (</ + 2 х) &
Выразив значение х из условия максимума скорости
16л е0цmg 2
окончательно получим
umax = |"J—2—^-2? +ng<d. (2)
i 4л e0 m d 4n e0 m J
Очевидно, что результаты (1) и (2) справедливы только в случаях, если в начальном
положении Fyi > = ц N, т.е.
д2 д2
Т^2>^т^ или ц<т-------------^—2-
4л Eqd 4itE0mgd
• Ответ: S = ~---------у; г>тах = {-—2—2 q + ц g</}
8л е0 d ц т g 2 I 4л е0 та 4л е0 т J
д2
приц<------2----J.
4л е0 т g d
12.285. Частица массой т = 1 г с зарядом q = 10‘6 Кл движется в электри-
ческом поле одноименного закрепленного заряда Q = 2-10"6 Кл так, что на рас-
237
стоянии /] = 5 см ее скорость и0 = 30 м/с составляет острый угол с линией, со-
единяющей заряды. Определить величину скорости частицы, когда она будет
на расстоянии /2 = 4 см от заряда Q. Сопротивление воздуха и гравитационное
взаимодействие не учитывать.
12.286. По гладкой наклонной плоскости, составляющей угол а = 30° с го-
ризонтом, с высоты h = 1 м, соскальзывает небольшое тело массой т = 10 г, за-
ряженное отрицательным зарядом q = - 1 мкКл. В точке пересечения вертика-
ли, проведенной через начальное положение тела, с основанием плоскости за-
креплен положительный заряд Q - 2 мкКл. Найти скорость, с которой тело до-
стигнет основания плоскости.
12.287. Две маленькие бусинки надеты на непроводящий стержень, распо-
ложенный вертикально вблизи поверхности земли, причем нижняя из них за-
креплена. Бусинки раздвинули на расстояние /0, сообщили каждой одинаковые
одноименные заряды q и отпустили. Какую максимальную скорость будет
иметь подвижная бусинка, если ее масса равна ml Трением пренебречь.
12.288. Два одинаковых шарика мас-
сой т, имеющие одинаковые заряды q, начи-
нают скользить по двум одинаковым непо-
движным и непроводящим спицам. Спицы
расположены в вертикальной плоскости,
причем каждая наклонена к горизонту под
углом а (рис. 12.136). На какую максималь-
ную высоту над первоначальным уровнем
поднимутся шарики? В начальный момент
шарики удерживались на расстоянии L друг от друга и на расстоянии I от кон-
цов спиц. Трением пренебречь.
12.289. На горизонтальной поверхности закреплен заряд qx. Тело мас-
сой т, имеющее заряд q2 (причем > 0), может перемещаться по поверх-
ности. На каком расстоянии от заряда qx тело остановится, если в начальный
момент оно покоилось и находилось на расстоянии /0 от заряда 9,? Коэффици-
ент трения о плоскость равен ц.
12.290. Два одинаковых маленьких шарика, соединенные невесомой и не-
проводящей пружиной жесткостью к, лежат на гладком горизонтальном столе.
На какое максимальное расстояние раздвинутся шарики, если каждому из них
сообщить одинаковые заряды 9? Длина пружины в недеформированном состо-
янии /0.
12.291. Три одинаковых одноименно заряженных тела, заряд каждого из
которых равен 9, а масса т, соединены невесомыми нерастяжимыми и непро-
водящими нитями длиной / так, что нити образуют равносторонний треуголь-
ник. Одну из нитей пережигают. Найти максимальные скорости тел.
238
12.292. Три маленьких одинаковых шарика массой т каждый, имеющие
одинаковые заряды q, могут скользить по очень длинному гладкому стержню.
Какую скорость будут иметь шарики на очень большом расстоянии друг от
друга, если в начальный момент они удерживались на расстоянии /?
12.293. Два небольших тела, связанные нитью длиной I, лежат на горизон-
тальной плоскости. Заряд каждого тела равен q, масса равна т. Нить пережига-
ют, и тела начинают скользить по плоскости. Какую максимальную скорость
приобретут тела, если коэффициент трения равен ц?
12.294. В вершинах правильного 1998-гранника со стороной а = 5 см были
закреплены небольшие одинаковые шарики с равными зарядами. В некоторый
момент времени один из шариков был освобожден, а через достаточно боль-
шой промежуток времени был освобожден шарик, соседний с первым освобож-
денным. Оказалось, что на большом расстоянии от многогранника кинетичес-
кие энергии освобожденных шариков различаются на величину AW = 0,01 Дж.
Определить заряд каждого шарика.
12.295. Небольшой шарик массой т, имеющий заряд q, вращается в гори-
зонтальной плоскости на непроводящей нити длиной I (рис. 12.137). Опреде-
лить период обращения шарика, если в центре окружности, описываемой ша-
риком при вращении, расположен точечный заряд q. При вращении нить обра-
зует с вертикалью угол а.
• Решение. На шарик в произвольный мо-
мент движения будут действовать три силы:
сила тяжести т g) сила натяжения нити 7^и
сила взаимодействия между зарядами .
направленные так, как показано на рис.
12.137, причем 2
р ------i—
г эл - , 2 ’
4л ед г
где г = 1 sin а - радиус окружности, описы-
ваемой шариком.
Запишем уравнение движения шарика г.
динат (см. книгу «Механика», §4), направленную по нормали к траектории тела, и ось
OZ, перпендикулярную плоскости вращения:
ОХ-. --^-=Tsina-F3n,
OZ: 0 = 7'cosa-mg.
С учетом выражений для радиуса окружности г и значения силы Рэл, получим
m о2 ^2
-----= mgtga-------\—р .
1 sm а 4л б011 sin" a
Откуда находим скорость движения шарика:
-i/ /sin a ( ' q2 1
о = У------- m g tg a-------3;—-z— j.
m 4n e0/‘sin2 a
239
Следовательно, период обращения
2яг___________________________2я “У / sin а
° Vgtg"--
а-
4л Eq m / sin а
„ 2л V / sin а
• Ответ: т = . 2 ...
-----q2 2
4ne0m/ sm а
12.296. В однородном электрическом поле напряженностью Е на невесо-
мой нерастяжимой нити удерживается шарик массой т и зарядом q > 0 (рис.
12.138). Найти натяжение нити при движении шарика, если первоначально он
был отклонен от вертикали на угол а0. Силовые линии поля направлены верти-
• Решение. На шарик в произвольный момент
движения будут действовать три силы: сила тя-
жести т gt сила натяжения нити ?и сила, причем
Еэл = 4 Е-
Запишем уравнение движения шарика на
ось ОХ «сопровождающей» системы координат:
- T + mg cos а - F3n cos а.
Для определения скорости о шарика в дан-
ном положении воспользуемся теоремой о полной
механической энергии в виде
^2 ~ ^1 = -4(^стор ),
где = О, W2 = т g h + Ц т и2 - начальная и конечная механические энергии шарика (ну-
левой уровень потенциальной энергии выбран на уровне начального положения);
^стор = .
При движении шарика сила Гработы не совершает, так как она направлена перпенди-
кулярно траектории. Работа силы Х,л не зависит от формы траектории перемещения шари-
ка и может быть определена как
^(^эл)=^эл h = qEh.
Следовательно,
т g h + [/i т v? - q Е h
и уравнение движения можно переписать в виде
2 (я £ - m я) Л „ , „
—j— = Т - (q Е - m g) cos а,
или
Т = (q Е - т g) [2 (cos а - cos а0) + cos а] = (q Е - т g) (3 cos а - 2 cos а0),
где учтено, что
h = I (1 - cos do) - / (1 - cos а) = I (cos а - cos а0).
Очевидно, что полученный результат имеет смысл только в случаях, если
q Е > т g.
• Ответ: T=(q Е-т g)(3 cos а - 2 cos а0) при q Е> mg.
240
12.297. Вокруг точечного заряда q0 = -5 нКл равномерно движется по ок-
ружности радиусом R = 3 см маленький заряженный шарик. Чему равно отно-
шение заряда шарика к его массе, если угловая скорость вращения шарика
равна (0 = 5 рад/с?
12.298. В атоме водорода электрон движется вокруг протона с угловой
скоростью со = 1016 рад/с. Определить радиус орбиты электрона. Заряд электро-
на |е| = 1,6-10'19 Кл, масса электрона т = 9,1-10'31 кг.
12.299. Отрицательно заряженная частица движется по окружности радиу-
са R = 1 м со скоростью и = 100 м/с вокруг положительно заряженной непо-
движной частицы. Величины зарядов частиц одинаковы и равны q = 100 мкКл.
Найти массу движущейся частицы.
Рис. 12.139
12.300. В плоскости симметрии двух протонов, расположенных на рас-
стоянии R друг от друга, по круговой орбите радиусом г движется электрон
(рис. 12.139). Определить угловую скорость его вращения. Заряд электрона
|е|, масса электрона т.
12.301. Два одинаковых точечных заряда величиной q и массой т каж-
дый движутся по окружности постоянного радиуса R вокруг отрицательного
заряда (-0) так, как показано на рис. 12.140. Найти угловые скорости враще-
ния зарядов.
12.302. В боровской модели атома водорода электрон движется по круго-
вой орбите радиусом R = 5-10'11 м, в центре которой расположен протон. Чему
равна полная энергия электрона? Заряд электрона |е| = 1,6-10'19 Кл.
12.303. Вокруг тяжелого ядра с зарядом Z |е| на расстоянии R вращается
по круговой орбите электрон. Какую минимальную энергию нужно сообщить
электрону, чтобы он оторвался от ядра?
12.304. К плоскости, заряженной с поверхностной плотностью заряда о,
привязан на невесомой непроводящей нити
длиной I маленький шарик массой т, имею-
щий заряд q. Шарик отводят от положения
равновесия и заставляют двигаться так, что
нить описывает круговой конус (рис.
12.141) . Найти период обращения шарика,
если угол при вершине конуса мал. Силой
тяжести пренебречь. Рис. 12.141
241
Рис. 12.142
Рис. 12.143
12.305. Небольшой шарик массой пг, подвешенный на непроводящей нити,
вращают в вертикальной плоскости (рис. 12.142). Найти максимальную раз-
ность натяжений нити, если в пространстве создано постоянное однородное
электрическое поле напряженностью Е, направленное вертикально вниз, а ша-
рику сообщен положительный заряд q.
12.306. Небольшой шарик массой т, подвешенный на непроводящей
нити длиной I, вращают в горизонтальной плоскости. На оси вращения в
точке, расположенной симметрично точке подвеса относительно плоскости
вращения, помещен точечный заряд q (рис. 12.143). Такой же по величине
заряд сообщен шарику. С какой скоростью вращается шарик, если при враще-
нии нить образует с вертикалью угол а?
12.307. Небольшой шарик массой т = 10 г, имеющий заряд q = 5 мкКл,
подвешен на непроводящей нити. Шарик отклоняют на натянутой нити от по-
ложения равновесия до горизонтального положения и отпускают. Определить
натяжение нити в тот момент, когда нить составляет угол а = 30° с вертика-
лью, если в пространстве создано постоянное однородное электрическое поле
напряженностью Е = 2 кВ/м, направленное вертикально вниз.
12.308. Небольшой шарик массой т = 6 г,
имеющий заряд q = 1 мкКл, подвешен на непроводя-
щей нити длиной I = 40 см. Над точкой подвеса на
расстоянии h = 30 см от нее помещен точечный за-
ряд 0 = 2 мкКл (рис. 12.144). Шарик отклоняют на
натянутой нити от положения равновесия до гори-
зонтального положения и отпускают. Определить
скорость шарика в момент прохождения им положе-
ния равновесия.
12309. На тонкое диэлектрическое кольцо радиусом R надета бусинка
массой т, которой сообщен заряд q. Кольцо расположено в вертикальной плос-
кости и вся система находится в однородном вертикальном электрическом
поле напряженностью Е. Какой по величине точечный заряд следует располо-
жить в центре кольца, чтобы бусинка, соскользнувшая с вершины кольца, не
давила на него в иижней точке? Трения нет.
242
12.310. Две одинаковые маленькие бусинки, имеющие одинаковые заря-
ды, могут без трения скользить по непроводящему кольцу радиусом R, распо-
ложенном вертикально в поле тяжести Земли. Первоначально бусинки удержи-
ваются на горизонтальном диаметре кольца. Бусинки отпускают. Найти их мак-
симальные скорости, если положение равновесия между ними находится на
хорде, равной радиусу кольца.
12.311. Найти период малых колебаний математического маятника, состо-
ящего из шарика массой m с зарядом q > 0, подвешенного на нити длиной I,
если маятник помещен в электрическое поле, векторы напряженности которого
Е, направлены: а) вдоль силы тяжести; б) под углом 90° к направлению силы
тяжести.
• Решение. На маятник в произволь-
ный момент движения будут действо-
вать три силы: сила тяжести m gt сила
натяжения нити ? и сила , при-
чем
^эл — <}Е
и F3n направлена вдоль силовых ли- /и> 1
ний электрического поля.
Период гармонических колеба-
ний математического маятника, иа
который, помимо силы тяжести и на-
тяжения нити, действует постоянная
внешняя сила , равен (см. книгу
«Механика», §8):
mg
^эл
а)
б)
Рис. 12.145
I
где Йэфф = I g'+ Рзл/m | •
В случае, когда векторы напряженности электрического поля направлены вдоль силы
тяжести (рис. 12.145, а):
£эфф = g + Еэл/т = g + q Е/т.
Следовательно, в первом случае период колебаний маятника будет равен
T=2n
Т=2пУ——— .
mg + qE
Если силовые линии электрического поля направлены горизонтально (рис. 12.145, б),
то
.^эфф = g2+(q Е/т)2.
Следовательно,
Т - т I
* 2 ТС V /25 •
У т2 g2 + q2 Е2
• Ответ: а) Г= 2 n'V - -т ; б) Т = 2 у , ? '.
mg + qE ymg2+q2E2 i
12.312. Найти период малых колебаний гантели длиной I с шариками мас-
сой «^расположенной вдоль однородного электрического поля напряженнос-
тью Е. Заряды шариков гантели равны q и (-q). Силой тяжести пренебречь.
243
12313. Небольшой металлический шарик массой т, подвешенный на не-
проводящей нити длиной /, колеблется по закону математического маятника
над бесконечной равномерно заряженной горизонтальной плоскостью с плот-
ностью заряда (+ о). Определить период колебаний маятника, если на шарике
находится заряд (- д').
Рис. 12.146
Рис. 12.147
12314. Между обкладками большого плоского конденсатора подвешен
на непроводящей нити маленький металлический шарик массой т (рис.
12.146). Как изменится период колебаний такого маятника, если на шарик по-
местить заряд q, а пластины конденсатора зарядить с поверхностной плотнос-
тью ±о? Колебания считать гармоническими.
12315. Решить задачу №12,314, если маятник подвешен между пластина-
ми так, как показано на рис. 12.147.
12316. Вблизи вертикальной стенки, заряженной положительно с по-
верхностной плотностью заряда о, подвешено на непроводящей нити длиной
1 маленькое тело массой т и зарядом q > 0. Найти период колебаний тела, счи-
тая их гармоническими.
12.317 . Две маленькие бусинки, имеющие одинаковые заряды, надеты на
непроводящий стержень, расположенный вертикально вблизи поверхности
Земли, причем нижняя из бусинок закреплена. В положении равновесия рас-
стояние между бусинками равно /0. Найти период малых колебаний подвиж-
• Решение. Если пренебречь тре-
нием, то при колебаниях подвиж-
ной бусинки на нее будут дейст-
вовать две силы: сца тяжести
т ^и сила Кулона ^эл > направ-
ленные в противоположные сто-
роны. Так как сила тяжести оста-
ется постоянной, а сила Кулона
изменяется обратно пропорцио-
нально квадрату расстояния меж-
ду бусинками, то легко заметить,
что при колебаниях результирую-
щая сила
^=^эл + т?
244
все время будет направлена к положению равновесия, т.е. будет возвращающей.
Для определения периода колебаний сместим подвижную бусинку из положения рав-
новесия на некоторое расстояние и предоставим самой себе. Тогда в некоторый момент
времени смещение бусинки от положения равновесия будет равно х (рис. 12.148, б). Если
ось ОХ направить в сторону смещения, то результирующая сила в проекции на эту ось
будет иметь значение:
Fx = F3H2~mg,
где сила Кулона F3„ 2 будет равна 2
р________
ГЭЛ 2 - _ 2 '
Следовательно, 71 ( о 4
Fx =----%-----Г ~ т g-
4ne0(Z0 + x)~
Учитывая, что в положении равновесия (рис. 12.148, а)
mg = F3sit’ U)
где 2
^л^у^Ч’ (2)
получаем 2 п®° 0 2
s’______2_____..—2______
ИдЛ 4л Ео (Zo + X) 4л Ео 10
F д2 ;________I____1 1 д2 [102-(!о + х)2}
Х 4лео1(/о + х)2 /02 ' 4пе0 1 Z02(/0+x)2'
Так как рассматриваются малые колебания, то х «и выражение для результирую-
щей силы Fx можно записать в виде
F = <?2 ( 102 - 102 -210х-х2} = । -x(2Z0 + x) > = г - 2Zoх , = _ _х
х 4яе0 Zo2 (Zq + x)2 ! 4п г(| /02 (Z0 + x)2j 4ле0’ Zo4 ’ 2ле0 Zo3 ’
Откуда следует, что сила Fx пропорциональна смещению х бусинки из положения
равновесия и, как было отмечено выше, действительно является возвращающей. Это оз-
начает, что бусинка будет совершать гармонические колебания. При таких колебаниях
сила Fx связана с коэффициентом к возвращающей силы соотношением:
Fx = -kx. (4)
Следовательно, из (3)-(4) находим
к = ~^.
2я е0 Zo
Выражая величину заряда q бусинок из соотношений (1)—(2)
д2— 4л е0 т g 1„,
получаем
k-l”L8.
10 ’
Используя связь коэффициента возвращающей силы с периодом гармонических ко-
лебаний
Т - 2 л у -г
окончательно имеем r-j—
гт- Т=2пУ-^.
• Ответ: . %
2g
12.318. На концах тонкого непроводящего горизонтального стержня дли-
ной Z закреплены две маленькие бусинки, а третья надета на стержень, по кото-
245
торому она может перемещаться без трения. Всем бусинкам сообщают одина-
ковые заряды q. Найти период малых колебаний подвижной бусинки, если ее
масса рвна т.
12.319. Тонкое кольцо радиусом R = 1 м равномерно заряжено положи-
тельным зарядом q = 10"16 Кл. Определить период малых колебаний электро-
на, находящегося на оси кольца на расстоянии х « R от его плоскости. Заряд
электрона |е| = 1,610'19 Кл, масса электрона пг = 9,1-)0"31 кг. Силой тяжести
Рис. 12.150
Рис. 12.151
12.320. Найти период малых колебаний тела массой т, заряд которого q,
внутри гладкой сферы радиусом R, если в верхней точке сферы закреплен
заряд Q (q-Q)>0 (рис. 12.149).
12.321. Горизонтальный желоб выгнут по цилиндрической поверхности:
слева по радиусу R, справа - по радиусу 2R (рис. 12.150). На дне желоба нахо-
дится бусинка массой т и зарядом q, а в точке О закреплен такой же по знаку
заряд величиной Q. Найти период малых колебаний бусинки. Трением прене-
бречь.
12.322. Определить период малых колебаний четырех заряженных тел,
связанных одинаковыми нитями длиной I и движущихся так, как показано на
рис. 12.151. Массы и заряды тел равны т и q.
12.323. На какое минимальное расстояние смогут сблизиться два электро-
на, если они движутся навстречу друг другу из бесконечности с относитель-
ными скоростями иогн = 10б м/с. Заряд электрона |е| = 1,610"19 Кл, масса элек-
трона т = 9,1 10"3! кг.
• Решение. При движении одной заряженной частицы в электрическом поле другой сила
взаимодействия между ними будет изменяться обратно пропорционально квадрату расстоя-
ния между' зарядами. Для читателя, хорошо обладающего навыками интегрирования, работу
такой силы при произвольном перемещении зарядов определить не сложно. Однако гораздо
проще решать подобные задачи, если воспользоваться законом сохранения механической
энергии.
П^сть электроны на бесконечном расстоянии друг относительно друга имеют ско-
рости и) и «2- Тогда в исходном положении полная механическая энергия системы двух
рассматриваемых зарядов будет равна сумме их кинетических энергий:
= '/2 т и? + 'Л т 1>2,
где учтено, что в начальном положении частицы не взаимодействуют.
246
При движении электронов навстречу друг другу их скорости будут уменьшаться, так
как движение каждой из частиц будет происходить в тормозящем поле другой. Однако
предполагать, что в момент сближения электронов на минимальное расстояние скорости
обеих частиц станут равными нулю, нет никаких оснований. Считая, что рассматриваемые
две частицы образуют замкнутую систему, на основании закона сохранения импульса, за-
писанного в виде
Др>=Й-Р1=0>
(где pi, р2 - начальный и конечный импульсы системы соответственно) можно сделать
вывод, что на минимальном расстоянии скорости частиц станут равны нулю (т.е. = 0)
только в случае, если в начальный момент импульсы частиц будут равны по величине и про-
тивоположны по направлению. В общем случае этого не происходит. Следовательно, запи-
сав импульсы в развернутом виде
р\ = т i?| + т ,
р, ~ (т + т) i?
(где v?- скорость электронов на минимальном расстоянии между ними), получим
(т + т) i?- (т u'i + т и2) - 0.
Откуда найдем скорость о:
о = M>(i?i + {?г). (1)
Теперь можно записать выражение для полной механической энергии системы в ко-
нечном положении:
Н2
^2 = -2^
2 4л е() гmjn
где второе слагаемое представляет собой потенциальную энергию взаимодействия частиц,
rmin ~ минимальное расстояние, на которое сблизятся электроны.
На основании закона сохранения энергии получим
т i>2 _ 2 m _____________________________________[еГ__
2 + 2 2 + 4л с0 rmin '
Скорость о электронов на минимальном расстоянии найдем из закона сохранения
импульса (1), записав его в проекции на произвольную ось, параллельную векторам
i?i и \}2:
= И>2,
(2)
и = 4 (v>i - 1>2).
Подставляя значение скорости и из (3) в (2), получаем
т (ui + °г)2 _ je|2
4 471 Ео rmin '
Следовательно, искомое минимальное расстояние между электронами
г _____________________________й!________ 1П-» м
rmm~ 2 —Юм,
л г.о т Ос™
где учтено, что при сближении электронов вдоль одной прямой их относительные скорости
равны оотн = О| + о2-
• Ответ '. rmjn =-—2— « 10‘9 м.
71 ео т °отн .
12.324. Электрон находится на расстоянии R = 5-10"“ м от неподвижного
протона. Какой должна быть скорость электрона, чтобы он мог улететь на беско-
нечность? Заряд электрона |е| = 1,6-1 О’19 Кл, масса электрона т = 9,1 10'31 кг.
12.325. Расстояние между закрепленными разноименными зарядами qt
и q2 равно I. Частица массой т, имеющая заряд q3 одного знака с q2, летит по
(3)
247
прямой, соединяющей закрепленные заряды. Какую наименьшую скорость
должна иметь частица на большом расстоянии од зарядов qt и q2, чтобы до-
стичь заряда <?}?
12.326. Два электрона находятся на расстоянии а друг от друга, причем
скорость одного из них равна нулю, а скорость другого - и* и направлена к
первому электрону вдоль линии их соединяющей. На какое минимальное рас-
стояние они сблизятся? Заряд электрона !<?!, масса электрона т.
12.327. Из бесконечности навстречу друг другу с одинаковыми скоростя-
ми г? движутся два электрона. Определить минимальное расстояние, на кото-
рое они сблизятся. Заряд электрона lei, масса электрона т.
12.328. Два электрона движутся вдоль одной прямой. На расстоянии а
друг от друга их скорости направлены в одну сторону и равны и, и и2, причем
Uj > и2 . На какое минимальное расстояние смогут сблизиться электроны?
Заряд электрона |е|, масса электрона т.
12.329. С большого расстояния навстречу' друг другу со скоростями соот-
ветственно и< ио2 движутся два электрона. Определить минимальное рассто-
яние, на которое они сблизятся. Заряд электрона |е|, масса электрона т.
и/ Хр' 12.330. Скорости двух элек-
аХ. тронов равны и. лежат в одной
у т~е плоскости и при расстоянии между
электронами d образуют углы а с
Рис. К. 152 прямой, соединяющей электроны
(рис. 12.152). На какое минимальное расстояние смогут сблизиться электро-
ны? Заряд электрона ie|, масса электрона т.
12.331. С большого расстояния к металлической плоскости движется тело
массой т, имеющее заряд q. Определить скорость тела в тот момент, когда
оно будет находиться на расстоянии d от плоскости. Начальная скорость тела
равна нулю, а его размеры много меньше d.
12.332. Частица массой т, имеющая заряд q, со скоростью и0 приближа-
ется с большого расстояния к заряженному незакрепленному кольцу, двигаясь
по его оси. Радиус кольца R, заряд Q (Qq > 0), масса М. Вначале кольцо поко-
ится. Чему будет равна скорость частицы, когда она проходит через центр
кольца? Как изменится ответ, если кольцо закрепить?
• Решение. Решение задачи проведем аналогичным способом, который был рассмотрен в за-
даче №12.323.
Считая систему «частица-кольцо» замкнутой, закон сохранения импульса
~ (т т 1% = 0,
(где и,и- скорости частицы н кольца в момент времени, когда частица проходит через
центр кольца) запишем в проекции на направление движения тел системы:
т о + Ми - т Од = 0. (1)
В начальный момент полная механическая энергия тел равна кинетической энергии
частицы:
Д'] = '/г т oj,
а в момент, когда частица находится в центре кольца,
248
W2=l/imv2+l/iMu2 + (Рю,
где IFB3 - энергия взаимодействия частицы с кольцом в рассматриваемом положении, рав-
ная
»вз = 9Ф-
Потенциал <р, создаваемый кольцом в центре, легко определить, разбив заряд Q иа
элементарные заряды Д0, каждый из которых можно считать точечным. Так как все за-
ряды Д(2 находятся на равных расстояниях от центра кольца, то потенциал, создаваемый
ими, будет равен
_ у sj)_______(/
где R - радиус кольца. Ч>-2'4лео.К-4л8о.К’
Следовательно,
W2 = ’Л т и2 + 'Л Ми2 + -
4л Sq Л
и закон сохранения механической энергии примет вид
IT, = W2.
или
л» up mu2 Л/к2 д Q
2 2 + 2 + 4л g0 R'
(2)
Выразив скорость кольца и из закона сохранения импульса (1)
и(и0-и)
М
н подставив в закон сохранения энергии (2), получим
Up mu2 т2(и2 - 2 и0 и + и2) qQ
2 ~ 2 + 2М +4леоЯ’
После не сложных преобразований уравнение (3) примет вид
^2 _ 2 m и,, - М— щ ____д QM_______Q
Л/+ т ° М+ т U° 2л е0 т (М+ т) R
Откуда получаем ________________
о=±л/ qQM
Л/+в> (Л/+т)2 2nz(sm{M+m)R ’
Для того, чтобы частица пролетела сквозь кольцо, ее скорость о должна быть больше
скорости и кольца. Очевидно, что частица догонит удаляющееся от нее кольцо, если от-
носительная скорость Doth = о - и > 0, или с учетом (1) и (4):
1----5—j-------------------
_ л»up т о _ л»Qp М+ ту] М up __________________д QM л>ир
Оотн-v- м + м - м ± м (М+т)2~ 2п е0 т (М + т) R ~ М '
Легко видеть, что условию «отн й 0 соответствует перед радикалом знак «+». Сле-
довательно, ____________________________
т up ^2°о gQM
М+т (Л/+в>)2 2л е0 т (M+m)R
Если кольцо закреплено, то полагая М»т, из (5) получаем
(5)
O = (6)
М 2л Ер л> R 2л sp m R
Выражение (6) можно также получить, записав закон сохранения энергии в виде
Л1 Up т\>2 q Q
2 ~ 2 +4ле0Я'
Ответ-, и = ------1.Qц =д/о2--^Ц- .
М+т (М+т)2 2пе^т(М+ т) R 2ite<imR
249
12333. Частица массой т, имеющая заряд q, движется по оси заряженно-
го закрепленного кольца, приближаясь к нему. Какую наименьшую скорость
должна иметь частица на большом расстоянии от кольца, чтобы пролететь
сквозь него? Масса кольца М, радиус R, заряд Q.
12.334. Закрепленная сфера радиусом R}, имеющая равномерно распреде-
ленный по поверхности положительный заряд qt, окружена металлической
сеткой радиусом R2, на которую нанесет положительный заряд q2 (рис.
12.153). Протон, находящийся вблизи поверхности сферы, не имея начальной
скорости, пролетает через сетку и удаляется на бесконечность. Найти ско-
рость протона на бесконечности. Отношение заряда q к массе М для протона
считать известным.
12.335. В закрепленной металлической сфере радиусом R = 10’2 м, имею-
щей заряд q ~ - 10'8 Кл, проделано очень маленькое отверстие (рис. 12.154). То-
чечный заряд q0 = 10'9 Кл массой т = 10'6 кг влетает в отверстие по направле-
нию к центру сферы, имея начальную скорость вдали от сферы v>0 = 1 м/с.
Найти скорость заряда в центре сферы.
12.336. Две закрепленные сферы радиусом R имеют одинаковые заряды
Q, распределенные равномерно по поверхностям сфер. Какую минимальную
энергию нужно сообщить электрону на поверхности одной из сфер, чтобы он
достиг второй сферы? Расстояние между центрами сфер I. Заряд электрона |е|.
Рис. 12.155
12.337. В закрепленном шаре радиусом
R = 1 м, равномерно заряженным с объемной
плотностью заряда р = -10’12 Кл/м3, просвер-
лен по диаметру узкий канал (рис. 12.155). В
центре шара находится электрон. С какой ско-
ростью вылетит из шара электрон, если ему
сообщить начальную скорость и0 = 1 м/с, на-
правленную по радиусу вдоль канала? Заряд
электрона 1е| = 1,6-10'19 Кл, масса электрона
т = 9,1-10'3 кг.
12.338. Частица массой т, имеющая заряд q, движется с большого рас-
стояния к центру равномерно заряженной незакрепленной сферы. Радиус
сферы R, заряд Q (Qq > 0), масса М. Какой скоростью должна обладать части-
250
ца на большом расстоянии от сферы, чтобы через небольшое отверстие проле-
теть сквозь нее?
12.339. Частица массой т, имеющая заряд q, приближается с большого
расстояния к равномерно заряженному незакрепленному шару, двигаясь по
направлению к его центру. Радиус шара R, заряд Q (Qq > 0), масса М. Внача-
ле шар покоится. Какую минимальную скорость должна иметь частица на
большом расстоянии от шара, чтобы пройти через его центр?
§13. Постоянный ток
При движении заряженных частиц в проводнике происходит перенос
электрического заряда с одного места на другое. Поскольку заряженные час-
тицы совершают беспорядочное тепловое движение, то в обычных условиях
через любую воображаемую площадку в проводнике за произвольный про-
межуток времени проходит в обе стороны в среднем одинаковое количество
носителей зарядов противоположных знаков. Если же каким-либо образом
упорядочить движение зарядов так, чтобы через эту площадку переносился
суммарный заряд, отличный от нуля, то говорят, что через эту площадку течет
электрический ток. При этом за направление тока условились считать на-
правление движения положительных зарядов. Если ток образован движением
отрицательно заряженных частиц, то направление тока считают противопо-
ложным направлению движения частиц.
Для существования электрического тока необходимо наличие в провод-
никах свободных заряженных частиц, которые называют носителями тока.
Таковыми, например, в металлах являются электроны, утратившие связи с
атомами (свободные электроны илн электроны проводимости), в проводящих
растворах (электролитах) - это положительные или отрицательные ионы, а в
ионизованных газах - ими одновременно являются и электроны, и ионы. Од-
нако наличия свободных носителей зарядов еще недостаточно для возникно-
вения тока - необходимо также существование силы, действующей на заряды
в определенном направлении. Если эта сила перестанет действовать, то упоря-
доченное движение зарядов прекратится из-за сопротивления, оказываемого
их движению кристаллической решеткой металлов или нейтральными моле-
кулами электролитов. Причиной, вызывающей и поддерживающей упорядо-
ченное движение заряженных частиц, служит электрическое поле напряжен-
ностью Е, которое существует внутри проводника до тех пор, пока между раз-
личными точками проводника имеется разность потенциалов, которую назы-
вают напряжением.
Легко понять, что независимо от знака носителей тока, ток в проводнике
всегда направлен от точки с большим потенциалом к точке с меньшим потен-
циалом. Действительно, электрическое поле направлено в сторону убывания
потенциала (см. §12) и если свободные заряды положительны, то они будут
двигаться по направлению силовых линий поля, если отрицательны - то про-
251
тив них. Поэтому согласно договоренности о направлении тока, его направле-
ние будет совпадать с направлением электрического поля.
Движение носителей тока непосредственно невидимо. Однако это движе-
ние вызывает различные явления, по которым можно судить о наличии тока.
Так, электрический ток вызывает нагревание проводников, может изменять
химический состав проводника - выделять его химические составные части
(при прохождении тока через электролиты), а также оказывать силовое воз-
действие на соседние токи и магниты (см. §14).
Сила тока и плотность тока
Чтобы получить наглядное представление о движении электронов и
ионов, образующих ток, используют понятие линий тока - линий, вдоль кото-
рых перемещаются заряженные частицы. Если внутри проводника мысленно
выделить некоторую трубку, у которой боковая поверхность состоит из линий
линии тока
трубка тока
Рис. 13.1
тока, то заряженные частицы при движе-
нии не будут пересекать боковую поверх-
ность трубки, т.е. не будут выходить из
трубки наружу, или входить в трубку
извне. Такую трубку называют трубкой
тока (рис. 13.1). В частности, трубкой то-
ка является боковая поверхность металли-
ческой проволоки.
Рассмотрим проводник поперечным сечением 5. Величина заряда, проте-
кающего через поперечное сечение проводника за единицу времени, называ-
ется силой тока. Если за одинаковые промежутки времени Л/ через попере-
чное сечение проводника протекают равные заряды Д<у, то сила тока в провод-
нике равна
1 = ^L
At ’
(13.1)
при этом ток называют постоянным (стационарным).
Если сила тока изменяется с течением времени, то формула (13.1) опре-
деляет среднее значение силы тока за промежуток времени Аг. Для определе-
ния мгновенного значения силы тока в (13.1) необходимо перейти к пределу
при Дг —> 0:
Z=lim =
д/ -> о Дг at
(13.2)
Единицей измерения силы тока в системе СИ служит ампер [А] (подроб-
ное определение будет дано в §14).
Как известно (см. §12), сила, действующая на заряды в проводнике со
стороны электрического поля напряженностью Е, определяется формулой
q Е. Поэтому при отсутствии других сил заряды должны двигаться с уско-
рением. Однако из-за столкновений носителей тока с атомами и молекулами
проводника возникает тормозящая сила, пропорциональная скорости < <?>,
252
которую называют средней скоростью направленного (упорядоченного) дви-
жения или средней скоростью дрейфа.
Пусть в проводнике имеются носители тока одного знака, средняя ско-
рость направленного движения которых постоянна и равна < {?>. Если провод-
ник цилиндрический, то площадка 5, совпадающая с площадью поперечного
сечения проводника, будет располо-
жена перпендикулярно к линиям то-
ка, а значит, и перпендикулярно к на-
правлению скорости < {?> заряжен-
ных частиц. Построим на этой пло-
щадке цилиндр длиной AZ = < и > Аг рис и 2
(рис. 13.2). Если через равные по пло-
щади участки поперечного сечения S проводника в единицу времени протека-
ют равные заряды, то число заряженных частиц, которые пройдут через пло-
щадку S за время Аг, будет равно числу частиц в рассматриваемом цилиндре:
Sq = q0 п S &!, или \q = q0 п S < и > <\t,
где q6 - заряд одной частицы, и - их концентрация в проводнике. В этом
случае распределение тока называют равномерным.
Электрический ток может быть распределен по сечению S неравномерно.
Более детально ток можно характеризовать с помощью вектора плотности
токау^Если распределение тока по сечению проводника равномерное, то вели-
чина вектора плотности тока численно равна заряду, протекающего через еди-
ницу площади поперечного сечения проводника за единицу времени:
j = ~, или j = qon<v>>. (13.3)
Поскольку за направление тока принято направление движения положи-
тельных зарядов, то направление плотности тока совпадает с направлением
скорости < (?>. Поэтому соотношение (13.3) в векторной форме записывают в
виде
?=qon<\?>. (13.4)
Если плотность тока не одинакова во всех точках поперечного сечения
проводника, то поверхность S можно разбить на бесконечно малые элементы
dS, в каждой точке которых плотность тока одинакова. Тогда ток через каждую
такую площадку dS будет равен
dl=j dS,
а сила тока, протекающего через сечение S
I=jdI-^JdS, (13.5)
где интегрирование производится по всей поверхности S сечения проводника.
253
Закон Ома для однородного участка цепи.
Электрическое сопротивление
1
a .„z=r—
Фа R
Рис. J3.3
Рассмотрим металлический проводник
(рис. 13.3), между концами которого имеет-
-• ся разность потенциалов Лфа-/> = Фа - Ф/>
Фб (т.е. напряжение или падение напряжения
U= фа - фу). Если фа > фу, то ток в провод-
нике будет направлен от точки а к точке Ь.
Если состояние проводника остается неизменным, то существует однозначная
зависимость между напряжением, приложенном к концам проводника, и силой
тока в нем. Эту зависимость называют вольт-амперной характеристикой дан-
ного проводника. Для металлических проводников эта зависимость особенно
проста: сила тока I в проводнике прямо пропорциональна разности потенциа-
лов U на его концах
(13.6)
41
где коэффициент R называется электрическим сопротивлением (или просто
сопротивлением) проводника, которое представляет собой меру противодей-
ствия данного проводника протеканию в нем электрического тока. В системе
СИ единицей измерения сопротивления служит ом [Ом = В/А].
Формула (13.6) была экспериментально установлена Омом и выражает
закон Ома для однородного участка цепи (определение однородного участка
будет дано ниже).
Электрическое сопротивление - основная электрическая характеристика
проводника, зависящая от его формы и размеров. Для металлических провод-
ников постоянного сечения установлено, что сопротивление прямо пропорцио-
нально длине I проводника и обратно пропорционально площади S его попере-
чного сечения:
Л = Р”. (13.7)
где р-удельное сопротивление проводника, характеризующее свойства и со-
стояние вещества, из которого он изготовлен. Удельное сопротивление зави-
сит не только от химической природы вещества, но и от температуры про-
водника: как правило, сопротивление металлов возрастает с ростом темпера-
туры и для всех металлов при обычных температурах
р = ро(1+аО, (13.8)
где р0 - удельное сопротивление при 0°С, а - температурный коэффициент
сопротивления, t - температура проводника в [°C].
Значения температурного коэффициента сопротивления являются таблич-
ными величинами. Однако для всех чистых металлов и многих сплавов в облас-
ти температур 0°С-Н00°С можно считать а » 1/273 [град'1].
254
Используя понятие удельного сопротивления, закон Ома (13.6) можно за-
писать по-другому.
Рассмотрим проводник длиной I и площадью поперечного сечения 5,
представленный на рис. 13.2. Если на концах этого проводника поддерживает-
ся постоянное напряжение U, то внутри него существует электрическое поле
напряженностью
E-U
I ’
направленное вдоль оси проводника. Если плотность тока одинакова в любой
точке, то сила тока в проводнике
I=jS.
На основании (13.6) и (13.7) получим
.с EIS
J о - ,
р/
или
/ = (13.9)
где о = 1/р - удельная электрическая проводимость (или просто проводи-
мость) проводника. Единицей измерения а является сименс [См = Ом^-м'1].
Поскольку в проводнике упорядоченное движение носителей тока проис-
ходит в направлении вектора Е, то направления J и Е совпадают. Поэтому со-
отношение (13.9) записывают в виде
7= о 2? (13.10)
и называют законом Ома в дифференциальной форме.
Последовательное и параллельное соединение проводников
!n
Рис. 13.4 Рис. 13.5
Несколько проводников могут быть соединены между собой. При этом
так же, как у конденсаторов, различают последовательное и параллельное со-
единения (см. рис. 13.4 и рис. 13.5 соответственно).
Прн последовательном соединении проводников через каждый из них
течет одинаковый ток (в противном случае заряд накапливался бы в некото-
рой точке):
/ = / = /2 = 7з = ... =
255
Разность потенциалов Дф = <рА - <рв на концах соединения равна сумме
разностей потенциалов на каждом из проводников:
Дф = S Дфр
в чем легко убедиться, введя потенциалы ф(у точек между проводниками со-
противлениями Rj и Rj.
Дф = Фл - Фв = (Фл - ф|,г) + (Ф1.2 - Фг,з) + (Фг,з - Фз.д) + • • (Фм-ijv- Фв)>
или
и= их + U2 + и3 + ... + UN,
где U - напряжение на концах участка, Ц - падения напряжения на каждом из
проводников.
Общее сопротивление всего соединения найдем, используя закон Ома
(13'6); „ и ux + u2 + u3 + ... + uN и, и2 и, и»
"пОСЛ. J ~ ] 1 + 1 + 1 ++ 1 ’
или л.
^посл ~ R[ R2 + 5 "Ь ... 4- RN — Rj. (13.11)
При параллельном соединении напряжения на концах всех проводников
одинаковы
U=lJx-U2=U3 = ...= UN=tya- ф^,
а сила тока до точки а и после точки Ь (см. рис. 13.5) по закону сохранения
заряда будет равна сумме токов в каждом из проводников:
7=/[ + /2 + 4 + • • + Л/-
Следовательно, при параллельном соединении общее сопротивление
1 h , h , h , Av 1 1 1 1 v 1 zi, nx
Лзар. U U -^U Rx+ R2 + R3+--' + RN &Rj- (13'k)
Электродвижущая сила источника.
Закон Ома для неоднородного участка цепи и замкнутой цепи
Легко понять, что нельзя получить в проводнике постоянный ток, если для
создания напряжения на концах проводника использовать заряженный конден-
сатор. Наличие тока будет сопровождаться переходом зарядов с одной обклад-
ки на другую в таком направлении, чтобы разность потенциалов между обклад-
ками уменьшалась. При этом сила тока в проводнике быстро упадет до нуля.
Рассмотрим проводник, между концами А м В которого существует раз-
ность потенциалов Дф = фл - фя, причем фл > <рв (рис. 13.6). В проводнике воз-
никнет электрическое поле, под действием которого носители заряда будут
перемещаться таким образом, чтобы уменьшить потенциал фл и увеличить по-
тенциал фв. Через некоторое время, если не принять мер для поддержания раз-
256
ности потенциалов, перемещение
носителей заряда проведет к то-
му, что поле внутри проводника
исчезнет и ток прекратится. Для
того, чтобы поддержать ток, нуж-
но непрерывно перемещать при-
носимые на один конец провод-
ника заряды на другой его конец, 13 6
т.е. необходимо осуществить круговорот зарядов, чтобы они двигались по
замкнутому пути. Очевидно, чтобы заставить двигаться положительные заря-
ды от меньшего потенциала к большему, а отрицательные - от большего к
меньшему, необходима сила, имеющая неэлектрическую природу. Поэтому в
замкнутой цепи наряду с участками, на которых заряды движутся под дейст-
вием сил электрического поля (такие участки называют однородными), долж-
ны существовать участки, где перенос зарядов происходит против сил поля.
Перемещение зарядов на таких участках возможно лишь с помощью сил не-
элекгростатического происхождения (т.е. не кулоновских), которые называют
сторонними, а участки, на которых они действуют - неоднородными. Эти
силы, например, могут быть обусловлены химическими процессами (всевоз-
можные аккумуляторы) или иметь электромагнитное происхождение (генера-
торы тока).
Сторонние силы характеризуют работой, которую оии совершают над
перемещаемыми зарядами. Величина, равная работе сторонних сил над еди-
ничным положительным зарядом, называется электродвижущей силой (э.д.с.),
действующей в контуре или на участке цепи:
(13.13)
Из сопоставления формул (13.13) и (12.19) следует, что размерность э.д.с.
совпадает с размерностью потенциала, т.е. э.д.с. измеряется в вольтах.
Любое устройство, в котором возникают сторонние силы, называют ис-
точником тока. Реальный источник тока имеет э.д.с. <?и сопротивление г, ко-
торое обычно называют внутренним сопротивлением источника в отличие от
внешнего сопротивления R цепи (в генераторе г — это сопротивление обмоток,
в аккумуляторе - сопротивление раствора электролита и электродов). При
расчете цепей реальный источник заменяют идеальным источником с э.д.с. S,
внутреннее сопротивление которого равно нулю, и последовательно включен-
ным с ним сопротивлением г.
Источники, используемые в цепях постоянного тока, имеют два электро-
да (один электрод положительный, а другой - отрицательный) и предназначе-
ны для перемещения положительных зарядов от электрода с меньшим потен-
циалом к электроду с большим, а отрицательные наоборот. Поэтому работа
стороних сил Ястор > 0 (а значит и э.д.с. S> 0), если положительные заряды
257
внутри источника переносятся от отрицательного электрода к положительно-
му. В противном случае А^р < 0 и 8< 0.
Рассмотрим участок цепи, содержащий источник э.д.с. 8 с внутренним
сопротивлением г и внешнее сопротивление R (рис. 13.7), по которому течет
ток I в указанном направлении.
Работа, совершаемая всеми силами при перемещении заряда q на участке
а-b цепи, равна
Аа-b = ^эл. + ^стор.>
где Аэя = q (сра - ф/,) - работа сил электрического поля (согласно указанному
на рисунке направлению тока, полагаем, что фо > ф/,); А^р - работа сторон-
них сил. Следовательно,
Л-ft = <7 (фа-ф*)+ '?<?•
Величина, численно равная работе, совершаемой электрическими и сто-
ронними силами при перемещении единичного положительного заряда, назы-
вается падением напряжения (напряжением) U на данном участке цепи. Поэ-
тому для участка а-6
Ц^ = ^ = (Фа-<Рй) + « (13-14)
Если источник включен так, как показано иа рис. 13.8, то работа сторон-
них сил будет отрицательной, поскольку внутри источника заряды будут
перемещаться в направлении убывания потенциала. В этом случае
Ц^ = ^ = (Фв-Фй)-«
Выражения (13.14) и (13.15) можно объединить:
Ua_b = ^a_b±8, (13.16)
где знак «+» перед э.д.с. соответствует случаю, если источник способствует
движению положительных зарядов в направлении тока иа участке, а знак
«-» - если препятствует.
Разделив напряжение Ua_b на полное сопротивление Ra_b = R + r участ-
ка, получим
дФо-й ± 8
/=^-- (13-17)
Формула (13.17) выражает закон Ома для неоднородного участка цепи.
Понятно, что если участок содержит N сопротивлений Rt и М источников
Э.Д.С. 8р то
(13.15)
(13.18)
258
где Дф/ - разность потенциалов на кон- ___।—ц—. с г J <g
цах сопротивления R,. Следовательно, — . .... * 1 _*|+
падение напряжения на неоднородном 1
участке цепи равно алгебраической сум-
ме падений напряжений на однородных
участках и действующих э.д.с. ^>мс- 13-9
Если цепь замкнута (рис. 13.9), то, положив в (13.17) Афа_/, = 0, получим
выражение закона Ома для замкнутой цепи:
а
/=i77- (1319>
Разность потенциалов между точками а и с цепи равна падению напряже-
ния на сопротивлении R
IR- S-Ir
и совпадает с разностью потенциалов между точками би с (так как (ра = ф/,)
которая равна напряжению на зажимах источника.
Итак, замкнутая цепь, в которой ч>
течет постоянный ток, должна содер-
жать источник, внутри которого поло-
жительные заряды движутся под дей-
ствием сторонних сил в направлении
возрастания потенциала (от отрица-
тельного электрода к положительно-
му), а во всей остальной цепи - в на-
правлении убывания потенциала. На
рис. 13.10 показано распределение по-
тенциала в замкнутой электрической
цепи, содержащей реальный источник
и внешнее сопротивление R.
Разветвленные цепи постоянного тока. Законы Кирхгофа
Определим некоторые понятия, принятые в электротехнике:
- узел - это точка, в которой сходятся более, чем два проводника;
- ветвь — это последовательное соединение сопротивлений, конденсаторов и
источников тока, расположенное между двумя узлами;
- контур - это замкнутый участок цепи, содержащий несколько последова-
тельных ветвей;
- независимый контур — контур, который содержит хотя бы одну ветвь, не
принадлежащую другим контурам, т.е. его нельзя получить наложением дру-
гих контуров друг на друга.
Расчет электрической цепи в общем случае предполагает нахождение
токов во всех ветвях цепи.
Существует два способа расчета разветвленных электрических цепей.
Один состоит в том, чтобы путем эквивалентных преобразований (замены
259
последовательно и параллельно соединенных элементов цепи эквивалентны-
ми) свести исходную разветвленную цепь к одному контуру, а затем, приме-
нив закон Ома для замкнутой цепи, найти ток в неразветвленной части. Далее,
применяя законы Ома для однородных и неоднородных участков цепи, обрат-
ными преобразованиями нужно вернуться к исходной цепи, последовательно
вычислив падения напряжения на каждом из участков и токи во всех ветвях.
Однако не все схемы можно преобразовать к одному замкнутому контуру,
поэтому этот путь не является универсальным.
Другой способ, не требующий преобразований цепи, основан на приме-
нении законов Кирхгофа. Первый из них относится к узлам цепи: алгебраичес-
кая сумма токов, сходящихся в узле, равна нулю:
11, = О, (13.20)
при этом ток, текущий к узлу, считается имеющим один знак (плюс или
минус), а ток, текущий от узла - имеющим другой знак (минус или плюс).
Первый закон Кирхгофа вытекает из закона сохранения заряда: поскольку в
узле не может происходить накопления зарядов, то суммарный заряд, прихо-
дящий в узел за любой промежуток
времени, должен быть равен заряду,
вытекающему из узла за это же время.
Выделим в разветвленной цепи
какой-либо контур (рис. 13.11) и запи-
шем закон Ома (13.17) для отдельных
его участков в виде:
Л (Я1+П) = Ф1-Ф2 + *1
h (^2 + ri) = Фг _ Фз + <?2 (13.21)
А(Лз+гз) = Фз-Ф1-<*з
Складывая левые и правые части
уравнений (12.21), получаем
Л (^1 +ri) +h (&2 + r2) +h (^з + гз)~ + &2~ ^з>
или
1L (R; + rd = 1 Sj. (13.22)
' J J
Соотношение (13.22) выражает второй закон Кирхгофа: для любого зам-
кнутого контура алгебраическая сумма падений напряжений в ветвях конту-
ра равна алгебраической сумме э.д.с. в этом контуре.
Применяя законы Кирхгофа к узлам и к различным замкнутым контурам,
входящим в состав разветвленной цепи, можно получить систему уравнений
для определения всех токов. Можно показать, что число независимых уравне-
ний всегда равно числу неизвестных токов. Если цепь содержит N узлов и В
ветвей с различными токами, то система должна содержать В уравнений, при-
чем N- 1 из них составлены по первому закону Кирхгофа, а К = В - (N - 1) -
260
по второму, где К - число независимых контуров. Прежде чем составлять сис-
тему уравнений по законам Кирхгофа, необходимо задать произвольным об-
разом направления токов в каждой ветви и выбрать направления обхода неза-
висимых контуров (по часовой стрелке или против, причем для каждого кон-
тура можно выбрать свое направление обхода). При составлении уравнений
по второму закону Кирхгофа соблюдают правила знаков: падения напряжений
на однородных участках контуров считаются положительными, если направ-
ления токов в них совпадают с направлением обхода, и э.д.с. считают положи-
тельными, если они действуют в направлении обхода, т.е. направление движе-
ния пожительных зарядов внутри источника (от «минуса» к «плюсу») совпа-
дает с направлением обхода контура.
Измерение токов и напряжений
Для измерения тока в проводнике и па-
дения напряжения на нем в электрическую
цепь включают амперметр и вольтметр, при-
чем амперметр включают последовательно с
этим проводником, а вольтметр - параллель-
но к нему (рис. 13.12). ^ис- НИ
Основной частью этих приборов является гальванометр, принцип работы
которого основан на том, что магнитное поле оказывает ориентирующее дей-
ствие на виток с током (см. §14), причем отклонение стрелки прибора пропор-
ционально силе протекающего через него тока.
Для измерения токов и напряжений гальванометры включают по схеме
амперметра или вольтметра. Поскольку измерительные приборы не должны
менять токи и напряжения на участках цепи, то внутреннее сопротивление ам-
перметра должно быть очень малым, а вольтметра - большим.
Каждый гальванометр рассчитан на из- j
мерение определенного максимального тока у /"ч*
/тах, соответствующего отклонению стрелки------------(G)------------
прибора на всю шкалу. Такой гальванометр 7Ш
можно непосредственно изпользовать для I дш
измерения токов силой I < Чтобы изме- । ।
рять токи I > /тах, параллельно гальваномет- у у j
ру включают дополнительное сопротивле-
ние Яш, которое называют шунтам (рис. 13.13). Необходимое значение Яш
для измерения тока I>Imax подбирают таким образом, чтобы через прибор
протекал ток силой 1тях, а ток 1Ш = I -отводился через шунт (по первому
закону Кирхгофа: I -- 7Ш = 0). Поскольку прибор и шунт подключены к
одним и тем же точкам цепи, то падение напряжения на внутреннем сопротив-
лении Rc гальванометра (сопротивлении витка) и шунте Яш одинаково:
Iraax Rg = 1ш Ицг
261
Рис. 13.14
Следовательно, через шунт потечет ток
. АпахЛ;
Ап_ р >
являющийся частью тока в цепи, равного &
I=Апах + Ап* или 1 = /щдх { 1 + }•
Лш
Откуда получим
Лш = -Л, (13.23)
где н = ///тах. ”
По закону Ома для однородного участка цепи предельно допустимое на-
пряжение, которое может измерить прибор, равно
Цпах = Алах &G-
Если необходимо измерить падение на-
пряжения U на сопротивлении R, которое
больше t/max, к гальванометру последова-
тельно подключают дополнительное сопро-
тивление Лд, которое называют добавочным
(рис. 13.14). Величину добавочного сопро-
тивления выбирают так, чтобы через прибор
и Лд тек ток силой 1тах. Напряжение на со-
противлении R будет равно падению напряжения на добавочном сопротивле-
нии и внутреннем сопротивлении прибора:
Ял + Кп
{RG + Яд), или U=Una№ -2=-* .
nG
Откуда получим
Лд = Л0(«-1), (13.24)
где п = U/Umax.
Из сказанного следует, что гальванометр с внутренним сопротивлением
Rg, рассчитанный на измерение тока /тах, можно использовать для измерения
токов 1< п /щах, если параллельно к нему подключить шунт, рассчитанный по
формуле (13.23). Если этот прибор нужно изпользовать как вольтметр для из-
мерения напряжений U<nImaxRc, то к нему необходимо последовательно
подключить добавочное сопротивление, величина которого должна быть оп-
ределена по формуле (13.24).
Работа и мощность постоянного тока. Закон Джоуля-Ленца
Рассмотрим произвольный однородный участок цепи (см. рис. 13.3),
между концами которого имеется разность потенциалов U= фа - фй. Через со-
противление R участка будет течь ток силой I, и за промежуток времени Az
через поперечное сечение проводника пройдет заряд 1щ = 1 Az. Силы электри-
ческого поля при этом совершат работу
262
A = Aq (<pfl - фй) = Д? U=IU At, (13.25)
которую принято называть работой тока.
Рассмотрим теперь неоднородный участок цепи, представленный на рис.
13.7-13.8. При наличии на участке цепи источника тока работу по переносу
заряда будут совершать силы электрического поля и сторонние силы, причем
если источник способствует движению положительных зарядов в направле-
нии тока (рис. 13.7), то работа сторонних сил положительна, в противном слу-
чае (рис. 13.8) - отрицательна:
Л = (фо - Фй) ±Лтор. = А$ (Дфа-Й ± <?) = /Афа-i At±ISAt,
где первое слагаемое представляет собой работу тока на участке цепи, а вто-
рое - работу источника.
Прохождение тока через проводник, обладающий сопротивлением, всег-
да сопровождается выделением теплоты. Нагревание проводника с током объ-
ясняется столкновениями носителей тока с узлами кристаллической решетки:
при столкновении часть кинетической энергии носителей тока передается ре-
шетке, увеличивая энергию теплового движения атомов вблизи положений
равновесия, это и означает увеличение температуры (см. формулу (II.7)).
Для однородных участков цепи, на которых не совершается механичес-
кая работа н ток не производит химических действий, работа тока будет затра-
чена на увеличение внутренней энергии проводника. Поэтому количество теп-
лоты Q, выделившейся в проводнике сопротивлением R за время At, будет
равно работе тока за это время:
Q = IUAt. (13.26)
Используя закон Ома (13.6), работу тока (13.25) и количество теплоты
(13.27) можно выразить любым из трех эквивалентных способов:
U2 ->
A = Q = IUAt = ^Ai = I2RAt. (13.27)
К
Выражение для Q в виде
Q = I2RAt (13.28)
было получено экспериментально и носит название закона Джоуля-Ленца.
На неоднородных участках цепи выделяющаяся теплота в общем случае
не равна работе тока: на таких участках протекание тока обычно сопровожда-
ется не только нагреванием проводников, но и другими процессами, связан-
ными с превращением энергии.
Рассмотрим в качестве примера зарядку и разрядку источника тока, на-
пример аккумулятора. В цепи, представленной на рис. 13.8, при указанном на-
правлении тока будет происходить зарядка источника, сопровождаемая хими-
ческими процессами. Работу тока
Л=7Дфа_6Дг, (13.29)
используя закон Ома для неоднородного участка цепи (13.17)
263
R + r
можно представить в виде
[(Дфо-л)2 - <?Дфо-л] & 2
А = ---*a-w_ = [ / <? + /2(Л + r)j д,
Л *+* г
Слагаемое 1S Аг представляет собой часть работы тока, затраченную на
увеличение энергии источника (зарядку аккумулятора), a I2(R + г) Аг - тепло,
выделившееся за время Аг на сопротивлении R и внутреннем сопротивлении
г аккумулятора (см. (13.28)).
В цепи, представленной на рис. 13.7, при указанном направлении тока
будет происходить разрядка аккумулятора. В этом случае ток на участке цепи
равен
^9a-b+S
R + r ’
и работу тока можно представить в виде
, гл л, [(Лфа-й)2 + ^ДФа-б]^ , . ,2(В
А=1 Ьфа_ь & = —-------—-----------= [ -1 S + I2(R + г)] АГ.
Л + Г
Слагаемое Istst представляет собой энергию, выделяемую аккумулято-
ром при его разрядке.
Как видим, независимо от направления тока на участке, количество теп-
лоты, выделившейся за время Аг на всех сопротивлениях (включая внутреннее
сопротивление источника) неоднородного участка цепи, будет равно
б = /2(Я + г)ДГ. (13.30)
Если цепь замкнута (рис. 13.9), то Дфа-б = 0 и работа источника тока
A = IS\t. (13.31)
Поскольку в замкнутой цепи носители тока перемещаются блогодаря ис-
точнику, то работа (13.31) определяет полную работу источника за время Аг.
Если ток в цепи не производит никаких действий, кроме нагревания провод-
ников, то количество теплоты, выделившейся в цепи (на внешнем сопротивле-
нии и внутреннем сопротивлении источника) за это время, будет равно
л2
0 = /<?АГ = ^—Ar = /2(j? + r)Af, (13.32)
при этом на внешнем сопротивлении R цепи будет выделено тепло
S2 о
а=7~^лаг=/2ядг. (1333)
+ Г)
Работа, совершаемая источником за единицу времени
А
N=~ = 1S, (13.34)
называется полной мощностью источника тока, а количество теплоты, выде-
ляющейся в проводнике сопротивлением R за единицу времени
264
ЛГК = £, (13.35)
тепловой мощностью тока.
Если цепь замкнута, то на внешнем сопротивлении (которое часто назы-
вают нагрузкой) выделяется тепловая мощность
ЛГ = ^ = —R = I2R, (13.36)
R М (R + r)2 v 7
называемая полезной мощностью. Для такой цепи разность
7
Nr = N-Nr = —~ г = 12г
r (R +г)2
определяет тепловую мощность, выделяющуюся внутри источника (это часть
полной мощности источника, которая тратится бесполезно на выделение
тепла внутри источника).
Для замкнутой цепи отношение полезной мощности NR к полной N назы-
вают коэффициентом полезного действия (к.п.д.) источника'.
_^r_ R
Л N R + r'
Очевидно, что к.п.д. источника может быть определен как
Qr
п=е‘>
Рассмотрим более подробно, как зависит полезная мощность и к.п.д. ис-
(13.37)
(13.38)
точника от внутреннего сопротивления г источника и внешнего сопротивле-
ния R цепи.
Полная мощность N (13.34) с учетом закона Ома (13.19) может быть за-
писана в виде
N=-^—.
R + r
Откуда следует, что полная мощность источника достигает максимально-
го значения при R = 0, т.е. при коротком замыкании источника. Полезная
мощность и к.п.д. источника при этом становятся равными нулю (см. форму-
лы (13.36), (13.37)).
Полезная мощность в зависимости от тока изменяется по параболическо-
му закону, в чем легко убедиться, если представить NR в виде
ArR = AT-Ar,. = M-72r.
Для нахождения значения максимальной полезной мощности исследуем
зависимость NR на экстремум:
dNK S я1
= 21тг = 0, /т=2^, Мттах= •
Очевидно, что ток в цепи будет равен Zm = S/2r, если внешнее сопротив-
ление R равно внутреннему сопротивлению источника г (см. формулу (13.19)).
265
К.п.д. источника
л 1
П ” R + г ~ 1 + r/R
увеличивается при возростании сопротивления внешней цепи и при токе, со-
ответствующем максимальной полезной мощности, равен т|т = Vi.
Зависимости N, NR, ц от величи-
ны внешнего сопротивления пре-
дставлены на рис. 13.15. Как видим,
условия получения максимальной
полезной мощности и максимального
к.п.д. источника несовместимы: ког-
да NR достигает наибольшего зна-
чения, к.п.д. равен r|m = Vi. Когда же
к.п.д. близок к единице, мощность
R Nr мала по сравнению с максималь-
ной мощностью, которую мог бы раз-
вить данный источник.
Как следует из зависимости NR от R, любую полезную мощность No
(меньшую максимальной) можно получить при двух разных сопротивлениях
/?! и R2 внешней цепи. Очевидно, что для получения заданной полезной мощ-
ности следует выбирать большее внешнее сопротивление, так как к.п.д. источ-
ника при этом выше.
Для получения большого к.п.д. источника должно выполняться условие
1 + r/R я 1, т.е. внешнее сопротивление должно быть R » г. Если же R « г,
то практически вся мощность будет выделяться в источнике, что может при-
вести к его перегреву и выходу из строя.
Электролиз
Рассмотрим некоторые особенности электрического тока в проводящих
жидкостях - электролитах. В общем случае электролитами называют раство-
ры и расплавы солей, щелочей и кислот, способные проводить ток. В этих сре-
дах носителями тока являются положительно и отрицательно заряженные
ионы, которые образуются в результате электролитической диссоциации -
процесса распада электролита на ионы
при растворении, никак не связанного
с наличием тока.
Прохождение постоянного тока в
электролитах всегда сопровождается
выделением на электродах химических
составных частей электролита. Этот
процесс называется электролизом.
Рассмотрим два электрода, поме-
щенные в электролит (рис. 13.16). По-
266
ложительно и отрицительно заряженные ионы под действием электрического
поля будут двигаться в противоположные стороны: положительные ионы (их
называют катионами) к отрицательному электроду - катоду, а отрицательно
заряженные (анионы) - к положительному электроду - аноду. Достигая анода,
отрицательный ион передает свой заряд электроду, отчего один или несколько
электронов (в зависимости от величины заряда иона) проходят по внешней
цепи, и ион превращается в нейтральный атом или молекулу, выделяющуюся
на аноде. Положительный ион, напротив, заимствует от катода один или не-
сколько электронов и, нейтрализуясь, выделяется на катоде. Эти процессы
были впервые изучены Фарадеем, который экспериментально установил, что
масса т вещества, выделившегося на каком-либо электроде, пропорциональна
заряду Ад, прошедшему через электролит:
/п = £Ад, пат m = kltst, (13.39)
где к - электрохимический эквивалент вещества.
Фарадей обратил внимание, что электрохимические эквиваленты различ-
ных веществ всегда пропорциональны атомной массе А и обратно пропорцио-
нальны валентности п, и установил зависимость к от отношения А/п (в химии
отношение А/п называют химическим эквивалентом):
1 Л
к=р~, (13.40)
где атомная масса А вещества выражена в [кг/моль], а коэффициент пропор-
циональности F = 9,6494-104 Кл/моль называется постоянной Фарадея.
Выражения (13.39) и (13.40) часто называют первым и вторым законами
Фарадея для электролиза.
Рекомендации по решению задач
Задачи, в которых неизвестная величина (сила тока, плотность тока, средняя скорость
упорядоченного движения носителей тока и т.п.) может быть найдена на основании оп-
ределений, решаются по формулам (13.1)-(13.5) и никаких особых трудностей не вызы-
вают.
Большая часть задач связана с расчетом параметров сопротивлений проводников и
образованных нз них цепей. Если в условии задачи указано, из какого материала изготов-
лен проводник, даны его геометрические размеры (длина, площадь поперечного сечения
илн объем) или масса, то для определения сопротивления проводника достаточно восполь-
зоваться формулой (13.7) и известными соотношениями между массой, плотностью и объ-
емом. Для решения задач о температурной зависимости сопротивлений проводников, как
правило, достаточно формул (13.7) и (13.8).
Прн расчете общего сопротивления цепи, составленной из нескольких проводников,
поступают таким же образом, как при расчете емкости батареи конденсаторов:
- прежде всего, нужно выяснить тип соединений (для этого, возможно, нужно будет нарисо-
вать схему по-другому); понять, какие из проводников соединены между собой последова-
тельно, а какие - параллельно;
- последовательно заменяя два (или более) сопротивления одним эквивалентным (при пос-
ледовательном соединении по формуле (13.11), при параллельном - по (13.12)), цепь посте-
пенно упрощают, пока не будет найдено общее сопротивление;
267
- если соединение проводников не относится ни к последовательному, ни к параллельному,
то общее сопротивление соединения можно найти сравнительно просто только в тех случа-
ях, когда в схеме имеются точки с одинаковым потенциалом: такие точки можно соединять
и разъединять, поскольку через проводник, включенный между ними, ток не течет. Соеди-
няя (если они были разъединены) и разъединяя (если они были соединены) точки с равным
потенциалом, можно сложное соединение проводников свести с комбинации последова-
тельных и параллельных соединений. Как и в случае батарей конденсаторов, точки с одина-
ковым потенциалом есть всегда в соединениях, обладающих осью или плоскостью симмет-
рии относительно точек входа и выхода (т.е. относительно точек подключения источника
тока). При этом если точки входа и выхода лежат на плоскости симметрии, то точки одного
потенциала находятся на концах проводни-
ков, которые «перечеркиваются» этой
плоскостью. Если плоскость симметрии
перпендикулярна линии, на которой лежат
точки входа и выхода, то равные потенциа-
лы имеют все точки пересечения этой плос-
кости с проводниками. Например, в извест-
ной схеме - мост сопротивлений, пред-
ставленной нарнс. 13.17, если Я] =Л2 и
/?з = /?4, то плоскостью симметрии является
Рис. 13.17
плоскость, проходящая перпендикулярно
рисунку через точки входа А и выхода В. При этом плоскость симметрии «перечеркивает»
сопротивление R5 и потенциалы в точках а и b будут одинаковы. Это означает, что через
проводник сопротивлением R5 ток не течет: его можно не учитывать удалив из цепи, или со-
единив между собой точки а и Ь. Если /?1 = R3 н R2 = Л4, то плоскость симметрии проходит
через точки а и Ь, которые будут иметь равные потенциалы. Легко понять, что рассмотрен-
ные случаи можно объединить: если /?1 R4 = R2 R2, то точки а и b имеют равные потенциа-
лы. Мост, в котором ток через сопротивление R5 отсутствует, называют уравновешенным
или сбалансированным.
В общем случае, когда нет точек с равным потенциалом, общее сопротивление цепи
определяют на основании законов Кирхгофа.
Задачи на определение силы тока в ветвях цепи или падения напряжения на отдель-
ных проводниках можно разделить на дае группы: первая из них охватывает цепи, которые
могут быть приведены к одному контуру (путем замены нескольких проводников одним
эквивалентным), другая - разветвленные цепи, которые простыми преобразованиями при-
вести к одному контуру нельзя.
Задачи первой группы можно решать в следующей последовательности:
а) начертить схему цепи, на которой отметить все узлы и проставить направления токов во
всех ветвях (в общем случае во всех ветвях токи разные); если направления токов неизвест-
ны, то в таких ветвях направления токов можно проставить произвольно (если при расчетах
окажется, что ток отрицателен, то это означает, что направление тока противоположно тому,
которое указанно на рисунке);
б) путем эквивалентных преобразований (замены последовательно и параллельно соедннен-
. ных проводников эквивалентными) свести
а________I-------1________1^ h исходную цепь к одному контуру, содержа-
, J +|1 щему источник тока и общее сопротивление
Яцепи Цепи (рис. 13.18);
I ^цепи в) применив закон Ома (13.19) для замкнутой
-----------1 I------------------ цепи, найти ток /, текущий через сопротивле-
ние. 13.18-----------------------ние ^цепи и источник;
268
г) применяя законы Ома для однородных (формула (13.6)) и неоднородных (формула
(13.17)) участков цепи, определить падения напряжения на внешнем участке цепи и источ-
нике: — I Т^цепи, ^а-Ь ~
д) если сопротивления Rj, составляющие ЛцеПи> соединены между собой последовательно,
то, зная ток I, по закону Ома (13.6) определить падение напряжения на каждом из них:
Uj = 7R/; если сопротивления Rj, составляющие Лцепи> соединены между собой параллель-
но, то, зная падение напряжения Ua-/» по закону Ома (13.6) для однородного участка опре-
делить токи через эти сопротивления: /, = U^f/Rj;
е) зная падения напряжения Uj между узлами цепи, по закону Ома (13.6) вычислить токи во
всех ветвях, включенных между этими узлами; зная токи I, в отдельных ветвях, по закону
Ома (13.6) определить падения напряжения на каждом из элементов, содержащихся в этих
ветвях;
ж) если падения напряжения н токи определены не на всех элементах цепи, то пункт е) сле-
дует повторять до тех пор, пока не будут найдены все необходимые по условию задачи па-
дения напряжения и токи.
Если цепь не замкнута (т.е. рассматривается участок цепи), то при решении задач
можно руководствоваться пунктами а)-ж), за исключением пункта в), в котором следует
использовать закон Ома (13.6), если цепь не содержит источников тока, илн (13.17), если
цепь содержит источник.
Задачи второй группы нужно решать на основании законов Кирхгофа. Общие пра-
вила расчета разветвленных цепей таковы:
а) начертить схему цепи, на которой отметить все узлы и произвольно проставить направле-
ния токов во всех ветвях;
б) написать уравнения, выражающие первый закон Кирхгофа для всех узлов, кроме одного;
при этом ток, текущий к узлу, считается имеющим один знак (плюс или минус), а ток, теку-
щий от узла - имеющим другой знак (минус или плюс);
в) произвольно выбрать направления обхода независимых контуров (одно и то же для всех
илн разные для каждого контура); прн составлении уравнений по второму закону Кирхгофа
нужно тщательно соблюдать правила знаков: падения напряжений на однородных участках
контуров считаются положительными, если направления токов в них совпадают с направле-
нием обхода н э.д.с. считают положительными, если они действуют в направления обхода;
г) если цепь содержит N узлов н В ветвей с различными токами, то составить для
К = В - (У - 1) независимых контуров уравнения, соответствующие второму закону Кирх-
гофа;
д) решить полученную систему уравнений; если в результате решения какие-либо токи ока-
жутся отрицательными, то в действительности их направления противоположны указанным
на рисунке.
К этой же группе можно отнести задачи на расчет цепей, содержащих сопротивления
н конденсаторы. Обычно в таких задачах требуется определить напряжение на конденса-
торе или его заряд. Для этого поступают следующим образом:
- поскольку в ветви, содержащей конденсатор,
ток течет лишь до тех пор, пока конденсатор не
зарядится (в течение очень малого промежутка
времени), то при расчете цепи ветвь, в которую
включен конденсатор , не учитывают, н схему
рисуют без нее (например, в цепи, представ-
ленной на рис. 13.19, это ветвь a-C-b-Rj-d);
- далее находят токи во всех ветвях и падения
напряжения между всеми узлами цепи (если
они остались в цепи после удаления из нее
ветви с конденсатором);
269
- затем цепь восстанавливают, т.е. включают в нее ветвь с конденсатором, и для опреде-
ления падения напряжения Uq на конденсаторе обходят любой из контуров, содержащих
конденсатор. Например, для контура a-C-b-R\~d-R-a при обходе по часовой стрелке
получим: (<ра - Фй) + (ф/, - -IR = 0, где фа - <рь = Uc - падение напряжения на конден-
саторе, ф/>-ф(/ = 0, поскольку ток в ветви a-C-b-Ry-d не течет. Следовательно,
Uc - IR = 0. Падения напряжения Uc на конденсаторе можно найти также, рассмотрев дру-
гой контур, содержащий источник. Рассмотрим контур a-C-b-Ri-d-'E-a. Обходя его про-
тив часовой стрелки, получим: (фа - ф£>) + (<р/> - Ф<у) + (ф<^ - фе) - Е = 0, где <ра - <р/> = Ос,
Ф2> - ф</ = 0, ф</ - фе = I г. Откуда находим: Uq + Ir - Е = 0. Если учесть, то ток в цепи равен
7= Е/(Л + г), то в обоих рассмотренных случаях Uc = Е R/(R + г);
- наконец, заряд конденсатора определяют по формуле: q = С Ис.
При решении задач, связанных с расчетами шунтов и добавочных сопротивлений для
гальванометров, можно использовать формулы (13.23)—(13.24). Если шкала гальванометра
с внутренним сопротивлением Rq рассчитана на максимальный ток 7тах, то им можно
измерять токи I < /тах н напряжения U < /тах Лд. Чтобы расширить пределы измерения
токов в п раз, параллельно гальванометру нужно подключить шуит, сопротивление кото-
рого рассчитывается по формуле (13.23). Для увеличения в п раз пределов измерения на-
пряжений к гальванометру последовательно подключают добавочное сопротивление, рас-
считанное по формуле (13.24). Прн этом следует помнить, что для измерения тока в про-
воднике амперметр включают последовательно с этим проводником, а вольтметр - парал-
лельно к нему.
Задачи на работу, мощность н тепловое действие можно разделить на две группы.
Задачи первой из них решаются аналогично задачам на расчет токов в ветвях цепи и па-
дений напряжений иа ее элементах. Для их решения составляют те же уравнения, но к
ним добавляют формулы (13.25)—(13.38):
- работа тока на однородном и неоднородном участках цепи определяется формулами
(13.25), (13.29); для нахождения полной работы источника тока в замкнутой цепи нужно ис-
пользовать формулу (13.31);
- количество теплоты, выделившейся иа однородном участке цепи, можно определить по
любой из формул (13.27); количество теплоты, выделившейся на всех сопротивлениях не-
однородного участка цепи - по формуле (13.30), а в замкнутой цепи (если ток не производит
никаких действий, кроме нагревания проводников) - по формулам (13.32)—(13.33);
- если в задаче речь идет о тепловой мощности тока, полной или полезной мощности источ-
ника тока, то необходимо использовать формулы (13.34)—(13.36);
— для определения к.п.д. источника нужно найти полную и полезную мощность или количе-
ство тепла, выделившегося во внешней цепи и во всей цепи, н воспользоваться формулами
(13.37) или (13.38).
К задачам первой группы относятся также задачи на расчет цепей, содержащих на-
гревательные приборы (электрические кипятильники, плитки и т.п.). Так как нагреватель-
ные приборы обычно подключают к источнику постоянного напряжения, величина кото-
рого ие зависит от внешней цепи, то для расчета количества теплоты (или мощности),
выделяющегося на разных проводниках, удобно использовать формулу (13.27) в виде
6= U2&/R (или Л’= U2/R).
К задачам второй группы отнесем задачи о превращении электрической энергии в
механическую и тепловую. Решение таких задач основано на совместном использовании
законов постоянного тока и закона сохранения энергии.
Последнюю часть задач на постоянный ток составляют задачи на электролиз. В боль-
шинстве случаев для решения таких задач достаточно законов Фарадея (13.39)—(13.40) и
некоторых соотношений, связывающих данные задачи с величинами, входящими в законы
Фарадея: ими могут быть зависимости толщины слоя металла, выделяющегося на электро-
270
де, скорости роста этого слоя, расхода электроэнергии от массы вещества и времени
электролиза и др. Если в задаче рассматривается выделение газа при электролизе, то со-
вместно с законами Фарадея нужно использовать уравнения состояния идеального газа.
Задачи
Сипа и плотность тока
13.1. Определить величину средней скорости направленного движения
электронов вдоль медного проводника поперечным сечением 5 = 1 мм2, по ко-
торому течет ток силой 1= 10 А. Заряд электрона |е| = 1,610'19 Кл, плотность
меди р = 8,9 г/см3, относительная атомная масса А = 64 а.е.м. Считать, что на
каждый атом меди приходится один электрон проводимости.
• Решение. При наличии электрического тока за время А/ через поперечное сечение $ про-
водника пройдет заряд
Ад = |е| п $<и > (1)
где < и > - средняя скорость направленного движения электронов.
Поскольку сила тока в проводнике равна
А/ ’
а концентрация электронов (см. §9)
т ЪТ
где т = р К-масса проводника, ц=Л-10 кг/моль - молярная масса меди, товыражение (1)
можно представить в виде
7Д/ = |е|—— NAS<v>At,
Л-ИТ3 К А
или
/=|е|7^ NKS<M>.
Л-10 3
Откуда находим среднюю скорость направленного движения электронов:
< и > = » 7,5- 10"4 м/с.
|е|рЯЛГА
„ 7Л40~3 - , л-4 /
• Ответ-. <и> = ——7,540 м/с.
|e| р S Na
13.2. Конденсатор емкостью С= 100 мкФ, заряженный до напряжения
U = 300 В, разряжается в течение времени Дг = 0,1 с. Определить среднее зна-
чение силы тока при разряде конденсатора.
13.3. Сила тока в лампочке карманного фонаря равна 7= 0,32 А. Сколько
электронов проходит через поперечное сечение нити накаливания за t = 0,1 с?
Заряд электрона |е| = 1,610'19 Кл.
13.4. Через поперечное сечение проводника 5=5 мм2 за время t= 10 с
прошел заряд q = 100 Кл. Определить плотность тока в проводнике.
13.5. При плотности тока J = 10‘2 А/м2 в пучке электронов средняя ско-
рость их направленного движения равна < и > = 5103 м/с. Определить объем-
ную плотность заряда в пучке.
13.6. Определить среднюю скорость направленного движения электронов
в проводнике при силе тока в нем 1= 10 А. Площадь поперечного сечения
271
проводника 5=1 мм2, концентрация свободных электронов п = 1028 м*3. Заряд
электрона |е| = 1,6-10’19 Кл.
13.7. По прямому проводнику длиной 1= 1 м течет ток силой 1= 10 А.
Определить средний суммарный импульс электронов в проводнике. Заряд
электрона |е| = 1,6-10"19 Кл, масса т = 9,1-10’31 кг.
13.8. Определить ток, создаваемый электроном, движущимся в атоме во-
дорода по орбите радиусом г = 0,5-10'10 м. Заряд электрона |е| = 1,6-10’19 Кл,
масса т = 9,1-10‘31 кг.
13.9. Определить заряд, который прошел через поперечное сечение про-
водника в течение времени t = 10 с при равномерном возрастании силы тока в
проводнике за это время от /0 = 0 до / = 3 А.
13.10. На обкладках плоского конденсатора с площадью квадратных
пластин 5 = 400 см2 и расстоянием между ними d = 2 см поддерживается на-
пряжение U = 120 В. В пространство между обкладками со скоростью
и = 10 м/с вдвигают диэлектрическую пластину толщиной d и проницаемос-
тью е = 2. Определить силу тока в цепи.
• Решение. Если диэлектрическая пластина вдви-
нута в конденсатор на расстояние х (рис. 13.20),
то полученную систему можно рассматривать как
два конденсатора емкостями
eeolx sol(l-x)
С2= d
(где / = Vs - длина обкладки конденсатора), со-
единенных параллельно. При этом их общая ем-
кость равна
„ с . с Еео/х ер/(/-х) eU
С — С] + Сп — * + * — , (с х + Z — х).
а а а
Заряд конденсатора емкостью С, на обкладках которого поддерживается напряжение
U, равен
q = CU,
или
£п /
9=t/-^-[(e-l)x + Z].
Очевидно, что при увеличении х заряд будет расти, т.е. конденсатор будет заряжаться.
При этом ток в цепи будет равен
da Snl, U ел (е - 1) и Vs »
си d d
dx
где учтено, что о = .
{/^(e-lJoVs ...........
• Ответ'. 1=—--------j---= 10,6-10 8 А.
а
13.11. В электрической цепи после зарядки конденсатора емкостью
С = 1 мФ и расстоянием между обкладками d = 1 см до напряжения U= 100 В
272
начинают сдвигать обкладки с постоянной скоростью и = 10 м/с. Определить
величину и направление тока в цепи в начальный момент сдвига обкладок.
13.12. На обкладках плоского конденсатора поддерживается напряжение
U= 12 В. Одна из пластин движется навстречу другой таким образом, что рас-
стояние между ними меняется по закону d=dQ-ot [м], где Jo = O,l м,
и = 20 м/с, t - время в секундах. Определить направление тока и зависимость
силы тока в цепи от времени. Площадь каждой из пластин конденсатора
5= 7,2-10’3 м2.
Электрическое сопротивление.
Параллельное и последовательное соединение сопротивлений
13.13. Два проводника - медный и алюминиевый - имеют одинаковую
массу. Во сколько раз отличаются их сопротивления, если длина медной про-
волоки в 10 раз больше длины алюминиевой? Плотность меди в 3,3 раза боль-
ше плотности алюминия, а удельное сопротивление - в 1,65 раза меньше.
• Решение. Сопротивление проводников зависит от их формы и размеров. Если проводник
имеет форму цилиндра постоянного поперечного сечения, то его сопротивление равно
где р - удельное сопротивление проводника, Z - длина проводника, $ - площадь его по-
перечного сечения.
Следовательно, отношение сопротивлений медного н алюминиевого проводников
равно
*м Рм /м ...
^а Ра /а
где индексы «м» и «а» относятся к меди и алюминию соответственно.
Если массу проводника выразить через плотность материала р0 и объем
т = ро V, или т = р01S,
то выражение (1) можно представить в виде
rm РмАи тАРОм Рм/м Ром
Ра /а тмР0А Ра/а2 Роа
где учтено, что ты = тА.
С учетом условия задачи
/“-Ю Рм 1 РОм - -
‘а Ра ’ 1-65’ Р0А-3’3’
получим
/с»
— = 200.
я ra
• Ответ: -г— = 200.
ЛА
13.14. Во сколько раз изменится сопротивление проводника, если его
длину уменьшить на и = 20%, а площадь поперечного сечения увеличить на
т = 50%?
273
13.15. Определить массу медного проводника, площадь поперечного се-
чения которого S=6-10’3 см2, а сопротивление R-3 Ом. Плотность меди
р0 = 8,9-Ю3 кг/м3, удельное сопротивление р = 1,8-10'8 Ом-м.
13.16. У проводника длиной I н площадью поперечного сечения S удель-
ное сопротивление меняется вдоль него по закону р = ах, где а - известная
постоянная, х - расстояние, отсчитываемое от одного из концов проводника.
Определить сопротивление проводника.
13.17. Нихромовая спираль нагревательного элемента должна иметь со-
противление R = 30 Ом при температуре накала t = 900°С. Какой длины надо
взять проволоку поперечным сечением S = 0,6 мм2, чтобы сделать эту спи-
раль? Удельное сопротивление нихрома при t0 = 0°С равно р0 = 1,1-1 О’6 Ом-м,
температурный коэффициент сопротивления а = 10-4 град’1. Тепловым расши-
рением проволоки пренебречь.
• Решение. Сопротивление проволоки длиной I и поперечным сечением S при t0 = 0°С
равно
Ro- s
При повышении температуры удельное сопротивление проволоки увеличится и при
температуре t станет равным
р = р0(1 +а0-
Поскольку по условию задачи изменением длины и площади поперечного сечения
проволоки можно пренебречь, то при температуре t сопротивление проволоки
ро(1+<хг)/
Л= .
Следовательно, для изготовления нагревательного элемента с заданным сопротивле-
нием R при температуре t нужно взять проволоку длиной
, R S , г-
I = —-------- «15 м.
Ро (1 + “ О
хч 1 R S ,
• Ответ: I = — ----- «15м.
РО (1 + а О
13.18. Вычислить отношение сопротивлений вольфрамовой проволоки
при температурах t0 = 0°С и t = 2400°С. Температурный коэффициент сопро-
тивления вольфрама а = 4,8-10’3 град’1. Тепловым расширением проволоки
пренебречь.
13.19. При какой температуре сопротивление серебряного проводника
станет в п - 2 раза больше, чем при t0 = 0°С? Температурный коэффициент со-
противления серебра а = 4,1-10’3 град’1. Тепловым расширением проводника
пренебречь.
13.20. На сколько отличаются сопротивления телеграфной линии длиной
I = 100 км летом и зимой, если она проложена железным проводом попереч-
ного сечения 5=10 мм2? Температуру летом считать равной tt - 25°, зимой -
t2 = - 20°С. Удельное сопротивление железа при Zo = 0°С равно р0 = 9,8-10’8 Ом-м,
температурный коэффициент сопротивления а = 6,2-Ю’3 град’1. Тепловым
расширением провода пренебречь.
274
13.21. Два проводника, соединенные последовательно, имеют сопротив-
ление в п = 6,25 раза больше, чем при их параллельном соединении. Опреде-
лить, во сколько раз сопротивление одного проводника больше сопротивле-
ния другого.
• Решение. Общее сопротивление двух проводников, соединенных последовательно, равно
^ПОСЛ. = + R2, (V
Где Я|, R2 - сопротивления каждого из проводников.
При их параллельном соединении общее сопротивление равно
*1 ^2
или с учетом выражения (1):
Лпа₽- ~R, + R2'
Ri R2
(2)
^пар._ р
япосл.
Поскольку по условию задачи
^посл. „ „
„ -п, или «поел._ п лпар.>
лпар.
то соотношения (1) и (2) можно представить в виде
п ^пар. = + ^2» п ^пар.= -^2*
Откуда получаем
Rt + R2 R-i + 2/Jj R2 + R2
= i „ - , или n =------------.
a/ R[ R2 R\ r2
Если обозначить отношение Ri/R2 через x, то последнее выражение преобразуется к
уравнению
п=х + 2 + 1/х, или х2-(л-2)х+1 =0.
Окончательно находим
Л1 л - 2 +'У (л - 2)2-4 . Rt Я-2-^(и-2?-4 „„
-£- = х =-----Ъ---i--= 4, или -б~ = х~---------т--------= 0,25.
Л2 Z Л2 Z
Ri л - 2 ± V (л — 2)^ — 4 R\ Ri
• Ответ: — =------i---1--; — = 4, или ~х~ = 0,25.
Л2 2 ix'2. *'‘2
13.22. Общее сопротивление двух проводников, соединенных последова-
тельно, равно 7?! = 5 Ом, а соединенных параллельно - R2 = 1,2 Ом. Опреде-
лить сопротивление каждого проводника.
13.23. Из куска проволоки сопротивлением Ro= 10 Ом сделано кольцо.
Где следует присоединить провода, подводящие ток, чтобы сопротивление
кольца равнялось R = 1 Ом?
13.24. Как нужно соединить три сопротивления Й1 = 2 Ом, R2 = 3 Ом и
R3 = 6 Ом, чтобы их общее сопротивление было равно R = 4 Ом?
13.25. Двенадцать проводников сопротивлением R= 16 Ом каждый со-
единены по три последовательно в четыре параллельные цепи. Определить
общее сопротивление цепи.
13.26. Последовательно соединены п равных сопротивлений. Во сколько
раз изменится сопротивление цепи, если их соединить параллельно?
275
13.27. На сколько равных частей требуется разрезать проводник, чтобы
при параллельном соединении частей получить сопротивление в п раз мень-
шее?
13.28. Из одинаковых сопротивлений по R = 5 Ом каждое требуется полу-
чить сопротивление Ro = 3 Ом. Как их следует соединить для того, чтобы
обойтись наименьшим числом сопротивлений?
13.29. Найти сопротивление между точками А и В цепи, изображенной на
рис. 13.21, а, если R = 4 Ом.
• Решение. Три сопротивления R, 2R и R, подсоединенные к точкам с и d цепи, соединены
между собой последовательно. Их общее сопротивление
RX=R + 2R + R = 4R.
Заменив указанные сопротивления одним эквивалентным Л। (рис. 13.21, б), легко за-
метить, что оно оказывается включенным параллельно сопротивлению 2R. Следовательно,
общее сопротивление участка цепи между точками с и d
111 в *12R 87? 4 „
R<^d~Rx + 2R’ или Rc~d~ RX^2R 6 3R'
С учетом сопротивления Rc-d цепь можно преобразовать к виду, показанному иа рис.
'<3.21, в, откуда видно, что сопротивления R, Rc_j и R соединены между собой последова-
тельно. Заменив эти три сопротивления одним
R2 = R + Rc_d + R = R + *6R + R = l06R,
цепь преобразуем к виду, представленному иа рис. 13.21г.
Очевидно, что сопротивления 2R и R2, включенные между точками а и Ъ, между собой
соединены параллельно. Их общее сопротивление
-1_ = -L + -L
Ra-b R2 2R’
D R*2R l0AR2R 5 „
н™ Ra~b R2 + 2R iaAR + 2R 4Л-
276
После замены сопротивлений 2R и на эквивалентное сопротивление Ra-b получаем
цепь (рис. 13.21, д), содержащую три сопротивления R, R&_b и соединенных последова-
тельно. Искомое сопротивление цепи
^цепи = + R-a—b + R ~ R + ^4 R + R = R = 13 Ом.
13.30. Найти сопротивление цепи между точками А и В, изображенной на
рис. 13.22, если Rt = Т?4 = 5 Ом, R2 = 2 Ом, R3 = 4 Ом.
13.31. Найти сопротивление цепи между точками А и В, изображенной на
рис. 13.23, если Rt = 5 Ом, R2 = 15 Ом, R3 = 10 Ом.
13.32. Найти сопротивление цепи между точками А и В, изображенной на
Рис. 13.25 Рис. 13.26
13.33. Найти сопротивление цепи между точками Ли В, изображенной на
рис. 13.25, если R = 4 Ом.
13.34. Определить сопротивление цепи, показанной на рис. 13.26.
Рис. 13.27 Рис. 13.28
13.35. Найти сопротивление цепи между точками А и В, изображенной на
рис. 13.27, если R = 1 Ом.
13.36. Каким должно быть сопротивление г в цепи, изображенной на рис.
13.28, чтобы суммарное сопротивление цепи было так же равно И?
277
13.37. Найти сопротивление цепи между точками А и В, изображенной на
рис. 13.29, а, если R = 1 Ом.
• Решение. На первый взгляд в представленной цепи нет ни последовательных, ни парал-
лельных соединений сопротивлений. Действительно, между любой парой сопротивлений
имеется узел, к которому подсоединен проводник или третье сопротивление.
Однако нетрудно заметить, что в данной схеме сопротивления включены симметрич-
но - в схеме есть продольная ось симметрии, проходящая через точки А и В, и поперечная
ось симметрии CD, проходящая через средние сопротивления 2R. Это означает, что в цепи
имеются точки с равными потенциалами, разъединив или соединив которые, можно свести
задачу к расчету более простой цепи.
Продольная ось симметрии АВ указывает, что потенциалы в точках а и Ь, а также
в точках cad будут равны. Поэтому разности потенциалов Д<ра~/, = Q Д<рс_</ = 0 и по со-
противлениям R ток не пойдет. Следовательно, не нарушая режима работы цепи, эти
точки можно разъединить или соединить, выбросив сопротивления R.
Если рассматриваемые точки разъединить, то цепь преобразуется к виду, показаному
на рис. 13.29, б. Преобразованная цепь содержит две параллельно соединенные ветви
А-а-с-В и A-b-d-B, в каждой из которых по три сопротивления, соединенные между
собой последовательно. Сопротивление одной ветви равно
278
RA-a-c-B = ^A-W-в - 27? + 2R + 2R = 6R,
а общее сопротивление цепи
11 1 RA-a-c-B RA-b-d~B , „ , Л
® = о + о > ^цепи - „ „ -3R-3 Ом.
лцепи лА-о-с-В лА-о-я-В лА-о-с-В + ла-5ч7-В
Если же точки а и Ь, с и d соединить между собой, то исходная цепь может быть
представлены в виде трех последовательно соединенных звеньев, каждое из которых со-
держит два сопротивления, соединенные параллельно друг другу (рис. 13.29, в). Сопро-
тивление каждого звена равно
1_____L 1 о 27? 2Я
7?звена 2Я + 2Я’ *звена 27?+ 27? ’
а общее сопротивление цепи
^цепи = ^звена + ^звена + ^звена = 3 7? = 3 Ом.
Рассмотрим теперь ось симметрии CD. Чтобы найти точки с равными потенциалами,
на наличие которых указывает эта ось, нарисуем цепь по-другому, заменив сопротивления
27?, которые перечеркивает ось CD, двумя сопротивлениями R, соединенными последова-
тельно (рис. 13.29, г).
Точки е и f имеют одинаковые потенциалы, поэтому их можно соединить и цепь
преобразовать к виду, показанному на рис. 13.29, д. Легко заметить, что теперь цепь со-
держит два одинаковых моста сопротивлений, соединенных между собой последовательно,
причем оба моста уравновешены. Поэтому сопротивления R, включенные между точками
а-Ь и c-d, можно изъять из цепи, а схему преобразовать к виду, показанному на рис.
13.29, е.
Сопротивление каждого из мостов сопротивлений равно
1 _ 1 1 о =3
7?моста 277 + 7? 2R + R’ моста 2*'
а абщее сопротивление цепи
^цепи = 2 7?моста = 37? = 3 Ом.
• Ответ: 7?цепи = 3 Ом.
13.38. Три равных сопротивления были соединены последовательно.
Затем вход цепи соединили проводником с точкой, лежащей между вторым и
третьим сопротивлениями, а выход - с точкой между первым и вторым сопро-
тивлениями. Начертить схему и определить, как изменилось сопротивление
цепи. „
7? Ы
Рис. 13.30 Рис. 13.31
13.39. Определить сопротивление цепи, показанной на рис. 13.30.
13.40. Определить сопротивление цепи, показанной на рис. 13.31.
13.41. Найти сопротивление цепи между точками А и В, изображенной на
рис. 13.32, если R = 3 Ом.
13.42. Найти сопротивление цепи между точками А и В, изображенной на
рис. 13.33, если R = 3 Ом.
279
Рис. 13.34
13.43. Найти сопротивление цепи между точками АиВ, изображенной на
рис. 13.34, если R = 8 Ом.
13.44. Найти сопротивление цепи между точками А и В, изображенной на
рис. 13.35, если Я = 1 Ом.
13.45. Найти сопротивление проволочного каркаса, имеющего форму
куба (рис. 13.36, а), при включении его в цепь между точками 1-7. Сопротив-
ление каждого ребра каркаса равно R.
• Решение. Расчет общего сопротивления каркаса куба аналогичен расчету цепи, рассмот-
ренной в задаче №13.37.
Нетрудно заметить, что в данной схеме имеется продольная ось симметрии, прохо-
дящая через точки 1 и 7. Поэтому точки 2, 4, 5 имеют одинаковые потенциалы и их можно
соединить в одну. Аналогично для точек 3,6, 8. В результате получим схему, содержащую
три последовательно соединенных звена, в каждом из которых содержатся параллельно
соединенные сопротивления (рис. 13.36, б). Общие сопротивления крайних звеньев оди-
наковы и равны 1111 R
й[ = Я + Я + Я’ ил Л1=У’
280
а сопротивление среднего звена
R2~ R R R R R R' “ *2=6‘
Следовательно, полное сопротивление каркаса
^каркаса в ^1 + R2 + R\ = Л + Л + 1*5 Л = R.
Рис. 13.37
13.46. Определить сопротивление цепи, изображенной на рис. 13.37,
между точками А и В. Сопротивление каждого звена равно R.
13.47. Определить сопротивление цепи, изображенной иа рис. 13.38,
между точками А и В. Сопротивление каждого звеиа равно R.
13.48. Решить задачу, аналогичную №13.45 при включении каркаса в
цепь между точками 1-2.
13.49. Решить задачу, аналогичную №13.45 при включении каркаса в
цепь между точками 1-3.
13.50. Цепь составлена из бесконечного числа ячеек, состоящих из трех
одинаковых сопротивлений R (рис. 13.39, а). Найти сопротивление цепи
между точками А и В.
а) б)
Рис. 13.39
• Решение. Так как цепь содержит бесконечно много ячеек, тц отделив от нее первую ячей-
ку, мь. получим ту же цепь, сопротивление которой равно сопротивлению Яцепи исходной.
Поэтому сопротивление всей цепи можно найти как (рис. 13.39, б)
^цепи = R + + R> или ^цепи ~ 7.R Лцепи - 2R2 = 0.
Лцепи + Л
Решив последнее уравнение относительно Лцепи, получим
_ 2Я + ^4Я2+8Я2 —
Кцепи =-------г-------= R (1 + <3).
• Ответ'. Лцепи - R (1 +
281
Рис. 13.40
Рис. 13.41
13.51. На рис. 13.40 пока-
зана бесконечная цепь, образо-
ванная повторением одного и
того же звена - сопротивлении
Я1 = 4 Ом и R2 = 3 Ом. Найти
сопротивление цепи между
точками А и В.
13.52. При каком сопро-
тивлении Rx в цепи, представ-
ленной на рис. 13.41, сопротив-
ление между точками А и В не
зависит от числа ячеек?
Закон Ома для однородного участка цепи
13.53. Чему равно удельное сопротивление проводника, если при силе
тока 7= 1 А падение напряжения иа нем равно U = 1,2 В? Диаметр проводника’
d = 0,5 мм, длина I = 47 мм.
• Решение. Поскольку иа участке цепи ие содержится источников э.д.с., то силу тока I
можно найти из закона Ома для однородного участка:
/="
1 R *
где сопротивление проводника
S
Выразив площадь S поперечного сечения проводника через его диаметр
4
получим
I-us_1tdu
pl 4 pl '
Откуда находим
Р = П^г 5,1 • 10"4 Ом м.
,2и 411
• Ответ', р = » 5,1-Ю"4 Ом-м.
13.54. Определить сопротивление проволоки, если по ней течет ток силой
1 = 0,1 А, а напряжение на ее концах равно U = 2 В.
13.55. За время t = 5 мин по проводнику прошел заряд q = 180 Кл. Опре-
делить падение напряжения иа проводнике, если его сопротивление равно
Л=ЮОм.
13.56. Какой величины ток пройдет по графитовому стержню, если на его
концы подать напряжение 17=6 В? Длина стержня 1 = 20 см, его диаметр
d=2 мм, удельное сопротивление графита р = 4-1 О'4Ом-м.
13.57. Обмотка реостата изготовлена из никелиновой проволоки длиной
I = 50 м пощадью поперечного сечения S = 10"6 м2. Определить напряжение на
282
зажимах реостата, если по нему протекает ток силой 1 = 6 А Удельное сопротив-
ление никелина р = 4-10"7 Омм.
13.58. По участку цепи, состоящем из четырех одинаковых параллельно
соединенных проводников, течет ток силой /0 = 4,8 А. Какой ток будет течь по
участку, если эти проводники соединить последовательно при том же напряже-
нии иа его концах?
• Решение. Сопротивление участка цепи, состоящего из четырех параллельно соединенных
проводников сопротивлением R каждое, равно
Поскольку на участке нет источников э.д.с., то ток /д, протекающий до разветвления по
такому участку, можно найти из закона Ома для однородного участка:
7° Rt ~ 'AR R ’ (1)
где U - напряжение иа концах участка.
Если проводники соединить последовательно, то общее сопротивление участка станет
равным
R2 = R + R+R + R = 4Л,
а ток
U_ =и_
1 ~ R2 ~ 4R ’
Из выражения (2) с учетом (1) получаем
/ = ^/о = О,3 А.
• Ответ'. 1= */|б /д = 0,3 А.
13.59. В электрическую цепь включены последовательно сопротивления
R! = 50 Ом, Т?2 - 30 Ом и Л3 = 20 Ом. Определить падение напряжения на всем
участке цепи и на каждом сопротивлении в отдельности, если сила тока в цепи
равна7=4А.
13.60. В электрическую цепь параллельно включены три сопротивления
7?j = 2 Ом, R2 = 3 Ом и Л3 = 12 Ом. Определить силу тока в неразветвленной
части цепи, и токи, текущие по каждому из этих сопротивлений, если падение
напряжения на участке равно U= 12 В.
13.61. Падение напряжения на участке цепи, содержащем четыре одинако-
вых сопротивления, соединенных последовательно, равно U. Как нужно изме-
нить напряжение на концах участка, чтобы при параллельном соединении этих
сопротивлений сила тока в неразветвленной части цепи увеличилась в п = 2
раза?
13.62. Электрическая цепь, на которую подается постоянное напряжение,
состоит из двух параллельно соединенных сопротивлений, подключенных пос-
ледовательно к третьему. Все сопротивления одинаковы. Во сколько раз изме-
нится напряжение на третьем сопротивлении, если одно из параллельно соеди-
ненных сопротивлений сгорит?
283
2
Рис. 13.42 Рис. 13.43
13.63. Определить сопротивление реостата и лампочки (рис. 13.42), если
наименьший ток в цепи равен Ц = 1,5 А, а наибольший -12 = 2,5 А. Напряжение
на зажимах цепи равно U= 12 В.
13.64. Найти токи через сопротивления Л] = 1 Ом, Л2 = 2 Ом и Л3 = 3 Ом
участка цепи, представленного на рис. 13.43, если потенциалы точек 1, 2, 3
равны ф] = 10 В, <р2 = 9 В, фз = 6 В соответственно.
r2 13.65. Падение напряжения на
участке а-с цепи, представленном
с на рис. 13.44, равно 11 = 12 В. Най-
ти падение напряжения на сопротив-
лении Л] = 10 Ом, если R2 = 5 Ом,
Рис. 13.44 Л3=ЮОм.
• Решение. Сопротивление участка b-с цепи, содержащей два сопротивления R2 и R3, со-
единенных параллельно, равно
ь
*1
а —I
R3
R2 R$
r^=r^r3’
а полное сопротивление участка а-с & &
^участка = + Rb-c = + д +дз •
Применяя закон Ома для однородного участка а-с, найдем силу тока в неразветвлен-
ной части цепи:
U(R2 + R3)
j = u = и =
^участка „ R2R3 R[ R2 +R[ R3+R2R3’
Ri + R2 + R3
которая равна току, текущему через сопротивление R\.
Еще раз записав закон Ома, но теперь для участка а-b, найдем падение напряжения на
сопротивлении Л|:
п U(R2+R3}Ri qr
Oa-h = 1 R\= ~ „ = 9 В.
R2 + R3 R3 + R2 R3
U(R2 + R3)Rl
• Ответ: U^b = IRt= „ J' “' „ « 9 B. .
/?i R2 + R{ R3 + R2 R3
13.66. Для регулирования напряжения собрана схема, представленная на
рис. 13.45. Сопротивления нагрузки и регулировочного реостата одинаковы и
равны R. Нагрузка подключена к половине реостата. Напряжение на входе цепи
неизменно и равно U. Определить, как изменится напряжение на нагрузке, если
ее сопротивление увеличить в п = 2 раза. '
284
Рис. 13.45
Рис. 13.46
13.67. Ток, текущий через сопротивление Rt = 10 кОм участка цепи, йзо-
браженого йа рис. 13.46, равен 7, = 2 А. Определить ток через сопротивление
R2, если R2 = R3 = 20 кОм.
Закон Ома для неоднородного участка цепи и замкнутой цепи
13.68. В схеме (рис. 13.47) э.д.с. источника равна <?= 5 В, внутреннее со-
противление г = 0,1 Ом. Найти токи и 12, текущие через сопротивления
/?! = 4 Ом и R2 = 6 Ом. j R
• Решение. Сопротивление внешней цепи, содержа- ---—| |------—
щей два сопротивления R{ н R2, соединенных па- j R
раллельно, равно а —~ ।------—>________
R2 ------
Яцепи = о , п , „.
л। + л2 . ‘ <У I .г__________
Для определения тока I в неразветвленной I
части цепи, содержащей источник э.д.с., применим Рис. 13.47
закон Ома для замкнутой цепи:
j _8 (R\ + ^2)
^цепи + r R\ R2 + r(R\ + ^2)
Применив закон Ома для однородного участка а-b цепи, найдем падение напряжения
на сопротивлениях Rt н R2:
Г, _______S Й1 R2
U^l>-^UenH-RiR2 + r{Ri+R7)-
Напряжение Ua~b = <ро - <pj можно также найти, записав закон Ома для неоднородно-
го участка b-8-a цепи:
8 — Оa—b 8 Ri R2
Ir = <pb-<pa + S, 1 =----U^.b = 8-Ir = 12
" Л| Л2 + г (Л|
Зная напряжения на концах сопротивлений Rt н R2, можно найти токи Ц н 12:
j _ Ue-b_________££2________1 2 А I - ________S ^1______
^1 R\ R2 + г (Л| + Л2) 2 R2 RiR2 + r(Ri-¥R2)
8 R2 г 8 R\ _ _
• Ответ'. Ц = ——----—----—- = 1,2 А, 12 = ~—z-—---~ = 0,8 А.
R । R2 + г (R । + R2) R1 R2 + г (R । + R^)
13.69. В проводнике сопротивлением R = 2 Ом, подключенном к источни-
ку э.д.с. <?= 1,1В, сила тока равна 1= 0,5 А. Определить силу тока при корот-
ком замыкании элемента.
13.70. Во сколько раз напряжение на зажимах источника отличаетси от его
э.д.с., если внутреннее сопротивление источника в п = 3 раза меньше сопротив-
ления внешней цепи?
285
13.71. Напряжение на зажимах источника с э.д.с. S = 30 В равно U- 18 В,
а сила тока в цепи 1= 3 А. Определить внутреннее сопротивление источника и
сопротивление внешней цепи.
13.72. Определить э.д.с. батареи, если известно, что при увеличении со-
противления нагрузки, подключенной к батарее, в п раз напряжение на на-
грузке увеличивается от Ц до U2.
13.73. Сила тока в цепи, содержащей источник э.д.с. и сопротивление
Л, = 4 Ом, равна Д = 0,2 А. Если же внешнее сопротивление равно R2 = 7 Ом,
то ток в цепи 12 = 0,14 А. Какой ток будет в цепи, если источник замкнуть на-
коротко?
13.74. Определить внутреннее сопротивление аккумулятора, если извест-
но, что при замыкании его на внешнее сопротивление R{ = 1 Ом напряжение
на зажимах аккумулятора равно Ц = 2 В, а при замыкании на сопротивление
R2 = 2 Ом напряжение на зажимах U2 = 2,4 В.
13.75. Два одинаковых сопротивления R = 5 Ом подключены параллельно
к источнику э.д.с. S= 16 В. Сила тока в каждом сопротивлении равна 7 = 2 А.
Чему равно внутреннее сопротивление источника?
13.76. Кусок проволоки сопротивлением R = 10 Ом свернули в кольцо и
подключили к источнику с э.д.с. <$"= 1 В и внутренним сопротивлением
г = 0,5 Ом в двух точках, лежащих на противоположных сторонах диаметра
кольца. Определить силу тока через источник.
13.77. Два одинаковых сопротивления подключены последовательно к
источнику напряжения. Одно из сопротивлений увеличили в п = 4 раза, а дру-
гое - во столько же раз уменьшили. Во сколько раз изменилась сила тока в'
цепи? Внутренним сопротивлением источника пренебречь.
Рис. 13.48 Рис. 13.49
13.78. Чему равна разность потенциалов между точками А и В в схеме,
представленной на рис. 13.48, если э.д.с. источника <$=80 В, сопротивления
R\ = 2 Ом, R2 = 8 Ом, внутреннее сопротивление пренебрежимо мало?
13.79. Определить силу тока, текущего через сопротивление Rx=2 кОм в
цепи, изображенной на рис. 13.49, где R2 = 1 кОм, = 2 кОм, э.д.с. источника
<$"= 24 В, внутреннее сопротивление источника пренебрежимо мало.
13.80. Какой ток течет через каждое из сопротивлений цепи, изображен-
ной на рис. 13.50, если R{ = R2 = R3 =Л4 = 1 Ом, э.д.с. источника в= 12 В,
внутреннее сопротивление источника пренебрежимо мало.
286
Рис. 13.50
______ R __________
“Г Ь
тНЬ-----£----------
11 Г| е>2 ~2
Рис. 13.52
13.81. Для схемы, изображенной на рис. 13.51, подобрать такое сопротив-
ление Rx, чтобы ток, текущий через это сопротивление при замкнутом ключе
и разомкнутом ключе К2, был в три раза больше тока, текущего через это
сопротивление при разомкнутом ключе и замкнутом ключе К2. Сопротив-
лением источника пренебречь.
13.82 Батарея состоит из п = 8 элементов, соединенных последовательно.
Э.д.с. каждого элемента <?= 1,5 В, внутреннее сопротивление г =0,25 Ом.
Внешнюю цепь образуют два параллельно соединенных проводника сопро-
тивлениями Rt = 10 Ом и R2 = 50 Ом. Определить напряжение на зажимах ба-
тареи.
• Решение. Батарея, содержащая несколько соеди-
ненных последовательно источников э.д.с., может
быть заменена одним эквивалентным источником.
Рассмотрим цепь, содержащую два источни-
ка тока с э.д.с. <?|, <?2 и внутренними сопротивле-
ниями гь г2, замкнутую на внешнее сопротивление
R (рис. 13.52). Запишем закон Ома для однородно-
го участка a-R-b цепи н неоднородных участков
a—R—b—^^^Cy с-ё\-a-R-b'.
j _ <Ра ~ <РЛ» j = (фа~Фс)+<?2 j = (фс~Фд)+<?1
Поскольку R ’ R + r^ ’ R*r'
(фа - Ф*) = (Фа - Фс) + (фс “ Фй)>
ТО
7Я = 7(Я + Г2)-<?2 + 7(Я + г,)-<?„ или 7= + .
Л+Г1+Г2
Сравнивая полученное соотношение с законом Ома для замкнутой цепи, видим, что
два последовательно соединенных источника тока действуют как один источник, у которого
э.д.с. и внутреннее сопротивления равны соответственно
ё[ + <^2’ Г = Г| + Г2*
Очевидно, что прн соединении источников разноименными полюсами, их э.д.с. будут
вычитаться.
Легко сообразить, что э.д.с. и внутреннее сопротивление источника, эквивалентного
п последовательно соединенным источникам, равны
*^ЭКВ. ~ + ^2 + • + &П ’ ГЭКВ. = Г| + г2 + ... + гл.
Закон Ома для замкнутой цепи, содержащей и источников э.д.с. и внешнее сопротив-
ления R, можно записать в виде
J ё экв.
+ гэкв.
287
л
а
А
Sr г 8г г #1 г
Рис. 13.53
Следовательно, ток в цепи
, _____п 8
В нашем случае п одинаковых источников тока
(рис. 13.53)
'экв. = П+'-2 + -.+'п = пг>
^ЭКВ. = *^1 + *^2 + • • • + вП — п
I пв
~ R + nr’
Я] 1?2
R-^i-
где
П & (Л| + Лз)
^1 ^2 Л] ^2 + И Г (Л| + J?2)
R^R^nr
Напряжения U = <ро - <pj на зажимах батарее можно найти двумя способами:
1) на основании закона Ома для однородного участка a-R-b цепи:
<Ра-<Р6 п SR, R2
1= а .г— , U=IR = —--------L-3 а 9>7 в;
R Rt R2 + nr(Ri+ Rq)
2) на основании закона Ома для неоднородного участка b-8-a цепи:
. (<Р6<Ра) + <?экв. . п & R\ R2 Q-7D
^экв. " 7?| Т?2 + д г (Ri + R2)
г (Ri+R-dnr 1
• Ответ: U=n #11- ——-------—----— г = 9,7 В.
RtR2 + nr (R। + R^)
13.83. Имеется два последовательно соединенных гальванических эле-
мента с одинаковыми э.д.с., но разными внутренними сопротивлениями Г]
и г2. При каком внешнем сопротивлении R разность потенциалов на зажимах
одного из элементов равна нулю и на каком?
13.84. При каком условии ток, даваемый двумя соединенными последова-
тельно разными гальваническими элементами, обладающими соответственно
э.д.с. и <У2 и внутренними сопротивлениями г, и г2, будет меньше тока, да-
ваемого первым из них, если они замкнуты на одно и то же внешнее сопро-
тивление Я?
13.85. Две батареи соединили последовательно и замкнули на сопротив-
ление R = 4 Ом. Прн этом ток в цепи оказался равным 1{ = 1,83 А. Затем один
из источников перевернули, включив навстре-
чу другому источнику. Ток в цепи стал равным
12 = 0,34 А. Каковы э.д.с. и внутренние сопро-
тивления батарей, если при замыкании каждой
из них на сопротивление R через него идут
токи /3 = 1 А и /4 = 1,3 А соответственно?
13.86. Какова будет разность потенциалов
между любыми двумя точками цепи, изобра-
288
женной на рис. 13.54? Э.д.с. каждого элемента S, а внутреннее сопротивле-
ние г. Сопротивлением проводов пренебречь.
Разветвленные цепи постоянного тока
13.87. Найти э.д.с. и внутреннее сопротивление источника, эквивалентно-
го двум параллельно соединенным элементам с э.д.с. и S2 и внутренними
сопротивлениями Г] и г2.
а) б)
Рис. 13.55
• Решение. Для решения поставленной задачи подключим к источникам сопротивление
нагрузки R н рассмотрим два варианта соединения источников друг с другом: одноимен-
ными (рис. 13.55, а) и разноименными (рис. 13.55, б) полюсами. Такую цепь (разветвлен-
ную) рассчитать, используя только законы Ома, нельзя; здесь используют законы Кирх-
гофа.
Рассмотрим первое соединение.
Выберем направления токов на участках цепи так, как показано на рис. 13.55, а, и ус-
ловимся обходить контуры по часовой стрелке.
Как видим, в цепи протекает три разных тока /ь 12 и I. Поэтому для решения задачи
нужно составить три уравнения.
Рассматриваемая схема содержит два узла Я и В. Поэтому по первому закону Кирхго-
фа можно составить только одно уравнение для любого из узлов. При составлении уравне-
ний по первому закону Кирхгофа необходимо соблюдать правило знаков: ток, подходящий
к узлу, входит в уравнение со знаком «плюс»; ток, отходящий от узла, - со знаком «минус»
(или наоборот). Поэтому, например, для узла В:
Ц+12-1=0. (1)
Уравнение для узла А будет следствием уравнения (1).
Недостающие два уравнения получим по второму закону Кирхгофа. Число независи-
мых уравнений всегда меньше количества контуров. Поэтому, чтобы уравнения были неза-
висимыми, контуры необходимо выбирать так, чтобы в каждый новый контур входил хотя
бы один участок, не участвовавший ни в одном из ранее использованных контуров. В нашей
задаче можно использовать два из трех контуров: A-£t-B-g2-A, AS^-B-R-A, A-S2-B-R-A.
При составлении уравнений по второму закону Кирхгофа необходимо соблюдать сле-
дующие правила знаков: если ток по направлению совпадает с выбранным направлением об-
хода контуров, то соответствующее произведение IR входит в уравнение со знаком «плюс»,
в противном случае - со знаком «минус»; если э.д.с. повышает потенциал в направлении об-
хода контура, т.е. если при обходе контура приходится идти от «минуса» к «плюсу» внутри
источника, то соответствующая э.д.с. входит в уравнение со знаком «плюс», в противном
случае - со знаком «минус».
289
Запишем уравнения, выражающие второй закон Кирхгофа, для независимых контуров
A—8 i—B—R—A, :
/,П+//?=<?!, (2)
I2r2 + IR = 82. (3)
Выразив токи Д и 12 из уравнений (2) и (3)
и подставив их значения в (1)
8^-IR + 82-IR _j_q
П Ъ
получим уравнение относительно тока 1, решая которое, находим
*Г2+<?2П
П г2 + Г) R + r2 R
Если заменить источники 8[ и <?2 эквивалентным источником с э.д.с. 8 и внутренним
сопротивлением г, то ток I будет равен
Очевидно, что внутреннее сопротивление г эквивалентного источника определяется
как сопротивление двух параллельно соединенных сопротивлений rt и г2:
Следовательно,
_ <?(П + Г2)
ri r2 R И г2 + Г| R + r2 R '
г1 + г2
Приравнивая правые части выражений (4) н (6), получим
<Sj г2 + в2 Г| = g (Г| + г2).
Откуда находим
» _ <?1 г2 + <?2 П
П+Гг
Соотношение (7) можно переписать в виде
g 82
r~ ri r2’
где г определяется выражением (5).
(5)
(6)
(7)
(8)
Если имеется более двух соединенных параллельно источников э.д.с., то, заменяя пос-
ледовательно каждую пару эквивалентным источником по формулам (5) и (8), придем к вы-
ражениям для внутреннего сопротивления н э.д.с. эквивалентного источника:
111 1
--= — + — + . . . + — ,
'•экв. И г2 га
<^экв. 8\ g2 gn
-------= — + — + ... + — ,
гэкв.--rl r2 rn
(9)
где л-количество источников.
Если рассмотреть случай соединения двух источников, показынный на рис. 13.55, б, то
мы придем к выражению для тока I в виде
290
<?1Г2~<?2П
rtr2 + rt R + r2R'
Легко сделать вывод, что формулы (5) и (8) здесь остаются справедливыми, если
учесть правило знаков: э.д.с. источников, которые создавали бы ток того же направления,
что и ток, идущий в цепи, берут со знаком «плюс», а э.д.с. источников, которые давали бы
ток противоположного направления, - со знаком «минус».
„ . <?1Г2+<?2П
• Ответ: г =----, ® =---------.
П+Г2 П + г2
13.88. Два гальванических элемента соединены параллельно одинаковы-
ми полюсами. Э.д.с. элементов и <S2, внутренние сопротивления одинако-
вы. Определить разность потенциалов между зажимами элементов.
13.89. Два аккумулятора с э.д.с. = 1,3 В и S2 = 2 В и внутренними со-
противлениями Г] = 0,1 Ом и г2 = 0,25 Ом соединены параллельно одинаковы-
ми полюсами. Найти силу тока в цепи и напряжение на зажимах аккумулято-
ров.
13.90. Два гальванических элемента с э.д.с. <?] = 1,5 В и <?2 = 2 В соедине-
ны параллельно одинаковыми полюсами. Вольтметр, подключенный к клемам
батареи, показал напряжение 17= 1,7 В. Определить отношение внутренних
сопротивлений элементов. Током через вольтметр пренебречь.
13.91. В цепь параллельно включены одинаковыми полюсами два гальва-
нических элемента с э.д.с. = 1,9 В и S2 = 1,1 В и внутренними сопротивле-
ниями Г| = 0,1 Ом и г2 = 0,8 Ом. Элементы замкнуты на внешнее сопротивле-
ние R = 10 Ом. Чему равны токи, текущие через элементы? Определить па-
дение напряжения на внешнем сопротивлении.
13.92. Два гальванических элемента с равными э.д.с. S = 2 В соединены
параллельно одинаковыми полюсами и замкнуты на внешнее сопротивление R
Внутренние сопротивления элементов равны соответственно Г] = 1 Ом и
г2 - 2 Ом. Чему равно внешнее сопротивление R, если ток, текущий через пер-
вый элемент, равен /, = 1 А? Найти силу тока 12, текущего через второй эле-
мент, а также силу тока /R через внешнее сопротивление.
13.93. Батарея из N одинаковых аккумуляторов замкнута на внешнее со-
противление R. Каково внутреннее сопротивление г одного аккумулятора, ес-
ли сила тока, текущего по сопротивлению, одинакова и при параллельном и
при последовательном соедининии аккумуляторов в батарею?
13.94. Есть две батареи: одна составлена из нескольких одинаковых галь-
ванических элементов, соединенных параллельно, другая - из того же числа
таких же элементов, соединенных последовательно. На какие одинаковые со-
противления R нужно замкнуть каждую из батарей, чтобы токи через эти соп-
ротивления были равны? Внутреннее сопротивление каждого элемента рав-
но г. Сопротивлением подводящих проводов пренебречь.
13.95. Из N = 400 одинаковых элементов составлена батарея так, что об-
разовано п соединенных последовательно групп, в каждой из которых содер-
291
жится т элементов, соединенных параллельно. Внутреннее сопротивление
одного элемента г = 1 Ом. При каких значениях п и т батарея, будучи замкну-
та на внешнее сопротивление R = 100 Ом, даст максимальную силу тока?
13.96. Определить силу тока через сопротивление R2 (рис. 13.56, а) и на-
пряжение между точками А и В, если э.д.с. источников равны = 4 В и
<?2 = 3 В, а сопротивления R} = 2 Ом, R2 = 1 Ом, R3 = 6 Ом. Внутренними со-
противлениями источников пренебречь.
Ri л r2
Рис. 13.56
• Решение. Прн решении задачи можно воспользоваться законами Кирхгофа или заменить
два источника э.д.с. одним эквивалентным и использовать законы Ома.
Рассмотрим оба способа решения.
Выберем направления токов 7|, I2, 73 на участках цепи так, как показано на рис. 13.56, а,
и условимся обходить контуры по часовой стрелке. Поскольку в цепи протекает трн разных
тока, то для решения задачи нужно составить трн уравнения.
Рассматриваемая схема содержит два узла Л и В. Поэтому по первому закону Кирхго-
фа можно составить только одно уравнение для любого из узлов, например, для узла Л:
7, +12 -13 = 0. (1)
Недостающие два уравнения нужно составить, используя второй закон Кирхгофа для
двух из трех контуров: A-Rz~f2~B-6t-Rt~A, A-R^B-^-R^A, A-R2-£2-B-R3-A. Тогда
для контуров A-R^B-^-Ry-A и A-R2-£2-B-R3-A получим
71+73 Я3 = <?|, (2)
-727?2-73 7?3 = -<?2. (3)
Из уравнений (2)—(3) находим
Подставив выражения для токов Ц и 13 из (4) в (1)
- <?2 + h r2 . ^2 ~ Л Д; _
7?! +/2 7?3 -°’
получим уравнение относительно тока 12:
Rj - @2 R3 + 4 R2 R3 + 4 R3 “ &2 Rl + h Rl R2 = 0.
Откуда находим
j C&2~ &l)R3+&2Rl g
2 7?! 7?2 + 7?! R3 +R2R3
Падение напряжения между точками А и В найдем из закона Ома для однородного
участка A~R3 -В цепи:
292
t/д-в = h ^з>
где ток
g (.^2~gi)R3+g2Ri
2 7?) т?2 + ^1 R3 + ^2 ^3^1 Т?2 + &2 Rj
R2 +1?| R3 + R2 R3
*з
Следовательно,
.. _ (<?[ Т?2 + ^2Д1) ^3 _ , в
АВ Я) R2 + Ri R3 +R2R3.
Рассмотрим теперь второй способ.
Для расчета э.д.с. <?экв. н внутреннего сопротивления гэкв эквивалентного источника
будем считать, что сопротивления Л| н R2 являются как бы внутренними сопротивлениями
источников и <?2 соответственно (если бы источники имели внутренние сопротивле-
ния Г| и г2, то прн расчетах гэкв н <?экв мы считали бы, что их внутренние сопротивления
равны (Г| + Л|) н (г2 + Л2)).
Воспользуемся результатами решения задачи №13.87. Так как источники соединены
друг с другом одинаковыми полюсами, то
R\ R2 R2 + <^2
Гэкв-= R^~R2 ’ <?ЭКВ'= Л1+Л2 '
С учетом эквивалентного источника цепь можно преобразовать к виду, представлен-
ному на рнс. 13.56, б.
Используя закон Ома для замкнутой цепи, найдем ток 13 через сопротивление R3:
<^1 R2 + ^2
J _ <^ЭКВ.Д1 + ^2^1 1?2 + ^2 ^1
3 гэкв.+ ^3 Rj ^2 „ R{ R2 +Я1 R3 + Я2Я3
-----+ Л1
Rt+R2
Падение напряжения между точками А и В равно
Я3 (<^| R2 + $2 ^1)
Т/А_в = h R3 = .V' = 3 В.
П. В J J В В | в в . в в
Л | Л2 + Л | Л3 Т Л2 Л3
Далее, применив закон Ома для неоднородного участка цепи A-R2-^2~R> найдем ток
через источник S2, который равен току через сопротивление /?2:
s ^3 (<^t ^2+ <^2^1)
у _ <^2~ Цу-в _ 2 g2 + ^1 ^3 + ^2^3 _ (<?2~ ^1)^3 + ^2^1 _ g
^2 ^2 1?| R2 + R3 + &2 ^3
(<^2 ~ R3 + <^2 Rl (^1 R2 + ^2 ^1) R3
• Ответ: 7, = -7-^--^-7---—L = О, Т/А_в = „ 1 2----2 17 = 3 В.
R\ R2 + R3 + Т?2 R3 Rt R2 +Ri R3 + R2R3
13.97. Какой ток будет течь через амперметр с пренебрежимо малым
внутренним сопротивлением в схеме, показанной на рис. 13.57, а, если
/?! = 15 Ом, R2 = R3 = Л4 = 10 Ом, э.д.с. источника S= 7,5 В. Внутренним сопро-
тивлением источника пренебречь.
• Решение. Так как сопротивление ЙА амперметра очень мало, будем считать его равным
нулю. Тогда ток /д через амперметр найти по закону Ома
293
Рис. 13.57
для однородного участка цепи b-с нельзя. В таких задачах силу тока определяют, используя
первый закон Кирхгофа, записанный для любого из узлов, к которому подходит нли от ко-
торого отходит ток /л. В нашей задачи можно использовать улел h или узел с:
/-/4-ZA = 0, 1А-Ц-13 = 0, (1)
где токи /, /], 13, Ц соответствуют обозначениям на рис. 13.57, а
Поскольку RA = 0, то при расчете токов в цепи точки b и с соединим, выбросив ам-
перметр.
Сопротивления R3 и R$ соединены параллельно (рис. 13.57, б), поэтому сопротивле-
ние участка d-c „ „
Сопротивление Rrf-c соединено с сопротивлением R2 последовательно (рис. 13.57, в).
Поэтому сопротивление участка а-с
Ra-c = Я2 + Rd-c = r2 + ’
К3 + Л4
а полное сопротивление цепи (сопротивления Ra^. и Я, соединены параллельно (рис. 13.57,
г)):
7?1 Кр-с Я । [Я2 (Я3 + Я4) + Я3 Я4]
цепи ~ Я, + Ra^ ’ (Я1 + Я2) (Я3 + Я4) + Я3 Я4 '
Записав закон Ома для замкнутой цепи, содержащей источник э.д.с. и сопротивление
•Кпепи. найдем ток I:
в _<У[(Я|+Я2)(Яз + Я4) + Я3Я4]
^цепи Я, [Я2 (Я3 + Я4) + Я3 Я4]
Далее, используя второй закон Кирхгофа для контура a-S-c-d-a (рис. 13.57, в), най-
дем ток /2:
(2)
Ё (£? (/?з + /?4)
7?3 7?4 (^3 + ^4) + Я3 /?4
+ /?4
4 Ra-
294
Из закона Ома для участка d-c цепи найдем падение напряжения на участке
£ R4
Ud-c = I2Rd~c = R2(R}+R4) + R3R4 ’
а затем ток /4:
Ud—c £R3
4 ^4 А2 (Л3 + Л4) + R3 Л4
Следовательно, из (1) с учетом (2) и (3) получим
. _ . <? l(Ai + ^2) (A3 + А4) + A3 А4]__* А3_______
А 4 Л, [Л2 (й3 + Л4) + й3 Л4] R2 (К3 + Л4) + R3 Л4
, **1*4
А ^1 А] [А2 (А3 + Л4) + R3 Л4]
S 6R, R.
• Ответ: /*=-=- + „ г„ ~, = 0,75 А.
А] Л] [R2 (A3 + Л4) + А3 Л4]
(3)
а1
^2|, г2
R
Рис. 13.58
Рис. 13.59
13.98. Две батареи с э.д.с. <?| = 10Ви<?2 = 8Ви внутренними сопротив-
лениями Г] = 1 Ом и г2 = 2 Ом соединены с сопротивлением R = 6 Ом так, как
показано на рис. 13.58. Найти силу тока, текущего через сопротивление R.
13.99. Две батареи с э.д.с. <?|=8Ви<?2 = 6Вн внутренними сопротивле-
ниями z-j = 2 Ом и г2 = 1,5 Ом соединены с сопротивлением А = 10 Ом так, как
показано на рис. 13.59. Найти силу тока, текущего через сопротивление R.
Рис. 13.60 Рис. 13.61
13.100. Три батареи с э.д.с. = 1,5 В, <?2 = 2 В, <?3 = 2,5 В соединены с
сопротивлениями А] = 10 Ом, А2 = 20 Ом и А3 = 30 Ом так, как показано на
рис. 13.60. Найти ток через сопротивление Ар Внутренние сопротивления ба-
тарей пренебрежимо малы.
13.101. Какой ток будет течь через амперметр в схеме, изображенной на
рис. 13.61? Э.д.с. источника <?, сопротивление А известно, внутренними со-
противлениями амперметра и источника пренебречь.
295
Рис. 13.62 Рис. 13.63
13.102. Какое показание будет у амперметра в схеме, изображенной на
рис. 13.62? Как изменится показание амперметра, если его и источник э.д.с.
поменять местами? Элементы цепи равны Ry = 2 Ом, R2 = 4 Ом, Я3 = 6 Ом,
<₽= 5 В, внутренние сопротивления источника и амперметра пренебрежимо
малы.
13.103. В схеме, изображенной на рис. 13.63, найти силу тока, текущего
через гальванометр при Sy = 1,5 В, S2 = 6 В, Ry = 3 кОм, R2 = 6 кОм. Внутрен-
ними сопротивлениями гальванометра и источников тока пренебречь.
Рис. 13.64 Рис. 13.65
13.104. Какой ток протекает через амперметр в схеме, изображенной на
рис. 13.64? Значения Я,, Я2, ^з> <^i, <®2 известны. Внутренними сопротивления-
ми источников и амперметра пренебречь.
13.105. Найти значение и направление тока через сопротивление R в
схеме (рис. 13.65), если <?, = 1,5 В, <?2 = 3,7 В, Ry = 10 Ом, Я2 = 20 Ом,
R = 5 Ом. Внутренние сопротивления источников пренебрежимо малы.
Рис. 13.66 Рис. 13.67
13.106. Найти силу тока через сопротивление R в схеме (рис. 13.66). Зна-
чения R, R}, R2, R3, S{, S2 известны. Внутренние сопротивления источников
пренебрежимо малы.
13.107. Три сопротивления Ry = 5 Ом, R2 = 1 Ом, Я3 = 3 Ом, а также ис-
точник тока Sy = 1,4 В соединены, как показано на рис. 13.67. Определить
э.д.с. источника тока, который надо подключить в цепь между точками А и В,
296
чтобы в сопротивлении R3 шел ток силой 1= 1 А в направлении, указанном
стрелкой. Сопротивлением источника тока пренебречь.
Конденсатор в цепи постоянного тока
13.108. Определить разность потенциалов между точками Л и Вв схеме,
изображенной на рис. 13.68. Значения емкостей конденсаторов С,, Съ С3, С4
и величина э.д.с. источника ^известны.
• Решение. При расчете электрических цепей, содержа-
щих конденсаторы, следует помнить, что постоянный
ток через конденсатор не течет, и в ветви, в которую он
включен, тока нет. Падение напряжение между произ-
вольными точками цепи в таких задачах можно найти,
пройдя от одной точки к другой по произвольному пути.
Рассмотрим конкретную задачу.
Для определения разности потенциалов между
точками А и В
Рис. 13.68
^л-в - Фа _ Фв
пройдем по цепи из точки А в точку В, например через точку а. Используя потенциал <ра
промежуточной точки а, выражение для t/A_B можно записать в виде
^А-В = Фа - Фа + Фа - Фв = (Фа - Фа) + (Фа “ Фв)-
Поскольку точка а соединена с положительной клеммой источника э.д.с., то потен-
циалы <рА < <ра и <рв < <ра, поэтому разность потенциалов (<рА - <ра) равна падению напря-
жения U} на конденсаторе Сь взятому со знаком «минус»:
Фа ~ Фа = _ ^1.
а разность потенциалов (<ра - <рв) - падению напряжения U2 иа конденсаторе С3:
Фа~Фв=
Следовательно,
t/A-B = -^ + t/3- (1)
Для нахождения падения напряжения U\ = (<ра - Фд) нужно пройти по произвольному
замкнутому контуру, походящем через точки aw А, например по контуру a-A-b-6-a:
(Фа-ФА) + (ФА-Фб)-<®'=О, (2)
где ф/, - потенциал в точке Ь, (фА - ф/,) = U2 - падение напряжения иа конденсаторе С2.
Аналогично, для нахождения падения напряжения U2 = (фа - фв) пройдем по контуру
а-В-Ь-^-а'.
(Фа - Фв) + (Фв - Фб) - <®'=°, (3)
где (фв - Фб) = - падение напряжения иа конденсаторе С4.
Выражения (2) и (3) можно записать в виде
+ U2 — <?, U2 + U< = <£ (4)
Конденсаторы С, и С2 соединены последовательно, поэтому заряды на них одина-
ковы: _ ГТ - __ ^1=^2» ИЛ11 CiUl = C2U2, Яз ~ Я^ Илн <^3 ^3 ® ^4 ^4» Решая систему уравнений (4)-(6), получаем с2 8 С\ё С4 <? и,- Сз* (5) (6)
и‘ с, + с2’ U2 cl + c2’ 3 с3 + с4’ С3 +С4
297
Следовательно, подставив значения напряжений Ut и U3 в (1), получим
_ _ ^2 ^4 _ g Q Q ~ ^2 Q
А в Ct + C2 С3 + С4 (С| + Cj) (С3 + С4)
Рис. 13.69 Рис. 13.70 Рис. 13.71
13.109. Как изменится заряд и разность потенциалов на обкладках кон-
денсатора С3 (рис. 13.69) при пробое (коротком замыкании) конденсатора С2?
Во сколько раз?
13.110. Определить разность потенциалов между точками А и В в схеме,
изображенной на рис. 13.70. Значения емкостей конденсаторов Сь С2 и вели-
чины э.д.с. <₽], <₽2 источников известны.
13.111. Три источника э.д.с. = 6 кВ, S2 = 3 кВ и S3 = 2 кВ) и три кон-
денсатора (С] = 3 мкФ, С2 = 2 мкФ и С3= 1 мкФ) соединяются между собой
последовательно в замкнутую цепь, чередуясь друг с другом (рис. 13.71).
Найтинапряжениенакаждомконденсаторе.
Рис. 13.72 Рис. 13.73 Рис. 13.74
13.112. КконденсаторуС,заряженномудоразностипотенциалов U, под-
соединена батарея из таких же конденсаторов (рис. 13.72). Найти заряд на
каждом конденсаторе.
13.113. Когда к батарее, показанной на рис. 13.73, подвели напряже-
ние U, заряд среднего конденсатора оказался равным нулю. Какова емкость
конденсатора С4, если емкость первого конденсатора С, второго - 2С, третье-
го - ЗС?
13.114. Найти заряды конденсаторов в цепи, показанной на рис. 13.74.
Значения емкостей конденсаторов С1( С2, С3 и величины э.д.с. <₽,, <₽2 источни-
ков известны.
298
13.115. Найти заряд конденсато-
ра в схеме, показанной на рис. 13.75.
Внутренним сопротивлением источ-
ника пренебречь.
• Решение. По участку цепи a-d, содержа-
щем конденсатор емкостью С, электричес-
кий ток будет течь до тех пор, пока конден-
сатор не зарядится. После этого ток в
узле а разветвляться не будет и весь пойдет
через сопротивление R. В узле Ь ток развет-
вится на токи /2 и Ц. Далее ток /3 = /2 пойде'
током /4, образуя ток 1\.
Рис. 13.75
через сопротивление ЗЯ и в узле п сольется с
Чтобы определить заряд иа конденсаторе, нужно найти разность потенциалов на его
обкладках. Как видно из рис. 13.75, оиа равна разности потенциалов между точками and
(потенциал <ра > <р^, так как точка а соединена с положительной клеммой источника):
Uа-d ~ fa fd-
Найти разность потенциалов Ua_j непосредственно используя закон Ома нельзя, по-
скольку ток /|, выходящий из точки а, на пути к точке d разветвляется. Рассмотрим путь
a-b-d, по которому ток приходит из точки а в точку d. Используя потенциал <pj промеж-
уточной точки Ь, выражение для можно записать в виде
Ua-d= Фа - fb + fb ~ fd = (.fa ~ fb) + (fb ~ fd)-
Разность потенциалов (я>а“ Фб) равна падению напряжения иа сопротивлении Я:
Фа"Ф6 = Л R-
а разность потенциалов (<pj - <pd) - падению напряжения на сопротивлеииии 2Я:
fb~fd = 122R-
Следовательно, нахождение разности потенциалов на конденсаторе
Ua~d= I1R + I2 2R
фактически сводится к определению токов Д и /2, т.е.к решению стандартной задачи по рас-
чету токов на участках цепи (см., иапример, задачу №13.97).
Участок b-d-n содержит два сопротивления, соединенные последовательно. Общее
сопротивление участка
Rb—rf_n ~ ^-R + ^R ~ 5Я.
Сопротивление Rb-d-n соединено параллельно с сопротивлением 4Я. Поэтому со-
противление участка цепи между точками Ь-п
Rb-d-n*R 20-
Я*^_„+4Я 9 ’
а полное сопротивление цепи
29
^цепи = Rb-n + R = "<j~ R-
Применяя закон Ома для замкнутой цепи, найдем ток 7р
. <? 9<?
’ Яцепи 29Я-
Падение напряжения между точками b-п цепи
г » 20<?
иЬ-п ~ Ч кЪ-п - “29” ’
299
Следовательно,
. Ub-n 4______
Rb^.n~ 29R-
Используя значения токов It и /2, найдем разность потенциалов на обкладках кон-
денсатора:
и заряд на нем:
• Ответ: q = |7/>9 С<?.
Ua-d-29RR + 29R2R~ 29
Рис. 13.76
q = C Ua-d=
Рис. 13.77
Рис. 13.78
13.116. Найти падение напряжения на каждом конденсаторе участка
цепи, представленного на рис. 13.76, если С} = 1 мкФ, С2 = 2 мкФ, <₽= 10 В, а
разность потенциалов между точками А ив равна Д<рА_в = 5 В.
13.117. Найти заряд конденсатора на участке цепи, представленном на
рис. 13.77, если величины <?], <?2, С, R, / известны и > S2.
13.118. Напряженность электрического поля в конденсаторе, встроенном
в схему (рис. 13.78), равна Е = 50 В/м. Расстояние между пластинами конден-
сатора d = 0,5 мм, площадь каждой из пластин
5= 100 см2, сопротивление нагрузки R - 5 Ом,
внутреннее сопротивление источника г = 0,1 Ом.
Какова э.д.с. батареи и сила притяжения пластин
конденсатора? Чему равен заряд на пластинах
конденсатора?
13.119. Определить величину сопротивле-
ния R в цепи, представленной на рис. 13.79, если
напряженность электрического поля между об-
кладками конденсатора Е = 2,25 кВ/м. Э.д.с. ис-
точника <?=5 В, внутреннее сопротивление
г = 0,5 Ом. Расстояние между пластинами кон-
денсатора d = 0,2 см.
13.120. Определить заряд конденсатора ем-
костью С = 1 мкФ в цепи, представленной на
рис. 13.80, где Я, = 1 Ом, Я2 = 4 Ом, <?=6 В,
внутреннее сопротивление источника г = 1 Ом.
13.121. В схеме (рис. 13.81) сопротивления
равны Я] = 1 Ом, Я2 = 5 Ом, емкость конденсатора
4П
пС
R R
Н——h в.
1_Л_____
Рис. 13.79
------г
*2 |
Рис. 13.80
Рис. 13.81
300
С= 1 мФ,,э.д.с. источника 100 В. Определить минимальное и максималь-
ное значения силы тока в цепи после замыкания ключа К. Внутренним сопро-
тивлением источника пренебречь.
Рис. 13.82 Рис. 13.83
13.122. Найти заряд на обкладках конденсатора емкостью С = 1 мкФ в
цепи, представленной на рис. 13.82. Э.д.с. источника S= 10 В, внутренним со-
противлением пренебречь.
13.123. До какой разности потенциалов зарядится конденсатор, включен-
ный в цепь по схеме, изображенной на рис. 13.83? Какой заряд будет при этом
на обкладках конденсатора, если его емкость равна С = 2 мкФ? Э.д.с. источни-
ка Е = 3,6 В, сопротивления равны R{ = 4 Ом, R2 = 7 Ом, Я3 = 3 Ом. Внутрен-
ним сопротивлением источника пренебречь.
Рис. 13.84 Рис. 13.85
13.124. Найти заряд на обкладках конденсатора емкостью С= 1,5 пФ в
цепи, изображенной на рис. 13.84. Э.д.с. источника S- 6 В, внутренние сопро-
тивление г = 1 Ом, сопротивления Я, = 8 Ом, Я2 = 2 Ом.
13.125. Найти заряд на обкладках конденсатора, включенного между точ-
ками Аи В в цепи, изображенной на рис. 13.85. Э.д.с. источника <?= 10 В, ем-
кость каждого конденсатора С = 1 мкФ. Внутренним сопротивлением источ-
ника пренебречь.
13.126. Найти разность потенци-
алов между точками А и В в цепи,
изображенной на рис. 13.86. Величи-
ны Яр Я2, Сь С2, S известны. Внут-
ренним сопротивлением источника
пренебречь.
с1ц А|[с2
В ,
---------q-----------
Рис. 13.86
301
Рис. 13.87
Рис. 13.88
13.127. В схеме, изображенной на рис. 13.87, известны величины Ru R2,
С2, U. Какой заряд пройдет через ключ К, если его замкнуть?
13.128. Определить заряд на конденсаторе при замкнутом ключе К (рис.
13.88) , если <₽= 500 В, г = 10 Ом, R} = R2 = R3 = Я4 = 20 Ом, С= 10 мкФ.
Рис. 13.89
Рис. 13.90
13.129. Определить заряд, который пройдет через сопротивление Rx (см.
условие задачи №13.128) после размыкания ключа К.
13.130. При переключении ключа К из положения 1 в положение 2 ток
через сопротивление R} (рис. 13.89) не меняет направления, но увеличивается
в и = 5 раз. Как изменится заряд на одной из обкладок конденсатора при таком
переключении? Внутренними сопротивлениями источников пренебречь.
13.131. При переключении ключа К из положения 1 в положение 2 ток
через сопротивление Я, (рис. 13.90) увеличивается в и = 3 раза и меняет на-
правление на противоположное. Как изменится
заряд на одной из обкладок конденсатора при
таком переключении? Внутренними сопротив-
лениями источников пренебречь.
13.132. Во сколько раз изменится заряд
конденсатора в цепи, представленной на рис.
13.91, если ключ К переключить из положения 1
в положение 2? Все сопротивления одинаковы,
внутренним сопротивлением источника прене-
бречь.
13.133. Найти заряд на конденсаторе (рис.
13.92). Внутренним сопротивлением батареи
пренебречь. Величины Я, С и S известны.
302
Рис. 13.93
13.134. Найти разность потенциалов между обкладками конденсатора С в
цепи, представленной на рис. 13.93, если =4 В, <?2= 1 В, R} = 10 Ом,
Я2 = 20 Ом, R3 = 30 Ом. Внутреннее сопротивление источника пренебрежимо
мало.
13.135. Найти заряды q, и q2 на
конденсаторах С} и С2 в цепи, пред-
ставленной на рис. 13.94. Внутренни-
ми сопротивлениями батареи прене-
бречь.
13.136. Плоский конденсатор с
пластинами длиной / и расстоянием
между ними d включен в цепь так,
Рис. 13.94
как показано на рис. 13.95, а. В конденсатор параллельно пластинам влетает
электрон со скоростью и0. Найти величину отклонения электрона от первона-
чального направления движения при вылете из конденсатора. Э.д.с. источника
<?, внутреннее сопротивление г, все сопротивления R одинаковы. Силу тяжести
не учитывать. Масса электрона т, заряд |е|.
Рис. 13.95
• Решение. Задачу можно разделить на две части. Решение первой части задачи сводится к
определению падения напряжения на конденсаторе, зная которое, во второй части рассмот-
рим движение электрона в электрическом поле между обкладками.
По участку цепи c-d, содержащему конденсатор емкостью С, электрический ток не
идет. Поэтому, при расчете токов и падений напряжений иа отдельных участках цепи
участок c-d можно выбросить. Тогда преобразованная схема становится очень простой
(рис. 13.95, б).
Разность потенциалов на обкладках конденсатора равна разности потенциалов между
точками с и d (потенциал <ре > так как точка d соединена с отрицательной клеммой
источника):
303
Uc-d - Фе ~ *Pd-
Общее сопротивление цепи равно
_ _ 2R R _ 2а g
Лцепи"2Л + Я’^ ’
а сила тока в ее неразветвленной части
<? _ 3<?
Дцепи. + г + Зг
Падение напряжения на участке а-Ь
^Л-^цепи.-2Л + 3г.
а токи /| и 12:
I _ Ua~b _ ё ] _ Ua~b _ 2 ё
1 2Я 2Д + Зг’ 2 R ~2R + 3r
Так как точки d и b соединены проводником, то они имеют одинаковые потенциалы.
Поэтому искомая разность потенциалов
Uc-d=<?c-<?d = 9c~<Pb
равна падению напряжения на сопротивлении R, включенном в цепь между точками с и Ь:
и^-^-^зг-
Теперь рассмотрим вторую часть задачи.
Напряженность электрического поля между обкладкими конденсатора, заряженного
до разности потенциалов Uc~d> равна
Uc-d _ RS
d d(2R + 3r)
н на электрон будет действовать сила
Т’=|е|£ = —
11 d(2R + 3r)
сообщая ему ускорение
a_F_ |е| Д <?
т md (2R + Зг) ’
направленное перпендикулярно пластинам.
Записав уравнения движения электрона в момент вылета нз конденсатора в виде
2
I = v>o t, &h = ^,
найдем величину его отклонения от
., al2
Лп = —» ,
2«о
|е|Д<?/2
• Ответ: Ап =-----UJ-------~ .
или
первоначального направления движения:
2т d (2R + Зг) Uq
Рис. 13.96
13.137. Плоский конденсатор с пласти-
нами длиной I и расстоянием между ними
d включен в цепь так, как показано на рис.
13.96. В конденсатор параллельно пластинам
влетает электрон со скоростью и0. Под каким
углом к пластинам вылетит электрон из кон-
денсатора? Э.д.с. источника S, сопротивления R и г считать известными. Силу
тяжести не учитывать. Масса электрона т, заряд |е|.
304
Рис. 13.97
13.138. Плоский конденсатор с пластинами длиной I и расстоянием
между ними d включен в цепь так, как показано на рис. 13.97. В конденсатор
параллельно пластинам влетает электрон со скоростью и0. Э.д.с. источника S,
внутреннее сопротивление г. Каким должно быть сопротивление R, чтобы
электрон вылетел из конденсатора под углом а к его пластинам? Силу тяжес-
ти не учитывать. Масса электрона т, заряд |е|.
13.139. Плоский конденсатор с пластинами длиной I и расстоянием
между ними d включен в цепь так, как показано на рис. 13.98. В конденсатор
параллельно пластинам посередине между ними влетает электрон. При каком
значении скорости электрона он не упадет на пластину конденсатора? Э.д.с.
источника в, внутреним сопротивлением пренебречь, сопротивление R из-
вестно. Силу тяжести не учитывать. Масса электрона т, заряд |е|.
Измерение токов и напряжений
13.140. Имеются два сопротивления. Если амперметр зашунтировать
одним из них, то цена его деления увеличится в И] раз, если зашунтировать
другим, то цена деления увеличится в п2 раз. Как изменится цена деления ам-
перметра, если для шунта использовать оба сопротивления, включив их
между собой: а) последовательно; б) параллельно?
• Решение. Предельно допустимый ток в цепи, который может измерить амперметр без
шунта, равен
/А = ^, (1)
где t/A - максимальное падение напряжения на приборе, при котором стрелка отклоняется
на всю шкалу; ЯА - внутреннее сопротивление амперметра.
Для увеличения диапазона измеряемых токов к
амперметру параллельно подключают шунты. При
этом часть тока «отводится» через шунт (рис. 13.99).
Поскольку прибор и шунт подключены к точкам
цепи параллельно, то падение напряжения на внут-
реннем сопротивлении амперметра ЯА и шунте Яш
одинаково:
_ Лп
Следовательно, через шунт потечет ток
I
JU1~ р
являющийся частью тока в цепи равного
ш-
Рис. 13.99
305
ft
/=/а + Лш и™ /=/а{ 1+Т5г4-
Если подключить первый шунт Л|, то максимально допустимый ток, измеряемый
прибором, станет равным
/1тах = 4{1+^}» (2)
а с другой стороны: 1
A max = П1О
Следовательно, из выражений (2) и (3) получим
Лд /?д
И1 = !+-£-, или Ri=----------.
Я1 «! - I
Аналогично, при подключении шунта А2:
f Лд 1 •
4max = ^Al 1 + J’ Лтах = п2^А> ^2 = j •
Если оба сопротивления и R2 соединить последовательно и подключить к ампер-
метру, то вновь образований шунт будет иметь сопротивление
^посл. = ^1 +
или с учетом полученных выше соотношений:
Яа("|+”2~2)
посл- (Л,-1)(Л2-1)-
Теперь амперметр может измерять токи до значений
4пак = Л. {1 + ~п }>
япосл.
или с учетом (4):
Апах-4Н+ „|+И2_2 !
Следовательно, цена деления прибора изменится в
(4)
Алах . (”i - 1) («2 - 1) «1 «2 -1
ипосл. -г -1 + „ ) ~ _ п Ра3-
•*д Л] + ^2 — 2 Л| + ^2 — 2
Если сопротивления Rx и Я2 соединить параллельно, то сопротивление шунта будет
равно
Rx R2 Ra
^пар. д|+д2 Л|+Л2-2
и амперметром можно измерять токи до значений
I ^А 1
Алах = ^АI 1 + ~п р
япар.
(5)
или с учетом (5):
'max - 'а I 1 v‘l "2 ~
При этом цена деления прибора изменится в
Алах ,
Япар. = -7- = «1 + «2-1 Раз-
*А
7^2 —’ 1
• Ответ: а) изменится в Лпосл =------~ раз; б) изменится в Лпар = Л) + п2 -1 раз.
И] + />2 “ 2 к’
13.141. Источник э.д.с. замкйут на сопротивление R = 100 Ом. При вклю-
чении в цепь амперметра с внутренним сопротивлением ЯА = 1 Ом, последний
306
показал силу тока I = 10 А. Определить силу тока в цепи до включения ампер-
метра. Внутренним сопротивлением источника пренебречь.
13.142. В схеме, изображенной на
рис. 13.100, сопротивления R2 = 80 Ом,
R3 = 30 Ом. Через сопротивление R2 течет
ток силой 12 = 1,5 А. Найти значение со-
противления Rb если амперметр показы-
вает ток I = 6 А. Рис. 13.100
13.143. Амперметр с внутренним сопротивлением ЯА = 0,02 Ом и шунтом
сопротивлением Яш = 0,005 Ом может измерять силу тока до I = 10 А. Опреде-
лить предельную силу тока 1к для самого амперметра.
13.144. Зашунтированный гальванометр может измерить ток силой до
7= 1 А. Определить сопротивление шунта, если сопротивление гальванометра
Ra = 20 Ом, максимальная сила тока через прибор без шунта IG = 50 мА.
13.145. Шкала амперметра имеет 100 делений с ценой п = 1 А каждого.
Каким сопротивлением следует зашунтировать прибор для измерения им
токов до 7= 1000 А? Внутреннее сопротивление амперметра ЯА = 90 Ом.
13.146. Для шунтирования амперметра используют два одинаковых со-
противления. Если сопротивления соединены между собой последовательно,
то цена деления увеличивается в п = 10 раз. Во сколько раз изменится цена де-
ления, если сопротивления соединить между собой параллельно?
13.147. К гальванометру, сопротивление которого Rq = 290 Ом, присо-
единили шунт, понижающий чувствительность гальванометра в п= 10 раз.
Какое сопротивление надо включить последовательно с шунтированным галь-
ванометром, чтобы общее сопротивление осталось неизменным?
13.148. Микроамперметр имеет шкалу из ТУ = 100 делений. Цена деления
70 = 1 мкА. Внутреннее сопротивление микроамперметра г = 200 Ом. Какой
величины шунт нужно присоединить к этому прибору, чтобы им можно было
измерять ток до 7= 1 мА?
13.149. В цепь, состоя-
щую из источника тока,
гальванометра и сопротив-
ления й] = 350 Ом (рис.
13.101, а), включили шунт
7?ш = 10 Ом и вместо сопро-
тивления й] включили со-
противление Я2=ЮООМ
Рис. 13.101
(рис. 13.101, б). При этом величина тока через гальванометр не изменилась.
Определить сопротивление гальванометра. Сопротивлением источника прене-
бречь.
307
13.150. Гальванометр подключают к источнику напряжения последова-
тельно с сопротивлением Я, и фиксируют отклонение стрелки прибора. Затем
параллельно гальванометру подключают шунт сопротивлением Rm. Для того,
чтобы получить прежнее отклонение стрелки прибора, необходимо заменить
сопротивление Л] наЛ2- Определить сопротивление гальванометра. Сопротив-
лением источника тока пренебречь.
13.151. Имеются два сопротивления. Если к вольтметру подключить одно
из них, то цена его деления увеличится в И] раз, если подключить второе, то
она увеличится в п2 раз. Как изменится цена деления вольтметра, если эти со-
противления использовать одновременно, включив между собой: а) последо-
вательно; б) параллельно?
• Решение. Предельно допустимое напряжение, которое может измерить вольтметр без до-
бавочных сопротивлений
I/v = Аг «V, (1)
где /v - максимальный ток через прибор, при котором стрелка отклоняется на всю шкалу;
Av - внутреннее сопротивление вольтметра.
Для увеличения диапазона измеряемых напряжений к вольтметру последовательно
подключают добавочные сопротивления. При этом шкала прибора становится грубее. Если
подключить первое сопротивление то максимально допустимое напряжение, измеряе-
мое прибором станет равным
Ul max = Аг (Ry + ^1)> (2)
а с другой стороны:
Ul max = nl Цг- (3)
Следовательно, из выражений (2) и (3) с учетом (1) получим
ГГ| Яу = Лу + Л], ИЛИ Я] = (Л] — 1) Яу.
Аналогично, при подключении добавочного сопротивления R2:
U2 max = Аг ОАг + ^г)> U2 max = п2 Uy, Я2 = (и2 - 1) &у-
Если оба сопротивления н R2 соединить последовательно и подключить к вольт-
метру, то вновь образованное добавочное сопротивление будет равно
^посл. ~ Я| +^2>
или с учетом полученных выше соотношений:
^посл. = (Л| + n2-2)Rv. (4)
Теперь вольтметр может измерять напряжения до значений
^Апах = Аг (*v + ^посл.)>
или с учетом (4):
Цпах = Аг Ry (”i + ”2 ~ О = Щ (Л) + п2 - 1).
Следовательно, цена деления прибора изменится в
^Апах ,
, «посл.=~ц^ = ”1+П2- 1 Раз.
Если сопротивления Rt и R2 соединить параллельно, то добавочное сопротивление
будет равно
RtR2 Яу(я,-1)(л2-1)
АпаР“Я1 + Я2_ п(+и2-2 W
и вольтметром можно измерить предельное напряжение
308
или с учетом (5):
Цпах _ Аг (*v + ^пар.)>
Стах = Аг Аг
(П|-1)(п2-1) tl тг Ь,п2~1
~ + 1 [ = Uy
П| + «2 - 2 1 П| + «2 - 2
Прн этом цена деления прибора изменится в
Стах n, и2 - 1
"пар. = -ТТ- = —---Г Раз.
uv п. + п2 - 2 ,
л. п2 - 1
• Ответ: а) изменится в ппосл = П| + п2 - 1 раз; б) изменится в ппар =- раз.
н' П| + л2 - 2
13.152. Вольтметр со шкалой на U= 100 В имеет внутреннее сопротивле-
ние Rv= 10 кОм. Какое максимальное падение напряжения можно измерить
этим прибором, если к нему присоединить добавочное сопротивление
Яд = 90 кОм?
13.153. Вольтметр имеет три предела измерения: Ц = 3, В, U2 = 15 В и
U2 = 75 В. Наибольший допустимый ток прибора 7V = 0,3 мА. Найти добавоч-
ные сопротивления Яр Я2 и Я3, если внутреннее сопротивление вольтметра
Яу= 103 Ом.
13.154. Для измерения падения напряжения на сопротивлении Я, подклю-
ченном к батарее с внутренним сопротивлением г, использовали вольтметр.
Оказалось, что падение напряжения на сопротивлении Я (до подключения
вольтметра) больше показания прибора в п раз. Определить сопротивление
вольтметра.
13.155. Вольтметр, включенный последовательно с сопротивлением
Я] = 7 кОм, показывает 17= 50 В при напряжении на концах цепи 170 = 120 В.
Какое показание дает при этом же напряжении Uo вольтметр, если включить
его последовательно с сопротивлением Я2 = 35 кОм?
13.156. Цепь состоит из аккумулятора с внутренним сопротивлением г
и нагрузки сопротивлением Я. Вольтметр, подключенный последовательно,
а затем параллельно к сопротивлению дает одно и то же показание. Опреде-
лить сопротивление вольтметра.
13.157. Цепь состоит из последовательно включенных батареи, перемен-
ного сопротивления и вольтметра. Если сопротивление уменьшить втрое, то
показание вольтметра возрастет вдвое. Во сколько раз изменится показание
вольтметра, если сопротивление уменьшить до нуля?
13.158. В схеме, изображенной на рис. 13.102, вольтметр измеряет напря-
жение на сопротивлении Я2 = 300 Ом. Каким должно быть сопротивление
вольтметра для того, чтобы его показания отличались не более, чем на ц = 2%
от действительного значения напряжения на сопротивлении Я2? Сопротивле-
ние Я] = 100 Ом. Внутренним сопротивлением источника пренебречь.
309
Рис. 13.102 Рис. 13.103
13.159. К сопротивлению подключили параллельно два вольтметра так,
как показано на рис. 13.103. После подключения зажимов цепи к источнику
э.д.с., первый элемент показал Ц = 6 В, а второй - U2 = 12 В. Определить со-
противление второго вольтметра, если сопротивление первого R} = 50 кОм.
13.160. В схеме, изображенной на рис. 13.104, при подключении вольт-
метра к точкам АВ, он покажет значение напряжения Ut = 6 В. Если вольтметр
подключить к точкам ВС, то - U2 = 4 В, а если к точкам АС, то - U3 = 12 В.
Пренебрегая внутренним сопротивлением источника, определить действи-
тельные значения напряжений между точками А, В, С.
13.161. Для измерения напряжения сети t/0 = 120 В последовательно со-
единили два вольтметра с номинальными напряжениями U= 100 В и сопро-
тивлениями й] = 20 кОм и R2 = 15 кОм. Определить показания каждого вольт-
метра и наибольшее напряжение, которое можно измерять вольтметрами.
13.162. В схеме (рис. 13.105) все вольтметры одинаковы. Э.д.с. батареи
9 В, ее внутреннее сопротивление пренебрежимо мало. Вольтметр V] по-
казывает напряжение Ц = 2 В. Какие значения напряжений показывают ос-
тальные вольтметры?
13.163. Если к амперметру, рассчитанному на максимальную силу тока
1А = 2 А, присоединить шунт сопротивлением Яш = 0,5 Ом, то цена деления
шкалы амперметра возрастает в п = 10 раз. Определить, какое добавочное соп-
ротивление необходимо присоединить к тому же амперметру, чтобы его
можно было использовать как вольтметр, рассчитанный на измерение напря-
жений до U = 220 В?
• Решение. При наличии шунта стрелка амперметра будет отлоняться на всю шкалу при токе
в неразветвленной части цепи равном
1 = If, + Ап»
где 1т - сила тока через шунт.
310
Поскольку по условию задачи
/=л/А,
то через шунт протекает ток силой
D-
Так как падение напряжения на приборе и шунте одинаково
= 4п
то внутренее сопротивление амперметра
Ла = гЦ^“=Лш(п-1) = 4,50м
'А
и максимально допустимое падение напряжения на нем
14пах — ЛА — Лщ (п 1) —9 В.
Следовательно, для измерения напряжений до U = 220 В к амперметру необходимо
присоединить последовательно добавочное сопротивление Адоб., величину которого най-
дем из условия, что при максимально допустимой силе тока через прибор падение напря-
жения на сопротивлении (ЛА + Адоб) равно U:
U -Ifi (ЛА + Лдоб.)-
Откуда находим:
Ядоб. = Т"*А = Т-*ш(«-!) = Ю5,5 Ом.
U * А
• Ответ: Ядоб. = ~г ~ Лщ (”-!) = Ю5,5 Ом.
* А
13.164. Гальванометр с сопротивлением RG, шунтированный сопротивле-
нием Яш и соединенный последовательно с сопротивлением R, применен в ка-
честве вольтметра. Он дает отклонение стрелки в одно деление на Ц = 1 В.
Каким сопротивлением R2 следует заменить Яь чтобы гальванометр давал от-
клонение в одно деление на U2 = 10 В?
13.165. Имеется прибор с ценой деления п = 1 мкА. Шкала прибора имеет
N= 100 делений, внутреннее сопротивление r = 1 кОм. Как из этого прибора
сделать вольтметр для измерения напряжения до 17= 100 В или амперметр для
измерения тока до I = 1 А?
13.166. При использовании гальванометра в качестве вольтметра после-
довательно с прибором включили добавочное сопротивление Ядод При даль-
нейших измерениях оказалось необходимым увеличить предел измерений в
п= 10 раз. Однако по ошибке дополнительное сопротивление, необходимое
для этого, припаяли параллельно Ядоб,- Во сколько раз изменилось предельное
напряжение, измеряемое прибором? Внутренним сопротивлением гальвано-
метра пренебречь.
13.167. Определить сопротивление R на ।__/у)___
участке цепи, представленном на рис. 13.106, 4—
если амперметр показывает силу тока I = 5 А, а /д\ I ...,
вольтметр - напряжение U = 100 В. Внутрен-
нее сопротивление вольтметра R,, = 2,5 кОм.
v Рис. 13.106
311
13.168. Амперметр и вольтметр подключили последовательно к батарее с
э.д.с. S= 6 В. Если параллельно вольтметру подключить некоторое сопротив-
ление, то показание вольтметра уменьшается в п - 2 раза, а показание ампер-
метра во столько же раз увеличивается. Найти показание вольтметра после
подключения сопротивления. Внутренним сопротивлением батареи прене-
бречь.
Рис. 13.107
13.169. Для измерения
величины сопротивления с
помощью амперметра и вольт-
метра используют различные
схемы включения приборов.
На рис. 13.107, а, б представ-
лены две из них. По какой схеме нужно включить приборы, чтобы измерить
сопротивление R более точно?
Работа и мощность тока
13.170. Электроплитка содержит три спирали с сопротивлениями
R = 120 Ом каждая, соединенные параллельно друг с другом. Плитку включа-
ют в сеть последовательно с сопротивлением г = 50 Ом. Как изменится время,
необходимое для нагревания на этой плитке чайника с водой до кипения, при
перегорании одной из спиралей?
• Решение. Независимо от количества спиралей в электроплитке и их соединения между
собой количество тепла, необходимое для нагревания воды до кипения во всех случаях
должно быть одинаковым.
При первоначальном соединении спиралей плитки общее сопротивление цепи
А| = ЦЯ + г
и в цепи протекает ток силой
I и _ и
'~Rt VsR + r'
При этом на спиралях за время Д/| выделится количество тепла
б! = /2Я, Л/) = - U -i ЛА/, = — R Д/j.
(’/5Я + г)2 (Я + Зг)2 1
Если одна из спиралей перегорит, то общее сопротивление цепи станет равным
R2 = '6R + r
и в цепи будет течь ток силой
. U U
2 R2 ’ЛЯ + г’
а на спиралях за время выделится количество тепла
q2 = i22r2 &t2 = , u 2 Ц Я Д/2 = - Я Дт2.
(’ЛЯ+r)2 (Я + 2г)2 2
Поскольку Qi = Q2, то
зи2
(Я + Зг)2
2U2
ЯДт.=—-тЯД/2,
' (Я + 2г)2 2
312
нли 3 2
---Д/| =-------ДГ>.
(А + Зг)2 (А + 2г)2
Откуда находим
Д*1_2(А + Зг)2_2 f Ач-Зг )2_ 243
Ы2 3(А + 2г)2 3 *А + 2г> 242
_ 243
• Ответ: уменьшится в раза.
13.171. Можно ли две лампочки накаливания мощностью Nx = 40 Вт и
# 2 = 60 Вт, рассчитанные на напряжение Uo = 110 В, подключить к сети с на-
пряжением U = 220 В, соединив их последовательно? Ответ обосновать.
• Решение. Поскольку каждая лампочка рассчитана иа работу от напряжения С/о, то для нор-
мального накала лампочки мощностью Nt по ней должен протекать ток силой 1Ь величину
которого найдем из выражения1 для мощности:
Откуда получаем
7, =-/==0,36 А.
о'О
Аналогично для лампочки, рассчитанной на мощность #2:
#2
72 = -”~0,55 А.
ио
Если лампочки соединить последовательно, то их общее сопротивление станет рав-
ным
А = А1+А2,
где А|, А2 - сопротивления лампочек мощностью и N2 соответственно.
Сопротивления лампочек можно найти, записав выражение для мощности через на-
пряжение Uo:
N U°2
Аналогично
Следовательно,
U2
R^'
R
R1~n2-
nx+n2-
При подключении лампочек к сети с напряжением U по ним потечет ток силой
г U U N,N2U
!=% = - <- ,= - J 2-------------------« 0,44 А.
R Ug uj U02(Nl+Ni)
#i+#2
. Так как 7| < 7, то лампочка мощностью Nt перегорит.
• Ответ: нельзя, так как лампочка мощностью Nt перегорит.
13.172. Лампочку мощностью No = 16 Вт, рассчитанную для работы при
напряжении Uo = 12 В, включили в цепь с напряжением на зажимах U-9 В.
Какая мощность будет выделятся в лампочке?
13.173, Лампочка мощностью #=500 Вт рассчитана на напряжение
UQ = 110 В. Определить величину дополнительного сопротивления, позволяю-
313
щего включить лампочку в сеть с напряжением U = 220 В без изменения ее
мощности.
13.174. В электрическую цепь с напряжением на зажимах U= 127 В
включены параллельно несколько лампочек сопротивлением R = 420 Ом каж-
дая. При этом потребляемая мощность N = 500 Вт. Определить число лампо-
чек в цепи.
13.175. Десять параллельно соединенных лампочек сопротивлением
R = 0,5 кОм каждая, рассчитанных на напряжение Uo = 120 В, соединенных
последовательно с реостатом, подключили к сети напряжением U = 220 В. Оп-
ределить мощность электрического тока в реостате, если лампочки горят нор-
мальным накалом.
13.176. Некто хочет изготовить гирлянду из пяти электрических лампо-
чек, рассчитанных на напряжение Uo = 110 В, с мощностями = 40 Вт (три
лампочки) и N2 = 60 Вт (две лампочки). Каким образом следует их соединить
для включения в сеть с напряжением U = 220 В, чтобы все они горели нор-
мальным накалом?
13.177. Электрическая лампа с вольфрамовой нитью в момент включения
потребляет мощность = 500 Вт. Какую мощность она будет потреблять
после того, как ее нить нагреется до t2 = 2500°С? Комнатная температура
Z] = 20°С. Температурный коэффициент сопротивления вольфрама равен
а = 4,810'3 град .
13.178. Два источника с одинаковыми э.д.с. 120 В и внутренними со-
противлениями Г] = 0,5 Ом и г2 = 0,6 Ом соединены параллельно одинаковыми
полюсами и замкнуты на сопротивление R = 10 Ом. Найти мощность, разви-
ваемую каждым источником, и мощность, выделяющуюся на внешнем сопро-
тивлении.
• Решение. Используя решение задачи №13.87, заменим два источника одним эквивалент-
ным с внутренним сопротивлением
гэкв. -
и э.д.с.
вг2 + вГ\ „
^экв.= =
Г1 +г2
Применив закон Ома для замкнутой цепи, найдем ток через внешнее сопротивление
J ^экв.(rl + гз)
Гэкв. + R rlr2 + rlR + r2R
и падение напряжения на нем (оно равно напряжению на зажимах батареи):
U-IR- g^+rl>R .
Г] г2 + Г| R + r2 R
Следовательно, мощность, выделяющаяся на сопротивлении R, равна
. , e1(rl + ri)1R
Nr = J2R =------5-!--------5 » 1,36 кДж.
(rt r2 +R + r2 R)2
314
, Для расчета мощности, развиваемой каждым источником, найдем токи 7] и /2, при-
менив закон Ома для неоднородного участка цепи:
«(Ti+r^R
ff— -II
U И г2 + Л / + / _______&Г2
1 Г| Г2 ^"1 ^2
s e(ri+r$R
j s~v rxr2 + rxR + r2R grx
2 r2 r2 rl r2 + rl R+fyR
Мощность, развиваемая источником, может быть найдена по одной из формул:
л 2
ЛГ=/^=:72(Д + г) = -^-.
Поэтому
Ni=Iig =
в2г2
лг2г.
~ 764,6 Дж, N2 = I2S=-------------—---------~~ 637,2 Дж.
г\ г2 + R + r2 R
gl r2
— 1,36 кДж, Ni =---------------------- ~ 764,6 Дж,
Г| г2 + т*1 R + r2 R
Г1 г2 + Г1 + г2 R
„ „ #2(Г1+Г2)2Я
• Ответ: NR =----------------5
(Г1Г2 + Г1Л+Г2Л)
2
<? Г.
Л^2 =--------„----- = 637,2 Дж.
rIr2 + rlR + r2R
13.179. Проволочный предохранитель перегорает, если напряжение на
нем равно Uo = 10 В. При каком напряжении перегорит предохранитель, изго-
товленный из того же материала, если его длину увеличить в и = 2 раза, пола-
гая, что все выделившееся тепло идет на нагревание и плавление проволоки, а
предохранители перегорают при равных мощностях, выделяющихся на сопро-
тивлении предохранителей?
13.180. Две электрические лампочки включены в сеть параллельно. Со-
противление первой лампочки R} = 360 Ом, второй -R2 = 240 Ом. Какая из
лампочек поглощает большую мощность и во сколько раз?
13.181. Источник э.д.с. S= 12 В с внутренним сопротивлением г = 4 Ом
замкнут на сопротивление R = 8 Ом. Определить мощность, выделяющуюся
во внешней цепи.
13.182. Э.д.с. источника S- 2 В, внутреннее сопротивление г = 1 Ом. Оп-
ределить силу тока, если во внешней цепи выделяется мощность W= 0,75 Вт.
13.183. Напряжение на зажимах аккумулятора с э.д.с. S- 10 В и внутрен-
ним сопротивлением г = 1 Ом, подключенного к некоторому сопротивлению,
равно U = 6 В. Какая мощность выделяется на внутреннем сопротивлении ак-
кумулятора?
13.184. Напряжение на зажимах аккумулятора с э.д.с. S= 2,5 В равно
U= 2 В. Какая доля мощности аккумулятора выделяется во внешней цепи?
13.185. Аккумулятор с внутренним сопротивлением г = 0,08 Ом при силе
тока 7j = 4 А отдает во внешнюю цепь мощность = 8 Вт. Какую мощность
он отдаст во внешнюю цепь при токе 12 = 6 А?
315
13.186. Определить ток короткого замыкания для аккумуляторной бата-
реи, если при токе 7] = 5 А она отдает во внешнюю цепь мощность N3 = 9,5 Вт, а
при токе 12 = 8 А - N2 = 14,4 Вт.
13.187. К аккумулятору с внутренним сопротивлением г = 1 Ом подклю-
чили сопротивление R = 8 Ом. Затем параллельно с первым подключили вто-
рое такое же сопротивление. Найти отношение мощностей, выделяющихся во
внешней цепи в первом и втором случаях.
13.188. При поочередном присоединении к аккумулятору двух разных со-
противлений тепловая мощность, выделяющаяся во внешней цепи была равна
А] = 30 Вт и ?72 = 60 Вт. Какая мощность будет выделяться, если к аккумуля-
тору подключить оба сопротивления, соединенные последовательно? Внут-
ренним сопротивлением аккумулятора пренебречь.
13.189. Два параллельно соединенных сопротивления Я] = 6 Ом и
R2 = 12 Ом включены последовательно с сопротивлением R3 = 15 Ом и под-
ключены к зажимам аккумулятора, э.д.с. которого равна <?= 200 В, а внутрен-
нее сопротивление r = 1 Ом. Определить мощность, выделяющуюся на сопро-
тивлении Лр
Рис. 13.108 Рис. 13.109
13.190. В схеме, представленной на рис. 13.108, э.д.с. источника S- 10 В,
сопротивления Rx = 2,6 Ом, R2 = 6 Ом, показание амперметра 1= 1,2 А. Опре-
делить мощность, выделяющуюся на сопротивлении R3. Внутренними сопро-
тивлениями источника и амперметра пренебречь.
13.191. В схеме, представленной на рис. 13.109, сопротивления
/?! = 3 Ом, R2 = 4 Ом, R3 = 6 Ом, показание вольтметра 17= 12 В. Определить
мощность, выделяющуюся на сопротивлении R2. Внутренним сопротивлением
источника пренебречь. Сопротивление вольтметра много больше R}.
13.192. Четыре одинаковых сопротивления Rt,R2, R3, Я4 подключены к
источнику напряжения так, как показано на рнс. 13.110. При этом на сопро-
тивлении Я( выделяется мощность = 0,9 Вт. Какая мощность будет выде-
ляться на сопротивлении Я], если сопротивление Я2 отключить? Внутренним
сопротивлением источника пренебречь.
13.193. Два гальванических элемента с э.д.с. = 10 В и в2 = 6 В н оди-
наковыми внутренними сопротивлениями г = 1 Ом соединены параллельно и
замкнуты на внешнее сопротивление Я = 0,5 Ом. Какая мощность выделяется
внутри первого элемента в виде тепла? .
316
Рис. 13.110 Рис. 13.111
13.194. Два сопротивления г и R подключены к источнику напряжения
так, как показано на рис. 13.111. При замыкании ключа К мощность, выделяю-
щаяся на сопротивлении R, увеличивается в два раза. Чему равно сопротивле-
ние г, если R = 10 Ом? Внутренним сопротивлением источника пренебречь.
13.195. п одинаковых источников э.д.с. S с внутренними сопротивления-
ми г сначала соединили последовательно и замкнули на некоторое сопротив-
ление R, а затем параллельно и замкнули на то же сопротивление. Определить
величину сопротивления R, если выделившаяся на нем мощность изменилась
в ц раз.
13.196. Проводник сопротивлением R присоединен к источнику напряже-
ния с э.д.с. S. От проводника отрезали некоторую часть и присоединили па-
раллельно оставшейся части. Какая это должна быть часть исходного провод-
ника, чтобы во внешней части образовавшейся цепи выделялась бы в и = 4
раза большая мощность, чем в первоначальной? Внутренним сопротивлением
источника пренебречь.
13.197. Линия электропередачи сопротивлением R = 250 Ом подключена
к генератору постоянного напряжения мощностью N = 25 кВт. При каком на-
пряжении на зажимах генератора потери мощности в линии составят т| = 4%
от мощности генератора?
13.198. Потери мощности в линии электропередачи составляют ctj = 5%
от мощности, получаемой потребителем. Как нужно изменить напряжение на
входе линии и сопротивление потребителя для того, чтобы при той же мощ-
ности, получаемой потребителем, потери в линии снизились до а2 = 1%?
13.199. Источник постоянного тока замыкается один раз сопротивлением
/?! = 4 Ом, другой раз - сопротивлением R2 = 9 Ом. В том и другом случаях
количество тепла, выделяющегося на сопротивлениях за одно и то же время,
одинаково. Определить внутреннее сопротивление источника.
• Решение. Количество тепла, выделяющегося за время t на сопротивлении R, подключен-
ном к источнику тока с э.д.с. ё и внутренним сопротивлением г, может быть рассчитано
по одной из формул
U2
Q = IUt = I2Rt = % t,
ix.
где 7- сила тока, протекающего через сопротивление R; U- падение напряжения на нем.
317
Воспользуемся, например, первой из этих формул.
Силу тока найдем из закона Ома для замкнутой цепи:
7=^-.
R + r
Следовательно, ,
(R + r? .
Так как по условию задачи на сопротивлениях Rt и R2 за одинаковое время выделяется
одинаковое количество тепла, то
#1_______&2
или (Rl + r? = (R2 + r?’
Яь&2 + г) = уПЪ(П1 + гУ
Откуда получаем
г = V Л, R2 = 6 Ом.
• Ответ: г = R\ R2 = 6 Ом.
13.200. При замкнутом и разомкну-
том ключе К на участке а-b цепи, пред-
ставленной иа рис. 13.112, выделяется
одинаковая мощность. Найти величину
сопротивления Rx, если напряжение на за-
жимах источника постоянно.
13.201. Сопротивление внешней цепи увеличили в и = 2,25 раза. При этом
мощность, выделяющаяся на нем, осталась прежней. Найти, во сколько раз от-
личается внутреннее сопротивление г источника от первоначального сопро-
тивления R внешней цепи.
13.202. На двух одинаковых сопротивлениях, каждое из которых при на-
пряжении U = 220 В потребляет мощность W= 800 Вт, выделяется одинаковое
количество тепла за одно и то же время при их параллельном и последова-
тельном подключении. Чему равно сопротивление подводящих проводов?
13.203. Какой величины ток пойдет по подводящим проводам при корот-
ком замыкании источника напряжения, если на двух сопротивлениях
R{ = 200 Ом и /?2 = 500 Ом выделяется при поочередном включении одинако-
вая мощность W= 200 Вт?
13.204. Два сопротивления по R = 100 Ом каждое подключаются к источ-
нику напряжения сначала последовательно, а затем параллельно. В обоих слу-
чаях тепловые мощности, выделяющиеся на каждом сопротивлении, оказа-
лись одинаковыми. Найти э.д.с. источника, если ток, протекающий в цепй при
последовательном включении сопротивлений, равен 1= 1 А.
13.205. Как при последовательном, так и при параллельном соединениях
двух одинаковых батарей на внешнем сопротивлении выделилась мощность
318
No = 80 Вт. Какая мощность будет выделяться на этом сопротивлении, если
замкнуть на него лишь одну батарею?
13.206. Батарея состоит из и = 5 последовательно соединенных источни-
ков с э.д.с. S= 1,4 В и внутренним сопротивлением г = 0,3 Ом каждого. При
какой силе тока мощность, выделяющаяся на нагрузке, равна # = 8 Вт? Чему
равна наибольшая мощность которую можно получить от батареи?
• Решение. При последовательном соединении источников тока э.д.с. всей батареи равна
алгебраической сумме э.д.с. отдельных источников (см. решение задачи №13.82) Следо-
вательно,
<^бат. — и 8.
Полное сопротивление цепи равно сумме внутренних сопротивлений источников н со-
противления R нагрузки:
^цепи = nr + R.
При таком соединении источников тока и нагрузки в цепи протекает ток
= (О
"цепи и г + R
и иа сопротивлении R выделяется мощность
N=I2R. (2)
Выражая из соотношения (2) величину сопротивления нагрузки
R = N/I2,
н подставляя ее в (1)
, п8
~ nr + N/I2
после несложных преобразований получим
пг I2—п <?/+У=0.
Решив последнее уравнение относительно /, найдем силу тока в цепи, соответствую-
щую мощности N~.
. п8 + г? 8 2 -4nr N п 8 - п282-4п г N - ,
/ =----------------И 2,67 А, или I =---------х---------» 2 А.
2п г ’ 2пг
Для ответа на второй вопрос задачи, т.е. определения максимальной мощности, кото-
рую можно получить от данной батареи источников, необходимо исследовать зависимость
мощности N, выделяющейся на внешней цепи, от величины сопротивления R нагрузки. Для
этого выражение (2) перепишем с учетом (1) в виде
N=I2R^-^\2R = 2^LL_
'nr+R1 (nr + R)2
(3)
Следовательно,
— -п282
dR~n 4 S
Откуда получаем
(nr + R)2-2R(nr + R) _Q
(nr + R)2
R = nr,
(4)
т.е. для получения максимальной мощности Nmax во внешней цепи сопротивление нагруз-
ки должно быть равно внутреннему сопротивлению батареи.
319
Из (3) с учетом (4) находим
и2#2 и г и#2
Л'тах = ----л = -ТГ- “8,16 Вт.
(и г + и г)
_ . И <? ± 'V И2 <?2 - 4и Г У пвг
• Ответ-. 1=------------------,7» 2,67 А, или2 А; Утях = ~.;— “ 8,16 Вт.
2и г 4г
13.207. Источник напряжения замкнут на некоторое внешнее сопротив-
ление. При этом на нем выделяется наибольшая мощность Утах = 9 Вт, а сила
тока в цепи равна 7=3 А. Найти величину э.д.с. источника и его внутреннее
сопротивление.
13.208. Источник с э.д.с. <%= 6 В может дать максимальный ток 1тах = 3 А.
Определить максимальную мощность, выделяющуюся во внешней цепи, и
внутреннее сопротивление источника.
13.209. Источник с э.д.с. S= 2,2 В и внутренним сопротивлением г = 1 Ом
замкнут медной проволокой, масса которой т = 30,3 г. Сопротивление прово-
локи подобрано таким образом, что на нем выделяется максимальная мощ-
ность. На сколько нагреется проволока за т = 5 минут? Удельная теплоемкость
меди с = 378 Дж/(кг-К).
13.210. При подключении некоторого сопротивления R к источнику на-
пряжения к.п.д. последнего равен р = 20%. Сколько таких сопротивлений
нужно взять и как их надо соединить, чтобы мощность, выделяющаяся на
этом соединении, была максимальной?
13.211. К источнику э.д.с. S= 10 В с внутренним сопротивлением.
г = 1 Ом подключена система из п = 4 сопротивлений по R = 1 Ом каждое.
Как требуется подсоединить эти сопротивления, чтобы в системе выделялась
максимальная мощность?
13.212. Какую наибольшую мощность Nn^ можно получить от источ-
ника с э.д.с. S= 100 В и внутренним сопротивлением г = 20 Ом? Какую наи-
большую мощность Л'к j можно получить, если максимально допустимый ток
через источник составляет ц = 0,1 от тока короткого замыкания?
13.213. Ток в проводнике сопротивлением R = 100 Ом равномерно нарас-
тает от 70 = 0 до 7тах = 10 А в течение времени t = 30 с. Чему равно количе-
ство теплоты, выделившееся за это время в проводнике?
• Решение. При переменном по величине токе в цепи на сопротивлении R за равные
промежутки времени будет выделяться разное количество тепла. Поэтому непосредствен-
но применять закон Джоуля-Леица в виде
Q = I2Rt
нельзя.
Рассмотрим бесконечно малый промежуток времени dt, в течение которого ток / в
цепи можно считать постоянным. За время dt в проводнике будет выделено количество
тепла
dQ = I2Rdt,
где сила тока I в момент времени t равна
320
Алах ~ A) t
т
Следовательно,
ф = {Апюс2о t^Ra
Суммарное количество тепла, выделившееся в проводнике за конечный интервал вре-
мени т найдем, проинтегрировав полученное выражение в пределах от 0 до т:
q = 4nax_J> , fR л = { fR Jрл>
О т т О
или
3
Q = | ^А) = (Алах -= 105
• Ответ-. Q = И (/max - I$2R т = 105 Дж.
13.214. Ток в проводнике сопротивлением R = 12 Ом равномерно убывает
от /0 = 5 А до / = 1 Ав течение времени т = 10 с. Какое количество теплоты
выделится в проводнике за это время?
13.215. Ток в проводнике сопротивлением R = 15 Ом равномерно нарас-
тает от /0 = 0 до некоторого максимума в течение времени т = 5 с. За это время
в проводнике выделилось количество теплоты 0-10 кДж. Найти среднее зна-
чение силы тока в проводнике за этот промежуток времени.
Нагревательные приборы
13.216. Какой длины надо взять никелиновый проводник диаметром
d = 0,5 мм, чтобы изготовить электрический камин, работающий от сети на-
пряжением U = 220 В, чтобы в нем выделялось Q = 1,68-108 Дж тепла в час?
Удельное сопротивление никелина р = 4-10"7 Ом-м.
• Решение. Поскольку тепловая энергия, выделяющаяся за время т на нагревательной спи-
рали камина, зависит от ее сопротивления по закону
то для решения задачи достаточно найти длину проводника, сопротивление которого
Величина R может быть выражена через длину и площадь поперечного сечения про-
водника:
Следовательно,
или с учетом S = ’/4 я d2:
, nd2 U2
Ответ: I =---- т « 0,5 м.
4р0
Я s .
. SU2
1 =—~ Т,
PQ
, ltd2 U2 п,
Z ==-— т « 0,5 м.
4ре
321
13.217. При ремонте электроплитки спираль была укорочена на г| = 10%
первоначальной длины. Во сколько раз при этом изменилась мощность плит-
ки?
13.21$. Утюг рассчитан на некоторую мощность при напряжении
Uo = 220 В. Как надо изменить включение нагревательной спирали, чтобы
утюг нормально эксплуатировался прн напряжении 17= 110 В?
13.219. Требуется изготовить нагревательную спираль для электрической
плитки мощностью У= 0,5 кВт при рабочем напряжении U = 220 В. Какую
длину нихромовой проволоки диаметром d = 0,4 мм надо взять для спирали?
Удельное сопротивление нихрома р = 1,05-Ю'5 Ом м.
13.220. Из комнаты в течение суток «уходит» Q= 8,7-107 Дж тепла. Какой
длины надо взять нихромовую проволоку диаметром d= 10’3 м для намотки
электрического обогревателя, поддерживающего постоянную температуру в
комнате? Удельное сопротивление нихрома р= 1,05-Ю"6 Ом-м. Наряжение в
сети U = 220 В.
13.221. Спираль, изготовленную из провода длиной / = 100 м, подключи-
ли к сети с напряжением 17= 100 В на т = 10 с. На сколько градусов нагреется
спираль? Плотность материала провода р0 = 7,8-103 кг/м3, удельное сопротив-
ление р = 0,12-10"6 Ом-м, удельная теплоемкость с = 460 Дж/(кг-К).
13.222. Какова мощность нагревательного элемента электрического чай-
ника, если V= 2 л воды, имевшей первоначальную температуру t = 15°С, заки-
пают через т = 5 мин? Напряжение в сети U = 220 В. Определить сопротивле-
ние нагревателя. Удельная теплоемкость воды с = 4200 Дж/(кг-К).
13.223. В электрическом чайнике мощностью N= 1 кВт кипит вода. Оп-
ределить скорость истечения пара из носика чайника, считая пар идеальным
газом. Атмосферное давление р0 = 105 Па, площадь поперечного сечения но-
сика чайника S = 1 см2. Удельная теплота испарения воды г = 2250 кДж/кг, мо-
лярная масса ц = 0,018 кг/моль. Считать, что вся энергия нагревателя переда-
ется воде.
13.224. Спираль свернута в кольцо и включена в цепь, по которой течет
ток силой I. Контакты делят кольцо в отношении 1:2, а на спирали выделяется
мощность 7V= 108 Вт. Какая мощность выделилась бы на спирали (при том же
токе во внешней цепи), если бы контакты были расположены по диаметру
кольца.
13.225. Электрокипятильник имеет две обмотки. При включении одной
из них вода в сосуде закипает через ^ = 10 минут, а при включении другой -
через Г2 = 20 минут. Через какое время закипит вода в том же сосуде, если обе
обмотки включить: а) последовательно; б) параллельно?
13.226. Две электроплитки, включенные в цепь параллельно, потребляют
мощность N. Какую мощность No будут потреблять эти плитки, включенные
последовательно, если одна из них потребляет мощность У,?
322
К.п.д. источника тока
13.227. Определить к.п.д. источника при силе тока в цепи 7= 0,8 А, если
ток короткого замыкания равен 7КЗ = 2 А.
• Решение. При подключении к источнику э.д.с. некоторого сопротивления R в цепи по-
течет ток и на участках, содержащих сопротивления, будет выделяться тепло. При этом
коэффициент полезного действия источника тока можно определить как отношение коли-
чества тепла <2r, выделяющегося во внешней цепи, к кожгчеству тепла Q, выделяющегося
во всей цепи (включая источник):
0R
Q '
Если источник тока закорочен, то ток 7К 3 определяется лишь э.д.с. ^источника и его
внутренним сопротивлением г.
Лез.
г ’
(1)
а при наличии внешней цепи сопротивлением R:
R + r
(2)
Используя закон Джоуля-Ленца, найдем количество тепла, выделяющегося за время
Д/ на сопротивлении R:
qr=i2rm={~^-}2R£j= g2RtJ
* * 1Я + г’ (Я + г)2
и во всей цепи:
Q^\R + r^-{^-r\\R + r^-^.
Подставляя эти соотношения в выражение для к.п.д., получим
R
или с учетом (1) и (2):
ц = ~ = 0,4 = 40%. .
• Ответ: Г] = ///к 3 = 0,4 = 40%. К'3'
13.228. К.п.д. источника с э.д.с. S= 100 В, к которому подключили сопро-
тивление R = 10 Ом, равен ц = 25%. Определить мощность выделяющуюся на
сопротивлении.
13.229. К источнику с э.д.с. S= 20 В с внутренним сопротивлением
г = 0,25 Ом подключили некоторое сопротивление. Определить к.п.д. источ-
ника, если ток в цепи равен 1 = 8 А.
13.230. Аккумулятор, замкнутый на сопротивление R = 5 Ом, имеет к.п.д.
Л = 50%. Каким станет к.п.д. аккумулятора, если его замкнуть на сопротивле-
ние 2R?
13.231. Во сколько раз сопротивление внешней цепи больше внутреннего
сопротивления источника, если к.п.д. источника равен т| = 80%?
13.232. Электродвигатель, приводящий в действие насос, подключен к
сети напряжением (7=220 В. Насос подает К=500 м3 воды на высоту
323
h = 20 м. Какое минимальное количество электричества протечет по обмотке
электродвигателя, если к.п.д. установки (двигателя с насосом) т) = 44%? Плот-
ность воды р = I О3 кг/м3.
• Решение. При работе электродвигателя, включенного в сеть постоянного тока, электри-
ческая энергия превращается в механическую и внутренную (тепло). К.п.д. установки
равно отношению полезной работы А, совершаемой ею за некоторый промежуток времени
ДТ, к энергии Q, потребляемой от сети:
А
ГДе
A = mgh = pVgh, Q=UIAt.
Следовательно,
Откуда с учетом, что сила тока I связана с зарядом Д? соотношением Лц = 1 полу-
чим
Ag = Р » 106 Кл.
и т]
• Ответ: Ла = Р » 106 Кл.
1/п
13.233. Электромотор питается от батареи с э.д.с. <$= 12 В. Какую меха-
ническую работу совершает мотор за время т = 1 с при протекании по его об-
мотке тока 1= 2 А, если при остановке якоря мотора по цепи протекает ток
70 = ЗА?
13.234. Троллейбус массой М= 11 т движется равномерно со скоростью
и = 36 км/час. Найти силу тока в обмотке двигателя, если рабочее напряжение
U = 550 В, а к.п.д. двигателя г, = 80%. Силу сопротивления движению принять
равной а = 0,02 силы тяжести троллейбуса.
13.235. Электродвигатель трамвайного вагона потребляет ток силой
/= 98 А при напряжении U = 500 В и развивает силу тяги F= 3,92 кН. Опре-
делить среднюю скорость движения трамвая, если к.п.д. электродвигателя и
механизмов передачи равен ц = 60%.
13.236. Через обмотку якоря электродвигателя, подключеного к сети на-
пряжением U = 110 В, протекает ток силой 1= 10 А. Чему равна потребляемая
мощность и к.п.д. электродвигателя, если сопротивление обмотки якоря равно
Л = 2 Ом?
13.237. Лифт массой т = 1 т равноускоренно поднимается на высоту
/1=15 м за 1 = 30 с. Напряжение на зажимах электромотора U = 220 В, его
к.п.д. т| = 80 %. Найти силу тока в обмотке мотора.
13.238. В электрическом чайнике мощностью N = 800 Вт можно вскипя-
тить У= 1,5 л воды, имевшей температуру t - 20°С за время т = 20 мин. Найти
к.п.д. чайника. Удельная теплоемкость воды с = 4200 Дж/(кг К).
324
13.239. На изготовление кипятильника израсходована нихромовая прово-
лока объемом V= 10 см3. Какую массу воды можно нагревать ежеминутно
этим кипятильником от = 10°С до /2 = 100°С при плотности тока в цепи
J = 3 А/мм2? К.п.д. кипятильника г, = 70%. Удельное сопротивление нихрома
р = 1,05-Ю’5 Ом-м, удельная теплоемкость воды с = 4200 Дж/(кг-К).
13.240. Нагревательная спираль электрического чайника при температуре
/= 100°С имеет сопротивление R = 10 Ом. Какой силы ток нужно пропустить
через спираль, чтобы испарить т = 100 г воды, взятой при температуре кипе-
ния, за т = 1 мин, если к.п.д. чайника г, = 70%? Удельная теплота парообразо-
вания г = 2,3 МДж/кг.
13.241. Какую массу нефти нужно сжечь на тепловой электростанции,
чтобы по телевизору, потребляющему ток силой 1= 1,2 А при напряжении
i/=220 В, посмотреть фильм продолжительностью т = 1,5 часа? К.п.д.
электростанции т| = 35%. Удельная теплота сгорания нефти q = 4,6-107 Дж/кг.
Электролиз
13.242. Через раствор азотно-кислого серебра проходит ток плотностью
j - 0,7 А/дм2. Сколько времени нужно пропускать ток, чтобы на катоде обра-
зовался слой серебра толщиной d = 0,05 мм? Относительная атомная масса
серебра равна А = 108 а.е.м., валентность и = 1, плотность р = 10,5 г/см3.
• Решение. При прохождении электрического тока силой I через раствор азотно-кислого
серебра за время t на -катоде откладывается масса серебра
А m = klt, (1)
где £ = —р - электрохимический эквивалент серебра.
Если серебро плотностью р осаждается равномерно по всей поверхности электрода
площадью S и образует слой толщиной d, то масса выделившегося серебра
m = pSd.
С учетом этого формулу (1) перепишем так:
pSd=-^It,
nF
или, используя связь I=JS между силой тока и его плотностью:
pSd = ^jSt.
П г
Откуда получаем
. nFpd , о,
t = —* 1,86 часа.
_ . nFpd , А}
• Ответ’, t = —7-5— » 1,86 часа.
А J
13.243. Вычислить число Фарадея и заряд электрона, если известно, что
при прохождении через электролит тока в I = 3 А в течение t = 20 мин на ка-
тоде выделилось т = 1188 мг меди. Относительная атомная масса меди равна
А = 64 а.е.м., валентность - и = 2.
325
13.244. При силе тока 1= 5 А за время t = 10 мин в электролитической
ванне выделилось т = 1,02 г двухвалентного металла. Определить его относи-
тельную атомную массу.
13.245. Какое количество алюминия выделится на катоде площадью
S= 1 см2 за Г = 6 час при электролизе A12(SO4)3 при пропускании через
электролит тока плотностью j = 15 кА/м2? Относительная атомная масса алю-
миния А = 27 а.е.м., валентность - п = 3.
13.246. Две электролитические ванны соединили последовательно. В пер-
вой ванне выделилось = 3,9 г цинка, во второй за это же время т2 = 2,24 г
железа. Цинк двухвалентен. Какова валентность железа? Относительные
атомные массы цинка и железа равны А\ = 56 а.е.м. и Л2 = 65 а.е.м. соответст-
венно.
13.247. Определить валентность железа, если при прохождении через же-
лезный вольтаметр q = 60 Кл электричества на катоде выделилось т = 11,6 г
железа. Относительная атомная масса железа А = 56 а.е.м.
13.248. Через раствор азотной кислоты проходит ток 7= 1 А. Какое коли-
чество электричества переносится в единицу времени ионами каждого знака?
13.249. Какое количество атомов двухвалентного цинка можно выделить
за t = 5 мин при пропускании тока силой 1= 2,5 А через раствор сернокислого
цинка? Электрохимический эквивалент цинка к= 3,39-10'7 кг/Кл.
13.250. Электролиз раствора NiSO4 протекал при плотности тока
j = 0,15 А/дм2. Какое количество атомов никеля выделилось за t = 2 мин на
площади S = 1 см2 поверхности катода? Электрохимический эквивалент нике-
ля к = 3,04-10"7 кг/Кл.
13.251. При никелировании пластины ее поверхность покрывается слоем
никеля толщиной <7=0,05 мм. Определить среднюю плотность тока, если
время никелирования t = 2,5 часа. Плотность никеля р = 8,9-103 кг/м3, относи-
тельная атомная масса А = 58,7 а.е.м., валентность - п = 2.
13.252. Через какое время медный анод станет тоньше на Sd = 0,03 мм,
если плотность тока при электролизе j = 2 А/дм2? Электрохимический эквива-
лент меди к= 3,3-10"7 кг/Кл, плотность меди р = 8,9-Ю3 кг/м3.
13.253. При какой плотности тока в растворе FgNO3 толщина выделяю-
щегося серебра растет со скоростью и = 1 мм/час? Электрохимический экви-
валент серебра к= 11,18 кг/Кл, а его плотность р = 10,5-103 кг/м3.
13.254. За какое время при силе тока 1= 1 А разложится т = 1 г воды.
Электрохимический эквивалент водорода к = 10‘8 кг/Кл.
13.255. При электролизе раствора серной кислоты за время т = 30 мин
выделилось т = 2-1 О'4 кг водорода. Определить максимальную силу тока, про-
текающего через электролит, если ток нарастал по линейному закону, а
электрохимический эквивалент водорода к = 10'8 кг/Кл.
326
• Решение. Поскольку сила тока при электролизе не постояна, то по закону Фарадея можно
найти массу dm водорода, выделившегося за бесконечно малое время dt, в течение кото-
рого ток можно считать постоянным:
dm = kldt,
где сила тока в момент времени t равна
4пах ~ { 4nax f
т т
Следовательно, за время т выделится масса водорода, равная
f , /max . , Лпах т
т= к------tdt = k—-—.
0J ' 2
Откуда получаем
/max = ^«22,2 А.
• Ответ: /тах = — » 22,2 А.
ат
13.256. В электролитической ванне с раствором медного купороса в тече-
ние t = 1 мин ток менялся по закону 1= 0,05-/. Какое количество меди выде-
лилось на катоде за это время? Электрохимический эквивалент меди
£=3,3-10’7 кг/Кл.
13.257. При никелировании изделия ток в течение первых = 15 мин
равномерно увеличивался от нуля до /тах = 5 А, затем в течение времени
t2 = 1 час оставался постоянным и последние /3 = 15 мин равномерно умень-
шался до нуля. Определить массу выделившегося никеля. Электрохимический
эквивалент никеля к = 0,304 мг/Кл.
13.258. Сколько электроэнергии нужно затратить для получения из воды
К =2,5 л водорода при температуре Г=298 К и давлении р= 105 Па, если
электролиз ведется при напряжении U=5 В, а к.п.д. установки равен
т| = 75%? Электрохимический эквивалент водорода к= 10'8 кг/Кл.
• Решение. К.п.д. любой установки равно отношению полезной работы А, совершаемой
ею за некоторый промежуток времени А/, к потребляемой энергии Q:
А
^Q-
Если бы к.п.д. установки был равен единице, то на электродах выделилась бы масса
М водорода, пропорциональная количеству потребляемой энергии Q н равная
M=klt.
Поскольку ц < 1, то на электродах выделится масса т водорода, пропорциональная по-
лезной работе установки. Следовательно, из пропорции
т^_ Л
М~ Q
с учетом выражения для к.п.д. находим
т = т|М или m = r\klt. (1)
327
С другой стороны, массу водорода можно выразить из уравнения Менделеева-Клапей-
рона через параметры состояния газа:
„v-SLpt РУ»
pV=-RT, т- RT .
Учитывая это, выражение (1) можно представить в виде
Следовательно, электролиз нужно проводить прн силе тока
т рУу-
r\ktRT
и затратить энергию
Q = IUt=P VpU кДж.
и i)kRT
• Ответ-. Q = 134 кДж.
и r\kRT
13.259. Какое количество электричества нужно пропустить через элект-
ролитическую ванну с подкисленной водой, чтобы получить V = 1 л водорода
при температуре t = 20°С и давлении р = 105 Па? Валентность водорода п = 1.
13.260. При электролизе воды через ванну прошел заряд q = 103 Кл. Оп-
ределить температуру выделившегося кислорода, если в объеме V = 0,25 л он
создает давление р = 129 кПа. Валентность кислорода п = 2.
13.261. Медь выделяется из раствора CuSO4 при напряжении 1/= 10 В.
Найти расход электроэнергии на т = 1 кг меди. Электрохимический эквива-
лент меди к= 3,3-10'7 кг/Кл.
13.262. Какая мощность расходуется на нагревание раствора азотно-кис-
лого серебра, если за t = 6 ч из него выделяется в процессе электролиза
т = 120 г серебра. Сопротивление раствора R = 1,2 Ом, электрохимический
эквивалент серебра к= 1,12 мг/Кл.
13.263. Алюминий добывают из окиси А12О3 с помощью элекролиза.
Оценить количество энергии, необходимой для получения из воды т = 1 т ме-
талла, если к.п.д. установки, работающей при напряжении (7=6 В, равен
т| = 70%. Относительная атомная масса алюминия А = 27 а.е.м., валентность -
« = 3.
13.264. При электролизе раствора серной кислоты за время t = 50 мин
выделилось т = 3-1 О'4 кг водорода. Определить количество теплоты, выделив-
шейся при этом в электролите, если его сопротивление R = 0,4 Ом, а электро-
химический эквивалент водорода к = 10'8 кг/Кл.
328
§14. Магнетизм
Хорошо известно, что если поднести два магнита друг к другу, то между
ними появится сила; магниты будут либо притягивать друг друга, либо оттал-
кивать. Взаимодействие магнитов ощущается даже тогда, когда они не сопри-
касаются. Любой магнит имеет два полюса - северный и южный. Если к се-
верному полюсу одного магнита поднести северный полюс другого, то магни-
ты будут отталкиваться; то же самое будет, если магниты сблизить южными
полюсами. Но если к северному полюсу одного магнита поднести южный
полюс другого, то между магнитами возникнет притяжение. Это напоминает
взаимодействие зарядов: одноименные полюса отталкиваются, а разноимен-
ные притягиваются.
Многочисленные опыты, проводимые с токами, показали, что электри-
ческие токи взаимодействуют друг с другом подобно магнитам.
Рис. 14.1
Рассмотрим два прямолинейных проводника, расположенных в одной
плоскости параллельно друг другу (рис. 14.1). Опыты показывают, что при
пропускании по проводникам токов одного направления, проводники будут
притягиваться; если же токи имеют протипоположные направления - провод-
ники будут отталкиваться. Однако если ток течет лишь по одному проводни-
ку, то силы взаимодействия между проводниками отсутствуют.
Рис. 14.2
Обратимся к другому опыту. Поместим вблизи длиною прямолинейного
проводника с током компас и будем его перемещать вокруг проводника. Мы
обнаружим, что в любой точке магнитная стрелка компаса установится по ка-
сательной к окружности, очерченной вокруг проводника (рис. 14.2, а, где N -
329
северный полюс магнитной стрелки, S- южный). Теперь заменим магнитную
стрелку на маленькую проволочную рамку, которая может свободно вращать-
ся вокруг оси, параллельной проводнику с током. При наличии тока в рамке
она повернется и расположится так, что проводник будет находится в плос-
кости рамки (рис. 14.2, б). Таким образом, проводник с током оказывает ори-
ентирующее действие на рамку с током так же, как и на магнитную стрелку.
Если изменить направление тока в проводнике, то и стрелка и рамка повер-
нутся на 180°.
Как позже было установлено, природа взаимодействия магнитов друг с
другом, токов друг с другом, магнитов и токов, одна и та же - в ее основе
лежит тот факт, что магниты и токи наделяют окружающее пространство осо-
быми физическими свойствами.
Магнитное поле
Для объяснения взаимодействия неподвижных зарядов (см. § 12) требова-
лось наличие некоторой материальной среды, порождаемой зарядами в окру-
жающем пространстве, которую назвали электрическим полем. Появление сил
магнитного взаимодействия также объясняют возникновением вокруг магни-
тов, и токов некоторой материальной среды, порождаемой магнитами и тока-
ми, которую называют магнитным полем. При этом магнитное поле сущест-
вует, даже если магнитное взаимодействие не наблюдается. О наличии в про-
странстве магнитного поля можно судить только по его действию на другие
магниты, движущиеся заряды или токи.
Из рассмотренных опытов следует, что магнитное поле имеет направлен-
ный характер и должнохарактеризоваться векторной величиной. Ее называют
магнитной индукцией В (или вектором индукции магнитного поля). Единицей
измерения вёличины магнитной индукции в системе СИ служит тесла [Тл].
Sg Ориентирующее действие маг-
--------------► нитного поля на рамку с током ис-
пользуют для определения направ-
:—ления вектора магнитно^ индукции.
™ За направление вектора В в том мес-
те, где расположена рамка с током
а) б) (которая может свободно ориенти-
Рис. 14.3 роваться), принимают направление
перпендикуляра к плоскости рамки. Так как перпендикуляр можно провести в
ту или иную сторону, то условились за направление перпендикуляра прини-
мать то направление, в котором будет поступательно двигаться буравчик (пра-
вый винт), если его рукоятку вращать по направлению тока в рамке (рис.
14.3, а). Этот перпендикуляр называют положительной нормалью. При этом в
магнитном поле направление положительной нормали 7?рамки с током совпа-
дает с направлением от южного полюса S к северному N магнитной стрелки
(рис. 14.3, б). .
330
С помощью магнитной стрелки или рамки с током можно на опыте опре-
делить направление вектора магнитной индукции в каждой точке поля. При
этом можно убедиться, что изменение формы проводника с током влияет на
направление вектора В. Опыт дает, что для магнитного поля, как и для элект-
рического, справедлив принцип суперпозиции: индукция магнитного поля, по-
рождаемого несколькими токами, равна векторной сумме индукций полей,
создаваемых каждым из токов в отдельности:
Поскольку любой проводник может быть
представлен в виде отдельных прямолинейных
участков (в общем случае бесконечно малых)
длиной dl, то магнитная индукция В проводника
с током в каждой точке будет равна векторной
сумме элементарных индукций dB, создаваемых
отдельными участками. Изменение расположе-
ния этих участков приведет к изменению на-
правлений векторов dB и вектора В в целом. По-
нятно, что если буравчик расположить вдоль
участка тока и рукоятку вращать так, чтобы по-
ступательное движение буравчика совпало с направлением тока в дроводнике,
то направление вращения рукоятки укажет направление вектора dB магнитной
индукции (рис. 14.4). Это правило называют правилом буравчика.
Магнитное поле так же, как и электрическое, можно изображать графи-
чески при помощи линий индукции (силовых линий магнитного поля). Линия-
ми индукции называют линди, касательные к которым в каждой точке направ-
лены так же, как и вектор В в данной точке поля. Очевидно что через каждую
точку магнитного поля можно провести лишь одну линию индукции (в про-
тивном случае вектор В одновременно должен иметь два или более направле-
ния). Следовательно, линии индукции нигде не могут пересекаться. Для на-
глядности на рисунках линии индукции изображают гуще в тех точках поля,
331
где больше величина В. При этом на линии индукции изображают стрелку в
направлении вектора индукции.
Обратимся к рис. 14.2, а, б. По действию магнитного поля прямолинейно-
го тока на стрелку и рамку с током можно заключить, что линии индукции
магнитного поля прямолинейного проводника с током представляют собой
концентрические окружности, в центре которых находится проводник. Ис-
пользуя правило буравчика, можно легко изобразить картину линий индукции
поля такого тока (рис. 14.5) и поля кругового тока (рис. 14.6).
Рис. 14.7
Рис. 14.8
Представление о линиях индукции можно получить с помощью магнит-
ной стрелки или рамки с током для любых токов. Еще удобнее воспользовать-
ся железными опилками, которые в магнитном поле намагничиваются и ста-
новятся подобными маленьким стрелкам компаса. На рис. 14.7 и 14.8 приведе-
ны полученные таким способом картины линий индукции поля кругового
витка с током и соленоида (так называют длинную катушку с большим чис-
лом витков). Из рис. 14.8 видно, что в средней части внутри соленоида линии
индукции параллельны друг другу и расположены на равных расстояниях.
Такие магнитные поля называют однородными.
Несмотря на некоторое сходство описания электрических и магнитных
полей между ними имеется принципиальное отличие: линии магнитной ин-
дукции непрерывны (они не имеют ни начала, ни конца) и замыкаются сами
на себя. Это имеет место для любых магнитных полей, порождаемых какими
угодно токами. Векторные поля, обладающие такими свойствами, называют
вихревыми.
Обратимся теперь к количественному описанию магнитного поля тока.
Если известна величина и направление векторов dB каждого участка dl
тока I, то величину и направление вектора В можно найти как векторную
сумму элементарных индукций dB, создаваемых отдельными участками. Фор-
мула для определения величины магнитной индукции dB* бесконечно малого
участка тока была получена опытным путем и выражает закон Био-Савара—
Лапласа:
332
4я №
где г — расстояние от участка тока до рассматриваемой точки поля (см. рис.
14.4), а - угол между током и направлением в данную точку поля, коэффи-
циент pg = 4тс-10'7 Н/А2 называется магнитной постоянной.
Определение количественных значений индукции магнитного поля даже
для простейших токов, достаточно трудоемкая задача, решение которой связа-
но с интегрированием. Поэтому ограничимся лишь результатами решения
такой задачи для трех рассмотренных выше токов:
а) индукция магнитного поля прямолинейного бесконечно длинного провод-
ника с током I на расстоянии г от него:
(14.3)
2 тс г
б) индукция на оси тока силой I, текущего в круговом проводнике радиусом
R, на расстоянии х от плоскости проводника:
в=Ы
2 (Я2 + х2)'5’
п .
. 2Л ’
в) индукция на оси бесконечно длинного соленоида с током силой /:
В = JJ.Q п 1,
где п - число витков, приходящихся на единицу длины соленоида.
(14.4)
в его центре (х = 0):
(14.5)
(14.6)
Сила Лоренца. Движение заряженных частиц в магнитном поле
Магнитное поле в отличие от электрического не оказывает действия на
покоящиеся заряды. Сила, с которой магнитное поле индукцией В действует
на электрический заряд q, движущийся со скоростью 1?, называется силой Ло-
ренца. Опытным путем установление, что величина этой силы
Fn = q и В sin а, (14.7)
где а - угол между векторами I? и it. Сила Лорен-
ца направлена перпендикулярно плоскости, в ко-
торой лежат векторы с? и В. Если заряд положи-
тельный, то направление силы Лоренца можно
определить по правилу левой руки: если располо-
жить левую руку таким образом, чтобы выпрям-
ленные пальцы были направлены по вектору ско-
рости частицы, а составляющие линий индук-
ции магнитного поля, перпендикулярные xt, вхо-
дили в ладонь, то отогнутый большой палец пока-
жет направление силы (рис. 14.9, а). Очевидно,
что направление силы Лоренца, действующей на
отрицательный заряд, будет противоположным
(рис. 14.9, б).
333
Из выражения (14.7) следует, что сила Лоренца действует на движущиеся
заряды только в том случае, если вектор скорости заряда не параллелен лини-
ям индукции (а * 0 и а * 180°). В противном случае Fn = 0.
Поскольку сила Лоренца все время перпендикулярна скорости частицы,
то ее проекция на направление перемещения частицы в любой момент равна
нулю. Это означает, что Fn не совершает работы над частицей и не меняет ее
кинетическую энергию (см. книгу «Механика», §3).
Рис. 14.10
Рассмотрим движение частицы с зарядом q > 0 в однородном магнитном
поле с индукцией В. Пусть скорость t? частицы направлена перпендикулярно
линиям индукции.
Так как сила Fn перпендикулярна то она будет менять только направ-
ление скорости частицы, сообщая ей нормальное^ускоренне. При этом вектор
скорости останется перпендикулярным вектору В. Это означает, что частица в
магнитном поле будет двигаться по окружности и в любой момент времени
сила Лоренца будет оставаться постоянной по величине
Fл = « и В
и направленой перпендикулярно плоскости, в которой лежат векторы В и к
центру окружности радиуса R (рис. 14.10). Записав уравнение движение час-
тицы в проекции на нормаль 7?к траектории (см. книгу «Механика», §4)
2
С т U D
ma„ = F„ или = q и В,
получим значение радиуса окружности, по которой будет двигаться частица
R = ~
qB
и ее период обращения:
2тг R 2п т
и ~ qB '
Как видим, период обращения частицы не зависит от ее скорости и кине-
тической энергии.
Рассмотрим случай, когда скорость частицы составляет угол а с направ-
лением линий индукции (рис. 14.11). Разложим вектор скорости t?частицы на
две составляющие, одна из которых Uj_= и sin а направлена перпендикуляр-
334
но силовым линиям поля, а другая - ин = и cos а параллельна им. На частицу
в магнитном поле действует сила Лоренца, обусловленная составляющей и±,
Fn = q Ч1Л
направленная к центру некоторой окружности радиуса R. Эта сила заставит
частицу двигаться по окружности. В направлении силовых линий на частицу
никакие силы не действуют, поэтому составляющая ( скорости не будет ме-
нять-ся ни по величине, ни по направлению. Наличие составляющей 0ц приве-
дет к тому, что частица будет двигаться равномерно вдоль силовых линий
, поля. В результате наложения этих двух движений траекторией частицы ста-
нет цилиндрическая спираль, изображенная на рис. 14.11. Радиус R спирали*
легко найти из уравнения движения частицы
2
т и I _ _ т иj т и sin а
R -q и±В, R - в - ,
а период Т обращения частицы и шаг h спирали - из очевидных условий:
_ 2 tiR 2 пт , _ 2 тг Я cos а
Т=-----= —й = и||Г=и||------------=------------.
о± qB 11 oj_ qB
Независимость периода обращения заряженной частицы в магнитном
поле от энергии частицы используют для устройства ускорителя заряженных
частиц - циклотрона. Он предназначен для ускорения тяжелых частиц без
применения большой разности потенциалов.
Рассмотрим другой пример
действия силы Лоренца. Поместим
проводник прямоугольного сече-
ния, по которому течет ток плот-
ностью J, в однородное магнитное
поле, перпендикулярное направле-
нию тока в проводнике (рис. 14.12).
На движущиеся электроны в про-
воднике будет действовать сила Лоренца /7, направленная вниз, и электроны
будут отклоняться к поверхности 1-1 проводника. Вследствие этого между
поверхностями 1-1 и 2-2 возникнет разность потенциалов Дер и электрическое
поле напряженностью Е. Разность потенциалов будет увеличиваться до тех
пор, пока силы F3n электрического поля не уравновесят силы, действующие
на заряды со стороны магнитного поля:
|Мл1 = Й> или |е| <и>В = |е|£,
где < и > - средняя скорость направленного движения электронов в проводни-
ке (см. §13)
<и> = т^~,
Iе!п
Е - величина напряженности электрического поля между рассматриваемыми
поверхностями, равная
335
Е = ^.
и
Следовательно, между поверхностями 1-1 и 2-2 проводника установится
разность потенциалов
, j В а
Д<р = Yi— •
1е1 п
Рассмотренное явление называют эффектом Хома для металлов, а воз-
никающую между поверхностями разность потенциалов - э.д.с. Хома, кото-
рую принято записывать в виде
Дф = RX j В d,
где величина Rx = 1 /|е| п, зависящая от концентрации п электронов в провод-
нике, называется постоянной Хома.
Сила Ампера
Как бьию отмечено выше, магнитное поле действует не только на движу-
щиеся заряженные частицы, но и на токи. В наиболее простом случае прямо-
линейного тока У «зла, действующая со стороны однородного магнитного
поля с индукцией В, направленного так, что линии индукции составляют угол
а с направлением тока, равна
FA = У В / sin а, (14.8)
где / - длина участка проводника с током. Эту силу называют силой Ампера.
Рис. 14.13 Рис. 14.14
Опыт показывает, что сила_^мпера перпендикулярна плоскости, в кото-
рой лежит проводник и вектор В. Направление силы Ампера можно опреде-
лить по правилу левой руки, сформулированному для силы Лоренца, если
вместо направления скорости частицы использовать направление тока (рис.
14.13).
Рассмотрим два прямолинейных параллельных тока, расположенных на
расстоянии Ь друг от друга (рис. 14.14). Пусть токи имеют одинаковые на-
правления и равны /| и /2- Проводник с током Д создаст на расстоянии b маг-
нитное поле с индукцией (см. формулу (14.3))
2 л b
направленное так, как показано на рисунке. Проводник с током 12 окажется в
магнитном поле, силовые линии которого направлены перпендикулярно про-
336
воднику от нас. В результате этого на участок длиной I проводника с током
12 будет действовать сила Ампера
Цо А
ка = Т7Г/- <14-9)
2 тс О
Понятно, что при изменении направления тока в одном из проводников
направление силы Fh изменится на противоположное, и проводники будут от-
талкиваться.
Заметим, что на основании силы (14.9) в системе СИ устанавливается
единица измерения силы тока - ампер [А]: это сила тока, который, проходя по
двум параллельным прямолинейным проводникам бесконечной длины, распо-
ложенным на расстоянии 1 м друг от друга в вакууме, вызывает между про-
водниками силу взаимодействия, равную 2-10’7 Н на каждый метр длины.
Рис. 14.15 Рис. 14.16
Рассмотрим теперь квадратный контур с током I, расположенный в одно-
родном магнитном поле с индукцией В так, что его плоскость перпендикуляр-
на линиям индукции (рис. 14.15). На каждый прямолинейный участок тока
будут действовать силы Ампера, направленные перпендикулярно току и лежа-
щие в плоскости контура. Если направления тока в контуре и поля таковы, как
показано на рисунке, то силы Ампера будут растягивать контур, стремясь его
разорвать; если направление тока или поля изменить на противоположное, то
силы Ампера будут сжимать контур.
Легко понять, что независимо от ориентации такого контура в магнитном
поле сумма действующих на него сил Ампера будет равна нулю. Это означа-
ет, что однородное поле не может заставить двигаться контур поступательно.
Однако если нормаль к плоскости контура составляет некоторый угол а с на-
правлением поля, то силы Ампера будут направлены так, чтобы, во-первых,
растянуть (сжать) контур, а во-вторых, повернуть его и расположить в плос-
кости, перпендикулярной силовым линиям. Например, в положении контура,
показанном на рис. 14.16, относительно оси OZ на контур действует момент
сил
Mz = F] I sin а + Fa I sin а = IВ12sin а,
337
который стремится развернуть контур. При а = тг/2 он максимален
Mmsx = IBl2 = IBS (14.10)
Шал к /
(где S - площадь, ограниченная контуром) и обращается в ноль при а = 0 или
а = тс (в первом случае контур с током будет находиться в положении устой-
чивого равновесия, во втором - в положении неустойчивого равновесия).
Величина
Pm = IS (14.11)
называется магнитным моментом контура с током. Магнитный момент /?т
принято записывать в виде вектора
^ = /5^ (14.12)
где л*~ положительная нормаль контура с током.
Опыт показывает, что в данной точке поля момент сил, действующих на
контур с током относительно произвольной неподвижной оси, зависит от рас-
положения контура, его геометрических размеров и от силы тока в нем, но не
зависит от формы контура. Поэтому для любого плоского контура справедли-
во:
Мг=ртВ sina., ^max=Pm^- (14.13)
Следовательно, на контур с током в магнитном поле в общем случае дей-
ствует момент сил Ампера (называемый механическим моментом), который
стремится расположить контур так, чтобы направление магнитного момента
р^ контура совпало с направлением вектора индукции поля в данной точке.
Магнитное поле в веществе
До сих пор мы рассматривали магнитное поле в вакууме. Если проводник
с током находится не в вакууме, а в некотором веществе, то, как показывает
опыт, магнитное поле изменяется. Это указывает на тот факт, что различные
вещества в магнитном поле сами становятся источниками магнитного поля
(говорят, намагничиваются). Результирующее поле в веществе является сум-
мой полей, создаваемых проводником с током и намагниченным веществом, и
поэтому не равно полю в вакууме. Вещества, способные намагничиваться, на-
зывают магнетиками.
Намагничивание тел Ампер объяснял наличием в веществе мельчайших
круговых токов (молекулярных токов). Каждый такой ток создает в окружаю-
щем пространстве магнитное поле и обладает магнитным моментом р^. При
отсутствии внешнего поля магнитные моменты молекулярных токов ориенти-
рованы беспорядочным образом (рис. 14.17, а). Под действие внешнего поля
Во магнитные моменты молекул преимущественно ориентируются в одном
направлении (рис. 14.17, б). В этом случае молекулярные токи, текущие по со-
прикасающимся участкам, имеют противоположные направления и взаимно
компенсируются; не скомпенсированными остаются лишь токи на участках,
примыкающих к поверхности магнетика. Поэтому действие всех молекуляр-
338
Рис. 14.17
ных токов будет такое же, как действие некоторого тока Г, текущего по по-
верхности магнетика (рис. 14.17, б, в). Этот ток создаст магнитное поле В', на-
правленное параллельно внешнему. Результирующее поле внутри магнетика,
равное
В = Во + В', В = Во + В
будет больше внешнего Во. Можно показать, что для однородного магнетика,
заполняющего все пространство, отношение р. = В/Во есть величина постоян-
ная, определяющая магнитные свойства вещества. Ее называют магнитной
проницаемостью вещества: она показывает, во сколько раз величина магнит-
ной индукции внутри магнетика больше величины индукции внешнего поля:
В = цВ0. (14.14)
Следует отметить, что не все магнетики усиливают внешнее поле: суще-
ствуют вещества, у которых магнитная проницаемость ц< 1. Соотношение
(14.14) справедливо лишь для магнетиков с ц> 1 (к ним относятся железо, ко-
бальт, никель и многие сплавы).
Электромагнитная индукция
Выше мы обсудили две стороны связи между магнитными и электричес-
кими явлениями: а) электрический ток создает магнитное поле и б) со сторо-
ны магнитного поля на электрический ток или движущийся заряд действует
сила. Закономерно задаться вопросом: если электрический ток создает маг-
нитное поле, то не может ли магнитное поле привести к возникновению тока?
Ответ на него был независимо получен Дж. Генри и М. Фарадеем.
На рис. 14.18 схематически представ-
лена установка одного из опытов Фарадея.
Фарадей обнаружил, что при замыкании и
размыкании ключа К стрелка гальваномет-
ра сильно отклоняется то в одну, то в дру-
гую сторону. Однако при замкнутом клю-
че, когда через катушку протекал постоян-
ный ток, стрелка оставалась неподвижной.
Исходя из этого Фарадей сделал вывод, что
339
постоянное во времени (стационарное) магнитное поле катушки не приводит
к появлению тока в рамке; для его возникновения необходимо, чтобы магнит-
ное поле, пронизывающее рамку, менялось со временем, т.е. было нестацио-
нарным. Дальнейшие опыты (например, быстрое введение постоянного маг-
нита в проволочный виток, или удаление его из витка) подтвердили догадку
Фарадея: в проводящем контуре возникает электрический ток только в случае,
если меняется магнитное поле, которое его пронизывает.
Появление тока в контуре равносильно наличию в контуре источника
э.д.с., которую назвали э.д.с. электромагнитной индукции, а возникающий в
контуре ток - индукционным током.
It
Рис. 14.19
Количественные измерения э.д.с.
индукции привели к выводу, что ее вели-
чина зависит от быстроты изменения ин-
дукции магнитного поля, площади, огра-
ниченной контуром, и ориентации конту-
ра в магнитном поле. Если магнитное
поле изобразить с помощью линий маг-
нитной индукции, то их густота будет
пропорциональна величине индукции.
Проводящий контур в таком поле будет
охватывать некоторую часть силовых линий (рис. 14.19). Если величина ин-
дукции изменится, то число силовых линий, охватываемых контуром, также
изменится (увеличится или уменьшится). Такой же результат будет при изме-
нении площади контура и изменении его ориентации в магнитном поле (часть
силовых линий станет параллельна плоскости контура или, наоборот, ранее
паралельные плоскости контура силовые линии будут теперь охвачены конту-
ром). Во всех этих случаях полное число линий, проходящих через площадь,
ограниченную контуром, изменится, и в контуре возникнет индукционный
ток.
Рассмотрим плоскую поверхность S
в однородном магнитном поле с индук-
цией В (рис. 14.20). Потоком вектора ин-
дукции магнитного поля (или магнитным
потоком) через поверхность S называют
скалярную величину
Ф = В S cos а - Вп S, (14.15)
где а - угол между вектором В и норма-
лью rt к поверхности S; Вп = В cos а -
проекция вектора 2? на нормаль.
Если магнитное поле неоднородно, а рассматриваемая поверхность S не
плоская, то ее можно разбить на бесконечно малые плоские элементы dS так,
чтобы индукция магнитного поля в каждой точке такого элемента была оди-
340
наковой. Очевидно, что в зависимости от значения проекции Вп поток может
быть положительным, отрицательным или равным нулю, а поток Ф магнитной
индукции через всю поверхность S равен алгебраической сумме потоков
<1Ф = В dS cos o. = BndS. Можно показать, что величина суммарного потока Ф
не зависит от формы поверхности S.
Единицей измерения величины потока магнитной индукции в системе
СИ служит вебер [Вб = Тл-м2].
Вернемся к опытам Фарадея. Используя определение потока, можно сде-
лать вывод, что э.д.с. индукции и индукционный ток возникают в контуре вся-
кий раз, когда меняется магнитный поток, который пронизывает поверхность,
натянутую на контур. Это явление, открытое Фарадеем, называется электро-
магнитной индукцией. Математически результаты опытов Фарадея можно за-
писать в виде
d<t>
= (14.16)
Следовательно, э.д.с. электромагнитной индукции, возникающей в прово-
дящем контуре, находящемся в магнитном поле, равна скорости изменения
потока индукции магнитного поля через произвольную поверхность, натяну-
тую на этот контур. Это утверждение называется законом электромагнит-
ной индукции.
Величина э.д.с. Sj индукции не зависит от того, какие причины привели к
возникновению нестационарного потока индукции магнитного поля. Из опре-
деления потока (14.15) видно, что изменение величины магнитной индукции
В, площади поверхности, охватываемой контуром, или изменение ориентации
контура в магнитном поле (т.е. изменение угла а) приведет к тому, что вели-
чина потока изменится и если границей поверхности служит проводящий кон-
тур, то в нем потечет ток.
Индукционный ток, возникающей в контуре, создаст собственное маг-
нитное поле, линии индукции которого также будут пронизывать поверх-
ность, ограниченную контуром. В зависимости от направления индукционно-
го тока суммарный поток индукции внешнего и собственного магнитних
полей будет равен их сумме или разности. Направление индукционного тока
определяется правилом Ленца, индукционный ток направлен всегда так,
чтобы противодействовать причине, его вызывающей. Поэтому, если маг-
нитный поток внешнего поля увеличится, то в контуре возникнет индукцион-
ный ток такого направления, чтобы собственный магнитный поток ослаблил
внешний. И, наоборот, уменьшение внешнего магнитного потока приведет к
возникновению индукционного тока такого направления, чтобы собственный
магнитный поток поддержал внешний. Именно по этой причине в правой
части формулы (14.16) стоит знак «минус».
Если контур, в котором индуцируется э.д.с. индукции, состоит из N вит-
ков, то в каждом витке возникнет своя э.д.с. Поскольку все витки соединены
341
Рис. 14.21
/
последовательно, то будет равна сумме э.д.с., индуцируемых в каждом из
витков в отдельности:
* аФ1 d*
— ~2j , —----Ф1.
' (=1 dt dti=i '
Величину
¥ = ?,*,• (14.17)
называют полным магнитным потоком или потокосцеплением. Если поток,
пронизывающий каждый из витков, одинаков, то
у = N Ф,
а э.д.с. индукции в таком контуре
Рассмотрим контур, образованный
согнутым в форме буквы П проводником
и стержнем АС, который может сколь-
зить по проводнику (рис. 14.21). Помес-
тим контур во внешнее стационарное
магнитное поле с индукцией В, направ-
ленное перпендикулярно плоскости, в ко-
торой расположен контур. Если стержень
АС перемещать со скоростью и* в плос-
кости контура, то площадь, охватываемая контуром, и магнитный поток, про-
низывающий поверхность, ограниченную контуром, будут меняться со време-
нем по законам
S = vtl, Ф = В8 = В\м1.
Согласно закону электромагнитной индукции, в контуре возникнет э.д.с.
1^1 =в"1- (14-19)
Сторонней силой, которой обусловлена э.д.с. индукции в рассмотренном
случае, служит сила Лоренца. При движении стержня вправо с такой же ско-
ростью будут перемещаться носители тока в стержне - электроны. В резуль-
тате на каждый электрон начнет действовать сила Лоренца, направленная
вдоль стержня, и электроны начнут перемещаться к его концу С: в контуре
возникнет индукционный ток. Перераспределившиеся в стержне заряды со-
здадут между точками АиС разность потенциалов, равную |<?; |. Очевидно,
что в данном случае для возникновения разности потенциалов между концами
стержня вовсе не требуется контур. Действительно, появившийся избыток
электронов у конца С стержня и их недостаток у конца А, приведет к появле-
нию в стержне электрического поля напряженностью Ей силы Еэл = |е| Е, на-
правленной противоположно силе Лоренца Ел = |е| и В. Если эти две силы ста-
нут равными по величине (Еэл = Fn, или Е = и В), то движение электронов в
стержне прекратится и между его концами установится разность потенциалов
Д<р = Е/ = Ви/. (14.20)
342
Как видим, разность потенциалов (14.20) между концами стержня, дви-
жущегося в магнитном поле, совпадает с величиной э.д.с. индукции (14.19),
возникающей в контуре, который пронизывает переменный магнитный поток,
обусловленный изменением площади контура за счет движения этого стерж-
ня.
Рассмотрим другой пример возникновения э.д.с. индукции в контуре,
представленном на рис. 14.21. Теперь стержень ДС будет оставаться непо-
движным, а будет меняться величина индукции В магнитного поля. В этом
случае магнитный поток Ф = В S, пронизывающий поверхность ограниченную
контуром, также будет меняться. По закону электромагнитной индукции это
приведет к появлению в контуре индукционного тока и э.д.с. т.е. в контуре
появятся сторонние силы. Ясно, что в нашем случае это не силы Лоренца:
привести в движение покоящиеся заряды эти силы не могут. Известно, что за-
ставить двигаться покоящиеся заряды в проводнике может только электричес-
кое поле (см. §13). Максвелл предположил, что изменяющееся со временем
магнитное поле приводит к появлению в пространстве электрического поля,
причем это поле существует независимо от наличия проводящего контура.
Последний лишь позволяет обнаружить это поле по возникающему в контуре
индукционому току. Электрическое поле, порождаемое переменным магнит-
ным, отличается от полей, рассматриваемых в электростатике: его силовые
линии, как и у магнитного поля, представляют собой замкнутые кривые, т.е.
оно является вихревым.
Никакого принципа, объединяющего оба рассмотренных случая вознико-
вения электромагнитной индукции (за счет действия на носители тока силы
Лоренца или вихревого электрического поля), не обнаружено. Поэтому закон
электромагнитной индукции нужно понимать как совместный эффект двух со-
вершенно различных явлений. При этом формула (14.16) автоматически учи-
тывает оба фактора.
Самоиндукция
Явление электромагнитной индукции наблюдается во всех случаях, когда
изменяется магнитный поток, пронизывающий контур. В частности, нестаци-
онарный поток может создаваться током, текущим в самом рассматриваемом
контуре.
Рассмотрим контур (состоящий из одного или нескольких витков), по ко-
торому протекает ток. Наличие тока приведет к появлению магнитного потока
хр собственного магнитного поля, пронизывающего поверхность, ограничен-
ную контуром. При изменении силы тока величина индукции магнитного
поля, созданного этим током, изменится и, как следствие, изменится магнит-
ный поток. Вследствие этого в контуре возникнет эд.с., которую называют
э.д.с. самоиндукции, и связаные с ней токи — экстратоками самоиндукции.
Из закона Био-Савара-Лапласа (14.2) и определения магнитного потока
(14.15) следует, что величина потока хр растет линейно с током в контуре:
343
y=LI, (14.21)
где коэффициент пропорциональности L называют индуктивностью контура.
Единицей измерения индуктивности в системе СИ служит генри [Гн = Вб/А].
Величина индуктивности зависит от геометрии контура, а также магнит-
ных свойств окружающей контур среды. Найдем, например, индуктивность
очень длинного соленоида площадью поперечного сечения S, заполненного
магнетиком с магнитной проницаемостью ц. При протекании по соленоиду
тока силой I внутри него возникнет однородное магнитное поле, индукция ко-
торого равна 5 = ц go и / (см. формулы (14.6) и (14.14)). Поток через каждый
из витков равен Ф = В S = ц ц,, и IS, а полный магнитный поток
\|/ =NФ = Nji y^nlS,
где N - число витков в соленоиде, равное N=nl(l - длина соленоида). Следо-
вательно, \|/ = ц ц0 и21 / S, а индуктивность соленоида
Z = ^=ppo«2 IS. (14.22)
Рассмотрим контур индуктивностью L = const, по которому протекает ток
силой I, величина которого меняется с течением времени. Подставляя значе-
ние потока ц/ индукции, пронизывающего поверхность ограниченную конту-
ром, из (14.21) в формулу (14.16), получаем
Ss dt L dt’ (14-23)
где Ss - э.д.с. самоиндукции, а знак «минус» в правой части обусловлен пра-
вилом Ленца.
Из (14.23) вытекает, что при уменьшении (увеличении) силы тока в кон-
туре в нем возникнет э.д.с. самоиндукции, направленная так, чтобы поддер-
жать (ослабить) значение тока. Поэтому наличие самоиндукции проявляется в
замедлении процессов исчезновения и установления тока в цепи, содержащей
контур (в общем случае, катушку) индуктивностью L.
Энергия магнитного поля
L
Рис. 14.22
Рассмотрим электрическую цепь, представлен-
ную на рис. 14.22. При замкнутом ключе К в поло-
жение 1 в катушке индуктивностью L установится
некоторый ток. Если ключ замкнуть в положение 2,
то ток в катушке должен исчезнуть. Однако вслед-
ствие самоиндукции исчезновение тока произойдет
не мгновенно. Убывающий ток будет поддерживать-
ся возникающей в катушке э.д.с. самоиндукции:
Работа, совершаемая экстратоком за бесконечно малое время dt, будет
равна (см. §13, формула (13.31)):
dA = SsIdt = -LIdI,
344
а за время, соответствующее полному исчезновению тока в цепи:
г LI2
А=-jLIdI=~ , (14.24)
где I- значение силы тока в момент размыкания ключа из положения 1.
Работа (14.24) идет на приращение внутренней энергии сопротивления R.
Совершение этой работы сопровождается исчезновением тока в цепи и маг-
нитного поля, которое первоначально существовало в окружающем простран-
стве. Поскольку никаких других изменений не произошло, то можно сделать
вывод, что магнитное поле является носителем энергии, за счет которой и со-
вершается работа (14.24). Поэтому контур (в нашем случае катушка) индук-
тивностью L, по которому течет ток силой I, обладает энергией
£ г2
W=~, (14.25)
которая сосредоточена в возбуждаемом током магнитном поле. Ее называют
энергией магнитного поля.
Используя выражение (14.22), энергию магнитного поля соленоида с
током I, можно записать в виде
или с учетом (14.6): ц ц0 п 1S Г w=-^~ V, 2 Ц Ро 2 ц ц0
где V=SI- объем соленоида. Величина
w в2 w- - , (14.26) v 2ppo
равная энергии поля, сосредоточенной в единице объема, называется объем-
ной плотностью энергии магнитного поля.
В общем случае неоднородного поля выражение для объемной плотности
энергии магнитного поля совпадает с (14.26). Энергию, заключенную в неко-
тором объеме V, можно найти, вычислив интеграл
W=\wdV. (14.27) И Электрические колебания
Рассмотрим один пример проявления э.д.с. самоиндукции.
Зарядим конденсатор емкостью С, поместив на обкладки разноименные
заряды ± qQ, и подключим его к катушке индуктив-
ностью L так, как показано на рис. 14.23. В результа-
те конденсатор будет разряжаться и в цепи потечет
ток, появление которого приведет к возникновению
в катушке э.д.с. самоиндукции и экстратока. При
этом энергия электрического поля конденсатора бу-
дет уменьшаться, но зато возникнет все возрастаю-
щая энергия магнитного поля катушки, обусловлен-
345
ная током. Полагая сопротивление катушки и соединительных проводов ни-
чтожно малым, можно утверждать, что полная энергия (энергия электрическо-
го поля конденсатора и магнитного поля катушки) останется неизменной и
равной начальной энергии конденсатора:
2С 2 2С‘
Поэтому в момент, когда заряд конденсатора и энергия электрического
поля обратятся в нуль, энергия магнитного поля и ток в цепи достигнут наи-
большего значения. В дальнейшем ток будет уменьшаться и, когда заряды на
обкладках конденсатора достигнут первоначального значения ± q0 (заряды на
обкладках поменяются местами), сила тока в цепи станет равной нулю. После
этого процессы потекут в обратном направлении. В ходе каждого из процес-
сов будет менятся заряд на обкладках конденсатора и сила тока, текущего
через катушку. При этом будут происходить взаимные превращения энергий
электрического и магнитного полей.
Можно показать, что эти изменения будут происходить периодически с
периодом
Г= 2п <LC. (14.28)
Поэтому цепь, представленную на рис. 14.23, называют колебательным
контуром (контуром Томсона). Заряд конденсатора и ток в катушке в таком
контуре будут изменяться по гармоническим законам:
? = ?тахСО8(ю0г + аХ /= “ ?тах “о sin (“о 1 + а)> (14.29)
где а>0 = 1/^ L С называется собственной частотой контура; gmax - макси-
мальное значение величины заряда на обкладках конденсатора; a - начальная
фаза. Значения qmax и а можно найти из начальных условий (т.е. из величины
заряда конденсатора q0 и тока 10 в катушке в начальный момент):
?0 = ?шах cos a’ А) = _ “Утах ®0 s'n a-
Откуда получаем ______
Яшах =^4)+^. tga = -77T’ (143°)
а>о Яо “о
Колебательный контур является неотъемлемой частью любого устройст-
ва, передающего или принимающего радиосигналы. В процессе периодичес-
ких превращений энергии электрического поля в энергию магнитного и на-
оборот, колебательный контур будет излучать электромагнитную волну с час-
тотой
v = — (14.31)
w СО л
и длиной волны и
Х = с7’=^-£, (14.32)
8 Ю°
где с = 3-10 м/с - скорость света в вакууме. Если собственная частота контура
совпадает с частотой электромагнитной волны, передаваемой некоторой ра-
346
диостанцией, то говорят, что в контуре наблюдается резонанс. Например, вра-
щая рукоятку настройки радиоприемника, мы изменяем параметры его прини-
мающего контура (обычно емкость конденсатора) до тех пор, пока не услы-
шим устойчивый сигнал. В этот момент собственная частота нашего контура
совпадает с частотой принимаемого сигнала, и мы говорим, что радиоприем-
ник настроен на волну передающей станции. Колебания зарядов и токов в
принимающем контуре будут происходить по законам, отличным от (14.29),
поскольку причиной их возникновения служат внешние факторы. О таких ко-
лебаниях говорят, что они вынужденные (см. книгу «Механика», §8).
Переменный ток
Рассмотрим теперь электрические колебания, возникающие в том случае,
если в цепи имеется источник тока, э.д.с. которого изменяется периодически
(такой источник будем называть генератором). Такие колебания подобны ме-
ханическим вынужденным колебаниям.
Все реальные генераторы тока имеют э.д.с., изменяющуюся по закону,
очень близкому к синусоидальному, и создаваемые ими токи практически яв-
ляются синусоидальными. С другой стороны, теория синусоидальных токов
наиболее проста. По этим причинам мы будем рассматривать только такие
токи, сила которых меняется по закону
7=/0 sin cot, (14.33)
где 10 - амплитудное значение тока, со - его частота.
Сопротивление в цепи переменного тока
R
Рассмотрим цепь, состоящую из генератора и со-
противления R (рис. 14.24), которое в случае перемен-
ных токов называют активным сопротивлением. а,
Напряжение на участке a-R-b цепи будет равно
U =1 R = I0R sin со/ = Uo sin cot, (14.34)
где Uq = IqR- максимальное значение напряжения на
участке.
Таким образом, напряжение на концах участка изменяется по закону си-
нуса, также как и ток в цепи. Причем разность фаз между колебаниями тока и
напряжения равна нулю: напряжение и ток одновременно достигают макси-
мальных значений и одновременно обращаются в нуль.
Конденсатор в цепи переменного тока
Рассмотрим теперь цепь, состоящую из генерато-
ра и конденсатора емкостью С.
Заряд конденсатора и силу тока будем считать по-
ложительными, если они соответствуют рис. 14.25.
Напряжение на участке а-C-b цепи будет равно
U=q/C,
где q =jldt - заряд конденсатора (см. формулу (13.2)).
а
Рис. 14.25
347
Если сила тока в цепи изменяется по закону (14.33), то заряд на конден-
саторе в любой момент времени равен
f k
q= llasincotdt = - — coscot,
(0
4 4
U= - —— cos cot = —- sin (cot - тг/2) = Uo sin (cot - тг/2). (14.35)
co С co C
Как видим, напряжение на конденсаторе изменяется также по закону си-
нуса, но колебания напряжения отстают по фазе от колебаний тока в цепи на
тг/2 (когда ток, возрастая, проходит через нуль, напряжение достигает мини-
мума и начинает увеличиваться; когда сила тока становится максимальной,
напряжение проходит через нуль и т.д.).
Амплитудное значение напряжения на конденсаторе С70 = /о/соС обычно
записывают в виде
UO=1OXC, (14.36)
где %с = 1/соС называют реактивным сопротивлением емкости. Величина
Хс тем меньше, чем больша частота тока и в цепи постоянного тока
%с -> оо.
Индуктивность в цепи переменного тока
L Рассмотрим, наконец, цепь, состоящую из генера-
тора и катушки индуктивностью L (рис. 14.26).
При наличии переменного тока в цепи в катушке
возникнет э.д.с. самоиндукции
„ г dl
S'~ L dt'
Поскольку активное сопротивление цепи равно
нулю, то напряжение на участке a-L-b цепи будет
равно
U= -£,=L .
5 dt
цепи изменяется по закону (14.33), то
U= - Io со L cos cot = Io со L sin (cot + тг/2) = Uo sin (cm + ic/2). (14.37)
Как видим, напряжение на индуктивности изменяется также по закону
синуса, но колебания напряжения опережают по фазе колебания тока в цепи
на тг/2 (когда ток, возрастая, проходит через нуль, напряжение уже достигает
максимума и начинает уменьшаться; когда сила тока становится максималь-
ной, напряжение проходит через нуль и т.д.).
Амплитудное значение напряжения на индуктивности Uo = I0coL обычно
записывают в виде
<70 = 70%l. (14.38)
где XL = coL называют реактивным сопротивлением индуктивности. Величи-
на XL растет линейно с частотой тока и в цепи постоянного тока XL = 0.
а-----U------- Ь
Рис. 14.26
Если сила тока в
348
Векторные диаграммы. Закон Ома для цепи переменного тока
Рассмотрим систему координат XOY
и вектор длиной А, составляющий с осью
ОХ угол а (рис. 14.27). Пусть этот вектор
равномерно вращается против часовой
стрелки с угловой скоростью со. Т^огда в
любой момент времени вектор А будет
составлять и осью ОХ угол <р = at + а, а
проекции этого вектора на оси ОХ и OY
будут равны
Ах = A cos <р = A cos (at + а),
Ay = A sin <р = A sin (сот + а).
Поэтому колебания с амплитудой А и постоянной частотой со, про-
исходящие по закону косинуса, можно наглядно представить графически в
виде проекции равномерно вращающегося с угловой скоростью со вектора
длиной А на ось ОХ, а синусоидальные колебания - в виде его проекции на
ось OY.
Можно показать, что сложение двух колебаний одного направления и
одинаковой частоты графически можно выполнить по правилам сложения
двух векторов.
R
Рис. 14.27
С L
ЧН~
а' •
b
и
Рис. 14.28
Вернемся к цепям переменного тока и рассмотрим последовательное со-
единение с генератором активного сопротивления R, конденсатора емкостью
С и катушки индуктивностью L (рис. 14.28). При таком соединении напряже-
ние между точками а-b участка a-R-C-L-b цепи будет равно сумме падений
напряжений на элементах участка. Выше мы видели, что ток в цепи, напряже-
ния на активном сопротивлении, конденсаторе н катушке меняются по зако-
нам синуса с одинаковой частотой. Для сложения напряжений воспользуемся
векторной диаграммой напряжений. Выберем ось диаграммы таким образом,
чтобы вектор, изображающий колебания тока, был направлен вдоль этой оси
(рис. 14.29). Тогда вектор, соответствующий колебаниям напряжения на ак-
тивном сопротивлении, будет иметь длину IqR и будет направлен вдоль оси
токов, поскольку разность фаз между током и напряжением равна нулю. Век-
тор длиной I^/аС, изображающий колебания напряжения на конденсаторе,
349
будет направлен относительно оси токов с отставанием на угол тг/2. Анало-
гично, вектор длиной IaaL, изображающий колебания напряжения на катуш-
ке, будет направлен относительно оси токов с опережением на угол тг/2. Скла-
дывая вектора, соответствующие двум последним напряжениям, получим зна-
чение так называемой реактивной составляющей напряжения:
Up = I0(a L-1/а С). (14.39)
С учетом (14.39) амплитуда напряжения на участке a-R-C-L-b цепи
Uo = у/ U% + 1/р2= 10 ^/г2 + (со £ - l/о Q2, (14.40)
где Ua = IQR- активная составляющая напряжения.
Формула (14.40) имеет сходство с законом Ома в том смысле, что ампли-
туда напряжения Uo пропорциональна амплитуде тока 10. Поэтому выражение
(14.40) часто называют законом Ома для участка цепи переменного тока.
Следует помнить, что эта формула справедлива лишь для амплитуд, но не для
мгновенных значений тока и напряжения.
Величину
Z = ^ = V /f2 + (ш £ - 1/0 Q2 (14.41)
называют полным сопротивлением цепи для переменного тока или импедан-
сом цепи, а величину
1
УГ=-£ = о£-Ч; (14.42)
'О 0 с
реактивным сопротивлением или реактансом цепи.
Из векторной диаграммы и проведенных вычислений понятно, что напря-
жение между точками а-b участка a-R-C-L-b цепи меняется по закону
U = Uo sin (at + ср), (14.43)
где сдвиг фаз ср между током и напряжением (см. рис. 14.29)
. . a L-1/0 С ,, . ...
ср = arctg = arctg ----------. (14.44)
Работа и мощность переменного тока
Найдем работу, совершаемую в цепи, представленной на рис. 14.28, при
наличии в ней переменного синусоидального тока.
Поскольку сила тока в цепи и напряжение на ее концах непрерывно ме-
няются, то сначала найдем работу dA за бесконечно малый интервал времени
dt, в течение которого ток и напряжение можно считать постоянными:
dA=IUdt.
Разложим напряжение U на активную и реактивную составляющие сле-
дующим образом (см. рис. 14.29):
1/а = Uo cos ф sin at, Up = Uo cos ф sin (at ± л/2),
где учтено, что реактивная составляющая напряжения Up смещена относи-
тельно тока на угол ±тс/2 (если aL > 1/аС, то Up смещена на угол +тг/2, в
350
противном случае - на -тг/2). Тогда работа за период Т = 2тг/со, обусловлен-
ная активной и реактивной составляющими напряжения, будет равна
Ай- Jt7a7c& = /0 t70cosq> Jsin2atdt = у TIQ t70cosq>, (14.45)
° T ° T
Ap= flJpIdt = ±I0 t70sin<p |sino)/cosa)/c& = 0. (14.46)
о о
Следовательно, полная работа тока в рассматриваемой цепи за период
определяется только активной составляющей напряжения.
Средняя мощность переменного тока за период равна
Ая 1
tf = ^ = |/0t/0cos<p, (14.47)
где величина cos <р называется коэффициентом мощности. Очевидно, что в
случае, если цепь переменного тока содержит только активные сопротивле-
ния, то сдвиг фаз между током и напряжением отсутствует и cos <р = 1. В этом
случае выражение для средней мощности примет вид
1 IqR Uo2
*=|/olZO= 2 =2/Г (14.48)
Такую же мощность в этой цепи развивает постоянный ток силой
4
/д=^=, (14-49)
который называют действующим (или эффективным) значением силы тока
(действующее значение синусоидального тока численно равно значению тако-
го постоянного тока, при котором за время, равное периоду синусоидального
тока, во внешней цепи выделится такое же количество теплоты.) Аналогично
величина ТТ
= (14.50)
называется действующим (илн эффективным) значением напряжения.
Выражение для средней мощности (14.47) через действующие значения
силы тока и напряжения примет вид
N = 7Д Ua cos ф. (14.51)
Рекомендации по решению задач
В задачах на расчет индукции магнитного поля, создаваемого несколькими токами,
обязательно нужно использовать рисунок, на котором требуется изобразить векторы индук-
ции отдельных токов в рассматриваемых точках поля. При этом особое внимание следует
обратить на направление векторов индукции. В общем случае для определения направления
вектора индукции произвольного прямолинейного участка с током можно воспользоваться
правилом буравчика. Поскольку в рамках школьного курса физики изучаются магнитные
поля лишь бесконечно длинных прямолинейных и круговых токов, то достаточно запомнить
как направлены векторы индукции этих токов (см. рис. 14.5, 14.6). Определив направления
векторов индукции всех токов, далее нужно найти их количественные значения в рассмат-
351
риваемой точке поля по известным формулам (14.3) или (14.4)-(14.5) и вычислить индук-
цию магнитного поля, создаваемого всеми токами, воспользовавшись принципом суперпо-
зиции (14.1).
Большую часть задач по магнетизму составляют задачи, связаные с определением си-
лового действия магнитного поля иа движущиеся заряды и токи.
При решении задач иа движение заряженных частиц в магнитных полях нужно по-
мнить, что:
- если вектор скорости частицы не параллелен вектору индукции магнитного поля, то
частица будет двигаться вокруг силовой линии;
- если скорость частицы перпендикулярна линиям индукции, то ее траекторией будет
окружность постоянного радиуса;
- если скорость частицы направлена под некоторым углом к линиям индукции, то ее
траекторией будет цилиндрическая спираль;
- независимо от направления скорости частицы и направления магнитного поля сила Ло-
ренца не меняет величину скорости частицы.
При решении таких задач можно придерживаться следующей последовательности:
1) сделать чертеж, на котором изобразить силовые линии магнитного поля и вектор на-
чальной скорости частицы;
2) если начальная скорость частицы направлена под углом к линиям индукции магнитного
поля, то ее следует разложить на две составляющие, одна из которых должна быть
нал- равлена перпендикулярно векторам индукции, а вторая и*. - параллельно им. Такое
разложение позволяет представить достаточно сложное движение частицы в магнитном
поле в виде наложения двух более простых: наличие составляющей проводит к движе-
нию по окружности постоянного радиуса, а наличие - к прямолинейному движению
вдоль силовых линий поля;
3) изобразить силы, действующие на частицу в произвольный момент движения. Для оп-
ределения направления силы Лоренца следует воспользоваться правилом левой руки, ко-
торую нужно расположить так, чтобы силовые линии поля входили в ладонь, а пальцы
были направлены по составляющей скорости частицы; если частица имеет положитель-
ный заряд, то отогнутый большой палец укажет направление силы Лоренца; если заряд
отрицательный, то сила Лоренца будет направлена в противоположную сторону;
4) ввести сопровождающую систему отсчета, направив одну из осей системы координат
по составляющей скорости частицы, вторую - по составляющей Bf , третью (обычно в
такой оси нет необходимости) - перпендикулярно первым двум;
5) записать уравнение второго закона Ньютона в проекции на оси выбранной системы
координат, дополнив их развернутыми выражениями для сил, действующих на частицу;
6) при необходимости записать уравнения кинематики и решить систему уравнений.
При решении задач, в которых рассматривается движение проводников с током в маг-
нитном поле, можно воспользоваться рекомендациями, предложенными в книге «Механи-
ка», поскольку эти задачи ничем принципиально не отличаются от задач механики; единст-
венное отличие, которое может быть, это наличие силы Ампера. При известных токах, теку-
щих в проводниках (если же токи неизвестны, то для их определения следует воспользовать-
ся законами постоянного тока) и индукции магнитного поля (если она неизвестна, то ее тре-
буется предварительно рассчитать), величину силы Ампера можно найти по формуле (14.8),
а ее направление - по правилу левой руки. Если в задаче рассматривается контур с током
или его часть, то значение силы Ампера и ее направление следует найти для всех прямоли-
нейных проводников. Следует помнить, что контур с током в магнитном поле силы Ампера
352
будут растягивать или сжимать (но ие то и другое одновременно), и, если плоскость контура
не перпендикулярна линиям индукции, то на контур будет действовать механический мо-
мент сил Ампера (14.13), разворачивающий контур так, чтобы расположить его в плоскости,
перпендикулярной силовым линиям.
Самую сложную часть задач этого параграфа составляют задачи на закон электромаг-
нитной индукции (включая и самоиндукцию). При их решении следует помнить, что:
- при движении проводника в магнитном поле э.д.с. индукции обусловлена действием на
носители тока силы Лоренца;
- прн изменении магнитного потока через поверхность, ограниченную контуром, э.д.с.
индукции обусловлена вихревым электрическим полем; ее появление не зависит от того,
какая из величин, входящих в выражение (14.15) для потока Ф, изменилась (величина В
индукции поля, площадь S контура, его ориентация в магнитном поле, две или все три
нз этих величин);
- независимо от причин возниковения э.д.с. индукции ее величина может быть найдена
по формуле (14.16);
- появление э.д.с. индукции приводит к возникновению в контуре индукционного тока,
направление которого определяется правилом Ленца; если магнитный поток увеличивает-
ся, то в контуре возникает индукционный ток такого направления, чтобы собственный
магнитный поток ослабил внешний, т.е. магнитное поле индукционного тока должно быть
направлено противоположно внешнему; если магнитный поток уменьшается, то индукци-
онный ток будет направлен так, чтобы поддержать внешний, т.е. магнитное поле индук-
ционного тока будет направлено по внешнему. При этом векторы индукции внешнего и
собственного магнитных полей не обязательно будут параллельны;
- на элементы контура, в котором возникает индукционный ток, будет действовать сила
Ампера. Поскольку направление индукционного тока определяется правилом Ленца, то и
сила Ампера будет направлена так, чтобы противодействовать причине, вызывающей по-
явление э.д.с. индукции. Если магнитный поток возрастает, то сила Ампера будет направ-
лена так, чтобы его уменьшить; так как сила Ампера не может изменить величину индук-
ции внешнего поля, то она будет направлена так, чтобы уменьшить площадь, ограничен-
ную контуром, т.е. сжать контур. И, наоборот, при уменьшении магнитного потока, сила
Ампера будет направлена так, чтобы растянуть контур.
Если проводник движется в магнитном поле, то иа электроны, находящиеся в провод-
нике, будет действовать сила Лоренца, и электроны будут перемещаться к одной из границ
проводника: в результате у одной границы проводника окажется избыток электронов, а у
другой - их недостаток. При этом между противоположными границами проводника воз-
никнет электрическое поле и разность потенциалов, значения которых нужно определить,
используя формулы электростатики. Другой способ решения таких задач основан на непо-
средственном применении закона электромагнитной
индукции (14.16). В этом случае проводник следует
дополнить проводящей рамкой до замкнутого конту-
ра, все части которого (кроме проводника) неподвиж-
ны. При этом контур должен иметь такую форму,
чтобы места контакта с рамкой у проводника не меня-
лись; если проводник движется поступательно, то
рамка может иметь форму буквы П (см. рис. 14.21);
если проводник вращается вогруг одного из концов, то
рамка должна иметь форму части сектора (рис. 14.30).
353
Переменный магнитный поток через поверхность S, ограниченную таким контуром, будет
обусловлен изменением площади контура. Поэтому, если магнитное поле направлено пер-
пендикулярно плоскости контура, то закон электромагнитной индукции (14.16) может быть
записан в виде
= •
' dt
Относительно просто решаются задачи, в которых причиной появления э.д.с. индук-
ции является вихревое электрическое поле, порождаемое изменяющимся со временем маг-
нитным полем, а параметры контура (его площадь и ориентация в магнитном поле остаются
неизменными). Для их решения достаточно правильно вычислить величину магнитного по-
тока в произвольный момент времени н воспользоваться законом электромагнитной индук-
ции (14.16).
Часто встречаются задачи, в которых нестационарный магнитный поток и э.д.с. индук-
ции возникают в контуре при изменении его площади за счет движения одной из сторон кон-
тура (одной из сторон контура является подвижный проводящий стержень). Обычно такие
задачи требуют привлечения законов механики. Решая их, можно придерживаться следую-
щей последовательности:
1) сделать чертеж, на котором изобразить силовые линии индукции магнитного поля н
контур;
2) проанализировав условие задачи, установить причины изменения магнитного потока,
пронизывающего поверхность, ограниченную контуром;
3) воспользовавшись правилом Ленца, определить направление индукционного тока в кон-
туре, указав его на рисунке;
4) если в задаче идет речь о движении контура или его части, указать направления всех
сил (в том числе н силы Ампера), действующих на интересующие нас элементы контура;
5) записать развернутые выражения для потока Ф магнитной индукции, э.д.с. «У; индукции,
индукционного тока н силы Ампера. Если контур содержит только сопротивления, то
величину индукционного тока нужно определить по закону Ома для замкнутой цепи, со-
держащей источник э.д.с., равный <S): 1= Sj/R. Если в контуре содержится конденсатор
емкостью С, то силу тока нужно выразить через заряд q конденсатора: I=dq/dt, где
q —
6) записать необходимые законы механики и решить систему уравнений относительно
искомых величин.
При решении задач на самоиндукцию нужно помнить, что э.д.с. 8S самоиндукции воз-
никает в контуре при изменении силы тока в нем н препятствует увеличению или уменьше-
нию тока в цепи. Задачи на расчет э.д.с. самоиндукции решаются или очень просто (по ос-
новным определениям), или очень сложно, причем эти сложности математические. По-
скольку э.д.с. самоиндукции существует лишь до тех пор, пока в контуре течет нестационар-
ный ток, то любые уравнения, связанные с Ss (например, ток в цепи, напряжения на участках
цепи, количество выделившегося на них тепла и т.п.) будут содержать зависимости от вре-
мени. Решение таких задач чаще всего требует навыков интегрирования. Найдем, например,
закон изменения тока в цепи, представленной на рис. 14.22, при замыкании ключа К из по-
ложения 1 в положение 2 (в этом случае источник эд.с. «Убудет отключен от цепи). Посколь-
ку ток в катушке индуктивностью L исчезнет не мгновенно, то в цепи будет действовать
э.д.с. самоиндукции <%: ,.
Запишем закон Ома для замкнутой цепи:
354
IR = Ss, или =
Разделив переменные I nt, получим уравнение
, I L
интегрируя которое (слева по току I, справа по времени), находим
R г R 1
In/=- — / +In const, или /= const • exp (- .
Значение постоянной интегрирования найдем, воспользовавшись условием, что в мо-
мент времени t = 0 (момент размыкания цепи) сила тока в катушке была равна 1= S/R:
в
~ = const
Следовательно, ток в цепи будет уменьшаться по закону:
, е t R ,1
/=7exPt-Z'b
При замыкании ключа К из положения 2 в положение 1 в цепь будет включен источник
э.д.с. <?и ток в катушке индуктивностью L станет возрастать, при этом в цепи наряду с э.д.с.
«Убудет действовать э.д.с. самоиндукции 8S. Таким же образом, как при замыкании ключа из
положения 1 в положение 2, можно показать, что теперь сила тока в цепи будет увеличи-
ваться по закону
7=/{l-exp{-fr}}.
К задачам на самоиндукцию можно также отнести задачи на электрические колебания.
Колебания даже в самом простом контуре - контуре Томсона - описываются дифференци-
альными уравнениями. Поэтому в рамках школьного курса физики используются их гото-
вые решения: период колебаний определяется формулой (14.28), заряд на конденсаторе и
ток в катушке изменяются по законам (14.29), максимальное значение заряда на обкладках
конденсатора н начальную фазу колебаний можно найти по формулам (14.30). Обычно этих
формул достаточно, чтобы решить любую задачу на свободные незатухающие электричес-
кие колебания. В некоторых случаях необходимо также использовать закон сохранения
энергии.
Задачи на определение частоты или длины волны, на которую настроен колебательный
контур, решаются непосредственным применением формул (14.31) и (14.32).
Наконец, особую часть составляют задачи на цепи переменного тока, изменяющегося
по закону синуса (14.33). В силу математических сложностей здесь также рассматривается
очень узкий класс задач, в которых электрические цепи содержат не более чем активное со-
противление, конденсатор и катушку, соединенные последовательно с генератором. При
расчете таких цепей следует помнить, что:
- напряжение на концах активного сопротивления изменяется по такому же закону, что
и ток в цепи, причем сдвиг фаз между током н напряжением равен нулю;
- напряжение на конденсаторе меняется по такому же закону, что и ток в цепи, но отстает
по фазе от тока на л/2; реактивное сопротивление Хс = 1/<оС конденсатора уменьшается
с ростом частоты тока;
- напряжение на катушке меняется по такому же закону, что и ток в цепи, но опережает
ток по фазе на л/2; реактивное сопротивление ~ &L катушки увеличивается с ростом
частоты тока;
- амплитудное значение Uq напряжения на концах цепи определяется из векторной диа-
граммы (см. рис. 14.29) или по формуле (14.40); активная составляющая напряжения С/а
совпадает по фазе с током в цепи, а реактивная ~ смещена относительно тока на угол
±я/2;
355
- напряжение U на концах участка цепи меняется по такому же закону, что и ток в цепи,
но существует сдвиг фаз <р между током н напряжением; если цепь переменного тока
содержит лишь активное сопротивление, то сдвиг фаз равен нулю;
- полное сопротивление Z цепи для переменного тока не определяется простым арифме-
тическим сложением активного н реактивных сопротивлений: его значение может быть
найдено по формуле (14.41); полное сопротивление цепи минимально н равно активному
сопротивлению, если частота тока такова, что выполняется условие ш£=1/шС, т.е.
Rl = Rc>
- полная работа (средняя мощность) реактивной составляющая напряжения за период
равна нулю;
- полная работа (средняя мощность) перемениного тока за период равна работе (средней
мощности) активной составляющая напряжения и определяется формулой (14.45) (или
(14.47));
- действующее значение синусоидального тока численно равно значению такого постоян-
ного тока, при котором за время, равное периоду синусоидального тока, во внешней цепи
выделится такое же количество теплоты.
Задачи
Магнитное поле тока
14.1. Два бесконечно длинных прямых проводника скрещены под пря-
мым углом (рис. 14.31). По проводникам текут токи /, = 80 А и /2 = 60 А. Рас-
стояние между проводниками d= 10 см. Чему равна магнитная индукция в
точке А, одинаково удаленной от обоих проводников?
• Решение. Прямолинейный бесконечно
длинный проводник с током I создает на
расстояния г от своей оси магнитное поле
индукцией
направление которого можно определить
по правилу буравчика (правого винта).
Проводники, рассматриваемые в
задаче, находятся на равных расстояниях
от точки А, поэтому индукции, создавае-
мые токами 7] и 12, будут равны
п Ио-Л 1*оЛ д 1*о 4
1 2лd/2 nd ’ 2 nd
соответственно.
Вектор индукции В] тока Ц в точке А будет направлен параллельно проводнику с
током /2 вертикально вниз, а вектор индукции В2тока 12 - параллельно проводнику с
током /] на нас (рис. 14.31). Индукция магнитного поля в точке А будет равна их векторной
сумме:
2? — + 1?2 •
Поскольку векторы % и 2?2 составляют между собой прямой угол, то
в = у!в^+в^,
356
или
В = ^5- Il+12 = 41 О'4 Тл.
л d 1 z
• Ответ: В = ~ ^Л2+/22 = 4-1 О’4 Тл.
л d
14.2. По прямому бесконечно длинному проводнику течет ток 7= 50 А.
Чему равна магнитная индукция в точке, удаленной на расстояние г = 5 см от
проводника?
14.3. Два длинных параллельных проводника находятся на расстоянии
d = 5 см один от другого. По проводникам текут в противоположных направ-
лениях одинаковые токи силой 1= 10 А каждый. Найти магнитную индукцию
в точке, находящейся на расстоянии = 2 см от одного и г2 = 3 см от другого
Рис. 14.32
проводника.
14.4. Расстояние между двумя длинными параллельными проводниками
равно d=5 см. По проводникам в одном направлении текут токи силой
7= 30 А каждый. Найти индукцию магнитного поля в точке, находящейся на
расстоянии Г] = 4 см от одного и г2 = 3 см от другого проводника.
14.5. По двум бесконечно длинным пря-
мым проводникам, скрещенным под прямым
углом, текут токи 7[ = 30 А и 72 = 40 А. Рассто-
яние между проводниками <7 = 20 см. Опреде-
лить магнитную индукцию в точке А (рис.
14.32), одинаково удаленной от обоих провод-
ников на расстояние, равное d.
14.6. В однородное магнитное поле с ин-
дукцией В - 1-10"4 Тл помещен перпендикуляр-
но к линиям индукции прямолинейный длин-
ный проводник с током 7 = 50 А. Найти геомет-
рическое место точек, в которых индукция маг-
нитного поля равна нулю.
14.7. Найти величину индукции магнитно-
го поля в центре петли радиусом R = 10 см, об-
разованной бесконечно длинным тонким про-
водником с током 7= 50 А (рис. 14.33.).
• Решение. Вектор индукции магнитного поля беско-
нечно длинного прямолинейного тока на расстоянии R-
от него по величине равен .
D РФ
В1 = Гл7
н направлен в центре (тодже О) петли перпендикулярно ее плоскости на нас.
Вектор индукции В2 магнитного поля кругового тока в центре петли по направлению
совпадает с sj и по величине равен
2R'
Следовательно, индукция поля, создаваемого проводником и круговым витком в рас-
сматриваемой точке, равна
Рис. 14.33
357
+ или В = В1+В2.
Окончательно находим
„ М . 1V Ш>7(1+л) 414
В = -—- + VK -~~~Z———«414 мкТл.
2nR 2R 2nR
Ио/(1 + л)
• Ответ: В = —-—-— « 414 мкТл.
2tiR
14.8. Какова магнитная индукция в центре тонкого кольца, по которому
течет ток 1= 10 А? Радиус кольца R = 5 см.
14.9. В центре кругового тока радиусом R = 5,8 см индукция магнитного
поля равна В = ЬЗ-Ю^Тл. Определить силу тока.
14.10. Индукция магнитного поля в центре кругового тока силой 1= 10 А
равна В = 10"4 Тл. Определить диаметр окружности, по которой течет ток.
14.11. По тонкому кольцу радиусом R = 10 см течет ток 1= 80 А. Опреде-
лить магнитную индукцию в точке, равноудаленной от всех точек кольца на
расстояние г = 20 см.
Рис. 14.34
14.12. Два круговых проводника одинакового радиуса с общим центром
О расположены во взаимно перпендикулярных плоскостях (рис. 14.34). Ин-
дукция магнитного поля в точке О равна Во = 2-1 О'4 Тл. Индукция магнитного
поля первого проводника с током 7, = 8 А в этой же точке Вх = 1,6- КГ4 Тл. Оп-
ределить индукцию В2 магнитного поля второго проводника в точке О и силу
тока 12 в нем.
14.13. Найти величину индукции магнитного поля в центре петли радиу-
сом R= 10 см, образованной бесконечно длинным тонким проводником с
током 1= 50 А (рис. 14.35).
14.14. Найти величину индукции
магнитного поля в точке О, если бес-
4 конечно длинный тонкий проводник с
— током 1= 20 А изогнут так, как пока-
зано на рис. 14.36. Радиус изгиба за-
_1_ гругленной части R = 50 см.
• Решение. Для определения индукции маг-
нитного поля тиса I в точке О разобьем про-
водник иа три участка, как показано на рис. 14.36, а индукцию В результирующего поля най-
дем на основании принципа суперпозиции.
Рассмотрим полубесконечный участок 1-2 проводника.
358
Бесконечно длинный прямолинейный проводник с током I, расположенный на месте
участка 1—2, на расстоянии R создавал бы магнитное поле с индукцией
й *>f
°°~2nR’
направленное перпендикулярно плоскости рисунка от нас. Поскольку бесконечный провод-
ник с током можно представить как два полубесконечных, каждый из которых вносит оди-
наковый вклад в индукцию Вх поля, то участкок 1-2 проводника в точке О создаст магнит-
ное поле с индукцией .
и _1 п >*0'
В'-2 2В”_4лЛ-
Участок 2-3 проводника представляет собой дугу окружности данной, равной %
длины окружности радиуса R. Каждый участок тока этой дуги в точке О создает магнитное
поле, направленное перпендикулярно плоскости рисунка от нас. Поэтому индукция маг-
нитного поля дуги 2-3 проводника будет равна
й 3Мо7
Но/ 2’3~ ° '
где Вкр = - индукция кругового тока в точке О. Следовательно,
Вг-з = ^кр.<
Индукция магнитного поля участка 3-4 проводника в точке О равна нулю. Дейст-
вительно, радиус-вектор, проведенный от любого элемента этого участка в точку О, со-
ставляет с направлением тока угол а = 180°. По закону Бно-Савара-Лапласа такой элемент
тока в рассматриваемой точке магнитного поля не создает (поскольку sin а = 0). Поэтому
индукция магнитного поля всего участка 3-4 проводника в точке О
В3_4 = 0.
Следовательно, индукция поля, создаваемого проводником в рассматриваемой точке,
равна
2? — 2^1—2 + ^2—3 » ИЛИ В — В|_2 + ^2-3-
Окончательно находим
М 3(V РоЛ2 + Зл)
В =---- + „ „ =-----------® 22,8 мкТл.
4лВ 8Я 8лЯ
14.15. Решить задачу №14.14, если бесконечно длинный тонкий провод-
ник с током 7= 20 А изогнут так, как показано на рис. 14.37. Радиус изгиба за-
груженной части R = 20 см.
14.16. Решить задачу №14.14, если бесконечно длинный тонкий провод-
ник с током 7 = 10 А изогнут так, как показано на рис. 14.38. Радиус изгиба за-
груженной части R = 40 см, угол <р = 90°.
359
14.17. Решить задачу №14.14, если бесконечно длинный тонкий провод-
ник с током 1= 50 А изогнут так, как показано на рис. 14.39. Радиус изгиба за-
груженной части R = 50 см.
14.18. Найти величину индукции магнитного поля в точке О, если тонкий
проводник с током 7= 10 А изогнут так, как показано на рис. 14.40. Радиус
R = 50 см.
14.19. Длинный прямой соленоид из проволоки диаметром d = 0,5 мм на-
мотан так, что витки плотно прилегают друг к другу. Какова магнитная ин-
дукция внутри соленоида при силе тока в нем I = 4 А? Толщиной изоляции
проволоки пренебречь.
14.20. Найти индукцию магнитного поля внутри длинного соленоида при
силе тока в нем 1= 8 А, если на / = 40 см его длины намотано N= 400 витков
проволоки. Во сколько раз изменится индукция магнитного поля, если внутрь
соленоида поместить железный сердечник, магнитная проницаемость которо-
го ц = 2000?
Сила Лоренца. Движение заряженных частиц в магнитном поле
14.21. В однородном магнитном поле с индукцией 5= 100 мкТл по вин-
товой линии движется электрон. Определить скорость электрона, если радиус
винтовой линии равен R = 5 см, а шаг й = 20 см. Масса электрона равна
т = 9,1-Ю'31 кг, его заряд |е| = 1,6-10‘19 Кл.
• Решение. При движении заря-
женной частицы в магнитном
поле на нее действует сила Лорен-
ца, направленная в любой момент
перпендикулярно вектору скорос-
ти частицы. При этом сила Лорен-
ца не совершает работы над час-
тицей и не меняет ее кинетичес-
кую энергию. Поэтому скорость
частицы будет оставаться неиз-
Рис. 14.41 менной в течение всего времени
движения в магнитном поле.
Известно, что при движении заряженной частицы в магнитном поле по винтовой
линии, ее скорость 1? направлена под некоторым углом а * 0 к линиям индукции поля
(рис. 14.41).
Разложим вектор скорости 7? электрона на две составляющие, одна из которых
= о sin а направлена перпендикулярно силовым линиям поля, а другая и|( = о cos а — па-
360
раллельна им. На электрон в магнитном поле действует сила Лоренца, обусловленная со-
ставляющей Ор
^л = МЧ1В.
Под действием этой силы частица будет двигаться по некоторой окружности радиуса R.
Наличие составляющей ои скорости приводит к тому, что частица будет двигаться
равномерно вдоль силовых линий поля. В результате наложения этих двух движений тра-
ектория электрона будет представлять собой цилиндрическую спираль.
Для нахождения радиуса R спирали запишем уравнения движения электрона на нор-
маль л к траектории: 2
т г>1 . , _
—^ = |е|Ч1В-
Откуда получаем
m Qi m о sin а
|е|В" |е|В '
Шаг h спирали - это расстояние, на которое сместится электрон вдоль силовой линии
поля за время Т одного оборота. Поскольку i>u = const, то
, 2nR 2 л m о cos a
|e|5—-
Следовательно,
или
. 2 R2\e\2 В2
sin а = —H-z- ,
т о
Откуда находим
2 h2 |е|2 В2
cos а = —2 '
4 тС т2 о2
. 2 2 R2\e\2 В2 h^efe2
sin а + cos а =—i-4- +——?•
т2 о2 4л2т2о2
о = R2+~ « 1,04-106 м/с.
------г т 4 л2
» Ответ: о = V R2+ » 1,04-10® м/с.
т 4я2
14.22. а-частица, ускоренная разностью потенциалов Дф = 10 В, влетает
в однородное магнитное поле перпендикулярно силовым линиям. Индукция
поля равна В = 0,15 Тл. Найти силу, действующую на частицу в магнитном
поле. Масса а-частицы т - 6,7-10'2' кг, ее заряд q = 3,2-10‘19 Кл.
14.23. Электрон, прошедший разность потенциалов Дф = 182 В, движется
параллельно бесконечно длинному прямому проводнику на расстоянии
/= 10 мм от него. Определить величину силы, действующей на электрон,
когда по проводнику потечет ток 7= 0,5 А. Масса электрона т = 9,1-1(Гэт кг,
его заряд |е| = 1,6-10"19 Кл.
14.24. Электрон движется по окружности радиуса R = 1 см в однородном
магнитном поле с индукцией В= 10"4 Тл. Определить скорость движения
электрона. Масса электрона т = 9,1-10"31 кг, его заряд |е| = 1,6-10'19 Кл.
14.25. Электрон влетает в область однородного магнитного поля с индук-
цией В = 1 мкТл перпендикулярно к силовым линиям. Определить частоту обра-
щения электрона. Масса электрона т = 9,1 10'31 кг, его заряд |е| = 1.6-10'19 Кл.
14.26. Протон, пройдя ускоряющую разность потенциалов Дф= 1 кВ,
влетает в однородное магнитное поле с индукцией В = 0,2 Тл перпендикуляр-
361
но линиям индукции. Определить радиус окружности, по которой будет дви-
гаться протон, и его период обращения. Масса протона т = 1,67-10’27 кг, его
заряд q = 1,6-10"19 Кл.
14.27. Частица массой т = 10'22 кг, и зарядом q = 10’16 Кл движется по
дуге окружности радиусом R = 1 см в магнитном поле индукцией В = 0,1 Тл.
Чему равна кинетическая энергия частицы?
14.28. Электрон влетает со скоростью и = 4-104 м/с в однородное магнит-
ное поле с индукцией В = 10'8 Тл перпендикулярно линиям индукции. Опреде-
лить нормальное и тангенциальное ускорения электрона. Масса электрона
т = 9,1 • 10'31 кг, его заряд |е| = 1,6-10’19 Кл.
14.29. Электрон проходит ускоряющую разность потенциалов Дф = 1 кВ
и влетает в однородное магнитное поле с индукцией В = 10'2 Тл под углом
а = 30° к силовым линиям. Определить радиус спирали, по которой будет дви-
гаться электрон. Масса электрона т = 9,1-10'31 кг, его заряд |е| = 1,6-10"19 Кл.
14.30. Электрон влетает в область маг-
нитного поля шириной I. Скорость электрона
г? перпендикулярна как вектору индукции
поля В, так и границам области (рис. 14.42).
Под каким углом к границе области электрон
вылетит из магнитного поля? Масса электро-
на т, его заряд |е|.
• Решение. Поскольку скорость электрона перпенди-
кулярна силовым линиям, то в области магнитного
поля на него будет действовать сила Лоренца
= |е| о В,
и электрон будет двигаться по дуге окружности неко-
торого радиуса R с центром в точке О. Учитывая, что
сила Лоренца в любой момент будет направлена по ра-
диусу окружности, запишем уравнение движения электрона в проекции на нормаль п*к тра-
ектории:
Откуда получим
т о2 . . _
п
|е|В'
Из равенства углов, обозначенных на рисунке а, находим
leLBZ
cos а = J-J—
т о
/
cos а = у., или
Л „
Следовательно, если электрон пролетит сквозь область, занятую магнитным полем,
то он вылетит из нее под углом
leLBZ
а = arccos J-J-
т о
к ее границам.
Легко заметить, что прн небольших скоростях, сильных магнитных полях или до-
статочно протяженной области, занятой полем, электрон не сможет пролететь сквозь поле:
в какой-то точке поля он развернется и вылетит из области под углом а = 90° с той же
стороны, с которой влетел.
362
Условия, при которых электрон пролетит сквозь область, занятую полем, можно
найти из условия ограниченности функции
lelBl . .
cosa = J-J—< 1,
т о
Следовательно, электрон покинет область
]е! В/ ]е| ВI
а = arccos J-1— при о > —,
ни т
\e\Bl
т
поля под углом
ЛЛО к| В I
или а = 90 при о < —
т
„ 1е!В/ |е| Я/ п.о |е| Я/
• Ответ: а = arccos J-1—, если о > J-1—; а = 90 , если о < J-J—.
mo т т
14.31. Однородное магнитное поле с индукцией В локализовано между
двумя параллельными плоскостями, расстояние между которыми / (рис.
14.42). Какую скорость должен иметь электрон, налетающий на эту «стенку»,
чтобы он мог пройти ее? Масса электрона т, его заряд |е|.
14.32. В однородном магнитном поле с индукцией В = 0,1 Тл по окруж-
ности некоторого радиуса со скоростью и = 104 м/с движется частица массой
т = 10'12 кг и зарядом q = Ю'10 Кл. Какой путь пройдет частица за время, в те-
чение которого направление ее скорости изменится на противоположное?
мишень
R
т
q
т, q
Рис. 14.43
®В
Рис. 14.44
14.33. Из точечного источника А (рис. 14.43) вылетают частицы массой
т = IO'20 кг и зарядом q = 10'16 Кл и движутся в однородном магнитном поле
с индукцией В = 0,1 Тл, силовые линии которого перпендикулярны вектору
скорости частиц на вылете из источника. На расстоянии / = 20 см от источни-
ка находится фотопластинка шириной /0 = 1 см. При каких скоростях частиц
они смогут попасть на фотопластинку? Силу тяжести не учитывать.
14.34. Из точечного источника вылетают частицы массой т - 2-1O"10 кг и
зарядом q = 10‘8 Кл с начальной скоростью и0 = 104 м/с и движутся в однород-
ном магнитном поле с индукцией В = 0,05 Тл, силовые линии которого пер-
пендикулярны и0 (рис. 14.44). На некотором расстоянии от источника нахо-
дится мишень радиусом R = 10 см, расположенная перпендикулярно . При
каких расстояниях от источника до мишени частицы попадут на ее поверх-
ность? Силу тяжести не учитывать.
14.35. Для определения отношения величины заряда |е| электрона к его
массе т пучок электронов разгоняют между катодом и анодом электронно-
лучевой трубки. При вылете из трубки электроны попадают в область одно-
родного магнитного поля с индукцией В = 5-1 О’4 Тл, силовые линии которого
перпендикулярны скорости пучка. При этом светлое пятно на экране, находя-
щемся за анодом, смещается на Л/ = 7,5 мм (относительно положения, когда
363
магнитное поле отсутствует). Определить отношение если напряжение
между анодом и катодом трубки равно U-10 кВ, а расстояние между анодом
и экраном I = 10 см. Силу тяжести не учитывать.
14.36. Электрон со скоростью <? влетает в
однородное магнитное поле с индукцией В, созда-
ваемое длинным соленоидом радисом R, перпенди-
кулярно оси соленоида (рис. 14.45). Какой угол с
первоначальным направлением будет составлять
скорость электрона после прохождения соленои-
да? Масса электрона т, его заряд |е|.
14.37. По обмотке длинного соленоида радиуса R = 5 см протекает посто-
янный ток, создающий внутри соленоида однородное магнитное поле с индук-
цией В = 5-10''° Тл. Между витками соленоида (перпендикулярно его оси)
вдоль радиуса в него влетает электрон со скоростью и = 10 м/с (рис. 14.45).
Определить время движения электрона внутри соленоида. Масса электрона
равна т = 9,110’3i кг, его заряд |е| = 1,6-Ю'19 Кл.
14.38. Протон влетает в однородные электрическое и магнитное поля, си-
ловые линии которых параллельны друг другу. Начальная скорость протона
перпендикулярна этим полям. Во сколько раз шаг второго витка траектории
протона больше шага первого витка?
Z • Решение. Пусть начальная
скорость протона равна а
напряженности электрического
и магнитного полей равны со-
-=у* ответственно
с Если бы электрическое
поле отсутствовало, то протон в
магнитном поле двигался бы по
окружности некоторого радиу-
са Л, при этом его скорость ос-
тавалась бы неизменной. Наличие электрического поля, направленного параллельно маг-
нитному, приведет к появлению у протона составляющей скорости v параллельной векто-
рам ?иД и частица будет двигаться вдоль силовых линий этих полей по спирали. Посколь-
ку величина и (с течением времени будет увеличиваться, то шаг спирали будет возрастать.
На протон при движении будут действовать две силы: сила Лоренца
Гл = ?и0 В,
направленная по радиусу окружности, и сила
Fjn = Ч F
направленная вдоль линий напряженности электрического поля.
Запишем уравнения движения протона на нормаль 7?к траектории и ось OZ, параллель-
ную векторам £ и Л (рис. 14.46):
7И Uq
или
364
-R- = qv0B, maz = qE,
где учтено, что составляющая скорости, перпендикулярная к направлению полей, при дви-
жении частицы не меняется.
Следовательно, вдоль оси OZ протон будет двигаться с постоянным ускорением
<?£
z т
и расстояние, пойденное им вдоль оси OZ, будет менятся по закону
az/2
Радиус R спирали и период Т обращение равны соответственно
„ m ио _ 2nR 2пт
ЧВ ’ о0 " ЧВ •
Как видим, период обращения не зависит от энергии протона. Расстояния, пройден-
ные протоном вдоль силовых линий за время первого и второго оборотов
„ az 2т? тЕ „ az(27")2 8я2йЕ
S'= 2 = ’ *2 = 2 •= ’
равны соответствующим шагам витков. Поэтому
, h\~
• Ответ: h2/h] = 4.
14.39. Первоначально покоящийся электрон разгоняется электрическим
полем напряженностью Е. Через Д/= 0,01 с после начала движения электрон
влетает в однородное магнитное поле с индукцией В= 10 мкТл, силовые
линии которого перпендикулярны Е. Определить отношение нормального и
тангенциального ускорений электрона в этот момент времени. Масса электро-
на равна т = 9,1-10'31 кг, его заряд \е\ = 1,6-10"’9 Кл.
14.40. Первоначально покоящийся электрон разгоняется электрическим
полем напряженностью Е = 1,6 кВ/м. Пройдя путь S электрон влетает в одно-
родное магнитное поле с индукцией В = 0,03 Тл, силовые линии которого пер-
пендикулярны скорости электрона, и далее движется по окружности радиуса
R = 2 мм. Определить путь, пройденный электроном в электрическом поле.
Масса электрона равна т = 9,1-10*31 кг, его заряд |е| = 1,6-10'19 Кл.
14.41. Электрон движется по окружности радиуса R = 0,1 м в однородном
магнитном поле с индукцией В = 0,1 Тл. В момент времени to-O включают
электрическое поле, векторы напряженности которого параллельны векторам
магнитной индукции. Через какое время кинетическая энергия электрона воз-
растет в и = 2 раза? Напряженность электрического поля равна Е = 100 В/м.
14.42. Перпендикулярно однородному магнитному полю с индукцией
В = 0,1 Тл возбуждено однородное электрическое поле с напряженностью
Е = 103 В/м. Перпендикулярно обоим полям движется, не отклоняясь от пря-
молинейной траектории, заряженная частица. Определить скорость частицы.
14.43. В простейшей схеме магнитогидродинамический генератор пред-
ставляет собой плоский конденсатор с площадью пластин 5 и расстоянием
между ними d, расположенный в потоке проводящей жидкости с удельным
365
Рис. 14.47
сопротивлением р, движущейся с постоянной скоростью и параллельно плас-
тинам. Между пластинами конденсатора создано магнитное поле с индукцией
В, которое параллельно пластинам и перпендикулярно вектору скорости тече-
ния жидкости. Конденсатор замкнут на сопротивление R. Какая мощность вы-
деляется на этом сопротивлении?
14.44. Небольшой шарик массой т = 10 г
и зарядом q = 10'6 Кл вращается в горизон-
тальной плоскости на невесомой диэлектри-
ческой нити длиной I = 50 см. В пространстве
создано однородное магнитное поле с индук-
цией В = 0,1 Тл, силовые линии которого на-
правлены вдоль силы тяжести вниз (рис.
14.47). При движении нить образует с верти-
калью угол a = 30°. Найти период обращения
шарика.
• Решение. При движении заряженного тела в магнитном поле на него будет действовать
сила Лоренца. В зависимости от того, в какую сторону вращается шарик, сила Лоренца
будет направлена или к центру окружности, описываемой шариком, или в противополож-
ную сторону. Пусть в положении, показанном на рисунке, скорость шарика направлена на
нас; тогда сила Лоренца будет направлена по радиусу окружности от ее центра.
Запишем уравнения движения шарика в проекции на нормаль 7? к траектории и ось
OZ, перпендукурярную плоскости движения:
т о2
—— = Nsina-q и В, 0 = Ncosa-mg,
R
где учтено, что = q о В. Исключая силу нвтяжения нити
cos a
получаем
m u2 _ , .
—+ 9 и В - m g tg a = 0,
Л
Тогда период обращения шарика
^_2nR
о
или с учетом, что R = I sin a:
-qB + 4 q2 B2 + 4 m2gtg a/R
° " 2 m/R
____________4-e.m________
V?2B2 + 4OT2gtga/« -9-8’
Т= 4 —---------------« 1,32 с.
У q2 В2 + 4 п? g/l cos a “9 8
Если шарик вращается в другую сторону, то сила Лоренца будет направлена к центру
окружности. Легко понять, что в этом случае
q В + V <?2 В2 + 4 /и2 g tg a/R
Ответ-. Т =
Т = _ 41т=----------------« 1,31 с.
У q2 В2 + 4 т2 g/l cos a + 9 8
______________________ — ; Т » 1,32 с или Т » 1,31 с.
V q2 В2 + 4 m2 g/l cos a ± 98
2m/R
4 n m
366
тп, q
l 1
9 Й
m,q i) °0
Puc. 14.48
Puc. 14.49
Puc. 14.50
14.45. Небольшое тело массой m = 20 г и зарядом q = 10’6 Кл подзешено
на невесомой диэлектрической нити длиной I = 50 см и помещено в однород-
ное магнитное поле с индукцией В = 0,1 Тл, силовые линии которого перпен-
дикулярны силе тяжести. Тело отклонили на натянутой нити от положения
равновесия до высоты h= 10 см в плоскости, перпендикулярной вектору
В (рис. 14.48) и отпустили без начальной скорости. Найти натяжение нити при
движении тела, когда оно проходит положение равновесия.
14.46. Шарик массой т = 10 г и зарядом q = 10"6 Кл подвешен на невесо-
мой шелковой нити длиной I = 50 см и помещен в однородное горизонтальное
магнитное поле с индукцией В = 0,1 Тл. В положении равновесия шарику со-
общают скорость и0, направленную перпендикулярно вектору В и силе тяжес-
ти (рис. 14.49). При каких значениях величины скорости и0 шарик совершит
полный оборот вокруг точки подвеса?
14.47. По наклонной плоскости с углом при основании а = 30° начинает
соскальзывать без начальной скорости небольшое тело массой т = 10 г и заря-
дом q = 10‘6 Кл (рис. 14.50). Какую максимальную скорость будет иметь тело
в процессе движения, если в пространстве создано однородное магнитное
поле с индукцией В = 0,1 Тл, силовые линии которого параллельны наклонной
плоскости и перпендикулярны силе тяжести? Коэффициент трения тела о
плоскость равен ц = 0,1. т
14.48. Небольшое тело массой т = 50 г
вать без начальной скорости с вершины
гладкой полусферы радиусом R = 50 см
(рис. 14.51). На какой высоте над центром
а»)»)»»»»»»»»!»»»/)»»/»)»»»/»»,
полусферы тело оторвется от ее поверхнос-
ти, если в пространстве создано однород- ?ис- 14.51
ное магнитное поле с индукцией В = 0,1 Тл? Магнитное поле направлено пер-
пендикулярно плоскости, в которой происходит движение тела.
Сила Ампера. Проводник с током в магнитном поле
14.49. Металлический стержень массой т = 0,5 кг и длиной I = 1 м со-
скальзывает с наклонной плоскости, составляющей угол а = 30° с горизонтом.
367
В пространстве создано однородное магнитное поле с индукцией В = 0,1 Тл,
силовые линии которого направлены вертикально вниз. Определить ускоре-
ние этого стержня, если по нему пропустить ток силой 1= 5 А в направлении,
показанном на рис. 14.52, а. Коэффициент трения между стержнем и поверх-
ностью наклонной плоскости равен ц = 0,2.
/•
а) б)
Рис. 14.52
• Решение. При движении стержня с током в магнитном поле иа него будут действовать:
сила тяжести m~g, силы реакции 1?и трения между стержнем и поверхностью наклон-
ной плоскости и сила / д Ампера. Направление силы Ампера определяется правилом левой
руки: расположим левую руку так, чтобы силовые линии магнитного поля входили в ла-
донь, а пальцы были направлены по току. Тогда отогнутый большой палец будет направ-
лен горизонтально и укажет направление силы Ампера (рис.’!14.52, а, б).
Запишем уравнения движения стержня в проекциях на оси системы координат
XOY:
ОХ: т а = т g sin а - F^ - FA cos a,
OY: 0=N-mg cos a -FA sin a.
С учетом связи
Гтр = рЛГ,
получим
N= т g cos a + FA sin a, F^ = \i(mg cos a + FA sin a),
m a = m g sin a - p (m g cos a + FA sin a) - FA cos a.
Поскольку сила Ампера в нашем случае равна
Fa = 1BI,
ТО
ma = mgsina-y,mg cos а-ц/B/sina-ZB/ cos а,
или IQ I
a-g (sin а - ц cos а) --(ц sin а + cos а)« 2,2 м/с2.
IВ I 2
• Ответ-. a = g (sin а - ц cos а) --(ц sin а + cos а) и 2,2 м/с2.
т
14.50. На прямой проводник длиной I = 50 см, по которому течет ток
силой 1= 2 А, в магнитном поле с индукцией В = 0,1 Тл действует сила
F = 0,05 Н. Определить угол между проводником и вектором магнитной ин-
дукции.
368
14.51. Два параллельных проводника с одинаковыми токами, находящие-
ся на расстоянии г = 8,7 см друг от друга, притягиваются с силой F = 25 мН.
Определить силу тока в проводниках, если длина каждого из них I = 320 см.
14.52. Прямой проводник укреплен горизонтально. Параллельно ему в
той же вертикальной плоскости ниже расположен другой прямой проводник
массой т = 1 кг и длиной / = 9,81 м. По нему пропускают ток силой 1=2 А.
Расстояние между проводниками г = 0,1 м. Какова должна быть сила тока в
верхнем проводнике, чтобы он уравновешивал вес нижнего проводника?
14.53. На столе лежит прямой проводник длиной 1 = 2 м и массой
т = 10 г, по которому течет ток силой I = 10 А. Над поверхностью стола созда-
ется однородное магнитное поле, силовые линии которого перпендикулярны
направлению тока. При некоторой величине индукции магнитного поля про-
водник приподнимается над поверхностью стола. Определить величину ин-
дукции этого поля.
14.54. Проводник длиной / = 0,2 м подвешен горизонтально к двум дина-
мометрам и помещен в горизонтальное однородное магнитное поле с индук-
цией В = 0,5 Тл, силовые линии которого перпендикулярны к проводнику. На
сколько изменятся показания каждого динамометра при прохождении по про-
воднику тока силой I = 5 А?
14.55. Проводящий стержень массой т = 0,1 кг и длиной / = 0,25 м лежит
на горизонтальной поверхности перпендикулярно к силовым линиям однород-
ного горизонтального магнитного поля с индукцией В = 0,2 Тл. Какую гори-
зонтальную силу нужно приложить перпендикулярно оси стержня для его
равномерного поступательного движения, если по стержню течет ток силой
1= 10 А? Коэффициент трения между стержнем и поверхностью ц = 0,1.
14.56. Проводник массой т = 0,2 кг и длиной / = 0,6 м лежит на горизон-
тальных рельсах, расположенных в однородном магнитном поле с индукцией
В = 0,1 Тл, силовые линии которого горизон-
тальны и направлены вдоль рельсов (рис.
14.53, вид сверху). Если пропустить по про-
воднику ток силой 7=20 А в указанном на
рисунке направлении, то для того, чтобы
сдвинуть проводник влево, требуется прило-
жить горизонтальную силу F = 0,5 Н. Какая
минимальная сила потребуется для этого,
если направление тока в проводнике изме-
нить на противоположное?
14.57. Проводник массой т = 1 кг и дли-
ной / = 0,5 м расположен на наклонной плос-
кости, составляющей угол а = 30° с горизон-
том, перпендикулярно к однородному гори-
зонтальному магнитному полю с индукцией
369
В = 0,1 Тл (рис. 14.54). Какую минимальную силу нужно приложить к провод-
нику параллельно наклонной плоскости для удержания его в состоянии покоя,
если ток в проводнике 1= 10 А? Коэффициент трения равен ц = 0,1.
14.58. На наклонной плоскости, составляющей угол а = 30° с горизонтом,
находится проводящий стержень массой т = 0,5 кг и длиной I = 30 см. В про-
странстве создано однородное магнитное поле. Какова должна быть мини-
мальная величина индукции этого поля, чтобы стержень двигался вверх по на-
клонной плоскости с ускорением а= 0,1 м/с2, если по нему пропустить ток
силой 1= 50 А? Коэффициент трения ц = 0,2. Стержень расположен в горизон-
тальной плоскости.
14.59. На непроводящем клине с углом
наклона к горизонту а = 30° параллельно
ребру клина лежит тонкий проводник мас-
сой т = 5 г и длиной /= 10 см. Концы про-
водника соединены с неподвижными стой-
ками двумя одинаковыми пружинами жест-
костью £=0,2 Н/м (рис. 14.55). К клеммам
стоек подводят постоянное напряжение
U= 4 В. Определить, на какую максималь-
ную величину изменятся длины пружин, если в пространстве создать одно-
родное магнитное поле с индукцией В = 0,1 Тл, направленное вертикально
вверх. Коэффициент трения проводника о плоскость клина равен ц = 0,1, его
сопротивление В = 20 Ом.
14.60. На двух легких проводящих нитях горизонтально висит металли-
ческий стержень длиной I = 0,25 м и массой т = 0,015 кг. Стержень находится
в вертикальном однородном магнитном поле с индукцией В = 0,3 Тл, силовые
линии которого направлены вертикально вниз. Определить угол отклонения
нитей, если по стержню пропустить ток силой I = 0,2 А.
14.61. Проводник длиной /= 24 см и сопротивлением R = 36 Ом согнут в
форме квадрата и помещен в однородное магнитное поле с индукцией
В = 0,1 Тл, перпендикулярное плоскости квадрата. Какая сила будет действо-
вать на проводник, если на соседние вершины образованной фигуры подать
напряжение U = 5,4 В?
• Решение. Точки а и Ъ, на которые подано напряже-
ние U, разделят проводник на две части с сопротив-
лениями
Ra-b = *А R-a-c-d-b = 3А £>
по которым будут течь токи
. С _4С/ U _4U
' Ra_b R ’ h Ra-c-d-b 3R
Поскольку стороны квадрата представляют
собой проводники с током в магнитном поле, то на
каждую из иих будут действовать силы Ампера,
направленные так, как показано иа рис. 14.56, и
а
Л
Л
12 Я®
h
h
d
С
Рис. 14.
370
равные \
f{ = 1auxb, f2 = 1aii2b, f3 = 1aii2b, f4 = 'aii2b.
Так как силы и 7^ направлены в одну сторону, а силы и ?4 равны по величине и
противоположны по направлению, то результирующая сила, действующая иа проводник
/=?1+?2 + ?з + А
по величине будет равна
г=г1+г2,
Н” F = % IBQi +/2) = 1А1В{ + = ±Гр = 4,810'3 Н.
л тт 1 п Л э К ' ЭЛ
• Ответ: F=^‘B = 4,810‘3 Н.
3 л
14.62. Решить задачу №14.61, если проводник согнут в форме равносто-
роннего треугольника.
14.63. Решить задачу №14.61, если проводник согнут в форме правильно-
го шестиугольника.
Контур с током в магнитном попе
14.64. Проводящее кольцо радиусом R = 1,5 м поместили в однородное
магнитное поле, перпендикулярное плоскости кольца. По кольцу пропустили
ток силой 1= 10 А. При какой величине индукции магнитного поля кольцо ра-
зорвется, если проволока, из которой кольцо изготовлено, выдерживает мак-
симальное натяжение Т = 2,5 Н? Магнитным полем тока в кольце пренебречь.
• Решение. Рассмотрим настолько малый элемент
кольца длиной А/, чтобы его можно было считал^
прямолинейным. В магнитном поле с индукцией В,
перпендикулярном плоскости кольца, на него будет
действовать сила Ампера:
FA = IB&1,
которая будет растягивать кольцо или сжимать его. I
Для того, чтобы кольцо разорвалось ток в кольце и
магнитное поле должны быть направлены так, как по-
казано на рис. 14.57^
Кроме силы на элемент А/ кольца будут
действовать со стороны соседних участков силы на-
тяжения Т. Очевидно, что при этом выполняется ра-
венство
/д = 2 Г sin а, или IB А/ = 2 Т sin а.
Поскольку длина А/ элемента кольца
., I о 2 л R а . „
А/ = — 2 а =-----= 2а R,
2л л
а угол а мал (можно положить, что sin а « а), то
IB2aR = 2Ta.
Следовательно, если индукция магнитного поля
В>ут«0,167 Тл,
то кольцо разорвется. к
• Ответ: В >-^-<=0,167 Тл.
1 л
371
14.65. По проводящему кольцу радиусом Л = 50 см течет ток силой 1= 10 А.
Кольцо поместили в однородное магнитное поле с индукцией В = 0,1 Тл, пер-
пендикулярное плоскости кольца. Определить величину силы, действующей
на кольцо. Магнитным полем тока в кольце пренебречь.
14.66. Определить силу, с которой дей-
ствует бесконечно длинный прямой провод
на прямоугольный контур, если по контуру
течет ток силой 10 = 10 А, а по проводу -
1=5 А. Провод расположен в плоскости
контура, направления токов указаны на рис.
14.58. Стороны контура AD = ВС = а = 50 см
параллельны проводу. Расстояние от прово-
да до стороны AD равно I = 20 см, длины
сторон АВ = DC =b = 20 см.
14.67. Проволочный виток радиусом R = 5 см находится в однородном
магнитном поле с индукцией В = 0,1 Тл. Плоскость витка составляет угол
Р = 60° с направлением поля. Определить магнитный момент витка и механи-
ческий момент, действующий на виток, если по нему течет ток силой I = 5 А.
• Решение. На виток с током, расположенный в магнитном поле так, что его плоскость
ие перпендикулярна направлению силовых линий поля, относительно произвольной непо-
движной оси OZ будет действовать механический момент Mz, который стремится повер-
нуть виток так, чтобы магнитный момент Хп витка был направлен по полю. Величина
магнитного момента произвольного плоского контура с током зависит лишь от силы тока
и площади, ограниченной контуром. Следовательно, для витка радиусом R, по которому
течет ток /,
рт = 1 S = lit Л2 « 0,04 А-м2.
Величина механического момента, действующего на виток в магнитном поле относи-
тельно произвольной оси, зависит от магнитного момента, величины индукции магнитного
поля и ориентации контура в магнитном поле:
A7Z = рт В sin а,
где а - угол, который составляет нормаль к плоскости контура с направлением поля. В
нашем случае а = л/2 - р. Следовательно,
Wz = I it R2B sin (л/2 - p) = I it R2B cos p » 2-Ю'3 Нм.
• Ответ: pm = 7л Л2» 0,04 А-м2, Mz = Iit R2Bcos p » 2-Ю"3 Н-м.
14.68. По проволочному витку радиусом R = 50 см течет ток силой
I = 50 А. Определить магнитный момент витка.
14.69. По катушке радиусом R = 50 см, содержащей N = 100 витков про-
вода, течет ток силой I = 1 А. Определить магнитный момент катушки.
14.70. Катушка радиусом R = 10 см, содержащая N = 200 витков провода,
находится в магнитном поле с индукцией В = 10‘2 Тл. Определить магнитный
момент катушки и максимальный механический момент, действующий на ка-
тушку относительно произвольной оси, если в ней течет ток силой 1= 1 А.
Электромагнитная индукция
14.71. В однородном магнитном поле с индукцией В = 0,1 Тл вокруг од-
ного из своих концов вращается с постоянной угловой сюростью <в = 10 рад/с
стержень длиной I = 50 см. Чему равна разность потенциалов между концами
стержня? Магнитные силовые линии перпендикуляпны плоскости вращения.
• Решение. Появление сторонних сил внутри стерж-
ня и возникновение разности потенциалов иа его
концах в данном случае вызвано действием силы
Лоренца иа электроны, находящиеся в проводнике,
движущемся в магнитном поле.
Рассмотрим произвольный электрон, находя-
щийся внутри стержня иа расстоянии г от оси вра-
щения (рис. 14.59). Если стержень вращается в
однородном магнитном поле с постоянной угловой
скоростью со, то линейная скорость рассматривае-
мого электрона равна
и = со г
и направлена по касательной к окружности, описываемой электроном вместе со стержнем.
Известно, что на заряженную частицу, движущуюся в магнитном поле, действует
сила Лоренца. Поскольку плоскость вращения стержня перпендикулярна силовым линиям
магнитного поля, то
Fn = |е| и В = |е| со г В,
и направлена вдоль стержня (в зависимости от взаимного направления вращения стерж-
ня и индукции магнитного поля или к одному, или к другому концу). Под действием этой
силы электроны будут перемещаться вдоль стержня к одному из его концов. В результате
между концами проводника возникнет некоторая разность потенциалов и электрическое
поле напряженностью Е, которое будет расти до тех пор, пока силы электрического поля
£Эл = |е| Е
не уравновесят силы Лоренца во всех точках стержня:
Еп = Езл, <огВ = Е.
При этом иа одном конце стержня окажется избыток электронов, а иа другом - их
недостаток и возникнет постоянная разность потенциалов Дер, зиачение которой можно
найти несколькими способами.
1. Поскольку электрическое поле в стержне в зависимости от расстояния г до оси
вращения меняется линейно, то
Д<р = < Е > /,
где среднее значение напряженности электрического поля равно
,, со/В
<£> = —2~.
Следовательно,
. со Г В - _
Дф = —j— = 0,125 В.
2. Появление разности потенциалов Дф иа концах стержня эквивалентно наличию
источника э.д.с., в котором роль сторонних сил играют силы Лоренца. Работа этих сил
иад единичним положительным зарядом q
как раз будет равна искомой разности потенциалов.
373
3. Дополним стержень ОС проводником ОАС до замкнутого контура (рис. 14.59),
имеющего форму сектора, причем проводники ОА и АС неподвижны, а проводник ОС
(стержень) вращается с постоянной угловой скоростью со.
При движении стержня угол а между стержнем и проводником ОА будет меняться
по закону а = со с, а площадь 5 сектора, ограниченная контуром ОАС,
„ l2a l2<ot
При этом появится нестационарный магнитный поток
Ф = ВВ=В^,
пронизывающий поверхность, натянутую на контур, н в контуре возникнет э.д.с. электро-
магнитной индукции , „ л
, . d<D В1<о
а - 2 ,
равная искомой разности потенциалов.
• Ответ: Дер = 0,125 В.
14.72. Реактивный самолет, имеющий размах крыльев I = 50 м, летит го-
ризонтально со скоростью и = 800 км/час. Определить разность потенциалов,
возникающую между концами крыльев, если вертикальная составляющая ин-
дукции магнитного поля Земли равна В = 5-10"5 Тл.
14.73. Металлический стержень длиной I = 20 см движется в однородном
магнитном поле с индукцией 5 = 0,1 Тл так, что его ось составляет угол
а = 30° с магнитными силовыми линиями. Как нужно двигать этот стержень,
чтобы разность потенциалов на его концах равномерно возрастала со скорос-
тью Дф/А/ = 1 В/с?
Рис. 14.60 Рис. 14.61
14.74. Металлический брусок размерами а* Ь*с движется горизонтально
со скоростью и = 20 м/с в вертикальном магнитном поле с индукцией
5 = 0,1 Тл (рис. 14.60). Определить поверхностные плотности зарядов на всех
поверхностях бруска. Распределение зарядов по поверхностям бруска считать
равномерным.
14.75. На непроводящем диске радиусом Л = 20 см закреплена на радиусе
проволока длиной ViR так, как показано на рис. 14.61. Диск вращается с по-
стоянной угловой скоростью со = 2 рад/с. Перпендикулярно к диску направле-
но магнитное поле с индукцией В = 0,01 Тл. Найти разность потенциалов
между концами проволоки.
14.76. Незаряженный металлический диск радиусом Л = 50 см вращается
в магнитном поле с угловой скоростью со = 20 рад/с вокруг своей оси. Индук-
ция магнитного поля направлена вдоль оси диска. Найти разность потенциа-
лов между осью диска и точками на его ободе, если индукция магнитного
поля равна В = 0,1 Тл.
14.77. Металлический стержень массой т = 100 г и длиной I = 1 м распо-
ложен горизонтально и подвешен за середину к пружине жесткостью
k = 1 Н/м. Стержень совершает в вертикальной плоскости гармонические ко-
лебания с амплитудой А = 0,1 м. Определить максимальную разность потен-
циалов, возникающую между концами стержня, если в окружающем про-
странстве создать однородное магнитное поле с индукцией В = 10'2 Тл, сило-
вые линии которого направленны перпендикулярно плоскости колебаний.
14.78. Замкнутая квадратная рамка из гибкой проволоки расположена в
магнитном поле с индукцией В = 0,1 Тл, силовые линии которого направлены
перпендикулярно к плоскости рамки. Какой заряд протечет в рамке, если, не
меняя плоскости расположения, придать ей форму окружности? Длина прово-
локи I = 1 м, ее сопротивление R = 100 Ом.
• Решение. Рассмотрим более общую задачу: определим, какой заряд протечет в контуре со-
противлением R, если по каким-либо причинам изменился магнитный поток, пронизываю-
щий площадь, ограниченную контуром.
По закону электромагнитной индукции в контуре возникнет э.д.с., равная
Появление э.д.с. электромагнитной индукции приведет к возникновению в контуре
тока силой
1 ЛФ
R R dt '
С другой стороны, сила тока по определению равна
dt'
Следовательно,
da I dФ , 1
j = — , или dq = — dФ.
dt R dt 4 R
Если изменение потока магнитной индукции через поверхность, ограниченную кон-
туром, на величину dф приводит к тому, что в контуре протечет заряд dq, то, очевидно,
при изменении потока на ДФ в контуре протечет заряд
= д ЛФ>
причем его величина не зависит от причин изменения потока.
Вернемся к нашей задаче.
Поток вектора магнитной индукции через поверхность, ограниченную контуром, за-
висит от величины магнитной индукции, площади, охватываемой контуром, и ориентации
плоскости контура относительно направления силовых линий магнитного поля. По усло-
вию задачи магнитное поле и плоскость, в которой расположен контур, не менялись, а
изменилась площадь, им ограниченная. Действительно, если рамка имела первоначально
форму квадрата площадью
то после преобразовании рамки в окружность радиуса R (I = 2л R) площадь круга стала рав-
ной
375
с „ t>2 I2
Oj — 71 л -
4 л
Поскольку 5|* S2, та поток вектора магнитной индукции через поверхность, ограни-
ченную рамкой, изменился иа величину
Дф = ф2-Ф1=Д52-Д5,=Д-^--Д-^ = Дг j4~”)
4 я io 16 я
и по контуру протек заряд „,2л,
= 4 Д//4~Л^ 1,710'5 Кл.
2 Д 16 л
• Ответ: Д^ = -^ 1,7-10'5Кл.
л 16 л
14.79. Проволочное кольцо расположено в однородном магнитном поле с
индукцией В = 0,6 Тл так, что плоскость кольца составляет с силовыми линия-
ми угол а = 30°. При этом магнитный поток через кольцо равен Ф = 24 Вб.
Определить радиус кольца.
14.80. Проволочный контур в форме равностороннего треугольника со
стороной / = 1 м расположен в магнитном поле с индукцией 5= 0,1 Тл так,
что силовые линии поля перпендикулярны плоскости контура. Определить из-
менение магнитного потока через контур, если не меняя плоскости располо-
жения преобразовать его в квадрат.
14.81. Проводящее кольцо радиусом г = 6 см и сопротивлением
R = 0,2 Ом помещено в магнитное поле с индукцией 5=20 мТл, перпендику-
лярное плоскости кольца. Кольцо складывают так, что получается два одина-
ковых кольца в виде восьмерки. Какой заряд протек при этом через кольцо?
Рассмотреть все возможные случаи.
14.82. Проволочную рамку площадью 5=20 см2 и сопротивлением
5 = 5 Ом поворачивают в однородном магнитном поле с индукцией В = 10"4 Тл
из положения, когда плоскость рамки перпендикулярна силовым линиям, в
положение, когда плоскость рамки параллельна полю. Какой заряд протек при
этом в рамке?
14.83. В однородном стационарном магнитном поле располагается прово-
дящая рамка. Ось рамки проходит через середины противоположных сторон и
направлена перпендикулярно линиям индукции магнитного поля. Сравнить
заряды, протекающие по рамке при повороте ее на угол а = 30°, если угол из-
меняется: а) от 0° до 30°; б) от 30° до 60°. Первоначально плоскость рамки
располагается перпендикулярно линиям индукции магнитного поля..
14.84. Лежащее на столе металлическое кольцо перевернули. Радиус
кольца г = 10 см, его сопротивление 5 = 2 Ом. Какой величины заряд протек
при этом через кольцо, если вертикальная составляющая магнитного поля
Земли равна В = 5-1O"5 Тл?
14.85. Из проволоки сопротивлением 5 = 20 Ом и длиной I = 0,5 м сдела-
ли кольцо и поместили в магнитное поле, индукция которого меняется по за-
кону В = a t, где а = 10"4 Вб/с, t — время в секундах. Определить, какая мощ-
ность выделяется в проволоке, если плоскость кольца перпендикулярна лини-
ям индукции магнитного поля.
376
• Решение. Поскольку магнитное поле, в котором находится кольцо, нестационарно, то
магнитный поток, пронизывающий поверхность 5 = 2n г2 (I = 2л г), ограниченную кольцом
Ф = В8,
будет менятся со временем по закону 2
Ф = а(-~-.
4 л
Это приведет к появлению в кольце э.д.с. электромагнитной индукции
j 1<У/1 _ al2
~ R 4 nR '
Прн этом в кольце будет выделяться тепловая мощность
N=12R= «2-10'|3Вт.
2,4 16л2Я
• Ответ-. N= а , «210~|3Вт.
16 л2 Я
14.86. Проводящий квадратный контур со стороной а = 10 см расположен
в однородном магнитном поле с индукцией В = 0,5 Тл, перпендикулярном
плоскости контура. Контур выводят из поля за Дг = 0,5 с. Определить среднее
значение э.д.с. электромагнитной индукции, возникающей в контуре.
14.87. Магнитный поток, пронизывающий проводящий контур, равно-
мерно изменяется на ДФ= 0,6 Вб так, что э.д.с. индукции в контуре равна
Sj = 1,2 В. Найти время изменения магнитного потока н силу индукционного
тока в контуре, если его сопротивление R = 0,24 Ом.
14.88. Квадратная рамка со стороной а = 10 см помещена в однородное
магнитное поле так, что нормаль к плоскости рамки составляет угол а = 60° с
направлением магнитного поля. Найти индукцию магнитного поля, если сред-
нее значение э.д.с. индукции, возникающей при включении поля в течение
времени Дг = 0,01 с, составляет Sj = 50 мВ.
14.89. Какой величины магнитный поток пронизывает каждый виток зам-
кнутой накоротко катушки, содержащей из «= 1000 витков, если при равно-
мерном исчезновении поля в течение времени г = 0,1 св катушке индуцирует-
ся э.д.с. Sj = 10 В?
14.90. Замкнутая накоротко катушка диаметром D- 10 см, содержащая
п = 200 витков, находится в однородном магнитном поле, индукция которого
увеличивается от В\ = 2 Тл до В2 = 6 Тл в течение времени Дг= 0,1 с. Опреде-
лить среднее значение э.д.с. индукции в катушке, если плоскость витков пер-
пендикулярна силовым линиям поля.
14.91. Квадратный контур со стороной а = 50 см, изготовленный из алю-
миниевой проволоки, помещен в магнитное поле, индукция которого меня-
ется по закону В = а Г, где а = 0,02 Тл/с, t - время в секундах. Определить из-
менение температуры витка за время Дг= 100 с, полагая, что выделяющееся
в проволоке тепло целиком идет на ее нагрев. Плоскость контура перпенди-
. 377
кулярна линиям индукции магнитного поля. Плотность алюминия равна
р = 2,7-103 кг/м3, удельное сопротивление р0 = 2,9-10'8 Ом-м, удельная тепло-
14.92. Проволоку длиной Z = 1 м согнули в
виде кольца, затем замкнули по диаметру пря-
мым проводником (рис. 14.62). Сопротивление
проволоки R = 200 Ом. Перпендикулярно плос-
кости кольца создано магнитное поле, индук-
ция которого зависит от времени по закону
В = a t, где а = 0,02 Тл/с, Г - время в секундах.
Найти тепловую мощность, выделяющуюся в
проволоке.
14.93. Проводящий квадратный контур со стороной а = 10 см вводят с по-
стоянной скоростью и = 70 см/с в зазор электромагнита. Индукция магнитно-
го поля в зазоре равна В = 0,1 Тл. Считая поле внутри зазора однородным, а
вне зазора равным нулю, определить количество теплоты, выделившейся в
контуре, при полном введении его в зазор, если протяженность зазора b > а, а
сопротивление контура равно R = 2 Ом. Плоскость контура перпендикулярна
линиям индукции магнитного поля.
• Решение. При введении ковтура в магнитное
поле часть площади, пронизываемой силовыми
линиями поля, будет увеличиваться по закону
S = ax,
тех- длина части контура, находящейся в зазоре
в данный момент времени (рис. 14.63), равная
х = v t.
Магнитный поток, пронизывающий поверх-
ность S, ограниченную контуром
Ф = В S=В a v t,
будет изменяться с течением времени, что приве-
дет к появлению в контуре э.д.с. <?, электромаг-
нитной индукции и тока I:
d<P „ , W Вам
W^ = Bav, 1=-Т = ~Г
Как видим, ток в контуре будет постоянным. Поэтому количество тепла, выделив-
шегося на сопротивлении Я, будет равно
O-Pr, -BWt
(J-1 к to---g---t0,
где t0 = а/м - время, затраченное на введение контура в зазор. Следовательно,
2 3
6 = ^-!г»3,5-10"6Дж.
п2 3 л
• Ответ: Q = —» 3,540"® Дж.
л
14.94. Эластичное проводящее кольцо помещено в однородное магнитное
поле с индукцией В = 20 мТл, перпендикулярное плоскости кольца. Радиус
кольца увеличивается с постоянной скоростью и = 2 см/с. Определить значе-
378
ние силы тока в кольце в момент времени / = 2 с, если начальный радиус коль-
ца г0 = 16 см, а его сопротивление R = 5 Ом не меняется при растяжении коль-
ца.
® ® ®|
®
®
®
®
®
®
Рис. 14.64
Рис. 14.65
14.95. Проводящий квадратный контур со стороной b = 80 см выводят с
постоянным ускорением а = 0,1 м/с2 из однородного магнитного поля с индук-
цией 5=10 мТл. Считая, что в начале движения одна из сторон контура рас-
положена на границе области магнитного поля (рис. 14.64), построить график
зависимости э.д.с. индукции, наводимой в контуре, как функцию времени.
Плоскость контура перпендикулярна линиям индукции магнитного поля.
14.96. Квадратная проволочная рамка со стороной а = 5 см движется со
скоростью и = 100 м/с в положительном направлении оси ОХ так, что две ее
стороны все время перпендикулярны оси ОХ. Силовые линии неоднородного
магнитного поля перпендикулярны плоскости рамки. В точке с координатой
X] = 0 величина индукции магнитного поля равна В} = 0,2 Тл, а в точке с коор-
динатой х2 = а - равна В2 = В, (рис. 14.65). Считая, что поле изменяется
равномерно в направлении оси ОХ и при х < 0 равно нулю, найти э.д.с., инду-
цируемую в рамке в момент времени, когда рамка займет положение, показан-
ное на рисунке.
14.97. В магнитном поле Земли с достаточно большой высоты падает
плоский проволочный контур (кольцо) площадью 5 и сопротивлением R. Вер-
тикальная составляющая магнитного поля Земли изменяется с высотой по за-'
кону В = Во (1 + а у), где а, Во -известные постоянные, у - высота, отсчиты-
ваемая по вертикали. Установившаяся скорость падения контура равна и0-
Считая, что плоскость кольца остается все время горизонтальной и пренебре-
гая сопротивлением воздуха, определить индукционный ток в контуре.
14.98. Длинный провод, расположенный в горизонтальной плоскости, со-
гнут под углом а = 30°. В вершине угла расположен металлический стержень,
перпендикулярный биссектрисе угла. Стержень может без трения скользить
по проводу. Система помещена в вертикальное внешнее однородное магнит-
ное поле индукцией В - 0,05 Тл. К стержню прикладывают горизонтальную
силу F=kx, направленную вдоль биссектрисы угла, которая растет линейно с
расстоянием х, отсчитываемым от вершины угла (рис. 14.66, вид сверху). Оп-
ределить максимальную скорость стержня, если сопротивление единицы его
379
длины равно р = 0,2 Ом/м, а коэффициент пропорциональности к= 0,1 Н/м.
Сопротивлением провода пренебречь.
• Решение. Если к стержню приложить силу X
то при его перемещении будет меняться пло-
щадь треугольника ACD, ограниченного про-
водом и стержнем, н, следовательно, возник-
нет изменяющийся со временем поток индук-
ции магнитного поля:
Ф = В8,
где S = х2 sin (а/2) - площадь контура (рассто-
яние х отсчитывается от вершины угла ZCAD).
Наличие нестационарного магнитного потока
приведет к возникновению в контуре э.д.с.
электромагнитной индукции
|<ЭД = = В = 2В х sin (а/2) ~ = 2В х sin (а/2) о,
что, в свою очередь, вызовет появление индукционного тока / и силы Ампера ?А.
Поскольку прн движении стержня магнитный поток, пронизывающий контур, уве-
личивается, то по правилу Ленца в контуре возникнет индукционный ток такого направ-
ления, чтобы его собственный магнитный поток ослаблял внешний (в нашем случае маг-
нитное поле тока I, пронизывающее площадь А4С£>, будет направлено на нас, а ток в
стержне - от точки D к точке Q. Направление силы Ампера, действующей на стержень
с током I в магнитном поле с индукцией В, можно определить по правилу левой руки:
расположим левую руку в плоскости рисунка так, чтобы силовые линии поля входили в
ладонь, а пальцы указывали направление тока; при этом отогнутый большой палец пока-
жет направление силы Ампера (см. рис. 14.66), равной
Fa = IB 2 х sin (а/2).
Сила тока в стержне по закону Ома равна
•* ’
где R = 2р х sin (а/2) - сопротивление части стержня между точками С и D контакта с про-
водом. Следовательно,
j W 2В х sin (а/2) о _ Ви
2pxsin(a/2) 2pxsin(a/2) р
С учетом выражения для силы тока FA можно представить в виде
„ 2В2х и . , ...
гА =--------------------------------- sin (а/2).
Запишем уравнение движения стержня на ось ОХ системы координат:
„ „ , 2В2х о . .
та = F-гА, или та = кх---------- sin(а/2).
Скорость стержня будет максимальна в момент времени, когда его ускорение станет
равным нулю. Следовательно,
2В2отах
0 = к -------- sin (a/2).
„ Р
Откуда получаем
Рк ,С АС /
Vmav— л ® 15,45 м/с.
к тах 2B2sin(a/2)
• Ответ: отях = —е-Р—— и 15,45 м/с.
2B2sin(a/2)
380
14.99. Проволока длиной I и сопротивлением R согнута в виде буквы П.
На серединах двух ее противоположных сторон лежит проводящая перемычка
АВ длиной 10. Вся система расположена горизонтально и помещена в верти-
кальное однородное магнитное поле с индукцией В. Перемычку начинают
двигать с постоянной скоростью так, как показано на рис. 14.67. Найти за-
висимость тока в перемычке от времени. Сопротивлением перемычки прене-
бречь.
14.100. Проводник АВ длиной Z = 0,5 м и сопротивлением R = 2 Ом лежит
на двух горизонтальных проводящих стержнях, замкнутых источником э.д.с.
S= 1 В (рис. 14.68, вид сверху). Вся система находится в вертикальном маг-
нитном поле с индукцией В - 0,2 Тл. Определить силу тока в проводнике,
если он движется: а) вправо; б) влево со скоростью и = 5 м/с. Внутренним со-
противлением источника и сопротивлением стержней пренебречь. Проводник
перпендикулярен стержням. ----------------------------
14.101. Длинный проводник согнут
в виде буквы П. На параллельных сто- .
ронах проводника лежит проводящая ®В -------------- I
перемычка (рис. 14.69). Проводник на-
ходится в однородном магнитном поле
с индукцией В, силовые линии которого —F------------—
направлены перпендикулярно плоское- /4.(59
ти проводника. Длина перемычки равна /, ее сопротивление R. Какую силу г
нужно приложить к перемычке, чтобы двигать ее с постоянной скоростью и?
14.102. Длинный проводник согнут в виде буквы!!. По параллельным
сторонам проводника под действием постоянной силы F скользит проводящая
перемычка (рис. 14.69). Проводник находится в однородном магнитном поле
с индукцией В, силовые линии которого направлены перпендикулярно плос-
кости проводника. Длина перемычки равна /, ее сопротивление R. Пренебре-
гая сопротивлением проводника, определить максимальную скорость пере-
мычки.
14.103. Два параллельных проводника расположены в однородном маг-
нитном поле с индукцией В = 1 Тл так, что силовые линии поля перпендику-
лярны плоскости, в которой лежат проводники. По проводникам перпендику-
лярно к ним скользит металлическая перемычка, приближаясь к вольтметру с
381
Рис. 14.70
Л
Рис. 14.71
очень большим внутренним сопротивлением, включенному между проводни-
ками (рис. 14.70). Скорость движения перемычки и = 10 м/с, ее длина / = 1 м.
Определить показание вольтметра.
14.104. Металлический стержень АС, сопротивление единицы длины ко-
торого г, движется с постоянной скоростью перпендикулярной А С, замыкая
два проводника OD и (ЭЕ, образующие друг с другом угол а. Длина ОЕ равна
I, а Л С перпендикулярна ОЕ (рис. 14.71). Вся система помещена в однородное
постоянное магнитное поле с индукцией В, перпендикулярное плоскости сис-
темы. Найти полное количество теплоты, которое выделится в цепи при дви-
жении стержня А С от точки О до точки Е. Сопротивлением проводников OD
и ОЕ пренебречь.
14.105. По двум параллельным проводящим стержням, образующим угол
а с горизонтом, соскальзывает горизонтальная проводящая перемычка массой
m и длиной I (рис. 14.72, а). В верхней части стержни замкнуты сопротивле-
нием R. Вся система находится в однородном магнитном поле с индукцией В,
силовые линии которого направлены вертикально вниз. Определить макси-
мальную скорость движения перемычки, если коэффициент трения между по-
верхностями стержней и перемычкой равен ц. Сопротивлением стержней и
перемычки пренебречь.
Рис. 14.72
• Решение. При соскальзывании перемычки возникнет переменный магнитный поток
Ф = В S cos а,
обусловленный тем, что меняется площадь
S=lx,
382
ограниченная контуром, где х - координата перемычки, отсчитываемая от верхнего края
контура. Это приведет к возникновению в контуре э.д.с. электромагнитной индукции
.„I d<i> „ dS п, dx
= “ST = « cos а -г — В / cos ат = Bl» cos a
ar dt dt
и вызовет появление тока в контуре н силы Ампера, направленных так, как показано на
рис. 14.72, а, б (направления тока в контуре и силы Ампера определяются правилами Ленца
н левой руки соответственно; см. решение задачи №14.98).
По закону Ома ток в контуре будет равен
' i в! и cos a
R ' R
Следовательно, сила Ампера, действующая на перемычку, при ее движении будет
меняться: 2
FA=IBl=l v,^asa .
Запишем уравнения движения перемычки в проекции на оси ОХ н OY системы ко-
ординат:
OX: ma = mgs.na-FAcosa-Ftp,
OY: 0=N-mg cos a - FA sin a,
где F™ = p N.
Решая уравнения движения относительно ускорения перемычки, получаем
N=mg cos а + FA sin a, F^ = p (m g cos a + FA sin a),
ma = mgsina~ii(mg cos a + FA sin a) - FA cos a,
или с учетом выражения для силы Ампера:
, . . В112» cos a, .
т а = т g (sin a - р cos a) -----(p sm a + cos a).
R
Скорость перемычки будет максимальной в момент времени, когда ее ускорение ста-
нет равным нулю: - 2
5^/ Umax cos a
О = т g (sm a - р cos a) --------(p sin a + cos a).
R
Откуда окончательно находим
mgR (sin a - p cos a)
umax- -2,2 , .•
B^ Z cos a (p sm a + cos a)
Легко понять, что такая максимальная скорость будет у перемычки при р < tg а. В
противном случае перемычка останется в покое.
„ mgR (sin a - p cos a)
• Ответ: umax = - Л "— --------- при p < tg a.
в I cos a (p sm a + cos a)
14.106. По двум гладким параллель-
ным проводящим стержням, образую-
щим угол а с горизонтом, соскальзывает
горизонтальная проводящая перемычка
массой т и длиной / (рис. 14.73). В верх-
ней части стержни замкнуты сопротив-
лением R. Вся система находится в од-
нородном магнитном поле с индукцией
В, силовые линии которого направлены
вертикально вниз. Определить силу тока в цепи и скорость установившегося
движения перемычки. Сопротивлением стержней пренебречь.
383
14.107. На двух гладких парал-
лельных проводящих стержнях, обра-
зующих угол а с горизонтом, находит-
ся горизонтальная проводящая пере-
мычка массой т и длиной I. В верхней
части стержни замкнуты сопротивле-
нием R (рис. 14.74). Вся система нахо-
дится в однородном магнитном поле с
индукцией В, силовые линии которого
направлены вертикально вверх. Перемычку тянут вдоль стержней вверх с
силой F. Определить максимальную скорость перемычки. Сопротивлением
стержней пренебречь.
14.108. По двум параллельным проводящим стержням, образующим угол
а с горизонтом, соскальзывает горизонтальная проводящая перемычка массой
т и длиной I (рис. 14.75, а). В верхней части стержни замкнуты конденсато-
ром емкостью С. Система находится в однородном магнитном поле с индук-
цией В, силовые линии которого направлены вертикально вниз. Найти ускоре-
ние перемычки, если коэффициент трения между поверхностями стержней и
перемычкой равен ц. Сопротивлением стержней и перемычки пренебречь.
• Решение. Поскольку условие нашей задачи в точности совпадает с условием задачи
№14.105, за исключением того, что вместо сопротивления стержни замкнуты конденсато-
ром, то решения этих задач на начальном этапе совпадают.
При соскальзывании перемычки возникнет переменный магнитный поток
Ф = В S cos а = В lx cos а,
обусловленный тем, что меняется плошадь S, ограниченная контуром, где х - координата
перемычки, отсчитываемая от верхнего края контура. Это приведет к возникновению в кон-
туре э.д.с. электромагнитной индукции
।»। _ dS D, dx „,
<?,1 = = В cos а — = B/cosa-r = B/ ocosa
dt dt dt
и вызовет появление тока в контуре и силы Ампера, направленных так, как показано на
рис. 14.75, а, б. При этом ток будет заряжать конденсатор.
384
Силу тока в контуре можно определить через заряд на обкладках конденсатора. Учи-
тывая, что напряжение на обкладках конденсатора U = в,, а заряд конденсатора q = CU,
получаем
/=^ = -^j(C £i) = C ВI cos а-^ = С ВI a cos а,
где а - ускорение перемычки.
Следовательно, сила Ампера, действующая на перемычку в любой момент, будет
равна
FA = IВI = С В2 l2a cos а.
Уравнение движения перемычки в проекции на оси системы координат можно запи-
сать в виде
OX: ma = mgsina-FAcosa-FTp,
OY: 0 = У-m g cos а - FA sin а,
гае F-m = р У.
Решив уравнения движения относительно ускорения перемычки с учетом выражения
для силы Ампера, находим
ma = mg sin а - ц (mg cos а + FA sin а) - FA cos а,
или
mg (sin а - ц cos a)___m g (sin а - ц cos а)
m + Fa (p sin a + cos a) m + C I2 tf cos a (p sin a + cos a)
.Ответ: a =--------------------------
m + C rtf cos a (p sin a + cos a)
14.109. Проволочный контур площадью S= 10 см2 подключен к конден-
сатору емкостью С = КГ6 Ф и помещен в однородное магнитное поле, индук-
ция которого меняется со временем по закону В = a t, где a = 1 Тл/с, t -время
в секундах. Определить заряд конденсатора. Силовые линии магнитного поля
перпендикулярны плоскости контура.
14.110. По двум параллельным проводящим шинам, расположенным в го-
ризонтальной плоскости на расстоянии I = 60 см друг от друга, может сколь-
зить без трения металлический стержень массой т = 100 г. С одного конца
шины замкнуты на конденсатор емкостью С = 10 мкФ. Система помещена в
однородное магнитное поле с индукцией В = 10"2 Тл, направленное перпенди-
кулярно плоскости, в которой расположены шины и стержень. В некоторый
момент времени на стержень начинает действовать постоянная горизонталь-
ная сила F = 0,5 Н, направленная перпендикулярно стержню. Определить ус-
корение стержня. Сопротивлением шин и стержня пренебречь.
14.111. Используя условие задачи №14.110, определить энергию конден-
сатора в момент времени, когда стержень пройдет путь S = 40 см. Первона-
чально конденсатор не заряжен.
14.112. По двум параллельным проводящим стержням, образующим угол
а с горизонтом, соскальзывает горизонтальная проводящая перемычка массой
т и длиной I (рис. 14.76). В верхней части стержни замкнуты конденсатором
емкостью С. Система находится в однородном магнитном поле с индукцией
В, силовые линии которого направлены перпендикулярно плоскости, в кото-
рой движется перемычка. Найти ускорение перемычки. Сопротивлением
стержней и перемычки, а также трением пренебречь.
385
Рис. 14.77
14.113. По двум гладким металлическим стержням, установленным па-
раллельно друг другу на расстоянии I = 0,4 м и под углом а = 45° к горизон-
ту, может скользит под действием силы тяжести проводящая перемычка мас-
сой т = 0,4 кг (рис. 14.77). Стержни замкнуты конденсатором емкостью
С = 50 мкФ. Система находится в однородном магнитном поле с индукцией
В = 0,1 Тл, силовые линии которого вертикальны. Первоначально перемычку
удерживают на расстоянии b = 50 см от основания стержней. Определить ско-
рость перемычки у основания стержней, если ее отпустить. Сопротивлением
стержней и перемычки пренебречь.
Самоиндукция. Энергия магнитного поля
14.114. По катушке индуктивностью L = 0,03 Гн течет ток 7 = 0,6 А. При
размыкании цепи сила тока изменяется практически до нуля за ДГ = 10’3 с. Оп-
ределить среднее значение э.д.с. самоиндукции, возникающей в катушке.
• Решение. При размыкании цепи ток в катушке начнет уменьшаться, что приведет к изме-
нению магнитного потока, пронизывающего витки катушки. При этом в катушке возникнет
э.д.с. самоиндукции
^ = -Л ~dt'
За бесконечно малое время Л сила тока в катушке изменится на величину
,, I «si Л
.. I«sl АГ
М L ’
Следовательно, за время уменьшения тока до нуля в катушке будет действовать э.д.с.
самоиндукции, среднее значение которой равно
|«S| = Z^=18B.
а/
а за время А/ на
• Ответ: |<?$| = Z = 18 В.
14.115. С помощью реостата ток в катушке индуктивностью £=10 мГн
равномерно увеличивают на А/ = 0,1 А за время Аг = 1 с. Определить среднее
значение э.д.с. самоиндукции, возникающей в катушке.
14.116. Катушку индуктивностью L = 3 мГн подключают к источнику по-
стоянного напряжения с э.д.с. S= 1,5 В. Через какое время ток в катушке до-
стигнет значения 7=50 А? Внутренним сопротивлением источника прене-
бречь.
386
14.117. Э.д.с. самоиндукции, возникающая в катушке индуктивностью
L = 2 Гн, изменяется с течением времени по закону Ss = 10 + 4t [В]. По како-
му закону меняется сила тока в катушке?
14.118. В электрической цепи, представ-
ленной на рис. 14.78, индуктивность катушки
равна L = 9 мГн, сопротивления Rx = 5 Ом,
R2 = 25 Ом. Первоначально ключ К замкнут и в
цепи течет ток силой I = 2 А. Какое количество
электричества будет индуцировано в катушке
после размыкания цепи ключом К? Внутрен-
ним сопротивлением источника и катушки пре-
небречь.
• Решение. До размыкания цепи в ней тек установившийся ток, силой
где R - общее сопротивление цепи. Поскольку катушка не обладает сопротивлением
постоянному току, то
Следовательно,
а э.д.с. источника
Ri R2
R=
+ Л2
г g(Rf + R2)
Rt R2
&=Iп Z .
Rf + R2
При этом через сопротивление Rt и катушку будет течь ток
j s , R*
/lm“-R1-',R1 + R2-
После размыкания цепи ток через катушку будет уменьшаться и в ней возникнет
э.д.с. самоиндукции
dll
#S-~L л >
где /[ - ток в цепи в произвольный момент после размыкания ключа К.
Записав закон Ома для полной цепи, содержащей сопротивления Rb R2 и катушку,
с учетом э.д.с. самоиндукции получим
/1(R1+R2) = -Z^,
или
dll (Ri + .
Ix~ L Л'
Проинтегрируем полученное уравнение (слева по току If, справа по времени):
(Ri+Rj) ( Rj + R2 1
In If = ---f + In const, или If = const exp | ‘ j •
Значение постоянной интегрирования найдем, воспользовавшись условием, что в мо-
мент времени t = 0 (момент размыкания цепи) сила тока в катушке была равна If max:
R2
h max _ 7 - const.
Ki + K2
Следовательно, ток в цепи будет уменьшаться по закону:
387
По определению тока
А2 [ Л| + Я2
— ехр| ——
dt'
следовательно, индуцированный в катушке за бесконечно малое время dt заряд dq будет
заряд
dq = I ——ехр {--Ц—-11 dt.
Ri+R2 1 L J
К моменту практически полного исчезновения тока в катушке будет индуцирован
( R2 [ R,+R2
------------------
j Rj+R2 i
‘ Rl+R2RJ+R2eXP^ L '
• Ответ: q =---5-10"4 Кл.
(Й1 + Й2)2
14.119. В электрической цепи, представленной на рис. 14.78, э.д.с. источ-
ника равна <£=15 В, индуктивность катушки £= 10'3 Гн, сопротивления
А] = 10 Ом, А2 = 20 Ом. Определить максимальное и минимальное значения
тока через сопротивление Rt и катушку после замыкания ключа К. Внутрен-
ним сопротивлением источника и сопротивлением катушки пренебречь.
14.120. В электрической цепи, представленной на рис. 14.78, э.д.с. источ-
ника равна <£=3 В, индуктивность катушки L = 2 мГн, сопротивлении
А] = 100 Ом, А2 = 200 Ом. Первоначально ключ К замкнут. Какое количество
тепла выделится в цепи после размыкания цепи ключом К? Внутренним со-
противлением источника и катушки пренебречь.
14.121. Источник тока замкнули на катушку с индуктивностью L = 1 Гн и
активным сопротивлением А = 10 Ом. Через какой промежуток времени сила
тока в катушке достигнет значения а = 0,9 от максимального?
14.122. Определить индуктивность длинного соленоида, в котором при
увеличении тока от 7, = 4 А до /2 = 6 А энергия магнитного поля увеличивает-
ся на &W = 10"2 Дж.
• Решение. Энергия магнитного поля внутри соленоида с индуктивностью L при увеличении
тока в нем от Ц до 12 увеличится от 2
ll2 Hi2
д^=у2-у,=-^-у.
, 2 ДУ щ-3 г
L =—2--2® *0 Гн.
12-1\
Rl L
L ‘J“‘-
= ILR1 - « 510~4 Кл.
(Й1+Й2)2
до
По условию задачи
Откуда получаем
г 2 ДУ ,п-з „
Ответ: L = —^—10 Гн.
/22-/12
388
14.123. По длинному соленоиду с индуктивностью L = 2 мГн течет ток
силой I = 1 А. Определить энергию магнитного поля внутри соленоида.
14.124. Индуктивность длинного соленоида равна L = 0,1 мГн. При какой
силе тока энергия магнитного поля внутри соленоида равна W= 10 мкДж?
14.125. По длинному соленоиду течет ток силой 1= 10 А, создающий
внутри соленоида магнитное поле энергией W = 0,5 Дж. Определить величину
магнитного потока, пронизывающего витки соленоида.
14.126. Соленоид с индуктивностью L = 4 мГн содержит N= 60 витков
провода. Определить энергию магнитного поля внутри соленоида и магнит-
ный поток, пронизывающий каждый из витков соленоида при силе тока в нем
1= 12 А.
Электромагнитные колебания и волны
14.127. Колебательный контур состоит из катушки индуктивностью
L = 0,2 мГн и двух одинаковых конденсаторов емкостями С, = С2 = 4 мкФ, со-
единенных последовательно. Определить период свободных колебаний в кон-
туре, максимальный заряд конденсатора и максимальное напряжение на
каждом конденсаторе. Максимальный ток в цепи Zmax = 0,1 А.
• Решение. Период колебаний в контуре, содержащем катушку и конденсатор, равен
Т=2я<ГС.
Поскольку наш контур содержит два конденсатора, соединенных последовательно,
то их общая емкость
Cj С2
с=—5.
п С] + С2
Следовательно,
Т= 2я У L „ --z- » 125 мкс.
Q + C2
Для определения максимального заряда ?тах на конденсаторах воспользуемся зако-
ном сохранения энергии: энергия конденсаторов будет максимальна в момент времени,
когда энергия магнитного поля катушки станет равной нулю:
, .2 2
Jmax _ "max
2 ~ 2С '
Откуда получим
9шах = Лпах LC.
При последовательном соединении конденсаторов заряд каждого из них равен заряду
всей батареи. Поэтому
I Q
‘Углах 1 ~ ‘Утах 2 = 4nax ’ L / ./ ~ мкКл.
C1 +C2
Максимальное напряжение на каждом из конденсаторов можно определить через его
заряд и емкость. Поскольку напряжение на конденсаторе прямо пропорционально заряду
на его обкладках, то
J сГсГ
^4nax 1 — 9 max 1 Ci — lmax * 0>5 В,
С] + С2
389
/ С С
t/max 2 = ?max 2 C2 =/щах C2 V Z « 0,5 В.
J C,C2 J C|C2
• Ответ: T= 2я ’ L-— ~ « 125 мкс; <7max 1 =?max2~Anax ’ L n г в2мкКл;
Ч + С2 Ч+с2
Цпах 1 ~ Anax Q ® 0,5 B; (/max2 = 4nax C2 ~ 0,5 B.
Gj + C2 Gj + G2
14.128. Определить период и частоту собственных колебаний в контуре,
составленном из конденсатора емкостью С = 2,2 мкФ и катушки индуктивнос-
тью L = 0,65 мГн.
14.129. Как изменятся период и частота собственных колебаний в конту-
ре Томсона, если его индуктивность увеличить в два раза, а емкость в четыре
раза?
14.130. Колебательный контур состоит из катушки индуктивностью
L = 1 мГн и конденсатора емкостью С = 10 мкФ. Конденсатор заряжен до мак-
симального напряжения t/max= 100 В. Определить максимальный заряд кон-
денсатора и максимальный ток в контуре.
14.131. Конденсатор емкостью С = 2 мкФ, заряженный до разности
потенциалов U = 2000 В, разряжается через катушку индуктивностью
£=100 мГн. Каково максимальное значение силы тока в катушке? В какой
момент времени после начала разряда достигается максимальное значение
тока?
14.132. В колебательном контуре с индуктивностью L = 10 мГн и емкос-
тью С= 100 мкФ конденсатор заряжен до максимального напряжения
(7тах = 100 В. Каким будет ток в тот момент, когда напряжение на конденса-
торе уменьшится в два раза? Колебания считать незатухающими.
14.133. В колебательном контуре конденсатор емкостью С = 10 мкФ
имеет максимальный заряд = 10'4 Кл. Какое количество тепла выде-
лилось в контуре к моменту полного затухания колебаний?
14.134. Конденсатор емкостью С=2-10‘5 Ф, заряженный до напряжения
UQ = 103 В, разряжается через катушку индуктивностью L = 410‘3 Гн и каким-
то активным сопротивлением. Через некоторое время напряжение на конден-
саторе равно U = 600 В, а ток в катушке достиг значения I = 20 А. Какое коли-
чество тепла выделилось к этому моменту в катушке?
14.135. Определить длину волны, на которую настроен колебательный
контур Томсона, если максимальный заряд конденсатора ^тах = 2-10’8 К л, а
максимальный ток в контуре /щ— = 1 А. Какова емкость конденсатора, если
индуктивность контура L = 2-10"'Гн?
• Решение. Частота собственных колебаний в контуре Томсона определяется формулой
Ио=7Тс-
При совпадении частоты вынуждающей силы с собственной частотой в контуре на-
ступает резонанс. Поэтому собственную частоту контура часто называют резонансной.
Используя закон сохранения энергии в виде
390
получаем
£ Алах 4max
"~2~ = 2С ’
Imax = '^c' ““
Алах
4max
Следовательно, длина волны, на которую настроен колебательный контур, и емкость
конденсатора соответственно равны
, 2яи 2листах , 1 4тах _ ,„-9 А
Л. =---= —z------« 37,7 м, С = —j— = -5--= 2-10 Ф,
ш0 'max ю0 L /тах L
где и = 3-108 м/с - скорость света.
2 я и <7тах „„ „ „ Чтах. ~ , „-9
• Ответ-. Л. = —--« 37,7 м, С = -j-= 210 Ф.
max Апах £
14.136. Определить частоту, на которую настроен колебательный контур,
содержащий катушку индуктивностью £=10 мГн и конденсатор емкостью
С= 10 мкФ. Активным сопротивлением контура пренебречь.
14.137. Резонансная частота колебательного контура равна v = 4,2 кГц.
Определить индуктивность катушки, если емкость конденсатора С = 2,2 мкФ.
Активным сопротивлением контура пренебречь.
14.138. Резонансная частота колебательного контура с конденсатором ем-
костью С= 10 мкФ равна Vj = 4 кГц. Когда параллельно данному конденсато-
ру подключают конденсатор неизвестной емкости Сх, то резонансная частота
становится равной v2= 1 кГц. Определить неизвестную емкость Сх и индук-
тивность контура. Активным сопротивлением контура пренебречь.
14.139. Какой длины электромагнитные волны в вакууме создает колеба-
тельный контур емкостью С = 2,6 пФ и индуктивностью L = 12-10"3 мГн, когда
в нем происходят колебания с собственной частотой?
14.140. Определить резонансную частоту колебаний в контуре, если мак-
симальный ток в нем 1тах = 5 А, а конденсатор емкостью С = 10 мкФ заряжен
до максимального напряжения t/max= 100 В. Активным сопротивлением кон-
тура пренебречь.
14.141. На какую длину волны настроен колебательный контур с индук-
тивностью L = 4-10'2 Гн, если максимальный ток в контуре /тах = 10 А, а мак-
симальное напряжение на конденсаторе Umax = 50 В? Активным сопротивле-
нием контура пренебречь.
14.142. В колебательном контуре происходят свободные незатухающие
колебания. Найти длину волны, на которую настроен контур, если максималь-
ный заряд конденсатора qtaax = 10"6 Кл, а максимальный ток в катушке
Апах = Ю А
14.143. На какой диапазон длин волн рассчитан приемник, если индук-
тивность его приемного контура равна L = 1,5 мГн, а емкость может меняться
от Ci = 75 пФ до С2 = 650 пФ? Активным сопротивлением контура прене-
бречь.
14.144. Входной контур радиоприемника состоит из катушки с индуктив-
ностью £ = 2 мГн и плоского конденсатора с площадью пластин 5=10 см2 и
391
расстоянием между ними d= 2 мм. Пространство между пластинами заполне-
но слюдой с относительной диэлектрической проницаемостью б = 7,5. На
какую длину волны настроен радиоприемник?
Переменный ток
14.145. Контур сечением S = 400 см2, состоящий из ?/= 100 витков прово-
да, равномерно вращается в однородном магнитном поле с индукцией
В = 0,01 Тл, силовые линии которого перпендикулярны оси вращения. Опре-
делить максимальное значение э.д.с., возникающей в контуре, если угловая
скорость контура <о = 1 рад/с.
• Решение. При вращении контура в магнитном поле, си-
\ 7? ловые линии которого не параллельны оси вращения,
ш X \ / магнитный поток сквозь контур с течением времени
( X. \ / будет изменяться и в контуре возникнет э.д.с. электромаг-
^Х-Уа т/ нитной индукции.
'ХсСу Пусть в некоторый момент времени нормаль к
। "С ................ плоскости контура образует с силовыми линиями поля
уХ. угол а (рис. 14.79). За время t контур повернется так, что
\Х. этот Угол станет равным
. \ Ф = шГ + а,
Рис 14 79 - _
г ие. 1 -г. / а магнитный поток, пронизывающий один виток контура,
Ф = В8 cos q> = В S cos (<о t + а).
Поскольку все витки одинаковы, то полный поток через N витков:
Ф = = ATB,Scos(<о Z + a).
Следовательно, э.д.с. индукции, возникающей в контуре
{N В S cos (<о Z + a)} = - ZV 5 S’ <о sin (<о z + a)
меняется с течением времени по синусоидальному закону, т.е. контур будет являться гене-
ратором переменного напряжения, максимальное значение которого равно
Si шах =N В S <0 = 0,04 В.
• Ответ-, в, тах = W В S к> = 0,04 В.
14.146. Какая максимальная э.д.с. наводится в контуре площадью S, вра-
щающемся в однородном магнитном поле с индукцией В так, что угол ф
между нормалью к площади рамки и силовыми линиями магнитного поля из-
меняется по закону <р (t) = <р0 + to t, где ф0, <о - известные постоянные, t -
время в секундах.
14.147. Электромотор постоянного тока, подключенный к источнику с
э.д.с. So = 24 В, делает = 600 оборотов в минуту при токе в цепи I = 0,2 А.
Полное сопротивлении цепи равно R = 20 Ом. Какую э.д.с. разовьет этот
мотор, работая в качестве динамомашины, делая и2 = 1400 оборотов в минуту?
14.148. Действующее значение напряжения в сети переменного тока час-
тотой v = 50 Гц равно Ua = 120 В. Какое время будет гореть неоновая лампоч-
ка в течение одной минуты при включении ее в сеть, если она зажигается и
гаснет при напряжении (70 = 84 В?
392
• Решение. При включении лампочки в сеть с частотой v напряжение на ией будет меняться
по закону
U = Цпах sin о> Г,
где С/щах = "^2 ид - максимальное значение напряжения в сети, со = 2nv.
Так как лампочка зажигается и гаснет при напряжении Uq, то в течение одного полу-
периода она будет гореть время
Д/ = Г2-Г(,
где Г|, t2 - интервалы времени, прошедшего от начала периода до момента зажигания лам-
почки и ее гашения соответственно, которые найдем из условий
Uo = V3 Un sin (2п v Г,), t2 = Т/2 -
где Г= 1/v - период тока. Откуда получаем
/. =~—arcsm-f=^—« 1,6710'3 с, t2= l/2v-/i «8,33-10‘3 с, Аг «6,6610’3 с.
2я v V 2 ид 2 1
Следовательно, за время Ат = 1 минута лампочка будет гореть в течение времени
т = 2 А/ = 2v Ат А/ « 40 с.
• Ответ-, х « 40 с.
14.149. В схеме (рис. 14.80) актив-
ное сопротивление равно R = 2 Ом, ин-
дуктивность катушки £ = 50 мГн, ем-
кость конденсатора С = 25 мкФ. Опреде-
лить полное сопротивление цепи и сдвиг
фаз между током и напряжением при ?ис U-80
частоте переменного тока v = 50 Гц. При какой частоте сопротивление цепи
минимально? Чему оно равно?
• Решение. Полное сопротивление цепи, содержащей соединенные последовательно актив-
ное сопротивление, катушку и конденсатор, для переменного тока
Z=^R2 + (XL-X(f,
где Xq = to Z, Xq = 1/ш С - реактивные сопротивления катушки и конденсатора соответст-
венно, со = 2nv. Следовательно,
Z = ’'I R2 + (2п v L ~ l/2n v С)2 « 111,6 Ом.
Сдвиг фаз между током и напряжением в такой цепи
, el-1/fflC , 2nv£-l/2nvC опо
Ф = arctg --&----= arctg -----R------« 89°.
Из выражения для полного сопротивления цепи видно, что минимальное сопротив-
ление цепи равно
Zmin — Л — 2 Ом
при частоте тока v0, для которой полное реактивное сопротивление равно нулю:
2я v0L - 1/2я v0 С = 0, или v0 = -—? « 142,4 Гц.
2п у L С
• Ответ: Z = Ч R2 + (2я v Z - 1/2п v Q2 « 111,6 Ом, ф = arctg v и 89°,
Zmin = 2 Ом, v0 = « 142,4 Гц.
R
393
14.150. Частота переменного тока равна v = 50 Гц. Чему равен его пери-
од?
14.151. Сила тока изменяется по закону 1= 8,5 sin(314 г+0,661) [А]. Оп-
ределить амплитудное значение силы тока, его начальную фазу и частоту.
14.152. Конденсатор емкостью С = 250 мкФ включается в сеть перемен-
ного тока. Определить его сопротивление при частоте тока v = 50 Гц.
14.153. Катушка индуктивностью L = 35 мГн включается в сеть перемен-
ного тока. Определить ее сопротивление при частоте тока v = 50 Гц.
14.154. Ток в катушке индуктивностью L = 0,5 Гн изменяется по закону
1= 0,1 sin (628 Г) [А]. Определить зависимость напряжения на катушке от вре-
мени и реактивное сопротивление катушки данному току.
14.155. Катушка с активным сопротивлением R = 15 Ом и индуктивнос-
тью L = 52 мГн включена в сеть переменного тока с частотой v = 50 Гц после-
довательно с конденсатором емкостью С = 120 мкФ. Действующее значение
напряжения в сети Ua = 220 В. Определить амплитудное и действующее зна-
чения тока в цепи, а также среднюю за период мощность тока.
• Решение. Полное сопротивление цепи, содержащей соединенные последовательно катуш-
ку с активным сопротивлением и конденсатор, для переменного тока частотой v равно (см.
решение задачи №14.149)
Z= "7л2 +(2л v Z - 1/2л v 02.
Из закона Ома для участка цепи переменного тока
7° Z ’
где /0, Uo - максимальные значения тока в цепи и напряжения на концах участка.
Используя связь между действующим и максимальным значениями напряжения
f/0 = V2 Пд,
получим величину амплитудного
V2 U„
/о = । £ ' , »17,2 А
V/f2 + (27tvZ-l/27tv02
и действующего
z 7° 1 -> J л
/л = тх = 15 ч х 12,3 А.
д ’2 у/г +(2л vZ - 1/2л v 02
значений тока в цепи.
Для определения средней мощности переменного тока воспользуемся формулой
N= иЛ1Л cos <р.
Значение коэффициента мощности cos ф можно найти, воспользовавшись известным
выражением для сдвига фаз между током и напряжением в цепи, представленной на
рнс. 14.80:
. ятф "V 1 - cos2 <о 2л v L - 1/2л v С
COS ф COS ф л
Откуда после несложных преобразований получим
394
008Ф + vi-l/2nvQ2 '
Значение cos <p можно найти и по-другому. Об-
ратимся к векторной диаграмме токов и напряжений.
Из рис. 14.81 видно, что
иа
cosq> = -j7-,
или Uq
IqR R
008Ф"Zoz V/l2* (2л vt-1/2л v 02 '
Следовательно,
N=-^---------------:
Я2 + (2яу1-1/2яу0‘
Vi u„
Ответ: In = .— д » ® 17,2 A, la = , , --- . ® 12,3 A,
Vlt2 + (2fl v£-l/2n v02 д V7T + (2fl у£-1/2л vQ2
Я2 + (2л v L - l/2n v 02
» 2250 Вт.
14.156. Действующие значения напряжения и тока в катушке равны соот-
ветственно (7Д = 127 В, /д = 0,5 А. Определить индуктивность катушки при
частоте переменного тока v = 50 Гц.
14.157. На участке цепи с активным сопротивлением R = 4 Ом сила тока
изменяется по закону 7= 6,4 sin (314/) [А]. Определить действующее значение
силы тока н активную мощность, выделяющуюся на этом участке.
14.158. Катушка с индуктивностью L = 0,02 Гн присоединена к источнику
переменного напряжения с частотой v = 50 Гц. Действующее значение напря-
жения (7Д= 100 В. Определить зависимость мгновенного значения тока от
времени и сдвиг фаз между током и напряжением. Активным сопротивлением
катушки пренебречь.
14.159. К городской сети переменного тока с действующим напряжением
t/д = 127 В присоединена цепь, состоящая из последовательно включенных
активного сопротивления Я= 100 Ом и конденсатора емкостью С =40 мкФ.
Определить амплитуду тока в цепи.
14.160. В городскую сеть переменного тока с действующим напряжением
t/д = 127 В включили лампочку от карманного фонаря и конденсатор, соеди-
ненные между собой последовательно. Какой должна быть емкость конденса-
тора, чтобы лампочка горела нормальным накалом? Лампочка рассчитана на
постоянное напряжение Un = 3,5 В и ток 1 = 0,28 А.
14.161. По участку ABD (рис. 14.82) цепи протекает синусоидальный ток.
На участке АВ действующее значение напряжения равно t/AB = 30 В, а на
участке BD - t/BD = 40 В. Определить действующее значение напряжения на
участке AD.
395
Рис. 14.82 Рис. 14.83
14.162. По участку ABD (рис. 14.83) цепи протекает синусоидальный ток.
На участке АВ действующее значение напряжения равно t/AB = 20 В, а на
участке BD - UBD= 10 В. Определить действующее значение напряжения на
участке ЛО.
НС в 1 , R С L
Рис. 14.84 Рис. 14.85
14.163. По участку ABD (рис. 14.84) цепи протекает синусоидальный ток.
Индуктивность катушки L = 0,25 Гн, емкость конденсатора С= 100 мкФ. Пре-
небрегая активным сопротивлением участка, определить частоту тока, при ко-
торой сопротивление участка будет равно нулю.
14.164. Для неразветвленной цепи переменного тока (рис. 14.85) сопро-
тивления равны: R = 3 Ом, XL = 6 Ом, Хс = 2 Ом. Определить полное сопро-
тивление цепи и коэффициент мощности.
14.165. В неразветвленной цепи переменного тока (рис. 14.85) напряже-
ния на участках цепи соответственно равны: UR = 40 В, UL = 80 В, Uc = 50 В.
Определить напряжение между точками АиВ цепи и коэффициент мощности.
14.166. Последовательно соединенные элементы R, L, С подключены к
источнику напряжения U= Uo cos co t, где Uo = 179 В. Ток в цепи максимален
при частоте v = 10 кГц. Найти индуктивность цепи и мощность, выделяющую-
ся в этом случае на активном сопротивлении, если R = 50 Ом, С = 0,05 мкФ.
14.167. Спираль электрического чайника имеет индуктивность L = 30 мГн
и активное сопротивление R = 30 Ом. В каком случае и во сколько раз быстрее
закипит вода в чайнике: а) при включении в цепь переменного напряжения
U = 311 cos со t, где со = 314 рад/с, или б) при включении в цепь постоянного
напряжения 17=311 В?
14.168. Электрический кипятильник со спиралью индуктивностью
L = 30 мГн и активным сопротивлением R = 10 Ом помещен в ведро с водой и
включен в цепь переменного напряжения l/= Uo sin со t, где [70= 179 В,
со = 628 рад/с. При этом V= 10 л воды закипает за время Г, = 40 мин. За какое
время закипит и полностью испарится вода, если два таких кипятильника со-
единить последовательно и подключить к источнику постоянного напряже-
ния, величина которого равна действующему значению напряжения в первом
случае? Начальная температура воды в обоих случаях одинакова. Плотность
воды р = 103 кг/м3, удельная теплота парообразования г = 2,26-106 Дж/кг.
396
Ответы указания
ГЛАВА II
МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ
§9. Основы молекулярно-кинетической теории газов.
Уравнение состояния идеального газа
9.2. У= p V ~A « 3,34-1022 молекул. 93. п& = я 2,54-1028 м'3.
К К
9.4. N = -Na* 1,37-Ю24молекул; т0 = -^-.7,31-Ю'26кг,п = — «2.71-1025м'3.
Ц ’А М
Мт,о р VNa ,,
9.5. = ---------- » 1,86 1019.
Л цЛ
ДЕВОЛЫ pl НТ
9.6. Т7-— =----» 0,82; Уводы < Уптути > следовательно, больше молекул в стакане ртути,
'’ртути Щ Р2 н
Р 1^5 Т Р V р. .
9.7. N= Na » 1,03-Ю3 молекул. 9.8. У = » 5,610s молекул.
и К>Уа ik т
9.9. N=-------- ~ 4,4-10’° молекул, где и = А-10 3 кг/моль.
В У
9.11. Увеличилась в (1 + и) = 1,5 раза.
9.13. < е > = я 1,24-10’20 Дж.
2уУа
(п ~ О То
9.12. Уменьшилась на ДГ =---------я> 66,7 К.
и
9.14. < е > = 3Л N к Т « 6,62-10'16 Дж.
9.15. v = » 0,13 моля.
Зл 1
9.П. < е > = 3Лр Р= 3 Дж.
9.20. иср цв = 'J 3R Т/ц и 2,15 км/с.
9.16.р = ^у|Л = 8105Па.
9.18. N=^ » 4,83-1019; < е > = ~р Г= 0,3 Дж.
к 1 2.
9.21. ц = 2^ и 4-Ю'3 кг/моль.
иср.кв.
9.23. иср цв = 3/i к Т/лрг3и 1,69 м/с.
9.22. «ср-кв, = Зк Т/т = 1 м/с.
9.24. <р > = Зрк T/NA и 2,4-10'23 кгм/с. 9.25. Дртах = 2 ^ЗкТ p./NA ~ 10'23 кг-м/с.
9.26. Т=^г« 1,410s К.
з^А
938. В л2 = 2,25 раз.
^^ = 0,53м3.
Зр
„2
1,76410s Па.
1.91023 молекул.
Зл i
9.29. оСр кв 2 — ^ср.кв. 1 М-1/Ц2 ® 492 м/с. 931. V=-
932. иСр.кв. = Зр V/m = 100 м/с. 933.р = -
934. иср цв, = т/ Зр V/v ц я> 1936 м/с. 935. У=
936. п = 3~Na- » 9,03-1025 м”3. Н иср.кв. 937.
ив = V ЗЯ Г N/m NA ® 468 м/с.
397
9.38. исркв = V Зр/р. 939. Оср.кв = N Зр/р » 482 м/с.
9.40. v = V -=Ц; я 0,59 м/с. m к Т 9.42.рг >р], К2 > К], Г2 > Гр
HPnV з 9.43. Не сможет, тх масса воздуха в зале m - „ т « 3,8-10 кг.
9.44. Г=Х^«40м3. Р D V 9,45, у = » 2 моля. К 1
pVN. 0 9.46. У- у, «1,02-109 молекул. Р VNb 14 9.47^= ЯГА я 3,21014 молекул.
рГУА 9.48. Т = » 302 К. 9.49.р = ^^-я 237 Па.
9.50. р = ^ = 0,33 кг/м3. 9.51. т0 = я 6,78-Ю'27 кг.
9.52. р = = 1 кг/м3. К 1 9.53. р = я 0,46 кг/м3. Л 1
9.54. Т'= Т — = 3200 К. Р2 9.55.р = £-^я 1,410* Па. Н
9.56.и = Дя2,7 1025м'3; Г=Х^.»22,4л. кТ р 9.57. то = я 6,7-10’27 кг.
9.59. р = & я 3,07 105 Па, ц = m0 NA = 4410'3 кг/моль, газ СО2.
9.60. и = ~ 116,007 кг/моль; и = 2000. э pv 9.61. ц = и 1710'3 кг/моль; газ N Н3 Р
9.62. Газ С Н4; тс я 11,25 г, тн = 3,75 г. 9.64. т = р К(1 -p\/pi) “ Ю5 г.
9.66. Увеличилось на tsp = = 2-104 Па. 9.68. В и2 = | ср ,кв'2 | =1,44 раза.
9.69. В^ = (’^^12 = 4ра3а.
Pt иср.кв. 1
„ Др гАиср.кв. , 12
9.70. Увеличится на = I---— + 1 -
Р иср.кв.
9.71. Увеличилась в 'Гп = 4 раза.
9.72. В Ср кв'2 = Js раз; увеличится в =
иср.кв. 1 ‘ I
9.74. Увеличилась в 'Гп = 2 раза.
9.76. ДГ= (и - 1) Т= 1980 К.
9.78. На т| = Г2/Г| - 1 я 0,115 = 11,5%.
9.80. m = р К(1 - Тг/Т\)я 38,8 г.
9.82. / =/0 Г/Го я 10,7 см.
иср.кв. 1
1 =0,44 = 44%.
5 раз.
9.75. К2 = И Тг/Тх я 1,114 м3.
9.77. Г=лГ0 = 546 К.
9.79. V=llT'~1' T2S~ 1,0610'4м3.
Тг-Тх
Ц2 Т,
9.81. т2 = mi----— = 1 кг.
«Н1
9.84. W= я 1,2-1023 молекул.
398
9.85. р = (1 - а)р0 = 105 Па.
р Кц» 2ц»
9.87. иВЫ11. = - m —» 2,66 г.
к 1 2р| + ц2
Т, tm RT2 .
9.89. Р2 =Р| ~ -----г/ « 3,64-105 Па.
li р И
9.92. а = 1 - 7,/72 « 0,17 = 17%.
Д/Я R Та Т
9.94. И=-------5— « 103 м3.
НРо^-^о)
Др г,
9.96. р, =1-----------= 25 атм.
(1 -П)^2-Л
И т2
9.99. В п = ~/ = 6 раз.
r2 11
Рт
9.101. Г2 = Г, — « 932 К.
2 ‘«Pi
9.86. V=~ = 0,1м3.
ир
9Л8.а=1-^^ = |.
Pi ?2 3
9.91. На т| = 1 - Tt/T2 « 0,04 = 4%.
9.93. Ди = - р « 1,5 г.
л h ‘2
оо<* ЦрУ(Т2-Тх)
9.95. Ди =--_ _ -z;---я> 6 кг.
К h ‘2
V т
9 91р = р|+'р2 {ро 7^ “ Ар }я °>33 а™
9.100. T = Tt/nk = 800 К.
9.102. p2 =Р) » 64,4-Ю3 Па.
И2
9.103. Уменьшилось на г| = 1 - + и 0,06 = 6%.
» 3500 м3.
9.104. Увеличилась на ДГ= Т2 - [Vt (р2 -pt) -р2 ДР] я> 48 К.
м К
9.105. Увеличился на ДК = V\ ——/ 0
Р ‘о
9.107. Ди = ^//'«40 г.
Л 1
9.109. иСп = ^~~«9м/с.
Ср' V^pSt
nV0 ,
9.112.р=р0—/ = 3105Па.
9.114. и = тг {- 1 | = 20 качаний.
К) 1 Ро 1
9.117. р0 = 3Лр = 24 кПа.
Ис 1
9.119./ =---------«0,37.
(Р(/Р) -1
9.108. о2 = и Т2/Т\ я> 2,4 м/с.
9.110. Д/ = я> 2,6 часа.
Ли Я Т
9.113. Др =р0 = 5-105 Па.
9.115. п = к (р/р0 - 1) = 120 качаний.
9.118. В (1+а)2 =1,21 раза.
( V+ f'o I6
9.120. Ро =р | —у— J» 83,4 мм рт.ст.
9.123. См. рис. 1.
399
9.124. См. рис. 2. 9.125. Т2 = Т0 .
'оРо
У f
9.126. В два раза. 9.127.р4=р, 1,6-Ю6Па.
„ 'л Г| К4
( ft 1 <5 Ц| Lb ,
9.128. Уменьшится в I —к— f = 2 раза. 9.130. цсм =---------------------» 10,3-10 кг/моль.
1 1 - а1 <Х| + а2 Ml
ixI хь (И| + ль) ч а но
9.131.11сМ = —— 1--------- ~ 28-10 3 кг/моль. 9.132. р =р0-----~ 2235 Па.
»!] Ц2 + OT2 Ml “ М2 + Ml
9.133. а, = И‘ ~ = 0,276 = 27,6%; а2 = 100% - а, » 72,4%.
М(М1-М2>
2 Dt 00 1 9.134. р = Н1 ' = 0,48 кг/м3. Pl +Р2 9.136. р = « 1.3106 Па. V VM| М21
9.138. р = ~ U 87,2 кПа. v 1 Ml М2 yA 1
Я (И, M2 + W2M1)
„„„ Д»(М2-2Ц1)ЯГ 9.139, р = » 2,1 ата. Ml М2^ 9.140. р = х 0,48 кг/м3. Л 1 ГП2 + М2 т1
Ро М2 ” (М2 - Ml) .3 9.141. р - _ _ .. * 0,6 кг/м , К То Na где р0 = 105 Па, TQ = 273 К.
Р(И + Рг)~Р2 ^2 , ,.5П 9.143./?!- у -510 Па. 9.144. р = —— = 2-105 Па. 7И|/Р| +т2/р2
Л/. +-^2 Pi V
9.145. р = ——!---т—. 9.146. и = .- ~ 400.
V|/Pi + N2/p2 5/бро^о
9.147. В сторону части сосуда, первоначально заполненной углекислым газом на величину
/(2М2-М1)
Д/ = —---—— * 0,13 /. Указание. На систему «сосуд-азот-углекислыи газ» внешние силы
4(Mt+2p2)
в горизонтальном направлении (например, пусть это будет ось ОХ) не действуют. Поэтому
ускорение центра масс системы ас х = 0. Следовательно, скорость центра масс ос х = const. Так
как вначале сосуд был неподвижен, то v>c х = 0 и хс = const. Определив положение центра
масс системы до и после перемешивания газов, найдем смещение Д/ сосуда.
Т2 4
9.149. р2 = 2р, = 4-104 Па.
' . зь
9.150. Уменьшилось на г| = 1 - у-=- = 0,25 = 25%.
271
9.151. л = m/п - 1 = 0,05 = 5%. 9.152. р0 = =83 кПа.
400
9.153. a = £-^4-l« 0,34.
Ш К 1
9.154. а = ^^--1«0Д8.
m Л 1 j
9.155. р « 57,6 кПа.
9.157. pt = I — + —}« 4,65-106 Па,
И 12ц, p2J
Ро Цо + Ц.
9.158. тг = = 3.
И М2-М1
m R AT/p-pah S
9.161. М=---------« 8,36 кг.
gf>
>И1 R Т z
р2 = -^у« 1,55 1 06Па.
О1<л ph(p<>S + Mg)
9.160. m =---------------
9.163. T/T0 = nm = 3.
9.165. P2 = Pj + po S = 260 H.
RT
9.162. ДЛ = —» 7,6 см.
pQS + (M+m)g
9.164. Am=- "ft-1),
л- 1
(pnS+mg)bl
9.166. ЬТ= —--- » 1 К.
vR
9.168. й » 0,55 I.
9.169. АЛ = I ('11 + рЬьр1 -p/bp).
9.170. И/Г2 » 1,86.
гелий
’..’.РГ.
кислород
h + bx
Puc. 3
P. .'
гелий - -
; Pr
кислород'
гелий’.'.
h
h
g
9.171. р' = Vip = 50 Па, Дх = е-^« 10 см.
mg
Решение. До того как поршень стал проница-
ем для гелия, на него действовала сила тяжес-
ти и силы давления гелия (сверху) и кислорода
(снизу). После того как поршень стал прони-
цаем для гелия, гелий на него больше «не
давит» и он переместится вверх на некоторое
расстояние Дх (рис. 3), где сила тяжести
будет равна силе давления кислорода в новом объеме. Так как в новом положении гелий рас-
ширится и займет весь объем сосуда, то, очевидно, его давление уменьшится в два раза, т.е.
р' = р. Уравнение состояния кислорода при начальном н конечном положениях поршня
pihS = vKRT, p2(h + bx)S=vKRT,
где давления pt ир2 кислорода под поршнем:
Р1=Р + ^, Р2 = П^-
Следовательно, (pS + mg)h = mg(h + Дх), или Дх = .
(nil2 М D n mg
9.172. v = | — j уу. Решение. В положении равновесия поршня:
Pi S-p2S + Mg = 0, lApi I S = vi RT, pi IS = vi R T,
где pt, V], p2, v2 - давление и число молей газа над и под поршнем соответственно. Откуда
получаем
2(yi-V2)RT/l + Mg = 0.
При смещении поршня из положения равновесия на малое расстояние х вниз:
р( (’/У + х) S = vi Я Т, pi - х) S = vz R Т.
Результирующая сила, действующая на поршень в этом положении, будет равна
401
Л Tf'/XV! - Vj) I-(Vj + Vj)x]
----------------------------+ Afg,
F=pjS-piS+Afg =
или, с учетом малых колебаний (x « */У):
2R T(yi - V2) 4RT (vt + vj
F я-----j-----+ Mg--------------
где к - коэффициент возвращающей силы. 47?7(v+V2)
С учетом условий равновесия поршня получаем: к =----
Из выражения для периода колебаний
('/У)2-?
—z-----х = -кх,
I2
I2
j л 112 М
находим: v = vt + v2 = j — J jjy.
«2 Ml 1
9.174. t] =-----—------= у.
7И1 Ц2 + m2 Ml J
к
А/
(vj + v2) R Т
9.175. ц2 = -Ц р,
10~1
~ 4 г/моль.
9.176. Д/| = 6ЛI, А1г = 5Л /.
9.177. АЛ =
И, Уг ат
—=-------- -«6,7-КГи.
л г2 [Г, Т+У2(Т+АТ)]
T2 Vi + Л К,
’л78-р=Р1Т7гТ7Г=1147гПа-
9.179. д/=7 ^9<Pos-t-”,g)2~8Pos",g~3Pos~'”g
Im g
9.180; Г = 4Г0 = 1200 К.
9.182.р =р0 + » 1,Ы05 Па.
О
•Ро
'А1
О
ггт.
Ах
3А1+'Ах-Ах
lA I + х - Ах
Р
Р
Puc.4
9.181. AZ =--<P~Po)S12o----.
(S] - S2) (p St ~Pq S2)
9.183. AZ = 0,37/.
9.184. Ax = ^y- = 5 см. Решение. При нагрева-
нии воздуха, например в левой части сосуда и
охлаждении в правой, поршень сместится в сто-
рону более холодного газа. Но в целом центр
масс системы останется на прежнем месте (в на-
правлении оси ОХ система замкнута, см. рнс. 4).
Найдем смещение поршня внутри сосуда. Для
этого запишем обобщенный газовый закон для
воздуха в обеих частях сосуда:
PpS’Al pS(lAl + x)
Т ~ Г+ДГ ’
PqS'AI _pS(lAl-x)
!АТ т ~ т~*т ’
нли X = -JjT
Найдем начальную и конечную координаты центра масс системы:
_ m */4 / -ют 34 / _ l_ _ m (1/41+^Лх- Дх) -ют (3/4 / + х - Ах) __ Z-2Ax + x
хс 1 “ . — о» хс 2 “ — 2 »
ffl + ffl м + м
где m - масса воздуха в каждой части сосуда. Следовательно,
I 1-2Ьх + х . х I АТ
----2----’ ““ Дх=2=’4Г-
402
9.189. В — = { 1 +£^}'/l 1,26 раза.
И 1 Ро 1
г рл 7\ 1
9.191. г2 = п -----г— » 1,86 см.
(Po + pg*)ri1
9.193. VQ=v{ - 1} - 1,8 м3.
l(Po + Pg*)^i 1
31
9.185. Увеличилось в ——гг = 5 раз. Указание. Координа ты центра масс системы не изме~
31 — оЬ
вились (см. решение задачи №9.184).
9.186. Т= 2л V J” С . Указание. См. решение задачи №9.172.
2р0 о
ока Фо + Р8*)М
9.188. р =----------« 1,32 КГ/М .
Л л
Р1 ^2 1
9.190. У2 = К = 800 м3.
Р2 *1
• Pn + Pgh
9.192. V = V « 13,6 л.
Ро ___________________________
owe ль A/pg+f -\l (p</pg + l)2 Pol Ti-T2
2 4 Р8 Л
9.196. Уменьшить в п =--——; раз. 9.197. Уменьшить в о = « 2,6 раза.
2p0-pgZ 4H-3h
9.198. йд = Vi [(Z + h + р</pg)- V(Z + й + pj/pg)2 -4й Z] я 12 см.
9.199. р0 = -^« 105 Па.
nd2
9.200.1 = Vi (pt/p g+l0)~ */4 (po/p g + Z0)2 ~ [P</(P g) + Л - Zo] й и 2,8 см.
l2 + It <
9.201. ро = Р g h 7—7• 0,95-105 Па.
*2“Ч _______________________
9.202. р=1Л(р0 - pgl) + V !4 (ро - Р g Z)2+ Ро Р g zo ~И,5 кПа.
Z, Z2
9.203. Z = -LA-.
2Z2 - Z,
9.204. T = % То. Решение. Запишем уравнение Менделее-
ва-Клапейрона для двух состояний воздуха (рис. 5):
phS=vRTo, px(h+x)S=v RTX,
где х - изменение уровня ртути в трубке прн нагрева-
нии воздуха до некоторой температуры Тх,р = р$ + р g й,
Рх = Ро + Р g (л - х) - давление воздуха в трубке при тем-
пературе Tq и Тх соответственно. Следовательно,
(Ро + Р g h) h/To = [Ро + Р g (л - X)J (л + х)/тх<
илн с учетом связи давления в [Па] с давлением в [мм рт.ст.) р0 = р g й:
2й2/7Ь = (2й-х)(й + х)/7’х.
Откуда получим зависимость температуры Тх от х:
7* = ~2й2х2 + 2йХ + Г°’
исследуя которую на экстремум, находим: х = Vi й. Это означает, что при медленном вытес-
нении ртути температура воздуха будет достигать наибольшего значения при х = Vi й. В
этот момент она будет равна: Тх = 7 * 9/g То. Для дальнейшего вытеснения ртути воздух доста-
точно поддерживать при этой температуре (легко показать, что температуру воздуха даже
можно понизить).
403
9ДО7.ДЛ = Л-Ро 9.209. АЛ = у {1 + 2pgA , }.
2pg 2' Zpo+pgh*
9.210. Л = — « 10,2 м. 9.211. Л = Я+ — » 10,3 м.
Pg Pg
9213.р = - р « • °’46 105 Н"-
z /q + ZVl] — ДЛ
р, ДЛ-Оъ-рЛОъ-/)
9.214. р0 ------;------------~ 761 мм рт.ст.
ЛЛ-(Р2-Р1)
9.215. ДЛ] = - >Л (Л- Ай +рд) + V Vi (Л-Дй+pg)2 + Л АЛ » 21 см.
9.117. АЛ = -J-{pq+^ + 2p«Ao -|р, 1 1 IPgAfl(J- 8‘
4p g 1 о 1 о 1 о 3
9.218- p = |- pg ДЛ} • { F+S(Ло - >Л ДЛ)}-Po^ •
9.219. p = |{p0 + -2pgho + >/{ро + ^^-2р«ЛоГ+ 8р«ЛоР0 }•
* Pl О Pld
9.221- p = 3mRJ « 1.25 107 Па.
4 n г u
Pq Vg (g2 ” Hi)
9.222. Сможет, так как подъемная сила шара Fn =-jry------т g « 5040 Н, а вес груза
P = Afg= 1470Н.
9.223. М=[(1 - а) Ц2 - Иг] - 385 кг- 9224. р =р0~~ « 3,16-Ю5 Па.
Л 1о Р! щ V
9.225. F=PgpF
Л 1 1 j
9.227. F„ = mg (р2/1*1 - D-
9.230. р = ^К
r mR
9.232. Tt = Т2 V2/V-i = 300 К.
«2
9.235. Tjnax - .
2v К а р
9.236. Гтах = -^- [К], р = -^ [Па], [м3].
XV А 1 Z х X
9.237. Гщщ = 3А v R То2/3(2 а)1/3, Т= 3Л р = (Т(/2а)1/3.
9.238. Pmin = 2v R л/ а 7g, Т— 2 7g, V— Ч Tq/o,.
9.240. T2 = Tt V22/Vt2.
9326. Уменьшилась в ----= 1,08 раза.
НЗ - 1*2
9.229. Увеличивается.
9231. Т = —
vR
9234 Т =-^~уГ^
9.234.7тах 3уЛХ3а.
404
9.241.1)р = а V, прямая; 2)р2 = a R Т, парабола; 3) V2 = R Т/а, парабола. См. рис. 6.
9.242.1)р = aA/W; 2)р - а/Т, гипербола; 3) V= R Т2/а, парабола. См. рис. 7.
9.243.1)р = A/VaT; 2)р = R/aT, гипербола; 3) F= a Т2, парабола. См. рис. 8.
9.244. См. рис. 9. 9.245. См. рис. 10. 9.246. См. рис. 11.
9.247. См. рис. 12. 9.248. См. рис. 13.
405
3
Р
р2------£
Pl
Рис. 16
9.251. 72 = ^Т| 73 «346 К.
у
9.250. См. рис. 15 (процесс 1-2: р ~Т *).
v Г4К2-Г|К| з
7) Г2/К) + 74-2 7|
vJ?7, r vRT2
9.253. Kmjn = V2 =-, /max = м =------ Указание. Решение задачи очевидно, если
Pi Pl
цикл 1 -2-3-4-1 представить на р-V диаграмме (рис. 16).
§10. Теплота и работа.
Физические основы термодинамики
п — А
10.2 .1)=^^ = 0,6 = 60%.
10.4. U = = — R 7= 9,3510s Дж.
2 ц
10.7. Ui = U2 = 3Л pi И = 1,5 кДж.
10.8. U} = U2 = 3Л vR 7«7,5-106 Дж; AU= 0;А = 0= 10 кДж.
10.9. Q = v R 7 In (р2/р{)« 1,73 кДж.
10.12. » 0,27 = 27%.
Р 3vRT
10.14. Q = 3Z> v R T(n2 - 1)« 10,3 кДж.
10.17. А = v R (Г2 - Г)); Д(/ = 3Л v R (t2 - Г,).
10.18. А = 2/sQ = 480 Дж; Ср = 5ЛЛ = 20,8 кДж/(кмоль-К).
10.19. Д7=-----------« 2 К.
m(pcv + R)
mRT.-iiA ,
10.21. V2 =---—— » 0,43 м3.
УР
10.3. A=MJ -—9 = 16 кДж.
П
10.5. U = 3Л (ро + т g/S) К» 660 Дж.
10.11. У= 2&и «8,3 л.
3 (Р2~Р1)
10.13. bU = 3Л р0 V = - 900 Дж.
10.16. п = 0,4 = 40%.
10.20. A = — RT —i к 10 кДж.
ц п
10.22. Vi = А\ = 0,3 м3.
1 Р(п-1)
406
1033. Г, = —» 241 К.
* ЗуА(л-1)
10.26. А = — R ЛТ*> 4,15 кДж.
Н
10.28. Д 7=^ = 45,5 К.
pF
10.24.А = vR Г, » 5 кДж.
10.27. v =
А
R(T2-Tt)
10.29. ДТ= «1,4 К; О = 5АМg h » 1,1 кДж.
jn к
1030. Q = %- R ДТ» 10,4 Дж; Л=|”^А^'» 3>8 см-
2 1* p^S + Mg
1О31.Т2 = Т1Л2/Л1=48О К.
Ро л d2+ 4(М + ш) g I 4RT, 1 3
10.32. Т= —---75-----—{----------h » 316К;Д1/ = 4R (Т- Г.) « 133 Дж.
4Л lp0nd2+4mg 1 2
? л л
1034. ДТ= = 7 К. 10.35. Д1/= - А = 300 Дж; ДГ = « 4 К.
5v R m cv
10.36. p2 =Р\ Ух/УгУ » 2,5 МПа, где у = 7/s.
1037. Т2 = Т, (F/F^" ’« 227 К;р2 = Рх (Ух/У^« 380 кПа, где у = 7/з.
_2_р2
10.39. Д17= 3Л (р2 F2-p| F|)= 1,05 кДж. 10.40.Л 3106Дж.
10.41. Я = 'Л a (У2 - F|2)= 49,5 Дж; 0 = 2а (F22 - f/) = 198 Дж.
10.42. Q = 2v R То (л2 -1) « 36,3 кДж. 10.43. Д1/= 3Л v R Г, (F/Fj - 1)« 2,5-106 Дж.
10.44. А = Ч> a v R (F22 - F,2) . 10.46. А = 0,4 R V2 « 1,ЗЗ Ю’3 Дж.
10.47. А = 7Л? R F,3 » 58,2-10’9 Дж. 10.48. А = » 11,1-109 Дж.
10.49. А = 6R « 35,25 Дж. 10.50. А = 1 R\- 24,4 Дж.
10.52. ц = ™ R-yT = 32-10-3 кг/моль; кислород О2.
Qp ~ Qv
10.53. ц = mR^T = 210'3 кг/моль. 10.54. В и = Q\/Qi = 1>67 раза.
Д0
10.55. Я = v R Т(п - 1) = 8,31 кДж.
10.56. Д1/=О;Я = 0 = уЛГ = 1,25-106 Дж.
10.57. В первом случае выделится теплоты на Д£2 = (pi -p^-CF] - F^ = 4105 Дж больше,
чем во втором.
10.58. Q = | (Р2 - Pi) F, + |р2 (F, - И). 10.59. а = / f 1 а 1,4, где т = 7/5.
(у — 1) ш л
10.61. Увеличилась в г, = U2/Vi = m/n = 1,4 раза.
(л -1) v R Тп з < и, т21 j
10.62. у = 1 + -7 - , «1,4. 10.64. U = 4 — + — Л 7 « 2,1 104 Дж.
е-уАТ01пл 2 1 Hi 1*2 1
407
3 т. 1Ь + Лиш
10.66. с = R —« 5,6 Дж/(кгК).
2 Ц! ц2 («1 + «2)
10.65. Д(/=11 — + —} R At» 623 Дж.
2 1 Hi F*2
10.67. А = 3v/(TS&h и 7
7* Г
10.68. Т2 = -° *_ = 262,5 К. Решение. Из уравнений состояния газов в сосудах, записанных
2Т| - То
до открытия крана:рх V=vx RTq,p2V=v2RTqH после открытия (в момент, когда давления
сравнялись):р V= vf R Тх,р V= v2 R T2, (me vb v2, v/, v2 - число молей газа в первом и вто-
ром сосудах до и после открытия крана соответственно; рх,р2,р - давления в сосудах в этих
же состояниях), получим
(Р!+Р2) F=(V| + Уг) А То, 2р И= (v/Т| + v2 Тг) А. (1)
С другой стороны, так как оба газа одноатомные, а сосуды теплоизолированны, то из за-
кона сохранения энергии:
3Л vj А То + 3Л V2 А То = 3/i vf А Т\ + 3Л vi А Тг, или (vj + уг) То = vi Ti + V2 Тг.
Торца из уравнений состояния (1) получим
р,+Р2 = 2р.
Записав закон сохранения числа молей: V] + v2 = v, + v2 в виде
Pl V P2V pV p V
RT0 + A To “ A T, + A T2 ’
(2)
с учетом (2) получаем
2£._2_ + 2_ щи, г,__________T0Tt
Тй~Тх + Т2' "ЛИ Тг~2Тх-Тй
10.70. Т= То 11 + Po + ffl^} ж «о К.
1O.71. t4to4^ + ^/5)^
vR
10.72. Q = 13Лу R То.
10.75. Т= То {1+тЦг}.
1 Зро К) >
10.76. и,=>/ 3^о ^. О2 =
(mj + m2)
10.77. Tmax = То + 2m v2/3R.
» 275 К; V= j Го + | УДГ° «4-Ю'3 м3.
5 0 5Po + Mg/S
Зро S + kl
10.80. А =р0 Го = 51О4Дж.
_ 3p0 Vo
m2 (ml + m2)
10.78. Q= 5/4 m u2.
10.81.Я = —А ^2~Г|^ .
H T\
10.83. A = v А ДТ« 250 Дж.
10.82. А = v R (,'ГТ^ - <Т7)2-
10.84. Q\ = 3Л (р2 Vi -р\ И) +р2 (V2 - И);02 = 3Л (pi И -р2 ty+pi (И - И2).
10.85. А = 0; газ получает тепло иа участке 1-2-3—4, отдает - на участке 4—5-6-1.
408
Рис. 17
10ЖЛ = ЗА Т,-2,25Л0.
2 2
10.87. Л = - 2-=—— • ~—— ——" 750Дк. Указание. Работу можно найти как раз-
2 Po~.Pi
иость площадей нижнего и верхнего треугольников
Л = «Л (У2 - ИХро-Pl) - 'Л (У4 - ГзХл -ро),
где разность объемов (К4 - У2) легко найти из подобия этих треугольников.
10.88. А = 12,5 кДж. Решение. Обозначим длину
половины диагонали квадрата буквой ft (рис. 17).
Тогда уравнения состояния газа в точках 1, 2, 3,
4 цикла примут вид
p(P-aft) = vATi, (р + pft) V=vRT2,
p(V + a.b) = v RT3, [p~$b)V=vRT4,
где a = 1 м3, p = 1 кПа. Откуда легко видеть, что,
если Т4 - минимальная температура в цикле, то
Т2 - максимальная температура. Следовательно,
Т2 = ЗТ4, или
р У+ р ft У= 3 (р V- р ft У).
Откуда получаем: Р Ь = 1Ар. Так как работа за цикл может быть определена как пло-
щадь в петле цикла:
А = 2а р ft2,
то А = 'Ла Рр2 = 12,5 кДж.
10.89. А = 2 кДж. Указание. См. решение задачи №10.88.
10.90. А = 'Л л R Гщах и 1044 Дж. Указание. Максимальная температура в цикле достигается
на участке 2-3. Объем и давление газа, соответствующие Ттах легко определить из условия
а2р2 + р2К2= (2у а)2 (где 2а - радиус кривизны кривой 2-3, где a = 1 м3, Р = 1 Па ,у = 1 Дж)
н уравнения Менделеева-Клапейрона рУ= vATmax, а работу газа как площадь в петле цик-
ла: Л = Иг [л (2у а)2 - л у2 а2].
10.92. A =2v R То = 3324 Дж.
10.94. А = v R Т4.
10.96. Л = v R (Тз - Т4) - Q = 999,5 Дж.
10.93. А = Q - v R (Т4 - Т,) = 1767,5 Дж.
10.95. А = — R (Т2 - Г,)« 1163 Дж.
10.97. Л4-3-5-6-4/Л1-2-3-4-1 = 2.
10.99. Л] 2 = Q + -4т v R Г] » 285 Дж.
3
V R (Т2 - Г.)2 Р .
10.100. А =-——— « 104 Дж. Р,— 1
mini j _ л _ <Р2 +Р1) (^2 ~ И) _
10.101. /1 щах--^1-2— 2 — 750 Дж; i
р2Р2 р2К2 Рг ----[------^]2
Т2=^^2=120К;Т3 = ^2-52 = 60К; „ „ 3
2 R ’ i nR Рз=Р4------ь------F—
р2 Vi -------1---------1_
Тл = —5* = 120 К; графики процессов на к у. = у,
П К \ 2, 3
р-V- диаграмме представлены на рис. 18. Рис'
409
10.103.112 = ^- = 25%;
2 “’ll
10.105.1) |/т)2 = 5Л.
10.107. i) = -Ц- = 0,1 = 10%.
n+ 1
1 вч 2
10.104.1)2 = г2-= 20%; ^= — -1=4.
2’ll лз ’ll
10.106. Т)|_2-3_| <’11-4-2-1 •
10.108. р4 = 1 МПа.
10.110. и
(Р2 ~PlX^2 ~ И) _ 2
3Л(Р2^-Р1И)+Р2(^2-И) 13 '
10.111. Т)1-2-3-4-1'/’11-5-6-4-1 - ^9
Рис. 19
10.112.1) = 2Л» 22,2%.
ко 2К0
Рис. 20
4-15 1,2
10.113.1)1 = -———. Цикл нар - V— диаграмме представлен иа рис. 19.
9- 15 1)2
10.114.1) = 2/\з » 15,4%. Цикл нар - V- диаграмме представлен на рис. 20.
10.115. О = - А = - 600 Дж. 10.116. п = 2/гз» 8,7%.
5i]
10.117. а = 9; Q2/Qi = %.
10.118.1) = - - р 1—-—, при любых Р > 1
р-1+а-1
10.119.1) = 3/>2 « 13,6%.
10.122. 1) = 10%.
10.124. и = 5/м.
10.126. При понижении температуры холодильника.
10.127. и * 0,4 = 40%; на А/» 947°С. 10.128. 1\ = Т2/а = 460 К.
10.129.1) = 1 - а = 0,2 = 20%; А = (1 - а) 0, = 1256 Дж.
Т\ — Т2 т2
10.130.1) = 2 « 0,27 = 27%; Q2 = А „ \ » 200 кДж.
71 ~1-~2
10.131. А = Qi (1 - T2/Ti) = 500 Дж; Q2 = 0, T2/Ti = 500 Дж.
Л^т Т, Л^т Т2
10.132. Qn = -—V и 987 мДж; Qx = = 722 МДж.
2|-/2 У1-у2
10.133. А =-^— = 5 Дж.
1 -П
т.-т2
10.134. п ='---
, “ > 1, следовательно, 1) < Vs, т.е. 1) < 20%.
р- 1
р2 3 п,/п. - 1
10.120. — =-----S-И—— = 2.
Pl 5, 5i)2/’li-3,5
10.123. п = 7Лг.
т2
= 0,5 = 50%; О2 = А -=г=100кДж.
410
1П_ 3(Т|-Тз)(Т2-7з) 1 ... ,-0,
1U.135.Т| = ———— —_ " ~~ = т«U,33 = 33%.
1 3 Т| Т2-Т2Т3-2Т|Т3 3
.(L.1Z 3 Т)! + Т]2 — 4 T]l Т|2 п._,
10.136. п =---------------» 0,156 = 15,6%.
4-ЗП2-П1
97
10.137.1, =^«0,8 = 80%.
§11. Уравнение теплового баланса.
Изменение агрегатного состояния вещества. Влажность
11.2. V =--------я 1,83 л, где /кип = 100°С - температура кипения воды,
с Р ('кип -')
т, 0-/2 71
113. Т2 = Г| [1 - и (m,/m2 +1)]я 291 К. 11.4. ± .
рК('2-'1)
11.5. т =--;-----я 16,5 кг, где Гкип = 100 С - температура кипения воды,
'кип ~ 'г
с, ди. с-i m-i (h - ti)
11.6. т ,/m2 = с2/С|. 11.7. Q = 1 1 z z z—- » 5850 Дж.
с. р V(Q - Л)
11.9. с2 = / -а;— = 1265 Дж/(кгК).
т (t2 - 0)
11.8. t = Г| + С^' * 32,5°С.
1 с т
CiM+Cimid-ti с-, m-i
11.10. тА =----------------------— я 96 г; тм = т2 - дяА я 84 г.
С] — С2 t2 — 0 С| — с2
11.12. Q = т [с (Тпд - Т) + Х] = 351 кДж, где Тщ, = 273 К - температура плавления льда.
11.13. т = » 11,7 кг.
А. + с ('2 -13)
с р V (/кип — ')
11.14. т =-----------я 3 кг, где Г^ц = 100 С - температура кипения воды.
„ X(m2-m3)-c2m2t2
11.15. =-----------^-7-----я 198 г.
с, /1
11.16. V= Ко - — + С Ив ('2 ~f|) -PB~fy » 1,06-Ю'4 м3.
Рв Л Рв Рл
„ rz_ 17 , Л<Х1 + С1 '1)(Р~Рг)
- —} я З Ю'5 м3.
Р1 ’
11.20. дг=—ИА£1_212__ ж 1 (43.1 о-4 мз
''г ('i ~f2)- И ('i _'i)
'• г — ' о ' .
^2 Р2 Р
с т & (р -р0)
11.18. Дда =--—-------— * 5,37 г.
X Др
11.21. t0 = -1,11 — - 30 » -53,6°С.
сл сл"
11.23. т =------------* 410'5 кг, где Гкип = 100°С - температура кипения воды.
с ('кип - ') +г
11.24. Д/ = — «36°С. 11.25. т = 2-^ » 13,7 кг.
твс X
11.26. Q = т [Сд^пд - Т() + X + св (t2 -+ г] я 6,06 МДж, где = 0°С- температура плав-
ления льда.
411
1137. Л/=-^«707 г.
r + 1
11.29.0 = 0°С. Указание. Поскольку количество тепла, необходимое для нагревания льда до
температуры плавления /пл = 0°С Qn” = сл тг (tun -ti) = 420 кДж больше, чем количество
тепла, которое может выделиться при остывании воды до 0°С Qb^ = св mi (t\ - 0°С) =
= 42 кДж, но меньше, чем количество тепла, которое может выделиться при остывании и за-
мерзании воды Q/в^ + ммеР3 = св т\ (ti - 0°С) +1 mi = 702 кДж, то вода в калориметре ос-
тынет до 0°С и часть ее замерзнет. В результате в колориметре будут находиться лед и вода
при температуре фазового перехода.
Ami + c(mi + /И2)('з-'1) ,.
ИЗО. т = mi + тг +-------1;-----—-------- » 14 кг.
Г + с(/2-/з)
1131. 0 = 100°С. Указание. Поскольку количество тепла, необходимое для нагревания льда
до температуры плавления /пл = 0°С, плавления льда и нагревания образовавшейся воды от
0°С до температуры кипения /кип = 100°С Qn = m2 (А + св ц - сл ti) « 76 кДж, меньше ко-
личества тепла, которое может выделиться прн конденсации пара Qn = г mi « 112 кДж, то
не весь пар сконденсируется.
1132. 0 = 36,6°С. Решение. Количество тепла, необходимое для нагревания калориметра и
льда от температуры /|=-10°С до (пл = 0°С и плавления льда равно рнагР + плавл =
= ci mi (/пл - /1) + сг тг (/пл - /1) + А тг = 351,8 кДж. Количество тепла, необходимое для
нагревания калориметра и образовавшейся воды до /кип = Ю0°С равно gHarp =
= ci mi (/кип - /пл) + с m2 (/кип - /пл) = 420,08' кДж. Количество тепла, которое выделится
при остывании пара от температуры /2=110°С до температуры /кип - 100°С равно Qtn™ =
= сз тз (/2 - /кип) = 3,34 кДж. Количество тепла, которое выделится при остывании пара н
его конденсации равно рвст +конд = сз тз (/2-/кип) + г т3 = 455,34 кДж. Так как
рнагр + плавл + ^нагр _ 77 jgg кДж больше (Зв” + ковд = 455,34 кДж, то пар остынет и скон-
денсируется. Следовательно, в калориметре будет находиться вода при некоторой темпера-
туре 0, значение которой можно найти из уравнения теплового баланса:
С1 И1 ('пл - '1) + с2 и2 ('пл - '1) + k»2 + С1 (е ~ 'пл) + с и2 (е - 'пл) =
= Сз тз (!г - 'кип) + гтз + с m3 (z^n - е)-
срК('кип-') о
1134. ц =----------= 0,525 = 52,5%, где Z^n = 100 С - температура кипения воды.
tN
т, <
1135. А = с — — (z2 - z.) » 3,3-Ю5 Дж/кг.
тг Tj
.. т 1сл ('пл _') + + св ('кип ~ 'пл) + 0,25 г] о
1136. ц =------------------------------------= 0,424 = 42,4%, где Z^ = О С - тем-
А/с
пература плавления льда, /кип = Ю0°С - температура кипения воды.
1137. А = с (/j - tj) т2/Т| - с t2 » 3,3-Ю5 Дж/кг. 1138. N=N$-m [с (Zg - /|) + А]/т » 286 Вт.
1139. св = [Х + с(Г2~Гз)1Т1 * 4130 Дж/(кг-К). 11.40. г = С(<~<о)Т2 » 2,24 МДж/кг.
(71 — Ту Т2 Т1
11.41. т2 = -----» 60 мин, где /кип = 100°С - температура кипения воды.
с ('кип-'о)
412
11.43. n = * 0,03 « 3%.
’ 2qm
N 9
11.45. m =----= 5 кг, где 5=1 км.
11.47. S = n P ^gU » 270 km.
Nx
11.44. m = —» 26,1 кг.
11.46. q =----» 46,2 МДж/кг.
т| mu
NT.
11.48. m = - ' .
«(Tl-Tj)
(cM + С)(Ь -ti) 4napK0u „
11.49. n = i----—----!'« 0,317 = 31,7%. 11.50.0 = t + —, »76,3°C .
m4 nd2cpoxRT
„ c2 Опл “ <1) + ^ + cl (,2_,пл) + г . . AOr>
11.51. M = m-----------------------» 0,6 кг, где Гщ, = О С - температура плавления
льда.
11.53. h = c &/g » 428,6 м.
11.54. h = X/ng« 42 км.
11.55. NT=gh/c« 0,12 К.
11.56. h = [c (Гкип - Го) + r]/g « 265 км, где Гкип = 100°С - температура кипения воды.
11.57. ДГ = » 0,023 К. 11.58. ДТ = и ^-Tgh „ о 9 к.
2с 2с
n g (к. - йт)
11.59. ДТ = » 0,12 К.
с
Vi И (и? - и?) - с (fnn - л) Ол с(Т-Т0) + к
11.60. а =----------- ПЛ. 1 » 0,06=6%. 11.61. Л = - —--------» 283 м.
X 2« П8
2
11.62. Omin = т/2 [сСГдл- То) + Х]/п » 2,9 км/с. 11.63. ДТ= = 20 К.
2
11.64. ДГ = HJL-OzJZsl ж 7 25 К.
ОС________________________________________
11.65. umm = 'J 2 [С| (Гдл - г) + X + с2 ((кип - (пл) + И * 2,58 км/с, Гдл = 0°С - температура
плавления льда, <кип= Ю0°С - температура кипения воды.
11.68. ^=1^ — » 0,92. 11.69. Дй = л{^-^-1}«58м.
Qn гр 1 ЦРн ’
11.70. Дт = Д4» 12 г.
К 1
,, „ , ~ с и (/кип - 0] Я Ткип lnno„ т IT,,,
11.71. h =---------------------» 13,7 см, где Гкип = 100 С, = 373 К - температура
кипения воды. г^°
Дл Ту
11.73. /тах = ^-« 14 м. _______________________________
Г, Ро J л/ 1(Ро_Рн , , )2 Ро ~Рн , 1 (РО Рн , ,1 . ,
11.74. Внутрь пробирки на Дй = N ------+1-Л | +--------Л - --------+ /-AJ я 1,2 м.
Р S Р 8 Р 8
11.75. х = |+11 - >/1|p«2£h + /}2_p«ZAiA . 1 м.
2 1 Pg ' 41 Р8 1 Р8 ___________________________________
.. ., _ [Р 81 (2г + Л) +Ро Л1 +^1Р8( (Т’г + Т’О+Ро + 4Р g IpoTi (T2-Tt)
11.7n. У =---------------------------------------------------------------as пл CM.
„ __ Рн Ppi . . VP2 I p Рн I . .
11.78. ^эфир “ w 0>® кг, ^возд “ ' T*- 7q W
413
11.81. ф = р/рн = 0,388 = 38,8%. 11.82. Р = ££ « 53,6-Ю’3кг/м3.
К 1
11.83. р = фрн = 9,84 кПа.
Рн j Т\ Рн 2 1*^ Р
11.84. ф=^^ = 0,54 = 54%, от=нД, «1,38 кг.
Phi 12 к12
11.85. р = 2р0 Т/Тй « 1,5-105 Па. 11.86. Дот = (ф р, - pj Р= 2710 кг.
11.89. р = <р рн = 1,15-Ю"2 кг/м3.
ЦРн 3 3
11.87. р2 = ~—= 9,410 кг/м . Указание. Поскольку Р2 <pi, то часть паров сконденсиру-
л ±2
ется и абсолютная влажность будет определяться плотностью насыщенных паров.
Рн V, Т2
11.88. ф = » 0,42 = 42%.
Ро ?2 Л
11.90. В июле в — = <?2-P27j и 3,4 раза.
Р1 Ф1Р1 *2
11.91. Ф =----2------« 0,325 = 32,5%.
J. мВНп]
Рн 1 +-----
1 wn Рв
11.92. р= —|^-рв}®0,0133 кг/м3; ф = «0,494 = 49,4%.
Р2 - Ц| “ 2 Рн
11.93. V=-------»870 см3. 11.94.p» = !!L~«2,33 кПа.
М1(р-фРн) + Р2ФРн РГФ
11.95. от = отв = 20 кг,р =, в и 8,37-105 Па.
11.96. ф = фо + —-^RT, „ « 0,494 = 49,4%.
[с(/-/1) + г]ц Грн
Лт Рн Pi Л от л г, ,
11.97. — = » 0,17. 11.98. р2 = ~ « 2,26-105 Па.
от mRT /1 fiV
,, „„ lnn„. ,, . нК(ф2Рн2 Ф1 Рн 1 1
11.99. ф= 100%. 11.100. Дот = „ | —=—- —— «0,31 кг.
л 1 12 1\ J
„ . РнР^(Ф2-Ф1) по. РнР^О-ф) ,
11.101. Дот =---« 0,21 кг. 11.102. Дот =---------------^-=--и 6 г.
К 1 К 1
11.104. ф = Ф| + ф2 V1 = 0,27 = 27%. 11.106. Уг = К, - I ~ }« 0,066 л.
У\ + И2 рл1 ч Л J
11.107. Дот = 1« 9,210'3 г.
л 1 12 11 J
11.108. Дот = (Фг Рн 2 ~ Ф1 Рн 1) 29,2-10"3 г.
11.109. ДР~ 0,164 см3. Указание. При температуре t2 для насыщения пара необходимо до-
полнительно испарить массу воды меньшую, чем р V = 1,5 г.
11.111. ф =2о(1-1.|:>вл/Рс^. „ о,487 = 48,7%. 11.112. а = ~ » 8,84-10’3 = 0,88%.
РнО - Рп/Рв) Р Р1
Рвл (Р1 - Из) Ф Рн к т
11.113. = 1 - ----и 0,987:
Рсух Р0Р1Р2
414
ГЛАВА III
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ
§12. Электростатика
12.2. $ = — Р R » 5,6-104 Кл. 123. а = «3,66-10'12.
3-10‘3Л mZNA
12.4. F=(2Z|+^ N* f 2,57-109Н. 12.5.у- = ----------«2,27-1039
4лв0р2г2 *1 4пг9утМ
12.6. г = I Je!2 ,}/б« 7,6-Ю'5 м. 12.7. q = К л р г3>14пео7 » 1,6-10’19 Кл.
104 nJyEopJ
12.9. q = 2 г 'ПГЁ^Ё « 1,05-Ю'5 Кл. 12.10. и = г2/<Ё « 17,3 см.
12.12. ?о = ^Ц-~ 1,33-Ю’9 Кл, где/ = г . ^Jgl) ==1м.
г2 V|?l|+V|?2|
12.13. На расстоянии х = I j - от заряда qt .
12.14. F = —2—2>/ (9, - q3)2 + (q2 - q4)2.
2 ne^a
12.15. £9 = 0,96 9.
32 л e0 m g Й 2
12.16. Q >-----------. Указание. Шарик будет находиться в положении устойчивого рав-
новесия, если при малом смещении его возникает возвращающая сила.
12.18. Q = - 4 л е0 (и - 1) т g l2/q « - 5,6-10’7 Кл.
tt tn т <l\Wq2 + q3) д3(Я\+^Ч2)
12.19. 9 = ± It 4 л Bq mg « ± 1,5-10 Кл. 12.20. Г]_2 =----2~;Г2_3=----------5-.
16 Л Ед Z 16 Л Bq I
, .2/з п2 г о -JT1
12.21. а = 2 arctg {q/Q} , р = л - а. 12.22. Т =-----—j- I— + —}.
8 л Ед Г 4
12.23. Уменьшится в л = Z|/Z2 = ^2 cos а » 1,3 раза.
12.25. Z0 = -r +Дх.
у 4 л е0 Л Дх
а/ 16^2 (VI- ВяЛеоо3 г—------------т
12.26. 9 = V---2 <2 + 1------ ” 1,56 " *Ео °
12.28. а. = 15°52, а2 = 7°5б'. 12.29. g =---2—5 « 9,99 м/с2.
_____У 8лвот12
12.30. 9= У ^П-.'П- а «б^З-Ю^Кл. 12.31. р = рк—^—= 1,6103 кг/м3.
А/ЗО/2-^) s-1
1233. F = -г4— IА + —+ -^--2}« 8,9-10"4 Н.
4 л во 4а2 (6-а)2 (6 + а)21
1234.9 = 4 (Л - АЛ) -V л ЕдЛДЛ.
415
1235. q = 4 (о -1 sin a) V л mgtg a « 7,9-10"* Кл.
1237. R = ..... 1238. AT=—g^ .
8 л EqT inegR
1239.? = <2?0-
12.41. E = = 2,45-10s В/м; силовые линии электрического поля должны быть направлены
по силе тяжести.
12.42. Т= mg + qЕ = 20,6мН. 12.43. Т= Jm2g2 + ?2£2« 22 мН.
12.44. Уменьшится на Да = a - arctg [(1 - r|) tg а] ~ 3°.
12.45. Уменьшится на Ах = . 12.46. Е = .
к Ч
ПАТ. Е = 4npgr . 12.48. Е = —-Ф~Ро^г .
3? Зд
TiZlelpK.V. , о п
12.50. ? = —- ,А«3,5-1О3Кл, Е =-------*—?«3,141013В/м, гдеZ = 26,А = 56а.е.м.-
ЛЮ-3 4 л go г
зарядовое число и относительная атомная масса железа соответственно.
12.51. ? = 4л е, г2 £ «4,2-Ю"8 Кл; Е2 = £ (г}/г^)2 = 37,5 кВ/м.
4£, <71+1 <7? I <
12.52. £ = ..... 1-z = 16 В/м. 12.53. £ = -- 21 « 5-Ю5 В/м.
[<£,/£, + 1]2 тг во Г
12.54. х = 341 = 6 см. 12.55. £ =-------------j- » 10* В/м.
2+ 2±----- 4 Л Е0 (Г2 + '/4 /2) Л
12.56. £ = ——£lS2. _ где знак <<+)> соответствует qrq2 > 0, а знаке-» - 9г?2 < 0.
4 л е0 а
12.57.4/ = у -4£2 ~£12 12.58. £ = —^^Ц« 81 В/м.
2 Et 4 л е0 о2
12.59. £ = 246 В/м. 12.60. £ = « 5,1 103 В/м или £ = 0.
ЛЕоЯ
4 Q
12.61. £тах = —J-------2 • Указание См. решение задачи №12.49.
3 у 3 л Е0а
12.63. £ =------------j-. 12.64. £ =-------------j-.
4лео(£2+й2Г 4ле0(£2+й2)^
12.66. £ = |е| £ = 3,2-10"14 Н.
Z |е| р d N. 13
12.67. £ =--5------» 1,54-10 В/м, где Z= 6, А = 12 а.е.м. - зарядовое число и относи-
6-10 ЕоЛ
тельная атомная масса угля соответственно.
12.68. £> = 4лео££2« 4,56-105 Кл. 12.69. £ = » 2,26-103 В/м.
16 Eq
12.70. а, б) £ = 0; в) £ = —« 1,2-104 В/м.
Бо
— ^о) 13 3
12.71. р =--ь------«-4,3 10‘ Кл/м . Указание. Вблизи поверхности Земли электричес-
' кое поле создается только зарядом Земли, а на высоте h над поверхностью — зарядом Земли
и зарядом слоя атмосферы, заключенном в сфере радиусом (R + й).
416
ПЛ2.Е =------Q_—
8 л EqR2
12.73. Е(г <£)= ?grD3 , Е(г >£)= —2—
4леоЯ 4леог
график £(г) представлен на рис. 21.
12.75. q = во S' Е = 2,655 • 10’5 Кл.
12.76. Уменьшится на ЕР = q Е (в - 1)/е + pg V* 8,84-Ю’3 Н.
Г
12.77. р = р0 —.
Е — 1
12.78. T=^l т2 g2 + [<з q/2 е0]2, а = arctg —.
___________________ 2 Ео»И g
2 (ч 2 “ 1) Ел tng чч по j
12.79. о = - —------’ °- -- » - 7,2-10 7 Кл/м2. 12.80. F = » 2,26-10* Н.
9 Ео
12.81. 0] = е0 (£] + £j) = 3^4-Ю’8 КлЛ?,о2 = е0 (£2 -£]) = - 1,77-10"8 Кл/м2. Указание. Элект-
рические поля £| и £3 заданных направлений и значений соответствуют отрицательному
заряду на верхней пластине и положительному - на нижней.
12.82. £в = £| sin a, Eq = 2 £] sin а. Решение.
Дополним обе полуплоскости справа такими же
заряженными полуплоскостями, как исходные
(рис. 22). Тогда напряженность электрического
поля в точке А будет равна £А = о/в0. Так как
относительно оси ОО' правая и левая системы
зарядов равноправны, то в результирующее
поле 11А обе они будут вносить одинаковый
вклад, т.е. £| = Е{ и 5^ = £?] + £^. Следователь-
но, £А = 2 £| sin а, или o/eq = 2 £| sin а. В точ-
ке В бесконечные плоскости создали бы поле
напряженностью £в = £А = 2 £] sin а, направ-
ленное вертикально вниз. Легко видеть, что £в = Vi £в = Е{ sin а. В точке С поле полуплос-
костей можно считать однородным и £с = <т/е0 = 2 £| sin а.
, 3£ F 3F
12.84. F= Vi ? |£2-£] |. 12.85.£а = -^, Еъ = -±, Ес = ^.
пи 2eoSF2 E2-Fx
12.87.91=—; q2 = q—рг~.
О'
Рис. 22
Гв.
12.86. Д£ = -£.
12.89. q = e0 S E. 12.90. qi2 = ± 'Л Q.
12.91. £a = £B = £d = - £F = 5,6104 В/м, £c = 2,8105 В/м.
12.93. £ = £q/<2 . 12.94. a) E = <3 £0; б) E = £0.
12.95. £ = <2 £0. 12.97. qp = - q .
E ~ 1 £ — 1
12.98. qp = - q -- вблизи заряда +?; qp = q --------- вблизи заряда -q.
417
Рис. 23
?1 41
12.99. <rD = -<т 12.100. <з_ = -<т —.
н 2е н е
£ — 1 £ — 1
12.101. qk = - q-, q" = q-----вблизи пластин с зарядами 4^ и ~q соответственно.
н е и е
12.103. <р = » 2,7 В. 12.104. <р = 9| + 92 + 2з + 9* + 95 + ?б и 40 $ в
2л Ео / 4 л Ео I
12.105. Дф =—2— | 1<2 11,9В. 12.106. Дф = —2--^—^» 4,5 кВ.
ЛЕо/ 1 <5 1 4л Ед г! г2
12.107. В системе координат, изо-
браженной на рис. 23, искомое гео-
метрическое место точек представ-
ляет собой окружность радиусом
R = 4 а, центр которой имеет коор-
динаты х = - 2 а, у = 0. Указание.
-V Так как заряды q\ = q и q2 = -2q раз-
22 ноименные, то в некоторой точке А
потенциал поля равен
= и =_______т____ _ ?
'Иа 4леоГ1 4леоГ2 4nE0Vx2+y2 4л в0 ^(6а-х)2+у2
Откуда получаем: 4 (х2+у2) = (6а-х)2+у2, или (х + 2а)2 +у2 = 16а2.
_ ma>2r . та>2 R2 .. „
12.108. Е =------; Дф =-------.Указание. При определении разности потенциалов
[е 2 |е|
между поверхностью цилиндра и осью следует учесть, что напряженность электрического
поля внутри цилиндра изменяется линейно в зависимости от расстояния до оси.
12.110. ф = .
4 Л Eq R
12.111. Ф = £А = 300кВ;= 471 Е°£й *2,1 • 1013.
И
12.112. ф = фо = 220 В; ? = 4 л eq (Р + /)ф0 » 2,410’9 Кл.
К
12.113. Я = йф2~°Ф1 = 0,1 м;? = 4 ЛЕ0Ф1(А + а) = 4 леоФ2(А + 6)«210'8 Кл;
ф,-ф2
Фо = й—®—й и 1,8 кВ.
4 л Eq Я
12.114. ф =-^2—_ = - 3,6 кВ. Указание. Учесть, что заряд и объем получившейся капли
4 л eqT д'9
равны сумме зарядов и объемов исходных капель соответственно.
12.116. Е =-^±2— „1,124 кВ/м, ф = ,^+2 и 4>5
4 Л Eq (R + г)2 4 Л Eq Я
12.117. Е. = О, £, = —» 74,7 кВ/м, Е3 = ^' + ^. « - 16,7 кВ/м;
4лео/22 4лео/32
Ф1=Т^~ {р + ^}«2,383кВ,ф2 = -^-{^ + ^}«-607В,фз = ^1^-«-1кВ.
4 л ео 1 А] Л2 4лбд1»2 "2 4лео/з
418
12.118. ф1 = , <f2 = ,^9D .
4ne0rR 4педЯ
12.120. <p j = —2— q>2 = 2—, Фз = 0.
4яеог 8iteor
12.123. qx = ± 2,67-10'7 Кл, q2 = + 0,67-Ю’7 Кл.
12.125. q2 = - 3,2- 10’19Кл.
Л, — Л]
12.127. Уменьшится иа А© = фл —=—.
Л2
Л1 -Л2
12Л29-9, = еГ7К’92 = еГ7Г'
Л| + «2 Л| + Л2
12.119.91=-8лЕогф, <?2 = 16 л е0 г ф.
12.122./ = г
91 + 92
2 '/919г ’
12.124. Ъ « 0,63 а » 3,15 см.
(91+ 9г)2 - .,
12.126. е = —:------«2,16.
4 9i92
12.128. R2 = Rx 46,7 cm.
Фо
12.131. ф = —2—-. Указание. Учесть, что потенциал на поверхности металлического шара
4 л е0 I
равен потенциалу в его центре.
12.132. Q = - 9 R/1. Решение. Потенциал шара складывается из потенциала точечного заря-
да 9 и потенциала заряда Q, распределенного по поверхности шара. Так как заряд Q распре-
делен по поверхности шара неравномерно, то удобно определить потенциал фо в его цент-
ре, разбив заряд Q на элементарные заряды bQ, расстояние от каждого из которых до центра
шара одинаково и равно R. Так как шар заземлен, то фо = 0 = —2—; + S----. Откуда
получаем: Q = L bQ = -q R/l. и
Л2 ~
12.133. ф = фо
12.134. ф = Г\ « 225 В.
4ле0л
12.135.Е(г<Л]) = 0, E(Rx<r<R£ =------s—i, E(r>R£ = 0-,
Inzer
1 Q R-2 ” Г
-, ф(Л] <r<R2) = —2------Г—, Ф(r>Л2) = 0.
4 П Eq Г Л2
12.139. Дф = — « 5,65 кВ.
eo
12.142. ф = Дф = 75 В; E = = 25 B/cm.
a a
ф(г<Л1) = 77----R~R~'
4neo Л|Л2
2
12.137. Уменьшится в I 1 + —з2-— I раз.
1 г^ЕоРо1
12.141. Дф =--------------------------
2ео
12.143. Е. , = а; £2-з = ?-
12 a L i b
12.144. Ex = —----—, E2 = —— ; ; O| =---------, o2 = -
Eo (a + b) ^(a + b) a + b
a b
a + b
12.146. <? = ± Ео £ S.
12.148. ДФ1 = Дфз = -^4-
10 Eq О
1,1И Л (Дф1+Дфг)а
12.150. Дф =------;-----.
a + d
12.152. ? = це.
ст а
a + b'
12.147. Дф = 6а^~-^.
Eq о и
12.149. Дф = -^-.
о Eq О
~d — 2 а
12.151.9 = 6-^-.
12.153. q = Q^-
419
izi56.9=e-^-.
а — Ь
12.159. <?пйп = S ед Е « 2,7 мКл.
12.161. Уменьшить на &d = d -—- = 1,5 мм.
CoS' "
12.163. С = ~Г-
d-2a
12.166. С = | = 2,91О’10 Ф.
2 4
(е-1)е08
12.169. Увеличится на ДС =--j----« 2,2 пФ.
4
12.171. Уменьшили в е/(1 + ц) ~ 1,43 раза.
12.173. Д<р = Ч> Дф0 — = 45 В.
£
Дф Ео dt
= 37,5 кВ/м, Дф. = ; = 375 В;
</] е2 + d2 В]
Дф Е| dj
= 131,25 кВ/м, Дф2= J ' = 2625В.
«] Ej + «2 Е]
2 в вп8
12.177. С = —~г— « 740 пФ.
d
«м л <^“2 а — Ь
,2л55-?=ет(^г
12.158. Дф = ^ = 5104 В.
12.160. Уменьшится в т/п » 1,7 раза.
12.162. а), б) С = Со
d — a
12.165. С = | ^=1,ЗЮ'|0Ф.
3 d
12.167. Увеличится в два раза.
12.170. Увеличится в в/и =1,4 раза
12.172.в = —= 6.
Дф]
12.175. £,= -АфЕ2
“1 Е2 + “2 Е1
г Д<РЕ1
£>2 = "j-----------
«1 Б2 + ^2б1
di Е|
12.176.-у-=
«2 Е2
Ел (Ео — Ei)
12.178. С = —-------. Решение. Так как проницаемость диэлектрика изменяется линей-
d In (s2/8]) _ _ _
но, то на расстоянии х от одной из обкладок оиа будет равна | е = Е| + —— х J, а напряжен-
ность электрического поля:
Е = —3— = —------2----------,
ее08 [в, + (в2 - erfx/d] e0S
где q - заряд конденсатора. Следовательно, разность потенциалов между обкладками равна
Дф = Je <& = J------— ---------dx = --—- In —,
о o (Ei + <62~Ei)Eo(e2-ei)eos ei
а емкость конденсатора _. .
c_ q _eoo(E2~ei)
Дф dlnfe/Ei)
3 E + 1
12.180. Увеличилась в ----—=1,25 раза.
2(s+l)
12.183. С = 3- = 510'2 Ф, R = —2— = 4,5 см.
Ф 4 л Ед ф
С. Сз (С! + 2 Сг)
12.186. С = „ „ = 2.4мкФ.
Q С2 + (С| + Сз) (С| + Сз)
12.179. С = 'Л Со (s + 1).
12.182. С = 2 л s0 d ~ 1,7 пФ.
12.184. С =
12.187. С =
12.188. С =
b-a
С, (С, + 2 С,) (С2 + С3) =
С] С2 + (С, + С2) (С, + С2 + С3)
2С, С2(С,+ С3)
12.189. С =
» 2,6 мкФ.
2С1С2 + (С1 + Сз)(2С1+С2)
С,Сз(4С)+С2)
2 С] С3 + (С] + С3) (4 Ci + Сг)
« 1,6 мкФ.
420
12.191. е = 2. 12.192. д = (е-1) С Дф.
12.193. Увеличится в (б + 1) раза. 12.194. Увеличится в « 1,33 раза.
6 + 1
,, . . Л (е -1) . . t (е -1)
12.195. Дфпар - Дф Е + Афпосл - Дф п
12.197. Дф = 2ЛДф0= 100 В.
С. С2
12.198. Qt = (?1 - ?2) —J—, Q2 = (?1 - ?2) —.
С| + С2 С| + (_>2
12.199. а) Дф/ = Дф2' = ’Л (Дф) + Дфг) = 150 В; б) Дф/ = Дф2 = ’Л (Дф) - Дфг) = 50 В.
С) С2 С)2 С2 .
12.200. Дф' = 2 Дф -—» 266,7 В, q) = 2 Дф -------!« 2,67-10'8 Кл,
(Ci+C,)2 (С,+С2)2
С С
о2 = 2 Дф ---*—Ц » 5,33-10‘8 Кл.
(С. + С,)2
12.201. Дф = |{ ^1+4аАФоЫ} = 20 В. 12.203. Со = С, + С2 + С3.
а
12.204. Со = С. 12.205. Со = 1Л (С, + С£.
12.206. Со = 2С.
12.207. С0 = 63Лб С.
Рис. 24
12.208. Со = 'Л С (V~5 - 1). Указание. Поскольку система кондеи-
саторов бесконечно длинная, то, отделив от нее первое звено, мы
получим ту же систему, емкость которой Со равна емкости исход-
ной системы. Поэтому емкость всей системы (рис. 24) можно
найти как
(С + Со) С 7 7
’ ипи Со2+ССо-С2=О.
(С + Со) + С
12.209. Со = 6/з С. Указание. Точки, лежащие в вершинах К, L, N, М «куба», имеют равные
потенциалы, поэтому их можно соединить.
2
12.210. Со = 'А С п. 12.212. А = Ч°Г « 2,25 1 О’6 Дж.
Ео (а + г)
12.213. Дф = - = 7 кВ. 12.214. А = (?2 ? + Г* ~Z)«3,6 Дж.
? 4лео/7Л7Т
л ?0(?2-?1)(^2-/1) ,п п . 9(?2-?1)(^2-1) псо п
12.215. Лт;п =--------—-------« 30 мДж. 12.216. А =----77^---------« 0,58 мкДж.
т1П 4 л е0 Л12 4<2лЕ0а
п д2 I 13 10 1 „ , 1911+72 (1 11
12.217. e-4jteJ/() 2/+ 2/2|« 0,135 мДж. 12.218. Лтк1-? ^R~^Ri + di
12.221. Лтй1 = - q -f-1 sin a » -3,4- IO-6 Дж. 12.222. Лтй1 = | q | = 0,35 Дж.
2eo c
O2 1
12.224. На Д1К= 12.225. W= (q, q2 + qtq3 + q2 q3).
421
1X226. ЫР= 2 л so (<pi - Фг)2. «l+«2 12028. Д1Р= и U710’4 Дж. 2а
а2 е-1 12O29.fi = z с е ..... QQ (Аф1-Дфг)2 х<п-3тт
н 1 к: । Р + ьо 1 a с *
Ct Ст Дф| ,, 12031. W=-^- -? = 0,4 Дж. С] + Cj ~ 12032. А = = 0 J5 Дж. 2 п
Ел 5 Д/ Д<р2 12.233. А= — =5-. 2d2 12035. w = » 2,2-102 Дж/м3.
12.236. Лщщ ='ЛеоКо2 * S- 12037. Лтщ = - 2 Е Eq Ео S d.
12038. Лт(п = - 'Л Ео (Ео - E?s d- 12.239. Л,™ = 'Л Ео (е - 1) (е Е2 - Eo)Sd.
2 12.240. Л = 2^. 12241.Amin = a Sh . 2ео
12.242. Лщц] = « 25 мкДж. 2 12043.На ДИ'=-2-^» 1,13 Дж. 4е&5
2 . 12.244. fimin = ^« 4,5 мДж. 12045. Увеличиться в 5Д раза.
12046. fi = ~ 27 Дж. 2 , 12047. Л™, = ^«2,26 Дж. 2 Е()О
12048. Hmin = ^«6,78 Дж. 2 Eq о 12050. JKmin_^pL«l Дж. 0 Я Eq А 12.252. В и раз.
12051. Лтт - (1 Л ) о Л Eq Л
12.253. А3 = ЗА; Ап = 'Л п (п - 1) А. 12055. Дф = -^= 100 В. 1*1
12056. Д«р = 1,02-106 В, гае с = 3-10 |е| 8 м/с - скорость света в вакууме.
12057. и ug - 2W— ~ 1,7-104 м/с; г = и т т ил < T7V® 3,8-10’5 с. |е|Е
12058.и, =Vи? + glglZ ~ 1,25-103м/с. тво 12059. и ="V 2lgl^ » 4,7-103 м/с. тС
12О60.ДфЮщ = ^-284В. 12 761 г l<?lfi(Af+>n)
4 л E0E(m fi + 3/| ^ |)
4 я е0 /2 глЕо^/г^ + ^-г/о)’
12065. р = arcsin {tg а V 1 + |e|(?2~?l) }. 1 т и sin a J ,,,,, д/2 |е| Фо 12.266. Dmin — ’ т
12067.5тах = u"V-^ » 0,25 м. а И 12 26ЙП V 2 Iе! Аф 1 “2/4
т 16 Дф2'
о1 „ _ q1
12069. ошш прп 2 umin — 0 иРи . ,2 4лео/ 4лео/
422
Указание. На шарик при движении будут действовать: сила тяжести т gt направленная вниз,
и сила Кулона FK направленная вверх. Пусть в исходном положении Fx > т g. Тогда в нача-
ле движения ускорение <? шарика будет направлено вверх. Однако при движении сила Ку-
лона будет уменьшаться (так как будет увеличиваться расстояние между зарядами) и, если
шарик достигнет положения равновесия, то после этого вектор ускорения <? изменит на-
правление на противоположное и шарик упадет на поверхность Земли. Следовательно, для
падения на Землю шарику достаточно достичь с нулевой скоростью точки, где его ускоре-
ние равно нулю (положение равновесия).
mg + gE
12.272. дх = ”»>2«
|е|£
т Op sin2 а т op sin 2а
max=2(mg+?£)’ S= mg + qE~'
« 2,84 м. 12.273. и0 2 .
т cos а
12.274. о = opV 1 , Р = arcsin
ШОр
12.275. W=-----?-qEl---------.
2 cos а (tg а + tg Р)
12.277. Ах = lelA<pf= 5,5 мм.
2md\>2
12.279. А/= — 2~.^2 .
о0 2
и0 sin а
V ор + 2 7 £ d/m
к d/P sin 2а , „
12.276. Д<р = гтт— = 150 В.
|е|/
12.278.1 < ^2WCd2/qQ .
12.280.о = л/2ИДд>+Л1^
т imlty
tn g d Дфл q
12.281. Д? =----------= 1,6-10‘19 Кл. 12.282.5 = 7 см.
Дф (Дф + Дф0)
12.283. п = ^4 • 100% = 0,08%. 12.285. о ="V иЗ + —|--М « 26,8 м/с.
Г___________________ 2 л ер т 1 ‘i ‘г1
12.286. и = 'V2g£ + a^^1—«4,25м/с.
2л&отл
12.287. umax = ^2 g^ -—тг: ...г - 1 . Указание. Подвижная бусинка будет иметь мак-
<о V 4 л Ер т g
симальную скорость на расстоянии I от неподвижной, соответствующем положению равно-
весия, т.е. когда сила тяжести бусинки будет равна силе электрического взаимодействия бу-
синок.
2 2
________ , . 2 a /cosasm a
12.288. йтах = Z sm a cos a + --“-———-------.
4nEpmg£(£ + 2 / cos a)
12.289. / = -—2 -. 12.290. /тах = + V
4 л Ep m g ц /0 m“ 2 4 2 л e01 /0
12.291. D| = u2 = 21>3 = , =. Указание. Скорости тел будут максимальны в момент
у 6 п Eq lit I
прохождении ими положений равновесия.
12.292. и =
Я ’-----------
8 л Ер т I
423
12л’3- ип>‘“ = {н«/ + т-^-;-29Л^ё1}Л Указа-
/ Wz ние. См. решение задачи №12.284.
j 01 12.294. 9 = 2 я Ео a Д1К « 2,3-10'7 Кл. Решение. Рассмот-
‘ । рим первый из освобожденных шариков. На большом рас-
I 0Л стоянии от многогранника, в вершинах которого закрепле-
\ / ны заряды, освобожденный шарик будет свободен и иметь
\ 0N- ^скорость иь величину которой можно найти из закона со-
jOUV-2 хранения энергии:
Рис. 25 —1— J _1_ + + + __1——!— + —5— +... + —— + ...} =
4 л Ео 1 “1-2 “1-3 O\-N “2-3 “2-4 a2-N
т«1 О2 ( 1 1 1 11 1 1
---=— + —---1 + . . . + + . . . + + + . . . +
2 4 Л Е0 “2-3 “2-4 a2-N “3-4 “3-5 a3-N
где aj_j - расстояния между зарядами с номерами i н j. Легко заметить, что
1 1 + 1 4 1 .ио?
4 Л Eq “1-2 “1-3 al-N 2
Для второго шарика, когда он станет свободен:
<?2 1 11 1 11 1
1 + ...+ +...+-------+------к . . . + + . . .
4 Л Eq “2-3 “2-4 a2-N “3-4 “3-5 a3-N
т «2 ?2 1 1 1 1 11 1
= —=— + —-— ------+------... +-----+ ... + — + — +... +--------
2 4 Я Е0 Дз-4 аЗ-5 a3-N а4-5 а4-6 ab-N
ИЛИ
4л Е0 “2-3 “2-4 a2-N 2
ПОСКОЛЬКУ “]-2 = Л2-3’ “1-3 = “2-4. “1-4 = “2-5 и т д- (РИС. 25), ТО
т и? т и? а2 1 а2
^=—1—^=-2-----------------------------------—•
2 2 4 л Eq ai-N 4 леоа
Следовательно, q = 2 ‘V л EqO Д1К.
a 4nenR3a>2 < 12.297. = гЦ « 1,5-10‘5 Кл/кг. т 1 ?о 1 12.299. т = 2 у «9 г. 4 л е0 R и 12.298. R = I —j }Л« 1,36-1О'10 м. 4 Л Eq т <0 12300. ш = г- . з/2лЕ0т(г2+‘/4Л2)'4
12301. о> = "V 2 т 11 Q | - '/4 q }. 4 леошЛ 12.302. W= - « 14,4 эВ. 8 Л ЕоЯ
12305. ДГтах = 6 (q Е + т g).
- / 2 Еп »1 /
12.304. 2 л V —------.
?о
, -J / sin a j , о2 sin а ]
12.306. и = V------i т gtg а - *----, | .
т 1 2 л Eq/'
424
12307. Т= 3 (m g - q E) cos a « 0,3 H. 12308. v =^2gl + -S-@— | , ,' , -y-M •
2яео»1 Н/2 + й2 l + b‘
12309. Силовые линии напряженности электрического поля направлены:
„ 20леоR2(Е-mg) л 20ле0Л2(| </|£+mg)
вверх: Q =------------ при qE*mgnq>0,Q =---------j-j-j-----при q < 0;
20л Ео R2 (qE + mg) 20л enR2 (m g-| q I E)
wsb:Q =---“ ---------- при <7 >0,£) =---pyj------ при| q | £# mgnq <0.
। 2
12310. umax = ’ 2 gg sin a - —, где a = 60°.
8 л Eo m R cos a
12312. Т=2л"7^4 .
2 q E
12314. Уменьшится вА/ 1 + ' 'CT раз.
^>mg
12316. T= 2 яА/ .1.
g2 + q2a2/4 г20 m2
12313. T = 2 л V-----v— .
2 geo +1 q I a
2 2
12315. Уменьшится в I1 + г г } 1
еош g
12318. T= ”/2 2 ” £o"L.
<7
</4ne«mgJ
12319. T= 2 л V-----— « 0,016 c.
?|e|
12320. T=2 я If +
l Л
qQ Г‘Л
32 л e0 m R3
m
_______ ... -г . Указание. Период колебаний бусинки
1 g mg/R + qQ/32m0R3!
равен половине суммы периодов колебаний в желобах с радиусами кривизны R и 2R.
12321. T=n
m I3
12324. и > -j- Iе' = 3,2-106 м/с.
N 2 Я Gq m R
12325.umin = { 2g3 (>/1?21 -^11911)} "PH Ift I >l«i I; u = 0 при |?2|S|9,].
4 4 Я Cq m I 1
a[e\2 |л|2
л E0 a m u2 + |e|2
_________"H2
л Eo m (и, - иг)2 + |e|2
_________И2**
|e|2 + 4 л Eo m u2 d cos 2 a
12322. Г=2 л
12326. rmjn =
12328. Tmjn —
12330. rmjn -
12.327 r ---------“______
rmm — . 2 ’
4 л Gq m и
|л12
12329. rmin =------------j.
(uj +D2)
12331. и = -/= ?
у 8 л Gq m d
12333. vmin = N при ? 2>0; u = 0 при ^g<0.
2я Gq m R
12334. и =
2я Cq M 1 Aj ^2
_\e\Q(l2-41R + 4 R2)
4neQlR(l-R)
12338. и
2 я Cq R m M
12336. lPmjn =
12335. и =N uo + ——— « 4,4 м/с.
2л ео шЯ
12337. и =а/ d2 + klleIZ\ 80 км/с.
3 MEo
12339. umin =л/3(Л/+д|Й5
mm 4леоиЛ/Л
425
§13. Постоянный ток
си
13Л.</> = ^«0>ЗА.
ш
13.4./ = ^ = 2 МА/м2
13.6. < и > = т-Ц = 6.25-10'3 м/с.
|е|и$
13.8.1=-----К « 1,5 мкА.
4nrVneo»ir
133.Ne=^“21017.
13.5. р = -^— - 2-Ю"6 Кл/м3.
<и>
13.7. <р > = « 5,7-10'" кг-м/с.
|е|
13.9. А? = ’Л (/0 + 7) / = 15 Кл. Указание. Сила тока в проводнике нарастает по линейному за-
кону. Заряд, прошедший через поперечное сечение проводника за время /, завей А? = < I> t,
где < 7> = 'Л (4 + /) - среднее значение тока за рассматриваемый интервал времени.
13.11. /= —j— = 100 А, ток заряжает конденсатор.
e0SUv 1,53-10”" ...
13.12. 1 =-----г = —-------, [А], ток заряжает конденсатор.
(4)-и0 (0,1-20 О2 F
1 + /и pn R S
13.14. Уменьшится в т] = --= 1,875 раза. 13.15. т =----» 534 г.
а/2 1-я р
13.16. Я = . Указание. Сопротивление dR части проводника длиной dx равно: dR = р dx/S,
где р = ах - удельное сопротивление этой части проводника на расстоянии х от одного нз
концов. Полное сопротивление будет равно сумме элементарных (интегралу по всей длине
проводника).
13.18. R/Rn = 1 + a t« 12,5. 13.19. t = — « 244°С.
а
13.20. ДЯ = р0 Z а (/j - t^/S « 273 Ом.
R,+4Ri-4R,R2
13.22. г, = = 3 Ом, г2 = Я, - г, = 2 Ом.
13.23. В точке, делящей кольцо на две части, длины которых относятся как
13.24. Сопротивления Я2 и Я3 параллельно, а Я| к ним последовательно.
13.25. Яцепи = 3/4 Я = 12 Ом. 13.26. Уменьшится в л2 раз.
5-VT5
5 + >П5'
Рис. 26
Я
13.27. На Гп частей.
13.28. Схему соединения см. на рнс. 26.
1330 R___________Я1Я4(Я2+Я3)_______
1з^.яцепи-(я1+я4)(я2+яз)+я1я4
Я] + я,
1331. Яцепи = 2 +R2 = 22,5 Ом’
« 1,76 Ом.
(я. + гяля,
13.32. Яиепи = -А-!------« 2,22 Ом.
цепи Я,+2(Я2 + Я3)
13.34. Яцепи = Я.
13.36. г = 77 Я.
1333. Яцепи = 54 Я = 2,5 Ом.
13.35. Яцепи = Л = 1 Ом.
426
Рис. 27
13.44. Лцепи = 2R = 2 Ом.
13.47. Лцепи = 13Л R.
13.49. /{цепи — R-
13.38. Уменьшилось в 9 раз.
Схема соединения представле-
на на рис. 27 ,а, б.
1339. /{цепи = R'
13.40. /{цепи e R-
13.41. Лцепи = 2Л R = 2 Ом.
13.42. Яцепи = 2ЛЯ = 2Ом.
13.43. /{цепи = 3AR = 6 Ом.
13.46. /{цепи = /{-
13.48. /{цепи = ^12 R-
13.51./{цепи = 'ЛЛ] (1 + V1 +4Л2/Л1) = 6Ом. 13.52.Rx = R (<3 - 1).
13.54. R = U/I= 20 Ом. 13.55. U = q R/t = 6 В.
13.56./=-5/-^« 0,24 А. 13.57. С/=^=120В.
4р/ о
13.59. U = I(Ri + R2 + Л3) = 400 В, (/, = IRt = 200 В, U2 = IR2 = 120 В, U3 = IR} = 80 В.
13.60.1- Л| + + Я} - 1 A, Il - - 6 A, I2 - - 4 А, 13 - - 1 А.
13.61. Уменьшить вт]=р*- = -^ = 8 раз. 13.62. Уменьшится в т] = раза.
13.63. R = Т’Т = 3>2 Ом, R л = 7^4,8 Ом.
Ji h h
-- r (<Pi-фг)Лз+ (<Pi "<Рз)Л2 . a
13.64. I\ = —— — — = 1 A,
Л i R2 + R1 R$ + R2 R3
j - (Ф2 - Фз) д| + (<Pl - <Рз) R2 _ 1 A
Rt R2 + Ri R3 + R2 R3
13.66. Увеличится в 10/9 раза.
<?/
13.69. /кз =- ,„- = 5,5 А.
кз- S-IR
13.71. Л =-у = 6 Ом, г = ^7^ = 4 Ом-
(<Р1 - <Рг) Дз+(<Рз-<Рг)д1 _0
Л] R2 + /?| r3 + R2 r3
. Л h № ~ *1) ПД7Д
13» 73. Lv <» — _ • 0,47 А.
к-3- 4Л2-/.Л,
13.75. г = = 1,5 Ом.
1-9 " V 1 + Л2 17
13.77. Уменьшилась в rj = раза.
£ R2
13.67./2 = -5|-=|Л/| = 1А.
л2 + «3
13.70.Меньше в т] = И* * = j раза.
„ Ц1/2(и-1)
nUj- U2
RlR2(.^2~^l) псп.
Ui R2 -U2Rt
13.76. /== т-4— => 0,33 А.
lAR + r
Ri — Ri
13.78. &<?А-В= в~~~^ = 48 В.
л| + Л2
13Л0./!=72 = /з = /4 = ^ = 6А,/3 = 0.
13-79-1 = ---гЧг—Г-7Г - 3 “А-
Л| R.2 + Rj + R2 Я3
427
13.81. RX = R.
13.83. При R = Г| - r2 на элементе с внутренним сопротивлением Г|, при условии Г] > г2; прн
R = г2 - Г| на элементе с внутренним сопротивлением г2, при условии r2 > Г|.
,, ал п <?2 <?1
13.84. При — <---------.
(А ~ 4) (h + 4 —А) + (4 *“ А) (4 — А “ А)
13.85. <?, = (г. + Д) /3 = 5,14 В, г> = R .'J/ , ,\ А = М* Ом;
(А ~ А) (А ~ 4) + (4 ~ А) (А + А)
А — А ~ А А + А
^2 = (Г2 + Л) 4 = А5 В, r2 = R . . - п 7—~ = 1,76 Ом.
А -4 А - 4
13.86. Дф/J = 0. 13.88. £7 =•/*.(<? l + ^2>.
13.89. 1 = <?2~<?| = 2 A, U = <?1 Гг + —-Г| = 1,5 В.
г, St-U 1
13.90. — = —--= 4.
r2 U-S2 3
13.91.7, = ±^-R(g2-SA) t о5 А> h = ^г.-Д^,-^ a _ о g7 А
П r2 + R (г, + rj г, r2 + R (г, + г£
U = R---1,8 В.
г! r2 + R (г, + гг)
S - 7, г, 7 г,
13.92. R = ---~~r2 = ^ Om,/2 = /, —= 0,5 А,7К = /,
/1(г1+гг) 2 3 2 ’г2
13.93. г = R.
= 1,5 A.
13.94. Л = г.
13.98. /= —*2 Г|+-1Г2 = 1,4 А.
R Г| +R Г2 +п г2
13.95. и = 200, m = 2.
13.99. /=—Г2- = 0.
R2 (1 "1S + R\ ( g I — £ г)
13.100. J= ——» 0,06 A.
R\ R2 +й| R2 +R2 R2
13.101./=/-.
4 r
13 .104.1 =
Л) R2 + Л] Ry + ^2 *з
13.102.1- ----------=--------= 0,45 А; не изменится.
Л] R2 + Л] Л3 + R2 r^
13.103. / = ^2 Д | ~^2 = 0,5 A.
Л| к2
<?2 ^1 — ^2
13.105./= ^ & + д = 0’02 А; против часовой стрелки (или слева направо).
1Т 1 ПЛ Г - ^2 Д2 + ( <^1 + <^г) дз
• • R(R2 + R3') + R2R3
/ (Л| R2 + Л] Л3 + R2 R^y ~ <?i ^2 -
13.107. ® =--------------------------------- 3,6 В; положительный полюс источника при-
соединить к точке В. + &2
428
13.109. Заряд и разность потенциалов увеличатся в ц =
раз.
<?1 С1 — <?з Со
13.110. Дф = ' 1 2 2.
Ci + с2
13 111 и - Сг С3 ( <?1 + Ф + ^з) _ 2 в у _ СхС3(вх + вг + в3)
1/1 схс2+схс3 + с2с3 'U1 СХС2 + СХС3 + С2С3 ’
тт С| С2 ( <?1 + <?2 + <?з) й п
Ui = г г = 6 кВ-
13.112. q = q3 = 'Д С U, qx = q2 = gt = q5 = '/б С. 13.113. С4 = 6С.
«Тил г {в1~в\)С2~в\С3 _ (<?i -<?г) С]-в2С3 <?|С|+<?2С2
13.114. q, = Cj -------------, q2 = С2 -ТГ, , ft = Ч - Z. ТГ
И-Д<Р)С2 (<?-Д<р)С,
13.116. Ux = — — ® 3,3 В, и2 = — « 1,7 В.
13.118. <F=
13.119. R =
13.117. q = (I R + в2 - <?,) C.
Rd£R + r) = 2 55 B>F=^=i;i.io6H,9 = e0S'£ = 4,410'lotoi.
К 2
f d E £CR\ £
« 2,25 Ом. 13.120. q =--—!- = 1 O’6 Кл.
2(g-dE) 4 r + Rx+R2
13.121. /min = -f = 20 A, /max = 120 A. 13.122. q = 'A C S « 3,3-W6 Кл.
Л2 Aj Л2
R2 S C R2 £
13.123. Д<р =-—= 2,1 В, q =-----—V = 4,2-10"° Кл.
г + Rx + R2 t + Л] + R2
>С(Й,-Й2)
13.124. q = - - -« 4,510' 2 Кл.
2г + й(+й2
C2 R2 — C. Rx
VAB (Сг+С^^+Лг)
CR2 Rj
13.125. q = 2Л С S = 6,67-10'6 Кл.
С| Л, — С2 r2
13.127. q = U !
4 rx+r2
13.128.0= е
Г (Л2 + Л3 + Л4) + Л4 (/?2 + Я3)
CR2 Л4
1,43-10'3Кл.
CR3 „3
—-—«3,4310'э Кл.
13.129. о =<£ ,
r (R2 + R3 + й4) + й4 (R2 + Л3)
13.130. Увеличится в 10 раз н изменить знак. 13.131. Увеличится в 6 раз.
13.132. Увеличится в 2 раза. 13.133. q = Ц С <?.
niu Az. <?1 Л| (Л2+Л3)-<?2Л3 (Л|+^2)
13.134. Дф =-----------------------------= 1 В.
Л] R-2 + Л| Ry + /?2 л3
( <?1 - <?2) G (Л1+Лз) ( <?i - <?г) С2 R3
13л35'91" r,+r}+r4 '92 = Л, + Лз+Л4
13.137. a = arctg -g 1—
m d ио (2Л + r)
m d Un r tg a
13.138. R =-------------------------
|e| <? I - m d u0 tg a
429
13139 Vn>—е~^~ M.13S.v0>rf 29 m ’ 13.142. Я] = р Vffi'pT = 240 /Дз-/2(Д2 + Дз) Д + Да 13.141. /0 = Z-vA = А 1, .4» г /ЛШ 10,1 А. 2 А.
Да + Дщ
1X144. Лш = —^«Юм. Z~/G 100 л ЯА 13Л45-Л“ = /-100.п = 10 Ом.
13.146. Увеличится в ипар = 4п - 3 = 37 раз. 13.147. R = Rq = 261 Ом.
Уг/0 „ RJU(Ri~R2)
13.148.Rm = - -°- = 22,2 Ом. 13.149.Rq = ------- = 25 Ом.
I-NI0 «2
ЯпДЯ.-ЯЛ ЩЯу + Яд)
13.150. Rq = , прн Я, > Я2. 13.152. l/max = —= 1000 В.
Я2 лу
U1 т /у Ry Uy — /у Лу U3 ~~ ly Ry
13.153. Л1 = -• • v = 9 кОм, Ry = - - = 49 кОм, R3 = -r -• = 249 кОм.
/у /у /у
13.154. Ry = . (и-1)(Я + г) Uo U, R, 13.155. t/2= 01 1 =15 В. С/j ^Л| - Kq) + C/q л2
13.156. Яу = Я г/г. 13.157. Возрастет в 4 раза. U2
13.158. Яу^ 3675 кОм. и. 13.159. Я2 = Я] ^=100 кОм.
13.160. С/дв = -—= 7,2 В, U3C = U3 - СТдв = 4,8 В, UAC = U3 = 12 В. Решение. Пос-
1 +
кольку C7j + С72 * ^з>то это означает, что измерительный прибор (в данном случае вольт-
метр) вносит погрешность. Если вольтметр подключен между точками АВ цепи, то полное
сопротивление цепи равно:
п Л]Ry п
Дцепи 1 = R + Л2>
где Ry - сопротивление прибора. В этом случае в цепи протечет ток
<? в
1 Дцепи 1 Д| Ду „
Я,+Яу 2
и вольтметр покажет напряжение, равное его падению на участке между точками А н В:
U Д1 ДУ__________________________?_____Д1 Ду __________£______
1 1 Л| + Ry Ri Ry „ Ri + Ry Д2(Д,+Ду)
Rt + Ry 1 RiRy
Аналогично в случае, когда вольтметр подключен между точками В и С:
U S Дд ДУ ______________________________________<?___
2 ^2 Ду Ri + Ry Я] (Я2 +Яу)
Я2 + Яу 1 + Я2Яу
При включении вольтметра между точками А н С:
У_________£ (Д1 + Дг) Ду _ £
з (R\ + R2) Ry Я|+Я2 + Яу
Д| + Я2 + Ry
430
13.166. Уменьшилось в r| = —— = раз.
и —1 9
Действительные значения напряжений между соответствующими точками цепи могут
быть найдены из полученных соотношений, если положить Ry = »:
^АВ = » J» = » 1 ₽ ^2’ ^АС ~ &
Решив полученную систему уравнений, придем к ответу.
П161 II URi 6ft 6 П II URl 51 4R II +Rd 175 R
13.161. C/] - +jj2 “68,6B, -51,4 B, Umax- — - 175 B.
Лл 72m
13.162. U2 = 8- 2Ut = 5 B, U3 = 17, = 2 B. 13.164. R2 = 10 72, + 9 D .
72q + 72ш
13.165. а) Включить последовательно добавочное сопротивление 72доб. = у^,ИГ ® Ю6 ^м;
„ ____ „ nN г п. „
б) включить параллельно шунт сопротивлением 72ш =-—— = 0,1 Ом.
I — Nn
URy
13.167. R = ---- « 20 Ом.
I Ry-U
U2 - и02
13.173. Лдоп = ——у= 72,6 Ом.
13.168. t7 =—~ = 2 B.
и +1
13.169. Если R 2 > Ry 72A, то более точно сопротивление можно измерить по первой схеме,
если R 2 < Ry 72А, то по второй.
U2
13.172. N=N0 ~ = 9Вт.
ио
13.174. и = =13.
U2
13.176. Три лампочки мощностью Nb а также две лампоч-
ки мощностью N2, соединить параллельно в два звена н
между собой соединить последовательно (рис. 28).
1 + а /1
13.177. N2 = Nt ------L « 44,5 Вт.
2 1 1 + а /2
13.175. N =
13.180. Лампочка сопротивлением R2 в п = 1,5 раза.
<?2Й
13.181. N=----^=8 Вт.
(R + г)2
13.182. /|>2 = ^~4 —, Л = 0,5 А, 72 = 1,5 А.
13.183. N= ( g~ = 16 Вт.
Г
13.185. N2 = j' Г) 12 Вт.
13.187. — = ^ t 2r^ « 0,62.
n2 2(R + r)2
13.184. ц=-^ = 0,8 = 80%.
NiI2-N2I^
13-186-z-=ithvr=62A-
TV, №
13.188. N= 1 2 = 20 Вт.
JVj +
431
jgp D D 2
13.189. N =--------—~------r « 266,6 Вт. 13.190. У « 3,84 Вт.
[(r + ^X^+^ + ^V
25
13.191. У« 23 Вт. 13.192. N=у У] = 2,5 Вт.
13.193. N = г { Г “ 36 Вт- 13.194. г = Л (<2 - 1) • 4,14 Ом.
13.195. R = -ИГ(1~Я)^С(1-»Ъ^П 13.196. а = п±2^^4п=
1-т)У 2"
13.197. U= 'ItyNR = 500В.
13.198. Напряжение на входе линии и сопротивление потребителя нужно увеличить соответ-
13.200. Ях = Я/<2.
а,
— = 5 раз.
“2
13.201. В -£ = = 1,5 раза.
Л \ п - 1
5 j?i + VЯ. Ло 1—
13.202. г =С72/У«60,5Ом. 13.203./кз = —----т=М- <У«5,16А.
К ' Л] <«2
13.204. <?= ЗЯ / = 300 В. 13.205. N = ’/16 Уо = 45 Вт.
13.207. <?=2Утах// = 6В, г = Утах /I2 = 1 Ом.
13.208. Утах = Ц <?/тах = 4,5 Вт, г = 7-= 2 Ом.
Jmax
13.209. ДТ»~ *•« 31,7 К. 13.210. п = 4; последовательно.
4т с г
13.211. В два последовательно соединенных звена, в каждом из которых по два параллельно
соединенных сопротивления.
13.212. Утах = = 125 Вт, Укз. = т? — = 5 Вт.
2
13.214. Q = (/°~р Дт = 640 Дж. 13.215. <I> = 'Л 3Q/R т « 10 А.
13.217. Увеличилась в —-— «1,1 раза.
1 -Т]
13.218. Разделить спираль на две равные части, которые соединить параллельно.
13.219.1 = ”—^« 1,16 м. 13.220.1 = *а2и^ « 36 м.
4рУ 4р0
(72т
13.221. ДТ= - « 23,2 К.
Р Ро I с
13.222. N =---—-« 2,88 кВт, Я = - - -------« 20,34 Ом, где 1КИП = 100°С.
т c»” ('кип.-О
Л'ЯТ'и.п , „
13.223. и =J« 7,65 м/с, где Т^п = 373 К. 13.224. N= % N= 121,5 Вт.
И rpo S
432
= 400 с.
• 2
13.228. Ar = п2 = 62,5 Вт.
К
13.230. п'= " 0,67 = 67%.
1 + Ц
gI(I0-T)t „„
13.233. А = —Ду—— = 8 Дж.
4)
13.235. и = = 72 км/час.
Г
82%. 13.237.1 = « 28 А.
П Ut
т. = юо°с.
13.225. a) t3 = r, +12 = 30 мин; 6) t3 =
Nii.N-Nd
13.226. Nq -.
g___/ T
13.229. T] =-— = 0,9 = 90%.
g
13.231. В= 4 раза.
1 -Т]
13.234./=£^££«49А.
П и
13.236. #=£//= 1,1 кВт, n = U~JR « 0,82
13.238. т] = 0,52 = 52%, где /,
13.239. т = « 15-Ю"4 кг.
13.240.1=У « 23,4 А.
т)Лт
и It
13.241. m = 88,5 г.
П9
13.243. F = — « 97 кКл/моль, |е| = А1‘ « 1,6-10'19 Кл.
тп 1 mnNA
13.244. А = 103 * 65,6 а.е.м. 13.245. т = « 3 г.
/ I П г
13.246. п2 = «1 -г—* = 3. 13.247. п = = 3.
1 1 Л| тг mF
13.248. <? = /Д/=1 Кл.
13.249. N = й 2,35-1021, где ц = 65-10'3 кг/моль - молярная масса цинка.
М
13.250. -« 5,68-Ю17, где ц = 59-10"3 кг/моль - молярная масса никеля.
И
13.251. </ > = Р-^Р—-« 1,6 А/дм2.
13.253. / = ^ = 2,61 кА/м2.
13.256. т = 0,025 к t2 « 30 мг.
13.259. q = 2р^’~ -- « 8-103 Кл.
К i
13.261. Q = = 3,03-107 Дж.
к
13.263. Q = т UnF « 9,2-107Дж.
13.252./ = £^ = 67 мин.
*1
13.254./ = ^у = 3 часа.
13.257. т = (/, + 2/2 + /3) « 4,1 кг.
13.260. Т= 2£Г„и^« 1500 К.
р
13.262.#=«29,6 Вт.
Л2/2
13.264. Q = « 120 кДж.
433
§14. Магнетизм
143. В = ^ —» 1,67 кг4 Тл.
2 я П г2
14.12. В2 = 1,2-101* Тл, 12 =
143.В»^- = 210‘4Тл.
2яг
14.4. В = «2,5-1 0-4 Тл 14.5. в = 4l}2 + l} = 5-10’5 Тл.
2 я rtr2 2nd 1 2
14.6. На прямой, параллельной проводнику и проходящей иа расстоянии 5 см от него.
14.8.8 = ^ я 126мкТл' 14.9./=^^ я 12 А.
2Я р°
14.10. d = я 12,6 см. 14.11. В = ^4 я 62,8 мкТл.
В 2 г3
ijBf-B?
—в;--------бА-
14.15. В = ^я 31,4 мкТл.
....... МоЛя + З) „
14.17. В = —-—~— « 51,4 мкТл.
4 nR
14.19. В = ^ я 0,01 Тл.
а
11а/(я - 1)
14.13. В = » 214 мкТл.
2яЯ
14.16. В = ~~ » 11,8 мкТл.
О Л
3 Цп/
14.18. В = я 9,4 мкТл.
О л
V
1430. В = Цо /у я 0,01 Тл; увеличится в 2000 раз.
1432.В=дВ''/^4^Е я4,710’|3Н. 14.23.V-W Аф я 13810~|7Н.
т 2п1 т
14.24. v = я 1,7610s м/с. 1435. v = « 2,8-Ю4 с*.
т 2 я т
1436. R = | yl2m&lf я 2,3-10'2 м, Т=„ з^810’7 с.
Bq qB
1437. w=g2^2« 510~|7Дж. 1438.ап = ^-^я7107м/с2,ах = 0.
L т Щ
1439. R = * 3 > je[BZ
В |е| ’ т
1432. S=я 3142 м.
1433.100 (м/с) = S v i + = 105 (м/с)
2 М 2 М
1434.1 <. в 28з м 14.35 И = «1,8-1 о" Кл/кг.
qB । 2m и0' т д^/’+д/2)2
1436.а = 2arctg 1437.,= 2« ЙА?я02Зс.
mv И я mu
1439. — = И^?я 1,76-10*. 14.40.5 = Ц^-2 я 19,8см.
а, т 2 т Е
434
14.41.Д/ = ^з/л-1 »1(Г*с. 14.42.1>=Л=104м/с.
Е В
2 п2 j2 п
14.43.N= u . 14.45. Т = mg(1 + 2h/l) + qB 'Ilgh •0,27H.
( R + p d/S)
14.46. u0 'VsgZ + ^y- { l-'Vl+V^ I » 5 м/с.
2m2 1 q2lB21
14.47. umax = mg (sin a-geos а) в4 lo6
B9-B
, 2 „ qBR {qBR , ~ q2 R2 B2 \ ,, ,,,
14.48. n = zrR-\— 3---+ V 6ял + 3--=— H 33,331 см, если тело соскальзыва-
3 9m I mg 6 m2 ___L—
ет влево (см. рис. 14.51); Zi = 7 В - ^ПД - I - Д-"''16gR+^ R >&- } = 33,334 см, если
j 9 m 1 mg т
тело скальзывает вправо.
14.50. a = arcsin 7^7 «30°. 14.51.1 = V - 58,3 A.
l*ol
14.52. /0 = = 250 kA. 1453. В = = 4,9-10’3 Тл.
Hq/I / <
14.54. В зависимости от направления тока в проводнике относительно направления магнит-
ного поля, уменьшатся или увеличатся на AF = 1ЛIВI = 0,25 Н.
14.55. F = ц(т g±I В /); в зависимости от направления тока в проводнике относительно на-
правления магнитного поля, F, = 0,148 Н или F2 = 0,048 Н.
14.57. Втщ = (т g + I Bl) (sin a - p cos a) » 0,6 H.
14.58. Bmin = '"° ^g.(sin«.^cosa) Тд
11 (cos a + |i sin a)
14.59. Уменьшатся на Axmax = m * <sin a ~ C0S- a> + Z <C0S * + H ^/R « 11 cm.
14.60. a = arctg — = 5,8°. 14.62. F = 3^'B = 5,4-10’3 H.
mg 2. к
14.63. Г=6^рД=4,3210'3 H. 14.65. F = IBR = 0,5 H.
J Л
l,25 10'3 H; контур притягивается к проводнику.
14.68. рт = I п R 2 = 39,3 А-м2.
14.69.рт = NIn R2« It,5 A m2.
14.70. pm = I n R 2 « 6,28 A m2, = I n R 2 В » 6,28-10'2 Н м.
14.72. Aq> = В Z v » 0,55 В.
14.73. С ускорением а = ——А— =100 м/с2.
1 Д/ В/sin a
435
14.74. Ci = ео о В » 17,7-10'12 Кл/м2, c2 = c3 = 0.
14.75. Aq> = 34 ш R2B = 3-10~* B. 14.76. Дф = 'Л ш R2B = 0,25 В.
14.77. Афтах=-4 IВ Тк7т « 3,1610'3 В. 14.79. R = ® => 5 м.
тшал- л В sin а
14.80. Увеличится на ДФ = в 13. ю'2 Вб.
10
_ я
14.81. В зависимости от того, как кольцо преобразуют в восьмерку q = « 0,56 мКл, или
2. л
пг2В ... т.
4 р »1,13мКл.
л
14.82. Д9 = ~ = 4-1 О'8 Кл.
К
14.84. Д9 = -П'2~ » 3,14- Ю’6 Кл.
К
14.87. Д/ = ^
<?,
0,5 с,/=-^ = 5 А.
Л
Sit ,
14.89. Ф =-=10"3B6.
n
14.91. AT= -/2д — w 9-10'3 K.
16cpp0
2 л и (rn + w /)
14.94.1 =---« 5-10 3 A.
14.83. = 0,366.
о _2
14.86. |<£,|= — « 0,01 В.
Д/
<?,Д/
14.88. В = ---------= 0,1 Тл.
аг cos а
_ я D2n (Bi - В,)
14.90. <?j =-------------И „ 62 8 в
4Д/
а2/4 «
14.92. N= -- » 1,27-10'° Вт.
16я2Я
R
14.95. См. рис. 29.
S-Blv _ .
---й---= 0,25 А.
К.
FR
14.102. umax =-y~-.
I В
14.96. <?, = а и (В, - Bj) = 0,5 В.
14лп./=^ио.
Л
14.99.7(0= •
R (1о +2 °о 0
14.100. a) 1= g + ?-!'3 = 0,75 А; б) 1 =
14.101.
К
14.103.1/= В Zu = 10 В.
шла п S2Z2utga „г. -> „
14.104. Q = ,Решение. Если стержень перемещать со скоростью и, то будет ме-
няться площадь контура, образованного проводом и стержнем, и, следовательно, возникнет
изменяющийся со временем поток индукции магнитного поля <P = BS, где 5 = х2 tg a -
площадь контура (расстояние х отсчитывается от вершины угла Z DOE до точки А стержня)
и э.д.с. электромагнитной индукции
t/Ф „aS dx
W’=~^ = B-^ = Bxtga-^ = Bxtga\3.
436
Сила тока в стержне по закону Ома равна
где R = г х tg а - сопротивление части стержня между точками контакта с проводниками
OD и ОЕ. Следовательно,
j fixtgau Bu
rxtga г
Как видим, в контуре будет течь постоянный ток.
В момент времени t сопротивление участка стержня между точками контакта с проводника-
ми будет равно R = г о t tg а. Поэтому, за бесконечно малый промежуток времени Л в
стержне выделится
dQ = I2R dt=г о t tg a dt = t dt
г r
тепла, а за все время At = Z/o движения стержня от точки О до точки Е
“if
a В2 Z2otga
2r
14 107
14.10/. Ощах- 2,2 2
В Г cos a
14.110. a =--^-5—5 ® 5 м/с.
m + Cl2B2
, . mg sin a
14.112. a =-----------.
m + CB‘r cos a
14.115. <?. = Z^=10 3B.
s At
14.106./ = ^^, о =
Bl B2/2cosa
14.109. q = CaS= 10’9Кл.
14.111. W= C l- —«7,2-10'" Дж.
m + Cl2B2
14.113.и = у! 2'ng-6^ina «0,75 м/с.
m + CZ2Bzcos2a
14.116. Дг = ^ = 0,1 с.
________ _ в (fa + RD
- —• 2max ~ о d ~ 'min _
14.117. ДО = А 5 Т [А].
14.119. /тах = ~ ~ = 2,25 А, /т;п = = 0,75 А. Указание. В начальный момент вре-
Aj Л2 Л2
мени после замыкания ключа ток будет течь только через сопротивление R2.
Lg2(Ri+R-2)2 6
14.120. О =-----z—;----«2-10 Дж. Указание. Ток в цепи в момент размыкания равен
2 Л) Л2
/= + Rq)/R\ R2 (см. решение задачи №14.118). Количество выделившегося тепла будет
равно энергии магнитного поля в катушке в этот момент времени.
14.121. At = 0,23 с. Указание. См. решение задачи №14.118 и указания к решению задач в
теоретическом введении.
14.123. W = = 1О'3 Дж. 14.124.1= У ~ я °>45 А-
14.125. у = = 0,1 Вб. 14.126. W= 0,288 Дж, Ф = = НО4 Вб.
14.128. Г = 2 л <ГС = 0,24 мс, v = ~ = 4208 Гц.
14.129. Период увеличится в Л раз, а частота уменьшится в Vs раз.
437
14.130. Фтах - С ^Апах — Ю Кл» Anax ~ ^Anax C/L — 10 А.
14.131. Anax = UTC/L я 8,9 А, г = И> я <ГС я 7-Ю"4с.
14.132. /=1/тах'У-|^ » 8,7 А. 14.133. 0 = ^ = 51О'4 Дж.
C(Ua2-U2)-LI2 1
14.134. Q = ’-----= 5,6 Дж. 14.136. v = -—Ц== я 503,3 Гц.
2 2 л V L С
14.137. L = —Д-х— ~ 65Q мкрн
4я2у2С
14.138. Сх = I (v./vj2 - 1} С< = 150 мкФ, L = —уЦ— я 1,58 мГн.
1 1 11 4n2vfC1
14.139. Х = 2 я с 'i LC я 10,5 м, где с = 3-108 м/с-скорость света в вакууме.
Апах о г’ «4««« л 2я£/тах Л Л_
14.140. vp =* -———--» 795,8 Гц. 14.141. X = ——----® 0,05 м.
г 2 я С с/тах Цпах
2 я с 9шах 8
14.142. X = —-------« 188,5 А, где с « 3-10 м/с - скорость света в вакууме.
Алах
14.143. От Xjnin = 2 я с 'TlC^ я 632,2 м до = 2 я с 'I LC2 я 1861,2 м, где с = ЗЮ8 м/с
скорость света в вакууме.
14.144. А. = 2 л с eegS L/d » 485,6 м, где с = ЗЮ8 м/с - скорость света в вакууме.
14.146. gm!a=BSa>.
14.150. Г = — = 0,02 с.
V
14.152. Хс = - —- » 12,7 Ом.
с 2яуС
14.147. 8= (<?0 -1R ) « 46,67 В.
14.151.10 = 8,5 А, а я 40°, v = 0,02 с.
14.153. = 2 я v Z я 11 Ом.
14.154. U= 31,4 sin (6281 + я/2) [В], XL = 314 Ом.
14.156. L = — *- я 0,81 Гн. 14.157.1„ я 4,5 А, У = 82 Вт.
2яу/д
<2 U„ п
14.158. /=---* sin 2 я v t = 22,5 sin 3141 [А], <p = £.
2яу£ 2
<2 Un г
14.159. /0 = —7 -5- -А-* «1,4 А. 14.160. С =--------А-т.---» 7 мк<
2 +1/(4 я2 v2 С2) 2 я v V t/д2 -
14.161. t/до = Vt/^+^BD = 50 В. 14.162. t/до = Vt/^+^BD - 22,4 В.
14.163. v я 31,8 Гц.
2, Я у Lt С.
14.164. Z = ^Л2 + (Агь-ДГс)2 = 5 Ом, cos <р = ~ = 0,6.
14.165. {/= ^1 и£ + (t/L - ад2 = 50 В, cos ф = = 0,8.
438
1 и
14.166. L = - J » 510'3 Гн, ^=я 320,4 Вт.
4 п2 v2 С 2 R
14.167. В случае б) в п = я 1,1 раза.
R
4R2h it
14.168. (j = ~5—~+ г р V —я 8,42 часа.
/?2 + (шЛ)2 к 1/02
Учебное издание
Демков Владимир Павлович
Третьякова Ольга Николаевна
В ПОМОЩЬ ПОСТУПАЮЩИМ В ВУЗы
ФИЗИКА
МОЛЕКУЛЯРНАЯ ФИЗИКА. ТЕПЛОВЫЕ ЯВЛЕНИЯ.
ЭЛЕКТРИЧЕСТВО И МАГНЕТИЗМ