Г. И. Просветов
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ:
ЗАДАЧИ И РЕШЕНИЯ
Учебно-практическое пособие
2-е издание, дополненное
Москва
'Альфа-Пресс|
2009
УДК (519.64+514.12X075)
ББК 22.14+22.151.5я7
П 82
П 82 Просветов Г. И.
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ: ЗАДАЧИ И РЕШЕНИЯ: Учебно-практическое пособие. 2-е изд., доп. — М.: Издательство «Альфа-Пресс», 2009. — 208 с.
ISBN 978-5-94280-421-3
В учебно-практическом пособии рассмотрены основные методы и приемы линейной алгебры и аналитической геометрии. Книга содержит как теоретический материал курса линейной алгебры и аналитической геометрии, так и практические примеры и задачи, позволяющие успешно овладеть знаниями по изучаемой дисциплине.
Пособие содержит задачи для самостоятельного решения с ответами и задачи для контрольной работы, соответствующие программе курса.
Для преподавателей и студентов различных специальностей, изучающих высшую математику.
ISBN 978-5-94280-421-3
9 7 8 5 94 2 8 04 2 1 3
УДК (519.64+514.12X075) ББК 22.14+22.151.5я7
© Просветов Г. И., 2009
© ООО Издательство «Альфа-Пресс», 2009
Предисловие
Математическая истина остается на вечные времена, а метафизические призраки проходят, как бред больных.
Вольтер
В настоящее время существует ряд обстоятельных руководств по линейной алгебре и аналитической геометрии, предназначенных для студентов высших учебных заведений. Но ощущается потребность в пособии, которое на простых и конкретных примерах способно показать читателю со скромной математической подготовкой весь арсенал современных методов линейной алгебры и аналитической геометрии. Одна из попыток решить эту задачу — перед вами, уважаемый читатель.
Предлагаемое пособие знакомит читателя с важнейшими разделами линейной алгебры и аналитической геометрии и призвано помочь тем, кто осваивает этот курс, особенно в системе заочного и вечернего образования.
Цель этой книги — просто и доходчиво на конкретных примерах изложить людям, которые, возможно, совершенно незнакомы с математической литературой, основные методы и приемы линейной алгебры и аналитической геометрии.
В пособии рассмотрены такие темы, как матрицы, определители, системы линейных уравнений, векторы, полярные координаты, комплексные числа, плоскость, прямая, кривые второго порядка, преобразования координат, поверхности второго порядка, линейные пространства, линейные операторы, многочлены, собственные векторы, жорданова нормальная форма, функции от матрицы, минимальный многочлен, евклидовы пространства, метод наименьших квадратов, билинейные функции, квадратичные формы, модель Леонтьева.
Весь материал разбит на главы, а главы — на параграфы. Каждый параграф — это отдельная тема. В начале параграфа приводится необходимый минимум теоретических сведений, затем подробно разбираются модельные примеры. Показано, как с помощью встроен
3
ных функций пакета Excel можно избежать долгих и утомительных вычислений. После каждого примера приводится задача для самостоятельного решения. Ответы ко всем задачам помещены в конце книги. Также в конце книги приведены программа курса и задачи для контрольной работы.
За основу пособия принят материал курсов, читаемых автором в Российской академии предпринимательства. Всем студентам, прослушавшим эти курсы, автор выражает благодарность за продуктивную совместную работу. Материал книги в 1998—2002 гг. использовался автором в Московском государственном институте электроники и математики (техническом университете), а в 1996—1998 гг. — в Московском государственном открытом университете.
Автор выражает искреннюю признательность В. М. Трояновскому за многочисленные замечания, способствовавшие улучшению книги.
Хочется надеяться, что знакомство с книгой будет как приятным, так и полезным.
Автор
Глава 1
МАТРИЦЫ
Матрицей (точнее числовой матрицей) размера т^п (произносится «эм на эн») называется таблица чисел, содержащая т строк и п столбцов.
Будем обозначать матрицы латинскими буквами А, В, С, ...
Числа, составляющие матрицу, называются ее элементами. Каждый элемент аиимеет два индекса i и у, которые показывают, что элемент находится в z-й строке иу-м столбце. В экономической практике элементами матриц являются вещественные числа.
Пример 1. Элемент а12 расположен в 1-й строке и 2-м столбце, а элемент я31 находится в 3-й строке и 1-м столбце.
Задача 1. Что можно сказать о расположении элемента я24?
Используют следующие обозначения матрицы:
#12
#21	#22
ат\ Я т2
®\п а2п
@тп
или А = (а,у).
Пример 2. Матрица А = I
имеет размер ( 4
2x4, так
как она содержит 2 строки и 4 столбца. Матрица В =
7 '
-1
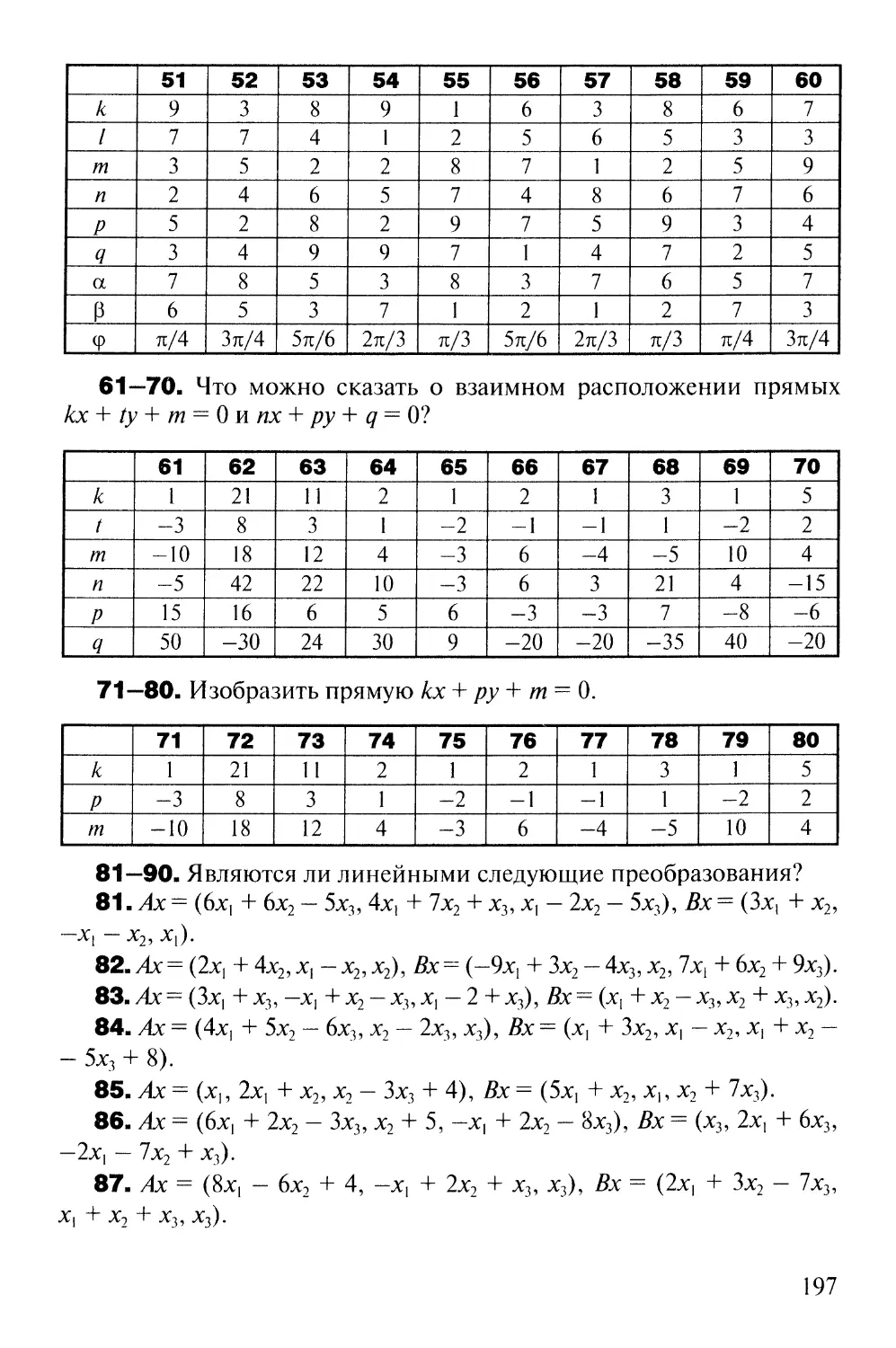
8
име-
ет размер 3x2, так как она содержит 3 строки и 2 столбца.
Задача 2. Привести пример матрицы размер 2x3.
Матрица, у которой число строк равно числу столбцов (т = п) называется квадратной матрицей порядка п. Иначе матрица называется прямоугольной.
5
Пример 3. Матрицы А и В из примера 2 прямоугольные. Матри-
ца С =
3 -1
1 2
5 6
— это квадратная матрица порядка 3. Она со-
2
держит 3 строки и 3 столбца.
Задача 3. Привести пример квадратной матрицы второго порядка.
Нулевая матрица — это матрица из одних нулей. Квадратная мат
рица следующего вида
1	0	0	...	(Г
О	1	0	...	О
.	О	0	0	...	1 ,
(элементы ан = 1, i = 1, ..., гц на диагонали равны 1, все остальные
элементы равны 0) называется единичной матрицей порядка п и обозначается латинской буквой Е.
1 о о
о о
1 о
0 1
1 о
0 1
Пример 4. Е2 =

— это примеры еди-
ничных матриц порядков 2 и 3 соответственно.
Задача 4. Как выглядит единичная матрица четвертого порядка?
§1.1. ДЕЙСТВИЯ С МАТРИЦАМИ
1.	Умножение на число. При умножении матрицы А = (а^ на число а каждый ее элемент умножается на это число: qlA = (ося/7).
Пример 5. Матрица Л =
"12 3 1
° 4 5 J ’
Тогда 2А =
2X1 2x2 2x31
2X0 2X4 2X5J
4 6 1
8 10/
г 2
0
Задача 5. Для матрицы А =
'2 5 Г
3 4 1
найти матрицу 5А.
2.	Сложение. Это действие применимо только к матрицам одинакового размера. Сумма матриц А = (аи) и В= (Ь^ размера тх п есть матрица С размера т^п, элементы которой есть сумма соответствующих элементов матриц А и В\ С = А + В = (си = аи + bt).
6
Пример 6. Даны матрицы А =	.
[ 7 5 9 J [ 16 11 6 J
Размер матриц А	и В	одинаков (2 X 3).	Матрица С = А +	В =
= Г1 2 31 + ( 4 8	lo'l	= Г 1 + 4 2 + 8	3 + 101 = С 5 10	131
[7 5 9J [16 11	6 J	[ 7 + 16 5 + 11	9 + 6 J [23 16	I5J
также имеет размер 2x3.
[10 17 И1	Г ДО 18 7 1
и В= \
8 9 7	1 5 19
3.	Вычитание. Это действие применимо только к матрицам одинакового размера. Разность матриц А = (а^ и В = (6/7) размера т X п есть матрица D размера тХ п, элементы которой есть разность соответствующих элементов матриц Аи В: D = A- B = (d^ = ац - b,).
Пример 7. Для матриц А и В из примера 6: D = А — В =
Г 1 2 31	f 4 8 101	Г 1 - 4 2 — 8 3 — 101 _ f —3 —6 —7'
L7 5 9J	[16 11 6 J	[7 -16 5-11 9-6 J [-9-6 3/
Задача 7. Найти разность матриц А и В из задачи 6.
4.	Транспонирование. Из матрицы А = (я/7) размера тХ п получается матрица А* размера пХ т следующим образом: А{ = (а*ц = а^), то есть надо строки матрицы А записать в виде столбцов.
Пример 8.
			< 1 5 13"	
	' 1 2 3 4 '			
			2 4 7	
Матрица А =	5 4 6 9	. Тогда А =	3 6 18	
	J3 7 18 19,			
			<4 9 19,	
			11 12 13	14'
Задача 8. Транспонировать матрицу А =			15 4 6	19
			3 7 8	9 ,
5.	Умножение. Произведение матриц А = (а/5) размера т X к и В = (Д7) размера кх п есть матрица С = (с/7) размера тх п. элементы к
которой Су = Е ciisbSp то есть для получения элемента си нужно z-ю строку матрицы А умножить поэлементно на J-й столбец матрицы В и полученные произведения сложить. АтХкВкХп = СтХп.
7
Порядок умножения матриц А и В очень важен. Число столбцов (к) 1-го множителя должно равняться числу строк 2-го множителя. Вообще говоря, АВ # ВА.
Пример 9- Даны матрицы А = Н
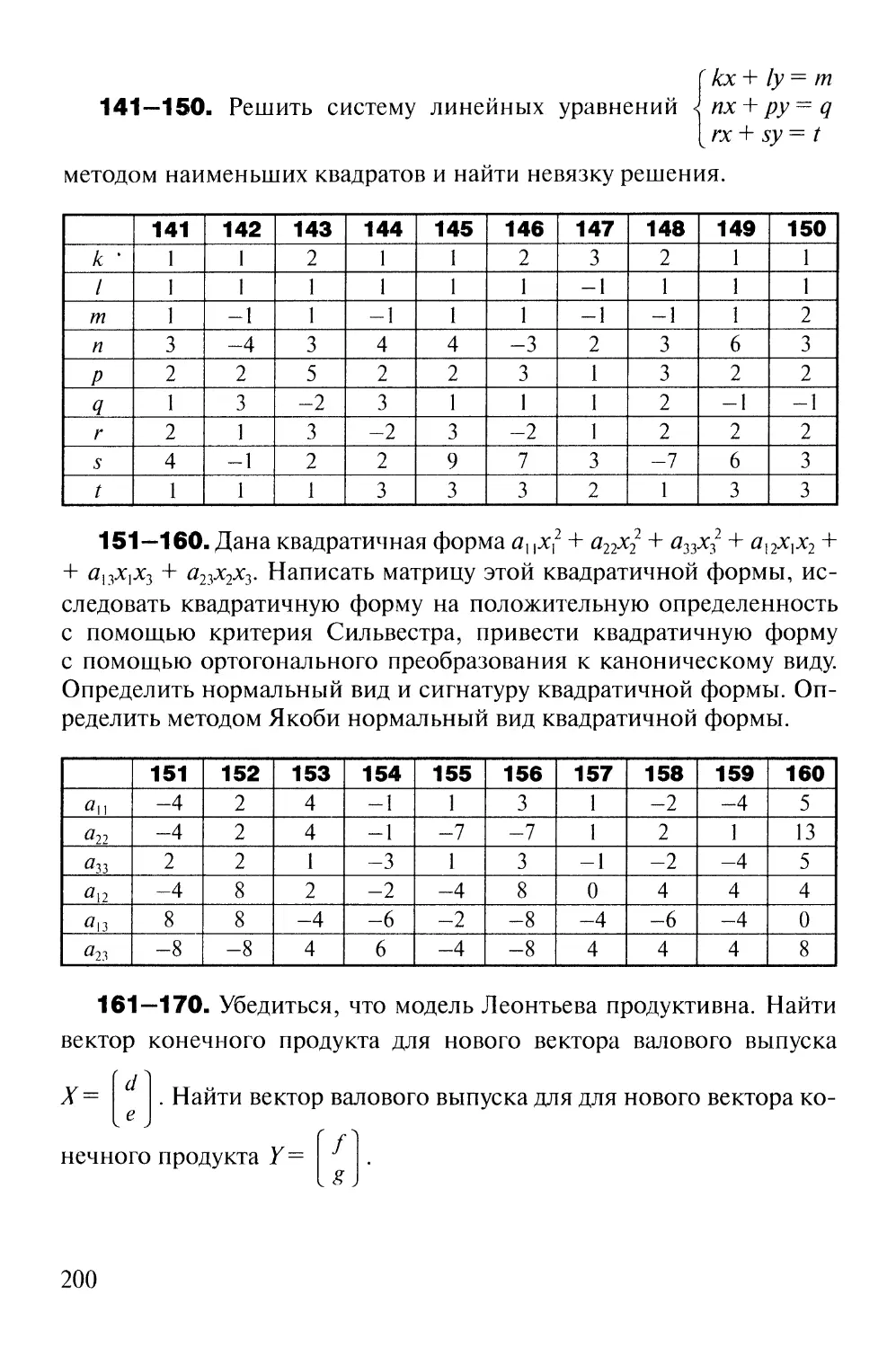
8 10 9 1 '
3 4 0 2
6 11 12 10>
2 3
4 5
и В —
Тогда Л2ХЗ-^ЗХ4 р2Х4
С12	С13
С22	С23
С|4
С24
Для нахождения элемента (1-я строка, 1-й столбец) нужно 1-ю строку матрицы А умножить поэлементно на 1-й столбец матрицы В и полученные произведения сложить: с,| = 1 х8 + 2х3 + 3х6 = 32.
Для нахождения элемента с12 (1-я строка, 2-й столбец) нужно 1-ю строку матрицы А умножить поэлементно на 2-й столбец матрицы В и полученные произведения сложить: сп = 1 х 10 + 2Х4 + ЗХ 11 = 51.
Для нахождения элемента c2J (2-я строка, 1-й столбец) нужно 2-ю строку матрицы А умножить поэлементно на 1 -й столбец матрицы В и полученные произведения сложить: с21 = 7х8 + 4хЗ + 5х6 = 98. И т. д.
с= Г 32 51 45 35 '
[ 98 141 123 65
Произведение же матриц в другом порядке (5зх4/12хз) не существует, так как 4^2.
5 1
9 3
8 7
Задача 9. Даны матрицы А =
. Найти
произведения АВ, ВА.
Пример 10. Пусть А =
, В =
I I 2
Тогда АВ =
3 4
Г IХ5 + 2Х6 [ЗХ5+4Х6
I х 9 + 2 х 7
ЗХ9+4Х7
17 23 пЯ f 5 9 . В А =
39 55	67
32 46
27 40
. Мы получили, что
' 1 2
3 4
АВ* ВА.
Задача 10. Привести пример матриц А, В, для которых АВ* ВА.
Замечание. Математическая функция МУМНОЖ мастера функций fx пакета Excel позволяет быстро перемножить матрицы. Перед
8
вызовом этой функции надо выделить мышкой диапазон ячеек нужного размера, куда после выполнения процедуры будет помещен ответ. fx -+ Математические —► МУМНОЖ —► ОК. Появляется диалоговое окно, которое нужно заполнить. В графах массив I и массив 2 указывается ссылка на ячейки, содержащие значения 1-го и 2-го матричных множителей соответственно. После этого нажимается не ОК. а одновременная комбинация клавиш Ctrl + Shift + Enter.
§ 1.2. СВОЙСТВА ДЕЙСТВИЙ С МАТРИЦАМИ
При условии, что операции имеют смысл, справедливы следующие свойства:
1)Л + В = В + А;
2) А + (В + С) = (А + В) + С;
3)АВ*ВА;
4)	(АВ)С = А(ВС);
5)	(а + Р)Л = аА + (ЗА;
6)	а(А + В) = аА + аВ;
7)	(а₽)Л = а(рЛ);
8)	(А +В)С = АС + ВС;
9)	С(А + В) = СА + СВ.
Глава 2
ОПРЕДЕЛИТЕЛИ
Понятие определителя вводится только для квадратной матрицы. Определитель — это число, которое считается для квадратной матрицы по некоторым вполне определенным правилам. Порядок определителя — это порядок квадратной матрицы. Если при задании матриц использовались круглые скобки, то в теории определителей используют прямые скобки.
§ 2.1. ОПРЕДЕЛИТЕЛИ ВТОРОГО ПОРЯДКА
Дана матрица А =
11	12 I 'Т'
. Тогда определитель второго порядка
#21 а22 I
det А вычисляется по следующему правилу:
det Л =
#12
а2\ а22
#11#22 — #12#21’ ИЛИ
*r>	__	*т'	Zp
Соединенные числа нужно перемножить и полученное произведение взять с указанным знаком.
1 2
3 4
Пример 11.
= 1 х 4 — 2 х 3 = —2.
Задача 11. Вычислить определитель
§ 2.2.	ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА
Дана матрица А =
#12 #13
#21	#22 #23
#31	#32	#33
. Тогда определитель третьего по-
рядка det А вычисляется по следующему правилу:
10
det Л =
#11	#12	#13
#21 #22 #23
#31 6Z_32 #33
#11#22#33	#31#12#23	#13#21#32 “
“ #13#22#31 ~ #11#23#32 ~ #21#I2#33, ИЛИ
❖ ❖ ❖ ❖ ❖ ❖ ❖ ❖ ❖
& Ф Ф # sk
❖ ?K ❖
>'< >'<	>'< ф т ❖ Ф
- #y£bk
❖ V*
#* ❖
В каждом произведении нет чисел из одного столбца или одной строки. Произведение чисел на одной диагонали берется со знаком «+» (это главная диагональ матрицы), а на другой — со знаком «—». Одна из сторон треугольника должна быть параллельна диагонали матрицы (и соответствующее произведение берется со знаком «+», если это главная диагональ, и со знаком «—», если нет).
I 3 2
Пример 12.
5 4 6 = I х 4 х 9 + 8 х 3 х 6 + 2 х 5 х 7-
8 7 9
-2х4х8-1х6х7-9хЗх5 = 9.
Задача 12. Вычислить определитель
3 I 2
4 6 7
5 8 9
§ 2.3.	АЛГЕБРАИЧЕСКИЕ ДОПОЛНЕНИЯ И МИНОРЫ
Минором Мц квадратной матрицы А называется определитель матрицы, полученной из матрицы А вычеркиванием z-й строки и /-го столбца.
	13 2			
			5 6	
Пример 13. /1	5 4 6	. Минор Мп =	8 9	(вычеркнули
	8 7 9 ^			
1-ю строку и 2-й столбец) = —3. Минор М23 =			1 3 8 7	(вычеркнули
2-ю строку и 3-й столбец) = —17.				
П
Задача 13. /1
3 12
4 6 7
5 8 9 ^
. Найти миноры Л/ц, Л/32 и Мп,
Алгебраическое дополнение Ду = (— Полезно запомнить, что (-1)2* = 1 и (—1)2Л+1 = -1.
Пример 14. В примере 13
4з = (-1),+3
5 4
8 7
= 3, Л2] = (-1)2+1
= -13.
Задача 14. В задаче 13 найти алгебраические дополнения Л22, Д2 и 41-
§ 2.4.	РАЗЛОЖЕНИЕ ОПРЕДЕЛИТЕЛЯ ПО СТРОКЕ ИЛИ СТОЛБЦУ
Верны следующие формулы, которые позволяют свести вычисление определителя /7-го порядка к вычислению определителей порядка п — 1:
det А =	+ ai2Ai2 + ... +	= Еа,747 = Е(-1У^а,Ми
/= 1	j= 1
— разложение определителя по i-й строке. Каждый элемент /-й строки аи умножается на свое алгебраическое дополнение Ау (вычеркиваются /-я строка и у-й столбец (то есть строка и столбец, содержащие элемент я/У), вычисляется определитель полученной матрицы и умножается на (—1)/+/). Полученные произведения суммируются.
det А = а|уЛ17 + а27Л2у + ... + anjAnj = ЕаиАи = Е (-!)''% Д7
— разложение определителя по j-му столбцу. Каждый элемент у-го столбца ач умножается на свое алгебраическое дополнение Ду (вычеркиваются z-я строка иу-й столбец (то есть строка и столбец, содержащие элемент я/у), вычисляется определитель полученной матрицы и умножается на (—1)/+у). Полученные произведения суммируются.
Пример 15. В примере 12 разложим определитель по 1-й строке.
3 2
4 6
7 9
1
5
8
4 6
7 9
= 1 х (-1)1+1
(вычеркнули 1-ю строку и 1-й столбец, содержащие элемент = 1)
12
6
9
+ 3x(-l)l+2 5
S 4
+ 2 х (—1)1+3
(вычеркнули 1-ю строку и 2-й столбец, содержащие элемент Я]2 — 3)
(вычеркнули 1-ю строку и 3-й столбец, содержащие элемент я13 = 2)
= 1 х (-1)2 Х(4Х9-6Х7) + ЗХ (-1)3 Х(5Х9-6Х8) + 2Х (-1)4 х х (5X7-4X8)-9.
Разложим определитель по 3-й строке.
1 3 2
5 4 6
8 7 9
= 8х(-1)1+| 3
+ 7 х (-1)3+2
+ 9х(—1)3+3 1 3
(вычеркнули 3-ю строку и 1-й столбец, содержащие элемент «31 = 8)
(вычеркнули 3-ю строку и 2-й столбец, содержащие элемент а32 ~ ?)
(вычеркнули 3-ю строку
и 3-й столбец, содержа- = 9. щие элемент я33 = 9)
2
6
Разложим определитель по 1-му столбцу.
1 5 8	3 4 7	2 6 9	= 1 X (-1)|+|	4 7	6 9	(вычеркнули 1-ю строку и 1-й столбец, содержащие элемент «11 = 1)
+ 5 х (-1)|+2 + 8 х (-1)1+3 Независимо от способа р;				3 2 7 9 3 2 4 6 1 зло же		(вычеркнули 2-ю строку и 1-й столбец, содержащие элемент «21 = 5) (вычеркнули 3-ю строку и 1-й столбец, содержащие = 9. элемент = 8) ;ния всегда получается один и тот
же ответ.
Задача 15. В задаче 12 разложить определитель по 1-й строке, по 2-й строке, по 3-му столбцу.
§ 2.5.	СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ
1.	Определитель транспонированной матрицы равен определителю исходной матрицы, то есть det А! = det А.
13
2.	Если поменять местами две строки (два столбца) определителя, то он изменит знак.
3.	Если определитель содержит две одинаковых строки (два одинаковых столбца), то он равен нулю.
4.	Если определитель содержит нулевую строку (нулевой столбец), то он равен нулю.
5.	Общий множитель в строке (в столбце) можно выносить за знак определителя.
6.	Определитель не изменится, если к любой строке прибавить (из любой строки вычесть) любую другую строку, умноженную на любое число. Аналогичное свойство верно и для столбцов.
§ 2.6. ВЫЧИСЛЕНИЕ ОПРЕДЕЛИТЕЛЕЙ
Выбирается строка (или столбец) определителя, содержащая больше всего нулей. Используя свойство 6, зануляют в этой строке (или столбце) все элементы, кроме одного. После чего разлагают определитель по этой строке (или столбцу). К полученному определителю применяют эту же схему.
Пример 16. Вычислим определитель
2-5 4
3-4 7
4-9 8
-3 2 -5
3
5
5
3
Мы видим, что все элементы отличны от нуля. В таком случае можно начать с любой строки или любого столбца. Например, с 1-го столбца. Наша цель — занулить все элементы, кроме одного, в 1-м столбце.
Прибавим 2-ю строку поэлементно к 4-й строке, а из 3-й строки вычтем поэлементно 1-ю строку, умноженную на 2:
2	-5	4	3		2	-5	4	3
3	-4	7	5		3	—4	7	5
4-2X2	-9-2 х (-5)	8-2Х4	5-2x3		0	1	0	-1
-3 + 3	2 + (-4)	-5 + 7	3 + 5		0	—2	2	8
Вынесем из последней строки общий множитель (2) за знак опре-
делителя: 2 х
2-543
3-475
0 10-1
0-114
14
Мы получили в 1-м столбце два нуля. Также два нуля получены в 3-й строке. Прибавим 2-й столбец поэлементно к 4-му столбцу:
	2	-5	4	з + (-5)		2	-5	4	—2
2х	3	—4	7	5 + (-4)	= 2 х	3	—4	7	1
	0	1	0	-1 + 1		0	1	0	0
	0	-1	1	4 + (-1)		0	-1	1	3
Разложим определитель по 3-й строке:
	2 4-2		2 4-2
2 х 1 х (-l)v2 х	3 7 1 0 1 3	= -2х	3 7 1 0 1 3
Вынесем из 1-й строки общий множитель (2) за знак определителя:
	1 2 -1		1 2 -1
-2 х 2 х	3 7 1	= —4 х	3 7 1
	0 1 3		0 1 3
По одному нулю в 1 -м столбце и 3-й строке. Вычтем из 2-й строки 1-ю строку, умноженную на 3:
	1	2	-1		1
—4 х	3-3x1	7-ЗХ2	1 — 3 х (—1)	= -4 х	0
	0	1	3		0
2 -1
1 4
1 3
Разложим определитель по 1-му столбцу:
-4 х 1 х (-1),+1 х	1 4	= -4 х	1 4	= 4.
	1 3		1 3	
Пример 17. Вычислим определитель
-3 9	3	6
-5 8	2	7
4 -5 -3 —2
7 -8 —4 -5
-I
= 3 х (-1) х (-1) х
—7
3
8
5
8
1
2
3
4
2	-13
7 =3х ~5	8
2	-4	5
5	-7	8
1 2
2 7
3 2
4 5
13 12
5 8 2 7
4 5 3 2
7 8 4 5
1	3-3X1	1-1
5	8-ЗХ5	2-5
4	5-3x4	3-4
7	8-3x7	4-7
2-2x1
7-2x5
2-2x4
5-2Х7
15
Задача 16. Вычислить определитель
-3 7 -I 5-9 2 4 -6 I
2
4
7
2
Задача 17. Вычислить определитель
3-3-5 8
-3 2	4 —6
2-5-7 5
-4 3	5 -6
Замечание. Математическая функция МОПРЕД мастера функций fx пакета Excel позволяет быстро вычислить определитель матрицы. fx —> Математические —> МОПРЕД-* ОК. Появляется диалоговое окно, которое нужно заполнить. В графе массив указывается ссылка на ячейки, содержащие элементы определителя. ОК.
Глава 3
ОБРАТНАЯ МАТРИЦА
Квадратная матрица называется невырожденной, если ее определитель отличен от нуля. Если при умножении квадратных матриц А и В в любом порядке получается единичная матрица (АВ = ВА = £), то матрица В называется обратной матрицей для матрицы А (очевидно, что матрица А — обратная матрица для матрицы В) и обозначается А~1, то есть АА~~[ = А~[А = Е.
Теорема. Для невырожденной матрицы существует обратная матрица.
§ 3.1.	АЛГОРИТМ НАХОЖДЕНИЯ ОБРАТНОЙ МАТРИЦЫ
Дана квадратная матрица А = (а^. Вычисляем определитель det А. Если det А = 0, то А~[ не существует. На место каждого элемента аи матрицы А нужно поставить его алгебраическое дополнение Д7. Получим матрицу (Ду). Транспонировав полученную матрицу и умножив ее на число I /det А, мы и найдем обратную матрицу:
Ап A2i ... Д1
Ап А22 ... Ап2
А~] =
det А
§ 3.2.	НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ ДЛЯ МАТРИЦ ВТОРОГО ПОРЯДКА
Дана матрица А = \ а Воспользовавшись тем, что det А = ad — be, I с d J
Alt = d, Д2 = -с, Л21 = -b, А22 = а, мы сразу получим следующую фор-
мулу: А 1 =
1 f d -b ad — be [ — с а
17
Пример 18. Найдем обратную матрицу для матрицы А =
Здесь а = 1, = 2, с = 3, d = 4.
т _	1 Г d -b]	1 Г 4 -21
°ГДа ad—bc [ - с a J 1 х 4 - 2 х 3 [ -3 1 J
= Г -2	11
I 1,5 -0,5 J *
Убедимся, что это действительно обратная матрица:
лл-U1 2 И-2 1 1 = f1 °1 =£-
[	3 4 J [ 1,5 -0,5 J	[о	1 J
,	[	-2	1	1 Г 1 21	Г 1	01
[	1,5 -0,5 П 3 4 J	[ 0	1 J
Задача 18. Найти обратную матрицу для матрицы А =
§ 3.3.	НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ ДЛЯ МАТРИЦ ТРЕТЬЕГО ПОРЯДКА
Пример 19. Найдем обратную матрицу для матрицы
3
2
3
А =
—4 5 '
-3 1
-5 -1
Определитель матрицы det А =
3-4 5
2 -3 1
3 -5 -1
= 3 х (-3) х (-1) +
+ 3 х (-4) х 1 + 5 х (-5) х 2 - 3 х (-3) х 5 - 3 х (-5) х 1 - 2 х (-4) х х (-1) = -1 * 0. Поэтому существует обратная матрица.
Вычисляем алгебраические дополнения Ah\
л„ = (-1)|+1	-3 -5	1 -1	= 8. Л12	= (-1)'«	2 3	1 -1	-5.
4з = (-1),+3	2 3	1 1	= — 1. А21	= (-1)2+|	—4 -5	5 -1	= -29.
яи = (-1)2+2	3 3	5 -1	= -18.ЛИ	= (-1)2+3	3 3	1 1 izi 4^	= 3.
18
= 11. Л32 = (-1)3+2
Л33 = (-1)3+3
5
5
1
-1
Составим из них матрицу —29 —18	3
11	7	-1
Транспонировав полученную матрицу и умножив ее на число 1/det А = 1/(— 1) = — 1, мы и найдем обратную матрицу:
= 1/(-1)
' 8
5
-1
-29 11 '
-18	7
3 -1 >
' -8
-5
1
29 -1Г
18	—7
-3 1 .
Задача 19. Найти обратную матрицу для матрицы ' 2 7 3 '
А= 3 9 4 .
1 5 3^
Замечание. Математическая функция МОБР мастера функций fx пакета Excel позволяет быстро найти обратную матрицу Перед вызовом этой функции надо выделить мышкой диапазон ячеек нужного размера (порядок обратной матрицы равен порядку исходной матрицы), куда после выполнения процедуры будет помещен ответ. fx —> Математические -> МОБР —► ОК. Появляется диалоговое окно, которое нужно заполнить. В графе массив указывается ссылка на ячейки, содержащие элементы исходной матрицы. После этого нажимается не ОК, а одновременная комбинация клавиш Ctrl + Shift + Enter.
§ 3.4.	СВОЙСТВА ОБРАТНОЙ МАТРИЦЫ
1.	(АВ)~Х = ВЛА\ где А, В — невырожденные квадратные матрицы одинакового порядка.
2.	(Л"1)"1 = А.
3.	(ЛУ1 = (Л"1)'.
4.	беЦЛ-1) = 1/det Л.
Глава 4
СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ
S 4.1. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
Система уравнений следующего вида:
'aIlx, + al2x2 + ... + a^„ = b{,
^21*^1	^22^2	^In^n ^2?
<
. amlx, + ат2х2 + ... + атл = Ьт,
где ау, — коэффициенты, xz — переменные, называется системой линейных уравнений. Решить систему линейных уравнений — значит указать все решения системы, то есть такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется:
а)	совместной, если она имеет хотя бы одно решение;
б)	несовместной, если она не имеет решений;
в)	определенной, если она имеет единственное решение;
г)	однородной, если все bt: = 0;
д)	неоднородной, если есть 6Z 0.
§ 4.2. ПРАВИЛО КРАМЕРА
Правило Крамера применяется к системам, у которых число уравнений т равно числу переменных п, то есть т = п.
§ 4.2.1. Случай п = 2
Рассматривается система линейных уравнений:
J апх + 4712у = Ь},
1 а21х + о22у = Ь2.
20
Вычисляются определители:
^1 й12 д —	а\\
^2 а22 У а2\
Ьх
1.	Если Д * 0, то система имеет единственное решение х = AJA, У = А/Д.
2.	Если Д = 0, а хотя один из определителей Дх, Д>; отличен от нуля, то система не имеет решений.
3.	Если Д = Дх = Д, = 0, то система имеет бесконечно много решений.
Пример 20- Решим с помощью правила Крамера систему урав-
нений:
2х 4- 4у = 7, Зх + 5у = 8.
2
3
4
5
Д =
= -2^0.
Поэтому система имеет единственное решение.
Тогда х = Д/Д = 3/(—2) = -1,5; у = Д/Д = —5/(—2) = 2,5.
Задача 20. Решить с помощью правила Крамера систему уравне-
ний:
5х 4- бу = 4, Зх+7у = 1.
Пример 21. Решим с помощью правила Крамера систему урав-. f Зх 4- 5у = 7,
нении: ]6х+10у=1.
Поэтому система не имеет решений.
Задача 21. Решить с помощью правила Крамера систему уравне-. f 3x4-7у = I, нии: < n ~ 1	~
9х 4- 21у = 2.
Пример 22. Решим с помощью правила Крамера систему урав-„ [ Зх 4- 5у = 4, нении: 9x+15j,= 12.
21
Поэтому система имеет бесконечно много решений.
Разделив коэффициенты 2-го уравнения на 3, получим:
f Зх 4- 5у = 4,
| Зх 4- 5у = 4.
Оставим только одно из этих уравнений: Зх 4- 5у = 4. Выразим у через х: у = (4 — Зх)/5, значение х — любое. Это и есть ответ.
Задача 22. Решить с помощью правила Крамера систему уравне-
f Зх 4- 7у = 1, ний:
[ 12х 4- 28у = 4.
§ 4.2.2. Случай п = 3
Рассматривается система линейных уравнений:
^нх+ я12у + a]3z = Ьъ <	4" Я22У 4” ^23^	^2?
ча31х + а31у + a33z = b3.
	а\\ ап а\з		я12 Ап
Вычисляются определители: Д =	а21 а22 а23	, Дх =	/?2 ^22 ^23
	а31 а32 а33		Ьз а32 азз
	ап	й13		а\\ ап ^1
	#21	^2	а23	мг =	б?21	^22	^2
	аз\ t)3 а33		Й31 а32 Ьз
1.	Если Д * 0, то система имеет единственное решение х = А*/А, у = Д/Д, z =
2.	Если Д = 0, а хотя один из определителей Дх, Ду, Дг отличен от нуля, то система не имеет решений.
3.	Если Д = Дх = Д , = Дг = 0, то возможны случаи:
а)	система не имеет решений;
б)	система имеет бесконечно много решений.
Пример 23. Решим с помощью правила Крамера систему урав-
Г X 4- 5у 4- 2z = 1,
нений: < 2х 4- Зу 4- 2z = — 3,
х 4- Зу 4- 4z = -3.
22
5 2
3 2
3 4
1
2
1
Д =
= -18^0.
Поэтому система имеет единственное решение.
5 1
3 -3
3 -3
Тогда х = Д/Д = 36Д-18) = -2; у = Д/Д = — 18/(— 18) = 1; z = Д/Д = = 18/(—18) == — 1.
Задача 23. Решить с помощью правила Крамера систему уравне-
2х - у + 3z = 9,
ний: < Зх - 5у + 2z - —4,
4х- 7у + z= 5.
§ 4.3. МАТРИЧНЫЙ МЕТОД
Матричный метод применяется к системам, у которых число уравнений т равно числу переменных п, то есть т = п.
Пример 24. Вернемся к примеру 23.
Введем следующие обозначения: матрица из коэффициентов сис-
темы А =
столбец неизвестных X =
у , столбец
Z
свободных членов В = —3
х + 5у + 2z 2х + Зу + 2z
х + Зу + 4z
то есть АХ = В — это матричная запись нашей системы. Так как det А = Д = —18 0, то существует А”1.
Умножим слева на А~1 наше матричное уравнение:
А ]АХ= А ]В, ЕХ= А 1 В, Х= А 1 В. Мы получили формулу для нахож-
дения решения.
Найдем А~1 методами, изложенными в главе 3.
23
— 14 4 '
2	2
2	—7
Тогда X = у = А }В
^бх 1 + (-14) х (-3) + 4 х (-3)' -6 х 1 + 2 х (-3) + 2 х (-3) 3 х I + 2 х (-3) + (-7) х (-3)
1
-18
" 36 '
-18
18
-2'
1
-1
то есть х = —2, у = 1, z = — 1.
Задача 24. Решить систему уравнений из задачи 23 матричным методом.
§ 4.4. СТУПЕНЧАТЫЙ ВИД МАТРИЦЫ. РАНГ МАТРИЦЫ
Нулевая строка — это строка из одних нулей. Ненулевая строка содержит хотя бы один ненулевой элемент. Главный элемент строки — это первый слева ненулевой элемент.
Пример 25. В строке (0023549000) главный элемент равен 2.
Задача 25. В строке (0004357600) найти главный элемент.
Ступенчатый вид имеет матрица, у которой:
1) все ненулевые строки расположены выше нулевых строк;
2) в каждой строке, начиная со второй, главный элемент расположен правее, чем главный элемент предыдущей строки.
Пример 26. Приведенные ниже матрицы являются ступенчатыми
(главные элементы каждой строки обведены):
3 0 ' о Ш о о
[ощо]
0 0 0
0 0 0
4 '
0
0
[ о Ш о о . о о
Задача 26. Какие из следующих матриц являются ступенчатыми?
'4	1	О'
0	0	2
0	5	0
12 3'
1	2	4
0 0	0
1	2 0]
0 0 0 J ’
2	1	0
0 0 0
24
' 0 1 о
О О 1
ООО
12 3
О	1	2
О	1	3
Главные столбцы ступенчатой матрицы — это столбцы, содержащие главные элементы.
Пример 27. В примере 26 главные столбцы содержат обведенный элемент.
Задача 27. Для ступенчатых матриц из задачи 26 указать главные столбцы.
Главный ступенчатый вид матрицы — это ступенчатый вид матрицы, для которого выполнены два условия:
1) все главные элементы равны 1;
2) в главных столбцах все элементы, кроме главных, равны 0.
Пример 28. Приведенные ниже матрицы имеют главный ступенчатый вид.
r 1
0
0
о о '
1 о
0 1
' о о о
1
о о
О 3 Г 1 5 О 1,001 0 J [ о о о
Г О 1 4 3
L о о 0 J ’
Задача 28. Какие из матриц задачи 26 имеют главный ступенчатый вид?
Всякую матрицу можно привести к главному ступенчатому виду, используя следующие преобразования (именно эти преобразования мы и использовали при вычислении определителей):
1)	любые две строки можно поменять местами;
2)	любую строку можно умножить на любое число, отличное от нуля;
3)	к любой строке можно прибавить (из любой строки можно вычесть) любую другую строку, умноженную на любое число.
Ранг матрицы — это число ненулевых строк в ее ступенчатом виде, то есть для нахождения ранга матрицы нужно с помощью указанных выше преобразований привести матрицу к ступенчатому виду и сосчитать число ненулевых строк.
25
S 4.5. МЕТОД ГАУССА
Для системы уравнений следующего вида: 'апх, + апх2 + ... + а|лх„ = Ь}, аихх + а22х2 + ... + а2ях„ = Ь2, <
.атХхх + ат2х2 + ... + атпхп = Ьт,
составляется расширенная матрица
^11 #12
^21 ^22
ат\ вт2
а{п Ь} ' а2п ^2
@тп
Здесь 1-й столбец — коэффициенты при хъ 2-й столбец — коэффициенты при х2 и т. д. Эта матрица приводится к главному ступенчатому виду. Если в процессе решения возникла ситуация, когда главный элемент расположен за вертикальной чертой, то такая система уравнений не имеет решений.
Нулевые строки будем просто вычеркивать. Главным столбцам соответствуют главные переменные. Остальные переменные называются свободными.
Если свободных переменных нет, то решение единственно. Если свободные переменные есть, то решений бесконечно много и нужно главные переменные выразить через свободные переменные.
Пример 29. Решим методом Гаусса систему уравнений:
' Зх\ — 5х2 + 2х3 + 4х4 = 2, < 7Х] — 4х2 + х3 + Зх4 = 5,
. 5Х] + 7х2 — 4х3 — 6х4 = 3.
Мы видим, что число уравнений (3) меньше числа переменных (4). Поэтому правило Крамера и матричный метод применять нельзя. Составляем расширенную матрицу:
7
< 5
-5 2	4
—4 1	3
7 —4 -6
2' 5
3.
Главные элементы равны 3 (1-я строка), 7 (2-я строка) и 5 (3-я строка). Мы видим, что матрица не является ступенчатой. Приведем ее к ступенчатому виду
Из главных элементов 1 -го столбца выбираем наименьший по модулю и, поменяв в случае необходимости строки, добьемся, чтобы этот элемент был расположен в левом верхнем углу матрицы. Этот
26
элемент назовем разрешающим элементом, а строку и столбец, содержащие разрешающий элемент, — разрешающими.
В нашем случае разрешающий элемент — это 3. Строки менять здесь не надо, элемент 3 расположен в 1-й строке. Поэтому 1-я строка не меняется. Под элементом 3 в 1-м столбце пишем одни 0. Нужно просчитать новые элементы (кроме 1 -й строки и 1 -го столбца) по правилу прямоугольников: новый элемент = (старый элемент) X (разрешающий элемент) — A X V.
Элемент А находится в разрешающей строке в одном столбце со старым элементом. Элемент V находится в разрешающем столбце в одной строке со старым элементом.
Для (—4) (клетка (2,2)) новый элемент = клетка (2,2) х клетка (1,1) — - клетка (1,2) х клетка (2,1) = (—4) х 3 - (—5) х 7 = 23.
Для 7 (клетка (3,2)) новый элемент = клетка (3,2) х клетка (1,1) — - клетка (1,2) х клетка (3,1) = 7 х 3 - (-5) х 5 = 46.
Для 1 (клетка (2,3)) новый элемент = клетка (2,3) X клетка (1,1) — - клетка (1,3) X клетка (2,1) = 1 X 3 — 2 х 7 = -11. И т. д.
	' 3	-5	2	4	2
Получаем матрицу	0	[23]	-И	-19	1
	0	46	-22	-38	-1
После 1-го шага отчеркнем 1-ю строку и 1-й столбец, а к оставшейся части применим алгоритм. Теперь 23 — разрешающий элемент.
	г 3	-5	2	4	2 '
Получим матрицу	0	23	-11	-19	1
	0	0	0	0	-69
	X,	х2	х3	х4	
Мы видим, что в 3-й строке главный элемент расположен за вертикальной чертой, что соответствует уравнению Ох, + 0х2 + 0х3 4- 0х4 = = -69.
Система не имеет решений.
Задача 29. Решить методом Гаусса систему уравнений:
2х - у 4- 3z = 9, < Зх - 5у 4- z = -4, 4х - 7у 4- z = 5.
27
Пример 30- Решим систему уравнений из примера 23 методом
Гаусса.
5
2	3
. 1	3
2
2
4
3-ю строку разделим
Умножим 2-ю строку на (—1), а
Получим матрицу:
на (-2).
' 1	5	2 11
О Г~7 2~ 5
0	1-12
Поменяем местами 2-ю и 3-ю строки. Получим матрицу:
О Ш -1
0 7	2
2	1 '
-1	2
9 -9
0 ш о о
И И 5	2
Ш -1 о Ш
1 '
2
-1
1	5 2
Г
2
5

1 о о
5
1
О
Это ступенчатый вид матрицы. Все столбцы (до черты) главные. Поэтому нет свободных переменных.
Приведем матрицу к главному ступенчатому виду. Применяем алгоритм, двигаясь от последней строки к первой. Это так называемый обратный ход.
Задача 30. Решить методом Гаусса систему уравнений из задачи 23.
Пример 31. Решим методом Гаусса систему уравнений:
"	4- Зх2 + 2х3 4- Зх4 + 4х5 = 5,
4%! 4- 2х2 4" х3 4- 2х4 4- Зх5 = 4, 4xj + 2х2 4- Зх3 4- 2х4 4- х5 — О, 2хх 4- х2 4- 7х3 + Зх4 4- 2х5 — 1.
Составляем расширенную матрицу и поменяем местами 1 -ю и 4-ю строки:
28
' 6 4		3 2	2 1	3 2	4 3	5 ' 4		ги 4	1 2	7 1	3 2	2 3	1 4
	4	2	3	2	1	0		4	2	3	2	1	0
	2	1	7	3	2	1		. 6	3	2	3	4	5 >
	2	1	7	3	2	1		' 2	1	7	3	2	1
	0	0	-26	-8	—2	4	—s	0	0	13	4	1	—2
	0	0	-22	-8	-6	—4		0	0	11	4	3	2
1	0	0	-38	-12	—4	4 .		. 0	0	19	6	2	-2,
Мы видим, что в отчеркнутой части главные элементы расположены в 3-м столбце. Наименьший из них равен 11. Поменяем местами 2-ю и 3-ю строки:
2	1	7	3	2	1 '		г 2	1	7	3	2	1
0	ЕЁ	]п	4	3	2		0	0	11	4	3	_2
0	0	13	4	1	—2		0	0	0	-8	-28	-48
0	0	19	6	2	—2>		0	0	0	-10	-35	-60
2	1	7	3	2	1
О	0	11	4	3	2
О	0	0	2	Т~ 12
0	0	0	2	7	12
Вычтем из 4-й строки 3-ю строку:
2	1	7	3	2	1	'
0	0	11	4	3	2
0	0	0	2	7	12
0	0	0	0	0	0
Последняя строка соответствует уравнению 0^ + 0х2 + 0х3 + 0х4 + + 0х5 = 0, то есть 0 = 0. Вычеркнем ее.
| Х\ |	Х2	| Х3 |	| Х4 |	Х5
'И	1	7	3	2	1 '
0	0	11	4	3	2	.
о	0	О	И	7	12
Это ступенчатый вид матрицы. Главные переменные: хь х3, х4. Свободные переменные: х2, х5. Система имеет бесконечно много решений.
Главные переменные нужно выразить через свободные переменные. Приведем матрицу к главному ступенчатому виду. Применим обратный ход.
29
' 2 1 7 3 2 001143 О О О Ц] 7
11	Г 4
2	=> О
12 О
J	V
2	14
О 22
О О
О -17
О -22
2	7
-341
-44
12
Числа в каждой строке разделим на главный элемент строки:
0	0
И о о
Ш
х5 -0,75
-1
3,5
-1,5 '
—2
6
Это главный ступенчатый вид матрицы. Отсюда:
"%! 4- 0,5х2 — 0,75х5 = —1,5, < х3 — х5 = —2,
х4 4- 3,5х5 = 6.
' Х| = -1,5 — О,5х2 + 0,75х5, ; х3 = -2 + х5, х4 = 6 — 3,5х5,
ч х2, х5 — любые.
Задача 31. Решить методом Гаусса систему уравнений: " X] 4- 2х2 + Зх3 — 2х4 + х5 = 4, ЗХ] 4- 6х2 4- 5х3 — 4х4 4- Зх5 = 5, X) 4- 2х2 4- 7х3 — 4х4 4- х5 = 11, 2х( 4- 4х2 4- 2х3 — Зх4 4- Зх5 = 6.
§ 4.6. НАХОЖДЕНИЕ ОБРАТНОЙ МАТРИЦЫ МЕТОДОМ ГАУССА
Припишем к матрице А единичную матрицу £ такого же порядка, что и А: (А | Е). Преобразованиями из метода Гаусса (§ 4.5) получим на месте А единичную матрицу Е. Тогда на месте Ебудет /Г1: (Е |/Г‘).
Пример 32. Найдем обратную матрицу для матрицы А из примера 24.
[Ш (Л|£) =	2 . 1 '15 2	5	2	10 3	2	0 1 3	4	0 0 1	0	0?	0 1	Г 1 5 2	10 0 0	0-7-2-2 1	0 1 J	[ 0 -2 2 -1 0 1 Г 1	5	2	1	0 0	' 0	[2]	-2	1	0-1 0	7	2	2	—1 0
0 7 2 0 2-2	2-10 1	0	-1	
30
гш 0 . о	5 И 0	2 —2 □и	1 1 -3	0 0 —2	0 ' -1 7 ,		' 1 0 0	5 2 0	2 —2 03	1 1 -3	0 0 —2	0 ' -1 7
' 18	90	0	24	4	-14'		' 9	45	0	12	2	-7'
0	36	0	12	—4	—4		0	0	0	3	-1	-1
0	0	18	-3	—2	7		0	0	18	-3	—2	7
г 81	0	0	-27	63	-18'		[0	0	0	-3	7	-2'
0	9	0	3	-1	-1		0	а	0	3	-1	-1
0	0	18	-3	—2	7		0	0		-3	—2	7 .
г 1	0	0	-1/3		7/9	-2/9 '						
0	1	0	1/3		-1/9	-1,	/9	= (Е|Л-').				
0	0	1	-1/6		-1/9	7/18						
То есть Л 1 = 1/18
'-6 14 -4"
6 —2 -2 -3 -2 7
Задача 32. Найти обратную матрицу для матрицы А из задачи 24.
Глава 5
ВЕКТОРЫ НА ПЛОСКОСТИ
Есть величины, которые полностью определяются заданием своих числовых значений. Например, масса, длина, площадь, объем. Это скалярные величины. Но есть величины, для задания которых необходимо знать еще и направление. Например, сила, скорость, ускорение. Это векторные величины.
Вектор АВ — это направленный отрезок: А — начальная точка вектора, В — конечная точка вектора.
Также будем обозначать векторы маленьки- д ми латинскими буквами со стрелкой: а, Ь, с.
Модуль вектора |а| — это длина отрезка, изображающего вектор: \АВ\= АВ.
Векторы АВ и ВА называются противоположными.
Если начальная и конечная точки вектора совпадают, то такой вектор называется нулевым и обозначается б. Конечно, |б| = 0.
Два вектора называются равными, если они имеют общее направление и одинаковые длины.
§ 5.1. ДЕЙСТВИЯ С ВЕКТОРАМИ
I. Сложение. Векторы можно складывать по правилам треугольника и параллелограмма.
При нахождении суммы векторов а + b по правилу треугольника от конечной точки вектора а откладывают вектор Ь. Тогда вектор а + b направлен от начальной точки вектора а к конечной точке вектора Ь.
32
При нахождении суммы векторов а + b по правилу параллелограмма нужно отложить векторы а и от одной точки и построить на векторах а и b параллелограмм. Тогда вектор-диагональ параллелограмма, выходящий из общей начальной точки векторов а и Ь. — это и есть вектор а + Ь.
2. Умножение на число. Если X > 0, то нужно отложить от начальной точки вектора а в направлении вектора а вектор длины Х|а|. Если X < 0, то нужно отложить от начальной точки вектора а в направлении, противоположном направлению вектора 3, вектор длины |Х||3|.
—> Пример 33. Дан вектор а = АВ. Изобразим векторы За и —0,5 а.
—0,5я а	3~а
 .	 —О————................
D А В	С
За = АС .АС = ЗАВ. -0,5 И =AD.АВ= 2AD.
Задача 33. Дан вектор а = АВ. Изобразить векторы 4Н и —2а.
§ 5.2.	БАЗИС
Линейной комбинацией векторов а{.а2..... ап называется вектор вида ocjflj + ос252 + ... + (лпап. где ос1? ос2, .... ап — это числа.
Если можно так подобрать числа ОС], ос2,..., осл, что ОС]2, + а2а2 + ... + + а„ап = би не все oczравны нулю, то говорят, что векторы а{. а2...., ап линейно зависимы.
В противном случае (равенство ОС|И] + ос2б2 + ... + апап ~ 0 возможно только при о,! = ос2 = ... = ос3 = 0) векторы al9 а2. .... ап называются линейно независимыми.
Пусть V— некоторое множество векторов. Линейно независимые векторы аь а2..... ап из множества ^называются базисом множества V. если для любого вектора а е Еможно так подобрать числа ОС], ос2,.... ап. что а = ОС]И| + а2а2 + ... + апап.
33
Числа ОС], ос2,ая, зависят от вектора а.
Равенство а = ot]Zz\ + а2а2 + ... + апап называется разложением вектора а по базису а{,а2,...,ап.
Для каждого вектора a g V разложение по базису 2,, 32,ап единственно. Числа (ос], ос2, ..., ос„) называются координатами вектора а в базисе аъ аъ ..., ап.
Теорема. Любой базис на прямой состоит из одного ненулевого вектора.
Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
Теорема. Любой базис плоскости состоит из двух неколлинеарных векторов.
Векторы, лежащие в одной плоскости или в параллельных плоскостях, называются компланарными.
Теорема. Любой базис пространства состоит из трех некомпланарных векторов.
§ 5.3.	ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Декартова система координат задается с помощью точки О (начало координат) и базиса аъ а2, ..., ап. Тогда координаты произвольной точки М — это координаты вектора ОМ в базисе аъ а2,..., ап.
Очень часто при задании декартовой системе координат используют ортонормированный базис, когда длина каждого базисного вектора равна единице и угол между любыми двумя базисными векторами равен 90°. Это декартова прямоугольная система координат.
Как правило, мы будем работать с декартовой прямоугольной системой координат.
§ 5.4.	СИСТЕМА КООРДИНАТ НА ПРЯМОЙ
На прямой выбирается точка О — начало координат. От этой точки откладывается вектор ех единичной длины. Он задает положительное направление и масштаб. Направление, противоположное направлению вектора е\, — это отрицательное направление. Координатам точек справа от точки О приписывается знак «+», а координатам точек слева от точки О приписывается знак «—». Координата точки А — это длина отрезка ОА. Координата точки В — это длина
34
отрезка ОВ, взятая со знаком «—». Положение точки на прямой определяется заданием одной координаты.
В О е}	А
х
О 1
Пример 34- Изобразим на прямой точки Л(3), Z?(-l), С(2), Э(-2,5), 0(0).
D ВО	С	А
-с------О----о--------о---о---X
-2,5	-10	2	3
Задача 34- Изобразить на прямой точки Л(-3), Z?(-2), С(4), 0(1).
§ 5.5.	ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ НА ПЛОСКОСТИ
Выбираются две взаимно перпендикулярные прямые на плоскости. Точка О их пересечения — это начало координат. На каждой из прямых выбираются векторы единичной длины et и е2 соответственно. Первая прямая Ох — это ось абсцисс, а вторая прямая Оу — это ось ординат.
кУ
Положение точки М на плоскости определяется двумя числами (координатами): абсциссой х и ординатой у. М(х, у). Как определить координаты точки М? Проведем из точки М прямые, параллельные осям, до пересечения с другими осями, получим точки Мх и Му. Используя материал § 5.4, определим х и у — координаты соответственно Мх и Му. Это и есть координаты точки М: М(х, у).
АУ
м
9
У
1
-4 о
\мх х о---о----
1 X
35
Пример 35. Изобразим на плоскости точки /1(2, 3), /?(-!, 2), С(-3,-4), £>(1,-1), 0(0,0).
Задача 35. Изобразить на плоскости точки А (—2, 1), В (У 4), С(2,-1), £>(-1,-3).
§ 5.6.	ДЕКАРТОВА ПРЯМОУГОЛЬНАЯ СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
Выбираются три взаимно перпендикулярные прямые в пространстве. Точка О их пересечения — это начало координат. На каждой из прямых выбираются векторы единичной длины z, j, к соответственно. Первая прямая Ох — это ось абсцисс, вторая прямая Оу — это ось ординат, третья прямая Oz — это ось аппликат.
Положение точки М в пространстве определяется тремя числами (координатами): абсциссой х, ординатой у и аппликатой z- М(х, у, г).
Как определить координаты точки М? Опускаем перпендикуляр из точки М на плоскость Оху. Получим точку Мху. Используя материал § 5.5, определим х и у — координаты точки Мху. Точка Mz — это точка пересечения прямой Oz и плоскости, проходящей через точку М параллельно плоскости Оху. Используя материал § 5.4, определим z — координату точки Mz. Тогда упорядоченная тройка (х, у, z) и задает координаты точки М.
36
Координаты базисных векторов i= (1,0, 0),/= (0, 1,0), к — (0, 0, 1).
§ 5.7.	КООРДИНАТЫ ВЕКТОРА. ПРЕОБРАЗОВАНИЯ КООРДИНАТ ВЕКТОРА ПРИ ОСНОВНЫХ ОПЕРАЦИЯХ
Дан вектор АВ . Известны координаты точекЛ (х15 у}, ^), В(х2, у2, z2). Тогда координаты вектора АВ вычисляются по следующему правилу. Из координат конечной точки нужно вычесть координаты начальной точки: АВ = (х2 - х1? у2 - уь z2 - £i).
Пример 36. Даны точки >4(1, --2, 3), В(3, 5, 8). Определим координаты вектора АВ .
Координаты вектора АВ = (х2-х}, у2-у}, z2~ zd = (3 - 1,5- (-2), 8-3) = (2, 7, 5).
Задача 36. Даны точки А (2, 5, 6), В(— 1, 8, 4). Определить координаты вектора АВ .
При умножении вектора а = (аь аъ а3) на число X его координаты умножаются на это число: Ха — каъ ка3).
Пример 37. Дан вектор а = (1,2, 5). Определим координаты вектора За.
Координаты вектора За = (3 X 1, 3 X 2, 3 X 5) = (3, 6, 15).
Задача 37. Дан вектор а = (2, -4, 7). Определить координаты вектора 5 а.
При сложении векторов а = (аь а2, а3) и b = (Ьь Ь2, Ь3) складываются соответствующие координаты: а + b =	+ Ьъ а2 + Ьъ а3 + Ь3).
37
Пример 38. Даны точки А(3, 4, 5), В(2, -3, 7), С(1,6, 9). Определим координаты вектора 2АВ + ЗСА .
Координаты вектора АВ = (2 - 3, —3 — 4, 7 — 5) = (-1, —7, 2).
Координаты вектора G4 = (3 - 1,4 - 6, 5 — 9) = (2, —2, -4).
Тогда 2АВ + ЗСА = 2(-1, -7, 2) + 3(2, -2, -4) = (-2, -14, 4) + (6, -6, -12) - (—2 + 6, -14 + (-6), 4 + (-12)) = (4, —20, -8).
Задача 38. Даны точки А(4, 2, 1), В(5, -1,6), С(3, 7, 9). Определить координаты вектора ЗВС — 2 АС .
§ 5.8.	МОДУЛЬ ВЕКТОРА. РАССТОЯНИЕ МЕЖДУ ДВУМЯ ТОЧКАМИ
Дан вектор а =	а2, а3). Модуль вектора а вычисляется по следующей формуле: |Н| = V я? +	+ аз •
Пример 39. Дан вектор а = (1,4, 5). Определим модуль вектора а.
Модуль вектора равен |а| = V я2 + я2 + аз = д/12 + 42 + 52 =^~42 .
Задача 39. Дан вектор а = (3, 4, 2). Определить модуль вектора а.
Известны координаты точек A (х15 yh Zi), В(хъ у2, z2)« Расстояние р(А, В) между этими точками равно длине вектора АВ :
р(Л, В) = \АВ | = V(х2 - х,)2 + (у2 - у})2 + (z2 - г,)2 •
Пример 40. Даны точки А (2, 5, 4) и В(3, 7, 1). Определим расстояние между этими точками
Расстояние между точками А и В равно р(А, В) =
= V (х2 - X,)2 + (у2 - у,)2 + (г2 - Zl)2 = У (3 - 2)2 + (7 - 5)2 + (1 - 4)2 =
= дГм .
Задача 40. Даны точки Д(4, 7, 5) и B(-i, 6, 2). Определить расстояние между этими точками.
§ 5.9.	НАПРАВЛЯЮЩИЕ КОСИНУСЫ
Направление вектора а =	а2, а3) определяется углами ос, р, у,
образованными вектором а с положительными направлениями осей Ох, Оу и Oz соответственно. Косинусы этих углов называются на
38
правляющими косинусами вектора а и определяются по следующим формулам:
cos ос = а}/\а\, cosp = а2/|а|, cosy = а3/|2|.
Пример 41- Определим направляющие косинусы вектора а = = (1,4, 5).
Модуль вектора равен | а \ = V л? + al + aj = "V I2 + 42 + 52 = V42 .
Тогда cos а = ах/\а\ = 1/V42 , cosp = а2/|а| = 4/V42 , cosy = а3/|Л| =
= 5/V42.
Задача 41- Определить направляющие косинусы вектора И = = (2, 3, 7).
Направляющие косинусы удовлетворяют следующему соотношению: cos2oc + cos2p + cos2y = 1.
Пример 42. Определим, может ли вектор а составлять с координатными осями углы ос = 45°, р = 30° и у = 120°.
Так как cos2oc + cos2p + cos2y = cos245° + cos230° + cos2120° = = ( 1/VI)2 + (VI/2)2+ (-l/2)2= 1/2+ 3/4 + 1/4 = 3/2 + 1, то вектор a не может составлять с координатными осями углы ос = 45°, р = 30° и у= 120°.
Задача 42. Определить, может ли вектор а составлять с координатными осями углы ос = 30°, р = 60° и у = 150°.
§ 5.10.	КРИТЕРИЙ КОЛЛИНЕАРНОСТИ ВЕКТОРОВ
Критерий коллинеарности векторов. Векторы а = (аъ аъ а3) и b = (Ьь Ь2, Ь3) коллинеарны тогда и только тогда, когда а}/Ь} = а2/Ь2 = = ау/Ь3.
Пример 43. Исследуем на коллинеарность векторы а = (1, 2, 3) и b = (3, 6, 9).
Так как для векторов а и b выполняется условие коллинеарности векторов (1/3 = 2/6 = 3/9), то векторы а и b коллинеарны.
Задача 43- Исследовать на коллинеарность векторы a = (5, 4, 3) и К = (25, 20, 15).
Пример 44. Исследуем на коллинеарность векторы а = (2, 4, 5) иЬ =(8, 16, 15).
39
Так как для векторов и не выполняется условие коллинеарности векторов (2/8 = 4/16	5/15), то а и b не являются коллинеарными
векторами.
Задача 44- Исследовать на коллинеарность векторы а = (3, 8, 2) и£ = (6, 12, 5).
§ 5.11.	ДЕЛЕНИЕ ОТРЕЗКА В ДАННОМ ОТНОШЕНИИ
Даны точки М}(хь yh zj и М2(х2, у2, z2). Проведем через эти точки прямую т. Пусть М(х, у, z) — любая точка прямой т, отличная от М{.
Точка М делит отрезок М}М2 в отношении I от к Мъ если мри = хмм2.
При X > 0 точка М лежит между точками Мх и М2. При X = 0 точки Ми Mi совпадаютПри X < 0 точка М лежит вне отрезка МХМ2.
Из равенства МХМ = ХММ2 находим координаты точки М:
х = (х} + Хх2)/(1 + X), у = (yI + Ху2)/( 1 + X), z = (Zj + Xz2)/( 1 + X).
Это формулы деления отрезка в данном отношении.
. Пример 45. Даны точки , 2, 7) и А/2(-4, 6, 5). Определим координаты точки Л/, делящей отрезок М}М2 в отношении X = 2 от к М2.
Координаты точки М:
х= (Xj + Хх2)/(1 + X) = (1 + 2 х (_4))/(1 + 2) = -7/3;
У = (У + Ху2)/(1 + X) = (2 + 2 х 6)/(1 + 2) = 14/3; z= (Z1 + Xz2)/(1 + X) = (7 + 2 х 5)/( 1 + 2) = 17/3. Тогда Л/(—7/3, 14/3, 17/3).
Задача 45. Даны точки (2,4, 5) и М2( 1, -3, 8). Определить координаты точки М, делящей отрезок МХМ2 в отношении X = 3 от М, к М2.
При X = 1 получаем координаты середины отрезка :
х = (Xj + х2)/2, у = (у, + у2)/2, Z = (г, + z2)/2.
Пример 46. Определим в примере 45 координаты середины отрезка М\М2.
Координаты середины отрезка равны:
X = (X, + х2)/2 = (1 + (-4))/2 = -3/2; у = (у, + у2)/2 = (2 + 6)/2 = 4;
Z = (z, + z2)/2 = (7 + 5)/2 = 6.
Тогда точка Л(-3/2, 4, 6) — середина отрезка МХМ2.
Задача 46. Определить в задаче 45 координаты середины отрезка Л/| М2.
40
Глава 6
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
§ 6.1.	ОПРЕДЕЛЕНИЕ И СВОЙСТВА СКАЛЯРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Даны векторы а иЬ. Обозначим угол между этими векторами через ф.
Скалярным произведением (а, Ь) векторов а и b называется число, которое определяется по следующему правилу: (a, b) = |а\|b |со8ф.
Основные свойства скалярного произведения:
I)	(а, а) = \а|2;
2)	(5, Ь) = (Ь, «);
3)	(Ха,/) = (о, М) = Х(о Д );
4)	(а, b + с) = (а, Ь) + (а, с).
Пример 47- Известно, что \ а | = 5, 0| = 3, а угол между векторами а и b равен ф = л/6. Определим скалярное произведение векторов За — 2Ь и 5а 4 7 Ь.
Скалярное произведение векторов равно (За — 2Ь, 5 а + 7Ь) = = (За, 5 а) - (2Ь,5а) + (За, 7 b) - (2 b, 7Ь) = 3 х 5(а, а) - 2 х 5(Ь, а) + + 3 х 7(а, Ь) — 2 х 7(Ь, Ь) = 15\а |2 - 100, Ь) + 210, Ь) - 14|Л|2 = = 15 х 52 + 110, Ь) - 14 х З2 — 375 + 11011b\cosф - 126 = 249 + = 11 х 5 х 3COS7T/6 = 249 + 165^3/2.
Задача 47- Известно, что 0| = 6, 0| = 4, а угол между векторами а и b равен ф = л/3. Определить скалярное произведение векторов 2а +7Ь иЗа — 5Ь.
Зная координаты векторов а = (а}, а2, а3) и b = (Ь{, Ь2, Ь3) в декартовой прямоугольной системе координат, для вычисления скалярного произведения векторов а и b можно воспользоваться следующей формулой: (а, Ь) = а}Ь\ + а2Ь2 + а3Ь3.
Пример 48- Даны векторы а = (2, 3, 5) и Ъ> = (4, 7, 1). Определим скалярное произведение этих векторов.
41
Скалярное произведение равно (3, Ь) = ахЬх + а2Ь2 + а3Ь2 = 2x4 + + 3X7 + 5X1=34.
Задача 48- Определить скалярное произведение векторов а = = (3, 8, 7) и 2> = (—1, 4, 2).
Пример 49- Векторы 3 и Ъ = (2, 3, 5) коллинеарны. Скалярное произведение векторов а и b равно 4. Определим координаты вектора а.
Так как векторы а и b коллинеарны, то соответствующие координаты этих векторов пропорциональны. Пусть X — коэффициент пропорциональности. Тогда И = kb = Х(2, 3, 5) = (2Х, ЗА,, 5Х).
Так как скалярное произведение векторов а и b равно 4, то 4 = = (а, Ь) = Тк х 2 + ЗХ х 3 + 5Х х 5 = 38Х. Отсюда к = 4/38 = 2/19.
Тогда И = (2А., ЗХ, 5Х) = (2 х 2/19, 3 х 2/19, 5 х 2/19) = (4/19, 6/19, 10/19).
Задача 49- Векторы И и b = (3, 1,7) коллинеарны. Скалярное произведение векторов а и b равно 3. Определить координаты вектора а.
§ 6.2.	УГОЛ МЕЖДУ ВЕКТОРАМИ
Из равенства (И, Ь) = |П||b\coscp можно определить значение косинуса угла между векторами а и Ь:
cos ср =
(а, Ь)
|а||+
Пример 50- Определим значение косинуса угла между векторами из примера 48.
Длина вектора а равна |И| = V 22 + З2 + 52 = V38~- Длина векто-
ра b составляет | b | = д/ 42 + 72 + I2 = л[б6 .
Тогда косинус угла между векторами а и b равен:
(И, И) 34	17
coscp = ------7 = ----- ----- =	•-----
|3||Z>|	\38\66	у627
Задача 50- Определить значение косинуса угла между векторами из задачи 48.
42
§ 6.3.	ПРОЕКЦИЯ ВЕКТОРА НА ОСЬ
Проекцией прs АВ вектора АВ на ось s называется длина отрезка пр(А)пр(В), взятая со знаком «+», если векторы пр(А)пр(В) и f оди-наково направлены, и со знаком «—», если направления векторов пр(А)пр(В) и s противоположны. Здесь пр(А) и пр(В) — это ортогональные проекции на ось 5 точек А и В соответственно.
При вычислении проекции вектора АВ на ось 5 пользуются следующей формулой: npsAB = (АВ , ?)/|?|.
Пример 51-Даны векторы И = (1,2, 4), b = (3, 5, 6) и с = (-1, -2, 7). Определить проекцию вектора а + b на ось с.
Так как а + b* = (1 + 3, 2 + 5, 4 + 6) =_(4, 7, 10), то скалярное произведение векторов а + b и с равно (а + /л с) = 4 х (-1) + 7 х (—2) + + 10X7 = 52.
Длина вектора с составляет | с | = (-1)2 + (-2)2 + 72 = V54 .
Тогда проекция вектора а + Ъ на ось с равна:
пр^а + Ь) = (а + Ь, с)/|с | = 52/^54 .
Задача 51-Даны векторы а = (2, 3, 5), b = (-1,4, -3) и с = (6, 7, I). Определить проекцию вектора b — 2с на ось а.
§ 6.4.	ОРТОГОНАЛЬНЫЕ ВЕКТОРЫ
Ортогональные векторы — это векторы, угол ср между которыми равен 90°, то есть cos ср = 0.
Условие ортогональности векторов. Два ненулевых вектора ортогональны тогда и только тогда, когда их скалярное произведение равно 0.
Пример 52- Выясним ортогональность векторов а = (1, 3, 5)
и Ь = (—2, 4, —1).
Так как скалярное произведение векторов а и hравно (И, Ь) = = 1 х (—2) + 3х4 + 5х(—1) = 5^0, то векторы а и b не ортогональны.
Задача 52. Выяснить ортогональность векторов а = (—2, 3,-1) и 3 = (7, 2, —8).
Глава 7
ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
§ 7.1. ПРАВЫЕ И ЛЕВЫЕ ТРОЙКИ ВЕКТОРОВ
Упорядоченная тройка некомпланарных векторов а, Ь, с называется правой тройкой, если наблюдателю, находящемуся в конечной точке вектора ?, поворот от вектора а к вектору b на кратчайший угол виден совершающимся против часовой стрелки. Если поворот от вектора а к вектору b виден совершающимся по часовой стрелке, то векторы а, Ь, с образуют левую тройку.
Пример 53. Тройка векторов /, у, к это правая тройка, так как наблюдатель из конечной точки вектора к видит, что поворот от вектора i к вектору j на кратчайший угол (90°) совершается против часовой стрелки.
Задача 53. Верно ли, что тройка векторов у, к, i — это правая тройка?
Пример 54. Тройка векторов к, j, i — это левая тройка, так как наблюдатель из конечной точки вектора / видит, что поворот от вектора к к вектору j на кратчайший угол (90°) совершается по часовой стрелке.
44
Задача 54- Верно ли, что тройка векторов /, к, j — это левая тройка?
§ 7.2. ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Векторным произведением [а, Ь] векторов а и b называется вектор, удовлетворяющий следующим условиям:
1)	|[а, /?]| = |а||61sin ср, то есть модуль векторного произведения векторов равен площади параллелограмма, построенного на этих векторах (геометрический смысл векторного произведения векторов)',
2)	вектор [а, Ь] перпендикулярен плоскости векторов а и Ь;
3)	векторы а, Ь, [а, Ь} образуют правую тройку векторов. Основные свойства векторного произведения векторов:
1)	[а, а] = 6;
2)	[d, b] = —[b, 5];
3)	[Ха, b] = [d, X/?| = XIя, b}, где X — это число;
4)	[а + b, с] = I а, c| + [b, с].
Пример 55. Известно, что \а | = 5, |/?| = 4, а угол между векторами а и Ь равен ср = л/6. Определим модуль векторного произведения векторов 2а - ЗЬ и ба + 7Ь.
Векторное произведение векторов 2 а — ЗЬ мба + 7Ь равно [2d - 3b, ба + 7Ь\ = [2d, 6а\ - [ЗЬ, 6а] + [2d, 7Ь\ - [ЗЬ, 7Ь\ = = 2 х 6\а, а} — 3 х б[Ь, а] + 2 х 7[а, ~Ь\- 3 х 7[Ь, Ь] = О + 18 [а, Ь] + + 14[Н, К]-0 = 32[а, К].
Поэтому модуль векторного произведения векторов 2а — ЗЬ и ба + 7Ь равен \\2а - ЗЬ, ба + 7£]| = 132[a, Z>]| = 32|fl||/?|sin(р = = 32 х 5 х 4 sin я/6 = 640 х 0,5 = 320.
Задача 55. Известно, что |”а| = 3, |/> | = 5, а угол между векторами а и Ь равен <р = 5л/6. Определить модуль векторного произведения векторов 4 а + 2b и7 а — 9b.
S 7.3. ВЫЧИСЛЕНИЕ ВЕКТОРНОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Зная координаты векторов а = (а{, а2, а3) и b = (Ь\, Ь2, Ь3) в декар-говой прямоугольной системе координат, для вычисления векторного произведения векторов а и b можно воспользоваться следующей
45
формулой: [d, b] =
'	j	к
d\	a2	a3
b\	b2	b3
Нужно разложить этот определи-
тель по первой строке.
Тогда коэффициенты при 7, j и к равны соответственно первой, второй и третьей координатам вектора [а, 6].
Пример 56- Определим векторное произведение векторов а и b из примера 48.
Векторное произведение векторов а = (2, 3, 5) и b = (4, 7, 1) равно
Р, Ь] =
i j к
2 3 5
4 7 1
= (-1)ж/
3 5
7 1
+ (-i)1+27
+ (-i)1+3£
= (3 х 1 - 5 х 7)7- (2 х 1 - 5 х 4)7+ (2 х 7 - 3 х 4)к = —327 + 187+ + 27= (-32, 18,2).
Задача 56- Определить векторное произведение векторов и из задачи 48.
Пример 57- Даны точки А(1, 2, 3), В(—2, 5,4) и С(7, 6, -5). Определим площадь треугольника АВС.
Из геометрического смысла векторного произведения векторов следует, что площадь треугольника АВС равна 0,51[ АВ , AC J|.
Найдем координаты векторов АВ и АС .
~АВ = (—2 - 1, 5 - 2, 4 - 3) = (-3, 3, 1).
~АС = (7 - 1, 6 - 2, -5 - 3) = (6, 4, -8)^ __	__ __
Тогда векторное произведение векторов АВ и АС равно [ АВ , АС] =
i
-3 6
7 к
3 1
2 —4
= 2(—127+ 37- 6к- 9к — 27- 127) =
= 2(—147 — 97- 157) = -287 - 187- 307 = (-28, -18, -30). Отсюда
|[ АВ , АС ]| = д/ (—28)2 + (—18)2 + (—30)2 = V 2008 = 2^502 . Поэтому площадь треугольника АВС равна 0,5\{АВ , АС]\ = 0,5 х 2^502 = = V502.
Задача 57. Даны точки Л (-1, -3, 2), В(2, 4, 5) и С(1, -2, 6). Определить площадь треугольника АВС.
Пример 58. Вектор с, перпендикулярный векторам а = (— 1,3, 2) и b = (5, 4, 1), образует с осью Ох тупой угол. Модуль вектора ~с равен 26д/Т. Определим координаты вектора с.
46
Из свойств векторного произведения векторов получаем, что векторное произведение {а, К] перпендикулярно векторам а и Ь. Поэтому векторы с и [а, Ь \ коллинеарны.
Ь] =
i j к
-1 3 2
5 4 1
= 37+ юу— 4£ — 15Х-87+ j = -57+ 11J-
- 19Х= (-5, 11,-19).
Тогда модуль векторного произведения [а, Ь] равен |[я, /?]| = = V(-5)2+ II2 + (-19)2 = V507 = 13VT.
Так как векторы с и [а, /?] = (—5, 11, —19) коллинеарны, то соответствующие координаты этих векторов пропорциональны. Пусть X — коэффициент пропорциональности. Тогда координаты вектора с = = (-5Х, ИХ, -19Х).
Так как вектор с образует с осью Ох тупой угол, то соответствую-
-5Х	-5Х
щий направляющий косинус меньше нуля: cos а =----=-----— < 0.
26 у 3 Тогда X > 0.
Модуль вектора с равен |с| = д/ (-5Х)2 + (1IX)2 + (-19Х)2 = = Л/507Х2 = 13<|Х| = 2бУТ. Отсюда |Х| = 2.
Но X > 0. Поэтому X = 2.
Тогда вектор с — (—5Х, ИХ, — 19Х) = (—5 х 2, И х 2, —19 х 2) = = (-10, 22, -38).
Задача 58. Вектор с, перпендикулярный векторам а — (3, 1, 2) и b = (-2, -3, 1), образует с осью Оу острый угол. Модуль вектора с равен 5. Определить координаты вектора с.
Условие коллинеарности векторов. Ненулевые векторы а и b коллинеарны тогда и только тогда, когда [a, /?| = 0.
Глава 8
СМЕШАННОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ
§ 8.1.	ОПРЕДЕЛЕНИЕ И ОСНОВНЫЕ СВОЙСТВА СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Смешанным произведением векторов а, Ь, с называется число (а, b, 3), которое равно скалярному произведению векторного произведения [а, 3] и вектора 3: (а, b, 3) = ([2, Ь], с).
Основные свойства смешанного произведения векторов:
I)	(3, 3, с) = ([3, Ь], с) = (а, [Ь, с |), то есть порядок двух операций (скалярное произведение векторов и смешанное произведение векторов), дающих смешанное произведение векторов, не является существенным;
2)	(3, Ь, с) = (3, 3, а) = (3, 3, 3) = -(3, 3, 3) = -(3, 3, 3) = — —(3, 3, 3);
3)	(k[al + Х232, 3, 3) = Ь, с) + Х2(32, 3, 3), где X, и Х2 — числа.
§ 8.2.	ВЫЧИСЛЕНИЕ СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Зная координаты векторов 3 = (ah а2, а3), b = (Зь 32, З3) и 3 = = (С], с2, с3) в декартовой прямоугольной системе координат, для вычисления смешанного произведения векторов 3, 3, 3 можно вос
пользоваться следующей формулой: (3, Ь.с) =
а{	а2	а3
3]	32	З3
С	с2	с3
Пример 59. Определим смешанное произведение векторов а = = (-3, 4, 1),3 =(5, 2,3) и с =(1,4, 6).
Смешанное произведение векторов 3, 3, с равно (3, 3, 3) =
-3 4 1
5 2 3
1 4 6
- -36 + 12 + 20 - 2 + 36 - 120 = -90.
48
Задача 59- Определить смешанное произведение векторов а = = (5, 1,4), Ь= (2, -1, 3) и с = (6, 2, -3).
§ 8.3.	УСЛОВИЕ КОМПЛАНАРНОСТИ ВЕКТОРОВ
Условие компланарности векторов. Векторы а, Ь,с компланарны тогда и только тогда, когда их смешанное произведение равно нулю: (а, b, ?) — 0.
Пример 60. Исследуем векторы а,Ь ,с из примера 59 на компланарность.
Так как смешанное произведение (а, Ъ,с) = —90 + 0, то векторы а, Ь,с не компланарны.
Задача 60- Исследовать векторы а,Ь,с из задачи 59 на компланарность.
§ 8.4.	ГЕОМЕТРИЧЕСКИЙ СМЫСЛ СМЕШАННОГО ПРОИЗВЕДЕНИЯ ВЕКТОРОВ
Смешанное произведение векторов а,Ь,с равно объему параллелепипеда, построенного на векторах а, Ь,с, взятому со знаком «+», если а, Ь,с — правая тройка, и со знаком «—», если а, Ь,с — левая тройка. Это геометрический смысл смешанного произведения векторов.
Пример 61. Даны точки Л(3, 4, 2), Л(-1, 3, -2), С(5, 4, 3) и Р(2, 6, 3). Определим объем пирамиды ABCD.
Так как объем пирамиды ABCD, построенной на векторах АВ , АС, AD , составляет 1 /6 часть объема параллелепипеда, построенного на этих векторах, то объем пирамиды ABCD равен \(АВ , АС , AD )|/6.
Найдем координаты векторов.
= (-1 - 3, 3 - 4, -2 - 2) = (-4, -1, -4).
АС =(5 -3,4 -4, 3-2) = (2,0, 1).
AD = (2 - 3, 6 - 4, 3 - 2) = (-1, 2, 1).
Тогда смешанное произведение векторов АВ, AC, AD равно
4
1
1
(АВ, AC, AD) =
-4 -1 —4
2 0 1
-1 2 1
4 1
2 0
-1 2
= -(0-1 + 16-0-
- 8 - 2) = -5.
Отсюда объем пирамиды A BCD равен \(АВ , АС , AD)\/e = \—5\/G — = 5/6.
49
Задача 61- Даны точки Л(2, 3, 4), Z?(-5, 4,'2), С(6, —I, 3) и Z)(l, 3, 4). Определить объем пирамиды ABCD.
Воспользовавшись геометрическим смыслом смешанного произведения векторов, можно определить тип тройки векторов по знаку смешанного произведения векторов. Если (5, Ь,с) > 0, то а, Ь, с — правая тройка векторов. Если (Н, b, с) < 0, то 3, b, с — левая тройка векторов.
Пример 62. Определим тип тройки векторов из примера 59.
Так как смешанное произведение (И, b, с) = -90 < 0, то а,~Ь,с — левая тройка векторов.
Задача 62. Определить тип тройки векторов из задачи 59.
Глава 9
ПОЛЯРНЫЕ КООРДИНАТЫ
Говорят, что на плоскости введена полярная система координат, если заданы:
1)	точка О (полюс);
2)	полупрямая О А (полярная ось);
3)	масштаб для измерения длин.
Положение точки М на плоскости определяется полярными координатами: полярным радиусом г = ОМ (г > 0) и полярным углом (р между полупрямыми ОА и ОМ. Считают, что (р > 0 при повороте от ОА к ОМ против часовой стрелки и (р < 0 при повороте от ОА к ОМ по часовой стрелке. Понятно, что полярный угол не определен однозначно. Значение полярного угла, удовлетворяющее условию 0 < ср < 2л, называется главным.
Пример 63. Изобразим точки, заданные полярными координатами: В(3, 0), С(1, л/2), D(2, -п/4), Е(4, л).
С
Е	| В
Задача 63. Изобразить точки, заданные полярными координатами: В(2, п/6), С(1, 0), Р(3, Зл/4), £(4, -л/3).
Определим связь между декартовыми координатами на плоскости и полярными координатами.
Совместим начало координат и полюс, а полярную ось направим по положительной полуоси абсцисс. Тогда декартовы координаты (х, у) и полярные координаты (г, (р) произвольной точки М связаны следующими соотношениями:
| х = rcoscp, f tgф = у/х,
[y=rsincp | г = д/х2 + у2'
51
При нахождении полярного угла необходимо учитывать, в какой координатной четверти расположена точка М. и подбирать соответствующее значение ф.
Пример 64. Определим декартовы координаты точки по полярным координатам (2, Зя/4).
Здесь г= 2, ф = Зл/4.
Тогда х = гсозф = 2cos3ti/4 = 2(-VT/2) = -VT, у = rsin(p =
= 2 sin Зл/4 = 2л/7/2 = У?.
Декартовы координаты точки равны (—VT VF).
Задача 64. Определить декартовы координаты точки по полярным координатам (3, л/6).
Пример 65. Определим полярные координаты точки М по де-
картовым координатам (—1, Vn
Изобразим точку с координатами (—1, Уз”) на координатной пло-СКОСТИ.

ф X
Полярный радиус точки Мравен г = д/ %2 + у2 = у (-1)2 + (Уз")2 =
= 2.
1£ф = УА = Уз~/(-1) = -Уз”. Точка Мнаходится во второй координатной четверти. Поэтому полярный угол равен ф = 2л/3.
Задача 65. Определить полярные координаты точки Мпо декартовым координатам (—2, —2).
Глава 40
КОМПЛЕКСНЫЕ ЧИСЛА
S 10.1. ВОЗНИКНОВЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ
Комплексные числа впервые возникли при вычислении корней кубических уравнений.
В шестнадцатом веке были получены формулы корней кубического уравнения. Корень кубического уравнения 7 = рх + q может быть найден по формуле х= у и + у у , где w и v — решения системы - f и + V = (L уравнении J 3 Д’ [ uv = р727.
Оказалось, что для некоторых кубических уравнений такая система не имеет действительных решений, хотя корень самого уравнения легко угадывается. Например, х = 4 — корень уравнения 7 = 15х + 4, - [ и + v “ 4, а система уравнении	’	не имеет действительных ре-
[ uv = 15727 = 125 шений.
Для разрешения возникшего противоречия итальянский математик Бомбелли в 1572 г. ввел в математику комплексные числа, в множестве которых выполнима операция извлечения квадратного корня из отрицательного числа. Но только после появления в девятнадцатом веке работ Гаусса и Бесселя использование комплексных чисел стало общепринятым.
§ 10.2. АЛГЕБРАИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Говорят, что комплексное число z задано в алгебраической форме, если оно имеет следующий вид: z = х + yi, где х и у — действительные числа, а мнимая единица i определяется условием z2 = — 1. Число х называется действительной частью комплексного числа z = х + yi и обо
53
значается х = Re z- Число у = Im z — это мнимая часть комплексного числа z — х + yi.
Пример 66. Определим действительную и мнимую части комплексного числа z = 5 + 3/.
Действительная часть комплексного числа z = 5 + 3i равна Re(5 + 3/) = 5. Мнимая часть комплексного числа z = 5 + 3/ — это Im(5 + 3/) = 3.
Задача 66. Определить действительную и мнимую части комплексного числа z = 6 — 7/.
§ 10.3. ДЕЙСТВИЯ С КОМПЛЕКСНЫМИ ЧИСЛАМИ
Число ~z = х — yi называется комплексно сопряженным к комплексному числу z = х + yi. При нахождении комплексно сопряженного числа надо изменить знак мнимой части исходного числа.
Пример 67. Определим комплексно сопряженные к следующим числам: 2 + 3z, -1 — 4/, 5, 7Z, -9/, 3 — 8/, — 10, -7 + 6/.
2+~3/ = 2 — 3/, — 1 — 4Z = -1 + 4/, 5 = 5, Ti = —7/, ^9/ = 9/,
3 — 8/ = 3 + 8/, -10 = -10, —7 + 6/ = -7 - 6/.
Задача 67. Определить комплексно сопряженные к следующим числам: 21 + 25/, -12 - 14/, 18, 8/, —15/, 14 - 9/, —7, -5 + 19/.
Даны комплексные числа Zi = х{ + ур и z2 = х2 + y2i. Сумма этих чисел определяется по следующему правилу:
Z, + Z1 = Xj + yj + х2 + y2i = Х'+х2 + (ух + y2)i.
Пример 68. Найдем сумму комплексных чисел Z\ = 5 + 3/ и z2 = = 7 - 2/.
г, +г2 = 5 + 3/ + 7-2/= 12 + /.
Задача 68. Найти сумму комплексных чисел г, = —2 + 4/ и = = -8 + 3/.
Разность комплексных чисел zt = х{ + y{i и z2 = х2 + y2i определяется по следующему правилу:
Z, - Z2 = X, + y}i - (х2 + y2i) = xt-x2 + (yt - y2)i.
Пример 69. Найдем разность комплексных чисел из примера 68.
г, - z2 = 5 + 3z- (7 - 2z) = 5 + 3i-7 + 2z = -2 + 5z.
Задача 69. Определить разность комплексных чисел из задачи 68.
54
При нахождении произведения комплексных чисел ад = (xf + ур) (х2 + У20 нужно раскрыть скобки и воспользоваться равенством /2 = — 1.
Пример 70. Определим произведение комплексных чисел из примера 68.
Z& = (5 + 3/)(7 - 21) = 35 + 21/ - 10/ - 6/2 = 35 + 11/ - 6 х (-1) = = 41 + 11/.
Задача 70. Определить произведение комплексных чисел из задачи 68.
При делении Z\/Zi комплексных чисел нужно умножить числитель и знаменатель дроби на комплексное число = х2 — у21, которое является комплексно сопряженным к знаменателю z2 = х2 + После этого надо раскрыть скобки в числителе и знаменателе дроби.
Пример 71. Определим в примере 68 результат деления числа на число Z2-
Z2 = 2 - 2/. Отсюда г2 = 7 + 2/.
Z\ _ 5 + 3/ _ (5 + 3/)(7 + 2/) _ 35 + 21/+10/-6 _ 29 + 31/ _
Тогда - - 7_2;. - (7 _ 2/)(7 + 2/) -	49 +4	53
= 29/53 + 31/53/.
Задача 71. Определить в задаче 68 результат деления числа Zi на
ЧИСЛО Z2-
Комплексные числа Z\ = х, + ур и г2 = х2 + ур считаются равными, если равны их действительные и мнимые части: х{ = х2, у} = у2.
Пример 72. Определим действительные корни уравнения
(2 - i)x + (-5 + 7/’)у = 1 - 8/.
Выделим в левой части уравнения действительную и мнимую части.
(2 — /)х+ (—5 + 7/)у = 1 — 8/-* 2х— ix— 5у + 7iy = 1 — 8/ -* (2х — 5у) +
+ (—х + 7у)/ = 1 — 8/.
Из равенства комплексных чисел получаем условия на действи-f 2х - 5у = 1, тельные и мнимые части:	z
[ -х + 7у = -8.
Решим эту систему линейных уравнений с помощью правила Крамера.
А =	2 -5 -1 7	= 2 х 7 — (—]) х (—5) = 9 0.
ал.=	1 -5 -8 7	= 1X7- (-8) X (-5) = -33.
55
Av—
= 2 x (—8) — 1 x (—1) = —15.
Тогда x = Лх/Л = -33/9 = -11/3, у = Д/Д ==—15/9 = -5/3.
Задача 72. Определить действительные корни уравнения (4 + 5i)x — (3 - 7i)y = 2 - 9/.
Комплексное число z — х + 0/ считается совпадающим с действительным числом х. Комплексные числа вида yi (у — действительное число) называются чисто мнимыми.
При решении квадратных уравнений в случае отрицательного дискриминанта нужно воспользоваться тем, что z2 = —1.
Пример 73. Решим квадратное уравнение г2 + 4^ + 13 = 0.
Здесь а = 1, b = 4, с = 13.
Тогда дискриминант D— Ь2 — 4яс = 42 — 4x1x13 = —36 < 0.
—b ± ’y/~D	—4 ± 6/	—4 ± 6/	—4 — 6/
Z =---------= ——' =  , то есть Zi = ~ = — 2 — 3/
2а 2X1	2	1	2
—4 + 6/
и z2 =------= -2 + 3/.
Задача 73. Решить квадратное уравнение z2 + 6z + 45 = 0.
§ 10.4.	ТРИГОНОМЕТРИЧЕСКАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Каждому комплексному числу z = х + yi поставим в соответствие точку с координатами (х, у) на координатной плоскости Оху. Это геометрическая интерпретация комплексных чисел.
Перейдем от декартовых координат (х, у) к полярным координатам (г, <р): х = г cos ф, у = rsin ф.
Тогда z = х + yi = г cos ф + zrsin ф = r(cos ф + isin ф). Форма записи комплексного числа z = х + yi в виде z = г (cos ф + i sin ф) является тригонометрической формой комплексного числа.
Полярный радиус r= Vх2 + у2 называется модулем комплексного числа z = х + yi и обозначается |г|.
Полярный угол ф, определяемый из условия tgф = у/х, называется аргументом комплексного числа z = х + yi и обозначается Arg г.
Главное значение аргумента arg z — это аргумент комплексного числа г, удовлетворяющий условию 0 < arg z < 2л.
56
Пример 74. Определим тригонометрическую форму комплексного числа z = — 1 — /.
Здесь х = — 1 и у = — 1. Тогда модуль комплексного числа равен г = = у X2 + / = у (-1)2 + (-1)2 = УТ
Изобразим комплексное число z = — 1 — / на плоскости Оху.
Мы видим, что комплексное число z = -1 — i принадлежит третьей четверти, a tg ф = у/х = (— 1)/(— 1) = 1. Поэтому главное значение аргумента комплексного числа z = — 1 — i равно 5л/4.
Получаем тригонометрическую форму z = r(cos(p + /sin ср) =
/— 5л 5л = у 2 (cos——Н / sin——). 4	4
Задача 74. Определить тригонометрическую форму комплексного числа £ = — 1 + i V?.
При умножении комплексных чисел Z\ = rXcoscp! + /sinср,) и z2 = r2(cos <р2 + i sin (р2) модули перемножаются, а аргументы складываются: Z\Zi = /^(cosCcp! + (р2) + /sin(cp! + (р2)).
Пример 75. Определим произведение комплексных чисел Zi = 5л 5л	л л
= 6(cos ——н /sin — ) и z2 = 2(cos— + /sin—), об	3	3
5л 5л	л л	5л л
ZiZ2 = 6(cos-— + /sin—-) х 2(cos— + /sin — ) = 6 x 2(cos(— + —) + oo	3	3	о 3
5л	л	7л	7л	I—	I—
+ zsin(— + —)) = 12(cos— + zsin—) = 12(—у 3 /2 — z/2) = —бу 3 — 6/.
6	3	6	6
Задача 75. Определить произведение комплексных чисел Zi = 2л 2л	л л
8(cos— + zsin —) и z2 = 4(cos— + / sin — ).
При делении комплексного числа Z\ = г |(cos cpj + zsin ф|) на комплексное число г2 = r2(cos (р2 + z sin ср2) нужно найти частное соответствующих модулей и разность соответствующих аргументов комплексных чисел: Z\/z2 = (cos(<Pi — Ф2) + Zsin((pj — ф2)).
57
Пример 76. В примере 75 определим результат деления числа z} на число г2.
5л	5л	л	л	5л	л
zjz2 = (6(cos— + Zsin—))/(2(cosy + Zsin—)) = 6/2(cos(— - y) + 0	0	J	J	О	J
5л	л	л	л
+ zsin(— - —)) = 3(cos— + / sin—) = 3(0 + /) = 3/.
о	j	2	2
Задача 76. В задаче 75 определить результат деления числа Z\ на ЧИСЛО Z2-
Пример 77. Определим множество точек, удовлетворяющих условию |z — 1 + 2Z| < 2.
Пусть z = х + yi. Тогда z - 1 + 2/ = х + yi - 1 + 2/ = (х — 1) + (у + 2)/.
Поэтому модуль |z — 1 + 2Z| = |(х — 1) + (у + 2)71 =
= У (х — I)2 + (у + 2)2 < 2, то есть (х — I)2 + (у + 2)2 < 4. Это внутренность круга радиуса 2 и с центром в точке (1, —2). Граница круга (то есть окружность) в ответ не включается.
Задача 77. Определить множество точек, удовлетворяющих условию |г + 5 - 4/| > 9.
§ 10.5.	ПОКАЗАТЕЛЬНАЯ ФОРМА КОМПЛЕКСНОГО ЧИСЛА
Верна следующая формула Эйлера'. е‘(? = coscp + Zsin ср. Тогда комплексное число z - г (cos <р + i sin ф) можно представить в виде z ~ ге1\ Это показательная форма комплексного числа.
Пример 78. Вычислим е'л/3.
е'л/3 = cosy + Zsin— = 1/2 + /‘Уз~/2.
Задача 78. Вычислить е'5л/6.
Пример 79. Определим показательную форму комплексного числа из примера 74.
Так как модуль г = УТ, а аргумент ф = 5л/4, то показательная форма комплексного числа равна z = re"* = УУе'5л/4.
Задача 79. Определить показательную форму комплексного числа из задачи 74.
58
§ 10.6.	СТЕПЕНЬ КОМПЛЕКСНОГО ЧИСЛА
При нахождении /z-й степени комплексного числа нужно записать это комплексное число в тригонометрической форме z = r(coscp + + z sin (р) и воспользоваться формулой Муавра zn = r"(cos /нр + Z siп /нр).
Пример 80. Возведем комплексное число z = — I — / в степень /7 = 5.
Тригонометрическая форма комплексного числа £ = — 1 — / равна
I— 5л 5л
Z = У 2 (cos— + zsin—) (см. пример 74).
/—	5 х 5л 5 х 5л
Тогда по формуле Муавра z = (у2 ) (cos—-----Ь / sin—-—) =
4	4
I—	25л	25л	I—	л	л
= 4y2(cos-^- + zsin-^j-) = 4 у2 (cos(6л + —) + шп(6л + —)) =
= 4’V2’(cos^- + /sin j) = 4'V2’(1/V2’ + i/~\[2) = 4(1 + /).
Задача 80. Возвести комплексное число z = — 1 + / Уз" в степень
/7 = 6.
§ 10.7. КОРЕНЬ п-Й СТЕПЕНИ ИЗ КОМПЛЕКСНОГО ЧИСЛА
При нахождении корня /7-й степени из комплексного числа нужно записать это комплексное число в тригонометрической форме Z = r(coscp + z sin <p) и воспользоваться следующей формулой: VT = «/—z ф + 2лк , . . ср + 2л±ч / /а 1
= у г (cos—---+ z sin------), где к = О, I, п - I.
п	п
Геометрически эти п значений корня представляют собой вершины правильного /z-угольника, вписанного в окружность радиуса с центром в начале координат.
Пример 81. Определим корень степени п = 3 из комплексного числа z = — I -
Тригонометрическая форма комплексного числа z = — I — i равна г— 5л	5л
z = у2 (cos~—н zsin — ) (см. пример 74).
з г- з / j— 5л/4 + 2л£	5л/4 + 2л£
Тогда у^ = у у 2 (cos-----Н- Zsin-------),где£ = О, 1,2.
59
Ьг- 5л/4 + 2л X О
При к = О получаем значение корня = \2 (cos------------Ь
5л/4 + 2л х О б,— 5л 5л + i sin---------) = V 2 (cos— + i sin—).
6,—	5л/4 + 2л x 1
При к = 1 получаем значение корня Z\ = V 2 (cos--------Ь
5л/4 + 2л X 1	б[—	13л	13л
+ zsin----------) = \2(cos— + zsin—).
6,—	5л/4 + 2л X 2
При к = 2 получаем значение корня z-i = \2(cos---------н
5л/4 + 2л х 2	6/—	21л	21л
+ zsin----------) = \2(cos— + zsin—).
Задача 81. Определить корень степени п = 4 из комплексного числа z= -I +
Глава 11
ПЛОСКОСТЬ
§ 11.1. ОБЩЕЕ УРАВНЕНИЕ ПЛОСКОСТИ
Говорят, что уравнение F(x, y,z) = 0 является уравнением фигуры G, если:
1) координаты (х, у, z) любой точки фигуры Gудовлетворяют этому уравнению;
2) координаты (х, у, z) любой точки, не принадлежащей фигуре G, не удовлетворяют этому уравнению.
Дана плоскость л. Известны точка Л/0(х0, у0, Zq) в этой плоскости и вектор п = (А, В, С), перпендикулярный плоскости л. Тогда плоскость л можно задать следующим уравнением:
А(х - х0) + В(у - у0) + C(z - Zo) = °-
Вектор п называется нормальным вектором (или просто нормалью) плоскости л.
Раскроем скобки и сгруппируем слагаемые: Ах + By + Cz — (Ах0 + + Ву() + С^о) = 0. Обозначим — (Лх0 + Ву(} + С^) через D. Тогда общее уравнение плоскости имеет следующий вид:
Ах + By + Cz + D = 0.
Пример 82. Определим уравнение плоскости л, зная точку
7И0(1, 2, 3) в этой плоскости и нормаль п = (—4, 5, 7) плоскости.
Уравнение плоскости л имеет следующий вид: А(х - л^) + В (у - у0) +
C(z-^о) = 0 -> —4(х — 1) + 5(у— 2) + 7(z- 3) = 0 - -4х+ 5у + lz~ 27 = 0.
Задача 82. Определить уравнение плоскости л, зная точку
Л/0(2, 3, —1) в этой плоскости и нормаль п = (6, 8, —3) плоскости.
Пример 83. Определим, принадлежат ли точки /ИДО, 4, 1)
и М(1, 4, 3) плоскости л, заданной уравнением 2х + Зу - 5z - 7 = 0. Подставим координаты точек в уравнение плоскости.
Так как 2х0 + Зх4-5х1-7 = 0, то точка принадлежит плоскости л.
61
А вот точка М2 не принадлежит плоскости л, потому что 2x1 + + 3x4 — 5x3 — 7 = —8 + 0.
Задача 83. Определить, принадлежат ли точки Л/,(— 1, 3, 2) и Л/2(9, -2, 1) плоскости л, заданной уравнением х - 2у + 2z + 3 = 0.
Плоскость Ах +By+Cz+D = 0 делит все пространство на два полупространства. Для координат точек одного полупространства выполнено условие Ах + By + Cz + D > 0. Координаты точек другого полупространства удовлетворяют условию Ах + By + Cz + D < 0.
Пример 84. Даны точки ЛД-5, 3, 1), 2V(2, 4, 6) и уравнение плоскости 2х + 7у — 3z + 5 = 0. Определим, пересекает ли отрезок MN плоскость.
Подставим координаты точек М и N в уравнение плоскости:
2(—5) + 7ХЗ-ЗХ1+5=13>О, 2Х2 + 7Х4-ЗХ6 + 5=19>О.
Так как получены числа одного знака, то точки М и N лежат в одном полупространстве относительно плоскости. Поэтому отрезок Л/У не пересекает плоскость.
Задача 84. Даны точки Л/(6, -4, 1), N(—3, 1,7) и уравнение плоскости 4х — 5у — 6z + 2 = 0. Определить, пересекает ли отрезок MN плоскость.
§ 11.2. ЧАСТНЫЕ СЛУЧАИ РАСПОЛОЖЕНИЯ ПЛОСКОСТИ
Плоскость Ах + By + Q = 0 проходит через начало координат.
Если в уравнении плоскости Ах + By + Cz + D = 0 коэффициент при какой-то переменной равен нулю, то при D + 0 плоскость параллельна соответствующей координатной оси, а при D = 0 плоскость проходит через соответствующую координатную ось.
Пример 85. Что можно сказать о расположении плоскости 2х - Зу + 5 = 0?
Так как в уравнении плоскости нет переменной z, а коэффициент D = 5 + 0, то плоскость параллельна координатной оси Oz.
Задача 85. Что можно сказать о расположении плоскости Зх + 5z - 6 = 0?
Пример 86. Что можно сказать о расположении плоскости 2х - Зу = 0?
Так как в уравнении плоскости нет переменной г, а коэффициент
D = 0, то плоскость проходит через координатную ось Oz.
62
Задача 86. Что можно сказать о расположении плоскости Зх + 5z = О?
Если в уравнении плоскости Ах + By + Cz + D = 0 коэффициенты при двух переменных равны нулю, а коэффициент D 0, то плоскость параллельна соответствующей координатной плоскости.
Пример 87. Что можно сказать о расположении плоскости Зх + 7 = О?
Так как в уравнении плоскости нет переменных у и z, а коэффициент D = 7 0, то плоскость параллельна координатной плоскости Oyz.
Задача 87. Что можно сказать о расположении плоскости 5у - 9 = О?
х = 0 — это уравнение координатной плоскости Oyz. Уравнением координатной плоскости Оху будет z = 0. у = 0 — это уравнение координатной плоскости Oxz.
§ 11.3.	УРАВНЕНИЕ ПЛОСКОСТИ В ОТРЕЗКАХ
Если известны абсцисса а, ордината b и аппликата с точек пересечения плоскости с координатными осями Ох, Оу и Oz соответственно, то можно составить уравнение плоскости в отрезках х/а + y/b + z/с = 1.
Пример 88. Плоскость проходит через точки (2, 0, 0), (0, -3, 0)
и (0, 0, 4). Составим уравнение плоскости в отрезках.
Здесь а = 2, b = — 3 и с = 4. Тогда уравнение плоскости в отрезках равно х/а + y/b + z/с = 1, то есть х/2 + у/(-3) + z/4 = 1.
Задача 88. Плоскость проходит через точки (-1, 0, 0), (0, 5, 0) и (0, 0, —3). Составить уравнение плоскости в отрезках.
Из общего уравнения плоскости Ах + By + Cz + D = 0 можно получить уравнение плоскости в отрезках. Для этого надо перенести коэффициент D в правую часть и разделить обе части полученного уравнения на —D.
Пример 89. Из уравнения плоскости Зх + 4у - 5z + 9 = 0 получим уравнение плоскости в отрезках.
Выполним следующую цепочку преобразований: Зх + 4у — 5z + 9 = 0 -^3x+4y-5z = -9^(3x + 4y-5z)/(-9)= 1 - -х/3 - 4у/9 + 5z/9 = 1 х/(—3) + у/(—9/4) + z/(9/5) = 1.
Задача 89. Из уравнения плоскости 2х- Зу + 8z - 7 = 0 получить уравнение плоскости в отрезках.
63
§ 11.4.	НОРМАЛЬНОЕ УРАВНЕНИЕ ПЛОСКОСТИ
Уравнение плоскости х cos ос + ycosp + г cos у — р = 0, где cos а, cosp, cosy — это направляющие косинусы нормали плоскости, ар — расстояние от начала координат до плоскости, называется нормальным уравнением плоскости.
Из общего уравнения плоскости Ах + By + Сг + D=0 можно получить нормальное уравнение плоскости, умножив обе части общего уравнения плоскости на нормирующий множитель - sgn D/^A2 + в2 + С2, где sgn/) — это знак коэффициента D.
Пример 90. Приведем уравнение плоскости Зх + 4у - 5z + 9 = О к нормальному виду.
Здесь А = 3, В= 4, С = — 5, D= 9. Тогда нормирующий множитель
-sgn Z)/V А2 + В2 + С2 = -sgn(9)/V З2 + 42 + (~5)2 = -1/V50.
Умножим обе части уравнения плоскости Зх + 4у — 5z + 9 = 0 на нормирующий множитель — 1/V50. Получим нормальное уравнение плоскости -3X/V50 - 4 v/VsO + 5г/У50 - 9/V50 = 0.
Задача 90. Привести уравнение плоскости 2х — Зу + 8г — 7 = О к нормальному виду.
§ 11.5.	РАССТОЯНИЕ ОТ ТОЧКИ ДО ПЛОСКОСТИ
Расстояние от точки Л/0(х0, у(), г») до плоскости Ах +By+Cz+D = 0 равно |4xq + Ву0 + Czg + D^\l А2 + В2 + С2.
Пример 91. Расстояние от точки Л/о( 1, 2, 3) до плоскости Зх + 4у —
- 5z+ 9 = 0равно|3 X I +4 х 2 - 5 х 3 + 9|/V З2 + 42 + (-5)2 =5/^50 =
= i/VT.
Задача 91. Определить расстояние от точки Л/о(—3, 4, I) до плоскости 2х - Зу + 8г - 7 = 0.
§ 11.6.	УРАВНЕНИЕ ПЛОСКОСТИ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТРИ ТОЧКИ
Даны три точки М\(хь yh zj, М2(х2, у2, г2) и М3(х3, у3, г3), лежащие в одной плоскости л. Пусть М(х, у, г) — произвольная точка плоскости л.
64
Из условия компланарности векторов , МЛМ2 и МХМ3 получаем уравнение плоскости л: (МХМ, М{М2, М}М3) = 0, то есть
X - Xj у - yl z-Zt
*2-*1 У2-У1 Z2-Z1
Х3 - У3 ~ у} Z3 - Zi
= 0.
Если точка М совпадает с точкой Мх, то первая строка определителя состоит из нулей. Поэтому определитель равен нулю. Если точка Мсовпадает с точкой М2, то первая и вторая строки определителя одинаковы. Поэтому определитель равен нулю. Если точка М совпадает с точкой М3, то первая и третья строки определителя одинаковы. Поэтому определитель равен нулю.
Следовательно, плоскость л, задаваемая этим уравнением, проходит через точки М2 и М3.
Пример 92. Определим уравнение плоскости л, проходящей через три точки Л/|(1, 2, 3), Л/2(- 1,4, 6) и Л/3(2, 4, 5).
Пусть Л/(х, у, z) — произвольная точка плоскости л. Определим координаты векторов:
— (х — 1, у - 2, z- 3), ЯМ =(-1 - 1,4 -2, 6-3) = (—2, 2, 3),
= (2 - 1, 4 - 2, 5 - 3) = (1, 2, 2).
Векторы М\М2 и компланарны. Поэтому их смешанное произведение равно нулю:
(М(Л/, Л/^2, А/1М3) = 0, то есть
х-1 у-2 г- 3
-2	2	3
1	2	2
= 4(х- 1) +
+ 3(у - 2) - 4(г - 3) - 2(г - 3) - 6(х - 1) + 4(у - 2) = -2(х - 1) + + 7(у-2) - 6(г-3) = 0.
Тогда уравнение плоскости л равно —2х + 1у — 6г + 6 = 0.
Задача 92. Определить уравнение плоскости л, проходящей через три точки A/j(2, 5, 3), М2(-2, 7, 6) и Л/З(3, -4, 1).
§ 11.7.	ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПЛОСКОСТЕЙ
Две плоскости Л] и л2 заданы своими общими уравнениями Дх + Вху + Qz + D, = 0 и А2х +	+ C2z + D2 = 0.
Плоскости л, и л2 совпадают тогда и только тогда, когда А}/А2 = = BJB. = С./С, = Z>,/Z)2.
65
Пример 93. Определим взаимное расположение плоскостей
Зх + 4у - 5z + 9 = 0 и 6х + 8у - 1 Qz + 18 = 0.
Так как 3/6 = 4/8 = — 5/(—10) = 9/18, то плоскости совпадают.
Задача 93. Определить взаимное расположение плоскостей бх - 9у + 24г - 21 = 0 и 2х - Зу + 8г - 7 = 0.
Плоскости Л! и л2 параллельны тогда и только тогда, когда А{/А2 = = В,/В2 = CJC2 * djd2.
Пример 94. Определим взаимное расположение плоскостей
Зх + 4у — 5z + 9 = 0 и 9х + 12у — 15z + 14 = 0.
Так как 3/9 = 4/12 = -5/(-15) ^9/14, то плоскости параллельны.
Задача 94. Определить взаимное расположение плоскостей
4х — бу + 16г — 19 = 0 и 2х - Зу + 8г - 7 = 0.
Плоскости Л| и тг2 перпендикулярны тогда и только тогда, когда перпендикулярны их нормали п} = (Аъ Въ С}) ип2 = (А2, Въ С2), то есть скалярное произведение (пь п2) = А}А2 + В}В2+ СХС2 = 0.
Пример 95. Определим взаимное расположение плоскостей
Зх + 4у — 5г + 9 = 0 и 2х — 4у — 2г + 3 = 0.
Нормали плоскостей равны л, = (3, 4, —5) и п2 = (2, —4, —2). Скалярное произведение (л,, п2) = 3 х 2 + 4 х (-4) + (-5) х (-2) = 0.
Поэтому векторы и п2 перпендикулярны. Следовательно, и плоскости перпендикулярны.
Задача 95. Определить взаимное расположение плоскостей 2х — Зу + 8г — 7 = 0 и х + бу + 2г — 5 = 0.
Пример 96. Определим уравнение плоскости ль проходящей через точку А/о( 1, 2, 3) параллельно плоскости л2, заданной уравнением Зх + 4у — 5г + 9 = 0.
Нормаль п2 = (3, 4, —5) перпендикулярна плоскости л2. Плоскости
л, и л2 параллельны. Поэтому вектор п2 перпендикулярен плоскости л, и является нормалью этой плоскости.
Воспользуемся уравнением плоскости, проходящей через данную точку: А(х - х0) + В(у — у{]) + С(г - го) = 0- Здесь А = 3, В = 4, С = —5, *0= 1,Л = 2, Zo = 3.
Тогда уравнение плоскости л! равно 3(х — 1) + 4(у — 2) — 5(г - 3) = 0, то есть Зх + 4у — 5г + 4 = 0.
Задача 96. Определить уравнение плоскости ль проходящей через точку Л/0(-4, 2, 1) параллельно плоскости л2, заданной уравнением 2х — Зу + 8г — 7 = 0.
66
Пример 97. Определим уравнение плоскости ли проходящей через точки ЛУ|(1, 2, 3), Л/2(—4, 6, 5) перпендикулярно плоскости л2, заданной уравнением Зх + 4у — 5z + 9 = 0.
Способ I. Нормаль плоскости л2 равна п2 = (3, 4, —5) и перпендикулярна плоскости л2. Плоскости Я| и л2 тоже перпендикулярны. Поэтому вектор п2 параллелен плоскости л,.
Вектор М{М2 = (-4 - 1, 6 - 2, 5 — 3) = (-5, 4, 2) лежит в плоскости Л].
Пусть М(х, у, z) — произвольная точка плоскости лР Тогда вектор М}М = (х- 1, у - 2, z - 3) лежит в плоскости Л|.
Условие компланарности векторов М}М, М}М2 и ri2 задает уравнение плоскости л,:
(М\М, М\М2, п2) = 0, то есть
х- 1 у—2 z-3 '-5	'4	2
3	4-5
= -20(х — 1) +
+ 6(у-2) - 20(г-3) - 12(г-3) - 8(х- 1) - 25(у- 2) = -28(х- 1) -- 19(у — 2) — 32(г — 3) — —28% — 19у-32г + 162-0.
Тогда уравнение плоскости л равно 28% + 19у + 32г —162 = 0.
Способ 2. Векторное произведение [М{М2, п2] перпендикулярно векторам МХМ2 и п2, каждый из которых параллелен плоскости Л] (см. рассуждения выше). Поэтому вектор [Л/,Л/2, п2] перпендикулярен плоскости Л[ и может быть принят за нормаль плоскости лк
Найдем координаты вектора [М2, п2]:
[М}М2,п2] =
i j к
-5 4 2 3 4-5
= -207+ 6j- 20к- V2k- 87- 25 J =
= —28Г— 19/- 32& — (-28, -19, -32).
Возьмем за нормаль к плоскости Л| вектор п — (28, 19, 32), колли
неарный вектору [М\М2, п2\. Зная точку (1, 2, 3) в плоскости л4 и нормаль п, получаем уравнение плоскости л,: 28(х — 1) + 19(у — 2) + + 32(г - 3) = 0, то есть 28х + 19у + 32г- 162-0.
Задача 97. Определить уравнение плоскости лн проходящей через точки Л71(4, 2, 1), Л/2(—3, 5, 6) перпендикулярно плоскости л2, заданной уравнением 2х — Зу + 8г — 7 = 0.
67
§11.8. УГОЛ МЕЖДУ ДВУМЯ плоскостями
Угол ф между плоскостями А}х + By + С,г + Z), = 0 и А2х + By + + C2z + D2 = 0 равен углу между их нормалями пх = (Al9 Вь С}) и ri2 =
<Л D Г. П	(«1> «2>
= (Л2, В2, С2). Поэтому COS ф = --2—.
Пример 98. Определим косинус угла ср между плоскостями
2х — у + Зг — 5 = 0 и 4х + Зу — z — 6 = 0.
Нормали к плоскостям равны п} — (2, — 1, 3) и п} ~ (4, 3,-1) соответственно.
Скалярное произведение (nh п2) = 2 х 4 + (— 1) х 3 + 3 х (— 1) = 2.
Длины нормалей равны |я,| = V 22 + (— I)2 + З2 = Vt4 и |и2| ==
= д/ 42 + 32 + (-1)2 = V26.
(п„п2)	2	2	1
Тогда cos ф =-----=	= —__ -р_	__ = ——.
I"ill"2l	V14\26	-V2V7V2V13
Задача 98. Определить косинус угла ср между плоскостями
Зх - 4у + 5z - 1 = 0 и 2х - у + 4г + 3 = 0.
Глава 12
ПРЯМАЯ В ПРОСТРАНСТВЕ
§ 12.1. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Если известны точка Л/(х0, у0, го) на прямой т и направляющий вектор s = (ос, р, у), коллинеарный этой прямой, то можно написать канонические уравнения прямой т\
х~х0 = Т~Уо а Р	Y ’
Пример 99. Известны точка М(\, 2, —3) на прямой и направляющий вектор Г = (-2, 6, 5) этой прямой. Определим канонические уравнения прямой.
Здесь х0 = I, у() = 2, Z() = —3, а = —2, р = 6, у = 5.
х — 1 у — 2
Тогда канонические уравнения прямой равны —— = —-— =
z - (-3) х - 1	у-2 г + 3
=-------, то есть —— = ——- = ——.
Э	—2 о Э
Задача 99. Известны точка М(—2, 4, 1) на прямой и направляющий вектор Г = (4, 7, —9) этой прямой. Определить канонические уравнения прямой.
Пример 100. Определим канонические уравнения прямой, проходящей через точки М,(2, —3, I) и Л/2(—4, 5, 6).
За направляющий вектор прямой примем вектор = (—4 — 2, 5 — (—3), 6 — I) = (—6, 8, 5), а в качестве координат точки на прямой можно взять координаты любой из точек Мь М2 (например, х—2 у+ 3
Тогда канонические уравнения прямой равны —— = —-— = —о 8
_ Z- I
= 5 '
Задача 100. Определить канонические уравнения прямой, проходящей через точки М}(—4, 3, 2) и Л/2(6, 7, 5).
69
§ 12.2. ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ
Зная точку Л/(х0, у0, Zo) на прямой т и направляющий вектор ? = = (а, р, у), коллинеарный этой прямой, можно написать параметри-
' х = х0 + at ческие уравнения прямой т\ X у = У о + Р^ •
I Z=Zo + jt
Придавая параметру t различные значения, получим координаты точек прямой.
Пример 101. Определим параметрические уравнения прямой из примера 99.
х = I — 2t
Параметрические уравнения прямой равны < у = 2 + 6/ . г = -3 + 5г
Задача 101. Определить параметрические уравнения прямой из задачи 99.
Пример 102. Определим, какие точки прямой из примера 101 соответствуют значениям 0, 1,-2 параметра /.
При t = 0 получаем точку с координатами (1 — 2x0, 2 + 6x0, —3 + 5 х 0) = (1, 2, —3). Параметру t= 1 соответствует точка (1 —2x1, 2 + 6 х 1, —3 + 5 х 1) = (-1, 8, 2). При / = —2 получаем точку с координатами (1 - 2 х (-2), 2 + 6 х (-2), -3 + 5 х (-2)) = (5, -10, -13).
Задача 102. Определить, какие точки прямой из задачи Ю! соответствуют значениям 0, 2, —I параметра /.
§ 12.3. СВЯЗЬ МЕЖДУ ПАРАМЕТРИЧЕСКИМИ И КАНОНИЧЕСКИМИ УРАВНЕНИЯМИ ПРЯМОЙ
' х — х{} + at
Из параметрических уравнений прямой 2 у = у0 + Р/1 можно по-= +
лучить канонические уравнения прямой. Для этого надо выразить в каждом уравнении параметр t и приравнять полученные выражения.
Пример 103. Определим канонические уравнения прямой х - 2 +- 3/ < у = -6 + 4/. z= 1 - 5t
70
х—1	у + 6
Из 1-го уравнения t= —-—. Из 2-го уравнения I — ——. Из 3-го
Z- 1 уравнения t— ——.
Приравняв эти выражения для Л получим канонические уравне-х — 2 у + 6 z — 1 ния прямой —~~— = ——.
Задача 103- Определить канонические уравнения прямой х=-4 + 9/ < у = 3 — 8/ . Z=5 + 7/
„	.	„ X — Xq У~Уо Z-Zo
Из канонических уравнении прямой------- = —-— =-----------
ару можно получить параметрические уравнения прямой. Для этого надо приравнять канонические уравнения прямой параметру t:
Х~Хр =	У — Уо = Z-Zq	=
а	₽ Y
х-Ъ	t	У~Уй . Z-Zq
и выразить из равенств —-—	= /,	—।— = /,	—-— = t перемен-
ные х, у, z соответственно.
Пример 104- Определим параметрические уравнения прямой
х- I у + 4 z— 8
3 ~ 7 “ -5 ‘
Приравняем канонические уравнения прямой параметру Г.
х- 1 у + 4 г- 8 3 = 7 = -5 =
х - 1	у + 4
Из равенства —-— = t получаем х= 1 + 3t. Равенство —-— = /поз-
г-8
воляет сделать вывод, что у = — 4 + 7/. Из равенства —— = /получа-
ем z = 8 - 5/.
х = 1 + 3t
Тогда параметрические уравнения прямой равны < у----4 + 7/ .
z = 8 - 5/
Задача 104- Определить параметрические уравнения прямой х + 9 у - 4 z — 2
7 ~ 5 = 6 '
71
§ 12.4. ПРЯМАЯ КАК ЛИНИЯ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ
Прямую в пространстве можно задать как линию пресечения плоскостей Ахх + 2?!^ + Cxz + Д = 0 и А2х + By + C2z + D2 = 0:
J Ахх + By + C\z + Д = 0 A2x + By + C2z + D2 = 0
Для перехода к каноническим или параметрическим уравнениям прямой нужно знать координаты какой-нибудь точки на прямой и направляющий вектор прямой.
Приравняв одну из переменных нулю (например, z= 0) и найдя из системы значения двух других переменных, получим координаты точки на прямой.
За направляющий вектор прямой можно взять векторное произведение нормалей пх = (Al9 В{, Д) и п2 = (Л2, В2, С2) плоскостей.
Пример 105. Определим канонические уравнения прямой
2х + Зу — 9z + 5 = О
-4х + 7 у + 8^ - 6 = 0 '
f 2х + Зу + 5 = О J 2х + Зу = -5 ПУстьг= 0. Тогда| _4% + 7у_ 6 = Q -1 _4% +	= 6 .
Решим полученную систему с помощью правила Крамера.
	2 3	
А =	—4 7	= 2 х 7 - 3 х (-4) = 26 + 0,
	-5 3	
Ах =	6 7	= —5 х 7 — 3 х 6 = —53,
	2 -5	
А},=	—4 6	= 2X6- (-5) х (-4) = -8.
Тогда х = Ал/А = -53/26, у = Ау/А = -8/26 = -4/13.
Точка с координатами (—53/26, —4/13, 0) принадлежит прямой.
Нормали к плоскостям равны пх = (2, 3, —9) и п2 = (—4, 7, 8).
За направляющий вектор прямой возьмем векторное произведе-
i j к
2 3-9
-4 7 8
ние [/7Н п2] =
= 247+ 36/ + 14? + 12? + 637 — 16/ =
= 877+ 20/+ 26?= (87, 20, 26).
72
X - (-53/26)
Тогда канонические уравнения прямой равны -------—------
87
у-(-4/13) z- 0	х+53/26 у+ 4/13 z
20	~ 26 ’ Т°еСТЬ 87	=	20	= 26-
Задача 105. Определить канонические уравнения прямой
Зх - 4у + 5z - 7 = 0
2х + 5у - 8г + 9 = 0 '
§ 12.5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ
А = х0 + at
Дана плоскость Ах• + By + Cz + D = 0 и прямая < у — То + Р^
 Под-
z = ъ + yt
ставив в уравнение плоскости вместо переменных х, у, z их значения из параметрических уравнений прямой, получим уравнение относительно параметра t.
Если уравнение относительно t не имеет решений, то прямая параллельна плоскости.
В этом случае Ах0 + ByQ + Czq + D 0, а Аа + 2?р + Су = 0.
Если уравнение относительно / примет вид 0 = 0, то прямая лежит в плоскости.
В этом случае Ах() + Ву() + Cz# + D = 0, а Аа + /?р + Су = 0.
Если уравнение относительно t имеет единственное решение /0, то подставим это значение параметра в уравнения прямой и найдем точку пересечения прямой и плоскости.
Пример 106. Определим взаимное расположение плоскости х = —1 - 4/
2х + Зу — 4г + 5 = 0 и прямой < у = 2 + 4/ . г = 5 -+ /
Выполним следующие действия: 2х + Зу — 4г + 5 = 0 2(—I — 4/) + + 3(2 + 4/) - 4(5 + /) + 5 = 0 -> -2 - 8/ + 6 + 12/ - 20 - 4/ + 5 = 0 -> — 11=0 (ложно).
Поэтому прямая параллельна плоскости.
Задача 106. Определить взаимное расположение плоскости
Зх + 4у - 2г — 7 = 0 и прямой < у = 2 + t . г=3 + 5/
73
Пример 107. Определим взаимное расположение плоскости х= I — 4/
2х + 3j’ — 4г + 5 = 0 и прямой < у = — I 4- 4/.
z= I + t
Выполним следующие действия: 2х + Зу — 4г + 5 = 0	2( I — 4/) 4-
4- 3(—I 4- 4/) - 4(1 + t) + 5 = 0	2 - 8г- 3 + 12/- 4 - 4/4- 5 = 0 —
0 = 0 (верно).
Поэтому прямая лежит в плоскости.
Задача 107. Определить взаимное расположение плоскости
х = 1 4- 2/
Зх 4- 4у — 2г — 7 - 0 и прямой < у — 2 4-1 .
z = 2 4- 5/
Пример 108. Определим точку пересечения плоскости 2х 4- Зу — rx= I 4-5/
— 4г — 5 = 0 и прямой < у = I — 2/ .
г=-1 4-2/
Выполним следующие действия: 2х 4- Зу — 4г - 5 = 0 -* 2(1 4- 5/) 4-4-3(1 -2/)-4(-1 4-2/)-5 = 0 — 24-10/4-3 — 6/4-4 — 8/—5 = 0 — 4 - 4/ = 0. Отсюда t = 1.
Подставив это значение параметра в уравнения прямой, получим ко-
ординаты точки пересечения прямой и плоскости: < у= 1 —2X1 = — 1 . г = -1+2х1==1
Задача 108- Определить точку пересечения плоскости Зх 4- 4у —
х = I 4- 2/
— 2г — 7 = 0 и прямой < у — I 4- /
Z = -I 4- 4/
Перпендикулярность плоскости Ах 4- By 4- Cz + D = 0 и прямой
' х = х0 4- а/
< У =	+ Р^ означает коллинеарность нормали плоскости п = (А, В, Q
5 = + у/
и направляющего вектора прямой ? = (а, р, у), т. е. А/а = B/fr = С/у.
Пример 109. Выясним перпендикулярность плоскости 4х 4- бу -
х = I 4-2/
— 8г — 5 = 0 и прямой < у = — 2 — 3/ .
г = 3 - 4/
Нормаль плоскости ~п = (4, 6, —8), направляющий вектор прямой
Г =(2,3, -4).
74
Так как соответствующие координаты нормали и направляющего вектора пропорциональны (4/2 = 6/3 = — 8/(—4)), то векторы п и 7коллинеарны. Следовательно, плоскость и прямая перпендикулярны.
Задача 109. Выяснить перпендикулярность плоскости 6х + 8у —
Г х = 5 + 3/ — 4г — 7 = 0 и прямой < у = 2 + 4/ . z~ I -2/
Пример 110. Определим проекцию точки Л/(1,2, 3) на плоскость 2х + Зу - 4г - 5 = 0.
Проведем через точку М прямую, перпендикулярную плоскости. Точка пересечения этой прямой и плоскости будет проекцией точки М на плоскость.
За направляющий вектор прямой У возьмем нормаль плоскости: s>= п = (2, 3, —4).
х = 1 + 2t
Тогда параметрические уравнения прямой < у = 2 + 3/ . г = 3 - 4/
Найдем точку пересечения прямой и плоскости.
Выполним следующие действия: 2х + Зу - 4г — 5 = 0 — 2( 1 + 2t) + + 3(2 + 3/) - 4(3 - 4/) - 5 = 0 — 2 + 4/ + 6 + 9/ - 12 + 16/ - 5 = 0 — —9 + 29/ = 0. Отсюда t = 9/29.
Подставив это значение параметра в уравнения прямой, получим ко-
rx = 1 + 2x9/29 = 47/29
ординаты проекции точки М на плоскость: < у = 2 + 3 х 9/29 = 85/29 .
z = 3-4Х9/29 = 51/29
Задача 110. Определить проекцию точки М(—2,4,1) на плоскость Зх + 4у — 2г — 7 = 0.
Пример 111. Определим проекцию точки Л/(1, 2, 3) на прямую х = 3 + 2t < у = — 1 + 4/.
г = 5 — г
Проведем через точку М плоскость, перпендикулярную прямой. Точка пересечения этой плоскости и прямой будет проекцией точки М на прямую. За нормаль п возьмем направляющий вектор прямой: п = s = (2, 4, —1).
Тогда уравнение плоскости будет 2(х — 1) + 4(у — 2) — (г — 3) = 0, то есть 2х + 4у — г — 7 = 0.
Найдем точку пересечения прямой и плоскости.
Выполним следующие действия: 2х + 4у — г — 7 = 0 -* 2(3 + 2t) + + 4(_1 +4/)- (5- /) - 7 = 0 — 6 + 4/ - 4+16/- 5 + / - 7 = 0 — -10 + 21/= 0. Отсюда /= 10/21.
75
Подставив это значение параметра в уравнения прямой, получим ко-
ординаты проекции точки Мна прямую: <
х= 3 + 2x10/21 =83/21
у = -1 +4x10/21 = 19/21.
Z = 5 — 10/21 =95/21
Задача 111- Определить проекцию точки М(—2, 4, I) напрямую х = 3 — t < у = 5 + 2t.
5= i + 3/
Пример 112- Определим уравнение плоскости тс, относительно которой симметричны точки /1(0, 2, 1) и /?(—3, 4, 5).
Так как точки А и В симметричны относительно плоскости тс, то середина отрезка АВ принадлежит плоскости тс, а за нормаль плоскости можно взять вектор АВ = (—3 — 0, 4 - 2, 5 — 1) = (—3, 2, 4).
Точка С(х0, +(), го) — середина отрезка АВ. Тогда х{) = (0 + (—3))/2 = = -1,5; +о = (2 + 4)/2 = 3; = (1 + 5)/2 = 3.
Отсюда уравнение плоскости тс, относительно которой симметричны точки /1(0, 2, 1) и #(-3, 4, 5), будет -3(х - (-1,5)) + 2(у - 3) + + 4(z - 3) = 0 -> -Зх + 2у + 4г - 22,5 = 0.
Задача 112- Определить уравнение плоскости тс, относительно которой симметричны точки /1(2, 1, 3) и В (4, 0, 5).
Пример 113. Определим, симметричны ли точки А(], 3, 2) и В(—3, 5, 4) относительно прямой (х — I)/2 = (у + 3)/1 = (г — 6)/3.
Если точки А(1, 3, 2) и В(—3, 5, 4) симметричны относительно прямой (х— 1 )/2 = (у 4 3)/1 = (z — 6)/3, то вектор АВ = (—3 — 1,5 — 3, 4 — 2) = (—4, 2, 2) перпендикулярен направляющему вектору? = (2, 1,3) прямой, а середина С отрезка АВ принадлежит этой прямой.
Скалярное произведение (АВ , /) = (—4) х 2 + 2 х 1 + 2x3 = 0. Отсюда векторы АВ и 5 перпендикулярны. Первое условие выполнено.
Найдем координаты точки С.
х= (1 + (—3))/2 = - 1, у = (3 + 5)/2 = 4, z~ (2 + 4)/2 = 3.
Подставим эти координаты в уравнение прямой: (—1 — 1)/2 = = (4 + 3)/1 = (3 — 6)/3, то есть —1 = 7 = — 1 (ложно).
Поэтому середина С отрезка АВ не принадлежит нашей прямой. Следовательно, точки А(1, 3, 2) и В(—3, 5, 4) не симметричны относительно прямой (х- 1)/2 = (у + 3)/1 = (г- 6)/3.
Задача 113. Определить, симметричны ли точки А(2, 3, 5) и В (—4, I, 6) относительно прямой (х + I)/3 = (у — 4)/2 = (г + 2)/Ю.
Пример 114. Определим уравнение какой-нибудь прямой, лежащей в плоскости 2х + Зу — 4г - 12 = 0.
76
Для задания прямой нужно знать две точки этой прямой.
Пусть у = z = 0. Тогда 2х + Зу - 4z - 12 = 0 -> 2х + 3 х 0 - 4 х 0 -— 12 = 0 2х — 12 = 0 ^ х = 6. Точка А (6, 0, 0) принадлежит нашей плоскости.
Пусть х = z = 0. Тогда 2х + Зу — 4z — 12 = 0-^2x04-Зу — 4x0 — — 12 = 0 -* Зу — 12 = 0 у = 4. Точка Z?(0, 4, 0) принадлежит нашей плоскости.
За направляющий вектор прямой АВ возьмем вектор АВ = (0 — 6, 4 — 0, 0 — 0) = (-6, 4, 0). Точка А (6, 0, 0) принадлежит прямой АВ.
Тогда канонические уравнения прямой АВ, лежащей в плоскости 2х + Зу — 4г - 12 = 0, будут следующими: (х - 6)/(—6) = (у — 0)/4 = = (г — 0)/0 —> (х — 6)/(—6) = у/4 = г/0. Здесь нет никакого деления на 0. Это просто условная запись.
Задача 114- Определить уравнение какой-нибудь прямой, лежащей в плоскости Зх + 2у + 6z — 18 = 0.
Пример 115- Определим уравнение плоскости л, проходящей х-2	у+3 г- 8
через точку Л/,(1,2, 3) параллельно прямым —-— = —j— = —-— (гщ)
х+2 у - 9	г-5
и = ~Т~=	(/"2)-
Так как плоскость л параллельна прямым т, и т2, то направляющие векторы этих прямых = (4, — 1, 3) и = (2, 4, 5) параллельны плоскости л.
Пусть Л/(х, у, г) — произвольная точка плоскости л. Тогда вектор М{М = (х — 1, у - 2, г - 3) лежит в плоскости л.
Условие компланарности векторов М, s\ и s2 позволяет получить уравнение плоскости л: (МХМ, s\, s2) = 0.
	х- I	у-2 г-3	
То есть	4	-I 3	= —5(х -1)4- 6(у - 2) 4- 16(г - 3) +
	2	4	5	
+ 2(г-3) - 12(х- 1) — 20(у — 2) = —17(х — 1) - 14(у-2) + 18(г-3) = 0. Отсюда уравнение плоскости л равно 17х + 14у — 18г + 9 = 0.
Задача 115. Определить уравнение плоскости л, проходящей х + 3 у — 8 г—2 через точку М(—2,4, I) параллельно прямым —-— = —-— = ——
х + 4 у - 5	г-7
77
§ 12.6.	УГОЛ МЕЖДУ ПРЯМОЙ и плоскостью
„•*-•*() У~Уо z - Zo
Угол (р между прямой ——— = —।— = —-— и плоскостью Ax+By+Cz+D = 0 вычисляется по следующей формуле:
где п = (А, В, С) — нормаль плоскости, а У = (а, р, у) — направляющий вектор прямой.
х — 2 у + 3
Пример 116. Определим синус угла между прямой —-— = —j— = z —8
= —-— и плоскостью 2х + Зу — 4т + 5 = 0.
Нормаль плоскости п = (2, 3, —4), направляющий вектор прямой / = (4, -1, 3). Тогда их скалярное произведение равно (и, У) = 2 х 4 + + 3 х (-1) + (-4) х 3 = -7. Длины векторов \п\ = V 22 + З2 + (-4)2 = = V29, | = V 42 + (-1)2 + З2 = V26.
Тогда синус угла между прямой и плоскостью равен:
(л, Т) |—7|	I--
sin ср =-= = —=—т= = 7/у 754 .
И1И ^[29 V26
х + 3 у — 8
Задача 116. Определить синус угла между прямой —-— = —-— =
Z-2
= —j— и плоскостью Зх + 4у — 2z — 7 = 0.
§ 12.7.	РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
х — х0 У - То Расстояние от точки М/х,, уъ Zi) до прямой —-— = —-— = ________________________________>
=------ вычисляется по формуле |[A/0Ml, ?]|/|?|, где у0, Zo),
а ? = (а, Р, у) — направляющий вектор прямой.
Пример 117. Определим расстояние от точки Л/,(2, 5, —I) до х-I у-2	z~3
прямой —— = —j— = -у-.
78
Здесь Л/о( 1, 2, 3), а направляющий вектор прямой равен У = (4, 1,2).
Тогда координаты вектора =(1,3, -4).
Векторное произведение [	, Г] =
J к
3 —4
1 2
= 6 i — 16 j +
+ к- Пк + Ai-2j= IO?— 187- 117 = (Ю, -18, -11).
Длины векторов равны |[Л/0Л/], Г]| =	102 + (— 18)2 + (— 11 )2 =
= V545, |?| = VT+ 12 + 22 = дТГ.
Тогда расстояние от точки до прямой составляет | [	, Т]|/| $ | =
= V5457 V2? = V 545/21 .
Задача 117- Определить расстояние отточки 4^(2, 3, - I) до пря-
х-1 у +2 z-5
МОЙ —-— = —7— = —“—.
4	6	3
§ 12.8.	ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ
х-х{	У ~ У\	Z-Z1 . ч X — Х2	у-у2
Даны прямые-------- = —-— = ----- (т}) и ----= —-— =
«I Pl Yl	«2	Р2
- —
Прямые т} и т2 параллельны тогда и только тогда, когда их направляющие векторы 7 = (ocj, yj и s2 = (ос2, р2, Уг) коллинеарны, то есть а,/а2 = р,/р2 =
х - 9 у + Ю
Пример 118. Определим, параллельны ли прямые —-— = —-— =
Z — 5	х+5 у - 11 г + 7
=----м-------=------—-------
—4	4	6	-8 ’
Так как направляющие векторы = (2, 3, —4) и Г2 = (4, 6, —8) коллинеарны (2/4 = 3/6 = —4/(—8)), то прямые параллельны.
х + 8 у — 12
Задача 118. Определить, параллельны ли прямые —— = —j^~ =
г + 7 х - 6 у + 11 z - 5 = --- ы ----- = ———— = -----
16	3	-6	-8 
79
Пример 119. Определим уравнение прямой проходящей через точку +/(!, 2, 3) параллельно прямой т2, заданной каноническими х- 9 у + 10 z - 5 уравнениями —-— = —-— — ——.
Так как прямые и т2 параллельны, то можно взять направляющий вектор s2 = (2, 3, —4) прямой т2 за направляющий вектор прямой Тогда прямая задается каноническими уравнениями х- I у-2 г- 3
2 ~ 3	—4 ’
Задача 119. Определить уравнение прямой проходящей через точку Л/(4, 7, 2) параллельно прямой т2, заданной канонически-х — 6 у + 11 г — 5 ми уравнениями —-— =----— = —-—.
3 —о о
Прямые тх и т2 перпендикулярны тогда и только тогда, когда их направляющие векторы 5] = (ос,, рн уО и У2 = (ос2, р2, у2) перпендикулярны, то есть (Tj, Г2) = 0.
х — 9 Пример 120. Определим, перпендикулярны ли прямые —-— =
у + IО	г - 5 х + 6 у - 12	г+5
= ----- = ---- ы --- = ------ = --
3	-4	-1	2	1 ’
Направляющие векторы равны У] = (2, 3, —4) и s2 = (— 1, 2, 1). Их скалярное произведение (У15 У2) = 2 х (— 1) + 3 х 2 + (—4) х 1 = 0. Поэтому прямые перпендикулярны.
х - 6 Задача 120. Определить, перпендикулярны ли прямые —-— =
у+П	г-5	х+7	у-9	г+2
—------—------pj----=------—------
-6	8	2	-3	-3 ’
Прямые, лежащие в одной плоскости, называются компланарными.
Прямые т} и т2 компланарны тогда и только тогда, когда (М\М2, 5], У2) = 0, где М}(х}, yh Zi) и М2(х2, у2, г2) — точки на прямых т\ и т2 соответственно.
Прямые называются скрещивающимися, если они не имеют общих точек и не являются параллельными.
Прямые и т2 являются скрещивающимися тогда и только тогда, когда (М\М2, У], У2) + 0.
Расстояние между скрещивающимися прямыми и т2 определяется по формуле |(Л/,М2, У,, J2)l/lf?b ?2ll-
80
х-1	у-2 Z-3
Пример 121- Покажем, что прямые —-— = —— = —j— х + I у — 5 z + 3
и —-— = —— = —-— являются скрещивающимися, и определим
расстояние между ними.
Здесь Л/,(1, 2, 3), Л/2(— 1, 5, -3), я, = (2, -3, I), 5, = (4, -2, 3). Тогда = (—2, 3, -6).
Смешанное произведение (МЛМ2, Г,, s*2) =
—2 3 -6
2 -3 I 4-2 3
= 18 +
+ 12 + 24 — 72 — 4— 18 = —40 + 0. Поэтому прямые являются скрещи-
вающимися.
Векторное произведение [5Н Т2] =
/ J к
2 -3 1
4-2 3
= -9 / + 4j - 4£ +
+ 12£ + 2i — 6j= -11- 2J + 8к = (-7, -2, 8).
Модуль векторного произведения |[Т(, s2]| = V (—7)2 + (-2)2 + 82 =
= VH7 .
Тогда расстояние между прямыми равно |(Л/|Л/2, Г,, $2)|/|[$|, Г2]| = = |-40|/VTn =40/(зУТз).
х+ 1 у — 2 г + 4
Задала 121- Показать, что прямые —~~— = —j— и х— I у + 3 г — 5
—-— = —~~— являются скрещивающимися, и определить расстояние между ними.
§ 12.9. УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ
x-Xi	y-Ti	Z-Zt	х — х2	у-у2
Угол ср между прямыми-----=	— =------и-------= —— =
(Xi	pi	Yi	ос2	Р2
z- z2
=----- — это угол между направляющими векторами 5] = (ан Yi)
72
и s2 = (а2, р2, у2) этих прямых.
Тогда cos ф = —-,-?2-.
I^il И
81
Пример 122- Определим косинус угла между прямыми —-—‘ =
у-2	г-3	х+1	у-2	г+4
— ---- = ---- ц ---- — ----- — ----
-3	13	4	-1
Направляющие векторы прямых равный = (2, -3, 1) и Т2 = (3,4, -1). Их скалярное произведение (7[, Г2) = 2 х 3 + (-3) х 4 + 1 х (-1) = -7.
Длины векторов равны:
|Г,| = V 22 + (—З)2 + I2 = V14,1s2| = V З2 + 42 + (—I)2 = V26.
Тогда косинус угла между прямыми равен:
cos <р = (5|’5г) = =	~7.__= -0,5^7/13.
l/.llsj V14V26
Задача 122- Определить косинус угла между прямыми
у+3 г-5 х+1 у-5 г+3
---—-----и----=-----=-----
2	4	4	-2	3
Глава 13
ПРЯМАЯ НА ПЛОСКОСТИ
§ 13.1. РАЗЛИЧНЫЕ ВИДЫ УРАВНЕНИЙ ПРЯМОЙ НА ПЛОСКОСТИ
Если известны точка Л/(х0, у0) на прямой т и направляющий вектор Г = (а, р), параллельный этой прямой, то можно написать каноническое уравнение прямой т\
= У~Уо а р
Пример 123- Известны точка М(1,2) на прямой т и направляющий вектор 7 = (3, 5) этой прямой. Тогда каноническое уравнение х - 1 у - 2 прямой пг. —-— = —-—.
Задача 123. Известны точка Л/(2, 5) на прямой т и направляющий вектор 5 =(—1,3) этой прямой. Найти каноническое уравнение прямой т.
Если известен ненулевой вектор п = (А, В), перпендикулярный прямой т, то можно написать общее уравнение прямой т\ Ах + By + С = 0. Вектор п называется нормалью. Для определения константы С нужно знать какую-нибудь точку на прямой т.
Уравнение Ах + By = 0 задает прямую, проходящую через начало координат.
Уравнения х = 0иу = 0 — это уравнения осей Оу и Ох соответственно. Уравнения х = const и у = const задают прямые, параллельные осям Оу и Ох соответственно.
Пример 124. Изобразим прямую 2х + Зу - 12 = 0. Для задания прямой нужно знать две ее точки. Подставим в уравнение прямой значение х = 0: 2 х 0 + Зу — 12 = 0, то есть у = 4. Точка 4/(0, 4) принадлежит этой прямой. Подставим в уравнение прямой значение у = 0: 2х + 3 х 0 - 12 = 0, то есть х = 6. Точка У(6, 0) принадлежит этой
83
прямой. Отмстим точки М и N на координатной плоскости и проведем через них прямую.
Задача 124- Изобразить прямую Зх + 4у — 12 = 0.
Пример 125. Изобразим прямые х = I и у = 2.
Задача 125. Изобразить прямые х = — I и у = 3.
Прямая Ах + By + С = 0 делит плоскость на две полуплоскости. В одной из них выполнено условие Ах + By + С > 0, в другой — условие Ах + By + С < 0.
Выразив из уравнения Ах + By + С = 0 прямой т переменную у через переменную х, мы получим уравнение прямой в форме с угловым коэффициентом: у = кх + Ь. Угловой коэффициент к равен тангенсу угла наклона прямой т к оси Ox: k = tga.
§ 13.2. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ПРЯМЫХ НА ПЛОСКОСТИ
Пусть две прямые тх и т2 заданы своими общими уравнениями
Ахх + Вху + Ci = 0 и А2х + В^у + С2 = 0 соответственно. Тогда:
I)	прямые тх и т2 совпадают (тх = т2) <=>	= Вх/В2 = Сх/С2,
2)	прямые тх и т2 параллельны (т, || т2) о Ах/А2 - Вх/В2 Сх/С2,
3)	прямые тх и т2 перпендикулярны (тх ± т2) <=> АХА2 + ВХВ2=: 0.
84
Для нахождения точки пересечения прямых т{ и т2 нужно ре-u [ Л|Х + В{у + С = О, шить систему уравнении: j д* +	+	= q
Пример 126- Что можно сказать о взаимном расположении прямых х+ 2у — 3 = 0 и 5х + Юу -2 = 0?
1/5 = 2/10 + (—3)/(—2). Прямые параллельны.
Задача 126- Что можно сказать о взаимном расположении прямых 2х + Зу - 6 = 0 и 8х + 12у +3 = 0?
Пример 127. Что можно сказать о взаимном расположении прямых х + 2у - 3 = 0 и 5х + Юу — 15 = 0?
1/5 = 2/Ю = (—3)/(—15). Прямые совпадают.
Задача 127- Что можно сказать о взаимном расположении прямых 2х + Зу - 6 = 0 и 8х + 12у - 24 = 0?
Пример 128- Что можно сказать о взаимном расположении прямых 2х + 4у — 3 = 0 и —6х + Зу + I = 0?
А\А2 + Bl В2 = 2 х (—6) + 4x3 = 0. Прямые перпендикулярны.
Задача 128- Что можно сказать о взаимном расположении прямых 2х + бу — 3 = 0 и 9х — Зу + 4 = 0?
Пример 129- Найдем точку пересечения прямых 2х + 5у — 9 = 0 и Зх + 4у — 2 = 0.
2х + 5у — 9 = 0,	f 2х + 5у = 9,
Зх + 4у — 2 = 0.	| Зх + 4у = 2.
Решим эту систему по правилу Крамера (см. § 4.2).
Тогда х = ДУД = 26/(—7) = -26/7, у = Д/Д = —23/(—7) = 23/7. Точка пересечения (-26/7, 23/7).
Задача 129- Найти точку пересечения прямых Зх + 4у — 2 = 0 и 5х + 7у - 9 = 0.
§ 13.3- УРАВНЕНИЕ ПРЯМОЙ, ПРОХОДЯЩЕЙ ЧЕРЕЗ ДВЕ ДАННЫЕ ТОЧКИ
Уравнение прямой, проходящей через две данные точки (х,, yj
У~У'
ч М2(х2, у2) имеет следующий вид: - = -.
Х2 ~	Уг~ У\
85
Пример 130. Найдем уравнение прямой, проходящей через две данные точки 3) и Л/2(4, 5).
х — х,	У ~У\	х — I	у — 3	х—1 у — 3
Х2 - X,	у2 - у,	4 - 1	5 - 3	3	2
о 2(х — 1) — 3(у — 3) <=> 2х — Зу + 7 — 0.
Задача 130. Найти уравнение прямой, проходящей через две данные точки М}(2, 5) и Л/2(6, 4).
§ 13.4.	РАССТОЯНИЕ ОТ ТОЧКИ ДО ПРЯМОЙ
Расстояние р(Л/0, т) от точки Л/0(х0, у0) до прямой т, заданной уравнением Ах + By + С = 0, вычисляется по формуле:
\а2+ в2
Пример 131. Найдем расстояние р(Л/0, т) от точки Л/()(1, 2) до прямой т, заданной уравнением Зх + 4у — 7 = 0.
|Лх0+5у0+С|	|Зх1+4х2-7|
р(Ч, т) =----.------— =-----=====----= 0,8.
УА2 + В2	у З2 + 42
Задача 131. Найти расстояние р(Л/0, т) отточки Л/о(2, 5) до прямой т. заданной уравнением Зх + Ту — 2 — 0.
§ 13.5.	УГОЛ МЕЖДУ ДВУМЯ ПРЯМЫМИ НА ПЛОСКОСТИ
Угол <р между прямыми Л,х + Bty + С, = 0 и А2х + В^у + С2 = 0 равен углу между нормалями Я, = (А{, В{) ип2 = (А2, В2).
Тогда cos (р =	- .
I«ill«2l
Пример 132. Определим косинус угла между прямыми 2х + 5у —
- 9 = 0 и Зх + 4у - 2 = 0.
Нормали прямых равны = (2, 5) и п2 = (3, 4) соответственно. Их скалярное произведение (пь п2) = 2 X 3 + 5 х 4 = 26.
Длины нормалей равны |л,| = V 22 + 52 = V29 и |л2| = V З2 + 42 = 5.
(ль п2)	26
Тогда косинус угла между прямыми cos (р = —-= —т=.
1«1И 5 у 29
86
Задача 132. Определить косинус угла между прямыми 2х — Зу + + 5 = 0 и 4х + 7у - 8 = 0.
При определении угла между прямыми у = к}х + А, и у = к2х + Ь2 Zc2 ~
можно воспользоваться следующей формулой: tgcp =
1 + ktk2
Из этой формулы получаем условие перпендикулярности прямых к^к2 = —1.
Пример 133. Определим тангенс угла между прямыми у = 2х + 5 и у = Зх — 8.
Здесь = 2, к2 = 3. Тогда тангенс угла между прямыми равен tg(p =
— к}
I + к}к2
3-2
I +2X3
-1/7.
Задача 133. Определить тангенс угла между прямыми у = —Зх + 4 и у = 7х + 6.
Пример 134. Определим уравнение прямой проходящей через точку Л/(1, 3), перпендикулярно прямой тъ заданной уравнением у = 2х + 4.
Здесь х0 = 1, у0 = 3, к2 = 2. Так как прямые перпендикулярны, то клк2 = — 1, то есть угловой коэффициент прямой равен к} = — \/к2 = = -1/2 - -0,5. Тогда уравнение прямой будет у - у0 = кх(х — х0) —► у - 3 = —0,5(х - 1) - у = —0,5х + 3,5.
Задача 134. Определить уравнение прямой проходящей через точку М(—2, 5), перпендикулярно прямой тъ заданной уравнением у = — 4х + 7.
Глава 14
КРИВЫЕ ВТОРОГО ПОРЯДКА
Кривая второго порядка — это кривая, уравнение которой в декартовой прямоугольной системе координат имеет вид
Ах2 + Вху + Су2 + Dx+ Еу + F= 0, где А2 + В2 + С2 0.
К вырожденным кривым второго порядка относят пустое множество, точку, прямую, пару прямых. Невырожденные кривые второго порядка — это эллипс, гипербола и парабола.
§ 14.1. ЭЛЛИПС
Эллипс — это геометрическое место точек М плоскости, сумма расстояний от которых до двух фиксированных точек Fx и F2 (фокусов) есть постоянная величина 2а, превышающая расстояние между фокусами 2с: MF{ + MF2 = 2а> 2с.
Выберем систему координат Оху так, чтобы координаты фокусов были Fx(—с, 0) и F2(c, 0). Пусть Ь2 = а2 — с2. Тогда каноническое (простейшее) уравнение эллипса будет х2/а2 + y2/b2 = 1.
Начало координат совпадает с центром эллипса. Точки (±а, 0) и (0, ±Ь) — это вершины эллипса. Числа а и b являются соответственно большой и малой полуосями эллипса. Тогда 2а и 2Ь — это соответственно большая и малая оси эллипса.
88
Величина а = с/а, называемая эксцентриситетом, характеризует меру сжатия эллипса. Так как а > с, то для эллипса с < 1. При с = О эллипс превращается в окружность.
Прямые х = ±а/г называются директрисами эллипса.
Теорема. Отношение расстояния г от точки эллипса до фокуса к расстоянию d до ближайшей к этому фокусу директрисы равно эксцентриситету: r/d = 8.
Пример 135- Для эллипсах2/!00 + у1/(А = I определим большую и малую полуоси, большую и малую оси, координаты фокусов, расстояние между фокусами, эксцентриситет, директрисы.
Так как а2 = 100 и Ь2 = 64, то большая полуось а= Ю, малая полуось b = 8, большая ось 2а = 2 X 10 = 20, малая ось 2Ь = 2 X 8 = 16.
Тогда с2 = а2 — Ь2 = 100 — 64 = 36. Отсюда с = 6, координаты фокусов (±с, 0) = (±6, 0), а расстояние между фокусами составляет 2с = = 2x6 = 12.
Эксцентриситет равен 8 = с/а = 6/10 = 0,6. Директрисы х = ±а/г =
= ±10/0,6 = ±50/3.
Задача 135. Для эллипса jc/289 + у2/225 = 1 определить большую и малую полуоси, большую и малую оси, координаты фокусов, расстояние между фокусами, эксцентриситет, директрисы.
Пример 136. Составим уравнение эллипса, фокусы которого расположены на оси Ох симметрично относительно начала координат, большая ось равна 20, а расстояние между директрисами 40.
Большая ось 2а = 20. Отсюда а = 10.
Расстояние между директрисами равно 2а/г = 40. Тогда эксцентриситет 8 = 2я/40 = (?/20. Но 8 = с/а.
Отсюда с = аг = а х я/20 = Ю х Ю/20 = 5.
Поэтому Ь2 = а2 ~ с2 = Ю2 - 52 = 75.
Уравнение эллипса х2/а2 + у2/Ь2 = 1,то есть х2/100 + у2/75 = 1.
Задача 136. Составить уравнение эллипса, фокусы которого расположены на оси Ох симметрично относительно начала координат, большая ось равна 16, а расстояние между директрисами 32.
Пример 137. Расстояние от точки М эллипса до фокуса F2 равно г = 15, а эксцентриситет эллипса 8 = 0,25. Определим расстояние от точки М до ближайшей к фокусу F2 директрисы.
Пусть d — искомое расстояние. Тогда r/d = 8. Отсюда d = г/г = = 15/0,25 = 60.
Задача 137. Расстояние от точки М эллипса до фокуса F2 равно г= 20, а эксцентриситет эллипса 8 = 0,5. Определить расстояние от точки Мдо ближайшей к фокусу F2 директрисы.
89
Оптическое свойство эллипса. Лучи света, вышедшие из одного фокуса эллипса, после отражения от эллипса соберутся в другом фокусе.
§ 14.2. ГИПЕРБОЛА
Гипербола — это геометрическое место точек Мплоскости, модуль разности расстояний от которых до двух фиксированных точек F] и F2 (фокусов) есть постоянная величина 2а, меньшая расстояния между фокусами 2с: \MF} — MF2\ = 2а< 2с.
Выберем систему координат Оху так, чтобы координаты фокусов были F}(—с, 0) и F2(c, 0). Пусть Ь2 = а2 — с2. Тогда каноническое (простейшее) уравнение гиперболы будет х2/а2 — y2/b2 = I.
Начало координат совпадает с центром гиперболы. Точки (+а, 0) — это вершины гиперболы. Числа а и b являются соответственно действительной и мнимой полуосями гиперболы. Тогда 2а и 2Ь — это соответственно действительная и мнимая оси гиперболы.
Величина с = с/а называется эксцентриситетом. Так как а < с, то для гиперболы с > I.
Прямые х = ±a/s — это директрисы гиперболы.
Прямая называется асимптотой гиперболы, если расстояние отточки М(х, у) гиперболы до этой прямой стремится к нулю при х -+ или х +оо. У гиперболы две асимптоты у = ±Ь/ах.
Теорема. Отношение расстояния г от точки гиперболы до фокуса к расстоянию dдо ближайшей к этому фокусу директрисы равно эксцентриситету: r/d = с.
Пример 138. Для гиперболы ?г/64 — У/36 = I определим действительную и мнимую полуоси, действительную и мнимую оси, координаты фокусов, расстояние между фокусами, эксцентриситет, директрисы, асимптоты.
90
Так как а2 = 64 и Ь2 — 36, то действительная полуось а = 8, мнимая полуось b = 6, действительная ось 2а = 2 х 8 = 16, мнимая ось 2Ь = = 2X6 = 12.
Тогда с2 = а2 + Ь2 = 64 + 36 = 100. Отсюда с = 10, координаты фокусов (±с, 0) = (±10, 0), а расстояние между фокусами составляет 2с = 2х 10 = 20.
Эксцентриситет равен е = с/а = 10/8 = 1,25.
Директрисы х = +а/ с = ±8/1,25 = ±6,4.
Асимптоты у = +Ь/ах = ±6/8х, то есть у = ±0,75х
Задача 138. Для гиперболы л^/144 — у2/81 = 1 определить действительную и мнимую полуоси, действительную и мнимую оси, координаты фокусов, расстояние между фокусами, эксцентриситет, директрисы, асимптоты.
Пример 139. Составим уравнение гиперболы, фокусы которой расположены на оси Ох симметрично относительно начала координат, асимптоты у = ±3/4х, а расстояние между фокусами равно 8.
Расстояние между фокусами равно 2с = 8. Отсюда с = 8/2 = 4.
У гиперболы две асимптоты у = +Ь/ах. У нас асимптоты равны у = ±3/4х Тогда b/а = 0,75 и b = 0,75<з.
Так с2 = а2 + Ь\ то 42 = а2 + (0,75я)2- Отсюда а2 = 10,24 и Ь2 = с2 - а2 = = 16 - 10,24 = 5,76.
Уравнение гиперболы х2/а2 —у^Ь2 = 1, то есть х2/10,24 — у2/5,76 = 1.
Задача 139. Составить уравнение гиперболы, фокусы которой расположены на оси Ох симметрично относительно начала координат, асимптоты у = ±5/8х, а расстояние между фокусами равно 16.
Пример 140. Расстояние от точки М гиперболы до директрисы равно d= 20, а эксцентриситет гиперболы е = 1,25. Определим расстояние от точки Мдо ближайшего к директрисе фокуса.
Пусть г — искомое расстояние. Тогда r/d = е. Отсюда г = d х е = = 20 X1,25 = 25.
Задача 140. Расстояние от точки М гиперболы до директрисы равно J= 15, а эксцентриситет гиперболы е = 1,6. Определить расстояние от точки М до ближайшего к директрисе фокуса.
Оптическое свойство гиперболы. Лучи света, вышедшие из одного фокуса гиперболы, после отражения от ближайшей ветви гиперболы распространяются так, будто вышли из другого фокуса.
91
S 14.3. ПАРАБОЛА
Парабола — это геометрическое место точек плоскости, равноудаленных от фиксированной точки плоскости (фокуса) и фиксированной прямой плоскости (директрисы).
Начало координат — это вершина параболы. Ось Ох является осью параболы.
Пусть F(p/2, 0) —- фокус, а х = —р/2 — уравнение директрисы. Тогда каноническое уравнение параболы в такой системе координат у2 = 2рх. Число р называется параметром параболы.
Пример 141. Определим фокус и директрису параболы у2 = 16х
Так как 2р — 16, то параметр параболы равен р = 16/2 = 8. Отсюда р/2 = 8/2 = 4.
Тогда фокус параболы F(4, 0), а уравнение директрисы х = —р/2 = =—4.
Задача 141. Определить фокус и директрису параболы у2 = 12х
Пример 142. На параболе у2 = 24х найдем точку М, удаленную от фокуса параболы на расстояние 15.
Пусть (х, у) — координаты точки М. Так как 2р = 24, го параметр параболы равен р = 24/2 = 12. Отсюда р/2 = 12/2 = 6.
Уравнение директрисы х = —р/2 = -6. Точки параболы равноудалены от директрисы и от фокуса. Поэтому расстояние от точки М до директрисы равно расстоянию от точки М до фокуса: х + 6 = 15. Отсюда х = 15-6 = 9.
Тогда у2 = 24,v =24х9 = 216иу = ±~\[216 = ±6 Уб~.
Задача 142. На параболе у2 = 36х найти точку М, удаленную от фокуса параболы на расстояние 16.
Оптическое свойство параболы. Лучи света, вышедшие из фокуса параболы, после отражения от параболы параллельны оси параболы.
92
Глава 15
ПРЕОБРАЗОВАНИЯ КООРДИНАТ
§ 15.1. ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
При параллельном переносе точка 0х(а, Ь) выбирается за новое начало координат и происходит переход от декартовой системы координат Оху к декартовой системе координат О^у,. При этом сохраняется направление осей координат.
Связь между старыми координатами (х, у) и новыми координатами (X], у,) задается формулами:	Xl + f и J Xl х а.
[у = ух + b [ух= у-Ь
Пример 143. При параллельном переносе за новое начало координат принята точка 0,(2, 3). В старой системе координат задана точка (—3, 5). Определим новые координаты этой точки.
Здесь а = 2, Ь=3,х=— 3, у = 5. Тогда новые координаты точки равны (-3 — 2,5 — 3)== (-5, 2).
Задача 143. При параллельном переносе за новое начало координат принята точка 0,(—I, 7). В старой системе координат задана точка (8, 3). Определить новые координаты этой точки.
Пример 144. Определим старые координаты точки при параллельном переносе из примера 143, если новые координаты точки равны (1, 7).
Здесь X] = 1, У) = 7. Тогда старые координаты точки равны (1+2, 7 + 3) = (3, 10).
Задача 144. Определить старые координаты точки при параллельном переносе из задачи 143, если новые координаты точки равны (2, 9).
Пример 145. При параллельном переносе точка Л(1, 2) переходит в точку Л^З, 7). Определим, в какую точку при этом параллельном переносе перейдет точка В(5, 8).
Для точек А и получаем, что х = 1, у = 2, х} = 3, у, = 7.
93
\ Х\ ~ х — а з = 1 - а а = -2
Тогда | У| = У - b	|7 = 2 - Л	[Ь = -5 •
Новое начало координат — это точка О,(—2, —5). Тогда точка £?(5, 8) при параллельном переносе перейдет в точку В^5 - (-2), 8 - (-5)), то есть Z?,(7, 13).
Задача 145. При параллельном переносе точка Л (4, I) переходит в точку А}(2, 9). Определить, в какую точку при этом параллельном переносе перейдет точка В(3, 7).
§ 15.2. ПОВОРОТ ОСЕЙ КООРДИНАТ
При повороте осей координат на угол а против часовой стрелки начало координат не меняется, а связь между старыми координатами (х, у) и новыми координатами (х15 yj задается формулами:
х = X[COsa — j^sinoc [ Xj = xcosoc + ysina и <
у = XjSin ОС + T]COS 01 I y} = — xsin oc + у cos ОС
Пример 146- Определим новые координаты точки (3, 4) при повороте осей координат на угол а = л/6.
Здесь х = 3, у = 4, cos а = cos у- = Уз~/2, sin а = sin — = 1/2. Тогда 6	6
новые координаты точки равны (ЗдД/2 + 4/2, -3/2 + 4VT/2) = = ((ЗУУ + 4)/2, (-3 + 4Уз’)/2).
Задача 146. Определить новые координаты точки (7, 2) при повороте осей координат на угол а = л /3.
Пример 147. При повороте осей координат на угол а = 2 л/3 новые координаты точки равны (4, 9). Определим старые координаты
точки.
Здесь х, = 4, X! = 9, cos а = cos = -1 /2, sin ос = sin = д/Т/2.
Тогда старые координаты точки равны (4 X (-1/2) - 9д/Т/2, 4“\Аз~/2 + + 9 х (-1/2)) = ((-4 - 9УТ)/2, (4дД - 9)/2).
Задача 147. При повороте осей координат на угол а = 5л/6 новые координаты точки равны (7, 5). Определить старые координаты точки.
Глава 16
ПРИВЕДЕНИЕ УРАВНЕНИЯ КРИВОЙ ВТОРОГО ПОРЯДКА К КАНОНИЧЕСКОМУ ВИДУ
мулами:
Дано общее уравнение кривой второго порядка Ах2 + Вху + Су2 + + Dx + Еу + F=^ 0, где В 0. Наша цель — привести уравнение кривой второго порядка к каноническому виду.
С помощью поворота осей координат на подходящий угол ос можно добиться, чтобы в новой системе координат О\Х}у{ в уравнении кривой второго порядка не было произведения хд^. После этого нужно выделить полные квадраты по переменным х}, и сделать параллельный перенос.
Пример 148. Приведем уравнение кривой второго порядка 14/ + 24лу + 21/ - 4х + 18у — 139 = 0 к каноническому виду.
Совершим поворот осей координат на угол а. Связь между старыми координатами (х, у) и новыми координатами (xb yj задается фор-
X = XjCOSOL — j^sino, у = Xjsin а + y(cosoc
Подставим эти выражения в уравнение кривой.
14(X|Cosoc — ytsina)2 + 24(X|Sina + y(cosa)(X|Cosa — y,sinoc) +
+ 21(X]Sina + y,cosa)2 — 4(X]Cosoc — y^ina) + 18(x,sina + y,cosa) — 139 = 0
-+ (14cos2a + 24 cos a sin a + 21sin2a)x2 + (-28 cos a sin a + 24cos2a -
— 24sin2a + 42 cos a sin a^y, + (14sin2a - 24cosasina + 21со82а)у/ +
+ (—4 cos a + 18sina)X| + (4sinct + 18cosa)yi — 139 = 0.
Коэффициент при х,у| приравняем нулю: — 28 cos a sin a + 24cos2a — — 24sin2a + 42 cos a since = 0 -* 24cos2a + 14cosasinoc — 24sin2a = 0 12sin2a — 7 cos a sin a — 12cos2a = 0.
Если cos2oc = 0, то из полученного уравнения sin2a = 0, что противоречит тождеству cos2oc + sin2oc = 1. Поэтому cos2a 0. Разделим обе части уравнения на cos2oc:
12tg2a - 7tgoc - 12 = 0. Отсюда tga = -3/4 и tga = 4/3.
95
Пусть tg ос = 4/3. Тогда cos а = 1/V 1 + tg2oc = 1/V 1 + (4/3)2 = 3/5, a sin ос = cos ос tg ос = 3/5 х 4/3 = 4/5.
Тогда (14cos2oc + 24 cos a siп ос + 21 sin2oc)x2 + (14sin2oc — 24 cos oc sin oc + + 21cos2a)y,2 + (—4cosoc + 18sinoc)x, + (4sinoc + 18cosoc\yi — 139 = 0 (14 + 24 cos a sin а + 7sin2oc)x2 + (14 — 24cosoc since + 7cos2oc)_y,2 + + (—4cosoc + 18sina)x, + (4sin oc + 18cos oc)jP| — 139 = 0 * (14 + 24X 3/5 x x 4/5 + 7 x (4/5)2)x2 + (14 - 24 x 3/5 X 4/5 + 7 x (3/5)2)y2 + (-4 x 3/5 + + 18 x 4/5)x, + (4 x 4/5 + 18 x 3/5)y, — 139 = 0 — 30x2 + 5y/ + 12x, + + 14y, - 139 = 0.
Выделим по каждой переменной полный квадрат.
30(,v2 + 2/5x0 + 5(у2 + 14/5^) - 139 = 0 -* 30(х2 + 2х{ х 1/5 + (1/5)2 -- (1/5)2) + 5(у}2 + 2У1 х 7/5 + (7/5)2 - (7/5)2) - 139 = 0 - 30(х, + 1/5)2 -- 30 х (1/5)2 + 5(_у, + 7/5)2 - 5 х (7/5)2 - 139 = 0 -> 30(х, + 0,2)2 + + 5(у, + 1,4)2 = 150 -> (х, + 0,2)2/5 + (^ + 1,4)2/30 = 1.
Введем следующие обозначения: х2 = х} + 0,2; у2 = yi + 1,4.
Тогда х2/5 + у?/!® = 1. Это каноническое уравнение эллипса.
Повернув оси координат на угол arctg4/3 и перенеся начало координат в точку (—0,2; —1,4), мы получили в новой системе координат каноническое уравнение эллипса х27^ + >7/30 = I.
Задача 148- Привести уравнение кривой второго порядка I lx2 — — 20ху — 4у2 — 20х — 8j- + 1 = 0 к каноническому виду.
Глава 17
ИНВАРИАНТЫ КРИВЫХ
ВТОРОГО ПОРЯДКА
Для кривой второго порядка
+ 2я12ху + Й22У2 + 2<7пх + 2<72зУ + Язз “ О
можно вычислить следующие однозначно определяющие тип кривой инварианты'.
	«11	«12	«13
II < II ю	«12	а22	«23
«12 а22	«13	«23	«зз
а\\ а\з +
«13 «33
«22 «23
а23 а33
/, ап + tz22, /2
Мы уже знакомы с такими кривыми второго порядка, как эллипс, гипербола и парабола. Но есть и шесть других кривых второго порядка.
Мнимый эллипс — это кривая второго порядка, которая в надлежащей системе координат, называемой для нее канонической, имеет уравнение х21а2 + у21Ъ2 = — 1.
Пара мнимых пересекающихся прямых — это кривая второго порядка, которая в надлежащей системе координат, называемой для нее канонической, имеет уравнение х^/а1 + у2/Ь2 = 0.
Пара пересекающихся прямых это кривая второго порядка, которая в надлежащей системе координат, называемой для нее канонической, имеет уравнение х^/а1 — у2/Ь2 = 0.
Пара параллельных прямых — это кривая второго порядка, которая в надлежащей системе координат, называемой для нее канонической, имеет уравнение х2 — а2 = 0.
Пара мнимых параллельных прямых — это кривая второго порядка, которая в надлежащей системе координат, называемой для нее канонической, имеет уравнение х2 + а2 = 0.
Пара совпавших прямых — это кривая второго порядка, которая в надлежащей системе координат, называемой для нее канонической, имеет уравнение х2 = 0.
97
Теорема.
1.	Если 8 > 0, 7]А < О, то это эллипс.
2.	Если 8 > О, Z]А > 0, то это мнимый эллипс.
3.	Если 8 > О, А = 0, то это пара мнимых пересекающихся прямых.
4.	Если 8 < О, А 0, то это гипербола.
5.	Если 8 < О, А = 0, то это пара пересекающихся прямых.
6.	Если 8 = О, А 0, то это парабола.
7.	Если 8 = А = 0, /2 < О, то это пара параллельных прямых.
8.	Если 8 = А = 0, /2 > 0, то это пара мнимых параллельных прямых.
9.	Если 8 = А = /2 = 0, то это пара совпавших прямых.
Пример 149. Определим тип кривой второго порядка, заданной уравнением 5.x2 + 4ху + бу2 — 12х - 10у + 3 = 0.
Здесь аи — 5, я12 = 4/2 = 2, а22 — 6,	= —12/2 — —6, а23 — —10/2 —
= —5, а33 = 3.
8 =	а\\	«12	—	5	2	= 26 > 0.	
	ап	а22		2	6		
	«и	«12	«13		5 2-6		
А =	«12	а22	а23	=	2 6-5		= 90 + 60 + 60-216- 125-12 =
	«13	а23	«33			6 -5 3	
= -143.
A = а} j + а22 = 5 + 6 = 11.
АД = их (-143) =-1573 <0.
Так как 8 = 26 > 0 и А А = —1573 < 0, то это эллипс.
Задача 149. Определить тип кривой второго порядка, заданной уравнением Зх2 - бху + 2j/ + 4х + 8у — I = 0.
Глава 18
ПОВЕРХНОСТИ
ВТОРОГО ПОРЯДКА
Уравнение поверхности второго порядка в декартовой прямоугольной системе координат имеет следующий вид:
Ах2 + By2 + Q2 + Dxy + Exz + Fyz + Gx+ Ну + Kz+ L = 0,
где A2 + В2 + С2 + Z)2 + E2 + F2 0.
К вырожденным поверхностям второго порядка относят пустое множество, точку, прямую, плоскость, пару плоскостей.
Уравнение невырожденной поверхности второго порядка преобразованием координат может быть приведено к одному из следующих видов:
1)	х2/а2 + у2/Ъ2 + z2/с2 = 1 (эллипсоиду
2)	х2/а2 + y2/b2 — z2/c2 = 1 (однополостный гиперболоиду
3)	х2/а2 + y2/b2 — z2/c2 = —1 (двуполостный гиперболоиду
4)	х2/а2 + y2/b2 — z2/c2 = 0 (конус второго порядкаУ
5)	z — х2/а2 + у2/Ь2 (эллиптический параболоиду
6)	z = х2/а2 + у2/Ь2 (гиперболический параболоиду
7)	х2/а2 + y2/b2 = 1 (эллиптический цилиндру
8)	х2/а2 — у21Ъ2 = 1 (гиперболический цилиндру
9)	у2 = 2рх (параболический цилиндр).
Пример 150. Определим тип поверхности второго порядка £ = ху.
Сделаем замену переменных х = (xj — у,)/УУ, у = (х, + У|)/\Т,
Z = Z\.
Тогда z2 = ху z2 = (х, - yjXxj + у{)/2 -> z2 = х^/2 - y2J2 z2 -
-хЦ2+У1/2 = Ъ.
Введем следующие обозначения: Z\ = х2, х} = ^2, У| = Уг- Тогда уравнение нашей поверхности примет вид х22 + у//2 — z2/2 = 0. Это конус второго порядка.
Задача 150. Определить тип поверхности второго порядка z = ху.
99
Если лежащая в плоскости Оху кривая F(x, у) = 0 вращается вокруг оси Ох, то уравнение полученной таким образом поверхности второго порядка будет F(x, ±Vу2 + Z2 ) = 0.
Пример 151. Эллипс ^/9 + у2/4 = I вращается вокруг оси Ох.
Определим уравнение и тип полученной поверхности второго порядка.
Уравнение поверхности второго порядка будет:
*79 + (±V/ + z2 )2/4= I,
то есть х2/9 + у2/4 + //4 = I. Это эллипсоид.
Задача 151. Парабола у2 = 16х вращается вокруг оси Ох. Определить уравнение и тип полученной поверхности второго порядка.
Если лежащая в плоскости Оху кривая F(x, у) = 0 вращается вокруг оси Оу, то уравнение полученной таким образом поверхности второго порядка будет F^^lx2 + z2, у) = 0.
Пример 152. Гиперболах2^ — //16 = 1 вращается вокруг оси Оу. Определим уравнение и тип полученной поверхности второго порядка.
Уравнение поверхности второго порядка будет: (±-y/x2 + z2 )79-//1б = 1, то есть х2/9 — у2/16 + г2/9 = 1. Это однополостный гиперболоид.
Задача 152. Прямая у = 2х вращается вокруг оси Оу. Определить уравнение и тип полученной поверхности второго порядка.
Форму поверхностей второго порядка исследуют с помощью сечений поверхностей плоскостями, параллельными координатным плоскостям.
Глава 19
ЛИНЕЙНЫЕ ПРОСТРАНСТВА
В данной главе мы обобщим понятие вектора, рассмотрению которого была посвящена глава 5.
Рассмотрим множество L чашек кофе с молоком. Введем в этом множестве операции умножения на число и сложения. Если к приготовленной порции кофе добавить точно такую же, то содержимое сосуда увеличится вдвое. Будем говорить, что мы умножили порцию кофе на 2. Аналогично можно определить умножение на любое положительное число.
Теперь возьмем две разные чашки кофе, приготовленного по различным рецептам, и сольем их вместе (да простят кофеманы этот кощунственный акт). Будем говорить, что мы произвели сложение двух элементов нашего множества. Заметим, что в результате всех этих действий мы получаем элемент нашего множества (кофе с молоком), а не компот и не кисель.
Каждой чашке кофе можно поставить в соответствие пару чисел (х, у), где х — количество молока (в стаканах) в этой чашке, а у — количество черного кофе (в стаканах) в этой чашке. Изобразим это в декартовой системе координат.
Соединив точки с началом координат, мы получим те объекты, с которыми уже хорошо знакомы, — векторы. А введенные нами операции во множестве чашек кофе — это умножение вектора на число и сложение векторов (например, по правилу параллелограмма).
Но интерпретация векторов на языке чашек кофе с молоком поможет нам лучше изучить свойства операций над векторами. При
Ю!
объединении содержимого двух чашек кофе мы получаем элемент нашего множества (кофе с молоком), а не компот и не кисель. На математическом языке это звучит так.
Аксиома 7. х + у лежит в L для любых х, у из L.
Можно добавить содержимое 2-й чашки к 1-й, а можно добавить содержимое 1-й чашки ко 2-й. Результат от этого не изменится.
П7 + \2/ =\2j +Ш
Аксиома 2. х + у = у + х для любых х, у из L.
Эта аксиома выполняется не для всякого множества, в котором введена операция сложения. Заменим кофе и молоко на воду и концентрированную серную кислоту. Тогда Н2О + H2SO4 = раствор серной кислоты, a H2SO4 + Н2О = опасность!
При сложении векторы можно объединять в любые группы. Можно объединить сначала содержимое 1 -й и 2-й чашек кофе, а затем добавить содержимое 3-й чашки кофе. А можно объединить сначала содержимое 3-й и 2-й чашек кофе и добавить все это к содержимому 1-й чашки кофе. Результат от этого не изменится.
(W + W) + W = W + (W + W)
Аксиома 3. (х + у) + z = х + (у + г) для любых х, у, z из L.
Эта аксиома выполняется не для всякого множества, в котором введена операция сложения. Для приготовления водного раствора кристаллического йода сначала нужно йод растворить в спирте, а затем полученный раствор разбавить водой: Н2О + (12 + С2Н5ОН) = раствор. При изменении порядка сложения результат будет другим: с водой йод образует взвесь, которая не превратится в раствор при добавлении спирта. (Н2О + 12) + С2Н5ОН = взвесь.
В нашем множестве чашек кофе с молоком есть особый элемент (пустая чашка), прибавление которого к любой другой чашке кофе с молоком не влияет на содержимое чашки кофе.
Аксиома 4. Во множестве L существует нулевой элемент 0 такой, что х + 0 = х для любого х из L.
Английскому физику Полю Дираку однажды предложили шуточную задачу на смекалку. Три рыбака ловили рыбу. Ловля закончилась затемно, и рыбаки решили разделить добычу утром при свете дня. Один рыбак проснулся раньше других и решил, не будя остальных,
102
взять причитающуюся ему треть улова и уйти. Число рыб на 3 не делилось. Рыбак выкинул одну рыбу и, забрав треть улова, ушел. Затем проснулся другой рыбак и, ничего не подозревая, принялся вновь делить добычу на 3 части. Число рыб на 3 не делилось. Рыбак выкинул одну рыбу и, забрав треть улова, ушел. Последний рыбак поступил так же, как и предыдущий. Какое минимальное число рыб поймали рыбаки?
Легко проверить, что ответ задачи 25. Но Дирак дал другой и, как ни странно, правильный ответ: —2. С точки зрения математики Дирак прав (—2 < 25 и —2 подходит, —2 — 1 = —3, -3/3 = —1, —3 — (-1) = = -2 ит. д.).
Конечно, ответ Дирака не имеет физического смысла. Но для нас ценен то факт, что Дирак не делает различия между положительными и отрицательными числами. И мы не будем делать различия между положительными и отрицательными числами при определении умножения на числа. Появляются отрицательные чашки кофе — кофе по-дираковски.
Из физики известно, что две взаимно противоположные силы при сложении дают нулевую силу. Для всякой силы можно подобрать противоположную силу.
Аксиома 5. Для всякого х из множества L существует противоположный элемент —х такой, что х + (—х) = 0.
Аксиома 6. Во множестве L введена операция умножения на числа такая, что для всякого х из множества L и для любого числа X элемент Хх лежит в L.
Сформулируем и другие аксиомы.
Аксиома 7. 1 х х = х для всякого х из множества L.
Аксиома 8. ос(Рх) = (осР)х для всякого х из множества L и любых чисел ос, р.
Аксиома 9. ос(х + у) = осх + осу для любых х, у из множества L и любого числа ос.
103
Аксиома 10. (сс + р)х = ах + рх для всякого х из множества L и любых чисел сс, р.
Множество L, в котором введены две операции, удовлетворяющие аксиомам 1 — 10, называется л инейным (векторным) пространством. Элементы линейного пространства называются векторами.
Пример 153. Множество всех чашек кофе с молоком, в котором введены выше операции сложения и умножения на числа, является линейным (векторным) пространством.
Пример 154. Множество всех векторов на плоскости с операциями сложения и умножения на числа является линейным пространством. Нулевой элемент — это нулевой вектор.
Пример 155. Множество всех целых чисел (0, ±1, ±2, ...) не является линейным пространством, так как 0,5 х 1 = 0,5 — не есть целое число (не выполняется аксиома 6).
Задача 153. Изменится ли ответ в примере 155, если произведение целого числа х на число X определить по правилу X X х = [Хх] (целая часть от произведения х)?
Пример 156. Множество всех векторов на оси Ох с операциями сложения и умножения на числа является линейным пространством.
Пример 157. Множество всех квадратных матриц 2-го порядка с обычными операциями сложения и умножения на числа является линейным пространством. Нулевой элемент — это нулевая матрица 2-го порядка.
Пример 158. Рассмотрим множество L всех положительных чисел и определим в нем сумму чисел и умножение на действительное число X по следующим правилам: х © у = ху (обычное произведение) и X х х = х\ Выясним, является ли это множество с введенными операциями линейным пространством.
I)	х © у — ху > 0 при х > 0 и у > 0, то есть сумма любых двух элементов из L снова лежит в L.
2)	х © у = ху = ух = у © х для любых х, у из L.
3)	(х © у) © г = ху © г = {xy)z = x(yz) = х(у® z) = х® (у® z) для любых х, у, z из L.
4)	х © I = х х I = х для любого х из £, то есть за нулевой элемент в пространстве L надо взять I.
5)	1/х © х = (1 /х)х = 1, то есть противоположный элемент для элемента х — это 1/х.
6)	X х х = Xх > 0 при х > 0, то есть X х х принадлежит L для любого х из £ и любого действительного числа X.
7)	1 х х = х1 — х для любого х из L.
104
8)	а(|3х) = ах3 = (хр)а = хар = (ар)х для любого х из L и для любых действительных чисел аир.
9)	а(х © у) = а(ху) = (ху)а = хауи = ха © уа = ах © ау для любых х, у из Ли любого действительного числа а.
10)	(а + р)х = ха+р = хахр = ха © хр = ах © рх для любого х из L и для любых действительных чисел аир.
Мы видим, что введенные операции удовлетворяют всем аксиомам линейного пространства. Поэтому множество L всех положительных чисел с введенными операциями является линейным пространством.
Задача 154, Рассмотрим множество L всех отрицательных чисел и определим в нем сумму чисел и умножение на действительное число Л по следующим правилам: х © у = — |х| |у | и Л X х = —|х|\ Выяснить, является ли это множество с введенными операциями линейным пространством.
Задача 155, Привести пример линейного пространства.
Задача 156, Привести пример множества с двумя операциями («сложение» и «умножение на числа»), которое не является линейным пространством.
Рассмотрим множество L упорядоченных наборов из п действительных чисел, то есть множество L состоит из элементов х = (х(, х2,хп). Элемент х называется п-мерным вектором.
Введем операции сложения х + у = (х1 + yh х2 + у2,х„ + уп) и умножения на число осх = (осхь ссх2, ахп) для всех х = (х15 х2,	х„),
у = (У\, у2, уп) из множества L и любого числа ос. Такое множество L будем обозначать Rn.
Задача 157, Показать, что R" является линейным пространством, то есть проверить выполнение аксиом 1 — 10.
Пример 159, Покажем, что в линейном пространстве при умножении нулевого элемента на число Л снова получается нулевой элемент.
Пусть ЛО = х. Тогда х + х = ЛО + ЛО = Л(0 + 0) = ЛО = х —> х + х = х
х + х + (—х) = х + (—х) v х + 0 = 0 ^ х = 0.
Пример 160, Покажем, что в линейном пространстве при умножении любого элемента на ноль получается нулевой элемент линейного пространства.
Пусть Од = х. Тогда х + х = 0а + 0а = (0 + 0)д = Од = х --> х + х = х
—> х + х + (-х) = х + (-х) х + 0 = () > х 0.
Пример 161, Покажем, что в линейном пространстве один нулевой элемент.
105
Пусть в линейном пространстве два нулевых элемента: 0, и 02. Тогда ()| + 02 = 0, (так как 02 — нулевой элемент линейного пространства) и 0] + 02 = 02 (так как 0] — нулевой элемент линейного пространства). Отсюда 0| = 02.
Задача 158. Показать, что в линейном пространстве Х(-я) = —X а.
Задача 159. Показать, что в линейном пространстве Х(я — Ь) = = гка- +Ь.
§ 19.1. ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ.
БАЗИС
Рассмотрим линейное пространство L. Выберем векторы х{, хъ хп в пространстве L и рассмотрим их линейную комбинацию — выражение вида о,)*! + сс2х2 + ... + сс^, где ос1? сс2,..., сс,? — какие-то числа. Это будет некоторый вектор из пространства L. Нас интересует случай, когда этот вектор нулевой, то есть можно ли так подобрать числа сс}, сс2, ..., ос,,, чтобы сцХ] + ос2х2 + ... +	= 0 (нулевой вектор).
Один ответ очевиден: все сс, = 0. Если других вариантов нет, то векторы %i, х2, ..., хп называются линейно независимыми.
Если можно подобрать числа сс2, ..., ап, где хотя бы одно ocz 0 и apci + сс2х2 + ... + af1xn = 0, то векторы х2,..., хп называются линейно зависимыми.
Пример 162.
2| а\ = | b |, 2d + 6 = 0. Векторы а и 6 линейно зависимы.
Пример 163.
Вектор а линейно независим, так как равенство аа = 0 возможно лишь при а = 0.
Пример 164. Х| = (1, 2, 3), х2 = (-3, -6, -9). Зх, + х2 = (0, 0, 0).
Векторы Х|, х2 линейно зависимы.
106
Пример 165.
Векторы el9 е2 линейно независимы, так как равенство а,е] + а2е2 —
= 0 возможно лишь при Q] = а2 = 0.
Задача 160. Привести пример линейно независимых векторов.
Задача 161. Привести пример линейно зависимых векторов.
Если v = оцХ] + а2х2 + ••• + ВД» то говорят, что вектор vлинейно выражается через векторы х{, х2, ..., хп.
Система векторов xh х2, хп линейного пространства L называется базисом, если:
I) векторы х{, х2, хп линейно независимы;
2) любой вектор v из пространства L линейно выражается через векторы %], х2, ..., хп (у = СС]Х| + сс2х2 + ... + сс/гх„).
Числа СС|, сс2, ..., ап называются координатами вектора v в базисе хь х2, хп.
Конечно, в линейном пространстве L очень много всевозможных базисов. Но все базисы содержат одинаковое число элементов. Это число называется размерностью линейного пространства L и обозначается dim L.
Пример 166. Цветное телевидение избрало в качестве базисных зеленый, красный и синий цвета, то есть оно трехмерно.
Пример 167. В полиграфии для цветной печати используют голубую, пурпурную, желтую и черную краски, то есть цветная полиграфия четырехмерна.
Пример 168. В «кофейном» пространстве за стандартную основу приняты стакан черного кофе и стакан молока, то есть «кофейное» пространство двумерно.
Пример 169. Любой кулинарный рецепт — это разложение по базису.
Пример 170. Множество векторов на плоскости двумерно. Базис образуют векторы е, = (1,0) и е2 = (О, I).
Пример 171. Пространство /Г л-мерно. Векторы = (I, 0,..., 0), е2 = (0, 1, 0, ..., 0), ..., еп = (0, 0, ..., I) образуют базис.
107
х = (x„ x2,..., xfl) =%,(!, 0,0) + x2(0, 1,0,..., 0) + ... + x„(0, 0,1) = = x,e, + x2e2 + ... + xnen, то есть любой вектор x из пространства R” линейно выражается через векторы еь е2. ..., еп.
Проверим линейную независимость векторов eh е2, ..., еп. с^е, + + ot2e2 + ... + апе„ = 0 = (0, 0,..., 0) « at(l, 0, ..., 0) + a2(0, 1, 0, ..., 0) + + ... + a„(0, 0, ..., 1) = (0, 0,..., 0) « (a1? 0, ..., 0) + (0, a2, 0, ..., 0) + ... + + (0, 0, ..., a„) = (0, 0, ..., 0) « (a„ a2, ..., a„) = (0, 0, ..., 0).
Отсюда a, = a2 = ... = a/; = 0.
Задача 162. Привести пример базиса.
Пример 172. Исследуем на линейную зависимость систему векторов Х| = (5, 4, 3), х2 = (3, 3, 2), х3 = (8, 1, 3).
Имеем: oqx, + а2х2 + а3х3 = 0 = (0, 0, 0).
Распишем это векторное равенство для каждой из координат.
' 5оС] + Зос2 + 8ос3 = 0, < 4ос! Н- За2 + ос3 = 0,
Зое, + 2ос2 + За3 = 0.
8	0 '
I 0
3	0
5 3
4 3
3 2
I о
3 8	0	1	Г	5	3	8
3 -27	0	=>	0	1	-9
1-9	0	J	[	0	0	0
(ос! = —7а3, а2 = 9а3, а3 любое.
0	5 0 35 0
0	10 1-90
Система векторов линейно зависима.
0	7	0 j
1-90]
Задача 163. Исследовать на линейную зависимость систему векторов X] = (2, -3, I), х2 = (3, -1, 5), х3 = (I, -4, 3).
Важным является следующий критерий линейной зависимости: векторы а = (аъ а2, а3), Ь= (Ь{, Ь2, Л3), с = (cb с3) линейно зависимы
а । а2 а3
ь2 by
Cs
Пример 173. В примере 172 определитель
5 4 3
3 3 2
8 I 3
— 0.
Теорема. Ненулевые векторы a = (a,, а2, а3), b= (bh b2, Ь3) линейно зависимы a[/bl = a2/b2 = а3/Ь3.
Пример 174. Векторы а = (I, 2, 3) и b = (3, 6, 9) линейно зависимы, так как I/3 = 2/6 = 3/9.
Задача 164. Исследовать на линейную зависимость векторы а = (5, 4, 3) и (25, 20, 15).
108
Глава 20
ПОДПРОСТРАНСТВА
ЛИНЕЙНОГО ПРОСТРАНСТВА
§ 20.1. ПРИМЕРЫ ПОДПРОСТРАНСТВ ЛИНЕЙНОГО ПРОСТРАНСТВА
Множество Я векторов линейного пространства L называется подпространством, если:
1) сумма любых двух векторов из Я принадлежит множеству Я;
2) произведение любого вектора из Я на любое число X (действительное или комплексное в зависимости от вида линейного пространства) принадлежит множеству Я.
Пример 175м Множество, состоящее из нулевого вектора линейного пространства, является подпространством линейного пространства. Само линейное пространство одновременно является и подпространством. Это несобственные подпространства линейного пространства. Остальные подпространства линейного пространства (если они есть) называются собственными подпространствами.
Пример 176. Рассмотрим в линейном пространстве Rn множество векторов Я= {(хн хп_}, 0)| %), ..., хп_} — действительные числа}.
Для любых векторов х = (хь ..., х„_,, 0) и у = (уь ..., уп_ъ 0) из множества Я сумма х + у = (х(, н 0) + (у1? ..., у„_,, 0) = (х, + ун ..., хп । + Уп |, 0 + 0) = (х, + У],..., х„. j + у„_,, 0) принадлежит множеству Я.
Произведение любого вектора х= (хь ..., хл_н 0) из множества Я на любое действительное число X равно Хх = Х(х,, ..., х„_,, 0) = (Ххн ..., Ххм_н X х 0) = (ХХ|, ..., Хх„_,5 0) и принадлежит множеству Я.
Поэтому множество Я является подпространством линейного пространства Rn.
Пример 177. Рассмотрим в линейном пространстве матриц второго порядка с обычными операциями сложения матриц и умноже-
Г7 ( f	I I
ния матриц на число множество матриц Я = {	“ | а{ и а2 —
t —а2 а{ J действительные числа}.
109
п	г	л ( ^1	^2 ]	г> (	^2 1
Для любых матриц А -	и В= I , из множе-
—а2 а} J [ —b2 b\ J
и А , „ Г а\ + Ь} б/2 + ^2 1	и
ства Я сумма Л + В= \	'	. принадлежит множеству Я.
— а2 — b2 а} + b\ J
Произведение любой матрицы А —	6/1	6/2 из множества Н
L~^2 Щ J
на любое действительное число X равно кА — X |	1	6/2	=
[ -^2 Щ
=	^2 и принадлежит множеству Н.
I	ЛаС1 । J
Поэтому множество Н является подпространством линейного пространства матриц второго порядка с обычными операциями сложения матриц и умножения матриц на число.
Пример 178. Рассмотрим в линейном пространстве Rn множество векторов Н= {(х}, ..., x„_b 1)| хь ..., хп_{ — действительные числа}.
Для векторов х = (х|?..., х„_,, 1) и у = (уь ..., уп1) из множества Н суммах + у- (х,, ...,x„_h 1) + (уь ..., К-н 0 = (*i + Уь -Vi + К-н 1 + 1) = (х, + yh ..., х„_, + у„_], 2) не принадлежит множеству Я.
Поэтому множество Я не является подпространством линейного пространства Rn.
Задача 165. Привести пример множества, которое является подпространством линейного пространства.
Задача 166. Привести пример множества, которое не является подпространством линейного пространства.
Задача 167. Определить, является ли подпространством линейного пространства матриц второго порядка с обычными операциями сложения матриц и умножения матриц на число множество Я = {А = = " О 6Z,
Задача 168. Определить, является ли подпространством линейного пространства Rn множество векторов Н- {(X] , ..., хп_ь 2)| хи ..., х„_, — действительные числа}.
С1\ I	о	ч
' | а, — действительное число}.
ПО
§ 20.2. СПОСОБЫ ЗАДАНИЯ ПОДПРОСТРАНСТВ
Подпространство Н можно задать как линейную оболочку системы векторов.
Выбирается система векторов аь ..., ат, Число векторов такой системы не превышает размерности пространства. Тогда всевозможные линейные комбинации ос^ + ... + атат образуют подпространство
<ах, ..., ат>. Число линейно независимых векторов среди векторов аъ ..., ат называется размерностью подпространства Ни обозначается dim И
Подпространство можно задать и системой линейных однородных уравнений относительно координат векторов.
Нужно уметь переходить от одного способа задания подпространства к другому способу задания подпространства.
Предположим, что подпространство задано как линейная оболочка системы векторов. Запишем координаты векторов в виде столбцов матрицы. Тогда в строках матрицы указаны соответствующие координаты векторов (в первой строке — первые координаты, во второй строке — вторые координаты и т. д.). Приведем полученную матрицу к ступенчатому виду. Тогда нулевым строкам ступенчатого вида матрицы соответствуют условия, накладываемые на координаты векторов подпространства. Система таких равенств и определяет подпространство.
Пример 179. Подпространство является линейной оболочкой векторов а, = (I, 2, 3, -4), а2 = (2, 3, -4, 1), а3 = (2, -5, 8, -3), а4 = = (5, 26, —9, —12), а5 = (3, -4, 1,2). Найдем уравнения, определяющие подпространство.
Запишем координаты векторов в виде столбцов матрицы. Справа от матрицы укажем номера координат.
г 1	2	2	5	3 '	
2	3	-5 26	—4	*2
3	—4	8 -9	1	
. -4	1	-3 -12	2 .	х4
Приведем полученную матрицу к ступенчатому виду. Соответствующие действия производим и над координатами.
г 1	2	2	5	3 ^		1	2	2	5	3 '	
2	3 -5 26 —4	х2	0	-1	-9	16 -10	%2	2Х|
3	-48-91	*з	0	-10	2	-24 -8	х3 — Зх,
. —4	1 -3 -12 2	х4	. 0	9	5	8	14	х4 + 4Х)
111
" 1	2		2	5	3 "	
0	-1		-9	16	-10	х2 — 2%[
0	0		92 -	-184	92	х3 - Зх! - 10(х2 - 2х,)
0	0		-76	152	-76 ,	х4 + 4Х| + 9(х2 — 2х,)
' 1	2	2	5	3		X,
0	-1	-9	16	-10		х2 — 2х,
0	0	1	—2	1	1/92(х3 + 17х, - 10х2)	
. 0	0	-1	2	-1 >	1 /76(х4 — 14х, + 9х2)	
1	2	2	5	3 '		
0	-1	-9	16	-10		х2 — 2Х|
0	0	1	—2	1		1/92(х3 + 17х, - 10х2)
0	0	0	0	0 ,	1 /76(х4 - 14х, + 9х2) + 1 /92(х3 + 17х, - 10х2)	
Выражения, соответствующие нулевым строкам, нужно приравнять нулю и записать в виде системы.
У нас одна нулевая строка. Поэтому подпространство задается уравнением 1/76(х4 - 14х, + 9х2) + 1/92(х3 + 17х, - 10х2) = 0, то есть х} + 17х2 + 19х3 + 23х4 = 0.
Задача 169- Подпространство является линейной оболочкой векторов = (2, -I, 3, 5), а2 = (4, -3, I, 3), а2 = (3, -2, 3, 4), а4 = = (4, - I, 15, 17), а5 = (7, —6, -7, 0). Найти уравнения, определяющие подпространство.
Пусть подпространство задано системой линейных однородных уравнений. Для задания подпространства как линейной оболочки векторов нужно найти фундаментальную систему решений — базис пространства решений линейной однородной системы.
Для этого решаем систему методом Гаусса и применяем метод бегущей единицы (поочередно одну свободную переменную приравниваем единице, другие свободные переменные приравниваем нулю и находим соответствующие значения главных переменных).
линейной однородной системы <
Пример 180. Подпространство задано как множество решений
%! + 2х, + 4х3 - Зх4 = О
3 %, + 5х2 + 6х3 — 4х4 = О
4х, + 5x2 - 2х3 + Зх4 = 0 ' ОпРеде-
Зх, + 8х, + 24%, — I 9х4 = О
лим базис подпространства.
Решим систему методом Гаусса.
112
1
о
х2 х3 х4
О -8 7 I ОI
. Это главный ступенчатый вид матрицы.
Главные переменные: х1 и х2. Свободные переменные: х3 и х4.
' х} = 8х3 — 7х4
Тогда < х2---6х3 + 5х4
х3, х4 любые
Для нахождения фундаментальной системы решения применим метод бегущей единицы (поочередно одну свободную переменную приравниваем единице, другую свободную переменные приравниваем нулю и находим соответствующие значения главных переменных).
<х] = 8х1—7x0 = 8
х2 = -6 х 1 + 5 х 0 = -6
х3 = 1
х4 = 0
= 8 х о - 7 х 1 = -7 х2 = - 6ХО + 5Х1 = 5 х3 = 0
х4 = 1
(8, —6, 1, 0) и (—7, 5, 0, 1) — это фундаментальная система решений, то есть базис пространства решений. Тогда общее решение линейной однородной системы имеет следующий вид: ^(8, —6, 1,0) + + С2(-7, 5, 0, 1), где С] и С2 — произвольные постоянные.
Задача 170- Подпространство задано как множество решений
г 2%| — 4х2 + 5х3 + Зх4 = 0
линейной однородной системы к ЗХ| — 6х2 + 4х3 + 2х4 — 0
4х, — 8х2 + 17х3 + 11х4 =
0
Определить базис подпространства.
113
§ 20.3. БАЗИС СИСТЕМЫ ВЕКТОРОВ
Для нахождения базиса системы векторов нужно записать координаты векторов в виде строк матрицы и привести полученную матрицу к ступенчатому виду Справа от матрицы указываются векторы и регистрируются проводимые преобразования матрицы.
Тогда ненулевые строки ступенчатого вида матрицы определяют базис системы векторов, а нулевые строки ступенчатого вида матрицы позволяют получить разложение остальных векторов системы по базисным векторам.
Пример 181. Определим базис и разложение остальных векторов по базису для системы векторов из примера 179.
Запишем координаты векторов в виде строк матрицы и приведем полученную матрицу к ступенчатому виду.
' 1 2	2 3	3	—4 ' —4	1		«1 «2		' 1	2	3 —4 ? 0 -1 -10 9	а2 — 2Л|
2	-5	8 -	-3	а	“*	0	-8 12 —4	а3-а2 ~*
5	26	-9 -	-12	а,		0	16 -24 8	5 а ।
. з	—4	1	2	а		. 0 -10 -8 14 .	а5 - За,
" 1	2	3		4			
0	-1	-10	9			а2 — 2tZj	
0	0	92	-76		«з‘	- tz2 — 8(tz2—2fl])	
0	0	-184	152		^4“	5а{ + 16(tz2~ 2а{)	
. 0	0	92	-76 ,		^5~	Зах — 10(tz2 - 2д()	
г 1	2	3		L	4 л		«1	
0	-1	-10	9			а2 — 2а}	
0	0	92	-76			- 9я2 + 16«]	
0	0	-184	152		^4“	- 37а} + 16tz2	
0	0	92	-76		а5 + 17tz, - 10я2		
' 1	2	3	—i	1 '			
0	-1	-10	9			а2 — 2а{	
0	0	92	-76			а3 - 9я2 + 16Л]	
0	0	0	0		0,5(я4 - 37 а} + 16я2) + а3		— 9tz2 + 16tZ|
. 0	0	0	0	>	tz5	+ 17л, - 10я2 — («з —	9я2 + 16/9^)
г 1	2	3	-4 1				
0	-1	-10	9			а2 — 2Л|	
0	0	92	-76		а3 - 9tz2 + 166?!		
0	. 0	0	0		0,5ц	4 — 2,5«| — аг + а,	
. 0	0	0	0		а	s + at - а2 - а}	
114
Ненулевым строкам ступенчатого вида матрицы соответствуют векторы ах, а2 — 2аъ а3 + 16Я| — 9я2- Поэтому векторы а2, а3 образуют базис линейной оболочки векторов.
Нулевым строкам ступенчатого вида матрицы соответствуют равенства 0,5tz4 — 2,5я, - а2 + а3 = 0, а5 + ах — а2 — а3 = 0. Отсюда получаем разложения векторов я4 и а5 по базису аъ аъ а3: а4 = 5ах + 2а2 — 2а3 и а5 = —ах + а2 + а3.
Задача 171. Определить базис и разложение остальных векторов по базису для системы векторов из задачи 169.
S 20.4. СУММА И ПЕРЕСЕЧЕНИЕ ПОДПРОСТРАНСТВ
Пусть в линейном пространстве L заданы подпространства L{ и £2. Суммой подпространств Lx + £2 называется множество всех векторов вида хх + х2, где g х2 g Ь2.
Пересечением L{ A L2 подпространств Lx и L2 называется множество всех векторов, каждый из которых одновременно принадлежит обоим подпространствам.
Формула Грассмана: dim(Lx + Z2) = dim Ц + dim L2 — dimCZj A £2).
Пример 182. Даны подпространства Lx = <ax = (0, 1, 1, 0), a2 = = (1, 1, 0, 0), a3 = (0, 0, 1, 1)> и L2 = <b} = (1, 2, 1, 2), b2 = (1, 0, 1, 0), b3 = (0, 2,1,1)>. Определим базис и размерность подпространств Lx + L2 и Гх A Z>2*
Запишем координаты векторов в виде строк матрицы и приведем полученную матрицу к ступенчатому виду. Справа от матрицы указываются векторы и регистрируются проводимые преобразования матрицы.
' 0 1 1 О'	«1	"110
110 0		0 1 1
0 0 11	«з	0 0 1
	—>	
12 12		1 2 1
10 10	Z>2	1 0 1
0 2 1 1 ,	Ь.	^021
1 10 0'		?2	(
0 110		
0 0 11	а3	
		—>
0 0 0 2	Ь\ — а2 — ах	
0 0 2 0	Ь2 — а2 + ах	
. 0 0-1 и	Ьз-	-2й,
0 '	л2	' 1	10 0^	«2
0		0	1 1 0	Л,
1	«3	0	0 1 1	«з
				
2	bl	0	1 1 2	^\~а2
0	^2	0	-1 1 0	Ь2 а2
1	Ь.	. 0	2 11,	Ьз
1	1 0	0 '	^2	
0	1 1	0	«1	
0 1	3 1	1	«з	
				
0 1	3 0	2	bi - а2 -	ах
0 1	3 0 -	-2	Ьг — а2 + ах	— 2а3
0 1	3 0	2 ,	Ь3 — 2ах “I- а3	
115
' 1 1	0 0	«2
0 1	1 0	«1
0 0	1 1	«3
		
0 0	0 2	Ь\ — а2 — ах
0 0	0 0	Ь2 — а2 + ах — 2а3 + Ьх — а2 — ах
. о 0	о о.	b3 - 2tZj + а3 - (Ьх - а2 - ах)
' 1 1	0 0 '	tz2
0 1	1 0	
0 0	1 1	^3
0 0	0 2	Ьх — а2 — ах
0 0	0 0	b2 — 2а2 — 2tz3 + bx
. о 0	о о	Ь3 — ах + а3 — Ьх + а2
Ненулевым строкам ступенчатого вида матрицы соответствуют векторы tz2, Я|, я3, Ьх — а2 — а}. Поэтому векторы я,, а2, а3, Ьх образуют базис подпространства L} + L2. Следовательно, размерность подпространства Lx + L2 равна dim(Zj + Z2) = 4.
Нулевым строкам ступенчатого вида матрицы соответствуют равенства Ь2 — 2а2 — 2а3 + Ь} = 0 и Ь3 — а} + а3 — Ьх + а2 = 0.
Соберем векторы подпространства L} в левой части равенств, а векторы подпространства L2 — в правей части равенств: + Ь2 = = 2а2 + 2tz3, b3 — Ьх = ах — а2 — а3.
Введем следующие обозначения: сх = b} + b2 = 2а2 + 2я3 = (2, 2, 2, 2) и с2 = Ь3 — Ь} = ах — а2 — а3 = (—1, 0, 0, —1).
Вектор сх принадлежит подпространству Lx (как 2а2 + 2я3) и принадлежит подпространству L2 (как Ьх + Ь2). Поэтому вектор сх принадлежит подпространству L} О L2. Аналогично вектор с2 принадлежит подпространству Lx A Ь2.
Получаем, что размерность подпространства A L2 равна dim(£] А £2) = 2. Мы можем принять векторы 0,5с, = (1, 1, 1, 1) и с2 = (-1,0, 0, — 1) за базис подпространства Lx A L2.
Задача 172. Даны подпространства L, = <Я| = (I, -I, I, -I), а2 = (I, 1, — 1, — 1), л3 = (1, 1, 1, 1)> и Z2 = </>j = (2, —2, 0, 0), Ь2 = (3,-1, 1, 1), b3 = (1, — 1, — 1, 1)>. Определить базис и размерность подпространств Z) + L2 и Lx A L2.
Если в пересечении подпространств Lx А Л2 содержится только нулевой вектор пространства Z, то сумма подпространств Lx и Z2 называется прямой и обозначается Lx © Z2.
Глава 21
ПРЕОБРАЗОВАНИЯ БАЗИСА
$21.1. МАТРИЦА ПЕРЕХОДА
Пусть ах, ап и Ьх, ...,Ьп — два различных базиса линейного пространства L.
Матрица Т, столбцы которой равны координатам векторов Ьх, ...,Ьп в базисе ах, ап, называется матрицей перехода от базиса аъ ..., ап к базису Ьх. ..., Ьп. Тогда (Ьх ... Ьп) = (ах ... ап)Т.
Определитель матрицы перехода отличен от нуля: det TV 0.
Пример 183. Определим матрицу перехода от базиса ах = (I, 2), а2 = (3, 5) к базису Ьх = (— 1, 3), Ь2 = (4, 6).
Запишем координаты векторов в виде строк матрицы и приведем полученную матрицу к ступенчатому виду. Справа от матрицы указываются векторы и регистрируются проводимые преобразования матрицы.
1 2 '	а.	' 1 2 '	О)	' 1 2 '	
3 5	°2 _	0 -1	«2“За,	0 -1	^2 — ^а\
-1 3		0 5	Z>, + а.	0 0	bx + ах + 5(я2 —Зя,)
4 6 .	Ьг	< 0 -2,	— 4я,	.00.	b2 — 46/j — 2(а2 — 3«|)
г 1 2 '	1				
0 -1	«2-	- Зах			
0 0	bx - 14й| + 5я2				
. о 0 .	Ь2 + 2ах - 2а2				
Нулевым строкам ступенчатого вида матрицы соответствуют равенства bx - 14tZ] + 5а2 = 0 и Ь2 + 2ах — 2а2 = 0. Отсюда bx = 14tz, — 5я2 и Ь2 = —2ах + 2а2.
Получено разложение векторов Ьх и Ь2 по базису а2. Записав коэффициенты этого разложения в виде столбцов матрицы, получим Г 14 -2 1
матрицу перехода Т=	J . Тогда (Ьх Ь2) = (ах а2)Т.
117
Задача 173- Определить матрицу перехода от базиса а1 = (2, 4), а2 = (1, 6) к базису Ь} = (2, —3), Ь2 = (7, 2).
§ 21.2. СВЯЗЬ МЕЖДУ КООРДИНАТАМИ ВЕКТОРА В РАЗНЫХ БАЗИСАХ
Пусть X =
%!
иТ =
— координаты вектора х в базисах
а15 ..., ап и Ьъ ..., Ьп соответственно. Известна матрица перехода Тот базиса аъ ап к базису Ьъ ..., Ьп. Тогда Х= ТХ'. Отсюда X' = Т~]Х.
Здесь Х=
Пример 184. В примере 183 известны координаты вектора х- (6, 7) в базисе а{, а2. Определим координаты вектора х в базисе Ь}, Ь2.
т ( 14
, матрица перехода Т=	J .
1	Г 7 ? )	( 7	7 3
I 5 ыН'Чз 14 ] *СМ'
§ 3.2).
Тогда координаты вектора х в базисе Ь{, Ь2 равны
-izisf2 2 М61 -1/1яГ2Х6 + 2Х71 - Г13/91 1/181 5 14 J L 7 J - l/l8L5 X 6 + 14 х 7 J " I 64/9 J '
Т~хХ =
Задача 174. В задаче 173 известны координаты вектора х = (9, 8) в базисе а2. Определить координаты вектора х в базисе Ьъ Ь2.
Глава 22
ЛИНЕЙНЫЕ ОПЕРАТОРЫ
Оператор — это отображение/линейного пространства L в себя, то есть/ L-> L Оператор /называется линейным, если выполнены следующие два условия:
!)/(* + У) +f(y) для всех х, у из Ц
2)/(ах) = а/(х) для всех х из L и любого числа ос.
Рассмотрим случай L = Rn. Пусть еъ е2,..., еп — базис пространства Rn.
Матрица следующего вида А = (/(е^) /(е2) .../(ej) (координаты векторов/(е;) в базисе е{, е2, ..., еп записаны в виде столбцов) называется матрицей линейного оператора/в базисе еъ е2, еп.
Если рассмотреть другой базис e'h е2, е'п пространства Rn, то у оператора/в этом базисе будет матрица А' = Т^АТ, где Т — матрица перехода от базиса еъ е2, ..., еп к базису е\, е2, ..., е’п (координаты векторов е\, е2, ..., е’п в базисе е2, ..., еп записаны в виде столбцов).
Пример 185. Оператор/переводит вектор х = (хь х2, х3) в вектор /(х) = (%] + х2, х2, 2%] - х2 + Зх3). Покажем, что/ — линейный оператор, и найдем его матрицу.
/(х) = (Х| + х2, х2, 2Х] - х2 + Зх3).
У = (Уъ У2, Уз),Яу) = (У| + Ун У2, 2^! - у2 + Зу3).
f(x) +f(y) = (X! + Х2 + + у2, Х2 + уъ 2х! - х2 + Зх3 + 2у1 - у2 + Зу3).
х + у = (х, + у15 х2 + уъ х3 + у3),
/(х + у) = (Xj + У] + х2 + у2, х2 + у2, 2(Х] + yt) - (х2 + у2) + З(х3 + у3)).
Мы видим, что/(х + у) = /(х) + /(у).
(XX = ((XX), (ХХ2, (ХХ3),
/(ах) = (аХ| + ах2, ах2, 2ах, — ах2 + Зах3).
а/(х) = а(Х| + х2, х2, 2Х] — х2 + Зх3) = (а(Х) + х2), ах2, а(2х, - х2 + Зх3)).
Мы видим, что /(ах) = а/(х). Оба свойства выполнены. Поэтому /— линейный оператор.
Какова его матрица? Найдем образы базисных векторов ех = (1,0, 0), е2 = (0, 1, 0), еъ = (0, 0, 1) под действием оператора/
119
А =
полученные координаты в виде столбцов матрицы: О '
О .
3
1
1
/(е,) = (1 + 0, 0, 2 х 1 - 0 + 3 х 0) = (1, 0, 2).
/(е2) = (0 + 1, 1,2X0 - 1 + ЗХО) = (1, 1,-1).
/(е3) = (0 + 0, 0, 2 х 0 - 0 + 3 х 1) = (0, 0, 3).
Запишем
' 1 0 2
Это и есть матрица линейного оператора/в базисе е,, е2, е3.
Задача 175. Оператор/переводит вектор х = (х,, хъ х3) в вектор /(х) = (2х, - х2, х3, Зх, - х2 + х3). Показать, что/ — линейный оператор, и найти его матрицу.
Пример 186- Оператор f переводит вектор х = (х,, х2, х3) в вектор f(x) — (х, + 1, х2, х3). Определим, является ли /линейным оператором.
Дх) = (х, + 1, х2, х,).
У = (Ун Ун Уз)ЛУ) = CFi + 1, У2, Уз)-
ЯД +Ду) = (*i + 1 + У1 + 1> х2 + у2, х} + л).
X + у = (Х| + yt, х2 + у2, х3 + л),
Дх + у) = (х, + у, + 1, х2 + у2, х} + у}).
Мы видим, что f(x + у) /(х) + f(y). Поэтому/не является линейным оператором.
Задача 176. Оператор/переводит вектор х = (х,, х2, х3) в вектор f(x) = (х,, х2 + 2, х3). Определить, является ли /линейным оператором.
Пример 187. Дана матрица линейного оператора А =
I 2 | в
3 4
базисе е} = (I, 0), е2 = (0,1). Найдем матрицу этого линейного опера-
тора в базисе е\ = (5, 3), е2 = (2, 1).
е\ = 5е, + Зе2, е2 = 2е, + е2. Матрица перехода состоит из записан-f 5 2 ' ных в столбцы координат векторов е\, е2 в базисе еъ е2\ Т=	.
Тогда матрица линейного оператора в базисе е\, е'2 вычисляется по формуле А' = Т ХАТ.
1	1 —2	—1 2 1 , л э
7 ==------------- =	/см. § 3 2).
5 х 1 - 2х 3 [-3 5 J [ 3 —5J
'r-U'r Г-1 2 И 1 2 П 5 2 I	f 43	16 1
[ 3 -5J [ 3 4 J [ 3 1 J	[-102 -38 J
(перемножать матрицы можно в любой последовательности, не меняя порядка множителей).
120
I 4 5 1
Задача 177. Дана матрица линейного оператора А = I
в базисе ех = (I, 0), е2 = (0,1). Найти матрицу этого линейного оператора в базисе е\ = (1, 2), е’2 = (2, 5).
Пример 188. В пространстве геометрических векторов {v= vf i + + v2y + v2k} задан линейный оператор A v = [v, у]. Определим матрицу этого линейного оператора в базисе /, У, к.
Найдем образы базисных векторов под действием линейного оператора.
j к 0
1
0
0
0
= к = (О, О, 1).
Ак = [к, 7] =
Aj= 177] = 0 = (0, О, 0). j к 0 I
(-1,0,0).
0
0
о
Тогда матрица линейного оператора в базисе /, у, к равна ' о о -Г
ООО.
1 о о
Задача 178. В пространстве геометрических векторов {v= vxi + + г2У + v2k} задан линейный оператор A v = [v, £j. Определить матрицу этого линейного оператора в базисе /, у, к.
Пример 189. В пространстве матриц второго порядка с обычными операциями сложения матриц и умножения матриц на число дей
ствует линейный оператор по правилу
а b с d
a b f I с d
Определим матрицу этого линейного оператора в базисе Ех =
2'
4 ’
О' о ’
3
1 о
'0 I ' о о Найдем образы базисных векторов под действием линейного оператора.
\ О' 0 0 — (1,2, 0,0).
,Е3 =
,Е4 —
— 1£] + 2Е2 + 0Е3 + 0Е4 —
Ei =
0 0
1 0
r I 0 П I 2 о о
3 4
о о
0 1
1 2
0 О
121
Г ° 11 fo
1° °J " 1° = (3,4,0, 0).
fO OlfO
[1 °J " I1 = (0, 0, 1,2).
'0 0]	fO
o ij	[o
1 Hl 21
Oj [з 4 J
°И1 2'I
0 J [ 3 4 J
0H1 2] 1J L 3 4J
— 3E\ + 4E2 + OjE*3 + 0/?4 —
= OE, + 0E2 + 1E3 + 2E4 =
= OE] + 0E2 + 3E3 + 4E4 =
= (0, 0, 3, 4).
Тогда матрица линейного оператора равна
13 0 0
2 4 0 0
0 0 13
0 0 2 4 ,
Задача 179. В пространстве матриц второго порядка с обычными операциями сложения матриц и умножения матриц на число дей
ствует линейный оператор по правилу
с d
Л 5] fa b 6 7 Д с d
Определить матрицу этого линейного оператора в базисе Е{ —
ч
о
о о
^0 I ' о о

Г I 0 0
, к =
3	10
^0 О'
° 1
,е4 =
Пример 190. Найдем матрицу линейного оператора, переводящего векторы Д] = (2, 3, 5), а2 = (0, I, 2), а3 = (I, 0, 0) в векторы Ь} = = (I, I, I), b2 = (I, I, —I), Ь3 = (2, I, 2), в том же базисе, в котором даны координаты векторов.
Составим из координат векторов следующую матрицу:
г 2 3 5
0 I 2
I о о
111' I I -I
2 1 I ,
Преобразованиями из метода Гаусса (§ 4.5) получим из этой матрицы матрицу вида (Е| С), где Е— единичная матрица. Транспонировав матрицу С, мы и найдем матрицу линейного оператора в нужном базисе.
' 2 3 5
0 1 2
10 0
111'
1 1 -1
2 1 1
10 0
0 1 2
2 3 5
2 12'
1 1 -1
1 1 1 .
122
r 1
о о
О 2 1 2 1 Г 1
2	11-1-0
5 -3 -1 -3J [О
О о 1 2
О -1
2 12
1 1 -1
—6—4 О
2 12 1	Г 1
11-1- О
6 4 О J	f О
-11 —7 -1
Тогда матрица линейного оператора в нужном базисе равна
г 2	1	2 '	t	' 2	-И	6
-11	—7	-1	=	1	—7	4
6	4	0 .		2	-1	0
Задача 180. Найти матрицу линейного оператора, переводящего векторы = (2, 0, 3), а2 = (4, I, 5), а3 = (3, I, 2) в векторы Ьх = = (1, 2, — I), Ь2 = (4, 5, —2), b3 = (I, — I, I), в том же базисе, в котором даны координаты векторов.
Пример 191. Определим, могут ли матрицы
быть матрицами одного линейного оператора в разных базисах.
Матрицы одного линейного оператора в разных базисах связаны соотношением А = Т~}АТ, Так как определитель матрицы перехода
отличен от нуля (det Т 0), то и det Т 1	0. Поэтому из условия
det А 0 следует, что det А * 0.
Так как
= -2 * 0, а
= 0, то указанные матрицы не
о
1
3
1 О О
О 1 2
О 0 1
О 1 о
о о
1
2	1	2
6	4	0
2 2
3 3
и
I 2
3 4
1 2
3 4
2 2
3 3
могут быть матрицами одного линейного оператора в разных базисах.
Задача 181. Определить, могут ли матрицы д и з 2 J быть матрицами одного линейного оператора в разных базисах.
Пример 192. Задан линейный оператор А проектирования на плоскость 2х + Зу + А = 0. Определим матрицу этого линейного оператора в базисе е\ = (1, 0, 0), е2 = (0, 1,0), е3 = (0, 0, 1).
Нормаль плоскости 2х + Зу + 4z = 0 равна п = (2, 3, 4).
Тогда линейный оператор А действует по следующему правилу:
_ п .	(а, п) п _
Аа = а-пр-а-----= а -  ---------= а-----— п.
1«1	|и| |л|	|я|
Квадрат модуля нормали равен | и | = 22 + З2 + 42 = 29.
Найдем образы базисных векторов под действием линейного оператора.
123
Ae, = et- n = (1, 0, 0) - 1 x 2 + 0 x 3 + 0 x 4 (2, 3, 4) = |л|2	29
= (1, 0, 0) - 2/29(2, 3, 4) = (25/29, -6/29, -8/29).
_	_	(e2,fl)- /a i nx 0X2+ 1 x3+0x4 ,, , ..
Ae2 = e2-	= (0, 1, 0)-------------—-----------(2, 3, 4) =
I я I
= (0, 1,0) - 3/29(2, 3, 4) = (-6/29, 20/29, -12/29).
Ae,	= (0, 0, 1) - 0X2 + 0X3+1X4 (2, 3, 4) =
|«|	29
= (0, 1,0) - 4/29(2, 3, 4) = (-8/29, -12/29, 13/29).
Г 25 -6 -8
Тогда матрица линейного оператора равна 1/29 —6
20 -12
— 12 13
-8
Задача 182. Задан линейный оператор А проектирования на плоскость Зх — у + 2z = 0. Определить матрицу этого линейного оператора в базисе в| — (I, 0, 0), е2 = (0, I, 0), = (0, 0, I).
Множество тех векторов линейного пространства £, которые под действием линейного оператора А переходят в нулевой вектор линейного пространства £, называется ядром линейного оператора А и обозначается Кег А.
Пример 193. Определим ядро линейного оператора А из примера 192.
Ядро линейного оператора А — это множество точек, которые проектируются в начало координат (начало координат принадлежит плоскости), то есть прямая х/2 = у/3 = г/4, проходящая через начало координат и перпендикулярная плоскости.
Задача 183. Определить ядро линейного оператора А из задачи 182.
Глава 23
МНОГОЧЛЕНЫ
Функция вида р(х) = апхп + я„_]Хя 1 + ... + ахх + а0, где ап 0, называется многочленом степени п.
Пример 194. 5х4 + 2х + I — это многочлен четвертой степени.
2Х5 + бх8 — jc + 3 — это многочлен восьмой степени.
Задача 184. Определить степень многочлена lx' + 4.x6 + х5 + х + + Зх2 + 2.
§ 23.1. ДЕЙСТВИЯ С МНОГОЧЛЕНАМИ
I. Сложение. При одинаковых степенях коэффициенты суммируются.
Пример 195. Найдем сумму многочленов р(х) — 2л3 + Зх2 — 4х +
5 и q(x) = 7xi - Зх2 - 9.
р(х) + q(x) = (2х3 + Зх2 - 4х + 5) + (7Х3 — Зх2 — 9) = (2 + 7)х* + (3 +
+ (—3))х2 - 4х + (5 + (-9)) = 9Х3 - 4х - 4.
Задача 185. Найти сумму многочленов р(х) = 4Х3 + 8Х2 - 5х + 9
и q(x) = I Ох3 — I Зх2 + 18х - 6.
2. Умножение. При умножении многочлена р(х) на многочлен q(x) просто раскрывают скобки, руководствуясь правилом Ах" X Вхт = = (А х В)х"+т, и приводят подобные слагаемые.
Пример 196. Найдем произведение многочленовр(х) = 2х3 + 5х2 +
+ 4х + 3 и q(x) = 7Х2 + 6.
p(x)q(x) = (2х3 + 5Х2 + 4х + 3)(7х2 + 6) = Их5 + 35х4 +
+ 28Х3 + 21Х2 + 12Х3 + ЗОх2 + 24х + 18 = Мх5 + 35х4 + 40Х3 + 51Х2 + + 24х+ 18.
Задача 186. Найти произведение многочленов р(х) = Зх3 — 4Х2 +
5 и q(x) = 2Х2 + 7х + I.
125
3. Деление с остатком. Для любых многочленов р(х) и q(x) можно так подобрать многочлены т(х) (частное) и г(х) (остаток), что р(х) = m(x)q(x) + г(х), причем степень остатка г(х) меньше степени многочлена q(x).
Обычно деление с остатком производят «столбиком». Если остаток равен нулю, то говорят, что многочлен р(х) делится на многочлен
Пример 197. Разделить с остатком многочлен р(х) = 2х5 — 2х4 —
— 18х3 + 28л2 + 20х + 7 на q(x) = Xs — Зх2 + 2.
2№ - 2х4 - 18х’ + 28л2 + 20х + 7 х1 - Зх2 + 2
2л5- 6х4+	4Х2	|2х2 + 4х—6
4х4 - 18л3 + 24Х2 + 20х + 7
4х4 — 12х3 +	8х
—бх3 + 24Х2 + 12х + 7
- бх3 + 18Х2	- 12
6х1+ 12х + 19
р(х) = (2Х2 + 4х - 6)<?(х) + (бх2 + 12х + 19). Каждый раз нужно умножать q(x) на множитель вида ахк, подобранный так, чтобы после выполнения вычитания степень вновь полученного многочлена понизилась.
Задача 187. Разделить с остатком многочлен р(х) = 12Х5 — 14х4 + + 22Х3 - 4Х2 - 4х + 3 на q(x) = Зх3 - 2Х2 + 1.
§ 23.2. СХЕМА ГОРНЕРА
Схема Горнера позволяет быстро разделить с остатком любой многочлен р(х) на многочлен вида х — с (с = const).
Пример 198. Использование схемы Горнера рассмотрим на примере многочленов р(х) = 4х3 + Зх2 + х + 5 и х - 2. Составляем таблицу.
4	3	I	5
2 4 3 + 4 x 2 =11	1 + 11x2 = 23	5 + 23 x2 = 51
В 1-й строке записаны коэффициенты многочлена р(х) в порядке убывания степеней, а во 2-й строке перед чертой — константа с = 2.
2-й строка заполняется слева направо. Переписываем число сверху и к нему прибавляем число слева (во 2-й строке), умноженное на число за чертой (то есть на 2).
126
Во 2-й строке получены коэффициенты частного в порядке убывания степеней, причем степень многочлена-частного на 1 меньше степени многочлена р(х). В последней клетке 2-й строки указан остаток.
4л3 + Зх2 + х + 5 = (х - 2Х4Х2 + Их + 23) + 51.
Задача 188. Применить схему Горнера к многочленам р(х) = lx2
+ + Зх2 — 4х + 1 и х — 5.
Если остаток равен нулю, то р(х) = (х — с)т(х). В этом случае р(с) = 0. Говорят, что х = с является корнем многочлена р(х).
Целые корни многочленар(х) = апх" + я^х"-1 + ... + ape + а{} с целыми коэффициентами а, могут быть только среди делителей коэффициента aQ.
Если р(х) = (х - с)кт(х), где т(с) 0, то говорят, что х = с является корнем кратности к многочлена р(х).
Глава 24
СОБСТВЕННЫЕ ВЕКТОРЫ
Если при действии линейного оператора f на ненулевой вектор х получается тот же вектор х, умноженный на какое-то число X, то такой вектор х называется собственным вектором линейного оператора f. f(x) = Хх. Число X называется собственным значением.
§ 24.1. НАХОЖДЕНИЕ СОБСТВЕННЫХ ВЕКТОРОВ И СОБСТВЕННЫХ ЗНАЧЕНИЙ
В матрице А порядка п линейного оператора/на главной диагонали вычитается число X. Определитель полученной матрицы приравнивается нулю, то есть det(^ — ХЕ) = 0. Это характеристическое уравнение. Его решения и есть собственные значения X,, Х2, Хк.
Для каждого X,- решается однородная система (А — к/Е)Х= 0, где
0 =
0
0
Выражаем главные переменные через свободные переменные и методом бегущей единицы (поочередно одну свободную переменную приравниваем единице, остальные свободные переменные приравниваем нулю, находим значения главных переменных) получаем все собственные векторы, соответствующие собственному значению Xz.
Пример 199. Найдем собственные векторы и собственные зна-
чения линейного оператора, заданного матрицей
' 3 4
5 2
det (Л - ХЕ) =
3-Х	4
5	2-Х
= (3 - X) х (2 - X) - 4 х 5 = X2 - 5Х —
— 14 = 0. Собственные значения: X] = —2, Х2 = 7. Найдем собственные
векторы.
128
Xi = —2. Тогда
3 - (-2)
5
4
2 - (-2)
'*i
х2
Г о ]	г 5 41 [ х< 1 = Г ° 1
[ о J	15 4 JI ъ J 10 J
Воспользуемся методом Гаусса.
%! Х2
Г 5 4 О [540
Г 5 4
I5 4
=>(
х2
0,8 |0)^
х} = —0,8х2.
х2 любое.
0 '
0
1
У нас одна свободная переменная х2. Приравняем ее единице и найдем соответствующее значение главной переменной Хр х2 = 1, Xj = —0,8. Х\ = Х_2 = (—0,8; 1) — собственный вектор, соответствующий собственному значению X] = —2.
Пусть теперь Х2 = 7. Тогда
Г 3-7
[ 5
4
2-7
Г О'
—4 5
4
-5
Xi
^2
Г о'
I 0 >
Применим метод Гаусса.
х,
-4
х2
4
1 -1
1 -1
X) х2
1 -1 | 0) =>
X, = х2, х2 любое.
5
0 '
0
0 '
0
У нас одна свободная переменная х2. Приравняем ее единице и найдем соответствующее значение главной переменной х,:х2= 1, Xj = 1. Х^ — Xq— (1; 1) — собственный вектор, соответствующий собственному значению Х2 = 7.
Задача 189. Найти собственные векторы и собственные значе-
Л 2 11
ния линейного оператора, заданного матрицей
Пример 200. Найдем собственные векторы и собственные зна-
	г 7	-12	6
чения линейного оператора, заданного матрицей	10	-19	10
	12	-24	13
det(/l - Х£) =
7-Z	-12	6
10	-19-Z	10
12	-24	13-Z
= (7 - Z)(—19 - Z)(l3 - к) + 12 х (—12) х 10 + 6 х (-24) х 10 -- 6 х (-19 - Z) х 12 - 10 х (7 - Z) х (-24) - 10 х (13 - Z) х (-12) = = -Z3 + X2 + Z - 1 = 0, то есть Z3 - Z2 — Z + 1 = 0.
129
Целые корни могут быть только среди делителей свободного члена 1, то есть среди ±1. Применим три раза схему Горнера.
1
1
-1
1-1-1 1
10-10
1	1	0
1	0
Z12 = 1 Дз = “1- Это собственные значения. Найдем собственные
векторы.
			7 -	1	-12	6		х	।		0 '		
Xj>2 = 1. Тогда ' 6 —12 6			10 12		-19—1 -24 " 0 '	К 13-	) - 1	х х	> 5	—	0 0		
10 -20 12 —24 X! х2 г 6 -12	10 12 X 6	1	Х2 О'		0 . Воспс 0 Г 1 -2 1		эльзу О'	емс:	я методом Taj Г 1 -2 1				/сса. О'
10 -20 12 -24	К К	) )	0 0		1 —2 1 —2	1 1	0 0^			0 0	0 0	0 0	0 0
X] Х2 х3
( 1 —2 1 10)
X, = 2х2 — х3, х2, х3 любые.
У нас две свободные переменные (х2 и х3). Применим метод бегу-
щей единицы (поочередно одну свободную переменную приравниваем единице, другую свободную переменную приравниваем нулю и находим соответствующее значение главной переменной).
X] = 2 х 1 - 0 = 2, х2 = 1, х3 = 0.
<х1 = 2х0— 1 = -1, < х2 = 0,
х3 = 1.
Х^} 2 =	= (2, 1, 0) и Х^ 2 = X™ = (—1, 0, 1) — собственные век-
торы, соответствующие собственному значению Х1>2 = 1.
	7~(—1)	-12	6			г 0 '
Х3 = -1. Тогда г 8 -12 6 10 -18 10 12 -24 14	10	- 12 х2 = Д *3 J	-19 —(-1)	10 -24	13-(-1) г 0 ' 0 . Применим метод 0 < у	х2 Гаус<	за.	0 0
130
X, Х2 Ху
8 —12 6
10 -18 10
12 —24 14
01 Г 4 —6 3
—6
—6
-12
3
5
10
4 -6
О -6
О -6
0 1	[4-63
О =>	0 -6 5
О J [ООО
О —2
-6 5
О '
О
О
О '
О
XI Х2 Ху
' 1 0 -0,5
О 1 —5/6
"х, = 0,5х3.
=> J х2 = 5/6ху,
Ху любое.
0 => 5 -9 5
ОJ [ 6 -12 7
О '
О
О
г 4
О о
3
5
5
О
О
О ' о о
г 4
О
У нас одна свободная переменная х3. Приравниваем ее единице и
находим соответствующие значения главных переменных:
Г%! = 0,5,
J х2 = 5/6,
I Ху = 1.
А/3 = ^-1 = (0,5; 5/6; 1) — собственный вектор, соответствующий собственному значению А3 = — 1.
Задача 190. Найти собственные векторы и собственные значе-
f О I
ния линейного оператора, заданного матрицей —4 4
-2 1
0 '
0
2
Множество всех собственных значений линейного оператора называют спектром линейного оператора.
Каждый собственный вектор связан со своим собственным значением. Действительно, если Ах = и Ах = Х2х при Aq # А2, то А,х = А2х (А] — А2)х = 0 -»х = 0, но нулевой вектор не может быть собственным вектором (по определению).
Множество всех собственных векторов, отвечающих данному собственному значению линейного оператора, не является подпространством, так как не содержит нулевого вектора.
Глава 25
ЖОРДАНОВА НОРМАЛЬНАЯ ФОРМА
Пусть L — конечномерное линейное пространство над множеством комплексных чисел.
Квадратная матрица &-го порядка
	р	1	0	0	... 0	0	0 '
	0	X	1	0	... 0	0	0
	0	0	X	1	... 0	0	0
Л(Х) =	0	0	0	0	... X	1	0
	0	0	0	0	... 0	X	1
	.0	0	0	0	... 0	0	
называется жордановой клеткой, соответствующей комплексному числу X.
Жордановаматрица — это матрица J= diag^pj, Л (Х2),Л (XJ) с жордановыми клетками Л (Х2),Л (A,w) на диагонали.
Для матрицы А линейного оператора существует жорданов базис, в котором матрица линейного оператора является жордановой матрицей: J= Т~ХАТ, где Т— матрица перехода. В этом случае матрица J называется жордановой нормальной формой матрицы А.
Напомним, что ранг rk А матрицы А равен числу ненулевых строк ступенчатого вида матрицы.
Алгоритм нахождения жордановой нормальной формы квадратной матрицы порядка п.
1.	Находим собственные значения матрицы А.
2.	Число всех жордановых клеток, соответствующих собственному значению X, равно N(E) = rk(4 — ХЕ), где Е — единичная матрица порядка п.
3.	Число жордановых клеток &-го порядка, соответствующих собственному значению X, равно М(Х) =	- 2^(Z) + ^+1(Z), где
гДХ) = гк(Д-ХЕ/, г0(Х) = и.
132
Жорданова нормальная форма матрицы определена однозначно с точностью до порядка жордановых клеток на диагонали.
Для нахождения жорданова базиса, в котором матрица линейного оператора является жордановой матрицей, нужно найти матрицу перехода Т (det Т # 0), решив относительно Т матричное уравнение: J = Г ’ЛГ, то есть TJ-AT=0.
Пример 201. Определим жорданову нормальную форму матри-
цы А =
3
9 0
0
-3 о о
1
—7
4
2
—7
-1
-8
—4
Характеристическое уравнение det (Л - Х£) = 0.
Тогда
3-Х
9
0
0
-1
-3-Х о о
1
—7 4-Х
2
—7
-1
-8
-4-Х
= (3- Х)(-1)
= (3 - Х)(—3 - X)
-3-Х о о
4-Х 2
-1
-8
2 -4-Х
—7 4-Х
-8
-4-Х
= (X2 - 9 + 9)
4-Х	-8
2	-4-Х
= X4 = 0.
-1
0
0
4-Х
2
7
4-Х
2
-8
-4-Х
—7
-8
-4-Х
+ 9(-l):
-9(-l)
Отсюда X = 0.
Число всех жордановых клеток, соответствующих собственному значению X = 0, равно: N(0) = ^(0) = гк(Л - 0Е) = гкЯ =
= rk	" 3 -1 9 -3	1 —7" —7 -1	= rk	г 3 0	-1 0	1 —7 ' -30 60	= rk	' 3 -1		1 -7" 1 —2	
								0	0		
	0 0	4 -8		0	0	1 —2		0	0	1 -2	
	. 0 0	2 -4.		. 0	0	1 -2 .		. 0	0	0 0 .	
	r 3	-1	1 -7'	
	0	0	1 —2	
= rk	0	0	0 0	= 2, так как матрица ступенчатого вида содер-
	0	0	0 0	
жит две ненулевые строки.
Число жордановых клеток 1-го порядка, соответствующих собственному значению X = 0, равно ^(0) = г0(0) — 2^(0) + г2(0) —
133
= n- 2f|(0) + + г2(0) = 4-2x2 + г2(0) = г2(0) = гк(Л - ОЕ)2 = гк А2 =
гк(
3 9 О О
ООО' ООО ООО
О О О >
= О, то есть
жорданова нормальная форма не содержит клеток 1-го порядка, соответствующих собственному значению X = 0.
Порядок матрицы равен 4, всего 2 жордановых клетки и нет клеток 1-го порядка. Поэтому жорданова нормальная форма матрицы содержит только две жордановых клетки 2-го порядка (4 = 2 + 2):
' О
О
о
. О
ООО' 1 о о
О 0 1 о о о „
= diag (
) = diag(J2(O), J2(0)).
О 1
о о
Задача 191. Определить жорданову нормальную форму матри-
	' 1 -3	0	3
цы А =	—2 -6	0	13
	0 -3	1	3
	-1 —4	0	8 ,
Пример 202. Определим жорданову нормальную форму матри
цы А =
-3 4
1 О
6 —6
-2'
1
5
и жорданов базис.
Характеристическое уравнение det (Л — ХЕ) — О,
	-3-Х	4	—2	
то есть	1	-X	1	= 0. Отсюда X) = -1, Х2 = 2, Х3 =
	6	—6	5-Х	
Так как порядок матрицы равен 3, а число собственных значений
f—1
О 2 О
О '
О
1
также равно 3, то жорданова нормальная форма J =
О
О
Найдем жорданов базис. Для этого надо решить матричное урав-
			г	*11 *12 *13			
нение TJ — у	4Г= 0, где Г=			*21	*22	*23	и det Т + 0.		
				*31	*32 *33			
*11 *12 *13	-10 О'			'-Ъ 4 -2'	*11 *12 *13		ООО'
*21 *22 *23	0 2 0	—		1 0 1	*21 *22 *23	=	ООО
*31 *32 *33 „	0 0 1			6 -6 5	*31 *32 *33		0 0 0
134
“61 2/|2 /13 ”61 2/22 6з —/3) 2/32 /33
' О О О '
ООО.
ООО
—3/ц +4/2| — 2/31 —3/i2 + 4/22—2/32 —3/|з + 4/2з—2/3з
61 + /3|	/12 + /32	бз+^ЗЗ
6/(1 — 6/21 + 5/3) 6/12 — 6/22 + 5/32 6/|з — 6/23 + 5/33
~6i + 3/ц — 4/21 + 2/3] О 2/]2 + 3/12 — 4/22 + 2/32 — О 6з + 3/|з — 4/23 + 2/33 = О
~” 61 ~ 61 = О
Тогда < 2/22 — /|2 — 62 О
6з ~ 6з ” 6з О
”61 — 6/ц + 6/21 — 5/3) — О 2/32 — 6/|2 + 6/22 — 5/з2 — О
6з “ 6/]з Т 6/23 — 6/33 = О
г /ц — 2/21 + /31 = О 5/12 — 4/22 + 2/32 = О 2/|з — 2/23 + /33 = О 61 + 61 4" 61 = о —2/22 + /]2 + /32 = О ”6з + 6з + 6з ~ О 61 4" 61 ~ 61 = о 62 4* 2/12 — 2/22 = 0 . 2/3з + 3/1з — 3/23 — О
Можно решить эту громоздкую систему линейных уравнений методом Гаусса. Но мы получим соотношения между переменными иначе.
Из 1-го и 4-го уравнений системы получаем, что /2i = 0. Отсюда 61 + /31 = 0, то есть /31 = —Zu-
Из 3-го и 6-го уравнений системы получаем, что /п — /23 = 0, то есть 6з = 6з-
Из 2-го и 5-го уравнений системы получаем, что /12 = 0. Отсюда 62 “ 2/22 = 0, то есть /32 = 2/22.
Так как /23 = /13, то из 9-го уравнения системы /33 = 0.
Получены следующие соотношения между элементами матрицы Г. /21 = 0, /3| = -61, 6з = 6з> 62 = 62= 2/22, 6з = 0. Тогда матрица пе-
рехода Т=
61 О
О 62 2/22
6з
6з О
Пусть /н = /22 = 63 = 1. Тогда матрица Т=
1 О -1
. Опреде-
О
1
2
1
1
О
литель det Т=
1 О
О 1
-1 2
1
1 О
= -1^0.
В столбцах матрицы перехода Т указаны координаты базисных векторов ef = (1, 0, — 1), е/ = (О, 1, 2), е3' = (1, 1, 0). Это жорданов базис.
135
Задача 192- Определить жорданову нормальную форму матри-
Г О I
О '
О 2
цы А = -4 4
О О
и жорданов базис.
136
Глава 26
ФУНКЦИИ ОТ МАТРИЦЫ
Очень часто возникает ситуация, когда нужно вычислить какую-нибудь функцию от матрицы (синус, косинус, экспонента, логарифм и т. д.). В этом случае можно воспользоваться следующим алгоритмом. Мы ограничимся рассмотрением квадратных матриц второго порядка.
Дана матрица А и функция /(х). Находим собственные значения Zj и Х2 матрицы А.
Если собственные значения различны (Xj Х2), то получим значе-,	f/(Z.) = аХ{ + b
ния а и b из системы ДД Л1
[/(Х2) = аХ2 + b
Тогда /(Л) = аА + ЬЕ, где Е = q '
Если собственные значения одинаковы (Xj = Х2 = X), то получим значения а и b из системы J аХ + b уогда = ад +
1 /W = а
Пример 203. Для матрицы А =
определим ел.
Здесь/(х) = ех. Найдем собственные значения матрицы А.
Характеристическое уравнение det (А — ХЕ) =
3-Х	-1
1	1-Х
= (3 - Х)(1 — X) + 1 = X2 - 4Х + 4 = 0, то есть X = 2.
Решим систему относительно а и Ь\
Г /(X) = аХ + b _f е2 = la + b _f е2 = 2е2 + b	Г b = — е2
(/'(X) = а	\е2 = а \а = е2	\а = е2
Тогда еА = аА + ЬЕ =
= Л3 Л-Л1 °Л fЗе?2 ~е2К(е2 °] = f2е2 .
1 1 ] [о 1 ] Л2 е2 j Л ^2> Л2 о J
137
I 3
Задача 193. Для матрицы А =
Пример 204. Для матрицы А =
Характеристическое уравнение det (А — ХЕ) =
1	I	А
$ определить е .
2	3
7 определим А100.
Здесь/(х) = х100. Найдем собственные значения матрицы А.
6-Х	2
3	7-Х
= (6 - Z)(7 -X) -6 = Х2 - 13Х + 36 = 0, то есть X] = 4, Х2 = 9. Решим систему относительно а и Ь:
Г/(Z.) = аХ} + b	Г 4100 = 4а + b	f 4100 = 4а + b
[f(X2) = aX2 + b	[ 9'00 = 9я + Z>	[ 9100 - 4100 = 5я
дюо _ 4 х 0,2(9100 - 4100) = b а = О,2(9100 - 4100)
1,8x41oo-O,8x9,oo = Z> а = О,2(9100 - 4100)
Тогда Л,оо = яЛ + ЬЕ =
= О,2(9100 - 41(Ю:
+ (1,8 х 4100 - 0,8 х 9100) I 1 0
0 1
1,8Х4|0(|-0,8Х9|0(|	0
0	1,8X4IMI-O,8X9"I(I
0,4 х 9100 + 0,6 х 41|)0	О,4(9100 - 4100)
О,6(9100 - 4100)	0,6 х 9100 + 0,4 х 4|0\
Задача 194. Для матрицы А =
0 2
-3 5
определить Д'00.
Глава 27
МИНИМАЛЬНЫЙ МНОГОЧЛЕН
Пусть А — квадратная матрица и р(х) = апхп + ... + ахх + а0 — многочлен степени п (ап — старший коэффициент).
Еслир(А) = апАп + ... + ахА + aQ = 0, то многочленр(х) называется аннулирующим многочленом матрицы А.
Теорема Гамильтона-Кэли. Матрица является корнем своего характеристического многочлена.
Пример 205. Убедимся, что матрица А из примера 199 является корнем своего характеристического многочлена.
Ы	а (3 41
Матрица А = I , характеристический многочлен равен
X2 — 5Z - 14.
ТогдаЛ2 — 5Л — 14Е:	= [ З 4 ' I5 2>	<3 5	4 ' 2	-5	'3 4 1		V1 °1 [о 1J	=
					L5	2 J		
= [29 201 _ [ 15 20'	_ [ 14 ।	0 '		0 0				
[25 24 J ^25 10	1 0 1	4		0 0				
Задача 195. Убедиться, что матрица А из задачи 189 является корнем своего характеристического многочлена.
Наименьшим общим кратным ненулевых многочленовpt(x), ..., pk(x) называется многочлен со старшим коэффициентом I, который делится на Р\(х), ..., рк(х), причем его степень минимальна среди всех многочленов, одновременно делящихся на р,(х), ..., рк(х).
Минимальный многочлен матрицы А — это аннулирующий матрицу А многочлен наименьшей степени со старшим коэффициентом I.
Теорема. Минимальные многочлены матриц А и В= Т~[АТ (det TV 0) совпадают.
Минимальный многочлен жордановой клетки Jk(K) равен (х- К)к. Минимальный многочлен матрицы равен наименьшему общему
139
кратному минимальных многочленов жордановых клеток жордано-вой нормальной формы матрицы.
Пример 206. Жорданова нормальная форма матрицы равна diag (j2(3), J2(3), /|(-2)). Определим минимальный многочлен матрицы.
Минимальные многочлены жордановых клеток У2(3), J,(3), J0(-2) равны соответственно (х — З)2, х — 3, х + 2. Наименьшим общим кратным этих многочленов будет многочлен (х - 3)2(х + 2). Это и есть минимальный многочлен матрицы.
Задача 196. Жорданова нормальная форма матрицы равна diag(J2(l), (I), «/0(~3)). Определить минимальный многочлен матрицы.
Глава 28
ЕВКЛИДОВЫ ПРОСТРАНСТВА
Линейное пространство L называется евклидовым пространством. если на нем задана функция двух переменных (х, у) — скалярное произведение, для которого выполнены следующие свойства (х, у, z — любые векторы из L, ос — любое число):
2)	(х, у + z) = (х, у) + (х, z);
3)	(ох, у) = сс(х, у);
4)	(х, х) > 0 и (х, х) = 0 « х = 0 (нулевой вектор пространства L).
Пример 207. Пространство Rn = {х = (х,,	х„)} является евкли-
довым пространством. Скалярное произведение задается формулой (х, у) = ху! + ... + хх, где х = (х15 ..., х„), у = (у15 ..., у,). Проверим выполнение всех свойств скалярного произведения.
Так как (х, у) = х^ + ... + хпуп, а (у, х) = у^ + ... + у„х„ = ху, + ... +
+ XX, то (х, у) = (у, х).
Пусть Z = U1, zj. Тогда у + z = (У\ + Z(, ..ад + 4)-
Отсюда (х, у + z) = х,(у, + z,) + ... + х„(у„ + 4) = xyj + х^ + ... +
+	+ ад-
Так как (х, у) + (х, z) = ху, + ... + хх + x}z} + ... + ад, то (х, у + z) =
= (х, у) + (х, Z).
ах = а(Х|, ..., х„) = (otXj, ..., ах„).
Так как (ах, у) = аху, + ... + ахх, a а(%, У) = a(xyj + ... + хх) =
= аху, + ... + ахх, то (ах, у) = а(х, у).
(х, х) = Х\ + ... + х/г2 > 0. Равенство здесь возможно тогда и только тогда, когда Xi = ... = х/; = 0, то естьх= (0,..., 0) — нулевой вектор пространства Rn.
Задача 197. Привести пример евклидова пространства.
Длина вектора х — это число |х| = V (^, *) •
Пример 208. Длина вектора х = (1, -2, 3, 4) равна |х| = V(х, х) =
V I2 + (—2)2 + З2 + 42 =7зо.
141
Задача 198. Найти длину вектора х = (5, 1,2,3).
Неравенство Коиш-Буняковского\ |(х, у)| < |х|[у|.
Неравенство треугольника'. |х + у| < |х| + |у|.
Угол ср, для которого cos ф = г (()мр < 2л), называется углом ММ
между векторами х, у.
Пример 209. Найдем угол между векторами х = (1, О, —1, 2) и
У =(2, 3,5,4).
(х, у) = 1 X 2 + 0 х 3 + (-1) Х5 + 2Х4 = 5.
|х| = У (х, х) = У12 + О2 + (—I)2 + 22 = У?.
|у| = У 22 + З2 + 52 + 42 = Ум = зУб.
(*,у)	5
COS(p = ---,7-;- =" “7=-7= = 5/18.
klbl V? х зУГ
Задача 199. Найти угол между векторами х = (2, О, —I, 3) и
У = (I, 2, —4, 5).
Векторы х, у, скалярное произведение которых равно нулю ((х, у) = 0), называются ортогональными (х ± у).
Пример 210. Векторы х, у из примера 209 не являются ортогональными, так как (х, у) = 5 0.
Задача 200. Определить, ортогональны ли векторы х, у из задачи 199.
Ортогональный базис евклидова пространства L — это базис пространства £, в котором все базисные векторы попарно ортогональны, то есть скалярное произведение любых двух векторов базиса равно нулю. Ортонормированный базис евклидова пространства L — это ортогональный базис, в котором длина любого базисного вектора равна единице.
§ 28.1. ПРОЦЕСС ОРТОГОНАЛИЗАЦИИ ГРАМА-ШМИДТА
Процесс ортогонализации Грама-Шмидта позволяет из любого базиса/, ...,/ изготовить ортонормированный базис й|9 ..., hn.
Сначала по/, ...,/ строим ортогональный базис gb ..., gn по формулам (к = 2, ..., п):
142
g\ =f\,gl =fl -
(fl, gl)
(gl’gl)gl
_ , (fl, gl)
& — h ~ ~r S\ ~ (gl,gl)
„ _f	(fk, gl) „
ok Jk	/	\ 61
(g\,g\)
(fl, gl)
(gl, gl)
(fk, gl) _	_ (fk, gk-t)
(gl,gl)82	(gk-l,
Затем из ортогонального базиса^, gfl получаем ортонормиро-ванный базис й15 ..., hn по формуле hk = gjJ\gk\ (каждую координату вектора нужно разделить на его длину), к = 1, ..., п.
Пример 211. Применим процесс ортогонализации Грама-Шмидта к системе векторов/ = (1,2, 2),/2 = (1, 1, -5),/3 = (3, 2, 8). Сначала по/,/2,/3 строим ортогональный базис g2, gn-
£,=/; = (1,2, 2), (g]? g,) = I2 + 22 + 22 = 9.
(/2,gl) = lxl + lx2 + (-5)x2 = -7.
& =fi -	= (1, 1, -5) - ^(1, 2, 2) =
(ghgi)	9
1 1
= — (9(1, 1, -5) + 7(1, 2, 2)) = - (9 x 1 + 7 x 1, 9 x 1 + 7 x 2,
1
9 x (-5) + 7X2) = -(16, 23, -31).
Умножим g2 на 9 (угол между векторами gx и g2 от этого не изменится) и полученный вектор вновь обозначим g2: g2 = (16, 23, —31).
Проверим, что g| ± g2:
(g15 g2) = 1 х 16 + 2 х 23 + 2 х (-31) = 0.
(&,&)= 162 + 232 + (-31)2 = 1746.
(/j, g,) = 3 х 1 + 2 х 2 + 8 х 2 = 23.
(4&) = 3х 16 + 2Х23 + 8 х (-31) = -154.
f (fi,g\)	(fi,gi)
& = fl - -----rgl - -----Г& =
(gl,gl)	(gl,gl)
23	-154	1
= (3, 2, 8) - -(1, 2, 2) - — (16, 23, -31) = -^(1746(3, 2, 8) --4462(1, 2, 2) + 154(16, 23, -31)) = —L.((1746 X 3 - 4462 X 1 +
+ 154 x 16, 1746 x 2 - 4462 X 2 + 154 x 23, 1746 X 8 - 4462 X 2 + 1	270
+ 154 x (-31)) =------(3240, -1890, 270) =-----(12, -7, 1).
1746	1746
143
Умножим g3 на — •  и полученный вектор вновь обозначим g3:
& = (12, —7, 1).
Проверим, что g} ± g,:
(gi, g3) = 1 х 12 + 2 х (-7) + 2 х 1 = 0.
Проверим, что g3 ± g2:
(g3,&) = 12 х 16 + (—7) х 23 + 1 х (—31) = 0.
Построен ортогональный базис gh g2, g-,. Получим из него орто-нормированный базис hx, h2, h3.
Л, = , ' ....-g, = -У(1, 2, 2) = (1/3, 2/3, 2/3).
V(ghgi)	V9
h2 =	'..g2 = —= (16, 23, -31).
V(g2,g2)	V1746
h, = —7===g3 = ,	 '	~(12, —7, 1) = —=(12, —7, 1).
V (g3, g3)	VlF +	(—7)2	+ I2	yl94
Задача 201. Применить процесс ортогонализации Грама-Шмидта к системе векторов/ = (1, 1, -1),/2 = (5, -2, -3),/3 = (1,3,1).
Глава 29
ПРОЕКЦИЯ ВЕКТОРА НА ПОДПРОСТРАНСТВО
Пусть V — евклидово пространство, L — подпространство пространства И
Вектор х ортогонален подпространству Z (х ± £), если вектор х ортогонален любому вектору у подпространства £, то есть (х, у) = 0. Множество всех векторов, ортогональных подпространству L, образует £1 — ортогональное дополнение подпространства L.
Пример 212. Дано подпространство L = <ах = (I, 2, I, —3), а2 = = (—1, 2, 3, 4)>. Определим базис ортогонального дополнения £±.
Пусть х = (xj, х2, х3, х4) — вектор из ортогонального дополнения А1.
[ (х, ад = 0 f х, 4- 2х2 + х3 - Зх4 = 0
Тогда х 1 L, то есть |	= Q -1	+	+	+ 4^ = 0-
Мы задали ортогональное дополнение I1 в виде системы линейных однородных уравнений. Найдем фундаментальную систему решений этой системы.
r 1 2 1 -3 01	Г1 2 1 -3 О'
-1 2 3 4 0J	[0 4 41 0>
4 0 -4 -14 О'
0 4 4	1	0
r 1 0-1 -3,5 О' 0 1 1 0,25 0
' X' = х3 + 3,5х4
< х2 == — х3 — 0,25х4.
х3, х4 любые
Применим метод бегущей единицы.
Xj== 1 4~ 3,5 х 0 = 1
х2 = —1—0,25x0 = —1
х3= 1
х4 = 0
<х1=04-3,5х 1 =3,5
х2 = -0 - 0,25 х 1 = -0,25
х3 = 0
х4 = 1
Векторы (1;—1; 1; 0) и (3,5; —0,25; 0; 1) образуют базис ортогонального дополнения I1.
145
Задача 202. Дано подпространство L = <а} = (-1, 3, 4, 2), а2 = (2, 5, —2, 3)>. Определить базис ортогонального дополнения L1.
Вектор у подпространства L называется проекцией вектора х на подпространство Z, если вектор х — у ортогонален подпространству L. В этом случае используется обозначение у = npLx. Вектор х — npLx называется ортогональной составляющей вектора х относительно подпространства L.
Для нахождения проекции вектора х на подпространство L нужно построить ортонормированный базис hm подпространства L. Тогда npLx = (х, hx)hx + ...+ (х, hm)hm.
Пример 213. Определим проекцию вектора х = (—2, I, 3, 4) на подпространство L = <f = (1, 2, 0, 2),f2 = (— 1, — 3, 4, -2)> и ортогональную составляющую вектора х относительно подпространства L.
Так как координаты векторов/ и/ не пропорциональны, то векторы/ и/ образуют базис подпространства L. Применим к этому базису процесс ортогонализации Грама—Шмидта.
Сначала по/, / строим ортогональный базис g1? g2.
g, =f = (1, 2, 0, 2), (g„ g,) = I2 + 22 + О2 + 22 = 9.
= x 1 + (—3) X 2 + 4 X 0 + (—2) X 2 = —11.
(/2,g,)	-И	1
&=/2-7—~+i = (—1, —3,4, —2) — ——- (1,2, 0, 2) = — (9(—1, —3, ta,gi)	9	9
1
4, -2) + 11(1, 2, 0, 2)) =—(—9 + 11, -27 + 22, 36 + 0, -18 + 22) =
= | (2, -5,36,4).
Умножим g2 на 9 (угол между векторами gx и g2 от этого не изменится) и полученный вектор вновь обозначим g2: g2 = (2, —5, 36, 4).
Проверим, что g, ± g2: (gH g2) = 1 х 2 + 2 х (—5) + 0x36 + 2x4 = = 0.
(&,&) = 22 +(-5)2 + 362 + 42 = 1341.
Построен ортогональный базис gj, g2 подпространства L. Получим
из него ортонормированный базис й,, й2 подпространства L.
й, = ...' ’..g, = _L(1, 2, 0, 2) = (1/3, 2/3, 0, 2/3).
V(gi,gi) V?
11	2-5
th = .------& = -== (2, -5, 36, 4) = (-==,
y(g2,g2) У 1341	V1341 V1341
36	4
^=>-
•у 1341 У 1341
146
(х, й.) = -2 х 1/3 + 1 х 2/3 + 3 х 0 + 4 х 2/3 = 8/3.
2	-5	36	4
(х, й2) = -2 х ——= + 1 х ——= + 3 х--------------— + 4 х-----------
V 1341 V 1341 V 1341 V 1341
115
V 1341
Тогда проекция вектора х на подпространство L равна пр,х =
8 1 2	2	115	2	-5	36
= (х, /г,) + (х, Л2) =	0, -) 4- -----1-----. —..........    .
3 3 3	3 v 1341 V1341 л/1341 v 1341
4
-------) = (8/9, 16/9, 0, 16/9) 4- (230/1341, -575/1341, 4140/1341,
V 1341
1
460/1341)= — (158, 201, 460, 316).
Отсюда ортогональная составляющая вектора х относительно под-
1
пространства L равна х - npLx = (-2, 1, 3, 4)-(158, 201,460, 316) =
1
= -----(-456,-52,-13,280).
149
Задача 203. Определить проекцию вектора х = (3, 1,4, -2) на подпространство L = <f = (1, -2, 2, l),j^ = (—2, 4, 0, 1)> и ортогональную составляющую вектора х относительно подпространства L.
Минимальное свойство проекции вектора х на подпространство L: |х — у| > |х — npLx\ для любого вектора у из подпространства L. Это свойство используется для обоснования метода наименьших квадратов.
Глава 30
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ
УРАВНЕНИЙ МЕТОДОМ НАИМЕНЬШИХ КВАДРАТОВ
Довольно часто система линейных уравнений не имеет решений. Особенно этим отличаются так называемые переопределенные системы (число уравнений больше числа переменных). В этом случае систему решают приближенно методом наименьших квадратов (МНК).
Записывают систему в матричной форме АХ= В и умножают слева обе части на транспонированную матрицу А‘\ А‘АХ= А(В. Решив полученную систему, найдем приближенное решение исходной системы.
Подставив это приближенное решение в исходную систему, мы получим невязку (отклонение) для каждого уравнения системы. Суммировав квадраты отклонений для каждого уравнения системы, мы найдем невязку решения.
Доказано, что решение, полученное описанным методом наименьших квадратов, — это решение, для которого невязка является минимальной среди всех возможных решений.
Пример 214- Решим систему линейных уравнений методом наименьших квадратов и найдем невязку решения:
f х — у = 2, J 2х + у = О, [х + у = 1.
Введем обозначения А =
1
2
1
. Тогда
матричная запись нашей системы АХ— В.
Умножим слева обе части матричного уравнения на транспониро-
ванную матрицу А{ =
1
1
148
А‘АХ = А'В
Гб 2 1 Г х
I2 3Jь.
2 '
О
1
Г 1 2 [-1 1
Г 3 1 -1
1 -1
2 1
1 1
Г 1 2 1
[-1 1 1
1
1
6х + 2у = 3, 2х+Зу=-1.
При транспонировании матрица полученной системы не должна меняться. Мы получили систему
Решим ее по правилу Крамера.
2
3
Д =
= Н,А,= 2 Д =-12.
х = Ах/А = 11/14, у = Д^/Д = —12/14 (у дробей в ответе лучше пока оставить общий знаменатель).
Найдем невязку решения. Перепишем исходную систему в следу-
ющем виде: <
х —у—2 = 0, 2х 4- у = О, х + у- 1 = 0.
Подставим в нее полученные значения х, у
' Ъ}=х-у-2=\ 1/14 - (— 12)/14 - 2 = -5/14,
<	82 = 2х 4- у = 2 х 11/14 4- (— 12)/14 = 10/14,
<	83 = х + у- 1 = 11/14 4- (_12)/14 — 1 =-15/14.
Понятно, что для точного решения все 8Z = 0.
Невязка 82 = 82 + 822 4- 832 = (-5/14)2 4- (10/14)2 4- (-15/14)2 = 175/98.
Задача 204. Решить систему линейных уравнений методом наименьших квадратов и найти невязку решения:
<	%4-у = 2,
< х — 2у = 1,
Зх 4- у = 0.
Глава 31
БИЛИНЕЙНЫЕ ФУНКЦИИ
§31.1. ПРИМЕРЫ БИЛИНЕЙНЫХ ФУНКЦИЙ
Пусть L — линейное пространство. Билинейная функция f(x, у) (х, у е L) — это числовая функция двух аргументов, для которой выполнены следующие свойства (х, у, z — любые векторы из L, а — любое действительное число):
1)	f(X + z, у) =f(x, у) +f(z, у);
2)	/(ах, у) = а/(х, у);
3)	/(%, У + Z) =f(x, у) +f(x, z\,
4)	/(х, ау) = а/(х, у).
Пример 215. Скалярное произведение в евклидовом пространстве — это пример билинейной функции.
Пример 215. Рассмотрим линейное пространство R\ Пусть х = = (хь х2), у = (уь у2). Определим функцию f следующим равенством:
Дх, у) =
X) х2
У1 У2
Убедимся, что/(х, у) является билинейной функцией.
Пусть z = Ui, z2) — вектор пространства R2.
Так как х + z = (х,, х2) + (гн z2) = (Х| + х2 + г2), то/(х + г, у) =
Х\ + Z\ x2 + z2
У1 У2
= (*1 + Zi)y2 - (х2 + г2)У1 = Х'У2 + г(у2 - Х2У1 - г2у, =
= х}у2 - х2у1 + г,у2 - z2y} =
X! х2
У1 У2
4-
Za Z2
У1 У2
^f(x, у) +f(z, у).
ах — а(хн х2) = (axh ах2). Тогда /(ах, у) =
аХ] ах2 _ X] х2
У1 У2 У1 у2
= а/(х, у).
Так как у 4- z = (ун у2) 4- (г„ z2) = (у, 4- у2 4- г2), то/(х, у + z) =
Х| х2
У1 + zt у2 + Z2
= Х,(у2 + Z1) - Х2(у, + г,) = ху2 + Х& - ХзУ, - X2Zi =
150
а.у = а(>>|, уг) = (аун ау2). Тогда fix, ау) =
X, х2 _ хх х2
ау} ау2 ух у2
= а/(х, у).
Задача 205. Рассмотрим линейное пространство квадратных матриц второго порядка с обычными операциями сложения матриц и умножения матриц на число. Определим функцию/следующим равенством: f(A, В) = tr(v42?) (матрицы Л, 2? перемножаются, а затем вычисляется сумма элементов на главной диагонали). Показать, что f(A, В) является билинейной функцией.
Задача 206. Привести примеры билинейных функций.
S 31.2. СИММЕТРИЧЕСКИЕ И КОСОСИММЕТРИЧЕСКИЕ БИЛИНЕЙНЫЕ ФУНКЦИИ
Билинейная функция/называется симметрической, если /(х, у) = = /(у, х) для всех векторов х, ^линейного пространства L.
Пример 217. Скалярное произведение в евклидовом пространстве — это пример симметрической билинейной функции.
Задача 207. Убедиться, что билинейная функция из задачи 205 является симметрической билинейной функцией.
Билинейная функция / называется кососимметрической, если f(x, у) = —f(y, х) для всех векторов х, у линейного пространства L.
Пример 218. Покажем, что билинейная функция из примера 216 является кососимметрической билинейной функцией.
f(x, у) =
*1 х2
У] У2
У\ У2
х} х2
= —f(y, х) для всех векторов х, у ли-
нейного пространства R2.
Задача 208. Привести примеры кососимметрических билинейных функций.
5 31.3. МАТРИЦА БИЛИНЕЙНОЙ ФУНКЦИИ
Пусть ех, ..., еп — базис линейного пространства L.
Матрица А = (ау = /(е,, еу)) называется матрицей билинейной функции/в базисе ех, ..., еп.
151
Пример 219- Рассмотрим линейное пространство R3. Пусть х = = (*i, х2, х3), у — (у,, у2, Уз). Билинейная функция f задана равенством /(х, у) = xtyt + ЗХ2У2 + 2хзу3. Определим матрицу этой билинейной функции в базисе ех = (1, —1, 1), е2 = (2, 1, 0), е3 = (—1, 3, 2).
Так как размерность линейного пространства А3 равна трем, то порядок квадратной матрицы билинейной функции /в базисе е,, е2, е3 равен трем. Вычислим элементы матрицы:
«н =/(<+ ej) = 1 х 1 + 3 х (-1) х (-1) + 2 х 1 х 1 = 6;
«12 =/(^ь е2) = 1 х 2 + 3 х (-1) х 1 + 2 х 1 х 0 = -1;
б7,з =Ж, е3) = 1 х (-О + 3 х (-1) х 3 + 2 х 1 х 2 = —6;
«21 =Ж, е,) = 2 х 1 + 3 х 1 х (-1) + 2 х 0 х 1 = -1;
«22 =/(е2, e2) = 2x2 + 3xixl+2xoxo = 7;
«2з =/(е2, е3) = 2 х (-1) + Зх1хЗ + 2х0х2 = 7;
б?з, =/(е3, е,) = (-1) х 1 + 3 х 3 х (-1) + 2 х 2 х 1 = -6;
«32 =/(^3, е2) = (-О x2 + 3x3xl+2x2x0 = 7;
б?зз =/(е3, е3) = (-1) х (-1) + 3X3X3 + 2X2X2 = 36.
Тогда матрица билинейной функции f в базисе е,, еъ е3 равна
А =
«Н	«12	«13
«21	«22	«23
«31	«32	«33
6 -1-6'
-17	7
-6 7 36
Задача 209- Определить матрицу билинейной функции из примера 219 в базисе е, = (1, 2, 3), е2 = (—1, 4, 5), е3 = (-2, —3, 4).
9 31.4. ПРЕОБРАЗОВАНИЕ МАТРИЦЫ БИЛИНЕЙНОЙ ФУНКЦИИ ПРИ ПЕРЕХОДЕ К НОВОМУ БАЗИСУ
Пусть е\,..., е'п — еще один базис линейного пространства L. Известна матрица перехода Тот базиса е,,..., еп к базису е[,..., е'п. Тогда матрицы А и А' билинейной функции в базисах ..., еп и е'х, ..., е'п соответственно связаны следующим соотношением: А' = Т*АТ.
Пример 220. Дана матрица билинейной функции А =
1 2 '
3 4.
в базисе е, = (1, 0), е2 = (0,1). Найдем матрицу этой билинейной функ-
ции в базисе е\ = (5, 3), е2 = (2, 1).
е[ = 5е, + Зе2, е2 = 2е, + е2. Матрица перехода состоит из записан-
f 5 2
ных в столбцы координат векторов е[, е2 в базисе е,, е2: Т=
152
Отсюда Г' = 2 j •
Тогда матрица билинейной функции в базисе е[, е2 равна А' = Т‘АТ=
Г136 50 1
f 5 2 1
5 3
1 2
(перемножать матрицы
[2 1 J ( 3 4 Д 3 1 J [49 18 J
можно в любой последовательности, не меняя порядка множителей).
Г 4 5 '
Задача 210- Дана матрица билинейной функции А = I
в базисе ех = (I, 0), е2 = (0, I). Найти матрицу этой билинейной функции в базисе е\ = (1, 2), е2 = (2, 5).
Теорема. Билинейная функция является симметрической (кососимметрической) тогда и только тогда, когда для матрицы А билинейной функции выполнено условие А' = A (Af = —А), причем выполнение этого условия не зависит от выбора базиса линейного пространства.
Пример 221. Так как матрица билинейной функции из примера 219 при транспонировании не меняется, то это симметрическая билинейная функция.
Задача 211. Матрица билинейной функции в некотором базисе равна Q j . Какая это билинейная функция: симметрическая или кососимметрическая?
Глава 32
КВАДРАТИЧНЫЕ ФОРМЫ
S 32.1. СООТВЕТСТВИЕ МЕЖДУ СИММЕТРИЧЕСКИМИ БИЛИНЕЙНЫМИ ФУНКЦИЯМИ И КВАДРАТИЧНЫМИ ФОРМАМИ
Пусть /(х, у) — симметрическая билинейная функция. Функция q(х) =f(x, х) называется квадратичной формой, ассоциированной с симметрической билинейной функцией/(х, у).
Пример 222. Дана симметрическая билинейная функция/= х,у, + + 2x^2 + 2хзУ| - Зх2У2- Определим квадратичную форму, ассоциированную с этой симметрической билинейной функцией.
Заменим в формуле симметрической билинейной функции букву у на букву х. Тогда квадратичная форма равна q — Х\ + 2х,х2 + 2х2х} — Зх22 = = X2 + 4Х]Х2 — Зх22.
Задача 212. Дана симметрическая билинейная функция/= 2xtyt — — Xjy2 — Х2У1 + 4х2у2- Определить квадратичную форму, ассоциированную с этой симметрической билинейной функцией.
В координатах квадратичная форма записывается в виде q(xh ...,хп) =
= Z Z ChjXiXj-
При п = 2 получаем q(xb х2) = anxf + апххх2 + a22xl.
При п = 3 будет q(x{, х2, х3) = ЯцХ2 + а22х2 + я33х32 + fl12XjX2 + апххх3 + + я23х2х3.
Квадратичные формы обладают легко проверяемым свойством:
<7(ах,, ах2,ах„) = а^х,, х2,	х„).
Симметрическая билинейная функция/может быть восстановлена по квадратичной форме с помощью формулы
/(х, у) = 0,5(<?(х + у) - q(x) - q(y)).
В этом случае функция f называется поляризацией квадратичной формы q.
154
Пример 223. Определим поляризацию квадратичной формы q(x) = Ху + 4Х|Х2 + 2х22, где х = (х1? х2).
Пусть у = (уи у2). Тогда х + у = (х} + ун х2 + у2).
Поляризация квадратичной формы равна 0,5(<?(х + у) — q(x) — q(y)) =
= 0,5((х, + у,)2 + 4(xj + уу)(х2 + у2) + 2(х2 + у2)2 - (х^ + 4xjX2 + 2х22) -
- (У12 + ^У1У2 + 2у22) = *1Т1 + 2х,у2 + 2у]Х2 + 2хзУ2.
Задача 213. Определить поляризацию квадратичной формы q(x) = Ху — 5Х|Х2 + Зх22, где х = (х,, х2).
Таким образом, существует взаимно однозначное соответствие между симметрическими билинейными функциями и квадратичными формами. Поэтому все понятия, относящиеся к симметрическим билинейным функциям, переносятся на квадратичные формы.
S 32.2. МАТРИЦА КВАДРАТИЧНОЙ ФОРМЫ
Из коэффициентов квадратичной формы можно составить матрицу квадратичной формы. Это квадратная матрица порядка п(п — число переменных квадратичной формы). Коэффициент при х] пишется на главной диагонали на пересечении z-й строки и /-го столбца. Коэффициент при XjXj (z j) делится пополам и пишется на пересечении /-й строки и у-го столбца.
Пример 224. Найдем матрицу квадратичной формы q(xy, х2, х3) =
= 17х2 + 14х22 + 14х32 - 4Х|Х2 - 4х,х3 — 8х2х3.
Порядок матрицы равен 3, так как квадратичная форма содержит
3 переменные. На главной диагонали расположены числа 17, 14, 14 (коэффициенты при квадратах), на пересечении переменных х„ ху (j J) пишем ац/2, где аи — коэффициент при xpcj (i j) в квадратичной форме.
х, Г 17
х2 —2
х3 —2
—2
—2
*2
-2
14
-4
*3
—2 '
-4 = А.
14
Заметим, что при транспонировании полученная матрица не меняется: А = А.
Задача 214. Найти матрицу квадратичной формы q(x}, х2, х3) = = Ху + х2 + х2 + 4Х|Х2 + 4Х|Х3 + 4х2х3.
155
§ 32.3. ПОЛОЖИТЕЛЬНАЯ ОПРЕДЕЛЕННОСТЬ КВАДРАТИЧНОЙ ФОРМЫ. КРИТЕРИЙ СИЛЬВЕСТРА
Квадратичная форма называется положительно определенной, если: q(xi, х2, хп) > 0 при (хь х2, хп) (0, 0,..., 0).
Критерий Сильвестра. Квадратичная форма положительно определена <=> все угловые миноры матрицы квадратичной формы положительны: Az > 0.
Пример 225. Исследуем на положительную определенность квадратичную форму из примера 224 (отчеркнуты угловые миноры).
Матрица квадратичной формы А =
47 |-2 —2'
—2 14 |-4
—2 —4 14
Aj = 17 > 0, Д2 =
17 —2
—2 14
= 234 > 0, Д3 =
17 —2 —2
—2 14 —4
—2 —4 14
= (-2)(-2)
17 —2 —2
1 —7 2
1	2 —7
= 2916 > 0.
Все угловые миноры положительны. По критерию Сильвестра квадратичная форма положительно определена.
Задача 215. Исследовать на положительную определенность квадратичную форму из задачи 214.
S 32.4. КАНОНИЧЕСКИЙ ВИД КВАДРАТИЧНОЙ ФОРМЫ. ПРИВЕДЕНИЕ КВАДРАТИЧНОЙ ФОРМЫ ОРТОГОНАЛЬНЫМ ПРЕОБРАЗОВАНИЕМ
К КАНОНИЧЕСКОМУ ВИДУ
Если квадратичная форма не содержит произведений вида х,ху (z у), то это канонический вид квадратичной формы.
Рассмотрим приведение квадратичной формы q(x},x2, ..., xw) = = Z Z a^Xj в евклидовом пространстве ортогональным преобразованием к каноническому виду
Находим для матрицы А квадратичной формы собственные значения Х2,..., 4 (с учетом кратности). Тогда канонический вид квадратичной формы — это q(yx, уъ ..., к) = Z W-z=i
156
Для нахождения базиса, в котором квадратичная форма имеет канонический вид, нужно для каждого собственного значения найти собственные векторы и применить к ним процесс ортогонализации Грама-Шмидта. Это и будет искомый базис.
Пример 226. Приведем квадратичную форму из примера 224 ортогональным преобразованием к каноническому виду.
Матрица квадратичной формы А =
17 —2 —2
—2 14 —4
. Найдем для
—2 —4 14
нее собственные значения (см. § 24.1).
17 -X —2	—2
det (А — ХЕ) =
-2	14 — X —4
—2	—4	14 —X
= 0, то есть X] = 9, Х23 = 18.
Это собственные значения.
Канонический вид квадратичной формы q(y l9 у2, у3) = Х|у2 + Х^2 + +	= Яг? + 18у2 + 18у32.
Найдем собственные векторы для каждого собственного значе-
ния.
Z] = 9. Тогда
17 — 9 —2	—2
—2 14-9 -4
-2	—4	14-9
О'
О О
8
—2
—2
—2 5
-4
-21 Г х,
-4 х2
5 Jl*3
^0'
0 о
Применим метод Гаусса.
*1 х2 х3
"8 -2-2
—2 5 —4
—2 —4 5
4 -1 -1
—2 5 —4
—2 —4 5
"-2
О о
5 —4
9 -9
-9 9
О '
О
О
О '
О
О
0 ' о о
—2 5—4
О 1 -1
О] Г-2 0 1
О J [ 0 1 -1
X,	х2	х3
О К	Г	1	0	-0,5
0 J	[	0	1	-1
о' о
%! = 0,5х3,	Г Х| = 0,5,
р2=Х3,	=> л Х2 — 1,
чх3 любое.	1х3= 1.
Х| = 1,
х2 = 2,
. х3 = 2.
Собственный вектор v9 = (1, 2, 2). Применим к нему процесс ортогонализации Грама-Шмидта, то есть изготовим из него вектор еди-
ничной длины h = -г-=	----(1, 2, 2) = (1/3, 2/3, 2/3).
Iv9l V I2 + 22 + 22
157
Х2,з =18. Тогда
Г17-18 —2	—2
—2 14-18 -4
'X,
X?
-2	—4 14-18
^-2
—2
—4
—4
-2"
-4
—4
*1
*2
*3
Г(Г о о
О
О
О
Применим метод Гаусса.
X, х2 х3 '-1 —2 —2 —2 —4 —4 —2 —4 —4
2
О о
1
О О
О '
О
О
2	О	х1	х2	х3
о	О	=>(	1	2	2	10) ]
О	О
Г Xj = — 2х2 — 2х3, 1 х2, х3 любые.
У нас две свободные переменные (х2 и х3). Применим метод бегущей единицы (поочередно одну свободную переменную приравниваем единице, другую свободную переменную приравниваем нулю и находим соответствующее значение главной переменной).
= -2 х 1 - 2 х 0 = -2, Г х, = -2 х 0 - 2 х 1 = -2,
J х2 = 1,	2 х2 = О,
х3 = 0.	^х3 = 1.
fj = (—2, 1,0) и/2 = (—2, 0, 1) — собственные векторы, соответствующие собственному значению Z2 3 =18. Применим к ним процесс ортогонализации Грама-Шмидта.
Сначала nofhf2 построим ортогональную систему gb g2.
g, =Z = (—2, 1, 0). (g„ g,) = (-2)2 + I2 + 02 = 5.
(£, gl) = (—2) x (—2) + 1 x 0 + 0 x 1 = 4.
& =Л -	= (-2, 0, 1) - 4 (—2, 1, 0) = 1 (5(-2, 0, 1) -
Ui-g.)	5	5
- 4(—2, 1, 0)) = 1(5 x (-2) - 4 x (-2), 5 x 0 - 4 x 1, 5 x 1 - 4x0) = = 1(—2, —4, 5).
Умножим g2 на 5 (угол между векторами g] и g2 от этого не изменится) и полученный вектор вновь обозначим g2: g2 = (—2, —4, 5).
Проверим, что g| ± g2:
(gi,g2) = (-2)x(-2)+ 1 х(-4) + 0х5 = 0.
Построена ортогональная система gb g2. Получим из него орто-нормированную систему Л15 h2.
11	-2	1
^ = -7=^^= ^=((-2, 1,0) = ( —, — ,0).
V(g!,gi) \5	\5 \5
158
1
1
= .-----fc = .	=(-2, —4, 5) =
У (g2, &)	У(-2)2 + (—4)2 + 52
1	-2-45
= “7=(—2, —4, 5) = (—-±=).
зУУ	зу? Зд/Т зу?
1	2 2
Мы получили ортонормированный базис h = (у,	у), h\ =
1 АХ /	/ -2	-4	5 ч
= ( — , — , 0) и п2 = (———— ——) нашего пространства.
V? V5	3“У5 Зу5 3-<5
Именно в нем наша квадратичная форма имеет канонический вид д(У1, Уз, Уз) = 9у, + 18у22 + 18у32.
Матрица перехода от базиса в] = (1, 0, 0), е2 = (0, 1,0), е3 = (0, 0, 1), в котором была задана исходная квадратичная форма q(x}i х2, х3) = = 17х,2 + 14х2 + 14х32 — 4х,х2 - 4х,х3 - 8х2х3, к базису h, hb h2 будет следующая (нужно координаты векторов A, h]9 h2 записать в столбцы матрицы):
'1-2	—2 '
3 У? зу?
2	1	-4
Т =	-	—	  .
3 У? зУ~5
2	5
3 0 зуГ
Мы привели квадратичную форму ортогональным преобразованием к каноническому виду.
Координаты векторах,, х2, х3 были даны в базисе е, = (1, 0, 0), е2 = = (0,1,0), е3 = (0, 0, 1). Теперь у,, уъ у3 — это координаты вектора в базисе Л, А,, Л2. Замена переменных происходит так:
159
Л____2л___2л
3	У?	3V5
2л	У1___4л
3	У?	ЗУ?
2^i 5л
3 зу?
Ti _ 2л _ 2л 3 V5 ЗУ?
то есть
2л У? 4у3 з VI зу?
2л 5т3
3 3V?’
Задача 216. Привести квадратичную форму из задачи 214 ортогональным преобразованием к каноническому виду.
S 32.5. НОРМАЛЬНЫЙ ВИД КВАДРАТИЧНОЙ ФОРМЫ
С помощью нормировки и перестановки базисных векторов квадратичную форму можно привести к нормальному виду
q(x) = Х(2 + ... + хк - x2k+l - ... х2к+1.
Числа к и / называются соответственно положительным и отрицательным индексами инерции квадратичной формы.
Закон инерции. Индексы инерции квадратичной формы не зависят от выбора базиса, в котором квадратичная форма имеет нормальный вид.
Пара (к, /) называется сигнатурой квадратичной формы.
Пример 227. Определим нормальный вид и сигнатуру квадратичной формы из примера 226.
Канонический вид квадратичной формы равен 9у,2 + 18у22 + 18у32.
Положим Зу, = г,, VTsy2 = £2> л/Т8Уз = Ъ-
Тогда 9j>i2 + 18л2 + 18л2 = (Зл)2 + (УТ? л)2 + (УТ? л)2 = У + У + Z2.
Это нормальный вид квадратичной формы.
160
Так как нормальный вид квадратичной формы содержит три квадрата со знаком «+», то положительный индекс инерции квадратичной формы равен к = 3. Нормальный вид квадратичной формы не содержит квадратов со знаком «—». Поэтому отрицательный индекс инерции квадратичной формы равен / = 0. Следовательно, сигнатура квадратичной формы будет (3,0).
Задача 217- Определить нормальный вид и сигнатуру квадратичной формы из задачи 216.
§ 32.6. МЕТОД ЯКОБИ
В методе Якоби утверждается, что отрицательный индекс инерции квадратичной формы равен числу перемен знака в последовательности угловых миноров До = 1, Д1, Д2? • ••, Дл матрицы квадратичной формы. При этом предполагается, что все Д; 0.
Пример 228. Определим методом Якоби нормальный вид квадратичной формы 2х2 + х22 + Зх3 — 2Х|Х2 + 4х,х3 — 8х2х3.
Матрица квадратичной формы равна А =
2—12
-1 1 —4 2-4 3
Тогда угловые миноры Ао = 1 > 0, Л( = 2 > 0, Д2 =
2 -1
-1 1
= 1 >0,
-1 1 —4 2-4 3
= 6 + 8 + 8 — 4 — 32 — 3 = -17 <0.
В этой последовательности одна перемена знака. Поэтому отрицательный индекс инерции квадратичной формы равен / = 1. Тогда положительный индекс инерции квадратичной формы к = п — 1 = 3— 1=2.
Поэтому нормальный вид квадратичной формы будет г,2 + zl — Z3 •
Задача 218. Определить методом Якоби нормальный вид квадратичной формы х2 + 2х22 + Зх3 — 4х,х2 — 6xjX3 + 8х2х3.
Глава 33
ПРИМЕНЕНИЕ
КВАДРАТИЧНЫХ ФОРМ В ТЕОРИИ КРИВЫХ ВТОРОГО ПОРЯДКА
Уравнение кривой второго порядка Лх2 + Вху + Су2 + Dx+ Еу + F= О можно привести к каноническому виду с помощью теории квадратичных форм. Находим канонический вид квадратичной формы Ах2 + Вху + Су2 и выделяем полный квадрат по каждой переменной.
Пример 229. Приведем уравнение кривой второго порядка из примера 148 к каноническому виду с помощью теории квадратичных форм.
Уравнение кривой второго порядка Мх2 + 24ху + 21У — 4х + 18у — — 139 = 0. Приведем квадратичную форму Мх2 + 24ху + 21^ к канони-
ческому виду.
Матрица квадратичной формы равна А =
14
12
12
21
. Найдем соб-
ственные значения этой матрицы.
Характеристическое уравнение det (А — ХЕ) =
14 —X 12
12	21 —X
= (14 - Х)(21 - X) - 122 = X2 - 35Х + 150 = 0. Отсюда 2ц = 30, Х2 = 5.
Тогда канонический вид квадратичной формы будет ЗОх2 + 5у2.
Найдем соответствующие собственные векторы.
Если X] = 30, то (А — X, Е)Х= 0
14-30	12
12	21—30
IV
1°>
г-16 12 ] [х'
12 -9 J
-4х + Зу = 0
х = 3/4у у любое
0
Положим у = 1. Тогда х = 3/4 х 1 = 3/4.
Собственный вектор v30 = (3/4,1). Изготовим из него вектор единич-1 1
ной длины: А, =  - -_-----~Узо =---------(3/4, 1) = (3/5, 4/5).
V(v3o, Vjo) V(3/4)2+ I2
162
Если Z2 = 5, то (А - Х.Е)Х= 0 — | 14 5	12
2	2	12	21—5
Г °] [°]
Г 9 121
[12 16J
[01
1° J
Зх + 4у = О
Г х = — 4/Зу 1 у любое
Положим у = 1. Тогда х = -4/3 х 1 = -4/3.
Собственный вектор у5 = (—4/3,1). Изготовим из него вектор единич-
ной длины: /?2 = -...,	у5 = -----------(-4/3, 1) = (-4/5, 3/5).
V(v5, v5)	V(-4/3)2 + I2
Запишем координаты векторов hb h2 в виде столбцов матрицы.
Получим матрицу перехода Г=
Тогда |	= Т
[Т J
^11 Г 3/5
J Н/5
' 3/5 -4/5' 4/5 3/5 -4/51 Г х,' 3/5 J
Отсюда
х = 3/5%! - 4/5у, у = 4/5х, + 3/5^!
Уравнение кривой второго порядка в координатах (хь j^) примет следующий вид: ЗОх2 + 5у2 - 4(3/5xj - 4/5у0 + 18(4/5х] + 3/5yi) — 139 = О — ЗОХ]2 + 5у2 + 12xj + 14у! - 139 = 0.
Выделив по каждой переменной полный квадрат (см. пример 148), получим каноническое уравнение эллипса х22/5 + у22/30 = 1.
Задача 219- Привести уравнение кривой второго порядка из задачи 148 к каноническому виду с помощью теории квадратичных форм.
Глава 34
ПАРА КВАДРАТИЧНЫХ ФОРМ
В евклидовом пространстве Изаданы квадратичная форма q{ и положительно определенная квадратичная форма q2. Пусть G— это поляризация квадратичной формы q2.
Теорема. Существует ортонормированный относительно определяемого функцией С скалярного произведения базис, в котором квадратичная форма qx имеет канонический вид, а квадратичная форма q2 приводится к нормальному виду.
Находим матрицы А и В квадратичных форм qx и q2 соответственно и определяем решения Xl5 ..., уравнения det (Л — ZZ?) = 0. Тогда канонический вид квадратичной формы qx —	+ ... + к„у^ а нор-
мальный вид квадратичной формы q2 = ух + ... + у%.
Соответствующие базисные векторы находятся из системы уравнений (А —	0 для каждого Zz.
По матрице В строим поляризацию G квадратичной формы q2. Симметрическая билинейная функция G определяет скалярное произведение. К полученным базисным векторам применяется процесс ортогонализации Грама-Шмидта относительно этого скалярного произведения.
Составляем матрицу перехода из координат ортонормированных векторов и получаем формулы замены координат.
Пример 230. Для квадратичных форм f = 1 lx2 — 6xjX2 + х2 и g = 1 Зх2 — 10Х]Х2 + Зх22 определим базис, в котором одна из этих квадратичных форм имеет канонический вид, а другая квадратичная форма приводится к нормальному виду, и соответствующую замену
координат
Матрица квадратичной формы /равна
11 -3
-3 1
миноры этой матрицы положительны (И > О,
Так как угловые
И -3
-3 1
= 2 > 0),
164
то квадратичная форма f положительно определена (по критерию Сильвестра).
Обозначим q{ = 13х1 2 - 10x^2 + Зх22 и <?2 = 1W - 6Х]Х2 + х22. Матри
цы квадратичных форм и q2 равны соответственно А =
и В =
' 11 -31
-3 1 ]’
Г 13 —51 [—5 3 J
Решим уравнение det (А — ХВ) = 0:
, Г 13 —51 л f 11 —31ч j . z
det(	— Z	) = det (
[-5 3 J [-3 1 J v
13 -51 _ Г HZ -3Z1.
-5 3 J [-3Z 1Z /
13- HZ -5 + 3Z -5 + 3Z 3 - Z
= (13 - 11Z)(3 - Z) - (-5 + 3Z)(—5 + 3Z) = 0,
то есть Z2 — 8Z + 7 = 0.
Отсюда Zj = 1, Z2 = 7. Тогда канонический вид квадратичной формы q} = Zj)/2 + Z^2 = у2 + 7у22, а нормальный вид квадратичной фор-мы q2 = Уг + у2.
Для каждого из чисел Zj = 1, Z2 = 7 решим матричное уравнение
(A — ^lB)X= 0 относительно %=
4-Z£ =
13 — 11Z -5 + 3Z'
-5 + 3Z 3 - Z
При Z| = 1 получаем A — ^B —
13-llxl
-5+3x1
3-1
2 -2'
—2 2
I 2
Тогда (А - ^В)Х= ° —	2
—2 2
0
0
= 0
1 x2 любое’
При x2 = 1 получим Xj = 1. Тогда первый базисный вектор равен £> = (1, О-
13-11Х7
-5+ЗХ7
-5+ЗХ7 3-7
-64 16
16 —4
При Z2 = 7 получаем А — Z2^:=
Г—64
Тогда (А - Х2В)Х= 0-
I 16
[х2 = 4х, 1 xt любое ’
При X] = 1 получим х2 = 4. Тогда второй базисный вектор равен й = (1Л).
16'
—4
х2
4Х[ - х2 = 0
0
0
165
I 11 —31
По матрице В =	I строим поляризацию G квадратичной
формы q2. Пусть х = (х,, х2) и у = (у,, у2).
' И
-3
х2
-3
1
У\
Уг
Симметрическая билинейная функция С(х, у) = 11х,У| — Зх^ — — ЗХ|У2 + х^2 задает скалярное произведение. Векторы g} = (1, 1) и g2 = (1, 4) ортогональны относительно этого скалярного произведения: G(gx, g2) = 11x1x1-3x1x1-3x1x4+1x4 = 0.
1 1
Тогда векторы h} = 	gx и h2 = —===rg2 образуют орто-
Vc(gl,gl)	Vc(g2,g2)
нормированный базис относительно скалярного произведения, определяемого функцией G.
G(gx,gx} = 11X1X1-3X1X1-3X1X1 + 1X1 = 6.
G(g2, g2) = 11x1x1-3x4x1-3x1x4 + 4x4 = 3.
1	1	11
h,= . ....g, = — (1, !) = ( — , —)•
TG(gi,gl)	V? Л/6	Уб
1	1	14
h2 = .	—	(1,4) = ( —,	—).
Ус(&,&)	Уз Уз	Уз
Тогда G(h„ /г,) = G(h2, h2) = 1, G(h„ h2) = 0.
Запишем координаты векторов /г, и h2 в виде столбцов матрицы.
' i/У? 1/УТ1
i/У? 4/УУ J 
Отсюда получаем замену переменных:
= ' 1/У? i/УТ 1 г у,'
ч 1/У? 4/УТ J [ у2 J ’
Получим матрицу перехода Т=
1 = т х2 I
Ут.
ToecTbU=wy? + wyr
Задача 220. Для квадратичных форм f = хх + 1ххх2 + Зх22 и g = 4х2 + 16xjX2 + 6х22 определить базис, в котором одна из этих квадратичных форм имеет канонический вид, а другая квадратичная форма приводится к нормальному виду, и соответствующую замену координат.
Глава 35
ЛИНЕЙНЫЕ ОПЕРАТОРЫ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
S 35.1. СОПРЯЖЕННЫЙ ОПЕРАТОР
Пусть V— евклидово пространство со скалярным произведением (х, у). А — линейный оператор в пространстве V.
Линейный оператор А\ действующий в евклидовом пространстве И, называется сопряженным к оператору А, если (А х, у) = (х, Л* у) для всех х, у из пространства И
Пример 231- В пространстве геометрических векторов {у = у, i + + у2у + v3k} задан линейный оператор Ау = [у, у]. Определим сопряженный к оператору А оператор.
Используя свойства смешанного произведения, получаем (A v, w) = = ([v, j], w) = (у, у, w) = -(у, w, Л = (v, -liv, у]) = (у, —Aw).
Поэтому сопряженный к оператору А оператор равен Л* = —А.
Задача 221. Рассмотрим множество С0°°[я, бесконечно дифференцируемых на отрезке [а, Ь] функций/(х), для которых f(a) =f(b) = 0. Скалярное произведение определяется с помощью формулы ь
(/(х), g(x)) = ^f(x)g(x)dx. В этом евклидовом пространстве действует а
линейный оператор Af(x) = f'(x). Определить сопряженный к оператору Л оператор. (Указание. Воспользоваться формулой интегрирования по частям.)
Теорема. Линейный оператор# является сопряженным к линейному оператору f тогда и только тогда, когда в ортонормированном базисе их матрицы удовлетворяют условию Ag = А}.
Пример 232. Матрица линейного оператора в ортонормирован-
r I
5
И
4 '
7
9
ном базисе равна А =
3 —2
2
. Определим матрицу сопряжен-
ного оператора в этом базисе.
167
Матрица сопряженного оператора получается транспонировани-
ем матрицы линейного оператора и равна А' =
1 5 1Г
3-2 2
4 7 9
Задача 222. Матрица линейного оператора в ортонормирован-
5
7
9
ном базисе равна А =
' 1 3
-6 8
1 10
Определить матрицу сопряжен-
ного оператора в этом базисе.
Пусть аъ ..., ак — векторы евклидова пространства. Матрица
Г (д„ а,)
G(a„ ак) =
(ак, «|)
(^1, а2)
(ак, а2)
(Яь акУ
(^akj а^)
называется матрицей
Грама векторов аъ ак.
Теорема. Для любых векторов аъ ак евклидова пространства
справедливо неравенство det G(ab аД > 0, причем det G(abа^ = 0
тогда и только тогда, когда векторы ах, ^линейно зависимы.
Матрица А линейного оператора f и матрица Л* сопряженного оператора/* в данном базисе связаны соотношением Л* — G}AG, где G — матрица Грама базисных векторов.
Пример 233. В базисе = (— 1, 1), а2 = (1, —2) евклидова прост-
ранства R2 известна матрица А =
1 2
3 4
линейного оператора. Опре-
делим матрицу сопряженного оператора в этом базисе.
Скалярное произведение в евклидовом пространства R2 задается формулой (х, у) =	+ х?уъ где х - (х15 х2), у = (у,, у2).
Определим элементы матрицы Грама G =
>11
&|
#12
&2
базисных век-
торов й|, а2.
£н = (_1)2 +12 = 2, g12 = (-1) х 1 + 1 х (-2) = -3, g21 = 1 х (-1) +
+ (—2) х 1 = —3,g22 = 12 + (—2)2 = 5. Тогда 6 =
' 2 -3
-3 5
Вспомним, что с d
1
ad — be
Отсюда G 1 =
1 f 5
2 x 5 - (—3)(—3) [ 3
d —b
.~c a
3 1 = f 5 3 '
2 J [З 2^
168
Поэтому матрица сопряженного оператора в этом базисе аь а2
_ f5 ЗП1 2М 2 -31 Г—38 68 1 z равна А = G AG = I II I	=	_ (пере-
[ 3 2 J [ 3 4 J [-3 5 J [—24 43 J
множать матрицы можно в любой последовательности, не меняя порядка сомножителей).
Задача 223. В базисе а{ — (2, 1), а2 = (-2, 3) евклидова простран-[2 — 11
линейного оператора. Опре-
делить матрицу сопряженного оператора в этом базисе.
§ 35.2.	СИММЕТРИЧЕСКИЙ ОПЕРАТОР
Линейный оператор Л, действующий в евклидовом пространстве V, называется симметрическим, если (Ах, у) = (х, Ау) для всех х, у из пространства V.
В ортонормированном базисе матрица симметрического оператора симметрична, то есть не меняется при транспонировании.
Теорема. Для любого симметрического оператора существует ор-тонормированный базис из собственных векторов.
Построение такого базиса показано в примере 226.
Симметрический оператор называется положительно определенным, если все его собственные значения положительны.
§ 35.3.	ОРТОГОНАЛЬНЫЙ ОПЕРАТОР
Линейный оператор А, действующий в евклидовом пространстве V, называется ортогональным, если (Ах, Ау) = (х, у) для всех х, у из пространства К Так как для ортогонального оператора (Ах, Ах) = (х, х), то ортогональный оператор сохраняет длину вектора.
Пример 234. Поворот в плоскости на угол <р — это пример opto-г.	I COS ф —sin (D
тонального оператора. Его матрица равна т т .
[ sin (р coscp
Задача 224. Привести примеры ортогонального оператора.
В ортонормированном базисе матрица ортогонального оператора ортогональна: АА{ = AfА = Е, то есть для ортогонального оператора А~1 = А'.
169
Теорема. Для любого ортогонального оператора существует ортонормированный базис, в котором матрица ортогонального оператора имеет канонический вид
/7(ф1)
-I
т-J, , f COS(pz где/7(ф,) =	. vz
sin срz
—sin ф/ cos ф,-
Так как Я(я) =
COS 71 —sin 71 sin 71 cos тс
cos 0 -sin О sin 0 cos О
= 1 О' О 1
ного элемента —1 и не более одного элемента 1.
Следствие. В трехмерном евклидовом пространстве матрица ортогонального оператора в подходящем r 1 О . О о
—sin ф COS ф
, то при желании на диагонали можно оставить не более од-
имеет один из следующих
видов:
ортонормированном базисе
О 0 ' со8ф — sin ф sin ф cos ф
(поворот во-
круг некоторой оси) и
fl О
О СО8ф sin ф
(зеркальный поворот — no-
ворот, совмещенный с отражением относительно плоскости, ортогональной оси поворота).
Пример 235. Для ортогонального оператора, заданного в неко-
тором ортонормированном базисе матрицей А =
' 2/3 -1/3
2/3 2/3
— 1/3 2/3
2/3 ' -1/3
2/3
определим канонический вид и ортонормированный базис, в котором матрица ортогонального оператора имеет канонический вид.
В трехмерном евклидовом пространстве матрица ортогонального
оператора в подходящем ортонормированном базисе имеет один из
170
следующих видов: =
'-1 О О cos ср О sin ср
О '
—sin ср cos ср
и А2 =
О cos ср
О sin ср
О
—sin ср cos Ср
След матрицы (то есть сумма элементов на главной диагонали матрицы) линейного оператора — это инвариант линейного оператора, который не зависит от базиса.
Для матрицы А след tr^ = 2/3 + 2/3 + 2/3 =2.
Для матрицы А' след tr^j = — 1 + 2 cos ср.
Для матрицы А2 след tr^2 =1+2 cos ср.
Равенство tr^ = tr^f невозможно (2 = -1 + 2 cos ср -* 3 = 2 cos ср -+ cos ср = 1,5 противоречие). Поэтому канонический вид матрицы op-
f 1 О
fl О 0 1
тогонального оператора равен А2 = 0 cos ср —sin ср
0 sincp cos ср
Так как tr^ = tr/l2, то 2 = 1 + 2 cos ср. Отсюда cos ср = 1/2 и ср = л/3.
	Поэтому А2 —	1 0	0	0 ' cos ср —sin ср	=	' 1 0	0	0 cos л/3 —sin ти/З	=
		0	sincp cos ср		0	sin л/3 cos л/3	
	ДО	0						
=	0 1/2 -V3/2 0 V3/2	1/2						
	Собственные значения матрицы			А равны		1 и cos ср ± isincp =	
= 1/2 ± z уЗ/2. Найдем соответствующие собственные векторы.							
Пусть X = 1.
					'2/3-1		-1	/3	2/3				' 0		
Тогда (А	-ХЕ)Х =			()>		2/3	2/3	-1	-1Л		х2	—	0		—
						-1/3	2/3		2/3 —	1^	Лз.		0		
'-1/3 -1/3	2/3		О'		' 1	1	—2	О'		' 1	1 -	-2	О'		
2/3 -1/3	-1/3		0	—>	—	2 1	1	0	—*	0	3 -	-3	0		
-1/3 2/3	-1/3		0		1	-2	1	0		< 0	-3	3	0		
11—2 0 1 -1 ООО	О' 0 0.	[ 1		1 1 - 3 1 -	-2 -1	0 1 0 J	—>	1 0	1 -1 1 -1	О' 0		л х2 ЛЗ'	= х3 любое		
Положим х3 = 1. Тогда = х2 = х3 = 1. Собственный вектор, соответствующий X = 1, равен (1, 1, 1).
Пусть X = 1/2 + z VV2. Тогда (А - \Е)Х= 0 —
'2/3-1/2-/V3/2	-1/3	2/3
2/3	2/3—1/2—/УЗ/2	-1/3
-1/3	2/3	2/3-1/2-/УУ/2
'х, '
'О'
о о < У
171
Положим х = 1 и отбросим третье уравнение системы (оно является следствием первых двух уравнений системы). Тогда
f (1/6 - i^/2)Xl - l/3x, = -2/3	Г О ~ ЗУ!/)^ - 2х2 = -4
[ 2/Зх, + (1/6 - /УТ/2)х2 =1/3	[ 4х, + (1 - зУУ/)х2 = 2 ’
Применим правило Крамера.
A|
1 - ЗУТ/ -2
4	1 - З-уТ/
—4	—2
2 1 - ЗУ1/
1 - зу!/ —4
4	2
= -18-6^37.
= 18-бУГ/.
Тогдах, =Д|/Д, х2 — Д2/Д, х3 = 1. (Д,/Д, Д2/Д, 1) -* (Д,, Д2, Д).
"	12^3/
18-6VT/ -18-бУУ/
" о '
18
-18
12 VI
+ -бУУ/ /
-бУУ/
д =
^2

Так как у нас действительное линейное пространство, то возьмем за два других собственных вектора действительную и мнимую части полученного вектора, то есть (0, 1, — 1) и (2, — 1, — 1).
Базис из собственных векторов g{ = (1, 1, 1), g2 = (0, 1, -1), g3 = = (2, —1, —1) является ортогональным:
(gl, g2) = 1 X 0 + 1 X 1 + 1 х (-1) = 0, (g„ g3) = 1 X 2 + 1 х (-1) + + 1 х (-1) = 0, (g2, g3) = 0 х 2 + 1 х (-1) + (-1) х (-1) = 0.
Изготовим из базиса g2, g3 искомый ортонормированный базис /г,, Л2, hy
2, |&| =
ортонормированном базисе матрицей А =
/ 22 + (—I)2 + (—I)2 =Уб-
= l/4d. 1.1) = ('/VI. 1/VI, 1/VI)-h2=g2/\g2\ = l/VI(0, 1, -1) = (0, i/VI.-i/VI). hy = &/|&| = 1/V?(2, -1, -1) = (2/Уб , - l/Уб , - l/Уб )-Задача 225. Для ортогонального оператора, заданного в некотором ' 1/2	1/2	-<2/2'
1/2	1/2	У2/2	,
У2/2 -У1/2	0
172
определить канонический вид и ортонормированный базис, в котором матрица ортогонального оператора имеет канонический вид.
§ 35.4.	ПОЛЯРНОЕ РАЗЛОЖЕНИЕ
Линейный оператор называется невырожденным, если его ядро состоит только из нулевого вектора.
Теорема о полярном разложении. Любой невырожденный линейный оператор в евклидовом пространстве единственным образом можно представить в виде произведения положительно определенного симметрического и ортогонального операторов.
Умножим матрицу А линейного оператора на матрицу А'. Из мат-эицы АА' извлечем квадратный корень и получим симметрическую матрицу R.
С помощью элементарных преобразований из матрицы (/? |Л) изготовим матрицу (Е\ О). Тогда А= RO.
Пример 236. Определим полярное разложение для матрицы Л ( 2 -П
А = I । линейного оператора, действующего в евклидовом про-
странстве.
Матрица R2 = АА1 =
-1
1
' 2
-1
Г 2
I 2
2
1
Г 5
[ 3
3
5
Тогда R = 'у/ R2 = aR2 + ЬЕ. Определим значения коэффициентов а и Ь.
Найдем собственные значения матрицы R2. Характеристическое
уравнение det (R2 — ХЕ) = 0, то есть
5-Х 3
3 5-Х
= 0. Тогда Xj = 2,
Х2 = 8. Мы видим, что собственные значения различны.
Функция f(x) = ~\J~x. Составим и решим систему относительно а и Ь.
f(Xd = aX, + b
/(Х2) = аХ2 + b
^2 = 2а + Ь 2"\СГ= 8ц + b
« = VT/6
6 = 4"VI/6 '
УТ= 2а + b
= 8ц + b
Тогда R = aR2 + ЬЕ = <2/6 [ | | 1 + 4<1/61 J °
f 5VI/6 3^2/61 + C4VI/6 0 If З/V? 1/VI ' [ 3<I/6 51/1/6 J [ 0	4<Т/б]	[ l/VT 3/Vl,
173
..	р,_ f 3/VI 1/VI l'_ f 3/VI l/VI 1 _ „
Мы видим, что R	j [ х/^ 3/^ j R.
В матрице (А|Л) получим на месте матрицы А единичную матрицу.
1
3
/П| ЛА	f 3/V2 1/V2
(SMI	[ 1/УУ 3/V7
2VT V? I _ f 1
3
-8
з 1 2V2 -V2I
1 з 2V2 V2 J
2W W 1
-4VI -4VIJ
1 0 VI/2 -VI/21 0 1 VI/2 VI/2 J ’
-11
_2-V2 2 л/2
2
2
3
0
2 0
О 2
Мы видим, что 001 =
[V2/2 v2/2 J
'VI/2-VI/21 f VI/2 Vl/2
_VI/2 VI/2
'1 (Г 0 1
-VI/2 VI/2
Получено полярное разложение А = RO, то есть
2 “И = [ 3/V2 l/VI 1 Г VI/2 -VI/2 '
2 1 J [ l/VI 3/V2 J [ VI/2 V2/2
Задача 226. Определить полярное разложение для матрицы л [ 1 -41
А =	линейного оператора, действующего в евклидовом про-
1 4
странстве.
Глава 6
МОДЕЛЬ ЛЕОНТЬЕВА
Есть п отраслей. Рассматривается процесс производства за один год. Пусть X/ — общий (валовой) объем продукции z-й отрасли, х0 — объем продукции z-й отрасли, потребляемыйу-й отраслью в процессе производства, у,- — объем конечной продукции z-й отрасли для не-
производственного потребления. Имеют место соотношения баланса п
х, = xti + xl7 + ... + xin + у =	z = 1, ..., п (продукция z-й отрас-
7 = 1
ли используется другими отраслями и потребителями).
Коэффициенты прямых затрат atj = хч/Х) показывают затраты продукции z-й отрасли на производство единицы продукцииу-й отрасли.
п
Считаем, что ау = const. Тогда = аух} их,- = SatJXj + у, i = 1, п.
Введем следующие обозначения: Х = •
— вектор валового вы-
«II ...
пуска, А = .......
.«л! ...
fУ11
рица),У= ••• — вектор конечного продукта.
IK J
••• — матрица прямых затрат (структурная мат-
Получаем матричное уравнение X = АХ + У. Матрица А > 0 (все элементы неотрицательны) называется продуктивной, если для любого вектора У> 0 существует решение Х> 0 этого уравнения. В этом случае и модель Леонтьева называется продуктивной.
п
Утверждение. Матрица Л > 0 продуктивна, если шах ^ау < 1 и су-j /=1 п
ществуету такой, что S «/, < 1, то есть наибольшая из сумм элементов : - 1 '
в столбцах матрицы А не превосходит 1, причем есть хотя бы один столбец, где сумма меньше 1.
175
Пример 237.
Имеем х} = 400, х2 = 500, у, = 150, у2 = 250, х}, = 50, х12 = 200, х21 = = 100, х22 = 150.
Отсюда а,, = Хц/х, = 50/400 = 0,125, я12 = Х|2/х2 = 200/500 = 0,4, я21 = х2]/х, = 100/400 = 0,25, а22 = х22/х2 = 150/500 = 0,3.
Структурная матрица А =
«н
«21
«12
«22
0,125 0,25
0,4
0,3
. Тогда
max (0,125 + 0,25; 0,4 + 0,3) = 0,7 < 1. Матрица А продуктивна.
X = АХ + К Пусть новый вектор валового выпуска Х=
300 1
450 J’
Тогда соответствующий вектор конечного продукта У— X— АХ =
= EX — АХ= (Е — А)Х —
' 0,125	0,4 f| Г 300 1
0,25	0,3 JJ [ 450 J
' 1
0
1
П зоо'
J I 450 >
' 1 -0,125 0-0,25
0 - 0,4
1 -0,3
f 0,875
I -0,25
г 300
450
Г 0,875X300 + (—0,4)х4501
[ -0,25X300 + 0,7X450 J
82,5
240
Замечание. Математическая функция МУМНОЖ мастера функций fx пакета Excel позволяет быстро перемножить матрицы. Перед вызовом этой функции надо выделить мышкой диапазон ячеек нужного размера, куда после выполнения процедуры будет помещен ответ./* Математические МУМНОЖОК. Появляется диалоговое окно, которое нужно заполнить. В графах массив 1 и массив 2 указывается ссылка на ячейки, содержащие значения 1-го и 2-го матричных множителей соответственно. После этого нажимается не ОК, а одновременная комбинация клавиш Ctrl + Shift + Enter.
П ~	V Г 200 1
Пусть новый вектор конечного продукта +=	.
176
Найдем соответствующий вектор валового выпуска X (это можно сделать, так как матрица А продуктивна).
У= (Е — А)Х. Тогда Х = (Е — Л)”1 Y. Матрица (£ — А)~1 называется матрицей полных затрат.
„ Л f 0,875 -0,4 1
£-^=[-0,25 0,7 J ’
Вспомним, что обратная матрица для матрицы В =
1 f d -b] числяется по формуле: В =----
ad — be I — с а
вы-
Тогда JT (Е А) У 0,875х0 7 _ (_0>25)Х(-0,4)
xf 0,7	0,4
[ 0,25	0,875
200 1 =	1	[ 260 1 Г 507 1
300 J 0,5125 [ 312,5 J ~ [ 610
Замечание. Математическая функция МОБР мастера функций fx пакета Excel позволяет быстро найти обратную матрицу. Перед вызовом этой функции надо выделить мышкой диапазон ячеек нужного размера (порядок обратной матрицы равен порядку исходной матрицы), куда после выполнения процедуры будет помещен ответ. fx Математические МОБР -> ОК. Появляется диалоговое окно, которое нужно заполнить. В графе массив указывается ссылка на ячейки, содержащие элементы исходной матрицы. После этого нажимается не ОК, а одновременная комбинация клавиш Ctrl + Shift + Enter.
Задача 227. Убедиться, что модель продуктивна. Найти вектор ко-v f 500 1 нечного продукта для нового вектора валового выпуска X =	.
Найти вектор валового выпуска для нового вектора конечного про-
200
Пик увлечения моделью Леонтьева прошел в семидесятые годы двадцатого века. Тогда стало ясно, что с использованием коэффициентов прямых затрат возникают проблемы из-за слишком быстрых изменений численных значений этих коэффициентов под действием научно-технического прогресса. Но модель Леонтьева и сейчас остается в арсенале методов, которыми должен владеть квалифицированный экономист. Ведь умение составлять и анализировать модели Леонтьева — это неотъемлемый элемент экономической культуры в целом, способствующий выработке экономического стиля мышления.
Ответы
1- Во 2-й строке и в 4-м столбце.
(12 3 0 4 7
3. Например, j
10 0	0
.	0	10 0
‘	0	0 10‘
.0	0 0	I
-	Г 10	25	35 '
‘	[ 15	20	5
6	Г 40	35	15 '
‘	[ 9	14	26 ’
- Г—20 -1 11 1
‘ [ 7	4-12/
—4
2
1 2
8 9
4 6
5 8
16. -9.
17.
+ 6
- 7
3
5
3
5
1
8
2
9
- 7
+ 9
3
4
3 1 .
5 8 ’
1
6 ’
18.
19.
18.
Г-1
2
1
-1/3]
-1/3 .
1
	' 11	15	3 '
о	12	4	7
Ов	13	6	8
	. 14	19	9 ,
20.
21.
22.
23.
25.
26.
3 ] -5
'—7/3 2 5/3 -1 —2
х = 22/17, у = -7/17.
Нет решений.
у = (1 — Зх)/7, х любое.
х=22,6;у = 11; z= - 8,4.
4.
2-я, 4-я и 5-я.
27. 2-я (1-й столбец), 4-я (1 -й столбец) и 5-я (2-й и 3-й столбцы).
28. 4-я и 5-я.
				' 12
9.	48	24	И	30
	[ 128	64		57
11. -13.
12. -3.
13. —2; 13; 2.
14. 17;-1;-5.
20 16'
42 36
59 58
15. 3
6 7
8 9
4 7
5 9
29. Нет решений.
' х, = — 15/4 — 2х2 — 0,5х5,
31 х х3 =-3/4 + 0,5х5, х4 = —5 + х5, х2, х5 — любые.
	' 9	-20	13 '
32. 0,1	5	-10	5
	-1	10	—7
34. £	в	0 D	С
-3	-2	0 1	4
179
36.	(-3, 3, —2).
37.	(10, -20, 35).
38.	(-4, 14, -7).
34. V29.
40.	У 35.
41.	2/Уб2,3/Уб2,7/Уб2.
42.	Нет.
43.	Коллинеарны.
44.	Не коллинеарны.
45.	(1,25; 5; 5,5).
46.	(1,5; 0,5; 6,5).
47.	-212.
48.	43.
49.	(9/53, 3/53, 21/53).
50.	43/У2562.
51.	-81/V38.
52.	Ортогональны.
53.	Да.
54.	Да.
55.	375.
56.	(-12, -13, 20).
57.	0,5л/782.
58.	(-V5/3 , Vs/T, V5/3 )•
59.	49.
60-	Не компланарны.
61-	1,5
62.	Правая.
64. (ЗУз/2, 3/2).
65.	(4V2,5л/4).
66.	6 и -7.
67.	21 - 25/, -12 + 14/, 18, -8/, 15/ 14 + 9/ —7, -5 - 19/.
68.	—10 + 7/.
69.	6 + /
70.	4 - 38/.
71.	28/73 - 26/73/.
72.	-13/43 и-46/43.
73.	-3 ± 6/.
2л . 2л
74.	2(cos— + zsm—).
11л 11лч
75.	32(cos— + zsin—).
5л . 5л .
76.	2(cos— + zsin — ).
77-	Внешность круга радиуса 9 с центром (-5, 4). Граница круга (то есть окружность) в ответ не включается.
78.	-V3/2 + //2.
78. ei2^\
80.	64.
4 г- 2л/3 + 2л£
81.	V2(cos-^-----+
. . 2к/3 + 2кк
+ zsin-------), к = О, I, 2, 3.
82.	6х+8у-Зг-39 = 0.
83.	Принадлежит; не принадлежит.
84.	Да.
85.	Параллельна Оу.
86.	Содержит Оу.
87.	Параллельна Oxz.
88-x/(-l) + у/5 + г/(-3) = I.
89.	х/(7/2) + у/(—7/3) + ^/(7/8) = 1.
90.	2x/V77 - З_у/Ут7 + Sz/^П - 7/V77 = 0.
91.	17/V77.
180
92.	23х-5у + 34г- 123 = 0.
93.	Совпадают.
94.	Параллельны.
95.	Перпендикулярны.
96.	2х - Зу + 8z + 6 = 0.
97.	13х+22у + 5г- 101 = 0.
98.	6/^42.
99.	(х + 2)/4 = (у — 4)/7 =
= а- D/(-9).
100.	(х + 4)/Ю = (у — 3)/4 = = а-2)/з.
101.
х = -2 + 4/
< y = 4 + 7t
1-9/
102.	(-2,4, I), (6, 18, -17), (-6, -3, Ю).
103.	(x +4)/9 = (у—3)/(—8) = = a- 5>/7.
fx = —9 + 7/
104.
< y = 4 + 5t Z = 2 + 6t
105.	(x- 7l/23)/7 =
= (y- l3/23)/24 = V23.
106.	Параллельна.
107.	Прямая лежит в плоскости.
108.	(-1,0, -5).
109.	Не перпендикулярны.
110.	(-62/29, 112/29, 31/29).
111.	(39/14, 38/7, 23/14).
112.	2x-y + 2z- 13,5 = 0.
113.	Нет.
114.	(х-6)/(-6)=у/9 = г/0.
115.	13х — 19у + z + Ю1 =0.
116.	19/^406.
117.	^3526/61.
118.	Параллельны.
119.	(х—4)/3 = (у — 7)/(—6) =
= U-2)/8.
120.	Перпендикулярны.
121.	V38/3.
122.	Ю/29.
123.	(х — 2)/(—I) = (у — 5)/3.
126.	Параллельны.
127.	Совпадают.
128.	Перпендикулярны.
129.	(-22, 17).
130.	х + 4у-22 = 0.
131.	39/V58.
132.	-0,2.
133.	0,5.
134.	у = 0,25х + 5,5.
135.	17; 15; 34; 30; (±8, 0); 16;
8/17;х= ±289/8.
136.	х2/64 + у2/16 = 1.
137.	40.
138.	12; 9; 24; 18; (±15, 0); 30;
1,25; х = ±9,6; у = 0,75х. х2	у2
139.	—---------------= I.
4096/89 I600/89
140.	24.
141.	(3, 0),х=-3.
142.	(Ю, бУТо).
143.	(9, -4).
144.	(1, 16).
145.	(I, 15).
146.	((7 + 2л/У)/2, (-7^3 + 2)/2).
181
147.	(-(7^3 + 5)/2, (7 - 5V3 )/2).
148.	Гипербола л2/(5/9) — -_у22/(5/16) = 1.
149.	Гипербола.
150.	Гиперболический параболоид.
151.	Эллиптический параболоид у2/\6 + Z2/16 = X.
152.	Конус второго порядка 4х2 + 4^2 -у2 = 0.
153.	Нет.
154.	Да.
157. Пусть х = (хь х2, хи) е R”, У=(УьУ2,е Rn- Тогдах + у = = (х1+у1,х2+у2,...,х„+у,1)иу + х= = (Г1 + *1, У2 + *2, Уп + то есть х + у = у + х. Аналогично проверяется выполнение и других аксиом.
163. Линейно независимы.
164. Линейно зависимы.
167.	Да.
168.	Нет.
169.	6х, + 7х2 — х4 = 0.
170.	(2, 1,0,0) и (2, 0, -5,7).
171.	Базис аъ а2, а3. а4 = 2а{ — За2 + + 4я3, а5 = а{ + 5я2 — 5я3.
172.	<al9 аъ аъ Ь}>, <аъ а3>.
173.	[ 15/8 5 ] [-7/4 -3 ]’
174.	(-21,44; 9,84).
	' 2	-I 0 '
175.	0	0 1
	3	-1 1
176. Не является линейным оператором.
177 ( 60	141 '
‘ [ -23 -54 , ’
	г 0	1	0 '
178.		1 0	0 .
	0	0	0
		! 2	5	0 '
179.	(	) 0	0 5
		> 6	7 0
	. С	) 0	0 7 .
		—6	И 5
180. 1	/3	-12	13	10
		6	-5 -5
181. Нет.			
		' 5	3 -6'
182. I	/V	1 3	13 2
		-6	1	10
183. л/3		= +/(-	-l) = z/2.
184.	6.
185.	14л3 — 21л? + 13л+ 3.
186.	6л5 + 1 Зх4 - 25л3 + 6л2 +
+ 35л + 5.
187.	р(л) = (4л2 — 2л + 6)<?(л) +
+ (4л2 —2л—3).
188.	2л3 + Зл2 — 4л + 1 = = (л —5)(2л2 + 13л+ 61)+ 306.
189.	1 h3;Aj = (-1, 1),%з = (1, О-
190.	2;	= (1/2, 1,0),Х,(2> =
= (0, о, 1).
191. diag(/3(l),/,(!)).	1 1 O'
192. diag(J,(2), J2(2)),	2 2 1
	1 0 0
f 0 p4 'I 193.	4	.	
[	2e4 J	
гЗх2100__2х3100 2(3100__2100)
—3(3100—2100) 3ioi_2loi
196. (л + 3)(л- I)2.
198. V39 •
199. 1,5^7/23 .
182
200. Нет.
201. — (I,1,-1),—!—(3,-4,-I), VT V26
^=(5, 2, 7).
78
202. (26, -6, 11,0)и(1,-7,0, 11).
203. 1/129(65, -130, 222, 134) и 1/129(322, -259, 294, -392).
204. (9/31, -3/31), 4068/961.
209.
'31
53
4
53 4 '
99 6
6 63
210.
24
53
57 '
126
211.	Кососимметрическая.
212.	2x2 — 2x,x2 + 4x22.
213.	x^ - 2,5x^2 - 2,5xjy, + Зх^.
214.
12 2'
2 1 2
2 2 1
215. He является положительно
определенной.
216. 5у2-^-у/;
'X,' х2
n/VT-i/V6 -i/VI) 1/VT-1/V6- 1/V2 1/VI 2/V6 О
УГ
У2
Ук
217.	Zi2-^-Z32,(l,2).
218.	г2 - z2 - Zj.
219.	Гипербола ^7(5/9) -_p22/(5/l6) = 1.
220.	у2 + у2, —4у2 + 5j22, Г X, = -У) + 3/VT8^2 |х2 = 2/Зу, + 1/VW
221. —А.
'2—6 1 '
222. 3 8 10 .
5 7 9
223- 1/64[б1 »Г-
'1 0 0)
225. 0 0 -1 , 1/VI(1, 1, 0),
0 1 0
1/2(1, -1, —VI), 1/2(—1, 1, -VI).
226.	5/V2 -3/V2' ч -з/VI 4/V2		
i/VI -i/VI' i/VI i/VI, 227. Модель npoz		1уктивна,	
Г 2751 Г 530,6' [ 400 J И (710,2
Программа учебного курса «Линейная алгебра и геометрия»
1.	Матрицы (прямоугольная, квадратная, единичная, нулевая). Действия с матрицами (умножение на число, сложение, вычитание, транспонирование, умножение). Свойства действий с матрицами.
2.	Определители второго и третьего порядков.
3.	Алгебраические дополнения и миноры. Разложение определителя по строке или столбцу.
4.	Свойства определителей.
5.	Вычисление определителей порядка п.
6.	Невырожденная матрица. Обратная матрица. Алгоритм нахождения обратной матрицы. Свойства обратной матрицы.
7.	Нахождение обратной матрицы для матрицы второго порядка.
8.	Нахождение обратной матрицы для матрицы третьего порядка.
9.	Системы линейных уравнений (совместная, несовместная, определенная, однородная, неоднородная).
10.	Правило Крамера (п = 2).
11.	Правило Крамера (п = 3).
12.	Матричный метод решения систем линейных уравнений.
13.	Главный элемент строки, ступенчатый вид матрицы, главные столбцы, главный ступенчатый вид матрицы. Приведение матрицы к главному ступенчатому виду. Ранг матрицы.
14.	Метод Гаусса.
15.	Нахождение обратной матрицы методом Гаусса.
16.	Векторы на плоскости. Нулевой вектор, противоположные векторы, равные векторы. Действия с векторами (сложение (правила треугольника и параллелограмма), умножение на число).
17.	Линейная комбинация векторов. Линейно зависимые векторы. Линейно независимые векторы. Базис. Разложение вектора по базису. Координаты вектора. Базис на прямой. Коллинеарные векторы. Базис на плоскости. Компланарные векторы. Базис в пространстве.
18.	Декартова система координат. Начало координат. Ортонормированный базис. Система координат на прямой.
19.	Декартова прямоугольная система координат на плоскости. Декартова прямоугольная система координат в пространстве.
20.	Координаты вектора. Преобразование координат вектора при основных операциях.
21.	Модуль вектора. Расстояние между двумя точками.
22.	Направляющие косинусы. Какому соотношению удовлетворяют направляющие косинусы?
184
23.	Критерий коллинеарности векторов.
24.	Деление отрезка в данном отношении. Формулы деления отрезка в данном отношении. Координаты середины отрезка.
25.	Скалярное произведение векторов. Основные свойства скалярного произведения. Нахождение скалярного произведения векторов с помощью координат векторов в декартовой прямоугольной системе координат.
26.	Угол между векторами.
27.	Проекция вектора на ось.
28.	Ортогональные векторы. Условие ортогональности векторов.
29.	Правая и левая тройки векторов. Примеры.
30.	Векторное произведение векторов. Правые и левые тройки векторов. Основные свойства векторного произведения векторов. Геометрический смысл векторного произведения векторов.
31.	Вычисление векторного произведения векторов.
32.	Смешанное произведение векторов. Основные свойства смешанного произведения векторов. Вычисление смешанного произведения векторов.
33.	Условие компланарности векторов.
34.	Геометрический смысл смешанного произведения векторов. Определение типа тройки векторов с помощью смешанного произведения векторов.
35.	Полярные координаты. Полярная система координат. Полюс. Полярная ось. Полярный радиус. Полярный угол. Главное значение полярного угла.
36.	Переход от полярных координат к декартовым координатам.
37.	Переход от декартовых координат к полярным координатам.
38.	Комплексные числа. Возникновение комплексных чисел. Алгебраическая форма комплексного числа. Действительная и мнимая части комплексного числа. Мнимая единица. Чисто мнимые комплексные числа.
39.	Действия с комплексными числами (комплексное сопряжение, сумма, разность, умножение, деление). Равенство комплексных чисел. Решение квадратных уравнений с отрицательным дискриминантом.
40.	Тригонометрическая форма комплексного числа. Модуль, аргумент и главный аргумент комплексного числа. Умножение и деление комплексных чисел в тригонометрической форме.
41.	Показательная форма комплексного числа. Формула Эйлера.
42.	Степень комплексного числа. Формула Муавра.
43.	Корень д-й степени из комплексного числа.
44.	Уравнение фигуры. Плоскость. Общее уравнение плоскости. Нормаль плоскости. Расположение точек относительно плоскости.
45.	Частные случаи расположения плоскости. Когда плоскость проходит через начало координат? Когда плоскость параллельна координатной оси? Когда плоскость проходит через координатную ось? Когда плоскость параллельна координатной плоскости? Уравнения координатных плоскостей.
46.	Уравнение плоскости в отрезках. Переход от общего уравнения плоскости к уравнению плоскости в отрезках.
47.	Нормальное уравнение плоскости. Переход от общего уравнения плоскости к нормальному уравнению плоскости. Нормирующий множитель.
185
48.	Расстояние от точки до плоскости.
49.	Уравнение плоскости, проходящей через три точки.
50.	Взаимное расположение плоскостей. Случай совпадения плоскостей. Случай параллельности плоскостей. Случай перпендикулярности плоскостей.
51.	Уравнение плоскости, проходящей через заданную точку параллельно заданной плоскости.
52.	Уравнение плоскости, проходящей через две заданные точки перпендикулярно заданной плоскости.
53.	Угол между двумя плоскостями.
54.	Прямая в пространстве. Канонические уравнения прямой. Направляющий вектор прямой.
55.	Параметрические уравнения прямой.
56.	Переход от параметрических уравнений прямой к каноническим уравнениям прямой.
57.	Переход от канонических уравнений прямой к параметрическим уравнениям прямой.
58.	Прямая как линия пересечения двух плоскостей. Переход к каноническим уравнениям прямой.
59.	Взаимное расположение прямой и плоскости. Когда прямая параллельна плоскости? Когда прямая лежит в плоскости?
60.	Нахождение точки пересечения прямой и плоскости.
61.	Перпендикулярность прямой и плоскости.
62.	Нахождение проекции точки на плоскость.
63.	Нахождение проекции точки на прямую.
64.	Нахождение уравнения плоскости, относительно которой симметричны две данные точки.
65.	Установление симметричности двух данных точек относительно данной прямой.
66.	Нахождение уравнения какой-нибудь прямой, лежащей в данной плоскости.
67.	Уравнение плоскости, проходящей через данную точку параллельно двум данным прямым.
68.	Угол между прямой и плоскостью.
69.	Расстояние от точки до прямой.
70.	Взаимное расположение прямых. Условие параллельности прямых.
71.	Уравнение прямой, проходящей через данную точку параллельно данной прямой.
72.	Условие перпендикулярности прямых.
73.	Компланарные прямые. Условие компланарности прямых.
74.	Скрещивающиеся прямые. Когда прямые являются скрещивающимися? Расстояние между скрещивающимися прямыми.
75.	Угол между двумя прямыми.
76.	Прямая на плоскости. Различные виды уравнений прямой на плоскости (каноническое, общее, с угловым коэффициентом). Геометрический смысл углового коэффициента прямой.
186
77.	Взаимное расположение прямых на плоскости (параллельность, совпадение, перпендикулярность, нахождение точки пересечения).
78.	Прямая на плоскости. Уравнение прямой, проходящей через две данные точки.
79.	Прямая на плоскости. Расстояние от точки до прямой.
80.	Угол между двумя прямыми на плоскости.
81.	Условие, которому удовлетворяют угловые коэффициенты перпендикулярных прямых. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой.
82.	Кривые второго порядка. Вырожденные кривые второго порядка. Невырожденные кривые второго порядка. Эллипс. Фокусы. Расстояние между фокусами. Каноническое уравнение эллипса. Большая и малая полуоси. Большая и малая оси. Центр эллипса. Вершины эллипса. Эксцентриситет. Эксцентриситет как мера сжатия эллипса. Директрисы. Чему равно отношение расстояния от точки эллипса до фокуса к расстоянию от этой точки до ближайшей к этому фокусу директрисы? Оптическое свойство эллипса.
83.	Гипербола. Фокусы. Расстояние между фокусами. Каноническое уравнение гиперболы. Действительная и мнимая полуоси. Действительная и мнимая оси. Вершины гиперболы. Эксцентриситет. Директрисы. Асимптоты гиперболы. Чему равно отношение расстояния от точки гиперболы до фокуса к расстоянию от этой точки до ближайшей к этому фокусу директрисы? Оптическое свойство гиперболы.
84.	Парабола. Фокус. Директриса. Вершина параболы. Ось параболы. Каноническое уравнение параболы. Параметр параболы. Оптическое свойство параболы.
85.	Преобразования координат. Параллельный перенос. Связь между старыми и новыми координатами.
86.	Преобразования координат. Поворот осей координат. Связь между старыми и новыми координатами.
87.	Приведение уравнения кривой второго порядка к каноническому виду.
88.	Инварианты кривых второго порядка. При каких значениях инвариантов кривая второго порядка является эллипсом? При каких значениях инвариантов кривая второго порядка является гиперболой? При каких значениях инвариантов кривая второго порядка является параболой? Мнимый эллипс. При каких значениях инвариантов кривая второго порядка является мнимым эллипсом? Пара мнимых пересекающихся прямых. При каких значениях инвариантов кривая второго порядка является парой мнимых пересекающихся прямых? Пара пересекающихся прямых. При каких значениях инвариантов кривая второго порядка является парой пересекающихся прямых? Пара параллельных прямых. При каких значениях инвариантов кривая второго порядка является парой параллельных прямых? Пара мнимых параллельных прямых. При каких значениях инвариантов кривая второго порядка является парой мнимых параллельных прямых? Пара совпавших прямых. При каких значениях инвариантов кривая второго порядка является парой совпавших прямых?
187
89.	Поверхности второго порядка. Вырожденные поверхности второго порядка. Невырожденные поверхности второго порядка. Канонические уравнения эллипсоида, однополостного гиперболоида, двуполостного гиперболоида, конуса второго порядка, эллиптического параболоида, гиперболического параболоида, эллиптического цилиндра, гиперболического цилиндра, параболического цилиндра.
90.	Уравнение поверхности второго порядка, полученной при вращении кривой вокруг оси Ох.
91.	Уравнение поверхности второго порядка, полученной при вращении кривой вокруг оси Оу.
92.	Линейные пространства. Примеры.
93.	Пространство R".
94.	Показать, что в линейном пространстве при умножении нулевого элемента на число получается нулевой элемент. Показать, что в линейном пространстве при умножении любого элемента на ноль получается нулевой элемент. Показать, что в линейном пространстве один нулевой элемент.
95.	Линейно зависимые и линейно независимые системы векторов. Линейная комбинация векторов. Базис. Размерность линейного пространства.
96.	Условие линейной зависимости трех векторов в пространстве R3. Условие линейной зависимости двух векторов в пространстве R3.
97.	Подпространства линейного пространства. Примеры. Собственные и несобственные подпространства.
98.	Подпространство как линейная оболочка системы векторов. Размерность подпространства. Нахождение системы линейных однородных уравнений, определяющих подпространство, в случае задания подпространства в виде линейной оболочки векторов.
99.	Задание подпространства с помощью системы линейных однородных уравнений. Фундаментальная система решений. Общее решение системы линейных однородных уравнений.
100.	Базис системы векторов.
101.	Сумма и пересечение подпространств. Формула Грассмана. Нахождение базиса суммы и пересечения подпространств.
102.	Преобразования базиса. Матрица перехода. Что можно сказать про определитель матрицы перехода?
103.	Связь между координатами вектора в разных базисах.
104.	Линейные операторы. Матрица линейного оператора. Матрица перехода. Связь между матрицами линейного оператора в разных базисах. Ядро линейного оператора.
105.	Многочлены, степень многочлена. Действия с многочленами (сложение, умножение, деление с остатком).
106.	Схема Горнера. Корень многочлена. Кратные корни.
107.	Собственные векторы и собственные значения линейного оператора. Нахождение собственных векторов и собственных значений. Характеристический многочлен. Спектр линейного оператора. Связь собственного вектора и собственного значения. Образует ли множество всех собственных
188
векторов, отвечающих данному собственному значению линейного оператора, подпространство?
108.	Жорданова нормальная форма. Жорданова клетка. Жорданова матрица. Жорданов базис. Алгоритм нахождения жордановой нормальной формы. Однозначно ли определена жорданова нормальная форма? Нахождение жорданова базиса.
109.	Функции от матрицы. Примеры.
110.	Аннулирующий многочлен матрицы. Теорема Гамильтона-Кэли. Примеры.
111.	Минимальный многочлен матрицы. Наименьшее общее кратное ненулевых многочленов. Минимальный многочлен жордановой клетки. Нахождение минимального многочлена матрицы.
112.	Евклидовы пространства. Примеры. Скалярное произведение. Длина вектора. Неравенство Коши-Буняковского. Неравенство треугольника. Угол между векторами. Ортогональный и ортонормированный базисы.
113.	Процесс ортогонализации Грама-Шмидта.
114.	Ортогональность вектора и подпространства. Ортогональное дополнение подпространства. Нахождение базиса ортогонального дополнения.
115.	Проекция вектора на подпространство. Ортогональная составляющая вектора относительно подпространства. Нахождение проекции вектора на подпространство. Минимальное свойство проекции вектора на подпространство.
116.	Решение систем линейных уравнений методом наименьших квадратов. Невязка.
117.	Билинейные функции. Примеры билинейных функций.
118.	Симметрические и кососимметрические билинейные функции.
119.	Матрица билинейной функции. Как по матрице билинейной функции определить симметричность (кососимметричность) билинейной функции?
120.	Преобразование матрицы билинейной функции при переходе к новому базису.
121.	Квадратичные формы. Взаимно однозначное соответствие между симметрическими билинейными функциями и квадратичными формами. Квадратичная форма, ассоциированная с симметрической билинейной функцией. Запись квадратичной формы в координатах. Поляризация квадратичной формы.
122.	Матрица квадратичной формы.
123.	Положительная определенность квадратичной формы. Критерий Сильвестра.
124.	Канонический вид квадратичной формы. Приведение квадратичной формы ортогональным преобразованием к каноническому виду. Ортогональное преобразование.
125.	Нормальный вид квадратичной формы. Положительный и отрицательный индексы инерции квадратичной формы. Сигнатура квадратичной формы. Закон инерции.
126.	Метод Якоби.
189
127.	Применение квадратичных форм в теории кривых второго порядка. Приведение уравнения кривой второго порядка к каноническому виду с помощью теории квадратичных форм.
128.	Пара квадратичных форм. Нахождение базиса, в котором одна из двух заданных квадратичных форм имеет канонический вид, а другая квадратичная форма (положительно определенная) приводится к нормальному виду. '
129.	Линейные операторы в евклидовом пространстве. Сопряженный оператор. Матрица сопряженного оператора в ортонормированном базисе. Матрица Грама системы векторов. Определитель матрицы Грама. Когда определитель матрицы Грама равен нулю? Матрица сопряженного оператора в произвольном базисе.
130.	Симметрический оператор. Матрица симметрического оператора в ортонормированном базисе. Построение ортонормированного базиса из собственных векторов симметрического оператора. Положительно определенный симметрический оператор.
131.	Ортогональный оператор. Примеры. Сохранение длины векторов под действием ортогонального оператора. Матрица ортогонального оператора в ортонормированном базисе. Канонический вид ортогонального оператора. Ортогональный оператор в трехмерном пространстве. Поворот и зеркальный поворот. Построение ортонормированного базиса, в котором матрица ортогонального оператора имеет канонический вид. След матрицы как инвариант линейного оператора.
132.	Невырожденный линейный оператор. Полярное разложение.
133.	Модель Леонтьева многоотраслевой экономики (балансовый анализ). Соотношения баланса. Коэффициенты прямых затрат. Вектор валового выпуска, вектор конечного продукта. Матрица прямых затрат (структурная матрица), матрица полных затрат, продуктивная матрица. Продуктивная модель Леонтьева. Уравнение Леонтьева. Критерий продуктивности матрицы.
Задачи для контрольной работы по курсу «Линейная алгебра и геометрия»
1—10- а) Для матриц А =
' к Н иВ= \р г
I п J q s
найти сумму А + В,
разность А — В, произведения АВ и ВА, определители, транспонированные и обратные матрицы.
б)	Дано подпространство L = <а{ — (—к, /, т, п), = (р, q, —г, s)>.
Определить базис ортогонального дополнения L1. Определить проекцию вектора х = (т, п, р, —q) на подпространство L и ортогональную составляющую вектора х относительно подпространства L,
в)	Рассмотрим линейное пространство R3. Пусть х = (хь х2, *з)>
у = (у,, у2, Уз). Билинейная функция f задана равенством /(х, у) = = 2х1у1 + 5%2у2 + Зх3у3. Определить матрицу этой билинейной функции в базисе в| = (—к, /, т), е2 = (р, q. —г), = (т, и, р).
г)	Дана симметрическая билинейная функция f= кхху{ — Ix^ — — Ixyy^ + т%2у2. Определить квадратичную форму, ассоциированную с этой симметрической билинейной функцией.
д)	Определить поляризацию квадратичной формы рх2 — тх{х2 + пх2.
е)	В базисе ах = (-Л, /), а2 = (/?, q) евклидова пространства R2 из-
вестна матрица г s
линейного оператора. Определить матрицу
сопряженного оператора в этом базисе.
ж)	При параллельном переносе точка Л(£, /) переходит в точку С(/л, п). Определить, в какую точку при этом параллельном переносе перейдет точка В(р, q).
з)	Определить уравнение плоскости, относительно которой симметричны точки А(к, /, т) и В(п, р, q).
и)	Определить, симметричны ли точки A(q, г, s) и В(т, п, р) относительно прямой (х + к)/р = (у — l)/q = (z + m)/r.
к)	Определить уравнение какой-нибудь прямой, лежащей в плоскости тх + пу + pz — к = 0.
191
	1	2	3	4	5	6	7	8	9	10
к	9	3	8	9	I	6	3	8	6	7
/	7	7	4	I	2	5	6	5	3	3
т	3	5	2	2	8	7	I	2	5	9
п	2	4	6	5	7	4	8	6	7	6
Р	5	2	8	2	9	7	5	9	3	4
Я	3	4	9	9	7	I	4	7	2	5
г	7	8	5	3	8	3	7	6	5	7
S	7	8	5	3	8	3	7	6	5	7
11—20. Для матрицы А = и найти обратную матрицу.					к п г ' Ips вычислить определитель т q t					
	11	12	13	14	15	16	17	18	19	20
к	9	3	8	9	I	6	3	8	6	7
1	7	7	4	I	2	5	6	5	3	3
т	3	5	2	2	8	7	I	2	5	9
п	2	4	6	5	7	4	8	6	7	6
Р	5	2	8	2	9	7	5	9	3	4
Я	3	4	9	9	7	I	4	7	2	5
г	7	8	5	3	8	3	7	6	5	7
S	6	5	3	7	I	2	1	2	7	3
t	7	3	6	3	6	7	4	8	9	7
21—30. Решить систему уравнений J + [пх + ру = q.
а)	с помощью правила Крамера;
б)	матричным методом;
в)	методом Гаусса.
	21	22	23	24	25	26	27	28	29	30
к	9	3	8	9	I	6	3	8	6	7
1	7	7	4	I	2	5	6	5	3	3
т	3	5	' 2	2	8	7	I	2	5	9
п	2	4	6	5	7	4	8	6	7	6
Р	5	2	8	2	9	7	5	9	3	4
Я	3	4	9	9	7	I	4	7	5	2
192
kx+ ly + mz = n,
31—40. Решить систему уравнений s рх 3- qy 3- rz = s,
Vtx+fy + gz = h.
а) с помощью правила Крамера;
б) матричным методом; в) методом Гаусса.
	к	/	т	п	р	Q	г	5	t	f	g	h
31	I	I	1	0	2	1	0	4	1	-1	-2	5
32	I	I	-1	—4	2	3	1	-1	1	-1	2	6
33	2	I	1	3	5	—2	3	0	1	0	2	5
34	I	1	-1	0	2	3	—2	2	3	—2	0	1
35	I	1	1	4	2	1	3	9	3	3	-1	0
36	2	1	1	-3	3	1	—2	7	3	1	0	1
37	3	-1	-1	2	1	1	1	0	2	2	3	7
38	2	1	-1	3	3	2	2	—7	1	0	1	—2
39	I	1	1	6	2	-1	2	6	3	1	-1	2
40	I	1	2	3	2	-1	0	3	3	-1	0	1
41—50. а) Методом Гаусса решить систему уравнений
' апХ{ +	Я,2Х2 + #13*3	+	#14*4 + #15*5	=
«2|Х| 3“	3“ ^23-^3	^24-^4	^25“^5	^2
6f3]X] +	a32x2 + a33x3	3-	«34X4 + a35x5	=	b3 *
«4jX| 3“	«43X3 3” £/43X3	"3“	Д44Х4 “I” «45x5	b4
б) Подпространство задано как множество решений линейной
	' аихх + «12х2 + а]3х3 + Я|4х4 + а]5х5 = 0
однородной системы <	а2|х, + а22х2 + а23х3 + а,Л + а25х5 = 0	е a3iXi + д32х2 + азЛ + а34х4 + азЛ = 0	р " 6?4|Х| З- $42X2 З- Д43Х3 З- Д44Х4 З- 6Z45X5	0
делить базис подпространства.
в) Определить тип кривой второго порядка, заданной уравнением ЯцХ2 + 2«12ху + «22У + 2«13х + 2«2зГ + #зз = 0.
	«н	Л12	«в	«14	Л15	bl	Л21	«22	а23	«24	а25	ь2
41	2	1	1	2	4	7	3	3	2	5	8	15
42	5	3	3	6	И	20	3	3	2	5	8	15
43	4	3	2	5	9	16	2	3	1	4	6	11
44	2	3	0	3	5	8	0	3	-1	2	2	3
45	I	3	0	3	4	7	-1	3	-1	2	1	2
46	2	3	1	4	6	И	0	1	0	1	1	2
	«н	«12	«,з	«14	Я15	ь.	«21	а22	«23	«24	а25	*2
47	5	3	3	6	11	20	3	2	2	4	7	13
48	3	3	2	5	8	15	1	3	1	4	5	10
49	3	3	1	4	7	12	1	3	0	3	4	7
50	5	3	2	5	10	17	3	3	1	4	7	12
	Й31	«32	«зз	й34	«35	by	«41	й42	й43	«44	й45	by
41	1	1	2	3	4	9	3	2	2	4	7	13
42	5	4	3	7	12	22	4	3	4	7	11	22
43	2	2	1	3	5	9	1	1	1	2	3	6
44	1	2	0	2	3	5	2	2	1	3	5	9
45	1	4	0	4	5	9	1	2	1	3	4	8
46	2	4	1	5	7	13	1	1	1	2	3	6
47	5	4	2	6	11	19	2	1	2	3	5	10
48	3	4	2	6	9	17	3	2	3	5	8	16
49	3	4	1	5	8	14	3	2	2	4	7	13
50	5	4	2	6	11	19	4	3	3	6	10	19
51—60. а) Даны точки А (к, /, р), В(т, п, q), С(р, q, т). Найти координаты вектора а АВ + р АС, скалярное произведение векторов АВ и АС, длину вектора АВ, косинус угла между векторами АВ и АС, уравнение прямой АС, расстояние от точки Б до прямой А С. Определить направляющие косинусы вектора АВ. Определить координаты точки М, делящей отрезок АВ в отношении X = р от А к В. Определить координаты середины отрезка АВ. Определить проекцию вектора АВ на ось а = (п, р, q). Выяснить ортогональность векторов АВ и АС. Определить векторное произведение векторов АВ и ВС. Определить с помощью векторного произведения площадь треугольника АВС.
б)	Известно, что |а| = к, \b\ = I, а угол между векторами а и b равен (р. Определить скалярное произведение векторов та + пЬира — qb. Определить модуль векторного произведения векторов та + nb и pa - qb.
в)	Векторы а и b = (к, I, т) коллинеарны. Скалярное произведение векторов а и b равно п. Определить координаты вектора а.
г)	Вектор ?, перпендикулярный векторам а = (к, I, т) и b = = (—п, —р, q), образует с осью Оу тупой угол. Модуль вектора с равен ос. Определить координаты вектора с.
д)	Определить смешанное произведение векторов а = (к, I, т), b = (—п, —р, q) ис = (р, п, —к). Исследовать векторы а, Ь, с на компланарность. Определить тип тройки векторов.
194
е)	Даны точки А(к, /, /?), В(т, /7, q), С(р, q, т), D(—n, —р, q). Определить объем пирамиды ABCD. Определить уравнение плоскости, проходящей через точки А(к, /, р), В(т, п, q), С(р, q, т).
ж)	Определить декартовы координаты точки по полярным координатам (р, ср).
з)	Определить действительную и мнимую части комплексного числа z = т — ni. Определить комплексно сопряженное к числу z-Найти сумму, разность, произведение и частное комплексных чисел Z} = — к + // и <2 = —т + ni.
и)	Возвести комплексное число z = /?(coscp + zsinср) в степень п. Определить корень степени п из комплексного числа г.
к) Определить уравнение плоскости л, зная точку М^к, /, т) в этой плоскости и нормаль п = (р, q, т) плоскости. Определить, принадлежат ли точки М^—1, 3, 2) и М2(9, —2, 1) плоскости л. Определить, пересекает ли отрезок М{М2 плоскость л. Составить уравнение плоскости л в отрезках. Привести уравнение плоскости л к нормальному виду. Определить расстояние от точки D(—n, —р, q) до плоскости л. Определить уравнение плоскости л1? проходящей через точку С(р, q, т) параллельно плоскости л. Определить уравнение плоскости л2, проходящей через точки А(к, I, р), В(т, п, q) перпендикулярно плоскости л. Определить проекцию точки D(—n, —р, q) на плоскость л. Задан линейный оператор А проектирования на плоскость л. Определить матрицу этого линейного оператора в базисе = (1,0, 0), е2 = (0, 1,0), = (0, 0, 1). Определить ядро этого линейного оператора.
л) Известны точка Л(£, /, р) на прямой и направляющий вектор Г = (m, п, q) этой прямой. Определить канонические уравнения прямой. Определить параметрические уравнения прямой. Определить, какие точки прямой соответствуют значениям 0, 2, —1 параметра t. Определить проекцию точки В(т, п, q) на прямую. Определить синус угла между построенной прямой и плоскостью л из пункта «к». Определить расстояние от точки С(р, q, т) до построенной прямой. По-
х + 1	у-2 г + 4
казать, что построенная прямая и прямая.----- = -у- = —р явля-
ются скрещивающимися, и определить расстояние между ними.
м) Определить канонические уравнения прямой, проходящей через точки А (к, /, р) и В(т, п, q).
н) Определить канонические и параметрические уравнения пря-[ rx — ly + mz — 7 = 0 мои, п п.
[ пх + ру + qz + 9 = О
195
Определить взаимное расположение этой прямой и плоскости из пункта «к».
о) Определить косинус угла между прямыми тх — пу + / = О и кх + ру — q = 0.
п) Определить тангенс угла между прямыми у = —рх + q и у = кх + /. Определить уравнение прямой ть проходящей через точку М(—сс, Р), перпендикулярно прямой у = кх + /.
р) Для эллипса х?/р + y*/q = 1 определить большую и малую полуоси, большую и малую оси, координаты фокусов, расстояние между фокусами, эксцентриситет, директрисы. Эллипс вращается вокруг оси Ох. Определить уравнение и тип полученной поверхности второго порядка.
с) Для гиперболы х?/к — y*/l = 1 определить действительную и мнимую полуоси, действительную и мнимую оси, координаты фокусов, расстояние между фокусами, эксцентриситет, директрисы, асимптоты. Гипербола вращается вокруг оси Оу. Определить уравнение и тип полученной поверхности второго порядка.
т) Определить фокус и директрису параболы у2 = тх.
у) При параллельном переносе за новое начало координат принята точка 0{(—р, q). В старой системе координат задана точка (т, п). Определить новые координаты этой точки. Определить старые координаты точки при этом параллельном переносе, если новые координаты точки равны (к, /).
ф) Определить новые координаты точки (т, п) при повороте осей координат на угол ср. Определить старые координаты точки (£, /) при повороте осей координат на угол ср.
х) Подпространство является линейной оболочкой векторов «1 = (£, /), а2 = (/я, — ri), а3 = (—р, q). Определить базис подпространства и разложение остальных векторов по базису.
ц) Определить матрицу перехода от базиса а} = (к, к), а2 = (т, п) к базису Ь\ = (-р, q), b2 = (п, р + q). Известны координаты вектора х = (ос, Р) в базисе а}, а2. Определить координаты вектора х в базисе Ьь Ь2. Найти матрицу линейного оператора, переводящего векторы аъ а2 в векторы Ь{, Ь2, в том же базисе, в котором даны координаты векторов.
ч) Жорданова нормальная форма матрицы равна diag(J2(w), J}(m), ^(-/v)). Определить минимальный многочлен матрицы.
196
	51	52	53	54	55	56	57	58	59	60
к	9	3	8	9	I	6	3	8	6	7
1	7	7	4	I	2	5	6	5	3	3
т	3	5	2	2	8	7	I	2	5	9
п	2	4	6	5	7	4	8	6	7	6
Р	5	2	8	2	9	7	5	9	3	4
Q	3	4	9	9	7	I	4	7	2	5
а	7	8	5	3	8	3	7	6	5	7
р	6	5	3	7	I	2	I	2	7	3
<р	л/4	Зтт/4	5л/6	2тг/3	п/З	5л/6	2п/3	7г/3	я/4	Зтг/4
61—70. Что можно сказать о взаимном расположении прямых кх + ty + т = 0 и пх + ру + q = О?
	61	62	63	64	65	66	67	68	69	70
к	I	21	И	2	I	2	1	3	1	5
t	-3	8	3	I	—2	-1	-1	1	—2	2
т	-ю	18	12	4	-3	6	—4	-5	10	4
п	-5	42	22	Ю	-3	6	3	21	4	-15
Р	15	16	6	5	6	-3	-3	7	-8	—6
Q	50	-30	24	30	9	-20	-20	-35	40	-20
71—80. Изобразить прямую кх + ру + т = 0.
	71	72	73	74	75	76	77	78	79	80
к	I	21	И	2	1	2	1	3	1	5
Р	-3	8	3	1	—2	-1	-1	1	—2	2
т	-ю	18	12	4	-3	6	—4	-5	10	4
81—90. Являются ли линейными следующие преобразования?
81.	Ах — (6х, + 6х2 — 5х3, 4х, + 7х2 + х3, х, — 2х2 — 5х3), Вх = (Зх, + х2, ~Х] — Х2, X,).
82.	Ах = (2Х| + 4х2, X! - х2, х2), Вх = (-9х, + Зх2 — 4х3, х2, 7х, + 6х2 + 9х3).
83.	Ах^ (Зх, +х3, -х, + х2-х3,х, — 2 +х3), Z?x= (х, +х2 — х3,х2 + х3,х2).
84.	Ах = (4х, + 5х2 — 6х3, х2 — 2х3, х3), Вх = (х, + Зх2, х, — х2, х, + х2 — - 5х3 + 8).
85.	Ах = (хь 2х, + х2, х2 — Зх3 + 4), Вх = (5х, + х2, х,, х2 + 7х3).
86.	Ах = (6х, + 2х2 - Зх3, х2 + 5, — х, + 2х2 — 8х3), Вх = (х3, 2х, + 6х3, —2х, — 7х2 + х3).
87.	Ах = (8х, — 6х2 + 4, — х, + 1х2 + х3, х3), Вх = (2х, + Зх2 — 7х3, Х| + х2 + х3, х3).
197
88.	Ax = (—5x, — 2x2 + x3, 7x{ + 2x2, x{ + x2 — x3), Bx = (X] + x2, —2X] + 3x2 + 5, X] — x3).
89.	Ax = (4x, + 5x2 - 9x3, x, + x2 + x3, x2), Bx = (7x, — 2x2 + 4x3, —2xj + 3 — 4x3, X! + x3).
90.	Ax = (—9Xj + x2 — Зх3, X], 6x2 + 5x3), Bx = (xj + 3x2 — 4x3, 2xx + + 3x2 - 7, X] + 3x3).
91—100. Решить уравнение Ax3 + /лх + wx + /? = 0.
	91	92	93	94	95	96	97	98	99	100
к	2	6	6	5	6	7	5	5	5	5
Р	И	7	—7	—4	—4	-8	—4	—4	—4	—4
т	19	-I	-I	-12	-12	14	-14	-15	-16	-17
п	10	—2	2	-3	—2	-13	-5	—6	—7	-8
101—110. а) Дана матрица линейного оператора Л =	I вба-
[ / п\
зисе ех = (1,0), е2 = (0, 1). Найти матрицу этого линейного оператора в базисе е[ = (р, q), е2 = (г, s).
б) Дана матрица билинейной функции А = \ ? г в базисе ех = I Я $ J
= (1,0), е2 = (0, 1). Найти матрицу этой билинейной функции в бази-
се е\ = (Л, /), е2 = (т, п).
	101	102	103	104	105	106	107	108	109	110
к	9	3	8	9	1	6	3	8	6	7
1	7	7	4	I	2	5	6	5	3	3
т	3	5	2	2	8	7	I	2	5	9
п	2	4	6	5	7	4	8	6	7	6
Р	5	2	8	2	9	7	5	9	3	4
Q	3	4	9	9	7	I	4	7	2	5
г	7	8	5	3	8	3	7	6	5	7
S	6	5	3	7	1	2	I	2	7	3
111—120. Найти собственные векторы и собс линейного оператора, заданного матрицей \ т L * п > поненту от матрицы	т . Убедиться, что матри I 1 п\ ся корнем своего характеристического многочлене								двенные значения . Определить экс- к in I [ца	являет- / п J а.		
198
	111	112	113	114	115	116	117	118	119	120
к	3	I	5	I	4	-5	I	—7	8	—2
1	3	7	I	7	2	2	5	-I	2	4
т	2	—2	3	-3	I	I	-3	3	-3	-3
п	4	-8	3	-9	5	—4	9	-3	3	-9
121 НИЯ ли б) равна в этом	-130. а) нейного о Матрица л ' к п г ' Ips т q t базисе.		Найти собственные векторы и ператора, заданного матрицей инейного оператора в ортоно . Определить матрицу conpj					собственные значе-к п г' Ips. т q t рмированном базисе жженного оператора		
	к	/		т	п	Р	q	г	5	t
121	4	-1		1	-2	3	-2	-1	-1	2
122	2	-1		1	-1	2	-1	0	0	1
123	3	0		0	-1	2	-1	1	-1	2
124	5	0		0	-1	4	-1	-1	-1	4
125	6	-1		1	—2	5	—2	-1	-1	4
126	3	2		—2	1	2	1	-1	-1	4
127	2	1	1	-1	0	1	0	-1	-1	2
128	2	1		-1	1	2	1	0	0	3
129	4	1	1	-1	1	4	1	0	0	5
130	5	—2		—2	1	4	1	-1	-1	6
131—140- Применить процесс ортогонализации Грама-Шмидта к системе векторов/ = (к, /, т),/2 = (я, Р, = (z3 •*, О-
	131	132	133	134	135	136	137	138	139	140
к	-I	I	I	I	I	I	2	0	1	I
1	2*	I	—2	0	I	0	0	I	2	4
т	I	4	0	5	0	2	I	3	-1	I
п	2	0	-I	-I	0	-I	I	I	3	-3
Р	0	-3	I	3	I	0	I	2	0	2
q	3	2	3	2	—2	1	0	-1	2	0
г	I	2	I	0	I	2	4	2	-1	I
S	I	I	0	-I	0	5	I	0	1	-I
t	I	1	4	1	3	3	2	1	1	2
199
141—150. Решить систему линейных уравнений
' кх+ 1у= т
< пх + ру= q rx + sy= t
методом наименьших квадратов и найти невязку решения.
	141	142	143	144	145	146	147	148	149	150
к ‘	I	I	2	I	I	2	3	2	I	I
/	I	I	I	I	I	I	-I	I	I	I
т	I	-I	I	-I	1	I	-I	-I	I	2
п	3	—4	3	4	4	-3	2	3	6	3
Р	2	2	5	2	2	3	I	3	2	2
Q	I	3	—2	3	1	I	I	2	-I	-I
г	2	I	3	—2	3	—2	I	2	2	2
S	4	-I	2	2	9	7	3	—7	6	3
t	1	1	1	3	3	3	2	1	3	3
151—160. Дана квадратичная форма «цХ|2 + а22х2 + аззхз + #i2xix2 + +	+ 6/23X2X3. Написать матрицу этой квадратичной формы, ис-
следовать квадратичную форму на положительную определенность с помощью критерия Сильвестра, привести квадратичную форму с помощью ортогонального преобразования к каноническому виду. Определить нормальный вид и сигнатуру квадратичной формы. Определить методом Якоби нормальный вид квадратичной формы.
	151	152	153	154	155	156	157	158	159	160
Я] I	—4	2	4	-I	I	3	I	—2	—4	5
а22	—4	2	4	-1	—7	—7	I	2	I	13
«зз	2	2	1	-3	1	3	-1	—2	—4	5
«12	—4	8	2	—2	—4	8	0	4	4	4
Я|3	8	8	—4	—6	—2	-8	—4	—6	—4	0
а23	-8	-8	4	6	—4	-8	4	4	4	8
Х =
161—170. Убедиться, что модель Леонтьева продуктивна. Найти вектор конечного продукта для нового вектора валового выпуска d е
. Найти вектор валового выпуска для для нового вектора ко-
нечного продукта Y= \ J
I 8
200
	161	162	163	164	165	166	167	168	169	170
*1	500	400	200	600	700	800	900	700	900	200
*2	700	900	300	300	400	300	300	600	600	900
Х,1	50	30	45	20	75	85	150	120	200	100
х12	100	40	90	80	125	95	70	150	400	75
*21	60	70	100	70	70	170	40	80	20	50
*22	90	120	70	100	150	100	120	75	125	120
d	400	200	600	700	800	900	700	600	200	500
е	900	300	300	400	300	400	600	900	700	700
f	800	900	700	600	200	500	400	200	600	700
g	300	400	600	900	700	700	900	300	300	400
201
Литература
Беклемишева Л. А., Петрович А. Ю., Чубаров И. А. Сборник задач по аналитической геометрии и линейной алгебре. М.: ФИЗМАТЛИТ, 2004.
Бурмистрова Е. Б., Лобанов С. Г. Линейная алгебра с элементами аналитической геометрии. М.: ГУ ВШЭ, 1998.
Винберг Э. Б. Курс алгебры. М.: Факториал Пресс, 2002.
Клетеник Д. В. Сборник задач по аналитической геометрии. СПб.: Специальная литература, 1998.
Просветов Г. И. Математика в экономике: Задачи и решения. 2-е изд. М.: Издательство РДЛ, 2005.
Просветов Г. И. Математика для гуманитариев: Задачи и решения. М.: Издательство «Альфа-Пресс», 2008.
Просветов Г. И. Математические методы и модели в экономике: Задачи и решения. М.: Издательство «Альфа-Пресс», 2008.
Просветов Г. И. Прогнозирование и планирование: Задачи и решения. 2-е изд. М.: Издательство «Альфа-Пресс», 2008.
Просветов Г. И. Статистика: Задачи и решения. М.: Издательство «Альфа-Пресс», 2008.
Просветов Г. И. Экономика предприятия: Задачи и решения. М.: Издательство «Альфа-Пресс», 2009.
Проскуряков И. В. Сборник задач по линейной алгебре. М.: Наука, 1974.
Цыпкин А. Г. Справочник по математике для средних учебных заведений. М.: Наука, 1988.
202
Содержание
Предисловие ........................................................ 3
ГЛАВА 1. Матрицы ................................................... 5
1.1. Действия с матрицами......................................... 6
1.2. Свойства действий с матрицами................................ 9
ГЛАВА 2. Определители.............................................. 10
2.1.	Определители второго порядка................................ 10
2.2.	Определители третьего порядка............................... 10
2.3.	Алгебраические дополнения и миноры........................... И
2.4.	Разложение определителя по строке или столбцу .............. 12
2.5.	Свойства определителей...................................... 13
2.6.	Вычисление определителей ................................... 14
ГЛАВА 3. Обратная матрица ......................................... 17
3.1.	Алгоритм нахождения обратной матрицы ....................... 17
3.2.	Нахождение обратной матрицы для матрицы второго порядка 17
3.3.	Нахождение обратной матрицы для матрицы третьего порядка 18
3.4.	Свойства обратной матрицы................................... 19
ГЛАВА 4. Системы линейных уравнений................................ 20
4.1.	Основные определения ....................................... 20
4.2.	Правило Крамера............................................. 20
4.3.	Матричный метод решения систем линейных уравнений .......... 23
4.4.	Ступенчатый вид матрицы. Ранг матрицы....................... 24
4.5.	Метод Гаусса................................................ 26
4.6.	Нахождение обратной матрицы методом Гаусса ................. 30
ГЛАВА 5. Векторы................................................... 32
5.1.	Действия с векторами........................................ 32
5.2.	Базис....................................................... 33
5.3.	Декартова система координат................................. 34
5.4.	Система координат на прямой................................. 34
5.5.	Декартова прямоугольная система координат на плоскости .	35
5.6.	Декартова прямоугольная система координат в пространстве ...	36
5.7.	Координаты вектора. Преобразование координат вектора при основных операциях.......................................... 37
203
5.8.	Модуль вектора. Расстояние между двумя точками ........... 38
5.9.	Направляющие косинусы..................................... 38
5.10.	Критерий коллинеарности векторов ........................ 39
5.11.	Деление отрезка в данном отношении ...................... 40
ГЛАВА 6. Скалярное произведение векторов ........................ 41
6.1.	Определение и основные свойства скалярного произведения векторов ................................................... 41
6.2.	Угол между векторами ..................................... 42
6.3.	Проекция вектора на ось................................... 43
6.4.	Ортогональные векторы .................................... 43
ГЛАВА 7. Векторное произведение векторов......................... 44
7.1.	Правая и левая тройки векторов............................ 44
7.2.	Определение и основные свойства векторного произведения векторов ................................................... 45
7.3.	Вычисление векторного произведения векторов............... 45
ГЛАВА 8. Смешанное произведение векторов ........................ 48
8.1.	Определение и основные свойства смешанного произведения векторов ................................................... 48
8.2.	Вычисление смешанного произведения векторов............... 48
8.3.	Условие компланарности векторов........................... 49
8.4.	Геометрический смысл смешанного произведения векторов ....	49
ГЛАВА 9. Полярные координаты .................................... 51
ГЛАВА 10. Комплексные числа ..................................... 53
10.1.	Возникновение комплексных чисел.......................... 53
10.2.	Алгебраическая форма комплексного числа.................. 53
10.3.	Действия с комплексными числами ......................... 54
10.4.	Тригонометрическая форма комплексного числа.............. 56
10.5.	Показательная форма комплексного числа .................. 58
10.6.	Степень комплексного числа............................... 59
10.7.	Корень д-й степени из комплексного числа ................ 59
ГЛАВА 11. Плоскость ............................................. 61
11.1.	Общее уравнение плоскости ............................... 61
11.2.	Частные случаи расположения плоскости ................... 62
11.3.	Уравнение плоскости в отрезках........................... 63
11.4.	Нормальное уравнение плоскости........................... 64
11.5.	Расстояние от точки до плоскости ........................ 64
11.6.	Уравнение плоскости, проходящей через три точки ......... 64
11.7.	Взаимное расположение плоскостей......................... 65
11.8.	Угол между двумя плоскостями ............................ 68
204
ГЛАВА 12. Прямая в пространстве ............................... 69
12.1.	Канонические уравнения прямой ......................... 69
12.2.	Параметрические уравнения прямой ...................... 70
12.3.	Связь между параметрическими и каноническими уравнениями прямой ................................................... 70
12.4.	Прямая как линия пересечения двух плоскостей .......... 72
12.5.	Взаимное расположение прямой и плоскости............... 73
12.6.	Угол между прямой и плоскостью ........................ 78
12.7.	Расстояние от точки до прямой ......................... 78
12.8.	Взаимное расположение прямых........................... 79
12.9.	Угол между двумя прямыми .............................. 81
ГЛАВА 13. Прямая на плоскости ................................. 83
13.1.	Различные виды уравнений прямой на плоскости .......... 83
13.2.	Взаимное расположение прямых на плоскости ............. 84
13.3.	Уравнение прямой, проходящей через две данные точки ... 85
13.4.	Расстояние от точки до прямой ......................... 86
13.5.	Угол между двумя прямыми на плоскости ................. 86
ГЛАВА 14. Кривые второго порядка.............................   88
14.1.	Эллипс...............................................   88
14.2.	Гипербола ............................................. 90
14.3.	Парабола .............................................. 92
ГЛАВА 15. Преобразования координат............................. 93
15.1. Параллельный перенос................................... 93
15.2. Поворот осей координат ................................ 94
ГЛАВА 16. Приведение уравнения кривой второго порядка к каноническому виду ....................................................... 95
ГЛАВА 17. Инварианты кривых второго порядка ................... 97
ГЛАВА 18. Поверхности второго порядка.......................... 99
ГЛАВА 19. Линейные пространства .............................. 101
19.1. Линейно зависимые и линейно независимые системы векторов. Базис ............................................. 106
ГЛАВА 20. Подпространства линейного пространства ............. 109
20.1.	Примеры подпространств линейного пространства......... 109
20.2.	Способы задания подпространств ....................... 111
20.3.	Базис системы векторов ............................... 114
20.4.	Сумма и пересечение подпространств ................... 115
205
ГЛАВА 21. Преобразования базиса.............................. 117
21.1. Матрица перехода..................................... 117
21.2. Связь между координатами вектора в разных базисах ... 118
ГЛАВА 22. Линейные операторы................................. 119
ГЛАВА 23. Многочлены ........................................ 125
23.1. Действия с многочленами ............................. 125
23.2. Схема Горнера ....................................... 126
ГЛАВА 24. Собственные векторы................................ 128
24.1. Нахождение собственных векторов и собственных значений ... 128
ГЛАВА 25. Жорданова нормальная форма......................... 132
ГЛАВА 26. Функции от матрицы................................. 137
ГЛАВА 27. Минимальный многочлен ............................. 139
ГЛАВА 28. Евклидовы пространства............................. 141
28.1. Процесс ортогонализации Грама-Шмидта................. 142
ГЛАВА 29. Проекция вектора на подпространство ............... 145
ГЛАВА 30. Решение систем линейных уравнений методом наименьших квадратов.................................................... 148
ГЛАВА 31. Билинейные функции ................................ 150
31.1.	Примеры билинейных функций........................... 150
31.2.	Симметрические и кососимметрические билинейные функции 151
31.3.	Матрица билинейной функции .......................... 151
31.4.	Преобразование матрицы билинейной функции при переходе к новому базису ............................................ 152
ГЛАВА 32. Квадратичные формы................................. 154
32.1.	Соответствие между симметрическими билинейными функциями и квадратичными формами ................................ 154
32.2.	Матрица квадратичной формы .......................... 155
32.3.	Положительная определенность квадратичной формы. Критерий Сильвестра.............................................. 156
32.4.	Канонический вид квадратичной формы. Приведение квадратичной формы ортогональным преобразованием к каноническому виду................................................... 156
32.5.	Нормальный вид квадратичной формы ................... 160
32.6.	Метод Якоби ......................................... 161
206
ГЛАВА 33. Применение квадратичных форм в теории кривых второго по-
рядка .............................................. 162
ГЛАВА 34. Пара квадратичных форм............................. 164
ГЛАВА 35. Линейные операторы в евклидовом пространстве....... 167
35.1.	Сопряженный оператор ................................ 167
35.2.	Симметрический оператор.............................. 169
35.3.	Ортогональный оператор .............................. 169
35.4.	Полярное разложение ................................. 173
ГЛАВА 36. Модель Леонтьева................................... 175
Ответы....................................................... 179
Программа учебного курса «Линейная алгебра и аналитическая геометрия» ....................................................... 184
Задачи для контрольной работы по курсу «Линейная алгебра и аналитическая геометрия».......................................... 191
Литература .................................................. 202
Учебно-практическое пособие
Просветов Георгий Иванович
ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ: ЗАДАЧИ И РЕШЕНИЯ
Санитарно-эпидемиологическое заключение № 77.ФЦ.15.953.П.000115.06.03 от 16.06.2003 года
Подписано в печать 27.04.09 г. Бумага офсетная. Формат 60x84/16. Гарнитура «Ньютон». Печать офсетная. Печ. л. 13,0. Тираж 1500 экз.
Зак. № 4809.
ООО Издательство «Альфа-Пресс»
117574, Москва, а/я 117 Тел.: (495) 777-40-60, 926-73-03 e-mail: book@bestbook.ru
Отпечатано в ФГУП «Производственно-издательский комбинат ВИНИТИ» Адрес: 140010, Моск, обл., Люберцы, Октябрьский пр-т, 403. Тел.: (495) 554-21-86.