Основы теоретической физики. Том 1. Механика. Электродинамика - Савельев И.В.

Author: Савельев И.В.

Tags: физика механика электродинамика

ISBN: 5-02-014455-Х

Year: 1991

Similar

Основы аналитической механики

Теоретическая механика

Вариационные принципы механики. Их развитие и применения в физике

Теоретическая механика

Text

И. В. САВЕЛЬЕВ
ОСНОВЫ
ТЕОРЕТИЧЕСКОЙ
ФИЗИКИ
В ДВУХ ТОМАХ
Том 1
МЕХАНИКА
ЭЛЕКТРОДИНАМИКА
ИЗДАНИЕ ВТОРОЕ. ИСПРАВЛЕННОЕ
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1991

ББК 22.31
С12
УДК 530.1@75.8)
Рекомендовано Государственным комитетом СССР
по народному образованию
для использования в учебном процессе
студентами физических специальностей
высших учебных заведений
Рецензент:
доктор физико-математических наук, профессор С. Я. Алли-
луев
САВЕЛЬЕВ И. Б. Основы теоретической физики: Учеб. ру-
руководство: Для вузов. В 2 т. Т. 1. Механика и электродинами-
электродинамика.— 2-е изд., испр. — М.: Наука. Гл. ред. физ.-мат. лит., 1991.—
496 с.
ISBN 5-02.014455-Х (Т. 1)
Содержит сжатое и ясное изложение основ механики, тео-
теории относительности и электродинамики. С большой строгостью
и подробностью проводятся все математические выкладки, что
облегчает усвоение материала. Математическое приложение ос-
освобождает читателя от необходимости обращаться к учебникам
по математике.
1-е изд.— 1975 г. Во втором издании внесены исправления
и уточнена терминология.
Для студентов кетеоретических специальностей вузов. Мо-
Может быть полезна преподавателям физики втузов.
Табл. 6. Ил. 71.
1604030000—059
С асо/аоч м $\-Ъ\ ©«Наука». Физматлит, 1975;
053@2)-91 с изменениями, 1991
ISBN 5-02-014455-Х (Т. 1)
ISBN 5-02-014454-1

ОГЛАВЛЕНИЕ
Предисловие ко второму изданию . . 6
Часть первая. МЕХАНИКА 7
Глава I. Вариационный принцип в механике 7
§ i. Введение 7
§ 2. Связи Ю
§ 3. Уравнения движения в декартовых координатах . • 13
§ 4. Уравнение Лагранжа в обобщенных координатах . . 17
§ 5. Функция Лагранжа и энергия 24
§ 6. Примеры на составление уравнений Лагранжа ... 28
§ 7. Принцип наименьшего действия 33
Глава II. Законы сохранения 36
§ 8. Сохранение энергии 36
§ 9. Сохранение импульса 37
§ 10. Сохранение момента импульса 39
Глава III. Некоторые задачи механики 42
§ 11. Движение частицы в центральном поле сил .... 42
§ 12. Задача двух тел 48
§ 13. Упругие столкновения частиц 52
§ 14. Рассеяние частиц 57
§ 15. Движение в неинерциальных системах отсчета ... 62
Глава IV. Малые колебания ... 69
§ 16. Свободные колебания системы без трения 69
§ 17. Затухающие колебания . 7t
§ 18. Вынужденные колебания , 76
§ 19. Колебания системы со многими степенями свободы . . 79
§ 20. Связанные маятники 85
Глава V. Механика твердого тела 91
21. Кинематика твердого тела 91
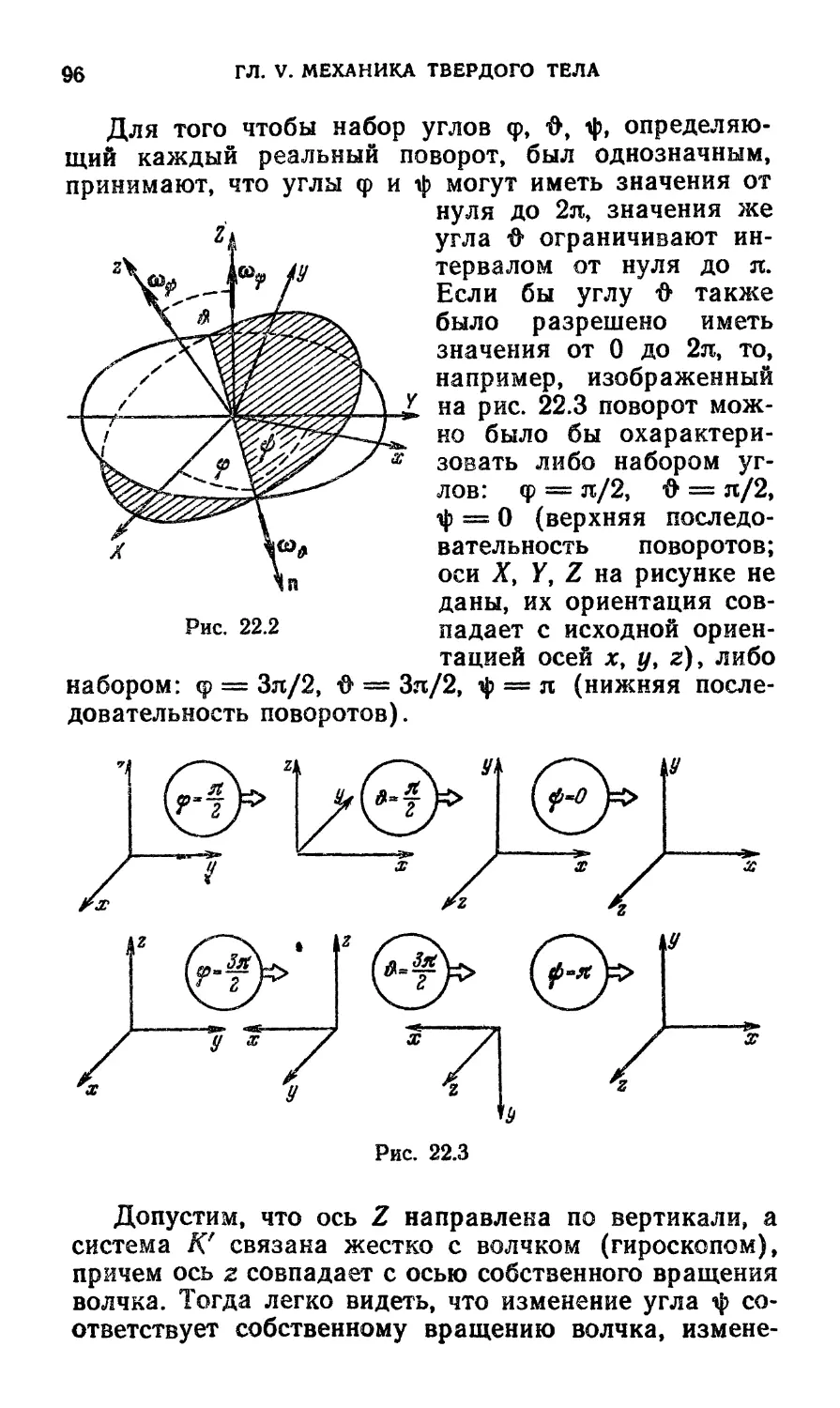
22. Эйлеровы углы 95
23. Тензор инерции 98
24. Момент импульса твердого тела . 106
25. Свободные оси вращения 112
§ 26. Уравнение движения твердого тела . . * .... 114
§ 27. Уравнения Эйлера 118
§ 28. Свободный симметричный волчок 120
§ 29. Симметричный волчок в однородном поле тяжести . .125
I*

4 ОГЛАВЛЕНИЕ
Глава VI. Канонические уравнения 130
§ 30. Уравнения Гамильтона 130
§ 31. Скобки Пуассона 134
§ 32. Уравнение Гамильтона — Якоби 136
Глава VII. Специальная теория относительности .... 141
§ 33. Принцип относительности 141
§ 34. Интервал 144
§ 05. Преобразования Лоренца 148
§ 36. Четырехмерные скорость и ускорение 153
§ 37. Релятивистская динамика 155
§ 38. Импульс и энергия частицы 158
§ 39. Действие для релятивистской частицы 161
§ 40. Тензор энергии-импульса 166
Часть вторая. ЭЛЕКТРОДИНАМИКА .177
Глава VIII. Электростатика . . 177
41. Электростатическое поле в пустоте . . * 177
42. Уравнение Пуассона 179
43. Разложение поля по мультиполям 182
44. Поле в диэлектриках 188
45. Описание поля в диэлектриках 192
46. Поле в анизотропных диэлектриках 198
Глава IX. Магнитостатика 200
§ 47. Стационарное магнитное поле в пустоте 200
§ 48. Уравнение Пуассона для векторного потенциала . . 203
§ 49. Поле соленоида 206
§ 50. Закон Био—Савара 210
§ 51. Магнитный момент 212
§ 52. Поле в магнетиках 220
Глава X. Нестационарное электромагнитное иоле . . . 226
53. Закон электромагнитной индукции 226
54. Ток смещения 227
55. Уравнения Максвелла , 229
56. Потенциалы электромагнитного поля 231
57. Уравнение Даламбера 236
58. Плотность и поток энергии электромагнитного поля . . 237
59. Импульс электромагнитного поля 240
Глава XI. Уравнения электродинамики в четырехмерной
форме 247
§ 60. Четырехмерный потенциал 247
§ 61. Тензор электромагнитного поля 251
§ 62. Формулы преобразования полей 253
§ 63. Инварианты поля 257
§ 64. Уравнения Максвелла в четырехмерной ферме . . .261
§ 65. Уравнение движения частицы в поле 263

ОГЛАВЛЕНИЕ 5
Глаза XII. Вариационный принцип в электродинамике 266
§ 66. Действие для заряженной частицы в электромагнитном
поле 267
§ 67. Действие для электромагнитного поля 269
§ 68. Вывод уравнений Максвелла из принципа наименьшего
действия 272
§ 69- Тензор энергии-импульса электромагнитного поля . . 275
§ 70. Заряженная частица в электромагнитном поле . . . 281
Глава XIII. Электромагнитные волны 285
§ 71. Волновое уравнение 2S5
§.-72. Плоская электромагнитная волна в однородной и изо-
изотропной среде 287
§ 73. Монохроматическая плоская волна 293
§ 74. Плоская монохроматическая волна в проводящей среде 300
§ 75. Немонохроматические волны 306
Глава XIV. Излучение электромагнитных волн 310
§ 76. Запаздывающие потенциалы . 310
§ 77. Поле равномерно движущегося заряда 314
§ 78. Поле заряда, движущегося произвольно 318
§ 79. Поле, создаваемое системой зарядов на больших рас-
расстояниях ... 326
§ 80. Дипольное излучение 332
§ 81. Магнитно-дипольное и квадрупольное излучения . . # 336
Приложения . . 342
I. Уравнения Лагранжа для голономной системы с идеаль-
идеальными нестационарными связями 342
II. Теорема Эйлера для однородных функций 345
III. Некоторые сведения из вариационного исчисления . . 345
IV. Конические сечения 356
V. Линейные дифференнцальные уравнения с постоянными
коэффициентами 361
VI. Векторы 365
VII. Матрицы . 382
VIII. Определители « 39!
IX. Квадратичные формы . . . * . ....... 402
X. Тензоры . 412
XI. Некоторые сведения из векторного анализа .... 430
XII. Четырехмерные векторы и тензоры в псевдоевклидовом
пространстве 458
XIII. Дельта-функция Дирака 481
XIV. Ряд и интеграл Фурье 483
Предметный указатель 490

ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
Предлагаемый вниманию читателей двухтомный
курс «Основы теоретической физики» является введе-
введением в теоретическую физику.
В соответствии с тем, как принято в теоретической
физике, изложение ведется в гауссовой системе еди-
единиц. В механике уравнения Лагранжа выводятся не
из принципа Даламбера (как это обычно делается), а
из уравнений Ньютона. Изложение электродинамики
ограничено средами, в которых отсутствует дисперсия,
а проницаемости е и |д не зависят от Е и В.
Более сложными являются § 40 и 69, посвященные
рассмотрению тензора энергии-импульса. Они вклю-
включены в книгу, потому что содержат превосходную
иллюстрацию к вопросу о том, каким способом осу-
осуществляется обобщение лагранжева формализма на
немеханические системы. Читатель, которому эти па-
параграфы покажутся слишком трудными, может про-
пропустить их без ущерба для понимания остальных
параграфов книги.
Большое внимание в книге уделено вариационному
принципу. При этом последовательно использован сле-
следующий прием — сначала требуемый результат полу-
получается с помощью методов, знакомых уже читателю,
а затем тот же результат получается с помощью ва-
вариационного принципа. Тем самым преследовалась
цель выработать у читателя отношение к вариацион-
вариационному принципу как к вполне надежному и мощному
средству исследования.
Работа над книгой значительно облегчается тем,
что она снабжена обстоятельными математическими
приложениями. Это избавляет читателя от необходи-
необходимости обращаться к руководствам по математике и
разыскивать в них необходимые сведения.
По сравнению с 1-м изданием текст в основном
остался неизменным. Сделана небольшая стилистиче-
стилистическая правка и устранены некоторые неточности и за-
замеченные опечатки.
Октябрь 1989 г, И. Савельев

Часть первая
МЕХАНИКА
Глава I
ВАРИАЦИОННЫЙ ПРИНЦИП В ЭДЕХАННКВ
§ 1. Введение
В зависимости от характера изучаемых объектов
механику можно подразделить на механику матери-
материальной точки, механику твердого тела !) и механику
сплошной среды. Последняя в свою очередь подразде-
подразделяется на гидродинамику, газовую динамику, теорию
упругости, теорию пластичности и т. д.
В механике самым сложным для изучения объектом
является сплошная (непрерывная) среда, поскольку
она представляет собой систему с бесконечно боль-
большим числом степеней свободы. Кроме того, при реше-
решении ряда задач, рассматриваемых механикой сплош-
сплошной среды, наряду с методами и уравнениями теоре-
теоретической механики используются также методы и
уравнения термодинамики, электродинамики и т. д.
Эти обстоятельства и служат причиной того, что ме-
механика сплошной среды является самым сложным
разделом механики. В данной книге вопросы меха-
механики сплошной среды затрагиваться не будут.
В курсе общей физики задачи механики решаются
с помощью уравнений Ньютона. В этой главе мы по-
познакомимся с другим подходом к описанию и изуче-
изучению движения механических систем. Под механиче-
механической системой мы будем понимать совокупность ма-
материальных точек, движение которых может быть
либо свободным, либо ограниченным связями. В част-
частности, совокупность материальных точек, объединен-
объединенных жесткими связями, образует твердое тело. В даль-
дальнейшем мы будем материальные точки для краткости
называть частицами.
*) Имеется в виду абсолютно твердое тело.

8 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
В соответствии с упомянутым подходом каждой
механической системе сопоставляется некая функция
обобщенных координат и обобщенных скоростей си-
системы, а также времени:
L — L (координат, скоростей, времени),
называемая функцией Лагранжа. Обобщенными коор-
координатами ци называются любые величины, с помощью
которых может быть задано положение системы в
пространстве. Обобщенными скоростями 4*
называются производные обобщенных координат по
времени1).
Функция Лагранжа может быть использована для
характеристики не только систем с конечным числом
степеней свободы, но и систем с бесконечным числом
степеней свободы — сплошных сред, электромагнит-
электромагнитных и других физических полей. Таким образом, зна-
значение функции Лагранжа выходит за рамки классиче-
классической механики.
Установив для рассматриваемой механической си-
системы вид функции Лагранжа, можно описать движе-
движение системы с помощью уравнений, связывающих
частные производные функции L по координатам и
скоростям. Эти уравнения, называемые уравнениями
Лагранжа, заменяют уравнения Ньютона.
Использование уравнений Лагранжа вместо урав-
уравнений Ньютона обладает тем преимуществом, что ко-
количество уравнений Лагранжа равно числу степеней
свободы системы, которое при наличии связей, огра-
ограничивающих движение системы, будет меньше чем
утроенное число частиц, входящих в систему. Количе-
Количество же уравнений Ньютона, необходимых для описа-
описания системы из N частиц, равно 3N. Кроме того, в
уравнения Лагранжа не входят реакции связей2), ко-
которые заранее неизвестны. Таким образом, при ис-
использовании уравнений Лагранжа реакции связей ав-
автоматически исключаются из рассмотрения, что суще-
существенно упрощает решение соответствующей задачи.
*) Напомним, что точки над символом величины означают
производную по времени: х « ~jr» %s
2) Это справедливо только для идеальных связей, т. е. связей
без трения.

§ 1. ВВЕДЕНИЕ
9
Правда, решение дает в этом случае сведения лишь
о движении системы, значения реакций остаются не-
неустановленными. Но в большинстве физических задач
значения реакций не представляют интереса, так что
данных, получаемых методом уравнений Лагранжа,
оказывается вполне достаточно. ,
В качестве примера можно указать
на задачу о колебаниях математи-
математического маятника (рис. 1.1). Урав-
Уравнение второго закона Ньютона для
частицы т имеет вид
mr — mg-\- R,
где R— реакция нити. Проектируя
все векторы на оси ху у и z (ось z
направлена за чертеж), мы полу-
получим три скалярных уравнения:
тх = Rxy my = mg + Rg, mz = 0.
Если же характеризовать положе-
положение системы обобщенной координа-
координатой ф, то вместо трех уравнений оказывается доста-
достаточным только одно:
тРф = — mgl sin q>, A-1)
которое и есть уравнение Лагранжа для данного слу-
случая1). Реакция R в него не входит. Решив уравнение,
мы найдем <р как функцию t Вида функции L для
рассматриваемой системы мы пока касаться не будем
(см. пример 1 в § 6).
Итак, движение механической системы может быть
описано либо с помощью уравнений Ньютона, либо
с помощью уравнений Лагранжа. Естественно, что
к уравнениям Лагранжа можно прийти, исходя из
уравнений Ньютона (что и будет сделано в § 4 этой
главы). Однако весьма существенным является то об-
обстоятельство, что уравнения Лагранжа можно полу-
получить с помощью весьма общего вариационного прин-
принципа— принципа наименьшего действия. Этот прин-
принцип может быть положен в основу классической
f) Обобщенная скорость ф входит в зто уравнение в вида
¦аг»-

10 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
механики вместо законов Ньютона. Достоинство прин-
принципа наименьшего действия состоит в том, что его
можно легко распространить на системы, не являю-
являющиеся механическими или чисто механическими, на-
например на упругие среды, электромагнитные поля,
поля элементарных частиц и т. д.
Резюмируя, можно сказать, что излагаемый в дан-
данной главе подход к изучению движения механических
систем обладает гораздо большей общностью, чем ме-
метод, основанный на законах Ньютона.
§ 2. Связи
Для системы частиц с массами т<1\ тB), ... урав-
уравнения второго закона Ньютона можно записать сле-
следующим образом:
= Л (/=1,2, ...,д), B.1)
где т\ =тг — тз = т1х) — масса 1-й частицы, Ш4 =
= тъ — гпь = тB) — масса 2-й частицы, ..., х\ — ко-
координата jc 1-й частицы, Х2 — координата у 1-й час-
частицы, Хъ — координата z 1-й частицы, х4, хь, хв— де-
декартовы координаты х, у, z 2-й частицы, ..., F\—
проекция на ось х результирующей силы FA>, дей-
действующей на 1-ю частицу, F2— проекция силы FA> на
ось у, Fs — проекция той же силы на ось г, F4, Fs, Fe —
х-* y-t г-компоненты силы FB\ действующей на 2-ю
частицу, и т. д. Число п уравнений, содержащихся
в B.1), равно утроенному числу частиц, входящих в
систему.
На положения и скорости частиц системы могут
быть наложены ограничения геометрического или ки-
кинематического характера. Эти ограничения называют-
называются связями.
Примерами систем со связями геометрического ха-
характера могут служить:
1) частица, которая при своем движении не мо-
может покинуть заданную поверхность или заданную
кривую. Поверхность или кривая могут быть непо-
неподвижными (стационарная связь) или перемещаться
заданным образом (нестационарная связь);
2) две частицы Л и В, связанные жестким невесо-
невесомым стержнем длины /. В этом случае ограничение»

§2. СВЯЗИ If
накладываемое связью, может быть записано в виде
уравнения
(хА - *вJ + (У а - У вJ + (гА - zBf = Р; B.2)
3) две частицы, связанные невесомой нитью дли-
длины L Аналитическое выражение такой связи имеет
вид
(хл - xBf + (уА - УвУ + (гА - zBf < Р; B.3)
4) абсолютно твердое тело, которое можно рас-
рассматривать как систему частиц с неизменными вза-
взаимными расстояниями, т. е. подчиненных связям вида
B.2).
Примером системы со связью как геометрического,
так и кинематического характера может служить шар,
катящийся без скольжения по шероховатой поверхно-
поверхности. Ограничение кинематического характера заклю-
заключается в том, что скорость точки касания должна
быть равна нулю.
В общем случае связь геометрического характера
можно представить уравнением
/fa, х2, ..., ха% 0 = 0 B.4)
(п = 3iV, где N — число частиц в системе).
Когда ограничения наложены не только на коор-
координаты частиц, но и на их скорости, уравнение связи
имеет вид
<р(*1, хъ ..., хт хи хъ ..., хп, /) = 0. B.5>
Если уравнение B.5) может быть проинтегрировано
по времени, оно, очевидно, эквивалентно уравнению
вида B.4).
Связи вида B.4) и сводящиеся к ним интегрируе-
интегрируемые связи вида B.5) называются голономными (или
интегрируемыми). Голономными называют также си-
системы с подобными связями. Системы, фигурирующие
в рассмотренных выше примерах 1, 2 и 4, относятся
к числу голономных.
Итак, в случае голономных связей накладываемые
ими ограничения выражаются в виде равенств, связы-
связывающих координаты частиц и время (см. уравнение
.B.4)).

12 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
Неинтегрируемые связи вида B.5), а также связи,
выражаемые в виде неравенств (см. пример 3), назы-
называются неголопомными.
Связи, не изменяющиеся со временем, называются
стационарными (или склерономными). Связи, изме-
изменяющиеся со временем, носят название нестационар-
нестационарных (или реономных).
Уравнение голономной стационарной связи имеет
вид
f(*i, **..., *«) = 0. B.6)
Оно отличается от уравнения B.4) голономной неста-
нестационарной связи тем, что в него не входит явно
время t.
Для задач с неголономными связями общих мето-
методов решения не существует. Требуется индивидуаль-
индивидуальный подход к каждой задаче. Неголономных систем
мы рассматривать не будем.
Каждая голономная связь, т. е. связь, выражаемая
уравнением B.4) или B.6), позволяет представить
одну из координат как функцию остальных. Следова-
Следовательно, каждая такая связь уменьшает число незави-
независимых координат на единицу.
Напомним, что число независимых величин, необ-
необходимых для определения положения системы в про-
пространстве, называется числом степеней свободы си-
системы. Поэтому можно сказать, что каждая голоном-
голономная связь уменьшает число степеней свободы системы
на единицу.
Если связи отсутствуют, то система из N частиц
обладает числом степеней свободы, равным п = 3N.
При наличии г связей число степеней свободы будет
равно s = n — r = 3N — г.
Связи действуют на частицы системы с силами R<a>,
которые называются реакциями. Связь без трения на-
называется идеальной. Суммарная работа, совершаемая
реакциями над частицами системы с идеальными ста-
стационарными связями, равна нулю. В качестве примера,
подтверждающего это утверждение, можно привести
систему, изображенную на рис. 1.1. У этой системы
реакция R направлена вдоль нити, а скорость час-
частицы v перпендикулярна к нити; поэтому сила R ра-
работы над частицей не совершает. Если связь (даже

§ 3. УРАВНЕНИЯ ДВИЖЕНИЯ В ДЕКАРТОВОЙ ФОРМЕ 13
идеальная) зависит от времени, совершаемая ее реак-
реакцией работа, как правило, отлична от нуля.
Выражение для элементарной работы, совершае-
совершаемой над частицами системы реакциями связей, имеет
вил dA^=Yi Hi dxi. Для системы с идеальными ста-
стационарными связями эта работа равна нулю. Следо-
Следовательно, для таких систем
E*,rf*,-0, B.7)
где dxi — проекции на координатные оси перемещений
частиц, совместимых со связями, наложенными на час-
частицы1).
§ 3. Уравнения движения
в декартовых координатах
Рассмотрим систему, состоящую из взаимодей-
взаимодействующих друг с другом частиц. Пусть на частицы
действуют также внешние силы. Воспользуемся для
координат частиц и компонент сил теми же обозначе-
обозначениями, которые мы применяли в предыдущем пара-
параграфе (см. первый абзац § 2).
В некоторых случаях силы, действующие на час-
частицы (или хотя бы часть этих сил), могут быть пред-
представлены в виде
Ъ—щ- <зл>
где
U = U(xu хъ ..., хЯ9 t) C.2)
— функция координат частиц и времени, называемая
потенциалом системы. Если в функцию U не входит
явно время ty она представляет собой потенциальную
энергию системы.
*) Во встречающихся в теоретической физике суммах индекс,
по которому осуществляется суммирование (немой индекс), как
правило, повторяется дважды. В связи с этим принято символ
Л опускать и подразумевать суммирование по дважды повто-
повторяющимся индексам. Например, вместо J] afii пишут просто
афь Однако, хотя такой способ записи отличается краткостью,
мы им пользоваться не будем. Суммирование будут подразуме-
подразумеваться только там, где написан символ У^.

|4 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
Сила, определяемая формулой C.1), называется
потенциальной. Следует различать стационарные и не-
нестационарные потенциальные силы. Стационарными
называют силы, зависящие только от координат час-
частицы и не зависящие явно от времени. Таким силам
отвечает функция U9 не содержащая времени явно.
Когда t входит в U явно, сила зависит не только от
координат, но и от времени и, следовательно, будет
нестационарной. Стационарные потенциальные силы
называют консервачивными. Системы, в которых дей-
действуют только консервативные силы, также называют
консервативными.
Отметим, что в соответствии с C.1) силу, дей-
действующую на частицу с номером а, можно предста-
представить в виде градиента функции C.2):
F«--V«tf(*,, О1)- C.3)
Здесь Va — оператор, компоненты которого равны
частным производным по координатам a-й частицы.
Формулу C.3) можно записать также следующим об-
образом:
где ra — радиус-вектор частицы 2).
Пусть часть сил, действующих на частицы систе-
системы, потенциальна, а часть — непотенциальна. Тогда
уравнению B.1) можно придать вид
тА^-^ + Ъ (/=1, 2, ..., и), C.5)
где F] — компоненты непотенциальных сил, п — утро-
утроенное число частиц.
Уравнение C.5) можно написать в форме, очень
удобной для обобщений. С этой целью вводится в рас-
рассмотрение упоминавшаяся в § 1 функция Лагранжа,
которая для рассматриваемой нами системы частиц
*) Через х/ в символах функций мы будем обозначать сово-
совокупность всех координат: хи хг, ..., х„.
2) Под производной скаляра <р по вектору а понимают век-
вектор с компонентами д<р/дах, ду/да^, ду/даг. Следовательно, сим-
символ ду/дт означает вектор с компонентами: ду/дх9 дф/ду, ду/дг
(т.е. grad<p или V<p; см. Приложение XI).

§ 3. УРАВНЕНИЯ ДВИЖЕНИЯ В ДЕКАРТОВОЙ ФОРМЕ 15
определяется следующим образом:
Продифференцировав по времени частную производ-
производную от L по *,, получим левую часть уравнения C.5):
d dL d
Частная производная от L по х* дает /-ю компоненту
потенциальной силы:
dL _ dU
Следовательно, мы приходим к соотношениям
которые носят название уравнений Лагранжа.
Для систем, в которых действуют только потен-
потенциальные силы, уравнения Лагранжа имеют вид
4^~Д- = ° (' = 1. 2,...,«). C.8)
В некоторых случаях уравнения Лагранжа можно
представить в форме C.8) даже тогда, когда силы,
действующие на частицы, зависят от скоростей (при-
(примером таких сил служит сила Лоренца). Это удается
сделать при условии, что такие силы можно получить
из некоторой функции U* (xt, xit t) с помощью соотно-
соотношения
(проверку этого утверждения предоставляем чита-
читателю) .
Функцию if* (xif ?i, t) называют обобщенным потен-
потенциалом. Силы, отвечающие этому потенциалу, мы бу-
будем называть обобщенно-потенциальными. При нали-
наличии таких сил функция Лагранжа записывается сле-
следующим образом:
L (xl9 ku t) = ? -^ - U (xh t) - U* (*ь *ь 0-

IS ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
К числу сил, зависящих от скоростей частиц, отно-
относятся и так называемые диссипативные силы. Этим
термином обозначают силы, всегда направленные про-
противоположно скоростям частиц и, следовательно, вы-
вызывающие их торможение. К числу диссипативных сил
относятся, например, силы трения. При наличии дис-
диссипативных сил полная механическая энергия систе-
системы уменьшается (рассеивается1)), переходя в другие
немеханические формы энергии (например, во внут-
внутреннюю энергию тел).
Во многих случаях диссипативные силы F(d> бы-
бывают пропорциональными скоростям частиц, так что
их компоненты по координатным осям определяются
равенством
Ff=-kixi (/=1,2, ...9п). C.11)
В этом случае диссипативные силы могут быть выра-
выражены через диссипативную функцию Рэлея2), равную
?- C.12)
i
Действительно, сопоставив выражения C.11) и C.12),
легко получить, что
*Р—Щ' <злз>
Подставив это выражение в формулу C.7) вместо F\
предполагая, что других непотенциальных сил нет, по-
получим уравнение
4t-?r+f=°- <314>
Функция D имеет простой физический смысл. Ра-
Работа, совершаемая диссзшативными силами за вре-
время dt, равна
йА=Е *ф dXi - Z F*)jti dt=- Е !f*<rf/= ~2Z> dt
(мы воспользовались теоремой Эйлера об однородных
функциях; см. Приложение II). Эта работа совер-
'¦!
Слово диссипация (лат.) означает рассеяние.
Обычно эту функцию обозначают буквой F или R. Однако
во избежание путаницы мы предпочли обозначение D.

§ 4. УРАВНЕНИЯ ЛАГРАНЖА В ОБОБЩЕННЫХ КООРДИНАТАХ 17
шается за счет запаса энергии системы. Следователь-
Следовательно, величина —dA/dt = 2D дает скорость рассеяния
энергии.
Преимущество уравнений Лагранжа перед уравне-
уравнениями Ньютона C.5) заключается в том, что они, как
будет показано в следующем параграфе, остаются
теми же по форме при переходе от декартовых к лю-
любым обобщенным координатам. При переходе же к не-
независимым обобщенным координатам из уравнений
выпадают реакции идеальных голономных связей, что
сильно облегчает решение задач.
§ 4. Уравнения Лагранжа
в обобщенных координатах
Обобщенными координатами qk называются лю-
любые величины (длины, углы, площади и т. д.), кото-
которые определяют положение механической системы в
пространстве. В качестве примера можно указать на
сферические координаты частицы: г, О, <р. Очевидно,
что декартовы координаты представляют собой част-
частный случай обобщенных координат.
Производные по времени от обобщенных коорди-
координат, т. е. величины qk называются обобщенными ско-
скоростями системы.
Число независимых обобщенных координат, необ-
необходимых для задания положения системы, равно числу
ее степеней свободы. В дальнейшем мы всегда будем
выбирать обобщенные координаты так, чтобы их число
совпадало с числом степеней свободы системы (т. е.
чтобы все они были независимы друг от друга).
Отметим, что обобщенные координаты часто бы-
бывают полезными и в системах без связей (в этом слу-
случае их число совпадает с числом декартовых коорди-
координат). Так, при решении задачи о движении частицы
в центральном поле сил сферические координаты г,
#, <р более удобны, чем декартовы координаты х, у, z.
Весьма полезным оказывается следующее пред-
представление. Введем в рассмотрение систему координат
в воображаемом 5-мерном пространстве (его назы-
называют конфигурационным пространством или <7*ПР°"
странством). По осям этой системы будем отклады-
откладывать значения координат <?*@- Тогда для каждого
момента времени t положению системы в обычном

18 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
пространстве будет соответствовать точка в конфигу-
конфигурационном пространстве. Движению системы в реаль-
реальном трехмерном пространстве будет соответствовать
движение точки в воображаемом s-мерном про-
пространстве.
Докажем, что уравнения C.7) остаются справед-
справедливыми при переходе от декартовых координат xi
к обобщенным координатам q^ а также что в урав-
уравнения Лагранжа, написанные в независимых обоб-
обобщенных координатах, реакции связей не входят.
Рассмотрим голономную систему с идеальными
стационарными связями. Разделим непотенциальные
силы, действующие на частицы системы, на две кате-
категории: реакции связей /?* и прочие непотенциальные
силы F*r Тогда уравнения C.7) будут выглядеть сле-
следующим образом:
-&Щ-Щ-** + * <*-1.2....,п). D.1)
Пусть на систему наложены г связей, выражаемых
условиями
М*ь*2, ...,*л) = 0 (/=1,2, ...,г) D.2)
(поскольку связи стационарны, в функции ft время
явно не входит).
Декартовы координаты лс,-, определяющие положе-
положение частиц системы, могут быть представлены как
функции обобщенных координат q^ Если время t не
входит явно в уравнения связей, всегда можно вы-
выбрать Ць так, чтобы / не вошло и в функции» выра-
выражающие Xi через </*, т. е. чтобы эти функции имели
вид
Xi = Xi(qu цъ ..., qs) (i=l, 2, ..., п) D.3)
(s — число степеней свободы, равное п — г). В даль-
дальнейшем для сокращения записей выражения типа
*/(<7ь<72, . ., qs) мы будем записывать в виде *i(<7*).
В соответствии с D.3) производные функций xL{qk)
по времени имеют вид
?&> D-4>

§ 4. УРАВНЕНИЯ ЛАГРАНЖА В ОБОБЩЕННЫХ КООРДИНАТАХ 19
Суммирование производится по всем qk, т. е. индекс k
пробегает все значения от 1 до s. Выражение D.4)
может быть написано для любого i от 1 до п. В даль-
дальнейшем, когда это не сможет привести к недоразуме-
недоразумениям, мы не будем указывать значения, пробегаемые
индексом, по которому производится суммирование.
Этот индекс называется немым. Отметим, что в фор-
формулах суммирования немой индекс может обозна-
обозначаться любой буквой — замена одного индекса другим
не изменяет суммы. В частности, выражение D.4) мо-
может быть с таким же успехом записано, например,
в виде
Величины dxi/dqk не содержат обобщенных скоро-
скоростей qk. Поэтому на основании D.4) можно утверж-
утверждать, что
Отметим также, что поскольку функции D.3) не со-
содержат величин дь, частные производные от xi по этим
величинам равны нулю:
=»•
Наконец, получим еще одно соотношение, которое
нам понадобится в дальнейшем. Величины dxi/dqk
суть функции только координат qk (скоростей qu эти
величины, как уже отмечалось, не содержат). По-
Поэтому
d дх{ y1 д (dxi
L
Теперь продифференцируем выражение D.5) по q^
Поскольку производные &qifdqk равны нулю, получим
dqk

20 гл. i. вариационный принцип в механике
Сопоставив это выражение с D.8), придем к соотно-
соотношению
dqk ~ dt dqk *
Получив все необходимые соотношения, приступим
к доказательству. Умножив обе части каждого из
уравнений D.1) на dxi/dqk и сложив все уравнения
вместе, получим
dL \ dxt ^ dL dxt
2
Y» / d dL \ dxt ^ dL dxt
2-r \di 1*1) Iq^~~ 2л dxi ^
e+Z':
Первая из сумм в правой части этого выражения
равна нулю. Чтобы доказать это, умножим ее на dqk*
Здесь dxi — приращения декартовых координат, воз-
возникающие в том случае, когда qk получает прираще-
приращение dq^ остальные же обобщенные координаты оста-
остаются неизменными. Однако согласно B.7) сумма
2 Ri dxi для любых dxtf совместимых со связями,
t
равна нулю (напомним, что мы предполагаем связи
стационарными и идеальными). Таким образом,
и, поскольку dqk Ф 0, мы приходим к выводу, что
?«,%_„. D11)
Величину
(см. второе слагаемое в правой части уравнения
D.10)) называют обобщенной силой. Основанием для

§ 4. УРАВНЕНИЯ ЛАГРАНЖА В ОБОБЩЕННЫХ КООРДИНАТАХ 21
такого названия служит то обстоятельство, что выра-
выражение
дает работу, совершаемую силами F\ при перемеще-
перемещениях частиц, обусловленных увеличением обобщенной
координаты <7* на dqk.
Таким образом, правая часть уравнения D.10) есть
просто Q*k. Рассмотрим теперь левую часть этого
уравнения. Прибавим к уменьшаемому и вычитаемому
E3L дх?
-тр-у*-. Тогда слева в D.10)
i * k
будет стоять разность выражений
дх. dq. + L дх, dqk '
Последнее выражение представляет собой производ-
производную функции Лагранжа по обобщенной координа-
координате qk: dLfdqk.
Выражение D.13) можно с учетом D.9) записать
в виде
d dL \ dxt « dL / d dx{ \ d ^ dL dx§
)+2J
Наконец, произведя замену dxi/dqk в соответствии
с D.6), придем к выражению
d ^> dL dxt
которое есть не что иное, как -л- -jt- - Действительно,
по правилам дифференцирования сложной функции
dL хтл dL дх.

22 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
но согласно D.7) все dxi/dqk равны нулю, так что
первая из сумм дает нуль. Таким образом, мы пока-
показали, что выражение D.13) равно -jf-jp"-.
Итак, разность выражений D.13) и D.14) есть
просто -п--^ -з— - Подставив это значение в D,10),
r dt dqk dqk
придем к уравнениям
-ZfWk-wrQ* (k = 1'2 s)' DЛ5)
которые отличаются от уравнений D.1) тем, что вме-
вместо декартовых координат xi в них входят обобщен-
обобщенные координаты qk, а вместо сил F* — обобщенные
силы Q\. Реакции связей Rt в уравнения D.15) не
входят.
Если все силы, действующие на частицы системы
(кроме реакций связей), потенциальны, уравнения
D.15) имеют вид
d dL dL
wwk-Wk=0 (*=1'2 s)- D16)
Уравнения D.15) и D.16) суть уравнения Лагран-
жа в обобщенных координатах. Фигурирующая в них
функция L = L(qu q2, ..., qs, qu fo qs) есть функ-
функция, получающаяся из (S.6) путем замены величин Xi
и xi функциями D.3) и D.4).
Можно показать (см. Приложение I), что уравне-
уравнения D.15) и D.16) остаются справедливыми и для го-
лоиомных систем с идеальными нестационарными
связями.
Итак, мы доказали, что уравнения Лагранжа
имеют одинаковый вид как в декартовых, так и в об-
обобщенных координатах.
Из выражения C.6) для функции Лагранжа в де-
декартовых координатах вытекает, что производная L
по it равна pi — проекции импульса соответствующей
частицы на одну из координатных осей:
_ = т^ =Рь D.17)

§ 4. УРАВНЕНИЯ ЛАГРАНЖА В ОБОБЩЕННЫХ КООРДИНАТАХ 23
а производная L по xt равна Ft — проекции потенци-
потенциальной силы» действующей на частицу:
dxt
По аналогии с D.17) и D.18) величину
p
<419>
называют обобщенным импульсом, а величину
ъ-Ц-; <420>
— обобщенной силой.
С использованием этих величин уравнения D.16)
могут быть представлены в виде
D.21)
аналогичном уравнениям Ньютона
dpi р
4T = F
Отметим, что определение D.20) является более
общим, чем определение D.12), введенное нами для
непотенциальных сил. Если бы мы распространили
определение D.12) на потенциальные силы, т. е. силы,
которые могут быть представлены в виде Т7,—
— —dU/dxu то пришли бы к выражению
Согласно же определению D.20)
a 0L _ dJL-чо дт ди
Выражение D.23) отличается от D.22) слагаемым
dT/dqk, которое, как будет показано в следующем па-
параграфе, вообще говоря, отлично от нуля (см. фор-
формулу E.9)).

24 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
§ 5» Функция Лаграяжа и энергия
Функция Лагранжа ?(?*, ?*, f) есть характеристи-
характеристическая функция механической системы. Естественно,
что через эту функцию могут быть выражены не
только импульсы и силы (см. формулы D.19) и
D.20)), ко также и энергия системы.
Выражение полной энергии системы через функ-
функцию Лагранжа имеет вид
ZI^^/)- EЛ)
Основания для того, чтобы определить ? именно та-
таким образом, выяснятся ниже. Выражение E.1) яв-
является более общим, чем известное из курса общей
физики выражение
E^T + U. E.2)
Определение E.1) остается пригодным и в том слу-
случае, когда полная энергия не может быть представ-
представлена в виде суммы кинетической и потенциальной
энергий.
Вычислим полную производную по времени от ве-
величины E.1):
dE _ 5Г* j3L_ - i Y1 • d dL — V dL •
dt — L* dqk 4* "Г JL qk dt dqk jL dqk 4k ~
dqk4k dt 2
В соответствии с уравнением Лагранжа D.15) выра-
выражение в скобках равно непотенциальной обобщенной
силе Q*k. Следовательно,
к
где W* — мощность всех непотенциальных сил, дей-
действующих на частицы системы.
В случае, когда функция Лагранжа не содержит
явно времени, dL/dt — O и формула E.3) переходит
в coot шение
dt ~w 9
д>е из курса общей физики.

§ б. ФУНКЦИЯ ЛАГРАНЖА И ЭНЕРГИЯ 26
Как следует из E.3), для того, чтобы имело место
сохранение полной энергии системы, недостаточно от-
отсутствия непотенциальных сил. Кроме того, нужно
еще, чтобы время не входило явно в функцию Лаг-
ранжа, т. е. чтобы система была консервативной.
Итак, мы выяснили, что для замкнутой системы, в ко-
которой действуют только консервативные силы, вели-
величина, определяемая формулой E.1), остается посто-
постоянной. Это и послужило основанием для того, чтобы
назвать величину E.1) полной энергией системы,
В механике функции величин qk и q^ сохраняю-
сохраняющие при движении системы постоянное значение, опре-
определяемое начальными условиями, называют интегра-
интегралами движения. Следовательно, можно сказать, что
энергия консервативной замкнутой системы является
интегралом движения.
Найдем условия, при которых определение E.1)
переходит в E.2). С этой целью исследуем выраже-
выражение Т в обобщенных координатах. Связи будем счи-
считать голономными. Выразим декартовы координаты Xi
частиц системы через обобщенные координаты q^
Xi = Xi(ql9 q2, ..., qs, i) (/=1, 2, ..., n). E.4)
Отметим, что время будет входить явно в эти соотно-
соотношения только в случае нестационарных связей.
Найдем полные производные функций xi по вре-
времени. Поскольку величины qk суть функции от t, ис-
искомые производные имеют вид
dx. дх, х-ъ дх,
ь-тг—эг + Ъ-щЬ (f==1'2 nY
Подставим эти выражения в формулу для кинетиче-
кинетической энергии:

26 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
В соответствии с E.4) выражения dxi/dt и /q
суть функции от qk и t, величины qk в них не входят.
Следовательно, первая из сумм в формуле E.5) есть
также функция от qk и t. Обозначив эту функцию
буквой а, напишем
Изменив во второй из сумм в формуле E.5) поря-
порядок суммирования по i и k, приведем ее к виду
Q ъ 3 ж Tf%t ' " " " '
1 tm^ dt Qfl,
где
i
Наконец, представив один из множителей в третьей
сумме в формуле E.5) в виде У-—-^, а другой
множитель — в виде V -^-qi, а затем, изменив по-
l
рядок суммирования по /, k и /, запишем третью сумму
так:
дх, «г* дх,
L^
где
Итак, выражение кинетической энергии можно
представить в виде
Г . а (^, 0
В случае стационарных связей / не входит явно
в функции E.4). Поэтому dx{/dt = O, так что коэффи-

§ 5. ФУНКЦИЯ ЛАГРАНЖА И ЭНЕРГИЯ 27
циенты а(<7/, t) и |М<7/» t) превращаются в нуль. В ко-
коэффициенты yki в этом случае время не входит явно.
В итоге
Г=?уы(<7/)<М/. E.10)
Таким образом, для системы со стационарными
связями кинетическая энергия есть однородная квад-
квадратичная функция обобщенных скоростей qk-
В § 3 мы выяснили, что для системы частиц функ-
функция Лагранжа в декартовых координатах имеет вид
L(xi9±i9 0-
i
При переходе от декартовых к обобщенным коорди-
координатам первый член написанного уравнения превратит-
превратится, вообще говоря, в выражение E.9). Если же огра-
ограничиться рассмотрением стационарных связей, пер-
первый член нужно заменить выражением E.10). Второй
член примет вид U(q^ t). В случае стационарных свя-
связей время будет входить явно в U при условии, что
потенциальные силы нестационарны.
Итак, в случае стационарных связей функция Лаг-
Лагранжа системы частиц, написанная в обобщенных ко-
координатах, выглядит так:
L (Яь <fk, t) = T (qk, qk) - U {qk9 /),
где Т определяется формулой E.10). Подставив это
выражение в формулу E.1), получим
f). E.11)
В соответствии с E.10) Т есть однородная квадратич-
квадратичная функция величин q^. Следовательно, для нее со-
согласно теореме Эйлера (см. Приложение II) справед-
справедливо соотношение
Произведя такую замену в E.11), придем к формуле
Е о. 2Г - Т + U = Т (дк, <jfc) + U (</*, /).

28 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
Эта формула была получена при одном лишь предпо-
предположении, что связи стационарны. Если, кроме того, и
потенциальные силы будут стационарными, потенциал
U{<!kft) превратится в потенциальную энергию U(qk)
и формула E.1) перейдет в E.2).
Итак, определение E.1) совпадает с E.2) в слу-
случае, когда и связи, и потенциальные силы стацио-
стационарны.
§ 6. Примеры на составление
уравнений Лагранжа
Выбрав независимые обобщенные координаты,
удобные для описания рассматриваемой системы,
нужно установить вид функций
*i = *i (<Ik, О и xt = xt (qk, qky t)
и подставить их вместо величин xt и xi в выражение
для функции Лагранжа
L = Г(*,)-?/(**, *> = ?¦?¦**-U(xt, t).
i
В результате получится функция Лагранжа в обоб-
обобщенных координатах:
L = L(qk, qk, t) = T(qk, qk, t) - U(qk, t).
Если в получившемся выражении для L окажутся
слагаемые, не зависящие от qk и #*, эти слагаемые
можно отбросить, так как они не внесут вклада в ве-
величины dL/dqk и dL/dqk и, следовательно, не окажут
влияния на вид уравнений Лагранжа.
Иногда операцию нахождения функции T(qk,qk,t)
удается сильно упростить. Это бывает возможно в тех
случаях, когда легко устанавливается связь между
элементарным перемещением частицы ds и прираще-
приращениями обобщенных координат qk. Так, например, в по-
полярных координатах на плоскости (рис. 6.1) переме-
перемещение ds является диагональю прямоугольника, по-
построенного на сторонах dr и rdq> (нужно помнить
о малости d(p). Следовательно, ds2 = dr2 + r2dq>2. Раз-
Разделив эту величину на dt2, получим квадрат скорости
частицы: v2 = г2 + г2ф2. Наконец,
T = \tnv2 = ±rm{r2 + г2ф2). F.1)

§ б. ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИИ ЛАГРАНЖА 29
В случае цилиндрических координат к предыдущим
двум (г и ф) добавляется третья координата z. Пере-
Перемещение ds является диагональю прямоугольного па-
параллелепипеда со сторонами drt rdq> и dz. Следова-
Следовательно,
Г = }т(г2 + г2ф2 + z2). F.2)
Приращениям полярных координат г, д, ф соответ-
соответствуют три взаимно перпендикулярных отрезка
(рис. 6.2) с длинами dr, drfr,
г sin ftdq> (последний отре-
/•sin#
Рис. 6.1
Рис. 6.2
зок направлен за чертеж1)). Перемещение ds со-
совпадает с диагональю прямоугольного параллелепи-
параллелепипеда, построенного на этих отрезках. В итоге
F.3)
\
Т = \ m Vя + r2h2 + г2 sin2
Рассмотрим несколько примеров.
1. Математический маятник (см. рис. 1.1). Переме-
Перемещение частицы m равно ds = /dcp. Поэтому Т =
= l/2ml2^2. Потенциальная энергия U =— mgl cos ф.
Следовательно, функция Лагранжа имеет вид
L = ЧътРцр + mgl cos ф.
Предоставляем читателю написать уравнение Лаг-
Лагранжа и убедиться в том, что оно совпадает с урав-
уравнением ( 1.1).
*) Отрезки, перпендикулярные к плоскости чертежа, мы бу-
будем изображать кружком с точкой, если отрезок направлен на
нас, и кружком с крестиком, если отрезок направлен на чертеж.

30 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
Найдем обобщенный импульс и обобщенную силу.
Согласно формуле DЛ9)
Таким образом, в данном случае обобщенный импульс
совпадает с моментом обычного импульса mv относи-
относительно точки подвеса маятника.
Согласно формуле D.20)
что есть момент N силы mg относительно точки под-
подвеса. Заметим, что элементарная работа равна
Последнее выражение совпадает с выражением для
работы при вращательном движении, известным из
элементарной механики.
Наконец, найдем энергию маятника по формуле
E.1) (в данном случае это можно сделать, так как
связь стационарна):
Е = -^ф-ф — L = т/2ф2 — у тРф2 — mgl cos <p =
= у т (/фJ — mgl cos <p,
2. Маятник с равномерно движущейся точкой под-
подвеса. Пусть точка подвеса математического маятника
движется в горизонтальном направлении с постоянной
скоростью v, лежащей в плоскости качаний маятника
(рис. 6.3). Уравнение связи имеет вид
f(xt у, t) = (x-vtJ + y2-P = 0
(связь не стационарна).
Из выражений для декартовых координат
х = / sin ф + vt, y = l cos ф
следует, что
jc ===== / cos ф • ф + v, у = — I sin ф • ф.
Отсюда
Т = V2m (/V + 2vt cos ф • ф + v2).
Потенциальная энергия U-— mgy = — mgl cos у.

§ 6. ПРИМЕРЫ НА СОСТАВЛЕНИЕ УРАВНЕНИИ ЛАГРАНЖА 31
При составлении функции Лагранжа постоянно
слагаемое xkmv2 можно отбросить. Следовательно,
L = -J (Рф2 + 2vl cos ф • ф) + mgl cos q>.
Несмотря на нестационарность связи, время не вошло
явно в функцию L.
Нахождение уравнения Лагранжа в этом и сле-
следующих примерах предоставляем читателю.
у-
Рис. 6.3
Рис. 6.4
3. Маятник с точкой подвеса, движущейся с по-
постоянным ускорением. Рассмотрим математический
маятник, точка подвеса которого движется вдоль пря-
прямой, наклоненной к горизонту под углом а, с посто-
постоянным ускорением а (рис. 6.4). Координаты точки
подвеса равны
acosat29 yn = ^asina-12,
а координаты точки т:
х = у a cos а • t2 + / sin ф, у = у а sin а • t2 + I cos ф«
Продифференцируем л: и у по /:
х = a cos а • t + / cos ф • ф, у = а sin а • t — Z sin ф • ф.
Подставив эти значения х и у в выражение для кине-
кинетической энергии, получим
Т — у та2/2 + та/ (cosacos ф — sin a sin ф) ф/ + -^ /

32
ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
Потенциальная энергия равна
U = — mgy — — mg (Чъа sin a • t2 + / cos ф).
При написании выражения для функции Лагранжа
можно опустить слагаемые х/2таЧ2 в Г и
—х h^ttga sin а-/2 в ?/, так как эти слагаемые не со-
содержат ф и ф, вследствие чего не могут повлиять на
вид уравнений Лагранжа. В результате найдем, что
L — mat (cos a cos ф — sin a sin ф) ф/ -f Ч^пгРу2 + mg/созф.
Рис. 6.5
Функция Лагранжа зависит явно от t (это обуслов-
обусловлено нестационарностью связи), причем время вошло
в L через кинетическую энер-
энергию Т.
4. Частица, перемещающая-
перемещающаяся по равномерно вращающей-
вращающейся прямой. Пусть на частицу
массы т наложена нестацио-
нестационарная связь, заключающая-
заключающаяся в том, что частица может
двигаться только вдоль пря-
прямой, вращающейся с постоян-
постоянной угловой скоростью (ф =
= со/) в вертикальной плоско-
плоскости (рис. 6.5). Кроме реакции связи, на частицу дей-
действует потенциальная сила mg. Декартовы коорди-
координаты частицы равны
х = г cos со/, у = г sin со/.
Соответственно
х = г cos ш/ — г© sin <о/, у = г sin со/ + по cos ш/.
Кинетическая энергия:
mgr sin со/
Потенциальная энергия:
U = mgy
(когда мы перешли от декартовых координат к обоб-
обобщенной координате г, в выражение для U вошло явно
время /).
Наконец, функция Лагранжа:
L я= y т (г2 + rW) — mgr sin ®t.

§ 7. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ 33
Она оказалась зависящей явно от t9 причем на этот
раз время вошло в L через потенциальную энергию ?Л
Обобщенный импульс:
дЬ
где v — скорость перемещения частицы по прямой.
Обобщенная сила:
Qr = -— = mm? — mg sin ю/
состоит из двух слагаемых, из которых первое mm2
есть центробежная сила инерции, а второе —
mg sin ®t — проекция силы mg на направление г.
5. Частица, перемещающаяся по прямой, вращаю-
вращающейся с ускорением. Пусть прямая, обусловливающая
связь (см. рис. 6.5), вращается не равномерно, а с
ускорением (ф==с^2). Тогда
х — г cos а/2, у — г sin а/2,
х == г cos at2 — r2oi sin at2,
у = f sin a^2 -f-
(/ = tngy = mgr sin a/2.
Соответственно
L = V2m (r2 + r24a2r2) — mgr sin at2.
В этом примере время вошло явно в L и через Г,
и через U.
§ 7, Принцип наименьшего действия ')
В основу механики вместо законов Ньютона мо-
может быть положен принцип наименьшего действии
или принцип Гамильтона2). Действием S за проме-
промежуток времени от i\ до i% называется интеграл
и
S-$I(<fc,*bO<«. G.1)
и
где L(?«, 9*»0 —ФУП]ВДИЯ Лагранжа рассматриваемой
*) Прежде чем приступить к изучению этого параграфа, сле-
следует ознакомиться с Приложением III.
2) Этот принцип был установлен ирландским математиком
Гамильтоном в 1834 г.
2 И. В. Савельев, т. !

34 ГЛ. I. ВАРИАЦИОННЫЙ ПРИНЦИП В МЕХАНИКЕ
системы. Интегрирование производится от момента
времени tu в который положение системы характери-
характеризуется значениями координат qk(t\)> до момента U>
в который положение системы определяется значения-
значениями координат Qk{i%\.
Согласно принципу наименьшего действия система
между положениями quih) и Цк{$ъ) движется таким
образом (т. е. функции quit) имеют такой вид), что
действие G.1) имеет наименьшее возможное значе-
значение. Воспользовавшись представлением о конфигура-
конфигурационном пространстве, можно сказать, что точка, изо-
изображающая положение системы, движется в этом
пространстве по той кривой, мя которой действие S
минимально.
Принцип Гамильтона представляет собой наиболее
общую формулировку закона движения механических
систем. Достоинство этой формулировки состоит в
том, что ее можно легко распространить на системы,
не являющиеся чисто механическими, например на
упругие среды, электромагнитные поля и т. п.
Как следует из G.1), размерность действия равна
размерности произведения энергии на время (или им-
импульса на перемещение). Такой же размерностью об-
обладает постоянная Планка, которую называют также
квантом действия.
Из принципа наименьшего действия легко полу-
получить уравнения Лагранжа. Действие S представляет
собой функционал (см. Приложение III). Согласно по-
положениям вариационного исчисления функционал до-
достигает экстремального значения при условии, что его
вариация равна нулю. Следовательно, принцип наи-
наименьшего действия можно выразить условием
и
Ь$ = 6 J L (qk9 qkf i) dt = 0. G.2)
По этой причине принцип наименьшего действия на-
называют вариационным принципом механики.
Из вариационного исчисления известно (см. При-
Приложение III), что вариация функционала типа G.1) *)
*) Ср. с A11.20). В данном случае роль f {х, yk, #?) играет
L (i, qk, <jk). Роль независимой переменной х играет tt роль у* (х)
играет ф*@ и роль у% (х) — функция qk(t).

§ 7. ПРИНЦИП НАИМЕНЬШЕГО ДЕЙСТВИЯ 35
обращается в нуль, если в качестве q^(i) взять функ-
функции, удовлетворяющие уравнениям Эйлера (III. 25).
В данном случае уравнения Эйлера имеют вид
"?^^8 (&=1, 2, ...,$), G.3)
т. е. совпадают с уравнениями Лагранжа.
Таким образом, мы убедились в том, что принцип
Гамильтона приводит к уравнениям Лагранжа,
В Приложении III было показано (см. текст, сле-
следующий за формулой (III. 19)), что прибавление в
G.2) к подынтегральной функции полной производной
по t от любой функции обобщенных координат и вре-
времени не изменяет условий экстремума, т. е. уравнений
G.3). Следовательно, функцию Лагранжа следует
определять с точностью до аддитивных слагаемых,
представляющих собой полную производную по вре-
времени от произвольной функции обобщенных коорди-
координат и времени (константа является частным случаем
такой функций). Зто обстоятельство нами уже отме-
отмечалось в § 4 и было использовано в § 6,

Глава II
ЗАКОНЫ СОХРАНЕНИЯ
§ 8. Сохранение энергии
В основе законов сохранения, рассматриваемых
в механике, лежат свойства пространства и времени.
Сохранение энергии связано с однородностью време-
времени, сохранение импульса — с однородностью простран-
пространства и, наконец, сохранение момента импульса нахо-
находится в связи с изотропией пространства *).
Начнем с закона сохранения энергии. Пусть си-
система частиц находится в неизменных внешних усло-
условиях (это имеет место, если система замкнута либо
подвержена воздействию постоянного внешнего сило-
силового поля); связи (если они есть) идеальны и стацио-
стационарны. В этом случае время в силу своей однородно-
однородности не может входить явно в функцию Лагранжа. Дей-
Действительно, однородность означает равнозначность
всех моментов времени. Поэтому замена одного мо-
момента времени другим без изменения значений коор-
координат и скоростей частиц не должна изменять меха-
механические свойства системы. Это, конечно, справедливо
лишь в том случае, если замена одного момента вре-
времени другим не изменяет условий, в которых нахо-
находится система, т. е. в случае независимости от времени
*) Однородность означает одинаковость свойств но всех точ-
точках. Изотропия означает одинаковость свойств в каждой точке
по всем направлениям. Однородность н изотропия независимы
друг от друга. Среда может иметь разные свойства в разных
точках, причем в каждой точке свойства будут иными, чем в
других точках, но одинаковыми по всем направлениям. Такая
среда будет неоднородной, но изотропной. Возможна среда, свой-
свойства которой одинаковы во всех точках, ко различны (одинако-
(одинаковым образом во всех точках) по разным направлениям. Такая
среда будет однородной, но анизотропной. Разумеется, возможны
среды однородные и изотропные» а также неоднородные и ани-
анизотропные.

§ 9. СОХРАНЕНИЕ ИМПУЛЬСА 37
внешнего поля (в частности, это поле может отсут-
отсутствовать) .
Итак, для замкнутой системы или системы, нахо-
находящейся в стационарном силовом поле, dL/dt = Q.
Следовательно,
dL Y1 dL A r V dL z /on
Lq^^kq^ (8Л)
Если система консервативна, движение частиц под-
подчиняется уравнениям D.16). Заменим в соответствии
dL d dL ^
с этими уравнениями «?— через -^ гр-. Тогда выра-
выражению (8.1) можно придать вид
dL y* d ( &L \ • j V dL d • d V dL °
Последнее соотношение можно записать следующим
образом:
d V dL - dL — d /V dL • /
1FZjJ^qk~~~dF~ dt уЬ~дГкЯк~
Согласно формуле E.1) величина, стоящая в скобках,
есть энергия системы ?. Таким образом, мы пришли
к утверждению, что dE/di — 0, откуда
Е — const. (8.2)
Итак из однородности времени вытекает закон:
энергия замкнутой (или находящейся в стационарном
внешнем силовом поле) консервативной системы час-
частиц остается постоянной.
Из определения E.1) следует, что Е есть функция
обобщенных координат qk и обобщенных скоростей ф*.
Как мы уже отмечали, функции величин q* и цн> со-
сохраняющие при движении постоянное значение, опре-
определяемое начальными условиями, называют интегра-
интегралами движения. Таким образом, энергия замкнутой
системы является интегралом движения.
§ 9. Сожранение имнульса
Рассмотрим замкнутую систему частиц. Замкну-
Замкнутость означает, что воздействие внешних тел на час-
частицы системы пренебрежимо мало. В силу однородно-

дВ ГЛ. П. ЗАКОНЫ СОХРАНЕНИЯ
сти пространства перемещение всех частиц системы
на одинаковый отрезок 6г не должно изменить меха-
механические свойства системы — функция Лагракжа
должна сохранить свое прежнее значение. Для неза-
незамкнутой системы такой перенос вызвал бы изменение
расположения частиц по отношению к взаимодей-
взаимодействующим с ними телам, что отразилось бы на меха-
механических свойствах системы. Таким образом, только
для замкнутой системы частиц можно утверждать, что
параллельный перенос системы как целого не сопро-
сопровождается изменением функции L(SL = 0).
Полагая перемещение бг очень малым, можно на-
написать
{а — номер частицы). Мы воспользовались тем об-
обстоятельством, что перемещения частиц бга одинако-
одинаковы и равны 6г.
По предположению 8г^0. Поэтому из (9.1) выте-
вытекает, что
Е-§^ет0- <9-2>
В соответствии с уравнениями Лагранжа C.8) можно
написать
dL _^_ d dL d jdL
dx7~~f dxa~~di"dv^9
dL d dL d dL
dya dt dya dt dvay *
dL d dL d dL
dza ~ dt dta ~ dt dvaz *
Умножив первое из этих уравнений на орте*, второе
на орте^, третье на орте*2) и сложив их вместе, по-
получим соотношение
1^?
дга ~ dt dva *
J) Си. подстрочное примечание на стр. 14. В соответствии
со асазаккым в этом примечании
-~21 dt«: --Х. dx + -r^- d и + -— dz.
dr dx ^ dy * ^ dz
2) Вместо символов i, j, k мы будем обозначать орты коор-
координатных осей символом е с соответствующим индексом.

§ 10. СОХРАНЕНИЕ МОМЕНТА ИМПУЛЬСА 39
Таким образом, уравнению (9.2) можно придать вид
а
Величина -^— есть вектор с компонентами ^— ==»
JJL dL — dL dL — dL Согласии (А \7
произведения суть проекции на координатные оси
обычного (не обобщенного) импульса ра частицы с
номером а. Следовательно,
С учетом этого обстоятельства уравнение (9.4) запи-
запишется следующим образом:
d
а
Отсюда вытекает, что
P=Efla==8«>nsti (9.6)
a
где р — суммарный импульс системы.
Итак, исходя из однородности пространства, мы
пришли к закону: суммарный импульс замкнутой си-
системы частиц остается постоянным. Следовательно,
импульс замкнутой системы есть также интеграл дви-
движения.
§ 10. Сохранение момента импульса
Вследствие изотропии пространства механические
свойства замкнутой системы частиц не должны изме-
изменяться при произвольном повороте системы как целого
в пространстве. В соответствии с этим не должна из-
изменяться и функция Лагранжа FL —0). Найдем
приращение функции Лагранжа 6L при произвольном
очень малом повороте системы на угол вф. Вместе
с системой повернутся все векторы, характеризующие
систему, вследствие чего эти векторы получат некото-
некоторые приращения, которые будут того же порядка, что
и бф. Согласно формуле (VI. 48)
бГа = [йф, Гa], 6va = [вф, VJ. (ЮЛ)

40 ГЛ. II. ЗАКОНЫ СОХРАНЕНИЯ
Ввиду малости величин бга и 6v«
(напомним, что L = L(ra, ra)==L(ra> va), время t в L
явно не входит). С учетом (ЮЛ)
Из векторной алгебры известно, что в смешанном
(векторно-скалярном) произведении трех векторов до-
допустима циклическая перестановка сомножителей
(см. формулу (VI. 3)). Произведя такую перестановку
в A0.2), получим
Вынесем Sq> за знак суммы, одновременно заменив
в соответствии с уравнениями Лагранжа (9.3) -^—
d dl Га
через df
По предположению бф ф 0, поэтому условие 6L=0
эквивалентно условию
или
а
Согласно (9.5) -~- есть обычный импульс ра. Ве-
Величина М —[гр] есть момент импульса частицы отно-
относительно начала координат. Следовательно, мы при-
пришли к утверждению, что
М ===== 2 Ма ===== 2) [Гера] == Const, A0.3)
а

§ 10. СОХРАНЕНИЕ МОМЕНТА ИМПУЛЬСА 41
В этом соотношении Ма — момент импульса частицы
с номером а, М — результирующий момент импульса
системы.
Итак, исходя из изотропии пространства, мы при-
пришли к закону: результирующий момент импульса
замкнутой системы частиц остается постоянным. Зна-
Значит, момент импульса замкнутой системы, так же как
ее энергия и импульс, является интегралом движения.
Пусть система частиц находится во внешнем цен-
центральном поле сил, т. е. в таком поле, в котором сила,
действующая ка любую из частиц, имеет направление,
проходящее через одну и ту же неподвижную точку О
(центр поля), а модуль силы зависит только от рас-
расстояния г частицы до этой точки. Потенциальная энер-
энергия частицы в таком поле имеет вид
?/ = ?/(г). A0.4)
Произвольный поворот системы в пространстве во-
вокруг точки О не изменяет механических свойств си-
системы (расположение частиц по отношению к сило-
силовому центру О остается при таком повороте неизмен-
неизменным). Следовательно, хотя в данном случае система
частиц и не является замкнутой, ее момент импульса
будет постоянным. Правда, это справедливо лишь для
момента, взятого относительно точки О. В случае же
замкнутой системы сохраняется момент импульса, взя-
взятый относительно любой точки.
Если внешнее поле обладает осевой симметрией
(это значит, что потенциальная энергия частицы за-
зависит лишь от расстояния частицы до заданной оси),
то механические свойства системы не будут изме-
изменяться при повороте вокруг оси поля. Следовательно,
будет постоянным момент импульса системы относи-
относительно этой оси (напомним, что моментом относи-
относительно оси называется проекция на эту ось момента,
взятого относительно любой из точек оси)„

Глава III
НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
§11. Движение частицы
в центральном поле сил
Рассмотрим движение частицы в центральном поле
вида
tf(r)«7-. (ИЛ)
где а — константа, которая может быть либо положи-
положительной, либо отрицательной. Положительная кон-
константа отвечает случаю отталкивания частицы от си-
силового центра (например, кулоновской силе отталки-
отталкивания), отрицательная константа —случаю притяже-
притяжения частицы к центру (кулоновской силе притяжения
или силе гравитационного взаимодействия данной час-
частицы с неподвижной частицей, помещающейся в цен-
центре коля).
В § 10 мы установили, что в центральном поле
остается постоянным момент импульса частицы:
const.
Векторное произведение перпендикулярно к плоско-
плоскости, в которой лежат перемножаемые векторы. Отсюда
следует, что при неизменном направлении вектора М
вектор г всегда лежит в одной плоскости, перпендику-
перпендикулярной к М, и траектория частицы является плоской
кривой. Будем определять положение частицы с по-
помощью полярных координат г и <р, совместив начало
координат с центром поля. В этих координатах функ-
функция Лзгранжа имеет вид (ем. формулу F.!))
В функцию L не вошла явно координата ср. Обоб-
Обобщенные координаты, не входящие явг.э в функцию

§11. ДВИЖЕНИЕ ЧАСТИЦЫ В ЦЕНТРАЛЬНОМ ПОЛЕ СИЛ 43
Лаграяжа, называются циклическими. В отсутствие
непотенциальных сил уравнения Лагранжа, соответ-
соответствующие циклическим координатам, выглядят сле-
следующим образом:
dt dqk ~~U-
Отсюда
ft=~« const A1.2)
Таким образом, обобщенные импульсы, соответствую-
соответствующие циклическим координатам, оказываются постоян-
постоянными, т. е. являются интегралами движения.
В рассматриваемой нами задаче уравнение A1.2)
имеет вид
рф^||^шг2ф^М^ const A1.3)
Это уравнение можно было написать сразу, учтя, что
тг^щ есть момент импульса частицы относительно на-
начала координат, который должен сохраняться в цен-
центральном поле сил.
Энергия частицы в центральном поле также яв-
является интегралом движения. Поэтому, произведя вы-
вычисления по формуле E.11), можно написать
Е »1 т (г2 + г*ф*) + 7 = const. (! 1.4)
Для нахождения траектории частицы лучше исхо-
исходить из уравнений A1.3) и A1.4), чем из уравнений
Лагранжа. Такой путь проще, так как уравнения Лаг-
Лагранжа содержат вторые производные координат, урав-
уравнения же A1.3) и A1.4) — первые производные коор-
координат по времени.
Исключив из уравнений A1.3) и A1.4) ф, получим
откуда
Из уравнения A1.3)
dy l м
Ф

44 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
Исключив dt из последних двух уравнений, най-
найдем, что
{М/гг) dr
Vn „ , ( am \2
am , М \2
Введя обозначения
№)'-* *+¦?— (-¦?*-*).
можно написать
arccos у + ф0,
где фо — постоянная интегрирования.
Возвращаясь к прежним обозначениям, мы полу-
получим уравнение траектории частицы в полярных коор-
координатах
ат/М + М/г
Ф~юо= arccos ; ¦ =
(ат/МJ
arccos .'H^g^jm. (IL5)
Vl + 2EM2/ma2 K '
Из уравнения A1.5) следует, что при заданной ве-
величине г разность ф — фо может иметь два отличаю-
отличающихся знаком значения (cos(—а) = cos а). Отсюда
легко заключить, что кривая, описываемая уравне-
уравнением AL5), симметрична относительно прямой, обра-
образующей с осью, от которой отсчитывается ф, угол ф0.
Чтобы выяснить характер кривой, описываемой
уравнением A1.5), введем обозначения
-y|j^==P> A1.6)
Vl+2?M2/ma2W. (П.7)
Тогда уравнение траектории примет вид
ф — фо = arccos —
а

§11. ДВИЖЕНИЕ ЧАСТИЦЫ В ЦЕНТРАЛЬНОМ ПОЛЕ СИЛ 45
или, после несложных преобразований,
(верхний знак соответствует случаю отталкивания,
нижний — случаю притяжения частицы к центру сил).
Полученное нами уравнение есть уравнение кони-
конического сечения (см. Приложение IV) с фокальным
параметром р и эксцентриситетом е.
Рассмотрим сначала случай отталкивания (а X)).
В этом случае U > 0, так что полная энергия Е не
может быть отрицательной. Поэтому согласно A1.7)
е> 1. Таким образом, в случае отталкивания траек-
траекторией частицы может быть только гипербола. Взяв
в A1.8) верхний знак (минус), получим уравнение
траектории
— Р
г —
— е cos (ф — ф0)
Значение <р0 определяется выбором начала отсчета <р.
Если угол ф отсчитывать от оси симметрии кривой (от
прямой, проходящей через фокусы), то г не должно
изменяться при изменении знака <р. Это имеет место
лишь при фо = 0 или фо = я. Положив фо = 0, получим
уравнение
Гв= не
! — е cos ф '
совпадающее с уравнением (IV. 14), которое описы-
описывает правую ветвь гиперболы (при условии, что на-
начало координат, т. е. силовой центр, помещено во
внешнем (левом) фокусе гиперболы).
Положив фо = л; и учтя, что соз(ф — я) ——со$ф,
получим уравнение
е cos
совпадающее с уравнением (IV. 13), описывающим
левую ветвь гиперболы (при условии, что начало ко-
координат помещено во внешнем (правом) фокусе ги-
гиперболы; рис. 11.1).
Теперь обратимся к случаю притяжения (а<ГО).
Ему соответствует в формуле A1.8) нижний знак

46 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
(плюс). Следовательно, уравнение траектории имеет
вид
I — е cos ф \ • * /
для фо = О и
ДЛЯ фо я= Я.
Как показано в Приложении IV, оба уравнения
описывают либо эллипс, либо одну из ветвей гипер-
гиперболы, либо параболу (см. уравнения (IV. 11) и
(IV. 12)). С какой из этих кривых мы имеем дело,
определяется значением е.
Рис-ИЛ
В случае притяжения U < 0, следовательно полная
энергия Е может быть как положительной, так и от-
отрицательной, в частности, она может оказаться рав-
равной нулю. Как следует из формулы A1.7), при ?>0
эксцентриситет оказывается больше единицы и траек-
траектория будет гиперболой. Уравнение A1.9) дает пра-
правую ветвь гиперболы, уравнение A1.10) —левую. При
этом, в отличие от случая отталкивания, начало ко-

§ П. ДВИЖЕНИЕ ЧАСТИЦЫ В ЦЕНТРАЛЬНОМ ПОЛЕ СИЛ 47
ординат, т. е. центр сил, помещается во внутреннем
для данной ветви фокусе (рис. 11.2) 1).
При ? = 0 эксцентриситет оказывается равным
единице, и траектория будет параболой. Этот случай
осуществляется, если частица начинает свое движение
из состояния покоя на бесконечности.
f
Е>0, жврболз
Е^О, трпбш
?<Qf шиле
Рис. 11.2
Наконец, при ? < 0 эксцентриситет меньше еди-
единицы, и траектория будет эллипсом. В этом случае
кривые, описываемые уравнениями A1.9) и A1.10),
отличаются положением силового центра. Кривая
A1.9) получается, если центр сил (начало координат)
помещается в левом фокусе эллипса. Кривая A1.10)
соответствует расположению центра сил в правом
фокусе.
4) Сплошные кривые на рис. 11.2 изображены для одного
и того же значения момента импульса М, а следовательно, для
одинакового значения фокального параметра р. Штриховой эл-
эллипс соответствует меньшему значению М. Для меньшего значе-
значения М вершина параболы может оказаться правее вершины
гиперболы, соответствующей большему М.

48 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
Если 1-Н2?М8/та2) = 0, т, е. Е =¦— tna*/2M29 то,
как следует из формулы A1.7), эксцентриситет обра-
обращается в нуль —траектория представляет собой
окружность. При заданном М такое значение энергии
в данном силовом поле является минимально возмож-
возможным (меньшим Е отвечает мнимое значение е).
Когда частица движется в ограниченной области
пространства (частица не уходит в бесконечность),
движение называется финитным. Если частица при
движении уходит в бесконечность, движение назы-
называется инфинитным. Движение по эллипсу является
финитным (напомним, что в этом случае Е < 0)» дви-
движение по гиперболе и параболо —инфинитным
§ 12. Задача двух тел
Рассмотрим замкнутую систему, состоящую из
двух взаимодействующих частиц с массами ш\ и ш2.
Потенциальная энергия такой системы зависит от рас-
стояния между части-
частицами г, которое можно
рассматривать как мо-
модуль вектора г, прове-
проведенного от одной час-
частицы (скажем, т^) к
другой (mi): U—U(r)
(рис. 12.1).
Система имеет
шесть степеней свобо-
свободы. В качестве обоб-
Рис. 12.1 щенных координат
возьмем три декартовы
координаты центра инерции С системы (которым эк-
эквивалентен радиус-вектор R точки С) и три проекции
вектора г на координатные оси. Вектор г можно пред-
представить в вкде
г = г,-г2, A2.1)
где fi и Г2 —радусы-векторы частиц относительно цен-
центра инерции. В соответствии с определением центра
инерции
+/И2Г2 == 0. A2.2)

§ 12. ЗАДАЧА ДВУХ ТЕЛ 49
Решая совместно уравнения A2.1) н A2.2), можно
найти, что
Положение частиц относительно начала координат
определяется векторами R + fi и R + iy
Напишем функцию Лагранжа системы:
Осуществив возведение в квадрат и приняв во внима-
внимание, что согласно A2.2) гп\Г\ + т2Г2 = 0, получим
Наконец, заменив ri и г2 через г в соответствии с
A2.3), придем к выражению для L в принятых нами
«координатах» R и г 1):
L^JSl+JSLip + JLit-uir), A2.4)
где
^l = _2Ll?^ A2.5)
— величина, называемая приведенной массой системы.
Функция A2.4) распадается на два независимых
слагаемых:
L(r, г).
Первое из них описывает поведение центра инерции
системы, второе — движение частиц относительно цен-
центра инерции.
Как вытекает из A2.4), координата R оказывается
циклической (она не входит явно в L; см. предыдущий
параграф). Следовательно,
Р# = {щ + щ) R = const
(импульс системы сохраняется; это можно было пред-
предвидеть заранее, ибо система замкнута). Центр инер-
а) Координатами без кавычек являются не сами векторы R
и г, а их проекции на координатные оси.

50 ГЛ. Ш. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
дни системы движется прямолинейно и равномерно
(либо покоится).
Движение частиц относительно центра инерции
описывается функцией
I—f r*-U(г). A2.6)
Ее можно рассматривать как функцию Лагранжа час-
частицы массы |д, движущейся в центральном поле с не-
неподвижным центром. Положение частицы относитель-
относительно силового центра определяется радиусом-вектором г.
Таким образом, задача о движении системы из двух
взаимодействующих частиц (задача двух тел) оказа-
оказалась сведенной к задаче о движении одной частицы
в центральном поле сил. Эту задачу мы рассмотрели
в предыдущем параграфе. Мы выяснили, что в случае,
когда U — а/г, траекторией частицы будет коническое
сечение. Следовательно, конец радиуса-вектора г —
— И—г2 скользит при движении частиц по кривой,
представляющей собой коническое сечекие. Согласно
A2.3) радиусы-векторы Т\ и г2 пропорциональны ра-
радиусу-вектору г1). Таким образом, каждый из этих
векторов также описывает коническое сечение. В за-
зависимости от характера взаимодействия (притяжения
либо отталкивания) и величины полной энергии си-
системы траекторией каждой из частиц будет либо эл-
эллипс, либо парабола, либо гипербола.
Допустим, что вспомогательная воображаемая час-
частица |х движется по эллипсу, описываемому уравне-
уравнением
— е cos
Согласно A2.3) вектор ri в любой момент времени
имеет такое же направление, что и г (q>i = q>), а мо-
модуль его в m2/(mi + m2) раз больше. Следовательно,
частица т\ движется по эллипсу:
"-1-Л,У1- <12-7>
где р\ = pm2/(mi + m2).
*) По этой причине воображаемый силовой центр, под дей-
действием которого движется частица \i, нужно предполагать поме-
помещающимся в той точке, от которой откладываются векторы г4
и г2, т. е. в центре инерции системы С.

§ 12. ЗАДАЧА ДВУХ ТЕЛ
51
Вектор г2 в каждый момент времени направлен
противоположно вектору г (см. A2.3)). Поэтому, ко-
когда вектор г ориентирован под углом q>, вектор г2
ориентирован под углом <р2 = п + Ф- Модуль вектора г2
в т\/(т\ + т2) раз больше. Следовательно, учтя, что
\
Рис. 12.2
Рис. 12.3
соз(ф2 — я) ——соэф2, уравнение эллипса, по кото-
которому движется частица /га2, нужно записать в виде
Г2 =
в COS
A2.8)
где
р р1 ( )
В сл)гчае, соответствующем уравнению A2.7), ка-
качало координат (т. е. центр инерции С) помещается
в левом фокусе эллипса (см. формулу (IV. 11)). В слу-
случае, отвечающем уравнению A2.8), качало коорди-
координат (точка С) помещается в правом фокусе эллипса

52 ГЛ- III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
(см. формулу (IV. 12)). Следовательно, траектории
частиц выглядят так, как показано на рис. 12.2 х).
Предоставляем читателю самому убедиться в том,
что в случае движения по гиперболам траектории час-
частиц будут выглядеть так, как показано на рис. 12.3, а
(в случае взаимного притяжения частиц), и на
рис. 12.3,6 (в случае отталкивания).
§ 13. Упругие столкновения частиц
Столкновением называется процесс, заключаю-
заключающийся в том, что взаимодействующие друг с другом
частицы, придя из бесконечности (т. е. с такого рас-
расстояния, при котором их взаимодействием можно пре-
пренебречь), сближаются, а затем либо расходятся снова
на бесконечность, либо остаются на конечном рас-
расстоянии друг от друга. В первом случае столкновение
называется рассеянием частиц, а во втором — захва-
захватом частиц. Очевидно, что захват может наблюдаться
только в том случае, если взаимодействие частиц
имеет характер притяжения.
Когда говорят о столкновениях частиц, отнюдь не
предполагают, что частицы приходят в соприкоснове-
соприкосновение, как это бывает, например, при столкновении двух
шаров. Имеется в виду лишь то, что вследствие взаи-
взаимодействия частицы изменяют направление или харак-
характер своего движения.
Рассмотрим упругое столкновение двух отталки-
отталкивающихся частиц. Столкновение называется упругим,
если оно не сопровождается изменением внутренней
энергии частиц. Следовательно, при упругих столкно-
столкновениях механическая энергия системы сталкивающих-
сталкивающихся частиц остается постоянной.
Проще всего процесс столкновения рассматривать
в системе отсчета, связанной с центром инерции час-
частиц (ее называют ц-спстшой). Однако на практике
наблюдения за столкновениями производятся в систе-
системе отсчета, относительно которой центр инерции час-
частиц движется со скоростью vc. Эту систему отсчета
называют лабораторной системой или, короче, л-систе-
мой. Обычно в лабораторной системе одна из частиц
до столкновения покоится.
*) Рис. 12.2 и 12.3 выполнены для mt/mz = 2/3; е = 0,8
(рис.12.2) ие=1,5 (рис. 12.3).

§ 13. УПРУГИЕ СТОЛКНОВЕНИЯ ЧАСТИЦ 53
Между скоростью i-й частицы в л-системе (мы бу-
будем обозначать ее символом vi) и скоростью той же
частицы в ^-системе (ЭТУ скорость обозначим v(^C))
имеется очевидное соотношение
v^Vc + vf). A3.1)
Из определения центра инерции следует, что
_ miVi -f
С ГП\+
В дальнейшем мы ограничимся рассмотрением слу-
случая, когда в л-системе вторая частица до столкнове-
столкновения покоится. Тогда, обозначив скорость первой час-
частицы до столкновения символом Ую, получим, что
A3-2)
Подставив это значение vc в формулу A3.1), получим
следующие выражения для скоростей частиц в ч-си-
стеме до столкновения:
mi + ? ° A3.3)
w on i __ » j л •
*v fill i fW>2
Умножив первую из этих скоростей на ть а вторую —
на /пг, найдем импульсы частиц до столкновения
в ^системе:
Здесь \х—т{т<г/{т\-\-т2)—приведенная масса частиц.
Как это и должно быть, суммарный импульс час-
частиц в ц-системе до столкновения равен нулю. Из за-
закона сохранения импульса следует, что и после столк-
столкновения импульсы частиц в ^-системе могут отличать-
отличаться лишь знаком: р';с*== — р^С).
Суммарная кинетическая энергия частиц в резуль-
результате упругого столкновения не может измениться (мы
считаем, что до и после столкновения частицы нахо-
находятся друг от друга настолько далеко, что их взаим-
взаимная потенциальная энергия пренебрежимо мала).

54 ГЛ. Ш. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
Поэтому можно написать соотношение
9
Pi
(мы опустили верхний индекс «(С)» при символах им-
импульсов). В сочетании с условием, что | Р^* j — | Р2011
и |р<с)| = jpBC)j, написанное нами соотношение указы-
указывает на то, что импульсы (а следовательно, и скоро-
скорости) частиц в результате столкновения лишь повора-
поворачиваются в ^-системе на некоторый угол %, оставаясь
неизменными по величине. Обозначим символом е* еди-
единичный вектор скорости первой частицы в q-системе
после столкновения. Тогда в соответствии с форму-
формулами A3.3) можно написать для скоростей частиц
после столкновения следующие выражения:
Чтобы получить скорости частиц после столкнове-
столкновения в л-снстеме, воспользуемся формулой A3.1), под-
подставив в нее выражение A3.2) для vc- В результате
получим
V = V +
ttl\
Для импульсов частиц в л-системе после столкнове-
столкновения получаются выражения
\lo.4)
Полученные соотношения можно сделать очень на-
наглядными с помощью следующего геометрического
построения. Изобразим вектор рю отрезком AD
(рис. 13.1) и отметим на нем точку О, которая делит
длину вектора в отношении т\: т^. Из точки О, как
из центра, проведем окружность, проходящую через

§ 13. УПРУГИЕ СТОЛКНОВЕНИЯ ЧАСТИЦ
55
конец вектора
/(
ю- Радиус этой окружности равен
Если гп\ < т2, точка Л попадает
внутрь окружности (рис. 13.1,о); если т\ > т2, точ-
точка Л оказывается вне
окружности (рис. 13.1,
б); при гп\ = т% точка
Л лежит на окружно-
сти (рис. 13.1,в).Отло-
13.1,в).Отложим из точки О под
углом % по отношению
к рю единичный вектор
ei направления, в кото-
котором по предположению
летит относительно
Ч-системы первая час-
частица. Тогда отрезок
ОВ будет изображать
вектор eipi0m2/(/ni +
+ т-г) и в соответст-
соответствии с формулами
A3.4) отрезок А В даст ^
вектор рь а отрезок
BD — вектор р2.
Угол 6i между век-
векторами pi и рю назы-
называется углом рассеяния.
Он характеризует от-
отклонение первой части-
частицы, наблюдаемое в
л-системе. Угол 82 меж-
между векторами р2 и рю
называется углом от-
отдачи. Сумма Bi-f-02 на-
называется углом раз-
разлета частиц после
столкновения. Углы 8i
и 02 можно выразить
через % — угол откло-
отклонения первой частицы
в ^-системе. Учтя, что
длина отрезка ОВ равна рют2/{гп\ + ^г), можно на-
написать
+ Юг)] sin х
[mi -jr tn?\ cos % •
Рис. 13.1

56 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
ИЛИ
tltt
A3.5)
Из равнобедренного треугольника OBD получается
соотношение
Из рис. 13Л,а видно, что более легкая частица
может рассеяться на более тяжелой (т\ < т2) в лю-
любом направлении (точка В может находиться в любом
месте на окружности). Угол разлета частиц в этом
случае всегда больше я/2.
В случае, когда гп\ > т2 (рис. 13.1,6), угол рас-
рассеяния не может превысить некоторое предельное зна-.
чение Bimax (ему соответствует точка В' на рисунке).
Синус этого угла равен отношению отрезков ОВ' и
О А, т. е.
При т\ > тг угол разлета частиц всегда меньше л/2.
Если массы частиц одинаковы (mi = m2), частицы
разлетаются после столкновения под прямым углом
друг к другу Fi + 02 = я/2; рис. 13.1, в).
При лобовом ударе частицы разлетаются под уг-
углом Oi + 02, равном либо зх (при ш\ < т2; рис. 13.1, а),
либо нулю (при т\> т2; рис. 13.1,6). Угол % ПРИ
лобовом ударе равен я. Когда массы частиц одина-
одинаковы (mi==m2), Pi оказывается равным нулю, а
р2 = р10 (см. рис. 13Л,в; в рассматриваемом случае
точка В совпадает с точкой А). Следовательно, час-
частицы одинаковой массы при лобовом ударе обмени-
обмениваются импульсами. Этот результат легко получить
также из формул A3.4).
Полученные нами результаты являются следствием
законов сохранения энергии и импульса и не зависят
от характера взаимодействия частиц. Для того чтобы
определить, под каким углом % рассеивается частица,
нужно знать закон взаимодействия частиц и их вза-
взаимное расположение при столкновении. Рассмотрению
этого вопроса посвящен следующий параграф.

§ 14. РАССЕЯНИЕ ЧАСТИЦ
57
§ 14. Рассеяние частиц
В § 12 было показано, что задача о движении двух
взаимодействующих частиц сводится к задаче о дви-
движении частицы с массой \i (\i—приведенная масса)
в центральном поле сил, причем расстояние этой час-
частицы от центра сил равно расстоянию между рассмат-
рассматриваемыми частицами. Найдя траекторию воображае-
воображаемой частицы массы ц, легко найти траектории обеих
частиц.
Воспользуемся этим приемом для изучения про-
процесса рассеяния частицы т\ частицей тг, которая
Рис. 14.1
первоначально неподвижна в л-системе. Перейдем
в ^-систему и рассмотрим частицу |х, движущуюся
в силовом поле, центр которого совпадает с центром
инерции системы С. На больших расстояниях от цен-
центра поле будем полагать столь слабым, что движение
частицы вдали от центра можно считать прямоли-
прямолинейным.
Введем в рассмотрение прицельный параметр или
прицельное расстояние 6, равное тому расстоянию, на
котором пролетела бы частица мимо силового центра,
если бы поле не оказывало ка нее воздействия
(рис. 14.1). Ясно, что угол отклонения частицы есть
функция прицельного расстояния: х = %(&), причем
чем меньше 6, тем, вообще говоря, должен быть боль-
больше %. Обратив эту функцию, можно написать
A4.1)

68 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
Предположим, что на силовой центр С падает пу-
пучок одинаковых частиц, летящих вдали от центра в
одном и том же направлении и с одинаковой ско-
скоростью vq. Этот пучок можно охарактеризовать плот-
плотностью потока частиц /, под которой подразумевается
число частиц, пролетающих за секунду через перпен-
перпендикулярную к пучку единичную площадку. Будем по-
полагать, что пучок частиц однороден, т. е. что вдали от
рассеивающего центра плотность потока одинакова во
всех точках поперечного сечения пучка.
Частицы пучка отклоняются на разные углы %
в зависимости от того, с каким прицельным расстоя-
расстоянием приближается к центру та или иная частица.
Частицы, прицельное расстояние которых окажется
в пределах от Ь до Ъ + dby будут рассеяны в пределах
углов от х до х+ d%. Обозначим поток таких частиц
(т. е. число частиц, рассеиваемых под углами от %
до х + d% в единицу времени) через dN%. Отношение
2 A4.2)
называют дифференциальным эффективным сечением
(или поперечником) рассеяния. Одним из оснований
для такого названия послужило то обстоятельство, что
da, как следует из A4.2), имеет размерность площади.
Легко видеть, что do определяет относительное коли-
количество (долю) частиц, рассеиваемых в данном интер-
интервале углов.
В случае однородного по сечению пучка поток час-
частиц, прицельное расстояние которых попадает в пре-
пределы от Ъ до Ъ + db, равен j2nbdb (поток = плотность
потоках площадь). Этот поток рассеивается под уг-
углами от х ДО X + d%. Следовательно, dN% = }2nb db.
Подставив это значение в формулу C4.2), получим
или, перейдя от переменной b к % (см. A4.1)),
% A4.3)
db db
ПОСКОЛЬКУ
(db
МЫ ВЗЯЛИ МОДУЛЬ -г—, ПОСКОЛЬКУ

§ 14. РАССЕЯНИЕ ЧАСТИЦ 59
Величину dN% в формуле A4.2) можно трактовать
как поток частиц, летящих в пределах телесного угла
йп = 2к sin % d% (такую величину имеет телесный
угол, заключенный между конусами с углами раствора
X и % + d%). Заменив в A4.3) 2nd% через dQ/sin%,
можно привести формулу для дифференциального эф-
эффективного сечения рассеяния к виду
Формула A4.3), равно как и A4,4), является са-
самой общей — она определяет дифференциальное эф-
эффективное сечение рассеяния в случае любого цен-
центрального рассеивающего поля. Величины Ь{%) и
dh/d% определяются характером силового поля, т. е.
характером взаимодействия частиц. Следовательно, da
определяется видом рассеивающего поля и является
важнейшей характеристикой процесса рассеяния. Ис-
Исследовав экспериментально da, можно получить све-
сведения о характере силового поля.
До сих пор шла речь о рассеянии пучка частиц
на одном рассеивающем центре. Практически же на-
наблюдают рассеяние на совокупности одинаковых рас-
рассеивающих центров. В связи с этим отметим следую-
следующее обстоятельство. На заметные углы % отклоняются
только те частицы, которые летят достаточно близко
от рассеивающего центра (для которых прицельное
расстояние мало). Поэтому если на пути частиц ока-
окажется п одинаковых не перекрывающих друг друга
и достаточно разреженных рассеивающих центров, то
эти центры будут осуществлять рассеяние независимо
друг от друга и поток частиц, рассеиваемых в преде-
пределах углов от % до % + d%, будет в п раз больше, чем
при наличии только одного центра. Таким образом,
в случае п центров
dN% = njdo. A4.5)
Перейдем от частицы с массой \х, рассеиваемой не-
неподвижным силовым центром, помещающимся в точ-
точке С, к реальным частицам п%\ и тъ Траектории этих
частиц геометрически подобны траектории частицы \х.
Действительно, согласно A2.3) радиус-вектор первой
частицы, проведенный из точки С, в rn%l{m\ + m2) раз
длиннее радиуса-вектора частицы ц, проведенного из

60 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
той же точки. Аналогичное соотношение справедливо
и для второй частицы. Значит, в ^-системе частица т\
отклоняется на тот же угол %, что и частица \i. В ка-
качестве прицельного расстояния нужно брать расстоя-
расстояние, на котором пролетела бы первая частица мимо
второй, если бы частицы не взаимодействовали (ра-
(радиус-вектор г частицы (л, проведенный из силового
центра С, совпадает с Т\ —г2).
Таким образом, формула A4.3) оказывается спра-
справедливой (в ^-системе) и для пучка частиц ти рас-
рассеиваемых частицей т^ Для того чтобы перейти от
Ч-системы к лабораторной системе, в которой наблю-
наблюдается рассеяние, необходимо в формуле A4.3) пе-
перейти от переменной % к переменной 6ь Этот переход
осуществляется по формуле A3.5). Формула, которая
при этом получается, в общем случае оказывается
очень громоздкой.
В частном случае, когда т\ <С га2 (рассеиваемые
частицы много легче рассеивающих), 6i ?s % (см. фор-
формулу A3.5)), так что формулы A4.3) и A4.4) можно
записать в л-системе:
A4.6)
sin 6i I d%
Отметим, что в этом случае \i ^ т\ и г & s*i (траекто-
(траектория частицы т\ практически совпадает с траекторией
частицы \i).
Рассмотрим случай кулоиовского рассеивающего
поля, т. е. поля вида U — a/г, полагая т\ <С tri2. Энер-
Энергию рассеиваемой частицы можно представить выра-
выражением Е — 72^i#e» где v0 — начальная (и конечная)
скорость частицы ni\. Момент импульса частицы т\
относительно центра рассеяния (совпадающего с час-
частицей /пг) равен № — m\Voh (см. рис. 14.1). Подставив
эти значения Е и М в формулу A1.5), придем к со-
соотношению:
^^. A4.7)
Из рис. 14.1 видно, чю при г = со имеются два
значения <р —нуль и 2фо. В первом случае левая час!ь

§ 14. РАССЕЯНИЕ ЧАСТИЦ 61
формулы A4.7) обращается в —фо, во втором в +фо.
Поэтому, положив в A4.7) г = ооэ можно написать
Фо= arccos1 _
откуда
cos2<Po= , Л,.ц- A4.8)
Далее из рис. 14.1 следует, что % — я — 2фо, т. е. фо =
= я/2 — х/2 = я/2 — Gi/2 (мы воспользовались тем,
что в рассматриваемом случае можно положить
0i =Х)- Подставив это значение фо в формулу A4.8),
получим
в 1
2 1 + (»
Разрешив это соотношение относительно Ъ, придем
после несложных преобразований к выражению
= —^-o-ctg —. A4.9)
Дифференцирование по 9i дает
db a 1
mxvl 2 sin2
A4.10)
Наконец, подставив выражения A4.9) и A4.10) в
A4.6), получим формулы для дифференциального эф-
эффективного сечения рассеяния частиц массы т\
в кулоновском поле, создаваемом частицей массы
da^n(^Y^EiELdQit (i4.li)
UJ •ш8(в1/а)
_«.. A4.12)
sin^e^)
Мы получили известную из общего курса физики
формулу Резерфорда для рассеяния а-частиц на тя-
тяжелых ядрах. В этом можно убедиться, заменив а че-
через 2Ze% и умножив формулы A4.11) и A4.12) на
плотность потока а-частиц / и число атомов рассеи-
рассеивающего вещества п, приходящееся на единицу

62 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
площади поперечного сечения пучка а-частиц. Тогда в
левой части формулы получится выражение njda, кото-
которое дает dNet — поток а-частиц, рассеиваемый в ин-
интервале углов от Oi до Qi + dQu либо dNu — поток
а-частиц, рассеиваемых в телесный угол dQ (см. фор-
формулу A4.5)).
Заметим, что найденные нами выражения для da
не зависят от знака а, так что полученный результат
справедлив не только для случая кулоновского от-
отталкивания частиц т\ и ть но и для случая их куло-
кулоновского притяжения.
§ 15, Движение в неинерцнальных системах
отсчета
Функция Лагранжа одной частицы имеет вид
A5.1)
только в икерциальных системах отсчета. Найдем
вид L в произвольной неинерциальной системе отсче-
отсчета. На рис. 15.1 изобра-
/^ " h31 жена инерциальнзя си-
система отсчета К и систе-
система К\ начало которой
(точка Of) движется в си-
системе /{ со скоростью
*' Vo(/), а сама система К'9
кроме того, вращается от-
относительно системы К с
*# угловой скоростью &{t).
Рис. 15.1 Выразим функцию A5.1)
через радиус-вектор г7,
определяющий положение частицы в системе К\ и
через скорость v' частицы, наблюдаемую в той же
системе.
Предположим сначала, что vo(/)sO и начала
обеих систем отсчета совпадают. Тогда между скоро-
скоростями частицы в обеих системах имелось бы соот-
соотношение
v =: у' -|» [©г'3 A5.2)
(частица, неподвижная в системе К\ имела бы в си-

§ !5. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА 63
стеме К скорость, равную [зг'] !}}. Если же vo{t) от-
личка от нуля, соотношение A5.2) примет вид
v = vo(/) + v' + [<»r']. A5.3)
Подставим полученное нами выражение лля v
в формулу A5.1). В результате получим
(/) v' + mv0 (t) [»r'J + mv' [er']. A5.4)
Первое слагаемое в этой формуле есть заданная функ-
функция времени, которая может быть представлена как
полная производная по t от некоторой другой функ-
функции. В § 7 мы установили, что функцию Лагранжа
следует определять с точностью до аддитивных сла-
слагаемых, представляющих собой полную производную
по времени от произвольной функции обобщенных ко-
координат и времени. Поэтому слагаемое (m/2)[vo(Ol2
следует опустить.
Рассмотрим четвертое и пятое слагаемые в фор-
формуле A5.4). Вынеся за скобки общий множитель, эти
слагаемые можно представить в виде
(,5.5)
Здесь dY— приращение г', наблюдаемое за время dt
в системе К' (напомним, что v' — скорость частицы,
наблюдаемая в системе /СО» ^Ф — угол, на который
поворачивается система К' за время dt.
Если одна из систем отсчета вращается относи-
относительно другой, то приращение некоторого вектора а,
наблюдаемое в обеих системах, будет неодинаковым.
Это легко понять, предположив, что по отношению
к вращающейся системе вектор не изменяется, т. е.
приращение вектора в этой системе (обозначим ее
К') равно нулю: d'a = 0. Тогда приращение вектора
*) Это выражение получается из формулы (VI. 46), если
положить в ней а = г' и разделить получившееся соотношение
на dt.

64 ГЛ. III. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
в неподвижной системе (системе К) можно записать
в виде
rfa = [tfq), a]
(см. формулу (VL46)). Если же наблюдаемое во вра-
вращающейся системе приращение вектора d'a отлично
от нуля, то приращение, наблюдаемое в неподвижной
системе, будет равно
а] A5.6)
(положив а = г7 и поделив на di, мы придем к фор-
формуле A5.2)).
Сопоставив A5.6) с выражением, стоящим в фи-
фигурных скобках в правой части формулы A5.5), при-
приходим к выводу, что это выражение представляет со-
собой приращение вектора г', наблюдаемое в системе К,
т. е. dt\ Таким образом, сумме четвертого и пятого
слагаемых формулы A5.4) можно придать вид
Преобразуем это выражение следующим образом:
mv0 (t)^- = ~ {mv0 @ г'} -mr'^f-.
Первое слагаемое как полную производную по t от
функции координат и времени можно отбросить. Во
втором слагаемом dvo/dt есть wo(t) — ускорение на-
начала координат системы К\ наблюдаемое в си-
системе /С
Таким образом, мы приходим к следующему вы-
выражению для функции Лагранжа в переменных г' и v':
V -= mv/2/2 + т [©гТ/г - тг^0 (/) + тч' [©г'] - U (г').
A5.7)
Мы получили общий вид функции Лагранжа час-
частицы в произвольной неинерциальной системе отсчета.
Функцию U теперь нужно считать заданной в пере-
переменных г' (в формуле A5.1) она была задана в пере-
переменных г). Переход от одних переменных к другим
осуществляется по формуле
г-МО + г7, A5.8)
где го(О —РаДиУс-вектоР начала координат системы/С
(см. рис. 15.1),

§ 15. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА 65
Отметим, что даже если в функцию A5.1) время
не входило явно (оно могло входить в силовую функ-
функцию {/), то в функцию A5.7) время будет входить,
так как w<> и © суть, вообще говоря, функции /; кроме
того, время войдет явно в слагаемое ?/(г') в резуль-
результате перехода от г к г', осуществляемого по фор-
формуле A5.8).
Прежде чем приступить к составлению уравнения
Лагранжа, заменим второе слагаемое выражения
A5.7) в соответствии с формулой (VI. 6). В резуль-
результате получим
V = m?/2/2 + mmV2/2 - т (wr'f/2 -
- пя/wo @ + mv' [mf] - U (г'). A5.9)
Воспользовавшись циклической перестановкой со-
сомножителей (см. формулу (VI. 3)), предпоследнее
слагаемое, равное mv'[wr'], можно было бы записать
в виде
m[v'o]r'. A5Л0)
Уравнение Лагранжа в системе К' выглядит сле-
следующим образом:
JL.L=L (l5in
(см. формулу (9.3) и подстрочное примечание на
стр. 14). Из выражения A5.9) следует, что
откуда
ЧГ !? = mv' + т [т'] + т [т?]'
Напомним, что с тех пор, как мы выразили L в пере-
переменных г' и v', мы «живем» в системе отсчета К'.
Следовательно, под v' нужно понимать ускорение
частицы w', наблюдаемое в системе /С', а под г'-— ско-
скорость частицы v7 в той же системе. Таким образом,
4-47- = mw' + mM + m[©v1. A5.12)
Что касается о, то это есть производная по времени
функции <a(t), которая задана нам в системе К*
3 И. В. Савельев, т. I

66 ГЛ. Ш. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
При вычислении dU/ckf будем предполагать, что
предпоследнее слагаемое в формуле A5.9) представ-
представлено в виде A5.10). Тогда получим
g- т (©гО ® - mw0 @ + m [ v'®J - |р-.
A5,13)
Первые два слагаемые в этом выражении представ-
представляют собой написанное по формуле «бац минус
цаб» (см. (VI.5)) двойное векторное произведение
т[ю, [г7®]]. Следовательно, выражение A5.13) можно
записать в виде
jgl = щ [», [г*©]] - mw0 @ + w W&\ - |р- • A5.14)
Подставив выражения A5.12) и A5.14) в фор-
формулу A5.11) и произведя преобразования, придем
к уравнению движения частицы в системе К':
mw' = —dUjdt' — raw0 @ + т [гЪ] + m [»[r'©]] +
+ 2m[v'ce]. A5.15)
Мы видим, что ускорение частицы в системе К'
определяется, кроме обусловленной силовым полем
силы — ди/дт\ рядом дополнительных сил, называе-
называемых, как известно, силами инерции. Слагаемое
пг[& [г'©]] дает центробежную силу инерции, а сла-
слагаемое 2m [v'®] — кориолисову силу. Сила т [г'ф]
связана с неравномерностью вращения; она специаль-
специального названия не имеет.
Если система К' движется относительно системы К
поступательно (в этом случае ©==0, а значит, и
© = 0), в уравнение движения входит только одна
сила инерции, равная
ffo —-mwo(O. A5.16)
Замечательно то, что эта сила, как и сила тяжести
trig, пропорциональна массе частицы. Это обстоятель-
обстоятельство лежит в основе общей теории относительности.
В случае равномерно вращающейся системы коор-
координат, не имеющей поступательного ускорения
(wo(O —0> © = 0), функция Лагранжа имеет вид (см.
V . шИ/2 + т [©гТ/2 + mv' W\ - U. A5.17)

§ 15. НЕИНЕРЦИАЛЬНЫВ СИСТЕМЫ ОТСЧЕТА 67
Найдем импульс, момент импульса и энергию частицы
для этого случая. В соответствии с формулой (9.5)
* dv
Взяв производную от функции A5.17), получим
р' = тч' + т {m'l =^m{v' + [&?]}. A5.18)
Если система К' не имеет не только поступательного
ускорения, но и поступательной скорости (?о = 0), то,
как видно из A5.3), выражение, стоящее в A5.18)
в фигурных скобках, есть скорость частицы v относи-
относительно инерциальной системы К. Таким образом, р'
оказывается равным mv, т. е. совпадает с импульсом р
частицы в инерциальной системе:
р' = р. A5.19)
Далее, если начала систем К и К' совпадают (см.
рис. 15.1), то совпадают и радиусы-векторы г и г'.
Отсюда с учетом A5.19) вытекает, что момент им-
импульса М' — [г'р'1 в системе К' совпадает с моментом
импульса М = [гр] в системе К:
М/ = М. A5.20)
В соответствии с формулой E.1) энергия частицы
в системе К' определяется выражением
где х\ — координаты (декартовы) частицы в системе
К'. Согласно D.17) дЩдк\ есть р\ — проекция им-
импульса частицы р' на j-ю координатную ось; х\ —
проекция на ту же ось скорости частицы v'. Следова-
Следовательно, выражение для энергии молено записать в виде
e = pW — L'. A5.21)
Подставив сюда значение A5.18) для р' и выраже-
выражение A5.17) для Z/, получим следующую формулу:
A5.22)
Вращение системы отсчета проявилось в появлении
в выражении для энергии дополнительного, не зави-

68 ГЛ. Ш. НЕКОТОРЫЕ ЗАДАЧИ МЕХАНИКИ
сящего от скорости частицы v\ слагаемого
t/цб-—5-[«/р. A5.23)
Эту дополнительную «потенциальную» энергию назы-
называют центробежной.
Заменим в формуле A5.22) v7 через v — [©r'] (см.
A5.3); полагаем Vo(t) — Q). В результате получим
Е' = mv2/2 + U - mv [©г']. A5.24)
Первые два слагаемые дают энергию частицы Е в си-
системе /С. Если начала систем К и К' совпадают, г'
можно заменить через г. Тогда последний член в
A5.24) с помощью циклической перестановки можно
привести к виду
mv [в>г] = © [г, mv] = e>IVl.
Таким образом, между энергиями частицы Е (в си-
системе К) и Е' (в системе К') имеется соотношение
?' = ?-<оМ. A5.25)
Напомним, что эта формула получена в предположе-
предположении, что начала обеих систем отсчета совпадают. Сле-
Следовательно, вместо М в формуле A5.25) можно пи-
писать М' (см. A5.20)).
Итак, если система отсчета К' равномерно вра-
вращается относительно инерциальной системы К и на-
начала обеих систем совмещены, то импульс и момент
импульса частицы в обеих системах совпадают, а
энергия частицы в системе К' меньше энергии в си-
системе К на величину скалярного произведения векто-
векторов ш и М.

Глава IV
МАЛЫЕ КОЛЕБАНИЯ
§ 16. Свободные колебания системы без трешш
Рассмотрим систему с одной степенью свободы,
в которой отсутствуют силы трения. Потенциальная
энергия такой системы имеет вид U = U(q), где q —
обобщенная координата. Известно, что в положении
устойчивого равновесия потенциальная энергия имеет
минимум. Будем отсчитывать q от этого положения.
Разложим функцию U(q) в ряд по степеням q в ма-
малой окрестности точки q — Q. Ввиду малости q огра-
ограничимся первыми членами разложения:
U(q) = U @) + (Г @) q + ¦/»?/" @) <?2.
Из условия равновесия ?/'@) = 0. Условимся от-
отсчитывать потенциальную энергию от положения рав-
равновесия, т. е. положим t/@) = 0. Наконец, введем
обозначение: ?/"(Q) = x (напомним, что в точке мини-
минимума вторая производная положительна; следователь-
следовательно, % > 0). В итоге придем к выражению
Будем считать связи стационарными. Тогда со-
согласно E.7)
При прохождении через положение равновесия Т не
обращается в нуль. Следовательно, <у@) отлична от
нуля. Разложив y{q) в ряд и сохранив ввиду мало-
малости q только нулевой член разложения, можно на-
написать
T = *f. A6.2)
где A = 27@) (не путать с приведенной массой!).

70 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
Составим функцию Лагранжа:
L-Jf-Si. A6.3)
Уравнение Лагранжа:
lig + Щ — О пли q-\~®lq = 0 A6.4)
(©* = (и/и) > 0) представляет собой линейное одно-
однородное дифференциальное уравнение второго порядка
с постоянными коэффициентами (см. Приложение V).
Применив подстановку q = exp(Xt), придем к харак-
характеристическому уравнению1)
Корни этого уравнения равны Х\ = +koo, Jt2 = —/©о-
Следовательно, общее решение имеет вид
q = С$ ехр (/©с/) + С2 ехр (—ОД), A6.5)
где Ci и С2 — комплексные постоянные величины.
Значения q должны быть вещественными; это зна-
значит, что должно выполняться условие q* — q (q* —
величина, комплексно-сопряженная с q). Подставив
в это условие выражение A6.5) для q, получим
С] ехр (—ОД) + Сг ехр (ОД) =
= Ci ехр (ОД) + С2 ехр (—ОД).
Полученное соотношение выполняется, если С, == С*
(соответственно С\ = С2). Учтя это, представим коэф-
коэффициенты С\ и С% в виде
Ci = (а/2) ехр (id), С2 = (а/2) ехр (~т) A6.6)
(а и а — произвольные вещественные постоянные).
Подстановка этих значений в формулу A6.5) дает
= а cos (©о* + а). A6.7)
Итак, свободное движение системы вблизи поло-
положения устойчивого равновесия носит характер гармо*
нического колебания (разумеется, при условии, что
в процессе движения q остается малой).
*) См. формулы (V.7) в (V.9).

§ 17. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ 71
Из общего курса физики известно, что а назы-
называется амплитудой, а —начальной фазой колебания;
©о — собственная частота системы1).
Преобразуем выражение A6.7) по формуле для
косинуса суммы:
q = a (cos a cos ш^ — sin а sin ®J)
и введем обозначения
С\ ===== a cos а, с2 = —a sin а.
Тогда решение уравнения A6.4) можно представить
в виде
q = c{ cos g>o? + c2 sin ©q/, A6.8)
где С\ и с% — вещественные постоянные, значения ко-
которых определяются из начальных условий (из до
и (q)о).
Наконец, приведем еще одну форму записи гармо-
гармонического колебания2):
A6.9)
где
A6.10)
— так называемая комплексная амплитуда; ее модуль
равен обычной амплитуде, а аргумент — начальной
фазе колебания. Подставив в A6.9) значение A6.10)
и взяв вещественную часть получившегося выражения,
придем к формуле A6.7).
Итак, гармоническое колебание может быть пред-
представлено в виде любой из трех формул: A6.7), A6.8),
A6.9).
§ 17. Затухающие колебания
Во всякой реальной колебательной системе дей-
действуют силы, тормозящие движение системы и приво-
приводящие к постепенному уменьшению размахов (затуха-
(затуханию) колебаний. Механическая энергия системы при
1) Как правило, мы не будем приводить тех сведений по
рассматриваемому вопросу, которые могут быть найдены в учеб-
учебниках общей физики.
2) Крышечкой над буквой мы будем обозначать комплекс-
комплексные величины.

72 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
этом переходит во внутреннюю энергию системы и
окружающей среды (обычно кратко, но не вполне
строго говорят, что энергия переходит в тепло). Та-
Такой процесс называют диссипацией энергии.
Мы ограничимся рассмотрением случаев, когда
тормозящая движение системы обобщенная сила тре-
трения пропорциональна обобщенной скорости системы:
Эта сила непотенциальна, поэтому уравнение Лагран-
жа будет иметь вид D.15), причем в качестве L нужно
взять функцию A6.3). Итак, затухающие колебания
описываются уравнением
(смысл величин ц и х тот же, что и в предыдущем
параграфе). Представим это уравнение в виде
<j + 2M + <i%q = 0, A7.1)
где
Подстановка <? = exp(Ai) приводит к характеристи-
характеристическому уравнению
Я2 + 2ря + а>| = 0. A7.2)
При условии, что р2 < ©*, корни характеристического
уравнения оказываются комплексными:
Общее решение уравнения A7.1) имеет вид
q = С, exp {^t) + C2 exp {X2t) =
= exp {-№ {С, exp (Ш) + С2 ехр (-/©0}.
где © = /^©2 —р2. Найденное нами решение отли-
отличается от функции A6.5) множителем ехр(—fit) и за-
заменой шо на со. Требование вещественности q приводит
к условию С{ = С?- Введя обозначения A6.6) и про-
произведя элементарные преобразования, придем к из-
известному из общего курса физики выражению для

§ 17. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
73
затухающих колебаний:
q = а ехр (—РО cos (ad
A7.3)
В случае, когда р2 > ю2, корни характеристического
уравнения A7.2) оказываются вещественными:
(поскольку
величина а
/ —- ю2 < р, величина ai положительна;
также положительна, причем a2>ai).
Рис. 17.1
Решение в этом случае имеет вид
q = Cx ехр (—akt) + С2ехр (—a^t), A7.4)
где С\ и Сг — вещественные постоянные.
Итак, при сильном трении (при р2 > ю§) колеба-
колебания не возникают — выведенная из положения равно-
равновесия система возвращается в это положение асимп-
асимптотически. Оказывается, что движение системы может
иметь характерр описываемый либо кривой /, либо
кривой 2 (рис. 17.1). В последнем случае система вна
чале проходит через положение равновесия, откло-
отклоняется в другую сторону и только потом прибли-
приближается асимптотически к положению равновесии.

74 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
Такое движение системы называется апериодиче-
апериодическим1) затуханием (или апериодическим процессом).
Как будет происходить возвращение системы в по-
положение равновесия (в соответствии с кривой 1 или
с кривой 2), зависит от соотношения коэффициентов
d и С2, которое в свою очередь определяется началь-
начальными условиями (т. е. значениями обобщенной коор-
координаты #0 и обобщенной" скорости vo — (q)o в началь-
начальный момент времени).
Выясним условия, при которых апериодическое
движение имеет тот либо иной характер. Выразим
коэффициенты С\ и С2 через #о и г>о« Положив в A7.4)
t = 0, получим
^-Ci + C2. A7.5)
Продифференцировав A7.4) по времени и положив
в получившемся выражении ? = G, найдем, что
Щ = (<7)о = — ЩСХ — «А. A7.6)
Из уравнений A7.5) и A7.6) следует, что
Приравняем выражение A7.4) кулю:
С, ехр (—axt) + С2ехр(~а^) = 0. A7.8)
В случае, когда апериодическое затухание происходит
в соответствии с кривой 2 (см. рис. 17.1), уравнение
A7.8) должно- иметь конечное положительное реше-
решение. Решив это уравнение относительно U получим
f — \ -- |п ( _
а он V
(мы подставили значения A7.7) для С\ и Сг). Раз-
Разность а2 — «1 больше нуля (см. выше). Поэтому /
будет положительным, когда выражение, стоящее под
знаком логарифма, больше +1- Последнее условие
соблюдается, если выражения (aifo+^o) и (еадо+Ро)
имеют одинаковые знаки и, кроме того, модуль пер-
первого выражения больше чем модуль второго2)
sign (ад + Щ) = sign (сад, + vQf),
+ vl { }
1) То есть непериодическим.
8) Символ sign означает «знак».

§ 17. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ
75
Коэффициенты cti и а2 положительны, причем
<&2 > аь Поэтому для выполнения второго из условий
A7.9) необходимо, чтобы q0 и vq имели разные знаки.
Это имеет место, если начальная скорость направлена
к положению равновесия (когда система отклонена
вправо (#о>О), скорость направлена влево (оо<0)
и наоборот). На рис. 17.2 показаны графики функций
у = (%1^о Ч~ Uo и у^с&г^оЧ"
+ Щ- Графики построены
ДЛЯ #о > 0, ПОЭТОМУ Vq <
<: 0. Значения, пробегае-
пробегаемые до, подразделены на
три области. Легко ви-
видеть, что оба условия
A7.9) выполняются лишь
в области /, т. е. при qQf
не превышающих —х)^/а%.
В области // не соблю-
соблюдается первое из условий,
в области /// не соблю-
соблюдается второе условие.
Таким образом, апе- Рис. 17.2
риодическое затухание
происходит в соответствии с кривой 2 (рис. 17.1) в
тех случаях, когда vq и #о имеют разные знаки и,
кроме того,
A7.10)
илн
(напомним, что а2 = р + ^/ §)
Следует особо рассмотреть случай, когда характе-
характеристическое уравнение A7.2) имеет кратные корни.
Это происходит при условии, что р2 = ©2. Тогда Х\ =
= Х2 = —р. Согласно формуле (V. 11) общее решение
уравнения A7.1) имеет в этом случае вид
q=*Cx exp (-P0 + С2^ехр (-ДО = (С{ + CJt) exp (-ДО.
Проделав соответствующие выкладки, найдем, что
Из условия q = 0 получается (кроме t» оо) значение

76 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
Это значение будет положительным, если
^<0 или -gr%-<
(умножение на р не изменяет знака величины, так
как р>0). Последнее условие выполняется, когда
знак v0 противоположен знаку qo и, кроме того,
|о0|>р|?о1-
Таким образом, и в случае кратных корней апе-
апериодическое затухание может происходить как моно-
монотонно (кривая / на рис. 17.1), так и с прохождением
через положение равновесия (кривая 2 на рис. 17.1).
Последний случай имеет место, если выведенная из
положения равновесия на q0 система получает толчок
к положению равновесия, сообщающий ей достаточно
большую начальную скорость (скорость, удовлетво-
удовлетворяющую условию A7.I1I)).
§ 18. Вынужденные колебания
Пусть на систему, рассмотренную в предыдущем
параграфе, действует периодически изменяющаяся
внешняя обобщенная сила
Q' = Q0cosM + a), A8Л)
которую мы будем для краткости называть вынуж-
вынуждающей силой. Тогда уравнение Лагранжа D.15) вы-
выглядит следующим образом:
М + Щ = — rq + Qo cos (erf + a).
Преобразуем его к виду
= f0 cos (со/ + a), A8.2)
где /o = Qo/m смысл остальных величин известен из
предыдущих параграфов.
Мы пришли к линейному неоднородному диффе-
дифференциальному уравнению с постоянными коэффициен-
коэффициентами. Согласно теореме (V. 6) его общее решение
можно получить, прибавив к общему решению соот-
соответствующего однородного уравнения, т. е. к функции
') В случае разных корней скорость должна удовлетворять
условию A7.10).

§ 18. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ 77
A7.3), какое-либо частное решение уравнения A8.2).
Для нахождения частного решения поступим в соот-
соответствии со сказанным в конце Приложения V, а
именно: прибавим к правой части A8.2) мнимую
функцию ifosin(<dt-\-a) и будем искать комплексное
решение # получившегося уравнения; найдя #, возь-
возьмем от него вещественную часть; она и будет пред-
представлять собой решение уравнения A8.2). Итак, бу-
будем решать уравнение
Его правую часть можно представить в виде
/о ехр {/ (®t + а)} = fо ехр (ОД
где
f A8.3)
— комплексная амплитуда 1) вынуждающей силы (точ-
(точнее, силы, деленной на ji, но мы для краткости будем
называть Q*/\i просто силой). Напишем дифференци-
дифференциальное уравнение в новых обозначениях:
q + 2W + «fr = h ехр (Ш) A8.4)
• (чтобы не усложнять обозначений, мы опустили кры-
крышечку над q).
Будем искать решение уравнения A8.4) в виде
9 = 4ехр(ОД A8.5)
где й — комплексная амплитуда колебания. Диффе-
Дифференцируя по ty найдем
q = тй ехр (/©/),
q = (toJ й ехр (Ш) = — ®?й ехр (ОД
Мы видим, что при комплексной записи гармонически
изменяющихся величин дифференцирование по вре-
времени сводится к умножению величины на т (при ин-
интегрировании — к делению на ко).
Подставив в уравнение A8.4) выражения A8.5)
и A8.6) и сократив на общий множитель ехр(Ш)>
придем к уравнению
—ый + 2/pcad -f щй — fо,
*) Ср. с A6.10).

78 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
из которого находим
©5 - <*г) + 2/р©
Представим комплексное число, стоящее в знаме-
знаменателе, в виде
(©2 — ®2) + 2фю = р ехр (/ф), A8.7)
где р —модуль, а ф —аргумент этого числа. Тогда
Из соотношения A8.7) вытекает1), что
^^-. A8.9)
Подставив в A8.8) значения р и f0 (см. A8.3)),
получим для комплексной амплитуды колебания сле-
следующее выражение:
=• ехр {/ (а — ф)} = аехр {/ (а — ф)}.
Наконец, подставив значение $ в формулу A8.5), най-
найдем комплексное выражение для q:
^ == аехр {i (orf + а — ф)}-
Его вещественная часть совпадает с известным из об-
общего курса физики выражением установившихся вы-
вынужденных колебаний:
У» сов^ + а-ф) A8.10)
2J + P22
(в учебниках общей физики обычно полагают а = 0).
Общее решение уравнения A8.2) получим, сложив
функции A7.3) и A8.10). Анализом этого решения и
ч) Напомним, что комплексное число может быть изображе-
изображено точкой Р на плоскости; абсцисса этой точки х равна веще-
вещественной части числа, ордината у — мнимой части. Модуль ком-
комплексного числа равен модулю р радиуса-вектора точки Р, а
аргумент ф есть угол, образуемый радиусом-вектором с осью
бсцисс. Отсюда следует, что р « л/х* -f У2, tg <р =* у/х.

§ 19. СЛУЧАЙ МНОГИХ СТЕПЕНЕЙ СВОБОДЫ 79
рассмотрением явления резонанса мы заниматься не
станем, поскольку это делается достаточно подробно
в курсах общей физики.
§ 19. Колебания системы
со многими степенями свободы*)
Рассмотрим консервативную систему с s степенями
свободы, обладающую положением устойчивого рав-
равновесия. В этом положении потенциальная энергия
системы (/== U(qu Цъ •••» <7«) имеет минимум. Обоб-
Обобщенные координаты qt будем отсчитывать от положе-
положения равновесия. Имея в виду, что мы ограничимся
рассмотрением малых колебаний, разложим потенци-
потенциальную энергию в ряд по степеням #*, причем прене-
пренебрежем членами более высоких порядков малости:
i i,k
В положении равновесия все обобщенные силы
Q* = — (-х—j равны нулю. Энергию UQ также поло-
положим равной нулю. С учетом сказанного выражение
для потенциальной энергии можно представить в виде
где
суть положительные величины (в минимуме вторые
производные больше нуля). Поскольку U отсчиты-
вается от минимального значения, принятого за нуль,
квадратичная форма A9.1) положительно-опреде-
положительно-определенная.
В случае стационарных связей кинетическая энер-
энергия определяется положительно определенной квадра-
квадратичной формой переменных qi (см. E.10)):
*. к
*) Прежде чем приступить к чтению этого параграфа, сле-
следует ознакомиться с Приложениями VII, VIII и IX.

80 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
где
суть нулевые члены разложения коэффид иеитов q
Согласно формуле E.8) y«* — У^> следовательно,
Вычтя из A9.2) выражение A9.1), получим функ-
функцию Лагранжа:
4- Y ¦*»*'** - т Y
Чтобы найти производные L по qt и ф, напишем вы-
выражение полного дифференциала функции A9.3):
^^tZi^'^ + i
i.k i,k
Индексы ink являются немыми, поэтому каждый из
них можно обозначить любой буквой. Воспользовав-
Воспользовавшись этим, поменяем местами индексы ink* первой
и третьей суммах:
1 y» ,. , 1
1%к U к f,k
i.k i.k itk
(напомним, что ftos|fc*, х« = хлк). Полученное нами
выражение можно представить в виде
dL = Z dqt ( Z |i^) - Z rfflfi ( E ^g,). A9.4)
В выражении полного дифференциала функции не-
нескольких переменных множитель при дифференциале
какой-либо переменной равен частной производной
функции по этой переменной. Следовательно, из A9.4)
вытекает, что
dL

§ 19. СЛУЧАИ МНОГИХ СТЕПЕНЕЙ СВОБОДЫ 81
Поскольку величины \цк суть константы, производ-
производная -Tr-jp-— A VtkQk- Поэтому уравнения Лагранжа
выглядят так:
Z Vikqk + Е ЩьЯъ = 0 (/ = 1, 2, ..., 8) A9.5)
(ср. с уравнением A6.4) для одной переменной).
Мы пришли к системе линейных однородных диф-
дифференциальных уравнений с постоянными коэффици-
коэффициентами. Попробуем искать неизвестные функции qk(t)
в виде (ср. с A6.5))
A9.6)
где Си — комплексные постоянные, которые требуется
определить. Функции A9.6) комплексные, обобщен-
обобщенные же координаты являются вещественными. Поэто-
Поэтому, завершив вычисления, нужно будет взять веще-
вещественные части функций A9.6) (см. Приложение V).
Подстановка выражений A9.6) в уравнения A9.5)
дает
Z №* (-<*2) Ck ехр (Ш) + ? %lkCk ехр (Ш) = О
(/ = 1, 2, ...,s).
Сократив все уравнения на ехр(ко?), получим
0. A9.7)
Мы пришли к системе s линейных однородных ал-
алгебраических уравнений с неизвестными Сь С2, ..., Cs.
Для того чтобы эта система имела ненулевое реше-
решение, необходимо и достаточно равенство нулю ее опре-
определителя:
(см. Приложение VIII, текст, следующий за форму-
формулой (VIII. 26)).
Уравнение A9.8) называется характеристическим.
Оно представляет собой уравнение s-й степени отно-

82 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
сительно о2. В общем случае это уравнение имеет
s различных1) вещественных положительных корней:
of, <»|, ..., <af. Найденные таким способом величины
оо<х (о&= 1, 2, ..., s) называются собственными час*
тотами системы.
Докажем вещественность и положительность кор-
корней уравнения A9.8). С этой целью умножим каждое
из уравнений A9.7) на С* (т. е. на величину, комп-
комплексно-сопряженную коэффициенту С/), а затем сло-
сложим вместе все уравнения. В результате получим, что
ИЛИ
откуда
В числителе и знаменателе найденного нами выраже-
выражения стоят квадратичные формы вида (IX.21). Как
показано в Приложении IX, такая форма равна сумме
квадратичных форм У! Щка1ак + Z1 *«/А** соответ-
ственно X V>ikaiak + X Vikbibk Aai — вещественная
i.k i,k
часть d, hi — мнимая часть Ct). Последние же фор-
формы, во-первых, очевидно, вещественны и, во-вторых,
положительно определенные (см. A9.1) и A9.2)). Та-
Таким образом, мы доказали, что числитель и знамена-
знаменатель выражения A9.9), а следовательно, и ю2 веще-
вещественны и положительны.
Итак, решив характеристическое уравнение A9.8),
мы найдем 5 собственных частот системы: соь оJ, ...
..., ю5. Подставляя поочередно значения ю? в систему
уравнений A9.7) и решая эту систему, найдем С*,
отвечающие различным соа. Если ранг матрицы систе-
системы A9.7) будет равен s— 1 (что обычно имеет ме-
*) В частных случаях могут получиться кратные корня.

§ 19. СЛУЧАЙ МНОГИХ СТЕПЕНЕЙ СВОБОДЫ 83
сто), то согласно (VIII. 28) решения системы имеют
вид
где са— произвольная комплексная постоянная,
алгебраическое дополнение элемента %mk — ®2a№mk в
определителе системы (т выбирается произвольно, но
так, чтобы хотя бы одно A^k было отлично от нуля).
Поскольку все элементы этого определителя веществен-
вещественны, величины А{?1 также будут вещественными.
Таким образом, для каждой обобщенной коорди-
координаты qk получается s различных решений вида
Як = саА{т1 ехр (/©а0 (а = 1, 2, ..., s)t A9.10)
где А{*1 — вещественные постоянные, определяемые
значениями коэффициентов х** и рм, а также час-
частот @а.
Общее решение получим, сложив все выражения
A9.10):
Qk= E caA(l
Перейдя к вещественной части этого выражения, по-
получим
Як = Re { S caA{U ехр (i<*J)] = ? ЛИ Re {ca exp (
Наконец, представив са в виде aaexp(i6a) (aa — мо-
модуль с^ т. е. вещественная положительная величина),
придем к выражению
Як Z cos (ша/ + 6«). A9.11)
Следовательно, изменение каждой обобщенной ко-
координаты qk со временем представляет собой наложе-
наложение s гармонических колебаний, частоты которых рав-
равны собственным частотам системы. Величины аа и ба
определяются из начальных условий.
При специальном выборе обобщенных координат
выражения A9.11) могут быть сильно упрощены.
В Приложении IX показано, что в случае, когда име-
имеются две квадратичные формы — одна от перемен-
переменных qk, а вторая от переменных qk* причем первая из

84 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
них положительно определенная, то существует такое
линейное преобразование переменных д^ которое при-
приводит обе формы к диагональному виду (см. схему
(IX. 37)). Перейдем с помощью такого преобразова-
преобразования от переменных q* к переменным g*. Тогда квад-
квадратичные формы A9.1) и A9.2) станут диагональ-
диагональными:
*й- <19Л2>
В новых переменных функция Лагранжа имеет вид
а уравнения Лагранжа запишутся следующим об-
образом:
1* + *А-0 (*-1, 2,...,5). A9.13)
Таким образом, в координатах |& уравнения дви-
движения распадаются на 5 независимых друг от друга
уравнений, каждое из которых тождественно уравне-
уравнению A6.4). Отметим, что в силу положительной опре-
определенности квадратичной формы, выражающей потен-
потенциальную энергию ?/, все коэффициенты %k положи-
положительны. Поэтому их можно представить в виде
где со* — вещественные величины.
Напишем решения уравнений A9.13):
$* = a*cos(©*/ + **) (fc=l, 2, ...,«) A9.14)
(см. формулу A6.7)).
Мы нашли, что обобщенные координаты g* совер-
совершают независимо друг от друга простое гармониче-
гармоническое колебание, каждая со своей частотой ©?. Опре-
Определенные так обобщенные координаты называются
нормальными (или главными), а совершаемые ими
простые гармонические колебания — нормальными ко-
колебаниями системы.
Отметим, что нормальные координаты |* связаны
с произвольными обобщенными координатами q* с по-

§ 20. СВЯЗАННЫЕ МАЯТНИКИ
85
мощью линейных преобразований, т. е. преобразова-
преобразований вида
I A9.15)
Следовательно, |* можно получить как линейную ком-
комбинацию координат qi.
§ 20. Связанные маятники
Рассмотрим малые колебания системы из двух оди-
одинаковых математических маятников, связанных неве-
невесомой пружиной (рис. 20.1). Предположим, что маят-
маятники могут совершать колебания только в плоскости
чертежа, так что система имеет две степени свободы.
В качестве обобщенных
координат выберем <pi и
фг — углы отклонения ма-
маятников от вертикального
направления. Длина каж-
каждого из маятников равна
/, масса т. Концы пружи-
пружины закреплены на стерж-
стержнях маятников на рассто-
расстоянии Ь от точки подвеса.
Пружина подобрана так,
что при ф1 = ф2 ее натя- Рис- 20-1
жение равно нулю.
Напишем выражение для потенциальной энергии
системы U, полагая U в положении равновесия рав-
равной нулю:
U — mgl(\ —cost
+ mgl (I — cos
+ l/2k (b sin
При малых колебаниях можно положить
COS ф = Vl — 81П2ф = Vl — ф2 = 1 —• !/2ф2-
выражение для U примет вид
U =
— b sin q>iJ.
sinqp = q),
ПОЭТОМУ
— V2 [(mgl + kb2) ф? -
. B0.1)

86 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
Кинетическая энергия в том же приближении
равна
ТЧ[Р] + 1Щ. B0.2)
Сравнение выражений B0.1) и B0.2) с выраже-
выражениями A9.1) и A9.2) дает для коэффициентов и,*
и \цк следующие значения:
Xj! = %22 = mgl + kb2, xl2 = %2{ = — kb2,
-2 _ ~ B0.3)
Подстановка этих значений коэффициентов в уравне-
уравнения A9.5) приводит к дифференциальным уравнениям
тРфх + (mgl + kb2) ф[ — kb2($2 =: 0»
т/2ф2 — kb2q>{ + (mgl + kb2) <p2 == 0. ^2°'4^
Будем искать решения этих уравнений в виде
ф1 = d ехр (Ш), <Рг = С2 ехр (Ш). B0.5)
Подставим эти выражения в уравнения B0.4). После
сокращения на еш и приведения подобных членов,
получим систему уравнений для определения постоян-
постоянных С\ и С2:
(mgl + kb2 — ml2®2) C{ — kb2C2 = 0,
—kb2d + (mgl + kb2 — m/2co2) C2 = 0.
Для того чтобы эта система имела ненулевое решение,
необходимо равенство нулю ее определителя:
I mgl + kb2 - m/2©2 -kb2 _ п
I — kb2 mgl + kb2 ~ ml2m2 ~ U>
т„ е. должно выполняться условие
(mgl + kb2 — m/2©2J — (-kb2J = 0.
Последнее уравнение после несложных преобразова-
преобразований можно привести к виду
О»2J - 2 [g/l + (k/m) (Ь2/12)] ш2 +
+ [Я2//2 + 2 (я//) (k/m) F2//2)] = 0,
Мы пришли к квадратному уравнению относи-
относительно ш2. Корки этого уравнения равны

§ 20. СВЯЗАННЫЕ МАЯТНИКИ 87
Следовательно, собственными частотами системы
будут
и <*2^*JJ/l+2{k/m)(b2jFj. B0.7)
Подставим в уравнения B0.6) вместо о>2 квадрат
первой собственной частоты, т. е. о]. После упроще-
упрощений система B0.8) принимает вид
Решения этой системы очевидны:
Сх == С2 = сг = 4 exp (/60, B0.8)
где Ci — произвольная комплексная постоянная, а\ —
ее модуль, 6i — аргумент.
Подстановка значения B0.8) в B0.5) дает комп-
комплексные решения дифференциальных уравнений
B0.4), соответствующие частоте щ:
ф0) = сх exp (i®xt) = ах exp {i (®{t + Ьх)},
qf> = ct exp (ш^) = a, exp {/ (©,^ + 6,)}.
Взяв вещественную часть от найденных нами функ-
функций, получим
qf> = ax cos (mxt + 6t), ф^ = ах cos (ю^ + б,). B0.9)
Теперь подставим в уравнение B0.6) вместо со2
квадрат второй собственной частоты, т. е. ©|. В ре-
результате получим
Система удовлетворяется значениями
Сх = — С2 = с2 — fl^ex
Соответственно функции B0.5) будут равны
ф<2) = с2 exp (to2t) = a2 exp {/ (m2t + 62)},
ф^2) „ _ c^ exp ^to^j = — a2 exp {/ (g>2^ + 62)}f
а их вещественные части
2). B0.10)

88 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
Общее решение системы B0.4) получим, сложив
решения B0.9) и B0.10). Следовательно,
B() и)
Ф2 = Ф2° + Ф22) = ах cos (©j/ + 6j) —a2 cos (ш2/ + 62).
Перейдем от обобщенных координат ф1 и ф2 к но-
новым переменным gi и ?г, которые определим так:
Ъ\ = Ч* (Ф1 + фг), h = V2 (Ф1 ~ фг).
С учетом B0.11) получаем
1{ = ах cos
Г / .Та! B0-12)
12 = Оз cos (оэ2/ + 62).
Таким образом, переменные %х и |2 суть нормальные
координаты системы связанных маятников. Обобщен-
Обобщенные координаты ф1 и ф2 выражаются через gi и |2
с помощью линейных соотношений
<Pi = 6i + 62, ф2 = gi — ё2. B0.13)
Предположим, что в системе совершается только
первое нормальное колебание. Это значит, что g2 = 0.
Из B0.13) вытекает, что в этом случае
<Pi = Ф2 = 1\ = ^i cos
т. е. оба маятника колеблются как одно целое с час-
частотой (oi, будучи в каждый момент времени отклонены
в одну и ту же сторо-
сторону на одинаковый угол
(рис. 20.2, а). Пружина при
этом не деформирована, так
что каждый маятник колеб-
колеблется так, как если бы вто-
второго маятника не было
(
Рис. 20.2 Теперь предположим, что
в системе совершается толь-
только второе нормальное колебание. Как следует из
B0.13), в этом случае
Ф1 = ~ <Рг = h — <h cos (<u2i + б2).
В каждый момент времени маятники отклонены на
одинаковый по величине угол, но в противоположные
стороны (рис. 20.2,б).

§ 20. СВЯЗАННЫЕ МАЯТНИКИ 89
Связь между маятниками можно охарактеризовать
с помощью коэффициента жесткости пружины k. На-
Назовем его коэффициентом связи. Рассмотрим случай
слабой связи, т. е. малого k. Если k/m <C gjU Раз-
Разность собственных частот будет много меньше самих
частот
@2 — Щ<.Щ. B0.14)
Отведем первый маятник на угол фю = а, второй ма-
маятник при этом удержим в нулевом положении. Затем
предоставим системе совершать колебания. Очевидно,
что начальные условия в этом случае имеют вид
Найдем значения постоянных а\, аг, 6i и б* Для
этого положим в B0.11) / = 0; в результате получим
Фю = а = а\cos si + <h cos б2,
ф20 == о = а{ cos 6] — а2 cos б2.
Теперь продифференцируем выражения B0.11) по вре-
времени и положим в получившихся формулах t = 0. Это
приводит к соотношениям
(ФОо = 0 = — а{щ sin 6Х — а&>2 sin б2,
(Фг)о = 0 = — ахщ sin 6Х + 02% sin д2-
Решив совместно уравнения B0.15) и B0.16), найдем,
что
ах = а2 = а/2, 6{ = б2 = 0.
Таким образом, в рассматриваемом случае коле-
колебания имеют вид
Ф,« !¦ (cos щг + cos ш20 = a cos
ф2 = -j (cos щг — cos ©20 = а sin @2 2 (Dl
В случае слабой связи (®2 — coi)<C (co2 + <oi) (см.
B0Л4)). Следовательно, можно считать, что каждый
из маятников совершает гармоническое колебание час-

90 ГЛ. IV. МАЛЫЕ КОЛЕБАНИЯ
тоты (<O2 + o>i)/2 « coi с медленно меняющейся ампли-
амплитудой. Значит, движение каждого из маятников но-
носит характер биений. Амплитуды изменяются со сдви-
сдвигом по фазе на я/2. Когда амплитуда одного из маят-
маятников достигает наибольшей величины, амплитуда
второго обращается в нуль и наоборот, В процессе
колебаний происходит как бы перекачка энергии от
одного маятника к другому.
В тех случаях, когда возбуждено только одно нор-
нормальное колебание 1\ или ?2, перехода энергии от од-
одного маятника к другому не происходит.

Глава V
МЕХАНИКА ТВЕРДОГО ТЕЛА
§ 21. Кинематика твердого тела
Разбив сплошное твердое тело ка элементарные
объемы массы pdV (p — плотность тела), его можно
представить как систему частиц с жесткими связями.
Твердое тело, как известно, обладает шестью сте-
степенями свободы—-тремя поступательными и тремя
вращательными. Для описания движения твердого
тела выберем инердиалькую систему отсчета К (с ося-
осями Х\у Х2, Х3), которую будем считать неподвижной.
С телом свяжем жестко другую систему К' (с осями
Х\> %2> #з), поместив ее начало в точку А тела. В ка-
качестве обобщенных координат, определяющих поло-
положение тела, удобно взять три координаты качала си-
системы К' (им отвечает радиус-вектор R0 и три угла,
характеризующих ориентацию осей хи х2, х$ по отно-
отношению к осям Хи %2> ^з- Названные оси образуют
друг с другом девять углов, однако независимыми
оказываются только три из них, остальные шесть мо-
могут быть выражены через значения первых трех1).
Обычно в качестве трех углов, определяющих взаим-
взаимную ориентацию осей систем К и К\ используются
так называемые эйлеровы углы <р, #, ty (см. следую-
следующий параграф).
Любое элементарное перемещение твердого тела
можно представить как сумму поступательного пере-
перемещения, при котором все точки тела смещаются на
одинаковый отрезок cIRa, и поворот на угол d<D во-
вокруг оси, проходящей через точку Л.
*) Между косинусами этих углов а« имеются шесть соотно-
соотношений (см. формулу (VI. 39));
Z агт4т *~ *ik <*. * - L 2, 3; t < k)
т
(а** =» cos(*i, Xk)).

92 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Поскольку скорости точек тела v в системе К'
равны нулю, формула A5.3) для скорости точки, по-
положение которой в системе К! определяется радиусом-
вектором Г(ЛI), принимает вид
У = Ул + К4)Г(Л)], B1.1)
где \а — поступательная скорость тела (скорость точ-
точки Л, наблюдаемая в системе К), со(>?) = ^Ф/^ — уг-
угловая скорость вращения тела вокруг оси, проходя-
проходящей через точку А. Первое слагаемое в этой формуле
одинаково для всех точек тела, второе есть функция
точки.
Если бы мы поместили начало системы К' в дру-
другую точку тела, скажем, в точку В, формула B1.1)
выглядела бы следующим образом:
V = Vb + [W(b>], B1.2)
где У в — скорость точки В, наблюдаемая в системе /С,
<&(в) — угловая скорость вращения тела вокруг оси,
проходящей через точку В.
*) Условимся об обозначениях. В этой главе мы будем
пользоваться индексами двух видов: 1) индексами без скобок и
2) индексами, взятыми в скобки. Индексы без скобок будут слу-
служить для указания частицы или точки, к которой относится дан-
данная величина. Например, та — масса частицы с номером а,
га — радиус-вектор той же частицы, R* — радиус-вектор точ-
точки А.
Индексы в скобках будут указывать точку, из которой про-
проведен радиус-вектор, либо точку, относительно которой берется
момент, и т. п. В зависимости от обстоятельств эти индексы мы
будем располагать то внизу, то вверху соответствующего сим-
символа. Так, например, Г(а> или т{А) будет обозначать радиус-век-
радиус-вектор, проведенный из точки А; М(д> или М(/1) — момент импульса
относительно точки А, Отсутствие при символе г или М индекса
в скобках будет означать, что соответствующая величина берется
относительно центра инерции тела С. Таким образом, радиус-
вектор, проведенный из точки С, мы будем обозначать либо
символом Г(о, либо просто г, момент относительно точки С —
символами М(о и М и т. д.
Символом R мы будем пользоваться только в одном вполне
определенном случае —для обозначения радиуса-вектора, прове-
проведенного из начала неподвижной системы координат К (с осями
X, У, Z). Поэтому в данном случае нет надобности в индексе
в скобках и мы его писать не будем.
Малыми буквами (г, х, у, г и т.д.) мы будем обозначать
радиусы-векторы, проведенные из начала системы координат К\
жестко связанной с телом, координаты в системе К* и т. д.

§ 21. КИНЕМАТИКА ТВЕРДОГО ТЕЛА 93
Положение произвольной точки тела в системе /С
определяется в обоих случаях одним и тем же радиу-
радиусом-вектором:
R = Яа + Т{А) = Rb + Г(В).
Отсюда следует, что радиус-вектор Г(в> можно пред-
представить в виде
Г(В) = а + г(ль B1.3)
где а = Ra — Kb есть радиус-вектор, проведенный из
точки В в точку Л, т. е. величина, не зависящая от
того, для какой из точек тела мы пишем формулу
B1.3).
Подставив значение B1.3) в формулу B1.2), по-
получим
V = VB + [<о(В)а] + Кв)Г(л)]. B1.4)
В этом выражении первые два слагаемые одинаковы
для всех точек тела, третье есть функция точки.
Формулы B1.1) и B1.4) определяют одну и ту же
величину — скорость рассматриваемой точки тела в
системе К. Следовательно, при любом Г(л> правые ча-
части этих формул должны совпадать. Это возможно
при условии, что
B1.5)
B1.6)
(знак тождества подчеркивает, что равенство должно
иметь место при любых г(л>).
Из тождества B1.6) вытекает, что
®{А) — ЩВ),
т. е. что угловая скорость вращения вокруг любой оси
одна и та же и можно говорить просто об угловой
скорости тела «о, безотносительно к выбору системы
отсчета /С7. Поступательная же скорость, как видно из
соотношения B1.5), не имеет абсолютного характе-
характера—она зависит от положения начала системы
К'(УАФУв).
Опустив ненужный индекс при &>, запишем соотно-
соотношение B1.5) следующим образом:
ув =..уА — [©а]. B1.7)

94 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Возможны два случая: 1) векторы VA и в> взаимно
перпендикулярны, 2) векторы Уд и © образуют угол,
отличный от я/2. Легко заметить, что в первом слу-
случае векторы Va и [©а] компланарны. Следовательно,
будут компланарными также векторы VB и VA. Зна-
Значит, вектор V5, как и вектор Уд, перпендикулярен
к вектору ©. Отсюда можно заключить следующее:
если векторы Va и © взаимно перпендикулярны при
каком-то выборе начала системы К', то эти векторы
будут взаимно перпендикулярными и при любом дру-
другом выборе начала системы К' (при любом другом
выборе точки А).
Теперь обратимся к формуле B1.1), записав ее
в виде
V = VA + [m{A)}. BL8)
Из нее следует, что при взаимной перпендикулярно-
перпендикулярности векторов Va и © (которая, если имеет место, то
наблюдается при любом выборе точки А) векторы V
и VA будут компланарными, причем скорости V всех
точек тела лежат в плоскостях, перпендикулярных
к вектору ©. Варьируя выбор точки Л, можно добиться
того, чтобы
[] B1.9)
стала равной нулю1) (при этом точка А может ока-
оказаться вне тела). В итоге движение твердого тела
окажется представленным как одно лишь вращение
вокруг оси, которую называют мгновенной осью вра-
вращения тела (см. B1.8)).
Когда векторы VA и © не перпендикулярны друг
к другу, точку А можно выбрать так, чтобы эти век-
векторы были коллинеарными. В итоге движение тела
в каждый момент времени будет наложением двух
движений: вращения вокруг некоторой оси с угловой
скоростью © и поступательного движения со ско-
скоростью Va вдоль той же оси. На доказательстве этого
утверждения мы останавливаться не будем.
Отметим, что формулы динамики твердого тела
принимают особенно простой вид, если начало систе-
*) Оба члена в правой части выражения B1.9) являются
функциями точки тела (V — скорость точки тела в системе К,
Гм> — радиус-вектор этой точки в системе /С'). Разность же этих
членов для всех точек тела одна и та же и равна Va.

§ 22. ЭЙЛЕРОВЫ УГЛЫ
95
мы К' совместить с центром инерции тела С. В даль-
дальнейшем мы обычно будем поступать именно так. По-
Поэтому формулу B1.8) будем писать в виде
B1.10)
§ 22. Эйлеровы углы
Эйлеровы углы определяются следующим образом.
Пусть первоначально оси связанной с телом систе-
системы Kf совпадали с осями системы /С. Затем тело со-
совершило некоторый поворот, в результате чего ориен-
ориентация осей К' в пространстве изменилась. Любой
такой поворот можно осуществить с помощью трех
поворотов, показанных на рис. 22.1.
1. Поворота вокруг оси Z на угол ср (рис. 22.1,а).
Направление п, которое примет при этом ось х, назы-
называется линией узлов.
2. Поворота вокруг линии узлов на угол д
(рис. 22.1,6).
3. Поворота вокруг оси z на угол ф (рис. 22.1,в).
Направление каждого из поворотов связано с на-
направлением оси, вокруг которой он осуществляется,
правилом правого винта.
Из рис. 22.2 видно, что линия узлов есть не что
иное, как линия пересечения координатных плоско-
плоскостей XY и ху. Угол ф образован осью X и линией уз-
узлов, угол ф — линией узлов и осью х и, наконец,
угол Ф есть угол между осями Z и г. Углы & и <р суть
полярные координаты точки пересечения оси z со сфе-
сферой единичного радиуса. Эту точку называют апексом.

96
ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Для того чтобы набор углов <р, #, if, определяю-
определяющий каждый реальный поворот, был однозначным,
принимают, что углы <р и if могут иметь значения от
нуля до 2я, значения же
угла Ф ограничивают ин-
интервалом от нуля до я.
Если бы углу # также
было разрешено иметь
значения от 0 до 2я, то,
например, изображенный
У на рис. 22.3 поворот мож-
можно было бы охарактери-
охарактеризовать либо набором уг-
углов: ф = я/2, Ф = я/2,
ф sss 0 (верхняя последо-
последовательность поворотов;
оси X, У, Z на рисунке не
даны, их ориентация сов-
Рис. 22.2 падает с исходной ориен-
ориентацией осей х, у, z)y либо
набором: <р = Зя/2, Ф = Зя/2, ф = я (нижняя после-
последовательность поворотов).
Рис. 22.3
Допустим, что ось Z направлена по вертикали, а
система К' связана жестко с волчком (гироскопом),
причем ось z совпадает с осью собственного вращения
волчка. Тогда легко видеть, что изменение угла -ф со-
соответствует собственному вращению волчка, измене-

§ 22. ЭЙЛЕРОВЫ УГЛЫ 97
ние угла ф —повороту вертикальной плоскости, в ко-
которой лежит ось г, т. е. прецессии волчка и, наконец,
изменение угла Ф— движению оси волчка, называе-
называемому нутацией1). В соответствии с этим угол <р на-
называют углом прецессии, угол Ф— углом нутации,
а угол ф — углом собственного вращения (или углом
чистого вращения) 2).
Скорость изменения угла <р можно охарактеризо-
охарактеризовать вектором угловой скорости ©ф, направленным по
оси Z (см. рис. 22.2); модуль этого вектора есть ф.
Разложим вектор <оф на две составляющие, одна из
которых направлена по оси г (ее модуль равен
ф cos*), а вторая перпендикулярна к оси z, т. е. ле-
лежит в плоскости ху (ее модуль равен фвтФ). Оче-
Очевидно, что эта вторая составляющая перпендикуляр-
перпендикулярна к линии узлов п и, следовательно, образует с ося-
осями х и у углы к/2 — ^ и ^ Из сказанного можно за-
заключить, что проекции вектора <&ф на оси системы К'
равны
(g><p)i = Ф sin Ф cos (зх/2 — ф) = ф sin Ф sin t|>,
(юфJ = ф sin Ф cos ф, B2.1)
К>)з = Ф cos Ф.
Скорость изменения угла Ф характеризуется век-
вектором <&$, направленным по линии узлов; его модуль
есть Ф. Линия узлов перпендикулярна к оси г, а с
осями х и у образует углы ф и ф+я/2. Следовательно,
проекции вектора <&& на оси системы К' имеют зна-
значения
(щ)г = Ф cos ф,
(<о<>J == ф cos (ф + я/2) = — Ф sin ф, B2.2)
Наконец, скорость изменения угла ф харак-
характеризуется вектором щ, направленным по оси г
*) В курсах общей физики обычно рассматривается только
так называемая регулярная прецессия, для которой характерно,
что угол между осью волчка и вертикалью остается неизменным.
В действительности ось волчка, как правило, совершает коле-
колебание в плоскости Zz около некоторого среднего положения.
Это колебание и есть нутация.
2) Иногда буквой ф обозначают угол прецессии, а буквой
ф —угол собственного вращения.
4 И. В. Савельев, т. I

98 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
(его модуль есть ф). Проекции этого вектора на оси
системы К' равны
*. B2.3)
Вектор угловой скорости <», с которой вращается
тело относительно системы К1), можно представить
как сумму угловых скоростей каждого из трех враще-
вращений, отвечающих изменениям эйлеровых углов
Поэтому для проекций угловой скорости ® на оси си-
системы К' с учетом формул B2.1), B2.2) и B2.3) по-
получаются следующие значения:
щ — ф sin # sin ф + Ь cos ф,
©2 = ф sin d cos ф — Ь sin ¦$, B2.4)
% — ф cos Ф + «ф.
Эти формулы нам понадобятся в дальнейшем.
§ 23. Тензор инерции2)
Пусть мы наблюдаем движение твердого тела в не-
неподвижной системе координат К (оси которой будем
обозначать Х%9 Яг, Xs или X, К, Z). В соответствии
со сказанным в § 21 свяжем жестко с телом систему
координат К' с осями х\, #г, *з (или ху у, г). Разобьем
мысленно тело на частицы массы та3). Согласно фор-
формуле B1.10) скорость частицы с номером а запишется
следующим образом:
Va = Vc + [<ora]. B3.1)
Вычислим кинетическую энергию тела. Она равна
a a
a a
*) Относительно системы /С7 тело всегда неподвижно.
2) Прежде чем приступить к изучению этого параграфа,
нужно ознакомиться с Приложением X.
3) Индекс а указывает номер частицы. Латинские индексы
/, к, I, ... мы используем для нумерации координатных осей,
компонент векторов и т. п.

§ 23. ТЕНЗОР ИНЕРЦИИ 99
В первом слагаемом можно вынести за знак суммы
множитель V2C. В итоге это слагаемое примет вид
xl2tnV2cy где т= ? та~~ масса тела. Во втором сла-
слагаемом произведем циклическую перестановку сомно-
сомножителей (см. (VI. 3)), после чего вынесем постоян-
постоянный множитель за знак суммы. В результате получим
выражение [Fc, ©] ? mara = [Vc, &]тгс, где гс — ра-
радиус-вектор центра инерции С. Если поместить, как
мы условились, начало системы К' в точку С, то вто-
второе слагаемое обращается в нуль.
Таким образом, кинетическая энергия твердого
тела распадается на два слагаемых. Первое слагаемое
B3.2)
представляет собой кинетическую энергию поступа-
поступательного движения. Второе слагаемое
Гвращ = У, Z ma[maf B3.3)
a
есть кинетическая энергия вращательного движения.
Подчеркнем, что обе эти энергии совершенно не-
независимы— одна зависит только от Vc, вторая —
только от ©. Благодаря совмещению начала систе-
системы К' с точкой С слагаемое, в которое входили и Vc,
и ©, обратилось в нуль.
Преобразуем выражение B3.3) к другому виду.
Прежде всего заменим квадрат векторного произведе-
произведения в соответствии с (VI. 6) :
= Vt ? пга {*>Va - (шга)*}. B3.4)
га
Теперь запишем это выражение, используя проекции
векторов <*> и та на оси системы /С'. Проекции ra на
оси системы К' равны просто координатам частицы:
х\а, *2а, *зс&. Обозначим проекции вектора в» на оси
системы К! символами a>i, co2, ©з. Тогда выражение
B3.4) в компонентах векторов примет вид
д вращ
-V, z «•{(? «>?) (? *)-(? -а.) (?

100 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
(напомним, что немой индекс можно обозначать лю-
любой буквой).
В полученном нами выражении величины со, и <о*
не зависят от индекса а и их можно было бы вынести
за знак суммы по а. Однако зтому препятствует то
обстоятельство, что в первый член выражения входит
сумма квадратов ©f, а во второй член — сумма про-
произведений ш/Ол. Это препятствие можно устранить, за-
заменив сумму величин <*>| выражением E^V^A*» к0~
торое, очевидно, эквивалентно Е®?- Тогда формула
для вращательной энергии примет вид
ГВращ — 72 Е ГПа U ? ЩЩбцЛ ( Е Х*Л — Е ЩЩХшХкЛ
а l\f. k / \ I / i, k }
B3.5)
f заметим, что ? доесть просто некоторый скаляр !V
зависящий от индекса а; каждое из слагаемых (О/одб^
умножается на этот скаляр ).
В выражении B3.5) сначала производится сумми-
суммирование по индексам i и к. а затем уже по индексу а.
Изменим порядок суммирования так, чтобы суммиро-
суммирование по индексам ink осуществлялось в последнюю
очередь, т. е. перепишем B3.5) следующим образом:
2"вРащ= !/2 Е «мо* Е пга
Если ввести обозначение2)
hk = Е ma {б,А ( Е ^/a) - W*«}» B3.6)
выражение для кинетической энергии вращательного
движения можно записать в виде
V2 ?/**«?*>*. B3.8)
2) При вычислении величин /« для сплошного тела нужно
вместо та взять pdV и суммирование заменить интегрированием.
Тогда
B3.7)
'/* - J К* Р

§ 23. ТЕНЗОР ИНЕРЦИИ \Q\
Величина, определяемая формулой B3.6), есть не-
некоторое число (но не инвариант!), зависящее от ин-
индексов i и к. Всего имеется девять таких чисел. Вид-
Видно, что совокупность величин /** образует тензор вто-
второго ранга1). Действительно, произведение скаляра
Y, #|а на единичный тензор б<* будет тензором (см.
формулы (X. 17) и (X. 19)), произведения XiaXka суть
произведения компонент вектора га, т. е. тоже тензор
(см. (X. 16)). Наконец, разность соответствующих
компонент двух тензоров также дает компоненты не-
некоторого тензора (см. X. 18)).
Итак, величины B3.6) суть компоненты тензора.
Этот тензор называют тензором инерции. При пере-
перестановке индексов ink величины B3.6) не изме-
изменяются. Следовательно, тензор инерции является сим-
симметричным (Iik — /a*).
Напишем компоненты тензора инерции, применив
обычные обозначения декартовых координат:
]? m {у2 + г2) — ]Г пгху — ]Г) тхг
]Г тгх — ]Г mzy ?,т
B3.9)
(чтобы не усложнять формул, мы опустили индекс а
при т и координатах дс, у, г; все суммы берутся по
этому индексу).
Диагональные компоненты тензора называют осе-
осевыми моментами инерции. Они совпадают с извест-
известными из курса общей физики моментами инерции тела
относительно соответствующих координатных осей.
*) К этому выводу можно также прийти путем следующих
рассуждений. Представим выражение B3.8) в виде
Написанное нами выражение может быть инвариантом лишь в
том случае, если величины 2л ^кфк будут t'-ми компонентами
некоторого вектора (см. Приложение VI, текст, следующий за
формулой (VI. 28)). Последнее, в свою очередь, возможно толь-
только в том случае, когда величины 1щ будут компонентами тензора
(см. Приложение X, текст, расположенный между формулами
(Х.22) и (Х.23)).

102 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Недиагональные компоненты называют центробеж-
центробежными моментами инерции.
Геометрическим образом симметричного тензора
является эллипсоид. В рассматриваемом нами случае
это есть эллипсоид инерции. Направления в теле, со-
совпадающие с полуосями эллипсоида инерции, назы-
называются главными осями инерции тела. Эти
оси пересекаются в центре инерции тела. Если напра-
направить оси системы К' (т. е. оси х, у, г; напомним, что
эти оси жестко связаны с телом) по главным осям
инерции тела, то тензор инерции окажется приведен-
приведенным к диагональному виду
/Л о 0 \
\0 О 1Ъ)
(/**) = ( ° '• ° • B3.10)
Значения /ь /2, h диагональных компонент тен-
тензора (в том случае, когда он приведен к диагональ-
диагональному виду) называют главными моментами инерции
тела (их можно было бы обозначить символами /х,
/*/ж).
Если в качестве связанных с телом осей х, у, z
выбраны главные оси инерции, выражение B3.8) для
кинетической энергии вращательного движения упро-
упрощается следующим образом:
гвраи - V* (/,•?+Л*+/3Ц) B3-10
либо
B3-12>
(напомним, что <оь ю2, од суть проекции на оси лс, уУ г
вектора <л — угловой скорости вращения тела, наблю-
наблюдаемого в системе с осями X, У, Z).
В случае, когда вектор <*> совпадает с одной из
главных осей инерции, вдоль которой мы направим,
скажем, ось г, выражение для энергии становится еше
проще:
Г/2 B3.13)
Выражение, аналогичное B3.13), получается также
в том случае, когда тело вращается вокруг проходя-
проходящей через центр инерции фиксированной относительно
тела оси1). Направив вдоль этой оси, скажем, ось г,
*) Если эта ось не совпадает ни с одной из главных осей
инерции, то ее нужно удерживать с помощью подшипников.

§ 23. ТЕНЗОР ИНЕРЦИИ ЮЗ
мы получим, что ю* = щ = 0, a co* = g>. Тогда из де-
девяти слагаемых формулы B3.8) отличным от нуля
будет только одно, в котором i — k = z, так что
V2/2,co| - У21гг<*\ B3.14)
где 1г2, вообще говоря, не является одним из главных
моментов инерции.
Отметим, что, например, у такого тела, как одно-
однородный шар, эллипсоид инерции вырождается в сфе-
сферу. Следовательно, главные оси инерции оказываются
не фиксированными относительно тела. Это значит,
что в качестве главных осей могут быть взяты любые
три взаимно перпендикулярные оси, проходящие че-
через центр шара. В этом случае все главные моменты
инерции оказываются одинаковыми: 1\ = h = h == /
и тензор инерции можно записать так:
(Л*) «/•<*!*>. B3.15)
где (8ik)—единичный тензор (см. X. 17)), а / —
скаляр.
Все то, что мы сказали в отношении шара, оказы-
оказывается справедливым и применительно к однородному
кубу. Действительно, для него, очевидно, справедливо
соотношение B3.15). Следовательно, эллипсоид инер-
инерции у куба вырождается в сферу. Поэтому любая ось
(а не только ось симметрии), проходящая через центр
куба, может рассматриваться как главная ось инер-
инерции. По этой причине куб наряду с шаром и другими
телами, у которых Л = 1% = /з, называют шаровым
волчком *).
Тело, у которого равны друг другу два главных
момента инерции (например, 1\= 1гФh)> называют
симметричным волчком. Наконец, тело, у которого все
три главные моменты инерции различны, называют
асимметричным волчком.
До сих пор, рассматривая тензор инерции, мы
предполагали, что начало связанной с телом си-
системы К' помещается в центре инерции тела С. Од-
Однако тензор инерции можно определить по формуле
B3.6) также и по отношению к связанной с телом
') Для шарового волчка энергия всегда выражается форму*
лой B3.13), причем под 1г следует понимать скалярный множи-
множитель /, входящий в выражение тензора инерции B3.15).

104
ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
системе К[А) с началом, помещающимся в произволь-
произвольной точке А. Компоненты тензора в этом случае будут
равны
- ? *.
Значения I\f оказываются связанными простыми со-
соотношениями с значениями Iik компонент тензора,
определяемых по отношению к системе К{С) с нача-
началом в точке С и осями,
параллельными осям си-
системы К{А) (рис. 23.1).
Для того чтобы найти эти
соотношения, обозначим
символом а радиус-век-
радиус-вектор точки А в системе
К{су Тогда для любой
точки тела Т(А) = г — а и,
следовательно,
Х1р=*хг — а,, B3.17)
Рис. 23.1 где di есть *-я координата
точки А в системе К[су
Подставим значения B3.17) в формулу B3.16):
Первая из пяти сумм есть Iik. Во второй сумме ни
одна из величин в фигурных скобках не содержит ин-
индекса а. Кроме того, 2 а? есть квадрат вектора а,
т. е. а2. Поэтому вторую сумму можно представить
в виде m(a2&ik — axafe). Третью сумму можно напи-
написать в виде X 26/fea/ J) maxia- Но 2 maxta — яг#/С=0,
I - a a
так что третья сумма равна нулю. Аналогично, вы-
кеся в четвертой и пятой суммах не зависящий от a

§ 23. ТЕНЗОР ИНЕРЦИИ {qk
множитель за скобки и приняв во внимание, что
xic я= хне = 0, установим, что обе эти суммы также
равны нулю. Итак, мы приходим к соотношению
'$ - /« + w (о^ - аЛ), B3.18)
которое представляет собой тензорную запись тео-
теоремы Штейнера. Чтобы убедиться в этом, найдем ком-
компоненту 1$ — 1{?. Согласно B3.18)
B3.19)
где а±— расстояние между осями z и s/*\
Вычислим кинетическую энергию тела, вращающе-
вращающегося с угловой скоростью с* вокруг неподвижной (в
системе К) фиксированной относительно тела оси, не
проходящей через его центр инерции. Если центр
инерции находится от оси вращения на расстоянии ах,
его скорость Vc = юал. Следовательно,
где т — масса тела. Вращательную энергию найдем
по формуле B3.14), направив ось г параллельно не-
неподвижной оси вращения. Сложив обе энергии, по-
получим
+I<»2 (mal + 7K
B3.20)
(см. формулу B3.19)). Мы пришли опять к фор-
формуле B3.14).
Таким образом, формула B3.14) для кинетической
энергии вращающегося тела справедлива не всегда,
а только в двух случаях: 1) когда тело вращается
вокруг одной из своих главных осей инерции (см.
формулу B3.13)); 2) когда тело вращается вокруг
неподвижной, фиксированной в нем оси (см. формулы
B3.14) и B3.20)).
В заключение найдем вид тензора инерции в слу-
случае, когда только одна из координатных осей, скажем,
ось z совпадает с одной из главных осей инерции
тела. Переход от системы, все оси которой совпадают
с главными осями, к интересующей нас системе осу-

106 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
ществляется поворотом вокруг оси z на угол q>. Легко
убедиться в том, что таблица коэффициентов преоб-
преобразования выглядит в этом случае следующим об-
образом:
|<*п <*is 01 I cos ф sin ф 01
«21 С*22 0 | = И — Sin Cp СОЗф 0|.
0 0 1 | 8 0 0 1 I
Компоненты тензора инерции в интересующей нас
системе координат получим из компонент тензора,
приведенного к главным осям, по формуле преобразо-
преобразования (X. 10). Представим компоненты тензора B3.10)
в виде 11т — б/m/m. Тогда, обозначив компоненты тен-
тензора в новой «штрихованной» системе просто /4* (без
штриха), можно написать
Согласно этой формуле
Аналогичные выкладки дают, что /22 = sin2 <p/i
+ cos2 ф/2, /зз — ^з, /12—/21—sin ф cos ф (/2 —1\),
s=s /31 = 0, /гз = /зг = 0. Таким образом, тензор инер-
инерции в новой системе имеет вид
/12 0 \
/21 /22 0 1. B3.21)
.0 о h /
<;
Отметим, что в случае, когда I\ = h = /, из полу-
полученных нами формул вытекает, что /ц=/22 = /, /12=
s=s /21 as 0, т. е. что новый тензор не отличается от
исходного. Так и должно быть, поскольку при равен-
равенстве моментов 1\ и /2 главные оси х и у оказываются
не фиксированными.
§ 24. Момент импульса твердого тела
Как и в предыдущих параграфах, будем рассмат-
рассматривать движение твердого тела в системе координат К
с осями X\f ^2, ^3. С телом свяжем жестко систему /С',
начало которой сначала поместим в произвольную
точку А. Оси этой системы обозначим хи x2t Хг (или
х, yt z). Тело разобьем мысленно на частицы массы ma.

* 24. МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА Ю7
Согласно формуле B1.8) скорость частицы с но-
номером а в системе К равна
B4.!)
где V*— скорость начала системы К\ © — угловая
скорость вращения тела в системе /С, г*** — радиус-
вектор частицы, проведенный из точки А.
Найдем момент импульса тела М<л> относительно
начала системы К' (относительно точки Л). Радиус-
вектор, проведенный из точки А к частице с номе-
номером а, есть г?А). Следовательно,
Подстановка в это выражение значения B4.1) для
Va дает
М(Л) = L [г<*. maVA] + L №>, ma [<<>] ]. B4.2)
a a
Второе слагаемое в B4.2) представляет собой значе-
значение М('Л), которое имел бы момент при условии, что
точка А была бы неподвижна. Следовательно, М[Д)
есть момент, обусловленный только вращением тела.
Преобразуем первое слагаемое в B4.2), восполь-
воспользовавшись дистрибутивностью векторного произве-
произведения:
и-
Здесь m — масса тела, г^ — радиус-вектор центра
инерции в системе К' (радиус-вектор, проведенный
из Л в С).
Таким образом, выражению B4.2) можно придать
вид
М^-М^ + де.тУ,]. B4.3)
Слагаемое М^, как мы уже отмечали, обусловлено
вращением тела. Его можно назвать собственным мо-
моментом тела. Второе слагаемое обусловлено поступа-
поступательным движением тела.

108 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Если начало системы К' (т. е. точку А) поместить
в центр инерции тела, г<^ будет равен нулю, вслед-
вследствие чего из B4.3) получается М(С) = М[С). Отсюда
следует, что наблюдаемый в неподвижной системе К
момент импульса тела относительно его центра инер-
инерции совпадает с собственным моментом, т. е. опреде-
определяется только вращением и не зависит от того, дви-
движется центр инерции тела или покоится.
Найдем выражение для момента импульса') тела
относительно центра инерции. Если точка А совпадает
с С, первое слагаемое в B4.2) обращается в нуль.
Следовательно,
Щс) — ? "*а [гв M\J ] B4.4)
(напомним, что га — радиус-вектор частицы, проведен-
проведенный из точки С). Преобразуем это выражение по фор-
формуле «бац минус цаб» (см. (VI. 5)):
(мы выразили скалярные произведения через проек-
проекции соответствующих векторов на оси связанной с те-
телом системы /С').
Вычислим компоненты вектора М(С) по осям си-
системы /(' (в дальнейших формулах индекс «С в скоб-
скобках» мы опустим). Для компоненты по 1-й оси по-
получаем
Представим со, в виде
©* = ?
к
Тогда
*) Наблюдаемого в системе /С. В системе К' тело покоится,
так что момент импульса в этой системе всегда равен нулю.

§ 24. МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА 109
Наконец, изменим порядок суммирования по индек-
индексам а и k:
Выражение в квадратных скобках есть компонента
тензора инерции Jik (см. формулу B3.6)). Таким об-
образом, для проекции вектора М на i-ю ось связанной
с телом координатной системы получается следующее
выражение:
]E tf-1,2,3) B4.5)
(напомним, что ю*— проекция вектора <*> на k-ю ось
системы /С').
Из формулы B4.5) вытекает, что векторы М и со,
вообще говоря, не коллинеарны друг другу. Если оси
системы К' (т. е. оси х, у, г) направить по главным
осям инерции тела, формула B4.5) упрощается сле-
следующим образом:
M^I&i (i = x,ytz). B4.6)
Здесь It — 1-й главный момент инерции.
Пусть тело вращается вокруг, например, третьей
главной оси инерции. Тогда о* = <% = 0, <ог = <о, так
что
Последнее соотношение можно записать в векторной
форме:
М = /г®. B4.7)
Из формулы B4.6) видно, что в случае шарового
волчка (т. е. тела, для которого 1\ = /2 = h = I) век-
векторы М и <о также будут коллинеарными, причем
М = /сй.
Если тело вращается вокруг фиксированной в нем
оси г, не совпадающей ни с одной из главных осей
инерции, то со* = щ — 0, <ог = <о. Тогда формула
B4.5) дает
Подчеркнем, что сам вектор JVI в этом случае не кол-
линеарен с вектором о> и поворачивается вокруг на-
направления со вместе с осями х п у.

110
ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Проекция вектора М на ось, проходящую через
точку, относительно которой определен М, называется
моментом импульса относительно этой оси. Следова-
Следовательно, момент импульса относительно, например,
оси г равен
B4.8)
(О
В заключение рассмотрим случай, когда тело вра-
вращается вокруг неподвижной (в системе /С), фиксиро-
фиксированной в нем оси, не проходящей через его центр
инерции С (рис. 24.1). Возь-
** мем на оси вращения про-
произвольную точку Л. Прове-
Проведем из этой точки в точку
€ вектор, который обозна-
обозначим символом а. Тогда для
каждой из частиц тела
= а + г, B4.9)
Рис. 24.1
где Tjj4 — радиус-вектор час-
частицы с номером а, прове-
проведенный из точки А, га — ра-
радиус-вектор той же час-
частицы, проведенный из точ-
точки С.
По предположению ось вращения неподвижна. По-
Поэтому скорость У* равна нулю. Найдем момент им-
импульса тела относительно точки Л, т. е. М<л>. В соот-
соответствии с формулой B4.2)
B4.10)
Подставим сюда значение B4.9) для t^h
Ща) = Е [а + га, та К a + г„] ].
Воспользовавшись дистрибутивностью векторного
произведения, можно после несложных преобразова-
преобразований привести выражение B4.10) к виду
B4.11)
+ [S тата,
+ Z [гв, ma [<»гв] ].

§ 24. МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛА |Ц
Поскольку X) тата = пгтс = 0, второе и третье сла-
слагаемые в полученном нами выражении равны нулю.
Применение формулы «бац минус цаб» и замена
X) пга массой тела m превращает первое слагаемое в
пг [ш2 — а (<оа)] = m \{а\ + а\) ю — afi©a],
где аи — составляющая вектора а, параллельная в>,
а± — составляющая а, перпендикулярная к <о (а± есть
расстояние между осью вращения и параллельной ей
осью г, проведенной через точку С).
Наконец, сравнение с формулой B4.4) показы-
показывает, что последнее слагаемое в B4.11) есть М(с> —
момент импульса тела относительно точки С. Таким
образом, в изображенном на рис. 24.1 случае
Ш(А) - « W + 4) • - "«V* + Micy B4.12)
Найдем момент импульса тела относительно оси
вращения (которую мы будем обозначать буквой <о).
Для этого нужно спроектировать вектор B4.12)
на ось со. Проекция первого слагаемого равна
m (ajj + а2±) cd. Проекция второго слагаемого равна
— пиг^(оай — — та]-©. Согласно формуле B4.8) проек-
проекция третьего слагаемого есть /<*>©, где /<,С) — момент
инерции тела относительно оси г, проходящей через
точку С. Следовательно,
т(а\ + а\) со — + г
та\) © = /^>©. B4.13)
Здесь /^> — определенный по теореме Штейнера мо-
момент инерции тела относительно оси со, проходящей
через точку А.
Таким образом как бы ни была выбрана непо-
неподвижная ось вращения, жестко связанная с телом,
момент импульса тела относительно выбранной оси
равен произведению момента инерции тела относи-
относительно этой оси на модуль угловой скорости (см. фор-
формулы B4.8) и B4.13)). Отметим, что, если ось, на
которую проектируется момент, и вектор со направ-
направлены в противоположные стороны, то в формуле
B4.13) появится знак минус.

112
ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
§ 25. Свободные оси вращения
Свободными осями вращения тела называются, как
известно, оси, которые сохраняют свое положение
в пространстве без воздействия на них внешних сил.
В этом параграфе мы докажем, что свободными осями
вращения могут быть только глав-
«> кые оси инерции тела.
Допустим, что тело вращается
с угловой скоростью ю вокруг неко-
некоторой связанной с ним неподвиж-
неподвижной оси (рис. 25.1). При этом каж-
каждой частице тела должно быть со-
сообщено ускорение
wa = —ш2ра,
где ра—перпендикулярная к оси
вращения составляющая радиуса-
вектора га данной частицы (ra про-
проведен из точки О, лежащей на оси
вращения !)).
Для того чтобы сообщить частице такое ускорение,
необходимо приложить к ней силу
а, B5.1)
Рис. 25.1
момент которой относительно точки 0 равен
а—¦ |Та> га1 ~~"—™а® 1Та» РаЬ (ZO.Z;
Сложив все силы B5.1), получим результирующую
внешнюю силу, которая должна быть приложена
к телу, чтобы обеспечить вращение его вокруг рас-
рассматриваемой оси 2):
F = ? Fa = - ©2 Z таРь. B5.3)
а а
*) В соответствии с принятыми нами обозначениями этот
вектор следовало бы обозначить символом г^\ Однако, по-
поскольку в этом параграфе нам не встретятся радиусы-векторы,
проведенные из точки С, мы, чтобы не усложнять обозначений,
опустим индекс «О в скобках» при символах векторов и коор-
координат.
2) Силы Fa включают в себя как внешние, так и внутренние
силы, но результирующая внутренних сил, как известно, равна
нулю.

§ 25. СВОБОДНЫЕ ОСИ ВРАЩЕНИЯ ИЗ
Результирующий момент внешних сил должен быть
равен сумме моментов B5.2):
N = Е Na = - со2 ? ma [ra, pj. B5.4)
a
Свяжем с телом систему координат, поместив ее
начало в точку 0, а ось г направив вдоль вектора «о.
Компоненты вектора ра по осям такой системы равны
*а> Уа, 0. Следовательно,
ь Pal :
*а Уа
г Уа О
так что компоненты вектора [га, ра] равны:
На» PaJnp. х === У а ' " ~~~ %аУа === Уа?а>
[га, ра]пр. у == zaxa — ха • 0 = л:ага, B5.5)
I* a> PaJnp. z ~~ ^аУо. ~~" Уа^а === ^*
Теперь напишем компоненты результирующей
силы F и результирующего момента N. Согласно фор-
формуле B5.3)
Fx = — ш2 2 таха = — <аРтхс,
a
где хс и ус — координаты центра инерции тела. Если
ось вращения проходит через центр инерции, эти ко-
координаты будут нулями, так что все компоненты силы,
а значит и сама F будут равны нулю.
Согласно формулам B5.4) и B5.5)
Nx =
, = —СО2
где 1уг и /xz — центробежные моменты инерции тела
(см. формулу B3.9)). Если ось 2, вокруг которой про-
происходит вращение, является одной из главных осей
инерции, центробежные моменты Ixz и 1уж равны нулю

114 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
(см. B3.21)), так что все компоненты результирую-
результирующего момента сил, а значит, и сам момент N будут
равными нулю.
Итак, мы доказали, что в случае, когда тело вра-
вращается вокруг одной из своих главных осей инерции,
результирующая внешних сил и результирующий мо-
момент этих сил равны нулю. Значит, для того чтобы
такая ось вращения сохраняла свое положение в про-
пространстве, необходимости во внешних силах нет.
§ 26. Уравнение движения твердого тела
Возьмем в качестве обобщенных координат, опре-
определяющих положение тела в неподвижной системе /С,
декартовы координаты центра инерции Х\С, Х2с, Язе
(им соответствует радиус-вектор Re) и эйлеровы углы
Ф, #, ф, причем оси связанной с телом системы К
направим по главным осям инерции тела.
В § 23 мы установили, что кинетическая энергия
твердого тела слагается из энергии поступательного
движения B3.2) и энергии вращательного движения,
которая при сделанном нами выборе осей К' опреде-
определяется формулой B3.11). Таким образом, для функ-
функции Лагранжа твердого тела можно написать сле-
следующее выражение:
L « i/,mV» + Vi (/,«? + /2©1 + /3Ц) - U. B6.1)
Чтобы получить выражение L в принятых нами
обобщенных координатах, заменим Vc через Re, a
проекции вектора ш на оси системы К' выразим через
эйлеровы углы (см. B2.4)). В результате получим
L = V2mRc + Vi Ух (Ф sin * sin ф + Ь cos фJ ~f
+ /2(Ф sin #cos \|> - Ь sin aj>J + /3 (ф cos d + -фJ} —
-?/(Rc, Ф, «, *) B6.2)
(напомним, что Iи /2, h — главные моменты инерции
тела).
Зная вид функции f/(Rc, <p, #, tp), можно составить
уравнения Лагранжа и решить соответствующую за-
задачу о движении твердого тела. Уравнение Лагранжа,

§ 26. УРАВНЕНИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА 115
соответствующее координатам центра инерции, имеет
вид
откуда получается уравнение движения центра инер-
инерции тела:
mRc — F, B6.3)
где F — результирующая внешних сил, действующих
на тело.
Чтобы получить уравнение, определяющее поведе-
поведение со временем момента импульса тела М, вспомним,
что для отдельной частицы
Ма = [raFa] = Na,
т. е. производная по времени от момента импульса
равна моменту силы, действующей на частицу. Про-
Просуммировав по всем частицам тела, получим
•aFa] = N, B6.4)
где N — сумма моментов всех действующих на тело
внешних сил относительно точки С (моменты внут-
внутренних сил в сумме дают нуль).
Запишем уравнение B6.4) в проекциях на оси си-
системы К' (на главные оси инерции тела):
J^M^Nt (*-1,2,3). B6.5)
Проекцию Ni можно представить в виде
B6-6)
где 6Ф* — угол поворота тела вокруг i-й главной оси
(un = dQ>i/dt). Действительно, при повороте тела на
угол вф/ силы, приложенные к телу, совершают ра-
работу
ЬА = ? F 6R = ? F [6Ф<еь т].
Здесь суммирование производится не по индексу /, а
по всем внешним силам, действующим на тело, 6R —
перемещение точки приложения соответствующей

И6 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
силы, е, — орт 1-й главной оси, г — радиус-вектор
точки приложения силы, проведенный из точки С (R
проводится из начала системы /С). Осуществив цикли-
циклическую перестановку сомножителей и вынеся общий
множитель бФ/е* за знак суммы, придем к выражению
6А = 6Ф,е, ? [rF] — 6O,e,N = Nt 6Ф
*,
где Ni — проекция результирующего момента сил на
ось, вокруг которой произведен поворот на угол 6Ф,.
Вычисленная нами работа 6Л совершается за счет
убыли потенциальной энергии (/, т. е.
откуда и следует формула B6.6).
Мы получили формулу B6.6), рассматривая пово-
поворот вокруг одной из главных осей инерции тела. Од-
Однако эта формула справедлива в самом общем слу-
случае— для поворота вокруг произвольной оси (конеч-
(конечно, при условии, что сила, момент которой рассмат-
рассматривается, является потенциальной).
Из формулы B6.6) следует, что величины Ni суть
обобщенные силы, отвечающие обобщенной коорди-
координате Ф, (см. D.20)).
Теперь продифференцируем функцию B6.1) по ш,-.
В результате получим
(см. формулу B4.6)). Проекцию угловой скорости т
можно представить как Ф* (см. текст, следующий за
формулой B6.6)). Следовательно, можно написать,
что
Mt-?—3jL B6.7)
dooj дФ1
(ср. с формулой A1.3)). Из формулы B6.7) вытекает,
что величины Mt суть обобщенные импульсы, отве-
отвечающие обобщенным координатам Ф,- (см. D.19)),
Воспользовавшись соотношениями B6.6) и B6.7),
формулу B6.5) можно представить в виде
J^JI^-JL, /oft»

§ 26. УРАВНЕНИЕ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА Ц7
т. е. как уравнение Лагранжа, отвечающее обобщен-
обобщенной координате Ф,.
Следует иметь в виду, что при сделанном нами вы-
выборе осей системы К' только эйлеров угол *ф соответ-
соответствует повороту вокруг главной оси. Остальные же
углы соответствуют поворотам вокруг неподвижной
оси Хъ и вокруг линии узлов.
Продифференцировав функцию B6.2) по ф, най-
найдем выражение для проекции момента импульса на
ось лез (на ось г) через эйлеровы углы
Мф = М3 = /3 (ф cos # + i). B6.9)
Допустим, что эйлеров угол О равен нулю. Это
означает, что оси Z и z все время совпадают — тело
вращается вокруг связанной с телом оси, которая не-
неподвижна в системе /О В этом случае сумма углов
Ф + ф определяет полный угол поворота тела вокруг
оси г. Положение линии узлов в этом случае оказы-
оказывается неопределенным — эта линия может быть распо-
расположена в любом месте между осями X и х. В частно-
частности, можно совместить линию узлов с осью X, тогда
Ф = 0 и поворот тела вокруг оси z будет характе-
характеризоваться углом собственного вращения ф. Если со-
совместить линию узлов с осью х, будет равен нулю
угол ф и поворот вокруг оси 2 будет описываться уг-
углом прецессии ф.
При Ф=0 формула B6.9) принимает вид
где соз — угловая скорость вращения тела вокруг оси г.
При Ь = п/2 формула B6.9) упрощается следую-
следующим образом:
где ©ф — угловая скорость собственного вращения
тела.
В заключение составим уравнение Лагранжа для
тела, вращающегося вокруг жестко связанной с ним
оси, неподвижной в системе /(. Для большей общно-
общности будем считать, что ось вращения не проходит че-
через центр инерции тела С и не параллельна ни одной
из главных осей инерции тела.
Направим оси Z и z по оси вращения тела. Тогда
эйлеров угол Ь будет равен нулю. Поскольку линия

118 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
узлов в этом случае не фиксирована, совместим ее
с осью х, тогда угол ф также обращается в нуль. При
сделанном нами выборе оси г (по направлению век-
вектора ®) (Ох = % — 0, <йг — <0 в Ф-
Кинетическую энергию для подобного случая мы
вычислили раньше. Она оказалась равной значению
B3.20). Следовательно, функция Лагранжа имеет вид
L = 72Яг>2 - U (ф) = Vi/ЙУ - U (Ф) B6.10)
(А — не совпадающая с С точка, в которой находится
начало системы К').
Составим уравнение Лагранжа:
d dL _ dL
dt дф д<$ *
Из B6.10) следует, что левая часть равна /^(о. Со-
Согласно B6.6) правая часть, равная — dU/ду, есть
проекция результирующего момента сил на ось вра-
вращения, т. е. Nz. Таким образом, мы приходим к урав-
уравнению
§ 27. Уравнения Эйлера
Уравнения Лагранжа, соответствующие эйлеровым
углам (т. е. описывающие вращение тела), оказы-
оказываются, как легко заключить из вида функции B6.2),
весьма сложными. Иногда бывает удобнее пользо-
пользоваться другими уравнениями, полученными Эйлером
и носящими его имя. Чтобы прийти к этим уравне-
уравнениям, будем исходить из соотношения B6.4):
TT-N. B7.1)
Уравнение B7.1) справедливо в инерциальной системе
отсчета (т. е. в неподвижной системе К). Мы попы-
попытаемся найти уравнение, справедливое во вращающей-
вращающейся вместе с телом системе /С', оси которой совпадают
с главными осями инерции тела.
В уравнении B7Л) dTA есть приращение вектора М
за время dtf наблюдаемое в системе К. Согласно
A5.6) это приращение можно представить в виде

$ 27. УРАВНЕНИЯ ЭЙЛЕРА ] 19
где d'PA — приращение вектора М за время dt, наблю-
наблюдаемое в системе К\ d<p — угол, на который поворачи-
поворачивается система К' за время dt. Разделив последнее
уравнение на dt, получим
4г~тг + 1*мЬ <27-2>
где dNi/dt — скорость изменения вектора М, наблю-
наблюдаемая в системе К, d'Ni/dt — скорость изменения
того же вектора, наблюдаемая в системе К7, со =
= dyfdt — угловая скорость вращения системы К'
(т. е. угловая скорость вращения тела).
Формула B7.2) справедлива для любого вектора,
в частности она справедлива и для вектора в>. В по-
последнем случае имеем
— = -^- 4- f ©в>1
Поскольку [ю©] з=г 0, мы приходим к соотношению
~ЗГ = ~Ш~' <273)
из которого следует, что скорости изменения век-
вектора ю, наблюдаемые в системах К и /С', одинаковы.
Заменим левую часть формулы B7.1) выраже-
выражением B7.2). В результате получим уравнение
Спроектируем все векторы на i-ю ось системы К',
учтя, что проекция вектора М на эту ось Mi = /,ю*
(см. B4.6)):
Приняв во внимание, что U = const, a d'&/dt = d&/dt
(см. B7.3)), можно записать полученное нами уравне-
уравнение следующим образом:
Представим проекцию векторного произведения на
ось xt по формуле (VI. 33):
Е шЩi Е

120 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
и подставим это выражение в B7.4). В итоге придем
к уравнениям
7< ТГ + Е *ш1**№ - Ni (I - 1, 2, 3), B7.5)
л, /
которые и представляют собой уравнения Эйлера. По-
Положив последовательно I = 1, i = 2, i = 3 и произведя
суммирование по ft и /, получим три уравнения:
B7.6)
Отметим, что каждое следующее уравнение получает-
получается из предыдущего с помощью циклической переста-
перестановки индексов 1,2,3.
Легко видеть, что в случае шарового волчка урав-
уравнения B7.6) превращаются в уравнение /<о = N.
§ 28. Свободный симметричный волчок
Применим уравнения Эйлера для исследования
движения симметричного волчка (т. е. тела, у кото-
которого Л =/г ^/з)» не подверженного действию внеш-
внешних сил. В этом случае центр инерции тела движется
с постоянной скоростью или покоится (см. формулу
B6.3)). Поэтому можно из всех инерциальных систем
выбрать ту систему /С, начало которой совмещено
с центром инерции тела С. В этой системе поступа-
поступательное движение тела отсутствует и остается выяс-
выяснить только характер вращательного движения.
В отсутствие внешних сил момент импульса тела М
остается по отношению к неподвижной системе К не-
неизменным по величине и направлению. Выберем на-
направление вектора М в качестве оси Z. Относительно
связанной с телом системы К' вектор М, как мы уви-
увидим, вообще говоря, все время изменяет свое направ-
направление.
Поскольку /i = /2 и момент внешних сил равен
нулю, уравнения B7.6) выглядят следующим об-

§ 28. СВОБОДНЫЙ СИММЕТРИЧНЫЙ ВОЛЧОК 12!
разом !):
ТГ-(//)ад-О, B8.1)
= 0.
dt
Из третьего уравнения сразу получается, что @3 =
= щ = const. Это означает, что проекция вектора уг-
угловой скорости на связанную с телом ось г остается
постоянной.
Введя обозначение
О = ^=^-ш0, B8.2)
запишем первые два уравнения B8.1) в виде
щ ——
Легко убедиться в том, что полученная нами система
удовлетворяется функциями
t + «)> ©2 = ®jl s*n (Of + а)> B8.3)
где ©х и а — константы, причем сэ± = д/of + ю| есть
величина проекции вектора со на плоскость ху, пер-
перпендикулярную к оси собственного вращения тела г.
Из B8.3) следует, что перпендикулярная к оси г со-
составляющая ©х» оставаясь постоянной по величине,
вращается равномерно в плоскости ху с угловой ско-
скоростью fi, определяемой формулой B8.2). Параллель-
Параллельная оси z составляющая щ тоже остается, как мы ви-
видели, постоянной по величине. Отсюда заключаем, что
вектор о) вращается относительно тела с угловой ско-
скоростью Q, описывая конус вокруг оси г, причем мо-
модуль вектора & не изменяется (рис. 28.1 2)).
*) Напомним, что уравнения Эйлера пишутся в системе ко-
координат, оси которой совпадают с главными осями инерции тела.
2) Практически в качестве симметричного волчка берут тело
вращения. Однако мы изобразили на рисунке тело неправильной
формы с целью подчеркнуть, что единственным условием того,
чтобы тело было симметричным волчком, является равенство
двух его главных моментов инерции.

122
ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Согласно B4.6) проекции вектора М на оси х, у9 г
равны
М х — Л<°1 > Му = 1{щ, Мг
Следовательно,
М =
где tXi ey, ъг — орты соответствующих осей (эти оси
вращаются вместе с телом). Сумма (Diex + o^ дает
перпендикулярную к оси z составляющую <&х; юзе*
есть параллельная оси z составляющая щ. Таким об-
образом,
М/ + ^ B8.4)
Направления векторов М и <о проходят через об-
общее для систем К и К' начало — точку С. Значит, эти
векторы определяют не-
некоторую плоскость (пло-
Рис. 28.1
Рис. 28.2
скость Zz). Для того чтобы могло выполняться ра-
равенство B8.4), вектор &± должен лежать в этой же
плоскости. Следовательно, и вектор <о = ох + Щ\ ле-
лежит в плоскости Zz. Отсюда заключаем, что век-
векторы М, со и ось собственного вращения тела z в каж-
каждый момент времени лежат в одной плоскости (на
рис. 28.1 эта плоскость заштрихована). Эта плоскость
вращается вокруг направления М. Вместе с ней пово-
поворачивается ось г, описывая вокруг оси Z круговой
конус. Такое вращение оси тела z называется регу-
регулярной прецессией. Для регулярной прецессии харак-
характерно постоянство угла нутации #.
Вектор ©, как мы установили, вращается относи-
относительно тела вокруг оси z с угловой скоростью Q. Вме-

§ 28. СВОБОДНЫЙ СИММЕТРИЧНЫЙ ВОЛЧОК 123
сте с тем этот вектор остается в плоскости Zz. Отсюда
следует, что относительно плоскости Zz тело вра-
вращается вокруг оси z в противоположную сторону с той
же скоростью Q.
На рис. 28.2 изображены составляющие /i«oi и
и, которые в сумме дают момент импульса Ж (см.
B8.4)). Из рисунка видно, что
**•-¦&¦• B8-5)
Ранее мы установили, что ®х и Щ — константы. Сле-
Следовательно, tgft, а значит, и сам угол нутации Ф оста-
остается неизменным. Угол между вектором со и осью z
также постоянен (его тангенс равен шх/соц).
Величины о>1 и щ определяются энергией тела Т
и моментом импульса М. Действительно,
т=4 с.-?+'м+« - т ел+w- B8 6)
Решив эту систему уравнений относительно шх и сои,
найдем выражения этих величин через Т к М:
VM2 — 2Г/, / М2 - 2773 /оо ,-
Допустим, что тело сплюснуто вдоль оси г, тогда
/з > /i и знаменатель под корнем в щ будет положи-
положительным, а в сох — отрицательным. Значит, для того
чтобы щ и со± были вещественными, необходимо вы-
выполнение условий М2 — 2Т1\ ^0, М2 — 2Г/3 < 0, ко-
которые можно объединить в одну формулу
*? B8.8)
Значений, выходящих за указанные пределы, энергия
свободного симметричного волчка иметь не может
(при данном М). Если энергия имеет наименьшее воз-
возможное значение, т. е. при М2 = 2Г/3, сох обращается
в нуль (см. B8.7)). Из формулы B8.5) следует, что
в этом случае # = 0 — оси Z и z совпадают, направ-
направления векторов М и о также совпадают, вектор ш не
перемещается ни относительно тела, ни относительно

124 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
системы /С Отметим, что в этом случае имеет место
соотношение
Теперь допустим, что энергия имеет наибольшее
возможное значение, т. е. М2 — 2Т1\. Тогда обращается
в нуль <оц (см. B8.7)). Согласно формуле B8.5) в
этом случае # = я/2 — оси Z и z взаимно перпендику-
перпендикулярны, вращения вокруг оси z нет, вектор ю —©х
совпадает по направлению с вектором М, энергия свя-
связана с моментом соотношением
Г = -?--. B8.10)
Полученным нами соотношениям можно дать кра-
красивую геометрическую интерпретацию. Перепишем
формулы B8.6) следующим образом:
Каждое из этих уравнений есть уравнение эллипсои-
эллипсоида вращения. Если, как мы предположили, /3 > /ь
оба эллипсоида сплющены вдоль оси а>3, которая со-
совпадает с осью z (эллипсоид инерции в этом случае,
наоборот, вытянут вдоль оси z). Легко сообразить1),
что первый эллипсоид (назовем его эллипсоидом энер-
энергии) сплющен меньше чем второй (который мы назо-
назовем эллипсоидом момента). На рис. 28.3 изображены
оба эллипсоида. Значения ©i, <ог, а>з> удовлетворяю-
удовлетворяющие уравнениям B8.11) и B8.12), определяются ли-
линиями пересечения обоих эллипсоидов. Отсюда выте-
вытекает, что конец вектора со должен скользить по этой
линии пересечения. Следовательно, вектор «о враща-
вращается относительно осей ©i, ©2, ©з, описывая конус во-
вокруг оси ©з. Напомним, что ©* есть проекция © на
t-ю главную ось инерции тела. Значит, оси ©t совпа-
совпадают с осями #, у, z. Таким образом, вращение отно-
относительно осей ©* означает вращение относительно
самого тела.
') Для этого нужно принять во внимание, что /|//i >

§ 29. СИММЕТРИЧНЫЙ ВОЛЧОК В ОДНОРОДНОМ ПОЛЕ 125
Увеличивая М при неизменном Г, можно добиться
того, чтобы эллипсоиды энергии и момента имели
только две общие точки. Это осуществляется при усло-
условии, что Y277/3 = Af//3 (ср. с B8.9)). В этом случае
вектор о) совпадает по направлению с осью г. Если
еще увеличить М, т. е. положить М2/21$ > Г, эллип-
эллипсоиды перестанут соприкасаться и система уравнений
Эллипсоид
энергии
Эллипсоид
момента
Рис. 28.3
B8.11) и B8.12) не будет иметь общих решений. Та-
Такой случай не может реализоваться. Следовательно,
мы получили нижнюю границу для Т (см. B8.8)).
Уменьшая М при неизменном 7*, придем к такому
положению, когда обе линии пересечения эллипсоидов
сольются в одну линию касания, лежащую в эквато-
риальной плоскости. Это осуществляется при условии,
что a/ZTIIx = Mjlx (ср. с B8.10)). В этом случае век-
вектор со вращается вокруг оси 2, оставаясь все время
к ней перпендикулярным. Если еще уменьшить М, т. е.
положить Т > М2/21\, эллипсоиды перестанут сопри-
соприкасаться и система уравнений B8.11) и B8.12) не бу-
будет иметь общих решений. Таким образом, мы прихо-
приходим к верхней границе для Т (см. B8.8)).
§ 29. Симметричный волчок
в однородном поле тяжести
Рассмотрим поведение симметричного волчка с од-
одной неподвижной точкой, находящегося в однородном
поле тяжести. Отметим, что общее решение1) задачи
*) То есть решение, получаемое с помощью квадратур при
произвольных начальных условиях.

126 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
о движении тела с одной неподвижной точкой в одно-
однородном поле тяжести может быть получено только
в трех случаях:
1) для асимметричного уравновешенного волчка
(волчок называется уравновешенным, если неподвиж-
неподвижная точка совпадает с центром инерции тела). Этот
случай называется задачей Эйлера;
2) для симметричного неуравновешенного волчка
(неподвижная точка не совпадает с центром инерции),
у которого центр инерции лежит на оси z — задача
Лагранжа;
3) для симметричного неуравновешенного волчка,
у которого 1\ = /2 = 2/з, а центр инерции лежит в пло-
плоскости ху — задача С. В. Ковалевской.
Мы рассмотрим задачу Лагранжа. Уравнения дви-
движения в этом случае интегрируются очень сложно.
Поэтому мы ограничимся написанием исходных урав-
уравнений и обсуждением их решений.
Начала обеих координатных систем К и К' помес-
поместим в неподвижную точку А волчка (в точку опоры).
Ось Z неподвижной системы К направим по вертикали,
ось z связанной с волчком системы К' направим вдоль
третьей главной оси инерции тела (Л = /2 ф h). При
таком выборе координатных осей потенциальная энер-
энергия волчка имеет вид U = mgl cos Ф, где / — расстоя-
расстояние от точки опоры до центра инерции С (предпола-
(предполагаем, что координата z центра инерции, т. е. Zc
больше нуля).
Найдем выражение кинетической энергии для дан-
данного случая. Учтя, что точка А неподвижна, напишем
и проделаем те же преобразования, какие мы выпол-
выполнили для выражения B3.3). В итоге мы придем к фор-
формуле, которая будет отличаться от B3.5) лишь тем,
что вместо координат дс/а, #*а и т. д. в ней будут
стоять координаты x^f х{?> и т. д. Следовательно,
для кинетической энергии получится выражение, ана-
аналогичное B3.8):

§ 29. СИММЕТРИЧНЫЙ ВОЛЧОК В ОДНОРОДНОМ ПОЛЕ J27
где /<Д> — компоненты тензора, определяемые по фор-
формуле B3.16). Согласно B3.18) эти компоненты равны
В нашем случае aiasa^ —О, Яз ——а=—/ (а —
есть i-я координата точки А в системе К'{С); см.
B3.17)). Кроме того, поскольку ось г совпадает
с третьей главной осью инерции, а оси х и у парал-
параллельны двум другим главным осям1), //* = /Д*. От-
Отсюда можно заключить, что тензор /<? будет диаго-
диагональным, причем отличные от нуля компоненты его
равны
Таким образом, учтя, что 1\ = /г, получим для ки-
кинетической энергии следующее выражение:
Подставив в это выражение значения B2.4) для ком-
компонент ©, получим
Т = Vt {(/i + ml2) (ф2 sin2 О + ?) + /3 (ф cos О + фJ}.
Напишем функцию Лагранжа2):
L = V« (/i + ml2) (ф2 sin2 # + а2) +
+ Vi/з (Ф cos Ф + -фJ - mgl cos -0. B9.1)
Координаты ф и ф являются циклическими (см. § И,
текст, связанный с формулой A1.2)). Поэтому обоб-
обобщенные импульсы рф и p^ оказываются интегралами
движения. Третьим интегралом движения является
энергия Е. Итак, мы имеем три уравнения:
рф = dL/дф = [(Л + ml2) sin2 # + /3 cos2 О] ф + /3 cos #^=
= М z — const,
/3 (ф cos # + *) = Мг = const3),
*) У симметричного волчка любые две взаимно перпендику-
перпендикулярные оси, перпендикулярные к оси симметрии, могут служить
главными осями инерции.
2) Сила, приложенная к волчку в точке опоры, есть реакция
связи, которая, как нам известно, в уравнения Лагранжа не
входит.
3) Ср. с B6.9).

128 ГЛ. V. МЕХАНИКА ТВЕРДОГО ТЕЛА
Анализ решений этих уравнений приводит к сле-
следующим результатам. Угол # изменяется периодиче-
периодически в пределах от #1 до #2, определяемых начальными
условиями (в частности, соотношением между энер-
энергией и моментом импульса волчка). Колебания оси
волчка, отвечающие изменениям угла <К называются
нутацией. Одновременно ось волчка прецессирует, т. е.
поворачивается вокруг оси Z. В итоге апекс, т. е. точка
пересечения оси z (оси волчка) со сферой единичного
А
радиуса, вычерчивает одну из кривых, изображенных
на рис. 29.1. Знак производной ф либо остается неиз-
неизменным (рис. 29.1,а и б), либо меняется (рис.29.1,в).
Случай б) имеет место, когда ф и © одновременно об-
обращаются в нуль.
Характер поведения ф, как и значения <h и #2,
зависит от начальных условий. Такое движение оси
волчка, как в случае б), соответствует естественным
начальным условиям, при которых волчок сначала
приводится во вращение вокруг своей оси, после чего
ось освобождается и начинает свое движение. В мо-
момент освобождения оси и <р, и Ф равны нулю. При
этих начальных условиях волчок сначала наклоняется,
а по достижении граничного угла #2 начинает подни-
подниматься (см, рис. 29.1,6).
При совершенно специфических начальных усло-
иях оба граничные значения #i и О2 совпадают, так
что ось волчка прецессирует без нутации. Такая пре-
прецессия называется, как мы уже отмечали, регулярной.
Чтобы получить регулярную прецессию, нужно сооб-
сообщить волчку начальный толчок вполне определенной
величины и направления.

§ 29. СИММЕТРИЧНЫЙ ВОЛЧОК В ОДНОРОДНОМ ПОЛБ 129
В случае «быстрого» волчка (т. е. в случае, когда
кинетическая энергия собственного вращения волчка
велика по сравнению с его энергией в поле тяжести)
действием сил тяжести можно в первом приближении
пренебречь. Следовательно, движение волчка можно
представить как рассмотренную в предыдущем пара-
параграфе свободную прецессию оси волчка вокруг на-
направления момента А/1 (эта прецессия соответствует
нутации тяжелого волчка), на которую наклады-
накладываются малые возмущения, обусловленные действием
силы тяжести. Эти возмущения вызывают медленную
прецессию момента НА вокруг вертикали.
Расчет показывает, что чем быстрее вращается
волчок, тем меньше амплитуда нутации. Кроме того,
у реального быстрого волчка нутация погашается тре-
трением в опоре. Поэтому практически нутация доста-
достаточно быстрого волчка бывает незаметной и волчок
представляется равномерно прецессирующим вокруг
вертикальной оси. Так как подобная прецессия яв-
является регулярной только приближенно, то она полу-
получила название псевдорегулярной прецессии.
5 И. В. Савельев, т. 1

Глава VI
КАНОНИЧЕСКИЕ УРАВНЕНИЯ
§ 30. Уравнения Гамильтона
При решении задач о движении системы с s сте-
степенями свободы с помощью уравнений Лагранжа при-
приходится решать систему s дифференциальных уравне-
уравнений второго порядка. Независимыми переменными
в этих уравнениях являются обобщенные коорди-
координаты д& и обобщенные скорости щ*.
Гамильтон получил уравнения движения, в кото-
которых независимыми переменными являются обобщен-
обобщенные координаты ци и обобщенные импульсы р*. Урав-
Уравнения Гамильтона или, как их еще называют, кано-
канонические1) уравнения (соответственно q*, и рц назы-
называются каноническими переменными), в отличие от
уравнений Лагранжа, являются дифференциальными
уравнениями первого порядка. Но зато число их, не-
необходимое для описания системы с s степенями сво-
свободы, оказывается равным 2s.
Уравнения Гамильтона можно вывести либо из
уравнений Лагранжа, либо непосредственно из прин-
принципа наименьшего действия (ниже мы приведем оба
вывода). Естественно, что они не дают ничего нового
по существу. Однако канонические уравнения симмет-
симметричнее уравнений Лагранжа и, кроме того, будучи
инвариантными по отношению к каноническим преоб-
преобразованиям, они открывают большие возможности
*) Уравнения Гамильтона называются каноническими в связи
с тем, что они остаются инвариантными при весьма общих пре-
преобразованиях переменных. С помощью таких канонических пре-
преобразований можно перейти от переменных q* и рь к другим
каноническим переменным Qi(qbf pa, t) и Pi(qk, рн, t). При этом
уравнения Гамильтона сохраняют свою форму, правда, с неко-
некоторой новой функцией Гамильтона H'(Qt,Pitt)9 которая заме-
заменяет функцию H(qk, Pa, t). Переменные Q* и Pt могут иметь
другой физический смысл, чем переменные $& к ph.

§ 30. УРАВНЕНИЯ ГАМИЛЬТОНА 131
для обобщений, играющих важную роль в электроди-
электродинамике, статистической физике и квантовой механике.
В качестве функции, характеризующей механиче-
механическую систему, Гамильтон взял энергию E.1), выра-
выраженную через переменные ф* и р*. Учтя, что
Pk=4t <30Л>
(см. D.19)), запишем эту функцию следующим об-
образом:
Я (</*, р*, 0 = Z PkQk - L (qky qh9 t) C0.2)
(qk предполагаются выраженными через ?* и р*). Ха-
Характеристическую функцию Н называют функцией
Гамильтона или гамильтонианом.
В качестве примера приведем гамильтониан час-
частицы, движущейся в потенциальном поле U =
U()
У> г> О- C0.3)
Для частицы, движущейся в стационарном поле, Я
имеет тот же вид, но U не зависит явно от t.
Выведем уравнения Гамильтона, исходя из урав-
уравнений Лагранжа. С этой целью найдем полные диффе-
дифференциалы левой и правой частей формулы C0.2) и
приравняем эти дифференциалы друг другу. Полный
дифференциал левой части равен
-J^dt. C0.4)
Дифференциал же правой части имеет вид
idPk-}g-&rdqk-
В силу соотношения (ЗОЛ) первая и четвертая суммы
взаимно уничтожаются. Из уравнения Лагранжа

132 ГЛ. VI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
D.16) *) следует, что
dL d dL .
P
C0-6)
Заменим в третьей сумме формулы C0.5) dL/dqk че-
через рк. В итоге выражение C0.5) примет вид
-WdL Cа7)
Для того чтобы выражения C0.4) и C0.7) были
равны при произвольных dqk, dpk и dt, необходимо
выполнение условий:
C0.9)
Уравнения C0.8) суть искомые уравнения Гамиль-
Гамильтона или канонические уравнения. Они, как уже отме-
отмечалось, являются дифференциальными уравнениями
первого порядка. Общее число их равно 2s.
Для частицы, описываемой гамильтонианом C0.3),
уравнения Гамильтона имеют вид
дх * ш
Теперь получим уравнения Гамильтона из прин-
принципа наименьшего действия. Напомним, что согласно
этому принципу система движется так, что действие S
(см. G.1)) имеет наименьшее возможное значение.
Это утверждение записывается в виде
L (фд, 4д, t) dt = 0.
Подставим сюда значение L, получающееся из соот-
соотношения C0.2):
и
6 \ (Е Р^к ~ И) dt те °' <30Л0>
*) Мы предполагаем, что все силы, действующие в системе,
потенциальны, поэтому используем уравнение D.16), а не D.15).

§ 30. УРАВНЕНИЯ ГАМИЛЬТОНА 133
Вариацию, стоящую в левой части C0.10), можно
представить в виде
и
Проинтегрируем по частям первое слагаемое:
и и и
|
Г мы воспользовались тем, что bqk = -тг (bqk); см. фор-
формулу (III. 4)). Вариации 6qk при подстановке преде-
пределов интегрирования обращаются в нуль1). Поэтому
первый член полученного выражения нужно отбро-
отбросить. Следовательно, условие C0.10) запишется так:
В силу произвольности вариаций 8qk и 6р* это усло-
условие может выполняться только в случае, если выра-
выражения в круглых скобках будут нулями. Отсюда сразу
получаются уравнения C0.8).
Исследуем функцию Гамильтона Я. Найдем пол-
полную производную от этой функции по времени
dH дН . \s дН . . v* дН .
+ 2^ + 2^
Приняв во внимание значения C0.8) для qk и /)*, по-
получим, что
Таким образом, если функция Н не зависит явно от
времени, она сохраняет свое значение. Этого следо-
следовало ожидать, поскольку Н есть полная энергия си-
системы, которая сохраняется при условии, что
dLfd^O (см. C0.9)).
!) Напомним, что при варьировании траекторий в конфигу-
конфигурационном пространстве (см. § 4) начальная и конечная точки
этих траекторий предполагаются закрепленными.

134 ГЛ. VI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Заменим во втором из уравнений C0.8) р* в соот-
соответствий с C0.6). В результате найдем, что
-^- = -#~. C0.12)
Отсюда следует, что те обобщенные координаты, ко-
которые являются циклическими, т. е. не входят явно
в функцию I, не войдут явно и в функцию Н. Выше
(см. A1.2)) мы установили, что обобщенные импуль-
импульсы, соответствующие циклическим координатам, яв-
являются интегралами движения. Из сказанного можно
заключить, что обобщенные импульсы, соответствую-
соответствующие координатам qk, не входящим явно в гамильто-
гамильтониан (т. е. циклическим относительно функции #),
остаются постоянными
/?? = const при условии, что dHfdqk = Q. C0.13)
§ 31. Скобки Пуассона
Возьмем некоторую функцию канонических пере-
переменных qk и рку а также времени t, т. е. f(<7*, Р*>0 и
выясним, при каких условиях эта функция будет ин-
интегралом движения1). Для этого вычислим полную
производную от этой функции по времени:
*f — df 4- V ( df л JL df
Заменим производные цк и рк их значениями C0.8):
JL ILmV(JLJ L
dt ~ dt ~*~ Ls\dqk dpk dpk
Если есть две функции <р(9*»Р*,0 и ф (?*• Р*» *), то
выражение
называют скобками Пуассона для функций <р и tf2).
В случае необходимости при символе скобок Пуассона
*) Напомним, что интегралами движения называются такие
функции динамических переменных (ф* и 4k либо Як и /?*), ко-
которые остаются постоянными при движении системы.
%) Для обозначения скобок Пуассона используются иногда
вместе фигурных квадратные и даже круглые скобки.

§ 31. СКОБКИ ПУАССОНА 135
указывают в виде индексов независимые переменные,
по которым берутся частные производные, т. е. запи-
записывают, например, скобки C1.2) так: {<р, ф}?,р. Легко
видеть, что
{ф, *}«, р = - (Ф> ФЬ, < — {*, Ф>р, <г C1.3)
Применив скобки Пуассона, выражение C1.1)
можно представить в виде
или в виде
¦аг—аг+<*•»*•• <315>
Из C1.4) следует, что условие, при котором функ-
функция f будет интегралом движения, выглядит так:
-2- + {/.Я>-0. C1.6)
Отсюда заключаем, что в случае, когда интеграл дви-
движения / не зависит от времени явно, его скобки Пуас-
Пуассона с функцией Гамильтона равны нулю.
Приведем некоторые очевидные свойства скобок
Пуассона:
(Ф, *} = -М>, ФЬ C1.7)
{Ф, Ф} = О, C1.8)
C1.9)
ф2), ^} = Ф1{Ф2, 1|?} + Ф2{ф1, Ф), C1.10)
В частности, в качестве ф или ф, либо их обеих можно
взять канонические переменные. Тогда получаются
следующие соотношения:
ill,
{Pi,
{
{J
{<
Яи ^*} = 0,
G,, pk}=0,
Jh pk) = б<л.
C1.12)
C1.13)
C1.14)
C1.15)
C1.16)

136 ГЛ. VI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Рекомендуем получить формулы C1.12) —C1.16) в по-
порядке упражнения. При их выводе следует учесть, что
dpi/dqk — 0; dqi/dpk = 0 (так как qk и рк — независи-
независимые переменные).
Очень важным свойством скобок Пуассона явля-
является их инвариантность относительно канонических
преобразований. Это означает, что
{Ф, Ф},,Р = {<Р, Ъ)я,р, C1Л7)
где Q, Р — переменные, полученные из q, p с помощью
канонических преобразований.
В квантовой механике мы познакомимся с кванто-
квантовыми скобками Пуассона, которые являются кванто-
вомеханическим аналогом рассмотренных в этом па-
параграфе классических скобок Пуассона.
§ 32. Уравнение Гамильтона — Якоб и
Варьирование действия
и
Ldi C2.1)
при нахождении истинной траектории движения си-
системы (имеется в виду траектория в конфигурацион-
конфигурационном пространстве, т. е. в пространстве 5 измерений;
s — число степеней свободы системы) заключается в
сравнении значений S для близких траекторий с за-
закрепленными концами, т. е. с одинаковыми значения-
значениями qk(i^=:qM и дк^^д{2) Наглядно это можно
представить с помощью рис. 32.1. Лишь та траекто-
траектория, для которой S минимально, отвечает действи-
действительному движению (на рисунке она изображена
сплошной линией).
В этом параграфе мы будем рассматривать дей-
действие S как величину, характеризующую движение по
истинным траекториям, и исследуем, как эта вели-
величина ведет себя при изменениях точки ф*> (при /2 =
= const), а также при изменениях t2 (символ qB)
означает совокупность всех q%]). Таким образом, мы
будем обращаться с действием как с функцией:
t). C2.2)

§ 32. УРАВНЕНИЕ ГАМИЛЬТОН А — ЯКОБИ 137
где <7л — координаты конечного положения системы,
a t—момент времени, когда это положение дости-
достигается.
Возьмем вблизи точки #B) точку с координатой
qB) _j_ g^ B которую система попадает в тот же мо-
момент времени t2> в который она приходит в точку ?B>
(рис. 32.2). Действие для траектории, приводящей си-
систему в точку qi2) + 6q, отличается от действия для
Рис. 32.2
траектории, по которой система приходит в точку
на величину
и
C23)
Здесь 6*7* ест« ^зность значений qkf взятых для обеих
траекторий в один и тот же момент времени /; анало-
аналогично dqk — разность qk в момент /.
Проинтегрируем по частям второе слагаемое в
C2.3):
Для истинной траектории dL/dqk представляет собой
обобщенный импульс р*. Начала обеих траекторий
совпадают, поэтому б<7*(М = 0. Величину б^(^)
можно обозначить просто 6^*. Следовательно, первый
член в правой части C2.4) можно представить в виде
рв<7

138 ГЛ. VI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Подставим C2.4) в выражение C2.3):
Истинные траектории удовлетворяют уравнениям Лаг-
ранжа. Поэтому подынтегральная функция, а значит,
и сам интеграл будет нулем. Таким образом, мы по-
получаем для приращения действия S, обусловленного
изменением координат конечного положения системы
на bqk (при неизменном времени движения), значение
6S = ? Рк *?*• C2.5)
C2.6)
Здесь pk — величина импульса в момент
Из выражения C2.5) вытекает, что
Следовательно, частные производные от действия по
обобщенным координатам равны соответствующим об-
обобщенным импульсам.
Теперь допустим, что верхний предел интегрирова-
интегрирования в C2.1) не фиксирован. Чтобы подчеркнуть это,
запишем действие в виде
C2.7)
Представленное так действие является функцией верх-
верхнего предела интегрирования, т. е. 5 — 5A). Из C2.7)
следует, что
-§—*-- C2.8)
Вместе с тем, в соответствии с C2.2) можно напи-
написать, что
C2.9)
(»ш учли соотношение C2.6)). Приравняв правые ча-
— выражений C2.8) и C2.9), получим для частной

§ 32. УРАВНЕНИЕ ГАМИЛЬТОНА — ЯКОБИ
производной от S по t значение
¦S—
Выражение в скобках есть гамильтониан Н. Следова-
Следовательно,
-f?---tffo»,P*,/). C2.10)
В соответствии с формулами C2.6) и C2.10) диф-
дифференциал функции C2.2) можно представить в виде
dS=TiPkdgk-Hdt. C2.11)
Заменим в уравнении C2.10) ри их значениями из
C2.6) и запишем это уравнение следующим образом:
dS i и („ „ „ dS dS dS
ST + nyqu ft, .., Яе, -^Г- Sb* •••» 157;
C2.12)
Мы получили дифференциальное уравнение, которому
должна удовлетворять функция S (qu q2, ..., qs\ <)•
Его называют уравнением Гамильтона — Якоби. Оно
является уравнением в частных производных первого
порядка.
Уравнение C2.12) лежит в основе некоторого об-
общего метода интегрирования уравнений движения. Од-
Однако рассмотрение этого метода выходит за рамки
нашего курса.
В случае консервативной системы со стационар-
стационарными связями время не входит явно в функцию Я
и // = ? = const (см. C0.9)). Поэтому согласно
C2.10) зависимость S от / выражается слагаемым
—Et, Следовательно, действие распадается на два
члена, один из которых зависит только от обобщен-
обобщенных координат, а другой — только от времени
EL C2.13)
Функцию So{qk) называют укороченным действием.
Подставив S в виде C2.13) в уравнение C2.12), при*
дем к уравнению Гамильтона — Якоби для укорочен-
укороченного действия

140 ГЛ. VI. КАНОНИЧЕСКИЕ УРАВНЕНИЯ
Уравнение Гамильтона — Якоби играет важную
роль в оптике и квантовой механике. Оно лежит в ос-
основе оптико-механической аналогии, которая привела
Шредингера к формулированию волновой механики.
Напишем уравнение Гамильтона — Якоби для час-
частицы, движущейся в нестационарном потенциальном
поле. Приняв во внимание формулы C0.3) и C2.12),
получим
+ U(x9y9z,t) = --^L. C2.15)
Если поле, в котором движется частица, стацио-
стационарно, вместо C2.15) рассматривается уравнение для
укороченного действия So
C2.16)

Глава VII
СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
§ 33. Принцип относительности
Основу специальной теории относительности обра-
образуют два постулата, сформулированные Эйнштейном:
1. Все законы природы одинаковы во всех инерци-
альных системах отсчета. Иначе можно сказать, что
уравнения, выражающие законы природы, инвариант-
инвариантны1) по отношению к преобразованиям координат и
времени от одной инерциальной системы отсчета
к другой.
2. Свет в пустоте всегда распространяется с опре-
определенной постоянной скоростью с, не зависящей от
состояния движения излучающего тела.
Первый постулат носит название принципа отно-
относительности Эйнштейна, второй постулат называют
принципом постоянства скорости света.
Ньютоновская механика исходит из предположе-
предположения о мгновенной передаче взаимодействий от одних
тел к другим. Это, в частности, проявляется в том, что
взаимодействие частиц описывается с помощью потен-
потенциальной энергии G(гьг2, ...), которая зависит
только от координат частиц. Тем самым предпола-
предполагается, что изменение положения одной из частиц от-
отражается на остальных частицах в тот же момент.
В действительности, как показывает опыт, мгно-
мгновенных взаимодействий в природе не существует. Если
изменяется положение одной из частиц, то на другой
взаимодействующей с ней частице это изменение нач-
начнет сказываться спустя конечный промежуток вре-
времени, необходимый для того, чтобы распространяю-
распространяющееся с конечной скоростью взаимодействие прошло
') Инвариантность уравнения означает неизменность вида
уравнения при замене в нем координат и времени одной систеш*
отсчета координатами и временем другой системы.

142 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
путь, равный расстоянию между частицами. Таким об-
образом нужно признать существование предельной ско-
скорости распространения взаимодействий. Из опыта сле-
следует, что эта скорость равна с — скорости света
в пустоте.
Из второго постулата вытекает также, что ско-
скорость распространения взаимодействий одинакова во
всех инерциальных системах отсчета, т. е. является
универсальной постоянной.
Согласно механическому принципу относительно-
относительности Галилея законы механики инвариантны по отно-
отношению к преобразованиям Галилея:
(uo — скорость движения системы К' по отношению
к системе /С). Из этих преобразований вытекает клас-
классический закон сложения скоростей:
C3.2)
Последнее соотношение, а следовательно, и урав-
уравнения C3.1), из которых оно вытекает, не согласуется
со вторым постулатом Эйнштейна, согласно которому
для светового сигнала с = cf.
кУ
К'
0г
Рис. 33.1
Рассмотрим две инерциальные системы отсчета К
и К'. Координатные оси этих систем выберем так»
чтобы оси х и х' были направлены вдоль скорости vo
системы К', а оси у и z были параллельны осям у'
и г' (рис. 33.1). Отсчет времени в обеих системах нач-
начнем с того момента, когда начала систем совпадали.
Пусть в момент t — f ==0 из совпадающих начал ко-
координат был послан световой сигнал, распространяю-
распространяющийся по всем направлениям. К моменту времени t

§ 33. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ 143
сигнал в системе К достигнет точек, отстоящих от О
на расстояние / = ct. Координаты этих точек удовлет-
удовлетворяют уравнению
c2t2 — *2 — #2 — г2 = 0. C3.3)
Аналогично, к моменту времени V сигнал в системе К9
достигнет точек сферы радиуса cf. Координаты этих
точек удовлетворяют уравнению
С2,'2 _ х,2 _ у,2 _ ^2 e 0 C3 4)
Уравнения C3.3) и C3.4) имеют одинаковый вид,
что является проявлением инвариантности закона
распространения света по отношению к преобразова-
преобразованию координат и времени от одной системы к другой.
Если подставить в C3.3) значения нештрихованных
координат и времени, определяемые формулами C3.1),
получается соотношение
су2 _ х* _ f _ г'* _ 2v</t' _ vlt'2 = 0,
не совпадающее с C3.4). Следовательно, мы снова
пришли к выводу, что преобразования Галилея не со-
совместимы с принципом постоянства скорости света.
Согласно принципу относительности Эйнштейна
все законы природы, в том числе законы механики и
электродинамики, должны быть инвариантными по от-
отношению к одним и тем же преобразованиям коор-
координат и времени, осуществляемым при переходе от
одной системы отсчета к другой. Однако уравнения
Ньютона и уравнения Максвелла этому требованию
не удовлетворяют. В то время как уравнения Ньютона
инвариантны по отношению к преобразованиям Гали-
Галилея, уравнения Максвелла, как легко убедиться непо-
непосредственной проверкой, по отношению к этим преоб-
преобразованиям оказываются не инвариантными. Это об-
обстоятельство привело Эйнштейна к выводу о том, что
уравнения Ньютона нуждаются в уточнении, в ре*
зультате которого законы механики и электродина-
электродинамики оказались бы инвариантными по отношению
к одним и тем же преобразованиям. Необходимое ви-
видоизменение законов механики было осуществлено
Эйнштейном. В результате возникла механика, согла-
согласующаяся с принципом относительности Эйнштейна,,

144 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
которая получила название релятивистской механики.
Изложению основ этой механики и посвящена эта
глава.
§ 34. Интервал
Событие, происходящее с некоторой частицей, ха-
характеризуется местом, где оно произошло (т. е. сово-
совокупностью значений х, у, г), и временем U когда оно
произошло. Если ввести воображаемое четырехмерное
пространство D-пространство), по осям которого от-
откладываются пространственные координаты х, у, г и
время t (или пропорциональная t величина), то собы
тие изобразится в этом пространстве точкой. Точка,
изображающая событие в 4-пространстве, называется
мировой точкой, С течением времени мировая точка,
соответствующая данной частице, перемещается в
4-пространстве, описывая некоторую линию, которую
называют мировой линией.
Рассмотрим два события, первое из которых за-
заключается в испускании светового сигнала из точки
с координатами хи Уи *\ в момент времени tu а вто-
второе— в приходе этого сигнала в точку с координа-
координатами х2, у2у z2 в момент времени t2. Между координа-
координатами и временем этих двух событий имеется следую-
следующее соотношение:
с* (t2 - hf - (х2 - xxf - (у2 - yxf - (г2 - z{f=0. C4.1)
Величина
Ъ - (** ~ *,J + (У. - Уд2 + (Ч ~ г.J C4-2)
представляет собой квадрат расстояния (интервала)
между двумя точками в обычном пространстве. Ана-
Аналогично можно говорить о расстоянии (интервале)
между двумя точками в 4-пространстве. Интервалом
между двумя событиями называют величину S\2, квад-
квадрат которой определяется формулой
~'гУ-Пг <34'3>
Для двух бесконечно близких событий квадрат ин-
интервала имеет вид
C4.4)

§ 34. ИНТЕРВАЛ 145
Для двух событий, заключающихся в испускании
светового сигнала в одной точке и приходе его в дру-
другую точку, интервал равен нулю:
AS2 в С2 д/2 _ д/2 = 0 C4.5)
(см. формулу C4.1)). Вследствие постоянства скоро-
скорости света равенство C4.1) должно быть справедливо
в любой инерциальной системе отсчета. Следователь-
Следовательно, если интервал равен нулю в системе /С, то он бу
дет равен нулю и в любой другой системе /('.
Итак, интервал должен обращаться в нуль одно-
одновременно во всех системах отсчета. Отсюда вытекает,
что интервал As между некоторыми событиями, вы-
выраженный в системе К, должен быть связан с интер-
интервалом As' между теми же событиями, выраженным
в системе /С', соотношением
As = a As'. C4.6)
Но в силу полной равноправности систем К и К'
можно с тем же основанием написать, что
As' = a As, C4.7)
где а имеет то же значение, что и в формуле C4.6).
Перемножив соотношения C4.6) и C4.7), найдем,
что
откуда а=±1. Естественно предположить, что знак
интервала во всех системах отсчета должен быть оди-
одинаков. Поэтому значение а, равное —1, нужно отбро-
отбросить. Таким образом, мы приходим к выводу, что ин-
интервал между двумя событиями есть инвариант:
As = As'. C4.8)
Полученный нами результат свидетельствует о це-
целесообразности принятого нами определения интер-
интервала между двумя точками 4-пространства. Интервал,
определяемый формулой C4.3), оказывается инва-
инвариантным по отношению к преобразованиям коорди-
координат и времени от одной системы отсчета к другой, т. е.
ведет себя подобно расстоянию C4.2) между двумя
точками в обычном пространстве.
Подчеркнем, что вывод об инвариантности вели-
величины C4.3) является логическим следствием из по-
постулатов Эйнштейна.

146 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Основываясь на инвариантности интервала, можно
написать
Д52« с2 At2 - АР = с2 At'2 - Д/'2. C4.9)
Допустим, что As2 > О, т. е. интервал вещественный.
Тогда можно найти такую систему отсчета /С', в ко-
которой AV будет равен нулю. В этой системе события,
разделенные интервалом As, произойдут в одной точке.
Промежуток времени между событиями в системе К'
равен
Д/'= —. C4.10)
с
Вещественные интервалы называются времениподоб-
ными.
Теперь допустим, что As2 < 0, т. е. интервал мни-
мнимый. Тогда можно найти такую систему отсчета К'>
в которой Д/' = 0, т. е. события происходят одновре-
одновременно. Расстояние между точками, в которых произо-
произошли события в системе К\ равно
Al' = iAs. C4.11)
Мнимые интервалы называются пространственнопо-
добными.
События, происходящие с одной и той же части-
частицей, могут быть разделены лишь времениподобным
интервалом. Действительно, поскольку частица не мо-
может двигаться со скоростью, большей с, пройденное
ею за время At расстояние Д/ не может превзойти
с At, т. е. Д/ ^ cAt. Отсюда As2 ^ 0.
Пространственноподобным интервалом могут быть
разделены лишь причинно не связанные события. Дей-
Действительно, если As2 < 0, то Д/ > cAt. Следовательно,
никакое воздействие, вышедшее из одной точки про-
пространства, не может достигнуть за время At другой
точки и оказать влияние на событие, происходящее
в этой точке.
Рассмотрим некоторую частицу, движущуюся рав-
равномерно со скоростью v относительно системы К (ла-
(лабораторной системы). Пусть с этой частицей проис-
происходят два события, разделенные промежутком
времени, который в системе К равен dt. Введем си-
систему К\ относительно которой частица покоится.
В этой системе промежуток времени между рассмат-

§ 34. ИНТЕРВАЛ 147
риваемыми событиями будет равен
(см. C4.10)).
Легко видеть, что промежуток времени dt' изме-
измерен часами, движущимися относительно К вместе с
частицей. Время, отсчитываемое по часам, движущим-
движущимся вместе с телом, называется собственным временем
этого тела. Обозначив собственное время буквой т,
можно написать
*/т = ^р. C4.12)
Поскольку ds есть инвариант, а с — константа, соб-
собственное время dx оказывается инвариантом.
Найдем связь между собственным временем dx и
временем dt, измеренным по часам системы К, отно-
относительно которой частица и связанные с ней (соб-
(собственные) часы движутся со скоростью v. Для этого
подставим в C4.12) выражение ds через координаты
и время системы К:
• ds «Jc2 dt2 — dl2
(см. формулу C4.4)). Преобразуем полученное выра-
выражение следующим образом:
Но dl/dt есть скорость'частицы v. Таким образом,
dx^dt^/T^v*]?. C4.13)
Из C4ЛЗ) заключаем, что собственное время частицы
всегда меньше соответствующего промежутка времени
в неподвижной (лабораторной) системе.
Формула C4.13) получена нами для случая равно-
равномерного движения частицы. Однако она оказывается
справедливой и в случае неравномерного движения.
Следовательно, лля конечных промежутков времени
C4.14)
где v = v(t)—скорость тела, для которого вычисля-
вычисляется собственное время.

148 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
§ 35. Преобразования Лоренца
В предыдущем параграфе мы установили, что ин-
интервал As между двумя точками в 4-пространстве яв-
является инвариантом, т. е. ведет себя подобно модулю
вектора в евклидовом пространстве. Это дает основа-
основание рассматривать As как модуль («длину») 4-век-
тора, проведенного из одной мировой точки в другую.
Если ввести обозначения
x° = ct, jc' = jc, jc2 = #, y? = z% C5.1)
то квадрат интервала примет вид
As2 = (А*0J - (Да:1J - (Д*2J — (Д*3J.
Для расстояния А/ между двумя точками в евкли-
евклидовом пространстве имеет место соотношение
т. е. Д/ равно модулю разности радиусов-векторов то-
точек. Аналогично интервал As можно представить как
модуль разности 4-радиусов-векторов соответствую-
соответствующих мировых точек. Следовательно, координаты x?f
xlt x2t дс3 суть компоненты 4-радиуса-вектора мировой
точки. Квадрат модуля этого радиуса-вектора равен
(х0J -(xlf -(х2J -(х3J.
Сравнение последнего выражения с формулой (XII. 5)
показывает, что пространство, в котором событие изо-
изображается мировой точкой с координатами C5.1), об-
обладает псевдоевклидовой метрикой, определяемой тен-
тензором (XII. 4).
Следовательно, квадрат 4-радиуса-вектора может
быть представлен в виде
з
*% + х{хх + х2х2 + Лез — ? *»% C5.2)
|А~0
(см. формулу (XII. 31)).
Преобразование компонент 4-радиуса-вектора осу-
осуществляется по формуле
э
^=Е <*й*у* C5,3)

§ 35. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
149
Возьмем в качестве координатных систем К и К'
в псевдоевклидовом пространстве две инерциальные
системы отсчета. Оси этих систем направим в соответ-
соответствии с рис. 33.1. Тогда, как показано в Приложе-
Приложении XII, матрица коэффициентов преобразования вы-
выглядит следующим образом (см. (XII. 21)):
а0 «1 О (
а, а0 О О
0 0 10
.о о о i_
причем
«2 — а2=1
C5.4)
C5.5)
(см. формулу (XII. 22)).
Коэффициенты ао и си могут зависеть только от
относительной скорости систем vq. Чтобы найти вид
этой зависимости, напишем формулу C5.3) для х'1.
Приняв во внимание C5.4), получим
Заменим хп через х'9 х° — через ct и х1—через х
(см. C5.1)):
C5.6)
Напишем полученное выражение для точки О' —
начала координат системы К! (см. рис. 33.1). Для
этой точки хг = 0, а х = vot. Подстановка в C5.6)
дает
0 = axct + OqV^,
откуда
«i = -*¦?. C5.7)
Подставив это значение ai в соотношение C5.5),
найдем, что
или
— щ
C5.8)

150 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Из C5.7) получим, что
а,
— Ур/С
C5.9)
Таким образом, матрица C5.4) в интересующем
нас случае будет иметь вид
-Р
К1-
о о
о о
C5.10)
Мы ввели обозначение
с
C5.11)
Таблица обратного преобразования [dJJ] отличает-
отличается от C5.10) лишь тем, что перед р в числителе стоит
знак плюс (см. матрицу (XII. 23)).
Подстановка найденных нами значений а» в {35.3)
приводит к формулам преобразования компонент 4-ра-
диуса-вектора:
х == ¦
X "*Г**~ -
[ - р2 '
C5.12)
Формулы обратного преобразования имеют вид
Ar ^~ ЫЛ | ПЛ "T~ Л о /2 О /3
C5.13)
Перейдя в формулах C5.12) и C5.13) к обычным
обозначениям t, jc, ^, г, получим
#' = у; г' = г.
C5.14)
C5.15)
Формулы C5.14) и C5.15) называются преобразо-
преобразованиями Лоренца, Предоставляем читателю убедиться

§ 35. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА 151
в том, что эти преобразования оставляют инвариант-
инвариантным интервал s^ между двумя событиями.
Формулы обратного преобразования C5.15) отли-
отличаются от формул прямого преобразования C5.14)
только знаком при vo. Этого следовало ожидать, при-
приняв во внимание полную равноправность обеих си-
систем отсчета, а также то обстоятельство, что для дан-
данных К и /С' проекции скорости относительного движе-
движения на оси х и х/ отличаются знаком. Действительно,
если скорость системы К! относительно системы К на-
направлена вправо (и ее проекция на ось х положитель-
положительна), то скорость системы К относительно К' направ-
направлена влево (и ее проекция на ось х1 отрицательна).
При скоростях vq настолько малых, что отноше-
отношением vo/c можно пренебречь по сравнению с едини-
единицей, преобразования Лоренца переходят в преобразо-
преобразования Галилея.
Из преобразований Лоренца можно получить фор-
формулы преобразования длин и промежутков времени
при переходе от одной инерциальной системы отсчета
к другой (это делается в любом курсе общей физики).
Мы ограничимся тем, что напомним формулу для
лоренцева сокращения длины тела (в направлении
его движения):
l = lo^Jl—v2/c2. C5.16)
Здесь /о — собственная длина тела, например стерж-
стержня (т. е. длина тела в той системе отсчета, в которой
оно покоится), I — длина тела в системе отсчета, отно-
относительно которой оно движется со скоростью v.
Поскольку поперечные размеры тела при его дви-
движении не изменяются, объем тела уменьшается в со-
соответствии с формулой
V =• VQ ^T^lFj?, C5.17)
где Vo — собственный объем тела, V — объем тела
в системе, относительно которой оно движется со ско-
скоростью V.
Найдем формулы преобразования компонент ско-
скорости частицы. Из формул C5.14) получаем
a? dt ~ <po/g2) dx
dyf = dy, dz' = dz*

152 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Следовательно,
, dx^ dx — v0 dt dx/dt — v0 vx —
— dt' dt - (vQ/c2) dx~\- (vo/c2) (dxfdt) ~ 1 - vovx/c2 *
Таким образом,
Аналогичные выкладки приводят к формулам преоб-
преобразования для двух других компонент скорости:
Формулы обратного преобразования имеют вид
/2 • v« ТЛ Г/2'
C5.20)
Пусть скорость частицы v образует с осью х угол в,
а с осью jc7 — угол 8' (оси хи? всегда можно путем
параллельного переноса привести в такое положение,
чтобы они оказались лежащими в одной плоскости
с v). Найдем связь между углами в и в7. Расположим
оси у и у* в плоскости, определяемой осью х и направ-
направлением вектора v. Тогда вектор v будет лежать в пло-
плоскости ху и можно написать
vx = v cos в, vy = v sin в,
v'x = v9 cos в', v'u = vr sin 6',
где v — модуль скорости в системе /С, v'—модуль
скорости в системе К'.
С помощью формул C5.18), C5.19) получаем, что
0COS6
Эта формула позволяет по известным v и в найти
угол в', который образует вектор v7 с осью xf. Анало-
Аналогично можно найти формулу, позволяющую по из-
известным v9 и 6' найти угол 6 между вектором v и

§ 36. ЧЕТЫРЕХМЕРНЫЕ СКОРОСТЬ И УСКОРЕНИЕ 153
осью х. Воспользовавшись формулами C5.20), по-
получим
^yjEI^'r'fr*. C5.22,
x 0x + t>o ° cose + о
§ 36. Четырехмерные скорость и ускорение
В Приложении XII мы определили 4-вектор как
совокупность величин а0, а1, а2, а3, которые при пере-
переходе от одной системы координат к другой преобра-
преобразуются по тем же правилам, что и компоненты 4-ра-
диуса-вектора. Следовательно, формулы преобразова-
преобразования величин а* аналогичны формулам C5.12):
,»,. + «. а,2 а,3
Vi-P2
C6.1)
Формулы обратного преобразования отличаются от
C6.1) знаком при р.*
C6.2)
Рассмотрим четырехмерные векторы скорости и
ускорения. В нерелятивистской механике предпола-
предполагаются инвариантными как пространственные интер-
интервалы dlt так и промежутки времени dt. Поэтому сово-
совокупность величин, получающихся после деления
компонент трехмерного вектора dx на инвариант dty
образует трехмерный вектор v — вектор скорости час-
частицы. Аналогично совокупность величин, получающих-
получающихся после деления компонент вектора dv на инвари-
инвариант dt, представляет собой вектор ускорения w.
В действительности как мы видели, ни dl, ни dt
не являются инвариантными. Инвариантом оказыва-
оказывается интервал dsy связанный с dl и dt соотношением
ds2 = c2dr — dl2. Инвариантность интервала дала воз-
возможность ввести в рассмотрение 4-радиус-вектор с
компонентами х°, х1, х2, х8, который является анало-
аналогом трехмерного радиуса-вектора с компонентами хи
Х2, *з- Попытаемся найти четырехмерные аналоги
3-векторов v и w.

154 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Очевидно, что совокупность четырех величин dx^/dt
не будет обладать свойствами 4-вектора, так как dt
не является инвариантом и ^(dx^/d^idxjdt) не бу-
будет сохранять свое значение при преобразованиях Ло-
Лоренца. Однако нам известен «родственный» dt инва-
инвариант. Им является собственное время dx = ds/c (см.
C4.12)). Поскольку dx— инвариант (т. е. скаляр),
величины
?? <36-3>
обладают свойствами компонент 4-вектора. Его назы-
называют четырехмерной скоростью частицы *).
Аналогично 4-вектор с компонентами
--?—?—'¦?¦ 0М»
называют четырехмерным ускорением частицы.
Приняв во внимание значения dx», а также то об-
обстоятельство, что
dx = dt Vl ~v2jc* C6.5)
(см. C4.13)), легко получить для компонент 4-скоро-
сти следующие значения:
Ь 2,3), C6.6)
что можно записать в виде
(см. формулы (XII. 34) и (XII. 35)). Здесь v — обыч-
обычная трехмерная скорость частицы, vu — ее проекции
на оси х, у, z. Существенным для дальнейшего изло-
изложения является тот факт, что при v «С с простран-
пространственная часть 4-скорости переходит в обычную ско-
скорость V.
Из формул C6.6) легко получить, что
Л
= с2 C6.8)
*) Эйнштейн определил 4-скорость как вектор с комлонен-
тами и** «х dx^/ds. Очевидно, что определенная так скорость
есть безразмерная величина, аналогичная vjc.

§ 37. РЕЛЯТИВИСТСКАЯ ДИНАМИКА 15&
(если определить и* так, как это сделал Эйнштейн,
1>0
Продифференцировав формулу C6.8) по т, придем
к выражению
+ L
\i \l И- М-
Согласно (XII. 33) обе суммы эквивалентны, так что
1>^ = 0. C6.9)
м-
Из последнего соотношения следует, что векторы
4-скорости и 4-ускорения взаимно перпендикулярны.
§ 37. Релятивистская динамика
Уравнения Ньютона инвариантны по отношению
к преобразованиям Галилея, но не инвариантны по
отношению к преобразованиям Лоренца. Поэтому для
того чтобы удовлетворить принципу относительности
Эйнштейна, второй закон Ньютона нужно заменить
более общим законом. Приняв во внимание, что при
р->0 (т. е. при vq/c-*Q) преобразования Лоренца
переходят в преобразования Галилея, нужно потребо-
потребовать, чтобы релятивистски-инвариантные уравнения
движения при v <tC с переходили в ньютоновские урав-
уравнения:
-?(т*,) = Л (/=1, 2,3). C7.1)
Естественным четырехмерным обобщением этих
уравнений являются соотношения
-?-(ти11)-К11 <|*-0, 1, 2, 3), C7.2)
где т — собственное время, т — инвариантная величи-
величина, характеризующая инертные свойства частицы
(масса частицы), Ф — компонента 4-скорости части-
частицы и, наконец, /С*4 — некоторый 4-вектор, называемый
силой Минковского. Величины К» должны быть опре-
определены таким образом, чтобы при у «С с простран-
пространственные компоненты уравнений C7.2) переходили в
уравнения C7.1), подобно тому как в этом случае

156 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
пространственные компоненты 4-скорости переходят
в обычную скорость v.
Приняв во внимание выражения C6.5) и C6.6)
для х и Ф, представим уравнения C7.2) в виде
~ v*/c2 dt V л/l-vVc2 )
(
*/c2 dt V л/l-vVc2
-Гл (/=1,2,3).
Умножив эти уравнения на л/\ —v2fc2f получим
=/C°Vr:ri;^' C7-3)
Если определить пространственные компоненты
силы Минковского Ki так, чтобы они были связаны
с компонентами обычной трехмерной силы F, соотно-
соотношениями
Ft = Ki Vl - v2/c2 (i = 1, 2, 3), C7.5)
то уравнения C7.4) примут вид
Видно, что при v <S с уравнения C7.6), как и тре-
требуется, переходят в уравнения Ньютона C7.1).
Чтобы определить временную компоненту силы
Минковского /С0, умножим уравнение C7.2) на 4-ско-
рость иР. В результате получим, что
= т
г(мы учли, что т — инвариант и, следовательно, ее
можно вынести за знак производной). Просуммиро-
Просуммировав полученные уравнения по (л, придем к формуле
з з
Л /Сй«1а = tn J) гЛ» ===== О
и=*о и=о
(см. C6.9)). Подстановка значений C6.6) для и* и
получающихся из C7.5) значений для Ki приводит

§ 37. РЕЛЯТИВИСТСКАЯ ДИНАМИКА
157
к соотношению
с
— v2fc2 f^ Vl — v2/
откуда
Fv
-. C7.7)
Теперь мы можем написать все компоненты силы
Минковского. Приняв во внимание формулы C7.5) и
C7.7), получим
Таким образом,
JT-( nF\>
V t- V1 ~ v2/c
C7.9)
Скалярное произведение трехмерных векторов F
и v дает работу силы F, совершаемую над частицей
в единицу времени. Эта работа равна скорости изме-
изменения энергии частицы, т. е. dE/dt Следовательно,
выражению C7.7) для К° можно придать вид
К0-
1
dE
- v2/c2 dt
C7.10)
где Е — энергия частицы.
Итак, мы установили, что релятивистски-инвари-
релятивистски-инвариантное1) уравнение динамики частицы имеет вид
C7.2), где и* — 4-скорость с компонентами C6.6),
К* — 4-сила (сила Минковского) с компонентами
C7.8). Пространственные компоненты уравнения
C7.2) можно представить в виде C7.4) либо C7.6).
В пределе при и<с эти уравнения переходят в урав-
уравнения Ньютона (см. C7.1)).
Временная компонента уравнения C7.2) (см.
C7.3)) после подстановки значения C7.10) для /С0
х) Поскольку иР и К* — 4-векторы, вид уравнения C7.2)
при преобразованиях Лоренца остается неизменным (т — инва-
инвариант по определению).

158 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
приобретает вид
( ™ ^L*L C7.11)
dt VVl -v2lc2) с dt
Отсюда заключаем, что релятивистское выражение
для энергии частицы выглядит следующим образом:
% C7Л2)
§ 38. Импульс и энергия частицы
В ньютоновской механике импульсом частицы на-
называется трехмерный вектор с компонентами
pt^rnvi (/=1,2,3). C8.1)
Четырехмерным аналогом этого импульса является
4-вектор с компонентами
р* = ти* (|г = 0, 1,2, 3). C8.2)
где и& — компоненты 4-скорости 1). Подставив значе-
значения C6.6) для и**, получим
- 1, 2, 3), C8.3)
что можно представить в виде
™ Л (з8.4)
При и<с формула для пространственных компо-
компонент релятивистского импульса переходит в ньютонов-
ньютоновскую формулу C8.1). Это дает основание принять
в качестве релятивистского выражения для обычного
трехмерного импульса формулу
Теперь обратимся к временной компоненте 4-им-
пульса. В конце предыдущего параграфа мы получили
формулу C7.12) для энергии частицы ?, причем оста-
*) Если 4-скорость была определена как tP^dx^/ds (см.
сноску на стр. 154) 4-импульс определяют как р^

§ 38. ИМПУЛЬС И ЭНЕРГИЯ ЧАСТИЦЫ 169
вили открытым вопрос о значении постоянной инте-
интегрирования. Сравнив выражение C8.3) для р° с фор-
формулой C7.12), легко обнаружить, что, положив const
равной нулю, можно получить соотношение
Р° = 4- <38-6>
В этом случае выражение 4-импульса приобретает вид
где р — величина, определяемая формулой C8.5).
Таким образом, энергия и импульс (обычный) ока-
оказываются компонентами одного 4-вектора 1)—4-им-
1)—4-импульса частицы. Это обстоятельство дает возможность
применить формулы C6.1) для нахождения правил
преобразования ?ир при переходе от одной инерци-
альной системы отсчета к другой. Подставив соответ-
соответствующие значения р** в C6.1), легко получить
e' + vqp', _ р'х + уо(е'/с*)
Ру = Ру> Рг = Р'г- C8.8)
Обратные преобразования отличаются знаком при vq.
Найдем квадрат 4-импульса. Из C8.7) получим
(см. формулу (XII.38)). Вместе с тем
3 3 3
? Р»Р» = ? (тР) (™О = т2 Z и*Ч — т2с2 C8.9)
0 0 0
(см. C6.8)). Таким образом, мы приходим к соотно-
соотношению
il-p2=m2c2. C8.10)
Отметим, что квадрат 4-импульса, как и квадрат лю-
любого 4-вектора, представляет собой инвариант.
!) Этот 4-вектор называют иногда вектором энергии-им-
энергии-импульса.

160 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Положив в формуле C7.12) const = 0, получим
для энергии частицы выражение
C8.11)
Величину ?, определяемую выражением C8.11), на-
называют полной энергией частицы. Следует иметь в
виду, что Е не включает в себя потенциальную энер-
энергию частицы во внешнем поле сил *).
Для покоящейся частицы (т. е. при у = 0) выра-
выражение C8.11) переходит в
C8.12)
где через Ео мы обозначили значение Е при v = 0.
Это значение называют энергией покоя частицы. На-
Напомним, что частицей для краткости мы назвали ма-
материальную точку, т. е. тело, размерами которого
можно пренебречь. Энергия покоя такого тела сла-
слагается из энергий покоя входящих в состав тела час-
частиц2), из кинетических энергий этих частиц и энергии
их взаимодействия друг с другом. Отсюда следует, что
me2 > ? тас2,
а
где m — масса тела, пга — массы покоя образующих
тело частиц. Таким образом, масса тела не равна
сумме масс его частей.
В свое время Эйнштейн затратил много усилий для
того, чтобы обосновать правомерность предположения
о равенстве нулю const в C7.12) или, другими сло-
словами, чтобы обосновать утверждение, что в массе m
запасена энергия тс2 (см. C8.12)). С этой целью он
рассмотрел несколько конкретных явлений и показал,
что в каждом из них изменение энергии тела на Д?
приводит к изменению его массы на Дт = ИЕ/с2.
В наше время дело обстоит гораздо проще. Чтобы
обосновать соотношение АЕ = с2Дт, достаточно, на-
например, рассмотреть процесс превращения покоя-
1) Напомним, что согласно C7.7) и C7.10) dE/dt = Fv.
В ньютоновской же механике работа результирующей всех сил,
действующих на частицу, равна приращению ее кинетической
энергии 7\ а не суммарной энергии Т + U.
2) В термин «частица» мы вкладываем теперь иной смысл»
чем вкладывали до сих пор.

§ 39. ДЕЙСТВИЕ ДЛЯ РЕЛЯТИВИСТСКОЙ ЧАСТИЦЫ \Q{
щихся электрона и позитрона в два 7~квапта* Соот-
Соответствующие измерения показывают, что суммарная
энергия этих 7-квантов в точности равна сумме энер-
энергий покоя электрона и позитрона.
Разность между полной энергией C8.11) и энер-
энергией покоя C8.12) дает кинетическую энергию час-
частицы
W C8ЛЗ)
При малых v эта формула переходит в ньютоновское
выражение для кинетической энергии
Г « тс2 A + -~ v2jc2) — тс2 = ~ mv2. C8.14)
В заключение отметим, что из формулы C8.10)
вытекает соотношение
& = р2с2 + т2с\ C8.15)
Энергия, выраженная через импульс, называется
функцией Гамильтона (см. § 30). Следовательно, ре-
релятивистское выражение функции Гамильтона час-
частицы имеет вид
Я = с ^pT+T^F, C8.16)
если частица свободна, и
Я = с Vp2 + т2с2 + U, C8Л 7)
если частица находится во внешнем силовом поле
(U — потенциальная энергия частицы в этом поле; см.
абзац, следующий за формулой C8.11)).
§ 39. Действие для релятивистской частицы
Найдем выражение действия для свободной (т. е.
не подверженной воздействию каких-либо сил) час-
частицы. Интеграл, выражающий действие, должен быть
инвариантным относительно преобразований Лоренца.
Следовательно, его нужно брать от скаляра, причем
скаляр должен иметь вид дифференциала в первой
степени. Единственный скаляр такого вида, который
можно сопоставить свободной частице, есть величина,
пропорциональная интервалу ds. Обозначив коэффи-
6 И. В. Савельев, т. 1

162 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
циент пропорциональности через а, получим для дей-
действия следующее выражение:
« | ads — | ®c^l~v2/c2di C9.1)
(мы воспользовались формулой C4.4) для ds% и учли,
что dl/dt равно скорости частицы v).
Сопоставив C9.1) с выражением G.1), приходим
к выводу, что функция Лагранжа для свободной ре-
релятивистской частицы должна иметь вид
C9.2)
В пределе при v < с эта функция должка переходить
в ньютоновское выражение
C9.3)
Разложим функцию C9?2) в ряд по степеням v/c.
Пренебрегая членами высших порядков, получим
L — ac<sfl — v2jc2 &* ас —- av2/2c.
Постоянное слагаемое ас можно отбросить (см. § 7).
Следовательно, в ньютоновском приближении ? =
= —av2/2c. Сравнение с C9.3) показывает, что а
нужно положить разной — тс. Таким образом, мы
установили вид функции Лагранжа для свободной
частицы!): _____
L=~mc2^l- v2jc2. C9.4)
Зная вид функции Лагранжа, легко найти импульс
и энергию частицы. Воспользовавшись формулами
(9.5) и E.1), получим
C9.5)
4) Для частицы, находящейся во внешнем потенциальном
коле сил,
L = — тс2 Vb- P2fc- — ?/,
где U — потенциальная энергия частицы. Отметки, что в реляти-
релятивистской механике L не равна Г — U.

§ 39. ДЕЙСТВИЕ ДЛЯ РЕЛЯТИВИСТСКОЙ ЧАСТИЦЫ 163
Итак, мы пришли к тем же формулам для им-
импульса и энергии частицы, которые были получены
в предыдущем параграфе. Однако следует иметь
в виду, что формулы C9,5) и C9.6) мы получили для
свободной частицы, в то время как в § 38 аналогич-
аналогичные формулы были получены в предположении, что
на частицу действуют силы.
Обратимся снова к выражению C9.1). Учтя най-
найденное нами значение а, напишем действие в виде
2
ds. C9.7)
Истинная траектория частицы определяется условием
63 = 0. C9.8)
Для вариации действия имеем выражение
2
mc
Интервал равен
— —mc6 \ ds —
1
Согласно (XII. 40) вариация подкоренного выраже-
выражения может быть представлена в виде
б ]? dx& dxp = 2
Следовательно,
2
6S == — тс \ б
Производная dxjds есть и^/с (см. C6.3)). Кроме
того, 6(dxP) = d(bxP') (см. (III.4)). Поэтому мы при-
приходим к выражению
2
6*

164 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Проинтегрируем это выражение по частям:
2 .
(мы представили du^ в виде (dull/dx)dx9 где т —соб-
—собственное время частицы). На концах траектории
6 = 0. Поэтому условие C9.8) принимает вид
C9.11)
Для того чтобы это условие выполнялось при про-
произвольных 6xv, необходимо равенство нулю величин
du^/dX) т. е. постоянство 4-скорости частицы, что, оче-
очевидно, справедливо для свободной частицы.
Найдем действие как функцию координат частицы
(т. е. как функцию верхнего предела интегрирования;
см. § 32). Для реального движения du^/dx = 0, следо-
следовательно, второй член в C9.10) обращается в нуль.
Нижний предел интегрирования мы считаем фиксиро-
фиксированным, поэтому Fx^I=0. Таким образом, действие
как функция координат частицы удовлетворяет соот-
соотношению
з
6S = — т Л и»
ц0
(мы опустили индекс «2» при бх*1). Величины ти^
дают ковариантные компоненты 4-импульса частицы
(см. C8.2)), так что приращение действия можно
представить в виде
з
6S=-S />u*^. C9.12)
В § 32 мы получили для приращения действия, обус-
обусловленного изменением конечного положения частицы
в обычном (трехмерном) пространстве, выражение
з
65=Ер/6^ C9 Л 3)
(см. формулу C2.5)). Легко заметить, что слагаемые
формулы C9.12), соответствующие пространственным

§ 39. ДЕЙСТВИЕ ДЛЯ РЕЛЯТИВИСТСКОЙ ЧАСТИЦЫ 165
координатам, после опускания индекса у их* дают
сумму C9.13).
Из C9.12) вытекает, что ковариантные компонен-
компоненты 4-импульса можно определить следующим образом:
*<39Л4>
(ср. с C2.6)).
В предыдущем параграфе было установлено, что
2 р^Рр = т2с2. Опустив индекс у первого сомножи-
сомножителя, т. е. заменив контравариантные сомножители со-
соответствующими ковариантными, найдем, что
Подставив сюда вместо pl3L их значения C9.14), при-
придем к релятивистскому уравнению Гамильтона —
Якоби:
C915)
(мы заменили х° через ct9 xl через хит. д.).
Фигурирующее в C9.15) действие S отличается от
нерелятивистского действия S'. Это легко понять, если
учесть, что действие связано с энергией выражением
Е = —(dS/dt) (см. формулу 'C2.10)). Нерелятивист-
Нерелятивистская же энергия Ег отличается от релятивистской энер-
энергии Е членом гпс2(Е = Е' + тс2). Отсюда
dt ~ at
или
Подставив это соотношение в C9.15), получим урав-
уравнение для S':
2m SA dx ) ^K dy
которое в пределе при с->оо переходит в нереляти-
нерелятивистское уравнение Гамильтона — Якоби для свобод-
свободной частицы (см. формулу C2.15), в которой нужно
положить ?/ = ())•

166 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
§ 40. Тензор энергии-импульса
В этом параграфе мы осуществим очень важное
обобщение выражения для действия. В таком обоб-
обобщенном виде выражение ждя действия оказывается
применимым не только к чисто механическим систе-
системам, ко также к электромагнитному полю и другим
физическим системам.
До сих пор мы писали выражение для действия
в виде
2
\ jk9 t)dt, D0.1)
где L — функция Лагранжа, qk = qk(t)— обобщенные
координаты, определяющие положение частиц, входя-
входящих в систему, ци — обобщенные скорости, равные
dqk/dt. Величины qk и qk предполагались зависящими
только от времени.
Когда мы записываем уравнения в четырехмерной
форме, мы имеем дело с четырьмя формально равно-
равноправными переменными ж0, х1, х2, х?, которые должны
входить в уравнения сходным образом. Чтобы отра-
отразить это обстоятельство, представим выражение для
действия в виде
, х\ х\ x?)dx°dx*dx2dx?, D0.2)
где под qa подразумевается совокупность величин
Яи 92, • • •, определяющих состояние системы (пара-
(параметров системы). Число этих параметров может быть
любым, в частности бесконечно большим. Под qav под-
подразумевается совокупность частных производных па-
параметров ца по координатам хУ:
¦—$ Cil;t.i"i)- <40-з)
Множитель \/с введен для удобства.
Величины qa и qav рассматриваются как функции
координат jfi9 х\ х2, jc3. В частности, может оказаться,
что параметры qa зависят только от х°. Тогда мы при-
придем к уже известному нам случаю, когда qa = qa\t)\

§ 40. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА 167
Отметим, что поскольку д2да/дх?дх& = d2qa/dx^dxvt
имеет место соотношение
2tL-2*2L. D04)
dxv K V
Чтобы установить соответствие между выражения-
выражениями D0.2) и D0.1), примем во внимание, что элемент
4-объема dV* связан с элементом объема в обычном
пространстве dV и интервалом времени dt следующим
соотношением:
dV% = dx°dxldx2dxd ^cdt dV. D0.5)
Подставив это значение dV* в D0.2), получим выра-
выражение
2
S =* J Vdt dV = J dt J l*dV. D0.6)
Интегрирование по dt ведется о заданном промежутке
времени, по dV—по всему трехмерному объему.
Сопоставление выражений D0.1) и „D0.6) дает, что
dV. D0.7)
Таким образом, функция L* есть «плотностью функции
Лагранжа рассматриваемой системы.
Для замкнутой механической системы функция
Лагранжа не зависит явно от t (см. § 8). Аналогично
математическим выражением замкнутости системы
должно быть отсутствие явной зависимости L* от ко-
координат x?f х\ х2, х3. Таким образом, для замкнутой
системы действие имеет вид
5 = 7$ Г (?., qa,)dV\ D0.8)
Найдем уравнения движения замкнутой системы.
Для этого вычислим вариацию действия D0.8) и при-
приравняем ее нулю.
Вариация выражения D0.8) равна
a, v

168 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
По аналогии с соотношением 6#' =
Осуществив такую замену, получим
Vr- D0.9)
По правилам дифференцирования произведения
b^L^ + L^
Первая сумма в правой части тождественна со вторым
членом подынтегрального выражения в формуле
D0.9). Поэтому можно написать
7%
Вторая из сумм:
есть 4-дивергенция вектора, v-я компонента которого
равна
Поэтому, воспользовавшись четырехмерным аналогом
теоремы Остроградского — Гаусса (см. (XII.72)),вто-
(XII.72)),второй из трех интегралов в формуле D0.10) можно за-
заменить интегралом по замкнутой гиперповерхности,
ограничивающей 4-объем, по которому осуществляется
интегрирование в D0.10):
D0.11)
Однако на границе рассматриваемого 4-объема ва-
вариации 8qa = 0. (Подобно этому в механике вариа-

§ 40. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА 169
ции 6<7/ в граничных точках равны нулю). Поэтому
интеграл D0.11) равен нулю, так что в формуле
D0Л0) остаются только первая и третья суммы. Мы
объединим их, вынеся за скобки общий множи-
множитель 8qa:
В силу произвольности вариаций 8qa полученное
нами выражение может равняться нулю только в том
случае, если равны нулю все выражения в квадрат-
квадратных скобках. Таким образом, мы приходим к следую-
следующим уравнениям движения:
V
Эти уравнения являются обобщением уравнений Лаг-
ранжа:
dL d dL /Afl |оч
*--л"з#- <40ЛЗ>
(см. формулу G.3)). В правой части D0.12) стоит
сумма четырех производных в соответствии с тем, что
роль, которую исполняла одна переменная /, теперь
играют четыре переменные xv. Легко убедиться в том,
что при условии, что qa зависят только от лс°, т. е. от t9
уравнение D0.12) переходит в уравнение D0.13).
Умножим уравнение D0.12) на qavL и произведем
суммирование по а:
-Уд
-Уд д dL*
к
****-
Правую часть можно преобразовать по формуле
dv d (uv) da
U
В результате получим
— • == V д (• dL* \ — V
'#/» 1 ***** dxv V"а*ь ДЛЛ„) *Lj
*,—- дху
D0.14)

170 ГЛ. VI!. СПЕЦИАЛЬНАЯ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Осуществим замену аац~дда/дх» в сумме слеза и
dqan/дхУ = dqav/dx» (см. D0.4)) во второй сумме
справа, а также сгруппируем иначе члены выражения
*40.14). В итоге придем к соотношению
ILL ЁЯ± + V ILL UhyL ^У-±-(л
^ dqa дх* f^dVav дх* ?^ dxv V **
ЛеЕая часть полученного выражения есть dL*/dxv.
Следовательно, мы пришли к формуле
Левую часть этой формулы можно записать в виде1)
v v
в результате чего получим соотношение
Это соотношение можно преобразовать следующим
образом:
Уравнение D0.15) представляет собой совокуп-
совокупность четырех уравнений, отвечающих разным значе-
значениям индекса \х (|х == 0, 1, 2, 3). Выражения в квад-
квадратных скобках обладают свойствами смешанных
компонент 4-тензора второго ранга. Обозначив этот
тензор символом ?У\ получим
Использовав это обозначение, можно записать урав-
уравнение D0.15) в виде
0 0х = 0, 1,2, 3). D0.17)
!) Напомним, что dyfdxv есть ковариантная компонента
4-вектора.

§ 40. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА 171
Напомним, что уравнение D0.15) мы получили, при-
приравняв нулю вариацию действия D0.8).
Тензор ?У\ удовлетворяющий уравнению D0.17),
определяется не однозначно. Всякий тензор вида
где QUP — тензор, антисимметричный по индексам v
и р (Q?p = — Q[T), также удовлетворяет уравнению
D0.17). Действительно, в силу антисимметрии тен-
тензора Ql9
и, следовательно,
у д
дхр
р V,
С _0
др
Поэтому из D0.17) будет вытекать условие
Надлежащим выбором тензора Qjlp всегда можно
добиться того, чтобы тензор D0.18) оказался симмет-
симметричным. В дальнейшем мы будем предполагать, что
это условие выполнено и
D0.20)
Отметим, что поскольку QjT = O»
Г/ = Г/, D0.21)
т. е. ТцР определяется по формуле D0.16).
Перемещение в D0.19) индекса р, вверх либо оста-
оставит все Tj без изменений (если «л = 0), либо изменит
у всех Ту? знак на обратный (если fi.== 1,2,3). Сле-
Следовательно, из D0.19) вытекает, что
{SA==0> *•% 3)- D0-22)

172 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Тензор Т**» называется тензором энергии-импульса
системы. Основания для этого выяснятся ниже.
В Приложении XII показано, что в случае, когда
тензор T»v удовлетворяет условию D0.22) и все 7>v
обращаются на бесконечности *в нуль, остается досто-
достоянным во времени (сохраняется) вектор с компонен-
компонентами:
(см. формулу (XII. 86)), где a — произвольная кон-
константа, dfv — компонента 4-вектора элемента гиперпо-
гиперповерхности. Интеграл D0.23) берется по произвольной
гиперповерхности, включающей в себя все трех-
трехмерное пространство. Если в качестве гиперповерхно-
гиперповерхности, по которой осуществляется интегрирование, взять
гиперплоскость jfi = const, то все rffv, кроме dfo = dV,
будут равны нулю и выражение D0.23) упростится
следующим образом:
= a J T^dV. D0.24)
Мы знаем, что для замкнутой системы сохраняется
полная (т. е. взятая по всему объему) энергия и пол-
полный (т. е. взятый по всему объему) импульс. Энергия
и импульс представляют собой компоненты 4-импуль-
са. Следовательно, 4-импульс замкнутой системы так-
также должен сохраняться. Это обстоятельство дает нам
основание отождествить вектор, определяемый форму-
формулами D0.23) и D0.24), с 4-импульсом системы. Кон-
Константу а нужно выбрать так, чтобы формулы D0.23)
и D0.24) согласовывались с прежним определением
4-импульса (см. C8.7)), в соответствии с которым,
например, р° = Е/с. Положив в формуле D0.24)
|л == 0, получим
ро в a J Twdv e Ejc D0.25)
Воспользовавшись формулами D0.21) и D0.16),
можно написать

§ 40. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА 173
где qa = dqa/dt (мы учли, что qao = d
d/d() (l/Y{d/d) (/))
q/() (/Y{q/) (/)q)
Интеграл д L*dV дает функцию Лагранжа L. По-
Поэтому мы приходим к соотношению
Согласно формуле E.1) выражение, стоящее в пра-
правой части, определяет энергию системы Е. Следова-
Следовательно,
J E, D0.26)
а Т00 есть плотность энергии до:
Т°° = до. D0.27)
Подстановка значения D0.26) в формулу D0.25)
приводит к заключению, что а = 1/с. Итак,
V
если интегрирование производить по произвольной ги-
гиперповерхности, включающей в себя все трехмерное
пространство, и
если интегрирование производить по гиперплоскости
х° = const.
Чтобы выяснить смысл компонент Г0*, напишем
соотношение D0.22) для|а = 0:
arOv дт00 у» дток п
дх° f
или
dTok
^ dxk
Умножение полученного соотношения на с и инте-
интегрирование по некоторому объему V дает
J
—51
D0.30)

174 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Интеграл в левой части равен энергии, заключенной
в объеме V. Справа под знаком интеграла стоит обыч-
обычная (трехмерная) дивергенция некоторого вектора S
с компонентами
Sx = cTQ\ Su = cT*\ S2 = cT<*. D0.31)
Таким образом, формулу D0.30) можно предста-
представить в виде
Применив к правой части теорему Остроградского —
Гаусса, получим
где интеграл берется по замкнутой поверхности, огра-
ограничивающей объем V.
Убыль энергии в объеме V за единицу времени
должка быть равна потоку энергии через поверхность.
Следовательно, S есть вектор плотности потока энер-
энергии. Согласно D0.31)
"]HQl «__ . Q *PQ2 .7_ О 7*03 Q IAf\ QO\
с х* с У* с z х '
В силу симметрии тензора Тр* выполняется соот-
соотношение Tk0 = TOk, так что
T0 JL Q 7*20 С 7*30 — С (Л(\ *Х*Х\
Л " ^~* О», X ¦ ™'¦ "~— Ом» * ~"~~ ~""~ О». lTrvl.OOf
с л> с у> с z \ /
Таким образом, компоненты TOfc и Tk0 с точностью
до множителя \/с равны соответствующим компонен-
компонентам вектора плотности потока энергии.
Пространственные компоненты вектора D0.28)
равны
Отсюда заключаем, что вектор g с компонентами
Тк0/с определяет плотность импульса системы:
fo-7r" Л-Т2*' Ьа7л <40-34>

§ 40. ТЕНЗОР ЗНВРГИИ-ИМПУЛЬСА 176
D0.35)
Сопоставление D0.34) с D0.33) дает, что
или, в векторном виде,
Итак, мы пришли к выводу, что между потоком
энергии и импульсом имеется связь — плотность им-
импульса равна плотности потока энергии, деленной
на с2.
Чтобы установить смысл компонент Г'*, напишем
соотношение D0.22) для р, = к
dTiv dTi0 . у dfik п
Отсюда, приняв во внимание, что х° = ct9 Тш
находим, что
dTik
at -fa d%k -
Проинтегрируем полученное выражение по некото-
некоторому объему V. Приняв во внимание, что VgdK = p
(р — импульс части системы, заключенной в объ-
объеме V), получим
*ь шаттл r\rw*ik.
dV.
_ dxk
V k-l
Преобразуем правую часть по теореме Остроград-
Остроградского—Гаусса:
Zf DО7)
где а — вектор с компонентами
oik = Tik. D0.38)
В левой части формулы D0.37) стоит скорость
убывания 1-й компоненты импульса системы, заклю-

176 ГЛ. VII. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
ченного в объеме V. Следовательно, правая часть
имеет смысл потока компоненты pi через ограничи-
ограничивающую V поверхность f, a a — плотности потока ри
Величина D0.38) есть k-я компонента вектора плот-
плотности потока компоненты р,. Таким образом, трехмер-
трехмерный тензор D0.38) определяет плотность потока им-
импульса. Отметим, что плотность потока скалярной ве-
величины (например, энергии) есть вектор; плотность
же потока векторной величины (например, импульса)
является тензором.
Импульс, переносимый через единичную площадку
в единицу времени, равен силе, действующей на эту
площадку, т. е. напряжению в том месте, где распо-
расположена площадка. По этой причине тензор atk назы-
называется тензором напряжений.
Итак, мы установили смысл всех компонент тен-
тензора Т»\ Объединив D0.27), D0.32), D0.33) и D0.38),
получим
(w Sx/c Sgfc S2/c\
Sx/c axx axy охг I D039)
Sy/C <JyX Gyy Оуг J X '
S2/c ozx ozy azz '
Компоненты тензора 7^v характеризуют плотность
энергии и импульса, а также плотности потоков этих
величин, чем и обусловлено название T»v — тензор
энергии-импульса.

Часть вторая
ЭЛЕКТРОДИНАМИКА
Глава VIII
ЭЛЕКТРОСТАТИКА
§ 41. Электростатическое поле в пустоте
Вообще говоря, электрическое и магнитное поля
тесно связаны друг с другом, образуя единое электро-
электромагнитное поле. Однако в случае стационарных (т. е.
не изменяющихся со временем) полей электрическое
поле и магнитное поле можно рассматривать раз-
раздельно. Мы начнем с рассмотрения электростатиче-
электростатического поля в пустоте.
Основной (силовой) характеристикой электриче-
электрического поля является напряженность поля Е, связан-
связанная с силой, действующей на точечный заряд е в дан-
данной точке поля, соотношением
F = eE. D1.1)
Это соотношение можно рассматривать как определе-
определение величины Е.
Из курса общей физики известно, что электроста-
электростатическое поле потенциально. Это означает, что работа,
совершаемая силами этого поля над зарядом на лю-
любом замкнутом пути, равна нулю:
= 0. D1.2)
Из формулы D1.2) следует, что циркуляция век-
вектора напряженности электростатического поля по лю-
любому контуру Г равна нулю. Воспользовавшись тео-
теоремой Стокса (см. (XI. 23)), можно написать
-0, D1.3)
где / — произвольная поверхность, ограниченная кон-
контуром Г, d\— вектор элементарной площадки, взятый
на этой поверхности.

178 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
Условие D1.3) должно выполняться для любой
произвольно выбранной поверхности f. Это возможно
лишь в том случае, если подынтегральная функция
в каждой точке равна нулю. Таким образом, мы при-
приходим к выводу, что ротор вектора напряженности
электростатического поля равен нулю в каждой точке
поля:
0. D1.4)
Равенство нулю ротора напряженности является
отличительной особенностью электростатического поля,
выражающей его потенциальность.
Из векторного анализа известно, что ротор гра-
градиента скалярной функции всегда равен нулю (см.
(XI. 43)). Поэтому напряженность электростатиче-
электростатического поля можно представить как градиент некото-
некоторой скалярной функции ср:
E=-Vq> D1.5)
1((знак «—» не меняет дела, он взят из физических со-
соображений). Функцию ф называют потенциалом элек-
электростатического поля. Очевидно, что <р определен с
точностью до произвольного постоянного слагаемого.
Следовательно, потенциал может отсчитываться от
любой точки поля, для которой его значение прини-
принимают равным нулю. В электродинамике обычно пола-
полагают потенциал равным нулю на бесконечности.
Потенциал поля точечного заряда е равен, как из-
известно,
Ф(г) = т-, <4L6)
где г — радиус-вектор, проведенный из точки, в кото-
которой помещается е, в точку, для которой опреде-
определяется ф.
Взяв градиент от выражения D1.6) и изменив
у него знак на обратный, найдем напряженность поля
точечного заряда:
Е—V(-f)-?f~Jr*. D1.7)
где ег — орт радиуса-вектора г (см. (XI. 51)).
Пусть поле создается системой точечных заря-
зарядов еа, помещающихся в точках, определяемых радиу-
радиусами-векторами г^, ,(рис. 41.1). Тогда согласно прин-

§ 42. УРАВНЕНИЕ ПУАССОНА 179
ципу суперпозиции потенциал поля, создаваемый этой
системой, в точке, определяемой радиусом-вектором г,
равен
а \Т Г° I
а напряженность поля
Если создающий поле заряд распределен в про-
пространстве с плотностью р = р(г'), вычисление потен-
потенциала и напряженности поля можно осуществить по
формулам, аналогичным D1.8)
и D1.9):
?(Г)=Л Р1Г-> <г - г/> dy/
D1.11)
где d V = Cxfdy'dv! есть эле-
элемент объема в точке г'(ж', #',
z' — компоненты переменного Рис. 41.1
вектора гг).
Переход от системы точечных зарядов еа к за-
заряду, распределенному в пространстве с плотностью
р(г), осуществляется с помощью б-функции Дирака
(см. Приложение XIII). Эта функция позволяет пред-
представить систему точечных зарядов еа> помещающихся
в точках с радиусами-векторами т'а, с помощью плот-
плотности заряда:
P(r)=l>e6(r-r'e). D1.12)
Очевидно, что, подставив функцию D1.12) в выра-
выражения D1.10) и D1.11) и произведя интегрирование,
мы придем к формулам D1.8) и D1.9).
§ 42. Уравнение Пуассона
Из курса общей физики известна теорема Гаусса,
которая в случае поля в пустоте может быть сформу-
сформулирована следующим образом: поток вектора Е через

180 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
замкнутую поверхность пропорционален алгебраиче-
алгебраической сумме зарядов, заключенных внутри поверхно-
поверхности. Коэффициент пропорциональности зависит от вы-
выбора системы единиц. В гауссовой системе, исполь-
используемой обычно в теоретической физике, он равен 4я.
Следовательно,
§? D2.1)
f
Если распределение зарядов внутри поверхности /
охарактеризовать с помощью плотности заряда
р = р(г), теореме Гаусса можно придать вид
D2.2)
где V — объем, ограниченный поверхностью f.
Применив к левой части формулы D2.2) теорему
Остроградского — Гаусса (см. (XI. 13)), придем к со-
соотношению
Последнее соотношение должно выполняться для лю-
любого произвольно выбранного объема V. Это возмож-
возможно только в том случае, если в каждой точке поля
D2.3)
Выразив в формуле D2.3) напряженность поля через
потенциал согласно D1.5), получим
V(V<J>)—— 4зхр.
В Приложении XI показано (см. (XI. 38)), что
V(Vq>) = Aq>, где Д — оператор Лапласа. Таким обра-
образом, мы приходим к соотношению
D2.4)
которое называют уравнением Пуассона. В разверну-
развернутом виде это уравнение выглядит следующим образом:
& + Ф + 3—** Н2.В,
Уравнение Пуассона позволяет по заданному рас-
распределению зарядов в пространстве ((по заданной

§ 42. УРАВНЕНИЕ ПУАССОНА 181
функции р) найти потенциал в каждой точке поля.
Зная ф, можно по формуле D1.5) определить Е.
Для точек поля, в которых р = 0, уравнение D2.4)
имеет вид
Дф = 0. D2.6)
Соотношение D2.6) называется уравнением Лапласа.
В соответствии с формулой D1.10) решение урав-
уравнения D2.4) имеет вид
где интегрирование распространяется на всю область,
в которой распределены заряды, создающие поле. Это
утверждение может быть доказано строго математи-
математически путем применения оператора Лапласа к инте-
интегралу D2.7).
Заметим, что выражение D2.7) будет удовлетво-
удовлетворять уравнению Пуассона и в том случае, если к нему
добавить произвольную постоянную (A const = 0).
Так что, вообще говоря, для того чтобы решение урав-
уравнения Пуассона было вполне определенным, необ-
необходимо задать граничные условия. Решение D2.7)
(с const = 0) получается в том случае, если принять
потенциал на бесконечности равным нулю.
Можно показать, что решение уравнения Пуассона
при заданных граничных условиях является един-
единственным. Однако это доказательство выходит за
рамки данной книги.
Покажем, что функция ф(г)=1/г удовлетворяет
уравнению Лапласа (уравнению D2.6)) во всех точ-
точках, кроме г —0. Согласно (XI.51) Vy = —j3~~ =
= ~"Г- Применим к этому выражению еще раз
оператор V:
Согласно (XI. 49) Vr = 3. Следовательно.
3 J
что и требовалось доказать.

№ ГЛ. VIII. ЭЛЕКТРОСТАТИКА
Можно найти значения ДA/г) во всех точках,
включая и г = 0. Для этого воспользуемся тем об-
обстоятельством, что в случае точечного заряда е, поме-
помещающегося в начале координат, р~— ?б(г), а потен-
потенциал ф = е/r. Подставив эти значения в уравнение
D2.4) и сократив на е, придем к следующему матема-
математическому соотношению:
Д-1 = _4яб(г). D2.8)
§ 43. Разложение поля по мультиполям
Рассмотрим систему зарядов, размещенную в огра-
ограниченном объеме, и исследуем поле, создаваемое та-
такой системой на расстояниях, больших по сравнению
с размерами системы. Поместив начало координат
внутри объема, занимаемого системой, получим для
потенциала выражение
D3Л)
где по предположению г^га (см. D1.8); мы опустили
ШТрИХ ПрИ Го).
Разложим выражение D3.1) в ряд по степеням
величин га/г. Для этого выразим <р(г) через компо-
компоненты векторов гига:
Ф (*i. хъ х3) - У еа D3.2)
(индекс i пробегает значения 1, 2, 3, индекс а — зна-
значения 1,2, ..., /г, где п — число зарядов в системе).
Рассматривая величины (—xat) как малые прираще-
приращения координат %и можно представить функцию D3.2)
в виде
D3.3)

§ 43. РАЗЛОЖЕНИЕ ПОЛЯ ПО МУЛЬТИПОЛЯМ 183
(раскладывается в ряд каждое из слагаемых суммы
D3.2)).
Выражение D3.3) называется разложением потен-
потенциала по мультиполям. Первый член разложения
Фо = ^~ D3.4)
(мы заменили VX Л через г) имеет вид потенциала
точечного заряда. Суммарный заряд ? еа представ-
представляет собой мультиполь нулевого порядка (его назы-
называют также монополем). В случае, когда этот муль-
мультиполь отличен от нуля, член <ро вносит основной
вклад в потенциал D3.2).
Чтобы выяснить вид мультиполя первого порядка,
преобразуем второй член разложения D3.3) следую-
следующим образом:
д ( еа \ t „ ч V* д ( \
Сумма X eaxak представляет собой проекцию на k-ю
а
координатную ось вектора
Р = Z Ve. D3.5)
а
Этот вектор есть не что иное как дипольный момент
системы зарядов1). Он и является мультиполем пер-
первого порядка.
Выражение
dxk
!) Если заряд распределен по объему системы с плотностью
р, то дипольный момент определяется интегралом:
р = { р (г) г dV. D3.6)
Напомним, что для системы, суммарный заряд которой J^ ea
равен нулю, дипольный момент не зависит от выбора начала
координат. Действительно, перенеся начало координат в точку
с г = Ь, мы получим для радиусов-векторов отложенных из
нового начала координат, значения та = rfl — b. Дипольный мо-
момент в новой системе равен р' = ?) еата = 2 еата ~~ 2 еоР в
=« р — b ^ еа. Так как ^ еа = 0, получаем, что р' *= р.

184 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
дает k-ю компоненту градиента 1/л Таким образом,
Формулу для ф! можно получить сразу в вектор-
векторной форме, воспользовавшись тем обстоятельством,
что согласно (XI.5) с точностью до членов первого
порядка
f( ) /()
Применим эту формулу к каждому слагаемому в
D3Л), рассматривая —та как бг. В результате по-
получим
??ЛуТ- D3.8)
Первое слагаемое совпадает с D3.4), второе —
с D3.7).
Отметим, что V(!/r) пропорционален 1/г2. Следо-
Следовательно, слагаемые второй суммы в D3.8) будут по
сравнению со слагаемыми первой суммы величинами
порядка та/V.
Вычислив V(l/r) и подставив его в D3.7), придем
к выражению для потенциала поля диполя:
9i = -pV^=-p(-^f)=^. D3.9)
Теперь найдем напряженность поля диполя:
(см. (XI. 25)). Воспользовавшись формулами (XI. 51)
и (XI. 37), получим
Е = !!?>. f - -1 {[р [Vr]] + [г [VP]] + (rV) P + (PV) r}.
Рассмотрим выражение в фигурных скобках:
[Vr] =0 (см. (XI. 50)), [Vp] =0, так как р не зави-
зависит от г; (rV)p = 0 по той же причине. Таким обра-
образом, из четырех слагаемых отлично от нуля только
последнее, которое согласно (XI. 34) равно р. Итак,
3(рг) г р Зег (рег) — р ( Q - .
Ь = —j; р *7*~ Н • 14*5.10)
где ег — орт радиуса-вектора г.

§ 43. РАЗЛОЖЕНИЕ ПОЛЯ ПО МУЛЬТИПОЛЯМ 185
Отметим, что поле диполя обладает осевой сим-
симметрией относительно направления р.
Может случиться, что не только суммарный заряд
X еа> но и дипольный момент р = X еата будет равен
нулю. Это имеет место, например, для изображенной
на рис. 43.J системы зарядов, называемой квадрупо-
лем. В этом случае поле определяется следующим
членом разложения функции D3.1), квадратичным от-
относительно величин Гд/г.
Запишем <р2 следующим образом (см. D3.3)):
^2 2 Zj Zj dxk dxm \ г )
a Km
1 V д2
kt m
Величина, стоящая в фигурных скобках, есть k, m-я
компонента симметричного тензора второго ранга
(см. Приложение X). Этот тензор +е а -е
можно было бы принять в качестве | ¦-¦f
соответствующего мультиполя. Од-
нако, как мы покажем ниже, из де-
\а
вяти компонент этого тензора неза-
независимыми являются не шесть ком-
компонент (как это бывает у симмет- А-—
ричного тензора), а только пять. ~е *е
Чтобы подчеркнуть это обстоятель- Рис. 43.1
ство, тензор, характеризующий свой-
свойство системы, определяющее q>2, записывают в ином
виде. В предыдущем параграфе мы видели, что функ-
функция \\г удовлетворяет уравнению Лапласа, т. е. что
(по предположению г ^> rGf так что г=0 исключается
из рассмотрения). Легко убедиться в том, что эту
формулу можно написать в виде
k% m
Умножим полученное нами соотношение на ojf^b
и просуммируем затем по а. В результате

185 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
получим
a kt m
что можно записать следующим образом:
дхкдхт
к,т
Вычтя полученное выражение из D3.11), прида-
придадим формуле для ф2 вид
D3.12)
Совокупность величин
Q = ? *а (ЗхвЛя| - rfl6,m) D3.13)
а
называется тензором квадрупольного момента систе-
системы. Вычислим след этого тензора, т. е. сумму его диа-
диагональных компонент:
sP (Qkm) = E Qkk - Z Z 6fl C4fe - r») -
==: 2j ea Zrf V^^afe "~ ra) "^
= Z ea /3 Z 4* - 3r») = 0. D3.14)
Равенство нулю Sp(Qfem) означает, что из трех
диагональных компонент тензора Qkm независимыми
являются только две, а следовательно, всего незави-
независимых компонент — пять.
Если привести тензор Qkm к главным осям, то
в силу условия D3.14) независимыми будут только
два из трех главных значений. Если система зарядов
обладает осью симметрии порядка выше второго, то
эта ось (обозначим ее буквой z) будет одной из глав-
главных осей тензора Q*m, положение двух других глав-
главных осей будет произвольным. В этом случае, оче-
очевидно Qxx = Qyy и в силу D3.14)
QXx = Qyy=--YQzz. D3.15)

§ 43. РАЗЛОЖЕНИЕ ПОЛЯ ПО МУЛЬТИПОЛЯМ jg/
Главное значение Qzz называют в этом случае просто
квадрупольным моментом системы. Можно показать,
что, когда суммарный заряд и дииольный момент си-
системы равны кулю, квадрупольный момент не зави-
зависит от выбора начала координат.
Применив обозначение D3.13), потенциал поля,
обусловленного квадруполем, можно записать сле-
следующим образом:
?fem—-^ -. D3.16)
k,m
Вычислим вторые производные, входящие в это
выражение:
д2 1 _ д / д \\ _ а / \ дг
dxk dxm г дхь \ дхт г ) dxk \ г2 дхт
dxk \ 7*")"" W~ ¦ "
(дхщ/dxk = 8*m). Подставим эти значения производ-
производных в D3.16):
™ 1 У* Qkm ( 3xmXk * Л (Аъ 17ч
к, т
Из D3.17) следует, что потенциал квадруполя убы-
убывает с расстоянием как 1/г3. Напомним, что потен-
потенциал монополя убывает по закону 1/г (см. D3.4)),
а потенциал диполя — по закону 1/г2 (см. D3.9)).
Вообще потенциал мультиполя /г-го порядка убывает
с расстоянием по закону l/rn+l.
Итак, поле системы зарядов можно представить
как наложение полей, создаваемых мультиполями раз-
разных порядков:
ср(г) = ф0 + Ф1 + Фг + • • - =
_ Е е* „ 1 , 1 V п & 1 «
~~7 P^T + "bLQkm дхкдхт Т+ •••
Мультиполи более высоких порядков мы не будем
рассматривать. Отметим лишь, что мультиполь треть-
третьего порядка называется октуцолем. В качестве при-
примера октуполя можно указать систему из восьми
одинаковых по величине разноименных зарядов, раз-
размещенных в вершинах куба таким образом, что ближай-
ближайшими соседями оказываются заряды разного знака.

188 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
§ 44. Поле в диэлектриках
До сих пор мы рассматривали электростатическое
поле, создаваемое заданной системой зарядов в пус-
пустоте. При этом предполагалось, что заряды, создаю-
создающие поле, могут перемещаться на макроскопические
расстояния (например, в пределах всего проводящего
тела). Такие заряды мы будем называть свободными.
В случае поля, возбуждаемого под воздействием
свободных зарядов в диэлектриках, положение сильно
усложняется, так как на поле свободных зарядов на-
накладывается поле, создаваемое зарядами, входящими
в состав атомов и молекул диэлектрика. Поскольку
эти заряды не могут покидать пределы атомов и мо-
молекул, в состав которых они входят, их называют
связанными.
Если обозначить поле свободных зарядов симво-
символом Есвоб, а поле связанных зарядов — символом ЕСВя3,
то напряженность результирующего поля Ерез можно
представить в виде
Даже если свободные заряды неподвижны, поле
D4.1) не будет стационарным (т. е. не зависящим
от времени), так как связанные заряды совершают
движение внутри молекул и, кроме того, участвуют
вместе с молекулами в тепловом движении. Таким об-
образом, очевидно, что поле ЕСВЯз есть быстроперемен-
ная функция времени. Кроме того, ЕСВяз сильно ме-
меняется в пространстве между двумя соседними моле-
молекулами. Оба вида зависимости (от времени и от точки
в промежутке между молекулами) исчезают, если рас-
рассматривать значение ЕСВяз, усредненное, во-первых, по
промежутку времени, много большему, чем период
внутримолекулярного движения и тепловых колеба-
колебаний, и, во-вторых, по объему, значительно превосхо-
превосходящему объем одной молекулы. Следовательно, поле
<ЕСвяз> будет стационарным. Кроме того, оно плавно
меняется в пределах объема, включающего много мо-
молекул. Поле <ЕсВяз> называют макроскопическим, в
отличие от микроскопического поля ЕСВЯз.
Мы будем называть напряженностью поля в ди-
диэлектрике макроскопическую величину
D4.2)

§ 44. ПОЛЕ В ДИЭЛЕКТРИКАХ 189
В отсутствие внешнего поля (т. е. поля свободных
зарядов) поле <ЕСвяз> обычно равно нулю. Под воз-
воздействием внешнего поля средние положения связан-
связанных зарядов смещаются тем сильнее, чем больше
действующее на них поле. В результате поле <ЕСВяз>
становится отличным от нуля. При вычислении поля
D4.2) положение усложняется тем, что среднее сме-
смещение связанных зарядов определяется не полем
Есвоб, а результирующим полем Е, которое включает
в себя <ЕСвяз>.
Электрическое состояние диэлектрика принято ха-
характеризовать дипольным моментом единицы объема
диэлектрика, который называют поляризованностью
и обозначают символом Р. Очевидно, что Р можно
определить как
i <44-3>
где AV — физически бесконечно малый объем1), р,- —
дипольный момент отдельной молекулы, суммирова-
суммирование осуществляется по всем молекулам, заключенным
в объеме Д1Л
Определив Р таким образом, мы по существу про-
произвели то усреднение, о котором шла речь выше в
связи с обсуждением ЕСВяз (Р — макроскопическая ве-
величина, р, — микроскопическая).
При воздействии на диэлектрик электрического
поля связанные заряды смещаются (оставаясь каж-
каждый в пределах «своей» молекулы) — положительные
по полю, отрицательные в противоположную сторону.
В результате на поверхности диэлектрика образуются
связанные заряды. Кроме того, могут возникать также
и объемные связанные заряды.
Найдем выражение для рсвяз — объемной плотно-
плотности связанных зарядов. Выделим мысленно в диэлек-
диэлектрике физически бесконечно малый объем АV. Пусть
в отсутствие поля связанные заряды еа (а = 1, 2, ...),
заключенные в этом объеме, помещаются в точках,
*) Физически бесконечно малым называют объем AV, заклю-
заключающий в себе достаточно большое число молекул для того,
чтобы можно было пренебречь дискретностью вещества, и вме-
вместе с тем достаточно малый для того, чтобы макроскопические
величины, например Е или Р, можно было считать в пределах
AV постоянными.

190 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
определяемых радиусами-векторами гао. Поскольку в
отсутствие поля диэлектрик не поляризован, выраже-
выражение 2 ^ага0 равно нулю (сумма бсоется по AV). Дей-
Действительно, с точностью до 1/Д V эта сумма совпадает
с поляризовакностью Р, которая у неполяризованного
диэлектрика равна нулю.
Предположим, что при включении поля связанные
заряды смещаются на отрезки Ага (отметим, что эти
отрезки много меньше линейных размеров объема
AV). В результате возникнет поляризация, характери-
характеризуемая вектором
Р =
Ж
Связанные заряды, входящие в состав диэлектри-
диэлектрика, можно разбить на несколько групп, в каждой из
которых величина заряда еа и смещение Дга одина-
одинаковы. Пронумеруем такие группы индексом р. Коли-
Количество зарядов группы р, приходящееся на единицу
объема диэлектрика, обозначим щ. Тогда поляризо-
ванность можно написать еле-
/ дующим образом:
<44-5)
р— число зарядов группы
Р, заключенных в объеме AV).
* Вычислим алгебраическую
сумму связанных зарядов, пере-
пересекающих при включении поля границу объема ДУ.
На рис. 44.1 показан элемент df поверхности, огра-
ограничивающей AV. Элемент df пересекут (и выйдут
наружу или войдут внутрь) те заряды группы с но-
номером р, которые заключены в элементарном объеме
величины Ar$di. Они унесут с собой заряд
я^АГрЛ. D4.6)
Это выражение является алгебраическим. Его знак
зависит от знака е$ и от знака скалярного произведе-
произведения Ar^df, т. е. от направления Дгр по отношению

§ 44. ПОЛЕ В ДИЭЛЕКТРИКАХ
191
к внешней нормали к df (на рис. 44.1 она обозначена
буквой о).
Просуммировав выражение D4.6) по р, получим
полный заряд, пересекающий df:
X м§ея Arp di = P df D4.7)
(см. D4,5)).
Проинтегрировав выражение D4.7) по поверхно-
поверхности /, найдем суммарный связанный заряд, выходящий
из объема AV при включении поля. Таким образом,
при включении поля объем AV, который был прежде
нейтральным, приобретает связанный заряд
(приобретаемый заряд равен взятому с обратным зна-
знаком вышедшему наружу заряду). Применив теорему
Остроградского — Гаусса, получим
J
dV = -VP
Отсюда для плотности связанных
зарядов получается выражение
-VP. D4.8)
пг**.
С помощью формулы D4.8)
можно найти и поверхностную
плотность связанных зарядов сгсвяз.
Для этого рассмотрим цилиндриче- рИс. 44.2
ский объем, заключенный между
двумя бесконечно близкими поверхностями вели-
величины А/, расположенными по разные стороны
от поверхности диэлектрика (рис. 44.2). Связанный
заряд <7связ, заключенный в этом объеме, можно пред-
представить ЛИбО В ВИДе \рсвяз^> ЛИбО В ВИДе СсзязА/.
Использовав формулу D4.8) и теорему Остроград-
Остроградского— Гаусса, можно написать
= - J VP dV = - J Ря, df,
где и' — внешняя нормаль к поверхности цилиндра.
Интеграл по поверхности можно разбить на три

192 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
части: интеграл по внешнему основанию цилиндра, ко-
который равен нулю, поскольку вне диэлектрика Р = 0;
интеграл по боковой поверхности цилиндра, которым
можно пренебречь в силу бесконечной малости этой
поверхности; и, наконец, интеграл по внутреннему
основанию цилиндра. Последний равен — /VA/, где
п' — нормаль к поверхности, направленная внутрь ди-
диэлектрика. Если вместо п' взять внешнюю нормаль п,
то —-Рл' нужно заменить на +Рп. Таким образом,
мы приходим к соотношению <тСвязА/ = P«Af, откуда
<W = *V D4.9)
Здесь Рп — проекция поляризованности Р на внеш-
внешнюю нормаль к поверхности диэлектрика.
Заметим, что заряды плотности, определяемой
формулами D4.8) и D4.9), являются не воображае-
воображаемыми, а вполне реальными зарядами.
Итак, при наличии диэлектриков на поле, созда-
создаваемое свободными зарядами (их плотность мы обо-
обозначим р), накладывается поле связанных поверхност-
поверхностных (см. D4.9)) и объемных (см. D4.8)) зарядов.
Следовательно, потенциал в точке, определяемой ра-
радиусом-вектором г, будет равен
V
0 Д R
D4.10)
где для краткости применено обозначение R=\r— г'|;
dVf — элементарный объем, взятый в окрестности точ-
точки г', df — элемент поверхности диэлектрика, взятый
в окрестности точки г'; дивергенция от Р(г') берется
по штрихованным координатам, поэтому оператор V
снабжен штрихом (см. (XI. 52)). Первый интеграл
берется по всему объему, где р отлична от нуля, вто-
второй интеграл берется по всем поверхностям, ограни-
ограничивающим диэлектрик, и, наконец, третий интеграл
берется по всему объему диэлектрика.
§ 45» Описание поля в диэлектриках
Если VP отлична от нуля, каждый элементарный
объем диэлектрика эквивалентен точечному заряду
величины —VPrfV и вносит соответствующий вклад

§ 45. ОПИСАНИЕ ПОЛЯ В ДИЭЛЕКТРИКАХ 193
в макроскопическое поле Е. Поэтому при наличии ди-
диэлектриков уравнение D2.3) нужно писать в виде
VE = 4я (рсвоб + рсвяз) = An (p - VP) D5.1)
(под р подразумевается плотность свободных заря-
зарядов). В таком виде уравнение малопригодно для на-
нахождения Е, так как определяет Е не только через
плотность свободных зарядов, но и через характер
поляризации диэлектрика. Поляризация же есть в
свою очередь функция Е.
Легко заметить, что если ввести вспомогательную
величину
D5.2)
то для нее будет справедливо уравнение
D5.3)
т. е. VD определяется только плотностью свободных
зарядов.
Величину D называют электрической индукцией.
Сопоставление уравнений D5.1) и D5.3) показы-
показывает, что операция нахождения D гораздо проще, чем
операция нахождения Е. Однако от величины D было
бы мало проку, если бы не то обстоятельство, что
в большинстве практически важных случаев D оказы-
оказывается пропорциональной Е. Поэтому удается осуще-
осуществить «обходный маневр»: вместо основной характе-
ристики поля Е вычисляют сначала вспомогательную
величину D, а затем совершают переход от D к Е.
Введение величины D целесообразно также по той
причине, что многие формулы, написанные с исполь-
использованием О, оказываются много проще, чем они вы-
выглядели бы, будучи выраженными через Е и Р.
Опыт дает, что во многих имеющих практический
интерес случаях поляризованность пропорциональна
напряженности поля
Р = кЕ D5.4)
(мы пока ограничимся рассмотрением изотропных ди-
диэлектриков). Величина х называется диэлектрической
восприимчивостью вещества. Она всегда положительна.
7 И. В. Савельев, т. 1

194 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
Подставив D5.4) в D5.2), найдем, что
D = Е + 4якЕ = еВ, D5.5)
где
е = 1 -f 4зш D5.6)
есть диэлектрическая проницаемость вещества.
Таким образом, D и Е во многих случаях пропор-
пропорциональны друг другу. Этим и обусловлена целесооб-
целесообразность введения D.
Основываясь на уравнении D5.3), можно, каза-
казалось бы, заключить, что D определяется только плот-
плотностью свободных зарядов. Однако это не так. Од-
Одного уравнения D5.3) для определения D недоста-
недостаточно. Чтобы отчетливее это понять, вспомним, как
осуществляется нахождение Е в отсутствие диэлектри-
диэлектриков. Кроме уравнения VE = 4яр, мы, воспользовав-
воспользовавшись тем, что [VE] = 0, положили Е = —Уф. Подста-
Подставив это выражение в уравнение для дивергенции, мы
пришли к уравнению Пуассона: V2cp = —4лр. Решение
этого уравнения позволяет найти <р, а затем и Е.
Если идти тем же путем при нахождении D, нужно
в дополнение к D5.3) рассмотреть уравнение
[VD]=-[V, eE] = [Ve, Е] + е [VE] = [Ve, EJ
(мы применили формулу (XI. 27) и приняли во вни-
внимание, что [VE] = 0). Это уравнение переходит в
[УВ] = 0 только в том случае, когда Ve = 0, т. е. ди-
диэлектрик однороден. В общем случае [VD] зависит
от Е, т. е. в конечном счете от связанных зарядов.
Однако, хотя D, вообще говоря, зависит от связан-
связанных зарядов, совокупность уравнений
[VE] = O,
позволяет по известному распределению в простран-
пространстве свободных зарядов вычислить Е и D.
Воспользовавшись соотношением D5.4), можно
выяснить, при каких условиях рСВЯз отлична от нуля.
Подставим значение D5.4) в формулу D4.8):
Рсвяз = —VP = - V (иЕ) = — xVE — EVh D5.7)
(см. (XI. 26)). Согласно D5.1) УЕ = 4я(рСВОб + рсвяэ).
Заменив этим значением VE в формуле D5.7), по-
получим
Ревю — -~*4я (Pe^ + рСЕ J - Е V*.

§ 45. ОПИСАНИЕ ПОЛЯ В ДИЭЛЕКТРИКАХ 195
Теперь разрешим получившееся уравнение относи-
относительно рсвязГ
= — Т [4яирсвоб +
Из найденного нами соотношения следует, что pCB*3
отлична от нуля, во-первых, в тех точках, где отлична
от нуля рсвоб» и, во-вторых, в тех точках, где УкфО9
т. е. в местах неоднородности диэлектрика. Отметим,
что в однородно-поляризованном диэлектрике (Р==
= const) объемные связанные заряды не возникают.
Рассмотрим поле в однородном диэлектрике. До-
Допустим, что в отсутствие диэлектрика при данном рас-
распределении свободных зарядов возникает поле, харак-
характеризуемое напряженностью Ео и потенциалом фо. Мы
знаем, что Ео и фо являются решениями уравнений
D5.8)
D5.9)
(см. D2.3) и D2.4)).
Теперь, не изменяя расположения свободных заря-
зарядов (т. е. р), заполним все пространство, в котором
поле отлично от нуля, однородным (е== const) изо-
изотропным диэлектриком. Тогда напряженность поля
станет равной Е, а потенциал примет значение q>. На-
Напишем уравнения для Е и ф. Согласно D5.3)
VD = V (вЕ) = 4яр. D5.10)
Заменив в этом уравнении Е через —Уф и приняв во
внимание, что е = const, можно написать
—V (еУф) = —V2 (бф) = 4яр,
или
=»—4яр. D5.11)
Сравнение D5.10) с D5.8) и D5.11) с D5.9) по-
показывает, что уравнение для еЕ совпадает с уравне-
уравнением для Ео, а уравнение для вф— с уравнением для
Фо. Отсюда следует, что заполнение пространства, в
котором имеется поле, однородным изотропным ди-
диэлектриком приводит к уменьшению как напряженно-
напряженности поля, так и потенциала в е раз. В частности, для
поля точечного заряда, помещающегося в однородном

196 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
диэлектрике,
D5.12)
Отметим, что согласно D5.11) уравнение Пуассо-
Пуассона D2.4) для поля в однородном изотропном диэлек-
диэлектрике выглядит следующим образом:
Аф=--?-р. <45ЛЗ>
Приведем без вывода 1) условия, которым должны
удовлетворять Е и D на границе двух диэлектриков:
(индекс х применен для обозначения тангенциальной
составляющей вектора, индекс п — для обозначения
нормальной составляющей).
Нахождение поля путем решения уравнений D2.4),
D5.3) и т. п. в общем случае представляет очень
трудную задачу. В случаях, обладающих симметрией,
удается установить вид поля, не решая уравнений.
Покажем это на следующем примере. Пусть имеется
плоская граница двух пол у бесконечных однородных и
изотропных диэлектриков с проницаемостями г\ и е2-
В первом диэлектрике на расстоянии а от границы
имеется точечный заряд q. Требуется найти поле в
обоих диэлектриках.
Поле в первом диэлектрике составим из полей то-
точечного заряда q и его зеркального изображения —
воображаемого заряда q'. Это допущение удовлетво-
удовлетворяет основному условию, что в первом диэлектрике
имеется только один источник D — заряд q (q' лежит
вне первого диэлектрика). Итак, будем искать потен-
потенциал в первом диэлектрике в виде
<45Л5>
(значения гиг7 ясны из рис. 45.1).
Поле во втором диэлектрике представим как поле
воображаемого заряда qf\ помещенного там же, где q.
*) Вывод можно найти во многих учебниках общей физики.

§ 45. ОПИСАНИЕ ПОЛЯ В ДИЭЛЕКТРИКАХ
197
Это допущение согласуется с тем фактом, что во вто-
втором диэлектрике нет источников D (q" лежит вне вто-
второго диэлектрика). Таким образом, будем искать по-
потенциал во втором диэлектрике в виде
82Г
D5.16)
Попробуем подобрать значения qf и cfr так, чтобы
удовлетворялись граничные условия D5.14) для D.
По сделанным нами предположениям D имеет в пер-
первом и втором диэлектри-
диэлектриках значения:
D5.17)
На границе диэлектриков
Jr| = ]r'|. Следователь-
Следовательно,
D5.18)
Найдем нормальные составляющие векторов в
D5.18). Вектор п направим от первого диэлектрика
ко второму. Приняв во внимание, что проекция г на п
равна а, а проекция т' равна —а, получим
С учетом того9 что тангенциальные составляющие
векторов гиг' одинаковы: г ~/%, можно написать
А
IX'
D6.19)
Из равенства Di« —Ds« вытекает, что
q-qr = q'\ D5.20)
Из соотношения Du/si—D2x/b2 (см. D5.14)) после
подстановки в него значений D5.19) получается, что

198 ГЛ. VIII. ЭЛЕКТРОСТАТИКА
Решив совместно уравнения D5.20) и D5.21), най-
найдем значения qf и <jr", удовлетворяющие граничным
условиям:
5? ? <4522>
Нам удалось «сконструировать» функции Di и D2
(см. D5.17)), каждая из которых в своей области
удовлетворяет уравнению VD = 4rcp. Кроме того, эти
функции удовлетворяют граничным условиям. Значит
функции D5.17) и соответственно D5.15) и D5.16)
будут (после подстановки в них значений D5.22) для
q' и q") решениями задачи. В силу теоремы о един»
ственности (см. § 42) никаких других решений не су-
существует.
§ 46. Поле в анизотропных диэлектриках
В анизотропных диэлектриках направления векто-
векторов Ри Е, вообще говоря, не совпадают (см. Прило-
Приложение X). Связь между компонентами этих векторов
дается соотношениями
Pt=E*tkBu (/=1,2,3), D6.1)
где *&ik — симметричный тензор второго ранга, назы-
называемый тензором диэлектрической восприимчивости.
Согласно D5.2) В = Е + 4яР или, в компонентах,
Подставив Р§ из D6.1), получим
/>, —Е| + 4я?
Если представить Ei в виде ? &<*?*» можно написать
Величины
D6.2)
очевидно, суть компоненты симметричного тензора
второго ранга. Его называют тензором диэлектриче-

§ 46. ПОЛЕ В АНИЗОТРОПНЫХ ДИЭЛЕКТРИКАХ 199
ской проницаемости (или, кратко, диэлектрическим
тензором). С его помощью связь между векторами
D и Е может быть написана в виде
ikEk (f-1,2,3). D6.3)
Симметричный тензор имеет шесть независимых
компонент. Если его привести к главным осям, он
выглядит следующим образом;
(в,*)
(б! О 0\
О 82 О I.
О 0 е3/
Отметим, что поскольку главные значения тензора х**
положительны, главные значения тензора &ik всегда
больше единицы.
В кристаллах триклинной, моноклинной и ромби-
ромбической систем все три главные значения тензора е^,
а следовательно, и полуоси тензорного эллипсоида
различны. Такие кристаллы называются двухосными.
В кристаллах тетрагональной, ромбоэдрической и
гексагональной систем два главных значения совпа-
совпадают: si = 8г Ф ез. Тензорный эллипсоид в этом слу-
случае является эллипсоидом вращения. Такие кристал-
кристаллы называются одноосными.
В кристаллах кубической системы все три главные
значения тензора е^ одинаковы, так что тензор имеет
вид гбщ. Тензорный эллипсоид в этом случае вырож-
вырождается в сферу. По своим диэлектрическим (и опти-
оптическим) свойствам такие кристаллы не отличаются от
изотропных тел.

Глава IX
МАГНИТОСТАТИКА
§ 47. Стационарное магнитное поле в пустоте
На точечный заряд е, движущийся со скоростью v,
действует в магнитном поле сила *)
F--f[vB] D7.1)
(с — скорость света в вакууме). Векторная величи-
величина В, называемая магнитной индукцией, является
основной (силовой) характеристикой магнитного поля.
Соотношение D7.1) можно рассматривать как опре-
определение величины В.
Вследствие отсутствия в природе магнитных заря-
зарядов, аналогичных электрическим зарядам е2), линии
вектора В не имеют ни начала, ни конца. Поэтому
поток вектора В через любую замкнутую поверхность
всегда равен нулю:
§nrf/ = 0. D7.2)
Формула D7.2) является аналитическим выраже-
выражением теоремы Гаусса для вектора магнитной ин-
индукции.
Воспользовавшись теоремой Остроградского — Га-
Гаусса, выражению D7.2) можно придать вид
O. D7.3)
') Сумму сил D1.1) и D7.1) называют силой Лоренца.
*) Исходя из того, что уравнения природы вообще и уравне*
ния электродинамики в частности должны быть симметричными,
Дирак высказал предположение, что в природе должны суще-
существовать магнитные заряды (монополи Дирака). Поиски этих
зарядов пока не дали никаких результатов, так что вопрос
о существовании монополей Дирака остается открытым.

§ 47. СТАЦИОНАРНОЕ МАГНИТНОЕ ПОЛЕ В ПУСТОТЕ 201
Условие D7.3) должно выполняться для любого про-
произвольно выбранного объема V. Это возможно лишь
в том случае, если подынтегральная функция в каж-
каждой точке равна нулю. Таким образом, мы приходим
к выводу, что дивергенция вектора магнитной индук-
индукции равна нулю в каждой точке поля:
VB = 0. D7.4)
В векторном анализе доказывается (см. (XI. 44)),
что дивергенция ротора векторной функции всегда
равна нулю. Поэтому магнитную индукцию можно
представить как ротор некоторой векторной функ-
функции А:
D7.5)
Функцию А называют векторным потенциалом маг-
магнитного поля.
Векторный потенциал, так же как и скалярный
потенциал <р, определяется неоднозначно. Действи-
Действительно, поскольку ротор градиента любой функции
есть нуль (см. (XI. 43)), добавление к векторному по-
потенциалу величины Уф (ф— произвольная функция)(
не изменяет значения [VA], т. е. В. Таким образом,
если А есть векторный потенциал, отвечающий дан-
данному магнитному полю, то и функция
A' = A + V$ D7.6)
также будет векторным потенциалом данного поля.
Свойство D7.6) позволяет выбирать потенциал
наиболее удобным образом, например, накладывать
определенные условия на дивергенцию А. Действи-
Действительно, из D7.6) следует, что
VA' = VA -f V (Щ) = VA + Ai|?,
так что подбором ф можно придать VA' любое напе-
наперед заданное значение. В рамках магнитостатики мы
будем выбирать ф так, чтобы
VA = 0. D7.7)
В качестве иллюстрации к сказанному рассмотрим
векторный потенциал однородного магнитного поля:
В = const = Во. Направим ось г вдоль Во* Тогда
Вх = Ву = 0, BZ = BO и уравнение D7.5), написанное

202
ГЛ. IX. МАГНИТОСТАТИКА
в компонентах, будет иметь вид
dAz
* лТ~ == ^> Ви
дАх
дг
дАг
D7.8)
дАу дАх
г дх ду °*
Видно, что этим уравнениям удовлетворяет, ска-
скажем, такое значение потенциала:
Ах=— Воу, ^ = 0, Аг — 0. D7.9)
На рис. 47.1, а изображены линии вектора А, имею-
имеющего компоненты D7.9).
1
У
X
J
J
j
а б б
Рис. 47.1
Решение D7.9) не является единственным. Урав-
Уравнениям D7.8) удовлетворяет также следующий по-
потенциал:
Лг = 0. D7.10)
Линии А в этом случае показаны на рис. 47.1,6. Оче-
Очевидно, что решением будет также
Ах = —aBQy9 Ау = A — a) BqX, Az = 0,
где а — любое число. В частности, уравнениям D7.8)
удовлетворяют
4 Т Аг = 0. D7.11)
Последнее решение можно представить в виде
Ах = ~- (Byz -
^~ (8zx - Bxz\

§ 48. УРАВНЕНИЕ ПУАССОНА 203
(напомним, что Вх = Ву = 0), откуда
44 D7Л2)
где R — составляющая радиуса-вектора г, перпенди-
перпендикулярная к оси г. Линии вектора А, отвечающие
D7.12), даны на рис. 47.1, в.
Все приведенные нами значения потенциала удов-
удовлетворяют условию D7.7). Отсюда заключаем, что
уравнения D7.5) и D7.7) не полностью определяют А.
Для того чтобы определение векторного потенциала
было однозначным, необходимо задать граничные
условия для А.
§ 43. Уравнение Пуассона
для векторного потенциала
Из курса общей физики известно, что циркуляция
вектора В по любому замкнутому контуру Г, взятому
в стационарном магнитном поле (в поле постоянных
токов), пропорциональна алгебраической сумме токов,
охватываемых контуром:
*
D8.1)
Формулу D8.1) мы будем рассматривать как соотно-
соотношение, установленное опытным путем.
Введя плотность тока j, сумму токов можно пред-
представить как поток вектора | через поверхность, огра-
ограниченную контуром Г. Тогда формула D8.1) примет
ВИД
г С f
Преобразуем левую часть полученного нами соотно-
соотношения по теореме Стокса. В результате получим
$[УВ]Л«-^Jjrfl. D8.2)
Предположим, что интегрирование слева и справа
ведется по одной и той же поверхности (хотя равен-
равенство D8.2) выполняется и для различных поверхно-
поверхностей, лишь бы они опирались на один и тот же кон-

204 ГЛ. IX. МАГНИТОСТАТИКА
тур Г). Соотношение D8.2) должно выполняться для
любой произвольно взятой поверхности f. Это воз-
возможно только в том случае, если в каждой точке поля
[VB] = ^-j D8.3)
(напомним, что рассматривается лоле постоянных
токов).
Уравнение D8.3) играет в магнитостатике такую
же основополагающую роль, как уравнение D2.3)
в электростатике. Совместно с уравнением D7.4) оно
позволяет вычислить поле заданных стационарных
токов.
Подставим в формулу D8.3) вместо В ротор А
(см. D7.5)):
Согласно (XI. 45) [V[VA]] = V(VA)—ДА. Положив,
как было условлено (см. D7.7)), VA = 0, получим
для А дифференциальное уравнение
AA=-±Lj. D8.4)
Это векторное уравнение эквивалентно трем скаляр-
скалярным уравнениям:
АЛ* = - Ц- h (к - х, у, г)9 D8.5)
каждое из которых аналогично уравнению Пуассона
для ф (см. D2.4)). С математической точки зрения
уравнения D2.4) и D8.5) тождественны. Следова-
Следовательно, заменив в решении уравнения D2.4) ср на Л*,
а р на jt/cf мы получим решение уравнения D8.5).
Приняв во внимание формулу D2.7), получим
Л* - Т 5 У-r'V (k = *• * Z)> D8'6)
где интегрирование распространяется на всю область,
в которой текут токи, создающие поле.
Три выражения D8.6) можно объединить в одно
векторное:

§ 48. УРАВНЕНИЕ ПУАССОНА 205
Формула D8.7) позволяет по известному распре-
распределению токов в пространстве вычислить векторный
потенциал поля, создаваемого этими токами. В каче-
качестве примера рассмотрим поле прямого тока. Извест-
Известно, что потенциал электрического поля, создаваемого
тонкой бесконечно длинной равномерно заряженной
нитью, имеет вид1) (рассматривается поле вне нити)
Ф (R) = -2Я In {R/Ro) « -2ро In (RjR0)f D8.8)
где R— расстояние от нити, R® — расстояние до то-
точек, потенциал которых принят за нуль (в данном
случае нельзя положить ш — 0 на бесконечности, так
как при такой нормировке потенциал при конечных R
получается бесконечно большим), % — линейная плот-
плотность заряда, которую, предположив, что заряд рас-
распределен равномерно по всему поперечному сечению
нити, можно представить в виде ра {с — площадь по-
поперечного сечения нити).
Теперь допустим, что имеется тонкий беско2*ечно
длинный прямой провод, по которому течет равно-
равномерно распределенный по сечению а ток плотности /.
Направив ось z вдоль провода, будем иметь /* =
= jy = 0, \z = /. Основываясь на идентичности урав-
уравнений D2.4) и D8.5), можно получить выражение для
Аг, заменив в D8.8) р через jz/c = j/c:
^ in(i?/i?) D8.9)
где t = /a —сила тока, текущего по проводу. Подста-
Подстановка в D8.8) jx = 0 и jy = 0 вместо р дает для ком-
компонент Ах и Аи нулевые значения. Следовательно,
вектор А можно записать в виде
где ez — орт оси г.
Взяв ротор от выражения D8.10), найдем В:
D8.10)
D8.10), найдем
B-IVA] f [v. !„-?¦«,]
=-f["
(мы воспользовались формулой (XI. 27)). Поскольку
*) С помощью теоремы Гаусса легко найти, что E(R) =з
= 2Х/#. Следовательно, dyldR =* - 2Я/Л. Интегрирование при*
водит к формуле D8.8).

206 ГЛ. IX. МАГНИТОСТАТИКА
ez = const, второй член равен нулю. Так как
В соответствии с полученным нами результатом
вектор В в каждой точке лежит в плоскости, перпен-
перпендикулярной к проводу, и направлен по касательной
к окружности, охватывающей провод. Модуль В равен
2*
§ 49. Поле соленоида
Вычислим поле бесконечного соленоида, предста-
представив этот соленоид как бесконечный цилиндр радиу-
радиуса а, в поверхностном слое которого толщины Ъ
4F <С а) течет ток плотности / (bj эквивалентно ш\
где i — сила тока в соле-
соленоиде, п — число витков на
единицу длины).
Выберем прямоугольные
координатные оси, совмес-
совместив ось z с геометрической
осью соленоида (рис. 49.1).
Проекции вектора j на ко-
координатные оси равны
-/sin
— /-J-,
Рис. 49.1
а
D9.1)
Из /г = 0 сразу следует, что Лг = 0. В соответ-
соответствии со сказанным в предыдущем параграфе состав-
составляющая Ах совпадает с потенциалом <р, создаваемым
зарядом, который распределен в поверхностном слое
цилиндра с плотностью рх — jx/c — — (j/c) (у/а) =
«ев—ро(у/а). Мы ввели обозначение
Аналогично, составляющая Ау совпадает с потенциа-
потенциалом заряда, распределенного в поверхностном слое
с плотностью ру = ]м/с — ро(#/а).

49. ПОЛЕ СОЛЕНОИДА
207
Плотность, изменяющуюся по закону —у/а, можно
получить следующим образом. Вставим один в другой
два цилиндра, один из которых заряжен равномерно
с объемной плотностью +ро, а другой — с плотностью
—р0. В целом система двух цилиндров будет в каж-
каждой точке нейтральной. Теперь сместим отрицательно
заряженный цилиндр на отрезок 6/2 в направлении
Рис. 49.2
оси у, а положительно заряженный цилиндр на та-
такое же расстояние в противоположную сторону
(рис. 49.2, а). Поскольку На (а радиус цилиндров),
образовавшуюся систему можно рассматривать как
цилиндр, в поверхностном слое которого толщины Ь
распределен заряд с переменной плотностью рх. В дей*
ствительности плотность заряда в поверхностном слое
постоянна и равна ро (или —р0), изменяется же тол-
толщина некомпенсированного слоя. Как видно из
рис. 49.2, а, эта толщина меняется по закону Ь sin а,
так что заряд, приходящийся на единицу поверхности
цилиндра, равен — po6sina = — рфу/а. Однако мы не
сделаем заметной ошибки, если будем считать

208 ГЛ. IX. МАГНИТОСТАТИКА
толщину заряженного слоя всюду одинаковой и рав-
равной 6, а плотность заряда в этом слое изменяющей-
изменяющейся по закону
/ D9.3)
Чтобы получить плотность, изменяющуюся по за-
закону х/а, сдвинем цилиндры, как показано на
рис. 49.2,6. В этом случае плотность заряда в вооб-
воображаемом поверхностном слое толщины b изменяется
по закону
fa D9.4)
В рассматриваемых случаях поля представляют
собой суперпозицию двух одинаковых по величине, но
противоположных по знаку полей +Фо и —<р0, сдви-
сдвинутых друг относительно друга на очень малый отре-
отрезок Ь (в случае рх вектор Ь направлен противопо-
противоположно оси у, в случае ру— по оси х). Пусть первона-
первоначально поля точно накладывались друг на друга,
вследствие чего потенциал в точке, определяемой ра-
радиусом-вектором г, был равен (+фо(г)) + (—фоО*)),
т. е. нулю. Теперь сдвинем поле +фо на Ь/29 а поле
—фо на —Ь/2. Тогда в точке с радиусом-вектором т
будет тот потенциал -j-фо, который был в точке
(г — Ъ/2), и потенциал — фО„ который был в точке
(г + Ь/2). Таким образом9
Ввиду малости b оба члена полученного нами вы-
выражения можно преобразовать по формуле (XI. 5),
т. е. написать
В случае рх вектор b имеет компоненты: &* =
Ъг = 09 by — —by так что
Ф(г) = -^-6 для Ах, D9.5)
в случае рв: Ьи — Ьг = 0, Ьх = Ь, так что
^ Аг D9.6)

§ 49. ПОЛЕ СОЛЕНОИДА 209
Теперь осталось найти <р0 и подставить в D9.5)
и D9.6) его производные. Напомним, что ф0 —это по-
потенциал поля, создаваемого цилиндром радиуса а, за-
заряженным с постоянной объемной плотностью +ро.
Потенциал внутри и вне такого цилиндра опреде-
определяется разными формулами.
Поле внутри соленоида. С помощью теоремы Гаус-
Гаусса легко найти, что поле внутри заряженного ци-
цилиндра равно E = 2npoRt где R— расстояние от оси
цилиндра (/?<а). Этому полю отвечает потенциал
Фо = — npoR2 + const = —про(х2 + у2) + const. Его про-
производные:
Подставим найденные значения производных в
D9.5) и D9.6):
Ф (г) = — 2прфу для АХУ
ф (г) = 2пр0рх для Ау.
Заменив в этих выражениях р0 через ni/bc (см.
D9.2)), получим выражения для Ак и Ау (выше было
установлено, что Аг = 0):
- 2nni 1 / 4пт
лу 1
В § 47 было показано (см. D7.11)), что потенциал
D9.7) определяет однородное магнитное поле с маг-
магнитной индукцией
В^Dя/с)т9 D9.8)
параллельной оси г, т. е. оси соленоида.
Поле вне соленоида. Потенциал вне цилиндра, за-
заряженного с плотностью ро, равен
где i? — расстояние от оси цилиндра (J?>a), Rq —
константа (ср. с D8.8)). Производные ф0 имеют вид

210 ГЛ. IX. МАГНИТОСТАТИКА
Подстановка этих значений в D9.5) и D9.6) дает
<р (г) = — 2р0яа2& ^дг для Ах,
Ф (г) = 2pQna2b -j-E- для Ау,
Заменив р0 через ni/bc, получим Ах и Ау. Напишем
значения всех трех компонент:
л -- 2nnia2 у — К у
л — 2лп1а2 х — к х D9-9)
л|г"" с R2 A R2 •
Лг = 0.
Величина /?2 = х2 + У2 не содержит г. Следова-
Следовательно, дАх/дг = дАу/дг = 0. Из Лг = 0 вытекает, что
дА2/дх = дАг/ду — 0. Таким образом, Вх и В«/ р%авны
нулю. Найдем В2:
R дАу дАх
Итак, мы получили, что поле вне бесконечно длин-
длинного соленоида равно нулю. Векторный же потенциал
вне соленоида отличен от нуля. Совокупность формул
D9.9) может быть представлена в виде одной вектор-
векторной формулы:
A—*g?fc.R]. D9.10)
Сравнение с формулой D8.11) показывает, что поле
вектора А вне соленоида имеет такой же характер,
как поле вектора В вокруг прямого длинного провода
с током.
§ 50. Зако&з Б&ш — Савара
Выражение
позволяет, зная распределение токов в пространстве,
определить векторный потенциал магнитного поля

§ 60. ЗАКОН БИО — САВАРА 211
(см. D8.7)). Попытаемся найти формулу, которая по-
позволяла бы по заданным токам найти сразу В. Для
этого вычислим ротор функции E0.1). Необходимо
иметь в виду, что интегрирование в E0.1) осуществ-
осуществляется по штрихованным координатам х\ у*\ г', диф-
дифференцирование же при взятии ротора производится
по нештрихованным координатам ху у, г. Поэтому
операции интегрирования и взятия ротора можно ме-
менять местами. Приняв это во внимание, получим
В (г)-(у. A(r)]-i-J[v. -ff^h
Рассматривая j(r7)/|r — г'| как произведение век-
векторной функции j(r') и скалярной функции 1/|г—г'|,
воспользуемся формулой (XI. 27):
V. -i^t] - [V fr^FT' J <г'
Второе слагаемое равно нулю, так как j(r') не содер-
содержит нештрихованных координат. Градиент, фигури-
фигурирующий в первом слагаемом, равен
_ 1 Г — Г'
Таким образом, мы приходим к формуле
1 f ЦПг-г^
с 3 | г — г' |з
(мы вынесли скалярный множитель за знак вектор-
векторного произведения и, кроме того, поменяли местами
сомножители, вследствие чего исчез знак минус).
Полученная формула решает поставленную нами
задачу — позволяет по заданным токам вычислить В.
Формула E0.2) упрощается, если токи текут только
по тонким проводам. На рис. 50.1 изображен участок
такого провода. Из рисунка видно, что выражение
\dV можно представить в виде
j dV =~\adl = ja d\ = I rfl, E0.3)
где a — поперечное сечение провода, i — сила тока,
rf! — вектор, совпадающий с элементом провода dl и

212 ГЛ. IX. МАГНИТОСТАТИКА
направленный в ту сторону, куда течет ток. Заменив
в E0.2) ]dV через idlt получим
В^4^А E0.4)
(интегрирование производится по длине всех про-
проводов) .
Рис. 50.1
Формула E0.4) является аналитическим выраже-
выражением закона Био — Савара. Рис. 50.2 поясняет, что
г — г' представляет собой вектор, проведенный из
точки, в которой расположен элемент тока dl, в точку,
для которой вычисляется В.
§ 51. Магнитный момент
Прежде чем обратиться к теме данного параграфа,
получим так называемое уравнение непрерывности, ко-
которое является следствием закона сохранения заряда.
Пусть в некоторой области текут токи, характери-
характеризуемые плотностью j = j(r). Выделим в этой области
воображаемый объем V, ограниченный поверхностью/.
Заряд, вытекающий через эту поверхность наружу
в единицу времени, можно представить в виде
f
Написанное выражение равно скорости убывания за-
заряда, заключенного в объеме V, которая определяется
выражением

§ 61. МАГНИТНЫЙ МОМЕНТ 213
(мы написали частную производную по /, поскольку р
есть функция не только времени, но и координат).
Приравняв оба выражения, получим
Написанное нами соотношение должно выполняться
для любого произвольно выбранного объема. Это воз-
возможно лишь при равенстве подынтегральных выраже-
выражений в каждой точке пространства. Таким образом,
мы приходим к соотношению
VJ—-Й-. E1-1)
которое называется уравнением непрерывности в диф-
дифференциальной форме. В интегральной форме уравне-
уравнение непрерывности имеет вид
[ E1.2)
Теперь рассмотрим систему стационарных токов,
циркулирующих в пределах ограниченного объема V,
и вычислим магнитное поле, создаваемое этой систе-
системой на расстояниях, больших по сравнению с разме-
размерами системы. Эта задача аналогична задаче, рас-
рассмотренной в § 43.
Прежде всего отметим, что в силу стационарности
токов ни в одной из точек системы не может происхо-
происходить накапливания или рассасывания зарядов, т. е.
должно быть всюду dp/df = O. Отсюда согласно
E1.1) вытекает, что в пределах системы
Vj = O. E1.3)
Далее, за пределами системы токов нет. Отсюда
следует, что всюду на поверхности, ограничивающей
систему,
/•-О E1.4)
(токи не пересекают поверхность).
Наконец, докажем, что
dV^Q, EI.5)

214 ГЛ. IX. МАГНИТОСТАТИКА
где интеграл берется по всему объему системы. В силу
стационарности и ограниченности системы все трубки
токов1), которые можно выделить внутри системы,
будут замкнутыми. Значит, весь объем системы можно
разбить на замкнутые трубки токов. Для каждой из
трубок интеграл по ее объему можно преобразовать
следующим образом:
J ldV = \ladl = $ldl = i§dl = O E1.6)
по трубке
(а — поперечное сечение трубки, i— сила тока, d\ —
элемент длины трубки; см. формулу E0.3)). Просум-
Просуммировав выражение E1.6) по всем трубкам тока, по-
получим формулу E1.5).
Выберем начало координат внутри системы и на-
напишем выражение для векторного потенциала:
Здесь г — радиус-вектор точки, для которой вычис-
вычисляется А, г' —радиус-вектор точки, в окрестности ко-
которой расположен элементарный объем dV'\ интегри-
интегрирование производится по штрихованным координатам
в пределах объема системы.
Воспользовавшись тем, что по предположению
г' «С г, разложим выражение EL7) в ряд по степеням
отношения г*/г2). С точностью до членов первого по-
порядка
Первый член этого выражения в силу E1.6) равен
нулю. Следовательно, подставив значение V(l/r), по-
получим
*) Под трубкой электрического тока понимается то же» что
и под трубкой тока в жидкости, т. е. объем, ограниченный ли-
линиями, касательные к которым в каждой точке совпадают с на-
направлением вектора j.
е) Рассматривая —г' как малое приращение радиуса-век-
радиуса-вектора г, мы представляем функцию /(г) = 1/г для значения аргу-
аргумента г «—г' в виде

§ 61. МАГНИТНЫЙ МОМЕНТ 215
Напишем k-ю компоненту потенциала:
\ - -s* J и (о (? ***;) «^ —sr Е ** $ />;^
E1.9)
(мы выразили скалярное произведение rr' через ком-
компоненты радиусов-векторов). Произведения jkx'. суть
компоненты тензора второго ранга *). Представим этот
тензор в виде суммы симметричного и антисимметрич-
антисимметричного тензоров:
. / hxi + hxk , ikxi — Ux% c , а /к 1 1 га
/Л = 2 ' 2 — Skt + Akt E1.10)
(см. (Х.27)).
Докажем, что интеграл от симметричной состав-
составляющей тензора E1.10) равен нулю. Для этого вос-
воспользуемся тождеством
V {x'/^W {х'(х'к) + *XVJ F1-11)
(см. (XI. 26)). В силу E1.3) второй член правой ча-
части есть нуль. Запишем выражение V7 (*!*?)» исполь-
используя формулу для градиента произведения скалярных
функций (см. (XI. 25)):
* L~i m дх &-* дх *-~*
m m m m m
(мы учли, что дх'к]дх'т = bkm). Выражение в скобках
есть m-я компонента градиента функции х[х'к.
Теперь вычислим второй член выражения E1.11):
O = EUv'(*X*)}m=E/
J) Интеграл /fei == \ \hx\ &V также представляет собой ком*
поненту тензора. Следовательно, вектор А с точностью до мно-
множителя \/сг* является произведением тензора hi на вектор Xi
(см. (Х.22».

216 ГЛ. IX. МАГНИТОСТАТИКА
В первой сумме отлично от нуля лишь слагаемое
с /п = 4, а во второй — слагаемое с т = /. Следова-
Следовательно,
Итак, согласно E1.11)
Возьмем интеграл от этого выражения
SkidV'= Tjv (xixiA)dv =Т
(мы применили теорему Остроградского — Гаусса) ¦
В силу E1.4) последний интеграл равен нулю. Таким
образом, мы доказали, что интеграл от симметричной
составляющей подынтегральной функции в E1.9) есть
нуль. С учетом этого обстоятельства выражение E1.9)
можно записать так:
Ak = -r
E112)
Покалсем, что подынтегральная функция равна
Л-й компоненте двойного векторного произведения
1Г [J1*'] 1 • Введя вспомогательное обозначение Ь = [jr']
и использовав формулу (VI. 33), можно написать
2jkili 2-r 1тп?тп= . 2* BkilemnlXiJmXn
if l tnt n t, i, m, n
(напомним, что при циклической перестановке индек-
индексов значение г1тп не изменяется). Произведем сумми-
суммирование по индексу /, причем воспользуемся соотно-
соотношением (VI. 16)
Теперь произведем суммирование по индексам т
и л. В первой сумме отличными от нуля будут ела-

§ 51. МАГНИТНЫЙ МОМЕНТ 217
гаемые с т = & и /г = /, во второй сумме — слагаемые
cn = knm = i. Следовательно,
[г [\г'])к=Е *л*1 - ? *,/,*; = s *< (/>; - />;)•
Сравнение с E1.12) позволяет написать
или, в векторной форме,
±[±\ ] E1.13)
', г]
(мы поменяли местами сомножители в обоих вектор-
векторных произведениях).
Величину
^$ E1.14)
называют магнитным моментом системы1).
Для системы дискретных зарядов выражение маг-
магнитного момента имеет вид
m = ±Zea[r'ava). E1.15)
Это выражение получается из E1.14), если положить
j (г') = р (г') v (г') = Е eav (О б (г' - г'в)
а
(см. D1.12)) и учесть, что \ еа\ (г') б (г' — г^) dV\ взя-
взятый в малой окрестности точки т'а, превращается
в еа\а.
Магнитный момент зависит только от свойств си*
стемы и, как легко убедиться, не зависит от выбора
системы координат. Действительно, сместим начало
f) Мы опустили штрих при dV, так как подынтегральное вы*
ражение не содержит нештрихованных координат. В выраже-
выражениях, содержавших и г', и г, штрих при dV указывал на то,
что интегрирование осуществляется по штрихованным координа-
координатам. В дальнейшем в этом выражении мы будем опускать штрих
в при г.

218 ГЛ. IX. МАГНИТОСТАТИКА
системы координат на отрезок Ь. Тогда радиусы-век-
радиусы-векторы в новой системе будут равны г" = г' — Ь. Маг-
Магнитный момент в новой системе имеет вид
Первый член равен т, второй член можно предста-
представить в виде
Но согласно E1.5) \ \dV равен нулю. Следователь-
Следовательно, мы пришли к равенству моментов т' и т, что и
требовалось доказать.
С учетом E1.14) выражение E1.13) можно запи-
записать следующим образом:
A(r)—l^ [m, vf] E1.16)
(ср. с формулой D3.7)).
Чтобы найти В, нужно вычислить ротор выраже-
выражения E1.16). Положив в формуле (IX.29) а = m, a
b = г/г3, получим
— (~r v) m - (mv)-pr + т (v-Jr) --?(Vm)
Вектор m не зависит от г, поэтому первый и послед-
последний члены равны нулю. Согласно (XI. 26)
Поэтому и третий член равен нулю. Таким образом,

§ 51. МАГНИТНЫЙ МОМЕНТ
В соответствии с формулой (XI. 33)
(mv)тг — г (m ' V-p-) + тг (mV) r =
219
(см. (XI.34), ег — орт вектора г). Следовательно,
Вв8М!^)-тв (Б1Л8)
Сравнение с формулой D3.10) показывает, что
магнитное поле выражается через магнитный момент
такой же формулой, какой электрическое поле выра-
выражается через электрический ди-
польный момент.
В заключение вычислим маг-
магнитный момент тока, текущего по
тонкому проводу, образующему
плоскую петлю. Начало коорди-
координат выберем в плоскости петли
(рис. 51.1). Согласно определе-
определению E1.14)
Й1 =
\dV.
Рис. 51.1
В рассматриваемом случае можно произвести замену:
ldV — id\ (см. формулы E0.3) и E1.6)). Следова-
Следовательно, выражению для m можно придать вид
Обозначив орт нормали к плоскости петли буквой п
(на рис. 51.1 этот орт направлен за чертеж), подынте-
подынтегральное выражение можно записать как nrsirmd/,
так что
¦ sin a dl
Из рис. 51Л видно, что подынтегральное выраже-
выражение равно площади заштрихованного треугольника.
Поэтому интеграл равен площади петли /. Таким

220 ГЛ. IX. МАГНИТОСТАТИКА
образом, мы пришли к выражению для магнитного
момента:
§ 52. Поле в магнетиках
При наличии магнетиков на поле токов проводи-
проводимости В/ накладывается поле, создаваемое молеку-
молекулами, Вмол, так что результирующее микроскопическое
поле можно представить в виде
Вр.з-Ву + В^. E2.1)
Поле Врез, подобно определяемому формулой D4.1)
полю Ерез, является быстропеременной функцией вре-
времени. Кроме того, оно сильно меняется в простран-
пространстве между двумя соседними молекулами. Поэтому
в качестве характеристики магнитного поля в магне-
магнетиках берут макроскопическую величину
В = В/ + <ВМОЛ>, E2.2)
которую называют магнитной индукцией в магнетике.
Усреднение микроскопического поля ВМол произво-
производится таким же способом, как и усреднение поля ЕСВяз
(см. §44).
Состояние магнетика принято характеризовать
магнитным моментом единицы объема магнетика, ко-
который называют намагниченностью. Мы будем обо-
обозначать ее символом М. Очевидно, что М можно опре-
определить как
дц = —_ 9 E2.3)
где dV — физически бесконечно малый объем, не-
немагнитный момент отдельной молекулы; суммирова-
суммирование осуществляется по всем молекулам, заключенным
в объеме dV.
Вклад, вносимый магнетиком в макроскопическое
магнитное поле, можно вычислить по формуле E1.16).
Согласно E2.3) элемент объема магнетика dV' обла-
обладает магнитным моментом dm «NLdV. Следователь-
Следовательно, в точке, определяемой радиусом-вектором г, этот
элемент объема создает магнитный потенциал
rr-/] dV E2.4)

§ 52. ПОЛЕ В МАГНЕТИКАХ 221
(г' — радиус-вектор точки, в которой расположен эле-
элемент объема dV, М(г')—намагниченность в этой
точке).
Интеграл от выражения E2.4), взятый по всему
объему магнетика, даст вклад, вносимый магнетиком
в макроскопический магнитный потенциал. Его нужно
прибавить к магнитному потенциалу, обусловленному
токами проводимости (см. формулу D8.7)). Следова-
Следовательно, поле при наличии магнетика, будет характери-
характеризоваться потенциалом
А (г) - ±- [\ (г'> «У! + \ [М <**>¦ r~A dV ~ /, + /,.
W С J Г — Г | * J Г— Г3 112
E2.5)
Второй интеграл в этом выражении можно преоб-
преобразовать следующим образом:
(штрих при V означает, что при взятии градиента диф-
дифференцирование осуществляется по штрихованным
координатам).
Положив в формуле (Х1.27)ф == 1/|г — г'| и а =
= М(г/), получим, что
откуда
IV', М(г')] Г„, M(r') "I
-f7^71 [V, jf—ttJ
Следовательно, второе слагаемое в формуле E2.5)
можно представить в виде
Преобразуем интеграл 1 по формуле (XI. 60):
Если магнетик занимает конечный объем или М(г')
достаточно быстро убывает при удалении от начала

222 ГЛ. IX. МАГНИТОСТАТИКА
координат, последний интеграл равен нулю (в случае
локализации магнетика в конечном объеме поверх-
поверхность интегрирования можно выбрать вне магнетика
и тогда всюду на поверхности Щг'^О).
Таким образом, при наличии магнетиков вектор-
векторный потенциал определяется выражением
AW —Л + '2 = ТЗ |г-г'Г+
Г
E2.6У
Полученный нами результат можно истолковать
так, что намагниченность вносит в векторный потен-
потенциал такой же вклад, как и ток плотности
Jai = c[VM] E2.7)
(мы опустили штрих при V» соответственно JW рассмат-
рассматривается как функция не г', а г). Отсюда вытекает,
что при наличии магнетиков уравнение D8.3) нужно
писать в виде
f E2.8)
Объединив члены, содержащие ротор, получим
[V, В-4яМ]=™].
Величина
Н = В — 4пШ E2.9)
называется напряженностью магнитного поля. Она
представляет собой вспомогательную макроскопиче-
макроскопическую характеристику магнитного поля, аналогичную
электрической индукции D (см. D5.2)). Для Н имеет
место уравнение
[VH]--f-J. E2.10)
Опыт дает, что для так называемых диа- и пара-
парамагнетиков, намагниченность пропорциональна напря-
напряженности поля:
М = хН. E2.11)
(Предполагается, что магнетик изотропный. Кроме
того, имеются в виду поля, при которых намагничение
далеко от насыщения.)

§ 62. ПОЛЕ В МАГНЕТИКАХ 223
Величина % называется магнитной восприимчи-
восприимчивостью вещества. Для парамагнетиков % положитель-
положительна, для диамагнетиков — отрицательна. Подстановка
выражения E2.11) в формулу E2.9) дает, что
В = Н + 4яхН = [хН, E2.12)
где
E2.13)
есть магнитная проницаемость вещества.
Соотношения E2.11) — E2.13) распространяют и
на ферромагнетики, рассматривая % и [i как функции
напряженности поля Н.
Целесообразность введения Н обусловлена теми же
соображениями, какие были изложены в § 45 для
обоснования целесообразности введения D.
Рассмотрим поле в однородном изотропном магне-
магнетике. Предположим, что в отсутствие магнетика дан-
данные токи проводимости возбуждают поле, характери-
характеризуемое индукцией Во и потенциалом Aq. Известно, что
Во и Ао являются решениями уравнений
^j, E2.14)
*Ч <52Л5>
(см. D8.3) и D8.4)).
Теперь, не изменяя токов проводимости, заполним
все пространство, в котором поле отлично от нуля,
однородным ((л = const) изотропным магнетиком. То-
Тогда индукция поля станет равной В, а потенциал при-
примет значение А. Напишем уравнения для В и А. Со-
Согласно равенству E2.10)
|] ^-|. E2.16)
Заменив в этом уравнении В через [VA] (см. D7.5))
и приняв во внимание, что \i = const, можно написать
Развернем левую часть полученного выражения по
формуле (XI. 45). В результате получим

224 ГЛ. IX. МАГНИТОСТАТИКА
Однако мы условились выбирать А так, чтобы VA
равнялась нулю (см. D7.7)). Следовательно, первый
член в фигурных скобках равен нулю и мы приходим
к уравнению
АТГ-—т-J- E2Л7>
Сравнение E2.16) с E2.14) и E2.17) с E2.15) по-
казывает, что уравнение для B/\i совпадает с уравне-
уравнением для Во, а уравнение для А/ц— с уравнением для
Ао. Отсюда следует, что заполнение пространства, в
котором имеется поле, однородным магнетиком при-
приводит к увеличению как магнитной индукции, так и
магнитного потенциала в ^ раз.
Согласно равенству E2.17) уравнение Пуассона
D8.4) для поля в однородном изотропном магнетике
будет иметь следующий вид:
E2.18)
В случае, когда однородный изотропный магнетик
с (i = const (т. е. с |i, не зависящей от Н) заполняет
все пространство, в котором поле отлично от нуля,
справедливо соотношение
Н—J-IVAI-IVA'], E2.19)
где А/ — A/jjl
Подчеркнем, что напряженность поля И можно
представить в виде ротора функции A/ji только в том
случае, когда магнетик однороден и fi = const. Маг-
Магнитную же индукцию В можно представить в виде
В — [VA] всегда, поскольку при любых условиях
VB=0.
Напомним, что на границе двух магнетиков век-
векторы В и Н должны удовлетворять следующим усло-
условиям:
®ni — Вп2, B%lfiix = ?,2/1*2,
Вывод этих граничных условий можно найти в учеб-
учебниках общей физики.

§ 52. ПОЛЕ В МАГНЕТИКАХ 225
В анизотропных магнетиках связь между М и Н
дается соотношениями
3
Mt = Zt tikHk (i - 1, 2, 3), E2.21)
где %ik — симметричный тензор второго ранга, назы-
называемый тензором магнитной восприимчивости.
Соответственно уравнения, связывающие векторы
В и Н, выглядят следующим образом:
Bt = Ej \iikHk (i = 1, 2, 3), E2.22)
где величины
E2.23)
суть компоненты тензора магнитной проницаемости
(ср. с формулами § 46).
В И. В. Савельев, t. !

Глава X
НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
§ §3. Закон электромагнитной индукции
При изменении потока магнитной индукции через
замкнутый контур Г в этом контуре возникает ЭДС
индукции, равная
^l~ c dt с dt
f
(Ф — магнитный поток, пронизывающий контур).
Если поверхность, по которой берется интеграл, не из-
изменяется со временем, операции дифференцирования
по t и интегрирования по координатам можно поме-
поменять местами. Поэтому выражению для S% можно при-
придать вид
* * " i\ E3.1)
(мы написали частную производную по tt потому что
В, вообще говоря, есть функция и времени, и коор-
координат).
ЭДС по определению есть циркуляция по данному
контуру вектора напряженности поля сторонних сил
Ест- В данном случае напряженностью Ест является
напряженность Е вихревого электрического поля, воз-
возбуждаемого изменяющимся магнитным полем В. Сле-
дoвafeльнo,
Ш% = § Et dl = J [VEJ dt E3.2)
г f
(мы применили теорему Стокса).
Приравняв правые части выражений E3.1) и
E3.2), придем к соотношению
JJ-Л. E3.3)

§ 54. ТОК СМЕЩЕНИЯ 227
Допустим, что оба интеграла берутся по одной
и той же поверхности (равенство E3.3) выполняется
и для разных поверхностей, лишь бы эти поверхности
опирались на один и тот же контур Г). Соотношение
E3.3) должно выполняться для любой поверхности f.
Это возможно лишь в том случае, если подынтеграль-
подынтегральные функции имеют одинаковое значение в каждой
точке пространства. Таким образом, мы приходим
к уравнению
™ —TTF- <534>
В полученное нами уравнение не входят пара-
параметры контура, с рассмотрения которого мы начали
этот параграф. Естественно предположить, что это
уравнение должно выполняться для любой точки поля,
независимо от присутствия в этом поле физически вы-
выделенного (в частности, проводящего) контура. Как
известно, это предположение оправдывается на опыте.
Из уравнения E3.4) следует, что изменяющееся во
времени магнитное поле В должно порождать элек-
электрическое поле Е. Действительно, для того чтобы [VEJ
был отличен от куля, необходимо наличие неоднород-
неоднородного (т. е. меняющегося от точки к точке) поля Е.
§ 54. Ток смещения
Анализируя уравнения, описывающие электромаг-
электромагнитные явления, Максвелл обратил внимание на то,
что в нестационарном случае уравнение
[VH] = ^-j E4.1)
(см. E2.10)) несовместимо при др/д(фО с уравне-
уравнением непрерывности
Vj = --|r E4.2)
(см. E1.1)). Чтобы убедиться в этом, возьмем дивер-
дивергенцию от обеих частей уравнения E4Л). Поскольку
дивергенция ротора всегда равна нулю (см. (XI. 44)),
мы придем к выводу, что дивергенция j, а следова-
следовательно, и dp/dt не могут быть отличными от нуля. Од-
Однако заключение о том, что dp/dt всегда равно нулю,

228 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
не согласуется с опытом: при нестационарных процес-
процессах плотность зарядов сплошь и рядом изменяется
с течением времени.
Уравнения E4.1) и E4.2) можно согласовать, до-
добавив в E4Л) к j некоторую величину (обозначим ее
}смещ), имеющую размерность плотности тока. Эту ве-
величину нужно определить так, чтобы всегда соблюда-
соблюдалось условие
Из него с учетом E4.2) следует, что слагаемое jCMem
должно удовлетворять соотношению
VW--VJ—|г E43>
Продифференцировав по времени уравнение D5.3),
получим уравнение
или, переставив порядок дифференцирования D по
времени и координатам,
»№)-*•*•
Подставив получающееся из этого соотношения выра-
выражение для dp/dt в формулу E4.3), придем к равен-
равенству
Из этого равенства следует, что в качестве ]СМещ долж-
должно быть взято выражение
1смещ = 1^"^Г E4.4)
(в общем случае нужно добавить к правой части про-
произвольную функцию времени f(t), но мы положим ее
равной нулю).
Таким образом, Максвелл пришел к выводу, что
в случае нестационарного поля уравнение E4.1) сле-
следует писать в виде

§ 55. УРАВНЕНИЯ МАКСВЕЛЛА 229
ИЛИ
№4—Т-1+71Г
—Т-1+71Г- <545>
Величину |Смещ Максвелл назвал током смещения,
а Сумму | + jciaeiu — ПОЛНЫМ ТОКОМ.
Из уравнения E4,5) следует, что магнитное поле
может порождаться не только токами проводимости,
но также и меняющимся со временем электрическим
полем. Таким образом, введение тока смещения сде-
сделало поля Е и В равноправными в отношении способ-
способности порождать друг друга.
§ 55. Уравнения Максвелла
Совокупность уравнений D5.3), D7.4), E3.4) и
E4.5) образует систему уравнений Максвелла. Эти
уравнения принято группировать попарно, причем
уравнения
4
VB = 0 E5.2)
называют первой парой уравнений Максвелла, а урав-
уравнения
IVHl-^-J + i-f- E5.3)
И
VD = 4яр E5.4)
носят название второй пары уравнений. Заметим, что
в первую пару уравнений входят только основные ха-
характеристики поля: Е и В. Во второй же паре фигу-
фигурируют вспомогательные величины ОиН.
Уравнения Максвелла составляют основу всей
электродинамики. Они играют в классической элек-
электродинамике такую же роль, какую в классической
механике играют законы Ньютона.
Система уравнений Максвелла включает в себя
8 скалярных уравнений (каждое из векторных уравне-
уравнений E5.1) и E5.3) эквивалентно 3 скалярным), в ко-
которых содержится 12 неизвестных скалярных функций
(компонент векторов Б, В, D и Н). Поэтому сами по
себе уравнения E5.1) —E5.4) недостаточны для

230 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
определения электромагнитных полей в веществе.
В этом смысле система уравнений Максвелла являет-
является неполной- Для того чтобы можно было произвести
вычисление полей, уравнения Максвелла нужно до-
дополнить уравнениями, связывающими друг с другом
величины D, j и Е, а также И и В. Эти уравнения 1)\
имеют вид (см. D5.5) и E2Л2))
D = eE, E5.5)
В = ^Н, E5.6)
j = оЕ E5.7)
(а — электропроводность среды). Для решения задачи
должны быть известны характеристики среды: е, ц и сг,
которые в простейшем случае являются константами.
Отметим, что уравнения Максвелла можно напи-
написать так, чтобы в них не входили вспомогательные
величины D и Н. Для этого нужно во второй паре
уравнений заменить эти величины их значениями
D5.2) и E2.9). Предоставляем читателю убедиться
в том, что после такой замены уравнения Максвелла
приобретают вид
[VE]-—1-|5-, VB-0; E5.8)
E5.9)
Для того чтобы решить систему уравнений E5.8),
E5.9), нужно знать вид функций Р —Р(Е), М =
М(В) j j(E)
() j j()
В дальнейшем нам придется рассматривать элек-
электромагнитные поля в однородных и изотропных сре-
средах, проницаемости которых е и ц постоянны. В этом
случае проницаемости можно выносить из-под знаков
производных либо, наоборот, вносить их под знак про-
производных. Поэтому уравнениям E5.1) — E5.4) можно
придать вид
J|t, VB-0; E5.10)
ijLj + i.*. VE = i2Lp. E5.11)
*) Их называют иногда уравнениями состояния.

§ 66. ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 231
В отсутствие поляриззлощихся и намагничиваю-
намагничивающихся сред е и |i равны единице, так что уравнения
Максвелла для поля в вакууме выглядят следующим
образом:
^ E5.12)
f § E5.13)
Поскольку в гауссовой системе для поля в вакууме Н
совпадает с В, в уравнениях E5.12) и E5.13) можно
в этом случае писать Н вместо В.
§ 58. Потенциалы электромагнитного поля
В § 47, воспользовавшись тем, что VB=0, мы
представили магнитную индукцию в виде
B = [VA], E6.1)
где А — вспомогательная функция, называемая век-
торным потенциалом. Выражение E6.1) остается в
силе и для нестационарного поля. Однако в этом слу-
случае А следует считать функцией не только координат,
но и времени: А== А (г, г).
Подставим E6Л) в уравнение E5.1). В результате
получим
Это соотношение можно записать так:
Поскольку ротор вектора E + (l/c)dk/dt оказы-
оказывается равным нулю, этот вектор можно представить
в виде градиента некоторой функции <р:
E + ~4^ = -V<p. E6.2)
Функция ф называется скалярным потенциалом элек-
электромагнитного поля. В нестационарном случае она
зависит от г и от /. Из E6.2) следует, что потенциалы
Ф и А имеют одинаковую размерность.

232 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
Согласно E6.2)
E = -Vq> — 4r. E6.3)
С 01
Таким образом, напряженность электрического поля
в общем случае определяется не только скалярным
потенциалом <р, но и векторным потенциалом А. Вто-
Второе слагаемое в E6.3), очевидно, обусловлено явле-
явлением электромагнитной^вюндукции. В случае стацио-
стационарного поля dA/dt = O и формула E6.3) переходит
в D1.5).
Соотношения E6.1) и E6.3) выражают магнитное
и электрическое поля через векторный и скалярный
потенциалы.
Найдем уравнения, с помощью которых можно вы-
вычислить потенциалы А и <р для поля в однородной и
изотропной среде с постоянными г и \i. С этой целью
заменим в уравнениях E5.11) Е выражением E6.3),
а В ротором А:
Приняв во внимание, что [V[VA]]== V(VA) — ДА
(см. (XI.45)), a V(V<p) = A<p, запишем полученные
нами уравнения в следующем виде:
^) E6.4)
A<p==_J|iL_l_|.(VA) E6.5)
(в некоторых членах уравнений мы поменяли поря-
порядок дифференцирования по координатам и времени).
Уравнения E6.4) и E6.5) и суть искомые уравне-
уравнения для нахождения А и <р. Эти уравнения довольно
сложны. Особенно неприятно то, что они взаимосвя-
взаимосвязаны— в каждое из них входит и А, и <р. Однако, как
мы увидим ниже, потенциалы можно выбрать так,
чтобы эти уравнения сильно упростились.
Потенциалы А и q> определяются неоднозначно.
Поэтому имеется некоторая свобода в их выборе.
В частности, например, к А можно прибавить произ-
произвольный постоянный вектор, а к ср — произвольную

§ 56. ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 233
постоянную без того, чтобы изменились значения
В и Е. Разумеется, выбор потенциалов следует осу-
осуществлять наиболее удобным для данного случая об-
образом. Такой наиболее целесообразный подбор потен-
потенциалов называется их калибровкой. Заметим, что мы
уже пользовались возможностью калибровки потен-
потенциалов в магнитостатике: в § 47 мы выбирали А так,
чтобы его дивергенция была равна нулю (см. фор-
формулу D7.7)).
Определим самый общий вид калибровочных пре-
преобразований, т. е. таких преобразований потенциалов
А и ф, при которых поля Е и В остаются неизмен-
неизменными. Поле В —fVA) не изменится, если к А доба-
добавить градиент произвольной скалярной функции f
(ротор градиента равен нулю), т. е. перейти от А к А',
равному А + Vf:
A-*A' = A + V/. E6.6)
Для того чтобы при этом не изменилось электрическое
поле Е ==—Уф — (l/c)dA/dt9 одновременно с перехо-
переходом E6.6) нужно совершить переход
Ф-ф'=Ф-|-§Г. E6.7)
где / — та же функция, что и в E6.6). Действительно,
поле Е', определяемое потенциалами А' и ф', будет
в этом случае равно
В'— V-MSr-
(напомним, что V(df/dt) = d(Vf)/dt)). Таким обра-
образом, преобразование потенциалов по формулам E6.6)
и E6.7) не изменяет значений В и Е.
Преобразования E6.6) и E6.7) представляют со-
собой калибровочные преобразования наиболее общего
вида. Поскольку при осуществлении этих преобразо-
преобразований поля В и Е остаются неизменными, все уравне-
уравнения, описывающие эти поля, должны быть инвариант-
инвариантными по отношению к калибровочным преобразова-
преобразованиям. Эта инвариантность называется калибровочной
(или градиентной) инвариантностью.

234 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
На практике, как уже отмечалось, применяется ка-
калибровка, наиболее целесообразная в каждом кон-
конкретном случае. В частности, можно выбрать потен-
потенциалы так, чтобы выполнялось условие
VA + iu-J-O. E6.8)
называемое условием Лоренца.
Для поля в вакууме условие Лоренца имеет вид
VA + 4-^ = 0. E6.9)
Покажем, что условие E6.8) может быть удовлет-
удовлетворено надлежащим выбором функции f в формулах
E6.6) н E6.7). Для этого подставим в уравнение
E6.8) значения А' и <р', определяемые этими форму-
формулами:
r(V(V/) = A/). Отсюда получается уравнение для на-
нахождения функции f:
&f-3r$—F(r9t)t E6.10)
где F(r, 0 = —VA — (z\i/c)d^)/dt есть заданная функ-
функция ги/. Подставив функцию f, получающуюся из ре-
решения этого уравнения, в формулы E6.6) и E6.7),
мы найдем значения потенциалов А' и <р', удовлетво-
удовлетворяющие условию E6.8).
Калибровка потенциалов, удовлетворяющая усло-
условию E6.8), называется лоренцевой калибровкой.
Этот вид калибровки является наиболее употреби-
употребительным.
Условие Лоренца сильно ограничивает набор зна-
значений потенциалов, пригодных для описания данного
поля, но все же не делает выбор потенциалов вполне
однозначным. Действительно, не нарушая условия
E6.8), можно осуществлять преобразования
E6.11)

§ 56. ПОТЕНЦИАЛЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 235
(оба набора потенциалов — А, <р и А', ф'— предпола-
предполагаются удовлетворяющими условию Лоренца), где
функция ф является решением уравнения
A*-?M?-«0. E6.12)
Действительно, подставив в левую часть E6.8) вме-
вместо А и ф штрихованные потенциалы из E6.11), по-
получим выражение
V*+ *¦ + ¦? &-ЗМй*~
которое в силу E6.8) и EG.12) равно нулю. Таким
образом, если потенциалы А и <р принадлежат к ло-
ренцевой калибровке, то и определяемые преобразо-
преобразованиями E6.11) (с tf\ подчиняющейся E6.12)) потен-
потенциалы А' и ф' принадлежат к той же калибровке. Это
обстоятельство позволяет наложить на потенциалы,
кроме условия E6.8), еще одно дополнительное усло-
условие. Например, можно потребовать, чтобы потен-
потенциал ф был равен нулю. Для этого согласно второму
из уравнений E6.11) достаточно выбрать функцию ф
так, чтобы ее производная по времени была равна сф.
В качестве дополнительного условия может быть
также принято требование
VA = 0. E6.13)
Из E6.11) следует, что VA' = VA + Аф- Поэтому для
того чтобы выполнялось требование VA' —0, необхо-
необходимо соблюдение равенства
Вместе с тем из E6.12)
Поэтому, если взять в качестве ф решение уравнения
и подставить это решение в E6.11), мы получим зна-
значения А' и ф', удовлетворяющие и условию Лоренца,
и требованию E6.13).

236 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
Лоренцева калибровка, удовлетворяющая дополни-
дополнительному условию E6.13), называется кулоновской
(или поперечной) калибровкой. В гл. IX мы пользо-
пользовались именно этой калибровкой (см. D7.7)). Из
E6.5) следует, что при кулоновской калибровке ска-
скалярный потенциал удовлетворяет уравнению Пуас-
Пуассона
(см. уравнение D5.13)), т. е. является кулоновским
потенциалом. Отсюда и происходит название «куло-
новская калибровка».
§ 57. Уравнение Даламбера
При соблюдении условия E6.8) последний член
в уравнении E6.4) обращается в нуль. Кроме того,
производная по времени от VA имеет значение
— (гуь/^дРу/дР. Следовательно, уравнения E6.4) и
E6.5) приобретают вид
АА-7Г-5^ = -], E7.1)
Дф---^-^г = Г- <57-2)
Таким образом, вместо двух взаимосвязанных
уравнений мы получили два раздельных уравнения,
причем уравнения для А и <р приобрели сходную
форму.
Дифференциальное уравнение вида
называется уравнением Даламбера (ср. с E6.10)).
Его можно записать в очень компактной форме, если
ввести так называемый оператор Даламбера:
-. А ец д2 д* , а2 . д2 ец д2
Тогда уравнение E7.3) выглядит следующим образом:
? f = F(r, 0. E7.5)
В стационарном случае производные по времени
обращаются в нуль и уравнение Даламбера перехо-

§ 58. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 237
дит в уравнение Пуассона (см. уравнения D5.13) я
E2.18)).
С использованием символа E7.4) уравнения E7.1)
и E7.2) приобретают вид
С
m m 4яР
С математической точки зрения уравнения E7.6}
и E7.7) проще, чем уравнения Максвелла. Поэтому
легче бывает вычислить потенциалы А и ф, чем непо-
непосредственно поля В и Е. Если же потенциалы извест-
известны, нахождение полей по формулам E6.1) и E6.3)
не составляет большого труда. Это обстоятельство
служит оправданием введения вспомогательных вели-
величин Аи ф. Кроме того, как мы увидим в следующей
главе, введение потенциалов позволяет придать урав-
уравнениям электродинамики очень компактную и изящ-
изящную форму.
§ 58. Плотность и поток энергии
электромагнитного поля
Из опыта следует, что электромагнитное поле об-
обладает энергией, которая распределяется в простран-
пространстве с некоторой плотностью w и может перетекать
из одного места в другое. Кроме того, эта энергия мо-
может превращаться в другие виды энергии, например»
затрачиваться на совершение работы над частицами
вещества.
Выделим в веществе, в котором имеется макроско-
макроскопическое электромагнитное поле, объем V, ограничен-
ограниченный поверхностью /. В этом объеме сосредоточена
энергия поля, равная
^ E8.1)
v
Энергия может вытекать наружу из объема V че-
через ограничивающую его поверхность f. Если ввести
вектор плотности потока энергии S, то поток энергии*
вытекающий наружу через f, можно представить

g$g ГЛ. X НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
следующим образом:
E8.2)
(мы воспользовались теоремой Остроградского —Га-
—Гаусса) .
Найдем работу, совершаемую в единицу времени
силами поля над частицами вещества. Над частицей,
имеющей заряд еа и движущейся со скоростью va,
силы поля совершают в единицу времени работу:
Na - еа { Е + \ [vflB]} ve- eavaE
(смешанное произведение vflfveB] равно нулю). Про-
Просуммировав это выражение по всем частицам, заклю-
заключенным в единице объема, получим плотность мощно-
мощности, развиваемой силами электромагнитного поля при
совершении работы над частицами вещества. Обозна-
Обозначив плотность мощности буквой N, можно написать
ЛГ—Еа^еЕ eava.
Взятая по единице объема сумма J1 еа^а есть
плотность электрического тока j (если все частицы
одинаковы, движутся с одинаковой скоростью и число
их в единице объема равно п, то ^ eava превраща-
превращается в известное выражение: j = ?ot). Таким образом,
tf = Ej. E8.3)
Заключенная в объеме V энергия W может умень-
уменьшаться за счет вытекания энергии наружу через по-
поверхность f и за счет совершения работы над части-
частицами вещества. Следовательно, должно выполняться
соотношение
(напомним, что iV есть плотность мощности, т. е. мощ-
мощность, развиваемая в единице объема). Подставив вы-
выражения E8.1) — E8.3) для W, Ф и N, получим
J jj \
V V
JL J w dV = - jj VS dV - \ Ej dV.

§ 58. ЭНЕРГИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 299
Поменяем местами в первом интеграле дифферен-
дифференцирование по времени и интегрирование по координа-
координатам, а также объединим все три интеграла в один.
В результате получим
) = O E8.4)
(мы применили символ частной производной, потому
что w в общем случае является функцией не только
времени, но и координат).
Условие E8.4) должно выполняться для любого
произвольно выбранного объема V. Отсюда заклю-
заключаем, что подынтегральная функция должна быть
равна нулю в каждой точке. Следовательно, мы при-
приходим к дифференциальному уравнению, которое
можно написать в виде
Ej = --^--vs. <58-5>
Плотность энергии w и плотность потока энергии S
являются функциями величин, характеризующих поле.
Чтобы найти вид этих функций, попытаемся преобра-
преобразовать выражение Ej так, чтобы оно стало суммой
двух слагаемых, одно из которых было бы производ-
производной по времени от некоторой скалярной величины, ко-
которую мы сможем отождествить с w, а второе — ди-
дивергенцией от некоторой векторной величины, кото-
которую мы отождествим с S.
Воспользовавшись уравнением Максвелла E5.3),
выразим j через характеристики поля Н и D:
Теперь умножим скалярно это выражение на Е:
^^E^-. E8.6)
Согласно формуле (XI. 28) V[EH] = H[VE] —
— E[VHJ, откуда E[VH]=H[VE1—V[EH]. Подста-
Подставив это значение в E8.6), получим
-^E-f}. E8.6')
Воспользовавшись уравнением Максвелла E5.1), за-
заменим [VEJ на —(l/c)db/dt. В результате выражение

240 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
в фигурных скобках примет вид
Наконец, используем соотношения E5.5) и E5.6):
E
dt + c dt
8я
(мы предположили, что в и \х не зависят от времени).
Итак, формулу E8.7) можно записать следующим
образом:
vl
Сопоставление полученного соотношения с формулой
E8.5) дает для до и S выражения
«_???. E8.8)
S = ^[EH]. E8.9)
Определяемый формулой E8.9) вектор S назы-
называется вектором Пойнтинга.
Отметим,, что выражение E8.8) включает в себя
как собственно энергию поля, равную
так и энергию, затраченную на поляризацию и на-
намагничивание среды.
§ 59. Импульс электромагнитного поля
Из существования давления света вытекает, что
электромагнитное поле обладает не только энергией,
но и импульсом. Импульс, как и энергия, может «пе-
«перетекать» из одного места в другое. Этот процесс
можно охарактеризовать, введя понятия потока и
плотности потока импульса.
Поток импульса, в отличие от потока энергии, яв-
является не скаляром, а вектором. Следовательно, плот-
плотность потока импульса должна быть величиной та-
такой природы, чтобы при умножении на вектор dt

§ 59. ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 241
(df — элемент поверхности) давать вектор. В прило-
приложении X показано, что скалярное произведение тен-
тензора второго ранга на вектор представляет собой
вектор. Отсюда заключаем, что плотность потока им-
импульса есть тензор. Обозначим компоненты этого тен-
тензора символом Oik- Тогда поток i-й компоненты импуль-
импульса через площадку df будет определяться выражением
а поток вектора импульса — формулой
Z е* ? <*ik dfk.
В системе, состоящей из свободных заряженных
частиц и электромагнитного поля, должен сохраняться
суммарный импульс, слагающийся из импульса час-
частиц и импульса поля. Следовательно, обозначив сум-
суммарный импульс частиц символом Р, а плотность им-
импульса (т. е. импульс единицы объема) электромаг-
электромагнитного поля символом g, можно написать
Левая часть дает скорость возрастания суммарного
импульса, содержащегося в объеме У, правая часть —
поток импульса поля, втекающий в объем V через
ограничивающую его поверхность /. Предполагаем, что
частицы не пересекают эту поверхность, так что пере-
переноса через нее импульса частицами не происходит.
Представим написанное нами соотношение в сле-
следующем виде:
j4 ZfS E9.1)
Скорость изменения импульса частицы определя-
определяется силой, действующей на частицу:
Просуммировав это выражение по частицам, заклю-
заключенным в единице объема, получим, что

242 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
где ро — плотность импульса частиц. Наконец, проин-
проинтегрировав это соотношение по всему объему системы,
найдем скорость изменения суммарного импульса
частиц:
4 Р - \ рЕ dV + \ \ ЦВ] dV. E9.2)
v v
Исключим из этого выражения р и j с помощью
уравнений Максвелла. Среду, в которой находятся
частицы и поле, будем предполагать однородной и изо-
изотропной с постоянными г и fuu Из уравнений E5.11)
следует, что
Подстановка этих значений в E9.2) дает
BrBR <593>
Преобразуем полученную формулу, воспользовав-
воспользовавшись соотношением
откуда
Заменим здесь dB/dt через —c[VEJ согласно первому
из уравнений E5.10). В итоге получим
Подставив полученное значение в E9.3), придем
к соотношению
Произведем во втором и третьем интегралах замену:
В = |дН, кроме того, во втором интеграле поменяем

§ 59. ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 243
местами сомножители (при этом знак изменится на
обратный):
jL
dt
Р в -5Г \ EvE dV ~ -te \
Чтобы сделать это выражение симметричным по
Е и Н, добавим к его правой части слагаемое
(ц/4я) \ HvHrfl/. От этого выражение не изменится,
так как это слагаемое равно нулю (p,VH = V(mH) =
= VB всюду есть нуль). Наконец, сгруппировав над-
надлежащим образом члены, получим
+ -~ \ {еЕуЕ + HHVH - в [Е [VE]] - ц [Н [VH]]} dV.
E9.4)
Второй интеграл, как мы убедимся ниже, можно
преобразовать в интеграл по поверхности f, ограничи-
ограничивающей объем V. Таким образом,
1
+ интеграл по поверхности f. E9.5)
Из сравнения найденного соотношения с E9.1)
следует вывод, что плотность импульса электромаг-
электромагнитного поля определяется выражением
? E9.6)
Приняв во внимание E8.9), можно написать, что
g—?-St E9.7)
где S — вектор Пойнтинга. В вакууме это соотноше-
соотношение имеет вид
g = 4s. E9.8)

244 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
Отметим, что выражение E9.7) кроме собственно
импульса поля включает в себя импульс связанных
зарядов, входящих в состав среды, в которой создано
поле. Чтобы получить импульс одного только поля,
следует в формуле E9.1) под Р подразумевать меха-
механический импульс не только свободных, но также и
связанных зарядов. Тогда в качестве Е и В нужно
было бы взять не усредненное макроскопическое поле,
а микроскопическое поле и соответственно пользо-
пользоваться при преобразованиях уравнениями Максвелла
для поля в вакууме1). Это равнозначно тому, чтобы
положить во всех формулах данного параграфа е ==
= [л—1. В результате мы пришли бы к формуле
E9.8). Таким образом, плотность импульса одного
только поля во всех случаях (и в вакууме, и в веще-
веществе) определяется формулой E9.8). Сопоставление
этой формулы с формулой D0.36) показывает, что
между плотностями потоков энергии и импульса элек-
электромагнитного поля существует точно такая же связь,
какая была получена в § 40 для произвольной си-
системы.
Теперь рассмотрим второй интеграл в формуле
E9.4), т. е. интеграл
4~- J {eEVE + JiHvH - e[E[VE]] - »[H[VH]]}dV. E9.9)
Попытаемся преобразовать его в поверхностный ин-
интеграл.
Подынтегральная функция содержит два анало-
аналогичных выражения вида
ava — [a[va]].
В одном из них вместо а стоит Е, в другом — Н.
Положив в формуле
V (ab) = [a [Vb]] + [b [Va]] + (aV) b -f (bv) a
(cm. (XI. 37)) b = а, получим
Va2 = 2 [a [Va]] + 2 (aV) a. E9.10)
Найдем значение выражения (Va)b, в котором
предполагается, что V действует на оба стоящие после
') Мы не сделали этого с самого начала, чтобы получить
более общее выражение для максвелловского тензора натяжений
(см. ниже)» пригодное также и для поля в среде.

§ 59. ИМПУЛЬС ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 245
него сомножителя. По общему правилу вычисления
таких выражений имеем
(Va) b — (Vfla) b + (V*a) b = bVa + (aV) b
или, положив b = a,
(Va) a = ava + (aV) a.
Выразив из последнего соотношения (aV)a, подста-
подставим его в формулу E9.10):
Va2 = 2 [a [Va]] + 2 (Va) a — 2aVa.
Отсюда
ava — [a [va]] = (Va) a — у Va*-
Применив такое преобразование к интегралу
E9.9), приведем его к виду
В написанном нами интеграле оператор V действует
на все стоящие за ним функции. Поэтому мы можем
с помощью преобразования
(см. (XI. 65)) превратить этот интеграл в поверх-
поверхностный
-^ ф { еЕ (Е di) + jxH (H di) - у (ef2 + ц#2) dt}
E9.11)
(поскольку di не обладает свойствами дифференци-
дифференциального оператора, сомножители в выражениях вида
(diа)а можно менять местами).
Раскроем выражение E9.11) через компоненты
входящих в него векторов. В результате получим
Представим в последнем члене dfi как X 6^ dfk и вы-
вынесем dfk за скобки. Кроме того, заменим выражения

246 ГЛ. X. НЕСТАЦИОНАРНОЕ ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ
вида zEi через Д, а вида \iHi через В*. В итоге придем
к выражению
~к ? е< § Z { ?^ + Я<В* ~ у (ED + НВ) 6ik
которое совпадет с последним членом формулы E9.1),
если положить
aih = ~ { EtDk + HtBk ~ 1 (ED + НВ) 6ik }. E9.12)
Как было выяснено в начале этого параграфа, тен-
тензор dk характеризует плотность потока импульса (см.
также § 40). Тензор а/*, компоненты которого опреде-
определяются формулой E9.12), называют максвелловским
тензором натяжений (или напряжений).
Чтобы подчеркнуть симметричность тензора с,*,
его компоненты пишут иногда в виде
<sik = JL {EtDk + EkDt + HtBk + HkBt ~(ED+ НВ)в«}.
Для поля в вакууме формула E9.12) упрощается
следующим образом:
^ } E9.13)
Тензор dk позволяет свести задачу о нахождении
силы, действующей в электромагнитном поле на неко-
некоторый объем вещества, к вычислению поверхностного
интеграла

Глава XI
УРАВНЕНИЯ ЭЛЕКТРОДИНАМИКИ
В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
§ 60. Четырехмерный потенциал !)
Согласно принципу относительности уравнения
электродинамики, равно как и все другие уравнения,
выражающие законы природы, должны быть реляти-
релятивистски-инвариантными, т. е. сохранять свою форму
при преобразованиях Лоренца (при переходе от од-
одной инерциальной системы отсчета к другой). Путем
непосредственной проверки можно убедиться в том,
что уравнения Максвелла удовлетворяют этому требо-
требованию. Однако мы выберем другой путь — покажем,
что уравнения электродинамики могут быть написаны
в четырехмерной форме, в виде соотношений между
4-векторами и 4-тензорами, откуда и будет следовать
их релятивистская инвариантность.
Отправным пунктом для нас послужит принимае-
принимаемое в электродинамике (в соответствии с опытом) по-
положение о том, что электрический заряд представляет
собой инвариант, т. е. что величина заряда частицы
одинакова во всех инерциальных системах отсчета.
Отсюда следует, что величина pdV также будет инва-
инвариантом:
р dV = p dx{ dx2 dx* = inv. F0.1)
Трехмерный объем dV не является, как мы знаем,
инвариантом (см. формулу C5.17)). Следовательно,
из F0.1) заключаем, что плотность заряда р также
не является инвариантной, а преобразуется при пере-
переходе от одной системы отсчета к другой по какому-то
*) В этой главе рассматриваются поля в вакууме, т. е. пред-
предполагается, что е «в 1, [I = 1.
Советуем перед тем, как приступить к чтению этой главы,
просмотреть Приложение XII и гл. VII.

248 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
закону. Чтобы установить этот закон, примем во вни-
внимание, что четырехмерный объем есть инвариант
dV* = dx° dxx dx2 dxb = cdtdV = inv, F0.2)
Действительно, при переходе к другой системе от-
отсчета dt и dV преобразуются по формулам
V1 —• v /с
так что dfdV' = dtdV.
Из сопоставления F0.1) с F0.2) следует, что р
преобразуется по такому же закону, что и dx°, т. е.
как временная компонента некоторого 4-вектора.
В Приложении XII показано, что контравариант-
ные компоненты 4-оператора Гамильтона равны
(см. формулу (XII. 45)).
Согласно (XII. 38) символический квадрат век-
вектора V* равен
V2 = i^-V2 = 7^-A, <60-3>
где Д — трехмерный оператор Лапласа.
Сравнение F0.3) с E7.4) показывает, что опера-
оператор Даламбера для поля в вакууме (е = 1, |л=1)
2
отличается от V*2 только знаком:
F0.4)
Из всего сказанного вытекает, что уравнение
E7.7) можно записать в виде
7*2<р = 4яр. F0.5)
Выше мы выяснили, что р обладает свойствами вре-
временной компоненты 4-вектора, V*2, как и квадрат
любого 4-вектора, ведет себя при преобразованиях
Лоренца как инвариант. С учетом этого на основании
F0.5) заключаем, что потенциал <р должен преобра-
преобразовываться по такому же закону, как р, т. е. как вре-
временная компонента 4-вектора.

§ 60. ЧЕТЫРЕХМЕРНЫЙ ПОТЕНЦИАЛ 240
Рассмотрим вектор плотности тока j = pv. Его
компоненты равны:
/* - РЧ - р -?? (к = 1, 2, 3). F0.6)
При преобразованиях р ведет себя подобно ct либо
cdt. Следовательно, /* будут вести себя подобно dxk
(k = 1,2,3), т. е. как пространственные компоненты
4- вектора.
Итак, при преобразованиях координат р ведет себя
как временная компонента 4-вектора, а величины
jk — как пространственные компоненты 4-вектора. По-
Поэтому, умножив р на скаляр с (чтобы получить вели-
величину такой же размерности, какую имеют /*), можно
объединить р и j в один 4-вектор, называемый 4-век-
тором заряда — тока или просто 4-вектором тока. Его
компоненты имеют значения:
что можно записать кратко следующим образом:
1» = (с9> j). F0.7)
Заметим, что компоненту j° = ср можно предста-
представить подобно компонентам F0.6) как
(x° — ct). Поэтому компоненты 4-вектора тока можно
определить следующим образом:
^Г ^ = 0> !'2, 3). F0.8)
Вытекающее из сохранения заряда уравнение не-
непрерывности имеет вид (см. E1.1))
С учетом F0.7) это уравнение можно записать в че-
четырехмерной форме:
Левая часть последнего соотношения представляет
собой четырехмерную дивергенцию 4-вектора тока.

250 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
Действительно, по аналогии с трехмерной диверген-
дивергенцией 4-днвергенцию вектора а* нужно определить как
скалярное произведение векторов V* и а*\ т. е. как
(см. выражение (XII. 42) &ля ковариантных компо-
компонент вектора V*).
Равенство нулю 4-дивергенции вектора /м- является
аналитическим выражением закона сохранения заря-
заряда. То обстоятельство, что введенный нами вектор
F0.7) удовлетворяет столь простому условию, яв-
является еще одним доводом в пользу объединения р
и j в один 4-вектор.
Учтя, что ? = — V*2, напишем уравнения E7.6)
и E7.7) следующим образом:
У2А = ^Ч, F0.10)
У'2ф = ^(ср). F0.11)
Из уравнения F0.10) вытекает, что величины Л& ве-
ведут себя так же, как величины /*., т. е. подобно про-
пространственным компонентам 4-вектора. Это обстоя-
обстоятельство дает возможность объединить <р и А в один
4-вектор:
Л* = (ф. A), F0.12)
называемый 4-потенциалом электромагнитного поля.
Тогда уравнения F0.10) и F0.11) можно представить
в виде одного уравнения
v*V==±Lf F0.i3)
либо
-i^f (й = о, I, 2, 3). F0.14)
Ковариантные компоненты 4-потенциала выглядят
следующим образом:
Лй = (ф. -А). F0.15)
Напомним, что 4-потенциал определяется неодно-
неоднозначно. Согласно D7.6) значения пространственных

§ 61. ТЕНЗОР ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 251
компонент Ан могут быть заменены величинами
Д, « Л* + ?^*'v**\ F0.16)
а значение компоненты Aq — величиной
А0=А0 + С F0.17)
(С — константа; см. текст, следующий за формулой
D1.5)) без того, чтобы изменились характеристики
ноля В и Е.
Лоренцево условие калибровки (см. E6.8)) в че-
четырехмерной форме имеет вид
3
?¦§?-0. F0.18)
JA = 0
Это означает, что 4-потенциал выбирается так, чтобы
его 4-дивергенция равнялась нулю (ср. с D7.7)).
§ 61. Тензор электромагнитного поля
Перейдем от потенциалов к силовым характери-
характеристикам поля Е и В. Этот переход осуществляется по
формулам E6.1) и E6.3). Для удобства выпишем
эти формулы еще раз:
B = [VA), F1.1)
E_v **A (б1.2)
х с ot
Напишем выражения для компонент вектора Е:
?, д<р 1 дАх
h*~~lfx~~~T~dr9
dq> 1 дАу
« дф I дАг
^г~ дг с dt '
В четырехмерных обозначениях эти формулы можно
представить в виде
~ дх» дх1
дА<> —у9л
дх9 ~ уолз

252 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
(см. формулы (XII. 42) для ковариантных компонент
4-оператора градиента и формулы F0.15) для кова-
ковариантных компонент 4-потенциала. Согласно послед-
последним формулам, например, Лж==—А\ и т. д.).
Теперь напишем выражения для компонент век-
вектора В. Согласно F1.1)
дАг
дАх
дг
дх
дАу
дг ~
дАг
дх
дАх
ди ~
дА2
дАг
дх1
дАг
дх2
дАг
дА{
дх*
дА2
дх'
Из тензорной алгебры известно, что выражения
вида a^bv — #v&n, суть ковариантные компоненты ан-
антисимметричного тензора второго ранга (а^ и bv —
ковариантные компоненты произвольных векторов).
Из формул F1.3), F1.4) следует, что компоненты
векторов Е и В можно трактовать как ковариантные
компоненты антисимметричного 4-тензора
Этот тензор называется тензором электромагнитного
поля.
Переместив в обеих частях равенства индексы \i
и v, получим выражение для контравариантных ком-
компонент тензора электромагнитного поля
e4avдАу
Сопоставление формул F1.3) и F1.4) с выраже-
выражением F1.5) дает, что
Ех = Ли = — Ло> Еу =s F02 ass — FgQ, Ег == Fq3 == —• F^
Bx === F32 == — /^гз» By = F13 = — F3U Bz == F2i == — F12.
F1.7)
Таким образом, тензор F^v выглядит следующим об-
образом:
(О Ех Еу Ег \
~-t I ~Во* _Й I F1-8)

% 62. ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ПОЛЕЙ 253
Приняв во внимание формулы (XII. 58), напишем
значения контравариантных компонент тензора элек-
электромагнитного поля
(О ~ЕХ -Еу -?г\
Ех О -Вг Ву\ ( , эд
Еу Вг О -Вх) \*1Л§>
Ег -Ву Вх 0 /
Итак, в четырехмерном пространстве электромаг-
электромагнитное поле описывается не посредством двух векто-
векторов (Е и В), а с помощью одного антисимметричного
тензора второго ранга.
Отметим, что в то время, как 4-потенциал А& опре-
определяется неоднозначно, компоненты тензора F^ ока-
оказываются однозначными. Действительно, произведем
в F1.5) замену компонент А^ величинами А^ согласно
формулам F0.16) и F0.17). Если р и v равны 1, 2, 3,
получим
- dAv д\ дА v д?*(х\х\х3)
дх» ^jcv dx» l dx»dxv
dxv дх* дх* dx* дху
Если один из индексов (например, ^i) равен нулю,
получим соотношение
dAQ dAv д д$ (лс1, я2,
V -у V |
99 ~1? l*-!?^!? as
дА0 дС
дх* d*v дх° дх* w*
Таким образом, мы доказали, что величины F^v
определяются однозначно.
§ 62. Формулы преобразования полей
Формулы преобразования компонент антисиммет-
антисимметричного 4-тензора выведены в Приложении XII (см.
формулы (XII. 62)). Подстановка значений C5.8) и

254 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
C5.9) для а0 и ах приводит эти формулы к виду
*02 о л\9 лОЗ а л 13
л/01 „01 у|/02 А — рА л/03 _..._ А •— рЛ
"» ^* П ао
ia_ Л^-рЛ03 Л^=Л23 F2Л)
Написав формулы F2.1) для тензора F1.9), по-
получим
F'Oi = F01, т. е. Е'Х = ЕХ,
02 f02 - pF12 , ?^ - №z
и т. д. Выписав соотношения F2.1) для всех компо-
компонент тензора F»v и заменив F»v соответствующими
значениями Ek и Вк, придем к формулам преобразо-
преобразования компонент векторов Е и В при переходе от од-
одной инерциальной системы отсчета к другой:
Е*= vr^F * /лляч
Формулы обратного преобразования отличаются от
этих формул лишь знаком при членах, содержащих
множитель р (т. е. знаком при vq).
Разложив векторы Ей В на составляющие парал-
параллельные оси х (а значит, и вектору vo) и перпендику-
перпендикулярные к этой оси (т. е. представив, например, Е
в виде Ей + Е±), можно записать формулы F2.2)
в векторном виде1)
F'_F р/ - Ei
0 а' "~
х) Заметим, что поскольку Вц и v0 коллинеарны, [v0B] ==
* [v0Bfl] + [v0B±] — [v0B±]# Аналогично [v0E] = [VoE±]- Поэтому
в векторных произведениях формул F2.3) можно опустить ин-
индекс «_1_» при Вх и Е^.

§ 62. ФОРМУЛЫ ПРЕОБРАЗОВАНИЯ ПОЛЕЙ 255
"(напомним, что vx — tfo, vy = иг = 0). Из этих формул
видно, что продольные1) составляющие полей при пе-
переходе от одной системы отсчета к другой не изме-
изменяются, а преобразуются только поперечные состав-
составляющие.
Если р «С 1 (т. е. &fo<Cc), выражение \/л/Т™—$2
приближенно равно 1 -}-{!/2)р2. Следовательно, с точ-
точностью до членов порядка р = Vo/c формулы F2.2)
выглядят следующим образом:
E'J = Ex, E*,-E,-(vJe)B.. К = Ея + Щс)Ва.
К = Вх, В'у = Ву + (vQ/c)Ez,B'z^Bz-(vo/c)Ey.
Легко убедиться в том, что эти формулы могут быть
записаны в векторном виде
E' = E + -i[voB], B' = B—I[v0E] F2.5)
(ср. с формулами F2.3)).
Если в системе К имеется только электрическое
поле (т. е. Е ф О, В = 0), то в системе К' будут суще-
существовать оба поля. Согласно формулам F2.5) эти
поля равны
Е'-Е, B' = -i-[v0E].
Учтя, что Е = Е', можно написать, что
l F2.6)
Последнее соотношение 2) указывает на то, что поля
В' и Е' взаимно перпендикулярны. Из этого соотноше-
соотношения вытекает также, что поле В' перпендикулярно
к вектору vo, т. е. к оси х.
Аналогичным способом можно показать, что в слу-
случае, когда в системе К имеется только магнитное
поле, векторы В' и Ег связаны соотношением
| F2.7)
*) Так мы будем называть для простоты составляющие, па-
параллельные вектору относительной скорости систем К и К' (век-
(вектору vo). Перпендикулярные составляющие мы будем называть
поперечными.
2) Рекомендуем убедиться в том, что такое же соотношение
между векторами В' и Е7 получается в рассматриваемом случае
и из точных формул F2.2).

256 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
Следовательно, и в этом случае поля В' и Е' взаимно
перпендикулярны. Кроме того, Е' перпендикулярно
к vo, т. е. к оси х.
Таким образом, если в системе К существует лишь
одно из полей (Е или В), то в любой другой системе К!
поля В' и Е' взаимно перпендикулярны. Справедливо
и обратное заключение: если в некоторой системе от-
отсчета К поля В и Е взаимно перпендикулярны (и ве-
величины полей удовлетворяют условиям, указанным
ниже), то существуют такие системы К\ в которых
поле будет чисто электрическим, а также такие си-
системы, в которых поле будет чисто магнитным. Най-
Найдем скорости соответствующих систем, начав с рас-
рассмотрения случая, когда Vq «С с.
Пусть векторы В и Е взаимно перпендикулярны.
Из формул F2.5) следует, что для того, чтобы в си-
системе К' поле было чисто электрическим (т. е. В'
было равно нулю), вектор vo должен удовлетворять
условию
В—J-IvoE].
Это условие будет соблюдено, если вектор vo перпен-
перпендикулярен к В (Е перпендикулярно к В по предполо-
предположению) и, кроме того, VqE sin a = сВ, где а — угол
между векторами vo и Е. Таким образом, поле будет
чисто электрическим во всех системах, движущихся
в направлениях, перпендикулярных к В, при условии,
что скорость vo данной системы равна сВ/Е sin а. По-
Поскольку скорость системы vo не может превзойти с,
рассматриваемые системы отсчета существуют лишь
при условии, что сВ < Е sin а. Если Е ^ сВ, указан-
указанное условие не выполняется ни при каком угле а.
Следовательно, в этом случае, несмотря на взаимную
перпендикулярность В и Е, систем, в которых поле
является чисто электрическим, не существует.
Легло убедиться в том, что полученный нами ре-
результат справедлив без оговорки, что v0 <C с. Для
этого обратимся к формулам F2.3). Пусть В и Е
взаимно перпендикулярны. Возьмем систему К\ ско-
скорость Vo которой перпендикулярна к В и равна по ве-
величине сВ/Е sin а (а — угол между векторами Vo и Е).
Вследствие взаимной перпендикулярности векторов vo
и В составляющая Bfl равна нулю. Согласно формулам

§ 63. ИНВАРИАНТЫ ПОЛЯ 257
F2,3) By также будет нулем. Рассмотрим числитель
формулы F2.3) для В'±. При выбранном нами на-
направлении vo вектор В± равен В. Векторное произве-
произведение векторов vo и Е можно представить в виде
[v0Ex] - [v0E J
(первое слагаемое равно нулю, так как векторы
v0 и Е. коллпнеарны). Таким образом, формулу для
В^_ можно в рассматриваемом случае написать сле-
следующим образом:
* _!^OMIv«e.L. F2>8)
По условию вектор Е перпендикулярен как к Es
так и к v0. Поэтому вектор fv0E] коллинеарен век-
вектору В. Выбрав надлежащим образом направление
вектора v0 (вправо или влево), можно сделать так,
чтобы векторы [v©E] и В имели одинаковое направ-
направление. Тогда в числителе формулы F2.8) будет стоять
разность двух одинаково направленных векторов, мо-
модули которых равны В и (l/c)voEs\na. Если i>o —
= сВ/Е sin а, модули этих векторов окажутся одина-
одинаковыми и числитель в формуле для В^ обратится
в нуль. Таким образом, и BJ, и В^ в этом случае бу-
будут отсутствовать. Аналогично можно показать, что
в случае взаимной перпендикулярности полей В и Е
в системах К', движущихся в направлениях, перпенди-
перпендикулярных к вектору Е, со скоростью vQ, равной
cE/Bsina (а — угол между векторами vo и В), поле
будет чисто магнитным. Это утверждение справедливо
при условии, что сЕ < В sin а. Если В ^ сЕ, систем,
в которых поле является чисто магнитным, не суо^е-
ствует.
§ 63. Инварианты поля
Образуем выражение
Заменим в нем величины B'k и Е'к их выражениями
9 И. В. Савельев, т. !

258 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
через нештрихованные компоненты (см. F2.2)):
Легко убедиться в том, что правая часть приводится
к виду
Таким образом, мы приходим к заключению, что
разность квадратов векторов В и Е имеет одинаковое
значение во всех инерциальных системах отсчета, т. е.
является инвариантом
F3.1)
Теперь образуем скалярное произведение векторов
Е' и В', т. е. сумму 2 ?*^*« Подставим в эту сумму
вместо Пк и Bk их значения F2.2). В результате по-
получим соотношение
Следовательно, скалярное произведение векторов Е
и В также является инвариантом
ЕВ = inv. F3.2)
Из F3.2) следует, что в случае, когда в какой-
либо системе отсчета поля В и Е взаимно перпендику-
перпендикулярны (т. е. ЕВ ==0), то они будут взаимно перпен-
перпендикулярными и во всякой другой инердиальной си-
системе отсчета.
Из F3.1) вытекает, что в случае, когда в какой-
либо системе отсчета модули векторов В и Е одина-
одинаковы (т. е» В2— Е2 —0), то они будут одинаковыми
в* любой другой системе отсчета..
Кроме того, из инвариантности выражений F3.1)
и F3.2) можно сделать следующие выводы. Если в

§ 63. ИНВАРИАНТЫ ПОЛЯ 259
какой-либо системе отсчета векторы В и Е образуют
острый (или тупой) угол (ЕВ больше либо меньше
нуля), то они будут образовывать острый (или тупой)
угол во всякой другой системе. Если в какой-либо си-
системе В > Е (или В < Е) (т. е. В2-— Е2 больше либо
меньше куля), то и в любой другой системе будет
сохраняться такое же соотношение между модулями
векторов В и Е.
В случае, когда оба инварианта равны нулю, век-
векторы В и Е во всех инерциальных системах отсчета
взаимно перпендикулярны и равны по величине.
Если равен нулю только инвариант F3.2), т. е.
ЕВ = 0, то можно найти такую систему отсчета, в ко-
которой равно нулю одно из полей, В или Е, какое
именно, определяется знаком выражения В2—-Е2.
Справедливо и обратное соотношение: если в какой-
либо системе равно нулю одно из полей, В или Е, то
во всякой другой системе поля будут взаимно перпен-
перпендикулярными (к этому заключению мы уже пришли
ранее, анализируя формулы преобразования полей).
Надо иметь в виду, что поля В и Е, вообще говоря,
меняются от точки к точке. Поэтому инварианты
F3.1) и F3.2) могут иметь в разных точках поля раз-
разные значения. Высказанные выше утверждения о свой-
свойствах полей относятся к тем точкам поля, для кото-
которых выполняются принимаемые предположения (на-
(например, равенство нулю данного инварианта и т. д.).
Если эти предположения выполняются во всех точках
поля, то, разумеется, и утверждения о свойствах по-
полей также будут относиться ко всем точкам.
Приняв во внимание сделанные замечании, допус-
допустим, что в системе К в некоторой точке поля произ-
произведение ЕВ отлично от нуля, т. е. что поля в данной
точке не перпендикулярны друг другу. Тогда можно
найти такую систему отсчета К', в которой поля в дан-
данной точке параллельны друг другу. В этой системе
Е'В' = Е'В\ так что получается два уравнения:
?'2 _ ?/2 = В2 _ ?2f еВГ = ЕВ
Решив совместно эти уравнения, найдем значения ве-
величин Е/ н Bf в той системе отсчета, в которой поля
Е' и В' параллельны (векторы Ей В заданы).
Инварианты поля можно найти, исходя из общих
свойств тензоров, В Приложении X показано, что при

260 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
перемножении тензоров т-го и n-го рангов получается
тензор (т + п)-го ранга, а также что свертывание
тензора по любой паре индексов понижает ранг тен-
тензора на две единицы. В частности, свертка тензора
второго ранга, равная сумме его диагональных компо-
компонент, называется следом (шпуром) тензора и пред-
представляет собой инвариант (см. формулы (X. 21) и
(XII. 63)).
В случае антисимметричного тензора, каковым яв-
является тензор электромагнитного поля, след равен
нулю, так что этот инвариант интереса не пред-
представляет.
Образуем произведение тензоров F1.8) и F1.9),
т. е. тензор с компонентами F]XVF^°. Он представляет
собой тензор четвертого ранга. Произведем двойную
свертку этого тензора, положив равными индексы \&
и р, а также v и о и произведя суммирование по этим
индексам. В результате ранг тензора понизится на
четыре единицы (каждая из двух сверток понижает
ранг на два) и мы получим тензор нулевого ранга,
т. е. инвариант:
Подстановка сюда значений F^ и F»v из F1.8)
и F1.9) приводит к соотношению
? F F»* 2Z?S + 2E ?$I = 2(B2-E2) = inv,
Ьх *' F3.3)
что согласуется с формулой F3.1).
Теперь образуем 4-тензор восьмого ранга
Ф^Р^Р*. F3.4)
где e**vpa — абсолютно антисимметричный единичный
4-псевдотензор четвертого ранга (см. Приложение XII,
текст, следующий за формулой (XII. 68)). Отличные
от нуля компоненты этого тензора равны +1 или —1
в зависимости от того, каким числом перестановок —
четным или нечетным — может быть получена данная
последовательность индексов ц, v, p, а, из последова-
последовательности 0, 1, 2, 3. В табл. 63.1 приведены все пере-
перестановки индексов с указанием знака при единице,
который им соответствует.

§ 64. ЧЕТЫРЕХМЕРНЫЕ УРАВНЕНИЯ МАКСВЕЛЛА
Таблица 63.1
251
После-
дователь-
довательность
0 12 3
0 13 2
0 2 3 1
0 2 13
0 3 12
0 3 2!
Знак
+
—
+
—
+
—-
После-
дователь-
довательность
13 2 0
13 0 2
12 0 3
12 3 0
10 3 2
10 2 3
Знак
+
—
-L.
—
После-
дователь-
довательность
2 0 13
2 0 3 1
2 i а о
2 10 3
2 3 0 1
2 3 10
1
Знак
!
+
+
—
—
После-
дователь-
довательность
3 2 10
3 2 0 1
3 10 2
3 12 0
3 0 2 1
3 0 12
Знак
+
«
—,
—
Четырехкратная свертка тензора F3.4) представ-
представляет собой инвариант:
Fpe===inv. F3.5)
JA. Vt 0, 0
Написав 24 отличных от нуля слагаемых суммы
F3.5) (знак слагаемых нужно взять из табл. 63.1),
легко убедиться в том, что их можно подразделить на
шесть групп, включающих в себя по четыре совпа-
совпадающих выражения:
]Г = 4F01F23 — 4F0sF32 + 4Fe2F31 —
-4F02F134-4F03F12-4F03F2l. F3,6)
Вследствие антисимметричности тензора Fp» произве-
произведения F01F32 = — F0iF23 и т. д. Поэтому выражение
F3.6) упрощается следующим образом:
? — 8 (FQlF23 + FQ2Fsl + FM = inv.
Инвариантным будет, очевидно, и выражение в скоб-
скобках. Подстановка значений F1.8) для JVv дает
Ех (- BJ + Еу (- Ву) + EZ(-B2)== inv,
что совпадает с F3.2).
§ 64. Уравнения Максвелла
в четырехмерной форме
Первая пара уравнений Максвелла (т. е. уравне-
уравнения E5.12)) может быть записана в виде одного урав-
уравнения для компонент тензора F1.8)
дх*
F4.1)

262 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
Заметим, что индексы в каждом из слагаемых обра-
образуют циклическую перестановку последовательности:
I*. v> P-
Выражение F4.1) представляет собой совокуп-
совокупность четырех уравнений, первое из которых полу-
чается при |i, v, p, равных соответственно 0, 1, 2, вто-
второе—при |л, v, р, равных 1, 2, 3, третье — при ц, v, p,
равных -2, 3, 0, и, наконец, четвертое — при р, v, p,
равных 3, О, I. В силу антисимметрии тензора F^,
уравнение, получающееся при любой другой комбина-
комбинации трех несовпадающих индексов, сводится к одному
из указанных четырех.
Напишем уравнение F4.1), положив [г = 0, v=l,
р = 2,
Подстазив значения F^ и координат хР9 получим
ду с dt дх
откуда
дЕу дЕх 1 dBz
дх ду с dt
Найденное соотношение представляет собой г-ю
компоненту векторного уравнения E5.12). Аналогич-
Аналогично, уравнения для р, — 2, v = 3, р = 0 и & = 3, v = 0,
р — I дают х-ю и у~ю компоненты того же уравнения.
(Получается уравнение для той компоненты, индекс
которой отсутствует в наборе значений ц,, v, p.)
Положив (i=l,v==2tp = 3, придем к формуле
которая после подстановки значений F^ и jc^ перехо-
переходит в соотношение
дг дх ду и>
эквивалентное второму из уравнений E5.10).
Таким образом, мы убедились з том, что уравне-
уравнение F4.1) эквивалентно первой паре уравнений Макс-
Максвелла.

§ 65. УРАВНЕНИЕ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ 263
Вторая пара уравнений Максвелла, т. е. уравнения
E5ЛЗ), может быть записана в виде
t *?—*-? <И-0. 1.2.3). F4.2)
Действительно, положим, например, |i=l. Тогда
уравнение F4.2) запишется следующим образом:
дх° + дх* i- ajc* с 1
(Fn=0). Подставив значения F^v и х&, а также
сгруппировав надлежащим образом члены, получим
уравнение
дВг дВу 4к 1 д8х
__ . _ _ _ j + _ —^
__ . _ _. jx + _ —^^
представляющее собой х-ю компоненту векторного
уравнения E5.13). Аналогично, уравнения для $л,==2
и {а = 3 дают у-ю и z-m компоненты того же урав-
уравнения.
При [4 = 0 уравнение F4.2) имеет вид
Подстановка значений F^v и х» дает
дд: ~~ ду дг —
что совпадает со вторым из уравнений E5.13).
Таким образом, мы показали, что уравнение F4.2)
эквивалентно второй паре уравнений Максвелла.
§ 65. Уравнение движения частицы в поле
Согласно C8.16) уравнение движения заряженной
частицы в электромагнитном поле имеет вид
dt \ V1 —
F5.1)
Разделив обе части равенства на *J\ —- v2jc% и приняв
во внимание, что dt^/l — v2jc2 есть dx (см. формулу

264 ГЛ. XI. УРАВНЕНИЯ В ЧЕТЫРЕХМЕРНОЙ ФОРМЕ
C4.13)), получим
d / mv \ _ е_ сЕ -f [vB]
dx \ <s/\—v2fc* } ~ с <>/Г^
или, в компонентах,
d / ти„ \ е сЕ
dx V
dx
»2/c2/" с Vl — »2/c2
Ho Bj/Vb^ = и*, cl's/T^WJ? = и0 (см. C6.6)).
Далее, ?, = Fi0, ?а = F20, Ez = F30, B, = F32 = - F23,
Be=:Ff3==_/?3ii ^^^i^.j^ia Поэтому уравне-
уравнения F5.2) можно написать следующим образом:
тЧГ
m Si
-Sir
Справа мы использовали ковариантные компоненты
4-скорости для того, чтобы все слагаемые были со
знаком «+>.
Теперь воспользуемся тем, что быстрота изменения
энергии частицы равна работе, совершаемой в еди-
единицу времени силами, действующими на частицу,
- F54)
Разделив обе части этого уравнения на с <\/\ — i>2
получим
4
Совокупность уравнений F5.3) и F5.5) можно за^
писать в виде одного уравнения
1Г ет Т Е Л* 0*" °> ! • 2> 3>- <65-6>

§ 65. УРАВНЕНИЕ ДВИЖЕНИЯ ЧАСТИЦЫ В ПОЛЕ 265
Это и есть уравнение движения частицы в поле, запи-
записанное в четырехмерной форме. Его пространственные
компоненты эквивалентны уравнению F5.1), а вре-
временная компонента эквивалентна уравнению F5.4).
Уравнению F5.6) можно придать несколько иной
вид. Опустим в обеих частях формулы F5.6) свобод-
свободный индекс р, вниз. Кроме того, переместим одновре-
одновременно немой индекс v при F^v вниз, а при uv вверх*
В результате получим
du в т—*
т ЧГ - 7 Z F^ (|х=0, 1, 2, 3). F5.7)
Последнее уравнение можно получить непосред-
непосредственно из уравнений F5.1) и F5.4), если заменить
в них левую часть ковариактными компонентами
4-скорости, а величины Ek и Вк представить как ком-
компоненты тензора F1.8).

Глава XII
ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
§ 66. Действие для заряженной частицы
в электромагнитном поле
Согласие с опытом получается в том случае, если
в качестве действия для частицы в поле принять вы-
выражение
JA-0
dx4>
где т-—масса частицы, е — ее заряд, Лд, —4-потен-
цнал поля. Обращаем внимание на то, что под зна-
знаком интеграла стоит, как это и должно быть, инва-
инвариант. При Л1*;= 0 выражение F6.1) переходит в дей-
действие или свободной частицы (см. формулу C9.7)).
Отметим, что неоднозначность потенциала не ока-
оказывает влияния на уравнения движения. Действи-
Действительно, заменив А& в F6.1) величинами Лц (см. фор-
формулы F0.16) и F0.17)), получим под знаком инте-
интеграла дополнительные слагаемые
7 ft
При интегрировании этих слагаемых получается по-
постоянная величина
2
JL
которая при варьировании действия дает нуль.

§ 66. ДЕЙСТВИЕ ДЛЯ ЧАСТИЦЫ В ПОЛЕ 267
Выражение F6.1) состоит из двух членов. Первый
зависит только от свойств частицы (от т). Второй
описывает взаимодействие частицы с полем, в соот-
соответствии с чем содержит как величину, характеризую-
характеризующую частицу (заряд е), так и величину, характери-
характеризующую поле (потенциал Ар). Вообще говоря, нужно
было бы включить еще член, описывающий само поле.
Но, рассматривая движение частицы в заданном поле,
этот член можно не принимать во внимание, так как
он в силу определенности поля не должен варьиро-
варьироваться. Правда, это утверждение оказывается спра-
справедливым лишь при условии, что заряд частицы
настолько мал, что его влиянием на поле можно пре-
пренебречь. При рассмотрении движения частицы в за-
заданном поле мы будем предполагать, что это условие
выполнено.
Получим уравнения движения частицы, исходя из
принципа наименьшего действия. Согласно этому
принципу для истинной траектории частицы выпол-
выполняется условие
(мы произвели замену: ds2 = 2 ^*ц dx&). Осуществив
варьирование, получим
1
2) = 0 F6.5»
(см. формулу C9.9); напомним, что ( ())
Проинтегрируем первые два члена в подынтеграль-
подынтегральном выражении по частям. В результате первый член
примет вид
тле х — собственное время частицы, е%-~
частицы (см. формулу C9.11)). Интегрирование

268 ГЛ. ХИ. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
частям второго члена дает
2 2 2
Первое выражение справа есть нуль, так как на кон-
концах траектории дх^ — О. Следовательно, после инте-
интегрирования по частям первых двух членов выражение
F6.2) приводится к виду
(как сейчас выяснится, в третьем члене целесообразно
обозначить немой индекс буквой v).
Теперь произведем замены:
dAp, = V —~ dxv == V —~ av dx — во втором члене,
дху
V
6AV == У\ —?- 6х* и dx"9 = uv йт — в третьем члене.
В итоге получим
2
что можно записать следующим образом:
с
V
Для того чтобы написанное условие выполнялось при
произвольных Ьх^> необходимо равенство нулю всех

§ 67. ДЕЙСТВИЕ ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 269
выражений, стоящих в круглых скобках. Отсюда вы-
вытекают соотношения
или
т
т
du.
dx
е
е
с
V
аи., е v—«
"St" = TE f^v (I* = 0, 1, 2, 3) F6.3)
(см. формулу F1.5)), что совпадает с F5.7).
Таким образом, мы получили уравнение движения
частицы в поле, исходя из принципа наименьшего
действия.
§ 67. Действие для электромагнитного поля
В предыдущем параграфе мы считали поле, в ко-
котором движется частица, заданным, в связи с чем сла-
слагаемое в действии, описывающее свойства самого
поля, мы не учитывали. Теперь рассмотрим систему,
состоящую из частиц, находящихся в электромагнит-
электромагнитном поле, и попытаемся, исходя из принципа наимень-
наименьшего действия, найти уравнения, определяющие поле.
При этом мы можем отказаться от предположения
о малости зарядов частиц и получить уравнения для
истинного поля, т. е. поля, получающегося при сложе-
сложении внешнего поля с полем, созданным самими заря-
зарядами. Следовательно, величины Лц должны будут за-
зависеть от положений и скоростей частиц.
Действие для системы поле + частицы должно со-
состоять из трех частей:
S = Sf + Sm + Smf. F7.1)
Здесь Sf есть та часть действия, которая зависит
только от свойств самого поля, т. е. действие для поля
в отсутствие зарядов; Sm — та часть действия, которая
зависит только от свойств частиц, т. е. действие для
свободных зарядов. И, наконец, Smf есть та часть
действия, которая обусловлена взаимодействием
между частицами и полем.
Что касается последних двух членов, то их значе-
значения можно получить, сложив выражения F6.1) для

270 ГЛ. XII. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
всех частиц. Следовательно,
F7.2)
F7.3)
Здесь а — номер частицы, N — число рассматривае-
рассматриваемых частиц, А^а — потенциал поля в той точке 4-про-
странства, где находится частица с номером а. Ин-
Индекс а следует отличать от применяемых яля обозна-
обозначения компонент 4~векторов и 4-тензоров индексов щ
v, р, ... Для последних индексов нужно различать
верхнее и нижнее положение. Для индекса а такое
различие не имеет смысла.
Выражению F7.3) можно придать другой вид.
С этой целью заменим в нем dx* через (dx^dt) dtt
т. е. напишем
Далее представим совокупность точечных зарядов
еа как заряд, распределенный в пространстве с плот-
плотностью
а
{см. D1.12)). Тогда заряд, заключенный в элементе
объема dV9 можно записать как de — pdV и сумму
вида X) eafixa> Уа> za) заменить интегралом
(x, y9 г)f{x9 у, z)dV.
В результате получим
Теперь учтем, что p{dx*/dt) — /**, где /¦* — компо*
неата 4-тока (см. формулу F0.8)). Значит, можно

§ 67. ДЕЙСТВИЕ ДЛЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ 271
написать
S"f- ~ 7 S I Vх dV dt - - Д- J ? Л,/ *Г, F7.4)
где dV = dx°dxldx2dx* ^
Чтобы получить выражение для слагаемого Sf,
примем во внимание, что, как показывает опыт, элек-
электромагнитное поле подчиняется принципу суперпози-
суперпозиции. Поэтому уравнения для поля должны быть ли-
линейными дифференциальными уравнениями. Уравне-
Уравнения поля получаются варьированием действия, при
варьировании же степень подынтегрального выраже-
ния понижается на единицу. Следовательно, уравне-
уравнения окажутся линейными в том случае, если в дей-
действии под знаком интеграла будет стоять выражение,
квадратичное по полю. Кроме того, это выражение
должно быть инвариантным. Простейшими квадратич-
квадратичными инвариантами, которые можно образовать из
характеристик поля, являются два: ? А^А* и
2 ^iav^V- Первый инвариант для нашей цели непри-
непригоден, так как 4-потенциал определен неоднозначно.
Таким образом, мы приходим к выводу, что под зна-
знаком интеграла в действии должен стоять инвариант
Ц ^nv^v- Чтобы получить действие для всего поля,
нужно произвести интегрирование по всему 4-про-
странству, где поле отлично от нуля. Итак, мы при»
ходим к выражению
I*. V
где а — некоторая константа, dV^^cdVdi Интегри-
Интегрирование по координатам осуществляется по всему
трехмерному пространству, а по времени • между
двумя заданными моментами t\ и ^
Из найденного нами выражения получаются пра*
вильные уравнения поля, если положить (в гауссовой
системе) a — — 1/16зхс, Тогда
'Bvrv<*r. F7.5)

272 ГЛ. XII. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
Сложив выражения F7.2), F7.4) и F7.5), полу-
получим действие для системы поле + частицы:
F7.6)
Согласно формуле F3.3) ? FayF*v = 2 (В2 - Е2).
Подставив это значение в F7.5)-, а также заме-
заменив dV* через с dV dt9 можно привести выражение
для Sf к виду
\\ JL (E2 - Щ dV. (87.7)
и
Из этой формулы вытекает, что функция Лагранжа
для поля определяется выражением
F7.8)
Итак, мы установили вид действия &ля электро-
электромагнитного поля. Как найти уравнения поля, исходя
из принципа наименьшего действия, будет объяснено
в следующем параграфе.
§ 68. Бывед уравнений Максвелла
из принципа наименьшего действия
Найдем уравнения поля, считая движение зарядов
заданным. В этом случае член Sm в действии можно
не принимать во внимание, поскольку он в силу опре-
определенности движения зарядов не должен варьиро-
варьироваться. Итак, будем исходить из выражения
(см. F7.5) и F7.4)).

§ 68. ВЫВОД УРАВНЕНИЙ МАКСВЕЛЛА 273
Вычислим вариацию выражения F8.1) и прирав-
приравняем ее нулю. При этом учтем, что в связи с опреде-
определенностью движения зарядов ток /»* не должен варьи-
варьироваться. Следовательно,
(Z V) dV* -k)Z Г М, dr.
F8,2)
Определим вариацию, стоящую вод знаком пер-
первого интеграла,
* Z V - Z /V. 6<ciiV + Z ^v wv
Поднимем индексы у первого сомножителя первой из
сумм и одновременно опустим их у второго сомножи-
сомножителя. В результате получим
Приняв во внимание формулу F1.5) для F^,, на-
напишем это выражение следующим образом:
6 У F.J»" - 2
2 У F**V6 -^ — 2 У F
Lj '$& Lj
дх
у
Воспользовавшись антисимметричностью тензора F^vt
заменим в первой сумме Fw через—Fv&, а затем поме-
поменяем в этой сумме индексы р, и v. В итоге первая сум-
сумма станет тождественной со второй и мы получим, что
6^. F8.3)
Изменив последовательность дифференцирования
и варьирования величин А^ приведем F8.3) к виду
Теперь преобразуем полученное выражение по фор-
формуле uvf = (uv)' — u'v\

274 ГЛ. XII. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
Подставив это выражение в F8.2), придем к следую-
следующей формуле для вариации действия:
— \ / ёЛп F dv \ / / ол» dv
Первый из трех интегралов можно преобразовать
по формуле Остроградского — Гаусса в поверхност-
поверхностный интеграл:
д
На границе рассматриваемого 4-объема 6Л^ = 0. По-
Поэтому написанный нами интеграл исчезает. Таким об-
образом, в формуле F8.4) нужно сохранить только вто-
второй и третий члены. Объединив их вместе и вынеся
за скобки общий множитель 6Ац, получим
В силу произвольности вариаций дА^ найденное
нами значение 65 может оказаться равным нулю
только в том случае, если все выражения в круглых
скобках будут нулями. Следовательно, мы приходим
к уравнениям
Е 7JT — Т ^ 0» - 0. 1. 2, 3), F8.5)
которые представляют собой вторую пару уравнений
Максвелла (см. уравнения F4.2)).
Отметим, что связь между полями В и Е, с одной
стороны, и зарядами и токами, с другой стороны,
определяется именно второй парой уравнений Макс-
Максвелла (см. уравнения E5.13)). Первая же пара урав-
уравнений Максвелла выражает свойства полей В и ? и
их связь друг с другом (см. уравнения E5.12)),

§ 69. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА ПОЛЯ 275
§ 69. Тензор энергик-импульса
электромагнитного поля !)
В § 67 мы установили, что действие для электро-
электромагнитного поля определяется выражением
16ж?
'(см. формулу F7.5)).
Сопоставление формул (89.1) и D0.2) показывает,
что в качестве плотности функции Лагранжа для поля
нужно взять выражение
kZV^. F9-2)
U, V
В качестве обобщенных координат qa для поля
следует принять компоненты потенциала Л^, а в ка-
качестве обобщенных скоростей — производные этих
компонент по координатам xv. Чтобы упростить за-
запись формул, введем обозначение
•^7=«W F9.3)
Приравняв вариацию действия нулю и проделав
такие же выкладки, какие в § 40 привели нас к урав-
уравнениям движения D0.12), придем к соотношениям
ТГ - 2 lh IT" 0* - 0. 1. 2, 3). F9.4)
Уравнения F9.4) суть уравнения поля. Чтобы опре-
определить значения входящих в них производных, напи-
напишем вариацию функции L*. По общим правилам вы-
вычисления вариации
4) Перед тем как приступить к чтению этого параграфа,
следует восстановить в памяти содержание § 40,

276 ГЛ. XII. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
С другой стороны, вариация функции F9.2) равна
16я JL* *v Ал
^, v u, v
|А, V
(см. формулу F8.3)).
Сравнение полученного выражения с формулой
F9.5) позволяет заключить, что
<69-6>
Заменив во втором выражении F*v на —Fvv и затем
поменяв местами индексы \i и v, найдем, что
.|?L_ * F*v F9.7)
Подстановка значений F9.6) в формулу F9.4)
приводит к следующим «уравнениям движения» для
электромагнитного поля:
?S~=0 <*i=o>i'2'3> <69-8>
V
(мы опустили множитель 1/4я). Полученное уравнение
есть уравнение Максвелла F4.2), написанное для слу-
случая /> = 0. Такого результата и следовало ожидать,
поскольку мы исходили из действия для одного лишь
поля без зарядов.
Теперь установим вид тензора энергии-импульса
электромагнитного поля. Подставив в формулу D0.16)
вместо с/ац, величины аРМ, (см. D0.3) и F9.3)), полу-
получим для компонент этого тензора следующее выра-
выражение:
Заменим в соответствии с F9,7) dL*/dapv через
— A/4я)/^р. Кроме того, подставим вместо арм# ее зна-
значение F9.3), а вместо L*—выражение F9.2). В ре-
результате получим
9. V

§ 69. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА ПОЛЯ 277
(во второй сумме нельзя обозначить немые индексы
буквами ц, v, как это сделано в формуле F9.2), по-
поскольку в формуле F9.9) \i и v были уже выбраны
в качестве свободных индексов).
Тензор F9.9) несимметричен. Для его симметри-
симметризации прибавим к нему тензор
дх? N
р
который, как мы сейчас покажем, можно представить
в виде
р
(см. формулу D0.18)). Действительно, применим квы-
ражению F9.10) преобразование uv' — luv)' — ufv:
Вторая сумма в силу F9.8) равна нулю (Лр, можно
вынести за знак суммы). Следовательно, мы привели
тензор F9.10) к виду
д f*±-A
Поскольку выражение в скобках антисимметрично по
индексам v и р, прибавление к тензору F9.9) выра-
выражения F9.10) допустимо (см. формулу D0.18) и свя-
связанный с нею текст).
Сложив выражения F9.9) и F9.10), получим
тензор
Р. У

278 ГЛ. XII. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
Выражение в круглых скобках есть F^p (см. F1.5)).
Следовательно, формула для смешанных компонент
тензора энергии-импульса приобретает вид
V=- т-г Z V+тяг « Е W"- <69-!!)
Р Э. Y
Чтобы перейти к контравариантным компонентам,
поднимем во всех членах формулы F9.11) индекс \i
вверх. При этом 6JJ, превратится в gv* (см. (XII. 66)
и (XII. 67)). Таким образом,
P Э. Y
Поднятие какого-либо индекса у одного из сомножи-
сомножителей при одновременном опускании этого же индекса
у второго сомножителя не изменяет произведения. По-
Поэтому с равным основанием можно написать, что
v"- F913)
Р Р, Y
Сопоставление выражений F2.12) и F2.13) позво-
позволяет заключить, что тензор 7>v действительно сим-
симметричен.
Вычислим след тензора Т*™. Согласно формуле
F9.11)
р /цЧ Р. V
Во втором члене все множители, кроме 6{1, можно
вынести за знак суммы по [д. Сумма же 2 бЦ равна
четырем. Таким образом,
Т.П — i
и IX, р ?, у
Последнее выражение равно нулю. Следовательно, мы
установили, что след тензора T&v равен нулю:
Е^Я — О. F9.14)
у,
Найдем выражения компонент тензора Т»-у через
компоненты векторов Е и В. Для этого подставим

§ 69. ТЕНЗОР ЭНЕРГИИ-ИМПУЛЬСА ПОЛЯ 279
в F9.S3) значения компонент F^v. Эти значения мы
возьмем из F1.9), причем будем учитывать, что опус-
опускание временного индекса не изменяет компоненты
тензора, а опускание пространственного индекса из-
изменяет знак компоненты на обратный. Примем также
во внимание, что сумма ]? ^Vv^ есть инвариант, ко-
который мы вычислили в § 63. Он равен
? F^v = 2 (В2 - Е2) (80.131
(см. формулу F3.3)).
Начнем с вычисления Г00. Согласно F9.13), F1.9)
и F9.15)
(g _j. CM (XII. 67)). Мы получили уже известный
результат: компонента Г00 равна плотности энергии w
(см. формулу D0.27)).
Теперь найдем компоненту Г01. Поскольку g° — 0,
г01 — 1
1 ~~~~&
1 Г111
j * / p о с* ?j \ ____ у Г I* Rl % ,.„, о 1чС1 1 ^ •
где Sx — х-я компонента вектора Пойнтинга в ва-
вакууме Н —В). Аналогичные выкладки дают, что
Т02 = Sy/cy Г03 = 8г/с (ср. с формулой D0.32)).
Наконец, вычислим, например, Г12. Согласно
(XII. 67) ?I2 = Q. Поэтому
~Л2 1
I s=s: 2—
где а^ — компонента максвелловского тензора натя-
натяжений (см. формулу E9.12)). Легко проверить, что

280 ГЛ. ХП. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
все остальные компоненты вида Tik совпадают с соот-
соответствующими компонентами тензора E9.12):
{ (Е* + в2) б Е$ вв} <69-*7>
(при проверке надо учесть, что g" = — 1=—6,г, см.
(XII. 67)).
Рассмотрим вопрос о приведении тензора 7>v к
диагональному виду. В евклидовом пространстве та-
такое преобразование симметричного тензора возможно
всегда. В псевдоевклидовом же пространстве, как мы
сейчас увидим, дело обстоит иначе. Согласно F9.16)
компоненты вида Ты = Г*° будут равны нулю при
условии, что
[ЕВ]=0. F9.18)
Согласно F9.17) компоненты вида Tik {1ФЩ будут
равны нулю при условии, что
?<?* = () и BtBk^0 {1фЩ. F9.19)
Таким образом, для того чтобы привести тензор
к диагональному виду, нужно перейти к системе от-
отсчета, в которой векторы В и Е коллинеарны либо
один из них равен нулю (тогда будет выполнено усло-
условие F9.18)). В § 62 мы выяснили, что такая система
существует всегда, за исключением случая, когда В
и Е взаимно перпендикулярны и одинаковы по мо-
модулю. В указанной системе отсчета одну из коорди-
координатных осей нужно направить вдоль поля. Тогда ока-
окажется выполненным условие F9.19). В итоге тензор
примет диагональный вид. Найдем компоненты Ти,
предположив, что ось х выбрана в направлении полей
и, следовательно,
Тогда согласно F9.17)
15Г
Г22 -= Г33 —gL (?2 + В2) =* w.
Компонента Г00, как мы знаем, тоже равна w. Итак,
будучи приведен к диагональному виду, тензор энер-

§ 70. ЗАРЯЖЕННАЯ ЧАСТИЦА В ПОЛЕ 281
гии-импульса электромагнитного поля выглядит сле-
следующим образом:
' w 0 0 0 \
° -;: :• №9.20)
0 0 w'
Если векторы В и Е взаимно перпендикулярны и
одинаковы по модулю, тензор T^v не может быть при-
приведен к диагональному виду (взаимная перпендику-
перпендикулярность не дает возможности преобразовать В и Е
так, чтобы они стали коллинеарными, а равенство мо-
модулей— так, чтобы одно из полей обратилось в нуль).
Отметим, что в смешанных компонентах тензор
F9.20) имеет вид
(w 0 0 0 \
0 0 0 —ш'
Из F9.21) сра?зу следует, что след тензора Г? равен
нулю. Этот результат мы получили ранее в общем
случае (см. F9.14)),
§ 70. Заряженная частица
в электромагнитном поле
Действие для заряженной частицы в электромаг-
электромагнитном поле определяется, как мы знаем, выражением
G0.1)
(см. формулу F6.1)).
Ковариантные компоненты 4-потенциала можно
представить в виде
(см. F0.15)). Компоненты 4-радиуса-вектора равны
х» = (с/, г).
Следовательно,
з
2 A* dx» = фс dt — А йт = (сф — Av) dt.
йо

282 ГЛ. XII. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
Подставим это значение суммы в формулу G0.1).
Кроме того, заменим ds в соответствии с C4.4) через
с Vl — v2fc2dt. В результате получим
+ у Ay - ар) dt.
Отсюда заключаем, что функция Лагранжа яля заря-
заряженной частицы в поле имеет вид
L = — tnc2 ^T^lFjJ2 + - Ay — ар. G0,2)
Первый член представляет собой функцию Лагран-
Лагранжа для свободной частицы (см. C9.4)). Остальные
два члена описывают взаимодействие частицы с полем.
Зная функцию Лагранжа, можно вычислить энер-
энергию и импульс частицы. Согласно формулам D.19)
и E.1) обобщенный импульс определяется выраже-
выражением
а энергия — выражением
W^^v-L. G0.3)
Следовательно, продифференцировав функцию G0.2)
по v, получим обобщенный импульс частицы:
Здесь р — обычный импульс частицы (см. формулу
C8.5)). Из полученной нами формулы следует, что об-
обобщенный импульс отличается от обычного слагаемым
(е/с)А. В отсутствие поля обобщенный импульс со-
совпадает с обычным.
Теперь определим энергию частицы. В соответ-
соответствии с G0.3) и G0.2)
G0.5)

§ 70. ЗАРЯЖЕННАЯ ЧАСТИЦА В ПОЛЕ 283
Первый член полученного выражения представляет
собой энергию свободной частицы (см. формулу
C8.11)), второй член — дополнительную энергию, ко-
которой обладает частица, находясь в поле.
Заменив в выражении для энергии скорость v че-
через обобщенный импульс Р, найдем функцию Гамиль-
Гамильтона частицы. Чтобы исключить v из формул G0.5)
и G0.4), представим эти уравнения в виде
тс
Если возвести эти уравнения в квадрат и вычесть из
верхнего нижнее, то справа получится т?с2. Следова-
Следовательно, заменив W на Ж, получим
G0.6)
¦ч *» г "ч v у
откуда
<Ж = с -д/лА2 + (р — -f AJ + ар. G0.7)
Это и есть функция Гамильтона для частицы в поле.
В § 32 было установлено, что компоненты обоб-
обобщенного импульса равны производным действия по
соответствующим обобщенным координатам (см. фор-
формулу C2.6)). В нашем случае роль обобщенных коор-
координат играют декартовы координаты хь Следова-
Следовательно,
или Р==
Далее, согласно C2.10) производная действия по вре-
времени дает функцию Гамильтона, взятую с обратным
знаком:
as _ у
dt ~ <т'
Заменив в формуле G0.6) Ж на —dS/dty a P на
VS, придем к уравнению Гамильтона — Якоби для час-
частицы в электромагнитном иоле:
S-4AV-mV = 0. G0.8)
с /

284 ГЛ. ХП. ВАРИАЦИОННЫЙ ПРИНЦИП В ЭЛЕКТРОДИНАМИКЕ
В ньютоновском приближении, т. е. при v <C с,
функция G0.2) переходит в
L^Tf + ±AY^e(p G0.9)
(мы разложили G0.2) по степеням v2/c2 и отбросили
константу —тс2).
Продифференцировав G0.9) по v, найдем обоб-
обобщенный импульс
P_mv + ~A = P4-~A, G0.10)
где р —обычный импульс.
Для энергии в этом приближении получается зна-
значение
W = Pv — L =
mv + — AJ ? — -у~- — — Av + еф » -j- + еф.
G0.11)
Из G0.10)
Подставив это значение v в G0Л1)9 придем к выра-
выражению для функции Гамильтона:
2 <70Л2>
Уравнение Гамильтона— Якоби в ньютоновском
приближении имеет вид
J 0. G0.13)

Глава XIII
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
§ 71 • Волновое уравнение
В § 57 было показано, что при наложении на по-
потенциалы Аиф условия Лоренца
*А+^^=0 G1.1)
(см. формулу E6.8)) они удовлетворяют уравнению
Даламбера 1):
^ G1.2)
G1.3)
(см. уравнения E7.6) и E7.7)). Здесь ?—оператор
Даламбера, равный
п А 8М2 д2 . д2 . д2 eji д2 ,-. лх
(см. E7.4)).
В отсутствие зарядов и токов (т. е. при р = 0 и
j as 0) уравнения для потенциалов приобретают вид:
DA-0, G1.5)
Пф = 0 G1.6)
или, с учетом G1.4),
1) Напомним, что уравнения E7.6) и E7.7) были получены
в предположении, что среда, в которой рассматривается поле,
однородна и изотропна и, кроме того, е и \и не зависят от Е и Н.

286 гл. хш. электромагнитные волны
Аналогичные уравнения получаются также для
векторов Е и В:
АЕ-^-даг-О, G1.9)
?_ о G1Л0)
(см, §74).
Уравнения G1.7)— G1.10) имеют ненулевые реше-
решения. Следовательно, электромагнитные поля могут су-
существовать и в отсутствие зарядов. Электромагнит-
Электромагнитные поля, существующие в отсутствие зарядов, назы-
называются электромагнитными волнами.
Уравнение вида
л/--ггжв0' Gi.il)
rjxe v — константа, называется волновылг. Из курса
общей физики известно, что v представляет собой фа-
фазовую скорость волны. Следовательно, скорость элек-
электромагнитных волн равна
ч = -7^« —, G1.12)
где
л*=Увц G1.13)
есть показатель преломления среды, в которой рас-
распространяется волна.
Волновое уравнение легко получить в четырехмер-
четырехмерном виде. Сделаем это для поля в вакууме. Согласно
F4.2) уравнения Максвелла в отсутствие зарядов и
tokos имеют вид
'!'2> 3)- G!Л4)
V
Подстановка вместо F^v их значений F1.6) дает
или

§ 72. ПЛОСКАЯ ВОЛНА В ОДНОРОДНОЙ СРЕДЕ 287
Первую сумму можно записать следующим об-
образом:
Ea2^v _ д у ^Ц
dxlkdxv дх» " dxv
Если 4-потенциал удовлетворяет условию Лоренца
F0.18), то J^ (dAv/dxv) = Q и в уравнении G1.15)
первый член будет отсутствовать. Таким образом, мы
приходим к уравнениям
?^ = 0 (|А = 0, 1, 2, 3). G1.16)
Поднятие индекса при дху равнозначно умноже-
умножению каждого из слагаемых в G1.16) на g™ (см.
(XII. 30)). Поэтому уравнениям G1.16) можно при-
придать вид
Наконец, приняв во внимание, что недиагональные
компоненты тензора g9*— нули, можно написать
=о (fi = 0, 1, 2, 3). G1.17)
Уравнения G1.16) и G1.17) представляют собой
волновое уравнение в четырехмерной форме. Подста-
Подстановка в них значений gvf> и xv приводит, как легко
убедиться, к уравнениям G1.7) и G1.8).
§ 72. Плоская электромагнитная волка
в однородной и изотропной среде
Решение волнового уравнения значительно облег-
облегчается, если поле зависит только от одной координа-
координаты, скажем, х. Волна в этом случае называется плос-
плоской. Вместе с тем, на примере плоской волны можно
выяснить все характерные особенности электромагнит-
электромагнитных волн. По этим причинам мы ограничимся в этой
главе рассмотрением только плоских волн.
Будем подразумевать под f любую из компонент
векторного потенциала А либо скалярный потенциал ср

288 ГЛ. ХШ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
(с равным основанием можно подразумевать под f
любую компоненту вектора Е или вектора В). В слу-
случае плоской волны функция f зависит только от х и /
и, следовательно, является решением уравнения
d2f ер d2f _п /79 П
дх2 с2 dt2 ч '
Это уравнение можно написать в виде
D/ = 0, G2.2)
где D— дифференциальный оператор, определяемый
формулой
дх2 с2 dt2 *
Предстдвим этот оператор в виде
D = (JL _ JL1Л (А„ 4- — JL^j G2.3)
G2.4)
где /t==V^T (см. G1.13)).
Введем новые переменные
т. е. заменим х и t по формулам
Согласно G2.5)
_а_ ^ , _LjeL —— JLJL д.-L-iL
~ ^ d| "+" ^ d| ~ 2» <9jc + 2 a*
с dt
Следовательно, при переходе к переменным g и ц пер-
первый множитель в G2.3) нужно заменить на
{2/)д/дЬ
Аналогично
JL~JLJ?*-jl.JL JL — J. L.JL.LJ.
дт\ дх дц "*" dt дц 2п дх "*" 2 а^
2п
/ а , п д \
Ч ajc + с dt)*

§ 72. ПЛОСКАЯ ВОЛНА В ОДНОРОДНОЙ СРЕДЕ 280
так что второй множитель в G2.3) нужно заменить на
Bп/с)д/дц. В итоге получим, что
U~ с2 д\ дц ~ с2 д1дц *
Подставим найденное нами значение D в уравне-
уравнение G2.2), опустив множитель —An2/с2. В результате
получим дифферешщалышеуравнение
= 0. G2,6)
Очевидным решением этого уравнения является
функция, зависящая только от одной переменной |
или tj, т. е. функция fi(g) либо /2A1). Сложив функ-
функции /1 и f2s получим общее решение уравнения G2.6):
Мы не стали умножать f\ на Сь а /2 на С2, поскольку
f\ и /г суть произвольные функции соответствующих
переменных.
Подставив в G2.7) выражения G2.4) для | и т|,
придем к решению уравнения G2.1):
+¦?)- G2-8)
Первый член в этом выражении представляет собой
волну, бегущую со скоростью с/п в направлении
оси х. Действительно, значения f\ одинаковы для всех
значений t и х, связанных соотношением
t ?- = const или х — — t —— const,
с/п п п
откуда и следует, что любое заданное значение функ-
функции /i перемещается вдоль оси х со скоростью с/п.
Аналогично второй член в выражении G2.8) пред-
представляет собой волну, бегущую со скоростью с/п в
направлении, противоположном оси х.
Форма волны G2.8), т. е. вид функций f\ и f2, яв-
является совершенно произвольной.
Рассмотрим плоскую волну, распространяющуюся
в направлении оси х. Выберем потенциалы так, чтобы
<р = 0, VA = 0. G2.9)
Ю И. В. Савельев, т. I

290 ГЛ. ХШ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Такая калибровка потенциалов удовлетворяет усло-
условию Лоренца G1.1) и, следовательно, не сказывается
на значениях векторов В и Е (см. § 56). При наложе-
наложении на потенциал ф условия G2.9)
Е —Т-? G210)
(см. E6.3)).
Для рассматриваемой волны все характеризующие
поле величины, в том числе и А, имеют вид
(^) G2.11)
так что
дА. дА,
В частности, равны нулю дАу/ду и dAzfdz. Таким об-
образом, второе из условий G2.9) принимает в рассмат-
рассматриваемом случае вид
дЛх
дх
--Q.
Подстановка последнего соотношения в уравнение
?72.1), написанное для Л*, дает, что
?de0
dt2
Согласно последнему уравнению
^2.:= const. G2.12)
Производная dAx/dt определяет компоненту поля Ех
(см. G2.10)). Поэтому соотношение G2.12) означает,
что Ех — const Таким образом, мы пришли к заклю-
заключению, что отличная от нуля компонента Ех может
быть обусловлена только постоянным и однородным
электрическим полем. Такое поле не имеет отношения
к электромагнитной волне. Значит, можно считать, что
АХ9 а следовательно, и Ех равно нулю.
Из G2.11) вытекает, что
EJOL — E^- <^ — E^J*L — --.JLilL /79 i^
dt ~ dl ' дх ~ dl дх ~ с 61 ' \'*А6)

§ 72. ПЛОСКАЯ ЗОЛ ПА В ОДНОРОДНОЙ СРЕДЕ 291
Согласно первой из этих формул
Поскольку А зависит только от одной коорди-
координаты х, в выражении Е = [VA] нужно сохранить
только компоненту У, равную гх(д/дх). Следователь-
Следовательно, можно написать, что
Е_Ге JL А1_Ге ±L1
или, согласно второй из формул G2.13),
Наконец, приняв во внимание G2.14), получаем
В = я [е„ Е] = VifT [е„ EJ, G2.15)
откуда вытекает, что вектор В перпендикулярен как
к вектору Е, так и к оси х. Ранее мы показали, что
у рассматриваемой нами волны EX = Q и, следова-
следовательно, вектор Е перпендикулярен к оси х. Таким
образом, мы приходим к заключению, что в плоской
волне векторы Е и В перпендикулярны к направлению
распространения волны. Следовательно, электромаг-
электромагнитные волны являются поперечными.
В формуле G2.15) е* представляет собой орт на-
направления, в котором распространяется волна. Обо-
Обозначив этот орт символом ко, придем к формуле
E], G2.16)
которая не зависит от выбора направлений коорди-
координатных осей.
Заменив В через цН, получим
V?H = [ko, У? El. G2.17)
Из G2.17) вытекает, что векторы Н и Е взаимно пер-
перпендикулярны, причем их модули связаны соотноше-
соотношением
У]1 /Я. G2.18)
Кроме того, из G2.17) легко заключить, что векторы
Е, II и к0 образуют правовинтовую последователь-
последовательность.
10*

292 ГЛ. XIII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Электромагнитная волна несет с собой энергию,
поток которой определяется вектором Пойнтинга
S-?-[EH].
Выразим Н через Е согласно G2.17) и применим фор-
формулу «бац минус цаб» (см. (VI. 5)). Тогда
Поскольку векторы Е и к0 взаимно перпендикулярны,
Еко = 0, так что
S - "Г" л/^?2Ьо=
4 V
Г л/?Ьо А
4л V |i An
Воспользовавшись соотношением G2.18), можно на-
написать
An уец An
Наконец, приняв во внимание, что (еЕ2 + \iH2)J8n
есть плотность энергии волны ш, получим
S = —?=• who = trwko. G2.19)
В вакууме
S — cwko. G2.20)
Таким образом, плотность потока энергии, перено-
переносимой волной, равна плотности энергии, умноженной
на скорость распространения волны. Направление
вектора плотности потока энергии совпадает с на-
направлением распространения волны.
Поток импульса определяется максвелловским
тензором натяжений, компоненты которого вычисля-
вычисляются по формуле
*"* - i {EiDk+я а - т(ED + нв) *«}

§ 73. МОНОХРОМАТИЧЕСКАЯ ПЛОСКАЯ ВОЛНА 293
(см. E9.12)). Направим ось х вдоль ко, ось у вдоль Е
и ось z вдоль Н (при этом векторы Е, Н и к0 будут
образовывать правовинтовую последовательность).
Тогда Еу = ±Е9 EX = ES = О, Dy = ±D, DX^DZ = О,
#г = ±#, #, = #,, = 0, Вг = ±?. B*==B,, = 0. Вид-
Видно, что при таком выборе осей все недиагональные
компоненты тензора aik будут нулями. Поскольку
ExDx и НХВХ равны нулю, получим, что
Так как Я^ = ED, а #„?, = 0э то
(согласно G2.18) ED = НВ). Аналогично
Таким образом, при сделанном нами выборе коор-
координатных осей отлична от нуля лишь одна компонента
максвелловского тензора натяжений — компонента
Охх—, причем она равна плотности энергии волны w9
взятой с обратным знаком. Напомним, что в соответ-
соответствии с тем, как это принято в подавляющем боль-
большинстве руководств по электродинамике, мы опреде-
определили тензор out так, чтобы он характеризовал поток
импульса, не вытекающий из данного объема, а вте-
втекающий в этот объем (см. § 59). Это равнозначно из-
изменению направления нормали к площадке на проти-
противоположное. Таким образом, поток импульса, перено-
переносимого в направлении оси х через перпендикулярную
к этой оси площадку df, определяется положительной
величиной: охх{—df) = wdf.
% 73. Монохроматическая плоская волна
Волна, у которой поле в каждой точке изменяется
со временем по гармоническому закону (т. е. по за-
закону косинуса), называется монохроматической.
Для монохроматической волны решение уравнения
G1.11) имеет вид
4'i). G3 Л)

294 ГЛ. ХШ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
где а — величина, ке зависящая от f, i?i — функция
от г. В этом случае d2f/dt2 = —со2/. Подстановка этого
значения в Gl.ll) приводит к уравнению
которое определяет зависимость / от г.
Введем величину
G3.2)
fff-ko, G3.3)
называемую волновым вектором (ко —орт направле-
направления, в котором распространяется волна). Тогда урав-
уравнение G3.2) можно написать следующим образом:
д/4-?2/ = 0. G3.4)
В дальнейшем мы ограничимся рассмотрением пло-
плоской монохроматической волны. Выберем ось х в на-
направлении распространения волны. Тогда уравнение
J[73.4) примет вид
g G3.5)
Решением этого уравнения будет функция
f = acos(±A* + iJ>2), G3.6)
где а — величина, не зависящая от х, ф2 — функция
от t.
Выражения G3.1) и G3.6) можно согласовать,
положив
f = a cos (Ш ±kx + a), G3.7)
где а и а — величины, ке зависящие ни от t, ни от х.
Разные знаки перед kx отвечают разным направле-
направлениям распространения волны. Мы будем рассматри-
рассматривать волны, бегущие в направлении возрастания х,
в связи с чем будем писать перед kx знак минус.
При произвольном выборе координатных осей фор-
формула G3.7) переходит в
f = a cos (iut — kr -f- a). G3.8)
По такому закону изменяется любая величина, харак-
характеризующая монохроматическую плоскую волну, в

§ 73. МОНОХРОМАТИЧЕСКАЯ ПЛОСКАЯ ВОЛНА 205
частности, и векторный потенциал А. Таким образом,
имеем
А = Ао cos (erf — кг + а). G3.9)
Здесь Ао—-амплитуда, ш — частота, к-—волновой век-
вектор, а — начальная фаза волны.
Выражение (©/—кг+а), которое называют фазой
волны, есть инвариант. Действительно, тот факт, что
поле в данной точке пространства в данный мо-
момент временя приняло, например, нулевое значение
t(cos(©f — kr -f~a) = 0), не может зависеть от выбора
системы отсчета. Отсюда следует, что для двух произ-
произвольно выбранных систем отсчета должно выполнять-
выполняться условие
arf - кг + a = ©Y — kV + a'.
Если положить * = 0 и г=0, то, как вытекает из
преобразований Лоренца, будут равны нулю также f
и г'. Следовательно, должно быть a — af = inv, из
чего заключаем, что и величина
Ф = ©/ — кг, G3.10)
которую также называют фазой, является инвари-
инвариантом.
В случае электромагнитной волны, распространяю-
распространяющейся в вакууме, фаза G3.10) может быть представ-
представлена в виде
ф = i (d) — kr = ±jp — kr. G3.11)
Поскольку Ф есть инвариант, из G3.11) следует, что
&/с и к образуют четырехмерный волновой вектор
G3Л2)
Это обстоятельство позволяет найти закон преоб-
преобразования частоты волны <о при переходе от одной
инерциальной системы отсчета к другой. Согласно
первой из формул C6.1)
откуда после подстановки значений k* = <o/c, kl =
= kx = (©/с) cos d (d — угол между направлением

296 ГЛ. ХШ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
распространения волны и осью х), р = v/c (v — ско-*
рость системы /С' относительно системы К) находим, ^
ц/_ О {I ~ (У/С) COS ft)
Из этой формулы при # = 0 получается формула
для продольного эффекта Доплера
При * = я/2 приходим к формуле для поперечного
эффекта Доплера
VI - v2jc2
Отметим, что, поскольку модуль волнового вектора
есть ©/с, квадрат 4-вектора kP равен нулю:
Обратимся снова к выражению G3.9). Его можно
представить в виде
А = Re {Aoexp [I (<ot - кг)]} = Re {A}, G3.13)
где Ао—постоянный комплексный вектор
> G3.14)
а А — комплексный вектор, стоящий в фигурных скоб-
скобках (ср. с A6.9) и A6.10)).
Изменение знака при показателе степени выраже-
выражения вида ехр(п|>) не изменяет вещественной части этого
выражения. Поэтому формулу G3.13) можно напи-
написать следующим образом:
А = Re {Аоexp [i (кг - ©0]} = Re {A}. G3.15)
В этом случае под фазой волны нужно понимать вы-
выражение, отличающееся от G3.10) знаком. Кроме
того, следовало бы изменить знак в аргументе экспо-
экспоненты G3.14). Однако ввиду произвольности а этого
можно не делать.
Выражение G3.15) оказывается в некоторых отно-
отношениях удобнее выражения G3.13) и, кроме того,

§ 73. МОНОХРОМАТИЧЕСКАЯ ПЛОСКАЯ ВОЛНА 297
имеет больше сходства с волновой функцией, описы-
описывающей движение свободной частицы в квантовой Ме-
Механике.
Легко убедиться в том, что производя над опреде-
определяемой формулой G3.15) величиной А линейные опе-
операции, например дифференцирование, можно осуще-
осуществлять эти операции над комплексным вектором А
и затем брать вещественную часть получившейся ве-
величины. Так, например,
— J = Re {—- шА). G3.16)
Вычислим ротор вектора А. Взятие ротора есть ли-
линейная операция. Поэтому
[VA] = Re {[vA]} = Re {[V, Ao exp (* (kr - <ot))]} =
= Re{Vexp(?(kr-<oO), Ao}. G3.17)
Поскольку kr = Yt kfXf,
^ exp (/ (kr - со/)) = ikt exp (/ (kr - Ш)).
Следовательно,
V exp (* (kr — ©0) = i exp (* (kr ¦— со/))
Подставив это значение градиента в G3.17), получим
[VA] = Re {[/к ехр (/ (кг - ©/)), Ао]} =
= Re{[ik, Aoexp(i(kr~<oO)]} = Re{/[kA]}. G3.18)
Теперь мы можем написать выражения для полей
J G319)
В = [vA] = Re {i [kA]} G3.20)
(если бы мы исходили из выражения G3.13), в по-
последних двух формулах появился бы знак минус). Из
сравнения этих двух выражений заключаем, что век-
векторы В и Е колеблются в одинаковой фазе.

298 ГЛ. ХШ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Приняв во внимание, что к = (со VW^) ^o> Ф°Р"
мулу G3.20) можно представить в виде
Второй множитель в векторном произведении есть Ё
(см. G3.19)). Таким образом, для вектора В, веще-
вещественная часть которого дает В, получается соотно-
соотношение
B = V^[feoE]. G3.21)
Введя обозначение i (щ'с) Ао — Ёо, выражение
G3.19) можно представить в виде
Е = Re {Ёо ехр (/ (кг - ©0)}. G3.22)
Если ось х направить вдоль вектора к, то вектор Е,
а значит, и Ёо будут лежать в плоскости уг. Позтому
Ёо можно представить как линейную комбинацию ор-
ортов еу и е2:
где | и ц — комплексные числа.
Покажем, что при надлежащем выборе а послед-
последнее выражение можно преобразовать следующим об-
образом:
>ехр(-т), G3.23)
где ?#о и Его — вещественные величины. Для этого на-
напишем для квадрата вектора Ёо, который, вообще го-
говоря, является комплексным числом, выражение
Ёо = вещественное число • ехр (—2/а)-
Представим вещественное число в виде квадрата
некоторой векторной величины. Этой величиной может
быть не только вещественный вектор, но также и
комплексный вектор а ± ih при условии, что а и Ь
взаимно перпендикулярны. Действительно, в случае,
когда аЬ = 0,
(а + /bJ = a2 -f 2тЬ + Ь2 = а2 + Ь2 =
«= вещественное число.

§ 73. МОНОХРОМАТИЧЕСКАЯ ПЛОСКАЯ ВОЛНА 299
Таким образом, мы получили выражение
откуда
Ео = (а + tb) exp (- la) (a ± Ь).
Направив ось у вдоль вектора а, а ось z — вдоль век-
вектора Ь, придем к формуле G3.23).
Подставим выражение G3.23) в формулу G3.22):
Е = Re {(RgQty + №л) exp (— I (mt — kx + a))}
(при выбранных нами направлениях осей kr =
Отсюда
Еу = EyQCos (mt — kx -f a), Ez — E& sin (cirf — kx + a).
G3.24)
Из этих формул следует, что
i?- + -iiB=I. G3.25)
Все рассуждения и формулы, начиная с G3.22),
справедливы и для вектора В.
Полученный нами результат означает, что вектор Е
вращается в плоскости, перпендикулярной к направ-
направлению распространения волны, описывая своим кон-
концом эллипс (аналогично ведет себя и вектор В). На-
Направление вращения зависит от того, какие (одинако-
(одинаковые или разные) знаки имеют Еу0 и Ez0 в формулах
G3.24). Такая волна называется эллиптически-поля-
ризованной. При ЕУо = ±Ег0 эллипс G3.25) превра-
превращается в окружность. В этом случае волна поляризо-
поляризована по кругу. Наконец, может случиться, что одна
из величин Ёуо и Ег0 равна нулю. Тогда вектор Е
(а также и В) направлен все время вдоль одной и
той же прямой. Волна в этом случае называется ли-
линейно-поляризованной или плоско-поляризованной.
Итак, монохроматическая волна обязательно поля-
поляризована (эллиптически, по кругу или линейно). Это
означает, что колебания в волне упорядочены тем или
иным способом.

300 гл. хш. электромагнитные волны
§ 74. Плоская монохроматическая волна
в проводящей среде
Уравнения G1.7) и 'G1.8) были получены в пред-
предположении, что в среде отсутствуют избыточные сво-
свободные заряды (р = 0) и токи проводимости (j = 0).
В предыдущем параграфе мы установили, что в слу-
случае плоской монохроматической волны решением
уравнения G1.7) является функция G3.9) с постоян-
постоянной амплитудой. Независимость амплитуды от коор-
координат означает, что распространение плоской волны
в диэлектрике не сопровождается изменением ее ин-
интенсивности.
Теперь допустим, что среда обладает электропро-
электропроводностью <х, так что в ней могут возникать токи про-
проводимости j, равные аЕ. Избыточные свободные за-
заряды будем по-прежнему считать отсутствующими
(р=0). При сделанных нами предположениях урав-
уравнения Максвелла E5.10) и E5.11) запишутся следую-
следующим образом:
[VEJ---J-U-. VB = 0; G4.1)
[VB]—*aL <* + -»-?. VE==O G4.2)
(мы заменили j через сгЕ).
Возьмем ротор от первого из уравнений G4.1):
f^ G4.3)
Согласно (XI.45) [V[VE]] = V(VE) —ДЕ. Но VE = 0,
так что остается только второй член, равный —АЕ.
Заменим им левую часть уравнения G4.3). Кроме
того, подставим в правую часть этого уравнения зна-
значение [VB] из G4.2). В результате получим
ер, д2Е
Напишем это уравнение следующим образом:
Уравнение G4.4) называется обобщенным волно-
волновым уравнением. Оно отличается от уравнения G1.9)
дополнительным слагаемым, содержащим первую

§ 74. МОНОХРОМАТИЧЕСКАЯ ВОЛНА В ПРОВОДНИКЕ 301
производную искомой функции по времени. При 0=0
это слагаемое исчезает и уравнение G4.4) переходит
в G1.9).
Считая волну монохроматической, будем искать
решение уравнения в виде
Е = Re {Е (г) ехр (- Ш)} — Re {Ё}, G4.5)
где Ё(г)—комплексная векторная функция от г, Ё—»
функция, стоящая в фигурных скобках. Дифференци-
Дифференцирование функции G4.5) по t дает
л2Р . л G4.6)
?i = Re {- ш2Е (г) ехр (- Ш)} = Re {- ©2Е}.
Подстановка в уравнение G4.4) значений G4.5)
и G4.6) приводит после сокращения на общий мно-
множитель ехр (—Ш) к следующему дифференциальному
уравнению для Ё(г):
> = 0. G4.7)
Умножим числитель и знаменатель в третьем слагае-
слагаемом на ею и заменим гумР/с2 через k2 (см. G3.3)).
В результате, объединив второе и третье слагаемые,
получим уравнение
АЁ (г) + к2 A + i ^) Ё (г) = 0. G4.8)
При а — 0 это уравнение переходит в уравнение вида
G3.5).
Представим коэффициент при Е(г) в уравнении
G4.8) в виде квадрата комплексного волнового числа
П, = ki -f- ik2:
Приравняв вещественные и мнимые части, придем
к системе двух уравнений для k\ и Jfe2:
>. G4.9)

gO2 ГЛ. XIIL ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Решение этой системы имеет вид
G4.10)
В случае, если Dпа/г®J < 1 (т. е. при малой а и
большой (о), формулы G4.10) сильно упрощаются:
величину k\ можно принять равной k, а в выражении
для k2 положить Vl + Dзш/есоJ « 1 + A/2)Dяа/е©J,
в результате чего для fe2 получится значение 2жт&/е(©.
Таким образом, при малой проводимости и большой
частоте
k = k + /2шт?/е©. G4.11)
Итак, уравнение G4.7) можно представить в виде
?Ё=0, G4.12)
где Ъ = &i + *&2 — комплексная величина, веществен-
вещественная и мнимая части которой определяются форму-
формулами G4.10).
Рассмотрим плоскую волну. Ось х выберем в на-
направлении распространения волны. Тогда Е(г) будет
зависеть только от х и уравнение G4.12) упростится
следующим образом:
Решением этого уравнения будет функция
Ё(г) = Ёоехр(±/Ь:), G4.13)
где Ёо — постоянный комплексный вектор. Знаки плюс
и минус соответствуют разным направлениям распро-
распространения волны. Нас будут интересовать волны, бе-
бегущие в направлении оси х. Поэтому мы возьмем в
экспоненте знак «+» (зависящий от / множитель мы
написали в виде ехр(—• Ш)).
Подставив найденное нами решение G4.13) в
G4.5), получим следующее выражение для Е:

§ 74. МОНОХРОМАТИЧЕСКАЯ ВОЛНА Б ПР0&0ДНШШ ВОЗ
Представим в этой формуле комплексный век-
вектор Ёо в виде Еоехр(—/а), где Ео — вещественный
постоянный вектор. Кроме того, выразим комплексное
число k через его вещественную и мнимую части (J? =
= k% + flfe2) • В результате получим
Е = Re {Бо ехр (— ia) exp (/ {kx -f ik2) х) ехр (— Ш)}.
Запишем это выражение следующим образом:
Е === Re {Eoexp(— fe2x)exp{— i(mt — kxx + а))}. G4.14)
Взяв вещественную часть выражения в фигурных
скобках, получим
Е = Ео ехр (— k2x) cos {ш — kxx + a). G4.15)
Выражение G4.15) описывает волну, амплитуда
которой убывает по закону ехр(—k%x). Фазовая ско-
скорость этой волны равна
о—-?-. G4.16)
Таким образом, вещественная часть комплексного вол-
волнового числа k определяет фазовую скорость волны,
а мнимая часть — затухание волны.
Согласно G4.10) при малом затухании k\ »
« k = (g>/c) V8f*> a коэффициент затухания
<74Л7>
Получим решение уравнения G4.7) еще одним
способом. Представим это уравнение в виде
Если ввести комплексную диэлектрическую проницае-
проницаемость
можно написать
Умножим это уравнение на ехр(—Ш) и примем
во внимание, что ш2Ё(г)ехр(— ш*)= — д*Ё/дР9 где

304 ГЛ. XIII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Б = Е(г) ехр(—Ш) (см. G4.6)). В итоге придем
к уравнению
АЕ-4МйГ-0, G4Л9)
отличающемуся от уравнения G1.9) лишь тем, что
напряженность электрического поля и диэлектриче-
диэлектрическая проницаемость являются не вещественными, а
комплексными. Поле Е представляет собой веществен-
вещественную часть решения уравнения G4.19).
Решение уравнения G1.9) мы кашли в предыду-
предыдущем параграфе, оно имеет вид
Е = Re {Еоехр (~ * (©/ — kx + а))} = Re {§},
где k = Vер, (й/с (волна предполагается бегущей в на-
направлении оси х). Следовательно, при вещественной е
решением уравнения G4.19) является функция
Е = Еоехр(- i((ot — kx + a)). G4.20)
Замена вещественной е комплексной не изменяет
вида решения. Однако вещественное волновое число k
должно быть заменено в ней комплексным числом,
определяемым по формуле
? = kx -f ik2 = V^a Ф, G4.21)
где в — величина из G4.18). Подстановка в формулу
^G4.20) вместо k комплексного числа й = k\ + ik% при-
приводит к выражению, совпадающему с G4.15).
С учетом G4.18) квадрат комплексного числа
G4.21) равен
, 2 I \ i_ •
' /v 1 1 I *
V
8(9 С2 V 8<д
Это значение совпадает с й2, стоящим в формуле
G4.8).
Таким образом, в случае проводящей среды и вол-
волновое число, и диэлектрическая проницаемость стано-
ьлтся комплексными. Комплексным будет также по-
показатель преломления A = V^- Запишем его в виде
п -f ft* — V^i* = V(e + '4na/®)l*' G4.22)

§ 74. МОНОХРОМАТИЧЕСКАЯ ВОЛНА В ПРОВОДНИКЕ 305
Возведем это соотношение в квадрат:
(п + Ы? = п2-х2 + 2inn = (е + /4я<у/ю) \i =
— ер, + Мястец/ше.
Приравняем вещественные и мнимые части:
п2 —• х2 = вц, 2пу, = 4яоге|х/8ю.
Получившаяся система уравнений тождественна
с системой G4.9). Поэтому ее решения можно найти,
заменив в формулах G4.10) k2 через ер. В результате
получим
G4.23)
2
Сопоставление формул G4.10) и G4.23) дает, что
= i%, fc2 =-JL-x-r—х G4.24)
{k мы определили как со \)
Подставив значение G4.24) для k\ в формулу
G4.16), придем к соотношению
v == —
из которого следует, что вещественная часть комп-
комплексного показателя преломления п есть обычный по-
показатель преломления среды п. Вторая из формул
G4.24) показывает, что мнимая часть А пропорцио-
пропорциональна коэффициенту затухания волны (x°°^2).
До сих пор мы говорили об электрическом поле
волны. Магнитное поле можно получить из соотноше-
соотношения G3.21), подставив в него комплексное значение
диэлектрической проницаемости и комплексную функ-
функцию Ё. Согласно G4.14)
Е = Ео ехр (— k2x) ехр (— / (©/ — kxx + a)).
Следовательно,
В = V^Ja [ко, Ео ехр (— k2x) ехр (— / (Ы — k{x + о))].

3Q6 ГЛ. XIII. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Комплексное число л/щ можно представить в виде
VIS = п + Ы == V^+l?exp (nf)).
где ф = arctg(«/n). Воспользовавшись этим, можно
написать формулу
B=V'?+k* №о» Ео ехр (— й2*) ехр (— / (ев/ — kxx+a—^))]
из которой видно, что колебания векторов В и Е про-
происходят не в одинаковой фазе (как это было в ди-
диэлектрике), а с разностью фаз ф, определяемой выра-
выражением
-~. G4.25)
Соотношение между амплитудами электрического
и магнитного полей определяется формулой
Во =
которая после подстановки значений G4.23) для п и %
принимает вид
Во = Ео Vefl У1 + Dясг/8соJ G4.26)
(ср. с G3.21)).
§ 75. Немонохроматические волны1)
Всякую немонохроматическую волну можно пред-
представить как суперпозицию монохроматических волн
различных частот. Эта операция называется спек-
спектральным разложением волны.
Если поле волны описывается строго периодиче-
периодической функцией, оно может быть разложено в ряд
Фурье. В этом случае спектральное разложение со-
содержит частоты, образующие дискретный ряд значе-
значений: соьш^шз, ••• Частоты юя (пФО) являются це-
целыми кратными основной частоты ©о, т. е. о)„ = жоо.
Основная частота определяется периодом Т функции,
описывающей поле: со0 = 2я/7\
Рассмотрим плоскую немонохроматическую волну,
распространяющуюся в вакууме в положительном на-
*) Прежде чем приступить к чтению этого параграфа, сле-
следует ознакомиться с Приложением XIV.

§ 75. НЕМОКОХРОМАТИЧЕСКИЕ ВОЛНЫ 307
правлении оси х* Любая величина, характеризующая
такую волну (Е, В и т. д.), описывается функцией
f^fQ-xjc) G5.1)
(см. G2,8)). Зафиксировав дс, мы получим функцию
от t, описывакщую колебания поля в данной точке.
По предположению эта функция является строго пе-
периодической. Пусть период ее равен Т:
Согласно (XIV. II) f{t) можно представить в виде
?
f@- ? Слехр(-/#шо0, G5.2)
где Сп — константа, вычисляемая по формуле
Ч-Г/2
\
-Г/2
(см. (XIV. 14)).
Согласно формуле (XIV. 15) разложение функции
f (t) можно представить также в виде
/@= I Cnexp(inmot). G5.3)
Лея ОО
Средняя интенсивность волны пропорциональна
среднему значению квадрата Е или В, т. е. пропор-
пропорциональна выражению
+г/2/ +о° \
= T ) f ? Слехр(-/то0/))х
-Г/2 \l= оо '
)/. G5.4)
Подынтегральное выражение равно [f(t)]2. Один из
множителей мы взяли в виде G5.2), второй — в виде
G5,3), причем во второй сумме немой индекс обозна-
обозначили буквой m вместо п.

308 ГЛ. ХШ. ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ
Преобразуем выражение G5.4) следующим об-
образом:
m-f ) exp(i(m-n)%t)dt
n, m=*-oo —Г/2
Я, /71—-ОО
G5.5)
(мы воспользовались ортогональностью системы функ-
функций ехр(тюоО; см. (XIV. 13)).
Полученный нами результат означает, что средняя
интенсивность немонохроматической волны слагается
из интенсивностей монохроматических компонент.
Теперь рассмотрим случай, когда волна, а следо-
следовательно, и колебание f (t) существуют в течение огра-
ограниченного промежутка времени (а не от *==—оо до
f = -fcx>). В этом случае f(t) не является периодиче-
периодической и может быть разложена не в ряд, а в интеграл
Фурье, содержащий непрерывный ряд различных час-
частот. Согласно (XIV. 22)
=- \ C.exp(-toO«fo, G5.6)
где Сю — функция частоты <о, определяемая выраже-
выражением v)
+оо
\ G5.7)
(см. (XIV. 21)). Очевидно, что
С-^С G5.8)
*) Обычно в формуле G5.7) переменную интегрирования
обозначают буквой t. Мы обозначили ее другой буквой, чтобы
подчернуть, что С<» есть величина, не зависящая от /.

§ 75. ИЕМОНОХРОМАТИЧЕСКИЕ ВОЛНЫ 309
Полная интенсивность волны за время от —оо до
+°о определяется выражением
[f(t)]2dt= J f(t)f(t)dt.
Замена одного из сомножителей выражением G5.6)
дает
+ ОО
В полученной нами формуле предполагается интегри-
интегрирование сначала по со, затем по t. Изменим порядок
интегрирования, т. е. напишем
+ 0О ^ +ОО
+ 0О ^ +О
Сравнение с G5.7) показывает, что интеграл, стоя-
стоящий внутри фигурных скобок, представляет собой
С_ю, т. е. С^. Следовательно,
+ ОО -f ОО ОО
h= \ CmCmd*= \ IC.pdB^JlC.p*». G5.9)
О
Из полученной нами формулы вытекает, что вели-
величина | C^}2 характеризует долю полной интенсивно-
интенсивности, приходящуюся на единичный интервал частот.
В качестве примера поля, которое может быть раз-
разложено в интеграл Фурье, можно привести излучение
заряда, испытывающего торможение.

Глава XIV
ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
§ 76. Запаздывающие потенциалы
В предыдущей главе мы предполагали, что заряды
и токи отсутствуют, в связи с чем правую часть в
уравнениях Даламбера G1.2) и G1.3) полагали рав-
равной нулю. Теперь займемся изучением переменных по-
полей при наличии произвольно движущихся зарядов.
В этом случае потенциалы поля удовлетворяют урав-
уравнениям
^^ G6.1)
4л
Из теории линейных дифференциальных уравне-
уравнений известно, что общее решение неоднородного урав-
уравнения равно сумме общего решения однородного урав-
уравнения и частного решения неоднородного уравнения.
Общие решения однородных уравнений были исследо-
исследованы в предыдущей главе. Поэтому, чтобы получить
общее решение уравнений G1.1) и G1.2), достаточно
найти их частные решения.
Разделим все пространство, в котором имеются
заряды и токи, на элементарные объемы dV и опре-
определим поле, создаваемое каждым из зарядов de, за-
заключенных в данном dV'. Вследствие линейности
уравнений искомое поле будет суперпозицией полей
создаваемых всеми зарядами de.
Заряд de, заключенный в данном элементарном
объеме dV\ есть, вообще говоря, функция времени:
de = de(t). Если отвлечься от наличия других заря-
зарядов de, то плотность заряда, обусловленную рассмат-
рассматриваемым точечным зарядом, можно представить

§ 76. ЗАПАЗДЫВАЮЩИЕ ПОТЕНЦИАЛЫ 311
в виде
p'(r,t) = de(tN(r-r% G6.3)
где г' — радиус-вектор, определяющий положение за-
заряда de(t). Мы обозначили эту плотность символом
р', чтобы отличить ее от плотности р(г, t), определяю-
определяющей de(t) по формуле de(t) — p{rt t)dV.
Подстановка выражения G6.3) в уравнение G1.3)
дает
Й - -4я de (t) 6 (R), G6.4)
где R = г — г'.
Во всех точках, кроме той, для которой R = О,
плотность р' = 0 и уравнение G6.4) имеет вид
Дф--рг$—0. G6.5)
Очевидно, что в этом случае поле обладает централь-
центральной симметрией относительно точки R = 0 и, следо-
следовательно, является функцией лишь R. Поэтому напи-
напишем уравнение G6.5) в сферической системе коорди-
координат. Воспользовавшись выражением (XI. 88) для опе-
оператора Лапласа, получим
Будем искать решение в виде
Ф = *(/?, О/Я- G6.7)
При этом условии
i? ¦ I а*
dR ~ R2 "^ R OR •
» + *«)-

312 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Подстановка этих значений в уравнение G6.6) приво-
приводит после сокращения на 1/R к уравнению !)
OR2 с2 dt2 ~u'
Как было установлено в § 72, общее решение та-
такого уравнения имеет вид
) ( ) G68)
(см. формулу G2.8); в рассматриваемом нами сейчас
случае л= 1).
Первое слагаемое в G6.8) описывает расходя-
расходящуюся сферическую волну, второе слагаемое описы-
описывает сферическую волну, сходящуюся к точке R = 0.
Нас интересует частное решение. Возьмем в качестве
такого решения первый член формулы G6.8). Под-
Подставив его в G6.7), найдем выражение для <р:
G6.9)
Решение G6.9) удовлетворяет уравнению G6.5)
при произвольном выборе функции f(t — R/c). Попы-
Попытаемся выбрать эту функцию так, чтобы выражение
G6.9) удовлетворяло уравнению G6.4) и в точке
R = 0. Заметим, что при /?->0 функция G6.9) стре-
стремится к бесконечности. Следовательно, ее производ-
производная по координатам становится для малых R очень
большой, так что членом A/с2) (d2y/dt2) можно пре-
пренебречь по сравнению с Аф и написать уравнение
G6.4) в виде
Мы пришли к уравнению Пуассона D2.4) для по-
потенциала точечного заряда. Таким образом, вблизи
точки R = 0 функция G6.9) должна переходить в вы-
выражение вида ф = e/R. Это будет иметь место, если
положить f(t — Rfc) — de(t — R/c). Итак, искомое ре-
решение имеет вид
*) Напомним, что точка, для которой R « 0, пока исклю-
исключена из рассмотрения.

§ 76. ЗАПАЗДЫВАЮЩИЕ ПОТЕНЦИАЛЫ 313
Очевидно, что в непосредственной близости к точке
R = 0 это выражение переходит в
Чтобы найти потенциал для произвольного распре-
распределения зарядов, описываемого функцией р(г, /), про-
просуммируем решение G6.10) по всем de = pdV'. Тогда
получим
G6.11)
Уравнение G6.2) отличается от G6.1) лишь тем,
что в правой части вместо функции р стоит j/c. По-
Поэтому можно сразу по аналогии с G6.11) написать
выражение для А:
(
A(r,0—J-1— |г-г-| • С76.12)
Выражения G6.11) и G6.12) называются запаз-
запаздывающими потенциалами. Название обусловлено
тем, что значения потенциалов в момент времени t
определяются значениями р и j в более ранние мо-
моменты времени, опережающие t на время запаздыва-
запаздывания т = |г— г'|/с, необходимое для того, чтобы элек-
электромагнитное возмущение дошло от точки г' в точку г.
Чтобы получить общее решение уравнений G6.1)
и G6.2), нужно к запаздывающим потенциалам при-
прибавить общие решения однородных уравнений, кото-
которые были найдены в предыдущей главе. Эти решения
не связаны с полем, возбуждаемым системой. Они
описывают внешнее поле, действующее на систему и
накладывающееся на поле, создаваемое системой.
В стационарном случае (т. е. в случае, когда р и j
не изменяются со временем) формулы G6.11) и
G6.12) переходят соответственно в выражения D1.10)
и D8.7).
Отметим, что, выбрав в качестве частного решения
функцию f2 (см. G6.8)), мы получили бы вместо за-
запаздывающих опережающие потенциалы. Подробнее
на этом мы останавливаться не будем.

314 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
§ 77. Поле равномерно движущегося зарвда
Пусть заряд е движется с постоянной скоростью v
относительно системы отсчета К. Свяжем с зарядом
систему отсчета /('. Эта система, как и заряд, дви-
движется относительно системы К со скоростью v.
Относительно системы К' заряд покоится. Следо-
Следовательно, потенциалы поля в этой системе равны
9(^0 = 7' А (г', 0 = 0. G7.1)
Самым общим решением было бы А = const, но в
силу калибровочной инвариантности эту константу
можно положить равной нулю.
Чтобы найти потенциал в системе К, осуществим
преобразование 4-вектора
Л* = (<р, А)
к системе К. Для этого нужно взять формулы обрат-
обратного преобразования C6.2), согласно которым
а _ Ф (г\ П + $АХ (г', П _ Ф (г', П
РФ {*'* П 4- Ах (г', Г) Рф (г", П
>" ^^P =
Подставив в эти формулы значение G7.1) для <р, по-
получим
Поскольку отлична от нуля лишь компонента Ах,
а вектор v направлен по оси х, выражение для век-
векторного потенциала можно записать так:
G7-3)
Теперь нужно перейти в формулах G7.2) и G7.3)
от штрихованных координат (т. е. от г') к нештрихо-

§ 77. ПОЛЕ РАВНОМЕРНО ДВИЖУЩЕГОСЯ ЗАРЯДА 316
ванным. Согласно преобразованиям Лоренца C5.14)
.j X—Vt ,
Следовательно,
=V[(*-^o/Vi-p212+!/2+
Подстановка в G7.2) и G7.3) дает
Ф(г, 0 = -
е
- ЫJ + (\- Э2) (у2 + i
ev
г2). G7.4)
-. G7.5)
W G7-6)
Сравнение G7.5) с G7.6) показывает, что между
потенциалами имеется соот-
соотношение
Тот
А =
G7.7)
Формулы G7.5) и G7.6)
можно упростить, выразив
их через длину вектора R,
проведенного от заряда в
точку наблюдения, и угол Ф
между направлением этого Рис. 77.1
вектора и осью х. Если от-
отсчет времени начать с момента, когда заряд был в
рачале координат, то, как видно из рис. 77.1,
Поэтому согласно G7.4)
1
'\ -§2

316 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Отношение (y2 + z2)/R2 равно sin2fl (см. рис. 77.1),
Следовательно,
r' = -^WVl-4
ч-р2
Подставив это значение в G7.2) и G7.3), получим:
ф= п „ 1. ,А. G7-8>
А = . ev . G7.9)
cR л/l - р2 sin2 G
Зная потенциалы, можно по формулам:
e = -v<p-4-|t' ^77Л°)
G7.11)
(см. E6.3) и E6.1)) вычислить поля Е и В. Записав
G7.10) в компонентах, получим
F - <?Ф 1 dAj
c'i~ dxi с dt '
Следовательно,
Р __^Ф. LM*.— _^2 1 д
с*~ дх с dt ~ дх с dt
Согласно G7.5) и G7.6) ф и А имеют одинаковый
вид
а
'(Г, О —
где а—константа (скалярная или векторная). Обо-
Обозначив х — vt = ?, можно написать, что
д* а| ддр ~ d| ' dt — дЪ dt
откуда заключаем, что

§ 77. ПОЛЕ РАВНОМЕРНО ДВИЖУЩЕГОСЯ ЗАРЯДА 317
Заменив в G7.12) dyfdt согласно G7.14), придем
к формуле
G7.15)
Подстановка производных по координатам от вы-
выражения G7.5) в формулы G7.15) и G7.13) дает
G716)
Эти формулы можно записать в векторном виде
где R — радиус-вектор, проведенный из точки, где на-
находится заряд, в точку наблюдения (см. рис. 77.1).
Для модуля Е имеем
?-/?2A_ ^„2 0K/2- G7.18)
Из этой формулы вытекает, что на оси, вдоль которой
движется заряд (т. е. при # = 0 ил),
G7.19)
а в направлениях, перпендикулярных к скорости за-
заряда (т. е. при Ф = я/2),
? = / G7.20)
Поле как бы сплющивается в направлении движения
заряда, причем тем сильнее, чем больше v.
Найдем магнитное поле. Согласно G7.11) и G7.7)
В - [VA] = [v, *f\ - ~- [УФ, v] - - 4- [v, УФ] G7.21)
(напомним, что v — константа).

318 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
В соответствии с G7.10)
-уфа~ fc + T —— E +
E (#7.^.2)
(мы приняли во внимание соотношение G7.7), а так-
также то обстоятельство, что скорость не зависит от /).
Подставим выражение G7.22) для — Щ в G7.21):
•-¦5-МЯ+-И». ?¦*]•
Второй член является векторным произведением кол-
линеарных векторов и, следовательно, равен нулю.
Таким образом,
B = 4-[vEl. G7-23)
с
Мы видим, что вектор В в каждой точке перпендику-
перпендикулярен как к вектору v, так и к вектору Е. На оси х
векторы v и Е коллинеарны. Следовательно, на этой
оси В = 0.
Если в формулу G7.23) подставить выражение
G7.17) для Е, получается
При о<с G7.24) переходит в формулу
В е
Заметим, что выражения G7.17) и G7.25) можно
получить с помощью формул преобразования полей
F2.2), исходя из того, что в системе К? Е' = &'//*,
В' = 0. Рекомендуем сделать это в порядке упраж-
упражнения.
§ 78. Поле заряда, движущегося произвольно
Найдем поле заряда, движущегося с ускорением.
Пусть движение происходит по траектории го = го(О
(рис. 78.1). Вычислим поле в точке наблюдения /\
определяемой радиусом-вектором г. Вследствие за-
запаздывания потенциалы в точке Р в момент t будут
определяться положением и скоростью заряда не в
тот же момент времени /, а в более ранний момент to.

§ 78. ПОЛЕ ЗАРЯДА, ДВИЖУЩЕГОСЯ ПРОИЗВОЛЬНО 319
Момент /о должен удовлетворять условию
сх = с (t — /л) = /? (D G8 I)
где R(to)—расстояние от точки, в которой находится
заряд в момент *0, ДО точки наблюдения Р. Запазды-
Запаздывание определяется временем т, которое требуется для
того, чтобы возмущение до-
дошло от точки Го (to) до точки Р.
Легко видеть, что сх и век-
вектор R(/o) образуют 4-вектор e^^J^^—^р
ie = {cx9 R). G8.2)
Действительно, 4-векторы
суть два 4-радиуса-вектора. Рка 7g.l
Вектор G8.2) равен разности
этих двух 4-векторов и, следовательно, сам является
4-вектором.
Из G8.1) вытекает, что квадрат 4-вектора G8.2)
равен нулю
Е0^р — Р2Х2 if — о GR $\
(это выражение есть по существу квадрат интервала
между событиями возникновения сигнала в одной
точке и прихода его в другую точку).
Свяжем с зарядом систему отсчета К'. В этой си-
системе заряд покоится и, следовательно, потенциалы
определяются выражениями
Ф' (г', О —Jr - ¦?-, А' (т\ Г) = 0, G8.4)
где г7 и f—место и время наблюдения, определенные
в системе К\ R' — расстояние между точкой, в кото-
которой находится заряд, и точкой наблюдения. Таким об-
образом, 4~потевциал поля в системе К' имеет вид
Попытаемся найти такое выражение для 4-потен-
циала, которое при v = 0 обращалось бы в выраже-
выражение G8.5). Очевидно, что в произвольно взятой
системе отсчета потенциалы должны зависеть от

320 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
скорости заряда v. Поскольку мы ищем четырехмер-
четырехмерное выражение потенциала, скорость нужно взять в
виде 4-скорости
Если положить 4-потенциал пропорциональным
4-скорости, то при v = 0 векторный потенциал А
также будет равен нулю. Далее, в знаменателе вре-
временной компоненты 4-потекциала G8.5) стоит времен-
временная компонента 4-вектора G8.2). Следовательно, в
знаменатель искомого выражения для А» следует вве-
ввести 4-вектор /?*\ причем для того чтобы получилась
правильная размерность, его нужно умножить на
4-скорость (в числитель мы уже ввели 4-скорость).
Таким образом, 4-потенциал нужно определить
следующим образом:
'-Тит (Ж6)
V
Подстановка значений /?v и uv дает, что
Следовательно, выражение G8,6) можно записать
в виде
ей1*
откуда
Нетрудно заметить, что при v = 0 выражение G8.7)
действительно переходит в G8.5).
Приняв во внимание, что ст = /?, запишем выра-
выражения потенциалов следующим образом:
O=(/?_eRp)fa, G8.8)
А (Г> f) = i
(мы применили обозначение 0 = v/c).

§ 78. ПОЛЕ ЗАРЯДА. ДВИЖУЩЕГОСЯ ПРОИЗВОЛЬНО 32!
Выражения G8.8) и G8.9) называются потенциа-
потенциалами Лиенара — Вихерта. Чтобы получить значения
потенциалов в момент времени tt значения v и R
в правых частях G8.8) и G8.9) нужно брать в мо-
момент to, определяемый условием
0 с с
Запишем это условие в виде
F(x, у, z, /, /0) = /-/0-
{[* - Хо (to)f + [у-уо (to)]2 + \г -
. _Оф
G8.10)
Правые части выражений G8.8) и G8.9) суть
функции от /о, которое в свою очередь есть функция
от *, у, z и / (х, у, z — координаты точки наблю-
наблюдения)
*о = /<*. У. *, t). G8,11)
Соотношение G8.10) представляет собой неявное вы-
выражение функциональной зависимости G8.11).
При нахождении полей по формулам
надо вычислять выражения вида ду/dxt, dk/dt и
dAk/дхц где xi — координата точки наблюдения. По-
Поскольку функции ф и А зависят от х, у, г, t сложным
образом — через to = f(xty,z,t), вычисления придется
производить по следующей схеме:
дф dq> dt0 ,-o ,m
дк dA dtp г7Л |qv
Ж~1Нр~~дГ' {(оло)
дАк _ дАк dtp GfK 14,
dxt —~dtp~ dxt ' l/o. l*|
Из соотношения G8.12) вытекает, что
fJ G8.15)
11 И. В, Савельев, т. I

322 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Таким образом, нам понадобятся значения произ-
производных dto/dxi и dto/dt9 которые можно найти с по-
помощью соотношения G8.10). Запишем это соотноше-
соотношение в виде
х х t П t t
= o. G8.16)
с
По правилам дифференцирования неявной функции
Продифференцировав G8.16) по tOt получим
dF _ %{Xt-Xoi)(dXoildto)
Приняв во внимание, что Xi — xoi = Rit a дхы/dto есть
/-я компонента скорости заряда в момент ?<ь придем
к выражению
Аналогичные вычисления дают
dxi — cR ' УЬЛЬ)
Разделив G8.18) на G8.17) и изменив знак на об-
обратный, получим
dxi c(R~ RP) •
откуда следует, что
Теперь найдем dio/dt. По правилу дифференциро-
дифференцирования неявной функции
dt ~ df/dt0 '
Производная функции F (см. G8.16)) по t равна еди-
единице: dF/dl — h Производная OF/dto определяется

§ 78. ПОЛЕ ЗАРЯДА, ДВИЖУЩЕГОСЯ ПРОИЗВОЛЬНО 323
выражением G8.17). Следовательно,
_^=а=___в G8.20)
Приступим к вычислению значений dq>fdto и
Согласно G8.8)
Из соотношений J? = с(/ — *0). R = г — Го (<о) выте-
вытекает, что
Кроме того, dfi/dto — Р = v/c, где v — ускорение за-
заряда в момент /0. Следовательно,
Согласно G8.9)
Подстановка выражения G8.2!) для dq>/dis и G8.8)
для ф дает
дА еср (I - р2 + RP'/c) , __?Р___ _
РA — Р2Ч- М/с) 4- (Р>) (/? - Щ) GЛ9*\
= се пГ=Ш * G8>22)
Наконец, мы получили возможность написать вы-
выражение для ?:
IS — V<p — c -gf — dt<> Wo c a<0 л
(см. формулы G8.15) и G8.13)). Подстановка сюда
выражений G8.21), G8.19), G8.22) и tG8.20) дзет
— « О - Р* + М/е) Г
~~ («-Rpf" L
. Р A - Р* + Rp/c) + (р/с) (Я -
е RP)8
A - Р2 + R
_
G8,23)

324 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Сгруппировав вместе члены, содержащие ускоре-
ускорение заряда v (т. е. р), можно привести выражение
для Е к виду
^_^ (R —/?Р)A — Р2) , ^ (RP/c) (R - R») - №с) (R - Rp)
Числитель второго слагаемого можно представить
в виде двойного векторного произведения [R[(R —
— ЯЭЬР/cJL в этом можно убедиться, раскрыв это
произведение по формуле «бац минус цаб» (см.
(VI. 5)). В результате получим окончательное выра-
выражение
р _,. « - ЯР) О - Р2) » r IR KR - *Р), Ь1с)\ ,7
Напомним, что значения R, р (т. е. v) и р (т. е. v)
в это формуле должны быть взяты в момент вре-
времени to = t — т.
Поле, описываемое выражением G8.24), состоит
из двух частей. Первая зависит только от скорости
заряда и на больших расстояниях убывает как I//?2
(т. е. как кулоновское поле). Вторая часть зависит,
кроме скорости заряда, также и от его ускорения и
на больших расстояниях убывает как \/R (т. е. как
напряженность поля в сферической электромагнитной
волне).
Если заряд движется равномерно, второе слагае-
слагаемое в формуле G8.24) обращается в нуль и поле
определяется следующим выражением:
Е _ (Rq~/?oP)(l-P2) Gg 25)
* (Яо-RoP)8 ' (/bZ)
Здесь индекс «О» при R подчеркивает то обстоятель-
обстоятельство, что значение R берется в момент времени to,
при р индекс «О» мы не поставили, поскольку при
равномерном движении р не зависит от t.
В § 77 мы получили для поля равномерно движу-
движущегося заряда формулу G7.17), которую можно за-
записать в виде
Е в е J4^^?7^W' G8'26)
Внешне формулы G8.25) и G8.26) сильно отличаются
друг от друга. Однако легко показать, что на самом

§ 78. ПОЛЕ ЗАРЯДА, ДВИЖУЩЕГОСЯ ПРОИЗВОЛЬНО 325
деле они тождественны. Дело в том, что в формуле
G8.25) поле выражено через расстояние от заряда до
точки наблюдения, взятое в момент времени to—t — т.
В формуле же G8.26) поле выражено через расстоя-
расстояние от заряда до точки наблюдения, взятое в момент
наблюдения t.
Чтобы доказать тождественность формул G8,25)
и G8.26), обратимся к рис. 78.2. Расстояние ОР есть
/?о, еР равно R, отрезок Ое есть путь, проходимый за-
зарядом за время запаздывания т. Приняв во внимание,
что т = Ro/c, этот путь можно представить в виде J?op.
Векторы Ro, R и i?op связаны соотношением R =
= Ro — i?oP> из которого следует тождественность чис-
числителей формул G8.25) и G8.26).
Длина отрезка OQ равна проекции вектора
на направление вектора Ro
Следовательно,
G8.27)
(ср. со знаменателем формулы G8.25)).
Выразим отрезок QP через R. Из рис. 78.2 видно,
что
(QPf = #2 _ ь2 = R2 - (J?op sin aJ.
Далее, опять-таки из рисунка следует, что /?osina =
= R sin Ф, так что
откуда
G8.28)

326 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Наконец, приравняв правые части выражений
G8.27) и G8,28), придем к соотношению
из которого следует тождественность знаменателей
формул G8.25) и G8.26). Таким образом, мы пока-
показали тождественность выражений G8.25) и G8.26).
Перейдем к нахождению поля В. Согласно фор-
формуле (XI. 56)
_ г д А
L дг& J
(А зависит от координат через f0, подобно тому как
в формуле (XI. 56) а зависит от координат через |).
Подставив выражения G8.19) и G8.22), получим
Rg/C) + ф/с) (R _
C6f (R-WJ
-/?Р A - Р2 4- ЪЬ/с) - (R&c) (R -
Добавим в числителе второго сомножителя слагаемое
R(l — P2 + Rp/c). От этого выражение не изменится,
так как [RRj = O. Однако второй сомножитель при
этом превратится в Е (см. G8.23)). Таким образом,
мы приходим к соотношению
] G829)
Здесь R —R(^o). Из G8.29) вытекает, что вектор В
в каждой точке перпендикулярен к вектору Е и к век-
вектору, проведенному из точки, в которой находился за-
заряд в момент to, в точку наблюдения.
§ 70. Поле, создаваемое системой зарядов
на болышж расстояниях
Пусть имеется система движущихся зарядов, не
выходящих при своем движении за пределы некото-
некоторого объема. Систему будем предполагать в целом
нейтральной. Рассмотрим поле, создаваемое такой си-
системой на расстояниях, больших по сравнению с ее
размерами. Поместим начало координат внутри си-
системы. Распределение заряда охарактеризуем с по*

§ 79. ПОЛЕ ЗАРЯДОВ НА БОЛЬШИХ РАССТОЯНИЯХ 327
мощью функции p = p(r',f). Тогда заряд, заключен-
заключенный внутри объема dV\ расположенного в точке с ра-
радиусом-вектором г', будет равен de(t) = p(r',t)dV.
Радиус-вектор точки наблюдения Р обозначим через г.
Кроме того, введем обозначение R = r — г'. Очевидно,
что R есть вектор, проведенный из de в точку Р.
Напишем выражения G6.11) и G6.12) для запаз-
запаздывающих потенциалов поля, создаваемого системой,
G9.2)
По предположению г >> г'. Поэтому величину R —
= |г — rf\ можно рассматривать как значение функ-
функции f(r) = |r| —r в точке r + бг, где бг = — г'. Вос-
Воспользовавшись формулой f (г + &0 = f (t) + Vf (r)Sr,
можно написать
-r') = r--.-f г'^г-пг', G9.3)
где п есть орт радиуса-вектора г.
Подстановка значения G9.3) в формулы для по-
потенциалов дает
Ф (г. 0 - $
G9.5)
Мы видим, что время запаздывания т слагается из
двух частей. Одна из них, равная то — г/с, не зависит
от г' и называется временем запаздывания системы.
Она определяет время, которое требуется для того,
чтобы электромагнитное возмущение прошло путь от
начала координат до точки наблюдения. Вторая часть,
равная i/ = —пг'/с, называется собственным запаз-
запаздыванием. Она характеризует время, необходимое для
распространения возмущения в пределах системы.
Разложим подынтегральное выражение в G9.4)
в ряд по степеням отношения г'/г. Рассматривая

328 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
величину —пг' как малое приращение бг аргумента г,
получим
г — пг' г ' "*"
... G9.6)
Для выяснения вопроса о том, можно ли ограни-
ограничиться в разложении написанными членами, нужно
произвести оценку последующих членов. В эти члены
будут входить старшие производные р по г. Легко за-
заметить, что производные р по г пропорциональны про-
производным р по t. Действительно, положив t — г/с = ?,
можно написать
дг ~ д% дг ~~ dl \ с )' dt ~ dl dt ~~ д% *
откуда
^ G9.7)
Аналогично
_ ( 1 \2 д2р дтр _( 1 \т дтр
— \ Т) HF* •••» ИР^— \Г~Т) 1Р^'
Последовательное дифференцирование функции р/г
по г с последующей заменой производных по г произ-
производными по t дает
дг\г)~ 75*"" г \~~ТI)Г'
i(b последней строке мы выписали только последнее
слагаемое).
При больших г первые члены в написанных нами
производных много меньше последних. Поэтому наша

§ 79. ПОЛЕ ЗАРЯДОВ НА БОЛЬШИХ РАССТОЯНИЯХ 329
задача сводится к оценке относительной величины вы-
выражений вида
(в разложении G9.6) т-я производная умножается
на (бг)от).
Допустим, что р изменяется со временем по гармо-
гармоническому закону р оэ cos (of. Тогда m-я производная р
по / будет порядка сотр. Подстановка в G9.8) дает
где / — линейные размеры рассматриваемой системы
зарядов.
Следующий член разложения будет порядка
717J
Таким образом, отношение последовательных членов
разложения G9.6) по порядку величины равно Ы/с.
Заменив частоту периодом изменений р (по формуле
со as 2я/Г), получим
<ol/c = 2nl/cT~l/cT.
Из сказанного вытекает, что последующими чле-
членами в разложении G9.6) можно пренебречь, если вы-
выполняется условие
1. G9.9)
Отношение 1/с определяет собственное запаздыва-
запаздывание т/. Следовательно, условию G9.9) можно придать
вид
т'<Г. G9.10)
Из G9.10) следует, что ограничиться первыми чле-
членами разложения G9.6) можно в том случае, когда
время, необходимое для распространения электромаг-
электромагнитного возмущения в лределах системы, много мень-
меньше времени, за которое распределение зарядов в си-
системе меняется заметным образом.
Условие G9,9) можно написать ещ/е дьуд^я спо-
способами. Произведение сТ дает длину волны к

330 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
излучения, возбуждаемого системой. Поэтому соотно-
соотношению G9,9) можно придать вид
/<А G9.11)
(размеры системы должны быть много меньше длины
волны).
Наконец, приняв во внимание, что 1/Т по порядку
величины равно скорости v движения зарядов в си-
системе, можно вместо выражения G9.9) написать
Же. G9.12)
Из последнего соотношения видно, что, оборвав
разложение G9.6) на втором члене, мы ограничи-
ограничиваемся рассмотрением излучения нерелятивистской
системы зарядов.
з Обратимся снова к вычислению потенциалов, по-
полагая условия G9.10)—G9.12) выполненными. Под-
Подстановка G9.6) в G9.4) дает
Ф(г, 0—xT\/)
i{f$(fK} <79ЛЗ>
{напомним, что интегрирование производится по
штрихованным координатам, поэтому г можно выне-
вынести за знак интеграла; кроме того, мы изменили по-
порядок дифференцирования по г и интегрирования).
Под знаком первого интеграла стоит плотность за-
заряда в момент времени t — (г/с). Следовательно, этот
интеграл дает суммарный заряд системы, который
ввиду предполагаемой электронейтралькости системы
равен нулю. Таким образом, в формуле G9.13) нужно
сохранить только второй член. Вынеся в нем и за
знак интеграла и производной, придем к выражению
Интеграл в этом выражении есть не что иное, как ди-
польный электрический момент, которым обладала
система в момент t — г/с,

§ 79. ПОЛЕ ЗАРЯДОВ НА БОЛЬШИХ РАССТОЯНИЯХ 331
(ср. с D3.6)). Поэтому можно написать
,<r.O—n?Mz-?L. G9.14)
Наконец, осуществив дифференцирование и приняв во
внимание, что dp/dr = — (l/c)dp/dt = — (l/c)p (ср.
с G9.7)), получим
Первый член в этой формуле совпадает с потен-
потенциалом D3.9) статического диполя (п=г/г). Отме-
Отметим, что отвечающее этому члену поле на расстоя-
расстоянии г в момент t определяется значением дипольного
момента в момент t — r/c. Первый член убывает с рас-
расстоянием г гораздо быстрее, чем второй член. По-
Поэтому, рассматривая поле на больших расстояниях,
можно положить
^/)- G9.15)
Перейдем к определению векторного потенциала.
Формула G9.2) отличается от G9.1) лишь тем, что
вместо p(r', t — R/c) под знаком интеграла стоит
j(r'f< — R/c). Поэтому, разложив подынтегральную
функцию в ряд, получим выражение, аналогичное
G9.13),
<79Л6>
Если бы токи были стационарными, т. е. не зави-
зависели от t, то первый интеграл был бы равен нулю
(см. E1.5)). Однако для нестационарных токов этот
интеграл отличен от нуля. Поэтому в разложении
G9.16) можно сохранить лишь первый член1). Таким
образом, можно положить
!) В формуле G9.13) мы ке могли пренебречь вторым чле-
членом, поскольку первый был равен нулю.

332 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Докажем, что \j(r', t — rjc)dVf равен производ-
производной по времени от дипольного момента системы, взя-
взятой в момент t — rfc. Доказательство проще всего
осуществить, перейдя от непрерывного распределения
зарядов к прерывному. Произведем замену
(скорости зарядов, как и функцию pv, нужно взять
в момент t — г/с). Однако
Таким образом,
A<r.0-i?=^. G9.17)
Сравнение с G9.15) позволяет написать
Ф = Ап. G9.18)
Потенциалы G9.15) и G9.17) определяются зна-
значением производной по времени от дипольного момен-
момента системы. Поэтому они называются потенциалами,
вычисленными в дипольном приближении. Дипольное
приближение допустимо при соблюдении условий
G9.10)—G9.12).
§ 80. Дипольное излучегше
Область поля, отстоящая от излучающей системы
на расстояние г, много большее не только размеров
системы /, но и длины волны излучения (г » К >> /),
называется волновой зоной.
В волновой зоне выполняются условия, при кото-
которых справедливо дипольное приближение, рассмот-
рассмотренное в предыдущем параграфе. В этом прибли-
приближении
^пЦ-г/^ А=Р?^?). (80Л)
(см. G9.15) и G9.17)).
Чтобы вычислить Е, нужно найти Уф и dK/dt. При-
Применив формулу (XI. 51), получим

§ 80. ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ 333
(напомним, что п = ег = г/г). Следовательно,
(мы воспользовались тем обстоятельством, что
/ = -(l/c)dp/dt).
Первый член в полученном нами выражении убы-
убывает с расстоянием гораздо быстрее, чем второй. По-
Поэтому на больших расстояниях им можно пренебречь
и считать, что
Производная dk/dt = р/cr. Таким образом,
Е = _„ 1 дА __ (пр)п 1 *р __ (nji) п -- р
*ф с flf C2r c cr J5p •
Числитель этого выражения можно представить в виде
[п[пр]]. В этом легко убедиться, раскрыв двойное
векторное произведение по формуле «бац минус цаб»
и приняв во внимание, что пп = 1. Итак, электриче-
электрическое поле определяется формулой
Перейдем к вычислению магнитного поля. Вектор-
Векторный потенциал является функцией от г. Поэтому со-
согласно (XI. 56)
B = [VAl = [vr, 4?-] = [n, Щ. (80.3)
Дифференцирование выражения (80.1) для А дает
дг ~ дг \ сг ) сг2
(ср. с (80.2)). Отбросив член, пропорциональный
получим, что дА/дг = —р/<А\ Таким образом,
Напишем окончательные выражения для Е и В.
[[рп]п1 В [ря] (S0.4)

334 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
(напомним, что значения р должны быть взяты в мо-
момент t — г/с). Сопоставление этих выражений приво-
приводит к заключению, что
Е = [Еп], (80.5)
откуда вытекает, что вектор Е перпендикулярен к век-
вектору В. Из выражений (80.4) следует, что векторы Е
и В перпендикулярны к вектору п (перпендикуляр-
(перпендикулярность Екп следует также и из (80.5)). Таким обра-
образом, как и в плоской волне, векторы В, Е и п взаимно
перпендикулярны (см. формулу G2.16) *)). Кроме
того, векторы В и Е, как и в плоской волне, одина-
одинаковы по величине, причем
i?j*» (80.6)
где # — угол между направлениями векторов р и п.
В том, что для изучаемого наги поля оказались
справедливыми соотношения, наблюдаемые для пло-
плоской волны, нет ничего удивительного. На расстоя-
расстояниях, больших по сравнению с размерами излучаю-
излучающей системы, волна должна быть сферической. Вме-
Вместе с тем при условии, что г ^> Я, небольшие участки
сферической волны практически совпадают с плоской
волной.
Как следует из (80.4), поля Е и В определяются
второй производной от дипольного момента системы.
Поэтому рассматриваемое излучение называется ди-
ПОАЬНЫМ.
Дйиолвый момент определяется выражением р —
в* Yj ет'° Следовательно, р ===== X ет' ^ 21 ^v- Отсюда
вытекает, что заряды излучают электромагнитные
волны только в том случае, когда они движутся
с ускорением.
Чтобы уяснить себе картину поля на больших рас-
расстояниях, введем сферическую систему координат,
причем полярный угол # будем отсчитывать от на-
направления вектора p(t — г/с) (рис. 80.1). Согласно
*) Умножим соотношение (80.5) слева на п и используем
формулу «бац минус цаб»:
(«Bj «¦ [п [Вп] ] -= В {пи) — п (иВ) = В.
Мы пришли к ф*РмУле G2.16) (в пустоте ч/гр. = 1, Н = В).

§ 80. ДИПОЛЬНОЕ ИЗЛУЧЕНИЕ
335
(80.4) вектор В перпендикулярен к плоскости, опре-
определяемой векторами р и п. Следовательно, В направ-
направлен по касательной к «параллели», причем векторы р,
п и В образуют правовинтовую систему.
Из (80.5) следует, что векторы В, п и Е образуют
правовинтовую систему. Отсюда вытекает, что Е на-
направлен по касатель-
касательной к «меридиану»,
причем на «экваторе»
направления р и Е про-
противоположны. Еще раз
подчеркнем, что изо-
изображенные на рис.
80.1 векторы относятся
к разным моментам
времени: р к моменту
/—г/с, а В и Е — к мо-
моменту t. Модуль век-
векторов В и Е пропор-
пропорционален sin Ф (см.
(80.4)). Следователь-
Следовательно, поля имеют наи-
наибольшую величину на «экваторе» и обращаются в
нуль на «полюсах».
Чтобы определить интенсивность излучения в раз-
разных направлениях и общую мощность излучения, вы-
вычислим вектор Пойнтинга. Приняв во внимание
(80.6), получим
(80.7)
Рис. 80.1
Таким образом, интенсивность излучения диполя про-
пропорциональна sin2 д. Соответствующая диаграмма на-
направленности излучения имеет вид лепестка.
Для определения мощности излучения / найдем
поток энергии через всю сферическую поверхность.
Площадь сферического пояска угловой ширины <ft>
равна 2nr2 sin Od<h Следовательно,
Зс3
(80,8)

336 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Пусть из всех зарядов системы ускорением обла-
обладает только один. Тогда р = J) eava = ev и мощность
излучения равна
§ (80.9)
Эта формула справедлива и в том случае, когда име-
имеется только один заряд, движущийся с ускорением v.
§ 81. Магнитно-дипольное и кзадрупольное
излучения
Если свойства системы зарядов таковы, что р = 0,
дипольное излучение не возникает. Однако это не
означает, что излучения нет вообще. В этом случае
нужно учесть те члены разложения потенциалов, ко-
которыми мы пренебрегли в дипольном приближении.
В предыдущем параграфе было выяснено, что
в волновой зоне волна в небольших областях близка
к плоской волне, для которой справедливо соотноше-
соотношение (80.5). С помощью этого соотношения, зная В,
легко найти Е. Для нахождения же В достаточно
знать только А. Поэтому мы ограничимся нахожде-
нахождением векторного потенциала.
Рассмотрим второй член формулы G9.16), кото-
которым мы пренебрегли в дипольном приближении. По-
Поскольку в интересующем нас случае первый член в
G9.16) равен нулю, векторный потенциал имеет вид
А(г. 0—-?
Осуществив дифференцирование по г, мы получим два
слагаемых. Одно из них будет пропорционально 1/г2,
второе пропорционально 1/г. Первое слагаемое убы-
убывает с расстоянием гораздо быстрее, чем второе. По-
Поэтому мы пренебрежем им, как это делали уже неод-
неоднократно. Кроме того, мы учтем, что dj/dr=*
«=—(l/c)dj/dt В результате получим
«-зГ^$1(г', t-r/c)(nr')dV.
Чтобы упростить дальнейшие выкладки, перейдем
от непрерывного распределения зарядов к дискрет*

§ 81. МАГНИТНО-ДИПОЛЬИЫЕ И КВАДРУПОЛЬНЫЕ ПОЛЯ 337
ному. Тогда выражение для А примет вид
iX>eva«). (81.1)
Значения vfl и т'а берутся в момент t — г/с.
Выражение, стоящее в (81.1) под знаком суммы,
можно представить следующим образом:
V* К.) - Ж К (О) " *'а (»*.)• (81-2)
Разобьем va(nr^)Ha две равные части и заменим одну
из них половиной выражения (81.2):
ve К) - т ve «) + -j-|r К «)} - Т < («ve)-
Первый и третий члены можно представить в виде
двойного векторного произведения: */2 [n [vfl, г^] ] (в
этом можно убедиться с помощью формулы «бац
минус цаб»). Таким образом,
- т [»[VX]] + т ж К К.)}.
Подстановка этого выражения в формулу (81.1)
дает
eXK) = Am + AQ. (81.3)
Смысл индексов m и Q выяснится в дальнейшем.
Вынесем в первом члене п за знак суммы н поме-
поменяем местами vfl и т'а% В результате этот член при-
примет вид
Первый множитель есть магнитный момент m системы
(см. формулу E1.15)). Поэтому можно написать, что
^ (81.4)

338 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
где m—dm/dt берется в момент времени t — r/c. Та-
Таким образом, потенциал Aw определяется изменениями
магнитного дипольного момента. Поэтому соответ-
соответствующее излучение называется магнитно-дипольным.
В случае магнитно-дипольного излучения магнит-
магнитное поле равно
(ср. с (80.3)). Если пренебречь в дАт/дг членом, про-
пропорциональным 1/г2, и заменить д/дг на (-—l/c)d/dtl),
получим
Воспользовавшись эквивалентным (80.5) соотно-
соотношением G2.16), получим, что
Итак, поля при магнитно-дипольном излучении
равны
! .. (81.5)
Сравнение полученных результатов с формулами
(80.4) для дипольного излучения показывает, что Вт
выражается через m точно такой формулой, какой Е
выражается через р. Формулы для Ет и В отличаются,
кроме замены р на т, еще и знаком. Отсюда сле-
следует, что картину поля при магнитно-дипольном излу-
излучении в волновой зоне можно получить, заменив на
рис. 80.1 р на ш, Е на Вт и В на — Ет.
Обратимся ко второму члену формулы (81.3), т. е.
к выражению
Напоминаем, что ш«ш((-г/с).

§ 81. МАГНИТНО-ДИПОЛЬНЫЕ И КВАДРУПОЛЬНЫЕ ПОЛЯ 339
Добавление к AQ выражения f(r)n (f{r) — любая
функция от г) не изменит BQ, так как [V,f(r)n]~0
(см. (XI.54)). Возьмем в качестве f(r) функцию
(г'а есть функция аргумента (t — г/с), которая при
воздействии на нее оператора V ведет себя как функ-
функция от г). Умножив эту функцию на п и прибавив ее
к (81.6), получим
Напишем выражение для i-й компоненты век-
вектора Aq!
ь (Z ч^
Последний член в фигурных скобках можно предста-
представить в виде X гд2^|Л- Тогда AQi будет выглядеть
следующим образом:
Но сумма по а есть Q,* — компонента тензора квад-
рупольного момента системы (см. формулу D3.13)).
Следовательно,
л — 1 д* V п „ 1 д% п
где Qi — компонента вектора, получающегося при ум-
умножении вектора и на тензор Qik. Обозначив этот век-
вектор символом Q, можно написать
Потенциал Aq определяется изменениями квадру-
польного момента системы. Поэтому соответствующее
излучение называется квадрупольным.

340 ГЛ. XIV. ИЗЛУЧЕНИЕ ЭЛЕКТРОМАГНИТНЫХ ВОЛН
Магнитное поле квадрупольного излучения равно
При вычислении дАо/дг пренебрежем членом, пропор-
пропорциональным 1/г2, и заменим производную по г произ-
производной по t. В результате получим
(мы переставили сомножители, чтобы не писать ми-
минус, вносимый множителем —1/с).
Воспользовавшись соотношением (80.5), найдем,
что
]. (81.9)
По сравнению с формулами (80.4) выражения
(81.8) и (81.9) имеют дополнительный множитель 1/6с.
Кроме того, вместо р в них стоит Q. В остальном
формулы для полей при квадрупольном излучении
тождественны аналогичным формулам для дипольного
излучения.
Соответствующие вычисления дают, что суммарная
мощность всех трех видов излучения (включая ди-
польное) определяется выражением
i (81Л0>
i, к
Произведем оценку относительной интенсивности
излучения различных видов. Для простоты предполо-
предположим, что заряды системы движутся по гармониче-
гармоническому закону. Тогда
г' = / cos ©/, t; ===== /о> sin etf,
где / — величина порядка размеров системы, Средние
значения модулей cos <$t и sin ®t — величины порядка
единицы. Поэтому в окончательных выражениях, ха-
характеризующих порядок величины рассматриваемых
выражений» множители cos со/ и sin&t мы будем от-
отбрасывать. Например, если не иметь в виду необходи-
необходимость дифференцирования по t9 можно написать, что
г'~ U v~l®. (81ЛI)

§ 81. МАГНИТНО-ДИПОЛЬНЫЕ И КВАДРУПОЛЬНЫЕ ПОЛЯ 341
Из определения D3.5) следует, что р есть величина
порядка ег\ т. е.
р ~ el cos ®t, р ~ el® sin ®t, p ~ el®2 cos ®t.
Отсюда получаем, что по порядку величины мощность
дипольного излучения определяется выражением
(см. (81.11)).
Из определения E1.15) следует, что магнитный
момент имеет величину порядка er'v/c, т. е.
т ~ — el2® cos ®t sin ®t ~ — el2® sin 2®t,
с с
loo loo
m ~ — el2®2 cos 2®t, m ~ — erar sin 2®t.
с с
Отсюда
Сопоставление выражений (81.12) и (81.13) дает,
что
Напомним, что вычисления полей излучаемых волн
мы осуществили для нерелятивистского случая (т. е.
для i/«<c). Следовательно, в исследованном нами
случае интенсивность магнитно-дипольного излучения
много меньше интенсивности электрического диполь-
дипольного излучения.
Согласно определению D3.13) квадрупольный мо-
момент (а значит, и вектор Q) есть величина порядка
ег'2, т. е.
Q ~ eP cos2 ®t, Q ~ eP® cos ®t sin ®t ~ el2® sin 2©/,
Q ~ eP®2 cos 2urf, Q ^ e?P®3 sin 2®t.
Следовательно,
*q -jr — ^r~- (81.14)
Таким образом, квадрупольное излучение обладает
интенсивностью того же порядка величины, что и маг-
нитно-дипольное излучение.

ПРИЛОЖЕНИЯ
1. Уравнения Лагранжа для голономной системы
с идеальными нестационарными связями
В случае нестационарных связей условия D.2)
имеют вид
/|<*ь х2, .... хЯ9 0 = 0 (/=1, 2, ..., г). A.1)
В соответствии с этим время входит и в функции D.3):
Xi = xt(qu Яъ ••-, Ч» 0 (/= 1, 2, ..., л). A.2)
В формулах D.4) и D.5) появляется еще одно сла-
слагаемое
дх. «—<i дх.
Из (I. 3) следует соотношение
^L_ifL (l4)
совпадающее с D.6). Формулы D.7) также остаются
без изменений:
дх,
° AБ)
дх.
Поскольку величины ~- будут содержать не
только qkt но и t, выражение D.8) немного услож-
усложнится:
Lffv
д2х.

I. УРАВНЕНИЯ ЛАГРАНЖА ГОЛОНОМНОИ СИСТЕМЫ 343
Продифференцировав выражение A.3) по qk, получим
dqjt — dqk\dt )^ L, dqk \dqt ) It ~
dqk dt^Li dqk dq{ 4l'
Сопоставив это выражение с A.6), приходим к соот-
соотношению
dqk dt dqk ' ^ i}
совпадающему с D.9).
Умножим уравнения
dt dxt дХ1~К1^Рг [l—l9 *, ..., П)
дх.
(см. D.1)) на ~- и просуммируем их по i:
d dL
\1f dx. ) dqk
Поскольку использованные в § 4 при преобразовании
левой части этого уравнения соотношения D.9), D.6)
и D.7) остались без изменений (см. A.7), A.4) и
A.5)), не изменится и результат. Следовательно, ле-
левая часть A.8) может быть представлена в виде
d dL dL
dt dqk dqk
(см. абзац, предшествующий формуле D.15)).
Прежде чем перейти к рассмотрению правой части
формулы A.8), обсудим следующий вопрос. В случае
стационарных связей */ —х*07*) и приращение коор-
координаты xi за время dt будет равно

344 ПРИЛОЖЕНИЯ
где dqk — приращения обобщенных координат за вре-
время dt. В случае нестационарных связей х/ = ^(^ t)
и приращение xi за время dt равно
* Aю)
где опять-таки dqk — приращения координат qk за
время dt.
дх.
Если бы связи вдруг перестали изменяться, -¦—-
обратилась бы в нуль и формула A.10) совпала бы
с A.9). Следовательно, второе слагаемое в A.10)
представляет собой воображаемое перемещение си-
системы, которое получилось бы при «замороженных»
связях. Его называют виртуальным (или возможным)
перемещением и обозначают bxi. Таким образом, ис-
истинное перемещение dxi может быть представлено
в виде суммы виртуального перемещения бдс/ и сла-
слагаемого, равного ~- dt,
dxt^bXi + '^jf-dt. (I. 11)
При стационарных связях виртуальное перемещение
совпадает с истинным.
Теперь рассмотрим первое слагаемое в правой ча-
части формулы A.8). Умножив его на dqk, получим
где bxi — виртуальное приращение координаты х$9
возникающее в том случае, когда изменяется только
одна обобщенная координата q^
Работа реакций Ri при фиксированных нестацио-
нестационарных связях (так же как и при стационарных свя-
связях) равна нулю. Поэтому J) /^ 6xi = 0 и так .как
dqk^Q, то из (I. 12) вытекает» что

III. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 345
Заметим, что истинная работа реакций нестацио-
нестационарных связей согласно A.11) и A.13) равна
и, вообще говоря, отлична от нуля.
Итак, согласно A.13) первое слагаемое в правой
части формулы A.8) равно нулю — реакции связей
опять выпали из уравнений. Что же касается второго
слагаемого, то оно по определению представляет со-
собой обобщенную cилyQ^ (см. формулу D.12)). Таким
образом, и для нестационарных связей мы пришли
к уравнениям Лагранжа
dt dqk dqk V*'
II. Теорема Эйлера для однородных функций
Функция любого числа переменных называется од-
однородной функцией этих переменных степени т, если
при умножении всех переменных на произвольную ве-
величину а функция умножается на aw, т. е.
/(а*,, ахъ ..., axn) = amf(x{i хъ ..., хп).
Продифференцируем это тождество по а:
Положив а = 1, получим
Мы доказали теорему Эйлера, которая гласит:
сумма произведений частных производных однородной
функции на соответствующие переменные равна про-
произведению самой функции на степень ее однородности.
III* Некоторые сведения
из вариационного исчисления
1. Функционал. Если каждому числу х из чисел
некоторого класса сопоставлено другое число у> то,
как известно, мы имеем дело с функцией у--у(х).

346 ПРИЛОЖЕНИЯ
Если каждой функции у(х) из некоторого класса
функций сопоставлено некоторое число Ф, то говорят,
что задан функционал Ф [у (х) ].
Для наглядности мы будем иногда говорить вместо
функции о кривой.
Итак, функция устанавливает соответствие:
число -> число,
функционал же устанавливает соответствие:
функция (или крива я) —> число.
Таким образом, в случае функционала роль аргумента
играет функция (или кривая).
Поясним сказанное следующим примером. Пусть
даны на плоскости х% у две фиксированные точки /
и 2 (рис. III. 1). Расстояние Л2
между точками, отсчитанное
вдоль соединяющей их кри-
кривой, есть функционал. Чтобы
найти аналитическое выраже-
выражение, связывающее величину 1Х2
с функцией # = !/(#), описы-
описывающей кривую, учтем, что
элемент кривой dl связан cdx
и dy соотношением dl2 ==
Рис. III. 1 — dx2 -f dy2. Представив dy
в виде y'(x)dx, получим, что
dl = ^dx2+(yf(x)Jdx2^ <s/r+(y'(xWdx. Наконец,
проинтегрировав и обозначив li2 через Ф}у{х)], при-
придем к выражению
2
®[у(х)) = \ л/T+VWdx. (III. 1)
Беря разные кривые, т. е. разные функции у(х), мы
будем получать разные числа Ф.
Подобно тому как бывают функции не одной, а не-
нескольких переменных, существуют функционалы, за-
зависящие от нескольких функций: Ух(х),У2(х), ...
*) Существуют также функционалы, зависящие от функций
нескольких переменных хи *2, ..., хп. Однако такие функцио-
функционалы нам не понадобятся, в мы их рассматривать не будем.

III. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 347
Если функционал удовлетворяет условиям
Ф [су (х)] = сФ [у (х)] (с - константа),
Ф \Ух (х) + У* (х)] = Ф [у, (х)] + Ф [у2 (*)], (HL 2)
он называется линейным. Линейные функционалы мы
будем обозначать символом Флин или Fnnn и т. п.
Функционалы, зависящие от нескольких функций,
могут оказаться линейными по отношению к одним
функциям и нелинейными по отношению к другим.
В этом случае, например, символ
Флин. по у, [У\ (Х), у2 (Х), . . . ]
будет означать функционал, линейный относительно
функции уъ{х).
Задачей вариационного исчисления является раз-
разработка методов нахождения экстремальных (т. е.
максимальных, минимальных или стационарных) зна-
значений функционалов. Эта задача во многом сходна с
задачей нахождения экстремумов обычных функций.
2. Вариация функционала. Выберем из рассматри-
рассматриваемого класса функций произвольную функцию у(х)
(чтобы отличить выбранную функцию от остальных
функций данного класса, мы воспользовались значком
тильда). Затем выберем из того же класса другую
функцию у(х). Разность этих двух функций назы-
называется вариацией функции у(х). Вариацию обозна-
обозначают символом 6у(х) или, короче, Ьу. Таким образом,
вариация функции определяется следующим выраже-
выражением
йу = У(х)-9(х). (Ш.З)
Вариация функции аналогична приращению Ах
(или dx) аргумента обычной функции: Дх = х — х.
Вариация 8у функции у(х) есть, очевидно, функ-
функция от х. Продифференцировав эту функцию по х,
найдем согласно (Ш.З), что
Правая часть этого выражения представляет собой
вариацию функции у'(х). Следовательно, мы прихо-
приходим к соотношению
F*/)' = б/ (III. 4)
(производная вариации равна вариации производной).

348 ПРИЛОЖЕНИЯ
Выясним, какая величина в вариационном исчис-
исчислении соответствует дифференциалу обычной функ-
функции. Напомним, что если функция непрерывна1), то
ее приращение &у, равное у(х)— у(х), можно пред-
представить в виде суммы линейного относительно Ах сла-
слагаемого и бесконечно малой величины порядка выше
первого по отношению к Да::
Ау — у' (х) Ах + 8 Ах,
где е — величина, обращающаяся в нуль вместе с Ал:
(иначе можно сказать, что lim е = 0). Первое сла-
до
гаемое в этом выражении называется дифференциа-
дифференциалом функции. Таким образом, дифференциалом функ-
функции называется та часть приращения функции, кото-
которая линейна относительно Ад:.
Для функции у = х дифференциал совпадает
с приращением. Следовательно, Ал: = dx, так что вы-
выражение для дифференциала функции можно напи-
написать в виде
dy = / (л:) Ал; либо dy = /(х) dx. (III. 5)
Если малому изменению функции (малой Ьу) со-
соответствует малое изменение функционала, то функ-
функционал называется непрерывным. Для непрерывных
функционалов можно ввести величину, аналогичную
дифференциалу обычной функции.
Приращение функционала АФ = Ф [у (х) + 8у] —
— Ф [#(*)] есть величина, зависящая от двух функ-
функций: у{х) и Ьу, Следовательно, АФ —также функцио-
функционал. Этот функционал, вообще говоря, будет нелиней-
нелинейным. Если АФ[у(х)] можно представить в виде
суммы линейного относительно Ьу функционала
^лин.поьу[у(х)>®у] и бесконечно малой величины по-
порядка выше первого по отношению к J6z/|ma* (макси-
(максимальному значению модуля функции б#), то главную,
линейную относительно 6у, часть приращения функ-
функционала называют вариацией функционала. Таким
!) Более строго, нужно было бы потребовать, чтобы функ-
функция была не только непрерывной, но также и дифференцируемой.
Однако функции, рассматриваемые в физике, как правило, если
непрерывны, то и дифференцируемы. Хотя, вообще говоря, в
математике известны непрерывные функции, которые недиффе-
ренцируемы.

III. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 349
образом,
АФ[у (х)] = 6Ф[у (х)] + г\6у |тах, (III. 6)
где
6Ф [у (х)] = Рлт. по ьи [У (*), Ьу] (III. 7)
есть вариация функционала, а е — величина, обра-
обращающаяся В НуЛЬ ВМеСТе С |6#|тах.
Вариация функционала является аналогом диф-
дифференциала функции, определяемого выражением
(III. 5).
Определение (III. 7) легко обобщить на случай
функционалов, зависящих от нескольких функций:
6Ф [*/,(*), у2(х\ ..., у.(х)] =
= /W по byv 6у2 <Sys [У\ (*), У2(Х)9 . . .
..., У*(х), *Уи Ъуъ ..., Ьуш\. (III. 8)
В качестве иллюстрации найдем приращение функ-
функционала
ъ
ФЫх)]=\[у(х)]Чх. (III. 9)
а
Это приращение равно
ъ ь
= \ [У (х) + byf dx~\[y (x)f dx =
a a
b b b
\ &У (x) by + Fy)*] dx = \2y (x) by dx + \ Fyf dx.
b
Интеграл \{byfdx не превосходит величину
\byLAb-a)~{\by\m&%{b-a)}\by\m^ где
максимальное значение модуля функщш Ьу в интер-
интервале а ^ х ^ 6. Выражение в фигурных скобках об-
обращается в нуль вместе с |5у|тах. Следовательно,
ь
\ (byfdx можно представить в виде s|6j/|max> где

350 ПРИЛОЖЕНИЯ
в-^0 при | ду\ шах -*-0. Тогда
ь
(ср. с (III. 6)). Первое слагаемое в этом выражении
представляет собой функционал, зависящий от функ-
функций у{х) и 6#,
ъ
/W по бу [У (х), Ьу] - J 2у (х) by dx. (III. 10)
Легко проверить, что этот функционал линеен *) по
отношению к 8у (см. условия (III. 2)). Таким обра-
образом, выражение (III. 10) дает вариацию функционала
(III. 9).
3. Необходимое условие экстремума функционала.
Начнем опять с аналогичных понятий из анализа.
О функции f(xuX2, ..., хг) говорят, что она имеет
в точке х\9 x2f ..., хп экстремум, если приращение этой
функции
Д/ = / (#ь &ъ • • • э хп) — f (х{, хъ ..., хп)
имеет один и тот же знак для всех точек
(хи x2i ..., Хп), принадлежащих окрестности точки
[х\, х2, ..., хя). При А/ ^ 0 в данной точке имеет ме-
место максимум, при А/ ^ 0 — минимум.
В анализе доказывается, что необходимым усло-
условием для существования экстремума в некоторой
точке является равенство нулю дифференциала функ-
функции в этой точке:
Аналогично говорят, что функционал Ф[у(*)] до-
достигает экстремума при у — у{х), если приращение
функционала
*) Данный функционал линеен также и по отношению к
у{х), но это не существенно — важна линейность лишь по отно-
отношению к бу.

III. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 351
имеет один и тот же знак для всех кривых у(х)у до-
достаточно близких к кривой у{х). При ДФ ^ О наблю-
наблюдается максимум функционала, при ДФ ^ О — ми-
минимум.
Найдем условие, необходимое для достижения
функционалом Ф [#(*)] экстремума при у — у(х).
Рассмотрим для определенности случай максимума.
Если Ф [#(*)] достигает максимума при # = |/(х), это
значит, что
Ф [У (х) + &у] - Ф [у (х)] < 0 (III. 12)
для всех 8у = 8у(х), для которых |б#|тах достаточно
мал. Согласно (III. 7) к (III.8)
ДФ =
= /W по ьу [у (х)9 Ьу] + е\6у |гаах (III. 13)
Выделим из всех возможных вариаций 6у те, ко-
которые могут быть представлены в виде 6у = аб#о, где
Sf/o—некоторая фиксированная достаточно малая ва-
вариация, а а — переменная алгебраическая величина.
Подставив эту вариацию в (III. 13) и учтя, что в силу
линейности F [у (х), абуо] — aF [у {х), буо] 9 можно на-
написать
Дф = aF [у (х), 6у0] + ва \ ёу0 |тах.
В последнем выражении F[y(x),8y0] есть просто
какое-то число. Если это число отлично от нуля, то
при достаточно малых а знак ДФ будет определяться
знаком выражения aF[y(x),6yo] (слагаемоеea|6j/0|max
убывает гораздо быстрее, чем первое слагаемое1)),
а это выражение будет изменять знак вместе с а (ко-
(которая может быть и положительной, и отрицатель-
отрицательной). Таким образом, для выполнения условия (III. 12)
необходимо равенство нулю величины F [у (х), буо].
Условие (III. 12) должно выполняться для всех без
исключения достаточно малых вариаций ёу. Мы же
обнаружили, что при 6Ф ф 0 хотя бы для части ва-
вариаций, имеющих вид абе/о, указанное условие не со-
соблюдается. Поэтому можно высказать следующее ут-
утверждение: для достижения функционалом Ф[у(х)]
максимума при у — у(х) необходимо, чтобы его
') Условие е~>0 при |6#jraaa~>G в данном случае приобре-
приобретает вид lim e = 0.
а->0

352 приложения
еираация (если она существует) обращалась в нуль
при у = у{х):
6Ф = Fm. по ьу [у (*), &у] в> 0 '). (III. 14)
Видно, что, повторив рассуждения для случая ми-
минимума функционала, мы придем к тому же заключе-
заключению. Следовательно, формула (III. 14) выражает усло-
условие не только максимума, но и минимума, т. е. экстре-
экстремума вообще. Эта формула является аналогом
формулы (III. 11).
4. Простейшая задача вариационного исчисления.
Найдем экстремум функционала вида
Ф [У(х)] = J f [x, У (х), у' (хI dx. (III. 15)
Х\
Граничные точки допустимых кривых предполагаются
закрепленными — для всех допустимых кривых
У(Х1) = Уи #(*2) = #2. (HI .16)
Приращение функционала равно
Хч Х2
АФ=^[х, у + бу, y' + 6y')dx- \f[x, у, y'\dx.
Х\ Х\
Разложим подынтегральную функцию в первом инте-
интеграле по степеням малых величин Ьу и 8у'. В резуль-
результате получим
х2
{П*. у, /1 + -^-*у + -^в
Хч
-\f[x,y,y'\dx,
где гFу,Sy') объединяет члены порядка выше пер-
первого относительно величин Ьу и 8у'. Это выражение
упрощается следующим образом:
. 17)
Хх
1) Знак тождества подчеркивает то обстоятельство, что ус-
условие (III. 14) должно выполняться для всех 6у.

III. СВЕДЕНИЯ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ 353
Проинтегрируем ею частям второе слагаемое в пер-
первом интеграле. Для этого представим его в виде
Х2 Хг
(напомним, что 8/ —(%)'; см. формулу (III. 4)). Обо-
Обозначив ~т через a, a (8y)'dx через dv и воспользо-
воспользовавшись формулой V и dv = uv —- \ v du9 получим
Вследствие того, что граничные точки допустимых
кривых закреплены, вариация &у в этих точках долж-
должна обращаться в нуль: 6y(#i) = 0, 8#(#2) = 0. Поэтому
первый член правой части равен нулю. Следовательно,
X?
Подставим найденное значение / в формулу (III. 17),
вынеся б# за скобки,
И
Х\
Главную часть АФ образует первый интеграл, ко-
который представляет собой функционал, линейный от-
относительно Ьу. По определению этот интеграл есть
вариация функционала Ф. Итак, вариация функцио-
функционала (III. 15) имеет вид
<ШЛ8>
а условие экстремума (III. 14) запишется следующим
образом:
Ху
12 И. В. Савельев, г, 1

354 приложения
Полученное тождество должно выполняться яля лю-
любых достаточно малых функций б#~б*/(дг). Это воз-
возможно только при условии, что функция, стоящая под
знаком интеграла в фигурных скобках, будет равна
нулю:
ду dx ду' —и* 1|И- iy>
Это уравнение называется уравнением Эйлера. Оно
представляет собой условие экстремума функциона-
функционалов вида (III. 15). Кривые у = у(х, Си Сг), являю-
являющиеся решениями этого уравнения, называются экс-
экстремалями (Сг и Сг — постоянные интегрирования).
Заметим, что прибавление в (III. 15) к подынте-
подынтегральной функций полной производной по х от любой
функции ij>(#, x) не изменяет условий экстремума
(III. 19). Действительно, это слагаемое после интегри-
интегрирования дает величину
•~|- dx = ¦ fe, x2) — $ (у
вариация которой равна нулю (по условию (III. 16)
кривые на концах не варьируются). Таким образом,
добавление d^f/dx изменяет лишь значение экстремума
функционала, но не влияет на вид функции у(х), при
которой этот экстремум достигается.
Воспользуемся формулой (III. 19) цля нахождения
экстремума функционала (III. 1). В этом случае
f (х* У\ У') = Vl + W (х)}2 - Следовательно,
o
ду ' ду' V
и уравнение (III. 19) примет вид
J
Решением этого дифференциального уравнения бу-
будет функция, для которой у" = 0, а у' — а. Следова-
Следовательно, сама функция есть линейная функция: */ =
= ах + 6, коэффициенты которой нужно подобрать
так, чтобы выполнялись условия (III. 16). Значит,
функционал (III. 1) достигает экстремума (в данном

III. СВЕДЕНИЕ ИЗ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ В55
случае, очевидно, минимума), если в качестве у(х)
взять прямую линию, соединяющую точки / и 2 (см.
рис. III. 1).
5. Экстремум функционалов, зависящих от не-
нескольких функций. Рассмотрим функционал вида
Уъ •••> У.] —
где Ук-Ук(х) {k = 1, 2, ..., s)— кривые, закреплен-
закрепленные в граничных точках, т. е„ удовлетворяющие гра-
граничным условиям
) = У*2 (й = 1, 2, ..., s). (III. 2i)
В соответствии со сказанным в п. 4 вариация
функционала (III. 20) определяется выражением
22>
где б#& — достаточно малые функции от х, обращаю-
обращающиеся в нуль в граничных точках
0. (IIL 23)
Требуется найти такую совокупность функций
Ук{х)* удовлетворяющих условиям (III.21), при кото-
которых функционал (III. 20) достигает экстремума. Не-
Необходимым условием экстремума является равенство
нулю вариации функционала (III. 22).
Интегрируя по частям каждое из s слагаемых вида
входящих в формулу (III. 22), можно привести его
к виду
Произведя такую замену в (III. 22) и приравняв нулю
получившееся выражение для 6Ф, придем к необхо-
12*

356
ПРИЛОЖЕНИЯ
условию экстремума:
.-±Лг
к dx dy'
(III. 24)
Это тождество должно выполняться для любых
выбранных независимо друг от друга достаточно ма-
малых функций %й = б^(х), что возможно лишь при
условии, что все s выражений, стоящих под знаком
суммы в круглых скобках, будут равны нулю. Таким
образом, мы пришли к системе уравнений Эйлера:
Л L.Jf-^0
дук dx dy'k
=l, 2, ..., s). (III. 25)
Совокупность функций Ук~Ук{х)> удовлетворяющих
этим уравнениям и граничным условиям (III. 21), при
подстановке в функционал (III. 20) даст его экс-
экстремум.
IV. Конмчеекне
Коническими сечениями называются линии пере-
пересечения кругового конуса с плоскостью. В зависимо-
зависимости от ориентации плоскости по отношению к оси ко-
конуса эти линии представ-
представляют собой эллипс (круг),
гиперболу или параболу.
Эллипсом (рис. IV. 1) на-
называется геометрическое
место точек, сумма расстоя-
расстояний которых до двух фик-
фиксированных точек F, и F2
называемых фокусами, есть
величина постоянная:
Рис. IV. 1
Каноническое уравнение эллипса имеет вид
*2 д. У2 _ 1
(IV.
(IV. 2)
где а и Ь~ большая к малая полуоси эллипса. Ве-
Величина
с
(IV. 3)

IV. КОНИЧЕСКИЕ СЕЧЕНИЯ
357
где с — половина расстояния между фокусами, назы-
называется эксцентриситетом эллипса. При =0 эллипс
вырождается в окружность. Величины a, b m с свя-
связаны соотношением
&2 = а2-Л {IV. 4)
Гиперболой (рис. IV. 2) называется геометрическое
место точек, модуль разности расстояний которых до
Рис. IV. 2
двух фиксированных точек F\ и F2, называемых фоку-
фокусами, есть величина постоянная:
ki —г2|=*2а. (IV, 5)
Гипербола имеет две симметричные ветви. Канониче-
Каноническое уравнение гиперболы выглядит следующим об-
образом:
где а и Ъ — действительная и мнимая полуоси гипер-
гиперболы. Величины а и Ь связаны с с (половиной рас-
расстояния между фокусами) соотношением
&2 = <*-<?. (IV 7)
Эксцентриситет гиперболы определяется той же
формулой (IV. 3), что и эксцентриситет эллипса. Вид-
Видно, что для эллипса е < 1, а для гиперболы е > 1.
Параболой (рис. IV. 3) называется геометрическое
место точек, расстояние которых г до фиксированной
точки F (фокуса) равно расстоянию d до фиксирован-
фиксированной прямой ?), называемой директрисой параболы:

358
ПРИЛОЖЕНИЯ
г sss5 d. Каноническое уравнение параболы имеет вид
у*^2рх, (IV. 8)
где р — параметр параболы, равный расстоянию от
фокуса до директрисы (ось х направлена по оси сим-
симметрии параболы, а начало координат совпадает
с вершиной параболы). Эксцентриситет параболы сле-
следует, как мы увидим ниже, принять равным 1.
r/d~e-f
Рис IV. 3
Рис. IV. 4
Любое коническое сечение можно определить как
геометрическое место точек, яля которых отношение
расстояния г (рис. IV. 4) до точки F (называемой фо-
фокусом) к расстоянию d до прямой D (называемой ди-
iv.i ректрисой) есть постоян-
постоянная величина е (назы-
(называемая эксцентриситетом
кривой):
¦?««. (IV. 9)
В зависимости от зна-
значения эксцентриситета е
получается то либо иное коническое сечение
(табл. IV. 1).
У эллипса и гиперболы имеются по два фокуса и
по две директрисы. Условие (IV. 9) выполняется для
каждого из фокусов и соответствующей ему дирек-
директрисы. На рис. IV. 5 показаны фокусы и директрисы
эллипса а) и гиперболы б) (ср с ркс IV. 3 для па-
параболы).
Значение в
<1
I
>i
Вид кривой
эллипс
парабола
гипербола

IV. КОНИЧЕСКИЕ СЕЧЕНИЯ
359
Расстояние рг от фокуса до директрисы называет-
называется параметром кривой. Величина
р^р'е (IV. 10)
называется фокальным параметром. Легко сообра-
сообразить, что он равен половине хорды, проходяхцей через
фокус и параллельной директрисе (рис. IV. 4). Для
параболы р — р'.
Расстояние между директрисами эллипса (гипер-
(гиперболы) равно 2(а/е)9 где а— большая (действитель-
(действительная) полуось кривой.
г(ф)
Рис. IV. 5
Напишем уравнение конического сечения в поляр-
полярных координатах, поместив начало координат в од-
одном из фокусов кривой (рис. IV. 4). В соответствии
с (IV. 9)
откуда
р' + r cos ф
p
1 — е cos <p
(IV. И)
(р = //е;сн. (IV. 10)).
Уравнение (IV. 11) описывает эллипс (с началом
координат в точке Fi; рис. IV.5,а)у правую ветвь ги-
гиперболы (с началом координат в точке F2;
рис. IV. 5, б) и параболу. Отметим, что фокус F2 яв-
является для правой ветви гиперболы внутренним.

360
ПРИЛОЖЕНИЯ
Если поместить начало координат в правом фо-
фокусе эллипса (точка F% на рис. IV.5,а), то, как сле-
следует из рис. IV. 6, уравнение эллипса имеет вид
р — г cos ер
или
1 + e cos \
(IV. 12)
(р = р'е). Это же уравнение описывает левую ветвь
гиперболы (см. рис. IV. 5, б) при условии, что начало
координат помещено в
точку Fx (во внутрен-
внутренний по отношению к
этой ветви фокус), а
также параболу, яв-
являющуюся зеркальным
Рис. IV. 6
Рис. IV. 7
относительно D) отражением параболы, изображен-
изображенной на рис. IV. 3. Фокус F такой параболы лежит сле-
слева от директрисы D.
Найдем уравнение одной из ветвей гиперболы
(скажем, левой) при условии, что начало координат
помещено во внешний по отношению к этой ветви фо-
фокус (в точку F2 для левой ветви; рис. IV. 5,б). В этом
случае (рис. IV. 7)
&' = г cos (я — ф) — 2 — — pf — —- г cos ф — 2 ~ —• р'.
Согласно определению гиперболы (IV. 5) г — г'==2я,
откуда

V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 361
Подставив найденные нами значения df и г' в соот-
соотношение (IV. 9), придем к формуле
г' г - 2а
— /* cos (р — 2 — —
После несложных преобразований получим искомое
уравнение
(р = р'е). Следует иметь в виду, что для левой ветви
Ф > — (см. рис. IV. 7), т. е. cos ф < 0. Кроме того,
для всех точек |^созф|> 1, так что значения г, по-
получаемые по формуле (IV. 13), будут положительными.
Предоставляем читателю убедиться в том, что ана-
аналогичное уравнение для правой ветви (начало коор-
координат в точке F\) имеет вид
— е cos
(IV. 14)
В этом случае ф < -=-, так что cos ф > 0; кроме того,
есозф> !, так что значения г положительны.
V. Линейные дифференциальные уравнения
с постоянными коэффициентами
Линейным дифференциальным уравнением п-ro по-
порядка с постоянными коэффициентами называется
уравнение вида
f (x). (V. 1)
т. е. уравнение, линейное относительно неизвестной
функции у{х) и ее производных (а,- — постоянные ве-
величины, которые могут быть и нулями).
Если правая часть уравнения тождественно равна
нулю (f(#)sssO), то линейное уравнение называется
однородным, в противном случае — неоднородным.
Однородное уравнение имеет вид
У{п) + ая_х#п-1> +...+ щу' + щу — 0. (V. 2)
Общим решением дифференциального уравнения
называется множество решений, включающее все без

362 ПРИЛОЖЕНИЯ
исключения частные решения. Общее решение вся-
всякого дифференциального уравнения п-ro порядка со-
содержит п произвольных постоянных (постоянных ин-
интегрирования), т. е. имеет вид
у = у{х,СиСъ ...,СЙ), (V.3)
Придав постоянным Си С2, ..., Сп определенные
значения, получим частное решение. Частное решение
не содержит произвольных постоянных величин.
В теории линейных дифференциальных уравнений
доказывается, что если уи #2, . ¦., Уп суть линейно не-
независимые !) решения однородного уравнения (V. 2),
то общее решение этого уравнения можно предста-
представить в виде
у (х, Си С2, ..., Сп) - Е Ciyi (х), (V. 4)
где А, С2, ..., Сп — произвольные постоянные.
Пусть у (х) есть одно из частных решений неодно-
неоднородного уравнения (V. 1), а у{х) — общее решение
того же уравнения. Если ввести обозначение и(х) —
— у(х)—У(х)* то общее решение можно записать сле-
следующим образом:
У(х, Си С2, ..., Сп)^и(х9 Си С2 Сп) + у(х).
(V.5)
Подставим эту функцию в уравнение (V. 1) и сгруп-
сгруппируем отдельно слагаемые вида uw и слагаемые
вида у&к
иМ + ^_,«с«-1) + ... + ахи' + щп +
+ W™ + в»-1^ "> + . ¦. + *xff + аоу] = / (х).
Функция у(х) есть частное решение уравнения.
Следовательно, выражение, заключенное в квадрат-
квадратные скобки, равно правой части уравнения. Отсюда
вытекает, что функция и(х9 Си С2, ..., Сп) удовлет-
удовлетворяет условию
= 0.
fl) Совокупность функций f i, /г, ..., fn называется линейно
независимой, если соотношение вида
0
выполняется только при условии, что все щ равны нулю.

V. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ 363
Таким образом, и является общим решением однород-
однородного уравнения (V.2), соответствующего неоднород-
неоднородному уравнению (V. 1), т. е. имеющего такие же ко-
коэффициенты а*, что и уравнение (V.1).
Полученный нами результат можно сформулиро-
сформулировать следующим образом: общее решение линейного
неоднородного уравнения равно сумме общего реше-
решения соответствующего однородного уравнения и ка-
какого-либо частного решения неоднородного уравнения:
#(общ., неоднор.) =
= у (общ., однор.) + у (части., неоднор.). (V. 6)
Линейные однородные дифференциальные уравне-
уравнения с постоянными коэффициентами решают с по-
помощью подстановки
у(*)-ехр(Ял), (V.7)
где % — постоянная величина. Продифференцировав
эту функцию m раз (т = 1,2, ..., п), получим
?<«>=« я» exp(fcx). (V.8)
Подставив значения функции (V. 7) и ее производных
(V. 8) в уравнение (V. 2) и сократив на отличный от
нуля множитель ехр(Хх), придем к так называемому
характеристическому уравнению
O. (V.9)
Корни этого уравнения представляют собой те значе-
значения X, при которых функция (V, 7). удовлетворяет
уравнению (V. 2).
Если все п корней характеристического уравнения
будут различными (будут отсутствовать кратные, т. е,
совпадающие корни), п частных решений вида
ехр(Я*к) окажутся линейно независимыми. Следова-
Следовательно, при отсутствии кратных корней общее реше-
решение уравнения (V. 2) выглядит следующим образом:
(Си Сг, ..., Сп — произвольные постоянные).
Можно показать, что в случае, когда характеристи-
характеристическое уравнение (V. 9) имеет кратные корни, то рй
линейно независимых частных решений, отвечающих

364 ПРИЛОЖЕНИЯ
корню Я|г кратности р^9 должны быть взяты в виде
exp (к^х), * ехр (Я^*), х2 ехр (Яйл), ..., хр*~х ехр (к^х\
гак что соответствующий им вклад в общее решение
равен сумме
Следовательно, если корень Х\ будет кратности рь
^2 — кратности р2, .... Лт—кратности рт{р\+р2+ ...
... +/?т = /г), то общее решение можно представить
в виде
И ). (V. 11)
Допустим, что коэффициенты ak в уравнении
(V. 1) действительные, а функция f(x) комплексная.
Представив ее в виде
получим уравнение
У{п) + ап~хУ{п-1) + • • • + ад' + (кУ = f i (*) + if 2 №•
(V. 12)
Будем искать решение этого уравнения в виде
y(x) = yi(x) + iy2(x).
Подстановка в (V. 12) дает
-fiW + 'faW- (V.13)
У равных друг другу комплексных чисел равны
порознь действительные и мнимые части. Следова-
Следовательно, уравнение (V. 13) распадается на два незави-
независимых уравнения вида (V. 1). В одном из них справа
стоит функция !\{х)9 его решением является функция
ух(х). В другом справа стоит функция f%(x), его реше-
решением является функция #2(я). Это свойство уравне-
уравнения (V. 13) обусловлено его линейностью. Оно позво-
позволяет воспользоваться следующим приемом, иногда

VI. ВЕКТОРЫ 365
значительно облегчающим вычисления. Пусть в ре-
решаемом нами уравнении (V. I) правая часть действи-
действительная. Прибавим к ней произвольную мнимую
функцию. Найдя затем комплексное решение получив-
получившегося уравнения, возьмем его действительную часть.
Она будет представлять собой решение исходного
дифференциального уравнения.
Очевидно следующее утверждение: если линейное
однородное уравнение (V. 2) с действительными коэф-
коэффициентами имеет комплексное решениеу{х)*=*у\{х) +
-\-iy%(x)% то каждая из функций у\(х) и уъ(х) в от-
отдельности является решением этого уравнения.
VI. Викторы
1. Основные определения. Векторами называются
величины, которые характеризуются численным зна-
значением (модулем) и направлением и, кроме того, скла-
складываются геометрически (т. е. по правилу параллело-
параллелограмма). Ниже мы дадим более общее определение,
позволяющее распространить понятие вектора на про-
пространство п измерений.
Скалярным произведением двух векторов а и b на-
называется скалярная величина
, Ь). (VI. 1)
Скалярное произведение коммутативно: аЬ = Ьа и ди-
дистрибутивно: а (bi + b2 + ...) = ab| + аЬ2 + ..., но
не ассоциативно: а(Ьс)=?ЦаЬ)с.
Векторным произведением называется вектор *)
[ab]==a&sin(a, Ь) • nf (VI. 2)
где п — орт (единичный вектор) нормали к плоскости,
в которой лежат векторы а и Ь, причем последова-
последовательность а, Ь, п образует правовинтовую систему.
Векторное произведение не коммутативно: [bj
Ф [Ы], дистрибутивно: [a(bi + b2 + ...) ] =
+ [ab2]+ ... и не ассоциативно: {[blj^fl]]
Рассмотрим смешанное (векторно-скалярное) про-
произведение трех векторов: a [be]. Применив формулы
{) Наряду с записью [ab], которой мы будем пользоваться,
для обозначения векторного произведения применяется также
символ ХЬ

ПРИЛОЖЕНИЯ
(VI. I) и (VI 2), получим
a [be] s= a {be sin (b, с)} cos (a, n).
Из рис. VI. 1 легко видеть, что полученное нами
выражение равно объему параллелепипеда, построен-
построенного на перемножаемых векторах1). Действительно,
Рис. VI. 1
Ьс sin (fe, с) дает площадь основания параллелепипеда,
a a cos (а, и) — его высоту.
В качестве основания параллелепипеда можно
взять также грань, стороны которой образуют век-
векторы с и а либо векторы а и Ь. Тогда объем будет
определяться смешанными произведениями b [ca] и
c[ab]. Поскольку объем во всех трех случаях один
и тот же, можно написать
a [bej =- Ь [са] = с [аЬ]. (VI. 3)
Таким образом, смешанное произведение допускает
циклическую перестановку сомножителей, т. е. замену
каждого из сомножителей следующим за ним или
предшествующим ему сомножителем. Следующим за с
следует считать вектор а, а предшествующим а — век-
вектор с, что нагляднее всего вытекает из следующей
схемы:
а-*Ь
ЧУ (VI. 4)
с
Отметим, что во всех трех выражениях формулы
(VI. 3) векторы идут в той же последовательности,
что и на схеме (VI. 4). Если взять векторы в последо-
последовательности, противоположной изображенной на схеме
(VI. 4), то смешанное произведение изменит знак.
1) Предполагается, что угол (а. п) острый. Если зтот угол
тупой, то смешанное произведение раэно объему параллелепи-
параллелепипед а, взятому со знаком минус.

VI. ВЕКТОРЫ 367
Двойным векторным произведением называется
вектор [а [Ьс]]. Можно показать (мы сделаем это
ниже), что
[a [be]]» b (ас) - с (ab) (VI. 5)
(эта формула читается «бац минус цаб»).
В соответствии с определениями (VI. 2) и (VI. I)
квадрат векторного произведения векторов а и Ь мо-
может быть преобразован следующим образом:
= аЧ2 - a2b2 cos2 (a, b) = a2b2 - (abJ.
Мы пришли к формуле
(VL6)
2. Формулы векторной алгебры, выраженные че-
через проекции векторов на координатные оси. Все при-
приведенные выше определения и формулы не зависят от
выбора системы координат, в которой ведется рас-
рассмотрение. Если установить систему координат (мы
будем рассматривать только прямоугольные, т. е. де-
декартовы системы), то каждый вектор может быть за-
задан тремя числами— его проекциями на координат-
координатные оси1). Следовательно, вектор а эквивалентен
тройке чисел ах, йу, аг, вектор Ь —тройке чисел bXt
byj bz и т. д.
Зная проекции вектора на координатные оси, можно
найти сам вектор. Обозначив орты координатных
осей2) символами е*9 е#, ег, можно представить вектор
в виде
а == ел + ъуау -f eA. (VI. 7)
Чтобы получить возможность записывать формулы
в компактной форме с помощью знака суммы 2 > бу-
будем в дальнейшем пользоваться следующими обозна-
обозначениями. Вместо координаты х будем писать х\9 вме-
вместо у — Х2 и вместо z — х$. Аналогично для ортов осей
введем обозначения: ei, e2, е3. Соответствие между
*) Мы рассматриваем так называемые свободные векторы,
для которых не фиксированы точка приложения и прямая, вдоль
которой направлен вектор.
2) Эти орты обозначают также символами i, j, k. Однако
принятые нами обозначения, как будет видно из последующего
изложения, имеют несомненное преимущество.

388 ПРИЛОЖЕНИЯ
Прежними и новыми обозначениями дано на приводи-
приводимых ниже схемах:
х->хи
(VI. 8)
i =
J = e,-»e*, (VI. 9)
В новых обозначениях формула (VI. 7) может
быть записана в виде
а—Еад* (VI. Ю)
(во всех случаях, когда не будет оговорено противное,
мы будем предполагать, что ин-
индекс, по которому производится
суммирование,— немой индекс —
пробегает значения I, 2, 3).
Тройка векторов еь е2, е3 об-
образует базис координатной си-
системы. Задание этих векторов
полностью определяет систему.
Рис VI. 2 Поскольку еь е2 и е3 взаимно
перпендикулярны, а модули их
равны единице, из формулы (VI. 1) вытекает, что
е*ек-Л1Ь (VIЛ1)
где bit — так называемый символ Кронвкера, который
определяется следующим образом:
, если i = fe,
I, если * Ф k.
Отметим1), что 6/* = бы.
Из формулы (VI. 2) следует, что (рис. VI. 2)
(VI. 13)
4) В Приложении X будет показано, что совокупность вели-
величин б» образует симметричный тензор второго ранга.

VI. ВЕКТОРЫ 369
Отметим, что каждое из соотношений (VI. 13) может
быть получено из предыдущего (или последующего)
с помощью циклической перестановки индексов по
схеме
1->2
\/ (VI. 14)
3
Введем символ г)
еш, (VI. 15)
обозначающий набор из 27 чисел, которые опреде-
определяются следующими правилами:
1) если значения хотя бы двух индексов совпа-
совпадают, то 8ш:=0 (например, еш = 62^2=6/33=8222=0);
2) если все индексы разные и образуют цикличе-
циклическую перестановку последовательности 123, то гш =
= 1 («123 = 8231 ~ е312 = 1) ;
3) если все индексы разные и образуют цикличе-
циклическую перестановку последовательности 3 2 1, то гш=
= —1 F321=6213 = 8132 = —!)•
Таким образом, из 27 значений гш 21 равно нулю,
3 равны +1 и 3 равны —1.
Заметим, что любая циклическая перестановка чи-
чисел I 2 3 может быть получена из 12 3 посредством
четного числа перестановок (транспозиций) двух ин-
индексов, а любая циклическая перестановка чисел 3 2 1
может быть получена из 1 2 3 посредством нечетного
числа перестановок двух индексов. Действительно, по-
поменяв, например, в последовательности 1 2 3 местами
1 и 2 (что даст 2 13, т. е. циклическую перестановку
чисел 3 2 1), а затем поменяв местами 1 и 3, получим
перестановку 2 3 1.
Следовательно, значения символа вш можно опре-
определить так: 1) они равны нулю при совпадении зна-
значений хотя бы двух индексов, 2) они равны +1 или
—1 в зависимости от того, каким — четным или не-
нечетным— числом перестановок может быть получена
последовательность ikl из последовательности 1 23.
х) Его называют иногда кососимметричным символом Кро-
иекера. В Приложении X будет показано, что совокупность ве-
величин ziki образует абсолютно антисимметричный тензор третьего
ранга.

370 ПРИЛОЖЕНИЯ
Для определения знака 8ш можно пользоваться
также следующим правилом. Назовем беспорядком
в перестановке тот факт, что большее число стоит
впереди меньшего. Так, например, в перестановке 2 1 3
содержится один беспорядок: 2 стоит впереди 1, а в
перестановке 32 1 три беспорядка: 3 стоит перед 1,
3 стоит перед 2 и 2 стоит перед 1. Припишем еш зна-
значение + 1, если число беспорядков в перестановке
ikl является четным, и —1, если число беспорядков
нечетное. Легко убедиться в том, что все три рассмот-
рассмотренные нами правила определения знака еш дают
одинаковый результат.
Докажем следующее очень полезное соотношение
между символами е и б:
binfikn — &iAm- (VI. 16)
Раскроем сумму, стоящую в левой части:
(VI. 17)
и выясним, при каких значениях индексов i\ k, m9 n
эта сумма отлична от нуля. Очевидно, что для отли-
отличия хотя бы одного слагаемого от нуля должны вы-
выполняться одновременно условия
I ф k и т Ф п. (VI. 18)
Кроме того, должно быть
i = mt k — n или / — я, & —т. (VIЛ 9)
Действительно, если при соблюдении условия (VI. 18)
не будет соблюдаться условие (VI. 19), то в каждом
из слагаемых в (VI. 17) в числе значений первых двух
индексов обоих сомножителей будут фигурировать и
1, и 2, и 3. Поэтому немой индекс / в каждом из сла-
слагаемых совпадет со значением одного из индексов i9
k, m, я, так что все слагаемые будут нулями.
Объединим условия (VI. 18) и (VL 19) в одно, вы-
выражаемое формулами
i = m^k = n, (VI.20)
i^n^k^m. (VI. 21)
В случае, соответствующем соотношениям (VI. 20),
сумма (VI. 17) имеет вид

VI. ВЕКТОРЫ 371
Очевидно, что отличным от нуля будет только одно
слагаемое (для которого m, n и / различны), причем
оно равно +1.
В случае, соответствующем соотношениям (VI. 21),
сумма (VI. 17) имеет вид
"Г ЪптФтпЪ i едт3ет«3*
В этой сумме также отлично от нуля только одно сла-
слагаемое, причем оно равно произведению +1 на —1,
т. е. — 1 (при перестановке двух индексов znmi меняет
знак).
Теперь обратимся к правой части формулы (VI. 16),
т. е. к выражению
в|«**ц-*|А«- (VI. 22)
Если i — k (или гп = п), это выражение принимает
ВИД bkmbkn — SkrSkm (либо бщбкп — б/„б*я). Оба ЭТИ
выражения равны нулю. Отсюда следует, что для от-
отличия выражения (VI. 22) от нуля должны одновре-
одновременно выполняться условия
1фк и тфп (VI. 23)
(ср. с (VI. 18)). Кроме того, должно соблюдаться одно
из двух следующих условий:
i = m9 * = л, (VI. 24)
/ = п, k = m. (VI. 25)
При соблюдении условия (VI. 24) первый член вы-
выражения (VI.22) равен +L Поскольку i = m, а тфп
(см. (VI. 23)), то гФп и второй член выражения
(VI. 22) равен нулю. Следовательно, при соблюдении
условия (VI. 24) выражение (VI. 22) равно +1. Сово-
Совокупность условий (VI. 23) и (VI. 24) эквивалентна
условию (VI. 20), при котором, как мы установили,
левая часть формулы (VI. 16) также обращается в
+ 1
+
При соблюдении условия (VI. 25), которое в соче-
сочетании с (VI. 23) эквивалентно условию (VI. 21), вы-
выражение (VI. 22) обращается в —1.
Таким образом, соотношение (VI. 16) нами дока-
доказано.
С помощью символа еш совокупность соотноше-
соотношений (VI. 13) может быть представлена в виде одного

372 ПРИЛОЖЕНИИ
выражения
Z (VI. 26)
Действительно, при /= 1, ft = 2 отличным от нуля бу-
будет только слагаемое еж**, равное ез, при i — 2, & — 3
отлично от нуля слагаемое 823iei — ei и, наконец, при
i г» 3, & = I отлично от нуля слагаемое взиСз — ©2.
Выражение (VI. 26) дает даже больше чем сово-
совокупность трех соотношений (VI. 13). Оно содержит
9 соотношений. Из него следует, что векторное про-
произведение любого орта на самого себя равно нулю —
при i = k все слагаемые в правой части формулы
(VI. 26) обращаются в нуль. Кроме того, в (VI. 26)
содержатся выражения, получающиеся из (VI. 13) пе-
перестановкой сомножителей. Так, например, при l = 2t
k = 1 справа в (VI.26) отлично от нуля слагаемое
т. д.
Образуем скалярное произведение векторов а =
Z 2)
Воспользовавшись свойством дистрибутивности, мож-
можно написать
ab -=
г,
(см. формулу (VI. 11)). В соответствии с определе-
определением б** в последней сумме отличны от нуля лишь
слагаемые с одинаковыми значениями индексов i и k.
Следовательно,
ab =?<ii*i (VI. 27)
или, переходя к обычным обозначениям,
ab = ахЬ% + a^fty + azbz. (VI. 28)
Для заданных векторов а и Ь их проекции на ко-
координатные оси зависят от выбора системы коорди-
координат, но само произведение аЬ от этого выбора не за-
зависит. Отсюда заключаем, что выражение аА +
+ Q>yby + а*** есть инвариант, т. е. величина, одина-
одинаковая во всех системах координат.

VI. ВЕКТОРЫ 373
Пусть нам дана совокупность трех чисел u, v, w,
о которых известно, что в комбинации с проекциями
некоторого вектора а они дают скаляр, т. е. инва-
инвариант:
иах + vay + waz = inv.
Тогда на основании сказанного выше можно утверж-
утверждать, что и, vy w суть компоненты 1) некоторого век-
вектора.
Образуем векторное произведение векторов а~
= X е,а, и Ь = X
В силу дистрибутивности можно написать
[] ?
Заменим [е/е*] в соответствии с формулой (VI. 26):
[аЬ] = Е (hh Z еш«/ =
Итак, векторное произведение может быть пред-
представлено в виде
Z (VI. 29)
Из 27 слагаемых этой суммы отличны от нуля только
шесть. Выписав эти слагаемые, получим
[ab] =
Наконец, объединив слагаемые с одинаковыми ор-
ортами, придем к выражению
[ab] = ei (a2fe3 — аф2) + % (аф{ — a{b3) + еа (а^з — a2bx),
(VI. 30)
которое может быть записано в виде определителя
(см. Приложение VIII)
[ab] =
е3
а2
(VI. 31)
*) Так для краткости мы будем называть проекции вектора
на координатные оси.

374 ПРИЛОЖЕНИЯ
или, в обычных обозначениях,
I j к
ах пу аг
b% by bz
(VI. 32)
Отметим, что согласно (VL 29) /-я компонента век-
векторного произведения определяется формулой
= Z bik№ibk — Z
(мы осуществили циклическую перестановку индексов
при е, которая, как известно, не изменяет числового
значения этого символа). Чтобы иметь дело с более
привычной последовательностью буквенных индексов,
напишем выражение для i-й компоненты векторного
произведения
lab], = E e,*Aft/. (VI. 33)
k, i
Докажем с помощью соотношения (VI. 16) фор-
формулу (VI. 5) («бац минус цаб»). Для этого запишем
векторное произведение в соответствии с формулой
(VI. 29):
= Z
Теперь заменим [Ьс]Пр. / его выражением, получаю-
получающимся из формулы (VI. 33) :
Z 4lb?l Z mnnfiv
ft, I, i m, n
Осуществим циклическую перестановку индексов при
символах е, чтобы общий для них индекс / оказался
на последнем месте. Кроме того, сгруппируем сомно-
сомножители таким образом, чтобы суммирование по /осу-
/осуществлялось в первую очередь:
d = Z *i<*kbmcn Z ъшътп1 —
i, к%т%п I
= Z eiakbmcn (bim6kn — bin6km)
i, kt m, n

VI. ВЕКТОРЫ 375
(мы применили соотношение (VI. 16)). Дальнейшие
преобразования дают
т п
_ Е ^inCn Е eftm^m — Zl ......
?, ft « m i, ft t\
= E ® A E я^ — E ^ E #/A = b (ac) — с
i k i ft
что и требовалось доказать.
3. Истинные векторы и псевдовекторы. Различают
два вида векторов: полярные (или истинные) и акси-
аксиальные (или осевые), иначе называемые псевдовекто-
рами1). При инверсии координатных осей, т. е. при
изменении направлений координатных осей на обрат-
обратные (рис. VI. 3) компоненты
полярного вектора меняют '
знак. Это означает, что такой
/
/(*)
вектор при инверсии остается
без изменений. Компоненты
псевдовектора при инверсии «« •
знака не изменяют. Это озна- ^ / ! ^
чает, что псевдовектор при ин-
инверсии изменяет свое направ-
направление на обратное (т. е. ме- ^
няет знак). ^
Из рис. VI. 3 видно, что Рис. VI. 3
при инверсии координатных
осей правая система координат переходит в левую.
Поэтому различие между полярным вектором и
псевдовектором можно определить следующим об-
образом: полярный вектор не изменяется при переходе
от правой системы координат к левой, псевдовектор
же при таком переходе изменяет направление на об-
обратное. В Приложении X будет показано, что псевдо-
псевдовектор представляет собой антисимметричный тензор
второго ранга.
Если оба вектора а и b полярные, компоненты
векторного произведения (VI. 30) при инверсии знака
не изменяют (at и Ьи в отдельности меняют знак, но
их произведение остается без изменений). Следова-
*) «Псевдо» — первая составная часть сложных слов, озна-
означающая: ложный, мнимый (соответствует русскому «лже»).

376 ПРИЛОЖЕНИЯ
телыю, векторное произведение полярных векторов
является псевдовектором.
Скаляры также нужно делить на два вида: истин-
истинные скаляры и псевдоскаляры. Истинные скаляры не
изменяются при переходе от правой системы коорди-
координат к левой (или при инверсии координатных осей).
К их числу относятся, например, масса, электрический
заряд, температура. Псевдоскаляры при переходе от
правой системы координат к левой меняют знак. К их
числу принадлежат скалярные выражения, получаю-
получающиеся в результате математических операций над век-
векторами. Так, например, скалярное произведение (см.
(VI. 27)) полярного и аксиального векторов при ин-
инверсии меняет знак и, следовательно, является не ис-
истинным скаляром, а псевдоскаляром.
Если векторы а, Ь, с полярные, то выражение
(VI. 3) будет псевдоскаляром — при инверсии оно ме-
меняет знак. Таким образом, смешанное произведение
полярных векторов есть псевдоскаляр.
4. Преобразования компонент векторов. Найдем
формулы преобразования компонент вектора при пе-
переходе от одной системы координат к другой. Возь-
Возьмем две системы прямоугольных координат К и К',
задав их базисами е,, е2, е3 и е,, е^, е^. Произволь-
Произвольный вектор а можно представить в виде а = 2 е&#ь
тле uk — проекции а на оси системы /С, либо в виде
а — Л ?'ka'k> r#e a'k ~~ проекции а на оси системы К'.
Таким образом,
Z« = Z VV (VI. 34)
k k
Умножим (VI. 34) на орт е*:
е,е.а. = & ь&ьак- (VI. 35)
k
Согласно (VI. 11) е^ —6ife. Следовательно, из трех
слагаемых в левой части будет отлично от нуля только
слагаемое с k == /, которое равно biia'i = a\.
Скалярное произведение e'tek равно косинусу угла
между осью х\ системы К и осью xk системы /(. Обо-
Обозначив этот косинус символом a4fe, можно написать
aik = t'*k = cos (*' xk) (i> k = 1, 2, 3). (VI. 36)

VI. ВЕКТОРЫ 377
Воспользовавшись этими обозначениями, соотно-
соотношение (VI. 35) можно представить в виде
<=Е«<Л (*=1, 2, 3). (VL37)
Формула (VI. 37) позволяет по известным проекциям
вектора а на оси системы К вычислить проекции а
на оси системы /('. Чтобы получить формулы обрат-
обратного преобразования (от К' к /С), умножим (VI.34)
на орт е*. Повторив рассуждения, приведшие нас
к формуле (VI. 37), получим, что
я,= Е«ы< (/=1,2,3). (VI. 38)
Формулы (VI. 37) и (VI. 38) различаются лишь
тем, что в одном случае суммирование производится
по второму индексу при а^, в другом случае — по
первому.
Девять величин а** не являются независимыми.
Образуем сумму Е a/m°W Учтя (VI. 36), получим
Величину е,ет можно рассматривать как проекцию
вектора е, на ось хт системы /С, аналогично e'feem есть
проекция вектора e'k на ось хт. Таким образом, сумму,
стоящую справа, можно представить в виде
Е (^)пр. хт Юпр. хт = « = \k
(см. формулу (VL27)). Отсюда следует, что
Е —в,Л. (VI. 39)
Аналогично можно доказать (рекомендуем это сде-
сделать читателю), что
Eomia^-6,*. (VI. 40)
m
Преобразования (VI. 37) и (VI. 38) могут быть
приняты в качестве определения вектора: вектором
называется совокупность величин аи a2t аз, которые
при переходе от одной системы координат к другой

378 приложения
преобразуется по формулам (VI. 37) и (VI. 38), где
aik, — величины, определяемые формулой (VI. 36).
Последнее определение вектора легко распростра-
распространить на пространство любого числа измерений. Пусть
имеется пространство п измерений. Возьмем в этом
пространстве систему координат, оси которой вза-
взаимно перпендикулярны. Это означает, что орты осей
еьег, ..., ел удовлетворяют условию (VI. II). Тогда
вектором в n-мерном пространстве (n-вектором) на-
называется совокупность п величин а\9 а^ ..., #«, кото-
которые при переходе от одной системы координат к дру-
другой преобразуются по формулам (VI. 37) и (VI. 38).
Немой индекс пробегает при суммировании в этом
случае не 3, а п значений. Число уравнений в (VI. 37)
и (VI.38) также будет не 3, а п.
Скалярное произведение векторов также легко об-
обобщается на пространство п измерений. Аналогично
(VI. 27) назовем скалярным произведением двух век-
векторов с компонентагМИ аи а%, ..., ап и Ь\, &2, .-., Ьп
выражение
(VI. 41)
которое представляет собой инвариант. Векторы, ска-
скалярное произведение которых равно нулю', назы-
называются взаимно ортогональными (или взаимно пер-
перпендикулярными) .
Понятие векторного произведения на пространства
иного, чем три, числа измерений не распространяется.
Инверсию координатных осей (см. рис. VI. 3)
можно рассматривать как преобразование от систе-
системы К к системе /<', коэффициенты которого имеют
значения
— 1 при i = kt
О при i Ф k
или
<*i* = -6a. (VI. 42)
Согласно формуле (VI. 37) компоненты вектора
преобразуются при инверсии по закону

VI. ВЕКТОРЫ 379
т. е. изменяют знак на обратный (об этом была уже
речь выше).
Найдем закон преобразования компонент вектор-
векторного произведения при инверсии координатных осей.
Напишем выражение (VI. 33) в системе координат К'
(получающейся в результате инверсии осей систе-
системы/С):
[ab]J - Z *'ikta'kb\ - Z в1ЫвДО. (VI. 43)
Мы воспользовались тем, что величины еш опреде-
определяются одинаково для всех систем координат, вслед-
ствие чего при любых преобразованиях координат
*ш = *ш- (VI. 44)
Выразим в формуле (VI. 43) а'к и Ь\ через не-
штрихованные компоненты соответствующих векто-
векторов, воспользовавшись соотношением (VI. 37)
- I еш ? (~ 6кт) ат I (- Ь1р) Ьр
2
kt I, m, p
Произведя суммирование по индексам тир, получим
В соответствии с (VI. 33) последнее выражение есть
[ab]/. Таким образом, мы установили, что
[ab]J-[ab]|t
т. е. что компоненты векторного произведения при
инверсии не изменяются. Отсюда следует, что вектор-
векторное произведение истинных векторов является псевдо-
псевдовектором.
Напишем смешанное произведение трех векторов.
Согласно формулам (VI. 27) и (VI. 33)
a [be] = ? at [be],- = ? at
i i k.
- iLbikiafikCt. (VI. 45)

380
ПРИЛОЖЕНИЯ
Выясним, как ведет себя эта величина при инверсии.
В системе К' будем иметь
Z
I, k, I
6iM) am I (- 6hp) Ьр Е (- &ts) c
p s
= — S
i, k,
У
Мы получили уже известный нам результат; смешан-
смешанное произведение истинных векторов при инверсии ме-
меняет знак, т. е. является псев-
псевдоскаляром.
5. Приращение вектора при
повороте» Найдем приращение,
которое получает вектор а
при повороте на бесконечно
малый угол Ар. Введем две си-
системы координат К и К', кото-
которые выберем так, чтобы их
оси г и г' совпадали с векто-
вектором dq> (рис. VI. 4). Пусть си-
система К' повернется вместе с
вектором а на угол d<p относи-
относительно системы /С. При этом
относительно системы К' век-
вектор а остается неизменным, от-
относительно же системы К век-
вектор а получает приращение da.
Будем сначала предполагать, что начало вектора а
помещается на оси z (рис. VI. 4). Если а лежит пер-
первоначально в плоскости уг, то приращение rfa колли-
неарно с осью х. Модуль этого приращения, как видно
из рисунка, равен asinat/ф. Из сказанного следует,
что приращение вектора а может быть представлено
в виде
Л = [Лр, а]. (VI. 46)
Докажем, что найденная нами формула остается
справедливой при произвольном расположении век-
вектора а относительно систем координат К и К'. Вве-
Введем в рассмотрение орты е*, еу, е2 системы К и орты
е*> е^» ez системы К'. Тогда вектор а можно задать
i е„
Рис. VI. 4

VI. ВЕКТОРЫ 381
выражением
а = еА + ел + еА (VI. 47)
либо выражением
а » еХ + « + е'Х, (VI. 48)
где ах> аУ9 аг — проекции вектора а на оси системы /С,
а'х> а'у> К ~~ пРоекВДи вектора а на оси системы /('.
При повороте вектора вместе с системой /С' на
угол а'ф вектор получает относительно К приращение,
которое можно записать в виде приращения выраже-
выражения (VI. 47):
da ~ ©Л d&x ~Ь е^ duy -j- ег A2Z
либо в виде приращения выражения (VI. 48):
da, — а'х de'x + а'у dz'y + a'z a'e^, (VI. 49)
где rfe^, defy9 defz — приращения ортов осей системы
К\ наблюдаемые в системе Л' (напомним, что проек-
проекции а'х, а'г а'г при повороте
остаются неизменными). с*1 /
При выбранном нами на- I /
правлении оси г' приращение
орта е^ равно нулю (rfe^ = 0).
На рис. VI. 5 показаны при-
приращения А? н dey, которые
получают орты е^. и е^ при по- 2°^^J^^^
вороте системы координат К'
на угол ^ф. Из рисунка вид- Рис. VI. 5
но, что направление dtx
совпадает с направлением орта е^. Модуль же dt'x
равен Лр [модуль (т. е. длина) любого орта равен
единице]. Следовательно, приращение орта е?, на-
наблюдаемое в системе /С, может быть представлено
в виде
Аналогичные рассуждения приводят к формуле
(знак «—» вызван тем, что векторы dt'y и t'x направ-
направлены в противоположные стороны).

382 ПРИЛОЖЕНИЯ
Подставив найденные нами значения приращений
ортов в формулу (VI. 49), получим, что
Покажем, что найденное нами выражение эквива-
эквивалентно векторному произведению [dtp, а]. Для этого
выразим последнее произведение через проекции пе-
перемножаемых векторов на оси системы /С', учтя, что
dap направлен по оси z!\ В соответствии с формулой
(VI. 32)
О 0 dq>
ах а'у а'г
Таким образом, мы пришли к формуле (VI. 46).
VII. Матрицы
Определение матрицы. В Приложении VI были по-
получены формулы преобразования компонент вектора
при переходе от системы координат К к системе К':
<=Е^А С-1.2,3), (VII. I)
°* = 5а*'а* (/=1> 2> 3) (VH-2)
(см. формулы (VI. 37) и (VI. 38)).
Коэффициенты перехода можно записать в виде
квадратной таблицы
<х2, а22 о2»! (VII. 3)
Ost C&32 «33 В
которая называется матрицей преобразования. Вели-
Величины ant именуются элементами матрицы. Первый ин-
индекс указывает номер строки, в которой стоит дан-
данный элемент, второй индекс — номер столбца.
Условимся об обозначениях. Элементы матрицы
мы будем обозначать строчными буквами с двумя ин-
индексами, а матрицу — соответствующей прописной
буквой (например, элемент а**, матрица А1)). Компо-
Компоненты вектора будем обозначать строчными буквами
*) Так пишется прописная прямая греческая буква «альфа».

VII. МАТРИЦЫ 383
с одним индексом, а вектор —такой же строчной бук-
буквой, но прямого полужирного шрифта (например, а,-—
компонента вектора, а —вектор).
Операцию (VII. 1) преобразования компонент век-
вектора можно записать символически в виде умноже-
умножения вектора на матрицу:
а'-=Аа. (VI 1.4)
Коэффициенты обратного преобразования (VII. 2)
образуют матрицу
|ап a2i аз! |
«12 «22 O»t|v (VII. 5)
«is ct2s «за II
называемую обратной матрицей. Обозначив элементы
обратной матрицы символом aJA, можно написать со-
соотношение
«!*-«¦*,. (vh. в)
Матрица, получаемая из А заменой строк столб-
столбцами, называется транспонированной и обозначается
А. Если обозначить элементы транспонированной
матрицы символом а**, можно написать
a^-aw. (VII. 7)
Из формул (VII. 6) и (VII. 7) следует, что мат-
матрица обратного преобразования (VII.5) совпадает
с транспонированной матрицей прямого преобразова-
преобразования (VII. 3):
А" —А. (VII. 8)
Соотношение (VII. 8) справедливо не для любых
матриц1). Матрицы, удовлетворяющие условию
(VII. 8), называются ортогональными.
Обратное преобразование (VII. 2) запишется сим-
символически в виде
а —A'V. (VII. 9)
Не меняя формальной математической стороны
дела, соотношения (VII. 4) и (VII. 9) (иными слова-
1) Вообще говоря, не всякая матрица имеет обратную. Мат-
Матрица, для которой обратной не существует, называется особенной
или вырожденной. Но даже если матрица не вырождена, ее об-
обратная и транспонированная матрицы могут не совпадать.

384 ПРИЛОЖЕНИЯ
ми, соотношения (VII. 1) и (VII. 2) можно рассмат-
рассматривать не как операции перехода от одной системы
координат к другой, а как операции, преобразующие
один вектор в другой, причем оба вектора рассматри-
рассматриваются в одной и той же системе координат. Имея
в виду такую трактовку, запишем формулы преобра-
преобразования следующим образом:
Ь = Аа, (VII. 10)
a = A"!b. (VILII)
Таким образом, матрицу А можно рассматривать
как линейный оператор, который, воздействуя на век-
вектор а, превращает его в вектор Ь.
Напишем в явном виде преобразования (VII. 10)
и (VII. 11), причем для большей общности будем счи-
считать, что векторы а и Ь определены не в трехмерном
пространстве, а в пространстве п измерений. По ана-
аналогии с (VII. 1) и (VII. 2) получим
hi = ]C Oitflu (i = 1, 2, ..., л), (VIL 12)
t JA (* = 1. Z, ..., /г), (VII. 13)
где a'ik — элементы матрицы обратного преобразова-
преобразования (матрицы А). Для ортогональной матрицы
Матрицы А и А-1 теперь будут иметь п строк
и п столбцов, например,
(VII. 14)
Матрица (VII. 14) является квадратной — число
строк в ней равно числу столбцов. Кроме квадратных
рассматриваются также прямоугольные матрицы, чи-
число строк которых т не равно числу столбцов п:
A = A{m,n) = |
«22
(VII. 15)

vii. матрицы 385
Первый индекс при символе матрицы указывает число
строк, второй — число столбцов. В случаях, когда это
не сможет привести к недоразумениям, мы эти ин-
индексы будем опускать.
Итак, в общем случае под матрицей понимается
совокупность т-п элементов, расположенных в ви-
виде прямоугольной таблицы. Элементами матрицы мо-
могут быть функций, числа либо иные величины, над
которыми можно производить алгебраические опера-
операции. Матрица с т строками и п столбцами называет-
называется (тX я)-матрицей, или матрицей порядка тХ«,
или, наконец, матрицей размера тХ^. Матрицу
порядка т X 1, т. е. матрицу с одним столбцом,
иногда называют просто столбцом. Матрицу порядка
1 X п, т. е. матрицу с одной строкой, иногда называют
просто строкой.
Две матрицы А и В называются равными (А=В),
если соответствующие элементы этих матриц равны
ДРУГ Другу (<*;* = &*).
Матрицы Аи В считаются отличающимися только
знаком, (А — —В), если соответствующие элементы
этих матриц связаны соотношением а^ = —р,*.
Квадратная матрица (VIL 14) (т. е. матрица по-
порядка пУ^п) есть частный случай матрицы (VII. 15).
Матрица, преобразующая вектор в пространстве п из-
измерений в другой вектор в том же пространстве, оче-
очевидно, будет квадратной.
Если элементы квадратной матрицы удовлетво-
удовлетворяют условию
** = <%„ (VII. 16)
матрица называется симметричной. Симметричная
матрица, очевидно, совпадает со своей транспониро-
транспонированной
(VII. 17)
Квадратная матрица, элементы которой удовлет-
удовлетворяют условию
а,*»-*,, (VII. 18)
называется антисимметричной или кососимметричной.
Антисимметричная матрица отличается от своей
транспонированной только знаком:
Аантисимм — Ааитисиш4. (V U • i 9/
13 И. В. Савельев, т. 1.

386 ПРИЛОЖЕНИЯ
Квадратная матрица, у которой отличны от куля
лишь элементы а^ с одинаковыми значениями индек-
индексов i и ky называется диагональной. Диагональная
матрица имеет вид
Я, О ... О |
О Я2 ... О (VII. 20)
О О ... hn 1
Элементы этой матрицы можно представить следую-
следующим образом:
*i*~*A*. (VII. 21)
где bik — символ Кронекера (см. (VI. 12)).
Если изменить систему координат (т. е. базис
еьег, ..., ел), то компоненты векторов а и Ь (см.
формулу (VII. 10)) станут другими. Изменятся также
и элементы матрицы-оператора. Оказывается, что в
некоторых случаях (в частности, в том случае, когда
матрица А симметрична) можно так выбрать базис,
что матрица А делается диагональной.
При переходе от одной системы координат к дру-
другой элементы матрицы меняются, однако остается не-
неизменной сумма диагональных элементов, называемая
следом матрицы (обозначается SpA; немецкое Spur
означает след). Таким образом, след матрицы одина-
одинаков во всех системах координат, т. е. является инва-
инвариантом:
Sp А = X о,, = Jnv. (VIL 22)
i
Остается неизменным также определитель матрицы
(см. (VIII. 3)):
det!!a^!j=-inv. (VIL 23)
Назовем единичной матрицей Е такую матрицу1),
которая при умножении на вектор по правилу
(VR 10) дает тот же вектор
Легко сообразить, что элементы единичной матрицы
должны быть равны б** (подстановка в (VII. 12)
*) Иногда единичную матрацу обозначают символом I.

vii. матрицы 387
a>ik ==6te приводит к соотношению hi^ui). Таким
образом,
i о ... о |
°..l;v.°|. (vn. 24)
О 0 ... 1 I
Отметим, что эта матрица является диагональной.
Алгебра матриц. Матрицы суть алгебраические
объекты, над которыми можно совершать операции
сложения, вычитания и умножения (операции деления
матриц не существует).
Суммой двух матриц А и В называется матрица
Гг^А-f-B1), элементы которой определяются фор-
формулой
(VII. 25)
Разностью матриц называется матрица Г = А — В
с элементами
Yi* = <*,*-?,*. (VII. 26)
Очевидно, что складывать и вычитать можно
только матрицы одинакового порядка, т. е. матрицы
с одинаковым числом строк и одинаковым числом
столбцов.
Произведением матрицы А на скаляр ц называется
матрица В = цА с элементами
(VIL 27)
Перейдем к рассмотрению перемножения матриц.
Предположим, что действие матрицы А на вектор а
превращает его в вектор Ь, а действие матрицы В на
вектор b превращает его в вектор с. Естественно на-
назвать произведением матриц А и В такую матрицу Г,
которая, действуя на вектор а, превращает его в век-
вектор с. Таким образом,
b = Аа, т. е. Ьт = ]? amkak,
с г» ВЬ = ВАа, т. е. ct = Е $imbm = E Ptm Z *mtflk —
т т k
ak E P<jn<*mft*
') Произносится: матрица «гамма» равна матрице «альфа»
плюс матрица «бета» (В — прописное греческое «бета», Г — про-
прописное греческое «гамма»).
13*

388 ПРИЛОЖЕНИЯ
С другой стороны,
т. е. С| =
Сравнение обеих формул для с и с(- приводит к пра-
правилу умножения матриц:
Г я» ВА означает, что yik = ]? $im®mk- (VII. 28)
т
Согласно этому правилу для получения элемента мат-
матрицы Г, стоящего на пересечении t-й строки и &-го
столбца, нужно умножить каждый элемент i-ft строки
матрицы В на соответствующий элемент fe-ro столбца
матрицы А и все произведения сложить. Это можно
пояснить следующей схемой:
_ ^р^*1
(VII. 29)
Ч-я строка, к-и столбец'
Заметим, что произведение матриц, вообще говоря,
не коммутативно, т. е.
ВА Ф АВ.
Матрицы, для которых выполняется условие
ВА = АВ, (VII. 30)
называются коммутирующими.
Легко показать, что произведение матриц ассоциа-
ассоциативно:
(ГВ)А = Г(ВА). (VII. 31)
Это означает, что умножив сначала В на Г, а затем
А на (ГВ), мы получим тот же результат, какой по-
получился бы при перемножении сначала матриц А и В
и последующем умножении матрицы (ВА) на Г. Дей-
Действительно, по правилу перемножения матриц
{(ГВ) А}** - Е (ГВ)|яЛв4 - I ( S
» ( S

VII. МАТРИЦЫ
389
(в ходе преобразований мы изменили порядок сумми-
суммирования по индексам т и /). Таким образом, свой-
свойство (VIL31) доказано.
Можно умножать друг на друга и неквадратные
(прямоугольные) матрицы. Как следует из схемы
(VII. 29), перемножение таких матриц возможно
только в том случае, когда число столбцов матрицы В
(второй матрицы1)) совпадает с числом строк мат-
матрицы А (первой матрицы). Матрица-произведение бу-
будет иметь столько строк, сколько их имеет вторая
матрица (матрица В) и столько столбцов, сколько их
имеет первая матрица (матрица А). Поясним это сле-
следующим примером:
Если вторая матрица квадратная, т. е. имеет по-
порядок п X я* а первая матрица содержит только один
столбец с п элементами, то матрица-произведение
также состоит из одного столбца с п элементами:
PlI Pl2 •
P2I P22 •
.. fa
«1
а2
(VII- 32)
При умножении матрицы с одним столбцом на
матрицу с одной строкой получается просто число
(или функция, если элементами матрицы являются
функции):
a\
(VL33)
*) В произведении матриц ВА первым сомножителем нужно
считать матрицу А, стоящую справа. На нее умножается вектор
в первую очередь, а затем уже на результат воздействует вторая
матрица В.

390 ПРИЛОЖЕНИЯ
В частности, если в качестве матрицы IIр!! взять транс-
транспонированную матрицу Ца||, то (VII. 33) переходит в
I«ж 0а — ап\
0,1
а2
¦z*
Следовательно, для матрицы А(«, о, имеющей только
один столбец, справедливо соотношение
VdVi)88^!. (VII. 34)
Если в качестве элементов матрицы с одним столб-
столбцом взять составляющие вектора а, а в качестве квад-
квадратной матрицы — матрицу-оператор А, то соотноше-
соотношение (VII. 32) примет вид
«И «12 •-. Щп II | Q>\ J
а2! а22 ... а2л а2 б | Ь2
I
! I в#
«яг • •. аля II 1 «я 1 I ^
где 6f ===== ^ а<&ал (ср. с (VII. 12)). Легко заметить,
что соотношение (VII. 35) эквивалентно соотношению
(VII. 10). Следовательно, вектор можно представить
как матрицу с одним столбцом.
Рассмотрим произведение единичной матрицы Е
на произвольную матрицу А. Согласно правилу
(VII. 28)
(AE)ik — Z-j A*mdmfe
m
(8mk — элементы матрицы Е). В этой сумме отличным
от нуля будет только одно слагаемое, у которого
m —]fe. Следовательно, (АЕ)**вА/*. Аналогично
Из сказанного следует, что умножение на единичную
матрицу (при любом порядке сомножителей) не изме-
изменяет матрицы А:
ЕА-АЕ = А. (VII. 36)
Последнее соотношение означает, что единичная мат-
матрица коммутирует с любой матрицей А.

VIII. ОПРЕДЕЛИТЕЛИ 39!
Очевидно, что, применив к какому-либо вектору
сначала преобразование А, а затем обратное ему пре-
преобразование А-1, мы должны вернуться к исходному
вектору
а — А'Аа. (VII. 37)
Отсюда вытекает, что произведение прямой и обрат-
обратной матриц должно быть равно единичной матрице:
А-!А = Е!). Произведение прямой и обратной мат-
матриц, очевидно, коммутативно, следовательно,
А-'А —АА^ — Е. (VII. 38)
Записав элементы произведения матриц А и А-1
по формуле (VII. 28), можно найти соотношение
между элементами прямой и обратной матриц:
? <А* = ? «i«<* - б<*- (VH. 39)
Для ортогональной матрицы, т. е. матрицы, удовлет-
удовлетворяющей условию (VII. 8), «^ = а^| (см. (VII. 6)).
Произведя в (VII. 39) такую замену, получим
Е *ш (VII. 40)
«iS. (VII- 41)
т
Таким образом, элементы ортогональной матрицы
удовлетворяют соотношениям (VII. 39) и (VII. 40)
(ср. с формулами (VI. 39) и (VI. 40)).
VIII. Определители
Пусть нам дана квадратная матрица
Л __- it fl2t **22 • • • **2»
(VIII. 1)
Образуем из элементов этой матрицы выражение
--*-» ОЛИ. 2)
*) Из этого соотношения становится понятным обозначение
А ', употребляемое для обратной матрицы (Е — «единица»).

392 приложения
где i, kt ..., rn — перестановка из чисел 1,2, ..., п,
a bik.^m— величина, равная + Ь если число беспо-
беспорядков !) в перестановке /, &, ..., т является четным,
и —1, если число беспорядков нечетное (ср. с
(VI. 15)). Число перестановок из п чисел, как извест-
известно, равно п\. Следовательно, можно составить л! раз-
различных выражений вида (VIII. 2).
Сумма всех выражений вида (VIII. 2) обозначается
символами
«11 «12 ••• «1П
«22 ••- «2Я __
Uft™ m)
(VIII. 3)
и называется определителем (или детерминантом),
соответствующим матрице (VIII. 1). Сумма (VIII.3)
берется по всем перестановкам чисел itkt ..., m. Сле-
Следовательно, она содержит п\ слагаемых.
Если дополнить определение Ык...т условием,
чтобы этот символ обращался в нуль при совпадении
значений хотя бы двух из п индексов, детерминант
D(A) можно определить как сумму
п
<ftZra=ie«...maua2ft...anOT, (VIII. 4)
в которой все индексы /, kt ..., m пробегают значе-
значения от 1 до п.
Из (VIII. 3) следует, что определитель можно за-
записать в виде таблицы, аналогичной (VIII. 1), с тем
отличием, что по бокам вместо двойных вертикаль-
вертикальных линий ставятся одинарные.
Число строк (или столбцов) определителя назы-
называется его порядком.
Отметим, что определитель диагональной матрицы
(VII. 20) равен произведению ее диагональных эле-
элементов:
detУ*Ж*II»*!*,... *я. (VIII.5)
*) Напомним, что беспорядком в перестановке называется
тот факт, что большее число стоит впереди меньшего.

VIII. ОПРЕДЕЛИТЕЛИ
393
а определитель единичной матрицы равен единице:
D (?)=!. (VIII. 6)
на примере определителя
Поясним сказанное
третьего порядка:
0Ц
031
012 013
022 023
032 033
Из вторых индексов элементов этого определителя
можно сделать 3! = 6 перестановок:
123
231
312
321
213
132
О
2
2
3
1
1
беспорядков
безпорядка
беспорядка
беспорядка
беспорядок
беспорядок
Согласно формуле (VIII. 4) определителем третьего
порядка будет выражение
— 013022^31 — «12«2i«33 — «11^23 «32-
Если в определителе я-го порядка вычеркнуть /-ю
строку и &«й столбец, получится определитель
(п—1)-го порядка, который называется минором ис-
исходного определителя, соответствующим элементу а,*.
Этот минор принято обозначать символом Д*&. Вели-
Величину
Л«*-(-1)'+*Д|* (VIII. 7)
называют алгебраическим дополнением элемента а<*.
Свойства определителей. Приведем без доказа-
доказательства основные свойства определителей.
1. При замене строк столбцами величина опреде-
определителя не изменяется:
0ц
021
0/11
012 ...
022 ...
0/12 «.
01»
02П
0/1/1
«яг-?
0ц
012
01/1
021 -..
022 • •
а2п
0Л2

394 приложения
или, в более компактной записи,
i = detail. (VIII. 8)
Замена строк столбцами называется транспониро-
транспонированием. Определитель, в котором призведена такая
замена, называют транспонированным. Таким обра-
образом, можно сказать, что транспонированный опреде-
определитель равен исходному.
Из свойства 1 вытекает, что определитель транс-
транспонированной матрицы равен определителю исходной
матрицы:
(VIII. 9)
Действительно, эти определители отличаются только
заменой строк на столбцы, что не изменяет величины
определителя.
2. При перестановке двух строк или двух столбцов
изменяется лишь знак определителя.
3. Определитель с двумя одинаковыми строками
или столбцами равен нулю (это следует из свой-
свойства 2).
4. Определитель является линейной формой1)
элементов какой-нибудь строки или какого-либо
столбца:
«let II О** В =
п
Л (линейная форма элементов f-й строки)
(VIII. 10)
либо
Ш
(линейная форма элементов fe-ro столбца),
(VIIIЛ1)
причем коэффициентами Aik линейных форм (VIII. 10)
и (VIII. И) являются алгебраические дополнения
(VIII. 6) соответствующих элементов.
!) Линейной формулой переменных хих2> ..., хп называется
однородная функция этих переменных, т. е. выражение
/ + а2х2 + ...

VIII. ОПРЕДЕЛИТЕЛИ
395
5. Если элементы одной строки (или столбца) ум-
умножить на алгебраические дополнения элементов дру-
другой строки (столбца) и полученные произведения сло-
сложить, то сумма будет равна кулю (эта сумма пред-
представляет собой определитель с двумя одинаковыми
строками или столбцами; см. свойство 3).
Свойства 4 и 5 можно объединить в виде соотно-
соотношений:
Е Aikamk = det || aik \\ • 6im,
Д (VIII. 12)
6
Из свойства 4 непосредственно вытекают еще два
свойства F и 7):
6. Если все элементы некоторой строки (или столб-
столбца) содержат общий множитель, то его можно выне-
вынести за знак определителя:
*\т
аа
п ...
. . . CM?,
«fe
л\п
ап\ '•• ank •'• апп
(VIII. 13)
7. Если элементы некоторой строки (или столбца)
являются суммой двух (или большего числа) слагае-
слагаемых, то определитель равен сумме определителей, в
которых элементами данной строк&$ (данного столбца)
служат соответствующие слагаемые, например,
41 ••
1
Чк
. •• an
а\\
а1к
а2к
... (Zi
а21
... a«
. (VIII. 14)
8. Значение определителя не изменится, если к эле-
элементам некоторой строки (шли столбца) прибавить

396 ПРИЛОЖЕНИЯ
соответствующие элементы другой строки (столбца),
предварительно умножив их на один и тот же мно-
множитель.
Это свойство вытекает из свойств 7, 6 и 3.
9. Произведением двух определителей одинакового
порядка det||a**|| и det||6^|| является определитель
того же порядка det|k/*||, элементы которого выра-
выражаются формулами
*и-Е «%«*«*. (VIII. 15)
m
Сравнение этой формулы с формулой (VII. 28) пока-
показывает, что определители перемножаются так же, как
и соответствующие матрицы. Следовательно, опреде-
определитель матрицы-произведения совпадает с произведе-
произведением определителей матриц-сомножителей.
Из свойства 9 вытекает, что определитель ортого-
ортогональной матрицы равен ±1. Действительно, для ор-
ортогональной матрицы А = Л-1 (см. (VII. 8)), вслед-
вследствие чего АА == Е. Согласно сказанному выше
(см. (VIII.6)). Но в соответствии с (VIII.9) D(A) =
= D{A), так что можно написать
откуда
D(A) = ±l. (VIII. 16)
Системы линейных неоднородных уравнений. Рас-
Рассмотрим систему п линейных алгебраических уравне-
уравнений с п неизвестными Х\, x2t ..., хп:
a2lxl+a22x2+ ...
Эту систему можно записать в виде одного выра-
выражения
= Ьг (/ - 1, 2, ..., п). (VIII. 17)
Видно, что коэффициенты при неизвестных обра-
образуют квадратную матрицу, аналогичную матрице

VIII. ОПРЕДЕЛИТЕЛИ 397
(VIII. 1). Допустим, что определитель этой матрицы
(мы будем его называть определителем системы) от-
отличен от нуля
#11 6l2 • • • О.\п
an a$8 ... #2л
/)
апп
(vm. 18)
Умножим первое из уравнений (VIII. 17) на Аш —
алгебраическое дополнение элемента aim, второе
уравнение — на Л2от, ..., п-е уравнение — на Апт п
сложим вместе получившиеся выражения. В резуль-
результате получим
п п п
Е Aimbl.
Поменяем порядок суммирования в левой части ра-
равенства:
п п а
^С Ч Е| Altrfllk — I! Aimbl-
п
Согласно второй из формул (VIII. 12) Е А1тщк^л
= <1е1||а<л||6тЛ = ?6тЛ, где D — определитель систе-
системы. Следовательно, полученное соотношение можно
представить в виде
Просуммировав слева по А, получим произведение
xmD. Сравнение суммы, стоящей справа, с формулой
(VIII, 11) позволяет сделать вывод, что эта сумма
представляет собой определитель, который получается
из определителя (VIII. 18) заменой элементов т-го
столбца свободными членами системы (VIII. 17). Обо-
Обозначив этот определитель символом D^m\ молено на-
написать, что
откуда
(замена т на k осуществлена для того, чтобы индекс
при х в данной формуле и формуле (VIII, Г/j б
чался одной и той же буквой).

398
ПРИЛОЖЕНИЯ
Мы пришли к теореме Крамера, которая гласит:
если определитель системы отличен от нуля, то она
имеет одно определенное решение, причем значение
неизвестного Xk равно дроби, знаменателем которой
является определитель системы D, а числителем —
определитель D<ft>, получающийся из D заменой эле-
элементов k-го столбца свободными членами системы:
f = l
D
«22
апп
aXk ••• aln
•• a2k
л
(VIII. 19)
Решение системы уравнений (VIII. 17) можно сде-
сделать очень наглядным, воспользовавшись следующим
представлением. Неизвестные %\,Хъ ..., хп можно
рассматривать как компоненты некоторого вектора х
в пространстве п измерений, а свободные члены
b\fb2, ...» 6Я —как компоненты заданного вектора Ь.
Тогда систему (VIII. 17) можно символически пред-
представить в виде соотношения
Ах^Ъ, (VIII. 20)
где А — матрица, составленная из коэффициентов
уравнений (VIII. 17):
л —
Оц п\2
&2\ &22
«ЯП
Действительно, раскрыв соотношение (VIII. 20) по
формуле (VII. 12), получим п уравнений:
= Ьг (/=1,2 п),
С
совпадающих с системой (VIII. 17).

VIII. ОПРЕДЕЛИТЕЛИ 399
Следовательно, задачу нахождения неизвестных хг
можно сформулировать следующим образом: даны
матрица А и вектор b в пространстве п измерений;
требуется найти такой вектор х, который, будучи умно-
умножен на матрицу Л, преобразуется в заданный вектор Ь.
Умножим уравнение (VIII. 20) на матрицу А"К
Тогда слева получится искомый вектор х (см. фор-
формулу (VII. 37)) и мы придем к соотношению
х = Л~!Ь. (VIII. 21)
Таким образом, для нахождения решений системы
уравнений (VIII. 17) нужно поступить следующим об-
образом: найти матрицу, обратную матрице системы, и
подставить элементы этой матрицы в формулы
** = ? <А (VIH. 22)
(см. формулы (VII. 11) и (VII. 13)).
Сопоставив формулы (VIII. 19) и (VIII. 22), мы
приходим к выводу, что элементы обратной матрицы
определяются выражениями
а'м-^Г- (VIII. 23)
Укажем еще одну форму записи рассмотренных
нами соотношений. Представив векторы киЬв виде
матриц с п строками и только одним столбцом, си-
систему уравнений (VIII. 17) можно записать в виде
или, кратко,
V«)-^.i)-Bo..i) (VOL 25)
(ср. с (VII. 35)).
Системы линейных однородных уравнений. Система
уравнений (VIII. 17), у которой все свободные членыbi
равны нулю, называется однородной. Таким образом,
однородная система имеет вид
апхг + а12х2 + ... + alnxn «= 0,
(h\*\ + аж4 + . • - + <%я*и — 0. (VIII, %Ц

400 приложения
(мы рассматриваем только системы, у которых число
уравнений равно числу неизвестных).
Если определитель этой системы отличен от нуля,
то согласно теореме Крамера система имеет одно
определенное решение, которое в данном случае бу-
будет нулевым:
1, 2, ..., п)
(см. (VIII. 19)).
Следовательно, для того чтобы однородная си-
система уравнений имела ненулевое решение, необхо-
необходимо, чтобы ее определитель был равен нулю. Можно
доказать, что это условие является не только необхо-
необходимым, но и достаточным.
Чтобы иметь возможность рассказать о характере
решений системы (VIII. 26), нужно познакомиться
с понятием ранга матрицы. Если число строк т не
равно числу столбцов п матрицы, для нее нельзя со-
составить определитель (VIII. 4). Однако, вычеркивая
кз матрицы некоторые строки и столбцы, можно из
оставшихся строк и столбцов составить определитель.
Полученные таким способом определители называ-
называются входящими в состав матрицы. Наивысший воз-
возможный порядок этих определителей равен минималь-
минимальному из чисел тип, определяющих размер матрицы,
а наименьший порядок этих определителей равен еди-
единице, причем определители первого порядка суть эле-
элементы матрицы.
Предположим, что все определители порядка /,
входящие в состав матрицы, равны нулю. Легко сооб-
сообразить, что тогда и все определители порядка A+1)
также равны нулю (это вытекает из свойства 4 опре-
определителей). Следовательно, если все определители не-
некоторого порядка /, входящие в состав матрицы, рав-
равны нулю, то и все определители более высокого по-
порядка также равны нулю.
Наивысший порядок отличного от нуля определи-
определителя, входящего в состав матрицы, называется ее ран-
рангом. Таким образом, тот факт, что ранг матрицы ра-
равен г, означает, что среди определителей порядка г,
входящих в состав матрицы, имеется хотя бы один от-

VIII. ОПРЕДЕЛИТЕЛИ 401
личный от нуля; определители же более высокого по-
порядка все равны нулю.
Понятие ранга применимо, разумеется, и к квад-
квадратной матрице. Так, например, при соблюдении усло-
условия (VIII. 18) ранг матрицы, составленной из коэф-
коэффициентов неоднородной системы уравнений (VIII. 17),
равен п.
Для того чтобы однородная система (VIII. 26)
имела ненулевое решение, требуется равенство нулю
ее определителя. Иными словами, необходимо, чтобы
ранг матрицы, составленной из коэффициентов систе-
системы, был меньше п. Пусть ранг матрицы системы ра-
равен г A^г<п). В этом случае существует п — г
линейно независимых решений
(а= 1, 2, ..., п - г).
Наиболее общим решением будут значения неизвест-
неизвестных, определяемые выражениями
*, = Е ?а4а) (* = *, 2, ... п), (VIII. 27)
а
*,
где са — произвольные постоянные.
В частном случае, когда ранг матрицы системы
г=^п—1, имеется только одно линейно-независимое
решение. Можно доказать, что этим решением будут
значения неизвестных
х, = cAku х2 = сАк2, • • •, хп = сАка, (Vlll. 28)
где Ам — алгебраическое дополнение элемента а*,-
в определителе системы D, с — произвольная постоян-
постоянная; k выбирается так, чтобы хотя бы одно из Аи
(/=1,2, ..., п) было отлично от нуля. Значения Ак%%
получающиеся при разном выборе k, отвечающем ука-
указанному условию, отличаются друг от друга на общий
множитель, который может быть включен в постоян-
постоянную с. Таким образом, от выбора k вид решения
(VI 11.28) не зависит.
Пусть некоторая совокупность значений xi = gi
удовлетворяет системе (VIII. 26). Легко заметить, что
значения х/ = %9< (Я — произвольная постоянная)
также удовлетворяют системе. Этим объясняется на-
наличие множителя с в формулах (VIII. 28). Из сказан-
сказанного следует, что системой (VIII. 26) однозначно опре-
определяются только отношения х*/х*, сами же значе-

402 приложения
ния Xi определяются с точностью до произвольного
множителя.
Задаче о решении системы однородных уравнений
можно дать следующую геометрическую интерпрета-
интерпретацию. Совокупность величин (агьдс2, ..., хп) будем
рассматривать как n-вектор х, аналогично совокуп-
совокупность величин (aiu а<2, . ¦., ain) будем рассматривать
как n-вектор а* (таких векторов будет л). Тогда си-
систему (VIII. 26) можно представить в виде
0 (/=1, 2, ..., п)
(см. формулу (VI.41)), а саму задачу сформулиро-
сформулировать так: в пространстве п измерений заданы п век-
векторов а,. Требуется найти такой вектор х, который
был бы перпендикулярен ко всем векторам а/.
Очевидно, что умножение вектора х на скаляр с
не нарушает его ортогональности к векторам а*. По-
Поэтому неизвестные хи *г, • •» *п определяются систе-
системой (VIII. 26) с точностью до произвольного множи-
множителя с, так что значение одного из неизвестных можно
выбрать произвольно (например, принять #i = 1); то-
тогда значения остальных неизвестных определятся од-
однозначно (они будут выражены через х\).
IX. Квадратичные формы
Квадратичной формой f от переменных х\9 #2, ...
..., хп называется однородный многочлен второй сте-
степени от этих переменных. Такой многочлен можно за-
записать в виде
п
где
aik = aki (IX. 2)
суть постоянные величины, которые могут быть как
вещественными, так и комплексными. Если все коэф-
коэффициенты am, вещественны, то квадратичная форма
называется вещественной. Если же хотя бы один из
коэффициентов является комплексным, то квадратич-
квадратичная форма называется комплексной.
Вещественная квадратичная форма называется по-
положительно определенной (отрицательно определен-
определенной), если для любых вещественных значений пере-

IX. КВАДРАТИЧНЫЕ ФОРМЫ 403
менных Хи %2, ...» хП9 не равных одновременно нулю,
эта форма имеет положительные (отрицательные)
значения.
В дальнейшем мы будем рассматривать только ве-
вещественные квадратичные формы.
Симметричная матрица
ап п\2 ... &\п
составленная из коэффициентов многочлена AХЛ),
называется матрицей квадратичной формы. Очевидно,
что квадратичная форма вполне определяется своей
матрицей.
Определитель
(IX. 4)
составленный из коэффициентов квадратичной формы,
называется ее дискриминантом.
Квадратичную форму можно представить в виде
произведения трех матриц:
f _.— v х х х I! I ^2I ^22 ** * агп II х* Я = X АХ
(IX. 5)
где X — матрица с одним столбцом, К — транспониро-
транспонированная с ней матрица. Действительно, произведение
матрицы с одним столбцом на квадратную матрицу
представляет собой матрицу с одним столбцом (см.
(VII.32)), элементы которой в рассматриваемом нами
случае равны
J^j aifeXfe \i === 1, dt ..., ft)*
k
Произведение же матрицы с одним столбцом на мат-
матрицу с одной строкой есть просто функция (см.
(VII. 33)). В данном случае это — функция
Видно, что последнее выражение тождественно
с выражением (IX. 1).

404 ПРИЛОЖЕНИЯ
Квадратичная форма вида
/кан=1 VI (IX. 6)
не содержащая членов с произведениями различных
переменных, называется канонической. Такая форма
имеет диагональную матрицу и поэтому называется
также диагональной квадратичной формой. Очевидно»
что если все %k больше (меньше) нуля, форма (IX. 6)
будет положительно определенной (отрицательно
определенной).
Всякая квадратичная форма при помощи неособен-
неособенного линейного преобразования1) переменных может
быть приведена к диагональному виду. Перейдем от
переменных хи jc2, ..., хя к новым переменным
У и 1/2» •«> Уп, связанным с прежними переменными,
с помощью линейных соотношений
*!-?*'***• (IX. 7)
Рассматривая совокупность величин xi и совокупность
величин ун как матрицы с одним столбцом, формулу
(IX. 7) можно записать в виде
X = BYy (IX. 8)
где В — матрица линейного преобразования, элемен-
элементами которой являются коэффициенты bik.
Подставив значения xiy определяемые соотноше-
соотношениями (IX.7), в формулу (IX. 1), найдем выражение
квадратичной формы в новых переменных:
f = Е <*ik Z buyi ? Ьктут = ? ytym E о>1кЬцЬкт =
I к I L rn itk
Y, (IX. 9)
где
^ (IX .10)
Легко убедиться в том, что из условия а^ — аы вы-
вытекает Cim = Cm/.
*) Неособенным называется такое линейное преобразова-
преобразование В (В — матрица), определитель которого отличен от нуля:
Оф)ф0

IX. КВАДРАТИЧНЫЕ ФОРМЫ 405
Запишем выражение (IX. 10) следующим образом:
Clm = ?4 biiYj <*llfikm ~ S bti 2
i к Ik
(мы заменили элементы матрицы В соответствующими
элементами транспонированной матрицы В\ см. фор-
формулу (VII. 7)). Согласно (VII. 28) Y*aikbkm представ-
представляет собой (AB)im — элемент матрицы, получающейся
в результате перемножения матриц В и А. Анало-
Аналогично X Ьц (AB)im представляет собой (BAB)tm — эле-
элемент матрицы, получающейся в результате перемно-
перемножения матриц (АВ) и В. Следовательно, матрица С,
элементы которой определяются формулой (IX. 10),
может быть представлена в виде
С = ВАВ. (IX. 11)
В соответствии с (VIII. 15) определитель D(C\
матрицы С равен
Поскольку матрицы В и В отличаются заменой столб-
столбцов строками, а определитель при такой замене не
изменяется (см. (VIII.8)), то D(B) = D(B) и можно
написать
D(C)^D(A)[D(B)f. (IX. 12)
Таким образом, при линейном преобразовании пере-
переменных дискриминант квадратичной формы умно-
умножается на квадрат определителя преобразования от
новых переменных к первоначальным.
Если преобразование В ортогонально (это озна-
означает, что коэффициенты bik удовлетворяют условиям
(VII.40) и (VII.41)), то транспонированная матрица
совпадает с обратной: б==В-~1 (см. (VII. 8)). Поэтому
в случае Ортогонального преобразования формула
(IX. 11) выглядит следующим образом:
С = В~1АВ. (IX. 13)
Матрица С, определяемая соотношением (IX. 13),
представляет собой матрицу квадратичной формы
в новых переменных у*. Попытаемся найти такое

406 ПРИЛОЖЕНИЯ
ортогональное преобразование /J, чтобы матрица С
была диагональной, т. е. имела вид
|Я, 0 ... 0 IJ
0 .я\*7 .° • (ix. н)
о о ... ял ||
Тогда квадратичная форма в новых переменных у*
будет иметь канонический вид (см. формулу (IX.6)).
Умножим обе части формулы (IX. 13) на В. По-
Поскольку ВВ-1 = ?, а умножение на единичную мат-
матрицу не изменяет второго сомножителя (см. (VII. 36)),
мы придем к соотношению
или
? bimCmk = ? aimbmk (/, k - 1, 2, ..., п). (IX. 15)
В соответствии с (IX. 14) элементы ст* могут быть
представлены в виде cm* = WW Подставив это зна-
значение cmk в формулу (IX. 15), получим
Е ЬшК^тк^ Z Gimhtnk (*\ * = 1, 2, . . ., л).
В сумме, стоящей слева, будет отлично от нуля лишь
слагаемое с т = ft, которое равно 6<Д*. Таким обра-
образом, мы приходим к уравнению
bikK = I a?m6m, (/, fe = 1, 2, ..., n). (IX. 16)
Последнее выражение можно рассматривать как
совокупность п2 уравнений с п2 неизвестными &,*. Эти
уравнения можно подразделить на п групп (отличаю-
(отличающихся значениями индекса к). Каждая из этих групп
состоит из п уравнений, отличающихся значениями
индекса L Перенеся в (IX. 16) все члены в одну сто-
сторону, k-ю группу уравнений можно представить в виде
= 0,
+ «пА* + -.. + («ян — К) ЬПк = 0.
(IX. 17)

IX. КВАДРАТИЧНЫЕ ФОРМЫ 407
Для того чтобы система уравнений (IX. 17) имела
отличные от нуля решения, ее определитель должен
быть равен нулю (см. Приложение VIII):
и -— Я п\г ... ахп
апх аП2 ... апп — Я,
0 (IX. 18)
(мы опустили индекс при Л,, поскольку аналогичные
условия получаются при любом k). Последнее выра-
выражение представляет собой алгебраическое уравнение
я-й степени относительно неизвестной X. Его называют
характеристическим уравнением матрицы Л.
Уравнение (IX. 18) имеет п корней: Я1Д2, ..., ХП9
которые представляют собой элементы искомой диа-
диагональной матрицы (IX. 14). Подставляя поочередно
значения Я* в систему (IX. 17) и решая эту систему
относительно неизвестных &/*, найдем элементы мат
рицы перехода от переменных #*, в которых квадра-
квадратичная форма имеет диагональный вид, к прежним
переменным xi (см. (IX. 7)). Переход от перемен-
переменных Xi к переменным ук может быть осуществлен с по-
помощью обратной матрицы В"*1. Так как по условию
О(В}Ф0 (преобразование В неособенное), то обрат-
обратная матрица существует; ее элементы можно вычис-
вычислить по формуле (VIII. 23).
Корни уравнения (IX. 18) (т. е. величины X*) бу-
будут вещественными. Это сразу следует из соотноше-
соотношений (IX. 16), если учесть вещественность величин а**
и Ьм. Таким образом, матрица (IX. 14) будет веще-
вещественной.
Рассмотрим диагональную квадратичную форму
вида
f=E4 (IX. 19)
Эта форма положительно определенная. Ее матрицей
будет единичная матрица
A=E = \\6ik\\. (IX. 20)
Применим к переменным Xi произвольное ортого-
ортогональное преобразование В и посмотрим» какой вид бу-
будет иметь в новых переменных квадратичная форма
(IX. 19). Согласно (IX. 13) матрица С квадратичной

408 ПРИЛОЖЕНИЯ
формы в новых переменных определяется выражением
(см. формулы (VII.36) и (VII.38)). Следовательно,
квадратичная форма (IX. 19) в новых переменных
имеет вид
Таким образом, всякое ортогональное преобразование
переменных оставляет без изменений квадратичную
форму вида (IX. 19).
Рассмотрим вещественную квадратичную форму
вида
fe, пг
где Z\yZ2, ..., zn — комплексные величины1). Пред-
Представим zm в виде хт + iym, соответственно г* — в виде
xk — iyk. Тогда
/ = ? Clkm(Xk — iyk)(xm + 1Ут) — Z «fern (***m + УкУт)+
k, m k, m
+ i ? akm (xkym - xmyk) = h + if* (IX. 22)
ft, m
Произведем в сумме, определяющей мнимую часть /2
полученного нами выражения, взаимную замену не-
немых индексов k и т:
/2 = ? я*т (жду,,, - *т#а) = ? amJfe (A:m//fe ~ xkym) =
k, m m, k
Z — ^mf/ft) = ~ f2
(мы воспользовались тем, что am* = ^^m; см. (IX. 2)).
Соотношение f2 = —/2 возможно только в том случае,
если ^ = 0. Таким образом, мы доказали, что квад-
квадратичная форма (IX. 21) при любых комплексных z
') Напомним, что вещественной называется квадратичная
форма с вещественными коэффициентами akm- Форма (IX. 21)
является частным случаем так называемой формы Эрмита, у ко-
которой коэффициенты, вообще говоря, комплексные и удовлетво-
удовлетворяют УСЛОВИЮ efft—Gftf-

IX. КВАДРАТИЧНЫЕ ФОРМЫ 409
имеет вещественные значения. Согласно (IX. 22) за-
запишем ее в виде
/ = Е актхкхт + ? akmykym = f0 (xk) + f0 (yk), (IX. 23)
k, m k, m
где
(напомним, что квадратичная форма полностью опре-
определяется своей матрицей, от обозначения переменных
она не зависит).
Одновременное приведение двух квадратичных
форм к диагональному виду. Пусть имеются две квад-
квадратичные формы:
Л =?*<**Л. (IX. 24)
ОХ. 25)
Покажем, что если одна из них, скажем, f\ положи-
положительно определенная, то можно найти такое линейное
преобразование переменных, которое приводит обе
формы к диагональному виду. Осуществим искомое
преобразование в несколько этапов. Сначала с по-
помощью ортогонального преобразования F перейдем
к переменным viy в которых форма (IX. 24) примет
диагональный вид
f.=? *tf
(такое преобразование подробно рассмотрено выше).
Теперь перейдем от переменных vi к переменным
Щ = v'i Vi*7
(легко убедиться в том, что при хотя бы одном щ ф 1
это преобразование неортогонально). Поскольку фор-
форма /i положительно определенная, все коэффициенты
№ положительны, так что переменные т будут веще-
вещественными. В этих переменных
h=?«?-
значит, матрицей f\ будет Е.
Наконец, перейдем с помощью ортогонального пре-
преобразования G от переменных щ к таким перемен-

410 ПРИЛОЖЕНИЯ
ным уи чтобы форма f2 стала диагональной. Форма f\
при этом останется диагональной, ибо, как было
показано выше, квадратичная форма с матрицей Е
(см. (IX. 20)) не изменяется при любом ортогональ*
ном преобразовании. Следовательно, в переменных yi
квадратичные формы (IX. 24) и (IX. 25) будут диаго-
диагональными:
Z E .26)
Вся последовательность преобразований может
быть представлена схемой:
(преобразование F) (X УиТ) (преобразование G)
xi->vi -> ut-> у(
Ew*-*E*v? - !>?->!>? (ix. 27)
I, k i i i
E bik*t*k -* E b\kvivk -* E b"kutuk -* E %1у1
i, k i, k I, k i
Чтобы установить способ нахождения коэффициен-
коэффициентов Я/, образуем вспомогательную квадратичную
форму
f = fа - *f 1 = .Е {bih - haik) xtxk =%(\- Я) y%
(IX. 28)
коэффициенты которой содержат параметр К. Дискри-
Дискриминант этой формы в переменных xi имеет вид
det || *,*-*<*„ ||, (IX. 29)
а в переменных ijt
det i| (lk - X) 6ik (I = (lx - I) (k2 - Я)... (Xn - Я). (IX. 30)
Обозначив преобразование непосредственного пе-
перехода от переменных xi к переменным yi буквой В
(это преобразование, вообще говоря, не будет ортого-
ортогональным), напишем для матрицы квадратичной фор-
формы (IX. 28) в переменных yi выражение
С = ВАВ,
где через А обозначена матрица формы (IX. 28) в пе-
переменных Xi (см. формулу (IX. 11)). Согласно (IX. 12)

IX. КВАДРАТИЧНЫЕ ФОРМЫ 411
где D(C) есть определитель (IX.30), D(A) — опреде-
определитель (IX. 29), D(В) — отличный от нуля определи-
определитель матрицы преобразования В, который не содер-
содержит параметра К (О(В)Ф0, так как преобразова-
преобразование В неособенное).
Итак,
(К - *) (Я* -*)... (К - *) = det (| bik - Kaik \\ [D (В)]2.
Подстановка вместо h любого из значений %k обра-
обращает в нуль левую часть уравнения, а следовательно,
и множитель det lift/* — Ха<*||. Таким образом, вели-
величины Xk суть корни уравнения
Ь\\—
Ku 6 ^2 Ьг 'кй _q /?v qi\
— %an\ bn2 —-
Итак, задача приведения квадратичных форм (IX. 24)
и (IX. 25) к диагональному виду сводится к нахожде-
нахождению корней уравнения (IX. 31).
Рассмотрим наряду с квадратичной формой от пе-
переменных
Е (IX. 32)
аналогичную квадратичную форму от переменных it
E . 33)
E
i, k
где Xi — производная переменной xi по какому-либо
параметру t. Назовем xi i-й скоростью.
При линейном преобразовании
*i=I,cimym (IX. 34)
от переменных xi к новым переменным iji скорости
испытывают такое же преобразование
it - S cim$M. (IX. 35)
Выразим формы (IX. 32) и (IX. 33) в новых пере-
переменных. Для этого подставим в формулы (IX, 32) и

412 ПРИЛОЖЕНИЯ
(IX. 33) выражения (IX. 34) и (IX. 35):
f = Z <*ik*iXk = Z a/Jfe Z cimym Z c-kiyi =
*, & i, k m I
= Z #mj// Z uikClmCki = Z b
m, I i, k m, I
где
&m* = Z VikCimCkl- (IX. 36)
2 &
Аналогично
Г = Z ^Л^ = Z (hk Z ^m»m Z
i, k i, k m I
= Z У mill Z <htfitnfiu = Z bmlymyh
m, t I, k m, I
где 6т/ имеет те же значения (IX. 36), что и в преды-
предыдущем случае.
Таким образом, при всяком линейном преобразо-
преобразовании от переменных xi к новым переменным yi ко-
коэффициенты квадратичной формы от скоростей к{ пре-
преобразуются точно таким образом, как коэффициенты
аналогичной квадратичной формы от xt. На этом осно-
основании схему (IX. 27) можно видоизменить следующим
образом:
(преобразование F) (X У N Ь (преобразование G)
а«*л -* Z ***°? -* Z и* -^ Z ^ их.37)
t.k i it
Z bikxlxk ""* Z bikvivk -* Z bikuiuk -* Z ^^?"
i. Л i, ft i, fe i
Предполагается, что квадратичная форма Z ®tk%i%k
положительно определенная.
X. Тензоры
1. Определение тензора. Чтобы прийти к понятию
тензора, рассмотрим поляризацию анизотропного ди-
диэлектрика.
В изотропном диэлектрике поляризованиость Р про-
пропорциональна напряженности электрического поля Е:
Р=%Е, (Х.1)

X. ТЕНЗОРЫ 413
где и — диэлектрическая восприимчивость. Согласно
(X. I) векторы Р и Е коллинеарны,
В анизотропном диэлектрике поляризуемость по
разным направлениям различна. Вследствие этого на*
правление вектора Р, вообще говоря, не совпадает
с направлением вектора Е. Как показывает опыт, в
любом анизотропном диэлектрике имеются три вза-
взаимно перпендикулярных направления таких, что при
совпадении направления Е с одним из них вектор Р
оказывается коллинеарным
с Е. Эти направления на-
называются главными. На-
Направим оси координат
вдоль главных направлений
диэлектрика (рис. X. 1).
Произвольно направленный
вектор Е можно разложить
на составляющие Ех, Ъу и
Е* (последняя составляю-
составляющая перпендикулярна к
плоскости рисунка). Состав-
Составляющая Ех создаст коллинеарную с ней поляризован-
ность Р* = ИхЕх, где кх — восприимчивость в направ-
направлении оси х. Аналогично две другие составляющие со-
создадут Ру — КуЕу и Рг = хгЕ2. Нетрудно заметить, что
при различных по величине пх, v.y и х* результирующий
вектор Р = Рх + Ру + Р« будет неколлинеарен с Е.
Рассмотрим анизотропный диэлектрик, который мы
будем считать однородной неограниченной средой.
Свяжем с ним декартову систему координат, оси кото-
которой ориентированы совершенно произвольно и не со-
совпадают ни с одним из главных направлений диэлек-
диэлектрика. Тогда при поле ?*, направленном по оси х, от-
отличными от нуля будут не только Рх, но также Ри
и PZ9 причем
Рх — *ххЕх> Ру — Мух^х* Рг — y»zxBx> (X. 2)
где Кхх, Щх и кгх — коэффициенты пропорциональности
между Ех и соответствующими компонентами Р.
Аналогично поля Еу и Ez вызовут поляризован-
мости:
* X ™ МхуЕу9 л у = КууЕу, Рг ass %гуЬу>
Р = кЕ Р-вкЕ Р-х? { ' '

414 ПРИЛОЖЕНИЯ
В случае поля Е, не совпадающего ни с одной из
координатных осей, одновременно будут существовать
Ех, Еу и ?*, так что возникнут все Р/, определяемые
формулами (X. 2) и (X. 3). Объединив соответствую-
соответствующие составляющие вектора Р, получим
Рх = %ХХЕХ -+- %Xyty -J- кхгЕг,
Ру = %ухЕх + Хв1,Ев + КугЕ» (X. 4)
Рг = %гхЕх "Т MZyfcy "
Перейдя от буквенных индексов к цифровым, за-
запишем уравнения (X. 4) в компактном виде
Pi=HxikEk (/ = 1,2,3). (Х.5)
k
Из сказанного выше вытекает, что для характери-
характеристики анизотропного диэлектрика необходимо задать
девять величин %ш (в случае изотропного диэлектрика
достаточно было одной величины к).
Перейдем от прежней системы координат хь х2, х$
(системы К) к новой системе xfv x'v x'3 (системе К'),
оси которой также не совпадают с главными направ-
направлениями диэлектрика. Выясним, как преобразуются
величины Kik при таком переходе. В новой системе
координат уравнения, связывающие Pft и Е'&, анало-
аналогичны уравнениям (X. 5):
Здесь n'ik ~~ девять величин, характеризующих ди-
диэлектрик в новой системе координат.
Согласно формулам (VI. 37) и (VI. 38) компонен-
компоненты вектора Р при переходе от системы К к системе К'
преобразуются по формуле
*Л' (Х.7)
а компоненты вектора Е при переходе от системы К'
к системе К преобразуются по формуле
(Напомним, что а^==«/ел есть досинус угла между
1-й штрихованной и k-й нештрихованной осями коор-
координат.)

X. ТЕНЗОРЫ 415
Заменим в (X, 7) Р/ через Ет согласно соотноше-
соотношению (X. 5). В результате получим
Р[ = Е «,Л = ?Ч* Е *,„*„ = Е <*„*,„?„.
I * /n I, m
Теперь подставим сюда Ет из формулы (X. 8):
р'й = Е <*„*,„ Е «fem?; = Е ?i E *«<ww
Сопоставив полученное выражение с выражением
(X. 6), получим
Совокупность девяти величин 7\-ft, преобразую-
преобразующихся при переходе от системы координат К к си-
системе К' по формуле
называется тензором второго ранга (или тензором
второго порядка, или, наконец, тензором второй ва-
валентности).
Обратное преобразование (от системы К' к си-
системе К) осуществляется по формуле
Тензор записывают одним из следующих трех спо-
способов:
/ ^11 ^12 7*13 \
Т = (Г«) = { г„ т22 т„\. (X. 12)
\ Г31 7*32 Т$г /
Величины Tik называют компонентами тензора. Ком-
Компоненты Гц, Г22 и Г3з называются диагональными.
Таким образом, свойства анизотропного диэлек-
диэлектрика описываются тензором диэлектрической воспри-
восприимчивости
%i W22 «23 S (X. 13)
%3l V.32 «33 /
Особый интерес представляет случай» когда оси
координат совпадают с главными направлениями

416 ПРИЛОЖЕНИЯ
диэлектрика. При этом условии составляющая поля
Ei порождает только i-io составляющую поляризован-
ности, причем
Р^*цЕл (/=1, 2, 3).
Сопоставление с (X. 5) приводит к выводу, что в рас-
рассматриваемом случае отличны от нуля только диаго-
диагональные компоненты тензора, так что тензор диэлек-
диэлектрической восприимчивости имеет вид
о о
/щ О О \
= 0 х2 О I
\0 0 из/
(мы оставили при отличных от нуля компонентах
тензора только один индекс, так как у диагональных
компонент оба индекса одинаковы).
Тензор, у которого отличны от нуля только диаго-
диагональные компоненты1), называется приведенным
к главным осям. Значения диагональных компонент,
которые получаются в этом случае, называются глав-
главными значениями тензора.
Отметим, что у изотропного диэлектрика все три
главные значения тензора диэлектрической восприим-
восприимчивости одинаковы: щ = %% == щ = и. Это значение
диагональных составляющих тензора и представляет
собой диэлектрическую восприимчивость, рассматри-
рассматриваемую в курсе общей физики. В качестве главных
направлений изотропного диэлектрика могут быть
взяты любые три взаимно перпендикулярные направ-
направления.
Рассматриваются тензоры не только второго, но и
других рангов. Так, например, тензором третьего
ранга называется совокупность 27 величин Гш, пре-
преобразующихся при переходе от одной системы коор-
координат к другой по формуле
*ш- JE;в«,Лрв|/«мг (Х-15)
Аналогично определяются тензоры других рангов. Тен-
Тензор г-го ранга имеет Зг компонент. Легко видеть, что
вектор есть тензор первого ранга (он имеет 31==3ком-
*) Заметим, что это возможно лишь при специально выбран-
выбранных координатных осях.

х. тензоры 417
поненты), а скаляр — тензор нулевого ранга (он имеет
3°= 1 компоненту).
Понятие тензора легко распространить на про-
пространство п измерений. Тензором r-го ранга в таком
пространстве (л-тензором r-го ранга) называется со-
совокупность пг величин Tik.mfp (всего г индексов), пре-
преобразующихся по формуле, отличающейся от фор-
формулы (X. 15) лишь тем, что немые индексы пробегают
при суммировании не три, а п значений.
Приведем еще несколько примеров тензоров вто-
второго ранга. Возьмем два вектора а и Ь и образуем из
их компонент произведения вида
Легко убедиться в том, что эти произведения преоб-
преобразуются по формуле (X. 10), т. е. обладают свой-
свойствами компонент тензора второго ранга.
Тензор
<*|*>
/1 о о
= [ 0 1 0
\0 0 1
называется единичным тензором. Согласно формуле
преобразования (VI. 39) его составляющие в новой
системе координат равны
i, tf
««faAm = ? aitakt = 6ik
, tfl I
(мы воспользовались свойством коэффициентов a,*,
выражаемым формулой (X. 39)). Таким образом, ком-
компоненты единичного тензора одинаковы во всех систе-
системах координат. Тензоры, обладающие таким свой-
ством, называются инвариантными.
2. Тензорная алгебра. Рассмотрим основные опе-
операции с тензорами.
Суммой тензоров Tik и G,* называется тензор
с компонентами
В соответствии с (X. 18) любой тензор можно пред-
представить в виде суммы двух (или более) тензоров.
Произведением тензора Tik на скаляр а называется
тензор Gik с компонентами
U И. В. Савельев» т. !

418 ПРИЛОЖЕНИЯ
Произведением тензоров Г^ и G/m называется тен-
тензор четвертого ранга Пшт с компонентами
r«Gi«. (X.20)
Аналогично определяется произведение тензоров иных
рангов, в частности, выше (см. (X. 16)) было рассмот-
рассмотрено произведение тензоров первого ранга, т. е. век-
векторов. Из определения (X. 20) следует, что ранг тен-
тензора-произведения равен сумме рангов тензоров-со-
тензоров-сомножителей (могут перемножаться и тензоры неоди-
неодинаковых рангов).
Свертыванием тензора называется следующая опе-
операция: два индекса при компонентах тензора пола-
полагаются одинаковыми и по ним осуществляется сумми-
суммирование. Получившаяся в результате такой операции
величина называется сверпсой тензора. Очевидно, что
свертывание понижает ранг тензора на две единицы.
Операция свертывания может применяться к тензо-
тензорам ранга не ниже второго1). В случае тензора вто-
второго ранга свертка представляет собой теизор нуле-
нулевого ранга, т. е. скаляр. Этот скаляр называется сле-
следом (или шпуром) тензора (ср. со следом матрицы;
стр.386). Он равен сумме диагональных компонент:
Скаляр не изменяется при преобразовании координат.
Следовательно, след тензора представляет собой ин-
инвариант. Например, след тензора (X. 16) есть не что
иное, как скалярное произведение векторов а и Ь, ко-
которое, как мы знаем, инвариантно относительно пре-
преобразования координат (см. текст, следующий за
формулой (VI. 28)).
В физических приложениях обычно применяется
умножение тензоров в сочетании с последующим свер-
свертыванием получившегося выражения. Результат этих
операций называется скалярным произведением тен-
тензоров2). Типичным примером может служить только
*) В случае тензора, ранг которого г выше второго, сверты-
свертывание можно производить несколькими способами (по разным
парам индексов). В результате будут получаться различные тен-
тензоры ранга г — 2.
2) Иногда последнее произведение называют внутренним, в
то время как выражение (X. 20) называют внешанм произведе-
произведением тензоров.

X. ТЕНЗОРЫ 419
что упоминавшееся скалярное произведение векторов
(тензоров первого ранга): тензор аф* свертывается
по паре индексов i и k, в итоге получается выражение
Е афк.
В соответствии со сказанным, скалярным произве-
произведением тензора Tik на вектор ak называется вектор Ьх
с компонентами
h = Е Tikak. (X. 22)
Убедимся в том, что определенная таким способом со-
совокупность величин bi действительно образует вектор.
Для этого найдем закон преобразования величин &*.
Очевидно, что
Ъ' = У V а'
Подставим в последнее соотношение выражения Т\к
и а'к через нештрихованные компоненты:
ь\ = Z т>; - Е Zmwkjtm E %sas=
Согласно свойству (VI. 40) ]Е afemafes= *ms- Следова-
Следовательно,
m, s * т /
Полученный нами результат означает, что вели-
величины bt преобразуются по закону преобразования
компонент вектора. Таким образом, определяемые вы-
выражением (X. 22) величины bi действительно образуют
вектор.
Аналогично можно убедиться в справедливости
следующего утверждения: если вырах*ение Е %ikak>
образованное совокупностью 9-ти величин Xik и ком-
компонентами некоторого вектора пь представляет собой
компоненты другого вектора Ьи то величины Хш суть
компоненты некоторого тензора. С подобной ситуа-
ситуацией мы столкнулись в начале этого Приложения. Со-
Совокупность девяти величин х/*, взятая с компонентами
14*

420 ПРИЛОЖЕНИЯ
вектора ?* в сочетании (X. 5), дала компоненты
вектора Pi. На этом основании мы показали, что ве-
величины Kik преобразуются по закону преобразования
компонент тензора, т. е. что диэлектрическая воспри-
восприимчивость является тензором.
В результате скалярного умножения вектора а на
тензор Т мы получили новый вектор Ь:
b = Ta. (X.23)
Поэтому тензор Т можно рассматривать как линейный
оператор, осуществляющий преобразование одного
вектора в другой.
Найдем произведение единичного тензора на век-
вектор а*. Согласно формуле (X. 22)
Таким образом, при умножении на единичный тензор
вектор не изменяется.
3. Симметричные и антисимметричные тензоры.
Тензор Siky компоненты которого удовлетворяют
условию
Sik = Ski9 (X.24)
называется симметричным. Отметим, что рассмотрен-
рассмотренный выше тензор диэлектрической восприимчивости
является симметричным.
Тензор А(ь, компоненты которого удовлетворяют
условию
i*i*--4w. (X.25)
называется антисимметричным.
Свойство симметрии или антисимметрии является
свойством самого тензора. Это следует из того факта,
что оно сохраняется при любых преобразованиях ко-
координат. Для доказательства приведем следующие
выкладки:
$'ik = Z *iPkmSlm — Zf «IjAAiI — Z *ktaimSlm = S'ki
(сначала мы произвели взаимную замену немых ин-
индексов / и т, а затем заменили Sm[ равным ему Sim).
Мы доказали, что тензор, симметричный в некоторой
системе /С, будет симметричным в любой другой си-
системе /С'.

X. ТЕНЗОРЫ 421
Аналогично
At *V Ч jl V -
*ft A«rf ** К/71 *f7J itmA itfi kl ttti
it m m, I
(после взаимной перестановки немых индексов мы за-
заменили Ami равным ему —Л/т). Мы доказали, что тен-
тензор, антисимметричный в К, будет антисимметричным
и в К'.
Любой тензор Tik можно представить в виде суммы
симметричного и антисимметричного тензоров. Дей-
Действительно, представим Г/* в виде
Tik = - g + 2 •
Правомерность такой записи очевидна. Вместе с тем,
первое слагаемое не изменяется при перестановке ин-
индексов I и ?, т. е. обладает свойствами компонент
симметричного тензора; второе же слагаемое при пе-
перестановке индексов меняет знак, т. е. обладает свой-
свойствами компонент антисимметричного тензора.
Таким образом, всегда можно считать, что
Tih=*Sik+Aik9 (X.26)
где
Понятия симметрии и антисимметрии применимы
и к тензорам более высокого ранга. Так, например,
Tiki называется симметричным (антисимметричным)
относительно индексов ink (или / и /, или k и /),
если при перестановке этих индексов компоненты тен-
тензора не изменяются (соответственно изменяют знак
на обратный). Если компоненты тензора не изме-
изменяются (или изменяют знак на обратный) при пере-
перестановке любой пары индексов, то тензор называется
абсолютно симметричным (соответственно абсолютно
антисимметричным).
Введенная в Приложении VI совокупность 27 ве-
величин ъш образует абсолютно антисимметричный тен-
тензор третьего ранга. Напомним, что величины еш:
1) равны нулю, если любые два индекса имеют оди-
одинаковые значения; 2) равны +1, если все индексы

422 ПРИЛОЖЕНИЯ
различны и образуют циклическую перестановку по-
последовательности 1, 2, 3; 3) равны —1, если все ин-
индексы различны и образуют циклическую переста-
перестановку последовательности 3, 2, 1. Из 27 компонент
этого тензора 21 равна нулю, три равны +' и три
равны — 1. Путем несложных, но громоздких вычис-
вычислений можно показать, что
т, р, s
т. е. что тензор еш инвариантен.
4. Истинные тензоры и псевдотензоры. Выясним,
как преобразуются компоненты тензора при инверсии
координатных осей. Коэффициенты преобразования
имеют в этом случае значения
(см. (VI. 42)). Поэтому формула преобразования
компонент тензора r-го ранга Tik..mt (всего г индек-
индексов) при инверсии имеет вид
=(-ir Е б,л- ^/mP...s=(-i)r^...r
m, p, .... s
Таким образом, компоненты тензора r-го ранга1) при
инверсии преобразуются по формуле
Согласно (X. 23) величины ziki при любом преоб-
преобразовании координат (а следовательно, и при инвер-
инверсии) остаются инвариантными, т. е. знака не изме-
изменяют. Компоненты же истинного тензора третьего
ранга должны при инверсии изменить знак на обрат-
обратный. Поэтому совокупность величин еш образует не
истинный тензор, а псевдотензор,
Превдотензором г-го ранга называется совокуп-
совокупность Зг компонент Pib...u которые при поворотах
системы координат ведут себя как компоненты обыч-
обычного тензора, а при инверсии преобразуются по фор-
формуле
*) Имеются в виду тензоры в пространстве трех измерений.

X. ТЕНЗОРЫ
423
Приведем примеры псевдотензоров разных рангов.
С псевдоскалярами и псевдовекторами мы познакоми-
познакомились в Приложении VI. Выше был рассмотрен псев-
псевдотензор третьего ранга вш. Совокупность величин Р**,
образованных из произведений компонент истинного
вектора щ и псевдовектора р*: Put = dip и, представ-
представляет собой псевдотензор второго ранга. Действитель-
Действительно, при инверсии величины щ меняют знак, а величи-
величины pk остаются неизменными. Следовательно, Р,а при
инверсии будет менять знак. В то же время, мы знаем,
что компоненты истинного тензора второго ранга при
инверсии знака не изменяют. Значит, Put есть псевдо-
псевдотензор.
Легко сообразить, что результатом свертывания
псевдотензора будет также псевдотензор (четность
или нечетность ранга тензора при свертывании не из-
изменяется, а формулы преобразования компонент ис-
исходного тензора и свертки отличаются на множитель
(-—1) s). Например, при свертывании псевдотекзора
Pik мы получим скалярное произведение истинного
вектора и псевдовектора, т. е. псевдоскаляр.
Произведение псевдотензора любого ранга Pik. л
на истинный тензор любого ранга Tmp...s представ-
представляет собой псевдотензор
тт Р Т
LLik ... Imp ...s rlk... Г mp.,.s-
Для проверки этого утверждения составим таблицу:
Pik..j
* mp...s
^ik...lmp...s
Ранг
Четный
четный
нечетный
нечетный
четный
нечетный
четный
нечетный
четный
нечетный
нечетный
четный
Знак прн инверсии
изменяется
изменяется
не изменяется
не изменяется
не изменяется
изменяется
не изменяется
изменяется
изменяется
не изменяется
не изменяется
изменяется

424 ПРИЛОЖЕНИЯ
Аналогично можно убедиться в том, что произве-
произведение двух псевдотекзоров любых рангов представ-
представляет собой истинный тензор.
5. Свойства симметричного тензора второго ранга.
У симметричного тензора второго ранга из девяти
компонент независимыми явля-
являются только шесть (Si2 = S21,
Si3 — S3!, S23 = S32).
Симметричный тензор второ-
второго ранга допускает важную гео-
геометрическую интерпретацию.
Прежде чем перейти к ее рас-
рассмотрению, отметим, что вектор
а можно представить не только
направленным отрезком, но и
плоскостью, уравнение которой
имеет вид
Рис Х.2 ar—I, (X.29)
где г — радиус-вектор точки плоскости (рис. Х.2).
Поскольку
аг = ага — 1, то га — 1/а.
Следовательно, уравнение (X. 29) определяет плос-
плоскость, перпендикулярную к вектору а и отстоящую от
начала координат на расстояние 1/а. Выражение
(X. 29) можно также представить в виде агг= 1, от-
откуда г = 1/а,. Таким образом, на прямой, проходя-
проходящей через начало координат и имеющей направление п
(см. рис. Х.2), плоскость (X.29) отсекает отрезок
длины
Теперь обратимся к симметричному тензору S. Со-
Сопоставим ему поверхность, определяемую уравнением
r(Sr)=l. (X.31)
Очевидно, что эта поверхность не зависит от выбора
системы координат, в которой определяются компо-
компоненты тензора S и радиуса-вектора г. Характер по-
поверхности зависит только от свойств тензора S.
Выберем произвольную систему координат хи х*, #з
и выразим левую часть уравнения (X. 31) через ком-

х. тензоры 425
поненты г и S в этой системе. Согласно (X. 22)
Умножив скалярно г на вектор Sr, получим
2а Xl (S*)* == 2-» Xi dL Sikxk == 2-i
Следовательно, уравнение (Х. 31) имеет вид
l. (X.32)
В развернутом виде это уравнение выглядит следую-
следующим образом (напомним, что S/* = S«):
5!1*? + S22Xl + S33*3 + 2S12*1*2 + 2S2SX2XZ
(X. 33)
Уравнение (Х. 33) есть уравнение поверхности вто-
второго порядка, центр которой помещается в начале ко-
координат. В приложениях тензорного исчисления к фи-
физическим задачам диагональные компоненты Su бы-
бывают больше нуля (это например, имеет место для
Рис. Х.З
величин х«). В этом случае поверхность (X. 33) пред-
представляет собой эллипсоид. Этот эллипсоид и является
геометрическим образом симметричного тензора вто-
второго ранга (разумеется в пространстве трех измере-
измерений), подобно тому как направленный отрезок или
плоскость (X. 29) дают геометрический образ тензора
первого ранга, т. е. вектора.
Найдем расстояние от центра эллипсоида до то-
точек, лежащих на его поверхности. Для этого прове-
проведем из центра эллипсоида произвольную прямую
(рис. Х.З), которую примем за ось х\. Тогда расстоя-

426 ПРИЛОЖЕНИЯ
кие р от центра эллипсоида до точки Р будет р
значению Х\ при Х2 = Хз —0. Положив в уравнении
(X. 33) х2 = х% — О, получим, что Snx\ = 1, откуда
(ср. с (X. 30)). Таким образом, расстояние р есть ве-
величина, обратная корню квадратному из компоненты
тензора 5ц, вычисленной при условии, что направле-
направление, вдоль которого отсчитывается р, принято за
ОСЬ Х\.
При преобразованиях координат изменяются коэф-
коэффициенты Sik в уравнении (X. 33), однако сам эллип-
эллипсоид от выбора системы координат не зависит. Если
направить оси координат вдоль полуосей эллипсоида,
уравнение эллипсоида, т. е. уравнение (X. 33), как
известно, упрощается и принимает вид
Это означает, что при указанном выборе координат-
координатных осей недиагональные компоненты тензора обра-
обращаются в нуль. Следовательно, главные оси тензора
совпадают с полуосями тензорного эллипсоида.
Если координатные оси направить вдоль главных
осей тензора (т. е. вдоль полуосей тензорного эллип-
эллипсоида), тензор принимает диагональный вид
Я, о о
(Л, О О \
о о х3/
Мы ввели обозначения: 5ii=%i, S22 = A,2, S33 = A,3.
Величины %и ^2, &з суть главные значения тензора.
В случае, когда Х\ = &2 ~ ^з = К тензорный эллип-
эллипсоид превращается в сферу. В частности, единичному
тензору fob соответствует сфера единичного радиуса*
Умножим некоторый вектор а на тензор (X. 34).
В результате получится вектор Ь, составляющие кото-
которого определяются по формуле (X. 22). Компоненты
тензора (X. 34) можно представить в виде S,*
Следовательно,
= a
(X. 35)

х. тензоры 427
Пусть вектор а направлен вдоль первой главной оси
тензора. Тогда a\ = af а2 = а3 = 0 (взяв тензор в
виде (X. 34), мы предположили, что оси координат
направлены по главным осям тензора). Согласно фор-
формуле (X. 35) компоненты вектора b будут равны
6i=Xiai, 62 = 63 = 0. Это означает, что направление
вектора b совпадает с направлением вектора а, мо-
модуль же вектора b в к\ раз больше чем модуль век-
вектора а. То же справедливо и для двух других главных
осей. Таким образом, если вектор а направлен по од-
одной из главных осей тензора, то справедливо следую-
следующее равенство:
Sa = Xa, (X.36)
где X — соответствующее главное значение тензора.
Мы пришли к следующему результату: при умно-
умножении вектора, имеющего направление одной из глав-
главных осей, на тензор направление вектора не изме-
изменяется, величина же вектора увеличивается в число
раз, равное соответствующему главному значению
тензора.
Равенство (X. 36) справедливо в любой системе
координат, лишь бы вектор а был направлен по одной
из главных осей тензора. Этим обстоятельством можно
воспользоваться для нахождения главных значений и
главных осей тензора. Для этого нужно варьировать
направление вектора а, пока вектор Sa не совпадет
по направлению с а. Соответствующее направление
даст главную ось тензора, а отношение Sa к а — соот-
соответствующее главное значение. Аналитически это вы-
выглядит следующим образом. Запишем равенство
(Х.Зб) в компонентах (мы пока еще не привели тен-
тензор к главным осям, так что, вообще говоря, все Sik
отличны от нуля) :
«$2202
Приведя подобные члены, получим
S12a2 + Si3a3 =0,
Л)а2+ 523аз =0, (X. 37)
Szla{ +

428 приложения
Мы пришли к однородной системе трех уравнений
с неизвестными <ц, 02, а3 — компонентами искомого
вектора а. Для того чтобы эта система имела ненуле-
ненулевое решение, требуется равенство нулю ее определи-
определителя (см. Приложение VIII; текст, следующий за фор-
формулой (VIII. 26)). Таким образом, должно выпол-
выполняться условие
-я
= 0. (Х.38)
Корни этого кубического относительно К уравнения
представляют собой главные значения тензора: К\,
%2> А*. Подставив один из этих корней в систему
(X. 37), мы сможем найти отношения a2/ai и а3/яь
которые определят направление вектора а, удовлет-
удовлетворяющего уравнению (X. 36), т. е. соответствующую
главную ось тензора. Проделав эту операцию для
всех трех А* найдем направления всех главных осей.
Мы предполагали, что все корни Ль %2 и А* раз-
разные. В случае, когда уравнение (Х.38) имеет кратные
корни, необходимо некоторое уточнение. При двух
кратных корнях (%2 = Яз == Аг, %\фА,) тензорный эл-
эллипсоид будет эллипсоидом вращения. Однозначно
будет определена только одна главная ось тензора,
совпадающая с осью симметрии эллипсоида. В каче-
качестве двух других главных осей можно взять две лю-
любые взаимно перпендикулярные оси, перпендикуляр-
перпендикулярные к оси симметрии эллипсоида. Если все три корня
уравнения (Х.38) одинаковы (А,] =А,2 = Я3 = Л), тен-
тензорный эллипсоид вырождается в сферу и в качестве
главных осей можно взять любые три взаимно пер-
перпендикулярные оси.
Рассмотрим свойства симметричного тензора как
оператора. Согласно (X. 36) воздействие S на век-
вектор а, направленный вдоль одной из главных осей
тензора, вызывает лишь изменение длины вектора
в А, раз. Воздействие S на произвольно ориентирован-
ориентированный вектор вызывает, вообще говоря, изменение как
длины, так и направления этого вектора (см., напри-
например, рис. X. 1).
6. Свойства антисимметричного тензора второго
ранга. Обратимся теперь к антисимметричному тен-
тензору второго ранга. Условие (X. 25) для диагональ-

х. тензоры 429
ных компонент имеет вид Ац = — Аи. Это возможно
лишь при Л// = 0. Следовательно, диагональные ком-
компоненты антисимметричного тензора равны нулю. Из
остальных шести компонент независимыми являются
только три. Таким образом, антисимметричный тензор
второго ранга определяется, как и вектор, тремя ве-
величинами:
А\2 = — Ам = Дз>
4b= — A32 = au (X.39)
Лз1 = — Л1з = #2»
Воспользовавшись этими обозначениями, можно запи-
записать антисимметричный тензор следующим образом:
(О а3 -а2\
-<*з О в, 1 (Х.40)
а2 — ах 0 /
Компоненты тензора (Х.40) можно представить
в виде
]? + eik2a2 + Booth, (X. 41)
где &ш — абсолютно антисимметричный псевдотензор
(см. текст, предшествующий формуле (Х.28)). Дей-
Действительно, определяемые этой формулой компоненты
Аи равны нулю, так как гш при любом / равно нулю.
Далее
+ «122^2 + е123аз = 0 • а{ + 0 • «2 + 1 • а3 = а3»
+ Б132Я2 + е,33Яз = 0 • «1 + (—1) • <h + 0 • (h =
и т. д.
Выше было показано, что при перемножении ис-
истинного тензора и псевдотензора получается псевдо-
псевдотензор. Произведение же двух псевдотензоров пред-
представляет собой истинный тензор. Тот факт, что вели-
величины aiy будучи умноженными на псевдотензор еш
(см. формулу (X.41)), дают компоненты истинного
тензора второго ранга, указывает на то, что эти ве-
величины обладают свойствами псевдотензора первого
ранга, т. е. псевдовектора.
Итак, всякому антисимметричному тензору второго
ранга может быть сопоставлен псевдовектор с компо-

430 ПРИЛОЖЕНИЯ
нентами а*, определяемыми формулами (X.39). И на-
наоборот, всякому псевдовектору а, может быть постав-
поставлен в соответствие истинный антисимметричный тен-
тензор второго ранга, компоненты которого выражаются
через компоненты псевдовектора по формуле (Х.41).
Применим оператор А (А — антисимметричный
тензор) к некоторому вектору Ь. Согласно (X. 22) и
(Х.41) мы получим вектор с с компонентами:
ci = Z Aikbh =
Сопоставив полученное выражение с формулой
(VI. 33), приходим к выводу, что с можно представить
в виде векторного произведения1) векторов b и а:
Вектор с перпендикулярен как к исходному век-
вектору Ь, так и к псевдовектору а, соответствующему
тензору А. Таким образом, воздействие тензора А вы-
вызывает поворот вектора на угол я/2. Кроме того, во-
вообще говоря, изменяется длина вектора.
XI. Некоторые сведения из векторного анализа
Градиент. Рассмотрим скалярное поле, т. е. об-
область пространства, каждой точке которой соответ-
соответствует определенное значение скаляра <р:
где г — радиус-вектор, а хи х2, #з — декартовы коор-
координаты точки Р.
Всем точкам поверхности, определяемой уравне-
уравнением
хъ х3) = const, (XI. 1)
соответствует одинаковое значение ф. Поверхность
вида (XI. 1) называется поверхностью уровня ска-
скаляра ф. Поверхность уровня можно провести через
любую точку поля.
*) Напомним, что векторное произведение представляет собой
полярный вектор только в том случае, если один из сомножите-
сомножителей является псевдовектором. Отсюда также можно было заклю-
заключить, что а есть не истинный вектор, а псевдовектор.

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 431
При смещении из точки Р на отрезок dv функция <р
получает приращение
Последнее выражение не зависит от выбора коорди-
координат хи т. е. представляет собой инвариант. Совокуп-
Совокупность величин dxi образует вектор dr. Поэтому (см.
текст, следующий за формулой (VI. 28)) можно ут-
утверждать, что величины dq>/dxi суть проекции некото-
некоторого вектора на оси хи Этот вектор называют гра-
градиентом скаляра ср и обозначают символом gradcp.
Итак,
или, в обычных обозначениях,
Определение (XI. 2) легко распространить на про-
пространство п измерений. В последнем случае число сла-
слагаемых в формуле (XI. 2) будет равно не трем, а я.
Докажем, что компоненты градиента преобра-
преобразуются по формулам (VI. 37). Взяв две системы коор-
координат К и К\ можно написать
?$ (Х13)
Выразим dxl через dx'kno формуле (VI. 38) и подста-
подставим эти выражения в (XI. 3):
ki k
dx\
Изменим в левой части порядок суммирования по ин-
индексам / и k:
( f дх\
Индексы ink являются немыми. Как уже отмечалось,
немой индекс можно обозначить любой буквой.

432 ПРИЛОЖЕНИЯ
Поэтому сумма слева не изменится, если переставить
индексы i и Л. В итоге получим
Из полученного нами соотношения следует
что совпадает с (VI. 37). Таким образом, мы пока-
показали, что величины дц/dxt при преобразованиях коор-
координат ведут себя как компоненты вектора.
Гамильтон ввел векторный дифференциальный опе-
оператор V (оператор набла) или оператор Гамильтона,
который представляет собой вектор с составляющими
д/дх, д/ду, д/дг:
Сам по себе вектор V смысла не имеет. Он приобре-
приобретает смысл, будучи применен к скалярной или вектор-
векторной функции. Так, при символическом умножении V
на ф получается градиент <р:
Следовательно, Тф = ?гас1ф. Согласно (XI. 3) прира-
приращение ф может быть представлено в виде скалярного
произведения векторов gra<^ и dv:
dq> = grad ф • dv = (Уф) dv. (XI. 5)
При перемещении по поверхности уровня ф остается
неизменной (Лр=0). Отсюда в соответствии с (XI. 5)
вытекает, что вектор Уф в каждой точке поля направ-
направлен по нормали к поверхности уровня. Найдем ско-
скорость изменения ф вдоль некоторого направления /,
т. е. dq>/dl. Согласно (XI. 5) приращение ф на отрезке
d\ равно (Тф)<Я = (Тф)/4/» где О^ф)/ — проекция гра-
<*ф (Уф); 4/
диента на направление /. Поэтому -5^ = —jf— —
= (Уф)/. Таким образом, проекция градиента на неко-

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 433
торое направление дает скорость изменения функции
в данном направлении.
Отметим, что вектор Vcp существует в каждой точке
скалярного поля <р. Следовательно, градиент образует
векторное поле, т. е. область пространства, каждой
точке которой соответствует определенное значение
вектора Vq>.
Дивергенция. Пусть нам дано поле вектора а. По-
Потоком вектора а через поверхность / называется вы-
выражение
где ап — проекция вектора а на положительную нор-
нормаль к площадке df, di— вектор элементарной пло-
площадки, его модуль равен величине площадки df, а на-
направление совпадает с направлением положительной
нормали к площадке. Направление положительной
нормали определяется в зависимости от обстоятельств.
Так, например, при вычислении потока через замкну-
замкнутую поверхность положительной считается внешняя
нормаль.
Название «поток» обусловлено тем, что в случае
поля вектора скорости жидкости интеграл (XI. 6) дает
поток жидкости через поверхность f, т. е. объем жид-
жидкости, протекающей через f в единицу времени.
Окружим точку Р поля замкнутой поверхностью f.
Вычислим поток Фа через эту поверхность. Отноше-
Отношение Фа к V будет характеризовать свойства поля в
окрестности точки Р, усредненные по объему V, за-
заключенному внутри /. Чем меньше линейные размеры
объема, тем ближе будет средняя характеристика к
истинной характеристике поля в точке Р. Скалярную
величину
lim ^ = lim 4r&andf (XI.7)
называют дивергенцией (или расхождением) вектор-
векторного поля в точке Р.
Определение (XI. 7) является самым общим, не за-
зависящим от выбора координатной системы. Найдем
выражение для дивергенции через проекции а на оси
декартовой системы координат. Возьмем в окрестно-
окрестности точки Р объем в виде прямоугольного параллеле-
1$ И. В. Смедм», т. I

434
ПРИЛОЖЕНИЯ
пипеда с гранями, перпендикулярными к координат-
ным осям (рис. XI. 1). Найдем поток вектора а через
грани 1 и 29 перпендикулярные к оси х. Внешняя нор-
нормаль к грани 1 совпадает по направлению с осью х.
Поэтому для этой гра-
грани ап = ах1 (индекс 1
указывает, что значе-
значение ах берется в точ-
точке, лежащей на гра-
грани /). Внешняя нор-
нормаль к грани 2 проти-
противоположна по направ-
направлению оси х. Поэтому
* для нее ап*=*—ах*
(индекс 2 указывает,
Рве XI. 1 что значение ах берет-
берется в точке, лежащей на
грани 2). Суммарный поток через грани 1 и 2 равен
(XL 8)
B)
где d/ = d/is=d/2 (см. рис. ХМ), ах\ и пх% берутся
для точек граней 1 н 2 с одинаковыми у п г. Инте-
Интеграл, стоящий справа, берется по поверхности f любой
из граней 1 и 2.
Разложим ах в ряд в окрестности точки Р:
Здесь Хр9 ц*% г* — координаты точки Р9 ахр — значе-
значение ах в точке Р, (дах/дх)Р и т. д. — значения произ-
производных в точке Р, гх — величина более высокого по-
порядка малости, чем разности (х — хР)9 (у — ур),
(г—2p)t т. е. величина, убывающая быстрее, чем ли-
линейные размеры параллелепипеда.
Положив в выражении (XI. 9) х «¦» хи найдем зна-
значения а% в точках грани /, т. е. аж\\ положив * = **,
получим значения а^ Вычтя эти значения друг из
друга, получим для противолежащих площадок dfi
ш d\% (значения у и г для них одинаковы)

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 435
где опять-таки е'х — величина, убывающая быстрее,
чем линейные размеры объема.
Подставив найденное нами значение в формулу
(XI. 8), получим
Из рис. XI. 1 видно» что произведение (х%—x2)f дает
объем параллелепипеда V. Поэтому
где г"х — величина более высокого порядка малости,
чем V. Аналогичные выражения получаются и для по-
потоков через пары граней, перпендикулярных к осям
Сложив вместе Ф*, Фу и Фг9 получим полный по-
поток вектора а через поверхность параллелепипеда.
Разделив согласно определению (XI. 7) этот поток
на V и сделав предельный переход1) V-+0, придем
к формуле
(за ненадобностью мы опустили индекс Р при произ-
производных).
Найденное нами выражение (XI. 10) для диверген-
дивергенции можно записать в виде
В такой форме понятие дивергенции может быть рас-
распространено на векторные поля в пространстве п из-
измерений. Определение (XI. 7) также можно распро-
'} При предельном переходе величины e"/V обращаются
в нуль.

436 ПРИЛОЖЕНИЯ
странить на пространство п измерений. В этом случае
под элементом объема следует понимать dV* =
= dx\dx2dxz ... dxn. Интеграл нужно брать по гипер-
гиперповерхности размерности п—1. Элемент гиперпо-
гиперповерхности, перпендикулярный к оси Хь, будет равен
df = dx\dx2 ... dxk~\dxk-y\ ... dxn. В пространстве че-
четырех измерений гиперповерхностью будет обычный
трехмерный объем.
Выражение (XI. 11) можно рассматривать как
сумму произведений величин V,- = d/dxi и а,-, т. е. как
скалярное произведение векторов V и а. Поэтому ди-
дивергенцию можно представить в виде
diva^Va. (XL 12)
Величина Va существует в каждой точке векторного
поля а. Следовательно, дивергенция образует скаляр-
скалярное поле, определенное в той же
части пространства, что и поле
вектора а.
Возьмем в поле вектора а ко-
конечный объем V, ограниченный
поверхностью f (рис. XI. 2). Ра-
Разобьем этот объем на элемен-
элементарные объемы АУ. Согласно
Рис. XI. 2 (XI. 7) для потока АФв через
поверхность такого объема мож-
можно написать ДФа ж diva-AV= Va-AK Сложим эти
выражения для всех элементарных объемов» При
суммировании АФв потоки через грани, разделяющие
два соседних объема, взаимно уничтожатся (для
смежных объемов потоки отличаются знаками, так
как внешние нормали п и п* имеют противополож-
противоположные направления). Некомпенсированными останутся
только потоки через участки внешней поверхности f,
так что в сумме получится поток вектора а через эту
поверхность. Сумма справа в пределе (при ДУ->0)
превратится в интеграл по всему объему. Прибли-
Приближенное равенство в пределе перейдет в строгое равен-
равенство. В итоге получим
<&dV. (XIЛ Э)
Полученное нами соотношение носит название тео-
теоремы Остроградского —Гаусса: поток вектора через

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 437
замкнутую поверхность равен интегралу от диверген-
дивергенции по объему, ограниченному этой поверхностью.
Ротор. Циркуляцией вектора а по контуру Г на-
называется выражение
ф ф (XI. 14)
Например, в поле консервативных сил циркуляция
вектора F равна работе сил на замкнутом пути Г.
Возьмем в окрестности точки Р контур Г, лежащий
в плоскости, проходящей через Р. Найдем циркуля-
циркуляцию Са по этому контуру. Отношение Са к поверхно-
поверхности f, охватываемой контуром, будет характеризовать
свойства поля в окрестности точки Р, усредненные по
поверхности f. Чем меньше линейные размеры поверх-
поверхности, тем ближе будет средняя характеристика к ис-
истинной характеристике поля в точке Р. В пределе,
при стягивании контура к точке Р, средняя характери-
характеристика превратится в истинную. Таким образом, свой-
свойства векторного поля в некоторой точке Р можно оха-
охарактеризовать величиной
lim ?*. = lim x & at dl. (XL 15)
Величина (XI. 15) зависит не только от свойств
поля в точке Р, но и от ориентации плоскости, в кото-
которой лежит контур. Ориентацию этой
плоскости в пространстве можно за-
дать нормалью к плоскости, связан-
связанной с направлением обхода по конту-
контуру Г при интегрировании правилом
правого винта (рис. XI.3) Для раз-
разных направлений п величина (XI.15)
будет иметь в одной и той же точке Р
разное значение, причем, как легко рнс# xi.3
сообразить, противоположным на-
направлениям п соответствуют значения величины
(XI. 15), отличающиеся только знаком. Следователь-
Следовательно, величина, определяемая формулой (XI. 15), ведет
себя как проекция некоторого вектора на направле-
направление нормали к контуру Г. Этот вектор называют ро-
тором (или вихрем) векторного поля в точке Р и

438
ПРИЛОЖЕНИЯ
обозначают символом rot а. Таким образом,
Са
(rota)*:
• lim
Г->0
г-м> f
(XI. 16)
Формула (XI. 16) дает самое общее определение
ротора, не зависящее от выбора координатной систе-
системы. Найдем выражение для
ротора через проекции векто*
ра а на оси декартовой систе-
системы координат. Начнем с опре-
определения проекции вектора
rot а на ось х. Для этого возь-
возьмем в окрестности точки Р
контур Г, лежащий в плоско-
плоскости, перпендикулярной к оси
х (рис. XI. 4). Направление
обхода по контуру выберем
так, чтобы оно образовывало
с направлением оси х правовинтовую систему. Тогда
направления п и оси х совпадут и выражение (XL 16)
даст (rota)*. Для выбранного нами контура
Рис. XI. 4
§ at dl = ф a d\ = ф (ау dy + а2 dz)
г г г
(для всех элементов контура dx = 0).
Значения ау для точек контура можно представить
в виде')
(дам \
где const включает в себя три слагаемых, не завися-
зависящих от у и г, гу — величина более высокого порядка
малости, чем линейные размеры контура. Следова-
Следовательно,
*) Смысл величин в этом выражении аналогичен смыслу ве-
величин в формуле (XI. 9); слагаемое с (х — Хр) отсутствует, так
как для всех точек контура х = хР.

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 439
Легко сообразить, что 4>d# = 0. Точно так же
равен нулю интеграл <у ydy = {l2§d(yz). Из рис. XI. 4
нетрудно заключить, что <у г dy = — /, где / — пло-
площадь контура. Таким образом
где гу — величина более высокого порядка малости»
чем площадь контура f.
Проделав аналогичные выкладки для аг, придем
к выражению
Ф аг dz = const ф dz
Интегралы &dz и &zdz = l/2§dB?) равны нулю,
&ydz = f. Поэтому
D^) . (XI. 18)
Выражения (XI. 17) и (XI. 18) в сумме дают
&atdL Разделив в соответствии с определением
(XI. 16) эту сумму на f и осуществив предельный пе-
переход1), получим
да„ даи
Рассмотрев циркуляцию для контуров» ориентиро-
ориентированных нормалью п по осям у и г, можно получить
выражения для проекций ротора на эти оси:
дах даг дау дах
Формулы для проекций ротора на координатные
оси легко запомнить, приняв во внимание, что в
') При предельном переходе величины е'// обращаются в
нуль.

440
ПРИЛОЖЕНИЯ
каждой из них индекс при rota и буквы, стоящие
справа в знаменателях, образуют циклическую пере-
перестановку, осуществляемую по схеме: х -*• у
Зная проекции, легко найти сам вектор:
С учетом того, что, например, даг/ду можно предста-
представить в виде Yvaz и т. д. (Vy — д/ду— проекция век-
вектора V на ось у), запишем формулу (XI. 19) следую-
следующим образом:
«х *у
д д д
дх ди дг
rota:
(XI. 20)
Наконец, сравнение с формулой (VI. 31) дает нам
право написать, что
(XI. 21)
Воспользовавшись формулами (VI. 29) и (VI. 33)
для векторного произведения, можно написать для ро-
ротора и его k-й компоненты следую-
? щие выражения:
[*•]- ?
i.k.l
да
Величина [Va] существует в каж-
каждой точке векторного поля а. Сле-
Следовательно, ротор образует векторное поле, опреде-
определенное в той же части пространства, в которой за-
задано поле вектора а.
Возьмем в поле вектора а произвольную поверх-
поверхность f9 ограниченную контуром Г (контур может
быть любым, не обязательно плоским). Разобьем эту
поверхность на малые элементы &f (рис. XI. 5). Со-
Согласно (XI. 16) для циркуляции АСа по границе эле-

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 441
мента Af можно написать выражение АСа « [Va] „Af,
где [Va] л —проекция [Va] на нормаль к данной АД
связанную с направлением обхода правилом правого
винта.
Сложим эти выражения для всех А/. При суммиро-
суммировании АСа интегралы \a/d/, взятые вдоль границы
раздела соседних площадок, взаимно уничтожатся
(для смежных площадок эти интегралы отличаются
знаком, так как берутся в разных направлениях).
Некомпенсированными останутся только интегралы
V a/ dl для участков, совпадающих с контуром Г»
ограничивающим f. Эти интегралы дадут в совокуп-
совокупности циркуляцию а по контуру Г. Сумма справа в
пределе (при Af-^O) превратится в интеграл по по-
поверхности. Приближенное равенство в пределе перей-
перейдет в строгое равенство. В итоге получим
V&]adf. (XL 23)
Найденное нами соотношение носит название тео-
теоремы Стокса: циркуляция вектора а по замкнутому
контуру Г равна потоку вектора [Va] через поверх*
ность, натянутую на контур Г.
Поверхность, по которой берется интеграл в пра-
правой части формулы (XI. 23), может быть любой»
важно лишь, чтобы она опиралась своей границей на
контур Г. Направление нормали п должно быть со-
согласовано с направлением обхода контура Г при
интегрировании.
Применение оператора V к произведению функций.
При составлении формул, в которые входит V, нужно
руководствоваться как правилами векторной алгебры»
так и правилами дифференциального исчисления.
Пусть, например, <р и ф — скалярные функции точки.
Тогда
(XI. 24)
(индекс при V указывает, на какую из функций она
действует). Сомножитель, на который в данном сла^
гаемом V не действует, можно вынести из-под знака V
(оператор V действует только на величины» стоящие
за ним). Тогда формула (XL24) примет следующий

442 ПРИЛОЖЕНИЯ
вид: ?(<рф) = фУ^ф-Ь-фУфф. В написанном нами вы-
выражении, очевидно, нет необходимости в индексах при
Vf так что окончательно
(XI. 25)
(читается: «фи градиент пси плюс пси градиент фи»).
Применим V к произведению фа. В этом случае
имеется две возможности — векторы V и фа можно
перемножить как скалярно, так и векторно. Соответ-
Соответственно получим
(XI. 26)
(«а градиент фи плюс фи дивергенция а»),
IV. (Фа)] - [?ф, (Фа)) + [V*, (<pa)J -
(XI. 27)
Теперь применим V к произведению [ab], перемно-
перемножив векторы сначала скалярно: V [ab] = Va [ab] +
+ V*[ab]. Осуществим в каждом из слагаемых цик-
циклическую перестановку (VI. 3) :
(во втором слагаемом мы поменяли местами b и V*,
чтобы вектор b оказался за оператором V&, который
на него действует; при этом у векторного произведе-
произведения изменился знак). Опустив ненужные уже индек-
индексы, придем к формуле
V [abj = Ь [?а] - а [?Ь] (XI. 28)
(«бэ ротор а минус а ротор бэ>).
Умножим [ab] на V вектор но: [V[ab]J=
= [Va[ab]]4-[V&[ab]]. Развернем каждое из слагае-
слагаемых по формуле «бац минус цаб» (см. (VI. 5)):
IV [ab]] =a(Veb)-b(Vea)+a(Vbb)-b(V6a). Рас-
ставив множители так, чтобы можно было опустить
индексы при V, получим
(XI. 29)
Выражения (aV) и (bV) суть скалярные диффе-
дифференциальные операторы. Например»
t

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 443
Эти операторы могут применяться как к скалярным,
так и к векторным функциям. В применении к ска-
скаляру ф оператор (XI. 30) дает
При действии оператора (а?) на вектор Ь получается
выражение
<Х132>
Применим оператор {XI. 30) к произведению ска-
скалярной функции ф и векторной функции Ь:
(aV) (ФЬ) - (аУф) (фЬ) + (*Vb) (ФЬ)*
Ь(а - ?Ф) + V(aV)b. (XI. 33)
Полезно знать значение выражения (aV)r, где г —
радиус-вектор, а — некоторый произвольный вектор.
Подставив в (XI. 32) г вместо b и приняв во внима-
внимание, что дхк/дх1 = 6,л, получим
= а. (XI. 34)
Формулы (XL 25)—(XL 29) мы получили легко.
Сложнее обстоит дело с нахождением градиента ска-
скалярного произведения двух векторов: V(ab), так как
неясно, что надо понимать под, например, выраже-
ниемУа(аЬ). Его нельзя трактовать как (Vaa)b, ибо
операции перемножения а с b и применения Va не пе-
переставимы. Это затруднение можно обойти, восполь-
воспользовавшись вспомогательными соотношениями, выте-
вытекающими из формулы «бац минус цаб»: ta[Vb]]e
= Vb (ab)—b (V&a) ¦¦ Vb (ab)—(aV)b, откуда
V6(ab) = (a[Vb]J + (aV)b. (XI. Щ
Записав таким же способом {Ь[Та]]9 придем к соот-
соотношению

444 приложения
Подстановка соотношений (XI. 35) и (XI. 36) в фор-
формулу
приводит к следующему выражению для градиента
скалярного произведения векторов а и Ь:
V (ab) = [a [Vb]) + [Ъ [Va]] + (aV) b + (bV) a. (XL 37)
Повторное применение оператора V. В результате
воздействия оператора V на скалярные или векторные
функции получаются новые векторные либо скалярные
функции, к которым в свою очередь может быть при-
применен оператор V.
Градиент функции <р есть вектор. Следовательно,
к нему могут быть применены операции и диверген-
дивергенции, и ротора. Вычислим дивергенцию градиента. Со-
Согласно формулам (XI. 2) и (XI. 11)
Таким образом,
A<p, (XL 38)
где А —оператор Лапласа:
Из проделанных нами выкладок вытекает, что
V2 = A. (XL 40)
Однако нужно иметь в виду, что такое соотношение
между операторами ? и А имеет место только в де-
декартовых координатах. В других системах координат,
например в цилиндрической или сферической, соотно-
соотношение (XI. 40) не выполняется. Самым общим опре-
определением оператора А, справедливым в любой системе
координат, является определение, вытекающее из со-
соотношения (XI. 38), которое можно записать в виде
Аф = div grad ф. (XL 41)

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 445
Найдем rot grad qx Согласно (XL 22)
• <XL42>
Поскольку d2q>/dXidxk = d2y/dxkdxit последнее выра-
выражение равно нулю, так что
rot grad ф = 0. (XL 43)
Этого и следовало ожидать, так как [V, Уф] = [W] <р,
а векторное произведение вектора на самого себя рав-
равно нулю.
Вычислим дивергенцию ротора. Согласно форму-
формулам (XI. 11) и (XI. 22)
= 2]d— ( 2 Ч
k k \т,п
Z Чтп
Так как д2ап/дхкдхт = д2ал/дхтдхк9 последнее выра-
выражение равно нулю. Следовательно,
divrota = 0. (XL 44)
К этому результату можно было прийти сразу, при-
приняв во внимание, что смешанное произведение векто-
векторов (каковым является V[Va]) равно объему парал-
параллелепипеда, построенного на перемножаемых векто-
векторах. Поэтому при совпадении двух сомножителей из
трех такое произведение равно нулю.
Для вычисления rot rot а будем исходить из фор-
формул (XL 22):
Произведем циклическую перестановку индексов при
е так, чтобы индекс k в обоих е оказался на послед-
последнем месте и воспользуемся соотношением (VI. 16).
В итоге получим
i U m n l
i, U m, n
I л» п l m
I, I. л», п
1.1, т.» * т LLm9n

446 ПРИЛОЖЕНИЯ
Осуществим суммирование по индексам т и п. В ре-
результате полученное нами выражение примет вид
д2^ ^ д2а1
что можно представить следующим образом:
Итак» мы пришли к формуле
[V [Va] ] = V (Va) - Да (XI. 45)
или
rot rot a = grad div a — Да. (XI. 46)
Легко убедиться в том, что соотношение (XI. 45)
можно получить, если развернуть [V[Va]] по фор-
формуле «бац минус цаб», обращаясь при этом с V как
с обычным вектором.
Из (XI. 46) вытекает, что
grad div a — rot rot a + Да. (XI. 47)
Дивергенция является скаляром. Поэтому никакой
операции, кроме операции нахождения градиента,
к ней применить нельзя.
Некоторые формулы векторного анализа. Найдем
дивергенцию и ротор радиуса-вектора г, а также гра-
градиент модуля г. Приняв во внимание, что г = (? х*)Чж,
получим согласно (XI. 2)
1> . 48)
где е, — орт радиуса-вектора г.
В соответствии с (XI. 11)
(XI. 49)
(мы использовали тот факт, что rt=Xi). В я-про-
странстве Vr = л.

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 447
Легко убедиться в том, что ротор радиуса-вектора
равен нулю:
[7г] = 0. (XI.50)
Для этого можно воспользоваться формулой (XI. 22),
заменив в ней а* через xk. Тогда получим
f. ft, / l I, kt I
Это выражение равно нулю, так как при одинаковых
значениях индексов ink обращается в нуль множи-
множитель eikiy а при различных значениях — обращается
в нуль множитель 6**.
Соотношение (XI. 50) вытекает также из того, что
циркуляция вектора г по любому контуру равна нулю.
Действительно, согласно (XL 14)
Под знаком интеграла стоит полный дифференциал,
поэтому интеграл равен нулю.
Теперь найдем градиент функции от г, т. е. V<p(r).
Частная производная от <р(г) по хк имеет вид1),
ду/dxk = ду/дг • дг/дхц = ду/дг • Xk/r. Следовательно,
Приняв во внимание формулу (XI. 48), можно напи-
написать
Пусть имеется функция расстояния между двумя
точками:
где
') Мы написали ду/дг вместо dq>/dr, поскольку может
чнться, что ф, кроме г, зависит еще, скажем, от L

448 ПРИЛОЖЕНИЯ
Операцию нахождения градиента можно применить
к этой функции двумя способами — можно произ-
производить дифференцирование либо по координатам дс/,
либо ао координатам х'г Чтобы различать эти два
градиента, в первом случае мы будем пользоваться
обозначением V, а во втором случае — обозначением
V. Компоненты градиента в обоих случаях имеют вид
), = dq>/dR • dR/dxlf (?», = dq>/dR - dR/dx'r
Очевидно, что производные dR/dxt и dR/dx\ отли-
отличаются только знаком. Отсюда заключаем, что
\ty=-vy (XI. 52)
Вычислим ротор орта ег=г/г. Представив г/г как
произведение ср=1/г на а = г, применим формулу
(XI.27). В результате получим: (V,r/r] = [V(l/r),r]-j-
+ (I/r)[Vr]. Согласно (XI.51) V(l/r)== — {l/r*)r/r.
Поэтому первое слагаемое равно нулю. Второе сла-
слагаемое равно нулю в соответствии с (XI. 50). Таким
образом,
[Vf r/r] = [Ver] = 0. (XI. 53)
Теперь найдем ротор функции ф(г)ег, где ф(г) —
произвольная функция от г. Применим снова формулы
(XI. 27) и (XI. 51):
tn сг] + Ф(г)[?ег] -0
(см. (XI. 53)). Итак,
[V, Ф(г)е,] = 0. (XI. 54)
Пусть нам дана векторная функция а(?) —
=*=?<** (I) е* скалярной величины I, которая в свою
очередь является функцией координат xiy ^ = ^(^/)-
Найдем ротор и дивергенцию этой функции. По пра-
правилам дифференцирования сложной функции
дак дак д%
'ЩЖ!Х~Щ~~дГ1- (XI.55)
Согласно (XI. 22)

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 449
Величина да*/<?? есть k-я компонента вектора да/<?|,
a dl/dxi есть /-я компонента градиента функции |.
Следовательно,
i.k.l
(мы воспользовались формулой (VI. 29)). Итак, если
а = а(?), где I = Цхих2,*з), то
, -ft]. (XI.56)
Для нахождения дивергенции функции а(|) будем
исходить из формулы (XI. 11). Учтя (XI. 55), получим
(XI. 57)
Положив в формулах (XI. 56) и (XI. 57) ? = г
(г—модуль радиуса-вектора), получим, что
?] = [ег, ?]. (XI.58)
Sirf <XL59>
(см. (XI. 48)).
Докажем формулу
\ [Va] dK - § [па] d/ = § [df, а], (XI. 60)
v f f
где а — некоторая векторная функция, V—произволь-
V—произвольный объем, f — ограничивающая его поверхность, п —
внешняя нормаль к элементу поверхности df. Для
этого умножим скалярно вектор [Va] на произволь-
произвольный постоянный вектор Ь. Из формулы V[ab] =
— b[Va] — a[Vb] (см. (XI. 28)) следует, что b[Va] =
=-V[abH~a[Vb]=V[ab] ([Vb]?=0, так как Ь =
* const). Теперь проинтегрируем полученное соотно-
соотношение по некоторому объему V и применим к правой
части теорему Остроградского — Гаусса:
b [?a] dV = J V [ab] dV «* § [ab] n df.

450 приложения
Выполнив в последнем интеграле циклическую пе-
перестановку перемножаемых векторов (см. (VI. 3)),
получим \ b [Vat] dV = ф b [na] df. Вынесем постоян-
v f
ный вектор b за знак интеграла:
b\[V&]dV =
v f
Полученное соотношение должно выполняться при
произвольном выборе вектора Ь. Поэтому на b можно
сократить. В результате мы придем к формуле
(XI. 60).
Интегральное определение оператора V. Рассмот-
Рассмотрим интеграл по замкнутой поверхности /:
(XI. 61)
где ф — произвольная скалярная функция, rff f
элементарный вектор площадки df. Возьмем в каче-
качестве поверхности, по которой вычисляется интеграл,
поверхность бесконечно малого прямоугольного па-
параллелепипеда со сторонами dx, dy$ dz. Тогда инте-
интеграл (XL 61) можно представить как сумму шести ин-
интегралов, каждый из которых вычисляется по одной
из граней параллелепипеда. Ввиду малости граней
значение ф в пределах каждой грани можно считать
постоянным. Следовательно,
=еЛф(^ + ^> У* *) — ф(х, У, z)]dydz +
еу [ф(х, у + dyt г) — ф(х> у, z)]dxdz +
еЛф(*, у, г + йг) — ф(*, у, z)\dxdy=*
Отсюда получаем, что
^ф (XI. 62)
к-ю
В соответствии с формулой (XI. 62) оператор V
можно определить следующим образом:
t. (XI. 63)

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 451
Возьмем некоторый объем V и разобьем его на
элементарные объемы AV. Согласно формуле (XI. 62)
для каждого объема выполняется приближенное ра-
равенство V<p • А V « ф ф d\.
Теперь просуммируем это равенство по всем эле-
элементарным объемам. При суммировании правые ча-
части, соответствующие поверхностям раздела соседних
объемов, взаимно уничтожатся. Останутся некомпен-
некомпенсированными только члены, отвечающие внешней по-
поверхности. Поэтому, перейдя к пределу, при котором
все ДУ->»0, мы придем к соотношению
(XI. 64)
Согласно (XI. 64) интеграл от скалярной функции ср
по замкнутой поверхности f можно преобразовать в
интеграл по заключенному в ней объему, заменив эле-
элемент поверхности di оператором VdV. При этом ком-
компоненты di претерпевают преобразование
Разумеется, возможно и обратное преобразование.
Аналогично обстоит дело и с интегралом от век-
векторной функции. Действительно, согласно теореме
Остроградского — Гаусса (см. (XI. 13)) \ Va dV —
v
ев фа di, что также согласуется с (XI. 65).
«j
f
Вообще преобразование (XI. 65) допустимо всегда,
независимо от конкретного вида выражений, стоящих
под знаком интегралов. Примером такого преобразо-
преобразования может служить соотношение (XI. 60).
Криволинейные координаты. Иногда бывает удобно
определять положение точки не декартовыми коорди-
координатами х\, Х2, Xzf а тремя другими числами <7ь фг, <7з>
более соответствующими характеру рассматриваемой
задачи. Эти числа называются криволинейными коор-
координатами точки.

452 ПРИЛОЖЕНИЯ
Наложив (если в том возникает необходимость)
ограничения на область изменения криволинейных ко-
координат, можно добиться взаимно однозначного соот-
соответствия переменных Xi и q^ Тогда qi = qi(x\tX2, х$),
Xi = Xi(q\y #2, ?з) (i = 1» 2, 3).
Поверхности, которые описываются уравнением
дс2> хг) = const, называются координатными по-
поверхностями. Линии пересечения двух координатных
поверхностей называются координатными линиями.
Вдоль координатной линии изменяется только одна
координата, остальные две остаются неизменными.
Примером криволинейных координат может слу-
служить сферическая система: г, Ф, <р. В этом случае ко-
координатными поверхностями являются: 1) сферы, г==
= const, 2) полуконусы, # = const, 3) полуплоскости,
ф = const. Координатные линии представляют собой:
1) радиусы — линии г, 2) меридианы — линии #, 3) па-
параллели— ЛИНИИ ф.
Если координатные линии в каждой точке взаимно
перпендикулярны, криволинейные координаты назы-
называются ортогональными. Мы ограничимся рассмотре-
рассмотрением только ортогональных координат. Сферические
и цилиндрические координаты принадлежат к их
числу.
Введем для каждой точки Р орты е*, е*, е^, на-
направленные по касательным к координатным линиям
в данной точке в сторону возрастания соответствую-
соответствующих переменных qt, В силу ортогональности для ор-
ортов е^ выполняются соотношения
« = 6ik- (XL 66)
Определим производную радиуса-вектора г =
= г(<7ь<72> <?з) по координате qi. Остальные две коор-
координаты при дифференцировании не изменяются. Сле-
Следовательно, при сообщении координате qi прираще-
приращения 8qi конец вектора г перемещается вдоль коорди-
координатной линии qi. Поэтому вектор dr/dqi направлен по
касательной к координатной линии qu т. е. коллинеа-
рен с е^. Обозначив модуль вектора dt/dqi симво*
лом Н^ можно написать, что
-5--ад (/-1,2,3). (XL 67)

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 453
Представив г в виде ? xktk (е* — орты декарто-
декартовых координатных осей), можно написать, что
Возведя это соотношение в квадрат, получим
(XI.68)
Величины Hi называются коэффициентами Ламе.
Их значения можно найти по формуле (XI. 68), если
известен вид функций х*—**(?{). Например, в слу-
случае сферической системы координат х\ = г sin О cos q>,
X2 = r sin d sin ф, Xz = r cos <K Отсюда
так что согласно (XL 68)
Н\ = (sin # cos фJ + (sin * sin q>J + (cos bf = 1.
Проделав аналогичные выкладки для Яг и Я3, по-
получим
Я, = 1, Я2 = г, Я3 = г8ш*. (XI. 69)
Найдем квадрат расстояния ds между двумя точ-
точками. Согласно (XI. 67)
dT = Z W d(li - Е Я«< ^г ДО- 70)
Z W
Следовательно,
rfs2 = | dr p = ? Я| dq]. (XL 71)
Для сферической системы координат эта формула
дает
ds2 = dr2 + r2d№ + r2 sin2 0 dqp. (XL 72)
Проведем через начало и конец вектора dr коор-
координатные поверхности. В результате получится беско-

454
ПРИЛОЖЕНИЯ
нечно малый параллелепипед, ребра которого согласно
(XI. 70) равны
dlt = Hi dqt (/ = 1, 2, 3). (XL 73)
Грани этого параллелепипеда будут иметь площадь
df\ = Н2Н$ dq2 dq$> df2 = Н%НХ dq$ dqXf
(XL 74)
(XL 75)
Объем же параллелепипеда равен
dV = HiH2Hzdqxdq2dqz.
Вместо вычисления по формулам (XI. 68) коэффи-
коэффициенты Ламе можно находить с помощью выражений
(XI. 73). Так, например, в случае сферических коор-
координат (рис. XI. 6) элементар-
элементарный параллелепипед имеет
ребра dU = dry dt2 = rdb%
dlz — r sin &/<p, откуда для ко-
коэффициентов Ламе сразу по-
получаются значения (XI. Ш).
Рис. XI. б
Рис. XI. 7
В случае цилиндрической системы координат
(рис. XL 7) ребра элементарного параллелепипеда
равны dl\ — ф, dl2 = р^ф, dk = dz, откуда
Я1 U Л И I /VI ТЛ
1 sbbs if fj^ = pt /7^— 1. \Л1. fO
Найдем выражение градиента в криволинейных ко-
координатах. Согласно формуле (XI. 5) проекция гра-
градиента функции ф на направление орта е* равна
:. Приняв во внимание (XI. 73), получим, что

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 455
Сам же градиент определяется формулой
Следовательно, в сферической системе координат
а в цилиндрической системе
^-^-^+}^+^- <Х1-79>
Для определения дивергенции в криволинейных
координатах будем исходить из определения (XI. 7),
согласно которому
Va = lim i <$ adt = lim -?-. (XI. 80)
V0 V j V0 V
V-+0
В качестве V возьмем объем бесконечно малого парал-
параллелепипеда, заключающего в себе точку Я, для кото-
которой вычисляется дивергенция. Рассуждая так же, как
при получении формулы (XI. 11), напишем выражение
для потока через грани, перпендикулярные к орту е*:
(см. (XI. 74)). Здесь щ — проекция вектора а на на-
направление е*. Одним штрихом помечены значения ве-
величин, относящиеся к одной из противолежащих друг
ДРУГУ граней, двумя штрихами — значения, относя-
относящиеся к другой грани.
Разложив а\Н2Иг в ряд в окрестности точки Р,
получим
где V — объем параллелепипеда (см. (XI. 75)), ei —
величина более высокого порядка малости, чем V.
Аналогично вычисляются потоки через две другие

456 ПРИЛОЖЕНИЯ
пары граней:
Подставив Ф = Ф1 + Ф2 + Фз в (XI. 80) и осуще-
осуществив предельный переход, придем к формуле
) )]
(XI. 81)
Приняв во внимание (XI. 69), получим выражение
для дивергенции в сферических координатах:
1 д(г\) 1 a(sinaa<>) I a%
va г2 дг "•" г sin * dft "*" г sin d дф *
(XI. 82)
В цилиндрических координатах
Согласно (XI. 16) проекция ротора на направление
орта е] определяется выражением
[Va]< = lim 4- $ a d\ = lim -^ f (XL 84)
где ft — площадка, перпендикулярная к е*, Ct — цир-
\$г+А?г куляция вектора а по контуру,
*\ м» \ ограничивающему эту площадку.
\ -L л Чтобы вычислить проекцию
[Va] на орт е*, возьмем ft в ви-
виде бесконечно малого криволи-
криволинейного прямоугольника со сто-
сторонами А/2 = #2Д?2 И Д^З =»
. Циркуляция а по кон-
^ ру
Риа XI. 8 туру этого прямоугольника мо-
может быть представлена в виде
четырех интегралов вида \adl. Два из них берутся
по противоположным сторонам Д/? и А/^, два — по
противоположным сторонам A/J и Ы? (рис. XI. 8),

XI. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОГО АНАЛИЗА 457
В итоге, учтя (XI. 73), получим
- к *? - «з К) - К К - < К) -
. 85)
Разложив азЯ3 и аг#2 в ряд в окрестности точки Р,
для которой вычисляется ротор, можно написать, что
Следовательно, выражение (XI. 85) можно предста-
представить в виде
с, ^
_ 1 {д(агНг) д (а2Н2)
— Я2#з1 ^2 дGз
где f\ — площадь прямоугольника (см. (XI. 74)), е —
величина более высокого порядка малости, чем f\.
Подставив найденное нами значение С\ в (XI. 84)
и осуществив предельный переход, придем к формуле
— \
- ITJh X дд2 ддь $ •
Аналогичные формулы получаются для двух других
проекций вектора [Va], Все три формулы можно объ-
объединить в одну
(индексы |, k9 l образуют циклическую перестановку
последовательности: 1, 2, 3). Наконец, найдем выра-
выражение для оператора Лапласа в криволинейных коор-
координатах. Согласно (XI. 41) А-ф = V(?$)= divgrad^.
Воспользовавшись формулами (XI. 81) и (XI. 77),
получим
L
dq

458 ПРИЛОЖЕНИЯ
Подставив значения (XI. 69), получим выражение для
оператора Лапласа в сферических координатах
В цилиндрических координатах
?& <XL89>
XII. Четырехмерные векторы и тензоры
в псевдоевклидовом пространстве
В Приложениях VI и X рассматривались векторы
и тензоры в евклидовом пространстве, в котором квад-
квадрат радиуса-вектора определяется выражением
? ! 4 ?
Если ввести тензор
(XII. 2)
о ...
выражение (XII. 1) можно представить в виде
gikx(xk. (XII. 3)
Тензор gik называется метрическим тензором.
Уравнения специальной теории относительности и
электродинамики приобретают особенно простой и на-
наглядный характер, если их представить в виде соот-
соотношений между векторами и тензорами в четырехмер-
четырехмерном пространстве, метрика которого определяется тен-
тензором
(I о о о\
°о -? l)
о о о -i/
По соображениям, которые выяснятся в дальней-
дальнейшем, мы будем пользоваться следующими обозначе-

хи. тензоры в псевдоевклидовом пространстве 459
ниями. Индексы при компонентах 4-радиуса-вектора
будем писать не внизу, а вверху. Символ Кронекера
будем записывать в виде 6$, т. е. один индекс ставить
вверху, а другой внизу. Индексы при компонентах
метрического тензора писать в зависимости от обстоя-
обстоятельств либо внизу, либо вверху.
При написании формул мы будем руководство-
руководствоваться следующими правилами:
1. В каждой паре немых индексов (т. е. индексов,
по которым осуществляется суммирование) один ин-
индекс ставить вверху, а другой внизу.
2. Свободные индексы (т. е. индексы, по которым
суммирование не производится) располагать так,
чтобы в обеих частях равенства они занимали одина-
одинаковое положение — вверху либо внизу.
У коэффициентов линейного преобразования ком-
компонент векторов и тензоров мы также будем ставить
один индекс вверху, а другой внизу1). Следовательно,
в отличие от формул преобразования «[-^А,
с которыми мы имели дело в Приложениях VI и X,
мы будем писать аналогичные формулы в видеа'1* —
V
Напомним, что согласно принятому нами условию
во всех случаях, когда знак ? отсутствует, суммиро-
суммирование даже по парным индексам не производится.
Пространство, свойства которого определяются
тензором (XII. 4), называется псевдоевклидовым
Координаты, а также компоненты векторов и тензо-
тензоров в этом 4-пространстве мы будем различать с по-
помощью греческих индексов |л, v и т. д., которые могут
принимать четыре значения: 0, 1, 2, 3. Латинскими
индексами *,&, ... (пробегающими значения 1, 2, 3)
мы будем снабжать координаты и компоненты векто-
векторов в обычном трехмерном пространстве (в простран-
пространстве с евклидовой метрикой). Иногда мы будем ис-
использовать латинские индексы при компонентах 4-век-
торов и 4-тензоров, чтобы подчеркнуть, что имеются
в виду ненулевые значения индексов.
*) В дальнейшем мы увидим, что один индекс вверху, а
другой внизу пишутся при смешанных компонентах тензоров.
Однако следует помнить, что коэффициенты линейного преобра-
преобразования свойствами компонент тензора не обладают.

460 ПРИЛОЖЕНИЯ
Определив квадрат радиуса-вектора в рассматри-
рассматриваемом 4-пространстве выражением, аналогичным
(XII.3), и приняв во внимание (XII.4), получим
з
^Wf-Wf-i*2?-(**?> (XII. 5)
|i,v«0
В качестве координаты jc° в теории относительно-
относительности принимается произведение времени t на скорость
света в пустоте, а в качестве остальных координат
х1— координаты в обычном трехмерном пространстве.
Таким образом,
x* = ct, xx = x, х2 = у, x* = z. (XIL6)
Приняв это во внимание, выражению (XII. 5) можно
придать вид
Е guvXW = (х°? - ? (jc1J = сН2 - г2. (XII. 7)
|i. v-0 /-1
Формулы преобразования координат. При переходе
к другой системе координат компоненты 4-радиуса-
вектора преобразуются по линейному закону
з
*'»=Е <etv. (XIL8)
v-0
Обратное преобразование осуществляется по формуле
s
**=? «S*/v, (XII. 9)
где а? — коэффициенты обратного преобразования.
Ввиду инвариантности квадрата 4-радиуса-век-
з
тора должно выполняться условие 2 ga^xv^ =
|А, V-0
3
= 21 gu^x^x^. Подставим сюда значения (XII. 8)
|i.V-0
для хг» и x'v:
jt,V-0 **v I», V-0 •* p-0 V 0-0

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 461
Поменяем местами справа немые индексы [i и р,
з
а также v и а. В результате получим J) g
3 3
Отсюда вытекают условия, которым должны удов-
удовлетворять коэффициенты линейного преобразования
(XII. 8),
з
Приняв во внимание, что gp0 отличны от нуля только
при р == а (см. (XII. 4)), это соотношение можно
упростить следующим образом:
Еогрр«де=gp, (», v=о, I, 2, з). (хи. ю)
Например, для р = v = 0 по этой формуле получается,
что
W - КJ - КJ - «У -1. (хи. 11)
а для \i= I, v = 2
0. (XII. 12)
Отметим, что, взяв в качестве gpa тензор (XII. 2),
мы смогли бы привести формулу (XII. 10) к виду
У!в?а? = б что совпадает с формулой (VI. 40).
р —
Очевидно, что для коэффициентов a!J также имеют
место соотношения, аналогичные (XII. 10).
Теперь найдем связь между коэффициентами пря-
прямого и обратного преобразований. Напомним, что в ев-
евклидовом пространстве эта связь имеет вид а/* = а«
(ср. формулы (VI.37) и (VI.38)).
Применим последовательно преобразования (XII. 9)
и (XII. 8). В результате получим
& — S og^— Е^Е <*?*v = S *v

462 приложения
Компоненту х* можно представить как ? *v*v. От-
v
сюда следует, что
^aga; = 6$ (ц, v = 0, 1, 2, 3). (XII. 13)
Легко убедиться в том, что система уравнений
(XII. 13) будет удовлетворена, если положить
ag = a<>, a°=-a<, a' = -aj, a?=a* (XII. 14)
(/, й=1, 2, 3).
Действительно, пусть p, = v=0. Тогда уравнение
(XII. 13) выглядит так:
з
р-о р °
или, с учетом (XII. 14),
что согласуется с (XII. 11).
Положим [л=1, v = 2. Тогда уравнение (XII. 13)
имеет вид
или, с учетом (XII. 14),
Е
что согласуется с (XII. 12). Аналогично можно убе-
убедиться в том, что и остальные 14 уравнений, содержа-
содержащихся в (XII. 13)«удовлетворяютсярешением (XII. 14).
Заметим, что совокупность соотношений (XII. 14)
можно записать в виде одного соотношения
Действительно, при ja = v = O имеем g\i\L = gw, по-
поэтому d°0 = aj; при ц == 0, v = i Ф 0, равно как и при
I* = /:??: О, v = 0, будет giisi=—gw, вследствие чего

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 463
oj — — aj и aj «* — a°; наконец, при \х = i Ф О, v =
«в й ф О оба множителя (g^ и gyv) равны — 1, так что
a? = a*. В итоге мы пришли к соотношениям (XII. 14).
В теории относительности рассматриваются обычно
такие преобразования, при которых координаты х2=у
и^ = 2 остаются неизменными (*'2=jc2 и / = л;3).
Очевидно, что матрица коэффициентов преобразова-
преобразования в этом случае выглядит следующим образом:
¦8 •?
[a!J] = | «о «I О О I (XII. 16)
[ag «? О 01
а? а| 0 0 I
0 0 1 0 Г
0 0 0 1 J
Матрица коэффициентов обратного преобразова-
преобразования имеет аналогичный вид.
Обозначим буквой р параметр, которым можно
охарактеризовать различие между системами К и /С'.
Этим параметром может быть, например, угол пово-
поворота одной системы относительно другой. В теории
относительности роль параметра р выполняет относи-
относительная скорость систем К и К'. Очевидно, что в ре-
результате предельного перехода, при котором р стре-
стремится к нулю, обе системы совпадут, так что матрица
(XII. 16) примет вид
10 0 0-
К1
110 0 0-1
0 10 0]
0 0 10 1'
0 0 0 1-1
Таким образом,
Iimag = limaj=l, Urn a? — lim cd — 0. (XII. 17)
р-Ю p->0 * p-M> p->Q
Четыре отличных от нуля и единицы коэффициен-
коэффициента а? не являются независимыми. Написав соотноше-
соотношение (XII. 10) для |i = v — 0, получим, что
Аналогичное соотношение имеет место и для коэф-
коэффициентов обратного преобразования: (ogJ — (a?J «¦
= 1, откуда с учетом (XII. 14) получается уравнение
i- <хп-19>

464 ПРИЛОЖЕНИЯ
Теперь напишем условие (XII. 10) для р, —0, v= 1
аЭД-аОД-0. (XII. 20)
Из сравнения уравнений (XII. 18) и (XII. 19) сле-
следует, что (а^J = (а?J> т- е. а10 = ±:а°{. Сопоставление
этого условия с уравнением (XII. 20) дает два воз-
возможных варианта соотношений между коэффициен-
коэффициентами:
1) а°0 = а}, если а° = aj, 2) a{J = — aj, если а° = — а'.
Со свойством коэффициентов, выражаемым форму-
формулой (XII. 17), согласуется первый вариант. Следова-
Следовательно, нужно принять, что о%=а\, а°=с^. Введя обо-
обозначения aj==a}^=ao, a°=aj=ap матрицу коэф-
коэффициентов преобразования можно представить в виде
о о-
К]
[а0 О| О 0"|
ot а0 О О I
О О 1 О Г
О О О 1 J
Эта матрица содержит только один независимый ко-
коэффициент (значение которого определяется конкрет-
конкретным видом преобразования), поскольку «0 = aJ и
а, =а° связаны соотношением (XII. 19)
a2-a2=l. (XII.22)
Согласно (XII. 14) fig —с{ —о^ a? = —a» = —ar
Следовательно, матрица обратного преобразования
имеет вид
Контраварнантные и ковариантные векторы* Под-
Подстановка в (XII. 8) значений а^ из (XII. 21) приводит
к формулам преобразования компонент 4-радиуса-
вектора:
(XII. 24)
Совокупность четырех величин ae, а1, а2, а8, преоб-
преобразующихся при переходе от одной системы коорди-

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 465
нат к другой по тем же правилам, что и компоненты
4-радиуса-вектора, т. е. но формулам
а=Е<с\ (XII. 25)
называется четырехмерным вектором D-вектором).
Коэффициенты ajj в (XII. 25) имеют те же значения,
что и в (XII. 8).
Компонента а0 соответствует компоненте 4-радиу-
4-радиуса-вектора х°, которая в теории относительности при-
принимается равной d (см. (XII. 6)). В связи с этим ком-
компонента а0 называется временной. Компоненты а1, а2,
а3 соответствуют компонентам хх = х, х2 — у, хг = z,
в связи с чем носят название пространственных.
Подстановка в ^XIL 25) значений a|J из (XII. 21)
приводит к следующим формулам:
(XIL26)
Квадрат 4-вектора определяется по аналогии с
квадратом 4-радиуса-вектора (см. (XII. 5)):
Е gw&tP - №? - (а1? - (a2f - (a3J. (XIL 27)
Отметим, что квадрат 4-вектора может быть как по-
положительным, так и отрицательным; в частности, он
может равняться нулю.
При написании векторных формул для псевдоев-
псевдоевклидова пространства мы сталкиваемся с большим не-
неудобством, вызванным тем, что квадрат 4-вектора
определяется выражением (XII. 27), которое не может
быть представлено в компактной форме как 2 (а**J-
Чтобы, устранить это неудобство, вводят два вида
4-векторов. Различают их тем, что у векторов одного
вида индекс пишут вверху, а у векторов другого
вида —внизу. Первые векторы называются контрава-
риантными, вторые —ковариантными. Таким образом,
поставив индекс при компонентах 4-радиуса-вектора
вверху, мы отнесли этот вектор к категории контра-
вариантных.
Каждому контравариантному вектору а& сопостав-
сопоставляется ковариантный вектор а& (и наоборот), причем
16 И. В. Савельев, т. 1

466 ПРИЛОЖЕНИЯ
принимается, что
<h> = gwP (XII. 28)
(см. (XII.4)), т. е.
^ = 0°, я, = -а1э Ог=-а2, а3=-а3. (XII.29)
Легко сообразить, что соотношению (XIL28)
можно придать вид
(XII. 30)
Таким образом, опускание или поднятие индекса и
при компоненте 4-вектора сопровождается умноже-
умножением компоненты ка g^^ или gw.
С использованием контравариактных и ковариант-
ных компонент квадрат 4-вектора (см. (XII. 27)) мо-
может быть записан следующим образом:
з
? «'«i + ^2 + <А%. (XII. 31)
По аналогии с формулой (XII. 31), которая дает
произведение 4-вектора на самого себя, определяется
скалярное произведение двух 4-векторов:
= tf°fe° - albx — a2b2 — а^3. (XII. 32)
Очевидно следующее соотношение:
з з
Е rffyi—E а„Л (XII. 33)
Вообще во всякой паре немых индексов можно вза-
взаимно менять местами верхний и нижний индексы.
Отметим, что при чисто пространственных поворо-
поворотах (т. е. преобразованиях, не затрагивающих компо-
компоненту а0) три пространственные компоненты 4-век-
4-вектора а& ведут себя как компоненты вектора в трехмер-
трехмерном евклидовом пространстве (компонента а0 ведет
себя при этом как трехмерный скаляр). В связи с этим
компоненты 4-вектора могут быть записаны в виде
а» = (a0, at) (i = 1, 2, 3) (XII. 34)
либо, короче,
а* = (а°, а). (XII.35)

XII. ТЕНЗОРЫ В ПС&ВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 467
Ковариактные компоненты того же вектора выгля-
выглядят следующим образом:
а,, = (а0, - щ) (х=1, 2, 3) (XII. 36)
или
пр = {сР, -а). (XII.37)
Для квадрата 4-вектора имеем выражение
Е <Л^ = (а0J - Е 4 = to0J - a2, (XIL 38)
а для скалярного произведения 4-векторов
Е d% — oPifi - ab. (XII. 39)
Легко убедиться в том, что приращение квадрата
4-вектора можно представить двумя способами:
6 Е &Н = 2 S aiX 5а!х = 2 S ац *^- (ХП. 40)
Четырехмерный градиент» Пусть нам дана скаляр-
скалярная функция величин х&:
!, х\
По правилам дифференциального исчисления прира-
приращение этой функции дается выражением
Приращение функции не может зависеть от того,
в какой системе координат оно вычисляется, т. е.
представляет собой инвариант. Отсюда заключаем, что
величины
ведут себя при преобразованиях координат как кова-
ковариактные компоненты некоторого вектора. Этот век-
вектор называется 4-градиентом функции <р.
Если мы захотим ввести 4-оператор градиента
(оператор V*), то его ковариантные компоненты нуж-
нужно определить следующим образом:
16*

468 ПРИЛОЖЕНИЯ
ИЛИ
<хи-43>
где V — оператор градиента в трехмерном евклидовом
пространстве. Тогда контравариантные компоненты
оператора V* будут иметь вид
v* _ JL. и*1 <L_ у*2 — <L-
V~"<°- - ,**•, - *'• (ХЧ.44)
W*3 i_
что можно представить следующим образом:
-V). (XII.45)
Теперь мы имеем возможность пояснить существо
различия между коктравариантными и ковариантны-
ми векторами. В соответствии с (XII. 8) производная
хф по xv равна а%:
^ (XII. 46)
Подставив эти значения а^ в (XI!.8), приведем
мулу преобразования контравариантных компонент
4 вектора к виду
дхч
Рассматривая некоторую скалярную функцию
как сложную фунвдию вида
Ф==Ф [*•(** х". ^'2, х'3), х« (Л х'\ х'\ х'3), ...]
можно написать, что
дх'\>- Z^ dxv дхФ '
Согласно (XII. 41) dyfdxf* есть jx-я ковариантиая со-
составляющая градиента ф, вычисленная в системе К9
(обозначим ее (^*ф)^), adф/дxv~v-я ковариантная со-
составляющая ?*ф8 вычисленная в системе К (обозна-

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 469
чим ее (V*cp)v). Следовательно, можно написать
з
1.48)
Сопоставление преобразований (XII. 47) и (XII. 48)
показывает, что они не тождественны. В одном из них
роль коэффициентов играют величины dxf^/dxv, в дру-
другом — величины dxv/dxf№.
Итак, контравариантными называются такие век-
векторы, компоненты которых преобразуются по закону
(XII. 47), т. е. как компоненты векторов х^ или dx&
(как дифференциалы координат). Ковариаитнылш же
называются векторы, компоненты которых преобра-
преобразуются по закону (XII. 43), т. е. как компоненты гра-
градиента (как .частные производные по координатам).
Выше мы видели, что если задан контравариант-
ный вектор а&% то всегда можно ввести по правилу
(XII. 29) соответствующий ему ковариантиый 'вектор
(и наоборот). Поскольку между величинами а& и а№
существует тесная связь, мы будем говорить о них Ее
как о компонентах двух разных векторов, а как о кон-
травариантных и ковариантных компонентах одного
и того же вектора.
В случае евклидовой метрики коэффициенты об-
обратного преобразования й% связаны с коэффициентами
прямого преобразования aij соотношением fig = aj[.
Следовательно, прямое и обратное преобразования ко-
координат имеют вид
откуда
dxv
dxv а*'1*
Таким образом, в случае, когда пространство обладает
евклидовой метрикой, коэффициенты преобразований
(XII. 47) и (XII. 48) совпадают и различие между
контравариантными и кооариантными векторами (а
также и тензорами) исчезает.
Преобразование &©в&риантных компонент. При пе-
переходе от системы К к системе К' ковариантные ком-
компоненты векторов, очевидно, преобразуются, как и

470 ПРИЛОЖЕНИЯ
контравариантные компоненты, по линейному закону.
Обозначив коэффициенты преобразования ковариант-
ных компонент символом й , можно написать
Z . 49)
Найдем связь между коэффициентами преобразо-
преобразований комтравариантных и ковариантных компонент,
т. е. между величинами а? и й^. Поднятие либо опус-
опускание индекса %i (или v) при компоненте вектора со-
сопровождается умножением этой компоненты на g^
(или gw). Поэтому выражение (XII. 49) можно пре-
преобразовать следующим образом:
a'4u = v|0№w)«v- (XH. 50)
Вместе с тем для контравариантных компонент имеет
место соотношение
Умножив его левую и правз'ю части на g^, получим
Сопоставление формул (XII. 50) и (XII. 51) дает
*&„ = <Зт- (XII. 52)
Приняв во внимание (XII. 4), легко получить
6o = aof й° = -с4, a? = -a«, a* = ai (/, й=1, 2, 3).
(XII. 53)
Сравнение соотношений (XII. 15) и (XII. 52) позво-
позволяет написать
S^a-, (XII. 54)
где 3* — коэффициенты обратного преобразования
контравариантных компонент.
Выше мы видели, что и&^дх^/дх* (см. (XII.46)).
Очевидно, что

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 471
Подставив это выражение в (XII. 54), получим коэф-
коэффициенты прямого преобразования ковариантных ком-
компонент
что согласуется с (XII. 48).
Четырехмерные тензоры, 4-тензором второго ранга
называется совокупность 16 величин Т»у, которые при
переходе от одной системы координат к другой преоб-
преобразуются по формуле
? #, (XII. 55)
р, а «О
где ag — коэффициенты из (XII. 21) (ср. с (X. 10)).
При обратном преобразовании
(XII. 58)
р, tf=0
Частным случаем 4-тензора является тензор с ком-
компонентами:
iF^aV, (XII. 57)
где а& и bv — компоненты 4-вёкторов.
Компоненты 4-тензора могут быть представлены
в трех видах: как контравариантные Т»у, ковариант-
ные Грд, и смешанные r*V По аналогии с (XII. 57)
поднятие или опускание временного индекса не изме-
изменяет знака компоненты, а поднимание или опускание
пространственного индекса изменяет знак компонен-
компоненты на обратный (ср. с (XII. 29)). Поднятие или опус-
опускание четного числа пространственных индексов, оче-
очевидно, оставляет компоненту без изменений. Таким
образом,
-Г»
y =7^ =-Г11, ... (XII.58)
Формулы преобразования ковариантных компонент
тензора (XII. 57) можно получить, приняв во внима-

472 ПРИЛОЖЕНИЯ
ние (XII. 49):
Аналогично
J^-jEW*' (XII. 59)
где коэффициенты а* определяются правилами
(XII. 53).
Таким же способом можно установить формулу
^. (XII. 60)
Из (XII. 58) видно, что, вообще говоря, нужно раз-
различать смешанные компоненты Т*\ и Т?*, т. е. следить
за тем, какой индекс — первый или второй — стоит
вверху, а какой внизу. Действительно, например, в об-
общем случае 'Л© = У10 Ф Г01 — Го1. В случае симмет-
симметричных тензоров S**v (для которых S^V=^SV^) сме-
смешанные компоненты S*\ и Sv*\ очевидно, совпадают,
так что индексы можно располагать один над другим.
В случае антисимметричных тензоров имеет место со-
соотношение Л^у ™ —А?*1.
У антисимметричного 4-тензора независимыми яв-
являются 6 компонент D диагональных равны нулю,
остальные удовлетворяют условию Ар* — —Av**). Сле-
Следовательно, таблица компонент антисимметричного
4~текзора выглядит следующим образом:
0 А01 Л02 Л03
jl _i» о" л- (ХН.61)
Лс3 -Л13 -Л23 0
Найдем формулы преобразования компонент тен-
тензора (XII. 61). Согласно (XII. 55) для компоненты Л01
имеем
А'01 = ? %?* 141 А
3Ч

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 473
Коэффициенты а° и а!}— нули (см. (XII.21)), поэто-
поэтому последние две суммы будут нулями. Из четырех
коэффициентов aj отличны от нуля только два: aj и
а{. Следовательно, в первых двух суммах отличны
от нуля только первые два слагаемых. Таким образом,
JP - «SCaU00 + aU01) + a? Цаю + «U'1).
Приняв во внимание, что Л°°=ЛИ = О, Л10 == —Лм,
и подставив о&о вместо ag и а}, а также а{ вместо а*
н *§, придем к формуле
(см. соотношение (XII. 22)). Аналогично могут быть
получены формулы преобразования для остальных
компонент тензора Ар*.
Формулы преобразования всех шести независимых
компонент выглядят следующим образом:
(XII. 62)
Отметим, что формулы обратного преобразования
отличаются от формул (XII. 62) лишь знаком при чле-
членах, содержащих множитель а% (см. (XII. 23)).
Формулы (XII. 62) понадобятся нам в электроди-
электродинамике.
Образуем из компонент тензора П^ — a^6v выра-
выражение
Это выражение представляет собой инвариант, т. е.
скаляр. Аналогично для любого тензора 7&v выра-
выражение
2 Т\ = Г°о + Т\ + Т\ + Т\ (XII. 83)
является скаляром (ср. с (Х.21)). Его называют сле-
следом тензора. Из (XIL 33) следует, что Е ПРц = Е П/-
Аналогично
Е^-ЕГЛ (XII. 04)

474 ПРИЛОЖЕНИЯ
Скалярным произведением 4-вектсра av на 4-тен-
зор Tw называется 4-век?эр 6>\ компоненты которого
определяются по формуле
У-XV. (XII. 65)
Инвариантные 4-тензеры. Тензор, который при ум-
умножении на вектор оставляет этот вектор без измене-
изменений, естественно назвать единичным. Очевидно, что
компоненты этого тензора следует принять равными
1, если n = v,
' • ' (XII. 66)
О, если [i Ф v. v '
(
Действительно, подстановка этих значений в формулу
(XII. 65) дает
как и должно быть для единичного тензора.
Из (XII. 66) следует, что б* = б?, т. е. что тензор
6v симметричный. Поэтому индексы мы расположили
один над другим. След тензора 6$ равен
Z 6U = 4.
Контравариантные и коварнантные компоненты
единичного тензора принято обозначать символами gv*
и g&v. Видно, что
(i 0 0 0\
2 "J -? Si
О 0 0-1/
Сравнение с (XII. 4) показывает, что тензор
(равно как и gy,y) есть метрический тензор.
Образуем выражение
Приняв во внимание (XII. 67), найдем, что при ji —0
это выражение равно а0 = aOt в при \i — i (i = 1,2,3)

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 475
получается —а1 == а/. Отсюда следует, что
Аналогично можно убедиться в том, чти
Поэтому скалярное произведение векторов а& и &v
можно записать любым из трех следующих способов:
Е А. = Z g^b- = Z g^A- (XII. 68)
Тензоры 6*J, g^, и gv» инвариантны — их компо-
компоненты одинаковы во всех системах координат. Инва-
Инвариантным является также абсолютно антисимметрич-
антисимметричный единичный 4-псевдотензор четвертого ранга s^vp<r.
Компоненты этого тензора определяются аналогично
компонентам псевдотензора 8ш в евклидовом про-
пространстве (см. (VI. 15)). При совпадении хотя бы двух
индексов e^vpor равен нулю. Следовательно, из 44 =
=256 компонент отличны от нуля только 4! = 24 ком-
компоненты. Полагают
еош = +1. (XII. 69)
Остальные 23 компоненты полагают равными +1 либо
— 1 в зависимости от того, каким числом перестано-
перестановок двух индексов — четным или нечетным — последо-
последовательность .и, v, р, а может быть получена из после-
последовательности 0, 1, 2, 3. Очевидно, что 12 компонент
имеют значение +1, а 12 — значение —L
По принятому нами выше правилу опускание всех
индексов у е*У1Ю должно изменить знак компоненты.
Поэтому ео12з = —1. Аналогично 8^00 = —е^р0 (из
четырех индексов один обязательно имеет значение 0,
остальные три —значения I, 2, 3). Отсюда следует,
что
Z в^е%^0 = -24. (XII. 70)
JA. v, p. a
Теорема Остроградского — Гаусса. В евклидовом
пространстве теорема Остроградского — Гаусса фор-

476 ПРИЛОЖЕНИЯ
мулируется следующим образом (см. (XI. 13)):
(интеграл по некоторому объему V от дивергенции
вектора а равен потоку этого вектора через ограничи-
ограничивающую V поверхность f). Величины dfi суть компо-
компоненты вектора df=ndf. Они имеют значения d/* =
== dydz7 dfy = dzdxf dfz — dxdy.
Обобщением теоремы Остроградского — Гаусса на
псевдоевклидово 4-пространетво является соотношение
<XIL72>
где аР — 4-вектор, dУ* = dx°dxldx2dx3 = cdt dV — эле-
элемент объема в 4-пространстве, df&— компонента 4-век-
fopa элемента гиперповерхности, ограничивающей
4-объем, по которому берется интеграл в левой части
формулы. Компоненты df* имеют значения df° =
= dxldx2dx? = dV, dfl=dx°dx2dx? = cdtdydz и т. д.
Докажем с помощью теоремы Остроградского —
Гаусса соотношение, которое нам понадобится в § 40.
Чтобы сделать доказательство более наглядным, про-
проведем его сначала для евклидова трехмерного про-
пространства, а затем выполним аналогичные выкладки
для 4-пространства.
Пусть имеется вектор at, дивергенция которого
равна нулю,
Ё
Полагаем, что вектор at отличен от нуля в ограничен-
ограниченной области пространства. Согласно (XII. 71)
Уравнение (XII. 73) справедливо для произвольно
взятого объема V и ограничивающей его поверхно-
поверхности f. Выберем в качестве V объем, заключенный
между двумя бесконечными плоскостями дгЕ = x|i) =

XII. ТЕНЗОРЫ В ПСЕВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 477
= const и хх = xf> = const (рис. XII. 1, а). Интеграл
по боковой поверхности этого объема равен нулю, так
как по условию на бесконечности а% = 0. Следова-
Следовательно, правую часть формулы (XII. 73) можно пред-
представить в виде
\ ах dfx — \ ах dfx = О
A) B)
(для плоскости хх = const компоненты rf/2 и dfz равны
нулю). Отсюда
\ ах dfx = \ ах dfx = const.
A) B)
Полученный нами результат означает, что инте-
интеграл V ах dfx, взятый по любой бесконечной плоско-
плоскости Х\ = const, имеет одинаковое значение. Заметим,
Рис. XII. 1
что координаты х2 и х$ при интегрировании прини-
принимают все значения от —оо до «f °°-
Теперь возьмем в качестве V объем, ограниченный
двумя поверхностями произвольной формы, для всех
точек которых координата хх конечна, координаты же
х2 и xz принимают значения от —оо до +оо. Таким
образом, края поверхностей лежат на бесконечности
(рис. XII. 1,6). В этом случае правая часть формулы
(XII. 73) может быть представлена в виде
U

478 приложения
откуда вытекает, что
(XII. 74)
т. е. имеет одинаковое значение лля любой поверхно-
поверхности, .включающей в себя все двухмерное пространство
х%хъ (пространство уг).
Теперь допустим, что имеется тензор Tikf удовлет-
удовлетворяющий условию
3 от
-^™^° (/-1,2,3). (XII. 76)
Компоненты Тм отличны от нуля в ограниченной об-
области пространства.
Образуем вектор а с компонентами
ak^%Tikbif (XII. 76)
где bt — компоненты произвольного постоянного век-
вектора F/ = const). Дивергенция вектора а будет ну-
нулем. Действительно»
Следовательно, вектор (XII. 78) удовлетворяет усло-
условиям, при которых выполняется соотношение (XII. 74).
Подстановка в (XII. 74) значений (XII. 76) дает
const <XIL 77>
(интегрирование производится по поверхности, вклю-
включающей в себя все двухмерное пространство )
Введя обозначение
соотношение (XIL77) можно записать в виде
И bipi = const.

XII. ТЕНЗОРЫ В ПСВВДОЕВКЛИДОВОМ ПРОСТРАНСТВЕ 479
В связи с постоянством и произвольностью величин hi
последнее соотношение может выполняться лишь при
условии, что все pi также постоянны.
Таким образом, мы пришли к следующему утверж-
утверждению: если тензор Ft& удовлетворяет условию
,(ХП. 75) и компоненты его отличны от нуля в ограни-
ограниченной области пространства, то значения компонент
вектора pi не зависят от того, по какой из поверхно-
поверхностей, включающих в себя все двухмерное простран-
пространство х%Къ, осуществляется интегрирование в формуле
1,(ХИ.78).
Теперь проведем аналогичные рассуждения для
4-пространства. Пусть имеется вектор av, 4-диверген-
ция которого равна нулю;
(XII. 79)
(av отличны от нуля в ограниченной области 4-про-
4-пространства). Согласно (XII. 72)
Это уравнение справедливо жля любой замкнутой ги-
гиперповерхности; интегрирование левой части произво-
производится по 4-объему, ограниченному этой гиперповерх-
гиперповерхностью. Выберем в качестве такого объема часть
4-пространства, заключенную между двумя бесконеч-
бесконечными гиперплоскостями л!° = x®t) = const и ^° = х®2) =
= const. Координаты х\ х9\ хг для точек таких гипер-
гиперплоскостей изменяются в пределах от — оо до +оо.
Следовательно, каждая из гиперплоскостей представ-
представляет собой все трехмерное пространство, взятое в мо-
момент tx = •??!)/? в случае первой плоскости, и в момент
t2 = х^/с в случае второй плоскости.
Для выбранного 4-объема правую часть соотноше-
соотношения (XII. 80) можно представить в виде
(О <2)

480 ПРИЛОЖЕНИЯ
(поскольку dx° = 0, все dp = 0). Отсюда
/о = const (XIL81)
\cPdf0
2§то означает, что значение интеграла (XII. 81) не за-
зависит от того, по какой из гиперплоскостей х° = const
осуществляется интегрирование.
Теперь возьмем 4-объем, ограниченный двумя ги-
гиперповерхностями произвольной формы, для всех то-
точек которых координата яа конечна, а координаты х1,
х29 ж3 принимают значения от —оо до +°°- Такие ги-
гиперповерхности включают в себя все трехмерное про-
пространство. Написав для такого объема правую часть
соотношения (XIL8G), получим
CD v B)
Отсюда следует, что интеграл
т. е. не зависит от того, по какой из гиперповерхно-
гиперповерхностей, охватывающих все трехмерное пространство, он
берется. Иными словами, этот интеграл не изменяется
со временем, его значение сохраняется.
Возьмем в качестве а? 4-вектор с компонентами
а = 2j i ^ц,> (XII.оЗ)
где by.— компоненты произвольного постоянного 4-век-
тора (d|i = const), а Т&» — 4-тензор, удовлетворяющий
условию
~~ """* (|i«09 1929 3). (XII. 84)
Компоненты этого тензора предполагаются отличными
от нуля б ограниченной области 4-пространства. Легко
убедиться в том, что вектор (XII. 83) удовлетворяет
условию (XII. 79) о Следовательно, для него должно
вшюлняться соотношение (XII. 82). Подстановка в

XIII. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА 481
(XII. 82) значений (XII. 83) дает
^ = const
p. v
(интегрирование производится по произвольной гипер-
гиперповерхности, включающей в себя все трехмерное про-
пространство).
Если ввести обозначение
<хп-85>
полученное нами соотношение можно представить
в виде
2 = const.
Вследствие произвольности и постоянства величин Ь^
последнее условие может выполняться только в том
случае, если постоянными (т. е. не зависящими от
времени) будут все р**. Таким образом, мы приходим
к следующему выводу. Если имеется тензор T^v9 ком-
компоненты которого отличны от нуля только в ограни-
ограниченной области 4-пространства и удовлетворяют усло-
условию (XII. 84), то компоненты 4-вектора (XII. 85) со-
сохраняются, т. е. не изменяют своего значения со
временем. Очевидно, что будет сохраняться также
4-вектор с компонентами
\ ]?vd/v, (XII. 86)
где а — произвольная константа.
XIП. Дельта-функция Дирака
Дельта-функцией Дирака (б-фуккцией) называется
функция, определяемая следующим образом: 6(дг)~О
при всех х, отличных от нуля; при х = 0 функция 6(х)
обращается в бесконечность, причем так, что
J 6(x)dx = l. (XIIIЛ)

482 ПРИЛОЖЕНИЯ
Дельта-функция оказывается полезной в силу сле-
следующего свойства:
f(xN(x)dx=*f@), (XIII. 2)
где f(x)-~ произвольная непрерывная функция от х.
Это свойство вытекает из определения б-функции.
Действительно, вследствие того, что б(*) = 0 при всех
хФО, отличный от нуля вклад в интеграл (ХШ. 2)
вносит лишь окрестность точки х = 0. В этой окрест-
окрестности f(x) можно положить равной /@). Вынеся f@)
за знак интеграла и приняв во внимание (XIII. I)» при
демк (XIII. 2).
Очевидно, что функция 8(х — а) обладает в окрест-
окрестности точки * = а теми же свойствами, что и функция
6(х) в окрестности точки х = 0. В частности,
f(xM(x-a)dx = f(a). <ХШ.З)
Область интегрирования в формулах (ХШ. 2) и
(ХШ. 3) не обязательно должна простираться от —оо
до +°°> достаточно, чтобы эта область включала в
себя особую точку, в которой б-функция отлична от
нуля.
Подобно тому как мы ввели 8(х), определяется
трехмерная б-функция, обозначаемая б (г). Она равна
нулю всюду, кроме начала координат. В начале коор-
координат б (г) обращается в бесконечность таким обра-
образом, что
J = 1. (ХШ.4)
Интегрирование производится по всему трехмерному
пространству.
Трехмерную б-функцию можно представить как
произведение трех одномерных функций:
б (г) — 6(х) б (у) 6 (г). (ХШ.5)
Из определения функции б (г) следует, что

XIV. РЯД И ИНТЕГРАЛ ФУРЬЕ 483
Область интегрирования в формуле (XIII. 6) не обя-
обязательно должна охватывать все трехмерное про-
пространство, достаточно, чтобы эта область включала
в себя точку, определяемую вектором г0.
XIV. Ряд и интеграл Фурье
Функцию, удовлетворяющую условию
f(t + Т) -/(О, (XIV. 1)
где Г— константа, называют периодической1). Вели-
Величина Г именуется периодом функции. Простейшим
примером периодической функции является гармони-
гармоническая функция f(t)= a cos ((at + а), где ш = 2я/Г—
круговая частота функции.
Подавляющее большинство периодических функ-
функций, встречающихся в физических задачах, можно
представить в виде ряда
/ @ = Е (ап cos rwHf + Ьл sin mV)- (XIV. 2)
о
Для краткости записи применено обозначение
щ = 2п/Т (Г — период функции). (XIV. 3)
Ряд (XIV. 2) называется рядом Фурье. Постоян-
Постоянные величины ап и Ьп называются коэффициентами
Фурье. Условия, которым должна удовлетворять
функция для того,, чтобы ее значения совпадали со
значениями ряда (XIV. 2), мы обсуждать не станем,
отослав интересующихся этим вопросом к руковод-
руководствам по математическому анализу.
Непериодическую функцию также можно предста-
представить в виде ряда Фурье. Однако такое представление
будет пригодно для непериодической функции лишь
на отрезке от — Г/2 до +Г/2.
Выражение (XIV. 2) представляет собой разложе-
разложение функции f(t) в ряд по функциям
1, cos ©Л sin<oo*, •••» соз/иц/, sinmoo*, ... (XIV. 4)
Система функций (XIV. 4) является ортогональной на
отрезке —Г/2, +Г/2. Это означает, что интеграл по
f) Имея в виду приложения, мы обозначили независимую
переменную буквой tt а не х.

484 приложения
этому отрезку от произведения двух различных функ-
функций системы равен нулю, а аналогичный интеграл от
квадрата любой функции отличен от нуля. Кратко
свойство ортогональности можно записать в виде
+Г/2
\
/
\
-*1
Здесь -фл и *фт — любые функции, принадлежащие си-
системе (XIV. 4). Легко убедиться в том, что qQ = Г,
<7„ = Г/2 (пфО). Для этого достаточно учесть, что
средние значения квадрата косинуса и квадрата си-
синуса равны 1/2.
Ортогональность системы функций (XIV. 4) позво-
позволяет найти значения коэффициентов Фурье. Умножим
соотношение (XIV.2) на функцию cosmos* (тФО)
и затем проинтегрируем на отрезке [—Г/2, -+-Г/2].
В силу ортогональности из всех интегралов в правой
части будет отличен от нуля только один, а именно
+ЗГ/2
-Г/2
+ 772
Поэтому мы придем к формуле \ f (t) cos тщ( dt«
= am-T/2, откуда
+Г/2
am = Y | f(t)cosmvrfdt (тФО). (XIV.5)
-Г/2
Аналогичные выкладки приводят к выражениям для
Ьт и а0:
+Г/2
= -Т \ f(t)sinm®Gtdi (тфО), (XIV.6)
+Г/2
fifidt, do=-O. (XIV.7)
-Г/2

XIV. РЯД И ИНТЕГРАЛ ФУРЬЕ 485
Ряд Фурье можно записать в комплексной форме.
Для этого заменим косинус и синус через экспоненты:
cos пщ[ = ехр (im»0° +
ехр (г/мир*) — ехр (—
Тогда выражение, стоящее под знаком суммы в фор-
формуле (XIV. 2), примет вид
ехр (tettoQ + ехр (— imM) ,
~* 2 ' '
j, • ехр (Intopt) — ехр (—
(XIV. 8)
Вместо коэффициентов а0, ап и 6/г мы ввели коэффи-
коэффициенты
(XIV. 9)
Заметим, что
С_п = С-п (XIV. 10)
(звездочка обозначает комплексно сопряженную вели-
величину).
Произведя в (XIV. 2) замену (XIV. 8), получим
f @ - Z Сл ехр (- Ш(М). (XIV. 11)
Р1
Выражение (XIV. 11) представляет собой разложе-
разложение функции f(t) в ряд по функциям
1, exp(d= to^)9 ехр(± /2сМ), ... (XIV. 12)
Система функций (XIV. 12) также является ортого-
ортогональной на отрезке [—Г/2, + Г/2]. В случае комп-
+772
.лексных функций это означает, что i ЪяФт&*=а
-Г/2
tssbnmqn ((/пфоу Действительно, легко убедиться

486 ПРИЛОЖЕНИЯ
В ТОМ, ЧТО
+Г/2*
\ ехр (/ (п — т) щг) dt = 6ят7\ (XIV, 13)
-Г/2
Ортогональность системы функций (XIV. 12) по-
позволяет найти значения коэффициентов Сп. Умножим
соотношение (XIV. И) на exp(i/na>of) и затем проин-
проинтегрируем на отрезке [—Г/2, -j-T/2}. В силу ортого-
ортогональности из всех интегралов в правой части будет
отличен от нуля только один, а именно
+ 772
\ Стехр (—i(m — m) ©00 dt = CmT.
-Г/2
+ Т/2
Поэтому мы придем к формуле V f (t)exp{im®dt)dt =
-Г/2
— CfnT, откуда
+ Г/2
^/n = у у f @exp {ьгпщг) dt. (XIV. 14)
-Г/2
Формула для C_m получается из (XIV. 14) заменой m
на —т. Значение коэффициента Со также можно
найти по формуле (XIV. 14), положив в ней т = 0.
Хотя все слагаемые в (XIV. 11) (кроме Со) комп-
комплексные, сама сумма в силу свойства (XIV. 10) яв-
является вещественной. Чтобы убедиться ш этом, напи-
напишем (XIV. 11) в виде
f (t) = Со + % (Сп ехр (- шщг) + С_пexp (ina^)) =
= Со + I {Cttexp (- itmdt) + (С.
(мы использовали соотношение (XIV. 10)). Но сумма
некоторой величины и ее комплексно сопряженной все-
всегда является вещественной величиной. Таким обра-
образом, вещественность суммы (XIV. 11) доказана.
Всякая вещественная величина равна своей комп-
комплексно сопряженной. Поэтому выражение (XIV. 11)

XIV. РЯД И ИНТЕГРАЛ ФУРЬЕ 487
можно видоизменить следующим образом:
+ ОО -f ОО
f (О = 2 С\ ехР (|#/мво0 ~ S С_п ехр (таHА.
fjtm—ОО П«ав—ОО
(XIV. 15)
Полученное выражение отличается от (XIV. 11) лишь
тем, что в нем слагаемые поставлены в обратной по-
последовательности. Если в (XIV. 9) поменять местами
обозначения Сп и С-п> то формула (XIV. 11) приняла
бы вид
f @ = п?ж Сп ехр (тшоО. (XIV. 16)
Одновременно формула (XIV. 14) изменилась бы сле-
следующим образом:
+ Г/2
Cn=^-jr \ f @ехР("~ ifWHf) dt. (XIV. 17)
-f/2
Очевидно, что формулы (XIV. 16) и (XIV. 17) эквива-
эквивалентны формулам (XIV. И) и (XIV. 14). В курсах ма-
тейатики обычно пишут ряд Фурье в виде (XIV. 16)
и соответственно формулу для коэффициентов в виде
(XIV. 17). В физике предпочтительнее формулы
(XIV. 11) и (XIV. 14).
Ряд (XIV. И) представляет периодическую функ-
функцию на бесконечном интервале (—оо, -f-°°)> либо не-
непериодическую функцию на ограниченном промежутке
[—Г/2, +Т/2]. Непериодическая функция может быть
представлена на бесконечном интервале с помощью
интеграла Фурье.
Введем обозначения
2ш/Т = пщ == шл, 2п/Т = со0 = А©. (XIV. 18)
Перепишем выражение (XIV. 14) с учетом этих обо-
обозначений. Кроме того, обозначим переменную интегри-
интегрирования вместо t буквой ?. Тогда
+Г/2
С„ 535 -— 1
JbSt 1
-Г/2

ПРИЛОЖЕНИЯ
(в соответствии с (XIV. 18) мы заменили 1/Г на
Дю/2я;). Подставим это выражение в (XIV. 11):
?Г Е «р(-* )
п«-со -Г/2
(XIV.19)
Теперь устремим Г к бесконечности. Согласно
(XIV. 18) Аш будет стремиться к нулю, так что сово-
совокупность дискретных значений ш« превратится в сово-
совокупность значений непрерывно изменяющейся пере-
переменной ш. Соответственно сумма по п превратится в
интеграл. В итоге формула (XIV. 19) примет вид
+ ОО -f СО
(XIV. 20)
Полученное нами выражение и есть интеграл Фурье.
Если ввести обозначение
/<&)exp(fo?)<ft, (XIV. 21)
интеграл Фурье запишется следующим образом1):
f(t) *=-!=. J ф(о)ехр(—йвО^ои. (XIV. 22)
Так же как и в случае ряда Фурье, в курсах мате-
математики формула (XIV. 22) пишется обычно со знаком
плюс в показателе степени. Соответственно в фор-
формуле (XIV. 21) в показателе степени пишут знак
минус.
Если две функции ф и f связаны выражением вида
ь
<p(x)=\f(t)K(x,t)dt, (XIV. 23)
*) Встречается также несимметричная запись интеграла
Фурье, а именно, формулы (XIV. 21) и (XIV. 22) пишутся в виде
+ 0© +00
= J f(t)axp(tog)<fg. /<0—5Г

XIV. РЯД И ИНТЕГРАЛ ФУРЬЕ 489
то функция ф(х) называется интегральным преобра-
преобразованием функции f(t), а функция К(х, t)—ядром ин-
интегрального преобразования.
Из сравнения формул (XIV. 21) и (XIV. 23) сле-
следует, что определяемая выражением (XIV. 21) функ-
функция ф(ю) представляет собой интегральное преобра-
преобразование функции f(?), причем ядро преобразования
имеет вид
Поэтому функцию ф(©) называют преобразованием
Фурье функции f(|). Определяемую выражением
(XIV. 22) функцию f(t) называют обратным преобра-
преобразованием Фурье. Отметим, что прямое (формула
|(XIV.21) и обратное (формула (XIV.22)) преобра-
преобразования Фурье отличаются только знаком при пока-
показателе экспоненты.
Функцию f(l) в выражении (XIV. 21) называют
также фурье-образом функции q>(<o).

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Алгебраическое дополнение эле-
элемента определителя 393
Амплитуда комплексная 71
Апекс 128
Апериодический процесс 74
Апериодическое затухание 74
Вариация функционала 348
Вектор в пространстве п изме-
измерений 378
— заряда — тока 249
— ковариантный 465, 469
— контравариантный 465, 469
— Пойнтинга 240, 243, 292
— четырехмерный 465
Виртуальное перемещение 344
Волновая зона 332
Волновое число комплексное
301
Волновой вектор четырехмер-
четырехмерный 295
Волчок асимметричный 103
— симметричный 103, 121, 125
свободный 120, 123
— шаровой 103
Восприимчивость диэлектриче-
диэлектрическая 193
— магнитная 223
Время запаздывания системы
327
собственное 327
Гамильтониан 131, 139
Гипербола 357
Главные оси инерции 102
Градиент 430
— четырехмерный 467
Движение инфинитное 48
— финитное 48
Действие 33, 136, 138
— для электромагнитного поля
271, 272
— укороченное 139
Дельта-функция Дирака 481
Детерминант 392
Дивергенция 433, 436
—t выражение в сферических
координатах 456
Дипольный момент системы
электрических зарядов 183
Дискриминант квадратичной
формы 403
Дисснпативная функция Рэлея
16
Диссипация энергии 72
Дифференциальное эффектив-
эффективное сечение рассеяния 58
Дифференциальный эффектив-
эффективный поперечник рассеяния 58
Задача Ковалевской 126
— Лагранжа 126
— Эйлера 126
Закон Био — Савара 212
— сохранения импульса 39
момента импульса 41
энергии 37
Заряды свободные 188
— связанные 188
Излучение дипольное 334, 341
— квадрупольное 339, 341
— магнитно-дипольное 338
Импульс обобщенный 23, 138,
282, 284
— релятивистский 158
— четырехмерный 158, 159
Инвариантность градиентная
— калибровочная 233
— уравнений 141
Инварианты поля 258
Индекс немой 13, 19
Индукция магнитная 200, 220
— электрическая 193
Интеграл движения 25, 37, 43
-— Фурье 488
Интервал 144

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
491
Интервал времениподобный
146
— пространственноподобный
146
Калибровка кулоновская 236
— лоренцева 234
— поперечная 236
— потенциалов 233
Канонические переменные 130,
135
Квадратичная форма 402
каноническая 404
Квадруполь 185
Квадрупольный момент систе-
системы зарядов 187
Квант действия 34
Колебания вынужденные 76
— гармонические 70, 71
— затухающие 71
— малые 69
— нормальные 84
— свободные 69
— системы со многими степе-
степенями свободы 79
Компоненты вектора 373
— тензора 415
— четырехмерного тензора ко-
вариантные 471
контравариаитные 471
— смешанные 471
Конические сечения 45, 356
Коэффициент затухания волны
305
— связи 89
Коэффициента Ламе 4СЗ
КриволипсйЕие координаты 451
ортогональные 452
Линейное дифференциальное
уравнение 361
, общее решение 361
Линия узлов 95
Л-система отсчета 52
Магнитный момент 217, 220
Масса приведенная 49
Матрица 382
— диагольнальная 386
— единичная 386
— квадратичной формы 403
— кососимметричная 385
— обратная 383
—,ранг 400
— симметричная 385
Матрица транспонированная
383
Матрицы коммутирующие 388
Маятник математический 29
Маятники связанные 85
Мгновенная ось вращения 94
Механическая система 7
Мировая линия 144
— точка 144
Моменты инерции главные 102
осевые 101
— — центробежные 102
Монополь 183
Монополи Дирака 200
Мультиполь нулевого порядка
183
— первого порядка 183
Намагниченность 220
Напряженность магнитного по-
поля 222
— электрического поля 177
Нутация 97; 128
Обобщенная координата 8, 17,
138
— скорость 8, 17
Обобщенные координаты глав-
главные 84
нормальные 84
— — циклические 43
Октуполь 187
Оператор Гамильтона 432
четырехмерный 248
— Даламбера 248, 2Ь5
— Лапласа 444
б сферкчесхчх координа-
координатах 458
— набла 432
, интегральнее определе-
определение 450
Определитель 392
—, входящей в состав матрицы
400
—, порядок 392
— транспонированный 394
Орты координатных осей 38
Парабола 358
Плотность импульса электро-
электромагнитного поля 243
— потока имульса 240
— связанных зарядов объем-
объемная 191
поверхностная 192

492
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Показатель преломления ком-
комплексный 305
Поляризованность 189
Постоянная Планка 34
Потенциал векторный магнит-
магнитного поля 201
— обобщенный 15
— поля диполя 184
— механической системы 13, 28
— четырехмерный 250
— электрического поля 178
Потенциалы запаздывающие
313
— Лиенара — Вихерта 321
Поток импульса 240, 292
Преобразование Фурье 489
Преобразования Галилея 142
— Лоренца 148, 150
Прецессия 97
— псевдорегулярная 129
— регулярная 97, 122, 128
Принцип вариационный 34
— Гамильтона 33, 34
— наименьшего действия 9, 33,
130
— относительности Галилея
142
Эйнштейна 141, 143
— постоянства скорости света
141
Прицельное расстояние 57
Прицельный параметр 57
Произведение аекторов вектор-
векторное 365, 373
скалярное 365, 372
смешанное 365
— двойное векторное 367
— тензоров внешнее 418
- внутреннее 418
— — скалярное 418
Проницаемость диэлектриче-
диэлектрическая 194
комплексная 303
— магнитная 223
Пространство конфигурацион-
конфигурационное 17, 34
— псевдоевклидово 459
Псевдовектор 375
Псевдоскаляр 376
Псевдотензор 422
Рассеяние частиц 52, 57
Реакции связей 8, 9, 12, 17
Ротор 437, 440
Ряд Фурье 483
Свободные оси вращения 112
Связи 8, 10
— геометрические 10
— голономные 11
— жесткие 7
— идеальные 8
— кинематические 10
— него лоном ные 1.2
— нестационарные 10
— реономные 12
— склерономные 12
— стационарные 10, 12
Сила диссипативная 16
— инерции центробежная 66
.— консервативная 14
— кориолисова 66
— Лоренца 15
— Минковского 155—157
— обобщенная 20, 22, 23
— потенциальная 14
Символ Кронекера 368
кососимметричный 369
Скаляр 417
Скобки Пуассона 134
Собственная длина 151
Собственное время 147
Соленоид 206—210
Спектральное разложение вол-
волны 306
Столкновение частиц 52
Твердое тело, 7, 11
Тензор 415
— абсолютно антисимметрич-
антисимметричный 421
симметричный 421
— антисимметричный 420, 429
—, главные значения 416, 426
— диэлектрической восприим-
восприимчивости 198
проницаемости 198
— единичный 417
— инвариантный 417
— инерции 98, 101, 106
— магнитной воспримчивости
225
проницаемости 225
— метрический 458, 474
— натяжений максвелловский
246, 279
—, приведенный к главным
осям 416
—, ранг 416
—,свертка 418
— симметричный 420, 424

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
493
Тензор след 418, 473
— четырехмерный 471
—, шпур 418
— электромагнитного поля 352
— энергии-импульса 176
электромагнитного по-
поля 276, 281
Теорема Гаусса для электриче-
электрического поля 179
— Крамера 398
— Остроградского — Гаусса
436, 476
— Стокса 441
—- Штейнера 105
— Эйлера 345
Угол нутации 97
— отдачи 55
—¦ прецессии 97
— разлета 55
— рассеяния 55
— собственного вращения 97
— чистого вращения 97
Уравнение волновое 286, 287
— Гамильтона — Якоби 136,
139, 140, 283
— Даламбера 236, 285
— Лапласа 181, 185
— непрерывности 213
— Пуассона 180, 196, 203, 224,
236, 237
— характеристическое 81, 82
Уравнения Гамильтона 130, 132
— канонические 130, 132
— Лагранжа 8, 9, 15, 179 22,
34, 1&)
— Максвелла 237
— в четырехмерной фооме
262, 263
— Ньютона 8, 9, 17
— Эйлера 118, 120, 121, 354,
356
Условие Лоренца 234
Условия на границе двух ди-
диэлектриков 196
— ¦ магнетиков 224
Фаза волны 295
Формула Резерфорда 6
Функционал 345, 346
— линейный 347
Функция Гамильтона 131, 283
— Лагранжа 8, 14, 24, 27, 35
для электромагнитного
поля 272
Фурье-образ функции 489
Циркуляция 437
Ц-система отсчета 52
Частота собственная 71
Частоты собственные системы
82
Четырехмерная скорость 153,
154
Четырехмерное ускорение 153,
154
Число степеней свободы систе-
системы 8, 12, 17
Эйлеровы углы 95
Электромагнитная волна 286
¦ немонохроматическая 306
¦ плоская 287
. _ монохроматическая
293
плоско-поляризованная
299
— —, поляризованная по кру-
кругу 299
эллиптически-поляризо-
ванная 299
Эллипс 356^
Энергия 24
— кинетическая 26, 27
— покоя 160
— полная системы 25
частицы 160
— потенциальная 13, 27, 28
— центробежная 68
— электромагнитного поля 240
Эффект Доплера 296

Учебное издание
САВЕЛЬЕВ Игорь Владимирович
основы теоретической физики
Том I
Механика. Электродинамика
Заведующий редакцией Я. А. Носсза
Редактор В. #. Дубнова
Художественный редактор Г. М. Коровина
Технический редактор Л. В. Лихачева
Корректор Я. Б. Румянцева
ИБ К* 41103
Сдано в набор 04.06.90. Подписано к печати 12.02.91. Формат
84X108/32. Бумага тип. № 2. Гарнитура литературная. Печать
высокая. Усл. печ. л. 26,04. Усл. кр.-отт. 26,04. Уч.-изд. л. 23,77.
Тираж 47 600 экз. Заказ № 553. Цена 3 р. 50 к.
Издателъско-пронзводственное и книготорговое
объединение «1^ука»
Главная редакция физико-математической литературы
117071 Москва В-71, Ленинский проспект, 15
Ленинградская типография № 2 головное предприятие ор-
ордена Трудового Красного Знамени Ленинградского объеди-
объединения «Техническая книга» им. Евгении Соколовой Госу-
Государственного комитета СССР по печати. 198052 г. Ленинград,
Л-52. Измайловский проспект, 29.