Author: Стеценко О.А.
Tags: электротехника общая радиотехника радиотехника
ISBN: 5-7339-0232-9
Year: 2000
Text
О.А. СТЕЦЕНКО
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
Часть 1
1..3
МОСКВА 2000 >
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ИНСТИТУТ
РАДИОТЕХНИКИ, ЭЛЕКТРОНИКИ И АВТОМАТИКИ
(ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ)
О.А. СТЕЦЕНКО
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
Часть 1
УЧЕБНОЕ ПОСОБИЕ
Рекомендовано Министерством образования РФ в
качестве учебного пособия для студентов
специальности ’’Радиотехника”
МОСКВА 2000
ББК 32.841
С 79
УДК 621.37
Рецензенты: д.т.н., проф. С. И. Баскаков
д.т.н., проф. В. Г. Карташов
С 79 Стеценко О. А. Радиотехнические цепи и сигналы. Ч. 1: Учебное по-
собие / Московский государственный институт радиотехники, электроники
и автоматики (технический университет) - М., 2000. - 148 с.
ISBN 5-7339-0232-9
Учебное пособие содержит материал разделов курса "Радиотехниче-
ские цепи и сигналы". Рассматриваются способы математического пред-
ставления и основные характеристики сигналов, применяемых в радиотех-
нике для передачи информации. Излагаются методы анализа прохождения
сигналов через линейные радиотехнические цепи, даегся оценка возни-
кающих при этом искажений сигналов. Обсуждаются условия неискажен-
ной передачи сигналов.
Табл. нет. Ил. 56. Библиогр.: 6 назв.
Печатается по решению редакционно-издательского совета Московско-
го государственного института радиотехники, электроники и автоматики
(технического университета).
2302020100-13
С-----------------Без объявл.
I К.8 (03) - 2000
ББК 32.841
ISBN 5-7339-0232-9
© О.А. Стеценко, 2000
ПРЕДИСЛОВИЕ
Дисциплина “Радиотехнические цепи и сигналы” (РТЦ и С)
является базовой для специальности “Радиотехника”. Она дает
студентам основной комплекс знаний, необходимых для понима-
ния принципов функционирования радиотехнических устройств
и систем. На ее материале основаны практически все последую-
щие дисциплины, входящие в типовой учебный план.
Предметом изучения в курсе РТЦ и С является теория сигна-
лов и их преобразования в радиотехнических цепях.
Изучаются следующие вопросы:
• основные характеристики и методы анализа сигналов, ис-
пользуемых в радиотехнике для передачи информации;
• основные виды преобразования сигналов, осуществляемых в
процессе передачи информации;
• способы построения и методы анализа радиотехнических
цепей, посредством которых выполняются определенные опера-
ции над сигналами.
Вопросы схемотехники не являются предметом изучения в
данном курсе.
Настоящее учебное пособие содержит материал, посвящен-
ный теории детерминированных сигналов и анализу их преобра-
зования в линейных радиотехнических цепях. В нем рассматри-
ваются основные характеристики и методы анализа детермини-
рованных сигналов. Излагаются методы анализа прохождения
детерминированных сигналов через линейные радиотехнические
цепи. Особое внимание уделяется возможным искажениям сиг-
налов при их прохождении через линейные цепи, обсуждаются
причины этих искажений.
Содержание учебного пособия отвечает соответствующим
разделам действующей типовой программы курса РТЦ и С. При
отборе и изложении материала автор руководствовался практиче-
ским опытом чтения лекций по данному курсу в МИРЗА.
-3-
1. ОБЩИЕ СВЕДЕНИЯ О
РАДИОТЕХНИЧЕСКИХ ПРОЦЕССАХ
1.1. ОСНОВНАЯ ЗАДАЧА И ПРИМЕНЕНИЕ
РАДИОТЕХНИКИ
Радиотехника представляет собой обширную область науки и
техники, решающую множество задач, главная из которых - пе-
редача информации на расстояние с помощью электромагнитных
волн (радиоволн). В общем понимании информация - это сово-
купность сведений о каких-либо событиях, явлениях или предме-
тах.
Развитие радиотехники началось с изобретения А.С. Поповым
в 1895 г. радиотелеграфии - телеграфной связи, осуществляемой
посредством электромагнитных волн. До этого телеграфная связь
осуществлялась по проводам.
В настоящее время области применения радиотехники весьма
обширны: радиосвязь, радиовещание и телевидение, радиолока-
ция, радионавигация, радиотелемеханика и др.
Радиосвязь - передача информации с помощью электромаг-
нитных волн между двумя или несколькими неподвижными или
подвижными объектами. Радиосвязь широко используется, осо-
бенно она важна для авиации, космонавтики, морского флота, где
невозможно использование других способов передачи информа-
ции.
Разновидностью радиосвязи являются радиовещание и те-
левидение - наиболее массовые средства распространения ин-
формации.
Радиолокация - обнаружение и опознавание различных объ-
ектов, определение их координат и параметров движения с по-
мощью радиотехнических средств. Такими объектами могут быть
самолеты, корабли, различные космические тела, грозовые обла-
ка и др.
Радионавигация - вождение летательных аппаратов, над-
водных и подводных кораблей и сухопутного транспорта с по-
мощью радиотехнических средств.
-4-
Радиотелемеханика - управление и измерение на расстоянии.
Управление различными объектами на расстоянии (например,
космическим кораблем) с помощью радиотехнических средств
называют радиоуправлением. Измерение на расстоянии - радио-
телеметрия. Системы радиотелеметрии применяются для контро-
ля за протеканием процессов на труднодоступных объектах (на-
пример, атмосферных радиозондах, искусственных спутниках
Земли и др.). Они нашли широкое применение и в медицине для
передачи на расстояние данных о состоянии людей, что особенно
важно в космической медицине.
Этот далеко не полный перечень применения радиотехниче-
ских методов и средств характеризует важную роль радиотех-
ники в жизни современного общества. В настоящее время трудно
указать область науки и техники, в которой не использовались бы
радиотехнические методы.
1.2. ПОНЯТИЕ СИГНАЛА
Все применения радиотехники связаны с передачей информа-
ции.
Для передачи информации необходимо представить ее в неко-
торой форме. Форму представления информации называют со-
общением. Сообщения могут быть самыми разнообразными. В
радиовещании передаются звуковые сообщения (речь, музыка), в
радиотелеграфии - текстовые сообщения (буквы, цифры, сим-
волы), в телевидении сообщением является движущееся изобра-
жение.
Для передачи и приема сообщений используются технические
устройства (передатчик, приемник, телефон, телевизор и др.).
Техническое устройство не может непосредственно воспринять
сообщение. Поэтому сообщение должно быть представлено в ви-
де физического процесса, который воспринимает данное уст-
ройство. Физический процесс, отображающий (несущий) переда-
ваемое сообщение, называют сигналом,
В качестве сигнала можно использовать любой физический
процесс, изменяющийся в соответствии с сообщением. В боль-
-5-
шинстве технических устройств носителями сообщений служат
электрические сигналы. Физической величиной, определяющей
такой сигнал, является ток или напряжение.
Преобразование сообщения в электрический сигнал осущест-
вляется с помощью специальных устройств (электрических, элек-
тромеханических, фотоэлектрических). Полученные в результате
этих преобразований сигналы принято называть первичными.
Различают два вида первичных сигналов - аналоговые и циф-
ровые.
Аналоговый.еигнал повторяет закон изменения передаваемого
сообщения (является его аналогом). Например, звуковое сообще-
ние (речь, музыка) преобразуется в аналоговый электрический
сигнал с помощью микрофона. Это означает, что электрический
ток в цепи микрофона изменяется во времени аналогично изме-
нению породившего его звукового давления перед микрофоном.
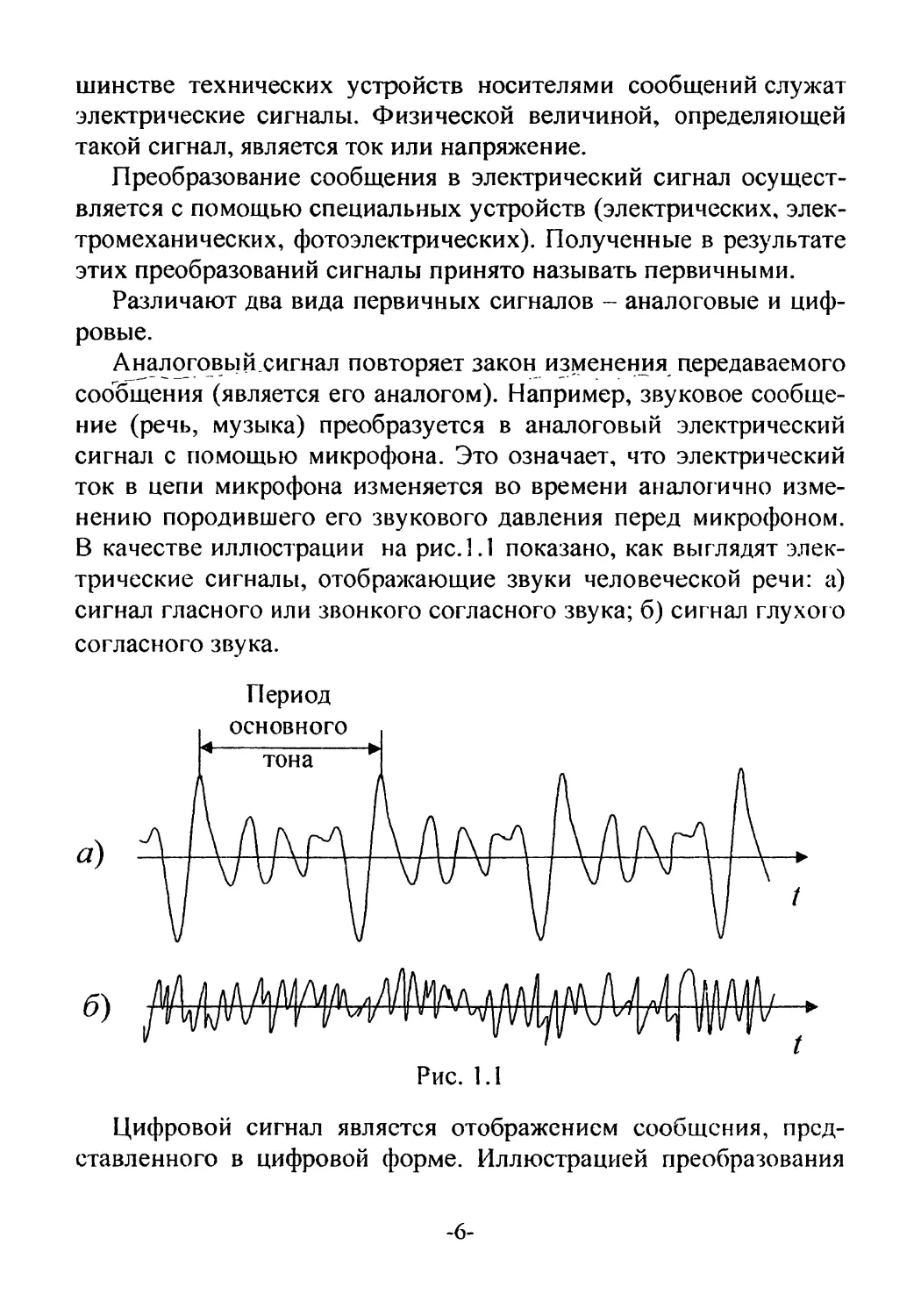
В качестве иллюстрации на рис. 1.1 показано, как выглядят элек-
трические сигналы, отображающие звуки человеческой речи: а)
сигнал гласного или звонкого согласного звука; б) сигнал глухого
согласного звука.
Период
основного
Рис. 1.1
Цифровой сигнал является отображением сообщения, пред-
ставленного в цифровой форме. Иллюстрацией преобразования
-6-
текстового сообщения в цифровой сигнал служит рис. 1.2.
Знаки Р Т С
Кодовые
комбинации
символов
1 и 0 01010 0 0 001 10100
Первичный _ г—1 гп п п
сигнал
Кодовая t
комбинация
Рис. 1.2
Видно, что сначала производится кодирование отдельных зна-
ков (букв) текстового сообщения. Кодирование заключается в за-
мене каждой буквы комбинацией из небольшого числа стан-
дартных символов. Правило, по которому..осуществляется такая
замена, называется ^одом. Наибольшее применение нашли дво-
ичные коды, символами которых являются две цифры: единица
(1) и нуль (0). Каждой букве сообщения соответствует некоторая
последовательность кодовых символов, называемая кодовой ком-
бинацией. В результате кодирования текстовое сообщение пред-
ставляется в виде последовательности единиц и нулей, т.е. в циф-
ровой форме. На рис. 1.2 использован международный теле-
графный код (МТК - 2). Далее символы кода преобразуются в
стандартные электрические сигналы. Например, наличие элек-
трического тока в цепи означает символ 1, а отсутствие тока -
символ 0. В результате получаем цифровой сигнал, вид которого
показан на рис. 1.2.
1.3. ПОНЯТИЕ РАДИОКАНАЛА
Радиоканал обеспечивает перенос информации из одной точки
пространства в другую. Основные элементы радиоканала - пере-
датчик, приемник и физическая среда, в которой распростра-
-7-
няются электромагнитные волны.
Рассмотрим в общих чертах процессы, обеспечивающие
функционирование радиоканала, на примере канала радиосвязи,
обобщенная структурная схема которого представлена на рис.1.3.
Рис. 1.3.
Источником сообщений может быть человек или какое-либо
устройство (автомат, вычислительная машина и т.д.).
Передаваемые сообщения с помощью различных преобразо-
вателей (микрофона, передающей телевизионной камеры, магни-
тофона и т.д.) преобразуются в первичные электрические сиг-
налы. Первичные сигналы, как правило, низкочастотные. Напри-
мер, звуковые колебания, воспринимаемые человеческим ухом,
лежат в полосе частот примерно от 20 Гц до 20 кГц. Эти же час-
тоты имеют электрические сигналы, отображающие речь и музы-
ку.
Низкочастотные электрические колебания не могут быть не-
посредственно использованы для возбуждения электромагнитных
волн. Так, частоте 20 кГц соответствует длина волны 15 км. А для
эффективного излучения электромагнитных волн размеры антен-
ны должны быть соизмеримы с длиной волны, что в данном слу-
чае практически неосуществимо.
Практическое применение электромагнитных волн для пере-
-8-
дачи информации оказалось возможным благодаря использова-
нию модуляции. Модуляция состоР1т_в_юменении параметров вы-
сокочастотного (несущего) колебания в соответствии с переда-
в^мым^сообщением. Иными словами, низкочастотный первич-
ный сигнал управляет параметрами высокочастотного несущего
колебания. В результате модуляции формируется модулирован-
ный сигнал. Формирование модулированного сигнала осуществ-
ляет передатчик.
Модулированный сигнал излучается передающей антенной,
т.е. создаются радиоволны. Радиоволной принято называть элек-
тромагнитную волну с частотой до 3 1012Гц, распространяю-
щуюся в пространстве без искусственных направляющих линий.
Радиоволну, несущую ту или иную информацию, называют ра-
диосигналомГ
Часть энергии распространяющихся радиоволн улавливается
приемной антенной.
Приемник - устройство, соединяемое с антенной, служащее
для приема радиосигналов и преобразования их к виду, позво-
ляющему использовать содержащуюся в них информацию. Од-
ним из основных преобразований принятого модулированного
сигнала является его демодуляция (детектирование) - операция,
обратная по отношению к модуляции. В результате на выходе
приемника возникает электрический сигнал, близкий к переда-
ваемому первичному сигналу.
В процессе передачи сигнал может быть искажен помехой,
вследствие чего принятый сигнал несколько отличается от пере-
данного сигнала. Поэтому при конструировании приемника пре-
дусматривается реализация какого-либо способа подавления по-
мех.
Получатель сообщений - человек или какое-либо устройство,
для которого предназначена передаваемая информация.
Краткое описание процессов, обеспечивающих функциониро-
вание канала радиосвязи, показывает, что в основном эти про-
цессы связаны с различными преобразованиями сигналов. В ра-
диотехнике преобразования сигналов осуществляются посредст-
вом радиотехнических цепей.
-9-
2. СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ
2.1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ
Сигнал передает сообщение во времени. Следовательно, он
всегда является функцией времени. Временные диаграммы от-
дельных сигналов приведены на рис. 1.1 и 1.2.
Исследование свойств и характеристик сигналов невозможно
без их математического описания. Математическое описание
сигнала всегда является некоторой его идеализацией, поскольку
оно отражает лишь отдельные свойства сигнала, наиболее суще-
ственные для данного исследования. Математическое описание
называют математической моделью реального сигнала. Матема-
тическая модель позволяет проводить исследование без учета фи-
зической природы сигнала, т.е. одна и та же модель пригодна для
описания тока, напряжения и т.д.
Различают детерминированные и случайные сигналы. Детер-
минированные сигналы описываются заданной функцией време-
ни, значение которой в любой момент времени известно, будем
обозначать ее s(7), Для описания случайных сигналов ис-
пользуется вероятностный подход, при котором сигналы рас-
сматриваются как случайные процессы. Например, из двух сиг-
налов, изображенных на рис. 1.1, сигнал (а) можно условно отне-
сти к детерминированным сигналам, а сигнал (б) - к случайным.
Реальные сигналы всегда являются в какой-то мере случайными.
Во-первых, сигнал искажается в цепях передатчика и приемника.
Эти искажения обусловлены несовершенством цепей, отличием
их характеристик от идеальных. Но если характеристики цепей
известны, то обусловленные ими искажения сигнала в прин-
ципе могут быть устранены. Случайным характером таких иска-
жений обычно пренебрегают. Во-вторых, сигнал подвергается
воздействию различного рода посторонних помех, мешающих
приему полезного сигнала. Поэтому в приемнике обычно учиты-
вается случайный характер принятого сигнала и производится его
обработка с целью подавления помехи и выделения полезного
сигнала.
-10-
Рассмотрение реальных сигналов как детерминированных во
многих случаях является оправданным. Оно позволяет получить
более ясное представление о свойствах и характеристиках реаль-
ных сигналов. Кроме того, проведенные на основе такого рас-
смотрения расчеты дают количественные результаты, которые
могут быть использованы для оценки реальных сигналов. В даль-
нейшем будем рассматривать детерминированные сигналы, на-
зывая их просто сигналами.
Детерминированные сигналы различают как периодические и
непериодические. Периодический сигнал s( f) с периодом Т дол-
жен удовлетворять тождеству s(t) = s(t+T) в интервале
— оо</<оо. Таких сигналов, естественно, не существует, так
как любой реальный сигнал имеет начало и конец. Однако на
практике часто встречаются сигналы, повторяющиеся во време-
ни: например, периодический характер сигнала виден на
рис. 1.1,а. Если условие периодичности выполняется на интервале
Zq < / < Zg + tfc, где »Г, то можно применять в качестве ма-
тематической модели таких сигналов периодическую функцию
времени. Все остальные сигналы относятся к непериодическим.
Среди них особый интерес представляют импульсные сигналы,
чаще называемые просто импульсами. Импульс - это сигнал,
значение которого отлично от нуля в течение ограниченного вре-
мени, определяемого как длительность импульса. Например, сиг-
нал на рис. 1.2 состоит из отдельных прямоугольных (прямо-
угольной формы) импульсов.
2.2. ОСНОВНЫЕ ПАРАМЕТРЫ СИГНАЛОВ
Описание сигналов с помощью известной функции s(t) явля-
ется наиболее полным, но оно требуется не всегда. Во многих
случаях достаточно знать несколько параметров, характеризую-
щих основные свойства сигнала. Целесообразно определить па-
раметры сигнала, которые являются основными с точки зрения
его передачи. Такими параметрами являются длительность сиг-
нала, его динамический диапазон и ширина спектра.
-11-
Длительность сигнала. Сигнал 5(/), как и всякий временной
процесс, имеет начало t\ и конец т.е. задан в ограниченном
интервале времени t\ < t < /2- Интервал времени, в пределах
которого сигнал существует, определяет его длительность:
Ти = ^2“ Л-
При описании сигналов иногда используют функции, задан-
ные на полубесконечном 0 < t < 00 или бесконечном —<*> < / <
со интервале времени. В этих случаях вводится понятие практи-
ческой или эффективной длительности сигнала. Применяются
различные способы ее определения.
Первый способ - определение длительности сигнала как ин-
тервала времени, в пределах которого его значение не меньше
некоторого заранее заданного уровня. Например, рассмотрим
сигнал, описываемый функцией
s(t) = Ue~at, />0,
(2.1)
его называют экспоненциальным импульсом (рис. 2.1).
Такой сигнал лишь условно можно назвать импульсом, по-
скольку он задан па полубесконечном интервале. Определим его
практическую длительность Ти из условия десятикратного
-12-
уменьшения уровня:
в =0,1 , откуда Ти= 2,303/(7.
Второй способ - энергетический. Энергия сигнала определя-
ется как
оо
Е= j s\t)dt.
—оо
Если s(t) - электрический сигнал, то Е - энергия, выделяемая
на сопротивлении в 1 Ом. Под практической длительностью сиг-
нала понимают интервал времени, внутри которого сосредоточе-
на заданная часть (например, 90%) энергии сигнала. Для экспо-
ненциального импульса это условие выглядит так:
Тц ОО
J (Ue~at )2dt = 0,9 J(Ue~at)2dt.
0 0
Отсюда нетрудно найти полученное выше значение Ти.
Динамический диапазон сигнала. Одной из энергетических ха-
рактеристик сигнала является его мгновенная мощность, опре-
деляемая как квадрат мгновенного значения:
p{f) = s2(f).
Если s(t) ~ электрический сигнал, то /?(/) - мгновенная мощ-
ность, выделяемая на сопротивлении в 1 Ом.
Динамический диапазон - это отношение максимального зна-
чения мгновенной мощности /?макс к тому минимальному значе-
нию рмпн, которое позволяет обеспечить заданное качество пере-
дачи. Он выражается обычно в логарифмической форме (децибе-
лах, дБ):
D= 10 lg(pMaKc/pмин )•
Например, динамический диапазон спокойной человеческой
речи составляет 25...30 дБ, а симфонического оркестра 70...95
дБ.
Выбор значения минимальной мощности сигнала связан с
уровнем помех: величина /?мин должна быть больше мощности
помехи. Оценкой помехоустойчивости сигнала служит также от-
ношение средних мощностей сигнала и помехи.
Ширина спектра сигнала является его важнейшим парамет-
ром. Понятие спектра и методы его определения рассматрива-
ются в § 2.3 и § 2.4. Спектры периодических и непериодических
сигналов имеют свои особенности и поэтому рассматриваются
раздельно.
Произведение трех основных параметров сигнала - длитель-
ности, динамического диапазона, ширины спектра - определяет
его объем. Чем больше объем сигнала, тем больше информации
можно «вложить» в этот объем.
Радиоканал, обеспечивающий передачу сигнала, имеет свои
собственные параметры. К ним относятся: длительность работы
канала, диапазон мощностей, на которые рассчитаны технические
устройства, и полоса пропускания этих устройств. Для неиска-
женной передачи сигнала его параметры должны быть согласова-
ны с параметрами радиоканала.
2.3. ПЕРИОДИЧЕСКИЕ СИГНАЛЫ И ИХ СПЕКТРЫ
2.3.1. ВВОДНЫЕ ЗАМЕЧАНИЯ
Периодическими называют сигналы, повторяющиеся во вре-
мени (например, как на рис. 1.1,а.). Периодический характер име-
ют сигналы, отображающие звуковые колебания различных му-
зыкальных инструментов. Например, звук ноты «ля», издаваемый
пианино, отображается сигналом, показанным на рис.2.2.
Установлено, что сложные несинусоидальные, но периодиче-
ские колебания можно рассматривать как сумму одного основно-
-14-
го синусоидального колебания и большого числа других сину-
соидальных колебаний с кратными частотами, которые называют
гармониками. Например, тон «ля» пианино состоит из следую-
щих синусоидальных составляющих: основное колебание с час-
тотой 440 Гц, вторая гармоника с частотой 880 Гц, третья гармо-
ника с частотой 1320 Гц и т.д. Такой эквивалент сложного сигна-
ла - совокупность воссоздающих его синусоидальных состав-
ляющих называют спектром данного сигнала.
< -МАЛАЛ
Первая гарм он и ка
Вторая гарм он и ка
Третья гармоника
Четвертая гармоника
П ятая гарм он и ка
Рис. 2.2
Существуют математические методы, позволяющие, зная сиг-
нал, вычислить его спектр, и есть приборы (спектроанализаторы),
позволяющие любой сложный сигнал реально разделить на экви-
валентный ему набор синусоидальных составляющих. Таким об-
разом, путем вычисления и измерения можно найти спектр любо-
го сигнала.
Рассмотрим математические методы вычисления спектра пе-
риодических сигналов.
-15-
2.3.2. СПЕКТРАЛЬНЫЙ АНАЛИЗ
ПЕРИОДИЧЕСКИХ СИГНАЛОВ
Из курса математики известно, что любую периодическую
функцию s(t) с периодом Т, удовлетворяющую условиям Ди-
рихле, можно разложить в ряд Фурье:
Т XC^cosww^ + Z^siiwtO)/).
(2.2)
где С0| = 2д/Т.
Коэффициенты ряда Фурье вычисляются по формулам:
2 7/2 2 т/~
ап=— J s^cosn^tdt, bn=— j 5(/)sin«G)1/t//.
-т/ 2 ?-Т/2
(2.3)
Заметим, что периодические функции, с которыми имеют дело
в радиотехнике, условиям Дирихле обычно удовлетворяют.
Так как
a„cosn(f\t + Z^sinnay = y4„cos(«(0|/ + ф„),
где
An=M+bl ^n=-^ctg(bn/an), (2.4)
то ряд Фурье (2.2) можно записать в другой (более удобной для
анализа) форме:
А 00
s(t) = — + £47c°s(mo/+ фп). (2.5)
2 n=i
Ряд (2.5) представляет сигнал s(f) в виде суммы постоянной
составляющей Aq / 2 и бесконечного числа гармонических со-
-16-
ставляющих (гармоник). Число И определяет порядковый номер
гармоники: /7-гармоника. Каждая /7-гармоника характеризуется
амплитудой Ап, частотой MDj и начальной фазой фп. Совокуп-
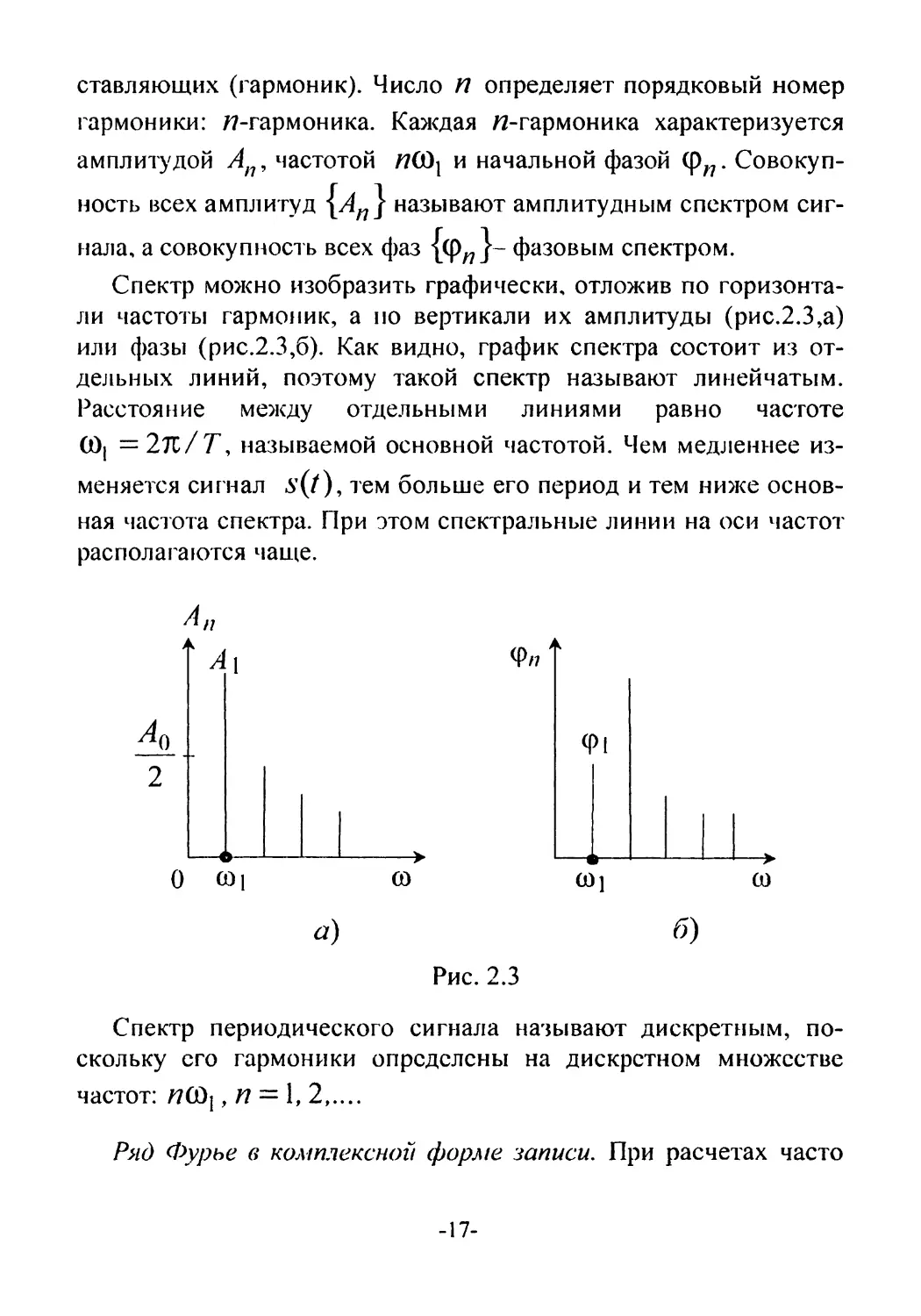
ность всех амплитуд называют амплитудным спектром сиг-
нала, а совокупность всех фаз {ф/7}~ фазовым спектром.
Спектр можно изобразить графически, отложив по горизонта-
ли частоты гармоник, а по вертикали их амплитуды (рис.2.3,а)
или фазы (рис.2.3,6). Как видно, график спектра состоит из от-
дельных линий, поэтому такой спектр называют линейчатым.
Расстояние между отдельными линиями равно частоте
CD| = 27l/7\ называемой основной частотой. Чем медленнее из-
меняется сигнал 5’(/), тем больше его период и тем ниже основ-
ная частота спектра. При этом спектральные линии на оси частот
располагаются чаще.
<0 б)
Рис. 2.3
Спектр периодического сигнала называют дискретным, по-
скольку его гармоники определены на дискретном множестве
частот: /7С0| ,/7 = 1, 2,....
Ряд Фурье в комплексной форме записи. При расчетах часто
-17-
оказывается предпочтительней комплексная форма записи ряда
Фурье. Учитывая, что COS X = {е^Х + е 'Х )/ 2, запишем
cos(„«v + <р„ ) = (е'(пт',+Ф" > + ) )/2.
Подставим это выражение в правую часть формулы (2.5) и обо-
значим
С» = Л / 2; С„=\/2 А„е^; С_„ = 1/2 А„е~^.
Тогда ряд (2.5) можно записать так:
оо
*(')= ЪС„е'"ш'1. (2.6)
/7=—оо
Здесь для вычисления коэффициентов ряда необходим всего
один интеграл:
1 7V2
С„=1 f (2.7)
1 -Т/2
что упрощает расчет. Коэффициент Сп есть комплексная ампли-
туда И-гармоиики:
C„=|C„P”=Re[C„]+/Im[C„].
где
| С„ |= 7Re2[C„] + Im2[C„],
Ф„ = arctg{ Im[C„ ]/ Re[C,? ]}.
Текущий индекс П принимает вес целые числовые значения
от — ©о до ©о. Однако, если функция s(f) является дсйствитсль-
-18-
ной (как и предполагается), то
Сп, |С_Л/| |С/7|, ф_н ф/7, (2.8)
где значок * обозначает комплексно-сопряженную величину.
Путем сравнения с ранее полученными результатами для
/7 > О можно установить, что
ап = 2Re[C„]; bn =-21т[С„]; А„ = 2|С„|.
Таким образом, периодический сигнал может быть представ-
лен или функцией $(/) или совокупностью коэффициентов ряда
Фурье, т.с. спектром сигнала. Эти представления равноценны.
Обычно их различают как временное (во временной области) и
частотное (в частотной области) представления.
Процесс определения коэффициентов ряда Фурье носит на-
звание спектрального анализа периодического сигнала.
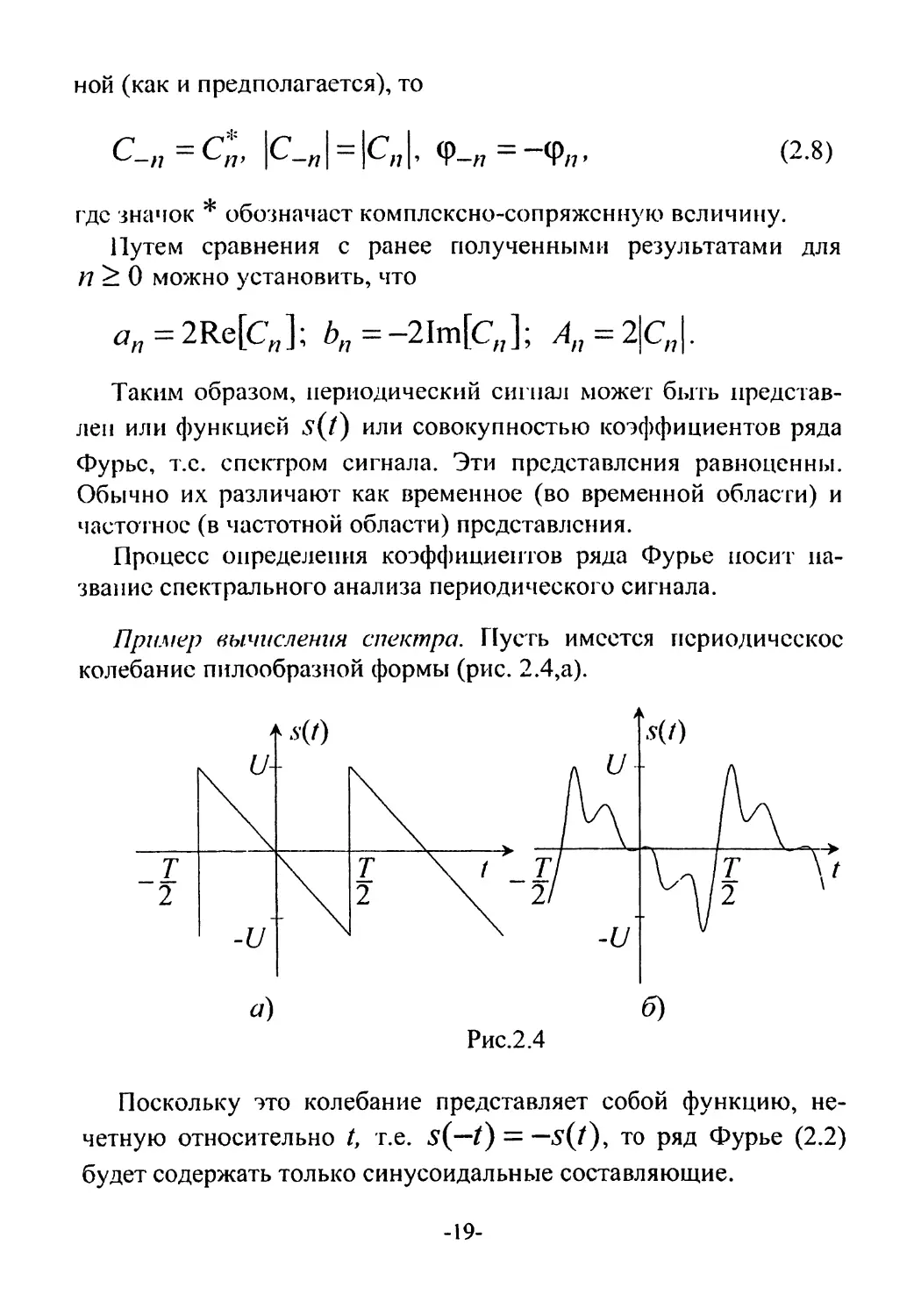
Пример вычисления спектра. Пусть имеется периодическое
колебание пилообразной формы (рис. 2.4,а).
Поскольку это колебание представляет собой функцию, не-
четную относительно т.е. 5(—Z) = —s(Z), то ряд Фурье (2.2)
будет содержать только синусоидальные составляющие.
-19-
Подставляя значение
5(/) = -(2С//Г)Л -T/2<t<T/2
в формулу (2.3), получаем
. 4UT‘2 . J 2U 2U . 1чИ
b„ =----z- t sinwcoi/ at -—cosnn =—(—1) .
T2 _r,2 nn mt
Таким образом, для данного сигнала ряд (2.2) принимает вид
277 00 1
s(t) = — У, (-1)” — sinwa)]/.
л „=1 и
(2.9)
Амплитуды гармоник, равные
Ап =\bn\ = 2U/mt,
убывают по закону \/ П. Соответствующий график приведен на
рис. 2.5,а.
-20-
Определение фаз гармоник упрощается, если записать ряд
(2.9) в форме (2.5):
О ТТ оо 1
$(/) = — S(-l)"+1 1 C0s(/7(0j/ + 71/2).
Tt /7-| п
Следует также учесть, что этот ряд является знакопеременным, а
изменение знака эквивалентно изменению фазы гармоники на 71.
Поэтому фазовый спектр имеет вид, показанный на рис. 2.5,6.
Ширина спектра. Ряд Фурье содержит бесконечное число
гармоник, т.с. теоретически спектр сигнала неограничен. Однако
расчеты показывают, что с увеличением порядкового номера
гармоники ее амплитуда, как правило, уменьшается. Поэтому при
анализе спектра достаточно учесть лишь конечное число гармо-
ник, а остальными можно пренебречь. Число учтенных гармоник
определяет так называемую практическую или эффективную ши-
рину спектра.
Допустим, что в (2.9) нужно учесть все гармоники, амплитуды
которых составляют не менее 1/5 (или 20%) от амплитуды первой
гармоники. Тогда номер высшей учтенной гармоники /7 = 5.
Ширина спектра Д(0с определяется разностью между верхней
С0в и нижней 0)н частотами: ДО)с = (Ов — С0н. В данном
случае (0в = 5СО|, (Он =(0|,т.е. Д(ОС = 4С0| (см. рис. 2.5,а).
Следует отметить, что принудительное ограничение ширины
спектра оказывает влияние на форму сигнала. На рис. 2.4,6 при-
веден график суммы первых пяти гармоник ряда (2.9). Заметим,
что имеется сходство колебаний, изображенных на рис. 2.2 и на
рис. 2.4,6.
Распределение мощности сигнала по гармоникам. Средняя
мощность периодического сигнала вычисляется по формуле
1 Т/2
Р = - J ?(/)<* =
1 -Т/2
-21-
2
£
Т
т''2 Г А
J — + У Ancos(n(i\t + <pw) dt.
-т 2[_ п=\
Раскрывая в этой формуле квадрат суммы и выполняя почлен-
ное интегрирование, можно показать, что
оо
Р=Л02/4+£^/2.
п=]
(2.10)
Здесь Aq /4 - средняя мощность постоянной составляющей,
А^г / 2 - средняя мощность Я-гармоники. Следовательно, сред-
няя мощность периодического сигнала равна сумме средних
мощностей его гармоник.
2.4. НЕПЕРИОДИЧЕСКИЕ СИГНАЛЫ И ИХ
СПЕКТРЫ
2.4.1. СПЕКТРАЛЬНЫЙ АНАЛИЗ
НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Непериодический сигнал можно рассматривать как предель-
ный случай периодического сигнала, когда его период неограни-
ченно возрастает Т —> сю.
Из разложения периодического сигнала в ряд Фурье (2.6) по-
средством предельного перехода при Т —> сю получают разло-
жение непериодического сигнала в интеграл Фурье:
5(Z) = — j5((D)e/oyJ(D,
2 л __
(2.1I)
где функция
-22-
оо
S(w)= р(/)е~/аУ<й
—оо
(2.12)
формально является предельным случаем (2.7) при Т —
Формула (2.12) известна как преобразование Фурье функции
s(t). При этом формулу (2.11) называют обратным преобразова-
нием Фурье.
Интеграл Фурье (2.11) так же, как и ряд Фурье (2.6), дает раз-
ложение сигнала на гармонические составляющие, представлен-
ные в комплексной форме. Принципиальное различие между ря-
дом (2.6) и интегралом (2.11) состоит в том, что ряд дает разло-
жение сигнала на гармонические составляющие е 1 с дис-
кретными частотами т?(0| (дискретный спектр), а интеграл дает
/ОУ
разложение сигнала на гармонические составляющие е с час-
тотой (О, принимающей непрерывные значения (непрерывный
спектр).
Таким образом, спектр периодического сигнала - дискретный,
а спектр непериодического сигнала - непрерывный.
Формула (2.11) выражает непериодический сигнал 5(/) в виде
бесконечно большого числа гармонических колебаний с беско-
нечно близкими частотами. Здесь представляет собой
вклад в S(t) от гармонической составляющей е . Функцию
5((0) называют спектральной плотностью сигнала s(t).
Для непериодического сигнала функция 5((0) играет ту же
роль, что и комплексная амплитуда (2.7) для периодического сиг-
нала.
В общем случае 5((0) принимает комплексные значения и
может быть представлена в форме:
ЗД = |5(со)|е/ф(со) = Re[5((0)]+zIm[S(co)],
-23-
где
|S(co) = 7Re2[5((d)]+Im2[S(co)],
ф(со) = arctg{lm[S(co)]/Re[S((o)]}. (2.13)
Частотную зависимость модуля |S((O)| называют амплитуд-
ным спектром непериодического сигнала. Функцию ф(со) опре-
деляют как фазовый спектр сигнала. Амплитудный спектр опи-
сывает плотность распределения амплитуд гармонических со-
ставляющих сигнала по частоте, а фазовый спектр - распределе-
ние их фаз. Заметим, что размерность |S(<0)| - это размерность
сигнала 6’(/), деленная на размерность частоты (например,
вольт/герц).
Поскольку s(t) - действительная функция, то
S(-СО) = 5*(СО), |S(-(0)| = |S((0)|, ф(-<0) = -ф((О), (2.14)
т.е. функция 5((0) обладает свойствами симметрии, аналогич-
ными (2.8).
Графическое изображение спектров приведено на рис. 2.6.
-24-
Вследствие симметрии можно ограничиться изображением
спектров в области положительных частот, которые являются фи-
зическими частотами. Следует подчеркнуть, что отрицательная
частота - лишь математическое понятие, используемое для пред-
ставления действительной функции в комплексной форме.
Таким образом, непериодический сигнал s(t) в частотной об-
ласти представляет его спектральная плотность 5(С0). Вычисле-
ние 5(со) составляет суть спектрального анализа непериодиче-
ского сигнала.
Условия существования Обратимся к формуле (2.12).
Интеграл с бесконечными пределами называют несобственным.
Если в результате интегрирования и подстановки пределов полу-
чают конечное число, то говорят, что интеграл сходится. В курсе
математики доказывается, что интеграл (2.12) сходится, если
функция s(t) является абсолютно интегрируемой, т.е.
J |5’(/]<7/<оо. (2.15)
—оо
Заметим, что условие (2.15) выполняется для всех сигналов
Л’(7), энергия которых конечна (/? < <*>).
2.4.2. ПРИМЕРЫ ВЫЧИСЛЕНИЯ СПЕКТРОВ
НЕПЕРИОДИЧЕСКИХ СИГНАЛОВ
Спектральная плотность прямоугольного импульса. В качест-
ве примера непериодического сигнала возьмем прямоугольный
импульс с амплитудой U и длительностью Ти. Пусть импульс
располагается симметрично относительно начала отсчета време-
ни (рис.2.7).
Подставляя значение
s(t) = U, -ти/2</<ти'2
-25-
в формулу (2.12), получаем
хи/2 . 07/
5(0)) - J Ue l(£tdt -—sin(coTH / 2).
-т л «>
Рис. 2.7
анализа форме:
Отметим, что 5*(С0) является
действительной функцией часто-
ты. Это характерно для сигналов,
представляющих собой функ-
цию, четную относительно t, т.е.
Полученное выражение S(CO)
запишем в более удобной для
S(co) = t/THsinc(coTH / 2).
(2.16)
Здесь использована функция
sinc(x)= (sinх)/х, где х = соти/2.
Ее значение равно единице при X = 0 и равно нулю при
X- ±71, ±271,... (рис. 2.8).
Согласно (2.16) график £((0) повторяет форму функции
Sllic(x). Следовательно, на нулевой частоте значение спек-
тральной плотности равно площади импульса: 5(0) = (7ТИ, а на
частотах C0Z7 = 2шс/Ти, Л7 = 1, 2,... значение 5(С0А7) = 0.
Амплитудный спектр определяется как
|S(a)j = t/TH|sinc((OTH /2)|.
(2.17)
График |s(tt>)| при (0> 0 изображен на рис. 2.9,а.
-26-
-27-
Видно, что амплитудный спектр имеет лепестковую структу-
ру. Ширина лепестка, равная Д(В= 2л/ти , обратно пропорцио-
нальна длительности импульса. Поэтому уменьшение длительно-
сти импульса равносильно расширению спектра и наоборот.
Фазовый спектр ф((о) имеет вид, показанный на рис.2.9,б.
Здесь изменение фазы скачком на 7С соответствует изменению
знака функции (2.16) (см. рис. 2.8).
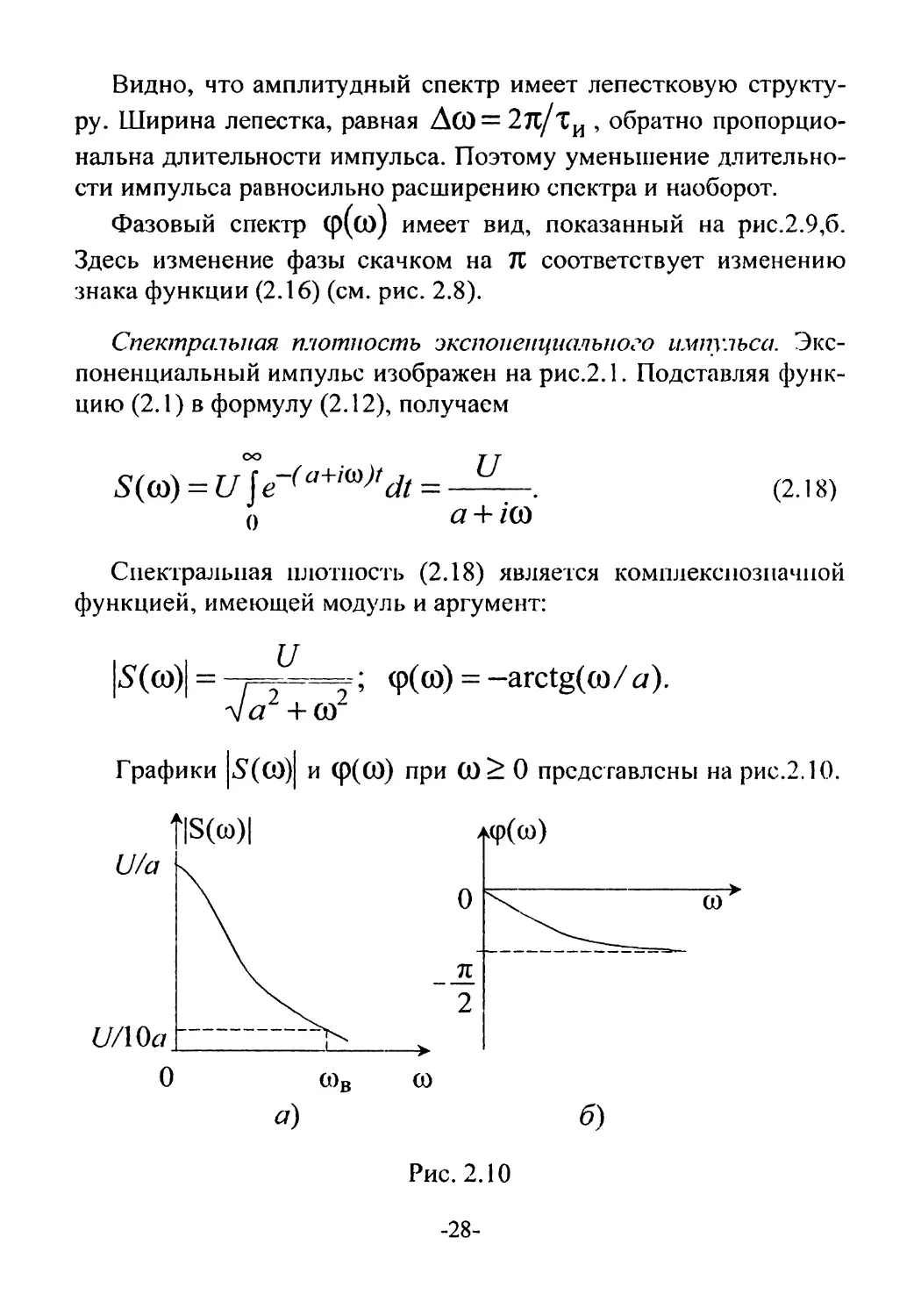
Спектральная плотность экспоненциального импульса. Экс-
поненциальный импульс изображен на рис.2.1. Подставляя функ-
цию (2.1) в формулу (2.12), получаем
S(co) = ule~(a+iw)tdt =
о а + /со
(2.18)
Спектральная плотность (2.18) является комплекснозначной
функцией, имеющей модуль и аргумент:
l-S'M = ТТ“Г; = “arctg(w/«)•
da + со
Графики |5(С0)| и (р(СО) при (0> О представлены на рис.2.10.
а) б)
Рис. 2.10
-28-
2.4.3. ЭНЕРГЕТИЧЕСКИЙ СПЕКТР СИГНАЛА.
ШИРИНА СПЕКТРА
Энергетический спектр. Выразим энергию сигнала через его
спектральную плотность. Подставляя интеграл (2.11) в выраже-
ние для энергии, запишем
оо оо
Е- \s\f)dt = j s(z)
—оо —оо
— JS((o)eZw/J(D dt.
2 л___
Меняя здесь местами порядок интегрирования, получим
| ОО оо
Е = — j 5(со) \s(t)eiiMdt d(a.
2 л___
*
Учитывая, что выражение в квадратных скобках есть 5 (СО), за-
пишем
1 7 *
Е- — р’((о)5 (<о) J(D.
2 л _оо
Поскольку S(о)5 (w) = |S((d)|" , то имеем
1 ОО 1 оо
Е-— /|5((о)|2<7(о = - J|5((d)|2Jcd. (2.19)
л о
Величину |S(w)|2, характеризующую спектральную плот-
ность энергии сигнала, называют энергетическим спектром.
Ширина спектра. Спектры, определяемые выражениями
(2.17) и (2.18), заданы на бесконечном интервале частот. Поэтому
вводится понятие практической или эффективной ширины спек-
-29-
тра. Возможны различные способы ее определения.
Первый способ - определение ширины спектра, как интервала
частот, в пределах которого модуль спектральной плотности не
меньше некоторого заданного значения.
Например, если ограничить амплитудный спектр прямоуголь-
ного импульса (рис. 2.9,а) первым лепестком, то верхняя гранич-
ная частота спектра будет равна
(Ов=2л:/ти или /в =сов/2л = 1/ти.
Отметим, что произведение /ъЪа = I.
Обратимся к спектру экспоненциального импульса (рис. 2.10).
Положим, что на верхней граничной частоте модуль спектраль-
ной плотности уменьшается в 10 раз по отношению к максималь-
ному значению:
1 / yja2 + (Og = 1 /10(7, отсюда находим
(Or = 499 а = 9,95(7 или Л = 1,584(7.
Поскольку практическая длительность экспоненциального им-
пульса равна Ти = 2,303/ <7, то произведение /ВТИ = 3,647.
На основании рассмотренных примеров можно сделать вывод:
чем меньше длительность импульса, тем шире его спектр. Отмс-
тим, что этот вывод справедлив для импульсов любой формы.
Второй способ определения практической ширины спектра -
энергетический. Ширину спектра определяют как интервал час-
тот, внутри которого сосредоточена заданная часть энергии сиг-
нала. Например, в полосе частот, занимаемой первым лепестком
спектра прямоугольного импульса, сосредоточено 90,2% его
энергии.
Используя выражение (2.19), запишем условие, определяющее
верхнюю граничную частоту спектра экспоненциального им-
пульса:
-30-
CDB оо
J |5’(со)|2<Усо = 0,9 J‘|*S'((»)|2 c7o>.
о о
Следует отметить, что рассмотренные способы определения
практической ширины спектра нс учитывают степени искажения
формы сигнала, вызванного ограничением спектра, а это может
привести к потере передаваемой информации. Поэтому при опре-
делении практической ширины спектра необходимо также руко-
водствоваться стремлением обеспечить требуемое качество пере-
дачи информации.
Например, при передаче сигналов, отображающих звуковые
сообщения (речь, музыка), необходимо прежде всего обеспечить
разборчивое восприятие их. Весь спектр звуковых колебаний,
воспринимаемых ухом человека, занимает широкую полосу час-
тот: 20...20000 Гц. Однако установлено, что при телефонной свя-
зи качество речи вполне удовлетворительно при ограничении
спектра частотами 300...3400 Гц. Для хорошего восприятия в ра-
диовещании необходимо передавать более широкую полосу час-
тот: для высшего класса 30... 15000 Гц, для первого класса
50... 10000 Гц, для второго класса 100...6300 Гц.
2.5. СООТНОШЕНИЕ МЕЖДУ СПЕКТРАМИ
ОДИНОЧНОГО ИМПУЛЬСА И
ПЕРИОДИЧЕСКОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
ИМПУЛЬСОВ
Для одиночного импульса, изображенного на рис. 2.7, форму-
ла (2.12) запишется в виде
Ти /2
5(со)= J s(f)e l(£>tdt. (2.20)
—Ти / 2
Образуем периодическую последовательность таких импуль-
сов (рис.2.11).
-31-
Рис. 2.11
Для вычисления ее спектра можно воспользоваться формулой
(2.7).
Из сравнения формул (2.7) и (2.20) следует, что комплексная
амплитуда 77-гармоники может быть определена как
= 5(иС0, )/7\ (2.21)
где S(w(0|) - значение спектральной плотности импульса на
частоте Ш= 77(D|. Из (2.21) следуют соотношения для амплитуды
и фазы 77-гармоники:
= = <2-22)
Эти соотношения полезно использовать для определения
спектра периодического сигнала: сначала находится спектральная
плотность одиночного импульса, а затем с помощью формул
(2.22) - спектр периодической последовательности импульсов.
Воспользуемся таким подходом для определения спектра пе-
риодической последовательности прямоугольных импульсов.
Спектр периодической последовательности прямоугольных
импульсов. Подставив функцию (2.16) в формулу (2.21), имеем
Сп =(k%/r)smc(«(0iTH/2). (2.23)
Определим амплитудный спектр как
-32-
АН = 2|CW| = (2^1 sinc(>m/<4
(2.24)
где ^ = 7"/ти - коэффициент, называемый скважностью им-
пульсной последовательности.
Коэффициенты Cw, определяемые (2.23), являются действи-
тельными, но знакопеременными. Это следует учитывать при оп-
ределении фазового спектра: ф/? =0, если Сп >0, и ф^ — 71,
если Сп < 0.
Графики амплитудного и фазового спектров приведены на
рис. 2.12, штриховой линией показана огибающая спектра, форма
которой совпадает со спектром, изображенным на рис.2.9.
Таким образом, непрерывный спектр одиночного импульса
является огибающей дискретного спектра периодической иосле-
Рис.2.12
-33-
2.6. СООТВЕТСТВИЕ МЕЖДУ ОПЕРАЦИЯМИ
НАД СИГНАЛАМИ И СПЕКТРАМИ
Известные из курса математики свойства преобразования Фу-
рье позволяют установить соответствие между операциями над
сигналами и спектрами.
Свойство линейности. Вследствие линейности преобразова-
ния Фурье при сложении сигналов 5*1 (?) и (?) их спектраль-
ные плотности ((D) и 52((о) суммируются. В краткой записи
это выглядит так:
s(t) = as\ (f) + b s2 (?) <-» 5,(со) = а5,1(со) + /)52((о). (2-25)
где а.Ь ~ произвольные постоянные. Знак <н> называют знаком
взаимно однозначного соответствия, которое устанавливается па-
рой преобразований Фурье (2.11) и (2.12). Заметим, что
амплитудный спектр |5((0)| Ф а|5] ((0)| + ^|52((о)|,
фазовый спектр ф((о) Ф1 (®)+ Ф2 (®)-
Смещение сигнала во времени. При смещении сигнала s(t) во
времени на интервал его спектр 5((о) получит приращение
фазы, равное (D/q :
s(t - /0)«-» 5,(со)е_/ОУо, s(t + /0 ) «-> . (2.26)
Отмстим, что при этом амплитудный спектр |s(<o)| нс меняется.
Изменение масштаба времени. При изменении временного
масштаба происходит обратное изменение частотного масштаба:
s(at) «-> (1/а )S(со/а), а > О, (2.27)
-34-
т.е. при сжатии сигнала во времени его спектр расширяется и на-
оборот. Например, при уменьшении длительности Ти прямо-
угольного импульса лепестки его спектра, ширина которых равна
2я/ Ти, расширяются.
Из (2.27) следует, что существует обратная пропорциональ-
ность между длительностью сигнала Тс и шириной его спектра:
Д/с ~ 1/Тс. Д/с=Д(0с/2л. (2.28)
Это соотношение имеет важное практическое значение.
Смещение спектра сигнала. При умножении сигнала 5*(/) на
комплексную экспоненту е/С°0^ его спектр 5(<о) смещается по
оси частот на интервал, равный (Oq:
s(t )el(aot S((f) - (00 ), s(t о S (w + w0).
(2.29)
Иными словами, происходит перенос спектра из одной области
частотного диапазона в другую.
Дифференцирование и интегрирование сигнала. При диффе-
ренцировании сигнала s(/) его спектр 5(со) изменяется как
<—> /CoS'(со), (2.30)
а при интегрировании сигнала
z 1
<-> — S(co), если S(0) = 0. (2.31)
о ™
Перемножение сигналов. При перемножении двух сигналов
^(/)и их СПСКТРЫ Si(®) и ^((о) подвергаются операции
-35-
свертки:
s(/)=Si(/)s2(/) S(m)= ~S{(w)0S2(co). (2.32)
Z71
Здесь знак ® используется для символической записи опера-
ции свертки, определяемой интегралом:
51 (со)® S2(co)= J ‘5'1(^)*S'2((O—хУ^х =
—оо
= J 5|(co-x)52(x)c/x. (2.33)
—оо
Свертка сигналов. Если сигнал 5(/) получен в результате
свертки сигналов 5] (/) и s2 (/), то его спектр 5(со) определяет-
ся как произведение спектров S| (со) и S2 (со):
5’(/)=51(0®52(/) <-> 5'(со)=51(со)5'2(со). (2.34)
Здесь
S] (/)® л’2 (?)= J5](x)52(^ — x)dx = J5](/ — x)s2(x)dx.
—оо —оо
(2.35)
Заметим, что свойство свертки часто используется при иссле-
дованиях.
2.7. ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ СВОЙСТВ
ПРЕОБРАЗОВАНИЯ ФУРЬЕ ПРИ
СПЕКТРАЛЬНОМ АНАЛИЗЕ СИГНАЛОВ
Вычисление спектров упрощается при использовании соот-
ношений (2.25) - (2.35). Рассмотрим примеры.
-36-
Спектральная плотность пачки импульсов. Пачка импульсов
- это сигнал в виде конечной последовательности одинаковых и
равноотстоящих импульсов. На рис. 2.13 изображена пачка пря-
моугольных импульсов.
Для определения спектральной плотности пачки импульсов
воспользуемся теми свойствами преобразования Фурье, которые
описываются соотношениями (2.25) и (2.26).
Сначала находим спектральную плотность 5*1 ((D) первого
импульса в пачке. Этот импульс отличается от симметричного
прямоугольного импульса (рис. 2.7) лишь смещением во времени
на интервал Тн / 2. Поэтому в соответствии с (2.26)
5, (ю) = 5о(со)е-/ОЛи 7 2, (2.36)
где ((О) определяется выражением (2.16).
Второй импульс в пачке смещен во времени относительно
первого на интервал Т. Его спектральная плотность
S2 (со) = S, (co)e"'wr. (2.37)
Далее находим спектральную плотность третьего импульса,
смещенного во времени относительно первого на интервал 2Т:
S3 (со) = S, (ю)е_/20)Г. (2.38)
-37-
Аналогично находим спектральные плотности всех после-
дующих импульсов в пачке.
Спектральная плотность пачки из N импульсов определяется в
соответствии с (2.25) так:
S(w) = 5, (со)[1 + e~iG)T + е~'2(дТ +... +
(2.39)
На частотах CD/? = 2пп / Т,п = 0, 1,2,... каждое слагаемое в
квадратных скобках равно единице. Следовательно,
S(2nn/T) = NS{(2iw/T).
Это означает, что на указанных частотах модуль спектральной
плотности пачки импульсов в Af раз больше модуля спектральной
плотности одного импульса.
Используя формулу суммы геометрической прогрессии,
представим спектральную плотность (2.39) в виде
5(®) = S', (со)(1 - - e~i(*T)
или после преобразования
S((0) = S| (co)[sin( NaT / 2) / sin((or / 2)]е~/( )(o7V 2.
(2.40)
Амплитудный спектр (модуль) определяется следующим об-
разом:
|S(co)| = |S, (co)||sin( ЛЬоТ / 2) / sin(w7 / 2)|,
где модуль |Sj (со)| описывается функцией (2.17).
В качестве иллюстрации на рис. 2.14 представлен график ам-
плитудного спектра пачки из четырех импульсов при Т — 4ТИ.
-38-
Рис. 2.14
Штриховой линией показан спектр одиночного импульса.
Следует отмстить, что с увеличением числа импульсов в пачке
лепестки спектра становятся все более узкими и в пределе при
N получаем линейчатую структуру спектра периодиче-
ской последовательности импульсов.
Спектральная плотность цифрового сигнала. Цифровой сиг-
нал может быть представлен в виде последовательности прямо-
угольных импульсов, сформированной в соответствии с двоич-
ным кодом. Наличие импульса означает символ 1, а отсутствие
импульса символ 0. Примерный вид цифрового сигнала показан
на рис. 2.15.
Цифровой сигнал можно описать следующим выражением:
N
И=1
-39-
где ал принимает значения 0 или 1 в соответствии с двоичным
кодом, прямоугольной импульс с амплитудой U и дли-
тельностью Ти:
гп^ =
и при (п - 1)ти < t < «ти,
О при других значениях t.
Импульсы Г] (/), Г2(0>--->гту(0 запаздывают один относительно
другого на интервал времени, равный Ти.
5(/)
О ти
Рис. 2.15
Для цифрового сигнала (2.41) в соответствии с (2.25) спек-
тральная плотность
N
5(со)= X (со), <2-42>
п=1
где Sn((d) - спектральная плотность импульса rw(/).
Спектральная плотность S) (СО) импульса Г\ (/) определяется
выражением (2.36). Для импульса ^(Z), сдвинутого относитель-
но Fj(Z) на интервал времени Ти, получим выражение спек-
-40-
тральной плотности ^(CD) в виде (2.37) при условии, что
Т — Ти. Аналогично из (2.38) при Т = Тп получаем выражение
спектральной плотности 5^ (б)) импульса Г3(/). В результате
имеем
5„((0) = 5| (сф-'^-1^". (2.43)
Подстановка (2.43) в (2.42) дает
N
5(ш) = 5|(ю)5>„е"'/"“|'|<от" . (2.44)
п-\
Формулу (2.44) представим в следующем виде:
5(ю) = 51(0))5код(0)). (2.45)
Функцию
W = (2-46)
/7=1
можно трактовать как спектральную плотность кодовой последо-
вательности б?!Как следует из (2.46), спектр кодовой
последовательности является периодическим с периодом на оси
частот, равным 2я/ Ти.
Таким образом, спектр цифрового сигнала, определяемый вы-
ражением (2.45), является результатом наложения на спектр оди-
ночного прямоугольного импульса 5] (СО) спектра кодовой по-
следовательности 5код(С0). На рис.2.16 показан примерный вид
модуля |5(со)|. Штриховой линией показан спектр одиночного
импульса.
-41-
2.8. ИСПОЛЬЗОВАНИЕ ОБОБЩЕННЫХ
ФУНКЦИЙ ПРИ АНАЛИЗЕ СИГНАЛОВ
При анализе сигналов иногда используют символические
функции, которые не являются функциями в обычном смысле, их
называют обобщенными функциями. Наиболее широкое приме-
нение получила 8-функция (дельта-функция) 8(/). Ес определя-
ют следующим соотношением:
оо
Js(/)8(/)c7/ = .s(O), (2-47)
—оо
понимая под 8(/) «функцию», равную нулю при всех t Ф 0 и об-
ращающуюся в точке t = 0 в бесконечность так, что
ОО
j8(/)cfr = l.
—оо
-42-
С помощью 8-функции можно выразить в математической
форме такое идеализированное понятие, как единичный импульс.
Так называют импульс с бесконечно малой длительностью, бес-
конечно большой амплитудой и площадью, равной единице. К
пониманию единичного импульса можно прийти, рассматривая
прямоугольный импульс с амплитудой 1/ти и длительностью Ти
при Ти —>0. Иногда единичный импульс называют 8-импуль-
сом.
Смещенная во времени 8-функция 8(/--/q) определяется
соотношением:
J s(/)8(/ —t^)dt= s(t$ ), (2.48)
—оо
где под 8(/ — /q ) понимают «функцию», которая равна нулю
всюду, кроме точки t = /q, где опа обращается в бесконечность
так, что
оо
)8(/-/0)с// = 1.
Соотношения (2.47) и (2.48) показывают, что 8-функция об-
ладает фильтрующим (выборочным) действием, выделяя значе-
ние сигнала в фиксированный момент времени.
Благодаря указанному выборочному свойству, вычисление
интегралов, содержащих 8-функцию в качестве подынтегрально-
го сомножителя, фактически не требуют интегрирования. Напри-
мер, можно сразу записать значение интегралов:
оо оо
Jе~‘ш5(/)dl = 1. Jе~‘ш8(t-t0)dt = e~ios'°.
—оо —оо
-43-
Сопоставление этих интегралов с интегралом (2.12) позволяет
формально ввести в рассмотрение спектральную плотность еди-
ничного импульса:
8(/)e»S(co)=l, 8(/-/0)<-> S((o)==e-KOZ°. (2.49)
Согласно (2.49) единичный импульс 8(/) имеет постоянную
спектральную плотность, равную единице, во всем диапазоне
частот от —00 до При смещении единичного импульса во
времени на интервал /д его спектральная плотность получает
приращение фазы, как и следует из (2.26).
Таким образом, единичный импульс является идеальным ши-
рокополосным сигналом: его спектр имеет постоянное значение в
бесконечной полосе частот. На рис. 2.17 изображен единичный
импульс и его спектральная плотность. Для 8-функции принято
символическое изображение в виде стрелки.
|5(/)
1
О t 0 io
Рис. 2.17
В теории сигналов используют также 8-функцию 8(со). Все
записанные выше соотношения для 8(?) можно отнести и к
8((й), если заменить в них 1 на СО.
Например, запишем
J8(co)e'wzc7(o = 1.
—оо
Сопоставление этого интеграла с интегралом Фурье (2.11) пока-
-44-
зывает, что имеет место соответствие:
s(t) = 1 <-> £(со) = 2л5(со),
(2.50)
т.е. функции •$(/), принимающей постоянное значение в интерва-
ле — <*></< 00, соответствует в частотной области функция
5((о). Таким образом, в обобщенном смысле постоянная величи-
на (ток, напряжение) является примером идеального узкополос-
ного сигнала: его спектр сосредоточен в точке С0=0 (рис.2.18).
1
8(ю)
1
0
0
t
(О
Рис. 2.18
Поскольку
J 8(со - co0)ezovd(o = e/w°?,
то имеет место соответствие:
e'W()Z 5(со)= 2я5((о- со0).
(2.51)
Аналогично
е W _ 2л5(со+ (00 ).
(2.52)
С помощью функции 5(со) можно выразить спектральную
плотность периодической функции. Например, для гармониче-
ского колебания
-45-
s(t)= cosco0/ = (e/<0°' + e~i<i>ot)/ 2
спектральная плотность с учетом (2.51) и (2.52) запишется в виде
5(со)= лЗ(®-СО0)+7Сб(сО + СО0). (2.53)
Таким образом, 6-функция дает возможность выразить в ма-
тематической форме спектральную плотность функций, для ко-
торых преобразование Фурье (2.12) не существует, так как не вы-
полнено условие (2.15) его существования.
2.9. ПРЕОБРАЗОВАНИЕ ЛАПЛАСА И ЕГО
ИСПОЛЬЗОВАНИЕ ПРИ АНАЛИЗЕ СИГНАЛОВ
Преобразование Лапласа - одно из интегральных преобразо-
ваний сигналов. Оно находит применение при анализе сигналов,
в частности, благодаря его связи с преобразованием Фурье.
Пусть имеется сигнал s(/), определенный при / > 0 и равный
нулю при t <0. Преобразование Лапласа этого сигнала опреде-
ляется как
оо
£(/?)= \s(t)e~ptdt, (2.54)
о
где р = (5 + /СО - комплексная переменная, получившая назва-
ние комплексной частоты. Сигнал s(l) называют оригиналом, а
функцию S(p) его изображением.
Функция S(j}) существует, если сходится интеграл (2.54).
Поэтому на функцию s(t) накладывается условие:
|s(/)|< Me~Q"', (2.55)
где М, CFq - положительные числа. При выполнении этого усло-
-46-
вия интеграл (2.54) абсолютно сходится для всех р, у которых
Re/? > (Jq. Минимальное значение числа (Уд, при котором усло-
вие (2.55) выполняется, называют абсциссой абсолютной сходи-
мости интеграла (2.54).
Если в (2.54) положить р = 7(0, то получим формулу (2.12)
для сигнала $(/), равного нулю при t < 0. Поэтому преобразова-
ние Лапласа можно рассматривать как обобщение преобразова-
ния Фурье на случай комплексных частот.
Основные свойства преобразования Лапласа совпадают с ана-
логичными свойствами преобразования Фурье, рассмотренными
в §2.6.
Заметим, что условие (2.55) обеспечивает сходимость инте-
грала (2.54) даже для тех сигналов, которые не удовлетворяют
условию (2.15). Это делает преобразование Лапласа более эффек-
тивным по сравнению с преобразованием Фурье.
Обратное преобразование Лапласа. Для перехода от изобра-
жения S(p) к функции времени s(t) может быть использовано
обратное преобразование Лапласа:
1 o+zoo
s(/)=—7 f S(p)ep'dp. (2.56)
2lc' a-i~
Здесь интегрирование проводится в плоскости комплексной
переменной р по любой прямой, параллельной мнимой оси, абс-
цисса которой (У >(5q. При практическом использовании этой
формулы интеграл в (2.56) заменяется контурным интегралом,
охватывающим все полюсы функции 5*(/?):
^6=-~-.jS(p)eptdp. (2.57)
2га с
Полюсами называют значения /?, при которых $(/?) обраща-
-47-
ется в бесконечность. В теории функций комплексного перемен-
ного доказывается, что правая часть формулы (2.57) равна сумме
вычетов (Res) подынтегральной функции во всех ее полюсах:
2~jS(p)eptdp = £Res S(p\pt.
В большинстве случаев 5(р) представляет собой дробно-
рациональную функцию, т.е. является отношением двух много-
членов по степеням р:
(2.58)
причем степень числителя не больше степени знаменателя. По-
люсами являются корни уравнения /?(/?)= 0. Допустим, что все
корни Рк> А: = 1,2,п различны. Тогда переход от изображе-
ния (2.58) к временной функции производят с помощью форму-
лы:
*(0= £Мл)/B'M]ePkt ’ <2-59>
к=\
где В'(р ) = dB/dp.
На практике для перехода от S'(z) к 5(р) или от 5(р)к s(l)
чаще всего пользуются готовыми таблицами преобразования Ла-
пласа. Эти таблицы, составленные для обширных классов функ-
ций, приводятся во многих математических и технических спра-
вочниках. Наличие таблиц делает способ анализа с помощью
преобразования Лапласа достаточно универсальным.
-48-
2.10. ОПИСАНИЕ СИГНАЛОВ С ИСПОЛЬЗОВАНИЕМ
ОРТОГОНАЛЬНЫХ СИСТЕМ БАЗИСНЫХ
ФУНКЦИЙ
Сигналы часто имеют довольно сложную форму, что весьма
затрудняет и,х описание. Сложный сигнал иногда удобно пред-
ставить в виде линейной комбинации некоторых заданных функ-
ций <P/?(Z)5 П = 0,1,2,..., называемых базисными. Такое пред-
ставление имеет вид
оо
*v(/)— <Z<Z2,
/7-0
(2.60)
где Сп- постоянные коэффициенты.
Выбор системы базисных функций зависит от вида сигнала и
цели исследования. Однако в любом случае функции (pZ7(z)
должны быть сравнительно простыми, обеспечивать простое вы-
числение коэффициентов С/7 и хорошую сходимость ряда (2.60) к
функции s[t\ Этим требованиям удовлетворяют базисные функ-
ции, которые образуют полную ортогональную систему. Кратко
напомним основные определения.
Функции (в общем случае комплексные) <pw(z),
П = 0,1,2,..., заданные на интервале [Zj ,Z2], называются орто-
гональными на этом интервале, если выполняется условие:
/2
J Ф/И )ф/7 0
>1
1Ы12>
о,
т = п,
т^п.
(2.61)
Здесь постоянная ||ф,7|| - норма базисной функции фл(/). Если
||фя|| = 1’ то система базисных функций называется ортонорми-
рованной.
-49-
При использовании ортогональной системы базисных функ-
ций коэффициенты ряда (2.60) вычисляются по формуле:
1
с„ =—тЬЖ
1ЫП
(2.62)
Разложение по ортогональной системе базисных функций
называют обобщенным рядом Фурье, а совокупность коэффици-
ентов {С„} такого разложения - спектром сигнала в выбранной
системе базисных функций или обобщенным спектром. Заметим,
что обобщенный спектр не является частотным спектром, т.е. он
нс определяет свойства сигнала в частотной области.
На практике при разложении сигналов верхний предел ряда
(2.60) берется конечным. При этом сигнал описывается с некото-
рой погрешностью, которую обычно оценивают среднеквадра-
тичной ошибкой:
(2.63)
Из курса математики известно, что ошибка 8 при заданном
N будет минимальной, если коэффициенты Сп вычисляются по
формуле (2.62).
Из (2.63) можно получить следующее неравенство:
N
]s2(l)dt> £С,;||<р„||2, (2.64)
которое известно как неравенство Бесселя. Это неравенство спра-
ведливо для любой ортогональной системы.
Ортогональная система называется полной, если при увсличе-
9
нии W среднеквадратичную ошибку 8“ можно сделать сколь
-50-
угодно малой. Иными словами, при N —> °° неравенство (2.64)
переходит в равенство:
^2 °°
Js2(t)dt= £С2||(р„|| , (2.65)
/|
известное как равенство Парсеваля. При этом ряд (2.60) сходится
в среднем квадратичном к функции Предполагается, что
функция ^(z) является квадратично интегрируемой на интервале
[/j ,Z2].
В представлении сигналов с помощью (2.60) применяются
разнообразные ортогональные системы функций: полиномы Че-
бышева, Лежандра, Лагерра, Эрмита, функции Уолша и другие.
Заметим, что ряд (2.2) дает разложение сигнала по ортогональной
системе тригонометрических функций.
2.11. ПРЕДСТАВЛЕНИЕ СИГНАЛОВ
С ОГРАНИЧЕННЫМ СПЕКТРОМ
Будем считать, что сигнал s(t) имеет ограниченный по часто-
те спектр: спектральная плотность 5((0) отлична от нуля лишь
для частот (0 при |(о| < Иными словами, при |(о| > (D/z/ спек-
тральная плотность S((O) = 0. Представление этого сигнала ин-
тегралом Фурье (2.11) выглядит так:
1
s(t) = — j S((d)eimtd(to. (2.66)
2К-(О
Разложим на интервале — (0w <(D<(DW функцию 5(С0) в
комплексный ряд Фурье. Для этого в формулах (2.6) и (2.7) нуж-
но аргумент Z заменить на (О, период Т заменить на величину
-51-
2(дт. В результате получим разложение спектральной плотности
в ряд:
оо in -со
5(со) = £ С„е 2<0'” . (2.67)
П—~ оо
Коэффициенты Сп определяются как
1 -in 2- и
С„ =------- j S(tt>) е -ы,п d(f). (2.68)
-й)т
Сравнивая правые части (2.66) и (2.68), видим, что имеет ме-
сто следующее равенство:
С„ = — s(-n— ) = Ts{-nT),
где Т = Я / .
С учетом (2.69) ряд (2.68) принимает вид
5(0)) = Г ^s(-nT)ei,J™
п--^>
или
5(со) = Т £ s(nT)e~inT(O.
п=-оо
(2.69)
(2.70)
(2.71)
Подставляя (2.71) в (2.66) и меняя порядок действия интегриро-
вания и суммирования, будем иметь
'7' оо
s(t) = ~~ J ^(пТ)е-1пТае,<я1с1м =
-ыт
-52-
rp оо . z, rr. .
= — E s(nT) j e1'"" "T'd(,> (2.72)
2я „=_
После вычисления интеграла в (2.72) получим следующее выра-
жение:
.s(/) = %s(nT)sinc[(»m(t-nT)], (2.73)
Л7=-оо
функция sinc(x)—(sin х)/х , X = (0w(/ — ПТ} уже использова-
лась ранее (см. § 2.4, рис.2.8).
Ряд (2.73) представляет собой разложение сигнала спектр
которого не содержит частот выше (0w, в обобщенный ряд Фу-
рье (2.60) по ортогональной системе функций вида:
Ф„(0 = sine [cow(/-пТ)]. (2.74)
Коэффициентами ряда являются значения (отсчеты) сигнала s(f)
в моменты времени t—nT\ Сп = s(nT). Этот ряд известен как
ряд Котельникова.
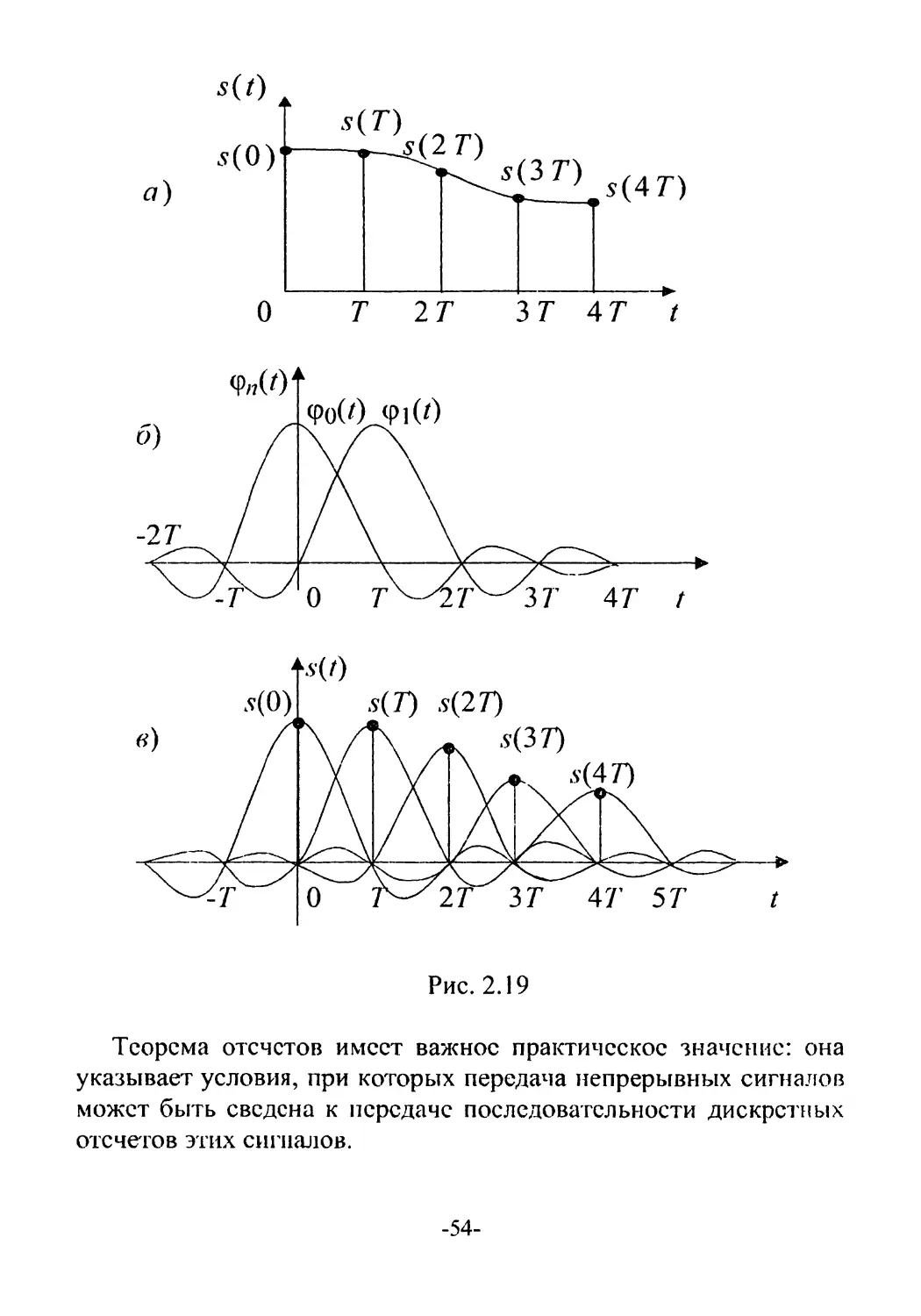
Иллюстрацией представления сигнала 5(/) рядом (2.73) слу-
жит рис. 2.19. Здесь изображены: а) сигнал s(/) и его отсчеты; б)
функции (2.74); в) сумма ряда (2.73).
Таким образом, для сигналов с ограниченным спектром спра-
ведливо представление (2.73). Полученный результат формули-
руется в виде гак называемой теоремы отсчетов: если спектр сиг-
нала ограничен максимальной частотой (Dw, то этот сигнал s(t)
полностью определяется последовательностью своих дискретных
отсчетов s(nT), п = 0, ± 1, ± 2,..., следующих с интервалом 7\
определяемым (2.70).
-53-
s(t)
Рис. 2.19
Теорема отсчетов имеет важное практическое значение: она
указывает условия, при которых передача непрерывных сигналов
может быть сведена к передаче последовательности дискретных
отсчегов этих сигналов.
-54-
3. МОДУЛИРОВАННЫЕ СИГНАЛЫ
3.1. ОБЩИЕ СВЕДЕНИЯ
Процесс передачи информации от источника заключается в
том, что сообщение превращается в сигнал, который передается
но радиоканалу получателю (см. § 1.3). Преобразование сообще-
ния в сигнал обычно проводится в два этапа: 1) преобразование
из неэлектрической формы в электрическую; 2) преобразование с
целью согласования характеристик сигнала с характеристиками
используемого радиоканала. На первом этапе образуется так на-
зываемый первичный сигнал (см. § 1.2). Задача второго - сфор-
мировать такой сигнал, который был бы наиболее удобен с точки
зрения обеспечения требуемого качества передачи и технических
возможностей, но с сохранением основных свойств первичного
сигнала.
Формирование сигналов, пригодных для передачи по радио-
каналу, осуществляется посредством модуляции. Модуляцией на-
зывают процесс изменения параметров одного сигнала под воз-
действием другого сигнала.
Обычно модулируемый сигнал представляет собой гармони-
ческое колебание
wH(/)=t70cos(co0/ + (p0),
его параметры (амплитуда Uq. частота (Од, начальная фаза фд)
постоянны. Это колебание называют несущим.
Результатом модуляции несущего колебания является моду-
лированный сигнал. В общем случае модулированный сигнал
можно описать выражением
u(t)= t/(/)cos[C00Z + <p(OL (3.1)
где (Од- несущая частота. Амплитуда U(f) и фаза ф(/) изме-
няются во времени в соответствии с изменением первичного сиг-
нала s(7), который при этом называют модулирующим сигна-
-55-
лом.
Принято различать амплитудную и угловую модуляцию. При
амплитудной модуляции изменяется только амплитуда (/(/), а
при угловой - только фазовый угол ф(/).
Процесс модуляции сопровождается переносом спектра моду-
лирующего сигнала в область около несущей частоты (Oq . Имен-
но это обстоятельство и обусловило широкое применение моду-
лированных сигналов вида (3.1) для передачи информации. Дело
в том, что первичные сигналы, как правило, низкочастотные. На-
пример, сигналы звукового вещания занимают полосу частот
примерно от 30 Гц до 15 кГц. Подобные сигналы не могут быть
непосредственно переданы по радиоканалу. Для эффективного
излучения электромагнитных волн необходимо использовать ко-
лебания высокой частоты. Поэтому предварительно спектр пер-
вичного сигнала должен быть перенесен в область высоких час-
тот. Такое преобразование спектра осуществляется путем моду-
ляции высокочастотного гармонического колебания низкочас-
тотным первичным (модулирующим) сигналом.
Модулированный сигнал u(jt) полностью эквивалентен моду-
лирующему сигналу в отношении содержащейся в нем ин-
формации, хотя они находятся в различных частотных диапазо-
нах.
Модулированный сигнал (3.1) занимает некоторую полосу
частот Асос около несущей частоты COq. Обычно выполняется
условие узкополосности: A(Oc/cOq«1. В этом случае можно
рассматривать модулированный сигнал как узкополосный сигнал.
Важное практическое значение имеет возможность посредст-
вом модуляции осуществить частотное разделение радиоканала,
при котором по радиоканалу на различных несущих частотах од-
новременно передается несколько сообщений (при условии, что
полосы частот сигналов не перекрываются). При этом происхо-
дит разделение полосы частот радиоканала на несколько более
узких нс перекрывающихся полос. Частотное разделение радио-
каналов является средством, с помощью которого имеющийся
-56-
диапазон радиочастот распределяется между различными служ-
бами.
Выбор несущей частоты осуществляется согласно Регламенту
радиосвязи, который является основным международным доку-
ментом, определяющим использование диапазона радиочастот и
их распределение между различными службами. Заметим, что
12
радиочастоты лежат в интервале от 3 кГц до 3 ТГц ( 3 • 10 Гц ).
Этот интервал разбит на девять диапазонов, каждый из которых
занимает полосу от 0,3-Ю” до 3 10” Гц, где 4 < П < 12. Для ра-
диоканалов различного назначения выделен определенный диа-
пазон радиочастот.
Радиоканал характеризуется пропускной способностью и по-
мехоустойчивостью. Можно увеличить его пропускную способ-
ность и помехоустойчивость соответствующим выбором вида
модуляции.
Рассмотрим основные виды модуляции гармонического несу-
щего колебания.
3.2. СИГНАЛЫ С АМПЛИТУДНОЙ МОДУЛЯЦИЕЙ
Амплитудная модуляция (AM) - наиболее простой и распро-
страненный вид модуляции. Например, AM применяют в радио-
вещании.
При AM амплитуда несущего колебания изменяется в соот-
ветствии с изменением модулирующего сигнала s(t). В резуль-
тате получаем амплитудно-модулированный сигнал
u(t) = Cz(/)cos((D0Z + ф0 ), (3.2)
где
U(t) = UQ + ks(t). (3.3)
Здесь к - постоянный коэффициент, выбираемый так, чтобы вы-
полнялось условие: U(t} > 0 (амплитуда U(f) не должна при-
нимать отрицательные значения).
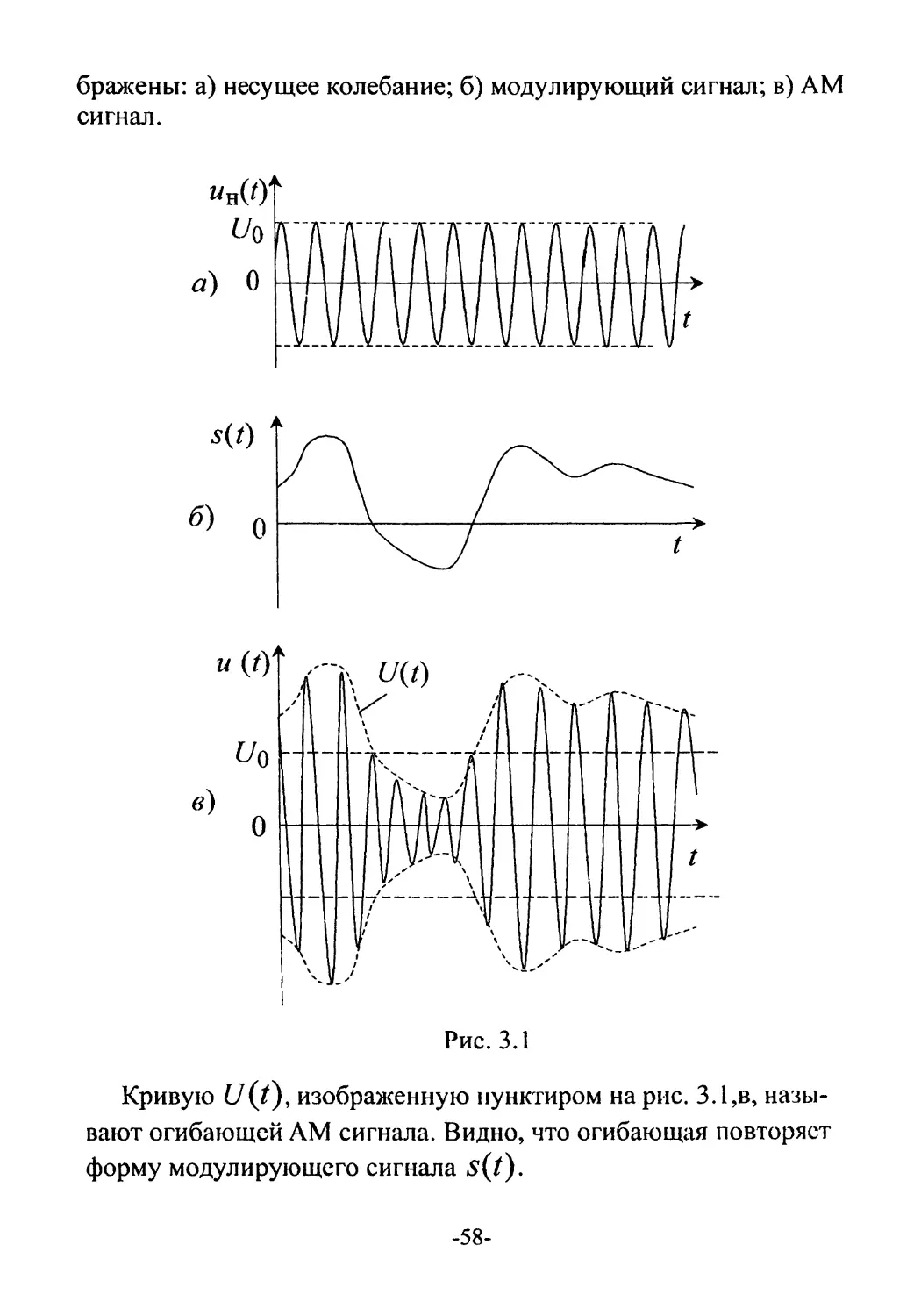
Формирование AM сигнала поясняет рис. 3.1, на котором изо-
-57-
бражены: а) несущее колебание; б) модулирующий сигнал; в) AM
сигнал.
Кривую U(7), изображенную пунктиром на рис. 3.1,в, назы-
вают огибающей AM сигнала. Видно, что огибающая повторяет
форму модулирующего сигнала s(7).
-58-
Для того чтобы огибающая AM сигнала достаточно точно по-
вторяла форму модулирующего сигнала, функция U(t} должна
изменяться медленно по сравнению с COSCDqZ. Это означает, что
несущая частота (Dq должна значительно превышать верхнюю
частоту спектра модулирующего сигнала.
Согласно (3.3) огибающая U(t) изменяется во времени отно-
сительно Uq. Размах колебаний U(t) относительно Uq характе-
ризует глубину модуляции. Для ее оценки вводят коэффициент
модуляции, определяемый как отношение амплитуды модули-
рующего сигнала к амплитуде несущего колебания. Коэффициент
модуляции является основным параметром AM сигналов.
3.2.2. ТОНАЛЬНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
Свойства AM сигналов удобно рассматривать, полагая моду-
лирующий сигнал гармоническим ( рис. 3.2,а ):
s(t) = cosQ/, (3.4)
где Q ~ частота модуляции, причем Q«(Oq. Считается, что
амплитуда сигнала s(/) равна единице. Модуляция гармониче-
ским сигналом звуковой частоты называется тональной.
Подставляя (3.4) в (3.3), запишем
£/(/) = С/о + At/cosQz = t/0(l + McosQ/), (3.5)
где М = Uq — коэффициент модуляции. С учетом (3.5) вы-
ражение (3.2) принимает вид
;/(/) =t/0(l + М cosQz)cos(a>0Z + (р0). (3.6)
Тональный AM сигнал изображен на рис. 3.2,б,в.
Для передачи информации без искажений форма огибающей
должна повторять форму модулирующего сигнала (рис. 3.2,6).
Поэтому необходимо, чтобы М < 1.
-59-
Если М > 1, наблюдается так называемая перемодуляция
(рис. 3.2,в). Здесь форма огибающей перестает повторять форму
модулирующего сигнала, что приводит к искажению передавае-
мой информации.
Спектр тонального AM сигнала. Для того чтобы определить
спектр ДМ сигнала, его нужно представить в виде суммы гармо-
нических колебаний с различными частотами. Используя триго-
нометрическую формулу
COSX COSJ' = [cos(x + у) + cos(x-у)]/2, (3.7)
-60-
преобразуем выражение (3.6) к виду
«(/) = [70COS(00Z +
cos((00 + Q)/ +
UQM /
—— cos(co0 - Q)/.
(3.8)
2
Выражение (3.8) дает спектральное представление тонального
AM сигнала. Здесь каждому слагаемому соответствует одна со-
ставляющая спектра, график которого изображен на рис. 3.3.
Как видно, спектр тонального AM сигнала содержит колеба-
ние на несущей частоте (Од и две составляющие на частотах
(Og + й и (Од - Йе равными амплитудами. Частоты (Од + й и
(Og-Q расположены по обе стороны от (Од, поэтому их назы-
вают боковыми частотами (соответственно верхней боковой и
нижней боковой), а составляющие спектра на этих частотах — бо-
ковыми составляющими.
Ширина полосы частот, занимаемая тональным AM сигналом,
простирается от нижней боковой частоты до верхней боковой
частоты (см. рис.3.3). Разность этих частот определяет ширину
-61-
спектра:
Дсос = (со0 +Q)-(co0 -Q)= 2Q.
Таким образом, ширина спектра тонального AM сигнала равна
удвоенной частоте модуляции.
Энергетические характеристики тонального AM сигнала. В
соответствии с формулой (2.10) средняя мощность AM сигнала
определяется как сумма средних мощностей его спектральных
составляющих:
Р = Uq /2+М-/8 + U^M2 /8 = Д + Рб,
где Ро = Uq /2 - мощность несущего колебания,
Pq ~ Uq М - мощность двух боковых составляющих.
Отмстим, что всю информацию несут боковые составляющие,
несущая не несет никакой информации. Отношение
Рй1Р0 = Мг/2
характеризует долю мощности боковых составляющих. Посколь-
ку М < 1 , ТО Р§/ Pq <12.
Таким образом, можно отметить неэффективность использо-
вания мощности передатчиков при передаче AM сигналов: толь-
ко незначительная часть мощности используется для передачи
информации. Основная часть мощности расходуется для переда-
чи несущего колебания. Эта особенность AM сигналов является
их существенным недостатком. Поэтому часто используются AM
сигналы, в которых несущее колебание подавляется, а передают-
ся только боковые составляющие. Такой вид AM называют ба-
лансной модуляцией.
Отметим еще один недостаток AM сигналов: низкую помехо-
-62-
устойчивость. Это связано с тем, что передаваемая информация
содержится в амплитуде сигнала, на которую прежде всего и
воздействуют помехи.
3.2.3. МНОГОТОНАЛЬНАЯ АМПЛИТУДНАЯ МОДУЛЯЦИЯ
Обычно модулирующий сигнал имеет сложный спектральный
состав (рис. 3.4,а) и может быть представлен в виде:
N
•*(/)= cos(Q„/ + 0„).
/7 = 1
(3.9)
Здесь Sn и 0Я - амплитуды и начальные фазы гармонических со-
-63-
ставляющих модулирующего сигнала; - частоты модуляции,
причем Q| <Q2 < ... « ^0- аналогии с (3.6) за-
пишем
м(0 = Uq
N
1+ X^//Cos(Q/7/ + 0;;)
/7=1
cos((00/ + (po), (3.10)
где коэффициенты Мп —ks^/U^, их называют парциальными
(частичными) коэффициентами модуляции.
Спектральное разложение многотонального AM сигнала (3.10)
проводится также, как и для тонального AM сигнала. В результа-
те выражение (3.10) при фо=О представляется так:
N и М
u(t) = t/0COS(O0/ + £ —-—- cos[(co0 + )/ + ]+
/7=1 2
А И. Д/
+ Z " cos[(<o0 - V - 0„ J. (3.11)
А7=1
Выражение (3.11) отличается от (3.8) лишь тем, что вместо
двух боковых составляющих имеем боковые полосы, располо-
женные по обе стороны от несущей, как показано на рис. 3.4,6.
Верхняя боковая полоса имеет спектр, который точно повторяет
спектр модулирующего сигнала, а нижняя боковая полоса явля-
ется зеркальной копией верхней. Каждая из боковых полос со-
держит одну и ту же информацию, что свидетельствует об избы-
точности передачи информации двумя боковыми полосами. Ши-
рина спектра равна удвоенной наибольшей частоте модуляции
Асос = 2£1Л/.
Отметим, что полосу частот, занимаемую AM сигналом, мож-
но уменьшить вдвое, если для передачи сообщения использовать
только одну из боковых полос - верхнюю или нижнюю. Такой
-64-
вид амплитудной модуляции называют однополосной. При одно-
полосной передаче в заданном диапазоне частот можно располо-
жить вдвое большее число информационных каналов, чем при
двухполосной передаче.
В радиовещании для удовлетворительного воспроизведения
речи и музыки достаточно, чтобы максимальная частота модуля-
ции Fm —£1т/2т1 нс превышала 4,5 кГц. В этом случае при
двухполосной модуляции каждая радиостанция занимает полосу
Д/с = 2F/?/ — 9 кГц. При такой относительно малой полосе час-
тот можно не использовать однополосную модуляцию.
В телевидении максимальной частотой модуляции считают
6,5 МГц и при двухполосной AM требуется большая полоса
Л/г — 13 МГц. Поэтому в телевидении используют однополос-
ную модуляцию.
Эффективность использования мощности передатчика можно
повысить, осуществив при однополосной модуляции частичное
или полное подавление несущего колебания.
J3.2.4. РАДИОИМПУЛЬСЫ
В радиотехнике важную роль играют импульсные сигналы
(импульсы), которые существуют лишь в пределах конечного от-
резка времени. При этом различают видеоимпульсы (рис.3.5,а) и
радиоимпульсы (рис.3.5,б)
-65-
Если s(f)- видеоимпульс, то ему соответствует радиоимпульс
w(/) = t/(/)cos(cD0/ + ф0), где U(t)= ks(t).
Таким образом, радиоимпульс можно рассматривать как AM сиг-
нал, огибающая которого имеет форму видеоимпульса.
Спектральная плотность радиоимпульса. Пусть 5р((Х)) -
спектральная плотность радиоимпульса, а S(cd) - спектральная
плотность видеоимпульса (огибающей). Установим связь между
5р(со) и
Для этого представим радиоимпульс в виде
w(/)=t7(/)cosco0/ = | W +|t/(/>"ROo/. (3.12)
Применяя к (3.12) преобразование Фурье и учитывая (2.29), по-
лучим для спектральной плотности радиоимпульса следующее
выражение:
5Р (®) = | S(o>- «о)+ |*S'(co+со0). (3.13)
Слагаемые в (3.13) описывают спектральную плотность видео-
импульса, смещенную из области частоты CD = О в области
CD = CDq (первое слагаемое) и CD = — CDq (второе слагаемое).
Если частота CDq достаточна велика, чтобы можно было пре-
небречь взаимным влиянием слагаемых в (3.13), то спектр радио-
импульса находится простым переносом спектра видеоимпульса
в область около + CDq, как показано на рис. 3.6. При этом в об-
ласти положительных (физических) частот
5'р(со) = ^5'((о-со()), со>0. (3.14)
-66-
В данном случае ширина спектра радиоимпульса равна удво-
енной ширине спектра видеоимпульса (см. рис.3.6).
Прямоугольный радиоимпульс и его спектр. В качестве при-
мера рассмотрим радиоимпульс с прямоугольной огибающей
(рис. 3.7).
Подставив выражение спектральной плотности прямоугольно-
го видеоимпульса (2.16) в формулу (3.13), находим спектральную
плотность прямоугольного радиоимпульса
Sp (w)=|t7THsinc[(w-(Ol))TH/2]+
+ itAHsinc[((o-(o0)TH/2]. (3.15)
-67-
Если несущая частота COq »2тс/ти, то можно пренебречь
взаимным влиянием слагаемых в (3.15) и считать, что в области
положительных частот
5р((о) = ^ти81пс[((о-(о0)ти/2], а)>0.
(3.16)
Иллюстрацией служит рис. 3.8, на котором изображены спектры
модулирующего видеоимпульса (а) и радиоимпульса (б).
Ширину спектра прямоугольного радиоимпульса можно при-
ближенно определить как полосу частот, занимаемую централь-
ным лепестком спектра (см. рис. 3.8,6):
Л(Ос=4л/ти. (3.17)
Таким образом, ширина спектра радиоимпульса равна удвоен-
ному значению ширины спектра видеоимпульса.
Из рассмотрения различных видов AM сигналов следует' важ-
ный вывод: ширина спектра AM сигнала равна удвоенному зна-
чению наивысшей частоты в спектре модулирующего низкочас-
тотного сигнала.
-68-
3.3. СИГНАЛЫ С УГЛОВОЙ МОДУЛЯЦИЕЙ
3.3.1. ОБЩАЯ ХАРАКТЕРИСТИКА
Другим распространенным видом модуляции является угловая
модуляция (УМ). Благодаря высокой помехоустойчивости УМ
применяют в звуковом сопровождении телевизионного вещания,
в системах радиосвязи, радиотелеметрии, радиоуправления, не-
которых системах радионавигации и радиолокации.
При угловой модуляции под воздействием модулирующего
-69-
сигнала изменяется фазовый угол гармонического нссУщего K0J
лебания. Амплитуда колебания остается постоянно Л. Примерный
вид сигнала с угловой модуляцией показан на рис. 3.9.
Сигнал с угловой модуляцией описывается вырая.экеНием
u(t) = t/0COs[(D0/ + ф(/ )] = (/0COS<t>(/ ). •1
Его мгновенная частота со(/) определяется как производная от
полной фазы Ф(/) по времени:
= <3.19)
’ dt 0 dt
Различают два вида угловой модуляции - фазсовУю и часгот-
ную, которые отличаются друг от друга весьма нсз -^амительно.
Фазовая модуляция. При фазовой модуляции (Ф^) модули-
рующий сигнал s(t) воздействует непосредственн о hia ФазУ ФМЛ
При этом
<рИ=Ш <3-2»>
где к - коэффициент пропорциональности. Под^1авив (3.20) в
(3.18), получим выражение для фазомодулированы^эГ0 сигнала
-70-
Z/(/)= t/0COS[(D0/ + fo(/)]. (3.21)
Заметим, что при ФМ изменяется и мгновенная частота сигнала
(3.21):
С0(/) = (0й+^^й. (3.22)
dl
Частотная модуляция. При частотной модуляции (ЧМ) моду-
лирующий сигнал воздействует непосредственно на мгновенную
частоту:
со(/)= со0 + ks(t). (3.23)
Используя формулу (3.19), найдем фазу
t
ф(/)= к\ s(tyit . (3.24)
О
Подставив (3.24) в (3.18), получим выражение для частотно-
модулированного сигнала
z/(/) = (70cos
/
+ k\s(t)dt
(3.25)
о
3.3.2. ТОНАЛЬНАЯ УГЛОВАЯ МОДУЛЯЦИЯ
Свойства и характеристики сигналов с угловой модуляцией
удобно рассмотреть на примере тональной угловой модуляции,
т.е. при гармоническом модулирующем сигнале (3.4).
В случае тональной угловой модуляции выражение
u(t) = + msinQ/) (3.26)
описывает как ФМ, так и ЧМ сигнал, поскольку производная и
-71-
интеграл от синуса отличаются лишь начальной фазой.
Фаза ф(/ ) в (3.26) изменяется по синусоидальному закону
<p(z)=wsinQz. (3.27)
Величину т, определяющую максимальное приращение фазы в
результате модуляции, называют индексом угловой модуляции.
Используя формулу (3.19), найдем мгновенную частоту
со(/) = со0 + mQcosQ/ = со0 + coAcosQ/, (3.28)
где величина С0д — т£1 характеризует максимальное отклонение
частоты от несущей CDq, ее называют девиацией частоты.
Спектр сигнала с тональной угловой модуляцией. Для того
чтобы определить спектр сигнала, выражение (3.26) надо разло-
жить в ряд по гармоническим составляющим. Заменив в (3.26)
косинус суммы двух углов по известной тригонометрической
формуле, запишем
«(/)= t/0cos(wsinQz)cosa)0Z -
-t/0sin(wsinQz)smco0Z. (3.29)
Воспользуемся следующими соотношениями:
cos(wsinQz) = J0(w)+2J2(w)cos2Q/ + ... ,
= 2JX (w)sinQZ + 2./3 (w)sin3Qz +....
Здесь Jn (m) - функция Бесселя первого рода П -го порядка от
аргумента т (рис. 3.10). Подставив эти соотношения в (3.29) и
выполнив необходимые преобразования, в результате получим
-72-
u(t) = U 0J 0(m)cos(O0/ + ^UqJ „(m)cos((i)Q +n£l)t +
n-\
+ U0Jn(m)cos((£>Q ~nQ,)t. (3.30)
n=\
Выражение (3.30) дает спектральное представление сигнала с
тональной угловой модуляцией. Оно показывает, что модулиро-
ванный сигнал содержит бесконечное число гармонических со-
ставляющих с частотами (Од + М1 и (Од — /7 £2, п = 1,2,..., кото-
рые образуют две боковые полосы, расположенные по обе сторо-
ны от несущей (Од. Амплитуды составляющих спектра равны
4 =ЦЛ(>и)-
-73-
Для вычисления значений Ап необходимо знание функций
Бесселя Jn(ni) при различных значениях П и т. Их можно най-
ти в математических справочниках. На рис. 3.10 приведены гра-
фики функций Бесселя при П = 0,1,...,6 и 0 < т < 9.
Строя по формуле (3.30) график амплитудного спектра сигна-
ла с тональной угловой модуляцией, следует обратить внимание
на равенство амплитуд верхних и соответствующих им нижних
боковых составляющих, а также на симметрию расположения
этих составляющих относительно несущего колебания (рис.3.11).
-74-
Примеры построенных по формуле (3.30) спектров, приведен-
ных на рис. 3.11, показывают, что амплитудный спектр симмет-
ричен относительно несущей, но его форма зависит от значения
индекса модуляции. Видно, что структура спектра является весь-
ма сложной.
Число составляющих в (3.30) бесконечно велико. Однако их
амплитуды с ростом номера П уменьшаются, как это видно из
графиков функций J п(т). Обычно считают, что можно пренеб-
речь всеми составляющими, номера которых п > т 4-1.
Практическая ширина спектра определяется как
Д(0с = 2(m + 1)Q.
Рассмотрим два крайних случая, когда т «1 и т » 1.
В первом случае ширина спектра равна Дсос =2Q, а во втором
Д(ОС = 2mQ, т.е. в т раз больше. Поэтому угловую модуляцию
при т «1 называют узкополосной, а при 777» 1 - широкопо-
лосной.
При значении /77 «1 можно принять, что
J0(/7?)~l; J}(m)~m/2; п>2.
Тогда выражение (3.30) сводится к следующему:
м(/) = (70cosco0/ + ууcos(co0 + - —у7 cos(to0 - Q)/.
Это выражение отличается от (3.8) лишь противоположной
фазой составляющей па частоте COq — Q. При этом амплитудный
спектр имеет такой же вид, как на рис.3.3, но амплитуды боковых
составляющих при /77 «1 малы по сравнению с амплитудой не-
сущей.
Приведенный анализ показывает, что даже в простейшем слу-
чае тональной угловой модуляции спектр оказывается сложным и
-75-
широким. Кроме того, при угловой модуляции не происходит
простого переноса спектра модулирующего сигнала в область не-
сущей (00, как это было при амплитудной модуляции.
Энергетические характеристики сигнала с угловой модуляци-
ей. Средняя мощность сигнала с угловой модуляцией равна сум-
ме средних мощностей его спектральных составляющих. Она
может быть определена из (3.30) как
г/2
Р = -^-[J02(w)+ 2J2 (m)+ 2 J2 (m)+...]. (3.31)
Воспользовавшись известной формулой для функций Бесселя,
согласно которой сумма в квадратных скобках равна единице, из
(3.31) имеем
Р = иЦ2 = Ра.
Таким образом, средняя мощность сигнала с угловой модуля-
цией равна средней мощности несущего колебания.
Сравнение сигналов при УМ и AM. Для передачи сигналов с
угловой модуляцией требуется значительно большая полоса час-
тот, чем при амплитудной модуляции. Например, при передаче
звука в ЧМ радиовещании используется индекс модуляции
т > 10. При максимальной частоте модуляции Fm =4,5 кГц
получаем, что ЧМ сигнал занимает полосу частот
= 2^/^ = 90 кГц, что в 10 раз больше полосы частот, за-
нимаемой AM сигналом. В этом существенный недостаток дан-
ных сигналов.
Следует отмстить важное преимущество сигналов с угловой
модуляцией перед AM сигналами: эти сигналы более помехо-
устойчивы. Поэтому применение ЧМ в радиовещании обеспечи-
вает лучшее качество звучания. Заметим, что для повышения по-
мехоустойчивости сигналов с угловой модуляцией необходимо
-76-
использовать эти сигналы с большим значением индекса модуля-
ции.
Известно также, что сигналы с угловой модуляцией обеспечи-
вают более высокие энергетические характеристики, чем AM
сигналы.
3.4. СИГНАЛЫ С ОБОБЩЕННОЙ МОДУЛЯЦИЕЙ
На практике часто применяются сложные сигналы с обобщен-
ной (одновременной амплитудной и угловой) модуляцией. Это
могут быть АМ-ФМ или АМ-ЧМ сигналы. Анализ таких сигна-
лов существенно упрощается, если ввести понятие комплексной
огибающей.
Колпгчекспая огибающая сигнала. Сигнал вида (3.1) можно
представить в комплексной форме
w(/)=Re[tf(/>w], (3.32)
где
;?(/)=(з.зз)
Функцию £/(/) называют комплексной огибающей сигнала (3.1).
Комплексная огибающая содержит всю информацию, заложен-
ную в сигнале (3.1) в результате как амплитудной, так и угловой
модуляции.
Следует отметить, что запись (3.32) возможна, если функция
U(t) изменяется медленно по сравнению с £Z0)°Z, т.е. для узко-
полосных сигналов. Заметим, что узкополосные сигналы пред-
ставляют широкий класс сигналов, которые применяются в ра-
диотехнике.
Спектральная плотность комплексной огибающей. Введем в
рассмотрение спектральную плотность комплексной огибающей:
-77-
(7(co) = i(Mdt. (3.34)
—оо
Так как комплексная огибающая U(t) определяется модулирую-
щим сигналом, то спектр (/(со) расположен в области низких
частот.
Установим связь между спектрами модулированного сигнала
и его комплексной огибающей.
Спектральную плотность модулированного сигнала можно
найти, применяя к (3.32) преобразование Фурье:
5(со)= jRe[tf(/>/COo/] е~’ш'dt. (3.35)
—оо
Для комплексной величины z = U(tсправедливо следую-
щее равенство:
Rez = (c + /y2, (3.36)
с учетом которого выражение (3.35) может быть представлено в
виде:
s(o>)= 1 л + 3 ’[u^tY^'^'dt.
—co —co
Отсюда следует соотношение, устанавливающее связь между
спектральными плотностями сигнала и его комплексной оги-
бающей:
S(w)= ^0 (со - (00 )+ -^0* (- ю - °)О )• (3.37)
Таким образом, для того чтобы определить спектральную
плотность сигнала вида (3.1), достаточно найти спектральную
-78-
плотность его комплексной огибающей и осуществить перенос ее
из области частоты (0 = 0 в область (0= (Од и (0=—(Од. При-
чем при (О<0 выполняется также операция комплексного со-
пряжения.
Допустим, что спектр U ((О) ограничен максимальной часто-
той (0w. При условии узкополосности ((Ow « (Од) взаимным
влиянием слагаемых в (3.37) можно пренебречь. Тогда в области
положительных частот имеем
S (со) = —О (ср - со0 ), со > 0.
2
(3.38)
При этом ширина спектра 5((0) будет равна
Д(0с = 2QW.
(3.39)
Радиоимпульс с частотной модуляцией. Рассмотрим в качест-
ве примера сигнал с угловой модуляцией, который существует
лишь в пределах конечного отрезка времени:
u(t) = C/0cos(co0/ + msinQz), -ти/2 < t < ти/2.
Такой сигнал можно рассматривать как прямоугольный радиоим-
пульс длительностью Ти, частота которого изменяется в соответ-
ствии с (3.28).
Комплексная огибающая данного сигнала имеет вид
U(d = Ue”nsm£lt, -ти/2</<ти/2. (3.40)
Найдем спектральную плотность комплексной огибающей.
Подставляя (3.40) в (3.34), запишем
Ти “ .
U(a>) = U f e"»s'n£i'e-'“'^.
(3.41)
-79-
Воспользуемся известным разложением по функциям Бесселя:
(3.42)
П-—©о
Подставив (3.42) в (3.41), получим интегралы вида
ти/2
J = 2ти8шс[(со-«0)ти/2]. (3.43)
“”ТИ 2
Таким образом, вычисление С7(СО) по формуле (3.41) приводит к
следующему выражению:
{7(со)=2{Ли £ У„(/и)зтс[(со-нН)ти/2]. (3.44)
/7=—оо
Выражение (3.44) представляет спектральную плотное»}
U (со) в виде последовательности спектральных плотное ! ей
(2.16), имеющих весовые коэффициенты Jп(т) и сдвинутых
одна относительно другой на Q.
По формуле (3.38) находим спектральную плотность радио-
импульса с частотной модуляцией
5(ю)=£/ти £ ,7/г (w)sinc[(co-со0 -нО)ти/2],
/?=—оо
СО > 0 . (3.45)
Таким образом, ограничение сигнала с угловой модуляцией во
времени приводит к существенному усложнению его спектра.
-80-
3.5. МАНИПУЛИРОВАННЫЕ СИГНАЛЫ
3.5.1. ОПИСАНИЕ И СВОЙСТВА МАНИПУЛИРОВАННЫХ
СИГНАЛОВ
Манипуляция - это вид модуляции, при котором модулируе-
мый параметр сигнала изменяется не плавно, а скачкообразно со-
ответственно скачкообразному изменению модулирующего сиг-
нала. Таким модулирующим сигналом может быть, например,
цифровой сигнал, отображающий двоичный код (см. рис. 1.2).
Полученный в результате манипуляции сигнал называют ма-
нипулированным.
В зависимости от того, какой из трех параметров (амплитуда,
фаза или частота) гармонического несущего колебания изменяет-
ся, различают три основных вида манипуляции: амплитудную
(АМн), фазовую (ФМн) и частотную (ЧМн).
На рис. 3.12 изображены временная диаграмма модулирующе-
го сигнала (а) и временные диаграммы манипулированных сигна-
лов.
Модулирующий сигнал принимает только два значения:
Vj(/)n s2 (/), которые в случае цифрового сигнала соответст-
вуют двум символам двоичного кода. При этом манипулирован-
ный сигнал также будет принимать только два значения: (t ) и
и 2 (f У Сигналы Wj (z) и и 2 (z )имеют одинаковую длитель-
ность.
При амплитудной манипуляции (рис.3.12,6) имеем
Z/](/)= t7cos(tt)0/ + (p0); U2(f) = 0. (3.46)
При фазовой манипуляции сигналы W] (/) и г/2 (/) различа-
ются лишь начальной фазой. Например, на рис.3.12,в фаза меня-
ется на Я при каждом переходе от (Z ) к и 2 (z) или наобо-
рот. В этом случае
И| (/) = (7cos(co0/ + ф0 ); M2(z)=-(7cos((D0/ + (p0), (3-47)
-81-
т.е. имеем противоположные сигналы. Предполагается, что от-
ношение длительности Ти каждого сигнала к периоду несущего
колебания Tq = 2я/COq является целым числом.
-82-
При частотной манипуляции (рис.3.12,г) сигналы их (/) и
г/ э 0 ) имеют различные частоты:
их (/) = t/cos(cD|/ + (р0 ); U2 (/) = £/cOs(0)2/ + ф0 ). (3.48)
Здесь CD] = СОО — (Од, (D2 = (О0 + (Од, где (Од - девиация часто-
ты. Обычно (Од выбирают так, чтобы спектры сигналов их (/) и
г/ о (/ ) мало перекрывались.
3.5.2. СПЕКТРЫ МАНИПУЛИРОВАННЫХ СИГНАЛОВ
Рассмотрим особенности спектров манипулированных сигна-
лов. На практике знания точной структуры спектра обычно не
требуется, достаточно определить лишь ширину спектра.
Сигналы и । (/ ) и и 2 0 ) ” это прямоугольные радиоимпуль-
сы одинаковой длительности, отличающиеся друг от друга зна-
чениями амплитуд (АМн), начальных фаз (ФМн) или частот
(ЧМн) гармонического несущего колебания.
Как известно (см. § 3.2.4), спектры радиоимпульсов хотя и
бесконечны теоретически, но все же сосредоточены около несу-
щей частоты (см. рис.3.8,б).
При амплитудной или фазовой манипуляции в состав манипу-
лированных сигналов входят радиоимпульсы с несущей частотой
(О0. Поэтому спектры АМн и ФМн сигналов сосредоточены
около частоты (Dq. Ширину их спектра обычно определяют как
(3.17).
При частотной манипуляции радиоимпульсы их (/) и (/)
имеют различные несущие частоты: CD] и (02. Спектр первого
радиоимпульса сосредоточен около частоты СО], а второго - око-
ло частоты (02. Спектр ЧМн сигнала образуется путем наложе-
ния этих спектров.
Пример определения спектра ЧМн сигнала. Возьмем в качест-
-83-
ве примера ЧМн сигнал, составленный из двух радиоимпульсов
(рис. 3.13,а).
Такой сигнал можно описать выражением
u(t}= Щ (/)+ u2(t - ти ). (3.49)
Первому слагаемому в (3.49) соответствует радиоимпульс на рис.
3.13,6, второму слагаемому - радиоимпульс на рис. 3.13,в.
Рис. 3.13
Применяя к (3.49) преобразование Фурье и учитывая (2.25),
(2.26), находим спектральную плотность данного сигнала
S((o)=5i(o))+1S'2(w>?"/WTm.
(3.50)
-84-
Здесь (б)) и S2 (со) - спектральные плотности радиоимпуль-
сов //](/) и W?(/) соответственно; они определяются анало-
гично (3.16):
5,((о) =
yt7THsinC [(со - со1 )ти /2], С0> 0;
(3.51)
52(со) = ^-t/THsinc [(со — со2 )ти /2]. со>0. (3.52)
На рис. 3.14 изображен амплитудный спектр |5'(со)|, постро-
енный в соответствии с выражениями (3.50) - (3.52). Видно, что
этот спектр является результатом наложения спектров (3.51) и
(3.52). Чем больше разность частот СО2 — COj = 2С0д, тем меньше
перекрываются эти спектры.
<0| «2 (0в ®
г Дсо^ п
Рис. 3.14
Ширину спектра ЧМн сигнала приближенно определяют как
полосу частот, занимаемую двумя главными лепестками (см.
рис. 3.14). Поскольку верхняя СОВ и нижняя С0п частоты равны
сов = со2 + 2к/ти , сон = СО] -2д/ти,
то имеем
-85-
Дсос = (Ов -(Он = (02 -со, +4л/ти = 2(0д + 4к/ти.
Таким образом, при любом виде манипуляции ширина спектра
манипулированного сигнала обратно пропорциональна величине
Ти.
Заметим, что при передаче цифрового сигнала Ти - это дли-
тельность посылки одного символа двоичного кода. Частоту
= 1/ти называют тактовой частотой. С ней связано такое по-
нятие, как скорость передачи цифровой информации, под кото-
рой понимается число переданных двоичных символов (бит) в
секунду (бит/с). Например, Д. = 1 кГц означает, что скорость
передачи двоичных символов равна 1000 бит/с = 1 кбит/с, т.с. за
одну секунду передается 1000 двоичных символов.
Следовательно, чем меньше длительность единичного элемен-
та (радиоимпульса) манипулированного сигнала, тем выше ско-
рость передачи цифровой информации. Однако увеличение ско-
рости передачи информации приводит к расширению спектра
манипулированного сигнала.
Наибольшее применение нашли ФМн и ЧМн сигналы, так как
фазовая и частотная манипуляции обеспечивают лучшую поме-
хозащищенность передачи информации, чем амплитудная мани-
пуляция.
3.6. АНАЛИТИЧЕСКИЙ СИГНАЛ
И ЕГО ПРИМЕНЕНИЕ
3.6.1. АНАЛИТИЧЕСКИЙ СИГНАЛ
Для многих исследований бывает полезно использовать ком-
плексное представление сигналов.
Например, комплексное представление гармонического коле-
бания дает формула Эйлера:
eoso)/ = (e'0)/ +e-/ow)/2.
-86-
Такое представление позволяет использовать методы теории
функций комплексного переменного, что значительно упрощает
расчеты.
Рассмотрим способ, позволяющий получить комплексное
представление произвольного сигнала.
Аналогично формуле Эйлера представим сигнал и (t) в виде
суммы двух составляющих, одна из которых содержит только
положительные, а другая только отрицательные частоты. Заме-
тим, что отрицательная частота - только математическое поня-
тие.
Для произвольного сигнала, имеющего спектральную плот-
ность S(co), запишем
1
u{t) = — JS(co) eiwtd(d=
2 л__
1 0 • 1 00
= — J^STcd) eiaitd(i)+—J5(co) d(&. (3.53)
2я_оо 2 л о
Выражение (3.53) можно записать и так:
(3.54)
где
z(/)= ei<atda,
л0
(3.55)
z*(/)=- j£(co) el(atd(i)=-/£(-со) e l(Otd&. (3.56)
Л-оо 71 0
Таким образом, выражение (3.54) представляет сигнал w(z) в
-87-
виде суммы сигнала z(t), содержащего только положительные
частоты, и комплексно-сопряженного с ним сигнала Z(/), со-
держащего только отрицательные частоты.
Сигнал z(/), определяемый формулой (3.55), называют анали-
тическим сигналом, соответствующим исходному сигналу z/(/).
Из сравнения формул (3.36) и (3.54) следует, что действитель-
ная часть аналитического сигнала представляет исходный сигнал:
u(t)= Re[z(/)]. (3.57)
Мнимую часть аналитического сигнала
wc(z)=Im[z(/)] (3.58)
называют сопряженным сигналом по отношению к исходному
сигналу u(t). При этом аналитический сигнал определяется как
z(t) = u(t)+iujt). (3.59)
Аналитический сигнал является обобщением комплексного
представления гармонического колебания на случай сигнала об-
щего вида.
Пример вычисления аналитического сигнала. Пусть исходный
сигнал z/(z) задан спектральной плотностью (рис. 3.15,а):
S((o)=SQ при — со,„ <(0<(0w.
Подставляя значение 5(С0) в формулу (3.55), находим анали-
тический сигнал:
С С / . \
z(z)=^ J е'ш'Жо = ^Це'“>«'-|)
тс 0 iTCt
или
-88-
£
z(/) = — [sina)w/ + z(1 - coscow/)].
nt
Рис. 3.15
Сравнивая это выражение с (3.59) видим, что
u(t) =—sinco^j/ = ^og>/w sinc(cD„/).
nt n
-89-
WC (0 = ~ 0 - cosov) = sin2 ((O„//2).
Tit nt
Графики u(t) и Z/c(/) изображены на рис.3.15,6.
Преобразования Гильберта. Однако чаще всего для определе-
ния аналитического сигнала используют следующие соотноше-
ния:
«с(0 =
1 7 «(т)
, 7 X 1 7 Wc(T) J
б/Т; «(/)=— Г (Ут.
Я 7 /-Т
—оо
(3.60)
Формулы (3.60) известны в математике как преобразования
Гильберта. При этом Z7C(/) называют сигналом, сопряженным по
Гильберту с u(t\
В частности, из формул (3.60) следует:
1) u(t)- cos со/, ис (/) = sinco/;
2) z/(/) = sin со/, uc (/) = -cosco/.
Таким образом, для того чтобы получить преобразование
Гильберта гармонического колебания, нужно сместить это коле-
бание на четверть периода в сторону запаздывания.
3.6.2. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ
АНАЛИТИЧЕСКОГО СИГНАЛА
На основании формулы (2.12) спектральная плотность анали-
тического сигнала
Sz(a>) = J dt.
—оо
В то же время спектральную плотность можно найти как преоб-
разование Фурье от (3.59):
-90-
Sz (co) = 5 (co)+ iSc (co),
(3.61)
где SC(CO) - спектральная плотность сопряженного сигнала.
Анализ формулы (3.55) показывает, что
2S(co)
О при со < 0 .
S;(co) =
(3.62)
Таким образом, спектральная плотность аналитического сиг-
нала существует лишь в области положительных частот, где она
равна удвоенному значению спектральной плотности исходного
сигнала.
Равенство (3.62) будет выполняться только при условии, что
М<») =
при СО > 0 ,
iS (со) при СО < 0 .
(3.63)
Из (3.63) следует, что сопряженный сигнал можно получить с
помощью так называемого квадратурного фильтра. На вход этого
фильтра подают исходный сигнал u(t\ Фильтр изменяет фазы
всех спектральных составляющих на —71/2 при СО>0 и на 71/2
при СО<0. В результате на выходе фильтра получаем сопряжен-
ный сигнал.
3.6.3. ОПРЕДЕЛЕНИЕ ОГИБАЮЩЕЙ И ФАЗЫ
УЗКОПОЛОСНОГО СИГНАЛА
Пусть имеется произвольный сигнал #(/), который необхо-
димо представить в следующем виде:
w(/)= t/(z)c0sO(/)= t/(/)cos[CD0/ +Ср(/)]. (3.64)
Можно показать, что огибающая C/(z) произвольного узконо-
-91-
лосного сигнала w(/) определяется как модуль аналитического
сигнала:
t/(/) = Jw2(z)+w2(/). (3.65)
Полная фаза узкополосного сигнала u(t) равна аргументу анали-
тического сигнала:
Ф(/) = arctg[z/c(z)/w(z)], (3.66)
а его мгновенная частота есть производная полной фазы по вре-
мени:
/ х d uAt)
^t)=- arctg
dt ult 1
?/'(/) w(/)-w'(/) Wc(z)
(3.67)
Определив частоту CQj как среднее значение функции (3.67),
можно записать ф(/)=(Ц)/+(р(/), где выделено линейное слагае-
мое.
Таким образом, для того чтобы произвольный узкополосный
сигнал w(/) представить в форме (3.64), необходимо сначала най-
ти функцию Wc(/), сопряженную с ним по Гильберту, а затем по
формулам (3.65)—(3.67) определить его огибающую, полную фазу
и мгновенную частоту.
Огибающая сигнала с однополосной AM. Поясним применение
преобразования Гильберта на примере определения огибающей
однополосного AM сигнала. Пусть в тональном AM сигнале (3.8)
отсутствует составляющая с нижней боковой частотой:
w(z)=t/0cosa)0/ + cos(tt)0 + Q)/.
2,
-92-
Изменив фазы гармонических составляющих на Тс/2 в сторону
запаздывания, получим сопряженный сигнал
wc(/) = t/os inco^z +
Подставив эти выражения в формулу (3.64), находим огибающую
u(t) = ujl + М2/а + Л/cosQ/.
(3.68)
Форма огибающей (3.68) при М = 1 показана на рис.3.16, для
сравнения штриховой линией изображена огибающая (3.5).
Как видно, огибающая одпополоспого AM сигнала не повто-
ряет форму гармонического модулирующего сигнала, что свиде-
тельствует о наличии искажения при передаче информации с по-
мощью однополосной AM.
-93-
4. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ
ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ
4.1. КЛАССИФИКАЦИЯ
РАДИОТЕХНИЧЕСКИХ ЦЕПЕЙ
Передача информации посредством сигналов сопровождается
различными преобразованиями этих сигналов (см.§1.3). В радио-
технике преобразования электрических сигналов осуществляются
с помощью радиотехнических цепей.
Радиотехнической цепью называют электрическую цепь,
предназначенную для выполнения каких-либо операций над
электрическими сигналами. Иными словами, радиотехническую
цепь можно рассматривать как совокупность отдельных элемен-
тов, связанных между собой таким образом, чтобы обеспечить
передачу сигналов в определенном направлении.
Анализ прохождения сигналов через радиотехнические цепи
сводится к установлению и исследованию зависимости между
сигналом Z/nv(7), поданным на вход цепи, и сигналом Z/KR,V(/),
полученном на ее выходе. В общем виде такую зависимость
можно описать с помощью оператора L:
WBb.x(O= i[wBX(O]- (4-1)
Запись (4.1) означает, что выходной сигнал есть результат воз-
действия оператора L на входной сигнал. Это схематически по-
казано на рис. 4.1. Конкретный вид оператора L определяется
характеристиками цепи.
Рис. 4.1
> ^вых(0
Заметим, что сигнал на входе обычно называют входным
-94-
воздействием, а сигнал на выходе - реакцией или откликом
цепи на данное воздействие.
Радиотехнические цепи, принято разделять на два класса -
линейные и нелинейные, отличающиеся по своим свойствам и
математическому описанию.
Цепь является линейной, если выполняемое ею преобразова-
ние (4.1) обладает следующими свойствами:
>
^[^вх! ^вх21 ^\и вх! ^[^вх2 Ь
L \ки вх ] kL \и вх ],
(4.2)
где к — любое действительное число.
Равенства (4.2) означают, что в линейных цепях может проис-
ходить линейное сложение или суперпозиция нескольких сигна-
лов. Поэтому линейные цепи можно определить как цепи, для ко-
торых справедлив принцип наложения (суперпозиции). Согласно
этому принципу реакция линейной цепи на сумму воздействий
равна сумме реакций от каждого воздействия в отдельности. Этот
принцип, в частности, означает, что в линейных цепях сигнал
можно рассматривать как результат сложения его спектральных
составляющих.
Если условие (4.2) не выполняется, то цепь является нелиней-
ной. Иными словами, к нелинейной цепи принцип наложения не-
применим.
В соответствии с разными свойствами линейных цепей их
разделяют на два подкласса - стационарные и нестационарные.
Линейные стационарные цепи удовлетворяют принципу инва-
риантности во времени:
^вых 'о) ~~ ^[^вх 'о)] (4-3)
при любом значении Это означает, что реакция стационарной
цепи не зависит от момента поступления воздействия.
Линейные нестационарные цепи не удовлетворяют условию
(4.3). Обычно линейные нестационарные цепи выделяют в от-
-95-
дельный класс так называемых параметрических цепей. Это объ-
ясняется тем, что параметрические цепи обладают некоторыми
специфическими свойствами, вследствие чего их применение ог-
раниченно специальными областями.
Поэтому в дальнейшем линейные стационарные цепи будем
называть сокращенно линейными цепями, а линейные нестацио-
нарные - параметрическими.
4.2. ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ
Линейные радиотехнические цепи состоят только из линейных
элементов с постоянными параметрами. По существу это линей-
ные электрические цепи, характеристики и методы анализа кото-
рых известны из курса «Основы теории цепей». Рассмотрим
кратко способы описания линейных цепей, их основные характе-
ристики. Будем называть основными те характеристики цепи, ко-
торые позволяют находить ее реакции для широкого класса воз-
действий.
4.2.1. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ
ЛИНЕЙНОЙ ЦЕПИ
Электрические цепи могут быть классифицированы по раз-
личным признакам, например, в зависимости от вида дифферен-
циального уравнения цепи.
Процессы в линейных цепях описываются линейными диффе-
ренциальными уравнениями с постоянными коэффициентами.
Эти уравнения составляются на основе законов Кирхгофа и зави-
симостей z(w) (Z—гок, и —напряжение) для всех элементов це-
пи.
Для произвольной линейной цепи дифференциальное уравне-
ние имеет следующий вид:
dmuBbK dmu3X „
Z а>”---= ^Ьт ,М\>М2, (4.4)
т=0 ш /я=0 dt
-96-
где ain, bm — постоянные коэффициенты, которые выражают-
ся через параметры элементов цепи. Порядок дифференциального
уравнения М\ характеризует порядок сложности цепи (порядок
цепи). Поскольку входной сигнал i/BX (/) задан, то правая часть
уравнения (4.4) является известной функцией, обозначим ее
j\t). Если 0, то уравнение (4.4) называется однород-
ным, в противном случае - неоднородным.
Для получения единственного решения уравнения (4.4) необ-
ходимо задать начальные условия, определяющие значения
функции WBbIX(/) и всех ее производных при t = 0. Если эти
значения равны нулю, то начальные условия называют нулевыми.
Из курса математики известны общие методы решения линей-
ных дифференциальных уравнений с постоянными коэффициен-
тами.
4.2.2. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
ЛИНЕЙНОЙ ЦЕПИ
Комплексная частотная характеристика //(/(О) представляет
реакцию линейной цепи на единичное гармоническое воздейст-
вие в установившемся режиме:
если = в/0)/ , то Wruiv =//(/СО) ezC0/ .
ЬХ ’ ьььх \ /
г1 IT
Если же Z/BX = U вх в , то
^вых вх £/C0Z вых (4.5)
где U ьх, U вых “комплексные амплитуды входного и выходно-
го сигналов. Из соотношения (4.5) следует, что
//(/СО) — Uвых / U вх • (4.6)
Таким образом, комплексная частотная характеристика це-
-97-
пи описывает частотную зависимость отношения комплексных
амплитуд выходного и входного сигналов. Очевидно, что в дан-
ном случае комплексная частотная характеристика имеет физиче-
ский смысл комплексного коэффициента передачи цепи по на-
пряжению.
Функция принимает комплексные значения и может
быть представлена в виде
H(zw) = H((0)e/(pw(w), (4.7)
где
//((d) = |//(/(о)|; (p/z ((d) = arg (4.8)
Частотную зависимость модуля //(СО) называют амплитудно-
частотной характеристикой (АЧХ) цепи. При постоянной ампли-
туде гармонического колебания на входе (7ВХ и изменении его
частоты АЧХ показывает, как изменяется амплитуда колебания
па выходе. Функцию (СО) определяют как фазочастотпую ха-
рактеристику (ФЧХ) цепи. Она показывает, как изменяется на-
чальная фаза колебания на выходе по отношению к начальной
фазе колебания на входе при изменении частоты входного коле-
бания.
Таким образом, если wBX = COS СО/, то
«вых = ^(CO)COS [(D/ + ф„ (со)]. (4.9)
Отсюда следует, что гармонические составляющие любого сиг-
нала проходят через линейные цепи без изменения формы и час-
тоты. Они претерпевают лишь изменения по амплитуде в соот-
ветствии с //(СО) и сдвиг по фазе в соответствии с фу/ (СО).
В качестве иллюстрации на рис.4.2 и 4.3 показан примерный
вид некоторых типовых частотных характеристик линейных це-
пей, применяемых для передачи сигналов.
-98-
л//(to)
Вид АЧХ //((D) показывает, что линейные цепи обладают
частотной избирательностью (селективностью). Такие цепи про-
пускают на выход лишь те составляющие спектра входного сиг-
нала, частоты которых лежат в пределах полосы пропускания це-
пи. Обычно полоса пропускания определяется как область часто г,
в пределах которой значение Н ((D) составляет не менее 1/^2
от своего максимального значения. По графику //((D) определя-
ем эту область частот: 0 < (D < (0^ (см. рис.4.2),
(0Гр| < (D< (Dpp2 (см- рис.4.3). В первом случае полоса пропус-
кания равна СОГр, а во втором "~((Drp2 ““®гр1)- Заметим, что
на границе полосы пропускания коэффициент передачи по
мощности, равный отношению мощностей выходного и входно-
го колебаний, уменьшается в два раза.
-99-
Цепи, предназначенные для выделения колебаний на одних
частотах и подавления на других, называют фильтрами. АЧХ,
приведенная на рис.4.2, соответствует фильтру нижних частот
(ФНЧ), который пропускает на выход только низкочастотные ко-
лебания. По виду АЧХ на рис.4.3 можно судить, что соответст-
вующая цепь является полосовым фильтром (ПФ), который про-
пускает на выход колебания в определенной полосе частот.
Частотные характеристики могут быть получены расчетным
или опытным путем.
Для произвольной линейной цепи выражение можно
найти из уравнения (4.4). Подставив в (4.4) значения 1/вх и z/BbIX
из (4.5) и выполнив необходимые преобразования, по формуле
(4.6) находим функцию
Л^2
ЖМ- Е М'®)” / Еат0<о)ш (4.10)
т=0 т~0
Характерный вид аргумента объясняется тем, что в (4.10) входят
различные степени выражения ZCO.
Переходя в (4.10) от вещественной частоты (0 к комплексной
частоте р путем формальной замены Z(D на р, получим функ-
цию
М2
Н(.р)-1Ь„рт/ Y«mpm. (4.11)
ли=0 т=0
которую называют операторной характеристикой (операторным
коэффициентом передачи) линейной цепи.
4.2.3. ИМПУЛЬСНАЯ ХАРАКТЕРИСТИКА
ЛИНЕЙНОЙ ЦЕПИ
Импульсная характеристика /z(Z) представляет реакцию
линейной цепи на воздействие единичного импульса 8(/)
при нулевых начальных условиях:
-100-
h(t) = L[S(/)], h{t)~0 при /<0.
(4.12)
Функцию A(Z) можно также ввести как обратное преобразова-
ние Фурье для Н (/СО):
1 °°
/?(/) = — скя. (4.13)
2^-оо
Тогда прямое преобразование Фурье от h(i)\
оо
tf(/co) = jA(z>"/w/f7z.
—оо
(4.14)
Знание/?(/) полностью эквивалентно знанию H(zCO), любая из
этих функций может быть вычислена, если известна другая.
На рис.4.4,а,б показан вид импульсных характеристик, преоб-
разованиями Фурье которых являются частотные характеристи-
ки, приведенные на рис.4.2 и 4.3 соответственно.
Рис.4.4
Видно, что функция /?(/) экспоненциально стремится к нулю
с ростом времени. Это характерно для физически реализуемой
линейной цепи. Иными словами, свидетельствует об ее устойчи-
вости.
-101-
Отметим, что интеграл (4.14) сходится, если выполняется
условие (2.15):
||Л(7)|б7/<оо.
(4.15)
4.3. МЕТОДЫ АНАЛИЗА ПРОХОЖДЕНИЯ
СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ
Анализ прохождения сигналов через линейные цени сводит-
ся к определению реакции цепи Ивых (/) на заданное входное
воздействие WBX(Z). Поскольку существуют различные способы
описания линейных цепей, то возможно применение различных
методов анализа. На практике при исследовании радиотехниче-
ских цепей дифференциальные уравнения используются редко.
Наибольшее применение нашли методы анализа, в основе кото-
рых - использование характеристик цепи и принципа наложения.
4.3.1. СПЕКТРАЛЬНЫЙ МЕТОД
Спектральный (частотный) метод основан на представлении
входного сигнала в виде суммы гармонических составляющих и
использовании частотных характеристик цепи для определения
выходного сигнала.
Допустим, что входной сигнал может быть представлен в виде
WBx(Z)= + (4.16)
Л=1
Анализ прохождения такого сигнала через линейную цепь
проводят путем нахождения реакции цепи на каждую из гармо-
нических составляющих в отдельности с помощью формулы
(4.9) и последующего суммирования этих реакций на основа-
нии принципа наложения. В результате получаем выходной сиг-
нал вида
-102-
N
S^(<o,,)^wcos[a)w/ + 0„+(p7/(a)w)]. (4.17)
77=1
В случае, если входной сигнал является непериодическим, то
его можно представить интегралом Фурье (2.11):
1 00
«,х(')= - 15вх(а»ЛШ.
2п-._
В соответствии с (4.1) выходной сигнал
^вых
(/) = £
1
2л
j5BX((O)ez<o/c/co
(4.18)
На основании принципа наложения линейный оператор L
может быть внесен под знак интеграла, поскольку интеграл есть
предельное значение суммы. Кроме того, следует учесть, что
оператор L действует лишь на величины, зависящие от текущего
времени t, а не от переменной интегрирования СО. Поэтому вы-
ражение (4.18) сводится к следующему:
1 °° Г 1
«,ь.х(О = —
(4.19)
По определению комплексной частотной характеристики:
Це/ю/] = Я(/(0)е/ю/.
Поэтому из (4.19) следует, что выходной сигнал определяется как
«вых 0) = V" J н('«^вх
____________
(4.20)
-103-
Выражение (4.20) запишем в виде
1 °°
^вых (0 ~ J ^вых (®)^ (4.21)
2^
где
^вых (со) = Н(/со)5вх (со). (4.22)
С помощью формулы (4.22) анализ прохождения сигналов че-
рез линейные цепи можно перевести из временной области в час-
тотную.
В теории и практике передачи сигналов описание сигналов и
цепей в частотной области обычно представляет больший инте-
рес, чем их описание во временной области. Именно благодаря
этому понятие спектра приобрело важное практическое значение,
а спектральный метод анализа получил широкое распростране-
ние.
4.3.2. ВРЕМЕННОЙ МЕТОД
Рассмотрим еще один метод анализа прохождения сигналов
через линейные цепи, в основе которого использование импульс-
ной характеристики /?(/).
Учитывая взаимно однозначное соответствие по Фурье:
/?(/) <-> Н[1(й) и ивх (/) <-> 5ВХ (со) ,
на основании (2.34) имеем следующее соответствие:
Н(io) SBX (со) h(t) ® ивк (/).
Поэтому, переводя соотношение (4.22) во временную область,
получаем для выходного сигнала следующее выражение:
^вых (0 wbx(0 '
-104-
которое в подробной записи выглядит так:
оо
"вых 0) = J h(x) "вх - *) dx =
—оо
= J Л(/- л) г/вх (jc) dx.
—оо
(4.23)
Формула (4.23) определяет выходной сигнал как свертку двух
функций - входного сигнала и импульсной характеристики цепи.
Следует отметить, что формулу (4.23) можно получить и дру-
гим путем. Запишем входной сигнал в виде
оо
"вх(0= JwBX(x)8(/-x)<&,
что соответствует его представлению с помощью последо-
вательности 5-импульсов. В соответствии с (4.1) выходной сиг-
нал определяется как
оо
"вых (0 = L J"вх (*) - *) dx =
—оо
= JwBX(.x) Л[б(/ — х)]б/х. (4.24)
—оо
Здесь учтено, что оператор L действует лишь на величины, зави-
сящие от текущего времени t, а не от переменной интегрирования
X. По определению импульсной характеристики:
h(f) = /,[§(?)], h(t -х) = £[8(Z - л:)].
Поэтому из (4.24) следует формула (4.23).
-105-
Для физически реализуемой цепи нижний предел в интеграле
(4.23) может быть заменен на нуль, а верхний предел - на теку-
щее значение:
t
^ВЫХ (О ~ J Л(.х) ^вх(^ “
О
t
= \h(t-x)uRX(x)dx. (4.25)
о
Интеграл (4.25) носит название интеграла наложения. Извест-
но также и другое название - интеграл Дюамеля.
4.4. ПРОХОЖДЕНИЕ ВИДЕОИМПУЛЬСОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ ЦЕПИ
4.4.1. ПОСТАНОВКА ЗАДАЧИ
Применим изложенные методы для анализа прохождения че-
рез линейные цепи видеоимпульсов.
Как известно, видеоимпульсы имеют спектр, сосредоточенный
в области низких частот. Поэтому для передачи таких сигналов
можно использовать лишь те частотно-избирательные цепи, ко-
торые пропускают на выход низкочастотные колебания.
В качестве примера возьмем линейную цепь, комплексная
частотная характеристика которой описывается выражением
//(/со) = = — "-°-....е~;,гс‘еют. (4.26)
1-нои TtW?
где Т—постоянная времени цепи. Из (4.26) получаем для
АЧХ и ФЧХ цепи следующие выражения:
Н (со) = , ф// (СО) = -arctg СОТ, (4.27)
71 +со т“
-106-
их вид показан на рис.4.2.
Полосу пропускания цепи определяет частота С0гр, на кото-
рой значение Н((д) уменьшается до уровня 7/q/V2. Из первой
формулы (4.27) следует, что (ОГрТ = 1, откуда
Югр=1/Т.
(4.28)
Заметим, что подобные частотные характеристики имеет RC -
цепь, схема которой изображена на рис.4.5.
WBX
о
-о
Рис.4.5
Комплексная частотная характеристика /?С-цспи определяет-
ся как
тт.. . 1 zcoC 1
Я(/со) = —--------=---------, т = RC .
/? + 1/о)С 1 +/сот
(4.29)
Видно, что выражения (4.29) и (4.26) при Hq = 1 совпадают.
Таким образом, задача сводится к анализу прохождения ви-
деоимпульсов через /?С-цепь. Следует обратить внимание на то,
как при прохождении через цепь искажается форма видеоим-
пульсов и при каких условиях эти искажения минимальные.
В качестве примера рассмотрим прохождение через 7? С-цепь
экспоненциального и прямоугольного импульсов.
4.4.2. ПРОХОЖДЕНИЕ ЭКСПОНЕНЦИАЛЬНОГО
-107-
ИМПУЛЬСА ЧЕРЕЗ RC -ЦЕПЬ
Дана /?С-цепь, схема которой изображена на рис.4.5. Вход-
ной сигнал - экспоненциальный импульс (рис.4.6, а):
WBX(/) —С7е at ПРИ ^0.
Выходным сигналом служит напряжение на конденсаторе.
Для определения Д/вых (/) применим спектральный метод.
В соответствии с (2.18) спектральная плотность входного
сигнала
5ВХ (w) = U/(a + i(o).
Подставляя значения /7(/С0) из (4.29) и 5'ВХ((О) в форму-
лу (4.22), находим спектральную плотность выходного сигнала
и
5Вых (<») =
вых (1 + /оя)(а + /со)
(4.30)
Переход от функции частоты (4.30) к временной функции
WBbjx(0 с помощью обратного преобразования Фурье (4.21)
требует громоздких вычислений. Вычисления упрощаются, если
-108-
заменив в (4.30) ZCO на р, перейти к преобразованию Лапласа
О / X U
SRMX (р) =---------------• (4.31)
ВЫХ (\ + pt)(a + p)
Теперь для перехода от (4.31) к функции ^вых(7) можно вос-
пользоваться формулой (2.59).
В результате для выходного сигнала получаем следующее вы-
ражение:
"вых (0 = 7-1— (e~at - е~^ )• (4-32)
1 — ат
На рис.4.6,б приведен график WBbIX(Z) при значении пара-
метра аТ = 0,5. Видно, что RC - цепь осуществляет сглаживание
входного сигнала, поскольку напряжение на конденсаторе при
нестационарном процессе всегда непрерывно во времени. Отме-
тим, что сглаживание входного сигнала будет тем заметнее, чем
больше значение параметра аТ.
4.4.3. ПРОХОЖДЕНИЕ ПРЯМОУГОЛЬНОГО ИМПУЛЬСА
ЧЕРЕЗ RC -ЦЕПЬ
Пусть входной сигнал - прямоугольный импульс, изображен-
ный на рис.4.7, а.
Для того чтобы найти выходной сигнал, воспользуемся инте-
гралом наложения (4.25).
Найдем импульсную характеристику RC -цепи. Подставив
выражение (4.29) в формулу (4.13), имеем
h(t)=— J—-—el<atckti =-e~t/x, t>0. (4.33)
271.^1 +ЙОТ т
Здесь использовано табличное значение интеграла.
-109-
Рис. 4.7
Подставляем во второй интеграл (4.25) вместе с импульсной
характеристикой (4.33) значение входного сигнала, равное U при
0< t < Ти. Следует иметь в виду, что функция WBX (х) в фор-
муле (4.25) обращается в нуль при х > Ти. Поэтому интервал ин-
тегрирования необходимо разбить на два промежутка:
1) при 0 < / < Ти
«вых(0 = -4^ ° х)/х dx = U0-e / т) ; (4.34)
т о
2) при t > Ти
гувых(/) = — J е (t х)/т dx = и(ет" т-1)е / т .(4.35)
1 о
Выражение (4.34) описывает процесс заряда конденсатора, а
выражение (4.35) - процесс разряда. Заметим, что длительность
каждого из этих процессов приближенно равна ЗТ.
На рис.4.7,б приведены графики WBblx(/) для двух значений
-НО-
постоянной времени RC -цепи. Видно, что RC -цепь осуществ-
ляет сглаживание прямоугольной формы входного импульса, ко-
торое тем заметнее, чем больше постоянная времени цепи по
сравнению с длительностью входного импульса.
4.5. ИСКАЖЕНИЯ СИГНАЛОВ В ЛИНЕЙНЫХ ЦЕПЯХ
4.5.1. ТРЕБОВАНИЯ К ЧАСТОТНЫМ ХАРАКТЕРИСТИКАМ
НЕИСКАЖАЮЩЕЙ ЦЕПИ
Передача информации осуществляется без искажений, если
сигналы, отображающие эту информацию, при прохождении че-
рез цепи сохраняют свою форму.
В идеальном случае выходной сигнал является копией вход-
ного сигнала:
'W (0('-'oh (4.36)
где /7 — некоторая постоянная, — время задержки (запаздыва-
ния) выходного сигнала относительно входного.
Сформулируем требования к частотным характеристикам це-
пей, обеспечивающих передачу сигналов без искажений.
Применяя к обеим частям равенства (4.36) преобразование
Фурье, получим
SBblx (Ш) =<Г'“» 5вх«0). (4.37)
Сравнение выражений (4.22) и (4.37) показывает, что частот-
ная характеристика неискажающей цепи имеет вид
77(zcd) —Н e~'wt° , (4.38)
отсюда следуют выражения для АЧХ и ФЧХ:
Н ((О) = Н , (со) = -С0/0, (4.39)
Таким образом, неискажающая цепь должна иметь равномер-
ную АЧХ и линейную ФЧХ (рис.4.8).
-111-
Н((О)А
Н
О
а)
Рис. 4.8
4.5.2. ПРИЧИНЫ ИСКАЖЕНИЙ СИГНАЛОВ
В ЛИНЕЙНЫХ ЦЕПЯХ
Частотные характеристики реальных цепей отличаются от
идеальных характеристик, изображенных на рис.4.8. Вследствие
этого передаваемые по радиоканалу сигналы могут искажаться.
Можно указать на три фактора, вызывающих искажение сиг-
налов в линейных цепях: ограничение спектра, неравномерность
АЧХ и нелинейность ФЧХ. Рассмотрим влияние на форму сигна-
ла каждого из этих факторов в отдельности.
Ограничение спектра. Реальные цепи имеют ограниченную
полосу пропускания, что может привести к ограничению (отсеч-
ке) спектра передаваемого сигнала.
Оценим искажения, вызванные ограничением спектра входно-
го сигнала. Пусть на вход цепи воздействует сигнал, изображен-
ный на рис.2.4,а. Такой сигнал можно представить рядом Фурье
(2.9). Допустим, что характеристики цепи близки к идеальным
характеристикам (4.39) в полосе частот 0<СО< 5(0]. Тогда на
выходе цепи получим сигнал, являющийся результатом суммиро-
вания первых пяти гармоник входного сигнала. Соответствую-
щий график приведен на рис.2.4,б. Видно, что при отбрасывании
высокочастотной части спектра сглаживается пилообразная фор-
ма сигнала.
Другой пример — сглаживание формы экспоненциального и
-112-
прямоугольного импульсов при прохождении их через RC -
цепь. Эти импульсы имеют широко протяженный спектр (см.
рис.2.9 и 2.10). Причем низкочастотная часть спектра формирует
медленно меняющиеся участки (например, плоскую вершину
прямоугольного импульса), а высокочастотная часть — фронты
импульсов. На рис. 4.6 и 4.7 видно, что 7?С-цепь, которая слу-
жит фильтром нижних частот, искажает главным образом фрон-
ты, делая их менее крутыми. Отметим, что длительность фронта
нарастания и спада импульса обратно пропорциональна полосе
пропускания цепи (4.28). Чем уже полоса, тем более затянут
фронт импульса (см. рис.4.7,б).
Как известно, импульсные сигналы конечной длительности и
их периодические последовательности имеют теоретически неог-
раниченный спектр. Отсюда следует, что задача неискаженной
передачи импульсных сигналов через цепи с ограниченной поло-
сой пропускания может решаться лишь приближенно.
Неравномерность АЧХ. Из-за неравномерности АЧХ цепи
возникают амплитудные искажения, они проявляются в измене-
нии амплитуд спектральных составляющих сигнала.
Пусть
z/BX (/) = t/j sine»,/н-t/2sin2ct>1/ .
На рис.4.9,а сплошной линией изображен входной сигнал, а
штриховой линией - временные диаграммы его первой и второй
гармоник. Допустим, что амплитуда второй гармоники сигнала
на выходе уменьшается вдвое:
&вых (0 = t/isina>iZ + 0,5t72sin2cD1Z .
Тогда, как показано на рис.4.9,б, форма wBbIX (0 (сплошная ли-
ния) не будет соответствовать форме Z/BX(Z) вследствие воз-
никновения амплитудных искажений.
-113-
о
б)
▲
^вых
«)
Рис. 4.9
Нелинейность ФЧХ. Вследствие нелинейности ФЧХ возник
ют фазовые искажения. Фазовые искажения вызваны нарушен
ем фазовых соотношений между отдельными спектральные
-114-
составляющим и.
Допустим, что у входного сигнала (рис.4.9,а) изменилась на-
чальная фаза второй гармоники. Тогда выходной сигнал
мвых (/) = Ux sincOj t + 0,5U2cos2cOj/ ,
изображенный на рис.4.9,в сплошной линией, имеет форму, от-
личную от формы ивх (/).
Фазовые искажения обусловлены тем, что различные спек-
тральные составляющие при прохождении через цепь задержи-
ваются не на один и тот же интервал времени , Для оценки
этих искажений иногда используется характеристика
z0((o) = <7(p// (ю)/б/со.
При этом фазовые искажения оцениваются неравномерностью
характеристики /0((0) .
Амплитудные и фазовые искажения сигналов называют ли-
нейными искажениями. Отметим, что линейные искажения не
сопровождаются появлением в спектре новых составляющих и не
зависят от амплитуды входного сигнала.
Важно, чтобы линейные искажения не вызывали существен-
ного искажения передаваемой информации. Очевидно, что ли-
нейные искажения тем больше, чем шире спектр входного сиг-
нала, поскольку в большей полосе частот заметнее проявляется
отличие АЧХ и ФЧХ цепи от идеальных. Поэтому существует
предельно допустимая полоса частот, в пределах которой данная
цепь передает сигналы без существенных искажений. Эта полоса
частот является полосой пропускания цепи.
-115-
5. ПРОХОЖДЕНИЕ
МОДУЛИРОВАННЫХ СИГНАЛОВ ЧЕРЕЗ
ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ
5.1. ЛИНЕЙНЫЕ УЗКОПОЛОСНЫЕ ЦЕПИ
Модулированные сигналы имеют спектр, сосредоточенный
около несущей частоты (Од и существенно отличный от нуля
лишь в определенной полосе частот, например, от нижней часто-
ты (0н до верхней частоты (0в. Поэтому для неискаженной пере-
дачи модулированных сигналов требуется, чтобы частотные ха-
рактеристики цепи имели вид, определяемый выражениями
(4.39), лишь в полосе частот от (0н до (Dn. Вне этой полосы же-
лательно, чтобы цепь не пропускала ненужных сигналов и помех,
т.е. АЧХ цепи должна быть равна нулю. Следовательно, частот-
ные характеристики цепи, осуществляющей неискаженную пере-
дачу модулированных сигналов, должны иметь вид, показанный
на рис. 5.1. Это характеристики идеального полосового фильтра,
который физически неосуществим.
Поэтому в реальных цепях неизбежны искажения модули-
рованных сигналов. Чтобы оценить характер этих искажений
возьмем в качестве примера цепь, комплексная частотная ха-
рактеристика которой описывается выражением
= —(5.1)
1 + г(со-сОр)т
где Т - постоянная времени цепи. Из (5.1) следуют выражения
для АЧХ и ФЧХ:
Я(а))-Я0/^1 + (СО-СОр)2Т2; (5.2)
<pz/ (со) = -arctg(co- (Ор )т. (5.3)
-116-
Эти выражения описывают АЧХ и ФЧХ, вид которых показан
на рис.5.2. Такая цепь может служить полосовым фильтром.
Полоса пропускания цепи определяется как полоса частот, в
которой //((О) > //0/V2. Из (5.2) определяем, что на границах
полосы пропускания, заданных частотами COrpj = (Ор—Д(О и
(0Гр2 = ^р + значение ДСОТ = 1. Следовательно, полоса
пропускания равна
-117-
АЮгр = (O^ -GVp, = 2Асо = 2/т. (5.4)
Линейные цепи можно считать узкополосными, если относи-
тельная полоса пропускания, определяемая как отношение
АсОрр / СОр, удовлетворяет условию:
Асо1р / С0р « 1.
Пример линейной узкополосной цепи. Рассмотрим колебатель-
ный контур (ЯЛС-цепь), схема которого изображена на рис.5.3.
Рис. 5.3
Комплексная частотная характеристика контура определяется
как
Я(/со) =
1/zcoC
R + zcoZ/ +1 zcoC
(5.5)
Это выражение можно преобразовать к виду:
Я(/со) =
-zgCOp/CO
1 + Z^(cO/ COp - (Op /со)’
(5.6)
где (Dp — 1/л/LC- резонансная частота, Q - добротность конту-
ра, равная
-118-
Q^VL_ 1
R (OpCT? R
Из (5.6) следует, что на резонансной частоте
H(i(dp) = —iQ = Qe~'K/2,
откуда находим резонансные значения АЧХ и ФЧХ:
Я(сор) = 2, ф„((0р)=-л/2.
(5.7)
На частотах, близких к резонансной (СО ~ СОр), имеем
2 2
СО С0п СО-СОп со+соп со-соп со-соп
_______Р _______Р _ ______Р_______Р _ 2______Р
СОр СО 2сосор СОр СОр СОр
при этом выражение (5.6) может быть заменено приближенным:
//(/со)«----—---------.
1 + z(co-(Ор)т
Здесь Т = 2 QlСОр - постоянная времени контура.
Из (5.7) следует, что АЧХ контура можно описать выражени-
ем (5.2), положив H^—Q, а ФЧХ контура отличается от (5.3)
лишь сдвигом по фазе на величину — 7U / 2.
Подставив значение Т в (5.4), находим полосу пропускания
контура:
Дсогр — СОр /Q-
Относительная полоса пропускания, равная ДС0Гр /СОр = 1 / Q,
тем меньше, чем больше добротность. Контур с добротностью
-119-
Q»\ является примером узкополосной цепи.
Линейные искажения модулированных сигналов. При прохож-
дении модулированного сигнала через линейную цепь с частот-
ными характеристиками (5.2)-(5.3) возникают линейные искаже-
ния сигнала, обусловленные неравномерностью АЧХ и нелиней-
ностью ФЧХ. Для того чтобы эти искажения минимизировать,
необходимо соблюдать ряд условий.
Очевидно, что спектр входного модулированного сигнала
должен быть расположен в пределах полосы пропускания цепи:
(0Гр| ^(0н, ^гр2 — ®в- (5-8)
Как известно, спектр модулированного сигнала симметричен
относительно несущей частоты (Dg. Для сохранения симметрии
спектра на выходе цепи ее АЧХ должна быть симметрична отно-
сительно несущей (Од, т.е.
Я((00-(0) = //(С00+(0). (5.9)
При этом для ФЧХ должно выполняться условие:
ф//((00 — (О) = —фу/((00 + (О). (5.10)
Частотные характеристики (5.2) и (5.3) удовлетворяют соот-
ветственно условиям (5.9) и (5.10), если (Од = (Ор. Положение
спектра входного модулированного сигнала относительно АЧХ и
ФЧХ цепи показано на рис.5.2.
При прохождении модулированных сигналов через цепь важ-
но установить характер возможных искажений и оценить, как при
этом исказится закон модуляции, поскольку именно он отобража-
ет передаваемую информацию.
Для передачи информации пригодны только те радиотехниче-
ские цепи, которые обладают способностью воспроизводить на
выходе закон модуляции входных сигналов с заданной точно-
стью.
-120-
5.2. ПРОХОЖДЕНИЕ
СИГНАЛОВ С АМПЛИТУДНОЙ МОДУЛЯЦИЕЙ
ЧЕРЕЗ ЛИНЕЙНУЮ УЗКОПОЛОСНУЮ ЦЕПЬ
Амплитудно-модулированный сигнал с несущей частотой (Dq
и максимальной частотой модуляции Qfn имеет спектр, ограни-
ченный частотами:
С0н = (00 — и (0в — ®0 + • (5.11)
Для передачи AM сигнала без искажений необходимо, чтобы
цепь имела частотные характеристики, соответствующие харак-
теристикам идеального полосового фильтра (рис.5.1), полоса
пропускания которого ограничена частотами (5.11).
В цепи с комплексной частотной характеристикой (5.1) усло-
вия неискаженной передачи AM сигнала могут быть выполнены
лишь приближенно в полосе частот (5.4):
^гр2~~^гр1 —-2/т>2£27Л. (5.11)
Оценим характер возможных искажений AM сигнала. При
этом основное внимание следует обратить на характер искажения
закона амплитудной модуляции, т.е. огибающей AM сигнала.
Прохождение тонального AM сигнала. При воздействии на
линейную цепь тонального AM сигнала
z/BX (0 = Щ1 + A/cosQ/)cos(d0Z
анализ можно проводить путем разложения его на гармонические
составляющие:
ТГ им , им z
wbx (0 = C/cosco0/ ч--cos((B0 + Qx +----cos(co0 - Q)/
2 2
нахождения реакции цепи на каждую из них в отдельности с по-
-121-
мощью формулы (4.9) и последующего суммирования этих реак-
ций на основании принципа наложения:
^вых (О = Н (со0 )O'cos[cd0/ + ФУ/ (со0)]+
+ Н (tt)0 + £2) cos[(co0 + Q)r + (р7У (со0 + £2)]+
+ //((й0 -Q)^^cos[((o0 -Q)f + (p/z (со0 -Q)J
2 (5.12)
Положим, что АЧХ и ФЧХ цепи описываются выражениями
(5.2) и (5.3), а несущая частота (Од = СОр. Тогда
//(С00) = /70; фя((О0) = 0;
Я(соо -Q) = H(cd0+Q) = Н6 = HQ/л/1 + О2т2 ;
ф7/ (со0 - Q) = -ф7/ (со0 + Q) = фб = arctg(Qx).
Смысл этих выражений поясняется рис.5.4. Подставляя эти вы-
ражения в (5.12), запишем
Ивых (0 = нQUcos(d0t + Н6 cos[(o)0 + - Фб ] +
+ #6 - COS[(со0 - О)/ + Фб ].
Выполнив элементарные тригонометрические преобразова-
ния, приходим к следующему выражению для выходного сигна-
ла:
-122-
«вых(О = H0C/[l + MBbIxcos(Q/-96)]cos(D0/, (5.13)
где коэффициент модуляции
Мвых = MHq /Hq = M/ 717q2t2 .
Рис. 5.4
Выражение (5.13) свидетельствует о сохранении формы оги-
бающей тонального AM сигнала на выходе цепи. Линейные ис-
кажения AM сигнала проявляются в уменьшении коэффициента
модуляции (Л/вых < М, так как Hq < Нq) и фазовом сдвиге
огибающей на угол
Прохождение многотоналъного AM сигнала. Аналогично при
входном сигнале
N
^вх (0 ““ U
1+^Mncos(£lnt + Qn) cosco0Z
п=]
на выходе цепи получаем измененный сигнал
-123-
WBblX
N
(t) = H(P 1+ £ A/';cos(Q„/+ -<Рб«) COS<*V>
n-\
(5.14)
где
Mn M n H 6n / ^0 ’
“ ^(®0 “ ^0 + )’
Фбя = Ф// (®0 - Q J = ~Фя (^0 + Q J-
В выражении (5.14) форма огибающей определяется видом £
Поэтому искажение формы огибающей будет тем меньше, чем
точнее выполняются условия отсутствия искажений:
/7 = 1,2,...^,
где /д - время запаздывания огибающей.
Влияние расстройки. В случае, когда несущая частота
(Do Ф СОр, в (5.12) Я(С00 +Q) Ф //((О0—Q). При этом нару-
шается симметрия спектра выходного сигнала, как показано на
рис.5.5.
-124-
Как известно, спектр AM сигнала симметричен относительно
несущей частоты. Следовательно, в выходном сигнале искажает-
ся закон амплитудной модуляции.
5.3. ПРОХОЖДЕНИЕ
СИГНАЛОВ С УГЛОВОЙ МОДУЛЯЦИЕЙ ЧЕРЕЗ
ЛИНЕЙНУЮ УЗКОПОЛОСНУЮ ЦЕПЬ
Сигнал с угловой модуляцией
wbx 0) = ^cos((o0/ + msinQ/)
имеет широко протяженный спектр (3.30). Однако можно пре-
небречь всеми составляющими, номера которых П > /77 + 1. При
этом спектр будет ограничен частотами:
СО,, = (О0 -(я?+ 1)0 и C0B =CO0+(w + l)Q. (5.15)
Передачу данного сигнала без искажений можно осуществить,
используя цепь с идеальными частотными характеристиками
(рис.5.1) в полосе пропускания, ограниченной частотами (5.15).
В реальной цепи неизбежны искажения сигнала с угловой мо-
дуляцией. Оценим характер возможных искажений на примере
прохождения сигнала WBX(^) через линейную цепь с комплекс-
ной частотной характеристикой (5.1). При этом полоса пропуска-
ния цепи (5.4) удовлетворяет условию:
согр2-(0гр) = 2/т > 2(m + l)Q, (5.16)
а несущая частота С00 = СОр.
Анализ прохождения сигнала с угловой модуляцией через ли-
нейную цепь в принципе можно провести, разложив г/вх(/) на
гармонические составляющие и суммируя реакции цепи на каж-
дую отдельную составляющую. Но поскольку в данном случае
число составляющих велико (3.30), то такой подход приводит к
-125-
громоздким вычислениям.
Метод мгновенной частоты. Для того чтобы определить вы-
ходной сигнал, применим приближенный метод, который назы-
вают методом мгновенной частоты. В основе этого метода лежит
допущение о медленности изменения мгновенной частоты ю(/)
входного сигнала, что справедливо при Q « COq. При таком до-
пущении входной сигнал можно представить в виде (3.32):
u^(t) = Re [а, (/)«'“"']. (5.17)
yjr / т r imsindt г
где U j (/) = Ue - комплексная огибающая входного сиг-
/соп/
нала, она изменяется медленно по сравнению се .
Выходной сигнал будем искать в виде, аналогичном (5.17):
«вых (') = Re[t7, (518)
где иг(!) = - комплексная огибающая выходного
сигнала. Таким образом, задача состоит в определении амплиту-
ды U2(/) и фазы ф2(0-
Поскольку на протяжении периода несущей частоты величи-
на (/](/) практически не меняется, то сигнал (5.17) в каждый
фиксированный момент времени t можно приближенно рассмат-
ривать как гармонический сигнал частоты COq, комплексная ам-
плитуда которого равна значению £/[(/) в данный момент вре-
мени. Тогда значение комплексной амплитуды выходного сигна-
ла в данный момент времени определяется как
U2(0=W[(<o(()K7|(/). (5.19)
Подобная запись возможна лишь для установившегося режи-
ма. Поэтому предполагается, что установление колебаний на вы-
-126-
ходе цепи происходит мгновенно с изменением частоты COj/J
сигнала на входе. Поскольку длительность процесса установле-
ния (переходного процесса) порядка ЗТ, то пренебрегая процес-
сом установления, тем самым предполагаем, что постоянная вре-
мени цепи Т значительно меньше периода модуляции
7т = 2ТС/£1. Отсюда получаем условие применимости метода
мгновенной частоты:
Qt «1.
Подставляя (5.19) в (5.18), запишем
«вь,х« = Ке{яН/)]с71(/>'ш»'}=
ИЛИ
z7Bbix (0 = ^[<XO]^cos{woz‘ + msinQr+(р7/ [co(z)]}
(5.20)
Здесь //[со(О] и ф7/[СО(/)] - соответственно значения АЧХ
/7(С0) и ФЧХ ф//(СО), в которых вместо текущей частоты (О
фигурирует мгновенная частота входного сигнала:
со(0 = % + wQcosQ/.
Сравнение выражений WBX(/) и МВЬ1Х(/) показывает, что в
выходном сигнале появились искажения. Оценим эти искажения.
Паразитная амплитудная модуляция. Из (5.20) следует, что
амплитуда выходного сигнала изменяется:
{/вых О’) = CW[co(/)] = UH[(&Q + mQcosQr], (5.21)
т.е. появляется паразитная амплитудная модуляция. Подставляя в
-127-
(5.2) вместо (О значение (О(/) и полагая (Oq = (Op, получим
^вых (0 = ^0 / a/1 + (wQt)2 cos2Q/ .
Амплитуда i/Bblx(7) изменяется от значения t/MaKC= UHq до
значения
=ин,/ф + (тах)2.
Форма 1/вых(0> полученная путем графических построений,
показана на рис.5.6. Как видно на рисунке, причиной появления
паразитной амплитудной модуляции выходного сигнала является
неравномерность АЧХ цепи.
Искажение закона угловой модуляции. Из (5.20) следует, что
-128-
закон угловой модуляции выходного сигнала, определяемый
Фвых (0 = WSinQ? + Фн [«(/)], (5.22)
отличается от тональной угловой модуляции входного сигнала
видом функции:
Ф // (0 = Ф// 1М0] = Ф/7 [юо + ^QcosQz].
Подставляя в (5.3) вместо СО значение С0(7) и полагая С00 = (Ор,
находим
Ф//(0 ~ -arctg(wQTcosQz).
Используя формулу разложения
arctgx = x-x3/3 + ... при |х| < 1,
запишем приближенное выражение
cpz/ (/) = -wQtcosQ/ +1 (wQt)3 cos3Qz +...
и, учитывая, что COS3X = (3COSX + COS3x)/4, получим
1 3
Ф// (О = [~wQt + - (wQt) ]cosQz +
1 3
+ - - (wQt) C0s3QZ +... (5.23)
Из (5.23) следует, что искажение закона тональной угловой
модуляции вызвано появлением гармоники на частоте 3Q. Но
поскольку (при выполнении условия (5.16)) величина < 1,
то амплитуда этой гармоники мала.
-129-
5.4.ПРОХОЖДЕНИЕ
ПРОИЗВОЛЬНОГО УЗКОПОЛОСНОГО СИГНАЛА
ЧЕРЕЗ ЛИНЕЙНУЮ УЗКОПОЛОСНУЮ ЦЕПЬ
Модулированный сигнал общего вида
«вх (0 = (OCOS[OV + Ф1 (')]
можно описать с помощью его комплексной огибающей:
и,(/) = (5.24)
Тогда
!1BX(/) = Re[ai(/)e'M»']. (5.25)
Спектр данного сигнала определяется как (3.37):
I ~ 1
5вх((0)=?-^|(со-соо) + 5^1 (-0)-С00). (5.26)
Если Q.tn - максимальная частота в спектре (7| (СО), то спектр
5ВХ (О)) занимает полосу, ограниченную частотами:
С0п =CO0-Q„z и C0B =COO+Q„r (5.27)
Для передачи сигнала UBX (t) без искажений нужно использо-
вать цепи с частотными характеристиками, близкими к идеаль-
ным (рис.5.1) в полосе пропускания:
сов сои 2Q/77.
(5.28)
В реальных цепях неизбежны искажения сигнала. Передавае-
мое сообщение, заложенное в сигнал Z/BX(^) в результате моду-
ляции (амплитудной и угловой), содержится только в По-
-130-
этому при передаче данного сигнала основной интерес представ-
ляет характер изменения С/| (/) в цепи и оценка возможных ис-
кажений.
При входном сигнале (5.25) на выходе цепи получаем изме-
ненный сигнал:
«BI„(/) = Re[(72(/k'“»']. (5.29)
Следовательно, задача сводится к определению комплексной
огибающей выходного сигнала.
Спектральный метод для комплексных огибающих. Выходной
сигнал будем искать спектральным методом. Полагаем, что АЧХ
Я ((О) цепи отлична от нуля лишь в полосе частот (5.28). Под-
ставив (5.26) в (4.20), получаем
1 00 ~
"вых (0 = — J (со- w0 )e'ovt/w+
— J (-to - w0
4rc_oo
Преобразуем эти интегралы, сделав замену переменной СО: в
первом интеграле (0 = COq 4-Q, а во втором СО = —СОд— Q. В
результате имеем
Z/BblX (0
J Я[-/((00 + £2)]Ц* (Q)e“'Qz d£i e~i(ad
Поскольку слагаемые здесь являются комплексно-сопряжен-
-131-
ными, то в соответствии с (3.36) можем записать
WBbIX
(/) = Re{
— JM/(cd0 +Q)]t/j(Q)ezQz<7Q
2^_oo
Z(1W
e 0
(5.30)
Сравнение правых частей (5.29) и (5.30) показывает, что
и2 (/) = —? Я[/(СО0 + ЩКЛ . (5.31)
2 л _
Из (5.31) следует, что комплексная огибающая сигнала на вы-
ходе цепи имеет спектральную плотность:
U2 (Q) = Яр(со0 + Q)]#( (Q). (5.32)
Соотношение (5.32) аналогично (4.22). Следовательно, если на
цепь с частотной характеристикой
Янч(/О) = Л[/(со0 + Q)] (5.33)
воздействует то откликом такой цепи будет (72(0- Пепь-
частотная характеристика которой определяется (5.33), называют
низкочастотным (НЧ) эквивалентом узкополосной цепи.
Временной метод (интеграл наложения) для комплексных
огибающих. Для определения комплексной огибающей выходно-
го сигнала можно воспользоваться также временным методом
(4.23):
оо
U2(t) =
(5.34)
где Л|1Ч(/) - импульсная характеристика низкочастотного экви-
-132-
валента, определяемая как обратное преобразование Фурье от
(5.33). Формулу (5.34) называют интегралом наложения для ком-
плексной огибающей.
5.5. ПРОХОЖДЕНИЕ РАДИОИМПУЛЬСОВ ЧЕРЕЗ
ЛИНЕЙНУЮ УЗКОПОЛОСНУЮ ЦЕПЬ
Пусть радиоимпульс длительностью Ти (рис.5.7,а):
WBX(z) = (71(?)cos©0? при 0</<Ти (5.35)
с прямоугольной огибающей (/) воздействует на цепь с ком-
плексной частотной характеристикой (5.1).
Рис. 5.7
Спектр прямоугольного радиоимпульса изображен на
-133-
рис.3.8,б. Как видно, спектр имеет широкую протяженность. По-
этому неизбежны искажения формы радиоимпульса на выходе
цепи, вызванные ограничением его спектра. Например, если
учесть только центральный лепесток, то спектр радиоимпульса
ограничивается частотами:
(Он =(00-2л/ти и (0в =(00+2л:/ти. (5.36)
При этом необходимо, чтобы полоса пропускания цепи (5.4)
удовлетворяла условию:
0)гр2 - югр1 = 2 / Т > 4л / ти, (5.37)
а несущая частота CDg = (Ор.
Тогда при входном сигнале (5.35) на выходе цени получим
измененный сигнал вида
wBbix(0 = ^2 0)cosa)0^ при (>0. (5.38)
Следовательно, задача сводится к определению огибающей
U2(/) выходного сигнала.
Функция может быть вычислена по формуле (5.31) или
(5.34).
Для этого сначала нужно найти функцию (5.33). Сделав в
формуле (5.1) замену: СО=СО0 + Й и полагая COq ^СОр, нахо-
дим
//1I4(zQ) = HQ /(1 + zQt) . (5.39)
Нетрудно заметить, что функция (5.39) эквивалентна (4.26).
Можно сделать следующий вывод: узкополосная цепь, АЧХ и
ФЧХ которой приведены на рис. 4.3, имеет своим низкочастот-
ным эквивалентом цепь, АЧХ и ФЧХ которой изображены на
рис. 4.2. Иными словами, фильтр нижних частот является низко-
частотным эквивалентом полосового фильтра.
-134-
Следовательно, огибающую ^(0 можно вычислить как ре-
акцию /?С-цепи на прямоугольный импульс (/|(?) (см. § 4.4.3).
Воспользовавшись формулами (4.34) и (4.35), сразу запишем вы-
ражение для огибающей:
U2(t) = HQU(\-e~t/X) при 0 < t < Ти ; (5.40)
U2(t) = Н^и(ех"/т - при ?>ти. (5.41)
Выражение (5.40) описывает процесс установления амплиту-
ды колебания на выходе цепи. За время порядка ЗТ амплитуда
достигает стационарного значения = H^U. После окончания
действия радиоимпульса на входе, при t > Ти на выходе цепи
будут свободные (собственные) колебания, амплитуда которых
уменьшается по экспоненциальному закону (5.41).
При выполнении условия (5.37) длительность импульса Ти и
постоянная времени цепи Т связаны так: Ти ~6Т. При этом
форма выходного сигнала имеет вид, показанный на рис.5.7,б.
Влияние расстройки. В общем случае частоты (Од и (0р мо-
гут отличаться друг от друга на некоторую величину 8(0. Уста-
новим характер возникающих при этом искажений.
Положив в (5.35) (Од = (Ор + 8(0, представим входной сигнал
в виде
wBX (?) = Ц (z)cos(GJp + 5(0)? = Ке[Ц (?>/<OpZ ], (5.42)
где
t71(?) = f71(?)e/5ov, 0<?<ти. (5.43)
Выходной сигнал будем искать в виде, аналогичном (5.42):
-135-
«вых (O = RefW, ]. (5.44)
Для определения комплексной огибающей воспользу-
емся формулой (5.34). Импульсная характеристика hm(t) опре-
деляется аналогично (4.33):
(5.45)
т
Подставив в (5.34) выражения (5.43) и (5.45), имеем
Cf2(') =
т о
Вычисление этого интеграла даст
(?,(/)= 0<(<Ти. (5.46)
1 + /Scot
Модуль комплексной величины (5.46) определяет огибающую
выходного сигнала на интервале 0 < t < Ти:
U2(/) = г-^-_.. 71 - 2e-z /Tcos(3co/) + e~2t'1. (5.47)
71 +(Scot)2
Выражение (5.47) показывает, что процесс установления ам-
плитуды колебаний на выходе цепи имеет колебательный харак-
тер, частота колебаний определяется величиной §С0, как показа-
но на рис.5.8.
Заметим, что при расстройке установившаяся амплитуда, рав-
ная
U2 =//0^/7ж5сот)2,
-136-
меньше, чем в случае, когда COq = СОр.
Из (5.46) находим фазу выходного сигнала на интервале
О < / < Ти:
ф2(0 = arctg{sin(5co/)/[cos(8co/)-e arctg(Scoz).
(5.48)
Как видно, процесс установления фазы выходного сигнала также
имеет колебательный характер.
После окончания действия радиоимпульса на входе, при
t > Ти на выходе цепи будут собственные колебания с частотой
СОр, амплитуда которых уменьшается по экспоненциальному за-
кону.
5.6. ПРОХОЖДЕНИЕ
ФАЗОМАНИПУЛИРОВАННЫХ СИГНАЛОВ
ЧЕРЕЗ ЛИНЕЙНУЮ УЗКОПОЛОСНУЮ ЦЕПЬ
Фазоманипулированные (ФМн) сигналы характеризуются
скачкообразным изменением начальной фазы гармонического не-
сущего колебания в определенные моменты времени (см.
рис.3.12,в). Как видно па рисунке, ФМн сигнал состоит из прямо-
-137-
угольных радиоимпульсов одинаковой длительности Ти, отли-
чающихся друг от друга только значениями начальной фазы гар-
монического колебания.
Спектр ФМн сигнала обычно ограничивают частотами (5.36).
Поэтому для передачи ФМн сигнала с минимальными искаже-
ниями нужно использовать цепи, частотные характеристики ко-
торых близки к идеальным в полосе частот (5.37).
Рассмотрим, какие искажения претерпевает ФМн сигнал в це-
пи с комплексной частотной характеристикой (5.1) и полосой
пропускания (5.37).
Пусть входной ФМн сигнал состоит из двух радиоимпульсов:
wBX(/) = (7cos(co0/ + (p()) при 0</<ти,
WBX (0 = -t/cos(av + Фо) ПРИ ти <z < 2ти•
Здесь фаза несущего колебания изменяется скачком на Л в мо-
мент времени t = Ти.
Такой сигнал удобно описать следующим образом:
ивх (?) = U] (?)cos((00z + Фо), (5.49)
где огибающая
и, 0</<ти,
-и, ти<г<2ти.
(5.50)
ее вид показан на рис. 5.9,а. При этом предполагается, чтс
Ти = 1ПП / COq, где п - целое число.
Если несущая частота С00 = (Ор, то на выходе цепи будет из
мененный сигнал вида
^вых (/)=C72(z)cos(<»0/ + <p0), z>°-
(5.5i:
-138-
Огибающую выходного сигнала U2 (Z) будем искать как ре-
акцию низкочастотного эквивалента — цепи с характеристиками
(5.39) и (5.45) на входное воздействие t/j (Z).
Как видно на рис.5.9,a, J7] (Z) состоит из двух одинаковых
прямоугольных импульсов разной полярности:
(71(/) = (71'(/)-Ц'(/-Ти). (5.52)
Можно использовать принцип наложения для нахождения
t/2(/). Тогда
(5-53)
где U2(t) и U2 (t — Ти) - реакции низкочастотного эквивалента
(7?С-цепи) соответственно на входные воздействия t7[(Z) и
Функция (72(Z) ~ это РеакЦия ЛС-цепи на прямоугольный
-139-
импульс, она определяется выражениями (5.40) и (5.41). Анало-
гично определяем функцию - реакцию 7?С-цепи на сме-
щенный прямоугольный импульс отрицательной полярности:
U2(t) = Hot/(l-e~('~T")/T) прити</<2ти; (5.54)
U2(t) = HQU(ex«/xпри />2ти. (5.55)
Объединяя (5.41) и (5.54), получим описание огибающей
U2(t) на интервале Ти < t < 2ТИ:
и2 (/) = HQU(ex* /т - 1)е-'/х - H0U(\ - 'х).
(5.56)
Это выражение свидетельствует о том, что в результате скач-
кообразного изменения в момент времени t = Ти фазы гармони-
ческого колебания происходит изменение его амплитуды. При-
чем в момент времени Zq, определяемый из уравнения
t/2 (Zo ) = 0, амплитуда колебания становится равной нулю.
На рис. 5.9,6 приведен график функции (5.53), построенный на
основании выражений (5.40), (5.55) и (5.56).
Таким образом, искажение фазоманипулированного сигнала
проявляется в том, что его амплитуда на выходе цепи изменяется
во времени как |(/2 (Z)|. Скачок фазы выходного сигнала проис-
ходит в момент времени Zg, когда функция t/2(Z) меняет знак
(см. рис. 5.9,6).
5.7. ПРОХОЖДЕНИЕ
ЧАСТОТНО-МАНИПУЛИРОВАННЫХ СИГНАЛОВ
ЧЕРЕЗ ЛИНЕЙНУЮ УЗКОПОЛОСНУЮ ЦЕПЬ
Частотно-манипулированные (ЧМн) сигналы являются ре-
зультатом скачкообразного изменения частоты гармонического
несущего колебания (см. рис.3.12,г). Они состоят из прямоуголь-
ных радиоимпульсов с различными несущими частотами.
-140-
Допустим, что на узкополосную цепь воздействует ЧМн сиг-
нал, составленный из двух радиоимпульсов (см. рис.3.13,а):
г/вх W = ^COSCOq? при 0 < t < Ти,
WBX(/) = C7cOS(tt)0 +5(0)/ при ти</<2ти. (5.57)
Здесь первый радиоимпульс (см. рис.3.13,6) имеет несущую час-
тоту (Do, а второй радиоимпульс (см. рис. 3.13,в) - частоту
(D0+8(D. Скачок несущей частоты ЧМн сигнала на величину
8(0 происходит в момент времени t = Ти.
Спектр такого ЧМн сигнала, изображенный на рис.3.15, обыч-
но ограничивают двумя главными лепестками, т.е. частотами:
(0п =(00-2к/ти и (0B =(D0 +5(О+2л/ти. (5.58)
Для передачи такого сигнала с минимальными искажениями
нужно использовать цепи с частотными характеристиками близ-
кими к идеальным в полосе частот (5.58).
Рассмотрим искажения ЧМн сигнала в цепи с комплексной
частотной характеристикой (5.1), полосой пропускания:
(0Гр2 “®гр1 =2/Т>8(О+4я/Ти (5.59)
и частотой (Dp = (Dq .
Входной сигнал (5.57) представим в виде
где комплексная огибающая
U при 0 < t < Ти,
< •£ (5.60)
ие при ти < t < 2ти.
Ц(0
На выходе цепи получим измененный сигнал:
-141-
«вьге(О = Ке[б?2(Ое'И°'] (5 61)
Теперь задача сводится к нахождению комплексной огибаю-
щей выходного сигнала U (f).
Определим функцию как Реакпию низкочастотного эк-
вивалента - цепи с импульсной характеристикой А|1Ч(/) (5.45) на
входное воздействие (/).
Входное воздействие (5.60) можно представить в виде суммы
двух составляющих:
где
С7(')=и при 0</<Ти, (5.62)
U"(t) = Ue^ при ти < t < 2ти. (5.63)
Воспользуемся принципом наложения и запишем
U2(t)=U2(t) + U2(t), (5.64)
где и U"(t) - реакции низкочастотного эквивалента на
входные воздействия £/[(/) и (/[{/) соответственно.
Для нахождения (/^(О и ^2(0 можно использовать резуль-
таты, полученные в § 5.5.
Функция как реакция низкочастотного эквивалента
(7?С-цепи) на прямоугольный импульс (5.62) описывается выра-
жениями (5.40), (5.41).
Входное воздействие (/[(/) отличается от (5.43) лишь смеще-
нием на временной интервал, равный Ти. На интервале
Ти < t < 2ТИ функцию U2^0 находим с помощью формулы
-142-
(5.34). Подставив в (5.34) выражения (5.45) и (5.63), имеем
= \e^e-^Hdx =
т
ТИ (5.65)
. [е'8оу _ е'5ок11 e“(z-Tii) / т 1
1 + /бсотL J
Приведенное рассмотрение позволяет сделать следующие вы-
воды.
На интервале 0 < t < Ти функция U2(/) определяется выра-
жением (5.40), которое описывает процесс установления ампли-
туды колебаний частоты COq до стационарного значения HrfJ.
На интервале Ти < t < 2ти комплексная огибающая U
является результатом наложения двух процессов, первый из ко-
торых описывается выражением (5.41), а второй - выражением
(5.65). Объединяя (5.41) и (5.65), получим при Ти < Z < 2ти:
/7,(0 = tf0//(eTti/т - +
/Зео/
1 + /бсот
_<?'8<эт11е-(/-тн)/т
(5.66)
После окончания действия сигнала на входе, при t > 2ТИ вы-
ходной сигнал определяется собственными колебаниями частоты
СОр, амплитуда 6/2(/) которых уменьшается по экспоненциаль-
ному закону.
Основной интерес представляют процессы, возникающие в
цени в результате скачкообразного изменения частоты входного
сигнала, т.с. на интервале Ти < t < 2ти. Здесь выходной сигнал
описывается выражением
-143-
«ВЫХ (?) = ^2 (Rostov + Ф2 WL
где огибающая и 4)аза ф?(0 определяются соответствен-
но как модуль и аргумент комплексной огибающей (5.66).
Запишем (5.66) в виде:
и2 (/) = H^U(A + iB) /(1 + /Scot),
где
А = cosSco? -e~t/x + (l- cos8coth )е-^-х" >/ т,
В - sin8co/-8coTe-z/T + (8coT-sin8coTM)e~(z~T,,)/x.
Теперь определив модуль и аргумент комплексной огибающей,
приходим к следующим выражениям для амплитуды и фазы вы-
ходного сигнала:
и2(?) = HQUy/A2+B2 /71 + (Scot)2 , (5.67)
ф2 (?) = arctg(5 / А) - arctg(ScoT). (5.68)
Из полученных выражений следует, что в результате скачко-
образного изменения частоты входного сигнала в момент време-
ни t = Ти в цепи возникает переходный процесс, обуславливаю-
щий колебательный характер изменения амплитуды (5.67) и фазы
(5.68) сигнала на выходе. Частота этих колебаний определяется
величиной скачка частоты входного сигнала 8СО. Длительность
переходного процесса порядка ЗТ. При выполнении условия
(5.57) к середине интервала Ти < I < 2ти амплитуда (5.67) и фа-
за (5.68) достигнут значений:
U2 = H^U / 71 + (Scot)2 ; ср2 = 8со? - arctg(ScoT).
При этом установится колебание
-144-
«вых (') = ^2c°s[(«o + 3(0)/ - ФО ].
где
<р0 =arctg(5coT).
Следовательно, при скачкообразном изменении частоты
входного сигнала в выходном сигнале переход от частоты CDq к
частоте CDq + 8СО происходит не скачкообразно, а плавно.
Таким образом, прохождение манипулированных сигналов
через линейную узкополосную цепь неизбежно сопровождается
искажениями, которые приводя! к сглаживанию скачкообразного
закона модуляции.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Баскаков С.И. Радиотехнические цепи и сигналы. Учебник для
вузов. - М.: Высшая школа, 1988. - 448 с.
2. Гоноровский И.С. Радиотехнические цепи и сигналы. Учебник
для вузов. - М.: Радио и связь, 1986. - 512 с.
3. Радиотехнические цепи и сигналы/ Под ред. К.А. Самойло.
Учеб, пособие для вузов. - М.: Радио и связь, 1982. - 528 с.
4. Денисенко А.Н., Стеценко О.А. Теоретическая радиотехника.
4.1: Детерминированные сигналы. - М.: Изд. стандартов, 1993.
-215с.
5. Баскаков С.И. Радиотехнические цепи и сигналы: Руководство
по решению задач. - М.: Высшая школа, 1987. - 207 с.
6. Радиотехнические цепи и сигналы. Примеры и задачи/ Под
ред. И.С. Гоноровского. - М.: Радио и связь, 1989. - 248 с.
-145-
СОДЕРЖАНИЕ
Предисловие...........................................3
1. ОБЩИЕ СВЕДЕНИЯ О РАДИОТЕХНИЧЕСКИХ
ПРОЦЕССАХ...........................................4
1.1. Основная задача и применение радиотехники........4
1.2. Понятие сигнала..................................5
1.3. Понятие радиоканала..............................7
2. СИГНАЛЫ И ИХ ХАРАКТЕРИСТИКИ...................... 10
2.1. Математические модели сигналов................. 10
2.2. Основные параметры сигналов.................... 11
2.3. Периодические сигналы и их спектры............ 14
2.4. Непериодические сигналы и их спектры........... 22
2.5. Соотношение между спектрами одиночного
импульса и периодической последовательности
импульсов..........................................31
2.6. Соответствие между операциями над сигналами
и спектрами........................................34
2.7. Примеры использования свойств преобразования
Фурье при спектральном анализе сигналов............36
2.8. Использование обобщенных функций при
анализе сигналов...................................42
2.9. Преобразование Лапласа и его использование при
анализе сигналов...................................46
2.10. Описание сигналов с использованием ортогональных
систем базисных функций............................49
2.11. Представление сигналов с ограниченным спектром.51
3. МОДУЛИРОВАННЫЕ СИГНАЛЫ............................55
3.1. Общие сведения..................................55
3.2. Сигналы с амплитудной модуляцией................57
-146-
3.3. Сигналы с угловой модуляцией.................69
3.4. Сигналы с обобщенной модуляцией..............77
3.5. Манипулированные сигналы.....................81
3.6. Аналитический сигнал и его применение........86
4. ПРОХОЖДЕНИЕ СИГНАЛОВ ЧЕРЕЗ ЛИНЕЙНЫЕ
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ............................ 94
4.1. Классификация радиотехнических цепей.........94
4.2. Линейные радиотехнические цепи...............96
4.3. Методы анализа прохождения сигналов
через линейные цепи............................ 102
4.4. Прохождение видеоимпульсов через
линейные цепи.................................. 106
4.5. Искажения сигналов в линейных цепях......... 111
5. ПРОХОЖДЕНИЕ МОДУЛИРОВАННЫХ СИГНАЛОВ
ЧЕРЕЗ ЛИНЕЙНЫЕ РАДИОТЕХНИЧЕСКИЕ ЦЕПИ...........116
5.1. Линейные узкополосные цепи.................. 116
5.2. Прохождение сигналов с амплитудной модуляцией
через линейную узкополосную цепь................. 121
5.3. Прохождение сигналов с угловой модуляцией
через линейную узкополосную цепь............... 125
5.4. Прохождение произвольного узкополосного
сигнала через линейную узкополосную цепь....... 130
5.5. Прохождение радиоимпульсов через линейную
узкополосную цепь.............................. 133
5.6. Прохождение фазоманипулированных сигналов
через линейную узкополосную цепь................. 137
5.7. Прохождение частотно-манипулированных сигналов
через линейную узкополосную цепь............... 140
библиографический список........................ 145
-147-
Ольга Алексеевна Стеценко
РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ
Часть 1
Редактор А.Н. Денисенко
Учебное пособие напечатано в авторской редакции
Изд. лицензия №020456 от 04.03.97
Подписано в печать 17.01.00. Формат 60x84 1/16.
Бумага офсетная. Печать офсетная. Усл. печ. л. 8,6.
Усл. кр.-отт. 34,4. Уч.-изд. л. 9,25. Тираж 300 экз. С62.
Московский государственный институт радиотехники,
электроники и автоматики (технический университет)
117454, Москва, просп. Вернадского, 78