Б.Шутц
ГЕОМЕТРИЧЕСКИЕ МЕТОДЫ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
Написанное английским математиком введение в геометрические методы
математической физики. Содержит основные сведения по дифференциальной
геометрии вплоть до понятий римановой геометрии и общей теории связностей, а
также некоторые физические приложения,— в частности, из общей теории
относительности и теории калибровочных полей
Для математиков и физиков, желающих ознакомиться с приложениями
геометрии в математической физике.
ОГЛАВЛЕНИЕ
От редактора перевода 5
Предисловие 7
1. НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ 13
1.1. Пространство Rn и его топология 13
1.2. Отображения 17
1.3. Вещественный анализ (вещественные функции вещественных 22
переменных)
1.4. Теория групп
1.5. Лниейиая алгебра
1.6. Алгебра квадратных матриц
1.7. Библиография
2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
2.1. Определение многообразия
2.2. Сфера как многообразие
2.3. Другие примеры многообразий
2.4. О свойствах многообразий "в целом"
2.5. Кривые
2.6. Функции наМ
2.7. Векторы и векторные поля
2.8. Базисные векторы и базисные векторные поля
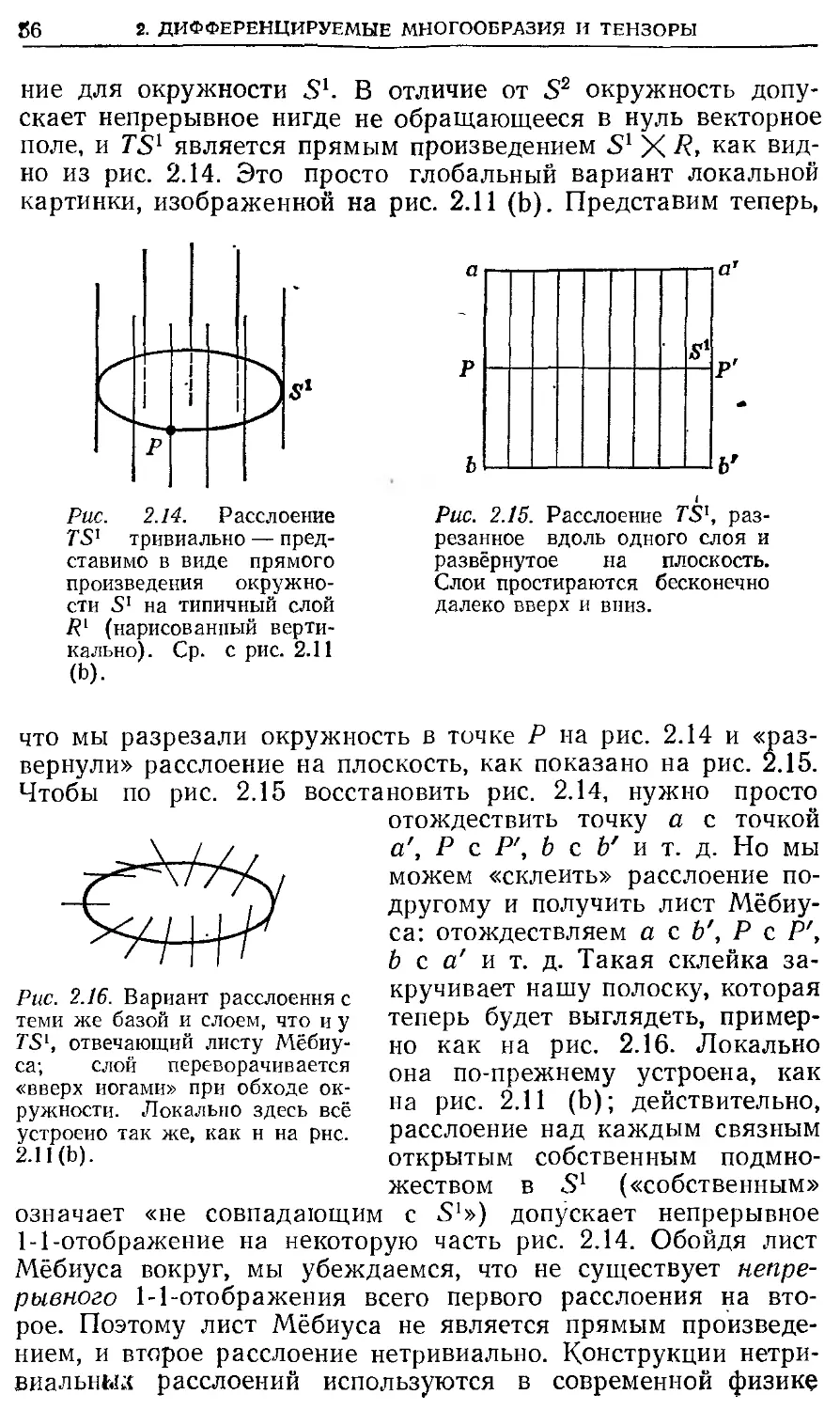
2.9. Расслоенные пространства
2.10. Примеры расслоенных пространств
2.11. Более глубокий взляд на расслоенные пространства
2.12. Векторные поля и интегральные кривые
2.13. Экспонента от оператора d/dA
2.14. Скобки Лии некоордниатные базисы
2.15. Когда базис является координатным
2.16. Одни-формы
2.17. Примеры одни-форм
2.18. Дельта-функция Дирака
2.19. Градиент и наглядное изображение одни-форм

2.20. Базисные одни-формы и компоненты одни-форм
2.21. Индексные обозначения
2.22. Тензоры и тензорные поля
2.23. Примеры тензоров
2.24. Компоненты тензоров и тензорное произведение
2.25. Свертка
2.26. Замена базиса
2.27. Геизорные операции над компонентами
2.28. Функции и скаляры
2.29. Метрический тензор в векторном пространстве
2.30. Поле метрического тензора на многообразии
2.31. Специальная теория относительности.
2.32. Библиография
3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
3.1. Введение как векторное поле отображает многообразие в себя
3.2. Действие переноса Ли на функции
3.3. Действие переноса Ли на векторные поля
3.4. Производные Ли
3.5. Производная Ли одни-формы
3.6. Подмногообразия
3.7. Теорема Фробениуса на языке векторных полей
3.8. Доказательство теоремы Фробениуса
3.9. Пример: генераторы вращений
3.10. Инвариантность
3.11. Векторные поля Киплинга
3.12. Векторы Киллингаи сохраняющиеся величины в динамике частицы
3.13. Осевая симметрия
3.14. Абстрактные группы Ли
3.15. Примеры групп Ли
3.16. Алгебры Лии отвечающие им группы Ли
3.17. Реализации и представления
3.18. Сферическая симметрия, сферические гармоники и представления
группы вращений
3.19. Библиография
4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
А. Алгебра и интегральное исчисление форм
4.1. Определение объема- геометрическая роль дифференциальных форм
4.2. Обозначения и определения, касающиеся антисимметричных тензоров
4.3. Дифференциальные формы
4.4. Обращение с дифференциальными формами
4.5. Ограничение форм
4.6. Поля форм

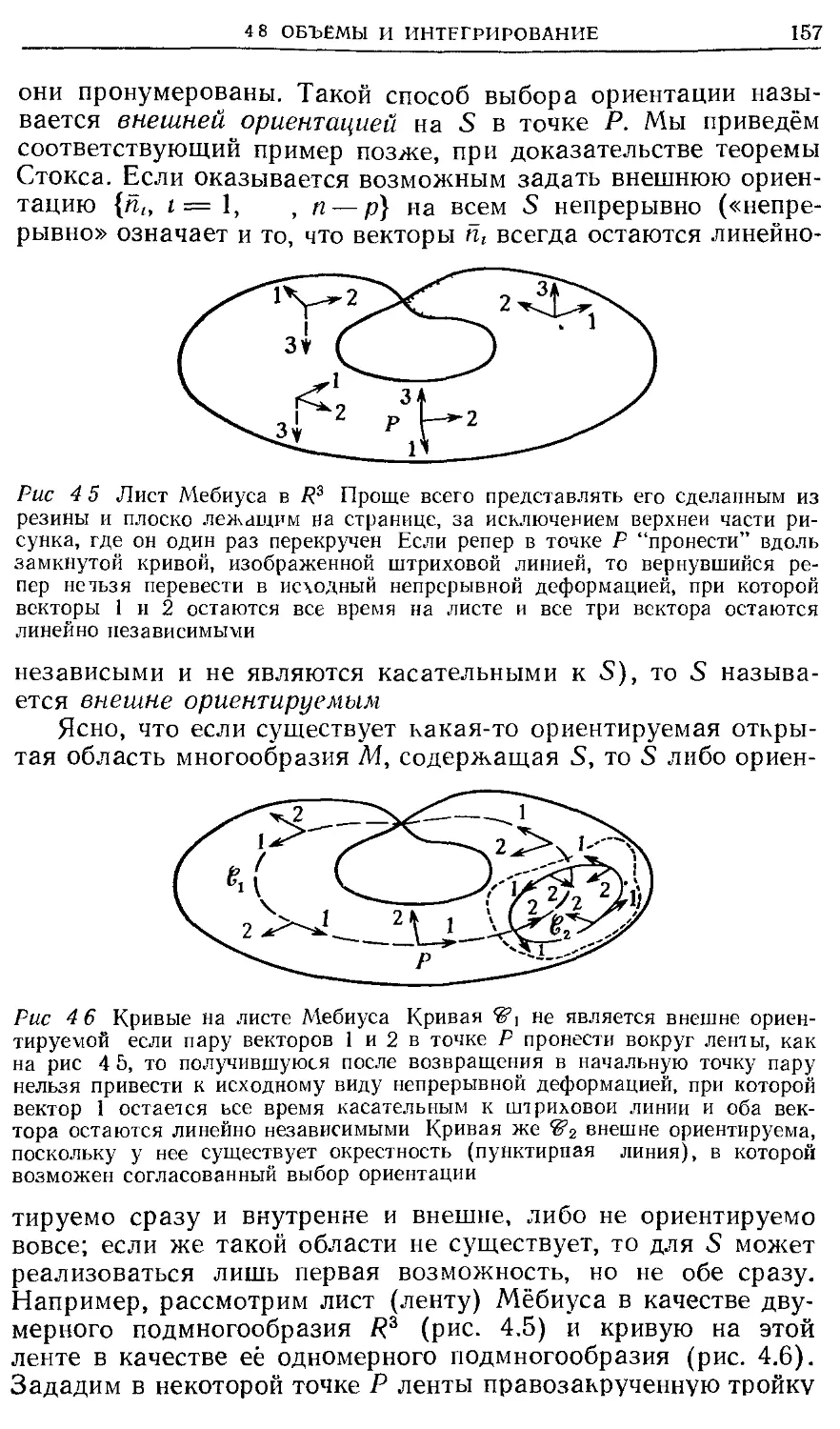
4.7 Ориентируемость
4.8. Объемы и интегрирование на ориентируемых многообразиях
4.9. N-векторы, дуальные величины и символ ?ij,...,k
4.10. Тензорные плотности
4.11. Обобщенные символы Кронекера
4.12. Определители и ?ij,...,k
4.13. Метрический элемент объема
В. Дифференциальное исчисление форм и его приложения
4.14. Внешняя производная
4.15. Обозначения для частных производных
4.16. Хорошо знакомые примеры внешнего дифференцирования
4.17. Условия интегрируемости дифференциальных уравнений в частных
производных
4.18. Точные формы
4.19. Доказательство локальной точности замкнутых форм
4.20. Производные Ли от форм
4.21. Производные Ли и внешние производные коммутируют
4.22. Теорема Стокса
4.23. Теорема Гаусса и определение дивергенции
4.24. Краткий экскурс в теорию когомологий
4.25. Дифференциальные формы и дифференциальные уравнения
4.26. Теорема Фробениуса на языке дифференциальных форм
4.27. Доказательство эквивалентности двух вариантов теоремы Фробениуса
4.28. Законы сохранения
4.29. Векторные сферические гармоники
4.30. Библиография
5. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
A. Термодинамика
5.1. Простые системы
5.2. Тождества Максвелла и другие математические тождества
5.3. Композитные термодинамические системы, теорема Каратеодори
B. Гамильтонова механика
5.4. Гамильтоновы векторные поля
5.5. Канонические преобразования
5.6. Соответствие между векторами и одни-формами, устанавливаемое
формой б
5.7. Скобка Пуассона
5.8. Многочастичные системы, симплектические формы
5.9. Линейные динамические системы, симплектическое скалярное
произведение и сохраняющиеся величины
5.10. Уравнения Гамильтона и расслоения
C. Электромагнетизм

5.11. Уравнения Максвелла на языке дифференциальных форм
5.12.Заряд и топология
5.13. Вектор потенциал
5.14. Плоские волны простой пример
D. Динамика идеальной жидкости
5.15. Роль производных Ли
5.16. Полная производная по времени
5.17. Уравнение движения
5.18. Сохранение вихрей
E. Космология
5.19. Космологический принцип
5.20. Алгебра Ли максимальной симметрии
5.21. Метрика сферически-симметричного трехмерного пространства
5.22. Построение шести векторов Киплинга
5.23. Открытая, замкнутая и плоская Вселенные
5.24. Библиография
6. СВЯЗНОСТИ НА РИМАНОВЫХ МНОГООБРАЗИЯХ И
КАЛИБРОВОЧНЫЕ ТЕОРИИ
6.1. Введение
6.2. Параллельность на искривленных поверхностях
6.3. Ковариантная производная
6.4. Компоненты, ковариантные производные базиса
6.5. Кручение
6.6. Геодезические
6.7. Нормальные координаты
6.8. Тензор Римана
6.9. Геометрическая интерпретация теизора Римана
6.10. Плоские пространства
6.11. Согласованность связности с объёмом или метрикой
6.12. Метрическая связность
6.13. Аффнииая связность и принцип эквивалентности
6.14. Связности и калибровочные теории на примере электромагнетизм
6.15. Библиография
Приложение. Решения и указания к некоторым упражнениям
Литература, добавленная при переводе
Именной указатель
Предметный указатель
Указатель обозначений
ИМЕННОЙ УКАЗАТЕЛЬ
Болл (S. Ball) 12 Галилей 7, 54

Декарт 7
де Рам (G. de Rham) 156
Дирак 68, 70
Каратеодори (С. Caratheodory) 204
Картан (Е. Cartan) 8, 144, 200, 266
Кеплер 7
Коминз (N. Comins) 12
Коперник 7
Ли (S. Lie) 62
Мниковский (Н. Minkowski) 95
Ньютон 54
ПРЕДМЕТНЫЙ
абелева алгебрами 121
— группа 25
автоморфизм внутренний 137
аксиальная симметрия 113, 116
алгебра Гроссмана 150
— Ли 131
абелева (коммутативная) 121
векторных полей 64
группы Ли 120
алгебраическое дополнение 32
аналитическая функция 22
аналитическое многообразие 60
аннулирует 153
аннулятор набора форм 191
антидифференцирование 169
антисимметричная часть 147
антисимметричный тензор 146, 147
антнэрмитова матрица 129 атлас 40
аффинная связность 242
аффинный параметр 250
база расслоения 53, 57
базис 28
— двойственный (дуальный) 74
— декартов 88
— координатный 50
— левозакрученный 153
— лореицев 88
— ортонормированный 87, 88
— правозакрученный 153
Оуэн (J Owen) 12
Птолемей 7
Соркии (R. Sorkin) 12, 219
Торн (К. Thome) 12
Уилер (J. A. Wheeler) 218
Уилкнисон (М. Wilkinson) 12
Уэйд (В. Wade) 12
Фрндмэн (J. Friedman) 12
Шутц(В. Schutz) б, 12
Эйнштейн 227
Эстабрук (P. Estabrook) 12
УКАЗАТЕЛЬ
— псевдоэвклидов 88
Бетти число 189
биекция 19
большой взрыв 240
бра-вектор 68
Бьянки тождества 254
Бейля тензор 260
вектор 48, 50
— ковариантный 68
— контр авариантный 68
—N-вектор 158
вектор-градиеит 94
векторное поле 50
гамильтоново 207
Киплинга ПА
левоинвариантное 120
— произведение 159
двойное 165
— пространство 27
вектор-потенциал 220
вес 163,164
взаимно-однозначиое отображение
18
вихрь 225
внешне ориентируемое многообразие
157
внешнее произведение 79, 149
внешняя ориентация 157
— производная 169

внутренний автоморфизм 137
времени-подобная кривая 93
Вселенная 227
— замкнутая 239
— открытая 239
— плоская 239
выделенная форма объёма 166
Гамильтона функция 206
— уравнения движения 206
гамильтоново векторное поле 207
гармоника осевая векторная 117—
118
скалярная 117
— сферическая 139
векторная 198—199
Гаусса теорема 184
Гельмгольца теорема о циркуляции
225
генерирует 207
геодезическая 250
геодезически полное многообразие
252
гиперповерхность 104
главное расслоенное пространство 59
гомеоморфизм 57
гомоморфизм 26
гравитационное поле 260 градиент
71,246
грассманова алгебра 150
группа 25
— абелева (коммутативная) 25
— изотропии 229
— когомологий де Рама 187
— Ли 44
— несвязная 126
— ортогональная 127
— полная линейная 123, 129
— специальная ортогональная 127
унитарная 129
— структурная
— унитарная 129
двойное векторное произведение 165
двойственное пространство 67
двойственность 68
двойственный базис 74 де Рама
группа когомологий 187
теорема 189
девиация геодезических 256
действие группы транзитивное 229
декартов базис 88
декартово произведение 55
дельта-символ 164
дельта-функция 69
детерминант 32
дивергенция 172
— ковариантная 257
ю-дивергенция 184
динамическая система 213
линейная 210
Дирака дельта-функция 69
дискретное множество 14
диффеоморфизм 45
дифференциальная структура 40
— форма 149
дифференциальный идеал 192
дифференцируемость класса Ск 21
дуализация 158, 160
дуальное пространство 67
дуальный базис 74
— тензор 159, 160
единица 24
естественные координаты 53
жорданова форма 124
закон преобразования 82
ковариантный 82
контр авариантный 82
— сохранения 196, 225
замкнутая Вселенная 239
— система (в термодинамике) 204
— форма 173
замкнутый набор форм 192
идеал дифференциальный 192
— полный 191

идеальная жидкость 222
изоморфизм групп 26
изотропии группа 229
изотропное многообразие 230
импульс 206
U-импульс канонический 213
инвариантное подпространство 139
инвариантность калибровочная 264
— относительно векторного поля 112
переносами 97
индуцирует (топологию) 15
интеграл от формы 154
интегральная кривая 59
— поверхность 197
нифинитезимальный генератор 124
— дифференциал 72
инъективное отображение 18
калибровочная два-форма кривизны
264
— инвариантность 264
калибровочное преобразование 220
калибровочио-ковариантная
производная 264
калибровочио-плоский 265
калибровочные теории 261
каноническая форма матрицы 124
канонический U-импульс 213
каноническое преобразование 207
Каратеодори теорема 204
карта 39
касательное пространство 50
— расслоение 53
касательный вектор 47
— пучок 53
квадратично-интегрируемая функция
23
кет-вектор 68
Кгиишнга вектор(ное поле) 114
— уравнение 259
ковариантная дивергенция 257
— производная 244
ковариантный вектор 68, 83
когомологий группа 187
— теория 174
кокасательное расслоение 71
коммутативная алгебрами 121
— группа 25
коммутатор 24
— матричный 127
коммутирующие операторы 24
композитная система 203 композиция
19
компонента единицы связная 126
компоненты вектора 28
— одни-формы 74
— преобразования (оператора 30
— тензора 79
конгруэнция 60
консервативная система 207
контр авариантный вектор 68, 82
конфигурациониое пространство 213
координатный базис 50
координаты 38
— естественные 53
— нормальные 252
Коперника принцип 230
космологический принцип 230
космология изотропная 230
— однородная 230
кососимметричный тензор 146
кососкалярное произведение 211
кривая 45
— параметризованная 45
кривизна 257
Кристоффеля символы 246
Кронекера символ 32
обобщённый 164
кручение 249
Лагранжа уравнение движения 206
— функция 206
Леви-Чивиты символы 162
левозакрученный базис 153
левоинвариантное векторное поле
120

Лейбница формула 102, 103
лемма Пуанкаре 175
Ли алгебра 64, 131
— группа 44
— производная 100, 101, 103
— скобка 62, 131
ли-инвариантность 97
линейная комбинация 27
— независимость 27
линейное преобразование 30
линейность (полилинейность) 76
ли-перенос 97 лист слоения 106
ли-тянутая конгруэнция 98
— функция 97
ли-тянутое векторное поле 98
— поле одни-форм 102
Лиувилля теорема 210
локальная тривиальность расслоения
55
локально-плоское метрическое
тензорное поле 91
Лоренца группа 88
— преобразование 88
лореицев базис 88
Максвелла тождества 202
— уравнения 215
максимально-симметричное
многообразие 232
матрица 30
— антнэрмитова 129
— вырожденная 32
— единичная 32
— невырожденная 32
— преобразования 81
— обратная 32
— транспонированная 32
матричное произведение 31
метрика 86
— индефинитная 88
— Минковского 88
— эвклидова 86
метрическая связность 258
метрический тензор 86
Мёбиуса лист 56
Минковского метрика 88
— пространство 93, 94
многообразие 37
— аналитическое 60
— внешне ориентируемое 157
— геодезически полное 252
— гладкое 40
— дифференцируемое 40
— изотропное 230
— класса С* 40
— максимально-симметричное 232
— однородное 229
— односвязное 131, 189
— ориентируемое 58, 153
— симплектическое 210
— сферически-симметричное 233
С^ -многообразие 40
модель заряда Соркииа 219
Уилера218
мультипликативность 253
на 19
накрывает 131
накрытие двулистное 133
непрерывность 19, 20
несвязная группа 126
норма 28
— эвклидова 30
нормальные координаты 252
нормированное векторное
пространство 28
нуль-форма 149
область определения 24
обобщённая функция 69
образ 18
образующие 28
обратное отображение 18
обратный элемент 25
объём 154
объёма форма 154
выделенная 166

— элемент 144
ограничение формы 152
одни-форма 67
однопараметрическая подгруппа 121
однородное многообразие 229
односвязное многообразие 131, 189
окрестность 14, 17
оператор 23
— момента импульса 111
определитель 32
опускание индексов 90
ориентация внешняя 157
ориентируемое многообразие 153
ориентируемость 58
ортогональная группа 127
ортонормированный базис 87, 88
осевая гармоника векторная 117—
118
скалярная 117
— симметрия 113, 116
осевое собственное значение 117
отделимость 15
открытая Вселенная 239
открытое множество 14
отношение эквивалентности 187
отображение 17
— взаимно-однозначиое 18
— дуализации 158, 160
1 -1-отображение 18
отражение 128
параллелограмма тождество 29
параллельный перенос 243
параметр 45
— аффинный 250
перенос вдоль конгруэнции 97
— Ли 91
— параллельный 243
плоская Вселенная 239
плоское пространство 257
плотность скалярная 163
— тензорная 164
площадь 144—147
повторяющиеся индексы 76
подгруппа 26
— однопараметрическая 121
подмногообразие 103—104
поднятие индексов 90
подобия преобразование 34
подпространство 28
поле векторное 50
— дифференцируемое 71
— тензорное 77
— форм 71, 153
полилинейность 76
полная линейная группа п-мерного
вещественного пространства
123
— комплексного
пространства 129
— производная по времени 222
— система функции 140
полный ндеал (набора форм) 191
порождает 28
правило запятой 170, 248
— разложения по строке 32
— сумирования Эйнштейна 16
правозакрученный базис 153
представление 136
— двузначное 142
— неприводимое 139
— присоединённое 137
— спииорное 142
— фундаментальное 142
преобразование калибровочное 220
— каноническое 207
— координат 39
— Лоренца 88
— присоединённое 137
принцип заурядности 230
— Коперника 230
— космологический 230
— минимальной связи 261
— эквивалентности сильный 261
присоединённая реализация 137

присоединённое представление 137
— преобразование 137
проекция расслоения 53, 57
произведение векторное 159
— внешнее 79, 149
— кососкалярное 211
— прямое 55
— тензорное 79
производная внешняя 169
— калибровочио-инвариантная 264
— ковариантная 244
— .Яы 100, 101, 103
— полная (по времени) 222
производящие функции
канонических преобразований
208
прообраз 18
пространственио-подобная кривая
93
пространственио-под обное
многообразие 192
пространство конфигурационное 213
— фазовое 43, 206
прямое произведение 55
псевдонорма 30
псевдоэвклидов базис 88
Пуанкаре лемма 175
Пуассона скобка 209
размерность векторного
пространства 28
— многообразия 37
ранг тензора 90
распределение на многообразии т-
мерное 108
— (обобщённая функция) 69
расслоение 52, 57
— касательное 53
— кокасательное 71
— реперов 59
иA)-расслоение 263
расслоенное пространство 52, 57
главное 59
расширение оператора 24
реализация 135
— главная 136
— присоединённая 137
— прогрессивная 136
— регрессивная 136
— точная 135
Римана тензор 253
Риччи тензор 259
ротор 171
свёртка 68, 80, 151, 178
связная компонента единицы 126
связность аффнииая. 242
связность метрическая 258
связность симметричная 248
сдвиг левый 119
— правый 119
сечение расслоения 53
сигнатура метрики 87
— поля 8 91
сильный принцип эквивалентности
261
символы Кристоффеля 246
— Кронекера обобщённые 164
— Леви-Чивиты 162
симметричная связность 248
— часть 232, 249
симметричный тензор 148
симметрия аксиальная 113, 116
— осевая 113,116
— сферическая 119, 138
— цилиндрическая 116
симплектическая форма 210
симплектическое многообразие 210
— скалярное произведение 211
скалярная плотность 163
скалярное произведение 29
симплектическое 211
скобками 62, 131
— Пуассона 209
след 34

слепляющее отображение 18
слоение 106
слой 52, 53, 57
собственное значение 34
осевое 117
собственный вектор 34
согласованность карт 39
— Уи g 258
— V и ЕВ 258
С^-согласованность 39
сопряжённое пространство 67
Соркина модель заряда 219
сохраняющиеся величины 115, 185,
196,210,225
специальная ортогональная группа
127
— унитарная группа 129
спин 142
спинор 142
спинорное представление 142
стереографическая проекция 42
Стокса теорема 183
структурная группа 57
структурные константы 120
сужение формы 152
сферическая гармоника 139
векторная 198—199
— симметрия 119, 138
сферически-симметричное
многообразие 233
сюръективное отображение 19
температура 201
тензор 76
— антисимметричный 146, 147
— Бейля 260
— дуальный 159, 160
— кососимметричный 146
— кручения 249
— метрический 86
— напряжений 78
— нулевой 83
— Романа. 253
— Риччи 259
— симметричный 148
(N'\
— Эйнштейна 260
N"\
-тензор 76
тензорная операция 85
тензорное поле 77
инвариантное относительно
векторного поля 112
— произведение 79
— равенство 85
— уравнение 85
теорема Гаусса 184
— Гелъмголъца с циркуляции 225
— де Рама 189
— Каратеодори 204
— Лиувшля 210
— о дивергенции 183
неподвижной точке на сфере
55,188
— об изменении полного заряда 218
обратной функции 22
— Стокса 183
— Фробениуса на языке векторных
полей 105—106
дифференциальных форм
192
— Эртеля 226
теория когомологий 174
тождества?ьян;ш 254
— Максвелла 202
тождественное преобразование 32
тождество Якоби 64, 131
топологическое пространство 15
топология 13
— глобальная 13
— локальная 13
точная форма 173
транзитивное действие 229

тривиальность расслоения 55
локальная 55
глобальная 55
тэйлорово разложение 23
увлечение 97
Угшера модель заряда 218
унитарная группа 129
уравнение девиации геодезических
256
— Киплинга 259
— Клейна—Гордона 213, 264
— неразрывности 185
— Эйлера (движения жидкости) 224
уравнение Максвелла 215
фазовое пространство 43, 206
факторпространство 187
Фарадея тензор 215—216
форма (дифференциальная) 149
— замкнутая 173
— объёма 154, 210
выделенная 166
— симплектическая 210
— точная 173
р-форма 149
1-форма 67
Фробениуса теорема на языке
векторных полей 105—106
дифференциальных форм
192
фундаментальное представление 142
функциональное пространство 69
функция 46, 85
— аналитическая 22
— Гамильтона 206
— дифференцируемая 46
— класса Ск 21
— Лагранжа 206
— обобщённая 69
Ск -функция 21
Сф -функция 23
С™-функция 21
хаусдорфовость 15
цилиндрическая симметрия 116
число Бетти 189
эвклидова метрика 86
эвклидово пространство 30
Эйлера уравнение (движения
жидкости) 224
Эйнштейна правило суммирования
76
— тензор 260
экспонента от оператора d/dX 61
экспоненциальное отображение 252
элемент объёма 144
энтропия 201, 224
Эртеля теорема 226
Якоби матрица 22
— тождество 64, 131
якобиан 22
Ск -многообразие 40
С -согласованность 39
Ск -функция 21
Сф -функция-23
С™-функция 21
N-вектор 158
N\
- тензор 76
р-дельта (-символ) 164
р-мерная группа когомологий 187
р-форма 149
?/-импульс канонический 213
U(T) -расслоение 263
ю-дивергенция 184
1-форма 67
1 -1-отображение 18

ОТ РЕДАКТОРА ПЕРЕВОДА
Учебная литература по дифференциальной геомет-
геометрии достаточно обширна. Однако в большинстве учеб-
учебников вопрос о приложениях дифференциальной гео-
геометрии к задачам математической физики даже не
ставится. Это и неудивительно. Необходимость освое-
освоения дифференциально-геометрических методов всеми
физиками-теоретиками (а не только теми, которые
избрали своей специальностью общую теорию относи-
относительности) была осознана лишь в самое последнее
время в связи с открытиями нетривиальных прило-
приложений геометрии и топологии в квантовой теории ка-
калибровочных полей, теории жидких кристаллов и
сверхтекучести, той же общей теории относительности
и других областях физики.
Предлагаемая вниманию читателей книга, напи-
написанная специалистом по общей теории относитель-
относительности, является одним из первых элементарных учеб-
учебников по дифференциальной геометрии, где при от-
отборе материала во главу угла ставился прикладной
аспект (это видно уже из её названия). Хотя она
предназначена для первоначального знакомства с
предметом, в ней обсуждается довольно много диф-
дифференциально-геометрических понятий. При сравни-
сравнительно небольшом объёме книги это определило стиль
изложения. Автор всюду стремится выделить главные
геометрические идеи, отсылая читателя к литературе
по поводу чисто технических деталей ряда доказа-
доказательств. Изложение сопровождается большим количе-
количеством упражнений, что особенно важно для актив-
активного овладения предметом.
Особо следует сказать о разбираемых в книге фи-
физических иллюстрациях и приложениях дифферен-
дифференциально-геометрических идей. Среди них имеются
ставшие уже общеизвестными, такие как изложение
основных положений гамильтоновой механики на язы-
языке симплектической геометрии, интерпретация термо-
термодинамических тождеств на языке дифференциальных

ОТ РЕДАКТОРА ПЕРЕВОДА
форм, тензорная запись уравнений Максвелла в про-
пространстве-времени специальной теории относительно-
относительности. Но есть и менее традиционные — вывод существо-
существования энтропии для составных систем из классиче-
классической формулировки второго начала термодинамики,
анализ геометрической структуры уравнений гидроди-
гидродинамики идеальной жидкости, элементы теории калиб-
калибровочных полей в свете общей теории связностей
и др. Широкий спектр подбора физических иллюстра-
иллюстраций позволит начинающим физикам разных специа-
специализаций уяснить важность геометрического аппарата
как одного из инструментов современной теоретиче-
теоретической физики. Начинающего же математика-геометра
чтение этой книги побудит, как нам кажется, к более
серьёзному изучению прикладных аспектов дифферен-
дифференциальной геометрии.
При переводе были исправлены замеченные опе-
опечатки, а также добавлен список ряда учебников на
русском языке по тематике глав книги.
В заключение отметим, что учебник Б. Шутца по-
получил ряд высоких отзывов специалистов-геометров
и физиков-теоретиков. О его популярности свидетель-
свидетельствует выход второго английского издания A982)
вскоре вслед за первым A980). Мы надеемся, что эта
книга получит признание и у наших читателей.
Б. А. Дубровин

ПРЕДИСЛОВИЕ
Зачем изучать геометрию?
Назначение этой книги — ввести начинающего или
уже работающего физика в весьма широкий круг
аналитических методов дифференциально-геометриче-
дифференциально-геометрического происхождения, которые ныне всё чаще и чаще
применяются в теоретической физике. В наши дни при
обучении физике «наглядное» и «интуитивное» рас-
рассмотрение физических явлений принято ставить во
главу угла. Однако при обучении студентов-физиков
математике геометрическими идеями и методами, за
исключением самых простейших, обычно пренебре-
пренебрегают. Это поразительное пренебрежение наглядностью
математического аппарата возникло не сразу, а яв-
является продуктом многовековой эволюции. Для ан-
античных и средневековых натурфилософов геометрия,
несомненно, была крайне важна; и Птолемей, и Ко-
Коперник, и Кеплер, и Галилей — все излагали свои рас-
рассуждения в геометрической форме. Но когда Декарт
ввёл в эвклидову геометрию координаты, геометрия
стала рассматриваться как приложение алгебры.
С той поры роль геометрии в подготовке ученого на-
начала сходить на нет, и в настоящее время студентам
старших курсов университетов — физикам или мате-
математикам-прикладникам— почти вовсе не приходится
сталкиваться с геометрией.
Одна из причин эюго очевидна: сравнительно про-
простая геометрия трёхмерного эвклидова мира (в кото-
котором, как думалось физику 19-го столетия, мы живём)
осваивалась легко, в то время как изучение огром-
огромного разнообразия аналитических приёмов, которые
необходимы для решения дифференциальных уравне-
уравнений физики, было делом весьма нелегким и отнимало
массу времени. Другая причина, наверное, состоит
в том, что сами эти аналитические приёмы и методы
разрабатывались, по крайней мере отчасти, на основе
глубокого убеждения физиков, что законы природы
могут быть записаны в виде дифференциальных урав-
уравнений, и это убеждение вплоть до самого последнего

ПРЕДИСЛОВИЕ
времени позволяло физикам с чистой совестью пре-
пренебрегать геометрией.
Однако два достижения науки нашего столетия
решительно изменили взгляды физиков 20-го века на
соотношение между геометрией и анализом. Первым
из них явилась теория относительности, согласно ко-
которой эвклидово трёхмерное пространство физика
19-го века — лишь приближение к правильному опи-
описанию физического мира. Вторым, лишь начинающим
играть свою роль, было осознание математиками
20-го века, вслед за Э. Картаном, того, что соотноше-
соотношение между геометрией и анализом двустороннее: с од-
одной стороны, анализ можно взять за основание при
изучении геометрии, а с другой стороны, изучение гео-
геометрии естественно приводит к развитию определён-
определённого аналитического аппарата (производная Ли, ис-
исчисление дифференциальных форм и т. д.) и опреде-
определённых понятий (многообразие, расслоенное про-
пространство, трактовка векторов как дифференцирова-
дифференцирований и т. д.), играющих чрезвычайно важную роль в
приложениях анализа. Согласно современным воззре-
воззрениям, геометрия остается подчинённой анализу. На-
Например, основное понятие дифференциальной геомет-
геометрии, понятие дифференцируемого многообразия, опре-
определяется на языке теории вещественных чисел и диф-
дифференцируемых функций. Но никакого вреда в этом
нет; наоборот, благодаря этому становится возмож-
возможным представить понятия анализа геометрически, а
это имеет огромное эвристическое значение.
Именно потому, что современная дифференциаль-
дифференциальная геометрия разрабатывает и эксплуатирует эту
тесную взаимосвязь между геометрическими и анали-
аналитическими понятиями и идеями, она становится всё
более и более важной в теоретической физике, упро-
упрощая математический формализм и углубляя физиче-
физическое понимание. Это возрождение геометрии оказало
влияние не только на специальную и общую теории
относительности, очевидно геометрические по своей
сути, но и на другие разделы физики, где на аван-
авансцену выходит уже не геометрия физического про-
пространства, а геометрия более абстрактных про-
пространств, — термодинамику, гамильтонов формализм,
гидродинамику и физику элементарных частиц.
Цели этой книги
В этой книге я хотел дать читателю представление
о наиболее важных понятиях дифференциальной гео-

ПРЕДИСЛОВИЕ
метрии 20-го века, стараясь при этом всюду использо-
использовать наглядный геометрический способ рассуждений,
столь полезный для развития физической интуиции.
Книга призвана научить математике, а не физике. Но
в неё включены разнообразные приложения этой ма-
математики к разделам физики, хорошо знакомым боль-
большинству студентов старших курсов. Надеюсь, что эти
примеры окажутся более чем просто иллюстрациями
к математическим теоремам, — новые математические
формулировки знакомых физических результатов
должны дать читателю более глубокое понимание фи-
физики.
Ниже будет более подробно обсуждаться, какая
подготовка требуется для чтения этой книги, а здесь,
пожалуй, полезно привести краткий список «знако-
«знакомых» понятий, которые будут показаны под новым
углом зрения: векторы, тензоры, скалярное произве-
произведение, специальная теория относительности, сфериче-
сферические гармоники и группа вращений (а также опера-
операторы момента), законы сохранения, объём, теория
интегрирования, ротор и векторное произведение, опре-
определитель, уравнения в частных производных и усло-
условия их интегрируемости, формулы Гаусса и Стокса
из векторного анализа, термодинамика простых си-
систем, теорема Каратеодори (и второе начало термо-
термодинамики), гамильтоновы системы в фазовом про-
пространстве, уравнения Максвелла, гидродинамика
(включая теорему о сохранении циркуляции), вектор-
векторный анализ в криволинейных координатах, квантовая
теория заряженного скалярного поля. Помимо этих
более или менее привычных тем есть и другие, о ко-
которых, хотя их обычно и не включают в обязательные
курсы, большинство читателей наверняка кое-что слы-
слышало: теория групп Ли и симметрия, открытая и замк-
замкнутая космологические модели, риманова геометрия и
теория физических калибровочных полей. То, что все
эти темы можно исследовать методами дифференци-
дифференциальной геометрии, служит явным указанием на ту
роль, которую она, по-видимому, будет играть в тео-
теоретической физике будущего.
Я считаю, что читателю важно выработать нагляд-
наглядный стиль мышления и развить в себе чувство «есте-
«естественности» того или иного геометрического аппарата
в определённых ситуациях. Имея это в виду, я по-
постоянно подчёркиваю идею, что тензоры — это гео-
геометрические объекты, определённые независимо от
какой-либо системы координат. Компонентам и коор-

10 ПРЕДИСЛОВИЕ
динатным преобразованиям неизменно отводится вто-
вторая роль — всюду, где только возможно, я записываю
уравнения в безындексной форме, с тем чтобы под-
подчеркнуть их независимость от выбора системы коор-
координат. Я не стремился дать логически замкнутое или
аксиоматическое изложение и потому оставил в сто-
стороне ряд аспектов, которые математик счел бы осно-
основополагающими. Разумеется, я даю доказательства
всех наиболее важных результатов, если эти доказа-
доказательства не слишком уже громоздки (в таком случае
я даю точные ссылки на литературу), но насколько
только это было возможно, я всюду старался добить-
добиться, чтобы главная геометрическая идея доказатель-
доказательства чётко выделялась на фоне выкладок. Я хотел по-
показать красоту, элегантность и естественность изла-
излагаемых математических приемов, не затемняя суть
дела излишними подробностями.
Как пользоваться этой книгой
Первая глава содержит обзор основных математи-
математических сведений, которые предполагаются известными
читателю, а также краткое введение в некоторые
разделы, в частности в топологию, с которыми стар-
старшекурсник может и не быть знаком. Следующие три
главы являются ядром книги; в них вводятся тен-
тензоры, производные Ли и дифференциальные формы.
По этим главам рассеяны и некоторые приложения
излагаемого аппарата, но большинство физических
приложений систематически разбираются в гл. 5.
В последней, шестой главе, посвященной римановой
геометрии, представлен более сложный материал,
имеющий непосредственное отношение к физике эле-
элементарных частиц и общей теории относительности,
для которых дифференциальная геометрия является
повседневным рабочим инструментом.
Материал этой книги может быть использован для
семестрового курса, при условии что наиболее слож-
сложные разделы будут представлены лишь выборочно, по
усмотрению лектора. Наиболее важные разделы мож-
можно использовать также для специального курса по
математическим методам физики, лекций на десять.
Я читал такой спецкурс для аспирантов, основываясь
на §§ 2.1—2.3, 2.5—2.8, 2.12—2.14, 2.16, 2.17, 2.19—
2.28, 3.1—3.13, 4.1—4.6, 4.8, 4.14—4.18, 4.20—4.23,
4.25, 4.26, 5.1, 5.2, 5.4—5.7 и 5.15—5.18. Надеюсь, пре-
преподаватели сами будут экспериментировать с отбо-
отбором материала для курса, учитывая аудиторию: для

ПРЕДИСЛОВИЕ 11
многих студентов геометрическое изложение понятнее
чисто аналитического, и для них только полезно как
можно раньше войти в круг геометрических идей.
Для того чтобы читателю было легче ориентироваться
в книге, заголовки параграфов набраны двумя раз-
различными шрифтами. Основной материал маркируется
жирным прямым шрифтом заголовков, а более слож-
сложный или дополнительный — жирным курсивом К по-
последней категории относится вся заключительная гла-
глава. Такие же шрифтовые выделения помогают отли-
отличить упражнения, лежащие в центральном русле
изложения, от периферийных.
Упражнения составляют неотъемлемую часть кни-
книги. Они расположены внутри текста, и имеется в виду,
что читатель решает их по мере их появления. Обычно
текст, следующий за упражнением, предполагает, что
это упражнение уже проработано и понято. Чита-
Читатель, у которого нет времени решать упражнение,
должен во всяком случае прочитать его и постарать-
постараться понять результат. В конце книги даны решения и
указания к некоторым упражнениям.
Требования, предъявляемые к читателю
Большая часть этой книги должна быть понятна
студентам-старшекурсникам или начинающим аспи-
аспирантам, специализирующимся в теоретической физике
или прикладной математике. Предполагается, что чи-
читатель достаточно уверенно владеет векторным ана-
анализом, дифференциальным и интегральным исчисле-
исчислением функций многих переменных, матричной алгеб-
алгеброй (включая собственные векторы и определители),
а также — немного — теорией операторов в том виде,
как она изучается в элементарной квантовой меха-
механике. Физические приложения брались из самых раз-
разных областей, так что не всякий будет чувствовать
себя как дома во всех из них. Многие приложения
можно пропустить при первом чтении без особого
ущерба для связности изложения, но, пожалуй, не-
нереалистично пытаться читать эту книгу без некото-
некоторого знакомства с классической механикой, специаль-
специальной теорией относительности и электродинамикой.
В библиографии в конце первой главы перечислен ряд
руководств, дающих достаточную подготовку для чте-
чтения этой книги.
Я хотел бы выразить признательность многим ли-
лицам— учителям и коллегам, которые помогли мне
оценить красоту дифференциальной геометрии и

предисловие
понять важность её для физики. Особая моя благодар-
благодарность Кипу Торну, Рэфиэлу Соркину, Джону Фрид-
мэну и Фрэнку Эстабруку. Мне хочется также побла-
поблагодарить первых двух из названных лиц и многих
прилежных студентов Университетского колледжа в
Кардиффе за замечания по поводу первых вариантов
этой книги. Двое из моих учеников, Нил Коминз и
Брайен Уэйд, заслуживают особого упоминания за
вдумчивые, конструктивные советы. Мне приятно по-
поблагодарить Сюзэн Болл, Джейн Оуэн и Маргрит
Уилкинсон за быструю и аккуратную перепечатку
многочисленных вариантов рукописи. Наконец, я бла-
благодарен жене за терпение и поддержку, особенно в по-
последние горячие месяцы.
Бернард Шутц
Кардифф, 30 июня 1979

1. НЕКОТОРЫЕ
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
В этой главе даётся обзор понятий из различных разделов
математики, на которых будут основываться геометрические
рассмотрения последующих глав. Большая часть излагаемого
ниже должна быть известна большинству читателей, но два
раздела — топология и теория отображений — наверняка не-
незнакомы многим читателям; с них мы и начнём. Главная
причина включения этих разделов — то, что это нужно для
строгого определения понятия многообразия, которое мы
вводим в самом начале гл. 2. Читатели, незнакомые с топо-
топологией, могут пропустить первые два параграфа при первом
чтении и вернуться к ним лишь после того, как почувствуют
в этом потребность, читая вторую главу.
1.1. ПРОСТРАНСТВО R" И ЕГО ТОПОЛОГИЯ
Пространство /?" — это обычное n-мерное пространство
векторной алгебры; точка в R" — это последовательность из
п вещественных чисел (х\,Х2, ..., хп). Интуитивно мы пред-
представляем себе это пространство непрерывным: для любой
данной точки в /?" существуют сколь угодно близкие точки,
и отрезок, соединяющий две любые точки, может быть раз-
разбит на сколь угодно много отрезков, концы которых также
являются точками /?". Эти свойства резко отличаются, ска-
скажем, от свойств решёток, таких как совокупность всевозмож-
всевозможных наборов из п целых чисел (iu 12, ..., in)- Понятие непре-
непрерывности в пространстве R" получает точный смысл при изу-
изучении его топологии. В математике слово «топология» имеет
два различных значения. Та топология, которую мы сейчас
будем изучать, может быть названа локальной. В противопо-
противоположность ей глобальная топология — это изучение свойств
пространства «в целом», отличающих, например, сферу от
тора. Мы немного поговорим о глобальной топологии позже,
в частности в главе о дифференциальных формах. Начнем
же мы с краткого обзора локальной топологии.
Основным понятием здесь является понятие окрестности
точки в R". Его можно определить, введя функцию расстоя-

14
1. НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
ния между точками х = (xi хп) и у = (уи ..., уп) в R":
d(x,y)= [(ъ- У1у + (Х2-у2у + ...(хп-уя)*у/*. A.1)
Окрестность радиуса г точки х в R" — это множество точек
N,(x), расстояние которых до х меньше г. Для случая R2 это
показано на рис. 1.1. Непрерывность пространства может
быть теперь более точно определена при помощи малых ок-
окрестностей. Множество точек в Rn дискретно, если каждая
точка этого множества имеет окрестность, не содержащую
лг,
Рис. 1.1. Функция расстояния
d(x, у) задаёт окрестность в R2,
представляющую собой вну-
внутренность круга, ограниченного
окружностью радиуса г. Сама
окружность не является частью
этой окрестности.
(а)
(Ь)
Рис. 1.2. (а) Любая окрест-
окрестность точки х = а содержит
точки, расположенные слева от
а, в то время как (Ь) любая
точка, лежащая справа от а,
обладает окрестностью, цели-
целиком расположенной по правую
сторону от а.
других его точек. Ясно, что само R" не дискретно. Говорят,
что множество точек S в R" открыто, если каждая точка х из
5 имеет окрестность, целиком содержащуюся в 5. Ясно, что
дискретные множества не открыты, и дальше мы их не бу-
будем использовать. Простой пример открытого множества в
пространстве R1 (последнее обозначается также просто че-
через R)— множество всех точек х, для которых а < х < Ъ для
двух заданных вещественных чисел а и Ь. Важно уяснить
себе, что множество точек х, для которых а ^ х < Ь, не от-
открыто, поскольку точка х = а не имеет окрестности, целиком
содержащейся в этом множестве: часть точек любой окрест-
окрестности точки х = а меньше, чем а, и поэтому они выходят
из этого множества (см. рис. 1.2). Это, разумеется, весьма
общее свойство: любой разумный «кусок» пространства /?"
будет открытым, если не включать в этот кусок его границу.

1.1 ПРОСТРАНСТВО НП И ЕГО ТОПОЛОГИЯ 15
Представление о том, что отрезок, соединяющий любые
две точки R", бесконечно делим, можно сделать точным, если
сказать, что любые две различные точки в /?" имеют непере-
непересекающиеся окрестности. (У них есть и такие окрестности,
которые пересекаются, но если сделать их достаточно ма-
маленькими, они пересекаться не будут.) Это свойство назы-
называется отделимостью (или хаусдорфовостью) пространства
R". Можно построить и неотделимые пространства, но для
наших целей они неестественны, и мы о них говорить не
будем.
Итак, мы использовали функцию расстояния d(x, у) для
гого, чтобы определить окрестности и, тем самым, открытые
множества. В этом смысле мы говорим, что d(x, у) индуци-
индуцирует топологию в R". Под этим мы подразумеваем, что она
позволяет определить открытые множества в R'\ обладаю-
обладающие следующими свойствами:
(Ti) если Oi и О2 открыты, то и их пересечение Ot П О2
открыто;
(Tii) объединение любой (возможно, бесконечной) сово-
совокупности открытых множеств открыто.
Для того чтобы свойство (Ti) было применимо ко всем от-
крытым множествам в Rn, будем считать пустое множество
открытым по определению. (В более обстоятельных курсах
топологическое пространство определяется как совокупность
точек с заданным набором открытых множеств, удовлетво-
удовлетворяющим (Ti) и (Tii). С этой точки зрения функция расстоя-
расстояния d(x,y) позволяет превратить пространство Rn в тополо-
топологическое.)
Уместно спросить, насколько индуцированная топология
зависит от точного вида функции d(x, у). Предположим, на-
например, что мы используем другую функцию расстояния
d'(x,y) = [4(xl-ytJ + 0.1(x2- у2J + ...
+ (х,г-упJ]]'2. A.2)
Она также определяет окрестности и открытые множества
в R2, как это изображено на рис. 1.3. Решающим здесь яв-
является то обстоятельство, что каждое множество, открытое
по отношению к d'{x,у), будет открыто и по отношению к
d(x, у), и наоборот. Это несложно доказать, основываясь на
том, что любая данная d-окрестность точки х содержит внут-
внутри себя некоторую d'-окрестность и наоборот. Другими сло-
словами, для данной d-окрестности точки х радиуса е можно
подобрать столь малое число б, что d'-окрестность точки х
радиуса 6 будет целиком содержаться в первой окрестности

16
I. НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
(см. рис. 1.4). Отсюда можно заключить, что каждое множе-
множество, открытое по отношению к d(x,у), открыто также и по
отношению к d'(x, у) и наоборот. Мы говорим поэтому, что
dad' индуцируют одну и ту же топологию в /?". Читатель
может проверить, что функции расстояния
d'" (х, у) = max (| х, — ух \, \х2 — у21, ..., \хп—уп\) A.4)
также индуцируют ту же топологию. Соответствующие ок-
окрестности в R2 изображены на рис. 1.&, Так что, хоть мы и
х,
Рис. 1.3. Функция расстояния
d'() [()s+fe
(,y)
— J/гJ]'2 определяет окрест-
окрестность в R2, состоящую из то-
точек, лежащих внутри эллипса
J+()г ^
Aг1)+(г)
Как и в случае рис. 1.1, сам
эллипс ие принадлежит к ок-
окрестности.
Рис. 1.4. В Р? rf-окрестность
радиуса е (ограниченная ок-
окружностью) целиком содержит
в себе rf'-окрестность радиуса б
(ограниченную эллипсом, пока-
показанным на рис. 1.3) при б < е.
При б > 2е включение заме-
заменяется на обратное.
начинали с обычной эвклидовой функции расстояния d(x, у),
топология, которую мы определили, не слишком зависит от
вида d. Она называется «естественной» топологией /?". Топо-
Топология— более «грубое» понятие по сравнению с расстоянием.
Нам не нужно знать точное значение расстояния между точ-
точками, поскольку расстояние можно определить по-разному.
Нужно лишь знать, что расстояние между точками может
быть сделано произвольно малым и что расстояние между
двумя различными точками никогда не может быть равно
нулю.
Наше определение окрестности было привязано к конк-
конкретной функции расстояния, но, поскольку топология много-
многообразия есть объект более общий, чем конкретная функция

1.2. ОТОБРАЖЕНИЯ
17
расстояния, слово «окрестность» будет часто использоваться
в другом смысле. Нам часто будет удобно считать окрест-
окрестностью точки х любое множество, содержащее открытое мно-
х.
(Ь)
Рис. 1.6. (а) В R2 функция расстояния d" задаёт круговые окрестности,
меньшие при том же радиусе, чем окрестности, задаваемые функцией d.
(b) Окрестность, отвечающая функции d"', ограничена квадратом со сто-
стороной 2г.
жество, содержащее х. Из контекста каждый раз будет ясно,
что именно имеется в виду под «окрестностью».
1.2. ОТОБРАЖЕНИЯ
Понятие отображения, хоть и очень простое, будет столь
полезно в дальнейшем, что стоит потратить немного времени
на его обсуждение. Отображение / из пространства М в про-
Рис. 1.6. Наглядное представление отображения f: M-
¦N; показано, что
странство N — это правило, сопоставляющее всякому эле-
элементу х из М некоторый единственный элемент f(x) из N. По-
Полезно представлять себе картинку типа показанной на
рис. 1.6. Простейший пример отображения — это обычная ве-
щественнозначная функция на R. Такая функция f сопостав-

,g 1 НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
ляет точке х из R точку f(x), снова из R. (Это служит иллю-
иллюстрацией того факта, что пространства М и N не обязательно
различны.) Подобное отображение обычным образом пред-
представлено на рис. 1.7. Отметим, что отображение даёт един-
единственное f(x) для каждого х, но вовсе не обязательно, чтобы
единственное х отвечало каждому }(х). На рисунке и х0, и
Xi отображаются в одно и то же значение. Такое отображе-
отображение назовем слепляющим '>. Более общо, если / отображает М
в N, то для любого подмножества 5 в М элементы из N,
в которые отображаются точки из 5, образуют множество Т,
f(x)
f(x0) -
Рис. I 7. Отображение (функция) из R в R, не являющееся взаимноодно-
взаимнооднозначным.
называемое образом S относительно f и обозначаемое через
f(S). Наоборот, множество S, состоящее из всех элементов,
отображающихся в Т, называется прообразом Т и обозна-
обозначается через /"'(Г). Если данное отображение переводит
несколько точек в одну, то прообраз точки из N не будет,
вообще говоря, точкой в М, так что в этом случае нет отобра-
отображения /-' из N в М, ибо отображение обязано быть однознач-
однозначным. Поэтому в общем случае обозначение /~'(^) может вос-
восприниматься лишь как единый символ — это не есть образ Т
относительно отображения f~l, а просто некое множество,
обозначаемое через f~l(T). Напротив, если каждая точка из
f(S) имеет одноточечный прообраз в S, то говорят, что /
инъективно или взаимно-однозначно (сокращенно: является
l-1-отображением); в этом случае имеется другое 1-1-отобра-
жение /¦"', называемое обратным к f, переводящее образ М
в М. Эти понятия известны из элементарного курса анализа,
хотя там они, возможно, так и не назывались. Функция
f(x) — sin л; не инъективна (является слепляющей), поскольку
f(x) = f(x-\- 2rat) — /(Bn+ 1)л — x) при любом целом п.
Следовательно, для неё настоящей обратной функции не су-
существует. Общепринятая обратная функция, arc sin у, полу-
получается, если ограничить обычный синус на область «главных»
В оригинале many-to-one — Прим. ред,

1.2. ОТОБРАЖЕНИЯ 19
значений, —я/2 < х < п/2, где он уже взаимно-однозначен
и обратим.
Другим примером Ы-отображения является географиче-
географическая карта данной части земной поверхности: точка поверх-
поверхности Земли отображается в точку на листе бумаги. Ещё
один пример отображения — это поворот сферы на данный
угол вокруг некоторого диаметра: точка сферы отображается
в другую точку той же сферы, находящуюся от неё на фик-
фиксированном угловом расстоянии по отношению к заданной
оси вращения.
Введём теперь для отображений некоторые стандартные
обозначения и терминологию. То что / отображает AI в N,
будет сокращённо записываться так: /: M-*-N. Для выраже-
выражения того факта, что / переводит данный элемент х из М в
элемент у из N, служит специальная запись /: х>—>у. Если
отображение обозначается через f, то образ точки х — через
f(x). Если отображение есть вещественнозначная функция,
скажем функция п переменных (т. е. f: Rn-^-R), то принято
среди физиков использовать один и тот же символ f(x) и
для значения f в точке х, и для самой функции /. Мы будем
следовать этой традиции там, где из-за этого не сможет про-
произойти недоразумений. Если имеются два отображения, fug,
f: M-+-N и g: N-*-P, то определено отображение, называе-
называемое композицией f и g и обозначаемое через gof, которое
отображает М в Р (gof: M-*-P). Оно строится очевидным
образом: берём точку х из М, находим точку f(x) из N и
отображаем её при помощи g в Р: (g of) (x) = g(f(x)). Ком-
Композицию g°f принято записывать именно в таком порядке,
так что отображение, действующее первым, стоит справа.
В общем случае мы говорим об отображении из М в N.
Если же каждая точка из N имеет прообраз (не обязательно
одноточечный), то мы говорим об отображении из М на ЛП>.
Как уже отмечалось выше, в случае если прообразы одното-
одноточечны, отображение инъективно. (Отображение, которое од-
одновременно является 1-1-отображением и отображением на,
называется биекцией.) Например, пусть N— единичный от-
открытый круг в R2, т. е. множество всех точек х, для которых
d(x, 0)<1 (где 0 — начало координат в R2), и пусть М —
полусфера 0 <; п/2 единичной сферы (см. рис. 1.8). Ясно, что
имеется взаимно-однозначное отображение М на N.
Введённая терминология теории отображений вместе с
тем, что мы уже знаем из топологии, позволяют дать полез-
полезное и короткое определение непрерывной функции или, фак-
фактически, произвольного непрерывного отображения. Отобра-
Отображение f: М-ь-N непрерывно в точке х из М, если любое от-
') Или о сюръективном отображении. — Прим. ред.

20
1. НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
крытое множество в N, содержащее f(x), содержит образ
некоторого открытого множества из М, содержащего точку х.
(Предполагается, конечно же, что М и N — топологические
пространства. В противном случае говорить о непрерывности
бессмысленно.) Далее, / непрерывно на М (или просто не-
непрерывно), если оно непрерывно во всех точках М. Посмот-
Посмотрим, как это связано с обычным определением непрерывной
функции из курса математического анализа.
М
Рис. 1.8. Рассматривая круг как
экваториальное сечение шара,
ограниченного сферой, легко
построить биективное отобра-
отображение верхней полусферы на
круг, используя ортогональную
проекцию.
Рис. 1.9. Непрерывная функция в том
смысле, как это было определено в
тексте. Отметим, что f переводит ок-
окрестность точки х0 радиуса б в ок-
окрестность точки f(xo) радиуса е, в
то время как прообраз этой послед-
последней окрестности содержит первую, но
не обязательно совпадает с ней. Он
может содержать другие области оси
х, например такие, как в правой ча-
части рисунка. Если f непрерывна и в
этой второй окрестности, то прообраз
будет открытым множеством.
Пусть / — вещественная функция одной вещественной пе-
переменной. Другими словами, f отображает R в R, переводя
число х в число f(x). (В наших обозначениях /: R-+R.)
С точки зрения элементарного анализа / непрерывна в точ-
точке хо, если для любого е > 0 существует 6 > 0, такое что
f(x)—f(*o)|<e для всех х, удовлетворяющих неравенству
x — xo\<i6 (см. рис. 1.9). Чтобы переформулировать это в
терминах открытых множеств, заметим, что для R функция
расстояния d'"(x, x0), введённая в § 1.1, сводится к
й'"(х,х0) = |х — хо\. Значит, согласно этому определению, f
непрерывна в точке х0, если каждая ^"'-окрестность f{x0) со-
содержит образ некоторой ^"-окрестности точки х0. Поскольку
эти окрестности являются открытыми множествами, непре-
непрерывность в смысле определения, данного в предыдущем аб-
абзаце, влечёт за собой непрерывность в смысле элементарного

1.2. ОТОБРАЖЕНИЯ 21
математического анализа. Наоборот, непрерывность в смысле
элементарного анализа влечёт за собой непрерывность в
смысле нового определения, поскольку любое открытое мно-
множество в R, содержащее f(x0), содержит d'''-окрестность
f(x0), которая в свою очередь содержит образ некоторого от-
открытого множества, содержащего х0 (а именно образ <Г"-ок-
рестности точки х0). Итак, эти два определения эквива-
эквивалентны.
Условие непрерывности отображения на всём М даже
легче формулировать, чем условие непрерывности в одной
точке: имеется теорема, что /: M-+N непрерывно, если и
только если прообраз каждого открытого множества из N от-
открыт в М. Доказательство этой теоремы несложно. Если /
непрерывно при всех х, то прообраз каждого открытого мно-
множества открыт, поскольку любая точка этого прообраза со-
содержится в некотором открытом множестве, содержащемся
в этом прообразе. Обратно, если прообраз каждого откры-
открытого множества из N открыт, то для каждой из своих точек
он содержит некоторое открытое множество, её содержащее,
так что / непрерывно в каждой точке.
Определение непрерывности на языке открытых множеств
намного легче использовать и понимать, чем определение на
языке «е-6», в особенности для функций многих переменных;
оно, несомненно, является единственно пригодным для общих
отображений топологических пространств.
Определив непрерывность, мы можем перейти к обыч-
обычному определению дифференцируемости функций. Если
/(*!, ..., хп)—функция, определённая на некотором откры-
открытом множестве 5 в Rn, то мы будем называть ее дифференци-
дифференцируемой класса Ck, если все её частные производные до по-
порядка k включительно непрерывны на S. Для краткости бу-
будем называть такую функцию С'-функцией. Частные слу-
случаи — класс С0 (непрерывные функции) и С°° (функции, у
которых существуют все производные; обычно они называют-
называются бесконечно дифференцируемыми). Очевидно, что функции
класса Ck являются и функциями класса С1 для всех 0 ^
^ / < k. Можно определить и понятие производной для та-
таких более общих непрерывных отображений. (Эти производ-
производные часто называют дифференциалами.) Интересующийся чи-
читатель может найти соответствующие определения в книгах
Choquet-Bruhat, DeWitt-Morette & Dillard-Bleick A977), или
Warner A971)х> (см. библиографию в конце главы).
Если 1-1-отображение переводит открытое подмножество
М в R" на другое открытое множество N в /?", оно может
'> Или у Зорича [5] (см. литературу, добавленную при переводе).-
Прим. ред.

22 1 НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
быть записано в виде
yi = ft(Xi,x2, ..., хп), или у = /(х),
где набор {Xi, i= I, ..., п} определяет точку х из М и на-
набор {t/i, i=l, ..., п} определяет аналогичную точку у из
N. Если функции {fi, i = l, ..., п) все класса Ск, то отобра-
отображение / называется отображением класса С" (или Cft-OTo6pa-
жением). Матрица Якоби С'-отображения — это матрица из
частных производных dft/dx,. Определитель / этой матрицы
называется просто якобианом и часто обозначается так:
J = d(fi, ..., fn)/d(xu ..., хп). A.5)
Если якобиан в точке х не обращается в нуль, то теорема об
обратной функции гарантирует взаимную однозначность ото-
отображения f на некоторой окрестности точки х (по поводу до-
доказательства этой теоремы см. Шоке-Брюа и др. A977)'>).
Если функции g(xi, ..., хп) и g*(yi, ..., уп) связаны
между собой формулой
g*(fl{Xu .-., Хп), -.., fn(Xl, ..., Xn)) = g(xX, ..., Хп)
(т. е. g* принимает такое же значение в /(х), что и g в х),
то интеграл g по М равен интегралу g+J по Л^:
[{x» • • •. хп) dx, ... dxn = ^gjiju ... уп) /d«/, ... йуп.
М Л'
A.6)
Поскольку g и g^ принимают одинаковые значения в соот-
соответствующих точках, часто говорят, что элемент объема
d*i ... йхп заменяется на Jdtj\ ... dyn- Эта точка зрения осо-
особенно полезна, когда / рассматривается как замена коорди-
координат. Хотя эта формула и общеизвестна из курса анализа, мы
разберем её более подробно в § 2.25 и 4.8.
1.3. ВЕЩЕСТВЕННЫЙ АНАЛИЗ
(ВЕЩЕСТВЕННЫЕ ФУНКЦИИ ВЕЩЕСТВЕННЫХ ПЕРЕМЕННЫХ)
Как уже отмечалось, предполагается, что читатель знаком
с теорией функций многих переменных. В этом параграфе мы
лишь выделим наиболее существенные моменты.
Вещественная функция одной вещественной переменной
f(x) называется аналитической в точке х = х0, если она об-
11 Или Зоорич [5]. —Прим. ред.

1.3 ВЕЩЕСТВЕННЫЙ АНАЛИЗ 2Ь
ладает в этой точке тэйлоровым разложением, сходящимся
к f(x) в некоторой окрестности х0:
Естественно, что функции, не являющиеся бесконечно диффе-
дифференцируемыми в точке х0 (т. е. такие, что (dnf/dxn)x0 не су-
существует для некоторого п), не аналитичны в х0. Но имеются
и бесконечно дифференцируемые функции, которые не анали-
аналитичны. Знаменитый пример — это функция ехр(—l/х2), зна-
значение и все производные которой равны нулю при х = О,
но которая отлична от нуля в любой окрестности х — 0.
(Это объясняется тем, что аналитическое продолжение этой
функции в комплексную плоскость имеет существенную осо-
особенность при г = 0; на вещественной же оси она ведёт себя
совершенно нормально.) Впрочем, несколько успокаивает то,
что аналитические функции дают хорошие приближения для
многих неаналитических функций в следующем смысле. Ве-
щественнозначная функция g(xi, ..., хп), определённая в не-
некоторой открытой области S в Rn, называется квадратично-
интегрируемой, если существует кратный интеграл
[g (xlt ..., xn)f dx, dx2 ... dxn. A.8}
s
Известна теорема функционального анализа, по которой каж-
каждую квадратично-интегрируемую функцию g можно аппрок-
аппроксимировать аналитической функцией g' так, что интеграл от
(g — g'J no S будет сколь угодно малым. В силу этого фи-
физики обычно не колеблясь предполагают данные функции
аналитическими, если только это помогает получить резуль-
результат; так же будем поступать и мы. Поскольку С°°-функции
не обязаны быть аналитическими, для аналитических функ-
функций имеется специальное обозначение: О. Разумеется,
Са-функция является С°°-функцией.
Оператор А на функциях, определённых на R", — это
отображение, переводящее одну функцию / в другую А (/).
Если А (/) имеет вид gf, где g — некоторая фиксированная
функция, то этот оператор есть простое умножение. Другие
примеры операторов на функциях на R — это обычное диф-
дифференцирование
= df/dx,

24 I. HFKOTOPblE ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
или интегрирование с заданным ядром g
х
(G(f)){x)=\f{y)g(x,y)dy,
о
или же более сложный оператор типа
Оператор может быть определён на всех функциях /, а мо-
может и не на всех. Например, D определён лишь на диффе-
дифференцируемых функциях, a G не определён на функциях, для
которых записанный выше интеграл не существует. Указа-
Указание множества функций, на которые оператор может действо-
действовать, составляет часть определения оператора; это множество
называется его областью определения.
Коммутатор двух операторов А и В, обозначаемый через
[А, В], — это новый оператор, определённый равенством
[A,B](f) = {AB-BA)(f) = A(B(f))-B{A(f)). A.9)
Если два оператора имеют нулевой коммутатор, то говорят,
что они коммутируют. Здесь нужно быть осторожным с об-
областями определения операторов: область определения опе-
оператора [А, В] может быть меньше, чем область определения
А пли В. Например, если А = й/йх и В = хй/dx, то в каче-
качестве их областей определения можно взять все С'-функции.
Но не для всех С'-функций / определено А (#(/)), так как
в это выражение входят вторые производные. В качестве
областей определения операторов АВ и ВА можно взять мно-
множество всех С2-функций, более узкое, чем множество С'-
функций. Тогда и коммутатор [А, В] будет иметь своей об-
областью определения лишь С2-функции. В данном случае
можно, однако, расширить область определения (это назы-
называется также расширением оператора), основываясь на сле-
следующем наблюдении. Легко проверить, что для любой
С2-функции /
[А, В] (f) = [d/dx, xu/dx]f = df/dx,
поскольку вторые производные в АВ и ВА взаимно сокра-
сокращаются. Поэтому можно отождествить [А, В] с d/d* (т. е.
с самим А) и тем самым расширить его область определения
до всех С'-функций. Мы видим, что коммутатор может ока-
оказаться определённым даже на таких функциях, на которых
произведения в коммутаторе не определены. При работе с
дифференциальными операторами часто бывает удобнее, по
крайней мере поначалу, брать в качестве их области опре-
определения С°°-функции. Позже мы именно так и будем посту-
поступать, и заботиться об областях определения не придётся.

(.4 теория групп 25
1.4. ТЕОРИЯ ГРУПП
Совокупность элементов G вместе с бинарной операцией
(обозначаемой точкой) называется группой, если удовлетво-
удовлетворяются следующие аксиомы:
(Gi) Ассоциативность: для любых х, у и z из G
х-(уг) = {х-у)-г.
(Gii) Наличие правой единицы: G содержит элемент 6,
такой что для любого х из G
х-е = х.
(Giii) Существование правого обратного: для любого х
из G существует элемент, обозначаемый через х~1,
также лежащий в G, такой что
Группа называется абелевой (коммутативной), если, кроме
того,
(Giv) х-у = у-х для любых х, у из G.
Стандартным примером группы с конечным числом элемен-
элементов является группа перестановок п объектов; бинарная ком-
композиция двух перестановок — это перестановка, получаемая
в результате их последовательного выполнения. В этой груп-
группе п\ элементов. Единичным элементом служит перестановка,
оставляющая все объекты неподвижными.
Из (Gi) —(Giii) можно вывести ряд простых следствий:
единичный элемент е единствен; е является также и левым
единичным {е-х = х)\ обратный элемент х-1 единствен для
каждого х; х-1 является также левым обратным (х~1-х = е).
Знак • обычно опускают, если нет риска ошибиться: вместо
х-у пишут просто ху.
В современной физике наиболее важны группы Ли, о ко-
которых мы будем много говорить ниже. Точное определение
будет дано в гл. 2, здесь же достаточно сказать, что это не-
непрерывные группы: каждое открытое множество элементов
группы Ли допускает 1-1-отображение на открытое множе-
множество в R" для некоторого п. Примером группы Ли является
группа трансляций (сдвигов) пространства Rn(x*—^x-\- а,
а = const). Каждой точке а пространства R" соответствует
элемент этой группы, так что фактически группа трансляций
взаимно-однозначно отображается на всё Rn. Групповым за-
законом является обычное сложение: пара элементов а =
(аи ..., а„) и b = (b\, ..., bn) переходит в с = (а{ +
Ь\, ..., пп + bn), или, коротко, c = a-f-b. Этот пример пока-
показывает, что не всегда символ • подходит для обозначения

26
I НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
групповой операции. Для абелевых групп, каковой является
разобранная нами группа, удобнее употреблять знак «+».
Подгруппа S группы G — это совокупность элементов из
G, сама образующая группу относительно той же бинарной
операции. (Приставка «под» всегда будет обозначать под-
подмножество, обладающее теми же свойствами, что и объем-
объемлющее множество. Мы столкнёмся с многими примерами
«подобъектов»: векторные подпространства, подмногообра-
подмногообразия, подалгебры Ли и подгруппы Ли.) Будучи группой, под-
подгруппа должна содержать единичный элемент. Поскольку
единичный элемент е группы единствен, любая подгруппа
должна его содержать. В примере с группой подстановок
легко придумать много подгрупп. Скажем, перестановки п
объектов, не меняющие положения первого объекта, обра-
образуют подгруппу полной группы подстановок, так как: (i)
тождественная перестановка е не двигает первый объект;
(ii) если данная перестановка не двигает первый объект, то
её обратная тоже такова; (ш) произведение двух таких пе-
перестановок опять же не двигает первый объект. Эта подгруп-
подгруппа совпадает с группой перестановок (п — 1) объектов. Пусть
читатель попробует доказать, что множество всех четных пе-
перестановок также является подгруппой в группе всех пере-
перестановок, а нечётные перестановки подгруппы не образуют.
Наше утверждение, что определённая подгруппа группы
перестановок п объектов «совпадает» с группой перестано-
перестановок п—1 объектов, есть пример изоморфизма групп. Две
группы Gi и G2 с бинарными операциями • и * соответствен-
соответственно изоморфны (это означает, что они неотличимы с точки
зрения их групповых свойств), если имеется 1-1-отображенис
/ группы d на d, сохраняющее групповую операцию:
f{x-y)=f(x)*f(y). A.10)
Для нашего примера изоморфизм / тривиален: элемент под-
подгруппы, переставляющий лишь последние п — 1 объектов из
п, переходит в ту же самую перестановку в группе переста-
перестановок п —¦ 1 объектов. Но изоморфизмы не всегда бывают
тривиальными. Пусть Gi — группа положительных веществен-
вещественных чисел с операцией умножения, a G2 — группа всех ве-
вещественных чисел с операцией сложения. (Почему это груп-
группы?) Тогда если х— число из G\, то f(x)—\ogx определяет
отображение f:Gi->G2, удовлетворяющее A.10):
log (xy)= log х+ log у.
Эти две группы изоморфны, и / — изоморфизм.
Другое полезное отношение между группами — это груп-
групповой гомоморфизм. Его определение похоже на определение
изоморфизма, может лишь нарушаться взаимная однознач-

1 S ЛИНЕЙНАЯ АЛГЕБРА 27
ность. Равенство A.10) по-прежнему должно быть справед-
справедливым. Тривиальный гомоморфизм группы в себя — это ото-
отображение, переводящее каждый элемент группы в единичный
элемент е. Менее тривиальный пример — гомоморфизм группы
перестановок на мультипликативную группу, состоящую из
двух элементов {1,—1}. Этот гомоморфизм переводит каж-
каждую чётную перестановку в 1, а каждую нечётную — в —1.
Читателю следует проверить равенство A.10) для этого при-
примера, т. е. проверить, что композиция двух нечётных пере-
перестановок есть чётная перестановка, нечётной и чётной — не-
нечётная и двух чётных — чётная.
1.5. ЛИНЕЙНАЯ АЛГЕБРА
Множество V называется векторным пространством (над
вещественными числами), если в нём задана бинарная опе-
операция, обозначаемая знаком „+", относительно которой оно
образует абелеву группу (см. выше), и если определено ум-
умножение (¦) его элементов (векторов) на вещественные чис-
числа, удовлетворяющее следующим аксиомам (ниже х и у —
векторы, а а и Ъ — вещественные числа):
(Vi) а-{х + у) = (а
(VH) {а + Ь)-х = {
(Viii) {ab)-x = a{b-x),
(Viv) 1-х — х.
Единичный элемент в группе V обозначается через 0 или
просто 0. Помимо стандартных примеров векторных про-
пространств отметим ещё, что векторными пространствами яв-
являются:
(i) множество всех п X п-матриц, где „+" обозначает по-
покомпонентное сложение, а „•" обозначает покомпонентное
умножение на вещественное число;
(ii) множество всех вещественных непрерывных функций
f{x), определённых на интервале а ^ х ^ Ъ.
Обычно опускают точку, обозначающую умножение на
число, и скобки, фигурирующие в аксиомах. Выражение вида
называется линейной комбинацией векторов х, у и 2. Множе-
Множество элементов {х\, х2, ..., хт) пространства V линейно-не-
линейно-независимо, если нельзя найти вещественные числа
{аи аг, ..., ат}, не все равные нулю, такие что
= 0 0-12}

28 1- НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Линейно-независимое множество называется максимальным,
.если добавление любого вектора из V делает его линейно-
зависимым. По определению это означает, что любой вектор
из V может быть представлен в виде линейной комбинации
элементов максимального множества, так что максимальное
множество образует базис пространства V. Например, если
V — множество вещественных п X «-матриц, то одним из ба-
базисов служит совокупность п2 различных матриц, у которых
все матричные элементы нулевые, кроме одного. В общем
случае число векторов базиса — это размерность простран-
пространства V. (Все базисы имеют одинаковое число элементов, если
оно вообще конечно.) Пусть векторы {xi, i— 1, ..., п} обра-
образуют базис. Тогда произвольный вектор у представим в виде
п
9= ?flj*j. A.13)
Числа {a,-,t=l, ..., п) называются компонентами вектора
у в этом базисе.
Подпространство векторного пространства V — это под-
подмножество в V, само являющееся векторным пространством.
(Сравните это определение с определением подгруппы в §1.4.)
В частности, оно должно включать в себя нулевой вектор и
линейные комбинации любых своих элементов. Говорят, что
некоторое множество векторов {у и ..., ут) порождает под-
подпространство в V, образованное всевозможными линейными
комбинациями
«i/7i + a2t/2 + •.. + amym
(векторы у* называются при этом образующими). Если
m < п, то это подпространство обязательно собственное, т. е.
не совпадает с V. В любом случае размерность подпростран-
подпространства равна максимальному числу линейно-независимых век-
векторов среди образующих.
Пока что ничего не было сказано о скалярных произведе-
произведениях или о длинах векторов. Эти понятия являются дополни-
дополнительными; они не всегда оказываются полезными в конкрет-
конкретных приложениях теории векторных пространств, так что нет
необходимости включать их в общее определение векторного
пространства. Один из способов ввести эти понятия — опреде-
определить норму на векторном пространстве. Нормированное век-
векторное пространство V — это векторное пространство с задан-
заданной на нём вещественнозначной функцией п (т. е. функцией,
которая сопоставляет каждому вектору х вещественное чис-
число п(х), называемое его нормой), удовлетворяющей следую-

1.5. ЛИНЕЙНАЯ АЛГЕБРА 29
щим аксиомам:
(Ni) п{х)^0 для всех х из V, причём п(х)=0, если и
только если х — 0;
(Nii) п(ах) = \а\п(х) для всех а из R и х из У;
(Niii) n(x + ^)^ п(х)+ п(у) для всех л, у из У.
Есть много функций, удовлетворяющих этим аксиомам. Рас-
Рассмотрим, например, само Rn как векторное пространство, где
сложение векторов задаётся равенством
Х + У = (*1 +Уъ ••-, хп-\-уп), A.14)
а умножение на вещественное число — равенством
ах = {ахи ..., ахп). A-15)
Тогда для трёх из четырёх функций расстояния, определён-
определённых в § 1.1, мы можем ввести норму как расстояние вектора
от начала координат:
. +Ы2]1/2, A.16)
+ ... +{xn)Y'\ A-17)
. \x2\ \хп\). A.18)
Читателю предоставляется возможность проверить справед-
справедливость аксиом (Ni) — (Niii) для каждой из этих норм. По-
Полезно также убедиться в том, что d"(x, у) не определяет
нормы.
Первые две нормы отличаются от третьей тем, что они
удовлетворяют еще одной, иногда весьма полезной аксиоме —
тождеству параллелограмма:
(Niv) [п(х + у)]>+[п(х-у)У = 2[п{х)У + 2[
Норма, удовлетворяющая этому тождеству, позволяет опре-
определить билинейное симметрическое скалярное произведение
двух векторов
} + y)]2-}[n(x-y)f. A.19)
Билинейность означает, что
) A.20)
и
z-(ax + by)=a(z-x)+b{z-y). A.21)
Симметричность означает, что
х-у — у-х, A.22)

30 1 НЕКОТОРЫЕ ОСНОВНЫЕ MATEi4ATH4ECKHE ПОНЯТИЯ
Кроме того, скалярное произведение является положительно-
определённым, т. е.
х-х ^ 0 к х-х = 0, лишь если х — 0. A-23)
Это очевидно, так как х-х= \п(х)]2.
Определённая выше норма п(х) на R" называется эвкли-
эвклидовой нормой. Векторное пространство R'\ рассматриваемое
вместе с этой нормой, мы будем обозначать через Еп и назы-
называть «-мерным эвклидовым пространством. Важно уяснить
себе различие между Rn и Еп: первое — это просто совокуп-
совокупность всех наборов (хи ..., хп) без привлечения какого-либо
расстояния или нормы. Полезность такого различения станет
понятной в гл. 2.
Для того чтобы ввести скалярное произведение и дока-
доказать его билинейность и симметричность, нужны только ак-
аксиомы (Nii) и (Niv). Если допустить нарушение свойств (№)
и (Niii), то мы получим псевдонорму; скалярное произведе-
произведение вектора с самим собой в этом случае не обязано быть по-
положительным. Примером физической теории, использующей
псевдонорму, является специальная теория относительности.
Ниже мы рассмотрим её более или менее подробно.
Хотя мы определили только векторные пространства над
вещественными числами, не составляет труда определить их
и над комплексными числами, просто дозволив числам а и Ь
в (Vi) — (Viv) быть комплексными. Тогда компоненты векто-
векторов будут комплексными. Такие векторные пространства ча-
часто используются в квантовой механике.
1.6. АЛГЕБРА КВАДРАТНЫХ МАТРИЦ
Линейное преобразование Т векторного пространства V —
это отображение V на себя, удовлетворяющее свойству ли-
линейности (ср. с A.20) и A.21))
¦- Т(ах + Ьу)=аТ{х) + ЬТ{у). A.24)
Если в V задан базис {et, i = 1, ..., п}, то
x=?ateit A-25)
г = 1
Т(х) = т(? аЛ = ? а{Г (ё,) = ? а, ? Тиё„ A.26)
\г=1 / i=\ i=i /=i
где каждый вектор Т(ё{) мы заменим его разложением вдан-
п
ном базисе X ^ifi- Числа Тц называются компонентами
l=i
(или координатами) преобразования Т (в базисе {?,-}); они
образуют квадратную п X п-матрицу.

i 6 Алгебра квадратных матриц 31
Отметим весьма важное алгебраическое соотношение, ко-
которое будет часто использоваться в дальнейшем:
п / т ч т / п ч
Z АЛ Z B^CA^ZCAZ BltAX
A.27)
Другими словами, порядок суммирования не играет никакой
роли. Поэтому обычно это выражение записывают в виде
п т
Z Z AtB4C, или просто Z AiBi,Ch A.28)
i=l/ = l I. i
подчеркивая тем самым, что эта сумма является просто сум-
суммой соответствующих произведений по всевозможным комби-
комбинациям индексов.
Два последовательных линейных преобразования Т и U,
действующих на пространстве V, дают новое преобразование
UT:
UT (х) = U{T (*)) = U ( Z atTltet) = Z щТии1кёк
k. A.29)
Z
ik
Отсюда вытекает, что компоненты произведения UT имеют
вид
Еад*. A-30)
Важно усвоить, что если мы запишем Тц в виде матрицы
(индекс i нумерует строки, а / — столбцы) и точно так же за-
запишем llju, то сумма A.30) в точности совпадёт с выраже-
выражением для матричного произведения соответствующих матриц.
В общем случае матричное произведение двух матриц Д„ и
Bij имеет вид
(AB)tk = Z Ai,Blk = Z B,kAtl, A.31)
(BA)ik = Z BtlAlk = Z AlkBir A.32)
Отметим, что третье выражение в равенстве A.31) равно
второму, поскольку Аи и В,] суть просто числа, а умножение
чисел коммутативно. Сравнивая третий член в равенстве
A.31) со вторым в равенстве A.32), мы видим, что важен не
порядок сомножителей, а взаимное расположение индексов
суммирования и свободных индексов. Различие этих двух
выражений означает, что матричное умножение, вообще го-
говоря, не коммутативно.

32 I НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Матричные элементы транспонированной к А матрицы Ат
имеют вид
(Ат)ц=Ац. A.33)
(Если матрица А комплексная, то её сопряженная А* опре-
определяется равенством (А*)ц = Ац, где черта обозначает комп-
комплексное сопряжение.) Единичная матрица / имеет всюду на
главной диагонали единицы, а вне главной диагонали —
нули; это записывается в виде
A)И = 8ц, A.34)
где bij — символ Кронекера, т. е. 8ц = 1 при i = j и 6,-; = О
при i Ф}. Тождественное преобразование переводит, по опре-
определению, каждый вектор х в себя. Его компоненты в любом
базисе равны 8ц. Матрица Л-1, обратная к матрице А, опре-
определяется равенством
Л-'Л = ЛЛ-1 ==/. A.35)
Не каждая матрица имеет обратную; очевидным примером яв-
является нулевая матрица. Если обратная матрица существует,
то она единственна. Ясно, что А будет обратной для А~х.
Если Л существует, то матрица Л называется невырожден-
невырожденной (в противном случае — вырожденной). Множество всех
невырожденных п X «-матриц образует группу относительно
операции матричного умножения. Её единицей является еди-
единичная матрица /. Эта группа служит очень важным приме-
примером группы Ли и обозначается через GL(n,R); мы изучим её
детально в гл. 3.
Определитель (детерминант) 2Х2-матрицы
Л =
обозначаемый через det (Л), определяется равенством
) = ad — bc. A.36)
Определитель п X n-матрицы определяется индуктивно при
помощи следующего правила разложения по строке. Алгеб-
Алгебраическое дополнение элемента ац матрицы А, обозначаемое
через а'1, — это число, равное взятому с коэффициентом
(—1)'+' определителю (п—1)Х(«— 1)-матрицы, получаю-
получающейся из матрицы А вычёркиванием строки и столбца, на пе-
пересечении которых стоит с,-/. Так, например, в матрице
A.37)

1 6 АЛГЕБРА КВАДРАТНЫХ МАТРИЦ 33
алгебраическое дополнение элемента а равно ek — fh, а эле-
элемента / равно bg—ah. Определитель матрицы А определяет-
определяется правилом
п
det(A)= X щ,а1' (для любого фиксированного i). A.38)
(=1
Для матрицы A.37), беря / = 1, получим
det (A) = a(ek — fh) + b(fg — dk) + c{dh — eg),
а взяв i = 2, будем иметь
det (Л) = d(hc — bk)+ e(ak — cg) + f(bg — ah);
оба эти выражения совпадают. Это правило выглядит весьма
загадочным при том способе изложения, который мы избрали.
Оно станет более понятным, когда мы снова вернёмся к нему
в § 4.12.
Каждую из строк (или столбцов) п X «-матрицы можно
считать координатами вектора в некотором л-мерном про-
пространстве. Определитель матрицы обращается в нуль, если
и только если п векторов, определённых его строками (или
столбцами), линейно-зависимы. Это вытекает из ряда дру-
других свойств определителя: если одну строку умножить на
константу %, то весь определитель умножится на К; определи-
определитель не изменится, если какую-нибудь одну строку заменить
на поэлементную сумму этой строки и произвольного крат-
кратного любой другой строки; при перестановке двух любых
строк определитель меняет знак. Все эти свойства остаются
верными, если заменить всюду «строка» на «столбец». Они
опять же станут более понятными после изучения § 4.12.
Построим по данной матрице А матрицу В, полагая
A.39)
Из A.38) вытекает, что
= I для любого фиксированного /.
Оказывается (вы можете убедиться в этом «эксперимен-
«экспериментально»), что
2_,
другими словами, матрица В, задаваемая формулой A.39),
является обратной для матрицы А. Следовательно, матрица
А невырожденна, если и только если det^)^ 0.

34 1. НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
Следом матрицы А называется сумма её диагональных
элементов:
tr(i4)=Ia«. A.40)
г
Преобразование подобия матрицы А при помощи невырож-
невырожденной матрицы В — это отображение А ¦<—> В~1АВ. Приведём
некоторые полезные формулы, которые могут быть доказаны
на основе данных выше определений:
(АВу = ВРА1, A.41)
(ЛВ)-1 = В-1 А-1, A.42)
det(Afi)=det(A)det(fii A.43)
tr(fi-Mfi) = tr(A), A.44)
det(fi-1Afi)=det(A), A.45)
det(AT)=det(A). A.46)
Говорят, что п X «-матрица А имеет собственное значение
к и (отвечающий ему) собственный вектор V ф 0, если
A(y) = lV, A.47)
где в левой части равенства А действует как линейное пре-
преобразование на V. В координатной форме это равенство запи-
запишется в виде п уравнений
Е(а„-а.в„)^ = 0. A.48)
Они имеют ненулевое решение V, если и только если
det(A — KI)=0. A.49)
Собственные значения А являются решениями уравнения
A.49), которое, очевидно, является уравнением п-й степени
по К. Каждому вещественному решению К отвечает собствен-
собственный вектор. Если некоторое решение комплексное, то отве-
отвечающих ему вещественных собственных векторов нет, так что
в случае, когда V пробегает вещественное векторное про-
пространство, имеется фундаментальное различие между веще-
вещественными собственными значениями и комплексными. Если
же рассматриваемое векторное пространство — и матрица
А — комплексные, то никакой разницы между вещественными
и комплексными решениями нет. Пусть {hi, ..., Хп}—все п
корней уравнения A.49) (каждый корень считается столько
раз, какова его кратность). Обратим внимание на следующие

1.7. БИБЛИОГРАФИЯ 35
три важных результата:
{собственные значения А7} = (собственные значения Л},
A.50)
det(A)=a,,Ae ...К, A-51)
Kl +K2+ ... +К. A.52)
Последние два утверждения можно доказать, явно расписав
многочлен в левой части A.49). Первое вытекает из A.46).
1.7. БИБЛИОГРАФИЯ
В перечисленных ниже руководствах материал излагается примерно
на том уровне сложности, который принят в данной книге. Назначение
этого списка — подвести читателя к уровню излагаемого в книге материа-
материала; он никоим образом не является исчерпывающим перечнем рекомен-
рекомендуемых книг для чтения.
Элементы математического анализа: G. В. Thomas, Calculus and Ana-
Analytic Geometry (Addison-Wesley, Reading, Mass., 1960).
Механика: К. R. Symon, Mechanics (Addison-Wesley, Reading, Mass.,
1953), или Н. Goldstein, Classical Mechanics (Addison-Wesley, Reading,
Mass., 1950) [имеется перевод: Голдстейн Г. Классическая механика. 2-е
изд. — М.: Наука, 1975] или Ландау Л. Д., Лифшиц Е. М. Механика.—
М.: Наука, 1965.
Термодинамика: М. W. Zemansky, Heat and Thermodynamics (McGraw-
Hill, New York, 1957) или Е. Fermi, Thermodinamics (Dover, New York,
1956) [имеется перевод: Ферми Э. Термодинамика. — Харьков: 1973].
Электродинамика: J. R. Reitz & F. J. Milford, Foundation of Electromag-
Electromagnetic Theory (Addison-Wesley, Reading, Mass., 1960) или J. В Marion, Clas-
Classical Electromagnetic Radiation (Academic Press, New York, 1965).
Специальная теория относительности: А. Р. French, Special Relativity
(Nelson, London, 1968) или E. F. Taylor & J. A. Wheeler, Spacetime Phy-
Physics (Freeman, San Francisco, 1965).
Квантовая механика: L. I. Schiff, Quantum Mechanics (McGraw-Hill,
New York, 1955).
Материал этой главы может быть более глубоко изучен по следую-
следующим книгам:
R. A. Dean, Elements of Abstract Algebra (Wiley, New York, 1967);
W. Rudin. Principles of Mathematical Anahsis (McGraw-Hill, New York,
1964) [имеется перевод: Рудин У. Основы математического анализа. —
М.: Мир, 1966];
E. W. Packel, Functional Analysis, a Short Course (International Textbook
Co., Glasgow, 1974);
F. Riesz & B. Sz.-Nagy, Functional Analysis (Ungar, New York, 1955)
[имеется перевод: Рисе Ф, Сёкефальви-Надь Б. Лекции по функциональ-
функциональному анализу.-—М.: Мир, 1979].
A. Wallace, Differential Topology: First Steps (Benjamin, Reading, Mass.,
1968) [имеется перевод в кн.: Милнор Дж., Уоллес А. Дифференциальная
топология. Начальный курс. — М.: Мир, 1972].
Приведём теперь список основных руководств, в которых излагается
материал последующих глав — излагается, как правило, более глубоко и
строго. Ниже мы будем ссылаться на эти руководства по фамилиям авто-
авторов.

36 1 НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ
У Choquet-Bruhat, С DeWitt-Moiette & М Dillard-Bleick, Analysis, Mani-
Manifolds and Physics (North Holland, Amsterdam, 1977) Исчерпывающий
курс, рассчитанный на математически подкованных физиков Особенно
хорошо изложены дифференциальные уравнения
R Abraham & I E Marsden, Foundations of Mechanics, rev 2nd ed (Ben-
jamin/Gummmgs, Reading, Mass, 1978) Эта книга, как видно из ее назва-
названия, охватывает меньше материала, чем предыдущая, зато с соответствен-
соответственно большей глубиной Отличается вниманием к глобальным проблемам, а
также обширной библиографией Второе издание существенно расширено
по сравнению с первым
F W Warner, Foundations of Differentiate Manifolds and Lie Groups
(Scott, Foresman, Glenview, 111, 1971) Доступное для студентов старших
курсов введение в теорию дифференцируемых многообразий и групп Ли.
Особенно сильны разделы, посвященные группам Ли и теории когомологий
М Spivak, A comprehensive Introduction to Diffeiential Geometry, four vo-
volumes (Publish or Perish, Boston 1970) Как показывает само название,
книга рассчитана па аспирантов-математиков Написана в свободной ма-
манере, местами с юмором много упражнений, разбирается много подробно-
подробностей
Есть и другие заслуживающие внимания книги по дифференциальной
геометрии Для первоначального знакомства полезны N J Hicks, Notes on
Differential Geometry (D Van Nostrand, New York, 1965) или R L Bishop
& S I Goldberg, Tensor Analysis on Manifolds (Macmillan, London, 1968).
В том же «современном» духе, и настоящая книга, написана книга
С Т J Dodson & Т Poston, Tensor Geometry (Pitman, London, 1977).
В ней обстоятельно обсуждаются многие вопросы, которых мы лишь ка-
касаемся, правда ничего не говорится об общих производных Ли или исчис-
исчислении дифференциальных форм Читатель, которому прыжок от данной
книги к, скажем,, Choquet-Bruhat el al покажется слишком далеким, мо-
может сперва попробовать почитать первую половину книги Dodson & Poston.
Заслуженным авторитетом почьзуются монографии S Kobayashi & К. No-
mizu, Foundations of Differential Geometry, two volumes (Interscience, New
York, 1963 and 1969) [имеется перевод Кобаяси Ш , Номидзу К Основы
дифференциальной геометрии —М Наука, 1981] и J A Schouten, Ricci
Calculus (Springer, Berlin, 1954), последняя написана в несколько старо-
старомодных обозначениях
Не удивительно, что одни из лучших изложений дифференциальной
геометрии для физиков содержатся в руководствах по общей теории отно-
относительности Рекомендую книгу С W Misner, К S Thorne & J A Whee-
Wheeler, Gravitation (Freeman, San Francisco, 1973) [имеется перевод Миз-
нер Ч, Торн К, Уилер Дж Гравитация —М Мир, 19761, в которой диф-
дифференциальная геометрия излагается на протяжении нескольких глав в том
же духе и примерно в тех же обозначениях, что и у меня здесь На более
высоком уровне сложности и более сжато написана глава по дифферен-
дифференциальной геометрии в книге S W Hawking & G F R Ellis, The Large
Scale Structure of Space —Time (Cambridge University Press, 1973). Вве-
Введением широкого диапазона является статья «Дифференциальнаи геомет-
геометрия» иаписаниая Ч Мизнером для сборника Relativity, Groups and Topo-
Topology, ed С DeWitt & В DeWitt (Gordon & Breach, New York, 1964) Дру-
Другое полезное введение — статья Б Шмидта в сборнике Relativity, Astro-
Astrophysics and Cosmology, ed W Israel (Reidel, Dordrecht, 1973) Также рас-
рассчитаны на физиков книги R Hermann, Differential Geometry and the Cal-
Calculus of Variations (Academic Press, New York, 1968), D Lovelock &
H Rund, Tensors, Differential Forms and Vanational Principles (Wiley, New
York, 1975), H Flanders, Differential Forms (Academic Press New York,
1963), Von Westenholz Differential Forms in Mathematical Physics (North-
Holland, Amsterdam, 1979).

2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ
И ТЕНЗОРЫ
Трудно представить себе физическую задачу, в которой не
приходится рассматривать какой-либо пространственный кон-
континуум. Это может быть физическое трёхмерное простран-
пространство, четырёхмерное пространство-время, фазовое простран-
пространство (для задач из классической или квантовой механики),
пространство всех термодинамически равновесных состояний
или даже ещё более абстрактное пространство. Все эти про-
пространства обладают различными геометрическими свойства-
свойствами, но есть в них и нечто общее, и это общее связано с тем,
что они являются непрерывными пространствами в отличие
от, скажем, решёток, состоящих из изолированных точек.
Дифференциальная геометрия именно потому важна для со-
современной физики, что она изучает как раз эти свойства, об-
общие для всех таких пространств. Наиболее фундаментальные
из этих свойств кладутся в основу определения дифференци-
дифференцируемого многообразия — точного математического эквивален-
эквивалента для слова «пространство».
2.1. ОПРЕДЕЛЕНИЕ МНОГООБРАЗИЯ
Как и в § 1.1, мы обозначаем через R" совокупность всех
наборов из п вещественных чисел (Х\,Хъ, ..., х„). Множество
(состоящее из «точек») М называется многообразием, если
каждая его точка имеет открытую окрестность, допускающую
непрерывное 1-1-отображение (называемое координатным)
на открытое множество в Rn для некоторого п. (Читателю,
который не вполне уверен, что смысл выражения «1-1-отобра-
«1-1-отображение на» ему понятен, стоит заглянуть в § 1.2.) Попросту
говоря, М локально «похоже» на Rn. Размерность многообра-
многообразия М — это, разумеется, число п. Важно, что в определении
участвуют только открытые множества, а не всё М или всё
Rn, так что мы не налагаем никаких ограничений на глобаль-
глобальную топологию М. Это станет ясно при разборе примера со
сферой в § 2.2. Обратим внимание, что от отображения тре-
требуется только взаимная однозначность и не требуется сохра-
сохранения длин, углов или других геометрических величин. На
этом уровне геометрии понятие длины просто даже не опре-

38
2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
делено, и мы встретимся в дальнейшем с примерами физи-
физических приложений, в которых и не нужно вводить понятие
расстояния между точками наших многообразий. На этом
элементарном («примитивном») уровне геометрии мы лишь
хотим добиться того, чтобы локальная топология нашего про-
пространства (как она описана в § 1.1) была такой же, как и для
Rn. Многообразие— это пространство с такой топологией.
По определению координатное отображение сопоставляет
точке Р многообразиям набор из п чисел (хх(Р) хп(Р))
Рис. 2.1. Отображение / взаимно-однозначно отображает область V из М
на область f(U) из Rn. Это отображение сопоставляет каждой точке Р од-
однозначно определённый набор п чисел (х\, хь ..., хп). Тем самым в U
возникает система координат, изображённая при помощи штриховых ли-
линий, являющихся образами при отображении f~l стандартной координат-
координатной сетки в R".
(см. рис. 2.1). Эти числа Xi(P), ..., хп(Р) называются ко-
координатами Р относительно этого отображения. Одна из воз-
возможных точек зрения на понятие «-мерного многообразия —
это просто считать его множеством, которое может быть за-
задано п независимыми координатами в некоторой окрестности
своей точки: именно, эти координаты на самом деле опреде-
определяют требуемое отображение в R". В дальнейшем мы будем
использовать стандартные обозначения для координат, нуме-
нумеруя их верхними индексами: xl(P), х2(Р), .... хп{Р) — это п
координат точки Р (а не степени х(Р)\) относительно коор-
координатного отображения.
В результате предшествующего обсуждения мы получили
некое общее представление о том, что такое многообразие,
но для того, чтобы получить что-нибудь большее, нужно рас-
рассмотреть более внимательно свойства координатных отобра-
отображений. Пусть / — инъективное отображение некоторой окре-
окрестности U точки Р из М на открытое множество f(U) в Rn.

2.1. ОПРЕДЕЛЕНИЕ МНОГООБРАЗИЯ
39
Как мы уже отмечали выше, окрестность U не обязана со-
содержать всё М (как мы увидим в § 2.2, в случае сферы она
и не может содержать всю сферу), так что должны быть и
другие окрестности со своими собственными отображениями,
причём каждая точка из М должна лежать по крайней мере
в одной такой окрестности. Пара «окрестность плюс её ото-
отображение» называется картой. Легко видеть, что эти откры-
открытые окрестности должны перекрываться, раз любая точка из
М должна содержаться по
крайней мере в одной из них:
именно эти перекрытия важны
для дальнейшей детализации
понятия многообразия (см.
рис. 2.2). Пусть окрестность V
частично покрывает окрест-
окрестность U, и пусть задано отобра-
отображение g окрестности V на от-
открытую область в R". Эта от-
открытая область может считать-
считаться совершенно отличной от той,
на которую / отображает окре-
окрестность U. Пересечение V и U
открыто (по аксиоме (Ti) из
§ 1.1) и задаётся двумя различ-
различными системами координат, от-
отвечающими отображениям f и
g. Имеется, стало быть, неко-
некоторая связь между этими коор-
координатными системами. Чтобы её найти, возьмём точку в об-
образе перекрытия относительно f (т. е. точку из R"), скажем
точку (xl,x2, ..., хп) на рис. 2.3. Отображение / обладает
обратным f~l, поэтому имеется единственная точка S, лежа-
лежащая в перекрытии, которая имеет именно эти числа своими
координатами относительно отображения f. Пусть теперь g
сопоставляет S другую точку в R", скажем (у1, у2, ..., у").
(Тем самым построено отображение R"-*~Rn— композиция
g-f~l.) В результате мы получаем функциональные соотно-
соотношения (преобразование координат)
y*=yl(x\x2 х"),
у* = уЦх\х\ ..., х"),
Рис. 2.2. Окрестности U и V из М
перекрываются (затушёванная об-
область). Соответствующие коорди-
координатные отображения f и g в R"
дают в зоне перекрытия два раз-
различных отображения (а, следова-
следовательно, две системы координат).
Соответствие мехщу этими коор-
координатами характеризует класс
гладкости многообразия.
уп = уп(х\х2, ..., X").
Если все частные производные порядка не выше k всех этих
функций {у1} по переменным {х1} существуют и непрерывны,
то отображения fug (более точно, карты (U,f) и (V,g))
называются Ck-согласованными. (Обозначение Ск было вве-

40
2 ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
дено в §1.2 длядифференцируемости.) Если можно построить
целую систему карт (называемую, вполне уместно, атласом)
так, чтобы каждая точка многообразия М содержалась по
крайней мере в одной окрестности и любая карта была Ск-
согласована с любой другой, с ней перекрывающейся, то мно-
многообразие М называется Ск-многообразием. Многообразия
класса С1 (а тем самым и класса Ск при k> 1) называются
дифференцируемыми (или гладкими) многообразиями.
Рис. 2.3. Увеличение рис. 2.2, демонстрирующее, как перекрытие порождает
отображение R" в R", являющееся композицией отображений f~l и g (и
обозначаемое через g ° f-1).
Дифференцируемость многообразия позволяет снабдить
его чрезвычайно богатой структурой: на нём можно опреде-
определить тензоры, дифференциальные формы и производные Ли.
Эта дифференциальная структура и будет для нас главным
предметом изучения. Напомним, что мы не вводили понятия
расстояния на М, поэтому у нас нет пока никаких представ-
представлений о «форме» или «кривизне» М. Мы знаем только, что
локально оно гладкое, и именно это нужно для дальнейшего.
В большинстве приложений мы будем иметь дело с С°°-
многообразиями, но обычно это не так уж и необходимо.
Иногда нам будет удобно предположить многообразие анали-
аналитическим (класса Си; функции {у1}—аналитические функции
от {х'}); как уже упоминалось в § 1.2, предполагать анали-
аналитичность всюду, где только удобно, вполне в духе физиков.
Наша точка зрения такова, что при первоначальном изучении
этого предмета лучше наложить более жёсткие ограничения
на многообразия, чтобы увидеть, в чём же суть дифферен-
дифференциальной геометрии. После того как изучающий лучше
освоится с предметом, он может подумать о том, как можно
было бы ослабить эти ограничения. В соответствии с такой

2 2 СФЕРА КАК МНОГООБРАЗИЕ
41
точкой зрения читатель этой книги всюду должен иметь в
виду, что все многообразия в этой книге дифференцируемы
столько раз, сколько нужно для наших рассуждений.
2.2. СФЕРА КАК МНОГООБРАЗИЕ
Одним из простейших примеров многообразия, иллюстри-
иллюстрирующим важность того обстоятельства, что допускается более
чем одна карта, служит сфера (поверхность шара). Рассмот-
Рассмотрим двумерную сферу (обозначаемую через S2)— множество
Рис. 2.4. Маленькая окрестность точки Р иа сфере S2 взаимно-однозначно
отображается на круг в R2.
точек в R3, для которых (х1J + (х2J + (х3J = const. Каж-
Каждая её точка имеет достаточно малую окрестность, допускаю-
допускающую 1-1-отображение на круг в R2 (см. рис. 2.4). Ясно, что
Рис. 2.5. Обычные сферические координаты задают отображение из S2 в
R2, "хорошее" для обыкновенных точек типа Р. А что является образом
северного полюса' И какую из двух указанных точек считать образом точ-
точки Q, лежащей на меридиане <р = О?
соответствующее отображение никоим образом не сохраняет
длины или углы. В качестве конкретного примера такого
отображения рассмотрим обычные сферические координаты
0 == х1, ф = х2. На первый взгляд может показаться, что вся
сфера отображается на прямоугольник 0 ^ х1 ^ п, 0 ^ х2 ^
^ 2л (рис. 2.5). Однако при более внимательном рассмотре-
рассмотрении видно, что здесь что-то не так. Во-первых, отображение

42 2 ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
портится в полюсе 0 = 0, где одна точка «отображается» в
целую линию х] = 0, 0 ^ х2 ^ 2л. Так что в полюсе, соб-
собственно, никакого отображения и нет. Второй трудностью
является то, что точки, для которых ф = 0, «отображаются»
в два различных места: х2 = 0 и х2 = 2л, чего опять-таки не
должно быть для настоящего отображения. Выйти из этого
затруднения можно, лишь ограничив координатное отображе-
отображение на открытую область 0 <с xl <z л, 0 < х2 < 2л. Тогда оба
полюса и соединяющая их полуокружность <р = 0 устраняют-
устраняются. Поэтому нужно хотя бы два отображения, чтобы покрыть
сферу" полностью. Второе мо-
может быть, скажем, другой сфе-
сферической системой координат,
у которой меридиан <р = 0 об-
образует часть экватора первой
системы. Ясно, что каждая точ-
точка на сфере лежит по крайней
мере в одной из двух этих
Q карт. Функции перекрытия, вы-
Рис. 2.6, Стереографическая проек- ражающие координаты второй
ция S2 в Я2. Сфера с выколотым системы через координаты пер-
северным полюсом N является от- вой довольно сложны, НО СО-
сТГотофГа^°";а7с^~ае: вершенно очевидно, что они
мой точке N отображение пере- аналитичны. Поэтому сфера
стает действовать является аналитическим мно-
многообразием.
Другим, более «хорошим» отображением сферы S2 на об-
область в R2, портящимся только в одной точке, является так
называемая стереографическая проекция сферы на плоскость,
изображённая в вертикальном сечении на рис. 2.6. Сфера ка-
касается плоскости, и из полюса N на сфере, диаметрально
противоположного точке касания, проводится прямая. Эта
прямая пересекает сферу в точке Р, а плоскость — в точке Q.
Этим и задастся координатное отображение: Р отображается
в Q; другими словами, координатами точки Р на сфере яв-
являются координаты точки Q на R2. Это отображение взаимно-
взаимнооднозначно всюду, кроме N, поскольку, когда проведённая
через N прямая делается горизонтальной (Р достигает N),
точка Q уходит на бесконечность. В каком бы направлении
ни уходила точка Q на бесконечность, точка Р будет стре-
стремиться к N. Таким образом, N отображается на всю «беско-
«бесконечность», и вблизи N нужно использовать другую коорди-
координатную систему. Нет никакого координатного отображения,
которое годилось бы для всей сферы S2. Обратим внимание,
что это обстоятельство связано только с глобальной тополо-
топологией S2: всё сказанное выше справедливо и для поверхности
кегли или бутылки, получающихся деформацией из S2. На-

2.3. ДРУГИЕ ПРИМЕРЫ МНОГООБРАЗИЙ 43
против, двумерная внутренность кольца, ограниченного двумя
концентрическими окружностями в R2, может быть покрыта
одной координатной системой. Попробуйте её найти!
2.3. ДРУГИЕ ПРИМЕРЫ МНОГООБРАЗИИ
Полезность понятия многообразия заключается в его общ-
общности: многообразиями оказываются такие множества, кото-
которые, не будь этого понятия, никому бы и в голову не пришло
считать пространствами. По определению любое множество
М, допускающее непрерывную параметризацию, является
многообразием, размерность которого равна числу независи-
независимых параметров. Например:
(i) Совокупность всех вращений твёрдого тела в трёх-
трёхмерном пространстве является многообразием, поскольку она
может быть непрерывно параметризована тремя «углами
Эйлера» (см. Goldstein, 1950).
(ii) Совокупность всех лоренцевых преобразований, зада-
задаваемых переходом к движущейся системе отсчета, устроена
как трёхмерное многообразие: параметрами служат три ком-
компоненты скорости движения.
(ш) Для N частиц величины, определяющие их положе-
положения CN величин) и скорости CN величин), задают точку
в 6iV-MepHOM многообразии, называемом фазовым простран-
пространством.
(iv) Если задано уравнение (алгебраическое или диффе-
дифференциальное) для величины у как функции от независимой
переменной х, то можно ввести структуру многообразия на
множестве всех пар (у, х): каждое частное решение есть кри-
кривая на этом многообразии. Этот пример легко обобщается на
случай произвольного числа зависимых и независимых пере-
переменных.
(v) Особенно часто встречающимся примером многооб-
многообразия служит векторное пространство, определение которого
было дано в § 1.5. (Мы рассматриваем здесь лишь векторные
пространства над вещественными числами.) Для того чтобы
убедиться в том, что векторное пространство является много-
многообразием, построим отображение его в некоторое R". Пусть
векторное пространство n-мерно, выберем в нём произволь-
произвольный базис {ё\, ..., ёп). Тогда любой вектор у представляется
в виде линейной комбинации
... +апёп. B.1)
Но у есть точка V; тем самым установлено отображение из V
в Rn, yi—>(ai, ..., ап). На самом деле каждой точке из Rn
отвечает при этом отображении единственный вектор из V,
так что V не только целиком покрывается одной координат-

44 2- ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
ной системой, которую мы построили, но просто совпадает
как многообразие с Rn. На языке теории групп (§ 1.4) V и Rn
изоморфны. Это важный результат. Он означает, что каждое
векторное пространство можно, когда это удобно, считать
просто пространством Rn.
(vi) Разобранный выше пример (i) служит примером
группы Ли, определение которой мы теперь в состоянии дать.
Группа Ли G — это группа, являющаяся к тому же С°°-мно-
гообразием, причём групповая операция должна индуциро-
индуцировать С°°-отображение этого многообразия в себя. Это озна-
означает следующее. Возьмём любой элемент а группы. Этот эле-
элемент индуцирует отображение G в себя, при котором любой
элемент b из G переходит в Ьа, by-^Ьа. Требуется, чтобы это
отображение было отображением класса С°°; на координат-
координатном языке это означает, что координаты точки Ьа должны
быть С°°-функциями от координат точки Ъ. В действитель-
действительности это требование есть требование согласованности: оно
гарантирует согласованность структуры многообразия с груп-
групповой структурой. В примере (i) совокупность всех вращений
твёрдого тела образует группу: нетрудно показать, что её
групповая структура согласована со структурой трёхмерного
многообразия. (Эта группа Ли называется группой 50C).)
Данное определение группы Ли может показаться поначалу
чересчур абстрактным и сухим: оно сделается более живым
после того, как мы разберём свойства групп Ли в гл. 3. Про-
Простым примером группы Ли является Rn. Это — векторное про-
пространство (см. пример (v) выше) и тем самым группа, а
также и многообразие: фактически R" служит простейшим
примером группы Ли.
2.4. О СВОЙСТВАХ МНОГООБРАЗИЙ «В ЦЕЛОМ»
Поскольку каждое многообразие локально устроено как
некоторое Rn, любые два многообразия одинаковой размер-
размерности (и одного класса гладкости) локально неразличимы на
данном уровне дифференциальной геометрии. Ситуация в
корне меняется при переходе к рассмотрению глобальных
структур, как это видно из сопоставления S2 с R2, проведен-
проведенного в § 2.2. Следовательно, многообразия делятся на раз-
различные классы в соответствии с их глобальными свойствами.
Например, поверхность сферы и поверхность мелка имеют
одинаковую глобальную структуру. Хотя ни одну из них
нельзя отобразить на R2, для каждой имеется прекрасное
1-1-отображение на другую, как это показано на рис. 2.7.
(Строго говоря, мелок должен иметь гладкие края для того,
чтобы его поверхность можно было отождествить с S2 как
С°°-многообразие.) Такое отображение непосредственно из

21! КРИВЫЕ
45
Рис 2 7 Поверхность гладкого
(класса С°°) цветного мелка
можно взаимно однозначно ото-
отобразить на сферу S2 Представ-
Представленное на рисунке отображение
определено глобально, а не
только на каком нибудь куске
поверхности Оно явтяется диф-
диффеоморфизмом (как и обрат
ное к нему)
одною С°°-многообразия М в другое N, являющееся взаимно-
взаимнооднозначным и класса С°" (отображение принадлежит к
классу С°°, если координаты точки из N являются бесконечно
дифференцируемыми функциями
от координат точки-прообраза
в М) и обладающее тем свой-
свойством, что его обратное тоже
является С°°-отображением, на-
называется диффеоморфизмом М
на N. Многообразия М и N, для
которых такое отображение су-
существует, называются диффео-
морфными Поверхность чайной
чашки диффеоморфна тору (по-
(поверхности бублика), поскольку
в каждой из этих поверхностей
есть ровно одна дырка- каждую
из них можно гладко продефор-
мировать в другую
Большая часть результатов,
излагаемых в этой книге, отно
сится к локальной геометрии, за-
зависящей только от дифференциальной структуры Но нам
встретятся и такие ситуации, например при изучении расслое-
расслоений и интегрирования функций, где
глобальные свойства многообразия
весьма существенны
2 5. КРИВЫЕ
Для нас будут очень важны
кривые на многообразиях. Обще-
Общепринятым является представление
о кривой как о непрерывном ряде
точек в М Нам здесь удобнее дать
несколько иное определение- кри-
кривая — это (дифференцируемое)
отображение открытого подмноже-
подмножества из R1 в М (см рис 2 8). Та-
Таким образом, каждой точке из R1
(являющейся вещественным чис-
числом, которое мы обозначим через К) отвечает точка
из М, называемая точкой-образом, отвечающей значению К.
Совокупность всех точек-образов и есть то, что понимается
обычно под кривой, но согласно нашему определению каждой
точке присваивается ещё некоторое значение К Ясно, что речь
идёт о параметризованной кривой, с параметром К Поэтому
Рис 2 8 Кривая в М — это
отображение из Ri в М
Точка Я из R1 переходит в
точку Р из М Образом от
крытого интервала с конца
ми а и Ь в R1 является на
рисованная линия в М

46
2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
две кривые различны, даже если они имеют совпадающие об-
образы в М, но одинаковым точкам отвечают различные значе-
значения параметров. Как и раньше, под «дифференцируемым» мы
понимаем такое отображение, для которого координаты то-
точек-образов {х'(к), i = l, ..., п} являются дифференцируе-
дифференцируемыми функциями от К.
2.6. ФУНКЦИИ НА М
Функция на М — это правило, сопоставляющее каждой
точке из М вещественное число (называемое значением функ-
функции). Если некоторая область в М отображается при помощи
гладкого координатного отображения на область в R", то
функция па М превращается в функцию на R" (см. рис. 2.9).
/(Р)
Рис. 2.9. Функция f на М есть отображение из М в RK Координатное ото-
отображение g из области U многообразия М, содержащей Р, на область
g(U) в R" обратимо. Составное отображение f ° g~l переводит R" в R1,
т. е. является функцией на /?". Это просто выражение f(P) через коорди-
координаты точки Р.
Если эта функция на Rn дифференцируема, то говорят,-что
она является дифференцируемой функцией на многообразии
М. То же можно выразить по-другому: абстрактно говоря,
наша функция может быть записана в виде f(P), где Р — точ-
точка из М. Но Р задана своими координатами, так что нашу
функцию можно записать в виде f(xl, x2, ..., хп). Если это
выражение дифференцируемо по своим аргументам, то функ-
функция называется дифференцируемой. Сами координаты, ко-
конечно же, являются непрерывными и бесконечно дифферен-
дифференцируемыми функциями. Например, х3 — это функция, для
которой хъ(Р) есть значение третьей координаты точки Р.
Начиная с этого места мы будем избегать упоминаний о
координатных отображениях из М в Rn, хотя и будем иногда
упоминать о координатах (задающих эти отображения).Цель
нашего изучения координатных отображений состояла в том,
чтобы по возможности строго сформулировать основные по-
понятия. Отныне нас будет больше интересовать использование

2.7. ВЕКТОРЫ И ВЕКТОРНЫЕ ПОЛЯ 47
этих понятий для построения дифференциальной структуры
на многообразиях, поэтому будем всюду в дальнейшем пред-
предполагать, что на рассматриваемом многообразии можно вве-
ввести координаты {xl, ?= 1, ..., п\ и что любая система до-
достаточно гладких функций у' = у'(х1), которая локально об-
обратима (т. е. якобиан которой отличен от нуля, см. § 1.2),
определяет допустимое преобразование к новым координатам
{у1, 1=1, ..., п).
2.7. ВЕКТОРЫ И ВЕКТОРНЫЕ ПОЛЯ
Рассмотрим кривую, проходящую через точку Р многооб-
многообразия М, задаваемую уравнениями х' = х'(Х), ?=1, .... п.
Далее, возьмём дифференцируемую функцию f(xl, ..., хп)
(сокращенно f(x1)) на М. В каждой точке кривой определено
значение функции f. Таким образом, на кривой возникает
дифференцируемая функция g(i), дающая значение f, кото-
которое та принимает в точке, отвечающей параметру X:
Дифференцируя, получаем по цепному правилу
dK ~ La 6K dxi ¦
I
Это равенство справедливо для любой функции g, так что
мы можем написать
_JL. B.3)
С точки зрения обычного векторного исчисления в эвкли-
эвклидовом пространстве можно считать набор чисел {Ax'/dX}
компонентами некоторого вектора, касательного к кривой
х*(к); это легко понять из того, что {Ах1} — бесконечно малое
перемещение вдоль кривой и деление его на АК меняет лишь
длину, а не направление этого перемещения. На самом деле,
поскольку кривая берётся вместе с вполне определённым па-
параметром, для каждой кривой однозначно определён набор
{Ах1/АХ}, о котором мы говорим, что это — компоненты каса-
касательного вектора к кривой. Итак, в силу нашего определения
кривой, каждая кривая имеет единственный касательный
вектор.
Разумеется, каждый вектор является касательным к бес-
бесконечному числу кривых, проходящих через точку Р, и для
этого имеются две различные причины. Во-первых, существует
много кривых, касающихся друг друга и имеющих одинако-
одинаковый касательный вектор в точке Р; во-вторых, данный путь
(траекторию) можно перепараметризовать так, чтобы каса-

48
2 ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТППОРЫ
тельный вектор в Р не изменился. Это изображено на
рис. 2.10. В качестве простого примера рассмотрим кривую
х'(Я) = Яа', где числа {а'}—константы. Тогда если Р — точ-
точка К = 0, то касательный вектор имеет вид йх1/йК — а1.
Другая кривая х'(ц) = у?Ъ1 + \аа1 также проходит через Р
при ц = 0и имеет такой же касательный вектор в этой точ-
точке, dx'/dn = а1. Перепараметризация первой кривой х1 =
(а;
\
\ г
A«
(Ь)
Л»
R1
Рис 210 (а) Две кривые с общим касательным вектором (Ь) Две кри-
кривые, совпадающие геометрически (имеющие общую траекторию), но задан-
заданные при помощи раз тачных параметризаций Если соответствующие ото-
отображения обозначить через hi и А2, то отображение К^ °hl задает связь
параметров Ki и Я2 Кг = K2(Xi) Если dX^dXi = 1 в Я, то в этой точке
касательные векторы совпадают
(ц3 + ц)а' даёт кривую, проходящую через те же самые точ-
точки и имеющую в точке Р (ц = 0) тот же самый касательный
вектор dxl/d\i = а1. Итак, в действительности каждый вектор
характеризует целый класс эквивалентности кривых, прохо-
проходящих через данную точку.
Полезность термина «вектор» связана с привычностью
этого понятия в геометрии эвклидова пространства, где век-
векторы определяются аналогично перемещениям Ах1. Однако
поскольку на многообразии понятие расстояния между точ-
точками вовсе не обязано быть определённым, необходимо дать
определение вектора, основанное только на рассмотрении ин-
фииитезимальных окрестностей точек М. Пусть а и Ъ — про-
произвольные два числа и х' = х1(ц)—другая кривая, проходя-
проходящая через точку Р. Тогда в этой точке мы будем иметь
dx' д
d|i dx1
UK dp,

2.7. ВЕКТОРЫ И ВЕКТОРНЫЕ ПОЛЯ 49
Итак, числа {adx'/dX-}- bdx'/dn} являются компонентами но-
нового вектора, который, конечно же, касается некоторой кри-
кривой, проходящей через точку Р. Следовательно, должна су-
существовать кривая с параметром, скажем, ф, такая что в
точке Р
dq> , \ dX du ) дх'
i
Сопоставляя полученные результаты, заключаем, что в точ-
точке Р
Л , , d d
Я-^т + о-г- =-т- .
dA d[i dф
Следовательно, операторы дифференцирования вдоль кривых
(типа d/dA,) образуют векторное пространство в точке Р '>.
В каждой системе координат имеются специальные кривые,
а именно сами координатные линии. Ясно, что операторы
дифференцирования вдоль этих кривых суть просто д/дх' и
соотношение B.3) показывает, что каждый оператор d/dA,
может быть представлен в виде линейной комбинации част-
частных производных д/дх'. Поэтому система {д/дх'} образует
базис указанного векторного пространства. Из равенства B.3)
вытекает, что вектор d/dX имеет в этом базисе компоненты
{dx'/dk}. Мы получаем, следовательно, замечательный ре-
результат: пространство всех касательных векторов в точке Р
и пространство всех дифференцирований вдоль кривых, про-
проходящих через Р, находятся во взаимно-однозначном соответ-
соответствии. По этой причине математики говорят, что d/dX и есть
касательный вектор к кривой х'(К). Мы будем следовать та-
такому соглашению, так как оно обладает тремя достоинствами.
Во-первых, оно является корректным, поскольку не привле-
привлекаются перемещения на конечные расстояния. Во-вторых,
в нём нет упоминания о координатах; в частности, не исполь-
используются понятия типа «преобразуется так же, как ...».
В-третьих, производная — это своего рода «движение» вдоль
кривой, порождаемое касательным вектором: такое соедине-
соединение понятия анализа — производной с понятием геометрии —
вектором имеет далеко идущие последствия.
Можно по-прежнему представлять себе наглядно вектор
как стрелку, касающуюся кривой, поскольку компоненты его
в точности те же самые. Теперь, однако, нужно иметь в виду,
что складывать можно лишь векторы, торчащие из одной
" Надо, конечно, убедиться в том, что для этих производных выпол-
выполняются и другие аксиомы векторного пространства (см. § 1.5); но лишь
проверка замкнутости относительно взятия линейных комбинаций является
не совсем тривиальной.

50 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
точки. Векторы, торчащие из разных точек, не имеют ника-
никакого отношения друг к другу. Касательные векторы лежат
не в М, а в касательном пространстве к М в точке Р, которое
обозначается через ТР. Для привычных многообразий, таких
как поверхность сферы, определённое выше касательное про-
пространство совпадает, как легко видеть, с касательной пло-
плоскостью к сфере в данной точке. Для более абстрактных мно-
многообразий такое наглядное представление получить труднее.
Мы будем использовать термин вектор для вектора, тор-
торчащего в данной точке Р многообразия М. Термин векторное
поле будет обозначать правило, задающее вектор в каждой
точке М.
2.8. БАЗИСНЫЕ ВЕКТОРЫ И БАЗИСНЫЕ ВЕКТОРНЫЕ ПОЛЯ •
Для любой точки Р пространство ТР является векторным
пространством той же размерности п, что и само многообра-
многообразие. Любая совокупность п линейно-независимых векторов в
ТР образует базис в Тр. Выбирая тот или иной базис в каж-
каждом ТР для всех точек Р из М, мы получаем базисные век-
векторные поля. Если в окрестности U точки Р задана система
координат {х1}, то в каждой точке из U определён коорди-
координатный базис {д/дх'}.
Но вовсе не обязательно работать с координатным бази-
базисом — векторы можно записывать и по отношению к произ-
произвольному базису {ё(}. Здесь индекс i используется для нуме-
нумерации базисных векторов. Он не обозначает компоненту чего-
либо. В точке Р произвольный вектор V может быть записан
в виде
Числа {]/'} являются компонентами вектора V относи-
относительно базиса {д/дх1}. Числа {V1}— компоненты V отно-
относительно {ё;}; они связаны с V' согласно обычному закону
преобразования векторов, о чём ещё пойдет речь ниже. Если
V и базисы {д/дх'} и {ё,} рассматриваются как векторные
поля, то компоненты {V1} и {V} поля V являются функ-
функциями на М. Векторное поле называется дифференцируемым,
если эти функции дифференцируемы.
Мы неявно предположили выше, что векторы {д/дх'} для
произвольной координатной системы линейно-независимы в
каждой точке Р из U. Какие у нас соображения в пользу
этого? Покажем, что это есть в точности условие того, что
координаты являются хорошими в точке Р, т. е. дают
1-1-отображение некоторой окрестности U точки Р на соот-

2.S РАССЛОЕННЫЕ ПРОСТРАНСТВА 51
ветствующую область V в Rn. Рассмотрим какую-нибудь хо-
хорошую систему координат на U, скажем {у1, i= 1, ..., п}.
Тогда отображение из {(х1 х11)} в 11 может быть запи-
записано в виде
у' = у1(х\ .... х"), /= 1, .... п.
По теореме об обратной функции (§ 1.2) это отображение
взаимно-однозначно, если и только если матрица Якоби
ду1 /дх1 невырожденна. Это означает, что в каждой точке из
U векторы с компонентами (дух/дх1, ду2/дхх, ..., дуп/дхх),
{ду1дх2,ду2/дх2, ..., дуп/дх2, (ду1/дхп,ду2/дхп, дуп/дхп)
линейно-независимы. Но это как раз и есть компоненты век-
векторов {д/дх1, i = l, ..., п) относительно координатного ба-
базиса для системы координат {у1}, поскольку, согласно цеп-
цепному правилу,
_а__ jV__d_ , jVLJL д. ¦ дуп д
дх' дх1 дух + дхх ду2 + ' *" "^ дхх ду"
и аналогично для остальных х'. Итак, действительно, система
{х1} координат в окрестности U является хорошей, если и
только если {д/дх'} образуют базис пространства касатель-
касательных векторов для каждой точки из U. Советуем читателю
рассмотреть базисные векторы, отвечающие сферическим ко-
координатам на сфере, и разобраться в том, как портится этот
базис в полюсах.
2.9. РАССЛОЕННЫЕ ПРОСТРАНСТВА
Очень интересное многообразие получится, если объеди-
объединить многообразие М с совокупностью всех его касательных
пространств ТР. Это проиллюстрировано на рис 2.11 для
простейшего случая: одномерное многообразие М (кривая)
и его касательные пространства (касательные к кривой в
каждой её точке). В части (а) рисунка изображены кривая
и несколько касательных пространств: это прямые, касаю-
касающиеся кривой, причём каждая мыслится неограниченно про-
продолженной в обе стороны, с тем чтобы векторы могли иметь
произвольную длину в каждой точке. Но если бы всё это
было нарисовано, то рисунок оказался бы неразборчивым,
поскольку различные касательные беспорядочно пересекали
бы друг друга и кривую М; эти случайные пересечения не
имеют никакого значения. Лучше изобразить всё так, как по-
показано в части (Ь), где касательные пространства располо-
расположены параллельно: они не пересекают друг друга и пересе-
пересекают М только в той точке, к которой они относятся. К сожа-
сожалению, этот рисунок не отражает того, что каждое ТР «ка-
«касается» кривой: это та цена, которую приходится платить за

52
2 ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
ясность рисунка. Каждая точка вертикальной прямой ТР
представляет вектор, имеющий данную длину н касающийся
М в точке Р. Глядя на рис. 2.11 (Ь), можно сделать ещё одно
наблюдение: каждая точка изображённой фигуры (двумерного
многообразия) является точкой одного п только одного каса-
касательного к М пространства, скажем TR для точки R из М.
Каждой точке фигуры отвечает один и только один вектор в
одной и только одной точке из М. Это наводит на мысль опре-
определить навое многообразие ТМ, состоящее из всех касатель-
касательных векторов во всех точках: в рассматриваемом случае это
Р
(a)
M
T
Рис. 2.11. (а) Одномерное многообразие и некоторые из его касательных
пространств. (Ь) То же самое, но касательные пространства нарисованы
параллельными друг другу, с тем чтобы исключить несущественные, слу-
случайные пересечения.
многообразие двумерно. Оно называется расслоенным про-
пространством (или просто расслоением); его слоями являются
пространства ТР для всех Р. Использование термина «слой»
объясняется картинками типа рис. 2.11 (Ь). Для того чтобы
убедиться в двумерности ТМ, построим систему координат
для небольшого куска этого пространства. Пусть одномерное
многообразие М имеет координату х; выберем координаты в
касательных пространствах, отвечающих точкам из М, лежа-
лежащим в интервале а < х < Ь, для некоторых а и Ь, предпола-
предполагая, что сама координата х является в этом интервале «хоро-
«хорошей». (Смысл такого предположения станет ясен из § 2.11
ниже.) Любой касательный вектор V в любой точке Р может
быть записан в виде
V = уд/дх,
B.4)
так что компонента у является координатой для ТР (см.
B.1)). Ясно, что она будет хорошей координатой на всём
слое ТР. Поскольку каждый слой отвечает фиксированному
значению х, координаты (х, у) однозначно определяют каса-
касательный вектор (у) и точку, к которой он относится (х). По-
Поскольку каждая точка расслоенного пространства должна,

2.10 ПРИМЕРЫ РАССЛОЕННЫХ ПРОСТРАНСТВ
53
по определению, лежать в некоторой области рассмотренного
вида, то мы доказали, что ТМ является многообразием. Ясно,
что эта конструкция легко переносится на касательные рас-
расслоения для многомерных многообразий. Координаты типа
описанных выше, где координаты для ТР определяются коор-
координатами на М в окрестности Р при помощи разложения
вектора по базису B.4), называются естественными коорди-
координатами для ТМ.
Далее, кривая в рассматриваемом расслоенном простран-
пространстве, изображённая штриховой линией на рис. 2.12, задаёт
Рис. 2.12. Сечение (штриховая линия) расслоенного пространства ТМ над
одномерным многообразием М (жирная линия).
некоторый вектор в каждой точке из М, поэтому такая кри-
кривая определяет векторное поле на М. Такая кривая назы-
называется сечением ТМ. Ясно, что, вообще говоря, не имеет
никакого смысла говорить о длине такой кривой, так что мы
имеем здесь пример многообразия, для которого не прихо-
приходится утруждать себя определением в нём метрики.
В общем случае расслоенное пространство состоит из мно-
многообразия, называемого базой (в разобранном случае это
была кривая Ж), и слоя, заданного для каждой точки базы.
Если база n-мерна, а каждый слой m-мерен, то размерность
расслоенного пространства равна m -f- п. Это многообразия
особого рода, обладающие свойством разложимости на слои:
точки одного слоя связаны друг с другом, а точки разных
слоев нет. Эта ситуация формализуется введением понятия
проекции л, отображающей каждую точку слоя в ту точку
базы, к которой «подвязан» данный слой. На произвольном
многообразии такой проекции определить нельзя. В следую-
следующем параграфе мы приведём много примеров многообразий,
являющихся расслоенными пространствами.
2.10. ПРИМЕРЫ РАССЛОЕННЫХ ПРОСТРАНСТВ
(i) Рассмотренное выше расслоенное пространство ТМ,
состоящее из многообразия и его касательных пространств,
называется касательным расслоением (или касательным пуч-
пучком). Это — один из важнейших для физики примеров аб-

54 2 ДИФФГРЕНПИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
страктных многообразий. Для «-мерного многообразия М
расслоение ТМ имеет размерность 2п.
(ii) Дальше в этой главе мы перейдём от случая вектор-
векторных полей к более общему случаю тензорных полей. Каж-
Каждому типу тензоров отвечают соответствующие расслоения
над гладкими многообразиями.
(iii) Слои не обязаны быть связанными с гладкой струк-
структурой на базе. Рассмотрим «внутренние» степени свободы,
описывающие состояние элементарной частицы, такие как
изоспин. Расслоение, слои которого
являются изоспиновыми простран-
пространствами, а база — пространством-
временем, может описывать как по-
^y ложение (х, у, z, t) частицы в про-
пространстве-времени, так и её внут-
внутреннее состояние (нзоспин).
(iv) С точки зрения ньютоновой
физики пространство-время есте-
Рис. 213 Естественная ственно наделено структурой рас-
структура расслоения нью- слоенного пространства. Для Нью-
Ньютонова (галилеева) про- Галилея время было абсо-
странства-времсни, слои ко- „ v
торого определяются фикса- лютпым: каждый может опреде-
цией единого мирового вре- лить, являются два данных собы-
менн. тия одновременными или нет, неза-
независимо от того, где они происхо-
происходят. Мы можем, следовательно, построить расслоение, базой
которого является R1 (время), а слоем — R3 (пространство).
Это изображено на рис. 2.13. Между точками различных
слоев (точками пространства в разные моменты времени)
нет никакой естественной связи, поскольку в ньютоновой фи-
физике нет абсолютного пространства: два различных наблюда-
наблюдателя, движущихся друг относительно друга, имеют различ-
различные точки зрения на то, какие точки пространства являются
неподвижными. Поэтому естественной структуры расслоения
с базой ^3 нет, а есть только расслоение с базой R1. Один из
эффектов эйнштейновской теории относительности — разру-
разрушение этой структуры расслоения и замена её другой струк-
структурой— метрической (см. § 2.31 ниже).
2.11. БОЛЕЕ ГЛУБОКИЙ ВЗГЛЯД НА РАССЛОЕННЫЕ
ПРОСТРАНСТВА
В теории расслоенных пространств имеются два связан-
связанных друг с другом аспекта, которые нам предстоит рассмот-
рассмотреть, с тем чтобы по-настоящему оценить богатство и Полез-
Полезность понятия расслоения. Это их глобальные свойства и
применение групп для их построения.

2 11 БОЛЕЕ ГЛУБОКИЙ ВЗГЛЯД НА РАССЛОЕНИЯ 55
Чтобы лучше разобраться с глобальными свойствами рас-
расслоенных пространств, определим сперва более простое поня-
понятие прямого произведения. Любым двум пространствам М и
TV можно сопоставить их прямое (декартово) произведение
М X N, состоящее из всех упорядоченных пар (а, Ь) с а из
М и Ъ из N. Например, R2 есть прямое произведение Rl X R1-
Если М и N — многообразия, то М X N также, очевидно, бу-
будет многообразием: координаты {х\ 2 = 1, ..., т} для от-
открытой области U в М вместе с координатами {у1, i = 1, ...
..., п} для открытой области V в /V дают набор tn -f- n коорди-
координат для открытой области U X V в М~Х N. Из приведённой
выше конструкции расслоенных пространств ясно, что по край-
крайней мере локально они являются прямыми произведениями ви-
вида Uy(F, где U — открытое множество базы В, a F представ-
представляет собой типичный слой (все слои тождественны F). На са-
самом деле это свойство — часть определения расслоенного про-
пространства; оно называется локальной тривиальностью рас-
расслоения (расслоение сводится к прямому произведению, если
ограничиться рассмотрением достаточно малой области базы
В). Интересен вопрос, является ли данное расслоение гло-
глобально тривиальным, т. е. может ли всё пространство рас-
расслоения в целом быть представлено в виде прямого прои?-
ведения BXF.
Обычно ответ оказывается отрицательным; мы приведём
два примера, иллюстрирующих и смысл вопроса, и смысл от-
ответа.
(i) Рассмотрим TS2, касательное расслоение для двумер-
двумерной сферы S2. Если бы оно было глобально тривиальным, то
существовало бы (^"-отображение (диффеоморфизм) TS2 на
S2 X R2, ибо типичным слоем является R2, касательная пло-
плоскость. Рассмотрим множество точек в S2 X R2 вида (Р, V),
где Р — произвольная точка из S2, а V — некоторый фиксиро-
фиксированный вектор из R2. Тогда прообраз этого множества дал
бы ненулевое сечение TS2, т. е. С^-векторное поле на S-,
нигде не обращающееся в нуль. Но такого поля на S2 нет
Это — следствие знаменитой (и трудной) теоремы о непод
вижной точке на сфере, согласно которой любое 1-1-отобра-
жение (диффеоморфизм) S2 на себя имеет на S2 по крайней
мере одну неподвижную точку. Нигде не обращающееся в
нуль векторное поле давало бы отображение без неподвиж-
неподвижных точек, как будет объяснено ниже в § 3.1. Поэтому TS2
в целом не является прямым произведением. Это пример,
в котором расслоение нетривиально в силу свойств тополо-
топологии базы (S2).
(и) Наш второй пример показывает, что нетривиальное
расслоение можно построить даже на базе, допускающей три-
тривиальное расслоение. Рассмотрим TS\ касательное расслое-

S6
2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
ние для окружности 51. В отличие от S2 окружность допу-
допускает непрерывное нигде не обращающееся в нуль векторное
поле, и TS1 является прямым произведением 51 X R, как вид-
видно из рис. 2.14. Это просто глобальный вариант локальной
картинки, изображенной на рис. 2.11 (Ь). Представим теперь,
1
р
Рис. 2.14. Расслоение
ТS1 тривиально — пред-
ставимо в виде прямого
произведения окружно-
окружности S1 на типичный слой
R1 (нарисованный верти-
вертикально). Ср. с рис. 2.11
(Ь).
Р'
Ь'
Рис. 2.15. Расслоение TS1, раз-
разрезанное вдоль одного слоя и
развёрнутое на плоскость.
Слои простираются бесконечно
далеко вверх и вниз.
что мы разрезали окружность в точке Р на рис. 2.14 и «раз-
«развернули» расслоение на плоскость, как показано на рис. 2.15.
Чтобы по рис. 2.15 восстановить рис. 2.14, нужно просто
отождествить точку а с точкой
а', Р с Р', Ъ с V и т. д. Но мы
можем «склеить» расслоение по-
другому и получить лист Мёбиу-
Мёбиуса: отождествляем а с Ь', Р с Р',
Ъ с а' и т. д. Такая склейка за-
закручивает нашу полоску, которая
теперь будет выглядеть, пример-
примерно как на рис. 2.16. Локально
она по-прежнему устроена, как
на рис. 2.11 (Ь); действительно,
расслоение над каждым связным
открытым собственным подмно-
подмножеством в S1 («собственным»
означает «не совпадающим с S1») допускает непрерывное
1-1-отображение на некоторую часть рис. 2.14. Обойдя лист
Мёбиуса вокруг, мы убеждаемся, что не существует непре-
непрерывного 1-1-отображения всего первого расслоения на вто-
второе. Поэтому лист Мёбиуса не является прямым произведе-
произведением, и второе расслоение нетривиально. Конструкции нетри-
нетривиальных расслоений используются в современной физике
Рис. 2.16. Вариант расслоения с
теми же базой и слоем, что и у
TS1, отвечающий листу Мёбиу-
Мёбиуса; слой переворачивается
«вверх йогами» при обходе ок-
окружности. Локально здесь всё
устроено так же, как н на рнс.
2.11 (Ь).

2.11. БОЛЕЕ ГЛУБОКИЙ ВЗГЛЯД НА РАССЛОЕНИЯ 57
элементарных частиц для определения так называемых «ин-
стантонов».
Пример листа Мёбиуса весьма поучителен: из него видно,
что недостаточно просто указать базу и слой, для того чтобы
задать расслоение, поскольку расслоение может определять-
определяться своими базой и слоем неоднозначно. Требуется более точ-
точное определение расслоения, и здесь на помощь приходят
группы. Различие между двумя указанными выше расслое-
расслоениями над S1 — в так называемой структурной группе рас-
расслоения. Чтобы сформулировать полное определение рас-
расслоенного пространства в компактном виде, нам потребуется
понятие гомеоморфизма; это просто 1-1-отображение одного
пространства на другое, непрерывное и имеющее непрерыв-
непрерывное обратное '>. (По поводу терминологии теории отображе-
отображений см. § 1.2.) Мы определяем расслоенное пространство как
пространство Е, для которого заданы следующие объекты:
многообразие В, называемое базой, проекция п: Е-*~В, ти-
типичный слой F, структурная группа G гомеоморфизмов F на
себя и семейство {[/,} открытых множеств, покрывающее В
(т. е. семейство открытых множеств, объединение которых
есть В), причём должны выполняться следующие требования.
(i) Локально расслоение является тривиальным; это озна-
означает, что расслоение над каждым множеством ?/,¦ (т. е.
лг1 (?//)) допускает гомеоморфизм на прямое произведение
U,- X F- Мы уже говорили об этом выше. Частью этого гомео-
гомеоморфизма является гомеоморфизм каждого слоя к~1(х), где
х — элемент базы В, на F. Обозначим его через h/{x), указы-
указывая тем самым не только точку х, над которой «висит» слой,
но также и индекс /, нумерующий окрестность U,-, содержа-
содержащую X.
(И) Если точка х содержится в области перекрытия ок-
окрестностей U,- и Uk, то возникают два гомеоморфизма h,-(x)
и hk(x) слоя над точкой х на F. Поскольку гомеоморфизмы
обратимы, отображение hj(x)ohk (х) является гомеоморфиз-
гомеоморфизмом F на F. Требуется, чтобы он принадлежал структурной
группе G.
Последнее требование содержит информацию о глобаль-
глобальной структуре расслоенного пространства. Чтобы увидеть,
как это работает, дадим полное определение расслоения TS1
(допускающее непосредственное обобщение на случай рас-
расслоения ТМ для любого М). Расслоение F = TS1 имеет базу
В = S1, типичный слой F = R1 и проекцию зт: (х, €7)i—»x, где
х — точка из 5" и »— вектор из Тх. В качестве открытого
Г) Гомеоморфизм — это диффеоморфизм без требований дифференци-
руемости. Для большинства физически интересных расслоений можно все
гомеоморфизмы считать диффеоморфизмами.

58 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
покрытия {?//} можно взять любой атлас на S1. Типичное
семейство {?/,} изображено на рис. 2.17. Каждое U\ имеет
«систему» координат, т. е. параметризацию S1, которую мы
обозначим через К/. Вектор d/dKj в точке х из U,- является
базисом для Тх, так что каждый вектор v из Тх представ-
представляется в виде К(,) d/dX, для некоторого фиксированного /, где
«(/) — вещественное число. Это не что иное, как соотношение
B.4). Гомеоморфизмы слоя Тх на R, входящие в определение
. , TS1, пусть по определению имеют
—771—^О вид Л'(*): ^1~>аФ- Если х содер-
содержится в двух окрестностях U, и
Uk, To имеются два таких гомео-
гомеоморфизма Тх на R, и, поскольку
Я/ и Xk никак не связаны между
собой, К(,) и 0С(й) могут быть дву-
Рис. 2.17. Совокупность откры- мя любыми ненулевыми веще-
тых множеств в S1, покрываю- J „
шая SK Границы этих мно- ственными числами. Гомеомор-
жеств указаны скобками. Мно- физм flj(x) о hi,l (x): F -> F ДеЙ-
жество U, имеет перекрытие с ствует так: а ^а и значит,
"о %: a^So'^p™ шляется умножением на число
с Uu r,-k = a.(f)/a,k- Поскольку rik мо-
может быть любым ненулевым ве-
вещественным числом, структурной группой здесь служит
^'\{0}—группа относительно умножения (фактически груп-
группа Ли). Отметим, что для общего «-мерного многообразия М
структурная группа расслоения ТМ есть совокупность всех
пХп-матриц с ненулевым определителем; эта группа обо-
обозначается через GL(n,R). Мы изучим её свойства в гл. 3.
Итак, TS1 определено. Но как оно выглядит? Можно вы-
выбрать координаты X,- таким образом, что любые две из них,
скажем Xt и Хь, возрастали на общей части окрестностей Uf
и Uk в одном направлении. (Мы выражаем этот факт, го-
говоря, что S1 ориентируемо, см. § 4.7.) При таком выборе ко-
координатных окрестностей все «числа перекрытия» г,-* будут,
как легко видеть, положительными, и структурная группа
сведётся к R+, группе положительных вещественных чисел
по умножению. Более того, можно добиться, чтобы
AXf/dhk = 1 в каждой области перекрытия. Тогда группа све-
сведётся просто к 1 — к одному единичному элементу. Последняя
структурная группа тривиальна, тривиальна и структура рас-
расслоения. Это и есть расслоение, изображённое на рис. 2.14.
Для того чтобы описать структуру листа Мёбиуса, нужно
использовать другие отображения h,(x), причём следует быть
внимательным, чтобы не «перепутать» это расслоение с каса-
касательным. Простейшая возможность — воспользоваться семей-
семейством {U,; 1=1, ..., 8}, изображённым на рис. 2.17, и поло-
положить г\2==\, г2з=1, ...1 г78=1. Но теперь закрученность

2 12 ВЕКТОРНЫЕ ПОЛЯ И ИНТЕГРАЛЬНЫЕ КРИВЫЕ 59
листа Мёбиуса вынуждает нас положить г&\ = —1. Струк-
Структурная группа состоит из двух элементов {1, —1} с умноже-
умножением в качестве групповой операции. Можно выбрать числа
г/й и по-другому, но уменьшить структурную группу невоз-
невозможно.
Касательное расслоение TS1 имеет своей структурной
группой /?ls\{0}—почти что типичный слой. Расслоение ре-
реперов на произвольном многообразии М — это расслоение,
у которого та же структурная группа, что и у ТМ, а слоем
является множество всех базисов в касательном пространстве
(т. е. в R"). Для одномерного многообразия типа S1 это есть
множество всех ненулевых векторов, совпадающее с /?1N\{0}.
Так что слои расслоения реперов на S1 гомеоморфны его
структурной группе; это верно для всех расслоений реперов.
Такие расслоения называются главными расслоенными про-
пространствами.
2.12. ВЕКТОРНЫЕ ПОЛЯ И ИНТЕГРАЛЬНЫЕ КРИВЫЕ
Как было определено в § 2.7, векторное поле — это пра-
правило, задающее вектор в каждой точке многообразия М.
В каждой точке — своё касательное пространство, так что
векторное поле «выбирает» по одному вектору из каждого
такого пространства. Далее, для каждой кривой в каждой её
точке определён касательный вектор, и возникает естествен-
естественный вопрос, нельзя лч, обратно, для заданного векторного
поля найти кривую, начинающуюся в заданной точке Р, ка-
касательный вектор к которой в каждой её точке принадлежит
векторному полю? Для векторных полей класса С1 ответ по-
положителен; такие кривые называются интегральными кри-
кривыми векторного поля. Доказательство состоит в следующем.
Пусть V'(P)—компоненты рассматриваемого векторного
поля (это функции от Р). В некоторой координатной системе
{х1} мы имеем V'(P) — v'(xi). To что это поле касается кри-
кривой с параметром л, означает, что
~ = ^{х'). B.5)
Мы получаем для х'(К) систему обыкновенных дифференци-
дифференциальных уравнений первого порядка, у которой всегда суще-
существует единственное решение в некоторой окрестности на-
начальной точки Р. (Теорема существования и единственноеги
для обыкновенных дифференциальных уравнений доказана в
большинстве руководств по дифференциальным уравнениям,
например в книге Choquet-Bruhat, DeWitt-Morette &Diilard —
Bleick A977) (см. библиографию в конце главы). Два при-
примера векторных полей представлены на рис. 2.18.

60 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
Отметим, что различные интегральные кривые могут пере-
пересекаться лишь в таких точках, где V' = 0 для всех i, в силу
единственности решения для системы B.5). Поскольку через
каждую точку Р проходит некоторая интегральная кривая
(она получается решением системы B.5) с начальным усло-
условием в точке Р), интегральные кривые «заполняют» всё М.
Например, если М трёхмерно, то на нём любое векторное поле
Рис. 2.18. Интегральные кривые для двух векторных полей на R2: (а) V =
= хд/ду - ydjdx; (b) V = (х + у (г) д/ду —(у — х/r) д/дх, где г = (х2 +
+ У2I'2.
задаёт двумерное семейство интегральных кривых, покры-
покрывающих всё М (за исключением, быть может, точек, где
Vl = 0 для всех t). Такое заполняющее многообразие мно-
множество кривых называется конгруэнцией. Отметим, между
прочим, что это множество кривых обычно само можно рас-
рассматривать как многообразие.
2.13. ЭКСПОНЕНТА ОТ ОПЕРАТОРА d/dX
Введём понятие, которое окажется полезным для после-
последующих вычислений. Пусть задано аналитическое многооб-
многообразие (класса Сш), и пусть координаты xl(K) точек каждой
из интегральных кривых поля У = d/dX являются аналити-
аналитическими функциями от К. Тогда координаты точек, отвечаю-
отвечающих значениям параметра Ко и Ко -f- e, связаны между собой
при помощи ряда Тэйлора:
где обозначение с «ехр» является очевидным и удобным со-
сокращением для «дифференциального оператора», который,
будучи применен к х'(К), даёт, после подстановки К = Ко, ряд

2 14 СКОБКИ ЛИ И НЕКООРДИПАТНЫЕ БАЗИСЫ 61
Тэйлора. Этот оператор называется экспонентой от оператора
ed/dX. Оператор ed/dX представляет бесконечно малое дви-
движение вдоль интегральной кривой, а его экспонента даёт ко-
конечное движение. Мы будем использовать на равных обозна-
обозначения
2.14. СКОБКИ ЛИ И НЕКООРДИНАТНЫЕ БАЗИСЫ
Если задана какая-нибудь координатная система х1, то
часто бывает удобно выбирать {д/дх1} в качестве базисных
векторных полей. Однако в качестве базиса можно брать лю-
любое линейно-независимое семейство векторных полей: нетруд-
нетрудно понять, что не все они происходят из каких-либо систем
координат. Дело в том, что операторы д/дх' и д/дх' комму-
коммутируют при всех I, j, а два произвольных векторных поля,
вообще говоря, не коммутируют: если V = d/dX и W = d/dji,
то
d d d _d
¦ivffj ( д д д ?
{.dx1 dx' dx' dx1.
д Х^ ш,| dVl д
dx1 dx' ?-i dx) dx1
1 B-7)
i. l
(последняя строчка получается из предпоследней переобозна-
переобозначением индексов суммирования во второй сумме предпослед-
предпоследней строчки). Таким образом,
da, ' dji J ~ dA dn
1 98
dji J ~ dA dn dn dl y ' '
является векторным полем, вообще говоря ненулевым. Если
d/dX и d/dp служат элементами некоторого базиса, то их
нельзя представить в виде дифференцирований по каким-либо
координатам. Такой базис является некоординатным.
Важно уяснить себе, что это различие между координат-
координатным и некоординатным базисами проявляется, лишь если
рассматривать некоторую область многообразия, а не одну
отдельную точку. Оно определяется производными от компо-
компонент векторов, а не только значениями в данной точке. Таким
образом, различие в свойствах координатных и некоординат-

62 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
ных базисов имеет значение, только когда мы имеем дело с
областями многообразия, и несущественно в задачах, где рас-
рассматривается лишь касательное пространство ТР в одной
точке Р.
Упражнение 2.1. Показать, что «единичные» базисные
векторные поля для полярных координат на эвклидовой
плоскости, определяемые формулами
г — cosBx + sinBy,
В = — sinBx + cosBy,
где х = д/дх и у = д/ду, образуют некоординатный базис.
Коммутатор [d/d>», d/d[x] называется скобкой Ли '> полей
V и W. Дадим её геометрическую интерпретацию.
На рис. 2.19 изображена типичная координатная сетка на
двумерном многообразии. За-
Заметим, что по определению х1
постоянно вдоль линий х2, яв-
ляющихся интегральными кри-
кривыми поля д/дх2. Именно по-
поэтому поля д/дх1 и д/дх2 и
коммутируют: каждое из них
является дифференцированием
вдоль линий, на которых дру-
хг=с x2'd гая координата фиксирована.
Рассмотрим теперь два произ-
произрос. 2.19. Типичная координатная вольных векторных поля V —
сетка на двумерном многообразии. =d/(& и №=d/dn, интеграль-
интегральные кривые которых изображе-
изображены на рис. 2.20. Интегральная кривая поля W не обязательно
будет кривой, на которой % постоянно, и наоборот. Дифферен-
Дифференцирование d/djx не является дифференцированием при по-
постоянном Я^поэтому 6/dK и d/d|i не коммутируют. Хотя кри-
кривые полей V и W выглядят как координатные, их параметри-
параметризация не такая, как в координатной системе. И даже то, что
они выглядят как координатные, есть лишь специфика раз-
размерности два: в трёхмерной ситуации может случиться, что
кривая A) пересекает кривые (а) и (Р), а кривая B) пере-
пересекает только (а).
[) И скобки Ли, н группы Ли обязаны своим названием одному и то-
тому же человеку — Софусу Ли, великому математику конца 19-го века.
Скобки Ли, как будет видно дальше, являются частным случаем произ-
производных Ли. Читатель, знакомый с теорией групп Ли, узнает в определе-
определении скобки Лн определение коммутатора векторных полей d/d>. и d/dfi,
являющихся генераторами некоторой группы Ли преобразований. Мы об-
обсудим эту связь в гл. 3.

2.14. СКОБКИ ЛИ И НЕКООРДИНАТНЫЕ БАЗИСЫ
63
Для вектора [V, W] можно дать геометрическую картинку
(рис. 2.21). Отправляясь от точки Р, сдвинемся на АК = е
вдоль интегральной кривой поля V, проходящей через Р; за-
затем сдвинемся на А[г = е вдоль интегральной кривой поля W.
A)
Рис. 2.20. Типичные интегральные кривые для двух векторных полей на
двумерном многообразии.
Пусть мы попадём в точку А. Начиная снова из точки Р и
сдвигаясь сначала на Д[г = е, а затем на Ah = е, мы придём
Рис. 2.21. Геометрическая интерпретация скобки Ли [V, Щ как "меры не-
незамкнутости" параллелограмма, стороны которого отвечают равным прира-
приращениям параметров вдоль интегральных кривых полей V и W.
в некоторую точку В Ф А. Покажем, что вектор, идущий из
А в В, есть е2[Р, W] с точностью до членов более высокого
порядка по е.
Удобнее всего использовать введённый выше экспоненци-
экспоненциальный оператор. Ясно, что
х<(Ю = ехр[е^-
Аналогично путь, идущий в точку В из точки Р, даёт

64 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
Поэтому разность координат точек Л и В
B.11)
справа стоит в точности коммутатор экспоненциальных опе-
операторов. Переходя к разложениям Тэйлора, получаем
т. е.
x'(fi) — х'(Л)=е2[Р, Щх*\Р + О(еР). B.12)
Это — i-я компонента скобки Ли: равенство B.12) подтвер-
подтверждает справедливость нашей геометрической картинки для
скобки Ли.
Упражнение 2.2. (а) Используя равенство B.6), докажите
формулу B.12).
(Ь) Докажите, что
ехр[ай/й1 + 6d/dn] == exp[ad/dfc] exp [bcl/dp] B.13)
при всех а и Ъ, если и только если [d/d?,, d/d^i] = 0.
Упражнение 2.3. Докажите, что любые три дважды диф-
дифференцируемые (т. е. класса С2) векторные поля К, Р, Z
удовлетворяют тождеству Якоби
[[*,?], Z] + [[F,Z], K] + [[Z,K], F] = 0. B.14)
Алгеброй Ли векторных полей в области U многообразия
М называется всякая совокупность А векторных полей на U,
являющаяся векторным пространством относительно сложе-
сложения (это значит, что любая линейная комбинация с постоян-
постоянными коэффициентами полей из А снова есть поле из Л) и
замкнутая относительно операции коммутирования (скобка
Ли двух полей из А снова есть поле из Л). Ясно, что сово-
совокупность всех векторных полей класса С°° на U является ал-
алгеброй Ли: гораздо интереснее, однако, когда выделенная по
той или иной причине меньшая совокупность векторных по-
полей тоже образует алгебру Ли. Такие совокупности тесно свя-
связаны со свойствами симметрии многообразия и с соответ-
соответствующими группами симметрии, которые обычно являются
группами Ли. Мы изучим их более подробно в гл. 3, где
будет также дано более общее определение алгебры Ли.

2Л5 КОГДА БЛЗИС ЯВЛЯЕТСЯ КООРДИНАТНЫМ? 65
2.15. КОГДА БАЗИС ЯВЛЯЕТСЯ КООРДИНАТНЫМ?
Пусть даны два векторных поля Л = d/dX и В =j3/d(a на
двумерном многообразии М; предположим, что А и В линей-
линейно-независимы в каждой точке некоторого открытого множе-
множества U из М, так что они образуют там базис векторных по-
полей. В каком случае можно быть уверенным, что этот базис
является координатным, другими словами, что % и ц, яв-
являются координатами на (У? Очевидно, необходимо, чтобы
наши поля коммутировали:
[А,Б] = 0.
Покажем, что это условие является также и достаточным.
Для этого обратимся непосредственно к определению много-
многообразия— построим соответствующее 1-1-отображение из V
Рис. 2.22. Описанное в тексте отображение из Я2 в М. Оно задаёт систему
координат в некоторой окрестности точки Р.
на некоторое открытое множество в R2. Отправляясь от не-
некоторой точки Р из U и используя произвольные координаты
(х1, х2) в LJ, сместимся вдоль поля А на «параметрическое
расстояние» Х\\ мы попадём в точку R с координатами (см.
B.6))
Если мы сначала сместимся на расстояние %\ вдоль А, а за-
затем на hi вдоль Е, то попадём в точку Q с координатами
Эта формула определяет отображение экспоненциального
типа из некоторой окрестности V начала координат в R2 в U;
данный элемент из V — пара (ки in) — отображается в точку
Q. Это отображение изображено на рис. 2.22. Для того чтобы
оно определяло координатную систему, оно должно быть
взаимно-однозначным, т. е. должно иметь обратное. Ниже мы
докажем, что обратное отображение на самом деле суще-

66 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
ствует всюду в U, но сначала покажем, что А а В являются
координатными базисными векторами этой координатной си-
системы, если они коммутируют в U. Перепишем наше отобра-
отображение в виде координатного преобразования от {а, р} к
X'(а Р) = gPd/dHead/d^jj-/1
Базисные векторы д/да и <Э/(Зр имеют (в системе координат
{х'}) компоненты дх'/да и дх1/д$ соответственно. Из B.6)
легко вытекает, что
pCtd/dA —— pudfdK .
da йХ '
и, поскольку d/dn и й/dk коммутируют, мы получаем
ар -
Но dx'/d^— это в точности компоненты поля d/йХ в коорди-
координатной системе {*'}. Поскольку они являются аналитическими
функциями на М, то после применения к ним оператора
exp(pd/d[x)exp(ocd/d^) мы получим их значение в точке, ко-
координаты которой равны (ос, Р). Следовательно, всюду на U
д/да = й/йХ и <Э/<Эр = d/dfr,
тем самым мы доказали достаточность условия [Л, Б] = 0 для
того, чтобы Л и В были координатными базисными векто-
векторами.
Обратимся теперь к обещанному доказательству того, что
{а, р} образуют координатную систему в U. Нужно доказать,
что отображение {a, p}t—>{x1} обратимо, и для этого мы ис-
используем теорему об обратной функции (см. § 1.2). Согласно
этой теореме, если матрица
дх1 дх2
да
дх2
ар
в некоторой точке {а, р) имеет ненулевой определитель, то
в некоторой окрестности этой точки указанное отображение
обратимо. Определитель обращается в нуль, если и только
если векторы дх1/да, дх'/dfi линейно-зависимы: из сказанного
выше ясно, что этого никогда не бывает, ибо А и Б линейно-
независимы в U. Таким образом, наше отображение обра-
обратимо во всём множестве U и, значит, задаёт систему коор-
координат.

2.16. ОДИН-ФОРМЫ 67
Интересно выяснить, в каком месте не пройдут наши рас-
рассуждения, если [А, В] Ф 0. В этом случае выражение дх*/д$
более сложно. По-прежнему наше отображение будет обра-
обратимым, по крайней мере в некоторой окрестности точки
а = р = 0. Но поскольку cbc'/dp уже не равно больше dxlfd\n
в изучаемой точке, векторы А и В не будут базисными век-
векторами построенной системы координат.
Проведённые выше рассуждения обобщаются на п-мерный
случай: если п векторных полей {?</>, /=1, ..., п} на
n-мерном многообразии М линейно-независимы и коммути-
коммутируют друг с другом в некоторой открытой области U на М,
то они являются координатными базисными векторами ко-
координатной системы {а,}, имеющей в произвольных коорди-
координатах {х1} вид
xl(au .... а„)
где в качестве «центра» Р берётся произвольная точка из U.
2.16. ОДИН-ФОРМЫ
Вернёмся к изучению ТР — пространства всех касательных
векторов в точке Р. В качестве первого примера тензоров
определим один-формы как линейные вещественнозначные
функции на векторах. Это означает следующее: один-форма
й в точке Р сопоставляет вектору V в точке Р некоторое ве-
вещественное число, обозначаемое через 5>(V). Обозначение с
волной подчёркивает то обстоятельство, что й является функ-
функцией на векторах. (Волна "* над буквой всегда обозначает
один-формы, точно так же как черта - над буквой всегда
обозначает векторы.) Линейность этой функции означает, что
B.15)
где а и b — вещественные числа. Непосредственно опреде-
определяются сложение один-форм и их умножение на веществен-
вещественные числа: аю есть один-форма вида
(aG>)(V) = a[<b(V)], B.16а)
а сумма й + 5 есть один-форма вида
(& + o)(V) = &(V)+6{V) B.16b)
(здесь V — произвольный вектор). Таким образом, совокуп-
совокупность один-форм в данной точке образует векторное про-
пространство; оно называется двойственным (дуальным, сопря-
сопряжённым) к ТР и обозначается через Т*Р. Термин «двойствен-
«двойственное» употребляется потому, что векторы также можно рас-
рассматривать как линейные, вещественвдзначные функции н&

68 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
один-формах. А именно, для любого вектора V мы полагаем
его значение на один-форме ю равным й(Р). Это линейная
функция, поскольку её значение на а© -4- Ьа равно, в силу
B.16),
(aS> + be) (V) = (об)
= а (значение V на й) + 6 (значение V на 5).
B.17)
Таким образом, именно мы можем рассматривать каждую из
этих величин как линейную вещественнозначную функцию,
аргументом которой служит другая величина; поэтому и го-
говорят, что векторы и один-формы двойственны друг другу.
Значения одних на других записывают разными способами:
¦ c5(V)s= р(б)шз<й, VY, B.18)
в последнем обозначении подчеркивается равноправие обоих
партнёров. Величина й (V) называется часто свёрткой с V.
В более старых руководствах по тензорной алгебре векторы
часто называются «контравариантными векторами», а один-
формы— «ковариантными векторами». Эти названия указы-
указывают на то, как ведут себя компоненты соответствующих
объектов при замене базиса, о чём будет идти речь в § 2.26.
2.17. ПРИМЕРЫ ОДИН-ФОРМ
Прежде чем излагать дальше математическую теорию,
рассмотрим несколько простых примеров один-форм. Один из
наиболее часто встречающихся примеров — это градиент
функции: о нём речь пойдёт в § 2.19. Приведём другие при-
примеры.
(i) В матричной алгебре, если считать «векторами», век-
вектор-столбцы, то вектор-строки будут один-формами. Действи-
Действительно, если их перемножить (в правильном порядке) по
обычным правилам матричного умножения, то получится ве-
вещественное число. Например, в двумерном случае вектор-
строку (—1, б) можно считать функцией, сопоставляющей лю-
любому вектор-столбцу вещественное число:
(-1, 5)
Легко проверяется линейность этой функции.
A1) В используемых в квантовой механике гильбертовых
пространствах аналогами вектор-строк и вектор-столбцов из
примера (i) являются так называемые кет-векторы |я1)> (век-
(векторы) и бра-векторы <ф| (один-формы) (названия и обо-
обозначения Дирака), свёртка <ф|яр> которых есть комплексное

2.18. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
число. (Обобщение векторной и тензорной алгебры на комп-
комплексный случай тривиально: нужно лишь заменить слово
«вещественный» на «комплексный». Обобщение построенной
выше теории вещественных многообразий на комплексно-ана-
комплексно-аналитический случай, где координатными отображениями слу-
служат комплексно-аналитические отображения в пространство
комплексных переменных (г',22 zn), также по большей
части не представляет труда. Но некоторые свойства комп-
комплексных многообразий, такие как глобальная структура и
кривизна, гораздо труднее поддаются изучению, и этих во-
вопросов в настоящей книге мы касаться не будем.) Обозначе-
Обозначение <ф|'ф> аналогично B.18), и это не случайно.
В обоих примерах (i) и (и) имеется возможность «пере-
«переводить векторы в один-формы (и обратно), сопоставляя дан-
данному вектору «сопряжённый», или «транспонированный»,
объект, являющийся один-формой. В § 2.29 мы увидим, что
это эквивалентно заданию метрики или скалярного произве-
произведения в рассматриваемом векторном пространстве. Это очень
важная дополнительная структура в векторном пространстве,
но читателю следует иметь в виду, что нет никакого априор-
априорного, «естественного» способа идентификации один-форм и
Векторов.
2.18. ДЕЛЬТА-ФУНКЦИЯ ДИРАКА
В квантовой механике часто приходится иметь дело с
функциональными пространствами (пространствами функ-
функций). Рассмотрим множество С[—1, 1] всех вещественно-
значных функций класса С00, определённых на интервале
—1 ^ х ^ 1 в R1. Это множество является группой относи-
относительно сложения (сумма двух С°°-функций снова есть С°°-
функция и т. д.) и векторным пространством над веществен-
вещественными числами (если / есть С°°-функция, то с/ также будет
С°°-функцией для любой вещественной константы с). Эле-
Элементы двойственного пространства (один-формы) называются
распределениями (или обобщёнными функциями). Примером
распределения служит дельта-функция Дирака 6(х), опреде-
определяемая как один-форма, значение которой на С°°-функции
f(x) естьДО):
<fi(*), «*)>=•/@). • B.19)
В одном смысле 8(х)— действительно настоящая функция:
она есть отображение С[—1, 1 ]-»-/?. Обычно термин «распре-
«распределение» используется только для непрерывных (линейных)
функций такого типа. Но понятие непрерывности требует
введения топологии, на этот раз топологии в С[—1, 1].Это —
бесконечномерное векторное пространство (в щш имеется

70 2 ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
бесконечное число линейно-независимых функций), а обсу-
обсуждение топологии таких пространств далеко выходит за рам-
рамки настоящей книги. Интересующегося читателя мы отсы-
отсылаем к Choquet-Bruhat et al. A977). Здесь важно отметить,
что мы понимаем дельта-функцию не в том смысле, который
вкладывали в это понятие Дирак и его современники. Чтобы
уяснить себе, что они имели в виду, разберём, как сделать
из функции — элемента пространства С[—1,1] — один-форму
на С [—1, 1].
Для любой функции g из С[—1,1] можно определить
один-форму g, значение которой на функции f из С[—1, 1]
равно
1
Q,f)=\g(x)f(x)dx. B.20)
\
Это, действительно, линейное отображение, переводящее f в
значение соответствующего интеграла. (Поскольку g и f не-
непрерывны на —1 ^х^ 1, этот интеграл всегда существует.)
Термин «дельта-функция» был использован как камуфляж
следующего обратного «рассуждения»: раз 8(х)— один-фор-
один-форма, то можно говорить о ней и как о функции от х в обычном
смысле слова, такой что интеграл от её произведения на f (х)
равен f@):
Эта идея была очень болезненно воспринята математиками,
некоторые из них даже заявили, что Дирак ошибается, не-
несмотря на то что он получал полезные и самосогласованные
результаты. Физики, однако, мудро отвергли эту крайнюю
точку зрения и больше прислушивались к своей интуиции.
Теперь мы в состоянии понять, почему они «ошибались» и при
этом получали верные результаты. Они «ошибались», по-
поскольку говорили о б (х) как о функции Rl^>-Rl, каковой су-
существовать не может ни в каком точном смысле слова, и по-
поскольку они манипулировали с ней, как с обычной функцией,
интегрируя её и даже дифференцируя
(*)/'(*)<**= -ПО).
Но они при этом были «правы», поскольку нигде не исполь-
использовали 8(х) без интеграла с достаточно гладкой функцией
f(x) — они нигде не использовали её иначе, как для того,
чтобы задать отображение функций в вещественные вдела,

2.19. ГРАДИЕНТ И НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ ОДИН-ФОРМ 71
Таким образом, они пользовались техникой, но не языком
теории обобщённых функций, которая была специально при-
придумана для того, чтобы подвести под дельта-функции солид-
солидный фундамент. Отметим, однако, что теория обобщённых
функций отличается от старой физической точки зрения сйоей
большой простотой: можно определить дельта-функцию без
привлечения правил типа B.20) для превращения функций
в один-формы. Как отмечалось в примере (п) выше, такое
правило есть дополнительная структура в векторном про-
пространстве, которая, как мы теперь понимаем, не нужна для
определения дельта-функции.
Стоит ещё. заметить следующее. Выше мы сказали, что
слово «распределение» используется только для непрерывных
один-форм, в соответствии с общепринятым определением
двойственного векторного пространства («топологического
сопряжённого»). Однако в наше определение один-форм в
§ 2.16 требование непрерывности мы не включили; не про-
проявили ли мы здесь непоследовательности? Нет, не проявили,
потому что на конечномерном векторном пространстве любая
линейная функция всегда непрерывна (см., например,
Choquet-Bruhat et al. A977) или Rudin A964) из библиогра-
библиографии к гл. 1).
2.19. ГРАДИЕНТ
И НАГЛЯДНОЕ ИЗОБРАЖЕНИЕ ОДИН-ФОРМ
Поле один-форм — это, по аналогии с векторным полем,
правило, задающее в каждой точке один-форму. Содержа-
Содержащиеся в формулах B.16) определения переносятся на поля:
в этом случае а есть функция на М, не обязательно постоян-
постоянная. Дифференцируемость полей один-форм можно опреде-
определить через дифференцируемость векторных полей и функций.
А именно, на С°°-многообразии заданная один-форма ю вм-
сте с векторным полем V определяют функцию 5> (V). Если
Эта функция принадлежит к классу С°° для любого С°°-поля
V, то ю называется один-формой класса С°°. (Более простое
определение дифференцируемости мы дадим после того, как
введём в § 2.20 компоненты один-форм.) Как и в случае век-
векторных полей, возникает расслоенное пространство, называе-
называемое кокасательным расслоением Т*М; базой этого расслое-
расслоения является М, а слоем над точкой Р служит Т*Р. Сечения
Т*М суть поля один-форм.
Наиболее полезный и поучительный пример один-формы —
Это градиент функции f, который мы обозначим через ctf.
Хотя в элементарных учебниках векторного анализа его и
называют вектором, на самом деле это всё же один-форма.
Итак, градиент uf (не путать с «инфинитезимальным диффе-

72 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
ренциалом» df, который мы изредка будем использовать1))
определяется равенством
¦ df{d/dk)=df/dk, B.21)
где d/d?» — произвольный касательный вектор. Другими сло-
словами, градиент функции / в некоторой точке Р_— это такой
элемент из Тр, значение которого на элементе V из ТР равно
производной f по направлении^ вектора V (т. е. вдоль кри-
кривой с касательным вектором V). Нужно проверить, что это
линейная функция на ТР, т. е. что выполнено B.15):
Линейность доказана. На первый взгляд может показаться,
что f сама есть один-форма, поскольку f и d/d?, дают число
df/dh. Но это неверно. Напомним читателю, что и Тр и Тр
заданы в точке Р, так что вся информация, необходимая для
вычисления df/d%, также должна быть задана в этой же точ-
точке. Но значение f в Р не влияет на df/dK. Чтобы вычислить
df/dX в Р, нужно знать df/dx' в Р, а это и есть, как мы уви-
увидим далее, компоненты градиента f.
Градиент позволяет нам дать наглядную интерпретацию
один-форм, дополняющую наглядную интерпретацию векто-
векторов как стрелок. На рис. 2.23 изображён кусок топографиче-
топографической карты местности, представляющий собой набор горизон-
горизонталей— линий равной высоты. Если обозначить через h вы-
высоту над уровнем моря, то градиент Ш, очевидно, наиболь-
наибольший в местах типа участка А, где линии наиболее плотно
сближаются друг с другом, и наименьший в районе В, где
горизонтали наиболее разрежены. Далее, пусть необходимо
выяснить, насколько придётся подняться, двигаясь из одной
точки в другую (близкую). Для этого на карте нужно про-
провести линию (вектор Ах) между этими точками. Тогда число
горизонталей, которые пересечёт эта линия, даст изменение
высоты. Например, линия 1 пересекает полторы горизонтали,
а линия 2 — две. Линия 3 начинается там же, где и 2, но идёт
в другом направлении, набирая высоты лишь на полгоризон-
полгоризонтали. Эти числа: 1 ^, 2, ^ — и есть Ah, причём ДА линейно
зависит от Ах:
J) Прекрасное обсуждение связи между 3f и df см. в книге Spivak
A970, vol. 1).

2.20. БАЗИСНЫЕ ОДИН-ФОРМЫ И КОМПОНЕНТЫ ОДИН-ФОРМ
73
Это — значение Sh на Дх (см. B.21) выше и B.27) ниже).
Следовательно, один-форму ю можно наглядно изобразить
в виде семейства поверхностей (рис. 2.24), а её свёртка
с вектором V есть число поверхностей, которые V пересекает.
Чем ближе друг к другу поверхности, тем больше й. Соб-
Собственно говоря, так же как вектор направлен по прямой, так
и поверхности один-форм прямые (плоские) и параллельные.
Это объясняется тем, что мы работаем с один-формами в точ-
точке, а не в протяжённой области, т. е. рассматриваем «каса-
«касательные» один-формы, по аналогии с касательными векто-
векторами.
3
Рис. 2.23. Топографическая кар- Рис. 2.24. "Касательная" один-
та холмистой местности. Кри- форма J может быть наглядно
вые на рисунке —это линии изображена в виде семейства
равной высоты над уровнем мо- параллельных плоскостей раз-
ря. Стрелками указаны возмож- мерности, на единицу меньшей,
ные пути подъема. чем размерность многообразия.
Число плоскостей, пересекае-
пересекаемых вектором V, равно свёртке
<й, V).
Из этих рисунков видно, почему, вообще говоря, нельзя
называть градиент вектором. Хотелось бы отождествить гра-
градиент с вектором, указывающим направление «вверх» по
склону, т. е. с вектором, который пересекает наибольшее чис-
число горизонталей на единицу длины. Но обратите внимание
на слова «на единицу длины». Если на многообразии имеется
мера длины, то градиенту можно сопоставить вектор. Но если
неизвестно, как сравнивать длины векторов, смотрящих в
разных направлениях, то определить направление самого
крутого подъёма нельзя, и в этом случае отличие градиента
от вектора существенно. Поскольку мы, вообще говоря, не
предполагаем наличие длины (или «метрики»), следует по-
постоянно помнить о различии между векторами и один-форма-
один-формами. Мы вернёмся к этому вопросу в § 2.29.
2.20. БАЗИСНЫЕ ОДИН-ФОРМЫ И КОМПОНЕНТЫ ОДИН-ФОРМ
В векторном пространстве Т*р один-форм в точке Р лю-
любые п Линейно-независимых один-форм образуют базис. Од-
рако если уже выбран базис (ё/, t=l, ,.., п) в простран-

74 2. ДИФФЕРЕНЦИРУЕМЫЦ МНОГООБРАЗИЯ И ТЕНЗОРЫ
стве Тр векторов в точке Р, то имеется привилегированный
базис {со', i= I, ..., п) в Т*р, называемый двойственным
(или дуальным) базисом. Его определение таково. Если V —
произвольный вектор в точке Р, то со' даёт его ?-ю компо-
компоненту:
Vl. B.22)
Легко видеть, что эта функция линейна по V, поскольку i-я
компонента, скажем, суммы V + W равна V' + W. Следова-
Следовательно, B.22) действительно определяет линейную функцию
на Тр. В частности, поскольку базисный вектор ё,- имеет лишь
одну, /-ю, ненулевую компоненту, то
й' (ё,-) = б'/. B.23)
При помощи этого равенства базис {й'} обычно и опреде-
определяется в учебниках. Отметим особо, что для нахождения
любого й' надо знать все векторы {ё,-}. Изменение какого-то
одного ёк меняет, вообще говоря, все базисные один-формы
й'. Мы построили соответствие между базисом и двойствен-
двойственным базисом, а не между индивидуальными векторами и со-
соответствующими один-формами.
Пока не было доказано, что один-формы {со'} линейно-
независимы и, значит, образуют базис. Это легко вытекает
из B.23), но мы пойдём другим, обходным путём. Рассмот-
Рассмотрим любую один-форму q, действующую на произвольный
вектор V:
q(V)=q(L V'e,) = Z Vq (ё,) = % &' (у) q (ё,). B.24)
Величины
q, = q(e,) B.25)
называются компонентами q в базисе, дуальном к {ё/}. Для
того чтобы убедиться в том, что это больше, чем просто ана-
аналогия с B.22), перепишем B.24) в виде
Поскольку один-форма определяется своими значениями на
векторах, из, этого равенства вместе с B.16) вытекает, ввиду
произвольности V, что
^ ?1=ЪЯ1<*'' B.26)
Отсюда следует, что {со'} действительно образуют базис, по-
поскольку их как раз п штук и любая один-форма q представима
в виде их линейной комбинации. Отсюда следует также, что

2.21. ИНДЕКСНЫЕ ОБОЗНАЧЕНИЯ 75
величины {<7,} на самом деле являются компонентами q отно*
сительно этого базиса в обычном смысле слова.
Самое важное то, что у нас есть теперь формула для вы-
вычисления значения q(V) известным компонентам q и V:
Zq,V'. B.27)
Как отмечалось выше, это есть свертка V и q.
- Разумеется, все эти рассуждения непосредственно перено-
переносятся на поля один-форм. Если совокупность векторных полей
{ё/} образует базис в каждой точке некоторой области U мно-
многообразия М, то поля {©'}, определяемые равенством B.23),
равным образом образуют базис в каждой точке из U. Дан-
Данная система координат {л;'} в области U определяет есте-
естественный базис векторных полей {д/дх'}. Она же определяет
естественное семейство один-форм — семейство, состоящее из
п градиентов {их'}. Эти один-формы фактически образуют
базис, дуальный к координатному базису векторов; действи-
действительно, в силу B.21)
dx<" (д/дх') = дх!/дх' = Ь1, B.28)
(второе равенство вытекает из свойств обычных частных про-
производных) .
В § 2.19 мы дали определение дифференцируемое™ поля
один-форм. Теперь легко доказать, что q есть форма класса
С°°, если и только если её компоненты {q'} относительно не-
некоторого базиса из векторных полей класса С°° являются
С°°-функциями.
2.21. ИНДЕКСНЫЕ ОБОЗНАЧЕНИЯ
Мы используем следующие соглашения, касающиеся рас-
расстановки индексов. Компоненты векторов, например V', ну-
нумеруются верхними индексами; компоненты один-форм, на-
например (о,-, — нижними. Базисные векторы нумеруются ниж-
нижними индексами (ё,), базисные один-формы — верхними (©')
(Для координатных базисов мы получаем согласно этим пра-
правилам, что один-формы (Ы нумеруются верхними индексами,
как оно и должно быть; векторы д/дх1 считаются имеющими
Нижние индексы, ибо они появляются в знаменателе как верх-
верхние.) Эти правила расстановки индексов очень полезны. Рас-
Рассмотрим свёртку

?б 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
¦"¦ _ , ¦
представляющую собой сумму произведений, в которых один
из сомножителей имеет верхний индекс, а другой — нижний.
Мы примем правило суммирования Эйнштейна: если в неко-
некотором выражении какой-нибудь индекс встречается дважды —
один раз как верхний, а другой — как нижний (такие индек-
индексы называют повторяющимися), то подразумевается, что по
этому индексу производится суммирование. Таким образом, в
выражениях
0Х
подразумевается суммирование. В выражениях
WWk, Wen,
никакого суммирования не производится; в первых двух во-
вообще нет повторяющихся индексов, а в последнем оба ин-
индекса верхние. Использование правила Эйнштейна очень
упрощает запись вычислений с компонентами, а наши пра-
правила расположения индексов минимизируют вероятность по-
появления случайной ошибки при использовании этого правила.
Теперь мы в состоянии перейти от векторной алгебры к
тензорной.
2.22. ТЕНЗОРЫ И ТЕНЗОРНЫЕ ПОЛЯ
Тензоры — естественное обобщение тех понятий, с кото-
которыми мы уже имели дело. Их алгебра устроена просто, и
они имеют множество разнообразных применений. Главная
проблема для тех, кто впервые сталкивается с тензорами, —
это невозможность их «визуализации»: их трудно нарисовать.
Выше мы выяснили, как изображать векторы и один-формы;
те же приемы можно в той или иной мере перенести на тен-
тензоры более высоких «рангов», но картинки делаются крайне
запутанными. По-видимому, в большинстве случаев лучше от-
отказаться от попыток рисовать тензоры и работать с ними в
рамках того определения, которое мы сейчас дадим, т. е. ду-
думать о тензорах как о линейных операторах на векторах и
один-формах.
Рассмотрим точку Р на М. Тензор типа I „, 1 в точке Р
определяется как линейная функция, аргументами которой
служат N один-форм и N' векторов, а значениями — веще-
вещественные числа. Это определение является обобщением дан-
данного выше для один-форм. Под «линейностью» мы понимаем
здесь линейность по каждому аргументу (это свойство назы-
называют обычно полилинейностью). Например, если F—тензор

2.22. ТЕНЗОРЫ И ТЕНЗОРНЫЕ ПОЛЯ 77
типа ( 2 J > то его значение на один-формах й и д и векторах
V и W записывается в виде
Свойство линейности здесь означает, что (для произвольных
чисел а и Ь)
F (аи + ЬЯ. а; К, w) = aF (ю, а; V, W) + bF (Л, а; V, W)
B.29)
и аналогично для других аргументов. В случае если мы хо-
хотим иметь дело с F, не указывая явно аргументы, мы будем
использовать обозначение F (, ; ,), где на пустые места мож-
можно поставить любые аргументы соответствующего типа (один-
формы до точки с запятой и векторы — после). Разумеется,
порядок аргументов, вообще говоря, существен, как это видно
уже на примере функций вещественных переменных (скажем,
у функции f(x, у) = Зл; -f- 5y значения /A,2) и /B,1) раз-
различны).
Как и в случае векторов и один-форм, тензорное поле
типа I „, I —это правило, сопоставляющее каждой точке
тензор типа ( N, J в этой точке. Свойство линейности тензо-
тензоров распространяется и на тензорные поля, причём числа а
и Ъ в B.29) в разных точках могут быть различными — они
являются функциями на М. Дифференцируемость тензорных
полей определяется так же, как и для один-форм (см.§ 2.19).
Отметим, что векторы суть тензоры типа f 0 ) • они яв-
являются линейными функциями на один-формах. Аналогично
один-формы суть тензоры типа ( , ) • Скалярные функции на
многообразии принято считать тензорами типа f 0 ) (см.
§ 2.28 «Функции и скаляры»). Тензор Т типа Г . J пред-
предполагает наличие двух аргументов. Значение Т (й; F) есть
вещественное число; при фиксированном б мы получаем
один-форму Т (й; ), поскольку сюда нужно подставить век-
вектор, для того чтобы получить вещественное число; Т (; V)
есть вектор. Таким образом, тензор типа f , J можно рас-
рассматривать как линейную функцию на векторах со значе-
значениями в векторах, а также как линейную функцию на один-
формах, принимающую значения также в один-формах. Та-
Такие трюки можно проделывать с любыми тензорами.

78 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
2.23. ПРИМЕРЫ ТЕНЗОРОВ
Хотя понятие тензора, как оно определено выше, может
показаться довольно абстрактным, оно весьма часто непо-
непосредственно приложимо к конкретным ситуациям. Мы приве-
приведём сейчас три примера, а чуть позже посвятим целый па-
параграф (§ 2.29) обсуждению одного чрезвычайно важного
тензора — метрического тензора.
(i) Наш первый пример — из матричной алгебры. Если
вектор-столбцы считать векторами, а вектор-строки — один-
формами, то матрицы суть тензоры типа Г ), так как, ум-
умножая матрицу на вектор, мы получаем вектор, а умножая её
на вектор с одной стороны и на один-форму — с другой, полу-
получаем число.
Упражнение 2.4. Линейное преобразование в смысле мат-
матричной алгебры (например, ортогональное преобразова-
преобразование (вращение)) преобразует одну матрицу в другую. По-
Покажите, что это индуцированное преобразование матриц
есть тензор типа ( 2 )•
(И) Второй пример относится к упоминавшемуся в § 2.18
функциональному пространству С[—1, 1]. Линейный диффе-
дифференциальный оператор (например, x2d/dx) переводит функ-
функции (векторы этого пространства) в другие функции (век-
(векторы). Будучи линейным, этот оператор является тензором
типа Г J в этом пространстве.
(iii) Третий наш пример — тензор напряжений. Читатели,
знакомые с теорией упругости, знают, что это такое. Если в
деформированном материале выделить мысленно некоторую
площадку, то тензор напряжений определяет вектор напря-
напряжения, действующий на этой площадке (силу на единицу
площади, с которой материал по одну сторону площадки дей-
действует на материал по другую её сторону). Так как площад-
площадка— это поверхность, а поверхности представляются один-
формами, то тензор напряжений оказывается линейной функ-
функцией на один-формах, принимающей значения в векторах,
т. е. тензором типа ( 0 ) •
2.24. КОМПОНЕНТЫ ТЕНЗОРОВ
И ТЕНЗОРНОЕ ПРОИЗВЕДЕНИЕ
Простейший пример тензора типа f . J строится так: бе-
берём два вектора V и W и определяем тензор F® W как тен-
тензор, значение которого на двух один-формах р и q равно

2.25. СВЁРТКА 79
произведению V(p)W(q):
V®W(p,q)=V(p)W(q). B.30)
Операция <8> называется тензорным (или внешним) произве-
произведением. Её обобщение на случай произвольного числа тензо-
тензоров произвольного типа очевидно. Тензорным произведением
/ N \ ( N' \ л
тензора типа I м I и тензора типа I м, \ будет тензор типа
N+N'
Компонентами тензора называются его значения на ба-
базисных векторах и один-формах. Скажем, если S — тензор
типа ( _ ), то его компоненты относительно базиса {ё/}
имеют вид
¦ S'/*/m = S (©', &', 5>k; ei, em). B.31)
Если порядок аргументов тензора S существенен, то суще-
существенным является и порядок индексов у компонент Siikim.
Обобщение понятия компоненты на тензорные поля и оп-
определение дифференцируемости тензорных полей совершенно
аналогичны случаю один-форм (см. § 2.20).
Упражнение 2.5. (а) Докажите, что общий тензор типа
( г.) нельзя представить в виде тензорного произведения
двух векторов. (Указание: подсчитайте число компонент
тензора типа @ )•)
(Ь) Докажите, что тензор V® й типа f J имеет компо-
компоненты К'со/.
Упражнение 2.6. Докажите, что тензоры типа ( - J в точ-
точке Р образуют векторное пространство относительно сло-
сложения, определённого аналогично B.16Ь). Докажите, что
тензоры et ® ej образуют базис этого пространства. (Та-
(Таким образом, хотя общий тензор типа Г Q J и не пред-
представляется в виде тензорного произведения, он представ-
представляется в виде линейной комбинации тензорных произведе-
произведений.) Это векторное пространство обозначается через
ТР ® Тр.
2.25. СВЁРТКА
Как было указано в упр. 2.5, величины {V'co/} являются
компонентами тензора типа Г J . Суммируя "диагональные"
компоненты (i = j), получим 1/'со/ — число, не зависящее от

Im
80 2 ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
базиса, а именно значение ю на V, которое можно считать
тензором типа ( 0 ) • Аналогично, если S'jk и Р1т — компо-
компоненты тензоров типа Q) и BЛ соответственно, то Б'1кР
суть компоненты тензора типа ( }, SljkP'm — компоненты
тензора типа ( , ). SllkP11 — компоненты другого тензора
типа ( ) и т. д. По аналогии с формулой B.27) эта опера-
операция называется свёрткой; она позволяет получать новые тен-
тензоры из уже имеющихся.
Дадим доказательство независимости свёртки от выбора
базиса. Рассмотрим тензор А типа Г 0 ). тензор В типа Г _ J
и их свёртку (относительно некоторого базиса) AliBlk. Мы
утверждаем, что это — компоненты тензора С типа ( , ). та-
такого что для произвольных вектора V и один-формы а
С (а; V) = ( Z Л<"%) a,Vb = Е А (а, &1) В (ё„ F).
В силу линейности А по второму аргументу это можно пе-
переписать в виде
так как величины В(ё,, V) суть просто числа. Но в § 2.20
мы по сути дела доказали, что независимо от выбора базиса
где правая часть является один-формой (при фиксирован-
фиксированном V)—на пустое место нужно подставлять вектор. Эта
один-форма стоит в качестве одного из аргументов в А, так
что
Л'/Б,* = #*<=> С (а; V) == А (а, В( , V)),
независимо от выбора базиса (см. упр. 2.8).
Упражнение 2.7. Сколько тензоров типа Г l ^ можно по-
получить свёрткой по паре индексов из тензора Qmim типа
( „ J ? Сколько тензоров типа ( 0 ). если выполнить ещё
одну свёртку?
Упражнение 2.8. Пусть А и В — два тензора типа Г
будем рассматривать их как линейные функции от

E.26. ЗАМЕНА БАЗИСА 81
торов со значениями в векторах: если V — вектор, то
A (F) и B(V) — векторы. Покажите, что если определить
С(V) равенством
С A7)= В (А (Г)),
то С—тоже тензор типа (ij- Покажите, что его ком-
компоненты имеют вид
Выясните связь всего этого с линейными преобразования-
преобразованиями (см. § 1.6).
2.26. ЗАМЕНА БАЗИСА
В фокусе старого определения тензора — поведение ком-
компонент тензора при замене базиса. Это определение было
позднее заменено на то, которое мы привели выше; насколько
же далеки друг от друга эти две концепции, раз мы только
сейчас дошли до замен базиса! Нельзя сказать, чтобы пре-
преобразования компонент тензора при замене базиса были не
важны. В большинстве практических вычислений с тензо-
тензорами используются их компоненты, и необходимо понимать,
как они преобразуются.
Рассмотрим векторы и тензоры, определённые в некоторой
точке Р многообразия М. Пусть у нас был один базис векторов
{ё;, ?= 1, ..., п} и мы хотим перейти от него к другому
базису {ej>, /'—1, ..., п}. (Штрихи у индексов будут слу-
служить признаком, позволяющим отличить то, что относится к
одному базису, от того, что относится к другому.) Тогда в ТР
возникает линейное преобразование Л от старого базиса к
новому:
ёг = А.1,-ёг B.32)
Матрица Л'у невырожденна (иначе векторы {е{>} были бы
линейно-зависимы), а в остальном произвольна. Это не есть
набор компонент какого-либо тензора, поскольку индексы от-
относятся к двум различным базисам. Эта матрица называется
^матрицей преобразования.
Старый базис один-форм удовлетворяет условию B.23) j
Умножая на Akf и используя B.32), получаем в силу линей-
линейности один-форм

-82 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
Далее, матрица Л'/- обратима. Обозначим обратную матрицу
через Ak't:
Л*> V = б*'/, Л*'гЛ'У = 6',, B,34)
Умножая B.33) на Л*';, получим
Ak'i&1 (ё/) = 6fe7;
сравнивая с B.33), заключаем, что
+ 5>k' = Ak'i&i. B.35)
Эта формула двойственна формуле B.32): базисные один-
формы преобразуются по закону, противоположному закону
преобразования базисных векторов (противоположному в том
смысле, что используется матрица, обратная к матрице пре-
преобразования); тогда в обоих базисах выполняется соотноше-
соотношение B.23).
Теперь уже совсем просто найти, как преобразуются ком-
компоненты:
yi' = ©*' (V) = Л1',€>1 (V) = А1'/У. B.36)
Чк' = Я (h') = <?(AV/) = AV<7 (e7) = Л'к'Ч, B.37)
и аналогично для тензоров более высокого «ранга» (см.
упр, 2.9 ниже). Мы видим, что компоненты векторов и базис-
базисные один-формы преобразуются по одному и тому же за-
закону, который противоположен (т. е. использует обратную
матрицу) закону, по которому преобразуются компоненты
один-форм и базисные векторы. Это и понятно, так как сум-
суммы вида Vlei, VI б] и т. д. не должны зависеть от базиса. Это
демонстрирует ещё одно преимущество наших правил рас-
расположения индексов и нашего правила суммирования: рас-
расположение индексов автоматически определяет закон преоб-
преобразования. Например, V' и б' подчиняются одному закону
преобразования, а именно
Матрицу А'/г здесь не поставишь, так как суммирование
должно вестись по нештрихованному индексу, который дол-
должен появляться один раз вверху и один раз внизу.
Эти взаимно противоположные законы преобразования в
более старой литературе именуются «контравариантными» и
«ковариантными». То, что мы называем просто векторами,
раньше называли «контравариантными векторами», посколь-
поскольку закон преобразования их компонент противоположен
(«контра»!) закону преобразования базисных векторов. Ана-

2.26. ЗАМЕНА БАЗИСА 83
логично один-формы назывались «ковариантными вектора-
векторами», поскольку их компоненты преобразуются так же, как
базисные векторы. При современном изложении подчёркивает-
подчёркивается тот факт, что ни векторы, ни один-формы не меняются при
замене базиса; это геометрические объекты, не зависящие от
выбора системы координат. Итак, ог использования старых
названий в современной терминологии отказались потому, что
в них делается чрезмерно сильный акцент на описаниях, за-
зависящих от выбора системы координат.
Упражнение 2.9. Покажите, что у произвольного тензора
типа ( „ J компоненты преобразуются так же, как у тен-
тензорного произведения двух векторов, т. е.
p'ir = At\Al'iTla. B.38)
Обобщите эту формулу на случай тензоров типа ( N, J.
Упражнение 2.10. Покажите, что если у тензора все ком-
компоненты в некотором базисе равны нулю, то они равны
нулю и в любом другом базисе (такой тензор является ну-
нулевой линейной функцией (см. § 2.22) и, естественно, назы-
называется нулевым). (Отсюда вытекает, что если компоненты
двух тензоров в некотором базисе совпадают, то эти тен-
тензоры равны.)
Упражнение 2.11. Для данного базиса {et} векторного
n-мерного пространства рассмотрим совокупность чисел
{A'i, i, j= 1, ..., ti). Для любого другого базиса {?/'},
связанного с исходным матрицей перехода Л'// построим
совокупность чисел вида А1'к- = Ai'iAlk'Ali. Докажите, что
существует тензор А , компоненты которого в базисе
(ё.Л равны А1\'. Из сказанного вытекает, что можно счи-
считать тензор просто набором, чисел Aljy преобразующихся
по определённому закону. Это другая форма того опре-
определения, которым мы пользуемся.
Особенно интересно рассмотреть эти преобразования ба-
базисов для случая, когда они происходят из координатных
"преобразований, о которых упоминалось в конце § 2.6. Пусть
в области U многообразия М задана координатная система
{xl, i=l, ..., п}; введём новые функции {у1', if=\, ..., п},
задаваемые формулами
/ = /'' (*', .... хп), i' = 1, ..., п, B.39)
или, кратко, yi' = ft'(xl). Эти формулы задают преобразова-
преобразование координат, если определитель матрицы Якоби дуг/дх> не

84 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
обращается в нуль в U. Данную точку Р е V можно описать
двумя различными совокупностями чисел: {*'} или {у1'}.
Равным образом в точке Р имеются два различных коорди-
координатных базиса: {д/дх1} и {д/ду1'}. В силу цепного правила,
ду1 ду1 дх1
Сравнивая с B.32), заключаем, что
Л7 = -^. B.41)
ду1
Аналогично, обратная матрица имеет вид *
как легко проверить, используя цепное правило для частных
производных:
дх1 ду'' дх1 .j
ду1' дхк ~~ дхк ~ к'
Важно уяснить, что B.42) охватывает лишь некоторый
специальный класс полей преобразований Ак') в U. В каж-
каждой отдельной точке Р из U можно произвольно выбрать все
п2 элементов Ak't (лишь бы не обращался в нуль определи-
определитель), но этого нельзя сделать в целой окрестности точки Р,
поскольку из B.42) вытекает, что
дАк',1дх1 = дАк\/дх', B.43)
а это равенство вовсе не обязано выполняться для произ-
произвольного поля Ак'j. Это — новая иллюстрация того, что не
каждый набор базисных векторных полей является коорди-
координатным.
2.27. ТЕНЗОРНЫЕ ОПЕРАЦИИ НАД КОМПОНЕНТАМИ
Пусть тензор Т в некотором базисе имеет компоненты
Т'•••/...}• Умножив эти компоненты на число а, получим
аТ1 •/...}. Ясно, что это — компоненты тензора йТ; отсюда
вытекает, что операция умножения всех компонент Т на а
инвариантна относительно замены базиса: начни мы вычис-
вычислять в других координатах {у1}, мы всё равно получили бы
компоненты тензора а Т в этих новых координатах. (Если бы
мы умножили на а лишь некоторые из компонент {Т'•••/...}.
то указанная инвариантность уже не имела бы места.) Таким
образом, операция {"Р •••/...} >—>{а"Р "•/...} в точности соот-

228. ФУНКЦИИ И СКАЛЯРЫ 85
ветствует инвариантной относительно выбора базиса опера-
операции Т *~>а Т. Аналогично операции взятия тензорного про-
произведения двух тензоров
А, В
отвечает однозначно определённая» операция над компонен-
компонентами (см. упр. 2.4.)
(независимо от того, является ли используемый базис коор-
д. натным или некоординатным). Более общо, операция над
компонентами, дающая компоненты одного и того же тен-
тензора, независимо от выбора базиса, называется тензорной
операцией; далее мы будем иметь дело только с такими опе-
операциями. Приведём список алгебраических тензорных опера-
операций (дифференциальные тензорные операции мы рассмотрим
попозже):
(i) сложение (и вычитание) компонент тензоров одина-
одинакового типа;
(и) умножение всех компонент тензора на данное число
(даёт тензор того же типа);
(in) умножение компонент двух тензоров (даёт тензор,
тип которого является «суммой» типов сомножите-
сомножителей);
(iv) свёртка по паре индексов, один из которых верхний,
а другой — нижний.
Уравнения (равенства), в которых тензорные компоненты
комбинируются только при помощи этих операций, назы-
называются тензорными уравнениями (равенствами). Из упр. 2.10
вытекает, что если в результате некоторой последователь-
последовательности тензорной операции над компонентами в некотором
базисе мы получили тензорное равенство, то это равенство
будет уместно и во всех других базисах. Ввиду этого базис
обычно выбирают из соображений удобства вычислений.
2.28. ФУНКЦИИ И СКАЛЯРЫ
Скаляры — это тензоры типа ( 0 ). т. е. функции на мно-
многообразии, определение которых инвариантно относительно
выбора базиса. Например, свёртка Vla>i — скаляр, поскольку
её значение не зависит от выбора базиса, в котором произво-
производится вычисление. Наоборот, хотя компонента V также яв-
является функцией на многообразии, у которой в каждой точке
определено численное значение, она — не скаляр, поскольку
это значение зависит от выбора базиса. Иначе говоря, суще-

86 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
ствует некоторая (скалярная) функция f(P), такая что
Vl(P) = f(P), где первая компонента (индекс 1) взята по от-
отношению к некоторому заданному базису; если выбрать дру-
другой базис, то новая Vl(P) не будет равняться f(P). Таким
образом, f(P) есть скаляр, значение которого случайно ока-
оказалось равным первой компоненте поля V в некотором ба-
базисе. Но сама эта первая компонента V1 не является скаля-
скаляром, поскольку её значения зависят от выбора базиса. Итак,
мы видим, что вопрос о том, является данная величина ска-
скаляром или же просто функцией, зависит от её интерпретации
в смысле поведения при замене базиса, а не от её численных
значений.
4
2.29. МЕТРИЧЕСКИЙ ТЕНЗОР
В ВЕКТОРНОМ ПРОСТРАНСТВЕ
Наиболее часто в векторной алгебре рассматривается ска-
скалярное произведение между векторами (см. § 1.5). Это —
правило, сопоставляющее число паре векторов. Это число ли-
линейно зависит от каждого из векторов. Значит, это есть тен-
тензор типа ( 2 1; его называют метрическим, тензором и обо-
обозначают через д. Итак, мы полагаем по определению
q(V,U) = q(U,V)b=O-V. B.44)
Первое из этих равенств выражает требование, чтобы вели-
величина U-V не зависела от порядка сомножителей О и V. Дру-
Другими словами, g— симметрический тензор. Его компоненты
в базисе {*?,} имеют вид
Qii = Q{ei,e,) = el-ei. B.45)
Эти компоненты образуют симметричную матрицу размера
п X п. По причинам, которые будут объяснены ниже, мы тре-
требуем также, чтобы матрица была обратимой. Если окажется,
что эта матрица единичная, т. е.
ёи = &л
то метрический тензор называется эвклидовой метрикой, а
векторное пространство — эвклидовым пространством. А как
быть, если gt/ не имеет такого простого вида? Всегда можно
попытаться выбрать новый базис {ё{}, в котором новые ком-
компоненты
gtr = A\,Alrgkl B.46)
принимают наиболее простой вид. Рассмотрим это соотноше-
соотношение как матричное уравнение. А именно перепишем его в виде

2 29. МЕТРИЧЕСКИЙ ТЕНЗОР В ВЕКТОРНОМ ПРОСТРАНСТВЕ gy
Из результатов § 1.6 ясно, что это — матричное уравнение
g> = Л^Л, B.47)
где Лт — матрица, транспонированная к матрице A = (Akt'),
Покажем, что если с умом выбрать матрицу Л, то матрицу
g' можно привести к весьма простому виду. Возьмём Л в виде
Л = OD, B.48)
где О — ортогональная матрица (ОТ = О~'), a D — диаго-
диагональная матрица (так что, в частности, DT — D). Из A.41)
вытекает, что
Лт = (OD)T = DTOT =
B.49)
Хорошо известно, что любую симметричную матрицу, и в
частности g, можно привести к диагональному виду ga пре-
преобразованием подобия, осуществляемым при помощи орто-
ортогональной матрицы; вот и возьмём в качестве О такую орто-
ортогональную матрицу:
gd = O-lgO,
g' = DguD.
Если gd = diag(gi, ..., gn) и наша пока ещё не определён-
определённая матрица D равна diag(di, ..., dn), то
g' = diag (gld\, g2d% ..., gndl). B.50)
Положим теперь d, = (|g;|)~I/2, так что каждый элемент диа-
диагональной матрицы g' равен +1 или —1. При помощи d/
можно изменять лишь величины диагональных элементов gj,
но не их знаки. Далее, диагональные элементы матрицы ga
являются собственными числами матрицы g и определены
однозначно с точностью до порядка. Более того, поскольку
матрица g обратима, ни одно из этих собственных чисел не
равно нулю. Если выбрать матрицу О так, чтобы сначала
шли отрицательные собственные значения, то мы приходим к
следующей теореме: любое векторное пространство с метри-
метрическим тензором обладает базисом, в котором этот тензор
представляется в каноническом виде diag(—1, ..., —1,
1, ..., 1). Такой базис называется ортонормированным. Сум-
Сумма этих диагональных элементов — след матрицы канониче-
канонического представления — называется сигнатурой метрики.
Упражнение 2.12. Найдите матрицы Л, приводящие сле-
следующие матрицы к диагональной форме:
2 1\ /0 1\ /4 0\
> <b4 > «Но -1>

88 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
Доказанная теорема очень важна. Из неё вытекает, что
имеется лишь весьма малое число различных типов метри-
метрических тензоров в данном векторном пространстве. Если мет-
метрика положительно-определённа, то в её канонической форме
всюду стоят +1 и пространство является эвклидовым. Если
метрика отрицательно-определённа, то она тоже называется
эвклидовой, так как существенно важно лишь то, одинаковы
все знаки или нет. Если не все знаки одинаковы, то метрика
называется индефинитной. Важный пример — каноническая
форма (—1, 1, ..., 1); такая метрика называется обычно
метрикой Минковского; такова метрика пространства специ-
специальной теории относительности (размерности п — 4), кото-
которое мы вскоре рассмотрим более подробно. ,
Ещё одно следствие теоремы о приведении к канониче-
каноническому виду — выделение одного привилегированного класса
базисов, векторного пространства, а именно класса ортонор-
мированных базисов. В эвклидовом пространстве Е" такие
базисы называют декартовыми. В таком базисе метрический
тензор имеет компоненты gij = б,/, или, в матричном виде,
g =/. Матрица преобразования Лс от одного такого базиса
к другому такому же :) удовлетворяет соотношению
/=--Лс/Лс, или Лс = Лс'. B.51)
Таким образом, преобразования между декартовыми бази-
базисами задаются ортогональными матрицами. Эти матрицы об-
образуют группу (произведение двух ортогональных матриц ор-
ортогонально), называемую ортогональной группой и обозна-
обозначаемую через О(п).
Аналогичным образом в пространстве с метрикой Минков-
Минковского выделены псевдоэвклидовы (или лоренцевы) базисы,
в которых компоненты метрики образуют матрицу вида
l,l, .... 1). B.52)
Матрица перехода Al от одного псевдоэвклидова базиса к
другому 2) удовлетворяет соотношению
¦n = AbiAL. B.53)
Такие преобразования называются преобразованиями Лорен-
Лоренца. Нетрудно показать, что они также образуют группу, на-
называемую группой Лоренца и обозначаемую L(n) или
О(п-1,1).
С точки зрения тензорной алгебры наиболее важная роль
метрических тензоров, о которой мы ещё не упоминали,—
это то, что они устанавливают взаимно-однозначное соответ-
11 Индекс С —от Cartesian (декартов). — Прим. ред.
г> Индекс L — от ^orentz. — Прим. ред.

2 29 МЕТРИЧЕСКИЙ ТЕНЗОР В ВЕКТОРНОМ ПРОСТРАНСТВЕ 89
ствие между векторами и один-формами Фиксируем какой-
нибудь вектор V Тогда g (F, ) является при этом фиксиро-
фиксированном V вещественнозначной линейной функцией от векто-
векторов, т. е. один-формой. Обозначим её через V:
V = q(V, ). B.54)
Невырожденность матрицы g4, которую мы потребовали
выше, гарантирует взаимную однозначность этого отображе-
отображения: имеется только один вектор V, который переходит в V.
Чтобы убедиться в этом, запишем последнее равенство в
компонентах Обозначим компоненты V через F,. Тогда
,, et)
= VlQ(el, et) = V'g,t=g4V'
(последнее равенство вытекает из симметричности д). Обо-
Обозначим через g4 матрицу, обратную к gtl:
¦ g"g,k = 6«ft. B.55)
Имеем
^lVt = gktgtlV' = 6klV' = Vk, B.56)
откуда и вытекает обратимость отображения V*—>V. Итак,
метрика позволяет однозначно отождествить векторы с один-
формами Соответствие между «отождествляемыми» вектором
и один-формой выражается так
¦ Vl = g.lV, B 57)
ф Vi = gi*Vk. B 58)
Обратим внимание на следующее обстоятельство То что мы
обозначили элементы обратной матрицы через g1', позволило
нам записать тензорное равенство B 58), следуя обычным
правилам суммирования Но для полноты следует показать,
что величины gl> действительно образуют компоненты тензо-
тензора типа ( 0) • Это и составляет содержание следующего
упражнения
Упражнение 2.13. (а) Покажите, что {g4} суть компоненты
некоторого тензора д типа ( 0 )> — либо удостоверившись,
что они преобразуются должным образом при замене ба-
базиса, либо установив, что они определяют билинейную
функцию на один-формах.
(Ь) Покажите, что если базис векторов {е,} ортонорми-
рован, то и дуальный базис один-форм {&'} тоже ортонор
мирован, в том смысле, что -Q~l (©', й') = бу

§0 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
Аналогично с помощью метрики можно превратить любой
тензор А типа f J в тензор типа Г , ) :
B.59)
Этот тензор в свою очередь можно превратить в тензор типа
(IY
(IY-
Ац = ginAml = glmgibA"*, B.60)
а от него вернуться к исходному тензору
A«' = gtlgkmAlm. /2.61)
Эти преобразования называются операциями поднятия и опу-
опускания индексов; принято обозначать все эти тензоры одной
й той же буквой (например, А), различая их между собой
только расположением индексов у компонент. В векторном
пространстве с метрикой иногда бывает неважно, имеет тен-
зор тип у N, ) , или [N, + j J , или (^ N, _ j J и т. д.; все
определяется в таком случае числом N + N', которое назы-
называется рангом тензора.
В эвклидовом пространстве в декартовом базисе gu = б,/,
так что g'>' — 8" и V' = Vi — между компонентами вектора и
ассоциированной с ним один-формы нет никакой разницы.
Именно этим объясняется то, почему в элементарных курсах
эвклидовой векторной алгебры не делается различия между
векторами и один-формами, а также то, почему в таких кур-
курсах ограничиваются ортонормированными базисами. Но в не-
ортонормированном базисе в эвклидовом пространстве и в
любом базисе в пространстве с индефинитной метрикой ком-
компоненты один-формы могут быть совсем отличными от ком-
компонент соответствующего вектора. Интересный пример такой
ситуации встретится нам в § 2.31, посвященном специальной
теории относительности.
2.30. ПОЛЕ МЕТРИЧЕСКОГО ТЕНЗОРА
НА МНОГООБРАЗИИ
Метрическое тензорное Поле g на многообразии — это сим-
симметрическое тензорное поле типа ( 2 ) ¦ обратимое в каждой
Точке. В каждой точке Р оно задает метрику в касательном
Пространстве ТР, для которой справедливы все свойства, об-
обсуждавшиеся в предыдущем параграфе. Но оно задаёт ещё
много сверх того.

2.30. ПОЛЕ МЕТРИЧЕСКОГО ТЕНЗОРА НА МНОГООБРАЗИИ 91
Выделение некоторого тензорного поля типа B/ на мно'
гообразии М в качестве его метрики снабжает М чрезвы-
чрезвычайно богатой структурой. Многообразие сразу же делается
«жёстким»; на нём становится возможным определить такие
понятия, как расстояние (см. ниже) и кривизна (см. гл. 6).
Эти понятия настолько важны для многих приложений, осо-
особенно для общей теории относительности, что всякий физик
почти наверняка знаком с такого рода геометрией. Но с точ-
точки зрения дифференциальной геометрии эти понятия яв-
являются структурами «более высокого уровня»: выделяя опре-
определённое тензорное поле на особое положение, мы выходим
за рамки «чистого» дифференцируемого многообразия. При
таком подходе можно проглядеть богатую геометрическую
структуру, которой обладает обычное многообразие. Такие
важные вещи, как производные Ли и дифференциальные
формы, не имеют никакого отношения к метрике. Соответ-
Соответственно мы будем стараться в этой книге всюду, где только
можно, обойтись без привлечения метрического тензора, даже
в приложениях к многообразиям, на которых он задан.
В этом параграфе мы лишь коротко рассмотрим его простей-
простейшие свойства, а более подробное изучение метрической гео-
геометрии отложим до гл. 6.
Метрический тензор может быть дифференцируемым
столько раз, сколько потребуется, но во всяком случае он
должен быть непрерывным. Отсюда следует, что его канони-
канонический вид должен быть всюду одинаков, поскольку он опре-
определяется целочисленными параметрами, которые не могут ме-
меняться непрерывно. Поэтому можно говорить о сигнатуре
поля д. Если допустить, что матрицу преобразования Л мож-
можно выбирать в каждой точке независимо, то можно перейти
от любого базиса векторных полей к глобально ортонормиро-
ванному базису, в котором компоненты g канонические. Но
такое преобразование Л не будет, вообще говоря, коорди-
координатным (т. е. не будет удовлетворять B.43)); на самом деле,
в общем случае нельзя найти координатный базис, являю-
являющийся также ортонормированным в некоторой открытой об-
области I) многообразия М (см. упр. 2.14). Очевидным исклю-
исключением является R", рассматриваемое как многообразие с
эвклидовой метрикой 6ц в каждой точке. Но даже и в этом
случае только декартовы координаты задают ортонормиро-
ванный базис. Соответствующий пример был дан в упр. 2.1,
где были рассмотрены полярные координаты в R2. Коорди-
Координатный базис ортогонален, но не нормирован. А если его нор-
нормировать, то он перестаёт быть координатным.
Упражнение 2.14. Покажите, что всякое метрическое тен-
тензорное поле g класса С°° является локально-плоским, в

92 2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
том смысле, что в некоторой окрестности любой точки
Р существует система координат, в которой компоненты
g,i обладают следующими свойствами:
(i) gi,(P)— ±8ij (ортонормированность в точке Р):
дх
жении вблизи Р);
(ш)
О (ортонормированность в первом прибли-
необязательно все равны нулю (система
дхк дх1
координат, вообще говоря, не является подлинно ортонор-
мированной).
Упражнение 2.15. Пусть на эвклидовой плоскости заданы
полярные координаты. Найдите компоненты метри'ки
(a) в базисе {д/дг, д/дв};
(b) в базисе г, 0 из упр. 2.1; выразите г, 0 через д/дг
и д/дв.
Упражнение 2.16. Найдите компоненты один-формы d/ и
соответствующего ей вектора df в обоих базисах из
упр. 2.15.
Здесь следует сделать одно предостережение. В большин-
большинстве руководств, где излагается векторное исчисление в кри-
криволинейных координатах в эвклидовом пространстве, исполь-
используются компоненты векторов в таких вот ортонормированных
(но, вообще говоря, не координатных) базисах. Это позво-
позволяет не делать различия между векторами и один-формами.
Но при сравнении выражений, которые мы получим ниже
для, скажем, дивергенции векторного поля через его компо-
компоненты, с выражениями, приводимыми в других руководствах,
следует иметь в виду возможное различие базисов.
Важным свойством метрики является то, что с её по-
помощью можно определить понятие длины на многообразии.
Если 17 = dx/d^ — касательный вектор к данной кривой, то
перемещению dk отвечает квадрат длины
= V ¦ V(dkJ = q (V, V) d^2 B.62)
(Здесь d — символ бесконечно малой величины, а не гра-
градиента.) Если метрика положительно-определённа, то
g (V, V) > 0 для всех V ф 0. В этом случае АР положительно,
и мы имеем для элемента длины кривой выражение
V)fl2dK. B.63)
Однако в случае индефинитной метрики квадрат длины уже
не имеет определённого знака. Кривые могут иметь как поло-

2.31. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ 93
жительное d/2 ("пространственно-подобные" кривые), так и
отрицательное ("времени-подобные"). В таком случае можно
считать вещественное число
d/ = |g(F, F)|1/2dA B.64)
"собственной длиной" для пространственно-подобных кривых
и "собственным временем" для времени-подобных. Эта вели-
величина равна нулю для "нулевых" кривых. При работе с инде-
индефинитной метрикой нужно следить за тем, чтобы не спутать
вектор с нулевой длиной с вектором, равным нулю {имеющим
нулевые компоненты).
2.31. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
Одним из важнейших для физики многообразий является
векторное пространство R4, снабжённое метрикой сигнатуры
+2 и рассматриваемое как многообразие; это — простран-
пространство Минковского, пространство-время специальной теории
относительности. В элементарных руководствах по специаль-
специальной теории относительности часто не вводят явно метриче-
метрический тензор, но в них содержится всё необходимое для того,
чтобы его ввести. В частности, мы знаем, что имеется приви-
привилегированное семейство систем координат в пространстве-
времени, называемых лоренцевыми системами отсчета, и что
если два события разделены координатным интервалом
(At, Ах, Ay, Az) в такой системе отсчёта, то величина
AS2 _ _С2(Д/J + {АхJ + (АуJ + (ДгJ B.65)
не зависит от выбора лоренцевой системы отсчёта. (Здесь
с — скорость света.) Изменим масштабы по осям координат,
полагая хР = ct, х1 = х, х2 = у, х3 = z. (В теории относитель-
относительности общепринято нумеровать координаты, начиная с 0, а не
с единицы.) Условимся также использовать для простран-
пространственно-временных индексов греческие буквы. Это поможет
нам отличать выкладки, относящиеся только к теории отно-
относительности, от более общих. Тогда равенство B.65) пере-
перепишется в виде
As2 = — (Дх0J + (Ax^A-f (Д*2JН- (А*3),2 = ЧвВДж«ДжР, B.66)
где т]ар — матрица вида
Пар = diag(—1,1,1,1). B.67)
Мы будем считать величину B.66) псевдонормой (§ 1.5) век-
вектора Ах с компонентами (Ах°, Ах1, Ах2, Ах3). Легко видеть,что
®та псевдонорма удовлетворяет аксиомам (Nii) и (Niv) из

94 2 ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ
§ 1.5 и, значит, ей отвечает скалярное произведение. Послед-
Последнее, очевидно, имеет вид
V-W = rto#V*W*, B.68)
так что фактически г]ар есть метрический тензор, записанный
в каноническом виде, а лоренцева система отсчёта есть соот-
соответствующий ортонормированный базис.
На примере этой метрики легко проиллюстрировать раз-
различие между компонентами вектора и ассоциированной с ним
один-формы. В лоренцевой системе отсчета
Uo = 4oaUa = —U°, B.69a)
0х = Vх, Uy = U», Uz = U*. r B.69b)
Рассмотрим вектор-градиент функции / — вектор, ассоцииро-
ассоциированный с один-формой d/. Градиент 3/ имеет компоненты
(df/dx°,df/dx\ ...), а вектор-градиент d/— компоненты
(—д[/дх°, df/дх1, ...). Во многих руководствах по специ-
специальной теории относительности градиент вводится как век-
векторный оператор с компонентами (—д/дх°, д/дх1, ...). Появ-
Появление неестественного знака «минус» объясняется именно
тем, что градиент в действительности является один-формой.
Многообразие М с метрикой g называется пространством
Минковского, лишь если в нём существует глобальная си-
система координат (покрывающая всё М), в которой компо-
компоненты g равны т]ар. С этой системой координат особенно
удобно работать, но она не является единственно возможной
для М. С тем же успехом можно рассматривать и другие си-
системы координат, например связанные с ускоряющимся на-
наблюдателем. Если следовать общим правилам дифференци-
дифференциальной геометрии, то при этом будут получаться физически
верные результаты.
2.32. БИБЛИОГРАФИЯ
По поводу более аккуратного н строгого обсуждения того, что пони-
понимается под многообразием, и в особенности по поводу важного понятия
расслоенного пространства, см. Y. Choquet-Bruhat, С. DeWitt-Morette &
М. Dillard-Bleick, Analysis, Manifolds, and Physics (North-Holland, Amster
dam, 1977). По поводу доказательства теоремы о неподвижной точке, ис-
использующего теорию когомологий, см. М. Spivak, A Comprehensive Intro-
Introduction to Differential Geometry (Publish or Perish, Boston, 1970), vol. 1,
pp. 8—54 (после прочтения § 4.24 ниже!). Касательное расслоение и свя-
связанные с ним структуры обсуждаются также в книгах: R. Hermann, Vector
Bundles in Mathematical Physics, two volumes (Benjamin, Reading, Mass.,
1970); R. Abraham & J. E. Marsden, Foundations of Mechanics, 2nd ed.
(Benjamin/Cummings, Reading, Mass., 1978). Обсуждение расслоенных про-
пространств в контексте современных исследований по квантовой теории поля
и гравитации можно найти в статье В. Carter, Underlying mathematical
Structure q{ classical gravitation theory, in: Recent Developments in Qra,vi-

2 32 БИБЛИОГРАФИЯ 95
tation, ed M Levy & S Deser (Plenum, New York, 1979) См также статью
A Trautman, Rep Math Phys, 10, 297 A976)
Функциональные пространства рассматриваются в Choquet-Bruhat et
al, а также во многих других руководствах по функциональному анализу,
например в книге F Riesz & В Sz-Nagy, Functional Analysis (Ungar, New
York, 1955) [имеется перевод Секефальви-Надь Б, Рисе Ф Лекции по
функциональному анализу - М Мир, 1979] Теория обобщённых функций
(дельта-функция Дирака и пр ) разбирается в книгах Choquet Bruhat et
al A977), G Friedlander, The Wave Equation on a Curved Space Time
(Cambridge Unicersity Press, 1976)
Результаты из матричной алгебры, используемые при приведении ме-
метрического тензора к каноническому виду, можно найти в книгах, указан-
указанных в гл 1 Хорошим справочником по векторному анализу в криволи-
криволинейных координатах в эвклидовом трехмерном пространстве может слу-
служить книга W Magnus & F Oberhettinger, Functions of Mathematical Phy-
Physics, ch 9 (Chelsea, New York, 1949) Метрическая структура многообра-
многообразия специальной теории относительности (пространства Минковского) опи-
описана на элементарном уровне в книге Е F Taylor & J A Wheeler, Space
time Physics (Freeman, San Francisco, 1963) Изложение этого вопроса,
принадлежащее самому Минковскому, см в The Principle of Relativity
edited and translated by W Perrett & G В Jeffrey (Dover, New York, 1924)
В качестве примера руководства, где градиенты в специальной теории от-
относительности обсуждаются без помощи один-форм, сошлемся на «Фейн-
мановские лекции по физике» (The Feynman Lectures on Physics, R P Fe-
ynman, R В Leighton & M Sands, vol 2, § 25 3 (Addison-Wesley, Reading,
Mass, 1950) [имеется перевод Фейнман Р , Лейтон Р , Сэндс М, Фейнма-
новские лекции по физике, вып 6 — М Мир, 1977]
Углы Эйлера и другие параметризации на группе вращений подробно
разобраны в книге Н Goldstein, Classical Mechanics (Addison-Wesley, Rea-
Reading, Mass, 1950) [имеется перевод Голдстейн Г Классическая меха-
механика 2-е изд —М Наука, 1975] Для изучающего предмет будет полез-
полезным сопоставить изложение Голдстейна с нашим анализом группы враще-
вращений в гл 3 ниже

3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
3.1. ВВЕДЕНИЕ: КАК ВЕКТОРНОЕ ПОЛЕ
ОТОБРАЖАЕТ МНОГООБРАЗИЕ В СЕБЯ
В предыдущей главе мы познакомились с системой индекс-
индексных обозначений. Эта система нужна для решения числен-
численных задач, но довольно часто она мешает раскрытию глубо-
глубоких геометрических идей, составляющих существо дела. В са-
самом начале мы дали определения векторов и тензоров, неза-
независимые от выбора базиса, а теперь, сохраняя тот же стиль,
опишем один из наиболее полезных инструментов, используе-
используемых в геометрии, — производную
Ли вдоль конгруэнции, опреде-
определяемой векторным полем.
Мы уже упоминали о понятии
конгруэнции в § 2.12; это — мно-
множество попарно непересающихся
кривых, заполняющих многообра-
многообразие или некоторую его часть. Каж-
Каждая точка из рассматриваемой
области многообразия М принад-
принадлежит одной и только одной кри-
кривой. Поскольку каждая кривая яв-
является одномерным множеством
точек, множество кривых, обра-
образующих конгруэнцию, имеет раз-
размерность п—1. (При соответ-
соответствующей параметризации это
множество кривых само ста-
становится многообразием.) Ключевым фактом, определяющим
все последующие результаты, является то, что конгруэнция
задаёт некоторое естественное отображение многообразия
в себя. Если параметр на кривых обозначить через Я, то вся-
всякое достаточно. малое число ДЯ будет определять отображе-
отображение, которое каждую точку переводит в точку той же кривой
на «расстоянии» ДЯ от неё (см. рис. 3.1). Это отображение
взаимно-однозначно, по крайней мере в области, где вектор-
векторное поле ведёт себя достаточно хорошо (хватает гладкости
класса С1). Если векторное поле — класса С00, то мы полу-
получаем диффеоморфизм (см. § 2.4). В случае когда такое ото-
отображение существует для всех ДЯ, мы получаем одномерное
Рис. 3.1. Отображение Много-
Многообразия М в себя, переводящее
каждую точку в точку той же
кривой данной конгруэнции,
отвечающую значению пара-
параметра, которое на некоторое
фиксированное число ДА боль-
больше значения параметра в ис-
исходной точке.

3 3 ЛЕПСТВНГ ПЕРЕНОС! ЛИ II \ ВЕКТОРНЫЕ ПОЛЯ 97
дифференцируемое семейство таких отображений (факти-
(фактически — однопараметрнческую группу Ли с законом компо-
композиции АА1 + АА,2). Такое отображение мы будем называть
переносом 1) вдоль конгруэнции или переносом Ли (ли-пере-
носом).
3.2. ДЕЙСТВИЕ ПЕРЕНОСА ЛИ НА ФУНКЦИИ
Пусть / — некоторая функция на многообразии. В резуль-
результате переноса вдоль конгруэнции на Да функции / очевид-
очевидным образом ставится в соответствие новая функция /*^:
если точка Р некоторой кривой (см. рис. 3.1) переходит в
точку Q той же кривой на параметрическом расстоянии АК
от Р, то значение новой функции f*AX в точке Q равно значе-
значению / в точке Р:
¦
(Здесь звёздочка в обозначении функции f^k означает просто
«новая».) Если случится так, что для каждой точки Q значе-
значение f\A (Q) окажется равным f(Q)—старому значению в точ-
точке Q, т. е.
f = F&v
то мы говорим, что функция f инвариантна относительно пе-
переноса Ли на AL Если функция инвариантна для всех Ал, то
говорят, что она является ли-тчнутой 2). Ясно, что всякая ли-
тянутая функция / должна быть постоянной вдоль любой
кривой данной конгруэнции, т. е. df/dh = 0.
3.3. ДЕЙСТВИЕ ПЕРЕНОСА ЛИ НА ВЕКТОРНЫЕ ПОЛЯ
Прежде чем говорить о действии описанного выше отобра-
отображения переноса Ли на векторные поля, напомним, что всякое
векторное поле определяется конгруэнцией кривых, для кото-
которой оно является касательным полем. На рис. 3.2 показаны
две конгруэнции: одна, для поля d/ёл, порождает отображе-
отображение данного многообразия; это порождённое ею отображение
действует на другую конгруэнцию, определяющую произ-
произвольное поле d/d(a. Действие это очень простое: любая кри-
кривая ц-конгруэнции отображается в новую кривую, получае-
получаемую в результате переноса Ли точек первой кривой; значе-
значения параметра ц также переносятся в новые точки. Итак, мы
" В оригинале dragging (буквально: волочение). Иногда используют
также термин «увлечение». — Прим. ред.
2) В оригинале Lie dragged. — Прим. ред.

98
3. ПРОИЗВОДНЫЕ ЛИ и ГРУППЫ ЛИ
определили новую конгруэнцию с параметром [i\k. Эта но-
новая конгруэнция имеет касательное векторное поле d/dM-^x,
которое и называется образом векторного поля d/df.i при
рассматриваемом переносе Ли.
Вообще говоря, [i*hl- конгруэнция будет отлична от ц-конг-
руэнцин. Если эти конгруэнции одинаковы, то мы всюду
имеем d/djx*u = d/djj, и в таком случае говорим, что вектор-
векторное поле и конгруэнция инвариантны относительно нашего
(А)
Рис. 3.2. Как новое векторное поле d/dfi^ получается из старого поля
d/dji в результате переноса Ли его путей (интегральных кривых) и его
параметра ц. Кривые A) —D)—это кривые А-коигруэнции. Кривая
(.4) — это ц-кривая, проходящая через точку Р; в результате переноса
Ли па расстояние А>. она отображается в кривую (А'), проходящую через
точку Q. Кривая (В)—это ц-кривая исходной конгруэнции, также прохо-
проходящая через точку Q. Образ кривой (В), получаемый в результате пере-
переноса, не показан. Вообще (В) и (А') — различные кривые. Если же они
совпадают, то мы говорим, что ц-конгруэнцня является ли-тянутой.
отображения переноса Ли на ДА,. Если эти векторное поле
и конгруэнция инвариантны при всех АХ, то мы говорим, что
они ли-тянуты векторным полем d/dA.
Ли-тянутое векторное поле имеет простой геометрический
смысл, который поясняется на рис. 3.3. Ясно, что (в пределе
для бесконечно малого АХ и бесконечно малого расстояния
между кривыми B) и C)) если поле d/djx в точке Р «ведёт»
по кривой (Л) точно из точки Р в точку R, то d/d|J.^ ведёт
по кривой (А') точно из точки Q в точку S. В случае когда
d/dp, — ли-тянутое векторное поле, кривая (В) (см. рис. 3.2)
совпадает с кривой (А') и (d/dn*^)Q = (d/dn)Q а следователь-
следовательно, d/d[i также ведёт из Q в S. Вспоминая наше обсуждение
скобок Ли в § 2.14, заключаем, что [d/dX, d/dn]= 0: вектор-

3 4. ПРОИЗВОДНЫЕ ЛИ
99
ное поле является ли-тянутым, если его скобка Ли с полем,
осуществляющим перенос («тянущим» полем), обращается
в нуль:
[d/db, d/dn] = O. C.1)
(A1)—
Можно посмотреть на дело и иначе. Предположим, что на
рис. 3.3 нам задана не вся конгруэнция, а лишь единственная
кривая (А) с параметром ц. Тогда, выполняя перенос Ли
этой кривой для всех возможных f
значений ДА, можно породить всю
конгруэнцию. Одной из таких по-
порожденных кривых будет (А').
Обозначим порождённое таким
образом поле через d/d(.iL. В си-
силу построения вектор d/dX всегда
касателеп к кривой с фиксиро-
фиксированным значением j.il, а вектор
d/d^L — к кривой с фиксирован-
фиксированным значением L Отсюда сле-
следует, что эти векторные поля
должны коммутировать.
Рис. 3.3. Средняя часть рис. 3.2.
Кривая (В) не изображена.
К кривым (.4) и (.4') в точках
Р н Q соответственно проведе-
проведены касательные векторы.
3.4. ПРОИЗВОДНЫЕ ЛИ
Понятие переноса позволяет
дать определение производ-
производной вдоль конгруэнции. Любые попытки определить произ-
производные векторных и тензорных полей сопряжены с опреде-
определёнными трудностями. Предположим, мы хотим определить
производную векторного поля как предел разности между
векторами в различных точках, поделённой на расстояние ме-
между ними. Первая проблема — определить «расстояние» между
точками. Если заданные точки лежат на одной кривой конг-
конгруэнции, то расстояние между ними можно определить как
разность значений параметра в этих точках. (В результате
мы получим производную по параметру; в случае многообра-
многообразий без метрики на большее рассчитывать и не приходится.)
Вторая и более серьёзная проблема — как сравнивать век-
векторы в различных точках, т. е. как ответить на вопрос, будут
векторы в разных точках «параллельны» или нет. В случае
эвклидовой плоскости ответ на этот вопрос прост и однозна-
однозначен. Для искривлённой поверхности ответ уже может не быть
однозначным. В случае же произвольного дифференцируе-
дифференцируемого многообразия вопрос о параллельности векторов в раз-
различных точках вообще не имеет смысла, поскольку не суще-
существует правил, по которым можно было бы осуществлять па-
параллельное перенесение векторов. Чтобы определить «абсо-

100 3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
лютную» параллельность, многообразие следует наделить
ещё одной структурой, называемой аффинной связностью.
Это делается в гл. 6, посвященной римановой геометрии.
Здесь мы рассмотрим другую конструкцию, полезную при ре-
решении любой задачи, в которой центральную роль играет
конгруэнция. Конгруэнция сама даёт возможность ввести по-
понятие параллельности в различных точках. Для сравнения
векторов в точках а и а + А?^, принадлежащих некоторой
кривой, достаточно выполнить перенос Ли вектора в точке
а -+- Ал обратно в точку а. В результате в точке а получится
новый вектор, вычитая который из старого можно найти раз-
разность между ними. Заметим, что эта разность определена од-
однозначно, следовательно, заданная конгруэнция однозначно
определяет производную. Но эта производная зависит от
конгруэнции.
Выведем аналитические формулы для вычисления произ-
производной. Для начала рассмотрим скалярную функцию. Вычис-
Вычислим значение скаляра в точке Ао + Ал, перенесем его обратно
в точку до, вычтем из него значение скаляра в точке Ао, раз-
разделим эту разность на Да и перейдем к пределу при Да-»-0.
Более подробно, значение скалярного поля f в точке л0 + ДЯ
равно /(ао + Дл). В результате переноса этого значения мы
получим новое (ли-тянутое) поле f*, удовлетворяющее соот-
соотношению df*/dk — 0. Очевидно, его значение в точке Яо то
же самое, что и в точке ло + Дл: /*(а0) =/(ао +ДЯ). Следо-
Следовательно, определённая выше производная имеет вид
.. Г (Яр) - f (К) ._ ,,_ f (Яр + АЛ) - / (Ао) / df \ , >
lim дг — Нт дт =1 —г,-I . F.2)
Полученная формула для производной Ли функции f не
является, конечно, неожиданной. Для оператора взятия про-
производной Ли имеется специальное обозначение: ?,-$¦¦> здесь
V — векторное поле, порождающее отображение переноса
(в нашем случае поле d/d^), Мы доказали, что для функ-
функций
¦ ?vf = V<f) = dffdb. C.3)
Теперь проделаем то же для векторного поля О = d/df.i.
Поскольку вектор определяется своим действием на функции,
мы используем в дальнейших рассуждениях произвольную
функцию /. В точке Яо поле О даёт производную (df/di^,
а в точке Я + Дл — производную Ш/^\0+Ак- Перенося
О(К0 + ДЯ), как в конце § 3.3, мы получаем новое, ли-тянутое
поле V* = d/djj-*, удовлетворяющее соотношениям [С*, V] = 0
и О* (а0 + Дл) = О (л0 + Дл). Из обращения коммутатора в

3 4 ПРОИЗВОДНЫЕ ЛИ Ю1
нуль следует, что всюду
dA d|x* ' ~ d|x* dA '• FЛ)
Поэтому (для аналитических векторных полей)
Определим производную Ли ?yU как векторное поле, дей-
действие которого на / задаётся соотношением
[?-vU] (/) = lim о [ V{ко)-
C.5)
Ясно, что разность между [i* и ц — первого порядка но А?.;
отсюда следует, что для получения предела последнего выра-
выражения нужно просто заменить ц* на ц. Поскольку это равен-
равенство верно для всех f, мы имеем
¦ ?уп = -?¦ О - -А- V = [V. Щ. C.6)
Этот результат также является совершенно естественным.
Действительно согласно определению производной Ли вдоль
V, векторное поле имеет нулевую производную Ли, если оно
ли-тянуто, т е. если оно коммутирует с V. Поэтому можно
было с самого начала ожидать, что производная Ли одного
векторного поля вдоль другого совпадает с их коммутатором.
В силу антисимметрии скобки Ли мы получаем
?-vU = -?jjV. C.7)
Упражнение 3.1. (а) Покажите, что для произвольных
дважды дифференцируемых полей V и V выполняется (на
функциях и полях) тождество

102 3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
(Ь) Докажите тождество Якоби для производных Ли
на функциях и векторных полях
[[?*, ?у]> ?z]+[[?f?z}> ?x]+[[?z> ?-x]> ¦?*]=<>;
C.9)
здесь X, ?, Z — произвольные трижды дифференцируемые
векторные поля.
[Указание: для проверки утверждения (а) на векто-
векторах покажите, что C.8) равносильно B.14); для проверки
утверждения (Ь) на векторах воспользуйтесь равенством
C.8) и непосредственно вытекающим из определения про-
производной Ли соотношением ?-^ + ?-g = ?-j+jf. ]
Упражнение 3.2. (а) Докажите формулу Лейбница
?v W = (?уП v + !?гД, C.10)
используя определения производной Ли ?-^ на функциях
и векторных полях.
(Ь) Из B.7) следует, что компоненты ?yU в коорди-
координатном базисе имеют вид
^У = у'^^-^'~у1- B-7)
Используя утверждение (а), покажите, что для векторных
полей, заданных в произвольном базисе {ё,},
(?yUy = V'e, (?/') - V% {V1) + V'Uk(?e-.ekI, C.11)
где ej(Ui)— производная функции U' вдоль векторного по-
поля Cj.
Упражнение 3.3. Рассмотрим систему координат, для ко-
которой V является одним из векторов координатного ба-
базиса, скажем д/дх1. Покажите, что для любого векторного
поля W выполняется соотношение
¦ (?T.wy^dW{/dx\ C.12)
т. е. определение производной Ли — это бескоординатная
форма определения частной производной.
3.6. ПРОИЗВОДНАЯ ЛИ ОДИН-ФОРМЫ
Поскольку поля один-форм и тензоров более высокого
ранга определяются через векторные поля и скалярные функ-
функции, можно из уже данных определений производной Ли для
векторов и скаляров получить определение производной Ли
для один-форм. Идея определения та же самая. Скажем, что
поле один-форм ли-тянуто, если erg значение на любом ли-

.4 6 ПОДМНОГООБРАЗИЯ ЮЗ
тянутом векторном поле постоянно •>. Чтобы найти производ-
производную Ли, переносим2) один-форму из точки Ко + АК обратно
в точку Ко, затем вычитаем один-форму в этой точке и т. д.
В результате мы получим, что если й — поле один-форм, то
?у-(Ь — производная Ли от й вдоль V — есть поле один-
форм, определяемое следующим правилом (правилом Лейб-
Лейбница для производных первого порядка):
?v Iй W)] = (?у&) (W) + й (?^W) C.13)
для произвольного векторного поля W. Поскольку й(W) —
просто функция, производная ?у& определена через уже
известные нам операции — через производные Ли от функций
и векторных полей.
Упражнение 3.4. Пользуясь формулой C.13) и соотношением
B.7) для компонент поля ?^W — [V, W], покажите, что
?-у5> имеет в координатном базисе компоненты, равные
т^)с = V -~г «' + */ -Ь yi- C-х 4>
Естественное обобщение формулы C.13) на тензоры более
высокого ранга приводит к следующим свойствам производ-
производной Ли:
), C.15)
>, ...; U, ...)) = (<?-Д)(й, ...; U, ...)
Й, ...;f7, ...)+... +Т(Й, ...;?$, ...)+...,
C.16)
где А, В, Т— произвольные тензоры, а й, ... и О, ... — про-
произвольные один-формы и векторы соответственно.
3.6. ПОДМНОГООБРАЗИЯ
Подмногообразие многообразия М — это такое многооб-
многообразие, которое является гладким подмножеством в М. Если
М — обычное трёхмерное эвклидово пространство, то обыч-
обычные гладкие поверхности и кривые служат его подмногообра-
подмногообразиями. Для четырёхмерного пространства-времени Минков-
ского (§ 2.31) подмногообразиями будут, например, трёхмер-
трёхмерное пространство событий, происходящих с точки зрения не-
некоторого фиксированного наблюдателя одновременно с дан-
данным событием (т. е. множество точек с одинаковой времен-
1; Вдоль интегральных кривых «тянущего» поля. — Прим. ред.
2) При помощи ли-тянутого поля один-форм. — Прим. ред.

104
3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
ной координатой {), а также гиперболоид всех событий, от-
отстоящих на постоянный интервал As2 от заданного события.
Иногда вместо слова «подмногообразие» употребляют слово
«гиперповерхность», в иных же учебниках под гиперповерх-
гиперповерхностью понимают только такое многообразие, размерность
которого на единицу меньше размерности М.
Рис. 3.4. Изображены двумерное подмногообразие S трёхмерного многооб-
многообразия Л) и система координат в окрестности точки Р, удовлетворяющая
определению, данному в тексте. Координатная линия х! пересекает S
только в точке Р.
Хотя понятие подмногообразия довольно наглядно, слово
«гладкий», которое мы употребили выше, нуждается в уточ-
уточнении. В разных руководствах предлагаются разные (и не
эквивалентные) определения гладкости. Мы примем такое
определение, которое обеслечива-
ет наибольшую гладкость и более
всего отвечает нашему определе-
определению многообразия. Итак, т-мер-
ное подмногообразие S л-мерно-
Рис. 3.5. Кандидат в одномер- го многообразия М — это множе-
ные подмногообразия двумер- ство точек многообразия М, об-
обладающее следующим свойством:
в некоторой открытой окрестно-
окрестности в М произвольной точки Р
из 5 существует такая система
координат для М, в которой
точки S, лежащие в этой окрест-
сти, определяются соотношениями х1 == х2 — ... = хп~т = 0
(см. рис. 3.4). Одномерные подмногообразия — это кривые;
предъявляемые к ним требования гладкости иллюстрирует
рис. 3.5. Из данного выше определения очевидным образом
вытекает, что всякое подмногообразие S само является мно-
многообразием, ибо покрывается соответствующими координат-
координатными окрестностями (картами). В том частном случае, когда
т = п, всякое открытое подмножество многообразия М бу-
будет его подмногообразием.
Наш интерес к подмногообразиям объясняется главным
образом тем, что решения дифференциальных уравнений,
записываемые обычно в виде {</, = /,(х1, ..., хт), t ==
1, ..., р), можно представлять себе как подмногообразия
иого многообразия, который не
проходит, так как пересекает
сам себя в точке Р. В этой точ-
точке нельзя построить требуемые
координаты. Таким образом, не
все, а лишь некоторые кривые
являются подмногообразиями.

3 7. ТЕОРЕМА ФРОБЕНИУСА НА ЯЗЫКЕ ВЕКТОРНЫХ ПОЛЕП Ю5
с координатами {х\ .... хт) некоторого большего многооб-
многообразия с координатами {уи ..., ур, х\ ..., х'п}. Однако изу-
изучение подмногообразий мы начнём в ином аспекте, и лишь
в гл. 4 увяжем его с дифференциальными уравнениями.
Пусть Р — точка подмногообразия S (размерности т)
многообразия М (размерности п). Всякая кривая в S, про'-
ходящая через точку Р, будет также кривой в М, проходя-
проходящей через Р; отсюда очевидным образом следует, что каса-
касательный вектор к такой кривой в точке Р является элемен-
элементом как пространства ТР, касательного к М в точке Р, так и
пространства ]/р, касательного к S в точке Р. В действитель-
действительности VP есть векторное подпространство размерности m в Тр.
С другой стороны, произвольный вектор, принадлежащий ТР,
но не принадлежащий VP, не имеет однозначной «естествен-
«естественной» проекции на VP (напомним, что в общем случае понятие
ортогональности не вводится).
Для один-форм в точке Р ситуация в точности обратная.
Пусть Т*Р — сопряжённое к ТР пространство; это совокуп-
совокупность всех один-форм в точке Р, каковые суть функции, опре-
определённые на всём ТР. Аналогично пусть V*P — сопряжённое
к VP, т. е. пространство один-форм в точке Р, рассматривае-
рассматриваемой уже как точка многообразия 5. Произвольная один-фор-
один-форма нзГр определяет один-форму нз V*p, получаемую просто
ограничением со всего ТР на его подпространство VP. Наоби-
рот, данному элементу из V*P нельзя однозначно сипоставшь
элемент из ТР, ибо, зная лишь значения одни-формы на Vr,
вообще говоря, нельзя сказать, каковы будут сё значения на
векторах, не принадлежащих Vp.
Итак, вектор, определённый на подмногообразии S, будет
также вектором на многообразии М, а один-форма иа М бу-
будет также один-формой на 5. Обратные же утверждения не-
неверны. К один-формам и подмногообразиям мы вернёмся
в гл. 4, а пока сосредоточим внимание на векторных полях.
3.7. ТЕОРЕМА ФРОБЕНИУСА НА ЯЗЫКЕ ВЕКТОРНЫХ ПОЛЕЙ
В произвольной карте подмногообразия S имеются коор-
координаты {//", а—1, ..., т) и базис {д/дуа} векторных полей
на 5. Эти базисные поля коммутируют:
[д/ду°, д/дуь] = О. C.17)
Упражнение 3.5. (а) Покажите, что если V и W — линей-
линейные комбинации (необязательно с постоянными коэффи-
коэффициентами) т попарно_коммутирующих векторных полей,
то и скобка Ли V и W будет линейной комбинацией тех
же т полей.

106
3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
(Ь) Докажите тот же результат для случая, когда по-
попарные скобки Ли т векторных полей не обязательно ну-
нулевые, а являются линейными комбинациями этих же т
полей.
Из упр. 3.5 (а) следует, что скобка Ли двух произволь-
произвольных векторных полей на подмногообразии S касается того же
подмногообразия S, ибо эти поля являются линейными ком-
комбинациями коммутирующих полей {д/дуа}. Важный факт со-
состоит в том, что верно и обратное утверждение: если т век-
(а)
Рис. 3.6. (а) Слоение многообразия R3, образованное параллельными пло-
плоскостями. Каждая точка R3 принадлежит одной плоскости данного слое-
слоения. Показано только несколько таких плоскостей. (Ь) Слоение многооб-
многообразия FP, образованное концентрическими сферами. Центр этих сфер яв-
является особой точкой слоения.
торных полей класса С°°, определённых в некоторой области
U многообразия М, имеют попарные скобки Ли, являющиеся
линейными комбинациями этих же m векторных полей, то
интегральные кривые этих полей образуют некоторое семей-
семейство подмногообразий. Размерность, которую имеет каждое
такое подмногообразие, равна размерности векторного про-
пространства, натянутого на эти поля в произвольной точке, т.е.
самое большее пг, но может быть и меньше (этот случай рас-
рассматривается в § 3.9). Каждая точка области V принадлежит
одному и только одному такому подмногообразию, при усло-
условии что размерность векторного пространства, порождённого
полями, одна и та же всюду в U. Такое семейство подмно-
подмногообразий заполняет U во многих отношениях вполне анало-
аналогично тому, как это делает конгруэнция кривых (см. § 2.12),
и называется слоением области 0. Каждое подмногообразие
является листом этого слоения. Два примера слоений можно
увидеть на рис. 3.6.
Сформулированное утверждение носит название теоремы
Фробениуса. Доказательство этой теоремы вкратце излагает-
излагается в следующем параграфе, но основную идею легко понять
И так. Если интегральные кривые различных полей опреде-

3 8 ДОКАЗЛТГЛЬСТВО ТЕОРЕМЫ ФРОБЕПИУСЛ
107
ляют некоторое подмногообразие, они должны оставаться ка-
касательными к нему: ни одна кривая не может начать «выпя-
«выпячиваться», «вылезать» из него. Такое касание может быть
гарантировано в том случае, если все указанные скобки Ли
сами будут касательными к нему, поскольку каждая такая
скобка Ли — это просто производная одного из нацшх век-
векторных полей вдоль другого. Если ни одно из векторных по-
полей не имеет производной, торчащей из данной гиперповерх-
гиперповерхности, то ни одна интегральная кривая не покинет этой гп-
Рис. 3.7. В R3 векторное поле dx/dX = —sin X, dy/dl = cos Я, dzldl = 1
"поднимается" по спирали в вертикальном направлении '>, с радиусом спи-
спирали 1. (а) Это спиральное поле и базисное векторное поле, отвечающее
координате х, образуют семейство поверхностей, причём каждая точка
пространства R3 принадлежит одной из поверхностей семейства. Одна та-
такая поверхность представлена на рисунке; она выглядит как волнистая
(но не закрученная в спираль!) лента. На рисунке мы смотрим на неё
чуть сверху (если считать плоскость х, у горизонтальной) и видим неко-
некоторые участки одной стороны ленты (горизонтальные линии) и некоторые
участки другой её стороны (спиральные линии). (Ь) Два векторных поля,
не образующих подмногообразия: спиральное поле и базисное поле, отве-
отвечающее координате z. Ни для какой точки плоскость, определяемая двумя
этими полями в этой точке, не будет касаться "соседних" (сверху или
снизу) спиральных кривых.
перповерхности. На рис. 3.7 представлено несколько приме-
примеров. Когда мы займёмся изучением дифференциальных форм,
мы познакомимся с еще одним вариантом теоремы Фробе-
ннуса и увидим, что эта фундаментальная теорема даст ус-
условия существования решений систем дифференциальных
уравнений в частных производных («условия интегрируемо-
интегрируемости») .
3.8. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ ФРОБЕНИУСА
Пусть в некоторой открытой области V многообразия М
заданы т' векторных полей, которые в каждой точке Р этой
области порождают некоторое подпространство пространства
" Надо представить себе, что горизонтальная плоскость (скажем, пло-
плоскость х, у) совершает поступательное движение вверх по спирали. —
Прим. ред.

Ю8 ч прснпводныг ли и группы ли
ТР, имеющее размерность tn^m'. (Множество * всех таких
подпространств называется m-мерным распределением на М;
эти распределения не следует путать с распределениями типа
дельта-функции, рассмотренными нами в § 2.18.) По крайней
мере в некоторой окрестности U произвольной точки Р из V
можно выбрать т полей, образующих линейно-независимый
базис для всего нашего множества полей; эти поля {V^,),
а=\, ..., т} будут (согласно упр. 3.5 (Ь)) обладать в О
следующим свойством:
[V{a), Уф)] = Z aabcV(c). C.18)
с
Поэтому на самом деле нет необходимости рассматривать
случай, когда эти поля не являются линейно-независимыми:
такое множество всегда сводится локально к линейно-незави-
линейно-независимому множеству меньшей размерности. Размерность много-
многообразия М пусть будет п.
Когда имеется только одно векторное поле V (т. е. т = 1),
теорема тривиальна. Ясно, что если У(Р)фО, то в U суще-
существуют интегральные кривые, и каждая кривая является од-
одномерным многообразием, подмногообразием многообра-
многообразия М.
Для случая т $г 2 доказательство проводится по индук-
индукции. Прежде всего установим одно полезное соотношение, ко-
которое нам понадобится при проведении индукции. Исполь-
Используя C.14), легко показать, что для произвольной функции /
и произвольного векторного поля V выполняется соотношение
?v&) = u(?-vf). C.19)
Кроме того, из C.15) вытекает, что для произвольного век-
векторного поля W
?-v(Af, W) - (??df, W) + (d/, ?-vW). C.20)
Объединяя эти соотношения и учитывая тот факт, что
?yW = [V, W], получаем нужное нам соотношение
Ш, [V, Щ) = ?-v(Sf, W) - (й(?уГ), W). C.21)
Возвращаясь к основному доказательству, заметим прежде
всего, что если все т векторных полей коммутируют (имеют
попарные нулевые скобки Ли), то в соответствии с конструк-
конструкцией, описанной нами в § 2.15, они определяют систему коор-
координат для точек, принадлежащих их интегральным кривым,
т. е. определяют искомое семейство подмногообразий много-
многообразия М. Чтобы доказать существование этих подмногооб-
подмногообразий в общем случае (когда скобки Ли линейно выражают-

-4 8 ДОК\3\ТГЛЬГТВО ТГОРГ МЫ ФРОБЕППУС\ 109
ся через поля), мы построим т линейно-независимых линей-
линейных комбинаций исходных полей, которые уже будут комму-
коммутировать. Итак, предположим, что мы имеем т линейно-не-
линейно-независимых векторных полей F(O), скобки Ли которых линейно
выражаются через них же. Рассмотрим одно из них, скажем
поле Vim) = d/d/.,,,. Параметр К{т) вдоль конгруэнции поля
V(m) определён в каждой точке и, следовательно, является
функцией в области U многообразия Л/, которую мы рас-
рассматриваем. Коль скоро это функция, определён её 1радиент
dh(m). Воспользуемся им следующем образом. Определим
т — 1 векторных полей ,Y@), являющихся линейными комби-
комбинациями всех исходных полей F(o) и удовлетворяющих соот-
соотношениям
(dX(m), Х(а)) = 0, а = 1, . .., т - 1. C.22)
Эти соотношения определяют векторные поля {X(k)} с точ-
точностью до их линейных комбинаций. Далее (согласно
упр. 3.5 (Ь)), мы имеем
_ _ m-l _ _
гу VI \ ' (XVI I/ /О 00\
[Л/а), Л(Ь)\— i_j РаЬсЛ(с) ~Г \аЬУ (т)» \б,?о)
с=1
_ т—\
[У(,„), Х(а)]= X liabXlb) + VaVim), C.24)
где Раьс, уаь, Цаь и vo суть функции в области U. Свернём эти
соотношения с сИ{т) и используем формулы C.21), C.22) и
простое тождество ¦>
(m)V1() = 0. C.25)
После свёртки левые части C.23) и C.24) дадут нуль, и в
конечном итоге мы находим, что ус,ь = \'„ = 0. Отсюда сле-
следует, что скобки Ли полей ,?(A) не содержат поля Г(Ш). Имен-
Именно этого мы и хотели добиться, когда налагали условие
C.22).
Используем теперь предположение индукции, а именно что
произвольные т — 1 векторных полей, скобки Ли которых
линейно выражаются через них же, порождают семейство
(т — 1)-мерных подмногообразий. Поскольку {Х(а), а = \, ...,
т—1}—как раз такие поля, они порождают семейство
(т—1)-мерных подмногообразий, заполняющее U. Опреде-
Определим множество векторных полей {F(o), а=\, ..., т—1},
!) Ниже и в некоторых других местах книги автор использует знак
просто как замену слов «откуда следует, что». — Прим. ред.

ПО 3. ПРОИЗВОДНЫЕ ЛИ II ГРУППЫ ЛИ
образующих координатный базис для одного из этих подмно-
подмногообразий, скажем S', таким образом, чтобы эти поля ком-
коммутировали на S'. Продолжим их до полей {2{а), a= 1, ...,
т —1}_ (определённых и вне S') при помощи переноса Ли
вдоль v{m):
'
Z(a) = YfB) на S
[V(m), Zfa)] = О в U вдоль всякой интегральной
кривой поля 1/(т), пересекающей S'
при а = 1, ..., т — 1. C.26)
Доказав, что поля Z(o) попарно коммутируют всюду, а не
только на S', мы получим полный набор коммутирующих
полей {F(,n), 2{а), а— 1, ..., т—1}, и теорема будет дока-
доказана. Но сначала надо установить, что каждое поле 2(а) по-
прежнему будет линейной комбинацией полей F(a). Фактиче-
Фактически мы покажем, что оно является линейной комбинацией од-
одних полей Х{а), без V{m)- Поскольку каждое поле 2{а) опреде-
определяется однозначным образом, попробуем искать решения си-
системы C.26) в виде линейной комбинации
Z(ct) = Z-i aabX(b)-
b
Используя C.24) при vo = 0, получаем
«ь»ьсХм, C27)
Ь be
где все суммы берутся в пределах от 1 до т—1. Переобо-
Переобозначая в последней сумме индексы суммирования (Ь-*-с, а
с->6), приходим к равенству
0= E fdaob/dXm + E aaciich) Xb.
b \ с )
Поскольку Х(а) линейно-независимы, мы получаем систему
обыкновенных дифференциальных уравнений
acVcb = 0. C.28)
Начальные условия (на подмногообразии S') для величин
ааь, состоящие в том, что соответствующая линейная комби-
комбинация полей Х(Ь) даёт поле У(О), определяют единственное ре-

3.9. ПРИМЕР: ГЕНЕРАТОРЫ ВРАЩЕНИЙ 111
шение этой системы, которое всегда существует. Следова-
Следовательно, в каждой точке поля Z(o) являются линейными ком-
комбинациями полей Х{ау
И наконец заметим, что после переноса Ли наши поля
продолжают коммутировать:
[Zlah Z{b)] = О, а, Ъ = 1 т — 1. C.29)
Это можно доказать, используя тождество Якоби (упр. 2.3)
для полей V(m), Z(a) и Z(b). Итак, мы имеем т полей
{V(m), Z(a), a= 1, ..., т—1}, которые попарно коммутируют
п, следовательно, образуют координатный базис для некото-
некоторого подмногообразия размерности т. Поскольку исходные
поля {Р(о)} являются линейными комбинациями этих т по-
полей, теорема доказана.
3.9. ПРИМЕР: ГЕНЕРАТОРЫ ВРАЩЕНИИ
Читатели, знакомые с моментом импульса в квантовой ме-
механике, могли обнаружить, что обсуждавшиеся выше поня-
понятия им хорошо известны. Рассмотрим в сферических коорди-
координатах (ненормированный) базисный вектор, отвечающий ко-
координате ф; часто его обозначают через <зф:
ёч = —уёх + хёи,
где ёх и ё„ — векторы обычного декартова базиса в R3.
В наших обозначениях это соотношение запишется следую-
следующим образом:
<Э <Э . <Э
—— = — //——\- х-т-.
<Эф •' дх ' ду
Обозначим левую часть этого равенства—так называемый
«оператор момента импульса» в 2-направлении — через 4:
(От формулы, принятой в квантовой механике, наша фор-
формула отличается отсутствием множителя ti/i.) Аналогичным
образом можно определить h и 1У и вычислить коммутаторы
(скобки Ли)
[h, Jy] = -h,
[Ту, U = -Ь, C.30)
[h, Тх] = — Ту.
Следовательно, эти три вектора определяют некоторое под-
подмногообразие. Поскольку векторов три, может создаться впе-
впечатление, что это подмногообразие непременно трёхмерное,

112 3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
т. е. должно совпадать со всем пространством. В действитель-
действительности же это подмногообразие двумерно. В самом деле, если
положить г з= (х2 + у2 + г2I'2, то 1х(г)=1у{г) = Ъ(г) = 0.
Иначе это можно выразить так:
= o. C.31)
В силу нашего описания градиента йг как множества поверх-
поверхностей постоянного г и в силу описания его свёртки, скажем
с 1Х, как числа поверхностей, которые 1Х «протыкает», из
C.31) вытекает, что все три оператора ~1Х, ~1у и 7г касательны
в сфере г = const. Следовательно, в любой точке эти опера-
операторы линейно-зависимы и порождают подмногообразие раз-
размерности два — эту самую сферу, конечно.
Упражнение 3.6. Покажите, что утверждение упр. 3.3
останется справедливым, если заменить W произвольным
тензорным полем.
Упражнение 3.7. Определим оператор L2 формулой
L2 = ?т?г х + ?г?1у + ?т?1г. C.32)
Докажите, что ?т и L2 коммутируют. По симметрии L2
должно также коммутировать с ?, и ?_ . Покажите,
1х 1у
что для любой скалярной функции /
-|^, C.33)
где 6 и ф — обычные сферические координаты. Таким об-
образом, L2) — «угловая часть» оператора V2/ на единичной
сфере.
3.10. ИНВАРИАНТНОСТЬ
С помощью производных Ли можно в удобной форме
записать, что означает инвариантность тензорного поля отно-
относительно тех или иных преобразований, и это один из основ-
основных случаев использования производных Ли в физике.
А именно, говорят, что тензорное поле Т инвариантно отно-
относительно векторного поля V, если
<?j>T = O. C.34)
В случае когда Т имеет физический смысл (скажем, являет-
является метрическим тензором, или скалярным полем, описы-
описывающим потенциальную энергию некоторой частицы, или век-
векторным силовым полем), все те векторные поля (если они

3 10. ИНВАРИАНТНОСТЬ 113
существуют), относительно которых Т инвариантно, также
представляют физический интерес. Например, в предыдущем
параграфе рассматривались векторные поля, связанные с вра-
вращениями сферы. Известно, что момент импульса полезно рас-
рассматривать лишь в том случае, когда задача инвариантна
относительно вращений вокруг хотя бы одной оси. Если си-
система инвариантна относительно вращений в некоторой пло-
плоскости, то говорят, что эта система аксиально-симметрична
(или осесимметрична), и момент импульса, отвечающий гене-
генератору этих вращений, является сохраняющейся величиной.
Как это получается, мы обсудим в упр. 5.8; здесь же рас-
рассмотрим инвариантность в общем случае.
Центральное место в изучении понятия инвариантности
занимает следующая теорема. Предположим, нам дано мно-
множество /7={Т1, Т2, • • •} тензорных полей, свойства инва-
инвариантности которых нчс интересуют. Множество всех вектор-
векторных полей V, относительно которых все поля из F инва-
инвариантны, является алгеброй Ли (определение алгебры Ли
было дано в § 2.14). Доказательство этой теоремы мы про-
проведём в два шага. На первом шаге, выполняемом в упр. 3.8,
доказывается, что указанное множество полей является век-
векторным пространством над вещественными числами.
Упражнение 3.8. Покажите, что если тензор Т инвариан-
инвариантен относительно каждого из векторных полей V и W, то
он будет инвариантен и относительно aV-\-bW, где а и
b — постоянные.
Наш второй шаг опирается на результат упр. 3.1 (а), при-
применимый ввиду C.13) и C.15) ко всем тензорным полям.
Если V и W—векторные поля из рассматриваемого множе-
множества, то для всякого тензорного поля Тг из F
?vTi=?wTf=Q*>[?v, ?w] Tf=o=^% w]t=o. (з.зб)
Следовательно, если V и W принадлежат нашему множеству,
то и [V, W] тоже ему принадлежит. Теорема доказана.
Вскоре мы увидим, что алгебры Ли очень тесно связаны с
группами Ли, и поэтому доказанная теорема отчасти помо-
помогает понять, почему группы Ли так полезны в физике. В сле-
следующих параграфах мы разберём несколько примеров инва-
инвариантности.
Весьма важно уяснить себе, какое именно векторное про-
пространство представляет из себя эта алгебра Ли. Под линей-
линейной комбинацией полей V и W обычно понимают векторное
поле dV-\-bW, где а и b — произвольные функции на дан-
данном многообразии. У нас же допускаются (см. упр. 3.8) лишь
линейные комбинации, в которых а и b — постоянные вели-

114 3 ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
чины. Для построенного нами векторного пространства поля
V и W служат элементами; это — не расслоенное простран-
пространство, для которого V и W служат сечениями. Это больше по-
похоже на конечномерные функциональные пространства (см.
§ 2.3). Возможно, этот момент может показаться несуще-
несущественным, но он важен для определения размерности рас-
рассматриваемого векторного пространства. Например, три век-
векторных поля 1х, 1У и Jz, о которых речь шла в предыдущем
параграфе, линейно-зависимы как векторные поля в R3, по-
поскольку все они касательны к S2. Но для представления од-
одного из эчи\ полей через два других приходится использо-
использовать линейные комбинации с переменными коэффициентами.
Поэтому эти три поля с\ть линейно-независимые элементы
алгебры Ли. никакая линейная комбинация этих полей с по-
постоянными коэффициентами (не все из которых нули) не
равна нулевому элементу алгебры, каковым является нуле-
нулевое векторное поле Поэтому мы говорим, что эти векторные
поля образуют базис трехмерной алгебры Ли Из других ал-
алгебр Ли мы знали до сих пор лишь одну, а именно алгебру
всех касательных векторных полей к некоторому многообра-
многообразию или подмногообразию Никакое конечное м южество та-
таких полей не может быть базисом относительно линейных
комбинаций с постоянными коэффициентами, поэтому мы го-
говорим, что эта алгебра Ли бесконечномерна.
3.11. ВЕКТОРНЫЕ ПОЛЯ КИЛЛИНГА
Многие многообразия, встречающиеся в физике, обладают
метриками, и случаи, когда метрика инвариантна относитель-
относительно некоторого векторного поля, представляют значительный
интерес Векторным полем Киллинга (или вектором Шил-
Шиллинга) называется гакое векторное иоле V, для которого
- C-36)
Можно показать, что координатная запись этого уравнения
в заданной системе координат имеет следующий вид (ср.
с C 14)):
= Vk-j?gt,+g*-?rVh + 8kt?; Vft = 0. C.37)
Часто удобно использовать такую систему координат, в ко-
которой семейство интегральных кривых векторного поля V яв-
является семейством координатных линий, скажем для коорди-
координаты л;1. Тогда, в силу упр. 3.6, мы имеем
==-^г^/ = о, C.38)

3 12. ВИКТОРЫ КНЛЛНПГА II СОХРАНЯЮЩИЙСЯ ВЕЛИЧИНЫ 115
т. е. метрические компоненты не зависят от координаты Xх.
И обратно, если в некоторой системе координат компоненты
метрики не зависят от какой-либо координаты, то базисный
вектор, отвечающий этой координате, будет вектором Киллин-
Киллинга. Довольно часто векторы Кнллинга находят именно таким
способом.
В качестве примера найдем векторные поля Кнллннга для
трехмерного эвклидова пространства. Его метрика имеет в
декартовых координатах компоненты
gu = б,/, C.39)
не зависящие от х, у и г. Поэтому д/дх, д/ду и д/dz суть
векторы Киллинга. Та же метрика в сферических координа-
координатах имеет компоненты
_ д _д .
&гг ~ дг ' дг '
_ д д
Следовательно, д/дср, т. е. /г, — вектор Киллинга. Ясно, что
~1Х и 1У—также векторы Киллннга. Эти шесть векторов Кил-
Киллинга образуют базис алгебры Ли векторных полей Кнллинга.
Доказательство этого утверждения будет дано в гл. 5, ч. Е,
где мы подробно рассмотрим максимально-симметричные про-
пространства.
3.12. ВЕКТОРЫ КИЛЛИНГА И СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
В ДИНАМИКЕ ЧАСТИЦЫ
Из классической механики известно, что если сила яв-
является градиентом аксиально-симметричного потенциала, то
момент импульса частицы относительно осп симметрии будет
величиной, постоянной вдоль траектории частицы. Подобным
же образом если потенциал не зависит от какой-нибудь из
декартовых координат, скажем от х, то л'-компопента импуль-
импульса сохраняется. Однако довольно редко отмечается, что если
потенциал имеет какую-либо другую симметрию (скажем,
постоянен на семействе подобных эллипсоидов), то с ней не
связано никакой сохраняющейся величины. Таким образом,
сохраняемость величин является не просто следствием инва-
инвариантности потенциала относительно некоторого движения
(кругового, линейного или эллиптического в наших трёх при-
примерах), необходимо также, чтобы это движение осуществля-
осуществлялось вдоль векторного поля Киллинга того эвклидова про-
пространства, которое используется для описания динамики. Мы

з. пропзводныг ли ii группы ли
пока не владеем достаточной математической техникой, чтобы
доказать это утверждение (его доказательство нам придётся
отложить до упр. 5.8), но в правдоподобности его можно
убедиться, рассмотрев уравнение движения. В общепринятых
векторных обозначениях оно записывается так:
т\ = — \Ф пли mV' = — УФ. C.41)
Но мы-то знаем, что для корректного определения вектора-
градиента необходимо вводить в дело метрику, так что в дей-
действительности это уравнение имеет вид
JL C.42)
дх'
Ясно, что все инварианты, которые можно построить для этого
уравнения, используют не только инвариантность Ф, но и ин-
инвариантность g
3.13. ОСЕВАЯ СИММЕТРИЯ
Для того чтобы продемонстрировать, каким естественным
образом появляются производные Ли в задачах с симметрией,
рассмотрим случай осевой симметрии. Осевая (или аксиаль-
аксиальная) симметрия — это инвариантность относительно вращений
вокруг некоторой фиксированной осн. (Её не следует путать
с цилиндрической симметрией, которая требует не только ин-
инвариантности относительно вращений вокруг оси симметрии,
но ещё и инвариантности относительно сдвигов вдоль этой
осн.) Обозначим через ср угол поворота относительно оси
симметрии. Довольно часто возникают задачи, в которых
имеется некоторая «фоновая» осевая симметрия. В качестве
примера можно указать частицу, двигающуюся в поле осе-
спмметрпческого потенциала, либо малые возмущения какой-
либо осесимчетрнческой системы. В этом случае мы получаем
линейное уравнение
Ц*Г)=-0, C.43)
где if— неизвестная величина, a L — оператор, инвариантный
относительно преобразования ф-> ср -J- const. Решения урав-
уравнения C.43) не обязаны быть осеспмметрическими: угол по-
поворота частицы относительно оси в какой-то момент имеет
одно значение, а в последующий момент — другое; рассмат-
рассматриваемое малое возмущение может иметь неосесимметричные
начальные данные. Тем не менее скалярные решения обла-
обладают тем прекрасным свойством, что коэффициенты их раз-
разложения в ряд Фурье по ф
со
C.44)

3 13 ОСЕВАЯ СИММЕТРИЯ
— функции tym (х>) (индекс j пробегает все координаты, кро-
кроме ф) — удовлетворяют следующему, тесно связанному с ис-
исходным дифференциальному уравнению:
0 = ^m(*m) = e-i'™PLA])me"'). C.45)
Операторы L и Lm, как правило, не тождественны, так как L
может содержать производные по ср, a Lm не должен. Для
примера рассмотрим оператор
г"
г2 дг дг г2 sin G <?6 <56 r2 sin2 6 дуг
Ясно, что этот оператор инвариантен относительно преобра-
преобразования ф-v ф -]- const. Применяя этот оператор к функции
f (r, 6)е'тФ, получаем
V2(/(r, 8)е1тф) —е'™?|-5--^-г2з~+ ¦> ¦ а ~^s sinB^-
" v ' ' ' I r2 dr dr r2 sin 6 dQ дв
Оператор в фигурных скобках есть оператор V2m в смысле
формулы C.45). Это разложение Фурье функции / не так уж
полезно в задачах о движении частицы, когда положение
частицы описывается дельта-функцией от ф, но чрезвычайно
удобно в случае непрерывных систем, таких, например, как
волны на осесимметричном фоне. Играющие ключевую роль
функции е" можно назвать скалярными осевыми гармони-
гармониками.
Скажем, что решение ^ уравнения C.43) имеет осевое
собственное значение т, если
¦ ?ё^ = ш^, C.47)
где ёс, 2= д/дц> — поле касательных векторов к окружностям
симметрии. Все эго очень просто, пока ф — скалярная функ-
функция, но предположим, мы имеем дело с векторным уравне-
уравнением, скажем с уравнением для векторного потенциала в тео-
теории электромагнетизма. И в этом случае опять полезны осе-
осевые гармоники, но это должны быть уже векторные осевые
гармоники, к построению которых мы и перейдём.
Рассмотрим подмногообразие хр = 0 (в действительности
это не просто подмногообразие, а так называемое подмно-
подмногообразие с краем; краем здесь служит ось симметрии).
В каждой его точке выберем какой-нибудь базис {ё,} векто-
векторов, касательных к подмногообразию. Дополним этот базис
вектором ёср, так что {ёф, ё,} будет базисом касательного про-
пространства к многообразию в точках нашего подмногообразия.
Теперь построим из него базис для всего многообразия, пе-

118 3. ПРОИЗВОДНЫЕ ЛИ I! ГРУППЫ ЛИ
ренося его по Ли вдоль векторного поля ёф> вокруг оси сим-
симметрии, как показано на рис. 3.8. Каждое из полученных
базисных векторных полей удовлетворяет уравнению
?в9ё, = О, C.48)
т. е. все они осесимметрические. Следует заметить, что в
обычных декартовых координатах компоненты вектора ё,- по
мере движения вокруг осп изменяются. Осевая симметрия
векторного поля совсем не означает, что его декартовы ком-
компоненты не зависят от ф, она означает лишь, что не зависят
от ф его компоненты в некоторой
системе координат, включаю-
включающей ф.
Итак, мы имеем базис векто-
векторов с осевым собственным значе-
значением 0 (см. C.48)). Ясно, что
ось» |—*. базисом с осевым собственным
ез значением т будет
ё{т), = ё,ётч,
ё1т)ч = ё<е1тч>. C.49)
Рис. 3.8. Базис (ё , еЛ, полу-
ченный в результате переноса Любое векторное поле, удовле-
Ли вдоль поля ?ф (вид сверху творяющее соотношению
вдоль оси симметрии). ?_ "у _ \ту
можно представить в виде линейной комбинации векторных
осевых гармоник с собственным значением т, задаваемых
формулой C.49), с коэффициентами, не зависящими от <р.
Упражнение 3.9. В эвклидовом трёхмерном пространстве
постройте осевые векторные гармоники для вращения
вокруг оси z, выбрав в плоскости ф = 0 базис {ёх,ёг}.
Найдите декартовы координаты трёх векторных гармоник,
отвечающих т = 2. Подобным же образом, отправляясь
ог базиса {Ах, Az} в плоскости ц> = 0, найдите базис один-
форм, являющихся осевыми гармониками с собственным
значением т — 2. Покажите, что если / — скалярная функ-
функция с осевым собственным значением 2, то её градиент d/
будет один-формой с осевым собственным значением 2.
Докажите, что ёх ± iey имеет осевые собственные значе-
значения ±1.
Хотя мы этим пока и не пользовались, ясно, что всё это
тесно связано с теорией групп. Существование осевой сим-
симметрии означает, что «фоновая» физическая ситуация инва-
инвариантна относительно переносов Ли вдоль д/ду, а эти пере-
переносы образуют группу Ли, как было описано в § 3.L Эта

3.M. АБСТРАКТНЫЕ ГРУППЫ ЛИ
119
группа, 50B), чрезвычайно проста. Больший интерес пред-
представляет группа всех вращений трёхмерного пространства
(симметрия относительно этой группы называется сфериче-
сферической симметрией); эта группа уже сложнее, поскольку про-
производные Ли вдоль U, ~1У и h попарно не коммутируют. Чтобы
исследовать этот случай, необходимо предварительно про-
провести систематическое изучение самих групп Ли, чему и по-
посвящена оставшаяся часть главы.
3.14. АБСТРАКТНЫЕ ГРУППЫ ЛИ
Мы уже несколько раз касались групп Лн и алгебр Ли.
Теперь займёмся их систематическим изучением. Использова-
Использование групп Ли и алгебр Ли в физике объясняется главным об-
образом тем, что, как мы уже видели, с их помощью выра-
выражаются свойства инвариантности некоторых физически важ-
важных тензоров. Этот вопрос бу-
будет рассмотрен в последующих
параграфах; в данном пара-
параграфе наша цель — исследо-
исследовать многообразие группы са-
само по себе. Необходимо совер-
совершенно чётко представлять себе,
что между многообразием
группы н каким бы то ни было
многообразием, снабжённым
тензором, свойства инвариант-
инвариантности которого описываются
группой, пет ничего общего.
Многообразие всех вращений
E0 C)) отлично от многооб-
многообразия, координатные системы жение векторов в точке е в век-
которого вращаются (Е3). торы в точке g.
Пусть нам дана конечномерная группа Ли, т. е. многооб-
многообразие класса С°° размерности п, на котором заданы следую-
следующие отображения класса С°° (диффеоморфизмы): любому
элементу g из G отвечает отображение h->gh (левый сдвиг
на (или посредством) g), а также отображение ln—^hg (пра-
(правый сдвиг на g). He предполагается, что данная группа яв-
является абелевой (коммутативной) (т. е., вообще говоря,
hg^gh). Единичный элемент группы будем обозначать че-
через е. Произвольная окрестность единичного элемента е ото-
отображается при левом сдвиге на данный элемент g в некото-
некоторую окрестность этого элемента (см. рис. 3.9). Поскольку это
отображение переводит кривые в кривые же, касательные
векторы в точке е (элементы касательного пространства Те)
отображаются в касательные векторы в точке g. Получаемое
Рис. 3.9.
Сражает
Левый сдвиг на g ото-
окрестность точки е на
1

120
3 ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
таким образом отображение Lg:Te-^Tg также представлено
на рис. 3.9. (Принцип здесь тот же самый, что и в случае
отображения переноса Ли, см. § 3.3.) Говорят, что векторное
поле V на G левоинвариантно, если Lg переводит значение V
в точке е в значение V в точке g (т. е. Lg : V{e)t—=» V(g)) для
всех g. В таком случае, в силу свойств группового закона
композиции, Ls: V(h)i->V(gh) для всех h из G, так что дан-
данное выше определение — это естественное определение «по-
сюянною» векторного поля на G. Также ясно, что каждый
Рис 310. Отображение незамкнутого параллелограмма на рис. 2.21 для
левоинвариаптпых векторных полей. Поскольку поля лсвоипвариантны,
смещения на параметрическое расстояние е в окрестности точки е отобра-
отобразятся в такие же сдвиги в окрестности точки g, и потому "зазор" в ок-
окрестности е, представляющий скобку Ли рассматриваемых полей, отобра-
шгея в зазор в окрестности g, нредставляющип скобку Ли сдвинутых по-
векгор из Те определяет единственное левоинвариантное век-
векторное поле, откуда следует, что левоинвариантные вектор-
векторные поля образуют n-мерное векторное пространство. (Как и
в случае линейных комбинаций, рассмотренных в § 3.10,
коэффициентами в линейных комбинациях этих полей яв-
являются константы, а не функции на G.) Далее, легко видеть
(см. рис. 3.10), что если V и W — два произвольных левоин-
вариантных векторных поля, то Lg переводит значение поля
[V, W] в точке е в значение того же поля в точке g, так что
поле [V, W] также оказывается левоинвариантным. (Те чи-
читатели, для которых приведённая картинка не кажется убе-
убедительной, могут, используя координаты на G, сами доказать
этот результат.) Этот факт весьма важен, ибо он означает,
что левоинвариантные векторные поля образуют алгебру Ли.
Это так называемая алгебра Ли группы G. Она обозначается
через 8(G) (некоторые авторы обозначают её через g). Эта
алгебра Ли полностью характеризуется своими структурными
константами с^, определяемыми следующим образом. Пусть
{F(()) /=1, .,., п) —какой-нибудь базис нашей алгебры Ли,

S 14 \БСТР\КТ11ЫГ ГРУППЫ ЛИ 121
т. е. линейно-независимое множество левоинвариантных век-
векторных полей. (Если эти поля линейно-независимы в одной
точке, скажем е, то в силу левоинварпантности они будут
линейно-независимы всюду.) Тогда можно записать
C.50)
(суммирование подразумевается). Если все структурные кон-
константы обращаются в нуль, то алгебра Ли называется абеле-
вой {коммутативной). Ниже мы увидим, что тогда и G оказы-
оказывается абелевой 1). Естественно, базис (F(fe)} не является един-
единственно возможным; можно показать, что при заменах базиса
числа с]ы преобразуются как компоненты тензора типа
( 2 ) ¦ П° кажД°й группе Ли с её алгеброй Ли однозначно оп-
определяется «тензор структурных констант» С. Имеет место
также ослабленный вариант обратного утверждения, а имен-
именно, множество структурных констант «почти-» однозначно оп-
определяет группу Ли, алгебре Ли которой они соответствуют.
Эго утверждение мы обсудим ниже в § 3.16.
Рассмотрим интегральную кривую левоинвариантного век-
векторного поля V, проходящую через е. Она имеет касатель-
касательный вектор Ve в точке е, и существует однозначно определён-
определённая параметризация этой кривой (с параметром, скажем, t),
для которой точке е соответствует значение параметра t = 0.
Как было показано в § 2.13, точки на этой кривой могут быть
получены экспоненцированием V, т. е. могут быть представ-
представлены в виде ехр(/Р). Здесь речь идёт попросту о диффео-
диффеоморфизме многообразия G на себя, порождённом векторным
полем V (см. § 3.1). В отличие от произвольного векторного
поля, поле V полностью определяется вектором Ve, поэтому
точки многообразия G, лежащие на указанной кривой, мож-
можно обозначить так:
ve \e. C.51)
Поскольку, по определению, для экспоненты выполняется со-
соотношение
exp (h V) ехр (/, V) | е = ехр [ (U + h) V] | е,
точки на нашей интегральной кривой образуют группу
= ехр (t2V) exp (t.V) \e = g^ (t2) g^ (/,), C.5 2)
которая называется однопараметрической подгруппой груп-
'' При условии её связности. — Прим. ред.

|22 Э. ПРОИЗВОДНЫЕ ЛИ II ГРУППЫ ЛИ
пы G. Эта подгруппа всегда будет абелевой: g\_ (^ -f <2) =
= g"_ (/2 + /j)—просто потому, что групповая операция со
ответствует сложению значений параметра. Каждому вектору
из Те соответствует единственная такая подгруппа. Далее,
поскольку каждая однопараметрическая подгруппа является
кривой в G класса Сж, проходящей через точку е (подгруппа
всегда содержит единичный элемент), то существует взаимно-
взаимнооднозначное соответствие между однопараметрическнмп под-
подгруппами группы G и элементами её алгебры Ли.
Упражнение 3.10. Дайте определение правопнвариантного
векторного поля. Покажите, что такие поля образуют ал-
алгебру Ли. Докажите, что их интегральные кривые, про-
проходящие через точку е, совпадают с интегральными кри-
кривыми левоинвариантных векторных полей. Покажите, что
их интегральные кривые, проходящие через другие точки,
вообще говоря, не совпадают с интегральными кривыми
левоинвариантных полей, за исключением случая, когда
группа является абелевой.
Упражнение 3.11. (а) Покажите, что произвольный базис
(V,(e), / = 1 п} в Те определяет линейно-независи-
линейно-независимое множество левоинвариантных векторных полей, ко-
которые мы обозначим череч {V,}.
(Ь) Рассмотрим касательное расслоение TG группы Ли
С В некоторой окрестности U точки е введём для него
следующие координаты. Пусть X — вектор в точке g из U.
Запишем Х= J^t а,1/г (g). Слоем в точке g служит Rn,
поэтому в качестве координат вектора X возьмём {а«}.
Координатами в расслоении TG над U будут тогда {{ко-
{{координаты точки g}, {а^}}. Показать, что этот выбор коор-
координат можно распространить на всё TG таким образом,
чтобы получилось 1-1-отображение TG на CXR", т. е. что
касательное расслоение группы Ли тривиально.
3.15. ПРИМЕРЫ ГРУПП ЛИ
(i) Простейшим примером группы Ли служит R", кото-
которое представляет собой многообразие и группу относительно
сложения векторов. Это абелева группа. Однопараметриче-
скими подгруппами являются прямые, проходящие через на-
начало координат. Левоинвариантные векторные поля парал-
параллельны этим прямым; очевидно, все они коммутируют между
собой. Отсюда следует, что соответствующая алгебра Ли есть
векторное пространство Те. снабжённое абелевой скобкой Ли:
[17, Щ = 0 для всех V и W из Те.
(и) Для физики одной из самых важных групп Ли яв-
является группа всех вещественных п X л-матриц с отличным

3.15. ПРИМЕРЫ ГРУПП ЛИ _123
от нуля определителем. Эта группа называется полной линей-
линейной группой п-мерноео вещественного пространства •> и обо-
обозначается через GL(n, R). Она является группой Ли по сле-
следующим причинам. Во-первых, это группа относительно опе-
операции умножения матриц, единичным элементом которой
служит единичная матрица. (Требование, чтобы определитель
был не равен нулю, необходимо, ибо оно обеспечивает суще-
существование обратного элемента для любой матрицы.) Во-вто-
Во-вторых, это многообразие. Для любой матрицы А из GL(n, R)
с элементами {a1,, i, /= 1, ..., п} можно рассмотреть окре-
окрестность радиуса е, состоящую из матриц В, для которых
|b'j — ali\ ¦< е при всех / и у, и е можно выбрать настолько
малым, чтобы каждая матрица В тоже имела отличный от
пуля определитель. В качестве координат в этой окрестности
можно взять x'i = b'j — а1,, и поскольку их п2 н все они не-
независимы, то размерность группы GL(n, R) равна /г2. В дей-
действительности это — подмногообразие пространства Rn'. По-
Поскольку R'1, подобно любому R'n, тождественно с касатель-
касательным пространством в любой из своих точек, то касательным
пространством к группе GL(n,R) в единице е будет Rn, и,
следовательно, любой касательный вектор представим в виде
матрицы. Например, кривая в GL(n, R), образованная матри-
матрицами diag(l + ехр(Я), 1, 1, ..., 1), где К — параметр, имеет
в точке 1 = 0 касательную diag(l,0, 0, ..., 0). Определитель
этой матрицы равен нулю, что иллюстрирует тот факт, что
в Те входят все матрицы и что любая матрица порождает
однопараметрическую подгруппу, левоинварпантное вектор-
векторное поле2) и некоторый элемент алгебры Ли группы Ли
GI(n.R).
Однопараметрическая подгруппа, порождённая произволь-
произвольной матрицей А, является проходящей через точку е интег-
интегральной кривой левоинвариантного векторного поля, значе-
значение которого в е совпадает с А. Обозначим матрицы из этой
подгруппы через gA(t), так что dgA (t)/dt\0 =A (это просто
означает, что d(g'4)'//W]o = о'/ для всех i, /). В силу C.52)
имеем
C.53)
C.54)
1} В оригинале Genera! Linear group in n Real dimensions. Отсюда
обозначение GL (n, R). — Прим. ред.
2) Следует помнить, что векторы, касательные к G, в действительно-
действительности являются матрицами п их не надо путать с «векторами-столбцами»,
которые здесь не играют никакой роли.

124
3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
Формула C.55) есть определение экспоненты от матрицы;
вместе с C.54) она даёт конкретную реализацию формулы
C.51). Таким образом, однопараметрические подгруппы груп-
группы GL(n, R) являются экспонентами произвольных пУ^п-
матриц. Матрицу А физики часто называют инфинитезималь-
ным генератором подгруппы gA(t). В упр. 3.12 приводятся
некоторые свойства экспоненты ехр(^4).
Упражнение 3.12. (а) Покажите, что C.55) удовлетворяет
соотношению C.53).
(Ь) Покажите, что из C.55) вытекает соотношение
ехр(В-1АВ) = В-1 ехр (А) В.
C.56)
(с) Известно (см., например, Hirsch & Smale, 1974 1J),
что для произвольной вещественной матрицы А можно
подобрать такую вещественную матрицу В, что В~1АВ бу-
будет иметь следующую каноническую (или жорданову)
форму (называемую также блочно-диагональной формой,
так как ненулевые элементы образуют квадратные блоки
вдоль главной диагонали)
В~1АВ =
'Р, О О
О Р2 О
О О Р3
C.57)
где каждый «блок» Р, является квадратной матрицей, при-
причём возможны следующие три случая2':
(i) P, является 1 X 1-матрицей
(li); C.58а)
ред.
') Или любой достаточно полный учебник по высшей алгебре. — Прим.
2> Возможен ещё один случай:
(iv) P/ является недиагональной 2п, Х2«; -матрицей вида
Р, Е
О Р]
О
Е
О
10
Р, Е
0 РП
где Р, имеет вид C.58Ь), а Е — единичная 2 X 2-матрица. — Прим. перев.

3.15. ПРИМЕРЫ ГРУПП ЛИ
125
(ii) P/ является недиагональной 2Х2-матрнцей вида
C.58b)
(iii) Pj является недиагональной щ X «/-матрицей
(пу ^ 2) вида
... 00
0 О
0
0
0
0
0
1
V-I
0
0
0
0
0
1
V,
0
0
0
о о
0
о
1
V-i J
C.58с)
При этом числа к/, \и и r;- ± is/ суть собственные значе-
значения матрицы А. Используя этот факт п C.55), покажите,
что exp(tB~lAB) также будет иметь блочно-диагональный
вид с соответствующими блоками:
(i) (e'W); C.59a)
C.59b)
< / costs, sin tsi\
а 11 I ¦
\— sin is, costsjj'
(iii)
I
0
0
0
t
1
0
0
1 /2
2! '
/
1
0
1
3!
W
t
I
C.69c)
Из (а) следует, что матрица В, приводящая А к канони»
ческой форме, приводит к канонической форме и exp(tA)
в случаях (i) и (ii), но в случае (iii) матрица, приводя-
приводящая ехр(/Л) к канонической форме, уже зависит от t.
Заметим, что не каждый элемент группы GL(n,R) при*
надлежит однопараметрической подгруппе. Это объясняется
тем, что такая подгруппа является непрерывной кривой в
GL(n, R), вдоль которой определитель изменяется непре-
непрерывно. Поскольку определитель в точке е равен 1 и обра-
обратиться в нуль на кривой не может, то этим исключается су*

126
3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
ществование непрерывной кривой, соединяющей точку е с
матрицей, имеющей отрицательный определитель. (Отметим,
что в C.59) представлены лишь матрицы с положительными
определителями.) Такие группы называют несвязными груп-
группами. Итак, мы видим, что для исследования группы Ли в
целом, вообще говоря, недостаточно рассматривать лишь её
однопараметрические подгруппы или её алгебру Ли. Те эле-
элементы, которые можно соединить с точкой е непрерывным
путём (не обязательно однопараметрической подгруппой),об-
подгруппой),образуют множество, называемое связной компонентой единицы
данной группы.
Упражнение 3.13. Покажите, что матрица
0 -\
принадлежит связной компоненте единицы группы
GL(n, R), но не принадлежит ни одной из однопараметри-
ческих подгрупп. (Указание: постройте непрерывный путь,
соединяющий эту матрицу с е = ( () J . J
Что представляет собой алгебра Ли группы GL(n, R)? Рас-
Рассмотрим касательный вектор Ае в точке е и соответствующую
однопараметрическую подгруп-
подгруппу g- (t); левый сдвиг fg_ (/)
Ае Ае
этой кривой, осуществляемый
посредством произвольной мат-
матрицы / из GL(n, R), даёт неко-
некоторую кривую из конгруэнции
левоинвариантного векторного
поля, отвечающего Ае, как по-
показано на рис. 3.11. Вот каким
образом Ае порождает левоин-
вариантное поле; мы обозна-
обозначим его просто через А. Если/
лежит на проходящей через е
кривой g_ (/), которая порож-
ве
дается матрицей Ве из Тс, то в силу B.12) скобка Ли [А, В]\е
этих двух векторных полей в точке е равна
Рис. 3.11. Левый перенос кривой
g- (t) посредством f.
Ае
и с помощью формулы C.55) легко вычислить, что
C.60}

3 15 ПРИМЕРЫ ГРУПП ЛИ 127
Таким образом, скобка Ли двух произвольных левоинвари-
антных векторных полей на GL(n,R) в точке е является не
чем иным, как обычным матричным коммутатором двух мат-
матриц, порождающих эти ноля. Лсвоинвариантное векторное
поле, порождённое этим коммутатором, есть элемент алгебры
Ли &(GL(n, R)), которая является скобкой Ли исходных
полей.
(iii) Мы уже знаем, что группа вращений есть группа Ли
(см. § 2.3 (vi)). Подробное исследование этой группы мы
проведем позже, а пока рассмотрим её как подгруппу груп-
группы GL(n,R). В § 2.29 было показано, что матрицы Л, для
которых А~1 = Л1, являются элементами группы О(п) — орто-
ортогональной группы в n-мерном пространстве'>. Поскольку
определитель обладает свойствами
det Л = l/det^-1), del(A)=dei(AT) C.61)
(см. § 1.6), у матриц из группы О(п) определитель равен ±1.
Матрицы, определитель которых равен +1, образуют под-
подгруппу, которая называется специальной ортогональной груп-
группой 2) и обозначается через SO(n). Мы сейчас покажем, что
это группа вращений. (Матрицы ортогональной группы О(п),
определитель которых равен —1, не образуют подгруппы, так
как единичная матрица не входит в их число. Подобно
GL(n, R) группа О(п) несвязна.)
Упражнение 3.14. (а) Покажите, что если А принадлежит
О(п), то её собственные значения совпадают с собствен-
собственными значениями обратной матрицы Л. (Воспользуйтесь
тем фактом, что для произвольной матрицы В выпол-
выполняется соотношение det В = det Br.) Читатели, позабыв-
позабывшие, что такое собственные значения, найдут их определе-
определение в § 1.6.
(b) Покажите, что собственные значения произвольной
невырожденной матрицы Л суть обратные величины к
собственным значениям матрицы А~1. (Используйте то об-
обстоятельство, что det (AB) = det A det В.) Выведите от-
отсюда, что собственные значения (Яь ..., ?Wi) произволь-
произвольной матрицы Л из О(п) бывают двух типов: либо
(i) А,/ = ±1, либо (ii) X,Kk = 1 для \ ф k. Покажите, что
в случае (ii) собственные значения встречаются парами
(ет, е~т), где G вещественно.
(c) Известно также, что каноническую форму мат-
матрицы Л из О (и) можно получить посредством преобразо-
преобразования б-'ЛВ, где б—матрица из SO(n). Используя этот
'' В оригинале Orthogonal group in n dimensions. Отсюда обозначе-
обозначение. — Прим. ред.
г> Special Orthogonal group. — Прим ред.

128 3 ПРОИЗВОДНЫЕ ЛИ II ГРУППЫ ЛИ
результат, докажите, что произвольная матрица из О(п)
имеет каноническую форму, состоящую из блоков
0) A); C.62а)
(И) (-1); C.62b)
,...* / cos 6 sin 6 Л /о со \
<•»> (-sine cose)- <3-62c>
(d) Покажите, что алгебра Ли группы О(п) состоит из
всех антисимметричных матриц. Используя этот резуль-
результат, докажите, что О(п) имеет размерность п{п— 1)/2.
Далее, всякую матрицу А из GL(n, R) можно рассматри-
рассматривать как обратимый тензор типа ( . 1 на Rn, переводящий
вектор-столбец V из R" в вектор-столбец А V (матричное умно-
умножение). Преобразование В~*АВ есть просто-напросто преоб-
преобразование компонент этого тензора (см. § 2.26) при замене
базиса {ei, ..., <?„} на базис {В~хёи ..., Вёп). Поэтому
можно считать, что произвольная матрица из SO(n) эквива-
эквивалентна последовательным вращениям в независимых двумер-
двумерных плоскостях, ибо каноническая форма C.62с), очевидно,
задаёт как раз такое вращение, а форма C.62Ь) должна
встречаться чётное число раз (чтобы определитель был поло-
положителен), так что, сгруппировав попарно соответствующие
направления, мы получим формы вида C.62с) с 6 — гг. Итак,
группа SO(n) есть группа вращений. (Заметим, что если п
нечётно, то каждая матрица из SO(n) оставляет неподвиж-
неподвижным по крайней мере одно направление.) Остальные мат-
матрицы из О(п) можно трактовать как отражения (с враще-
вращением), т. е. преобразования, изменяющие ориентацию вся-
всякого множества п линейно-независимых векторов. Это — тема
следующего упражнения. (Понятие ориентации базиса под-
подробно обсуждается в гл. 4.)
Упражнение 3.15. Покажите, что каноническая форма вся-
всякого элемента из О(п), не принадлежащего SO(n), есть
произведение матрицы diag(l, ..., 1, —1,1, ..., 1) (имею-
(имеющей ровно один элемент —1 на диагонали) и канониче-
канонической формы некоторой матрицы из SO(n). Выведите от-
отсюда, что она является отражением.
Упражнение 3.16. Покажите, что любая матрица из SO(n)
является элементом однопараметрическои подгруппы. До-
Докажите, что произвольная матрица из 50C) эквивалентна
одному повороту на некоторый угол G относительно не-
некоторой оси,

3 15 ПРИМЕРЫ ГРУПП ЛИ 129
Прежде чем расстаться с группой вращений, исследуем
её алгебру Ли, по крайней мере для группы 50C). Вектор-
Векторное пространство Те есть пространство всех антисимметрич-
антисимметричных матриц, имеющее размерность три (см. упр. 3.14 (d)).
Один из его базисов состоит из матриц
Li==\ 0 0—1, L2=\ 000, L3=
Упражнение 3.17. Покажите, что указанный выше базис
алгебры Ли группы SOC) имеет следующие скобки Ли:
[LuL2]=L3, [L2,U)=L1, [L3, Z.,] = L2. C.64)
Вскоре мы ешс вернемся к этой алгебре.
(iv) Ещё одна важная для физики матричная группа —
это SU(n), специальная унитарная группа в (комплексном)
«-мерном пространстве1*. Это подгруппа в группе GL(n,C)
всех комплексных п X n-матриц с ненулевым определителем
(так называемой полной линейной группе n-мерного комп-
комплексного пространства2'). Поскольку каждый элемент мат-
матрицы может быть комплексным, а каждое комплексное число
задаётся двумя вещественными, группа GL(n,C) имеет раз-
размерность (вещественную) 2п2. В ней имеется подгруппа U{n),
называемая унитарной группой, состоящая из унитарных мат-
матриц, т. е. матриц U, удовлетворяющих равенству ?/-' = U*,
где символ * обозначает переход к комплексно-сопряженной
транспонированной (эрмитово-сопряжённой) матрице. По ана-
аналогии со случаем О(п) алгебра Ли подгруппы U(п) состоит из
всех антиэрмитовых п X «-матриц. (Матрица А называется
антиэрмитовой, если Л* = —А.) Эта алгебра Ли имеет веще-
вещественную размерность и2, поскольку антиэрмитова матрица
имеет п (п — 1)/2 произвольных комплексных внедиагональных
элементов (задаваемых п{п—1} вещественными числами) и п
произвольных чисто мнимых диагональных элементов (кото-
(которые дают ещё п вещественных измерений, а в итоге полная
размерность получается п2). Подгруппа SU(n) в U(n)—это
множество всех матриц U(n) с единичным определителем.
Поскольку определитель любого элемента U (п) есть комп*
лексное число, по модулю равное единице, равенство еди-
единице определителя даёт одно дополнительное условие, по-
поэтому SU(n) имеет размерность п2 — 1. Алгебра Ли группы
'> Special Unitary group in n dimensions. — Прим. ред.
2) General Linear group in n Complex dimensions. — Прим. ред.

130 3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
SU(n) — это множество всех антиэрмитовых матриц с нуле-
нулевым следом. (След матрицы А есть сумма а1 г, см. § 1.6.)
Упражнение 3.18. Покажите, что алгебра Ли группы
SU(n) есть множество всех антиэрмитовых матриц с ну-
нулевым следом. (Можно воспользоваться тем фактом, что
произвольный элемент из U(n) имеет каноническую фор-
форму diag(e1<J\ е"Ч ..., еф"),где {ср,-, /=1, .... п}— веще-
вещественные числа.)
Упражнение 3.19. (а) Покажите, что следующие матрицы
образуют базис касательного пространства Те группы
St/B):
Jl~TKi о)' Js~T\i о)' Ji~\o -[)¦
C.65)
Докажите, что Те — трёхмерное вещественное векторное
пространство: хотя сами матрицы и содержат мнимые чис-
числа, лишь их линейные комбинации с вещественными коэф-
коэффициентами остаются в Те.
(Ь) Покажите, что указанный выше базис алгебры Ли
группы SUB) имеет следующие скобки Ли:
[/l, /2] = /s, [/2,/3]=/l, [/3, /l] = /2- C.66)
Формально это идентично C.66); как мы увидим в сле-
следующем параграфе, это указывает на тесную связь между
SUB) и 50C).
Упражнение 3.20. (а) Пусть tr(/4) = o', обозначает след
матрицы А. Докажите, что tr(?-M?)= tr(Л).
(b) Используя (а), а также: (i) тот факт, что опреде-
определитель обладает свойством det(AB)= det(y4)detF), (ii)
соотношение C.56) и (Hi) канонические формы C.55) —
C.59), докажите, что для произвольной матрицы А вы-
выполняется соотношение
det(exp(i4))=exp(trD)). C.67)
(c) Используя C.67), дайте более простое доказатель-
доказательство утверждения упр. 3.18.
3.16. АЛГЕБРЫ ЛИ И ОТВЕЧАЮЩИЕ ИМ ГРУППЫ ЛИ
Для каждой группы Jlu\G определена её алгебра Ли (д).
Поскольку каждый элемент g из G есть образ точки е при
левом сдвиге, порождённом g, и поскольку каждому вектору
из Те соответствует единственное векторное поле из этой ал-
алгебры Ли, то, следовательно, каждая точка g из G принадле-

3.16 АЛГЕБРЫ ЛИ И ОТВЕЧАЮЩИЕ ИМ ГРУППЫ ЛИ 131
жит некоторой кривой из каждой левоинвариантной конгруэн-
конгруэнции. Можно ли построить группу G, зная лишь её алгебру
Ли? Ответ в общем утвердительный, но прежде чем сформу-
сформулировать его, надо дать более совершенное определение ал-
алгебры Ли, нежели то, с которым мы до сих пор работали.
Алгебра Ли— это вещественное векторное пространство V,
снабжённое операцией билинейного умножения, обозначаемой
через [,] (и называемой скобкой Ли), которая двум произ-
произвольным векторам А и В сопоставляет вектор [Л, В], причём
должны быть выполнены следующие соотношения:
(i) [А,В]=-[В,А], C.68)
(ii) [А,[В,С]\ + [В,[С,А]]+[С,[А,В]} = 0. C.69)
Существенное различие между этим определением и опреде-
определением, которое мы дали в § 2.14, состоит в том, что здесь
скобка Ли определена формально, а именно как операция,
обладающая свойствами (i) и (ii), что позволяет работать
с операциями любой природы, лишь бы они обладали этими
свойствами. Одной из таких операций является взятие ком-
коммутатора векторных полей, и это была единственная опера-
операция, которую мы до сих пор использовали. Другим очевид-
очевидных примером служит векторное пространство ^3 с обыч-
обычным векторным произведением
[а,Б]=аХБ. C.70)
Упражнение 3.21. (а) Покажите, что C.70) удовлетворяет
тождеству Якоби C.69).
(Ь) Покажите, ^то базис ei = A,0,0), ёч = @,1,0),
ё3 = @, 0, 1) имеет следующие скобки:
[ёи ё2] = ё3, [ё2, ё3] = ёи [ё3, et] = е2. C.71)
Сравните C.71) с C.64) и C.66).
А теперь сформулируем без доказательства теорему,
имеющую фундаментальное значение для физики: за каждой
алгеброй Ли стоит группа Ли. Точнее, каждая алгебра Ли
есть алгебра Ли одной и только одной связной и односвяз-
ной группы Ли. (Многообр-азие называется односвязным,
если каждая замкнутая кривая может быть гладко стянута
в точку. Обсуждение и доказательство этой теоремы для не-
некоторых частных случаев можно найти в книгах Spivak
A970) и Warner A971).) Более того, любая другая связная
группа Ли с той же алгеброй Ли, но не односвязная накры-
накрывается этой односвязной группой Ли. (Связное многообразие
М накрывает многообразие N, если существует отображение
я многообразия М на N, такое что прообраз некоторой ок-

132 3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
рестности V произвольной точки Р многообразия N есть
дизъюнктное объединение открытых окрестностей точек из
лг1 (Р) в М. Пример накрывающего многообразия приведён
на рис. 3.12.) Это накрытие должно быть гомоморфизмом
групп. (Определение гомоморфизма в § 1.4.)
д1 К») К») 1С)—К») 10—К*
-4n -2rt 0 2п 4rt 6rt
Рис 3./2. Единичная окружность S1 бесконечное число раз накрывается
вещественной прямой /?' при отображении я: Z?1 —»- S1, переводящем точку
х в точку зт(дс) на S1, координатами которой в плоскости Я2 служат
(cos л:, sin л:). Множество n~l(V) является объединением всех указанных
на рисунке открытых интервалов в R'.
Прекрасной иллюстрацией этой теоремы служат группы
50C) и SUB). Прежде всего покажем, что группа 5?/B)
односвязна. Для этого рассмотрим множество Н всех матриц
вида
/ а Ь\
{ ), C.72)
где а и b — произвольные комплексные числа (черта обо-
обозначает комплексное сопряжение).
Упражнение 3.22. (а) Покажите, что#\|Г0 0)|. под-
подмножество множества Н, состоящее из матриц с ненуле-
ненулевым определителем, является группой по умножению и,
следовательно, подгруппой Ли в GLB, С).
(b) Покажите, что Н — вещественное векторное про-
пространство (относительно матричного сложения) размер-
размерности 4, один из базисов которого образуют матрицы /ь
/2, /з из упр. 3.19 и матрица / = ( Q J .
(c) Пусть А—произвольная матрица, принадлежа-
принадлежащая Н:
А = 2cti/i + 2а2/2 + 2а3/3 + а4/,
где {а;}—вещественные числа. Покажите, что А принад-
принадлежит SUB) тогда и только тогда, когда
| + o|=l. C.73)

3.16. АЛГЕБРЫ ЛИ И ОТВЕЧАЮЩИЕ ИМ ГРУППЫ ЛИ 133
(d) Используя этот факт, покажите, что группа $)
допускает 1-1-отображение на трёхмерную сферу S3, кото-
которая является односвязным многообразием. (Другими сло-
словами, S3 и SUB) диффеоморфны.)
Теперь построим отображение я: S?/B)->SOC), являю-
являющееся накрытием. Его легко построить, используя экспонен-
экспоненту от элементов алгебры Ли. В SUB) экспонента элемента
Ji равна
ехр (//,) = ( 0 J + T(. 0)+2гЫ( 0 _J
,i sin (//2)
Экспонента элемента L\ из SOC) равна
1 0 ON /0 0
exp(sZ.!) = | 0 1 0 |+s| 0 0 -
.0 1 О-
'О О ON
_: х-
coss —sins I. C.75)
sin s cos s /
Поэтому естественно задать отображение л правилом
я: SUB)->SOC),
'10 О
О cost — sin/ I. C.76)
COST
\0 sin/ cost.
Ясно, что это гомоморфизм двух однопараметрических под-
подгрупп, а также что два элемента t и t + 2я из SUB) имеют
один и тот же образ в SOC). Далее, значению параметра
t -\- 4гат, где п — произвольное целое число, отвечает та же
точка из SU{2), что и значению t. Тем самым мы доказали,
что exp(//i) — двулистное накрытие exp(sLi). Это утвержде-
утверждение распространяется на всю группу: отображение
Г. ехр ( Wj + hJ2 + t3J3)^> ехр (tiLi + t2L2 + t3L3) C.77)
есть двулистное накрытие группы SOC) группой SU{2).

134
з. производные ли и группы ли
Поскольку мы знаем, что у SUB) та же глобальная топо-
топология, что у трёхмерной сферы, построенное двулистное на-
накрытие даёт возможность разобраться в топологии группы
50C). Однопараметрическая подгруппа exp(//i) в SUB)
начинается в точке е при t = 0 и возвращается в неё при
t — 4n. На рис. 3.13 эта подгруппа представлена в виде боль-
большой окружности сферы 53. (Следует, однако, помнить, что
мы не вводим метрику на группе SUB). Нас интересует
лишь топология в целом, а не
метрические отношения.) Точки,
обозначенные / и t -f- 2л, диамет-
диаметрально противоположны друг дру-
другу. Они дают одну и ту же точку
из 50C), поэтому мы просто мо-
можем считать, что 50C) — это
верхняя полусфера сферы 53, при-
причём точки экватора, находящиеся
на противоположных концах диа-
диаметра (т. е. точки t = я и / =
= Зл), отождествлются между
собой. Эта верхняя полусфера
сферы S3 с указанным отождеств-
отождествлением уже не является одно-
связной. Такую кривую, как 'g',
можно гладко стянуть в точ-
точку, а вот кривую, задаваемую
подгруппой exp(^Li), — нельзя,
поскольку диаметрально противоположные точки на экваторе
нельзя свести вместе — они всегда будут оставаться диамет-
диаметрально противоположными. Эта конструкция делает очевид-
очевидным и тот факт, что в некоторой окрестности точки е группы
50C) и StyB) тождественны. Именно поэтому у них и со-
совпадают алгебры Ли. Такая идентичность в окрестности еди-
единицы имеет место для любых двух групп с одинаковыми ал-
алгебрами Ли.
Какой же из этих двух групп соответствует алгебра Ли,
определяемая соотношением C.70)? Это всецело вопрос ин-
интерпретации. Как абстрактная алгебра Ли она соответствует
обеим группам. Как конкретную алгебру векторов в R3 её
обычно связывают с группой S0C), а именно говорят, что
подгруппе exp(QL\) (поворот на угол Э относительно оси х)
соответствует «кривая» exp(Bei) в R3 (вектор вдоль оси х
длины Э). Это сопоставление повороту вектора общепринято
у физиков, особенно когда вращение происходит во вре-
времени— тогда скорости вращения сопоставляется вектор угло-
угловой скорости. Возможность такого удобного отождествления —
чисто случайная вещь, связанная с трёхмерностью нашего
Рис. 3.13. Двумерный „срез"
пространства S3, содержащий
однопараметрическую подгруп-
подгруппу exp(tJi) группы SUB).
Группа SOC) есть верхняя по-
полусфера, причём точки на про-
противоположных концах диамет-
диаметров отождествляются.

3.17. РЕАЛИЗАЦИИ II ПРЕДСТАВЛЕНИЯ 135
пространства; группа SO D) имеет размерность 6, а размер-
размерность векторного пространства R4, на котором эта группа дей-
действует, равна 4, и здесь подобное отождествление уже невоз-
невозможно. Но вернёмся к алгебре Ли R3 (с операцией вектор-
векторного произведения). Её можно отождествить и с алгеброй
Ли группы SUB), способом, аналогичным описанному выше.
В § 3.18 мы увидим, что это даёт возможность сопоставить
спину частицы некоторый вектор в Rs, хотя спин и не яв-
является элементом из Тр для какой-либо точки Р в Rz.
Заканчивая наш разговор об алгебрах Ли, отметим, что
мы теперь в состоянии доказать, что абелева алгебра Ли —
это алгебра Ли абелевой группы Ли. Абелева алгебра Ли
размерности п — это просто векторное пространство и как та-
таковое является алгеброй Ли группы Ли R" (см. § 3.15). По-
Поскольку группа Rn односвязна, любая другая группа Ли с
той же алгеброй Ли должна накрываться группой R" и
должна быть тождественна с ней в окрестности началу коор-
координат е. Поскольку Rn — абелева группа (V -f- W = W -\- V),
абелевой будет и любая другая (связная) группа, имеющая
абелеву алгебру Ли.
3.17. РЕАЛИЗАЦИИ И ПРЕДСТАВЛЕНИЯ
Обычно всякую группу лучше всего рассматривать как
абстрактную группу, всецело определяемую групповой опера-
операцией, а в случае групп Ли ешё и структурой многообразия.
Таким образом, S0C) как абстрактная группа — это просто
определённое трёхмерное многообразие, на котором действует
определённое правило, по которому паре элементов g и h
ставится в соответствие точка gh, их произведение; это пра-
правило должно подчиняться обычным аксиомам группы. Для
физиков эта абстрактная структура— не самый интересный
аспект теории групп. Для них важнее знать, где действует
группа и как. Группа 50C) играет такую большую роль
потому, что с каждой её точкой ассоциировано вращение на-
нашего трёхмерного пространства. Такое соответствие назы-
называется реализацией группы. Точнее, реализация данной груп-
группы G — это соотнесение каждому элементу g из G преобразо-
преобразования T(g) некоторого пространства М, при котором сохра-
сохраняются групповые свойства: (i) Г(е)=/ (тождественное
преобразование, оставляющее все точки М на месте);
(ii) 7'(g-') = [7-(g)]-1; (iii) T(g)oT(h)=T(gh). Если это
соответствие взаимно-однозначно, (T(g)^=T(h) при g?=h),
то мы имеем точную реализацию. В случае когда М — век-
векторное пространство, а каждое T(g) — линейное преобразова-
преобразование (т. е. тензор типа Г ) на этом векторном пространстве)',

136 з. производные ли и группы лИ
реализация называется представлением. Поясним эти понятия
на примерах.
(i) Рассмотрим вращения единичной сферы S2, заданной
уравнением х2 -f- у2 + г2 = 1 в R3. Предположим, выполнен
поворот относительно оси х на угол 6. В результате этого по-
поворота точка на сфере, имеющая координаты (х, у, г), ото-
отобразится в точку (х\ у', г') с координатами
х' — х,
y' = ycosQ — г sine, C.78)
г' = у sin 6 + z cos Э,
по-прежнему принадлежащую нашей сфере, поскольку
(х'J -\-(у'J -\-(z'J = 1. Это преобразование отвечает эле-
элементу exp(BLi) группы 50C), в обозначениях C.63). Лю-
Любому элементу этой группы соответствует некоторое преобра-
преобразование сферы S2 в себя. Поскольку S2 — многообразие, но не
векторное пространство, мы имеем реализацию группы .50C).
Но то же самое преобразование C.78) можно рассматри-
рассматривать и как отображение всего пространства R3 в себя, а не
только сферы S2 в себя. Поскольку R3 — векторное простран-
пространство, мы получаем представление группы S0C) посредством
матриц, преобразующих векторы пространства ^3 в векторы
того же пространства. С помощью этих самых матриц мы и
определили группу S0C) в самом начале. Этот пример слу-
служит демонстрацией весьма тонкого, но полезного подхода.
Как правило, группа определяется сначала при помощи той
или иной (точной) реализации либо представления, так как
это даёт возможность конкретно изучить все свойства груп-
группы. Затем, однако, целесообразно рассматривать её как аб-
абстрактную группу, ибо могут быть и другие полезные пред-
представления или реализации, которые до сего были неизвестны.
В следующем параграфе мы укажем также представления и
реализации для группы вращения.
(i'l) У каждой группы есть по меньшей мере две точные
реализации: левый и правый сдвиги по себе. Произвольный
элемент g группы G определяет её преобразование, при ко-
котором точка h отображается в точку gh (прогрессивная, или
главная, реализация), а также преобразование, при котором
h отображается в hg-1 (регрессивная реализация).
(iiiI) Все изучавшиеся выше матричные группы: GL(nR),
0(п), SO(n), GL(n,C), U(n), SU(n)—мы изучали при по-
помощи их точных представлений в виде матричных преобразо-
преобразований и-мерных вещественных либо комплексных векторных
пространств. Но каждая группа Ли G допускает ещё пред-
') Этот пример даётся в качестве дополнительного материала

3 17. РЕАЛИЗАЦИИ и ПРЕДСТАВЛЕНИЯ 137
ставление в виде линейных преобразований на своей соб-
собственной алгебре Ли; оно называется присоединённым пред-
представлением и определяется следующим образом. Рассмотрим
сначала отображение группы G в себя Ie:hi—>ghg-x. Это —
присоединенная реализация группы G; преобразование, отве-
отвечающее элементу g, состоит в левом сдвиге на g и правом
сдвиге на g~l. (Эта реализация не обязательно точная; если
G — абелева группа, то 1е — тождественное отображение
ht~>h для всех g.) Такие преобразования называются внут-
внутренними автоморфизмами группы С Заметим, что каждое Ig
Рис. 3.14. Что происходит с кривой, проходящей через точку е, при ото-
отображении h~ -gftg, показано в два этапа. Сначала действует отображе-
отображение h (- bgh, затем gfu—>ghg~'. Единичная точка е отображается в себя,
но близкие к ней точки h и / обычно изменяются, так что касательный
вектор в точке е отображается в некоторый другой вектор.
отображает единичный элемент е в себя, так что каждая кри-
кривая, проходящая через е, отображается в кривую, также про-
проходящую через е (вообще говоря, другую), см. рис. 3.14. По-
Поэтому /g индуцирует отображение произвольного касатель-
касательного вектора из Те в касательный же вектор. Это отображе-
отображение, обозначаемое через Adg, называется присоединённым
преобразованием пространства Те, индуцированным элемен-
элементом g. Если кривая, изображённая на рис. 3.14 сплошной ли-
линией, есть, скажем, однопараметрическая подгруппа ехр(^),
где X принадлежит Те, то её образ при действии внутреннего
автоморфизма Ig будет тоже однопараметрической подгруп-
подгруппой, поскольку g(fh)g~l = (gfg-*) {ghg-1). Следовательно,
штриховая кривая на рис. 3.14 есть однопараметрическая
подгруппа, порождённая вектором Adg(Z):
/g[exp(^)]=exp[?Adg(*)]. C.79)
Если элемент g сам принадлежит некоторой однопараметри-
однопараметрической подгруппе g(s) = exp(sF), то вектор Adg(Z) должен

138
3. ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ
некоторым естественным образом выражаться через У. Такое
выражение для Айв(Х) дано в следующем упражнении.
Упражнение 3.23. Покажите, что
Ads ,„ (X) = exp (s??) X. C.80)
3.18. СФЕРИЧЕСКАЯ СИММЕТРИЯ, СФЕРИЧЕСКИЕ ГАРМОНИКИ
И ПРЕДСТАВЛЕНИЯ ГРУППЫ ВРАЩЕНИЙ
Выше мы рассматривали векторы Киллинга и их связь
с симметриями эвклидова пространства. Конкретизируем те-
теперь эти понятия на примере сферической симметрии. Гово-
Говорят, что многообразие М с метрическим тензором g обладает
сферической симметрией, если алгебра
Ли её векторных полей Киллинга со-
содержит в качестве подалгебры (т. е.
подпространства, скобки элементов ко-
которого снова принадлежат ему же) ал-
алгебру Ли группы SO C). О подалгебре
приходится говорить, так как тензор
g может иметь и другие симметрии;
нас же интересуют здесь только те,
которые связаны с его сферической
природой. Обратим внимание читателя,
что было бы неверно говорить, что М
сферично «относительно некоторой
точки», так как «центры» соответ-
соответствующих сфер могут и не принадле-
принадлежать М (см. рис. 3.15). Наше опреде-
определение является внутренним: указанная выше подалгебра Ли
определяется через векторные поля на самом многообразии М.
В § 3.9 было показано, что алгебра Ли векторных полей
{h, 1у, 1г} задаётся соотношениями C.30). Полагая Vi = —1Х,
р2 = —}у и Fj = —/2, мы видим, что алгебра Ли векторных
полей {Vz} тождественна алгебре Ли группы 50C), зада-
задаваемой соотношениями C.64). Отсюда следует, что данное
нами определение сферической симметрии влечёт существо-
существование слоения многообразия М, слои которого имеют геомет-
геометрию сферы (определение слоений см. в § 3.7).
Рассмотрим теперь функции, определённые на двумерной
сфере S2. Всякая функция на М задаёт такую функцию на
каждой из её сфер — слоев симметрии. Определим простран-
пространство функций L2(S2) как гильбертово пространство всех
комплекснозначных квадратично-интегрируемых функций на
S2, т. е. функций, для которых существует
Рис. 3.15. Цилиндриче-
Цилиндрическая поверхность имеет
осевую симметрию, но
центры окружностей
симметрии не принадле-
принадлежат этой поверхности.

^_ 318 СФЕРИЧЕСКАЯ СИММЕТРИЯ 139
(норма /), где интеграл берётся по обычному элементу пло-
площади сферы. (Наше определение этого пространства не сов-
совсем аккуратно, но достаточно для тех целей, которые стоят
перед ними.) Пространство L2{S2) есть бесконечномерное
векторное пространство. Его элементами являются функции,
линейные комбинации которых берутся с произвольными по-
постоянными коэффициентами; никакое конечное множество
функций не образует базиса. Реализация элемента g группы
50C) как отображения R(g) сферы 52 порождает отобра-
отображение, переводящее произвольную функцию f(x') на сфере
в другую функцию на сфере, получаемую простым сдвигом
аргумента. Тем самым R(g) определяет представление группы
S0C) в векторном пространстве L2(S2),h это представление
будет уже бесконечномерным, поскольку L2(S2) бесконечно-
бесконечномерно. Возникает вопрос, существуют ли конечномерные под-
подпространства пространства L2(S2), также дающие представле-
представления группа S0C)? Каждое такое подпространство должно
быть инвариантным относительно группы 50C) в том смысле,
что функция R(g)[f] для любого элемента g из S0C) и лю-
любой функции /, принадлежащей этому подпространству, снова
должна принадлежать ему. Поедположим, такое подпростран-
подпространство существует и функции {/,, i = 1, ..., N} образуют его
базис. Это подпространство инвариантно тогда и только тогда,
когда для произвольных чисел {а1} существуют числа {Ь1},
такие что
R(g)[u>f,] = b% C.82)
Поскольку рассматриваемое отображение линейно, имеет
место соотношение
Ь' = gl,a>, C.83)
которое определяет матрицу g',t соответствующую элементу
g группы S0C). Эта матрица и будет представлением эле-
элемента g в данном подпространстве. Будем говорить, что пред-
представление группы 50C) в векторном пространстве V (а так-
также и само V) неприводимо, если V не содержит ни одного
конечномерного подпространства, инвариантного относи-
относительно S0C).
Конструкция неприводимых представлений группы 50C)
в подпространствах L2E2) описана во многих работах
(см. Гельфанд, Минлос и Шапиро, 1963). Базисные функции
неприводимых подпространств хорошо известны всем физи-
физикам как сферические гармоники Уш- Мы не будем зани-
заниматься построением этих гармоник, а просто попытаемся ис-
истолковать их в наших терминах. Утверждается следующее.
Каждое неприводимое подпространство пространства L2E2)
характеризуется некоторым целым числом /^0 и имеет раз-

140 3 ПРОИЗВОДНЫЕ ЛИ II ГРУППЫ ЛИ
мерность, равную 21+ 1. Функции {Ytm, m = —I, ..., /} суть
базисные функции для этого подпространства, которое мы
обозначим через V/. Далее, объединение всех этих базисов
для всех / служит базисом для самого пространства L2{S2)\
другими словами, сферические гармоники образуют полную
систему функций. Поскольку любое отображение R(g) сферы
S2 в себя является экспонентой от некоторой линейной ком-
комбинации векторов {2х,1у,1г}, подпространство Vi инвариантно
относительно группы 50C) тогда и только тогда, когда оно
инвариантно относительно 1Х, 1У и 1г. В тривиальном случае
/ = 0 базисная функция УОо = 1 имеет производные Ли
h(YOD)=Jy(Y0o)=U(Yoa)=0,
которые, разумеется, все линейно-зависимы с Yoo. Более со-
содержателен случай / = 1, где мы имеем три базисные функ-
функции
C.84)
Упражнение 3.24. (а) Покажите, что если х, у, г — декар-
декартовы координаты в R3, то на сфере S2, определяемой урав-
уравнением х2 + у2 + z2 = 1, выполняются следующие соотно-
соотношения:
з
(b) Вычислите все производные l,Ylk, в частности про-
проверьте, что
и^-1) = -'Т10/21/2, /1(У11) = 1У11, C.86)
и убедитесь, что пространство Y\ инвариантно относитель-
относительно 50C).
Почему для V\ берётся именно этот базис' В основном
ради удобства. Удобно, когда базис состоит из собственных
функций относящихся к делу операторов, т. е. функций, удов-
удовлетворяющих соотношению
Af = af, C.87)
где А — рассматриваемый оператор, а а — константа. Сфери-
Сферические гармоники пользуются предпочтением потому, что они
являются собственными функциями одновременно для опера-
оператора lz и оператора L2 = (o6ixJ + (?j J + (?:гJ> °преде-

3 18 СФЕРИЧЕСКАЯ СИММЕТРИЯ 141
ленного в упр. 3.7. Следующее упражнение показывает, что
это большее, на что можно рассчитывать: нельзя найти не-
нетривиальные собственные функции сразу для двух из опера-
операторов {7*, lv, Ц.
Упражнение 3.25. Предположим, что функция / удовлетво-
удовлетворяет условиям
U(f) = af, lv(f)=№
где а и |3 — некоторые константы. Используя C.30), пока-
покажите, что
Между прочим, полнота системы сферических гармоник
проистекает из того факта, что Пг и L2 — коммутирующие
операторы (см. упр. 3.7), которые являются самосопряжён-
самосопряжёнными операторами в L2(SZ) (точнее, могут быть «расширены»
до таких операторов). Спектральная теорема из функцио-
функционального анализа (см. Рисе и Сёкефальви-Надь, 1979) гаран-
гарантирует полноту системы их собственных функций.
В действительности представления группы SOC) можно
изучать гораздо более абстрактно, чем мы это делали выше.
В частности, для того чтобы развить большую часть относя-
относящейся сюда алгебры, нет нужды знать, что представляет
собой векторное пространство V. Например, наше исходное
представление группы SOC) в виде матриц, преобразующих
векторы пространства R3, безусловно неприводимо, поскольку
ни одно подпространство в R3, за исключением тривиального
подпространства {0}, не является инвариантным относитель-
относительно вращений. Оказывается, это представление формально
идентично представлению в пространстве, порождённом сфе-
сферическими гармониками с /== 1, размерность которого также
равна трём (=2/+1). Фактически соотношения C.85) — это
просто преобразование координат в R3, от (х, у, z) к (Fi-ь
Yiq, Yu). В это преобразование входят комплексные числа, но
если подходить к делу формально алгебраически, то матрицы
gli (см. C.83)). отвечающие базису из сферических гармо-
гармоник, можно преобразовать в матрицы, отвечающие обычному
декартову базису, и окажется, что это будут именно те мат-
матрицы, с помощью которых мы в самом начале определили
группу SOC).
Упражнение 3.26. Пусть {yi', /=1, 2, 3} обозначают функ-
функции (Y\-u Yio, Yu), а {х'}—функции {x,y,z}. Найдите
матрицу перехода A'"ft = dyi'/dxk и её обратную Akf. Ис-
Используя метод упр 3.24 (Ь), найдите матрицу Х1\> опе-
оператора 1Х в базисе сферических гармоник:

142 3 ПРОИЗВОДНЫЕ ЛИ II ГРУППЫ ЛИ
Вычислите, во что перейдет матрица Х!'к- при переходе
к декартовому базису:
и убедитесь, что получится в точности матрица —L\ (см.
C.63)).
Отметим, что представление, отвечающее /— 1, есть наи-
наименьшее точное представление группы SOC) (представле-
(представление, отвечающее 1 = 0, очевидно, не является точным). Его
обычно называют фундаментальным представлением группы
50C). В § 4.29, посвященное векторным сферическим гармо-
гармоникам, мы познакомимся ещё с одним множеством неприво-
неприводимых представлений группы S0C). Там пространство пред-
представления будет уже не пространством функций на сфере, а
пространством векторных полей на сфере.
И наконец, следует сказать несколько слов относительно
связи между представлениями группы S0C) и накрывающей
её группы SUB). (Те читатели, которые не проштудировали
§ 3.16, смело могут пропустить это место.) Поскольку суще-
существует единственный элемент группы 50C), ассоциирован-
ассоциированный с данным элементом группы SUB), то всякое представ-
представление R группы S0C) автоматически определяет представ-
представление 5 группы SUB): для произвольного элемента и из
SUB) в качестве преобразования 5(«) берём R(n(u)). Если
элементам и и и' отвечает один и тот же элемент группы
S0C), то для так построенного представления 5(«) —5(и').
Но у SU{2) имеются и другие представления, скажем Т, для
которых Т(и)фТ(и'), даже если л(и) = л(и'). Эти пред-
представления иногда называют двузначными представлениями
группы 50C). Снова мы просто приведём здесь результат:
неприводимые представления группы SUB) определяются ин-
индексом /г ^ 0, который может быть либо целым, либо по-
полуцелым числом. Те представления, для которых k — целое
число, являются представлениями группы 50C), отвечаю-
отвечающие тому же индексу (т. е. l = k). Прочие представления
суть двузначные представления группы 50C). Примером та-
такого двузначного представления может служить матричное
представление в двумерном комплексном пространстве, ко-
которое мы использовали для определения группы 5?/B).Для
этого представления k=-^, и называется оно спинорным
представлением со спином -%. Подобно представлению с / = 1
для группы 50C), данное представление является наимень-
наименьшим точным представлением для группы SLJB). Если взять
произвольный базисный вектор в пространстве этого пред-
представления (называемый спинором) и подействовать на него
однопараметрической подгруппой exp(tJ\), где t пробегает

3 19 БИБЛИОГРАФИЯ 143
значения от 0 до 4л, то, как нетрудно видеть, соответствую-
соответствующий путь в 50C), а именно exp(tLi) дважды пройдет от О
до 2л: когда мы дойдем до значения t = 2л, мы вернёмся
опять в начальную точку в группе S0C), но в группе SUB)
мы окажемся в точке —е. Поэтому говорят, что при повороте
на угол 2л спинор меняет знак (е-» е).
Поистине удивительно, что описанное выше соответствие
между представлениями — не просто математическая забава
Волновая функция элементарной частицы со спином -% есть
элемент пространства неприводимого представления группы
SUB) для соответствующего полуцелого k. Вот пример того,
что физик назвал бы изумительной простотой природы. Мы
начинаем с алгебры Ли группы вращений и находим, что
простейшей из групп, имеющих ту же алгебру Ли, т е. наи-
наиболее просто устроенной топологически, будет SUB), а не
50C). А затем мы находим, что, несмотря на трудности на-
наглядного представления действия группы SUB) в Rs, при-
природа посчитала именно её более фундаментальной, создав
частицы, соответствующие тем из её представлений, которые
не являются представлениями группы 50 C)!
3.19. БИБЛИОГРАФИЯ
Нсскочько старомодное, та весьма полное изложение теории произ-
производных Ли дает книга К Yano, The Theory от Lie Derivatives and its Ap-
Applications (North Holland, Amsterdam, 1955)
Теоремы о полноте для самосопряженных операторов можно найти в
«Лекциях по функциональному анализу» Ф Рисса и Б Сёкефальви-Надя
(М Мир, 1979)
Анализ тесной взаимосвязи, существующей между группами Ли и про-
производными Ли, дай в книгах F W Warnei, Foundations of Differentiate
Manifolds and Lie Groups (Scott, Foresman, Glenview, 111, 1971), M Spivak,
A Comprehensive Introduction to Differential Geometry (Publish or Perish,
Boston, 1970), vol 1, L Auslander & R E Mac Kenzie, Introduction to Dif-
ferentiable Manifolds (McGraw Hill, New York, 1963)
Более подробную информацию о группах Ли можно найти в моногра-
монографиях R Hermann, Lie Groups for Physicists (Benjamin, Reading, Mass,
1966) или Н Weyl, The Theory of Groups and Quantum Mechanics (Do-
(Dover, New York, 1950) Теория представления для наиболее важных групп
излагается в большинстве руководств по квантовой механике, например в
указанной выше книге Г Вейля, см также Н Lipkm, Lie Groups for Pe-
Pedestrians (North-Holland, Amsterdam, 1966), M А Наймарк, Линейные
представления группы Лоренца (М Физматгиз, 1958), И М Гельфаид,
Р. А Минлос и 3 Я Шапиро, Представления группы вращений и группы
Лоренца и их применения (М Физматгиз, 1958)
Полезным справочным пособием по матричной алгебре, на которое
мы неоднократно ссылались, является книга М W Hirsch, & S Smale, Dif-
Differential Equations, Dynamical Systems, and Linear Algebra (Academic
Press, New York, 1974).

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Исчисление дифференциальных форм, созданное в начале
этого века Э. Картаном, — один из наиболее полезных и пло-
плодотворных аналитических методов в дифференциальной гео-
геометрии. Перечень понятий, унифицированных и упрощённых
благодаря введению этих форм, поразителен: теория интегри-
интегрирования на многообразиях, векторное произведение, диверген-
дивергенция и ротор в трехмерной теории поля, определители матриц,
ориентируемость многообразий, условия интегрируемости для
систем дифференциальных уравнений в частных производных,
формула Стокса, формула Гаусса •> и ещё многое другое. Как
и в случае большинства действительно фундаментальных ма-
математических и физических понятий, математика дифферен-
дифференциальных форм очень проста. В этой главе мы сначала вве-
введём дифференциальные формы в том геометрическом контек-
контексте, в котором они возникают наиболее естественным обра-
образом, а затем на глазах читателя теория дифференциальных
форм (или просто форм) будет постепенно набирать свою
силу.
А. АЛГЕБРА И ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ ШОРМ
4.1. ОПРЕДЕЛЕНИЕ ОБЪЕМА:
ГЕОМЕТРИЧЕСКАЯ РОЛЬ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
До сих пор мы избегали «придавать» нашим многообра-
многообразиям какую-либо форму или жёсткость. Мы отметили, правда,
возможность введения метрических тензоров, но всё наше
внимание было сосредоточено на аналитических структурах,
которые можно было определять, не прибегая к метрике. Те-
Теперь мы обратимся к изучению одного чрезвычайно полезного
класса тензоров, а именно тензоров, с помощью которых
можно определять элементы объёма на многообразиях.
Рассмотрим объём в двумерном случае, называемый в этом
случае площадью. Любая пара (бесконечно малых) векторов
*> В отечественной литературе называемая также формулой Гаусса —
Остроградского. — Прим. ред.

4.1. ОПРЕДЕЛЕНИЕ ОБЪЁМА: ГЕОМЕТРИЧЕСКАЯ РОЛЬ ФОРМ 145
в эвклидовом пространстве определяет некоторую (бесконеч-
(бесконечно малую) площадь, а именно площадь, ограниченную парал-
параллелограммом, построенным на этих векторах (рис. 4.1). Одна
и та же площадь задаётся многими различными парами век-
векторов, которые могут отличаться друг от друга как длиной
Рис. 4.1. Две пары векторов и определяемые ими площади.
векторов, так и величиной угла между ними (рис. 4.2). От-
Отсюда видно, что площадь — понятие менее жёсткое, чем
метрика, ибо эвклидова метрика однозначно определяет и
длины векторов, и величину угла, заключённого между ними,
а площадь даёт всего лишь одно число, отвечающее двум за-
заданным векторам. Естественно, если метрика есть, то она
однозначно определяет и плошадь; позже мы покажем, как
/
1
Рис. 4.2. Три пары векторов, определяющие равные площади.
это происходит. Но для определения площади на двумерном
многообразии (либо объёма на произвольном многообразии)
вовсе не обязательно определять метрику на этом многообра-
многообразии. В самом деле, многие различные метрики могут опреде-
определять один и тот же объём.
Предположим, в некоторой точке двумерного многообра-
многообразия мы имеем два линейно-независимых бесконечно малых
вектора. Рассмотрим построенный на них параллелограмм.
Мы хотим приписать этой фигуре (малую) площадь, т. е.
двум заданным векторам сопоставить некоторое число. Это
число должно удваиваться, если будет удвоена длина одного
из векторов; кроме того, оно должно обладать свойством
аддитивности относительно сложения векторов, т. е. должно
выполняться соотношение
площадь (а, В) + площадь (а, с) = площади (а, В + с).
То что это соотношение выполняется для эвклидова про-
пространства, доказано геометрически на рис. 4.3. На предпо-

146 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
следнем шаге используется тот факт, что площадь паралле-
параллелограмма останется неизменной, если одну из его сторон
сместить на любое расстояние вдоль прямой, которую она
определяет. Таким образом, мы доказали, что площадь (,)
а
площадь (а,Ъ)
площадь (а,Ь+с)-
иплощадь(а,Ь) + площадь {а,с),
Рис. 4.3. Геометрическое доказательство того факта, что площадь парал-
параллелограмма является значением тензора.
билинейна по своим аргументам, т. е. является тензором. По-
Поскольку площадь — число, это тензор типа ( J . Далее, если
а и Б параллельны, площадь по-
ч строенного на них параллело-
\ грамма обращается в нуль. От-
^W сюда вытекает, что если а к Б
поменять местами, то наш тен-
Рис. 4.4. Площадь, определяв- зор должен изменить знак; этот
мая векторами v и W. факт доказывается в следующем
упражнении.
Упражнение 4.1. Докажите, что если В—тензор типа
( 2J, такой что В(Р, F) = 0 для всех V, то В (О, W) —
— В W, U) для всех О, W. (Указание: положите V =
D + V^.) Тензор В с таким свойством называется антисим-
антисимметричным (или кососимметричны,м) по своим аргументам.
Остановимся на этом поподробнее. На рис. 4.4 изображены
два вектора, задающие параллелограмм определённой пло-
площади. Эта площадь, выраженная через координаты векторов,
как известно, равна (с точностью до знака) следующему

4.2. АНТИСИММЕТРИЧНЫЕ ТЕНЗОРЫ 147
определителю:
Vх Vv
площадь =
Антисимметричность относительно V и W очевидна.
Обычно в приложениях знак игнорируют и под площадью
понимают абсолютное значение указанного выше определи-
определителя. Но нам будет удобнее сохранить знак, так как он даёт
информацию о том, какую ориентацию, правую или левую,
имеет заданная пара векторов. Позже мы будем подробно
говорить об этом. Кроме того, мы детально исследуем связь
между тензорами объёма и определителями матриц. Но
прежде нам надо построить алгебру антисимметричных тен-
тензоров. Сначала мы рассмотрим свойства таких тензоров в
произвольной фиксированной точке, а затем обобщим полу-
полученные результаты на тензорные поля.
4.2. ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ, КАСАЮЩИЕСЯ
АНТИСИММЕТРИЧНЫХ ТЕНЗОРОВ
Напомним ещё раз (см. упр. 4.1) что тензор типа ( J
называется антисимметричным, если при перестановке аргу-
аргументов его знак изменяется, т. е.
со антисимметричен <?=>-й(?/, V) =
—5>(V, U) для всех U, V. D.1)
Тензор типа ( ), р^З, называется антисимметричным,
если при перестановке любых двух своих аргументов он ме-
меняет знак. Из всякого тензора можно построить антисимме-
антисимметричный — его так называемую антисимметричную часть. На-
/0 \ _ /0 \
пример, если со — тензор типа I „ I, а р — тензор типа II,
то их антисимметричные части задаются формулами
¦ сод Ф, V) = ±- [со (V, 1/1 - со (V, О)], D.2)
¦ рА (U, V, W)=± [р Ф, V, W)+p (V, W,U) + p (W, U, ~V)
-p(V,U,W)-p(W, V,U)-pФ, W, V)]. D.3)
Общее правило состоит в том, что должны учитываться все
перестановки аргументов, причём нечётные перестановки бе-
берутся со знаком минус, а чётные — со знаком плюс. Множи-
Множители 1/2! и 1/3! суть традиционные нормировочные множи-

148 4 ДПФФЕРГНЦШЛЬНЫЕ ФОРМЫ
тели, позволяющие называть йд антисимметричной частью
тензора й В индексных обозначениях формулы D.2) и D.3)
перепишутся в виде
D.4)
y11, D.5)
Квадратные скобки [t ... k] используются для краткой
записи процедуры антнсимметризации, включая нормировоч-
нормировочный множитель В дальнейшем мы постоянно будем использо-
использовать это обозначение. Буква с волной над ней, например р,
всегда обозначает антисимметричный тензор. Один-формы,
для которых мы уже давно используем обозначение с вол-
волной, — «вырожденный» частный случай антисимметричных
тензоров, — у них всего один аргумент.
Упражнение 4.2. (а) Докажите, что если компоненты тен-
тензора р типа f v J антисимметричны относительно любой
пары индексов, то р — антисимметричный тензор.
(b) Пусть {Л,/%}—компоненты некоторого антисим-
антисимметричного тензора Покажите, что
(c) Пусть А — антисимметричный тензор типа (9)> а
В—произвольный тензор типа @ )¦ Покажите, что
т. е. что в свёртке А с В участвует лишь антисимметрич-
антисимметричная часть тензора В.
(d) Пусть тензор А тот же, что и в (Ь), а В — сим-
симметричный тензор типа Г „ J, т. е. В(й, 6) = В (а, со) для
любых один-форм й и а. Покажите, что
AtlB4 = 0. D.6)
Антисимметричные тензоры обладают следующим важным
свойством: антисимметричный тензор типа f J на п-мерном
векторном пространстве (р ^ п) имё|рт не более чем
15 У нас принято обозначать эту величину через С^. — Прим. ред.

4.3. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ 149
независимых компонент. Чтобы доказать это, заметим, что
всякая ненулевая компонента нашего тензора определяется р
различными числами, выбираемыми из множества A, ..., п).
(Числа должны быть попарно различными, ибо при любых
двух равных индексах компонента антисимметричного тензора
обращается в нуль; ср. с упр. 4.1.) Порядок, в каком выбраны
эти р чисел, т. е. порядок индексов компоненты, влияет самое
большее на её знак, следовательно, все компоненты, индексы
которых являются перестановками заданного множества р
чисел, можно считать известными, если известна хотя бы
одна из них. Таким образом, число независимых компонент
равно числу различных наборов из р чисел, выбранных из
множества п чисел, а это как раз и есть биномиальный коэф-
коэффициент, указанный выше.
Упражнение 4.3. Докажите, что если р > п, то все компо-
ненты антисимметричного тензора типа I J на п-мерном
векторном пространстве равны нулю.
4.3. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Дифференциальная форма степени р, или, короче, р-форма
(р^2), — это, по определению, антисимметричный тензор
типа ( ] . Как уже было определено ранее, один-форма —
это тензор типа ( J. Скалярные функции называются нуль-
нульформами.
Упражнение 4.4. Покажите, что множество всех р-форм
фиксированной степени р само является векторным про-
пространством относительно операции сложения, определён-
определённой в упр. 2.4. Следовательно, оно является подпростран-
подпространством пространства всех тензоров типаГ J. Какова его
размерность?
Точно так же, как тензоры типа ( „ J можно получать из
тензоров типа ( ) при помощи операции взятия тензорного
произведения <8>, так и два-формы можно строить из один-
форм при помощи операции Л (называемой операцией взятия
внешнего произведения), которую мы сейчас и определим.
Если р и q — один-формы, то их внешнее произведение за-
задаётся формулой
р Ag = p®q — q®p. D.8)

150 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
В отличие от формулы D.2) множитель 1/2! здесь отсут-
отсутствует]
Упражнение 4.5. Проверьте, что р A q есть два-форма. По-
Покажите, что р А р = 0.
Упражнение 4.6. Пусть {ё;, i= 1, ..., п) — базис данного
векторного пространства, а {й'}—двойственный ему ба-
базис один-форм. Покажите, что {й'Лй*, /, k—l, ..., п)
будет базисом векторного пространства всех два-форм.
Указание: для произвольной два-формы а рассмотрите
числа ач = а(ё,, ё,) и покажите, что
Л&'. D.9)
Обратите внимание на множитель 1/2! в D.9); он обуслов-
обусловлен тем, что в рассматриваемую сумму по (i, /) равный вклад
вносят со' <8> й' и й' ® й'. Появление этого множителя именно
здесь объясняется тем, что мы не ввели его в определение
внешнего произведения (см. D.8)), как это делается в неко-
некоторых руководствах. Это дело вкуса.
Формула для внешнего произведения естественным обра-
образом распространяется на три-формы:
р A(q Лг) = (р Л q) Лг=р Л q Л?
= p®q®>r + q®r®>p+— ...; D.10)
фигурирующие здесь перестановки и знаки те же, что и в пре-
предыдущем параграфе. Заметим, что эта формула и её обобще-
обобщение на случай любого конечного числа один-форм позволяют
определить внешние произведения для произвольных р- и
<?-форм, ибо, согласно упр. 4.6, произвольную р-форму можно
представить в виде линейной комбинации внешних произве-
произведений р один-форм (базисных один-форм).
Множество всех форм любой степени, снабжённое анти-
антикоммутативным умножением Л, называется алгеброй Грас-
смана (или грассмановой алгеброй).
Упражнение 4.7. Покажите, что сумма размерностей всех
пространств р-форм, р ^.п, равна 2". (Указание: исполь-
используйте биномиальную теорему.) Такова размерность про-
пространства грассмановой алгебры. )
Упражнение 4.8. Покажите, что если р — один-форма, а
q — два-форма, то
(Р A q)ijk = Pflik + Pfikt + Pfftn = Зр,^/Ч.

4 4. ОБРАЩЕНИЕ С ДИФФЕРЕНЦИАЛЬНЫМИ ФОРМАМИ 151
Вообще покажите, что для любых р-формы р и #-формы q
4.4. ОБРАЩЕНИЕ С ДИФФЕРЕНЦИАЛЬНЫМИ ФОРМАМИ
Алгебра форм достаточно проста, сложности связаны лишь
с необходимостью следить за знаками и факториалами. Как
будет видно из этого и последующих параграфов, лучший спо-
способ прийти к правильному результату — это действовать тща-
тщательно и неторопливо. Например, выведем правило коммута-
коммутации форм. Если р — р-форма, a q— g-форма, то
¦ p/\q = (—\)Mq/\p. D.12)
Чтоб убедиться в этом, представим р и q в виде суммы компо-
компонент, умноженных на внешние произведения форм б' Л ...
... Au;H6ftA ... Ли1 (р и q множителей в каждом внеш-
внешнем произведении соответственно), и покажем, что D.12)
выполнено для каждого простого произведения
(<Ь1 Л ... Л 3') Л (со* Л • • • Л со').
В силу ассоциативности внешнего произведения скобки в
этом выражении можно опустить. Если переставить два лю-
любых множителя (например, 5>' и со*1), то выражение
изменит знак. Переставляя со' с q множителями coftA ...
... Л й', мы изменим знак q раз, и в итоге
со' Л ... Л со'' Л coft Л ... Л со' =
= (-1)9со' Л •.. Л coft Л • • • Л &1 Л ©'_
Проделав то же самое с каждым из р множителей со' Л ...
...Л со', получим требуемый множитель [(—1)<7]р, что и до-
доказывает D.12).
В дальнейшем нам понадобится операция свёртки вектора
с формой. Чтоб получить из р-формы вещественное число,
требуется р векторов. Если же подставлен только один аргу-
аргумент, то р-форма превратится в (р—-1)-форму. А именно,
определим (р— 1)-форму, полученную свёрткой р-формы ее с
вектором |, следующей формулой:
¦ й(|) ^й (I, vLJ;;:j ), [5AI, ...* = «„...*б'- D-13)
р — 1 пустых мест
Заметим, что если мы поставим g вместо первого на какое-то
другое место, то это скажется только на знаке сс(|). Чтоб
понять, как это происходит, рассмотрим а = р Л q, где р и

152 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
q— 1-формы:
Таким образом, хотя ?, свёртывается с первым аргументом
р Л q, перестановки, которых требует операция внешнего про-
произведения, приводят к тому, что g свёртывается с каждой из
1-форм, входящих в это произведение. Аналогично для произ-
произведения р штук 1-форм мы находим
(й'Лй'Л.-. Л ю*)(|) = 1'й' Л ... Л со*
- g's' л ... л 6>k + ...
± |*©' Л &' Л •..
= р|['з'Л... Л©*1- D.14)
Из этой формулы и обобщения формулы D.2) следует, что
если а — р-форма, то
Этот ответ, конечно, прямо следует из D.13) и D.9). Анало-
Аналогично если ее — произвольная форма, а C — р-форма, то
¦ (РЛб)Ш = рA)б + (-1)рРЛбA). D.16)
Это можно доказать, рассматривая опять каждую компоненту
Р Л ее по отдельности.
Упражнение 4.9. Докажите D.16).
Для б(|) широко применяется и другое обозначение: ?j б
4.5. ОГРАНИЧЕНИЕ ФОРМ
Элементарным, но важным является понятие ограничения
(сужения) формы на подпространство исходного векторного
пространства V. Поскольку р-форма есть тензор типа f J,
её областью определения служит множество всех векторов
из V (точнее, областью определения служит произведение
^Х^Х ... УСУ р экземпляров пространства V). Ограниче-
Ограничение (или сужение) а на подпространство W пространства V —
это та же самая р-форма а, только её область определения
ограничена векторами из W. Мы обозначаем, её сс|ц?:
a\w(X, ..., ?)=а(Х, ..., У),
где все X, ..., Y — из W. Таким образом, форма a\w опреде-
определена лишь на W. Заметим, что если размерность W т меньше
р, то сужение а|к—просто нуль (при pi> m любая р-форма

I7" ОРИЕНТИРУЕМОСТЬ \53
на m-мерном пространстве — нулевая), а если р = т, то
a|iF имеет одну независимую компоненту. Операцию сужения
часто называют «сечением», поскольку наглядно векторное
подпространство W можно представлять себе в виде пло-
плоскости, рассекающей семейство поверхностей, представляю-
представляющих форму. Говорят, что форма аннулируется векторным
пространством, если её сужение на это пространство обра-
обращается в нуль.
4.6. ПОЙЯ ФОРМ
Как и для всякого тензора, поле р-форм на многообразии
М есть правило (удовлетворяющее соответствующим усло-
условиям дифференцируемости), сопоставляющее каждой точке
многообразия М р-форму. Поэтому все сделанные нами
раньше замечания применимы к формам, рассматриваемым
как функции на пространстве ТР в каждой точке Р многооб-
многообразия М. Лишь один пункт нуждается в уточнении: поскольку
любое подмногообразие 5 выделяет в каждой точке Р, при-
принадлежащей S, подпространство Vp касательного простран-
пространства ТР, мы определим сужение поля р-форм а на 5 как
поле, образованное сужением а на VP в каждой точке Р. Для
случая 1-форм мы уже имели пример такого сужения в § 3.6.
4.7. ОРИЕНТИРУЕМОСТЬ
На любом n-мерном многообразии пространство «-форм
в каждой точке одномерно (см. D.7)). Выберем некоторое
поле n-форм и обозначим его й- Рассмотрим векторный базис
{ёь ..., ёп) в точке Р. Поскольку векторы базиса линейно-
независимы, то со(ei, ..., ёп) отлично от нуля тогда и только
тогда, когда со -ф О в точке Р. Поэтому й делит множество
всех базисов в точке Р на два класса: базисы, на которых й
положительна, и те, на которых она отрицательна. На самом
деле эти классы не зависят от конкретного выбора формы со.
А именно, если со'— другая n-форма, отличная от нуля в точ-
точке Р, то существует число f?=0, такое что со' = /со. Если со
положительна на каких-то двух базисах, то и со' будет иметь
на них один и тот же знак (плюс, если / > 0, и минус, если
/ < 0) и оба базиса опять-таки окажутся в одном классе.
Итак, все базисы в данной точке попадают в один из двух
классов-.правозакрученные и левозакрученные. (Как называть
какой класс, конечно же, вопрос соглашения; важно то, что
сами классы чётко определены.) Многообразие называется
(внутренне) ориентируемым, если возможно определить за-
крученность согласованно (т. е. непрерывно) на всём много-

]54 4- ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
образии, иными словами, если существует п непрерывных
векторных полей {ei(P), ..., ёп(Р)\, таких что в каждой
точке Р они образуют базис одной и той же ориентации. По-
Понятно, что это эквивалентно существованию n-формы, всюду
непрерывной и отличной от нуля. Эвклидово пространство
ориентируемо, лист Мёбиуса нет.
4.8. ОБЪЕМЫ И ИНТЕГРИРОВАНИЕ
НА ОРИЕНТИРУЕМЫХ МНОГООБРАЗИЯХ
Вспомним, что формы связаны с элементом объёма. На
п-мерном многообразии набор из п линейно-независимых
«бесконечно-малых» векторов определяет область ненулевого
объёма, п-мерный параллелепипед. Объём этой области есть
значение я-формы. Можно выбрать любую n-форму в каче-
качестве формы объёма; этот выбор диктуется лишь рассматри-
рассматриваемой задачей.
Интегрирование функции на многообразии сводится по су-
существу к умножению значения функции на объём малого
координатного элемента, а затем к суммированию полученных
чисел. Возвращаясь к форме объёма, введем удобные обозна-
обозначения. Пусть со — это п-форма в области U «-мерного много-
многообразия М с координатами {х1, ..., хп}. Тогда, поскольку
все п-формы в данной точке образуют одномерное векторное
пространство, существует некоторая функция fix1 х"),
такая что
й = \йхх Л ... Л Зхп.
Чтоб проинтегрировать по области U, разобьём её на малень-
маленькие области («ячейки») — параллелепипеды, построенные на
п векторах {Аххд/дх1, ..., Ахпд/дхп}, где {Ах1}—малые чис-
числа. Интеграл функции f по одной ячейке аппроксимируем зна-
значением f, умноженным на произведение
.. Ax" = SxIA ... /\йхп(Аххд/дх\ ....
Ах"д/дхп).
Таким образом,
f(xl х") as S (ячейка). D.17)
ячейка
Просуммировав по всем ячейкам и взяв предел при стремя-
стремящемся к нулю размере ячейки, мы получим то, что будем
называть интегралом о по U:
+ (j й = \f(xl, ..., xn)dxl ...dx", D.18)

4.8. ОБЪЁМЫ И ИНТЕГРИРОВАНИЕ 155
где в правой части равенства стоит обычный интеграл диф-
дифференциального исчисления, а в левой части — наше новое
обозначение. Поскольку левая часть не зависит от координат
явно, то надо доказать, что она действительно не зависит от
выбора системы координат на U. Мы ограничимся в нашем
доказательстве случаем двух измерений, поскольку общий
случай из него тривиально вытекает. Рассмотрим координаты
Я, и |я. Тогда
Если перейти к другим координатам х и у, то из определения
д.К как градиента и правила дифференцирования сложной
функции следует, что
Итак, мы получаем (напомним, что dx Л dx = О в силу анти-
антисимметричности)
ь л fr_(?;u+? а») л (?а*+Ц«О
= (l7^---5757)dxAdi/.J D.19)
Множитель перед dx /\dy — это якобиан преобразования ко-
координат д(Я,, \\)/д(х, у). Мы знаем из обычного интеграль-
интегрального исчисления, что именно так и должен преобразовываться
элемент объёма. Таким образом, (К, ц) -интеграл от f связан
с. (х, у) -интегралом в точности так, как надо.
Однако значение \ й не является совершенно нечувстви-
нечувствительным к выбору исходной системы координат. Мы показали
лишь то, что оно не меняется при преобразованиях коорди-
координат, но уже в самой формуле D.17) имеется неопределённость
в знаке. На этой формуле основано само определение \ й,
и, следуя ему, мы получим \ й с другим знаком, если базис,
отвечающий исходной координатной системе, будет иметь
ориентацию, противоположную той, которую мы выбрали.
Правая часть D.17) останется той же — форма не зависит от
выбора базиса, но функция f в левой части изменит знак.
(Такое изменение знака не имеет ничего общего с только что

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
рассмотренными координатными преобразованиями: там dnx
умножилось бы на отрицательный якобиан, и всё было бы
в порядке. Изменение знака происходит в самом исходном
определении V со через обычный интеграл.) Избежать этой не-
неопределённости нельзя. Общепринятый выход из положе-
положения— выбрать на U некоторую ориентацию, т. е. определить,
какое из двух семейств базисов будет правозакрученным, и
использовать в определении D.17) только правые координат-
координатные системы. Итак, мы видим, что интеграл от со по области
U не зависит ни от чего, кроме ориентации.
Во всех этих рассуждениях существенную роль играло то
обстоятельство, что U можно покрыть единой координатной
системой. Можно ли распространить интеграл на всё М, ко-
которое может и не иметь глобальной системы координат? Ясно,
что если две координатные карты имеют односвязную область
перекрытия, то ориентация на одной карте однозначно инду-
индуцирует ориентацию на другой и интеграл по объединению
двух областей корректно определён. Ясно, что охватить всё М
таким образом можно тогда и только тогда, когда М ориен-
ориентируемо. С этого момента мы ограничимся интегрированием
на ориентируемых многообразиях; стоит, однако, заметить,
что теория интегрирования была распространена де Рамом и
на неориентируемые многообразия, и эта обобщённая теория
имеет интересные физические приложения (см. статью Сор-
кина A977), указанную в библиографии в конце главы).
Для интегрирования, которое мы определили, всегда тре-
требуются формы максимальной степени: л-формы на п-мерном
многообразии. Конечно, можно интегрировать и р-форму по
р-мерному подмногообразию, если оно внутренне ориенти-
ориентируемо. Как связана ориентируемость подмногообразия 5 с
ориентируемостью М? Предположим, что М ориентируемо и
Р — точка из S. Можно ли однозначно «индуцировать» ориен-
ориентацию р-форм в точке Р с помощью заданной п-формы со,
которую мы считаем «правозакрученной», или «положительно
ориентированной»? К сожалению, нет: сама по себе со на 5
не значит ничего, ведь её сужение на 5 — тождественный
нуль, так как р < п. Обычно делается следующее: форма со
редуцируется от п-формы до р-формы с помощью п — р ли-
линейно-независимых «нормальных» (т. е. не являющихся ка-
касательными к S) векторов в точке Р и, по определению, су-
сужение р-формы )
со (Я,, ..., п„-р)
на 5 считается правозакрученным. Это определение явно за-
зависит от выбора векторов {Я/}, включая и порядок, в котором

4 8 ОБЪЁМЫ И ИНТЕГРИРОВАНИЕ
157
они пронумерованы. Такой способ выбора ориентации назы-
называется внешней ориентацией на S в точке Р. Мы приведём
соответствующий пример позже, при доказательстве теоремы
Стокса. Если оказывается возможным задать внешнюю ориен-
ориентацию {п„ 1=1, , п — р} на всем 5 непрерывно («непре-
(«непрерывно» означает и то, что векторы nt всегда остаются линейно-
Рис 4 5 Лист Мебиуса в R3 Проще всего представлять его сделанным из
резины и плоско лежащим на странице, за исключением верхней части ри-
рисунка, где он один раз перекручен Если репер в точке Р "пронести" вдоль
замкнутой кривой, изображенной штриховой линией, то вернувшийся ре-
репер нечьзя перевести в исходный непрерывной деформацией, при которой
векторы 1 и 2 остаются все время на листе и все три вектора остаются
линейно независимыми
независыми и не являются касательными к 5), то S называ-
называется внешне ориентируемым
Ясно, что если существует какая-то ориентируемая откры-
открытая область многообразия М, содержащая S, то 5 либо ориен-
Рис 4 6 Кривые на листе Мебиуса Кривая 9^ не является внешне ориен-
ориентируемой если пару векторов 1 и 2 в точке Р пронести вокруг ленты, как
на рис 4 5, то получившуюся после возвращения в начальную точку пару
нельзя привести к исходному виду непрерывной деформацией, при которой
вектор 1 остается ьсе время касательным к штриховой линии и оба век-
вектора остаются линейно независимыми Кривая же <&2 внешне ориентируема,
поскольку у нее существует окрестность (пунктирная линия), в которой
возможен согласованный выбор ориентации
тируемо сразу и внутренне и внешне, либо не ориентируемо
вовсе; если же такой области не существует, то для 5 может
реализоваться лишь первая возможность, но не обе сразу.
Например, рассмотрим лист (ленту) Мёбиуса в качестве дву-
двумерного подмногообразия R3 (рис. 4.5) и кривую на этой
ленте в качестве её одномерного подмногообразия (рис. 4.6).
Зададим в некоторой точке Р ленты правозакрученную тройку

158 4- ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
векторов, два из которых лежат на ленте, а третий вне неё.
Обнесём эту тройку один раз вокруг ленты так, чтоб два
вектора всегда оставались касательными к ней. Тогда направ-
направленный наружу вектор вернётся в точку Р направленным в
противоположную сторону — лента Мёбиуса не является
внешне ориентируемой в R3. Аналогично, рассмотрим пару
векторов на ленте, один из которых касателен к кривой Фи
а другой нет. После переноса вокруг кривой вектор, направ-
направленный наружу, окажется по другую сторону кривой. Хотя мы
знаем, что наша кривая внутренне ориентируема, это свойство
не зависит от того, в какое пространство она погружена, её
нельзя внешне ориентировать в большем неориентируемом
многообразии. Напротив, кривая ^2 ориентируема и внутрен-
внутренне и внешне на ленте Мёбиуса, поскольку она не «чувствует»
неориентируемости ленты — у ^2 есть на ленте ориентируемая
окрестность.
4.9. W-ВЕКТОРЫ, ДУАЛЬНЫЕ ВЕЛИЧИНЫ И СИМВОЛ гц k
До сих пор мы ограничивались рассмотрением антисим-
метричных тензоров типа I N 1, но и для тензоров типа I „ 1
можно таким же образом построить грассманову алгебру.
Антисимметричный тензор типа ( „ J называется N-вектором.
Также как и в случае форм, векторное пространство всех
р-векторов в данной точке n-мерного многообразия имеет
размерность Спр.
Заметим, что в любой точке есть четыре векторных про-
пространства с одинаковой размерностью: пространства р-форм,
(п—р)-форм, р-векторов и (п — р)-векторов все имеют раз-
размерность Спр = Спп_р При соответствующих обстоятельствах
можно строить 1-1-соответствия между различными парами
этих пространств. Мы видели в § 2.29, что метрический тен-
тензор задает 1-1-соответствие между тензорами типа ( J и
типа ( q) • Нетрудно видеть, что это отображение сохраняет
антисимметричность, следовательно, оно обратимо отобра-
отображает р-формы в р-векторы. Вне зависимости от того, задана
метрика или нет, всякая п-форма объёма й (т. е. п-форма,
нигде не обращаются в нуль) обеспечивает существование
отображения р-форм в (п — р)-векторы. Это (Ьтображение на-
называется отображением, дуализации, и сейчас мы покажем,
как оно строится. (Не путайте это отображение, которое за-
/0\
висит от со и каждому отдельному тензору типа I I сопо-

49 ЛГ-ВЕКТОРЫ, ДУАЛЬНЫЕ ВЕЛИЧИНЫ И СИМВОЛ et/. ..ft 159
ставляет тензор типа ( п~1р ) и наоборот, с понятием дуаль-
дуального базиса один-форм, обсуждавшимся в гл. 2: там нет
зависимости от со и там набор из п тензоров типа ( 0) ото-
отображается в набор из п тензоров типа Г . J и наоборот.)
Для данного ^-вектора Т с компонентами Т' ь = т[1-к\
(q индексов) определим тензор А следующим соотношением:
¦ Ч..л=>,...*/.../'-*- D-2°)
Символически мы будем писать
Л = со(Т)
или проще
¦ 1 = *Т D.21)
Мы будем говорить, что А дуален к Т относительно со. Из
D.20) и антисимметричности со* . i относительно перестановки
любых двух индексов очевидно следует, что А—антисимме-
А—антисимметричный тензор степени п — q (это — число индексов со,
оставшихся свободными после свёртки с q индексами Т).
Таким образом, А есть (п — #)-форма. Описанное отображе-
отображение однозначно определяет (п — <7)~Ф°РМУ Для каждого <7-век-
тора. То что оно обратимо, мы покажем позже, а сейчас про-
продемонстрируем, что это отображение уже встречалось чита-
читателю при изучении векторного произведения в векторной ал-
алгебре трёхмерного эвклидова пространства.
Чтоб это понять, вспомним, что в эвклидовом пространстве
обычно не различают векторы и один-формы: в декартовых
координатах компоненты вектора и ассоциированной с ним
один-формы совпадают. Рассмотрим два вектора О и V и
отвечающие им один-формы О и V. Два-форма О Л V имеет
С|=3 независимых компонент V\V2—U2Vi, UiV3—U3V1,
U2V3—U3VT Вектор VXV имеет те же компоненты, и легко
показать, что
*(DXV)==OAV (размерность 3). D.22)
Упражнение 4.10. Докажите D.22), используя D.20).
Это проливает свет на странные обстоятельства, связан-
связанные с векторным произведением: почему оно вообще сущест-
существует, почему оно не существует в размерностях, не равных
трём (только в случае размерности 3 отображение дуализации
превращает векторы в два-формы), и почему VXV — «акси-
«аксиальный» вектор. Последнее объясняется тем, что в эвклидо-
эвклидовом пространстве принято определять й так, чтобы базису

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
(ei ё2,ё3) соответствовал положительный объём. Если ориен-
ориентация' базиса меняется, то то же происходит и со знаком й,
а следовательно, и со знаком О X У (который зависит от
знака ©, поскольку с помощью й вектор О X V отображается
в форму D AV, знак которой не должен меняться). Вот век-
векторное произведение и меняет знак при отражении координат.
Соответствие между Т и * Т обратимо, поскольку они
имеют по одинаковому числу компонент. (Иными словами,
свёртка Т с й в D.20) не приводит к потере информации, со-
содержащейся в Т поскольку Т уже был антисимметричен по
всем своим индексам.) Таким образом, для Данной р-фор-
мы А существует единственный (п — р) -вектор Т, такой что
А = * Т Это можно формально записать, введя п-вектор
со'"*, обратный к й, определяемый соотношением
со'"- feco. . ft = n!. D.23)
Множитель п\ необходим, поскольку сумма в D.23) содер-
содержит п\ одинаковых слагаемых со123 ••• па>12з... « = со213 •¦ • "со2|3 ...«
= ...; он обеспечивает нужную нормировку:
Ш12з...п=. 1 D.24)
«123.. .я
Мы говорим, что тензор S дуален к р-форме В относительно
б, и пишем
ф S = 'В, D.25)
если
* S'-* = ^-co/-m'-ftfl/...». D.26)
То что два введённых отображения дуализации взаимно об-
ратны, мы покажем сначала на примере числовой функции.
Функция /, рассматриваемая как 0-вектор, имеет дуальную
п-форму /й Этой п-форме дуален 0-вектор
Итак, мы доказали, что **/" = /.
В общем случае рассуждаем так. Начнём с р-формы Ё и
определим (п — р)-вектор S с помощью D.26). Применим
к S оператор дуализации:
S'"'k
«г
p\(tl-p)\ i-.-k
— (-Op(Д-р) ш ai...kr...s

4 9. Л/-ВЕКТОРЫ, ДУАЛЬНЫЕ ВЕЛИЧИНЫ И СИМВОЛ ВЦ.. Л 161
Чтобы получить последнюю строчку, надо было переставить
каждый из п — р индексов i ... к со всеми р индексами
г ... s, что и дало п — р множителей (—1)р. Дадим индексам
(/ ... /) конкретные значения, например A ... р). (Понят-
(Понятно, что несущественно, как именно они «называются».) Тогда
в сумме (при фиксированных (г ... s))
индексы i ... k надо выбирать из множества (р-\-\, ..., п).
Таким образом, в сумме получится (п — р)! ненулевых сла-
слагаемых и все они будут равны друг другу, в точности как в
D.23); следовательно,
Далее, это равно нулю во всех случаях, когда (г ... s) не
есть перестановка из A ... р), ибо тогда у второго со будут
иметься совпадающие индексы. В сумме по (г ... s)
есть р\ ненулевых слагаемых, опять-таки равных друг Другу.
Итак, мы получаем
Вместе эти формулы дают
(*S)i ... р = (—1)р(--р)сор+1 ... „,...
Но из D.24) вытекает, что
следовательно,
(*S),...P = (-l)p("~p)fii...P.
Поскольку метки 1 ... р могли представлять произвольные
индексы, то мы доказали, что
ф *'В = (-1)р1п~р)В. D.27а)
Аналогично если бы мы начали с ^-вектора Т то получили бы
ф •*Т = (-1)'?("-<?)Т. D.27Ь)
Заметим, что при нечётных п множитель (—1)р("-р) всегда
равен +1.
Как мы уже раньше отмечали, метрика отображает р-фор-
мы в р-векторы. В сочетании с отображением дуализации это
даёт отображение р-форм в (п — р)-формы, или ^-векторов
в (п — <7)-вект°ры. Обычно это отображение по-прежнему

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
обозначается просто через *. Нужна, правда, известная бди-
бдительность в отношении знаков в случае, если метрика инде-
индефинитна (когда, как в теории относительности, некоторые
длины положительны, а некоторые отрицательны). В деталях
мы обсудим это попозже. Один пример использования такой
операции дуальности дан в упр. 5.13.
В алгебре форм часто бывает удобно употреблять анти-
антисимметричные символы Леви-Чивиты
1, если ij... k — четная
перестановка чисел
1, 2,..., п;
1, если ij ... k — нечетная
перестановка чисел
1, 2 п;
О во всех остальных
случаях.
е = е«1-* = { D.28)
'•• ресаоа числ
Например, форма fix1 Л fix2 Л fixs на трёхмерном многообра-
многообразии будет иметь компоненты ецк в системе координат
(xl,x2, Xs) и компоненты Ыцк в любой другой системе коор-
координат, где h— некоторая функция. Предположим, что л-фор-
ма объёма ш имеет компоненты
со. . =fe.. , D.29)
где / — некоторая функция. Тогда обратный к ней п-вектор
имеет компоненты
со"---fc = ye" •••*. D.30)
4.10. ТЕНЗОРНЫЕ ПЛОТНОСТИ
Нами принята та точка зрения, что любая ненулевая
п-форма на п-мерном многообразии определяет элемент
объёма. В реальных задачах подчас встречается сразу не-
несколько таких п-форм. (Примером может служить течение
идеальной жидкости, рассматриваемое в гл. 5. На трёхмер-
трёхмерном многообразии эвклидова пространства есть три физи-
физически существенные три-формы: одна, интеграл от которой
задаёт объём области, другая — массу, а третья — некоторую
сохраняющуюся величину, связанную с завихренностью.) По-
Поэтому иногда удобнее соотносить все такие формы с одной
зависящей от выбора системы координат п-формой fix1 Л
Зх2 Л ... Л Зхп, компоненты которой суть просто ъц... k- Если
со — рассматриваемая n-форма, то соотношение D.29), пере-

4Л0 ТЕНЗОРНЫЕ ПЛОТНОСТИ 163
писанное в виде
0)г/ ... k = WBij ... k,
определяет величину ю, называемую скалярной плотностью.
Хотя Ю — функция на многообразии, она не является настоя-
настоящим скаляром, поскольку зависит от выбора координат. При
преобразовании координат х1' = !1(х') компоненты ю умно-
умножаются на якобиан / этого преобразования (см. D.19)), в то
время как е,-/... k no определению остаются неизменными. Та-
Таким образом, № преобразуется по правилу
ю' = Jro.
Это закон преобразования скалярной плотности веса 1. (Тер-
(Термин «вес» будет определён позднее.) Всё это можно обобщить
и на тензорные плотности. Предположим, например, что Т —
тензор типа ( j на и-мерном многообразии, антисимметрич-
антисимметричный по своим векторным аргументам:
п индексов
Тогда, после свёртки с двумя один-формами а и р, Т задаёт
форму объёма t(a, р):
*E, P) = T(a, P; ,...,),
(Такие тензоры появляются в физике. Например, тензор
напряжений, упоминавшийся в гл. 2, определяет плотность
напряжений, когда заданы две один-формы; полное напря-
напряжение есть интеграл от неё по всему объёму, интеграл от
свёртки тензора типа Г V полученного умножением тензора
напряжений на форму объёма.) Компоненты Т можно пред-
представить в виде
откуда определяются числа {?"}, являющиеся компонентами
тензорной плотности типа ( 0 ) • (Для обозначения тензорных
плотностей общепринято использовать готические буквы.) За-
Законом преобразования для такой плотности будет
a:l'//=»Ml'*A/'i2w, D.31)
где /, как и раньше,— якобиан (определитель матрицы Л*')').
Это закон преобразования для тензорной плотности типа
(I) веса 1.

4 ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
164 : __
Термин вес указывает, сколько якобианов / в законе пре-
преобразования. Например, число гс, преобразующееся по закону
п>' = Pro,
есть скалярная плотность веса два. Обобщение на тензорные
плотности и на другие веса очевидно. Обычные тензоры —
это плотности веса нуль. Интерпретация плотностей с весом,
отличным от нуля или единицы, довольно сложна, но такие
величины действительно оказываются иногда полезными.
В этой книге мы не будем работать с плотностями, отдавая
предпочтение формам как таковым.
4.11. ОБОБЩЕННЫЕ СИМВОЛЫ КРОНЕКЕРА
У символов Леви-Чивиты есть много полезных и интерес-
интересных свойств; некоторыми мы воспользуемся в этом и следую-
следующем параграфах. Как мы видели раньше, часто приходится
сталкиваться с произведениями нескольких е, такими как
в1'' - kzu... т- Возможно развить систематический и удобный
способ работы с ними.
Прежде всего заметим, что в двух измерениях для любой
ненулевой два-формы й мы имеем
са,7ш« = е17в*» == 6**6'/ — б*,*',-. D.32)
Первое равенство следует из D.29) и D.30). Простейший
способ установить второе равенство — это заметить, что обе
части антисимметричны относительно (k, l) и (i, /); поэтому
достаточно рассмотреть случай 1ф\, \ф1. С точностью до
знака есть только один такой член, а именно ei2e12 = 1. Легко
видеть, что правая часть тоже дает единицу, что и доказывает
равенство. Похожая цепь рассуждений приводит нас к от-
ответу в общем случае п измерений:
1т...г *1 c-m sf *1 sm sr ¦
ЕЦ ...kE = б |в / • • • б k — б /б 1..Р * + • • •
= лг!б^бту. .. 6rfe]. D.33)
Существует сокращённая запись для всего этого. Определим
р-дельта-символ как
¦ 6iy.;! = p!6/[fe...6/n, D.34)
где каждое из множеств (i .../') и (&... /) содержит по р
индексов. В частности,
¦ щ...&1т"г = ь\Г;;Л. D.35)

4 11. ОБОБЩЁННЫЕ СИМВОЛЫ КРОНЕКЕРА 165
Можно получить р-дельта-символ из (р+ 1) -дельта-символа
с помощью свёртки, например по первому индексу. Начнём с
fij&W.'e = (Р + 1)! в'[|в/тв*г • • • S's,.
Члены суммы можно перегруппировать следующим образом:
= р! fi'ifiV.e'r . ¦ • ail - р! в'тв'цв*, • • ¦ 6'si
— р! f>\{)'\m(>ki • ¦ • б'Я] — ... — р! б^б'[тб*г ... б'ч
= р! {лв'[тв*г •. • в',| - Ь\тЬ\ ... 6ls]
— б;[тбЙг . . . 6 Я] — . . . — 6'[m6 r . . . бг5|},
что даёт
¦ вй,-::.1,==(л-Р)б?,-::.1, D.36)
для один раз свёрнутой (р+ 1)-дельты в я-мерном простран-
пространстве.
Упражнение 4.11. (а) Обоснуйте каждый шаг в выводе
D.36).
(Ь) Получите р-дельту из я-дельты с помощью п — р
свёрток:
бг :::'Л:\: 1=(п-Р)\ бк:\{. D.37)
п — р р
В качестве примера использования этой алгебры вычислим
двойное векторное произведение в трёхмерном эвклидовом
пространстве. В декартовых координатах оператор * выра-
выражается через е, и
поэтому
V)]t =
Из D.34) и D.36) получаем
[W X (О XV)]t = (бгебт; - 6ljdml)W^UlV
Вывод настолько прост, что делает совершенно ненужным
заучивание формулы двойного векторного произведения.

166 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
4.12. ОПРЕДЕЛИТЕЛИ И еу k
Рассмотрим 2Х2-матрицу с элементами А11. Мы покажем,
что
сМ(Л)=е,7А1гЛ2'. D.38)
Чтоб в этом убедиться, выпишем явно сумму в правой части:
вцАиА*1 = е12ЛпЛ22 + е21Л12Л21;
мы воспользовались тем, что ец = е22 = 0. Кроме того, ей =
—Е21 = 1, и мы получаем
Л" Л22 — Л'М21,
что по определению и есть определитель нашей матрицы. Сле-
Следующее упражнение обобщает формулу на случай произволь-
произвольной матрицы размера «Хя.
Упражнение 4.12. (а) Покажите, что определитель п X п-
матрицы с элементами Ali (i, ] = 1, ..., п) равен
+ det(,A) = el,...kAllA2i...Ank. D.39)
(Указание: определитель п X я-матрицы выражается через
(п—1)Х(П—1) определители по правилу Лапласа. Ис-
Используя это правило, докажите D.39) по индукции, начи-
начиная с 2Х2-случая.)
(Ь) Покажите, что
det Л = -1 еаЬ... сви ... кАа1Аы ... Аск.
Упражнение 4.13. На многообразии с метрикой фиксируем
какой-нибудь ортонормированный базис один-форм {©'}
и определим выделенную форму объёма й формулой
й = й1 Л &2 Л ... йп.
Покажите, что в произвольной системе координат {х*'}
¦ & = | g |1/2 dx' Л rf/' Л ... Л dJf"', D.40)
где g — определитель матрицы, составленной из компо-
компонент g{,j, метрического тензора в этих координатах.
Снова интересно рассмотреть случай трёхмерного эвкли-
эвклидова пространства. Объём параллелепипеда, построенного на
трёх векторах а, Б и с, равен определителю матрицы, строки
которой составлены из компонент этих векторов. Следова-
Следовательно, в силу D.39):
объём = Ец^х1Ь1ск = а1 {ЕцФ!ск)
ещё одно хорошо известное выражение для объёма.

4.13 МЕТРИЧЕСКИЙ ЭЛЕМЕНТ ОБЪЕМА 167
4.13. МЕТРИЧЕСКИЙ ЭЛЕМЕНТ ОБЪЕМА
В упр. 4.13 наличие метрики на многообразии позволило
фиксировать некий ортонормированный базис {©'} и с его по-
помощью сконструировать n-форму & (см. D.40)), которую мы
назвали «выделенной формой объёма». Насколько эта форма
оправдывает название «выделенная»? Однозначно ли она
определена или зависит от выбора ортонормированного ба-
базиса (который, конечно, можно выбрать не единственным
образом), использованного при её построении? Ответ таков:
она определена однозначно с точностью до знака. Чтобы в
этом убедиться, заметим, что компоненты й в исходном ба-
базисе по определению равны е,;-... k- Если {5>г} — какой-то
другой ортонормированный базис, то компоненты й будут в
нём равны /ег/'... ft-, где /—якобиан преобразования от
{й'} к {й'}. Но поскольку оба базиса ортонормированные,
то / = ±1 (это будет доказано ниже). Таким образом, форма
й отличается от «выделенной» формы, задаваемой базисом
{й'"}, не более чем знаком. Если принять какое-либо согла-
соглашение об ориентации, то мы сможем определять & только
через правые ортонормированные базисы, и такое определе-
определение будет уже однозначным. Итак, метрика однозначно опре-
определяет форму объёма на ориентируемых многообразиях. С ин-
интуитивной точки зрения это, конечно, и не удивительно.
Чтобы прийти к этому результату, мы воспользовались
тем, что якобиан преобразования от одного ортонормироваи-
ного базиса к другому (а он есть не что иное, как определи-
определитель матрицы перехода Л'"/) по модулю равен единице. Это
нетрудно установить. Начнём с общего закона преобразования
координат метрического тензора
который можно записать в матричном виде так (см. § 2.29):
Взяв определитель от обеих частей закона преобразования,
получаем
Но в ортонормированном базисе g,j— это матрица, на диаго-
диагонали которой стоят ±1, а в остальных местах — нули. (На-
(Напомним, что если gi,-— индефинитная метрика, то не все диа-
диагональные элементы имеют одинаковый знак.) Следователь-
Следовательно, определитель матрицы gij равен ±1 и имеет один и тот
же знак во всех ортонормированных базисах. Таким образом,
для нашего якобиана мы имеем
det(A) = / = ±l.

4 ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
168
В случае индефинитной метрики оператор дуализации *
можно определить двумя разными способами; это связано
с тем, что для л-вектора со'7 - *, обратного форме объёма, есть
два «естественных» определения, отличающихся знаком.
Раньше мы стояли на той точке зрения, что
СО*' —*©//... к = П\,
т. е.
Но если имеется метрика, то можно определить n-вектор й'
п поднимая индексы у ю:
Из D.39) и D.40) следует, что
Теперь, поскольку (glm) — матрица, обратная к gi]t её опре-
опреD-41)
у
делитель равен g-\ и мы имеем
тогда как раньше мы имели
12" !='. D.42)
Если g отрицателен, то эти формулы отличаются знаком.
В теории относительности, где g как раз отрицателен, при-
принято использовать 6/ в соотношениях дуальности. Это вводит
дополнительный знак минус в формулы типа D.27).
В. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
ФОРМ И ЕГО ПРИЛОЖЕНИЯ
Где есть интегральное исчисление, должно быть и диффе-
дифференциальное, и мы сейчас введём так называемое «внешнее
дифференцирование», которое действует на формы и превра-
превращает их в формы же — их «внешние производные». Точный
смысл утверждения, что внешнее дифференцирование обратно
к интегрированию, содержится в доказываемой ниже теореме
Стокса, обобщающей основную формулу интегрального ис-
исчисления
= f(b)-f(a). D.43)

4 14 ВНЕШНЯЯ ПРОИЗВОДНАЯ 169
Потом мы продвинемся дальше и продемонстрируем тесную
связь между дифференциальными формами и уравнениями
в частных производных.
4.14. ВНЕШНЯЯ ПРОИЗВОДНАЯ
Мы хотим определить дифференциальный оператор на
формах, который бы сохранял их свойства как форм и был
обратным к операции интегрирования в смысле формулы
D.43). Заметим, что если М — одномерное многообразие, то
оператор Я, превращающий нуль-форму f в один-форму Я/,
конечно же, удовлетворяет D.43). Итак, нам требуется рас-
расширить й на формы старших степеней. По аналогии с опера-
оператором й на нуль-формах он должен повышать степень формы.
Таким образом, если а — р-форма, то da должна быть
(р + 1)-формой. Подходящий способ расширения Я заклю-
заключается в следующем (ниже а — р-форма, а р. у — ^-формы);
¦ (i)d(P + Y) = WP) + tfY).
¦ (И) rf(aAP) = (da)AP + (-l)paA#,
+ (iii) d (da) = 0.
Свойство (ii) — это не что иное, как правило Лейбница, если
отвлечься от множителя (—1)р. Этот множитель возникает
потому, что прежде чем подействовать оператором Я на C,
его надо «пронести» через р-форму а; это означает «переста-
«перестановку» его с р один-формами, а каждая перестановка дает
множитель —1. Это свойство гарантирует, что действие д. бу-
будет согласовано с законом D.12). (Дифференцирование,
удовлетворяющее условию (ii), называется антидифференци-
антидифференцированием.) Свойство (iii) на первый взгляд несколько неожи-
неожиданно, однако если посмотреть, что оно значит в случае,
когда а есть просто функция /, то станет очевидной его «ра-
«разумность». Один-форма Щ имеет компоненты df/дх1; компо-
компоненты второй производной должны быть линейными комбина-
комбинациями d2f/dx'dx'. Но чтобы образовать два-форму, эти вто-
вторые производные должны быть антисимметричны по i и /, в
то время как d2f/dx'dx' симметричны (частные производные
коммутируют); поэтому появление нуля совершенно есте-
естественно. Свойства (i)—(iii) вместе с определением действия
Я на функции однозначно определяют й. (Довольно длинное
доказательство этой теоремы можно найти, посмотрев любое
стандартное руководство по дифференциальным формам.)
Упражнение 4.14. (а) Покажите, что
dfAdg. D.44)

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
(b) Используя (а), покажите, что если
— запись р-формы а в каком-нибудь координатном ба-
базисе, то
1 д
р\ дхк
й = 4" "А («' - l) <*** Л ЗУ Л ... ЗУ
и, следовательно,
^</] D.45)
4.15. ОБОЗНАЧЕНИЯ ДЛЯ ЧАСТНЫХ ПРОИЗВОДНЫХ
Начиная с этого момента мы будем перманентно пользо-
пользоваться частными производными. Для них существуют удобные
стандартные обозначения. А именно, для любой функции f
на многообразии
-TT^f D46)
Заметим, что сама f может быть компонентой тензора, в этом
случае запятая ставится после всех индексов:
¦ 5= V',k- D-47)
Вторые производные дают дополнительный индекс после за-
запятой, дополнительные же запятые не ставятся:
5?Ь- = '- D-48)
Чтобы определить порядок действия производных, индексы
надо читать слева направо (для д/дхк правило обратное).
Особо отметим, что частное дифференцирование компонент
не есть тензорная операция в смысле определения § 2.27.
То есть функции {V'j,k} в общем случае не совпадают с функ-
функциями
полученными преобразованием частных производных, взятых
в другой системе координат. (Вспомните обсуждение в § 3.4
вопросов, связанных с определением дифференцирования тен-
тензоров на многообразии.) Единственное исключение из этого
правила — дифференцирование скалярной функции; как мы
видели, /, ,¦ являются компонентами один-формы df. (Здесь

4 16 ЗНАКОМЫЕ ПРИМЕРЫ ВНЕШНЕГО ДИФФЕРЕНЦИРОВАНИЯ 171
стоит вспомнить указанное в § 2.28 различие между скаля-
скалярами и функциями.) Пример использования наших новых
обозначений даёт скобка Ли:
Хотя каждое слагаемое в правой части само по себе тензора
не образует, их сумма есть тензор. Аналогично частные про-
производные в D.45) входят в такой комбинации, что тоже пре-
преобразуются как тензор.
Упражнение 4.15. Покажите, что при произвольных преоб-
преобразованиях координат V',k не преобразуются как тензор,
а [V, V]1 все-таки преобразуются как вектор.
Учитывая соглашение о том, что индексы производных пи-
пишутся после всех других индексов, можно переписать D.45)
в виде
(da)i .../* = (— 1)р(р+ 1)щ1...},к]. D.49)
4.16. ХОРОШО ЗНАКОМЫЕ ПРИМЕРЫ ВНЕШНЕГО
ДИФФЕРЕНЦИРОВАНИЯ
В точности так же, как внешнее умножение «превраща-
«превращалось» в трёхмерном пространстве в векторное произведение,
внешнее дифференцирование превращается в ротор. Рас-
Рассмотрим вектор а. Внешняя производная ассоциированной с
ним один-формы есть
da = d(a{ dx1 -\- a2 dx2 + a3dx3)
= a,, j dx1 A dx1 + а2. у dx1 Л dx2 + Og.,- dx' Л dx3.
Поскольку dx1 Л dx1 = 0 и то же верно для индексов 2 и 3, то
da = (а,, 2 — а2, у) их2 Л dx1 + (а2,3 — а3,2) dx3 Л dx2
+ (а3,1 — аь 3) dx1 Л dx3.
Ясно, что ротор здесь содержится. Чтобы выделить его как
вектор, возьмём дуальную величину:
*da = (a,, j — а2,}) *(йх2 Л dx1) + ...
213 д ,
== \а\, 2 — а2, l) ? ~дх^ ~Г ¦ • •
== (а2,1 а\, г) "^з" т • • • t
т. е.
*da = V X а. D.60)
Итак, ротор в трёхмерном пространстве есть *d.

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Не только ротор, но и дивергенция возникает из внешнего
дифференцирования. В этом случае соответствующий опера-
оператор будет d*. Возьмём вектор а и найдем дуальную ему
форму:
= у ахвт dV А dxk + ... = a1 (d.t2 ,A dx3) +
Её внешняя производная равна
й"а = а\, dx' A dx2 A dx3 + ...
= a',1dV A dx2 Adx3+ ...
= (а'.7) (Зл:1 Л dx2 A~dx3. D.51)
(При переходе от первой строчки ко второй во внешнем про-
произведении «выживает» только член с /= 1.) Таким образом,
мы показали, что
+ сГа = (У-а)й, D.52)
где ю= dx1 Л dx2 Л dx3 —эвклидов элемент объёма в декар-
декартовых координатах. В § 4.23 мы обобщим эту формулу для
дивергенции на случай произвольных р-векторов на произ-
произвольных многообразиях.
Упражнение 4.16. Используя D.50), D.52) и свойство (ш)
из § 4.14, покажите, что (в трёхмерном эвклидовом век-
векторном анализе) дивергенция ротора и ротор градиента
равны нулю.
4.17. УСЛОВИЯ ИНТЕГРИРУЕМОСТИ
ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ В ЧАСТНЫХ ПРОИЗВОДНЫХ
Внешнее дифференцирование, как и формы сами по себе,
тесно связано с хорошо известными понятиями дифференци-
дифференциального исчисления. В качестве примера рассмотрим систему
дифференциальных уравнений в частных производных
!?- = *(*.#) ¦%r = hix,y). D.53)
Если считать, что (х, у)—координаты на многообразии, то
её можно записать в виде
где ах = g и ау = h. Это уравнение в свою очередь можно
записать в бескоординатной форме
d7 = а, D.54)

4.18 ТОЧНЫЕ ФОРМЫ 173
гдей—один-форма с компонентами g и ft. Предположим те-
теперь, что / — решение этого уравнения. Тогда, действуя на
обе части оператором d, мы получим
d(d/)=da.
Но левая часть равна нулю в силу свойства (Ш) из опреде-
определения d, и мы видим, что необходимое условие существования
решения — равенство
"da = 0.
В компонентах оно имеет вид
«[*,/] = О,
что на самом деле есть одно равенство (у нас два-форма на
двумерном многообразии)
дах дау dg dh
~д7, aF ^ 0<^~д7 ~~д7:==0- ^4-55^
Как и следовало ожидать, это — хорошо всем знакомое усло-
условие совместности системы. Таким образом, внешнее диффе-
дифференциальное исчисление даёт нам геометрический вывод
этого условия, и, как правило, такой способ вывода благо-
благодаря компактности обозначений простейший. То что условия
совместности являются и достаточными условиями существо-
существования решения, гарантируется теоремой Фробениуса в том
варианте, в котором она изложена в § 4.26.
4.18. ТОЧНЫЕ ФОРМЫ
По определению внешней производной d из того, что а =
dp, следует, что da = 0. Естественно задать обратный вопрос:
если da = 0, то можно ли утверждать, что существует форма
Р, такая что a = dp? Форма а, для которой da = 0, назы-
называется замкнутой; ферма а, такая что a = dp, называется
точной. Является ли замкнутая форма точной? Мы докажем
в § 4.19, что ответ утвердительный в следующем смысле. Рас-
Рассмотрим окрестность 3) точки Р, в которой а определена
всюду и в которой da = 0. Тогда существуют достаточно ма-
малая окрестность точки Р и всюду в ней определённая форма
Р, такие что a = dp. Конечно, р определяется не однозначно:
Р +^v с произвольной формой у (нужной степени) тоже
подходит.
То что замкнутая форма точна, мы можем утверждать
только локально, глобально это имеет место вовсе не всегда.

174
4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Рис. 4.7. Кольцевая область в Я2.
Граничные кривые не входят в об-
область.
Если дана произвольная область 3), в которой а всюду опре-
определена и замкнута, то может оказаться невозможным найти
одну-единственную форму Р, определённую всюду в 3), та-
такую что а = dp.
Проиллюстрируем это примером в R2. Рассмотрим кольцо,
заключённое между кривыми 9>?\ и ^2 (рис. 4.7), и введём де-
декартовы координаты х и у с
началом координат Р, лежа-
лежащим внутри ??2. Один-форма
~_ хду — у их
О, 5—I 5
х + У2
определена всюду между кри-
кривыми и, как нетрудно убедить-
убедиться, обладает свойством йа=0.
Существует ли функция /, та-
такая что а = d/? Если мы вве-
введём обычные полярные коорди-
координаты гиб, то, как легко видеть, а = d6, так что на первый
взгляд ответ положителен. Однако дело не столь просто: 6 не
является однозначной непрерывной функцией во всей рассма-
рассматриваемой области между кри-
кривыми ^i и (&2- Таким образом,
хотя а корректно определена
всюду в области, нет такой
функции /, для которой всюду
ее = d/. Локально ответ «да»,
но глобально —• «нет». Вопрос
снимается, если мы уберем %?2
и будем рассматривать всю
внутренность кривой <&\, по-
поскольку а в точке х = у = О
не определена. Опять-таки,
если мы рассмотрим область,
изображенную на рис. 4.8, за-
задача решается: в этом случае
а определена всюду внутри ^ и функцию 6 можно выбрать
однозначной и непрерывной внутри W. Итак, на этом про-
простом примере мы обнаружили, что, хотя локально da = 0 =>
а = d/, ответ на глобальный вопрос (определена ли / всюду)
зависит от рассматриваемой области.
Очевидно, что мы имеем дело с одним из аспектов топо-
топологии областей или многообразий. Изучением топологических
свойств, которые определяют связь между замкнутыми и точ-
точными формами, занимается теория когомологий. После до-
доказательства теоремы Стокса мы будем иметь достаточно
Рис. 4.8. Область в R2, похожая на
область на рис. 4.7, но имеющая
границу, которая представляет со-
собой единую связную кривую.
Точку скачка 6 (в которой 6
"прыгает" от 2я до 0) на любом
круге г = const с центром в Р
можно вынести за пределы обла-
области SD.

4.19. ДОКАЗАТЕЛЬСТВО ЛОКАЛЬНОЙ ТОЧНОСТИ ЗАМКНУТЫХ ФОРМ 175
развитый -математический аппарат, который позволит нам
дать краткий экскурс в теорию когомологий в § 4.24.
4.19. ДОКАЗАТЕЛЬСТВО ЛОКАЛЬНОЙ
ТОЧНОСТИ ЗАМКНУТЫХ ФОРМ
Мы докажем следующую теорему, известную, под назва-
названием леммы Пуанкаре. Пусть а — замкнутая р-форма, опре-
определённая всюду в области U многообразия М, и пусть сущест-
существует гладкое 1-1-отображение U на открытый шар в R", т. е.
на внутренность сферы S", задаваемой уравнением (х1J-\~
(х2J + ••• -\-(хпJ= 1- Тогда в U существует (р—1)-форма
Р, для которой б = Яр.
Рис. 4.9. Отображение области на рис. <3.8 на открытый единичный шар в
R2 (внутренность единичного круга). Пунктирные линии переходят в пунк-
пунктирные, штриховые — в штриховые; показано несколько типичных точек.
Если граничная кривая 'в — класса С°°, то и это отображение можно вы-
выбрать класса С°°.
Прежде чем перейти к доказательству, посмотрим, в чём
смысл такого отображения. Очевидно, оно означает, что U
может быть покрыто единой топологической декартовой си-
системой координат. Это, действительно, — топологическое усло-
условие: для области, показанной на рис. 4.7, такой системы нет,
а для области на рис. 4.8 — есть, как это показано на рис. 4.9.
Такие отображения существуют и для многих других обла-
областей. Например, R" само по себе можно отобразить на его
единичный открытый шар по формуле
г^А^шх^ . 5
л г у '
г = [(Ху + (х2J + ... + (*»)*] '/2, D.57)
т. е. по формуле
2
г н-> — arctg r. D.58)

j7g 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Это — отображение класса С°° даже в начале координат, что
можно увидеть, разложив arctgr в ряд Тэйлора:
arctgr = r — -j rs + -^r5-\- ... .
Доказательство теоремы состоит в том, что, используя ко-
координаты х' на U, мы в явном виде построим искомую форму
р. Пусть
б = а,... н (*', .... хп) dV Л • • • Л йх\ D.59)
где каждая компонента ос,-... k имеет р индексов. Свернём а
с «радиус-вектором» г, который в каждой точке имеет компо-
компоненты (х1, ..., х") относительно координатного базиса, и обо-
обозначим полученную (р—1)-форму через р. В силу D.13)
имеем
Д = б (г) = аи ... kXl~6x' A ... Л dx\ D.60)
Теперь положим
i
Р/...*(*', .••. x?)=\t"-lat,...k(tx\ ..., txn)xlAt. D.61)
о
Интегрирование здесь идет вдоль радиуса, на котором лежит
точка {х'}. Эти функции определяют (р—1)-форму Р:
и мы утверждаем, что а = dp.
Доказательство этого утверждения сводится к простой
алгебре. В силу D.45)
Производная легко берется:
"•ij ... k \LX , . . ., IX ) Cxi
dxl
Чтоб это антисимметризовать, воспользуемся (впервые) замк-
замкнутостью а:
0 = 0,,/...*.,,=
аШ ... к. I] а[/|/| ... к. Л ~ a\ki... IIl.il a[i/...ftl. I' D.64)

4.20 ПРОИЗВОДНЫЕ ЛИ ОТ ФОРМ 177
где вертикальные черточки отделяют индексы, не участвую-
участвующие в антисимметризации, требуемой [ ]. Но компоненты а
сами по себе антисимметричны по своим индексам, поэтому
первые р членов равны между собой и мы заключаем, что
° = PatU... к,ц-%,-... щ, г D-65)
Подставляя это во второй интеграл антисимметризованной
версии D.63), а потом всё вместе в D.62), получаем
(dp)f/...* =
о
=««/... *(*' ¦*")- D-66)
Это доказывает теорему.
Упражнение 4.17. Докажите равенства D.64) и D.65).
Упражнение 4.18. Используя теорему о локальной точно-
точности, покажите, что (в трёхмерном эвклидовом векторном
анализе) векторное поле с нулевым ротором есть гра-
градиент, а векторное поле с нулевой дивергенцией есть ротор.
Тут надо сделать два замечания предостерегающего ха-
характера. Первое заключается в том, что, как отмечалось в
§ 4.18, построенная нами (р—1)-форма Р— не единственная
форма, для которой Яр = а. Второе же состоит в том, что мы
всего лишь нашли одно достаточное условие точности замк-
замкнутой формы. Теория когомологий открывает нам гораздо
более сложные многообразия, на которых всякая замкнутая
форма оказывается точной (см. § 4.24).
4.20. ПРОИЗВОДНЫЕ ЛИ ОТ ФОРМ
Мы выведем следующее удобное выражение для произ-
производной Ли р-формы й по направлению векторного поля V:
D.67)
Таким образом, р-форма ?у& есть сумма двух р-форм: пер-
первая— это внешняя производная от &(V)—свёртки й и V;
вторая — это свёртка йй с V. Доказательство довольно длин-
длинное, и при первом чтении его можно опустить. Ответ D.67)
выглядит вполне естественно:?v& есть р-форма, зависящая

178 4 ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
от V и со, и если вообще можно построить её с помощью д
(чего мы вправе ожидать, поскольку обе производные свя-
связаны лишь с дифференциальной структурой многообразия),
то она должна выражаться через те две единственные р-фор-
мы, которые удаётся построить из V, со и Я. Фактически она
оказывается просто их суммой.
Доказательство проводится по индукции. Ради простоты
записи не будем писать волны над буквами до конца пара-
параграфа.
Первая часть доказательства состоит в рассмотрении слу-
случая нуль-формы со, т. е. функции /. Её свёртка с V есть по
определению нуль, а внешняя производная есть df. Если V =
— d/dX, то, как мы знаем, df(V)=df/dX, но это же равно
?yf — V(f) =Af/dX, что и доказывает формулу в её про-
простейшем случае.
Следующий рассматриваемый случай — один-форма со. За-
Запишем в компонентах:
со (V) = co,-F(' =Ф- d [со (V)] = (OiV1). j dx',
dco = d (со, dx') = (dco,) Л dx1'
= со,-,;- dx' Л dx1 = со,-,;- (dx'© dx1 — dx1 © dx1)
=> (dco) (V) = со,,, [dx'' (V) dx' - dx1 (?) dx']
= cob jV1 dx1 — сог, jVl dx'.
Вместе эти выражения дают
d [со (V)] + da> (V) = [со,-, ,V' + (u,V'. ,-] dx1,
что как раз и есть <^^со в виде C.14).
Доказательство завершается выполнением шага индукции
по р. Поскольку произвольная р-форма может быть представ-
представлена в виде суммы функций, умноженных на внешнее произ-
произведение р один-форм:
co = -^-cuj... kdxl Л ... Л dx\
то достаточно доказать теорему для случая форм, имеющих
вид
и = fa Л Ь, D.68)
в предположении, что теорема имеет место для а и Ь. Тогда
?vv> = (?vf) аЛЬ + f (?va) Л b + fa Л (?vb)
-(da)(V)}Ab
-4- fa A id\b(V)} + (db)(V)}.

4 22 ТЕОРЕМА СТОКСА 179
Но кроме того мы знаем, что (если а — р-форма)
d [со (у)] = d [fa (V)Ab + (-l)pfaAb (V)]
= Af[(a Л b)(V)] +f{u[a(V)] Ab + (-l
= [d/ Л а Л b + fua A b + (-If fa A Ab](V)
= df(V)a Ab-dfA[(aA b)(V)] + f[da(V) A b
Складывая эти два выражения, мы получаем формулу для
?у<?>, приведённую выше, что и доказывает правильность
D.67) для форм общего вида.
4.21. ПРОИЗВОДНЫЕ ЛИ И ВНЕШНИЕ ПРОИЗВОДНЫЕ
КОММУТИРУЮТ
Важнейшее следствие формулы D.67) состоит в том, что
производные Ли и внешние производные коммутируют (см.
D.69) ниже). Чтоб доказать это, заметим, что для любой
формы со (мы опять опускаем волны)
поскольку ddco = 0. С другой стороны, формулу для произ-
производной Ли можно переписать так:
Таким образом (опять потому, что dd = 0), мы получаем
¦ ?у№) = А(?^)- <4-69)
Производная Ли и внешняя производная коммутируют! На
самом деле мы столкнулись здесь с частным проявлением
фундаментального свойства оператора d (устанавливаемым в
более полных курсах), которое заключается в том, что в не-
некотором смысле d коммутирует с любым дифференцируемым
отображением многообразия. (Это свойство коммутирования
значительно упрощает доказательство предпоследнего утвер-
утверждения упр. 3.9!)
4.22. ТЕОРЕМА СТОКСА
Теперь мы в состоянии показать, что внешнее дифферен-
дифференцирование и интегрирование — взаимно обратные операции.
Поскольку интегрирование на л-мерном многообразии опре-

4 ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
делено только для л-форм, то речь может идти лишь о внеш-
внешних производных (л—1)-форм Далее, поскольку мы ввели
лишь определенные интегралы от п форм (т е интегралы,
значение которых есть число, а не функция), то соотношение,
обобщающее формулу D 43), приведенную в начале части В
этой главы, должно связать нам интеграл от п-формы й© с
другим интегралом—от формы б Но (п—1) форму © мож-
можно проинтегрировать только по (п—I)-мерной гиперповерх-
гиперповерхности, следовательно, искомая формула должна связывать
Рис 4 10 \1ног^,обрэзио с ручкой Ни приват 9*i ни кривая "<?2 не яв
ляются границ ми, госкошку оич не де!ят М на две об 1асти ( внутри и
снаружи ) Их объединение rS>i\J'g'2 есть граница состоящая из дв\ к не
связанных между собой подмногообразий Кривая '&ъ—связная граница
интеграл or && по некоторой конечьой области с интегралом
от б по границе эюй области, которая (п—-1)-мерна Мы
подойдем к теореме Стокса (формула D 75) ниже) несколь
ко окольным путем, что позволит избежать длинных вычис-
вычислений, встречающихся в стандартных доказательствах Сна
чала исследуем (с точностью до первою порядка), что про-
происходит с интегралом при малой вариации области интегриро-
интегрирования
Итак, рассмотрим интеграл от п формы б по области b
n-мерного мноюобразия М Пусть U имеет гладкую ориенти-
ориентируемую границу, обознгчим ее дИ Под ориеншруемой гра-
границей мы подразумеваем (п—1)-мерное ориентируемое под-
подмногообразие в М, такое что M\dU распадается на два не-
непересекающихся множества U и CU (дополнение U) таким
образом, что любая кривая, соединяющая точки из U и CLJ,
обязательно содержит точку из dU Для простоты будем счи-
считать dU связной, хотя это и не обязательно Примеры ориен-
ориентируемых границ приведены на рис. 4 10 Пусть | — векторное
поле на М Рассмотрим изменение области интегрирования,
генерируемое переносом Ли этой области (но не формы б)

4 22 ТЕОРЕМА СТОКСА
181
вдоль g В результате мы получим семейство областей ?/(е)
и границ d(J(e), зависящее от параметра сдвига е, причем
U = U@) и dU = dU@). Это изображено на рис 4.11.
Изменение интеграла равно просто интегралу от й по об-
области 6LJ (е), заключённой между границами:
D.70)
U (е)
1/@)
61/(е)
Вычислим его. Пусть V—кусок dU с системой координат
{а2, хъ, ..., х11} С помощью переноса Ли мы можем ввести
Рис 4 11 Деформация области V = 1/@) в t/(e) при сдвиге точек много-
многообразия вдочь интегральных кривых поля | на параметрическое "расстоя-
"расстояние" е Стрелки изображают векторы ь| (для малых е) Область между
dU и db (г)— это 6{/(ь)
координаты {х1 = е, х2, х3, ..., х") в некоторой окрестности
V, если поле ? i.e является касательным к границе dU ни в
V=V@)
V(c)
Рис 4 12 Система координат в окрестности куска V границы dU, на кото-
котором g нигде не касается dil Область 6V(e) состоит из тех точек инте-
интегральных кривых поля |, проходящих через V, которые удалены от V на
параметрическое расстояние ^ е
одной её точке (см. рис. 4.12). Это задаёт координатную си-
систему в области 6F(e), заключённой между d(J(O) и dU(e)
«над» V= V@) Сначала мы вычислим интеграл от й по
этой области, а потом распространим его на всю область
61/(е).

J82 А. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
В выбранных координатах
со — / yx , ..., x ) ax / \ ... / \ ил .
Если е мало, то интеграл равен '>
J ©= J K/dx'ldx2... dxn
6V(e) V(O)Lo J
=e ^ /@, x2, ..., xn) dx2... dx" + o(e)
l'(O)
a (I) | +o(e). D.71)
Последняя строчка следует из D.13) и того, что д/дх1 = Ъ,.
Равенство D.71) не зависит от построенной системы коор-
координат, важно лишь, чтобы поле | не было касательным к dU
на V. Таким образом, оно очевидно применимо к любой части
dU, заключенной между точками, в которых | касательно к
dU. Если эти точки образуют подмногообразие dU меньшей
размерности (как на рис. 4.11), тогда вопросов не возникает:
они как раз разделят dU на области Ущ, в каждой из кото-
которых D.71) выполняется. Если же точки касания | к dU обра-
образуют открытую область в dU, тогда перенос Ли просто
отображает эту область в себя и вообще не меняет значения
интеграла, следовательно, D.71) опять-таки выполняется, так
как обе части равны нулю. Итак, мы можем применить D.71)
ко всей границе dU, что даёт вместе с D.70)
¦ чг \ й=иттГ S &~ S й1= Sб® ! • D-72)
С/(е) е">° Lc/(ei С/(Ю J dU dU
Но для (d/de) \ й можно получить и другое выражение,
следующее прямо из определения переноса Ли области по
направлению |. В каждой сдвинутой точке подынтегральное
выражение отличается от исходного на г?^& + о (г), и, сле-
следовательно,
¦ ? J й= J ?%S>. D.73)
U(e) U @)
Но в нашем случае формула D.67) для ?%& значительно
упрощается, поскольку d& есть (п+ 1)-форма и, значит, тож-
') Символ о(е) обозначает любую функцию g(e), такую что g(e)/e->-
-»- 0 при е -»- 0.

4 23 ТЕОРЕМА ГАУССА И ОПРЕДЕЛЕНИЕ ДИВЕРГЕНЦИИ 183
дественно равна нулю:
и и
Сравнивая эту формулу с предыдущим выражением для
(d/de) \ й, мы получаем теорему о дивергенции (причина та-
и
кого названия станет понятной в следующем параграфе):
D.74)
Поскольку й и I произвольны, то й (|) — произвольная
(п — 1)-форма, и мы можем переписать D.74) в виде теоремы
Стокса для произвольной (п — 1)-формы а, определённой
на М:
\ da =
U
J a, D.75)
dU
где в правой части стоит, конечно же, ограничение а на dU.
То, что это та самая формула, которая называется в эвкли-
эвклидовом векторном исчислении формулой Стокса, легко увидеть,
если взять М двумерным, как на рис. 4.11. Тогда а будет
один-формой: a = a,dx' и da = (a/, / — a,-,,-)dx>' ® dx'. Огра-
Ограничить а на dU — это значит рассматривать её значения лишь
на касательных к dU векторах I = d/AK. Поэтому мы полу-
получаем
\ (ai, 2 ~ a2, i) d*1 dx2 = & at -^- dh = & a,- dx1.
dU dU
Но это и есть стандартная формула Стокса.
4.23. ТЕОРЕМА ГАУССА И ОПРЕДЕЛЕНИЕ ДИВЕРГЕНЦИИ
В теореме Стокса содержится и то, что в векторном ис-
исчислении известно под именем теоремы Гаусса. Действительно,
вернёмся к формуле D.74) и рассмотрим координаты в неко-
некоторой области W многообразия М, в которых й= dx1 А ... Л
dx". Тогда её свёртка с | равна
йA) = |Мл;2 Л ... Л SxT — gux1 Л dx3... Л dxn± ...
D.76)
и
d [б (|)] =1'., dx1 Л dx2 Л • • • Л dxn
-T-!2BdV Л dx2 Л ... Л d*"+ • •• =1'.,S.

jg4 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
По аналогии с эвклидовой геометрией определим &-диверген-
цию векторного поля | формулой
¦ (diva|)«^d [«(!)]. D.77)
Если на области V, определённой в § 4.22, мы опять введем
координаты, в которых dU есть поверхность постоянного х1,
то ограничение й (?) на dll будет опять равно
а (|) \ди = I'd*2 Л • • • Л dxn = dx1 (I)Ял;2 Л ... Л Яж".
Более общо, если п — один-форма, нормальная к дИ, т. е.
n(fj) = O на любом касательном к dU векторе (т)), и если а —
произвольная (п— 1)-форма, такая что
й = Я Л а,
то мы получаем й(|) |а?/= Я(|)а |а?/. Это позволяет записать
D.74) в виде
(diva i) ю = jj ЯA)а, D.78)
и av
где а ограничена на 0U и пЛа = й. Если всё С/ покрыто
системой координат, в которой имеет место D.76), то мы
можем записать
%% &п~хх, D.79)
dU
а это и есть стандартная запись теоремы Гаусса в R".
Упражнение 4.19. Покажите, что хотя сама форма а опре-
определяется формулой D.78) неоднозначно, её ограничение
а\ди определено уже однозначно при фиксированной фор-
форме п. Покажите, далее, что Я единственна с точностью до
преобразования изменения масштаба nt—>fn, где f — про-
произвольная, нигде не обращающаяся в нуль функция, и,
следовательно, а\ди определено однозначно с точностью
до преобразования а\ди н->/~'б \ди- Выведите отсюда, что
ограничение Я (|) а \ди определено однозначно-.
Произвол в определении дивергенции |, связанный с вы-
выбором формы й, можно устранить, если имеется метрика,—
мы можем использовать тогда в качестве со метрический эле-
элемент объёма (§ 4.13). Он, правда, определён лишь с точ-
точностью до знака, но из D.77) видно, что на самом деле diva I
от этого знака не зависит. Из D.79) следует, что стандарт-
стандартная дивергенция в R" строится на основе формы dVЛ ...

4 23 ТЕОРЕМА ГАУССА II ОПРЕДЕЛЕНИЕ ДИВЕРГЕНЦИИ ^85
... Л dxnt являющейся элементом объёма в эвклидовой
метрике.
Упражнение 4.20. С помощью D.77) покажите, что если
выбраны координаты, в которых &=f<\x Л ••• Л йхп, то
divffl 1=! (#).!• D-80)
Упражнение 4.21. Рассмотрим в трёхмерном эвклидовом
пространстве выделенную три-форму объёма й = dx Л
йу Л Зг. Покажите, что в полярных координатах она имеет
вид й = г2 sin 6dr Л d6 Л dcp. Используя D.80), покажите,
что дивергенция вектора | = %гд/дг + %дд/д$ +
равна
Упражнение 4.22. В гидродинамике (и во многих других
областях физики) используется уравнение неразрывности,
которое на языке обычного тензорного исчисления запи-
записывается как
Здесь р — плотность массы (или другой сохраняющейся
величины), а V — скорость потока. Определив й = dx Л
cty Л иг, как в упр. 4.21, и используя оператор полной про-
производной по времени d/dt-{-?v (он подробно обсуждается
ниже в гл. 5), покажите, что уравнение неразрывности
можно записать в виде
Это позволяет смотреть на рй как на динамически сохра-
сохраняющуюся три-форму объёма в жидкости. «Объём», ко-
который она приписывает каждому элементу жидкости, есть
его масса.
Упражнение 4.23. (а) С помощью D.77) покажите, что
дивергенция вектора | может быть записана как
diva | = Ml, D.81)
где * обозначает введённый ранее оператор дуализации
относительно й.
(Ь) Для любого р-вектора F положим
diveF-^l^'^dT. D-82)

4 ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Покажите, что divaF есть (р — 1)-вектор. Покажите, что
если в некоторой системе координат й> имеет компоненты
е,-... /, то
j'-^F*1-7.* D.83)
в этой системе координат.
(с) Обобщите D.80) на р-векторы.
Упражнение 4.24. (а) Используя теорему Стокса, дока-
докажите, что два-форма й на сфере S2 точна (т. е. является
внешней производной другой формы) только тогда, когда
s2
(Указание: S2 не имеет границы.)
(b) Покажите, что интеграл от заданной в R3 два-фор-
мы
5> — х1Ах2 ЛАх3
по единичной сфере S2 равен
(Указание: что такое dco в R3?) Поскольку любая два-
форма на S2 замкнута (почему?), это доказывает, что не
всякая замкнутая форма на S2 точна.
(c) Покажите, что любая замкнутая один-форма р на
S2 точна. (Указание: проинтегрируйте dp по части S2.)
4.24. КРАТКИЙ ЭКСКУРС
В ТЕОРИЮ КОГОМОЛОГИИ
Приведённое выше упр. 4.24 показывает, как можно исполь-
использовать теорему Стокса для изучения тех глобальных свойств
многообразия, которые определяют соотношение между замк-
замкнутыми и точными формами. Обозначим через ZP(M) мно-
множество всех замкнутых р-форм на М (всех а, таких что
da = 0) и через Вр(М) множество всех точных р-форм на М
(всех а, таких, что а = dp). Оба эти множества являются
векторными пространствами над полем вещественных чисел
(например, если аир — замкнутые р-формы, то act + ftp
тоже замкнута для любых вещественных чисел а и Ь). Кроме
того, Вр — подпространство в Zp, так как ddp~ = O. Покажем,
как можно разбить ZP(M) на классы эквивалентности относи-

4.24 КРАТКИЙ ЭКСКУРС В ТЕОРИЮ КОГОМОЛОГИИ 187
тельно ВР(М). Будем говорить, что две замкнутые формы
at и а.1 эквивалентны (ai да аг), если их разность есть эле-
элемент из ВР(М):
СЦ «* а2 «?=>- б[ — a2 = dp. D.84)
Класс эквивалентности ai состоит из всех замкнутых форм,
эквивалентных ей. Множество всех классов эквивалентности
называется р-мерной группой когомологий де Рама много-
многообразия М и обозначается Нр(М).
Упражнение 4.25. (а) Отношение да называется отноше-
отношением эквивалентности, если оно удовлетворяет следующим
условиям: (i) для любого а имеем a да a; (ii) если
а да |3, то и (Г да a; (Hi) если а да р и |3 да у. то а да у.
Покажите, что D.84) определяет отношение эквивалент-
эквивалентности.
(b) Если Zp и Вр — произвольные векторное простран-
пространство и его подпространство соответственно, то множество
определённых нами классов эквивалентности называется
факторпространством пространства Z" по Вр и обозна-
обозначается Zp/Bp. Покажите, что это — векторное пространство.
(Прежде всего надо определить сложение классов экви-
эквивалентности. Докажите, а затем используйте следующее:
если ai и аъ — элементы из классов эквивалентности Ау и
А2 соответственно, то сумма двух любых элементов из Л[
и Л2 лежит в классе эквивалентности элемента ai + «2-)
(c) Рассмотрим векторное пространство R2 и его под-
подпространство Rlx, состоящее из всех векторов вида (а, 0)
с произвольным вещественным а. Покажите, что R2/Rlx
есть конгруэнция прямых, параллельных оси х.
Теперь мы можем сформулировать результат § 4.19 в виде
следующего утверждения: для любого открытого шара в
«-мерном пространстве или даже для любой области U, диф-
феоморфной такому шару, №(?/) = 0 при р^1, поскольку
все замкнутые р-формы эквивалентны друг другу и, следова-
следовательно, нулевой р-форме. Так же легко вычислить H°(U)
или даже Н°(М) для любого связного многообразия М.
Нуль-форма — это просто функция, поэтому Z°(M) есть про-
пространство всех функций /, таких что й/ = 0, т. е. постоянных
функций, оно по существу совпадает с R1. Далее, поскольку
(—1)-форм в природе не существует, то пространство В°(М)
состоит из одной нулевой функции. Таким образом, отноше-
отношение эквивалентности да превращается в обычное алгебраи-
алгебраическое равенство: константы / и g эквивалентны (f да g)
тогда и только тогда, когда они равны (f==g). Следова-
Следовательно, Н°(М) = Z°(M) = Rl. В случае несвязного М функ-

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
ции из Z°(M) должны быть константами на каждой компо-
компоненте связности М, но значения этих констант не обязательно
совпадают, и Н°(М)= Z°(M) = Rm, где т — число компо-
компонент связности М.
Упражнение 4.24 легко обобщить на случай произвольной
размерности и убедиться в том, что Hn(Sn)^0 (пункт (Ь))
и #"-1(S") = 0 (пункт (с)), а в целом картина такова:
Hn(Sn) = Rl
Нр (Sn) = О, 0 < р < п,
Н° (Sn) = /?'. D.85)
Доказательство этих формул, как и многие другие интерес-
интересные результаты, можно найти в книге Спивака A970, vol. 1).
Среди множества приложений теории когомологий в этой
книге есть теорема о неподвижной точке: для чётного п на
сфере S" не существует нигде не обращающегося в нуль век-
векторного поля.
Упражнение 4.26. Для нечётного п постройте всюду отлич-
отличное от нуля векторное поле на S". (Указание: Рассмотрите
сферу S2m+1 как подмногообразие в R2m+2 и исследуйте,
как действуют на ней вращения, отвечающие матрицам
Т из SO Bm + 2), имеющим следующий вид: Т =
diag(Au Л2, ..., Am+i), где каждая из матриц Л,- есть
одна и та же 2 X 2-матрица
(cos В — sinBN
)
sin В cos6/
Покажите, что векторное поле d/d6, порождённое этой
однопараметрической подгруппой, на сфере 52m+1 нигде
не обращается в нуль.)
Упражнение 4.27. (а) Обобщая результат упр. 4.24 (Ь),
покажите, что (п — 1)-форма в Rn
й = е,7... kx' dV A • • • Л dx\ D.86)
суженная на Sn~l, не имеет нулей (сфера Sn~l определена
уравнением (х1J + (х2J + ... +(*»)*= 1).
(Ь) Покажите, что из того, что //"-'(S"-1) — Rl l), сле-
следует, что для любой (п—1)-формы а на Sn~l форма
а—аа, где а = \ al \ й, точна.
Sn~l I sn~l
(с)Дуализуя это утверждение, покажите, что любую
функцию f на 5"-I можно представить в виде /V
См. D.85). — Прим. ред.

4.25. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ И УРАВНЕНИЯ 189
где с — некоторая константа, а V — векторное поле на
S
(d) Докажите, что Hl(S1) = R1, явно построив функ-
функцию f, для которой df — a — a& (см. (Ь)).
Упражнение 4.28. (а) Предположим, что один-форма а на
М такова, что \а = 0 для любой замкнутой кривой <& в
v
М. Покажите, что а точна, т. е. существует функция /, та-
такая что а — df.
(b) Связное многообразие М называется односвязным,
если любая замкнутая кривая на нём может быть непре-
непрерывно стянута в точку. Покажите, что М односвязно
тогда и только тогда, когда Hl (M) = 0.
Прежде чем расстаться с теорией когомологий, сделаем
два коротких замечания. Во-первых, размерность простран-
пространства Нр(М) называется р-мерным числом Бетти многообра-
многообразия М и обозначается через Ьр. Во-вторых, хотя наше опре-
определение Нр(М) основано на использовании дифференциаль-
дифференциальной структуры многообразия, одна из основных теорем тео-
теории когомологий (теорема де Рама) утверждает, что на са-
самом деле группы когомологий определяются исключительно
топологической структурой многообразия М, а от его диффе-
дифференциальной структуры не зависит. Подробное обсуждение
вопроса можно найти в книге Уорнера A971).
4.25. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
И ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Рассмотренный в § 4.17 пример того, как внешнее диффе-
дифференцирование связано с условием интегрируемости, показы-
показывает также, что по крайней мере для уравнений в частных
производных первого порядка можно естественным образом
трактовать эти уравнения как соотношения между формами.
Это обстоятельство чрезвычайно важно, и мы сейчас оста-
остановимся на нём подробнее.
Рассмотрим уравнение
представленное в виде
йу = /(*, у) Ах. D.87)
Так и хочется записать его как уравнение для один-форм на
двумерном многообразии М с координатами х и у
dy — fdx = Q, D.8.8)

4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
где / теперь — функция на М. Каков смысл этого уравнения?
Поскольку формы dy и их на таком многообразии линейно-
независимы, D.88) на самом деле не может быть верным —
оно не может быть тождеством. Но, с другой стороны, мы и
не обязаны понимать его как тождество. Уравнение D.87), из
которого мы его получили, — это соотношение между «при-
«приращениями» йу и их, выполняющееся только на решении. Ре-
Решение же D.87) имеет вид у — g(x) и определяет в М кри-
кривую (или, во всяком случае, путь), т. е. одномерное подмно-
подмногообразие в М. Коэффициент наклона векторов, касательных
к этому подмногообразию, Ау/йх, равен f(x,y). Рассмотрим
один такой вектор V в некоторой точке Р, имеющий компо-
компоненты A,/(Р)). Для него ay(V) = f(P) и ux{V)=\. Таким
образом, один-форма D.88) обращается на этом векторе в
нуль:
В этом и состоит смысл D.88): решения исходного диффе-
дифференциального уравнения определяют подмногообразие в М,
касательные векторы к которому аннулируют форму D.88).
Равенство D.88) выполняется, когда оно ограничено на это
подмногообразие. Верно и обратное: если существует подмно-
подмногообразие, касательные векторы к которому аннулируют
D.88), то это подмногообразие даёт решение D.87). Есте-
Естественно, существует не одно такое подмногообразие, а целое
семейство подмногообразий, отличающихся друг от друга, на-
например, «начальным значением» решения в некоторой задан-
заданной точке х = х0 (или постоянной интегрирования в решении
D.87)).
Эту картину легко обобщить. Любое заданное семейство
форм (не обязательно один-форм) {yi, i== I, ..., N} опре-
определяет в каждой точке Р подпространство в ТР, аннулирую-
аннулирующее эти формы. Решением (интегральным подмногообразием)
для этих форм (или для соответствующего дифференциаль-
дифференциального уравнения) будет многообразие, «склеенное» из таких
бесконечно-малых касательных подпространств. Вопрос о том,
когда такая склейка возможна, прямо связан с теоремой
Фробениуса, доказанной в гл. 3. В следующем параграфе мы
переформулируем эту теорему на языке форм.
Однако первый вопрос, который приходит в голову фи-
физику,— это как вообще найти тот самый (или некоторый)
набор форм, который соответствует данному набору диффе-
дифференциальных уравнений? Для уравнений первого порядка
пример того, как это делается, был дан в упр. 4.32. Более
сложный пример доставляется уравнением второго порядка

4.26. ТЕОРЕМА ФРОБЕННУСА НЛ ЯЗЫКЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 191
для гармонического осциллятора
-|^ + со2* = 0. ,4.89)
Для удобства будем считать со константой. Чтоб перевести
это уравнение на язык форм, представим его в виде системы
уравнений первого порядка
dt ~~y> At ~ ш
Теперь очевидно, что найти подмногообразие, аннулирующее
формы
а = dx — ydt, P =s Ay + a2xAt,
и решить D.89) — это одно и то же. Многообразие, на кото-
котором определены наши формы, — трёхмерное, с координатами
(х, у, t). Подмногообразие решений будет одномерным, по-
поскольку требование обращения в нуль аир налагает два
условия на вектор в данной точке многообразия. Другие по-
поучительные примеры можно найти в работах Estabrook A976)
и Harrison & Estabrook A971), указанных в библиографии в
конце главы, мы же переходим к вопросу существования ре-
решения таких уравнений.
4.26. ТЕОРЕМА ФРОБЕНИУСА
НА ЯЗЫКЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
Итак, мы возвращаемся к одной из важнейших теорем
дифференциального исчисления на многообразиях, теореме,
которую мы обсуждали в § 3.7, используя язык производных
Ли. Чтобы переформулировать её в терминах дифференциаль-
дифференциальных форм, нам понадобятся некоторые определения. Набор
форм {р(} (любой степени) определяет в каждой точке Р
подпространство Хр в ТР, состоящее из векторов, аннулирую-
аннулирующих каждую из форм JL Оно называется аннулятором дан-
данного набора форм в точке Р. Полный идеал набора в точке Р
состоит из всех форм в этой точке, ограничения которых на ХР
равны нулю. (Заметим, что в Р для любой формы у ограни-
ограничение формы у А р,- на аннулятор р,-!) есть нуль и, следова-
следовательно, содержится в нашем полном идеале.) В любом пол-
полном идеале есть семейство линейно-независимых один-форм
{а,}, которое его порождает в том смысле, что полные идеалы
{й,}> и {Ру} совпадают. В упр. 4.29 явно строится такое се-
семейство образующих.
" А тем более на Хр. —Прим. ред.

,92 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Упражнение 4.29. Пусть {ei ёт) — базис в ХР; до-
дополним его произвольным образом векторами {ёт+1,---,ёп}
до базиса в ТР. Покажите, что дуальный базис один-форм
{йт+1, ...,&"} порождает полный идеал. Покажите, что
любая форма из этого идеала записывается в виде
X Y' Л «' с некоторыми {у'}.
Упражнение 4.30. Пусть {а/, /=1, ..., ш}—набор ли-
линейно-независимых один-форм. Покажите, что форма \ со-
содержится в их полном идеале тогда и только тогда, когда
Л^Л ... Лат = 0. D.90)
Вся эта алгебра легко распространяется на поля форм.
Полный идеал набора полей {J3,} состоит из всех таких по-
полей, что в каждой точке Р их аннулирует ХР — аннулятор на-
набора (P(i)} в этой точке. Идеал называется дифференциальным
идеалом, если вместе с любой формой у в нём содер-
содержится и dy. Набор один-форм {а,} называется замкнутым,
если все формы dat содержатся в полном идеале, порождён-
порождённом этим набором.
Упражнение 4.31. (а) Покажите, что замкнутый набор
один-форм порождает дифференциальный идеал.
(Ь) Покажите, что любой линейно-независимый набор
из п—1 или из п один-форм на «-мерном многообразии
замкнут.
Теперь мы можем сформулировать теорему Фробениуса:
Пусть {а(-, i=l, ..., m) — набор линейно-независимых
полей один-форм в открытой области U м-мерного многообра-
многообразия М. Этот набор замкнут тогда и только тогда, когда су-
существуют функции {Рц, Q/, /, / = 1, ..., т), такие что
т
¦ Щ=?Рцй<},. D.91)
Это утверждение будет доказано в следующем параграфе,
а сейчас посмотрим, что оно означает. Напомним, что мы
ищем решение системы дифференциальных уравнений {а,=0}.
Как видно из D.91), она эквивалентна системе {dQ,- = 0}. Но
последняя легко решается: {Q,- = const}. Итак, функции
{Qi} являются решениями системы {щ = 0}. Каждый набор
значений {Q/} задает m-мерное подмногообразие в М. Его
касательные векторы по определению аннулируют {dQ,}, a
следовательно и {а,}. В этом и состоит связь с прежней вер-
версией теоремы Фробениуса. Требование, чтоб набор один-форм
был замкнут, дуально к требованию, чтоб набор аннулирую-

4.26. ТЕОРЕМА ФРОВЕНИУСА НА ЯЗЫКЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 193
щих их векторных полей составлял алгебру Ли. Ниже мы
подробнее обсудим эту связь.
Формы {ш}, удовлетворяющие D.91), можно было бы
назвать «образующими поверхность» '>. Теперь мы можем уста-
установить достаточность условия интегрируемости из § 4.17.
В рассмотренном там случае многообразие имело размерность
два, а многообразие решений — размерность один. Уравнение
имеет вид D.91); следовательно, f существует тогда и только
тогда, когда da = 0. Разберем более сложный пример.
Упражнение 4.32. Рассмотрим систему линейных неодно-
неоднородных дифференциальных уравнений для функций fug,
зависящих от переменных х и у:
Sr+A2f
7 D.92)
где Ai, Bi, Ci, Di, Ei, Fi (i = 1, 2) зависят от x и у. Мы
хотим найти условия интегрируемости для этих уравнений.
(a) На четырехмерном многообразии М с координа-
координатами (х, у, f, g) введем один-формы
a = df+fA+gB-C,
^dg + gb + fE-F, D.93)
где один-форма А определена равенством
Л=Л1Зх + ЛДг/ D.94)
и аналогично определены В, С, ... . Покажите, что реше-
решение системы D.92) эквивалентно построению двумерного
подмногообразия 36 в М, на котором a|^ = PI^ = 0.
(b) Из теоремы Фробениуса следует, что если пара
(а, р) замкнута, то существуют функции U, V, W, X, Y, Z
четырёх переменных (х, у, f, g), такие что
= YdU + ZdV.
¦' В оригинале surface-forming. — Прим. ред.

194 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Покажите, что
U (х, у, f, g) = const,
V(x, у, f, g) = const
задают решение системы D.92).
(с) Из (b) следует,что необходимое и достаточное
условие существования решения — это принадлежность
форм da и dp к идеалу (a, P). Покажите, что последняя
имеет место тогда и только тогда, когда
dA + B AE = dB + B AD + A Л В
^dC + BAF + AAC
= dD + E AB = dE + E AA + D АЁ
(Указание: учет того факта, что вследствие D.94) форма
йА пропорциональна Зх Л Зу, чрезвычайно упрощает вы-
вычисления.)
(d) Покажите, что условия пункта (с) приводят к
следующим условиям интегрируемости для D.92):
дВ{
ду дх
И Т. Д.
, - BXD2 - АХВ2 = О
Что следует из теоремы Фробениуса относительно сущест-
Ёования решения уравнения D.89)? Ответ простой: поскольку
любые две линейно-независимые один-формы на трёхмерном
многообразии автоматически имеют замкнутый идеал (см.
упр. 4.31 (Ь)), то должны существовать функции f, g, h, I, m,
n, такие что
P = md/ + ndg.
Тогда одномерные подмногообразия, задаваемые уравнениями
f = const, g = const, аннулируют формы а и р и, следова-
следовательно, являются многообразиями решений.
Рассмотренный нами вариант теоремы Фробениуса не при-
применим непосредственно к системам дифференциальных урав-
уравнений, которые описываются наборами форм, включающими
и формы старших степеней. В этом случае можно поступить,
как в упр. 4.29, т. е. найти набор один-форм, порождающий

4.27. ДОК-BO ЭКВИВАЛЕНТНОСТИ ДВУХ ВАРИАНТОВ Т-МЫ ФРОБЕНИУСА 195
тот же полный идеал. Отнюдь не всегда эти один-формы
будут алгебраически эквивалентны исходному набору, т. е.
соответствующая им система дифференциальных уравнений
может не быть эквивалентна исходной. Если такого не случи-
случилось, то можно прямо применять теорему Фробениуса, в про-
противном случае нужны более тонкие методы. Обсуждение этого
вопроса можно найти в книге Шоке-Брюа и др. A977).
427. ДОКАЗАТЕЛЬСТВО ЭКВИВАЛЕНТНОСТИ
ДВУХ ВАРИАНТОВ ТЕОРЕМЫ ФРОБЕНИУСА
Напомним, как выглядит теорема в её геометрически бо-
более прозрачном варианте, описанном в гл. 3: данный набор
векторных полей {FA), i= I, ..., q), образующий в каждой
точке р-мерное векторное пространство, задает р-мерную ги-
гиперповерхность тогда и только тогда, когда всевозможные
скобки Ли \V(i), V{,i] (i, / = 1, ..., q) суть линейные комби-
комбинации этих q векторных полей. В этой главе мы сформулиро-
сформулировали теорему на языке форм, в терминах замкнутости их
внешних производных. Эта «картинка» «дуальна», дополни-
дополнительна к картинке с векторами и условием замкнутости их
скобок Ли. Центральным моментом при установлении соот-
соответствия между ними является следующее наблюдение: если
указанные выше векторные поля определяют в некоторой
точке Р нашего п-мерного многообразия r-мерное подпро-
подпространство в ТР, то они же естественным образом определяют
(п — г) -мерное подпространство в Т*р (пространстве один-
форм в точке Р), состоящее из форм, аннулируемых этими
векторами. В точности так же набор q один-форм определяет
(п — q) -мерное подпространство в Тр. Итак, мы видим, что
подмногообразие можно описать, либо задав в каждой точке
r-мерное подпространство касательных к нему векторов из
ТР, либо задав (п — г)-мерное подпространство один-форм,
которые этими векторами аннулируются.
Собственно доказательство эквивалентности двух вариан-
вариантов теоремы Фробениуса проведем в два этапа.
A) Рассмотрим подмногообразие размерности р в п-мер-
ном многообразии; найдётся п-—р различных функций Q(k),
которые (локально) задают наше подмногообразие с по-
помощью п — р уравнений Q(k) = const. По предположению,
формы dQ(ft) линейно-независимы и аннулируются векторами
V, касательными к подмногообразию: <dQ(ft>, F> = 0. С другой
стороны, касательное пространство к подмногообразию есть
р-мерное векторное пространство, определяющее (п — р)-мер-
р)-мерное подпространство один-форм, состоящее из форм, аннули-
аннулируемых касательными векторами V^y. <р, F(()> = 0. Пусть
{a,(k), k— I, .t., n — р}—некий базис в этом подпростран-

196 4- ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
стве. Поскольку формы dQ(k) тоже образуют базис, то a(k)
можно представить в виде линейных комбинаций dQ(fe), как в
D.91). Поэтому, чтоб доказать эквивалентность, мы должны
теперь убедиться в том, что условие замкнутости относи-
относительно взятия скобок Ли, которому удовлетворяют векторные
поля Vm, эквивалентно условию замкнутости набора форм
{«<*>}•
B) С этой целью рассмотрим равенства
(Щц>У(п) = О (/ = 1, ...,п — р\ / = 1, .... р)
и возьмём от них производные Ли относительно всевозмож--
ных V(k):
По правилу ли-дифференцирования форм имеем
Первый член обращается в нуль, ибо си ?ннулируется векто-
вектором V(k), второй же как раз и есть fiaw (Ущ, V(l)) — значение
d на двух векторах из исходного набора. Итак, если
?v V<-\ — линейная комбинация F((), то он аннулирует am
и, следовательно, За(^ тоже аннулируются векторами {V(j)}.
Таким образом, da(() принадлежат нашему идеалу, и замкну-
замкнутость в смысле скобок Ли влечёт за собой замкнутость на-
набора форм. И обратно: легко видеть, что из замкнутости на-
набора форм (da,(i)(V(k), V(n) = 0) следует замкнутость в смысле
скобок Ли.
4.28. ЗАКОНЫ СОХРАНЕНИЯ
Формы дают нам чрезвычайно удобный способ получения
законов сохранения для дифференциальных уравнений. Бу-
Будем считать, что решение системы уравнений эквивалентно
нахождению поверхности, аннулирующей некоторый набор
форм {а,}. Предположим, что существует форма у, являю-
являющаяся линейной комбинацией {т}:
у == Ai&i + ...,
такая что
cfy = 0.
Тогда существует другая форма о, такая что

4.28. ЗАКОНЫ СОХРАНЕНИЯ 197
в некоторой области U поверхности решения (интегральной
поверхности) Я и, кроме того,
Yltf = do|// = 0. D.95)
Применяя теорему Стокса к интегралу от do по области V,
получаем
\ da = & д.
U dU
Но в силу D.95) интеграл в левой части равен нулю, и мы
заключаем, что
а [н = 0.
Это — некоторый интегральный закон сохранения, как мы
продемонстрируем сейчас на примере гармонического осцил-
осциллятора.
В этом случае интегральные поверхности, фигурирующие
в D.95), одномерны, следовательно, do должна быть один-
формой, а а соответственно — нуль-формой (функцией). По-
Поскольку do совпадает с у, рассмотрим форму (обозначения
те же, что и в § 4.25)
Y = со2 X а + #р.
Легко проверить, что
5у = 0 D.96)
и что фактически
) D.97)
Тогда на интегральной кривой, для которой й = р = 0 и,
следовательно, \>=0> мы имеем
где рх и р2 — концы отрезка интегральной кривой, по кото-
которому мы интегрировали. Итак, мы видим, что энергия
Т • У2 + 4" • g*2*2 сохраняется на интегральной кривой*

19g 4. ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
Читатель, интересующийся приложениями такого подхода
к уравнениям, имеющим солитонные решения, может найти
их в работе Estabrook & Wahlquist A975), указанной в биб-
библиографии в конце главы.
Упражнение 4.33. Проверьте равенства D.96) и D.97).
4.29. ВЕКТОРНЫЕ СФЕРИЧЕСКИЕ ГАРМОНИКИ
Теперь мы подведём итог обсуждению сферических гар-
гармоник, начатому в § 3.18. В этом параграфе мы показали, что
пространство конечномерного представления группы SO C)
квадратично-интегрируемыми функциями на S2, отвечающего
числу /, имеет базис {Yi,m, т==—/ /}. Как построить
аналогичный базис в пространстве векторных полей на S2?
Введем в этом пространстве естественную норму с помощью
метрического тензора g на S2, который имеет в обычной сфе-
сферической системе координат компоненты {^ее=1, g^^^sin2 в,
?е<р = О}. Пусть & — элемент объёма на S2, индуцированный
этой метрикой (§ 4.13) и пусть Li,o(S ) —векторное простран-
пространство, состоящее из всех векторных полей V на S2, имеющих
конечную норму
\V)&. D.98)
s»
Мы хотим найти векторные поля из Ь\ш o(S2), являющиеся
собственными функциями для ~lz и L2.
Воспользуемся тем, что, во-первых, g и соответственно й
инвариантны относительно 1г и L2, а во-вторых, внешняя про-
производная и производная Ли коммутируют. Из функции Ущ
мы построим один-форму AYim, а из неё — вектор VYim с ком-
компонентами (индексы А и В пробегают значения 1 и 2)
DYim)A=gAB(Ylm)-B. D.99)
Очевидно, что этот вектор есть собственная функция для
h и L2:
, D.100а)
lLYi.>n> D.100b)
Но мы не можем обойтись одним типом векторных гармоник,
поскольку интересующее нас векторное пространство дву-
двумерно. Однако на двумерном многообразии есть и другой
способ построения вектора из один-формы — операция дуа-
лизации. Таким образом мы получаем вторую собственную
функцию *dYim.

4.29. ВЕКТОРНЫЕ СФЕРИЧЕСКИЕ ГАРМОНИКИ, 199
Упражнение 4.34. Покажите, что VYim и *dF/m линейно-не-
линейно-независимы в каждой точке.
Как следует из теоремы о полноте, приведённой в § 3.18»
две системы векторных сферических гармоник
ф Ytm^VYtm, D.101а)
¦ YJm^AYm D.101b)
образуют полную систему в пространстве векторных полей
на двумерной сфере.
Можно пойти дальше и таким же способом построить сфе-
сферические гармоники для тензоров второго ранга. Однако это
потребовало бы привлечения ковариантных производных на
сфере, с которыми мы пока что не знакомы (см. гл. 6). Ин-
Интересующегося читателя отсылаем к работе Regge & Wheeler
A957), указанной в библиографии.
Отметим, что мы рассматривали скалярные и векторные
сферические гармоники лишь на сфере. В приложениях
обычно фигурируют большие многообразия со сферической
симметрией, для которых сферы являются подмногообра-
подмногообразиями. В качестве простого Примера рассмотрим трёхмерное
евклидово пространство Е3. Функцию на ?3 можно разложить
в ряд 2 ftm (r) X Yim, где вся зависимость от г сосредото-
сосредоточена в {fim}- Векторное поле V на Е3 можно расщепить на
два поля:
Где Рх перпендикулярно к сферам (параллельно ёг), a Vr
касательно к ним. Если мы представим V \_ в виде ver, где
v—некоторая функция, то при вращениях v преобразуется
как скалярная функция на сфере,_а VT преобразуется как
Векторное поле на сфере. Поэтому Vt надо разлагать по век-
векторным сферическим гармоникам, аи — по скалярным. (Мно-
(Многие авторы умножают скалярные гармоники на е~, и называют
получившуюся систему третьим типом векторных сфериче-
сферических гармоник.) Мы будем использовать эти разложения при
рассмотрении космологических моделей в части Е гл. 5.
Существуют и другие, эквивалентные определения вектор-
векторных сферических гармоник, имеющие на первый взгляд мало
общего с нашими. Например, их можно определить с по-
помощью методов теории групп (см. Edmonds, 1957). Построен-
Построенная здесь система удобна для работы с дифференциальными
уравнениями, где естественно возникают использованные
нами производные.

200 * ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ
4 30. БИБЛИОГРАФИЯ
Точка зрения самого Э Картана на дифференциальные формы чрезвы-
чрезвычайно ясно изложена в его книге Les Systemes Differentials Exteneurs et
Leurs Application Geometnques (Hermann, Pans, 1945) [имеется перевод
Картан Э Внешние дифференциальные системы и их геометрические при-
приложения — М Изд во Моек ун-та, 1962] Прекрасным введением в пред
мет с множеством деталей, для которых у нас не нашлось места, и с мно-
многочисленными приложениями к физике и технике может служить книга
Н Flanders, Differential Forms with Applications to the Physical Sciences
(Academic Press, New York, L963) Свежее и современное обсуждение во-
вопроса, не требующее большой математически подготовки, проведено в
книге М Schreiber, Differential Forms a Heuristic Introduction (Springer,
Berlin, 1977) Строгое и углубленное изложение теории форм можчс найти
в книге Y Choquet Bruhat, С DeWitt Morette & М Dillard Bleick Analysis,
Manifolds, end Physics (North Holland, Amsterdam, 1977)
Обсуждение теоремы Стокса на неориеьтируемых многообразиях, за-
затрагивающее вопрос о существовании магнитных монополей, см в статье
R Sorkin J Phys A 10, 717 A977)
Подробное изложение теории когомологии можно найти в книгах
М Spivak, A Comprehensive Introduction to Differential Geometry (Pub
lish or Perish, Boston, 1970), vol 1 или F W Warner, Foundations of Diffe-
rentiable Manifolds and Lie Groups (Scott, Foresman, Glenview, III, 1971)
Полезность форм при исследовании структуры дифференциальных ура-
уравнений продемонстрирована в статьях F В Estabrook & Н D Wahlquist,
Prolongation structure of nonlinear evolution equations, J Math Phys 16, 1
A975) и The geometric approach to sets of ordinary differential equations
and Hamiltonian dynamics, SIAM Review 17, 201 A975) См также
В К Harrison & F В Estabrook Geometric approach to invariance groups
and sohtons of partial differential systems, J Math Phys 12, 653 A971) и
F В Estabrook, Some old and new techniques for practical use of exterior
differential forms, in Backlund Transformation ed R N Miura Lectures
Notes in Math no 515 (Springer Verlag, Heidelberg, 1976)
Существует много определений векторных сферических гармоник Стан
дартное руководство по этой теме — A R Edmonds, Angular Momentum
in Quantum Mechnics (Princeton University Press, 1957) По поводу рас-
распространения наших методов на тензоры см Т Regge & J A Wheeler,
Phys. Rev 108, 1063 A957) Другие определения тензорных сферических
гармоник можно найти в статьях D A Akyeampong J Math Phys 20,
505—8 A979) и E T Newman & R Penrose, J Math Phys 7, 863 A96b)

б. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
А. ТЕРМОДИНАМИКА
5.1. ПРОСТЫЕ СИСТЕМЫ
Сначала рассмотрим однокомпонентиую систему (скажем,
газ), для которой закон сохранения энергии имеет вид
?/, E.1)
где U — внутренняя энергия, a 6Q — количество тепла, полу-
получаемое газом, когда он совершает работу P6.V и изменяет
свою энергию. Мы будем понимать это равенство (уравнение
состояния) как соотношение между различными один-фор-
один-формами на двумерном многообразии с координатами (V, U),
на котором определена функция P(V,U). Итак, dV и d?/
будут у нас один-формами, а следовательно, и 6Q тоже. Но
будет ли 6Q точной один-формой? То есть можно ли найти
функцию Q(V, U), такую что 6Q = dQ? Если бы это было
так, то мы имели бы SbQ = 0, что означало бы
о=Ър a dV = [(§)а <iv + (^)v л/] л d>
(Индексы у производных указывают, какая переменная при
дифференцировании фиксирована.) Таким образом, нужная
функция Q может существовать, только если (dP/dU)v всюду
обращается в нуль, — довольно странный это был бы газ!
Поскольку 6Q — один-форма в двумерном пространстве, то
её идеал автоматически замкнут, и из теоремы Фробениуса
(§ 4.26) следует, что должны существовать функции T(U, V)
и S{U, V), такие что 6Q = TdS. Таким образом, мы опреде-
определили функции температуры и энтропии для однокомпонент-
ной системы, находящейся в состоянии термодинамического
равновесия, просто как функции, фигурирующие в записи
один-формы из левой части E.1):
+ TdS = PdV + dU. E.2)
Важно понимать, что это — чисто математическое определе-
определение S и Г, не имеющее никакого' отношения ко второму за-

202 8 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
кону термодинамики, который мы немного погодя рассмотрим.
Математические тождества такого рода для многокомпонент-
многокомпонентной жидкости уже не имеют места. (Мы увидим, что второй
закон термодинамики эквивалентен требованию 6Q = 7dS
для композитных систем. Поскольку это тождество не выпол-
выполняется автоматически, то второй закон термодинамики яв-
является физическим законом: он налагает ограничения на
возможную математическую природу физической системы.)
5.2. ТОЖДЕСТВА МАКСВЕЛЛА
И ДРУГИЕ МАТЕМАТИЧЕСКИЕ ТОЖДЕСТВА
Взяв внешнюю производную от E.2), мы получим
$Т Л dS = АР A dV. E.3)
Предположим, что мы записали T=T(S, V), P = P(S, V),
Тогда E.3) даёт (поскольку dS Л dS = 0, dV Л dV == 0)
отсюда вытекает равенство
известное как одно из тождеств Максвелла. Аналогично, за-
записав S = S(T, V), P = P(T, V), мы можем вывести ещё
одно тождество Максвелла:
Разделив обе части E.2) на Г и взяв внешнюю производную,
получаем
j-dP AdV— jzdT AdV— ~UT A dU = 0.
Полагая U=U{T, V),P=*P(T, V), имеем
или

53. КОМПОЗИТНЫЕ СИСТЕМЫ; ТЕОРЕМА КАРАТЕОДОРИ 203
Упражнение 5.1. Выведите тождество
(ди
)т
т(дРЛ d (дР\ (диЛ (дР\
Т \Ж)т ~ Р = Ьт h Ы)т ~ Ы)
умножив E.2) на \/Р и продифференцировав.
Другое важное соотношение, которое легко получается е
помощью форм, — это
Соотношение такого вида верно для любой тройки из (Р, V,
U, T, S). Для доказательства запишем
T=T(P,S), S = SG\P), P^P(T,S), E.9)
что допустимо в силу двумерности нашего многообразия.
Тогда мы получаем последовательность тождеств
dTAdS = (j^)sdP AdS
из которых и следует E.8). Заметим, что весь вывод осно-
основан на возможности записать формулы E.9), поэтому такое
тождество в действительности верно для любых трёх функ-
функций на двумерном многообразии.
То, как просто мы вывели тождества Максвелла и E.8)
при помощи форм, указывает, насколько естественно введе-
введение их в термодинамику; один-формы dP, dS и т. д. ¦— это
математически точная замена расплывчатых физических по-
понятий бесконечно-малых dP, dS и т. д.
5.3. КОМПОЗИТНЫЕ ТЕРМОДИНАМИЧЕСКИЕ СИСТЕМЫ;
ТЕОРЕМА КАРАТЕОДОРИ
Теперь рассмотрим композитную (составную) термодина-
термодинамическую систему, части которой могут обмениваться энер-
энергией друг с другом и с окружающим миром. Для неё закон
сохранения энергии имеет вид (в случае системы из Лг частей)
6Q = P, d Vx + df/, + P2d V2 + dU2 + ...
Мы будем смотреть на него как на соотношение между один-
формами на 2Л^-мерном многообразии с координатами (Vi,

204 5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
?/,; i = 1, ..., лг) и предположим, что каждое Р, может быть
выражено как функция этих координат. Возникает вопрос,
можно ли определить энтропию и температуру для системы
в целом, т. е. существуют ли Т и S, такие что
+ 6Q = 7US. E.11)
Это равенство есть не что иное, как утверждение, что форма
8Q интегрируема (в смысле теоремы Фробениуса). И теорема
Фробениуса говорит нам, что условием, необходимым и доста-
достаточным для того, чтоб это было верно, является равенство
dSQ Л 6Q = 0. Как легко видеть из E.6), вообще говоря, это
не так, и мы заключаем, что для произвольной взаимодейст-
взаимодействующей системы нет глобальных функций температуры или
энтропии. Но положение может быть иным для равновесной
системы, поскольку условия механического и термодинамиче-
термодинамического равновесия между составными частями ограничат за-
задачу (как мы надеемся) на некоторое подмногообразие на-
нашего 2Л^-мерного многообразия. Впредь мы будем относить
слово «многообразие» к этому равновесному подмногообра-
подмногообразию и исследуем возможность интегрируемости на нём 6Q,
став на точку зрения Каратеодори.
Если 6Q интегрируема, то каждая точка многообразия
принадлежит одному и только одному интегральному под-
подмногообразию; эти подмногообразия суть поверхности 5 =
const, причём они попарно не пересекаются. Таким образом,
начав в некоторой точке и двигаясь по кривой с 8Q = 0, мы
не можем достичь произвольной точки многообразия. Иными
словами, если существует функция энтропии, то нельзя адиа-
адиабатически получить произвольное равновесное состояние. Фи-
Физически интересен вопрос: верно ли обратное, т. е. если мы
знаем, что не каждое состояние достижимо по пути с 8Q = 0,
то можно ли утверждать, что 8Q интегрируема? Этот вопрос
интересен потому, что второй закон термодинамики в одной
из своих версий утверждает, что в замкнутой системе тепло
не может передаваться от холодного тела к горячему, если
в остальном система остаётся неизменной. Под замкнутой
системой мы понимаем систему с SQ = 0, и, следовательно,
второй закон говорит нам, что не всякое состояние можно
достичь при 8Q = 0. Итак, следует ли из второго закона су-
существование функции энтропии? Теорема Каратеодори
утверждает, что да.
Мы докажем следующее: если 6Q не интегрируема, то все
точки, лежащие в окрестности некоторой начальной точки Р,
можно соединить с Р кривыми, аннулирующими 8Q По-
Поскольку 6Q не интегрируема, то из теоремы Фробениуса в ва-

5 3. КОМПОЗИТНЫЕ СИСТЕМЫ; ТЕОРЕМА КАРАТЕОДОРИ 205
рианте § 4.26 видно, что существует по крайней мере одна
пара векторных полей V и W, таких что bQ{V) = bQ{W) = 0
в окрестности любой точки Р, но 6Q([V, W)) Ф О в самой Р.
По-другому, один-форма 6Q определяет в любой точке Р под-
подпространство Кр касательного пространства ТР, состоящее
из векторов, аннулирующих 8Q. Неинтегрируемость SQ озна-
означает, что эти векторные поля нигде не задают гиперповерх-
гиперповерхность: по крайней мере одна из их скобок Ли не принадлежит
Кр (см. рис. 5.1). Поскольку условие аннуляции 6Q — это
только одно уравнение, то Кр
имеет размерность п— 1 (где п —
размерность равновесного много-
многообразия). Теперь вспомните вве-
введённую в § 2.13 экспоненциаль-
экспоненциальную запись разложения Тэйлора.
Взяв любое векторное поле О, Рис 51 Касательная
принадлежащее Кр во всех точ- плоскость Кр содержит векто-
ках Р, и сдвинувшись вдоль него ры> аннулирующие 6Q, но не
на «расстояние» е от Р, мы ока- все их скобки Ли.
жемся в точке с координатами
х'= ехр(еС7)л"'|р, где О—это оператор дифференцирования по
параметру кривой, действующий на функцию х1. Множество
точек в малой окрестности Р, которые достигаются таким об-
образом, можно обозначить ехр(е/СР); это образ векторного
пространства Кр в многообразии. Локально это множество
есть (п—1)-мерная гиперповерхность. Теперь покажем, что,
двигаясь по кривым определённых выше полей V и W, можно
попасть в точки, лежащие как «снизу», так и «сверху» этой
«гиперповерхности», т. е. все точки вблизи Р достижимы.
А именно, пройдём следующим путем: сперва сдвинемся на
«расстояние» е вдоль V, потом на е вдоль W, потом на —е
вдоль V и наконец на —е вдоль W. Это приведёт нас в точку
(см. формулу B.6))
==A + e2[W, V] + О(е3))*'|р- F.12)
Отсюда видно, что мы «почти что» вернулись в точку Р, не
дойдя до неё на е2 по направлению [V, W]. Эта точка не
лежит в ехр(е/\р), поскольку Кр не содержит [V, W]. Она
находится по какую-то сторону ехр(е/Ср); _чтоб попасть на
другую, надо просто сначала двигаться nojp, а потом по V.
А раз наш путь был все время вдоль V и W, значит, он был
адиабатическим: 6Q = 0 всюду. Таким образом, ясно, что
если 8Q неинтегрируема, то все состояния системы можно
достичь адиабатически. Тем самым мы доказали, что из

206 5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
второго закона термодинамики вытекает интегрируемость 6Q
на равновесном многообразии и существование функции эн-
энтропии у композитных систем, находящихся в равновесии.
В. ГАМИЛЬТОНОВА МЕХАНИКА
5.4. ГАМИЛЬТОНОВЫ ВЕКТОРНЫЕ ПОЛЯ
Построение гамильтонова формализма начинается с функ-
функции Лагранжа 2:(q, q,t) динамической системы с координа-
координатой q(t). Импульс определяется как
p = dse/d(q,t), E.13)
а функция Гамильтона — как
H = pq,, — 2 = H(p, q). E.14)
Лагранжево уравнение движения
Г  ¦ 3— —U E.15)
dt dqj dq y '
вместе с определением р эквивалентно системе
dq dt 'dp At ' U-i.ioj
Дадим теперь геометрическое истолкование гамильтоновых
уравнений, определив многообразие М с координатами р и q,
называемое «фазовым пространством». Определим на М два-
форму
¦ 6н=сГр Л d^- E.17)
Рассмотрим на М кривую {q = f(t), p — g(t)}, являющуюся
решением системы E.16). Касательный вектор к этой кривой
О = d/dt — f,td/dq + g,td/dp обладает свойством
¦ ?п& = 0, E.18)
которое мы сейчас докажем. Поскольку d& = 0, то из D.67)
получаем
?v<b=d\G>(U)]. E.19)
Но так как й = d^ <8> dp — dp <2> d^, то
U)dp~(dp, U)dq
df з dq 7 E.20)

5.5. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ 207
С другой стороны, поскольку / и g удовлетворяют E.16), мы
имеем
&{п) = ~^р+Щ-дЧ=^Н. E.21)
Таким образом, d[u@)] обращается в нуль и E.18) дока-
доказано. Векторное поле U, удовлетворяющее E.18), называется
гамильтоновым векторным полем.
Упражнение 5.2. (а) Докажите, что если О — гамильтоново
векторное поле, то существует некоторая функция #(р, q),
такая что уравнения E.16) выполнены на интегральных
кривых поля П.
(Ь) Докажите, что гамильтоновы векторные поля обра-
образуют алгебру Ли относительно операции коммутирования.
Упражнение 5.2(а) позволяет смотреть на гамильтоново
поле U как на поле касательных к траекториям системы в
фазовом пространстве. Заметим, что система консервативна,
поскольку из E.16) следует, что
?^0 <522)
5.5. КАНОНИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ
Координаты р и q задаются не однозначно. Определим
каноническое преобразование как преобразование, сохраняю-
сохраняющее вид й. Это значит, что новые координаты Р = P(q, р) и
Q = Q{q, p) будут каноническими, если
dq Л dp = 6Q Л dP. E.23)
Необходимое и достаточное для этого условие:
q dp dp dq ) w--"/
Пример канонического преобразования: Q = p, P = —q. Ме-
Менее тривиальный пример строится, если следовать процедуре,
использованной нами при выводе тождеств Максвелла в тер-
термодинамике. Запишем p = p(q, Q), P = P(q, Q); тогда из
E.23) находим
др/dQ — —dP/dq. E.25)
Следовательно, если взять произвольную функцию F(q, Q) и
положить
р == OF/dq, P = —dF/dQ,
то E.25) будет выполняться тождественно. Поэтому мы гово-
говорим, что F(q, Q) генерирует каноническое преобразование.

208 5. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Поскольку за независимые переменные в E.23) можно было
бы взять не (q, Q), а любую из пар: (q, P), (р, Q) или (р, Р),
то соответственно есть четыре типа производящих функций
канонических преобразований. Более полно этот вопрос иссле-
исследован у Голдстейна A975) (см. библиографию в конце главы).
5.6. СООТВЕТСТВИЕ МЕЖДУ ВЕКТОРАМИ
И ОДИН-ФОРМАМИ, УСТАНАВЛИВАЕМОЕ ФОРМОЙ й
Один из наиболее важных моментов описанного геометри-
геометрического подхода к гамильтоновой динамике состоит в том, что
форма й играет ту же роль, какую метрика играет на рима-
новых многообразиях, — задаёт обратимое 1-1-соответствие
между векторами и один-формами. Если V — векторное поле
на М, то мы определяем поле один-форм V формулой
Pssffi(F), E.26)
или
(?),- = Ю„У/. E.27)
Аналогично по заданному полю один-форм а определяется
(однозначно) векторное поле а:
а за б (а). E.28)
Упражнение 5.3. Докажите, что (V, V} = 0, так что б не
подходит в качестве обычной метрики.
Упражнение 5.4. Докажите, что если а — fdq + gdp, то
a = Baj-fw {5'29)
Упражнение 5.5. Докажите, что X — гамильтоново вектор-
векторное поле на М тогда и только тогда, когда X — точная
один-форма, т. е. тогда и только тогда, когда существует
функция Н, такая что К — АН, или X — АН.
5.7. СКОБКА ПУАССОНА
Предположим, что на многообразии заданы две функции
fag. Введём векторные поля Xf == d/ и Xg^= dg и рассмо-
рассмотрим скаляр
{f, g} з= 5>(Xf, Хв) = <d/. ХЙУ E.30)
Поскольку & = dq ® dp — dp <?> d^, мы имеем
у __ dg д dg д
Л8~ dq др~ ~д^Щг

5.8. МНОГОЧАСТИЧНЫЕ СИСТЕМЫ; СИМПЛЕКТИЧЕСКИЕ ФОРМЫ 209
в чём можно убедиться, проверив, что со {Xg) = dg. Таким об-
образом, мы получаем
u. §i — w л ле; — dq др др dq ¦
Справа стоит то, что обычно называют скобкой Пуассона
функций fug. Определение E.30) поясняет её геометрический
смысл и показывает, что скобка Пуассона действительно не
зависит от системы координат. Она зависит только от й.
Упражнение 5.6. (а) Положив Хн = &Н, покажите, что для
любой функции К
{К, Н) = ХН (К) = dK/dt, E.32)
где / — параметр, такой что Хн = A/At. Итак, скобка Пуас-
Пуассона произвольной функции с функцией Гамильтона есть
производная по времени от значений этой функции вдоль
траектории системы. В частности, интегралы движения
имеют нулевую скобку Пуассона с Н.
(b) Покажите, что скобки Пуассона удовлетворяют
тождеству Якоби:
{f, {g, h}} + {g, {h, ft} + {h, {f, g}} = 0 E.33)
для любых функций /, g, h класса С2.
(c) Используя это, покажите, что
[Xt, Xg} = -X{f.e}, E.34)
так что гамильтоновы векторные поля образуют алгебру
Ли.
5.8. МНОГОЧАСТИЧНЫЕ СИСТЕМЫ;
СИМПЛЕКТИЧЕСКИЕ ФОРМЫ
На практике мы сталкиваемся с системами, имеющими бо-
более чем одну степень свободы, так что имеется не одна, а не-
несколько пар р и q. У частицы в трёхмерном пространстве есть
три q и три р, и фазовое пространство шестимерно. Система,
содержащая N таких частиц, имеет 6Лг-мерное фазовое про-
пространство. Если мы рассмотрим систему общего вида с п
степенями свободы, то фазовое пространство будет 2«-мер-
ным, и все предыдущие результаты останутся в силе, если в
качестве два-формы б мы возьмем (локально)
п
б = X d qA Л d pA. E.35)
Л1

210
6. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Эта форма й называется симплектшеской формой, а фазовое
пространство с этой формой — симплектическим многообра-
многообразием.
Упражнение 5.7. (а) Покажите, что / является интегралом
движения, если функция Гамильтона Н ли-инвариантна
относительно поля Xf = df:
?JfH^0. E.36)
(См. упр. 5.6.)
(b) Определим форму объёма б в фазовом простран-
пространстве формулой
д = б Л ... Ли, E.37)
п раз
где 2п — размерность фазового пространства. Покажите,
что 5#0 и что всякое гамильтоново векторное поле U
имеет нулевую дивергенцию относительно этого -элемента
объёма. Иными словами, объём в фазовом пространстве
сохраняется при эволюции системы во времени. Этот ре-
результат известен как теорема Лиувилля.
Упражнение 5.8. Сейчас мы докажем правильность сделан-
сделанного в § 3.12 замечания относительно связи векторов Кил-
линга и сохраняющихся величин. Для движущейся ча-
частицы координаты фазового пространства суть {qA, pA} =
{xl, pi = mvi}, а функция Гамильтона равна Я =
(l/2m)giipipj-\-Ф(х'). Докажите, что если О — вектор
Киллинга и функция Ф постоянна вдоль U, то «сопряжён-
«сопряжённый момент» вектора Киллинга pjj^Uipi является сохра-
сохраняющейся величиной. (Указание: Используя упр. 5.7, опре-
определите Xf как векторное поле в фазовом пространстве,
у которого пространственные компоненты те же, что и у О,
а импульсные компоненты нулевые. Покажите, что
и найдите / из формулы E.31).)
5.9. ЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ;
СИМПЛЕКТИЧЕСКОЕ СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
И СОХРАНЯЮЩИЕСЯ ВЕЛИЧИНЫ
Особенно просто и наглядно формулируются законы со-
сохранения в случае линейных систем. Линейной называется
динамическая система, функция Гамильтона которой имеет
вид
Н= ? (ТАВрАрв + УавЯаЯ% E.38)
дв1

59 ЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ СИСТЕМЫ 211
где ТАВ и Vab не зависят от рд и qA. Такая система называется
линейной потому, что её уравнения движения линейны по
{q\ Pa}:
Заметим, что можно считать ТАВ = ТВА и VAB = Квл, по-
поскольку антисимметричная часть, скажем, 7ми, после свёртки
с симметричным выражением рдрв не даёт вклада в Н.
Линейность системы гарантирует, что если {яйу Ртд} и
К)' РB) а} - Решения, то и {си/Д + р^,арA) л + РРBМ} будет
решением при любых аир. Поэтому фазовое пространство —
это не просто многообразие, оно обладает естественной струк-
структурой векторного пространства. Конечно же, векторное про-
пространство— это частный случай многообразия, так как его
можно отобразить в R", но это такое многообразие, которое
может быть отождествлено с касательным пространством в
любой его точке. А именно, поскольку кривая в векторном
пространстве есть последовательность векторов, зависящая от
параметра, а касательный вектор есть просто результат диф-
дифференцирования по этому параметру, то он тоже является
элементом этого векторного пространства. Более того, все
касательные пространства ТР естественно отождествляются
друг с другом; мы можем говорить о равенстве векторов из
разных ТР, просто сравнивая их компоненты. (Это значит, что
векторное пространство является плоским многообразием, см.
гл. 6 )
Поскольку точка фазового пространства является векто-
вектором, мы можем использовать симплектическую форму й для
определения скалярного произведения элементов фазового
пространства. Если РA)— вектор с компонентами to4,., p., Aj
Л = 1 N\, а РB) имеет соответственно компоненты
{#B)> Р{2\д}> т0 их симплектическое скалярное произведение
(или кососколярное произведение) определяется как
qf2)Pw a). E.41)
Если ?(i)(t) и ?B)(t) — траектории системы, то их симплекти-
ческое скалярное произведение не зависит от времени. Чтоб
это доказать, мы просто подставим уравнения движения в
формулу для d6 (Г(п, KB))/d/ (по повторяющимся индексам

212 5. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
производится суммирование):
~п Ю (^A). У{2)) = -J7 (9A)) РB, л + <7(Ц J РB) Л
d_ , л , д d_
At K4W ПО Л 9B) rff РA) Л
Из симметричности ТАВ и V4b следует, что
^FF(S)) = O, E.42)
если P(i) и РB) — решения.
Симплектическое скалярное произведение позволяет до-
довольно изящно определить некоторые из сохраняющихся ве-
величин, связанных с решениями. На первый взгляд это не ка-
кажется очевидным: хотя симплектическое скалярное произве-
произведение и сохраняется, но, умножив решение само на себя, мы
получим тождественный нуль. Фокус заключается в том, что,
воспользовавшись инвариантностью системы (т. е. инвариант-
инвариантностью ТАВ и Vab), мы можем получить из одного решения Р
другое, тесно с ним связанное. Например, допустим, что ТАВ
и Vab не зависят от времени. Тогда уравнения движения по-
показывают, что если ?(t) — решение, то 6V/dt — тоже решение.
И мы определяем каноническую энергию Ес решения У как
E.43)
Легко проверить, что Ес(?) есть в точности значение функ-
функции Гамильтона на решении Р.
Так же легко получать и другие сохраняющиеся величины.
Обычно бывает, что ТАВ и Vab зависят от координат {х1} мно-
многообразия, на котором задана динамическая система (эвкли-
(эвклидово пространство для нерелятивистской динамики). Если,
как в упр. 5.8, найдётся векторное поле О, такое что
?1]T^ = 0 = ?vVABt F.44)
то существуют связанные с О сохраняющиеся величины. (Вы-
(Вычисляя ?jjTab, важно иметь в виду различие между индек-
индексами А, В, относящимися к координатам в фазовом простран-
пространстве, и тензорными свойствами ТАВ на исходном многообра-
многообразии. На нём величины ТАВ могут быть скалярами или тензо-
тензорами в зависимости от того, что представляют из себя qA.
Индексы А и В всего лишь метки, они вовсе не указывают на

5.10. УРАВНЕНИЯ ГАМИЛЬТОНА И РАССЛОЕНИЯ 213
то, что с ТАВ надо обращаться как с тензором типа (Qj при
вычислении производной Ли по направлению U, поскольку
О — это вектор в исходном многообразии, а не в фазовом
пространстве.) Как и раньше, если У— решение, то и ?,jjY —
решение. (Опять то же замечание: это производная в исход-
исходном многообразии, а не в фазовом пространстве.) Итак, опре-
определим канонический U-импульс формулой
¦ Рп<У) = й(?пУ-П E.45)
Читатель может на простых примерах, вроде того что дан
в упр. 5.8, убедиться •>, что обычные сохраняющиеся величины
действительно так получаются.
Хотя наше обсуждение ограничивалось системами с конеч-
конечным числом (N) степеней свободы, развитый формализм
прямо обобщается на непрерывные системы, такие как систе-
системы, описываемые волновым уравнением. Знакомый с уравне-
уравнением Клейна — Гордона читатель может узнать симплектиче-
ское скалярное произведение: интеграл от сохраняющейся
плотности тока -ф*-ф — -ф^з* как раз и есть (с точностью до по-
постоянных множителей) б(гр*, ty). Обсуждение канонических
сохраняющихся величин для случая волн в жидкости с при-
приложением к вопросам устойчивости можно найти в работе
Friedman & Schutz A978), указанной в библиографии в конце
главы.
5.10. УРАВНЕНИЯ ГАМИЛЬТОНА И РАССЛОЕНИЯ
В § 5.4 мы определили фазовое пространство как много-
многообразие с координатами р и q. Это определение таит в себе
множество важных и интересных структур. Пусть динамиче-
динамическая система имеет N координат {<?'}, отвечающих её N сте-
степеням свободы. Они определяют многообразие М, называемое
конфигурационным пространством, и эволюция динамической
системы во времени описывается кривой q'(t) в М. Функция
Лагранжа S1 зависит от q' и dql/At и, следовательно, является
функцией на касательном расслоении ТМ. Покажем, что им-
импульс
pt=*d&№\t) E.46)
есть поле один-форм на М, т. е. сечение кокасательного рас-
расслоения Т*М. Мы покажем это, установив, как преобразуется
импульс при замене координат. Введём на М новые коорди-
координаты
E.47)
" Это далеко не просто. — Прим. перев.

214 5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Тогда новые импульсы будут равны
Далее, как qk,t, так и Q' ,t, в каждой точке Р являются эле-
элементами слоя над этой точкой, и при замене переменных
E.47) координаты в этом слое соответственно преобразуются.
А именно, если V — вектор в Р, то для его компонент мы
имеем
Vi' = A>'Vk, Vk = AW'.
к ]
С тем же успехом формула применима и к вектору скорости
Подставив это соотношение в E.48), получаем
Pr = Afok, E.49)
и, следовательно, импульс действительно является один-
формой.
Итак, мы видим, что фазовое пространство с координа-
координатами {q\ pi) есть не что иное, как кокасательное расслоение
Т*М, а функция Гамильтона — функция ча этом расслоении.
Более того, симплектическая форма
й = d</ Л 2/э,
(суммирование подразумевается) не зависит от впбора коор-
координат на М. Пусть произведено преобразование
Q1' = Q1'(<?') => W = A,'dq\
ь - ь ~ / , - E.50)
Р,' = A,'pk=> d Pr = Л?. ipkd ql + Aj' d pk.
(Напомним, что оператор d действует на Т*М, а не на М и
что Akf — функции, зависящие, лишь от координат М.)
Тогда
W Л dPr = Ai'A}, lPkdql Л dql + A1-A)-dql Л dpk. E.51)
В то же время
и E.51) принимает вид
dQr Л dPv = - А[ lA^pkdq' Л dql + dq A dpt.

5 И. УРАВНЕНИЯ МАКСВЕЛЛА НА ЯЗЫКЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 215
Первый член в правой части обращается в нуль, поскольку
симметрично по / и /, а свёртывается с антисимметричной
формой ~dq' A~dql. Таким образом, от выбора координат на М
форма & не зависит и является естественной структурой на
кокасательном расслоении Т*М. Кроме того, Т*М всегда ори-
ориентируемо, поскольку форма объёма 5, определённая в
упр. 5.7(Ь), нигде не обращается в нуль.
Очевидно, что хотя в нашем примере мы обращались с
расслоенной структурой как с тривиальной (т. е. как с пря-
прямым произведением q- и р-пространств), можно рассматри-
рассматривать и нетривиальные многообразия М и расслоения Т*М,
для которых все приведённые выше координатные формулы
имеют смысл уже лишь локально. Даже в таком простом
примере, как шарик, движущийся по поверхности сферы, мы
имеем фазовое пространство с нетривиальной расслоенной
структурой, как было отмечено в § 2.11.
С. ЭЛЕКТРОМАГНЕТИЗМ
5.11. УРАВНЕНИЯ МАКСВЕЛЛА
НА ЯЗЫКЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ
Выпишем уравнения Максвелла в их традиционном виде
в системе единиц с с == \\0 = е0 = 1:
E.52а)
B=0, E.52b)
В = 0, (Б.Б2с)
E.52d)
При этом мы, конечно же, использовали операторы ротора и
дивергенции в обычном трёхмерном плоском пространстве,
Теперь мы хотим показать, что эти уравнения можно за-
записать, пользуясь лишь понятиями метрики и внешнего диф-
дифференцирования. Начнём с того, что перепишем уравнения в
их релятивистски-инвариантном виде •>, введя два-форму Фа-
'* Для читателя, который это не знал или забыл, напомним, что урав-
уравнения Максвелла правильно описывают распространение света, а специаль-
специальная теория относительности как раз и была изобретена для объяснения не-
некоторых свойств света; поэтому уравнения Максвелла уже релятивистские.
Всё, что мы здесь делаем, — это придаём им подходящую форму.

216 5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
радея F
v.
с компонентами
/0 -
, Ех
\ СУ
\Ег
-Ех
0
-вг
By
-Еу
Bz
0
-вх
-Ez
-By
вх
0
E.53)
(Здесь, как и в § 2.31, греческие индексы пробегают t, x, у, z.)
Упражнение 5.9. Докажите, что при пространственных вра-
вращениях F^v преобразуются таким образом, что Е и В пре-
преобразуются как трёхмерные векторы.
С помощью тензора Фарадея уравнениям Максвелла
можно придать чрезвычайно простой вид. Например, четыре
уравнения E.52b, с) записываются как
F = 0, E.54)
где квадратные скобки обозначают антисимметризацию.
Упражнение 5.10. (а) Докажите, что в E.54) содержится
четыре линейно-независимых уравнения.
(Ь) Докажите эквивалентность уравнений E.54) и
E.52Ь, с), воспользовавшись явным выражением E.53)
для компонент F.
Теперь перейдем к оставшимся уравнениям. Если мы вве-
введём метрику специальной теории относительности, имеющую
в нашей системе координат следующие компоненты:
— 1 0 0 0-
I о I о° I-
0 0 0 1
то мы можем определить антисимметричный тензор F типа
«)=
F F
— Ez Ву — Вх
Упражнение 5.11. Докажите формулу E.56),

6 11. УРАВНЕНИЯ МАКСВЕЛЛА НА ЯЗЫКЕ ДИФФЕРЕНЦИАЛЬНЫХ ФОРМ 217
Теперь оставшиеся уравнения можно записать так:
У*У = 4яЛ E.57)
где мы ввели 4-вектор тока с компонентами {/'==р, /' = (.!)'
для i = х, у, z}.
Упражнение 5.12. Докажите, что четыре уравнения
E.57) — это то же самое, что E.52а—d).
До сих пор мы были привязаны к лоренцевым координа-
координатам, поскольку, хотя E.54) и не зависит от координат, E.57)
не представляет собой тензорного равенства, верного в
любой системе координат (вспомните упр. 4.15). С другой
стороны, в упр. 4.23 мы видели, как определить дивергенцию
антисимметричного (п )-тензора, если у нас есть форма
объёма. Поскольку у нас есть метрика и {d/dt, д/дх, д/ду,
d/dz} образуют в этой метрике ортонормированный базис, то
выделенная форма объёма имеет вид
o5 = d? Л их Л йу Л Sz.
Дальнейшие рассмотрения проведем в форме упражнения.
Упражнение 5.13. (а) Определим два-форму *F как
свёртку
'P^±&{F), E.58)
т. е.
7"
Конечно же, это введённая в гл. 4 дуальная к F форма.
Выразите компоненты (*Р)^ через Е и В.
(Ь) Определите три-форму *7 как свёртку
7= йG) E.59)
и покажите, что E.57) эквивалентно
&(F) = AnJ. E.60)
Из упр. 4.23 следует, что это можно переписать так:
7 E.61)
Обратите внимание на то, как похоже выглядят две части
уравнений Максвелла в нашей новой записи:
+ d? = 0, E.54)
+ d *F = 4я7. E.60)

Б ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Также заметьте, что теперь они представлены в бескоорди-
бескоординатном виде и, следовательно, выглядят так же на любом
многообразии с метрикой (метрика была нужна, чтоб полу-
получить *Р из F). Сходство между E.54) и E.60) в уравнениях
Максвелла довольно глубокое. В самом деле, действие опера-
операции * на F сводится просто к взаимной замене Е и В (см.
упр. 5.13(а)), а 7— это плотность электрического тока. Если
бы существовали магнитные монополи, то у нас было бы
два тока 7е и 7т и уравнения Максвелла приняли бы сим-
симметричную форму
df = 4я*7т, $*Р = 4я*7е. E.62)
Упражнение 5.14. (а) Докажите E.62).
(Ь) Докажите с помощью внешнего дифференцирова-
дифференцирования, что уравнение E.60) гарантирует сохранение заряда,
т. е. что
divG) = 0. E.63)
Упражнение 5.15. Установите теорему об изменении пол-
полного заряда, действуя следующим образом.
(а) Возьмите произвольную ориентированную трёх-
трёхмерную гиперповерхность Ж и ограничьте на неё E.60).
Докажите, что операция ограничения коммутирует с внеш-
внешним дифференцированием, т. е.
(Ь) Возьмите на Ж какую-нибудь область 3) с грани-
границей дЗ>. Проинтегрируйте ограничение E.60) по 3) и, вос-
воспользовавшись теоремой Стокса, покажите, что (соответ*
ствующие ограничения подразумеваются)
3) дЗ)
(с) Докажите, что в случае, когда Ж — гиперповерх-
гиперповерхность t — const в пространстве Минковского, а дЗ) —
сфера, полный заряд, заключённый в 3), получается как
интеграл от нормальной компоненты электрического поля
по дЗ).
5.12. ЗАРЯД И ТОПОЛОГИЯ
Поскольку теперь мы можем говорить об уравнениях Мак-
Максвелла на любом многообразии с метрикой, стоит упомянуть
о двух попытках разрешить головоломный вопрос: «Что есть
заряд?», при помощи такого ответа: «Заряд —это топология».
Первое объяснение, принадлежащее Дж. Уилеру A962),

5 12 ЗАРЯД И ТОПОЛОГИЯ _219
чрезвычайно просто. Рассмотрим рис. 5 2, на котором изобра-
изображена гиперповерхность t = const некоего гипотетического
пространства-времени. Сплошные линии на рисунке — это
интегральные кривые поля Е Никаких зарядов нигде нет, и
эти интегральные кривые либо замкнуты (концы линий, «про-
«продетых» сквозь ручху, соединяются между отверстиями), либо
бесконечны (концы линий остаются свободными). Посмотрим,
что обнаружит экспериментатор, измеряющий Е на сфере S,
Рис 5 2 Червоточина', или 'ручка', прикрепленная к трехмерному мно-
многообразию (одна размерность на рисунке не представлена) Силовые ли-
линии могут пронизывать ручку, выходить наружу и вновь нырять в нее, в
результате чего каждое отверстие выглядит заряженным, хотя зарядов в
пространстве нет
окружающей одно из отверстий, интеграл Is^is, конечно же,
в нуль не обратится (всюду на S поле направлено наружу), и
он скажет, что отверстие имеет положительный заряд В точ-
точности так же сфера вокруг другого отверстия даст отрица-
отрицательный заряд, равный по величине предыдущему (Вычис-
(Вычисления упр 5 15 здесь силы не имеют, поскольку S не делит
многообразие на внешность и внутренность, см рис 4.10)
Итак, мы nociроили модель «заряда без заряда», получив
заодно объяснение того, почему положительный и отрицатель-
отрицательный заряды равны между собой У такой модели есть, однако,
два изъяна во первых, никому пока не удалось получить ре-
решение, скажем, уравнений Эйнштейна с похожей геометрией
пространства-времени, во-вторых, представление о том, что
два заряда (которые могут быть чрезвычайно сильно удалены
друг от друга) всегда соединены собственной специальной
«ручкой», неудовлетворительно в философском плане.
Второе, более изощренное объяснение использует много-
многообразие, сделанное неориентируемым при помощи специаль-
специальной конструкции ручки. Оно принадлежит Соркину A977)
(см библиографию в конце гл. 4). В его модели оба отверстия
имеют одинаковые по величине и знаку заряды, и можно

220 5. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
себе представить, что они близко сомкнуты и образуют нечто,
выглядящее для внешнего наблюдателя как один заряд, рав-
равный удвоенному заряду каждого отверстия. Здесь упр. 5.15
опять не работает, поскольку многообразие неориентируемо.
Такая модель свободна от второго изъяна модели Уилера —
но не от первого! И ни одна из моделей не объясняет, почему
два произвольных (не имеющих друг к другу отношения) за-
заряда должны быть равны. Несмотря на это, приведённые
примеры иллюстрируют становящуюся все более и более не-
несомненной идею, что в теоретической физике есть и ещё
что-то, кроме локальных дифференциальных уравнений!
5.13. ВЕКТОР-ПОТЕНЦИАЛ
Существование «вектор-потенциала» для уравнений Мак-
Максвелла прямо следует из E.54). Поскольку F — замкнутая
два-форма, то существует один-форма А, такая что
¦ F = dA E.64)
в некоторой окрестности каждой точки. С помощью метрики
этой один-форме- можно сопоставить вектор, который и назы-
называется вектор-потенциалом. Более естественно, конечно же,
пользоваться один-формой потенциала. Заметим, что А опре-
определена не однозначно: А' = А -\- Щ при любой функции / даёт
по формуле E.64) то же самое F. Такая замена называется
калибровочным преобразованием. Отметим также, что если
существуют магнитные монополи, то йР не может всюду обра-
обращаться в нуль. Как следует из нашего обсуждения точных
форм в гл. 4, в этом случае А можно определить лишь на
простых областях, не содержащих магнитных монополей.
В частности, в той области пространства-времени, где содер-
содержится мировая линия магнитного монополя, нельзя всюду
согласованно определить один-форму потенциала.
Упражнение 5.16. (а) Покажите, что если существует
один-форма потенциала А, то на нерелятивистском языке
ей соответствуют скалярный потенциал ф и вектор-потен-
вектор-потенциал Л' (трёхмерный), задаваемые формулами ф = Ло,
Л' (вектор-потенциал) = —Л,- (один-форма), где индексы
относятся к той же системе координат, что и в E.52).
(b) Выясните, как определённые в (а) потенциалы ф
и Л' преобразуются при калибровочных преобразованиях.
(c) Чтобы проиллюстрировать сложности с один-фор-
один-формой потенциала, вызываемые наличием магнитных моно-
монополей, рассмотрим случай, когда заряды есть, а монополей
нет, но один-форма потенциала а для F определена равен-
равенством

5.14. ПЛОСКИЕ ВОЛНЫ: ПРОСТОЙ ПРИМЕР 221
(Вследствие дуальности магнитных и электрических полей
относительно операции* присутствие электрического за-
заряда влечёт для а те же сложности, что и присутствие
магнитного для А.) Запишите уравнение Максвелла через
& и покажите, что а существует лишь в тех областях, в ко-
которых нет заряда и которые могут быть стянуты в точку.
Сделайте это, найдя а явно для случая одиночного стати-
статического изолированного заряда q.
5.14. ПЛОСКИЕ ВОЛНЫ: ПРОСТОЙ ПРИМЕР
Как известно, плоские электромагнитные волны движутся
со скоростью света. Рассмотрим специальный тензор Фарадея
Fa&, все компоненты которого зависят лишь от и = t — х (на-
(напомним, что мы используем систему единиц с с= 1):
/?оР = A<*V(t — х) = Л«Р(«). E.65)
При каких условиях он удовлетворяет уравнениям для пустого
пространства dF = 0, 6. Р = 0? Из E.65) следует, что
AF = А (^ F^Ax» A d>) = \ d (/>) d> A d>
== Y(dЛн,v/dы) Аи A d> Л d**.
Из E.53) легко вывести, что
№ = [±- [Bz - Еу) At Л Ах ЛАУ + +- (Вх) At А $у Л dz
— (— By — Ez) dif Л dx Л dzl,
и если это обращается в нуль, то (пренебрегая статическим
полем) мы получаем
Bz = Ey, Ву = —Ег, Ех = 0. E.66)
Упражнение 5.17. Покажите, что из уравнения й*Р = О
следует, что
Вг = Еу, By = —Ez, Ex = 0. E.67)
Теперь мы видим, что электрическое и магнитное поля пло-
плоской электромагнитной волны поперечны (т. е. перпендику-
перпендикулярны направлению её распространения) и задаются двумя
независимыми функциями Еу(и) и Ег(и), отвечающими двум
независимым поляризациям волны.

222 Б. ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
D. ДИНАМИКА ИДЕАЛЬНОЙ ЖИДКОСТИ
5.15. РОЛЬ ПРОИЗВОДНЫХ ЛИ
Под «идеальной» мы понимаем жидкость, не обладающую
вязкостью и движущуюся адиабатически, т. е. без теплооб-
теплообмена. Хорошо известно, что такая жидкость подчиняется опре-
определённым локальным законам сохранения: каждый элемент
жидкости в процессе своего движения сохраняет постоянную
массу, энтропию и, в некотором смысле, интенсивность вихрей
скорости. Эти законы сохранения обычно выводятся с по-
помощью традиционного векторного анализа и могут показаться
довольно сложными. С геометрической точки зрения наличие
некоего потока немедленно наводит на мысль использовать
производную Ли, и, действительно, мы сейчас продемонстри-
продемонстрируем, как проясняются локальные законы сохранения, если
работать с производными Ли.
5.16. ПОЛНАЯ ПРОИЗВОДНАЯ ПО ВРЕМЕНИ
Как мы видели в упр. 4.22, уравнение неразрывности,
обычно записываемое в виде
можно представить в виде
¦ Df + ?v)(pS>) = 0, E.68)
где й = dx Д dy Л dz — гри-форма объёма в эвклидовом
пространстве. Оператор (д/dt + ?у) естественно считать
оператором дифференцирования по времени, связанным с дан-
данным элементом жидкости. Чтобы это понять, представим себе
не наше обычное пространство, а галилеево пространство-
время— четырёхмерное многообразие с координатами (х, у,
z, t) (см. § 2.10). Любая гиперповерхность / = const есть
эвклидово пространство. Движение элемента жидкости опи-
описывается кривой в пространстве-времени, называемой миро-
мировой линией этого элемента. На рис. 5.3 изображены две такие
мировые линии (АА' и ВВ'). За бесконечно-малый промежу-
промежуток времени dt точка на этой кривой перемещается из поло-
положения с координатами [х, у, z, t) в положение с координатами
(х + Vxdt, у + Vydt, z -f- Vzdt, t-j-dt). Если обозначить через
U вектор, касательный к мировой линии в четырёхмерном
многообразии, то он, очевидно, будет иметь компоненты
(Vх, Vv, Vz, 1). Мы видим, что полная производная по вре-
времени, связанная с элементом жидкости, есть просто ?jj —

6.16. ПОЛНАЯ ПРОИЗВОДНАЯ ПО ВРЕМЕНИ 223
естественная производная вдоль мировой линии этого эле-
элемента.
Упражнение 5.18. Используя равенство B.7), покажите, что
, E.69)
где W — любое векторное поле на гиперповерхности t =
const, т. е. любое чисто пространственное векторное поле
(W 0)
Равенство E.69), очевидно, выполняется, и если мы
заменим W любым чисто пространственным тензором типа
II, т. е. тензором, «лежащим» в трехмерном пространстве
t = const. Понятие чисто пространственного тензора выглядит
Рис. 5.3. Два момента галилеева времени и мировые линии АА' и ВВ' двуз?
частиц. Вектор О касателен к кривой АА', параметризованной временем t.
неправомерным — оно неинвариантно относительно замены
координат в четырёхмерном многообразии, поскольку «чистая
пространственность» означает просто, что все ^-компоненты
тензора равны нулю. Но в нашем случае оно приемлемо, так
как в нерелятивистской физике между пространством и вре-
временем проводится чёткая грань.
Упражнение 5.19. Наиболее общий вид преобразований
координат, сохраняющих свою «естественность» по отно-
отношению к расслоенной структуре галилеева пространства-
времени (§ 2.10), — это
t' = g(tY, xl' = f(xl,t), /=1,2,3. E.70)
Покажите, что (". J-тензор А, не имеющий временных
компонент (А(..., S', ...) = 0), сохраняет это свойство
при таких преобразованиях и ( J -тензор В, не имеющий
пространственных компонент (т. е. лишь Bt...t не нуль),
тоже остается чисто временным.

224 S- ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
5.17. УРАВНЕНИЕ ДВИЖЕНИЯ
Условие адиабатичности движения означает, что полная
энтропия элемента жидкости должна сохраняться. Удобно ра-
работать с удельной энтропией S (энтропией на единицу мас-
массы). Очевидно, что при движении она должна оставаться по-
постоянной:
Движение жидкости с давлением р, находящейся в грави-
гравитационном поле с потенциалом Ф, описывается уравнением
Эйлера, которое в декартовой системе координат выглядит
так:
JLVt+VidV^±ep+dO==0. E.72)
dt дх' р дх1 дх1
Есть две причины, по которым это уравнение верно лишь в
декартовых координатах. Во-первых, некоторые индексы i —
верхние, а некоторые—нижние, а это безразлично лишь в
ортонормированном базисе. Во-вторых, член дУ/дх' преоб-
преобразуется как Г J-тензор, только если матрица преобразова-
преобразования Л/ не зависит от точки (упр. 4.5), что выполняется при
переходе от одной декартовой системы к другой. Стандартный
способ приспособить уравнение к произвольной системе коор-
координат заключается во введении ковариантной производной,
которая определяется в главе, посвященной римановой гео-
геометрии. Здесь мы покажем, что имеется другой, и весьма
поучительный, подход. Сначала заметим, что первые два сла-
слагаемых в E.72) можно записать как
dV{ 1 dvt
dt + V dxl ¦
поскольку в декартовых координатах нет разницы между V
и Vi. (Здесь мы, конечно же, воспользовались тем, что в
трёхмерном пространстве есть метрический тензор.) Затем
заменим производную V'dVi/dx' производной Ли (формула
C.14)) один-формы j/ = g(l/, ):
где мы опять воспользовались равенством V,- = V1. Итак, мы
получаем
yl bv *~&^—Ь?Л EJ3)

5.18 СОХРАНЕНИЕ ВИХРЕЙ 225
Оба слагаемых в правой части — это тензоры в произвольной
системе координат! Таким образом, E.72) приобретает бес-
бескоординатный вид
(± O. E.74)
Роль метрики в этом выражении несколько завуалированна,
но является решающей: она нужна, чтобы V превратить в V и
получить отсюда V2 = V(V).
5.18. СОХРАНЕНИЕ ВИХРЕН
Теперь мы можем заняться вопросом о сохранении вихрей.
В обычных обозначениях вихрь — это ротор скорости VXF.
Как мы видели в гл. 4, это по существу внешняя производная
dP. Раз внешняя производная и производная Ли коммутируют
(конечно, д. и d/dt тоже коммутируют, поскольку в d входят
только пространственные производные), то мы получаем из
E.74)
4г + ?у)*У = ±дрЛйр. E.75)
(Для простоты записи мы опустили волны.) Здесь имеются
два случая. Рассмотрим сначала более простой, когда жид-
жидкость подчиняется уравнению состояния р = р(р). Тогда
dp Л dp = 0, и мы находим, что два-форма вихря dV удовле-
удовлетворяет локальному (или конвективному) закону сохранения
E.76)
Это теорема Гельмгольца о циркуляции, представленная в её
наиболее естественном виде. Однако, если имеется более об-
общее уравнение состояния р = р(р, S), ответ будет иной.
В этом случае в нуль обращается не сама правая часть
E.75), а её внешнее произведение с 6S:
US Л dp A dp = 0. E.77)
Упражнение 5.20. Докажите E.77).
Внешнее дифференцирование E.71) даёт
E.78)
а умножив E.75) внешне на dS, мы получаем

226
5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Таким образом,
¦ Dг + ?v)dSAdV = 0. E.79)
Это наиболее общий закон сохранения вихрей. Он называется
теоремой Эртеля.
Смысл три-формы dSAdV непосредственно не очевиден,
но можно превратить E.79) в закон сохранения для скаляра.
Дело в том, что у нас есть и другая сохраняющаяся три-фор-
ма: рю, а в трёхмерном пространстве любые две три-формы
пропорциональны. Значит, найдётся скалярная функция а, та-
такая что
dSAdl/ = aP(D, E.80)
и из E.68) и E.79) получится скалярное уравнение
Можно показать, что в общепринятых векторных обозначе-
обозначениях
a=jVS-VXV. E.81)
Упражнение 5.21. Докажите E.81). (Указание: выразите
обе части E.80) через dx Л dy Л dz.)
В обозначениях гл. 4
S.(Kfcy. E.82)
Таким образом, а дуальна к dS Л dV относительно рю, и со-
сохранение а естественно следует из сохранения dSAdl/: то
что рсо сохраняется, означает, что операция дуализации отно-
относительно рю — это тоже сохраняющаяся, т. е. коммутирующая
с оператором (д/dt + ?-у), операция.
Упражнение 5.22. В декартовых координатах сдвиг поля
скоростей определяется формулой
<yi, = Vl,l+Vl,l-j6lfi, E.83)
где 8 — дивергенция поля скоростей:
6 = V-V. E.84)
Покажите, что в произвольной системе координат

5 19. КОСМОЛОГИЧЕСКИЙ ПРИНЦИП 227
Е. КОСМОЛОГИЯ
5.19. КОСМОЛОГИЧЕСКИЙ ПРИНЦИП
Большинство физиков знает, что общая теория относи-
относительности Эйнштейна дала современной физике последова-
последовательный и плодотворный подход, в рамках которого можно
заниматься космологией, изучением крупномасштабной струк-
структуры нашей Вселенной. Большинство из них знает также, что
(по крайней мере на простейшем уровне) существуют лишь
три основные космологические модели — «замкнутая», «пло-
«плоская» и «открытая» Вселенные. Однако то, что эта простота
выбора всего из трёх моделей вовсе не является, собственно
говоря, следствием уравнений Эйнштейна, известно гораздо
хуже. На самом деле это — следствие предположения об
однородности и изотропности крупномасштабных свойств Все-
Вселенной. (Точное определение однородности и изотропности бу-
будет дано ниже.) Подобно всем фундаментальным физическим
теориям, общая теория относительности — динамическая тео-
теория; по заданным начальным условиям она предсказывает
будущую эволюцию и восстанавливает предшествующую исто-
историю. Однородность Вселенной — это часть начальных усло-
условий, которые мы задаём при построении простейших моделей.
Главное, что даёт общая теория относительности, — это то,
что она позволяет нам выбирать геометрию пространства —
а именно поле его метрического тензора — как часть началь-
начальных условий. В ньютоновской теории гравитации такое, ко-
конечно, невозможно. Как только принято решение выбрать
наиболее однородные начальные условия, остальное — уже
дело дифференциальной геометрии; это она скажет нам, что
возможны лишь три типа полей метрического тензора. Найти
эти метрики и будет нашей задачей в следующих параграфах.
Нам понадобится математика симметрии и инвариантности,
развитая в гл. 3, но вовсе не понадобится знать что-либо ни
об общей теории относительности, ни о римановой геометрии.
Начнём с физики — с самой Вселенной. Несомненно, что
в малых масштабах Вселенная «комковата». На любых рас-
расстояниях, от ядерных A0~15 м) до межзвездных A017 м), для
нашего мира характерна тенденция к сосредоточению материи
в малых областях с отчетливыми границами между различ-
различными типами материи или между материей и вакуумом. Сами
звезды группируются в более или менее изолированные га-
галактики, галактики группируются в скопления от нескольких
десятков до нескольких тысяч в каждом, и даже скопления
группируются в разреженные суперскопления. Но современ-
современной астрономии доступны расстояния, превышающие раз-
размеры суперскоплений, и там мы видим, что по всем направ-
направлениям наблюдается тенденция ко всё большей и большей

228
6 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
однородности свойств Вселенной — после усреднения во всё
большем и большем масштабе. Поскольку именно эти крупно-
крупномасштабные усреднённые характеристики (например, сред-
средние плотность и скорость) важны для понимания динамики
Вселенной, космолог хотел бы включить эту однородность по
крайней мере в простейшие модели. Но каков реальный смысл
однородности? В конце концов, в развивающейся Вселенной
более удалённые от нас области должны выглядеть иначе,
чем близкие, хотя бы потому, что мы наблюдаем их в ранней
фазе их истории (см. рис. 5.4). В действительности так оно
и есть; число квазаров, например, гораздо больше в удалён-
удалённых областях, чем вблизи от нас. «Наблюдаемая» однород-
однородность— это ня самом деле экстраполяция в настоящее время
наблюдатель
сейчас- -
недавнее-
прошлое
далёкое- , -галактика
прошлое ' галактика
удалённая
Рис. 5.4. "Срез" у = г = 0 пространства-времени. Точки-события на нём
задаются координатами t (время) и х. Поскольку электромагнитные вол-
волны распространяются с конечной скоростью, то удалённые объекты мы ви-
видим на более ранних стадиях их истории, чем близлежащие.
состояния удалённых областей. Однако в теории относитель-
относительности и само понятие «настоящего времени» не является абсо-
абсолютным. Дальнейшее обсуждение этих вопросов выходит за
рамки данной книги; здесь можем только сказать, как они
решаются.
Основная идея заключается в том, чтобы разбить про-
пространство-время на семейство заполняющих его пространст-
пространственно-подобных подмногообразий (слоение). Эти подмного-
подмногообразия называются гиперповерхностями постоянного времени
(см. рис. 5.5). Фактически это эквивалентно выбору времен-
временной координаты. Метрический тензор пространства-времени g
как и любой тензор типа ( J , допускает естественное огра-
ограничение на каждую гиперповерхность, и гиперповерхность
будет пространственно-подобной, если g положительно-опре-
положительно-определён на всех касательных к ней векторах. Космологическая
«однородность» определяется в терминах векторов Киллинга
или изометрий этих гиперповерхностей.
Пусть G — группа Ли изометрий некоторого многообразия
S с метрическим тензором д. Алгебра Ли группы — это ал-
алгебра Ли векторных полей Киллинга для этой метрики. Эле-

5.19. КОСМОЛОГИЧЕСКИЙ ПРИНЦИП
229
менты G суть отображения S на себя (диффеоморфизмы).
Действие G на S называется транзитивным на S, если для
любых двух точек Р и Q из S найдется элемент g группы G,
удовлетворяющий условию g(P)=Q, т. е. переводящий Р
в Q. Многообразие S называется однородным, если его группа
время
пространство
Рис. 5.5. Расслоение пространства-времени на пространства постоянного
времени t.
изометрий действует на нём транзитивно (см. рис. 5.6). Это
и значит, что всюду в S геометрия одинакова.
Предположим, что в G существуют элементы, оставляю-
оставляющие неподвижной некоторую точку Р из S. Поскольку произ-
Рис. 5.6. Некоторая окрестность U точки Р изометрически отображается
посредством g на окрестность V точки Q = g(P); геометрия вблизи Р и
Q одинаковая.
ведение двух таких элементов тоже оставляет Р неподвиж-
неподвижной и тождественное преобразование е, очевидно, принадле-
принадлежит к числу таких элементов, они образуют подгруппу Нр
группы G, называемую группой изотропии точки Р. Очевидно,
что это хорошо нам знакомые вращения вокруг осей, проходя-
проходящих через Р. Так как группа изотропии оставляет Р на месте,
то любая кривая, проходящая через Р, отображается в кри-
кривую, также проходящую через Р (см. рис. 5.7). Это индуци-
индуцирует отображение пространства касательных векторов в точке

230 5 <J>H3H4FXKHE ПРИЛОЖЕНИЯ
P в себя: Тр^>-Тр. Эта группа отображений называется ли-
линейной группой изотропии точки Р. (Вспомните сходное об-
обсуждение присоединённого представления группы Ли в
§ 3.17.) Многообразие S размерности т называется изотроп-
изотропным в точке Р, если группа изотропии НР совпадает с
SO(tn)—группой вращения вокруг всевозможных осей, про-
проходящих через Р. Если S изотропно во всякой своей точке, то
оно называется изотропным.
Космологическая модель М называется однородной кос-
космологией, если у неё имеется слоение пространственно-подоб-
пространственно-подобных гиперповерхностей, каждая
из которых однородна; аналогич-
аналогично определяется изотропная кос-
космология. Как говорилось выше,
есть веские основания считать
нашу Вселенную однородной по
крайней мере в больших масшта-
масштабах в наблюдаемой нами окрест-
окрестности. Кроме того, мы не видим
никаких систематических откло-
ки^^об^жа^ТГпер:. нени« в её структуре, связанных
водя проходящие через эту точ- с выбором направления наблю-
ку кривые в другие кривые, дения. Это говорит о том, что во-
проходящие через ту же точку, круг нас, в точке, где мы жи-
живем, Вселенная изотропна. Но
современная наука не полагает, что мы живём в каком-то
особенно благоприятном месте во Вселенной. Это положение
часто возводится в ранг принципа (известного под разными
названиями: космологический принцип, принцип Коперника,
принцип заурядности): те свойства Вселенной, что мы наблю-
наблюдаем вокруг нас, увидел бы, в среднем, и любой другой
наблюдатель, расположенный в любом другом месте Вселен-
Вселенной. Этот принцип позволяет космологам распространить
свойства локальной однородности и изотропности на всю Все-
Вселенную — покуда, конечно, нет никаких противоречащих это-
этому фактов. Делать это, разумеется, не необходимо, и немало
сегодняшних исследований посвящено изучению неоднород-
неоднородной и/или анизотропной космологии. Но три основные мо-
модели — это единственно возможные модели, в которых трёх-
трёхмерные пространства являются однородными и изотропными.
Именно это мы и собираемся теперь доказать.
Упражнение 5.23. Как мы знаем из § 3.9, на сфере S2
поля 1Х, Ту, ~1г являются киллинговыми. Они образуют ба-
базис алгебры Ли группы изометрий S2, т. е. группы SOC).
Докажите, что S2 — однородное и изотропное много-
многообразие.

5 20 АЛГЕБРА ЛИ МАКСИМАЛЬНОЙ СИММЕТРИИ 231
5.20. АЛГЕБРА ЛИ МАКСИМАЛЬНОЙ СИММЕТРИИ
Мы начнем с изучения векторных полей Киллинга на трёх-
трёхмерном многообразии S. Если | — вектор Киллинга, то в лю-
любой системе координат его компоненты удовлетворяют урав-
уравнению
f. A, + f, frh = 0- E.87)
Нам будет удобнее пользоваться компонентами один-формы
Q(f, )
U = gktV. E.88)
Они удовлетворяют эквивалентному уравнению
= 0, E.89)
где, по определению
Г',у = у ёЫ (gmi, , + gmi, i ~ gtl. «)• E-90)
(Определение Г*,-/, включая множитель у. общепринято и
станет понятным после прочтения гл. 6. Для нас здесь
E.90)—всего лишь удобное сокращение.)
Уравнение E.89) симметрично относительно i и /, а сле-
следовательно, в случае п измерений в нём содержится я(п+1)/2
независимых дифференциальных уравнений, шесть при п = 3.
Поскольку ищутся всего три компоненты вектора |, то си-
система переопределена: у произвольного метрического тензора
g векторов Киллинга нет. Наша цель — выяснить, каким дол-
должен быть д, чтоб он допускал максимальное число векторов
Киллинга. Найдём, чему равно это максимальное число. Для
этого продифференцируем E.89):
1!.# + Бу.« = 2&Г1|/Ь, E.91)
прибавим к уравнению E.91) его же с перестановкой (i-*-k,
j-*-i, k-*-j) и вычтем с перестановкой (i-*-j, j-*-k, k-*-i).
В результате придём к равенству
h, ik = Hlfk It + Ktjk mh. m> E.92)
где Hijkl — сложного вида функция от компонент gu и их пер-
первых и вторых производных, а Кци1 подобным же образом
зависит от g,j и их первых производных. Главный смысл
E.92) состоит в том, что если мы знаем |,- и |,-_;- в некоторой
точке Р и gij заданы всюду, то из E.92) мы можем найти
Ъ, ik в Р, а последующее дифференцирование E.92) позво-
позволяет найти и высшие производные в этой точке. Если наше
многообразие аналитично (что мы предположим), то этого

232 Б ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
достаточно, чтобы определить векторное поле ?, всюду. Да-
Далее, мы знаем, что значения |, в точке Р определяют по фор-
формуле E.89) симметричную часть |(,, в этой точке. Следова-
Следовательно, каждое векторное поле Киллинга на S полностью
определяется заданием значений
ц,^Ь(Р) и А, -Е It,.,,(Р) E.93)
в одной какой-нибудь точке Р. Важно отметить, что, задав
{т],, Ач} в Р, мы вовсе не обязательно определим вектор Кил-
Киллинга, ведь может случиться, что у E.92) нет решений: пра-
правая часть может оказаться несимметричной по / и k. Но при-
приведённые соображения показывают, что число (линейно-неза-
(линейно-независимых) векторов Киллинга не может быть больше числа
независимых выборов {ц,, А,,}, которое в случае m измерений
равно
m + {m(m-l) = {m(m+l), E.94)
как следует из E.93). Многообразие называется максимально-
симметричным, если на нём имеется максимальное число век-
векторных полей Киллинга.
Легко показать, что максимально-симметричное связное
многообразие S однородно. В любой точке Р мы можем вы-
выбрать векторное поле Киллинга
по направлению любого касатель-
касательного вектора в Р. И однопара-
метрические подгруппы, связан-
связанные с векторами Киллинга, могут
отобразить точку Р в любую дру-
другую точку Q, принадлежащую
некоторой её окрестности U (см.
рис. 5.8). Последовательностью
таких отображений, очевидно,
Рис. 5 8 Выбрав подходящую можно перевести Р в какую угод-
однопараметрическую подгруп- но точку S Итак группа ИЗОме-
пу группы изометрии, можно « пи
отобразить Р в любую точку- ТРИИ переводит Р в любую точку,
хоть в Q, хоть в Q' — окрестно- и S однородно,
ста U. Теперь займёмся группой
изотропии точки Р. Преобразо-
Преобразования из этой группы оставляют Р на месте, стало быть, со-
соответствующие векторные поля Киллинга обращаются в нуль
в Р. Скобка Ли любых двух полей Киллинга V и W равна
[V, W]l= V\,Wi — Wl,,Vi,
или
[V, Щ, = V.,,W'— WhiV — ?,*.,(К*№'— WkW). E.95)

5 21 МЕТРИКА СФЕРИЧЕСКИ-СИММЕТРИЧНОГО ТРЁХМЕРНОГО П-ВА 233
Если оба поля V и W обращаются в нуль в точке Р, то то же
происходит и с [V, W]. Однако [V, W] — линейная комбина-
комбинация векторных полей Киллинга, и, чтобы обратиться в нуль,
она должна быть линейной комбинацией полей, которые тоже
обращаются в нуль в Р. Таким образом, эти поля образуют
подалгебру Ли, и ясно, что это — алгебра Ли группы изотро-
изотропии точки Р. Следующее упражнение показывает, что если 5
пространственно-подобно, то группа изотропии есть SO(m),
т. е. что максимально-симметричное пространственно-подоб-
пространственно-подобное многообразие изотропно.
Упражнение 5.24. Выберите в точке Р координатную си-
систему типа построенной в упр. 2.14, в которой для про-
пространственно-подобного многообразия giy(/5) = 6<7 и ёч и
JP)=0.
(a) Покажите, что вблизи Р изотропное векторное поле
Киллинга даётся формулой
у = А',х> + О(х2), E.96)
где А1, — произвольная антисимметричная матрица:
А', = —А',. E.97)
(b) Пусть W — другое изотропное векторное поле Кил-
Киллинга,
W = В',х1 + О (х2);
покажите, что
[V,W]'=[A,B] 1,х> + О (х2), E.98)
где через [А, В\1, обозначены элементы матричного ком-
коммутатора Л', и В1,. Отсюда видно, что алгебра Ли группы
изотропии совпадает с алгеброй Ли группы SO(m).
(c) Выведите из предыдущего, что группа изотропии
точки Р есть SO(tn).
(d) Покажите, что если g не является положительно-
определённым (или отрицательно-определённым), то груп-
группа изотропии с SO(tn) не совпадает. В частности, пока-
покажите, что группа изотропии точки Р в четырёхмерном про-
пространстве Минковского есть группа Лоренца LD).
5.21. МЕТРИКА СФЕРИЧЕСКИ-СИММЕТРИЧНОГО
ТРЁХМЕРНОГО ПРОСТРАНСТВА
Теперь ограничим своё внимание пространственно-подоб-
пространственно-подобными трёхмерными многообразиями. В таком случае группа
изотропии равна 50C) и мы говорим, что наше многообразие
сферически-симметрично в каждой точке. В этом параграфе

234
5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
мы построим систему координат, удобную для предстоящих
вычислений Мы знаем, что интегральные кривые векторныч
полей Киллинга на группе 50C) определяют сферы S2 По-
Поскольку каждая точка принадлежит одной такой сфере, оии
расслаивают многообразие 5 Выберем сферические коорди-
координаты с обычными углами 0 и ф на каждой сфере и с третьей
«радиальной» координатой, нумерующей сферы Для выбора
этой координаты имеется один особенно удобный способ
D
Рис 5 9 Окружности (парал
лели) на сфере нумер}ет ра
диальная координата, опреде
ленная как длина окружности
поделенная на 2я Это двумер
ный аналог описанной в тексте
ситуации Сначала радиальная
координата возрастает с удале
нием от Р (например когда мы
движемся от Л к В) а потом
начинает убывать (например
при движении от С к В) и об-
обращается в нуль в точке Р'
Рис 510 Выбор "почюса' на
каждой окружности г == const
на сфере рнс 5 9 посредством
требования, чтобы все полюсы
лежали на одной интегральной
кривой единичного нормального
поля п
Метрика на 5 индуцирует на каждой сфере метрический тен-
тензор, последний в свою очередь определяет два форму объема
и полную площадь (интеграл от два формы объема) Опреде-
Определим радиальную координату г, отвечающую данной сфере, ра-
равенством
площадь сферы = 4зтг2, г = (площадь сферы/4яI2. E 99)
Такая внутренним образом определенная координата не обя-
обязана монотонно возрастать всюду (см рис 5 9) Но в силу
теоремы о приводимости метрики к локально-плоскому виду
(упр 2 14) мы можем утверждать, что это будет хорошая
координата по крайней мере в некоторой окрестности Р (При
г = О она, конечно, сингулярна, но мы знаем, как с этим
справиться )

S 21 МЕТРИКА СФЕРИЧЕСКИ СИММЕТРИЧНОГО ТРЁХМЕРНОГО П ВА 235
Помимо радиальной координаты надо поаккуратнее опре-
определить 6 и ф Мы определили <р и 0 на каждой сфере, однако
мы не сказали, как связаны полюсы 0 = 0 двух разных сфер
А это значит, что при переходе от одной сферы к другой мы
можем свободно сдвигать систему координат Зафиксируем
полюсы следующим образом В каждой точке Q существует
вектор п, нормальный к поверхности сферы (д(й, V) = 0 для
каждого V из TQ(S2)), имеющий единичную длину (g(n, n) =
1) и направленный прочь от точки Р (такой выбор можно
корректно произвести вблизи Р, а на все 5 распространить
по непрерывности) Это векторное поле называется единич-
единичным нормальным полем, оно принадлежит классу С°° всюду,
кроме Р Выберем произвольным образом полюс на некото-
некоторой сфере S2, а затем фиксируем полюсы на всех остальных
сферах так, чтоб они лежали на интегральной кривой поля
п, проходящей через исходный полюс Эта процедура проил-
проиллюстрирована на рис 5 10 Очевидно, что при таком выборе
любая интегральная кривая поля Я будет линией постоянства
0 и ф, иными словами, она будет координатной линией ра-
радиальной координаты Поскольку векторы д/dQ и д/дц> каса-
тельны к сферам, из нашей конструкции следует, что
0, E 100a)
О. E 100b)
Далее, метрика каждой из сфер совпадает с метрикой еди-
единичной сферы, умноженной на г2 (именно этот множитель
дает площадь, равную 4пг2, см E 99))
gee = ''2. &еФ = 0, gw = r2sin20. E.100с)
Итак, у метрического тензора осталась лишь одна неизвест-
неизвестная компонента, grr
Упражнение 5.25. (а) Определим радиальное расстояние
от точки Р до сферы с координатой г как интеграл
!dr E.101)
вдоль линии 0 = const, ф = const Докажите, что компо-
компонента grr должна быть независимой от 0 и ф
(Ь) Покажите с помощью упр 2.14, что при прибли-
приближении к Р
hmgrr = l. E.102)

236 5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Как видно из упр. 5.25(а), grr = f(r), и мы получаем
метрику
¦fir) О О
(g)=| Or2 0 |. E.103)
О О
0 0ч
г2 О I.
D г2 sin2 6 У
Чтобы получить этот ответ, мы использовали лишь группу
изотропии Р, и нет оснований полагать, что с её помощью мы
сможем найти и /(г). Для этого нам понадобятся остальные
изометрии 5.
5.22. ПОСТРОЕНИЕ ШЕСТИ ВЕКТОРОВ КИЛЛИНГА
Есть несколько способов определить вид функции f(r),
гарантирующий однородность S. Предлагаемый же нами ме-
метод заключается в построении всех векторных полей Киллин-
га на 5 с использованием векторных сферических гармоник,
введённых в § 4.29.
Любое векторное поле V на 5 можно записать в виде
V = 1ш (г) У1т i + Ч1т (г) Yl + llm (r) YJm, E.104)
как здесь, так и в дальнейшем в каждом члене, где индексы
/ и т повторяются, подразумевается суммирование по ним.
Разложим эту формулу по компонентам. Из D.101) легко
получаем
JFlW <5-105a>
Отсюда следует, что
Vr = hmY[m, E.106а)
Vе = 4imYlm, е + Z,mY,m, «p/sin 0, E.106b)
Т/Ч> „ у /с1п2й Т. V, /«in ft ^ Ififiri
Эти компоненты должны удовлетворять уравнению Киллинга
Ки = Vkgih k + Vk,igk, + Vk,,glk = 0 E.107)
с ga, определённым формулой E.103).
В три уравнения {/Сев = 0, Квц> — 0, /^фф = 0} производ-
производные от |гт, Л'т и t,im не входят, ими мы и займёмся сначала,

В 22 ПОСТРОЕНИЕ ШЕСТИ ВЕКТОРОВ КИЛЛИНГА 237
Рассмотрим комбинацию (индексы подняты тензором E.103))
0 = Я ее + ft <Рф = ± Ьтуы + 24lmL2 (Ylm),
где оператор L2 определён равенством C.33). Используя
C.33), получаем
[ B/r)g,m — /(/ + O4im] Yim = 0.
В силу линейной независимости сферических гармоник отсюда
следует, что
Thm~l(t+l)mm = 0. E.108)
Теперь рассмотрим комбинации
= — {K e — K\) = Flmr\lm+ Glmllm, E.109a)
П * pr n у, _i_ p, г /к том
где через F;m и G;m обозначены следующие выражения:
^гт = Yim, ее — ctg QYtm, e — Кгт, vv/sin26,
Gim = 2кгт, eq)/sin e - 2 ctg eylm. ,/sin e.
Система E.109) имеет лишь тривиальное решение %tm = х\т
= 0 при отличном от нуля детерминанте. Последний равен
(FimJ + (GimJ и, значит, обращается в нуль, только если и
Fim и Gim — нули. Нетрудно убедиться, что это может быть
лишь при / = 0, 1 (т любое). Но, как видно нз E.106), при
/ = 0 ни г), ни ? ненулевого вклада не дают (опять теорема
о неподвижной точке для 52!), и в итоге мы получаем
l=l- Ilm. Sim ПРОИЗВОЛЬНЫ, E 11(П
В силу E.108) имеем
/ = 0: ?оо == 0'
f=l: glm = r4lm, E.111)
/>2: glm = 0.
Теперь займёмся тремя другими уравнениями в E.107).
Первое даёт скаляр относительно вращений:
0 = Кг, = Bfi,m., + /.,glm) У„и-
следовательно,

238 5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Два оставшихся уравнения Кгв =¦= Кпр = 0 относительно вра-
вращений образуют вектор. Дивергенция этого вектора (относи-
(относительно объёма на S2) равна
О = (sin е/сД е + (sin 6/сЛ ф =
откуда следует, что (при / > 0)
4lm.r+-^"/Slm = 0. E.113)
Наконец, для получения последнего уравнения можно взять
дивергенцию от дуальной к вектору на S2 величины:
О = Кгв, Ф - /Слр. е = г%ы. r sin QL2 (Ytm),
и очевидно, что
Zlm.r = 0. E.114)
Итак, мы приходим к выводу, что весь вклад от У[т опре-
определяется тремя произвольными постоянными {?im, т = —1,
О ,1}. Решение оставшихся трёх уравнений (относительно не-
неизвестных ?im, r\im и f) можно выразить через произвольные
постоянные К и Vm:
f = (l-Kr2)-\ E.115)
hm^Vm(l-Kr2I12, E.116)
Чш-\Ут^~Кг2I12. E.П7)
Упражнение 5.26. Проверьте формулы E.105), E.108),
E.109), E.112) —E.117).
Упражнение 5.27. Покажите, что векторы Киллинга с
Vm = 0 — это как раз векторы, отвечающие группе изо-
изотропии начала координат (г = 0).
Упражнение 5.28. Покажите, что сингулярность r)im при
г-*-0 — чисто координатный эффект: векторное поле кор-
корректно определено в этой точке.
Упражнение 5.29. Положите К = 0 в E.115—117) и пока-
покажите, что в этом случае 5 совпадает с Е3 (эвклидовым про-
пространством). Найдите постоянные Vm, определяющие век-
векторы Киллинга {д/дх, д/ду, д/дг), при условии что де-
декартовы координаты получены из наших полярных обыч-
обычным образом.

5.23. ОТКРЫТАЯ. ЗАМКНУТАЯ И ПЛОСКАЯ ВСЕЛЕННЫЕ 239
5.23. ОТКРЫТАЯ,
ЗАМКНУТАЯ И ПЛОСКАЯ ВСЕЛЕННЫЕ
Теперь мы располагаем полным описанием геометрии
однородных и изотропных пространств космологических мо-
моделей: они имеют метрический тензор вида
f(l-Kr2yl 0 О \
(ёц) = \ 0 г2 „ 0 . E.118)
V 0 0 r2sin2e/
Остаётся лишь понять, как эта геометрия выглядит, и помо-
поможет в этом нам следующая замена координат.
Упражнение 5.30. Найдите преобразование координат от
г к %, приводящее метрический тензор к виду
при К> 0:
0 0 \
Ы = х( ° Six ° ' E.119а)
0 sin2%sin26/
при К <0:
0 0 \
sh2x 0 I. E.119Ь)
.0 0 sh2xsh26/
Теперь видно, что геометрия фактически зависит лишь от
знака К. Абсолютная величина К служит просто всеобщим
масштабным множителем.
В случае К > 0 площадь сферы с координатой % равна 4л
X sin2 %/К. При увеличении %от% — 0до% = я она сначала
возрастает, достигая максимума при % = я/2, а потом убы-
убывает до нуля в точке %==Jt> что напоминает нам ситуацию на
сфере 52 (рис. 5.9). И действительно, фактически мы имеем
дело с метрикой сферы S3 радиуса К~1/2. Поскольку это про-
пространство конечно, такая Вселенная называется замкнутой.
Упражнение 5.31. Найдите в ?4 преобразование, перево-
переводящее декартовы координаты {х1} = {ш, х, у, z} в сфери-
сферические координаты {х'"} = {г, %, 0, <р}, в которых метрика
gij = 6,7, ограниченная на сферу S3: ш2 + х2 -\- у2 -\- z2 =
= К~\ будет иметь компоненты E.119а).
Случай К — 0 был разобран в упр. 5.29. Это — плоская Все-
Вселенная.
Случай К < 0 — это открытая Вселенная, и его труднее
всего представить. Площадь поверхности сферы с радиаль-
радиальной координатой х равна 4я8п2%/|/С| и растёт с ростом К
всё быстрее и быстрее. Эта Вселенная неограниченна.

240 S ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ
Упражнение 5.32. (а) Рассмотрев соотношение между пло-
площадью сфер х = const и расстоянием от сферы до начала
координат % = О (см. E.101)), докажите, что метрика
E.119Ь) не является ограничением эвклидовой метрики на
подмногообразие в Е" ни для какого п и ни для какого
подмногообразия в Е".
(Ь) Найдите подмногообразие в пространстве Минков-
ского, имеющее метрику E.119Ь).
В случае когда для уравнений Эйнштейна выбраны одно-
однородные и изотропные начальные данные (речь идёт не об
одной геометрии, а ещё и о переменных, описывающих мате-
материю), последующее развитие Вселенной эту симметрию со-
сохраняет. Следовательно, единственная геометрическая харак-
характеристика, которая может меняться со временем, — это мас-
масштабный множитель К: со временем Вселенная становится
«больше» или «меньше». Однако следует проявить осторож-
осторожность и не делать зависящих от координат утверждений.
В замкнутой Вселенной, имеющей конечный полный объём
изменение К вызывает изменение полного объёма. Но плоская
и открытая Вселенные бесконечны, и говорить об их полном
объёме не имеет смысла. Тем не менее общая теория отно-
относительности позволяет смотреть на систему координат, в ко-
которой записаны формулы E.119), как на «сопровождающую»:
в любой малой области Вселенной локальная система покоя
галактик не меняет своих координат {%, 0, ф} при изменении
времени. Отсюда следует, что изменения К приводят к изме-
изменению расстояния между галактиками, а это как раз то, что
имеют в виду, говоря о расширяющейся Вселенной. В «стан-
«стандартных моделях», предполагающих однородность, изотроп-
изотропность и ряд других свойств, все три типа Вселенной начинают
своё существование с нулевого «объёма» (К= оо) — с «боль-
«большого взрыва» — и затем расширяются. Замкнутая Вселенная
расширяется до некоторого максимума, а потом опять сжи-
сжимается, скорость расширения плоской Вселенной асимптоти-
асимптотически стремится к нулю, а открытая Вселенная расширяется
со скоростью, имеющей ненулевой асимптотический предел.
Все эти свойства следуют из уравнений Эйнштейна. Однако
для понимания этих уравнений необходимо ввести на много-
многообразии еще одну дополнительную структуру — аффинную
связность. Она составляет предмет гл. 6.
5.24. БИБЛИОГРАФИЯ
Краткое и прекрасно написанное введение в термодинамику — книга
Э Феоми, «Термодинамика» (Харьков: Изд-во Харьк. ун-та, 1973). Тео-
Теорема Каратеодори обсуждается в книге S. Chandrasekhar, An Introduc-
Introduction to the Studv of Stellar Structure (Dover, New York, 1958), а на более
современном уровне —в книге R Hermann, Differential Geometry and
the Calculu? of Variations (Academic Press, New York, 1968).

S.24 БИБЛИОГРАФИЯ 241
Наше обсуждение гамильтоновой механики близко по духу к изложе-
изложению, данному в R. Abraham & J. E. Marsden, Foundations of Mechanics,
2nd ed. (Benjamin/Cummings, Reading, Mass., 1978). Познакомиться с
теми же понятиями, но без всякой геометрии можно по книгам Голд-
стейн Г. Классическая механика (М.: Наука, 1975) или Ландау Л. Д.,
Лифшиц Е. М. Теоретическая физика, т. 1. Механика (М.: Наука, 1975).
Привлекая канонические сохраняющиеся величины^ проще понять некото-
некоторые явления неустойчивости в жидкостях, см. J. L. Friedman &
В. F. Schutz, Astrophys. J. 221, 937—957 A978); 222, 281—296 A978). Ряд
полезных статей по гамильтоновой механике с геометрической точки зрения
можно найти в сборнике Topics in Nonlinear Dynamics — A Tribute to Sir
Edward Bullard, ed. S. Jorna, American Institute of Physics, 1978; A. I. P.
Conference Proceeding no. 46. Интересный пример использования дифферен-
дифференциальных форм для вывода необходимых и достаточных условий того, что
система динамических уравнений имеет гамильтонову (т. е. симплектиче-
скую) структуру, приведён в книге R. M. Santilli, Foundations of Theoreti-
Theoretical Mechanics. I — The Inverse Problem in Newtonian Mechanics (Springer,
Berlin, 1978).
Введение в теорию электромагнетизма, включающее релятивистскую
формулировку теории, дано в книге Д. Джексона «Классическая электро-
электродинамика» (М.: Мир, 1965). Продолжение и развитие нашего изложения
можно найти в книге Ч. Мизнера, К. Торна, Дж. Уилера «Гравитация»
(М.: Мир, 1977). Развёрнутое изложение теории релятивистских волновых
уравнений см. в книге F. G. Fridlander, The Wave Equations on a Curved
Space Time (Cambridge University Press, 1976). Уилеров «заряд без за-
заряда» обсуждается в статьях, воспроизведённых в сборнике J A. Wheeler,
Geometrodynamics (Academic Press, New York, 1962). Неориентируемая
модель заряда, принадлежащая Соркину, описана в статье R. Sorkin, J.
Phys. A 12,403—421 A979).
Введение в гидродинамику, включающее теорему Гельмгольца, дано
в книгах: Ландау Л. Д., Лифшиц Е. М. Теоретическая физика. Механика
сплошных сред (М: Гостехиздат, 1954); Ламб Г. Гидродинамика (М.:
Гостехиздат, 1947). То, что мы назвали теоремой Эртеля, на самом деле
есть лишь частный случай результата, полученного X. Эртелем (Н Ertel,
Meteorologishe Zeitschrift 59, 277 A942)). Мы вкратце касались свойств
многообразия, называемого «галилеевым пространством-временем», на ко-
котором разыгрывается иерелятивистская физика. Исследование его струк-
структуры требует привлечения понятия аффинной связности, разбираемого в
следующей глэве; см. указанную выше книгу Мизнера, Торна и Уилера, где
содержится весьма прозрачное обсуждение вопроса, или книгу R. Hermann.
Topics in General Relativity (Maih-Sci Press, Brooklin, Mass., 1973), где
дано более техническое изложение. Использование производных Ли в меха-
механике сплошных сред особенно плодотворно в теории упругости. Действи-
Действительно, сформулировать обще-релятивистскую теорию упругости без помо-
помощи такого аппарата чрезвычайно трудно. См. В. Carter & Н. Quintana,
Proc. Roy. Soc. London, A331, 57 A972) или В. Carter, Proc. Roy. Soc. Lon-
London, A, to be published.
Космология рассматривается в большинстве учебников по общей тео-
теории относительности. В нашем изложении использованы элементы из книги
С. Вейнбсрга «Гравитация и космология» (М.: Мир, 1975) и всё той же
книги Мизнера и др. Более простое введение см. у М. Berry, Principles
of Cosmology and Gravitation (Cambridge University Press, 1977) С астро-
астрофизической и экспериментально-наблюдательной точек зрения космология
обсуждается в указанной книге Вейнберга и в книге P. J. E. Peebles, Phy-
Physical Cosmology (Princeton University Press, 1971) [имеется перевод:
Пиблс П. Физическая космология. — М.: Мир, 1975]. Однородные, но не
обязательно изотропные космологии исследуются с помощью методов тео-
теории групп в книге М. P. Ryan & L. С. Shepley, Homogeneous Relativistic
Cosmologies (Princeton University Press, 1975).

6. СВЯЗНОСТИ НА РИМАНОВЫХ МНОГООБРАЗИЯХ
И КАЛИБРОВОЧНЫЕ ТЕОРИИ
6.1. ВВЕДЕНИЕ
Предмет этой главы лежит несколько в стороне от основной
темы книги — изучения дифференциальных структур на мно-
многообразиях. Аффинная связность — это дополнительная струк-
структура, придающая многообразию кривизну и форму; она не
возникает естественно из дифференциальной структуры, она
даже не является тензором. Поэтому настоящая глава играет
роль дополнения. Однако без этой важной и злободневной
темы никакое изучение дифференциальной геометрии не будет
полным для физика. Особенно в физике элементарных частиц,
в калибровочных теориях, связности приобретают всё боль-
большую популярность. В основном мы будем обсуждать аффин-
аффинные связности (на римановых многообразиях) и лишь под
занавес отведём небольшой параграф вводного характера ка-
калибровочным связностям.
В предыдущих главах нам уже приходилось вводить до-
дополнительные структуры на многообразиях; мы делали это,
выделяя некоторое тензорное поле среди других, с тем чтобы
оно служило нам в качестве метрики или элемента объёма.
Задание элемента объёма совсем недалеко выводит за рамки
дифференциальной структуры многообразия. Метрика же, как
мы увидим в дальнейшем, порождает много дополнительных
структур и помимо аффинной связности. Правда, в описан-
описанных ранее приложениях можно было просто не обращать вни-
внимания на всё это и использовать метрику лишь в её роли
,- ( N \ ( N —\\
отображения тензоров типа I ^ I и тензоры типа I м . 1.
Аффинная связность не укладывается в рамки уже построен-
построенных структур. С точки зрения дифференциальной геометрии
это совершенно новая структура на многообразии, дающая
богатые новые возможности для физических приложений.
62. ПАРАЛЛЕЛЬНОСТЬ
НА ИСКРИВЛЕННЫХ ПОВЕРХНОСТЯХ
Как мы уже неоднократно подчёркивали, на дифференци-
дифференцируемых многообразиях нет само собой разумеющегося поня-
понятия параллельности векторов в разных точках. Аффинная
связность — это правило, посредством которого вводится по-

6.2. ПАРАЛЛЕЛЬНОСТЬ НА ИСКРИВЛЕННЫХ ПОВЕРХНОСТЯХ
243
нятие параллельности. Чтобы представить, какого сорта пра-
правила вообще возможны, рассмотрим понятие параллельности
на обычной двумерной поверхности, скажем на сфере. На
рис. 6.1 вектор V — это касательный вектор к большому
кругу ABC в северном полюсе, обозначенном А. Представим,
что мы «переносим» V вдоль ABC к южному полюсу С. Для
того чтоб вектор продолжал «лежать на сфере», он должен
всё время оставаться в касательной плоскости к сфере, и,
если по дороге мы не будем его поворачивать, он будет про-
просто оставаться касательным к кривой ABC. В точку С он
А
Рис. 6.1. Параллельный перенос
вектора V по большому кругу
на сфере.
Рис. 6.2. Другой путь параллель-
параллельного переноса, приводящий к
другому результату.
придёт вектором V', направленным с точки зрения нашего
трёхмерного мира точно противоположно вектору V. Должны
ли мы считать, что хотя бы с точки зрения геометрии сферы
векторы V и V параллельны? Прежде чем сделать оконча-
окончательный вывод, представим, что мы переносим V из точки А
в точку С по пути ADC, изображенному на рис. 6.2, где
ADC — другой большой круг, пересекающий ABC в обоих по-
полюсах под прямым углом. Поскольку в начале пути V пер-
перпендикулярен ADC, то естественно считать, что мы движем
его, не поворачивая, если он всё время будет оставаться пер-
перпендикулярным к ADC и касательным к сфере. Таким обра-
образом в точке С мы получим вектор V", который для нас, трёх-
трёхмерных, и в самом деле параллелен вектору V. Но векторы
V" и V в точке С направлены прямо противоположно! Кото-
Который из них параллелен V? Ясно, что если мы будем рассма-
рассматривать свойства сферы как таковой, ни один вектор не за-
заслуживает быть названным параллельным V. Понятия парал-
параллельности как таковой просто нет. Всё, что можно сделать,
и как раз это мы и делали, — это определить понятие парал-
параллельного переноса, понятие движения вектора вдоль кривой
без изменения его направления. Аффинная связность есть
правило параллельного переноса.

244 6 СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
6J3. КОВАРИАИТИАЯ ПРОИЗВОДНАЯ
Будем пока смотреть на аффинную связность как на чисто
абстрактное понятие; более конкретный облик она приобре-
приобретёт в следующем пункте, когда мы перейдём к компонентам.
Итак, предположим, что мы имеем кривую 'ё' и связность, г. е.
правило параллельного переноса. Обозначим через U =¦¦ d/d'k
касательный вектор к <&. Зафиксируем в точке Р произволь-
произвольный вектор V из Тр. Тогда связность позволяет нам задать
R
Рис 6 3. Аффинная связность позволяет определить V(Q) в_любой точке
Q кривой & как результат параллельного переноса вектора V из точки Р.
векторное поле V вдоль кривой ??, полученное параллельным
переносом V (см. рис. 6.3). Поскольку мы можем теперь ска-
сказать, что V не меняется вдоль <ё>, мы можем определить про-
производную, в смысле которой изменение V равно нулю. Она
Рис. 6 4 Векторное поле W на 1? не есть результат параллельного пере-
переноса. Сравнение с векторным полем, которое таковым является, позволяет
определить ковариантную производную поля W.
называется ковариантной производной по направлению О и
обозначается через Vfj; итак,
+ V-[jV = 0<^V есть результат параллельного
переноса вдоль ЯЗ. F.1)
Если W — произвольное векторное поле, заданное всюду на
<&*, то мы можем определить его ковариантную производную
вдоль ?? почти так же, как мы определяли производную Ли
(см. рис. 6.4). Чтобы определить V77W в точке Р, удобно все
векторы представить как функции от К. Пусть точке Р отве-
отвечает значение Ко. Определим поле W^+ei^) как результат
параллельного переноса (VyU^* = 0) вектора W из точки
А-о + 8, так что вектор Wko+e (^0) получается параллельным
переносом вектора iF(Ao + e) назад в точку Ко. Теперь, когда

6.3. КОВАРИАНТНАЯ ПРОИЗВОДНАЯ 245
сравниваемые векторы лежат в одном пространстве Тр, мы
можем записать определение производной:
F.2)
Хотя эта процедура напоминает ту, которую мы использовали
при определении производной Ли, важно уяснить имеющуюся
принципиальную разницу между ними: чтобы перенести на-
назад вектор при вычислении производной Ли, нужна полная
конгруэнция, т. е. D и W должны быть' определены в целой
окрестности кривой е&\ для параллельного переноса нам
нужны лишь кривая <&, векторные поля U и W на этой кривой
и, конечно, связность на этой кривой.
Как легко вывести из F.2), V^j —дифференциальный опе-
оператор:
^ (fW) = fVjjW + WWyf = fVvW + W^. F.3a)
(определение ковариантной производной для скаляров оче-
очевидно). Правило Лейбница позволяет распространить опре-
определение ковариантной производной на тензоры произвольного
типа:
¦ Vv (А ® В) = (yvA) ® В + А ® (VVB), F.3b)
4 Vy <S, A) = (VV5>, A) + E>, VjjA). F.3c)
Равенства F.3) гарантируют согласованность связности с
дифференциальной структурой.
Представим, что мы ввели новый параметр на кривой,
перейдя от параметра К к параметру ц. Тогда новым каса-
касательным вектором будет gU, где g = d^/d^. Из F.2) видно,
что коваригчтная производная тоже умножится на g, по-
поскольку е заменится на 6ц = ed^/dA, а №цо+бр(Ио) совпадает
с Wla+e(K)- (Это, строго говоря, входит в определение связ-
связности: понятие параллельного переноса вдоль кривой не
должно зависеть от выбора параметризации.) Отсюда можно
заключить, что для любой функции g
Vgi7^=^VI7#. F.4a)
Ещё одно условие, которому должна удовлетворять аффинная
связность, — это свойство аддитивности ковариантных произ-
производных по разным направлениям:
Щ )P. F.4b)

246 6- СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
Оно делает ковариантную V похожей на обычную V эвклидова
векторного исчисления. Соотношения F.4а, Ь) _в совокупности
показывают, что для любых векторных полей U, V, W и функ-
функций /, g
¦ Vf77+gFr = fVZ7r + gV7i\ F.4c)
Упражнение 6.1. Покажите, что из F.4с) и того, что WjjW
есть вектор, следует, что VW есть тензор типа ( . J, зна-
значение которого на аргументах О и со равно
; U) = {e, VVW). F.5)
Этот тензор называется градиентом поля W.
Тот факт, что VW есть тензорное поле, означает, что мы
можем совсем убрать кривую из определения ковариантной
производной. Тензор Vt^ определяется только связностью и
самим полем W. Есть искушение пойти дальше и сказать, что
V сама по себе есть тензорное поле типа Г . ), представляю-
представляющее связность, но это будет ошибкой. Хотя и можно считать,
что V представляет связность, тензорным полем она не яв-
является, так как У([Ш)ф fVW (см. F.3а)). Вот что не позво-
позволяет смотреть на связность как на тензорное поле.
6.4. КОМПОНЕНТЫ:
КОВАРИАНТНЫЕ ПРОИЗВОДНЫЕ БАЗИСА
Поскольку каждый тензор можно представить в виде ли-
линейной комбинации базисных тензоров, а эти последние в
свою очередь можно получить из векторного базиса {ёг}, то
связность полностью описывается градиентами базисных век-
векторов. Итак, положим
¦ V/=rV*- (е-6)
Функции Г*// называются символами Кристоффеля. При фик-
фиксированных (i, j) Tka есть k-я компонента векторного поля
Уё?ё/. Обратите внимание на порядок индексов у Г: связан-
связанный с производной индекс идёт последним. Часто мы будем
пользоваться сокращением
Ve, = V,. F.7)
На л-мерном многообразии я3 функций Ткц полностью опре-
определяют аффинную связность, и часто это самый удобный спо-
способ её описания. Отметим, что Tkji тензора не образуют: при

6.4. КОМПОНЕНТЫ: КОВАРИАНТНЫЕ ПРОИЗВОДНЫЕ БАЗИСА 247
преобразованиях базиса индексы k и i ведут себя как тензор-
тензорные (в силу F.5)), а / нет (в силу F.3а)).
Упражнение 6.2. Покажите, что
где под \iA.kj/ подразумеваются dAfe7'/dA,-, а ё,- = d/dA,- и
Aftj' рассматриваются как функции на интегральных
кривых полей ei.
Упражнение 6.3. Покажите с помощью упр. 6.1, что
есть набор п тензоров типа Г J. (Здесь {со'} — базис-
базисные один-формы, дуальные к {ei}.)
Упражнение 6.4. На единичной сфере обычные сферические
координаты 6 и ф задают базис {ее = d/dQ, ё,р = d/dcp}.
Развивая соображения, высказанные в § 6.2, докажите,
что
Гефф = - sin 6 cos 6, Гфеф = Г^е = ctgG,
а остальные Г равны нулю. (NB Это непростая задача.
Вы должны максимально использовать симметрию сферы
и догадаться (это совсем не тривиально!), как ведут себя
векторы при параллельном переносе.)
Упражнение 6.5. Выведите из F.6) и F.3с), что
; = - г'ыа*. F.8)
Теперь, когда у нас есть производные базисных векторов,
мы можем найти производные любых тензоров. Например,
если U = d/dX, то
i7= и1
В первом члене V — просто функция и UlVi(Vi) =
Поэтому
Чтоб получить окончательное выражение, нам пришлось пе-
переобозначить индексы суммирования в последнем члене. По-
Поскольку VV — тензор, можно найти его компоненты:

248 6 СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
Несколько слов относительно члена Vt(V')- Если ё, есть век-
вектор d/dp,, то S/,(Vl) = dV//dn, где V1 — просто функции, за-
заданные на кривой с параметром ц. Если ё, — координатные
базисные векторы, то ё, = д/дх1, и мы получаем
здесь использовано «правило запятой», введённое для диффе-
дифференциальных форм. Обычно правило запятой используется и
тогда, когда ё, не являются координатными базисными век-
векторами:
VeJ = etlf]^f., F.9)
для любой функции /. В случае когда ё, — координатные ба-
базисные векторы, Vi совпадает с обычной частной производной,
когда нет, это просто производная по направлению ё,. Итак,
мы можем записать
¦ (Wy.^V, , + r'hV'ej", ,; F.10)
мы ввели обозначение «точка с запятой» для ковариантной
производной. Хотя ни V11, ни T!ktVk не преобразуются как
тензоры, их сумма есть тензор.
Упражнение 6.6. Покажите, что если ю — один-форма, то
(Vu)t/ = <ot, , = ©,./ — Гк,,щ. F.11)
Упражнение 6.7. Покажите, что если Т — тензор типа
Ум)' ТО
Г1 . I rpl .. I I fit грП . . / |
к l,m = * k...l,m-rl nmJ ft . . / "Т •••
I Ti/ rpi .. n -pre rni . / r\ti rni .. /
"T-l nm' ft г — A ftm-* n ... I — • ¦• — I Iml k . «•
6.5. КРУЧЕНИЕ
Величины [U, V] и S/-gV—VyU обе представляют собой
векторные поля и обе антисимметричны по О и У. Связность
называется симметричной, если они равны:
¦ ^цУ — V^C? = [U, V] <?=> связность симметрична. F.13)
Название «симметричная» объясняется свойством, доказы-
доказываемым в следующем упражнении.

6.5 КРУЧЕНИЕ 249
Упражнение 6.8. Покажите, что в координатном базисе из
F.13) следует, что связность симметрична тогда и только
тогда, когда
¦ Г^ = Г%, F.14)
Для несимметричной связности определим кручение Ткц
формулой
V/ ~~ V' ~ ^' ёЛ Е Г*'Л> F-15)
Упражнение 6.9. Покажите, что {Tkji} образуют тензор
типа ( о ); мы будем называть его тензором кручения и
обозначать через Т:
VVV-VVU-[U, V] = T(;U, V).
Пустое место в скобках оставлено для аргумента — один-
формы.
Упражнение 6.10. Пусть на многообразии заданы две связ-
связности с символами Кристоффеля Тьц и Г"*у соответствен-
соответственно. Покажите, что
и ij = I t/ ~ 1 И
являются компонентами тензора типа Г J . Покажите, что
этот тензор D симметричен по своим векторным аргумен-
аргументам тогда и только тогда, когда тензоры кручения обеих
связностей совпадают.
Упражнения 6.9 и 6.10 показывают, что мы всегда можем
определить симметричную часть V(s> любой связности V. за-
задав её символы Кристоффеля формулой
Хотя кручение в принципе тоже полезная часть связности,
но в конструировании математических моделей физических
законов оно не так популярно, как симметричная часть. На-
Начиная с этого места мы будем иметь дело только с симметрич-
симметричными связностями, за исключением тех случаев, когда явно
оговорено противное. Одна из причин для такого решения
станет ясна из упр. 6.18. Заметим, что из определения F.13)
непосредственно вытекает следующее свойство.
Упражнение 6.11. Пусть на многообразии задана симмет-
симметричная связность. Покажите, что в любом выражении
для компонент производной Ли любого тензора все запя-

250 в- СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
тые можно заменить на точки с запятой. Например,
(Естественно, при этом надо заменять все запятые, а не
только некоторые.)
6.6. ГЕОДЕЗИЧЕСКИЕ
Геодезическая — это такая кривая, собственный касатель-
касательный вектор которой переносится вдоль неё параллельно.
Уравнение геодезической:
«. ^11 = 0. F.16а)
Если Я, —параметр кривой„и задана система координат {х'},
то оно принимает вид
F.16Ь)
или
¦
Последнее уравнение — это квазилинейная система дифферен-
дифференциальных уравнений относительно функций х'(К), задающих
геодезическую кривую.
Упражнение 6.12. Напомним, что наше определение кри-
кривой включает в себя задание параметра. Покажите, что
если F.16с) верно для параметра К, то при замене его на
li = aK + b, F.17)
где а и Ъ — постоянные, мы тоже получим решение F.16с).
По этой причине параметр геодезической кривой назы-
называется аффинным параметром.
Заметим, что в уравнение геодезической входит лишь сим-
симметричная часть связности. Это позволяет представить эф-
эффект кручения геометрически. Возьмём геодезическую с ка-
касательным вектором U, проходящую через точку Р. В ТР вы-
выберем какое-нибудь (п— 1)-мерное подпространство RP (раз-
(размерность многообразия п), состоящее из линейно-независи-
линейно-независимых от U векторов. Зафиксируем вектор | из RP и проведём
через Р геодезическую, касательную к |. Используя симме-
симметричную часть связности, перенесём U параллельно вдоль |
на малое расстояние (в смысле аффинного параметра) е.
Через эту новую точку проведём новую геодезическую, каса-

6.7 НОРМАЛЬНЫЕ КООРДИНАТЫ 251
тельную к U в этой точке (т. е. к U' на рис. 6.5). Эта геоде-
геодезическая будет почти что параллельна исходной. Таким спо-
способом мы можем провести геодезические, «параллельные» V,
через каждую точку из окрестности Р. Мы можем переносить
«связующий» вектор | вдоль этой конгруэнции геодезических
двумя разными способами: либо с помощью параллельного
Рис. 6.5. Две параллельные геодезические U и U' и вектор \, который со-
соединяет их в плоскости Rp и параллельно переносится вдоль О. Когда есть
кручение, он "откручивается" от V.
переноса, либо с помощью переноса Ли. Пусть | перенесён
параллельно. Тогда мы получаем из F.15)
Однако для исходного вектора | мы имеем v,S)gt/ = O, иначе
говоря, (V| Uy = у T'jkU'l11. Таким образом, в исходной точке
Это означает, что при параллельном переносе вдоль построен-
построенной нами конгруэнции геодезических векторов | будет оста-
оставаться «прикреплённым» к кривым конгруэнции, если связ-
связность симметрична. Но если связность не симметрична, он не
будет оставаться «прикреплённым». Грубо говоря, под дейст-
действием кручения вектор | «вращается» относительно ближай-
ближайших геодезических. И наоборот: если мы рассматриваем па-
параллельно переносимый вектор | как определяющий некое
«постоянное» направление, то конгруэнция «параллельных»
геодезических будет при движении | «закручиваться» вокруг
геодезической «несущей» |. (Нельзя, однако, придать точный
смысл словам «вращается» и «закручивается», если нет
метрики.)
6.7. НОРМАЛЬНЫЕ КООРДИНАТЫ
В дальнейшем будет удобно использовать систему коор-
координат, основанную на геодезических. Чтоб построить её, за-
заметим, что геодезические, проходящие через точку Р, задают

252 6 СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
1-1-оюбражение окрестности Р на окрестность нуля в ТР. Это
отображение строится так: каждый вектор из ТР однозначно
определяет геодезическую, проходящую через точку Р, и мы
можем сопоставить ему точку этой геодезической, находящую-
находящуюся на расстоянии ДХ = 1 (где К — аффинный параметр) от точ-
точки Р. (Напомним, что если два вектора из ТР параллельны,
то их геодезические суть совпадающие, но по-разному пара-
параметризованные кривые, и, следовательно, построенное отобра-
отображение «различает» точки на геодезической.) С помощью та-
такого отображения мы можем, выбрав в ТР некоторый базис,
определить нормальные координаты точки Q как компоненты
вектора, связанного с этой точкой. Вообще говоря, это ото-
отображение будет взаимно-однозначным лишь в некоторой
окрестности Р, ибо геодезические на искривлённом многооб-
многообразии могут пересекаться. Для некоторых связностей, таких
как связность плоского пространства, оно будет взаимно-одно-
взаимно-однозначным и на всём многообразии. (Отображение из ТР в мно-
многообразие корректно определено, даже если геодезические
пересекаются. Оно называется экспоненциальным отображе-
отображением. Если оно определено для всех элементов ТР во всех
точках Р, то многообразие называется геодезически полным.)
Основная ценность нормальных координат для нас связана
с тем, что в них Г',й = 0 в точке Р (но не всюду в окрест-
окрестности Р). Чтоб это увидеть, заметим, что если мы рассматри-
рассматриваем геодезическую, определяемую вектором D с компонен-
компонентами U'(P), то координаты точки на этой геодезической, от-
отвечающей аффинному параметру, равному X, будут просто
xt = kUl(P), если мы положили К = О в Р. Таким образом,
d2x'/dX2 обращаются в нуль, а из F.16с) видно, что
r",ftt/ft(P) t/'(P) должно обращаться в нуль на всей кривой.
Однако в точке Р направление U было произвольным, откуда
и следует, что Г',Й(Р)= 0.
Тот факт, что всегда можно выбрать координатную си-
систему так, чтобы Г',й обращалась в нуль в некоторой точке,
ниже будет нам чрезвычайно полезен при доказательстве не-
нескольких теорем. Поскольку в других точках Г',й не обязаны
обращаться в нуль, то и производные Г',б в точке Р нулю не
равны.
6.8. ТЕНЗОР РИМАНА
Можно ожидать, что коммутатор двух ковариантных произ-
производных
будет дифференциальным оператором. Однако на самом деле
он обладает следующим замечательным свойством: оператор

6 8 ТЕНЗОР РИМАНА 253
R, определённый формулой
¦ [%. VF] - VlZ7; щ ^ R (Jj, V), F.18)
есть мультипликативный оператор. Еще более замечательно
то, что R также не зависит от производных V и V. Эти
свойства объясняются и доказываются в следующем упраж-
упражнении.
Упражнение 6.13. Докажите, что для любой функции /
(a) R(ULVUW = fR(U, V)W,
(b) R (fU, V)W = fR (U, V) W.
Благодаря этим свойствам F.18) в действительности опре-
определяет тензор, называемый тензором Римана. Из F.18)
видно, что, при заданных векторах О и V, R (U, V) — это тен-
тензор типа ( | ). поскольку, действуя на вектор, левая часть
опять-таки даёт вектор. Если считать V и V аргументами, то
тензор Римана становится тензором типа C) • (Заметим,
что принятое нами определение тензора Римана (F.18) и
F.19)) отнюдь не является единственно возможным. Исполь-
Используются и другие определения, отличающиеся от нашего зна-
знаком или порядком аргументов. Справляясь в других книгах,
проверьте, знаете ли вы, какое было использовано определе-
определение. Мы следуем Мизнеру, Торну и Уилеру A977).)
Упражнение 6.14. Компоненты тензора Римана /?'/« опре-
определяются формулой
[V,, Ч,]ёк-Ч[е1.ф = Я1Ы1ёг FЛ9)
(a) покажите, что в координатном базисе
¦ Rlktj = Ttk,.t-Tlkili + Tmk,Tlmt-rmhtTlmi. F.20)
(b) В некоординатном базисе определим перестано-
перестановочные коэффициенты C',k формулой
[ё„ ek] = Cllket. F.21)
Покажите, что
А Ы1 — * ft/, г 4i.( + l ft/1 ml — 1 fci1 m/ ~L t/l ftm»
F.22)
где /,, = et [f].
(c) Покажите, что
Rlkun = j (R'kH + Rlk») = 0 F.23a)
и
R\ki,\ = 0. F.23b)

254 6. СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
(Указание: для доказательства F.23Ь) используйте нор-
нормальные координаты; ответ, конечно же, от выбора коор-
координат не зависит.)
(d) Используя (с), покажите, что на n-мерном много-
многообразии число линейно-независимых компонент /?'«/ равно
4 о П (П + 1) П(П— 1)(И — 2) 1 9/ |\ /л о«
п4 — п2 v 2 — п —- gp = у и («—!)• F-24)
Упражнение 6.15. Покажите, что
/?Wm] = 0. F.25)
Эти соотношения называются тождествами Бьянки. (Ука-
(Указание: опять работайте в нормальных координатах.) По-
Покажите, что в координатном базисе эти тождества экви-
эквивалентны тождествам Якоби для ковариантных произ-
производных
[V*. [V/, Va]] + [V/, [V*. V*]] + [Vft, [V,, V,]] = 0.
[См. B.14) и C.9).]
6.9. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
ТЕНЗОРА РИМАНА
Так же, как и при интерпретации другого встречавшегося
нам коммутатора, [D, V], речь пойдёт о замкнутой или почти
замкнутой петле. Наши рассуждения основаны на использо-
использовании экспонент от ковариантных производных и потому
идут практически параллельно тому, что было в случае ско-
скобок Ли. Если векторное поле А определено вдоль кривой с
касательным вектором V, то параллельный перенос позво-
позволяет нам перенести А из любой точки кривой Q в любую дру-
другую её точку Р. Полученный таким образом вектор A(Q^-P)
из касательного пространства ТР (вообще говоря, не равный
А(Р)) назовём образом A(Q) в Р; он, конечно же, зависит от
кривой. Действительно, если А и О аналитичны, мы можем
записать следующий ряд Тейлора:
A(Q -+ Р) = А(Р) + W
= екр[№и]А\Р, F.26)
где X — параметр кривой (U — d/dh), а обозначение «ехр»
опять всего лишь сокращённая запись предыдущей строки.
Теперь рассмотрим две конгруэнции с касательными век-
векторами U = d/dX и V = d/djx, такими что [О, V]—0. Тогда
при пересечении они образуют замкнутые петли (рис. 6.6).
Если мы параллельно перенесём вектор из некоторой точки R

6.9. ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ТЕНЗОРА РИМАНА 255
вдоль кривой V в точку Q, как показано на рисунке, то по-
получим вектор
где ц — изменение параметра при переходе от Q к R. Если
теперь мы параллельно перенесём полученный вектор из О
в Р, то в точке Р получим вектор
A(R -* Q -> Р) = ехр [Wv] exp fnVF] А \Р,
где К — изменение параметра при переходе от Р к Q. Но мож-
можно сделать перенос и по другому пути, а именно сначала
v
и
Рис. 6.6. В результате параллельного переноса вокруг замкнутой петли
получается вектор, вообще говоря, не совпадающий с исходным.
пойти в точку S («расстояние» к вдоль О-кривой), а потом —
в Р («расстояние» \х вдоль F-кривой). Значения К и \i будут
те же, поскольку О и V коммутируют. При втором способе
получаем
A(R->-S-:>-P) = exp\nVy]exp\kV-u]A \P.
При малых X и ц мы можем найти разность 6Л векторов, по-
получаемых этими двумя способами, с помощью разложения
Тейлора:
= [1 + Wv + \ 12VvVu, 1 + KiVF + 4" V?VVVV] А + О C),
где через 0C) обозначены члены, имеющие по \х и К суммар-
суммарную степень ^3. После некоторых преобразований приходим
к равенству
6Л"= Xjx [Vjj, Vy] A + О C); F.27)
но это как раз и есть тензор Римана, причём производные от
Л сюда не вошли. На 6А можно также смотреть как на изме-

256
6. СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
нение А при параллельном переносе его вдоль замкнутой
петли PQRSP. Это изменение как раз и равно значению тен-
тензора Римана, умноженному на «площадь» петли, Яц:
Другой существенный для геометрии аспект тензора Ри-
Римана связан с девиацией геодезических, т. е. с тем фактом,
что геодезические, бывшие в начале параллельными, теряют
в дальнейшем это свойство. Чтоб
измерить этот эффект, рассмо-
рассмотрим конгруэнцию геодезиче-
геодезических с касательным вектором
U(y^U = 0) и соединяющий
кривые конгруэнции вектор |,
который перемещается по кри-
кривым с помощью переноса Ли
(?т]% = 0) (см. рис. 6.7). Me-
^ ' геодезических бу-
Дет служить изменение вектора
|. Его первая производная
зависит от начальных условий, от того, параллельны
исходные геодезические или нет. Геометрия сидит во второй
производной VyVyi, которая говорит, как меняется исход-
исходная степень разделения геодезических. Итак, мы имеем
Рис. 6.7. Соединяющий кривые
конгруэнции геодезических век-
= VVV%U = | Vy, V
] I/ -f
На первом шаге использовано упр. 6.11. Последний член в
правой части обращается в нуль, поскольку О — геодезиче-
геодезическая, и мы получаем
\)U.
F.28a)
или в компонентах
Заметим, что левую часть можно упростить, поскольку f/^
= 0; это даёт
'• <6-28b)
Уравнение F.28) называется уравнением девиации геодези-
геодезических.

6.1!. СОГЛАСОВАННОСТЬ СВЯЗНОСТИ С ОБЪЁМОМ " 257
6.10. ПЛОСКИЕ ПРОСТРАНСТВА
Аксиома Эвклида о параллельных служит определяющей
аксиомой плоского пространства. Как ясно нз F.28), про-
пространство плоско тогда и только тогда, когда его тензор Ри-
мана равен нулю. Таким образом, тензор Римана есть мера
кривизны многообразия со связностью. В плоском простран-
пространстве, как следует из F.27), есть глобальное понятие парал-
параллельности: можно говорить, что вектор в точке Р параллелен
вектору в точке Q, ибо его можно параллельно перенести в Q
способом, не зависящим от пути. Поэтому в плоском про-
пространстве можно отождествить все касательные пространства
ТР. Более того, экспоненциальное отображение можно про-
продолжать бесконечно (при условии, что глобальная топология
многообразия не усложнена искусственно «резкой» и «склей-
«склейкой») и всё многообразие можно отождествить с его каса-
касательным пространством. Обратите внимание, что метрический
тензор во всём этом не участвует. Пространство Минковского
так же плоско, как и эвклидово пространство.
Упражнение 6.16. Рассмотрим двумерное плоское про-
пространство с декартовыми координатами х, у и полярными
координатами г, 6.
(a) Используя то, что векторы ёх и ёу параллельны
сами себе глобально (для любых Р и Q вектор ёх(Р) па-
параллелен вектору eA(Q)), покажите, что
ГГее = — г> Г ге = Г вг = 1/г,
а все остальные Г в полярных координатах равны нулю.
(b) Для произвольного векторного поля V выразите
ViV* и V,V' для случая полярных координат через V и Vе.
(c) Для базиса rs=d/dr, G = A/г)д/дв найдите все
символы Кристоффеля.
(d) Выполните задание (Ь) для базиса из (с).
Это упражнение устанавливает следующий важный факт:
хотя на плоском многообразии существуют системы коорди-
координат, в которых Yljk = 0 повсюду, можно выбрать координаты,
в которых они ненулевые.
6.11. СОГЛАСОВАННОСТЬ СВЯЗНОСТИ
С ОБЪЁМОМ ИЛИ МЕТРИКОЙ
Если на многообразии помимо связности задана ещё фор-
форма объёма или метрика, то, как правило, на неё налагаются
некоторые дополнительные ограничения. Например, как связ-
связность, так и форма объёма могут задавать дивергенцию век-
векторного поля V. Ковариантная дивергенция — это V-Г sa V;K'>

258
6 СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
а дивергенция относительно формы объёма определяется фор-
формулой
Мы говорим, что V ий согласованы, если div& F = V -V для
всех V.
Упражнение 6.17. (а) Покажите, что V и 5 согласованы
тогда и только тогда, когда Vco = 0. (Указание: для вычис-
вычисления ?у& используйте упр. 6.11.)
(Ь) Предположим, что coi2...n = f в координатах
(л;1, ..., хп). Покажите, что V и й согласованы тогда и
только тогда, когда для всех k
Аналогично если на многообразии задан метрический тен-
тензор, то имеется естественное требование согласованности.
А именно, для любых двух векторов Л_и В в точке Р опре-
определено скалярное произведение g (Л, Б). Мы говорим, что
V и g согласованы, если это скалярное произведение сохра-
сохраняется при параллельном переносе А и В вдоль каждой
кривой.
Упражнение 6.18. (а) Покажите, что Vug согласованы
тогда и только тогда, когда
Vg=0. F.29)
(b) Покажите, что в координатах (х1, ..., хп) условие
согласованности имеет вид
г'/* = ? а' ten. k + etk, I—gik. /)¦> (б.зо)
За'^ь ц" —элементы обратной к gim матрицы (см. B.55)).
/Указание: используйте симметрию Г',* = Г'*;.)
Упражнение 6.19. Напомним (см. упр. 4.13), что, когда
имеется метрика, можно определить выделенную форму
объёма. (Это ещё один вид согласованности, на этот раз
метрики и формы объёма.) Покажите, что если метрика
и связность согласованы, то выделенная форма объёма и
связность тоже согласованы. (Указание: надо убедиться в
том, чтоg,k = gngn,b\ для этого используйте D.19).)
Равенство F.30) выявляет тот замечательный факт, что
метрика однозначно определяет согласованную с ней связ-
связность. Такая связность называется метрической связностью.
Упражнение 6.20. Покажите, что для произвольного век-
вектора V

6.12. МЕТРИЧЕСКАЯ СВЯЗНОСТЬ 259
Следовательно, вектор Киллинга (см. § 3.11) удовлетво-
удовлетворяет уравнению Киллинга
V/F/ + VjVi = 0.
Ср. с уравнением E.89),
6.12. МЕТРИЧЕСКАЯ СВЯЗНОСТЬ
Поскольку F.30) налагает на связность жесткие ограни-
ограничения, метрическая связность обладает дополнительными
свойствами, которых у произвольной симметричной связности
нет. Вывести некоторые из этих свойств проще всего в нор-
нормальных координатах. Заметим, что из F.29) и F.30) сле-
следует, что
Tljk = 0 в точке P<=>gltnitl=0 в точке Р. F.31)
Упражнение 6.21. Покажите, что из F.20), F.30) и F.31)
вытекает, что в нормальных координатах в точке Р
Ri/ki = gimRmiki = т (#«. /ft ~~ Elk, ji + gik. и — g/i. ik)-
F.32)
Упражнение 6.22. (а) Покажите, что из F.32) следует
тождество
Riiki = Rkiu- F.33)
(b) Покажите, что из F.33) и F.23) следует, что на
и-мерном многообразии число линейно-независимых ком-
компонент Rijki равно
-^п(п-1)(п2-п+2)--~п(п-1)(п-2)(п-3) =
= ^п>2- 1).
Упражнение 6.23. (а) Определим тензор Rki, называемый
тензором Риччи, формулой
Rki = R'ku F.34)
и скалярную кривизну формулой
R = gklRki. F.35)
Покажите, что тензор /?,¦/ симметричен.
(Ь) Покажите, что из свёрнутых тождеств Бьянки
Rl,[il;m] = 0 И gilRii[U;m] = 0
следует, что
V) = 0- <6-36)

260 6. СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
(Индексы у /?" поднимаются с помощью метрики: R1' =
g"g>mRlm.)
(с) Определим тензор Вейля формулой
Си = Rliki - 26ltlkRnl} + ± 6[tlk6nt]R. F.37)
Покажите, что любая свёртка Сцы по индексам даёт
нуль — это «чистый» тензор четвёртого ранга.
Равенство F.36) играет важную роль в эйнштейновой тео-
теории гравитации — общей теории относительности. Простран-
Пространство-время в этой теории есть обобщение плоского простран-
пространства Минковского— четырёхмерное многообразие с метрикой.
Гравитационное поле (т. е. метрика) в пустом пространстве
(без материи) находится как решение дифференциальных
уравнений
G'' = ^'-i-^' = 0. F.38)
Тензор G'1 называется тензором Эйнштейна. Тождества F.36)
понижают число независимых уравнений в F.38) от 10
(=^п{п— 1), поскольку Gi} симметричен) до 6. Это гаран-
гарантирует, что решение gih тоже имеющее 10 независимых ком-
компонент, определяется с точностью до четырёх функциональ-
функциональных степеней свободы, которым в свою очередь соответствуют
координатные преобразования gij.
Упражнение 6.24. Покажите, что соединяющая точки Р и
Q геодезическая есть кривая экстремальной длины среди
всех кривых, соединяющих эти точки. А именно, покажите,
что с точностью до первого порядка
Q
г dx dx \ П/2
не меняется при отклонениях х1{к) от геодезической.
(Имейте в виду, что параметр каждой кривой определяется
однозначно; параметр геодезической должен быть аффин-
аффинным.) Обдумайте вопрос о необходимости знака модуля
в случае индефинитной метрики и отдельно обдумайте
случай нулевой геодезической (геодезической нулевой
длины).
6.13. АФФИННАЯ СВЯЗНОСТЬ
И ПРИНЦИП ЭКВИВАЛЕНТНОСТИ
Мы все обучались основам физики и геометрии, изучая
плоские многообразия: эвклидово трёхмерное пространство,
галилеево пространство-время (хотя, возможно, его так и не

6 14. СВЯЗНОСТИ И КАЛИБР. ТЕОРИИ НА ПРИМЕРЕ ЭЛЕКТРОМАГНЕТИЗМА 261
называли), а потом (если довелось) пространство-время Мин-
ковского. С другой стороны, общая теория относительности
использует искривлённое пространство-время, и кажется
естественным представлять себе плоское пространство как
простейший вид пространств. Но с точки зрения теории мно-
многообразий даже плоское пространство вовсе не просто: по
сравнению с обычным дифференцируемым многообразием
оно имеет гораздо более богатую структуру, ибо на нём за-
задана аффинная связность. В элементарной геометрии и физике
присутствие этой связности не ощущается, поскольку, как
правило, применяют прямоугольные системы координат, в ко-
которых символы Кристоффеля обращаются б пуль. Однако,
если физические законы сформулированы в плоском простран-
пространстве на языке криволинейных координат, в которых символы
Кристоффеля уже придётся использовать, связность стано-
становится наблюдаемой.
На первый взгляд это ненужное усложнение, но посмо-
посмотрим, какие в нём содержатся возможности для обобщений.
В большинство так записанных физических законов входят
символы Кристоффеля, а не тензор Римана, следовательно, их
уравнения осмыслены и выглядят одинаково вне зависимости
от того, плоско наше многообразие или криво. Таким обра-
образом, естественно постулировать, что математическая форма
физических законов в искривлённом пространстве-времени
общей теории относительности в точности та же, что и в кри-
криволинейных координатах плоского пространства Минковского.
Такой постулат называется принципом минимальной связи
(физических полей с кривизной пространства-времени) или
сильным принципом эквивалентности. Это широко принятый
постулат, который согласуется с экспериментом. Подробно он
обсуждается в книге Мизнера и др. A977). Здесь же стоит
подчеркнуть то весьма замечательное обстоятельство, что,
записывая «плоские» физические законы в криволинейной си-
системе координат, мы находим их вид в искривлённом про-
пространстве. Это обстоятельство объясняется тем, что плоские
пространства, хотя у них и нулевая кривизна, имеют вполне
определённую связность, а потому являются просто частным
случаем искривлённого пространства.
6.14. СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
НА ПРИМЕРЕ ЭЛЕКТРОМАГНЕТИЗМА
Под названием «калибровочные теории» объединяется це-
целое множество разнообразных теорий взаимодействия элемен-
элементарных частиц. Все они обладают одним общим свойством;
их физические предсказания инвариантны относительно груп-
группы преобразований основных полевых переменных. Наиболее
известный пример — это теория электромагнетизма: если вы-

262 6 СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
брать в качестве основной переменной один-форму («вектор»)
потенциала А, то физические предсказания теории инвари-
инвариантны относительно калибровочных преобразований А —>
А+ (Г/. Общее обсуждение калибровочных теорий выходит за
рамки этой книги (см. Trautman, 1973), и мы ограничимся
здесь электродинамикой, поясняя всё на примере уравнения
движения заряженной бесспиновой частицы массы т. Мы
увидим, что естественно появится связность, другая, но играю-
играющая ту же роль, что и аффинная, и эта связность приведёт
нас к «открытию» электромагнитного поля!
Сначала рассмотрим нейтральную скалярную частицу
массы т, волновая функция которой я|) удовлетворяет уравне-
уравнению Клейна — Гордона и (сохраняющемуся) условию нор-
нормировки:
$J F.39)
где греческие индексы пробегают (t, x, у, г); мы предполо-
предположили для простоты, что взята метрика Минковского. Оче-
Очевидно, что если я]? — решение, то и яре1'*, где <р — произвольное
вещественное число, тоже будет решением. Таким образом,
я|) -*- яре1* — калибровочное преобразование. Теперь проведём
аналогию, которой будем пользоваться на протяжении всего
последующего обсуждения. Наши калибровочные преобразо-
преобразования чрезвычайно ограниченны, поскольку <р не может за-
зависеть от точки. Это похоже на инвариантность относительно
выбора координат при описании некоторых (всех) физиче-
физических систем в прямоугольных координатах специальной тео-
теории относительности. Допустимые координатные преобразо-
преобразования— это вращения, лоренцевы бусты и трансляции, и все
они «жёсткие»: нельзя в одной точке выполнять одно преоб-
преобразование, а в другой — другое. Ослабление этого ограниче-
ограничения, необходимое, если мы хотим использовать произвольные
системы координат, заставляет нас, как мы видели в предыду-
предыдущем параграфе, ввести аффинную связность, — иначе мы не
сможем определить не зависящую от выбора координат ко-
вариантную производную. Но если уж уравнения движения
физической системы записаны в терминах связности, то есте-
естественно использовать их и тогда, когда связность уже не яв-
является плоской. И они оказываются подходящими уравне-
уравнениями для рассматриваемых систем в общей теории относи-
относительности. Итак, методика, основанная на использовании сво-
свободы в выборе системы координат, привела нас к теории,
описывающей, как система взаимодействует с гравитацион-
гравитационным полем. Подобным же образом мы увеличим теперь ка-
калибровочную свободу поля я]з — и автоматически придём к
теории, описывающей, как гравитационное поле взаимодейст-
взаимодействует с электромагнитным полем.

6.14. СВЯЗНОСТИ И КАЛИБР ТЕОРИИ НА ПРИМЕРЕ ЭЛЕКТРОМАГНЕТИЗМА 263
Обобщение очевидно: нам нужны калибровочные преоб-
преобразования общего вида
¦ф-э-гре"^, F.40)
где теперь ф — произвольная функция точки х в пространстве
Минковского. Но поскольку в уравнения поля входят произ-
производные, мы получаем
а^-^ф + гфЗф)^*). F.41)
Для того чтоб понять, как избавиться от лишнего члена, по-
посмотрим на дело более геометрически. Множитель е1^ — это
комплексное число на единичной окружности; калибровочное
преобразование — это представление группы И(\) (унитар-
(унитарной группы в одномерном комплексном пространстве) сё
действием на ф. Поэтому преобразование ф -*¦ tjre145-^ можно
представлять себе так: в каждой точке х выбирается элемент
из U (У) и действует на -ф. Геометрический объект, отвечаю-
отвечающий этой картине, — это расслоение, причём пространство
Минковского играет роль базы, а группа U{1) — слоя (его
можно представлять в виде единичной окружности на комп-
комплексной плоскости). Тогда калибровочные преобразования
F.40) будут сечениями этого расслоения, которое мы назо-
назовём 0 A) -расслоением.
Объект, которым мы теперь хотим заняться, — это не сама
¦ф, а УД> — элемент из 7*я, векторного пространства один-
форм в точке Р. Рассмотрим на базе кривую Ч? с параметром
К. Двигаясь по кркчои, мы последовательно встречаемся с
один-формами dij\ по одной в каждой точке. Если г|э удов-
удовлетворяет уравнению Клейна — Гордона F.39), то мы будем
говорить, что d\|) меняется вдоль <ё «правильным» образом.
У нас есть ограниченный набор калибровочных преобразова-
преобразований (ф = const), для которых новая форма dx|) тоже «пра-
«правильная». Но представим себе, что мы сделали произвольное
калибровочное преобразование. Тогда кривой Ч? на базе со-
соответствует кривая <&* в U(l)-расслоении: в каждом слое, ле-
лежащем над точкой х кривой Ф, она проходит через элемент
е«р(х)# Если преобразование не постоянно (если Ч/* не «парал-
«параллельна» '&), то градиент преобразованной t]j не будет «пра-
«правильным»: он не будет равен градиенту исходной ф с точно-
точностью до фазы. Поэтому мы определим на базе один-форму
связности Л, зависящую от кривой 9F* таким образом, чтобы
это «исправило» производную •ф. Определение будет следую-
следующее:
(i) Если ф —решение F.39;, ш А = 0.

6. СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
(ii) При преобразовании •ф->фе'ч)га один-форма связ-
связности преобразуется по правилу
Л-*-Л+<Г<р. F.42)
(Ш) Калибрсвочно-ковариантная производная т|) опреде-
определяется формулой
By = сЬф — tyA. F.43)
Свойства (п) и (iii) означают, что при калибровочном пре-
преобразовании Dty переходит в е'Ч'^О'ф; свойство (i) гаранти-
гарантирует, что Dty «правильна» на <ё.
Теперь поймём, почему Л называется связностью. Аффин-
Аффинную связность представляют символы Кристоффеля, которые
мы добавляем к обычной частной производной, чтоб получить
«правильную» производную —¦ производную, задающую парал-
параллельный перенос (ср. F.43) с F.10)). Чтобы эта «правиль-
«правильность» производной сохранялась, символы Кристоффеля
должны преобразовываться при замене координат специаль-
специальным образом (упр. 6.2), и формулы перехода очень похожи
на то, как меняется А при калибровочном преобразовании
F.42). Различаются эти связности тем, что они призваны со-
сохранять: аффинная связность сохраняет параллельность,
наша один-форма связности сохраняет градиент при калибро-
калибровочных преобразованиях.
Теперь мы можем записать уравнение Клейна — Гордона
в калибровочно-ковариантном виде:
ш\ = (V,, - iA,x) (v* - М") Ф - т% = 0. F.44)
Если фаза i]5 «правильна», то она превращается в обычное
уравнение Клейна —¦ Гордона, и любая -ф. полученная из «пра-
«правильной» калибровочным преобразованием, тоже будет реше-
решением F.44).
Задав какую-либо систему координат, мы можем опреде-
определить тензор кривизны формулой, похожей на F.18) i
Её аналогом для нашего случая будет
[D^Djq^F^. F.46)
Прямое вычисление показывает, что калибровочная два-фор-
ма кривизны F, имеющая компоненты f^v» — это просто
F = —idA. F.46).
Очевидно, F калибровочно-инвариантна (см. (ii) выше). (Тен-
(Тензор Римана был координатно-инвариантным.) Уравнение

6 15 БИБЛИОГРАФИЯ
265
Клейна — Гордона калибровочно-плоско (F — Q), поскольку
существует калибровка с Л = 0. Но поскольку есть явная
аналогия с электромагнетизмом (Л = один-форма потенциа-
потенциала, if = тензор Фарадея, см. гл. 5), естественно попытаться
посмотреть на F.44) как на обобщение уравнения Клейна —
Гордона на случай заряженной частицы, взаимодействующей
с внешним электромагнитным полем F. Такая гипотеза и в
самом деле верна, и F.44) можно прямо вывести из того фак-
факта, что канонический импульс классической частицы во внеш-
внешнем электромагнитном поле равен рс = р + (<?/с) А, где р —
«настоящий» 4-импульс частицы. В силу принципа соответ-
соответствия уравнение р-р-{-т2 = 0 переходит (в системе единиц
с Ь = с = 1) в уравнение
(—iVn — qA») (—iV^ — qAv) + m\\, = 0;
отсюда мы видим, что F.44) действительно есть волновое
уравнение для такой частицы с зарядом q= 1. Всё вышеска-
вышесказанное можно подытожить следующим образом: скалярная
частица с массой m и зарядом q, находящаяся во внешнем
электромагнитном поле с один-формой потенциала Л, подчи-
подчиняется уравнению
(Уц — iqAu) (W — iqA») i|) — m2i|) = 0. F.47)
Калибровочные преобразования состоят в следующем:
F.48а)
F.48Ь)
Один-форму Л можно рассматривать как связность на 1/A)-
расслоении, а Р — как её кривизну.
Упражнение 6.25. (а) Проверьте, что tty-*-eltM*)Bty при
калибровочном преобразовании.
(Ь) Проверьте F.46).
6.16. БИБЛИОГРАФИЯ
Весьма полное руководство по римановой геометрии — двухтомная мо-
монография Ш. Кобаяси и К. Номидзу «Основы дифференциальной геомет-
геометрия» (М.: Наука, 1981).
Хорошее современное введение в псевдориманову геометрию (метри-
(метрическая связность для случая индефинитной метрики) можно найти в кни-
книгах: Мнзнер Ч., Торн К., Уилер Дж. Гравитация (М.: Мир, 1977); The
Large-Scale Structure of Space-Time, S. W. Hawking & G. F. R. Ellis (Cam-
(Cambridge University Press, 1973); Вейнберг С. Гравитация и космология (М.:
Мир, 1975).
Более полное описание роли связностей в калибровочных теориях
имеется в статье A. Trautman, Infinitesimal connections in physics, in:
Proceedings of the International Symposium on New Mathematical Methods
in Physics, ed. K. Bleuler & A. Reetz (Bonn, 1973). См. также R. Hermann,
Vector Bundles in Mathematical Physics, в 2-х томах (Benjamin, Reading,

266 С. СВЯЗНОСТИ И КАЛИБРОВОЧНЫЕ ТЕОРИИ
Mass., 1970). По поводу «физического» описания калибровочных теорий
см. J. С. Taylor, Gauge Theories of the Weak Interactions (Cambridge Uni-
University Press, 1976). Математическое обсуждение связностей, понимаемых
в более широком смысле, можно найти в книге Y. Cnoquet-Brunat, С. De-
Witt-Morette & М. Dillard-Bleick, Analysis, Manifolds, and Physics (North-
Holland, Amsterdam, 1977). Связности на расслоенных пространствах рас-
рассматриваются в статье В. Carter, Underlying mathematical structures of
classical gravitation theory, in: Recent Developments in Gravitation, ed.
M- Levy & S. Deser (Plenum, New York, 1979).
Введение аффинной связности на многообразии вызывает к жизни мно-
множество других тем для исследования. Например, на группах Ли имеется
естественная аффинная связность, превращающая однопараметрические
подгруппы в геодезические группового многообразия. Эта конструкция изу-
изучается шаг за шагом в виде последовательности упражнений в указанной
выше книге Мизнера и др.
То что кручение может играть роль в гравитации, впервые было за-
замечено Картаном. Однако значительное внимание теория гравитации Эйн-
Эйнштейна — Картана привлекла лишь позднее; см. A. Trautman, Bull, de
l'Academie Polonaises des Sciences (math., astr., phys.) 20, 185—190 A972).
Тензор Римана не так просто вычислить по заданным компонентам
метрического тензора. Задача упрощается, если использовать метод по-
подвижных реперов Картана, использующий исчисление дифференциальных
форм; см. снова книгу Мизнера и др.
Хотя мы вовсе не рассматривали дифференциальную геометрию на
комплексных многообразиях, она интересна и может в будущем сыграть
существенную роль в физических приложениях. Введение в неё, рассчитан-
рассчитанное на физиков, дано в книге Е. J. Flahery, Hermitian and Kahlerian Geo-
Geometry in Relativity (Springer, Berlin, 1976); стандартное чисто математиче-
математическое руководство — S. S. Chern, Complex Manifolds Without Potential Theo-
Theory (D. Van Nostrand, New York, 1967).

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ
К НЕКОТОРЫМ УПРАЖНЕНИЯМ
2.1. [?, §] = —Ъ/гфО.
2.2. (Ь) Поскольку ad/6% + bd/djx = bd/djj, + ad/dk, то из
B.13) следует, что exp[ad/dX]exp [bd/djj,] = exp [bd/djj,]exp
[ad/dk], откуда получаем [d/dk, d/djj,] = 0. И наоборот, если
порядок d/dk и d/djj, в правой части B.13) роли не играет, то
с ними можно обращаться как с простыми числами, для ко-
которых B.13) выполнено.
2.3. Разверните каждое слагаемое (например, [ [X, У] ,1] =
XYZ—YXZ — ZXY + ZYX). Каждый член этого разложения —
дифференциальный оператор на функциях. Условие принад-
принадлежности классу С2 гарантирует, что каждый член разложе-
разложения существует. После того как все слагаемые в B.14) так
разложены, результат становится очевиден.
2.4. Чтобы получить из матрицы, являющейся тензором типа
( j J, число, нужны один вектор и одна один-форма. По-
Поскольку у нас в деле участвуют две матрицы, то, чтобы свя-
связать с преобразованием число, нужны два вектора и две один-
формы. Линейность проверяется легко.
2.6. В случае размерности п у тензора типа Г Q J имеется п2
независимых компонент, а у пары векторов — всего лишь 2п
компонент. Вообще говоря, этого недостаточно.
2.6. Линейная комбинация двух тензоров типа ( „ J опреде-
определяется своими значениями на двух произвольных один-фор-
один-формах: (afi'H- Pr) (р, q) = ah (p, q)-\- Pr (p, q). Она является ли-
линейной функцией от р и q, а следовательно, Г J-тензором,
Нулевой тензор равен нулю на любых двух р и q, и все ак-
аксиомы векторного пространства, очевидно, выполняются.
Наше пространство имеет размерность п2, поскольку любой
тензор полностью определяется своими компонентами
h(©', ©') = A". Тензоры {&®ё/} (их п2 штук) образуют ба-

268 ПРИЛОЖЕНИЕ РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
зис, поскольку они линейно-независимы: линейная комбина-
комбинация Р"ё, ® ё, обращается в нуль тогда и только тогда, когда
все р" — нули, что легко увидеть, подействовав этим тензо-
тензором на всевозможные пары базисных один-форм. На самом
деле, как нетрудно проверить, h= h"e, ®ё,.
2.7. Шесть. Шесть.
2.8. Линейность: C(aV + bW) = B(A(aP-f bW)) = B(oA(F)
+ bA(W))== aB{A{V))+bB{A(W))=aC(V) + bC(W).
Компоненты: если А(ё,) = Ак,ёк, то С(ё/) = В(Ак,ёк) =
В (ek) Ak, = BlkAk,e,, откуда и следует ответ.
Каждый ( - J-тензор — это линейное преобразование в Тр.
Из полученного результата видно, что линейные преобразо-
преобразования образуют группу относительно операции композиции
(с помощью которой мы получили С из А и В).
2.9. Т(б'', йО = Т(Л'*й\ Xl'i&t) = Al'kAl'lT(&k, б1). На слу-
случай N индексов (i' ... /') и Л/'индексов (&' ... /') это обоб-
обобщается так: V' ¦/V.../' = A'V ... Л;'5Л^ ... AuyTr---st.. „.
2.10. Это верно для любого векторного пространства: нулевой
элемент определяется однозначно.
2.11. Значение нашего «тензора» (в исходном базисе) на один-
форме р и векторе V есть A^VW,. В новом же базисе, исполь-
используя новые компоненты для всех величин, мы получаем:
A1','V''Pt' = (Л''ГЛ5,'Ars)(A''kVk)(Al\'Pi). Просуммировав по
i' и /', а затем использовав B.34), мы получим старый ответ.
Таким образом, наше правило сопоставляет вектору и один-
-форме вещественное число, не зависящее от выбора базиса.
2.12.
(a) Л = 1 ¦ ._ I /-) приводит к каноническому виду
/1 04
U \)-
(b) Л = f . ,— У,- 1 приводит к каноническому виду
I 0 I)'
(c) Л = Г . р J приводит к каноническому виду Г ~0 Л.
2.13. (а) Закон преобразования можно получить из B.55).
Как функция от один-форм g удовлетворяет равенству
9~'(Д 9) = Q (pi я)> откуда следуют B.55) и, очевидным об-
образом, свойство линейности.

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 269
(Ь) В таком базисе метрика имеет компоненты ±6,/, сле-
следовательно, обратная матрица д-1 имеет те же компоненты
2.14. Разложите g.f и А1,, в ряд Тэйлора в точке Р. Попы-
Попытайтесь удовлетворить (i) и (и), подобрав по произвольным
коэффициентам разложения gc, соответствующие коэффи-
коэффициенты разложения Л1,'. Подсчётом числа коэффициентов
покажите, что (i) — (Hi) имеют место. Обратите внимание на
то, что не все дА1 ^\дхк' в точке Р независимы, поскольку из
А*г = дхЧдхг следует, что дА'г/дхк' = дА\'/дхг.
2.15. (a) grr = 1, grQ = 0, gee =f-
(b) Базис ортонормирован; г = д/дг, 6 = г~1д/дв.
2.16. (a) df имеет компоненты (df/dr, df/dQ), d/ имеет компо-
компоненты (df/dr, r-2df/dQ).
(b) В этом ортонормированном базисе и df и df имеют
компоненты {df/dr, r~ldf/dQ).
3.1. (а) В случае функций_из C.3) следует, что в обеих частях
C.8) стоит оператор [V, Щ. В случае векторного поля_?7 из
C.6) следует, что левая часть имеет вид [V, [W, U]] —
[W, [V, О]], а правая часть равна [[V, W], О]. Наш резуль-
результат следует теперь из тождества Якоби (упр. 2.3) и антисим-
антисимметричности скобок Ли.
(Ь) В случае функций опять используем тождество Якоби
B.14). В случае векторов тождество C.8) превращает C.9)
в производную Ли по направлению нулевого вектора
[[X, Y], Z} + [\?, Z], Х\ + [[2, X], Y].
3.2. (b) ^7f7=^F(^4)
[V'e, (U1)] ё-п*?.{ (У!ё,)
Последний шаг требует переобозначения индексов. Используя
C.7) в последнем слагаемом, получаем требуемый ответ.
3.3. Это следует из B.7) при V'1 — Ь1\.
3.4. Из C.13) получаем
где индексы во втором слагаемом переобозначены. Ответ сле-
следует из произвольности W'.

270 ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
3.5. (a) [Z<VV ?Р<Ида
Z
3.6.
-TY ••• I т/г 5 Tl •¦¦ i тг ¦¦• < д i/'
4T
ox1
Положив У1 = Ь\, получим (^ТI' - 'k _, =dV ¦•¦ \ Jdxu
3.7. [L\ ?iz] = ?-lx[?h, ?iz] + [?ix- ?iz]?-tx+?iyX
\?j , ?j ] ?j = ?i ?j + ?-t ?-t - ?7 ?г -
j ?t]
?i?i =0.
lx ly
Второй шаг основан на тождестве C.8). Чтобы доказать
C.33), выведите следующие соотношения: 1Х = —эшфд/дб —
cos ф ctg 6<Э/йф; 1У = —cos ф<Э/д0 + sin Ф ctg 6<Э/<Эф; lz = д/dq.
3.8. Это тривиально следует из того, что ?ау = а?-у, если
а — константа. (Это неверно, если а — произвольная функ-
функция.)
3.9. При переносе Ли вдоль ф из ф = 0 вектор ёг не меняется,
а ёх превращается в ёг = costye* + s'm<pey. Третий базисный
вектор ёц> в декартовом базисе имеет вид —sin ц>ёх + cos ц>ёу.
Три векторные гармоники — это: ехрB1ф)ёг, ехр{2'vp) (cosуёх
+ s\nq>ey), ехрB1ф)(—81пфёл: + созфё^). Иногда удобнее пе-
перейти к их линейным комбинациям: ехрB1ф)ёг, ехр^ф) (ёх +
1ёу), ехр C1ф) (ёх — iey). Отсюда видно, что ёх + iey имеет
собственное значение +1, а ёх — iey — собственное значение
—1, что впрочем легко и прямо проверить. Перенос Ли не
меняет один-форму Sz, а их переходит в d7 = cosфdл¦ +
sin фЗг/. Третья базисная один-форма Эф в декартовом базисе
имеет вид —sin фdл; + cos qdy. Поэтому тремя гармониками
для один-форм будут: ехрB1ф)йг, ехрAф) (их + idy),
ехр Ciq>) (dx — idy). Поскольку ?eJ = 2lf, то d(?eJ) = 2idf.
Кроме того, как легко показать (используя цилиндрические
координаты), d(?gJ) = ?e^(df), что и завершает доказа-
доказательство. Последнее равенство есть частный случай общей
теоремы, которая будет доказана ниже, в § 4.21.
3.10. Правоинвариантное векторное поле инвариантно относи-
относительно отображений Де, которые порождаются правыми сдви-

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 271
гами так же, как Le — левыми. Рисунок 3.10 «верен», и в этом
случае, следовательно, такие поля образуют алгебру Ли.
Интегральные кривые правоинвариантных векторных полей,
проходящие через е, являются однопараметрическими под-
подгруппами по тем же причинам, что и в случае левоинвариант-
ных полей. Таким образом, однопараметрические подгруппы
находятся в 1-1-соответствии сразу с обоими семействами ин-
интегральных кривых; следовательно, кривые в этих семействах
одни и те же. Интегральные кривые левоинвариантного поля,
не проходящие через е, получаются левым сдвигом из кри-
кривых, проходящих через е, т. е. из однопараметрических под-
подгрупп. Кривая поля V, проходящая, например, через точку
/г, — это hgv (t). Тогда интегральная кривая правоинвариант-
*е
ного поля, проходящая через h, будет иметь вид gy (t) h. Эти
выражения различны, за исключением случая, когда gy {t)
и h коммутируют.
3.11 (а) Поскольку левые сдвиги на Ьгх взаимно-однозначно
отображают окрестность h на окрестность е, отображение
векторных полей Lh также будет взаимно-однозначным и об-
обратимым. Отсюда следует, что если {Р,(е)} линейно-незави-
линейно-независимы, то это верно для {LhVi{e)== V,(h)} при любом h.
(b) Дело в том, что поля {V,} образуют глобальный ба-
базис и любое векторное поле определяется заданием {()}
для всех g. Это отображает TG на G X Rn-
3.12. (b) Ключевой
B-lAB = B~lAnB.
(с) Экспонента от
вычисляется, поскольку
Р, 0 0 .
О Р2 0 .
О О Р3 .
момент: (В~1АВ)" = В'1 ABB-1 АВ ...
блочно-диагональной матрицы легко
О
О
о
(Р2)п
о
о
о
(РзГ
в случае (i) ехр (ft/) — это обычная экспонента. В случае A1)
ехр 111
Ч V-s, г,
Г 1 /1 -iVO + is, О
ех1ТуП1 Л о r,-i
*(.' ::Ь['(
г, + is,
О
Гу-1

272 ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
cos trt -f- i sin /5
- / sin /5/ О N
О cos tfj — i sin /5/ /
1 -i
откуда и следует ответ. В случае (Ш), немного повозившись
можно проверить формулу
л: 1 0 0 ..
О л: 1 0 ..
0 0*1 ..
Xя Xn
Ax
О хп
О О
2! 'их2
d
IF*
X"
3! d.v3
1 d2 n
2! d.v2
Умножив на t" и подставив в разложение экспоненты, полу-
получим C.59с).
3.13. Семейство матриц
cos t sin (//2) \
— sin / cos t )
— непрерывная кривая, содержащая е (при / = 0) и
/-1 14
\ о -\)
(при t = n). Рассматриваемая матрица не принадлежит ни-
никакой однопараметрическои подгруппе, поскольку не является
экспонентой ни от какой матрицы, что следует из упр. 3.12.
Легко проверить, что ни одну из матриц вида C.59) нельзя
преобразовать с помощью C.56) в рассматриваемую матрицу,
поскольку на диагонали стоят отрицательные числа.
3.14. (а) Собственное значение К матрицы А удовлетворяет
уравнению det (А — %1) = 0 = det (А — KI)т = det (Ат — Я/) =
det (Л-1 — Я/) и поэтому является собственным значением
4. Верно и обратное.

ПРИЛОЖЕНИЕ РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 273
(b) det(;4 — KI) = 0 => 0 = det{A~l)det{A — %1) =
det(/ — KA'1)= det(—AYJdetfX-1 — Я-1/). Так как det(A)=^O,
то все собственные значения отличны от нуля и, следова-
следовательно, det(A-! — К~Ч)=О. Таким образом, если А — из
О(п) и К — собственное значение А, то им будет и \/К. Но
поскольку уравнение det(i4 — kl) = 0 вещественное, то его
решения образуют пары комплексно-сопряжённых чисел. Что-
Чтобы два числа в такой паре были взаимно обратны, они долж-
должны иметь вид(е'е, е~'8).
(c) Такая форма есть как раз C.58а, Ь) при специальных
собственных значениях, причём C.62Ь) — это частный случай
C.62с). Случай C.58с) с ц, — ±1 следует исключить. Такая
форма невозможна, поскольку В~1АВ принадлежит О(п), а
C.58с), очевидно, нет.
(d) Чтобы найти алгебру Ли данной группы, достаточно
рассмотреть касательное пространство произвольного её эле-
элемента, например е, поэтому мы можем ограничиться рассмо-
рассмотрением генераторов однопараметрических подгрупп в SO(n).
Задачу можно решить, привлекая каноническую форму, но
быстрее следующий способ. Возьмём элемент exp(tA), где А
принадлежит алгебре Ли группы О(п). Тогда [ехр(/Л)]-! =
ехр(—tA) и [exp(tA)]T = exp(tAT). Эти выражения равны
при любом /, следовательно, Ат =—А. Обратное доказы-
доказывается так же. Размерность О (п) есть максимальное число
линейно-независимых антисимметричных матриц размера
п X п, а оно равно п (п — 1) /2.
3.15. Матрица А принадлежит SO(n) тогда и только тогда,
когда в её канонической форме C.62) чётное число блоков
(—-1). Элемент из О(п), не принадлежащий SO(n), имеет
нечётное число блоков (—1) и может быть тривиально полу-
получен из элемента SO{n) указанным преобразованием.
3.16. Как было сказано в указаниях к предыдущей задаче, в
канонической форме матрицы А из SO(n) чётное число бло-
блоков (—1), на которые можно смотреть как на частный случай
блоков C.62с) при 6 = л. Любая из канонических форм
C.62а), C.62с) есть частный случай экспонент C.59а) или
C.5%). В канонической форме для матриц из группы 50C)
один блок должен быть C.62а), а другой — C.62с). Собствен-
Собственный вектор для C.62а) — это ось вращения.
3.17. Воспользуйтесь C.60).
3.18. Матрица diag[exp(ioiO. exp(ia2*), ¦ • •] есть экспонента
от матрицы diag(iai?, \ait, ...). Определитель первой матрицы
равен exp(i/XjGy), и если он равен 1, то след второй
матрицы равен 0. Зададим соответствие между комплексными

274 ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
числами и 2Х2-матрицами правилом а-\- ib -*-*•(_ ^ а) •
Оно устойчиво относительно умножения: (с + ib) (с + id) ¦<-»•
¦*-*(_ 1 )(_j J • Таким образом, это групповой изоморфизм
между комплексными числами и матрицами специального
вида. (На самом деле это изоморфизм алгебр, так как он
устойчив и относительно сложения.) Эта конструкция обоб-
обобщается до изоморфизма между GL(n, С) и подгруппой в
GLBn, R), состоящей из матриц, построенных из 2Х2-бло-
коввидаГ^ а). Эрмитову сопряжению в GL(n,C), оче-
очевидно, соответствует транспонирование в GLBn, R). Итак,
мы можем считать U(n) подгруппой в ОBп). Поскольку ге-
генераторы ОBп) — это антисимметричные 2/?Х 2п-матрицы, то
генераторы U(n) — это антиэрмитовы матрицы. В силу нашего
первого замечания и упр. 3.20(а), эти матрицы должны иметь
нулевой след.
3.20. (a) (B~1AB)ik = (B-l)f,A'mBmk. Но (B~l)ilBmi = Wni, по-
поэтому tr(B-1AB) = tr(A).
(b) Поскольку det(B~1)= l/det(B), то det(expGl)) =
det (В-1 exp (A) B) = det (exp {B~lAB)); далее ехр (tr (A)) ==
exp(B-1(trA)B) = exp(tr(B~1AB)). Таким образом, доста-
достаточно доказать C.67) для различных канонических форм. Для
формы C.58а) это тривиально. Для C.58Ь) всё сразу следует
из рассмотрения C.59Ь). Аналогично обстоит дело с C.58с),
поскольку матрица в C.59с) имеет единичный определитель.
3.21. (а) Воспользуйтесь тождеством (аХ 5)Х с = (а-с)Б —
(Б-с) а.
3.22. (а) Учтите, что det ( _ ^ Й) = |а|2 + 1&Р обращается в
нуль только для нулевой матрицы.
(Ь) Размерность равна 4, так как для задания элемента
из Н нужны четыре независимых вещественных числа.
(d) Уравнение C.73) есть уравнение сферы S3, и искомое
1-1-отображение ставит матрице А в соответствие точку
(аь а2, а3, оц) сферы S3 в 7?4.
3.23. Поскольку [^(s)]" = ехр(—sY), мы можем записать
C.79) в виде
exp (s F) exp (tX) exp (—s У) = exp [ t Adg(s) (X) ].
Дифференцируя обе части по t, получаем при t = 0
(~ sY) = Ads(s) (Я).

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 275
Разложив левую часть по степеням s:
X + s[Y, X] + ~s2[Y, [Y,
получаем ответ.
3.24. (b)/x(K1_,) = iFm/V2; 1аA) Л/ i
L (K10) = i (K,_, - Ku)/V2; ly (K10)=- (У,., + Г,,)/V2;
ix(Yn) = -iYioN2; iy{Yn) = Yj^/2; 1гФи) = \Уи. Поэтому
любая комплексная линейная комбинация этих трёх
функций переводится дифференцированием вдоль 1Х, 1У, 1г
снова в линейную комбинацию этих функций.
3.25. Из первого равенства C.30) следует, что 7z(f)=0.
Тогда из двух оставшихся получаем lx (f) = ly (f) = 0. Итак,
f постоянна на сфере.
4.2. (a) p(..., U, .... W, ..-) = P...t...l..
= -p...j...i...uiwl = -p(---' w,..., u,...).
(b) следует из равенств Ат = — Ajik = Akij и т. д.
(c) AtlB" = i АИВ11 + 4 AtiBn=i (ЛцВН-АцВ») =А
Первый шаг сводится к перестановке немых индексов.
(d) В['"/] = -Н
4.3. Компоненты р-формы й> — это её значения на р базисных
векторах. Если р > п, то найдутся по крайней мере два сов-
совпадающих вектора. Их перестановка ничего не меняет, но в

276 ПРИЛОЖЕНИЕ РЕШЕНИЯ И УКАЗАНИЯ К HFKOTOPbIM УПРАЖНЕНИЯМ
то же время знак компоненты должен измениться. Единствен-
Единственное число, равное самому себе со знаком минус, — эго нуль.
4.4. Надо лишь показать, что сумма двух р-форм есть р-фор-
ма, т е является антисимметричной, и что р-форма, умно-
умноженная на число, — тоже р-форма. Размерность нашего про-
пространства— это число независимых компонент р-формы, рав-
равное Ср, как видно из D 7).
4.5. р A q(U, V) = p (U)jj (V)-q(U)p (V) =_~-_р Aq(V, U).
Очевидно, что р Л p{U, V) = 0 при любых U, V.
4.6. Проверка D.9): a (U, V) = \ ач [б' (U) б' (V)~ б' (U) &l(V))=
ja^iU'V -V'U^^^a^V + ^altVlU' = a,,t/T'. Число не-
независимых два-форм &' Л 6fc, равное n(n— 1)/2, и есть раз-
размерность пространства два-форм.
4.7. По формуле бинома Ньютона A + 1)" = J]p=0Cp. Обра-
Обратите внимание, что в сумме есть член с р = 0, отвечающий
одномерному пространству нуль-форм.
4.8. Из равенства D.9) и его обобщения мы знаем, что
q = (l/2l)qlkG>' A G>k и р Л q = (l/3l)(p Л qLk «' Л &' А 6>к. Но
р Л q = A/2!) ptq,kS>1 Л (©' Л ©fc) = A/2!) Plq,kS>1 A ©' Л б* =
A/2!) P1(<7;fe] й1 Л »' Л 6fe. Поскольку {©' Л а1 Л ©fc} образуют
базис, мы видим, что (р A q)l]k = C\/2\) p[iqik]=-^(piqjk +
РкЯч + Pflki — PAkt ~ РъЯл — Pftik) = PA,k + PkQij + Pflki-
Обобщение до D.11) прямо отсюда следует. Напомним, что
Cp+q — Cq+g, поэтому р и q входят в D.11) равноправно.
4.9. Обе части равенства D 16) билинейны по р и а, поэто-
поэтому достаточно доказать его в случае Р = б Л • •. Л бр и б =
©р+1Л...Лбр+<?. Тогда рЛаа) = (б1Л...Л»РЛбр+1Л...
... Лбр+<?)(|). В этом внешнем произведении имеется
(Р + Я)' членов, отвечающих всевозможным перестановкам
индексов. Те члены, где первой стоит форма б1, при свёртке
с I дают б1 (|) (б1 Л • • • Л бр Л бр+1 Л ... Л бр+<?). Каждый
член с б2, стоящей на первом месте, получается из членов со-
стоящей на первом месте б1 заменой б1 на б2, т. е. нечетной
перестановкой Итак, после свертки с | эти члены дадут
— п2Ш(п Л б3 Л ... Л бр Л бр+1 Л ... Л бр+9). Аналогич-
Аналогично рассматриваются свёртки 63(|)F1 Л б2 Л б3 Л ©4 Л •..)
и т. д. Первые р свёрток как раз и есть р (|) Л а, поскольку
в них входят лишь один-формы из р.

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И ОКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 277
Оставшиеся q свёрток суть, с точностью до (общего) зна-
знака, зависящего от степени р, свёртки один-форм из а с ?,
внешне умноженные слева на р. Таким образом, первый член
такого типа —это (-1)" ©р+1 (!)(©'Л ... Л йр Л «Р+2Л ...
...Лйр+9), и все остальные тоже имеют вид(—1)р,умножен-
вид(—1)р,умноженная на некий член разложения р Л а (|).
4.10. В декартовых координатах W — П\ V имеет компонен-
компоненты (U2V3 — U3V2, U3Vl — U1 V3, иу2— V2V1)._ Для Ш12з — 1
формула D.20) принимает вид *(?/Х V)l2 = (UX VK и т. д.,
что и доказывает равенство D.22).
4.11. (а) Правая часть равенства, следующего за D.35), есть
сумма (р + 1)! слагаемых. На следующей строке сначала вы-
выписаны р! слагаемых, у которых нижний индекс i идет пер-
первым. Дальше идёт взятая с правильным знаком сумма р!
членов, имеющих первым нижним индексом т. Последняя
строка получается после суммирования по i (б'г- = п).
(Ь) Чтоб перейти от «-дельты к р-дельте, применим D.36)
п — р раз и получим множитель 1-2- ... • (п — р), требуемый
в D.37).
4.12. (а) Ключевой пункт: e?/ kAHA2i... Ank=An (ef/ kA21...
Ank) + A*(e2i... И2/ • • • П+ ... = Л" (ee... И2" • •'• A"*) ~
Л12(еа рЛ2а ... Л"р) Ч ....причём в последней строчке
греческие индексы принимают лишь п — 1 значений: в первой
сумме пропускается 1, во второй 2 и т. д. Как следует из
D.39), р-й член в разложении — это определитель матрицы
размера (п—1)X(п —-1), полученный исключением первой
строки и р-ro столбца из исходной матрицы.
(Ь) Правая часть D.39), очевидно, меняет знак при взаим-
взаимной замене индексов 1 и 2; отсюда можно вывести требуемое
равенство.
4.13. Пусть Л'/' —матрица преобразований базисных один-
форм: а = А'г их1'. Тогда й = Л'г ... Л"^?;/ Л • •. Л dxk' =
А1 г ¦ ¦ ¦ Л\-вг - k'dxv Л . • ¦ Л dxn' = det(A) Ах' Л ... Л их11'.
Но закон преобразования метрики имеет вид gt,j, = Akt,Aljrgk[-f
если взять определитель от обеих частей этого матричного
равенства, то мы получим det (grr) = [det (Л)]2 det (gtl)- (За-
(Заметим, что, как следует из упр. 4.12 (Ь), определители матри-
матрицы и её транспонированной совпадают.) Далее, поскольку
исходный базис был ортонормированным, то det (gr, = ± 1),
откуда следует, что det(A) = | det(g-r/,)|1/2, чем требуемый ре-
результат и доказан.

278 ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
4.14. (а) Это частный случай свойства B), когда а есть нуль-
нульформа f; dug «исчезает» по свойству C).
(Ь) Это очевидно.
4.15. Vi',k' = Atk<(Ai'tVl),i = Aik'AriVl,j + А\'А1\,^1. Второй
член преобразуется не по тензорному закону. Далее, в [U, V]1'
два «неправильных» члена дают U'VlA' i, ;- — V'UlAl it,-. Эта
сумма равна нулю, поскольку Л' i, / = Л''/, i = д2х1'/дх'дх1.
4.16. rot (grad /) = *d (d/) = *(ddf) = 0.
div (rot a) = d* fdfi) = d Г da) = ddc = 0.
4.17. Первое выражение в D.64) — это da = 0, записанное в
компонентах. Следующий шаг делается так же, как в
упр. 4.11 (а). Второй член в правой части D.64) получается
из первого заменой / на /, это приводит к изменению знака
и показывает, что эти члены равны.
4.18. div (a) = d*c = 0 =>- *с = d5 при некотором Б =>- а =
T
rot(a)=*da = 0=*-da=0 => а = uf = grad (f).
4.19. Выберите векторный базис {ё\, ё2, ¦¦¦, ёп), такой что
(ёг, ..-, ёп) касательны к dU: Я(ёр) = О при 2 ^ р ^ п. Это
значит, что п(ё{)Ф0, поскольку у Я должна быть по крайней
мере одна ненулевая компонента. Так как й — n-форма, то
у неё всего одна независимая компонента, равная ё>(ёи ..., ёп)
= (п Ла) (ёи ..., ёп). Единственный ненулевой член здесь
отвечает свёртке Я с ё\, поэтому мы получаем n(ei)a(e2,..., ёп).
Но сс(ё2, •¦-, ёп) — это единственная компонента а\ои в этом
базисе, и, следовательно, она равна б(ё], ..., en)/n(ei). Сама
по себе а задается неоднозначно: при любой функции f форма
а + fn так же хорошо подходит. Далее, единственное усло-
условие на форму Я — это её ортогональность к дЦ. Это значит,
что в нашем базисе Я имеет компоненты (п1, 0, ..., 0), и оче-
очевидно, что для любых двух Я и Я' мы имеем Я = fn'. Но из
предыдущего рассмотрения следует, что a\ev переходит при
этом в \-la\ev, следовательно, п(Ъ,)а\зи не меняется.
4.20. Действуя так же, как в случае D.76), находим
] = №),рейх1 Л ... Adxn = f-*(fll),ie.
4.21. Используя упр. D.13), покажите, что метрика в сфери-
сферических координатах задаётся матрицей diag(l, r2, r2 sin26).
Тогда выражение для div | получается, если положить f =
г2 sin 6 в D.80).

ПРИЛОЖЕНИЕ РЕШЕНИЯ 11 УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 279
4.22. _Из D.67) следует, что ?v (рб) = d [рй (V)] = d [й (pV)] =
div(pV) й>.
4.23. (а) Поскольку й> (%) = •?, дуализация D.77) прямо даёт
D.81).
(b) *F —это (п — р)-форма, d*F — это (п — р+1)-фор-
р+1)-форма, следовательно, *d*F — это (р—1)-вектор. Равенство
D.83) доказывается простым обобщением D.76).
(c) ' I(W'
4.24. (а) Если © = Яс, то \й = ша, но последний интеграл
равен нулю, поскольку границы нет.
(b) d& = dx1 A dx2 A dxs — это обычная форма объёма,
поэтому если В — единичный шар (внутренность S2 в R3), то
\ Яй = объём шара = 4я/3. По теореме Стокса \ de =
\ 9 © )sj. Далее, любая два-форма на двумерном многообра-
зии замкнута, поскольку все три-формы тождественно равны
нулю. Таким образом, & замкнута, но (а) для неё не выпол-
выполнено, следовательно, она не точна.
(c) Нам дана форма р, определённая всюду на S2, такая
что йр = 0. Проинтегрировав йр по любой области на сфере
S2, ограниченной замкнутой кривой <&, мы находим,
что & р = 0 для любой <ё. Это может иметь место,
только если р = df; в противном случае нашлась бы кри-
кривая ^, по которой р имела бы ненулевой интеграл. На самом
деле f легко строится явно: положим f в некоторой точке Р
равным произвольному числу f0, в любой же другой точке Q
положим /(Q) = fo+ \ P, где интеграл берётся по произволь-
произвольной кривой, соединяющей Р и Q. Условие & р = 0 гаранти-
гарантирует, что f(Q) не зависит от выбора кривой.
4.25. (а) Свойство (i) и (ii) тривиальны. В случае (iii) поло-
положим a — p = djii, р — y — d[i2; тогда б — -у == rf (jjtt + &2).
(b) Докажите сначала, что если ^ «* щ и р2 ~ «2. то
afi1~\-b$2^adi-\-ba2 для любых вещественных чисел а, Ъ. Это
просто, поскольку существуют pi и 'р2, такие, что р, = 5i + rfjli
и ^2 = 62 + ^^2=^^1 + bp2 = aai + Ъщ-\-й(ащ + ЬД2). Итак,
мы можем самосогласованно определить линейную комбина-

280 ПРИЛОЖЕНИЕ РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
цию аА\ -f- ЬА2 классов эквивалентности Ах и Л2 как класс
эквивалентности, порождённый той же линейной комбина-
комбинацией любых двух элементов из этих классов. Теперь можно
смотреть на классы эквивалентности как на векторы из век-
векторного пространства: нулём будет класс нулевого вектора
из Zp, противоположным классу А — класс —А, и т. д.
(с) Возьмём вектор вида @, Ь) в R2. Что входит в его
класс эквивалентности? Это все векторы @, Ь)-\-(а, 0) с про-
произвольным а и заданным Ь. Геометрическое место точек, в
которых кончаются этн векторы, есть прямая, параллельная
оси х и удалённая от неё на расстояние Ь. В этом смысле мы
можем отождествить пространство классов эквивалентности
с конгруэнцией таких линий.
4.26. Указанное векторное поле нигде не может обращаться
в нуль, поскольку у нашего отображения нет ни одной не-
неподвижной точки: неподвижная точка соответствовала бы
блоку (+1) в канонической форме Т, но таких блоков там
нет. Заметьте, что решающим здесь является факт нечётной
размерности сферы.
4.27. (а) Это тривиально.
(b) Hlb~1(Sn-1) — это одномерное векторное пространство
(R1), поэтому два любых класса эквивалентности кратны
друг другу. Поскольку со не точна, она принадлежит ненуле-
ненулевому классу эквивалентности. Из упр. 4.25(Ь) следует, что в
любом классе найдется элемент кратный ю, поэтому для лю-
любой формы а существует число с, такое что форма а — аб«* 0,
т. е. точна. Проинтегрировав по. Sn-1, получим значение а.
(c) Если a —Gco = dp, то р — это (п — 2)-форма. Обозна-
Обозначим через V вектор, дуальный к ней относительно б : V = *р>
или р = (—l)nV.Тогда dp = (—l)"(div<sV)S. Если / — функ-
функция, дуальная к а, то мы получаем (/ — а) й = (— l)"(di\u V)e>.
Эта формула равносильна доказываемой.
(d) В этом случае со = хау — уйх — d~6 на единичной
окружности, где 6 — полярный угол. Любую другую один-фор-
один-форму а можно записать как §F)йб, и, следовательно, нам надо
найти функцию /F), такую что d/ = [grF)—c]d6 всюду. По-
Поскольку df = (df/d6)d6, то f есть решение уравнения df/d6 =
gF) — а, т. е. f = \ g d6 — ав. Чтоб f была непрерывна, потре-
потребуем, чтобы /@) = /Bл), или, что равносильно, 2ла= \ gdQ.
Jo
Это как раз то условие, которое было получено выше, в
пункте (Ь). Обращая рассуждения того пункта, мы можем
заключить, что ' ^1

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 281
4.28. (a) f строится так же, как в упр. 4.24(с).
(Ь) Предположим, что М односвязно, и пусть а — произ-
произвольное достаточно гладкое поле один-форм на М. Тогда \ б
гладко меняется при стягивании кривой ЯЗ. Но W всегда мож-
можно сделать достаточно малой, чтоб она оказалось внутри об-
области, в которой справедлива лемма Пуанкаре (§ 4.19), т. е.
S5 = 0. По непрерывности (объединяем несколько малых
кривых в одну большую) отсюда следует, что \ 6 = 0 для
любой замкнутой кривой W. Тогда из (а) следует, что Я1 (М)
= 0. Аналогично доказывается и обратное утверждение. Если
Н1(М)Ф0, то существует замкнутая один-форма а, которая
не точна. Из пункта (а) вытекает, что существует по крайней
мере одна замкнутая кривая ЯЗ в М, на которой \ а ф 0.
Если эту кривую можно гладко стянуть в точку, то для всех
достаточно малых её «стягиваний» ЯЗ' мы получим \ , а = 0.
Рассуждая, как раньше, приходим к противоречию: \ 5 = 0.
Следовательно, ЯЗ сжаться в точку не может.
4.29. Все линейные комбинации векторов {ei, ..., ёт} и толь-
только они аннулируются каждой из один-форм {©m+!, ..., б"},
поэтому полные идеалы этого набора и исходного совпадают.
Пусть р — д-форма, аннулирующая каждый вектор из Хр\
разложим её по базису один-форм. Каждый член разложения
будет внешним произведением q один-форм, причём он дол-
должен содержать хотя бы одну из форм {©m+1, ..., б"}. В про-
противном случае этот член не будет аннулировать все векторы
из Хр. Такое разложение р можно записать, как указано в
упражнении.
4.30. Как в упр. 4.29, разложим у по базису один-форм {щ,...
...,ат, 6m+1, ..., ©"}. Если у принадлежит указанному
идеалу, то в каждом члене разложения есть по крайней мере
одна из форм {аь ..., ат} и потому D.90) выполнено. Об-
Обратно, если у—д-форма (<7 ^ " — т)> удовлетворяющая
D.90), рассмотрим набор векторов {х, у2, ..., ym+q}, где х
принадлежит аннулятору Хр форм а,-, а у,- нет. Пусть (т + q)-
форма из D.90) действует на этот набор. Нетривиальные
члены будут получаться лишь тогда, когда х будет аргумен-
аргументом y- Если D.90) выполнено и в этом случае (при произволь-
произвольных yt), то у (х) = 0 для любого х из ХР. Это и значит, что
Y принадлежит нашему полному идеалу. Остаётся рассмо-
рассмотреть случай q + т > п, когда D.90) превращается в тож-

282 ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
дество. Но тогда разложение у по выбранному базису будет
содержать хотя бы одну а/ в каждом слагаемом и, следова-
следовательно, \ принадлежит идеалу.
4.31. (а) Пусть р принадлежит полному идеалу набора {а/}.
Тогда существуют {y1}» такие, что Р = ][]'У'Ла,- и Яр =
= Л (dy! А й/ + y' Л da,]). Первое слагаемое лежит в идеале;
то же верно и для второго, поскольку da/ можно представить
как 2 Й* Л ak.
(b) Используйте D.90) и то, что р-формы при р > п тож-
тождественно равны нулю.
4.32. (Ь) У каждой кривой, удовлетворяющей условиям U =
const, V = const касательный вектор аннулирует 3U и 3V,
а следовательно и а и р\ а потому лежит в Ж.
(c) Используйте критерий D.90), чтобы определить, при
каких условиях da и Яр принадлежат указанному идеалу.
Это потребует сложных вычислений, в которых будет полезно
данное в задаче указание. Имеем, например, BAdA=0.
В результате можем записать da А а Л Р = df A dg Л
-\- Б А Б)]. Это выражение должно обращаться в нуль всюду
на многообразии. Член в квадратных скобках пропорциона-
пропорционален форме их А д,у, не зависящей от df A Sg, поэтому он дол-
должен обращаться в нуль. Поскольку А, В и т. д. от f и g не
зависят, он обращается в нуль тогда и только тогда, когда
в нуль обращается каждое из трех его слагаемых. Отсюда
получаем три первых условия. Остальные получаются из
Ярлйлр = о.
(d) Вынесите dx Л dy из каждого члена.
4.33. dy = (a2(dx Л a
a>2x dy Adt + (й2х dy A dt + a2y dx A dt = 0. Так же легко про-
проверить D.97).
4.34. Рассмотрим скалярное произведение {VYim) ¦ (*dYim) =
=gABi&ACYim,c){^DBYlm,D)=^DCYlmtCYlm,D, которое обращается
в нуль в силу антисимметричности coDC. Поскольку метрика
положительно-определённа, эти векторы могут быть парал-
параллельны, только если они равны нулю, что может быть (при
1Ф0) лишь в изолированных точках.
5.1. Вынесите dS Л dt и умножьте на Р2.

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ ?83
5.2. (а) &цп> = 0 = d [й (?/)], поскольку dco = 0. Так как фа-
фазовое пространство удовлетворяет условиям леммы Пуанкаре
(§ 4.19), существует функция Н, такая что й(?/)=?#, от-
откуда и следуют E.16).
(b) Используя [?п, ?v] = ?[D^ Р), покажите, что если О
и у — гамильтоновы векторные поля, то то же верно и для
[О, V]. Это и есть скобка в алгебре Ли гамильтоновых век-
векторных полей.
5.3. й антисимметрична.
5.4. В компонентах всё получается тривиально.
5.5. Доказывается так же, как равенство й (U)— clH в
упр. 5.2(а).
5.6. (Ь) Устанавливается прямым вычислением.
(c) Используем E.32): {f, {g, h}} = X,Xg(h); {g, {ft, f}} =
~{g, {/. h}) = -XgXf(h); {h, {f, g}} = Xlf. e} (h).
5.7. (b) ?jj6 = 0, потому что ^й = 0, но ?^а = (dive U) ст.
5.8. Очевидно, что ?j H = 0, и, поскольку у X; нет им-
импульсных компонент, df/dx1 = 0 и df/dPi = —№. Итак, / =
—№Pi.
5.9. Используйте преобразование
10 0 (Г
0 cos 6 — sin 6 0
0 s{ne cose 0
0 0 0 1
5.10. (а) Три-форма в четырёхмерном пространстве имеет С
независимых компонент.
(Ь) Например: F[Xy,Z] — 0 =>¦ Fxy>z + Fzx, y + Fyz,x = 0 =
Вг,г + By,у + Вх,х. Это — E.52с).
5.11. Перемножьте матрицы.
5.12. Например: Ftv,v == Ftx,x + F'v,y + Ftz}Z = Ex,x + Ey,y +
EZiZ. Это даёт E.52d).
5.13. (a) CF)tx = ±
Искомая матрица совпадает с E.53), если Bi-*-Ei, ?,->—В,.
(Ь) Это следует из упр. 4.23.

284 ПРИЛОЖЕНИЕ. РЕШЕНИЯ II УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
5.14. (а) Покажите, что первое уравнение даёт V-B
и т. д.
(b) dd'/=0 =ф- d7 = 3[& (Т)] = (divs T) й.
5.15. (а) Это легко доказывается в компонентах.
(b) Поскольку для интегрирования нужно взять ограни-
ограничение на Ж, то *7 выступает как три-форма.
(c) Ограничение *7 на Ж — это Р dx /\dy A dz. Ограни-
Ограничение F на дЗУ (поверхность с постоянными t и г) — это
*Р6ф Яб Л Яф. Однако *Р6ф = 4 («^ес/"" + <*zte<s,Frt) = r2 sin 0?г.
(Вспомните равенство D.40) и упр. 4.21.) Таким образом, в
обычных обозначениях интеграл принимает вид \ pd3x —
) Err2 sin 6 rfe d<p.
5.16. (а) Рассмотрите, например, (t, x) -компоненту E.64):
FtK = Ax,t — At,x. Сравните это с обычным определением:
Ех = q>,x + Ax.t. Поскольку Ftx = —Ex, то всё отсюда и сле-
следует. С остальными уравнениями это совместно.
(b) ф->ф + Д*; A'^A' + Vif.
(c) Для статического заряда q в начале координат все
компоненты В равны нулю, а Е = qr~2e,. Отлична от нуля
лишь компонента (*^)вф, равная (как в упр. 5.15) ^ sin 6.
Отсюда аф,е — ае,Ф = <7 sin 0. Возможны два решения: {аф =
—q cos В, ае = at = ar = 0} и {ае = — qy sin 0, аФ = at =
аг = 0}. Они отличаются друг от друга на калибровочное пре-
преобразование и оба обращают в нуль все остальные компо-
компоненты да. Но ни одно не задаёт корректно определённой
один-формы: первое не определено в полюсах 6 = 0 и 0 = п,
второе многозначно.
5.17. Это очевидно.
5.18. (?VWI = [U, W]1 = U'W j - W\}. = U'W1 t + UaWl a -
WaU\a,rm сумма по а берётся только по (х, у, z). Ответ сле-
следует нз того, что U* = 1 и U\a = 0.
5.19. Ответ следует из того, что Л* х = dt'/dx = 0, А*Х' =
dt/d' O
5.20. dp = (dp/dp) dp + (dp/dS)dS. Это обращает E.77) в
нуль, поскольку dS Л dS = 0 = dp Л dp.
5.21. Возьмите дуализацию E.80), как в E.82), и найдите
компоненты.
5.22. Воспользовавшись C.37) в декартовых координатах, по-
покажите, что E.85) и E.86) принимают нужный вид. По-

ПРИЛОЖЕНИЕ. РЕШЕНИЯ П УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 285
скольку это тензорные равенства, то, будучи верны в одной
координатной системе, они верны и во всех системах.
5.23. В группе изометрии, 50C), очевидно, имеются элементы,
переводящие любую точку сферы в любую другую точку:
просто проводим через эти точки большой круг и выполняем
поворот вокруг оси, перпендикулярной плоскости круга. По-
Поэтому 52 однородна. Группа изотропии точки Р состоит из
всех вращений, оставляющих Р неподвижной. Очевидно, что
они образуют подгруппу 50B) в 50C), следовательно, S2
изотропна.
5.24. (а) Поскольку V' должны обращаться в нуль в точке Р
(группа изотропии оставляет Р неподвижной), их разложе-
разложение Тэйлора имеет вид E.96) с некоторыми матрицами А1,-.
Из E.89), учитывая, что в наших координатах Г',-,-== 0 и нет
разницы между верхними и нижними индексами, мы получаем
условие E.97): Л',- + Ah = 0.
(b) E.98) получается простым вычислением.
(c) Алгебры Ли группы изотропии и группы 50 (т) сов-
совпадают, следовательно, и сами группы совпадают, по край-
крайней мере в некоторой окрестности единичного элемента. Но
у точки Р есть малая окрестность, взаимно-однозначно ото-
отображающаяся на окрестность начала координат в Rm, а из
пункта (а) следует, что их поля Киллинга отображаются друг
в друга с точностью до 0(х2). Поэтому их преобразования
изотропии можно привести в 1-1-соответствие, и наши группы
совпадают.
(d) Если g не положительно-определённа, то в нашей си-
системе координат поднятие и опускание индексов может из-
изменить знак. Тогда правильно записанное E.97) — это Ац =
—Aji, а не А',- = —Ah, и алгебра Ли группы изотропии не
состоит из антисимметричных матриц.
5.25. (а) Геометрически линии 0 = const, q> = const опреде-
определяются как интегральные кривые поля Я. Если бы радиальное
расстояние между сферами было различно по разным направ-
направлениям, то многообразие не было бы изотропным. Поэтому
grr не зависит от 0 и ср.
(Ь) Около точки Р мы можем построить координаты, как
в упр. 2.14, а затем перейти к сферическим координатам та-
таким же преобразованием, как в плоском пространстве. Эти
новые координаты совпадают (при 2->0) с координатами
в E.100), поскольку площадь поверхности сфер определяет г.
Таким образом, E.102) выполнено.
5.26. Доказывается прямым вычислением.
5.27. Они соответствуют %\т = const. Легко видеть, что норма
такого вектора стремится к нулю при г~*-0, следовательно,

286 ПРИЛОЖЕНИЕ РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
он принадлежит алгебре Ли группы изотропии. Рассматри-
Рассматриваемая группа изотропии, 50C), трёхмерна, и множество
всех векторов Киллинга, порождённых тремя константами ?im,
тоже трёхмерно, поэтому такими векторами исчерпывается
вся группа изотропии.
5.82. Перейдите к декартовым координатам или вычислите
норму вектора с Vm—\ и t,lm = 0.
5.29. Очевидно, что f = \ => S есть Еъ. Далее, д/дх —
cos ф sin Qd/dr + r~l cos ф cos Qd/dQ — r~l sin ф cos 0 d/dq> — это
вектор Киллинга, порождённый V\ = V_i = Bя/3I/2, ?im = 0.
5.30. Из вторых и третьих диагональных компонент матриц
E.119) мы получаем r=sin%/V^ и r = sh%/-\/K соответ-
соответственно. Остаётся проверить, что первая диагональная ком-
компонента получится, какая надо. Например, в случае К > 0:
ёхх = grr(dr/d%y = A —Кг2)-1 cos2%/K = 1//C, как и требо-
требовалось.
5.31. w — г cos %, х = г sin % sin 0 sin ф, у — г sin x sin 0 cos ф,
z = rsinxcos 0. Тогда, например, gee = (dw/двJ + (<5х/<50J+
(ду/дбJ -j-(dz/d6J = г2 sin^. Для полного совпадения оста-
остаётся положить г2 = К~1.
5.32. (а) Центральный пункт состоит в том, что при К < О
площадь/4л(радиальное расстояниеJ = sh2%/%2 > 1. Рассмо-
Рассмотрим сферу в подмногообразии пространства Е". Вслед-
Вследствие положительности метрики в Е" расстояние от центра
сферы до её поверхности вдоль кривой в любом подмногооб-
подмногообразии Е" всегда больше, чем «настоящий» радиус сферы. По-
Поэтому для любого сферически симметричного подмногообра-
подмногообразия в Е" площадь/4зх(радиальное расстояниеJ ^ 1. Таким
образом, открытая Вселенная не может быть «погружена» ни
в какое эвклидово пространство с сохранением метрики. Это
верно даже тогда, когда открытая Вселенная имеет положи-
положительно-определённую метрику!
(Ь) Рассмотрим гиперболоид —t2 + х2 + У2 + z2 — K~l
(<0) в пространстве Минковского. Зададим обычные сфери-
сферические координаты: х = г sin 0 cos q>, у = г sin 0 sin q>, 2 =
r cos 0; тогда это подмногообразие задается как t= (г2—К~1I/2.
Компоненты метрического тензора будут grr = —(dt/drJ-\-
(дх/дгJ + (ду/дгJ + (dz/дгJ = A — Кг2)-1. Аналогично gee
= г2> &фф = г2 sin2 6. Таким образом, гиперболоид изометри-
чен открытой Вселенной.
6.1. Воспользуйтесь определением тензора.
6.2. Прямой подсчет по F.6) с учётом ey = Ami'em.

ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 287
6.3. Тривиально.
6.4. Базисный вектор ее на рис. 6.1 не меняется при переносе
по направлению 0: Veeee = 0. Поэтому мы получаем из F.6):
Гфее = Геее = 0. Представим, что вектор в точке D на рис. 6.2
это ёф. Тогда при переносе по направлению 0 будет оста-
оставаться неизменным лишь его направление, но не длина, по-
поскольку при приближении к полюсам ё,Р->0 в отличие от
переносимого вектора. А именно, |ёф| = sin 0, и мы получаем
ёф F + 60) — ёф F) = % @) [6 (sin 0) /sin 6], или
т. е. РРчв = ctg 6, Г\е = 0. Со-
Соответствующие производные по
направлению ё,г вычислить
труднее, поскольку кривые 0 =
const не являются большими
кругами. Рассмотрим точку Р:
ф = 0, 0 = 0О. На рис. П. 1 мы
изобразили окрестность Р так, ^^чбольшой круг
как её видит стоящий в этой Рис п t
точке наблюдатель. Линия
0 = 0О) проходящая через Р, — это кривая, касающаяся боль-
большого круга, который выглядит на рисунке как прямая линия.
Рассмотрим точку Q с q> = 6ф <С 1 на круге 0 = 60. Чтоб вы-
вычислить, скажем, уё ёт в Р, нам нужна разность ёф(О) —
ф
ёф (Р) с точностью до первого порядка по 6ф. Поскольку наши
координаты не декартовы, то мы не можем просто взять раз-
разность компонент векторов в двух разных точках. Вместо этого
мы зададим на большом круге векторное поле V, перенеся
ёф (Р) вдоль него параллельно, т. е. сохраняя вектор каса-
касательным и не меняя его длины. Точка R с координатой ф==6ф
очень близка к Q, расстояние между ними порядка ОFф2).
Поэтому с точностью до первого порядка мы можем взять за
основу вектор V(R) и аппроксимировать ecp(Q)— ёФ(Р) раз-
разностью ёф(ф)—V(R), которую мы уже можем вычислять,
просто взяв разность компонент. Итак, в наших координатах
ёф всюду имеет компоненты @, 1). Найдём V. Большой
круг — это пересечение сферы х2 -f- у2 + z2 — 1 с плоскостью
x = 2tg0o. Поэтому в сферических координатах уравнением
большого круга будет sin0 = sin0o(l—cos2 0o sin2 q>)I/2. Счи-
Считая ф параметром, находим касательный вектор (cffi/cftp, 1) =
(sin 0O cos 0o sin <p/ A — cos2 0O sin2 ф), 1). При <р = 0 (точка Р)
он равен ёф(Р), а при q> = 6ф (точка R) это будет
(sin Bo cos 0обф, 1), с точностью до первого порядка. С той же
точностью он имеет ту же длину, что и ёф(Р), значит, это на
самом деле вектор V(R). Таким образом, мы получаем
о (ёФ (Q) — V (/?))/бф = (— sin 0о cos 0O, 0). Отсюда

288 ПРИЛОЖЕНИЕ РЕШЕНИЯ II УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
следует, что rew = — sin 6 cos 0, Гффф=0. Аналогичные вы-
вычисления дляУёфёе дают I^e
6.5. <&', et> = 6'fc=J-<V,S', efc) = -<S', V,eft> = -r'fc,. Таким
образом, Viu' — это один-форма, k-я компонента которой рав-
равна —Г'ь, как и требуется в F.8).
6.6. Используйте упр. 6.5 и действуйте так же, как при вы-
выводе равенства F.10).
6.7. Действуйте, как в предыдущем упражнении.
6.8. В координатном базисе [ё,, ё,] = 0.
6.9. Надо показать, что Т линеен по своим аргументам. На-
Например^ по О: Т_( ;jU, V) = wfVV - V?(ff7) - [fU, V] =
= f (.Vvv - VvU ~ W, V]) - UVV (f) + U?y (f). Члены с произ-
производными от f сокращаются, следовательно, Т действительно
линеен по этому аргументу.
6.10. Доказательство аналогично доказательству упр. 6.9.
6.11. Достаточно показать это для скаляров (где оба значка
означают одно и то же) и векторов (что составляет содержа-
содержание F.13)). Поскольку оба правила дифференцирования
обобщаются на тензоры старшего ранга с помощью F.3), мы
получаем ответ для всех тензоров.
6.12. Очевидно.
6.13. Доказывается прямым вычислением.
6.14. (а) В координатном базисе [ёп ё,] = 0, У,У,ёА = V«r'fe,e,=
= r'fe/, ie[ + T'k/VA = T\h tei + TlklTmHem. Антисимметриза-
Антисимметризация no i и / и переобозначение индексов приводят к ответу.
(b) Очевидно.
(c) F.23а) сразу следует из F.19), но F.23Ь) надо до-
доказывать. В нормальных координатах в точке Р имеем
Г'/*(Р) = 0; значит, /?'*„(Р)= Г^ы — Г1*,,,. Тогда ЗЯ'и,,]^
Г1*/,* — Г1*..; + Г1»*./ — Г1;*.. + Г1;»,* — Г1,,,* = 0, поскольку Т1,к
= 1 ft/-
(d) To что индексов 4, означает, что мы начинаем с п4
компонент. Равенства F.23а) — это п2--^п(п+1) отдельных
соотношений, поскольку индексы Ink свободные, а симме-
симметричных пар (ij) имеется 4"п(п+ 1) штук. (Их столько же,
сколько независимых компонент у симметричной матрицы
размера пХ"-) Связи F.23Ь) совершенно не зависят от

ПРИЛОЖЕНИЕ РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ 289
F.23а), поскольку в них входят лишь RlkUu- Всего в этом ра-
равенстве п(п—1)(п — 2)/3' различных антисимметричных
троек (kij); с учётом произвольности / это дает третье сла-
слагаемое в F.24)
6.15. В нормальных координатах в точке Р имеем Rlku,m =
Rlku,m = rlk,,tm — Г1к1,,т; первый член симметричен по (im),
второй — по (//и), поэтому в F.25) оба обращаются в нуль.
Связь с тождеством Якоби следует из F.19).
6.16. (а) ёг = cos 6ёх + sin Ыу, ёе = — г sin Шх + г cos вёу =*¦
Ve-eer = — sin Вёх + cos вёи = r~% =>¦ Геге = r~\ Ггг6 = 0. Дру-
Другие равенства выводятся так же.
(b) Vr:r=Vr,r; Vr.e=Vr.e-rV*; V*mr=V*.r+V°/r;
V<>, ь = Vе, е + V/r; V\ , = Vr r + r~lVT + Vе, e = r~l (rV), r +
6.17. (a)
401 )У1 v Поэтому V1 / = divsl/ при всех V тогда и только
тогда, когда Vco = 0.
(b) со, ... fe. г = со, . к, i — Гттгсо, ... k = (f.i — frmmi)Bi.. k-
6.18. (a) VtJ \ _
fi) = (V79)(^' ^)- Это равно нулю для всех А, В, V тогда
и только тогда, когда уд = 0.
(Ь) Из равенства F.29) следует, что g,,,k = Tllkgij +
T'ikgii- Объединив различные g вместе, как в правой части
F.30), получаем нужный ответ.
6.19. Нам надо показать, что из F.30) следует T',k =
(ln|g|1/2),ft. Это будет нетрудно, если мы докажем, что g,k =
8"ёч,к- (Это справедливо для определителя любой матрицы.)
Начнем с равенства g = e1 kgu ... gnk = gw(e" ¦ kg2l ...
gnk). Отсюда видно, что если определить g'1 =g-1e"- kg2, ...
gnk, то мы получим 1 =giig'1. Далее, g2igu = 0 в силу анти-
антисимметричности е. Таким образом, мы имеем явное выраже-
выражение для матрицы, обратной к gil'.g''=::((n—l)\g)~lea mX
s'k ¦ rgim ¦ ¦ ¦ grm. Теперь воспользуемся результатом из
упр. 4.12(b): g — eft mElk rg,,gik . •• gmr/n\ и получим
g a = ПЕи mE<k rg,,,aglk ¦ . • gmr/tl\ = g,,,ag'1. Дальнейшее
просто.
6.20. Замените в C.37) запятые на точки с запятой и исполь-
используйте равенство V,g,k = 0.
6.21. Доказывается прямым вычислением.

290 ПРИЛОЖЕНИЕ. РЕШЕНИЯ И УКАЗАНИЯ К НЕКОТОРЫМ УПРАЖНЕНИЯМ
6.22. (Ь) Просто вычесть из F.24) число связей, содержа-
содержащихся в F.33), нельзя, поскольку среди новых связей не все
могут быть независимыми от старых. Вместо этого мы начнём
всё заново и займёмся парами индексов. Из F.23а) следует,
что имеется \п{п—1) независимых пар, а F.33) означает,
что R есть симметричная матрица в пространстве размер-
размерности -jti(n— 1) и, значит, имеет-j [п(п — 1)/2] [п(п — 1)/2+
1 ] = п (п — 1) (п2 — п -\- 2) /8 независимых компонент. Теперь
F.23Ь) содержит меньше независимых связей, чем раньше.
Рассмотрим всевозможные тройки (kij) (п(п—1) (о — 2)/3!
возможных наборов); будет ли каждый выбор / давать неза-
независимую связь? Нет, потому что F.23а) и F.33) позволяют
провести следующее преобразование: ЗЯцып — Rikij + Rim +
Rink = Ruin + Rkiij + Rkju = SRftiji]. Это значит, что новую
информацию мы получаем, только если все четыре индекса
различны, т. е. всего связей будет п(п—.1) (/г —2) (п — 3)/4!.
Этот ответ совпадает с данным в задаче.
6.23. (а) Это следует из F.33) и F.23а).
6.24. Геодезическая задаётся уравнением F.16а). Из него
видно, что VjjQ(U, ?/) = 0; следовательно, если g (О, С)Ф0,
то малые вариации пути не изменят знака g (dx/dA, dx/dX).
Сначала займёмся пространственно-подобной геодезической.
Из вариационного исчисления известно, что при вариации пу-
пути бх'(К) вариация б \ {g^X'X') d% с точностью до первого
порядка равна - -^ $ fi*' (Я) (- 2d (gtjX')/ db + gjk, iXrXk) X
1)-112^ = J 6x{ (A) (
(Точки обозначают здесь d/dA.) Отсюда следует, что геодези-
геодезическая является экстремалью. В случае времени-подобной
геодезической практически всё то же. В случае нулевой гео-
геодезической надо разбить интеграл на части так, чтобы в каж-
каждой из них вариация была или времени-подобной, или про-
пространственно-подобной, или нулевой.
6.25. (a) /VI> = V^-iVl>; й
(b) D^D^ = V^^ - iAvV^ - i (VHv) *- iA^-A^A^.
Поскольку УцУл/Ф == VvVn^, то мы получаем [?>„,, Dv]^ =

ЛИТЕРАТУРА, ДОБАВЛЕННАЯ ПРИ ПЕРЕВОДЕ
[1] Арнольд В. И. Математические методы классической механики. — М.:
Наука, 1974 (к гл. 4).
[2] Виленкин Н. Я. Специальные функции и теория представлений групп.—
М.: Наука, 1968 (к гл. 3).
[3] Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геомет-
геометрия.—М.: Наука, 1979 (к гл. 1—6).
[4] Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геомет-
геометрия. Методы гомологии. — М.: Наука, 1984 (к гл. 6).
[5] Зорич В. А. Математический анализ. В 2-х т. Т. 1.—М.: Наука,
1981; т. 2.—1984 (к гл. 1, 2).
[6] Ландау Л. Д., Лифшиц Е. М. Теоретическая физика, т. 2. Теория по-
поля.— М.: Наука, 1973 (к гл. 5—6); т. 3. Квантовая механика.—М.:
Наука, 1974 (к гл. 4); т. 5. Статистическая физика. — М.: Наука, 1974
(к гл. 5).
[7] Лихнерович А. Теория связностей в целом и группы голономии.—М.:
ИЛ. 1961 (к гл. 6).
[8] Масси У. Теория гомологии и когомологий. — М.: Мир. 1981 (к
гл. 4).
[9] Мищенко А. С, Фоменко А. Т. Курс дифференциальной геометрии и
топологии. — М.: Изд-во МГУ, 1980 (к гл. 1—4).
101 Новиков С. П. (ред.) Теория солитонов. — М.: Наука, 1980 (к гл. 5).
11] Понтрягии Л. С. Непрерывные группы. — М.: Наука, 1968 (к гл. 3).
121 Седов Л. И. Механика сплошной среды. — М.: Наука, 1976 (к гл. 5).
13] Славнов А. А., Фаддеев Л. Д. Введение в теорию калибровочных по-
полей. — М.: Наука, 1978 (к гл. 6).
[14] Стернберг С. Лекции по дифференциальной геометрии.—М.: Мир,
1970 (к гл. 1—4).
[15] Чжэнь Шэн-шэнь. Комплексные многообразия.—-М.: ИЛ, 1961 (к
гл. 6).

ИМЕННОЙ УКАЗАТЕЛЬ
Болл (S. Ball) 12 Оуэн (.1 Owen) 12
Галилей 7, 54 Птолемей 7
Декарт 7 Соркин (R. Sorkin) 12, 219
де Рам (G. de Rham) 156
Дирак 68, 70
Торн (К. Thorne) 12
Каратеодори (С. Caratheodory) 204
Картан (Е. Cartan) 8, 144, 200, 266 Уилер (J. A. Wheeler) 218
Кеплер 7 Уилкинсон (М. Wilkinson) 12
Коминз (N. Comins) 12 Уэйд (В. Wade) 12
Коперник 7
Фридмэн (J. Friedman) 12
Ли (S. Lie) 62
Шутц (В. Schutz) 6, 12
Минковский (Н. Minkowski) 95
Эйнштейн 227
Ньютон 54 Эстабрук (F. Estabrook) 12

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
абелева алгебра Ли 121
— группа 25
автоморфизм внутренний 137
аксиальная симметрия 113, 116
алгебра Грассмана 150
— Ли 131
— — абелева (коммутативная)
121
векторных полей 64
группы Ли 120
алгебраическое дополнение 32
аналитическая функция 22
аналитическое многообразие 60
аннулирует 153
аннулятор набора форм 191
антидифференцирование 169
антисимметричная часть 147
антисимметричный тензор 146, 147
антиэрмитова матрица 129
атлас 40
аффинная связность 242
аффинный параметр 250
база расслоения 53, 57
базис 28
— двойственный (дуальный) 74
— декартов 88
— координатный 50
— левозакрученный 153
— лоренцев 88
— ортонормированный 87, 88
— правозакрученный 153
— псевдоэвклидов 88
Бетти число 189
биекция 19
большой взрыв 240
бра-вектор 68
Бьянки тождества 254
Вейля тензор 260
вектор 48, 50
— ковариантный 68
— контравариантный 68
iV-вектор 158
вектор-градиент 94
векторное поле 50
гамильтоново 207
— •— Киллинга 114
левоинвариантное 120
— произведение 159
— — двойное 165
— пространство 27
вектор-потенциал 220
вес 163, 164
взанмно-олнозначное отображение
18
вихрь 225
внешне ориентируемое многообразие
157
внешнее произведение 79, 149
внешняя ориентация 157
— производная 169
внутренний автоморфизм 137
времени-подобная кривая 93
Вселенная 227
— замкнутая 239
— открытая 239
— плоская 239
выделенная форма объёма 166
Гамильтона функция 206
— уравнения движения 206
гамильтоново векторное поле 207
гармоника осевая векторная 117—
118
скалярная 117
— сферическая 139
— — векторная 198—199
Гаусса теорема 184
Гельмгольца теорема о циркуляции
225
генерирует 207
геодезическая 250
геодезически полное многообразие
252
гиперповерхность 104
главное расслоенное пространство
59
гомеоморфизм 57

294
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
гомоморфизм 26
гравитационное поле 260
градиент 71, 246
грассманова алгебра 150
группа 25
— абелева (коммутативная) 25
— изотропии 229
— когомологий де Рама 187
— Ли 44
— Лоренца 88
— несвязная 126
— ортогональная 127
— полная линейная 123, 129
— специальная ортогональная 127
— — унитарная 129
— структурная
— унитарная 129
двойное векторное произведение 165
двойственное пространство 67
двойственность 68
двойственный базис 74
де Рама группа когомологий 187
теорема 189
девиация геодезических 256
действие группы транзитивное 229
декартов базис 88
декартово произведение 55
дельта-символ 164
дельта-функцня 69
детерминант 32
дивергенция 172
— ковариантная 257
w-дивергенция 184
динамическая система 213
— — линейная 210
Дирака дельта-функция 69
дискретное множество 14
диффеоморфизм 45
дифференциальная структура 40
¦— форма 149
дифференциальный идеал 192
дифференцируемость класса Ск 21
дуализация 158, 160
дуальное пространство 67
дуальный базис 74
— тензор 159, 160
единица 24
естественные координаты 53
жорданова форма 124
закон преобразования 82
ковариантный 82
контравариантный 82
— сохранения 196, 225
замкнутая Вселенная 239
— система (в термодинамике) 204
— форма 173
замкнутый набор форм 192
идеал дифференциальный 192
— полный 191
идеальная жидкость 222
изоморфизм групп 26
изотропии группа 229
изотропное многообразие 230
импульс 206
(У-импульс канонический 213
инвариантное подпространство 139
инвариантность калибровочная 264
— относительно векторного поля
112
— ¦— переноса Ли 97
индуцирует (топологию) 15
интеграл от формы 154
интегральная кривая 59
— поверхность 197
инфииитезимальный генератор 124
— дифференциал 72
инъективное отображение 18
калибровочная два-форма кривизны
264
— инвариантность 264
калибровочное преобразование 220
калибровочно-ковариантная произ-
производная 264
калибровочно-плоский 265
калибровочные теории 261
каноническая форма матрицы 124
канонический О-импульс 213
каноническое преобразование 207
Каратеодори теорема 204
карта 39
касательное пространство 50
— расслоение 53
касательный вектор 47
— пучок 53
квадратично-интегрируемая функ-
функция 23
кет-вектор 68
Киллинга вектор (ное поле) 114
— уравнение 259
ковариантная дивергенция 257
— производная 244
ковариантный вектор 68, 83
когомологий группа 187
— теория 174
кокасательное расслоение 71
коммутативная алгебра Ли 121
— группа 25

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
295
коммутатор 24
— матричный 127
коммутирующие операторы 24
композитная система 203
композиция 19
компонента единицы связная 126
компоненты вектора 28
— один-формы 74
— преобразования (оператора 30
— тензора 79
конгруэнция 60
консервативная система 207
контравариантный вектор 68, 82
конфигурационное пространство 213
координатный базис 50
координаты 38
— естественные 53
— нормальные 252
Коперника принцип 230
космологический принцип 230
космология изотропная 230
— однородная 230
кососимметричный тензор 146
кососкалярное произведение 211
кривая 45
— параметризованная 45
кривизна 257
Кристоффеля символы 246
Кронекера символ 32
обобщённый 164
кручение 249
Лагранжа уравнение движения 206
— функция 206
Леви-Чивиты символы 162
левозакрученный базис 153
левоинварнантное векторное поле
120
Лейбница формула 102, 103
лемма Пуанкаре 175
Ли алгебра 64, 131
— группа 44
— производная 100, 101, 103
— скобка 62, 131
ли-инвариантность 97
линейная комбинация 27
— независимость 27
линейное преобразование 30
линейность (полилинейность) 76
ли-перенос 97
лист слоения 106
ли-тянутая конгруэнция 98
— функция 97
ли-тянутое векторное поле 98
— поле один-форм 102
Лиувиляя теорема 210
локальная тривиальность расслое-
расслоения 55
тен-
локально-плоское метрическое
зорное поле 91
Лоренца группа 88
— преобразование 88
лоренцев базис 88
Максвелла тождества 202
— уравнения 215
максимально-симметричное много-
многообразие 232
матрица 30
¦— антиэрмитова 129
— вырожденная 32
— единичная 32
— невырожденная 32
— преобразования 81
— обратная 32
— транспонированная 32
матричное произведение 31
метрика 86
— индефинитная 88
— Минковского 88
— эвклидова 86
метрическая связность 258
метрический тензор 86
Мёбиуса лист 56
Минковского метрика 88
— пространство 93, 94
многообразие 37
— аналитическое 60
— внешне ориентируемое 157
— геодезически полное 252
— гладкое 40
— дифференцируемое 40
— изотропное 230
— класса С* 40
— максимально-симметричное 232
— однородное 229
— односвязное 131, 189
— ориентируемое 58, 153
— симплектическое 210
— сферически-симметричное 233
С^-многообразие 40
модель заряда Соркина 219
Уилера 218
мультипликативность 253
на 19
накрывает 131
накрытие двулистное 133
непрерывность 19, 20
несвязная группа 126
норма 28
— эвклидова 30
нормальные координаты 252
нормированное векторное простран-
пространство 28
нуль-форма 149

296
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
область определения 24
обобщённая функция 69
образ 18
образующие 28
обратное отображение 18
обратный элемент 25
объём 154
объёма форма 154
• выделенная 166
— элемент 144
ограничение формы 152
один-форма 67
однопараметрическая подгруппа 121
однородное многообразие 229
односвязное многообразие 131, 189
окрестность 14, 17
оператор 23
— момента импульса 111
определитель 32
опускание индексов 90
ориентация внешняя 157
ориентируемое многообразие 153
ориентируемость 58
ортогональная группа 127
ортонормированный базис 87, 88
осевая гармоника векторная [17—
118
— скалярная 117
— симметрия 113, 116
осевое собственное значение 117
отделимость 15
открытая Вселенная 239
открытое множество 14
отношение эквивалентности 187
отображение 17
— взаимно-однозначное 18
— дуализации 158, 160
1-1-отображение 18
отражение 128
параллелограмма тождество 29
параллельный перенос 243
параметр 45
— аффинный 250
перенос вдоль конгруэнции 97
— Ли 97
— параллельный 243
плоская Вселенная 239
плоское пространство 257
плотность скалярная 163
— тензорная 164
площадь 144—147
повторяющиеся индексы 76
Подгруппа 26
— однопараметрическая 121
подмногообразие 103—104
поднятие индексов 90
подобия преобразование 34
подпространство 28
поле векторное 50
— дифференцируемое 71
— тензорное 77
— форм 71, 153
полилинейность 76
полная линейная группа «-мерного
вещественного пространства 123
— комплексного простран-
пространства 129
— производная по времени 222
— система функций 140
полный идеал (набора форм) 191
порождает 28
правило запятой 170, 248
— разложения по строке 32
— сумирования Эйнштейна 76
правозакрученный базис 153
представление 136
¦— двузначное 142
— неприводимое 139
— присоединённое 137
— спинорное 142
— фундаментальное 142
преобразование калибровочное 220
— каноническое 207
— координат 39
— Лоренца 88
— присоединённое 137
принцип заурядности 230
— Коперника 230
— космологический 230
—¦ минимальной связи 261
— эквивалентности сильный 261
присоединённая реализация 137
присоединённое представление 137
— преобразование 137
проекция расслоения 53, 57
произведение векторное 159
— внешнее 79, 149
— кососкалярное 211
— прямое 55
— тензорное 79
производная внешняя 169
— калибровочно-инвариантная 264
— ковариантная 244
— Ли 100, 101, 103
— полная (по времени) 222
производящие функции канониче-
канонических преобразований 208
прообраз 18
пространственно-подобная кривая
93
пространственно-подобное многооб-
многообразие 192
пространство конфигурационное 213
— фазовое 43, 206
прямое произведение 55
псевдонорма 30

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
297
псевдоэвклидов базис 88
Пуанкаре лемма 175
Пуассона скобка 209
размерность векторного простран-
пространства 28
— многообразия 37
ранг тензора 90
распределение на многообразии
«-мерное 108
— (обобщённая функция) 69
расслоение 52, 57
— касательное 53
— кокасательное 71
— реперов 59
U(l)-расслоение 263
расслоенное пространство 52, 57
главное 59
расширение оператора 24
реализация 135
— главная 136
— присоединённая 137
— прогрессивная 136
— регрессивная 136
— точная 135
Римана тензор 253
Риччи тензор 259
ротор 171
свёртка 68, 80, 151, 178
связная компонента единицы 126
связность аффинная. 242
связность метрическая 258
связность симметричная 248
сдвиг левый 119
— правый 119
сечение расслоения 53
сигнатура метрики 87
— поля О 91
сильный принцип эквивалентное!.
261
символы Кристоффеля 246
— Кронекера обобщённые 164
— Леви-Чивиты 162
симметричная связность 248
— часть 232, 249
симметричный тензор 148
симметрия аксиальная ИЗ, 116
— осевая 113, 116
— сферическая 119, 138
— цилиндрическая 116
симплектическая форма 210
симплектическое многообразие 210
— скалярное произведение 211
скаляр 85
скалярная плотность 163
скалярное произведение 29
симплектическое 211
скобка Ли 62, 131
— Пуассона 209
след 34
слепляющее отображение 18
слоение 106
слой 52, 53, 57
собственное значение 34
¦ осевое 117
собственный вектор 34
согласованность карт 39
— V и Q 258
— V и й 258
С*-согласованность 39
сопряжённое пространство 67
Соркина модель заряда 219
сохраняющиеся величины 115, 185,
196, 210, 225
специальная ортогональная группа
127
— унитарная группа 129
спин 142
спинор 142
спинорное представление 142
стереографическая проекция 42
Стокса теорема 183
структурная группа 57
структурные константы 120
сужение формы 152
сферическая гармоника 139
векторная 198—199
— симметрия 119, 138
сферически-симметричное многооб-
многообразие 233
сюръективное отображение 19
температура 201
тензор 76
— антисимметричный 146, 147
— Вейля 260
— дуальный 159, 160
— кососимметричный 146
— кручения 249
— метрический 86
— напряжений 78
— нулевой 83
— Римана 253
— Риччи 259
— симметричный 148
— типа
76
— Эйнштейна 260
Л/\
М') -тензор 76
тензорная операция 85
тензорное поле 77
инвариантное относительно
векторного поля 112

298
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
— произведение 79
— равенство 85
— уравнение 85
теорема Гаусса 184
— Гельмгольца с циркуляции 225
— де Рама 189
— Каратеодори 204
— Лиувиляя 210
— о дивергенции 183
неподвижной точке на сфере
55, 188
— об изменении полного заряда 218
обратной функции 22
— Стокса 183
— Фробениуса на языке векторных
полей 105—106
— • дифференциальных
форм 192
— Эртеля 226
теория когомологий 174
тождества Бьянки 254
— Максвелла 202
тождественное преобразование 32
тождество Якоби 64, 131
топологическое пространство 15
топология 13
¦— глобальная 13
— локальная 13
точная форма 173
транзитивное действие 229
тривиальность расслоения 55
локальная 55
глобальная 55
тэйлорово разложение 23
увлечение 97
Уилера модель заряда 218
унитарная группа 129
уравнение девиации геодезических
256
— Киллинга 259
— Клейна — Гордона 213, 264
— неразрывности 185
— Эйлера (движения жидкости)
224
уравнение Максвелла 215
фазовое пространство 43, 206
факторпространство 187
Фарадея тензор 215—216
форма (дифференциальная) 149
— замкнутая 173
— объёма 154, 210
выделенная 166
— симплектическая 210
— точная 173
р-форма 149
1-форма 67
Фробениуса теорема на языке век-
векторных полей 105—106
дифференциальных
форм 192
фундаментальное представление 142
функциональное пространство 69
функция 46, 85
— аналитическая 22
— Гамильтона 206
— дифференцируемая 46
— класса С* 21
— Лагранжа 206
— обобщённая 69
С*-функция 21
Сю-функция 23
С°° -функция 21
хаусдорфовость 15
цилиндрическая симметрия 116
число Бетти 189
эвклидова метрика 86
эвклидово пространство 30
Эйлера уравнение (движения жид-
жидкости) 224
Эйнштейна правило суммирования
76
— тензор 260
экспонента от оператора й/йХ 61
экспоненциальное отображение 252
элемент объёма 144
энтропия 201, 224
Эртеля теорема 226
Якоби матрица 22
— тождество 64, 131
якобиан 22
С*-многообразие 40
^-согласованность 39
С*-функция 21
С^-функция-гЗ
С°°-функция 21
Л/-вектор 158
(N \
к,')~тензор 76
р-дельта(-символ) 164
р-мерная группа когомологий 187
Р;форма 149
[/-импульс канонический 213
U(\)-расслоение 263
б-дивергенция 184
1-форма 67
1-1-отображение 18

УКАЗАТЕЛЬ ОБОЗНАЧЕНИЙ
При обозначениях указаны страницы, на которых они введены или полу-
получили новое толкование. По поводу соглашений о размещении индексов
см. § 2.21, по поводу правила суммирования Эйнштейна —§ 2.26.
Виды тензора
а 27
Б 67, 148
F 76
г 62
Ю 164
Специальные тензоры и т. п.
в ga 86
g-1 g'i 89
R( , ), R',u 253
ei...j, в'-' 162
6у 32
К'"{ '64
Г'/*246
Л'у,. Л''у 81, 82
Специальные пространства
Еп 30
GL(n, С) 129
GL(n, «) 58
L(n) 88
О(п) 88
« 14
R" 13
S" 41
SO(n) 44, 127
SU(n) 129
ГР 50
Г*Р 71
ТЛГ 52
Т*М 71
[/(и) 129
Операции
Г , ] 24, 63, 131
*Т, *Б 159, 160
X 55
® 78
154
Ат, Л-1 32
d 71, 169
del (A) 32
diva 184, 185
ехр( ) 60
/: M-+N 19
/: xt—>y 19
g°f 19
Lg 120
^p 100
tt(A) 34
V'j 170
VI-,i 248
o|r 152
ш Л Р 149
V, Vv, Vi 244—246
6@) 67, 151
(Й, O> 68
Различные обозначения
С, С~ 21
Си 23
C^ 148
18
N
76
(/i, .... fn)/d(X!
dt/ 180
22

ОГЛАВЛЕНИЕ
От редактора перевода 5
Предисловие ...... .7
1. НЕКОТОРЫЕ ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ . . 13
1 1. Пространство Rn и его топология 13
1 2 Отображения 17
] 3 Вещественный анализ (вещественные функции вещественных
переменных) ... . . . 22
1 4 1 еория гр> пп 25
15 Линейная алгебра 27
16 Алгебра квадратных матриц ... .... ... 30
17. Библиография .... 35
2. ДИФФЕРЕНЦИРУЕМЫЕ МНОГООБРАЗИЯ И ТЕНЗОРЫ ... 37
2.1 Определение многообразия .... . . 37
2 2 Сфера как многообразие 41
2 3 Другие примеры многообразий . . . . . . 43
2 4 О свойствах многообразий "в цеоом" .... .... 44
2 5 Кривые 45
2 6 Функции на М 46
2 7 Векторы и векторные поля 47
2 8 Базисные векторы и базисные векторные поля 50
2 9 Расслоенные пространства 51
2 10 Примеры расслоенных пространств .... 53
211 Более глубокий взляд на расслоенные пространства .... 54
2 12 Векторные поля и интегральные кривые ... .... 59
2 13 Экспонента от оператора й/йк 60
2 14 Скобки Ли и некоординатные базисы 61
215 Когда базис является координатным? 65
2 16 Один-формы 67
2 17. Примеры один-форм 68
218 Дельта-функция Дирака 69
2 19 Градиент и наглядное изображение один-форм 71
2 20 Базисные один-формы и компоненты один-форм 73
2 21 Индексные обозначения 75
2 22 Тензоры и тензорные поля 76
2 23 Примеры тензоров 78
2 24 Компоненты тензоров и тензорное произведение 78
2 25 Свертка 79
2 26 Замена базиса 81
2 27 Тензорные операции над компонентами . . 84
2 28 Функции и скаляры 85
2 29 Метрический тензор в векторном пространстве 86
2 30 Поле метрического тензора на многообразии . . . . 90
2 31. Специальная теория относительности .... . . . 93
2 32 Библиографии . . 94

ОГЛАВЛЕНИЕ 301
3 ПРОИЗВОДНЫЕ ЛИ И ГРУППЫ ЛИ 96
31 Введение как векторное поле отображает многообразие в
себя ... • • 9°
32 Действие переноса Ли на функции . . 97
3 3 Действие переноса Ли на векторные поля 97
3 4 Производные Ли 99
3 5. Производная Ли один-формы 102
3 6 Подмногообразия .... 103
3 7 Теорема Фробениуса на языке векторных полей . 105
3 8 Докаэате гьство теоремы Фробениуса ... .... 107
3 9 Пример генераторы вращений 111
3 10 Инвариантность . • "^
3 11. Векторные поля Киллинга ... .114
3 12 Векторы Киллинга и сохраняющиеся величины в динамиье ча-
частицы ... ..... .45
313 Осевая симметрия • .116
314 Абстрактные группы Ли .119
315 Примеры групп Ли ¦ 122
316 Алгебры Ли и отвечающие им группы Ли . . 130
3 17. Реализации и представления . 135
3 18 Сферическая симметрия, сферические гармоники и представ-
представления группы вращений .... 138
3 19 Библиография 143
4 ДИФФЕРЕНЦИАЛЬНЫЕ ФОРМЫ 144
А Алгебра и интегральное исчисление форм 144
4 1. Определение объема- геометрическая роль дифференциальных
форм . . 144
4 2 Обозначения и определения, касающиеся антисимметричных
тензоров . 147
4 3. Дифференциальные формы . 149
4 4 Обращение с дифференциальными формами . . . 151
4 5 Ограничение форм - 152
4 6. Поля форм . . 153
4 7 Ориентируемость .... 153
4 8 Объемы и интегрирование на ориентируемых многообразиях 154
4 9 N-векторы, дуальные величины и символ е„ * 158
410 Тензорные плотности 162
4 11 Обобщенные символы Кронекера 164
4 12 Определители и е„ k 166
4 13. Метрический элемент объема 167
В. Дифференциальное исчисление форм и его приложения . . . 168
4 14 Внешняя производная 169
4 15 Обозначения для частных производных 170
4 16 Хорошо знакомые примеры внешнего дифференцирования . 171
4 17. Условия интегрируемости дифференциальных уравнений в
частных производных 172
4 18 Точные формы 173
419 Доказательство локальной точности замкнутых форм . . 175
4 20 Производные Ли от форм 177
4 21. Производные Ли и внешние производные коммутируют . . . 179
4 22 Теорема Стокса 179
4 23 Теорема Гаусса и определение дивергенции ... . . 183
4 24. Краткий экскурс в теорию когомологий 186

302 ОГЛАВЛЕНИЕ
4 25 Дифференциальные формы и дифференциальные уравнения 189
4 26 Теорема Фробениуса на языке дифференциальных форм . . 191
4 27 Доказательство эквивалентности двух вариантов теоремы
Фробениуса . ¦ ¦ ¦ 195
4 28 Законы сохранения 196
4 29 Векторные сферические гармоники . 198
4 30 Библиография 200
5 ФИЗИЧЕСКИЕ ПРИЛОЖЕНИЯ .... 201
А Термодинамика 201
51 Простые системы 201
5 2 Тождества Максвелла и другие математические тождества 202
5 3 Композитные термодинамические системы, теорема Каратео-
дори .... . . . 203
В Гамильтонова механика 206
5 4 Гамильтоновы векторные поля 206
5 5 Канонические преобразования ... 207
5 6 Соответствие между векторами и один-формами, устанавли-
устанавливаемое формой й. . . . . 208
5 7 Скобка Пуассона 208
5 8 Многочасгичные системы, симплектические формы 209
5 9 Линейные динамические системы, симплектическое скалярное
произведение и сохраняющиеся величины . . . 210
5 10 Уравнения Гамильтона и расслоения 213
С Электромагнетизм 215
5 11 Уравнения Максвелла на языке дифференциальных форм . . 215
5 12 Заряд и топология 218
5 13 Вектор потенциал 220
5 14 Плоские волны простой пример .... 221
D Динамика идеальной жидкости 222
515 Роль производных Ли . . 222
5 16 Полная производная по времени 222
5 17. Уравнение движения 524
5 18 Сохранение вихрей 225
Е Космология 227
5 19 Космологический принцип 227
5 20 Алгебра Ли максимальной симметрии 231
5 21 Метрика сферически-симметричного трехмерного пространства 233
5 22 Построение шести векторов Киллинга 236
5 23 Открытая, замкнутая и плоская Вселенные 239
5 24 Библиография 240
6 СВЯЗНОСТИ НА РИМАНОВЫХ МНОГООБРАЗИЯХ И КАЛИБ-
КАЛИБРОВОЧНЫЕ ТЕОРИИ 242
61 Введение 242
6 2 Параллельность на искривленных поверхностях 242
6 3 Ковариантная производная 244
6 4. Компоненты ковариантные производные базиса .... 246
6 5 Кручение . . 248
66 Геодезические ... . . 250
6 7 Нормальные координаты . ... 251
6 8 Тензор Римана 252

ОГЛАВЛЕНИЕ 303
6.9. Геометрическая интерпретация тензора Римана "^4
6.10. Плоские пространства 257
6.11. Согласованность связности с объёмом или метрикой .... 257
6.12. Метрическая связность 259
6.13. Аффинная связность и принцип эквивалентности 260
6.14. Связности и калибровочные теории на примере электромаг-
электромагнетизма 261
6.15. Библиография 265
Приложение. Решения и указания к некоторым упражнениям .... 267
Литература, добавленая при переводе 291
Именной указатель 292
Предметный указатель 293
Указатель обозначений 29Э