Методы решения задач в общем курсе физики. Электричество и магнетизм - Корявов В.П.

Author: Корявов В.П.
Tags: тепло термодинамика строение материи физика электричество задачи по физике магнетизм
ISBN: 978-5-4363-0009-2
Year: 2011
Similar
Методы решения задач в общем курсе физики. Оптика
Методы решения задач в общем курсе физики. Атомная и ядерная физика
Методы решения задач в общем курсе физики. Строение вещества
Методы решения задач в общем курсе физики. Механика
Text
                    В.П. КОРЯВОВ
МЕТОДЫ
РЕШЕНИЯ ЗАДАЧ
В ОБЩЕМ КУРСЕ
ФИЗИКИ
ЭЛЕКТРИЧЕСТВО
И МАГН ЕТИЗМ
МОСКВА
«СТУДЕНТ»
2011

УДК 5362539
ББК 22.317+22.36
К 66
Корявов В.П.
К 66 Методы решения задач в общем курсе физики. Электричество
и магнетизм: Учеб. пособие / В.П. Корявов. — М. , Студент, 201 1. —
533 с.: ил.
1$ВМ 978-5-4363-0009-2
В учебном пособии подробно разобраны методы решения задач по курсу
электричества и магнетизма. Задачи систематизированы по разделам, каждый
из которых предваряется кратким изложением теоретического материала.
Для студентов технических вузов, а также преподавателей физики высших
и средних учебных заведений.
УДК 5362539
ББК 22.317+22.36
1$ВЫ 978-5-4363-0009-2 © ООО «ТИД «СТУдент», 2011

ПРЕДИСЛОВИЕ
Эта книга продолжает рассмотрение методов решения задач в
общем курсе физики, начатое в ранее вышедших книгах В.П. Коря-
вова: Методы решения задач в общем курсе физики. Механика, 2007;
Методы решения задач в общем курсе физики. Термодинамика и
молекулярная физика, 2009. Ссылки на них в дальнейшем будут
отмечаться 1 и 2. Здесь повторяем часть предисловия к вышедшим
книгам.
Особенности преподавания физики в Московском физико-тех-
ническом институте (МФТИ) заключаются, во-первых, в значитель-
ности затрачиваемого времени (шесть семестров) и, во-вторых, в
привлечении к преподаванию по совместительству сотрудников ис-
следовательских физических институтов Российской академии наук
и различных министерств, т. е. весьма квалифицированных специа-
листов.
Любая практическая деятельность физиков фактически сводит-
ся к решению конкретных задач. Понимание этого привело к тому,
что и в процессе обучения, и при проверке знаний на экзаменах на
кафедре общей физики МФТИ большое внимание уделяется уме-
нию решать задачи. Поэтому все экзамены включают письменные
контрольные работы. О достаточной сложности предлагаемых задач
свидетельствует то, что студентам на письменных экзаменах разре-
шается пользоваться учебниками, книгами, конспектами и другими
учебными пособиями.
Придумывать новые задачи — обязательное требование к сотруд-
никам кафедры общей физики. О числе задач можно судить, напри-
мер, по тому, что в первом семестре, посвященном изучению меха-
ники, надо иметь 20 задач (контрольная по первому заданию и экза-
менационная работа по два варианта из 5 задач). Эта трудная работа
(придумывание задач) проводится на кафедре более полувека. На-
коплено много хороших задач. Практически исчерпаны все возмож-
ные варианты. Лучшие и показательные (представительные) задачи
вошли в три тома сборника под редакцией В.А. Овчинкина. В пер-
3

вом томе (Сборник задач по общему курсу физики в трех частях /
Под ред. В.А. Овчинкина. В 3 ч. Ч. 1. Механика. Термодинамика и
молекулярная физика. — 2-е изд., испр. и доп. — М.: Изд-во МФТИ,
2002) содержится 1060 задач по механике и 827 задач по термоди-
намике и молекулярной физике. Во втором томе (Сборник задач
по общему курсу физики в трех частях / Под ред. В.А. Овчинкина.
Ч. 2. Электричество и магнетизм. Оптика. — М.: Физматкнига, 2004)
содержится 715 задач по электричеству и магнетизму и 627 задач по
оптике.
В предлагаемой книге систематизированы и приведены методы
решения задач по электричеству и магнетизму, содержащихся в упо-
мянутом сборнике. Каждый из 12 тематических разделов начинает-
ся с краткого изложения основных теоретических результатов.
В отличие от имеющихся различных задачников с решениями
здесь возможно впервые сделан акцент на изложении методов ре-
шения задач и соответствующей систематизации.
Предполагается, что основными читателями данной книги мо-
гут стать преподаватели и студенты физических специальностей
университетов и институтов, а также преподаватели школ.
Более 40 лет автор имел возможность общаться с сотрудниками
кафедры общей физики МФТИ и благодарен им за все полезное, что
смог от них почерпнуть, а таюке благодарен профессору А.Д. Гладу-
ну за поддержку работы, А.В. Гуденко за полезные замечания, сде-
ланные им после детального ознакомления с рукописью книги. За
помощь в издании книги автор выражает большую благодарность
Д.П. Корявову.
Автор

ВВЕДЕНИЕ
Методы решений новых задач создаются на основе общих сведе-
ний о рассматриваемых явлениях и известных методах решения по-
хожих задач.
Затруднения при решении задач следует преодолевать дополни-
тельными усилиями, чтением учебников, беседой с однокурсника-
ми, обсуждением на семинарских занятиях с преподавателями. Эта
книга таюке может быть полезна, если самостоятельные упорные
предварительные попытки найти решение не дают результата. Ав-
тор старался, чтобы книга не была решебником, а помогала бы ос-
воить методы решения, проясняла бы трудные вопросы. Если чело-
век не хочет научиться решать задачи, а стремится лишь к сдаче
тетради с заданием, он найдет, откуда переписать решения, может
быть и неправильные, и сделает это без настоящей пользы для себя.
Автор надеется, что, воспользовавшись этой книгой, даже ленивый
чему-нибудь научится.
В общем курсе физики электричество и магнетизм существенно
отличаются от школьной программы.
Решение задач полезно проводить по следующему плану:
1) хорошо понять условие задачи, используя рисунки и допол-
няя их затем по ходу решения;
2) обдумать условие задачи и возможные пути и варианты ре-
шений;
3) используя нужные физические законы, выписать уравнения,
и если они в векторном виде, то выбрать удобную систему коорди-
нат и записать уравнения в проекциях;
4) выписать дополнительные условия, которые необходимы для
решения задачи, и написать решение уравнений;
5) провести анализ результатов решения: по размерности, по
правильности предельных значений полученных зависимостей
(с учетом области применимости решения), по разумности поряд-
ков вычисленных величин (по грубым оценкам и здравому смыслу).
В данной книге автор не стремился доводить решения конкрет-
ных задач до численных результатов (за некоторым исключением).
5

Важно было проследить цепочки задач, попытаться их систематизи-
ровать и провести анализ различных вариантов. В скобках указыва-
ются номера задач из Сборника задач по общему курсу физики под
ред. В.А. Овчинкина (Ч. 2. — М.: Изд-во МФТИ, 2004), в которых
возможно применение излагаемых методов решения.
Наша цель — показать, как общие физические законы, кото-
рые будут кратко изложены, позволяют решить большое число
ЗЗДЗЧ .

1. ЭЛЕКТРИЧЕСКИЙ ЗАРЯД
И НАПРЯЖЕННОСТЬ ЭЛЕКТРИЧЕСКОГО поля.
диполь. ТЕОРЕМА ГАУССА
При изучении механики бьш рассмотрен закон всемирного тяго-
тения (гравитации), определяющий силу взаимодействия между дву-
мя точечными массами (см. 1, с. 135). Было введено поле тяготения,
напряженность поля, экспериментально получена теорема Гаусса.
Опыты показывают, что между телами могут быть взаимодей-
ствия, значительно превышающие гравитационные, связанные с
электрическими зарядами тел. Заряды на телах возникают в ре-
зультате явления, называемого электризацией (разделение зарядов).
В равных количествах появляются положительные и отрицательные
заряды. Между телами с зарядами одинакового знака существует
отталкивание, а между телами с зарядами разных знаков — притя-
жение. Электрические заряды изменяют свойства пространства,
окружающего заряженное тело, создают электрическое поле, кото-
рое проявляет себя тем, что действует на заряженные тела. Заряды
являются количественной мерой взаимодействия заряженных тел.
Экспериментально получен закон Кулона для силы взаимодействия
двух неподвижных точечных тел с зарядами 41 и 42 в зависимости от
расстояния между ними г:
ЬШ; (1.1)
Здесь векторы обозначены полужирным шрифтом: Ё — сила, дей-
ствующая на тело с зарядом 42; г — расстояние от тела с зарядом с],
до тела с зарядом 42. Величина (г/г) — единичный вектор в направ-
лении г, который определяет направление силы Р. Такое написание
формулы (1.1) показывает, что величина силы обратно пропорцио-
нальна квадрату расстояния между заряженными телами малых (то-
чечных) размеров. В этой формуле отсутствует влияние среды, ок-
ружающей тела, т. е. предполагается, что заряженные тела находят-
ся в вакууме. Однако сразу отметим, что влияние воздуха на силы
взаимодействия очень мало и им можно пренебречь.

Единицы измерения зарядов можно получить из (1.1). Исполь-
зуя системы СГС и Гаусса (расстояние в см, сила в дцнах) находим
единицу заряда (СГСЭ ед. заряда). Исторически практической еди-
ницей заряда (в системе СИ) стал кулон (1 Кл = 3 - 109 СГСЭ ед.
заряда). При этом закон Кулона (в системе СИ) имеет вид
_ 4142 Г
Р — ——т—= (12)
4ТЁЁОГ г
ЗДЕСЬ электрическая ПОСТОЯННЗЯ (диэлектрическая ПОСТОЯННЗЯ ва-
куума)
- 107 -8 85 10-12 Ф
80 _4лс2 — , ' /М‚
где с — скорость света; сила измеряется в ньютонах, расстояние — в
метрах; Ф — фарада.
В дальнейшем тексте для основных формул в системе Гаусса
будут приведены их аналоги в системе СИ (в фигурных скобках).
Сравнение электростатических (кулоновских) Рк и гравитацион-
ных Р; сил можно сделать для частиц с известными зарядами и мас-
сами, например протона и электрона (Не 1.1). Из таблиц в соответ-
ствующих единицах измерения зарядов, масс и постоянной грави-
тации находим
для протона это 1,24- 1036, для электрона 4,17 - 1047.
Для проверки зависимости (1.1) Кулон проводил измерения пе-
риода колебаний шеллаковой (не проводящей зарядов) стрелочки,
на одном конце которой был прикреплен небольшой кружок из зо-
лотой фольги с зарядом 4„ подвешенной на неупругой нити за центр
масс, с моментом инерции 1 относительно оси, проходящей через
центр масс в направлении нити. Колебания происходят из-за того,
что на расстоянии 11, которое значительно больше размера стрелоч-
ки, в плоскости колебаний находится точечный заряд 42 противопо-
ложного знака относительно 4,. Найдем зависимость периода коле-
баний Тот расстояния 11 (Мэ 1.18). Считая, что колебания малы и
фактически происходят в постоянном электрическом поле, получа-
ем уравнение колебаний стрелки
с12‹р
1__ Ф
= “Ч1Ч2['—

Отсюда для периода имеем
1 1/2
т = 21% ) .
611421
Заряженное тело меняет свойства окружающего ‘его простран-
ства — создает электрическое поле. Для неподвижного точечного
тела с зарядом 41 из (1.1) получаем для напряженности электростати-
ческого поля
Г
4пе0г
Такая сила будет действовать на точечное тело с единичным за-
рядом, называемое пробным заряженным телом. Реальное пробное
тело должно иметь настолько малый заряд, чтобы не возникали су-
щественные перераспределения зарядов на телах, создающих поле.
Для изображения полей удобно использовать линии, называе-
мые силовыми, касательными к которым являются векторы напря-
женности поля. Направление линий совпадает с направлением век-
тора напряженности поля — от положительного к отрицательному
заряду.
В декартовых координатах силовую линию определяют диффе-
ренциальные уравнения
ядам „4,
Ех Еу Е:
где с1х‚ с1у и. (12 — изменения декартовых координат вдоль силовой
линии; Ех, Еу и Е: -— декартовы компоненты вектора напряженности
электрического поля.
Для вывода этих соотношений вводим элемент длины вдоль си-
ловой линии с15 = (с1х2 + с1у2 + 4122)“? Учитывая, что
ф‘ _ З д)’ _ Е)’ ‘11 _ Е:
23" Е’ Ж’Т’ Ж’_Ё"
выражаем с15/Е и получаем (1.4).
Экспериментально установлено, что для сил взаимодействия за-
ряженных тел выполняется суперпозиция (геометрическое сложение
сил от разн_ых заряженных тел).
Для примера найдем, какой заряд О надо поместить в центре
квадрата со стороной а, чтобы нулю была равна сила, действующая
на каждый из зарядов (1, находящихся в вершинах квадрата (М9 1.2).
9

На рис. 1.1 показаны силы, действующие на один из
Ч
Ч ЗЗРЯДОВ В ВСрШИНС квадрата ОТ ДРУГИХ ЗЗРЯДОВ. ИЗ
равенства ГСОМСТРИЧССКОЙ СУММЫ НУЛЮ ПОЛУЧЗСМ
2 2
а а 061 Ч Ч 45 . 1+ Ъ/Ё
= + 2 9 О = Ч б-
Рис. 1.1 („д/ау ил)’ а 4
Здесь уместно напомнить теорему Ирншоу о том, что всякая
равновесная конфигурация покоящихся точечных электрических
зарядов неустойчива, если на них, кроме кулоновских сил притя-
жения и отталкивания, никакие другие силы не действуют. Убе-
диться в справедливости теоремы можно, рассматривая изменение
сил при смешении зарядов. Простейший пример устойчивой сис-
темы: два тела с зарядами одного знака, подвешенные на ниточках
в поле тяжести.
Силы взаимодействия между заряженными телами конечных
размеров и напряженности полей от больших тел можно найти пу-
тем сложения (интегрирования) сил, действующих от бесконечно
малых элементов тел.
Найдем напряженность поля на оси симметрии диска радиусом К,
заряженного равномерно с поверхностной плотностью о (Не 1.10).
На рис. 1.2 показан диск и выделено колечко радиусом ги шириной ф:
На элементе колечка площадью гдсрдг, который можно считать точеч-
ным, находится заряд, равный огдфдг, который создает напряжен-
ность поля на расстоянии 11 от поверхности диска на оси симметрии
с1г
а72Е = он! ———.
Ф #2 + г2
„н
«РЕ
т 52
Н:
дФ } Е]
Г — —:—
с1г _ -4
к _ ‚
г
Рис. 1.2 Рис. 1.3
10

Пользуясь симметрией относительно оси Ь, интегрируем по углу ~р,
учитывая, что сумма составляющих перпендикулярных оси Ь равна
нулю, а складывать надо только составляющие поля вдоль оси Ь
йЕ = 2титЫг
Ь
(~г „г)'1г
Интегрируя это выражение по г, получаем
Е = 2па(1
(1 )
Отсюда следует, что в центре диска на его поверхности напря-
женность поля
Е=2па; ~~Е=
(1 )
Важным примером суперпозиции является сложение полей от
двух равных по величине зарядов противоположных знаков на рас-
стояниях, значительно превосходящих расстояние между зарядами.
Система зарядов в таком случае называется диполем. Моментом ди-
поля р называется произведение абсолютной величины зарядов д на
вектор 1 вЂ” расстояние от заряда вЂ” д до заряда +д. На рис. 1.3 показа-
ны два заряда на расстоянии!. Напряженность поля К, в направле-
нии р = д1 на расстоянии г
(г + 1/2) вЂ” (г вЂ” 1/2) ~у р
(г вЂ” 1/2) (г+ 1/2) (г вЂ” 1/2) (г+ 1/2) г
В векторном виде
(1 )
Напряженность поля в направлении, перпендикулярном р:
гг + (1/2) („г (1/2)г)1 г' г'
В векторном виде
(1 )
2 3.

где г, вЂ” расстояние до силовой линии +ч
в направлении перпендикуляра к век-
1гору момента диполя (при 6 = я/2).
На рис. 1.5 показана система четы-
ех зарядов (двух положительных +д и
г
вух отрицательных вЂ” д, расположенных
+д
вершинах квадрата со стороной а). Г2
оле такой системы на расстояниях
г, » а называется полем квадруполя. Ис-
пользуя (1.9) и разлагая (1/»2' вЂ” 1/~') в ряд Тейлора, получаем для
напряженности поля в точке А (№ 1.6)
р р Нфг) а
вЂ” р (», вЂ” «) = вЂ” Зр вЂ”.
гЗ гЗ Й 2 1 г4
2 1
где р = да.
Сила, действующая на заряд д, находящийся в поле диполя р,
определяется (1.9). В частности, на заряд на расстоянии А по на-
правлению диполя (№ 1.7), используя (1.7),
г~р
3 '
Для положительного заряда получаем силу отталкивания, для отри-
цательного вЂ” притяжения. Отметим, что при взаимодействии заря-
дов сила уменьшается обратно пропорционально квадрату расстоя-
ния, при взаимодействии заряда с диполем вЂ” обратно пропорцио-
нально кубу расстояния, а при взаимодействии с квадруполемвЂ”
обратно пропорционально четвертой степени расстояния.
Поле диполя симметрично относительно его оси. Найдем на-
правление вектора г (угол 6 с осью диполя), для которого вектор
напряженности поля будет перпендикулярен направлению оси дипо-
ля. Эго условие выполняется, если скалярное произведение Ер = О.
Получаем
соя 0
Ер = З(рг) Р вЂ” РР = Зр г = О.
г5 гЗ г5 гЗ
Отсюда находим
1~2
созО =+вЂ”
3
13

Г=2р,, -2р,вЂ”,=вЂ”
бр1 р2
(1.10)
(А+() А А
Диполи, направленные в одну и ту же сторону, притягиваются, а
в противоположные вЂ” отталкиваются.
В постоянном по величине и направлению электрическом поле
силы, действующие на диполь, представляют пару сил. Они не
вызывают поступательное движение, а только вращение. При
отклонении диполя на угол а от направления поля момент сил (удоб-
но вычислять относительно положения отрицательного заряда вЂ” д)
М = дЕ( яп а = рЕ яп а. В векторном виде
М = [рЕ].
В изменяющемся по пространству электрическом поле возника-
ет сила, вызывающая поступательное движение диполя:
дЕ дЕ
Г = дЬЕ = д вЂ” (соБ а = р вЂ” сова.
дх дх
Здесь поле направлено по оси х. Если диполь направлен по полю, то
дЕ
=РвЂ”
дх
(1.11)
Из суперпозиции и (1.3) можно получить теорему Гаусса. Пото-
ком вектора называется скалярное произведение этого вектора на
вектор площадки (единичный вектор нормали на величину площад-
ки), через которую вектор как бы протекает. Поток через площадки
конечной величины в случае меняющегося по пространству вектора
надо вычислять интегрированием по бесконечно малым площадкам.
Используя выражение (1.3), для потока вектора напряженности
электрического поля от точечной массы с зарядом д, (точечного за-
ряда) через замкнутую поверхность, получаем
ф ЕЫЯ = ф ЕйБ = ф д, вЂ”,е = ф д~ ~(Й = 4щ1,
14
Следовательно, возможны круговые движения с постоянной ско-
ростью точечного электрического заряда вокруг оси точечного элек-
трического диполя на любом расстоянии от него в плоскости, пер
пендикулярной его оси (№ 1.8). Знак минус для положительног
заряда, знак плюс для отрицательного.
Найдем силу взаимодействия Г двух точечных диполей, если и
дипольные моменты р~ и р2 направлены вдоль соединяющей их пря
мой, а расстояние между диполями равно А (№ 1.9). Представи
р, = д( и найдем силу, используя (1.7):

ШЯ, вЂ” проекция площадки поверхности на направление поля;
вЂ” телесный угол из точечного тела на бесконечно малую пло-
ку поверхности.
Используя суперпозицию, для произвольного заряженного тела
которым распределением зарядов получаем теорему Гаусса для
ы зарядов д внутри замкнутой поверхности:
фЕШЯ=4кд; ~фЕШЯ= ~
~о
(1.12)
еорема Гаусса может быть использована для вычисления на-
пр енности поля в тех случаях, когда легко вычислить интеграл.
Например, в случае симметрии поля: сферической, цилиндричес-
КОЙ ИЛИ ПЛОСКОЙ.
В случае сферической симметрии распределения заряда напря-
женность на одном и том же расстоянии г от центра симметрии
одинакова по абсолютной величине для всех направлений, и для
переменной плотности заряда р получаем
Г
Е (г) 4пг2 = 4п~ р (г) 4пгтйг,
О
откуда
Г
Е(г) = вЂ” 4п/р(г) г~дг.
г
(1.13)
Для постоянной плотности имеем линейную зависимость
Е(г) = вЂ” прг.
4
3
В векторном виде
Е(г) = вЂ” прг; Е(г) = ~
3 Зео
(1.14)
Если плотность отлична от нуля только до некоторого Я, то для
г > Л из (1.13) следует
Е(г) = вЂ” пЛ р вЂ” = вЂ” вЂ”.
4 з г д г
=3
(1.15)
Это совпадает с выражением (1.3) для точечной массы. Отсюда
для взаимодействия двух сферически симметричных распределений
зарядов получаем силу взаимодействия такую же, как для точечных
15

заряженных тел. Логика такая: поле первого заряда такое же, как о
точечного, значит, сила взаимодействия та же, что для точечного
второго зарядов. Но силу со стороны второго заряда на точечно
заряженное тело вычисляем по полю от второго, которое такое ж ,
как для точечного, равного заряду второго тела.
На рис. 1.6 показано изменение напряженности электрическо
поля Е тела радиусом К с постоянной плотностью заряда.
В металлических телах есть электрические заряды, которые мо
свободно перемещаться. Под действием электрических полей в н х
может происходить перераспределение зарядов — поляризация. ЗЁ-
ряды, помещенные на металлический шарик, располагаются равн
мерно (при отсутствии влияния каких-либо других зарядов или по-
лей) на его поверхности. Внутри металлического шарика (как и любо-
то проводящего тела) электрическое поле отсутствует. Если вокруг такого
металлического шарика (радиусом К д), имеющего заряд О, концентри-
чески расположить незаряженную металлическую оболочку конеч-
ной толщины (внутренний радиус 122, наружный 123), то поле будет
меняться так, как показано на рис. 1.7. Напряженность поля падает
обратно пропорционально квадрату расстояния от центра шарика.
Внутри металлической оболочки поле отсутствует. На поверхностях
оболочки появляются заряды, по абсолютной величине равные заря-
ду шарика (на внешней с тем же знаком, а на внутренней с противо-
положным). Зависимость напряженности от расстояния за оболоч-
кой продолжает ту же зависимость, которая была перед ней.
Поле вокруг равномерно заряженной сферической поверхности
(с поверхностной плотностью заряда о) определяется (1. 15). На внеш-
ней стороне поверхности Е = 41во, на внутренней — поле равно
нулю. Найдем поле Ед, которое будет в центре небольшого отвер-
стия, вырезанного в этой поверхности (Мг 1.12). Воспользуемся прин-
ципом суперпозиции: сумма Е, и поля в центре площадки, которую
затем удаляют, определяемая (1.6), должна давать соответствующие
поля на заряженной сферической поверхности (внутри и снаружи).
Следовательно, Е, = 2тго и направлено от центра сферы.
Е
„1/‚2 Е=%
Ей
мг
7:: "“""‘
‘г Н
э‘
7::
м
д
Ч
Рис. 1.6 Рис. 1.7

1
При АЕ = 75 В/м и 11 = 1500 м получаем р = 1,33- 10 ‘9 ед. СГСЭ;
Измерения показали, что земное электрическое поле меняется вб
времени. Кроме регулярных (суточных и годичных) существуют й
нерегулярные изменения. В среднем напряженность электрическо-
го поля у поверхности Земли равна 130 В/м. Заряд Земли отрица-
тельный и равен 6- 105 Кл. Так как электрическое поле направлено
к поверхности Земли, отрицательные заряды будут двигаться вверх,
и в атмосфере появится положительный заряд (р > 0).
Рассмотрим две бесконечные плоскопараллельные металличес-
кие пластинки, помещенные в вакууме параллельно друг другу и
имеющие одна на единицу площади полный заряд (т. е. сумма заря-
дов на обеих поверхностях пластинки) 41, а другая — 42 (Не 1.13). На
рис. 1.9 показаны пластинки и соответствующие параметры (Е —
напряженности поля, 0 — плотности зарядов на поверхностях). Скла-
дывая поля от плоских зарядов, которые определяются (1.17), с уче-
том их направлений внутри металлических пластин, где они долж-
ны быть равны нулю, получаем
2п(0{ —0, -02 —05) = 0; 2п(0;+01+02 —0;) = О.
СКЛЗДЫВЗЯ И ВЫЧИТЗЯ ЭТИ СООТНОШЕНИЯ, НЗХОДИМ
По условию
а, =0{ +0,; 42 = 02 +03.
Отсюда
°1="°2 =-——-Ч1 342; 01:05 =—:Ч1ЁЧ2-
Используя эти результаты и теорему Гаусса (1.12), получаем из
потоков через поверхности 1 и 2
Е = 41:01 = 2п(с1‚—а2);
Е,’ = Е; = 41:01: 21т(с1,+с12).
Конструкция из двух проводящих
пластин, на которых можно помес-
тить заряды, называется плоским кон-
Рис. 1.9 денсатором.
У)
18

нности поля внутри и вне плоского слоя толщиной 1с равномер-
ным распределением положительных зарядов с объемной плот-
ноцстью р (Мг 1.15). На рис. 1.10 в плоскости, перпендикулярной
сл ю, показаны поверхности, через которые вычисляются потоки
вектора напряженности. Так как вектор напряженности имеет со-
ставляющую только в направлении оси х и существует симметрия
относительно средней плоскости (х = О), получаем для потоков
через поверхность с единичной площадью: для поверхности 1 име-
ем 2Е = 41ър2х, для поверхности 2 — 2Ед = 4пр1. Откуда находим
линейное возрастание напряженности внутри слоя Е = 4прх и
постоянную напряженность поля вне Е1 = 21ър1.
Теорема Гаусса является интегральным соотношением. В не-
которых случаях удобнее иметь дифференциальные соотношения.
Для этого надо рассмотреть бесконечно малый объем. На рис. 1.11
в декартовых координатах показан бесконечно малый объем дхдудг.
Чтобы не загромождать рисунок, поток вектора напряженности
поля Е показан только вдоль одной координаты х (проекция векто-
ра на эту ось Ех). По другим координатам потоки подсчитываются
аналогичным образом. Обозначая плотность заряда р, из (1.12)
получаем
Х; Воспользуемся теоремой Гаусса (1.12) для нахождения напря-
ж
фвдз = 4ш1 =
1
= ЭЕ ЭЕ
Е Е = дЕх дхдудг + —1 дудха’: + г дгдхду =
= сну Едхдуа’: = 4прдхс1уа72.
<-—{ —>
Е! Е]
2
Е н
2пр1 —-—
_; 0 щ Ё
2 2
Рис. 1.10 Рис. 1.11
2* 19

Здесь введено обозначение сйу, называемое дивергенцией (расходи-
мостью) вектора Е, ›
$33)“
Таким образом, теорема Гаусса в дифференциальном виде
саун: нт (
АУ-›0
с11уЕ=4пр; {синь-Е}. (1.19)
до
В декартовых координатах, как это получено ранее,
д Ех дЕу дЕ,
+ —— + .
Эх ду д:
В случае цилиндрической симметрии относительно оси 1, изоб-
раженном на рис. 1.12, получаем
ёйуЕ = (1.2О)
(Е, + дЕ‚/дг аг)(г + с1г)а7‹р д: - Ед с1‹р а; _
гдфдга’: ‘-
дЕ‚ Е, 1д(гЕ‚)
:———+::—-—:——‚
д!’ Г г д!‘
сНуЕ =
(1.21)
В случае сферической симметрии
(“у Е _ (Е, + ЭЕ, /дг с1г)4п (г + дг)2 - Е‚4пг2 _
4пг2с1г (1 22)
= г д.15; =_Ё_Э(’2Е*)
дг г ‚д дг °
При равномерном распределении заряда (плотность р) в беско-
нечной плоской пластине толщиной 2/2 напряженность поля можно
вычислить, пользуясь теоремой Гаусса в диф-
’ ференциальном виде (Мг 1.19). Из (1.19) и
дЕ’ (1.2О) внутри пластины
Е, + г дг
дЕ
с1г Е;
Постоянная интегрирования С определя-
ется из условия симметрии задачи: при х = О
напряженность поля равна нулю и, следова-
Рис. 1.12 тельно, С = О. Вне пластины заряда нет
=4пр и Е=4прх+С.
20

Для каждого из шаров поле определяется (1.14). В области их пере-
сечения (в некоторой точке А) для напряженности поля имеем
ЕО = Е, +Е2 = %пр(г, —г2) = —%пра. (1.24)
Таким образом, в области пересечения, где суммарная плотность
заряда равна нулю, поле постоянно и направлено противоположно
вектору а (из центра отрицательно заряженного шара к центру по-
ложительно заряженного шара). Если расстояние между центрами
шаров мало по сравнению с их радиусами (а << К), то нескомпенси-
рованные заряды распределены фактически по поверхности сферы.
Так как поверхности шаров в направлении вектора а сдвинуты на а,
то расстояние между ними по направлению 6 равно а сов 6. Плот-
ность заряда на единицу поверхности
о = ра сов 9.
Отметим, что при стремлении а к нулю произведение ар должно
оставаться конечным. Выражая ра из (1.24), находим, что для полу-
чения внутри сферической поверхности поля Ед распределение плот-
ности заряда на ней должно быть (Мг 1.23)
350 .
о = Жсозе, {о = ЗеОЕО сове}. (1.25)
Поле вне однородно заряженного шара определяется суммар-
ным зарядом
О = ЁпКЗр.
Два противоположно заряженных шара на расстояниях, зна-
чительно превосходящих расстояние между их центрами, создают
поле в области пересечения, соответствующее диполю с моментом
р = Оа. Из (1.24) находим р = —К3ЕО. Постоянное поле внутри
шара согласуется с полем диполя при г = К с учетом скачка поля,
связанного с зарядом (1.18).
На границе проводящего тела напряженность электростатическо-
го поля может быть направлена только по нормали к границе. В про-
тивном случае возникает движение и перераспределение зарядов.
На границе проводящего шара (радиусом К), находящегося в по-
стоянном электрическом поле Ео, вектор напряженности поля Ее
направлен по нормали к границе (поверхности), т. е. касательная
компонента равна нулю. Попробуем удовлетворить это условие с по-
мощью диполя р, помещенного в центре шара. Обозначая напряжен-
22

ность поля от диполя Ед, получаем, что суммарное поле Ее = ЕО + Ед
при г = В должно иметь только радиальную компоненту. Векторное
произведение этого поля на К должно быть равно нулю. Это позво-
лит найти величину р. Учитывая, что в выражении (1.9) остается
только второй член, имеем
[Еск] = [Е„к]- Нэп] = ПЕ, - %)к] = о.
Откуда
р = 11312,; {р = 4таоКзЕо}. (1.26)
Распределение зарядов по поверхности проводящего шара, по-
мещенного в постоянное поле с напряженностью Ед, определяется
(1.24) и (1.25), так как в проводнике поле внутри должно быть равно
нулю, т. е. распределение зарядов должно создать напряженность
постоянную и противоположную напряженности внешнего поля Ед.
Напряженность поля вне проводящего шара определяется суммой
напряженности внешнего поля Ео, в которое он помещен, и напря-
женности поля диполя, возникающего на шаре благодаря поляриза-
ции, р = К3Ео.
Поле вне шара
Е
в=но +3К3(Е0г)%—123:39-. (1.27)
Напряженность ПОЛЯ на ПОВСРХНОСТИ шара
1:01) = 35, со$6%. (1.28)
Видно, что на поверхности проводящего шара напряженность поля
всегда нормальна к поверхности и на оси симметрии (6 = О и 6 = п)
равна ЗЕО, а при О = 11/2 равна нулю (Мг 1.26). Направление, при кого-
ром напряженность поля по абсолютной величине равна Ео (М 1.25),
определяется сов В = 11/3, а 2Е0 — соответственно сов О = 12/3.
Найдем точки пространства, в которых поле равно 2Ео (Мг 1.27).
Из (1.27)
3 Г 3 Ео
Ед = ЗК (Е„г);3-— К ——.
‚З
Поэтому
Е, (1 + Ё) = 3113 (Еог)-Ё.
ГЗ ‚5
23

Отсюда направление г, для которого это условие выполняет-
ся, совпадает с направлением Ео. Проведя вычисления, находим
г = Я(2) '~з
Аналогичным образом найдем точки, в которых поле равно Е/3
(М 1.27). Получаем
~3
Е вЂ”, вЂ” вЂ” = ЗЯ' (Еог) вЂ”,.
О гз 3 О г5
дЕ р
Г = р вЂ” = вЂ” 6 вЂ” = вЂ” 6Е2 вЂ”.
д,. 4 О„4
(1.29)
Для сфер, находящихся в поле, перпендикулярном к линии, со-
единяющей их центры (Мо 1.30), как следует из (1.8) и (1.11), проис-
ходит отталкивание с силой
Г= р вЂ” =3 вЂ” =ЗЕ вЂ”.
дЕ р
дГ 4 О 4
(1.30)
Поле внутри равномерно заряженного (с объемной плотностью р)
бесконечного цилиндра находим с помощью (1.12)
Е=2прг; ~Е=
рг
2ЕО
(1.31)
Это линейная зависимость, как и (1.14), но с другим коэффици-
ентом. Для двух параллельных цилиндров с зарядами противопо-
24
Если предположить, что г направлено по Ео, то получаем г = вЂ” А(2)'~'.
Так как в случае сферической симметрии г не может быть отрица-
тельным, для удовлетворения уравнения используем Еог = О. В этом
случае г = Л(3/2)'~'. Следовательно, искомая напряженность поля
будет на окружности с радиусом г = Я(3/2)'~' в плоскости, перпен-
дикулярной вектору Ео, проходящей через центр шара.
Найдем величину и направление силы взаимодействия между
двумя незаряженными проводящими сферами радиусом Я, помещен-
ными в однородное электрическое поле Е, направленное параллель-
но линии, соединяющей центры сфер, расстояние между которыми
г» Л (М 1.29). Действие поля на проводящий шар, как получено
ранее, приводит к поляризации вЂ” возникновению дипольного мо-
мента р = Л'Ео. Постоянное по величине и направлению поле на
диполи не действует. Одинаково направленные диполи, как показа-
но ранее (1.10), притягиваются с силой, которую можно также най-
ти через градиент поля диполя (1.11)

ложных знаков в области перекрытия зарядов получаем постоянную
напряженность поля
Е, = Е, + Е, = 2яр(г, вЂ” г,) = вЂ” 2тц~а,
(1.32)
где а вЂ” расстояние между осями симметрии цилиндров. Используя
рис. 1.14, можем найти необходимое распределение плотности за-
ряда по поверхности цилиндра, чтобы получить постоянную напря-
женность поля Ео внутри цилиндра
а = расовО = вЂ” совО; ~а = расовО = 2в Ео совО~.
о
2я
(1.33)
(1.34)
2 '
Вместо (1.8)
(1.35)
2 2 '
Используя рис. 1.4, для произвольного угла О находим поле «плос-
КОГО» ДИПОЛЯ
Е = 4(рг) вЂ” вЂ” 2 вЂ”.
Р
г4 г2
(1.36)
Если в безграничном плоском слое толщиной 2Ь объемная плот-
ность заряда р изменяется по закону р = р х/Ь ( вЂ” Ь 5 х< Ь), где хвЂ”
25
Если бесконечно длинный проводящий цилиндр помещен в по-
стоянное электрическое поле, перпендикулярное оси цилиндра, с
напряженностью Е, то для отсутствия поля в проводящем цилиндре
на его поверхности должно быть распределение (1.33) (М 1.24).
Отметим, что поле на поверхности цилиндра в плоскости симмет-
рии (О = 0) увеличивается до 2Е, а при О = я/2 равно нулю. Силовые
линии подходят по нормали к поверхности цилиндра.
По аналогии с диполем можно рассмотреть систему двух разно-
именно заряженных (с одинаковым абсолютным значением заряда
на единицу длины) бесконечных прямолинейных нитей, находящихся
на очень близком расстоянии. В соответствии с (1.12) и (1.16), обо-
значая заряд на единицу длины нити ~, имеем для напряженности
поля Е = 2т/г. Если нити находятся на расстоянии 1, то можно вве-
сти вектор р = ~1, направленный от отрицательно заряженной к
положительно заряженной нити и являющийся аналогом дипольно-
го момента. Используя рис. 1.3 вместо (1.7), получаем

2. ПОТЕНЦИАЛ.
МЕТОД ЭЛЕКТРИЧЕСКИХ ИЗОБРАЖЕНИЙ
При изучении механики были введены понятия «работа» и «по-
тенциальная энергия». Работа вЂ” это скалярное произведение силы
на перемещение (работу совершает только сила, направленная по
перемещению)
ИА = РЛ = ГН сов 0 = Гйг,
(2.1)
где Нг вЂ” проекция перемещения Л на направление силы Е Куло-
новские силы, так же как и гравитационные, зависят только от ко-
ординат. Работа в поле сил (2.1) связана с перемещением точечного
заряда д, в поле неподвижного точечного заряда д, из точки 1 в
точку 2, которые определяются расстояниями г, и г от заряда д„
(2.2)
Силы, зависящие только от координат, называются консерва-
тивными, или потенциальными. Работа не зависит от формы пути,
и по замкнутому контуру она равна нулю. Величина гг называется
потенциальной энергией. Для малых перемещений
(2.3)
ЫА = вЂ” НК
Рассмотрим две одинаковые и одинаково заряженные капли не-
сжимаемой проводящей жидкости, находящиеся на большом (бес-
конечном) расстоянии друг от друга. Заряд, радиус и масса каждой
капли равны соответственно д, г и и. Найдем, какую минимальную
скорость ~~ вдоль прямой, соединяющей их центры, надо сообщить
каждой капле, чтобы они стали двигаться навстречу друг другу и
при столкновении соединились в одну, не учитывая поверхностное
натяжение и колебания формы (Ж 2.1). Когда капли соприкоснут-
ся, их потенциальная энергия достигнет величины
(
2д
2г
28

При СЛИЯНИИ ИХ ПОТСНЦИЗЛЬНЗЯ ЭНЕРГИЯ СТЗНОВИТСЯ равной
2 21
и/2 = ЦЁ.
п
где радиус Г] ОПРСДСЛЯСТСЯ ИЗ УСЛОВИЯ НССЖИМЗСМОСТИ ЖИДКОСТИ,
9
т. е. сохранения объема 113 = 2г3. Увеличение потенциальной энер-
гии происходит за счет имевшейся при соприкосновении капель
кинетической энергии
2тП/2
щ _ щ = _Ть.
В результате
2:22:43 _ 2тц2 _ _ 2 25/3
2 — 2 + И/ — И/д — 4 т.
Отсюда находим И).
Для характеристики поля электрического заряда, кроме введен-
ной ранее напряженности поля (1.3), вводится потенциал. Это рабо-
та, которую совершает поле при удалении из данной точки на бес-
конечно большое расстояние единичного точечного (пробного) за-
ряда. Из (2.2) находим изменение потенциала с расстоянием от
точечного заряда с]
41180!‘
‹р(г) = г; {ф (г) = 4-й (2.4)
Потенциал электрического поля можно определить и как работу
внешней силы (противоположной кулоновской) по перемещению
единичного пробного заряда из бесконечности, где поле отсутству-
ет, в данную точку поля.
Из суперпозиции полей следует сложение потенциалов в точке
на расстояниях г, от точечных зарядов 4,:
(р = ЕЁ. (25)
п
‚=1 Й
Связь потенциала с напряженностью поля находим из (2.1)
с1ср = —Е‹1| (2.6)
и, следовательно,
2 2
‹р‚-‹р2=[вал=]дд1.
1 1
29

В соответствии с (2.4) и потенциальностью поля получаем для
замкнутой траектории в электростатике
$ЕЛ =0.
(2.2)
Таким образом, циркуляция вектора напряженности в статичес-
ком электрическом поле равна нулю.
Приведем пример, когда возникающая разность потенциалов не
успевает выровняться. Оценим разность потенциалов У между го-
ловной и хвостовой частями стального керна бронебойного снаря-
да, возникающую вследствие его торможения в преграде. Считаем,
что керн длиной А = 25 см потерял скорость и = 1000 м/с, пробив
броню толщиной Н = 5 см (М 2.8). Обозначая замедление скорости
при торможении а, массу электрона т и заряд его е, для силы инер-
ции, действующей на электрон, получаем Г = та. Это приводит к
возникновению электрического поля Е = иа/е и разности потенци-
алов на концах керна У = Ей = таА/е. Предполагая, что вся кине-
тическая энергия снаряда тратится на работу на пути, равном тол-
щине брони, получаем
ИО
2
вЂ” = РН = шаН.
2
Подставляя это в выражение для разности потенциалов, имеем
У = вЂ” ЦеН = 14 мкВ.
030
2
Из (2.6) следует связь между напряженностью поля и потенциа-
лом в дифференциальном виде
дф
Е, = вЂ” вЂ”.
д1
Здесь производная от скаляра берется по направлению 1 и называет-
ся градиентом. В декартовых координатах вектор напряженности поля
можно представить
Е = вЂ” вЂ” 1+ вЂ” 1+ вЂ” Ы~ = вЂ” дгайд = -9д.
др. др. др
дх ду д~
(2.8)
Обозначение ~7 называется оператором градиента, или набла.
Поверхность, на которой потенциал постоянен, называется поверх-
ностью уровня, или эквипотенциальной поверхностью. Линии, пер-
пендикулярные к этим поверхностям, называются линиями градиен-
та и совпадают с силовыми линиями. Вдоль них происходит наи-
большее изменение ~р.
30

Найдем для цилиндрического (диаметром 1)) пучка частиц (это
может быть дейтрон, у которого заряд равен заряду протона, а масса
на нейтрон больше) с кинетической энергией И’ и силой тока в
пучке 1 (с равномерной плотностью по сечению пучка 1) напряжен-
ность электрического поля Е на поверхности и разность потенциа-
лов П между его границей и осью симметрии (Мг 2.9). Вводя плот-
ность зарядов р, получаем для плотности тока
41
°= у=_‚
1 р 1:02
Где
2и/ “2
т) =
ч
Из теоремы Гаусса (1.12) находим напряженность электрического
поля внутри пучка Е 2пг = 4лрпг2 и, следовательно, Е (г) = 2прг для
г 5 0/2. На поверхности пучка
41
Е = ——.
И)
Для разности потенциалов имеем
0/2
Н = [2пргс1г = 1:02 В =
О 4
Внутри металлических (и вообще проводящих) тел электроста-
тическое поле равно нулю и потенциал постоянен. Потенциал ме-
таллического заряженного шарика радиусом К можно вычислить в
его центре, используя (2.5). При г 2 К потенциал описывается (2.4).
Если заряд равен а, то потенциал в центре — ср = 4/12.
Рассмотрим систему из трех одинаковых металлических шари-
ков радиусом г, расстояния между которыми одинаковы и равны а
(очевидно, что они находятся в вершинах равностороннего треу-
гольника), и удаленный заряженный проводник, потенциал кото-
рого неизвестен (ф), но поддерживается постоянным. Поочередно
шарики соединяются проводом с удаленным проводником. Найдем
заряд на шарике, который присоединялся последним ((13), если на
двух присоединявшихся ранее оказались заряды 41 и (12 (Не 2.46).
Для первого шарика после присоединения к удаленному заряжен-
ному проводнику имеем (р = 41/12 Для второго шарика полный по-
тенциал (р складывается из потенциала от полученного в результа-
32
1
у.

ТС ПОДСОСДИНСНИЯ СОбСТВСННОГО заряда 42 И на-
ВСДСННОГО ОТ ПЕРВОГО заряда
$41.
г а
Ф
Для третьего шарика
= Ё + Д + Ё_
а а
Из этих трех уравнений находим
Ф
Рис. 2.2
= а
‘11 .
Найдем потенциал диполя с дипольным моментом р = 411. Ис-
пользуя рис. 2.2 и суперпозицию (2.5), имеем
43
"2 П Ч’2 Г2 Г2 ГЗ ,
_. р‘
{Ф 4118073}
Воспользуемся этой формулой, чтобы найти, на какое макси-
мальное расстояние Ь удалится Эквипотенциальная поверхность от
плоского заряженного конденсатора (расстояние между пластинами И,
площадь пластин З), если внутри конденсатора она проходит на
расстоянии 599/1/ 1200 от одной из пластин (Не 2.52). Обозначая раз-
ность потенциалов между пластинами сро и учитывая, что потенциал
равен нулю на половине расстояния между пластинами, находим
для данной эквипотенциальной поверхности
Ф=Ч(1 1)=Чц—г2 =4/со36=рсо$6=рг_
(2.14)
_ ‘Ро
Ф 1200‘
Поле вдали от конденсатора будет соответствовать полю диполя,
заряд которого равен заряду пластин, а расстояние между зарядами —
расстоянию между пластинами
ЕБ/т 5
р-с1/1-о5/2-П-ф0д.
Используя (2.14), получаем
1/2 1/2
д = (Е) =1о(ё) „
41: п:
33

‘Р А По известному распределению напря-
—<1/К женности поля с помощью (2.6) можно
(„д найти распределение потенциала.
° При равномерном распределении за-
ряда внутри шара радиусом К изменение
О к ‚ напряженности поля показано на рис. 1.6.
РИФ 2.3 При г2 К поле описывается (1.3)‚ и с
помощью (2.6) получаем (2.4). Внутри
шара поле описывается (1.14). Интегрируя, с учетом полученного
потенциала на поверхности шара, имеем
2
3
На рис. 2.3 показано распределение потенциала.
Для заряженного металлического шара, окруженного концент-
рической металлической незаряженной оболочкой, распределение
напряженности поля показано на рис. 1.7. На рис. 2.4 приведено
распределение потенциала (Не 2.3), полученное с помощью (2.6).
Потенциал оболочки равен
пр(3К2 42). (215)
_2
Ф кв.
Потенциал шара
1 1 1
= — - — + — .
Ф‘ ее к2 к)
В случае заземленной оболочки (потенциал ее равен нулю) рас-
пределение потенциала показано на рис. 2.4 пунктиром. В этом слу-
чае потенциал шара
ФН
34

В металлической оболочке любой формы в электростатике все-
гда поле равно нулю, и внешнее и внутреннее поля независимы.
Внутреннее поле не будет меняться, если снаружи подносить заря-
женный проводник. Это называется электростатической экраниров-
кой. Перемещение зарядов внутри металлической оболочки будет
изменять поле внутри, но не будет изменять снаружи (Мг 2.2).
Заряд на сферической металлической оболочке располагается на
внешней поверхности. Внутри поверхности поля нет. Потенциал ср
поверхности и всей оболочки определяется зарядом О и внешним
радиусом К:
Ф = 2-
К
Если незаряженный металлический шарик радиусом г, располо-
женный достаточно далеко, чтобы можно было не рассматривать
индукционные явления (перераспределение зарядов), соединить
металлическим проводом с заряженной оболочкой (рис. 2.5), то
происходит перемещение зарядов и выравнивание потенциалов шари-
ка и оболочки. Движение зарядов происходит благодаря разности
потенциалов даже в случае, если проводник через малое отверстие
присоединяется к внутренней поверхности оболочки, где зарядов нет.
После перемещения зарядов на шарике появляется заряд с], а на обо-
лочке остается (О — 4). Заряд с] находится из равенства потенциалов
(2-4
К
Поле от двух зарядов с; и —с1 можно вычислить, используя (1.3) и
(2.4). На рис. 2.6 показаны эти заряды, находящиеся на оси х сим-
метрично относительно оси у на расстоянии друг от друга 211. Кар-
тина поля симметрична относительно оси х. Из (2.4) следует, что на
Е:
Г
Рис. 2.5 Рис. 2.6
3*
35

плоскости, проходящей через ось у и перпендикулярной оси х, по-
тенциал равен нулю. Из (1.4) следует, что в плоскости нулевого по-
тенциала напряженность поля перпендикулярна этой плоскости.
Вводя угол 0 из условия сов 0 = Ь/г,, получаем изменение напряжен-
ности поля вдоль оси у (линии нулевого потенциала)
3
со~ 0
~2
(2.16)
Уравнения, описывающие положение силовых линий, можно
находить, используя дифференциальные связи. В декартовых коор-
динатах они имеют вид (1.4)
~у
Е„ Е Е,
(2.17)
где Шх, с1у и с1~ вЂ” изменения декартовых координат вдоль силовой
линии; Е„, Е,, и Е, вЂ” декартовы компоненты вектора напряженности
электрического поля. Решение этих уравнений громоздкая проце-
дура. Качественно ход силовых линий можно получить, зная, на-
пример, в данном случае, что из точки линии выходят симметрично
во все стороны, а на линии нулевого потенциала параллельны оси х.
Пунктиром, для примера, показаны на рис. 2.6 две силовые линии
поля.
Важным следствием полученной картины поля является то, что
при расположении заряда на расстоянии Ь от проводящей беско-
нечной плоскости в области положительных значений х возникает
такая же картина, как для двух зарядов. Если поля одинаковы, то и
воздействие проводящей поверхности на заряд д будет таким же,
как воздействие от заряда вЂ” д, помещенного симметрично относи-
тельно границы проводящей плоскости. Поэтому для нахождения
картины поля и сил взаимодействия можно заменить проводящую
плоскость зарядом-изображением « вЂ” О», расположенным симметрич-
но заряду д относительно положения проводящей плоскости. Метод,
использующий такую замену, называется методом электрических изоб-
ражений. Сила притяжения заряда к бесконечной проводящей плос-
кости равна
г г
(2Ы 4кко (2Ы ~
(2.18)
Если между зарядами Д, и О, было расстояние Л и между ними
посередине вставили перпендикулярно линии их соединяющей
36

бесконечную металлическую пластину толщиной К/2, то силы,
притягивающие каждый из этих зарядов, определяются по (2.18),
где 11 = К/4 (Не 2.12).
Для примера найдем напряженность поля в точке А (рис. 2.7),
если заряд с; находится на расстоянии 11 от проводящей бесконечной
плоскости (Мг 2.10). Из (1.3)
5:1; Е=_Ё1_‚
' и? 5112
ИЗ СООТВСТСТВУЮЩСГО треугольника
1
сове = —.
45
Величину напряженности определяем ПО теореме КОСИНУСОВ
52 = Е} + Е; - 215,5, сове.
Получаем
26 - ъ/З
Е = 4:7.
5/2
Наклон к горизонтали вектора Е (угол В) находим тапоке из тео-
ремы косинусов.
На рис. 2.8 показаны два одинаковых шарика массой т с заряда-
ми О, подвешенных на одинаковых нитях над горизонтальной ме-
таллической заземленной плитой на высоте И и соединенных ни-
тью длиной 1. Найдем натяжение нитей, если радиусы шариков
7%7
Рис. 2.7 Рис. 2.8
37

малы по сравнению с /1 и 1, которые значительно меньше размеров
плиты (Мг 2.13). Для получения нулевого потенциала на плите нуж-
но ввести два симметрично расположенных отрицательных заряда
(—О), как показано на рис. 2.8. Складывая силы, действующие на
заряженные шарики, получаем для натяжения горизонтальной нити
Е = Р, — 13 сов 6, вертикальной РВ = т3 + Р, + 173 51116. Здесь угол 6
определяется соотношением
2 2 2
к 6 - 2,1 — О Г — О — О
8 - —› 1 - ‘т, 2 — %‚
1 1 (м)
3 ‘ П.
12 + 4/12
Распределение плотности отрицательного заряда, наводимого на
проводящей плоскости зарядом 4, находящемся на расстоянии 11 от
нее, определяется теоремой Гаусса Е = 4110 и (2.16) (Не 2.11)
з
о = —с1 сов 29. (2.19)
21:}:
Угол 9 показан на рис. 2.6.
Интегрируя по всей плоскости, получаем, что полный индуци-
рованный заряд равен +4. Плотность индуцированного заряда на
оси симметрии (6 = О) равна
_ _ Ч
2пИ2
Если известно, что одна из силовых линий, идущая от точечного
заряда 6], НЗХОДЯЩСГОСЯ на ВЫСОТС 11 над бССКОНСЧНОЙ МСТЗЛЛИЧССКОЙ
ПЛЗСТИНОЙ (потенциал равен НУЛЮ), ПРИХОДИТ на ПОВЕРХНОСТЬ ПЛЗС-
тины на расстоянии Ь = ЙЛ от точки, над которой находится заряд,
то можно определить, под каким углом к горизонту эта силовая
линия выходит из заряда (М) 2.50). Чтобы вос-
пользоваться теоремой Гаусса для потоков векто-
ра напряженности поля, выберем поверхности,
через которые удобно вычислять поток. Сечения
этих поверхностей показаны на рис. 2.9. Через
поверхность, образованную силовыми линиями,
потока нет. Поле у поверхности пластины нахо-
2412
3/2
(х2 + #2)
числяем соответствующий поток. Поток через
Рис. 2.9 часть сферической поверхности у заряда опреде-
дим методом изображений (Е = и вы-
38

ляетсявеличиной заряда (4) и соответствующим телесным углом ($2).
Таким образом, используя теорему Гаусса (1.12), получаем
Н?
0 (х2 +112)
Отсюда находим (2 = 2л, т. е. силовые линии от заряда идут
горизонтально.
Рассмотрим похожую ситуацию для цилиндрического случая.
Длинный тонкий провод, имеющий заряд на единицу длины А, про-
ходит параллельно горизонтальной металлической поверхности на
высоте И. Поле находим, используя провод-изображение, имеющий
заряд на единицу длины —А, находящийся с другой стороны поверх-
ности на расстоянии 11 и обеспечивающий условие на металли-
ческой поверхности (см. рис. 2.9). Найдем, на каком расстоянии
от точки на плоскости под проводом (начало координат) прихо-
дит на плоскость силовая линия, уходящая от провода горизон-
тально (М: 2.51). Поток вектора напряженности поля, идущий от
провода между силовой линией и осью у, представляет четвертую
часть общего потока, т. е. равен п)». На оси х напряженность поля
(1.16) от двух проводов
2›„ 2;: = 4/0,
0:2 + И)!” (и? +х2)1/2 “2 + х?
Поток этого вектора при изменении х от О до Ь должен равняться
Ь
их = 41111 7457.
о 11 + х
Вводя обозначение х/Ь = 13 ос и интегрируя, получаем для грани-
цы потока ос = п/4. Это соответствует Ь = 11.
Найдем плотность индуцированного заряда в горизонтальном
листе металла под вертикально расположенным равномерно заря-
женным (полный заряд 0) тонким стержнем длиной 1, нижний ко-
нец которого находится от листа на расстоянии Н (М 2.17). Обозна-
чая вертикальное расстояние от листа у и пользуясь суперпозицией
для напряженности поля, находим
О = _Н]_+1 А — а
н 421103 ——2ПН(Н+[).
39

Сила отрицательная, поэтому диполь притягивается. Работа вне-
шних сил для отодвигания диполя от пластинки от расстояния 1,1 до
расстояния Ь2 при этом положительна и равна
А: _ГРс1х=%р2————1_ЦЗ/ЬЁ.
д, 51
Двугранный угол образуется при пересечении плоскостей. Это
позволяет применить для двугранных углов методы, использованные
для плоскостей. Найдем силу, действующую на точечный заряд (1,
помещенный на биссектрисе прямого двугранного угла между дву-
мя проводящими плоскостями (Ме 2.14). На рис. 2.11 показаны за-
ряды, с помощью которых обеспечивается нулевой потенциал на
плоскостях, которые образуют двугранный угол. Абсолютные зна-
чения сил
2 2
Ч. Ч
“дэ `f
Суммарная сила направлена К вершине двугранного УГЛЗ
2
г = ЗЭ-(Л - 1).
2а 2
Найдем силу, действующую на диполь, находящийся на биссек-
трисе прямого двугранного угла, образованного двумя проводящими
плоскостями на расстоянии а от вершины (М9 2.16). На рис. 2.12
показаны диполь в точке А на биссектрисе угла и диполи электри-
Рис. 2.12
41

ческих отображений в точках В, С и 1), которые обеспечивают нуле-
вые потенциалы на плоскостях, образующих прямой двугранный
угол. Напряженности поля от диполей находим по (1.9). От дипо-
лей в В и В две составляющие по р и по г. По направлению р в
сумме получаем ноль. Для удобства введем расстояние от точки С
до точки А х = 2а. Тогда расстояние от точек В и В до точки А равны
х/х/Ё. Напряженности поля Ед, и Ед, одинаковы по абсолютной ве-
личине и дают в сумме (геометрической)
Едд =6Л-Ё-.
Напряженность поля в точке А от диполя в точке С
Суммарная напряженность ПОЛЯ направлена К ВСРШИНС УГЛЗ
3Л-1
Действие поля на диполь определяется (1.11)
дв 3Л-1 3
’=Р5;=‘6Р2_;Г=5
23Л-1
р-т-
а
Рассмотрим три концентрические бес-
конечно тонкие металлические сферы с
радиусами К, < К, < Кз (рис. 2.13). Най-
дем распределение напряженности поля
и потенциала, если крайние сферы зазем-
лены (потенциал равен нулю), а на сред-
ней находится заряд О (М 1.11).
Так как заряженная сфера при от-
сутствии заземления на крайних сферах
создает на них потенциалы, отличные
от нуля, то при заземлении появятся за-
ряды, которые обозначим на внутренней
сфере О], а на внешней 92. Используя
суперпозицию (сложение потенциалов)
и то, что для заряженной сферы (ради-
Рис. 2.13 ус К, заряд О) внутри потенциал посто-
42

янек и равен О/Л, а снаружи падает как О/г, получаем из условия
заземления:
на внутренней сфере
0= О + 0+02
Я1 Яг Я3
на внешней сфере
Отсюда находим
О! =-0
~3/~2
02 = -0-0!.
~3/~!
Наведенные заряды отрицательные. Напряженности поля:
если 0<г<Я! и Я3<г<
Е= вЂ” О,, если Я,<г<Л„'
~3/~2
г2 1 вЂ” Я2/Я!
1 вЂ” Я ! /Я2
(1 !~ ! /~ 3 )
ЕСЛИ ~2 < Г ~3
На трех концентрических тонких металлических сферах радиу-
сами Л! < Л2 < Л„находящихся в вакууме, имеются соответственно
заряды О„О2 и О3. Найдем изменение потенциала в некоторой точ-
ке между первой и второй сферами на расстоянии г от их центра в
результате замыкания накоротко второй и третьей сфер (Мо 2.4). До
соединения потенциал определяется суперпозицией от трех зарядов
1~! + 1~2 + О3
91 =
Яг Я3
После соединения второй и третьей сфер у них будет одинако-
вый потенциал, поэтому напряженность поля между ними должна
равняться нулю. Следовательно, на второй сфере находится заряд,
противоположный заряду на первой сфере ( вЂ” Д!), а на третьейвЂ”
заряд, равный сумме всех зарядов О! + Д2 + 03. Суперпозиция дает
6 й 6+~2+О3
'Рг= я +
43

Изменение потенциала равно
1 1
92 ~! (9 +1~2) д д
На рис. 1.10 показано изменение напряженности поля в плоском
слое с постоянной плотностью заряда. Если расстояние отсчитывать от
одного края слоя толщины Ь, то для напряженности поля получаем
Е=4жр х вЂ” вЂ”.
Ь
2
Если этот слой поместить между двумя тонкими металлически-
ми пластинами (обкладками), образующими плоский конденсатор,
в котором одна обкладка заземлена (нулевой потенциал), а вторая
имеет потенциал до, то к напряженности поля добавляется постоян-
ная напряженность у /Ь. Постоянство напряженности между метал-
лическими пластинами следует из плоской картины и равномерно-
го распределения зарядов на пластинах. Таким образом, напряжен-
ность поля в конденсаторе
(ро
Е =4яр х вЂ” вЂ” вЂ” вЂ”.
2 Ь
Используя (2.6), получаем (М 2.5):
д(х) = вЂ” "+2ярЬ х вЂ” 2ярх .
Ь
Найдем, какой должна быть плотность объемного заряда (р) рав-
номерно распределенного между пластинами плоского конденсато-
ра (расстояние между пластинами Ь), которая получается, напри-
мер, при распространении равномерного потока электронов внутри
конденсатора параллельно пластинам, чтобы потенциал и напряжен-
ность поля на одной пластине были равны нулю, а на другой потен-
циал был равен <ро (М 2.б). Из (2.11) для плоского случая имеем
д <р
вЂ” = -4яр.
дх
Дважды интегрируя, получаем
(р = вЂ” 2ярх'+ С,х+ С.
Из условия при х = Ь имеем
<р = <ро = вЂ” 2ярЬ + С,Ь + С„

прих=0
<р=о=с,; Е=-%=-4лр.о+с‚ =о.
х
Откуда
= —;ро
2пЬ°
Разность потенциалов между обкладками цилиндрического кон-
денсатора (внутренний радиус 122, внешний радиус К д), между кото-
рыми находится заряд с постояннои объемнои плотностью р, мож-
но найти (Мг 2.7), используя (2.12) для потенциала
1 Щгдф/дг) _
г ф‘ _
Дважды интегрируя, получаем
—4пр.
‹р= С1пг+ С, —прг2.
Константы определяются, если задано, что при г = К, потенциал
‹р = (ро, а при г = К, потенциал ‹р = О.
Найдем поверхность нулевого потенциала для двух разноимен-
ных зарядов с; и —с1/п (п > 1) (Не 2.19). На рис. 2.14 изображены
заряды. Ось х, проходящая через них, является осью симметрии кар-
тины поля. Ось у проводим через точку расположения меньшего по
абсолютной величине заряда перпендикулярно х. Найдем линию
пересечения плоскости (х, у) с поверхностью нулевого потенциала.
Обозначая расстояния от зарядов до произвольной точки с нулевым
потенциалом г, и г2, находим
1 _
Ф=О=Ф] +Ф2 :—Ч.Ш_.’ДЁ_
Откуда следует, что г, = пгд. у“
Из рис. 2.14 находим (ху)
ц2=х2+у2; г22=(1—х)2+у2. к ‚1 ‚2 д
Отсюда ч
Их’ + у’) = (1 — х)2 + у?
ш
|
=|
\
Щ!
Окончательно < д — =
(х+ 1 )2+у2=( п’ т. (2.20)
„2-1 „2-1 Рис. 2.14
17
45

Это окружность радиусом
к = "’ (2.21)
п2—|.
Центр ее находится на расстоянии ОТ МСНЬШСГО заряда
1 122
И на расстоянии ОТ бОЛЬШСГО заряда
2121
Ь=н+1= 2 =пК. (2.23)
п—1
Получаем ПОЛСЗНОС СООТНОШСНИС
п:
=г|>ь
(2.24)
Ы:-
Вычислим силу, действующую между заземленным металличес-
ким шаром (потенциал равен нулю) и зарядом ((1), расположенным
от центра шара на расстоянии Ь. Воспользуемся тем, что поле вокруг
заряда будет таким же, как от этого заряда (а) и заряда-изображения
(-—с1/п), находящегося на расстоянии 1 от заряда с; (см. рис. 2.14).
Пользуясь законом Кулона (1.1), а также (2.24), (2.23) и (2.22), нахо-
дим силу, действующую на заряд 4 (М) 2.20):
2
Р = -кЬ—1—-. (2.25)
(В - 1292
ЗНЗК МИНУС ГОВОРИТ О притяжении заряда К заземленному шару.
Напряженность ПОЛЯ В ТОЧКС А равна
_Ч 1+ ЦК
А (Ь + К)2 ’
а в точке В
а К/Ь
в = *"т т Ч ———'т-
(Ь + К) (к + К2/Ь)
Для получения плотности зарядов в данных точках напряженно-
сти надо разделить на 41: (М9 2.42).
Если шар не заземлен и заряд его равен нулю, то можно воспользо-
ваться суперпозицией полученного ранее поля и поля от заряда а/п,
46

расположенного в точке, соответствующей центру шара. Заряд в этой
точке дает на сфере, соответствующей поверхности шара, постоян-
ный потенциал, который получаем также, если этот заряд равно-
мерно расположить на поверхности сферы:
Ч Ч
9= вЂ” =вЂ”
пЯ С
(2.26)
Это важный результат, заключающийся в том, что незаряжен-
ный проводящий шар в поле заряда имеет потенциал, который со-
здавался бы в точке, соответствующей центру шара, в его отсут-
ствии (теорема о среднем).
Внутри сферы сумма зарядов равна нулю. Сила, действующая на
заряд д от зарядов внутри сферы, равна (№ 2.20)
(2.27)
Если на шаре еще имеется заряд вЂ” д (№ 2.40), то в выражении
для силы появится еще член вЂ” д2/А2 и
Если на шаре полный заряд О, то сила равна
д Я Д+ дЯ/А
А(А вЂ” Я /Е)
Отсюда, чтобы сила взаимодействия была равна нулю (№ 2.41),
заряд должен быть равен
Я с,'-(~,'- Я')'
(А2 вЂ” Я2) А
гЯ~ ~'~~ 1~и Я~~~ -Я ) 1 ч Я
А еЕ вЂ” Я 2е (А2 Я2) 2А вЂ” Я
47
Для вычисления работы по удалению заряда д на бесконечность
(№ 2.21) надо проинтегрировать полученные выражения, учитывая,
что внешняя сила имеет противоположный знак.
В случае заземленного шара (2.25)

В случае незаряженного шара (2.27)
2 °° ш; 1 42123
Аг”д+ЧКГ-г=5"гЧ——г=
„Ь Ь(Ь-к)
Если внутри незаряженной металличес-
кой оболочки (внутренний радиус г, вне-
шний К) в точке А на расстоянии ОА = 11
от ее центра находится сосредоточенный
РИС- 2-15 заряд с; (рис. 2.15) и требуется вычислить
потенциал на внутренней поверхности обо-
лочки, то надо иметь в виду, что на внутреннюю поверхность обо-
лочки притягивается заряд, равный —с1, но неравномерно распреде-
ленный, а на внешней поверхности оболочки заряд, равный 4, рас-
пределяется равномерно с поверхностной плотностью
о = %‚
41:12
так как поле в проводящей оболочке равно нулю и влияние внут-
ренних зарядов отсутствует. Потенциал оболочки в сферически сим-
метричном поле (р = 4/12. Такой же и в точках В и С (М 2.22).
Поле внутри оболочки найдем, пользуясь методом электрических
изображений. Найдем вначале, какой заряд О и на каком расстоя-
нии х от сферической поверхности, находящейся на месте внутрен-
ней поверхности оболочки (см. рис. 2.15), надо поместить, чтобы
потенциал на этой сфере был постоянен и равен нулю. Можно вос-
пользоваться приведенными ранее формулами, а можно записать
соотношения для равенства потенциалов нулю в точках В и С
.д;+2=о Ч + 9
х 9
г — И г + 12 х + 2г =
Отсюда
г — Ь ‚ _ __ С
х - г 11 , О — с] И.
Напряженность поля в точке В от двух зарядов равна
_ 4(1 + /1/г)
В 1 а
(г - н?
Напряженность поля от тех же зарядов в точке С
=ч0-ИЛ
(г + Ь)2
48

Для получения распределения плотности зарядов надо эти вели-
чины разделить на 41:. Изменения потенциала на сферической повер-
хности на постоянную величину не изменяет картину поля внутри и
распределение заряда по поверхности. Если потенциал поверхности
не нулевой, а ‹р0 = 40/23 то потенциал, например, точки В равен
Чо Ч О
=—+——+—.
ФВ г г-Ь х
Получаем ТО Же Самое уравнение, ЧТО И раньше:
Ч О 40 О
г—/2+Ё=ФО—Т=
Рассмотрим теперь тонкостенную металлическую изолированную
сферу радиусом К с зарядом на ней (2 и зарядом 4 внутри нее на рас-
стоянии от центра, равном половине радиуса (рис. 2.16). Вне сферы
поле сферически симметрично и по теореме Гаусса (1.12) определя-
ется суммарным зарядом на сфере и внутри ее. На внешней поверх-
ности сферы напряженность поля и плотность заряда равны (Не 2.30)
„от; О=[_=0+‹1_
к 41: 41:18
Для обеспечения нулевого (и вообще постоянного) потенциала
на сфере надо использовать заряд-изображение О, = —пс1 на рассто-
янии Ь = пК от центра сферы (2.23) и (2.24). Если заряд 4 находится
на середине радиуса, то п = 2, О] = —2с1 и Ь = 21%. Поэтому сила,
действующая на заряд с], равна
42 Ай
2-[1-2
(ь- т)’ 9 к"
Поле на внутренней поверхности сферы в точке А равно
ч Низ
Е (к/2)2 к2 кг
Заряд на сфере поля внутри не создает.
Поле внутри металлической обо-
лочки должно быть равно нулю. Это
обеспечивается плотностью заряда в
точке А, равной
Е 3:1 Ь
о = —— = — 2 .
4% 21:12 Рис. 2.16
4-2073 49

В точке В на внутренней поверхности поле равно
д 2д 2д
(Я+ Я/2)' ЗЯ' 9 Я'
Плотность отрицательного заряда в точке В на внутренней по-
верхности
Е д
О= вЂ” =
4 т~ 18~д2
Плотность на внешней поверхности в случае О = вЂ” 2д (М 2.31)
д вЂ” 2д д
4кЯ 4т~Я
При заземлении сферы плотности зарядов на внутренней повер-
хности в точках А и В не изменяются, а на внешней поверхности
плотность заряда должна быть равна нулю, так как потенциал такой
же, как на бесконечности, и нет поля.
Найдем потенциал р металлического шара радиусом Л с зарядом
на нем О, когда точечный заряд д помещен на расстоянии А от цен-
тра шара (М 2.23). Пользуясь суперпозицией для потенциала в цен-
тре шара, можно написать
Здесь суммируются потенциалы от зарядов Ло,. на поверхности шара.
Потенциал металлического шара такой же, как в центре.
Для нахождения потенциала сферической проводящей оболочки
(или полого металлического шара) от собственного заряда О и заряда д,
находящегося на расстоянии Е от центра оболочки, также можно
использовать суперпозицию теоремы о среднем (2.2б) и решение
для постоянного заряда на сферической поверхности. В случае за-
ряда д вне сферической поверхности потенциал на оболочке
Если же заряд д переместить через малое отверстие внутрь оболоч-
ки (М 2.25), то потенциал на ней определяется ее внешним радиу-
сом и по теореме Гаусса суммарным зарядом
Д+д
91 =
50

Поле вокруг заземленного металлического шара, когда на рас-
стоянии Ь от его центра находится заряд а, такое же, как от этого
заряда и заряда —с1/п, расположенного, как показано на рис. 2.14, и
определяемого (2.24)‚ Можно вычислить напряженность поля на
поверхности шара и найти распределение заряда, который в сумме
равен —с1/п. В случае изолированного незаряженного металлическо-
го шара картина распределения напряженности поля не изменится,
и распределение заряда по поверхности будет таким же, но в центре
надо расположить заряд с1/п, который обеспечивает суммарный ну-
левой заряд на шаре и приводит к появлению потенциала на нем.
Если этот шар заземлить, то на него притечет заряд —с1/п, чтобы
нейтрализовать заряд, создававший потенциал (Не 2.26).
Если в поле заряда а находится заземленная проводящая сфе-
ра, то, используя (2.23) и (2.24)‚ для напряженности поля в точке А
(см. рис. 2.14) имеем
_ ч с; _ ‹1(1+ ЦК)
’ 2 + 2 2 “ 2 '
(Ь-К) „(к-к/Ь) (Ь-К)
Обозначая напряженность в точке А при отсутствии проводящей
сферы
ЕА
= Ч
(Ь - 102
получаем для изменения напряженности при внесении заземленной
проводящей сферы (Не 2.27)
0
Ё : 1 + Ь_
Ед К
Аналогичным образом находим для точки В (см. рис. 2.14)
Ед д
— = 1 — —.
Ео К
Для незаряженной проводящей сферы ищем поле от трех зарядов
(в центр сферы, как это получено ранее, надо поместить заряд с1/п).
В этом случае
Ё: ‹3_5)Ё_&= ‹3 5)
во 4 1,50 4 +Ь`
Полученные ранее решения для сферической и плоской про-
водящих поверхностей можно использовать для решения задачи,
4* 5!

Рис. 2.18 Рис. 2.19
ними (Мг 2.28). На рис. 2.19 показаны заряды и расстояния. Пользу-
ясь тем, что для диполя 1<< Ь, имеем для заряда
412
Ь+1зак
Ь Ь д? Ь дг
ИДЛЯ
Тытыъ
Таким образом, система изображений состоит из диполя
= ч/Ш = ЕЁ
р! Ь 113
и заряда
41 =“-
Диполь р притягивается к диполю р] и заряду 41. Для вычисле-
ния силы притяжения надо воспользоваться (1.1О) и (1.7):
брр, + 241р = 2р2К1„(2К2+Ь2).
(Ь - к2/1.)4 (Ь - К2/Ь)3 (В - 1:27
Если проводящая сфера радиусом К изолирована и не заряжена
и диполь с моментом р = 41, находящийся от центра сферы на рас-
стоянии Ь и направленный перпендикулярно линии, идущей от цент-
ра сферы к центру диполя, то расположение зарядов-изображений
53

Рис. 2.20
будет таким, как показано на рис. 2.20. Заряды в центре сферы,
создающие потенциал, не показаны, так как в сумме равны нулю.
Величина зарядов с] определяется (2.24)
_ЗЁ д _Ё 1‚1_(1}+Ё)ш„д
Ч]"'Ь1› |_Ь1› - 4 "' э
1/2 1:2 к 122 123
11=Ё=1Ь)› Р1=Ч1’1=Ч:1(:)=Р(2)-
Поле диполя в перпендикулярном направлении (1.8) зависит
только от расстояния. Из (1.11) следует (Не 2.34)
_ ЭЕ _ (КУ 3р _ р2К3
_ р‘ Ё ц Ё Ё _ Е
Знак минус указывает на притяжение диполей.
Приближенное решение данной задачи (оценка) может быть
получено в предположении, что изолированная незаряженная про-
водящая сфера помещена в постоянное поле, равное полю диполя в
данном месте. В этом случае поляризация приводит к диполю с мо-
ментом (1.26) р, = К3Е. Поле определяется по ( 1.9).
В таком же приближении можно оценить силу взаимодействия
между двумя маленькими металлическими шариками радиусом К,
из которых один имеет заряд с], а второй не заряжен, в зависимости
от расстояния между ними Ь. Поле от заряда Е = 4/19 поляризует
незаряженный шарик, создавая дипольный момент
3
р = КЗ Е =
Ь
54

Поле этого диполя определяется (1.7) и действует на заряд. В ре-
зультате сила притяжения (№ 2.36)
г~'я'
Если к металлическому шарику радиусом Л, на котором медлен-
но повышается потенциал д (увеличивается заряд), на тонкой не-
проводящей нити длины 1» Л подвешен нейтральный металличес-
кий шарик массой т и радиусом г «Л, то при некотором потенци-
але он притянется к верхнему. Этот потенциал находим из равенства
силы притяжения весу нижнего шарика. Для верхнего шарика заряд
О = уЛ и поле вблизи нижнего шарика
дЯ
(~+ я)'
Это поле поляризует нижний шарик, создавая дипольный мо-
мент р = г'Е. При этом поле считаем однородным. Но сила, дей-
ствующая на диполь, определяется неоднородностью поля вЂ” про-
изводной
дЕ
д(
Используя (1.11), получаем
т= 3 (Фя)
" ((+я)'
Откуда находим 9 (№ 2.43).
Такую же схему решения можно применить, если эти шарики
находятся вне поля тяжести и не скреплены между собой, а мень-
шему сообщается начальная скорость в направлении от большего
шарика. Найдем величину этой скорости, чтобы меньший шарик
мог уйти на бесконечность (№ 2.44). Благодаря поляризации созда-
ется дипольный момент р = г'Е, где Е вЂ” поле заряженного шарика:
Используя (1.11), получаем
2г Д~
55

Для работы внешней силы получаем
°° 3‘ 2
А=[гс11=1——’9 4,
1 2 (’ + к)
которую надо приравнять ти2/2, чтобы найти нужную скорость
(Мг 2.44). а
Подобным образом можно рассмотреть устойчивое положение
Небольшого НСЗЗРЯЖЁННОГО МеТаЛЛиЧеСКоГо Шарика радиусом Г, КО-
ТОРЬЁЙ может смещаться ТОЛЬКО ВДОЛЬ Оси ТОНКОГО однородно Заря‘
женного кольца радиусом К. Обозначая расстояние вдоль оси кольца
ОТ еГо Плоскости х И ПОЛНЬЁЙ Заряд Кольца О, Получаем ДЛЯ Напря‘
ЖеННОСТи ПОЛЯ ВДОЛЬ ОСИ
_ Ох
‘ 3/2 °
(122 + 2:2)
ЭТО ПОЛЕ ПОЛЯРИЗУСТ шарик, СОЗДЗВЗЯ ДИПОЛЬНЫЙ МОМСНТ
р = г3Е. Условие равновесия —— равенство силы, действующей на
шарик, нулю:
дЕ
= -— = О.
Р р дх
Дифференцирование Е дает
дЕ _ 1:2 - 2х2
— ' "_——5Ё'
ах (К2 + х2)
При х = О равны нулю и поле, и дипольный момент, а производная —
положительна. Однако при малейшем отклонении возникает диполь-
ный момент, т. е. равновесие неустойчивое. Устойчивое равновесие
будет при равенстве производной нулю, т. е. при (Не 2.37)
К
х = 1*——.
21/2
Поле вне конденсатора на большом расстоянии г >> (.5`)‘/3 (5 —
площадь пластин конденсатора, которые считаем дисками) можно
приближенно описывать как поле диполя с моментом
57
Р|—Ч[—СИ—Ё1?‚
где с] — заряд конденсатора; 1—- РЗССТОЯНИВ МЕЖДУ пластинами; С —
СМКОСТЬ КОНДСНСЗТОРЭ; у — напряжение на конденсаторе.
56

Напряженность поля диполя (1.7)
2
Е = -3’1‚
Г
изменение поля диполя
ЁЁ = _3 . 2_&_
дг ‚-4
Если на оси конденсатора на большом расстоянии находится
проводящий незаряженный шарик радиусом К << г, то происходит
поляризация и создается дипольный момент, величину которого
вычисляем в предположении постоянства поля конденсатора вок-
руг шарика р, = КЗЕ. Силу вычисляем, используя (1.11) (Мг 2.53):
дЕ 123 123
Р: р2——=-12‚0Е—Т=-3$2у2т
д’ г 41: г
Рассмотрим случай, когда диполь с моментом = [помещен в
Р Ч
центр проводящей незаряженной сферы (рис. 2.21). Зарядь1-изо-
бражения т; и —пс1 каждый в паре с соответствующим зарядом
диполя создают постоянный потенциал на сфере. Суперпозиция
дает полное решение. Сумма зарядов в центре сферы, создающих
потенциал на сфере, равна нулю (поэтому на рис. 2.21 не показана).
Из (2.24) и (2.22)
212
Т
Поэтому поле от зарядов т; вокруг сферы можно считать однород-
ным и равным
>>1.
п:
>о|ь
"Ч Р
Е = Т =?.
Напряженности поля от диполя
в точках А и В определяются соот- в
ветственно (1.7) и (1.8). Суммарное
поле в точке А равно
т! -а р ч А -т1
— р _}Д о о
Е""Ё+Ё_к3’ к 1
вточке В(М 2.33):
Ев=Т-—'?=О.
К К Рис. 2.21

-‹1|+‹1 —п‚‹1 314 _Ч
Рис. 2.23 Рис. 2.24
сила действия заряда на диполь (отталкивание)
= 24р = 2р2К
2 Ь-й /12(1.—/2)3
Суммарная сила (М 2.35) (притяжение)
рыдал 2+н2/к2
34 “(1412/122)”
На рис. 2.24 показана система зарядов изображений аК/а и —с1К/а
для двух зарядов с] и —4‚ расположенных на расстоянии 2а друг от
друга, и незаряженной проводящей сферы радиусом К, находящейся
посередине между зарядами (Мз 2.29). Величины зарядов-изображе-
ний определяются (2.24), их расстояния от центра сферы — (2.22).
Так как сумма зарядов равна нулю, имеем незаряженную сферу.
При а >> К заряды-изображения действуют на заряды с] и —9 как
диполь с дипольным моментом
21234
р = ——»
а2
Воспользовавшись (1.7)‚ получаем изменение (увеличение) силы,
действующей между зарядами,
р=д
4а2
на
32
Ар=%1=4к54 ‚
а а
59

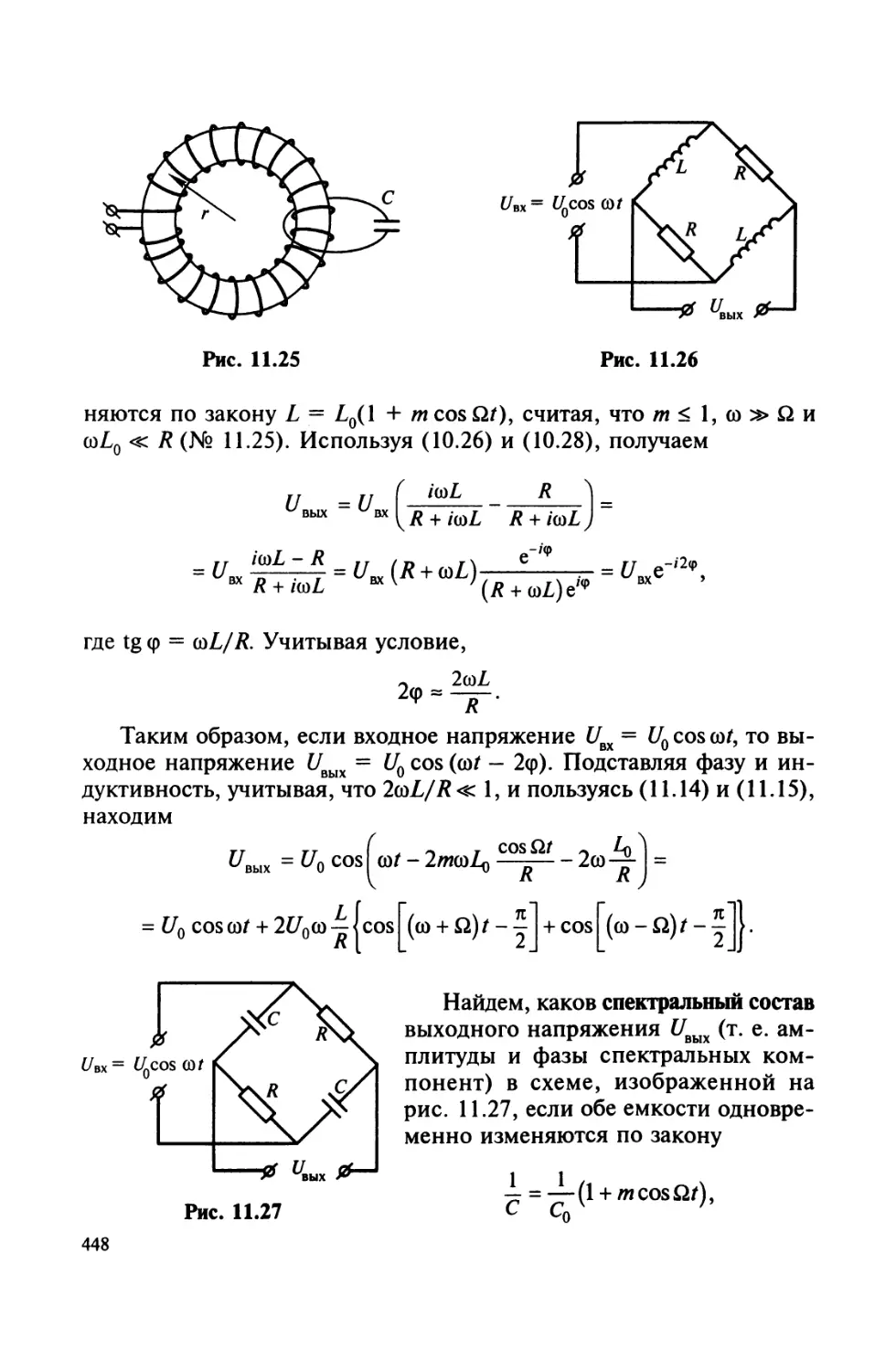
Рассмотрим систему двух параллельных бесконечно длинных
прямых нитей, находящихся на расстоянии 2а друг от друга и имею-
щих равномерные заряды противоположных знаков по абсолютной
величине равные х на единицу длины. Напряженность электричес-
кого поля на расстоянии г от заряженной прямой нити определяет-
ся (1.|6): Е = 2х/г. Между нитями действует сила притяжения, кото-
рая на единицу длины равна
2
Г=Ех=%—.
Отметим, что этим же способом можно вычислить силы и для раз-
ных зарядов на единицу длины. Из (2.8) и (2.10) для потенциала
получаем
(р = 2х|п г + фо. (2.28)
На рис. 2.25 показано сечение, перпендикулярное нитям. Ось х
проходит через нити, а ось у перпендикулярно к оси х через середи-
ну расстояния между нитями. Потенциал в точке с координатами
(х, у) равен
д.
\
ф = (р, +‹р2 = 2х1пц +‹р0 -2х|пг2 +‹р0 = 2х1п(%)+2‹р0.
2
Постоянное значение потенциала будет при
Г
4 = С = сопвт. (2.29)
"2
Значение С определяет различные линии постоянного потенци-
ала (сечение поверхностей равного потенциала). При С = 1 получа-
ем ось у. Для других значений С получаем
С2=ЦЁ_(“"")2+У2
г; _(а+х)2+у2.
Отсюда находим для сечения поверхностей равного потенциала
(2.3О)
у2+(х+аС2+1)2= 4а2С2 '
52 (с2-1)2
Это уравнение окружности.
Полученные результаты позволяют вычислить силу (на единицу
длины) взаимодействия между металлическим цилиндром радиусом г
60

_Х
г'йх| —7
Ч
Рис. 2.25 Рис. 2.26
и длинной тонкой проволочкой, расположенной на расстоянии К > г,
если на единице длины нити заряд х, а на единице длины цилиндра —х
(Не 2.45). Из (2.3О) находим положение и радиус для нашего метал-
лического цилиндра (линии равного потенциала). Центр сдвинут на
_ с2+1
с2-1
в сторону отрицательных иксов, а радиус равен
хн
С
г=2а .
с2-1
На рис. 2.26 показаны цилиндр и проволока (сечение в перпен-
дикулярной плоскости). Расстояние от центра цилиндра до прово-
локи К = а + х]. Так как поле вокруг цилиндра такое же, как от
проволочки на расстоянии —а, то сила взаимодействия между ци-
линдром и проволочками одна и та же. Из предыдущих соотноше-
ний получаем
2
0:51 и 2а=К(1-%].
г к
С помощью (1.16) получаем
г = 379: = ————2"2
2“ К(1— г2/К2).
Найдем, какую максимальную разность потенциалов можно под-
держивать между проводами бесконечной двухпроводной линии,
если напряженность пробоя воздуха Е = 30 кВ/см, диаметр прово-
дов 2а = 1 см, а расстояние между проводами Ь = 5 м (Мг 2.48).
Используя теорему Гаусса (1.12) для изолированного заряженного
цилиндра, как и в случае заряженной нити (1.16), получаем распре-
61

деление напряженности поля Е = 2~/г, где К вЂ” заряд на единицу
длины; г вЂ” расстояние от оси цилиндра. В случае двух противопо-
ложно заряженных цилиндров благодаря суперлозиции получаем на
линии, соединяющей их центры (расстояние х отсчитывается от оси
положительно заряженного цилиндра):
г~
= вЂ” +
Х О вЂ” Х
Исследуя эту зависимость, можно получить, что при х = Ь/2 она
имеет минимум. Таким образом максимальное значение напряжен-
ности поля на поверхности цилиндров равно
2КЬ
а(Ь вЂ” а)
Из (2.6) следует
О Ь
=2Е„а 1 вЂ” вЂ” 1п вЂ” вЂ” 1 =207 кВ.
а а
Заряд (д), находящийся в точке внешнего электрического поля с
потенциалом д, обладает энергией в этом поле, равной
(2.31)
Если в поле находятся два заряда +д и вЂ” д, образующие диполь
бесконечно малой длины 1, то энергия этих зарядов во внешнем
поле равна
где д и р' вЂ” потенциалы внешнего поля в полюсах диполя. С точно-
стью до величин второго порядка малости, учитывая (2.10),
(р = (р'+ вЂ” Р ( = ~р'+ 1ягад (р = ~р' вЂ” !Е.
д1
Поэтому
Ф'= вЂ” д!Е = вЂ” рЕ,
(2.32)
где р вЂ” момент диполя; Е вЂ” напряженность внешнего поля в месте
расположения диполя. В этом выражении не учитывается взаимная
энергия зарядов диполя, величина которой изменяется лишь при
изменении длины диполя 1.
62

Силы, действующие на диполь, представляют пару сил. Их мо-
мент определяется векторным произведением
.д .д д
7 =! вЂ” +] вЂ” + К вЂ”.
дх ду д~
(2.34)
Скалярным умножением р на ~1 получаем оператор
д д д
Ф)=р.вЂ” +л вЂ” +рвЂ”
" дх У ду ' д~
(2.35)
С помощью этого оператора можно обобщить формулу (1.11)
для силы, действующей на диполь,
Е = (рЧ)Е.
(2.36)
М = [!Р] = д[1Е] = [рЕ].
Используя сокращенное обозначение градиента в виде операто-
ра «набла».'

3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВЕЩЕСТВЕ.
ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ.
ЭНЕРГЕТИЧЕСКИЙ МЕТОД ВЫЧИСЛЕНИЯ
ПОНДЕРОМОТОРНЫХ СИЛ
Диэлектриками, или изоляторами, называются вещества, не прово-
дящие (или очень плохо проводящие) электрический ток. Имеющиеся
в них заряженные частицы могут под действием электрического поля
лишь смещаться (а не перемещаться свободно, как в проводниках).
Возникающая поляризация, как показывает опыт, пропорциональна
напряженности электрического поля, прикладываемого к диэлектри-
кам. Эго наблюдается и для веществ, у которых частицы, например
молекулы, обладают дипольными моментами (полярные диэлектри-
ки), но из-за хаотичности их направлений суммарный дипольный мо-
мент диэлектрика равен нулю, и появляется он только тогда, когда под
действием поля происходит выстраивание моментов в направлении
поля. Вектором поляризации (или поляризацией) Р называется суммар-
ный дипольный момент единицы объема диэлектрика
; ЛГ
( 1)
Возникающая в диэлектрике поляризация, как показывает опыт
при не очень больших напряженностях поля, пропорциональна при-
клады ваемому электрическому полю
(3.2)
Р = аЕ; (Р = еоаЕ).
64
Коэффициент пропорциональности называется поляризуемостью.
Отметим, что такая зависимость хорошо выполняется для изотроп-
ных вешеств. Для анизотропных веществ поляризуемость является
тензорной величиной и направления векторов Р и Е могут не со-
впадать. Отметим также, что поляризация может возникнуть и в
отсутствие электрического поля, например при механическом сжа-
тии (пьезоэффект).
При поляризации, несмотря на смещение, все заряды внутри
диэлектрика скомпенсированы, и только на границах остаются свя-

занные заряды. На рис. 3.1 показано сечение слоя
диэлектрика. Выделен объем А У с боковыми по-
верхностями, параллельными вектору поляриза-
ции Р, и торцевыми поверхностями площадью АЗ, _ С’
на которых плотность связанных зарядов о. Для ‚А у
дипольного момента этого объема имеем АЗ —0
РА у: оАШ. Ч В
Вводя угол В между нормалью к границе и
вектором Р, получаем
о = Рсоз [З = Рп = осЕд; {о = Р,’ = еоосЕп}. (3.3)
Для диэлектриков в дифференциальную теорему Гаусса (1.19)
необходимо включать и связанные заряды
Рис. 3.1
(Их/Е = 4пр+4пфоё`ё = 4пр—4пс11уР.
В общем для плотности связанных зарядов имеем
рев = —‹11у Р; {рев = —с11у Р}. (3.4)
Вектор электрической индукции (смещения) В вводится следую-
щим образом:
в = в + 4лР; {в = еоЕ + Р}. (35)
Вектор 1) является суммой различного рода физических вели-
чин: напряженности приложенного поля и поляризации единицы
объема диэлектрика, но использование его упрощает описание поля
в диэлектриках. В частности, для диэлектриков в дифференциаль-
ной теореме Гаусса (1.19) надо заменить вектор Е на 1) и учитывать
только свободные заряды
(Ну 1) = 4пр; {бйу В = р}. (3.6)
Соответственно для интегральной теоремы (1.12)
фраз =ф1›„с15 = 4114; {фраз = фцаз = 4}. (37)
Для равномерно заряженной пластины диэлектрика (с плотно-
стью заряда р) толщиной 2а получаем изменение В в зависимости
от расстояния от средней плоскости пластины х: внутри пластины
В = 41ърх, вне пластины постоянно и равно 1) = 4пра.
Для равномерно заряженного шара из диэлектрика (с плотнос-
тью заряда р) радиусом а в зависимости от расстояния от центра г:
5— 65

Потенциал сферы радиусом а, равномерно заряженной по поверх-
ности зарядом д:
вне сферы
Ч= вЂ” '
ЙГ
(3.13)
внутри сферы
%= вЂ”.
Для равномерно заряженной (плотность заряда р) пластины тол-
щиной 2а в зависимости от расстояния от средней плоскости х:
внутри пластины
х +а
ф =2яр +(р
Е
(3.14)
вне пластины
ах
у= вЂ” 4шр вЂ” +до при х >а;
Е
р =4пр вЂ” +до при х < а,
Е
где до вЂ” значение потенциала на средней плоскости.
Для бесконечного равномерно заряженного по объему цилиндра
(плотность заряда р) радиусом а в зависимости от расстояния от оси
цилиндра г
~р = вЂ” ~а вЂ” г ~+ до при г < а;
~Р~ 2
6
(3.15)
д= вЂ” 2 вЂ” а 1п вЂ” +до приг>а,
Е а
где до вЂ” значение потенциала на оси цилиндра.
Для бесконечной цилиндрической оболочки, равномерно заряжен-
ной с поверхностной плотностью а, в зависимости от расстояния до
оси оболочки
~р=до при г <а,
(3.16)
ЯО Г
у= вЂ” 2 вЂ” а1п вЂ” +у при г>а,
е а
где р вЂ” значение потенциала на оболочке.
5*
67

Введя обозначение а, = 4/6, можно для поля (3.1О) повторить все
выкладки, которые привели к формулам (2.2О)—(2.24)‚ и получить
обобщение теоремы о среднем (2.26) — потенциал проводящего шара
радиусом г, находящегося в поле заряда (на расстоянии Ь) в диэлек-
трической среде с диэлектрической проницаемостью е (Не 3.37):
_ 1
(р — ЕЬ . (3.17)
В электростатике было получено, что циркуляция электрическо-
го поля равна нулю (2.7):
фиат =фЕ‚а1 =о. (3.18)
Рассмотрим однородный изотропный диэлектрик с проницае-
мостью е, на плоской границе которого с вакуумом напряженность
электрического поля в вакууме равна ЕО и вектор Ед составляет угол 6
с нормалью к поверхности диэлектрика (рис. 3.2). Считая поле внут-
ри и вне диэлектрика однородным, найдем:
1) поток ФЕ вектора Е через сферу радиусом К с центром на
поверхности диэлектрика;
2) циркуляцию вектора В по прямоугольному контуру Г со сто-
ронами длиной 11 и 12, плоскость которого перпендикулярна к по-
верхности диэлектрика и параллельна вектору Ед (Мг 3.23).
Из (3.18) касательная к поверхности диэлектрика компонента
поля ЕО зйп 6 непрерывна на границе. Вследствие симметрии входя-
щий в сферу поток ее равен выходящему потоку. Нормальная ком-
понента поля ЕО сов 6 дает поток через поверхность сферы такой же,
как через ее диаметральное сечение. Из (3.7) следует сохранение
нормальной компоненты вектора электрической индукции
В = Еоп = еЕдп = ЕО сов 6.
Л
ОТСЮДЗ ДЛЯ НОРМЭЛЬНОЙ КОМПОНСНТЫ НЭПРЯЖСННОСТИ ЭЛЕКТРИ-
ЧССКОГО ПОЛЯ В ДИЭЛСКТРИКС имеем
ЕО СОЗЭ
Едп=Е0 8 '
д Поэтому поток вектора напряженнос-
----1 ‘2 ти электрического поля
А .
Касательная компонента вектора ин-
Рис. 3.2 дукции в вакууме равна касательной ком-

поненте напряженности поля ЕО зйп 9. В диэлектрике В, = еЕО зйп 6.
Поэтому циркуляция вектора электрической индукции (по контуру Г
из 11 и 12) равна
фваи = 1,5, 51п6(1 —е).
Г
Если в центре диэлектрического шара радиусом К с диэлектри-
ческой проницаемостью е, помещен точечный заряд с; и шар окру-
жен бесконечным диэлектриком с проницаемостью е, то на границе
диэлектриков появляются поляризационные заряды. Найдем их плот-
ность (Мз 3.22). Из (3.7) следует непрерывность В на границе. Из (3.8)
15:41.; „ф.
1 931122 2 82К2
Из (1.12) 4тсо = Е, - 15,. Откуда
Из (3.7) и (3.18) следует, что в плоских щелях (воздушных или
вакуумных, для которых диэлектрическая постоянная е = 1) напря-
женность электрического поля Ещ связана с напряженностью элек-
трического поля в диэлектрике (с диэлектрической проницаемос-
тью е) Ед следующим образом: в щели, параллельной полю, ЕЩ = Ед,
в щели, перпендикулярной полю, Ещ = еЕд. Аналогичным образом
связаны поля на границах диэлектрика в конденсаторах, частично
заполненных диэлектриком. Например, если плоский конденсатор
(две параллельные металлические пластины, имеющие противопо-
ложные заряды) частью опущен в диэлектрик так, что пластины
перпендикулярны поверхности диэлектрика, то поле в диэлектрике
равно полю в воздушной части конденсатора.
Используя (3.7) и (3.18), получаем, что при отсутствии на грани-
цах между диэлектриками свободных зарядов, при переходе через
границу сохраняются нормальные к границе ком-
поненты В и касательные к ней компоненты Е. д
На рис. 3.3 показано преломление силовой ли- 71 П
нии поля на границе двух диэлектриков с ди-
электрическими проницаемостями е, и 82. Учи- е<е
тывая, что д т,
В
Ё = 4 =
87 0„ 0„ Рис. 3.3
69

получаем
$Я '~1 Е~
~Ы у2 е2
(3.19)
Е = вЂ” пр1,
где р! вЂ” дипольный момент единицы объема, т. е. ( вЂ” Р). Поэтому поле
внутри шаров (при малом сдвиге это один как бы шар радиусом Л)
Е,. = вЂ” вЂ” шР; ~Е,. = вЂ” вЂ” ).
(3.20)
Это поле за счет поляризации. Дополнительного внешнего поля,
которое могло приводить к такой поляризации, нет.
Дипольный момент поляризованного шара равен
=иР=4 Я'Р.
3
(3.21)
Вне шара поле является полем диполя (1.9)
Е, = )г[(Рг) вЂ”,вЂ” вЂ”,
Г Г
(3.22)
На границе шара с внешней стороны
Е„, = 4л(Рп)п вЂ” вЂ” лР,
4
(3.23)
где и вЂ” единичная нормаль к поверхности шара. В точках поверх-
ности на оси симметрии
Е„о = вЂ” лР = вЂ” 2Е,
8
На диаметре, перпендикулярном оси,
Е„„= вЂ” вЂ” шР=Е,
4
70
Для определения поля равномерно поляризованного шара вос-
пользуемся формулой (1.14) для поля в равномерно заряженном
(плотность заряда р) шаре и суперпозицией его поля с полем от
такого же шара с отрицательным равномерным зарядом ( вЂ” р), сдви-
нутым на малое расстояние 1 относительно первого. Сложение по-
лей в области пересечения определяется (1.24) и дает

Равномерная поляризация диэлектрического шара получается при
помещении его во внешнее однородное электрическое поле (с на-
пряженностью Ед). Убедимся, что в этом случае сумма внешнего
поля и поля равномерно поляризованного шара ‚удовлетворяет ус-
ловиям на бесконечно большом расстоянии и на границе шара. На
бесконечно большом расстоянии суммарное поле Е = Ед + Ее пере-
ходит в Ео, так как поле шара (3.22) стремится к нулю. На границе
шара по разные стороны границы должны быть одинаковы касательные
составляющие векторов Е и нормальные составляющие векторов 1).
Суммарное поле внутри шара Е = Ед + Е‚‚ вне шара Е = ЕО + Ее. Как
видно из (3.20) и (3.23), касательные составляющие поля на границе
шара совпадают. Вне шара 1) = Ео + Ее. Внутри шара В = ЕО + Е, + 4лР.
Используя (3.20) и (3.23), находим, что на границе шара одинаковы
нормальные составляющие вектора 1). Таким образом, поле внутри
диэлектрического шара, находящегося во внешнем поле Ед,
в = во - ЁпР. (3.24)
Используя (3.2) и (3.9), находим
Ео
Е = 3 а + 2 (3.25)
Из (3.2) и (3.25)
Е
Р = 3(е - НТЁЩ. (3.26)
Дипольный момент диэлектрического шара радиусом а (У= 41ш3/3)
во внешнем поле
р = УР = а° (а - 0;}- (3.27)
2.
Введем координатную ось х, проходящую через центр шара (на-
чало отсчета) параллельно внешнему полю Ед. При этом потенциал
внешнего поля ‹р = —Е0х, а потенциал поляризованного шара опре-
деляется уравнениями (2.14) и (3.11), в последнем е = 1 для среды,
окружающей шар (г 2 а),
Ф‘, = 14,2 при г 2. а, (3.28)
Г
ГДС
4
И, =3тса3.
71

Внутри шара
Г = вЂ” дг .
4
3
Поэтому при г < а
4
р. = вЂ” яРг.
3
(3.29)
Окончательно, для потенциала поляризованного шара во внеш-
нем поле Ео получаем
Рг а
3
д, = вЂ” Едх + )ц вЂ” вЂ” вЂ” вЂ” Ецк 1 вЂ” Ь вЂ” 1) ~, г > а; ~3.30)
г (е+ 2)г
~р, = вЂ” Е„х + вЂ” нРг = вЂ” 3Е, г < а.
4 х
3 я+2'
(3.31)
Найдем напряженность поля Е„в сферической полости, выре-
занной внутри равномерно поляризованного диэлектрика. Обозна-
чим поле внутри диэлектрика, вызвавшее его поляризацию, Е. Если
полость заполнить тем же диэлектриком, то к полю в полости доба-
вится поле равномерно поляризованного шара (3.20). Их сумма дол-
жна равняться Е. Отсюда
Е„= Е+ вЂ” пР = (е+ 2) вЂ”; Е„= Е+ вЂ” = (е+ 2) вЂ” .
4 Е Р Е
Зео
(3.32)
Оценим силу взаимодействия между нейтральным диэлектричес-
ким шариком радиусом Л и точечным зарядом а, считая расстояние
между ними А большим, а диэлектрическую проницаемость шарика е,
такой, что е вЂ” 1 «1 (М 3.39). Предполагая, что при вычислении
дипольного момента шарика поле, его создающее (от заряда), мож-
но считать постоянным по величине и направлению, а при вычис-
лении силы учитывать его изменение, из (3.27) и (1.11) находим
(е вЂ” !) Л Д ~1(Д/А ) д Я е вЂ” 1
(~+ 2)~,2 сИ. А А е+ 2
При е вЂ” 1 «1 получаем
2 2 ~3
вЂ” вЂ” вЂ” вЂ” (е вЂ” 1) .
3 Е С
72

У11 Рассмотрим два однородных диэлектрика
В, д. с диэлектрическими проницаемостями е, и е2,
‹ граничащих друг с другом вдоль плоскости
1 (рис. 3.5). В точке Вд помещен точечный за-
" ряд 41. Найдем напряженность электрическо-
е! _ го поля в каждом из диэлектриков. В окрест-
ед Т ности В, поле должно описываться (3.1О)‚ т. е.
д 5 в выражение для поля должен входить член вида
(3.1О). Предположим, что поле от поляриза-
1 ционных зарядов на границе диэлектриков в
2 первом диэлектрике (ед) эквивалентно полю
Рид 35 заряда 42, помещенного в точку 82, зеркально
симметричную точке В, относительно границы.
В таком случае поле в первом диэлектрике описывается формулой
В
Е‘ = 4171 + 4252
51П3 52"2
Предположим также, что поле во втором диэлектрике можно
представить через некоторый заряд 43, помещенный в точку В],
_ 4351
Е2 - т.
52%
Оба предположения будут оправданы последующими вь1числе-
ниями. Должны удовлетворяться условия на границе диэлектриков:
непрерывность касательных компонент вектора Е и нормальных
компонент вектора 1)
51116 31116 _ э1п6_
‘11_"+‘12‘_‘т‘13__›
51 51 52
4, сове — 42 сове = 43 сов 6.
Видно, что угол 6 выпадает из обоих уравнений. Отсюда находим
е —е е
42 = 914; 43 = 241 2 - (3-36)
81 +82 Ё‘ +82
Подставляя их в выражения для полей, имеем
4 г е — е 4 г _
Е|=1Ё_(2 01%, `ǰ
514 51 (51+ 52)’:
24 г
Е2 = 4%. (3.38)
(51+ 52)’1
74

При 82 —› со получаем выражения для точечного заряда над про-
водящей плоскостью
81713 81723 '
Чтобы определить силу, действующую на заряд (11, который на-
ходится на расстоянии Ь от границы диэлектриков, находим поле от
заряда 42, равное
‘12
4/125, ’
и умножаем его на с],
‘1 (81 ‘ 52)
= Т. (3.39)
4/12 (е, + 82)
Опишем поля через потенциалы: (р, в первом диэлектрике и (р,
во втором диэлектрике. Из отсутствия заряда на границе диэлект-
риков и (2.8) и (3.1О) имеем
Ш - Ё
едк ау )у=0 - е2( ау )у=о. (3.4О)
Используя (3.6), (3.8) и (2.12), получаем уравнения Пуассона
Ш; щр, = -Ш. (3.41)
81 82
АФ1=_
Плотность зарядов равна нулю везде, кроме точки В1. Поэтому
Аф, = О. (3.42)
Другое уравнение из (3.41) можно удовлетворить, положив
ф, = Дни; Асрз = о, (343)
51%
Где г, = [х2 + (у — 102 + 1211”. Воспользовавшись (2.13), убеждаемся,
„что первый член устраняет особенность в точке В].
Потенциал в каждой точке пространства зависит от г и расстояния
от плоской границы раздела диэлектриков (у). Вместо у удобно ввес-
ти расстояние от точки В2, расположенной симметрично точки В,
относительно границы диэлектриков, г, = [х2 + (у + 102 + 22] 1/2. Гра-
75

ница диэлектриков описывается уравнением г, = г,. Решениями урав-
нений Лапласа из (3.42) и (3.43) являются суперпозиции сферичес-
ки симметричных решений (2.13), зависящих от г, и г,. При этом
потенциал дг во втором диэлектрике не может содержать членов,
пропорциональных 1/г2, а потенциал д, в первом диэлектрике соот-
ветственно членов, пропорциональных 1/г,. Решения ищем в виде
Ч . Ч
% =~~
Е1~~
где а, и а, вЂ” постоянные величины, которые определяем из условий
на границе. Равенство потенциалов ю, и д дает
1+ ~1 ~г
Е1 Ег
Из (3.40) имеем 1 вЂ” а, = а. Отсюда
1 2. а 2
Е вЂ” 6 2е
1
~1+~2 ~1+~2
Получаем для потенциала
Ч Ч(е~ ~г)
Ч=Ч! = +
е~Ф~ е~ (е~ + 62) г2
приу>0;
(3.44)
г~
'Рг
Е1+ Ег Г1
приу<0.
(3.45)
4 з (е вЂ” 1)К Е
= вЂ” П
3 3
(3.46)
76
Рассмотрим взаимодействие между сферическими пузырьками
(полостями) радиусом г внутри диэлектрика с диэлектрической прони-
цаемостью е, помещенного между обкладками плоского конденсатора,
имеющими разность потенциалов У. В первом варианте пузырьки рас-
положены на расстоянии 1 друг от друга в плоскости, параллельной
обкладкам конденсатора. Оценим величину и направление силы их
электростатического взаимодействия, предполагая, что наличие пу-
зырьков не изменяет однородной поляризации диэлектрика и рав-
номерного распределения заряда на обкладках (М 3.17). Дипольные
моменты пузырьков р„противоположны дипольным моментам, ко-
торые получились бы при заполнении их данным диэлектриком.
Поэтому (3.21) и (3.8) дают

Для диполей из (1.8) и (1.11) находим силу отталкивания
Зр„(е вЂ” 1) У г
(4 3( (4
Если пузырьки расположены вдоль прямой, перпендикулярной об-
кладкам конденсатора (№ 3.18), то возникает сила притяжения (1.10)
бр2 2(е вЂ” 1) У~г
(4 3Ь2(4
(е вЂ” 1) Е
Так как Р = пр, р = д(, д = е~, то
(е вЂ” 1) Е
р Р
д ле~
4япе~.
Отметим, что смещение для атома аргона в поле с напряженно-
стью Е = 300 В/м получается 2 10-" см, что значительно меньше
размера атома.
Предполагая некоторую структуру электронного облака в атоме,
можно вычислить коэффициент поляризуемости атома а в слабом
внешнем электрическом поле, пренебрегая деформацией электрон-
ного облака (№ 3.3).
Если плотность электронного облака описывается функцией
8 2г
р(г) = вЂ” вЂ”,ехр вЂ” вЂ”,
ка а
77
Некоторой моделью диэлектрика может служить среда, состоя-
щая из большого числа проводящих шариков радиусом Я. Предпола-
гая, что концентрация шариков и очень мала Л'и «1, можем найти,
на сколько отличается от единицы диэлектрическая постоянная (про-
ницаемость) среды (№ 3.1). Считая, что поле вблизи шариков равно
внешнему Е, из (1.26) находим дипольный момент шарика р = Я'Е.
Из (3.1) Р = пр, а из (3.8) находим е = 1 + 4ппЯ'.
Зная диэлектрическую проницаемость е некоторого одноатом-
ного газа с известным числом атомов в единице объема и, можно
оценить, на какое расстояние ( в заданном электрическом поле Е
сместится электронная оболочка (предполагаемая симметричной в
отсутствие внешнего поля) атома с известным зарядом ~е (№ 3.2).
В случае, когда Л = еЕ, имеем еЕ = Е+ 4яР. Откуда

где а — радиус первой боровской орбиты, то, используя теорему
Гаусса (1.12), имеем
Е(г)4пг2 = 4п_[ 4пг2р(г)а'г.
о
Откуда находим
Г 72
Е(г) = —%[1 - ехр(—ё)(1+ё+%л.
Отметим, что неопределенность при г, стремящемся к нулю, можно
раскрыть по правилу Лопиталя. Производная числителя: 4(г2/а2)е‘2’/“,
производная знаменателя: 2г/а. Поэтому Е(О) = О.
Так как наибольшая плотность заряда в основном находится при
г << а, то, разлагая экспоненту до кубического члена, получаем
4 ег
Е (Г) = -—т-
3 а
Это поле в электронном облаке. При наложении внешнего поля ЕО
облако сдвигается, и смещение его центра на го определяется поло-
жением нулевого поля из условия Ео + Е(г0) = О. Получаем
з
3 а Ео з
г =— —ег -—а Е
о 4 е ‚ Р о 4 о
и, следовательно,
3 3
а=—а.
4
Можно предположить, что электронное облако сосредоточено
внутри сферы радиусом а с постоянной плотностью (Мг 3.4)
Зе
41:03 .
По теореме Гаусса (1.12) получаем
ег
Е(7')="";3-.
При НЗЛОЖСНИИ ВНСШНСГО ПОЛЯ Ео В ДЗННОМ СЛУЧЗС СМСЩСНИС
центра облака ПРОИСХОДИТ также на ГО?
аз Ед
е
. _ _ 3
го: , р-его-аЕо
и, следовательно, ос = а3.
78

Из (3.2) и (3.9) получаем
—1.Е
15„ = (в 3) . (3.48)
Отметим, что поле в сферической полости определяется (3.32)
4 Р
Е„ = Е + E
Если диэлектрик состоит из диполей р по А! штук в единице
объема, то при отсутствии их взаимного влияния друг на друга по-
лучаем из (3.1) Р = А/р и из (3.2) Р = осЕ. Обозначая поляризуемость
диполей (например, молекул) В, получаем для диполей р = ВЕ и
связь с поляризуемостью среды ос = МВ. Влияние диполей друг на
друга можно учесть, считая, что поле вокруг одного диполя, созда-
ваемое другими диполями, соответствует (3.47), и вместе с прило-
женным описывается (3.32). В таком случае для поляризуемости
вводим око = МВ и для суммарного поля Ее
Р = А/р = А/ВЕС = осоЕс = оъ0Е+4поъ0%.
Отсюда получаем
р=щ=ав и а=д__9‘д__
1-4па0/3 1-4па0/3
Отметим, что осо — поляризуемость, вычисленная без учета отличия
Ее от Е.
Из (3.9) находим
4па0
1-4ла0/3'
Откуда следует формула Лоренц-Лорентца для определения а с
учетом влияния диполей в диэлектрике друг на друга (Мэ 3.16)
е—1_4пПВ
г + 2 “ 3
Эта формула хорошо подтверждается для диэлектрических жид-
костей, поляризуемость которых ос не мала по сравнению с еди-
ницей.
Рассмотрим газ из молекул, представляющих упругие диполи с
молекулярной поляризуемостью В, для которых дипольный момент
р = ВЕ. Если в такой газ, имеющий температуру Ти среднюю кон-
80
е=1+4пос=1+
. (3.49)

центрацию по, внести заряженный шарик, то в результате притяже-
ния молекул к шарику и их теплового движения установится боль-
цмановское распределение молекул в электрическом поле. Сила
притяжения определяется (1 . 1 1)
дЕ
Р = — —
р дх
где, по определению силы в потенциальном поле, И/— потенциаль-
ная энергия. Распределение Больцмана дает для распределения числа
молекул в единице объема от величины поля в случае малого возму-
щения концентрации (бп << по) (см. 2, с. 188)
5152 52
"="°°"Р(т)“ “ОЬЁ/й)
Для заряда в диэлектрической среде из (3.9) и (3.10) имеем
з
1) = % = еЕ = Е[1+4пп(г)В] = Е(1+4ппОВ)+4пп„В%.
Решаем это уравнение методом последовательных приближений.
В качестве первого приближения берем
В
и подставляем в предыдущее уравнение. В результате для зависимо-
сти напряженности поля от расстояния в газе, состоящем из диполей,
имеем (М9 3.21)
1 - [в(г)2/ (1 + 4лп„в)3]4пп„в’ /1‹т _
Е (г) = ВО‘)
1 +4пп0В
Если в пространство, первоначально занятое однородным элек-
трическим полем Ео, вносят длинный диэлектрический цилиндр
так, что его ось перпендикулярна начальному полю ЕО, то ди-
электрик поляризуется однородно, и в соответствии с (1.31) поле
за счет поляризации Е“ = —21:ра. Вводя вектор поляризации Р
(поляризация единицы объема), получаем для поля за счет поля-
ризации Еп = —2пР. Полное поле в диэлектрике включает прило-
женное поле Ед и равно Е = Ед — 21гР. Так как именно это поле
6-2073 8 1

вызывает поляризацию, с помощью (3.2) получаем Е = Ео вЂ” 2паЕ.
Учитывая (3.9), находим (Мо 3.20)
Ео 2Ео
и Р=аЕ=
(е вЂ” 1) Ео
1+ 2ла е+ 1 2п(е + 1)
При выключении внешнего поля в диэлектрике может остаться
так называемая замороженная поляризация. Связанные заряды на
границах диэлектрика создают электрические поля вне и внутри
диэлектрика.
В случае плоского слоя диэлектрика с замороженной поляри-
зацией Р, перпендикулярной границе, поле будет как в плоском
конденсаторе: снаружи нулевое (и Й = О), внутри из (3.5) получа-
ем Е = вЂ” 4яР.
Для шара из диэлектрика с замороженной поляризацией Р мож-
но воспользоваться (1.25) и (3.3) или сразу (3.20). Получаем, что
поле внутри шара
Е = вЂ” вЂ” яР.
4
Вне шара поле определяется диполем с моментом, равным про-
изведению Р на объем шара (3.21).
Если напряженность поля в диэлектрике Е, то поле в полости
внутри диэлектрика из суперпозиции (3.32)
Е„= Е вЂ” Е = Е+ вЂ” яР.
4
Найдем поля Е и Р для тонкого диэлектрического цилиндра дли-
ной 2( и радиусом г «( с замороженной поляризацией Р, направлен-
ной вдоль оси цилиндра (М 3.7, М 3.8). Электрическое поле созда-
ется связанными зарядами на торцах цилиндра. Из (3.3) получаем
плотность зарядов на торцах: а = Р на верхнем торце, если поляри-
зация направлена вверх, и а = вЂ” Р на нижнем (рис. 3.7, а). Напря-
женность поля на торцах определяется плотностью зарядов (1.17)
Е = 2яо = 2пР. Вдали от торцов поле меняется как от зарядов
а = шаг 2. В середине цилиндра Е= д/Р. Еще на больших расстояни-
ях поле превращается в поле диполя. На рис. 3.7, а показаны сило-
вые линии напряженности поля, на рис. 3.7, б вЂ” силовые линии
вектора Р = Е + 4пР. Видно, что вне диэлектрика линии Р совпада-,
ют с линиями Е, а на боковой поверхности резко меняют направле-
ние. Изменение вектора ЛР = 4шР. При переходе через торцы век-
тор Р не меняется.
82

Рис. 3.7
В случае короткого цилиндра радиусом К и высотой 12 << К с замо-
роженной поляризацией Р, направленной по оси цилиндра, напря-
женность поля близка к напряженности поля в плоском конденса-
торе: внутри Е = 4по = 4пР и направлена противоположно Р,
а снаружи поля нет. Если учесть конечность размера диэлектрика,
то, пользуясь для поля заряженного диска формулой (1.5), в центре
поверхности диэлектрика получаем напряженность поля (Мг 3.8)
2поЬ
К
Для бесконечной полоски диэлектрика шириной Ь и толщиной
1 << Ь с вектором замороженной поляризации Р, перпендикулярным
меньшей грани (рис. 3.8), найдем поле Е и индукцию В на сред-
ней линии (М 3.9). Поле на средней линии полоски будет как от
двух линий с зарядами на единицу длины линии, равными о! = Р!
и —о1 = —Р1. Это, как следует из (1.16), дает поле Е = —8Р1/[‚. Для
индукции из (3.5) получаем
Е:
В = 4(п-%)Р.
Если диэлектрический образец с замороженной поляризацией Р
имеет форму полого цилиндра радиусом К и толщиной стенки И « К
с разрезом ширины 1 << К (сечение его и направление вектора
поляризации показаны на рис. 3.9), то поле в точке А будет от
двух заряженных линий с зарядами на единицу длины 0/2 = Р}: и
д. 83

-„
Рис. 3.8 Рис. 3.9
—о/1 = —Р/1‚ отстоящими друг от друга на 1 и находящимися от
точки А на расстоянии 2К. Используя (1.16), из геометрического
сложения получаем
РЫ
Е = —7.
2К
Так как этот вектор направлен противоположно вектору Р А (в точке А),
получаем (Не 3.10)
Ы
13„ = (4п-—2к2)1>‚‚.
Аналогичным образом решается задача для желоба, сечение ко-
торого показано на рис. 3.10 (М) 3.11). Из (1.16) и геометрического
сложения находим в точке А
ЬР
Е =——4.
А к
ии3(3.4)
2/2
В = 4 —— Р.
А (п к)’
Рассмотрим тонкий диск из диэлектрика радиусом К с отвер-
стием радиусом гтолщиной И 4: г с замороженной поляризацией Р,
параллельной поверхности диска (рис. 3.11). В соответствии с (3.3)
плотность связанных зарядов на внешней поверхности о = —Рсов 9,
а на внутренней — о = Рсоз 6. Электрическое поле, создаваемое
84

“и
П И‘ —ь 0 л
Р 1
ними т:
ш
Рис. 3.12 Рис. 3.13
где х отсчитывается от средней плоскости пластинки. В силу симмет-
рии относительно средней плоскости по теореме Гаусса вне пластин-
ки имеем Евнеш = В = О. Из непрерывности нормальной компоненты
электрической индукции на границе диэлектрика и внутри пластин-
ки В = О. Из (3.5) Евнут = —4пР. Разность потенциалов между боковы-
ми поверхностями пластинки (М 3.13) находим из (2.6)
и л 2
(р, —‹р2 = [Едх=—4п1{д]д(1-%]с1х=
-л 4:
1’ х2 11
= —8п1ъ]’(1 —7)а’х = —161т1{, д.
о
Для диэлектрической пластинки с замороженной поляризацией Р,
перпендикулярной поверхностям пластинки, поле Е и индукция 1)
снаружи равны нулю. Так как индукция В на границе диэлектрика
непрерывна, то из (3.5) следует Е = —41тР. Если такую пластинку
поместить внутрь плоского конденсатора (рис. 3.14), пластины ко-
торого, находящиеся на расстоянии 1, соединены между собой, то
картина полей изменится. Наличие связанных зарядов на поверхно-
сти диэлектрика приводит к тому, что на пластинах
1 _ конденсатора наводятся свободные заряды плотнос-
тью о, разных знаков. Учитывая, что плотность свя-
занных зарядов на поверхности диэлектрика о = :Р
и что из непрерывности В для поля вне диэлектрика
имеем Евнсш = В = Е + 41гР, из (2.6) и равенства по-
тенциалов на пластинах конденсатора (по условию)
получаем Евнеши — И) + Е}: = 0. Решая это уравнение
_/1
Р
2}-
Ш совместно с предыдущим, находим (Не 3.19)
_ 4тгР/2_ _ 4пР(1—/1)
Рис. 3.14 В = Е""°"’ — 1 ’ Е 1

Плотность связанных зарядов на поверхности диэлектрика о = Р,
плотность свободных зарядов на пластинах конденсатора
с, = Ёшзш. = д,
41: 1
Важной характеристикой проводящих тел и конденсаторов (спе-
циальных технических устройств, предназначенных для накопле-
ния и сохранения электрических зарядов) является емкость. Это —
коэффициент пропорциональности между зарядом проводника или
конденсатора и потенциалом или разностью потенциалов, кото-
рый зависит от размеров и формы устройств и диэлектрической
проницаемости окружающего диэлектрика и ее распределения в
пространстве. ф
Емкость металлического шара радиусом К в вакууме из (2.4)
с = % = к; {с = % = меде}. (350)
Емкость такого же шара в диэлектрике с диэлектрической про-
ницаемостью е из (3.10)
С = еК; {С = 41180812}. (3.51)
Для двух металлических шаров (радиусами К, и 122), находящих-
ся в диэлектрике с диэлектрической проницаемостью е и располо-
женных на расстоянии 212 друг от друга, в точке, отстоящей от одно-
го на г], а от другого — на г2, из (3.10) и суперпозиции для потенциа-
ла получаем
‹р=1—1-+соп51.
и; ег2
В случае 11 >> К, и 11 >> К, имеем на первом шаре
Ч Ч
= — — —— + сопвт
Ф] 8121 8211
и на втором шаре
Ч Ч
= — — —— + сопзт.
Ф2 8211 8К2
Разность потенциалов
_ 4[ь(к, + к,)- к,к,] 2 4(к‚ + к,)
_ ещк, ещк, `
Ф1"‘Р2
87

Отсюда емкость такой системы
1 2 1 2
(3.52)
При Я, = Л = Л получаем
С=4тк,е вЂ” .
Я
О
(3.53)
Применение метода зеркальных изображений дает то же значе-
ние емкости для системы из проводящей плоскости и проводящего
шара на расстоянии Ь» Л.
Для концентрических металлических оболочек радиусами Л, и
Л„между которыми находится диэлектрик с диэлектрической про-
ницаемостью е (сферический конденсатор), из (3.10) получаем
~(1/~~ 1/~г)
~1 'Р2
(3.54)
Е
Отметим, что здесь д вЂ” абсолютная величина заряда, который нахо-
дится на внешней оболочке внутренней сферы и на внутренней повер-
хности внешней сферы. На внешней поверхности внешней сферы мо-
жет находиться любой заряд, и он не влияет на поле между сферами.
Из (3.54) емкость сферического (шарового) конденсатора
(3.55)
5' = 47~А, = 4нЯ'г = 4лЛ,Аг.
В этом случае для емкости получаем
Я
С =еое
Ь
4нЬ '
(3.56)
Естественно, что ту же самую формулу получаем и для плоского
конденсатора, если пренебрегать краевыми эффектами. Используя
(3.7) и (3.8) для напряженности между противоположно заряжен-
ными плоскими металлическими пластинами, получаем
4щ 4кдЬ
Е= и Ч,вЂ” фг=ЕЬ=
еЮ е5
Отсюда и следует (3.5б).
88
Если толщина зазора между обкладками Ь мала по сравнению с
радиусами, то для площадей обкладок имеем

Найдем емкость плоского конденсатора, пространство между
обкладками которого заполнено диэлектриком с линейно изменяю-
щейся диэлектрической проницаемостью от значения е, у одной об-
кладки до е, < е, у другой. Обозначая расстояние между обкладками Ь,
площадь обкладок Я и координату, перпендикулярную к обкладкам
х, получаем из (2.6) для изменения разности потенциалов
У =~И =4~~~ ~ =4 '~ '» вЂ” 4~" Ь
5 о е(») 5 о 82+ (е~ вЂ” е2)»/Ь 5 е1 вЂ” е~
Отсюда определяем емкость С = д/У (М 3.26).
Рассмотрим плоский конденсатор, на пластинах которого рас-
пределен заряд с поверхностной плотностью о, а между пластинами
вставлен диэлектрик с диэлектрической проницаемостью е, заря-
женный положительным пространственным зарядом так, что объем-
ная плотность заряда изменяется от О у одной пластины (положи-
тельной) до р, у другой по закону
Х
р(х) = а вЂ”,
~2 '
где Ь вЂ” расстояние между пластинами. Найдем полный простран-
ственный заряд в диэлектрике на единицу площади
Ь
Их д
о = ах вЂ” = вЂ”.
Ь
О
Используя (3.7), находим, что снаружи конденсатора поле, как
от заряженной плоскости 2Е,„, = 4на/2, т. е. абсолютное значение
Е „, = яа. Снова используя (3.7) для поверхности вне конденсатора
и внутри на расстоянии х, получаем
ОХ
па <- еЕ = 4п (а +
2Ь
Отсюда получаем Е(х) внутри конденсатора (Мо 3.27).
Если в изолированный заряженный конденсатор вдвигать плас-
тину (толщиной, равной зазору между обкладками) из диэлектрика
(проницаемость е), то заряды на обкладках не меняются, а перерас-
пределяется их плотность. Конденсатор можно рассматривать как
два конденсатора, соединенных параллельно. Суммарная емкость
при этом увеличивается, а разность потенциалов и напряженность
поля уменьшаются.
89

Электрическая индукция (смещение) в диэлектрике при вдви-
гании уменьшается и при заполнении конденсатора целиком стано-
вится равной значению без диэлектрика. На границе диэлектрика
меняется плотность заряда на обкладках так, чтобы напряженность
поля была одинаковой с обеих сторон границы. Обозначая пло-
щадь обкладок 5„ а площадь, занятую диэлектриком 52, и отно-
шение индуктивности в диэлектрике (В = еЕ) к его значению без
диэлектрика (ВО = Ед) буквой п = В/Ео, из сохранения заряда
получаем
_ 5150 _ (5252 +51“52)Е
41: 41:
Найдем, при каком отношении площади диэлектрика к площа-
ди обкладок получим заданное значение п (Не 3.30). Из приведен-
ных ранее соотношений
52 _ е-п
5, п(е 41)"
В плоском конденсаторе (расстояние между обкладками 1) мож-
но две пластины диэлектрика (диэлектрическая проницаемость е)
приложить к обкладкам так, что между ними остается небольшой
зазор 11. Найдем, при каком Ь поле в зазоре будет в п раз превышать
поле в отсутствие пластин, если конденсатор подключен к батарее
(Не 3.31). Обозначая поле в отсутствие диэлектрика Ед, в диэлектри-
ке Ед и в зазоре Е, из постоянства разности потенциалов на обклад-
ках и (2.6) находим
1501 = Ед(1 - и) + Ел.
Из непрерывности нормальной компоненты электрической ин-
дукции на границе диэлектрика следует Е = еЕд. Получаем
„ _ А _ __*1_
ЕО 1+ /2(е — 1)°
Откуда находим
н: !(е—п) Г‘
ЯГ 17) °
ж
Если металлический шар радиусом К, окружен шаровым слоем
диэлектрика с диэлектрической проницаемостью г толщиной 12
(122 = К, + 11) и помещен концентрично в металлической оболочке с
90

внутренним радиусом КЗ (Мг 3.24), то для разности потенциалов
такого конденсатора имеем
К:
“З не -1к
АФ=—1[%—Ч1%:Ч Ддд. .Ц_._; _
812,’ к_" 8 312 кз
Отсюда находим С = с1/Аср.
Найдем изменение напряженности электрического поля в сфери-
ческом конденсаторе (радиусы К1 и 122), который заполнен двумя одно-
родными диэлектриками (с диэлектрическими постоянными 81 и 52),
граничащими по конической поверхности (телесные углы $21 и $22).
Если на внутренней обкладке заряд О, то О = 82112101 + 52212202. Из
сохранения касательнои компоненты поля на границе диэлектри-
ков и (3.1О) получаем
Е = 41:12} Ш- = 4пк3 52.
ар‘ е2г
Откуда
Ш = Э__
81 52
Это позволяет найти
О
01-
к%(91+92 82/51)
и подставить его в выражение для напряженности поля (Мг 3.28)
Рассмотрим пустотелый металлический шар, заряд которого а,
а радиус К, плавающий в жидкости с диэлектрической проницаемо-
стью 81 так, что его центр находится на уровне поверхности жидко-
сти, и найдем плотность свободных зарядов на его поверхности,
считая диэлектрическую проницаемость воздуха равной в (Мз 3.38).
Для потенциала и напряженности поля вокруг шара имеем симмет-
ричную картину, описываемую уравнением Лапласа (2.13). Плотность
свободных зарядов на шаре и электрическая индукция меняются скач-
ком на границе диэлектриков. Обозначая плотность заряда на поло-
вине поверхности, находящейся в жидкости 01, а в воздухе о, можем
написать с] = 2пК2(о1 + о). Изменение электрической индукции из
(3.7) в воздухе
О’
1) = 4пК2
9
4пг2
91

а В ЖИДКОСТИ
в - магд-
Ц 1 о
4тсг2
Используя непрерывность напряженности электрического поля
на границе диэлектриков (2.7), получаем
2-2;
Е е!
Е
И ЗЗТСМ
б].
31
т|о
Подставляя это в выражение для суммарного заряда, находим соот-
ветствующие плотности.
Найдем емкость сферического конденсатора, т. е. отношение
заряда к разности потенциалов, при заданном значении заряда с],
если в него (радиусы обкладок соответственно К] и 122) помещен
неоднородный диэлектрик с поляризуемостью, зависящей от рас-
стояния от Центра сфер (г), ос = В|Е|г2. Из (3.7) В = 4/23. Из (3.2),
(3.5) и заданного соотношения для поляризуемости имеем
г’, = Е(1+ 4пВг2 |Е|).
При положительном заряде на внутренней обкладке Е > О получаем
41ЕВ(Г2Е)2 + г2Е — 4 = 0.
Решая это квадратное уравнение и беря (по смыслу) положитель-
ный корень, находим
_ -1 + (1 + 161169)
" ЗпВ
г2Е = А = сопвк.
С помощью (2.6) получаем
к„
'‹1г 1 1
А‹р=—А —=-А(—-—).
1,’; кл к:
Откуда емкость (Мг 3.33) С = а/Аср.
Найдем объемное распределение связанных зарядов в диэлектри-
ке, заполняющем сферический конденсатор (внутренний радиус К],
92

внешний Я,), проницаемость которого с расстоянием ог центра сфер (г)
изменяется по закону (№ 3.34):
Я2
1
Е = 61 вЂ” °
2
Из (3.7) и (3.8) имеем
В = вЂ” = Ее= Ее,вЂ” '.
д Я1
2 1 2
Откуда следует постоянство напряженности поля при изменении
расстояния от центра сфер
г'
я~Я~
Из (3.8)
4яе1 Я1
Используя (3.4) и выражение для дивергенции в сферических
координатах в случае сферической симметрии (1.22), получаем
2д
4тк1 Я1»
2
Если задан не заряд, а разность потенциалов (У), то
У = Е(Яг вЂ” Я,) = д
е~Я1
Емкость цилиндрического конденсатора, состоящего из коаксиаль-
ных цилиндрических металлических обкладок радиусами Я, и Я„
между которыми находится диэлектрик с диэлектрической прони-
цаемостью е, получаем, используя (3.7) и (3.8). Из (3.7) для едини-
цы длины цилиндра получаем еЕ2жг = 4шд. Для разности потенциа-
лов на обкладках имеем
~р вЂ” ег, = вЂ” 2 вЂ” вЂ” = вЂ” 2 вЂ” 1п вЂ” .
И»
е„г ~ Я,
1
93

Откуда для емкости цилиндрического конденсатора длиной [по-
лучаем
_ е! _ _ 4пе е!
С-2'“(К2/К1), {С_21“(К:/К1)}. (3.57)
При малом по сравнению с радиусами зазоре между цилиндра-
ми (11) (3.57) переходит в (3.56).
Найдем емкость цилиндрического конденсатора (на единицу
длины), т. е. отношение заряда к разности потенциалов, при задан-
ном значении заряда с] (на единицу длины), если в него (радиусы
обкладок соответственно К, и К 2) помещен неоднородный диэлек-
трик с поляризуемостью, зависящеи от расстояния от оси цилинд-
ров (г)‚ ос = В|Е|г. Из (3.7) В = 24/11 Из (3.2), (3.5) и соотношения
для поляризуемости имеем
2%: Е(1+4п|3г|Е|).
При положительном заряде на внутренней обкладке Е > О по-
лучаем
4пВ(гЕ)2 + гЕ — 2:1 = О.
Решая это квадратное уравнение и беря (по смыслу) положитель-
ный корень, находим
-1 + (1 + 3211134)
= = т.
8,26 А сопв
гЕ=
С помощью (2.6) получаем
к„
Аср =-А] ё = —А1п(%).
к, 1
Откуда емкость (М: 3.32) С = а/Аср.
Рассмотрим цилиндрический конденсатор (с радиусами обкла-
док К, и К2 и длиной 1), заполненный двумя разными диэлектрикаг
ми (с проницаемостями е, и 82), граничащими по плоскостям, про-
ходящим через ось цилиндра и образующим двугранные углы 6, и
92 = 21: — 6,. Найдем напряженность электрического поля между
обкладками, если заряд на внутренней обкладке равен О (М 3.29).
Обозначая плотности зарядов на внутренней обкладке о, и 02, име-
94

ем О = Кд/(Эдо, + 6,02). Из сохранения напряженности поля на гра-
нице диэлектриков (3.18) и (3.7) находим
Е = 41:53 = 415592.
’° 81 ’° 52
Откуда
& =ЕА
51 52 .
Используя выражение для О, получаем
4пО
(8161 + Ё2е2)1’° О
Найдем распределение объемной плотности поляризационного
(связанного) заряда, напряженность поля Е (г) и индукцию 1)(г) внут-
ри и вне в длинном цилиндре радиусом К с замороженной поляри-
зацией (Мг 3.35)
г
Пользуясь (3.4) и выражением для дивергенции в цилиндричес-
ки симметричном случае (1.21), получаем
__Ёд(1—г/К)(г2/К) _Ш(]_ 31‘).
дг = К Ж
Снаружи, так как свободных зарядов нет, 1) = О. Следовательно,
снаружи и Е = О. Из непрерывности на границе диэлектрика нор-
мальной компоненты В и (3.8) внутри Е = —4лР.
Если диэлектрический диск вращать, то силы инерции (центро-
бежные) вызывают смещение электронных оболочек и возникнове-
ние поляризации диэлектрика. Сила, действующая на электрон,
определяется угловой скоростью его вращения а), массой т и рас-
стоянием г от оси вращения, Е = тш2г. Эта сила дает ту же поляри-
зацию, что и электрическое поле Е = Е/е (е — заряд электрона). Для
нахождения поляризации воспользуемся (3.2) и (3.9)
рСВЯЗ
--.›
Е _.
Р = тш2г:,
4пе
где 8 -— диэлектрическая ПРОНИЦЗСМОСТЬ диэлектрика, а ВСКТОР ПО-
ляризации направлен К ОСИ вращения И на поверхности цилиндра
95

при ~ = Л будет отрицательный заряд. Объемная плотность связан-
ных зарядов определяется (3.4) и дивергенцией для цилиндричес-
ких координат. С учетом направления Р получаем (№ 3.36)
1 г ти (я вЂ” 1)/4пе ~ р вЂ” ]
Рсвнз у
4пе
Угловую скорость вращения можно выразить через число обо-
ротов
ОЭ
П = вЂ”.
2л
Для заряда на поверхности цилиндра получаем
д = вЂ” т2н~ (е вЂ” 1) и'А' вЂ”.
е
2
1ег
(3.58)
Из (2.6) получаем
2д 1пг
+ со~й.
Ы
(3.59)
В точке, которая находится от проволок на расстояниях г, и г„
потенциал
2д 1п)~ 2д 1пг~
Ч вЂ” ч 1+ Ч 2 +совью
1~ Ы
Вводя расстояние между проволоками 2Ь и действуя так же, как
ранее для шаров, получаем емкость системы
е! . 2ееОе1
2 1и (44 (я,я 2) 1п (44~ 1я,я ))
(3.60)
В случае одинаковых радиусов проволок
(3.61)
4 1п (2Ь/Я )
Емкость двух прямолинейных параллельных проволок длиной 4
~много большей диаметров проволок Л, и Л„чтобы можно было пре-
небречь краевыми эффектами), имеющих противоположные по знаку
заряды д, вычислим, используя суперпозицию и теорему Гаусса.
Из (3.7) следует

СИСТВМЗ ИЗ проводящей ПОВЕРХНОСТИ И ПРОВОЛОКИ, проходящей
параллельно ВЙ на расстоянии Й, ИМССТ СМКОСТЬ
е!
Это следует из предыдущей формулы при использовании метода
зеркальных изображений.
Конденсаторы можно соединять в батареи. Общая формула свя-
зи разности потенциалов на конденсаторе с зарядом и емкостью
Аф=Н=%. вью
При параллельном соединении конденсаторов (емкостями С,
и С2) разности потенциалов между обкладками обоих конденса-
торов одинаковые, заряд системы равен сумме зарядов конденса-
торов с] = 41 + 42. Разделив это на одинаковую разность потенци-
алов, получаем
с=ц+9. (мм
При последовательном соединении конденсаторов средние об-
кладки соединены между собой, поэтому их заряды равны по вели-
чине и противоположны по знаку, а разности потенциалов склады-
ваются Н = П] + 1/2. Поэтому
1 1 1
— = — + —. 3.65
с с, с, ( )
Если в плоский конденсатор, имеющий расстояние между об-
кладками 11, введена пластина из оптического стекла (е) так, что
остался зазор б, и приложена разность потенциалов П, то напряжен-
ность поля Е можно найти из соотношения
12-8
е .
П=Еб+Е
При отключении конденсатора от источника на нем сохра-
няется заряд. При удалении пластины напряженность поля, оп-
ределяемая плотностью заряда, не меняется. Напряжение будет
равно У = Е/т. Используя предыдущее соотношение, получаем
(Не 3.25)
Ус
“таит

В случае слоев диэлектрика в плоском конденсаторе можно
считать на границах диэлектриков обкладки и пользоваться резуль-
татами для последовательно соединенных конденсаторов. В данном
случае
5 _ _ 85
С‘“ББ’ С2`4п(л-в)'
Емкость системы С получаем с помощью (3.63)
= 85
С 41:“: +(е — 1)б]°
При удалении диэлектрика заряд с; = УС сохраняется, а емкость
конденсатора становится
5
С = ——.
3 41:11
Разность потенциалов
и = 1.
Сз
Перемещение ОДНОГО заряда В поле ДРУГОГО ПРИВОДИТ К измене-
нию энергии электрического взаимодействия зарядов (2.3). Для двух
точечных зарядов 4, и 42 можно вычислить, например, работу по
перемещению заряда а, в поле неподвижного заряда 42 из бесконеч-
ности в точку, находящуюся от него на расстоянии тю, потенциал
которой обозначим ф, = с12/гшдля энергии взаимодействия получаем
1
И’ = 2%‘ = 41% = ‘12Ф2 = 5(Ч1‘Р1 + 42%)’ (356)
Здесь ‹р2 = ад/гп.
Найдем энергию, запасаемую в конденсаторе при зарядке. Работа
совершается при перемещении заряда с одной обкладки на другую
Ч 1‘! 142
И’=]`‹ра’с1=Ё_|‘4с14=——=—5—=——, (3.67)
о о
где П — напряжение (разность потенциалов) на обкладках конден-
сатора.
Для плоского конденсатора
51521
ш: 81:
(3.68)
98

На единицу объема электрического поля (плотность энергии) в
плоском конденсаторе
(3.69)
0 ! 0 ! д2 О2
О 2 Я 8~~ОЯ
(3.70)
В случае распределения заряда в шаре с постоянной плотнос-
тью (р) получаем (М 3.43)
Ю = ~ (р(г, д) Й~ = ~ вЂ” пг р вЂ” 4пг р йг = вЂ” вЂ”. (3.71)
4 2 1 2 ЗД
3 г 5 Я
Те же результаты можно получить, если, воспользовавшись (З.б9),
(1.14) и (1.15), проинтегрировать по пространству, где имеется элек-
трическое поле:
л Я 4 2 - д 2
~К = вЂ” ~Е~НГ+~Е~ЙУ =/ вЂ” прг 4пг~йг+/ вЂ” 4пг~йг =
8ЖО я 03 я г'
(3.72)
1 Д ! Д 3 Д
10Я 2Я 5Я
Отметим, что при рассмотрении точечных зарядов в энергии
появляются бесконечно большие величины. В некоторых задачах,
где требуется найти разности энергий (работу), можно их вычитать.
Рассмотрим две удаленные друг от друга металлические сферы с
внешними радиусами Я, и Л2 и толщиной стенки Л, в центры кото-
рых помещены заряды д, и д,. Найдем работу, необходимую, чтобы
поменять заряды местами (М 3.47). Используя (3.72), можем напи-
сать энергию поля для первой сферы с зарядом
Я! вЂ” Ь
ОО Я1-Ь 2
Ч~
вЂ” / вЂ” +Д~ ~ вЂ” = вЂ” ф~ ~ вЂ” +вЂ”
2 о г гг 2 о г Я
Можно ввести и электрическую энергию одного заряда, подразу-
мевая под этим работу, требующуюся для его создания, например
путем последовательного переноса зарядов из бесконечности.
Вычислим электростатическую энергию заряда на шаре радиу-
сом Л в вакууме, если заряд шара Д равномерно распределен по его
поверхности. Можно заряды из бесконечности приносить на повер-
хность бесконечно тонкими симметричными слоями. Используя
(339), имеем (М 3.42)

Аналогичным образом можно написать и для второй сферы.
Суммарная энергия в начальном состоянии
Я1 вЂ” Д 2 2
В'„= вЂ” д, ~ вЂ”,+ вЂ” +д, ~ вЂ”,+ вЂ” .
1 2 дГ Д1 2 ЫГ Ч2
2 г я гг
В конечном состоянии
Я1-Д 2 я2-Д 2
1 2 ИГ Д2 2 дГ
вЂ” + вЂ” +Д
2 2
~ +
2 ~ Я, „ ~ Я2
Работа равна разности этих энергий
Предполагая, что масса электрона определяется из соотношения
И' = тс~, где И' вЂ” электростатическая энергия заряда электрона,
можно оценить его радиус:
1) в случае постоянной плотности заряда по обьему с помощью (3.71);
2) в случае заряда на поверхности с помощью (3.70) (М 3.44).
Если известна работа А, необходимая для перемещения заряда д
от поверхности равномерно заряженного (плотность заряда р) плос-
кого слоя на расстояние (, то, используя (1.12), получаем толщину
слоя (Ж 3.45)
А
2ярд(
Электрическая энергия конденсатора, определяемая (3.67), при
разряде передается среде, находящейся между обкладками. Если
между ними находился разреженный водород с начальными: объемом
~~ = 1О л, давлением ро = 10 ~ мм рт. ст. и температурой Т„= 300 К,
а напряжение на конденсаторе емкости С = 13 мкФ было У = 30 кВ,
то, обозначая число частиц в данном объеме Ж (после нагрева до
температуры Тих в результате диссоциации и ионизации станет 4Щ
можем написать закон сохранения энергии
СУ
= 4Ж вЂ” /сТ вЂ” Ж вЂ” ЙТО.
2 2 2

Используя уравнение состояния идеального газа (см. 2, с. 8)
А; = РОИ)
Щ
и пренебрегая начальной энергией газа (вторым членом), находим
(Мг 3.46)
_ 7ЬСН2
_ -.- 3-10’ к.
ПРОК)
Отметим, что температура газа может снизиться, если будут на-
греваться обкладки конденсатора.
Энергия трех проводящих шаров с радиусами 12„ К, и 123 и соот-
ветственно потенциалами ‹р‚‚ ф, и срз, далеко разведенных друг от
друга, равна
и, _ К1Ф?+К2ФЁ+КзФЁ
н _ 2 '
Если шары соединить тонкими проволочками, емкостями кото-
рых можно пренебречь, то потенциалы их станут одинаковыми. Его
можно найти из сохранения зарядов
Кдфд + К2‹р2 + Кзфз = (К, + 122 + Кз)‹р.
Энергия системы после соединения шаров
(К|+К2+К3)(р2
И/к = 2
Количество теплоты, выделившееся при прохождении токов (М 3.56):
О: и/н- `v
Рассмотрим диск радиусом К и толщиной 1 (1 4: К) из равно-
мерно заряженного диэлектрика (диэлектрическую проницаемость
положим е = 1) с объемной плотностью заряда р, который лежит
на большой металлической заземленной пластине. Вычислим энер-
гию электростатического поля диска, пренебрегая краевыми эф-
фектами (М: 3.49). Воспользуемся методом электрических изобра-
жений. Для удовлетворения условия на металлической пластине
надо под диском разместить такой же диск с объемной плотнос-
тью заряда —р. Используя теорему Гаусса (1.12), (1.19) и (1.20),
получаем, что вне диска поле отсутствует, а по его толщине меня-
101

ется линейно. Интегрируя по толщине с помощью (3.69) и умно-
жая на площадь, получаем
/
и/ = 11122 1 (41грх)2 Ё’: = ёп2р2к21з.
0
ЕСЛИ ВО ВНСШНСМ ПОЛС Е находятся два заряда ПРОТИВОПОЛОЖ-
НЬ|Х знаков, образующие ДИПОЛЬ С МОМСНТОМ р = а‘, ТО энергия ЭТИХ
зарядов ВО внешнем поле равна
И’= ЧФ — ст’ = ‹1(Ф — Ф’).
С ТОЧНОСТЬЮ ДО ВСЛИЧИН второго порядка малости
‹р =‹р’+%%1 =‹р’+|3гас1‹р=‹р’—|Е.
Откуда
И/= -с1|Е = —рЕ. (3.73)
Это энергия взаимодействия зарядов, поэтому она может быть от-
рицательной. Отметим, что это энергия жесткого диполя (расстоя-
ние между зарядами не меняется).
Для проводящего шарика радиусом К в поле Е дипольный мо-
мент р = К3Е, и поэтому при изменении поля
Е 3 2
и/=-к3[15аЕ=-КЕ. ‹3.74)
0
2
При внесении проводящего незаряженного шарика в заряжен-
ный плоский конденсатор его заряд с; не меняется, а емкость увели-
чивается (как бы уменьшается расстояние между пластинами 1). Из
сохранения энергии
42 _ 42 + кзЕ2 _ а + кзч2
2С 2(С + АС) 2 2(С + АС) 2С312'
Отсюда изменение емкости (Не 3.66) АС = 123/12. Заметим, что не
учтено исчезновение энергии поля в объеме шарика, которая равна
Е:
Ёпкзд, т. е. примерно того же порядка в случае В = 0,2 мм и
1 = 1 см.
Рассмотрим идеальный газ, полярзуемость молекул которого В,
находящийся в большом сосуде при температуре Т, где также нахо-
дится плоский конденсатор с напряженностью поля Е. Найдем от-
102

носительную разность концентраций молекул Ап/по в конденсаторе и
вне его, предполагая выполнение распределения Больцмана (М 3.6).
Дипольный момент молекул в электрическом поле равен р = ВЕ.
Формула (3.73) получена для жесткого диполя и связана с его пово-
ротом в поле. Получим энергию упругого диполя в процессе квази-
статического изменения дипольного момента при изменении внеш-
него поля. При изменении поля изменяется дипольный момент
др = 4:11 = ВаУЕ. Работа электрических сил с1Е‹11 = ВЕс1Е. Определяя
энергию упругого диполя ИС как работу внешних сил, имеем
ш=-_ВЕ’=-щ=_&
2 2 2`
Распределение Больцмана для числа молекул в единице объема
(см. 2, с. 188)
„ = „ ехр‹_!/_) = „ ехрцЁ)
° кт ° 2/сТ ’
где по — концентрация молекул вне конденсатора.
При малых отклонениях концентрации
А»: .. В?
„О 2кт°
Формулы (3.68) и (3.69) можно преобразовать для конденсато-
ров, заполненных диэлектриками. Используя (2.6) и (3.7), из (3.67)
получаем вдоль силовой линии
и! ьёщ=ёрзд1йрэд1з=ёдлвол1уьётдевёагу,
где д У = с11‹1.$`.
Для плотности электростатической энергии в диэлектрической среде
имеем
_ (во) _ еЕ’ _ 02 _ _ (во) _ еоеЕ2 _ 02
__’ {ш- 2 _ 2 _ 2808 7 (375)
Используя те же формулы, можно получить выражение для плот-
ности энергии, не предполагающее линейную зависимость между
Е и 1),
40„ _ вал), _
4“ 4/1 4“, {ими/рвал}. (3.76)
и/=[‹рд4=[Е1
103

Рассмотрим два удаленных друг от друга диэлектрических (с ди-
электрической проницаемостью е) шара радиусами Л, и Л„в цент-
ры которых помещены заряды д, и д,. Найдем работу, необходимую,
чтобы поменять эти заряды местами (М 3.48). Используя (3.75) и
(3.10), можем найти начальную и конечную энергии
2 2Я2 2
2е г 2Я, 2е г 2Я
2еог2 2Я, 2е Ог 2Я
Работа равна разности энергий
) 1/Я~ вЂ” 1/Я2
Рассмотрим плоский конденсатор емкостью С, подключенный пос-
ледовательно с некоторым сопротивлением (Л) к батарее с ЭДС Й.
Пластины конденсатора быстро сближают, так что расстояние между
ними уменьшается в два раза, причем настолько быстро, что заряд
конденсатора практически не меняется. Найдем джоулеву теплоту,
которая выделится на сопротивлении к моменту окончания переза-
рядки (Мо 3.58). В соответствии с (3.56) емкость увеличится в два
раза (ЛС = С), и, следовательно, при неизменном заряде разность
потенциалов уменьшится в два раза (станет равной Й/2). После окон-
чания процесса перезарядки разность потенциалов снова станет рав-
ной 11; а заряд увеличится в два раза, т. е. протечет заряд, равный
начальному на конденсаторе Лд = д = СЙ. Изменение энергии кон-
денсатора в процессе перезарядки
Из сохранения энергии следует, что работа батареи А = Лдй = СВ2
пошла на изменение энергии конденсатора ЛЖи нагрев сопротив-
ления ~О). Таким образом,
О = А вЂ” Л В' = вЂ” СФ'~.
4
Для того чтобы за время сближения пластин Л~ заряд конденса-
тора не изменился, необходимо выполнить условие Л~ «т = ЛС.
104

ВО ВТОРОМ СЛУЧЗС сохраняется заряд. ПОЭТОМУ
= 410142 < ш = 411/242
“ 28.5‘ " 25 °
Энергия увеличивается
2
_ _ = __ ‘1
АРУ-РУК И/н (е Омск.
При вычислении механической работы Ам в первом случае надо
учесть работу источника напряжения
А„ = и] (14 = НМ = (РАС. (377)
ЭТЗ величина отрицательная, ПОЭТОМУ энергия ИСТОЧНИКЗ УВОЛИ-
ЧИВЗСТСЯ за СЧСТ МСХЗНИЧССКОЙ работы. СЛСДОВЗТСЛЬНО,
1 2 2 1 2 Ски2
Ам =Ащ —А„ =5и АС-Н АС=-5П АС=(е-1) 2
Во втором случае механическая работа идет на увеличение энер-
ГИИ конденсатора
2
‚д, =Аи/ =(е—1) ‘1 =1е(е-1)С‚<П2.
’ 2еС 2
К
Пондеромоторными называются силы, которые действуют на ве-
сомые тела (диэлектрики и проводники), находящиеся в электри-
ческом поле. Сила, действующая на заряд, определяется напряжен-
ностью поля, в которое помещен этот заряд, а не того поля, которое
возбуждается им самим.
Рассмотрим заряженный проводник. Так как взаимно отталки-
вающиеся элементы заряда не могут покинуть проводник, к его по-
верхности будут приложены пондеромоторные силы, стремящиеся
ее растянуть. Обозначая поверхностную плотность заряда о, для на-
пряженности поля с внешней стороны элемента площади поверх-
ности (15 имеем из (1.12) Е = 4по. У поверхности проводника поле
направлено по нормали к поверхности. Это поле можно считать
суммой полей от заряженной площадки 415 (1.17) и поля, создава-
емого другими зарядами поверхности в отсутствие площадки. Это
поле равно 2по и направлено по внешней нормали к поверхности.
106

Таким образом, сила, действующая на единицу площади элемента
дБ’, равна
1:21:02 =1Ео=Ё. ’ (3.78)
2 81:
Если по поверхности сферы радиусом К равномерно распреде-
лен заряд О, то давление изнутри поверхности определяется по (3.46)
(Мэ 3.50)
А
8пк4 °
Силу отталкивания между двумя половинками проводящей сферы
радиусом К с общим зарядом О (М) 3.51) можно найти, используя (3.78):
р = 1“ = 21:02 = (3.79)
2
г = рпК2 = %. (3.80)
812
Если в центр проводящей сферы, рассмотренной ранее, помес-
тить заряд с], то он увеличит давление на поверхность на р, = ос1/К2.
Складывая это с давлением от заряда О, получаем (Не 3.52)
О (О + 24)
8122
Рассмотрим незаряженный проводящий шар (радиусом К), разре-
занный пополам, находящийся во внешнем однородном поле (Ео),
перпендикулярном плоскости разреза. Найдем силу, с которой оба
полушария отталкиваются друг от друга (Не 3.53). Поле на поверх-
ности шара описывается (1.28)
Г:
К
Е = ЗЕО сов6г,
где 6 — угол между направлением Ед и нормалью к поверхности.
Проекция силы давления на ось симметрии (направление поля ЕО)
из (3.78)
_ 2со$6
Д-Е 81: °
Силу отталкивания, действующую на каждую из половинок, на-
ходим интегрированием по углу
п/2 тг/2
. 9 . 9
Р = [д2пкзпп6кд6 = ЕЕЁЁ _[ 0053 63111646 = ЕЕЁКЁ
о о
107

Рассмотрим длинный проводящий шшиндр радиусом К, состав-
ленный из двух половинок. Найдем силу отталкивания Е действую-
щую на единицу длины каждого полуцилиндра, если на единицу
длины цилиндра приходится заряд х (Мг 3.54). Давление на единицу
поверхности определяется (3.78). На единицу длины каждой поло-
винки цилиндра действует сила
2
г = 21102212 = А,
1:12
так как
_ Х
о— 21:11.
ЕСЛИ на ОСИ ЦИЛИНДРЗ ПОМЕСТИТЬ ТОНКУЮ ЗЗРЯЖСННУЮ НИТЬ, на
СДИНИЦУ ДЛИНЫ КОТОРОЙ ПРИХОДИТСЯ ЗЗРЯД хо, ТО на СГО ПОВЕРХНОСТИ
2740
Ее = т
и дополнительное давление
27400
р0 = Та
Т. С. В СУММС ДЛЯ СИЛЫ ИМССМ
_ х(х+2хо)
Р-“эггт
Оценим силу, действующую на атом, находящийся на рассто-
янии 1 = 200 А от поверхности острия металлической иглы с ра-
диусом закругления К = 100 А. Потенциал на игле У= 100 кВ.
Поляризуемость атома ос — величина порядка его объема (М: 3.71).
Будем считать, что поле острия иглы совпадает с полем заряжен-
ного шара
Е = 1’- = Ё.
Г Г
Дипольный момент поляризованного атома р = осЕ. Используя
(1.11)‚ находим силу притяжения
108

Найдем силу притяжения между пластинами плоского конден-
сатора, на одной из которых плотность заряда о, а на другой вЂ” о.
Поле, создаваемое одной пластиной там, где находится вторая, равно
(1.17) Е = 2яа. Сила, действующая на единицу. поверхности второй
пластины,
г
вЂ” = р=2яа .
Я
(3.81)
Учитывая, что поле внутри конденсатора Е = 4яа, получаем, что
.г
Р=вЂ”
8к
Это можно назвать силой натяжения вдоль силовой линии, и ее
величина равна плотности энергии (3.69). Силовая линия как бы
старается сократиться, а расстояние между силовыми линиями, как
в дальнейшем будет показано, стремится увеличиться.
Рассмотрим плоский конденсатор, состоящий из двух квадрат-
ных пластин, расположенных в вакууме вертикально на расстоянии
Ь = 1 мм друг от друга, одна из которых закреплена, а другая может
двигаться без трения по гладким вертикальным направляющим.
Найдем, при какой разности потенциалов У между пластинами
подвижная не упадет вниз, если ее масса М = 1 г, а сторона квад-
рата (= 10 см (№ 3.69). Обозначая смещение подвижной пластины
у и пользуясь (3.68), получаем для энергии конденсатора
ЕИ(( вЂ” у)
Сила в направлении у равна
дИ~ ЕИ
ду 8к
Отсюда для разности потенциалов получаем
1(г
Г=ЕЬ= 8"М~" =4,71 кВ.
(
Если между пластинами конденсатора находится диэлектрик, то
поле от первой пластины, которое действует на заряд второй, равно
Е = 2па/е и сила
2жо аЕ
вЂ” =Р=
Я е Зя
(3.83)
109

И в этом случае величина силы натяжения вдоль силовой линии
равна плотности энергии (3.75).
Отметим, что в случае твердых диэлектриков, когда имеется хотя
бы небольшой зазор между диэлектриком и пластиной, сила притя-
жения определяется (3.81) и (3.82)‚ а для жидких диэлектриков, ког-
да зазор отсутствует, — (3.83).
В заряженном цилиндрическом конденсаторе сила притяжения
между обкладками может привести к разрушению обкладки. Рас-
смотрим цилиндрический конденсатор, состоящий из двух тонко-
стенных коаксиальных металлических цилиндров, пространство
между которыми заполнено жидким диэлектриком с диэлектричес-
кой проницаемостью е = 2. На конденсатор подается напряжение,
величина которого медленно увеличивается. Найдем, что наступит
раньше: механическое разрушение внутренней обкладки или пробой
диэлектрика, если известно, что пробой наступает при напряженно-
сти поля Еп = 30 кВ/мм, а разрывное усилие стенок цилиндров —
оразр = 500 /м и радиус внутренней обкладки К = 3 см (Не 3.60).
Отметим, что сила притяжения между обкладками растягивает внут-
реннюю обкладку и сжимает внешнюю. Так как материал на сжа-
тие обладает большей прочностью, чем на растяжение, то в пер-
вую очередь будет разрушаться внутренняя обкладка. На рис. 3.15
показаны силы, действующие на элемент обкладки (площадью 2осК,
умноженной на единицу длины вдоль образующей цилиндра): сила
притяжения 2оъКр, которая определяется по (3.83), и проекции сил
20% которые ее уравновешивают. Откуда
_ КгЕ2
х _ 81: '
Если Е= Ед , то/= 2- 105 дин/см. Это меньше, чем о ар = 500 Н/м =
= 5 - 105 дин/см. Поэтому раньше произойдет пробои диэлектрика.
Найдем силу притяжения между обкладками (площадью 5) плос-
кого воздушного конденсатора (разность потенциалов обкладок Н),
в который введена диэлектрическая пластина толщиной 12, и диэлек-
трической проницаемостью е так, что между обкладками и пласти-
ной еще остались зазоры, суммарная толщина которых 1 (Не 3.59).
Для разности потенциалов имеем
киви-д}.
Используя (3.82)‚ получаем
5112
Г _ 8л(1+ /1/е)°
110

:тффч‹——ф
1
Рис. 3.15 Рис. 3.16
На рис. 3.16 показано сечение плоского конденсатора, в кото-
рый параллельно его обкладкам вставлена диэлектрическая пласти-
на с проницаемостью е, толщина которой равна половине зазора
конденсатора (11), и приложено напряжение И Пунктиром изобра-
жен некоторый замкнутый контур Ь, пронизывающий конденсатор
и диэлектрическую пластину. Найдем циркуляцию 4319,41 вектора
электростатической индукции 1) по контуру Ь (М9 3.65). Круговой
интеграл (3.18) в электростатике равный нулю можно разбить на две
части. Часть, находящуюся вне конденсатора, обозначим А. Тогда
из (3.18)
Е}: Е}: _ __ е+1
А+7+Ё-О, А- Е/т 28.
Так как вне конденсатора 1) = Е, а внутри конденсатора 1) не-
прерывно, получаем
фцсл = мы = ЕЬШ = п/Ш.
2е е + 1
Рассмотрим плоский конденсатор, пластины которого имеют
площадь 5‘ и расположены на расстоянии И, заполненный диэлект-
риком с диэлектрической проницаемостью е и присоединенный к
батарее постоянного тока, поддерживающей на нем разность потен-
циалов Ы Одну из пластин отодвигают так, что образуется воздуш-
ный зазор. Найдем, на какое расстояние х отодвинута пластина,
если при этом совершена работа А (М9 3.57). Изменение напряжен-
ности электрического поля Е в воздушном зазоре можно опреде-
лить из условия
111

Аналогичным образом можно решить задачу с твердым диэлект-
риком. Найдем, например, силу, с которой пластина из диэлектри-
ка (е), также вставленная до половины конденсатора (с квадратными
пластинами), втягивается в него (М 3.63). Используя (3.85), имеем
,~~~ (е вЂ” 1) Е ~,~~2 (е вЂ” 1) 4Г
8п 8„(е + 1)
Если внутри конденсатора имеется диэлектрик с диэлектричес-
кой проницаемостью е, то его емкость (Со) увеличивается в е раз
С = еСО (3.56). Из (3.67) для энергии плоского конденсатора имеем
Д
2С 2яСо
Допустим, что в конденсаторе находился жидкий диэлектрик,
который слили, предварительно отсоединив конденсатор от батареи
(источника питания). Так как заряд на конденсаторе сохраняется,
его энергия станет равной
~~2
гс,
Такая энергия выделится при разрядке конденсатора (М 3.55).
Выливание диэлектрика вЂ” это работа силы тяжести против сил элек-
трического поля, которые в соответствии с (3.85) стремятся втяги-
вать диэлектрик. Она увеличивает энергию конденсатора.
На рис. 3.19 показано сечение конденсатора переменной емкости,
состоящего из двух неподвижных металлических пластин, располо-
женных на расстоянии Ь друг от друга, и подвижной диэлектричес-
кой пластины с диэлектрической проницаемостью е, которая может
поворачиваться и заходить в зазор между металлическими пласти-
нами. Все пластины имеют форму полукруга радиусом Л, причем
зазоры между диэлектрической пластиной и пластинами конденса-
тора пренебрежимо малы по сравнению с Ь. Пренебрегая краевыми
эффектами, найдем момент М сил, действующих иа диэлектрическую
пластину, когда она выведена из положения равновесия, а разность
потенциалов на пластинах конденсатора равна Г (М 3.67). Сила,
действующая на границе между диэлектриком и воздухом внутри
пластин конденсатора, втягивает диэлектрик в конденсатор и опре-
деляется (3.85). Момент ее равен
114

Рис. 3.19 Рис. 3.20
Как видим, момент сил не зависит от угла поворота диэлектри-
ческой пластины. Отметим, что когда угол поворота равен нулю,
можно считать, что внутри конденсатора находятся две границы
диэлектрика, на которых моменты уравновешивают друг друга, и
суммарный момент, действующий на пластину диэлектрика, равен
нулю (Не 3.68).
На рис. 3.20 показано сечение сферического конденсатора, у ко-
торого половина заполнена диэлектриком с проницаемостью е„ а
другая половина диэлектриком с проницаемостью е2. Найдем силу,
действующую на внутреннюю сферу радиусом К, если конденсатор
имеет заряд О (Не 3.70). Заряд перераспределится (разделится на
9, + О, = О) так, чтобы в соответствии с (3.18) на границе остава-
лась непрерывной напряженность поля
Е=&=_92__
81/‘2 827
Используя связь между зарядами, выражаем через суммарный
заряд '
Е=——9——.
(е, +е2)г2
Из (3.85) получаем давление на внутренней сфере, которое для
получения силы умножаем на площадь:
(е, - е2)О2 2пК2 О
Р:
8ТЁ(Ё| + Ё2)К4
Рассмотрим подъем жидкого диэлектрика (диэлектрическая про-
ницаемость е, плотность р) в вертикальном воздушном цилиндри-
ческом конденсаторе с радиусами обкладок К, и К, < К„ разность
8. 115

4. постоянный ток.
токи в НЕОГРАНИЧЕННОЙ СРЕДЕ
Электрический ток — это движение зарядов, которое возникает
в проводнике под действием электрического поля. Плотность тока]
определяется числом частиц в единице объема п, имеющих заряд е,
проходящих через единицу поверхности за единицу времени со ско-
ростью п:
3 = пеп. (4.1)
Поток электрического заряда через поверхность (15 (с нормалью п)
называется силой тока 1
= % = [оном = 1 дав. (4.2)
5 5
Изменение заряда, имеющего плотность рт, внутри объема И
охватываемого неподвижной поверхностью 5, описывается урав-
нением
д (1 рта!’ ]
у
д’ = -ф1„а$, (4.3)
где 1„ — проекция плотности тока на внешнюю нормаль поверх-
ности.
В дифференциальном виде отсюда имеем
д . .
р” + сну _| = 0. (4.4)
д!
Это называют законом сохранения заряда.
При постоянных токах распределение зарядов стационарно и из
(4.3) и (4.4) имеем
ф дав = о; (4.5)
агу 3 = о. (4.6)
117

Эти уравнения показывают, что постоянный ток не имеет ис-
токов, т. е. что линии тока всегда замкнуты или уходят в бесконеч-
ность.
Как показывает опыт, для многих проводящих сред (в частно-
сти, металлов) плотность тока 3 пропорциональна напряженности
электрического поля Е (закон Ома в дифференциальном виде)
3 = АЕ, (4.7)
где ж — постоянная для данной среды величина, называемая удель-
ной проводимостью, или электропроводностью, зависящая от свойств
сред и условий, в которых они находятся. Отметим, что это уравне-
ние остается справедливым и в переменных электрических полях.
Величина, обратная удельной проводимости, называется удельным
сопротивлением среды
р = —. (4.8)
Используя (4.6), (4.7), (3.8) и (3.6), получаем, что в случае стаци-
онарных токов макроскопические электрические заряды могут на-
ходиться только на поверхности или в местах неоднородности про-
водящей среды. В этом отношении электрическое поле стационар-
ных токов аналогично электростатическому.
Отметим, что закон Ома не является фундаментальным зако-
ном, а выполняется лишь для некоторых (может и многочислен-
ных) сред при определенных ограничениях. Приведем пример мо-
дельного представления, позволяющего получить зависимость (4.7)
и выражение для А.
В металлах проводимость связана с наличием свободных элект-
ронов (масса т, заряд е), которые под действием электрического
поля могут ускоряться в направлении поля (Е) и тормозиться при
соударениях с ионами решетки. Хаотическое (тепловое) движение
электронов не приводит к току. Ток — это дрейфовое (упорядочен-
ное) движение с ускорением
еЕ
т .
Предполагая, что при соударении дрейфовое движение пропада-
ет, находим, что за время т до следующего соударения скорость бу-
дет и = ат. Средняя скорость дрейфа
118

Для плотности тока получаем
_ пе2тЕ
1 = пеи 2,”
Это — закон Ома (4.7)‚ где выражение для проводимости
ж=”дГ (49
2т
Время между соударениями можно оценить из длины пробега 1и
скорости теплового движения с:
т=—. илщ
Работа, совершаемая в единицу времени (мощность) над элект-
ронами единицы объема, при дрейфовом движении
‘Е’
пиГ = д.
Эта энергия идет на увеличение внутренней (тепловой) энергии
среды. Тепловая мощность А’, создаваемая током в единице объема
проводящей среды:
_д_жг2
е _ е2 .
Н (4.11)
Или, так как Г = еЕ, используя (4.7), получаем
.2
м=#. мю)
А
Это закон Джоуля-Левша в дифференциальном виде.
Для поддержания постоянного электрического тока необходимы
электродвижущие силы неэлектростатического происхождения (хи-
мические, индукционные, термоэлектрические, контактные, инер-
циальные и т. д.). Работа этих электродвижущих сил (ЭДС), кото-
рые называются сторонними, компенсирует потери на джоулеву теп-
лоту. Для совокупного действия электростатического поля Е и поля
сторонних сил Е° в соответствии с (4.7) можем написать
3 = МЕ + Е°). (4.13)
Это обобщенный закон Ома в дифференциальном виде.
119

Применим полученные соотношения для токов вдоль проводов.
Сопротивлением провода на участке от поперечного сечения 1 до се-
чения 2 назовем величину
Ы1
12,~ у~ ~
1
(4.14)
при постоянных 5'и Х
( р(
Так как ток во всех сечениях одинаковый, то, используя (4.2),
(4.13) и (4.14), получаем
2 2
1Х!2 вЂ”вЂ” ~Б((+~ Е'СИ = ~!2+6!2. (4.1 5)
1 1
В стационарном поле постоянных токов электрическое поле Е
обладает потенциалом <р. Поэтому
1Х!2 Р1 ~Р1 + '12'
(4.16)
Для замкнутого контура
(4.17)
где Х вЂ” полное сопротивление контура (включая сопротивление ЭДС);
Ж вЂ” полная ЭДС контура (верхний индекс здесь опущен, так как это
обозначение будет использоваться только для сторонних электродви-
жущих сил). Это закон Ома для полной (замкнутой) цепи тока.
Интегрируя (4.12) по объему провода, получаем закон ДжоулявЂ”
Ленца в интегральной форме
(4.18)
У= 12Х.
Для разветвленной цепи проводов, включающих ЭДС, сформу-
лированы два правила Кнрхгофа:
1) в каждой точке разветвления проводов алгебраическая сумма
токов (например, входящие положительны, а выходящие отрица-
тельны) равна нулю
~1,. =0; (4.19)
Ю
2) сумма ЭДС в выделяемом контуре равна сумме падений на-
пряжений на всех участках контура
(4.20)
120

1= 1, + 12. Из (4.2О) ЁЗ, = 11:‘, + 112 и $2 = 125 + 112. Три уравнения и
три неизвестных тока. Решая уравнения, получаем
= ад + к(гг‚ 45)
= 1,05 А;
г‚г2+К(ц +5)
= ат + к(гк‚ 4972) 2 _О 87 А_
игл/Ш. +5) ’ ’
1 = 8,1‘: +852г, 2 0,18 А;
П’2+К(Ч +5)
У = Н? = 1,8 В.
Ток через второй элемент идет противоположно направлению,
указанному на рис. 4.2.
Для схемы, показанной на рис. 4.3 (М 4.3), пренебрегая сопро-
тивлением соединяющих проводов, из (4.2О) имеем
га, + $2 + 263
Г‘ + Г2 + 73
Откуда
516 ‘ ‘Ш * 31% ‘ дай
У=б—Л= р .
п + Г2 + 73
При
б, ад гад
‘1 ’°2 "з
получаем У= О.
Г‘ 81
Т
г- Ъ-
12
122

В схеме на рис. 4.4 сопротивления К, и К2 подобраны так, что ток
через гальванометр Г не идет. Считая известными 81, $2, К, и К2 и
пренебрегая внутренними сопротивлениями батарей по сравнению
с К, и К2, найдем 55019 4.4). Предполагаем направления токов таки-
ми, как показано на рис. 4.4. Так как ток через гальванометр не
идет, то 1, = 12 = 1. Используя (4.2О), находим
- щщ- е 29-112
-?_'› ‘1“2- 1-
к,+к,
Отсюда
2 ё,К2+ё2К‚
_ К1+К2 °
Найдем ток, проходящий через Ко, в схеме на рис. 4.5 (Не 4.5).
Предположим направления токов такими, какие обозначены на
рис. 4.5. Из (4.19) и (4.2О)
10 = 12 + 13; О = 13К3 — 12К2;
8, + 550 = 12КО + 13(К0 + Кд).
Откуда
1 ё1Ко+(?%+ёЬ)К2 1 Ё71К2+ёо(к2"'кз)
3 = д о = -
К0К3+КОК2+К2К3 К0К3+К0К2+К2К3
Для схемы на рис. 4.6 при заданных значениях К] и К2 найдем К,
при котором рассеиваемая на нем мощность максимальна, и опреде-
лим условие того, что ток, проходящий через К, равен нулю (Не 4.6).
Считаем направления токов такими, как обозначенные на рис. 4.6.
Из (4.19) и (4;20) имеем
1, = 1+ 12; 81 = 1(К + К1)+ 1дК1; $2 = 12К2 — 1К.
123

Откуда
к(к‚ + к‚)+ 12,122 `
Отсюда условие, чтобы ток был равен нулю:
н’, _ к‘
“2 32 .
Для мощности, рассеиваемой на К, имеем
А’ = Рк = Шт,
(к + В)
где
(дтк2‘ёёкл)2_ В: К,К2
(к‚+к2)2 ’ дик:
Вычисляя производную П по К и приравнивая ее нулю, получа-
ем, что максимальная мощность рассеивается при
= клк2 _
к‚+к2
На рис. 4.7 показана схема из двух батарей ЭДС 5%’, и $2 и четы-
рех одинаковых резисторов сопротивлением К каждый. Найдем мощ-
ность, рассеиваемую на этих резисторах (М 4.7). На рисунке обозна-
чены выбранные направления токов. Используя (4.19), получаем
1‚+ 16= 12; 12=13+ 15;13=14+1д;14+15=16.
Откуда
12+ 14=13+ 16.
из (4.20)
Д+Д+Д+Ь=Щ
ё):
552
124

В результате
Н’ +8 0hx —ё’
ЁК 2/3
Выделяемая мощность равна А’ = РК.
Существует принцип, согласно которому токи и напряжения в
цепи, состоящей из линейных (подчиняющихся закону Ома) эле-
ментов, распределяются таким образом, что диссипируемая в теп-
лоту мощность минимальна. Найдем с помощью этого принципа
напряжения на каждом из трех последовательно соединенных со-
противлений Кд, 12„ 12„ если суммарное падение напряжения на
них равно У(М> 4.10). Обозначим падения напряжений на сопро-
тивлениях И = 112„ 13 = 112,. Тогда падение напряжения на третьем
сопротивлении (У- У, — 13). Для диссипируемой в теплоту мощно-
сти, используя (4.18), получаем
=Ё+Ё+(У‘Й“У2)2_
12 ="14 =
А!
к, к, к,
Условие минимальности мощности определяется уравнениями
дитяти-ю) О. ш шути-га) д
аи к, к, ’ ау, к, к,
Решая их, находим
ук, кк, Ук,
и =————; га =————; и =——-——.
К‚+К,+К, К‚+К,+К, к‚+к,+к,
Если сопротивления соединить параллельно (Мг 4.11), то из (4. 18)
А’ = 1312? + 1312, +(1 - 11- 1,)К,.
Условие минимальности мощности
Ш_ш_2(1-1,-/,) ш_ш_2(1-1‚-1,)
д1‚ к, к, ’ д], к, к,
=0.
Получаем
_ 73233 . _ ‘кпд: .
‘ к,к,+к‚к,+к,к,’ 2 к‚к,+к‚к,+к,к,’
_ 132“:
к‚к, + к‚к, + к,к,'
13
125

Рис. 4.8
Рис. 4.9
В схеме на рис. 4.8 сопротивления Л„Л, и Л, подобраны так,
что ток через гальванометр Г не идет. Зная эти сопротивления и
ЭДС Ы'1 и Кз, найдем ЭДС Ы' и ток 1, проходящий через батарею Й„
пренебрегая внутренними сопротивлениями батарей (№ 4.8). На
рисунке показаны предполагаемые направления токов. Учитывая,
что ток через гальванометр не идет, из (4.20) получаем
2
'3 1 3 ~ "2 1 ( 2 3 ) "3
3
Ток 1 находим из уравнения
И'1 = 1Л, + 1,(Л, + Л,).
В схеме на рис. 4.9 сопротивления Л, и Л, подобраны так, что
ток через гальванометр Г не идет. Пренебрегая внутренними сопро-
тивлениями батарей и считая известными Й1 и Й2, найдем Ж (№ 4.9).
Выбранное направление тока указано на рисунке.
Используя (4.20), получаем
К1 вЂ” И;2 = 1(Л, + Л ); Й вЂ” Й1 = 1Л,.
Откуда
~1 + '2 ~1/~2
К=
1+ Я1/Я2
126
На рис. 4.10 показана схема включения неоновой лампочки в раз-
рыв подвижного проводящего диаметра СР окружности АСВР, сде-
ланной из однородной проволоки постоянного поперечного сече-
ния. Найдем, при каких положениях СР лампочка зажигается (по-
тенциал зажигания Г„) и гаснет (потенциал гашения Г„( Г ),

если между А и В поддерживается напря-
жение И а сопротивление проводов мало
по сравнению с сопротивлением неоновой
лампочки. При вращении диаметра по ча-
совой стрелке (от ос = О) получаем
Аналогично находим
‚К 1 _К д- =Ш
уж“ л(2+в) тс(2 л °
Поэтому (Не 4.12)
В = ЕЕ
У 2
В длинных сетях потери в проводах могут быть существенными.
Найдем, каким должен быть минимальный диаметр медного про-
вода В (удельное сопротивление меди р = О,О17- 10'4 Ом - см, дли-
на 10 км), чтобы потери энергии в сети не превышали 10 % от мощ-
ности источника (1\’= 5 кВт) с напряжением У= 110 В (М 4.31). По
условию теряемая мощность
й < д.
К 10’
где
- 91
К - 5 .
Откуда
192 < 491“ =1О см2.
10л1/2
Основными элементами прибора для измерения напряженности
электрического поля у поверхности Земли являются две проводящие
127

плотность зарядов на проводниках :р, то для стержней в отдельно-
сти из (|.|2) и (|.|6) Е = 5:2р/г. Разность потенциалов между про-
водниками находим, интегрируя напряженности от них по линии,
проходящей через их оси:
17-го
у=2рЦ1+ ' )аг=4рпп(”"°)=4р1п[д].
го г Ь ГО ‚О
—г
Величину тока находим, считая, что вблизи каждого Цилиндра
влияние другого мало и имеется цилиндрическая симметрия, т. е.
1 = 2пгоа] = 2пг0 аЖЕ = 4прЖа.
Следовательно, сопротивление
у „1п(1›/г0).
тгщ
1 пжа
Аналогичным образом можно найти сопротивление систем, изоб-
раженных на рис. 4.14 и рис. 4.15. В первом случае к цилиндричес-
ким электродам диаметром с! присоединен проводящий слой с про-
водимостью ж, намного меньшей проводимости электродов, и тол-
щиной б << д, находящийся на двух конусах, наибольший диаметр
которых 1), а во втором — такой же проводящий слой на поверхно-
сти цилиндра диаметром В и высотой 1.
Для изменения напряженности электрического поля в проводя-
щем слое на конусе имеем для компоненты поля, перпендикуляр-
ной оси симметрии,
Рис. 4.14 Рис. 4.15
130

РЗЗНОСТЬ потенциалов на конусе
0/2 В
у = -1 Ем = 2р1п(—).
и/2 ‘1 ›
На втором конусе еще такое же падение потенциала. Для тока
получаем
4прЖб
зйп ос
9
1 = 2л%б] = пазжв, =
где Е, — поле вдоль образующей конуса, компонентой которого яв-
ляется Е‚,
„О-д
21 '
Сопротивление системы (Мг 4.17)
_ 1 _ 211п(В/с1)
1 яка (в - а)’
В случае цилиндра (см. рис. 4.15) напряженность электрическо-
го поля на его основании Е = 2р/г и разность потенциалов (на
каждом основании)
это: =
В
У = 2 1п — .
1 р д
На бОКОВОЙ ПОВЕРХНОСТИ цилиндра поле ПОСТОЯННО, так же как
постоянна плотность тока. Следовательно, падение потенциала на
боковой поверхности
1
Полное падение потенциала
У =4р[%+1п(%)].
СИЛУ ТОКЗ вычисляем ПО ПЛОТНОСТИ ПОТОКЕ! ВбЛИЗИ электрода
1 = 2п%б] = пдбАЕ = 4лрж5.
Сопротивление системы (Не 4.18)
к _: _1/0+1п(0/с1)
` 1 ’ яма ‘
9 131

Найдем сопротивление между двумя металлическими шарами (ра-
диусами К, и 122), зарытыми на большую глубину и находящимися
на большом расстоянии друг от друга в земле, проводимость кото-
рой вблизи от шаров А] и А, значительно меньше проводимости
металлов (Не 4.32, 4.34). Воспользуемся тем, что токи вблизи шаров
близки к сферической симметрии
1 = ’ 2 и Е = 1 = $7,
41гг 7» 4ТЙГ
что приводит к быстрой сходимости интеграла {Еа/г. Для оценки
к
разности ПОТСНЦИЭЛОВ МЕЖДУ шарами ИМССМ
т?
К:
ЕД? + у %_ = [к
4ТЁ›\.|Г [22 41ЁЖ2Г
Откуда _
1 1
= + .
4ТЁЖ1К| 4ПЖ2К2
Если шары включить в цепь постоянного тока с источником ЭДС 85,
как показано на рис. 4.16, то, пренебрегая всеми сопротивлениями,
кроме сопротивления заземления, получаем для тока
41%
1 = .
1/Ж,К,+1/А2К2
Это позволяет найти напряженности поля на каждом шаре и по
теореме Гаусса (1.12) вычислить соответствующие заряды (знак оп-
ределяется направлением тока) (Не 4.36)
1 к21 2512
1:, О: = 3351 = | 2 = 2 3
° 4111113; к2/к1+7ч/7*2
1221 та,
О = К2Е = 2 = _
2 2 2 4пж2кё МИ: щ/М
7»
1 Сопротивление заземления можно найти и для
Рис. 4.16 электродов произвольной формы, если заданы
132

Очевидно, что все внутренние слои дают нулевой вклад и ре-
зультат определяют крайние. Используя (3.8)‚ получаем (Не 4.23)
5(д2 ‘ дн) “$252 ‘81511: $(52/7*2 ‘еж/М) 2 ’(®2/7*2 ‘81/11)
а = 41: =° 43: 41: 41:
Если электрическое поле направлено от стороны 1 к стороне 2 и
82 е,
_: > Т,
ж: ж,
то заряд положительный.
Если задан не ток, а разность потенциалов на пластинах (об-
кладках) И то в случае двух слоев диэлектрика толщиной 111 и 122
(М 4.25) плотность заряда на границе диэлектриков получаем сле-
дующим образом:
Е‚11‚+ Е2112 = У; 1 = 1„‚Е]= АЗЕ?
Откуда
ы/ ку
1 = г-—;————- и Е.) : Т
111% + ы, ' 111% + 1221»]
и, так как 02 — В‘ = е2Е2 — едЕд = 4110, то
_ (‘Уч ’ Ё17*2)У
_ 4п(ь‚›„2 + ярд)"
Рассмотрим цилиндрический конденсатор с радиусами обкладок
К, и 122, заполненный слабо проводящей средой (е = 1, 1» = 1с/г2‚ где
1с — некоторая постоянная), на который подано напряжение И Най-
дем распределение поля и плотности заряда (р) в конденсаторе и
его емкость (Не 4.24). Из постоянства тока через единицу длины
конденсатора
1 = 27:17 = 21сгАЕ = ИСКЕ = сопвт
г-
следует линейная зависимость напряженности поля от радиуса Е = Аг.
Для определения постоянной А вычислим разность потенциалов на
обкладках конденсатора
Ед‚.=___*‘<”3°“”.
У: 2
Э'—-.Э°
134

Откуда
2Н
~2 ~!
2 2'
Следовательно,
~2 ~!
2 2'
Из (3.6) и (1.21) при е = 1 имеем
(1/г) д (гЕ, )/дг
4к 4ж
2 2
~~2 1
Плотность заряда постоянна.
Величина заряда на единицу длины на внутренней обкладке д
определяем из уравнения
2 2~Я,
2 2'
Для определения емкости на единицу длины к этому заряду надо
добавить распределенный заряд в диэлектрике
Ря ~2 Я1
Отсюда емкость
д2
2
2 ~1
2 2'
Найдем, по какому закону должна меняться проводимость в та-
ком конденсаторе, чтобы напряженность электрического поля была
постипша. Из постоянства тока в конденсаторе имеем
Х= 2пг/= 2шгАЕ.
Отсюда (М 4.28)
1 1
2пЕг г
В случае сферического конденсатора (радиусы Я, и Я,), запол-
ненного диэлектриком с удельной проводимостью А, из постоян-
ства тока Х = 4шг~/для напряженности электрического поля имеем
У
4жг Х
135

Если в вакууме находятся п идеально проводящих тел с заряда-
ми 4„ 42, 43, ..., 4„ и соответственно потенциалами ф], ‹р2, срз, ..., срп,
то поле между телами определяется уравнением Лапласа, следую-
щим из уравнения Пуассона (2.1 1) при р = О. При заполнении про-
странства между телами однородной жидкостью с диэлектрической
проницаемостью е и слабой проводимостью А и поддержании потен-
циалов тел при прежних значениях электрическое поле между ними
не изменится. Найдем, какое количество теплоты будет выделяться
ежесекундно в этой жидкости (Мг 4.30). Для каждого тела выделяю-
щаяся теплота определяется током с его поверхности
1, = 951„ аз,
где д, — плотность тока по нормали к поверхности тела и разностью
потенциалов на теле и на бесконечности (О). Используя теорему
Гаусса (3.7)‚ для заряда на каждом теле имеем
_ щш_ цш_ дж
4* -95'2г'®фт'® 41:)» °
КОЛИЧЕСТВО ЕЖЕСЕКУНДНО ВЫДЕЛЯЮЩЕЙСЯ ТЕПЛОТЫ
4 А
О = ЕЙНР/с ="Ё“2‘1/‹Фк-
Ток может создаваться механическим переносом заряда, на-
пример на диэлектрической ленте. С помощь такой ленты заря-
жается высоковольтный сферический электрод (радиусом К) в
генераторе Ван-де-Граафа, изображен-
ном на рис. 4.17. Найдем максимальный
потенциал и ток, которые можно полу-
чить от такого генератора, если скорость
движения ленты и, ширина 1, а пробой в
атмосфере газа, вкотором находятся лен-
та и высоковольтный электрод, возни-
кает при напряженности электрическо-
го поля Епр (Мг 4.21). Максимальная плот- +
ность поверхностного заряда на ленте в + 1,}
определяется пробоем Ё +
_ Евр п "
°“Г“ Ф
п „х
Поэтому максимальный ток
Источник
Епр/и
1 = 0112 = .
2% Рис. 4.17
137

Максимальный потенциал на сфере
(р = % = КЕМ.
Атомный электрический элемент представляет собой две концен-
трические проводящие сферы. Внутренняя сфера сделана из радио-
активного материала, испускающего быстрые электроны. В простран-
стве между сферами скорость электронов и, следовательно, их иони-
зирующее действие можно считать постоянным. Пролетев воздушный
зазор, электроны поглощаются на внешней сфере. В отключенной
батарее устанавливается равновесие между потоком заряда, перено-
симым быстрыми электронами, и током проводимости в ионизиро-
ванном воздухе. Найдем напряженность электрического поля Е в
пространстве между сферами, если ЭДС элемента равна $5, радиусы
сфер равны К, и К, (Не 4.22). Так как проводимость А ионизирован-
ного газа пропорциональна концентрации ионов, которая пропор-
циональна потоку быстрых электронов, при равновесии равному току
проводимости, то из закона Ома (др = ЖЕ) следует постоянство на-
пряженности электрического поля
к,-к,
Постоянное поле в сферическом конденсаторе свидетельствует
о наличии пространственного заряда.
Если в пространстве между пластинами плоского конденсатора,
заполненного газом и подсоединенного к батарее, образуется пара
ионов с зарядами фе, то возникающее движение этих ионов приво-
дит к протеканию заряда (току) в цепи..Найдем этот ток (Мг 4.37).
Предполагаем постоянной подвижность ионов, т. е. их скорости и,
и 22,. Обозначим расстояние между пластинами 1. Тогда, если один
проходит путь до соответствующей пластины х, то другой ион про-
ходит до другой пластины путь 1 — х. У одного на это уходит время
Е
а у другого пусть большее время
1-х
12 =
02
Ток через конденсатор определяется (4.1), числом зарядов на
единицу длины, умноженным на скорость движения. Учитывая, что
138

движение заряда отрицательного знака в отрицательном направле-
нии дает ток в положительном направлении, получаем, пока двига-
ются оба иона (О < ~ < ~,), ток
е
~ = А = у("~ + "г)
а затем при 1, < 1 < 1,
е
~2 ~2
1
Таким образом, ток меняется скачком в момент прихода на пласти-
ну одного иона.
Простые правила вычисления суммарного сопротивления сис-
темы при последовательном =, и параллельном соединени-
1 1
ях вЂ” = ~ вЂ” иногда бывает трудно применить. В таких случаях
Я,. р,
надо искать некоторую симметрию, возможность где-то систему
разомкнуть. Рассмотрим такой пример. Фигура, изображенная на
рис. 4.18, сделана из проволоки постоянного сечения. Число впи-
санных друг в друга правильных треугольников очень велико. Сто-
рона самого большого треугольника а, = 1 м. Сопротивление одно-
го метра проволоки 1 Ом. Найдем сопротивление между клеммами
А и В (№ 4.19). В силу симметрии системы потенциал во всех точках
на вертикальной линии, проведенной из верхней вершины треу-
гольника, будет один и тот же (равный половине разности потенци-
алов между точками А и В). Поэтому ток, идущий от А к а„равен
току от а, к В, а ток от а, к а, равен току от а, к а,. В таком случае
можно в нижнем а, отделить внутренний треугольник от внешнего.
Для внутреннего треугольника ситуация теперь такая же, как была
для внешнего. Учитывая, что сторона его равна половине внешнего,
Рис. 4.18
Рис. 4.19
139

получаем, что и сопротивление его должно быть в два раза меньше
внешнего. Если искомое сопротивление А, то сопротивление систе-
мы, ограниченной первым внутренним треугольником, равно Я/2.
Обозначая сопротивление куска проволоки, равного длине стороны
внешнего треугольника г = а,р, получаем эквивалентную схему, изоб-
раженную на рис. 4.19. В результате
1 1 1
вЂ” = вЂ” +
г+ гЯ/(Я+2г)
Это квадратное уравнение относительно Л. Выбирая корень, кото-
рый дает положительное значение, получаем
Л = вЂ” ~Г7 вЂ” 1 г = О, 55 Ом.
3

5. МАЁНИТНОЕ ПОЛЕ.
ЗАКОН БИО-САВАРА-ЛАПЛАСА.
ТЕОРЕМА О ЦИРКУЛЯЦИИ В ВАКУУМЕ.
ИНДУКТИВНОСТЬ ПРОВОДНИКОВ.
ТЕОРЕМА ВЗАИМНОСТИ
В пространстве, окружающем электрический ток, создается маг-
нитное поле, проявляющее себя тем, что действует на движущиеся
заряды, в том числе и на токи. Название этого поля объясняется
тем, что оно того же типа, как у постоянных магнитов. Величина и
направление поля описываются вектором Н, называемым напряжен-
ностью магнитного поля. На основе опытов сформулирован закон
Био-Савара-Лапласа, позволяющий вычислить напряженность маг-
нитного поля от элементов тока:
С г 4пг3
ан=11@; {шиш}, (5.1)
где с — скорость света (электромагнитных волн) в вакууме (при
использовании для входящих в формулу величин гауссовой сис-
темы единиц); с1| — элемент проводника, по которому течет ток 1;
г — вектор расстояния, отсчитываемого от элемента тока. Из опыта
следует суперпозиция магнитных полей, которая нарушается лишь
при наличии в поле ферромагнетиков.
Для бесконечною прямолинейного проводни-
ка с током силовые линии магнитного поля пред-
ставляют окружности с центрами на оси прово- 1’
да. Из (5.1) интегрированием получаем напря-
женность магнитного поля на расстоянии Ь от
оси провода. На рис. 5.1 показан прямой беско-
нечный провод, по которому течет ток 1. Для
вычисления напряженности магнитного поля на
расстоянии Ь от провода пользуемся тем, что
Ё - сова - $0‘
г “ аи ' Рис. 5.1
141

А а расстояниях, больших К, поле является полем диполя типа
(1.9 . В таком случае поток поля
\
_ 1п2КЁ
` со 2 2
` 1: ‚-3 та’. — сК 1’0с
Магнитные стрелки, далеко отстоящие друг от друга, взаимо-
действуют как диполи. На рис. 5.3 показано, что в точке А закрепле-
на под углом ос = 45° к линии АВ одна стрелка. Найдем угол В, под
которым установится другая стрелка, которая может вращаться в
точке В (Не 5.27). Используя формулу (1.9) и обозначая
ъ
_Р
а- 3,
Г
находим вдоль направления г: Е, = За сов ос; вдоль направления р:
Ер = -а. Поэтому
авто: 1
13В=- =——т3ос.
Засоза-асоза 2
При ос = 45°13В = —1/2.
Магнитное поле в плоскости кругового витка с током неоднородно.
Для прямого провода оно уменьшается обратно пропорционально рас-
стоянию от оси провода. Но для искривленного провода оно могло бы
и возрастать. Покажем, что на оси оно имеет минимум (М: 5.9). Рас-
смотрим два элемента 1:11 на противоположных сторонах диаметра
витка (2К). Обозначим расстояние от центра витка х. Используя
(5.1), от двух противоположно расположенных элементов имеем
дН=Ё1аи ‘ 2 + А‘ 2
с (К — х) (К + х)
Поведение этого выражения вблизи центр витка (х = О) опреде-
ляет и поведение суммы всех элементов. Для выяснения этого надо
рассмотреть функцию
_ 1 + 1 .
/( )_ (К—х)2 (К+х)2
у/Ёа В 3а совет
А
143

Первая производная по х /
Вторая производная
‚‚ 6 6 Г
1‘ = 4 + д . %
(К—х) (К+х)
Так как при х = О первая производная равна нулю, а вторая
производная положительна, то здесь минимум функции. Минимум
даст и сумма всех элементов витка.
Для плоской катушки (как бы сжатой в один виток), имеющей А!
витков, в ее Центре в соответствии с (5.4) имеем поле
Н = 2л11\/ .
сК
Если в центр этой катушки подвесить, например, на жесткой нити
другую плоскую катушку, то при пропускании по ним тока возника-
ет взаимодействие. Предполагая, что подвешенная катушка значи-
тельно меньше неподвижной, имеет п витков с площадью 5‘ и в
равновесии плоскости катушек взаимно перпендикулярны, а мо-
дуль кручения нити ос, найдем угол поворота подвижной катушки в
случае одинакового постоянного тока в них 1 (Не 5.40). В данном
случае магнитный диполь с магнитным моментом р = 1п5/с нахо-
дится в поле Н. Момент сил, действующий на диполь, М = [рН].
Величина момента определяется синусом угла между векторами. Угол
поворота подвижной катушки ср предполагаем малым. Получаем урав-
нение для определения (р
2
М = рН созф = 2л$1\’-%(-Ё) = осср.
Аналогичным образом можно рассмот-
реть квадратную рамку, подвешенную внут-
°‘ ри соленоида (Мг 5.41).
Ь Найдем напряженность магнитного поля
"Ф Г в фокусе витка с током (1 ) в виде эллипса,
Ф уравнение которого в полярной системе ко-
у с | ординат (рис. 5.4) имеет вид
= Р
Рис. 5.4 1+ е сов (р ’
144

Где
— параметр;
с (а2 — 122 у”
е = Б = а < 1
— эксцентриситет (Не 5.1).
Используя (5.1) и вводя угол а между д! и г, находим
. а’!
с1Н =1-%с11$п1ос=11д—=11с1‹р.
с,- сг г сг
Так как
1_1+есов‹р
г _ р ’
получаем
Н =11т(1+есозср)с1ср=ш= мёд.
с р О ср сЬ
Рассмотрим также виток, представляющий «гофрированную ок-
ружность» (рис. 5.5), уравнение которой в полярной системе коор-
динат имеет вид
1 1
7 = Б+ Ьсо$(т‹р),
где а и Ь — постоянные величины; т — целое число (Мг 5.2).
Можно повторить сделанное ранее
с1Н =1%а7151пос=11ш=11с1‹р.
с ‚- с г г с г
Так как
%= %+Ьсо$(т‹р), А“
получаем
1 2“ 1 2 1
Н = -1_[ [—+Ьсо$(т‹р)]д‹р = д.
С о а с“ Рис. 5.5
1 0-2073 145

ОФ
А В
п ’ ’\
' Рис. 5.7
Найдем магнитное поле в центре окружности,
—<- если по провощ, изображенному на рис. 5.6, а,
А 5 протекает ток 1 (Не 5.3). Суперпозиция четырех
таких проводов, изображенная на рис. 5.6, б, по-
зволяет найти поле от круглого витка (5.4) и че-
тырех прямолинейных проводов (5.2)
Н = 1(Ш+4Е) = 211(3+2).
4 у сК сК с К 2
На рис. 5.7 изображена однородная тонкая металлическая плас-
тинка, имеющая форму равностороннего треугольника со стороной
а, по которой пропускают ток 1. Пренебрегая магнитным полем от
подводящих ток проводов, найдем магнитное поле в центре треуюль-
ника (Не 5.4). Три подобные системы утроят поле в центре. Из сим-
метрии и суперпозиции следует, что поворот второй системы на
12О°‚ а третьей — на 24О° ничего не должен изменить. При этом
оказывается, что через каждую вершину суммарный ток равен нулю.
Таким образом, для трех так расположенных пластин поле в центре
равно нулю. Следовательно, оно равно нулю и для одной пластины.
На рис. 5.8 показан длинный тонкий многовитковый соленоид с
поверхностной плотностью тока 1 и площадью поперечного сечения
5 = пг2 согнутый так, что его ось образует половину окружности ра-
диусом К. Найдем напряженность магнитного поля Н в центре этой
окружности (Не 5.12). Элемент соленоида на угле с!‹р представляет
магнитный диполь, магнитный дипольный момент которого в соот-
ветствии с (5.5)
Рис. 5.6
. 5
аГрт = жКсйрг,
и дает в центре окружности в соответствии с (1.9)
ан=Ё’%*-.
К
146

Рис. 5.9
Рис. 5.8
При интегрировании по длине соленоида (по углу у) компонен-
ты поля, перпендикулярные диаметру АВ, компенсируются, и окон-
чательное значение поля в точке 0 дает интеграл от компоненты
вдоль АВ
Я е я Я
2
Н =Г~ЙНБт ~р = вЂ” вЂ”,~яп байр = вЂ” 2ти вЂ”.
С Я С Я
Магнитное поле от витков, намотанных на немагнитную сферу
радиусом Л, можно найти, пользуясь формулой (5.3). Считаем, что
плотность поверхностного тока в таком «соленоиде» постоянна и
равна ~. Найдем напряженность магнитного поля в точке 0 (рис. 5.9),
подставляя в (5.3) ток в витке Ийр, радиус витка Л яппи, расстояние
от элементов витка до точки 0 равно Л:
ф НЛ = ф и, й! = ф и, сн„= ф Н.~п = вЂ” ф ~Юа = вЂ” ' Х.
С С
147
10*
. к/2 2 °
2ти . 2 я у
Н = вЂ” ~ я'и ~р~йр= вЂ”.
С 2с
Если обмотана вся сфера (№ 5.13), то поле будет в два раза больше.
Вычислим циркуляцию напряженности магнитного поля вдоль
произвольного замкнутого контура для бесконечного прямолиней-
ного провода с током, магнитное поле которого описывается (5.2).
На рис. 5.10 показана проекция контура на плоскость, перпендику-
лярную проводу. Интегрируя скалярное произведение вектора на-
пряженности магнитного поля Н на элемент длины контура Н по
длине замкнутого контура, с помощью (5.2) получаем

Суперпозиция позволяет написать
эту формулу (теорему о циркуляции в
интегральном виде) для суммы прохо-
дящих внутри контура токов
фна|=%21;
(5.6)
Рис. 5.10 Ж' Нс” =
Отсюда для цилиндрического провода радиусом К, по которому
течет ток с постоянной плотностью], получаем напряженность маг-
нитного поля внутри провода
2 . 2 1 ' 1
Н=-1‚г=--;; {Н=д= э}. (5.7›
с с к 2 2лк
Вне провода магнитное поле описывается формулой (5.2)‚ ко-
торую также можно получить с помощью теоремы о циркуляции
(5.6).
Здесь уместно ввести еще один дифференциальный оператор —
ротор. Напомним, что оператор градиента (набла)
д д д
= — ' — ° — к.
О (дхъ 145»), ”’(аг)
Оператор, примененный к скалярной величине — потенциалу (р,
дает напряженность электрического поля (2.8)
Е = —Ч7‹р; {Е = —К7‹р}. (5.8)
Скалярное произведение наблы, например, на Е дает диверген-
цию (1.20)
дЕ дЕ, дЕ,
=—4 : . 5.
УЕ дх + д)’ + д: ( 9)
Векторное произведение наблы, например, на Н дает ротор
а 3 к
д д д
Н Н Н
х у 2
| 48

Этот определитель раскрывается обычным путем по минорам
дн, дН
гогН=й[дН‘— *)+д(днх-днг]+к( У-днх]. (5.11)
д у д: д: Эх Эх д у
Так ротор записывается в декартовых координатах.
В цилиндрических координатах (р, ш, г на рис. 2.1)
ЭН ЭН дН ЭН д Н дН
го(Н=[}.;_ Ф]ер+{ Р ___$_]еш +(1_Ц_1_%)ег. (512)
р дш д: д: др
В сферических координатах (г, ш, Э на рис. 2.1)
1 двйп 9Н„‚ дне 1дгНе 1дН‚
ЮЁН-[гвйпб де дц: е” 7 дг 7’ де °‘*‘+
5.13
+ 1ан‚_1дгН.‚‚ ( )
зтэ дч; г дг е
Из циркуляции (5.6) ротор получается предельным переходом к
контуру с бесконечно малой площадью АЗ
_ . н,а1
готН - $110 (пф т), (5.14)
где п — единичный вектор нормали к поверхности АЗ.
Отсюда теорема о циркуляции в дифференциальном виде
тиф}; {го1Н=]}, (515)
где 1 — вектор плотности тока.
На рис. 5.11 показана широкая полиэтиленовая пленка (ди-
электрик) с равномерным поверхностным зарядом с плотнос-
тью о, которая движется по роликам со скоростью и. Движение за-
рядов создает ток плотностью] = он.
Перпендикулярно току и парал-
лельно поверхности пленки возни-
кает магнитное поле, которое на-
ходим с помощью теоремы о цир- `у
куляции (5.6) \
211 = Ш.
с Рис. 5.11

Откуда
Н = 21:02; Еи
а
С С
где Е — напряженность электрического поля у поверхности плен-
ки. При известном значении электрического поля пробоя можно
найти максимальные плотность поверхностного заряда и значе-
ние магнитного поля при заданной скорости протягивания плен-
ки (Мэ 5.6).
Если постоянный ток 1 течет вдоль длинной тонкостенной труб-
ки радиусом К, которая имеет тонкую прорезь шириной Ь, парал-
лельную оси трубки, то вокруг трубки возникает магнитное поле.
Найдем его напряженность (Мг 5.7). При отсутствии разреза внутри
трубки магнитного поля не было бы. Условие в разрезе удовлетво-
ряется, если предположить, что по нему, противоположно 1, про-
пускается ток силой
112 _ [Ь
2пК —[) и 21113.
Внутри трубки на расстоянии г от разреза с помощью (5.2) по-
лучаем
1Ь
псКг '
Вне трубки добавляется еще поле тока по всей трубке
_ 21
_ Ё,
где 1 — расстояние от оси трубки.
Найдем распределение магнитного поля вне и внутри длинного
цилиндрического провода, состоящего из двух проводящих сред,
имеющих удельное сопротивление р, от оси провода до К, и р, от К,
до К2, по которому идет ток 1 (Мг 5.8). Благодаря электрическому
контакту, стационарности токов, при котором электрическое поле
аналогично электростатическому, напряженность электрического
поля в проводе постоянна. Из (4.7) и (4.8) для плотностей тока в
частях провода получаем Е = р, 1, = р, 1,. Откуда
Н
1; = Щ
Л 92
Ток через первую среду
150

ток через вторую среду
~г = Лг~ Лг™! .
Для токов получаем
г
~1 Рг
Отсюда
~ (р! /рг) Лг/Л !
(1+ р! /р2) ~2/Л!
1
(1+ р!/рг) Лг/Л!
Из (5.7) и (5.2) при О < г < Л, магнитное поле
2Х!г
!
СЯ1
приЛ,<г< Л,
(2/с)(1/г)(1+ р!/рг) г /Я! вЂ” 1
(1+ р! /р2) ~2/~!
при г> Л
21
СГ
Найдем зависимость магнитного поля Н от расстояния г от оси
бесконечного прямого провода радиусом Л, по которому течет по-
стоянный ток 1, а удельное сопротивление его р зависит от расстоя-
иия от оси по закону р = р,г (М 5.38). Как и в предыдущей задаче,
электрическое поле Е в проводнике постоянно, поэтому
Е Е
р(г) = вЂ” = вЂ”.
р (г) рог
Используя закон Ома (4.7), (4.8), получаем
1 = ~ /(г)2ягдг =
0 РО
151

Из (5.б) внутри провода
К2пг = вЂ” ~ ~ (г)2лгНг = вЂ” 1 вЂ”.
4л' . 4л г
С с Я
Откуда
21
Н = вЂ” = сопя~.
СЯ
При г> Л
СГ
Если в плазменном цилиндре радиусом а распределение удельной
проводимости Х в зависимости от расстояния от оси цилиндра г
имеет вид
то плотность тока
2
! (г) = х (г) е = !', ~1 вЂ” вЂ”,
где ~о = ХОЕ; Е вЂ” постоянное электрическое поле, вызывающее по-
стоянный ток:
Х = ~~'2пЫг =
2
С помощью теоремы о циркуляции (5.6) находим распределение
магнитного поля (М 5.21). Внутри плазменного цилиндра
4ж
Г
г 4ж . 2 г
2 4
2пгН = вЂ” 2шд ~г 1 вЂ” вЂ”, Нг = вЂ” кд г вЂ” вЂ”,
с а с 2а
откуда
Вне плазменного цилиндра
4я1
2пгН =вЂ”
С
152

И, СЛСДОВЗТСЛЬНО,
н = д.
С!‘
На рис. 5.12, а показано поперечное сечение системы из двух
бесконечно длинных прямолинейных проводников из немагнитного
материала, изолированных друг от друга и ограниченных цилинд-
рическими поверхностями. Найдем величину и направление маг-
нитного поля (в данном случае, совпадающего с индукцией магнит-
ного поля) в полости (П), если токи с одинаковой плотностью 1
идут по одному проводнику к читателю, а по другому — от читателя
(Не 5.23). Используя (5.7), для цилиндра с током можем написать в
векторном виде
Н = Ёпг].
С
На рис. 5.12, б показаны все векторы. В результате получаем
О
2 . 2 .
Н = НА +Нв = %[1("А _ГВЛ = ЁЬГАВЪ
Эту же формулу можно применить и к нахождению магнитного
поля внутри бесконечной цилиндрической полости, сделанной в
бесконечном цилиндрическом проводе, вдоль которого течет по-
стоянный ток плотностью], равномерно распределенный по сече-
нию провода (М 5.24).
Рассмотрим плоский конденсатор, пластинами которого явля-
ются диски радиусом К, подключенный к источнику постоянного
153

напряжения И Объем между пластинами заполнен слабопроводя-
щим диэлектриком, диэлектрическая проницаемость которого
а ПРОВОДИМОСТЬ
мг) = м, ф)”,
где 11 — расстояние между пластинами, а 2 отсчитывается от нижней
пластины; г — расстояние от оси. Пренебрегая краевыми эффекта-
ми, найдем плотность заряда р(г, 2), а таюке полный свободный заряд
О, сосредоточенный‘ в диэлектрике, и магнитное поле В(г) (Мг 5.25).
Из (4.7) имеем Е = ]/А. Считая, что плотность тока не зависит от г,
получаем, что напряженность поля
= мг)
до (“душ
также не зависит от г, т. е. Е = У/Ь.
Из (3.6)
р _ дВ/д; _ д(еЕ)/д2 _ 2Е2 _ У:
41: 41: ил’ 2лл3 '
Интегрируя по объему, находим
дней/г д _1/к’
’ ("мг
О 21023 О
Из теоремы о циркуляции (5.6) следует
Г
г К!” 2 12 12 15 2 1/2
21тгН = 41ъЕ_[2тгг7я0( ) ф‘ = 81: ЕК/ Адг/ с1г =—5п Е(Кг) то.
о
Откуда, учитывая, что В = Н, находим
В = 8ТЁ%АО (туп .
При симметрии системы можно воспользоваться теоремой о
циркуляции (5.6) и в случае части провода конечной длины. Система,
изображенная на рис. 5.13, представляет однородную проводящую
154

”
Рис. 5.13 Рис. 5.14
В
сферу и провод вдоль диаметра. Ток 1 идет по проводу от В к А, а
затем по поверхности сферы (М9 5.10). Так как имеется симметрия
относительно АВ, то, обозначая расстояние от оси симметрии г, мож-
но из (5.6) внутри сферы получить Н2пг = 41ъ1/с. Снаружи сферы
поля нет, так как суммарный ток равен нулю.
На рис. 5.14 показан круговой тор прямоугольного поперечного
сечения с размерами а и Ь, на который навита обмотка тонкой про-
волоки, содержащая А’ витков (на рисунке не показана). На тор
надета кольцевая катушка с числом витков п, по обмотке которой
течет ток 1. Найдем магнитный поток, который посылает магнитное
поле катушки через обмотку тора с внугренним радиусом К (Не 5.35).
Предполагаем, что рассеяния магнитного потока от кольцевой ка-
тушки нет, т. е. весь поток идет внутри тора, и учитываем, что сило-
вые линии не пересекаются. Для силовой линии, проходящей на
расстоянии г от оси симметрии тора, из (5.6) 2пгН = 4пп1/с. Для
потока имеем
К+и 1 К+а дг 1 а
ф = ] Ньаг = 2—1п[›] — = 2-1пь1п(1+-).
к с к г с К
Умножая это на А’, получаем зацепленный поток через тор.
Если по оси полого цилиндра из немагнитного металла или диэ-
лектрика натянута заряженная нить, то на его поверхностях появят-
ся заряды. Вращение Цилиндра дает электрический ток и приводит
к появлению магнитного поля. Пренебрегая краевыми эффектами,
пьезоэффектом и всеми эффектами, вызываемыми центробежной
силой, найдем магнитные поля в случае металлического и диэлект-
рического (диэлектрическая проницаемость е) цилиндров, вращаю-
щихся с угловой скоростью $2 вокруг нити, на единицу длины кото-
рой приходится заряд х (Не 5.14). Так как суммарный заряд на ци-
линдре равен нулю, то и суммарный ток равен нулю. Поэтому в
155

полости и снаружи цилиндра магнитного поля нет. Поле внутри
цилиндра определяется плотностью заряда на внешней поверхности
цилиндра (радиус К). В соответствии с (1.16) напряженность элект-
рического поля на внешней поверхности цилиндра
2х
Е=—.
к
В случае металла плотность заряда из (1.12)
_ _ё_ _ х
" 41: ' 2лк’
а в случае диэлектрика из (3.3) и (3.8), так как
Е= В= еЕд= Ед+4пР,
то
_ _(е—1)Ед (е—1)Е_(е—1)х
од " В: " = _ '
47! 41ъе 2пеК
Ток на единицу длины цилиндра 1= 08212. Используя (5.4), по-
лучаем в случае металла Н = 2х$2/с‚ а в случае диэлектрика
Н _ 29552 (е — 1)
д — '———*-—.
СВ
Найдем магнитные поля, возникающие при вращении длинного
сплошного цилиндра из статически поляризованного диэлектрика,
вращающегося вокруг своей оси симметрии с угловой скоростью а).
Задано, что вектор поляризации во всех точках цилиндра направлен
радиально, а его величина пропорциональна расстоянию от про-
дольной оси цилиндра, т. е. Р = Кг (/‹ = сопвт; г — радиус-вектор,
проведенный от оси перпендикулярно к ней), радиус цилиндра К
(Мг 5.15). Из (3.4) следует для объемной плотности связанных зарядов
рСВЯЗ
= «цуг = «ат = -/‹(Ё+Ё) = -21‹‚
дх ду
т. е. постоянна во всем объеме цилиндра.
При вращении связанные заряды создают токи с объемной плот-
ностью
1 = шгрсвяз = —2/ссог.
Заметим, что на поверхности цилиндра при [с > О из (3.3) поло-
жительн ый поверхностный связанный заряд плотностью о = Р„ = КВ,
156

а внутренние связанные заряды отрицательные и в к
сумме равны поверхностному заряду, т. е., как и >
должно быть, свободных зарядов нет. Поэтому при
вращении цилиндра внешнего магнитного поля нет.
Для вычисления магнитного поля внутри цилиндра Н„а„= 0
воспользуемся теоремой о циркуляции (5.6). Кон- э
тур для циркуляции, показанный на рис. 5.15, бе-
рем вдоль образующей цилиндра на единице длины д \
по радиусам и линии на расстоянии г от оси Цилин-
дра. Получаем ток АЪ____
к к
1 = 1 мг + осоК = —2/‹со_[ га'г + кшкг = /«ог2
’ ’ Рис. 5.15
и магнитное поле Н = 41т1/с.
Если тонкостенная длинная дюралевая трубка заряжается элект-
рически и приводится в быстрое вращение относительно оси сим-
метрии, то возникают магнитные поля. Максимальная скорость вра-
щения трубки ш обусловлена механической прочностью дюраля спр.
На рис. 5.16 показана максимальная центробежная сила
г = рькашйк = 2о„,ь1'},
где р — плотность дюраля; И — толщина трубки; К — ее радиус.
Отсюда
2 О'
ш="р
2 .
рК
Обозначая заряд на трубке с], имеем из (1.3) для напряженности
электрического поля на поверхности трубки
ДЛЯ ПЛОТНОСТИ ТОКЗ при вращении
._ Как; _ с1(0„р/р)1/2
А 41:18 41:18
Этот ток, так же как в соленоиде, созда-
ет магнитное поле внутри трубки
_ 41:!
Рис. 5.16 Н ‘ Т‘
157

“д” Для наибольшего отношения магнит-
‘Р ного поля внутри трубки к электрическо-
му полю на ее внешней поверхности по-
к б/(р 1/2
лучаем Щ:- (Мз 5.16).
Для вращающегося заряженного шари-
ка магнитное поле вдали от него пред-
ставляет поле магнитного диполя. Най-
дем величину магнитного диполя при рав-
номерном распределении заряда 4 по
поверхности шарика радиусом К. Плот-
ность заряда на поверхности
Ч
4пК2
На колечке радиусом К вйп ср (рис. 5.17) имеется заряд оКс1‹р2пК со5‹р.
Этот заряд проходит за время поворота Т= 2п/ш. Отсюда получаем
ток и, в соответствии с (5.5)‚ магнитный момент
Рис. 5.17
1
др = ЁошпК‘ 0053 ‹рс1‹р.
Интегрируя по углам, находим магнитный момент, направлен-
ный по со,
_| 4 пр 2 . _1 20)
р-сошлК 2{со5‹рс151п‹р-сс112 3.
В случае равномерного распределения заряда по объему шара
для плотности заряда имеем
34
4пК3.
Заряд в кольце высотой 212 5111 (р, шириной Кедр зйпср и радиусом
К сов (р равен р2К $111 ср Кадр зйп ср 2пК сов ‹р. Этот заряд проходит за
время поворота Т= 2тс/со. Отсюда получаем ток и, в соответствии с
(5.5)‚ магнитный момент
р:
1 .
а/р = Ь-2ршпК5 сов’ ‹р зтв ‹рс1‹р.
Интегрируя по углам, находим магнитный момент, направлен-
ный по (о,
1 < #2 2 . 2 . 1 2 О)
=грсо1тд 2] сов срзт срдзшср =24К Ё.
о
158

Используя полученные магнитные моменты с помощью (1.9)‚
находим магнитное поле (М) 5.17).
Согласно современным данным, допустимое из опытов различие
абсолютных величин зарядов электрона 4‘, и протона ар таково, что
2:1 <10-2г
Чр
Таким образом, каждый атом с номером 2 может иметь заряд
Ххар, где
х = ар _ ее
чр
Считая, что для атомов, составляющих Землю, отношение от-
носительной атомной массы А к атомному номеру 2порядка 2, а
плотность Земли р = 5 г/см3, оценим, не может ли наличие заря-
да и вращение Земли создать существующее магнитное поле Земли
В = 3 - 1О‘5 Тл (Не 5.20). Так как масса атома равна массе нуклона
(протона или нейтрона) тн, умноженного на А, то отношение пол-
ного заряда Земли а к ее массе М равно
_1_д"...‘!г
М тнА.
ИСПОЛЬЗУЯ ПОЛУЧСННОС В предыдущей ЗЗДЗЧС СООТНОШСНИС ДЛЯ
МЗГНИТНОГО МОМСНТЗ ЗЕМЛИ, НЗХОДИМ
р-хг ч” 4про) КЗ
А тн 15С .
Если бы Земля обладала таким дипольным магнитным момен-
том, то из (1.9) для максимального значения на полюсе получим
2
В = ‘Ё’
а затем вычисляем
А т Т _
х = —4‘-15сВ-—%Т—7 = 2,6- 10 ‘9.
2 61„ 161: рК
Эта величина намного больше возможной, поэтому магнитное поле
Земли не может быть создано из-за разности зарядов.
159

Найдем магнитный момент квадратной рамки со стороной а, рав-
номерно заряженной с линейной плотностью р, вращающейся с уг-
ловой скоростью со вокруг одной из сторон (Мг 5.18). Сторона, па-
раллельная угловой скорости, дает момент в ее направлении
т —1 а—°3-па2 - (о:
1 с р 21: р 2с°
Каждая из радиальных сторон дает
1 и (О 2 1 аЗ
=_ „д__ =- _„
В сумме получаем
[п = 1Ёрша3
с 6 °
Для вращающегося с угловой скоростью (о равномерно заряжен-
ного (полный заряд О) диска радиусом К (рис. 5.18) магнитный мо-
мент находим (Не 5.19) интегрированием, используя (5.5):
р = 3991г2(к2 - за)” с1х1гх2‚
с 2п О
где
О
о = ——.
пК2
С помощью таблицы интегралов, либо
о) вводя обозначение х = В зйп (р, полу-
чаем
х
к = 1:2 31.
р о 8с
_ Вектор-потенциал магнитного поля
_ х Й Фг х можно получить из закона Би6—Сава-
ра-Лапласа (Не 12.1).
Используя связь 1 = 1:15, из (5.1) по-
2/ лучаем
11щшц 1. мс
дн = Ц-г- = -[дг]—;.
Рис. 5.18 С г С г
160

Интегрируя, находим
= вЂ” ~[~г вЂ”,.
1 . И~
си г
(5.16)
Входящий в (5.16) радиус-вектор г имеет начальную точку, где
находится элемент тока с плотностью 1, называемую истоком, и ко-
нечную точку, где вычисляют величину магнитного поля, называе-
мую точкой наблюдения. Найдем градиент численной величины
радиуса-вектора г. Можно при вычислении градиента оставлять не-
подвижной точку истока. В таком случае наибольшее возрастание
производной происходит в направлении радиуса-вектора (измене-
ние расстояния равно изменению длины вектора)
(5.17)
агам„ г = г/г.
При перемещении истока
(5.18)
угад„г = вЂ” г/г.
Так как для произвольной функции ~(г)
огай„~ [г) = агам„г,
д~ (г)
дг
то
1 1 Г
агам„вЂ” = вЂ” вЂ” угад„г = вЂ” вЂ”.
'г г2 ' гЗ'
(5.19)
Далее можно воспользоваться формулой, в справедливости ко-
торой можно убедиться просто вычислением,
го$(~а) =/'го$ а + [ягас1 ~а].
Подставляя в это соотношение~= 1/г и а = 1 и при дифференци-
ровании считая неподвижной точку истока вектора г, получаем
1
го1, вЂ” = [~гад„г~]+ вЂ” го1„].
Г г
Так как значение вектора1 в элементе ШГ(точка истока) не зави-
сит от перемещения точки наблюдения, в которой вычисляется поле,
то го1, 1 = О. Следовательно,
го1 вЂ” = дгас1
] 1 . [1г]
Г г Г
161

Внося это в уравнение (5.16), находим
Н=- го$„Х ЫГ.
1
С Г
Так как дифференцирование (образование ротора) проводится
по координатам точки наблюдения, а интегрирование вЂ” по объему
проводников, обтекаемых током, то возможно изменение последо-
вательности этих операций
Н = го~, ~ вЂ” ~ ~ ШГ~.
Вводя обозначение величины, называемой векторным потенциалом
магнитного поля,
А = вЂ” /~ вЂ” ~,
1 .Ы~
С Г
(5.20)
получаем
Н = го1 А; (Н = го1 А).
(5.21)
Найдем поле на оси соленоида (катушки) как сумму полей от
набора витков (№ 5.5). На рис. 5.19 показано сечение соленоида и
даны его размеры. Обозначая общее число витков Жи силу тока 1и
пользуясь (5.3), получаем поле в точке А от элемента соленоида Нх
ИН = вЂ” вЂ” я'и ~р; И=1 вЂ” Нх;
Н2к . з Ж
с Я ' 1
Ыхяп~р = ЛвЂ”
Иф
яп ~р
В результате
2Ы Ф
Н = вЂ” вЂ” ~я'п~рйр.
с 1
Откуда
2яУ Ф
Н = вЂ” вЂ” (соя р вЂ” соя а).
с 1
(5.22)
Для точек внутри достаточно длинного соленоида, чтобы можно
было пренебречь краевыми эффектами р = О, а = л:
4ж 1И
(5.23)
с 1
162

Из отсутствия магнитных зарядов (замкнутости силовых линий)
и, следовательно, сохранения магнитного потока, пользуясь (5.23),
имеем
Ш11Ъ(ВТ = ТН2пгс1г.
с 1 а д
Подставляя и интегрируя, получаем
ос2/
Т
В следующем разделе будет введено понятие вектора магнитной
индукции В, который подобно вектору напряженности электричес-
кого поля Е является силовым вектором, определяющим Пондеро-
моторные силы. Здесь ограничимся лишь указанием, что в отсут-
ствие магнетиков вектор магнитной индукции равен вектору напря-
женности магнитного поля
/1=
В = Н; {В = дон}. (5.25)
Здесь магнитная постоянная
до = 4п- 1О'7 = 1,256637О6144- 10"“ Гн - м“. (5.26)
Поэтому при отсутствии магнетиков поток вектора магнитной ин-
ДУКЦИИ
Ф=[Вс1$=]Нс15; Фцвазцдндз . (527)
5 5 5 8
Приведем пример вычисления потока магнитного поля (М9 5.32).
Найдем поток напряженности магнитного поля, создаваемого
квадратной рамкой со стороной а, по которой
течет ток 1, через полуплоскость, граница
(‚у которой расположена на расстоянии Ь от од-
дх ной из сторон рамки (рис. 5.21). Рамка лежит
на полуплоскости, граница которой начина-
Н ется от заштрихованной части. Очевидно, что
сумма потоков магнитного поля от сторон
рамки, перпендикулярных границе полуплос-
кости, равна нулю. Чтобы вычислить потоки
от сторон рамки, параллельных границе по-
луплоскости, воспользуемся тем, что поток
Рис. 5.21 от единичного отрезка стороны рамки через
7 у“
ап,
И!
7
1 4
164

все единичные площадки, лежащие на линиях, параллельных гра-
нице полуплоскости, равен потоку от провода бесконечной длины
через единичную площадку на этой линии, который вычисляется по
(5.2). В соответствии с (5.1) поток равен интегралу
Ф = гтгфсду1щ.
Введенные координаты показаны на рис. 5.21. Можно поменять
местами (11 и с1у и воспользоваться (5.2).
Отсчитывая расстояние х от стороны рамки, получаем, что ин-
тегрировать надо для ближней к границе стороны рамки от Ь до оо,
а для дальней стороны от а + Ь до со, так как ближайшие к сторонам
части дают интегралы с разными знаками (т. е. нуль). Интегралы
надо увеличить в а раз, так как результаты были для единичного
элемента стороны. Учитывая, что от ближней и дальней от границы
полуплоскости сторон потоки имеют разные знаки, получаем
х С Ь х С
ЧЪШ °°51д_ та: _21а"*”ах_21а1п(1+3)
— с Ьх а+Ь Ь о
Для замкнутого провода, по которому течет ток 1, можно вычис-
лить, используя (5.27) и (5.1), поток Ф вектора напряженности маг-
нитного поля Н через замкнутый контур площади 8
Ф = ёи; {Ф = и}. (5.28)
Здесь, как и в (5.1), используется множитель (1 /с), а другой мно-
житель (Ь), определяемый только геометрией системы (размерами
и конфигурацией провода) и не зависящий от силы тока, называет-
ся индуктивностью, а также коэффициентом самоиндукции провода,
или самоиндукцией.
Воспользовавшись полученной для длинного соленоида (длину
обозначим 1) зависимостью (5.23) и учитывая, что площадь витков
равна 5 и число их М т. е. поток через весь контур увеличивается в А’
раз и превращается в так называемый зацепленный поток ‘Р = ФА’,
находим самоиндукцию соленоида
Ь = мтё; {Ь = „от / (529)
Найдем индуктивность Ь проводника, показанного на рис. 5.22.
Ток течет по проволоке диаметром 2а, расположенной по оси доста-
165

точно тонкой металлической трубки диаметром 20, переходит на дно
трубки, к центру которой припаяна проволока, и возвращается об-
ратно по ее поверхности (№ 5.28). Пренебрегая краевыми эффекта-
ми для магнитного поля внутри трубки, из (5.2) получаем
21
С Г
Внутри провода из (5.7)
2УГ
са
На единицу длины трубки и провода получаем
вЂ” вЂ” вЂ” 2+ вЂ” = вЂ” 1+2 ивЂ”
Используя (5.28), находим
вЂ” =1+21п вЂ” .
о
(
а
Для единицы длины системы из двух параллельных одинаковых
проводов, по которым одинаковые токи текут в противоположных
направлениях (рис. 5.23), учитывая магнитное поле только вне про-
водов, из (5.2) и (5.27) получаем (№ 5.29)
Ь-и
Ф=2! / вЂ” =4У вЂ” 1и( );
и
вЂ” = 4 1и ~ ).
2а
Рис. 5.23
Рис. 5.22
1бб

Если имеются два замкнутых контура 11 и 1,2: первый с током 11,
а второй с током 12, то первый создает поток магнитного поля через
второй Ф12, а второй через первый Ф21. Используя теорему Стокса,
получаем
ф„ = 1 н‚„а$, = ф,4„‹л = фдаь;
3, 1,2 12
Фд = 1 н,„‹15, = фА„а1, = фмац.
51 1-1 14
Переходя в (5.2О) к току (1 = 1:15), находим
1 с1| _ _1_ Е:
Ф„=-Ё-Ё;Ёа|1%, Ф21- 3:11:11, Гл.
Интегрирование проводится по обоим контурам 11 и 12, причем
каждый элемент длиной с111 контура 1,1 должен быть скалярно умно-
жен на элемент длиной (112 контура 1,2, и полученное произведение
разделено на расстояние между элементами г. Двойной интеграл,
входящий в формулы для Ф12 и Ф21, носит название коэффициента
взаимной индукции контуров 11 и 12, обозначается 1,12 и 1,21,
а из их выражения следует теорема взаимности
1,12 = 1,21. (5.3О)
Если на один сердечник намотаны две катушки с индуктивнос-
тями 1,1 и 1,2 и известно, что рассеяния магнитного поля нет, то
можно найти их взаимную индукцию М (Не 5.30). Обозначим число
витков в катушках 1\/1 и А! , магнитный поток, который не рассеи-
вается, и поэтому одинаковый для обеих катушек Ф, сцепленный
поток первой катушки ‘111 = ФА/1, сцепленный поток от первой ка-
тушки через вторую ‘Р21 = Ф1\’2, сцепленный поток второй катушки
‘Р2 = Ф1\’2 и сцепленный поток от второй катушки через первую
‘Р12 = Ф1\’1. При токе 1 только в первой катушке имеем
=Ё=Ёа
“л “2
Надо иметь в виду, что формула (5.28) была написана для од-
ного витка. Если поток пронизывает А! витков, то вместо Ф надо
брать ‘Р = ФА’
т=%11,; {ч›= 11}. (531)
167

В данном случае
П, 1
Ч11=——1- И ‘Р71='_{2;.
С С
Отсюда, используя полученные ранее соотношения при сохранении
потока, имеем
1-1 _ “ж
121 ^’2 °
При токе / только через вторую катушку получаем
_Ь_Ч’л2
щ м,’
Используя (5.3|), находим
ища,
^’2 12
Из двух соотношений числа витков следует М = (Ь1Ь2)‘/2.
Найдем магнитный поток, который посылает поле маленькой
плоской катушечки площадью 5 с числом витков Нк, по обмотке
которой течет ток 1к, через обмотку соленоида длиной 1 с числом
витков Не (Мг 5.31). Используя (5.23) для зацепленного потока маг-
нитного поля от соленоида, по которому течет ток 1С, через кату-
шечку получаем
1
хук = А’к54п1\’с Ё = Ша.
С
Используя теорему взаимности (5.28), находим для зацепленно-
го магнитного потока через соленоид
‘гс = МВ = 4тс1\’к.5`1\’с Е.
с с!
Поле намагниченного стержня и витка с током на больших по
сравнению с их размерами расстояниях описывается полем диполя
с магнитным моментом (5.5)
1
ВИТЗВИТ
р:
Используя это, найдем магнитный поток, пронизывающий длин-
ный соленоид с плотностью намотки п и радиусом К, от намагни-
168

следовательном соединении катушек имеем 1, = 1,0 + 1,1 + 2М. Вза-
имную индуктивность М находим, вычисляя зацепленный поток через
меньшую катушку:
Ч’ = % = Но%1со56 = %1по1\’со56.
Отсюда
М = 4попА/со5 6.
В результате
Ь = 1,0 + 41гп218 + 81гоп1\/ сов 6.
Аналогичным методом можно вычислить индуктивность систе-
мы, когда внутри длинной катушки-соленоида индуктивностью Ь,
расположен соосно другой соленоид меньших размеров с тем же
числом витков, все линейные размеры которого в В раз меньше ли-
нейных размеров большого соленоида (подобные катушки) (М: 5.37).
Так как число витков одинаково, получаем из (529), что индуктив-
ность меньшей катушки
Для нахождения взаимной индукции записываем зацепленный
поток через меньшую катушку ` ‘
т = Ш = Н1\/%.
с В
Откуда, используя (5.29)‚
М = 0
В
В результате индуктивность системы
1 2
Ь = 1 + - + — .
14 В в’)
На основе опытов Фарадея и правила Ленца, следуя Максвел-
лу, можно сформулировать закон электромагнитной индукции: из-
менение магнитного поля во времени возбуждает в окружающем
пространстве электрическое поле. В неподвижном замкнутом конту-
170

ре ВОЗНИКЗСТ ЦИРКУЛЯЦИЯ напряженности ЭЛЕКТРИЧЕСКОГО ПОЛЯ Е,
определяемая ИЗМСНСНИСМ МЗГНИТНОГО ПОТОКЕ! Ф, ПРОНИЗЫВЗЮЩС-
го этот контур:
(532)
фЕдл = _1ЁЁ‚
с д!
где Ф — поток вектора магнитной индукции, Ф = ФВдБ. О магнит-
ной индукции будет подробно сказано в следующем разделе, сейчас
лишь заметим, что в отсутствие магнетиков В = Н (вектору напря-
женности магнитного поля).

6. МАГ НИТНОЕ ПОЛЕ В ВЕЩЕСТВЕ.
ВЕКТОРЫ В И Н.
ТЕОРЕМА О ЦИРКУЛЯЦИИ В ВЕЩЕСТВЕ.
СВЕРХПРОВОДНИК В МАГНИТНОМ ПОЛЕ
Вещества могут обладать магнетизмом, который возникает бла-
годаря орбитальному движению электронов вокруг атомных ядер,
собственному вращению (спину электрона), собственному вращению
ядер (спину атомного ядра). При беспорядочном тепловом движении
в отсутствие магнитного поля атомы вещества обычно ориентирова-
ны хаотически и возбуждаемые ими магнитные поля компенсируют
друг друга. Под воздействием магнитного поля некоторые вещества
(например, железо, никель, кобальт) могут сильно намагничивать-
ся. Они называются ферромагнетиками. Другие, например платина,
вольфрам, алюминий, намагничиваются, но слабо. Они называются
парамагнетиками. Среди слабо намагничивающихся веществ есть
такие (например, висмут, золото, серебро), которые приобретают
намагниченность, противоположную прикладываемому полю, и на-
зываются диамагнетиками. Замечательной особенностью ферромаг-
нетиков является то, что при снятии внешнего магнитного поля
они не размагничиваются полностью. Остается постоянное (остаточ-
ное) намагничивание. Здесь проявляется нелинейная зависимость
намагниченности от напряженности магнитного поля и гистерезис —
зависимость намагничивания от истории изменения магнитного поля.
Орбитальные и спиновые вращения электронов и спиновые вра-
щения атомных ядер можно рассматривать как молекулярные токи,
создающие магнитные поля. Таким образом макроскопическое маг-
нитное поле В возбуждается как обычными токами проводимости
(плотностью 1), так и токами намагничивания (плотностью ]т), по-
зволяющими описать вклад усредненных молекулярных токов. За-
метим, что токи намагничивания не испытывают сопротивления и
не приводят к джоулевым потерям на теплоту.
Отсутствие магнитных зарядов приводит к замкнутости силовых
линий магнитного поля. Применение аналога теоремы Гаусса дает
фваз = о. (6.1)
172

В дифференциальной форме
(Ну В = О. (6.2)
Теорему о циркуляции (5.6) и (5.15) надо дополнить включени-
ем токов намагничивания [т
фва =%(1+1„‚). (6.3)
ь
В дифференциальной форме
гоъв=%’Е(3+3„‚); {го1В=]+]‚„}. (6.4)
Намагниченность среды принято характеризовать вектором на-
магничивания М. Это средний магнитный момент единицы объема
магнетика, создаваемый молекулярными токами. Если рассмотреть
магнетик цилиндрической формы, магнитный момент которого на-
правлен вдоль оси цилиндра, и обозначить средний магнитный мо-
мент молекулы р, а число молекул в единице объемом п, то средний
магнитный момент единицы объема М_ = пр. Молекулярные токи
соседних молекул в местах их соприкосновения текут в противопо-
ложных направлениях и взаимно компенсируют друг друга. Неком-
пенсированными остаются только молекулярные токи, выходящие
на наружную боковую поверхность цилиндра и дающие ток 1,”. Для
цилиндра, имеющего объем И высоту 1и площадь основания 5 ( У=
15), магнитный момент
д? = ум = ям.
Направление 5 совпадает с направлением М. Поэтому [т = с1М.
Следовательно, поверхностный ток, приходящийся на единицу длины
цилиндра, равен
[т сМ; {Ем = М}. (6.5)
Если вектор М не направлен по оси цилиндра, то поверхност-
ный ток (6.5) определяется только проекцией М на ось цилиндра.
Поверхностный ток создает поле, которое можно найти по фор-
муле для соленоида (5.23) и следует добавить к полю, вызвавшему
намагниченность:
в = н + 4пМ; {в = н + м). (6.6)
Вектор В называется вектором магнитной индукции. Как выяс-
нится позднее, он подобно вектору напряженности электрическо-
173

го поля Е и является силовым. Название возникло исторически,
так как учение о магнетизме развивалось по аналогии с электро-
статикой.
Если намагниченность (М) пропорциональна напряженности
поля (Н)
М = ХН, (6.7)
то из (6.6) следует
В = иН; {В = пион}, (68)
где
и = 1 + 4тгх; {и = 1 + х}‚ (69)
магнитная постоянная до = 1,256637О614- 104 Гн/м.
Величина х называется магнитной восприимчивостью, а р. — маг-
нитной проницаемостью вещества. Вещества, для которых х > О и,
следовательно, р. > 1, называются парамагнетиками, а вещества, для
которых х < О и, следовательно, р. < 1, называются диамагнетиками.
В постоянном магните цилиндрической формы с постоянной на-
магниченностью М, направленной по оси цилиндра, плотность тока
намагничивания на боковой поверхности определяется (6.5). Чтобы
индукция В в длинном тонком однослойном соленоиде с плотностью
намотки п [витков/см] была такой же, как в постоянном магните
тех же размеров, должно быть 1п = Ем. И, как следует из (6.5), ток в
соленоиде 1= сМ/п (Не 6.1).
Между электрическими и магнитными полями, а также между
диэлектриками и магнетиками существует аналогия. Основное от-
личие при этом связано с отсутствием свободных магнитных заря-
дов. Для связанных «магнитных зарядов», возникающих при намаг-
ничивании, существует аналогия со связанными электрическими
зарядами при ПОЛЯРИЗЗЦИИ. На границе МЗГНСТИКЗ В СООТВЕТСТВИИ С.
(3.3) плотность «магнитных зарядов» равна нормальной к поверхно-
сти компоненте вектора намагниченности
о = М. (6.10)
И
Аналогии, существующие между законом Кулона (1.1) и зако-
ном Би6—Савара—Лапласа (5.1), между (3.8) и (6.6), между (3.7) и
(6.1), между (3.6) и (6.2)‚ между (5.32) и (5.6)‚ позволяют использо-
вать результаты, полученные для диэлектриков, также и для магне-
тиков. Картина полей В и Н для прямоугольного бруска с намагни-
ченностью М (Мг 6.2), показанная на рис. 6.1, совпадает с картиной
для 1) и Е, показанной на рис. 3.7.
174

имеющего форму цилиндра радиусом г, во внешнее однородное маг-
нитное поле Во, направленное вдоль оси стержня, имеем внутри очень
длинного цилиндра Н= В„В = рН = цВ, и из (6.6)
М = (р-1) вЂ”.
~0
4н
Для стержня длиной (, используя (5.22) и (6.5), в центре стержня
от токов намагничивания получаем
В,„= 2п!,, вЂ” 4пМ [1 вЂ” 2 вЂ” ~ = (р вЂ” 1) В~ [1 вЂ” 2 вЂ” ~
((/2) +г
В результате
2
В = В + В„= [рВ, вЂ” (р вЂ” 1)2 вЂ” В,.
Найдем длину 1, при которой полученное значение менее чем
на 1 % отличается от значения для стержня очень большой длины
(М 6.7). Для этого
Откуда
(>[ ~ )] 14г.
Если круглый диск (радиусом г), изготовленный из такого же
материала, поместить в однородное магнитное поле Во, то для беско-
нечно тонкого диска В = В . Оценим, при какой максимальной
толщине 1 индукция в центре диска отличается от этого значе-
ния не более чем на 1% (Мо 6.8). Так как в данном случае В = Во
и Н = Во/р из (6.6)
(И вЂ” 1) ВО
4лр
Используя формулы для витка (5.4) и тока намагничивания (6.5),
находим
В = 2н~ вЂ” = 2пМ вЂ” = (р вЂ” 1)~ вЂ”.
1 1 во
СГ Г 2РГ
176

Найдем поток индукции Ф через сечение (в виде квадрата со сто-
роной а) железного сердечника (магнитная проницаемость ц), име-
ющего форму тора (диаметром Х)), на который равномерно намота-
на проволока (Ж витков), по которой идет ток 1(М 6.10). Используя
(5.6), имеем
аВН = вЂ” ХФ.
С
Откуда
2
Ф = Ва' = 4И)рвЂ”
с0
Если в этом сердечнике сделать поперечный разрез (воздушный
зазор толщиной Ь), то поток изменится. Найдем его (Ж 6.11). Отме-
чая параметры в разрезе индексом «р», имеем В = цН= В = Н. Из
(5.6), предполагая, что нет рассеяния потока, следует
(кб вЂ” Ь) Н+ ЬН =
С
Откуда
(41/с)(Ф/В)
1+(~ вЂ” 1)Ь/ а
Отсюда поток Ф = рНа'.
Для вычисления коэффициентов индукции необходимо находить
потоки индукции Ф. Определим коэффициент самоиндукции А ко-
аксиала, образованного соосно расположенными железным стерж-
нем (ц = 1000) и медной (ц = 1) трубкой, замкнутыми на одном из
концов проводящим диском. Длина стержня и трубки ! = 10 см,
диаметр стержня 2г, = 2 мм, внутренний диаметр трубки 2г = 9 мм,
наружный вЂ” 2г, = 1О мм. Считаем, что в стержне и трубке токи
равномерно распределяются по сечениям (Ж 6.39). Обозначая ток в
цепи 1, в соответствии с (5.7) получаем внутри стержня на расстоя-
нии г от оси поле
Н =2ХвЂ”
сг'
и поток поля
Ф, = 2 и вЂ” г! вЂ”, = вЂ” !р,.
У Ыг 1
О с г1 с
178

В зазоре поле, как следует из (5.2),
21
СГ
И ПОТОК ПОЛЯ
Г1
Ф = 2~ вЂ” 1 вЂ” =2 вЂ” (1п
Ос г с г1
В трубке, как следует из (5.6),
4д У г вЂ” г2 4д 1 г3 вЂ” г
2 2 2 2
И2яг = вЂ” 1
гЗ г2 3 г2
Поток
2
т и ~ ~" ~~~ "1 "(~l~)
2 2 2 2
г2 г3 2 г3 2
Суммарный поток
Ф=Ф, +Ф, +Ф, = вЂ” ( и+21п вЂ” +2г, вЂ” 1
1 Г~ г 1и (Гзl~г)
с
г3 вЂ” г2
поэтому
Р +1п г +„г г г 1()4 см.
3 г2
2 2
г вЂ” г
Аналогичным образом можно вычислить индуктивность коак-
сиала, если стержень такой же проводник, как трубка, а простран-
ство между ними заполнено диэлектрическим магнетиком с маг-
нитной проницаемостью ц (М 6.40). В этом случае
г2 21П гЗ г2
1=2( 1г1п г +г~, ' г =58 см.
г3 вЂ” г2
Требуется построить электромагнит, который создает в зазоре
магнитную индукцию В. Длина железного сердечника (, ширина
воздушного зазора а, диаметр сердечника Н, магнитная проницае-
мость железа ц. Найдем, какое число витков должна иметь обмотка,
если используется медный провод (удельное сопротивление меди р)
179
12*

площадью сечения 5, по которому можно пропустить ток, не пре-
вышающий 1тах. Оценим также напряжение И которое нужно по-
дать на обмотку для получения максимального поля (М9 6.21).
Из (6.8) и (5.6)
В! А!
г+ Ва - 4п1тах ?.
Откуда
_ В(1/м + а)с
_ 41:! '
А’
ГПЗХ
Для напряжения получаем
1 А’ д
1/ = 1„‚,„к = ———та*:„ п .
Найдем индукцию магнитного поля в небольшом зазоре (толщи-
ной 11) электромагнита, изображенного на рис. 6.3 (М 6.12). По об-
мотке, имеющей А’ витков, протекает ток 1. Участки электромагни-
та, размеры которых указаны на рисунке (11 << 1), имеют одинаковые
площади сечения, а магнитная проницаемость его равна м. При раз-
ветвлении потока Ф = Ф] + Ф2, поэтому Н = Н] + Н, Отмечая
параметры в зазоре индексом «р», для циркуляции магнитного поля
из (5.6) имеем
н‚21+ н1= Н1+ н,(21_/2)+Н,л = ЁЁШ.
Из (6.1) и (6.8) Нр = Вр = В, = цН2. В результате
Т 21
в _
н_н‚+н‚ -н,+—=-д[2+ (" М],
ц 21
2Н1+Н=4п11\’,
с/
В = тс/Нц
Р с1[1+(3/8)(и-1)л/1]'
180

_ +1
Рис. 6.3 Рис. 6.4
На рис. 6.4 показан тороидальный сердечник, составленный из
двух половинок, сделанных из различных ферромагнитных материа-
лов с магнитными проницаемостями и, и д, Общая длина сердеч-
ников, включая два небольших зазора величиной 11, равна 1. По об-
мотке сердечника, имеющей А’ витков, течет ток 1. Найдем величи-
ну поля В в зазоре, предполагая, что рассеянием магнитного поля в
нем можно пренебречь (Не 6.13). Используя (6.1) и (5.6), имеем
В =„‚Н, =„,Н; 2нв+Н(%-л)+н(%-н]= 4":^’.
Откуда
= (41т/с)!1\’
2/1 + (1/2-л)(„‚ + дд/‚дд, '
Тонкий сердечник тороидальной катушки длиной 1 сделан из
ферромагнитного материала. Минимальная напряженность магнит-
ного поля, при которой материал достигает насыщения (М = Мнас),
равна Н = Нш. Найдем, какой минимальный ток 10 должен течь по
обмотке, имеющей А’ витков, чтобы намагниченность сердечника
достигла насыщения (Не 6.15). Из (5.6)
_ Ннасй’.
° ` 4п1\/ '
При создании воздушного зазора в сердечнике достаточной тол-
щины (дн) насыщения намагниченности не возникает при 1 > 10.
Найдем такую толщину (Не 6.15). При зазоре И из (5.6), обозначая
напряженность поля в зазоре На, имеем
Н,н+н(1-л)=4":“.
181

, \ Из (6.1) и (6.6)
Нз=В3=В=Н+4лМ.
’ ч Для тока получаем
_ Н1+ 4пМИ
° 4пс/\/ '
Ток, при котором наступает насыщение,
пн Г _ Ннас1+4пМнасЙ = 10 + Мнасйс.
1 — 4пс1\/ А’
Эта линия на плоскости (1, 11) (рис. 6.5)
отделяет область насыщения (заштрихованная) от области отсут-
ствия насыщения. Отсюда
Рис. 6.5
м, =—-——(":;;°)”.
Следовательно, насыщение отсутствует при Ь > дн.
На рис. 6.6 показан железный сердечник постоянного сечения
длиной 1 = 1 м, который изогнут в виде тора с зазором 11 = 1 мм и на
который намотана катушка с числом витков А’ = 1600, по которой
идет ток 1 = 1 А. Зависимость В(Н) материала сердечника представле-
на на рис. 6.7. Найдем магнитное поле в зазоре (М 6.17). Из (5.6)
вл-ьн1=%м.
Подставляя данные, находим 1ОВ + Н = 20,1. Эту линейную зависи-
мость наносим на рис. 6.7. Пересечение с заданной зависимостью
позволяет найти В = 15 кГс, которое и есть магнитное поле в зазоре.
На рис. 6.8 показан разрез достаточно длинной катушки с плотно-
стью намотки п витков на 1 см, по которым течет постоянный ток 1.
25
20
ё 15 1, п 5____п1____`
ч. 10 ооооооочоооо Е
7 7 Ё
ь 5 т д
0 5 10 15 2025 °°°°°°°4З_°°° З
Н, Э ‘п
Рис. 6.6 Рис. 6.7 Рис. 6.8
182

Если смотреть на катушку со стороны правого торца, то ток течет
по виткам в направлении по часовой стрелке. В катушку соосно
вставлен длинный магнитный стержень с площадью сечения о и
магнитной проницаемостью ц > 1. На рис. 6.8 пунктиром изображе-
на некоторая замкнутая поверхность 5, которая пересекает катушку
вдали от ее торцов. Найдем поток фН„ 415 вектора напряженности
3
магнитного поля Н, пронизывающий поверхность 5, и определим
его знак (М 6.16). Используя (6.1), получаем
фваз =1дназ+ 1 наз = о.
3 о $-
Откуда
1 наз = -„1на5.
5-0 о
Поэтому, используя (6.8) и (5.23)‚ имеем
[наз = дцнавцндв = (1 41)?- 1по.
8 о о
Тор квадратного сечения с поперечным разрезом шириной И
изготовлен из ферромагнитного материала, имеющего остаточную
намагниченность МО, коэрцитивную силу Но и зависимость М(Н) в
виде четверти окружности (рис. 6.9), представляет постоянный маг-
нит (внутренний радиус тора г], внешний — г2). Найдем величину
магнитного поля в центре зазора (Не 6.14). Из (5.6) И
Нрь + Н(21:г - и) = о,
где
_ Ч +"2
г - 2 ,
поле в разрезе отмечено индексом «р». Отсюда
21гг
Н = н(1- _).
Р д ‘М
Мо
Из (6.6) следует М
д=щ=н+мм
поэтому
т}
Н=_2ьм Н° Н
г ° Рис. 6.9
183

всю систему поместят в среду с магнитной проницаемостью ц
(равной магнитной проницаемости сердечника) (М 6.19). В ре-
зультате имеем постоянный магнит, который можно рассматри-
вать как магнитный диполь с дипольным моментом р = МУ, где
У — объем магнита. Вокруг магнита среда, являющаяся магнетиком
всюду, кроме небольшой области, заполненной диэлектриком. Ис-
пользуя формулу для поля диполя (1.8), а также полученное ранее
выражение для магнитного вектора, можем найти
в ь-ё.
(21?)
При заполнении разреза Б веществом с той же магнитной про-
ницаемостью и, что и сердечник, магнитное поле в центре тора из-
менится. Найдем, во сколько раз (Мз 6.20). При намагниченном
сердечнике поле в центре тора от пустых разрезов равно нулю. Если
один разрез заполнен магнитом (объем И намагниченность М), то
поле в центре тора можно вычислить в соответствии с (1.9) как поле
диполя
МУ
В‘ = @nT
Если второй разрез заполнить веществом таким же, как вещество
сердечника (с магнитной проницаемостью д), то, используя (5.6)
вместо (6.12), получаем
(в - 41гМ)Ь + %(2лк + н) = о,
и вместо (6.13)
= 4пМ/1
1: + (2пК + И)/ц°
В!
При ЭТОМ НЗМЗГНИЧСННОСТЬ сердечника
В/_В/ В!
М» = Д‘ 2 __
411 41:
ЭТУ НЗМЗГНИЧСННОСТЬ надо ВЫЧССТЬ ИЗ НЗМЗГНИЧСННОСТИ магнита
и снова воспользоваться формулой для поля. диполя
(р. >> 1).
(М - М’)У
В2 = кз
185

Таким образом,
В‚_ М _Ир.+2тсК+/1=1 Д
в2"м-м" 2пК+/1 21:12‘
При ПОМЕЩЕНИИ МЭГНСТИКЗ ЭЛЛИПСОИДЗЛЬНОЙ формы В ОДНОРОД-
НОС МЗГНИТНОС ПОЛС Но ВНУТРИ НСГО ВОЗНИКЗСТ однородное ПОЛО
н = но + нф. (6.14)
Поле Н ф ослабляет внешнее поле внутри магнетика. Оно назы-‘
вается размагничивающим, так как в ферромагнетиках и парамагне-
тиках оно направлено противоположно внешнему полю. Влияние
формы тела на его намагниченность М обычно представляют с помо-
шью коэффициента размашичивания (размагничивающего фактора)
в: шгдд‘; (6.15)
Рассмотрим стальной шарик, который намагничивается во внеш-
нем поле до насыщения, и затем поле выключается. Оценим оста-
точную намагниченность М шарика, если В и Н для данного сорта
стали связаны уравнением
Н
К
коэффициент размагничивания В (Не 6.22). Из (6.14) и (6.15), так
как НО = О, Н = —ВМ. Используя условие и (6.6), имеем
в=н+4лм=4лм-вм=в„( НЁМ].
К
Откуда
= ВОНК
вво + (41: - в)н„'
Изменение внешнего магнитного поля приводит к изменению
намагниченности находящегося в этом поле магнетика. Максималь-
ная намагниченность (все магнитные диполи направлены по внеш-
нему полю) достигается при Внас (поле насыщения). При уменьше-
нии внешнего поля до нуля в ферромагнетиках остается намагничен-
ность. Разный ход зависимости В(Н) для увеличения и уменьшения
внешнего поля называется гистерезисом. Часть работы, затрачивае-
186

мой на поворот магнитных моментов магнетика, А В
не возвращается, а уходит в теплоту. Воспользу-
емся аналогией между электрическими и магнит- В
ными процессами. Подобно (3.76) для потерь на " "°°
теплоту получаем О Н:
У Н
= — На/В ‚
47: 1 ‚ (6 16) _____
Тю
где У— объем магнетика. АН
Теплота, выделяющаяся в одном цикле на-
магничивания в единице объема, равна площади
петли гистерезиса, деленной на 41:.
На рис. 6.11 показана идеализированная петля (прямоугольник)
гистерезиса железного цилиндра (радиусом а, длиной 1), помещен-
ного внутрь соленоида, по которому пропускают переменный ток
(период Т), который перемагничивает цилиндр от Внас до —В„ас и
от —Внас до Вт. Найдем теплоту гистерезиса О, выделяющуюся за
время 1(М9 6.41). Используя (6.16)‚ получаем
Рис. 6.11
о = %вАН1а2;_-.
При быстро происходящих процессах, как следует из (5.32), со-
храняется (не изменяется) магнитный поток. Рассмотрим цилиндри-
ческий (радиус цилиндра К) магнетик (магнитная проницаемость ц),
помещенный внутрь соленоида (радиусом К), по обмотке которого
течет ток 10. Находящийся на оси магнетика детонационный шнур в
некоторый момент взрывается. Цилиндрическая взрывная волна
распространяется со скоростью и и, не разрушая магнетик, уменьшает
его магнитную проницаемость до 1. Найдем, как меняется при этом
ток в обмотке (М9 6.42). Используя (5.27), (5.23) и (6.8), получаем
1 1
Ф = пК2ц4п(Ъ9]п = пр“? — г2)+ г2]4п(—)п,
С
где г — расстояние, на которое распространилась взрывная волна в
момент времени г. Отсюда имеем
10
1= ‚
1-(и-0г2/нК2
где г = 121.
Удельное сопротивление проводников (р) уменьшается с умень-
шением температуры (Т). Для чистых (без примесей) металлов при
187

Сверхпроводни к
Идеальный
проводник
д б в
Т >Т„Тс Т„Н=О
Рис. 6.13
Рис. 6.12
188
низких температурах р вЂ” Т'. Замечательным свойством ряда веществ
является переход их при низких температурах в состояние сверхпро-
водимости, когда сопротивление скачком падает до нуля или, во вся-
ком случае, до очень малой величины. Такие вещества называются
сверхпроводннкамн. Температура перехода называется критической
(Т). Измерения показали, что переход происходит на очень узком
интервале температур вЂ” для чистых веществ порядка 10-'...10 4 К.
Интервал возрастает при наличии примесей или других дефектов
структуры. Однако сверхпроводник не является просто идеальным
проводником. Было установлено, что слабое магнитное поле не про-
никает в глубь сверхпроводника независимо от того, было ли поле
включено до или после его перехода в сверхпроводящее состояние
(эффект Мейснера). Направление намагничивания и в том и в дру-
гом случае противоположно направлению намагничивающего поля.
Эффект Мейснера связан с тем, что в поверхностном слое сверхпро-
водника под действием магнитного поля появляется электрический
ток, который компенсирует внешнее поле в толще сверхпроводника.
На рис. 6.12 сравнивается действие магнитного поля на сверхпро-
водник и идеальный проводник. При температуре Т > Т„(рис. 6.12, а)
магнитное поле захвачено обоими шариками. При температуре Т< Т„
(рис. 6.12, б) поле вытесняется из шарика, перешедшего в сверхпрово-
дяшее состояние. Если затем выключается магнитное поле (рис. 6.12, в),
то в идеальном проводнике будет остаточная намагниченность.
По поведению в достаточно сильных магнитных полях сверх-
проводники подразделяются на две группы. Их различие можно
видеть на примере зависимости намагничивания (М) длинных ци-
линдрических образцов, когда внешнее магнитное поле (Н) направ-
лено по оси цилиндров. На рис. 6.13 приведена зависимость для
сверхпроводннков 1-го рода. Начальный участок зависимости соот-
ветствует интервалу значений Н от нуля до Н„(критическое), на
котором имеет место эффект Мейснера и после которого поле скач-

ком проникает внутрь образца, и он во всем объеме переходит в
нормальное состояние. При этом удельный магнитный момент также
скачком уменьшается примерно в 105 раз. Критическое поле НК зави-
сит от температуры. Оно максимально при Т = О К и уменьшается
до нуля при Т = Тк. Если разрушение сверхпроводимости магнит-
ным полем проводится при адиабатической изоляции образца, то
он будет охлаждаться. Теплота поглощается сверхпроводником при
переходе в нормальное состояние. Отметим, что скачкообразный
переход наблюдается только в длинном цилиндре в продольном поле.
При произвольной форме образца и других ориентациях поля пере-
ход из сверхпроводящего состояния в нормальное оказывается рас-
тянутым по некоторому интервалу значений Н. Он начинается при
Н < НК и заканчивается, когда поле во всех точках образца превос-
ходит Нк. Образец расслаивается на чередующиеся области в нор-
мальном и сверхпроводящем состоянии.
Зависимость намагничивания М от магнитного поля Н для сверх-
проводников 2-го рода показана на рис. 6.14. Как и у сверхпроводни-
ков 1-го рода, начальный участок — линейная зависимость. Картина
разрушения сверхпроводимости магнитным полем в сверхпровод-
никах 2-го рода даже в длинных цилиндрических образцах в про-
дольном поле сложнее. Постепенное уменьшение намагничивания
начинается от значения магнитного поля Н” (нижнее критическое
поле), когда оно начинает проникать в толщу образца, и продолжа-
ется до значения НК, (верхнее критическое поле), при котором про-
исходит полное разрушение сверхпроводимости. Особенность сверх-
проводников 2-го рода заключается в том, что имеется смешанное
состояние, когда области сверхпроводящего состояния пронизаны
областями нормального состояния в виде нитей.
Найдем магнитное поле Н вне шара радиусом К из сверхпровод-
ника 1-го рода, внесенного в постоянное однородное магнитное поле
с напряженностью Но, которое еще не разрушило сверхпроводи-
мость в шаре, а также поверхностную плотность сверхпроводящего
тока] (Не 6.23).
Так как поле не входит в сверхпроводник
(эффект Мейснера), то на его границе оно -м(н)
должно быть направлено по касательной,
т. е. скалярное произведение НВ = О. Попы- Ё
таемся удовлетворить этому условию с помо- Ё
1
ЩЬЮ диполя р, помещенного в Центре шара: =
нк. нк На н
Н = Згд — 3-
д 5 3 '
г Г Рис. 6.14

Поле вокруг шара Н = НО + Нд. Для выполнения граничного
условия необходимо
нк = нов + зк (“Ёж -% = о.
Отсюда
к(н +2) = о,
р = -к3 , (6.17)
Для поля вокруг шара имеем
3
Н=(1+;—]Н0—%К3г-ЪЫ.
‚5
‚з (6.18)
Для получения напряженности поля на границе шара надо (6.18)
умножить на единичный касательный к поверхности шара вектор 1:.
Введем угол 6, как показано на рис. 6.15. Этот же угол определяет
точку на поверхности шара, если его отсчитывать от диаметра, па-
раллельного внешнему полю Но. Картина полей симметрична отно-
сительно направления этого диаметра. Для поля на границе шара
получаем
н, =Нт=%Н051п6=4п%. (6.19)
Это поле на оси симметрии (6 = 0) равно нулю, а на «экваторе»
(6 = п/2) поле равно (3/2)Н0. Плотность поверхностного тока 1 опре-
деляется из (6.19).
190

Если внутрь катушки поместить сверхпроводящий шарик, то ее
индуктивность изменится. Найдем, насколько изменится коэффи-
циент самоиндукции длинной однослойной катушки, в середину
которой поместили сверхпроводящий шарик, радиус которого гзна-
чительно меньше радиуса витков. Длина катушки 1, число витков А’
(Мг 6.28). Из (5.23) в середине пустой катушки
4п!\’1к
с! °
Магнитный момент шарика, определяемый (6.17)
рт=_г3%`›
В=Н=
ЗЗМСНЯСМ ВИТКОМ С ТОКОМ [в ПЛОЩЗДЬЮ ССЧСНИЯ 5, ДЛЯ КОТОРОГО
5
рв=1в_=рт'
С
Коэффициент взаимной индукции М определяется из условия
ч; = 35 = 41г1\’1к Ё = МВ.
с! с
Откуда
М = 4тсМ$`_
1
Таким образом,
1
ч; = ЬК-щмд: Ьк-Ь-„щппзд-
С С
1к м г3 4пАП 4„м)2г3 1
= — 4 -— —— " = — —— — Ф.
Ькс+л!(2 с! Ь"(! 2с
Откуда
2 3
Ад=_‹4п!\’) д_
! 2
Рассмотрим длинный сверхпроводящий Короткозамкнутый со-
леноид (плотность намотки п, радиус К, ток 1), на оси которого
вдали от концов соленоида находится маленький шарик (радиусом
г << К) из немагнитного материала, который при охлаждении пере-
водится в сверхпроводящее состояние. Найдем, где после этого бу-
13-2073 193

Его изменение (градиент)
1’: = _61 Е,
д’ сгз
Сверхпроводящий шарик радиусом К в этой точке в соответствии
с (6.17) приобретает дипольный момент
з
рш = -к3 Ё = 451. (6.20)
2 сгз
По аналогии с (1.11) для силы, действующей на шарик (Не 6.48),
ИМССМ
— д!’ С р7
2 3
г-рШ=6(Ё) 1. (6.21)
Шарик отталкивается от витка.
При помещении сверхпроводника в электрическое поле он ве-
дет себя как проводник — происходит поляризация (идет ток, вы-
равнивается потенциал). Проводящий шар радиусом К в электри-
ческом поле Ё в соответствии с (1.26) приобретает электрический
дипольный момент, равный рэ = К3Е. Два шарика, расположенные
вдоль электрического поля на расстоянии х >> К друг от друга, в
соответствии с (1.10) притягиваются как диполи с силой
г =6-’%=6К —. (6.22)
Если, кроме того, имеется еще и магнитное поле, перпендику-
лярное электрическому, то создаются магнитные дипольные мо-
менты (6.17)
_ ЗЕ
р_к29
которые в соответствии с (1.8) и (1.1 1) вызывают отталкивание ша-
риков с силой
1361’:
2
_ д-51
Е„_3х4- 4 х,. (623)
Сила взаимодействия шариков равна нулю (Не 6.46), если Р; = Рм,
т. е. Н = 2(2)‘/2Е.
13‘ 195

Если магнитное поле создается внутри соленоида, то.для равен-
ства электрических и магнитных сил в соленоиде, как следует из
(5.23), должен идти ток (М) 6.47)
1 = 2(2)"2 Ё-
41гп°
Если ток силой 1 идет по бесконечному прямому проводу, распо-
ложенному на расстоянии 11 параллельно плоской поверхности сверх-
проводящей среды, то распределение плотности поверхностных то-
ков 1 и силу, действующую на единицу длины провода, / можно
найти, используя условие отсутствия магнитного поля в сверхпро-
водящей среде (эффект Мейснера). Поле на плоской границе будет
иметь только касательную к границе составляющую Нт, если сим-
метрично под неи расположить провод с противоположным направ-
лением тока. Используя (5.2) и рис. 6.18, получаем
_Ш
сг2 О
н, = 2Н$йп6 (6.24)
Откуда (Мг 6.33; 6.37)
Н, _ 1/1
4“ 1:03 + х2)
Для дальнейшего необходимо воспользоваться законом Ампера
для взаимодействия тока с магнитным полем. Обозначая силу тока 1,
элемент тока аП, индукцию магнитного поля В и силу, действую-
щую на элемент тока, с117, имеем
](х)=
ат = Ё-[апв]; {ат = 1[апв]}. (6.25)
Из (5.2) и (6.25) сила, действующая на единицу длины провода
от параллельного провода с противоположным направлением тока,
является силой отталкивания, равной (Не 6.37)
. 1’
7 = Т‘
и н с 11
9 `\\Н‚ Если погонная плотность (масса на еди-
н 7 ницу длины) провода р„ то условие его па-
1’ рения над плоской поверхностью сверхпро-
Е, водника
| х 12
918 = Т = Т- (616)
Рис. 6.18 С Й
196

Отсюда можем найти высоту, на которой провод будет поддер-
живаться магнитным полем (Не 6.36).
Если над плоской поверхностью сверхпроводника 1-го рода на изо-
лирующем слое толщиной 11 лежит тонкое сверхпроводящее кольцо
радиусом К >› 11, по которому течет ток 1, то для каждого небольшо-
го элемента кольца можно силу рассчитывать, как для прямолиней-
ного провода. Найдем, при каком токе 1 кольцо начинает парить
над поверхностью, если его масса т (Мг 6.35). Ранее получена сила
на единицу длины (6.26). Поэтому
Вдали от витка с током (1) поле является полем магнитного ди-
поля (5.5). Если такой виток находится над сверхпроводящей плос-
костью, то для удовлетворения условия отсутствия проникновения
поля в сверхпроводник (эффект Мейснера) необходимо симметрично
от поверхности разместить соответствующим образом ориентиро-
ванный магнитный диполь (метод зеркальных отображений). Нали-
чие второго диполя изменяет поле вблизи первого и, следовательно,
изменяет индуктивность витка с током. Найдем изменение индук-
тивности (АЬ), когда плоскость витка параллельна поверхности сверх-
проводника (Ме 6.30) и когда она перпендикулярна ей (М 6.31). Ис-
пользуя формулы для поля диполя (1.7) и (1.8)‚ следующие из (1.9)‚ и
(5.28) для потока поля и индуктивности и обозначая радиус витка К и
расстояние витка от поверхности сверхпроводника 11 >> К, находим в
первом случае
2
АФ = -1-——"к 3 11122 = ЁАЬ.
с (2/2) С
Откуда
2 4
АЬ=-“Ё
8/2
Во втором случае
2
АФ = -21 "к, лк2 = ЁАЬ.
с (210 с
Откуда
2 4
АЬ - --—" Ё
411
197

Постоянный магнит со сверхпроводящей поверхностью взаимо-
действует подобно витку, имеющему такой же магнитный момент.
Используя метод зеркальных изображений и выражение для поля
диполя (1.8) и силы взаимодействия (1.11), обозначая массу магни-
та т, магнитный момент р, расстояние до поверхности 11, получаем
3р2
(2104 °
Отсюда находим магнитный момент р, а по нему магнитное поле
у поверхности сверхпроводника от двух диполей (Не 6.34)
Н = Ё ‹Щ)1/2
11 3 '
Рассмотрим кольцо (радиусом К) из тонкой проволоки радиусом
г<< К, находящееся в магнитном поле Н, которое перпендикулярно к
плоскости кольца. Кольцо охлаждением переводится в сверхпрово-
дящее состояние. При этом магнитное поле вытесняется из кольца,
а по поверхности его начинают течь токи намагничивания (рис. 6.19)
по внутренней поверхности в одну сторону, а по внешней в другую.
При уменьшении магнитного поля его силовые линии удаляются на
бесконечность. Но линии, проходящие внутри кольца, пройти через
сверхпроводник не могут. Поэтому остается поле внутри кольца и
ток на внутренней поверхности проволоки, как показано на рис. 6.20.
Используя (5.28) и известную формулу для индуктивности тонкого
проволочного кольца
т3=
Ь = 4лК[1п(ё) - 2],
можем найти силу тока в кольце (Мг 6.32)
1 = слК2 Z
Найдем распределение поверхностных токов 1„0В(6) на проволоке
(радиусом а), если поле Но, в которое она помещена, еще не раз-
\Н/
\
Рис. 6.19 Рис. 6.20
198

рушает сверхпроводимость в ней (М 6.25).
Поле внутри проводящего цилиндра, по ко-
торому течет однородный ток плотностью 1,
на расстоянии г от оси определяется (5.7)
Н-Ёш].
С
Используя метод наложения (рис. 6.21), по-
лучаем в полости, где ток отсутствует,
Н = %‘-[(г2 -г.)1]= Ёдьз].
Чтобы внутри сверхпроводника поля не было,
должно быть Н = —Но. Откуда следует
2 .
щ=%щ
Из геометрии имеем 1„овс11=]с1.5`=]с111›. Поэтому, используя рис. 6.15,
получаем распределение поверхностного тока
[ш = Л; зйпе = сНО %.
Ток течет параллельно оси проволоки.
Магнитное поле вне длинной сверхпроводящей проволоки, по-
мещенной во внешнее однородное магнитное поле Но, найдем, ис-
пользуя тот же прием, что и для сверхпроводящего шара. По анало-
гии с полем электрического «плоского» диполя (1.36) имеем для
«плоского» магнитного диполя
нд = 4(рг)1; - 2%. (6.27)
Г Г
Величину дипольного момента находим из условия, что сумма
внешнего поля и поля диполя на границе проволоки (г = К) имеет
только касательную к поверхности составляющую
нов + (рК)? - 7 = о.
Откуда
р = —Н0 —. (6.28)
Для поля вне проволоки получаем
к2

7. ЭЛЕКТРОМАГНИТНАЯ ИНДУКЦИЯ.
ЭНЕРГИЯ И СИЛЫ В МАГ НИТНОМ ПОЛЕ.
СОХРАНЕНИЕ МАГНИТНОГ О ПОТОКА
В СВЕРХПРОВОДЯЩИХ КОНТУРАХ
Открытие Фарадея заключалось в том, что в замкнутом проводя-
щем контуре при изменении потока магнитной индукции (В), охва-
тываемого этим контуром, возникает электрический ток, называе-
мый индукционным. Это означает, что в контуре появляется ЭДС
индукции
1 ЭФ
б’ = —-—, 7.1
с д! ( )
где Ф — поток вектора магнитной индукции через площадь 5,
Ф={Вс15.
Знак минус связан с выбором положительного направления об-
хода контура (направления тока и ЭДС). Положительным является
направление, при вращении в котором правый винт смещается в
направлении нормали к плоскости контура.
Для проверки правильности выбора направления тока можно
пользоваться правилом Ленца: ток идет так, чтобы возникающее от
него магнитное поле противодействовало изменению потока маг-
нитного поля. Помогает также использование формул, полученных
обобщением экспериментальных данных для сил Лоренца и Ампе-
ра. Сила Лоренца, действующая на заряд с], движущийся в магнит-
ном поле (индуктивность В) со скоростью у, равна
гм = Ёсдув]; {г„ = атм}. (72)
Если кроме магнитного поля действует еще и электрическое Е,
то сила Лоренца
г = 4(Е + гит); {г = до; + [чв])}. (73)
200

Сила Ампера действует на элемент тока И!
~~ = -[ЛВ]; (~~ = ~ [~1В]).
(7.4)
Следуя Максвеллу, можно переписать (7.1) для вихревого элек-
трического поля в проводнике в интегральном и дифференциаль-
ном виде
фел =--'~ вЂ” ',~л, ~~феы =-1',~л~;
(7.5)
1дВ
гойЕ = вЂ” вЂ” вЂ”,
с дР
дВ
гойЕ = вЂ” вЂ” .
дк
(7.6)
Изменение площади внутри контура не всегда предстает в яв-
ном виде. Рассмотрим медный диск (радиусом а), вращающийся в
однородном магнитном поле (с индукцией В, перпендикулярной к
плоскости диска) с угловой скоростью и. Две щетки, одна на оси
диска, другая на окружности, соединяют его с внешней цепью, в
которую включены реостат с сопротивлением Л и амперметр, со-
противлением которого, а также сопротивлением соединительных
проводов можно пренебречь. Найдем силу тока, идущего через ам-
перметр (Ж 7.1). Можно подумать, что площадь, охватываемая кон-
туром, не меняется, если не учитывать подвижность элементов дис-
ка, которые замыкают контур. Элемент поворачивается на беско-
нечно малый угол Ша = иаг за бесконечно малое время аг. При этом '
изменение площади
аБ = вЂ” аааа.
1
2
Из (7.1)
1дФ 1 д5 2 в
К' = вЂ” вЂ” вЂ” = вЂ” вЂ” В вЂ” = вЂ” Ва вЂ”.
с д~ с д~ 2С
Для тока получаем
Ф
Х= вЂ” =
Я
2
2сЯ
Появление тока свободных зарядов в проводнике можно объяс-
нить действием магнитной силы (7.2), так как заряды вместе с дис-
ком имеют скорости о = сог, где г вЂ” это расстояние заряда от оси
вращения. Напряженность электрического поля
Е = вЂ” игв,
1
С
201

нение потока магнитного поля через кольцо приводит к изменению
тока в соответствии с (5.28)
АФ = В05со$6 =%1‚А1.
Если известно, что в результате переноса кольца текший по нему
ток 1 обращается в нуль, то можно найти коэффициент его самоин-
дукции (М: 7.27)
Ь = сВОЗЁЁ-Ё.
1
Поток магнитного поля может меняться за счет изменения со
временем магнитного поля. Вычислим ЭДС Ё в квадратном прово-
лочном контуре со стороной а, в который включена лампочка, нахо-
дящемся на расстоянии Ь от длинного прямого провода (рис. 7.4), по
которому течет синусоидальный ток 1 = 10 сов (ш. В соответствии с
(5.2) и (5.27) поток через контур
Ф:
‹ъ|ю
ч|°д
а+Ь
1а 1 ’ =Ё1а1п(1+5’-).
Ь с Ь
Из .(7. |) находим
‘ . 2 . а
ё = —10ш$1пю1а1п 1+—.
с Ь
Если сопротивлением контура можно пренебречь и задано на-
пряжение И требующееся для нормального накала лампочки, то можно
найти эффективное (смотри разд. 10) значение силы тока (М 7.3)
1 _ с2У
эф _ 2аш1п(1 + а/Ь)’
Рассмотрим длинную катушку с плотностью витков п, по обмот-
ке которой течет ток 1 = 10 сов ш: и в которую вставлен стержень
радиусом К с магнитной проницаемостью д, обладающий слабой
удельной проводимостью А. Найдем среднюю мощ-
/ ность тепловых потерь в стержне на единицу длины в
: д Центральной части катушки (Не 7.87). В соответствии
‚ с (5.23) и (6.8) поле в сердечнике, вставленном по
а оси катушки, будет равно
1
В = 4тшп1со5 (т.
Рис. 7.4 с
204

Используя (7.5), находим вихревое электрическое поле
10 .
Е = Ъшптшг зт (т,
С
где г — расстояние от оси стержня (и соленоида).
В соответствии с (4.12) и (4.7) мощность тепловых потерь опре-
деляется интегралом по объему
м = 1 АЕЫУ.
У
Объем на единицу длины стержня равен с11/= 2пгс1г, и интегри-
ровать надо от О до К. Поэтому
12 .
А! = 2пзмх2п2 —%оэ2К4 51112 ил.
С
Усреднение за период изменения тока дает
‚2
(П) = п3м12п2 -%‹о2К4.
С
Аналогичным образом можно найти среднюю мощность тепло-
вых потерь в металлическом диске радиусом а, толщиной Ь и удель-
ной проводимостью А, находящемся в однородном магнитном поле,
перпендикулярном плоскости диска и изменяющемся по закону
В = Во 5111 со: (Не 7.86). Обозначая расстояние от оси диска г, из (7.5)
получаем
2пгЕ = —%пг2Вш созюг; Е = —%%В0шгсо5ю1.
В соответствии с (4.12) и (4.7) мощность тепловых потерь опре-
деляется интегралом по объему
м = 1 шил
У
Объем с1У= Ь21т1г‚ и интегрировать надо от О до а. Поэтому
1 53 2 2 ‘4
1\’=- АЬ——ш совала.
8 с2
Усреднение за период изменения тока дает
_ 1 4 33 2
(Н) —Е1га 16:70).
205

решением предыдущей задачи, в том числе и (7.7). Колебания стрелки
во внешнем поле описываются уравнением 10:” = — Орион. Здесь
штрихами обозначена вторая производная угла отклонения стрелки
по времени, а в правой части момент сил, действующих на магнит-
ный диполь во внешнем поле при малых углах отклонения. Из это-
го уравнения частота колебаний равна (о = (Ворм/1)‘/2, а закон коле-
баний стрелки ос(1) = 01.0 сов (т. Действуя далее, как в предыдущей
задаче, получаем для амплитуды переменной ЭДС на концах обмот-
ки соленоида
‚ 1 2
ЕЭС = 21тЁ прмосошс,
и для частоты (ос = ш.
Магнитик в виде цилиндра радиусом г и длиной 1 с остаточной
индукцией В и соответственно намагниченностью М = 8/41: имеет
магнитный момент рм = пг21М, которому соответствует виток с маг-
нитным моментом пгЧ/с. Откуда сила тока
В!
1 = Д.
— 41:
Если такой магнит вращается с угловой скоростью ш в центре
кругового витка радиусом В >> 1 >> г, то коэффициент взаимной
индукции находим, как для вращающегося витка. Используя (5.4),
(5.28) и (5.30), получаем, как и ранее, для коэффициента взаимной
индукции
2 2
1:
—С080)1`.
Ь=пг к
ИЗ (5.28)
Ф = п 2 %%созш.
Если виток радиусом К подключен к вольтметру переменного
тока, то, как будет в дальнейшем получено для переменного тока,
показание меньше максимального значения в 2 раз. Используя (7. 1),
получаем (Мг 7.16):
_ пг21шВ
2Лкс `
Магнитик такой же, как в предыдущей задаче (массой т и плот-
ностью р), расположен посередине между двумя параллельными тон-
144073 209

кими длинными проводниками, находящимися на расстоянии 21,
концы которых с одной стороны замкнуты, а с другой — подключе-
ны к милливеберметру. Ось магнитика перпендикулярна плоскости
проводников. Найдем изменение показаний прибора (изменение
магнитного потока АФ) после быстрого нагревания магнитика выше
температуры Кюри (полного размагничивания), если до этого оста-
точная индукция в нем была равна В (Мг 7.17). Объем магнитика т/р.
Поэтому магнитный момент
т т
д, = М— = ВТ.
Р “Р
Ему соответствует магнитный момент витка
- ' 15
рм "` 2
(площадью 5 с током 1). Взаимную индукцию (Ь) находим по магнит-
ному потоку Ф 5 от проводов с током 1” (5.2) через площадь 5. Имеем
21 5 1
Фз = сп 7 = tt
ОТКУДЗ ВЗЗИМНЗЯ ИНДУКЦИЯ
5
Ь — 47.
В соответствии с теоремой взаимности (5.3О) поток от магнитика
Ф=1Ы=4Ш=ВЦЪ
с 1 пр!
Если остаточная индукция стали стрелки компаса равна индук-
ции насыщения ВО, то ее намагниченность М = В0/4л, а магнитный
момент рм = М И где У- объем стрелки. Такой компас расположен
под прямым бесконечным проводом, по которому течет ток. Най-
дем, какая должна быть сила тока, чтобы стрелка поднялась над осью,
на которой она находится (Не 7.50). Магнитное поле тока определя-
ется (5.2). Оно увеличивается при приближении к проводу, поэтому
магнитный диполь (стрелка компаса) будет втягиваться в это поле.
Силу, действующую на диполь, находим по аналогии с (1.11) или из
того, что потенциальная энергия (1 = рмВ. Для предельной силы
имеем
аи д(р‚ В) ав 21
г=руг='т=’%=’рмэг=воуцд’
где р — плотность материала стрелки.
210

Отсюда
1 = 21грсг2 1.
Во
Стрелка компаса, направленная по горизонтальной составляю-
щей земного поля (ВО = 0,2 Гс), будет отклоняться, если к ней под-
нести (на расстояние Ь = 1 м) магнитный брусок (площадью сече-
ния 5‘ = 1 см2‚ длиной 1= 10 см, с остаточной индукцией материала
Вд = 10 кГс). При вычислении магнитного поля, действующего на
стрелку, брусок будем считать магнитным диполем в соответствии с
(6.6), равным
_ 8,15
_ 41: '
Максимальное поле в соответствии с (1.7) получаем в направлении
оси диполя
_ 8,15
_ 2Ьл
Поэтому, направляя диполь перпендикулярно полю Земли, полу-
чаем максимальное отклонение на угол ср = В/ВО = 0,1 рад (Не 7.65).
Стрелка компаса с магнитным моментом р может вращаться на
вертикальной оси, но связана со спиральной пружиной, модуль круче-
ния которой [ По большому горизонтальному листу, расположенно-
му под стрелкой, начинает течь поверхностный ток плотностью 3,
направление которого совпадает с направлением начального равно-
весного направления стрелки. Предполагая угол поворота ос малым,
найдем его величину (Мг 7.49). Магнитное поле, создаваемое током,
определяем с помощью (5.6) Н = 41: ]/с. Момент сил, действующий на
магнитный диполь в магнитном поле, в соответствии с (2.33) и ана-
логией между магнитными и электрическими полями равен
М = [рВ]. (7.8)
В данном случае при малых углах отклонения стрелки и почти
перпендикулярном направлении магнитного момента стрелки (р) к
направлению магнитного поля тока, учитывая, что В = Н, а также
связь момента сил, создаваемого пружиной, с углом поворота стрелки,
имеем
Н=в=2% =О,О16 Гс.
рВ = муё = т.
ОТСЮДЗ НЗХОДИМ УГОЛ ПОВОРОТЭ СТреЛКИ.
14- 21 1

Искусственный спутник Земли массой т выполнен в виде тон-
костенного шара. Для сообщения ему угловой скорости можно ис-
пользовать магнитное поле Земли, индукция которого В. Найдем
угловую скорость (о, которую приобретет спутник при быстрой раз-
рядке аккумуляторов, имеющих заряд О, через обмотку А’ витков,
уложенную на поверхности спутника вдоль окружности большого
круга, считая магнитное поле Земли параллельным плоскости об-
мотки (Мг 7.51). Спутник представляет магнитный диполь, на кото-
рый в магнитном поле, как и в предыдущей задаче, действует мо-
мент сил, приводящий к вращению с угловым ускорением с1ю/а'1.
Момент инерции полого шара массой т и радиусом К равен
1 =%тК2
Ш
(см.: 1, с. 190). Уравнение, описывающее вращение спутника,
до)
1„‚—
д!
так как магнитный диполь спутника при малом времени разрядки
аккумулятора практически перпендикулярен магнитному полю.
Используя для магнитного момента (5.5)‚ в которое подставляем
АО
1-7,
находим набранную угловую скорость.
Прецессия тяжелого гироскопа (гироскопа, подвешенного таким
образом, что на него действует момент силы тяжести) описывается
уравнением (см.: 1, с. 286) А
каш = [гтв], ‹7.9›
= РВ,
где 52 — скорость прецессии; Ьш — момент импульса собственного
вращения гироскопа; г — вектор расстояния от точки опоры до цен-
тра масс гироскопа; д — напряженность силы тяжести; т — масса
гироскопа. Если направление г совпадает с направлением Ьш, то
получаем
т:
$2=—г——.
Ь
О)
Скорость прецессии меняется, если гироскоп имеет намагничен-
ность М вдоль своей оси и находится в магнитном поле с индуктив-
ностью В, направленной, например, вертикально вверх. В этом слу-
212

чае в соответствии с (2.33) и аналогией между электрическим и маг-
нитным полем
[Й,Ь„] = [гтрк] вЂ” [рВ]. (7.10)
Обозначая плотность материала гироскопа р, для его объема по-
лучаем Г= т/р. Намагниченность, умноженная на объем, дает маг-
нитный дипольный момент р = МК Для изменения скорости пре-
цессии Ьй = И, вЂ” И имеем
[ЛЙЬ„] = -[МРВ].
Поэтому получаем (М 7.66)
МВ
И рот
Найдем скорость прецессии й однородно заряженного непрово-
дящего кольца (массой т, с зарядом д), быстро вращающегося вок-
руг своей оси с угловой скоростью и во внешнем однородном маг-
нитном поле В (М 7.47). Вращение заряда соответствует току
О
Т 2к
Введем обозначение радиуса кольца Я и угол между его осью и
направлением магнитного поля а. Собственный момент импульса
кольца А„= тЛ2и. Магнитный момент в соответствии с (5.5)
д2
~Р = ДИ вЂ”.
2С
Используя приведенные ранее формулы для скорости прецес-
сии, получаем [ЙЬ„] = вЂ” [рВ] = [Вр]. Так как направление скорости
прецессии совпадает с направлением магнитного поля, а направле-
ние момента импульса кольца совпадает с направлением его маг-
нитного момента, то
Й=
2тс
Отметим, что скорость прецессии не зависит от радиуса кольца,
угловой скорости его вращения и угла между его осью и направле-
нием магнитного поля.
Вместо рассмотренного кольца можно взять стержень. Если из-
вестно, что работа для поворота этого стержня, обладающего маг-
нитным моментом р, на 180' в магнитном поле В равна А, то в соот-
213

ветствии с приведенной далее формулой (7.31) и результатом для
электрического поля (3.73) А =: 2рВ. При раскручивании стержня
вокруг собственной оси до большой скорости вращения равной а)
стержню сообщается энергия вращения, равная 10 А:
1 2
%}=юА.
ОТСЮДЗ ДЛЯ МСХЗНИЧССКОГО МОМСНТЗ ИМПУЛЬСЗ ИМССМ
ц:1ш=Ё„
(1)
Используя приведенную ранее формулу для скорости прецессии,
получаем (Не 7.48):
_ А = Я
$2 - В Ь 40.
О.)
Для определения магнитной восприимчивости диамагнитного ма-
териала измеряют с помощью весов силу, выталкивающую малень-
кий образец из зазора между полюсами электромагнита (рис. 7.8).
Известно, что магнитное поле в зазоре меняется в зависимости от
расстояния (г) от оси симметрии В = ВО ехр (—осг2). Найдем, на ка-
ком расстоянии от оси нужно расположить диамагнитный образец
(абсолютное значение магнитной восприимчивости материала х << 1)
в виде небольшого тонкого диска объемом И ориентированного пер-
пендикулярно магнитному полю, чтобы сила его выталкивающая была
максимальной (М 7.76). Учитывая (6.7) и (6.9) (в данном случае д: 1),
для магнитного момента образца имеем
р = МУ= ХНУ: хВИ
В соответствии с (1.11) на магнитный диполь действует сила
дВ а'В
\ / Г - р;- —- 827.
Обычным образом (приравнивая нулю про-
изводную) находим экстремальную силу. Надо
удовлетворить
Ж
ав2 ат*
(Е)+вЕ7=о
И \ Вычисляя производные, имеем
Рис. 7.8 2осг2 + 2002 — 1 = О.
214

вычисляя с помощью. (5.3), где г = (l' + Л')[~' = (, поток от витка
через 5', предполагая, что по витку идет ток 1,:
откуда
Поэтому, учитывая, что ( = И, получаем с помощью (5.28) маг-
нитный поток через виток
Ф(~) = Е вЂ”" = 2шА'
с (,~)з
С помощью (7.1) находим ЭДС в витке и затем силу тока
1 = блЛ-р„
сг(
Намагниченная пуля пролетает вдоль оси тонкой (плоской) ка-
тушки (диаметром Р, с числом витков и), соединенной с баллисти-
ческим гальванометром через идеальный выпрямляющий элемент
(сопротивление цепи Л). Зная, что размеры пули малы по сравне-
нию с диаметром катушки и магнитный момент пули М направлен
вдоль оси движения, найдем его величину, если известны баллисти-
ческая постоянная гальванометра Ь (рад/Кл) и угол р, на который
стрелка гальванометра отклонилась после пролета пули (Мо 7.19).
Удобно перейти в систему координат, связанную с пулей. Тогда в
движущейся со скоростью о в магнитном поле пули, определяемом
(7.11), катушке под действием силы Лоренца (7.2) возникает движе-
ние зарядов (вихревое электрическое поле). Используя (7.11) для
силы Лоренца и напряженности электрического поля в системе СИ,
получаем
Е = Р„= [чВ[ = вЂ” ~~3[Мг[
где г вЂ” вектор от диполя к элементу катушки.
Второй член из (7.11) дает нуль, так как скорость параллельна
дипольному моменту.
Обозначая угол наклона вектора г к оси катушки а, имеем для
модуля напряженности электрического поля
Е = вЂ” вЂ” Мсоваи
Зи 81Й О,
4ж
3
216

Откуда находим (М 7.20, 7.21):
о>В,( )
Если к небольшой катушке с числом витков Ж и площадью вит-
ка 5', по которой течет переменный ток 1(действующее значение,
т. е. показание амперметра переменного тока, которое меньше мак-
симального значения в ~2 раз), поднести (на расстояние а) лист из
хорошо проводящего материала, то, как и в случае сверхпроводя-
щего «магнитного зеркала», возникает «отражение» катушки. Так
как она небольшая, можно поле, проходящее через нее, вычислять
по (5.3)
Н =2ЮвЂ”
' (га)'
Дополнительную ЭДС (действующее значение, которое так же,
как и ток, в ~2 раз меньше максимального) определяем по (7.1)
1с ууг 5г
4с2аз
Знак минус означает, что дополнительная ЭДС направлена против
поля катушечки, т. е. ЭДС убывает при экранировке (М 7.14).
Рассмотрим два соосных круговых витка радиусами Я и г «Я,
размещенных на расстоянии Я друг от друга. Найдем ток Х(~) в боль-
шом витке, сопротивление которого Я, если по малому витку про-
пускается ток ~ = ~, сов и1(М 7.15). В данном случае, используя (5.3),
легко найти поток через малый виток Ф„, если по большому идет
ток Кб,
Ф„= вЂ” тг 2шЯ'
с ( г г)г~г
Отсюда и из (5.28) для взаимной индукции имеем
к2г2
А=
Используя теорему взаимности (5.30) и (7.1), для тока в боль-
шом витке получаем
Я ~ ~ О ~ » 3 1 П О ~ »
/2ЛЯОС
218

На рис. 7.10 показан прямолинейный магнит Ж5',
расположенный на оси круглого кольца радиусом а,
состоящего из и витков проволоки, концы которой
соединены с баллистическим гальванометром. Рас-
стояние между центрами кольца и магнита равно Ь.
Размеры магнита малы по сравнению с и и радиусом
кольца. Найдем магнитный момент р, магнита, если
при его удалении от кольца стрелка баллистического
гальванометра отклонилась на угол у. Баллистичес-
кая постоянная равна о (рад/Кл), сопротивление цепи
(включая сопротивление гальванометра) Л (№ 7.22).
Магнит можно заменить соответствующим витком
небольшой площади Я с током 1„и магнитным моментом (5.5)
(р, = 1„5/с). Коэффициент взаимной индукции А находим, пользу-
ясь теоремой взаимности (5.30) и (5.28), а также вычисляя с помо-
щью (5.3), где г = (и'- + а')~~', поток от витка через 5', предполагая,
что по витку идет ток 1,:
Ф=2на 1,вЂ” = Е вЂ” '.
2 ~ ~в
' сг' с
Откуда
А = 2на вЂ”.
г 5
3 '
Поэтому с помощью (5.28) получаем магнитный поток через и вит-
ков (зацепленный)
2пиа
Ч'О) = пФ(~) = п1. вЂ”"вЂ”
с гЗ
С помощью (7.1) находим для цепи (с гальванометром)
й с Ж
Интегрируя по времени, получаем
д 2ла р„си
2
Зд
Отсюда находим магнитный момент.
Длинный соленоид, витки которого намотаны с плотностью и,
включен в цепь, общее сопротивление которой Л. В торцевых плос-
костях на оси соленоида помещены одинаковые магнитики малого
219

объема Е каждый и намагниченностью 4яМ, повернутые друг к дру-
гу разноименными полюсами. Найдем, какой заряд О протечет в
цепи соленоида, если магнитики, двигаясь по оси соленоида, сли-
паются в его центре (М 7.24).
Магнитик можно заменить соответствующим витком небольшой
площади 5, с током 1, и магнитным моментом (5.5) (Р = Х Я,/с).
Обозначая коэффициент взаимной индукции Е, который по те-
ореме взаимности (5.30) одинаков для витка и соленоида, и исполь-
зуя для поля соленоида (5.22), получаем для магнитного потока че-
рез виток (на торце соленоида)
4жл1, Ю,
Ч', = вЂ” ЕХ, =НБ, =
Откуда Е = 4ппБ,. Поэтому
~в 4йо5в ~в
Ч', =М вЂ” '= ' ' =4ппр.
С С
После слипания общий магнитный момент слипшихся магнити-
ков 2р. Поэтому поток через соленоид будет в два раза больше, а
изменение потока
ЛЧ' = Ч', = 4ппр = 4ппМК
Откуда
ЬФ
сЯ
Найдем силу, действующую на магнитный д~шоль с магнитным
моментом р, расположенный в центре торца длинного соленоида с
плотностью намотки и (витков/см), радиусом сечения Л, по обмотке
которого течет ток 1, если диполь ориентирован по оси соленоида
(М 7.80). Для поля на оси соленоида воспользуемся (5.22) и рис. 5.19.
Координату х отсчитываем от центра торца. Для силы, действующей
на диполь в переменном поле, подобно (1.11), можем написать
д И д~2тс Яс) п(соз и вЂ” сов Д)]
=Р вЂ” =Р
дх дх
1 . да . др
= р 2к вЂ” и вЂ” я'п а вЂ” + яп р вЂ” .
С дх дх
При х = 0 в1п а = 1, яп р стремится к нулю для длинного соленоида,
дп 1 дР
вЂ” вЂ” вЂ” вЂ” -э О.
дх = Я' ах
220

В результате
1 и
Г = р2н вЂ” вЂ”.
с Я
Если дипольный момент направлен так же, как поле в соленоиде,
то диполь будет втягиваться в соленоид.
Небольшой сверхпроводящнй шарик может свободно перемещаться
вдоль осн тонкого кольца радиусом Л, по которому течет ток. Най-
дем, при каком расстоянии между шариком и плоскостью кольца
сила, действующая на шарик, принимает максимальное значение и
как она направлена (№ 7.81). Обозначая расстояние от плоскости
кольца вдоль его оси х, из (5.3) имеем
У Я
К =2я
с( г г)
Дипольный момент сверхпроводящего шарика радиусом г в со-
ответствии с (6.28)
3 И
р= вЂ” г вЂ”.
2
Сила подобно (1.11)
Г=р вЂ” = 2я1 вЂ” -г
дН Я 3 з х
дх с 2 ( г г)4
Приравнивая первую производную по х нулю, находим экстре-
мумы. При х = Я/~/7 сила максимальна и направлена в сторону воз-
растания х (сила отталкивания). При х = -Л//7 сила по абсолют-
ной величине такая же, но направлена в сторону отрицательных
значений х (также сила отталкивания).
В экваториальной плоскости шара радиусом а находится тонкое
металлическое кольцо радиусом р > а с электрическим сопротивле-
нием Л. Внешнее однородное магнитное поле Во перпендикулярно
плоскости кольца. Пренебрегая индуктивностью кольца, найдем
заряд, протекший по кольцу, если охлаждением шар переводится
в сверхпроводящее состояние (№ 7.28). Предполагая, что вещество
щара является немагнитным, получаем для потока магнитного поля
через кольцо Ф„= Воярг. В результате превращения шара в сверх-
проводник магнитное поле из него вытесняется (эффект Мейснера).
221

По поверхности шара текут поверхностные токи. Для удовлетворе-
ния граничного условия на поверхности шара, как это следует из
(6.17), можно считать, что в центре шара имеется диполь с диполь-
ным моментом
1
Поле в экваториальной плоскости шара будет равно
Г
ДЛЯ ПОТОКЕ! В ЭТОМ случае ПОЛУЧЭСМ
р з
Фк = [В(г)2т°с!г = В0пр2 — В0т:%.
Используя (7.1), находим
_ _ Е__1Ё
а_т`кш_ сел’
Откуда
1АФ аз
На рис. 7.11 показан стальной магнитопровод длиной Ь с магнит-
ной проницаемостью р, в замкнутой сверхпроводящей обмотке ко-
торого возбужден ток 10. Найдем, как изменится ток в обмотке, если
имеющийся в магнитопроводе небольшой зазор 1, в котором рассея-
нием магнитного поля можно пренебречь,
уменьшить в два раза (М) 7.30). Из теоре-
мы о циркуляции (5.6), обозначая число
витков в обмотке п, находим
10-
4пп - НдЬ + Н21.
7
Из условия на границе с помощью
(6.1) имеем рН‚ = Н, Откуда
Миш = Н2 (Ь+ pS
С Р-
Рис. 7.11
222

Так как сопротивление обмотки и, следовательно, ЭДС Йравны
нулю, из (7.1) имеем постоянство магнитного потока и поэтому по-
стоянство напряженности магнитного поля. Отсюда
Э
1
4шп вЂ” = Н, вЂ” +-,
с 2 р 2
где 1 вЂ” новый ток в обмотке, для которого получаем
А/р + 1/2
' ~/И+1
Если не уменьшать зазор, а заполнить его тем же веществом, из
которого состоит магнитопровод (М 7.32), то второе уравнение при-
мет вид
1+1
4пп вЂ” = Н,
с и
Откуда
1+1
А+ 1р
Постоянство магнитного потока из (7.1) следует также для быс-
трых (при й стремящихся к нулю) процессов. Сильные магнитные
поля можно получить взрывным сжатием проводящей цилиндричес-
кой трубы, внутри которой создано начальное магнитное поле с
индукцией В . Предполагая материал трубы идеально проводящим
(магнитное поле не входит в него), найдем индукцию магнитного
поля внутри трубы В при сжатии ее по радиусу от начального внут-
реннего радиуса Л до г и давление р, необходимое для этого (М 7.31).
Из постоянства потока магнитного поля Вшг' = ВОБЛ' находим В.
Для плотности энергии (в) магнитного поля (напряженность Н, ин-
дукция В = цН), которое определяет давление (р), по аналогии с
(3.75) имеем
В В
р=в=Н вЂ”; р=и=Н вЂ” .
8л' 2
(7.12)
Поэтому в данном случае (ц = 1)
В ~ (Я/г)
р= вЂ” =Во
Зл; 8тс
Найдем давление р, действующее на боковую поверхность длин-
ного соленоида, имеющего плотность намотки и [витков/см], по ко-
223

торому течет ток 1(М9 7.34). Предполагая магнитную проницаемость
среды ц = 1, из (7.12) и (5.23) получаем
12п2
С2‘
С внешней стороны длинного соленоида магнитное поле отсут-
ствует. Отметим, что давление в случае магнитного поля действует в
сторону от него, в то время как в случае электрического поля, на-
пример в конденсаторе, давление направлено в сторону электричес-
кого поля (обкладки заряженного конденсатора притягиваются).
Давление можно найти и другим способом, используя закон
Ампера. Сила, действующая на элемент тока 1:11, находящийся в
магнитном поле Н, в соответствии с (7.4) при В = Н
р=2п
ат =%1[с1|Н], (713)
где Н — магнитное поле, создаваемое в данной точке всеми элемен-
тами тока соленоида, кроме самого рассматриваемого элемента.
Это поле можно найти из условия, что сумма его с полем На,
создаваемым элементом, равно полю внутри соленоида, а вне -
равно нулю (Н — На = О). Вычисляя Циркуляцию поля на единице
длины, из (5.6) имеем
Н+Нэ=4пп1.
С
Откуда
22
Н=21гп1 и р_с1Р 1п.
Если обмотка соленоида выполнена проводом диаметром с! в один
слой, то п = 1/4 и, следовательно,
р — 21: 12
с2 (12 °
В случае сверхпроводящей обмотки максимально возможный ток
определяется либо механической прочностью провода обмотки, либо
разрушением его сверхпроводимости. При разрушающем сверхпро-
водимость внешнем поле Вк = 15 кГс и диаметре провода обмотки
а’ = 0,2 мм, используя (5.23), находим
Вк, _ 3.10” -2.1о‘2.1,5.1о4
_ =240 А.
4тс з-1о°-2.3‚14
1тах1= с‘,
224

При прочности проволоки на разрыв
Р = 5 Н и диаметре соленоида В = 2 см,
Р
учитывая, что давление магнитного поля р ад р- — т
уравновешивается силой вдоль оси про- ‚гр *
вода, как показано на рис. 7.12, для пре-
дельной прочности получаем уравнение к
рс1-с1х
оъ/2
В
21% = рдаа,
находим (М 7.67)
Р а, п/2 Рис. 7.12
1тах2 = С(Ь)
1:0
ПО ЗЗДЗННЫМ ЗНЗЧСНИЯМ НЗХОДИМ
0,0 5 - 105 .2. 104/2 - 3,14
3 - 109
Таким образом, вначале разрушается сверхпроводимость (Не 7.68).
На поверхности сверхпроводящей сферы, находящейся в одно-
родном магнитном поле, напряженность магнитного поля определя-
ется (6.19)
1„‚,„, =3.1 =4оо А.
Н, = ЁНО 51116,
где 6 — угол отклонения радиуса, направленного в данную точку, от
направления магнитного поля (НО = ВО). Давление на поверхность
сферы определяется (7. 12)
„2
_ 15
р 81:
и направлено к Центру сферы. Если сфера радиусом К разрезана
вдоль диаметральной плоскости, перпендикулярной к направлению
магнитного поля, то для отрыва одной полусферы от другой требует-
ся сила (Не 7.69)
11/2
г = 1 р12$1п92п12с16со$6 = ёвдкё
0
В сверхпроводящем соленоиде отсутствует сопротивление и ЭДС
равна нулю. Поэтому из (7.1) следует неизменность потока магнит-
ного поля Ф. Если в короткозамкнутый длинный сверхпроводящий
154073 225

соленоид с начальным внутренним полем, равным ВО в его центре,
и площадью сечения 5 вставляют длинный сверхпроводящий сердеч-
ник с площадью сечения о, то, пренебрегая краевыми эффектами,
получаем, что индукция магнитного поля станет
5
В=В0$_О.
В соответствии с (7.12) и (7.13) давление на внутреннюю повер-
хность соленоида и боковую поверхность сердечника будет равно
(Мг 7.71)
=Ё = [в„5(5 —о)]2
р 81: 81: '
НЗЧЗЛЬНОС ДЭВЛСНИС ПОЛЯ бЫЛО
85
рО 87: °
В Общем СЛуЧае при адиабаТическом СЖаТиИ МЗГНИТНОГО ПОЛЯ
получаем из предыдущего соотношение типа адиабаты для газов
(Мг 7.72)
171512 = 17253-
На рис. 7.13 изображен полый цилиндр (конечной длины с радиу-
сами цилиндрических поверхностей К, и К2) из сверхпроводника, вдоль
оси которого расположен длинныи проводъшк, по которому идет ток
1. Найдем токи, текущие по внутренней и наружной цилиндрической
поверхности сверхпроводящего образца, и давление на стенки ци-
линдра (М9 7.73). Важной особенностью данной задачи является осе-
вая симметрия. Благодаря этому, исполь-
зуя (5.6), находим поле у внутренней стен-
2 ки цилиндра, как и в (5.2) имеем
к:
и Ж Н - 2:-
: _ сК, 0
Е 1А 1: Ч 12 Токи, идущие по поверхности сверх-
...... „в
‚‚‚/%‘:____:—гж\ ..— проводника, должны не впустить магнит-
' Д щ? ”2 ное поле внутрь. Вводя плотность тока на
поверхности 11, из (5.6) получим
Н-1=4 д.
Рис.7.13 “с

Откуда
1
21:12, .
По всей внутренней поверхности идет ток 1. Сверхпроводник в
поле проводника будет вести себя подобно тороидальной катушке.
На внешней боковой поверхности цилиндра полный ток также 1 и
соответственно
‚Д:
1
2пК2,
а за внешней боковой поверхностью Цилиндра магнитное поле опи-
сывается (5.2). Поэтому давления на боковые стенки цилиндра на-
ходим с помощью (7.12)
12:
12 12
р! = 2пс2К% , р2 = 2пс2КЁ.
Давления направлены внутрь сверхпроводника, причем р2 < рд,
а силы одинаковые.
Используя формулу для магнитного поля прямого провода бес-
конечной длины (5.2) и закон Ампера (7.4)‚ находим силу взаимо-
действия между двумя прямыми параллельными проводами беско-
нечной длины, расположенными на расстоянии 1, много большем
диаметров проводов, по которым текут постоянные токи 1, и 12. На
единицу длины сила равна
г=21,%; {гцодд}. (7.14)
с 1 21:!
Из векторных уравнений (5.1) и (7.13) находим направление силы.
При одинаковом направлении токов —— притяжение, при противо-
положном — отталкивание. Обратим внимание на то, что парал-
лельно движущиеся свободные заряды отталкиваются. Полученным
направлением силы взаимодействия между элементами тока можно
объяснить силы в витках соленоида (отталкивание) и между витка-
ми (притяжение).
Для двух параллельных длинных проводов с противоположными
направлениями тока силой 1 из (7.14) для силы отталкивания на
единицу длины имеем
д:
с2г .
19 227
17

Работа, которую совершает магнитное поле, при увеличении
расстояния между проводами (11) в два раза (М 7.43) равна
2;: 2 2
А =[%с1г=21,1п2.
д С Г С
На такую величину увеличится магнитная энергия единицы длины
системы двух проводов.
Если два параллельных цилиндрических провода из сверхпро-
водника находятся в однородном постоянном магнитном поле с
индукцией В, направленной вдоль проводов, то на их боковые
поверхности действует давление, определяемое (7.12). Сила взаи-
модействия между проводами отсутствует при отсутствии в них
тока (Мес 7.36).
Рассмотрим два провода в виде прямых плоских шин шириной а,
расположенных параллельно на расстоянии 1 << а, по которым
идут токи 1 в противоположных направлениях. На единицу ши-
рины шины ток 1/а. Используя (5.6), получаем магнитное поле
для шины
1
Н = 2л—-.
са
От двух шин, в которых токи идут в противоположных направ-
лениях, поле будет в два раза больше. С помощью (5.28)
=1Ь1=2Н1=4"”.
С Са
ОТКУДЗ НЗХОДИМ ИНДУКТИВНОСТЬ СИСТЕМЫ на СДИНИЦУ ДЛИНЫ
_Ш
а.
Сила взаимодействия (отталкивания) между шинами на едини-
цу площади (давление) определяем с помощью (7.12) (Мг 7.54):
2п12
С202 .
ЕСЛИ на ШИНЗХ задана ПЛОТНОСТЬ тока 1, ТО ПОЛС МСИСДУ ШИНЗМИ
Н=Ш.
С
При ЗЗПОЛНСНИИ ПРОСТРЗНСТВЭ МСЖДУ ШИНЗМИ ПЛОСКИМИ СЛОЯМИ
МЗГНСТИКОВ С МЗГНИТНЫМИ ПРОНИЦЗСМОСТЯМИ Дд И М? С УЧЕТОМ НС-
228

нитном поле В (М 7.40). Предполагая, что в трубе реализуется тече-
ние Пуазейля, воспользуемся соответствующей формулой для силы
трения в трубе (см.: 1, с. 364):
Г = 32т1А вЂ”.
~~г '
Приравнивая это силе в насосе (7.16), где а = Л, получаем
1 = 32т1сА вЂ”.
~~3 '
Применим формулу (7.15) для цилиндрического проводника, по
которому течет ток плотностью ~, и, следовательно, магнитное поле
в нем определяется (5.7)
2к .
В= вЂ” р.
С
ИГ = 5'с(г и р = вЂ” = ~йг.
ИР
5
Используя (7.15) и (5.7), с учетом знака имеем
2Я
Нр = вЂ” вЂ” ~-Ыг.
2
(7.17)
Найдем давление внутри жидкого (отсутствует сдвиговая проч-
ность) цилиндрического проводника радиусом а, в котором равно-
мерно по сечению (плотность тока постоянна) течет ток 1(М 7.38).
Интегрируя (7.17), имеем
г г г г
2л .г 2л .га -г г г
р= вЂ” вЂ” ~' п6 = вЂ” / =Х 1 вЂ” вЂ”, пас.
сг сг 2
а
и
На оси проводника при г =0
~г
с ла
232
Это поле, как следует из (7.15), давит на ток в направлении к оси
цилиндра. Токи, текущие по проводнику, имеют одинаковое на-
правление и поэтому притягиваются друг к другу, создавая давление
внутри проводника.
Обозначая цилиндрическую боковую поверхность элемента объе-
ма 5', имеем соответственно

магнитной энергии неподвижного контура, когда самоиндукция ос-
тается постоянной, получаем
2 с 2 с 2 Е
(7.20)
Используя (7.12), для магнитной энергии внутри соленоида пло-
щадью 5' и длиной ( можем написать
2
Ю = -А вЂ” = В~Я вЂ” = Г1,
2 с Зп
(7.21)
где
В'Ю
8я
вЂ” сила, действующая между витками соленоида вдали от концов.
Из (7.21) можем найти выражение для индуктивности соленои-
да, которое, конечно, совпадает с (5.29). Это так называемый энер-
еетнчесянй метод няяождення нддуятняностя. Воспользуемся нм, чтобы
найти индуктивность единицы длины коаксиального кабеля, состо-
ящего из толстого внутреннего провода радиусом а и тонкой внеш-
ней оболочки радиусом Ь (М 7.55). Исходим из (7.12) и (7.20). Объем
на единицу длины равен НГ= 2пгдг, где г вЂ” расстояние от оси внут-
реннего провода. Поле внутри провода определяется (5.7)
2Хг
1
са
Поле вне провода определяется (5.2)
21
сГ
В результате получаем
=-,'Ь вЂ” ' = ((И,злу +~Изду),
и
откуда
А = вЂ” +21п вЂ” .
1 О
2 а
Круговую петлю из сверхпроводннка индуктивностью Е, по кото-
рой течет ток, помещают внутрь длинного сверхпроводящего корот-
234

козамкнутого соленоида индуктивностью Ьс, с числом витков А’,
в котором тока вначале нет. Найдем, во сколько раз изменится при
этом ток в петле, если диаметры петли и соленоида одинаковы
(Мг 7.29). Обозначая начальный ток в петле 1„* и учитывая, что в
сверхпроводнике из-за отсутствия сопротивления нет ЭДС и, как
следует из (7.1), сохраняется поток (5.28)‚ для петли получаем
Ын = 1‚1К + М/с,
где М — взаимная индукция петли и соленоида; 1С — ток в соленоиде.
В сверхпроводящем соленоиде поток также сохраняется
Ьс 1С + М/к = О.
Учитывая, что поток через петлю от соленоида ВЗ = М/с,
а зацепленный поток (5.31) в соленоиде МВЗ = 1,0 с, находим
М = Ьс /1\’. Используя предыдущие уравнения, получаем
1„ Ь Ь
1„ Ь - М2/Ьс Ь - Ьс/А/2
Найдем, какую работу надо совершить для того, чтобы круговую
петлю из сверхпроводника поместить внутрь длинного сверхпрово-
дящего соленоида, замкнутого накоротко. Диаметры петли и соле-
ноида считаем равными, а их оси — параллельными. В отсутствие
круговой петли ток в соленоиде равен нулю, начальный ток в пет-
ле 1„. Индуктивность петли Ь, соленоида — Ьс, число витков соле-
ноида А’ (Мг 7.75). Используя (7.2О), для начальной энергии систе-
мы получаем
12
‘у! = д й
для конечной соответственно
1,3 13
1472 = ЬТ+ ЬСТ+М1К1С.
Работа, которую надо совершить, чтобы поместить петлю в со-
леноид, равна А = АИ/= Щ — И/д. Используя полученные в преды-
дущей задаче соотношения, находим
Ь Ад
2 Ь - Ь, /м
Формулами (7.19) и (7.2О) можно воспользоваться для вычисле-
ния работы, необходимой, чтобы кольцо из сверхпроводника надеть
235

Учитывая, что в случае магнитного поля давление является на-
тяжением (витки притягиваются друг к другу), а на внешнем конце
стержня нет сил, получаем силу втягивания стержня в соленоид
(7.22)
Если известна сила втягивания стержня в соленоид, в котором
течет ток (, можно найти коэффициент самоиндукции А соленоида
(без сердечника) при известной длине ((М 7.59). Используя (7.21) и
(7.22), находим
А = 2Г(с'
(р -1)('
В случае длинного соленоида (п витков), намотанного на тонко-
стенный капилляр, погруженный одним концом в парамагнитную
жидкость с плотностью р и магнитной проницаемостью и, найдем,
насколько изменится уровень жидкости в капилляре, если по соле-
ноиду пропустить ток ((М 7.60). Обозначая изменение уровня (вы-
соту подъема жидкости) А из (7.22), (5.23) и (6.8), получаем
(, = 2лУ'л' "
вЂ” 1
с ррах
Если в соленоид, по которому течет ток, вставлен тонкий стер-
жень из магнитного материала, то для вычисления сил, действую-
щих на стержень, надо пользоваться условием сохранения касатель-
ной составляющей напряженности магнитного поля на боковой
поверхности стержня: Н = Н, = Н. В таком случае для стержня
площадью сечения 5 получаем из (7.12) силу втягивания стержня
По заданному току в соленоиде (Х) и плотности намотки п (вит-
ков/см) с помощью (5.23) находим
Н =4пп вЂ”.
1
С
По заданной кривой намагничивания стержня
м = м„„[1 вЂ” ехр( вЂ” )]
238

и (6.6) получаем (Не 7.77)
ё
Г = ЕЗНМЮС [1 — ехр Pɢ
Если длинный сверхпроводящий цилиндр (из сверхпроводника
1-го рода) внесен в постоянное однородное магнитное поле с индук-
цией В, направленное параллельно оси цилиндра, то поле в сверх-
проводник не проникает, а создает давление на его поверхность,
определяемое (7.12). Предполагая, что для окружающей сверхпро-
водник среды Н = В, получаем давление (Не 7.82)
81: °
Для определения сил в магнитном поле существует энергетичес-
кий метод. Рассмотрим его на примере системы, состоящей из двух
контуров с токами 1, и 12. В соответствии с (7.20) магнитная энергия
такой системы может быть представлена в виде
_ 1 11Ф1 + 12Ф2
2 с ’
где Ф и Ф — полные магнитные потоки, п онизывающие кон ы
1 2
1 и 2 соответственно (индукции контуров Ь, и 1,2, взаимная индук-
ция Ьп = Ьд):
и/ (723)
в 1 1
ф] =ЬЁД`#Ё; ф, =ЁЕЁЦД (714)
Работа бА, которую совершают ЭДС, включенные в контуры, идет
на теплоту 8С, приращение магнитной энергии системы дИ/ (из-за
движения контуров или изменения токов в них) и механическую ра-
боту бАмех (вследствие перемещения или деформации контуров):
бА = за + дни вАш. (725)
Предполагая, что емкость и сопротивления контуров пренебре-
жимо малы, электрическую энергию учитывать не будем. Принима-
ем во внимание только работу ЗА“, которая совершается против ЭДС
индукции и самоиндукции:
5А„ = «ат + веда: - (д, + вед/дн.
Учитывая (7.1), т. е.
‚ с1Ф
*д=‘7г›
239

получаем
бАи = [ДФ] + 12аУФ2. (7.26)
Эта работа идет на приращение магнитной энергии и механи-
ческую работу
[да/Ф, + 12с1Ф2 = дИ/+ бАмех. (7.27)
Из этой формулы получаем в случае постоянных потоков
бАмех = —а!И/Ф. (7.28)
Если токи постоянны, то, используя (7.23) и (7.27), находим
бАмех = ащ. (7.29)
На рис. 7.22 изображен электромагнит, в сердечнике которого
имеется малый зазор 1, в который помещена пластинка из того же
материала, что и материал сердечника. Найдем, какую работу нуж-
но совершить против магнитных сил, чтобы удалить пластинку из
зазора. Длина сердечника равна Ь, сечение всюду одинаково и рав-
но 3, магнитная проницаемость р >> 1. Обмотка электромагнита имеет
А’ витков, по которым течет ток 1. Рассеянием магнитного потока
пренебрегаем (Мг 7.61). При наличии в зазоре пластинки из (5.6)
находим
1/с =
Цн+Пи
Из (7.|2) и (6.8) получаем
В, = 4п1\’
4тс1\’% и =ос д
Ь+1_ 2 5
_ 2
щ _В'$ 81ш _ад8п(1‚+1)°
При отсутствии пластинки
И
[‚+ц1<в1;
251,
2
—- - ос ——-—— < И’ .
- 28п ”8мЬ+„ц 1
В случае постоянного тока надо воспользоваться (7.29), учиты-
вая, что внешняя работа
11, 1-1 Ь 1
бАЪнеш=_бАмех=_ащ=_(щ_щ)=а2д5 j. + 0/ +|›‘)_
240

магнитной проницаемостью р? отличной от магнитной проницаемос-
ти верхней подковы п, (д, 1: цд) (Мг 7.63). Из (5.6) и (6.8) имеем
ВпК($-+-Ь)+ В2х = 41:11, *
д: #12 с
где х — величина возможного зазора между подковами.
Отсюда
1 А’
В _ 4“: пКП/ц, + 1/112) + 2х °
Из (7.12) и (6.8)
_2 ш а з- (ц 5
РУ-В [пК(ц1+и2)+2х:|8л-2п 1 с пк(1/ц1+1/р2)+2х.
Используя (7.3О)‚ получаем
(НУ/с? о
[пКО/ц, + 1/д2) + 2х]2
При х = О находим
(гм/ей _
[ЛЕН/пл + 1/Н2П2
Отношение сил: Р, при д, = р? Р, при р] 7* д,
Ё 4
‘Ё _(1+Н1/д2)2.
Аналогичным образом можно рассмотреть дру-
гие конфигурации электромагнитов (Не 7.64).
С помощью чувствительных весов измеряется
сила Р‚(х), втягивающая парамагнитный образец в
сверхпроводяшую короткозамкнутую катушку в за-
висимости от его положения (х) (рис. 7.26). Извест-
но, что при х = О индуктивность катушки равна 1,0,
а по ее виткам течет некоторый ток 1,. Найдем, ка-
кую зависимость 13(х) следует ожидать, если катушку
перевести в нормальное состояние и по ее виткам
пропускать ток 12 от внешнего источника (Не 7.78). Рис. 7.26
243
=%':Н
„Ы! Ь
3 х
тдттйдтд
ЬООООМ
16‘

Такое же выражение получим, если, считая магнитный момент
малой катушки
1
рм _М`;5›
будем вычислять энергию, по аналогии с (2.32)‚ как скалярное про-
изведение
И/= —рмВ. (7.31)
Обозначая момент сил М и используя (7.29), имеем
бА = Ра/х = Ма/Э = дИ/Г
Откуда находим
2
М = —4пп1\/5 @̯ зйп 6.
Малая катушка стремится развернуться, чтобы ее магнитный
момент (ее поле) был направлен по полю катушки-соленоида.
Найдем, на какой высоте 11 постоянный магнитик с магнитным
моментом р и массой т, который можно считать магнитным дипо-
лем, будет парить в горизонтальном положении над плоской гори-
зонтальной поверхностью сверхпроводника 1-го рода (Мч 7.83). Ус-
ловие на границе сверхпроводника — отсутствие проникновения в
него магнитного поля, можно обеспечить с помощью метода зер-
кальных изображений. Если симметрично относительно его грани-
цы расположить такой же диполь как заданный, то на границе маг-
нитное поле будет иметь только компоненту касательную к поверх-
ности. Расстояние между диполями найдем из равенства силы
отталкивания между диполями весу магнитика. Силу отталкивания
определяем из магнитной энергии взаимодействия диполей. Один
диполь создает поле, определяемое (7.11), а второй, находясь в
этом поле, в соответствии с (7.31) обладает энергией И’= —рВ.
Поэтому, используя (7.11), получаем
_ш : д(рВ) _ рд[3г(рг)/г5 — р/гз ]
дг дг — дг °
Так как Г В данном случае перпендикулярно р, ТО находим
17:
р = ` = Ñ: ¥Ï 21 2 Ñ,
Ð´â Ð³4 16/14 .
ÐÑÑÑÐ´Ð° Ð½Ð°Ñ Ð¾Ð´Ð¸Ð¼ 11. ÐÑÐ¼ÐµÑÐ¸Ð¼, ÑÑÐ¾ ÑÐ°ÐºÐ¾Ðµ Ð¶Ðµ Ð²ÑÑÐ°Ð¶ÐµÐ½Ð¸Ðµ Ð´Ð»Ñ ÑÐ¸Ð»Ñ Ð¿Ð¾-
Ð»ÑÑÐµÐ½Ð¾ Ð² (1.10) Ð¸ (6.23).
245

Шарик из сверхпроводника можно подвесить на магнитной по-
душке. Оценим его максимальный размер (К), если известны плот-
ность р, критическое магнитное поле (В) и такое изменение поля с
расстоянием, что на тыльной стороне шарика давлением магнитно-
го поля можно пренебречь. Используя (7.12), можем написать урав-
нение равновесия сил
пК2В2
81:
Отсюда находим максимальный радиус (Мг 7.74):
_ 4 з
-р3пК3.
_ 332
_ 321гр3'
Если магнитный компас, стрелка которого может вращаться в
горизонтальной плоскости, находится рядом с вертикальной сверх-
проводящей плоскостью, то, предполагая, что внешнее магнитное
поле отсутствует, действующие на стрелку силы можно найти, ис-
пользуя метод зеркальных изображений. Условие, которому должно
удовлетворять зеркальное изображение, заключается в отсутствии
нормальной к поверхности сверхпроводника компоненты магнит-
ного поля, т. е. симметричному относительно поверхности положе-
нию стрелки и ее зеркального изображения. Угол стрелки относи-
тельно поверхности при устойчивом равновесии определяется ми-
нимальной энергией взаимодействия стрелки и ее изображения.
Для нахождения энергии стрелку и ее изображение считаем точеч-
ными диполями (рис. 7.27). Из (7.31) и (7.11) для энергии взаимо-
действия имеем
И/ = _р[3 (рг)% _ `*S = _3р2г2 Сова со5(1:5— ос) + р2 со3(т:3— 20:) =
Г Г Г Г
_ 2 1 + сов2 а
‚з
Видно, что минимальная энергия при ос = п/2, т. е. устойчивое
равновесие стрелки, когда она параллельна сверхпроводящей плос-
кости (М9 7.85).
В ферромагнитном шаре пропилена узкая глубокая щель. Шар
намагничен до насыщения перпендикулярно плоскости щели, и за-
тем внешнее поле выключено. Кривая размагничивания материала
шара М (Н ) представляет собой четверть окружности (рис. 7.28). Из
щели выдергивается и удаляется на значительное расстояние плос-
246

м
О.
‘М
Мо
а“ М’
/ тг-оъ >
Но Н, Н
Рис. 7.27 Рис. 7.28
кая рамка площадью 5 с числом витков П. Рамка подключена к
гапьванометру. Найдем количество электричества О, протекшего
через гальванометр. Полное сопротивление цепи К. Заданы также
Но, Мо и размагничивающий фактор шара В = 4тв/3 (Не 7.23). Из
(7.1) получаем для цепи гальванометра
. (10 1 ЩФА’)
ё = К —— = — — .
а’! с (1!
Поток вектора магнитной индукции Ф меняется от начального,
определяемого начальной магнитной индукцией в щели В], до нуля
при значительном удалении рамки от шара. Поэтому
9 = 13,5%. (732)
Используя (6.15) для размагничивающего фактора и зависимость,
изображенную на рис. 7.28, получаем для поля внутри магнетика
4 4 2 в
Откуда определяем М]. В отсутствие внешнего поля для начальной
магнитной индукции в щели имеем
81: 81: М
3 3 (41т/3) +1
Эту величину подставляем в (7.32).
Для исключения потерь энергии на джоулеву теплоту в линиях
передачи постоянного тока предложено использовать коаксиальный
247

кабель, проводящие поверхности которого для внутренней жилы
(диаметр с!) и наружной оболочки (диаметр В) выполнены из сверх-
проводника. Максимально допустимая индукция магнитного поля
на поверхности сверхпроводника В, максимально допустимая на-
пряженность электрического поля в изолирующей прослойке ка-
беля Е“. Найдем, при каком соотношении диаметров х = В/с! мож-
но передать наибольшую мощность А’ и величину этой мощности
(М 7.52). Из (4.18) мощность тока А! = ПС где 1- сила тока, идуще-
го в разные стороны по оболочке и жиле и создающего магнитное
поле вокруг жилы, определяемое (5.2) и имеющее максимальное зна-
чение на ее поверхности
1.
В-Н—4Й‚
У — разность потенциалов между жилой и оболочкой, на которых
благодаря сверхпроводимости потенциал не меняется. Для однород-
ной изолирующей прослойки из (3.7) и (3.8) находим (для цилинд-
рического случая) Е 2пг = сопвт = А. Из (2.6) с1У= —Ес1г. Поэтому
А 0 У
У = —1п—° Е = ——.
21: с! ’ г1пх
Максимальное значение напряженности электрического поля на жиле
У У
Е„ = 2 _._ = д;
' а! 1п х 1) 1п х
Для мощности получаем
м = п/ = %свЕв2%1пх.
Х
Приравнивая производную мощности по х нулю, находим, что
максимальная мощность будет при х = е” и равно
_ свЕЫ
м - “п?
В длинном идеально проводящем соленоиде при изменении ин-
дуктивности сохраняется поток магнитного поля, и поэтому из (5.31)
следует [Ь = 10Ь0. Используя выражение (513) для соленоида, в слу-
чае изменения его длины 1= 10 + асов сшдля тока получаем (М 7.33)
А’
1=1 1=1 1+3со$ш1.
0,0 о [О

8. ДВИЙКЕНИЕ ЗАРШКЕННЫХ ЧАСТИЦ
В ЭЛЕКТРИЧЕСКОМ И МАГ НИТНОМ ПОЛЯХ.
ЭДС ХОЛЛА. ДВШКЕНИЕ ПРИ НАЛИЧИИ
ПОНДЕРОМОТОРНЫХ СИЛ
При рассмотрении движения заряженных частиц в дополнение
к силам, которые были введены в механике, надо учитывать дей-
ствие электрических и магнитных полей.
Сила взаимодействия между заряженными частицами определя-
ется законом Кулона (1.1), а потенциальная энергия — соответству-
ющей работой в электрическом поле (2.1). Напряженность поля
вокруг точечной заряженной частицы описывается (1.3), а потенци-
ал — работа, которую надо совершить, чтобы единичный заряд из
бесконечности перевести на расстояние г (2.4). Потенциал от элект-
рона, который считаем точечной частицей с зарядом е, на расстоя-
нии а от него равен е/а. Если в эту точку переместить из бесконеч-
ности второй электрон, то потенциальная энергия системы будет
равна е2/г. Потенциал в точке, находящейся на расстоянии а от каж-
дого из этих электронов, будет равен 2е/а. Чтобы в эту точку переме-
стить из бесконечности еще один электрон, нужно совершить работу
2е2/а. Таким образом, система из трех электронов, находящихся в
состоянии покоя в вершинах правильного треугольника со стороной а,
обладает потенциальной энергией 3е2/а. Если этим электронам пре-
доставить возможность свободно разлетаться под действием сил от-
талкивания, то вся их потенциальная энергия перейдет в кинетичес-
кую. Предполагая симметрию движения, получаем для определения
предельной скорости разлета (и) электронов массой т уравнение
2 2
е 1)
3:1- — 31717.
Отсюда находим скорость (Не 8.1). Здесь использовано нереля-
тивистское приближение.
В релятивистском случае (больших энергий и скоростей) кине-
тическая энергия имеет вид
Т: тсЧУ — 1),
249

где
_ 1 а _ у .
у_(1—В2)1/2› В-сэ
с — скорость света (см.: 1, с. 179.). Поэтому имеем
2
1: 2 _
а тс (у 1).
Откуда
е2 и 1 1/ 2 (1 + 2тс2 а/е2 )1/2
У=Нтс2а3 ;=(1"'3) = 1 2 /2
у +тс а е
Нерелятивистским приближением (М: 8.2) можно пользоваться,
если выполняется условие
82 2
— << тс .
а
Поэтому должно быть
92 -1з
а>>-—=г =2,8-1О см
2 КЛ
тс
(классический радиус электрона).
В плоском конденсаторе с напряженностью электрического поля Е
отрицательно заряженный электрон ускоряется при движении к
положительной пластине. Однако на вырвавшийся из отрицатель-
ной пластины благодаря термоэмиссии электрон кроме поля кон-
денсатора действует еще притяжение положительного заряда элект-
рического изображения. Обозначая расстояние электрона от отрица-
тельной пластины через х и используя закон Кулона (1.1)‚ получаем
уравнение движения электрона
Скорость вырвавшегося электрона будет вначале уменьшать-
ся, а затем увеличиваться. Минимальная скорость определяется
условием
до
т-О.
250

тронов. Предполагая, что поперечный размер пучков много меньше
расстояния между ними (а), и обозначая площадь сечения пучков о
и скорость электронов и, из (1.12), (5.6) и закона Ампера (7 .4) полу-
чаем (Не 8.9)
2
е е
Е2па = 4попе; Е = 2оп—; РК = 2о2п2 —;
а а
В=Н=2опе1; Г„=2о2п2е2%; &=(Ё)2.
са ' са Г С
К
Найдем частоту поперечных колебаний протонов, захваченных
релятивистским электронным пучком, имеющим сечение 1:12 2 и силу
тока 1 (Не 8.6). Обозначая плотность электронов в пучке п, для силы
тока в пучке получаем 1 = етлъК2 = епспК2, с учетом того, что 1) = с.
Используя теорему Гаусса (1.12), получаем электрическое поле в
электронном пучке
Е = 2еттг = 21%.
сК
На протон действует сила притяжения еЕ. Уравнение колебаний
протона (массой т)
с12г 21ег
т + т = О.
(1! сК
Отсюда частота колебаний
2 _ 21е ш
_ тсК2 и у 275
Две щели 5, и 52, которые будем считать бесконечно длинными,
шириной 1 каждая (рис. 8.3), установленные в эвакуированном со-
суде, выделяют плоский пучок электронов с энергией Ж Найдем,
на каком расстоянии х от щели $2 ширина электронного пучка удво-
ится из-за кулоновского расталкивания электронов, если электрон-
ный ток, приходящийся на единицу длины щели (за щелью 52), ра-
вен 1 (М9 8.5). Для скорости электронов (массы т) имеем
2и/ "2
и=‹-› -
т
Ё| 5! 52|__‚« Ток 1 = пеи1. Используя (1.12), получаем
:| I поле на границе пучка 2Е = 41гп1е. Откуда
д = Ш
Рис. 8.3 и °
254

Г = дЕ+ вЂ” д[тВ]; (Г = дЕ+ д [ГМВЦ,
(8.1)
где с вЂ” скорость света в вакууме.
При п «с для частицы с массой т получаем уравнение дви-
жения
т вЂ” =дЕ+ вЂ” д[тВ]; т вЂ” =дЕ+д[тВ] .
дч 1 Ыч
й с ' й
(8.2)
В дальнейшем будет показано, что движение с нерелятивистски-
ми скоростями может происходить при выполнении условия Е «В.
Так как в нерелятивистском приближении сила одинакова в
инерциальных системах координат, а второй член в (8.1) меняется
при изменении скорости, то разделение силы на электрическую и
магнитную зависит от выбора системы отсчета. Рассмотрим две си-
стемы отсчета: неподвижную 5' и движущуюся относительно нее со
скоростью и подвижную систему 5". Скорость частицы (и) в систе-
ме 5'связана со скоростью (п') в системе 5" преобразованием Гали-
лея о = и' + и. Из равенства сил имеем
Г = дЕ+ вЂ” д[тВ] = дЕ+ вЂ” д[т'В]+ вЂ” д[иВ = Р' = дЕ'+ вЂ” д[т'В].
1 1, 1,, 1
Отсюда следует
Е' = Е+ вЂ” [иВ].
(8.3)
Для получения закона преобразования магнитной индукции надо
привлекать теорию относительности. Приведем результат
В'= В вЂ” вЂ” [иЕ .
1
С
(8.4)
256
мал по сравнению с током накала, что обычно и бывает в лампах,
и учитывая, что нить имеет в разных точках различный потенци-
ал, получаем, что вылетающие из разных частей нити электроны
при движении до анода набирают различные скорости в соответ-
ствии с той разностью потенциалов, на которой они разгоняются
(от 56 до 60) (Мо 8.8). Такое распределение скоростей будет иметь
место, если анодный ток мал по сравнению с током накала, что
обычно и бывает.
Движение частицы, имеющей заряд д и скорость т, в электри-
ческом поле с напряженностью Е и магнитном поле с индукцией В
определяется, как следует из опыта, силой Лоренца

Соотношения (8.3) и (8.4) позволяют получить условия для вы-
бора систем, в которых существует либо только магнитное поле,
либо только электрическое.
В постоянном магнитном поле сила перпендикулярна скорости
и поэтому работы не совершает.
Если скорость перпендикулярна В, то движение происходит по
окружности. Вводя угловую скорость вращения ш и радиус окруж-
ности К, получаем с помощью (8.2) и уравнения движения по ок-
ружности (см. 1, с. 14; 45) для угловой скорости вращения, которую
называют циклотронной частотой
В
ш = 1. (8.5)
тс
ЗЗМВТИМ, ЧТО эта частота не зависит ОТ радиуса орбиты, КОТОРЫЙ
называется циклотронным, или ларморовским, радиусом
к = Ш. (8.6)
аВ
На рис. 8.5 показана траектория электрона, который влетает в
постоянное однородное магнитное поле В со скоростью у под углом ос
к направлению поля. Найдем расстояние АС, которое электрон про-
ходит за один оборот (Не 8.12). Обозначим компоненты скорости,
перпендикулярной и параллельной магнитному полю соответствен-
но и, = изйп ос и 222 = исоз ос. Тогда в соответствии с (8.2) для движе-
ния по окружности получаем
тП] 1
Т = 281218
Откуда
еКВ
1 тс
и период обращения
Т = 21:12 = 2птс. :
р] ЗВ
Поэтому
Ас = „27 = ЁЕШЗЁЁД
еВ
Найдем величину магнитного поля, необ- 7
ходимого для того, чтобы в ускорителе ультра- Рис. 8.5
17-2073 257

Дифференцируя первое уравнение по времени и подставляя вто-
рое, получаем
и: + ш2 (их - и) = О,
где
(о = Е.
тс
Общее решение их — и = А вйп о)! + Всоз (о! при начальных условиях
(1 = О) их = О, и: = О, а из первого дифференциального уравнения и
и; = О дает
их = 12(1 — сов (01); и, = —и51пш1.
Учитывая, что в начальный момент х = 2 = О, получаем
1 . _ и
х=221——$1пшг , 2=—(со5ш1-1).
О) О.)
Из полученных ранее соотношений видно, что максимальное
удаление от начальной точки по оси 2 по абсолютной величине
равно 2и/со, максимальная скорость их так = 212, а среднее значение
(Мг 8.87)
<и)=1?и а71=12
х ТО х '
Для моделирования траектории атомной частицы с зарядом е и
импульсом р, движущейся в магнитном поле, часто пользуются тем
обстоятельством, что очень легкий (невесомый) гибкий проводник е
током 1, находящийся под постоянным механическим натяжением 7,
занимает в том же магнитном поле положение, совпадающее с траек-
торией частицы. Найдем связь между е, р, 1 и Т, когда частица дви-
жется перпендикулярно магнитному полю, предполагая, что вне него
участки проводника прямолинейны и расположены вдоль соответ-
ствующих прямолинейных же участков траектории (Мг 8.14). Из (8.6)
для радиуса кривизны траектории частицы в магнитном поле полу-
чаем
к = 91.
еВ
На проводник с током действует сила Ампера (7.4). Сила на еди-
ницу длины '
17‘ 259

Используя рис. 7.24, находим для силы натяже-
ния (на рисунке она обозначена [) Т = РК], где
К — радиус кривизны провода. Для совпадения его с
радиусом кривизны траектории частицы должно быть
1р = еГ Если задана энергия частицы, то пользуемся
связью (Не 8.15)
р2
И/ - ж.
На рис. 8.7 показана схема масс-селектора, т. е. прибора, пред-
назначенного для разделения атомных частиц разных масс, состо-
ящего из цилиндрического конденсатора с внутренним радиусом
г, = 2,4 см и внешним г2 = 3 см. Ионные лучи (частицы) попадают
в селектор через узкую щель 5, расположенную посередине между
обкладками. Параллельно оси конденсатора (т. е. перпендикулярно
к плоскости чертежа) приложено однородное магнитное поле с ин-
дукцией В = 2000 Гс. Найдем, какую по величине и знаку раз-
ность потенциалов надо приложить к пластинам конденсатора,
чтобы однократно заряженный положительный ион 71.1, имею-
щий энергию И/= 1000 эВ, прошел по средней линии конденса-
тора, т. е. по окружности радиусом г = 2,7 см, а также напряжен-
ность электрического поля на этой окружности (М9 8.16). Масса иона
равна примерно семи массам нуклонов (протонов или нейтронов)
т = 7 - 1,67 - 10-24 г. Чтобы ион двигался по окружности радиусом г,
на него должна действовать сила
2
„П!
Р:
Г
(см. 1, с. 14; 45). Используя связь заданной энергии со скоростью
01112
2 9
находим скорость и = 1,65 - 107 см/с. Необходимая сила равна
Р = 11,7 - 10"” дн. Поэтому из (8.1) для магнитной силы получаем
Р = 5,12 - 10"° дн. Необходимо добавить еще электрическое поле
И
ЦИЛ И ндрическо ГО КОНДСНСЗТОРЗ
И/=
Е=——Р;’7“ =412 В/см.
Обозначив заряд на внутренней цилиндрической обкладке а, из
(1.12) находим Е = 2с1/г. Для обеспечения движения положительных
260

Интегрируя, находим
м=мт%
Отсюда != 2,5 г.
Сепаратор частиц может быть устроен так,
как показано на рис. 8.9. На вход цилиндри-
ческого конденсатора с радиусами г, и г, попа-
Рис. 8.9 дают ионы разных масс и, двигаясь по окруж-
ности, попадают затем в магнитное поле В.
Найдем отношение т/с; массы иона к его заряду, если он прошел
сепаратор при напряжении Н, а радиус его траектории в магнитном
поле равен гт (М 8. 18). Из (1.|6) напряженность электрического поля
в цилиндрическом конденсаторе с зарядом на единицу длины х рав-
на Е = 2х/г. Из (2.6) для разности потенциалов получаем
с/=2хт(Ё).
Й
Уравнение ДВИЖЕНИЯ ЧЗСТИЦЫ ПО окружности В КОНДСНСЗТОРС
а В МЗГНИТНОМ ПОЛЕ
По
то _Ч1)В
г, с’
ИСПОЛЬЗУЯ ВСС ПРИВСДСННЫС СООТНОШСНИЯ, ПОЛУЧЭСМ
В ускорителях заряженных частиц индукция В магнитного поля,
направленная вдоль оси симметрии, изменяется вблизи равновес-
ной орбиты по закону
а
В = т,
Г
где г —— радиус круговой орбиты; п — характерный показатель; а —
постоянная ВВЛИЧИНЗ. Найдем, при КЗКОМ СГО ЗНЗЧСНИИ обеспечива-
ется не только круговое движение на равновесной орбите, но и ра-
262

диальная устойчивость ее (Мг 8.23). Используя (8.1) и (8.6) для ско-
рости, магнитного поля и силы на равновесной орбите, получаем
2 2
_ЧВО’О. В_а. Г_Ч”ОВО_' Ча
”0‘_—" О"? 0" ‘ (2 -1)‘
Если с той же скоростью частица переходит на орбиту радиу-
сом г], то
П
1 "` _ | '
7] с стгё” И”
Таким образом, для равновесия на новой орбите
2 2
р = 4:.
1 (2п—1) ’
стц
а при СХОДС С нее
2 2
р =_Ш__
01 („_1) „ °
стго г]
Для устойчивости орбиты при увеличении радиуса эта величина
должна быть больше равновесной
_; > _;_
‚дн-Н п(п-1)
Чтобы это выполнялось, должно быть п — 1 < О, т. е. п < 1. Для
устойчивости орбиты при уменьшении радиуса Е” < Г, и получаем
то же самое соотношение.
Один из ранних методов определе-
ния отношения заряда к массе е/т для
электрона состоял в следующем. Элек-
троны, вырванные из алюминиевого
диска А, ускорялись разностью по-
тенциалов П, приложенной между А и
щелью 5 (рис. 8.10). Пройдя через
щель 5’, электронный пучок попадал в
однородное магнитное поле, перпен-
дикулярное к плоскости рисунка. Вся
система помещалась в вакуум. Изме-
няя величину магнитного поля, доби- Рис. 8.10
263

вались того, чтобы ток на коллекторе С, регистрируемый гальвано-
метром Г, был максимален. Измерив магнитное поле В в этот мо-
мент, можно вычислить е/т. Найдем е/т, зная длину хорды 5С = 1
и ее угол с начальным направлением скорости ос (Мг 8.19). Из сохра-
нения энергии имеем
и = 1.
е т 2
Из (8.6)
_ еВ°
г - те:
Из треугольника ОЗС
_ 1
_ 251па°
В результате находим
. 2
е э $111 (1
Я 8с Вт
В ускорителе прямого действия протон движется в практически
однородном электрическом поле внутри вакуумной трубки (ускоря-
ется от пренебрежимо малой энергии до энергии И/= 4 МэВ). Оце-
ним допустимое однородное внешнее магнитное поле в зоне такого
ускорителя, чтобы на длине трубки 1 = 2 м отклонение протонов от
осевой линии было меньше Ь = 1 см (Мг 8.20). При такой энергии
можно пользоваться нерелятивистскими соотношениями. При ма-
лых углах отклонения можно считать, что сила Лоренца и вызывае-
мая ею скорость иу перпендикулярны к горизонтальной составляю-
шей скорости их, приобретаемой за счет электрического поля. Для
продольного движения имеем
(112
Х
а: =4Е
т
Интегрируя это уравнение, находим
264

ей относительно 22. Удобно воспользоваться цилиндрическими ко-
ординатами (р, ш, 2 на рис. 2.1). В использованных ранее обозна-
чениях г в р. Из симметрии и (5.6) следует, что производные по ш
и В“, = НЧ, равны нулю. Поэтому из (5.12)
дан дн дн дн 1дрН дан
‘Н: _ г_ ч! р_ 1 _ ч!__ о =
Ю (о дш дг )е°+( дг до е” о др р дш е‘
=(днр_днг)е =О_
д: др ч’
Отсюда в использованных ранее обозначениях получаем
два, _ дв,
дг — д: '
Из условия
дВг_ п В”
_г_ -— ы: — г
д’- ‚(п+|) г
Для изменения компоненты В, по малому изменению 2 можем
написать
В, = ——’1 Ваз.
"о
Таким образом, увеличение 2 (от нулевого значения на равновес-
ной орбите) приводит к появлению компоненты В‚, которая в соответ-
ствии с (8.1) дает силу, возвращающую (как показано на рис. 8.11) к
плоскости 1 = О:
е е 2
Д = $228, = —Ёш0пВд2 = «лапта,
ГДС
и еВ
(00 -— _" = _"‘
го тс
(последнее из (8.5)).
Уравнение колебаний по 1 (штрихами далее обозначены произ-
водные по времени)
та” + тог, т: = О.
266

Колебательный режим возможен при п < 2. Частота колебаний
Эры ш0(2 п) .
Длинный соленоид намотан так, что магнитное поле вдоль его
оси меняется по линейному закону
В = Во (1 + 1%),
где х — расстояние от центра соленоида вдоль его оси; Ь — пара-
метр поля. Диаметр соленоида с! << 1„ поле В не зависит от времени.
Отметим, что указанную зависимость В(х) нельзя реализовать в ок-
рестности х = О, что не существенно для решения задачи. Заряжен-
ная частица движется так, что ее траектория полностью находится
внутри соленоида (для простоты можно считать, что траектория
симметрична относительно оси соленоида). Опишем картину дви-
жения частицы и найдем период и амплитуду ее колебаний вдоль
оси соленоида, если известно, что в цент-
д ральном поперечном сечении соленоида
она движется под углом 6О° к его оси со
скоростью и (Не 8.24).
На рис. 8.12, а показано изменение маг-
нитного поля с изменением х. С увеличе-
нием х, как следует из (8.5) и (8.6), увели-
чивается частота вращения и уменьшается
= радиус. На рис. 8.12, б показаны компо-
ненты скоростей частицы и магнитного
и Вт поля. Предполагаем, что скорость смеще-
ё ния к оси и, очень мала. Очень важным
и_ “х является наличие у магнитного поля состав-
‘ ляющей, направленной к оси вращения
частицы В‚. Благодаря ей магнитное поле
образует «ловушку», в которой частица за-
стревает, т. е. останавливается и идет на-
зад (рис. 8.12, в). Используя (8.1)‚ получа-
—д а о
ь .--..-
Е”
д П
2 __ о ем, что компоненты векторных произве-
1202 дений дают: ихВх = О; и‚В‚ = О; ихВ‚_ — силу
в направлении 122, которая увеличивает эту
00„ скорость, игВх — силу в направлении 22„
г которая в основном обеспечивает враще-
Рис. 8.12 ние относительно оси, 1218, — силу против
268

скорости их, которая замедляет движение, а затем обеспечивает дви-
жение к центру соленоида, цВх — силу в направлении 122, которая
при движении в положительном направлении х увеличивает ско-
рость вращения, а при возвратном движении — уменьшает. Так как
сила Лоренца (8.1)‚ представляющая сумму указанных сил, всегда
направлена перпендикулярно скорости, то она работы не соверша-
ет. Поэтому кинетическая энергия частицы сохраняется. Пренебре-
гая скоростью и, по сравнению с и: и вводя начальные скорости иго и
ухо (рис. 8.12, г), получаем из закона сохранения энергии
Медленность изменения орбиты вращения частицы позволяет
воспользоваться адиабатическим инвариантом (см.: 1, с. 127). Ки-
нетическая энергия вращения
2
1)
К = тд
2 3
угловая скорость вращения определяется (8.5). Инвариантность от-
ношения К/ш дает
2 2
Её. _”г°
в во '
ПОДСТЗВЛЯЯ ЭТО В СООТНОШЕНИЕ ДЛЯ МЗГНИТНОГО ПОЛЯ И ИСПОЛЬЗУЯ
ЗЗКОН сохранения энергии, ИМССМ при их = О МЗКСИМЗЛЬНОС ОТКЛО-
НСНИС
2
= Ьё = деду во‘:
“со
хтах
Период колебаний в 4 раза больше времени прохождения этого
расстояния
хтах ах — хтах ах
7:4] -
0 ”х 0 (2230 — 12%‘) х/Ь
)1/2 °
Один из предложенных ‘путей получения высоких температур,
необходимых для осуществления термоядерных реакций, использу-
ет так называемую «магнитную термоизоляцию». Уход быстрых час-
тиц из зоны высокой температуры предотвращается магнитным по-
лем. Найдем силу тока 1 в столбе газового разряда радиусом В = 3 см,
269

необходимую для того, чтобы электроны, обладающие средней ско-
ростью хаотического движения, отвечающей температуре Т= 106 К,
не могли удаляться от поверхности столба на расстояние больше,
чем г = 2 - 10-3 см (Не 8.25). Наибольший шанс уйти от столба имеет
электрон, у которого скорость
З/сТ ‘д
-‹-›
т
направлена перпендикулярно границе столба. Магнитное поле вблизи
поверхности столба (5.2)
1
В-2ад.
На расстоянии г поле можно считать постоянным и воспользо-
ваться (8.2)
В результате
акт/ту”
2ег
При пропускании мощных импульсов тока по коаксиальному
токопроводу, находящемуся в вакууме, когда между проводниками
коаксиала имеются мегавольтные напряжения, поверхность провод-
ников покрыта плазменной «подушкой» и приобретает неограни-
ченную способность к эмиссии электронов. Найдем, каким должен
быть ток в коаксиале с радиусом внутреннего провода К, = 0,6 см и
внешнего провода К, = 1 см (рис. 8.13) при напряжении между ними
Н = 600 кВ, чтобы не было «вакуумного пробоя» (Мг 8.81). Из теоремы
о циркуляции (5.6) находим величину магнитного поля между про-
водниками
1=с2К =1‚4.1о5 А.
3:31.
С!’
Меньшее значение поля при г = 122. Разность потенциалов
между проводами разгоняет электроны, а магнитное поле застав-
ляет их вращаться по окружности. При больших энергиях элект-
ронов (см. 1, с. 179) получаем в данном случае
у: 1 = Е =тс2+еП=
(1 — „2/‘32 )1/2 тс2 тс2
2,
270

Рис. 8.13 Рис. 8.14
откуда и/с = 1. А циклотронный радиус из (8.6)
тс2
еВ °
Чтобы не было «вакуумного пробоя», расстояние между провод-
никами должно быть больше циклотронного радиуса К, — К] > г“.
Поэтому для тока находим
гц=2
1 > 1Шс2уи——&——.
2 е к2 ’ кл
Вместо коаксиапа можно использовать две плоские параллель-
ные пластины шириной 1 = 5 см с зазором между ними б = 0,5 см
(рис. 8.14), на которых падение напряжения Н = 1 МВ. Найдем, при
каком токе в такой линии проводники окажутся эффективно изо-
лированными друг от друга (Не 8.82). Оценивая, как и раньше, энер-
гии электронов, получаем у = 3; и/с = 1. Магнитное поле в соответ-
ствии с (5.6)
1
В = 4л—.
с!
В результате получаем, что для отсутствия пробоя должно быть
1 > тс2уи141гбе.
По классическим представлениям электрон, вращающийся в ато-
ме, обладает механическим моментом количества движения Ь = тю.
Считая, что ток, соответствующий движению электрона, 1 = —е/ Т,
где Т — период обращения электрона, Т = 2лг/и. В соответствии с
(5.5) магнитный момент этого движения (тока)
5 и
р-[Ё-“е/‘ЕЁ.
271

1 и постоянном магнитном (В = 3- 103 Гс)
полях (рис. 8.15). Найдем частоту, при ко-
е) К торой ионы М; будут достигать коллекто-
ра К (контакта между обкладками конден-
сатора). При этой частоте радиус спирали
Ч будет возрастать до тех пор, пока ион не
достигнет коллектора на радиусе К = 1 см.
Рис- 3-15 Если частоту немного изменить, то ион
будет некоторое время раскручиваться, а
потом начнет скручиваться обратно к источнику. Оценим, на сколь-
ко надо изменить частоту, чтобы ток на коллекторе прекратился
(Мг 8.28). Электрическое поле будет способствовать увеличению ра-
диуса орбиты, если оно будет согласовано с изменением направле-
ния при вращении, т. е. его частота будет совпадать с частотой вра-
щения (8.5)
Ё = 163 кГц.
\) =
О 2тстс
Для оценки изменения частоты, приводящей к нарушению син-
хронизма, оценим вначале шаг спирали. Обозначая период обраще-
ния Т, из второго закона Ньютона получаем
тАи = еЕё.
Для скорости и на орбите радиусом К имеем
и = 21:12
Т 9
поэтому
АК=ТАЁ=Т2ЁЕ= с21:—-Ё—.
21: 4л:т (еду
При уменьшении периода изменения электрического поля до
величины Т], меньшей периода обращения Т, обозначая
_ ‘Щ
21: ’
можем написать
2 т
АТ=Т—7] =ЪЁ(к-к‚)=(к-к‚)д.
274

Если Л вЂ” Я, < ЬЛ, то раскручивания не происходит и ток в цепи
коллектора прекращается. Для изменения частоты колебания элек-
трического поля имеем
1 ЬТ
Ьч=Л вЂ” = вЂ” вЂ”.
т= т
Нарушение синхронизма будет при
Ьч ЬЯ
вЂ” )вЂ”
чо Я
Поэтому получаем
Лч = =15 кГц.
Е
Рассмотрим систему, состоящую из вертикально стоящего соле-
ноида и гладкой горизонтальной поверхности внутри него вдали от
концов, на которой на расстояНии Л от оси соленоида находится
шарик массой т с зарядом д, который может скользить по поверх-
ности без трения. Найдем радиус круговой траектории, по которой
будет скользить шарик, если быстро, пока шарик еще не успевает
заметно сместиться, в соленоиде устанавливается постоянное одно-
родное магнитное поле В (М 8.29). Из (7.5), используя симметрию,
находим
1 ЯЫВ
2с й
Подставляя это во второй закон Ньютона еЕй =- тджх и интегрируя,
получаем скорость шарика к моменту установления магнитного поля
В
о=дЛ
2тс
Дальнейшее движение шарика будет происходить по окружнос-
ти и описываться уравнением
иВ
2
т вЂ” =д вЂ”.
Г С
Отсюда следует г = Л/2 и Т= 2лг/и Период оказывается очень боль-
шим для макроскопических частиц.
В ускорителе электронов бетатроне роль ускоряющего напряже-
ния играет ЭДС индукции (7.1), возбуждаемая изменением магнит-
ного потока, пронизывающего орбиту электронов. Электроны дви-
275
18*

жутся при этом по орбитам приблизительно постоянного радиуса.
Считая радиус орбиты электрона неизменным, определим необхо-
димое для этого в данный момент времени соотношение между сред-
ним магнитным полем (В(1)), пронизывающим орбиту электрона, и
магнитным полем на орбите электрона В0(1) (Не 8.30). Из (7.5)
_ _ 1 с/(В)
с а’!
Используя второй закон Ньютона
а: 2с а: ’
находим
то = „Ш,
2с
учитывая, что нет поля, нет и скорости. Движение электрона по
окружности определяется полем ВО на орбите
12 иВ
т— = е—.
Г С
Из этих соотношений
В _ (в)
2 .
Магнитное поле некоторой нейтронной звезды (массой М =
= 1,5 - 1030 кг, радиусом КО = 10 км) имеет дипольный характер, т. е.
к 3
ватта)»
где ВО Ы 10” Гс. Оценим, какие силы будут доминировать в динами-
ке релятивистского электрона (И/н 3 МэВ) на расстоянии от звезды
порядка радиуса земной орбиты (150 млн км) (Мг 8.31). Для задан-
ной энергии электрона, у которого энергия покоя тс2 = 0,511 МэВ,
имеем (см. 1, с. 179),
Так как
276

получаем скорость порядка скорости
света (с). Из (8.1) для силы Лоренца
имеем „ „
ц-{ь к‘ 4:
3 90
КО -19
Р = еВО -— - 10 дн,
К
а ИЗ ЗЗКОНЗ ВСЕМИРНОГО ТЯГОТСНИЯ, УЧИТЫ- У]
ВЗЯ СЛЯТИВИЗМЁ
р Рис. 8.16
Г - Сути —— 10"” дн.
кз
Таким образом, доминируют электромагнитные силы.
Длинная катушка, по виткам которой течет ток, движется со ско-
ростью и, направленной перпендикулярно ее оси. заряженная час-
тица, имеющая скорость у (с >> и > и), догоняет катушку и, пролетев
между ее витками, вылетает под углом 9О° к первоначальному на-
правлению со скоростью, которую обозначим у] (рис. 8.16). Найдем
относительное изменение энергии частицы (Не 8.32). В системе от-
счета, связанной с катушкой, получаем начальную скорость части-
цы у, = у — п, а конечную уз = у, — и. При этом в магнитном поле
сила Лоренца (7.2) перпендикулярна скорости, не меняет ее вели-
чины, т. е. 123 = 122. Поэтому и — и = (и, + и)“. Откуда
122 —2ии+и2 = и? +и2.
Относительное изменение энергии частицы
АИ/ __и%-и2
и/ „2
=_2З_
1)
Энергия уменьшается, часть ее передана катушке.
Другой способ решения основан на использовании формулы (8.3).
В системе отсчета, которая движется относительно магнитного поля
со скоростью (—ц), для электрического поля
Е; = Е + [-“в]‚
С
для магнитного из (8.4)
В’ = В - ЁЪЦЕ].
277

Частица в этой системе имеет начальную скорость у. Так как в сис-
теме неподвижного магнитного поля электрическое поле Е = О, то
из (8.3) и (8.4)
= [—иВ1
С
Е’ В’ = В.
Чтобы поворот положительно заряженной частицы в поле В был
вниз (см. рис. 8.16), оно должно быть направлено к нам относитель-
но плоскости рисунка. При этом электрическое поле перпендику-
лярно и и В и направлено вверх, т. е. тормозит движение. Работа
этой силы и приводит к уменьшению энергии. Лоренцева сила ра-
боты не совершает. Значит, изменение энергии
АИ/=—4Виё.
Используя уравнение движения
т 122 _ Ч иВ
г с ’
ПОЛУЧЗСМ, КЗК И РЗНСС,
АИ/ _ 2 и
т122/2 71
Один из механизмов ускорения заряженных частиц (протонов и
ядер) в космических лучах в Галактике обусловлен их отражением от
движущихся «магнитных облаков» —— потоков ионизированной плаз-
мы, несущей сильные «замороженные» магнитные поля. На рис. 8.17
показана граница намагниченной области АА’ (область, заполнен-
ная магнитным полем, заштрихована), которая движется со скоро-
стью и. Магнитное поле в облаке направлено перпендикулярно ри-
сунку. Нерелятивистское заряженное ядро летит перпендикулярно
границе АА’ со скоростью у (и >> и). Найдем относительное измене-
ние энергии ядра при его отражении от магнитного облака, учиты-
вая действие магнитного и электрическо-
В ч го полей (Не 8.33). В системе отсчета, свя-
\ ‚ занной с магнитным полем, скорость ядра
А А
п. 121 = и + и. Для силы Лоренца (7.2) имеем
г 4
Р = — В .
Рис. 8.17 с м 1

При движении под действием силы Лоренца скорость не меня-
ется по величине. После выхода из магнитного поля в системе Га-
лактики 122 = и, + и = и + 2и. Относительное изменение энергии
АИ’ _ 123-122 _ 4ип+4и2 4и
И/ 02 02 7)
ДРУГОЙ МСТОД, КЗК И В ПРЕДЫДУЩЕЙ ЗЗДЗЧС, С рассмотрением ПО-
лей в системе Галактики, где начальная скорость ядра равна у. Из
(8.3) и (8.4) имеем
Е’=—ЁЁ- и В’=В.
ИСПОЛЬЗУЯ уравнение, ОПИСЫВЗЮЩСС ДВИЖСНИС ПО ОКРУХСНОСТИ
К с’
для работы электрического поля получаем
А = АИ’ = 4Е’2К = аиВё = 2ити.
Для относительного изменения энергии имеем
АИ/_2 12 __4и
ш ит т 122/2 11
В скрещенных однородных полях Е и В (Е _|. В) из некоторой
точки хо разлетаются электроны с одинаковыми скоростями и << с,
лежащими в плоскости Оху (рис. 8.18). Считая Е << В (СГСЭ) и
пренебрегая взаимодействием электронов друг с другом, найдем, на
каком расстоянии 1 и через какое время Тони снова соберутся в
одну точку, а также изобразим (качественно) траекторию частицы,
если известно, что в начальный момент она покоилась в точке хо
(Не 8.34). Перейдем в систему отсчета, в которой электрическое
поле равно нулю. В соответствии с (8.3) и заданными условиями
эта скорость направлена по оси х (см. рис. 8.18)
и равна
и=Е%.
В этой системе частицы движутся по окружнос-
тям с угловой скоростью
тс Рис. 8.18
279

любое значение. Выберем так, чтобы а было вещественным. Общее
решение уравнения (8.1О), учитывая, что е"‘°’ = сов (о! — 15111 шт,
можем записать
. .. Е
х’+1у’=асо5ш1—1а51пш1+сБ. (8.13)
Приравнивая действительные и мнимые члены, находим
/ Е ‚ / '
х =асо5ш1+сБ‚ у =—а51п‹ш. (8.14)
Видно, что в момент 1= О скорость направлена по оси х, а ком-
поненты скорости — периодические функции. Для средних по вре-
мени значений находим
ш7=о%; @7=0
Скорость дрейфа (х’) перпендикулярна обоим полям. В вектор-
ном виде
шт
= . 8.15
у с 32 ( )
Интегрируя (8.14), получаем
х=%51пш1+сЕ%; у=%(со5ш1—1). (8.16)
Это — трохоида. При а = -сЕ/В — это циклоида.
По двум параллельным проводящим плоскостям текут антипа-
раллельные токи с линейной плотностью 1. Они замыкаются через
соединяющую плоскости перемычку толщиной б с удельным сопро-
тивлением р (рис. 8.19). В пространстве между плоскостями совер-
шает дрейфовое движение свободный электрон. Найдем величину и
направление скорости дрейфа (Не 8.80). Обозначая ширину плоско-
стей 1, а высоту а, получаем:
для тока
1 = 11,
ДЛЯ СОПРОТИВЛЕНИЯ перемычки
ж:
К- 18’
ДЛЯ ПЗДСНИЯ напряжения
и=т=Е3
‘а’ июзлэ
281

ДЛЯ НЭПРЯЖСННОСТИ ЭЛСКТРИЧССКОГО ПОЛЯ
_ И _ В
Е - а -18.
Из теоремы о циркуляции (5.6)
в = 41:!
С
Из (8.15) получаем
› _ Ё. _ 2_&_
" ' с в ’ с 4пб°
Заряженный шарик движется в скрещенных однородных элект-
рическом Е и магнитном В полях (Е << В) в среде, сила трения в
которой пропорциональна скорости движения. Движение происхо-
дит в плоскости, перпендикулярной вектору индукции магнитного
поля. Найдем ‚величину и направление скорости его установивше-
гося движения, если известно, что в отсутствие магнитного поля эта
скорость равна и, (М9 8.42). Используя (8.2), для описания движения
шарика получаем
с1у с;
т— =4Е+—[\'В]—0ш. (8.17)
д! с
На рис. 8.20 показаны вектор-ы полей и скорости.
В установившемся движении производная скорости по времени
равна нулю. Поэтому при отсутствии магнитного поля с1Е = от].
При наличии магнитного поля запишем уравнение в проекциях
4Е—осих+%иуВ=0; —0сиу—%12„В=0. (8.18)
Из этих уравнений находим
КБФ=`=——-—' и=(1› +12 т: и]
их 5С’ х у [1+В1›%/Е2с2:|]/2.
Вместо электрического может быть грави-
тационное поле. Такое же условие в отсутствие
магнитного поля. Кроме того, при отсутствии
трения задана скорость дрейфа од (Мг 8.41).
Из решения уравнений (8.9) следует, что
х дрейф возникает при любой постоянной силе,
Рис. 8.20 например силе тяжести Р. В уравнении (8.2),
282

а потом и в (8.17) записываем Е = Р/е (в последнем соответственно
Е = Ё/а). Для скорости дрейфа из (8.15) следует
чд = ст. - (8.19)
В ч
Таким образом, при ОТСУТСТВИИ МЗГНИТНОГО ПОЛЯ Р: (1211, а ДЛЯ
скорости дрейфа получаем
_сЕ и
_::С —
йд ЧВ ЧВ.
Подставляя в уравнения (8.18) Е = Е/а и решая их, находим
1)
13ф=—1%=—%-; и=(их+иу) 2 21/2.
х д [1 + и, /ид:|
Однородный по плотности плоскопараллельный слой электро-
нов удерживается в вакууме однородным магнитным полем с индук-
цией В = 57 Гс (рис. 8.21). Поле параллельно поверхности слоя.
Толщина слоя б = 1 см. Плотность электронов в слое п = 107 см’3.
В этих условиях электроны движутся параллельно поверхности слоя
в плоскости, перпендикулярной магнитному полю (дрейф). Найдем
скорость дрейфа од в зависимости от расстояния х до плоскости
симметрии. А также определим разность потенциалов Аср между
плоскостью симметрии и внешними поверхностями слоя. Зная, что
для электронов е/т = 5‚27- 10” ед. СГСЭ (М9 8.36) однородный
слой заряженных частиц (в данном случае электронов) создает элек-
трическое поле. Учитывая симметрию и применяя теорему Гаусса
(1.12), получаем Е = —4пепх внутри слоя и Ее = —2пепб — вне слоя
(см. рис. 8.21). Движение электронов внутри слоя в скрещенных
электрическом и магнитном полях описывается уравнениями (8.9)‚
которые в данных наименованиях координат имеют вид
1/2 _ 711
тх” = -еЕ — вуё; ту” = егё; та” = О. (8.2О)
В соответствии с (8.16) получаем
_ - . _ _ 1 . юн
х-гыпшг, у-гсозшг сЕВ, х / 2
_ В (8.21) у _
‘ 03 — ЗРЯ. д/ Ё
Таким образом, заряд наряду с круговым
движением дрейфует вдоль оси у (перпенди- Рис. 8.21
283

кулярно Е и В). В слое частицы удерживаются в результате равнове-
сия электрической и лоренцевой сил
Е+у' вЂ” = О.
,В
С
Отсюда скорость дрейфа
СЕ
0
В
Колебания в линейно меняющемся поле описываются уравне-
нием
тх" + 4ше~пх = О.
Частота их называется плазменной частотой
(8.22)
и = 4яе вЂ”.
г
Р т
(8.23)
Воспользовавшись этим определением плазменной частоты, вы-
ражением для электрического поля
Е=и твЂ”
2 Х
е
и формулой для циклотронной частоты (8.5), получаем
г х
О = И
Рв'
(8.24)
Для разности потенциалов имеем
5/г ог
Л<р = 4яепх Ых = неп вЂ”.
2
(8.25)
Электронный пучок представляет собой тонкостенную трубку,
движущуюся в направлении своей оси и вращающуюся относитель-
но нее в вакуумированном пространстве между электродами соос-
ного с пучком цилиндрического конденсатора (радиус внутреннего
электрода г„внешнего г,). Считая пучок бесконечно тонкой заря-
женной поверхностью, свернутой в круглую трубу радиусом го, а
полную скорость электронного пучка заданной и равной оо, найдем
максимальный ток 1 „, который может быть проведен в таком пучке
через пространство, ограниченное электродами конденсатора. Кон-
денсатор электрически закорочен, его длина существенно превы-
шает зазор между электродами (М 8.37).
284

Обозначая поверхностный заряд пучка о, получаем заряд пучка
на единицу длины х = 2пгоо. Вводя заряд на единицу длины на
внутреннем электроде х‘, из выражения для напряженности элект-
рического поля, имеющего цилиндрическую симметрию, (1.16) по-
лучаем, что поле между г] и го равно
2
Едщ
Г
9
а ПОЛС МЕЖДУ ГО И Г2 равно
Е: = 2(Х+Х1)_
Г
Используя связь напряженности поля с потенциалом (2.6), на-
ходим
‹р(г„)-‹р(г‚) = 494,111“);
о
П
‹р(г2)—‹р(г0)=—2(х+х‚)1п(%).
Из условия закороченности конденсатора ‹р(г2) = ‹р(г1) получаем
_ 1"("2/"о)
Х; -‘хт-
СКОРОСТЬ ДВИЖСНИЯ ЭЛЕКТРОНОВ 120 СКЛЗДЫВЗСТСЯ ИЗ СКОРОСТИ вра-
ЩСНИЯ ПО окружности 1)“ И СКОРОСТИ ВДОЛЬ ОСИ пучка
_ 2 21/2
ип-(ио-иц) .
Для движения электрона с зарядом е (отрицательным) и массой т
по окружности имеем
“Е: 2761
т— = —е —- + 2110 .
ГО ГО
Используя полученные ранее связи, записываем
2
он = ах,
где
2
е 1“ (П "2/"о)
а: т ШИ/п) '
285

Соответственно
Д _ о
диц
НЗХОДИМ
2тиё
[так = 3Ле°
Вдоль оси находящегося в вакууме соленоида с плотностью на-
мотки п и током 1 из электронной пушки инжектируется цилиндри-
ческий пучок электронов (рис. 8.22). Вследствие пересечения части-
цами сходящихся магнитных силовых линий в области неоднород-
ного поля у торца соленоида пучок приобретает однородное
вращение. Полагая, что пушка находится вдали от торца соленоида,
и не принимая во внимание радиальные скорости электронов, при-
обретенные при движении в неоднородном магнитном поле, най-
дем угловую скорость вращения пучка (Мг 8.38).
Перейдем в систему отсчета, движущуюся со скоростью частиц,
вылетающих из пушки. В ней из-за движения неоднородной части
магнитного поля соленоида происходит изменение потока магнит-
ного поля, и появляется азимутальное электрическое поле. С помо-
щью (5.32) получаем
Е2лг=-1%.
С
Считаем, что это поле заставляет электроны вращаться по ок-
ружности постоянного радиуса г. Изменение момента количества
движения электрона (масса т, заряд е) связано с моментом сил
с1(тг2ш)__еЕ‚__:_4_9 КА
а’! - — 2пс а’! °
Начальный поток Фн = О, так как пушка на-
ходится вдали от соленоида. Рис. 8.22
287

Конечный поток
Фк = Втд,
где В — магнитное поле соленоида (5.21):
1
В = 4пп—.
С
После интегрирования имеем
_ еВ
к `_ Е?’
что в два раза меньше (8.5) — циклотронной частоты
еВ
и.
Металлическое кольцо радиусом г и массой т падает в магнитном
поле, вертикальная составляющая индукции которого зависит от
высоты И по закону В(/1) = В0(1 — а/т), где а — константа. Плоскость
кольца при падении горизонтальна, омическое сопротивление К.
Найдем зависимость скорости его падения от времени 1 (Мз 8.46).
Используя (7.1), получаем
г‘ ——-ТЕЁС1В -пг2Ва у
Е _ сК Ё — О Е?’
где
_ ат
_ Ж_
При таком токе кольцо представляет магнитный диполь с маг-
нитным моментом (5.5)
1)
2
Г
Р—]ТЁТ.
Сила, действующая на диполь в меняющемся по пространству
магнитном поле, в соответствии с (1.11) и (6.21) равна
‚из _ (пг2аВ0 )2
Р = —— — —
” си: за
Уравнение ДВИЖСНИЯ КОЛЬЦЗ В МЭГНИТНОМ ПОЛЕ И ПОЛС ТЯЖЕСТИ
(122 2 3 12
т— = — тсг аВО — — ту. (8.26)
Установившаяся скорость при ускорении, равном нулю:
с2К
пуст = -т3——;——-7.
(кг аВО)
288

Алюминиевое кольцо, сопротивление которого пренебрежимо
мало, надето на сердечник электромагнита и лежит на подставке в
верхней части сердечника (рис. 8.23). Магнитный поток, посылае-
мый сердечником через кольцо, нарастает от нуля до конечного зна-
чения ФО = 10 Гс › см3. Нарастание потока происходит настолько
быстро, что за это время кольцо практически не успевает сместить-
ся. Найдем высоту Н, на которую подскочит кольцо, если его масса
т = 100 г, а индуктивность Ь = 100 см (М 8.62). Изменение потока
магнитного поля через кольцо приводит к возникновению в кольце
тока 1 и появлению магнитного момента
_15
"Та
С
где 5 — площадь кольца. Благодаря градиенту внешнего поля Ввнеш
(от катушки с сердечником) на кольцо, являющееся магнитным ди-
полем, действует сила типа (1.1 1)
1;‘ = _р дВвнеш
фс
Координата х направлена по оси сердечника вверх. Так как по-
ток внешнего поля через кольцо равен Фвнеш = ВВНСШЗ, то ДЛЯ силы
получаем
1: = _1 дфвнеш _
с а'х
Используя (7.1) при быстром нарастании магнитного поля и
пренебрежимо малом омическом сопротивлении кольца, получа-
ем сохранение полного потока магнитного поля, который скла-
дывается из потоков внешнего поля и собственного поля кольца
Фподн = Фвнеш + Фсоб. Так как в начальный момент никакого поля не
было, то имеем Фвнеш = —Фсоб. Из (5.28)
1
Фсоб = Ь-Ф
С
где Ь — индуктивность кольца. Таким образом, для силы получаем
17 _ 1 Ф афвнеш
_ Т внеш Т
Отсюда находим работу, которая создает кинетическую энергию
кольца. Так как за время нарастания магнитного поля оно практи-
чески не успевает сдвинуться, то
_1Фё
- г? = т“
290

ф
Рис. 8.23 Рис. 8.24
Начиная двигаться, кольцо быстро уходит из области влияния маг-
нитного поля, и потоками магнитного поля там можно пренебречь.
Рассмотрим систему (рис. 8.24), представляющую диск из изо-
лятора, который может свободно вращаться на вертикальной оси
и на котором размещены заряды, суммарная величина которых
О = 4- 10"“ Кл, и в его центре вертикально закрепленный длинный
сверхпроводящий соленоид (радиусом го = 2 см), замкнутый нако-
ротко‚ по которому циркулирует ток, создающии в центре соленои-
да индукцию ВО = 104 Гс. Найдем момент импульса (Ь), который
получит система при разогреве соленоида, прекращении тока и ис-
чезновении магнитного поля (Мг 8.51).
При изменении магнитного потока вокруг него возникает элек-
трическое поле, которое можно найти из циркуляции (5.22)
Е 21:)’ = ޯ
с а’!
Магнитный поток в основном идет внутри соленоида, а вне его,
где расположены заряды, ИМ МОЖНО пренебречь. МОМСНТ электри-
ческой силы, действующей на заряд с], расположенный на расстоя-
нии г от оси, равен
_ 4 ш _ 2 ЁВ/(Й
— ЕЕ а’! _ О 2с
ВИДНО, ЧТО ОН не ЗЗВИСИТ ОТ расстояния Г, ПОЭТОМУ ДЛЯ НССКОЛЬ-
ких зарядов просто складывается. Суммарный момент сил изменяет
МОМВНТ КОЛИЧССТВЗ ДВИЖСНИЯ
Ё_ дав/д:
т’ ° 2с'
Отсюда
В _
Ь=@г02%=8-10 3 г-см2/с.
19’ 291

С точки зрения механики, кажется, что здесь нарушается закон
сохранения импульса. В действительности до прекращения тока в
соленоиде, благодаря наличию электрического и магнитного полей,
как будет далее показано, существует поток электромагнитной энер-
гии, определяемый вектором Пойнтинга, и соответствующий ему
момент количества движения, который затем при исчезновении
магнитного поля сохраняется.
Металлический шарик массой т, с зарядом с; подвешен на нити
длиной Ь и вращается вокруг вертикальной оси (конический маят-
ник). Обозначая расстояние шарика от оси вращения г, угловую ско-
рость вращения (по, ускорение в поле тяжести 3 и отклонение нити
от оси вращения ос, получаем
Г .
шё—=твос=вппос=
„е
Ы‘:
Откуда
1/2
шо = (%) ь
Если включить параллельное оси вращения однородное магнит-
ное поле с индукцией В, то на заряженный шарик будет действовать
вихревое электрическое поле с напряженностью Е, которая опреде-
ляется из циркуляции (7.5)
Е2пг = —1пг2Ё.
с а’!
Сила Р = с1Е. Импульс
Га’! = с1(ти) = 44%.
Для угловой скорости, если В направлено _так же, как (о, и сила
замедляет вращение, имеем
При противоположном направлении В вращение на столько же
ускоряется.
Для изменения кинетической энергии в случае одинакового на-
правления поля и угловой скорости получаем уменьшение, а в про-
тивоположном случае увеличение (Не 8.54) на
АИ’ = тг2 Ы = тг2 (Ю-юожиншо) = тг2 —Ё(2Ш `z^
2 2 4тс О 2тс
292

Если задан потенциал Н шарика (М: 8.53), то подставляем с; = Нг,
где г — радиус шарика. При вращении в постоянном магнитном
поле, направленном как со, сила Лоренца (8.1) уменьшает центрост-
ремительную силу. Без магнитного поля для угла отклонения нити
имеем
2 г._ г
030 Е ‘ 7.
Откуда
8
03% = 7.
При магнитном поле
В
(02 —с1шй = ё =ш3.
Таким образом,
_ в в
“то "Юта; “т;
Постоянный короткий магнит с магнитным моментом, ориен-
тированным вертикально, сначала удерживается над сверхпрово-
дящей плоскостью на расстоянии а = 2 см, а затем отпускается
(рис. 8.25). Оценим высоту 11, на которую он подскочит, если мас-
са магнита т = 15 г, объем У= 2 см3, намагниченность М = 103 Гс
(М?) 8.57). При оценке энергии взаимодействия магнита со сверх-
проводящей плоскостью воспользуемся методом «изображений»,
т. е. будем рассматривать взаимодействие его с другим, который
обеспечивает такие же граничные условия, как на поверхности сверх-
проводника. Для магнитного момента магнита
имеем р = УМ. В дипольном приближении из ё
(7.11) для нашего случая находим д,
11
= 2.2.5,
(2г)
где г — расстояние магнита от сверхпроводя-
щей плоскости. В соответствии с (1.1О) сила
отталкивания
2
= в-Ь. 8.27
(2г)‘ ( ) Рис. 8.25
293

Сила отталкивания и приобретаемая энергия положительны, так
как направление диполя «изображения» противоположно диполю
магнита. Энергия определяется работой этой силы с1И/ = Гдг. Надо
иметь в виду, что такая же работа тратится при перемещении «изоб-
ражения», фактически расходуясь на изменение токов, текущих по
поверхности сверхпроводника.
Из закона сохранения энергии после интегрирования следует
(иМ)2 _ 2 (иМ)2
: _ ——— н.
(2а)’ (2а + 2л)3 + тд
СЧИТЗЯ, ЧТО В верхнем ПОЛОЖЕНИИ ВЗЗИМОДСЙСТВИС МЗГНИТЭ СО
СВСРХПРОВОДНИКОМ МЭЛО ПО СРЗВНСНИЮ С начальным, НЗХОДИМ
Используя полную формулу, получаем 4,166 см, т. е. приближе-
ние оправдано.
Такой магнит может находиться над сверхпроводящей плоско-
стью в равновесии или совершать, например, малые гармонические
колебания. Используя (8.27), получаем для равновесия на высоте а
над сверхпроводящей поверхностью
2
3
ШЁ=6Д=Ё
(2а)4
При малом отклонении х (например, вниз) от равновесия
2
Е.
а4
2 21 4
тх”=тд_ёгр 4=т3-3———-—р( их“).
8(а-х) 8а
Отсюда получаем (Не 8.56)
х” +435 = О; а) = 45)“:
а а
Найдем отношение периодов колебаний двух аналогичных маг-
нитов одинаковой массы, если их магнитные моменты отличаются
в 16 раз и оси при колебаниях остаются параллельны сверхпрово-
дящей плоскости (М9 8.58). В случае диполя, параллельного сверх-
проводящей поверхности, диполь, соответствующий «изображе-
нию», параллелен первому диполю. Они отталкиваются. Силу на-
294

ходим с помощью (1.9) и (1.11). Она оказывается вполовину мень-
ше (8.27). Обозначая отклонение от равновесного положения х,
получаем
з 2 3 2 '
р = ___2_т „ _д(1_4:)„
16 а4 а
Уравнение ДВИЖЕНИЯ магнита С УЧЕТОМ СИЛЫ ТЯЖЕСТИ
тх” = Г- ту или х” + ю2х = О, (8.28)
где ЧЗСТОТЗ И ПОЛОЖСНИС равновесия
2 2 '/4
002 3%; а=(1-&-) . (8.29)
=3та
Поэтому (02 Н р“/2‚ период
1/4
То Ро
Если в 16 раз отличаются массы, а магнитные моменты одина-
ковые и перпендикулярные сверхпроводящей поверхности (Мэ 8.59),
то из (8.27) и (8.28) следует вместо (8.29) для частоты и положения
равновесия
1/4
(„2 = 311. а = 2:1
2 та5 э 8 т8 .
Поэтому 002 ‘ч т1/4, период
Т - тЧ/З и Д = ;
76 21/2 °
Рассмотрим сверхпроводящий шарик радиусом г и массой т, ко-
торый со скоростью и подлетает к области постоянного магнитного
поля В. Оценим максимальную скорость, при которой он отразится
от поля (Мг 8.63). При вхождении шарика на расстояние х в область
поля на него действует тормозящая сила давления (7.12)‚ равная
В:
Р=—п[г2—(г—х)2].
81:
Уравнение движения шарика
д„_ ‹1„_ в’ 2
тЖ-ти2;——-г(2гх—х lr
295

Если шарик не полностью погрузится в
поле (х < 2г)‚ то сила давления магнитного
‘х поля вытолкнет его. Интегрируя уравнение
х{; * движения (скорость от и до нуля, х от нуля
до 2г)‚ получаем
Вгш
' < и < от)“ '
Монополь Дирака (элементарная частица,
пока не обнаруженная, массой т, обладаю-
. щая магнитным зарядом Ь) находится строго
Рис_ 826 посередине зазора между пластинами незаря-
женного разомкнутого плоского конденсато-
ра, изготовленного из идеального сверхпро-
водника. Оценим частоту малых колебаний монополя в направле-
нии нормали к плоскостям. Все размеры конденсатора много больше
расстояния 11 между пластинами (Мг 8.60). Чтобы обеспечить отсут-
ствие нормальной к сверхпроводящей поверхности компоненты
магнитного поля, необходимо, чтобы «изображение» магнитного
заряда имело тот же знак и находилось в симметричном положении.
Так как сверхпроводящих поверхностей две, то потребуется целая
система зарядов. Для оценки сил, возникающих при небольшом
отклонении заряда от начального положения, достаточно учесть лишь
ближайшие изображения. На рис. 8.26 показаны заряд и изображе-
ния. При отклонении от средней линии, равном х, для силы, дей-
ствующей на заряд (подобно закону Кулона), получаем
Ь2 _ Ь2 и _ 21
(и + 2х)2 (и - х)2 из '
Уравнение колебаний заряда
тх” + 8Ь2 1 = о.
„З
Откуда для частоты получаем
2
(02 = 837.
т/х
В однородное магнитное поле с индукцией В помещена тонкая
металлическая лента шириной 1 (рис. 8.27) и толщиной а так, что
плоскость ленты перпендикулярна к индукции В. По ленте пропус-
кают ток 1. Найдем разность потенциалов П, возникающую между
296

Разность потенциалов
я2
2 1~ я2
г вЂ” вЂ” Шг =
1
~( ~! ~) [ 2 (д2 д2)~
2 я-,'/я,' вЂ” ~
У= |юг=
я
В простейшей схеме магнитного гидродиыамического генератора
плоский конденсатор с площадью пластин 5 и расстоянием между
ними ( помещен в поток проводящей жидкости с проводимостью Х
(рис. 8.28), двигающейся с постоянной скоростью т параллельно пла-
стинам. Система находится в магнитном поле с индукцией В, на-
правленной перпендикулярно плоскости рисунка. Найдем, какая мощ-
ность Ф выделится во внешней цепи, имеющей сопротивление Л
(№ 8.69). Сила Лоренца (8.1) вызывает движение заряженных частиц,
работает как электродвижущая сила й = иВ1. Для тока в цепи имеем
г+ Я
Здесь внутреннее сопротивление
1 1
Г = вЂ” вЂ”.
ХЮ
Мощность, выделяемая во внешней цепи (4.18),
~ В1Я
Длинная незаряженная пластинка из немагнитного металла дви-
жется равномерно в однородном магнитном поле В со скоростью о.
Векторы В и т взаимно перпендикулярны и параллельны плоскости
пластинки (рис. 8.29). Найдем поверхностную плотность электри-
Рис. 8.29
Рис. 8.28
298

ческих зарядов на плоскостях пластинки, возникающих вследствие
ее движения, и их знаки, если векторное произведение [тВ] направ-
лено вверх. Магнитным полем зарядов будем пренебрегать (Мо 8.70).
Используя (8.1), получаем, что электроны будут отклоняться к ниж-
ней стороне пластинки, а верхняя получит положительный заряд.
Плотность заряда а определяется из соотношения
Е = вЂ” = 4яа.
оВ
С
Откуда
вВ
а=
4т~с
Длинный сплошной алюминиевый цилиндр радиусом Л заря-
жен электричеством и вращается с постоянной угловой скоростью и
вокруг своей продольной оси. Заряд на единицу длины цилиндра
равен у,. Найдем разность потенциалов Умежду осью и поверхнос-
тью цилиндра, возникающую из-за его вращения, пренебрегая цен-
тробежной силой (Мо 8.67). За счет вращения заряда, который нахо-
дится на поверхности цилиндра, с периодом Т имеем круговой ток
на единицу длины цилиндра
Х Х®
Т 2ж
Из теоремы о циркуляции (5.6) следует, что снаружи цилиндра
магнитного поля нет, а внутри оно постоянно и направлено по оси
в ту же сторону, что и угловая скорость, и равно
Н =4п вЂ” =2у вЂ”.
С С
В соответствии с (8.1) на заряды внутри цилиндра действует сила
Лоренца, которая создает меняющуюся с расстоянием напряжен-
ность электрического поля
Е = вЂ” = 2уи вЂ”.
оИ 2г
с С2
Для нахождения разности потенциалов надо вычислить интеграл
2~ ~2
У = 2т вЂ” ~ г Нг = и вЂ” у,.
О
Длинный незаряженный цилиндр из немагнитного металла ра-
диусом Л = 12,56 см равномерно вращается в однородном магнит-
299

Интегрируя по объему единицы длины цилиндра, имеем
‚22 _п2
2с
Поверхностная плотность связанных зарядов на внутренней и
внешней поверхности цилиндра:
4 = [ржаи = -(е —1)(о›В)
о‚„,„, = —(е—1)(шВ)д—%; о,„,„, =(е—1)(шВ)%.
Диэлектрическая жидкость проницаемостью е протекает между
пластинами плоского конденсатора (расстояние между пластинами
равно 1) со скоростью и << с. Перпендикулярно направлению движе-
ния жидкости и параллельно обкпадкам конденсатора приложено
однородное постоянное магнитное поле В. Найдем напряжение Н
между обкладками конденсатора и поверхностную плотность заря-
дов диэлектрика о (Не 8.71). В системе отсчета, связанной с конденса-
тором, задано поле В, а электрическое поле вне конденсатора Е = О.
В системе отсчета, связанной с движущейся жидкостью, в соответ-
ствии с (8.4) и (8.3) магнитное поле не меняется, а электрическое
поле вне конденсатора
Е*=Е+1[чв]=1[ув].
С С
При отсутствии свободных зарядов на границе диэлектрика из (3.7)
имеем непрерывность электрической индукции 1)’ = Е’ = 1)” = еЕ”.
Таким образом, в системе отсчета, связанной с диэлектрической
жидкостью, имеем для напряженности электрического поля
Е„ _ [уВ]
ес '
ПСРСХОДЯ обраТнО В СИСТСМУ ОТСЧеТа, СВЯЗЗННУЮ С КОНДСНСЗТО-
ром, получаем внутри диэлектрика
Е=Е"-Ё!Ё=[чв]®“.
С 8С
Из (2.6) для разности потенциалов находим
и = -[ув] 8 ‘ 1.
ес
Из (3.8)
1) — Е
Р _ 41: ’
301

а из (3.3)
|о| = Р„ = НуВЦ Ёж;
Диэлектрическая незаряженная пластина с проницаемостью е = 3
движется между обкладками плоского конденсатора со скоростью
и = 1 м/с. Перпендикулярно направлению движения пластины и
параллельно обкладкам конденсатора приложено однородное по-
стоянное магнитное поле В = 1,5 Тл. Найдем поверхностную плот-
ность зарядов на обкладках конденсатора и поверхностную плот-
ность поляризационных зарядов диэлектрика, если к конденсатору
приложена разность потенциалов Н = 1 В. Расстояние между плас-
тинами конденсатора 11 = 2 см и равно толщине пластины диэлект-
рика (Не 8.84). Разность потенциалов создает внешнее поле внутри
конденсатора Е = 11/11. В системе отсчета, связанной с движущимся
диэлектриком, получаем из (8.3)
Е’=Е:1’Ё.
С
Знак зависит от направления магнитного поля. Для вектора поляри-
зации из (3.2) и (3.9) имеем
Р=(е—1)
Е!
41г°
Отсюда поверхностная плотность поляризационных зарядов в соот-
ветствии с (3.3)
ос = (е —1)————-—и/Й:п”В/с.
При знаке плюс это равно 0,91 - 10-9 Кл/м2, при знаке минус —
0,86 - 1О'9 Кл/м2. Для плотности свободных зарядов на обкладках
конденсатора из (3.7) и (3.8) получаем
0
о=——
41:’
где
В=Е+4пР=еЕ:(е—1)3Ё.
При знаке плюс плотность зарядов — 1,33 - 10-9 Кл/м2, при знаке
минус — 1,3- 10 ‘9 Кл/м2.
На рис. 8.30 показан вертикально расположенный цилиндричес-
кий конденсатор (радиус наружного цилиндра К, внутреннего — г,
302

Одна из пластин конденсатора жестко зак-
реплена, а вторая, имеющая массу т, связана с
пружиной жесткостью 1: (рис. 8.31). Расстояние
между пластинами при ненагруженной пружи-
не равно 10. При подключении к конденсатору
батареи в новом положении равновесия рассто-
яние между пластинами
Рис. 8.31 1 =%1О_
Найдем период малых колебаний пластины (М 8.79). Силу взаи-
модействия между пластинами найдем из закона сохранения энер-
гии: работа батареи (3.77) равна сумме механической работы и из-
менению энергии конденсатора 0:19 = аУИ/+ Рдх. При подключении
к батарее напряжение на конденсаторе 1! не меняется. Так как ем-
кость плоского конденсатора
а энергия
то с1с1 = Ца/С, и при постоянном напряжении на конденсаторе
_ 2519-- 2 5 Ё
д-11 щ- и виды)‘.
Считая отклонения от равновесия (х) при колебаниях малыми,
получаем уравнение колебаний
5
„ш = 4410 -1+х)+и2—_7.
8п(1 — х)
Из условия равновесия
5
81:12
Используя это, малость х и связь 10 и 1, получаем уравнение коле-
баний
и = то -1).
х”+%х =О.
304

Откуда находим период колебаний д, н
1/2
Т = 21432) . Ё >
к К
Электрический заряд О равномерно распреде-
лен по тонкому кольцу радиусом В (рис. 8.32). Рис. 8.32
Точечный диполь массой т с дипольным момен-
том р может перемещаться вдоль оси кольца (ось х), перпендику-
лярно его плоскости, причем дипольный момент диполя паралле-
лен оси кольца, а сила тяжести отсутствует. В начальный момент
времени диполь находится в центре кольца и имеет нулевую ско-
рость. Найдем:
1) максимальную скорость птах диполя при его движении вдоль
оси кольца;
2) положение равновесия хо диполя;
3) период малых колебаний диполя около положения равнове-
сия (Не 8.78).
Распределение потенциала вдоль оси кольца
__А_
(122 + 1:2)!” .
В соответствии с (2.6) или (2.8)
(р:
Е(х)=—Ё= Ох
дх (122 „г?“
Используя'(1.11)‚ для силы, действующей на диполь, получаем
дЕ 1:2 —2х2
Р" ”7‹"”9‹к2 +2?”
В ПОЛОЖЕНИИ равновесия сила равна НУЛЮ. ПОЭТОМУ
Вводя малое отклонение у от положения равновесия х = хо + у,
получаем уравнение колебаний
„ У _
у “идти-
20-2073 305

Откуда для периода колебаний находим
1/2
У 1 35/4 Д2
г
Для вычисления максимальной скорости воспользуемся тем, что
работа силы НА = ГШх = рйЕ. Сила разгоняет диполь от начального
положения х = 0 до положения равновесия
Я
ХО
2Л
Следовательно,
А = т ~'" = рЕ (х0) = 2р
Отсюда находим максимальную скорость.
Найдем период малых крутильных колебаний магнитного брус-
ка (5'= 1 мм', (= 10 см), подвешенного горизонтально на неупругом
подвесе в магнитном поле Земли (горизонтальная составляющая
В, = 0,2 Гс). Плотность стали р = 7,8 г/см', остаточная индукция
В = 1О кГс (№ 8.73). Момент инерции бруска относительно оси
вращения (см. 1, с. 191)
У = р5' вЂ”.
1
Магнитный момент бруска в соответствии с (б.б)
ВЯ
4я
(8.31)
В соответствии с (7.8) в магнитном поле Земли создается воз-
вращающий момент сил ВОВЯу/4я. Уравнение колебаний бруска
ВО В~~(~
ф +
(8.32)
Отсюда период колебаний
Т=2п(~ )
Два одинаковых железных бруска площадью сечения 5 = 0,1 см~ и
длиной ( = 5 см имеют остаточную магнитную индукцию В = 12 5бО Гс.
Бруски расположены на одной прямой на расстоянии А = 1 м. Один
306

брусок закреплен неподвижно, а дру- 0
гой может свободно вращаться вокруг 1 ‘ ‘ ‘ ‘ Щ
оси 00’, проходящей через его середи- 1 д ::3
ну и параллельной магнитному полю ‚ =
Земли ВО (рис. 8.33). Найдем период Т
малых крутильных колебаний бруска. РИС- 8-33
Плотность железа р = 7,8 г/см3 (Мг 8.74).
Магнитные моменты брусков можно вычислить по (8.31), а поле,
которое они создают на расстоянии 1„ —— по (7.11). Поле Земли
возвращающего момента не создает. Момент со стороны закреп-
ленного бруска равен 2Б212В2Ф/(16п2ЬЗ). Уравнение колебаний
‚‚ 252!2В2‹р _
1611213
После подстановки 1, как в предшествующей задаче, получаем
(2р1ц35)"2
Т=22Ь——————.
я в
Если бы бруски были перпендикулярны линии их соединяющей
(Мг 8.75), то изменился бы коэффициент (вместо двойки единица) в
выражении для магнитного поля, определяемого по (7.11).
В результате некоторого космического события образовалась
система, состоящая из звезды (масса М, магнитный момент ро) и
планеты (масса т << М, магнитный момент р). Планета движется по
круговой орбите радиусом К. Найдем возможный разброс величины
периода обращения в зависимости от ориентации магнитных мо-
ментов, считая плоскость орбиты, перпендикулярной магнитному
моменту звезды ро (М) 8.72). Из (7.11) получаем для поля звезды
Р
‚З
Используя (1.11), для силы магнитного взаимодействия звезды и
планеты получаем отталкивание при одинаковом направлении маг-
нитных моментов и притяжение при противоположном направле-
нии с силой ЗрОр/К“. Эта сила складывается с гравитационной. Для
ДВИЖЕНИЯ ПО ОКРУЖНОСТИ ИМССМ
2
т}; = у)”: + р А
К 1:2 ' ° к“ °
Учитывая, что период обращения
Т = 2п5‚
11
20‘ 307

зарядов диполя, будет создавать момент, стремящийся уменьшить
отклонения диполя от направления [уВ]. Для малых углов отклоне-
ния оъ имеем уравнение вращательных колебаний
м” + „в; = о.
Отсюда находим угловую частоту колебаний
032 = ир-Ё.
с!
Плоский воздушный. конденсатор помещен в горизонтальном
положении между круглыми горизонтальными наконечниками элек-
тромагнита (рис. 8.35). Между обкладками конденсатора в однород-
ном электрическом поле Е на расстоянии К от оси полюсных нако-
нечников неподвижно висит заряженная масляная капля с зарядом 4.
В обмотке включают ток, и магнитное поле доводят до постоянной
величины В. Предполагая, что за время нарастания магнитного поля
смещение капли пренебрежимо мало, найдем ее скорость и и траек-
торию движения после включения магнитного поля (М9 8.44). Для
вихревого электрического поля из (7.5) имеем
_ _1 2 ав
Ев2пК - с 1:12 д’ . (8.33)
Для скорости в направлении этого поля получаем
а: 2 с ‘7 а: ‘
ОТКУДЭ ДЛЯ ЭТОЙ СКОРОСТИ С УЧСТОМ НУПСВЫХ НЗЧЗЛЬНЪЁХ ЗНЗЧСНИЙ
получаем
(8.34)
_ _ё_ - а
и - 412 то - КВ ЖЕ. (8.35)
_ _ `ЁЬ
Оч-Е
О О
О О О | |
. . . ‹э——Ё
Рис. 8.34 Рис. 8.35
309

Здесь введено поле конденсатора Е из связи тд = аЕ. При такой
скорости из (8.6) находим радиус кривизны траектории
г = та: = В.
43 2
Электрический заряд с; равномерно распределен по твердому
непроводящему тонкому кольцу массой т. Кольцо может свободно
вращаться вокруг своего (закрепленного) центра. Вначале оно по-
коится, а магнитное поле равно нулю. Затем включают однородное
магнитное поле В = В(1), перпендикулярное к плоскости кольца и
произвольно меняющееся во времени. Найдем движение кольца в
магнитном поле (Не 8.45). Для него выполняются уравнения (8.33)‚
(8.34) и первая часть уравнения (8.35). Поэтому для угловой скоро-
сти вращения кольца имеем
_ и _ В
' т ' ‘1 т-
Тонкое металлическое кольцо быстро вращается вокруг верти-
кальной оси, проходящий через его диаметр и перпендикулярной
однородному магнитному полю с индукцией В = 100 Гс. Пренеб-
регая трением в оси, найдем время т, за которое угловая скорость
вращения уменьшается в е раз, если плотность материала кольца
р = 9 г/см3, проводимость А = 5- 105 Ом" - см“, считая потери
энергии за один оборот малыми (Не 8.76). Момент инерции кольца
относительно диаметра (см.: 1, с. 193)
(О
./= рпзг3,
где 5 — площадь сечения кольца; г — его радиус. Угловая скорость
вращения кольца о) изменяется при изменении кинетической энер-
гии вращения И/за счет потерь на сопротивлении
2пг
К = —-.
7.9
Из (7.1) находим ЭДС в кольце. Разделив ее на сопротивление,
имеем для тока в кольце
1 аГФ 1 _ Вжвшг зйп о)!
с а?! К 2с °
Потери на джоулеву теплоту равны аЮ = 12121. Усредняя их по
периоду вращения и приравнивая потерям кинетической энергии,
получаем
1 2 вгж 2 2:1:
д: = м, ‚м, = -_Д°_;_„
2 4с
310

Для краткости введем в (8.36) обозначения Р = а(1 - Ьх). В слу-
чаях а) и б) колебания будут описываться соответственно уравне-
ниями
тх” + (/‹ + аЬ)х = О и тх” + (К — аЬ)х = О.
Отсюда находим и частоты колебаний. Если конденсатор подсо-
единить к батарее, то сила Г будет постоянной (независящей от
отклонения) и скажется только на положении равновесия, а частота
колебаний будет как в отсутствие конденсатора (Мг 8.85).

9. ПЕРЕХОДНЫЕ ПРОЦЕССЫ
В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ.
СВОБОДНЫЕ КОЛЕБАНИЯ
Электрические цепи — это соединенные проводами какие-то
наборы сопротивлений, конденсаторов, катушек (соленоидов), де-
текторов, источников электричества и других устройств. Электро-
магнитное возмущение (например, изменение силы тока в цепи)
распространяется с большой, но конечной скоростью. Если время
распространения возмущения по цепи длиной 1 со скоростью с, рав-
ное т = 1/с, много меньше характерного времени Тизменения, на-
пример силы тока, то сила тока будет успевать, как бы мгновенно
выравниваться в цепи. Далее будем предполагать выполнение усло-
вия 1: << Т, т. е. считать системы квазистационарными. В частности,
будем считать мгновенные значения квазистационарных токов под-
чиняющимися закону Ома и для систем пользоваться правилами
Кирхгофа.
Рассмотрим цепь (колебательный контур), состоящую (рис. 9.1)
из последовательно соединенных источника ЭДС 25, активного со-
противления К, катушки (соленоида) с индуктивностью Ь и кон-
денсатора емкостью С.
В этом разделе удобно использовать практическую систему еди-
ниц (СИ). В некоторых случаях в фигурных скобках приводим фор-
мулы в системе Гаусса.
Падение напряжения на активном сопротивлении К при про-
хождении через него тока силой 1 определяется законом Ома
у, = 11:. (9.1)
Падение напряжения на индуктивности Ь опре-
деляется изменением зацепленного потока магнит-
ного поля ‘Р = [Ь [(5.27) и (5.28)]:
0711,
У = -—.
‘ д:
Эта ЭДС индукции здесь записана как падение
Рис. 9.1 напряжения на индуктивности и поэтому без минуса.
314
(9.2)

Падение напряжения на емкости С, заряженной зарядом д, (3.63):
С
С
(9.3)
По правилу Кирхгофа
НА д
+ П~+ вЂ” = Ы.
~й С
(9.4)
Приведем это уравнение в системе Гаусса
+/А+ вЂ” =Ф
с 1 ИП. д
С2 сй С
Заряд на конденсаторе и сила тока связаны соотношением
(9.5)
поэтому получаем
~ [~(й~~й)]
й й С
(9.6)
Ад" + Яд'+ ~ =Ж.
С
(9 7)
Это обыкновенное линейное неоднородное дифференциальное
уравнение второго порядка с постоянными коэффициентами. Для
нахождения решения необходимы еще два начальных условия. Удоб-
но ввести обозначения, смысл которых поясним позднее. Собствен-
ной (циклической) частотой колебательного контура называется
1
®О
(АС) ~
(9 8)
В системе Гаусса
(ЕС) ~
где с вЂ” скорость света. Коэффициентом затухания:
Я
2Е
Будем обозначать производную по времени штрихом. Тогда для
постоянной нноунтннностн имеем

В таком случае из (9.7) получаем
ф'
д + 2~3я~ + иод
Е
(9.10)
д +иоЧ=О.
(9.11)
Его решение
д = д сов(ио~+ а),
иначе
д = А в1п и,т+ В сов и,т.
Постоянные интегрирования д (амплитуда изменения заряда на
обкладках конденсатора) и а (начальная фаза колебаний) или А и В
определяются из начальных условий, а собственная частота колеба-
ний и, (9.8) вЂ” параметрами колебательного контура. Для периода
колебаний То и числа колебаний в секунду чо имеем
То вЂ” вЂ” вЂ” вЂ” вЂ” вЂ” вЂ” вЂ” 2ш(ЕС)
1 2я 1/2
о~о
(9.13)
Из (9.12) можно найти ток в контуре
дд Ж
I = вЂ” = -Д ~, Б~й (И~! + П) = Д Ио ~о~ вЂ” вЂ” Ир! вЂ” й).
й
е
2
Сравнивая это с (9.12), видим, что ток по фазе опережает на я/2
напряжение на конденсаторе, которое по фазе совпадает с зарядом.
Если (9.11) умножить на д', проинтегрировать и воспользовать-
ся (9.8), то получим закон сохранения энергии
д
вЂ” + вЂ” = сопв1.
2 2С
(9.14)
Сумма магнитной энергии в катушке и электрической энергии в
конденсаторе остается постоянной. Энергия из катушки переходит
в конденсатор, а потом возвращается обратно.
316
Рассмотрим различные виды колебаний и соответствующие им
решения уравнения (9.10).
Колебания называются свободными, если Ж = О. Они могут быть
незатухающими (собственными), если Я = О (и соответственно ~3 = 0),
либо затухающими при Л и р не равных нулю.
Для собственных колебаний имеем уравнение гармонического
осциллятора

Рассмотрим пример, когда электрическая цепь представляет со-
бой треугольник, каждая сторона которого содержит емкость С, а
вершины соединены с общей центральной точкой индуктивностя-
ми Ь (рис. 9.2, а). Найдем частоту возможных колебаний (Мг 9.31).
Удобно эту цепь перерисовать так, как на рис. 9.2, б. Сразу видна
симметрия. На одном конденсаторе нет разностипотенциалов, и
поэтому отсутствует заряд. Ток через него не идет. В центральной
точке одинаковые токи (обозначим их 1) складываются. По (9.2),
(9.3) и по Кирхгофу для суммы падения напряжений имеем
1,21’ + и’ +% = о.
Отсюда
314” + % = О.
Из (9.11) и (9.8)
_ 1
_ (3Ьс)"2`
На рис. 9.3 изображена система, в которой вначале через индук-
тивность Ь и замкнутый ключ К течет ток 10, а напряжение на кон-
денсаторе равно нулю. В момент времени г= О ключ размыкается.
Пренебрегая активным сопротивлением всех элементов цепи, най-
дем напряжение на конденсаторе и ток через него как функцию
времени (Не 9.32). Из (9.2) и (9.3) для цепи
после размыкания ключа имее л
д1*+1‚1*+%=о.
“до
Отсюда
317

Из (9.| 1) и (9.12) имеем решение в виде
4 = А 5111 (001 + Всоз (001.
Из условия, что напряжение на конденсаторе, а значит и заряд,
равно нулю, находим В = О. Для определения второй постоянной
рассмотрим момент времени, бесконечно близкий к начальному,
когда через конденсатор идет ток 10,. Из уравнения для токов, в
котором можно считать 4 = О, получаем
14101 ’" о) + [числ ’ О) = О-
Откуда находим
, _ д;
01 - -
д + 12
Подставляя этот ток как начальный в решение для тока
1 = 4’ = Асоо сов 0001,
находим А = ЬдС1о. Поэтому
_ Ь, 10 совшо!
д + 12
С одной из пластин конденсатора мгновенно испаряется тонкий
слой вещества, несущий заряд (40), который затем движется как целое
с постоянной скоростью и к противоположной пластине (рис. 9.4).
Найдем зависимость тока в ЬС-цепи от времени при движении слоя
в конденсаторе, если расстояние между пластинами конденсатора И,
площадь пластин 5‘ и индуктивность катушки Ь (М9 9.50). Конденса-
тор со слоем можно рассматривать как два последовательно соеди-
ненных конденсатора с изменяющимися емкостями и зарядами.
Обозначим заряд на левой пластине конденсатора 90) — 40, на ле-
вой стороне слоя 40 — Оп), на правой стороне слоя — 00), а всего
-на слое 40 ‚ на правои пластине конденсатора, -
00). Используя (3.56), для емкостей конден-
саторов имеем:
для начального
1 и и = % = д], эйпшог.
5
Со ' т
и для образовавшихся
5 5
‘Ё т т’ ‘г " тщ-
3!8

Из (9.4) получаем (в системе Гаусса)
вЂ”,А1'+ + вЂ” = О.
1, Д вЂ” до Д
с С~(х) С2(х)
Учитывая, что Д' = 1, х' = о, и вводя обозначение
2
0)' =вЂ”
~СО
(в системе Гаусса), получаем
+О~ 1 = Чо'овЂ”
Ь
Используя решение (9.12) однородного уравнения (9.11) и част-
ное решение неоднородного
а также начальное условие 1(О) = 1'(О) = О, находим
1 = до вЂ” (1 вЂ” сови~),
В однородное элекгрическое поле Ео перпендикулярно ему по-
мещены две плоскопараллельные незаряженные металлические пла-
стины (площадью Я, с расстоянием между ними Ь), образующие
плоский конденсатор. Найдем зависимость заряда конденсатора от
времени, если в момент времени ~ = О пластины закорачивают через
катушку индуктивностью А (М 9.51). На пластинах происходит раз-
деление зарядов (на +д и вЂ” д). Обозначая емкость конденсатора С,
находим поле внутри конденсатора
Е=Ео+ ~.
вЂ” 0 Ьс.
Используя (9.7), получаем в системе Гаусса
вЂ” Ад" + ЬЕ = вЂ” Ад" + ~ + ЬЕо = О.
Вводя обозначение
2
О)
2 С
ЕС
319

Найдем время, за которое ток достигает максимального значе-
ния, и это значение, если конденсатор емкостью С, заряженный до
напряжения ЭДС 8, в момент времени 1= О замыкается на катушку
индуктивностью Ь и сопротивление, равное критическому (9.21) для
образовавшегося контура (М9 9.36). При 1= О имеем с; = а = 8С, 1 = О,
Ь = аВ. Откуда 1 = —ВЬ!е“3’. Время максимума определяем из условия
(11 _‚
д: ВЬ(В1—1)е д =о.
Это дает
1 1 1/2 [b ‹С)1/2
= — = — = ЬС , 1 = — — .
‘м В то ( ) м е Ь
Чтобы рассмотреть случаи В 2 то, введем обозначение
1/2
у = (в? - (03) . (923)
Тогда из (9.17) и (9.18) х = Ае-У’ + Ве”, а из (9.16)
4 = pȒ + у)’ + Pѐ (у " В)’_
Постоянные интегрирования А и В определяются из начальных
условий.
Для характеристики затуханий вводится ряд величин. Время, за
которое амплитуда уменьшается в е раз, называется временем релак-
сации. Оно равно
1
т = Тb (9.25)
ДВКРОМВНТОМ ЗЯТУХЗНИЯ НЗЗЫВЗСТСЯ ОТНОШСНИС ЗМПЛИТУД Через
40)
период Й ‚ а логарифмическим декрементом затухания называется
(г) 1
›„=1 Ь: Т=—, 9.26
п[‹1(“7`) В А’, ( )
где А’, — число колебаний, за которое амплитуда уменьшается в
е раз.
добротностью О колебательного контура называют величину
1: 1: _ _:)_=Ш‚_
О-Х-ЁТ-пде-ш к. (9.27)
322

Следовательно, для добротности из (9.27) имеем
_ _ Ь(1+г/К)/ЬС
25 г 1+Ьржс ’
Отношение добротностей
0.. 1 +Ь/ГКС 3
— = ———— = 10 .
о’, 1 + г/К
Рассмотрим колебательный контур, который содержит катушку
с индуктивностью Ь и конденсатор емкостью С с утечкой, сопротив-
ление которой равно К. Пренебрегая активным сопротивлением
катушки и прочих проводов, выведем уравнение собственных коле-
баний контура, найдем собственную частоту колебаний (по и лога-
рифмический декремент затухания А (Не 9.35). На рис. 9.7 приведе-
на схема колебательного контура. Сопротивление утечки параллельно
емкости. Из (9.1)—(9.3) и (9.7)
Ы{+%=О, %=1„к, 1, =1„+4*.
Из второго соотношения 4’ = ВСЦ, из третьего 4” = 12 — 1;, из
первого
„ ч’ д _
9 + кс + ЬС О
Вводя обозначения
_ 1 2 _ 1
В "` кс’ “’° ’ ЬС’
приходим к стандартному уравнению затухающих свободных колеба-
ний (9.15). Его решение (9. 19). Из (9.26) получаем декремент затухания
_ _ лшс)“
А - ВТ _ —г.
Рис. 9.7
324

Число колебаний Не, за которое их амплитуда уменьшается в е раз,
определяется (9.27). Считая, что затухание слабое, найдем, во сколько
раз оно изменится, если в два раза уменьшить индуктивность и в два
раза увеличить емкость, сохранив неизменным активное сопротив-
ление (Не 9.33). Очевидно, что частота собственных колебаний (9.8)
при этом не изменится. Из (9.27)
А! =Ё=Ё=Д‹Ё)Ш =2_
е 1: пК лК С
Найдем добротность контура с емкостью С и индуктивностью 1„
если на поддержание в нем незатухающих колебаний, которые мож-
но считать малыми, с амплитудой напряжения на конденсаторе Н
необходимо подводить среднюю мощность (П) (Мг 9.37). Энер-
гия, содержащаяся в колебательном контуре, равна максималь-
ной энергии на конденсаторе СН2/2ЦВ соответствии с (9.13) пе-
риод колебаний
21:
Т = Т.
(Ьопр
Потери за период равны (НИТ Из (9.29) следует
си2/2 = Н, (с/Ь)”
(ШТ 2(1\/>
Колебательный контур составлен из конденсатора емкостью С и
катушки радиусом а и индуктивностью Ь, заполненной слабопрово-
дящим материалом с удельной проводимостью А и магнитной прони-
цаемостью р. Пренебрегая сопротивлением проводов и потерями
энергии на перемагничивание, найдем добротность колебательного
контура (Мг 9.57). В данном контуре потери энергии связаны не с
сопротивлением в нем, а с процессом нагрева вещества внутри ка-
тушки, которое не влияет на параметры собственных колебаний,
определяемых уравнением (9.11). Используя его, имеем для собствен-
ных колебаний тока и их частоты
0:27:
2 02
= П?‘
Потери будут уменьшать амплитуду тока 10. Они определяются
Циркулярными токами в веществе внутри катушки, связанными с
326
1 = 10 созсог, а)

что падение напряжения на С, противоположно падению напряже-
ния на С‘. Поэтому
Д—Ё+КЁ=О.
С] С, а’!
Из сохранения заряда 41 + 42 = 40. Исключая из дифференциаль-
ного уравнения 4, и учитывая, что в начальный момент 41 = 40,
получаем
1+ (с,/с,)ехр[-(с, + с,)г/кс,с,]
1+С2/С,
Ч = ‘10 -
40
1 + С2 /С,
К такому же значению стремится и конечное значение 41,‘ при
стремлении Времени гк бесконечности. Соответственно
При стремлении сопротивления к нулю 4, стремится к
Чо
Используя (3.67), получаем энергии конденсаторов. Потери энер-
гии на сопротивлении (на джоулеву теплоту) равны разности на-
чальной и конечной энергий конденсаторов
12С2/С1
=АИ/=И/—И/ И/ =— -———.
О о (1+ 2) 2Ч0С1+С2
Если задано напряжение По, которое равно 40/ С, а требуется най-
ти ток
__‹1‹1
1’ ан
(Мг 9.18), то, пользуясь полученной формулой, имеем
1 = Шехр{_ (С, +С2)1]'
кос,
Используя этот результат, можно прямым расчетом найти ко-
личество выделенной в соединительных проводах теплоты, пренеб-
регая индуктивностью проводов, например для случая С] = С, = С
(Мг 9.19). Из (3.18) (закон Джоуля-Ленца) имеем (10 = 12Ка71.
328

ет максимального значения, ключ К вновь размыкают. Найдем, ка-
кой заряд протечет через сопротивление К, если сопротивление дио-
да В в схеме в прямом направлении много меньше К, а в обратном —
бесконечно велико (М 9.27). После замыкания ключа ток идет только
через индуктивность, так как на диоде В потенциал в верхней точке
выше, чем в нижней. Из (9.7) для заряда на конденсаторе
ч” + М; = 0,
ГДЕ
2 _ 1
_ 2..6
Решение этого уравнения а = А зйп (о: + Всов юг. В начальный мо-
мент заряд на конденсаторе 40, а ток через индуктивность 4’(О) = О.
Используя это, находим с; = 40 сов юг, 1 = —4’ = ада) вйп ш. Откуда
[шах = чаш. В момент максимального тока (заряд на конденсаторе
равен нулю) после отключения конденсатора ток идет через диод.
Из (9.7) Ы’ + К1= 0. Интегрируя с учетом, что здесь в начальный
момент ток был максимальный, получаем 1 = [Шахе-ШК Для заряда,
протекшего через К,
О)
... Ь С 1/2
Ч =хйл= ’тах%=40&%'
Длинный соленоид, длина которого равна 1, а площадь витков 5,
замыкается в некоторый момент времени последовательно с сопро-
тивлением К на источник постоянною напряжения с ЭДС 8. В сред-
ней части соленоида находится небольшое короткозамкнутое коль-
цо, площадь которого равна о, сопротивление г. Плоскость кольца
перпендикулярна оси соленоида. Пренебрегая самоиндукцией коль-
ца, определим радиальное давление на него (т. е. радиальную силу
на единицу длины) в тот момент, когда оно максимально (Мг 9.23).
Из (9.4) имеем
1,411 ‚
Решая ЭТО уравнение, С УЧСТОМ ТОГО, ЧТО В НЗЧЗЛЬНЫЙ МОМЕНТ ТОК
равен нулю, находим
_ Е _ _ 2 Ш
1- к|:1 ехр( с `:
332

Используя (5.27) и (5.28)', находим индуктивность тора
г
Е = 27~о вЂ”.
т
т
ЭДС И:, в кольце определяется (7.1). Для тока в кольце 1, по-
лучаем
о1ЫВ ~ г Я~
1, = вЂ” = вЂ” вЂ” вЂ” = 2аУ вЂ” ехр вЂ” с вЂ” .
г гс й гЯЙ
Из (4.18) находим джоулевы потери
г
жс гЯ,Яг,
2 2
Два соленоида имеют одинаковые геометрические размеры, но
один из них изготовлен из проволоки вдвое большей площади
поперечного сечения и вдвое меньшей длины, чем другой. Мате-
риал проводов обоих соленоидов одинаков. Найдем, в обмотке
какого из них будет выделяться больше теплоты, если магнитные
поля в них одинаковы, а также у какого из них меньше время
установления магнитного поля (М 9.26). Обозначая сечение про-
водов а и их длину Ь, из (4.14) получаем для отношения сопро-
тивлений проводов
Яг "г ~~ 1
Я1 Ь1 Ог 4
При одинаковых диаметрах соленоидов отношение числа вит-
ков пропорционально длинам проволок
"г 1
у, Ь, 2
Так как по условию длины соленоидов одинаковые и устанавли-
ваются одинаковые магнитные поля, то из (5.23) следует
Используя (4.18), для отношений выделившейся теплоты имеем
334

В предыдущих задачах с помощью (9.4) были получены уравне-
ния установления тока и соответственно магнитного поля, куда вошли
характерные времена установления 1:. Используя (5.29) для индук-
тивн сти соленоида
1
1
к Ь=4лм2%,
НЗХОДИМ
172 _ 12 к1_(”2]2 31 _1
171 11 32 М 1 32
В схеме, приведенной на рис. 9.13 и состоящий из двух конту-
ров с известными Ё, г, Ь], 1,2 и М, в некоторый момент, когда в
первом контуре уже установился ток, одновременно и мгновенно ра-
зомкнули ключ К‘, а К2 замкнули. Вычислим энергию И/д, вьщелив-
шуюся на сопротивлении К, а также энергию ИЗ, полученную вторым
контуром, пренебрегая в нем омическим сопротивлением (М) 9.42).
Ток, установившийся через индуктивность Ь], равен 110 = ЁЁ/г. Для
второго контура можно написать (7.1), учитывая, что поток магнит-
ного поля через вторую индуктивность складывается из собствен-
ного и взаимного (5.25)
Интегрируя 12 от нуля до 122 и 1, от 110 до нуля, получаем 1‚212к = М1ю.
Второй контур получает энергию, которая в нем в результате содер-
жится
2 2 2
т-ь%=Мъ%:-=М2/‘:’2-
ИЗ сохранения ЭНЕРГИИ НЗХОДИМ
и/ гд-ё-щ =(1-Ё)1,Ё=(1 М: )Ь(Ё/’)2.
2 "Д"; 2
На рис. 9.14 изображена электрическая цепь, состоящая из бата-
реи 8, сопротивлений г и К и индуктивности 1,2. К катушке 1,1 изда-
335

(к. к;
ё м / ‘
1-й 2-й
контур д: 52 контур
Рис. 9.13 Рис. 9.14
лека приближают короткозамкнутую сверхпроводящую катушку с
индуктивностью Ь, Первоначально ток в ней отсутствует, а после
сближения с катушкой 1,1 он становится равным 12. После сближе-
ния катушек ключ К замыкают. Найдем, какая энергия выделится
на сопротивлении К в виде джоулевой теплоты (Не 9.43). Первона-
чально в катушке Ь, течет ток
д.
1 = ' .
ю К+г
Как и в предыдущей задаче, поток магнитного поля через вто-
рую индуктивность складывается из собственного и взаимного (5.27)
1
ф = 20,1, + М1,).
НО ЗДЕСЬ надо УЧЕСТЬ, ЧТО МЕНЯЕТСЯ взаимная ИНДУКТИВНОСТЬ М,
Т. Е.
си, дм},
1* д: + а:
Интегрируя 1, от нуля до 12К и М], от нуля до М/ю, получаем
Ь212к = ’М11о°
Энергия взаимодействия катушек
=О.
130 1% 130 13
шк = дТ+1о7+М1ю12 =14Т‘1«27-
Эта энергия и выделится в виде теплоты на сопротивлении К.
В схеме, изображенной на рис. 9.15, при замыкании ключа К
через гальванометр Г протек заряд 4. Определим коэффициент вза-
имоиндукции М катушек, обозначенных как Ь, и 1,2, если извест-
336

Рис. 9.21
график зависимости 1/(1) (Мг 9.54). Используем
решение предыдущей задачи. Соотношение соб- “$912
ственной частоты контура и длительности импуль-
са таково, что происходят два колебания (рис. 9.21).
Среднее значение напряжения на этом участке (И) = Е = 5 В. Через
Тповторяется изменение напряжения на конденсаторе. Среднее зна-
чение за Травно (Ут) = ( И) т/ Г Чтобы эта величина равнялась 2 В,
из последнего соотношения Т= 0,05 с.
После размыкания ключа в контуре (рис. 9.22) возникают мед-
ленно затухающие колебания, максимальная амплитуда напряжения
которых Нтах в п раз превосходит напряжение батареи ЕЁ. Найдем
собственную частоту контура ш, если уменьшение амплитуды коле-
баний в е раз происходит за время т: (М 9.30). Из (9.19) получаем
для затухающих колебаний
а = е-“(А зйп со: + Всов ил).
Как и в (99), (93) и (917),
К 1
В=Е‚ ЮЁ=Ёэ Ф2=ШЁ‘В2-
В начальный момент (1= О) имеем П = ё’, 1 = 4’ = 8/12. В резуль-
тате получаем
= див» 1 ; 1)-
П 4С Ее [соэшньокксдс этом].
При слабом затухании
1 1 1/2
В’ <<ш%„ ш ==ш0, т=—>>—=(ЬС) .
В (‚По
Используя это, имеем
С! = $65’ Ёшвйп ш.
340

Из условия и этого результата
Поэтому а) = 2п/т.
Постоянная времени разряда плоского масляного конденсатора
через некоторое сопротивление равна т1. После того как масло кон-
денсатора отсырела, постоянная времени разряда через то же сопро-
тивление оказалась равной т2. Найдем удельное сопротивление р
отсыревшего масла, если его диэлектрическая проницаемость е не
изменилась (М 9.6). Используя (9.1) и (9.3)‚ имеем
12% +% = о.
Откуда
4 = воет = Чае-т- ‹9.з0›
Таким образом, постоянная разряда конденсатора
т = КС. (9.31)
При прохождении тока через конденсатор схема цепи выглядит,
как на рис. 9.23. Конденсатор разряжается через параллельно со-
единенные сопротивления. С учетом (4.14) для нового сопротивле-
ния К] получаем
1 1 5
—= +—.
к, 1
Ё р
Таким образом, т, = НС, т2 = К1С. Учитывая выражение для ем-
кости (3.56)
85
С - та»
Находим ъ
р = 41:17,
(т1 — 12 ) Е . С
Сферический конденсатор с радиусами сфер 1-1 и 1-2 ::
заполнен слабо проводящей средой. Емкость конден-
сатора равна С, а разность потенциалов на конден-
саторе после отключения его от батареи уменьши-
лась в два раза за время 1. Найдем диэлектрическую Рис. 9.23
341

Интегрируя и используя условие, что в начальный момент с; = О,
находим
_$СК 1—ехр[—(кд +К2)1/СК1К2:|
_ 2 с(к,+к,) `
К контуру 1„ С, К (рис. 9.25) с малым затуханием в момент г= О
подключают источник постоянной ЭДС ЁЁ с ничтожно малым внут-
ренним сопротивлением. Найдем напряжение Н на конденсаторе С
в зависимости от времени г, а также, на какое минимальное напря-
жение он должен быть рассчитан (Мг 9.13). Изменение заряда на
нем с; = ПС описывается уравнением (9.7). Решение его представля-
ет сумму решения однородного уравнения (9.19) и частного реше-
ния уравнения (9.7), которое для разности потенциалов на конден-
саторе имеет вид П = ё. Таким образом, общее решение для напря-
жения на конденсаторе
П= ё’ + е-“(А $111 о): + Всоз оп).
В начальный момент 1= 0 заряда на конденсаторе нет, и поэто-
му П = О. Откуда следует В = —$. Так как индуктивность препят-
ствует увеличению тока скачком, то ток в начальный момент равен
нулю, т. е.
дП_1д‹1_О
д! С а’:
Дифференцируя и подставляя, получаем
А = -ЁЁ.
(0
Окончательно
О.)
П = 8[1— е’°' (совы: + В зйп 001)].
Так как по условию затухание мало, то г“ = 1 и, следовательно,
вт = 2пЁ < 1.
О.)
Поэтому Н = б’ (1 — сов (М). Напряжение, которое должен выдержи-
вать конденсатор, П = 28.
Рассмотрим вариант, когда катушка индуктивностью 1„ кон-
денсатор емкостью С и батарея с ЭДС ё’ и внутренним сопротив-
343

Л = 2,5 Ом и индуктивность Е = 10 ' Гн и подключена через кон-
денсатор емкостью С = 0,2 мкФ к источнику постоянной ЭДС
Й = 12 В. Отношение числа витков обмоток трансформатора
2 вЂ” 4О
Ф1
Найдем, через какое время после размыкания прерывателя (клю-
ча К) возникает разряд, если пробой зарядного промежутка свечи
происходит при напряжении У = 3 кВ (М 9.:-4). Используя (9.4),
получаем уравнение колебаний в контуре
Х.Х'+И+ ~ = г:..
В начальный момент ~ = 0 имеем д(0) = О, Х(0) = Й/Л и из урав-
нения колебаний 1'(О) = О. Дифференцируя уравнение колебаний,
получаем уравнение для тока в первичной обмотке и начальные ус-
ловия
Х" + 2рХ'+ и,'Х = О, 1(0) = вЂ” ', Х'(0) = О.
Здесь введены обозначения
1/2
р = вЂ” =1,25 10' с ', и2 = = 0,71 10' с '.
ы ' ' ' сс
Так как р «ио и рассматриваются времена, не превышающие
четверти периода колебаний (нарастание напряжения до величины
меньшей максимума), а период Т = 10-~ с, то можно пренебречь
затуханием и искать решение в виде
1(~) = Асоьи~+ Выпи~.
Используя начальные условия, находим
1(~) = вЂ” соки~.
Я
Напряжения на обмотках определяются зацепленными потока-
ми индукции магнитного поля Ч' = ЖФ. Поэтому из сохранения
потока для напряжения на вторичной обмотке, которое в момент
проскакивания искры равно напряжению на разрядном промеясут-
ке, получаем
Л2 ~ ~2 ~." ~2
У = вЂ” Х,Х' = вЂ” вЂ” иХ,япи~ = вЂ” Ос япи1.
Ж1 Ф1 ~ Ж1
345

никает импульс напряжения, величина которого измеряется с помо-
щью ооциллоцзафа. Найлом иипаецзую аоецриимаиаоеза з образца, еоли
Й = 4,5 В, Л = 10 Ом, Е = 1 Гн (пустой катушки), У = 6,8 мВ (М 9.3).
Из (9.4) следует, что при быстром удалении образца (Лг «Х./Л = 0,1 с)
сохраняется магнитный поток ЕХ= рАХО, где Х = фЛ. Таким обра-
зом, после удаления образца
1=ИХ, =1~ вЂ”.
Я
В итоге, используя (6.9) в системе СИ, получаем для напряже-
ния на катушке У = й вЂ” И = 1~'(1 вЂ” ц) = вЂ” ~Й Откуда
т, = вЂ” =1,5 10
-3
ф'
В контуре, состоящем из батареи с ЭДС Й, сопротивления Л и
конденсатора емкостью С = 10 'о Ф, очень быстро за время Л~ = 10 ' с
уменьшают расстояние между пластинами в два раза. Найдем, при
каком условии за это время заряд конденсатора практически не изме-
нится, а также определим джоулеву теплоту О, которая выделится в
сопротивлении Л к моменту перезарядки (Мо 9.1). Для того чтобы за
время сближения пластин изменение заряда, равное произведению
тока 1 на время М, было мало по сравнению с зарядом (д), необходи-
мо условие ХЛ~ «д = СЖ, т. е. должно быть Я» Л~/С = 10' Ом. При
уменьшении расстояния между пластинами в два раза емкость
увеличивается в два раза С, = 2С. Используя (9.1) и (9.3), получа-
ем уравнение, описывающее изменение заряда после раздвиже-
ния пластин,
Л вЂ” + вЂ” = Ж.
дд д
й
Решение его
д=бС1+Кехр вЂ” вЂ” .
ЯС,
Для определения постоянной К используем условие, что в на-
чальный момент заряд на пластинах д = ЖС. Поэтому получаем
д о'С 2 е-г/2лс
Работа батареи, равная А = Лдй = дй = СЖ2, идет на изменение
энергии конденсатора и джоулевой теплоты. Энергию конденсатора
347

после сдвигания пластин можно вычислить с помощью (3.67) из
постоянства заряда и увеличения емкости в два раза
1 Ч $2
И’ = — = С —.
' 4
Заметим, что при сдвигании разность потенциалов уменьшается
В два раза, И СНОВЭ
в ‘ : 2 2
1 ё б;
щ „Ы „с,
После работы батареи энергия конденсатора
1
В результате
е2
о=А-(%-И4)=С%-
На рис. 9.31 показан контур, состоящий из постоянной ЭДС 8,
сопротивления К и плоского конденсатора, из которого очень бы-
стро извлекают пластину из диэлектрика с проницаемостью е, кото-
рая заполняла весь объем конденсатора. Найдем зависимость тока
в цепи от времени, если после удаления пластины емкость кон-
денсатора равна С (Не 9.4). До удаления пластины заряд на кон-
денсаторе с; = ЁЁе С. В процессе удаления пластины в цепи идет ток
371 = ё’ —4/еС
д: к '
Так как справа стоит конечная величина, то при бесконечно
малом а’! должно быть бесконечно малое да, т. е. с; можно считать
постоянной величиной. Как следует из (9.7)‚ дальнейшее изменение
4 описывается уравнением
12% +% = 25
Ц С 8
к; :Г': Е] ——- Разделяя переменные и интегрируя при
’ условии, что в начальный момент заряд
ё; равен ёеС‚ получаем
Рис. 9.31 4 = 8С + 2$С(е -1)е"/“С.
348

Отсюда для тока находим
1 = вЂ” вЂ” 6(е вЂ” 1)е '~"с.
Я
Колебательпый контур содержит индуктивность и емкость. В не-
который момент времени из конденсатора быстро извлекают плас-
тину с диэлектрической проницаемостью е = 4, занимавшей весь
его объем. Найдем, как изменится частота колебаний контура, во
сколько раз изменятся максимальные величины заряда на конден-
саторе и тока в катушке, если пластину извлекают в момент, когда
заряд на конденсаторе:
1) отсутствует;
2) максимален (М 9.5).
В соответствии с (3.56) емкость конденсатора уменьшится в 4 раза
с,
4
Из (9.8) для изменения частоты колебаний получаем
Если при извлечении пластины заряд на конденсаторе отсут-
ствует, то в соответствии с (З.б7) энергия конденсатора равна нулю.
Вся энергия колебательного контура в этот момент находится в ка-
тушке. В соответствии с (7.20) она равна
2
~1м
2
Максимальные значения тока не изменятся 1,„= Х,„. Учитывая,
что при колебании вся энергия катушки переходит в энергию кон-
денсатора (конечно, когда нет потерь, т. е. сопротивления, как в
данном случае),
2 2 2
~гм ~Ам йм
2Сг 2 2С~
находим

Если на конденсаторе есть заряд, то при быстром извлечении
пластины он не успевает измениться. Значит, ад = ат. Используя
закон сохранения энергии, получаем
1/2
Щ = (Я) = 2_
11м С2
Другой вариант колебательного контура, в котором емкость не
изменяется, а из катушки индуктивности быстро вьщергивают сер-
дечник из сверхпроводника с радиусом в два раза меньшим радиуса
катушки. Найдем, как изменится частота колебаний контура, во
сколько раз изменятся максимальные величины заряда на конден-
саторе и тока в катушке, если сердечник выдергивают в момент,
когда ток в катушке:
1) отсутствует;
2) максимален (Не 9.10).
В соответствии с (5.29) для отношения индукции соленоида с
сердечником 1,0 к индукции без сердечника Ь, получаем
Из (9.8) следует, что отношение частот
1/2 1/2
щ = (д) = _<3>
‘до 10 2
В первом случае энергии В катушке НОТ, ВСЯ энергия В конденса-
торе, который не меняется, и поэтому а“ = дом = 4. Из сохранения
энергии (так потерями на сопротивление пренебрегаем)
Ё = ‚д = [д
2 2 2 '
Откуда
Щ- : (3)1/2 .
{Ом 2
Во втором случае в соответствии с (7.1) и (5.28)

Длинный тонкий соленоид радиусом го подключен к батарее, и
по нему течет постоянный ток 10. Сердечником в соленоиде служит
сплошной цилиндр из сверхпроводника радиусом г, = О,5г0. Сердеч-
ник быстро выдергивают из соленоида. Найдем значение 11 тока в
обмотке непосредственно после удаления сердечника и его дальней-
шее изменение (Мг 9.9). В соответствии с (5.29) для отношения ин-
дукции соленоида с сердечником 1.0 к индукции без сердечника 1„
получаем
[ч ’°о2
Используя (7.1) и (5.28), из сохранения потока магнитного поля
при быстром удалении сердечника получаем, как и в (9.32), 1,010 = Ьд/д.
Откуда
2
г 3
"о
Окончательно устанавливающийся ток определяется ЭДС ба-
тареи и сопротивлением соленоида и поэтому равен начальному
току 10. График изменения тока во времени качественно показан
на рис. 9.33.
Изменить индуктивность можно и простым растягиванием ка-
тушки (М9 9.17). Найдем, как изменится собственная частота коле-
баний в контуре, состоящем из индуктивности 1,0 и емкости С, в
котором совершаются колебания силы тока 1 = 10 сов то:
с частотой
1 1/2
“о = и ’
если в момент 1 = О длину катушки (10), представляющую спираль,
очень быстро растянуть в два раза. Из (5.19) по-
’ ц ЛУЧЗСМ, ЧТО при УВСЛИЧСНИИ ДЛИНЫ КЗТУШКИ В два
‚А раза индуктивность ее уменьшится в два раза
“тж
1„ ----- 11 10 1 .‚
Е)- = Т = 5 , а частота собственных колебании
1
7: 1 1/2 1/2
О) = —"— = (00 Г .
Рис. 9.33 Ь,С
352

В момент времени 1 = О сила тока максимальна (10). При быст-
ром растяжении выполняется (9.3О), поэтому сила тока практичес-
ки скачком увеличивается в два раза. При этом вся энергия колеба-
тельного контура находится в катушке. Для отношения энергий по-
лучаем
2
Ш = М. =
2
"Ъ 1010
Энергия ВОЗРЗСТЗСТ В ДВЗ раза за СЧЕТ РЗбОТЫ СИЛ ПО растяжению
катушки.
В колебательном контуре с малым затуханием одновременно уве-
личивают емкость конденсатора и самоиндукцию катушки в одно и
то же число раз, равное п. Увеличение проводится в произвольный
момент за время, малое по сравнению с периодом собственных ко-
лебаний контура. Найдем соотношение между амплитудами тока
11 и 12 до и после изменения параметров контура (Мг 9.40). При
быстром изменении индуктивности не изменяется магнитный по-
ток (7.1), поэтому энергия в катушке (7.2О) обратно пропорциональна
индуктивности
Ф2
И/ч = -—.
^ 2Ь
При быстром изменении емкости С не успевает измениться за-
ряд конденсатора с], поэтому энергия (3.67) обратно пропорциональна
емкости
42
э - 76-
Так как индуктивность и емкость меняются в одинаковое число
раз, то суммарная энергия И/изменится в такое же число раз. Мак-
симальные значения тока (амплитуды) определяются полной энер-
гией, поэтому
12 1 1 12
И/ = $ = _и/ = - 4.
2 19 2с п 1 п Ь‘ 2с
Так как И ИНДУКТИВНОСТЬ УВСЛИЧИВЗЮТ В п раз, ТО
1? п2.
1:;
- з
23 207 353

нежелательной перегрузке источника. Достаточно, чтобы Ум было
порядка И), т. е. г еч К.
Защитить аналогичную цепь можно и с помощью конденсатора,
как показано на рис. 9.35. Найдем напряжение на конденсаторе после
отключения источника электричества, считая, что 4Ь > СК2 (Мг 9.15).
Учитывая принятое условие, а также (9.8)‚ (9.9) и (9.17)‚ имеем в
цепи свободные затухающие колебания, описываемые уравнением
(9.15) и его решением (9.19). Начальными условиями при г= О яв-
ляются
ей; у
Ч=ЧО=%С и [:2;:—%_
Из первого получаем В = УС, а из второго
И, С
= —— У —.
А Ко) + В о ш
Таким образом,
5 11,643’ [сов ш: + — %дазйп ил].
Груз массой т подвешен на тонкой проволоке длиной !(рис. 9.36)
и сопротивлением К в однородном горизонтальном магнитном по-
ле В и совершает малые колебания в плоскости, перпендикулярной
полю. При этом проволока всегда остается замкнутой накоротко
неподвижной внешней цепью. Найдем число колебаний, по проше-
ствии которых амплитуда тока в цепи уменьшится в е раз (Не 9.39).
В уравнение колебаний маятника (см. 1, с. 244) надо Добавить мо-
мент силы Ампера (7.4)
1
тср” = —т31‹р — [х Ё с1хВ.
о
К `Ч ‘ъ
Рис. 9.35 Рис. 9.36
356

В контуре из-за изменения потока магнитного поля создается
ЭДС (7.1)
›_1 21
б-2В1с, .
которая создает ток 1 = 55/12. В результате получаем уравнение сво-
бодных затухающих колебаний
ф” + 2В‹р’ + шёф = О.
Здесь введены обозначения
12
В=В2—-—
2 (в единицах СГСЭ); 00% =
8тс К
Ё
1 .
Используя (9.19)‚ находим
ср = срое“”соз (а)! + б).
Изменение амплитуды отклонения фм = ‹р0е'°‘. Максимальный
угол отклонения достигается при а)! + б = О. Так как ЭДС и, следо-
вательно, ток пропорциональны ф’, то максимальный ток возникает
при (о! + б = п/2. Для тока имеем
1= ф’ = —‹р0е‘°’[Всо5 (а): + б) + шзйп (о)! + 8)].
Изменение амплитуды тока [м = фоте ‘В’. Время уменьшения ам-
плитуды тока в е раз
т = 1 = 8тс2К
В 3212
Так как
(_о2=(1)ё—В2=(оё=-ё, Т:ЁЕ,
1 („О
то можно вычислить число колебаний п = т/Т
Кольцо из тонкой проволоки, имеющее омичес-
кое сопротивление К = 104 Ом, массу т = 1 г и ра-
диус г = 1 см, подвешенное на упругой нити, совер- В
шает малые крутильные колебания с частотой у = 1 Гц
(рис. 9.37). Если поместить кольцо в магнитное поле,
параллельное плоскости кольца в положении равно- Ф
весия, то возникает сильное затухание колебаний.
Оценим магнитную индукцию поля, при которой Рис. 9.37
357

движение крутильного маятника происходит в критическом режиме
(т. е. колебательный режим переходит в апериодический), не учиты-
вая самоиндукцию кольца и затухание без магнитного поля (М 9.41).
В уравнение крутильных колебаний (см.: 1, с. 266) надо добавить
момент силы Ампера (7.4)
л/4
Ур" + Ау+4 ~ гяп01ЫОяпО вЂ” = О,
О
С
где 1 вЂ” момент инерции кольца, У = тг'/2; Й вЂ” модуль кручения
нити; 0 вЂ” угол между направлением тока в кольце и направлением
магнитного поля и одновременно из центра кольца на элемент тока
от вертикали; д вЂ” угол поворота кольца от положения равновесия,
который считаем малым (яп р = р). Момент силы Ампера в резуль-
2 В
тате равен лг У вЂ”.
С
В контуре из-за изменения потока магнитного поля создается
ЭДС (7.1)
1'. = Вяг вЂ”,
2 Ю
С
которая создает ток Х = фЯ. В результате получаем уравнение сво-
бодных затухающих колебаний аналогичное (9.1.5)
~р" + 2~3~р' + и,'~р = О.
Здесь введены обозначения
~3 = В, (в единицах СГСЭ), и
2( )
2
2С ЯУ О у'
Из (9.17) и (9.18) критический (апериодический) режим возникает
при ~3 = и,. Отсюда находим соответствующее этому магнитное поле
с(2Шио) с(2тиотЯ)
'ш' 7~Г
Конденсатор емкостью С присоединен к верхним концам двух
параллельных медных шин, расположенных вертикально на расстоя-
нии ( друг от друга. Однородное магнитное поле В горизонтально и
перпендикулярно к плоскости шин. Вдоль шин в магнитном поле
падает без начальной скорости медный проводник массой т так, что
всегда имеется контакт между проводником и шинами. Пренебре-
358

гая сопротивлением и индуктивностью проводников, а также тре-
нием проводника о шины, найдем:
1) ускорение проводника;
2) силу тока, заряжающего конденсатор (№ 9.45).
Из (8.1) следует, что в движущемся со скоростью х' проводнике
создается вдоль проводника электрическое поле Е = х'В и на кон-
цах проводника разность потенциалов
11= х'В1 = д/С.
(9.33)
На проводник, по которому идет ток 1, действует сила Ампера (7.4)
Г= Х1В.
(9.34)
Она направлена в соответствии с векторными произведениями в
(8.1) и (7.4) вверх. Уравнение движения проводника
тх" = тд вЂ” 11В = ту вЂ” СВ212х".
(9.35)
Отсюда находим ускорение проводника
х" =
т+СВ 1
и ток, заряжающий конденсатор,
туВ1С
и+ СВ21
Та же конструкция, но вверху вместо конденсатора присоединен
солеиони индуитивностью с с ничтожным солрогивлением. Найдем за-
кон движения проводника (№ 9.46). В данном случае падение напряже-
ния на проводнике вместо (9.33) равно падению на индуктивности
(9.36)
У= х'В1= АХ'.
Х" + В 1 вЂ” вЂ” В1 ~ = О.
тЕ Е
Используя начальное условие Х(0) = 1'(0) = О, получаем
1 вЂ” с08 и1
Х = ту
В1
где
и' = ВвЂ”
тЕ
359
Отсюда х"В1 = Х,Х". Для силы Ампера имеем снова (9.34). Под-
ставляя все соотношения в первую часть уравнения движения про-
водника (9.35), имеем

Из (9.36) и начальных условий имеем
1 — сов со!
3212
Если в той же конструкции вверху находится сопротивление К,
то вместо (9.33) и (9.36) получаем
Н = х’В1 = 112. (9.37)
Подставляя (9.37) в первую часть уравнения движения провод-
ника (9.35), имеем
х =т3Ь
х!
тх” = тд- ПВ = тд- 8212г.
При установившемся движении х” = О получаем для скорости
11-х 0
ÐÐ· (9.34) Ð¸ (9.37) Ð²Ð¸Ð´Ð½Ð¾, ÑÑÐ¾ ÑÐºÐ¾ÑÐ¾ÑÑÑ Ð¿Ð°Ð´ÐµÐ½Ð¸Ñ Ð±ÑÐ´ÐµÑ ÑÐ°ÑÑÐ¸ (Ð¾Ñ
Ð½ÑÐ»Ñ), Ð¿Ð¾ÐºÐ° ÑÐ¸Ð»Ð° ÐÐ¼Ð¿ÐµÑÐ° Ð½Ðµ ÑÑÐ°Ð½ÐµÑ ÑÐ°Ð²Ð½Ð¾Ð¹ ÑÐ¸Ð»Ðµ ÑÑÐ¶ÐµÑÑÐ¸ (ÐÐ³ 9.47).
Ð Ð°ÑÑÐ¼Ð¾ÑÑÐ¸Ð¼ ÐµÑÐµ ÑÐ»ÑÑÐ°Ð¹ (Ð: 9.48), ÐºÐ¾Ð³Ð´Ð° ÑÑÐ° ÑÐ¸ÑÑÐµÐ¼Ð° ÑÐ²ÐµÑÑ Ñ Ð·Ð°Ð¼-
ÐºÐ½ÑÑÐ° Ð¸Ð½Ð´ÑÐºÑÐ¸Ð²Ð½Ð¾ÑÑÑÑ, Ð° ÑÐ½Ð¸Ð·Ñ ÑÐ¾Ð¿ÑÐ¾ÑÐ¸Ð²Ð»ÐµÐ½Ð¸ÐµÐ¼ (ÑÐ¸Ñ. 9.38). Ð¢ÐµÐ¿ÐµÑÑ Ñ
Ð¿Ð¾Ð¼Ð¾ÑÑÑ (9.35)â(9.37) Ð¸Ð¼ÐµÐµÐ¼
ÑÑ â = ÑÑ + Ð²1(1, - 1â), Ð¸â = âÐÐ¬Ñâ, 121â = ÐÐ¬Ñâ.
ÐÑÑÑÐ´Ð°
Ñ â + (Ð1)2 âÐÐ + (Ð1)2 Ð¹ = 3.
ÐÐÐ¡ÐÐ¡ Ð¸Ð½ÑÐµÐ³ÑÐ¸ÑÐ¾Ð²Ð°Ð½Ð¸Ñ Ð¿ÑÐ¸ ÐÐ£ÐÐÐÐ«Ð¥ Ð½Ð°ÑÐ°Ð»ÑÐ½ÑÑ Ð£Ð¡ÐÐÐÐÐ¯Ð¥ ÐÐÐ¡Ð¡Ð
1 - Ð±Ñ ÑÐ¾Ð² Ð¾)!
Ñ = ÑÐ´Ð¬
(802
9
ÐÐÐ¡
Ð _ (302 Ð¤: =â¹Ð²1)2_
_ 2Ñ3 â Ñ1
ÐÑÐµ Ð¾Ð´Ð¸Ð½ ÑÐ»ÑÑÐ°Ð¹, ÐºÐ¾Ð³Ð´Ð° Ðº Ð²ÐµÑÑ Ð½Ð¸Ð¼ ÐºÐ¾Ð½ÑÐ°Ð¼ Ð¿ÑÐ¸ÑÐ¾ÐµÐ´Ð¸Ð½ÐµÐ½Ñ Ð¿Ð¾ÑÐ»Ðµ-
Ð´Ð¾Ð²Ð°ÑÐµÐ»ÑÐ½Ð¾ ÑÐ¾ÐµÐ´Ð¸Ð½ÐµÐ½Ð½ÑÐµ ÐºÐ¾Ð½Ð´ÐµÐ½ÑÐ°ÑÐ¾Ñ ÐµÐ¼ÐºÐ¾ÑÑÑÑ Ð¡ Ð¸ ÐºÐ°ÑÑÑÐºÐ° Ð¸Ð½Ð´ÑÐº-
ÑÐ¸Ð²Ð½Ð¾ÑÑÑÑ Ð¬ (ÑÐ¸Ñ. 9.39). ÐÑÐµÐ½ÐµÐ±ÑÐµÐ³Ð°Ñ ÑÐ¾Ð¿ÑÐ¾ÑÐ¸Ð²Ð»ÐµÐ½Ð¸ÐµÐ¼ ÐºÐ°ÑÑÑÐºÐ¸,
Ð¼ÐµÐ´Ð½ÑÑ ÑÐ¸Ð½ Ð¸ Ð¿ÑÐ¾Ð²Ð¾Ð´Ð½Ð¸ÐºÐ°, Ð° ÑÐ°ÐºÐ¶Ðµ Ð¸Ð½Ð´ÑÐºÑÐ¸Ð²Ð½Ð¾ÑÑÑÑ Ð¿ÑÐ¾Ð²Ð¾Ð´Ð½Ð¸ÐºÐ¾Ð² Ð¸
360

>< х
ХХХ
н" Ь
Х
ХХХХ ххх
ХХХ
{—.
О‘
Х
ХХХХ
„Ъ
ХХХХ
ш
ХХХХ
——:—
Рис. 9.38 Рис. 9.39
трением проводника о шины, определим закон изменения тока [(1),
а также координаты проводника х(1), начиная с момента начала па-
дения 1 = 0, х(О) = О (Не 9.49). Используя (9.33)‚ (9.35) и (9.36),
получаем
тх” = ту — 1В1, 1,1’ + а/С = В1х’.
Откуда, дифференцируя, имеем
1 х” В1/Ь
// р‘: = [ = .
1 + ЬС В Ь 3 - ви/т
Вводя обозначение
получаем
1”+ш21 = 31%.
Его решение при условии [(0) = О
— СОЗ (д)?
1
1 1 = В!
( ) 8 1,002
Для координаты проводника имеем
$0)!
1 — со
х” = __ 8212 у
8 8 тЬш2
Интегрируя и используя условия х’(О) = О и х(О) = О, получаем
1 В212 1— сов (от
х<’>=аг‘2["г‚г„т)*в2’2дтдг—

Для удовлетворения (1О.2) должно быть
Пшё — ю2)со5ш — 2Всо 5111 ш:|с1‚„ = Х0;_
Пшё - ш2)51п ч; + 2Всо со$ц!:|с1т = О.
Из (1О.5)
2Вю
каш = 10% _ш2.
ВОСПОЛЬЗУСМСЯ тригонометрическими ТОЖДССТВЗМИ
2 1
соз2 =———‚ зйп =——г.
ч, 1+тв2чл ч! 1+ст32ш
Получаем
со“! _ 2 2 2 2 2 1/2 ‚
“(по —ш) +46 т]
зйпц; = 26“)
“(на — (02 )2 + 4В2ю2 т” .
Подставляя в (10.4), находим амплитуду
Хо
[щ -„‚2)’ „ь 4В2ш2:|1/2 °
4„‚(ш) =
Максимальное значение амплитуды будет при ю = фрез,
емой резонансной частотой. Используя (1О.7), получаем
ш2 - 003-2132;
рез ‘
Хо
Чт = -
Р“ 2вшж
При со = О имеем
Х
‹1„‚(О) = %.
‘до
(1О.4)
(1О.5)
(1О.6)
(107)
НЗЗЫВЗ-
(1013)
(10.9)
00.10)
363

На рис. 10.1 показана зависимость амплитуды вынужденных ко-
лебаний от частоты вынуждающего воздействия. При уменьшении
затухания (уменьшении В) максимум становится острее и выше.
Частота резонанса при этом стремится к собственной частоте, а от-
ношение максимальной амплитуды к амплитуде при нулевой часто-
те приближается к добротности О (9.27).
Удобно в ( 10.7) ввести добротность и профиль пика. Обозначая
отклонение частоты от пика Аи) = |ш0 — оо| (при малых затуханиях
(при = то), из (10.7) и (9.27) получаем
ат: _ ЧтРез2 21/2. (10.11)
[1+(2А‹о/ш) С :|
На рис. 10.2 показано изменение фазы колебаний. При малых
частотах фазы совпадают. При резонансе отстают на п/2, а при боль-
ших частотах колебания происходят в противофазе воздействию.
Из ( 10.3) дифференцированием получаем изменение тока 1 в цепи
1= —шс1т$1п(‹о: + ш) = 1тсо$(ш1 + ш + п/2). (10_12)
Отсюда видно, что изменение тока опережает по фазе измене-
ние заряда на 112/2. При резонансе ток по фазе совпадает с вынужда-
ющим воздействием.
Для производной тока (второй производной заряда) по времени
получаем
1’ = ч” = с1тю2 сов (о): + ц; + 1:). (10.13)
Это изменение опережает на п/2 изменение тока и на я измене-
ние заряда.
отд
_ Хо
“гймз
д 13243, кип
|
д, (о) = Ё Ё (до Б
’" сед : в, _д.
2 . _ 2
юрсз] (по (О -ТС
шрсэ2
Рис. 10.1 Рис. 10.2
364

На рис. 10.3 показано изменение ампли- [ША
туды тока в зависимости от частоты вь1нуж-
дающего воздействия. Резонансное для тока
значение частоты равно собственной частоте.
Резонанс тока соответствует резонансу падения
напряжения на активном сопротивлении. Ре- к
зонанс заряда (1О.8) соответствует резонансу _
падения напряжения на емкости. Резонансу ‘до 0’
падения напряжения на индуктивности будет Рис_ 103
соответствовать резонанс второи производнои
заряда. Используя (10.3) и находя экстремум,
получаем
‘до
‘ 11 - 21111, П“
Установившиеся вынужденные колебания можно рассматривать
как протекание в цепи переменного тока.
Обозначая амплитуду прикладываемого напряжения Пт = ДЬ,
из (1О.13), (9.8) и (9.9) получаем для тока
(10.14)
= "т . (1о.15)
[[22 + (шЬ —1/‹1)С)2:|1/2
Формально это соотношение можно рассматривать как закон Ома
для амплитуд напряжения и тока. Величину, стоящую в знаменате-
ле, называют полным сопротивлением, или импедансом,
1 21/2
2=[к2+(юЬ-ЁЛ . (1о.1в)
Величину, стоящую в круглых скобках, называют реактивным со-
противлением (в отличие от активного сопротивления К), или релак-
тансом. индуктивным сопротивлением называют
2, = соЬ. (1о.17)
Емкостным сопротивлением называют
(1О.18)
АНЗЛИЗ колебательных процессов В МНОГИХ СЛУЧЗЯХ облегчается
при ИСПОЛЬЗОВЗНИИ КОМПЛЕКСНЫХ чисел. ЕСЛИ ДСЙСТВИТВЛЬНЫС ЧИСЛЗ
365

~=х+ гу,
где ~'= ~1.
Комплексное число можно записать в полярных координатах, введя
радиус-вектор р = (х' + у2)'~2 и угол <р из соотношения ф р = у/х.
Тогда получаем
~ = х + ~у = р(сов р + ~ яп <р).
(10.19)
Дифференцируя по р, получаем
вЂ” = р( вЂ” в1п<р+~'сову) = ~~.
И~
Ыф
Разделяя переменные и интегрируя, с учетом, что при 6 = 0 ~ = р,
находим так называемую формулу Эйлера
~ = р(сов<р + ~в1п<р) = ре'Р.
(10.20)
Комплексная (экспоненциальная) форма во многих случаях по-
могает упростить преобразования.
Для линейных уравнений всегда можно разделить действитель-
ную часть, для которой были получены решения, и мнимую. Вместо
уравнения (10.2) напишем уравнение для напряжения на конденса-
торе, предполагая его комплексной величиной
Г" + 2~3 Г'+ и'Е = Е и2е' '.
(10.21)
Частное решение ищем в виде
Г= Ае'"'.
(10.22)
Получаем
(10.23)
О вЂ” и +к2Р
2 2
Преобразуя с помощью формулы Эйлера знаменатель, полу ~аем
(10.24)
366
можно расположить на прямой линии вЂ” числовой оси, то для пред-
ставления комплексных чисел нужна плоскость, называемая комп-
лексной, на которой точкой определяется комплексное число (~),
имеющее действительную (по оси х) и мнимую (по оси у) части.
Оно записывается в виде

1) что покажет достаточно чувствительный амперметр переменного
тока с сопротивлением г, если его присоединить к двум из этих точек;
2) как изменится показание амперметра, если его перебросить в
положение, указанное штриховой линией на рис. 10.5 (М) 10.1).
Из (7.1) для ЭДС в кольце получаем
_ _1 дф
" _ Е?’
где Ф — поток магнитного поля в сердечнике.
Для обмотки из п витков в аналогичном соотношении надо
писать зацепленный поток ‘Р. Если рассеяние потока отсутствует,
то Ч’ = пФ. Поэтому 8 = пёк. В случае присоединения амперметра к
точкам А и С имеем контур из параллельно соединенных ампермет-
ра и третьей части кольца и последовательно к ним присоединен-
ных остальных двух третей кольца. Используя правило Кирхгофа,
получаем
П
._ 1 212 _1 9г+2К
$"_1(1/г+3/К+ з)-з’“з„к=
Обозначая ток через амперметр Д, а через часть кольца 11, по
правилам Кирхгофа имеем
1=1,+1„ 1г=—
И, СЛСДОВЗТСЛЬНО,
11: 31%} ЗЁЁ/п
1 = = - .
а 3г+К 9г+2К 9г+2К
ВО ВТОРОМ СЛУЧЗС ПОДСОСДИНСНИЯ, ОбОЗНЗЧСННОМ ПУНКТИРОМ,
ПОСТУПЗЯ ЗНЗЛОГИЧНЫМ образом, НЗХОДИМ
_ бё/п
а —9г+2К'
В опыте Мандельштама и Папалекси прямой однослойный со-
леноид с индуктивностью Ь совершает вынужденные крутильные
гармонические колебания вокруг своей оси ‹р = фсоз он. Соленоид
гибкими проводами присоединен к конденсатору емкостью С. Ра-
диус соленоида а, длина проволоки, из которой он изготовлен, 1,
сопротивление соленоида К. Найдем напряжение на конденсаторе
24-2073 359

при резонансе, когда частота о) равна собственной частоте колеба-
тельного контура (Мг 10.17):
1
(Ь С)1/2
В системе отсчета, связанной с витками соленоида, на электро-
ны действует переменная тангенциальная сила, равная массе элект-
рона, умноженной на ускорение, которое равно угловому ускоре-
нию (второй производной угла по времени), умноженному на ради-
ус витков. Разделив на заряд электрона, получаем напряженность
поля, а умножив на длину проволоки, получаем ЭДС, действующую
в контуре. Таким образом, приходим к уравнению (10.2), в котором
‘до
2
ХО = т1асро %.
Используя (10.7)‚ при и) = (по для амплитуды напряжения на кон-
денсаторе получаем
3
уо = т1аФ0 ‘йе.
Напряжение в соответствии с (1О.3) меняется гармонически
У= Щсоз (ст + ш),
но ц: здесь несущественно.
Рассмотрим подключение к источнику синусоидального на-
пряжения П = По зйп юг в момент времени 1 = О последовательно
соединенных сопротивления К и индуктивности Ь. Найдем силу
тока 1 как функцию времени и фазы ср, а также условие, при
котором сразу после замыкания цепи в ней установятсясинусо-
идальные колебания (Не 10.4).=Используя (9.4), для цепи полу-
чаем уравнение
1‚%+К1 = По зйпшг.
Решение этого уравнения можно составить из общего решения од-
нородного уравнения (правая часть равна нулю) и частного реше-
ния данного уравнения. Решение однородного уравнения
Ае`т
11 = Ь ‚
370

где А — постоянная, которую определим из начальных данных. Ча-
стное решение будем искать в виде 12 = 10 зйп (ш: + ф). Подставляя
это в общее уравнение, находим
иок
(122 + ш2Ь2)соз‹р
10 = и 51п‹р=—%со5‹р.
Общее решение
иок
1 = Ае'к'/" + .
(122 + ш2Ь2)сов‹р
Используя начальное условие — ток в начальный момент равен
НУЛЮ, И ПОЛУЧеННЫе ранее СООТНОШеНИЯ, имеем
‘КМ — эйп(ш! + ср)/зйп ср
[(2 + (0219 °
Заметим, ЧТО частное решение МОЖНО ОЫЛО ИСКЗТЬ В виде
1 = г/„шй
12 = 10 сов (о): + (р).
При Ь = О сразу устанавливаются колебания
' г
1 = до 31:21) _
Выделяемая мощность в случае переменного тока, как и для по-
стоянного (4.18), определяется силой тока 1 и напряжением У
1\’=1И
Для переменного тока У= И, сов а)! и 1 = 10 сов (ш! + ф), где ср —
сдвиг фаз между напряжением и током. Поэтому
А’ = 11,10 сов со: сов (со! + (р) = %И‚10|:сов‹р + сов (2001 +
Для средней за период мощности, так как среднее значение
сов (2ш1 + (р) равно нулю, получаем
(м) = Ёг/„д, совф. (1035)
При гармоническом изменении токов и напряжений их средне-
квадратичные значения, называемые эффективными, равны
эф - 75‘, эф - —'- ( - )
1 - ’° у - 10 36
24‘ 371

Эти величины показывают амперметры и вольтметры перемен-
ного тока.
Для средней мощности через эффективные значения имеем
(М) = Уэф/эф сов (р. (1О.37)
Для определения мощности, вьщеляемой переменным током в
катушке, у которой неизвестны индуктивность Ь и сопротивление г,
иногда применяют метод трех амперметров. Включение их показано
на рис. 10.6. Параллельно катушке включают известное сопротивле-
ние К. измеряют эффективные значения токов: 11 — через катушку,
12 — через сопротивление К и полный ток 1. Зная показания прибо-
ров, определим искомую мощность А! (Не 10.3).
В соответствии с (10.32) и (1О.33) нарисуем векторные диаграм-
мы для напряжений и токов. На рис. 10.7, а для последовательно
соединенных сопротивления г и индуктивности получаем, что паде-
ния напряжения на индуктивности #51 дсоЬ опережает по фазе паде-
ния напряжения на сопротивлении х/Йдг на п/2. Геометричес-
кая сумма этих падений (т. е. падение на катушке) равна 151212
(т. е. падению напряжения на сопротивлении К). Угол ср — это
сдвиг фаз между напряжением и током в катушке, который входит
в (1О.37). На рис. 10.7, б показано сложение токов по правилу
Кирхгофа 1 = 11 + 12. По теореме косинусов
12 = 13 + 13 -21,12 со$(п—‹р) = 1,2 +13 + 21,12 созср.
Пьк
о А А
С]? Ф 7
2 3 бы Пыль
Рис. 10.6 Рис. 10.7
372

Используя (10.37), получаем
12 -12 -1’ 1
(М) = 1’1,со$‹р= ЬК/‚ЙЁ-Ё =5
1г(12 -13 43).
Заметим, что при чисто реактивном сопротивлении катушки
(г = О) ‹р = п/2. Соответственно косинус и джоулевы (тепловые)
потери равны нулю.
Для определения мощности, выделяемой переменным током в
катушке, у которой неизвестны индуктивность Ь и сопротивление г,
применяют также метод трех вольтметров. Последовательно с ка-
тушкой включают известное сопротивление К и присоединяют к
цепи три вольтметра так, как показано на рис. 10.8. Измеряют с их
помощью Эффективные напряжения: 13 — на катушке, 13 — на со-
противбтении и 17- между концами цепи. Зная показания прибо-
ров, определим искомую мощность 1\’(М2 10.2). На рис. 10.9 приве-
дены соответствующие векторные диаграммы. Ток через катушку и
через сопротивление К один и тот же. По теореме косинусов
172 = 132 + 132 — 21313 со3(п —‹р) = 132 + 132 + 21313 со5‹р.
Используя (10.37), получаем
у 72-1/2-1/2 11/2-1/2-1/2
м =у1 =у4_;__2.=__;_;_
‹ 2 ‘СОЗФ ‘к 21413 2 к
Входящий в (1О.35) сов ‹р называют коэффшшентом мощности.
Пи _
Ь (р 7
б’; ‚. \/_21г Йод].
Рис. 10.8 "п Рис. 10.9
373

Обмотка электромагнита, полное сопротивление которой У= 10 Ом
и коэффициент мощности соя р = 0,6, присоединена к цепи пере-
менного тока. Найдем, каким будет коэффициент мощности сов р',
если параллельно обмотке присоединить конденсатор, реактивное
сопротивление которого равно У, = 7 Ом (№ 10.7). Используя ком-
плексные представления (10.27), (10.29), (10.31), (10.32) и (10.35),
изобразим их на векторной диаграмме (рис. 10.10). Получаем
У яп ~р вЂ” У~
~ач =
У соя ~р
Л = Усову,
Откуда
в1п~р вЂ” У~ У
соку' = соя агс1д
соя (р
1/2
С
Используя это соотношение, а также (10.27), (10.29) и (10.31), нахо-
дим импеданс параллельного соединения У
1 1 ] 2Я + ~(иА вЂ” 1/иС) ]
У Я+ йод Я+ 1/~иС 2Я+ ~Я(иЕ вЂ” 1/иС) Я
Это чисто активное сопротивление. Поэтому
81П И~
= ~о
Я Я
Рис. 10.11
Рис. 10.10
374
В приведенной на рис. 10.11 схеме в момент ~ = 0 замыкают
ключ К. Найдем зависимость от времени тока 1, текущего через ис-
точник синусоидальной ЭДС Й = Ж, яп и~, если параметры контура
связаны соотношением (№ 10.5)

Источник переменного тока с циклической частотой со и ЭДС ЕЁ
действует на колебательный контур (рис. 10.12). Определим силу
тока 1 и сдвиг фазы ср между 1 и б’ при резонансе (Мг 10.8). Используя
условие резонанса (9.8)‚ а таюке (1О.27), (10.29) и (1О.31), находим
импеданс параллельного соединения 2
1 1 . _ лоск
2=к+:шЬ+'шС”П7Ь'1Ё‘
Для тока получаем
до
^ . К шЬ — [К , е
1 - 81соС—————К + ЮЬ - $шСВ———-——к2 Нэп} - ёшСКрг.
Отсюда
_ С __1
10 _ ёшк(к2 +ш2Ь2)1/2 ’ щ) — ‘М.
Для цепи, изображенной на рис. 10.13, найдем ток 1 в цент (в ус-
тановившемся режиме при У= И, сов ш), а также значения час-
тот, при которых амплитуда установившихся колебаний будет мак-
симальна и минимальна, и значения максимума и минимума тока
(М 10.9). Обозначив импеданс параллельного соединения 21, имеем
Ь = ;+Ш›С =1-со21‚т(;.
21 шэЬ ш)1‚
ДЛЯ ПОЛНОГО ИМПеДаНСа ЦЕПИ ПОЛУЧЗСМ
1 . Ь _ 1(2о›2ЬС- 1)
2 =Ё”Ю1-ш21.с _ шс(1-ю21‚с)°
Еъсозо)!
ПЙ
одогл
П
|__
4
Рис. 10.12 Рис. 10.13
375

Пользуясь тем, что заданная зависимость напряжения есть ре-
альная часть от комплексного напряжения До” и (1О.33)‚ вычисля-
ем комплексный ток
А {ш 1(ш1-п/2)
1=У:=УшС1—ш2ЬС -3—-—.
° 2 ° ( )2‹о2ЬС—1
Получаем для действительной части
1 = У0шС(1—ш2ЬС)———ЁпШ‚ .
2ш ЬС -1
Минимальное значение
1
[шт = О при (02 =-Ё,
максимальное
1
[шах = со при 002 =5Ё.
индуктивностью резонансного контура (/= 10 МГц) служит длин-
ная однослойная катушка диаметром В = 10 мм. Найдем, во сколь-
ко раз изменится его резонансная частота, если внутрь катушки
вставлен на всю длину латунный цилиндр (удельное сопротивле-
ние латуни р = 8 - 1045 Ом - см) диаметром 0/2 (М) 10.10). При
высоких частотах колебаний электромагнитных полей они не про-
никают внутрь проводников. В данном случае, учитывая также,
что для латуни и порядка единицы в соответствии с (12.56) толщи-
на скин-слоя
а =———с ш = 4-10-2 мм.
(21цлш/р)
Индуктивность катушки меняется из-за уменьшения площади,
через которую идет магнитный поток (5.29)
5______”2 -
12 “02-02/4-
ы|4>
Используя (9.8)‚ получаем
%=&1'”=‹:›"®
376

В цепь, состоящую из последовательно включенных сопротив-
ления К, индуктивности Ь и емкости С, включен последовательно
источник синусоидальной ЭДС постоянной амплитуды и перестра-
иваемой частоты. Изменяя частоту источника, настраивают ее в ре-
зонанс с частотой Цепи, затем уменьшают емкость контура в два
раза и снова добиваются резонанса. Посмотрим, изменится ли сила
тока при резонансе. Найдем отношение резонансных частот, соот-
ветствующих первому и второму случаям (Мг 10.11). Из (9.8) следует
1 1
(01 =—-—-——, (02 :Т
ист“ (щ/гУ”
И СООТВСТСТВСННО
з; = 2 т
ш! ( )
Из (1О.15) находим
Сила тока одинакова.
Через баллистический гальванометр пропускается кратковремен-
ный импульс тока. При этом его рамка отклоняется на угол (ро. Спу-
стя половину периода, когда она вернется в исходное положение,
через него пропускается такой же импульс тока, но в противопо-
ложном направлении; через следующую половину периода пропус-
кается снова такой же импульс, но в первоначальном направлении
и т. д. Таким образом, всякий раз, когда рамка гальванометра про-
ходит через положение равновесия, она испытывает одинаковые
толчки в направлении своего движения. Найдем максимальный угол
ее отклонения ‹р при установившихся колебаниях, зная, что период
затухающих колебаний 7, а коэффициент затухания В (Мг 10.13).
Обозначая механический момент толчка рамки М, для изменения
момента количества движения (момент инерции 1, полученная уг-
ловая скорость (рд) имеем Мс11= Лрд. Пока нет толчка, колебания
затухают как свободные, и изменения угла описываются уравнени-
ем типа (9.15) и имеют решение типа (9.19). В начальный момент
угол равен нулю, а угловая скорость благодаря удару срд. Используя
это, находим
Ф = %е'°’ зйп шг, ф’ = 1301) сов ш: - Взйп ш1)е’°‘ .
377

Для определения сдвига фаз имеем
2к
шС(К2 -1/ш2с2)'
18Ф=-
Чтобы удовлетворить условие, должно быть юКС = 1.
Найдем, при каком соотношении между параметрами схемы,
изображенной на рис. 10.16, напряжение на выходе Н находится в
фазе с напряжением на входе У= И, сов со! и какова при этом ампли-
туда напряжения на выходе, а также построим векторную диаграм-
му напряжений на элементах схемы (М 10.55). Для делителей на-
пряжения имеем
УК У
=___ у=_____
у” кыш.’ С 1+1шСК
В результате
умет - 1.)
К(1— ш2СЬ)+1ш(СК2 + Ь).
При ш2 СЬ = 1 это выражение чисто действительное и
Иск’ - 1,)
ск’ + Ь `
Векторная диаграмма представлена на рис. 10.17.
Найдем, при каком соотношении между параметрами схемы,
изображенной на рис. 10.18,напряжение на выходе Н сдвинуто по
фазе относительно напряжения на входе Уна 9О° и какова при этом
амплитуда напряжения на выходе, а также построим векторную ди-
аграмму напряжений на элементах схемы (Не 10.56). Для делителей
напряжения имеем
П:
УК УКЁЩС
=К+1ш1‚’ к2_1+1‹оСк°
Рис. 10.16 Рис. 10.17
380

К Им
т» д д,
К К у
‘Ё Ив
Рис. 10.18 Рис. 10.19
В результате
г/к (1 + ш2ЬС)
Н=Ук1'ук2=
к(1- „Ест + 1о›(СК2 + 1,)’
При 032 СЬ = 1 это выражение чисто мнимое (поворот на 90°) и
_ шкив)”
СК2 + 1, '
Векторная диаграмма представлена на рис. 10.19.
Найдем, при каком соотношении между параметрами схемы,
изображенной на рис. 10.20, напряжение на выходе П находится в
фазе с напряжением на входе Уи каким при этом будет отношение
амплитуд напряжений (Мг 10.57). Обозначая импеданс параллель-
ного соединения 2, имеем
=%+1‹оС.
Ы|›—
Откуда
= К
1+1шСК°
И__Ё_| к к тк
к с у „у с| Тс| Тс| и
Т ч: и Т т” Т и
Рис. 10.20 Рис. 10.21
381

Для делителя напряжений имеем
72 _ у
к -1/шС + 2 “ 3 +1((оСК -1/шск)'
Н:
Это выражение будет чисто действительным, а следовательно, на-
пряжения будут в одинаковой фазе при шСК = 1. При этом У/Н = 3.
На вход фильтра (рис. 10.21) подано напряжение У= И, сов (01, где
;
КС °
Найдем амплитуду напряжения на выходе Н (Не 10.58). На ри-
сунке даны обозначения токов. Используя правила Кирхгофа, по-
лучаем
О):
1 1 1 1
1 = 1 1 . 1 = 2 . у = к 2 . = 1 _
3 1+ 2’ лтк +1юС ЮС ’ 13 +1шС ’ ёшС
ПОЛЬЗУЯСЬ условием ДЛЯ ЧЗСТОТЬЁ, Находим
и у
=1—т+1(т+2)'
ДЛЯ ЗМПЛИТУДЫ НаПрЯЖеНИЯ имеем
у у
НО = О 1/2 = О 1
[(1 — т)2 + (т + 2)2] (2т2 + 2т + 5)
/2°
К клеммам А и В (рис. 10.22) подводится произвольное пере-
менное напряжение Увхф‘), которое возбуждает между клеммами
М и А’ напряжение Увдхи). Параметры К, 1„ С подобраны таким
к 1.
Ад_1:_1_4м А М
С к
8% Т Им 352$ 2 И”
С к
АИ {Ё %М А М
ВИ 3 ИМ НИ 4 И“
Рис.10.22
382

образом, что напряжение на выходе в каждый момент времени
мало по сравнению с напряжением на входе в тот же момент.
Покажем, что при выполнении этого условия выходное напряже-
ние на схемах 1 и 2 приблизительно пропорционально интегралу,
а на схемах 3 и 4 вЂ” производной от входного напряжения по
времени (Мо 10.59). Цепочки 1 и 2 называются интегрирующими, а
3 и 4 вЂ” дифференцирующими.
Заметим, что между МЖ большое сопротивление (как в вольт-
метре) и ток идет только через конденсатор. Для схемы 1 ток через
конденсатор
Откуда
Ы1
ЯС
ых /
Для схемы 2 имеем
Откуда
Для схемы 3 получаем
Откуда
Для схемы 4 находим
Найдем входной импеданс бесконечной цепочки, показанной на
рис. 10.23, а также при каких частотах цепь не будет потреблять
мощность от источника (Мо 10.60). Импеданс части цепи, обведен-
ной пунктиром, обозначим У. Импеданс цепи после катушки с ин-
383

т т
Рис. 10.23 Рис. 10.24
дуктивностью Ь/2 также равен 2 Поэтому для параллельного со-
единения имеем
1 . 1
-- = шС + ————.
2 ' юЬ+2
Откуда
1/2
2 . _1‚_ _ __. Ь 1‚_ 25
2 +ю›1‚2 С-О, 2- шэ2:(с (о 4 .
Для положительного модуля импеданса годится только положи-
тельный корень. Учитывая сопротивление катушки с индуктивнос-
Ь 2 1/2
тью Ь/2, получаем, что импеданс цепи равен (— — (02 —) . Цепь не
С 4
потребляет мощности, если импеданс чисто мнимый. Это будет при
со › _3_
(Ь С)1/2
На вход схемы, изображенной на рис. 10.24, подается синусои-
дальное напряжение с частотой со. Исследуем зависимость ампли-
туды и фазы выходного напряжения от величины сопротивления К
(Мг 10.61). Так как параллельные участки одинаковые, по ним идет
одинаковый ток
= уВХ
К + ЕШЬ °
Тогда выходное напряжение
. им - к „т - кг + 2100112
увых=1(‘ш[’_к)=увхвш= вх к2+ш2д2 =
1/2 ‘Ф .
= Их [шт - т)’ + 4ш21Зк2] Рёв? = ждет.
384

При изменении частоты /' вынуждающей силы, действующей на
линейную колебательную систему, меняется фаза р установившихся
колебаний этой системы и запасенная в ней энергия ~К Пусть при
малом сдвиге частоты от резонансной Л/'= 1 Г1~ фаза колебаний и
изменилась на я/4. Найдем, как изменится при этом энергия ~К
Определим также, каково время затухания т системы в режиме
свободных колебаний (№ 10.15). При слабом затухании из (10.8)
следует, что резонанс при и „= ио. Изменение фазы от резонанс-
ного ( вЂ” ш/2) на п/4, как следует из (10.6), дает
И2 И2 вЂ” 2И2
Используя это и то, что отношение энергий равно отношению
квадратов амплитуд, выражаемых (10.7), получаем
(ио вЂ” и ) +4Р и
4Р~и~
Энергия уменьшится в два раза.
Используя полученное ранее соотношение, для характерного вре-
мени затухания свободных колебаний (9.25) получаем
1 2в 2в 1 1
$ ио и' (ио вЂ” и) (ио + и) Ьи 2кЬ~
В колебательном контуре с индуктивностью А = 1 Гн, настроен-
ном в резонанс, под действием внешнего синусоидального напряже-
ния с амплитудой ~~ = 200 В установился переменный ток с амплиту-
дой Хо = 20 А. Найдем сопротивление контура Л и время затухания т
(время, за которое амплитуда колебаний уменьшается в е раз) в ре-
жиме свободных затухающих колебаний (№ 10.16). Используя зави-
симость амплитуды колебаний в контуре от частоты внешнего воз-
действия (10.15), представленную на рис. 10.3, видим, что макси-
мальное значение будет при
1
0
(ЕС) ~
При этом сопротивление контура (10.16) чисто активное и равно
Л = вЂ” о =10 Ом.
~0
25*
387

При резонансе
4 -1.
о~ = о~о = 2тсА = вЂ” =10 с; 1 = 1О вЂ” вЂ” вЂ”.
ЕС ™~ Я
При высоких частотах
В результате
Л= вЂ” =10 0м; А= =01Гн; С= =10' Ф=01мкФ.
На колебательный контур с собственной частотой ио и логариф-
мическим декрементом затухания А = 0,02 действует внешняя пери-
одическая сила с постоянной амплитудой. Ее частота и, вначале
равная частоте собственных колебаний, изменяется настолько, что
мощность, расходуемая в контуре, падает вдвое. Найдем изменение
частоты в процентах к собственной (или резонансной) частоте ио
(Хо 10.65). Мощность, расходуемая в контуре, определяется (10.35).
Так как амплитуда внешней силы, т. е. амплитуда напряжения ~„
является постоянной, то отношение мощностей зависит от токов и
фазы. Используя (10.32) и (10.34) и обозначая и = ио + Ли, получаем
для модуля импеданса
Для фазы
Откуда
1
соз<р =
г г
(1+ 4Ли~1~/Я~)
Учитывая, что резонансу соответствует ди = О, получаем
О г С
г
вЂ” = 2 = 1+4Ли вЂ”.
Ф ~г
Отсюда
Ьа А 1
в 2ж т~
389

Емкостной датчик — это одно из наиболее чув-
ствительных радиотехнических устройств для реги-
страции малых механических смещений. Обычно он
представляет собой электрический колебательный
контур с воздушным конденсатором (рис. 10.30),
одна пластина которого подвижна. Оценим мини-
Рис- 10.30 мальное измеряемое перемещение пластины кон-
денсатора АИ, если контур настроен в резонанс.
Напряжение источника питания Н = 100 В, минимальное измеряе-
мое изменение напряжение на сопротивлении АН = 100 мкВ, доброт-
ность контура О = 100 и зазор между пластинами 11 = 1 мм (Мч 10.23).
Используя для емкости плоского конденсатора (3.56)
„$2.
_ 4пЬ°
и собственной частоты колебательного контура (9.8)
С
1
` пои’
можем получить (например, логарифмируя, а затем дифференцируя)
030
Из (10. 15) получаем для отклонения от резонансного значения
Н Н
А! =—— 2 2 ш.
[К +(ш1‚—1/щС) ]
К
Для ш = (по + Ащо получаем
юЬ—-1-=Ь(ш0+Аш0)——;——=
ЮС ((00 +АШО)С
(1О.38)
=ш0Ь 1+Аш° - 1 ггюо/ДЁЁ.
(по 1+Аш0/о›0 то
Используя соотношение на сопротивлении АН = КА! и выраже-
ние для добротности (9.27)‚ находим
Ё-Ёы- ' =1- 1 410.39)
{1+|:(ю01‚/К)2 Ашо /ш0 Тур [П + (02 Ашо /о›0 )2 т”

Так как затухание слабое, получаем
2
Ш=%(92&] _ ‚
и („о
ПОДСТЗВЛЯЯ СЮДЗ ПОЛУЧСННОС ранее СООТНОШСНИС, ИМССМ
м! 1 А]: 2
Т”5(97)'
Откуда
_ И ЁАП !/2_ _7
АЬ-б(Т-) _14.1о см.
Индуктивный датчик является радиотехническим устройством
для регистрации небольших изменений индуктивности. Обычно
он представляет собой электрический колебательный контур с из-
меняемой индуктивностью (рис. 10.31). Оценим минимальное изме-
ряемое относительное изменение индуктивности АЬ/Ь, если контур
настроен в резонанс. Напряжение источника питания П = 100 В,
минимальное измеряемое изменение напряжения на сопротивле-
нии АН = 10 мкВ, добротность контура О = 100 (Не 10.22). Исполь-
зуя выражение для собственной частоты колебательного контура (9.8)‚
находим
(о _ 2 Ь °
‘Асе _ 1 щ
Как и в предыдущей задаче, для падения напряжения на сопро-
тивлении (1О.39) получаем
2
% 21-{14г[(шоЬ/К):Ао3о/шо]2}1/2 ъ °
Откуда следует
1/2
%=ё(2%) =4‚4-1о-6. д
Так как в (1О.39) АП= П — (11, где Н — резо- С
рез рез
нансное значение; П, — на некотором интервале от К
резонанса, из (1О.39) получаем
П 1
П‘ = 2 ш. (10.4О)
рез {1+[о2Аш„/щ„] } Рис. 10.31
391

Для отношения энергий соответственно
щ _ 1
_ 2 _
И/рез 1 + [02 АШО /(1)0]
(10.41)
Характеристикой ширины резонансной кривой в случае слабого
затухания является ширина резонансной кривой (2Асо0) (Ашо называет-
ся расстройкой) при уменьшении энергии колебаний в два раза. Из
(10.41) получаем, что относительная ширина резонансной кривой
25% = 1. (1042)
(по О
Обратная величина называется избирательностью контура
“’° = . 10.43
2Аш0 о ( )
Найдем, как изменится избирательность контура, если вдвое
увеличить индуктивность Ь и вдвое уменьшить емкость, оставляя
неизменным активное сопротивление (Мг 10.18). Из (10.43), (9.27)
и (9.8):
‘°0 = 9 = Ё = 1%)!” .
2Аш0 К К С
Избирательность увеличится в два раза, так как О, = 291.
Считая добротность некоторого контура достаточно большой,
найдем:
1) расстройку Аи), (при снятии резонансной кривой), при кото-
рой потребляемая контуром мощность падает в два раза;
2) расстройку Аш2, при которой сдвиг фазы меняется на л/4,
если при свободных колебаниях этого контура амплитуда падает в
е раз за время т: = 1 с (Не 10.14).
Из (10.42), (9.27) и (9.25) следует
Аи), =Аш0 =5%= =%.
Из (1О.34), (10.38), (10.42), (9.27) и (9.25) получаем при ‹р = л/4
также Аи), =1/т = 1 с ‘1.
В определенном пункте напряженность электрического поля,
создаваемого радиостанцией А (на частоте 210 кГц), в пять раз боль-
ше, чем напряженность электрического поля радиостанции В (на
392

В контуре, состоящем из последовательно соединенных емко-
сти, индуктивности, сопротивления и синусоидальной ЭДС, амп-
литуда силы тока 1, существующая при отклонении частоты ЭДС
на небольшую величину АД которая называется «расстройкой»
(а АД]; — «относительной расстройкой»), от резонансной частоты Д),
в соответствии с (1О.15) и (9.27) будет связана с амплитудой силы
тока при резонансе 10 следующим соотношением (Не 10.12)
1 1
— = 1/2 '
’° [1+(о2Ал‚/л‚)2]
Для схемы, изображенной на рис. 10.32, а, определим частоты
источника ЭДС, соответствующие резонансам токов и напряжений, а
не тока и напряжения, как, например, в (1О.8). Построим график
сдвига фазы тока 1 относительно ЭДС 8 в зависимости от частоты
источника, считая внутреннее сопротивление последнего пренебре-
жимо малым (Мг 10.25). Используя (1О.29) и (1О.31), имеем для им-
педансов
(1045)
. 1 _ 1_1 .
21—1(Ш1ц“Ё), 22 — [ШЬ+1ШС.
В результате ИМПСДЗНС ЦСПИ 2 НЗХОДИМ ИЗ СООТНОШЕНИЯ
11121шС
ИЛИ
д (1 - ш2ЬС)2 - 2ш2ЬС
7 = юЬ (1 — ш2ЬС) (1О.46)
Обозначая оэ2ЬС = х, из (1О.46) получаем
1 1 + 4х + х2
Ё - $; (1О.47)
Резонансу напряжений соответствует наименьшее напряжение в
цепи при 2 = О, что получаем при
1
Ш=Т=Ш .
(ЬС)1/2 О
394

0
Н
7:” Ф
— т:
2 г т П г
0 > О т
|‘°1 ‘до (0200 ‘01 ‘00 (0200
_Д
2 б `% б
Рис. 10.32 Рис. 10.33
Резонансу токов соответствует минимальный ток, что будет при
1/2 = 0. Следовательно, надо удовлетворить уравнению х2 + 4 х + 1 = О,
решение которого х = 2 1 Л. Получаем
ш _ 2-6 "а 0,52 _ _ 2+Л „ 1,93
1“ “Г; "(дал/г 2“(ЬС)1/2 '“(ЬС)1/2°
Для тока имеем
1 _Ё_Ё1—4х+х2
"2 ' 1 ш[‚(1—х) °
В соответствии с (10.33)
1: е-1л/2_
1
На рис. 10.32, б показано изменение фазы, которая определяет-
ся знаком второй дроби предыдущего выражения. Оно положительно
при О < (о < (од и при (по < ш < 002, а отрицательно при (01 < (о < то и
032 < о). Изменение знака соответствует повороту фазы на т: (т. е.
знаку в показателе экспоненты).
Аналогичным образом можно действовать в случае схемы, изоб-
раженной на рис. 10.33, а (Не 10.26). Здесь
2 _‚(2Ь__1_). д 1_1_-_ш.7.Ь..С._
‘"2шс’22:ш1.'
395

В итоге
1 =Ё=_Ё1—4х+х2
2 1 ш1‚(1 — х) '
Изменения фазы показано на рис. 10.33, б.
Приведем пример, когда схему можно нарисовать по данным об
изменении тока. Дан черный ящик с двумя внешними клеммами.
Внутри него собрана схема из индуктивности с малыми омически-
ми потерями, емкости и сопротивления. Известно, что если по-
дать на клеммы постоянное напряжение По = 1 В, то ток будет
равен 10 = 10 мА. При переменном напряжении 1 В на частоте 50 Гц
ток равен 1 мА. С ростом частоты ток падает, достигает минимума
при частоте Д, = 500 Гц, а затем постоянно возрастает до предельно-
го значения 10 мА. Нарисуем схему черного ящика и определим ее
параметры (Мг 10.27). Для получения минимума тока, что соответ-
ствует резонансу токов, необходимо иметь параллельное соедине-
ние индуктивности и емкости, так как при этом
2, _ ЕШЬ
п " П‘
1 — (о ЬС
Так как по условию значение силы тока при (о —› со равно силе
тока при постоянном напряжении, то значит сопротивление вклю-
чено последовательно с параллельным соединением индуктивности
и емкости (рис. 10.34). В результате имеем
к =Ё9 = 100 Ом; ЬС =-1, =1о*7 с
о ‘до
При ш а: (по
. д д
2 = к + ———"”} .
1— (о ЬС 5% к
а
‘а
к —б`| од к —^'*Г^^—И
и—с:ъ—
-—с::›——
1, б
Рис. 10.34 Рис. 10.35
396

Откуда при 50 ГЦ
Ь 1/2
2: 1:2 ё =103 .
" [ “Ч-ог/шз] °”
Так как при этом 122 < |2|2 и 032 < 00%, то |2| = 00Ь, что дает Ь = 3,2 Гн
и С = 3,14-10‘2 мкФ.
Другой вариант такого же черного ящика. Известно, что если
подать на клеммы постоянное напряжение По = 1 В, то ток будет
равен 10 = 1 мА. При переменном напряжении 1 В на частоте 50 Гц
ток равен 10 мА. С ростом частоты ток растет и достигает максиму-
ма на частоте Д, = 500 Гц, а затем постоянно возрастает до предель-
ного значения 10 мА. Нарисуем схему черного ящика и определим
ее параметры (М 10.28). Так как ток достигает максимума, то, сле-
довательно, Ь и С включены последовательно. Чтобы был ток при
постоянном напряжении, сопротивление должно быть включено им
параллельно (рис. 10.35, а). Получаем
=Ё = 1000 Ом; ЬС = ё,- 104 с.
0 (00
К
ДЛЯ ИМПСДЗНСЗ ЦСПИ НЭХОДИМ
1
1/2 °
[1/122 + (шС/ш2ЬС -1)2]
При частоте [ = 50 Гц по условию получаем И = 102 Ом. Под-
ставляя это в предыдущее соотношение и учитывая, что
и =
2
-% «10-4 1/Ом и (Е) < 1,
К (00
находим 0›С= 104, С =.3,2-10‘5 Ф, Ь = 3,14- 10-3 Гн.
Имеется еще и другая возможная схема, когда сопротивле-
ние параллельно емкости, а индуктивность им последовательна
(рис. 10.35, б). Сопротивление и ЬС остаются теми же, а для модуля
импеданса цепи получаем
[1 — (со/то )2 + (‹0Ь/К)2 т”
[1/122 + (шсП/
2|=
397

Так как
1 - а
х_К”
то в случае г << х и соответственно К >> Х получаем г == К, а в случае
г>>химеем Х>> Ки х: 122/26
В цепь переменного тока с ЕЁ = 440 В и частотой [= 50 Гц вклю-
чены последовательно нормально горящая лампочка накаливания и
конденсатор. Найдем, чему равна емкость конденсатора С, если лам-
почка рассчитана на напряжение У = 220 В и силу тока 1 = 1 А.
Определим также, чему равен сдвиг фаз (р между током и пол-
ным напряжением в цепи (Не 10.30). Сопротивление лампочки
В = У/1= 220 Ом. Из (1О.32) получаем
- 1 1
Ёе” =1 К+—— =1 К———.
ЮС шС
Левая часть является представлением правой в экспоненциаль-
ном виде, поэтому
г: 1 1:2 1 ш 1
= —- ; к =———.
( Щей) у” Ф“
Отсюда
’ 2 =ггк2-12к2=г;2-у2; с: 1 „2 =8,4 мкФ.
(ЮС) [2л/(82 - 72)]
Поскольку
8 440 В
7-11,‘ -44О Ом-2К,
то
12:33?
(ЮС)
В таком случае гвф = — 3 и (р = —6О°. Ток опережает по фазе
напряжение.
Другой вариант, когда в цепь переменного тока с 55 = 440 В и
частотой / = 50 Гц включены последовательно нормально горящая
лампочка накаливания и катушка самоиндукции. Лампочка рассчи-
тана на напряжение У = 110 В и силу тока 11 = 1 А. При замене
1
399

лампочки другой, рассчитанной на 13 = 220 В и 12 = 0,8 А, оказалось,
что новая лампочка горит также нормальным накалом. Найдем со-
противление К и самоиндукцию Ь катушки (Мэ 10.31). Сопротивле-
ние первой лампочки
к, =Ё=11о Ом,
1
1
СО проти ВЛСНИС ВТОРОЙ ЛЗМПОЧ КИ
_72
2
к, = 275 Ом.
Из (1О.32) получаем
|2,| = [щ + к)’ + ш2Ь2:|1/2 = 4к,;
л/2
|2,| = [(19 + к} +со2Ь2] = 212,.
ВОЗВОДЯ В квадрат И решая СИСТСМУ, НЗХОДИМ
- 3———5к% ’ кг = 137 Ом
2 2 1/2
Рек, -(к, +12) ]
Ь = а = 1,16 Гн.
21:]
Найдем диэлектрическую проницаемость жидкости, если извес-
тно, что ее удельное сопротивление р = 10” Ом - см и при переходе
от постоянного тока к переменному с частотой 50 Гц (при том же
эффективном напряжении) ток, текущий через конденсатор, напол-
ненный этой жидкостью, возрастает в 7 раз (п = 7) (Не 10.32). Кон-
денсатор с утечкой представляет систему из параллельно соединен-
ных емкости и сопротивления. Импеданс этой системы 2 определя-
ем, пользуясь (1О.27) и (1О.31), 1/2= В + ЮС. Откуда
к
[1+(шск)2]
|2| = 1/2‘
По условию
400

Пользуясь (3.56) и (4.14), имеем С = 8066711 и К = р/т/Б и соответ-
ственно СК = еоер. Отсюда
2 1/2
е=———(п 4) =2‚5.
2л[е0р
Длинный однослойный реостат из нихромовой проволоки с удель-
ным сопротивлением р = 1,1 - 104 Ом - м намотан виток к витку с
плотностью витков п = 10 см“ на керамический каркас диаметром
1) = 5 см и включен в цепь переменного тока с частотой / = 50 Гц.
Найдем сдвиг фаз между током и напряжением на реостате, пренеб-
регая толщиной изоляции проволоки (Мг 10.33). Воспользовавшись
(5.29) и (4.14), находим
Ь = доп/УМУ; К = 4рВ1\’п2.
Используя (10.34), получаем
_ ЗЁ - 2 _2_ -
{эф - к - я [до Д)” - 0,025.
В схеме, представленной на рис. 10.37, емкость С подобрана та-
ким образом, что при замыкании ключа К ток 1, показываемый
амперметром А, не изменится. Найдем индуктивность катушки, если
известно, что 1= 0,5 А, П= 380 В,/= 50 Гц (Мг 10.34). Из (10.30)
шС = 1/(1 Используя (10.32), получаем
А ^. _ А _ ^1—шЬС+Еа›СК
1‚-Пщ›С, 12-(1 К+ЮЬ .
Амперметр показывает эффективные значения, т. е. меряет мо-
дули. Они и должны быть равны (удобно написать квадраты моду-
лей)
(1 - „На? + ш2С2К2
2С2 =
ш к’ + „т
Откуда
. _ 1 _ д’ _
2шЬС-1, -2шС-4пЛ-1,2Гн.
На рис. 10.38 показана принципиальная схе-
ма трансформатора — устройства для изменения
напряжения переменного тока. Первичная обмот-
ка, связанная с источником переменного на- Рис. 10.37
264073 401

11 12
5 < ›
1! Ё ’ 32
1) ‹ >
111
111 52
п‘ Ч’=ЛФ п2
Рис. 10.38
пряжения, и вторичная, связанная с нагрузкой (потребителем), нави-
ты на общий железный сердечник, в котором при вычислениях счита-
ем отсутствие рассеяния магнитного поля и ферромагнитизма. Индук-
ция магнитного поля В сердечника (площадь сечения 5) создает маг-
нитный поток Ф = ВБ. Число витков обмотки п дает зацепленный
поток ‘Р = пФ. Этим потоком определяется ЭДС индукции или индук-
тивное сопротивление ШРИ! (здесь и далее используется система СИ).
В соответствии с (5.31) имеется связь с коэффициентом индукции Ь и
током 1 в обмотке Ч’ = 11,. Для обмоток из (1О.32) получаем
д‘? д‘?
и, ьгыщд; 0=7А+к,1,. (1О.48)
При ОТСУТСТВИИ раССеЯНИЯ МЗГНИТНОГО ПОТОКЗ
ФЦЁ-Ё. (10.49)
"1 "2
Используя (5.31) и вводя собственную и взаимную индуктив-
ность, получаем для потоков
‘Р, = д], + Ь1212; ‘Р, = 1,211] + 1,212. (10.5О)
Подставляя это в (10.49) и учитывая, что полученное соотноше-
ние должно соблюдаться при любых токах, находим п2Ь1 = пдЬд и
п2Ь12 = п‚Ь2 и, следовательно, Ь], 1,21 = 1‚‚[‚2. Пользуясь теоремой
взаимности (5.3О), имеем
[12 = Ьд = Ьв = (Ь1Ь2)‘/2. (1О.51)
Для переменного тока частотой со из (1О.32) получаем
д, = (к, +100Ь,)Й, +1ш(Ь‚1‚,)‘/’ 2,; (1052)
0 =1‹„(1„1‚,)‘/’ 1, +(к, +1а)[‚д)Ё2. (1053)
402

Отсюда
1 = (К; +1‹0Ь2)С71 _ (1О.54)
3132 +"°(Ь1к2 + 1231),
А . /2 ^
1 — - мы” Н‘ (10.55)
2 _ 3132 +"°(Ь1к2 + 1231).
Если можно пренебречь активным сопротивлением в первичной
цепи (К, << юЬд), то имеем
1, = (кг ТМИН‘ ; (10.56)
ЁШЬ] К2
Ё2 =_(З)1/2Ш=_ЁЁ1 (1057)
д 32 "1 32
где учтено, что индуктивность катушки пропорциональна п3.
Для так называемого падения напряжения во вторичной цепи
получаем
и, = 1,11, = -Ёи,. (1058)
111 Ё
Разделительный трансформатор имеет две одинаковые обмотки,
у каждой из которых индуктивное сопротивление на рабочей часто-
те в п = 5 раз больше омического. Найдем, каково отношение мощ-
ностей, потребляемых в первичной цепи при замкнутой и разомк-
нутой вторичной цепи (М 10.37). Воспользуемся (1О.54) и (1О.55).
В случае замкнутой цепи (в соответствии с условием) К] = К, = К,
Ь, = 1,2 = Ь и 001, = пК. Поэтому получаем
>
_ (К + [со[‚)[7,_
'_ кдьшшлк’
2: клюв’
(1О.59)
(10.60)
Модуль тока в первичной цепи равен
[(1+ 2:3): + Ж]
1 + 4п2
26’ 403
1/2
П
1, =ЪЬ (10.61)

Ток отстает от напряжения. При п, = п, = 10 ‹р = —3°.
По первичной обмотке трансформатора течет ток 1 = 10 сов (ш.
Найдем, в какой момент времени следует разорвать вторичную об-
мотку трансформатора, чтобы в месте разрыва неюбразовалась ис-
кра, и чему будет равна сила тока 11 в первичной обмотке в этот
момент времени, если индуктивность вторичной обмотки Ь, сопро-
тивление К (Не 10.35). Из (1О.53)
А гшшьлй, „г стат
12=ТТ—:'=Ш(Ь|Ь) 11 1/2,
2 + "М? (122 +‹о21‚2)
где фаза определяется из равенства (3 ‹р = (оЬ/К.
Так как 1= 10 сов со! = Ке(1Ое“°’), то
1/2 сов (п/2 - ‹р + со!)
(к, + ш2Ь2)'/2
Чтобы не проскочила искра во вторичной цепи, напряжение и
ток должны равняться нулю в момент размыкания. Поэтому
п/2 — (р + (011 = п/2.
Отсюда (от, = (р. Так как
12 = [о (дд)
2 _ 1
сов ‹р - т,
1+13 (р
то для тока в первичной обмотке имеем
1 о
(1 + щт/к?
1, у, .
Если во вторичную обмотку дополнительно вкшочить конденса-
тор емкостью С, то во все соотношения, в которые входит ШЬ, доба-
вится —(1/соС) (М 10.36). В таком случае
шЬ—ПшС
1 к
тур: тещ, =—г—; 1, = °
[18 + (шЬ —1/шС)2]1
/2`
Видно, что 11 = 10 при
шЬ=
ш С/
405

Вблизи катушки колебательного контура с параметрами 1,1, С, К
расположена вторая катушка с индуктивностью 1,2. Взаимная ин-
дукция между ними равна М. Найдем, какой будет резонансная ча-
стота контура, если выводы второй катушки замкнуты накоротко,
считая, что ее индуктивное сопротивление на рассматриваемой
частоте значительно больше ее активного сопротивления, а также
при каком условии резонанс недостижим (М9 10.39). В соответ-
ствии с (9.4) и (7.1) для первого колебательного контура имеем
(11,
1 д!
1„ д, +К1,+-ё_[1,а71+Мд-
д: =О`
Для второго
(11, + си,
а: а:
ПОДСТЭВЛЯЯ второе СООТНОШЕНИЕ В первое, ПОЛУЧЗСМ
=О.
м2 (11
-— 4+к1,+11,‹1:=о.
д, д: с
Резонанс тока происходит при собственной частоте контура,
поэтому
1
Ь, -М2/1е)`
Резонанс не достижим, если М 2 = 1,11? как это бывает при от-
сутствии рассеяния магнитного потока через две катушки.
Две одинаковые катушки, намотанные на общий каркас, вклю-
чены последовательно в колебательный контур с емкостью С двумя
способами, изображенными на рис. 10.39. Резонансные частоты
колебательных контуров оказались равными ш, и (о, соответствен-
но. Найдем индуктивность Ь каждой из катушек и коэффициент их
взаимной индукции М (М) 10.40). В первом случае соединения вза-
2 _ 2_
шрез"ш0’с(
||
СП
1. Ь ЬТЬТ
Рис. 10.39
О

имные индукции действуют так же, как собственные (складываются
с собственными), а во втором случае — против собственных:
д! 1 д]
2ЬЁ+2„-[1с1::2МЖ=О.
В первом случае
2_ 1
ш‘ “ 2с(1„+м)’
а во втором
2 1
2
со =ЁЁ.
Отсюда
Ь = 1/(1)? +1/ш% _ М = 1/0)? —1/ш%
4С ’ 4С
Две одинаковые катушки, намотанные на общий каркас, вклю-
чены парадшельно в колебательный контур с емкостью С двумя спо-
собами, изображенными на рис. 10.40. Резонансные частоты коле-
бательных контуров оказались равными о), и (о, соответственно.
Найдем индуктивность Ь каждой из катушек и коэффициент их вза-
имной индукции М (М) 10.43). В первом случае соединения взаим-
ные индукции действуют так же, как собственные (складываются с
собственными), а во втором случае — против собственных. Так как
катушки соединены параллельно, то ток в них равен половине, иду-
щего через конденсатор. Поэтому
1 а’! 1 д!
5ЬЖ+д[1с1г:2М-д- .
В первом случае
00%: 2
С(Ь+М)
Ь Ь Ь Ь
| СТ | Ь См
П
Рис. 10.40
407

а во втором
Отсюда
1/0)? +1/ш% _ М _ 1/(1)? —1/(о%
С `_—б—_’
Ь=———‚
Высокодобротный колебательный контур (рис. 10.41) включает две
последовательно соединенные катушки с индуктивностями Ь, и 1,2.
После того как катушку Ь2 замыкают накоротко, частота собствен-
ных колебаний контура не изменяется. Определим коэффициент
взаимной индукции М (Мг 10.41). До замыкания накоротко
д] с11 1 д!
дд+цд+драг+2мдг=о. (10.63)
Откуда
(02 = 1 .
с(д + 12 + 2м)
При замыкании второй катушки два контура, для которых име-
ем уравнения:
б/д 1 6112 _ _
ДТ+-ё!1|СЛ+М-Е1Т—О,
д12 с11,_
1‚2—Ж+МШ -—-О.
ПОДСТЗВЛЯЯ ВТОРОЕ СООТНОШЕНИЕ В ПЕРВОЕ, ПОЛУЧЗЕМ
2
(д-%_]%+ё[1,а:=о.
/7<
|[
|д
П

Отсюда
2 1
' С(Ь. —М2/Ь2)°
По условию это равно полученному ранее. Откуда
М2+2Ь,М+1‚3 =(м+1,)2 =о
и, следовательно, М = —Ь2.
К высокодобротному колебательному контуру Ь], С, с известной
резонансной частотой со, может быть подключена ключом К после-
довательно цепочка с известными Ь2, С, (рис. 10.42). При этом ре-
зонансная частота контура не изменяется. Определим коэффициент
взаимной индукции М (Мг 10.42). До переключения
(02 1
1: 1‘1С1.
ПОСЛС ПОДКЛЮЧЕНИЯ суммарная СМКОСТЬ конденсаторов
_ С1С2
с, +с2'
Цепь описывается уравнением (1О.63). Приравнивая частоты,
получаем
СС
де. =‹1„ +14 плод-Ё.
Откуда
М=%Ё%Ё*’°Ё=%ЁЁ”°Ё°
Найдем добротность катуппш, намотанной на тонкую медную трубку
с внешним диаметром В = 2 см и толщиной стенок б = 0,05 см
(удельное сопротивление меди р = 1,8 - 10-5 Ом - см), подключенной
к цепи переменного тока частотой /= 50 Гц, если длины катушки и
трубки одинаковы и значительно больше диаметра (Мг 10.44). Вос-
пользуемся (9.29), (7.21), (4.18), (4.14) и (7.1). Потери энергии
связаны с вихревыми (кольцевыми) токами (Фуко) в стенках труб-
ки. Причина вихревых токов — ЭДС индукции
шф: 1 (из
:——__._—_:_ 1.
со’! с 717’

Откуда
Е = 118 югвйпшг.
2 с О
В соответствии с (4.7) и (4.12) мощность выделения энергии
’о 82 ш 2 ’о_
А’ = 1 жвтз = ж-Ч- - 51112 ил] 2лг3аг.
о 4 с о
Усредняя по периоду, получаем
„и = йщшу = Ёп2г2„ж(Ш)2
8 О с 81ш О с '
Энергия, запасенная в контуре за период (по двум полуперио-
дам) в соответствии с (1О.65):
32
и/=-9-2 21.
Зщл иго
Так как потери энергии АИ/= (1\’)Т= 1\’2п/то, то из (9.29) получаем
2
д: Фи’ = 2(‘/’°) ‚ (1О.66)
(М: щшо
Найдем, как изменится добротность контура при увеличении
емкости конденсатора в два раза (Мг 10.46). Из (9.8)
1
со=-———.
(ЬС)1/2
Используя (1О.66), получаем
Ё = [ау = 21/2,
91 С1
Катушка колебательного контура имеет добротность О = 100.
Если один виток катушки замкнуть накоротко, то ее индуктивность
почти не меняется, а добротность уменьшается вдвое. Определим
по этим данным число витков катушки 1\’(М9 10.45). ЭДС индукции
определяется зацепленным потоком, который в соответствии с (5.31)
равен ‘Р = 1,1 (в СИ произведению индуктивности на ток). В катуш-
ке зацепленный поток больше, чем в витке, в А’ раз. В соответствии
411

с (1О.29) падение на катушке НК = [м], а на витке На = Ьш1/А’.
С помощью (4.18) и (9.27), учитывая, что сопротивление витка рав-
но К/А’ (К - сопротивление катушки), находим мощность потерь
энергии в витке
м’, = "Ё -(9Е)21Ё = 92125.
к/м к А’ м
Так как по условию добротность при замыкании витка в два раза
меньше, то потери, которые в катушке равны 121%, в два раза боль-
ше, АМВ + 1212 = 21312. Откуда получаем 1\’= 92 = 10 ООО.
На рис. 10.44 изображена металлическая скоба длиной 1, шириной
а ы 1и с зазором И << 1, а. Ее можно рассматривать как колебательный
контур: конденсатор и полувиток, по которому заряд переходит с
одной пластины на другую. Оценим резонансную частоту такого ко-
лебательного контура (Не 10.48). Из (3.56) емкость конденсатора
__ 11
410$
Если по скобе идет ток 1, то из (5.6)
В - 4п1.
са
Поток индукции магнитного поля
Ф - 4л111
СЦ
и из (5.28)
1, - 41:15
а
Из (9.8)
1/2
ю-(Ё) „5-3409 с‘,
а -Ё
а
11
ш д; $4
„д
|<——Г—->| " ’* г"!
а В а
Рис. 10.44 Рис. 10.45
412

или /' вЂ” 500 Гц. Прямая оценка из условия 1 вЂ” Х/2, где А вЂ” длина
волны, дает Х вЂ” 20 см и частота и = 2шс/А вЂ” 10'о с -'.
Оценим приближенно резонансную частоту /'„тороидального
резонатора, размеры которого представлены на рис. 10.45, где изобра-
жено его меридианальное сечение: а = 20 см, Р = 10 см, Ь = 1 мм
(М 10.49). Предполагаем, что размеры резонатора малы по сравне-
нию с резонансной длиной волны. В таком случае можно пользо-
ваться формулами для квазистационарной цепи (9.8). Из (3.56) для
емкости плоского конденсатора в центральной части резонатора
Р2
4шЬ 16Ь
Из (5.6) получаем напряженность (равную индукции) магнитно-
го поля в зависимости от расстояния от оси тора (г)
Н= В= вЂ”.
СГ
Для потока магнитного поля имеем
О/2+и ~ у ~а
Ф=2а вЂ” ~ вЂ” "=2а вЂ” 1и 1+вЂ”
~/2 " 0
Из (5.28) получаем индуктивность тора
А = 2а 1и (1 + вЂ” .
2а
0
Из (9.8) резонансная частота
И С
Э 2 ~р~
(1/я)(с/Р)
~(1/2)(а/Ь) 1п(1+ 2а/Р)~~
я5 ла
2
4шЬ 4шЬ
413
Тороидальный резонатор электромагнитных колебаний представ-
ляет собой полый идеально проводящий тор круглого сечения. Внутри
него вырезан зазор (рис. 10.46), края которого затянуты двумя прово-
дящими сетками, имеющими форму круга радиусом и = 5 см, рассто-
яние между сетками Ь = 2 см, а средний радиус кривизны тора 2а.
Рассматривая резонатор как колебательный контур и считая, что е и ц
в нем примерно равны единице, оценим резонансную частоту (Мо 10.50).
Действуем, как в предыдущей задаче. Из (3.56) для емкости плоско-
го конденсатора в центральной части резонатора

д \
@jo к} к а Ь
<®ЁЧ ‘Н’ С
\`\:сЁТ‘ _______ -. [и 14
‚и """"" " с д
А С
Рис. 10.46 Рис. 10.47
Из (5.6) получаем напряженность (равную индукции) магнитно-
го поля
11-49-21.
са
Для потока магнитного поля имеем
1
Ф = Впа2 = Ёпа.
Из (5.28) получаем индуктивность тора 1, == па. Из (9.8) резонан-
сная частота
На рис. 10.47 показана схема. Пренебрегая активным сопро-
тивлением катушек, определим частоту резонанса токов в схеме,
когда генератор подключен к клеммам: 1) аЬ, 2) ас! и 3) ас (Не 10.51).
В соответствии с (10.31) и (1О.29) и их паршшельным соединением в
случае:
1) аЬ
т=дшс+ 1 = ш 1-‹„’ЬС
2 21ш[‚— Ж/шС 1_2(„2дс'
Для резонанса токов 2 = со. Для этого должно быть
2) ас!
1 2 2шС
В этом случае резонанс токов не возможен;
414

3) ас
1 1 1 Ь-ш?Ьс
2 цоЬ юоЬ — 21/шС ш дс _.2
Условие совпадает с первым случаем.
На рис. 10.48 изображена электрическая схема, в которой К = 6 Ом,
Ь = 0,01 Гн. Внешнее напряжение синусоидальное с круговой час-
тотой (о = 300 с“. Определим, при какой емкости конденсатора С
ток 1 находится в фазе с напряжением д/(Ме 10.53). Для импеданса
цепи 2 при параллельном соединении по (10.27), (10.29) и (1О.31)
имеем
1_ к-юь
2 122 +ш2Ь2
Для совпадения фаз тока и напряжения 2 должно быть веще-
ственным, т. е.
+Ео›С.
Ь
шС — ш = О
[(2 +ш2Ь2
Откуда
Ь
С =——-—.
122 +ш2Ь2
В одной из схем радиочастотного лампового генератора наличие
электронной лампы с нелинейной характеристикой в цепи обрат-
ной связи эквивалентно подключению к колебательному контуру
двухполюсника (так называют какое-либо устройство, имеющее вход
и выход — две клеммы) (рис. 10.49), комплексное сопротивление
которого зависит от амплитуды тока 1 и на частоте о) равно
а . 1
2 - 7 + та,
Т
В
С
то) Ё:
Т Ь
Рис. 10.48 Рис. 10.49
415

где а и Ь вЂ” известные константы. Найдем, при каких условиях воз-
никнут автоколебвния в такой схеме и какова частота и и амплитуда
А установившихся колебаний (№ 10.70). Импеданс колебательного
контура (без двухполюсника)
2
УО Л+1щА 1 Я+!ай 1 г
1 ®О
в СС И
Условие возникновения автоколебаний У + У= О. Должны нулю
равняться действительная и мнимая части этого выражения, поэто-
му получаем
Л+ вЂ” = О.
1
Отсюда видно, что а < О. Следовательно, амплитуда тока
1а!
Из равенства мнимых частей имеем
Откуда
г
= Ого
г
Конденсатор колебательного контура возбуждается периодичес-
кой последовательностью коротких импульсов, частота следования
которых равна собственной частоте контура, а их величина равна ~~.
Найдем, как изменится амплитуда вынужденных колебаний, если кон-
тур возбудить гармонической ЭДС той же частоты и амплитуды ~~
(ЭДС в этом случае включается последовательно с элементами
контура) (№ 10.68). На рис. 10.50 показаны прикладываемые
напряжения и схемы соединения элементов контура. В первом случае
(рис. 10.50, а) в соответствии с (9.19) максимальная амплитуда 1',
затухающих (с коэффициентом затухания р) колебаний через пери-
од Тбудет равна ~е Рг. Добавка (~~) возвращает амплитуду к мак-
симальному значению
1',е-~г+ Г, = Е.
416

Активное сопротивление г~ определяется суммарной потерей
мощности
Ул+ Упм
г, вЂ”, " = 9,81 Ом.
1
Используя (10.32), находим модуль импеданса цепи
У = вЂ” =220 Ом
У
1
и реактивное сопротивление конденсатора
У = вЂ” = У~ вЂ” г2 = 219,8 Ом.
с иС
Откуда
С= = 14,4 мкФ.
=г,~о=
Для изготовления трансформатора используется замкнутый маг-
нитный сердечник с площадью поперечного сечения Я = 5 см. Ин-
дукция насыщения материала сердечника равна В„„= 2 Тл. Найдем
минимальное число Ж витков первичной обмотки, предназначен-
ной для включения в сеть с действующим напряжением Г= 220 В и
частотой~= 50 Гц, чтобы в сердечнике еще не возникало насыщения,
пренебрегая рассеянием магнитного потока (М 10.77). Поток в сер-
дечнике не должен превышать Ф = ЯВ„„в1п и~. Возникающая ЭДС
индукции определяется зацепленным потоком Ж„~ = ЯВ„„Жисов и~.
Измеряемое вольтметром напряжение выявляется эффективным зна-
чением напряжения (10.36), т. е.
Г= "" =ЯВ„„Ф вЂ”.
При большем числе витков вЂ” меньшая индуктивность. При за-
данном насыщении минимальное число витков определяется
= 990 витков.
2ф5'В„„
На металлическую трубу с внешним радиусом г и толщиной Ь
намотана катушка (рис. 10.51). Число витков Ж, длина трубы (, удель-
ная проводимость ее материала А, магнитная проницаемость р = 1.
Считая обмотку идеально проводящей, найдем активное сопротив-
418

1 = [Осоз соо:
`&:-—
У = Ебсоз о)!
Рис. 10.52 Рис. 10.53
Для нахождения резонансной частоты амплитуды механических
колебаний можно воспользоваться соответствующими-формулами
(например, см. 1, с. 98—1ОО). Резонанс будет при
1 к "2
тЫ -
Амплитуда вынуждающей силы
ко’
д’ =1(8_1)16п/1°
Амплитуда колебаний
729
Хрю =1(е—1)1ё’пл.
Обратим внимание на сходство формул с (1О.9) и (9.27).
На рис. 10.53 изображена электромеханическая колебательная
система высокой добротности О, совершающая вынужденные коле-
бания. Система состоит из неподвижного соленоида с числом витков
на единицу длины п, по виткам которого протекает переменный ток
1 = 100050001. В катушку вставлен длинный магнитный стержень мас-
сой т, площадью сечения 5, с магнитной проницаемостью р, подве-
шенный на невесомой пружине. Известно, что собственная частота ме-
ханических колебаний стержня на пружине совпадает с частотой тока в
соленоиде. Определим амплитуду колебаний стержня (Не 10.80).
В соответствии с (7.22) и (5.23) сила, действующая на стержень:
1 + сов 2ш01‘
с2д
г = „(д -1)п2135
420

Амплитуда вынуждающей силы
Е.
С2Н. '
Е, = 1с(р. — 1)п21ё
Так как частота вынуждающей силы 2030 >> соо, т. е. далека от
резонанса, можно пренебречь затуханием и воспользоваться соот-
ветствующей формулой (например, см.: 1, с. 100) для нахождения
амплитуды колебаний:
Х _ шт _ а,
0 ‘ 2 2 “ 2 '
4ш0 — то Зтсоо
Металлическое проволочное кольцо площадью 5 с омическим
сопротивлением К и индуктивностью Ь подвешено в горизонталь-
ном однородном магнитном поле В = ВО сов со! и удерживается в нем
таким образом, что угол между вектором Во и нормалью п к плоско-
сти кольца равен ср (рис. 10.54). Найдем средний момент М сил,
действующих на кольцо со стороны магнитного поля, а также поло-
жения равновесия кольца и исследуем их устойчивость. Рассмот-
рим два предельных случая:
1) соЬ >> К;
2) со], << К.
Выясним, в каком случае при одинаковых Ь вращающий мо-
мент больше (М 10.75). Используя (7.1) и (9.4)‚ для тока в кольце
получаем
д! 1 .
ЬЁ+ К! - ёВо8созсрсозлпсог.
Решение ищем в виде 1 = А зйп со: + Всоз сог. Подставляя в урав-
нение и приравнивая коэффициенты при синусах и косинусах, по-
лучаем
К зйп со: - Ьсо сов со:
1:2 + Ь2со2
Используя (5.5) и (7.8)‚ находим момент сил
1 = ЁВОЗ‘ созср
М = [рВ] =
= Ь 805, сов Ф“) (К зйп со! сов со! — Ьсо соз2 шгцпво].
В к’ + Ь2ш2 с Рис. 10.54
421

При резонансе
2-;
°°'Ьс
И ПОЭТОМУ
‘лыс’ шС "сг с‘
Отсюда, во-первых, для модуля 2 из условия задачи и (9.28) на-
ходим
2 2 1/2
2 — 1[Ь +51] =
_—. = 2
—гс2 С Оп
Ь
Сг
Во-вторых, УЧИТЫВЗЯ, ЧТО ИЗ УСЛОВИЯ задачи при резонансе СЛС-
дует, что На)’ >> г’, и поэтому импеданс контура можно считать
некоторым активным сопротивлением, которое обозначим Кк. Обо-
значая ток от источника 1 и падение напряжения на контуре П],
получаем По = [(12 + Кк), Н, = ИСК. Откуда
К
к
П1=П°К+К°
к
При ВКЛЮЧЕНИИ ВТОРОГО СОПРОТИВЛЕНИЯ ПОЛУЧЗСМ
кК
° к/2 + кк’
2
По условию оно в 1,5 раза больше П]. Это позволяет найти
_к_ _21/2_к1/2
к„_5, 9_(_) _(5) „30.
Г

11. ЭЛЕМЕНТЫ СПЕКТРАЛЬНОГО АНАЛИЗА.
АВТОКОЛЕБАНИЯ.
ПАРАМЕТРИЧЕСКИЙ РЕЗОНАНС. ШУМЫ
При рассмотрении вынужденных колебаний уже было сказано о
важности представления воздействующей нагрузки (правой части в
уравнении вынужденных колебаний) в виде набора гармоник (си-
нусов и косинусов). Такое разложение нагрузки (произвольного
сигнала) называется спектральным анализом.
Периодическую функцию ~(~) можно разложить в ряд Фурье
ОО ОО
ф) = А + ~~ А„яп(пиГ)+ ~~ В„сои(тГ).
п=1 п=1
(1 1.1)
С круговой частотой и связан период основной гармоники
(11.2)
Коэффициенты определяются следующим образом:
Т(2
А = вЂ” ~ Д~)й.
вЂ” Т)2
(11.3)
Интегралы всех гармоник по основному периоду дают нули.
2 Т
А„= вЂ” ~ ~(~) яп (позГ) 11~.
вЂ” Т~2
(11.4)
2 ТР2
В„= вЂ” ~ Я(~) сок (пи~) ~й.
вЂ” Т~2
(11.5)
Легко проверить непосредственным вычислением, что в обоих
случаях только квадратичные члены отличны от нуля.
Можно разложение написать и для комплексной функции 5'(~),
для которой Д~) является действительной частью (в отличие от пре-
424

дыдущего раздела специальный значок «» используем для спект-
ральной функции):
Я~) = Ке5'(~).
(11.6)
(11.7)
Отрицательные частоты соответствуют вращению вектора в ком-
плексной плоскости по часовой стрелке
(1 1.8)
Для непериодической функции Д~) снова имеем (11.6) и интег-
рал Фурье
5'(~) = вЂ” ~ 5'(и)е' 'Ыи.
(11.9)
Функция 5'(и) называется спектром (или преобразованием Фу-
рье) функции 5'(1)
5'(и) = ~ 5'(~)е '"'сй.
(11. 10)
В спектроскопии принято в показателе (11.9) ставить минус, а в
показателе (11.10) соответственно плюс и 1/(2л) из (11.9) перенести
в (11.10).
Найдем, какую величину 5, получаем вместо (11.10) при сдвиге
(11.9) на Т, т. е. при 5'(~ вЂ” Т). Из (11.10) следует
5'(и) = ~ 5'(~ вЂ” Т) е ' 'Й.
Введем новую переменную ~' = ~ вЂ” Т. Производя замену, получаем
Откуда
5', (и) = 5'(и)е '"~.
5(~) =,'~ С„е'""'.
и=-
ОО ОО
5' (и) = ~ 5'(1') е '"~' ~~й' = е '"т ~ ЯЯе ' ' й'.
(11.11)
425

При сдвиге сигнала изменяется фаза спектральной характеристики.
Проведем спектральный анализ некоторых колебаний. Цель та-
кого анализа — найти коэффициенты при гармониках, входящих в
разложение (11.1).
Для квадратичного преобразования монохроматического (одной
частоты) сигнала [(1) = А со32ш1 (М: 11.1) даже не нужно пользовать-
ся приведенными ранее формулами для коэффициентов ряда Фу-
рье, а из простой тригонометрии получаем
[(1) = А 0052 со! = %+ %сов 2ш1,
т. е. сигнал представляет сумму постоянной величины и второй гар-
моники.
Если при колебаниях амплитуда или фаза, или и то и другое
меняются со временем, то они называются модулированными. Наи-
больший интерес представляют случаи, когда модуляция является
гармонической функцией с частотой, значительно меньшей часто-
ты колебаний, которая называется несущей частотой.
Для амплитудной модулящш с частотой $2 << о) (несущей) частоты
и отношением амплитуд т < 1 (т называется глубиной модуляции)
(М 11.1) получаем
[(1) = А(1+ тсозсщсозш: =
т т (11.12)
= Асо$ш1+ А3со$(ш +Е2)1+ А5сов(со -$2):.
Спектр этого колебания, показанный на рис. 11.1, называется
линейчатым. Это коэффициенты при соответствующих гармониках,
обозначаемые А(ю).
Удобно воспользоваться комплексной формой сигнала и век-
торными представлениями. Из ( 10.20)
А его: + е-юг
АЮ) сов (21 = —————
н 3
А Получаем
.5'(1) = А (1 + тсов Еще“ =
Аёп 1 1 ц = А(1 +_!;е:ш +%е-даг)едшг =
аэ-О ш (м!) (о
Рис. 11.1
(11.13)
= Аедш; +Шецш+оу ++АШе1(ш-9):.
2
426

Учитывая (1О.33), изображаем вектора на векторной плоскости
(рис. 11.3). При т << 1 амплитуда суммарного вектора не меняется,
а меняется его наклон, т. е. фаза.
Найдем, что зарегистрирует приемник радиоизлучения, если изве1
стно, что в нем осуществляется квадратичное преобразование прини
маемого сигнала с последующим усреднением за некоторое время ш;
подчиняющееся условию 2л/ю << А: << 2л/9, где (о — радиочастота;
$2 — частота модуляции ($2 << ю) в следующих случаях:
1) на вход поданы амплитудно-модулированные колебания (11.12);
2) на вход поданы колебания, модулированные по фазе (11.14);
3) на вход поданы колебания, модулированные по фазе с от-
фильтрованной (т. е. убранной) частотой (о;
4) на вход поданы колебания, модулированные по фазе, в ко-
торых фаза спектральной компоненты частоты со изменена на л/2
(т. е. фаза несущей изменена на л/2) (Не 11.2).
В первом случае введем обозначение В(1) = А(1 + т сов (21) для
величины, которая мало меняется на интервале от 1- А1/2 до 1+ А1/2.
В этом случае выходной сигнал, который регистрирует приемник,
будет
!+А!
до) = 020)) = Ё 1 В2(х)со$2шх‹1х =
82 !+А!
=—%2 1 со$2сохс1х=
Г-А!
В2 (г) = А2 (1 + тсоз $202
———— 2 .
Предполагается, что А! содержит целое число периодов несущей
радиочастоты о).
Можно воспользоваться комплексными представлениями
/(1)= 11650),
где $0) = х + [у = А(1 + т сов (21)е“”’. Усреднение модуля комплексно-
го числа по большому числу периодов (р2) = (х2) + (у?) = 2(х2). Поэто-
МУ
1 1 _ 1 + тсов $21 2
8=<х2> `)) =А2( 2 )
где 8* — вектор, комплексно сопряженный 5, 5* = х — 1у. При т << 1
получаем
9
__ А; 1 + 2тсо$$21
д. .
$0)
(11.18)
428

См;
‚. ` А 1
‘1’, [`\` Т
1/1 |"\
`__‚'—", 7 "\1`--’ /’,’ $
—2о› —о) О о) 20:) 30) (о
|
1
Рис. 11.5 ”
На рис. 11.5 показан линейчатый спектр этого сигнала.
В случае рис. 11.4, б для непериодического сигнала с помощью
интеграла Фурье (11.1О) получаем сплошной спектр
5'(ш) = Т 5(1)е"""’с1: =
ш ‘°° (1 1.19)
= А 1 е-яшгд’: А(е-!цп/2_е1шт/2)= Ат 51“(‘”Т/2)_
ч” —1ш сот/2
Этот спектр показан на рис. 11.6.
Интервал частот, в котором спектральная амплитуда существен-
но отличается от нуля, называется шириной спектра. В данном слу-
чае можно взять ширину главного максимума (2Аоэ), для которого
Аи) = 2п/т. (11.2О)
Так как т равно длительности сигнала Ай, то можно написать
общее соотношение, связывающее длительность сигнала с"шири-
ной спектра и называемое соотношением неопределенности:
АгАсо = 21:. (11.21)
Вводя обозначение $2 = 21г/ 7, в случае рис. 11.4, в получаем сплош-
ной спектр
. ‘д .
.$`(со)= 1 Асо5($21)е“‘°’с11=
—1:/2
А #2 . . . А т” . 72 .
= 7 1 (егд! + 6-19! )е—1ш!‘1’ = 3 у е-Кш -52)!д[ + 1 е-Кш +$`2)гд‘ =
—т/2 —т/2 —т/2
430

Зав)
Ёиот
Х /\ _
Чае о шиш ё “Г
| Т Т | Т Т
2Аш —О О ‘д
Рис. 11.6 Рис. 11.7
— А е-Кш —$2)1:/2 _ еЕ(ш —$2)т/2 + е—1(‹о +52)1:/2 _ е1(ш +9)1:/2 _
` 7 —1(ш - о) —1(ш + о) `
_ А»; в1п[(со — $2)т/2] + з1п[(ш + $2)т/2]
" 7 (и) - $2)т/2 (ш + $2)т/2 '
Отметим, что этот спектр представляет сумму двух спектров
от прямоугольных импульсов, сдвинутых на $2 в разные стороны
(рис. 11.7).
Плоский вакуумный диод подключен к источнику постоянного
напряжения с пренебрежимо малым внутренним сопротивлением
(рис. 11.8). Эмиссионная способность катода К столь мала, что ток
через диод протекает в виде одиночных импульсов отдельных элек-
тронов, калщый из которых имеет длительность 1:. Найдем спектр
сигнала на измерительном приборе при прохождении такого им-
пульса (М 11.4). При пролете заряда (14 работа источника
11:14 = и %ш = или.
Для электрона работа
и К А
еЕаЬс = етах, 9*”
где 1 — ширина зазора. Поэтому, обозначая ускоре-
ние электрона а, получаем
ах ваг 2е1
1 т = 5- = ——- - —
( ) 1 д‘ ат2/2 1:2
Рис. 11.8
431

В первом случае при
1
вам << ЯС
~ а во втором случае при
1
от!л >> ЯС
получаем У,„„= У .
Высокодобротный колебательный контур находится под действи-
ем внешней амплитудно-модулированной ЭДС, изменяющейся по
закону Й(~) = А(1 + т сов2 Ж) сов и ~. Резонансная частота контура
может перестраиваться с помощью изменения емкости. Считая ко-
эффициент затухания контура р заданным, найдем амплитуду вы-
нужденных колебаний в следующих случаях:
1) контур настроен на несущую частоту ио;
2) контур настроен на частоту и + 2Й (Мо 11.8).
Используя тригонометрические формулы, для входного сигнала
получаем
В(В) = А')1в вЂ” совивс+ вЂ” тАсов1и в-2й)в+
2 о 4
+ вЂ” тА сов (ио вЂ” 2Й) ~.
1
4
Спектр этого сигнала показан на рис. 11.5. В соответствии с (10.1),
(10.9) и (9.27) для выходного сигнал получаем в первом случае
А, =и,вЂ” )1~ вЂ” )А =и,(1в вЂ” ) вЂ”.
Во втором случае
А2 = (ио + 2Й) вЂ” вЂ” А = (ио + 2Й) вЂ” вЂ”.
На вход колебательного контура с высокой добротностью подаются
амплитудно-модулированные колебания Й(~) = А(1 + т сов Й~) сов и~.
При перестройке несущей частоты и наблюдается несколько резо-
нансов. Найдем резонансные значения частот и определим глубину
модуляции т, если известно, что амплитуда вынужденных колеба-
ний напряжения на контуре уменьшилась в п = 4 раза при пере-
стройке частоты и от значения и до ио + Й + р (ио вЂ” собственная
433
28-2073

Рис. 11.12 Рис. 11.13
В схеме, изображенной на рис. 11.13, действует переменная ЭДС,
изменяющаяся по закону ё’ = $50 сов’ $21. Найдем токи 1 и 11, если
известно, что параметры цепи удовлетворяют соотношению (Не 11.11)
1
`3Ё`
Можно воздействие представить
92
—Т+7С0$ .
ё‘ б‘) а’ 252:
Постоянный ток будет идти только через 1,. Он будет равен
ггь
` 2к'
Так как ЬС контур находится в резонансе токов, то переменный
ток через него не идет, а идет через К, и Сд. Поэтому
_ гвь/2
` к + к, + 1/2ос, °
1
1
Амплитуда его
ё’ 2:2
1, =—Ёсо$ „Ф
2 [Кн „ь 1102 +1/(2:2С1)2Т/2 ; и =
2(К + К,)+1/$2С‚ '
На КС-цепЬчку (рис. 11.14) подается гармо- р-——-|
ническое напряжение ПВХ = Ц, сов юг. Парамет-
ры цепочки подобраны так, что сдвиг фаз меж- ивх к Нм
ду Паш и/Пвх составляет 60°. Найдем спектраль-
ный состав выходного напряжения и фазовые
сдвиги между спектральными компонентами для Рис. 11.14
23* 435

Таким образом, в спектре имеем три гармонические компонен-
ты: основную с частотой о) и амплитудой 110/2 и с частотами со 1 $2
а
и амплитудами ПОЛЕ, которые по фазе сдвинуты относительно
основной на 51г/6.
Рассмотрим аналогичную задачу, в которой сопротивление и
емкость поменялись местами (рис. 11.15) и сдвиг фазы равен —45°
(Не 11.13). При этом
1/1юС0 _ П
(1 = _
вы‘ “кн/косо 1+1шС0К
и гвср = —‹оСдК = —1, т. е. ШСОК = 1. В результате
ВЫХ
и“ 1+1/(1+асов$21)” 1+[
П _ 1 __ 1 +1асо$(2!/(1 +1)
Представляя входное напряжение в комплексном виде Ё = Нов“ ‚
имеем
д =%е1(шг—тг/4)[1+де1(пг+тг/4)+__е_ед(—ш+1г/4)].
2Л 2Л
Таким образом, В спектре имеем три гармонические КОМПОНСН-
Н о
ты: основную с частотой со и амплитудой Ё и с частотами со 1 $2 и
а
амплитудами Пои, КОТОРЫЕ ПО ФЗЗВ СДВИНУТЫ ОТНОСИТСЛЬНО ОСНОВ-
ной на п/4.
На вход колебательного контура (рис. 11.16) подается амплитуд-
но-модулированпое напряжение
П“ = 1/„(1 + тсоза!) созщо! (т < 1).
Контур настроен в резонанс с частотои то. Вычислим Нвых,
если то = 2- 105 с“, $2 = 5 - 103 с", добротность контура О = 100
и-МГЁ
Н“ Пыд ивх к иных
ст
И л д‘ д
Рис. 11.15 Рис. 11.16
К
437

(М9 11.14). Используя (11.12), получаем для спектра входного сиг-
нала
П = По (1 + тсо591)со$ш1 =
“от
= По созшо: +у%п-со5(шо + 9)1+—5—со$(ш0 + $2)1.
Чтобы получить спектр тока, надо воспользоваться (1О.16) для им-
педанса‚ (9.27) и (1О.38) для связи с добротностью и (1О.34) для фазы:
1 2 1 ш ш» 2 и
2=1{1+(ш1‚—бб)й] нем-ф?” ;
шЬ —1/юС 2
2А
‘8Ф=—Т—— 9-2
9
ш
где для резонанса Аш = О, а для смещенных компонент |Аш| = $2.
Таким образом, спектр тока
(1 и со5(ш 1+$2!+‹р)
1 =-Ё‘1со5ш01+ Ёт ° 2 ш +
к[1+(о2о/ш„) ]
Нот со$(ш01-$21—Ф) = Шсозшот] + тсо5($21+ ф) ]
2 1/2 к 1/2 '
к[1 + (о 29/ш0)2:| [1 + (о 2о/ш„)2]
Отсюда
Н = По СОЗШО’ 1 + тсоз(ш p7Z = По сов шар + т, со5(52! +301”),
[ЬЧОДЁ/ШЮ] [Ншдд/ЮЮ]
где
т, = ”’ 2 ‚д =О‚9т; (во =о,5.
[1+(02$2/ш0) :|
На вход колебательного контура (см. рис. 11.16) подается пери-
одическая последовательность прямоугольных импульсов, длительность
которых (т) в 4 раза меньше величины периода (Т). Частота повто-
рения импульсов (со = 211/ Т) совпадает с резонансной частотой кон-
тура. Найдем отношение амплитуд второй гармоники к первой на
438

выходе контура, если его добротность О = 100 (М: 11.15). Для вход-
ного сигнала, используя (11.7) и ( 11.8), получаем
1 т/2
С = _
п Т —-т/2
где А — амплитуда импульса; ш = 2л/Т— первая гармоника.
Так как т = Т/4‚ то для первой гармоники
Ае"”"”'с1! = 1 3111 то 3 ,
т: 2
А . л А
Спи = ЁЗШЕ = П‘,
а для второй гармоники
А
Ст - Е.
Рассматривая схему как делитель напряжения, получаем для ре-
зонанса Сизых = Сдвх, а для
1
(д) : (д) = ч,
2 ж)”
используя (1О.16), находим
еды, _ к к А
1 к
во
Ст ` [32 ЦШЬЧ/шсплр ‘ [(9/4)ЦС+К2]1/2 39.
Окончательно
ЁЩ = о, 0047.
1вьгх
Сигнал с выпрямителя имеет вид Щ!) (половинки косинусоид)
(рис. 11.17 сплошная линия). Его подают на схему, изображенную
на рис. 11.18. Контур Ь, С настроен на частоту (по; К >> ШОЬ и К >> г.
110)
Рис. 11.17 Рис. 11.18
439

Рис. 11.19 Рис. 11.20
Генератор импульсов, имеющих форму, изображенную на рис. 11.17
(сплошная линия), включен в цепь колебательного контура Ь, С, К,
имеющего добротность О = 100 и настроенного на первую гармони-
ку генератора (по (рис. 11.20). Внутреннее сопротивление генератора
г = 50 Ом, а амплитуда ЭДС П = 100 В. Найдем максимально воз-
можное значение амплитуды первой гармоники тока 1, так в контуре,
если все высшие гармоники должны быть подавлены по крайней мере
в 100 раз (В = 11/12 2 100) (М) 11.18). Пользуемся разложением в ряд
Фурье (11.1). В соответствии с (11.5) для первой гармоники имеем
2 “4 2 1
=— с11‘=—.
В, Т-Тжмсоз под! 2
Для второй гармоники, используя четность формы импульсов,
находим
7/4
4 2
В2 =7 Е! соз2соогсозсоогс1 =Ё.
АМПЛИТУДЫ ВХОДНЫХ сигналов
П 211
д‘? “Рт
При резонансе, используя (9.8) и (9.27), имеем
шоЬ = # = он.
(ПОС
При резонансе сопротивление имеет активный характер (10. 16),
поэтому
_ д:
1 ц К + г '
441

Вторая гармоника —- ВНС резонанса. ПОСКОЛЬКУ ПО УСЛОВИЮ она
ДОЛЖНЗ бЫТЬ СИЛЬНО ПОДЗВЛСНЗ, ТО
1
К+г<ш2Ь-——.
одС
Таким образом,
_ “2 _ [12 _ 2д2
2 ш21‚—1/ш2С 2011 - (1/2)0К ЗОН"
Отношение гармоник тока
Откуда
к = 8 -—5-_.
В 9пО — 813
Считая, что В равно как минимум 100, получаем К = 20 Ом. Это
значение сопротивления К определяет максимально возможное зна-
чение амплитуды первой гармоники тока
_ (71 _ ‘1/2 ‚.
[Шах -Й- п? - 0,71 А.
Аналогичную задачу можно решить в случае генератора прямо-
угольных импульсов (рис. 11.21) с амплитудой П = 100 В и скважно-
стью ос = Т/т = 4 (Т- период следования; т — длительность импуль-
сов), имеющего внутреннее сопротивление г = 50 Ом, нагруженного
на последовательный контур с добротностью О = 100. Найдем мак-
симально возможное значение амплитуды первой гармоники тока
[так в контуре, если все высшие гармоники должны быть подавле-
ны по крайней мере в 100 раз (В = 11/12 2 100) (Мг 11.19). Пользуемся
П
П П,
ю|ч
Н
Н
ю|ч
Рис. 11.21
М2

разложением в ряд Фурье (11.1). В соответствии с (11.5) для первой
гармоники имеем (11.22)
/2
2 ‘ 2.
в, =_и у со$(‹оО1)с11=(/[—.
Т п:
—-1:/2
В силу выбранной четности зависимости импульсов члены с
синусами отсутствуют. В чем можно убедиться непосредственным
применением (11.4).
Для второй гармоники, используя четность формы импульсов,
находим
т/2
1 сов (2ш01) д! =
—т/2
Е
п .
В = —
2 Т
АМПЛИТУДЫ ВХОДНЫХ СИГНЗЛОВ
ТЕ П
Н] =
При резонансе, используя (9.8) и (9.27), имеем
1
(о Ь = — = К.
о („ОС о
При резонансе сопротивление имеет активный характер (1О.16),
поэтому
_ д 1
1 _ К + г '
Вторая гармоника —— вне резонанса. Поскольку по условию она
должна быть сильно подавлена, то
к + г < ш2Ь - -1—.
ш2С
Таким образом,
_ (12 _ [12 _ 2112
(021. — 1/(о2С 293 ’ (1/2ЮК 3013 О
Отношение гармоник тока
12
443

Откуда
к = вмщзо -в\/5).
Считая, что В равно как минимум 100, получаем К = 45 Ом. Это
значение сопротивления К определяет максимально возможное зна-
чение амплитуды первой гармоники тока
_ (71 _д\/5/д
‘та г+К г+К
Квадратичный детектор В преобразует входное напряжение
Н = П0(5йп ш: + зйп 20)!) по закону Нд = #02. К выходу детектора
подключена цепь, состоящая из последовательно соединенных ин-
дуктивности Ь и сопротивления К (шЬ/К = 1/3) (рис. 11.22). Найдем
отношение амплитуды гармоники с максимальной частотой к посто-
янной составляющей выходного напряжения, снимаемого с сопро-
тивления (М 11.20). Результат квадратичного преобразования проще
всего получить, воспользовавшись (10.20). Обозначив со! = ос, имеем
(его: _ е-Еа е12а _ 6420: )2
= 0,474 А.
2: " 2:
ед2а _ 2 + е-Па + еИа _ 2 + е-Иа + 2(е13а _ еда _ е-йа + е-Юа)
_4 .
(5111 о: + зйп 2002 =
Отсюда следует
Нд = КНЁ (1 + сова)! —- 1со52ш1 — со53ш1—%со$4ш1).
2
Как в делителе напряжения, на выходе получаем
К
П = П
вых п Д п 1/2 °
(18 + шёл’)
С учетом условия находим
ивых4 1 1 = А
Нвыхо 5(1+16Ш2Ь2/к2)1/2 10`
Если на квадратичный детектор поступает входное напряжение
(1 = С/„(сов ш: + сов 2со1), то, действуя, как в предыдущей задаче,
получаем
Нд = #05 (1 + сова): + %со52ш1 + соз3ш1 + ёсоз4шг).
444

1.
5*‘ ‘——> ‚б 1
и 1) ид к им и го
У _ 7
кг — и
Рис. 11.22 Рис. 11.23
В случае подключения к детектору цепи, изображенной на
рис. 11.23, используя (1О.27) и (10.31)‚ для амплитуд получаем
и =и ‘
выхп дп <1+шйЬ2к2)1/2 °
Если известно, что
1
Л’
то для отношения амплитуды гармоники с максимальной частотой
к постоянной составляющей выходного напряжения, снимаемого с
емкости (Мг 11.21), имеем
юКС=
ивых4 _ 1/2 _ Ь
ивыхО О + 16Ш2 С2[К2 )1/2 6
Дифференциальная магнитная проницаемость ц некоторого фер-
ромагнетика зависит от напряженности магнитного поля по закону
_1Ё
"На;
На тонкий тороидальный сердеч-
ник из такого материала равномерно
намотана катушка, имеющая А! витков.
Сечение сердечника 5, радиус тора г 1
(рис. 11.24). Через катушку течет по- ' 5
стоянный ток подмагничивания, вели-
чина которого такова, что зависимость
В(Н) достигает максимума. Катушка
охвачена короткозамкнутым проводом,
сопротивление которого К. Найдем Рис. 11.24
=Н1‘Н2Н2-
445

спектр тока 1 в проводнике (пренебрегая его индуктивностью), если
помимо тока подмагничивания через катушку пропустить слабый
переменный ток 1 = 10 51п со! (Мг 11.23). Из условия
дВ
(__ = о.
а/Н „о
н = (Шуи.
#2
Ток 1 дает добавку магнитного поля АН, для которой из (5.6)
следует
НЗХОДИМ
АН 2тсг -
_ 41с1\/1
с .
Откуда
АН = ш 1 = 2мо 3*" Ф’ = А51псо!‚
СГ СГ
Где
А = шд.
С’
Магнитную индукцию представим в виде ряда Тейлора (разло-
жения по АН относительно максимального В)
_ 1 аз 1 4213 1 2 1 азв 3
По условию
ав _ _ с12В _ _ _ _ 1/2_ с13В _ _2
‹т)о - Оэ @*s - 2112110 ' ДШЩ) ’ ( ‘до ° 112-
Более высокие производные равны нулю.
Поэтому, подставляя АН, получаем
В = ВО 411,112)” А2 51112 со! - ёАз 51113 со!.
Для изменения индукции со временем находим
ЭВ
Ё = 401,112)!” А2со $111 со! сов со! — % Азсо (1 — сов 2со!) сов ш! =
= _(„‚„2)'/2 АЗсд) 51п 2со! сов ш! — -‘%А3ш (сов од! — сов 3со!).

Рис. 11.25
Рис. 11.26
няются по закону А = Е (1 + т сов Й~), считая, что т < 1, и:ь Й и
иЕ, «Л (№ 11.25). Используя (10.26) и (10.28), получаем
йод Я
Я+ АХ, Я+ сои
е ''Р
= У . вЂ” У (Я+иЕ),. = У,„е '~~,
Я+ коЕ (Я+ иА) е'~
где ф р = иЕ/Л. Учитывая условие,
2вЕ
9=
У.„„= У, сов~и! вЂ” 2тшД, вЂ” 2ивЂ”
сов Й~
= У сов и~+ 2Г и вЂ” сов (и+ Й) ~ вЂ” вЂ” + сов (и вЂ” Й) ~ вЂ”вЂ”
о о
2 2
Найдем, каков спектральный состав
выходного напряжения У,„„(т. е. ам-
плитуды и фазы спектральных ком-
понент) в схеме, изображенной на
рис. 11.27, если обе емкости одновре-
менно изменяются по закону
Увх= УО
вЂ” = вЂ” (1+ тсоай~),
1 1
С С
Рис. 11.27
448
Таким образом, если входное напряжение У = У, соя и~, то вы-
ходное напряжение У,„„= У сов (и~ вЂ” 2~р). Подставляя фазу и ин-
дуктивность, учитывая, что 2иА/Л «1, и пользуясь (11.14) и (11.15),
находим

Из (11.27)
к
У=в
4
Для частоты (ио вЂ” Й) получаем
7$
~Р = вЂ”вЂ”
4
Поэтому
= О~ое совио~
Г,®,„„вЂ” вЂ” вЂ” У е '"/4 вЂ” сов(и, +Й)/;
~~„, о1вы, = ~~~ое 2 сов(ио ~2)/
Сигнал на выходе представляет амплитудную модуляцию с глу-
Ш
биной вЂ”. Суммарный сигнал
к 1 т Зж 1т Е
ДУ сов и ~ вЂ” вЂ” + вЂ” сов и ~+ Ж вЂ” вЂ” + вЂ” вЂ” сов и / вЂ” й~ вЂ”вЂ”
2 2 2 4 2 /2 4
= ДУ,и~пи,![1+ вЂ” сов ш вЂ”вЂ”
~2 4
Чтобы построить векторную диаграмму, запишем результаты в
комплексном виде:
У,,„„= ДГое '"/'ехр (/иог);
У~„, „,>,„„вЂ” вЂ” вЂ” Г вЂ” е '"/'е'~ ехр (тД;
Г( о1 „= д Уо вЂ” е е ехр(нуэог).
Суммарный выходной сигнал в комплексном виде
у ду е-/в/2 + 0 у е-язв/4е/ж + е-!л/4е-!ж ехр(~и /)
вых о ~~2 о
о
455

Аналогичным образом можно представить и входной сигнал
А
Н“ = [По + По —’;(е’9’ + е”9’ ехр (тог).
На рис. 11.28 этот сигнал показан горизонтальным вектором По
и двумя векторами, вращающимися в противоположные стороны.
Выходной сигнал представлен вектором ОНО, отстающим от вход-
ного на л/2‚ и двумя векторами, вращающимися в противополож-
ные стороны.
Индуктивность колебательного контура периодически изменя-
ется во времени по закону, указанному на рис. 11.29. Найдем, при
каком значении емкости колебательного контура возможен пара-
метрический резонанс, а также при каком максимальном значении
активного сопротивления контура произойдет возбуждение пара-
метрических колебаний (Мг 11.35). Для резонанса необходимо, что-
бы период вынуждающей силы 410 совпал с периодом собственных
колебаний
41:, = т = % = 2л(1„с)"2.
Откуда
4 2
С- ‚ТО .
“То
Чэт х
“о _ 1422‘,
и
1 ЧМ" и’
2 с
Ц!)
0110
1,0)“ АЬ
Ч
д _ Г__.1|`|;__:Г_ц__
ои т П он т °
° —‘Ь- то Зто 10 Зто то
2П щами, 2П = = = — г
Рис. 11.28 Рис. 11.29
456

Предположим, что изменение индуктивности происходит за счет
изменения длины катушки. При растягивании производится рабо-
та, так как витки в катушке притягиваются друг к другу (как парал-
лельные провода). Колебания поддерживаются благодаря этой ра-
боте, которая равна изменению энергии магнитного поля в катушке
и равна потерям на сопротивлении (4.18)
2 2
(Ь + АЬ)% - 1„% = %12К4т0.
Откуда
_ М
тах — 410 '
Для поддержания незатухаюших колебаний в ЬСК-контуре ем-
кость конденсатора быстро меняется на величину АС каждый раз,
когда напряжение на нем равно нулю, а через время 1: возвращается
в исходное состояние. Найдем величину и знак АС (Мг 11.36). Когда
напряжение на конденсаторе равно нулю, ток в индуктивности мак-
симален 1 и мало меняется. Если время т мало по сравнению с
тах
характерным временем изменения тока, ТО на конденсатор притечет
заряд с; = [тахъ
Изменение энергии электрического поля в нем связано с изме-
нением емкости от С, до С2‚ которое должно восполнить потери на
сопротивлении за половину периода колебаний
1612 1с12_ 2 2С1‘С2 12 Т
2С2 2С"1тахт 26.2 >21тахк2°
Отсюда
т. е. емкость надо уменьшить, для чего раз-
двинуть пластины, при этом совершив ра-
боту, так как заряженные пластины притя-
гиваются.
В схеме, изображенной на рис. 11.30,
анодный ток [а при малых колебаниях в кон-
туре линеино зависит от напряжения на сет-
ке И по закону [а = „ЧК + 10, где Зи 10 —
постоянные величины. Катушка колебатель-
ного контура Ь и катушка связи Ьсв намота- Рис. 11.30
457

ны на общем магнитном сердечнике. Считая величины Ь, 1.”, С и 5
заданными (Ь = 4- 1О‘4 Гн, Ьсв = 4- 1О’6 Гн, С= 10"“ Ф, 5= 2. 1О'3 А/В),
найдем, при каком максимальном значении активного сопротив-
ления К контура возможно возбуждение автоколебаний и какова
будет эффективная добротность контура, если выбрать К = 2Ктах
(Мг 11.37). Как видим, анодныи ток не зависит от потенциала ано-
да, а зависит от потенциала сетки. Это связано с тем, что сетка
находится ближе к катоду. Дифференцируя это соотношение, по-
лучаем
а], 411, аи аП/с
= = 5‘ _
а: щ а: а:
При изменении анодного тока в колебательном контуре через
[св в соответствии с (9.1) и (5.27) индуцируется ЭДС
(в аи ау
д” = _М д: = _М5 вис’
где М — коэффициент взаимной индукции. Предполагая, что рассе-
яние мало, из (5.3О) получаем
м = (деву/г.
ПОТСНЦИЗЛ на ССТКС равен ПОТСНЦИЗЛУ на КОНДСНСЗТОРС, ПОЭТОМУ
где с] и 1 — заряд на конденсаторе и ток через конденсатор. Следо-
вательно,
‚ 1
Ёинд = ‘МЗЁ.
Если М < О, то ‘дм и 1 имеют одинаковые знаки, колебания
нарастают (самовозбуждение). При М > О колебания подавляются.
Используя (9.4), получаем для колебательного контура
и” + Ка’ +% = 445%
Вводя обозначения
1 К МБ К МЗ
“Ё та " 2В=:+г=:('+а)›
458

Для данной модуляции из (11.12) имеем
Г(~) = Ео совио~+ о сов(ио + Й)~+ о сов(ио вЂ” Й) ~. (11.32)
Используя (10.26), (10.28) и (10.32), имеем
О=К =Е .; ф~р= вЂ”.
Я+,иу (Яг+ ~г) ~р ' Я '
Для отношения амплитуд боковых гармоник получаем
2 2 1/2
А-.+ а Я' + (ио - ~1) ~'
А, о Яг +(и„+ о) ~г (41)
Искомый сдвиг р = вЂ” <р, поэтому
'ОО +~
3
вЂ” 1КЧ
4' ®О
~ИЧ, о=
БИЧ, а=
4'
®О
О)О
Используя связь
получаем
1 1
~~„,, „= агс~д вЂ” вЂ”; Ьу, „= агс1ц вЂ” вЂ” .
~о
О Д~' 4
Используем (11.32). Из (10.26), (10.30) и (10.32) имеем
Г/с'и С
е'~;
Я + 1Ци С 1+ иг ягСг
ф~р = иЯС.
Для отношения амплитуд боковых гармоник получаем
2
Ао,,+о 1+(ио вЂ” Й) Я С 5
А о о 1+(ио+й) ЯгС (41)'
462
Аналогичным образом можно рассмотреть ЯС-цепочку (рис. 11.35).
Для такого же амплитудно-модулированного напряжения ~(~) =
= ~,(1 + ~л сов Й~) сов и~, и < 1, найдем отношение амплитуд $око-
вых спектральных гармоник выходного сигнала, а также начальные
фазы гармоник, если (№ 11.43)

к
ж с
т) С 1/(1) дог‘ ж | ‘ к -—
т к
11% й
1
1
Рис. 11.35 Рис. 11.36
ИСКОМЬПЙ СДВИГ ч! = —Ф, ПОЭТОМУ
_ ("о + 9 _ 5.
‘Бшшсря _ _ то “ Е)
_ ‘до ‘9 _ 3. _
[Ёшщо-ц __ („О —_2! ‘Ёшщо —_1'
На вход колебательного контура (рис. 11.36) подается сигнал в
виде периодической последовательности прямоугольных импульсов,
длительность которых равна 1: = Т/2 — половине периода Тих сле-
дования. Круговая частота следования сигналов $2 = 2тв/ Т = 50 с“,
колебательный контур настроен на частоту (по = 350 0*‘.
1) Определим добротность контура, если амплитуда УС напря-
жения на конденсаторе оказалось в 8 раз больше амплитуды им-
пульсов По.
2) Найдем, при каком значении $2 = 921 наступит ближайший
резонанс и во сколько раз при этом изменится амплитуда напряже-
ния на конденсаторе, если период Т следования импульсов начина-
ют плавно уменьшать, не изменяя отношения т/ Ти параметров ко-
лебательного контура (Не 11.44).
В соответствии с (11.1)—(11.5) разложение Фурье для сигнала
(четной функции) (рис. 11.37) имеет вид
[(1) = 2 А‚‚ сов под
где
7/2
А„ = 1 /(!)СО$п$21д1.
-т/2
Для нашей функции
463

Щ?)
М д
-— * к
; ' ‘г’ г
_1_1 о 1 131 751 ’ г ‚<<к к Р
2 4 4 2 4 4 —с::|—-4——г;
Рис. 11.37 Рис. 11.38
Из условия следует, что контур настроен на седьмую гармони-
ку сигнала и амплитуда колебаний напряжения на конденсаторе
равна 8110. Из (1О.9) получаем
2 ОНО
7 1:
Откуда О = 2811 = 88. При уменьшении периода и увеличении часто-
ты Целое значение сед/ш получаем дляц, = 70 с“ при п = 5. Для
амплитуды имеем
= ય
2110
Аз = Ё-
Отношение амплитуд
511 _ 7
А, ` 3`
В схеме, изображенной на рис. 11.38, ключ К периодически за-
мыкает и размыкает цепь на равные промежутки времени (круговая
частота переключений 52 = 2п/Т= 100 с"), и в колебательном кон-
туре возникают колебания. Контур настроен на частоту о) = 500 с“,
напряжение источника постоянного тока ё = 1 В, добротность кон-
тура О = 50.
1) Определим амплитуду УС вынужденных колебаний напряже-
ния на конденсаторе.
2) При каком значении (2 = $2, наступит ближайший резонанс и
какова при этом будет амплитуда 175 колебаний напряжения на кон-
денсаторе, если частоту переключений $2 начинают плавно увеличи-
вать, оставляя параметры схемы неизменными (Не 11.45). Эта зада-
ча аналогична предыдущей. Воспользуемся полученными там ре-
зультатами. Так как п = со/п, то п = 5 , п, = 2. Поэтому напряжение
на конденсаторе
у 425‘; 1/5=6‚4 в; У,=15,9 в.
И

12. УРАВНЕНИЯ МАКСВЕЛЛА.
ЭЛЕКТРОМАГНИТНЫЕ ВОЛНЫ.
ВОЛНОВОДЫ И РЕЗОНАТОРЫ. ПЛАЗМА
Обобщение опытных данных и гениальная догадка позволили
Максвеллу получить уравнения электродинамики, носящие его имя.
В интегральном виде
фнл= вЂ” '"/(г+ вЂ”,' ',~)шя, /фнл=/(г+',~)ня~; дг.11
фел = вЂ” вЂ” / вЂ” шя, /фел = -/ вЂ” шя~;
(12.2)
фвыя = 4ш/ршГ, фвшя =/рл~;
5 и 5
фвня = о, ~фвгя =о~.
(12.3)
(12.4)
Максвелл в дополнение к току проводимости (плотности 1), свя-
занному с движением заряженных частиц, ввел ток смещения с плот-
ностью
1 дР . дР
3 = вЂ” вЂ” ' 3
см 4~ Др см Др
(12.5)
ЗО-го7з
Этот ток существует только там, где меняется электрическая
индукция Р. Подобно тому, что изменение магнитного поля вызы-
вает появление электрического (12.2), изменение электрического
вызывает появление магнитного (12.1). На ток смещения не дей-
ствуют силы, и в нем не выделяется теплота, так как нет движущих-
ся зарядов. Он создает магнитное поле.
Фундаментальные уравнения Максвелла (12.1) вЂ” (12.4) не содер-
жат никаких характеристик среды, в которой возбуждается электро-
магнитное поле. Их необходимо дополнить материальными уравне-
ниями. Наиболее простые материальные уравнения имеем в случае
слабых электромагнитных полей, достаточно медленно меняющих-
465

ся в пространстве (заметные изменения происходят на расстояниях,
значительно превышающих межатомные и межмолекулярные) и во
времени (характерное время изменения велико по сравнению с пе-
риодами внутриатомных и внутримолекулярных колебаний). Для
изотропных сред, не являющихся ферромагнетиками или сегнето-
электриками, можно получить
В = гЕ, {В = еоеЕ}; (|2.6)
В = мн, {В = дядин}; (12-7)
3= АЕ, {3 = ЖЕ}. (12.8)
Приведенные уравнения Максвелла в интегральной форме спра-
ведливы и там, где напряженности полей или свойства среды меня-
ются скачкообразно.
При отсутствии скачков те же уравнения можно записать в диф-
ференциальной форме
41:. 161) . д1)_
готН=71+Ёы-, {готнднг}, (12.9)
1дВ ЭВ _
готЕ--Ёг, {гогЕ-—-ё7}, (12.1О)
с1йу1)=4пр, {с11у1)=р}; (12.11)
сНуВ = О, {сйуВ = О}. (12.12)
Отметим, что из четырех уравнений Максвелла два являются
векторными и два — скалярными.
Введение в уравнение (12.1) изменения потока вектора элект-
рической индукции (тока смещения) оказалось весьма плодотвор-
ным. Для похожести уравнений (12.1) и (12.2) во второе надо вве-
сти ток магнитных зарядов, которые возможно, как показывают
известные опыты, вряд ли существуют. Однако предпринимаются
попытки обнаружения гипотетического элементарного магнитно-
го заряда — монополя Дирака, величина которого в гауссовой сис-
теме единиц до = Ис/2е‚ — методом регистрации электрического
тока, возникающего в сверхпроводящем контуре после прохож-
дения сквозь него монополя. Оценим величину тока в кольце ин-
дуктивностью Ь = 0,1 мкГн (М) 12.14). Обозначая ЕЁ — ЭДС, воз-
никающая в контуре, Ф — поток магнитной индукции, 1м — ток
монополя, т. е. магнитныи заряд, протекающии через площадку,
466

Для потока электрического поля получаем
'1'мах
Ф = ~ Е„йз = 2я вЂ” ' / яп у ~3 сов' ~р вЂ” 1) ~йр =
5' О
СОВ Ц) вЂ” СОВ ф
3
= 2щ~,
Точка А соответствует р = л/4. Поэтому
81Й И1
~И = 7Ц2
Я
Из (12.1) находим
СОЯ Ы
Н = Р0)
2 2СЯ
Чтобы поле диполя можно было вычислять по электростатичес-
кой формуле (1.9), необходимо выполнение условия квазистатич-
ности Л «сТ= 2яс/и.
Аналогичным образом можно найти напряженность магнит-
ного поля, если величина диполя постоянна, а положение меня-
ется ~ = аип и~, где постоянная величина а «Л (№ 12.64). Из-за
нейтральности диполя ток при его движении не возникает. Это зна-
чит, что магнитное поле определяется опять потоком вектора на-
пряженности электрического поля. Найдем магнитное поле в точке В
(см. рис. 12.1) Для связи с углом ~~ имеем
р = с Щ ф, ~~~ = 2щ>~ф, ~ф =
~~Ч~
со~Ч~ соя ~р
Для потока при каждом ~ получаем
"~мах
Ф = ~ Е„й = 2ш вЂ” / яп у 3 сов~ у вЂ” 1 Шу =
з ~ о
со~ Чп~~ со~ Чп~~~
3
Щ~
г
Из рис. 12.1 видно, что при ~ «Л получаем
Ж
Ч
~а~
2 Я
Поэтому для потока имеем
2 Я2
Ф=2шр
Я

Из (12.1)
нагл-ЕЁ
_ с дг’
ПОДСТЗВЛЯЯ ЗЗВИСИМОСТЬ 2 ОТ времени, ПОЛУЧЗСМ
. 2ш1
Н = а2ш зт —.
р 0124
Из (12.2) следует, что изменение магнитного потока приводит к
появлению вихревого электрического поля, созданию ЭДС. Это про-
исходит, например, если в однородное магнитное поле, которое с
некоторого момента 1= 0 начинает уменьшаться по линейному зако-
ну со скоростью
с1В _
717 ‘ ’ ›
перпендикулярно полю поместить замкнутый круглый виток радиу-
сом г, индуктивность которого 1„ а омическое сопротивление К.
Используя (9.4) и (12.2), получаем
ЬЁ + К! = пуда.
(1!
Разделяя переменные и интегрируя, находим
1 = „И 5% + Ае“”’/‘.
Постоянная интегрирования А определяется из начального ус-
ловия: при 1= О, 1= О и
А = - 2 Е.
пг к
В результате для потока магнитной индукции через виток, ис-
пользуя (5.27), получаем (Не 12.21)
2 2 1 _ е-КГ/Ь
Ф: Вт +1,] =пг Во —а1‘+Ьа——7г—.
На самоиндукционный поток в витке наложен внешний поток
поля.
При переменном напряжении (У= И, сов со!) на обкладках кон-
денсатора (например, в виде круглых дисков, находящихся на рас-
469

стоянии 11) внутри возникает магнитное поле, которое из (12.1) и
(12.5) равно
,' —;-(0[/
2с/2 _ О 2С}: '
Если внутри такого конденсатора находится проволочная прямо-
угольная рамка (2а - 21)), одна сторона которой (21)) совпадает с осью
симметрии конденсатора, то по рамке будет идти ток. Найдем силу
тока 1, предполагая, что омическое сопротивление рамки К велико
по сравнению с индуктивным (Не 12.19). Из (7.1)
Н:
20
д [н(г)2ьаг д:
_ 1дФ/д! _ 1 0 _ 2 а
--Б—г-—Ё к -2о) Ьцдсоэшгш.
Рассмотрим такой же конденсатор (два круглых диска площа-
дью 5‘), в который помещена квадратная проволочная рамка со сто-
роной, равной а, причем одна сторона рамки совпадает с осью кон-
денсатора, а две другие направлены по радиусу диска. Конденсатор
заряжается от источника постоянной ЭДС до заряда 90 (постоянная
времени т = к‚с›. Считая, что омическое сопротивление рамки К
намного больше ее индуктивного сопротивления, найдем джоулеву
теплоту, выделяющуюся в рамке при зарядке конденсатора (М) 12.24).
При изменении заряда конденсатора меняется электрическое поле
в нем и в соответствии с (12.1) возникает меняющееся в зависимо-
сти от расстояния от оси конденсатора г магнитное поле
Е ‘г
2с °
Штрихом здесь и далее обозначены производные по времени. По-
ТОК МЭГНИТНОГО ПОЛЯ ЧЕРЕЗ рамку
Н:
а ‚аЗ
Ф =]’Нас1г = Е —.
О 4с
Из (12.2) находим ЭДС в рамке, которая создает ток в ней
1 Ф! 3 Е//
1 = — = а —-.
С к 4с2К
Поле в конденсаторе равно
Е = 411%.
470

Для тока получаем
Ток при зарядке конденсатора Х, = Д', идущий через сопротив-
ление Л„определяется (9.4)
Щ'+ вЂ” = Ж.
С
Разделяем переменные и интегрируем
В начальный момент заряд равен нулю, поэтому постоянная
К = вЂ” ЖС; Д = ЖС(1 вЂ” е '~').
При ~ = О = Оо. Следовательно, Д = Оо(1 вЂ” е-'~'). Отсюда
О" = вЂ” ®е '~'.
Для джоулевых потерь в рамке имеем
ОО
Ог
Ж = ~Х~Яй = тс'а о е ~'~'й = я~а
4 ~-2д 4
0 "' О
2с Я Ят~
а = ~ Хай = вЂ” Б1п и~
~о
471
Эта энергия берется от батареи, заряжающей конденсатор. Пре-
небрегать индуктивным сопротивлением можно, когда а/т «с.
Рассмотрим плоский конденсатор с обкладками в форме дисков
радиусом Я (расстояние между ними равно Ь), который заполнен
диэлектриком (диэлектрическая и магнитная проницаемости е и р)
и через который идет переменный ток смещения Х = Хо сов и1.
Этот ток создает в конденсаторе магнитное поле. Пренебрегая
краевыми эффектами, вычислим электрическую и магнитную
энергии, локализованные в конденсаторе, и найдем отношение
максимальной магнитной к максимальной электрической энер-
гии (№ 12.2).
По току смещения Х находим изменение заряда

и напряженность электрического поля
Е=4п ~.
еЮ
Плотность электрической энергии
8п ещ2дя4 '
а в объеме конденсатора
° 2
~, = пЯ~Ьи, = 2ЫО
И0'Я'
Для плотности тока смещения в конденсаторе имеем
1
./ =
жЯ
Поэтому из (5.7) и (12.1) магнитное поле
И =21
сЯ
где г вЂ” расстояние от оси конденсатора.
Плотность магнитной энергии
и„= вЂ” = р41~
уг ~г
м 8~ 8исгЯ4
Магнитная энергия в конденсаторе
Я
~„= ~ н„2пЬпБ = рЫ'
о
4с
Отношение максимальной магнитной энергии к максимальной
электрической энергии равно
2
~чдих
8 с
э мах
Для справедливости условия квазистационарности, когда выпол-
няются использованные ранее соотношения, должно быть иЛ «с.
Г1ри этом полученное отношение много меньше единицы.
472

Если бы была задана не сила тока в цепи, а переменное напряже-
ние на обкладках этого конденсатора Г= ~~ яп и~, то для тока сме-
щения из (12.5) получаем
1 дЮ дЕ/д~ дГ/д~
4~ д~ 4~ ~Ь
Из (12.1), пренебрегая краевыми эффектами, находим магнит-
ное поле (М 12.6, 12.7)
Н = е вЂ” = еиг1'о
д ~ ~ СО~О~1
д~ 2сД О 2Д~
Найдем отношение электрической и магнитной энергий внутри
длинного соленоида (длина /, радиус Л), состоящего из Ж витков
проволоки, заполненного веществом с диэлектрической и маг-
нитной проницаемостями е и р, по которому идет' неременный
ток 1= 1 соки~ (Ж 12.3). Из (5.23) магнитное поле в соленоиде
Н = 4пЖ вЂ” = 4пЖ10
с1 с1
Плотность магнитной энергии
Н2
~м
Зп
Пренебрегая краевыми эффектами, получаем магнитную энер-
гию внутри соленоида
2
Ж„= ч„пЯЯ1 = 2п~рЛ~У~1О
с1
Из (12.2)
Е2пг = вЂ” вЂ” пг = пг р4пЖ1ои
2 З1П О~
с д1
с
Откуда
Е = 2пцЖиг10
с1
Плотность электрической энергии
ЕЕ
Ж
э 8
473

Для вычисления всей электрической энергии внутри соленоида
(опять пренебрегая краевыми эффектами) интегрируем
2 2 2 2 2 31й И1
2
2 2 2 4 2 2 Б1П
И~, = е4ш~р~и~К~Х~О(,, 2шп1г = ц~~я~и~Я~К~Х
С (
Отношение максимальной электрической к максимальной маг-
нитной энергии равно
г
э мах ~Р
8 С
М ПАЯХ
В случае квазистационарности (иЛ «с) это отношение много
меньше единицы.
При изменении силы тока в соленоиде меняется поток магнитно-
го поля и в соответствии с (12.2) возникает вихревое электрическое
поле, силовые линии которого представляют окружности относи-
тельно оси соленоида. Например, при возрастании тока с постоян-
ной скоростью Н/Ы~ = Х' в длинном воздушном соленоиде с радиу-
сом намотки го, содержащим и витков на единицу длины, имеем для
потока, используя (5.23),
Ф = жг„~4яХ вЂ”,
С
и из (12.2)
ЕЛ = 2пгЕ = вЂ” вЂ” Ф' = иго 4шХ' вЂ”.
Откуда для г = 2г, (т. е. вне соленоида) находим электрическое поле
Е = яг Х' вЂ”.
2'
Если соленоид погрузить в диэлектрик с диэлектрической про-
ницаемостью е = 2, то в соответствии с (12.2) Е, = Е, а в соответ-
ствии с (3.8) Л, = 2Х) (М 12.20).
На рис. 12.2 показана система из двух длинных соленоидов (один
радиусом г, вставлен в другой радиусом г,) с одинаковой плотнос-
тью намотки л (витков на сантиметр), которые одними концами
подключены к батарее постоянного тока ЭДС, равной Ж, а друтими
замкнуты на сопротивление Л. Оценим, при каком сопротивлении
электрическая и магнитная энергии системы будут одинаковы (М 12.66).
Пренебрегая сопротивлением соленоидов, можем считать, что раз-
474

является магнетиком, но имеет меньшее удельное сопротивление,
зависит от величины р/р. Для меди ц вЂ” 1, р = 10 ' Ом м, для
железа ц вЂ” 1000, р = 10-' Ом м. Поэтому ток в железе больше в
1О 000 раз. Железный цилиндр будет нагреваться быстрее медного
вне зависимости от гистерезиса (М 12.16).
Для медного цилиндра радиусом а и высотой Ь в переменном
однородном поле В = Во сов и~ мощность теплоты, выделяющейся
из-за токов Фуко, равна
и
Д = Ь ) р/~2пЫг,
о
где г вЂ” расстояние от оси цилиндра.
Пользуясь законом Ома (4.7), (4.8) и (12.2), получаем
2
О = вЂ” пЬ вЂ” иВ,вЂ” яп и~.
1 1 а
р
При вычислении средней мощности теплоты надо учесть, что
среднее значение яп2и~ равно 1/2 (Ж 12.22).
Если в цепь переменного тока Х = Хо сов и~ входит конденсатор
(площадь пластин 5', расстояние между ними Ь), заполненный слабо
проводящим диэлектриком (диэлектрическая проницаемость е, удель-
ное сопротивление р), то токи проводимости и смещения идут па-
раллельно. Обозначая поверхностную плотность зарядов на пласти-
нах конденсатора о и плотность тока проводимости ~, получаем
да 1
й 5'
Используя (3.8) и (4.7), находим
вЂ” +4ш вЂ” = 4я вЂ”.
ЫЕ Е 1
й ре е5'
Для изменения напряжения Г на конденсаторе имеем
вЂ” + 4я вЂ” = 4яХ вЂ”.
Ы~ ~ Ь
й ре е5'
Для решения этого уравнения удобно представить правую часть
в комплексном виде ае' ' и соответственно искать Г= ~~е'"'. Под-
ставляя в уравнение, получаем
476
4ш1О Ь/еЮ (4ш1О Ь/еЯ) е '~
4пlРе+ ~о~ ~(4 / )2 + 2]~

Откуда (Не 12.23)
41:10 12/85
|:(4л/ре)2 + (02 т”
Можно воспользоваться представлениями об импедансе, пере-
писав (10.32) для параллельного соединения сопротивлений
_ К
_1+1‹1›СК’
где
11_ _ 5
К-рё, С-еда.
Получаем тот же результат, так как И, = 10|2|.
Рассмотрим плоский конденсатор в виде двух плоских дисков с
радиусами а и расстоянием между ними 11, заполненный слабо про-
водящей средой (е = и = 1) с электропроводностью А, который в
момент времени 1 = О подключается к батарее постоянного тока с
ЭДС, равной 85, и внутренним сопротивлением г. Найдем зависи-
мость от времени тока проводимости 1" и тока смешения [см в кон-
денсаторе, а также магнитное поле Н вбэлизи его боковой поверхно-
сти (М 12.72).
Обозначив напряжение на конденсаторе И его емкость С и со-
противление току проводимости
Ь
Ада
к:
В)
И ИМЕЯ В ВИДУ, ЧТО ТОК через конденсатор равен СУММЕ ТОКЗ ПРОВО-
ДИМОСТИ
1 1. у
пр ' Б
и тока смещения [см = СУ’ (штрихом обозначена производная по
времени), 1 = 1пр + 1“, из (4.2О) 8 = У+ 1г и, следовательно,
ггг-г/
‚ У
-СУ+Е.
Интегрируя это уравнение при условии 1/(0) = О, получаем
„ 1—е”“
17:81?-
К+`г ’
477

Если параметры схемы подобраны так, что юСК = 1, то
ё)
1 =1 = 2
[(К+ г)2 +г2]и
пр см
Из (12.1)
2
(Йпр + ]см)х ЁОШСК +1)
а2с
; Й=2х 2 .
а с(К+г+1о›СКг)
Й2пх = 41:
При шСК = 1 имеем
_ ЙЁЛХ
а2с [(К + г)2 + г2 т”
Проводящий шар радиусом а = 20 см (рис. 12.3, а), находя-
щийся при потенциале ПО = 3 - 104 В, разряжается через сопро-
тивление К = 5- 103 Ом. В квазистационарном (следующем изме-
нению тока) приближении найдем возникающее при этом маг-
нитное поле В(1, г, 6) вне шара (Мг 9.12). Заряд шара меняется, и
меняется создаваемое им электрическое поле (1.4). Из симметрии
картины и уравнения (12.1) получаем
до Едят)
флаг: = Н2т° = 14:.
с а‘!
С помощью рис. 12.3, б и (1.3) можно получить
1 Еда: = 4:2,
5
где а — заряд шара; 52 — телесный угол, для
которого из рис. 12.3, а находим
$2 = 2п(1 — сов О).
Изменение заряда шара за счет тока че-
рез сопротивление К описывается (9.3О), где
в соответствии с (2.4) С = а и с; = П0ае"/”".
Для магнитного поля
—!/Ка
В = Н = П0а(1 —со56)
саКг °
479

Возмущения электрических и магнитных полей распространя-
ются в виде волн.
Получим уравнение, описывающее распространение плоской
поперечной электромагнитной волны. Будем предполагать, что заря-
ды и токи отсутствуют (р = О, 1 = О), и волна распространяется
вдоль оси х в однородной бесконечной среде с диэлектрической и
магнитной проницаемостями е и ц. Из (12.9) и (12.10) получаем
гогН = вЂ” вЂ”;
едЕ
с д1
(12.13)
(12.14)
гог Е = вЂ” вЂ” вЂ”.
рдв
с дР
Используя правую систему координат и (5.13), проектируем
(12.13) на у, а (12.14) на ~
дН, едЕ
дх с дг
(12.15)
дЕ, ~дН,
дх с дг
(12.16)
Дифференцируя первое по г, а второе по х, получаем волновое
уравнение
сг дгЕ
ЕОЦ'Ор, дх
г
д~ ~И дх д~
(12.17)
Е =фх вЂ” И) +фх+ И),
(12.18)
где ~ и /, вЂ” произвольные функции своих аргументов (фаз); о вЂ” ско-
рость распространения фазы (фазовая скорость):
С С С С
О = О =
( )1/2 и ' ( )1/2 и
(12.19)
Здесь введен показатель преломления среды
С 1(г
и = вЂ” = еоерор
и = вЂ” = (ц~)
1/2,
(12.20)
480
Можно было бы продифференцировать (12.15) по х, а (12.16) по г
и получить аналогичное уравнение для Н,
Легко убедиться простой подстановкой, что решение уравнения
(12.17) имеет вид

Для волны, бегущей в положительном направлении оси х, из
(12.18) находим Еу =/3(х — 12:). Из (12.16) получаем
дд”г__Ё__‚ _ НЕ-‘ 11225
Ё д: _ дх _ Д“ т’? д: _Ё(ед) д:`
Отсюда
1/2ш&_ 1/236: (12.21)
(Щ д: 48) 3:‘
Интегрируя и учитывая, что постоянных составляющих в волне
нет, находим
1/2 1/2
(р) Н = (е) Е .
1 У
На рис. 12.4 показано, для примера, изменение электромагнит-
ного поля в очень важном случае плоской поперечной гармоничес-
кой (л — гармоническая функция: синус или косинус) волны.
Из (12.21), (3.75) и (7.12) следует одинаковая плотность энергии
в электрическом и магнитном полях. Эта энергия распространяется
со скоростью и.
Уравнения Максвелла дополним законом сохранения энергии.
Для этого умножим скалярно (12.13) на Е, а (12.14) на Н и сложим
д(еЕ’/2 + „112/2)
д:
Пользуясь векторной формулой, получаем
= -(НгогЕ—ЕготН).
1
С
Э(ЕЕ2 + “На/З” = —с11у$. (1222)
д:
31‘ 481

Введенный здесь вектор плотности потока энергии 8 называется
вектором Пойнтинга
[ЕН] _
41: ’
ПОСКОЛЬКУ ПЛОТНОСТИ ЭНерГИИ СООТВСТСТВУСТ ПЛОТНОСТЬ МЗССЬП,
ТО при раСПрОСТраНеНии ЭНЕРГИИ СО СКОРОСТЬЮ С, ДЛЯ ПЛОТНОСТИ Элек‘
тромаГниТноГо импульса 8 ПОЛУЧаеМ
3=%=%Ё1; {дЦЕШ}. (1224)
с пс с
Для двухпроводной линии из идеального проводника (без тепло-
вых потерь), соединяющей генератор постоянного тока с нагрузкой
(сопротивление К), найдем вектор плотности потока энергии (век-
тор Пойнтинга) (Не 12.25). На рис. 12.5 показаны направления век-
торов. При отсутствии сопротивления подводящих проводов их по-
тенциалы (р, и (р, постоянны и отличаются на величину напряжения
(падения потенциала) на сопротивлении нагрузки (К). Учитывая
направление магнитного поля, получаем из (12.23)‚ что поток энер-
гии идет от генератора к нагрузке между проводами линии.
Если учитывать, что подводящие провода обладают сопротивле-
нием, то у вектора напряженности электрического поля появляется
составляющая вдоль провода (М 12.26). Это приводит к потоку энер-
гии к проводу. Если провод имеет длину 1 и радиус г, а падение
напряжения на этой длине У и по нему идет ток силой 1, то на
поверхности провода
5 = с {5 = [ЕН]}. (1223)
Е-ё; Н-Ё,
СГ
а поток энергии через боковую поверхность, как следует из (12.23):
52пг1 = свнт! = пл
41:
Этот поток энергии равен мощности, выделяемой током в проводе
(в виде джоулевой теплоты).
Если в линии, изображенной на рис. 12.5, поменять направле-
ние тока, что соответствует как бы переворачиванию рисунка, то
направление потока энергии от генератора к нагрузке не изменится.
Поэтому в случае синусоидального тока, когда напряжение и сила
тока находятся в одной и той же фазе, т. е. одновременно меняют
направление (Не 12.39), направление потока энергии не меняется,
хотя величина его меняется вместе с изменением величины полей.
482

+ 5
Е? Е‘ —-- к
69
Рис. 12.5 Рис. 12.6
Если ток отстает по фазе от напряжения на 90° (п/2) (Не 12.40), то
результат меняется. Предполагая гармоническое изменение величин,
можем написать для напряженности электрического поля, которая по
фазе совпадает с напряжением, Е = Ед сов юг, а для напряженности маг-
нитного поля, которая по фазе совпадает с током, Н = НО зйп оп. Исполь-
зуя (12.23) и вычисляя плотность потока за период, получаем
з-ТЕНЁ-ТЕ созсогН запюгЁё-о
_О 411-0 О О 411- °
Каждые четверть периода вектор 3 меняет направление на об-
ратное. Энергия колеблется в отдельных участках, а не течет в од-
ном направлении. Это стоячая волна.
Найдем величину и направление вектора Пойнтинга (5) для си-
стемы из двух параллельных проводящих плоскостей (рис. 12.6), по
которым текут антипараллельные токи с линейной плотностью 1 и
которые замыкаются через соединяющую плоскости перемычку тол-
щиной б с удельным сопротивлением р (Не 12.71). Полный ток по
плоскости 1 = 11, полное сопротивление перемычки
к = 1,
915
падение напряжения между ПЛОСКОСТЯМИ
У = 11: =1р3‚
в
НЗПРЯЖеННОСТЬ электрического ПОЛЯ между ПЛОСКОСТЯМИ
Е = Е.
‘а
Из (12.1)
Н = 21111
с
483

и, следовательно,
. . р
5 = 12 —.
б
При подключении соленоида к источнику постоянного тока в
него втекает (от момента подключения до момента установления
постоянного тока) энергия. Найдем ее величину для длинного соле-
ноида (длина 1, радиус г, число витков А’), который подключается к
источнику постоянной ЭДС ё (Мг 12.28). Из (9.4) имеем
д! ‚
ЬЁ+1К-&6.
Разделяя переменные, интегрируя и используя, что в начальный
момент ток был равен нулю, получаем
1=%р_ытц.
Из (5.23) и (5.25) (в системе СИ)
Ш
1 .
Из (12.2) на боковой поверхности соленоида
В=НО
ё‘ к: Ь
Е = .М°——е` / .
”° 211. я
Используя (1223), для энергии, прошедшей через боковую по-
верхность соленоида за все время установления тока, получаем
12
Г
= 1‚—.
21122 2
их =12пгтЕНс1т = „ома-гл
О
На рис. 12.7, а изображена цепь, состоящая из резистора сопро-
тивлением К и длинной катушки радиусом г, и плотностью намотки
витков п [см"] и соосного с катушкой прямого провода радиусом гд,
по которому течет постоянный ток 1. Пренебрегая сопротивлени-
ем катушки и провода, найдем аксиальную 82 и азимутальную ЗФ
компоненты вектора Пойнтинга внутри катушки вдали от ее тор-
Цов (М 12.27). ‚
Разность потенциалов между катушкой и проводом Аср = 112. Это
значит, что на проводе имеется заряд, а из (123) следует

в Ё; 5:.
ФИФ ЭЗФ
Ф б)
Для определения постоянной А найдем из интеграла
2 г:
ф‘
[дф = А 1 —.
Г
1 Г|
Отсюда
Аф [К
Ф -‹р =-А1п[2]; А: - . .
2 ` п шит) ‘ПИ/Ф
Таким образом, для вектора Е имеем _
__$&__:
1“(’2/'3) "2 .
Для магнитного поля из (5.23) и (5.2) имеем
Н: май; НФ = 91.
С СГ
Е=—
На рис. 12.7, б показаны векторы полей и получающиеся на ос-
новании (12.23) плотности потоков энергии:
51-2 д
5 = Е -1 ———————;
1 с 471 2пг21п(г2/13)
п
н
5 = Е4=12К—————.
° с 4“ г1П(г2/п)
485

ПОЛНЫЙ ПОТОК энергии через КЭТУШКУ К СОПРОТИВЛСНИЮ К равен
’2
п = у удят/г = 1212.
"1
Это — мощность джоулевых потерь на сопротивлении.
Рассмотрим плоский конденсатор, состоящий из двух одинако-
вых дисков радиусом К, заряженный и отключенный от источника
электричества. Если среда внутри конденсатора обладает проводимо-
стью, то он будет разряжаться. При этом за счет изменения плотно-
сти заряда о идет ток проводимости плотностью
. _ а'о
1 с1г ’
направленный так же, как вектор электрической индукции 1), и ток
смешения
направленный, как вектор дВ/дг, т. е. противоположно вектору В.
Таким образом, суммарный ток через конденсатор равен нулю (Мг 12.4).
И вследствие (12.1) или (12.9) магнитное поле отсутствует.
Если же конденсатор разряжается посредством искры, проскаки-
вающей по его оси, то внутри него возникает магнитное поле. Это
связано с тем, что плотность тока смещения не зависит от расстоя-
ния от оси конденсатора, а ток проводимости 1 идет только по оси
и создает поле в соответствии с (5.2)
Н„р = д.
С!’
Учитывая изменение заряда конденсатора для тока смещения в
зависимости от расстояния от оси г, получаем
Отсюда и из (12.1) следует (М 12.5)
2 2
2лгН = 530 + 1„) = 21:11.
С д СГ
На рис. 12.8 показано изменение магнитного поля в зависимос-
ти от расстояния от оси. Вектор Пойнтинга определяем по (12.23).
486

Поток энергии направлен к оси конденсатора и нм
обеспечивает разогрев среды (в искровом кана-
ле) током проводимости (сопротивление искро-
вому пробою). На краях конденсатора, где маг-
нитное поле равно нулю, потока энергии нет
(Мг 12.8).
Разряд конденсатора может произойти за счет
соединения его обкладок проводом длиной 1 и
радиусом а, проходящим вне конденсатора. Пре-
небрегая краевыми эффектами и обозначая ток
в цепи 1 (в проводе это ток проводимости, в кон-
денсаторе — ток смешения) и заряд на конден-
саторе с] (и ток и заряд меняются со временем), находим, что на
краю конденсатора (из круглых дисков радиусом Ь, расстояние между
которыми 11) магнитное поле
Рис. 12.8
Н=Ё
ксЬ
И ЭЛЕКТРИЧЕСКОЕ
Ек =4п1—=1(1.
Из (12.23) получаем, что через боковую поверхность конденса-
тора вытекает поток энергии равный 441/2/122. Электрическое поле
вдоль поверхности провода
л
ц=ц„
1
а МЭГНИТНОЕ на ПОВЕРХНОСТИ провода
_Е
_са`
Н
П
Учитывая направление полей и (12.23), для потока, втекаюшего
в провод через его поверхность (21га1), получаем 441/1/122. Таким об-
разом, вся энергия, вытекающая из конденсатора, втекает в провод
и идет на его нагрев за счет омического сопротивления (М 12.9).
Найдем вектор Пойнтинга в зависимости от расстояния от оси
конденсатора (г) и времени и полную электромагнитную энергию,
вытекающую через боковую поверхность конденсатора за все время
разряда, если он заполнен диэлектриком с диэлектрической прони-
цаемостью а, а сопротивление провода К (М9 12.32).
487

Если конденсатор емкостью
2
С = 875%
разряжается через сопротивление К, то из (9.4)
(14 с; _ д!’ _
КЖ+Е-КС д’ +У-О.
Откуда
1/(1) = И‚е“/‘; т = НС.
Электрическое поле внутри конденсатора Е = У/Ь. Плотность
тока смешения в конденсаторе
= дв/а: = _ У„е""
см 475 тсЬ2К °
Из (12.1) имеем
е-г/т
сЬ2К ч
Вектор Пойнтинга направлен из конденсатора к сопротивлению
Н = мы г = 214,;-
-2!/т
__ Н __ 2 С
.5`(г‚ г‘) - сЕ 4” — гИ, Гит,‘
При г = Ь
—2!/т
_ 2 е
5 ' у° 2пььк‘
Полная электромагнитная энергия, вытекающая через боковую
поверхность конденсатора за все время разряда,
И’ = Тильда: = Тддет“ Ё = С-Ё.
о о О к 2
Это начальная энергия заряженного конденсатора.
В подобном конденсаторе, образованном двумя круглыми диска-
ми, расположенными на расстоянии 11 друг от друга, мысленно вы-
делим замкнутую цилиндрическую поверхность радиусом К (212 < И) и
длиной Ь меньше диаметра пластин конденсатора (рис. 12.9). В слу-
чае изменения напряжения на конденсаторе по линейному закону
488

1 {Е т
д н н
2к ед 9 Ь
‚ 5 5
—? ‘Ч-
- Ь =
11
Рис. 12.9
(от времени) У= А! (А — известная константа) найдем вектор Пойн-
тинга внутри него и вычислим полный поток энергии через цилин-
дрическую поверхность за время 1 (Кв 12.37).
Напряженность электрического поля
У А!
Е * ‘Я ‘_ Т-
Из (12.1) напряженность магнитного поля
А
Н = г——.
2с11
Магнитное поле со временем не меняется. С помощью ( 12.23)
НЗХОДИМ
1
8лл2`
Как видно из рис, 12.9, при положительном А поток энергии
идет к оси конденсатора (увеличивается энергия в конденсаторе с
увеличением заряда). Для подсчета полного потока через цилинд-
рическую поверхность воспользуемся тем, что энергия магнитного
поля в объеме цилиндра не меняется, так как напряженность маг-
нитного поля не зависит от времени, а меняется только электричес-
кая энергия за счет потока энергии. Из (3.69) энергия электричес-
кого поля внутри цилиндра
$=А2г
2
и/ = шпК2Ь = «инд.
81:
Ее изменение равно потоку энергии
П-11:К Ьд‘ к ЬА 4,1.
489

Подобный подсчет потока энергии можно использовать для объе-
ма внутри длинного соленоида, ток через который меняется по линей-
ному закону (от времени) 1 = А: (М 12.36). Из (5.23) для соленоида
Н = 4ппА 1.
С
Для электрического поля из (12.2) имеем
Е = 2ппА-3.
С
Оно со временем не меняется. Вектор Пойнтинга (12.23)
5’ = 2пп2А2гё.
С
Он направлен к оси соленоида и приводит к увеличению магнитной
энергии и напряженности магнитного поля с увеличением силы тока.
Для вычисления потока энергии через сферическую поверхность ра-
диусом К, центр которой лежит на оси соленоида вдали от торцов и
радиус меньше радиуса витков соленоида, учтем, что электрическая
энергия внутри сферы не меняется со временем, а меняется только
магнитная. Поток энергии обеспечивает изменение магнитной энер-
гии (3.69)
_ 4 3 Н2
И’ - 3 пК 8“ .
Откуда
п = Ш =16л2к3п2А2 Pj
д’ 3С
ЕСЛИ выразить п через ИНДУКТИВНОСТЬ Ь И ОбЪСМ КЗТУШКИ
2 _ Ь
у” _ 41:!’ ’
ТО
5 = ЬА2г 2 ; п = $лК3ЬА2+.
2с У 3 с У
Рассмотрим, как меняется ток проводимости в конденсаторе при
раздвигании его пластин с постоянной скоростью (Не 12.10). Пре-
небрегая краевыми эффектами и считая, что при движении пластин
расстояние между ними (х) остается всегда малым по сравнению с
490

их линейными размерами, для электрического поля Е (при отсут-
ствии диэлектриков равного индуктивности В), разности потенциа-
лов Уи заряда с; получаем
У
1) = Е = 4п$ = _
5 х
Учитывая (12.5), при постоянных с] и площади пластин 5 имеем
отсутствие тока смещения, а при постоянной разности потенциалов
на обкладках
и
4тгх2 ,
где и — скорость раздвигания пластин. При сдвигании пластин из-
менится направление тока смещения.
Рассмотрим плоский конденсатор, состоящий из двух одинако-
вых соосных дисков, подключенный к источнику постоянного на-
пряжения 8. В момент времени := О расстояние меищу дисками на-
чинает увеличиваться по некоторому закону 110). Найдем вектор
Пойнтинга 5 и электромагнитную энергию И/(г, 1), переносимую
через цилиндрическую поверхность радиусом г, расположенную
внутри конденсатора вокруг оси, как функцию времени, считая, что
расстояние между пластинами остается все время малым по сравне-
нию с радиусом (М 12.33).
Напряженность электрического поля в конденсаторе Е = 8/11.
Из (12.1)
1=4’
Н = —8г "д.
2с1:
ИЗ (1223)
. д’
5 — аут.
Для переносимой энергии получаем
1
и! = 1 $И2пгс11 = 8%’ `{N
о
По длинному отрезку коаксиального кабеля, у которого оболоч-
ка (радиусом Ко) и центральный проводник (радиусом го) изготов-
лены из разных сверхпроводников и замкнуты на торцах, вначале
циркулирует ток 10 (рис. 12.10). Найдем вектор Пойнтинга после
перехода внутреннего проводника (в результате нагрева) в нор-
491

При г= г
Учитывая, что погонная индуктивность кабеля
А = г1п~ вЂ” ~,
получаем
~2
г(,) = л вЂ” '".
2
На рис. 12.11 показана цепь, в которой источник постоянного
тока нагружен на сопротивление Я через коаксиальную линию (ради-
усы внутренний г, и внешний г,) длиной (» г,. В некоторый момент
ключ К, отключает линию от источника и одновременно К, замы-
кает накоротко нагрузку. Полагая все сопротивления, кроме Л, пре-
небрежимо малыми, а величины ЭДС (напряжение Г), (, г, задан-
ными, найдем, при какой величине г2 энергия, излученная линией
после срабатывания ключей, будет минимальной (М 12.41). В мо-
мент срабатывания ключей ток в цепи 1 = К/Л. В отсутствие оми-
ческой диссипации излучается вся энергия, имевшаяся в коакси-
альной линии:
г г
~=А вЂ” +С вЂ”.
2
Для определения индуктивности воспользуемся (12.1) и (5.31)
г2
2пгН = 4я вЂ”; Ч' = / 2Х( вЂ” = 2Х( 1п
С СГ г1 с
Г1
Откуда
ь = ги~(-"').
Обозначая заряд на внутреннем цилиндре О, получаем из (1.12)
или (12.3) для напряженности элекгрического поля в зависимости
от г (расстояния от оси симметрии)
2
1г
493

Для разности потенциалов находим
Г:
_ _ 2 2-9.
л/_{Е‹1г-2(1)1п-С.
Откуда
Таким образом, энергия, излученная линией,
и/=121 1“("2/’1)+ 1 О
02 (2/102 Ш (ъ/п)
Обозначая
Г
111-3 = х,
П
получаем, что для частного случая с = 2/13, надо найти минимум
у = х + 1/х. Приравнивая нулю производную, получаем минимум
при х= 1, т. е. при
Ё- = е = 2, 718.
Ч
Для цепи, изображенной на рис. 12.11, с замкнутым ключом К,
и разомкнутым К, найдем величину нагрузочного сопротивления,
при котором в случае заполнения пространства между проводника-
ми коаксиального кабеля диэлектриком с диэлектрической прони-
цаемостью е = 2 электрическая и магнитная энергии в диэлектрике
окажутся одинаковыми, если (М: 12.65)
Г
3-=2О=е3.
п
Используя (12.3), получаем Е = А/г. Постоянную А находим из
условия для разности потенциалов
П
г; г;
у: Ед: АЁ1=А1
Д г Д ‚ п

1: Потери за период на джоулеву тепло-
ту из (4.12) и (4.7)
и/„от = Ёж] 1 1 оЕ2а'У.
е т Добротность системы в соответствии
pM, pM, с (9.29)
А
И’ е
Рис. 12.12 9 = МЁД = т-
ПОТ
Электромагнитный импульс, описываемый (12.24), можно наблю-
дать в системе, изображенной на рис. 12.12, где заряженный конден-
сатор, в котором электрическое поле Е, помещен внутрь соленоида
прямоугольного сечения, находящегося вместе с батареей постоян-
ного тока и ключом, который включает ток в соленоиде и первона-
чально разомкнутый, на платформе, которая без трения может дви-
гаться по горизонтальным рельсам. Найдем импульс системы после
замыкания ключа (Не 12.12, 12.11). На рис. 12.12 показаны электри-
ческое Е и магнитное Н поля (после включения тока). В соответ-
ствии с (12.24) в объеме конденсатора Упоявляется электромагнит-
ный импульс
_ [Енп/
_ 4пс °
Для неизменности полного импульса системы, которого до
включения тока в соленоиде "не было, платформа должна двигать-
ся в направлении, противоположном Р.
Найдем вектор Пойнтинга, при распространении в свободном
пространстве цилиндрического электронного пучка радиусом К с кон-
центрацией электронов п и кинетической энергией каждого элект-
рона Е. Предполагая, что скорость электронов не очень большая
(нерелятивистский случай), получаем для скорости
2Е "2
и=‹-› э
т
где т — масса электрона. Обозначая заряд электрона е, для плотно-
сти тока в пучке получаем] = пеи. Используя (1.12), получаем элек-
трическое поле внутри пучка Ем = 2ппег и вне пучка
5„ = 21:18:23
496

где г вЂ” расстояние от оси симметрии пучка. Из (5.6) для магнитного
поля внутри пучка
Н,.„= 2пг вЂ” = 2ппеивЂ”
Г
С С
и для магнитного поля вне пучка
Н,„= 2пЛ~ ~ = 2пЯ~пе вЂ”.
ГС ГС
С помощью (12.23) получаем плотности потоков энергии:
внутри пучка
5'. = пи'е'пг'
и вне (М 12.29)
Г
Видно, что поток энергии идет со скоростью пучка.
Рассмотрим цилиндрический электрипый пучок с концентрацией п
и продольной скоростью электронов о, проходящий сквозь газ положи-
телып и неподвижных ионов с концентрацией, подобранной таким об-
разом, чтобы скомпенсировать силы взаимодействия электронов в
поперечном направлении. Найдем величину и направление вектора
Пойнтинга внутри пучка, а также концентрацию ионов и,. (М 12.35).
Из (12.1) находим азимутальную составляющую напряженности
магнитного поля
вЂ” еи, ит П~
2пгН =4п '; Н =-и2пге вЂ” '.
9
С С
Из условия равновесия электрических и магнитных сил
Н
Е„= вЂ” о вЂ” "=О
С
получаем
Е = вЂ” о 2пге вЂ”.
П
г 2'
С
Из (12.23) находим
з
Я=сЕ вЂ” =и вЂ” =пе п г вЂ”.
Ф 9 2 2 2 ~
4ж 4т~ с2
497

Чтобы найти концентрацию ионов п‚, вычислим Е, по теореме
Гаусса (1.12) или (12.3) 2пг1Ег = 4пе(п‚ — пе)пг21. Подставляя сюда Е‚,
полученное ранее из равновесия сил, находим
2
.= 1-З’-.
на ч л
В случае распространения в свободном пространстве электрон-
ного пучка «Ножевой» геометрии, т. е. имеющего вид тонкого плос-
кого слоя (М 12.31), вектор Пойнтинга можно найти тем же спосо-
бом, что и в случае цилиндрического пучка. На рис. 12.13 показаны
векторы полей и потоков энергии. Используя (1.12), получаем элек-
трическое поле внутри пучка Ем = 4ппех и вне пучка Е“ = 41теа‚ где
х — расстояние от плоскости симметрии пучка. Границы пучка при
х = м. Из (5.6) для магнитного поля внутри пучка
Н. = 41:’: = 4ппе3
"' 1 с с
и для магнитного поля вне пучка
‚а аи
На = 41:12 = 4ппеТ.
С помощью (12.23) получаем плотности потоков энергии: внут-
ри пучка Зт = 4пп2е2их2 и вне 5“ = 4пп2е2иа2. Видно, что поток
энергии идет со скоростью электронов в пучке.
Найдем величину и направление вектора Пойнтинга в произ-
вольной точке внутри проводника (и = 1), имеющего форму плоской
ленты (толщина много меньше ширины), по которой течет ток плот-
ностью 1, а носителями тока являются электроны (заряд — е) с кон-
Рис. 12.13 Рис. 12.14

обладает электромагнитным моментом количества движения М. Обо-
значая заряд конденсатора О его длину 1, из (1.16) находим электри-
ческое поле в зависимости от расстояния от оси конденсатора г:
5:2
[г °
Получаем
1 о к с1г 122
М = —2(-)]12лп_н = оН—.
/ О г 2с
4пс
Если конденсатор нагреть, то он быстро разряжается за счет тер-
моэмиссии. В результате электромагнитный момент быстро переда-
ется конденсатору, который приобретает кинетическую энергию
вращения
2 34
418 ’
М2
“$432”
где 1 — момент инерции конденсатора.
Эта кинетическая энергия переходит в упругую энергию закру-
ченной на угол (р нити
2
_ &
И’ -/ 2 .
Откуда (М 12.13)
к2
= ОН-г.
Ф жил“
В случае описания начальных или граничных условий гармони-
ческими функциями (синусами и косинусами) решения волнового
уравнения (12.17)‚ т. е. функции Д и д, входящие в (12.18)‚ также
будут гармоническими.
Рассмотрим подробнее гармонические бегущие водшы. Удобно вве-
сти круговую частоту, связанную с периодом гармонической волны,
21:
(о — Т (1225)
и волновое число, связанное с длиной волны,
21: 2 = .
= — = —. 12.26
[с 7». иТ ( )
500

Для волны, беГУЩей в положительном направлении оси х, имеем
Е}, = А сов (со! — /сх). (12.27)
Для магнитного поля из (12.21)
8 1/2
Н = (д) Асо$(ш1‘ - Кх). (12.28)
Для скорости распространения фазы (фазовой скорости) получаем
54%
12 = 9. (12.29)
[с
Как видно из (12.19), фазовая скорость зависит от характерис-
тик среды, по которой распространяется волна, и, в частности, эти
характеристики определяются зависимостью ш(/с) — дисперсионным
соотношением. При постоянной фазовой скорости говорят об отсут-
ствии дисперсии.
Для волны, распространяющейся в пространстве в направлении
вектора г с декартовыми координатами х, у и 2, вместо волнового
числа в (12.27) надо использовать волновой вектор (или вектор рас-
пространения) к. В таком случае
кг = Кхх + Куу + Как. (12.3О)
Рассмотрим отражение бегущей волны (12.27) и (12.28) от бес-
конечной плоской поверхности идеального проводника, перпенди-
кулярной к направлению распространения волны (рис. 12.16). Ось 2
направлена к читателю. Для удовлетворения условия отсутствия элек-
трического поля в идеально проводящей среде необходимо суще-
ствование отраженной от плоскости х = О волны, бегущей в проти-
воположном направлении:
Е; =—Асо$(о)1+/‹.х). (1231)
8 1/2
Н; = (д) А соз(ш1 + Кх). (12.32)
Здесь использовано, что обозначенный на рис. 12.16 вектор к’ = — к.
В диэлектрике над проводящей поверхностью получаем
Е, + Е; = А[со$(ш1 — /‹.х) i соз(ш1 + Ѐh = ЁА $111 Кхэйп юг;
Н‘+Н’- Ё1/2А[соз(шг /сх)+соз — в ш
— и — (сог+/сх):|—2 Е Асов/оссовсог.
501

| к‘ к
Еу Е;
Е}, , +
Ау
Идеальный проводник
{у х Н 1
Рис. 12.16 Рис. 12.17
Это стоячие электромагнитные волны. При х = О имеем узел
электрического поля и пучность магнитного. Внутри проводника
магнитного поля нет. Изменение магнитного поля на границе (от
величины в пучности до нуля) связано с токами проводимости вдоль
границы.
Аналогичным образом можно рассмотреть падение электромаг-
нитной волны на плоскую поверхность идеального проводника под
углом ос (рис. 12.17). Электрическое поле в волне направлено парал-
лельно оси у, которая направлена к читателю. Уравнение падающей
волны из (12.27) и (12.3О)
Еу, = А сов (о)! - Кхх - 192), (12.33)
где Ку = О; Кх = Ксоза; К: = [сзйп а.
Отраженную волну записываем в виде
;‚ = А’со5(со1 — /с‚;х — 1:3 + ф).
Условия при х = 2 = О требуют отсутствия электрического поля,
поэтому А’ = А, ср = п, непрерывность компоненты магнитного поля
касательной к границе, поэтому угол падения равен углу отражения
и, следовательно, /сх = К; и К: = —/‹;. Следовательно,
;, = —А сов (со! — Кхх + 192). (12.34)
Волна над проводящей стенкой представляет сумму (12.33) и (12.34)
Еу = Еу, + Е;, = -2А 5111 (/с22)$1п(ш1 — Кхх). (12.35)
Для этой волны выполняется условие отсутствия электрическо-
го поля при 2 = О. Это же решение годится в случае установления
502

странение фаз в направлении х вдоль волновода происходит с фазо-
вой скоростью
Ж ш
ОЭ
0
ф
й и лг и1
(12.40)
1 вЂ” и Хо 21 ш с вЂ” ®кр
где Хо вЂ” длина волны в вакууме, А = 2шс/и; значение и дано далее
в (12.43).
Из (12.40) следует, что фазовая скорость в волноводе больше
скорости света в вакууме. Напомним, что в теории относительности
для фазовой скорости нет ограничения. Для длины волны в волно-
воде получаем
2п ~о
д ~~О.
1 вЂ” А 21
(12.41)
Для того чтобы происходило распространение волны, Й„должно
быть действительным числом, т. е. должно выполняться
г г
г ~
вЂ” >и
1
(12.42)
Критической (или грани пюй) частотой является
ЕС
03
кр
(12.43)
Критическая длина волны
(12.44)
Критическим условиям отвечает угол а = ш/2. Образуется сто-
ячая волна.
В отличие от безграничных плоских волн, о которых говорилось
ранее, здесь электрическое поле меняется на конечном интервале.
Вычисляя циркуляцию магнитного поля вокруг электрического,
получаем, что при электрическом поле, имеющем только компо-
ненту вдоль у, магнитное поле имеет компоненты вдоль ~ и х, т. е и
в направлении распространения волны. Если у электрического поля
есть только компоненты, перпендикулярные направлению распР~с-
транения электромагнитной волны, то такой тип ~олн наз~~вается
504

поперечным электрическим (сокращенно ТЕ —
ггапвуегве-Ыестгйс). Магнитное поле в волне та- х 2
кого типа имеет компоненту в направлении рас-
пространения волны. На рис. 12.18 показаны .0
пунктиром, для примера, две силовые линии О
магнитного поля, лежащие в плоскости (х, 2). а
Если в электромагнитной волне магнитное поле у
в ограниченном пространстве имеет только Рис. 12.19
составляющие в плоскости, перпендикулярнои
направлению распространения волны, то та-
кой тип волн называется поперечным магнитным (сокращенно ТМ —
тгапзуегзе-тавпетйс). При этом у электрического поля есть составля-
ющая и в направлении распространения волны.
Найдем вектор Пойнтинга, описывающий плотность потока энер-
гии в волноводе квадратного сечения (сторона квадрата равна а) с
идеально проводящими стенками и вакуумным наполнением при
распространении бегущей электромагнитной ТЕ — волны с мини-
мальной частотой при заданном волновом числе К: (М9 12.50). Ось 2
направлена вдоль волновода, вектор Е параллелен оси х, а амплиту-
да поля равна Ео (рис. 12.19).
Из (12.39), учитывая минимальность частоты (п = 1) и переиме-
нование осей, для напряженности электрического поля в волне имеем
Е, = Е, $111 Ш $1п(оог 49:). (1245)
а
Из (12.1О) и (5.11) получаем
1 ЭН . ЭЕх дЕх _
‘257"°‘Е" а: “ ау’
1дН аЕ, .
_Ё д: ._‚ г = -Ео1с, в1псоз(оэ1 — 192);
1дН дБ, .
2 д‘: = 797. = ЕО %со$(%:)5т (и)! — 191).
интегрируем, учитывая, что постоянных составляющих в волне нет,
1 " - пу - .
БНУ = Ео Ё51п(7)ып(ю1— 1:22),
с 1 аш
33’ 505
1 Н = —ЕО дсоз со5(‹о1 — 192).

Используя (12.23) и (5.10), находим
Б = вЂ” ЕН] = вЂ” ( вЂ” ~Е„Н, + Ъ~Е,Н ) =
4к 4ш
2
=с~ ' ~ вЂ” яп 2п вЂ” я!п2(пП вЂ” Й~)+И,п1п' и вЂ” сов~(и~ вЂ” Й,С)].
4ки 4а а а
Для частоты из (12.38) имеем
Рассмотрим волновод с металлическими стенками квадратного
сечения со стороной а = 5 см, который возбуждается модулирован-
ными колебаниями
Е„(~) = Е (1 + сов Ж) сов ио1,
где
вЂ” о = 3001 МГц; вЂ” =4 МГц.
2ж 2ж
Пренебрегая потерями бегущих волн в волноводе, найдем, по
какому закону меняется поле Е,„„(~) на выходе волновода длиной А.
Поле Е перпендикулярно оси волновода и параллельно одной из
стенок (см. рис. 12.19). Определим также, чему равна фазовая ско-
рость волны с частотой ио (Мо 12.45). Из (12.43) следует, что гранич-
ной частотой для данного волновода является
ч = "Р = вЂ” 2998 МГц.
2к 2а
Из имеющихся в спектре модулированной волны гармоник
(ио вЂ” й, ио и и + й) проходят только две. Из (12.38) находим
(ио + ~)
2
С
Имея в виду, что
Е„(~) = Е, (1+ совй~)совио~ = Е, сови,~+ Ео совь,1~сови,~ =
1 1
= Ео совио~+ вЂ” Ео сов(й вЂ” ио)~+ вЂ” Ео сов(И+и,)~,
О
506

Т. С. ЗМПЛИТУДЫ бОКОВЫХ ВОЛН ВПОЛОВИНУ МСНЬШС, ПОЛУЧЗСМ ПОЛС на
ВЫХОДЕ ИЗ ВОЛНОВОДЗ
Е, вы,‘ (1) = Ед соз(оэог — КШЬ) + ё Ед сов “то + $2): — кед].
Из (12.4О) фазовая скорость волны с частотой (по равна
ш с с
0-4: = =22,4с.
дао [1—(пс)2/(ю0а)2:|]/2 р_<„‚‚,„„,у]'”
Если волна с несущей частотой уо имеет амплитудную модуляцию
с частотой ум, то в соответствии с (11.12) появляются еще волны с
частотами (уо — ум) и (уо + ум). Прохождение волн через волновод
определяется его размером. Для волновода квадратного сечения со
стороной, равной а = 5 см, из (12.43) (Не 12.46)
у = 1 = 2998 МГц.
“р 2а
Если задана несущая частота 2995 МГц, то она не проходит. Тем
более не проходит волна с частотой, равной разности частот. Чтобы
превзойти критическую частоту, частота модуляции должна быть
больше 3 МГц. Для фазовой скорости из (12.4О) при частоте моду-
ляции 5 МГц получаем
С
и = 2 2 ш =27,4с.
[1—\›кр (уо +ум)]
Рассмотрим распространение монохроматической волны слож-
ной пространственной структуры в прямоугольном волноводе, изоб-
раженном на рис. 12.20. Электрическое поле Е в волне перпендику-
лярно широкой стенке волновода размером а. Такую волну можно
представить как суперпозицию собственных мод волновода типа Нот,
поле Е которых в плоскости 2 имеет вид:
Е, (у, О, 1) = ЕСт 5111 (тп%)соз(шг + ост).
т
Предположим, что для всех мод вы- хд ‚
полнено условие т >›> 2а/Ао, где АО — дли- ‚И
на волны в свободном пространстве. ‚ ’
Докажем, что распределение амплитуды
колебаний по поперечному сечению вол-
новода Е(у, г) воспроизводится (повто- Рис. 12.20
507

а в моде Но вЂ” только у-компоненту
Е = Е я'и ш вЂ” сови~.
О
Считая, что частота много больше критических частот обеих
~д >> д вЂ”, л вЂ”, найдем, при какой минимальной длине волновода ори-
а
ентация вектора Е в любой точке (х, у) выходного сечения совпада-
ет с его ориентацией во входном сечении (в точке с теми же коор-
динатами х, у) (Мо 12.70).
Как видно из (12.40) фазовые скорости мод типа Н, и Но различ-
ны. Во входном сечении ~ = 0 моды в одинаковой фазе. Волна линей-
но поляризована. При распространении волны происходит сдвиг фаз
составляющих компонент. Они снова будут в фазе при условии
Л(р = [(Й,)О1 вЂ” (Й,) о](= 2л,
где
С С
Так как и » ш вЂ”, ш вЂ” и, следовательно, А ~ а, Ь, то совпадение
а
фаз произойдет при
1 1
вЂ” Хо! вЂ” вЂ” вЂ” = 2л.
40 2 Ь2
Откуда и находим 1.
Энергия, посылаемая через волновод к некоторой нагрузке, мо-
жет частично поглотиться, а частично отразиться. Обозначая коэф-
фициент отражения амплитуды а через г, для амплитуды отраженной
волны имеем аг. В результате отражения получаем подобие стоячей
~олны с отношением максимальной напряженности (в пучности) к
минимальной (в узле)
а+аг 1+г
а вЂ” аг 1 вЂ” г
Если заданы посылаемая мощность Жо и поглощаемая в нагруз-
ке Ж„, то, учитывая, что мощность пропорциональна квадрату амп-
литуды, имеем
2 ~о ~н
2 2
вЂ” =г
~о
2

. 3
Это уравнение подставляем в предыдущее соотно-
д шение (Не 12.52).
Волновод превращается в объемный резонатор,
д ’ если вход в него и выход из него закрыты проводя-
щими стенками.
Найдем резонансные частоты двух наинизших мод
объемного резонатора в виде прямоугольного па-
раллелепипеда со сторонами а = 1 см, Ь = 2 см, 1= 3 см (рис. 12.22).
Из (12.38), подставляя аналогично (12.37) Кх = тат/Ь и беря наи-
меньшие значения п = 1 и т = 1, чтобы получить наименьшее зна-
чение ю, имеем (Не 12.68)
Рис. 12.22
2
ш 1 1
7:18 (ТЧ-Т). (12.46)
с Ь 1
Здесь взяты наибольшие стороны (Ь и 1), чтобы о) было меньше.
Следующая наинизшая мода соответствует тому, что на наиболь-
шей стороне укладывается не половина длины волны, а целая длина
волны
Т: _—+_.__
с2 Ь2 12
(О? 2 1 22 ]
Предполагая, что электрические параметры воздуха, заполняю-
щего резонатор, не зависят от частоты, а потери энергии определя-
ются удельной проводимостью р, найдем отношение добротностей
резонатора при (о и со, (Не 12.68). Потери на джоулеву теплоту в
единице объема за период Тпри плотности тока 1 и напряженности
электрического поля Е равны
Аи/ - ]2рТ - 152%.
Запасенная энергия И/ы Е 2. Поэтому добротность
д„д;„51„:„
АИ’ 527 Т
Тогда
2 = 2,
91 (01
Волну в волноводе (12.45) можно записать в комплексном виде
Ех = Ед зйп (Куу) ехр [Кап - 1622)]. (12.47)
510

В трехмерном пространстве волновое уравнение имеет вид
д Е„ д Е„ д Е„ ] д Е„
дх ду д~ с д~
Подставляя сюда (12.47) и учитывая, что Е„не зависит от х, т. е.
при изменении х не меняется, получаем
г
вЂ” „= ~,', +Й,',
С
(12.48)
что согласуется с (12.37), (12.38) и (12.46).
Найдем вектор Пойнтинга Я(~, х, у, г) как функцию координат и
времени в резонаторе, который представляет собой кубик со сторо-
ной а, с идеально проводящими стенками и вакуумным наполнени-
ем и в котором возбуждена основная мода электромагнитных коле-
баний, причем электрическое поле с амплитудой Ео ориентировано
по оси ~ (Мо 12.47). Для основной моды электрического поля в дан-
ном резонаторе имеем
Е=е Е,в1п я вЂ” в1п пУ совиг,
вЂ” О
а а
где е, вЂ” единичный вектор в направлении оси ~. Далее будут упот-
ребляться единичные векторы вдоль осей х и у е„и е .
Из (12.10) получаем
ан
вЂ” = вЂ” сготЕ =
дю
й ° Х у х . у
= вЂ” сЕ,вЂ” е„вш к вЂ” сов я вЂ” вЂ” е,сов к вЂ” вш 2ж вЂ” сови~.
И а а а а
Отсюда можно найти выражение для поля Н. Из (12.46) частота
основной моды в резонаторе
2 2 ~ (2)ч2
а =с вЂ” + вЂ” =си
дг аг а
Используя (12.23), находим
Я(г,х,у, ~)=
Е2
=с о е„вш 2к вЂ” в1п2 ку +е вш' к вЂ” вш 2я вЂ” вш2и~.
16Яд " а а ~ а а
Найдем максимальную напряженность Ео электрического поля в
прямоутольном резонаторе с проводящими стенками объемом
511

Частота определяется из (12.46)
Откуда период
Подводимая мощность
_АИ/
__Т_
Волновод может быть заполнен слабо проводящей (удельная про-
водимость А) диэлектрической средой (диэлектрическая проницае-
мость е). Найдем добротность отрезка такого волновода с запаян-
ными торцами (прямоугольного резонатора с ребрами а < Ь < 1) для
самой низкой возможной резонансной частоты утш, считая, что по-
тери связаны только с проводимостью диэлектрика (Не 12.44). Учи-
тывая, что средняя энергия электрического поля за период Т равна
половине И/тах, получаем
Т .
и/ =Ыа4ДаЕ2%=%И/ШЩ.
Потери за период
и/„т = Ёшш АЕ2с1У.
о у
Добротность резонатора
2” И/тах 5
9=г=т=
ПОТ
Период надо выразить через самую низкую возможную частоту в
резонаторе. Из (12. 19) для фазовой скорости в диэлектрической среде
имеем с/(е)‘/2. Подставляем ее вместо с в (12.46) с учетом необходи-
мости получения наименьшей частоты. Период Т= 21ъ/ш.
Оценим силы, оказываемые электромагнитным полем на стен-
ки объемного резонатора, имеющего в плоскости ХО)’ квадратное
сечение со стороной а = 3 см, в направлении оси 02 сторона рав-
на Ь = 1 см в условиях, когда СВЧ-генератор непрерывно подводит
513

к резонатору мощность Ж = 1 Вт на наинизшей моде резонатора,
добротность резонатора О = 10' (№ 12.76). Из (12.46)
С
Я э
а
Из (9.29) энергия в резонаторе за период
ЛЗК
2ж
Потери за период
ЛИ'= ИТ= Ж вЂ”.
И
Давление вдоль оси бранно
где объем Г= а'Ь.
Рассмотрим распределение переменных токов по сечению про-
водников вЂ” скин-аффект. Так как в проводниках, по крайней мере
в мекдллах, можно пренебречь токами смещения по сравнению с
токами проводимости, то из (12.8) и (12.1) получаем
гогН = 4яАвЂ”
Е
С
Учитывая (12.7) и (12.50), находим
(12.50)
готго1Е =
и дгойН ф~ дЕ
вЂ” -4я вЂ” вЂ”.
с д~ с2 д
(12.51)
Рассматрим однородный проводник с постоянными А, р, е.
Непосредственным вычислением в декартовых координатах мож-
но получить
го1го1Е = ягадйч Е вЂ” ~2Е.
При отсутствии в проводнике свободных зарядов из (12.11) и
(12.6) получаем
Ч Е =4я вЂ” вЂ”.
~й дЕ
с2 д~
Подобным же способом можно найти
(12.52)
Ч Н=4ш вЂ” вЂ”.
г фдН
с2 д1
(12.53)
5!4

Рассмотрим поля
Е = Ео(х‚ у‚ 2)е’°”‚ Н = Н„(х‚ у, г)е"”’- (12.54)
Здесь амплитуды Ед и НО могут быть комплексными векторами,
но от времени не зависят.
Подставляя (12.54) в (12.52) и сокращая на временной множи-
тель, находим
. 2'Е
7213, = 4п%юэЕо = 5% (12.55)
где введено обозначение
Н
Предполагаем, что проводник занимает полупространство 1 > О,
так что его поверхность совпадает с плоскостью 2 = О, а электричес-
кое поле, следовательно, и ток направлены по оси х параллельно
граничной поверхности (Еу = Е: = О), причем напряженность поля
зависит только от расстояния 2 рассматриваемой точки проводника
от его поверхности, но не зависит от х и у. Из (12.55) получаем
д?Е Е
<7?Еь„ ==--91-==21 0*.
дд2 52
(12.57)
Общее решение этого уравнения
= к -/‹
Еох Ае 1 + Ве 1,
где А и В - постоянные интегрирования; 1: — корень уравнения:
21
18 = —,
82
Т. С
К_(шУ2_1+1
‘ 82 “ 82 °
Таким образом,
Ед, = Аё/бещб + ве-г/бе-‘г/б. (12.58)
Отметим, что в соответствии с (12.56) б — вещественная вели-
чина.
515

5
3.1
Для ограниченности решения надо считать А = 0. В результате
Е, = Еще“ = ве-г/бе’<°"'*/5>. (1259)
Опуская мнимую часть, получаем
Е, = Ве"/5 соз (со! — Pz (12.6О)
Для плотности тока находим
1, = ЖЕ, = 1062” соври! — Ё), (12.61)
где 10 = АВ — амплитуда плотности тока на поверхности провод-
ника.
Таким образом, амплитуды напряженности поля и тока убывают
в глубь проводника по экспоненциальному закону. Можно считать,
что поле и ток сосредоточены в слое толщиной б, который называют
скин-слоем.
При достаточно больших частотах электрическое поле в провод-
ник фактически не проникает. Воспользовавшись (12.53) и (12.54),
то же самое можем получить и для магнитного поля. Это похоже на
отсутствие проникновения в сверхпроводник. При этом поле на
проводник оказывает давление, определяемое (7.12), с учетом того,
что усреднение сов? со! дает 1/2.
Капля ртути на несмачиваемой горизонтальной поверхности стола
похожа на «блин». Если эту поверхность, предполагая, что она из
непроводяшего и немагнитного материала, поместить в вь1сокочас-
тотное (но удовлетворяющее квазистатичности со! << с , где 1 — ха-
рактерный размер, а с — скорость света) магнитное поле, то на кап-
лю, кроме поверхностного натяжения, будет действовать магнитное
давление, и она окажется менее сплющенной. Известно, что до по-
мещения в магнитное поле В = ВО сов шгдиаметр «блина» был равен
с! = 10 см. Найдем, какой должна быть амплитуда поля Во, чтобы на
частоте у = 1 МГЦ диаметр блина уменьшился в два раза (Мг 12.8).
Используя (1256), получаем толщину скин-слоя б = 0,005 см. Для
вычисления высоты «блина» до помещения в магнитное поле мож-
но воспользоваться решением, приведенным в книге 2, с. 342. Для
оценки приравниваем давление за счет поверхностного натяжения
на краях «блина» среднему давлению в капле. Откуда
О 1/2
ь=2(_) .
98
5|6

ЕЛ
где Ка/х — суммарное сопротивление элементов проводов АВ и СВ.
Используя эти соотношения и обозначая магнитный поток, прони-
зывающий контур АВСВ,
Ф: 1 Вс15=Ы,
АВСО
где Ь — индуктивность единицы длины линии, из (12.2) получаем
д“ __1 »=-Ь_9_!_
Жми- СФ ад‘. (12.63)
Вводя С = 4/0 — емкость на единицу длины линии, из (12.62)
имеем
д! __ Ш
Ж- С д’ . (12.64)
При К = О из (12.63) получаем
аи _ $31
Ж- с, д‘. (12.65)
Из последних двух уравнений следуют волновые уравнения
Ё_5ЗЁ- . &_:ЁЧ_-„
8:2 СЬ дх2 ’ ад СЬ дх2 °
ФЗЗОВЗЯ СКОРОСТЬ ВОЛН
с (12.66)
и = Т.
(сыт
В бегущей волне напряжение и ток связаны соотношением, сход-
ным с законом Ома:
П= 1 И/Ь (12.67)
Здесь введено волновое сопротивление линии
1 1„ 1”
и! = 4-] . (12.68)
с С
Сходство с законом Ома чисто внешнее, так как разность потен-
циалов берется не вдоль проводов, как в законе Ома, а между про-
водами.
518

Для тонких цилиндрических проводов радиусом а на расстоя-
нии 12 в среде с диэлектрической проницаемостью е и магнитной
проницаемостью и имеем
_ Й . _ 8
1“ " 4"1"(Б)’ С ` ищи/а)‘
Поэтому из (12.66) получаем
= ——9—. .
и (еду/з (12 69)
Эта фазовая скорость совпадает с фазовой скоростью электро-
магнитной волны в свободном пространстве.
При распространении гармонической волны, как следует из
(12.67) и (12.68), ток и напряжение колеблются в одинаковых фазах.
Так как в бегущей волне электрический и магнитный векторы пер-
пендикулярны проводам, вектор Пойнтинга параллелен проводам и
направлен от источника энергии.
Соединим провода лехеровой системы в некоторой точке мос-
тиком из последовательно соединенных катушки индуктивности,
омического сопротивления и емкости (с импедансом мостика 2).
Волновое сопротивление до мостика И/и после мостика И” могут
быть разными. Падающая на мостик волна может частично прохо-
дить, а частично отражаться. Найдем у мостика отраженную (1‚) и
прошедшую (1 д) волны тока, а также ток через мостик 1, если ток
падающей волны равен 18. Напряжение в падающей К, отраженной
И и прошедшей У‘, волнах у мостика:
ц= те; ц= -и/1‚; 14,: и/*1„.
Минус показывает, что отраженная волна идет назад.
Пользуясь правилом Кирхгофа для токов, имеем
4+д=1+д.
Напряжения между КОНЦЗМИ МОСТИКЗ МОЖНО ЗЗПИСЗТЬ
Ш=К+И=Ю-
Выражая напряжения через ТОКИ, ПОЛУЧЗСМ
21= и/(д- 1,), 21= И/Чд.
519

Решая эти уравнения вместе с уравнением для токов, находим
д_шшчтмит2„
1, А ’ 4 А’ 4 А’
где А = И/ИР + (И/+ И/’)2
Для мостика, поставленного в конце линии, получаем в случае
отсутствия прошедшей волны (И/’ = со)
1д_2И’2_ 1_2И’И”
1 =(и/-2)———’* - 1=——-2"/’г .
" И’ + 2 ’ И’ + 2
При закороченной линии (2 = О) и со свободными концами
(2 = оо) в обоих случаях отражение полное, но с разными фазами в
первом случае пучность, во втором узел. При чисто реактивном со-
противлении (2 = ЕХ) отражение также полное |1е| = |1‚|, а наличие
реактивного сопротивления сказывается только на положении уз-
лов и пучностей.
В стоячей волне, которая образуется при полном отражении, узлы
тока являются пучностями напряжения, а узлы напряжения — пуч-
ностями тока. В узлах вектор Пойнтинга равен нулю. Электромаг-
нитная энергия колеблется между узлами, не переходя через них.
Отраженной волны нет, если
2= ш (1270)
По системе распространяется только бегущая волна. Такое со-
противление называется согласованным.
Рассмотрим систему Лехера, в которой между проводами (диа-
метр 2а‚ расстояние между ними 12) поставлен плоский лист прово-
дящей пленки толщиной б с удельным сопротивлением р. Исполь-
зуя соотношения для индуктивности на единицу длины провода
Ь = 4„1п(Ё)
а
И СМКОСТИ На еДиНИЦУ ДЛИНЬП ПРОВОДЭ
с = ;_
41п(/1/а)
при е = 1 и и = 1, получаем для волнового сопротивления системы
_1Ь”_4 Ь
“ЕЮ "2‘“(2)°
520

При определении сопротивления из (4.23) емкость надо взять на
расстоянии б. В итоге имеем сопротивление между проводами
_ Р
к ‘ 4тсбС°
В случае отсутствия отраженной и проходящей волн 2 = К = Ж
Откуда (Не 12.75)
б=р2%.
Если для передачи электромагнитной энергии от генератора вы-
сокочастотных колебаний к нагрузке используется длинная линия,
состоящая из двух плоских шин (ширина их 1, расстояние между
ними 12), расположенных параллельно ДРУГ другу, то на единицу
длины емкость равна
1
_ _ 11
С-т, Ь-4тг1‚
Так Как ДЛЯ ПОТОКЕ!
Ф = 4111 В = 1.1.
с! с
Из (12.66) фазовая скорость волны и = с. Для отсутствия отражен-
ной волны должны выполняться (12.7О) и ( 12.68), т. е. (Не 12.67)
Торец линии можно закрыть пленкой толщиной б из полупро-
водникового материала с удельным сопротивлением р. Найдем,
при каком отношении р/б не будет отраженной и проходящей
волн (М 12.74). Так как
12
К = — = 2
р `.^ 9
то в соответствии с полученным ранее |
|
5 С . м Гъсоз (о! их, Г)
На рис. 12.24 показана система Лехера, нахо- | В ‚ д
дЯЩаяся в емкостной связи с генератором сину- Г |
соидальных колебаний, который поддерживает х
между концами А и В переменное напряжение Рис. 12.24
521

Г(х, 1) = вЂ” соь(Ы вЂ” йх вЂ” о)+ вЂ” сов(и1+ йх+ о) =
А А
2 2
= А сов и~ сов(Йх + О).
При х = ( напряжение должно равняться нулю, поэтому
Й(+о=п и+ вЂ” прип=О, 1, 2, ....
1
Откуда
Б=п и+ вЂ” вЂ” Ы.
1
2
Амплитуду колебаний находим из условия на АВ
1'(О, () = Госоьв(= Асовв(соьо.
Полностью ионизованная плазма состоит из электронов и тя-
желых положительных ионов, которые можно считать неподвиж-
ными. Допустим, что плазма находится между двумя плоскостями
(например, перпендикулярными оси х), заряд электронов е и число
их в единице объема п. Если все электроны сместятся из положе-
ния равновесия на расстояние х, то возникнет электрическое поле
Е = 4ппех. Сила, действующая на электрон, Г = 4пие'х. Обозначая
производную по времени штрихом, получаем уравнение движения
электрона тх" = вЂ” Г. Это уравнение колебаний элекгрона с так на-
зываемой плазменной частотой
и = ~1пл вЂ” ~
(12.71)
Эта частота зависит от числа электронов в единице объема
плазмы. Когда по плазме распространяется электрическое поле
522
Г, сов и~ ( Го и и вЂ” постоянные), а концы С и Р закорочены. Длина
лехеровой системы АС = ВР = (. Найдем распределение напряжения
Г(х, () между проводами как функцию координаты х и времени (,
предполагая, что колебания установились, а активное сопротивле-
ние всех проводов равно нулю (М 12.42). В системе установится
стоячая волна, представляющая сумму волн, бегущих в противопо-
ложных направлениях,

Е = Еде-т’ ‘ "д, то смещение электрона г описывается уравнением
тг” = —еЕ. Дважды интегрируя, получаем
е-Кшг-Кх) еЕ
г = еЕО 2 = 2 .
тю та)
Из (3.8), (3.1) и (12.71) находим
е2
2
О.)
е=1—4пп 2 ы-Ё. (1272)
тю
Такое изменение диэлектрической проницаемости надо учиты-
вать, например, при пропускании электронного пучка через про-
странство меэкду пластинами конденсатора, заполненное диэлект-
рической средой (е = 1). Если конденсатор входит в колебательный
контур с резонансной частотой то, то она изменится. Найдем, во
сколько раз изменится резонансная частота, предполагая, что пучок
сечением 8 с энергией электронов И’и полным током 1 идет парал-
лельно пластинам конденсатора, полностью заполняя пространство
между ними (Мг 12.56). Для плоского конденсатора емкость, как
следует из (3.56), увеличится в е раз. При этом, как следует из (9.8),
новая резонансная частота
Ш
СО = 0L
ИЗ (1272)
2 2
е(ш)=1—4лп3-3 =1—а9%.
тш (о
Откуда
о) =шо(1+а)ш,
где
е
= 4 1——————.
а п Зшё (тИ’)1/2
Если через волновод прямоугольного сечения со сторонами а < Ь
распространяется волна низшего типа (т. е. Нм), возбуждаемая ге-
нератором микроволнового излучения с частотой а), то для трехмер-
523

ного (пространственного) случая, учитывая диэлектрическую про-
ницаемость е, из (12.17) получаем
д2Е 2 д2Е, д2Е д2Е,
аж; Ц (дх2 + ау; ай ` (1273)
8
Обозначим ось волновода, по которой распространяется волна, 2.
Для бегущей волны Ех = Есоз (со! — |‹г) с учетом (12.3О) находим
птЗ п212
_ 2 2 2_ 2
—/Сх+/Су+/Сг —7+—Л +19,
2
ЕЮ
с2
где К, = 1с = 2п/А.
Для волны, имеющей наименьшую возможную частоту для дан-
ного волновода, при а < Ь должно быть т = О и 1= 1. Таким образом,
2 2
8“; = 37-48. (12.74)
с Ь
Известно, что воздух, для которого можно считать е = 1, остав-
шийся в волноводе после его вакуумирования, превращается в плазму,
для которой е определяется (12.72). Найдем концентрацию электронов
в плазме (п), если известно, что длина волны в волноводе после иониза-
Ции удваивается А, = Д, и соответственно К, = 19/2 (Не 12.54). Из
(12.74) для воздуха
002 1:2
— = — + 192
с2 Ь2
для плазмы, с учетом (12.6О) и того, что частота генератора не ме-
няется,
(1 —41:п:37]Ё = Ё+КЁ.
пир с2 Ь2
Следовательно,
(02 _ 1:2 02 /д2
п = 3т—————г—.
16пе
Рассмотрим плазму со средней концентрацией электронов и
ионов по и температурой 7, находящуюся между пластинами плос-
кого конденсатора, расстояние между которыми равно а, а разность
потенциалов ` Пренебрегая током через плазму, краевыми эффекта-
524

ми и считая еГ «ЙТ (Й вЂ” постоянная Больцмана; е вЂ” заряд
элекгрона), найдем зависимость потенциала в плазме между плас-
тинами от координаты, перпендикулярной пластинам р'(х) (№ 12.55).
В поле конденсатора энергия электронов ( вЂ” еГ), а энергия ионов
(е1'). В соответствии с распределением Больцмана концентрация
электронов
и, =«ее' ~' -ее(1+ вЂ” ); и,. -ее(! вЂ” вЂ” ).
Плотность заряда
р = 4пе(и„вЂ” и,) = 4н2иое вЂ” = вЂ”.
2
д
Здесь введена важная характеристика плазмы вЂ” дебаевский
размер (или радиус), который определяет размер экранировки
или расстояние, на котором электрическая энергия порядка теп-
ловой
(12.75)
Из (2.11) имеем уравнение Пуассона
И Е Е
х2 х2'
д
Его решение
!' = Р; ехр ( вЂ” ) е Р' ехр ( вЂ” ).
Граничные условия: при х = О Г= О, при х = а Г= ~~. Откуда
хе = Р; '(ехр( вЂ” ) вЂ” ехр( вЂ” вЂ” )) = 2р; хЬ( вЂ” ).
Окончательно
вЬ(х/( )
~ = ~о
вп(а/1 )
525

Когда по длинному плазменному цилиндру диаметром 212 течет
ток 1, то образующееся магнитное поле (5.2)
21
Н = —
сК
в соответствии с (7.12) создает давление
Если ток сосредоточен в поверхностном слое, а давление внутри
цилиндра в плазме больше магнитного давления, то плазменный
цилиндр будет расширяться (М 12.57).
Рассмотрим плазменный шнур (2-пинч), вдоль оси которого
течет ток 1. Считаем, что плазма нейтральна с однородным рас-
пределением плотностей частиц и тока по поперечному сечению
пучка и что магнитное давление собственного магнитного поля
пучка уравновешивается газокинетическим давлением плазмы. При
этом температура меняется по сечению пучка. Оценим темпера-
туру Т плазмы на оси пучка (Мг 12.58). Из закона Ампера плот-
ность силы магнитного давления в зависимости от расстояния г
от оси пучка
пю=%пщ.
Эта сила действует на объем а/И представляющий собой тонкое
кольцо толщиной с1г, высотой 1 (аП/= 21г1г4г). Из (5.7)‚ следующего
из теоремы о циркуляции,
в=Н=2щ%.
Магнитное давление, действующее на стенки элементарного объе-
ма (боковую стенку цилиндра радиусом г),
. ф’
с1р = —[с1г = —21у2г:—.
Здесь надо поставить минус, так как Г направлено противоположно г.
Интегрируя, найдем распределение магнитного давления внутри
плазменного пучка
Мг)- г а 2
_['с1р=2п_/2_[г-:=пк2]2 1—%
рог) к с к
526

Таким образом,
2 г
р(г) = р(Я)+ Х"
с жЯ
Магнитное давление, направленное к центру шнура, уравнове-
шивается газокинетическим давлением плазмы р(г) = п1сТ(г). Пред-
полагается, что для электрически нейтральной плазмы можно вос-
пользоваться уравнением состояния идеального газа. Следовательно,
Первый член в этой формуле вЂ” температура на периферии шну-
ра Т(Л), которой можно пренебречь по сравнению с температурой
на оси. Тогда
~2
Т(О) =,
сжЯпй
При заданной температуре можно найти необходимый ток или
магнитное поле (М 12.59).
Эгой же формулой можно воспользоваться, если задано число
частиц на единицу длины плазменного шнура Ж = лжЛ (М 12.62).
При быстром сжатии плазменного шнура сохраняется магнит-
ный поток. Когда по тонкой цилиндрической плазменной оболочке
течет ток Х, то магнитное поле определяется (5.2)
21
СГ
Если внутри оболочки предварительно создано продольное маг-
нитное поле Н„то внешним магнитным полем оболочка будет сжи-
маться от начального радиуса Я до некоторого радиуса г, при кото-
ром внешнее магнитное поле станет равным магнитному полю внут-
ри, которое получается в результате сохранения магнитного потока:
Я У
сг
Откуда получаем (М 12.61)
г = НОЯ' вЂ”.
2У
В цилиндрическом пропорциональном счетчике пучок частиц
вызывает объемную ионизацию. Найдем время собирания ионов в
527

таком счетчике, наполненном аргоном при нормальном давлении.
Радиус катода К, радиус анода а << К. Разность потенциалов между
анодом и катодом Ы Подвижность положительных ионов аргона Ь
(Мг 12.60). В случае цилиндрической симметрии электрическое поле
Е = А/г, где А — постоянная величина; г — расстояние от оси сим-
метрии. Разность потенциалов
Н=гЕа7г=А1п 5.
к а
Перемещение ИОНЗ описывается уравнением
дг _ ЩИ’)
Й;_ нцлиу
Интегрируя, найдем время перемещения иона на расстояние
порядка К
2ЬН
Если известно, что после накопления в резонаторе плазмы, об-
разующейся в результате ионизации оставшегося после откачки воз-
духа, частота наинизшей моды колебаний удваивается, то можно
найти концентрацию электронов плазмы (Мг 12.53). Используя
(12.73), (12.72) и (12.71)‚ находим в случае воздуха (е = 1)
В случае плазмы
С помощью (12.71) получаем
2 1/ь2 +1/12 _
п = Зптс 2
4е
Оценим силы Рх, Ру и 171, оказываемые электромагнитным по-
лем на стенки объемного резонатора, имеющего размеры в плос-
кости ХО)’: а, = а, = а = 3 см, по оси 02: Ь = 1 см, в условиях, когда
СВЧ-генератор непрерывно подводит к резонатору мощность 1\’= 1 Вт
на наинизшей моде резонатора. Добротность резонатора О = 10
528

(Мг 12.76). Из (9.29) для энергии за период имеем И’= ОЛ/ш. Плот-
ность электромагнитной энергии в объеме Уравна
ш = И//У= ОП/ФУ.
В соответствии с (7.12) эта энергия определяет давление.
Из (12.46) наименьшая частота
Л
о)=с1г—.
а
Электромагнитное поле представляет двумерную стоячую волну.
Энергия ш распределяется на четыре бегущие волны. На стенках,
перпендикулярных Х и 1С складываются две волны. Поэтому
гх = 13 = ёшад = % = 0,037 дин.
По оси 2 волны не идут, поэтому 12 = О.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Емкость 87
530
Амплитуда вынужденных коле-
баний 363
Амплитудная модуляция 426
Апериодичность 321
Баллистический гальванометр 377
Бетатрон 275
Вектор
вЂ” магнитной индукции 173
вЂ” намагничивания 173
вЂ” Пойнтинга 481
вЂ” поляризации 64
вЂ” электрической индукции
(смещения) 65
Векторная диаграмма 368
Векторный потенциал магнит-
ного поля 160
Вихревое электрическое поле 201
Волноводы 503
Волновое уравнение 480
Волновой вектор 501
Время релаксации 322
Гармоническая бегущая
волна 500
Гармоническая волна 481
Гистерезис 172, 186
Гиромагнитное отношение 272
Глубина модуляции 426
Градиент 30, 148
Давление поля 223
вЂ” магнитного 223
вЂ” электрического 109, 112, 113
Дебаевский радиус 524
Декремент затухания 322
Диамагнетики 172
Дивергенция 20, 148
Диполь 11, 25, 62, 63
Дисперсионное соотношение 501
Диэлектрик 64
Диэлектрическая проницае-
мость (диэлектрическая посто-
янная) 66
Добротность колебательного
контура 322
Дробовой шум 459
Закон Ампера 196
вЂ” Био вЂ” Савара вЂ” Лапласа 141
вЂ” Джоуля вЂ” Ленца в диффе-
ренциальном виде 119
вЂ” Джоуля вЂ” Ленца в интег-
ральном виде 120
вЂ” Кулона 7, 66
вЂ” Ома в дифференциаль-
ном виде 118
вЂ” Ома для цепи тока 120
вЂ” сохранения заряда 117
вЂ” сохранения энергии 316
вЂ” Фарадея 171
вЂ” электромагнитной ин-
дукции 170
Замороженная поляризация 82
Зацепленный поток 165
Избирательность контура 392
Изолятор 64
Импеданс (полное сопротив-
ление) 365
Индукционный ток 200
Интеграл Фурье 425

Квадруполь 13
Комплексная амплитуда 367
Коэрцетивная сила 183
Коэффициент взаимной ин-
дукции 167
— затухания 315
— размагничивания 186
— самоиндукции (индуктив-
ность) 165
Критическая (граничная) час-
тота 504
— длина волны 504
— температура 188
Критическое поле 188
— сопротивление 321
Кулон 8
Ларморовская частота 272
Линейчатый спектр 426, 430
Логарифмический декремент
затухания 322
Магнитная восприимчивость 174
— «ловушка» 268
— постоянная 164
— проницаемость 174
— «термоизоляция» 269
Магнитно-гидродинамический
генератор 298
Магнитное поле бесконечно-
го прямолинейного провода
с током 141
—— витка с током 142
—— соленоида 162
Магнитный диполь 142
Материальные уравнения 465
Метод электрических изобра-
жений 36
Модуляция фазы 427
Молекулярные токи 172
Момент диполя 11
Монополь Дирака 296, 466
Мощность переменного тока 371
— тепловых потерь 205
Набла 30
Напряженность электрического
поля 9
— магнитного поля 141
Несущая частота '426
Обобщенный закон Ома в диф-
ференциальном виде 119
Оператор Лапласа 31
Остаточная намагниченность 183
Отключение цепей 355
Парамагнетики 172
Параметрический резонанс 456
Переменный ток 365
Плазма 521
Плазменная частота 284, 522
Плоская поперечная электромаг-
нитная волна 479
Плоский конденсатор 18, 109, 110
Плотность тока 117
— энергии магнитного поля 223
—— электрического поля 103
Показатель преломления
среды 480
Поляризация 64
Поляризуемость 64
Пондеромоторные силы 106
Потенциал 29
— диполя 33
Потенциальная энергия 28
Поток вектора магнитной ин-
дукции 164
Правила Кирхгофа 120, 368
Правило Ленца 200
Преобразование Фурье 425
Пьезоэффект 64
Размагничивающий фактор 186
Расстройка 392
Реактивное сопротивление
(релактанс) 365
Резонанс напряжений 394
— токов 395
531

Резонансная частота 363
Резонаторы 509
Ротор 148
Ряд Фурье 424
Сверхпроводимость 188
Сверхпроводник первого рода 188
— второго рода 189
Свободные затухающие коле-
бания 320
— незатухающие колебания 316
Связанные заряды 65
Система Лехера 516
Сила Ампера 196, 201, 224
— Лоренца 200, 256
Силовая линия 9
Скин-эффект 515
Скорость дрейфа 281
Собственная частота колеба-
тельного контура 315
Согласованная нагрузка 495
Согласованное сопротивление 519
Солнечный ветер 258
Соотношение неопределен-
ности 430
Сопротивление провода 120
Спектральный анализ 426
Суперпозиция 9
Сферический конденсатор 88
Теорема взаимности 167
— Гаусса 15, 20, 65
— Ирншоу 10
— о среднем 47, 68
— о циркуляции 148, 173
Типы электромагнитных волн
(ТЕ и ТМ) 504
Ток смещения 465
— намагничивания 172
— Фуко 475
Толщина скин-слоя 515
Трансформатор 401
Удельная проводимость
(электропроводность) 1 18
Удельное сопротивление 118
Уравнение гармонических ко-
лебаний (гармонического ос-
циллятора) 316
Уравнения Максвелла 465
Уравнение Пуассона 31
— силовых линий точечного
диполя 12
Фазовая скорость 480
Фазовый сдвиг 378
Ферромагнетики 172
Формула Эйлера 366
Циклотронная частота 257
циклотронный (ларморовский)
радиус 257
Цилиндрический конденсатор 93
Ширина резонансной кривой 392
— спектра 430
Шумы 459
Экранировка 35
Электризация 7
Электромагнитные волны 479
Электромагнитный импульс 482
Энергия в конденсаторе 98, 103
Эффект Мейснера 188
Эффективные значения пара-
метров переменного тока 371

СОДЕРЖАНИЕ
редисловие .............. ° ..°...........................................................°........................ 3
П
ведение ...............................................................°............................................ 5
В
Электрический заряд и напряженность электрического поля.
иполь. Теорема Гаусса ............................................................................. 7
2.
Потенциал. Метод электрических изображений ................................... 28
3. Электрическое поле в веществе. Энергия электрического поля.
Энергетический метод вычисления пондеромоторных сил ................. 64
Постоянный ток. Токи в неограниченной среде ............................°... 117
4.
5. Магнитное поле. Закон Био вЂ” Савара вЂ” Лапласа. Теорема
о циркуляции в вакууме. Индуктивность проводников.
еорема взаимности ....°..........°............................................................... 141
Т
6. Магнитное поле в веществе. Векторы В и Н. Теорема
о циркуляции в веществе. Сверхпроводник в магнитном поле ........ 172
7. Электромагнитная индукция. Энергия и силы в магнитном поле.
Сохранение магнитного потока в сверхпроводящих контурах .......... 200
8. Движение заряженных частиц в электрическом и магнитном полях.
ЭДС Холла. Движение при наличии пондеромоторных сил ............. 249
9. Переходные процессы в электрических цепях. Свободные
олебания е ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° 3 1 4
К
10. Вынужденные колебания. Резонанс. Метод комплексных
мплитуд ...........................°...°.................................................................. 362
а
Элементы спектрального анализа. Автоколебания.
Параметрический резонанс. Шумы ...................................................... 424
Уравнения Максвелла. Электромагнитные волны. Волноводы
и резонаторы. Плазма .........................°........................°......................... 465
12.
П
° У
редметныи указатель ................................................................................. 530

Учебное издание
коряво: Владимир Павлович
МЕТОДЫ РЕШЕНИЯ ЗАДАЧ В ОБЩЕМ КУРСЕ ФИЗИКИ.
ЭЛЕКТРИЧЕСТВО И МАГНЕГИЗМ
Редактор 0. А. Кузнецова
Внешнее оформление Н. Е. Ильенко
Изд. Мг 036. Подп. в печать 06.04.11. Формат 60›‹88 И‘.
Бум. офсетная. Гарнитура «Ньютон». Печать офсетная.
Объем 32,83 усл. печ. л.‚ 33,57 усл. кр.-отг.
Тираж 1500 экз. Заказ Мг 352.
ООО «ТИД» «Студент».
109004, 1: Москва, ул. Земляной Вал, д. 64, стр. 2, офис 717 (31).
Тел. (495) 915-80-41; (495) 915-08-96.
Отпечатано ООО «Великолукская городская типография».
182100, Псковская область, 1: Великие Луки, ул. полиграфистов, 78/12.