Author: Dunford N.J. Schwartz J. T.
Tags: mathematics higher mathematics computer science john wiley & sons inc linear operators
Year: 1958
Text
PURE AND APPLIED MATHEMATICS
A Series 01 T exfs and Monographs
LINEAR OPERATORS
Edited by: R. COURANT . L. BERS . J. J, STOKER
PART I:
GENERAL THEORY
NELSON DUNFORD and JACOB T. SCHWARTZ
FORMER JAMES E. ENGLISH
FROFEsaOR OF MATHEMATICS
YALE 1.r""NIVERSl"1'Y
PROFESSOR OF MATHEMATICS
COURANT INSTITUTE
NEW YORK UNIVERSITY
VOLUME VIl
WITH THE ASSISTANCE OF
WiUiam G. Bade and Robert G. Bartle
FROFESSOR OF
'MATHF..MATICS
UNIVER9JTY OF
CALIFORNIA,BERKELEY
PROFESSOR OF
MATHEMATICS
UNIVERSITY OF
ILLINOIS
INTERSCIENCE PUBLISHERS, INC., NEW YORK
a division of John Wi1ey & Sons, Inc., New Y.ork .. London" Sydney
Preface
This volume is dedicaled to Virginia,
Sandra, Eleanor and Doris
ALL RIGHTS RESERVED
In the two parts of Linear Opn-ators we endeavor to give 3 com-
prehensive sunrey of the general theory of linear operations, toge-ther
with a survey of the application of this general theory to the diverse
fields of more classical analysis. It has been our desire to emphasize
the significance of the relationships between the abstract th""l"Y and
its applications, that has set the general tone and determined the gener-
al structure of the present work. Thus, .a very elaborate analysis
(Chapter XIII) ofthe spectral theory of ordinary self-adjoint differen-
tial operators is prf'tiented, while on the other hand the theory oflocal.
ly convex spaces is treated (Chapter V) rather briefly in its connection
with the theory of B-spaces. Applications of the general theory are
presented in two ways: as a part of the text, and as graded series of
exercises. Thus Chapter VIII is devoted to ergodic theory and to the
theory of semi-groups; Chapter XI to a variety of topics including the
theories of integral equations, harmonic analysis, closure theorems of
Wiener type.. singular integral operators.. and almost periodic func-
tions; and Chapters XIII, XIV. XIX, and XX to various aspects of the
spectral theory of differential operators_ On the other hand, part8 of
the theory of summability of series and integrals are given as graded
series of exercises in Chapters II and IV; the theory of orthogonal ex-
pansions as exercises in Chapter IV; the theory of inequalities In
Chapter VI; the theory of Tauberian theorems of Hardy-Littlewood
type in Chapter XI; etc. The exerClSe-_ (of which there are approxi-
mately one thousand) have been chosen with considerable care. They
are not normally routine drill problems but rather are designed to car-
ry forward the throry presented in the text and to emphasize its inter-
esting., and often surprising, appJications. The reader is encouraged
to read the exercises even though he may not care to work them out
in all detail.
The dIvision of the p:resent work into two parts has been baseu
on the following principle: all material relating to the topological
1 IS 14 13 12 11 10 9 8
LIBRARY OF CONGRESS CATALOG CARD NUMBER
.57-105.15
ISBN () 47() 22605
Printed in the Uni d Slates of America
v
vi
PREFACE
PREFACE
vii
theor:r of spaces and operators, and all material pertaining to the
spectral theory of arbitrary uperators into the first part; a1l material
rdating to the the<:>ry of completely reducible operators into the secoud
part. Of course. we have occasionally found it convenient to violate
this principle.
The pre8ent work is written for the student"" well as for the
mature mathematician. Much of the text has grown directJy out of lec-
tureS given by the authors over man)' years,. and the two parts are de-
signed to form suitable texts for a variety of graduate courses. Thus.
Chapters I, II, and selected topics from Chapters III and IV make a
comprehensive one-year course in the theory of functions of a reat
variable. The material contained in Chapters VI, VII, IX, and X, with
selections from V t VIIl t and Xl. has been used many times as the basis
for a one-year set of lectures in operator theory.. A vne.year course in
the 8pectral theory of self-adjoint differential operators and the asso-
ciated boundary value problems may be ba8edon Chapters IX. X, XII,
and XIII. Many other topics, such as harmonic analysis, ergodic theo-
ry, the the<:>ry of semi-groups, and the general theory of completely
reducible ("Spectral") operators in B-spaces developed in Chapters
XV through XX are suitable for detailed study in a graduate seminar.
The present treatise is relatively self-contained, and nearly every-
thing in it can be read by one who has studied the elementary alge-
braic and topological properties of the real and complex number sys-
tems, and those basic results of the theory of functions of a complex
variable which center around the Cauchy intrgral theorem. At a very
few isolated points, knowledge of certain less elementary results of
algebra and analysis (e.g., determinant theory, the Weierstrass pre-
paration tbeorem) is needed. Most of the notions and results from
general topology and ab8tract algebra needed are presented and ex-
plained in the text, though in such a way as to require of the reader
a considerable general mathematical maturity. It is desirabJe that he
have as much familiarity with these two subjects as would be the I\or-
mal fruit of one seme8ter of gradoote study of abstract algebra and
complex variable thC<Jf)'.
To facilitate access to the very large amount of material collected
in the present treatise, it has been furnitilied with a number of special
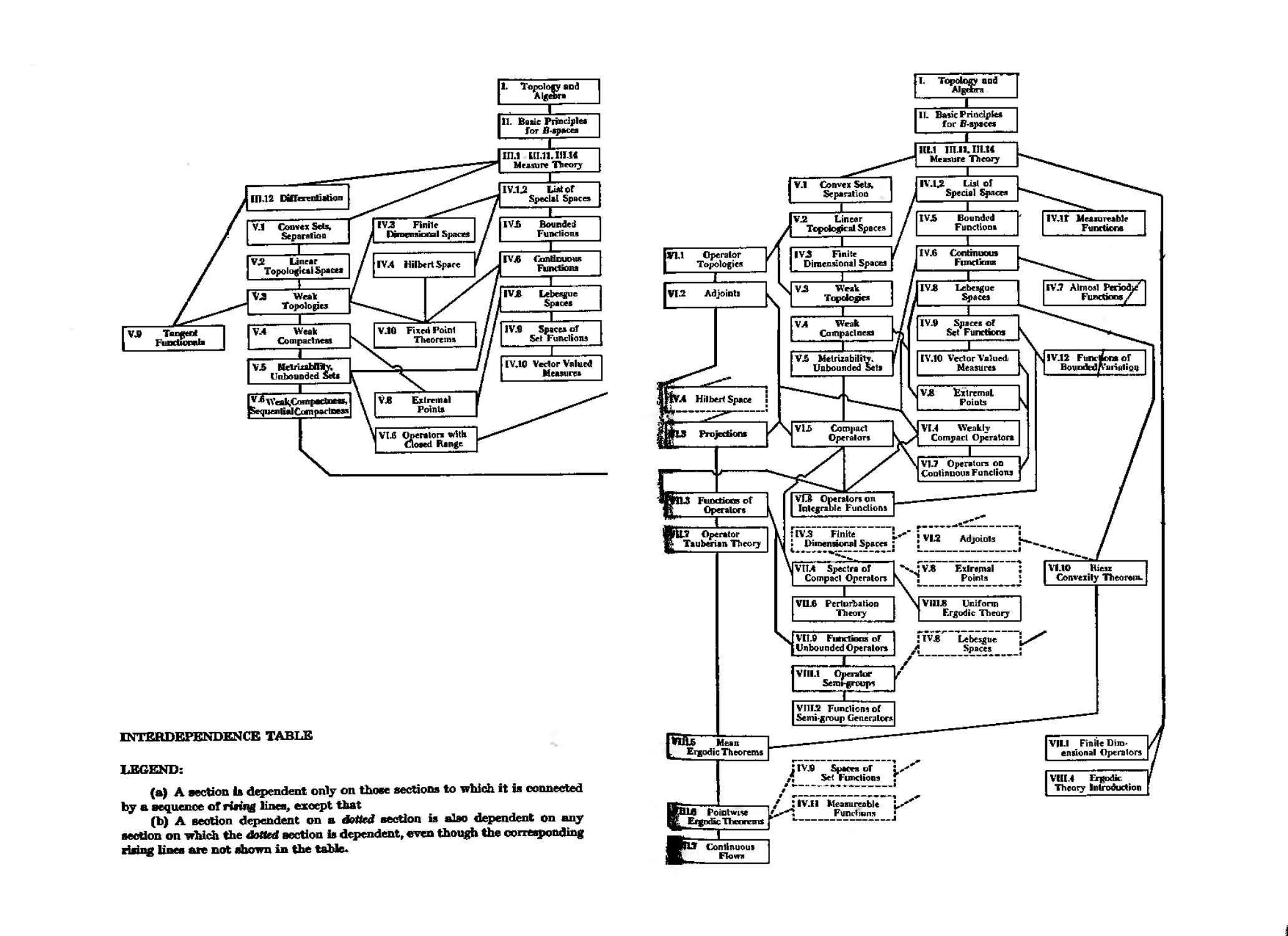
features. A table graphically shows the interdependence of the sec-
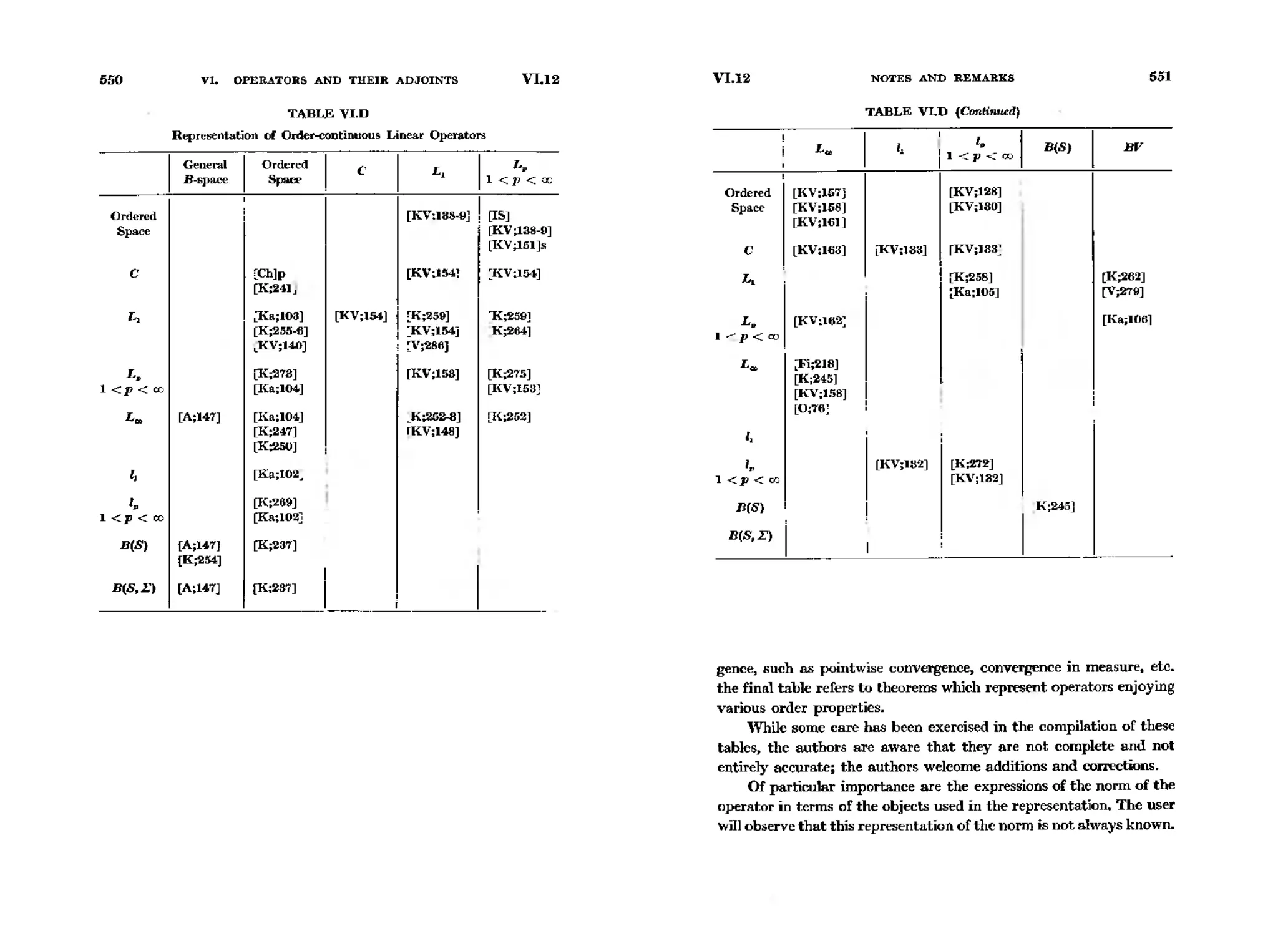
tions of the various chapters. Tables of the properties of a number of
special B-spaces and of operators mapping various of these spaces into
each other are given in Chapters IV and VI. Many of the chapters end
with sections entitled UNotes and Remarks" I which have a du.aI pur-
pose. On the one hand, they contain references to the original and
subsequent papers in which the principal results of the chapter in ques-
t.ion have been discussed in the literature. In addition, they contain
references to many results related to but not included among tbose
given in the text. In this capacity, the notes and remarks 8upplement
the bibliography on the one hand, the exercises on the other, and
furnish additional information for the research mathematician. To
facilitate study, those results presented in the text which are partic-
ularly important for the subsequent development have been marked
with 8 black tHrOw in the margin; such theorems and lemmas, some
of which might otherwise have seemed reJatively obscure. should be
noted with parti(!u]ar care. We have tried to adhere to con,'entiona1
terminology and notation exrept at those few points where the stand-
Brd conventions seemed particularly unfortunate t.o us; at any rate,
a general index and an index of notation have been provided to give
guidance on this score. The theorems. lemmas. and definitions which
compose the text are numbered serially in a single system that pro-
ceeds by sections. Lemma XI.5.4 is the fourth numbered item in the
fifth section in the ele,'enth chapter. In the course of Chapter XI. this
lemma is referred to as Lemma 5.4, and in the course of the f'd'th sec-
tion of Chapter XI it is referred to as Lemma 4.
The general character of the present work may be indicated by a
brief comparison with R number of the best.known books which have
dealt with some of the topics treated here. The famous treatise of Ba-
nach is the inspiration and the prototype for Chapters IV, V, and VI.
Stone's book on linear operators in Hilbert space contains substanti-
ally the material found in Chapters X and XII, though our treatment.
which is based on the devices introduced by various Russian mathe.
maticians and most notably by Gelfand, is quite different from that
of Stone. The recent book of Riesz and Nagy is close in spirit to our
work, and should be regarded as an excellent introduction to the much
more extensive theory presented in the prescnt Chapters III through
XII. Nai:mark's recent book on linear differential operators is ver,}'
viii
PREFACE
PREFACE
ix
close to Chapter XIII, and also discusses some points of the theory
given in Chapter XIX.
Surveying in retrospect the theories presented in the following
twenty chapters, it seems to the authors that the general theory of the
first seven chapters, aod the Hilbert space theory of self-adjoint opera-
tors given in Chapters IX, X, and XII, are theories which have now
reached a relatively final form. The theory of semi-groups, the general
harmonic analysis, and especially the theory of singular self-adjoint dif-
ferential operators, thougb they have re""hed a considerable degree of
maturity, should all still enjoy a substantial development. The new
theory of spectral operators presented in Chapters XV through XVIII
is, hy comparison with the con-esponding theory for 8elf-adjoint opera-
tors, in an early and incomplete stage of development. Chapters XIX
.and XX give evidence that non-se1f-adjoint and non-normal 5pectral
operators are of common enough occurrence among the interesting
objects of mathematics to justify serious study. It is the authors'
hope that the present treatise will indicate the location of the weak
and of the strong spots in the edifice of theory built up till now, and
thereby faciHtate both the study of the theory 8S it exists and future
research.
We have been especially fortunate in having the assistance of two
of our colleagues. Without the patient and unstinting work of Profes-
SOrS Robert Bartle and William G. Bade, who revised and edited near-
ly every chapter and who contributed a number of sections, it is cer-
tain that nothing on the scale of the present treatise could have been
completed. The great majority of the sections of "Noles and Re-
marks u , in particular, are due to Professor Bartle.
We have received valuable advice and criticism from many other
colleagues at Yale and at New York University. We have profited very
much, and particularly in connection with our treatment of ergodic
theory, from frequent contacts with Professor Shizuo KakutAni.
\Ve are indebted for many va]uable suggestions concerning the theory
of semi-groups to Professors Einar Hille and Ralph Phillips. who most
generou81y made portions of their forthcoming treatise on this .ubject
available to us. Innumerable contacts. both informal and in formal
seminars, with Professors Berkowitz. Friedrichs, Friedman, Helson.
Lax, Nirenberg, Rickart. and Wermer, and with Dr, Gian-Carlo Rota
have b€en of immeasurable value to us, Rnd we wish to thank all tJlese
friends for the help which they provided in the form of penni""ion to
quote manuscripts, help in revisin.gourownmanuscript orland written
criticism. The final two sections of' Chapter XIII, in particular, Bre due
to Dr. Rota. Dr. Rota and )\Jr. David }lc Garvey edited many por-
tions of the text, and, together with Drs. .John Barry and Robert
Christian, cht'cked the aITuraey of most of the problems in the text.
We also wish to thank Dr. Alfred B. Wilcox for his hdp on Chapter
IX, Dr. !\Iaric Lesnick for edIting Chapter V, and IIIr. .John Thompson
for checking the calculations with hypergrom.etric and confluent
hypergeometric func::tions made In Chapter XIII.
For most of thC' eight years that have gone into tl1t" "taiting of
this volume the work was assisted by the support of the Office of
:Naval He-:;earch and particular thanks are due the administrators of
its Mathematics Branch fur their understanding and ('ncQuragement.
NELSON nU FORD
JACOB ScHWARTZ
August. ] {)57.
La pensee n'est qU.'UR eclair au milieu de fa nltir.
Mob c'esf, ceJ" eclair qui est tout.
Content8
HENRI POINCABt
PART I. GENERAL THEORY
I. Prellrninary Concepts . 1
A. Set-theoretic PreIiminarie
. _ . . . . 1
1. N()tation and Elementary Notion
1
2. Partially Ordered Sy$U'tUS 4.
a._.......... 8
B. Topological PreIim.insrie
10
4. Definitions and Basic Properties 10
5. Nonnal and Compact Spaceft 14
6. Metric Space9 ........ 18
7. Convergence and Uniform Convergence {)of Generalized Se-
quences _ _ . . 26
8. Froduct Spaces . _ . . . . . al
9.-...... 38
c. Algebraic Preliminaries . 94
10. Groups 84
ll. Lineal" Spaces 35
12. Algebras 38
13. Detennina.nts 44.
14._. 4"
15. References 47
LINEAR OPERATORS IN THREE PARrs
PART I
Gen<7Bl Theory
PARTn
Spect.ra.l Theory 9 Self Adjoint Opera'tors in Hilbert Space
PART m
Spectral Operators
II. Three Basic PrIndptes or Linear Analysis 49
1. The Principle ot Unifonn Boundedness 49
2. The Interior Mapping Principk 55
S. The Hahn-flanach Theorem 58
4._ 70
5. Notes and remarks 79
Nelson Dunford and Jacob T. Schwartz
JII. Integ:rat1on and Set Functions 95
1. Finitely Additive Set Functions . g5
2:. Integration . . . . 101
8. The Lebesgue Spaces. . . . . _ 110
4. Conntahly Additive Set Functions . 126
5_ Extensions of Set Functions. _ . . . . . . . 132
6. It1tegration with Respect to a Countably Additive :\oIeasure . 144.
xi
Xli
COSTENTS
7. The Vitali-Hahn-Saks Theorem and Space!'o of Measures
8. Rc1ativit.ation (J{ Set Functions
9. Exerci!;:es #.. - - . .
IV. The Rn.don-
ikodYm Theorem
11_ Product l\Jeasures . . - - . .
12. Diffnentia.tiQn
13. Exercises . . . . . . - . . - .
14. Fundions lOr a Complex Varia'blf'
15. N"otes and Remarks
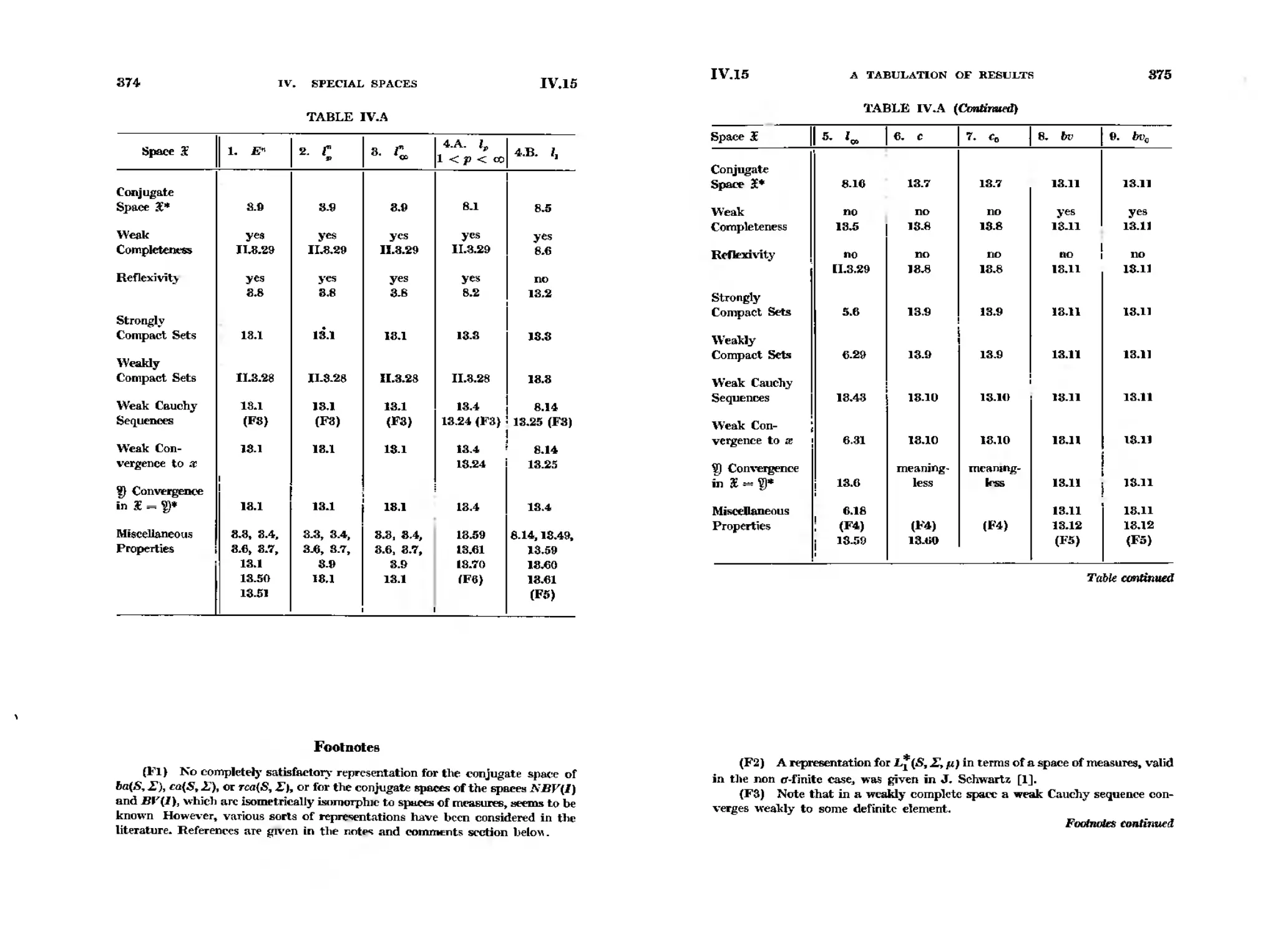
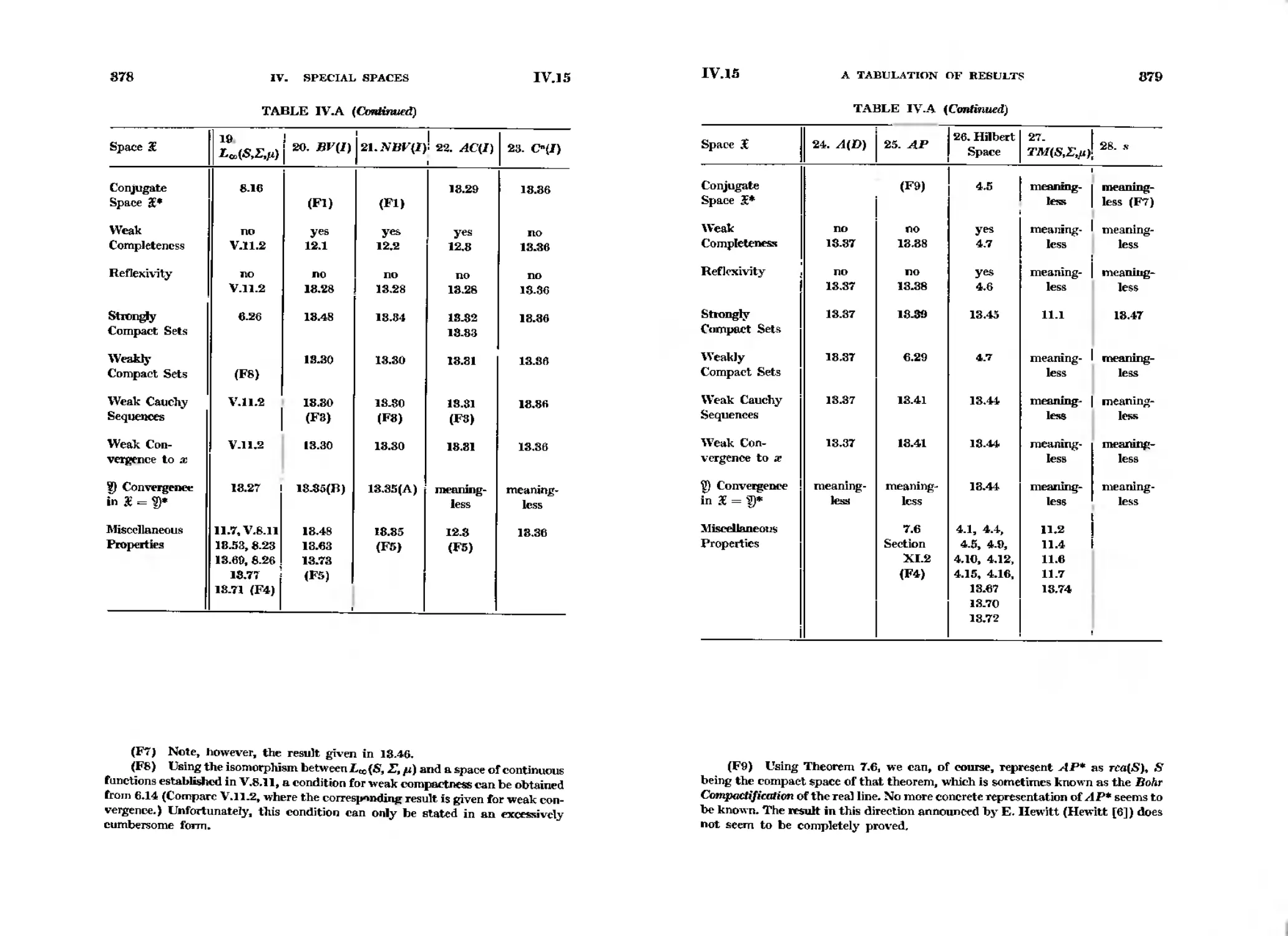
IV. Specia18paces .
1. Introduction. . . . . .
2. A List of SpttiaI Space..
3. Finit
Dimrnsional Spaa"'"
4. Hilbert Space . . . - . .
5. The S.....,.., B(S, I) and B(SI
6. The Space C(S) . -
7. The Space AP
8. The Space' L.(S, I,I') .
9. Spaces of Set Functions
10. Vector Vatued l\leasuR'S
II. The Spa.. 7'M(S, I,p)
12. Functions cf :Bounded V.ariation
18.Exenisrs..... .....
14. Exercises on Orthogonal
;;kries and AnRl
Functions .
15. Tabulation of Rcsults . . . . . . . - . . . . . .
16.
otes and Remarks
V. Cmtvex Sets and Weak Topologies
1. Convex Sets in LineaT Spaces .
2. UneaT Topological Spacl:S . - . . . . . . . . . .
3. Weak 'l'cp()logies. DcfinitiQlls :p.nd Funda.mrntal Properties.
4. \\'eak TQPologin. Compactness and Reflexhrity .
5. \V<,ak Topologies. 1fJetrizability. Unbounded Sets
(J. "teak Topologies. \\- eak Compactness
7. Exereises . . . . .
ti. Ext.remal Poinb .
D. Tangent Funct:ionals
10. Fixed Point Theorem>;
11. EXCI'"eises . . .
12. Xotes Rnd Remarks
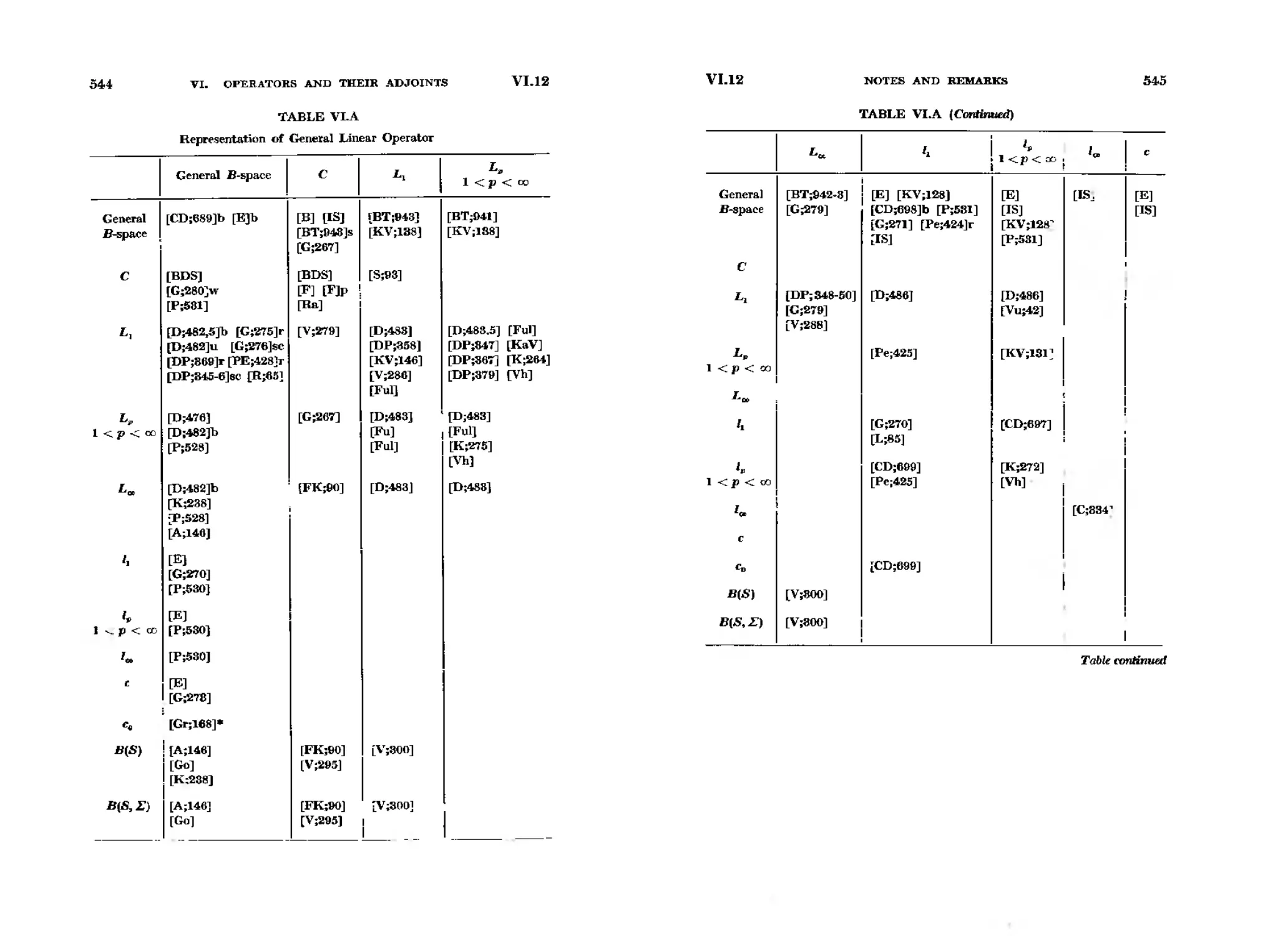
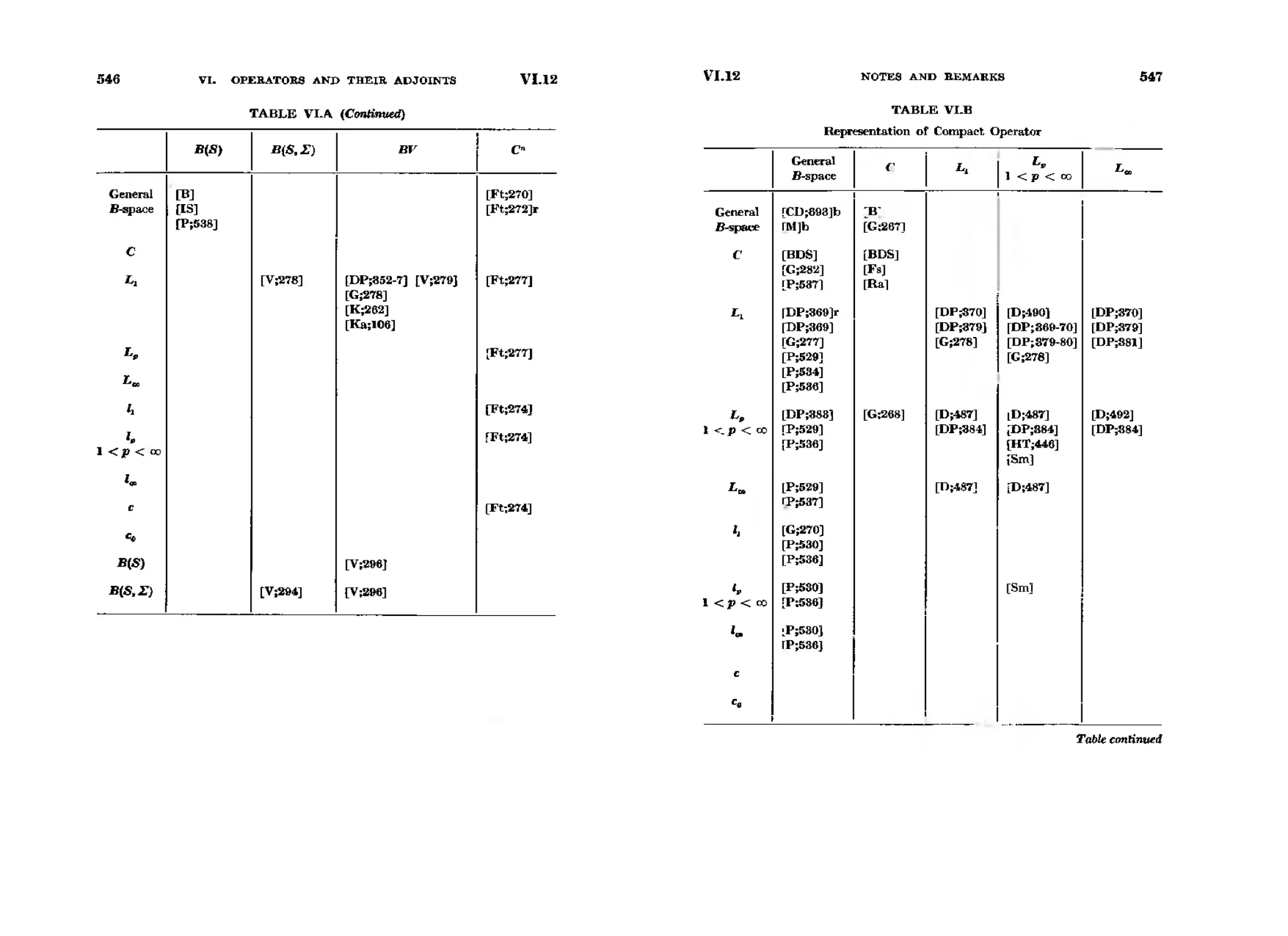
VI. Operators, and Their Adjoints .
1. The Sp.... B({, ?J).
2. .-\djoints . . . . .
CON'rENTS
15S
164
168
174
183
210
22.
224
232
S. Project1ons . . . . . . . .
4. \\'eakly Compact Operators .
5. Compact Operators
6. Operators with Closed Range
7. Representation of Opera.tors in C(S) . . . . .
8. The Representation of Operators in a Lebesgue Space
9.
..........
10. The Riesz Convexity Theorem
11.
on Inequalities
12. Notes and Remarks .
287
237
288
2+I.
247
257
261
281
285
305
BIB
829
VII. General Spectral Theory .
1. Spectra! Theory in .IL Finite Dimensoonal Space
2. Exercises . . . . .
3. Functions of an Operator
4. Spectral Theory of Compa.ct Operators
5. Exercises . . . . .
6. Perturbation Theory
7. Tauberian Theory
8. Exerc1ses . . . . . . . . . .
V. An Operational Calculus for Unbounded Clooed Operators
IU.Ex
__...
tIe Notes and Remarks
S37
338
357
S72
""'"
VIII. Applications
1. Semi-groups of Operators ....
.
2. Funct.ions of an Infinitegjmal Generator
3.-......__ ......
4. Ergodic Thfory .
5. Mean Ergodic 'I'beorem.s
6. Pointwise :Eqwdic Theorems
7. The Ergodic Theory of Continuous Flows
8. UnifoTlll Ergodic "lbeory . .
9. Exercises on Ergodic Thenry
10. :Kotes and Remp.rks.
409
409
413
418
423
425
430
486
480
445
4{i3
457
460
REFERE
CES
NOTATION Th'DEX
AUTHOR I:>IUEX
SUBJECT I=EX
475
475
.17S
xiii
480
482
485
487
489
498
511
-
526
538
555
556
.561
566
577
580
584
593
597
599
604
606
613
613
641
653
657
660
668
684
708
717
726
731
B27
829
837
xiv
CONTENTS
PART II. SPECTRAL THEORY
IX. B-AJg<oras
X. Bounded Nonna! Operators in llilbert Space
XI. Various Special Cla:'!lses: .of Operators in Lp
XII. Unoonnd<d Op<rators in Hilbert Space
XIII. Ordinary Differential Operators
XIV. Appljntin ns to Partial Differential Operators
XV. SpectrnI 0p<"-rs
XVI. Spectral Operators: Sufficieut Conditions
XVII. Algebras of Spectral Ope1'8tors
XVIII. UnooundOO Sp<ctTB1 Operators
XIX. Perturbations or Spectral Opera
rs with Ifucrete Spectra
XX. Perturbations vC Spectral Operators with Continuous Spectra
CHAPTER 1
Preliminary Concepts
The study of linear operations requires a familiarity with certain
basic concepts from the fields of set theory, topology and algebra.
Chapter I discusses all of the concepts and results of these theories
which win be used in this text. The exposition is complete, but briefi
it contains results Rnd proofs, with little accompanying illustrative
or explanatory material For the average reader, it win serve as R
concise review of the topics treated, and, at the same time, as B col-
lection of results available for easy reference. A reader familiar with
set theory, metric spaces,. and Hausdorff spaces, may prefer to start
with Chapter II. and use Chapter I only fur reference.
A. SET-THEORETIC PRELIMINARIES
1. Notation and Elementary Notioll8
Rather than list the undefined terms of set theory, the axioms
relating them. and the logical postulates governing the manipulation
of these axioms, we shall in this first section follow an intuitive ap-
proach. The theorems and their proofs wiD be carefully stated al-
though in an informal manner.
Upper or lower case Latm or Greek letters will usoolly be used
to denote Bets, roUecti01Ut, families, or clas8t's, as wen as to denote
functionB or mappings. The symbol. will indicate membership in a
set; thus",. A means that", is a member (or element) of the set A.
If P("') is a proposition concerning "', the symbol {"'!P("')} denotes
the set of all ",sati8fying the proposition P(",). The symbol {"" y, . . _, z}
is used for the set whose elements are :x, y, . . ., z. 'Vhere no danger
of confusion exists. we sometinles write :c in place of {a:}. In this
notation then {"'} = {YIY = "'}' The void Be! is the set with no mem-
bers: it is denoted by
. If C\'ery element of a set A is also an element
of a set B. th.en A is said to be incllld£d in B, or is said to be a subset
2
I. PRELUllNARY CONCEPTS
I.1
1.1
N01'ATIQS AND ELEMENTAllY NOT[O
S
3
of B, and B is said to confain A. This is dcnoted symbolically by
A C B. or B"J A. Two sets are the same if and only if they have
th; same elc;;;ents, i.e., A = B if and only if A
Band B
A.
The set A is said to be a propn subs£! of the set B if A
Band
A "* B. The notation ACE, or B J A, will mean that A is a proper
subset of B, The eompln1il"'t 01 a set A nlative In a 0.1 B is the set
who8e elcments are in B but not in A, i.e., the set {xix < B, X
A}.
This set is sometimes denoted by B-A. In a discussion where the
set B is clearly under>tood, we may simply employ the plu-ase
complmumt 01 A and use the symbol A' for this complemcnt; this is
stated symbolically A' = {xix f A}. If A is a set whose elements
are sets a, the set of all 3) such that tv E a for some- a E" A is called
the union, or .sum, of the sets a in A. This union is denoted by U A
or U a. The intl'rsn:tiun, or product, of the sets a in A is the set of
.,,,
all x in U A which aTe clements of every a < A. If A = {a, b, . . ., c}
we will sometimes write the union U A as au bU. . . U c, and the
inteTSCCtion n A as a n b n . . . n c, or simply as ab... c. The
operations of forming unions Rnd intersections are €OmmufaJi['C (i.e.,
aU b = bua,ab= ba), andassodutil'e (i.e., aU (bue)=(aub)u e ,
a(be}=(ab)c). Abo, intersection is distributive with respect to union,
and vice VCI'S8. This means that the following distributive laws hold:
xUa=U(xa), :rU(na)=n(xu<l}.
u£.A. ac:A "..II lie-A
Moreover, there are identities, known as the rules oj De 1J1organ.
which relate the operations of complementation, taking unions, and
taking intersections. The.e rules are expressed by the formulas
(U a)' = n a', (n a)' = U u',
"£A sEA A
A 4
A
where it is understood that all complements are taken relative to
some set b which contains every element a of A.
Two set:; are disjoint if their intersection is void. A family of
sets is a disjoint lamily if e,'ery pair of distinct sets in the famil! is
disjoint. A sequence {a,J of sets is a scqlietiCe of di8j{}int sets If an n am =
'" for" * 111. A set a is saId to i>lttrsed a set b if ab * "'.
The terms fum:l:ion, moppillg, trans/fJrmation, Bnd correspondence
will be used synonymously_ The symbols I: A --> B wIll mean that
J is 8 function whose domain is A, Rnd whose range is con tamed in B;
that is, for every a < A, the function t assigns an clcmcnt I(a) < B.
[f I : A --> Band g : B -+ C, then the mapping gl : A -+ C is defined
by the equation (gf)(a) = g(/(a» for a < A. If I : A -+ Band C
A,
the symbol I(C) is u8ed for the set of all elements of the form I(e)
where c < C. If I: A -+ Band D
B then I
I(D) is defined as
{xix <' A, I(x) < D}. The set I(C} is called the imnge of C and the sel
I
I(D) is called the inverse image of D. If f : A -+ A and C
A, then
C is said to be invariant t",uIer I in case that I(C)
C. The function
I is said to map A o.do B if I(A) = B and i>lta B if I(A)
B. The
function f is said to be an eldension of the function g and g a restriction
of I if the domain of I contains the domain of g, and I(x) = g(x) for
a; in the domain of g. The restriction of a function I to a subset A of
its domain is sometimes denoted by IIA. If I : A -+ E, and for eacb
b < I(A) tbere is only one a < A with I(a) = b, I is said to have an
inl'eT8e or to be one-In-OtlR. The inl...r.. /tmd;on has domain I(A} and
range A; it is defined by the equation a = I-I(b). Thus the domain
and range of I-I "re the range and domam, respectively. of I. The
dw.raderistic lunaion x" of" set E is the real function defined by the
equations X,,(8) = I, 8 <' E, and X,,(8) = O. 8f E.
SolIlf'times, when the range of a transformation / : A
B is to
be emphasized at the expense of t itself and its domain, we sh"ll
write I(a) a8 b.. Then I(A) is said to be an irult-xed set, and A is said
to be a sel 01 indices. If B is a collectiou of sets, the union U I(A} will
sometimes be written as Ub.. and n I(A), as nb..
GIEA faA
A relation in (or on) a set A is a collection T of ordered pairs
[x, y] of elements of A. It is customary to write :rry for [x, y] <'T.
Other symbols for relations are =, S, C,
, C'.J, and _ .
\Ve presuppose a farniharity with the real and complex number
systems. By the ewnded Teal numbtT system we mean the real numbers
with the symbols +ro and - co adjoined; by the emnded compl
.r
?lumber system we mean the complex numbers with the single symbol
CQ adjoined. If A is a. set of real numbers, then the 8ItpTemum, or the
least upper bound, of A is the smallest real number b such that a ,;: b
for all a in A; if no such number exists, we ta.ke + 0) as the supremum.
In either case we wrjte sup A or lub A to denote the supremum.
Similar definition. are given for thc inli,m'In, or the grea"..t lower
bound, of a set A which we denote by the notation-inf A or glb A.
4
I. PRELl1\ollNARV CONCEPTS
1.2.1
1.2.5
PARTIALLY ORDERED SYSTEMS
5
lim sup I(IX) = inf 8UP 1«0, a»,
_01- 6>0
similar fashion, the terms lower bound and /Jrealest u,wer bound may
be defined. As in the case of real numbers we denote the least upper
bound of F by sup F or tub F and the greatest lower bound of F
by inf F or glb F.
4 DEFINITION. An element a: in E is said to be ma.ximal if
:£ S; Y implies y :r.
The family A of all subsets of a set X affords an illustration ofthese
coneepts. The inclusion re1a.tion between the sets contained in X
makes the pair (A,!;;) a partially ordered system. An upper bound for a
8ubfamily B!;; A is any set containing U B, and U B is the only least
upper bound of B. Similarly, n B is the only greatest lower bound
of B. The only maximal element of A is X. In general, when dealing
with a family of subsets of a given set. it will be supposed that they are
ordered by inclusion, unless some other ordering is explicitly defined.
The following proof contains the central argument of this section.
5 THEOREM. Let I : E --+ E Mve the propt:rIy that I(:r) ::2: :r wha.
(E, S; ) is a '/Ion-void parlially ordired sys!em with the addiJional prop-
erties:
(ex) 11 a b and b a then a = b;
(P) every ww.Uy ordEred suhset of E hn.s a least upper bound.
Then there is a w in E milk w few).
PROOF. Let a be an element of E which will remain fixed through-
out the proof. A subset B of E with the following three properties
will be called admissible.
(i) aEB.
(ii) I(B)!;;B.
(iii) Every least upper bound of a totally ordered subset of B
is in B.
There exists a 8et, namely E itself, which has these properties. Also
an intersection of admissible sets is admissible. Hence the intersection
A of all8uch sets is a minimal admissible .et. The set {:£I:r E,:r ::2: a}
is an admissible subset of E, and thus
(iv) a < IX, :£EA.
Now let P = (IXj:£ A; YE A, Y <:r imply I(y) S; :r)
where y <:r means that y S; :r and y ""':r, It will be shown that
(v) IXE P, '1a A imply either z :r or z ::2: j(:r).
Fix :r in P, and define B to be the set of aU z in A such that
either z < jJ or z ::2: 1(:£). The condition (iv) shows that B has the prop-
erty (i). The set B has the property (ii). For if % > /(:£), then I{z) ::2:
% ;;; I(a:); ifz = :£ then 1(%) = 1(:£); and, finally, ifz < a:, then /(%) ":;:r
If ." is the void subset of the real numbers, it is conventional to take
- co = .up"', + co = inf"', If A is an infinite set of real numbers.
then the symlJollim sup A denotes the infimum of all numbers b with
the property that omy a finite set of numbers in A exceed b; the de-
finition of the symbollim inf A is similar. In particular. if A is a
sequence {an} then lim sup A and lim inf A are usually denoted by
lim sup U II . lim Inf a7j. I
.,-+IIJ IJ-rUJ
respectively. If a and b are extended real numbers, then the symbol
(a, b) denotes the open infcroal defioed by (lXla < x < b); the symbol
[a. b J denotes the closed interval defined by {xla ,.:; :r b); and the
Bemi-open infmJals (a. b] and [a, b) are given by {xln < x ;:;:; b} and
{:£Ia S; '" < b}, respectively. If I is a real function defined on an open
interval containing zeN then thf" equati.ons
lim sup I(x) = inf sup 1« - a, a),
D 0>0
lim inf I(IX) = sup inf 1« - a. a)),
e-+O b>O
lim inf I(:r) = sup inf 1((0, a»,
z__u+ 0>0
derme the symbols on their left sides. Similar definitions hold for
the symbols lim sup"...", I(x), lim inf"....--- I(x). Finally if z is a
complex: number and z = x +iy, where Of: Bnd yare rea', then :I: and 11
are called the real parI and the imaginary par! of z and are denoted
by $i(z) and -'(%), respectively.
2. Partially Ordered System.
1 DEFINITION. A parlially ord£red system (E, < ) (henceforth
abbreviated p,o.s.) is a non-empty set E, together with a relation S;
on E, such that
(a) if a :<::: band b S; c then a ;:;:; c,
(b) a < a.
The relation ,.:; is called an ordir nlalion in E. The notation y IX is
sometimes used in place of IX y.
2 DEFINITION. A "'tally ordem! subset F of a p.o.s. (E, ) is
n subset of E such that for every pair IX, y . F either IX ;:;:; Y or Y < IX.
8 DEFINITION. If F is a subset of a p.o... (E, ;:;:;), then an ele-
ment '" in E is said to be an upper bound for F if every I in F has the
prope y I ;;;; x. An upper bound '" for F is said to be a IeMt upper
nd of F f every upper bound g of F has the property x ;;;; g. In ..
6
t. PRELIMINARY CONCEPTS
1.2.6
1.2.8
PARTIALLy ORDERED SYSTEMS
7
sjnce x < P. The set B has the property (iii), for if u is a least upper
bound for the totally ordered subset F of B, then either y ,.,:; x for
eyery y £ F, in which case it-
r£, or else y
I(:r.) for some y £ F,
in which case u > I(a:). Thus B is an admis8ible subset of A. and there-
fore B = A. which p,m""" the assertJOn (v).
It will next be shown that P is admissible. The condition (i) is
vacuously satisfied by P. To prove that P has the property (ii), let
a:. P. It will be shown that if u A. and " < I(x), then fez) ,.,:; I(a:).
From (v). either z > I(x), or z < a:, so that if z < I(x), then z
a:.
Then. since x. P, if z < x. then fez)
a: ,.,:; f(x), and if z = x. then
fez) = f(x). To verify that P has the proJX'rly (iii), let v be a least
upper bound for the totally ordered set F!::: P. To show that v e P,
let z
A, Z < v. From (vl, it is seen that every a: £ F satisfies either
z
x, or x
f(x)
z. The second alternative cannot be valid for
every lV in F, for then v < z. Hence, for Borne m in F, Z < x. If z < x
then f(z)
x
v by the definition of P. If z = x, then since z *- v,
there is a y In F with z < y, in which case fez) ::£ y
v_ Thus, in
both C8Se-< f(") <- v, which proves that v. P, and that P has the pro-
perty (iii). Thus P is an admissible subset of A, and so P = A.
Ther€fore, by (v) it is seen that for Bny two elements x, z in A, either
" ,,;; a:. or z
I(x) ;;::; x. which shows that A is totally ordered. If w
is a least upper bound for A, then, since f(w). A, w
I(w) ;;; w.
and f(u-) = ro. Q.E.D.
6 THEOREM. (Hausdm-If n'(J.]);l1Ialily theorem). Every parliall y
m-ckml sysl£m eo"tains a llIa.ril1lol ''''<lIly urdn-ed 8ubsysl£m.
A more explicit statement of the theorem follows: Let the family
8 of totally ordel't'd subsets of a p.o.s. (E, < ) be made into a p.o.s.
(8, !:::), by using the relahon of inclusion between the elements of G
(which arc subsets of E). Then It has a maxima] clement.
PROOF. If C has no m:rxnru.I element. then to every A 0 It there
corresponds an f(A) < 8 containing A properly. Thus Thmrem 5 is
eontradicted by tbe function f : 8
C. Q.E.D.
7 THEOREM. (Zorn's lemma). A partially arJerNl 8ys'em has a
mn.rimal element il e-l't!ty rotally ordered 8"b8yst
m M8 au upper bound.
PROOF. Applying Tb<-orem 6, let x be an upper bound of a maxi-
mal totally ordered suhset E. of the p.o.s. (E. ;<; ). Let a: < y. Then,
if Y , Eo. the set E. u {y} is a totally ordered set containing Eo as 8
proper subset. Hence y < Eo' so that Y < x. Q.E.D.
8 DEFINITION. A p.o... (E, < ) is said to be well-ordeml if
(i) a
band b
a implies a = b.
(ii) Any non-void subset of E contains a lower bound for itself.
The positive int'.e{,.rcrs in their usual ot'der afford a familiar example
of a well-ordered 8ystem.
9 THEOREM. (Well-urdering tli-eorem of ZemU'lo) Every 8et may
be well-rmlrred.
The theorem means that for every set E there is an order re1ation
< in E such that the p.o.s. (E, ,,;; ) is well-ordered.
PROOF. Consider the famIly 8 of all well
rdered sets (E., :::; .)
such that E.!::: E, We define the ordering < inCbyplaeing (Eo, ,.,:;.)
< (E"
I) if and on]y if
(i) Eo
E.,
(ii) x, y < Eo, X ::£0 y imply", ::£1 y.
and
(iii) xoEo> YfE., yoEI imply X::£1Y'
Under this ordering every totally ordt'rf'd subfamily Go of G has an
upper bound. Indeed. it will be seen that this upper bound may be
defined as (u C.,
'), where x
. Y, whenever a: and y both belong
to some subset Eo e Co, and x
o Y in the ordering
o ofthat E.. It is
clear that if (UCo, < ') belongs to C it is an upper bound for Co. It
will now be shown that it is well-ordered and hence belongs to 8. The
statement 3J ::; .. 3J for It' E" U BfJ is clear. If :£
' Y and '!J < ' 2
then
::c, 11£ Eo
8 0 , lit 2£ El E" Co, J: < eY, and y
lZ. Sin
e Co is totally
ordered it may be supposed that (Eo,
.)< (El' S ,), and then it is
seen that x ::£, z, and thus that a:
. z. If x < ' y, and y
. x. then
or, y £ Eo. and a:, Yof" EI' with i'£
o y, and y
1:C. Then, supposing
that (E.,
o>"< (E,. ;<;1 ). it follows that x = y.
Now, let F!:::UC., and let F be non-void. Then, for some
Eo 0 Go, F n Eo oF 4>. The p.o.s. (Eo, ::£0) is well-ordered. Let
Xo e F n Eo be a lower bound for ,.. n Eo, under the ordering S O'
Then. if y < F, y f F n Eo, it f01l0ws that x., Y' E,. where (Eo, < 0)
< (E 1 , :<;;; 1)' so that xo ::£, y. Thus. Xo is a lower bound for F under
the ordering < '. Thus it has been shown that Co has an upper bound.
8
I. PRELIMINARY CONCEPTS
1.3.1
1.9.11
EXERCISES
9
Hence, by Theorem 7, there is a maximal well-ordered subset Eo
of E. Now Eo = E for if x is in E but not in E" the ordering
(J in
E. may be extended to the set E. U {x} by defining y
. x for
y . E.. Q.E.D.
x
y implies I(x) <::: I(y), then I has a flxed element x. (/(0:.) = x.j,
and the set of all fixed elements contains its least upper bound and
its greatest lower bound.
11 D£F1NlTIO". For eaeh '" in a set X let A. be a subset of aset
A. Then the Carksian product P .,X A. or P A. is defined to be the set
of all functions I on X to A for which
l(x).A., ",.X.
U X consists of a finite number of elenlentS1' X = {.xl'> . . "f 3:'"h P A
will sometimes be written Ax xA m X ... ,Aa:. fUX
.. .
12 If Xis the set{I, . . ., n}, then p.,x A.can be regarded as the
set of n.tuples of the form [ill' . . ., an], where il. . A,. If X is the set
of integers, then P A. may be regarded as the set of sequences [a,., a"
. . .], where a. E Ai-
13 Let Q., N., and 111. be subsets of A.. for", . X. Let 111 =
PM., N = PN., and Q
PQ.. Suppose that N *' '" *' Q. 111 =
N U Q, and N n Q =.p. Then there exists a uniquely determined
07'0 E X, such that
(a) lIl. =N. uQ., N. nQ. =.p,
'(} II II II II
(b) JU.=N.=Q" if x*,x., x.X.
14 DEF'NITION. If Y};;X the mapping which takes each I in
P
ExAa: Into its restriction flY is called the projection of P:uxA
onto P.,yA.. Thi. mapping is denoted by pry. If Y = {x} then pry
will be written as pr..
15 Lct X oF .p.
(a) P 111. is void if and only if some M. IS void.
.,x
(b) II' lIl.};; N, for or. X, P lIf.};; P 1'0'..
z£x Z£.X
(c) If P JU. "F.p, the converse of (b) is true, and equality ill the
'EX
conclusion of (b) implies equality in the hypothesis.
(d) A set F IS of the form P B. with B.};;A. if aad only if
1<' = P W.(F). uX
.,x
3. ExetUoes
1 If (E, <::: ) is a p.o.s. with the property that every totally
ordered set has a lower bound, then E contains a minimal element
2 [f a family Iff af subsets of a set has the property that A . Iff
if and only if every finite subset of A belongs to S, then S contains
a maximal clement.
S Derive Theorem 6 from the statement of Exert-ise 2.
4 Show that anyone of tIle following implies any other one:
Tbeorem 6 J Theorem 7, Theorem 9. and Exercise 2.
5 Prove that if A and B Bl'e sets, there exists either.a one-to-one
mapping of A into B, or a one-to-one mapping of B into A. This is
known as the comparability thevrem lor cardinals.
6 Show that there exists a one-to-one correspondence between
any infinite set A and the set af all pairs (a, n). where a
A and n is
an integer.
7 Let R he the set of real numbers. A subset S};; R is called a
Hamel basis if every real number T can be uniquely represented as
,. = ..Ei«
i' where Si
S and at is rational. (a) Show that there exists
a Hamel basis. (b) Show tIlat there exists a discontinuous real fuuc-
tion of a real variable satisfying the identity I("'+y) = l(x)+/(y).
8 A family..K of subsets ol'a set X is said to have property (0:) if
(0:) X IS not the union of a finite number of subsets in ..K.
Show that if..K has property (0:), there exists a maximal family
A - of subsets of X wIth property (0:) which contains..K. Also, show
that any maxlInal A r has the property
(fJ) If Ai
X, i = 1...., n, and A1n... nA. .,Ar, then .ome
A.£.i....
9 DU'lNIT10X_ A I"O'S. (E,
) is said to be complete if:
(i) a
band b
a imply a = b,
(ii) Every non-void subset ha
a least upper bound and a greatest
lower bound.
10 (Tarsk.) If (E,
) lS a complete p.o.s., I: E ..... E, and
10
I. PRELIMJKARY COXC'EPTS
1.4.1
1.4.7
DEFINITIO}l;S AND BA8IC PROPERTIES
II
B. TOPOLOGICAL PRELIMINARIES
hoods of a set A !;; X and every neighborhood of A contains a set in p,
then p is caIled a junlIammtd Jami!y oj nngh/>orhoods for A.
For exnmplc, the usual wpolDgy of the real li'le i8 the topology on
( - 00, + co) which has as a base all open inteITais (a, b), where a
and b .arc arbitrary real numbers. Another base for this topology is
obtained by taking a and b to be rational numbers. A subbase for this
topology is given by all infinite intervals (-co, a), (b, +co), where
a and b are either real or rational. The topvlogy vf the e.Et£ntkd real
number. bas as a base the sets [-co, a), (a, b), {b, +00], where
a and b are real numbers. The complex numbers and the extended
complex numbers are treated similarly.
4. Definitions and BlI8ie Propatie.
1 DEFINITION. A family -r of subsets of a set X is called a
ropolagy in X if -r contains the void set.p, the set X, the union of every
one of its subfamilies, and the intersection of everyone of its finite
subfamilies. The pair (X, -r) is called a Il>pOlogical'paee; but sometimes
if -r is understood, we refer to X as a topological space. If -r, -r, are two
topologies in X. -r is said to be 81ronger, or larger, than -r, and T, is
said to be weak/'T. or ..naIler, than -.if-.. 2 -r.. The sets in T are called the
opeaBels of (X, T). A neighborhood oftMpoimpisanopensetcontaining
p. A 71l:ighblJrhood of the Bet A is an open set containing A. If A is a
subset of X, then a point p is a limit poin
or a point 01 accumulation,
of A provided every neighborhood of p contains at least one point
q *' p. with q e A. The i_lor of a set in X is the union of its open
subsets; a point in the interior of a set is called an i1lterior poinl of the
set.
7 LEMMA. If fJ is a family oj 8Ub8rls oj X, and if r is the family
of all unions of s'"bfamili.. oj p, IhR" -r is a topology iJ ond olily if
(i) for et1/'T!f pair U, Vep and Ire un V there is a Wep, sueh
that a:eW!;;UnV, and
{ii)X=Up.
2 LEMMA. A Bel in a topologiad 'Pace is vptm if and tmly if iI
contui"" a nrighOOrhood of cach of ils points.
This lemma, Bnd a. number of those to follow, are immediate
consequences of the definitions involved. Where this i8 the case, the
proofs will be omitted.
3 DEFINITION. A set is said to be clased if its complement is
open.
4 LE"MA. Tlte Inkr8edion of any family of elosed Bels i3 closed,
the union oj any finite family of dosed sets is closed, and .p and X arl:
dosed.
8 LEMMA. A family p is a .ubbaBt" for the topology T iJ and only
if p
rand nJery vpen set is a union vffinite i1l1"sections of sels in p.
9 DEFI"ITION. The closure A of a 8et A i8 the intersection of all
closed sets containing A. The set of points in A and not in the intenor
of A is called the boundnry of A.
10 LEMMA. Tlte closure op<:ration Itas thR propertiu:
(a) AUB
AuB, (b)A:2A,
(c) A = A, (d) .if = A if A =.p,
(e) peA if and only if eiJ£ry neigltoorhood N (p) of p .ntRrsecls A.
PROOF. Statement (b) is self-evident. Since A is closed, (Lenuna
4), it follows that A = A. The set A UB contains A and is closed.
Thus A u B ;) A. and similarly A U B ;) 11. Therclore A U B :2
.it u B. Conv;'ely, Au 11 is closed (Lem
a4), so Au B2 A un.
which proves (a). Statement (d) means simply that.p is closed. State-
ment (e) follows immediately from Definitions 8 and 9. Q.E.D.
II LEMMA. Let d be tM family of all subsets of X, and let
A --->- A be a mapping d --->- d, whkh It"" the four properlU,B (a), . . .,
(d) oj 1..emma 10. TMn tM family :F = {AlA = .if} Iuu tM properlie11
5 LEMMA. If .'F is any family of Bubsels of X having the proJKrliea
of um'lIQ 4, and r is the family oj compltm<'nts of mnnhers of fF, then
(X, T) is a tvpological 'Pace, and g; is the family of closed sels of this
tQJJology.
6 DEF'''''TION. A family p of subsets of X is said to be a base for
the topology -r if P!;; -r and if every set in -r is the union of some sub-
family of p. The family p is said to be a ndlbast: for the topology T if-r
is the smallest topology containing p. If P is a collection of neighbor.
12
[. PRELIM(YARV COXCEl>'l'S
1.4.12
1.4.15
DEFINITIONS Al'D BASIC PROPERTIES
13
lured in Lemma 5, so Ihat 1M fam,1y of complemalls 0/ clements 0/ SF
is a topology. The set ..4 is tM C/csUTC of A in thu topology.
PROOF. Statements lO(b). (d) show that"', X e SF, and lO(a)
shows that A U B . SF if A. B. SF. It follows th..t any finite union
ofsets in SF is in SF. From 10(..), itfollows that A C B implics..4 C Ii,
and hence if Az £ !F, it is seen that
ngA.
Ag = Ag.
PROOF. Let Bu B., . .. rn, an cnumeration of p. Let Po be the
family of elements of P which are contained in some subset of <f. If
Bfl E /30' let C n be some set in (J which contains B 1It a.nd let 0'0 be the
family of all these C n , Then it is evident that
U<f
U<fo
UPo.
Sincc P is a basis, if peA e <f, there is a Bfi' P such that p . Bn
A,
and so UPo
U<f. Q.E.D.
15 DEFIN'TIOK. If (X, T) and (Y. T,) are topologIcal spaces. and
f : X -+ Y, then / is aJ1llinuous if 1
I(A) . T for every A in r.. In other
words a mapping between topological spaces is continuous if the in-
verse image of every open set is open. The function I is said to be
lJ01ilinuous al the point x if to every neighborhood V of fIx) there cor-
responds a neighborhood V of x with I(V)
V. If f is a continuous
one-ta-one map of X onto Y, and if the inverse function 1-1 is also
continuous" then f is called a hO'llleomorphism, or a topologiool iso-
morphism. In this situation, the spaces X and Y Bre said to be hunvo-
morphic.
16 LEMMA. Let X, Y be topological sp<1£fB and let f: X _ Y.
Then, Cilch of the loU_ing .tarelnents i. egunoalellt w th
continuity
r4 I:
(a) The funetion f i. continuous at ro.ch point a:. X.
(b) Tile itlVl'Tse image of a dasrd set is rlo.ed.
(c) 1/ A
Y, !hen I-'(A)
f-'(A).
(d) II A
X, thell/(..4)
/(A).
(e) ForCloery A in 'oTlleS1lbba1J
lortM lopology in Y theset/
I(A)
is open.
Thus
n.A.
n.A"
n.A.,
and the family SF has all of the properties listed in Lemma 5. From
that lemma it is seeo that the fllJl1ily of complements of clements of
SF form a topoJogy. It remains to be shown only that..4 is the closure
of A in this topology. Now if B is closed, and B:1 ..4, then ii d A = ..4,
which shows that A is closed
and is, in fact
the smallest ;losed set
containing A. Q.E.D.
12 DEFJNrT'OK. If Y
X, and r is a topology for X, then the
wpology
ry = {AlA = Bny, BeT}
IS called the ..mural relative topology 01' Y generated by r. A subset of
Y is said to be YE'Uztively npen if it is in Ty; relntively tlmJed if its com-
plement relativc to Y is relative]y open. Other terms like Tela1ive
dfJo'JUTe of a set are defined analogously. A topoJogical space X is
said to be cOnllel'ted if it is not the union of two non-void disjoint
closed sets.
13 LEMMA. II Y
X, and (X, r) is a topological spuc
, tho. the
Tela!ive closure 01 a sul>sd A of Y ;s the illler.eClion of the "''''litre of A
with }'.
A subset of a topological space will always be regarded as a
topological space with its rclath-c topology, unless some other topo.
logy is given explicit\
.
PRom', If f is continuous and V is a neighborhood of I(a:), then
V = f-I(V) is a neighborhood ofa: with/(V)!;; U. Tlllisfiscontinuous
ar. ea.ch point x. C.onversely, Lemma 2 shows that (a) implics the con-
tinuity of /. Since the inverse image of a complement is the comple-
ment of the inverse image, the continuity of / is equivalent to the
statement (b). _
Statement (b) implies (c), sin..... if 1-'(..4) is closed, thcllf
I(A)
f-I(..4). But (c) implies (b), since if A is closed, f-I(A)
f-I(A), so
that f-I(A) is closed.
H THEOREM. (Lindelof) Let (X, r) be a lopological.pace, alld let
r have a cOlmtable base p. Then e1.oery lamily u
T contai"s a coulltable
subfamily <fo witll U u = U "0'
14
I. PRELIMINARY CONCEPTS
1.4.17
1.5.1
XORMAL AND COMPACT SPACES
15
_..
tatem:.nts (c) and (d ) are e guivalent, for if I(A)
I{A), then
1(/- 1 (B»
B, and hence I-'(B) !;; r1{B). On the other hand, if
l-l(A)"; U-'(A) , then r' ct(B» )";;J,!-'(I(B» "2 B, and hence I(B) "2
I(B).
It is clear that (a) implies (e). Also, since the inverse image of an
inteIRdion (or union) is the intersection (or un1on) of the inverse
images, (e) implies (a). Q.E.D.
17 LEMMA. II X, Y. Z are topological spaces, and il I : X ..... Y
and g : Y ..... Z are continuous, tJum the campos;le Iwld;on Ig is coMnu.
ous.
The term 8calar win be used fot' a real or complex number; &
scalar fund;o" is a real or complex valued function. The topology in
the set nf scalars is always assumed to be that determined by the
base whose elements are neighborhoods of the form {fiIiP-exj < e).
18 LEMMA. Let I, g be continuous &adar funcli01l$ on a topulogirol
BptWe X, and let C1 be a Bea!ar. The.. the lunctions gi7Jfn by the e.rprt:8sion&
1 DEFINITiON. A topological space X is a HtlItsdorff space if
it has the properties (a), (b), listed below. It is a regular space if it has
the properties (a), (c), a nOmWspace, if it has the properties (a), (d).
(a) Sets consisting of single points are closed.
(b) For every pair of distinct points IX and y, there are disjOint
neighborhoods of IX and 1f.
(e) For every closed set A. and every IX f A. there are disjoint
neighborhoods of A and IX.
(d) For every pair of disjoint dosed sets A and B, there are dis.
jo;nt neighborhoods of A and B.
2 THEOREM. (UrY8iJhn) Let A and B be disjoin! clolfed BelS ;n a
1Wrmal topolngien! spau X. Then there is a COfliin= rea! /unctifJI. I
defi7u;d on X, such thai 0 .-;; I(IX) :::;; 1, I(A) = O./(B) = 1.
max 1f("'I, g(IXI),
a!sa define continuous funrtions.
min (1(",), g(IX»
PROOF. Let AlJ2 and B lj !. be disjoint open sets) containing A nnd
B respectively. Then we have
A!;;Al/,
Al/,!;;B;,'2' BfJ,;:JB.
Then A and A:/ 2 Bre disjoint closed sets, Rnd B
2 and B are disjoint
closed sets. Ernplo)-ll1g the hypoth""is of normality again, we con-
struct open sets Al/ 4t and AS}4. such that
A
A fJ ,!;; A./,!;; A,t,
AfJ'
A 3 },!;; A,/"
and A.}, n B =.J.. By induction. a family of open sets A, may be
defined for every. dyadic rational r. 0 < r < I, such that
(i) r < s imphes A,
A.
lI(re)I,
"/(IX),
1("')+g(IX),
are contillUoUS. II I, g are rea!, then the expresBions
5. Normal and Compact Spaces
Is there. on a given topological space, a contmuous real function
which is not a constant? If '" and 1f are distinct points of a topological
space X, is there a continuous real function on X with 1("') '¥= ICy)?
If the answer to this second question is in the affirmative for an arbi-
trary pair of distinct points, it is said that there are enough real con-
tinuous functions to distinguish between the points of the space. It is
not clear from any of the preceding remarks whether or not a given
topological space has this property. However, it wili be shown pre-
sently that the normal and the compact Hausdorff spaces introduced
in tm, section all have enough continuous real functions to distinguish
between their points.
and
(ii) A
A.. BnA.=.J..
Let I(x) = 0, if x is in all of the sets A,. Otherwise let
fIx) = sup {rl'"
A,}.
To verify that I is continuolls,let c = I(J:) he positi\'e. Then, for some
suitable arbitrarily small £ and 1) < E, t£ is ill the open setA.c+en A;_rr
If y is also in this open set, then 1f(..)-/(y)1 < 2e. If 1("') = 0 an
analogous proof of continuity holds. Q.E.D.
1\ THEOREM. (The Tirl::£ atmsi"" tluw'cm J II I is a bounded real
continuaus IUlldio" defined 011 a closed set A 01 a normat space X. there
16
I. P1lELIM'
ARY COXCEPTB
1.5.3
1.5.4
)lORMAL AND COMPACT SPACES
J'j'
is a CfmtinuOUB Teal fUndion F de(inro on X rritlz F(re) = fIre) fOT:r
in A, and sup IF(re)1 = sup If(re)l.
3:EX ze-A
.
If("') - I F.(re) I <: (I) ","11'..
;={)
x€A.
. e
I IF,("') - F.(Y)I < -, y
v,
1-0 2
and thus IF(",j-F(Y)1 < e for Y III V. Q.E.D.
i COROLLARY. A Teal continuo." fundion tkfined On a closed
81ket 0/ a nann a I "PIlce has a Teal continUOWl e""msion lkfined or> the
'Whole space.
PROOF. The only case where the theorem does not apply imme-
diately is the case where I is unbounded. If / is real and continuous on
the closed set A in the normal space X, the bounded function
arctan f("') has a continuous extension a!re) defined on X. The closed
sets A and B = ("'lIa(",)! = :n;J2} are di8joint, and hence there is a
continuous function fJ with 0 ,,;; {J(re) ;;;;; 1, which vanishes on B, and
has the constant value Ion A. Thus the function tanp!"')",!re) is a
continuous extension of /. Q.E.D.
5 DEFINITION. A CUt,<ring of a set A in a topological space X
is B family of open sets whose union contains A. The space X is said
to be compact if every covering of X contain8 a finite subset which is
also a covering_ A topological space X is said to be locally compact if
every point has a neighborhood whose closure is compact. A family of
sets Ju.s the finite inrersection property if every finite subfamily Ju.s a
non-void inten;ection. A subset of X is called conditi<mally compact
ifits closure is compact in its relative topology, It should be noted that
a subset A
X is compact in its relative topology if and only if every
covering of A by open sets in X contains a finite subcoverjng.
A well-known example of it loca.lly compact space is a ()losed set
of real or complex numbers. Such a spaoee is compact if and only if it
is bounded. These statements constitute the Heine-Borel theorem.
6 LEMMA. A topolngind space is compact if and only if every
lamily of closed Bela ",ilh Ihc linile i»ursec!ion property has a nan-void
inler8fd:ian.
This lemma follows immediately from the rules of DeMorgan,
and the next lernma follows readily from the definitions involved.
7 LEMMA. (a) A closed Btlbset 01 a compact spare i8 compacl.
(b) A continuous image 01 a compact space is cumpact.
(c) A compact Bubsrt of a H GusMrl/ space is cloaed.
PROOF. SInce the theorem is obvious if f is identically zero on A,
it will be assumed that this is not the case. Let f.(re) = /(re), 1'0 =
sup Ilo(re)l, A. = ("'Ix. A, Io(x)
-PolS}, and B. = (xlx
A, Io(x) >
z<A
I'./IJ}. Then Ao n B. = rJ>, and both axe closed. Applying the previous
theorem, we find a function 1<'0("') defined on aU of X such that
Fo(Ao) = -1'./3, F.(Bo) = 1'0/8. -1'018 <: Fo(re) ,,;; 1'0/3. Let/ I (",) =
Io(x)-F.(",) for re. A. Then f. is continuous, and 1'. ";; (2/3)1'0
where 1', = sup 1/.("')1.
..A
By applying to the pair /" 1'. the procedure applied to fo, P., and
then continuing inductively, one obtains a sequence F " i = I, 2, _ . .,
of real continuous functions on X, with the properties:
and
sup 1F.!re)l;;;;; l(!)."..
..x
These properties show that the series I:...o F n(x) converges and defmes
a function F on X which coincides with / on A. To ""my that F is
continuous, let, > 0 and fix n so that 21'0(2/3).+' < e/2. Then
.
IP(",) - F(Y)I <: IF("') - I F.(m)1
.-=0
. . .
+ I Z p.(:r) - I F,(y)1 + I I F,(y) - F(y)1
.-0 i=O j=(}
.
;;;; 2p.(i)","1 + I 1F,(m) - F,(y)!
i=Q
t .
< - + I IF.(x) - F,(y)J.
2 j"",v
The continuity of Jo' will be shown, using Lemma 4.16(a), by proving
that F 18 continuous at each point z. According to Lemmas 4.16 and
4.18, there is B neighborhood V of .x slich that
18
I. PRELIMINARY CONC:.E;PTS
1.5.8
I.ti.2
METRIC SPACES
19
8 LEMMA. A rontinuoUJ; one-ltrone map from a compact space 10 a
HaruJmjf space is a hmnemnorphism,
PROOF. Let X be a compact 8pace, Y a Hausdorff spaee, and I a
one-to-one continuous function on X, with f(X) = Y. According to
the p ng lemma, B dosed set A in X is compact, its continuous
image f(A) is compact, and, since Y is a Hausdorff space, I(A) is
clo8ed. Thus Lemma 4.16(b) shows that 1- 1 is continuous. Q.E.D.
I) THEOltEloL A oompad Hausdorff space is normal.
PROOF. Let A be a closed subset of the compact Hausdorff space
X, and let p f A. Then. if q e A, there is a neighborhood V. of q and
a neighborhood V. of p, such that V. n V. = .". Since A is compact,
a finite set U Q , . . 0. U(1 co,. ers A and
, .
S(ilI, s) = (Yle(x, y) < el
are called .phl'TCB in X. The sphere S(ilI. s) has a: for a center. and s
for a radius. The metric Ihpologg in X is the smallcst topology contain-
ing the spheres. The set X, with its metric topology. is calIed a metric
space. If X is a topological space such that there exists a metric func-
tion whose topology is the same as the original topology. we say that
X is metri:tnble.
If A and Bare subsets of a metric space, lete{A, B) = inf e(a, b).
ae:.1.()£B
If A is a suh-.et of a metric space, the e-m.ghhorhood of A is the set
SeA, e) = (xle(A, ill) < e}. Thc diamdn of a set A, in symbols (I(A),
is the number sup era. b).
a. "A
2 LEMMA. If e is a meltic fundion in lhe set X, lhe sph£res form
a /JaIIe for Ihe ",elm topology.
PROOF. Ifu e S(x_ e)S(y, e'), choose.5 > 0, so that e{x, u)+b < e,
e(y,u)+(1 <c'. Then ifveS(u..5),
e(x, v) ;:;; e(x, u)+e(u, v) < 1.'(a:.u)+" < e,
(V. u.. .uV. )n(V. n...n V.) =.".
,. J. .....
Thus any compact set A and any point P f A have disjoint neighbor-
hoods. Let A and B be closed and disjoint. Then if peA, there is a
neighborhood V p of p, and a neighborhood V. of B, such that
V p n V. =.,.. Then a finite set V. will Cover A, and the sets U U
.
V p u... u V. and V. n V. n. .. n V_ are dis J 'oint nei g hbor.
2 mIl: m
hoods of A and B, respectively, Q.E.D.
10 LEMMA. A rea! crmtintuJUS lundi"" on a oompact ,pact! attains
its supremum and its infimum.
P.ltoOF. Let f be a real continuous function on tbe compact space
X. By Lemma 1(b) the set f(X) is wrnpact and hence by Lemma 1(c)
it is closed, Hence I(X) is a bounded closed set of real numbers. and,
therefore. it contains both its supremum and its infimum. Q.E.D.
and
6. Metric Spaces
I DEFISI'l'roN. Let X be a. set, and let f! be a reaL function on
X X X. with the properties:
(i) 1.'(x,y);;;' 0,
(ii) 1.'(x, y) = 0 if and only if '" = y,
(Hi) 1.'(ilI, Y) = 1.'(y, ill), and
(iv) e(ilI, y) e(x, z)+ (z, V).
Then e is caUed a metric, or a metric jU1lction in X. Sets of the form
e(y, v) ;:;; e(y, u)+e(u, v) < 1.'(y, u)+b < e',
which show that S(u, (I) (; S("" elSey, e'). The desired conclusion
follows from Lemma 4.1. Q.E.D.
g THEOREM. A metric spaa is normal.
PROOF. Ifx "",y,S(ilI,(l/2)e(ilI,y» and Sty, (I/2)e("',y» are disjoint
neighborhoods of oX .and y respectiv ly; therefore a metric space is a
Hausdorff spare. If A and H are disjoint closed sets, the sets Al =
(xle("', A) < e(x, B)} and Bl = (a:Je(x, H) < 1.'(ilI. An, are disjoint
neighborhoods of A and B, respectively. Q.E.D,
4 LEMMA. In a metric space, any Itubset, with its relative topology,
is also a mdri apace.
PROOF. The restriction of the metric function to a subset deter.
mines a metric, the topology of which is the relative topology of
the subset. Q.E.D.
5 DEFINIT[O . A sequ nce {an} in a topological space is said to
converge to a point a in the space if every neighborhood of a contains
20
). l'RELlMIN_"RY CONCEPTS
1.6.6
1.6.10
METRIC SPACES
21
all but a finite number of the points an. This notion is written sym-
bolicaUy an -+ a, or Jiml'J_cc a,. = a. A sequence {at.} is said to be
€ouvergen.t if an -+ a for some o. A sequence {all} in B metric space
is a Cauthy seqru:ru:e if lim"... e(a." a.) = O. If every Cauchy se-
quence is convergent. a metric space is said to be complett;.
The next three lemmas are immediate consequences of the
definitions.
the centers Pm form a Cauchy sequence, and hence converge to a
point p. Since
e(p., p) ;;;; !'(P.. P..) + e(Pm, p)
6 LE....A. In a merric space, a oonvo-gem s..gum"" is a Cauthy
""'}",,,."". A Cauchy sequtma: converges ;J and only if ;t MS a convergt'llt
8tibseqlJen(;e. A point a is in lhe closure of a set A ;n a m£tri.c space if
and cmly ;f there ;s a sequ<:nce {a.} of poin/s of A CQnverging ro a.
Ell Ell
<"2 + !'(Pm,P) 2
it is seen that p S. for every n. This implies that p is in none of the
sets A,., and hence, that it is not in their union. This contradicts the
assumption that X = UA., Q.E.D.
10 DEFINITION. A subset A of a topological space X is se9""n-
tially eompacl, if every sequence of points in A has .. subsequence
converging to .. point of X.
11 DEFINITION. A set is said to be dense in .. topological space
X, if its closure is X. It is said to be nowhere dense if its closure does
not contain any open set. A space is 8eparable if it contains a denumer-
able dense set.
7 LEMMA. A closed subspace oj a complde .nmic space is com-
plete. A complete subspace of a mmic space i. cloud.
8 LEMMA. A mapping J: X --+ Y between metric spaces IS oontill-
uous at the point '" iJ and only if {I("'.)} converges to f("'), whenever
{"'.) C(J'lINtgC8 10 <C.
9 TIIEOREM. (The Bait< category theorem) If a complae .nelric
space is lhe tlEnumetabk union oj cw.ed subsetJ/, al least one oflhese
ewsed subsets rontaifts a non.void open set.
PROOF. Let X be a complete metric space with metric 1'("" y).
Let; {A.} be a sequence of closed sets whose union is X. For the
purposes of an indireet proof. it is assumed that no A. contains a
non-void open set. Thus .AJ #= X. and A is open and contains a
sphere S, = S(p" e,) with 0 < 8, < 1/2. By assumption. the set A.
does not contain the open set S(p" ",-/2); hence the non-void open
set A n SIp" 8,/2J contain8 a sphere S. = S(p" e.J with 0 < 8. <
1/2'. By induction, a sequence {S.) = {S(P., e.)} of spheres is ob-
tained with the properties
12 THEOREM. IJ a Wpowgical space has a countable base, it i8
separable. Conversely, ;,J a metric space is separable, ;t has a countable
base. Thus a subspace oj a separable metric $pac.. ;s separable.
PROOF. Let AI' A.. . . _ be a base for the topology in a topological
space X, and let P. A.. If V is open, there is a base element A"
contained in V. and hence a point Po in V. Thus the denumerable set
P = {Pt,,,., . . .} is dense in X. Conversely, let p" p" . . . be a count-
able dense set in a metric space. It will be shown that the denumerable
set of spheres S(p., T), with T rational, forms .. base. If 11 is in the
open set V, then S(p, 8J V for small 8. Some P. is in SIp, 8/4), and
for such P.
o < 8. < 1/2.,
S"'I S(P., 8.J2),
SfiA" = "' n = II 210 . . ..
p S(P.' T) SCpo 8)C V.
where T is any Tationa! nnmber between 8/4 and 8/2. The final state-
ment follows readily. Q.E.D.
18 THEOREM. A subset of a metric space is compact iJ and only
iJ il is closed and iJequentia11.y con.pacl.
PROOF. Let A be a compact subset of a metric space X. By
Lemma 5. 7( c), A is closed. If A is not sequentially compact, then some
sequence {a,.} contains no cOIlvergent subsequence. Hence each point
Since. for n < m,
e(p., Pm) ;;;; p(P., P,*1) + e(p,*" Po..) + . . . + !'(P_1' Pm)
I I I
<-+...+-<-,
2 n +1 2'JJ 21'
22
I. PRELIMINARY CONCEPTS
1.6.14
1.6.16
METRIC 81> ACES
28
in A has a neighborhood contaimng at most 11 finite number of an"
Since a finite number of these neighborhoods cover At the sequence
{a.} consists of only a fimte number of distinct points of A, and there-
fore most rertainJ.y does have 8 convergent subs.equence. This contra-
diction proves that A is sequentially compact.
Convcrsely, suppose that A is sequentially compact and closed.
It will first be shown that A is separable. Let P. be an arbitrary point
of A, and let do = sup e(p., p). The number d. is finite, for if
.<A
e(P., qfi) -i'- 00, there is a convergent subsequence CJVli .......,. 9.,. and hence
e(p., q) = lim e(P., V.) = 00, on impossibility.
Now, inductively: let P'+I be chosen so that mm e(Pn. P<+I) ;;"
d,/2., where O;S;n:$i
d, = sup min e(Pn' p).
pe-II O:iift l
It i8 clear that do d, ;;; _ . u If d n ;;; C> 0 for all n, then no sub-
sequence of Po' Pit' _ . is B Cauchy sequence; by Lemma 6 no sub-
sequence converges. Since this contradicts our hypothesis, it foUows
that d. -+ O. Thus, for every P in A and every e > 0, there is a P.
such that e(p., p) < e. Therefore, {Po. p" . . .} is a countable dense
set.
NowJ' as is seen from Theorems 12 Bnd 4.14, to prove that A is
compact, it suffices to show that every countable covering of A by
open sets G , G v . . . contains a finite 5ubcovering. If U _l G i *' At let
OVfl tjU :'_1 G tl "'n£ A. Let :£111. ---+3: be a. convergent subsequence of {m D }.
Then.. since the comp1ement of LJ =l G j is dosed" x 1- U G" so that
'" f U ::, G,; this contradicts the fnet that U , G, A. Q.E.D.
14 DEFINITION. A subset K of a metric space is towlly bomuIed,
if for every E > 0 it is possible to cover K by a fioite number of
spht"J1's S(k;, E), i = I, . . ., 11., with centers in K.
15 THEOREM. II K is a set in a metric space X. the lollDwmg
8I.atemmts are equitYJJent:
(a) K is 6eqlU:rrIinlJy compact:
(b) K is compact:
(c) K is totally bounded and K is compirle.
FtJ1'!knnore, a compacl metric space is comple/<! and separabk.
PROOF. By the preceding theorem, (b) follows from (a) if we
can show thatK is sequentially compact. Let (P.} be a sequence inK,
and let k n E K be such tlmt e(p., k.) < Iln, n = 1, 2, . ... Some
subsequence of {k n } converges, and it is readIly seen that the same
subsequence of {Ph} converges to the same point. This proves (b).
Suppose (b) is true and let e> O. Then. since K is dense in R:,
the spheres S(k, E), k £ K, cover K. Consequently, a finite number
S(k., E). . . ., S(k., E) of these spheres cover if and hence K, proving
that K is totally bounded. Let {P.} be a Cauchy sequence in R:; since
if is sequentially compact (Theorem 13), some subsequence of {Pn}
converges to a point p E K. It is readily seen that the entire sequence
{P.} converges to p" so K is complete.
Let (c) be valid, and let {k.} be a sequence in K. By the total
boundedness of K, for each number Iln n = 1, 2, ..., there is a
covering of K by a finite collection of spheres with center8 in K and
radius I/n. Thus some suhscquence {kl } of {k.} is contained entirely
in a sphere of radius OIlC; a subsequence {kz,n} of {Icj,n} is contained
entirely in 8. sphere of radius ] /2, etc. Continue this process and set
k n = k mn . By construction, {/in.} is a Cauchy sequence; since K is
con'lp]ete, it is convergent. Hence K is sequcntially compac.t, and the
equivalence of (a), (b) and (e) is provro.
To prove the final statement, observe that if a space X is com.
pact, then from the equivalence of (b) and (c) it follow8 that X is
complete. The fact that X is separable WaS proved in the course of
the proof of Theorem 13. Q.E.D.
The sejection procedure used to establish part (c) in the preceding
proof is known as the Cantor mag, mal 'P'"""ess.
16 DEFINITIO". A mapping I: X -+ Y between metric spaces
is said to be tlnijUTmly co-nlinuous on X, if to every e > 0 there
corresponds a (j > 0 such that e("'. ",') < (j implie8 (f("'),/(""» < e.
The next theorem is of an elementary character, and wiIJ be used
frequently throughout the text.
17 THEOREM. (PrinciplE 01 e:rumsion by continuity) Let X and Y
be metric spaces, and let Y br complde. III : A .... Y is uniformly con-
tinuous on the dell&C subset A 01 X, IMn I hw; a unique continuous
e.rt-ension g : X ......,.. Y. This unilJlk? extension is uniformly continuous
on X.
24
I.. PRELIMINARY CONCEPTS
1.6.18
1.6.19
METRIC SPACES
25
PROOF. If X < X. there is Q sequence of points an < A with an x.
Since {an} is Q Cauchy sequence, and 1 is uniformly continuous, the
sequence {/( an)} is also a Cauchy sequence. Since Y is complete. there
is a pointg(x) < Ywith I(a,,) -+ g(x). To verify thatg(x) depends only
upon x. "nd not upon the particular sequence a" -+ x, let {b n } be
another sequence in A with blJ. -+ ir. Then e(a n , b n ) -Jo. 0, .and, since f
is unifonnly continuous. e(j{a,,), I(b n » O. and therefore I(b.) -+g(x).
Now it is readily seen that e(x. ",') < {j implies e(g("'). g(.x')) ,;; e;
from this the uniform continuity of € follows. Finally, the uniqueness
of g is obvious. Q.E.D.
In general a continuous function is not uniformly continuous,
but on a compact metric space these two notions coincidt:.
18 TUEOREM. II I: X -+ Y u a conli",,,,,,,. mapping bdult'm
mdrir- spaces, and il X is rompad, then f i3 ulliformly continuous.
PROOF. If I is not uniformly continuous, there exists an t: > 0
e.nd two sequences ("'n} e.nd {z.} such that e(x.. z,.) < I/n and
e(/("'n). I(z..}} > e for n = 1, 2. . . .. Since X is sequentie.lly compact
(Theorem 13). there exist subsequences {x n ..} and {z,.,} which converge.
and it is evident that they converge to the same point. If 1 is contino
uous. then for 8ufficiently large k. we have e{/{xn,),/(zn,)) < e
which contradicts the above inequality. Thus if I is not uniformly
continuous, it is not continuous on X. Q.E.D.
The following result gives conditions under which the topology
of a space can be given by a metnc function.
19 THEOREM. (U ion theorem) A regular lopologirol
space with a countable bMe U mrlTimble. In pmtU:uJ.ar, a €ompacl
Hausdorff 6pU€e is metriJ!ahle il and tmly il it has a cmmJable bMe.
PROOF. We have seen in Theorem 15 that a compact metric
space is separable and, by Theorem 12. has a countable base. On thc
other hand. a compact Hausdorff space is normal (5.1J) and therefore
regular (5.1). so the second statement foHows from the first.
Let X be a regular space with a countable base {Un}' It will
first be shown that X is normaL Let A, B be closed and disjoint
sets m X. Since X is regular there is for each point x in A a set
U < (Un) with "'. U U B'. Thus if {V.} is the subsequence of{U n }
consisting of aU U. WIth U.I;;;B' we have AI;;; U:::., V.. Similarly
if {W.} romists of those U. with Un!;;A' then B U:., W.. Now
Jet Y. = VI' Z. = W. -1'1 and, inductively let Y n = V.- Ur-tZ"
Zn= W n - uj->Y,. Thus Y= U:'tYn "nd Z=U::"..,Zn are open
sets. ItIlJ<LY be seen that Y and Z are disjoint by showing that YnZ m =<f>
for all n, m :2: I. If n;:;; m then Z.. W..-Yn W.. -Yn and so
YnZ..=",.1f n> m then YnI;;;Vn-ZmI;;;Vn-Z.. and so YnZ,.=<f>.
To see that A r;; Y let", be " point of A "nd choose m with x in V m .
Then, since ZA Wn A' for n ], and since a: AVm' we have
x.y.. which proves that AI;;;Y. Similarly B Z and thus X is a
normal space.
Again let U,. U"... be a base for the open sets in X. If p,U",
then there exists a U. such that p. Un Un' U... Thus there exist
pairs (U., U m ) of sets selected from the base with the property that
U. C U..; but since there are only a countable number of sets in the
base. there can only be a countable number of such pairs. Let
(U.... U...). . . ., (U.., U m .). . . .
be an enumeration of such pairs, and for each k = I, 2, . . 0' by
Theorem 5.2 there exists a continuous function Ik with I.(U...) = 0,
MU:") = 1, 0 ;:;; t.("'} :S; 1. Let e be defined on X xX by
m
r{x. Y) = 1: 2--"1/.«10) - I.MI.
k=l
It is evident tlmt e satisfies (i). (iii) and (iv) of Definition 6.1. Sup-
pose that elx, y) = 0 for 80me pair x 0# 11; then /.(x) = /.(y), k =
I, 2, 0 . .. On the other hand there exists a. set U"'{ ) from the base
such thatx£U mi')' y Umlz)' By the regularityof espacethereissome
other set U ntao from the base with ",.U n ,.)!;;; U nl .) I;;; U..!%). so that
(U nl .). U mlz » i8 one of the pairs listed above. Hencef>(a;) 0# I.{y) for
Borne choice of k, and this contradiction shows that e is a metric
function on X.
Let '" be given and E > O. Then .t is readily seen that e(x, .} is
a continuous t"ea1 valued function on X. Hence there exists B set U
from the base with '" < U m such that if y. U.. then e{x,1}) < E. This
shows that the identity mapping of X with the given topology onto
X with the metric topology defined by e is a continuous function.
On the other hand if",. U m there is a U.such that x £ Un U. U...
Hence (U., U m ) occurs in the enumeration of the pairs, say in the
""y£X.
26
I. PRELIMINARY CO CEP'f8
(,7.1
1.7.2
CONVERGENCE OF GENERALIZED SEQUENCES
27
k-th tenn. Then if e(a:, y) < 2-< we have IMY)I < 1 ..nd so y £ U"'.
Thus S(a:, 2"') U"" which shows that the identity mapping of X
with the metric topology onto X with the given topology i8 continuou8.
Hence the identity is a homeomorphism and the space IS metrizabIe.
Q.E.D.
D X A mto X. Then the 8tatement limv/(d, a) = g(a) unilormly
on A or uniformly for a £ .AI means that for every e > 0 there exists
ad. £ D, such that !!(j(d, a), g(a» < .cord> d...nd for every a inA.
If I and g are two ,generalized sequences of real or complex num-
bers defined on the :same directed set D. then we write
7. Convergence Bnd Uniform Con""rgt'Ilce of Genenilized Sequences
The notion of convergence introduced in Definition 6.5 is not
sufficiently general for all our purposes. \Ve wish to indicate various
ways in which it can be generalized.
If X and Yare topologic..1 spaces and g : X -->- Y, the expression
lim g( w) = y is written to mean th..t for every neighborhood N. of y.
-.
there eXISts a neighborhoodN. of a:, such that g(N.) N.. The follow-
ing is a related, but more general notion: Let A be a set.. and l t X
and Y be topological spnces. Let f : A ->- X, and g : A .... Y. Then
lim g(a) = y IS written to mean that for every neighborhoodN.ofy,
11.a)_.J:
there exist8 a neighborhood N. of :r, such that g(/ l(Nv» N.. For
instance, the statement lim a: = oro is true in evft'Y metric space. Of
p{::e:.2.0)-O
course, if A = X. and f is the identity mapping, then lim g(a) = y
if and only if lim g( a) = y. flol-+.
.-+m
The following definition gives a third important and interesting
way in which tbe concept of conl."ergt'nce can be generalized:
1 DEFI!<ITION. A partially ordered sct (D, ) is said to be
direcl£d. jf every finite subset of D has an upper bound. A nmp
I : D .... X of a directed set D into a set X is called a gern!ralbRd
8t!tJUtm€.e of elements in X, or simply a generahzed sequence in X.
If I : D - X is a generalized sequence in the topological space X, it is
said to cOllverge to the poi..1 p in X, if to every neighborhood N of p
there corresponds a d. . D, such that d ;0;: d. implies I(d) N. In this
case, it is ..100 said th..t the limil 01 I ea:iIits and is egual to p, ,!r.
symbolically, lim f(d) = p, or, if D is to be emphasized,lim f(d) = p.
D
Each notion of convergence gives rise to a related notion of
uniform convergt'Tl££, For instance, let D be a directed set, A an arbi-
trary set. and X a metric space. Suppose that I = I( d, a) m..ps
1=0(11)
in case there exists an A> 0 such that I/(d)J Alg(d)1 whenever
d ;0;: d A . Similarly the symbol
I=o(g)
indicates th..t for ew-ry E> 0 there is a d, D such that I/(d)! S
flg(d)1 whenever d ;0;: d,.
In I..ter chapters we will ordinarily denote a generalized sequence
I : D ->- X by the notation {",.}, thus emphasizing the range of the
function.
Generalized 8equence8 may be used in .. general topological spa.ce
in much the same way as ordinary sequences are used in B metric
space. Several of the following lemmas illustrate this statement.
2 LEMMA. Let A be a 8et in a top<Jlogical 8pace. Then a point p
ia in the closure 01 A if and only il 80me generali2ed 8equence in A
rom;crge8 W p,
PROOF. If P = lim I(d). WIth I(d) in A, then every neighborhood
of p contains a point of A. Hence p . A. Conversely, let every neigh-
borhood of p contain a point of A. Let the family {N} of neighbor-
hoods of p be directed by defining N. ;0;: N. to mean that N. N..
Let I be a function on {N}, whose value I(N) is a point in NA. Then
p = lim I(N). Q.E.D.
3 LEMMA. A topoWgi<xl1 8pace ia a Hausdorff space il and only
il "" generalized segmnce 01 il8 elemenl8 has more than one limit.
4 LEMMA. II X and Yare Wpoll>giMl spacea, and I: X .... Y,
then I ia com;nu0U8 il and only il lim hId) = '" implies lim I(h(d») =
f("'} Irrr every gerwra[; d 6ftJ'1t'nu h 01 elements of X.
The proofs of these lemmas are left to the reader.
:Most of the notions related to the basic notion of convergence
can be carried over from sequences to generalized sequences: Let
28
1. PRELUUSARY CO CEPTS
1.7.5
1.7.7
CONVERGENCE OF GENERALIZED SEQUENCES
29
J : D --)- X be a gcnera1ized sequence of elements in a metric space X.
We callI a ge>leralized Cauchy srquen« in X, if, for each. > 0, there
exists a d.. D. such that e(f(p),/(q)) < . if l' ;;; d., q > d..
o LEMMA. III i8 a generaliz£d Cauchy sequeru:e in a compleu
meITic space X, there Mists a p. X Buch lluzt lim I(d) = p.
PROOF. Let do. D be ouch that e l , c. :2 do implies e(f(t;),/(c,» <
I/n. Let b n be an upper bound for the finite set {tf., d" . . ., do}. Then
it is evident that f(b.) is a Cauchy sequence. Hence there exists a
p. X such that limn c> I(b n ) = p. Let. > 0 be given, and choose n.
l1ch that 2"0 1 < " and such that e(/(b...), p) < .f2. Then if d ;;; bOn'
It IS apparent that e(/(d), p) <.. Q.E.D.
The reader who l'eviews the preceding discussion of metric spaces
win discover other results which can be carried over from sequences
to generalized scquences.
The following important result on interchange of limit operations
is due to E. H. Moore.
6 LEMMA. Let D, and D. be direded sels, and supJ1"S" Ihat
DI ... D. is directed by the relation (tf., d,) ,;;; (d , <I;,), ",hich is defined
L . ,
tv mea.. tunt d, d 1 and d, .;: d.. Let I : DI v D. X be a genera-
lized sequenu in the c<>mplete mdric space X. SuP'fJ'lB' that:
(a) lor each d,. D.. /he Umit g(d,) = lim I(tf., d,) exists, and
D,
(b) the limit h(tf.) = lim I(tf., d,) exi81s unifcnmly 0/1 D,.
D,
Then the three limits
sequence. By Lemma 5, hm f{d" d,) = p eXists. We have
DIXDS
e(p, I(d , d;» = !I( lim I(d" d,,), I(d , d;)) ;;;., d ;;; {j,. d; :2 "-.
D,XD,
Hence
e\p, g(d;» = e{p, lim I( , d;)) ;;; e, d; > {j.,
D,
limg(d,),
D,
aU exist and are equal.
PROOF. Let e> 0 be given. There is II {j. e D. such that d. ;;; {j,
implies !I(/(d,. d,), h(tf.)) < ef8 for all d, e D,. It follows that
e(/(tf., d,),/(tf., {j.» < e/4
for tf. . DI' Thus if {j, . D, is such that tf. ;;; {jl implies e(f(tf., {j,), g({;,»
< t/8, we have
e(f(tf., {j,), I({jl' {j.»< ./4,
so that e(/(d" d,), I({j" {j.» < .f2. Hence, if d,. d; ;;;; {j, and d" d; {j"
we have e(f(d" d.), fed;, <I;,)) < e. Thus. I is a generalized Cauchy
limh(tf.),
D,
lim f(tf., d,)
D xDI:
so that lim g{d,) = p.
D,
In the same way, we show that lim h(d,) = P Q.E.D.
D,
7 COROLLARY. Let D be a direded set, let X and Y be topologiul
spaces, and leI Y be complEU and metric. Let I; D X X Y, 80
that I( d, a;) is a generalized 8f'quence of lundin". on X, wi!h values in Y
Supposc that:
(a) far each d". D, the IIUIdion I(d., x) is continuo...-. and
(b) lhe limit g(a;) = lim I(d. a;) aists uniloTTllly on X.
Then g(a;) is continuous. D
PROOF. This follows readily from Lemmas 4 and 6. Q.E.D.
It is often convenient to have a characterization of compa.ctness
in terms of generalized sequences. We will find it convenient to use one
dealing with the notion of R cluster point.
8 DEFINITION. Let I ; D X be a generalized sequence in a
topological space X. A point p IS a cluster point of I if for each neigh-
borhood U of p and d.. D there is ad;;; d. such that fed) . U.
II LEMMA. A space X is compad if aOO onty il each gerrerulized
sequence in X has a cluster point.
PROOF. If I: D X is a generalized sequence in a compact
space X, for each d. D let
A,. = {YIY = I(d'), d' . D, d' ;,;; d}.
The collection {A,.} and hence the collection {A;,} have the finite
intersection property. By Lemma 5.6 there is a point p common to
their closures. Since ev"'1' neIghborhood of p interooets each A., the
point p is a cluster point of f.
Conversely" let each generalized sequence in X have a cluster
point. Let fF, be a given family of closed sets with the finite inter-
section property, and let fF be the set of all finite intersections of
30
I. PRELIMINARY COSCEP'tS
1.7.10
I.B
PRODUCT SPACES
31
sets in !F,. Then !iF has the finite intersection property and is directed
by inclusion. Picking a point in each set of :T we obtain B generalized
sequence which therefore has a cluster point. This cluster point
cleaJ:ly in each member of the family ff. Hence the sets in ff,
have a commOl' point and X is compact. Q.E.D.
There is another notion \'\o"hich is often of convenience in discus-
sions of con'''ergence.
10 DEFINtTION. A family Iff of subsets of a set is said to be a
/i1ter if it posse8ses the following properties:
(i) The void set '" is not in 8:
(ii) if A B and B£8, then A£8:
(iii) if A,B.8, then An B.C.
If 8 and C' are filters of subsets of a set, we say that C Telines ,c'
if C;) C'. A filter is called an .dtro{ilta if it is not refined by any
filter but it.clf. A filter C of subsets of a topo]ogical space X con-
''ITges tv a point p. X, if ewry neighborhood of p belongs to C.
The reader will observe that the collection of all subsets of a
topo]ogical space X which contain a neighborhood of a point p fonns
a filter -,V (p). Thus the filter Ii converges tn p if and nn]y if C ref"mes
-np}, i.e., C ..f"(p). In applying the filter theory the following
lemma, due to H. Cartan, is of considerable importance.
11 LEMMA. Evt'Ty lilta 01 B1.bsds of a set X ;s refined by some
"Ilra/ilter 01 s"bsets of X.
PROOF. Let Co be a filter in X, and let $ be the cnllectinn of all
filters 8 in X with Co!:;; Iff. Let!j3 be partially ordered by!:;;. If (\\ =
[C) is a totally ordered subset of !jJ, then C' = {EIE. C EIIJ} is
readily seen tn be a filter in $ and {f!;; C', for all C. ill. By 7..orn's
lemma (2.7) there is a maximal clement which is obvLOu81y an ultra-
filter in X and which refines 8 0 , Q.E.D.
It is evident that if & is an ultrafilter in X and if E!:;; X, then
preci<rely one of the sets E, E' is contained in 8.
12 LEMMA. A tap%giaIl space X is compact if and only -if
...,ay IIllra/ilf€T of s!dlsels of X converges 10 a point in X.
PROOF. Let & be an ultrafilter III a compact space X. If & does
not converge to p E X. then some neighborhood N" is not in C, and
thus Its complement N is in 4. If B does not converge to BRY point,.
then X is covered by N., p, X, and hence by a finite number N r , . . .,
Nfl of such sets. Therefore'" =N; n... nN = (N, U... UNfl)' = X',
being the intersection of a finite number of sets in If is also in C.
But this violates the definition of a filter.
Suppose that every ultrafilter of subsets of X converges. Let ff
be a family of closed subsets of X wIth the finite intersection property.
Let 8r be the cw. of all sets which eonta.n a finite intersectinn
F, n.. . n Fn of sets F,. fF. It is evident that C, is a filter. Let C
be an ultrafilter refining &r. and Jet p be a point to which & eonvcrg<:5.
Then. every neighborhood of p has a. non-void intersection with every
set of C. Hence. p i8 in the cl08ure of every set of C. In particular,
p . F if F £ !F. Hence p . n ff, 80 that n:F oF 4>. The desired result
fnllnws from Lemma 5.6. Q.E.D.
8. Product Spaces
Given a Cartesian product {cf. Definition 3.11} X = PaX" of
topo]ogical spaces X., it is natural to 8eek to define a topolngy in X.
For example, if Xl and X 2 both represent the space of real numbers,
the Cartesian plane X, X X. may be topologi7.ed by using sets of
the form U >' V, where U and V are open, as " base, With this
tnpolngy, X r Y X. is two-d,mensiona1 Euclidean space. Abstracting
a vita] property of this example, we seek a topology..- for the general
Cartesian product XI such that each projection pro: : X --}o- Xa is
continuous. It is readily seen that the maps pro: will be continuous if
and nn]y if each set of the form U = P.U... where U a Xa is npen,
and where Va = XJI t'xcept for some single a. = «.01 is in T. This
property is not suffici""t to characterize T completely. AmOl1g the
various topologies which make: the maps pTa. continuous we still
have the three topo]ogies determined by taking as a base the sets
U = PaUa with:
{Il} all U. open,
or
(b) all U a open. U. = X. for all but a cfJU1ItalJ<: set of rx,
or
(c) all U a open, U. = X. for all but a lini/£ set nf rx.
With a view to future applications, the topology (c), which is the
32
I. PRELIMINARY CONCEPTS
1.8,1
1.9,1
EXEBCI8EB
33
weakest topology for X which will guarantee the continuity of the maps
pra' is selected for fUTther anaJysis. The formal definition follows:
1 DEFINITION. Let (X.' -ra) be an indexed family of topological
spaces. Then the product topoWgy is the topology -r in X = P.X.
obtaincd by taking tile collection of all sets U = PaU., where each
Va. is open, and where Ua, = Xa except for a finite set of indices a.. as
a base. A product space is a Cartesian product of topological spaces
with its product topology.
It is apparent that a gencralized sequence f in the product 8pace
X converges if and only if the generalized sequence pr.! converges in
Xa. for each IX.
2 LEMMA. A product of Hausdorff spaces is a Hausdorfl space.
S LEMMA. If b a, then 111£ projre/ion pro (cf. 8.14) of P X. onl41
P Xa is CMltin1U)'U8, and maps open sets into open Bets. 4(1]
...
9. Exerci8et!
4 LEMMA. A dmumerable product 01 n>£tric spaces X n , n 1,2,
. . ", is a TI'ldri apa«.lj en is a 'Indrie: Jor X n , then a melri(" JOT the pro-
duct &pllU' X = P .X n i. given by th£ lormula
1 e.(pr n ,", prny)
e(tr,y) =.:- - .
_1 2'"-l+en(Jl7ft,xt pT",y)
If each 01 the spaces X n is oompllh. lhen 111£ produd space X milk this
mflric is a/so complcU.
The proofs of these lemmas are straightforward and elementary.
They will be left to the reader.
5 THEOREM. (Tychonoff) A Carlesinn product 01 compact spaces
is compact in its product topology.
PROOF. The proof is based upon Lemma 7.12. Let X. be compact,
and let 8 be an ultraCi1tet of subsets of X = P.X.. Then the set 8.
of all sets o£the form pr.(E) with E. 8 is an ultrafilter of sets in X,.
This is clear, since a proper refmement 4 of 8 a determines a proper
refinement
1 Any non-void open interval of reals is homeomorphic to the
set of all real numbers, but not homeomorphic taa half open or a closed
interval. A closed interval is not homeomorphic to the set of complex
nwnbers of absolute value one.
2 Let R be the space of real numbers. and let R. = R for each
'". R. Show that Q = p.." R. contains a countable subset whose
closure is Q. but that Q does not have a countable base.
3 Not every normal space is a metric space.
-I Let G, and G. be open sets in a normal 8pace, and let F be
a closed 8et with F G 1 U G.. Show that F is the union of closed 8ets
FI' F. with F, G, and F. G..
5 Let S be an abstract set, Show that the collection B(S) of all
bounded real or complex functions on S is a. complete metric space
under the metric function e defined by elf. g) = sUP"s If(s)-g(s)l.
If S is a topological space, then the collection C(S) of all bounded con-
tmuous real or complex functions on S is a closed subset of B(S).
6 Establish the existence of continuous real functions of " real
variable such that
I f(t+h)-/(t) I
lim sup = 00 for all t.
It_Of- h
Hint: Let S be the real line and let C(S) be the space of periodic
real continuous functions metrized as in Exercise 5. For m = I. 2. . . .
let C.. be the set of aliI in C(S) for which
I f(t+htf(t) i m
for some t and all h > O. Using the Baire category theorem, show that
C(S) is not the union of the sets Cm.
S' = (EIE = pr;;I(E.), E.. S;J
of 8. Lemma 7.12 shows that each 8. converges to some point
,"(",). X.. It follows readily from the definition of the product topo-
logy that 8 converges to the point'" = P ,..x("') in X. Q.E.D.
,
34
I. PRF;LIMINARV CONCEl>TS
1.10
1.11
LINEAR SPACES
35
C ALGEBRAIC PRELDUNARIES
quences of the above defmitions: In a group G the identity e IS unique;
the inv rsc a-I of a is unique; for every a and b in G. there are uniquely
determined elements x and y in G for which am = b. ya = b; the unit
e in G belongs to every subgroup of G; and (ab)-' = b ]a 1.
A mappmg h : A -+ B between groups A and B is called a IUJlno-
'JWrphism if h(ab) = h(a)h(b). A one-to-one homomorphism is called
an isomorphi..... If h : A --> B is an isomorphism and if heAl = B,
then A and B are said to be isomvrphic, or A c, said to be istrmorphi£
with B. An isomorphism of a group G with it5eH is called an mdmooT-
phism of G. If a 1S an element of the group G, the transformation
h. : G -+ G, defined by h.(.x) = a l.l'a, is an automorphism of G, and
is called the coni"ganon of G by a. Conjugations are called inner-
uutomorphisms; all other automorphisms are outer ardomorphiam.s.
The group oj aulomorphi,,,,,, of a group G is the set of all automorphisms
taken together with the binary operation of composition; toot is. the
product of two automorphisms is defined by the equation (hk){.x) =
h(k(x)). It is evident that the inner automorphisms form a .-ubgroup
of the group of automorphisms.
A subgroup A of a group G is said to be invarUm!, or normal,
in G if .x l Ax = A for every .x in G. If A is a subgroup of G. sets of the
form A.x are called Tight casrls of A, and sets of the form .xA are called
kIt caseu of A. Thus, if A is normal, the right coset A.x is the same as
the left coset xA. It is clear that the cosets of a normal subgroup A
form a group under the operation (A.x)(Ay) = A.xy, This group of
cosets of A is called the quotient group. or fCleWr group of G by A;
it is denoted by GIA. If G is Abelian then every subgroup is normal.
The algebraic results used in this book win be i01troduced, and
proved. as the are needed. This section will review basic notions, and
give fundamental definitions.
10, Groups
A group is a set G, togetller wIth a mapping p, : G X G -+ G.
which has the properties (i), . . _, (iii) listed below. The binaryopera-
tion II is often written as p(a, b) = ab, and, when this notation is used..
it is called multiplu:ation. The element ab is called the product of a and
b. The product ab is required to satisfy the followmg conditions:
(i) a(be) = (ab)e. a. b, c e G;
(ii) there is an element e in G. caned the idmfity or the unit of
G, such that ue = ea = a for every a in G,
(iii) to each a in G, there corresponds an element a I, caned the
inverse of a. such that t'Uc l = a-1a = €.
A "'Wgrowp of a group G is a subset of G which is itself a group
with respect to the binary operation in G. A proper subgroup is a
subgroup other than {e} or G. A commulative group, or an Abelian
group, is a group in which the commutative law ab = ba holds. In
the commutative case, the binary operation p is sometimes written
asp,(a, b) = a+b. and, when this notation is used, it is calledaddilion,
a+b is called the rum of a and b, and the group is cal1ed an additiVl!
group. The identity in an 'ldditive group is called the zero elernenl
of the group: its symbol is 0 instead of e. l\Ioreover, in an additive
group, -a is written instead of a 1, and a-b instead of a+(-b).
The additive notation for a group will be used only if the group is
commutative.
If A and B are subsets of a group G in which the group operation
is multiplication, and if g and h are elements of G, the symbol A 1is
written for the set of elements of the form a 1 where a. A, AB de-
notes the set of elements of the form ab with a e A and bE B, gA de-
notes the set of elements ga with a. A, and gAh denotes the set of
elements of the form gal. with a. A. The corresponding notations
-A, A+B, g+A are adopted for additive groups.
The followjng frequently used assertions are immediate ConSe-
n. Linear Spaees
A ring is Sll additive group R togethcr with a mapping T : R.< R
--+ Rwhich has the properties (i), (ii) and (iii) listed below. The binary
operation T is written as T(a, b) = ab, and is called 1n1/1tiplicau n.
Multiplication is required to satisfy the following identities:
(i) (ab)c = a(be);
(ii) a(b+c) = ab+ae;
(iii) (b+c)a = ba+ea.
In a ring a+b is called the 8l.m of a and b, and abthclrprad1/d. A ring
,
86
[. PRELIMINARY CONCEPTS
1.11
I.n
LINEAR SPACES
87
(i) «(x+y) = cx.r+«y,
(ii) (<<+P)x = "-,,,+px.
(iii) «(px) = (rxf]}"',
(iv) 1"'="',
«let]), a:.,YE:£;
a;,fJ£f/J, xEI;
OC,{JEt/J, xEl;
"'eX.
and if T(",+y} = T.x+Ty, T(cx.r) = "T", for every" e <1> and every
pair x, y of vectors in the domain of T. Thus a linear transformation
on a linear space.! is a homomorphism on the additive group I which
commutes with the operations of multiplication by scalars. If
T : X - ID and U : IJ) -.8 are linear transformations, and I, ID, .8 are
linear spaces over the same field <1>, the product UT, defined by
(UT)", = U(T",), is a liDear trarlsformation which map8 X into .8. If
T is B linear operator on I to £. it is said to be a lill£tlT optrntDr in I.
For such operators the symbol T' is used for TT, and. inductively.
T' for T' lT. The symbol I is used for the itkntity operalor, Ix = x,
and 0 for the 2ero opuat<>r, Ox = O. If P(;') = "'0+",;.+.. .+".", is a
polynomial, the symbol PIT} is used for the operator cx.,I +a 1 T +. . .
+cx,.T', If T, U are both linear on I to the linear space 'g), the sum
T-LU, defined as (T+U}x = Ta:+Ux, is Blso linear on I to \1). If T
is linear. and if 0; is a scalar. the operation «T defined by (aT).x=a(T:x)
is also linear. If I and ID are linear 8paces over the same field <1>, the
set of all linear operations from I to %I is a linear space over q; under
the operations T +U and "T. If I = ID this set is also a ring under the
operations T+U and TV, A linear operator E iD I is said to be a
projedion or a projedion i" I if E' = E. A projection is sometimes
called an itkmpo!J!nt opt7a1or. If I is a vector space, if A I. and if
« is a 8ealar, the symbol aA IS written for the set of elements of the
form a'" with x in A. If A, B X, and a: e I, then, since I is an additive
group, the symbols A +B. A - B, and a:+A have already been assigned
definite meanings. The vector 8pace I is said to be the direct Bum
of the vector spaces ID'l:" i = 1, . .", n; symbolicaUy 1. =IDl i ED .. .
E!J !JJ/n, if the spaces!JJ/, arc subspaees of I with the property that every
IE in has a unique representation a: = '11.I+.. .+m" with m i EIDl i .
i = I, .. ., n. The map E i :]:: -+!m,. given by the eqUAtion E,JJ = m i ,
is a projection of 1: onto IDe i -
If :£1' . . " In arc vector spaces over the field <1>, the set I =
I" < I, " . . . . I. is a vector space under the operations defined by the
equations
is rommutoJive if the identity a = ba is valid. A field is a commuta-
tive ring in which the non-zero elements fonn a group under multipli-
cation. The unit of this group in lL field will be written as 1 instead of c.
A linear vertOT BpD.f:.e'J linear spt1££, or vector BpO£e over a lieul is
an additive group I together with an operation m: <1> )( I -+ I,
written as m(oc.. x) = a..:x, which satisfy the fo]]owing four conditions:
The elements of a vector space are caUed vectors. The elements of tbe
coefficient field <1> arc called B<"alarB. The operations x -+ cx.r and
aJ -+ a +.T, where IX E f]J and a E I, are called 8cawT multiplication by iX,
and !ramlalum by a. respectively. A sum cx.r+fJy+. . '+1'z. where
0:., p. . . _, 'Y are scalars., is called a limar rombi7Ultion of the vectors
3:, Y. . . ., . A luUYlT BUb8paCt:; tJUhspace Or lin ar manifold in a vector
space, is a subset wbich contains all linear combinations of its vectors.
The subspace Bpllnnal by, or tkUrmined by a given set E, is the set of
all linear con.biDations of elements of E. Thi8 set is a linear manifold;
it is the smallest linear manifold containing E.
A set A in a linear space over a field <1> is said to be li,warly indeptnd--
ent ifthe only linear combination cx.r+Py+. , . +1'z of distinct elements
x, y, . . .,2 of A which "aniShf'S is that for which a = P = . . . =:r = 0,
It follows readily from Theorem 2.7 that in every linear vector space I
there is a maxirnallinearly indepeDdent set B. A subset B of the linear
space I is called a Hamel basis or a Homa base for I if every vector x
in 1: has B unique representation :x = a.zb J +. . . + Jlbft with a.. £ r]J and
b i e B. It is clear that a set B is a Hamel base if and only if it is a
maximal linearly independent set. The cardinality of a Hamel basis is
a Dumber indepeDdent of the Hamel basis; it is called the dim""..,;on
of the linear space. This independence is readily proved if there is a
finite Hamel basis. in which case the space is said to be finiu dimrn-
si(}nal. In a finite dimensional space" a Hamel basis is usually called
a basis.
A function T is said to be a linear opt'TfJtor, or a li.U!ar transforma-
tion, if its domain and range axe linear spaces over the same field {l).
[X., . . ., :X n ]+[Y1'" ., Yo] = [Xl +Y1" . .. :x,+y, ,
«[Xl' . . ., "'.J = [cx.r 1 . ' . " cU n ].
The space I IS the direct sum of the spaces " where!JJ/, is the set of
88
I. PRELIMINARY CONCEPTS
1.12
1.12
ALGEBRAS
89
those vectors [Xl' . . . xn] in I with Xi = 0 for i #=- i. Since there is a
one-to-one linear map between the spaces!m, and I" the space I
is oftcn called the direct GUm of the spaces 1,., . . '. In.
If!m is a subspace of the vector space I over the field (fJ, the
factor space II!m is the set of cosels of!m, i.e., the set of sets of the
form ",+!m with '" I. The algebraic opcrations in IlfIJI are defined
by the equations
(",+fIJI)+(y+!!JI) = ("'+y)+!!JI,
",(",+!m) = cxx+!!JI,
IX.E ,
<r,y£!,
"'E :£.
a; E R such that e = ax = .xa. Thus every non-7.ero clement of R has
an inverse, so R is a field.
A right (lcft. or two.sided) Ideal in a nng R is called a m=imal
right (!eft, or two-sided) idrol, if it is containcd in no other ideal of the
same type. If R contains a unit element e, than any right ideal 10 is
contained in a maximal right ideal. To see this, let C be the collection
of all right ideals in R which contain I. and which do not contain e.
Let G be ordered by ; if !iF is a totally ordered subsystem of C, then
it i8 easy to see that U !iF is aright idealin Rwhichdoes not contain e,
Zorn's lemma (2.7) applies to give a maxImal element in G, which is
readily seen to be a maximal right ideal containing I..
If I is a two-sided ideal in R, let x+I be defined as ",+1 =
rX--ryly E l}. If we define the operations
(a:+I)+(y-t-I) = (a:+y)+I,
(x-t-I)(y+I) = .J:y+I,
the sets x+I, tv E" R, form R ring which is caned the quotient ring and
denoted by Ril. It is an easy exercise for the reader to venfy that for
the above equations to define uniquely the operations in RII it is
necessary and sufficient that I be a two-8ided ideal. A mapping h
of one :ring RJ into another ring R2, is called a lunnomoryhitnn, Of a ring
honwmnrphism, if
With these operations the factor space II!m is a linear vector space.
The tenn qtWfient 8pOcc is sometimes used instead of factor space.
The mapping of I onto 1lfIJI, defined by '" -+ "'-t- 9)/. is ealled the natural
homommphiJnn of :£ onto I/fIJI. It is a linear transformation.
Unless otherwise stated, the coefficient field (fJ for a linear space
I win be eithef the field of real numbers. in which case :£ is alled a
T£aI linear space, or the field of complex numbers J in which case :f is
caned a comp/e'" [i"Far spaa. The term linear functional win be used
for .a linear transformation whose range IS in the coeffici,ent field.
12. Aigehras
If R IS a nng, th n a subset n. R i8 called a BlWring if the
elements in Hj form a ring under the operations defined in R. A sub-
ring I of R is called a right ideal of R if it has the additional properties
(a) Ix};,!, "'ER;
(1)) (0) #-1 #- R.
The definition of left idea! is similar. If I is both a right and a left ideal
of R it is ca1led a two-sided ideal. The suhrings (0) and R are frequently
mlIEd trivial, or improper, ideals and all other ideals proper ideal.
Condition (a) above evidently shows that if R has a unit c, then c is
not contained in any (proper) ideal. In addition, if R is a field, then R
contains no proper ideals. for if I is an ideal and a E I. ll- =1= 0, then.I
contains a(a-1.x) = J: for any x E R. Conversely, if R is a commutative
ring with unit e and if R has no proper ideals, then R is a field, To
prove this let a E R, a "" 0_ Then I. = taxlx E R} is a subring sati..
fying (a) which is not (0); therefore Ie = R, and so there exists an
hl"'+y) = h(",)+h(yJ
and
h(a:y) = h(;r)h(y).
A one-to-one homomorphism is called an isomorphism. 'l'hc kFrru:1 of a
homomorphism is the set of elements which are mapped into zero.
The mapping'" --+ x+l is a homomorphISm of R onto RII and is "a1led
the lIalural hom..m..rphitnn. The reader will observe that I is the kernel
of this natural homomorphism. We notIce that if J is a nght ideal and
1 a two-sided ideal with I!;; J, then the image of J under the natural
homomorphism h of R onto RII i8 a (possibly trivial) right ideal in
RII, whieh wc denote by JII. Conv rsely, if A is a right Ideal in RII,
the set J = h I(A) is readily seen to be a right ideal in R SUcll that
I!;; J and A = JII. Further, J/I is a proper ,deal If and only if
Ie J C R. This remark elUlbles Olle to ""c that If R is a commutative
ring wIth a unit, and I is an idcal III R, then HiI IS " f.eld If and only if
40
1. PREL1MINARV CONCEP1'S
1.12
1.12.1
ALGEBRAS
4.1
I is a maximal idea1. For if I is maximal, then Rjl is a commutative
ring with unit which has no proper ideals; by what we showed earlier
RII is 8 field. Conversely, if RII is a field, it contains no ideals alld
hence R has no ideal8 properly containing 1.
If R is a ring with unit e, then an element a in R is called (righi.
kit) regulnr in R in case R coutains a (right, left) inverse y for a, i.e.,
we have (ay = e, yx = e) u:y = yx = e. If a is regulBr, its uni'lue
inverse is denoted by a l. An element which is not {right, left) regular
is called (righi. kit) singular.
If <P is a field, then a set X is said to be an algebra over <P if X
is a ring as well as a vector .space over (J) and if
1 = a.,-1 = a'.,-I = a{a.. I) = '" . I = "'.
Any Boolean ring may be thought of as a commutative algebra over
the field <P" and in doing so we note that a set is a ring ideal if and only
if it is an algebraic ideal. If I is an ideal in a Boolean ring R, then RII
is .a Boolean ring. Further, from the above we see that if M is a
maximal ideal in a Boolean ring R with unit, then RIJ-f is isomorphic
with the field <P,.
An important example of a Boolean ring with a unit is the ring of
subsets of a fixed set. More precisely, let S be a set and let multiplica-
tion and addition of arbitrary subsets E and F of the set S be defined
by
o:(.ryJ = (""')Y = x(o:y),
x, y X,. ex tJ).
EF = EnF,
E+P = (EnP')v(E'nF) = (EvF)n(EnF)'.
A right (lefl, l'u!o-rided) ideal in an algebra is a right (I,.ft, two-sided)
ideal in the ring .sense which is also closed under multiplication by
scalars. If I is a two-sided ideal in an algebra X then the quotient ring
XII is an algebra. called the rp.wtient algebra, under the operations
defined above in tbe ring and the linear space Cases. A mapping of an
algebra X into another algebra over the Same field is a IwmvmurphillTh,
or an algebraic homomorphism, if it is both B linear transfonnation and
a ring homomorpbism. If the homomorphism is one-to--t>ne, it is called
an isvmvrphism. If <P is the field of complex numbers and if in the
algebra X there is a single valued map a a* with (",+y)* = a* +y*,
(h). = Xx., Ix.). = x, (u:y)* = y*a* then we say that X is an
algebra UJUh inwlutivn, and .,. is called the adjvin! of a.
An element x in a ring is said to be idemptJt<,nt if"" = a and to be
nilpotent if x" = 0 for some positive integer n, A Boolean rir!g is one in
which every element i. idempotent. The identity x+'" = 0, or equi-
valently '" = -"', hold8 in every Boolean ring. To see this, lIote that
2.. = (2x)2 = 4.1:' = 4.. so that 2x = x+x = O. A Boolean ring is
commutative, for",+y = ("'+y)2 = x 2 +"'Y+YX+Y' = ",+xy+y.x+y.
so that xII = -yx and thus u:y = yx.
The 8mallest Boolean ring with unit consists of the integers
modulo 2, i.e.., the two numbers 0, I. This Boolean ring, which we
denou, by <p., is actually a field. Conversely, every Boolean ring with
unit which is also a field i. necessarily isomorphic to the field <P,. To
prove this let 1 dcnote the unit and let x be a regular element. Then
The reader may verify that the colle tion of all subsets of S forms a
Boolean ring with S as unit element and the void set as zero. (The set
E+F defined above is u8ually called the symmetric diflerena of
E and F; in later chapters we will denote it by E..1 F). Other examples
of Boolean rings will be given in later chapters, but the important fact
is that every Boolean ring with unit may be represented as a Boolean
ring of Eiubsets of some set. This important result is due to Stone.
A topological space is said to be totally ch6OOn1!ected if its topology
has a base consisting of sets which are simultaneously open and closed.
1 THEOREM. (Stone represenlation theorem) Every Boolean ring
",ilk unil is isomorph", with the Bvvkan ring of all vpen ana elvsed
subsets vf a lotally diseonn£C!£d compad Hausdorff 8pO£e.
PROOF. If the Boolean ring B contains only one element so that
e = 0 1 the theorem is triviali hence we suppose that e =/:; o. Let H be
the set of aU non-zero ring homomorphisms of B into the Boolean
ring <1>.. For each",. B, let H(x) = (hlh. H, h(",) = I}. Throughout
this proof, if x. B, let x' = e+",; then H(x') = H(",)' where the 8ec-
ond prime denotes the complement in H of H(",). The relations
H(xy) = H(",) n H(y)
and
H(.x+y) = (H(",) n H(y)'} u (H{x)' n H(y}}
show that the mapping", --+ H(x} is a homomorphism of B into a
collection of subsets of H.
402
I. PRELIMINARY CONCEPTS
1.12.1
1.12.1
ALGEBRAS
48
As an aid for the remainder of the proof. we demonstrate the
following statement: Let B I !;; B have the properties
(a) if m, Y' Bj' then :r:y. B j ;
(b) if m. BI' then m 0# 0;
then there is a homomorphi8m k, : B -+ 11>. such that k, (m) = I for
"'. Bj' To prove this 8tatement let Ij be the set of all elements of the
form l13/ with a B, a: £ BJo To see that 11 is an ideal, observe that
are both open and closed. We have seen above that H(x)nH(y) =
H(:r:y) and H = H(e). so by Lemma 4.7 the col!ection {H(x)lx. B}
is a base for a topology. Since H(x}' = H(e+x), each set in the base
is both open and closed, so H is totally disconnected. To prove that H
is compact in this topology we will use Lemma 5.6. Since each closed
set in H is the intersection of sets in {H(m)lx. B}, it is sufficient to
prove that if Al is a subset of B such that n:'-I H(x,) '" </J for each
finite set {x" . . ., x.}!;; Ai' then n H(x) 0# </J. If B i is the set of all
!lE.h
finite pfoducts of elements in AJ' then B 1 evidently satisfies conditions
(a) and (b) above. Hence there exists all h,. H with hj(x) = I,
x. Aj' so that k, is in each H(x), u,. Aj' Therefore H is compact.
Finally, if G is any set in H wh,ch is both open and closed in H,
then since G is open we have G = U aH({£a)' Since G is compact, a
finite covering G = H(x,) u... U H(m.) = H«x .. . x:)') can he ex-
tracted. Thus every open and dosed set in H has the form H{x) for
some x. B. This completes the proof of the theorem. Q.E.D.
It is convenient to give another formulation of this result in
terms of order and lattice properties. A partmJly ordered set L is SOld
to be a lattice if every pair "', y of elements in L has a least upper
bound (2.3) and a greatest lower bound, denoted by '" v y and x A y,
respectively. The lattice L has a unit if there exists an element I such
that :c ;S 1, J: r: L, and a UTa if there exist8 an element 0 stIch that
o ;;; m. x E L. The lattice L is called distributio'e if
(ax' +by')(xy)' = (ax' +by')(e+:r:y)
= (ax' +by')+(ax' +by')xy
= (ax' +by')-t-(a+ax+b+by)xy
= (ax' +bY')+""'1I-t-""'1I+b:r:y+bxy
= ax'+by',
so that the sum of two elements in 11 is also In lr Since it is clear that
11 is invariant under mu]tip]ications by elements in B, 1 1 is an ideal.
Further II is a proper ideal, for if ax' = e, then
e = ax' = ax'al = ex' = z
from which it follows that x = 0 contradicting (h). Since B has a unit
element, It is contained in some maximal idea] M r Let be the na
tura! homomorphism k,: B -+ BfM I = 11>.. Now if x E Bl' then
a:' = e+.x € I. M 1 and hence
h,(e)+h.(x) h,(e+x) = 0
showing that h j (",) = h,(e) = 1. This proves the statem nt made
above.
We have seen that the mapping x ..... H(x) is a homomoq>bism.
To show that it is an isomorphism, let Xo YD' We wi1I prove that
there exists an ho' H with ho("'D) 0# ho(yD)' If x D Yo' then either
Xo 0# "'0110 or Yo '" "'01/0; we suppose the former is valid. Let .... =
xo+xo1ID = Xo1I ' so that.... 0# O. If Bl = {"oj. then by the preceding
paragraph there i8 an ho' H with ho(....) = I. Now Zo1fo = 0, so
h.(y.) = ho(z.)h.(y.) = h.(ZoYD) = h.(O) = 0; also I = h.(z.) =
ho(xo+xo1lo) = 11,,("'0). This proves that B is isomorphic to a Booletin
ring of subsets of H.
It remains to prove that H may be topologized in such a way that
it becomes a totally disconnected compact Hausdorff space in which
the sets H(",), '" E B, are precisely the collection of subsets of H which
"'A (yvz) = (x A y)v ("'AZ),
l£,y,zeL
and complemented if for every :.v in L there exists an .1/ in L such that
.rV ' = l
XA"" =0.
A lattice L ,s said to bc complete if enry subset hounded above has a
least upper bound, or equivalently, every subset bounded below has
a greatest lower bound It is aid to be a-complete if this I::; true fOJ'
denumerable subsets of L. A Boolean algebra IS a lattice ,,,th unit and
zero which is djstributi\"c and complemented.
Let B be a Boolean algebra, and define multiphcatloll nnd add..
tion as
ity = XI\Y,
.r+y = (XAY')V(,e AY).
Then it may be verified that with tht"S<, operations, B IS a Boo\can
44
I. PRELIMINARY CONCEPTS
1.18
£.18
DETERMINANTS
45
rlOg with I as unit. On the other hand, if B is a Boolean ring with unit
denoted by 1, then if a: :S; y is defined to mean", = "'Y. and ",' = 1 +x
then B is a Boolean algebra and
",vy = x+Y+"'Y. XAII = "'Y.
Thus the concepts of Boolean algebra and Boolean ring with unit are
equivalent.
If Band C are Boolean algebras and h : B ..... C, then h IS said
to be a hOlno>Mrph or R Boo/ron algebra Iwmomorphism, if
with j #- k; to be +1 if an even number of interchanges of adjacent
terms brings . . 0' in into the arrangement Is . . ", n; and to be -1
If an odd number of such interchanges brings '4'.."S in into the
arrangement 1,.... n, With this notation the number expressed by the
sum
ft ft
2... I fl..u,{. 0il,]'.'.' a , .'11
i 1 _1 f..-( ..
h(x A y) = h(x} A h(y),
htxvy) = h(a:) v h(y),
h!x')=h(a:)'.
is called the de1erminal1i 01 tM matria: (a,;). If T is a linear operator.
then it can be shown that the determinants of tbe matrices of T in
terms of any two bases are equaJ, and :so we maJt and shaH call their
common value the dt1erminanl of T. denoted by det (T). The deter-
minant satisfies the important multiplicative relationship det (T.T.)
= det (TI) det (T.). A linear operator T in I with a one-to-one in-
verse is said to be IWn- i,lgU1m. An important theorem in the theory
of det..rminants states that a linear <>pwator in a linile dimenaitmnl
8pace is non-siTl-glllar il and only il ils determinant is nol "",,"0.
If (aIJ) is an nXn matrix, then the colactor- of the element a" is
the product of ( I )'+' with the (n-I) X (n-l) determinant obtained
by deleting the ith row and the ith column in (a,,). Expressed differ-
ently, the cofactor of a" is obtained by replacing the element a" by 1
and all the other elements of the ith row and jth column by 0 and
calculating the resulting determinant. Denoting the cofactor of a" by
All' it may be seen that
If h is one-to-one, it is called an isomorphi1lm. If h is .an isomorphism
and h(B} = C, then we 8ay that B is isomorphic with C, or that Band
C are isomorphic. From the preceding paragraph, it will be 8een that
if h is a homomorphism of a Boolean algebra B. and if B is regarded as
B Boolean ring with unit, then h is .a ring homomorphism. The con
verse i also true.
As examples of Boolean algebras we mention the class (/'J. = {O, I},
or the colleetion of all 8ubsets of a given set where :S; is taken to be
set inclusion.. and 1\.. v are taken as intersection and union, r-espec-
tively.
In terms of these concepts, we can give the followmg formulation
to the Stone representation theorem: Every Boolean algebra is i801nQr-
phic with the Boolron algebra 01 aU open and rI_d wlJscts 01 a totally
discoruux:ted compacl Hausdorll space.
{*J
ft ft
det (a,,) = ! ai/A" ! ail A".
" l 1-1
13. Delenninants
The first sum is an expansion of det (a,,) in tenus of elements of the
jth column and the seeond is in terms of elements of the ith row,
Similarly, if i ,p k. then
Let J be a finite dimensional linear space, and let Xl' . . ", X'ft be a
basis for I. Suppose that T is a linear mapping of I into itself. The
coefficients (a,) in the formula
n
T:r. = }: aj.jXjl
3-1
i = I,.. _,n.
n n
0= I llilAjk = IaJiAkio
I-I i_I
completely determine the linear operator T. and are collectively caUed
the matrix 01 T in terms 01 tM basis Xl' ' , .. X., or (if the basis is under-
stood) simply the mQtri.v 01 T. If i k is an integer with 1 ;::;; i k ;::;; n, for
k = I,..., n, tet /j.........ft be defined to be zero if i j =1k for some pair
Cramer' B rule asserts that, if T is a nonsingu1a:r linear operator with
matrix (a,,), then the matrix (b,;) of T I, relative to the same basis,
may be calculated by the formula b il = A,,/det (a,,).
In the second volume we will need the Laplace expansion for a
detenninant. Let (ao;) be an n Xn matrix, let p be an integer with
46
I. PRELIMINARY CONCEPTS
1.H..1
1,14.3
REFERENCES
47
14. E,.erci8e.
3 If X is a vector space over t!>, and t!>' is a subfield of t!>. show
that X can be regarded as a vcctor space o'\'er rp'. \Vhat is the relation
between the two correspondmg values for the dimension of I?
4 The Ilnear space X is the direct um of the subspaces 9Jl i .
i = I. . J n, if and only if there Rre projection.... Et in with E,E 1 =O,
; * i, 1= E 1 +.. .+E., and E,3Z = !IJ1,.
5. Let T be a linear operator in a complex linear \'f,:cl:or space.
Let p. Q, R be polynomials with complex coefficients such that
P().)Q().) = R()') for all complex numbers A. Show that P(TIQ(T) =
R(T).
6 The family C of project;ons in a linear space may be partially
orden:d by defining A ,,;; B to mean that AB = BA = A. Show that
(6', ";; ) is a partially ordered set. For commuting projections A and B
let A A B = AB and A \ B = A +B-AB. Show that A 1\ B is a
projection which is the greatest lower bound of A and B and that its
range is the intersection of the ranges of A and B. Show that A v B
is a projection which is the least upper bound of A and B and that its
range is the Imear manifold spanned by the ranges of A and B.
7 Let the Boolean ringt!>2 = to, I} be topologized by taking all
subsets to be open. For each .t' in a Boolean ring B with unit, let
t!>2(m) = t!>2 and P = P1>2(m)- Let H be the family of all non-zero
..B
I P < n. and let i,. . , .. i and ii' . . ., i. be sets of imUces with
1 i, < .. < .. . < i. -0;: nand 1 il < i. < .. . < i. ";; !'O Let
h(, ' :, . 1 . , . ) d enote the P X P submatrix obtained from ( a, ,)
J_. . 0' ..".. I'.'"' {P
by retaining only the elements of the iI' . . ., ijlth rows and the 11' . . a,
i. th columns. and let B(.... . . .. i.; il' . . ., i ) denote the determinant
of h(i".... i ; i" . . ., i.). Then the colac!or of this submatrix is
the product of (-I ),,+...-+;.-tJ.+...+'. witb the determinant of the
(n-p) X (n-p) matrix obtained by suppressing the i", . . ., i.th rows
and the i" . . .. i.th columns. Denoting this cofactor by C(i,.. . . ., i.;
i" . . .. i.). tben the Laplace.=pansinn of det (a,,) in terms of the
elements of the i". . ., i.th roWS is given by the formulA
det (ail) = ! B( '.."7 iJl; 11' . - ., i p ) X C(i 1 ,. . 0' i.,,; 11' . . ",1.,,)..
'1>...o'JI
where the summation is extended over aU sets of p indices 1 '1 <
. . . < i. <: n. Similarly, det (a,,) may be calculated in terms of ele-
ments of the iI' . . ., i.th columns by summing over aUscts of p indices
1 ;1 < . . . < ;. ,,;; n. In case p = 1 the Laplace expansion reduces
to the expansion by row or column given as r*] above.
I Show that there is a correspondence between non-zero linear
functionals f on a vector space :E and snbspaces we snch that :EI!IJ1 is
one-dimensiona1. This correspondence is defined by
homomorphisms of B into tP z , and regard H as a subspace of P. Show
that P is a totalIy disconnected compact Hausdorff space. and tbat
H is a closed subset of 1'.
we = {mlt(m) = OJ.
How can f be defined in terms of!!J1? What class of t's corresponds to
a single !!J1?
2 Supply tbe detads of the proof that every vector space has a
Hamel basis. Prove that any two bases have the same cardinality.
(The finite Bnd infinite dimensional cases are to be handled separately.
For the infinite dimensional use the theorem of Bernstein which
states: If A and B are arbitrary sets, if the cardinality of A is at most
equal to the cardinality of B and if the cardinality of B is at most
equal to the cardinality of A, then these two sets have the same
cardinality. )
15. References
Since t.hf" discussion of many of the topics mentioned in this
chapter is not complete, we cite here some texts to which the reader
nmy wish to refer.
Set l/uory and logic. GOOel lI]. Hausdorff [I, 2}. Kamke [1, 2},
Rosenbloom [I]. Rosser [I], Wilder [I].
Topology. Alcxandroff and Hopt ll; Chap. I}. Bourbaki [5J.
Hausdorff [1. 2], Kelley [5]. Lefschetz [I; Cbap. I]. Pontrjagin [I;
Chap_ 2].
48
I. PRELIMJNARV CONCEPTS
1.15
Real t'Cl7iable8. Caratheodory [1,2], L. M. Graves [2], Hahn [4],
Hausdorff [I, 2 .
Compll!:lJ oo7whlFs. Ahlfors [1). Rieberbach [I], Knopp [IJ,
Titehmarsh [1].
Algebra. Birkhoff and MaeLane [1], Halmos [7], .Jacobson [1],
van der \Vaerden [I].
Lama theory and Boolean algebras. Birkhoff [8], Stone [1, 9J.
Dderminan!JJ. Birkhoff and MacLane [1; Chap. XJ, Dresden [1;
Chap. I], KowaJewski [1], and Veblen [1; Chap. IJ.
CHAPTER II
Three Basic Principles of Linear Analysis
The treatment of set theory in Sections 1-2 is on the intuitive
leveJ; the reader who wishes to approach this theory axiomatically
should refer to GodeJ [IJ. We do not expJicitly mention ZermeJo's
uaxiom of choice" (ef. Zenne]o [I, 2]);, since we do not mention any of
the other axioms of logic or set theory. The :reader will observe, how-
ever, that the use of this axiom is made in the proof of the Hausdorff
m8Jcima\ity principJe (Theorem 2.6) - it wilJ be used in the text
most frequently via Zorn's lemma (Theorem 2.7). The proof of
Theorem 2.5 goes back to ZermeJo's [2J second proof of the well-
ordering theorem. This paper is aJ80 interesting for its poJemicaJ dis-
cussion of his Rxiom. The first occurrence of a maximum principle
equivaJent to the weJl-ordering principle (as in Theorem 2.6) is in
Hausdorff [1; p. 140]. Zorn [IJ gave a theorem essentiaUy equivalent
to Theorem 2.7. A simiJar theorem is due to R. L, Moore [1; p. 84].
For proofs of the equivaJence of the weU-ordering theorem and other
theorems see TeichmuUer [I] and Rosser [1 J, Kelley [8] has proved
that the well-ordering theorem is equivalent to Tychonoff's product
theorem (Theorem 8.5).
In dosing. we observe that while GOde1 [2J has proved that if a
system of logic is adequate for present day mathematics, then there
can be no assurance that it does not contain a contradiction t he has
also proved (GOdel [1 J) that if the other axioms of set theory are con-
si,tent, then they remain consistent when the axiom of choice is added:
In linear spaces with R suitable topology, one encounters three
far-reaching principles roncermng continuous linear transformations.
These principles and their corollaries will be used repeatedly in the
remaining chapters of the text. They furnish the foundation for mauy
of the modern results in such fields of linear analysis as summability
ttJeary, the moment problem, ergodic theory, existence of invariant
measures, and integration theory. The first of these principles is
known as the principle of ..,,;form boundethit:s.. It estabJishes, among
other things,. that the limit of a sequence of continuous linear opera-
tors is continuous. The second is caUed the interior mapptflg principle;
it asserts that continuous linear mappings between certain types of
spaces map open sets onto open sets. The third, the Holm-Banach
theorem, is concerned with the existence of e:xt.ensions of a linear
functional. The Hahn-Banach theorem is the basis for several exist-
ence t)lCorems that will be used frequentJy in later chapters.
1. The Principle of Unifonn Boundedne88
Throughout the text, allli.u:ar vecwr spa",. wi!! be m.",- the field
of real or thE lidd of comple.r numbers. A Teal vector space is one for which
the field r]J is the set of real numbers; a complex {'€'dOT space is one for
which (/J is the set of complex numbers. \Vhen a statement is made
about a vector space. with no mention of the field. it is to be under-
stood that the statement appJies to both the real and the complex
cases.
I DEFINI1?ION. A group G is said to be a topological group if:
(i) G is a Hausdorff space:
(ii) The mapping (x,y) ...,.xy-l of GxG into G is continuous.
A linear space 3Z is said to be a linear tnpolog,eal splWe If '" IS a com-
49
50
11. rHREE BASIC PRINCIPLES
11.1.2
11.1.6
PRINCIPLE OF UNIFORM BOUNDEnXESs
51
mutative topological group under addition, and if the mapping
(0<, ",) ..... a.x of <PxI. into I is continuous.
\! LEMMA. (a) In a lopological group G, any algebraic combinali<m
of any numbn of ,oarialka "'" . . ., Xft is continuous as a map of C x, . ,
xC inlo G.
(b) In a linecu topological space iE, all linear oomlmu1ti<m8 of any
1fUJRbn- 01 scalar6 IXl' . . 0, CI n > and vectors Xl' . . ", a::''lJ1 are continuous
mappings of II)x.. .xll)xiEx.. .xI inlo 1:.
(c) In a limar IopolDgicd Bpacr I (group C), the mapping(s)
J) -+ CXX'(or -+ -ll X oz, or IE a;a) where IX is any scalar not zero, is a
IIom£ommphiam of I <mlo itself (C onto if3elf).
PROOF. Statements (a) and (h) are easily proved, by induction.
from the basic definitions. Statement (c) simply reflects the fact that
the mapping:v -0(.1! (a: _ -lt tV -..-ax. or x <t'a) has the inverse
x .... (II"');]) (;]) .... ", " x .... a 1x. or '" .... xa- 1 ). Q.E.D.
8 LEMMA. The elOIrure of a linear manifold in a linear ropol<>giool
apace is a linear manifold.
PROOF. Let B be the closure of the linear manifold ID in the linear
topological space iE. Let «. fJ be fixed scalars, and define the map
Ii; (".0) ...."'u-+Pv
of 1: X I into I. Since VJ is linear,
PROOF. Let 11). be a denumerable set dense in the scalar field <P,
and let B be a denumerable set in a linear topological space. Then the
denumerable set of vectors of the form ax+. . . +(Jy with at . . _, B in
<p. and x. . . ., y in B is dense in sp (B). Q.E.D.
6 LE"MA. If a h011wmorphi:m, 01 one tapological group inlo an-
vth r is continuou.s anywhere, it is continuous.
PROOF. Let the homomorphism I : G II be contmuous at "',
and let y< C. If V is a neighborhood of fly). then, by Lemma 2(c),
Vf{y l",) is a neighborhood of f{x). If U is R neighborhood of x such
that I(U) Vf(y- 1 x), then Ux- 1 y is a neighborhood of y such that
f(Ux-Iy) = f(U)f(x-ly) Vf(y-1x)f(x-ly) = V. Therefore, f is con-
tinuous everywhere Q.E.D.
7 DEFINITJO . A set B in R linear topological space I is bountl.ed
if, givcn any neighborhood "'" of the zero in X, there exists a positive
real number. such that O'.B V providing 10'.1 :S; E.
8 LE"MA. A compact 6Ubael of a linear topological.pace is bounded.
PROOF. Let B be a compact set in the linear topological space I,
Bnd let Vbe a neighborhood of the origin in I. Since (1.3} is continuous
in both variables, there is a {j > 0 and a neighborhood U of the origin
in .:E such that {JU C V if IfJl < {j. Kow, since xln 0, we have
ID :'. g) I(¥J) lffi).
m
I U nl.!, and since B is compact, Be u nU for some m. Let E = {jim.
,......1 ro-]
m
If hi < e. tben 1«71 [ < b for 71 = 1,. .,111, and xB C U '1.lIP C V.
Lemma 2 8hows that IB continuous. and thus E-lffi) is closed. Hence
I
B x.8 1ffi),
which shows that B IS linear. Q.E.D.
DEFINITION. The subspace spanned by a set B in a linear
space 3Z will be denoted by sp(B). If I is a linear topologica1space, the
closure of 8p(B), denoted by sp (B), is called the closed linear mani
fold dder",;ned by, or BpIm1Ied by, B. From Lemma 8, it is seen that
sp (B) is a linear space. If sp (B) = I. the set B is called /u1u1amentaL
5 LEMMA.. The closed linear manifold determined by a denumerable
ael in a ropologit:al linear apace i. aeparable.
Q.E.D.
9 COROLLARY. A CDtlt'€TfYllt sequence in a lifll!ur topolugical spa!'l'
is bounikd.
PROOF. A con\- ergent sequence together with its limit point is
compact. Q.E.D.
10 DEFDIITIO:<. An F-.pace, or 1\ space of 1y{J<' P, is a linear
space I which is also a metric space with the following properties:
(i) The metric (! in I is invarialll, i.e.,
(!(x, y) = (!(x-y, 0);
52
II. THREE :BASIC PRINCIPLES
11.1.11
11.1.12
PRINCIPJ.F. OF UNIFORM BOVSDEDNF.SS
53
(ii) The mapping (0:,02') <LX of <P <3, 1 is continuous in 0:
for each a' and continuous in x for each 0:.;
(iii) The metrIc space l' is complete.
The symbol IxJ, called the norm of 02'. is written for e(a:, 0). In
view of the invariance property stated in (i) above, it is readily seen
that the propertie8 e(x. y) e(x, 2)+(1('-, y), (I(x, y) = 0 jf and only
if .r = y, and e(.r, y) = e(y, .r), are equivalent to the propcrties
I"'+yl < jxl+lyl, ixl = 0 if and only if x = o. I\l1d I-xi = 14 of the
norm, respectively. Thus an F-spare may also be defined as a linear
space on which there is a non-negative function Ix] with these latter
tJlree properti<"S and where. in addition, the properties (ii) and (iii)
hold with reference to the metric function (! defined by e(x, y) =
I"'-yl.
In this definition, it i8 not assumed that the operation ("', x) <LX
of multiplication is a continuous function on the product space
(p X ; SO it is not immediately apparent that an F-space is a linear
topological space. This fact is established in Theorem 12. The notion
of a bounded set in an F-space will be needed. It is defined just as it is
in a linear topological space (cr. Definition 7).
The following theorem, a principle of etjUi-conti1wi!1J, is the basic
principle of this section. Because of the form which it assumes in the
special case of B-spaces (cf. Section S),. it is known in the literature as
the prindple 0/ uniform bounlkdness.
11 THEOREM. FOT each a in the Bet A,I£! T. be a conhnuouslirlnJr
map of an F -space 3: in!o an F -space W. If, fOT eadI x in 1, 1M sel
{T.xla. A} is bounded, Ih£n lim T.rI: = 0 7I:J.ifonJlly lor a. A_
. o
10(ii). Theorem 11 establishes the existence of a <I(e) > 0 dependmg
on e such that [<LX[ < e for 1"'1 < 1, and [rI:1 < <1(£). A moment's re-
flection shows us that this implies the continuity of the mapping
(..,,,,) cxa:. Hence the following statement has been established:
12 THEOREM. An F-space is a li1U'UT topologiarl space.
\-Ve return now to the proof of Theorem 11. Kate that it i8 clearly
.a consequence of the following lemma, which is concerned with func-
tions not necessarily linear, and which can be regarded as a refine-
ment of Theorem 1 I. While Theorem 11 wi1l suffice for the purposes
of the pre8ent chapter, the more general form of the lemma will be
used OCC'aSiona11y in later chapters.
18 LEMMA. For earh a in a sel A, let Va be a colltimwus map of
an F -space I in!o an F -space W. Let V. mtisfy 1M foUuwing rornJ;t;om:
(i) !V.(x+y)! ;:;-; !V.(x)1 +!V.(y)I, a:. y. '5.;
(ii) I"V.(.r) [ = lV.texxll, 0: .t/J, 0: 0, .re1'.
Th£n. if for each rI: in 1', th£ set {V."'la. A} is bounded. 1M limit
lim V.(x) = 0 aim uniformly for a in A.
. o
PROOF. For given {: > 0, and for each positive integer k, consider
x.={xll V'(X)I+I V.t-X}i , a.A.
Since V o is -continuous, it is n that each set X is closed. Moreover,.
m
from our assumption of boundedness, U X k = L Hence, by the Haire
1:=1
The value of Theorem II i. that it enables us to pass from two
statements, in each of which one of the parameters a and :c is fixed, to
One in which they can both vary simu1taneously. An application of the
tbeorem will illustrate this statement. Let the set A of indices be the
set of scalars of absolute value less than one. Let the corresponding
maps be T. : rI: <LX. By Definition 10(ii}. each of these mappings is
linear and continuous. Moreover,. for each fixed %, the set of all ctZ o
is bounded. Indeed, if {J is a small scalar, and if 10:1 < I, (Jo: is a small
.sca1ar, and hence the required boundedness follows from Defmition
category theo...m (1.6.9), some X.. contains a sphere S(.r.. <I}. That is,
if 1'1'1 < <I, then
I :. V.(rI:.+.,) 1 .
By assumptions (i) and (ii).
' 1 2.. VotrI:) I ;:;-;[ V o (a7.+a7) ' I +1 1 2.. V.(-rI:.) j .
ko ,k. ko
Thus
. ( 1 ) I .
[ IV a -,',V i= -V('I(x), {:
k. Ilk. I
Ixi <t" a..A.
54
11. THREE BASIC PRINCIPI ES
11.1.14
II.U8
INTERIOR MAPPING PRINCIPLE
55
Since the mapping x --+ xlk. is a homeomorphism of I with itself. b)'
10(ii). the proof is complete. Q.E.D.
\Ve now are in a position to prove a number of basIc results about
F-spaces.
ir in a Then lima:-+O Tnx = 0 'Uniformly fOT n = I, 2, . . ',. and T i{J a
eonlinuous linear map of !: inlo ID.
14 THEOREM. A linl'-ilr mappillg oj om F-s]JQrr into another is
roJltinuous if and only if it maps ba"ndrd sets into oollndtd sets.
PROOF. Let I. W be F -'pal"",,, let T : if -+- ID be linear and contin-
uous. and let B if be bounded. For every neighborhood Vof the
zero in Y, there is a neighborhood U of zero in!: such that T(U) V,
If a i8 a sufficiently small scalar. then aB U and hence cx.T(B) =
T(aB) V.
Conversely,. let T map bounded sets into bounded sets. In view of
Lemma 6, it suffices to show that T is continuous at 3' = 0 to pro""f'
continuity. Suppose that lim:Ci = 0; then lim !xil = 0, and there is
i i_c<>
PROOF, The linearity of T is an immeiliate consequence of the
linearity of the operators Tno For each IX, the sequence {Tft.T} is con
"ergent, and hence bounded (9 and 12). By Theorem 1I. for every
. > o there is a" > Osuch that IT."'I < . when Ixl < "forn = 1,2....
Hence ITxl ,;; £ for Ix[ < ". and the continuity of T follows from
Lemma 6. Q.E.D.
18 THEOREM, Let T. : I -+- ID be a generalizedsequena: of conlin-
w>u. linear map. bffween F-8'JXlCt!s. If lim" T,;v exi6ls for each x in a
fundamental set, and if f(jT each x in 3i the set {T.a:} is bounded, then the
limit T", = lim T,;v e",i.ts for elUJh X in if. and ;" oontint/CU$ and linear.
.
"«gent sequence {k....,} is bounded (9 and 12); so by hypothesis the
sequence {T(k.",,}} = (k.Ta:,} is bounded, Therefore,
1
lim T(",.)=lim - T(k,-a:,) = o.
i_o> '- Cf:lki
Q.E.D.
PROOF. Since T u. is linear,. and T jZ converges for x in 8 fundamen-
tal set, it also con" erges for ;x in a dense set D. By Theorem II, for
every e > 0 there is a" > 0 such that for all a we ha"e IT...I < e when
Izi < ". Now. for an arbitrary a:. 3::, there is a y. D with I x-yl < lI.
and an cx.(.) such that I T'y-Tpyl < . for cz, f3 ale). Therefore,
ITd"-T i"1 ,;; IT.(x-y)J+ITp(Y-"')I+IT.y-Tpyl <3.. a,f3 a(e).
Since ID is compJete, Lemma 1.7.5 shows that lim.. Td" exists for each
x.3::. It is evident that T is linear. Theorem 1I and Lemma 1.7.6 show
that
a sequence of integers k i such tbat Jim k£ = 00 while lim k..:]<t':il = o.
i-cx> i_O)
Now, Ik,"'.1 = 1"',+. . . +"',1 ,;; k,lx.l, so that lim k,-a:, = O. The con-
i_I):
The first corollary below follows from the first part of the proof
of Tht'Orcm 14; the second from tbe second part.
lim T", = lim lim Td" = hm lim Td" = O.
z_U z-).Q c a (J
15 COROL1.ARV4 Any continuous linrnr mapping from one liJI ar
topological spaf'C to anothn sends bouniI£d sets into ooul1ikd Bets4
By Lemma 6, T is everywbere contmuoUS 4 Q.E.D4
16 COROLLARY. Any linror mapping from one F-spaa to anothn-
wJdch sellds seqr.u:nces ct11lverging to zero into bountkd sets is ooulinuOlu.
The following two convergence theorems have important applica-
tions, and will be used frequently_
2. The Inrerior Mapping Principle
.
The interior mappmg principle is stated in the followmg theorem.
I THEOREM. Under a eonlinllollS linear map of one F-space oJlto
{II! of anatlur. the- image oll't't!ry open set is open.
PROOF. Let J, ID be F-spaces, Jet T : J: -+ ID be linear and conti-
nuous, and let T"£ = ID. It will first be shown that the dosure TG
17 TJlEORE3,I. Let {T'I'I} be a sequellce ()/ conlinUf.lusli"t'ar maps of
an F-s]Jllrt X iw.to an F-spu('e . anu lei To.r: = Jim Tni£ e;xist Jor each
56
II. THREE BASIC PRINCIPLES
II.2.I
11.2.2
INTERIOR MAPPING PRINCIPLE
5'7
of the image of any neighborhood G of the element 0 in '" contains a
neighborhood of t1)e element 0 in Il). Since a-b is a continuous func-
tion of a and b, there is a neighborhood M of 0 such that 111 M (;; G.
For every :l E , X/'/1 -+ 0, and &0 a; E nM for large n. Thus
Since T 1S continuous. it is seen from (b) that y=Tx. Thus it has been
shown that an arbitrary sphere X", about the origin in I maps onto
a. set TX 2Eo which contains a sphere Y g about the origin in W. Hence
the image under T of a neighborhood of the origin in 1: contains a
neighborhood of the origin in 2).
Now let G be a non-void open set in I, and let N be a neighbor-
hood of 0 in iE sucb that x,..N C G. Let M be a neighborhood of 0 in [)
such that TN d AI. Then
TG-;J T(x+N) = Tx+TN-;J Tx+lI-f,
which shows that TG contains a neighborhood of everyone of its
points. Q.E,D.
2 THEOREM. A crmtinuous limar <me-Io-one map of <me F-apace
01110 all of another Iuu a rontinuoU8 linMr invCTse.
PROOF Let 1:,. [) be F-spaces and T a continuous linear one-to-
ooe map with TI = Il). Since (T-I)-l = T maps open sets onto open
sets (Theorem 1), the operator T-1 is continuous (1.4.15). Let YI'Y" Il),
1X1"x,2£:!? TiJ.i = Yl' T.x 2 = Y I Bnd a€f/J. Then,
_I
2) = TI = UnTM,
n-I
iE = U nM,
and, by the Baire category theorem (1.6.9), one of the sets ..TM con-
tains a non-void open set. Since the map y --+..y is a homeomorphism
in 1lJ. TM contains a non-void open set V. Thus.
TG -;JTM-TM-;J TlII - TM -;J V-v.
Since a map of the form y ....a-y is a homeomorphism, theseta V
is open. Since the set V-V = U (a- V) is the union of open sets, it is
.,v
open, contains 0, and hence is a neighborhood of O. Thus the closure of
the image of a neighborhood of the origin contains a neighhorhood of
the qrigin.
For any. > 0, let X.. Y. be the spheres in I, ID, respectively,
with centers at their origins, and with radii E. Let EO > 0 be arbitrary,
and let " > 0 with 1;::, . < '0' Then, according to the result stated in
the preceding paragraph, there is a sequence {'I" i = 0, I, . . .} with
'1, > 0, '1, .... 0, and such that
(a) TX. ,::>Y.,. i=O,I, .n
Let y . Y",. It will be shown that there is an '" . X", such that Tx = y.
From (a), with i = 0, it is seen that there is an x.' X" such that
ly-Tx.1 < 'I,' Since y T",.. Y ",' from (a), with i = I, there is an
x"X" with Iy-Tx.-T."J <'I,' Continuing in this manner, a se-
quence {x.} may be defined for which x.. X., and
"
T(x. "''''.) = Tx 1 ,..T;r. = YI +y"
so that
TaxI = cxToc l = a.Yl'
(b)
.
Jy-T(1; x,)1 < '10+1'
'-0
n=O, I, ....
T '(YI+Y') = x.+x. = T 'Y1+T ly.,
and T-I(O<YI) = !XXI = u.T-I yl . The8e equations show that T 'lS linear.
Q,E,D.
8 DEFINITION, Let T be a linear map whose domain (T) 1S a
linear manifold in an F -space iE. and whose range lies in an F -space 'g).
The graph of T is the set of all points in the product space iE xllJ of
the form x, Tx] with x. (TJ. The operator T is said to be clO8t'd if
its graph is closed in the product space I x 1lJ. An equivalent state-
ment is as follows: The operator T is closed if x. . (TJ, x. ---> x.
Tx. .... y imply that x. (Tl and T;r = y.
.. 4 THEOREM. (Closed graph tkorem) A cWsed limar map defined
on all of an F -space, and with values in an F -space, is cantimWll8.
PROOF. Note first that the product 3::x'g) of two F-spaces is an
F-space, where the distance between two points, [.7.', y] and :.r', y'],
is defined as Ix-x'I+Jy-y'J. The graph (!J of T is a closed linear
Letz". = x.+.. '+"'m' so that for m > n, /:;,.-%.1 = 1"'.+.+.. .+iI;.l
< '0+1 +. _ . +e... This shows that {z.} is a Cauchy sequence, and that
the series x.+"2+" , converges to a point x with
Ixl = lim Iz.1 s: lim ('.+'1 +.. '+'.) < 2'0'
fi_CD "_CD
58
II. THREE BASIC PRINC1PLES
1I.2.5
IIJJ.l
HAHN-BASACH THEOREM
59
manifold in this product space; hence it is a complete metric space
(1.6.7). Thus @ is an F-space. The map prJ: : ["" T",J... '" of @ onto
£ is one-to-one, ]inear, and continuous (1.8.8). Hence, by Theorem 2,
its inverse pri1 is continuous. Thus T = pT'ftpril is continuous (1.4.17).
Q.E.D.
5 THEOREM. II a linear spa« is an F-.pace under each of two
metrics, and il one of tlu: rorrcsponding topolog s contains tM olMr,
the Iiro topologies are t'tJual.
PROOF. Let T I , TZ be meuic topologies in the linear space I for
whicll the spaces iE 1 = (I, "-1)' I. = (I, ..-.) are F-spltces. If..- 1 !;; ..-.,
then the one-to-one linear map .:t' aJ of 1,2 onto is continuous. By
Theorem 2, it is a. homeomorphism, and so 1"} = 1'2" Q.E.D.
6 DEFINI'fION. A family F of functions which map one vector
space I into another vector 8pace III i8 caUed total if '" = 0 is the only
vector in I for which f("') = 0 for all f in F.
7 THEOREM. Let 3:, , and iID be F-spoas and leI F be a total
family of conlilluou' linMr maps on I to 'f). Let T be a linear map fTom
!lli to I such that fT i8 Cf",ti"uousfQr 'Very fin F. Th£" T is continuous.
PROOF. W" shall show that T is closed, nnd apply Theorem 4. Let
lim It.. w, nnd let lim T""n = "'. Then lim I(Tw n ) = 1("') for each
t'i--Jo-W ..-+0'> t'i_m
scalar ex and every vector x An Investigation into the consequences of
this identity is the chief purpose of the present section.
I DEFINITIOX. A linear spacc t€ is a IlornU'd Utleflr spaC't: or a
lwrmcd space, if to each :I1 E .I corresponds R real number Ixl caUed the
norm of J' which satisfies the conditions
(i) 10) = 0; I"'i > 0, x * 0;
(ii) Ix+yl < :"'I+JyJ, x,y£I;
(iii) Icx.ri = J"lIxl, " . <P, a:e 1:.
The zero dement is called the urigill of I: the closed unit sph Te is the
set {xilxl ,;;; I}.
The properties (i), (ii), and (iii) show that the function e, defined
by p("" Y) = Ix-yi, is an invariant metric in 3:. The metric topology
in a normed linear space is sometim.es eaUed its norm or Kfrong topology.
2 DEFINITION. A romp/de nOTJned litlror space, a space of type B.
a B-spa«. or a Banach sptl.Ce, is B normerllinear space which is com-
plete in its norm topology.
The following is clearly an equivalent defmition:
A B-.pace is lm F-space ill uhU:h the identity I"xl = 1"lIxJ is sotisfied.
f- F, since each t _ F is continuous. On the other hand, lim f(Tw o ) =
n-+O>
a LEMMA. A set B in a 'llorm.t'd linear space is ooulliwd if and
only il snp Ixl < W.
.<li
I(Tw) = I(x)
for I _ F,
PROOF. A neighborhood V ot' 0 contains an 1J-neighborhood
S. = {xll"'l < 1J} of O. If a = sUP..u )xl's fimte, and £ = 1J!2a, then
"B!;; V when letl ;:i; £, which proves that B is bounded (d. 1.7). Con-
versely if B is bounded. there is an E > 0 such that rx.B is contained in
the unit sphere SI = {xllxl < I} for all 1"1;:;; £. Thus for .r. B,
£1"'1 I£.r) < I; so 1"'1 < Ife. Q.E.D.
f(Tw) since each of the functions IT is contmuous. Therefore.
and,. since F is tota1,. Tw = :JJ. This proves that T is closed. and Theo-
rem 4 gives the desired conclusion. Q.E.D.
3. The Hahn-Banach Theorem
A number of important F-spaces are li8ted at the beginning-'of
Chapter IV. The list includes spaces of continuous functions, functions
of bounded variation, almost periodic functions, integrable functions,
etc. :\lost of these spaces have a property not cnjored by P-spaces in
general: namely, the identIty I:<xJ = Ictl!orj, which is satisfied by every
..,.. -I I,EMMA. For a lilll:ar map T hrtz£een IIOTmed linear spaces the
follou..illg statements a.re t'fjltil'tllt"llt:
(i) T is continuous;
(Ii) T i8 continuous at some lJoint;
(ill) tltr supTcmu", Slip ITxl is lillite;
Ixi l
(iv) fOT so",e scilla.. J1, IT.r1 Mlxl fOT all ;r.
C!o
II. THREE BASIC PRI CIPI.ES
11.8.5
II,S,?
HAHN-BANACH THEOREM
61
PROOF. The equiva]ence of (i) and (ii) was proved in Lemma 1,6.
If T is continuous at 0, there is an E > 0 such that ITxl < I if Ixl < E.
For an arbitrary' x * O. the vector y = (Ex)!21"'1 has norm Iyl < E; so,
E
- IT"'I = ITyl < I
*1
2
IT"'I <-Ixi.
E
(i) and (ii) are satisfied, Lemma 8 shows that the hypothcses of Theo.
rem ].18 arc satisfi d. From that theorem it is seen that Tx exists for
each :£, and tbat T is continuous. Thus; Lemma 4 shows that T is
bounded. Now, when Tx eXIsts,
IT"'J = lim ITnxl lim inf ITn!!xl,
n4o:> n-+oo
This shows that (i) implies (iv). Statement (iv) clearly implies the
,-'OntinuityofT at 0; so (iv) imp]ies (ii). This (i), (ii), and (iv)areequiv-
alent. If _ [ = sup ITa:1 is finite, then for all arbitrary '" * 0,
I2:J 1
and thu8
ITI lim inr ITnl.
n_m
ITa:1 = I"'IIT (I:) I Mixi.
Finally, to verify that sup. ITnl < 00, if T is everywhere defined, we
apply Theorem 1.11. According to that theorem, there is a IJ> u
such that for an n = 1.2, . .., JTn",J < I if Ixl < IJ. Hence ITnl :S;; IjlJ
for n = I, 2. . . .. Q.E.D.
This shows that (iii) implies (iv). It is obvious that (iv) implies (iii).
Q.E.D.
7 DEFINITION. If I: and 'ID are linear topologiea] spaces. the
symbol B(I:. 'ID) win be used for the linear space of all linear continuous
maps of I: into 'ID. The symbol B(I:) will be written for B(I.I:), and
.1:. for B(I:.4». The linear space 1:. is called the l'01ljugate space,
adjoint $P<>ce, or dual space of 1:. Thus the elements of 1:. are the COn.
tinuous linear functionals on .
5 'DEFINITION. The bou.nd or norm of a linear map T between
normed linear spaces is the sUPr."..ITxl, denoted by ITI. The operator
T is said to be bDuntkd if ITJ < Ct).
Thus, according to Lemma. 4, a linear map between normed linear
spaces is contimw,u if and only if it is bOWldFd. 111is fact will be used
frequently, and the terms '"bounded'n and ""continuous'" when applied
to linear operators will be used interchangeably without reference to
Lemma 4. Another frequently used consequence of Definition 5 is the
inequality IABI :S;; IAIIBI, satisfied by linear maps betw<'ffi normed
spact'S, provided the domain of A contains the range of B.
8 LEMMA. If I: and 'ID are harmed linear $ptlL'l's, and if 'ID W oom-
plete, then the li1l€tlr space B(I:, 'ID). with the .lOnn given in Definitioll 5,
is a B-spat,"e.
. 6 THEOREM. Lei 1:, 'ID be B-sp<>tes, a1l<1 {T fi) a 8etJW'nee of bauru1ed
linear operators on :£ to . Then lhe limil T", = lim T fiX exi818 for evl!17J
'" in I if ahd ()lily if . m
(i) the limit T", e",i818 'or every '" in a fw,damental sel, and
(Ii) far each x in I: the supremum sup. IT".x1 < 00.
IVhen the limit T", exisUi for each '" in 1:, Ihe operalor T is bounded. and
ITj < lim int' ITnl sup ITnl < 00.
ft-tow n
PROOF. It is clear that ITI = 0 if and only if T = 0, and that
jaTI = jaliTI. Since
I(T+D)xl;:i; ITa:I+IU"'1 < (iTI+JDi>I.xI,
it follows that
IT+UJ < ITI+IUI.
To prove completeness, let JTn-Tml < E for n, m neE). Theu
T.x = lim T fiX exists for each .x, and
n '"
PROOF. If T.:v exists for each a:', then, since a convergent sequence
is bounded (1.9), statement (ii) foHows from Lemma 8. Converse]y, if
IT",-Tft"'l ITa:-Tm"'l+iTm-T.llxl.
Since the left side of this inequality is independent of m, it is seen by
letting '" --> Ct) that IT-Tnl ;,,-; E for n ;i; neE). This shows that
!T! < 00, and that jT-Tnl--+O. Q.E.D.
62
11. THREE BASIC PRISCIPLES
II.S.9
lI.s.n
HAHN-DANACH TIIEOREM
63
The fact that the field </J is a B-spaee yields the followmg corol.
lary.
yields
g\y)-g(.x) = g(y-.x) < P(y-.x) ;;;; P(Y+YI)+P( -Yl-.x)
9 COROLLARY. The nmiugatt' of a lwTmrn linear space is a B-
8pllt.Y.
This corona ' suggests the question: arc there any functionals
other than 0 in the cunjugate J:* of a B-1>J>""" J:? As will be seen, the
answer is in the affirmativei there are, in fact., enough functionals in
J:* to distinguish between the points of 3:. WhiJe this is not always the
case for F -spaces, there are c1asses of linear topological spaces other
than B-spaces for wbich it is true. These spaces are discussed in Chap-
ter V. The following theorem is of basic importance in the analysis of
questions concerning the existence of continuous linear functionals.
-pI --YI-X)-g(n:) ;;;; P(Y+YI)-g(y).
Since the left 8ide of this inequahty is independent of y and the right
side is independent of Of, there is a constant c with
(i) c ;;;; P(y+YI)-g(y),
(ii) -p( -YI-Y) g(y);;;; c,
yo
Y 0 21..
10 THEOREM. (Hahn-Balla"h) Let the real fundian p on tlw real
linear "pace I satisfy
For 11: = y+rzYI m the inequality
gl(n:) = g(y)+"" ..;; p(y+,,%) = p("').
which holds for rz = 0 by hypothesis, is obtained for rz > 0 by reo
placing y by y!rz in (i), and for rz < 0 by replacing y by y/rz in (ii).
Q.E.D.
p(.x+y) .,;; p(xJ+p(y), p(=) = rzp(x);
t".(. Ot Xty I.
]] TlIEOREM. Let \1) be a subapa<e of a nonru:d linear spaCR x.
Then to cwry y* in \1)* ctJrrf8pontU an ",* in 3:* with
Let f he a real liMur fUlIrliollal fJU a 811bapaU \1) of J: with
!x*1 = Iy*:;
n:*y = y*y,
yo\1).
f(.x) p(.xJ,
l1:<m.
F(",) = f(x), .x 01);
F(.x) :'C p(.x), "" J:.
PROOt' If}; IS a real space, this follow immediately fron1
Theorem 10, by placing p{x) ly*I[.xI, and f = y* (ef. Lemma 4 and
Definition 5). Now suppose that 3: is a normed space uver the field of
complex numbers. For each y in 11), let I.(y). f.(y) be real numbers
defined by the equation
Then !bere is a rrol lilll'llr fUlIrliollul F on J: for which
PROOF. Consider the fami.ly of all real linear extensions g of f for
which the inequality g(.x) ;;;; pIx) holds for.x in the domain of g. Th..
relation h > gt defined to mean that It is an extension of g, partially
orders tlLis family. Zorn's lemma (1.2.7.) implies the existence of a
ma."imal linear extension g of f for which the inequality g(.x) < p(l1:)
holds for J: in the domain uf g. It remains to be shown that the domain
Vo uf g is equal to I.
For the purposes of an indirect proof, RSSUlne the existence of a
vector Yl in a: but not in IDo. Every vector in the manifold 11. spanned
by 'DR and YI has a uniqll.t' representation In the form y+a.Yl with
y f: 1Jo. For any constant c, the function gl defined on IDl b}" the equA-
tion gl(y+a.YI) = g(y)+ac is a proper exwmion of g. The desired
contradIction ,',iII be rrwde and the proof finished when it is sbown
that c may be elu"",n so that g,(.x} ,;;; p(.x) for x in ?It. Let 11:, y be
arbitrary pomt. of 'l!o; then the inequality
y*y = fl(y)+if.(y}.
Then for rz, fJ renl and 11:, yo \1),
Max+fJy) = rzfr(.x)+NI(Y)'
IMy)l;;;; ly*yl ;;;; Iy*llyl.
yoW.
Thus, regarding I a8 a real linear space, and applying Theorem 10, a
:real linear function F I on I is obtained for which
:FII;;;; ly*l;
PI(y) = It(y),
yo\1).
Let the f..nction .x* on the complex linear space J: be defined by the
equation
.x*11: = PI(n:)-iFI(ix).
It will first be shown that n:'" is linear. It is clearly additive, and
64
II. THRl'.E BASIC PRINCIPLES
11,8.12
11.3.14
HAIIN-BA.NACH TRROREM
65
"'"(<LX) = o:x"", for 0: real. Also, ","(ix) = FI(ix) iFI( -x) = "'""';
thus oX. is linear. It will next be sbown that * is nn extension of y..
For y in ,
f,(iy)+i/.(iy} = y"(iy) = iy"y = i"(y)-f.(y).
which show" that MY) = -Miy), and hence that
y"y = My)-iMiy), y ID.
Thus :£* is an extension of y. . Finally,. let x.x = re ts . with r > 0
Rnd () rea1; then
I","xl = ",.(". ",) = F,I""",) :::;; ly.II"' "'1 = ly.II"'J,
which proves that Ix. I ly.l. On the other hand. since x. is an
extensinn of y", ,,,,", ;;;;; Iy'l. Thus /",'1 = Iy'l. Q.E.D,
12 LEMMA. Let ID be a .ub&pace of the n07l1led li,U'tIr $pilee J.
Let '" . J he tnU:h tJuzt
14 COROLLARY. For every :e =1= 0 in a IUJrlni'd lillt'QT space E,
there is an "," c J" with I",'j = 1 and ",.", = 1"'/.
PROOF. Apply Lemma 12 with ID = O. The x. required In the
present corollary may then be defined as fa:! times the z. whose
existence is established in Lemma 12. Q.E.D.
Corollary 14 shows that tMre are enough fuoolOnals in the con-
jugale "'. of a 7iOrmed space '" to distinguiah lIttwnn tM PQi1ll8 of :£, The
following result is an immediate consequen e of Corollary 14.
15 COROLLARY. FOT ellf'TY X it! a rwrmed linear space .I,
1"'/ = .up I"'""'"
a:.I!'S.
.r*x=l;
1..../ = lId;
:x*y= 0,
ycID.
wMre S" i. the d_d unit sphere in the sp<l.... I" cvnjugak tv :£.
L6 LEMMA. If tM conjugate ;E" of a normed linear space I is
sepl1TaJde.,so i. J:.
PROOF. Let {x:} be dense in :£*, and let "'. :£ be such that
1"'.1 ;;;; I, and Ix:"'.1 ;;;;; 1"'://2. The set L offin;te linear combinations
of the elements X n with rational coefficients IS a denumerable set. If II
is not dense, th re is, by Lemma 12, an oX. "# 0 with :x*L = 0. Let
3:: -+ oX*. Since
.
inE [y-"'I = d > o.
-<2)
Then there is a pc;nt ",." I" with
PJlOOF. Since '" ID, every point z in the linear manifold .B
spanned by ID and", is uniquely representable in the form z = y+<LX
with 0: . <1> and y . 'ID. ]i'or this z, let z"z = 0.. The function z* is clearly
linear on g. For <X -4 O.
1 11 I
Izl = 'y+o:xl = 10.1 ; +"'j ;;;;; I<xld,
and hence I,"zl < l'l/d, Iz"' < lId. Let Y." ID be sueh that
I"'-y.' --->- d. Then,
i = '*("'-Y.) ,,;; Iz.II"'-y.1 --->- ["Id.
and lId Iz*l. Thus 'z*1 = lId. Theorem 11 gives the existence of
the desired extension "," of ... Q.E.D. '.
... 18 COROLLAJlY. Let x be a vector not in tM dosed subspace ID vf
tM nonned linear space I. Tlu:n there i. a functional x' in 31* with
x'x = I; .c'y = 0, Y' ID.
Ix L ",=.1 ;;;; ;(.c*-",:.).x.,1 = Ix:.",.., ;;;;; 1"':.1/2,
we have x:. -+ 0, or* = 0 , a contradiction which proves the lemma.
Q,E,D.
There is an important interpretation of CoroUary 15. For ev ry
3J in a nonned linear space 1", the scalar X*:X depends linearly and con-
tinuously upon it'll, and thus d fines a continuous linear functional on
!*; i.e., each IV in 1: determines a unique point ,f in (I*)* such that
.fu:* = "'""'. ",.I. Bydefinition,li:1 = sup'zO,;>.lu'l, and thus, by Coml-
lary IS, 1.11 = Ix!- These observations suggest the following definitions.
17 DEFINITION. An ismnorphism between two normed linear
spaces'" and ID is a one.to.one continuous linear map T ::£ ..,. ID with
TI = ID. When .uch an isomprphism exists, the spaces :£ and ID are
caned €!Juivaknt. An iSQmetric i80rrwrphism between two norrned linear
spaces I and 'ID is an isolnorphism T bet1<..-.,n I and 'ID for which
IT"'I = Ixi. When such a T exists, the spaces are said to be i80tnetTical-
ly equivalent. or iSQrnl'lricall.?f isomQrphic.
66
II. THREE BASIC PRINCIPLES
11.8.18
11.8.23
HAHN-BANACH THEOREM
67
20 THEOREM. Let lea' a. E A be an indexed set oj f'lnnmts in a
normed linear apm:e 1_ If
sup Ix'x.1 < 00,
.<A
OV*E 1*,
28 THEOREM. A closed li'l£LIr ma"ilold in a reflexive 8-¥JXlf'f' is
reflexive.
PROOF. Let \[J be a closed linear manifold in thc reflexive space I.
Let : x'-+y' be defined by the equation (x*)y = x*y. Y' 'l1. Clear-
ly Ic{x*)1 ;;:: Ix*l, so that c : I' -+ \!)*. Let » : y** x** be defined
by »(y.*)"" = y'*(c(x*»), x*. 1*. It is evident that 1'1(y**)x*1
;;:: ly**II ("'*)1 ;;:: ly**I1"'*:; bence ?J : ID*' -+ I**. Let '" '" -+.t be
the natural isometric isomorphism of I into I**. Since 1 is teflcxive
each x** = Ii for some", . I. It will be shown that ,,-I'1(\!J*') k \!). If
x = ,c'?J(y**) 1'D there is, by Corollary 18, an ",*.1* with J!"x "" O.
x* ) = O. Since "'*'I!J = 0, c(oX*) = o. Thus,
o = y'*c(.x*) = ?J(Y**)x* = .tx* = "'*"',
a contradiction proving that " '?J(y**) k 'g). Now let rIo* . \!)** and
x * = '1J(y *). If y*. \!)*, let "'*.1* be any extensio; of yO. Then
y* = c("'*)' and
18 DEFINITION. Let I: be a normed lmear space, and if.. the
conjugate of the B-space 1*, The mapping": oX .t of I into I**,
defined by .tx* = "'*'" for "'* in :t*, is called the IU1ltIral .mh£dding of
I into I**. The range of " will be denoted by i.
Thus, according to the remarks preceding Definition 17, the
following theorem IS a corollary of Corollary 16.
19 THEOREM. The nal>l¥rJl nnbe<lding of a rommed. limar apace I
into ils second «J is an ioomdric isommphiBTll bt1nwen I and i.
In view of the property of the natural embedding given in Theo.
rem 19, the map x is sometimes called the natural istJmdric isomur-
phism of I mto I**
then
(Hi) sup ly*T.;r1 < co,
..A
:rEI,
y*.'l1*.
** y * ( ** ) * ** * - - . " * * )
Yo = TJ Yo '" = Xo .x = ""' = '" "'0 = Y "'0' Y '. *,
since "'0 = "-'?J(y:*). 'l1. This shows that 'l1 is reflexive. Q.E.D.
24 COROLLARY. A B-space is reflu,,:. if and only il ils conjugate
spa« is re/kril'f:.
PROOF. Let :f be reflexive, and let x be the natural isometric iso-
morphism of X onto 1:*11-. For an arbitrary point x*** £ (1*)** =
(I.*)*, the functional :1:. -= ,1:***" is in :I*, and
.:r.*x* = .fx* = 3*.t: = oX*"'*",x = x""''''J' = .t:"'**x*. x.* 1*'\
which shows that 1* IS Tr-flexive. Conversely, let 1* he refleXIve. Then
J'** is reflexive. and hence. by Theorem 23. the closed linear mal1ifo]d
i in.!**is reflexive. From this it follows that!, which is isometrically
equivalent to :i:. is reflexive. Q.E.D.
sup IX.I < co.
..d
PROOF. The functions 5:.. a. A, satisfy the hypothesis of Theorem
1.11, which is to he applied to the conjugate spaee ;r*. Then, by Theo.
rem 1.11. there is a 6> 0 such that Ix.;r.1 < 1 if Ix'i < lJ. Hence
15:.1 ;;:: I/lJ, a. A; and, by Theorem 19, I"' I s:. I/lJ, a. A. Q.E.D.
21 COROLLARY. Let I, 'ID"" B-spaces, and let Ta' a . A, be bounded
limaT maps from I to 'l1. Then 111£ Imlowing tdnlemenls are equWalem:
(i) sup ITal < co;
a'"
(ii) sup IT.;r1 < 00,
..A
31£1;
PROOF. Theorem 20 shows that (iii) implies (ii). Now assume
(ii). Lemma S shows that for each", the set (T.;rla. A) is hounded,
and Theorem 1.11 gives a lJ > 0 8uch that IT.;r1 < I if 1"'1 < lJ. Thus
IT.I ;;:: l/iJ, a. A. Q.E.D.
22 DEFINITION. A B-space I is rel/....ive if the natural embedding
" of Definition 18 maps ;r onto all of 1**.
25 D FINITION4 Let 1: be R linear topological spaCt". A genera-
lized sequence {.xa.} in is said to be "ll:'f'.llkly convergent if there is an
or in with ,x*x = IirIlu a:*x(I for every J:.£ *. The point x is called a
weak limit of the generalized sequence, and tJ}C generahzed sequence
{;t.) is said to <,",verge weakly to x. A set A !;; I is said to be 'U'Eakly
aequelltially compact if every sequence {XI'I} in A contains a subsequence
68
II. THREE EASIC PRJNCIPLES
11.13.26
11.8.29
HAHN-BANACH 'lIlEOREM
69
whieh cOIwerges ,,,'eakly to a point in 1. Ever)' sequence {.Tn} such that
{x*.x..} is 8 Cauch). sequence of scalars for each or* of" 1* is called a'lL'1"uk
Cauchy se/}Uence. The space I is said to be recaJdy complete if C\'erv
weak Cauchy sequence has a weak limit. ..
In Chapter V, a topology is introduced in certain linear spaces In
such a way that they become Hau:sdorff spaces in which the notion of
conveltrence of generalized sequences ("Oincides with the notion of
weak convergence as just defined.
26 LEMMA. In a nonned li..ear 811ace. a tt'eo1dy crmvergcnl genera-
lbi-d setJ1U'Rct: has a unique limit.
PROOF. If x and y are both weak limits of a generalized sequence,
then for each x*. 3::*, ",*x = ,,,*y, "'*("'-y) = 0 and '" = y, by
Corollary 14. Q.E.D.
27 LEMMA. A wrokly com"ergent .sequeru:e {a:'7.1} 01 points in a Twrmed
linrar 8pact' is buundnl. Its limit a: is in tM clO3ed li1J ar ,nani/old
ddffminrd by {r .}, and 1"'1 S; lim inf 1"'"[.
lim y:a:i = lim xiY: exists for each 11 = 1,2, . . .. Since {y:} is dense
.-+om i_"'
m *. and Ix,1 ;:;:; K, Theorem 6 shows that there is a y*. in '!.i** with
11m y*x i = y.*y*, y* E y)*.
Since V is reflexivc, there is a polnt y ID witb Y.Xi -+ y.y for every
y* . '{,i*. Now, any 3:* in 3::* determines a y* in 1'* such that x*y = y*y
for y in ; thus, since XhE ,. ;t*:r, x.y for -1'* in J;* and {.t''I'Il CQn-
,'erges weakl) to y. Hence bounded sets are weakly sequeututll)
compact. The con'\'cr c follows from the preceding lemma. Q.E.D.
29 COROLLARY. A refle",ive space is tuakly complete.
PROOF. If {xn} is a sequence in a reflexive space :f for whi h
Iim "'*"'_ exi.ts for each.,.. in I*. then, by Theorem 20, ("'.} is bounded.
.-'"
n_
By Theorem 28, there is B subsequence {a':nJ which converges weakly
to a point ;r in 1. Thus,
lim x*x R = Jim .x*.x 7l ;; = «*.x. oc* (; 1*.
PROOF. If in 'l'heorem 6, I, 1), Tn arc r<'placcd by 1.*,,z,, ,lr11' it is
seen that 1£1 ;;:; lim inf 1£.1. Theorem HI give8 the inequality 1"'1 S;
-'"
.
,
lim inf 1"'.1, and Theorem 20 shows that sup. 1"'_1 < 00. It follows
.-'"
which proves that iIZ is weakly complete. Q.E.D.
The reader is referred to Chapter V for additional discussion of
reflexive spaces and weak convergence. We conclude this section with
B lemma on weak sequential compactness which has useful applica-
tions to ergodic theory.
80 LEMMA. Let I, '{,i be B.ltpf1e," and let {T.} be a bounded 8e
quenu in B(i1Z, ID). T/U'n the set '.m af all",. 3:: for which {Tn"'ln = I, 2, }
is weakly sequentially compact is a closed li7leoT 811b8paec af 3::.
PROOF. An obvious argument shows that W1IS a linear space. It
will be demonstrated here that'.m is clo.ed. Let IT.I ;:;:; K, n = 1,2.. . .
Let,zn iEIDl, ,x71 4- x. An arbitrary sequence {n , } of integers contains a
subsequence {n 1 i] for whid1 Tn .X I converges weakly to some point
. iu
which will be denoted by Yl' Sm\ilarl), there i. a pomt Y. and a sub
sequence (n. ,} of {nH} such that T. ."'.... Y. weakly. Proceeding
,i I.,
by induction. a point Ym. and a sequence (Um.i} arc obtained fot' which
T Ji",.lm .....,.. y,rt. weakly. The sequence {mil defined by '111, = 1'i,( i'i a
subsequence of In,} for wh1Ch T mo'Ck ... Yk weakly for all k = I. 2, . . .:
the inequality .
from Corollary 13 that x is in the closed linear manifold determined
by {x.}. Q.E.D.
28 THEOREM. A set in a ref/e.rive spact: is weakly IltXJURlllinlly
c01ll1Hld i/ a7ld only if it is bounded.
PROOF. Let {y,,) be a bounded sequence in the reflexi1.'e space I
with IYnl ,;; K, '11 = 1,2, . ... Let ID be the closed linear manifold
detennined by the sequence {y.}. Then ID is separable, and, by Theo
rem 28, reflexive. Thus ) = ID** is separable and by Lemma 16
'{,i* is separable. Let {y:} be dense in W*. Since he s quenec {y:y.}
oundedl it. has a convergent subsequence {yiY l')' Since {y:y; .)
IS bounded, It has a convergent subsequence {yty",.)- In this manner
on(' obtajns by mduction, a sequence {Pn, i}, 'which is a subsequence of
{Pn-1, i}" for ""hidl the uence {Y:Y"ft.) IS convergent. Thus U1e se
qucnce {x,}, defined by "" Y.,.,' has the property that the limit
70
II. THREE BASIC PRINCIPLES
II. .1
n.4.7
EXF.RCISES
71
ly,-y,1 ;:;; KIXj-Xil, i, j = 1. 2, . . ..
follows from Lemma 27. Since {x,} is a Cauchy sequence, {Yi} is also.
Let y = limy.. For ",* y* and p = 1,2,....
I . f(p.)-f( )
,m-
u-+< I'-
-
exists for each . G.
7 DEFINITION. A sequence {x.} in an F-spare iE is mile<! a basis
for!: if to each (£ £ I there corresponds R unique sequence {ail of sca-
lars such that
I "'*T x "'. yl :<:; l x*r x-x*T '" 1 + l x"T x -x* y I +'x. y -x. y !
7/1. _ m, ""'il" moil) vi""
and hence
I,m sup Ix*T..,.r-;r.ul ;;; Klx*lIx-x.l+ix.lly-y.i.
f--'HX>
.
By letting p aJ. it is seen that T..,x _ y weakly. Thus e,'cry se-
qucnce {n,} of inugers has a subsequence {m i } for which T...x y
weakly. It fol1ows that T,,;r ---+- y weakly. Q.E.D.
lim Ix - l' 0;;$,1 = o.
n OO i=J
8 Let {x.} be a basis in the F -space iE. and let ID be the vector
:space of all sequences y = {a.i} for which the series !:l aix,
converges. Show that with the definitIon
4. Exerei8es
.
I A set C in .a linear space is said to be COlU'eX if (Xx + (I -ct.)y £ C
whenever x. y . C and 0 ;;;; " ;;;; 1. Show that 8pheres in a B-space
are convex. Show tbat the closed sphere {xllx-yl :<:; o} is the closure
of the open spherc {xllx-yl < e}. Show that the intersection of a
dPCreflSing sequence of closed spheres in a B-space is ne,r(T void.
2 Find a decreasing sequence of non-void, bound.ed, closed, con-
vex sets in some B-space whose intf"rsection is void.
8 Let \!J and .B be closed linear maoifo](\s in the B-space I.
Suppose that each a: in has a unique representation in the form
x = y+z. with y £ \!), Z £.8. Show that there IS a constant K, with
Iyl ;;;; Klxl, and Izi ;;;; Klxl, for each x io I.
4 Let I, and .8 be B-spaces, and let z = (x, y) be a function
on I .< 2J to.B which is linear III '" for eaell y, and linear in y for each x.
Such a function is caUed bilill<?ar. Suppose that, for each z. in .s*, the
function 2.(.x y) is continuous in y for each x. and continuous in x for
each y. Show that there is a constant K such that
I(x.y), :<:; KI"'lIyl.
5 Let and .s be B-apaC<"S, and let I : \!J -+ 8 be such that
z*' £ YJ. for eachz* .s*. Show that I B('f), .8).
6 Let I be a complex B-space. and let G be an open subset of
the complex plane. Let , : G _ .£ be surh that x*' is analytic in G
for each a;* I.. Show that
[yl = sup 1 I ......1.
fl i-l
ID is an F.space. and that ID is a B-space if iE is.
9 If {XII} is a basIs in the F-space £r and for ;x = :l a,<x, we
define x (:t'!) = air i = lr 2, . .,. then the linear functional a: is con-
tinuous. (Hint, Uae the natural mapping between I and 2J of Exercise
8.)
10 Show that no element of a basi in an F-space is in the
clUS("d linear manifold dett'rmincd by the remaining .el.ements of the
basi!J.
II DEFINITION. A paIr of sequences {x.}. "'. £ I, and {xn,
"' . I*, is called abiurthogonal system for a Banach spaceiE ifx (x,) =
{J".
12 Let {Xi}, {x } be a biorthogonal system for the B-space 3L
(a) Ifsup II -I x*(x.)x:1 < 00 for each x.oI*, the representation
"
'"
if: = xi(.x)x.
i"",l
IS valid for each x in the closed Imear span of thc sequence {x,}.
(b) IfsuPn 1l':'....lx:<x)x,! < aJ for each x£iE, the representation
.x* = I a:*(oci)xi
i_I
is vB1id for ach ;c* in the closed linear span of the seQuence {.x }.
13 Let! be a B-spacc (or an F-space), and let.8 be a closed
72
II. THR£E BASIC PRINCIPLES
II.4,H,
11.4.21
EXERCISES
73
linear manifold in i.t'. Then J:!.3 (cf. 1.11) IS a B-space (or an P-space)
with the metric
there exists a yo.J: such that x *(y*) =Y*(Yo) for all Y*'.8 L .)
21 Let m be the space of all bounded sequence. 8 = [8 i . 8.,. . .J.
Show that if the UOrm of 8 be defined as
IX +.81 = inf Ix+zl.
..g
(Hint: Given a Cauchy sequence in J:/.8, define a subsequence Ibr
which Ix.-x'+1 +.81 < 2-1<. k = I, 2, . . ., and show that a Cauchy
sequence in J: can be chosen which maps onto (x.+.8}.)
14 Let J: be an F -s!","" Or a normed spacc. (a) The natural
homomorphism I: I ->- 1:/.8 defined by I(x) = x+.8 is continuous,
maps open sets onto open set., and has norm III .,;; 1.
(b) If :£/.8 i8 given a topology actually stronger than the topo-
logy defined by the metric given above, then I will no longer be con-
tinuous.
(c) Thc function f map' the open unit sphere uf :£ onto the
open unit sphere of 1/.8.
15 (Banach). Let I and '!J be B-spares, and let T be a con-
tinuous linear mapping of I onto all of . Show that thcre is a
number N > 0 such tb:a.t for every sequence Yn -+ 'liD there is a se-
quence IZ'n -J>- &£1) with Iil'nl S NIYftl and TX n = y" n = 0, 1, . . n
16 Let I be a normed linear space which is not assumed to be
complete, and let .8 be a closed subspace of I. Then, if.8 and J:/E are
complete, show that J: is also.
17 DEFIKITION. If 1: is a normed linear space, and Z I, the
set ZL = (x*lx*. 1*, x*(Z) = O} is called the annihiw.wr or ortko-
gulUll comp/.nn£nt of Z.
18 (a) If J: is a nonned linear space, and .8 a linear manifold in
1) the mappingx*+.8.L z*, where 2* is defined by Z*.2 = a;:*z, %E"B,
is an isometric isomorphism of a;*t2.L onto all of .a*.
(b) If.8 is a closed subspace of a B-space J:, the mapping x* --+;j;*
where'x' is defined by.;;*("'+8) = x*(x), is an isometric isomorphism
of .8 L onto all of (J:/m*.
(c) If J: is a reflexive B-space and 8 is a closed subsp ce of
I. show that .8 LL = 1.8. Is the result true if I is not reflexive'!'
19 If J: is a reflexive B-space, and .8 is a closed subspace of I,
show, using Exercise 18, that both .8 and liS are reflexive.
20 If I is a B-space, with .B !;; J:, and both 8 and 1/.8 are re-
flexive, then J: is reflexive. (Hint: Given any x * . J:**, show that
Isl = lub [s,l,
1::;i<::
m is a B-space.
22 (Banach limits) Let mo be thc smallest closed subspace of
m (cf. Exercise 21) containing all sequmres of the form
t = [SI' 8.2--8 1 , 8:8-8.1:1'. .], where s = [8 1 , 8 2 , ...] is an lement of m.
Show that the sequence e = [I, I, .. .J is not in m", and that there
exists B ontinuous functionaI.:c* on tn such that 1:r*1 = 11 :r"(e) = lp
x'(x) = 0 if x e mo' Letting LIM 8. = X*(8). show that
n
(a) LI!\I8. = LI!I-I Sn+1;
ft_W 7j"""",*
(b) LIM (O<'.+PI.) = <> LIM 8n + P LIMt.;
.
. '"
.
(e) LIM 8. ;;;; 0 if [8.] is a non-negative sequence;
" W
(d) Iim inf 8. ;,; LIlU s. ,.;: lim sup 8. if ['.] is B rea! sequence;
11_00 n-+:'JJ n (X;
(e) If 8ft is a convergent sequence l then
LIJ\.I 8" = lim sn
II_W n-+OO
23 Show that there exists B method of assigning a "generalized
limit" LIM to every bounded complex valued function I of B rea!
w
variable s in such II way that
(a) LIM/(s) = LIM/{8+t) for each I;
B-Tct> tJ-+0:
(b) LIM (<>/(8)+Pg(s)} =" LIM/(s) + PLlMg(8);
._w
'"
,.,.
(c) LIM I(s) 2: 0 if I is a non-ncgativc function;
H
(d) Iim inf 1(8) LnI f(8) lim sup 1(8) if f is real;
'"
. '"
(e) LIM f(s) = lim /(8) if the right hand limIt eXISts.
'-00 _-'CD
'1'4
u. THREE BASIC PRINCIPLES
11.4.24
11.4.85
:EXERCISES
75
24 If W is a linear manifold which is dense in a B-space j;, show
that there is a natural isometric isomorphism between if. and W..
25 Let !II be a separable linear rnllnifold in j;.. Show that there
is a separable subspace .B j; such that !II i. isometrically isomorphic
to a 8ubspace of .s*.
26 If I is 8 linear topologIcal space, 8 linear functional on 1: is
continuous if and only if it is bounded on some neighborhood of the
ongln.
27 DEFINITION, A B-.pace if is uniformly conv,"" if 1"'..1 =
IYnl = 1, 1"'.+y.1 -.. 2 implies 1"'.-y.1 -+ O.
28 If J is uniformly convex, <En -to- a:a weakly, and IXnl -+-IZD!'
then 3J n -+ 3:'0 in the metric topology.
29 Let K be B closed iConvex set in a uniformly convex B-space.
Then the norm function f(x} = 1.x18ssumes its minimum exactly once
onK.
30 An infinite dimensional F -space never has a denumerable
Hamel basis.
(a) I, = a,o hmB, + !;':, a.;8" where T[B,.B.,...,]= ilz,I.,...J;
;-+01
(b) lub !;':o la,,1 = 111 < co:
lS.i<w
(c) lim ad exists for i = 1,. 2, .. .;
__'tIC
(d) 11m :o a;; exists;
;:-+0:>
(e) ITI = ill.
Conversely, if {a,,} is a double sequence satisfying (b), (c) and (d),
then (a) defines a bounded linear mapping T on c to c whose norm
ITj=lIl.
35 DEFINITION. Suppose that a matrIx {ad) defines a linear
transformation T of c into itself by means of the formula
0> 0>
Tes., B., . . .] = [Iz, I., . . .] [1: aus,,! a.,8" . . .].
1-1 I-I
then c is a B-space.
32 Let denote the space of .all sequences B = [B()I 8 1 , 8.1' . . . ]
sucb that !::'..IB,J < 00. Show that if the norm of 8' is defined as
If T preserves limits of sequences (i.e. if lim,-+-Cr;> Ii = lim Sj far every
[s,] c). then the matrix (ail) is said to define a regular .netlwd vf
summahilily.
86 (Silverman-Toeplitz). Show that a matrix (a.,) defines "-
regumr method of .ummability if and only if
(a) lub 1:;':, laill = M < co:
1:;;:1<0:.
The ""xl 8e1 vf cir:€TCisa fOTTnB a oonru:cted group p<:rlaining 10 !he
summnbility lheory of di>!crgeril 8f'rics.
81 Let c denote the space of aU convergent sequences 8 =-
[8 1 , BO' . . .] of scalars. Show that if the norm of 8 is defined a'
181 = lub 18,1,
l i<DCI
(b) lima" = 0 for 1 i < 00:
. O>
0>
(c) lim !;:. ail = I.
i-Jo-G:I
IBI = 1: "'I,
'-0
37 Let [P.J be a sequt,'IlCC of pusitive numbers, Rnd let Pi =
! _I Po. Show that the formula
then l, is a B-.pace.
88 For each B = [B., B,. B., . . .] £ l" and t = [Iz, I" . . .] £ c, let
0>
(gB Jet) = BO lim t. + 1: 8.1._
'I_IX> ,,_1
, 0>
" = Pi-l !PPi = Ia1jS J
;"". i_I
Show that g is an isometric isomorphism of 11 onto al1 of c..
84 Let T be a bounded linear map of c into c. Show that there is
s double sequence {au},. i = 1,2, . I., i = 0, 1, 2, . .. such that
defines a regular method of summabilityif and only if.l':", P. diverges.
(Irall P, = I, then this is called Cesaro (C.1)-su.mmahility, ('f. Exercise
39 below.)
38 (Norlund summnbility). Let [p.J be a sequence of po.itive
76
II. THREE BASIC PRIXCIPLES
11.4.39
11.4.46
EXEBC1SES
77
numbers, and Ict Pi = _I PI.;. Show that the: formula t f =
Pi' I:_I P' ;+lSj defines a regular method ofsummability if and only if
lim P;'P. = o.
k->
(1) 'nAmn converges for every n:
(2) I,,[lmn-1m,ft+J1 cOllverge:; for each mj
....
(3) sup I. I I (A".-Am,.+I)1 < 00.
M m.....o
89 {Cesaro (C, at)-summabihty). Show that the formula
The transformatIon preserves sumo;; of series (i.e. I (I:=oJ...l1'lnon) =..
I:...{I an) if' and onJy if the equation
(n Im;"". = I
holds for each n, in addItion to (2) and (8).
46 A matrix (Am,'), m, n = 0, I, 2, .. ., defines a tramformation
!:"=D an ,. !:'=(I Am"a n = 'm which maps convergent series into con-
vergent sequences if and only if
(1) lim ;.",. exists for each n;
.
I = ( Co+ I ) -, C' 9
n n £n-kk
defines .a regular method of summability for each complex number I;(
such that 9i'(at) > O. Here C = I and C = fJ(fJ+l).. .(fJ+m-l)fm!
for m > O.
40 Let:!:..o Pno;:.TI be the power-St'ries expansion of an entire
function. Suppose that P. > 0 for each n. Show that
P g x'
r I " .L n_O It tI
)tnS"" = 1111 (I;o II
n-+OI> Z_17J ,Ln-fi 'Prior
m
(2) sup I:.n IAm'-;"""+l1 < 00.
m
whenever the limit on the left exists.
41 Let :-o PrjzTI. be the power-series expansion of R function
analytic in the circle Izi < T. Suppose that P. 0 for each nand
lim L:""o Pn.X'" = a), where 0 < x < T. If lim slj exists, show that
r h m
Further, Jim 1m = 1:'-0 an if and only if the equation
m
(I') lim;"". I
m
r I I:".,(J pljs"a:TI.
IffiB n = Im QJ 1Ic
n_D:' ,. .£.,n-{) pna:
holds for each ?<, in addition to (2).
47 Show that
. '" m(m-I)
Ian =hm{a,,+--- a, + a,,+...}
,.,.{I m m+1 (m+l){m+2)
whenever the series on the left converges.
48 Show that
where the limit is taken through real values of iX.
42 (Abel summability) Show that if lim. Sn = S exists, then
(l z)I":"'lJsn converges to s as z con,.erges to I along any path inside
the circle C = {zllzj = I} not tangent to C.
43 (Abel) If the series L:...o Il n converges to II, if l:.ob n con-
verges to h, if I:'--o C n con\rf't-ges to C, and if C n = a,,_;b; show
that c = ab. (Hint: Use Exercise 42).
44 The mapping I;;" an -->- I. A.a n defined by the sequence {A.}
maps convergent series into conve:a-gent series if and only if
I::'..o IA.-AM.I < 00.
45 A matrix (AmnJ, m, n = 0, 1,2, .'., defif'les a transformation
L:"'...oD" -+ :""D(.I:-O ).l1tllan) which maps convergent series into con-
\.'ergent series If .and onJy if
( sin nh ) k
Ian=lim Ia. -
""",1 "-+0 ?I-I nh
whenever k > 1 and the series on the left con""erge-s.
49 (Schur.l\lertens). Let u = {an} and b = {b.} bc two se.
quences of complex numbers, and let c m = I:-o a;n bn' If I lanl
conve .. then I C n converges whene-\"er Ib n converges. Conversely,
if ! c,. converges whenever L b n convergE's, then lanl converges.
(Compare this result with that of Exercise 43).
50 (a) If a. converges and {P.} is a non-increasing sequence
.of positive numbers, then 2 anPn con,.erges.
78
II. THREE bASIC PRINCIPLES
11.4.51
11.5
NOTES AND REMARKS
79
(b) If {Pm.} is a sequence such that
I) 0 ;;;; Pm. :$; Pm. l:
2) Pm. ;;;; ]If for some fixed ]If < 00;
8) Jim Pm. = 1 for each ,,;
m_"
lim 2 -o a,JJm.n = ! o:AI an
m_"
5. Notes ami Remark.
Geru:ral rm.ark. and refnom«.. Although the proces>es of differ-
entiation .and integration can be regarded as operations defined on
.a class of functions, before the end of the last century this ,riewpoint
was employed as little more than a notational con,"enience. By the
tUn! of the century however, the work of Volterra and Fredholm on
integral equations had emphasized the utility of these "'operational"
techniques. As integral equations and related theorIes were advanced
by Hilbert. E. Schmidt, F. Riesz and other8, and the similarities with
roIT.:sponding algebraic problems emerged. the valuc of reganling a
function a::; a vector or as a point in a "space" of functions became
evident. This wa, rccognized clearly by Schmidt [1], for example.
\\ hose geometrical notation and terminology In Hilbert space is sub-
stantially that in current use. At approximately the same time the
foundations of modern point-set topolog,. were being laid by Freehet
[I], Hausdorff [I], and F. Riesz [1], and it was only natural that these
topological notions should bc applied to algebra and analysis. Thus
Kiirschak [1] introduced topology into the theory of fields by de-
fining a valuation. and thus the concrete Hilbert space and the LlJ
spa('t'ti. soon led to the general concepts of normed Rnd topological
linear spaces.
Considering the extent to which Lie and his foltoll'ers had deve-
loped the study of Ucontinuous groups." it is sonlcwhat surprising
that the Idea of a general topological gruup was so slow in taking
form. For it was not until 1926 that Schecter [1] defined an abstracl
topological group and established somc of Its properties. (See also
Leja [1].) A systematic treatment of the topologizing of abstract
group" ring" and fields was given by van Dantzig [I]. The concept of
B normed algebra was first used by Michal and Martin [1], Nagumo
[1] and Gelfand [1]. Frkhet [2, 3] appears to have originated the
concept of an F -'Space.
&/erences: Those int""",,1;ed in studying general topological
groups in detail will want to consult the treatises of Loomis [1],
Pontrjagin [1], and Weil [I]. The books of Cheralley [1, 2] arc con-
cerned with the more special Lte groups.
We particularly recommend the report III "Ole Eucyklopadie der
Mathematischen WiS>eIJSclmften n by Hellinger and Toeplitz [8: par-
then
whenever the series on the right converges.
51 (Hardy-Littlewood) Suppose that a(z) = I ... a".. con-
"erges for z = 1. If 0 < a; < 1, show that
., a l "("-')(I-"-')'
I.... kl
converges. (Hmt: Cse Exel't'ise 50.)
52 Let u. and v. be elements of I, (cf. Exercise 82) defined by
the fonnulae
u. [1,112. 1}8, . .., II", o. 0, ...]
v. = [(I-If,,), 112(1-11")',,..J
Show that {u.-v.} is bounded, but does not converge to zero.
58 Suppose {a.} is a sequence of complex numbers for which
(nu.} is bounded. and let a(z) = I -o a..... Prove the fnllowing state-
ments:
(a) a(a;} is bounded for 0 < a; < 1 if and only if the 8cquence,
{L =o Ilk} of partial sums of the series !:: Ok is bounded;
(b) a(.) is bounded in the circle 1'1 < 1 if and only if the se-
quence of partial sums of I: G n 2" is uniformly hounded for Izi = I.
1'1 = 1.
54 Suppose {a.} IS a sequence such that {ka.} converges to zero.
If a(.) = I:'o a...., show that
lim [I -o a.-a(I -If,,)] = O.
.-..
Hence show that I:.o a. converges if and only if a(,,-,) has a limit as
a: --+ 1. (This famous result, due to Tauber, is the prototype of all
dTauberian u theorems. Theorems of this type state conditions under
which Ustrong" (in this case Abel) summation reduces to ordinary
summat,on. Compare the result of Exercise 54 with that of Exercise
42.)
80
II. THREE RASIC PRJXCIPLES
II.5
11.5
NOTES AND REMARKS
81
tiCl1larly Sec. 24] 3.' a remarkably readable and complete bibliographic
account of the theory of integral equations, which erved as the pomt
of departure for much of linear pace theory. Also of more than n)ere
historical interest are tbe fundamental papt'ffi of Hilbert [1] on in-
tegral equations and the book of F. Riesz [6] on equations in infinitely
many unknowns. The older IIEncyklopadie u report of Pillcherle [1],
th volumes of E. H. Moore [1.2], and the work of Volterra [I] are
also related to much of this material. Finally, the book uf Davis [I]
cites many referellceti to operational methods such as the Heaviside
operational calculus, fractional differentiation Rnd integration, etc.
!\lost intimately related to this present work is the c1lUiSie treatise
of Banach [1] and th recent books of F. Riesz and Sz.-Nagy [I] and
of Zaanen [5]. The more special theory in Hilbert space is treated by
Stone [3]. Sz.-Nagy [3J. Halmos [6], and Cooke [I]. The volume of
Hille [1] also has many points of contact. 'I'hc treatises of Nakano
[I, 2], and Bourbaki [2] are more general in scope in that they arc
concerned principally with locally convex topological linear :spa<:es.
All of the.e books will be found useful as references.
Bvwull'd sels. Definition 1.7 is t'SSt'atially due to von Neumann
[I]. An equivalent dcfinition is: a set B is bou",led if for every se-
quence {xn}!;; B and every sequence of scalars {an} with ex" 0, it
follows that O:nxn -+ II. This latter condition waS US{>() by Mazur and
Orlicz [1]. In the case of B-spaces it is seen in Leulmn 3.3 that a set is
bounded if and only if It is contained in some sphere. An F-space ,
however, may have all of its .spheres unbounded.
The principle oj u.1iJorm bou,"l£dne88. (The comments in this
paragraph pertain to Theorems I.Il. 1.13. 1.17, and 1.18. and their
applications to Theorems 3.6, 3.20, and 8.21. See also Gal [3].) There
are many instanl'eS of results related to this theorem throughout
analysis, although because of their frequent special character they
are not always recognized as :such, nor ean they alwlL)'s be compared in
strength. Some results of this nature were proved by Lebesgue [I J In
his study ofsingular integrals, others by Hahn ,1; p. 678], Steinha;"8
[I], and Saks and Tamarkin [11. Certain consequences of Theorem
I.II which arc closely tied to the problems of represcntation of
lineal' funchonals and operators were proved in by Hcllinger and
Toeplitz [1,2] in lv, P > I, by Landau [I], in r by Tocplitt. _2], in
C[o, I] by Helly [1], and in L., p> I, by F. Riesz [2; p. 4.57].
Theorems 1.11, 1.17,. and 1.18 were proved for linear fUlictionals
on a general B-spacc by Hahn [2] who applied these results to a large
number of special spaces. The first really general proofs of Theorems
1.11 and 1.18 were given by Hildebrandt [2] in the case of a B-space.
Banach and Steinhaus [1; p, 53] ol>sen'cd that in the case of a B-
space Theorem 1.11 remains valid if {T.xla A} is bounded for x in
a set of the second category. Banach and Steinhaus [1; p. M] proved
the following theorem, often called the theorem of condensation of
sin,gularities.
THEOREM.IJ {U.,} is a douMe M<}UI!1IJ:8 oj bounded linear operators
between IWQ B-apac€s I alld IlJ such that
lim sup IU a'1 = 00, p = I, 2, . .-,
....'"
llIen Ih£re ,nsls a sel S of the second rotego'y in I 8ud! that for each
:XES,
!im sup IU..(x)j = 00,
....'"
p = 1,2. ....
Banach [3] proved Theorems 1.17 and 1.18 for B-.paccs and
gave [7] theorems related to these and the condensation theorem just
mentioned for complete metnc groups. (See also Banach [I; Chap. I].}
Tbc extension of Theorems 1.11 and 1.13 to F-spaees was made by
:!IIazur and Orliez [I].
Pettis [5; p. 300] has givcn a very general extenSIon of Theorem
1.13 to linear topo1ogical spaces. He has also shown that an extension
of Theorem 1.17 is valid for a sequence of continuous homomorphisms
between two topological groups.
Theorems 8.20 and 3.21 have been extendcd by Sargeut [I, 2]
so that thcy may be applied to a spRce of Denjoy integrable functions
on [0, I], which is of the first category.
A &&unifonn boundcdness theorem" for a collection of real-valued
functions on a metric space was proved by Goldstine [2]. Alexiewicz
[1] has made R systematic study of circumstances under which theo-
rems analogous to Theorcfns 1.17. 1.18, and the condensation theorem
are valid for classes of continuous Inappmgs between mt:"trJ<: spaces.
HIs comlltJons are such that they can be spet-;,alizcd to gh.e those
82
11 TitRE!:. lJAB1C' }>RI CIPLES
11.5
II.5
NOTES AND REMARKS
83
theorems or to givc genc....tlizations of some theorems of Saks [2, 3]
on sequences of measures. Alexiewi{:!z [Ii II] also discussed these
results in spaces where certain abstract notions of limit are available.
Mazunmd Odicz [2] (see also Alexiewicz [I; []) have e.uended these
three theorems to poLynomial operators in F-spaces. A]exiewicz [I;
III] has also treated polynomial operators in a lmear space in which
various notions of limit are present. Orlicz [7J proves a. theorem of the
condensation type where the double st't)uence of operators also de-
pends on a parameter in 8 complete metric spa . which includes the
following theorem.
THEOREM. Let D. be a continuous jundioll all J::. [0, I] to'[) and
lIuch riwl jor rorh t £ [0, I], D.(., I) £ B(J:, ¥J). Ij jor each t £ [0. I] thae
€xist8anxtsuchthatlimsuPn_o;> IU I1 (Xt,t)j =00, thenthereex-istsanxsuch
that lim sup.-->o> !CJ.(x, 1)1 = 00 jar all I in a 7wn-d.nlJlllerable perjecl
lie' in [0, I].
Gn! [I. 2] has extended the uniform boundedness theorem and
the condensation theorem to a class of non-linear homogeneous ma.p-
pings between B-spac.., under certain I.ypothcses that compensate
for the lack of linearity.
Let {Tnl'" . A} be a generahzed sequence of bounded linear opera.
tors from onc B-space J: into another B-8pace ). Day [9] has consi-
dered the question of when lim snp..A IT."'I < 00, x. J:, implies that
lim !'!UPc;tEA ITal-< 00. Among other results, he showed that this is valid
for any directed set A If and only if I is finite dimensional.
A numher of throl"t'ms of the uniform boundedness type together
with applications are provcd by Dunford [I; Chap. I]. It is seen (Dun-
ford [I; p. 808]) that thc closed graph theorem (11.2.4) together with
the Hahn-Banach theorem can be used to give a "\rery simple proof of
the uniform boundednt"SS theorem for B-spaces
Bourbaki :3] has demonstrated that Theorem 1.17 rema"'s valid
in a certain class of locally convex topological linear slJaccs. (See also
Dieudonne and Schwartz [I; p. 73].)
Co"tinuityoj ti..ear aprratiQ"8. (These remarks refer to Theorems
1.14-1.16 anti 8.4,) Although special cases of Theorem 1.14 had been
used befure, it was first proved for a general B-space by Banach
[3: p. 151]. Mazur and Orlicz [1; p. 153] cxtcnded this and 1.16 to
F-spaces. Wehausen [I: p. 161] observed that 1.16 remains true when
the range is any topological linear space. He also derived necessary and
sufficient conditions for the continuity of linear operators when the
domain is a locally convex :space. A:s may be surmised by analogy with
the real case. additivity plus "measurability" of a function should
imply continuity. That such results are valid in metric groups was
shown by Banach [7] (see also Banach [I: Chap. I] and Kuratowski
[I]). Conditions of this nature are extended to polynomial operators
by Mazur and Odicz [2].
It is sometimes useful to define a notion of "continuity'" of a li-
near mapping T between linear spaces 1 and YJ if T maps sequences of
I which converge in some sense into convergent sequences in V). This
is the case, for example, when 1:. and ID are concrete linear spaces
having one or more natural notions of limit, ur when J. and \9 have a
notion of order. The reader will find such oecasions in the references
on partially ordered spaces. He may also compare Alexiewicz [I; II,
III]. Fichtenholz [1, 2], and Orlicz [5. 6].
The i.."'ivr 7Jlappi7lg principle. This result and the closed graph
theorem are closely related to the notion of category. Theorem 2.2
was first proved by Banach [4; p. 238] for the case of a B-space; his
proof was different than the one given. Schauder [7] gave a proof for
B-spaces which is closer to the one in the text; be also stated Theorem
2.1. The validity of the theorems in Section 2 for F -spaces was proved
in Banach's treatise by essentially the same arguments.
It is an interesting and important fact that Theorems 2.1 - 2.5
remain valid for homomorphic mappings of separa.ble complete metric
groups with left-invariant metrics. This fact was proved by Banach
[7]. The hypothesis of separability is required in the group case, as is
shown by the example of the identity map from the additive group of
real numbers with its discrete topology into this group with its usual
topology.
Pcttis [5] has given sev'eral necessary and sufficient conditions
that a homomorphism h between two topological groups X and Y be
continuous, or that it be interior,. i.e., map open sets into sds with an
interior point. We mention the following result
THEOREM. II the topological group X is compu-r.- ",ilk respeel w
84
II. THREE lIASIC }>JllSC1PLES
II.5
11.5
NOTES AND REMARKS
85
so"", right-invarianl (possibly non-rkJinile) me/Tic, Ihen a ho.nomcnphism
h: X -->- Y is an inlc";"T map inlo Y and 1= a closed kf7M, h-1(0), iJ
and only il Ihe graph 01 h is closed. and h maps each "o","void open sel
onta « .set wbose clo&url" contains ah open 8et.
Pettis [5] pr""...J theorems extending 80me of the results of
Banach [7], Freudenthal [2], and Lorentz [IIJ, and which, when spe-
cialized to linear .spaces, contain most of the results of this section
The field of scalars can be any field with non-discrete absolute
value (see Bourbaki [2; p. 34] for details). Further extensions have
been made by Dieudono and Schwartz ); p. 72] and othe", (see
Dieudonne [18; p. 504]) to the t'aSC where the domain space if is the
union of a countahle number of expanding F-spaces II Is [; . . .,
and the topology of if is defined in a natural way, the range space ID
having certain completeness and neighborhood properties. See also
Kothe [7, 10] and Ptak [IJ.
Similar theorems may be proved III more general topological
spaces, which do not necessarily have a group structure. For instance,
Dunford [5] generalized the notion of category to derive conditions
which are sufficient that a one-to-one continuous function send 8.
non-void open set onto it. set wllicll contains an interior point. McShane
[4.] gave conditions for a set of the second category in a topological
space to contain an interior point. His results were improved by
Pettis [3. 5].
For systematic treatment of interior (or open) mappings in to.
pological spaces, the reader is referred to Whyburn, [1, 2].
Schau del' [4, 5] (8ee also Leray [3], and [I] for other references)
bas proved a theorem on the invariance of domain which is similar to
2.1 for a class of non.linear mappings in a B-spsce. but also closely
related to Ct'rtain fixed point theorems (see Sec. V. 10).
THEOREM. Let I be a cOJltinuous mnpping d£lined on tM cloBure of a
bounded "pm sr.Wsd 01 a B-spat:< if with values in a compact subse! vi
:£. Then, iJ 1M mapping", -->- "'--r/("'} is om-Io-one, 1M image oj an vpt;n
ad is open.
For a proof, the reader is refeITt.'d to Kagumo [2:. L. 1\1. Graves
[5] has shown that a continuous non-linear function J.': I -->- ID be-
tween B-spaces such that F(",o) = Yo; maps a neighborhood of "'0 into
a set containing a neighborhood of Yo- provided that ' Can be approxi-
mated near "'0 by a continuo"" linear operator mapping '" onto ID. The
approximation is taken in a sense generalizing the notion of the dif.
ferential. This extends tfuoon>ms of Hildebrandt and Graves [1 J. where
the approximating linear operator was taken to bave an inverse. In
this latter case. however, considerably more refined results can be
obtained.
The following theorem, a special case of one due to Bartle and
Gra,,'es [I]. is a generalization of Theorem 2.1.
THEOREM. LetK(I) he a amlinuous lillear map vi a B-BpUl'e'" onlo
a B-space ID lOl'l € [0, I], andsupposelhal 1M mapt -+K(t) is CfJ1llinu.
ous frOnl [0. I] to B(if, m) with Ihe unilvrm operator lopvIogy. Then
Ihere e:rists a constant N > 0 sueh tiuzl il \" is a wnlinuous map 01 [0, I)
imo m, !here e.<isls a continuvus map 'I' : [0, I] -->-:£ such lhat
K(I)9'(t) = '1'(1), 19'(1)1 1\'1\,,(/)1, t € [O,IJ.
An important special case of Theorem 2.4 1S the case where T is
a symmetric linear mapping on all of Hilbert spatT, i.e., where
(T"" y) = ("'. Ty) for all "', y. It follows readily that T is closed and
. hence continuous. In the terminology of bilinear forms in infinitely
many variables this was proved by Hellinger and Toeplitz ll; p.
321-7], and in an abstract setting by "On Neumann [7; p_ 107].
See also Stone [8; p. 59].
Hisroriml Comments. Axioms closely related to those of a normcd
linear space were introduced, in 1916, by Bennett [I] it. a generaliza-
tion of Newton's method for the location of roots. F. Riesz [4] ex-
tended much of the Fredholm theory of integral equations using the
axioms of a complete Ilormed linear space, and Lamson [I] proved .an
implicit function theorem for such s . In 1022, Banach [8],
Hahn [2], and Wiener fI] published papers using the same or 8imilar
sets of axioms. Though Banacb did not initiate the study of th,:sc
spaces. his contributions were many and deep-for that reason many
authors use the term Banach &part! to refer to a complete normed
linear space. Throughout this work. we will adhere more closely to
his own terminology and call them B-spaces.
The Hahn-Ballach Thearem. Both '1'hcorcms 8.10 and 8.Il are
called the Hahn-Banach theorem, but the reader should observe that
11.5
NOTES AND REMARKS
87
86
II. "j'HREE BASIC PRINCIPLES
11.5
the former applIes to any linear space (topologized or not) and the
latter is an application to normed spaces and yields thc cxist""ce of
mn!intUJus linear functionals. It wiU be seen in Chapter V that Theo-
rem 3.10 yie1ds the existence of many continuous Jjnear functionals
in any space when the topology can be derined by a family of OORt'U
neighborhoods of the origin. This plenitude of continuous linear
functionals wiJI be of utmost importance for much of what follows.
On the other hand, Theorem 8.10 has other applications to the ex-
tension of measures, integrals, etc.-see the references given below.
Though some of the res<'ar<'h of Helly [I, 2] and F. Riesz [2, 6]
dealing with the problem of solving an infinite system of linear equa-
tions is very closely related to this theorem, tbe extensIOn given by
Theorem 8.11 was first proved by Hahn [8; p. 217] for a real B-space.
Banach [4; pp. 212,226] (see al80 Banach [I; pp. 28. 55]) proved both
Theorem 8.11 and Theorem 8.10 and applied these results systema.
tically to real B",p"""", The trick involved in the case of a complex
space is due to Bohnenblu8t and Sobczyk [1] and, independently, to
Soukhomlinoff [1] who treated the mse of quatemion scalars as well.
The following theorem is due to Hahn [3; p. 216] and is a usefur
consequence of the Hahn-Banach theOJ"em. This result contains COf-
responding thromns proved by F. Riesz [2; p. 470] [6; p. 61] for L
and l , and by Helly [1; p. 271] for C[0,1].
scalars, {tr:, . . ., oX:} a finil£ set in ",.., and kit JI.f> o. Tmn, for any
£ > 0 tmre e;rim an tr 0 '" such that
rcj(;r) =C i ,
if and only if
i = 1, . . ., n, and !"'I < M +,
THEORE>I. LeI {c.} be a OO1lRtahle sel of scalars, and {oX.} a cmmtaM.e
set of elements in a B-'Pace I. Then tlwre exists an x" 0 "'.. such tlUlt
oX"(x.} = c. for all n, and such tlUlt I"'''' 11-1 if and only iJ
/1: ","c.1 s:. JI.f J 1: ",,,".1
for <very finil£ ooUecrWn of ecalare {o:,}.
A similar theorem dealing with the solution x . '" of the infinite
system
l1:o:...I 5:- M l1:o:,ol';1
far every fin.'" colkct;"n of scalars {o:,}.
We cite a related theorem of Yamabe [1].
THEOREM. Li!l K be a dense convex set in a 'lwTmed lillear space ..
Let :x £ I, 6 > 0, and 3:: t . . 'J oX: E 1* be arbib-ary.. Then there exiata a
y in K BUch that
Iy-trl < E; x;(y) = oX:'(oX), i = 1, . . ., n.
Theorems of this nature "-"" often useful in the theory of moments
or of approIimation.
The Hahn-Banach theorem can be sharpened to show the exist-
ence of c rtain invariant ljnear functionals. For examp]c, a special
case of a theorem of Agnew and Morse [1] reads:
THEOREM. In addition to the hypalhueR of Theorem 13.10 auppose
that G is an Al!I'lian (or a snlvabk) group oj linear trcmsforrJIQti<ms of I
which map ID into itself and that
p(g(x)} p(oX), goG, xd';
f(g(",)} = f("'), go G. tr. ID.
Tmn lhar ,,,,ists a rea! linear functional F on '" which mtell<U1 f and
such that
$:(:r) = C'21
n= 1,2,._ OJ
F(x} < pIx); F(g(.x» F(x). liE G, oXo:E.
For further generalizations of this nature and applicatIons to the
extension of measures, etc., the reader should consult Agnew [1],
Agnew and Morse [1], and Klee [5J.
Let P be a positive function as in Theorem 8.IOi then 1t IS of
interest to ask if there exists a real lioear functional f defined on '"
such thAt
is valid l'ro\"lded that the space I is reflexive. but not in general.
Tl1c following tbeorem, due to Helly [2; p. 73] is valid for general
spaces. (See Kakutani ;2] for an elementary proof.)
THEOREM. Let 1. be a narmed li'U'ClT space {CJ .."7 Cn} urbitnrry
f(x) < pCx), tr * O.
A necessary condition is that p(",) +p( -tr} * 0, for x * o. Aronszajn
[5] showed that if I is separable under the norm defined hy
88
u. THREE: BASIC PRINCIPLES
11.5
II.5
NOTES AND REMARKS
89
Ixl = p(x)+p(-a:).
then this condition is sufficient. BonsaU [I) showed that the separa.
bility condition cannot be dropped.
Ingleton [1] has given conditions for the Hahn-Banach theorem
to hold when the field of scalars is non-Archimedean. (See also Flei-
scher [I] and Ono [I].)
The Hahn-Banach theorem may be used to give short proofs of
the existence of Green's functions for the Laplace equation I and for
other boundary value problems. We refer the reader to the papers of
Garabedian [I]. Garabedian and Shiffman rI), Lax [I] and Miranda.
[2], for detnils and other refe1:ences.
Refle;rivi!y. The fact that the natural isomorphism of a B-space
:r into its second conjugate is isometric was proved by Hahn [8; p. 219]
who was the first to fonnulate the notion of thc conjugate space. Hc
used the tenn regular to describe what we. following Lorch [2], have
called reflu:;.'e. Examples of reflexive B-spaces are given in Chapter
IV, and a necessary and sufficient condition for reflexivity is given in
Theorem V.4.7. It is a consequence of Theorem V.6.I that a necessary
.and sufficient condition for reflexivity is that spheres be weakly
sequentially compact. This is due to Eberlein [1], and is tbe strongest
criterion known.
Theorems 8.23 and 8.24 are due to Pettis [1], Theorem 3.28 was
proved by Schmidt [I] for L. and by F. Riesz [2; p. 467] for L.; in
these spaces it is sometimes caUed the "Theorem of ChOlce4'" In the
case of abstra.ct Hilbert space, it was proved by von Neumann [2;
p. 881]; for a general reflexive B-spaee, Theorem 3.28 is due to Pettis
[1].
It must be emphasized that reflexivity involves the isometrIC
isomorphism of :r and I.. under the natural mapping" defined in
8.18, .James [4, 5] has proved the following startling theorem,
TIlEoaEM. Th£re erim a oeparable B-space which is isomorphic
and is(}metric with its MCOfld coniugak Bpace, but which is 110t refle.rive.
Fador spaces. Let:r be an F-space and!m a closed subspaeeol"3..
Let 11m be the factor, or quotient. 8pace as defined in section LB.
As is seen ill Exercise 11.4.18, JffJ1 becomes an .F-space under the
metric
This useful device was introduced by Banach [6; pp. 47-9] and Haus-
dorff [8]. It will be fundamental in the discussion of B-algebras.
Completion Qf spaces. In the definitions of F - and B-8paces, we
required the spaces to be complete in their metric topology. Occa-
sionally it is necessary to consider metric linear :spaces which are not
complete. In :such cases, the following theorem i:s often convenient.
THEOREM. Let:r be a linear space sa!isfyi-ng properties (i) and (ii)
of Defit,iJian 1.10. Then 3. is isurrwrphic and isomdrW with a dense linear
subsp<JCl' of an F-space i. Th£ space i is uniqudy ddermined up!o iso-
metrW isomorphism. It 3. is a normed linear space, rJu:n i is a B-space.
The proof of this thoorem plYKJfCds as in the Cantor completion of
the rational numbers to obtain the real numbers. Let'ID be the linear
space of all Cauchy :sequences in :fl whose vector addition and scalal"
multiplication in W are defined coordinatewise, and if y = torn} IE W.
let lyJ = sup 1"'.1. Then \1) is an F- (or a B-) space. Let.B be the dosed
.
subspace in 'V consisting of all Cauchy sequences in ! which converge
to zero. and let if = 'V/.3. The reader may verify that i has the stated
properties.
Direcl sums and products. Let 3i and 'V be two topological linear
spaces over thc same field of scalars. Let :r eo 'V be the direct sum of
tbe linear spaces :r and 'V in the sense of Section I. I I, with the product
topology of Section 1.8. Then J eo 'ID is readily 8een to be a topological
linear space. If ! and \lJ are B- (or F -) spaces, then J eo 'ID is a B-
(or an F -) space under either of the norms
If"', y]1 = rnax (Ixl. Iy/).
I[a:, y]j = {la:I +lyl }'I , I ,.,;; p < co,
Ix+!ml = mf {Ix+mllm .!D1}.
and these norms are equh'alent to the product topology. The space
J eo \lJ so obtained is called the direct sum of :r and \1) (although the
term dired product is used by some autbors). The extension to any
finite number of summands is immediate. By Lemma 1.8.4, the direct
sum of a denumerable number of B- (or F-) spaces can be made into
an F-space, but 1n general not into a B-space. Finally, one can deftne
the direct sum of an arbitrary family of 1opologicallinear sp8.ce , but
it is ordinarily not metric e""en if the summands are. It may be seen
90
II. 'tHREE BASIC PRINCIPLES
11.5
II.5
NOTES AND REMARKS
91
I* 0 \\)* (I ID)*
admits an equivalent metric under which it is complete, then G admits
an invariant metric and is complete under each invariant metric.
Thus every complete linear metl'ic Bpace can be metrized to be an
F-:space. Further, a Donned linear space is a B-space provided it is
complete under some equivalent metric. See also van Dantzig [1], [2].
Norms in linear Bpaces. We have seen that in a Donned linear
space there are many continuous linear functionals. LaSalle [I] (see
also Theorem V.2.8) showed that B non-zero continuous lineal' func
tional exists if and only if the space contains an open convex neigh-
borhood of the origin which does not contain the enhre space. How
ever. Kolmogoroff [1] proved that a topological linear space is
homeomorphic to a normed linear space if and only if there exists a
bG"rnkd convex neighborhood of the origin. Wehausen [1] showed
that if a topological linear space has a bounded neighborhood of the
origin (not necessarily convex) then it has an equivalent invariant
metric, but that an F-space may have no bounded sphere.
Eidelheit and Mazur [I] have proved that every F -spare can
be equipped with an invariant metric, equivalent to the original one.
such that if x oF 0, then the function 1=1 is a monotone increasing
function of the real 'variable a,
Isomd7y and linear di_ion, Mazur and Ulam [1] (see also Ba-
nach [1; p. 166] and Aronszajn [1]) have proved the interesting result.
that in the case of B spaces, if the norms are chosen appropriately.
'We have
:1'* m \\)* = (I m W.
For notational PIUJ'OS"S, let us denote the couple ["'. Y] . I ffi
by the symbol '" ffi y. Then we havc the linear relations:
"', e y, +"'. ffi Y. = ("" +"'2) m W, +y.),
"'('" e y) = = e "'Y'
We now ask if it is possible to construct a linear space from 1 and
in such a way as to make valid the bilinear relations;
'" 1;9 (YI+Y.) = '" 1;9 YI +x @Y"
("'1+"'.) 1;9 Y = X, @ Y + "'. @ y,
a{J(x (9 y) = (=) (9 (fJy)
This can be attained by taking the set :I' @ 'ID of all finite formal sumS
Ire, 181 Yf with suitable identifications. Such a space is caHed the direct
prod-1m (although the terms tensor. crGSs. and KronedreT producl are
also used). If I and 'ID are B-spaccs, it is desired to define a topology
on 1 (9 ID in such a manl1er that it becomes a B-spacel and such that
the relationship
is va1id. There are unexpected difficulties attached to this and aSSOa
ciated problems. These questions have been treated by a number of
authors; the reader may find the theory and further references in
Schatten [1] for the case of B-spaces. and in Grothendieck [8] for
general topological linear spoces.
Invariant mdriC8 in groups. A metric e on a (multiplicative) group
G is said to be left-invariant if r{gx. gy) = r(a::. y) for aU gin G. It is
said to be invariant if r{gx. gy) = e{a::. y) = e(xg. yg) for aU g in G.
If G is R topological group, we say it is metrizable if there is a metric
whose topology is eqU1valent to the original topology.
G. Birkhoff [5] and Kakutani [12] proved that a topological
group G admits a left-invariant metric if and only if the family of
neighborhoods of the identity can be defined by Q countable collection
(i.e., G satisfies the first axiom of countability).
Klee [6] showed that if G is an Abelian topological group which
THEOREM. Et"'Y mapping F of one Teal normed li1l£flr spa". onto
another which is istJ11U'tric. i.e., IF(a::)-F(y)1 = I"'-yl. and sIKh that
F(O) = o. is a linear mapping.
A proof for finite dimensional F-space has been given by Char-
zynski [IJ.
In Theorem V,8.S we will determine the form of the most general
isometric isomorphism between two spaces of continuous functions.
Banach [1; p. 174 -ISO] has represented such mappings in other
special B-spaces.
K. Borsuk (see Banach [1; p. 182-4)] showed that there is an
algebraic isomorphism which is also a homeomorphism between each
of the spaces L., 'D' P ;::.; J. c. cO. C[O. 1] and the direct sum of these
spaces with themselves. Mazur (4J demonstrated that L . and L
. "
are homeomorphic for I ;:,::;;: Pi :-;: P2'
92
11. THREE BASIC J"RINCJPI.ES
I1.5
11.5
NOTEs AND REMARKS
os
Banach [I; Chap. 12] defines! to be of sma/Jcr 1i>U'UT dimension
than ¥J if there is a one-to-one continuous linear map of.I onto a closed
linear manifold in \)), and writes dim, ! s dim,\)). A number of results
are obtained about the comparability of the L. spaces in the sense of
linear dimension. Banach and Mazur [1] have demonstrated that two
separable B-spaces can be of equal linear dimension but not be topo-
10gicaUy isomorphic.
Dillennti<d calculus in B-spaCl's. In Chapter III it will be """n
that a satisfactory theory of integration con be constructed for func-
tions with their domain in a Dleasure space and their range in a B-
space" and further that a theory of analytic functions of a <-'Omplex
lTariable with vatues in a complex B-space is also available. It is
appropriate to observe that at least the fundamentals of a theory of
the denvative exists for functions with both domain and range in
B-spaces. In the case of complex B-spaces the theory is relativel}
complete and reminiscent of the theory of analytic functions. For this
theory the reader i8 refClTt'd to Hille [1; Chap, 4]; the real case is
somewhat more complicated. Tbe central concept in both cases is
that of the FrtieM (or Iotal) differe1l/ial.
DEFINITION. Let 3i and \)) be B-sp8C'CS. Let D be an open set in 3:,
and F : D \)). Then F is said to have a Frlt-hd differential at the
point a < D if there is a linear operator dF(a,.) £ B(!, \))) such that
hm Ihi-IIF(a+h)-F(a)-dF(a, h)1 = o.
)111_0
L. 1\1. Graves [8] has proved the validity of a generalization of
Taylor'8 theorem with remainder. Kerner [1, 2] has extended Stokes'
theorem and developed a fonn of differential geometry-for the latter
see also IIlichal [I]. Differential equations have been treated by
Michal and Eleonin [I]. The implicit function theorem has been esta-
blished by Hildebrandt and Graves [1] other results along this line
are due to Michal and Chfford [1]. Cromn [1, 2] and Bartle [1].
For further references the reader should consult Hille [I] and
the expository articles of L. 1\1. Graves [I], Hyers [8], 1Iichal [1].
Rothe ,4], and Taylor [10].
Cvnr:etgtnce. A series I -1 X j is said to be unconditionally con-
1Jcrgenl if cvel1. ammgement of its terms converges to the same ele-
ment. It IS clear that a sufficient condition fot" unconditional conver-
gence is that the series be absolutcl.1I converge1l/, i.eoo that ::'I 1"'.1
eonverges. Dvoretzky and Rogers [1] have shown that absolute con-
vergence is equivalent to unconditional convergence if and only if the
B-space is finite dimensional. The Orlicz-Banach theorem states: a
SeNeS is unconditionally «m_gent il and only il every parlial sequence
conveTgCs rrellIdy 10 S01M eUm""t 01 tM spa<e. (See Banach [I; p. 240].
Dunford [I; p. 322]). In the ca8e when the space is weakly complete,
the series is unconditionally convergent if and only if I l IX* il
is convergent for each 3:'* in I*.
References on convergence: Dvoretzky and Rogers [1], Hilde-
brandt [1], Karlin [1], Macphail [I], Munroe [I], Nikod:fm [1],
Orlicz [I. 2],
For special types of convergence in abstract linear spaces:
Gagaev [1], Maddaus [I], Nachbin [I], Titov [1,2], Vulich [8].
Orthogtmalily. At least four definitions of orthogonality of ele-
ments of a real nonned linear space have beeu employed. Possibly
the most fruitful is the one introduced by Birkhoff and extensively
<leveloped by.James [2]: x is said to be orrhogonal to y if and only if
1"'1 -s: I'" +kyl for all real k. This notion has been related to concepts of
-strict convexity t weak compactness, differentiability of the norm..
.and various properties of linear functionals. In terms of it. several
necessary and sufficient conditions that an inner product can be de.
fined have been given by James [2, 3].
References on orthogonality: Birkhoff [I], Fortet [I, 2]. James
_I, 2, 3], Roberts [1].
Bases. A sequence {x.} of elements of a B-<space 3: is called"
-base (or basis) if for every '" £ ! there is a unique set {a,} of scalars such
that
n
lim 1"'- a,"'. I = O.
71_0;. i_I
This notion was mtrodu 'Cd by Schauder [1] and is convenient in
extending results from finite to infinite dImensional spa.ces, whenever
the base exists. A number of other types of bases have also been used
by various authors. It can be seen that this concept is closely related
to the problem of (biorthogonal) expansion of an arbitrary element.
It is clear that" B-space having a base in the sense defined above
94
II. THREE :BASIC PR!NCIPLES
II.5
rnust be separable. The converse question as to whether every separ.
able B"'pace possesses a base bBS not yet been solved, In the spaces
c G or 'II' I :5: P < co. the vectors {w.}. where iJ;,i = [6."J.' l}i2' . . .J,. form
a base. In c, these vectors with "'0 = [1,1, 1. . , .] added form a base.
Schauder [1] constructed a base In the space CEo, IJ, and proved
(Schauder [3]) that the Haar orthogonal system is a base for L.,
t ;,:; p < 00. In L.(O, 1) the trigonometric or Legendre polynomia1s
can be normalized to fonn a base; in L,,(O, 00) the Laguerre functions,
and in L 2 ( - 00. (0) the Hermite functions, are sometimes used.
For addition results on bases and biorthogonaI systems, see the
following: AI'tman :[1. 2], Babenko [1], Bari [1], Banach [I; Chap.
7], Boas [2], Bohnenblust [8], Dieudonne [16], Dixmier [7], Frink
[1], Gelbaum [1,2.8], Gdfand [6], Grinblyum [1. 2, 3. 4). Gurevic
[I], James [4], Kaczman and Steinhaus [1], Karlin [1.2]. Kostyu-
cenko and Skorohod [1], Kozlov [1, 2], Krein, Milman and Rutman
[1], Lorch [1]. Markouchevitch [I, 2, 8]. Nikol'skii [1], Orlicz [8],
ScbMke [1, 2J, Schauder [1,3], Tseng [IJ, Viuokurov [1) and Wi-
lansky [1].
CHAPTER III
Integration and Set Functions
I. Finitely Additive Set Functions
In contrast to the terms real function, complex function, etc.,
where the adjectives real and oom refer to the range of the func-
tion, the term 8e! fu'ltClion is commonly used in mathematics for a
function whose domam is a famny of sets. The theory of the integral
(E) = f ,)(s)l-'(ds)
.as developed in this chapter is based upon a set funct.ion p... In WJffie
cases that will be encountered the values of p are not scalars, but
customarily where integration is used in this text p is 8 scalar valued
function Bnd I a. vector (or scalar) valued function. Thu!!, even if the
integration process is defined with respect to a scalar valued set
function p, the resulting integral" may be a vector valued set function.
It is desirable therefore to formulate some of the basic and elementary
roncepts in such B way that vector as well as scalar ,-alued set func-
tion8 may be 8tudied. A discussion of some of the deeper properties of
vector valued set functions is contained in Section IV.IO. It is desirable
also to allow the set function I-' to have its values in the extended real
number system (which is not a vector space) but. since 00+(-00)
IS not defined and it will be necessary to add values in the range of 1-'.
it will be stipulated that an extended real valued set function has at
most one of the improper values 00 and - 00.
I DEFINITION. A set fuMtwtl is a function defined on a family
of scts, and having values either in a B-space, which may be the set
of real or complex numbers, or in the extended real number system,
In wInch case its range contams at m08t one of the improper values
+ 00 and - 00. A positive set function is a real valued or extended real
valued set function which has no negative values.
95
96
111. INTEGRATION AND SET FUNCTIONS
III.I.2
1II.1.4
FINITELY ADDITIVE SET FUNCTIONS
97
2 DEFINITION. A sot function I' defined on a family ..- of sets is
said to be additive or finitEly tu!ditive if T contains the void set "',
if I,(<J» = 0 and if
I'(A I U A... . U A.) = I'(A I )+fL(A.)+. . .+,u(A.),
for every finite family {A" . . ., A.} of disjoint subsets of T whose
union is in T.
For an example of a finitely additive set function, let S = [0, I)
and let T be the family of intervals I = [a, b), 0 < a < b < 1. with
1'(1) = b-a.
We will ordinarily require that the domain of an additive set
function be closed under the finite operations of union, intersection,
and complementation. If A and B are subsets of a set S it is conve.
nient to introduce the 8ymbol A-B to denote the set An B'. How.
ever this notation will be avoided whenever S is a group and there is
possibility of confusion with the group operation. We will use the
notation ALl B for the symmetric differetl£e (A-B)U(B-A).
s DEFINITION. Let S be a set. A ld of suli.e18 of S, or a Boolean
algebra of subsets of S, is a non-empty family of subsets of S which
contains the void set, lhe complement (relative to S) of each of its
members, and the union of each finite collection of its members.
A field of sets clearly contains the difference and the symmetric
difference of any two of its members, It follows from the rule8 of De
Morgan that
A,nA.n ...nA. = S-{(S-AI)U (S-A.Ju-..U (S-Aft)).
Thus a field of sets contains the intersection of each finite collection
of its members..
In the example above, let E be the family of all finite uniooo of
intervals I = [a. b) in T. ThenEisafieJd. If A E E, then A = U _,I"
where the interva1sI, are disjoint. If pIA) = Z:'-,p(I,), it can easily
be seen thatp(A) depends only on A and not on its particulardecom.
position into intervals, and that p is a finite1y additive set function
defined on the field E.
The next step in our anAlysis is to show that an arbItrarily given
set function p can be used to define a non-negative set function v(P),
called the total varia lion of I" The set function v(l') is defined so as to
be equal to p if p itself is non-negative and additive, to be additive
if ,u is additive, and to be bounded if ,u is bounded and add,l1ve.
The total variation v(P) of an additive set function p is important
because it dominates,u in the sense that v(p, E) ;;:: II'(E)I for E E E;
the reader should test his comprehension of Definition 4 below by
proving that v(l') is the smallest of the non-negative additive set
functiuns A such that A(E) ;;:: [,u(E)1 for E. E.
" DEFINITION. Let,u be a set function defined on the field E of
subsets of a set S. Then for every E in E the total rxn-ffition of p on E,
denoted by vip. E), i8 defined as
.
vip, E) = sup z 1,u(E,)I,
<--,
where the supremum is taken over all finite sequences {E,} of disjoint
sets in E with E,!;; E. The set function p is of bounded ooriation if
v(p, S) < co, And it is of Wunded variation on a set E in E if v(p, E)
< co.
5 LEMMA. If a .ear or complex valunl additive setfuru:tion definnl
on a field E 0/ subsets of a set S is baunded, ;r is of bouwled variation and
"(p, SJ S; "sup [I'(E»).
Eol:
PROOF. Let,u be an additive set function on E with 1,u(E)1 ;:;; lIef
for every E in X. If It is real valued then for any finite sequence
{E" . . ., Eft} of disjoint sets in E
.
z II'(E,)I = Z+ I'(E,)- Z- ,u(E,) = 1'( U E,)-I'{ U E,)
._1
where E+ and U + (2'- and u - J are taken over those t for winch
piE,) 0 (I'(E,) < 0). Thu8
v(ft, S) = sup (ft(A)-I'(B)} ;:;; 2"U.
A,Be!:
If p is complex valued its real and imaginary parts are additive real
set functions on E whose ahsolute values are bounded by IlL Thus ill
this case v(l', S) :;; 4.'11. Q.E.D.
If I' is understood we may write viE) instead of v(p. E). If p is
non-negative and additive, v(p, E) = I'(E)- It is often !ielpful to
think of viE) as the limit of a generalized sequence in the following
manner. Let the fomil}' of all finite sequences {E,} of disjoint sets in E
with E, E be ordered hy defining {E,} {F,} to mean thnt each E,
98
III. INTEGRA "1'ION AND SET FUNCTIONS
111.1.6
111.1.9
FINITEI,Y ADDITIVF. SET FUNCTIONS
99
is the union of some of the sets F,. ThenElp(E,)] ;:;; Elp(F,)1 and we
have viE) = limElI'(E,)f.
(E,I
6 LE....A. Th£ lotal variatwn of an addili.", Bel fundirm I' defi1led
on a field 1: of subsrlB of a Bel S i> also onditive rm E.
PRoOF. Let {A,} be a finite 8equence of disjoint sets in 1: with
A, EU F where E. F £ 1: and EF = 1>. Let E, = EA" F, = FA"
then
:lI'IA,)1 ;:;; III'(E,)I+III-'(F,)1 ;:;; v(l-', E)+v(,u, F),
wMre F is reatrided 101M domain 1: 011'. Th£ sel functions 1'+, f' are
additivt:, nnn--nf'gative, and fOT each E in 1:.
I'(E) = f'+(E)-p IE), v(,u, E) = I-'+(Ej +I-' (E).
PROOF. If F E, E, Fe 1: then
21-'(F) = I-'(F)+/-4E)-I-'(E .F)
:;;: I-'(E)+II'(F)I+lp(E-F)1
< I-'(E)+v(I-" E) = 2/-,f-(E}.
TItUS
and hence
sup I-'{F) ;:;; I-'f-(E).
F£E
On the ather hand let E > 0 and let E 1 , . . ., En be disjoint sets in 1:
with U E, = E and 1:11'(E,)1 > v(,u. E)-E. Then. in the notation of
Lemma 5,
(i)
Ii) v(l'. EU F) ,,;; v{p, E)+v(,u. F).
Thus if v(,u, E U F) co it follows that v(l-', E U F) = v(,u, E)+
v(l-'. F). If v(,u, EU F) < co there are finite sequences {E,}, {P,} of
disjoint sets in 1: with E, E. F, F and
v(,u, E) < 1:11-'(E,)I+., v(,u,P) < 1:11-'(F,)I+E
vI,." E)+v(,u, F) ;:;; 1:lp(E,)I+1:j,.,(F,JI+2e
:;;: v(,u, EU F)+2..
Since e:> 0 IS arbitrary, v{p. E)+v(,." F) ..;; v{p, E U F). whlCh taken
together with (i), show8 that v(,u, E) is additive for E in E. Q.E.D.
In the next. definition and theorem. we show how the total varia-
tion of a bounded additive real valued set function p can be used to
define the "'positive" and Unegativel'l parts of 1'_ The process is similar
to the decomposition of a function f(') into the difference of two non-
negative functions: if we put ff-(.) = (1/2)(1/(')1+/('» and f-(') =
(1/2>11/(')1-/('», then f+ and f- are non-negative, and f = ff--/ .
., DEFINITION. Let I-' be a bounded additive real set function
defined on a field E of subsets of a set S. The UppeT or pomive varia.
lion p+ and the lower or negative oorialion I' of I-' are set functions de.
fined on 1: by the equations
I-'f-(E) = Hvl,." E>+I-'(E)}, I-'-(E) = Hv(,u, E)-I-'IE)}.
8 THEOREM. (Jordan dero11lp(l8iti<m) If I-' is a hourukd addiliI'"
real Be! fundi.n defined rm a fkld 1:. tJU'n, fm €ach E in 1:.
I' (E) = StIp I,(F), I':(E) = - inf ,.,1 F).
F£!: F£E
2,.,f-{E)-" = v(l-', EI+I-'(E)-E ;:;; 1:II'IE,}I+"IE)
= 1-'( U +E,)-I-'( U E,)+iI« U f-E,)+I-'( U E,)}
= 21-'(u+E,) ;:;;2suPI-'IF).
E£E
Since E> 0 i8 arbitrary, I-'f-IE) ;:;; SUPF"E ,,(F), which, with Ii) above.
shows that I-'+(E) = SUPFCE I-'(F). Since 1'- = {-f'}+ it follows that
I-' (E) = - inf F .>;" "IF). The remaining conclusions of the theorem
follow readily from the defmitions. Q.E.D.
In the theory of an additive set function I-' certain non-empty
sets are likely to occur which are in many waY8 negligible as far as I-'
is concerned. These are the p-null sets as introduced in Definition 11
below. They may perhaps best be introduced by first considering a
certain (not necessarily additive) extension p. of a positive set fune.
tion I' which is defined as follows:
9 DEFINITION. Let I-' be a positIve extended real valued additIVc
set function defined on a field 1: of subsets of a set S. For all arbitrary
subset E of S the number p*(E) is defined by the equation
p*(E} = inf I-'IF),
F "
where F is restricted to the domain 1: of 1-"
1110
HI. IN'l'EGRATIOS AND SET FUNCTIONS
III.I.lO
111.11.1
INTEGRATION
101
10 LEMMA. L£I p be a p<JSitive ea1endcd real valued additive 8et
Jmu:tion defif'l£d on a field E of ..,Net" of a 8e' s. Then
(a) p*{E)=p(E), E£E;
(b) p*(AUB) < p*(A)+p*(B), A, B';;;S;
(c) p*(A) S; p*(B), A';;;B';;;S.
PROOF, If E. E, F. E, and F;;;) E, thenp(F) =1'(E)+p(F-E),
so that p(F) ;e;; pIE). Thus p*(E) pIE). On the other haod. since
E;;;) E, pIE) ;e;; p*(E). This proves (a). To prove (b) let e> 0 and
let AI' B I £ E be such that AI;;;) A, B I ;;1 Band
p(A I ) ,;;; IL*(A)+e/II, p(B I ) ;:;;; p*(BJ--t.e/2.
Then A I UB I ;;1AUB and
p*(A U B) S; peAl uBI)
= 1.(AI)+p(BI-A I )
;:;;; p(AIJ+p(B I )
S; p*(A)+p*(B)+e.
Since, > 0 is arbitrary, this proves (b). Statement (c) follows imme-
diately from the definition of p*. Q.E.D.
Definitions 4 and 9 allow us to Introduce one of the most fre-
quently occurring concepts In measure theory, namely, the concept of
a null set. This is done in the following definition.
11 DEFINITION. Let P. be an additive set function defined on a
field of subsets of a set S. A subset N of S is 8aid to be a p-null 8et if
v*(p, N) = H, where v* is the extension of the total variation I) of Jl
defined in Definition 9. It follows immediately from Lemma 10 that
every subset of a J.l-null set. and every finite union of ,u-null sets, is B
p-null 8et. Any statement concerning the pomts of S is said to hold
p.-all1!.vst f.'Vt7'Y'Wherr:, or. if p. is understood. simply almost evetyrt'hen?,
or for alrnost all B in S, if it is true except for those points 8 in a
p-null set. The phrase "almost eyerywhere" is customarily abbreviated
"a.e." Thus. if lim.f.(8) =/(8), s<S-N, whereN i8 ap-null set, -"'e
say that the sequeoce {fn) converges to f a11ll08l roeryw/Iere on S.
In addition to ' p-atmost everywhere" there is another expression
which is relatt-d to the notion of a p-null set and which is used in con-
nection with functions f on S where the emphasis is on the range of I
rather than 00 its domain S, Thus if there is a p-null set N such that
the restxi -tion of f to S-N is bounded, then f is said to be p-essentially
bournkd or simply essrnJ.ially boundnl. The quantity
jnf sup 1/(8)1.
1'1 £S-N
where N ranges over the p-null subsets of S is called the p-usential
suprt"fI"Il7n or p.e8senlialleMt upper bound of )f(')1 and is written as
ess sup If(s)1 or esS lub If(8)1.
$6 s
If for some null 8et N the restriction of f to S -N bas its values in a
separable set, the function f is said to be ;.<-e8BffItialJy separably valued.
Expressions such as essenliaJly etrll<pacl valued are defined similarly.
In the example above. where E is generated by intervals I = [a, b),
o S; a < b < I. and 1'(1) = I.-a. we note that any finite setofpoint.o;
as well as any com'ergent sequcnce of points in [0, 1) is It p-null set.
2. Integration
[n this section and the following on Lebesgue spaces, we will be
concerned with defining and developing the basic properties of the
integral f /(')1'(&). In these sections f will be a vector valued func-
tion defined on 8 set Sand p a finitely additive set function defined
on a field of subsets of S. It will not be assumed that I' is bounded.
Thus the basis for this material is a fixed Bet S, a field L of sub8ets of
S. and a finitely additive complex or extended real valued set func-
tion I' on L. The functions to be integratcd will have their values in a
real or complex B-space :f.
Thc first step in our analysis is to introduce a topology on the
set of all fundions defined on b" with values in a B-space :f. This
topology will be defined by a certain metric function, wbich will be
chosen so that two functions f and g are close together in tem!s of thc
metric if /(8) is close to g(8) except for thosc8 in asct E in Efor which
vIp. E) is small.
1 DEFINITION. For every E ';;; S, every « 0 and every func-
tion f on S to 1: we define the subset E( If I > «) of E by the equation
102
III. Th"TEGRATJON AND SET FUNCTIONS
111.2.2
111.2.11
INTEGRATION
103
E(I/I > 0:1 = {SIS. E, 1f(.)1 > O:},
and the norm 1/ I of I by
III = inf arctan {o:+v"(.u, SWI > o:»}.
_>0
space of III! functions which map S into I (see 1.5.1). Unfortmuttely,
this is rarely the case and so a slight detour wil! be made.
It should be remarked that we take the principal value of the
arctan; i.e., that value lying between 0 IInd "/2. The function
arctan in Definition 1 is used to insure that III < 00, even though
v.(S) = 00. In fact, arctan could be replaced by any continuous in-
creasing function <p such that <p(0) = 0, '1'("'1+"'.) <P("'1)+1"(""} for
"'., x. 0, and <p(co} = lim..-+", '1'("') exists; e.g_, <pIx) = ",(I+X)-I.
Ifv.(S)<co we may take
111= inf [o:+v.(I', S(I/I > «))].
a>O
3 DEFINITION. The function I on S to I is said to be a p.null
/undion or, when It is understood, simply a null function if the set
S<lfl > 0:) is a p-nul! set for each 0: > O.
It is important to observe that a null function with respect to a
finitely additive set function need not vanish almost everywhere.
For an example of such a function, let S = [0, I) and E be the field of
finite unions of intervals I = [a, h), 0;:;;; a < h < I, withl'(I) = b-a
as in Section 1. Let R denote the set of rational points in S. For r =
pfq . R in lowt'St terms, we define I(pfq) = Ifq, and set 1("') = 0,
S . S - k. Since for ellch 0: > 0, 8( III > «) is a finite set, I is a I"null
function. However, p.(R) = I.
The reader should avoid confusing the norm of I with the norm
I/(a) I of the values I(a) of the function I. If we wish to consider the
function defined by g(s) = I/(s)l, we may write it on occasion as
1/(')1, but ,,,,,,,,r as III. If the reader k<'Cp.< these notational conventions
in mind, he ""viII be spared considerable confUSIon.
Note also that, with the nonn just defined, the set of .all functions
on S to is not in general a linear topological spa«, since f}f need
not appruach zero as f} approaches zero (cf. Exercise 9.7).
4 LEMMA. A fundW" I "" S to I is a p.nuU fwnction il and only
ill/I = O.
PROOF. If II! = 0 1 then t for each £ > 0 1 there is an (It > 0 such
that o:+v"(.u, S()/I > 0:» < e. Thu8 0: < £ so that S(I/I > «);;)
8(111) £) and v*(.u, 8(111) e» < e. Since 8<1/1> ")!::; 8(111) £) for
" > e, we have v.(.u, 8<1/1 > "» < £ for" > e, which proves that
v*(.u,8<1/1 > II» = 0 for every" > O. Conversely, it is clear that
III = 0 provided that v*(I-" 8<1/1 > «)) = 0 for each 0: > O. Q.E.D.
2 LE""A.Iffandgareluru1itnlsonStoiftJu.n I/+gl :S: 1/1+lgl.
PROOF. Let «,f!>0. Then S(I/+g!>«+f!)!::;8(1/1>0:)u
S(lgl > P) and
I/+gl = inf arctan {o:+f!+v*(I-', 8(I/+gl > O:-j-f!))}
a.fJ>O
, inf ard:an {o:+v*(p, S(I/I > 0:»1
_>0
5 COROLLARY. The null fum:liOTUf lorm a linear subspace 01 tlu:
8piUT 01 all lunctionwn 8 to :£.11 I is a null fum:tion and il Ig(.)1 :S: I/(s) J
almoRt et.'i'rywhere on 8 t1u:n g is a nuU fundi",..
Lemmas 2 and 4 show that the relationship bet:ween two func-
tions I and g on S to I which is expressed by the statement that I-g
is a null function) is an equivalence relation. The linear set of all func-
tions on S to 1: can therefore be divided into mutually exclusive
equivalence classes. For an arbitrary function I on 8 to if let [I] denote
the class of functions equivalent to I (i.e. all g such that I-g is a
I'-null function), and let F(S, E, 1', I) denote the set of all such sets
[!]. If the following equations are used to define their left hand mem-
bers then Lemmas 2 and 4 show that F{S. E, 1', I) is a linear vector
space as well as a metric space with the distance function e([I], [g])
= I[lJ-[g]l:
;:;;; inf arctan (o:+v.(I-', SOIl> rx»+P+v.(f', 8(lgl > P))}
a,fJ>O
+ inf arctan {Ii +V.(I-'. S( Igl > P))}
p>o
= 1/1+lg:. Q.E.D.
If it were known that I = 0 whenever III = 0, the preceding
lemma would show that the function eU,g) = I/-gf is a metric in the
104
III. INTEGRATION AND SET FUNCTIONS
111.2.6
111.2.8
INTEGRATION
105
[/J+[g] = [/+g];
!X[/] = [!Xf);
1[/]1 = Ifl.
Since Igl = III it" [g] = [j). it is clear that the above equation defines
the norm uniquely. r.loreov rl' just as in the general case for a factor
space (see Section 1.11) the addition and scaJar multiplication of
equivalence classes is well defined.
It is customary to speak ofthe elements of F(S, E.I-" 1:} as if they
were functions rather than sets of equivalent functions and this we
shall ordinariJy do. Thus, we shaJJ write I instead of [/] and think of
F(S, E, 1-', 3:) as the set of all functions on S to 1:. No confusion should
arise if it is remembered that two functions which differ only by a
null funetion are considered to be the same. Thus a function 'I' can not
beeonsidered as defined on the space F(S, E,p, 3:). urness 'l'U> = 'l'1g)
whenever I-g is a nul] function, SimiJarly, if a function I on S to 3:
i. defined and is referred to as a point in the space F(S, E, p., 3:), whnt
should be understood is the class of all functions g on S to ;E which
differ from I by a null function. Where the vector space ;E is fixed
throughout a dis<-ussion, the 8ymbol F(S, E, 1') will80metimes be used
instead of F(8, E, 1', I). Likewise, if I and l' are clearly understood,
the symbol F(8) may be used in place of F(S, E,p).
(h) if v*tu. S!If.-/1 > eJ) > iJ > 0, e> O. then 1/.-/1 >
min [arctan iJ, arctan eJ. Q.E.D.
8 LEMMA. Let 1 and g be lu"ctilms on 8 to I,
(a) The muppi1lg 1, g I+g is a "",.li"",0"'8 map 01 F{S} X F(S)
inlo F(S).
(b) For a lixed scalar !X 1M map 1 !X1 is a ccmJ.in1UJU8 map 01
F(8) info ilsdl.
(c) II I. crm a 10 1 in l'-mrosure, then //.(')1 corwergt:8 to 11(')1
in p-mensu:re.
PROOF. If 1. I and g. --+-g, then, by Lemma 2,1/.+II.-(/+g)1
;;;; I/.-/I-+-Ig.-gi 0 and so I+g is a continuous function of I and g.
AlsoI' since (b) is trivia] if a: = O. we can assume a. =1= 0, in which case
6 DEFINITION. Convergence in the metric space F(8) is called
oom.ngena: in p.-m£nJJUT€, or simply convtTgcnce in mea8tlTe. A sequence
{I.} of functions on 8 to I converges inp-7rI€LU/Ut'r to the fum:tion 1 on S
to I if and only if
8(I!X/.-!X/I > eJ = S(I/.-/I <- e/l",I),
which shows that !XI. --+!XI if I. --+ 1. The last statement follows from
lhe inequality
111.(a)I-I/(8)1I ;;;; 11.(a)-I(a)l. Q.E.D.
Various linear subspaces of F(S) will be of particular importance
in the development of the theory of the integral. We shall, in fact,
first define the integral for functions of a very simple type, described
in the next definition. The domain of definition of the integral will
then be extended, by using its continuity properties, to a much larger
class of functions.
lim 1/.-/1 = o.
9 DEFINITION. Consider a function 1 on S to iE which has only a
finite set .xl' . . ., or,. of values and for whi h
I-'(x,) = {ala £ S, I(a) = x,} £ I, i = I, . . ., n.
AllY function g on S to I which differs from such an I hy a p-null
function is called a p-simple 1"'''ctiot!.
In accordance with our usual habit of saying "function" instead
of "equivalence cIass of functions". we shall of tell treat a I-'-sirnple
function as if it were necessarily a function taking on only a finite
number of values. and taking on these values on sets of E. If the reader
remembers tlmt we ordinarily make no distinction between two func-
tions differing by a null function, this will cause no difficulty,
It follows from Corollary 5 that the p-simple functions form a
linear manifold in F(S).
.-
7 LEMMA. A sequence {1ft} 01 Jundioru; on 8 to I convtrges in
meaaure 10 Ihe function I on 8 to I il and onlll if
lim v*tu. 8<11.-11> ej) = 0
ft_
lor t:Very e > O.
PROOF. The proof follows from the following elementary in-
equa1ities:
(a) if It.-/I>iJ>O and 0<e«1/2)taniJ, then
v*(,u. Slit., -II > e}) > (1/2) tan iJ;
106
III. INTEGRATION AND BB'1' FUNCTIONS
III.2.10
111.2.12
INTEGRATION
107
10 DEFINITIO>I. The functions wtally ",-mellSUl'lIble Olt S. or, if
'" is understood. wrally measurable on S are the functions in the
dosure TM(S) in F(S) of the ",-simple functions. If for every E in
E with vII', E) < <1:>. the product :lE1 of f with the characteristic
function XE of E is totally measurable, the function f is said to be
",-mnumrahk or. if I' is understood, simply measurable. A aet A is
m£iJ8Urahk if XA is measurable. Symbols for the set of measurable
functions are M(S. E. "', I), M(S, E. ",). M(S) and symbols besides
TlIf(S) for the set of totally measurable functions are TM(S. E, "', I)
and TM(S. E. ",).
n LEMMA. The totally rlWUUroble fwwtions as we!! as 1M
metJllUrahk functions form a dosed limar a-ub8pMe of F(S).
PItOOF. The set of p-simple functions forms a linear manifold in
F(S) and hence, by Lemma 8, its closure TlIl(S) does likewise. Since
if {In} converges in measure So does {f"xE} for any set E in E, it fol.
lows that the set M(S) is also a closed linear manifold in F(S). Q.E.D.
12 LEMMA, Let I, P be totally p-meaaurahk (I'- ) furn:.
litm8 I>n S wilh (J aeawr valued and let g be a ronti"uo.... funeli<m defined
tm lhe field of Malnrs. Then lhe lundwna Pf, If(' )1, and g(P(')) are
wrallyp- (p--17U!asuroble).lf one of {J and I is p,-null. whik lhe
ather is wtally p le. {Jf .. ",-null. Furlkermare lhe m<lppiflg
(J ->g({J('» i. a rnnti7luous map allhe apace alwtnlly mrostJ.rahk
acalar lundio7la ;'1110 ilself.
PROOF.. In view of the identitIes
XE(S)P(S)/(s) = (xE(a){i{a))(XE(a)/(a)), XE(s)l/(s)l = IXE(s)/(a)l.
XE(S)g(,8(s)} = g(XE{s)ft{a)) - g(O)XE.{a),
the statements made in the lemma concerning p-measurable functions
will follow from those concerning totally ",-measurable functions.
We now show that if {J and f are totally p-measurable so is their
product. Let {In} and {{in} be sequences of finitely valued p-simple
functions converging in measure to f and (J respectively, and let E be an
arbitrary positive number. For n sufficiently large, the function fi is ap-
proximated uniformly within Eon aset whose complemifot has measure
less than . by a bounded function P. of the sequence. and a similar
remark applies to I. Thus there is a constant M and a set Ao such tl1at
and v*(""A )<.. Now, there e"jgts an integerN.such that if ,, N.,
.
1/.(a)-/{a)1 < M '
.
1{J.(s)-{J(s)1 < M '
1{i(s)1 lit.
I/(s)1 $" M,
BEAO!
for all a in a set An for wl1icl1 v*(p, A:) < E. Tl1us,
I/n(a)ftn(s) - f(s){J(a) I ,;; 1/.(s) -/(s)!lftn(s)!
+ l{Jn(a) - fi{s)lI/(a)1
E: ,£ 6 2
,;; M (E+M) + lit lit = 2E + lIf
for a. A" n A., where ""(P. (A. n A.)') < 2., This shows that the
sequence {{i..!.} of p-simple function8 converges in p.measure to Pf.
The fact that If(')1 is totally p-mea8urable follows from Lemma 8.
Now let g be a continuous function defined on the field of scalars
and let (J be totally ",-measurable. Let {Pn} be a sequence of finitely
valued p-simple functions with P. -> P in ",-measure, Given . > 0
there is, as before, a constant M and a 8et A" such that ""(p. ) <.
and IP(s)j ;;;; M. s . Ao. Let <I be a positive number less than one such
that Ig(<<)-g(1')l <. if 1«-1'] < <I and 1«1. 1,,1 ,'11+1. There is a
sequence of sets {An} and an integer Nr. such that if n N ,
l{Jn(s)-P{s)! < <I, s. A.,
and v*(,u, A ) <.. Thus for" > N..
jg({Jn{s»-g({J(s»j < E, BE An n Ao,
and ""(p, (AnnAo)'} <2.. Thus g(Pn(')) ->g({J('» inp-measure and
therefore g({J(.)} is totally measurable. The argument of this para-
graph may be used to prove the last statement of the lemma.
Finally, let f be totally measurable and let {J be a scalar valued
null function. Given l: > 0 we can. by our previous remarks t find a
Cl>nstant M and a set Ao such that If(s)1 ;;;; 11/, a. Ao. v.(/<. .(,) < ..
Let <I > o and define B. = {all{J{a)/(s}1 > <I). The set AoBois a null set
since it is contained in the set of . for which 1{J{s)1 > <I{1I1. and
v*(A B.) < .. Consequently, v*(Bo) < " and Pf is ",-null. The case
in which {J is totally p-measurable and f is p-null can be handled in
exactly the same way. Q.E.D.
It is seen from Lemma II that the totally measurable fuuctions
form a linear space. Lemma 12 shows also that lhe equWo.lena elLusea 01
acawr valued torally meaauroble funclions Icrm an algebra.
IOS
III. INTEGRATION AND SET FUNCTIONS
111.2.18
111.2.15
INT£GRATION
109
18 DEFI>iITlON. A It.simple function is It-inkgrabk if it differs by
a null function from a function of t'he form
ft
1= L"'Xs,.
.=)
PROOF. Suppose that I and g are It-integrable simple functions
having the fonn given in the penultimate paragraph. Then the values
%.1) . . .J z of f+g .are found among the elements .:t'i+YJ' 1 ::;;: i '/1,
1 <;; i <;; m and
where E i = I-I(re,), i = I, . . 0' n, are disjoint sets in .E with union h'
and where x, = 0 ifv(u, Ed = co. The phrases "It-integrable It-simplc
function'" and u.u-integrable simple function" will be tlsed interchan-
geably. For an E.E the inlegra! over E of a It.integrable simple func-
tion h is defined by the equation
J h(s)lt(ds) = f f(s)p(ds) = i x,p(EE,).
E E 1
In this equation a tenn ll,p(EE,) with the fonn O. CO is defined to be
zero.
To see that the Integral is uniquely defined let
.
I+g = LZ,XB.'
1<-'
where B. is the union of all the sets E,A, for which x,+y, = 2,. If
z, oF 0 and if x, +y. = 2" then not both 11:, and y. are zero. and hence
v(,u, Bd < co. Thus I+g is a p-integrable simple function. If p. is the
set of an pairs (i. i) with x,+y, = z. then E,A. is void if (i, i) is in
none of the sets P", k = I. . . ., p.. and hence
L (f+g)dp. = . z.p(EB k )
'"
g = IY;XA,
'-1
where A j = -l(Yjl, i = I, . . ". m, .are disjoint sets in E whose union
18 Sand wherey, = 0 ifv(u, A,) co, and suppose that g also differs
from h by n null function. Then the function
.
I z. I p(EE,A,)
A=1 1:i,iJ€p k
n m
= I I (x,+y,)p(EE.A,)
....1 ;-1
n m n m
= I I x,p(EE,A,) + I 2.y.p(EE,A,)
1_11_1 i_ll_l
n m
ft m
= Ix./-l(EE,) + Iy,,u(EA,)
.--1 :1",,1
f-g = 2. I (x,-y.)X"....,
f-l J.,.1
= IBId!. + fEgd,u.
The remaining conclusions of the lemma are immediate. Q.E.D.
15 LEMMA. III is a I-'-inlegrable simple function then
IIEI(S)fL(ds)[ ;;; IE l/(s)lv(p, ds).
The sel function J.(E) = I I(s)p(ds) is an additive set IURdion an l:
whDse total variation is E
v(J., E) = Islf(s)lv(u.ds), EEl:.
F'urlhermme lim I "/(s)p(ds) = o.
-v!,. E)-+O
PROOF, Since Il(E>! < v(J.. E) for E E E, the """"nd statement
implies the first. To prove this second statement, let I have the
is a null function and hence tr,-y, = 0 if v(lt. E,A,) * O. Therefore
11 'fII n. m
I"';JL(EE,)- Iy,p(EA;) = L I (x,-y,)p(EE,A.) = 0,
pi j....] "...lj-]
which provesthatthedefinition given for JEh(S)It(ds) is independent
of the particular repro;enting function I which is uscrl. The symbol
JEhdfL will sometimes be used in place of J"h(s)lt(ds). The above ar-
gument also shows that J" hd,u J" kdp. if hand k are both It-integrable
simple functions with Ih-kl = 0 (see Lemma 4). Thus the integNlI
may be regarded a8 defined on a subset of the metric space PIS).
14 LEMMA. The p-iategrable simple fundions form a tl7iwr man;-
fold in F(S) and Ihe '-"Iegral J "Idp is a Ziaror mappi"g Irom tltis .nani-
lold into ;(. III and p. are bolk non-negative, so i8 Jsfdp.
110
III. INTEGRATION AND SET :J?"UNCTIONS
III.2, IS
111.2.16
[NTEGRATION'
111
dist1llct value8 "'I'" .. "'. and let E, = 1 1(",,). Since "'.p(EE,) is
additive for E in E so is the integral A(E) = 1::'_1 "",,(EE,). Next, let
E . E and let A" j = I, . . .. m. be disjointsets in E with A = U A!;;E.
Then. since the total variation v(u. E) i. additive in E (see 1.6).
The next lemma provides us with the key Uuniqueness theorem'
needed in extending the definition of the integral to a class of func-
tions larger than the class of simple integrable functions.
... m .
I IA(A,)I = I I I ""p(A,E,)1
1-1 1-1 '-1
16 LEMMA. If {f }. {f.} aTe 01 p-i71l£groble simple
lunetions both ctl'I'WeTfflng in p.-metl81JTe on S to the same limil and if
... n
:;:; I I 1"',lv(u. A,E,}
;-1 '-1
n
= I I-r.lv(u, AE,)
'_I
lim Is 1f"(s)-f,,,(s)lv(u. <Is) = o. i = 1,2,
....n
then the Iimi!8 lim i 1 (s)p(d8), i = 1.2, exi81 ur,;jomdy with respect
n E
to E in E and aTe equal.
PROOF. Using Lemma 15.
.
:;:; I Ix,lv(u. EE,)
<-1
IIE/ d;U - I,/:"d,ul Is 1/ (8) - f:"(s)lv(u. <Is) -+0, i = 1, 2.
= IE 1/(8)lv(,u. <Is)
which shows that v(A,E) IE I/(s)lv(u.<Is). Next let EjoI.
m = I, . . ., ffl" be disjoint subsets of E; with
Thus, the desired limits exist uniformly with respect to E in I and it
only remains to show that they are equal. In showing this, the
following abbreviations will be used:
8
.z.1p.(EEj)1 > V(I-', EE,) --
m_t At
v(E) = v(l'. E).
1'.(8) = 1/ (8)-f;(sH.
Pn(E) = fEP,dv.
n
where <is a given positive number and M = I 1"'.1. Then IA(EEj)1 =
1"';III-'(EEj)I. and ,-1
n m;
v(A, E) > I I IA(EEj) I
J lm-l
Since
IPn(8) - 1'...(811 :;:; 1/ (8) - I;.(s) I + 1f-(8) - f..(s) I
n ....
= I 1"',1 III-'(EEj)[
j".l mdl
.
> I 1"',lv(,u. EE,)-E
,-I
it is seen thatlim",m Is IPn(s)-p...(s)lv(ds) = O. and hence it follows
from the above argument thaUhe limit P(E) = lim" P neE) exists uni-
formly with respect to E in E. It will be 8hown that P(E) = 0 for
every E II and. consequently,. by Lemma 15,
= fE I/(s)lv(u, <Is) - 8,
which proves that vIA, E) ;;;" IE If(s)lv(u. ds) Bnd thus completes the-
derivation of the formula for v(.1. E), The final conclusion of the lemma
follows from the inequality
IIE/(S)fl(<Is)1 :;:; sup Ix,lv(I-', E). Q.E.D.
l i.:5ri
(i) If./ d;u - IE/ d,u[ < Pn(E) -+0,
E£E.
Since Iim.IE)-+O Pn(E) = 0 for each n = 1,2, . .., (Lemma 15), it
follows from 1.1.6 that lill1,,(£)-+o PIE) = O. Thus for E > O. there is
... 6 > 0 and an integer no such that
(ii) peE) < 8 for vIE) < 6, and
(iii) IP(E)-p.(E)1 < 8 for n no,
E£E.
112
III. INTEGRATIO:S _"-ND SET FUNCTIONS
111.2.17
111.2.18
INTEGRATION
lI8
Since P. ($) = 0 for $ in the complement A' of a set A. E with
.
vIA) < 00, we have P ..(A') = 0, and so (Hi) gives
(iv) P(A') < e.
(v)
e
p ($) <-.--,
., v(A)+1
SE B.
18 LEMMA. A fU1!£tiQn I on S i$ ,..-integraMe il and only if it i.
o{.u)-integrable. If I '" ,..-it1tegrable so.. 1/(')1, If (I.} i. a 8etJ1U7'Cf! 01
,..-iflkgi"abk 8imp junctWna determining I in with the preced-
ing <klinition. then the seqr=e {iI.(' JI} determine8 1/(')1 and furtho-
more
lim Is 1/.(8)-/(s)lv{.u, da) = O.
o
PROOF. If f/;k)} determines I, it is clear that {iI.(')!} determines
If('J! and, for a fixed m, {it.(-)-Im(-)!} determines If(')-lm(')I.
Since onvergt'nce in p-measure is the Same 8S convergence in
,,(p)-measure, this lemma follows diredl)' from Lemma II and Def-
inition 17. Q.E.D.
... 19 THEOREM. Let p be a finitely additive fu7l£tion <kfined en a
lield I 01 sub8ets of a aet So Then
(a) the aet L(S) of ,..-integrohl£ fundions on S i8 a linear space,
and for each E e I, the integral IE fd,.. i8 linear on L(S};
(h) it X. i8 the functWn 01 a set A.I, and I is
p-in!egrable. then Ix. i. p-integraMe and
LJ(8)xA8)p(ds) = I EA I(a)p(ds), E e E;
(c) if T i8 a bounded limar operator on £ to anoiMT B-space and
I i8 p-inUgraDk, then T/(') i8 p-integrable and
fETf(8)p(rIa) T JE/(S)p(ds), EeI.
PaooF. To prove statement (a) let {t.} and {g.} be sequences of
p-integrahle simple functions defining the elements I. g. L(S) in ac-
cordance with Definition 17. By Lemma 8. <1.1.+!3g. --,>«I+!3g in
measure on S. and if h. = «f.+!3g.. then
Is Ih.(a)-h".(8)lv(p, ria)
,;; 1,,1 Is 1/.(s)-lm(a)lv(p, ds) +1!31 Is Ig.(s)-gm(s!lv(P, ds) 0,
which proves that L(S) is a linear space. By Lemma 14
'" SEfdp +!3 I"gdp = lim (<1. IEI.d,.. +(J I"g.d!')
.
= lim IE hod!, = IE ("I +!3g)dp,
.
Now Pn -+ 0 in measure on S hy Lemma 8, and thus there is an integer
"-1 ;::0: ". and a set B. I with v(B') < h such that
Thus from (Hi) and (v)
(vi) P(AB);:iO LBP.,dv+s ';; 2s.
Since v(AB') ;:iO v(B') < h it follows from (ii). (iv), and (vi) that
PIS} = P(ABJ+P(AB'J+P(A') < 4e,
and since s> 0 is arbitrary and 0 PIE) ,;; PIS), it fnllows that
PIE) = 0 for every E in E, proving (i). This completes the proof of
the lemma, Q.E.D.
17 DEnNrnON. A function f on S to I is Winugrahls on S if
there is a sequence {I.} of p-integrable simple functions converging to
I in p-measure on S and satisfying in addition the equation
lim Is [tm(a)-I.($)lv{.u, ria) = O.
m,.
Such a sequence of p.integrable slmp]e functions will be said to de.
termim f. For each E.E, the integral over E, fE'd!,. of ap-integrable
function f i8 defined in terms of such a sequence {t.} of p-integrable
simple functions by the equation
JEf(a)p(da) = lim IEf.(a)p(rIa), E. E.
ft
The preceding lemma shows that this limit exists and is independent
of the particular sequence {lo} of p-integrable simple functions. The
set of all p-integrable functions I on S to 3: will be denoted by one of
the symbols: L(S, I, p, 3:), L(S, E. p), L(S. p), or L(S).
The remaining theorems of this section develop some of the basic
properties of the integral.
114
III. INTEGRATIO AND SET FUNCTIONS
111.2.20
111.2,20
INTEGRATION
115
v*(u, S(ITI-Tlnl > e») :s;: '-'*(}', SO/-/ftl > e/ITI)),
1,;It. g(S)}'(M) [ , IL. gft(S»)l(M) I I
:s;: i If egIs) -gn(S)]}'(M) 1
.-] '"
;;;; L Ig(s) - gn(S) I v!!" M) < e,
which prove. that the integral i. linear on L(S).
Statement (b) i. clear from the definitions.
Statement (c) is evident for }'-integrable simple functions; to
prove it in the general case. let I. be a sequence of finitely valued
I'",imple functions which deternrine I, Then the functions Tlft(") are
It-integrable simple functions. Moreover, since for each € > 0
Tfn('} TI(') in p-measure. The inequality
independently of the choice of El' . . ., E.. Let us for the moment fix
n > N. and choose A], . . ., Am such that
Is ITI.(s} - Tlm(s)lv(p, M) ;;;; ITI Is I/ft(s) - Im(s) Iv!!', M)
shows that (TI.J determines {TI}. Statement (c) foUows from these
observations. Q.E.D.
The next theorem extends the results of Lemma IS to arbitrary
integrable functions,
v(G. E) - i i f g(s)p(d,,) I < e,
.-1 A.
and BI'.' ., B such that
,,(G., E) - i Ii gn(S)p(M) 1 < e.
.._1 BI
.. 20 THEOREM. Let g be p-inregraUe and. lor E E, let G(E) =
Ieg(s}}'{M). Th£n
(a) G(E) is additive on E and has towl varia!ion
Let EI' . . ., E. be the family of all intersections of sets A. and
set. B.; then
v(G, E) IE Ig(8)lv(}', M),
E E;
v(G. E) - i I i g(8)}'(M} ] < e,
1-1 E
v{Gft, E) - i Ii gft(8)p(M} 1 < e.
'-1 ".
Hence Iv(G, E)-v(Gft, E)I < 8e. Consequently,
Hm ,,(G., E) = ,,(G, E), E E E.
in particular. il g and p are non-negative. ''''' integral G(E) i8 non-
negative;
(b) lim v(G, E} = 0;
.(Po EJ-+D
(c) For elUh e > 0 there are complementary selB A and A' in E
with v!!" A) < 00, v(G, A'} < e;
{d} Is Ig(s)lv{jl, M) = 0 il and only il g is a }'.null furu:tiim..
PROOF, Let (g.) be a sequence of p-integrable simple functions d .
termining g in aerordanee with Definition ]7. Since by Lemma 1.5
the set fun tions Gn(E) = IE g .(8)}'(M) are additive, it follows that
G(E)isadditive.LetE EbetheunionofdisjointsetsEl"'" E.,Eo
Given e > 0 there is by Lemma 18 an N. such that if n > N.
n "
Since by Lemma 15 and Lemma )8
v(Gft, E) = L 19,,(8)1 vI}', d,,) L Ig(8)lv{jl, d,,),
we have
v(G. E) = IE Ig(s)lv{jl, M),
Eel:.
Thus we have p oved (a).
To prove (b) let t; be IU'bitrary and select a finitely valued fL"
simple function II. such that
Is Ig(8) - g.(8)lv{,«. d,,) < Eo
110
III. INTEGRATION AND SET FUNCTIONS
111.2,21
III.2.22
INTEGRATION
117
v(G, E) = fE Ig(E)[V{u, rIa)
;;:; fE le(E) - g.(E)iV{u, ds)
+ f Ig,(E)lv(p, rIa)
AE
<. + Mv(p, AE) < 2.,
PROOF. Since g is p-integrable there is, for each integer nh 8-
p-integrable simple function gm assuming finitely many values on sets
of I: such that Ig(E) gm(E)1 < 11m except on " set E", with v{u, -8..)
< 11m. Since em vanishes outside a set Fm"I: with v(p.. Fm) < co.
I
Ig(E)1 ;;:; Ig(E) - e",(s)1 + Ig",(s)1 < -
m
Then there is a set _4. . I: with v{u. A) < co and a constant M with
le.(s)1 <]If for all 8. Sand e,(E) = 0 for 8 t A. Thus if v{u, E) <
ElM, E.l:.
En(CJ) = {sllg,.rs)1 > CJ}.
Then E.(CJ) E l: and
F.(CJ) = {s!lg(s}-e.{o)1 > CJ}.
for s t Am = E... u Fm' v(p, A",) < co. Consequentl}' if we define
Im{o) = I(s) if BE A.. and Jm(s) = 0 if st A.., the sequence {1m} eon.
verges in measure to J. By Lemma 11, J is totally p-measurable.
Q.E.D.
22 THEOREIL Lei P he Jinitely aMi/ive on a Jield I: oj subsets oj a
sel S. Thrn
(a) A p-measurahk junclion J is integrable iJ and onlg il the Junc-
tion If('}1 i. integrable.
(b) IJ e i. a p-integrahle Jum:tion on S to a B Bpace ID am! J i. a
p.-measurohk Jundion on S to a B-space :E, and IJ(E}I ;;:; Ig(s)1 almost
evn-!fWhn"e, Ihrn I is p.-inltgrohle.
PROOF. The direct part of (a) follows from Lemma 18. Since the
converse part of (a) clearly follows from (b), it is sufficient to prove (b).
By Lemma 21 it follows from the hypotheses of (b) that I is
totally p.-meMurable. Let {g.} be a sequence of p-simple functions con.
verging to J in p-measure. It wit! first be shown that a sequence {I.}
of p-simple functions ma}' be defined which converges to I in p-
measure and for which If.(s)1 ,,; 2If(s)1 for every s in S. There are sets
A". E];I n = I.. 2, . . ." for which VVtI An) -)0 0 and a sequence of con-
stants £n -+ 0 such that
proving (b). Since
v(G, A') ;;:; t. [g(s) - g.(s}[v(p, rIa) < 8
we have also proved statement (c).
Finally. to prove (d), let fs Ig(s}iv{u, rIa} = 0 and let {g.} be a
sequence of functions" each assulning B finjte set of values on sets of II
which determines g in accordance with Defmition 17. Then
lim J Ig.(s)lv{u. rIa} = O.
ft-»-O> S
Let CJ > 0 and define
Is Ign(s)lv(p, rIa) fE.(.) Ig.(s}lv{u, rIa) ;:;,; CJv(p, E.(CJ)).
Consequently, Iim,,--+co v{u, E.(CJ)) O. Since g. -+ g in p-meMure,
Iim,,--+co v*{u, F.(CJ)) = O. But
Ig(s}1 ,,; Ig(s)-g.(s}I+le.(s)1 ,,; 2CJ,
E t E.(CJ) u F.(6).
19,.(s)-/(s}1 < E.,
We now define In by the equations
I.(s} = gn(a} if a t A. and 19,.(s}1 > 28., I.(s) = 0 otherwise.
If 8 A. and Ig.(s)1 > 28. then 1/.(s)-f(E}1 < 8., while if Sf A. and
Ig.(s) I ;;:; 28. we have
If(s}1 < f/(s)-g.(s}I+lg.(s)1 < 38..
stA.,
Since lim,,-+co v*{u, E.(CJ) U F .(CJ» = 0 and CJ is arbitrary. it follows
tbat g is a null function. Q.E.D. c.
21 LEMMA. Let f he a IHneaaurable fwll:twn, let g he a p-integroble
Jun.ction, and suppose /hat If(s}1 Ig(s)1 almosl everyrvhert'. Tkn I
ia lotally p.-mrosurahle.
Thus
1/.(s)-/!s)j < 38.,
st A..
118
111. JNTEGRA'.rl0N AND SET FUNCT10NS
111.2.22
111.8.1
J.EBESGUE SPACES
n9
('A>nsequently I. approaches I in p-messure. Now if sEA. or if
Ig.(s)1 ;.:; 2e. then I.(s) = 0 and so j/.(s)1 ;,;: 21/(s>l while if s A.
and Ig.(a)l> 2e. then
I/{a)l> Ig.(s)I-lg.(s)-/(.)1 > Ig.{a)l-e. > ilg.(s)1 = ll/.(a)l.
Hence for all s in S we have 1/.(s) I ;,;: 21/(a»).
It will next be 8hown that I. is p-integrable. Let", be a non.zero
value of/. and Ethesetofall. inSfor which/.(a) =",. Since2jg[ III
we have Ig(')1 > 1"'1{2 on E. The argument of the preceding lemma
then shows that vIp, E) < 00.
l"'lv('u, E) = JE 1/.(')[v(P. ds) ;,;: 2 fE Ig(s>lv(P, ds) < 00,
from which it follows that v(p, E) < co. This shows that the function
I. is a p-integrable simple function. Since 1/.(a)1 ,;: 2Ig(a)1 we have
fEI/.(a)-I..(a)lv(P,ds);';:4 JE Ig(a)l'l>(p, ds), EEE.
Let e > 0 be given. By Theorem 20{ c) there IS a set FEE such that
vIp, F) < co and
fS-F Il.(a) -1..{a)lv(p, ds) < e, n. m ;;,: L
By Theorem 20(b) there is .. /j> 0 such that if EfiI and
vIp, E) < /j,
IE l!.I a ) - 1..(a)lv(p, ds) < e, n. m ;;,: I.
Since In - J in p-measure, there is an integer N and a. set En '''" if" 1;
such that v(p, E....I < /j and such that 1/.(s)-I..(s)[ < e{v(p, P) for
s;En,m and nJm N Hence. if n.'1n N.
(b) the function g defined by g{s) = I(a) if8 S+uS-, g("1 = 0
if S E S+ LJ S-, is p-measurable.
Next suppose that we consider a function I (vector Or extended
real-valued) which is def'"mtrl only on the complement of a p-nul! set
N S. Then we say that I is p-measurable if the function Ii defined
by g{a) = I(al if s N, g(s) = 0 if s. N, is ,,-measurahle. A discussion
similar to that preceding Definition 6 shows that b}" considering this
somewhat more extended class of functions we make no change in
F(S, E. p, I), or in any of the theorems or lemmas of this section.
Finally, suppose that I is a non-negative ,,-measnrable extended
rcal valued function. If lis notp-integrable, we write fs/{.)v(,u.dsl =
+co. It follows, from Theorem 22(bl, that if 0 ,;: I.(a) ;;;; 1.(.) for
almost all s, and if I. and I. are p;-measurable. we still have
fsA(')'I>(I" ds) ,.;; fsf.(a)v(,u. ds),
even though one or both of these integrals may be infinite.
3. The Lebesgue Spaces
(a) there exist p-null sets N+ and N- such that S+ LI N+ and
.<1- LI N both belong to E, and
The basis for this section is a finitely additive complex or ex-
tended real valued set function p defined on a field E of subsets of a
set S. The functions to be integrated with respect to p will have their
values in areal or complex B-spaceI. We shall define and discuss the
properties of various linear spaces of p-rneasurable functions.
1 DEF'NiTION. Let I ,;: l' < co. Then L:(S, I, ", I) (nr, if I
is understood, L:(S, I, "I), will denote the set of all p-measurable
functions I on S to I such that the function If(' W is p-integrable. By
the 1Iorm III of an element IE L:(S, E, ,,) we mean the quantity
III = [Is If(sJIPv(P, dsl]'/P.
When desirable for cwity, the symbol III. will be used for the nonn
of an element in L {S, E, Jl I.
. 2 LEMMA. (Holderl Let I be a scalar valw-d lunction and Ii a
vectorvallUdlUndi 01 1 with I. L:(S, I, pI, gE L (S,E'I'I, wherep > I.
q> I. and I!p+liq = I. 'l'hen the lunction Ig is p-int<'grabl£, and
I 1/.(a) - Im(sllv(,u, dB) = f + f + I ;;;; 3..
S S-F F-E.. FE,..
Thus the sequence {I.} detenninesl in accordance with Definition 17
and therefore I is integrable. Q.E.D.
For certain purposes, it is useful to extend the definition of
measurability and integrability in the following ways.
First suppose that I is an extended .real-valued function. Let
S+ = rl( + ro) and S = I-I( - ro). Then I is said to be p-triI!a.mrabl<
if
120
III. INTEGRATION AND BET FUNCTIONS
III.3.3
III.S,"
LEBESGUE SPACE.S
121
II s f(S)g(8)p(tIs)1 ;:;; Ifl lglv'
PROOF. In case either Ifl or Iglv is zero the lemma follows from
Lemmas 2.12, 2.21, and Theorem 2.20(d) and so we shall ...'<Sume that
neither of these nonns is zero. The function 'f(I) = IV/p+I-'/q has a
positive derivative for t > 1, and a negative derivative for 0 < t < I.
Hence its minimum value for t > 0 is q:;(l) = 1. Ifwe put, = a ll f.lb- 1 /'R
we obtain the inequality ab S; avfp+b'/'l, valid for a, b > 0; henee, the
inequality labl ;:;; la!"/p+lbjvf'l is valId for all sc:1lar. a,b. Putting a =
f(s)flfl . b = g(s)/lgl., we find that
1 I
I/(s)g(s)1 -If(s)l lfl -;lgl. +_lg(s)I'lg --1iIlI _
p q
It follows from Lemma 2.12, Thoorem 2.19(a), 2.20(a) and Theorem
2.22(b) that fg is integrable and thai
I Lf(S)g(S)p(tIs)1 ;:;; (; +;) Ifl lgl.. Q.E.D.
8 LEMMA. Let I S; P < co, lei fl' f. be in L:(S. E. 1')' ani!iel a
be a scaIM. Then
(a) the funcliotl «fl iies in L (S, E. pl. ani! 1"f.I = 1,,11/11.;
(b) the sum of It an" f. Ius in L (S, E, p), and 111 +I.I ;:;;
Ifll + 1/.1.;
(c) IA-f.l. = 0 if and cmly if fcl. is a nuU lunction.
The inequality in part (b) is known as lI-finkowski's inequalily.
PROOF. Part (a) IS obvious. Part (b) is obvious if p I; to prove
part (b) forp > 1, we reason as follows: the function (1+",)v/(I+"'v)
approaches I as u: -+ Oora: -+ co; consequent1y" it is bounded by some
con8tant c in the whole range 0 S; '" < co. Putting'" = alb, it follows
that we ha,'e (a+b). S; c(a"+b.) for all 0 a, b < co. Since tbis
implies
= Is IMs)IIMs>+f.(s)I. 'v(p. tis)
+ Is 1/.(s)III.(s>+f,(s)I.-'v(p, <1-8)
{il11. +I/.I } lIs (lMB)I+IMB)I},'v lIv(p.tIs)ll"
by Lemma 2, where Ifp+l/q = 1. Since q(p-l) = p.
{If 1 + f.I.}' {jAI. + If. I.} WI + f.!..}"'.
Thus,
If 1 + f.lv = Wl + f.I.}' v(' ;:;; )f,l + II.I ,
which proves (b).
Part (c) follows from Theorem 2.20(d). Q.E.D.
In view of Lemma 8(c) it is natural to consider the classes of
functions in L (S, E, 1',:£) equivalent under the relation: f is equiv-
alent to g if and only if f-g is a null function. Denoting the eqU1v-
a1ence class of f. L (S, E,p,. 30) by U], it follows from Corollary 2.5
and Lemma a( c) that the equivalence classes form a linear space in
which I [j] I = Ifl is a nonn. We refer the reader to the analogous dis.
rU8sion following Corollaty 2.5 for the space PIS, E, p, I),
4 DEFINITION. The symbol L (S, E, p, I) will denote tbe set
of equivalence classes [j] of functions f. L (S, E, p, if).
In view of the remarks above, we have the following theorem.
1/1+f.l: = Is IMs) + 1,(s)I'vlP, tis)
< Is {IM8) 1+1f.(s) I} It. (s)+/,(8)1"-'v (p, <Is)
5 THEORE!\(, The space L.(S. E, p. I) is a normei!linear space.
As in the case of the space F(S, E, p. if) it is customary to refer
to the elements of L.(S, E, p, I) as if they were functions, rather than
classes of equivalent functions. Thus where no confusion will result,
we 8hall speak simply of "a function in L.... In the sequel the symbol
f rather than [j] will be used for an element III L . We observe that
the inequality of Minkowski and (in the case of scalar valued func-
tions) the inequality of HOlder may be regarded as applying to the
spaces L . This observation is obvious in the case of Minkowski's
inequality. To :5ee that it is justified in case of HOlder's inequality,
note that HOlder's inequality implies that
IMs)+f.(811" {IMs)I+[f.{s)l}v ;:;; c{lf.{s)I'+If.(sW},
it follows from Theorem 2.22(b) that_
f. +f. . L (S, E, p).
Now,
Ifgll S; Ifl lgl. if f. L ,
g L:,
1 1
- + = I,
P q
122
111. INTEGRATION AND SE'l' FUNCTIONS
III.8.6
III,3.6
LEBESGUE SPACES
123
and at least one of I and g is scaJar-va1ued. Thus, if one of 1 and g is
p-nul!. so is Ig. Hence. if I.. I. " L:, g"g.£L , and f.-f. and g.-g, are
p-null functions. then f1ll1 f.g, is a p.null function.
The reader will more easily perceive the significance of the SOme-
what complicated cornlitions (ii) and (iii) in the following theorem. if
he reads the statement and proof of Theorem 7 after the statement of
Theorem 6 but before its proof.
which proves that {g.} is a Cauchy sequence in L,(S). To see that
g is integrable let h., n > 1, be integrable simple functions witb
f Ih.(s)-gn{s)jv(JL,ds) < ,
Js n
f"g.(s)v(}!, ds) <s,
n ]
and [h. -g. IF < l/n. where the norm is that of the space F(S,I,}!).
Since {g.} is a Cauchy sequence in LI(S) with g. g in measure
it fol1ows that {h n } is a Cauchy sequence in L,{S) which also con-
verges to g in measure. By Definition 2.17, g is integrable and this
proves that f is in L..
For convenience let us write IOQ = j. In view of Theorem 2.20.
conditions (ii) and (iii) hold uniformly for 1 ;;'; n S" <0. For each s> 0
there exists a set Fo such that If.(s)-I (s)1 < e for sf Fo and
such that 0(1', F.) _ 0 as n_ OJ. Consequently
1/.-11. = Us I/n(s)-f(s)j.v{p, ds)t J .
,;; IJ If.(s)I'v[p, ds» ) 'I.
S-CE.-5lJF,J
+ US-IE,UF., 1/ (s>i"v(p,ds)llJP
+ 1f£' F.lf.(s)-f",(s)l.v(p, ds) ]11'
+ IfFn 1/.(s)-/ (s)l.v(p, ds}t.
< 20". + s[v(l'. E.)]lJ.
+ IfF o {If.(s)I'v(p. ds) ! II.
+ [t.I/",(8)I'v(P, ds)J/.'
Now let l' > o. If we choose (J such that 2b"' < 1'. and then choose
ssuch that s[v(l', E.)]I1. <1'and{JFI/.(s)l.v(p,ds)}'I. <1',I S" n < oo,
whenever v(p. F) < s, then 11.-/1. < 4y for n> no, which proves
that Ifn-fl. O. This completes the proof of the sufficicncy.
ext we will prove the necessity of (i). If f€ L. nnd If.-fl. -+ 0
then for each £ > 0 there is .an integer 'i1o such that n 2 no implies
Jsg,,(s)v(p, ds) < E where g.(-}= 1/.(')-/['>1'. Now each g" is the
6 THEOREM.Ldl;;';p < 00; kt {I.} be a selJ"'l1!Ce 01 funcli<m3 in
L (S, E. 1', 1) and let I be a function on S to 1. Then f is in L. and
II. -II. conveTges 10 =0 if and only if the three lollowing conditi1m3 MId:
(i) ffl converges to f in 1ne/I$Ure;
(ii) 11m fE 1/.(s)l.v(!', ds) = 0 'Unifvrmly in fI;
'tI(IoJoEJ-+D
(iii) lor each s > 0 there is a set E. in I with vI!'. E.) < <0 and
such IIulI
J If.(s}I'v(!" ds) < s, n = 1. 2.....
S-E.
PROOF. Assummg (i), (ii), and (iii) let 11.= I/.('}I , g= 1/(,)1..
We win first show that {g.} is a Cauchy sequence in L,(S). For
s > 0 there is, by (iii), a set E, with v(p, E,) < <0 such that
JII.-/1.II ';:: 2s + Is Ig,.{s)-g.(sllv(,u. ds),
,
n,m l.
Thus to see that the sequence {go) is a Cauchy sequence in L,(S) it
wi1l suffice to prove that it is a Cauchy sequence in L,(E,). Hence
we may and shall assume that v(}!, S) < co. By (ii) there is a (J > 0
such that
provided that v(p, E) < (J. By Lemma 2.12 g. -+ g in measure, so
there are sets E.. in I with v(}!, Eom) < tJ for all large va1ues of
nand m and with 11I.(8)-gm(s)1 < E for every 8 in S-Enm. Thus,
for sufficientJy large nand m,
IlIn-gmll < 2s + fs-E.. Ig.(s) - /lm(s)!v(p. ds)
;;;; s(2+v{p,S»,
124
III. INTEGRATION J\.ND SET FUNCTIONS
111.8.7
III.S.8
LEBESGUE SPACES
125
limit in p-measure of a s quence {h ) of real valued simple functions,
eaeh assuming finitely many values on sets of E, such that
lim Jsh (s)v(.u, ds) = fsg n (s)vIJ1' ds)
. W
(cf. Lemma 2.18). Since we may replace h (') by Ih (' JI, it may be
supposed that h:(s) ;;0, 0, Consequently Is h:{s)v(.u,dsJ < 2e for all
sufficiently large Ie, and we may assume without loss of generality
that Is h:(s )v(.u, ds J < 2e for all k. By the simple form ofthe functions
h: the set
L.(S,E, 1-') SlUltthat If.(')1 Ig(sJI a!most e loreaclt 0:. Then
J. converges to I in 1-'-7nCa3UTe il and only if I i. in L_ and the no",,",
If.-/I. converge to zero.
E: = {alh:(sl > rJ
PROOF. Let us first consider the case when the generalized se-
quence is an ordinary 8equence {In}. Since I/n(s)l :S: Ig(s)1 almost
everywhere. (ii) and (iii) of Theorem 6 hold automatically, Conse-
quentIy the statements In --+- I in measure and In --+- I in L_ are equi-
valent by Theorem 6.
ft will now be shown that the statement of the theorem for a
generalized sequence follows from the case for sequences. We recall
that the topologies of the spaces F(S, E.I-" J:) and L_(S, E, 1-', J:) are
metric. Let I. --+- I in measure and 8uppose that I. does not converge to
I in LZ'. Then there is an £. > 0, and for each :x. a f1f£ 2: I such that
I/ . -fl. > e. The generalized sequence (f.), r = (l.. clearly converges
to I in measure. Now from each sphere of radius If.. about I in F
select an element f . Since I. -+ I in measure, it follows that f .... I
J'", 1ft Y"
in L l1 , contradicting the inequality above. The proof of the converse IS
similar. Q.E.D.
is in I fOT each y> o. Moreover"
yu(.u. E ) Is' (s)v(J1' ds) < 2e.
Consequently, v(J1, E ) < 281y. Smce {h:} converges in I-'-measure to
g.. for each sufficiently large k we can find a set F: £ E such that
v(.u, F ) < 8fr and ,h:(s)- g la)1 < r for B F . Thus 1/.(e)-f(a)1
< (2r)li- for s F: U E . Given o\,lJ. > 0, choose y so 8mall that
(21' )IJ. < 0\. and 8 so 8mall that 8efy < li.. Then for 11 ;;0, n.,
I/nla)-/(s)1 < 0\ except when a lies inasetG n such thatv(J1, G n ) < li..
Thus I. --+ / in measure and (i) is proved.
We now prove the necessity of (ii). By Theorem 2.20, for
each 8 > 0 there is a lJ 1 > 0 sucb that vlf', E) < lJ 1 implies
(fE I/(e)IPv(.u,ds»)IJ- <e. Let ''0 be such that I/n-/ip <e if.. ;:;' 1'0,
and let li. < 0\ be a positive quantity such that v(l-', E) < lJ" implies
UE 1/.(aJl-v(f"ds)j"- <e for 1 < .. 1'0.
8 CoROLLARY. Lei. 1 P < 00. The ael oll-'-simp!e wintegrable
functWns ia dims. i.. L.IS. E, 1-'. 1).
PROOF. Let I. L. = L.(S, E, p, J:) and 8> O. By 2.20 we can
find an E £ E such that v(JL, E) < 00, and such that
fS-E I/(s Jl-v(.u, ds) < eP.
Thus, if X" is the characteristic function of E, then XEt i8 an element
of L. and I/-x.:fl_ < e. By Definition 2.10. XEI is the limit in 1-'_
meaSure of a sequence {In} of I-'-simple functions. By using the argu-
ment presented in the proof of Theorem 2.22, we may and shall
assume that 1/.(a)1 2Ixe!a)ll/laJl, a.S. Since I.(s) vanishes for
"' E, I. is I-'-integrable and I-'-simple. By Theorem 7, ",-xEtl. < e
for sufficiently large ... Hence I/-Inl_ < 28 for sufficiently large 11
and the proof is complete. Q.E.D.
Then,
UE 1/.(SWV(.u,ds»)Ii. <28 for I n 00,
proving (ii).
Statement (iii) may be proved in thc same way to complete the
proof of the theorem. Q.E.D.
7 THEOREM. (Dominaled W1I""'g""'" theorem) Let I P < 00,
let g £ L.(S, 1:, 1-'), and let {I.} be a generalized 8fqUffl£f of de,,,,,,ts 01
126
IIJ, INTEGRATION AND SET FUNCTlQNS
UI.4.1
111.4.4
COUNTABLV ADDITIVE SET FUNCTIO S
127
4. Countably Adtlilive Set FWlctioDS
The basis for the present section is a countably additive set func-
tion defined on a <t-field of sub8ets of a set. In this case the results of
the pl'<'CCding sections can be considerably extended.
1 DEFINITION. Let J.l be .a vector valued, complex valued, or
extended real valued additive set function defined on a field I: of
subsets of a set S. Then I' is said to be countahly aJdilive If
n = 1, 2, _ ... It is evident that such a. sequence has the limit U :"1 En.
A non-i1UTaJ.Sing sequence {Eft} is one for which EI) En+l' n = 1,2,. . u
Such a sequence has the limit n:- 1 En' A monotone sequence is one
which is either non-decreasing or non-increasing. We note that the
intersection, union: limit inferior, and limit superior of every sequence
of mE':asurable sets is measurable.
'" '"
/l (U E,) = 'Ip(E,)
i-l t-l
4 LEMMA. The values of an eJ:tcm];,d rcal-valu<:d mrosure which
never assume8 the value + 00 have a finite upper bound.
PROOE. Suppose that p is not bounded above. Call a set E. E I:
unbounded if supplEE,) = +00: otherwise call it bounded. Then
either Eo(1:
(a) every unbounded 8et contains an uubounded set of arbitrarily
large measure, or
(b) there exi8ts an unbounded set F E I: and an integer N such
that F contains no unbounded set of measure greater than N.
In case (a), we can clearly apply induction, and find a d ing
sequence of unbounded sets such that /l(En) ;;;, n. Then
whenever Ell Ej, . . _ are disjoint sets in E whose union also belongs
to I:.
2 DEFINITION. A a-field is a field I: of subsets of a set 8 with the
pro ..-h. that U E , EI: whenever En < I:. n = I, 2,. ... In other
": i-I
words, a a-field is a field which is closed under the operation of forming
denumerable unions.
II DEFINITION. A triple (S, I:, p} consisting of a 8et S. a field I:
of 8ubsets of S, and a comp1ex valued or extended real valued additive
8et function p defined on I: is said to be a meaBUJ'C space if I: is a <t-
field, and p is countably additive. Oc<>nsioruilly, 8 itself is called a
measure space. The sets in E are called mRtJ8urable sets. Tbe measure
space is said to be finite if /l does not take on either of the values +00
or - co, and to be pogitive if p. never takes on a negative value. A
mecurnre is a complex or extended real valued countably additive set
function whose domain is a ii-field.
Throughout this section (8, I:. p} is assumed to be a measure
space.
Suppose that {En} is a sequence of sets. We define the limit
inferior and the limit sUp"rior of {En} by the equations
'"
p (n E,) + 'I/l(E, - E'+1} = peEn);
..,.1 i"'n
since p(E.) '" + 00, the series on the left converges to a finite quan-
tity, and we have
'"
p(nE,} = Iimp(E n } = +00,
t-:I O;I
'" '"
timinf En = U n Em'
which contradicts our hypothesIs.
In case (b) we let Fi be a measurable 8ubset of F such that
p(FI} > N. Then FI is not unbounded; since F i8 unbounded. F-F.
is unbounded. Let A. be a measurable subset of F - Fi such that
p(A.) > I. Then, since F contains no unbounded set of measure
greater than N, F. = F. U Al is bounded. so F - F. is unbounded.
Proceeding jnduc'lively we construct a sequence of disjoint measur-
able se s Ai' A", . . . such tnat p(A.) ;;" I for every k. It follows that
I'{ U: I A,} = +00, contrary to assumption. Q.E.D. .
5 COROLLARV. The set of values 01 a t'frt8r valued, cvrmWhly
additive sel fUndion <kfimd on a a-field of sets is bou.nded.
" 11='1171"'"
lim sup En = n u Em.
1i n-lm-71
If lim inf" En = lim sup" En' {En} is said to be convergent, and we
write the common value of the limit jnferior and the limit superior as
lim En. A nou-dt>r.reasing sequence {E..} is one for which En E n + 1r
"
128
III. INTEGRATION AND SET FUNCTIONS
111.4.6
111.4.9
COUNTABLY ADDIT£VE SET FUNCTIONS
129
PROOF. Let p be a set function defined on the ".field E, and with
values in the B-space X. Then, by Lemma 4, £)l"'-p(E) and -''''-p(X)
are both bounded for each ",- X-, so that by 11.8.20, p(E) is bounded.
Q.E.D.
6 COROLLARY. If (S, X, 1') is a finite measure space, p i. bounded,
7 LEMMA. If (8. E, p) is a finite measure spm;e, W lolal varia1w..
v(.u) is cowrtahly additive and bounded. II p is Teal val""d. W upper and
ImtJer variarivns 1'+ and p are also cuunWbly additive and bounded.
PROOF. The boundedness follows from Corollary 6 and Lemma
1.5, and only the countable additivity need be established. Since
1'+ = (1/2)(v(.u)+p) and p- = (1/2)(v(.u)-p), it is enough to show
that v(.u) is eountably additive. Let E. be disjoint sets in E and let
U:l En = E. Now, since 1'(11) is non-negative and additive,
p( u () Em) = lim p( () Em) ;;; \im mf p(En)'
.....1 m=n
fj m=n
fl
w
p (n u Em) = lim p (U Em) ;:;:; lim sup p(E.). Q.E.D.
n=ll'n""'n ,. _'I "
9 COROLLARV. If (S,X,p) is a finite measure space, and {E.}
a OOtWngetll sequence of measuroble sel8. 111m lim p(E n ) = p(lim E.).
n o.
w
w
PROOF. If P is positive, the conclusion follows from Lemma 8.
The general case is treated by splitting p into its real and imaginary
parts, and then decomposing each of these. with the aid of the .Jordan
decomposition theorem (1.8), into the difference of two p08itive
measures, and then applying Lemma 8. Q.E.D.
v(.u, E) ;:;:; I vIp, E.).
_1
10 THEOREM. (Hahn decomposition) To every e:J:lended Teal
measure p rorreJ/fJOTids a metl8Uroble set Eo sw:h Ihal p i. nan-negaJive ""
measurable subsets of Eo aTid nan-posirive on mel18W'tlbk subsets vI E;"
PnooF. Either p. or -I' fails to asSUme the value + 00. Hence it
may be ASsumed that p(E) < 00 for every E in the ,,-field X where
I' is defined.
Let P cOl1£ist of alJ sets E £ E for whkh p(AE) ;:., 0, A E X, Let
Eo. P be such that
.. ..
v(.u, E) > v(l-', U En) = l v(.u, Eo.},
,""",1 71-1
On the otber hand, let {F,} be a finite sequence of disjoint measurable
set., with F,!;; E, Then
J: k C,it) J:
IIp(F,)1 IIp(UF,E.)1 =l,Ip(F,E.)1
i_1 £0.1..-1 1'=1. n-1
.
,;; I IIp(F,E.)1 S lv(.u. E.),
n-l j-l n-l
p(E.} -->- sup peE).
E.P
Smce " IS countabl y additive the set E o = U E 18 P d
I _]A in an
fl
.
.
.
p(E.) = sup p(E).
E.P
It wiD now be shown by an indirect proofthatp(E A) ;;; 0 for every
A £ X. Suppose that Ao £ E, Ao!;; E , and p(A,,) > o. PartialJy order
the family
Q = fEIE.E, E!;;Ao,p(E) > p(Ao))
by defining EI E. to mean that either EI::> E. and plE I ) < u(E.),
or El = E.. Zorn's lemma (1.2.7) will be applied to show that Q con-
tains a maximal element. Let Qo be a totally ordered subset of Q, If
there is a Bo Q. witb p(B.) = sUPEoQ.p(E) then clearly Bo is an
upper bound for Q.. On the other hand, if
so that
m
vIp, EJ l v(.u, E.). Q,E.D.
._1
8 LEMMA. If (S. E, p) i8 a finite pori/ive mea8tlJ'e space, and
{E.} a sequence of measurable sets, 111m
p(lim inf En) ;;; lim inf It( E.) ;;; lim sup p(E.) S p(lim sup Eo.)'
PROOF. Observe first that if {E.} is a non-decreasing sequence
with limit E then E = EIU (E.-EIJU..., and pIE) = limp(E.).
By taking complements it follows that this equation holds also for
non-increasing sequences. Thus if /' is non-negative and {E.} is an
arbitrary sequence in I,
ISO
Ill. JNTEGI\AT:ION AND SET FUNCTIONS
111.4.11
111.4.12
COUNTA13LY ADDITIVE SET FUNCTlOKS
ISI
pIE) <6 = 8upp(E), E.Q.,
E<!I.
there is a sequence {Bn}CQ. with p(B n ) <p(B"'I) ---+-6. Since Q.
is tota1ly ordered, B.::> BR+I' .. = 1,2, . . .. Since p(Bn) < p(B... I )
< <X>, all the quantities p( B n ), .. ;;" 2. are finite. If C n = B. - B.. I .
and no = n :...1 BAt then Bfl = Be U U :...1t C'r> so that
12 DEFINITION. Let A,P. be finitely additive set functions defined
on a field E- Then A is said to be amtinno... with Tespect to p. or simply
p-C(mtinit()us if
'"
p(B.) = p.(B.J+ 1:p.(C.J,
....
.. 0;;2.
lim A(E) =0.
II( .E)
The fuoction A is said to be p-mngular if therc is a set Eo . L 8uch Ihat
v(l-'. E.) = 0; A(E) = AlEE.), E. E-
It is clear that the only set function which is both p-singular and
",-continuous is the set fun£'tion identicaUy zero.
If A, p are both scalar valued additive set functions on a field L
and if A is p.-continuous then the inequality (IILI.5)
VIA. E) 4 sup IA(A)I
A£E
shows that the lowl variation oj A i. ulso p-rorotinuoU$. Thus the positive
and .Iq{ative varianom of a Teal p-continu0U8 set furwtion aTe likfwi8e
1l-ron/.inuoU8. It is also dear that the Jl continuous set functions as
well as the p:-singuw set functions form 8 linear vector space under
the natural definitions of addition and scalar multiplication.
IS LEMMA, Let A, '" be co..rdaOlll addi1ire Bet f....ctions. compwor
eztendnl Teal valued, defined on the o-/ield L, and lei A be jinil£. Then A
is p-co"tinuo,,", if and vnly if vlf-', E) = 0 implies that A(E) = o.
PROOF. The necessity of the condition is obvious. To prove the
sufficiency of the condition we obsel"Ve first that a set function A
satisfies this condition if and only if the positive and negative varia-
tions of its real and imaginary parts satisfy the same condition. Thus,
it may be assumed that;' is non-negative. If .It is not p-continuous,
there is an E> 0 and sets EnE-I, n = 1,2,..", with ;t(E.",) e and
v(j.t, En) < 1/2'''. Let Eo = lim sup En. Then. for each 1 = 1,2, . . ",
'"
Thus lim p(B.) = p(B ). and the set Bo = n B. is inQ. andiJ = p(B ).
n-+m _1
Let E. Q.; then pIE) < 6 = p(Bo) and there is an .. with
pIE) <p(B.). Since Q. is totally ordered, E::> B.::> B.. Thus Bo is
an upper bound for Q.. Since every totally ordered subset of Q has an
upper bound. there is a maximal element M in Q. This maximal
elementMisinP,forotherwisethereisasetA .2".A M,p(A) < 0,
M -A Ao, p(M -A) = p(M)-p(A) :> p(M) 0;; p(.4,,), and thus
M-A ;;" M.
Since M E and M. P
p(M UE.) p(M)+p(E.):> supp(E),
E.P
a contradiction which proves that p(E;,A.) ,:;; 0 for every A. L. Q.E.D.
The Hahn decomposition a!lows us to extend the definition of tbe
positive and negative variations to extended real valued measures.
11 COROLI,ARY. Let (S. L. p) be a measure space. and p a.. ""'-
tended Teal valw:d measure. Tllen thne are .,m>-tu'gative measuT""
p., W. one vf whieh is finite and .tu:h thnt
P = p+-p-, vlf-') = 1'+ +p-.
PROOF. If E. is the sel whose existence is proved in the above
theorem, then the functions p+. p- defined by
p+(A) = p(EoA), p-(A) = -p(E;,A.), A. 2",
clearly have the desired properties. Q.E.D,
It is clear that ifp isa bounded function the set functions p+ and
p coincide with those of the .Jordan decomposition. We shall cootinue
to ca!l them, even if the p is an extended real valued measure as in
Corollary 11. the posilive and negaJive variations oj p.
n
m '"
v(I-', Eo) < vlf-', U Em) ;;;;; 1: 1/2'",
""""11 m-n
which shows toot vlf-', E.) = 0 and hence A(E ) = O. On the otIler
hand. by Lemma 8.
A(Eo) :;;, lim sup A(E.) E.
n
which is a direct contradiction, proving the lemma. Q.E.D.
182
111. INTEGRATION AND SET FUNCTIONS
III,4.14
III.5.1
EXTENSIONS OF SET FUNCTIONS
188
This lemma shows that if each member of a gena-alized sequenre
{l.} of finite, countably additive measures is p-continuous and if
lim" J.,.(E) = l(E), E£E. where l is also a finite, countably additive
measure, then A is also p-continllous..
It follows easily from Definition 12 that if ).. A., n = I, 2. . . ., are
finite countably additive measures with ).,,(E) A(E), E e E. and
if An' tl = 1, 2, . .. are .a-singular, then). is also p-singular.
I DEFINITION. Let ). be a vector or extended real valued set
function defined on a field E of sets in S for which l("') = O. A set E
is called a A-Bet if E . E and if
l(M) = l(ME)+A(ME'),
MeE.
14 THEOREM. (Lebesgue dtiwmposili<m) :&'1 (S,E,p) be a
measure 8poce. Then ev fini!e euuntably additive measure). defined On
E is uni'JU"ly representable as a BUm A = ex.+{J whete ex. is p-cantinu(JUIJ
and {J iB p-Bingular.
PROOF. The uniqueness of ex and (J is clear. In view of the .Tordan
decomposition, which may be applied to both the real and imaginary
parts of l if A is complex valued, we may and shall assume that A is
non-negative. Partially order the collection N of all sets E £ E with
v(p, EI = 0 by defining A B to mean that l(A) A(B). If
N. is a totally ordered subset of Nand (j = SUpg<NJ(E) then
either there is an upper bound E. of No in the set No itself or there is a
sequence (E.} in No with A(E.) < l(E.....) (j. In the latter case,
E. C E.+1> and E = U En is readily seen to be an upper bound for
No. It follows from Zorn's lemma thatN contains a maximal element
Eo' The function P defined on 1: by (J(E) = A(EEo) is p-singular. To
see that the function ex on E defined by the equation ex(E) =
A(E)-{J(E) = A(EE ) is p-continuous, suppose that E EN and
ex(E) = A(EE ) > O. Then E. E. U EE £ N which contradicts the
maximality of Eo, and proves that ex is p-continuous. Q.E.D.
2 LEMMA. Let A be any veclor valued or exrended real valued Bet
funttima defined on a fitW 1: of Be'" in S with A(",) = O. The family of
A--sets i. a subfield of E upon which l i. oMitive. Furlhermme. if E i.
lhe union oj a finite {EJ of disjoinl A-8el8, then
A(ME) = 1:A(ME.),
M£E.
PROOF. It is clear that the void set. the whole space, and the
complement of any l-set are A-sets. It will now be shown that the
product of two A-8ets A, B is also a l-set. Let It-l E E, Since A is ..
A-set,
(i) l(lt-lB) = A(MBA)+).(MBA').
Bnd since B is a A-set.
(ii) A(M) = A(MB)+).(MB'),
A(M(ABJ') = ).(M(AB)'B)+l{M{AB)'B'),
(iii) A(M(AB)') = l(1I1BA')+l(MB').
From (i) and (ii) it follows that
l(M) = A(MBA)+).(MBA')+).(MB'),
and from (iii) that
A(M) A(MBA)+A(M(AB)').
5. Extension. of Set Functions
Thus ABisaA-set, Since UAn = (n.(.)' we conclude thattheA.sets
form a field. Now if E, and E. are disjoint A-sets. it follows, by re-
placing M by M(E, U E.) in Definition I, that
l(1I1(E, U E.» = A(ME,)+A(ME.).
A given countably additive set function defined on a field Can be
extended to a countably additive set function defined on a a-field
containing the given field. This extension theorem of Hahn and
similar extension theorems. of importance in later applications, will
be discussed in this section. Finally, it is shown how the extension
theorems may be used to construct the clsssical measures of Borel,
Lebesgue. and Stieltjes.
The final conclusion of the lemma follows from this by induction.
Q.E.D.
3 DEFINITION. An outer measure in S is a non.negative extended
184
111. INTEGRATION AND SET FUNCTIONS
III.5.4
III.5.6
EXTE:s'SIONS OF SET FUNCTIONS
185
(i) A(<!» =0;
(ii)A(A);:£A(B),
A B,
A,BeE;
PROOF. The properties (i) and (ii) of Definition 3 are evident.
Let E he the union of an arbitmry sequence {En} of scts in S. Let
< > 0 and for each n = 1,2, . . . let the sequence {Em..} have the
properti s
real valued set function A defined on au-field 1: of sets in Sand satisf}.-
mg
m m
(iii) A (U E.) ,.;: }).(E.),
ft=l _1
{En} 1:.
Em.?I€I"
m m
E. C U Em., II'(E..,.) ;:£ p(E.I+</2.+I.
- ___1' fn""l
m
4 THEOREM. (Carathiodmy) If A i. an r measure tM" tM
family of A-sets i. a a-/ield upon which A i. countably additive.
PROOF. Smee the A-sets form a field (Lemma 2), to see that they
form a u.field it will suffice to show that the uoion E of any sequence
{E.} of disjoint A-sets is a A-set. It follows from Lemma 2 that, for
111 e 1:.
Then U Em,. E and thus
m,ft-]
m
i«E);;;; I I'(E m ..) ;"; I,ii(E.) + e.
ft,m=l n-l
_1
-.
which proves, since e> 0 is arbitrary. that p, has the property (iii)
of Definition 3. Thus jL is an outer measure defined on the u-field of all
subsets of S.
Now let E. E. Since E E, it follows that I'(E) ;,; PIE). If
Eno£:E. n = I. 2,...", and E U=-] En then the sets Al = Ell An =
En( UI<tt E;)', n> I, are disjoint sets inEwith UAn = U En- Thus
k .
A(M) = A(M U E.) + A(lII( U En)')
. .
= IA(ME.) +A(M(UE.Y>
_1 t'F-l
k
IA(ME.I +A(ME').
_1
m m m
I'(E) = f-l(EUA.) =" (U EA.) = II'(EA.}
71""'1 'PI""I 11-1
ThU8
m
m
;;;; II'(A.) ;;;; II'(E n ),
71...1 '11...1
A(ME) +A{ME') J.{M) IA(ME.) +A(1IIE')
n-'
which shows that I'(E) ;:£ ME). Thus I'(E) = PIE) if E is in E.
Finally. to show that t''Y("I'Y set E in L is a {l.-set.letM be an ar-
bitrary subset of S. Since jt is an outer measure, jz(ME)+P(lIfE')
P("U). Thus to prove that E is a fl-set it suffices to show that
A(lIIE) +J.(ME').
This proves that E is a A-set and shows also, by replacing It! by ME,
that
m
J.(1I!E) = I A{ME.).
-I
Q.E.D.
filM) ;,; ft{ME)+jt(ME').
5 LEMMA. Let p. be a 'IW1.-negaZn;e, eoun/ably additive errt<'1Ided
real valued set fundia" rk/im:d on a lield 1: of sets in S. Fot each A S
let
For £ > 0 there are sets En if I, n = I, 2, . . ., with ft,l U En and
..
II'(E ) ;:£ p(M)+e.
=1
Do
jt{A) = inf II'(E..),
0-'
"'Mre 1M inlimum i. /ok1l over all sequences {E.} 01 sets in E whose
union conlains A4 Then is an outer mffl.SrDe and every set in I is a
iNtI. Fur/Mrmore, pIE) = I'(E) JOT E in 1:.
Now, since 1I-IE UEE., and _llE' UE'E.,
m
m
e + {l(lII) > I p(E.) = I {pIE"E) + I,(E.E')}
"=1 '11=1
P(ME) + fl(ME').
Q.E.D.
186
III. INTEGRATION AND SET FUNCTIONS
111.5.6
III.5.10
EXTENSIONS OF SET FUNCTIONS
181
6 LEMMA. Thoe is a uniquely determined "",allest field and a
uniquely detennined smallesl a-field comaining a given family of sets.
PROOF. There is at least one field, namely the field of all subsets
of S, which contains a given family T. The intersection of all fields
containing T is readily seen to be a field and hence it is the smallest
field containing 7:. A similar argument shows the existence of a
smallest a-field containing 'C. Q.E.D.
The smallest field containing a family of sets will sometimes be
called the field ddermimd by, or grnn-aJnl by the family of sets, and
the smallest q-field containing a family of sets correspondingly caUed
the a-field ddrrmined by, or generated by tbe family.
7 DEFINITION. Let L be a field of suhsets of a set S, and I'- an
extended real va!ued function defined on L. Then I'- i8 said to be a-
finir. 1m L if S i8 the union of a sequence {En} of sets in I such that
v(p, En) < 00, n = 1,2, . ... A measure 8pace (8, I,I') is caUed
a-finite if I' is a-finite on I.
8 THEOREM. (Hahn e.rten.io..) &erycountahlyaddiriunorH'1"lt-
alive t101'tmded Teal valmd sel function p. 1m a field L has a cmt1ltably
additive nm.- ti"" e.rteru;ion to the a-field dd£rmined by L. If p. is
q-f,ni!e on L then this cXfe"sum i. mlique.
PROOF. Theorem 4 and Lemma 5 show that the outer measure
p. is one non-negative countably additive extension of p. to the G fie1d
LO determined by I. Suppose that 1'1 is another such extension. If
p. is q.finite on L to prove the uniqueness of the extension, it will
suffice to show that p(E) = p.,(E) for every set E in Io contained
in a set F in L for which p.(F) < 0".1. Let E.eI and E U E .
Then since p.,(E) II'1(En) = Ip.(E.), it follows that p.l(E) ;'(E).
Similarly p.1(F-E) p(F-E). Since
I'l(E)+p.(F-E) =I'-,(F) =p,(F) =p(E)+p(F-E)
the preceding j"equalities show that P.I(E) = p.(E). Q.E.D.
9 COROLLARY. Every bounded, oompk:c valued. countobly additivl!
aelfu.ldion 1m a field L has a unique countably addilive errJension to the
q-field determined by L.
PROOF. If P is a bounded countably additive set function on the
field I, the .Jordan decomposition (1.8) and Lemma 4.1 show that
its real and imaginary parts may be expressed as the difrerence of two
non-negative countably additive set functions on I. The desired
resuJt follows from Theorem 8. Q.E.D.
The next results on the extension of measures make use of inter.
esting relations between the topology of a space and certain measures
which may be defmed on it.
10 DEFiNITION. The smallest v.field I?l containing all the closed
sets of a given topological space S is called the Bore! field of 8, and
the sets in I?l a.re called the Borel sel8.
II DEFINITION. An additive set function p. defined on a field L
of subsets of a topological space S is said to be regular if for each
EeL and s > 0 there is a 8et F in I whose closure is contained in E
and a set G in I whose interior contains E such that 1,u(C)1 < s for
every C in L with C G-F.
For a complex or extended rea! valued additive set function it
IS seen, from Lemma 1.5, that
sup 1,u(C)1 v(p, G-F) :s; 4 sup IIi(C)],
Thus for such functions the requirement for regularity, that
sup 1,u(C)1 < s. may be replaced hy the equivalent conditIon:
v(,u.G-FJ <c.
12 LE....A. The tetal variation of a Tegular additive oompk:z or
c:cURded Teal valued sel function on a fuld is Tegular. lIforeooer, the
f'O$itive and negative ooriaIions of a bouruWJ. regular Teal valued additive
/tet juncticn are also reguJar.
PROOF, If I' is a regular additive complex or extended real valued
set function on a field I of subsets of a 8et S, then the regularity of
v(P) is ohvious from the remark followin Definition II. If P. is
bounded and real valued, let E e I,. "> O,and let F and G be sets in
I such that the closure of F is contained in E, E is contained in the
interior of G, and v(p, G-F) < c. Then since
v(p, G-F) = p.+(G F)+p. (G F),
p.+(G-F) and p. (G-F) are both less than E, and hence 1'-+ and p.-
a.re both regular. Q.E,D.
1118
III. INTEGRATION AND BET FUNCTIONS
BIoS.18
111.5.14
EXTENSIONS OF SET FUNCTIONS
189
18 THEOREM. IAle",androff) Let I-' be a bounded reguJar comple",
valued additit", aet fu1idion delined on a lield E 01 aubse18 01 a compacl
Wpological apace S. Thm P is rountalJIy additive.
PROOF. Let £ > O. Let {En} be a disjoint sequence of sets in E
with union E, E. There exists a set F, E such that F !; E and such
that v{p, E-F) < £. MOn'OWl" there exists a set Gn,Esueh that En
is contained in the interior a:: of G n , and such that v{p, G.-En)
< £/2" Since u:=-. G F, there is an integer m such that
U:;:., d.: F. Hence
shall assume that /1 is non-negative. By Theorem IS,p, is countably ad-
ditive in E. Thus the outer measure p 8S defined in Lemma 5 furnishes,
aN'Ording to Theorem 4, Theorem 8, and Lernma.5, a countably additive
extension to the u-field E, generated by Eo Thus for E, E , and E > 0,
there are sets E'fI E E with U :-1 En:j E and
fil u En-E) < ./2.
By Definition 11 there is an open set G n and a set An . E with En
!; G n An and
., ., '"
LV{P, En) LV(P, G n ) - E L vIp, G n ) -.
11_1 ..._1 11_1
I«A n En) < ./2n+l.
If G =UG n and A = UAn, then G is open, A,E" and
v{p, F)-e :::: v{p, E) - 2£.
E Gf,;;A,
'" .,
A - uEn f,;;u (An-En),
71_1 n",,]
.,
{t(A - E) filA - U En) + fi( U En - E)
This proves that L '/J(p, En) '/J(It, E). Since
_1
.,
n n
'/J(p, E) '/J(p, U E,) = L '/J(.u, E,),
1-1 {=]
n = 1,2, ...,
::;;; LI-'(A n - En) + £/2
.-,
w
it is seen that vI!', E) LVI!', E,), and thus that '/J(It) is conntably
additive. '_1
Since I-' is bounded, we see by Lemma 1,5 that v{p, E) < co.
Consequently, L::I v(p, E,) < co. and
::;;; L £/2 +' + £/2 = e.
n-'
.,
Applying the same argument to E', we construct a set B in E , whose
closure is contained in E, such thatfi(E-B) < e. This proves that,it
is regular on E,. Q.E.D.
Theorem 14 may be used to construct many interesting examples
of regular countably additive measures. One of the best known exam-
ples of such a measure is Borel-Lebesgue, or Borel measure. To con-
struct Borel-Lebesgue measure on the compact inte1'\'n! S = [a, b]
of real numbers, consider intervals I having one of the two forms
[a, d] or (e, el] where a < c < d b. For such intervals. place
p([a. d) = d-a, p((c, d]) = d-e. Let E consist of all finite unions of
such intervals. It is clear that E is a field and that if a set E, E
has the form
., .,
v(It, U E,) = L v(lt, E,) -+ 0, as n --+ co.
._" f_n
Consequently,
fa-1 oc (p
Ip(E)- !p(E,)1 = II-'(uE,1I S; v(p,UE,) --+0,
__1 f_:n i-n
proving that pIE) = LI-'(E n ). Q.E.D.
-,
14 THEOREM. Let P be a bounded regular complex valued additive
se! lunetifJ1l tklined on a field E 01 trubaets 01 a compact Wpolagieal apflCe
S. Thm I' ha" a unitpte regular eountahly additive e:rtensitm ro t1r£
u-jidd ddermined by E.
PROOF. Since p is regular if and only if the positive and negative
variations of its rea) and imaginary parts are regular. we may and
E =IIUI.U" .Ul .
where l,t i = 1, . . "J 11 are disjoint intervals of the type described
then pII , )+.. '+I-'II ) is independent of the particular family of
disjoint intervals II' . . .,In, whose union is E. The number pIE) may
thus be defined by the equation
140
III. INTEGRATION AND SET FUNCTIONS
1Ir.s.I5
III.5.16
EXTENSIONS OF SET FUNCTIONS
141
pIE) = 1-'(1 1 )+, . '+I-'[I.).
The hypotheses of Theorem l40 are readily verified. and thus by
that theorem there is a unique regular eountably additive extension
of I-' to the a-field of Borel subsets of S. This extension is known as
the Burel measure in [a, b].
The preceding construction can be generalized to several di-
mensions. It Can also be extended by defining the measure differentJy
on the basic field E. We s!mll illustrate this latter remark by describing
here the construction of B Radon measure On an interval.
IS DEFINITION. An inttroa1 is a set of points in the extended
real number system which has one of the forms:
[a. bJ = {Bla s: B b}. [a. b) = {sla s: s < b},
(a, bJ = {Bla < 8 ,;; b}, (a, b) = (sla < s < b).
The number a is called lhe left end point and b lhe right end point
of any of these intervaJs. An intervaJ is linite if both its end points
are finite; otherwise it is an inlinik interval. If I is a complex function
on an intervaJ I, the rotal variatim of I on I is defined by the equation
Let '. = an, -c. Since '(/, (c, c+,.J) > lJ there are points a" b"
;="1+1....,n. in (O,c+,.] = (c.a,.,J with c<a.. b... ..,
< (1n..+l b n .+ 1 $ c+e 2 = ana and such that
.
1 I/(b.)-f(a,)1 > lJ.
i-flJ.+ J
The argument may be repeated by defining E. = an" -c and
choosing appropriate points in the intervaJ (c, C+E.J. By induction.
it is clear that for every integer k = 1, 2, . . ", there B:re points ai' b f
with c < a., b., . . . s: a 1 s: b I s: c +'1 such that
n,
II/(b.)-f{a,)I> (k-l)lI,
'-1
k=l,2,....
.
v(f, I) = sup Ilf(b.) -/(a,)I.
'-1
where the supremum is taken over all finite sets of points al-. b i E I
with l1z ,;; b I ,;; a. ;:;;; b. ;:;;; . . . ;;:;: a. ;:;;; b.. If vU, I) < 00, f is said to
be of btmnded variar.ion on 1.
16 LEMMA.. Let f be a funetion of bounded variatim on an interval
1 and let c be any point in I except 111£ right end point. Then
lim vU. (c, c+eJ) = o.
.......
PROOF. If b is the right end point of 1 the function vU, (c, c+e])
is a non.decreasing function of , in the interval 0 < E < b c. We
may therefore make an indirect proof by supposing that for some
positive II,
This contradicts the fact that I is of bounded variation anI and proves
the lemma. Q.E.D.
Now let I be a function of bounded variation on the open interval
1 = (a, b) which may be finite or infinite. It is assumed that
(i) f(s) = liw/(s+I,IJ, ad;
e->U
I.e., I is continuous on the right at every point in the open interval I.
The closed intervali = [a. b] is a compact subset of the extended real
number system and we extend the domain of f to i by placing I(a)
I{b) = O. J"ust as in the above construction of Borel measure, we
let E be the field of all finite unions
(ii)
E =11UI.U.. .Ul.
of intervals IJI i = I, 2, . . ., n where each II has one of the two forms:
[a, dJ or (c, d] with a < c < d s: b. If the intervals I,. i = 1, . . .. n
in (ii) are disjoint we define p(E) for E. E by the equation
(iii)
.
/.I(E) = 11'(1,)
,-1
Thus if 0 < cJ < b-c there are ":t points a" b, in (c, c+'IJ
c < a., < b., ;? _ . . l1z ;? b 1 C+'I and such t!ult
n,
If(b,)-f(a,)1 > lJ.
'_1
\\'jth
where p([a. d]) = f(d)-/{a) and p(c. dJ) = f(d)-/(c) for a < c
< d b. It is readily seen that I-'(E) is independent of the particular
finite set {I,} used to represent E and that I" is additive on E. Sioce I
is of bounded variation on I, I-' is bounded. Moreover. if E consists of
a single intervaJ, then it follows readily from (i) tllat vIP, E) =
vU. E). From this equation and the preceding lemma. the regularity
v(f, (c, c + EJ) > 6.
O<,<b c.
142
III. INTEGRATION AND SET FUNCTIONS
III.5.17
IIL5.18
EXTENSIONS OF SE'l" FUNCTIONS
148
of l' on :E may be seen as follows: let E be given by (H) where If =
(OJ. b,]. a ;;;: "1 < b l ;:;;; a. < b. . . . ;:;;; an < bft ;:;;; b. and let
it is seen that
'"
(i)
U(E.UNft)= (UEn)UN
.
.-,
-,
E(€) = U (a,+€. b,].
,-,
o < € < inf (b,-a,).
where
'"
'"
Then, by Lemma 115. v(P,E-E(€» = I;_, U.(a"a,+€])---+-Owbicb
proves that p is regular on:E. (In the above expressions, ("1, bJ and
(a l . a,+€] are to be replaced by [a, b,j and [a. a+e] resptrlively if
"1= a.)
It follows from Theorem 14 that p has a regular countably
additive extension to the a-field of all Borel sets in [a. b]. The restric-
tion of this extension to the a.field of Borel 8ubsets of (a, b) is called
the Radan or Btwel-Stidt;es measure in (a, b) ddermin«l by the fun£I:ion
f.
The following extension theorem is elementary and independent
of tbe preceding extension theorems. It <Stabli:she5 a genera] form of
the relationsbip between the Bore]-Stie1tjes measures as just defined
and the Lebesgue-Stie]tjes measures to be defined presently.
17 THEOREM. Let P be a countahly additive VeelQr or et<Urulffl rea!
valtud setjundion <>II tlu! a-field:E. Let :E* CV1I8isl of all sets of 1M form
E U N where E is in :E and N is a subset of a set III in :E with v(/t, lU)
= O. Then:E* is a u-field and if 1M dcmain of p is extended to :E. by de-
fining pIE U N) = p( E). tM e.vtended "",man is co-untably additive on
:E*.
N=U(EnUN.)-U E .,
._1
._1
Thus :E. is a a-field. Now if E,uN, = E.UN. and N.!;;;lIl l .
N.!;;;M.. let M=MIUM. so that E,UM=E.UM and thus
p(E.) = p(EI U M) = p(E.). This shows that p is uniquely defined
on :E* and (i) 8hows that P is countably additive on :E*. Q.E.D.
'"
'"
'"
'"
18 DEFINIT1ON. Letp beacouutably Rdditivevectororextended
real valued function on the u-field :E and let :E* be defined as in tbe
preceding theorem. Then the function tt with domain I* is known as
the LfflFsgUl' e:rl,nsion 0/ p. The a-field :E* is known as the Lebrsgu£
,xteT!sion (relati.", to p) of the a-field :E. and the measure space
(S, :E*, p) is the Lebrsgu& extension of the mCB-'ure space (S,:E, pl.
Expressions such 8.8 p-simple function, totally p*measurable
function, p.measurable function. JL-integrable function. etc., do not
change meaning when p is reganled as defined on :E*. This is beeRuse
these expressions refer to equivalence classes of functions differing by
a p-null function rather than the functions themselves. Thus the use
of the symbol p for the measure on :E as well as for its extension on
X* should cause no confusion.
The measure of Lebrsgu£ in an interval [a, b] ofreR! number8 may
be defined as the Lebesgue extension of the Borel measure in [a. b].
The Lebesgue measurobk sefs in [a. b] are the sets in the Lebesgue
extension (relative to Borel measure) of the a-field of Borel sets in
[a, b]. Similarly, the Lebesgue-Stielljes metlSure determined by a func-
tion j of bounded variation on n finite or infinite interval is the Le-
besgue extension of the Borel-Stieltjes measure determined by /.
If P is either the Borel-Stieltjes or the Lebesgue-Stie1tjes measure
determined by the function / of bounded variation on the interval
I = (a, b) and if g isp-integrable then the integral f g(o)p(ds) is often
f " I
written g(o)dj(o}. In the case where f(o) = 0, i.e., if p is Borel or
. "
Lebesgue measure. f,hen this integral is sometimes written as f (J g(s )ds.
PROOF. It will first be sbown that the family :E* is a a-field.
Throughout the proof the symbol E with or without subscripts will
denote 0. set in:E. the symbol M with or without subscripts will denote
a set in :E for which v(Jt. M) = O. and N with or without subscripts
will denote a subset of a set M. To see that the complement of a set
EuN in:E* is also in :E.. let NGM so that
(EuN)' = E'N';2 E'M'. E'N'-E'M' = E'(N'-M')!;;; M.
Thus if N I = E'N'-E'M' then N1!;;;M and (EUN)' = (E'M')
U N 1 .. Hence 1:* contains the complement of everyone of its elements.
Next let {EftUN.}!;;;:E. and NftGMft. Then. since
U (E.UNft) - u Eft!;;;UN.!;;;U 11-1. = M,
.,-1 _1 tI-l fl'""l
144
III. INTEGRATION AND SET FUNCTIONS
111.6
111.6.1
COVNTABLY ADDITIVE :MEASUB}f;
145
The construction which we have given can be extended to mono-
tone functions (defined on an open interva]) which are not of bounded
variation. Suppose that J is finite valuedJ' real. monotone increasing,
and continuous on the right in ( - co. + co). By our previous construc-
tion, we have already assigned a non-negative measure p. to every
bounded Borel set B. Let In = {sl-n < 8 < +n}, Bnd put I-'(B)
= lim.- p(InB) for every Borel set (the limit exists as an extended
positive rea] numher. since V.«InB)} is an increasing sequence). To
see that I-' is countably additive. note that if B is writtm as the union
of a sequence of disjoint Borel sets B" we have
is the Lebesgue extension of (S. E.I-')' The functions f to be integrated
with respect to I-' ill be extended real valued. or will have their
values in a B.space I. It will be shown in this section that if (S. E.p)
is a measure space the various linear vector spaces of measurable and
integrable functions we have encountered are complete metric spaces.
Criteria for p:-measurability are given and almost everywhere con-
vergence is discussed.
m
1 DEFINITION. A sequence of functions Un} defined on 8 with
values in I converg.. I-'-unilormly if for ea h E > 0 there i8 a set E € E
such that v(l-'. E) < E and such that {/.J com'erges uniformly on
8 - E. The sequence U } CIJ1tVer1!UII-'-uniformly to tM furu:tion f if for
each E > 0 there is a set E € E 8uch that v(p, E) < E and such that
{I.} converges unifonnly to f on 8-E.
It is clear that I-'-uniform convergence of fn to f implies conver-
gence of I. to / in p-measurea The next lemma is a partial converse of
this relation. .
. .
I-'(B) p(BI ) = 1>(B,In) LI-'(B,In} -+ LI-'(B,).
1_] ;-1 J-I
so that
I-'(B» LI-'(B,).
;_1
while
m m
I-'(BI ) = LI-'(B;In) ";; !I-'(B,).
i-] 1-]
2 LEMMA. Let (8, E.I-') be a m£asure 8pIJu. Let Un} be a Beqrum.ce
of fU"""fio"" rkjimd on 8, and BWJYPOse that lim"..n-+ (/.-f..) = 0 in,,-
m£amre. ThEn tlur. exists a robseqrum.ce {In} of U.} IJnd a function f
,
such that {In} converg.. I-'-uniformly to f.
,
PROOF. If lim".,n (fn-f...) = 0 in measure, we can find a subse.
quence {In} and sets E.€E such that v(!',E,) <1/2' and such that
,
I/n,(B)-fn.+.(B)1 < 1/2' if B E.. Then if F. = U :':.E" we have
v(l-'. F.) < 1/2> 1. and. for s F..
so that
..
I-'(B} LI-'(B,).
,-'-
In this case also we adopt the notation
f"g(B)I-'(d8) = r: g(B)d/(s),
and speak of I-' Wi !he m£asure determined by f.
The reader will see without difficulty that the same constructi"i
can be carried out for an BYbitrary open interval I provided only that
i has finite real values, is monotone increasing, and is continuous on
the right at each point of I.
6. Inregration with Respeel to a Countably Additive Measure
I/ ,<B) - fn,CB)[ L I/n)B) -I...... (BII < 1/2>-1,
m-'
where i>i k. Thus if s\l n :'_1 F. then (In,(s)} is a Cauchy sequence
which converges to a function f uniformly on each of the sets 8 - F._
This sIJows that f , --+ f I-'-uniformly. Q.E.D.
3 COROLLARY, Let (S, E, 1-') be a tneasure 8pace. Let {In} be a
Beqrum.ce of fu"""tions defined o-n 8. and BUPP<'se that fn converges to f
in I-'-=asur.. ThEn BO"'" nce co-trlJI) B to f !,-uniformly.
4 COROLLARY. If (8. E,I-') is a meamre 8pace. tM 8pace
F(8. E, 1-'. x) is complete.
The basis for this section is 8 m asure space (8, I, p.), i.e., a
countably additive complex or extended rea] valued set function I-'
defined on a u-fieltlE ofsubsets of a set S. The measure space (S, EO,,.)
146
III. INTEGRATION AND SET FUNCTIONS
III.6.5
111.6.7
COUNTABLY ADDITIVE MEABUR:E.
147
PROOF. Let {I.} be a Cauchy sequence in F(S, E, f.I, I). By
Lemma 2, .. sub,equence {I.,} of fl.} COnV1'rge8 to a certain function I
in J'-measure. Let t > 0 be given. Then there exists an N such that
I/.-Iml < ./2 if m... N, and an n, N such that II... -II < ./2.
Consequently, 1/.-/1 I/.-I..I+I/.,-H <. for n N, so that
I. I in f.I-measure. Q.E.D.
fs E 1/.(sll"vel" de) < c. n = 1,2, .
By Theorem 8.6, I c L. and lim 1/.-/1. = O. Q.E.D,
.--+
M.",...m
7 LEMMA. A set is a null sf! il and only if it is a subset 01 some
mea.mrahk set F such thaI v{ft, F) = O.
PaOOF. If E is a null set, then v*ly., E) = 0 and there are mea-
surable sets E. containing E wIth v(Jl, E..} < l/n. Thus the set
F = nEB is a measurable set containing E and v(,u, F) = O. Q.E.D.
8 LEMMA. II (S, E,I-') is a mta8ure space, a junction I defined on
8 10 I is a null lunction il and tmly il it vanishes almost everywhere,
III is p-int£grohle then IE/(s)p(de) = 0 lOT every E inE if and only il
I vanisMs almost everywhere.
PROOF. It is clear that a function vanishing almost everywhere is
a null function. Conversely, if I is a null function then for each
n = 1,2,..., the set E. = {sll/(sJl > l/n} is a null set and thepreced-
ing lemma shows that the set u :_1 E. = {sl/(s} "* O} is contained in
a set of mea,ure zero, The final statement follows from parts (a)
and (d) of Theorem 2,20. Q.E.D.
The next two results provide useful £riteria for measurability.
9 LEMMA. Let (8, E*,I-') be 1M Lebesgue eaJtension 01 tM linit.
measure space (8, E, 1-'). Th£n a vector or e=ded ..eal valued lundio"
I delilWd on 8 is J'-meo.nu-able il and only il
(I) f is I-' separoJ;ly valued, and
(ii) I-I(G) is in E* IQr each open set G, or. equivalently,
(ii') I I(B) is in E* lor e<uk Bore! set B.
PROOF. First assume that I is ,u-measurable, and let U.} be a
sequence of simple functions converging to f in p-measure. By Lemma
2. we can suppose that UJ converges to II-'-unifonnly. Let E.. E
be such that vly., En) < l/n and I.(s) I(s) unifonnly on S-En.
and let n:"IE n = E. Then E is a null set, and I.(s)--+/(s) for
s; E. The set ./.(8- E) i, finite and hence the closure of the union
U I.(S-E) is a separable set containing I(S-E) which proves
(1.6.12) that I(S-E) is separable.
Now let G be an open set, and let G. be the set of '" such that
5 COROLLARY. II (S, E, p) is a mea.mre splU:e, 1M spaces
TM(8, E, p. I) and M(S, E,p, I) 01 !orally measurah!e and measurah!e
lunctions aTe coml'!et£.
PROOF. By Lemma 2.11, TAt and M are both closed subspaces of
F. Hence, by 1.6.7, these 8paces are complete. Q.E.D.
.. 6 THEOREM, If (S, E,p) is a measure space, and p 1, th£n
Lo(8, E,J', I) is crm>plete and thus a B-splU:e.
PROOF. We observe firstthat a sequence U.} in a,metrlc space is a
Cauchy sequence if and only if
Jim (f... -I. ) = 0
. 11+1
._
for every subsequence in,}. Thus if lim I/.-Iml. = 0, itfollows from
m.........CP
Theorem 8.6 that lim (fm-f.) 0 m ,u-measure. Consequently, by
Corollary 4, there exists an I such that lim I. = I in I-'-mea.mre. Let
.--+
£ > O. let N be so large that I/.-Iml. < e for n. m :2: N, and let
be so small that
lIE It.ls)l"v(P, de)]'" <.
for v(p, E) < and 1 :<;;; n :<;;; N, Then
lIE I/.(s)fov(u, de)II!' < 2.
for v{ft, E) < and 1 n < <0, proving that
lim IE If.(s)['v(Jl, de) = 0
lp.E)-+O
uniformly in n. In the same way, we can show that for each £ > 0
there is a set E. E such that v(,u, E) < CO and such that
148
III. INTEGRATION ASD SET FUNCTIONS
[11.6.10
1I1.6,1l
COUNTABLY ADDITIVE MEASURE
149
S("" Ifn) G. Let 8 E. Then 1(8). G if and only if /.(8) belongs to
some set G" for aU sufficiently large k, i.e.,
00 00
l l(G) - E = U n t;1(G n ) - E.
m,f1.-1l1>-m
Thus sup In is measurable. Similarly the inf In is measurable, and con-
sequent1y lim sup I'DJ lim inf 171 and lim f are measurable.
71_01 "_CO ,,_U>
Since I. is a simple function, we may suppose that the sets 1.I(G n ) are
in Z:. Thus, J-I(G)-E. z: and hence I '(G). Z:*.
Since/ l( U:;:". B.) = U :_lJ-'-{B.), the family of sets Bforwhich
l l(B). z:* is a o.field. From this the equivalence of (ii) and (ii') is
evident.
Conversely. suppose that (i) and (ii') hold. Let E be a nuU set
and {"'.} be a countable dense subset of I(S -E). Let e > 0 be given,
and let An be tbe set of 8 not in E for which 1/(8)-"'.1 < e, while
I/{a)-"',I e, I :;;; i < n. Then A,. .Z:*,andE u U :_IA. = S. Con-
8equently, we can find an N so large that v(p, u::'-N A,,) < £. Put
I.(a) = "'n if 8. An and n < N. and let 1.(8) = 0 otherwise. Tben I.
is a ,.,-simple function. Clearly, I. I in ,.,-measure as e O. Conse-
quently, I is p-measurable. Q.E,D.
10 THEOREM. Let (S, Z:..J') be the Lebeagm eitlm8ion of the
measuTe space (S, Z:. p). Tium a veclOT OT ext;m<kd real valmd fumti<m I
<kJined on S is "'-11U!a.mrab!. if and only if lor elU'h TI'IlXUItU'ahh set F
1J1JCh tlrnt v(I', F) < 00,
(i) I i. p-esoen1ia1ly BepaTably valmd On F;
(ii) F n I '{G) i. in Z:* lOT elU'h 0IM'" 8et G; or, equivakntly,
(ii') Fn/ I(B) is in Z:* lor each Bore! Bet B.
PROOF. This result follows immediately from Lemma 9 and
Definition 2.10. Q.E.D.
As a consequence of Theorem 10 we note the useful fact that an
extended real valued function I is measurable if for each set FEZ:
with (p, F) < 00, and real number c, the set F n (alf(8) > e} is in
Z:*, Equivalently. we may replace (BI/(B) > c} by {Blf(s);;:; e},
(Blt(a) < c}. or (Blt(a) c}. Eacb of these families of sets generates
the Borel sets. If U.} is a sequence of extended real valued measurable
functions and g = sup 1ft, tben
The next theorem applies specifically to vector valued functions,
and provides a method for reducing tbe study of measurability of
such funct:ions to the scalar valued case4 It is sometimes convenient
to npply this theorem rather than Tbeorem 10.
11 THEOREM. II (S, Z:.p) is a "","-'Ure space, tMn a lu1ldu»/ I
on S to a B--space I is p-1'T1£tl.BUn1ble il and only il
(i) lor every ""'''-'UTab!. Bet F with v(,." F) < 00, tM junctimt I
is ,.,-essentially 8eporobly valued on F. and
(ii) lor every linear Ilmcfirmal ",* in 1* the scalar lunction "'*1 on
S is J'-mmsuroble.
PROOF. The necessity of (i) is clear from Theorem 10. If I is
measurableand",* E I.,letr(') = "'./('), IfH is an open set of scalars,
G = ",. I(H) is open in I and r l(H) = I I(G) "Z:*, proving (ii). To
prove suff"lCiency we may suppose without loss of generality that
(S, Z:, p) is n finite measure space. Let {:e.} be a countable dense 8ub-
set of J(S - E), where E is a null set. Let toe:} be a sequence of linear
functionals which satisfy (cf. 11.3.14) Ix:1 = 1 and ",:(:e.) = 1"'.1.
Since If(a)1 = sup 1"':/(a)I, ",S-E, tbe function It(')1 is measurable.
n
n
By tbe same argument the function !I,(') = I/(')-"'nl is measurable.
Let G be an open set in I.If G = </>' I '(G) = </> E Z:*. If G oF </>, let
{y.} be that subset of {"'n} that is in G and let en be the radius of the
largest open sphere S(y., E) G. If G. = S(",., e.) then I '(G.) =
g;;1([O, eft» . Z:*, by applying Theorem 10 to gn' Since G = u : 1 G no
it follows that I I(G) = u :_1 I '(G.) . Z:*, proving, by Theorem 10,
that 1 is me.surablc. Q.E.D.
12 THEOREM. (Egoroff) II (S, z:, p) is a linire ""'''-'UTe space,
tMn a 8eqrumee {tft} 01 meaa-uroble jwu:tions defined on S with a!ma in
I i, I'-uniformly C<Jnvergent to a fu1ldion I il and only il I.(s) con:vcrg.a
to f(a) almost everywh£re.
PROOF. Suppose that I. II'-uniformly. Let Eft. Z:besucb that
v(l', E.) < Iln, and such thatf,.(a) -+ I(B) uniformly fora f En. Then
It = n ::'-1 En is a null set such that I.(s) -+- I(a) for a E.
(sJg(.) > c} = U (Blt.(a) > c}.
n_]
150
III. INTEGR..o\.TION AND SET FUNCTIONS
111.6.18
111.6.16
COUNTABLY ADDITIVE MEASVRE
151
Conversely, suppuse that E is a null set such that f.(s} - f(s}
for sf E. Let
Ek = {sls f E, !/,(s}-f(s}J < 11m for r ;;;; k}.
Then Ek+1,,,, E.,.., and, since f.(s) -f(s) for each sES-E,
U =='1 Ek.t>I = S- E for aU m Hence., for each E; > O. and each m we can
find an integer k", such that v(p, S-E.......) < ef'J'". If we let A.
= n :'IEk .'" then v{ft, S-A,} < E, while Il.(s)-f(s)1 < 11m for
k> k", and SE A., prov;ng that t.(s) _ f(s} uniformly in A,. Q.E.D.
It should be noted that the direct part of the proof does not use
the finiteness of (S,.E, p), so that we have shown that if (S,.E, p) is a
measure space., uniform Jl-convergence implies conv nce almost
everywhere..
13 COROLLARY. (a) If (S, E.p) is a 11!easure 8'fJ<JU.a sffJt"'nte of
measurable jundio,," OOnvergt:lll in measure has a ...bseqlte1lft which
converges almost evtT!fI1Jhue.
(b) If (S..E. p) i8 a fini'" mea8U" BJH1ff. an almo8t everywhue
oo &€qUellce of measurahk f"-lldions is COllloet"ge1lt in p-metU'UTe.
14 COROLLARY. If (S. E, p) is a mMIIUrt? 8pQC/', atld {t.} i8 a
""JUE"ce of meU81lmble vedor valued fltlldions defitled <m S «Jniffgillg
almos! e-verywhen to a f,,,,etian f defined <m S. f i8 measurable,
PROOF. This result follows from Theorem 12 and Definition 2.10.
Q.E.D.
I" lI(s)I'v{ft. ds) < 00 and lim I" If.{s)-f(sl!"v{ft, ds) = 0
.
follow easily from Corollary 18(b) and Theorem 8.6. Consequently,
limsup If.-f..l. limsup If" If.{s)-f..(s)!'v(.u,ds)jll, +2.,1,
m,n---'>- m.ft_Q).II
lim sup [ ( J If.(s)-f(s)J'v{ft. d8) 1 11.
m,t1-+w Er.
+ UE.1/",(s)-f(sWv{ft, ds}t'] + 2,,'"
= 2el/ p ,
SO that lim 1/.-1..1. = O. Since L.(S,.E, p, I) is complete. there
m ta-+
exists agE L, such that lim If.-gl, = O. Then by Tbeorem 8.6 and
. w
Corollary IS(a}, a subsequence of {I.} converge8 to g almost every-
where. Hence? g = f almost everywhere, and consequently f IE" L'fJ and
If.-fl. -->- o. Q.E.D.
IS THEOREM. (Vitali corwergence thfflrem) LeI I P < 00, let
(S,.E. p) be a m<'a.....e space and leI {I.} be a segue_ 01 Ju1U'tiom in
L,(S, E, .u, 1:) eonrx:rgi'l£ almost to a fund-ion f. Then f is
in L,(S, .E, .u, .t) aoo If. - fl, converges to zero if and only if
(i) lim I If.(s)l.v{ft, ds} = 0 unilorm!y i1l n;
tI(P,EJ-i>U E
(il) for each" > O. there is a Bel E. E.E such that v{,., E.) < 00
and such that
f If.{BI"v(l<, ds) < e, n = 1.2, .. ..
S-E
PROOF. The necessity of (i) and (ii) is an immediate consequence
of Theorem 3.6. Conversely, suppose that (i) and (ii) hold. If E is a set
such that v{ft, E) < 00, then
... 16 COROLLARY. (Lebesgue d071li.Ulted oorwergence th£orem) Let
I 0;: P < 00, leI (S, .E, .u) be a FlU'asurt: spa,,", and let {In} be a sequence of
/wlrti",," in L.(S,.E,.u, 3Z) ootlocrgillg al",ast t:N7!f'J'here to a fundi<m f.
Suppose that !here uists a f.nldion g in L.(S,.E,.u, J:} such that
If.(s)1 Ig(s)1 almost t:N!rymhere. Thm I is in L.(S, E,.u, J,} and
If.-/I, co./verges to ::.ero.
PROOF. This result fonows immediately from Theorem 15, as:
conditions (i) and (ii) are satisfied by ff.}. Q.E.D.
I7 COROLLARY. Let (S, E..u) be a pOBilive measure space. and
let {t.} be a fnOllotone ituwasing sequence of non-negative rrol measurable,
but not mcesmrily integrable, fum!irms tonverging a!m08! everywhere to
a fur",tion f. Then,
lim J f.(s)p(ds) = f f(s).u(ds).
. S s
PROOF. Since 0 < f.(s) 0;: f(s}, our result follows immediately
from Corollary 16 if Isf(s)l«ds) < co. Consequently, we have only to
show thllt if I s '.(8)I«ds} 111 < co, tben f.'(s)l«ds) < 00. But if the
152
III. INTEGRA'XION AND SET FUNCTIONS
111.6.18
111.6.20
COUNTABLY ADDITIVE MEASURE
158
sequence of integrals of {In} has a finite upper bound. for each e > 0
we can find an N such that
functions whose limit is lim inf In(s). Consequently, by Corollary 17,
n
Is/n(S)P(ds) ;;:: IsiN(S)p(ds) + e.
n=1 2.....
fsliminf/n(s)l'(dsl = lim f gn(')I'(ds).
n_w _ s
Since g.(s) ..;: 1.(')'
lim Is g,.(s)p(ds) < lim inf f I.(')p.(ds). Q.E.D,
'II._ fl_CIC S
\Ve next show that an arbitrary closed operator commutes. in a
certain sense, with the operation of integration. This supplements the
similar result stated for bounded operators in Theorem 2.19.
20. THEOREM. Let J:, 'V be B-spa&8 and kt T be a clo8ed linear
operaW>' on a do1lUlin J: and with range in 'V. Let (S, I, p) be a
meMUTe sp<u:e and I a I'--in grable fu.."non with value8 in . II TI i8
also p-integrable then J/(s)p(ds) i8 in and
T I s /{s)l'(ds) = I s TI(8)p(ds).
PROOF. Consider the product spo.ce B = I x'V with norm
1[....1IJ) = Ix[ +1111. By hypothesis the graph @ of T is a closed linear
manifold in .8 (cf. 11.2.3). It will fir8t be 8hown, using Theorem 11.
that the function II on S to @ defmed by the equation
g(s) = [f(s), TI(s)], S _ S.
is p-measurable. Let F be a measurable set with v(p. F) < co. Then
since I and TI are both p-measurable there is a null set E such that
I(F-E) and T/(F-E) are both separable. Since
g(F E) f(F-E)xT/{F-E),
g is p--<$SCntially 8eparably valued on F. To prove that g is p-measur-
ab1e it will suffice, in view of Theorem 11, to show that g*g is p-
measurable for every g* in <M*. Let 2* E.8* be an extension (see
Theorem 11.3.11) of g* to :E X 'V and let x* E I*, 1/* _ 'V* be defined
by the equations
Consequently
lim sup J fn(s)p(d8);;:: lim snp f IN('}p(ds)+E = E
(E)_O E ,.(£)_0 E
uniformly in n. This, since.r is arbitrary, implies that
lim J fn(s)p(ds) = 0 unifonnly ror n 1.
..un_n £
In the same way, we can establish the existence of a set E of finite
measure such that
Is_"f"{s)p(ds) < e, n :?: 1.
Thus, by Theorem 15, I- . Q.E.D.
Corollaries 16 and 17 are historicalIy important. and together
with Theorem 6 are the principal results of the classiCAl convergence
theory for Lebesgue integrals.
IS COROLLARY. If (8. I, p) is a pc3itive measure sp<u:e and f
is a non-TI£galiroe measurable function, the ftindibn G <kiined by
G(E) = fE f (8)p(ds), EEI,
is an u:le-nded Teal valtud sel fum:tWn which is CbI.U1tably additive,
PROOF. If E _ I is the union of an increasing sequence of mea.
surable sets Em let f" = XE f. Then
.
G(E) = J,j(s)p(ds) lim JE/n(S)p{ds) = lim G(E.)
n "
by Corollary 17. Q.E.D.
19 THEOREM. (Falou's lemma) Let (S,I, p) be a positioe mea-
sure opoce. and {In} a se'l'te-n<:e 01 fWtI-n£gaJivc mea8UTUble, but 7iOt
necessarily integrable, funri.Wr>s. Then
f lim inf 'n(s)p(ds) ..;: Jim inf f 1.(8)p(ds).
S ,"_Gel ",,_0:> S
.x*.x = z*[x:. 0],
1/*11 = "*[0, yJ.
Then
PROOF. Let gn(s} = inf /.(.). Then g. is an increasing sequence of
>.,"
g.g(8) = ,,*[1(8), Tf(s)] = x./(sJ+y*T/(s)
which shows that g*g is p-rneasurab1e and this proves that g is "'-
measurable. Since
154
III. INTEGRATION AND SET FUNCTIONS
111.6.21
111.7
VITALI-IIAHro:.SAXS THEOREM
155
Ig(B)1 = If(B)I+IT/(B)I,
( k+l )
"'.("') = IX -;;- ,
k k+1
- :c<-,
" "
I k " - 2;
it f01l0ws from Theorem 2.22 that g is I'-integrable. Since g(B) is in
(}I for every B in 8 it f01l0ws that the integral
I ,,-I
...("') = 0, if 0 < '" < - or - :"; '" < I.
n n
Isg(B)I'(da) = [I s /(B)I'(da}, Is T/(B)!-'(ds)]
i8 also in QJ. This means that Is/(B)!-'(da) is in SD and that
T Is/(B)!-'(da) = Is T/(B)p(ds). Q.E.D.
The convergence theory of this section may be used to prove a
useful reciprocal relation between Stieltjes integrals with respect to
two different functions of bounded variation, which is given by the
famou8 formula for integration by parts. Before stating it, we prove a
preliminary lemma.
fifi(3J)= fi m,
k k+1
-;0;:;",<-
n "
l:";k :";"-2;
1 ..-I
tln("') = 0, ifo < '" <-or -;O;:;3J < I.
n ..
Then clearly, ",.(x) --+ ex("'), fi.(") -.. fi(",), and
1",(")1 sup 1,,(x)l,
D<II<l
21 LEMMA. Let / be a lunction 0/ bounded wriation in the inlmJal
(a, b). Then I(a+) and I(b-) cn$!.
Ifi.(x)1 8UP lfi(x)!.
O<z<l
Consequently, by Corollary 16, both integrals are defined, and
J: IX(",)dfi(..) + J: fi(..)da.(..)
PROOF. Since it is clear that 1 is of bounded variation in (a. b) if
and only if its real and imaginary parts are of bounded variation on
(a, b), we may and shall assume that 1 is real. If
lim sup /(a+I"1> > lim mf/(a+I"I)+
0--+0 0--+0
where > 0 1 there are decreasmgsequences as" hi' with an > fin> an+l
n = 1,2, . . ., which converge to a, such thatf(afi)-/(b n ) > and this
clearly contradIcts the fact that 1 is of bounded variation on (a, b). Thus
lim sup l(a+1,,1) = lim inf /(a+I.I) = Iim l(a+I"1> = I(a+).
_U _U _0
fi-! ( k+l ) { ( k+l ) ( k ))
= n r: 1=, IX -;- fi -;- - fi ;;
+ n r: ],fi ( ) (IX (k:l ) - a ( ))
" ! { ( k+l ) ( k+l ) ( k ) ( k )}
= Iim L IX - fi - -IX - fi -
-+O' ,t...t '/1, n n n
= ,:Hl- ) tI(1 - ) -a( ) fiG))
[n the same way we can show that /(b-) exists, Q.E,D.
22 THEOREM. Let a(x) and fi(x) be t-ol!O fwwtiom c/ bountkd
vaTialion in an interval (a. b), Suppose tJuu one i8 oomi_ in (a, b),
and tJuzl tM cther i. eon/inU<>U$ on tM r-iglU, Then
J: lX{x)dp("') + I: fi(:c)da.(:c) = IX(b- )fi(b- )-IX(O+ ),8(0+).
= a(I-)fi(l-)-a(O +)fi(O+). Q.E.D.
7. The Vitali-Hahn-Sak. Theorem and Spa e. of Measure.
FROO.-. Clearly, it suffices to prove the result for every finite
subinterval of (a. b). For simplicity, and without loss of generality,
we will suppose that (a. b) = (0. 1). Pot
In this section a metric will be introduced in the ".field 1: of a
measure space (8,1:,1') in such a way that the corresponding metric
space E(i') is complete, The additive functions on E which are con-
tinuous on 1:(i') are precisely the Ii.continuous additive functions on
E. A basic result ccncerned with a sequence {v n } of such functions is
156
III. INTEGRATION AND SET FUNCTIONS
III,7
III.7
VITALl-HAHN SAKS THEOREM
157
tbe Vitali-Hahn-Saks theorem. It states that if (lOft(E)} converges for
each E in I, then the continuity of 10ft on tbe metric 8pace I(I') is
uniform witb respect to n = .1, 2, . . ._ The reader is already familiar
with a striking analogy to the Vitali-Hahn-Saks theorem the tbeo.
rem (U,l.17) asserting that continuity of the elements of a pointwise
convergent sequence {T9I} of continuous linear operators on an F-
space is uniform in fl = 1, 2, . . .. It is enlightening to compare the
proof of the Vita1i-Hahn-Saks theorem given here (which is that of
Saks) with the proof of the unifonn bounded..ess principle in F-spaces
(cf. 11.1.(3), for such comparison reveals a useful analogy between
a-fields and linear metric 8paceS. l\Iore direct relationships between
set functions and certain B-sp""es are explicitly discussed in the next
chapter. where it is shown that the conjugate spaces of some familiar
B-spaces may be represented in terms of set functions. In the present
section it will be shown that the spaces of bounded additive set func-
tions, and regular countably additive 8et functions are all B-spaces.
XA and XB differ by al'-null function. Thus the map E -+ X£ may be
regarded as a homeomorphism of I(P) onto a subset of bl(S, I, ,,).
It is clear that this homeomorphism maps Cauchy sequences into
Cauchy sequences. Thus if e(E.. Em) -+ o. there is, by Corollary 6.5,
a function X in M(S, I, ,,) with Xs -+ X. By Corollary 6.13 some sub-
sequence of {XE } converges alm st everywhere to X and thus for
almost.all 8 in S: X(8) is either 0 or I. Thus X = ZE for some E in E.
Since Xs -+X" in l1,t(S,I,,,}, equation (ii) shows that En -+E in
I(,,). The space I(I') is th....fore a complete metric space.
If A is an additive vector or scalar valued function on I which is
p-continuous , then}. is defined and continuous on the metric :space
I(,,). To 8ee this note first that the identities
v(p, ELI F) vIp, E - EF) + v(", F - EF),
A(E) - A(F) = A(E - EP) - A(F - EF),
The melrw space I(p)
Lct (S, I,!,) be a measure space, and for each pair A, E in I de-
fine the equivalence relation A E by the equation v(p, A LI E) = O.
wbere ALl E is tbe 8ymmetric difference (A U E) -AE of A and E.
The fact that is an equivalence relation follows readily from the
fact that the symmetric difference is a commutative and associative
operation with A LI A = .". The set I(P) of all equivalence classes
E(P) = {AlA E} is a metric space with the distance function
(i) e(E(,,), F(P» = arctanv(", ELI F).
For the sake of simplicity and convenience we shall speak of the sets
E in I as e1ements of I(P) just as we speak of tbe elerlIenls ofthe space
M(S, I, ,,) of measurable fW1ctions as functiorfs on S rather than
equivalence classes of such functions. Thus we will sometimes write.
instead of (i), the equation
(ii) erE, F) = arctan v(", ELI F).
It should be noted however that a function A on I cannot be regarded
as defined on I(p) unless A(E) = A(F) whenever v(p, ELI F) = o.
We note that A E if and only if the characteristic functions X..
and X8 are eqUIvalent as elements of M(S. I, 1'), i.e., if and only if
show that A(E) A(F) whenever v(p, ELI F) = 0, and so a ,,-con-
tinuous additive fuoction A on I is defined on the metric space I(P).
These !-lame identities show that such a 1 is continuous on E(!').. for
if Em -->- E in I(,,), then v(", E-EE m ) -+ 0 and v(p, Em- EEm) -+ o.
Thus A(E-EE m ) -+0 and A(Em-EEm) O and therefore '-(Em)
A(E). Thus a p-continuous additive function 1 is continuous on the
metric space I(P). Conven;eJy, an additive function on I which is
defined and continuous on I(,,) is ,,-continuous. This follow8 imme-
diately from the definitions.
It should also be observed that the binary operation8 AU B,
AB, ALl B are continuous maps of I(P)xI(P) into I(.a) and that
ilie unary operation of comp1ementation, A -+ AI, is a continuous
map of I(P) into I(P). These e1ementary hut important facts are
readi1y verifIed by an application of the ineqlUi1ity
v(.u, ELI F) < v(p, E)+v(p, F}
to the identities:
(AU B)LI (AI UBI) = (ALl A.)LI (BLI BI)LI A(BLI BI)LI BI(ALI AI)'
(AB)LI (AIBI) = A(BLI B1)LI B1(ALI Ad,
A'LI A; = ALlAr'
IA LI B) LI (AI LI B I ) = (A Ll Ad LI (B LI BI)'
158
III. IN'I'EGRATION AND SET FUNCTIONS
III.7.I
III.7.3
VITALI-HAHN-SARS THEOREM.
159
If V(p., S) < ro and if a sequence {En} in E converges to E in the
Sense that
PROOF. By Lemma 1, An is contmuous on E(p.) and so for each
€ > 0 the set>
(iii)
E = lim inf E = lim sup En'
En... = {E[E E, I)."(E)-J.,,.(E)I €},
nJ m = I, 2, . . _.
n
XI) = n LI'J,'tII.!
tl.tn;::
p=l,'2,...,
then e(E., E) -? O. i.e., E -? E in the metric space E(I-')' For con-
dition (iii) shows that XE (8) --+ xd8) for every 8 in S and hence, by
the dominated converge ce theorem of Lebesgue (6.16). it is seen..
using (ii). that
e(En.E) =arctan f IXE (8) XE(8Hv(I-"d,,) -?O.
5 .
are do:;ed in the complete metric space£(p.). Since the limit lim,. ).,,(E)
exists for each E E E we have £(p.) = U ;:'1 E . The Haire category
theorem (1.6.9) shows that one of the sets E has an interior point.
Thus there is an integer q, a positive numher r and a set A E I 8uch
that
The above statements which relate the usual point set operations with
the metric h. E(p.) show immediately that, when v(p, S) < co, the
dosure in E(I-') of a subfieJd £. of E is itseJf a <I-fieJd.
The remlU'ks above are summarized in the following lemmll.
I)."(E)-J.,,.(E)I :5;; €,
71,m q,
for every set E in the 8phere
K = {EIEEE. v(p., ALl E) < r}.
ft
Let 0 <" < r be chosen so that
I).,,(B)I < E, .. = 1,2, . . ., q,
for every B . E with v(p., B) < iI. Now let v(p., B) < iI 60 that the sets
AU B, A - B are both in K. The identity
).,,(B) = A_(B) + {).,,(B) - J..(B)}
= A.(B) I- ().,,(A U B) -J.,,(A U B)}-{).,,(A - B) - A_(A - B)},
shows that I}.,,(B)[ < 3€ for IlIJ n = 1, 2. . . .. Q.E.D.
8 COROLLARY, Unlkr tM. hypotheses of Theorem 2 and tM. add-
itiona! hypothesis v(,u, S) < co, the fundion A(E) = liml,.(E) is
counlalily additive em E. ft
PROOF. The additivity of A follows from that of An and therefore
to prove countable additivity it suffices to show that A( Em) --+ 0 for
every decreasmg sequence {Em} C E with void intersection, Since
v(I-', Em) = I:'m v(p., E.-E'+l)' it follows that for such sequences
v(p., Em) --+ 0 and thus. by the theorem, for every £ > 0 there is an
integer m. with
1 LEMMA, If (S, E, p) i8 a "",asu,.,. s-puce, the <I-field E (or more
precisely, tM qwJtierll set EIY, ",ktTeY i8 the itWal of all p-null sels in
E) is a complde m<:tric space u1ICur tM f1I£tric
e(A, B) = erctan v(/', A LI B).
An ooditive ""etor or 8ctJ/ar valued funrtion on £ is tkfi>letJ am! contin-
UOU8 on E(P) if and emly if it is I-'-oontinrwus. The operaJ.wns A U B,
AB, ALl B, A' are continuous fwtcti<>>l8 of A wid B. If v(p., S) < co
tM diJsure in I(p.) of a subfwld of E i8 a a-field.
The following theorem is one of the most important results in
the throry of set functions. The proof given here is thllt of Seks. and
consists of eppJying the Baire category theorem to the space I(p.)
in much the same way 8S it was applied to an F space in the proof of
the principle of uniform boundedness (cf. lI,l.IS),
2 THEOREM. (Vitali-Hahn-Sak8) Let (8, E, 1-') be a meUSUTe space
and {).,,} a seqtlClIce of ,u-amtinuous vct:for or scalar valued additive 8et
funclioWJ on E. If the lim,t lim A.(E) exists for each E in E IMn .
lim }.,,(E) =0,
"C,..E)-+D
uniformly for n = I, 2, . . ..
1}.,,(Em)1 <e,
m :2: m6'
'It = 1..2, ...
Hence
1)'{Em)1 ;;;€,
m;;;m e o
Q.E.D.
160
111. INTEGRATION AND SET FUNCTIONS
III.7.40
III.7.4
VJTALI-HAHN-SAKS THEOREM
161
Corollary 8 can be strengthened. as in the following roroJlsry,
which is stated here only for scalar valued functions. Actually, the
following result is true for vector valued functions. but the proof
is postponed until Section IV.IO, where B aeeper investigation into
the properties of ,-ector valued set functions is made.
,. € ba. For 5 > 0 choose n. so that Ip.-Pml 5 for m, n;;;:; n,. Then
p(E)-p.(E) = limm (.u".(E)-p.(E)), from which it follows that
11'-1'.1 ::;;; 5 for 'It :?: 'It" Hence 1-'. -+ ". which prov<s that ba(S, I. I)
is complete. It fonows. therefore, that ba(S, I. I) is a B-space.
If I is the 8et of real or complex numbers, then aecording to
Lemma 1.5,
4. COROLLARY. (Nikadfim) Lid {,u.} be a sequ<'nct? 0/ counWhly
additive 8calar jundi(Jt!8 on theo./ield I,l/ pIE) = lim.p,.(E) e",isls /OT
each E in I tlu:n I' I:s cauntab!y add!!ive On I and llu: oo...../abk additivity
oj 1-'11 is uniform in tt = 1, '2, . . ..
PROOF. The final conduslOn means that if {Em} i8 a decreasing
sequence in I with void intersection then limmPA(Em) = 0 uniformly
rorn = I, 2,.... To prove this we note first that since ILn is finite onI
the total variation v(p.. S) is also finite (LemTIUI. 4.7). Now let
A. = 0 if 1'. = 0 and otherwise let _
).,.(E) = v("". E)jV(PA' S). .A = L ).,./2.
.-1
sup Ip(E)j ;:;; v(p, S) 4 sup Ip(E)I.
EE1: BfF
This shows that v(p, S) is a norm in ba(S, I, 1') which is eqmvalent
to the norm sup Ip(E)I.
E,r
The set ca(S, E, 3::) of all countably additive set functions in
ba(S, E. I) is clearly a linear manifold in ba(S, E, I). To see that it is
a closed linear manifold, let I' . ba, and {,u.} be a sequence of elements
of ca(S, E, I) converging to p. Let {Em} be a sequence of disjoint sets
in I whose union E is also in I. Then as n -+ co.
Then A is countably additive on I and A(E",) -+ O. Since each p. is
l-continuous, the conclusions fonow from Theorem 2 and Corollary
8. Q.E.D.
TIu: sp""cs ba(S, E, 3::), Tba(S. E, 3::). ca(S, E. 30), Tea(S, E, I).
It will now be shown that severa! familiar spaces of set functions
are B-spaces.
Let E be a field of subsets of a set S, and let ;E be a B-space. By
ba(S, E. I) will be understood the family of all bounded finitely addi-
tive set functions with domain E and range in I. It is evident that the
sum of two functions in ba(S,1:. I) is again in ba(S, E, 3::), while if
p is in ba( = ba(S. E, I» and" is a scalar, then ap is in ba. Thus
ba is a linear vector space. If the norm of I' is dcfined by the equation
?II CE> 0. m
p.(E) - L p.(E,) = P. ( U EJ) -+ p ( U E,) = I'(E) - L pIE,),
1-1 :f-m+l 1=-4+] 1-1
uniformly for m = I, 2, . ... On the other hand, as m -).- 00,
pA(E)- LJ:.,p.(E,) O for each n = 1.2,.... Thus, by 1.7.6.
.-"
00
p(E} = LP(E,),
,-,
which proves that I' is countably additive on I, Thus ca(S, E. 3:) is a
closed linear manifold in ba(S. E, I) and is therefore a B-space.
If S is a topological space, Tba(S. E, ;E) will denote the set of all
regular set functions in ba(S, E. I). It is easily seen that Tba(S, E, 3:)
i8 a linear subspace of ba(S. E, I). Let I' (; ba(S. E, I), and let {PA} be
a sequence of elements of Tba(S. E, I) converging to I" Let 5 > 0
and E (; E be given, and fix 'It so large that Ip-p.1 ;:;; 5. Let F, G" I
be such thatF!;; E, Eis contained in the interior ofG, and Ip.(A)I;:;;"
for every A in Ewith A!;;: G- F. Then, for such A. we have Ip(A)1 ;:;;25,
which proves that 1''' Tba(S, I, 3::). Thus Tba(S, E. I) is a closed linear
manifold in ba(S, E. 3::) and therefore a B-space.
The set Tea(S. E, 3::) of all regular countably additive measures
in ba(S. E. J:) is the intersection of m(S, E, 3::) and Tha(S, E, 3::). Con-
Ipi = sup Ip(E)I.
E.r
then ba becomes a normed linear space. To see that it is mmpJete, let
{p.} be a Cauchy sequence in ba. Clearly {p.(E)} is a Cauchy sequence
in J: for each E" I, so that pIE) = lim I'A(E) defines an element
162
III. 11'TEGRATIOX AND SET }<'UNCTIONS
III.7.5
111.7.6
VITALl-1tAHN-BAKS THEOREM
163
sequent1y Tea(S, I, ;E} is also a closed linear subspace of bu(S, I, ;E},
and hence is also a B-space e
We Dote that if;E is the space of scalars (real or comp1ex} it will
usually be omitted from notat;ons likuu(S, I. ;E}. Thus cu(S. I} is the
space of all real or complex valued countably add;tive set funct;ons
defined on I.
We have just seen that the spaces OO(S, I) and ca(S. I) are B-
5p es_ For Some purposes it is useful to know that they are also C!om-
plete lattices. \Ve close this section with some observations concerning
their order properties and another decomposition theorem.
I.et I be a field of subsets of a set S, then if p. is an additive set
function such that p.(E} ;;;: 0, E E I, we say that p. is positi and
write p. o. If p,-p., 0 then we write P., ;;;: fl2 or p., ';; p.,. It is
readily seen that this gives a partial ordering (1.2.1) on the collectinn
of all real or complex va1ued additive set functions on I. The terms
"'upper bound" 11 "least upper bound''. etc" have the meanings given
in 1.2.8.
p.(EJ+p.{F) p.(EU F}.
Next let {B,}. {C.} be finite partitionings of E and F into disjoint sets
in :E with
:Ep..JB.) < p.(E) +.,
Ip.p,(C,) <p.(F}+e.
Then
5 THEOIU!:M, Every aubsrl 01 !Iu! partially ordered coIlecl.ian of
arMit"", scalar val""d set fundiDns on a /idd which '= an upper hound
(law<T hound) '= a least upper bound I,grrotest U;wer bound).
PROOF. To prove the theorem it will clearly suffice to show that
an indexed 8et {p..} of positive elements has a greatest lower bound p.
We define
p.(EU F} I,u",(B.}+:Ep.e,(C,} <p.(E}+p.(F}+2e,
.and so
p.(EU F) ;S; p.(E}+J4F},
which completes the proof of the additivity of p.. To see that p. is the
greatest lower bound of the set (.u.) let be an additive set fUIlction
with ;S; p.. for each a. Then for any fillite partitioning E" . . ., E.
of the set E and any choice "', . . ., a. of the indices we have (E.)
p",(E.) and thus
(E) = I (E.) :Ep..,(E.},
which proves that {E} pIE). Q.E.D.
We point out that the precediuj( theorem did not aSsume bound.
edness of the set functions.
6 COMLLARY. The laitkes ha(S, I) and ca(S, I) are complete.
PROOF. It suffices to show that if p.. ;;;; o. then the greatest lower
bouud p. of the subset {.u.} has the property of boundedness or of
countable additivity, If each p.. is in batS, I}, then since 0 ;S; p.(E)
;::;; p..(E), E e:E, we have,u e batS, I}. If P. e ca(S, I), and if {E.)k:E,
E.., k E., n E. = If> then lim.p..(E.} =O.SinceO ';; p.{E.) ;::;;p..(E.}.
it foUows that Iim. p.(E.) 0 and hence p. e ca(S, I}. Q.E.D.
p.(E} = inf{.u.,(E.} +... +p..{E.H. EeI,
where the infimum is taken over a1l finite subsets {a,} of indices and
aU finite families of disjoint sets {E.} in I whose union is E. It will
first be shown that p. is additive on I. Let E, F be disjoint sets in I
and let e> 0 be arbitrary. Let EU F be partitioned into disjoint
sets A",." A.. in I with
We now 8how that if}, e ba(S, :E}, then}. can be uniquely decom-
posed into the sum of a countab1y additive set function aud one
which is finitely additive in a certain maximal sense
7 DEF1NITION. If}. is in ha(S, :E} and if}, ::,: 0, we say that A is
purely linitily iUlditive in case 0 ';; ,u }. and p. e catS, I) imply that
p.=0.
8 THEOREM. If }. is in ha(S, I} and}, ::,: 0 th= there is a unique
deoompotrition }. = A, +J.", }., ;;;: 0, where A, i$ counlably arMitivc and
J." i. a purely finitely addilive sel ft-tndiDn in batS. I}.
p." (AI H.. .+p....(A..) ;S; p.(Eu F}+c
for an appropriate choice of the indices "'" . . ., .....' If E, = A.E and
F. = A,F then
p(E}+p.(F} < L'p..,(E.}+:Ep...(F,) = IP..(A,} p.(EU F)+e
which, since E > 0 is arbitrary, proves that
164
11[. INTEGRATION AND SET FUNCTIONs'
III.8
III.8.1
RELATIVlZATION OF .sET FUNC'I'{ON8
165
PROOF. Let C be the set of aI! I' in ca(S, I) such that 0 :::; I-' :;;: A.
Let 1-'.. n = 1.2, ' . .. be chosen from C in such a way thatlim"p;,,(S)
= suPp,c pIS) < co. Since 1', :;;: I;_II-'" i = 1, ..., n, it foHows from
Corollary 6 that {!-'J.' . . ',I-'.} has a least upper bound fin in ca(S. 1:).
Clearly A fi, < . . . :;;: fin . . .. Let I, be the .,.-field determined
by I and denote the unique extensions (5.8) of tbe mea8ures {,u.} to
II by the same symbols. Since tbe extension of a non-negative set
function on Ito I, is non-negative, itfollows that {U.{E)} is a bounded
non-decreasing set of real numbers for each E E II' We define A.(E)
= lim.p.(E), EEII' By Corollary 4, Al is countably additive on II'
and hence its restriction to I is in ca(S,I). We define A,,(E) =
A(E)-A,(E), E E I: clearly A. 2 O. If A" is not purely finitely additive,
there is a non-zero A' E ca(S, I) such tbat A' A-AI: hence Al
A.+A' :;;: A and sUP.,cl'(S) = (S) < (S)+A'(S). This is a contra.
diction. To prove the uniqueness, suppose that A = A. -rA. = '" +Yt
where AI' Y 1 are in ca(S, I) and A., y. are purely finitely additive nOn-
negative 8et functions. Now A,.- Y l = y.-A" and 80 8UP ( -YI' 0)
= sup (v.-A.. 0). By Corollary 6. sup (A,.-y 1 . 0). c,,(S. I) and
evidently 0 sup (AI-VI' 0) < Y. So that 8UP (A.-VI' 0) = 0, i.e..
A1(E) v,(E). EE1:. Similarly sup (Y1-A 1 , 0) = 0 and hence
VI (E) :;;: A 1 (E), E. I. Consequently Ai = v,. as desired. Q.E.D.
This result may be extended to complex valued set functions by
decomposing them into rea! and imaginary and positive and negative
parts by means of the .Jordan decomposition (1.8). We leave this to
the reader.
Since a l-'1-simple function is clearly "-8imple, it follows immediately
that .a /ll-measllrable function is p.-measurable.
If I is a l-'1-integrable simple function. it is evident that 1 is also
a p-integrablesimplcfunction.and that JE/(s)I-'1(d.s) = fE/(s)p(d.s) for
E . II' Let I be a I-'J.-integrable function and let fl.} be a sequence of
PI-integrable simple functions converging to I in PI-m....1lre, and such
that
lim Is 1/.(s) - 1..(sUPI(d.s) = o.
m.ft-+Q)
Then I. -+ I in ,,-measure. and
lim J 1/.(s) - 1..(s)II-'(d.s) = o.
m,n---)-CI'
Consequently,
JE/(S)1'1(d.s) = ! ':, IEI.(S)!'1(d.s) = IE/(S)I-'(ds)
for each E E I1"
These I'Pmarks are summarized in the following lemma.
8. Relativization of Set FunctiOlll!
1 LEMMA. ul S he u sel. I a lidd 01 subsets of S. and I-' a "'-'n-
negative liniliil!! addilive setlum:lion d£fined on 1:. LeI I, he a sublield
01 I, and PI the nslriclw" 0/ I-' Irom I to 1:,. Then
(a) corrcerg"'''''' in I-',-measure implies COf't>eTgence in I-'-measure:
(b) a p,.nu!! ftuwlion is a I-'-null I"'u:tw,,;
(c) a 1-'1-null set is a p-null set;
(d) a I-'J. fundion is fl'metl8WI"ahle;
(e) a p,-WtegrabIe IUnclion I is I-'-inlt:grahk and
Througbout this section, S is a set, I a field of subsets of S, and
I-' a finitely additive set function defined for E. E. The field II is a
subfield of I. and 1-'1 the restriction of l' from I to 1: 1 , There are anum.
ber of elementary but useful relations betweenl'- andPI-measurabi1ity.
1-'- and PI-mtegrability, etc.. which wiU bc discussed in the presE!ll1
section.
First. if p is non-negative. it is evident that V*V", E) v*!!'1. E)
for E k S. Thus, convergence in J"t-measure implies convergence in
It-measure, a. pcnuU function is p-null. and a Pl-null set is Jl-null.
JE/(S)PI(d.s) = IE/(S)p(d.s),
EEII'
Let I be an arbitrary B-space. It follows from (d) and (e) that a
function I E L.{S. II' 1-'1' 3:) is also in L.(S, I,I-" 3:), and that its norm
in both spaces is the same. Thus L.(S, II' 1-'1' 3:) has a natural iso-
rnetric embedding in L.(S, I, 1-'. :1'). and can be regarded as a sub-
space of L.(S. I. 1-'. 3:).
2 LE"MA, Under 1M hypolheses 01 umma 1 a wlally l-'1-meas1tr-
able functum in L.(S. E, 1-', 3:) is in L.(S, 1: 1 ,1-'" I).
166
III. INTEGRATION AND SET FUNCTIONS
111.8.2
III.8.B
BELATIVIZATION OF SET FUNCTIONS
167
PROOF. Let fin} be a sequence of ....-.imple functions converging
m I-'I-mEaSUre to a function I. Lp(l-') = L.(8, E. p, 1:). By the
argument presented in the proof of Theorem 2.22 we may and shall
as'Ume that If.(8)1 21/(8)1 for all 8 in 8. By the dominated conver-
gence theorem. In ..... I in L.(I-'), and hence {fn} i. a Cauchy .equence in
Lp(P) and {itn(' )Ip} is a Cauchy sequence in L,.(I-')' Since Ifn(' )Ip is a
Pt.-simple function its P1-integral coincides with its p-integral and
thus {Jf.{' )Ip} is a Cauchy 8equence in L,.(p,). Since 1/.(. >i" converges
to If(' >i" in ....-measure. it follows from Definition 2.17 that If(' W
is ....-integrable and thus that I' L.(....). Q,E.D.
In addition to the restriction of p to a subfield of E there is an-
other type of restriction of common occurrence in mtegration tbeory.
In the following oliscussion of this other type of restriction it is not
n " to aSSume that p is non-negative.
Supposc that Eis a set inE. IfweputE(E) = IF. EIF E} it
is clear thatE(E) is afield ofsubset8 of E, and thatE(E) is the family
of all.ets AE, A . E, and that if E is a .,..field, then E(E) is a .,.-field.
E(E) i. called the ustridWn 01 E to E. If E 1 is a field, E. E 1 . and E is
the .,.-field generated by E 1 , then we can easily .how that E(E) is the
.,.-field generated by E 1 (E). Indeed, E( E) is a .,.-field containing E 1 (E),
while, conversely, if E. is a a-field of subsets of E containing E 1 (E) it
is evident that the fumilyofunions of a set inE. with a set inE(S-E)
is a .,.-field containing E 1 . so that E.;;;!E(E).
The restrictzon A of I' to E(E) is sometimes caUecl the TeJJtrietion
011-' w E. It is clear that (E,E(E),.:I) is a measure space if (S, E, p) is.
The reader will have no difficulty in verifying that ViA, F) = v(p, F)
if F E. Tbe set of (vector or extended real valued) functions de.
fined on E is In an obvious one-to-one correspondence with the set of
functions defined on 8 and vanisbing outside E; we have only to
..>. nd the domain of definition of a function I defined only on E to
all of 8 in the natural way, by putting 1(8) = 0 for 6; E. Then a
sequence of functions defined on E converges in A-measure if and
only if the sequence of extensions converges in JL-measure. In this
case the original sequence of funcbons defined on E is said to amverge
in I-'-measure on E. Similarly, if tI,e domains of two functions I, g both
contain the set E, the statement 1(8) = g(s) p--alnwsr everywhere on E
means that there is a set A E with v*(I-', A) = 0 and 1(6) = g(s)
fb.. every .6 in E A. A function defined on E is A simple or A-measur-
able if and only if its natural extension to 8 is p-simple or p-measur-
able, respectively. The concepts of A-integrability and I-'-integrability
can be seen to be related in the same way Thus, L ( E, E( E), .:I. 1:)
i8 i80metrically equivalent to the set of all functions in L p (8, E, 1-'. I)
vanisbing outside E, .0 that the former space may be regarded as a
subspaee of the latter.
B LEMMA. LeI (8, l:, p) be a posilive measure spate and.... the
Testricticm 01 I-' to a subfield E 1 01 E. If E i. the .,.-field gel1£ro1ed by El
and ill-', i8 "'-linitr on El' then the ....-inkgrahh simple IUWJ!icrns aTe
dense in L.(S, E, p, 1:), 1 < P < ro.
PROOF. Since the ,u-integrab]e simple functions are dense in
L.(8, E, p, 1:) (by Corollary 8.8), it suffices to prove that the cllBJ'''''-
teristic function XE of a set E in E with I-'(E) < ro is the limit in
L p (8, E, po) of a sequence XE with En E,. Let.4,. be an increasing
.equence of sets inE" such that 1-',(.4,.) < ro and U:" l A.. = 8. Since
piE) < 00 we have IXEA -xl"l = {p(E-A..)}lJP ..... 0, and it win
therefore suffice to prove "'that XE.... i. the limit in Lp(S, E, p) of a
sequence XI" with En' E 1 for m = I, . . .. Since E(Am) is generated
by E 1 (A",). ur whole argument can be confined to the set. Am. Thus,
we may and shallllSSume without loss of generality that piS) < roo
Ey Lemma 7.1 the closure of E 1 in the metric 8pace E(p) is a a-field
containing 17 1 and thus every set E in I is the limit of B sequence
{En} of sets in Er Since p(8) < ro. the function identically equal to
one is in L p (8,E,pI and dominates XE.(8). Thus by Theorem 3.7,
XE ..... XI" in L.(8, E, 1-'). Q.E.D.
.
4 LEMMA. Tk lield generated by a cuulltable lamily 01 8efs is
it8ell COllnJnb/£.
PROOF. Let = {En" n = 1, 2, . . .} be a countable collection of
subsets of a set S. Let I be the family of all unions of finite sub-
collections of . 91 1 the family of all complcments A' in 8 of sets A
in 1' 'G'. the family of unions of finite subcollections of 9l l , 9l. the
family of all complements A' of sets A in 2' etc. It is clear that if A
and B arc in t'(f:n then
168
11[. INTEGRATION AND SET FIJNCTIONS
III.8.5
111.9.1
EXERCISES
169
9. Exem..es
I Show that f. TM(8, E, p) if and only if for each e > 0 there
exists a set E.. I and a finite collection of disjoint sets A., . , '. A..I
such that A. U. . . U A. = E., v{u. E.) < E, and sup 1/(8)-/(t)1 < e,
j = 1, . . ., n. _,ilEAl
2 Let A 8 be a p-nu!l set. Show that there need not eXIst any
set E. I containing A such that v(p, E ) = O.
8 Suppose that S is the interval (a, b], that E is the field
of finite sums of intervals half open on the left, and that I' is the
restriction of Lebesgue measure to E. Show that a real valued function
I is p..measurable if and only ifit is continuous at every point not lying
in a certain set E of Lebesgue measure zero, and p.-integrable if and
only if it is I"measurable and Lebesgue integrable.
4 Show that, even if p is bounded, a unifonnly bounded se-
quence (f,J of ,u-measurable real valued functions defined on Scan
converge to zero everywhere without converging w zero in p-measure.
5 Show that (i), (ii), and (iii) of Theorem 8.6 imply that I is in
L (8, 1:,1') and that If.-/I converges to zero even if (I.} is ageneral-
ized sequence.
6 Let I' be bounded. Suppose that the field I is separable under
the metric e(E, F) = v(p, EL1 F). Show that L (S, I, p.,;[) is se-
parable if the B-.pace ;[ is separable.
7 Show that F(8) need not be a linear topological space if I'
is not bounded, nor if I' is bounded but not countably additive.
8 Show that 8 can be the union of an inCl'CllSmg sequence of
null sets even if fL is not identically zero.
9 Show that if I is defined on S and has values in a compact
subset of 3:, and if I.I(G) is in E for each open subset G of 3:, then I is
totally p-measurable.
10 Find an example in which 4(8, E, p) is not complete, Show
that if TM(8. E, 1') is eomplete, so is 4(8, E, 1').
Il Show that if 10 L (S, I,p.) for some p ..ith I P < 00,
then loTM(8,I,,u).
12 Lct E generate the a-field I., and let I' be positive and count-
ably additive on E. Show that if the measure space (S,1:, 1') is not
a-finite, I' may have two distinct countably additive extensions to 1:..
18 Show that the map of TM(S,1:.,u)xTM(S.1:,p.) into
TM(S, E, 1') defined by U, g] ...h, where h(s) = I(e)g(s), is contin-
AUBo ., A'. .+l' AB= (A'UB')'o'if.+,.
Thus the family 1: = U :'1 . is a field. and clearly the smallest field
containing a An elementary induction sbows that C n . n = 1. 2, . . .,
is countable and thus E is a countable field. Q.E.D.
5 LEMMA. ut (8,1:. 1') be a 'jJfJSitive measure spt1£e and G
a 811parobk subset 01 L (8,1:, p, I), where I S; P < 00. Then there
is a eel Sl in 1:, a sub a'lield 1: 1 01 E(SI)' and a closed 8IpQTable
Mspace :f, 01 ;[ such Ihat 1M restrictiun 1'1 01 I' 10 I 1 has tJu
IQUQwing properlie:j;
(i) 1M "'rosIlTe space (Sl' I1,P-l) is a-finite;
(ii) 1M B-sp<u:e L,(Sl' E"Pl':f,) is 8t'paraJk;
(iii) G k L (81' 1: 1 ,1'1' :f,).
PROOF. Let {fn} be dense in G and Jet /';,,'111), m, n = 1, 2, . .'J be
p-integrable simple functions with lim I/ ...J -1.1. = O. Let X n be the
.._m
countable set of non-zero values of the funcbons j),m) and :f, the closed
linear manifold in I determined by Xo. By Lemma 1I.1.5, :f, is se-
parable. Let 'if be the countable colIection of sets Eo I which have
the fonn E = {sls c S. j),..J(s) = ",.}, where m. n are arbitrary positive
integers and "'. . X.. Let 8 1 = u 'if, let 1:. be the field of subsets of
SI generated by 'if and £1 be the a-field of subsets of 8. determined by
1:.. Since every E in has 1'( E) < 00 and all the functions I "')
vanish on the complement of 8 1 , statements (i) and (Ui) are lDllnediate.
If Po is the restriction of,u to I., then it foHows from Lemma 8 that the
set of l'1.integrable I,.-simple functions is dense in L,(SI' 1:., 1'1, 3: 1 ),
Since I. is countable (Lemma 4) and Il is separable, this set offunc-
tions is a separable 8et and hence its closure, i,e.. L (S., 1: 1 ,1'1, :f,),
is separable. Q.E.D.
In all the exercises below, unless the contrary is explicitly stated.
8 denotes a set. I a field of subsets of S, and I' a finitely additive
(complex or extended real valued) set function on I. The letter I wilI
denote a function defined on S with values in a B-sp""e I.
170
III INTEGRATION AND SET FUNCTIONS
III.D.lt
111.0.23
EXERCISES
In
AB=AnB,
A+B=A.dB
23 Suppose that 8 is a metric spacc, that E is a ,,-field, and that
p is countably additive and bounded. Supp08e that every continuous
function is p-measurable, Show that E' contains every Borel set.
2 Suppose that 8 is a compact topological space, with the
property that for evel)' covermg of 8 by a finite number of open sets
G 1 . & . "t Gr; there exists a covering EJ7 . . ., Em of S by sets in I such
that each Es is contained in..some G i " Show that if f is continuous, f is
p-measurable.
25 Suppose that (8, E, p) is a finite meaSUre space. Let E, be
a subfield of the ,,-field E which generates E, and p." the restriction of
p to L,. Show that v(/<1. E) = v(p, E) for E EEl'
26 Under the hypotheses of Exercise 25, let be a complex
valued countably additive set function defined on E. Let l be the
restriction of JI to LI" Show that 9' is p-continuous if Bnd only if 1. 1 is
,tt]-continuous.
27 Under the hypotheses of Exercise 26, T.I\1.(8, E, /<1.]0) is
dense In Tlfl(8, E./-" ]0).
28 If (8, E, /-,) is a measure space, TM(8, L, 1-', 1') is ao F-space,
but M(8. E.!,. 1'), though a complete metric space. is not necessarily
an F-space.
29 Define L F (8, E, /-,) for 0 < p < 1 ns the set of aU functions
for which
uous. Show that this is no longer the cnse if TM is replaced by M.
14 Let L, be n subfield of E. nnd 1-', the restriction of p to E,.
Show that v(P,. E) v(p. E) holds for every E £ L l , but that neither
v*(,u" E) v*(I" E) nOr v'(p, E) S; v*(I'1. E) need hold for every
subset E of S.
15 Show that Lemma 8.2 need no longer hold if we write
uPt-measurable" for UtotBlly J'l.measurable n .
16 Show that E forms an algebra in which A' = A if we define
nnd that the l"nuU sets nre nn ideal in this algebra.
17 Suppose that S is a normal topological space and that p
is regular and defined on the field E of Borel sets in 8. Show that if I
is separable, the set of continuous functions in TM(S, E. 1', IE) is
dense in TM(8, E. p, I), Show that for 1 P < ro, the set of con-
tinuous function8 in L,,(S,E,p,'i£) is dense in L F (S.E.p,1').
18 Let p be n finite regumr measure on the Borel subsets of a
compact space 8. Show thnt I is p-measurable if and only if for each
E there exists an open set E. such that v*(p. E.) < e and such that I
is continuous on S-E..
19 Find an example in which S is a metric space and p is regular
but not countably additive.
20 (Lnnglands) A regular complex valued additive set function
defined on a field of sets in a compact space is countably additive.
21 Let Sand 8, be compaet topologlCa' spaces with 8 1 a
Hausdorff space. Let 'P : 8 8, be a continuous mapping. Let I-'
be a regular bounded additive set fun<'tion defined on a field E
containing the open subsets of 8, and define the set function
.(El) = P('P 'El)
for each EI 8, with 9' I(El) £ L. Show that v is n regular additive
set function defined on the field {E,I<p-' E, £ I}.
22 Let 8 be a topological space. and p n bounded, countably
additive measure. Call a set E . E regulnr if for each e > 0 there exist
setsF 1 and F. £E. such thatF I E. F. S- E, v(p, S F.-Fa) <e.
Show that the regulnr sets form a ".field. Hence show that if S is a
metric space and p n hounded measure defined on the a-field of Borel
subsets of 8. then I' IS regular.
III = Is l/(s)l. p(m) < 00
Show that 1/1i-/.! 1/,1 +1/.1, while
II, +I.I'/F ;e, 1/ 1 1" F +lf.I 1J F
if /, and I. nre both positive.
80 Let (8, E./-,) be a measure space, and lct 0 < p < I. Show
that the space L.(8. E, p) of Exercise 29 is an Jo'-space.
81 Let 1 P < 00 and let /" I. be positive functions In L F .
Show that II, +I.IF ;:>; /I,[F+I/.!..
32 Find an example of a countably additive. bounded, Vector
valued function p defmed on a ,,-field E of subsets of S for which
v(u,8) = +ro.
33 Show that (8, I./,) can be n fmite positive measure spaee.
and {f.} a umformly bounded generalized sequence of non-negatIve
172
Ill. INTEGRATION AND SET FUNCTIONS
111.9.84
111.9.39
EXEBCISES
173
It-simple functions defined on S converging to zero for each.8 S hut
not converg1Rg to :zero in p-measure.
84 Let (8, I,p) be a ,,-finite positive measure space, and let I,
be a subfield of the a-field I, generating I and suppose that p is
,,-finite on II' Show that if E . I,
pIE) = inf Ip(E,),
,-,
where the infimum is taken over the family of all sequences {E,} of
sets in I, such that U ::',E, E.
85 Let (S, I, p) be a positive measure space. If f . L, (8, I, p),
and {I.} is a sequence of real valued fundions in £,(S, I, p), and
1/.(.)1 '$ f(.) for . _ S, then
J.liminf/.(o)p(ds) $ liminfj f.(o)p(da)
n CI:I 7I_OC 5
;:i; lim sup f fn(o)p(da)
a_to S
'$ f lim SUp In(o)J-'(da).
S ,.-+-
89 Let (S, I, p) be as in Exercise 88. Find a continuous mono-
tone increasing real function f defined on S such that I cannot be
represented as
1(.) = J:g(l)dt with g in £,(S,I,p).
4Q Under the hypotheses of Exercise 86, let ° < a. < I. and
suppose that G is defined on Sx8, and continuous for all (s, t) such
that 0 * I. and that
IG(a, 1)1 '$ la-II-I Isin (0-1) I.
Show that if h is a bounded. p-measurable function defined on S,
G(s. . )h(' J is p-integra.ble for each a, and
f +
_ G(s,l)h(l)dt
86 Let 8 be the real axis, I the field of Lebesgue measurable
subsets of S. and p Lebesgue measure. Show that if E _ I, and a and b
are rea.'-numbers, then aE +b _ I, and ,4aE +b) = lalp(E). Show that
if I is p-integrable, then the function g defined by g(s) = I(as+b) is
p-integrable, and
is a continuous function of .8.
.n Construct the Lebesgue extension of Borel meaSure by direct
use of Theorem 5.4.
42 Let 1 '$ P < 00. and let (S, I, p) be a positive measure
space. Let I_ L and g _ L. IIp+Ilq = I, and let h(a) = f(o)g(o).
If II.sh{o)p(da)1 = Ifl lgl., then g(s) = A;g;; (f(s»lf(s)I -l p-almost
everywhere. where the function sgn(re") of the complex number
" = re" is defined to be.... if r oF ° and zero if r = 0. (Hint; Examine
the cases of equality in the various steps of the proof of Lemma. 8.2).
43 Let 1 < p < 00, and let (S, I, p) be a measure space. Let
l,g.L,(S,I,p), and let I/+gj, = Ifl +lgl,. Show that. if g *0,
then I = rxg for some scalar a..
44 Let (8. I, p) be a measure space. Let {In} be a sequence of
p-measurable functions defined on 8, with values in I, and let f be a
function defined on S, with values in 30. Suppose that for each
.,* _ 1*. "*I.(s) .... .,*f{s) for each o. S. Show that I is p-measurable.
45 Let (8, I, p) be a meaSUl'C space. Show that conditions {i)
and (H) in Theorem 6.15 may be replaced by the single condition
lim J 1/.(s)I'v(p, tIs) = ° unifonnly in fI,
E_
Find a sequence {I.} of positive functions in LJ(S,I'f-I) for which
the preceding inequalities are nut all valid.
J +Oo f +
la] _00 f(as + bIds = _ f(o)da.
87 Let S be the rea.l aXIS, I the field of Borel subsets of S, and
p any Borel-Stieltjcs measure on I. Show that if the real function I
is of bounded variation, or is continuous on the left, or is continuous
on the right. then I is p-measurable.
88 Let S be the closed unit interval. I the field of Borel sets of
S, and II, Lebesgue measure. Find a p-singular non...negative measure
defmed for E £ I for wmch each point p £ 8 has zero measure. (Hint:
Use the Cantor perfect set.)
{E..} being an arbitrary decreasing sequence of sets with void inter-
section.
174
III. INTEGRATION AND BET FUNCTIONS
III.9.46
III.IO.I
RADON..NIKODYM THEOREM
1?5
46 Show that Lemma 8.3 need no longer bold if we omit the
hypothesis that p., is .,.-finite on E,.
47 Let]l.l be a metric space. Let A M; let ex, < > O. Then de.
fine A.(A,..) as glb I::',("(A,»", where {At} is an arbitrary sequence
of sets covering A wbose diameters "(At) are less than E. Show that
Ae(A, a.) is an outer measure, that A.(A,.ex) increases .as .£, d 1
and that A(A,..) = lirn.-..A.(A. ex) is an outer measure. (It can be
shown that every Borel set is A(A, a:) measurable; the Borel measure
derived from A(A,..) is known as Hausdmff a-measure.)
48 Let {An} and {B..} be sequences of subsets of 8, and let
An -+ A, Bn -+ B. both in the sense of the discussion following
Definition 4.3. Show that A.B...... AB, An U Bn -+ AU B.
S-A n --+S-A.
The set P may be partiaUy ordered by defining h :'£ g to mean that
h(8) ..:; g(s) almost everywhere. We wiU show. using Zorn's lemma,
that P contains a It1B.Ximal element. Indeed, let Q be a totaUy ordered
subfamily of P and.. = sUPA"1I s h(8)p(ds). Then 0:'£ a:'£ ;'(8). Let h.
be a sequence of elements of Q such that
10. The Radon-Nikodym Theon:m
We have seen that the integral IE f(8)p(ds) of a p-integrable
function is a p-.oontinuous set function. A partial converse to this state-
ment is the important Radon-Nikodym theorem which Mserts that
if (S, E. p) is a measure space then any finite scalar valued additive
set function}, which is p-continuous has the formA(E) = I" f(8)p(ds)
for some p-integrable function f. This theorem (Theorem 2) wiU be
proved first under the assumption that p is non-negative. and the
complex valued case (Theorem 7) wiU be proved after some general
results on change of measure have been established.
is h.(s)p(ds) :'£ is h,,-+-I(s)p(ds) .....a.
Then, since Q is totally ordered. it follows thath,,(s) :'£ hn+l(s) almost
everywhere and thus. without loss of generality, we may assume that
h,,(8) ..:; h..-r,{s) everywhere. By Corollary 6.17 h(s) = limn h n (8) is
integrable, Is h(s)p(ds) = "', and h,,:'£ h. n = I, 2, . . .. To see that h
is an upper bound for Q, let g be an arbitrary element of Q. Then
either g h. for some ", in which case g :'£ h. or g h" for every ",
in which case g hand
o isg(s)f1(ds) -a = is [g(8) - h(s)],u(ds) o.
and this implies that g(s) = h(s) almost everywhere. Thus h is an
upper bound for Q and Zorn'. lemma shows the existence of a maximal
element f in P.
Let
I.t(E) = A(E) - i"f(s)p(ds).
E.E,
I LE....A, Let (8, E, p) be a finil£ pollitive mea.mre 8pace. and'
A a finil£ positive ,u-c<mtinuous measure tkji""d on E. Thm there e.rists
a unique frmcticrt ! in Lx(8. E. /.t) such that
Then AIlS a p-continuous finite non-negative measure on E. To com-
plete the proof we demonstrate that ;',(E) = 0 for every E in E.
If this is not .0. then 1.t(8} > 0 and there i8 a positive number k such
that
(i)
peS) - kAleS) < O.
A(E) = iE!(8)p(ds),
Moreover, vIA. S) = If!,.
PROOF. Let P be the set of non.negative integrable functions h
such that
By the Hahn decomposition (4.10) there is a set A in E such that
E.E.
p(EA) - kAl(EA) S; 0,
p(EA') -kl.t(EA') > 0,
E.E,
and then, a fortiorI,
(ii) p(EA)-kAl(E) ":; 0, p{EA')-kJ.,{EA') O,
E.E.
Therefore
J.:h(s}p(ds) :'£ A(E),
E.E.
(iii)
I
kP(EA)-A,(E} :,£0,
E.E.
176
III. INTEGRATlO AND SET FUNCT10NS
111.10.2
111.10.8
BADON-NIKODYM THEOREM:
177
If pIA) = 0 then J,(A) = 0 and pIS) = p(A'),ll(S) = Al(A'); thm.
from (i) and (ii) we have
o ;;;; pIA') kAl(A') = pIS) - kA,(S) < O.
a contradiction. This proves that p(A) > O.
Let g be defined by the equations:
The inequality (iii) may then be written
fEg(S)p(rlo) :S: ),(E) = lIE) - fE/(S)p(rlo),
which shows that
EEl:,
may be assumed that A is real valued. A real valued set function can
be represented as the difference of its positive and negative variations
(4.II) and so we may also assume that A is positive, Let, then, {En}
be a sequence of measurable sets such that vlJl, E.) < 00, E. E.. I ,
and U ='1 En = S By Lemma 1, for each n =- I. 2, _ . . there is a
nODanega.tive integrable function In which vamshes on E and for
which
IE/n(s)p(<u) =.il(E), E E..
By the uniqueness of In' we have I.(s) = 1.+1(s) almost everywhere
in En; without loss of generality we may assume that I.(s) = 1_ 1 (s)
everywhere in E.. Then I. E 4(S, l:, 1'), I.(s);;;; 1.+1(s), and
f.I,,(s)p(tls) = A(E.) ;;: .il(S). Put I(s) = lim I.(s). Then, by Corollary
6.17, Ij._CD
lIE) = lim.il(E.E) = lim IEI.(S}p(ds) = IE/(S)p(ds)
n-+GO ",-+
for every E. E. Q.E.D.
The next results are u8eful complements to the Radon-Nikodym
theorem, and may be used to extend that theorem. The key theorems
in the set are 4 and 6, which give important Ii;change of measure"
statements.
g(S) = Ilk,
g(s) =0,
s£A;
SfA.
IE U(8) + g(s)Jp(rlo) ;;;; .il(E),
EEE.
Since I+g > I, this contradicts the maximality of I in P. Therefore
),(E) = 0 for every E in I:.
The equation v(.il, S) = 1/11 is simply Theorem 2.20(a). Un the
other hand, if I and g are two p-integrable functions such that
lIE) IE/(S)p(rlo) = IE g(s)p(rlo),
then, by Lemma 0.8, I and g differ by a p- null function, This estab.
lishes the uniqueness of I and completes the proof of the lemma.
Q.E.D.
. 2 THEOREM. (Radon-NikodYm) Let (S.E. 1') beao-liniw positiu
measure 81'lree, and .il a lini!e p-ronlintUJus measure delined on E. Then
lhere n;sls a unigue fwldicm I i.. L,.(S. E.",) such tluU
.il(E) = fE/(B)p(rlo), EEl:.
Moreover, vI;!. S) = 1/11'
PROOF. Once the e:ristence of I is established, the equality v(l, S)
= It I> follows from Theorem 2.20. Consequently, A(E) = 0 if and only
if It!, = 0; i,e., If and only if I is a p-null function. The uniqueness of I
fo]Jows immediately from this. Thus, all that must be shown is the
existence of I.
By separating Amto Its real and imagmary parts, we find that it
8 LEMMA. Let (S, E,,,,) be a measure 81'lree and let f be a p-
metuurable lunction definnl on S. Suppose that eilher
(a) (S, E, p) is posilWe and f is rum-mgmive, or
(b) I is corrqJk;c valued and i..ugroble.
Let
.il(E) = IE / (S)I'(ds), E.E,
and kt g be a function delined on S wirh values in a B-81'ace 30. Tlwn g
is .il-measvrable il and only il Ig is p-measurable.
PROOF. Let g be ;!-measurable. To show that Ig is p-measurable.
we shall.how that XFfg is totally ",-measurable, where X" is the char.
acteristic function of an arbitrary set F in E with v(p, F) < 00. \Ve
observe first that it may be assumed that v(A, F) < 00. For, if I is
integrable then v(.il, F) < 00 for all F . E; if I is only assumed to be
positive and measurable we can put F. = {sls, F, j(s) < n). Then
F = U:'_,F. and v(l. F.) < 00 for each n. Since
178
111. INTEGRATION AND SET FUNCTIONS
111.10.8
111.10.4
BAIJON-XIKCDYM 'rHEOREM
179
xp(s)/(s)g(s) = lim XP (s)/(s)g(s),
"
.
and the pointwise limit of B sequen e of measurable functions is
measurable, it will suffice then to show that xp.fg is measurable. Thus
we may and sball assume that v(l'. F) < ro and v(A, F) < 00,
Since Ii is A-measurable there is a sequence {g.} of simple functions
c nverging to g(s) for every s in F except nn a set E (;; F with
v(A. E) = 0 (by Corollary 6.l3(a}). But
vIA, E) = IE I/(s)fv(I', ds)
so that I(s) = 0 for s in E except in a set A with v(l', A) = U. Thus
BES,
4 THEOREM. Let (S, E, f<) be a positive measure apace, I a non-
negative IH,,,,,,..urobk lum:lwn defined on Sand
ME) = f I(s)",{ds),
."
EeE.
Let g be a IWIHlegalive A-measnabk I!lndion dsli/lefl on S. Then Ig is
p-measuTllble, and
J"g(s)),(ds) = I,.J(s)g(s)l'(ds),
EeE.
PROOF. The p-measurability of Ig follows from Lemma 3. If we
let H be the class of all non-negative A-measurable functions h for
which the equation
g,,(s)/(s) --+ g(sl/Cs),
s. F-A,
I"h(S)A(ds) = I p/(B)h(s)p(ds),
E.E,
and CoroUary 6.14 shows that Xl,fg is ,,-measurable.
Conversely, let Ig be ,,-measurable, and let (S, E*, ,,) and
(S, It, A) be the Lebesgue extensions of (S, E, ,,) and (S, E, A) l"espec-
tively. Then Et;;) EO. We note first that a given function is measur-
able with respect to a given measure if and only if it is measurable
with respect to the Lebesgue extension of the measure. Now let
N = {Bls E s, I(s) = OJ, so that A(E) = 0 for every E e E* with
E (;; N. Thus gXN is .I.-measurable. and it need only be proved that
gXN' is .I.-measurable. Thus we may and shall assume that I(B) never
vani8hes on S. Since
is valid, then H clearly contains all non-negative A-simple functions.
In view of Corollary 6.17 the class H is closed under the operation of
taking limits of increasing sequences. '.rhus to prove the theorem, it
wiU suffice to prove that a non-negative A-measurable function g is
the pointwise limit almost everywhere of an in asing sequence {gft}
of simple functions.
To define such a sequence, decompose the set E. = {slg(s) < n}
into the n' disjoint parts
{sllll(s), G} = {sl/(B) = lIz, z £ G},
Theorem 6.10 shows that 111 is p-measurable, and thus it follows from
Lemma2.12 that g is ,,-measurabJe. By Theorem 6.10, g is p-essentiaUy
separably valued, and hence it is .I.-essentially separably valued. Also
for G open in I we have. by 6.10, g-l(G). EO<. Thus, since E:2E*.
it is seen from Theorem 6.10 that g is .I.-measurable. In the preceding
statement we have implicitly used the fact that any F £ E with
( j-l i J
E(i,n) = sl- g(s) <- ,
Ii n
1 = I, . . ., n 2 .
Let
g.(s} = ( n ,
iln,
lifE""
s. E(j, n),
V(A. F) = Ip I/(sJlv(". ds) < ro
so that g,,(s) illere..,es to g(s) for each s in S. It follows from Theorem
6.10 that each g. is a simple function relative to the Lebesgue exten-
sion of .I. and thus the proof is £amplete. Q.E.D.
5 COROLLARY. Let (S, E, ,,) be a positive """"lire apace, I a non-
mgaJire lneasurable lunctioll dslilled on S, and
A(E) f"/(s),,(ds), EEE,
Then a lune/ion g on S to the B-spare :I: is A-integrable il and only il
Ig is ".irm:grable. and in this case,
may be decomposed into a denumerable union of sets
Fft = {sls £ F. I/(s)1 > lln}
with v(,u, F.) < roo Q.E.D.
180
HI. INTEGRATION AND SET FUNCTIONS
III.I0.6
111.10.'7
RADON-NIKODYM THF..oREM
181
[*]
IEI1(8}).(ds} = I"/(8)g(8},u(ds},
EEL,
is measurable, and hence 11 is ).-integrable if and only if Ig(')1 is
v(,u )-integrable. The v(,u }-integrability of )g(.)I, however, follows from
Theorem 4 just as in the preceding argument. Thus only formum [*]
remains to be verified. By the argument used in the proof of Corollary
5 it is seen that it will be sufficient to provc [*J in the case when g is
a positive real function, It is also clear that [*J holds for )'-integrable
simple functions. M in the proof of Theorem 4. there is an increasing
sequence {gll} of non-negative simple functions converging pointwise
to g. Since g.(s} ;;;; g(8), we have Ig.(8)/(8)1 s;: Ig(8)/(8)I for every s
in S. It follows from the dominated convergence theorem (6.16) that
fEg(S»).(ds) = IE / (8)g(8)p(ds),
EEL.
PROOF. Suppose that g is A-integrable. By Lemma S, Ig is measur.
ablc. The wintegrability of Ig foJlows from Theorem 2.22 when it is
observed (by Theorem 4) that If(.)g('}1 is wintegrable. Theorem 4
applies in the same manner to prove the .ii-integrability of g when it is
assumed that fg is p.integrable.
Since every rea] measurable function is the difference of two non-
negative measurable functions, it follows from the theorem that
for a real integrable function g, Since the real and imaginary parts of
B ornplex measurable function are themselves measurable, it follows
that ["] holds for complex valued function8 g. If g takes its values in
the B-space if, let;£* be a linear functional on if. Then using Theorem
2.19(c) and [*],
;£* IE g (8}).(ds} = IE "'*g(8»).(ds}
= IE ..../(8}g(8),u(ds} =... IEI(8)g(s),u(ds),
which, in view of Corollary II.S.I5, proves [*] in the desired generality.
Q,E.D,
f" )/(s}g.(s) f(8)g(8)lv(,u, ds) .... 0,
and
6 COROLLARY. Let (S,L,p) be a measure apace, fa compr...
valued p-inlegrahle futlCtion and
.iI(E) = I,j(S},u(ds), EEL.
Then a jutu:tWn g on Ii to the B-apace if is A il and only il fg
is p-mugrahh, and in this case we /lave
f"lg.(s}-g(s)jv(.iI,d8) ....0.
Since equation ["] holds for II = g this shows that it holds also for g.
Q.E.D.
The next result supplements Theorem 2 by allowing I' to be
complex valued.
.p. '7 THEOREM. Let (S, L, p) be a linite measure apace and .1. a p-
continuous comple", valued mentlUre on L. Then lhere is a unique p-
int£grahk /wld.on f lfUC" that
A(E) = IE / (8},u(ds), EEL,
PROOF. Using the Radon-Nikodym theorem (Them'em 2) we fInd
v(p).integrable functions II and" such that
E L.
A(E) = IEg(S}V(,u, ds),
peE) = IE h(8}V(p. ds),
EEL,
[*J
IE g(s)A(ds) = IEI(8)g(s},u(d8},
EEL.
Since
PROOF. Let g be A-integrable so that. by Lemma 8. fg is measur.
able. To show that Ig is p.integrable it wiU suffice. in view of Theorems
2.22 and 2.18. to show that 1/(.)g(')1 is v(,u}.integrable. But since
Ig(.)1 is v(,u}-integrable and viA. E) = h It(s}lv(l', d8), this is a con-
sequence of Theorem ,.
Conversely, suppose that Ig is f-l-integrable. Then, by Lemma 6, II
v(,u, E) = IE ih(s)lv(,u. ds},
It follows that
IE {I -lh(8J1}v(jt, ds) = 0, EEL,
from which it is seen that 1"(8)1 = 1 except on a set where v(,u)
vanishes. Thus I = gilt is p-integrable, and by the preeediDg corollary,
182
III. I:S'l'EGRA'f10N AXD SET FUNCTIONS
111.10.8
111.11
FRODUCT MEASURES
183
IE/(8IP(ds) = IEg(8IV(P, ds) = A(E). Q.E.D.
Nore: The unique p-integrable function I of Theorem8 2 and 7
is called the Radon-Nikodflm tkriwtive of A with respect to I-' and is
often denoted by dJ.fd,... Thus dA!d,.. is defined I-'-almost evel)",'here by
tbe fonnula
ACE) = L { : (s}) l1(ds),
EE:E.
it follows readily from the definition of v(l-'I) that vv.-" "' I(E»
v(P,. E). Conversely, since "'(E, u E.) = ",(E,) u "'(E.) and
",(E1E.) = "'(E"J.f>(E.) if E 1 , E. belong to :E I , v(I'2' "'(E» is a non-
negative additive set function defined for E E z:.. Since
v(p., "'(E» 11'2("'(E»1 = 1J'1(E)I,
it follows readily from the definition of vv.-,) that v(p., "'(EI) :e:
v(J'1, E). As it has also been shown that vCp., "'(E» vv.-" E), we
have v(I'2' "'(E» = V(J'1, E) for E E z:., and therefore v(I'2, E) =
v(J'1, <}> l( EI) for Ed:.. This proves (c).
It is a consequence of (c) that if (!ft) is a sequence of functions
defined on 8. and converging to a function I in I-'.-measure, then
(fn("'('))} converges to 1("'('» in f-'t-measure. Since g("'(' I) i8 J'1-simple
if g is l'2-simple, (d) follows immediately.
Clearly, g(<}>(. I) is a f-'t-integrable simple function if g is a f-'2-
integrable simple function. From the definition of 1-'1 it follows that
for such a function g we have
I g(8.)f-'2(ds.) = f I g("'(Bl))J'1(dsl)' E E :E."
£ - IE)
Thus (f) follows from the definition of integrability just as (d) from
the definition of measurability. Finally, (e) i8 a consequence of Theo.
rem 6.17 ans! the application of (f) to each member of an increasing
sequence of f-£2-integrab]e simple functions which converge pointwise
to the function I. Q.E.D.
'Ve close this section with a generalization of many '''change of
variable" theorems.
8 LEMMA. Lei SI and S. be 8e/8 and '" a mappmg 01 8 1 it/to SO'
II 2'2 is a lield (reop. (I-lield) 01 8e/8 in S.. thrn tM lamily 2'1 =
{"'-l(E)IE.2'.} is a lirld (Ye8p. (I-lield) 01 se/8 inS!" Foranaddwr€8e/
funetw" I-'t on 2'. the equation f-'t("'-I(E» = f',(E) delilU18 an addi/ive
8et junction f-'t on £1' ltfor
(a) il I-'z i. counf4bly additive, so i. f-'t;
(b) ill-', is bounded, J'1 is boundl-d;
(c) v(l-'l' "' t(E» = v(f'.. E), E. E.;
(d) il a furu;tUm I defined on S2 is f-'2-ttWa8Urahle, tlu:n 1("'(') i.
flsJ-meastU"Qblei
(e) il1-'2 is non-n.gative and counlably additive and a lut/own J
delirwd on 8, is 1-'.-measurolJlto and non..legt1/ive, lAm
I,/(s.ll'2(ds.) = t-'(EJ 1("'(8 1 ))J'1(ds , );
(f) il a lunction I deli>",d on S2 is f-'2-;megralJlto, tMn 1("'(')) is
f-'t-iategrabk, and
I £/(8.)f"(ds,) = t-'(£J I("'(S,»)I-'t(ds , ).
PROOF. Since "'("'-I(E)) = E it is clear that J'1 is well defined on
E" Since "'-I(EF) = "' I(E)"' I(F), "'-l(E') = {"'-I(E)}', and
"'_I( U::'I E,) = U :1 ",-I(E,), it is clear that 2'1 is a field and that
J'1 is additiw on :E1" These identities also show that £1 IS a a-field if
Eo is, and that 1-'1 is countably additi"e if I-'a is. Statement (b) i.
obvious. Since vv.-" "' l(E)) IS a non-negative set function defined
for E.:E. and
V(PI' "' I(E» If-'t(.,,-I(E»I = II',(EJI,
II. Produet Measures
Our principal objective in this section is to construct. from a
given family (8., E" Pi)' i = 11 . . .,. 71, of measure spaces, 8. measure
defined in the Cartesian product space SI X. . . X 8ft' and to investigate
the relations between integration in the product and integration in
the component spaces. The most fami1iar example is, of course. the
case of the Euclidean plane. the product of the real line with itself.
For a rectangle E with sides parallel to the coordinate axes one de-
fine. the two dimensional measure of E to be the product 0( ,the
lengths (one dImensional measure) oftwo adjacent sides. This measure
function is then extended to the a-field in the plane generated by
such rectangles.
184
III. INTEGRATION AND SET FUNCTIOKS
III.H.l
III.ll.2
PRODUCT MEASURES
185
In the latter half of the section the theory of product meaSures
and integration is extended to the product of an infinite family of
measure spaces.
Thc following notation will be convenient in the statements of the
theorclns of this section. Suppose that for i = I, . . . nJ' Ii is a fie1d
of 8ubsets of a set 8;. We shall denote by 4 the family of all sets in
the Cartesian product 8 = 8, " , . . X 8w of the form E = E, X .. .
)' En> where E j E Lt-
the restriction of " to I is an additive set function with the desired
properties.
To prave the uniqueness of" suppose that A is an additive set
function defined on I which agrees with" on each set of If. Let !B o
be the class of A-integrable functions I in \11" for which
f,/(o»),(w) = f ". [. . . [J ", !("" . . ., ".)!'t(w,)] , . .] ",(w.),
E= E,x...xE. for arbitrary E,.I., i=I, ...,n. Let 18;. be the
set of all I! . !B. such that II! . !B o for alii. 18 0 , Then 18, is a linear class
which is closed under products and contains the ch8I'8Cteristic func-
tion of each set in G. By the argument used before, It follows that
A(F) = Isx,,(s»),(w)
= Is, [. .. [Is 1 x"(s,,. .., s.IJ.t,(W,)] ...] 1l,,(w.1
for all F . I. Q.E.D.
Remark. T/w lieU I cmsu,f8 o! aU linite diojoint uni<ms o! sets in G.
For, if Eo is the coHection of all finite disjoint unions, then Eo is evi-
dently cloled under finite intersections. To prove that I. is a field it
suffices to show that it is closed under complementation. If n = 8,
this follows from the Identity
(E,xE.xE.)' = (E x8.'8.) v (E,xE;xS.) u (E,xE.,E ),
and the general case is similar.
2 THEOREM. Let (Si, Li. .u ), i = 1, . . "' n, be finite mea.mre
8pl1Ce.. Then there i. a unique reuntably additive measure J.t delimJd em
the sma/ln;t rJ-lield in S = 8, x. . . )( 8. containing 4 and such tlwt
..
J.t(E1x.. .xE.) = IT ,,(Ed
....1
1 LEMMA. FfJT i = I, . . .. n. let 1'; be a finitely additive remplex
valued set 'unction wjined on a lield I, 01 ...borl8 01 a sel S,. Tllen there
is a wUf}'M addiriDe sel !unction " dejined on the smallest !ieU I in
S = S,x.. .xS. containingC "uchthat,,(E) = II'_l,,;(E,J!or EinC.
Remark. The rcader may imagine that this lemma is best praved
by a direct construction. Such a proof can be given; but it is surpris
ingly cumbersome. Far this reason, we give a proof depending on tbe
theory of intl'gl"ltion.
PROOF. Let 'No be the family of bounded complex valued functions
I defined on 8 with the following property: For each fixed [s., . . " s,J
the function l(sl' . . ., 8,) is 1'1-integrable as a function of s.. for each
fixed [8.,...,8.] and E, in II the function
J l(sl"'" s.).u,(w.)
"1
is Jt:-integrabJe as a function of 9 2 : for each fixed[s,,-, ..., s,J, E[ ",.EI'
and E.. I.> the function
f [f 1(0.,.,., 8 w )!'t(W 1 } ] ",,(w.}
F. z E.
is ".,integrable as a function of 8., etc. We denote by 91 1 the class of
all I!' 'No with the property that the product Ig is in o for every
I. \11". Then 91 1 is a linear class of functions which contains the product
of any pair of its members, Now let 11> he the family of sets F S
whose characteristic functions X" belong to l" It follows that 11> is
dosed under inter.se<'tion and complementation and contains S. Thus
11> is a field of sets. Moreover, each set of If belongs to 11> and hence
11> ;;) I. If the set function p. is defined for F. <}J by the formula
p(F} Is, [... [Is, /.""(Sl'...' ".}p.,(ds,)] ...] J.t,(w.),
'M e{Uhset Elx. ..xE. in 4.
PROOF. Define lit, as in Lemma 1. It follows fram the countable
additivity of the measures ", and fram Theorem 6.16 that if U.} is a
uniformly bounded sequence in er J converging pointwise to a function
I. then I. lit, and
lim f [ ... [f I.(s"..., S,)pI(W,) ] .. . ] p.(ww)
,,_CXI S.. 51
= Is. [. .. [fs,/(s"..., S.)I'l(W)] .. .J p.(w.).
186
III. INTEGRATION AND SET FUNCTIONS
III.n.s
111.n.6
PRODUCT MEASURES
187
Thus. the fieJd <P of Lemma 1 is a a-field and the measure I'- of Lemma
I is eountabJy additive on <P. Consequently, the restrietion of I'- to the
a.field I generated by 8 is " measure with the desil'ed properties.
To prove the uniqueness of p, we note th"t it foUows in the same
way that the set 18 1 of Lemma I eontains the Jim,t of a convergent
uniform1y bounded .sequence of its e1ement&, Rnd hence contains the
eharacteristic funetion of each set F . I. Thus the argument used in
proving uniqueness in Lemma. I goes through withmIt change in this
ease. Q.E.D.
3 DEFINITION. The measure space (8, E, p) constructed in
Tbeorem 2 is caUed the prodru:! mrosure Bpace of the measure spa<'CS
(S.,I.,I'-.)' We write
I=Ilx...xI., 1'-=1',__><....,.1'-.,
(S, I,p} = (SI' I 1 .P:t)x... ': (S.. I., I'.),
6 COROLLARY. 1/ the mea.sUTe spaces (Sf' Lb Pi), i = 1, . . 0, n}
are positive and a-finite, lhere is a u";que meu.mre I' <kfined on the a-field
g",,.ra/td by 8 Buchlltlll pIE) = In , p,(E,) for E = P;',., E" E,.I"
&mark. It is undel'Stoo<! that In ,I'-,(E,) = + <XI if p,(E,) = + <XI
for some iand nop,(E,) = 0, while if some factor in a product is zero,
we take the produet to be zero.
PROOF. For each k = I.. . . ., n let Sk be the union of an In-
creasing sequence {E )} i = l . .", of pk-measurable seh of finite
fl.-measure. If EO) = PZ_, EL), then {EW} is an increasing sequence
of subsets of S whose union is S. For each k, let ' be thc field of
Pk measurable subsets of E ) and let f.l J be the restriction of Ilk to
E ). We have already seen how to form the finite measure spaces
and
(S,I.I'-} = P(S"I.,p,}.
i"",J
.
( E J Ifi) "fi) } = P ( E") ....,,) ,,1iJ }
". Ie l.Lfk 'rk "
k-'
It foHows from the uniqueness part of Theorem 2 that 1'(11 (F}
= p"+1'{F} if F E"'. LctI o be the family ofallsubs<>ts EofS such
that
In the course of the proof of Throrcm 2 we showed that the
characteristic function of every set E £ I = II X" . ">:I is in WI"
That is, we bave proved the following corollary, which is at the same
time the first of a sequence of th<Ore1US on thc relation between
"'multiple integrals" and "iterated integrals" to be proved in this
section.
EnE'j'.IW
for each j. Since each I'" is a a-field, Io is itself a a-field. Let I be the
a-fieJd generated by 8. Then I I'" for eacb j, and thus I I"
ClearJy I Io, and thu8 I = I..
If FE I define I'-(F) = lim,--+w pe;'(F nEe,,). Since this sequence
is increasing, the limit exists but IIlRY equal +00. To see that p is
countably additive on I, Jet F E I be the union of a sequenee { F.}
of disjoint sets in I. Then for each j and k
4 COROLLARY. Let (S, I, p) be Ihe prodru:t vf finite pvriUve
7lU'llBUre spMes (SI' II' J<,) and (S., I., ,u,}. Fvr each E in I and B.
in S. the sel E(B.} = {SllrSI' B.] e E} is PI-measurable. The fUMiun
p, (E{ s.» is ,u,-integrahk and
pIE) = f p,(E(s.)),u,(ds.),
s.
5 COROLLARY. The produd of finile positive metJBure spaces is a
finzte posUit'e 1fWastlre space.
PROOF. This fact follows immediately from the formuJa for
I'-(E) given in Corollar) 4. Q.E.D.
It is now easy to extend tie definition of the product measure
to the Case that the mt':lSure spaces (8., Lit Pi), i = l . . ". n. are
positive and u-fitlite rather than fimte.
p(F) p(j)(FnE"'} = p(j'(F.nEI")
l
.
1'-(j)(F.nE(j)}.
71=1
Thus p(F) <"" :., p(Fn}, and bence p(F} :_I p(P..). On the
other lumd, for caeh i,
'"
p(P.):;o; pIJI(F.n E"'}
1'J-l '11--1
=,,"'(l<'nE'''),
188
III. IXTEGRATION AND BET FUNCTIONS
I1I.ll.7
III.ll.8
PRODUCT MEASURES
189
..
So' l p(-"',.} :;?; p(F}. It is clear that the measure has the property
_1
n
p( P E,) = IIp,(E,).
i""'l .-1
Ej E;."
pll'(EE<I') = f,,'!SI J',(EE<l> (S.})p,.!ds 2 ).
.
:SlOe. #(E) = hm(,'IJ{EE<"1 and
,....'"
f ",p,(EE"'(B.»)f'2(ds.} = f p,(EE<II(s.»f'2(ds.),
EI
and it follaws from the uniqueness part of Theorem 2 far each of
the space8 (EW. EIII. pH'), that p is the unique countably additive
measure Qn E with this property. Q.E.D.
As in the case of finite measure spaces we shan call the measure
space (8. E. p) constructed in Corollary 6 from the O'-finite measure
spaces (8" E,. Pi) the prod,u;! mroSUTe sp""e and write (8, E. p) =
P -1 (8 4 , Iii p.1)'
The best knQwn example of Theorem 2 and its Corolliuy 6 is
obtained by taking (8" E" p,) to be the Borel-Lebesgue measure nn
the reallme for i = I, . . ", n. Then S = p _] Si is fl.-dimensional Eucli-
. dean space, and p = 1'1 X . . . X Pn is known as n-dimerutional Borel.
Lebesgue vneusure. The Lebesgue extension of p. is known as n-dimen-
sional Lebesgue measure. The characteristic property nf this measure
is then that the measure of an arbitrary ureC'tanglel'l
R = {[s,. . . ., s.]Ia.. ;:;;; sl ;;;; b., . . ., a. s. b n }
is the product (b,-a..).. (b.-a.).
The next coronary is the a-fmite analogue Qf Cnrollary 4.
7 CORQLLARY. Let (8. E. p) be !he prodnc! of two posiiWe O'-fini!e
measure spaces (S" E,. p,) and (8., E., f'2). For each E in E and s.
in S. !he set E(B.) = {BIllS,. B.] £ E} i. p,-m<'tIQUraUe. Tk fundWn
p,(E(B.)) iB f'2-rnt!asurabk, and
[*] PIE) = f p.(E(s.»f'2(ds.).
s.
formula [*] follows immediately from Caroltary 6.17. Q.E.D.
In proving the crucial Theorem 9 belnw, we will have use fnr the
following easy consequence of Corollary 7.
g CORnLLARY. Let (8, I, 1') be tk product 0' two positi... a"'ni!e
fnelUtlre spaces (8,. II' PI) and (8., E.. f'2). Le! N £ I be a p.-null Be!.
Tkn. for PI-almost all s, in 8 1 , tM se! N(s,) = {B.I[B,.B 2 ] EN} is a
f'2-null Be!.
PROQF. This follows immediately from the fQrmula gIVen by
Corollary 7, and from Lemma 6.8. Q.E.D.
At this point we make certain observations whicb will greatly
slmplify the Inter work nfthis section. Let (8 1 , I" p,), (8., E., f'2) and
(S" E 3 ,p.) he measure spaces and (8,E,p)= _1 (8,.E"J',). Thus 8
is the collection of points [SI' "2' Sa], at E Sa, and, strictly speaking, S
should not be confused with the space 8 0 = (8, ,8 2 ) ;.:8. whnseelements
have the fann [[s,. s.], S3]' However, it is reasnnable and cnnvenient
to regard 8 and S. as identical, as there is clearly a natural one-to-Qne
oolTt'Spnndence between their points. Moreover, as the reader will
easily verif,..., this correspondence induces a one-to-one co1'l'f':t-pondence
between the O'-fields E and Eo which is measure preseITing. Thus
(S. E. p) and (8 0 , ED' Po) may he identified as measure spaces. We may
de8cribc this situatiQn hy saying that the process Qf fnnning products
of measure spaces is ll$8QCiLdive. It is easily seen to be commtdative
also. These remarks clearly extend to the product nf any finite family
of measure spaces. Thus if (8.1 I" Ili), i = 1, . . _, n, are measure
space8 which are all finite or all positive and O'-finite, and a. is any sub-
set nf {I, . . .. n}, we may identify the measure spaces P -I (8" E" p;)
and (8., Eo' P.) X (8." E.,. Po')' where
(8.> E.. Po) = P (8,. E,. p,),
and I
(8." E.., Po') = P (8,. E" 1',).
i.
PROOF. \Ve shall use the notations introduced in the proof of
Corollary 6. According to the proof Qf that corollary, EE';' is in I'"
fnr each i, sO' that if EE"'(B.) = {B1lrs" s.]. EE"'} then PI(EE';'(so»
is f'2-measurable on E ). Since Jl1(EEUI(B 3 ») = 0 for sof EX'.
p,(EEII'(s.» is a f'2-measurable function Qf B.. Since {EEU'(s.)} is an
increasing seqnence of sets with' umon E(S2)' «,(E(s.)) =
lim,_", J'.(EE!IJ(s.» fnr each B.£8.. Thus by Corollary 6.14. pI(E(B.»
js a P2-measurablc function of 8 2 " Accordmg to Corollary 4,
190
III. INTEGRATION AND SE'l' FUNCTIONS
III.n.9
I11.n.l0
PRODUCT MEASURES
191
The next theorems concern the relationship between integration
in a product measure space and integration in the components of the
product. It is a consequence of the associativity of the product
measure that the discussion can. be restricted without Joss of genera.lity
to the case of the product (R, E R . (I) of two measure space" (S, Es.p)
and (T,ET,A).
... 9 THEOREM. (Fubini) Let (S. Es, p) and (T. LT' A) be two posi-
tive <I-/inile 11U'asure 8JX1L'f'S. Let (R,ER' (I) = (S.LS',u) x (T, E T , A)
and let I be in L,,(R. ER' (I. 3;). Then lor ,u-almDst all 8 in S, I(s, .) is in
L,,(T. E T .)., X). MoreOV<'T. h/('. t)A(d!) is in L I (S, Es',u. X). and
fs UT!(S, t)A(dt)1 peds) = fR,(r)(!(dr).
PROOF. Let 210 be the subspace of (I--simple functions
g . L,,(R, ER' (I, 3;). It follows from Corollary '1 that every g .210 satis-
fies the conc1usivn of the theorem. By Lemma 2.18.. we can find a
sequence {g.) of elements of 21. converging to I in the topology of
L" (R, E R' (I, X). TlJen we have
lim fs 1fT Ig.(s, t) - g,..(s, t)[)'(dl») peds)
m.ft-+w
= lim IR Ig.(r) - g",(7)1 (dr) = o.
m,1t-+ rn
Consequently, if we define the function G. n in
L I = LI(S. Es,p, L,.(T.L T , 1. I»
by G.(8) = g.(s, .), we have
hm Is IG.(8) - Gm(s)lp(ds)
,»,rI_CO
= lim J I f Ig.(s, t} - gm(" t)!l(dt}\ peds) = o.
m,1i_D) 5 T i
By.Corollary 6.6, there exists a G . LI such that G. --> G in the norm
of L,.. By Theorem 8.6(i) and Corollary 6.18(a), (and passing without
loss of generality to a subsequence) we can find a p-null set N E Es
such that G.(s) -+ G(s) for s; N.
At the same time, passage to a subsequence al10ws us to assume
that g,,(T) --> I{r) for all T not belonging to a certain (I.null set M. By
Corollary 8, this means that there exists a p.null set N I such that
g.(s. t) --> f(s. tJ- for 1-almost all t if s; N I .
By Theorem 8.6(i) and Corollary 6,I8(a), if s.; N is given. we
can find an increasing sequence of integers n. such that G..(so)(t)
-+ G(so)!t) for ),-almost all t; i.e.. such that .
g. (s., t) --> G(s.)(t)
.
for 1-a1most all t. Consequently, if so; N U N I , f(so' I) = G(s.)(t),
so that f(s., .) E L,.(T. E T . 1, X}.
The equation Uh = JTh(t}A(dt) clearly defines a continuous linear
mapping U of LI(T, E T ,).. J:') into I. In terms of the mapping U we
bave
fT/(SO' t)2(dt) = JTG(S.)(t)A(dt) = UG(so), so;NUN1'
Hence, by Theorem 2.19(c), h/(',t)A(dt)=UG is III LI(S,L,p.J:').
and we have
[*] fs IfT/(s, t)A(dt») peds) = J UG(s)p(ds)
= U fs G(s)p(ds)
= lim U fs G.(s)p(ds)
. OO
= lim fsUG.(s)p(ds)
.-+00
= lim J IJ g.(s,t)2(dt) ! ,u(ds).
tI........oC,> 5 T
Since We bave already observed that
fS.(fT g .(8, t)A(dt») peds) = tg.(r)(I(dr)
for the (I--simple functions g., and since g. --> I in the norm of
L,(R. ER' (I, I). the limit on the right is JR/(r)(I(dr). and the theorem
i8 proved. Q.E.D,
Theorem 9 can easily be extended to the product of two arbitrary
finite measure spaces. For this. the following three lemmas are con-
venient.
[0 LEMMA. Let (R,L R , (I) be the product 01 two <I-/inite positive
mrosliTe spaces (S. LS' p) and (T. LT' A), w,d let I be p-measurable on
S, w;,h values in a B-.pace I. Then the Iu"clin.. g .ro R to I, defined by
the lormula g(s, t) = Its) is (I-measo,rable.
192
IlL INTEGRATION AND SET FUNCTIONS
II1.I1,11
111,11.12
PRODUCT MEASURES
193
PROOF, Let I be an arbitrary p-measurable function; let Efi be an
inereasingsequenceofsetsinE s such that U Efi = S andp(E.} < co.
Let/.(sl = I(s}fors£ E. aod/fi(s) = o otherwise_ Letg.(s. t) = I.(s).
Then g.(r) -+ I(r) for each r and hence, by CoroJlary 6.14, it is suffi-
cient to show that each function g,. is e-measurable. Thus, there is no
loss in generality if we prove the lemma only for the case of the totally
p-measurable functions 1.-
Assume then that I is an arbitrary totally p-measurable function.
Using CoroJlary 6.18(a), let {I.} be a oequence of p-simple functions
convergmg to I p-almost everywhere. If gfi(S, t) = 1.(8) then
g.(r) -+ g(r) e.almost everywhere. Hence, by Coro]]ary 6.14, g i8
e-measurable. Q.E.D.
11 LEMMA. Let (B, E B . e) be the pToduct 01 the linite measure
spaces (8,E..p) and (T,ET"'-)' Then v(e) =v(.u):<v(A).
PaoOF, By the Radon-Nikodyro theorem (10.2) there is a p'
integrable function g with
pIA) = 1. g(s)v(.u, ds), A . E..
By Theorem 2.20, v(.u, A) = fA Ig(s)lv(,u, ds) and so Ig(s)! = 1 for
p-almost all s. Without loss of generality we may and shall assume
that Ig(s)1 = 1 for all s. Similarly, there is a A-integrable function h
with Ih(t)1 = 1 for a]] t and
A(B) = fBh(t)v(A. dt}, B.E T ,
For r = [s, t] let I(r) = g(s)h(t) so that I/(r)1 = I for all r in B. Let
v = v{p)xv(A), so that for A .E.. B.ET' and E = A:,B we have,
from Theorem 9,
12 LEMMA. Let (B, I R' e) be the product 01 linite measure 8p<JC£lt
(S, Es, p) and (T, E T , A). Let E be a e-nullset in R. Then lOT A-almoet
all t, the set E(t) = {sl [s, t] . E} .;. a p-nuIl set.
PROOF_ By Lemma 11 it may be assumed that the measure
spaces are positive, but in this case the desired conclusiOn was
established in Corollary 8, Q,E,D.
13 THEOREM. Let IS. E.,,u) and (T, ET,.i!) be linif£ mea.mTe
spilUS and let (B,ER' e) be their product. Let iE be a B-space and F bea
e-integrable function on R to I. Then, lor p lm&t aU s in S, the lunmon
F(s,') .;.A-integrableon TandthelUMtion ITF(', t)A(dt) isp-int£grab/£
en S. MMeover
f. 1fT F(s, t)A(dt») p(ds) = I" F(r)e(dr),
PROOF. By Lem"", 2.18, the function F is vIe )-integrable and
hence, by Theorem 9. F(s, .) is v(A)-integrable for v(.u)-almost all s
in S. From this and Lemma 2_18 it follows that F(s, .) is A-integrable
for p-almost all s in S. Now let the functions I, g, and h be defined as
in the proof of Lem"", n. Then. by Corollary 10.6,
fT F(s, t)A(dt) = IT F(s, t)h(t)v(A, dt).
Using this equation, Theorem 9, Lern"", 10, Lem"", 2.18, and Theo-
rern2.22(a), it is seen that ITF('. t)A(dt) isp-integrableon S. ByCorol-
Isry 10..6, Theorem 9 , and Lemma 11, we have
f../(r)v(dT) = L Usg(B)h(t)v(A. dt)1 v(.u, ds)
= IfAg(s)vC,u,ds)llfsh(t}v(A,dt)1
=.u(A).\(B).
Hence. by the uniqueness assertion in Theorem 2, e{E) = I "/(r)v(dr).
Since V(r)1 = I for all r we have. from Theorem 2.20,
fs Ifr F{s, t).i!(dt») peds)
= fs 1fT F(s, t)g(s)h(llv{A, dt») vIp, ds)
= f" F(r)f(r)v(e, dT).
Since, as was seen in the proof of Lemma II.
e(E) = f"/(T)V(e, dr),
it follows, from Corollary 10.6, that
f" F(r)/(T)v(e, dr) = t F(r}el dT ).
E.E",
Thus
t'(e, E) = f" I/lr)lv(d r ) = vIE).
Q.E.D:
Is 1fT F(B, t)A(dt») p{ds) = f R F(r)e(dr).
Q.E.D
194
Ill. INTEGRATION AND SET FUNC'J:'IONS
III.H.14
IIl.H. U;
PRODUCT MEASUIt.ES
195
The next result is a useful complement to the Fubini theorem
(Theorem 9).
. l4. THEOREM. (TO'I1£Ui) Let IR,I R , e) = (8,I s '«) x(T,Ir.l)
be the product 01 two positive a-finik measure space.. Let I be a poritive
e.measurable IUrrdion. Then, lor p-abnosl all . in S, the function I(s. .)
i8 1.,nea81JTl1h/,e. Mereover, the (emmded real valued) Iunction
J T 1(-, !)l(dt) i8 p-measurable amI
[*] fs IfTI(s, t)l(dt)1 pldsl = IR I(r)e(drj,
irreapedive 01 wkther the integrals have linite or injinu. value..
PROOF. Let {E A } be an increasing sequence of sets in I R such
that R = U E. and e(E.) < 00. Put IA(r) = 1(1') if Ilr} nand
r E E., I.(r) = 0 otherwise. By Theorem 6.10, I. is e-measurable, and
by Theorem 2.22(b), I. is e-integrable. If JRIlr)!!(dr) < 00, ourstate-
ment is merely Theorem 9. Hence, we have only to show that
JRllr)!!(dr) = 00 implies that the iterated integral on the right of [0]
is infinite. But thJs is obvious. since
Is IfTI(s, l)l(dt)1 peds} fs If.J.(s, t)j.(dt) I peds}
= fRI.(r}e(dr) --+ fRI(r)e(dr)
by Theorem 9 and Corollary 6.17. Q.E.D.
15 COROLLARY. Under the hypothesis 01 Tkorl!1l1 14, a e-measur-
able veclor valued fundion g lor which
Is 1fT Igls, t)ll(dl}j p(ds) < 00
i. e-integrabl.! on R and
fRglr)e(dr) = Is (fTg(S, t)l(dt)1 plds).
PROOF. This is an immediate corollary of the theorems of Tone1li
and Fubini and the fact that a e-measurable function g is e-integrable
if the function Ig(')1 is e-integrable (2,22), Q.E.D.
Tonelli's theorem has the important consequence that a non-
negative function measurable on the product of two positive ,,-finite
measure spaces yields the same value whether it be first integrated
with respect to one variable and then with respect to the other, or
vice versa. Indeed, according to Tonelli's theorem, both these inte-
grals are e\lual to the integral of I with respect to the product measuw
(and we have already remarked that the product of meaSUres is com-
mutative.) Generalizing this statement, and making use of the com-
mutativity and associativity of product measures, we can say that
the integral of a non-negative function measurable on the product
measure space of a finite collection of positive a-finite measure spaces
can be evaluated by . iteratedn integration over the various factor
spaces in any order. If either the function I or one of the mea..
spaces fails to be positive, we can no longer make this statement under
the mere hypothesis that 1 is measurable on the product space, But,
according to Theorems 9 and H. if we assume that I is inll'grable on
the product space, we can again evaluate its integral by Uiterated H
integration over the various factor spaces in any order. Thus tht>
Fubini and Tonelli theorems provide us with very general results on
uchange of order of integration".
It follows that if I is a function defined ou Euclidean n.dimen.
sional space E and integrable with re8pect to n-dimensional Lebesgue
measure J.. the "multiple" integral J E/(s )l( da) is equal to the "iterated"
integral J ::: {. . .{J ::: /('1'" ., s.)da,}. ..} da.. .Moreover, the order of
Integration in the iterated integral is immaterial. For this reason, both
multiple and iterated ,,-dimensional Lebesgue integrals are commonly
denoted by the incomplete notation
f +w f +w
. . 1(8 1 , . . .. SA} ds l . . .ds..
-0:;> -;Jt!
ColTt.ospondingly, if R is the ""rectangle'"
R = {[81' . . ., 8.]1a,. s, h" . . ., a. < SA b.},
tJI s Il( ds) is often written as
I .. .. . I ', 1[81' . . ., s.jda, . . - da..
G,!. 4...
It should aL be mentioned that just as in the one dimensional
case) a specific symbol for n-dimensional Lebesgue measure is often
omitted from the notation for ".dimensional Lehesgue integrals. Thus,
when no confusion can arise. h/ls)l(ds) is often written as JE/(S)da,
and JR/(s)l(ds} as J,,/(s}da.
106
III. INTEGRATION A:ND SET FUNCTIOSS
III.n.16
111.11.16
PRODUCT MEASURES
197
Next we study the relation between the theory of product me as--
ures and the theory of vector valued integrals. In the application of
the theory of vector valued integrals to concrete problems such as the
representation of operaters betwf-en Lebesgue spaces (cr. Section VI.8)
one is faced with the following situation. Suppose that (S, E, p) is a
measure space and .. is a ,u-measurable function whose values are in
L.(T, E T , A), 1 ;,; p < 00. For each B in S, F(B) i8 an equivalence
class of functions any pair of whose members coincide A-almost every-
where. If for each B we select a particular function I(s, .) E F(s), the
resulting function I(a, I) defined on
(R.ER,e) = (S,Es,p)x(T,ET,A)
wiJ] be caUed a repreamtation of the function F. It is important to
know whether F has Be-measurable representation, and, in ca:;;e F is
p-integrable. whether IsF(s)p(de) = Isl(s, . )p(ds). These questions
are answered by Theorem 17 below.
16 LEMM". Let IS. Es. p)and (T,Ep A) bemea.mrespacesU'hidl
are either both linif or both ]XHJilive and a-finUe; let (R, ER' e) belh£ir
produd and let I b. a B-spau.
(a) II F i8 a function on S 10 Li(T, LT' A, I) ""'Uki. p-integrable
on S, Ih£n there i. a e-iwgrab1.e lunc!io-n I on R to X lfUI:h that I(s, . )
= F(s) lor p-almost all s in S. Murt!mJt!T, Is/(s, t)p(ds) e:risfs lor A-al.
most 1111 I in T and, asalundian olt. i8e'JUl11 folhul_ JsF(s),u(ds)
01 L,,(T, LT> A, I).
(b) L.t 1 P < 00, and let I be a e-measurob1.e fumtion on
(R.E R , 1!)loa;lfUI:hthatF(s) = f(s, ')isinL.(T.ET' A, l)farp-almosl
all s in S. Then 1M V«ior valued fundwn F on (S,Es,p) w
L.(T, ET' A,:f) i8 ,.-mrosuralU.
PRoOF. For brevity we shall use the symbol 1. i for the space
L,,(S. Es, p, L,,(T, L T , A. :f). By Lemma 2.18 there is a sequence
{F.} ofp-.simple functions in 1. J with Fn --+ F in the norm of . Each
of the funct:ions F n is constant on each of a fimte collection of disjoint
sets E l), . . ., E;,"n) in E which together form a partition of S. Let
g ) be the va1ue of F n on E ' and define the functions fn. n = 1, 2, . . -t-
on R by the equations
I.(s, I) = g II), s £ E I.
It follows from Lemma 10 tbat In is I!-measurable, Moreover, it is clear
tbat In(s,') = Fn(s) for B in S. Also by Theorem 14
IR !In(r}lv((', dr) = Is (IT I/n{s,I)lv{A, tIt)j v(p, ds)
= Is IFn(s)I"(!', ds) < 00,
and so (2.18) In is ('-integrable on R. Since I.(B. .) = Fn(s) for sin S
we have. by Theorem II and Lemma 11,
lim IR I/nIT)-I..(T)lv«(', dr)
m,J'I...p
= lim Is 1fT (l/.(s. !)-/m(s, 1)lv(A, tIt)j V(Il, de)
m ,,-.m
= lim Is IFn(s)-F..(s)lv(P, tis)
m,n-+o-
= lim IFm-Fnl = O.
m,ft tQ
Thus. by Corollary 6.6. there is a e-mtegrable function I on R to .I
such that
lim J I/n(r)-/(r)jV«(J. dr) = O.
"-HII R
It IS seen, by using Theorem 0, Lemma II, and Lemma 2.111. that the
function G(s) = I(s, .} is in L. and that
IFn-GI = Is IFn(s)-G(s)jv(!" de)
= Is (IT I/n(S, I)-/(B, !)IV{J., tIt)1 V(!" tis)
= Is I/n(r)-/(r)lv(l!, dr) --+0.
Since Fn - F in Ii we have IF GI = 0 and therefore, (6.8), F(s)
= G(s) = I(B, .) for p-almost all s in S. Thus, the first assertion of
part (a) is proved.
Since I is ('-integrable on R it follows from Theorems 9 and 13 that
for A-almost aU I in T the function/{', t) isp-integrable onS and that
Js/(s,l)plde) is A.integrable on T, proving the second assertion of part
(a).
To prove the final assertion in la) we define, for each E in E T , the
bouoded linear operator DE on LJ(T, IT' A,.I) to I by the equation
198
11[. INTEGRATION AND SET FUNCTIONS
111.11.17
HI.n.17
PRODUCT MEASURES
199
UEg = IEg(t)).(dt),
g € (T, ET' A, if).
integral IsI(s, t)p(ds), 118 a Iltnclwn 01 I, is fYJUul 10 111£ dRme.u
Is F(s)p(ds) 01 Lp(T, 2"7-, A, if).
PROOF. Let E T be partitioned mto a sequence {E.} of disjoint sets
of inite A-measure. For 1 £ p £ 00 let L. = Lp(T,E T , A, if) and
defme thC' maps UTI, n = 1,2, . . ., of Lv into Ll by the equations
(U.g)(t) = g(/)X".{t), where X" is the characteri8tic function of E .
By Holder's inequality (8.2), . .
[U"gl, v(A, E.)"'lgl.,
where l/p+I/q = I. and thUg U. is a continuous linear map of L
nto LJ' By Th orem 2.I9(c), the function F.(,) = U.F(') is a fl
Integrable functIOn on 8 to LI' By applying Lemma I6(a) to F we
obtain a e-integrable function I. on R to I such that 1.(8, .) = F.(s)
for every 8 in S which is not in some ,u-null set N . Furthermore, for
A-almost Il t the fun ion/.(-, I) isp-integrablc on 8 and IsI.(s, t)p(ds)
as af nctIon oft defmes the SBme elernent in LJ as Is F.(s)p(ds). The
f nctJon I on R toI is now defined by the equation I(s, t) I.(s,t) for
t m E.. Theorem 6.10 shows that I is a e-measurable function on R to
I. Since F.(s)(t)=F(s)(t) fortin En' it is clear thatforeal'h s not in the
p-null set U;;:", N n . we have 1{8,t)=F(s)(t) forA.almostalltin T. Thus
I(s, .) = F(s) for p-almost all 8 in 8. Since In(', t) is p.integrable on 8
for A-almost all t the same must bc true for I{', t). The integral
Is I.(s. t)!-'(ds) as a function of t defines the same element in L as
i
Is Pn(s).u(ds) = Is UnF(s)!-,(ds) = Un fs F(s)p(ds).
From Theorems 9, 18. and 2,19(c), it is seen that
U E Is I(s, ')p(ds) = IE Ifs I(s, t)!-'(ds)J A(dt)
= f.xE/(r)!I{dT) = Is IfE/(s, t)A(dt)}p(ds)
= fs UEF(s),.(ds) = U E Is F(s)p(ds).
The final assertion of part (a) therefore follows from Lemma 15.8.
It suffices to prove (b) under the additional assumption that
v(.u, 8) and v(A, T) are finite. Since I is !I-measurable, there is a 8e-
quence {tn} of e-measurBble simple functions converging in !I-measure
to I. In virtue of Lemma 8.8 and the remark before Theorem 2 we may
suppose that each 1ft is a finite linear combination of characteristic
functions ofsets of the form A X B, where A € Is, B . IT' In addition,
we IllBY assume that I/.(B, 1)1 ;;;; I/(s. t)1 e-almost everywhere, and by
CoroI1My 6.1I!(a) we IllBY suppose that U.} converges e-almost every-
where to I. Put P.(B) = I.(s. -), B'S, so that each F. is a simple
function on (8. Is.!-') to L.(T, E T , A, if). By Corollary 8 or Lemma 12,
we conclude that for p...lm08t all 8 . 8 the sequence U.(B, t)} converges
to I(s, t) A-almost everywhere on T. It follows from the Lebesgue
dominated convergence theorem (6.16) that for p-almost all s € 8,
the sequence (F.(s)} converge8 to F(s) in the norm of the space
L.(T, E T , A, £). The p-measurability of F now follows from Corollary
6.14. Q.E.D.
In the following theorem the space Lm(T,IpA, if) i8 understood
to be the space of all A-measlUable, essentially bounded if-valued
functions on T. The norm of such a function is itsl.essentiat supremum
(cf. Def"urition l.n).
17 THEOREM. Let (8, Is, 1') and (T, ET' A) be measure space.
which are either both liflit< or buth positive and l1-linite, and let (R, E B' e)
be eMir produd. Let I ;;;; P ,,;: co and kt F be a p-irite{!,Toblt Jwnctinn on
810 L.(T, E T . A, 3i) where 3i i. a rea! oHomplex B-space. Then there is a
!I-mrogurable luru:tion I on R to I, which is uniquely ddero,inffi except
lor a set 01 e-measur. zero, and sw:h that 1(8, .) = F(s) lOT p-a!most all
Bin 8. MmeutJt?T 1(', t) is p-integTah!r on 8 fOT A-almo81 all t arn! th£
Since
IU n f F(BJI-'(M)J (t) = Us (F(s)p(dsJl(I), t. En,
it follows that
J I"(s, t).u(ds) = IL F(s)p(ds») (t), t. E.
and thus that
I../(s, t)p(ds) = Ifs F(s)p(ds») (I),
for A-almost an t in T_
To complete the proof ofthe theorem It only remains to show that
200
HI. INTEGRATION AND BET FUXCTIONS
III.n.n
III.n.I8
PRODUCT MEASURES
201
jls uniquely determined up to " set of ('-measure zero. To pro"e this
uniqueness it is evidently sufficient to show that a ('..measurable
function h on R to 3: fonvhich hIs, .) is " A-null function for p-almost
all s, must be a ('.null function. If h is such a function then, by Tonelli'8
throrem (14),
I R Ih(r)lv(e, dT) = Is (f. Ih(s, t)IV(A. tIt») V(fl. ds) = o.
so that. by Lemma 6.8. h(TI = 0 for ('.almost all T in R. Q.E.D.
Infinite pTrxhu:t8. The theory of measure in product spaces will
now be extended to the product of an infinite family (8 , I . ,u.),
c( to A. of measure spaces. We shall construct.a measure space (S, E. p)
called the prodiKt oj 1M measure sp<U"e8 (8a. I.. P.). "nd denoted by
p(E) = IT p (Ea)'
a.A
number of "irregular" factors and the theory to be developed In
what follows to the infinite family of regulAr factors and then, using
only the theory developed in the first part of this section, form the
product of these two separate parts.
Throughout the remaining part of this section the symbol A
will be used for an arbitrary set of indil'CS IX, and S for the product
P ..A 8 . For a suhset B of A we also write 8 B for P B 8 so that
a,
8 = 8 A' The symbol" will be reserved for an arbitrary finite subset
of A and ,,' will denote the complement A -:n; of" in A. The symbol
C n will be used for the family of those sets in 8 which have the form
n
Parn Ea with Ea in Ia, and the symbol In used for the smallest
field of sets in 8n which contains C n . There should be no confusion
bctween the symbols In and Ea. for if" reduces to the single element IX
then the field En is the a-field Ea' An ekmeJllary set in 8 is one of the
form Pa€A Eo. where Ea is in .Eo: and, for aU but a finite number of a;,
Eo. = Baa Equivalently, an elenlcntary set in S is one having the fann
Sn' X En for some:rr and some En in 8 . The family of elementary sets
in 8 will be denoted by C and the field of sets in 8 determined by &
will be denoted by EI" The symbol E will be used for the a-field of sets
in 8 determined by E,. The family of aU sets in 8 of the form 8n' X En
with En £ In will be denoted hy E".
(8, I,,.} = P (8a. I., fl.).
a_A
which has the following properties: S is the Cartesian product P Sa;
a,A
I is the a-field determined by all subsets of 8 of the form E = P Ea
a_A
where Ed. £ La and. with 8 finite number of exceptions. Eo. = See; and
p is a measure on I with the properly that
where E has the form just specified.
In order to avoid difficulties whIch might otherwise aTIse from
the presence of infinite products such as II Pa( Eo.:> it is convenient to
a_A
18 LEMMA. For each" lhe jamily E" is a field of 8et. in 8 and
II = u.E".
assume that for all but a finite number of II) fll1. is non-negative and
Pa(8 a J = 1. In this case the product IT Pa(Ea) i8 meaningful for the
a,A
PROOF. The identities
(8n' X En) U (8 n , ..: Fn) 8n' X (En U Fn)'
and
type of set P Ea mentioned above, since E-a = 8a and hence p.(8.) = I
ad
(8n,'..EnY = 8...xE:
show that I:' is a field. It is clear from its definition that II contains
all of the fields E". On the other hand, since E'" I:" if "1 "., the
union u En is a field. Thus E I = u I:'. Q.E,D.
n n
for all but a finite number of IX. We 8hall actua1!y restrict ourselves
somewhat more than this by assuming that. for all a., flfl. is non-nega-
tive and 1-'.(8a) = 1. No generality is really lost by abandoning the
posslbility of including a finite number of factors in which fla is not
necessarily positive and PlI.(StrJ is not necessarily on . In fact, we may
apply the theory developed in the first part of this section to the finite
19 LEMMA.. For efU'h IX in A let (8 a . I., P.) be a positive mel1$1U'e
BpfU'e ith p.(8 ) = I. Theil lhere i. a uniqlle additive seljum1ion p.
on E I wifl, Ihe property lhal
202
III. JXTEGRATJON AND SET FUSCTIONS
111.11.11)
111.11.20
PROnucr M£ASURES
203
p{ P E.) = II Po(E.),
:1f"A o: .4
p{E) = pn{E),
E€E"
for every elemmlnry sel p.. A E. in S.
PROOF. We will first show that I' is unique. Let A be another
additive set function on E I with the stated value on elementary sets.
For each Jet PilI Aft be set functions on E7J defined by the formulas
Pn(En) = p(EnxS n ,), J.,,(Enl = A(E"xS n ,), E.€En'
Then
is uniquely defined on the field E,. To see that I' is additive on E, let
El' Ej be disjoint sets in 1:'J- By Lemma 18, there are finite sets '1 1 ' :f't 2
in A with E, E E"'. E. € E"'. Thus, if" = "1 U "" we have E" E. € L-
and hence there are disjoint sets AI' A 2 in E7J with
El = A1xS n "
E. = A.xS n ,
and
.
.."
...
p(EIUE.) = p({AIUA.)',Sn') = 1-'.(A 1 U A .)
= Pn{A')+Pn{A.) = p(E,)+p(E.),
which proves that p is additive on E I . Q.E.D.
1'.( P E.) = II Po(E.) = J.,,( P E.),
and so. by Lemma 1, A(E) = p(E) for every E in En' This means that
A(E) = pIE) for every E In E". Thus, by Lemma 18, A{E) = pIE)
for every E in L 19 and p js unique. This uniqueness argument suggests
how we may prove the existence of p. For eaeh finite set n in A there
is, by Lemma 1, a unique additive set function Pn defined on ED which
has the property
Pn(P E.) = II I,.(E.),
EaE"Ea-
20 THEOREM. For each a in A leI (S., E., 1-'.) be a positive fi..ile
measuTe8jHlcelDithpo{S.) = 1. Then rlu:re is a u..iquecountablyaddirive
sel ftmdion I' defined on the a-field drlerllli..ed by lhe elemn1lary sc18 in
Smith the property thaI
1'( P E.) = II p.{E.)
a£A a£A
Cle1I D:E"Z
Let If' be defined on E" by the equation
If'(En/S n ,) = p.(En)'
We note that if "1 ", then
pn(PE.xS,.;}=ILn(PE.x P S.)
UoiJ'T.t a CVI-7I 1
= { II p.(E.)} { II p.(S.}}
UiPIJ. OiE1J-n1.
= II Po(E.}
En£E n "
for every elementary sel p." E. in S.
PROOF. Let I' be the set function on El whose eXIStence is asserted
in Lemma 19. If it can be shown that IL is countably additive on E,.
then Corollary 5.9 will yield a unique extension of IL to 1: with the
required properties, Let {E,} be a sequence of disjoint sets i" E I whose
union is also inEJ.Let F7J = U: l E i ; then n:_ 1 Fft is1"oid and it
is required to show thatlimn m p(Fn) = O. By Lemma 18, there exists
a sequence {".} of finite subsets of A such that Fn€E"-, n 1. Since
L- If' if '" ,;; we may assume that "" "0+1" Thus there is a
8equence {.x.} in A with ". = {aI' . . ., a..J. For each n, let 1',,- be
the set function on E.. defined by the formula
p..(E n ) = p{E. X Sn_')' En€En o '
Since F 71 is in p'4 there is an Eft in .!':1J a with Fn = En /. S ,. Thu::;, by
the Fubiui theorem,
(I) p{F.) = p..(E n )
= fs (.. .Us XEJS"',..., S...IIL.._ (dsa..>I...1 /,..(d8..).
Q;l .a: JI
.m.
=p"'(P E. xS-:},
I\':£:'fl
which shows tha/pn'(E) = pn(E) for every set E of the form E',Sni
with E in & ",. It follows from the uniqueneos argument presen.ted at
the beginning of the proof that p-"'(E) = pn{E) for every E III E".
Thus if", and ". are arbitrary finite sets in A and if E < :£'" n E'" then
p.'(E) = 1f"""'(E) = !'"'IE),
which shows, by Lemma 18, that the function
204
III. INTEGRATION AND SE'X FUNCTIONS
III.1l.20
111.11.2]
PRODUCT MEASURES
205
Since {F.} is a decreasing sequence so is I-'(F.). \Ve shall make an in-
direct proof by assuming that I'(F.) li > 0 for all n = 1.2, ,_..
By thc Fubini theorem, the iterated integra1
In(Sg)
= Is I... [Is XE.(sa,,"" s..)p...'ds....)].. .fl'..(ds a ,)
1%11 I\
Since F, is in I7" it has the form F, = E,xS", and thus (4) is true
for every t, inS . We no\Vlet:ngo= U:"1 1'€,. Bnd let 8 be an arbitrary
eJement of Sa for oc" ,, , It follows that
p 8 ot" Fj, i = 1,2, -. "'
a.A
is defined for 1'., -almost all a., in S.,. Since I-'(F.) = Js.jn(aa)Pa, (ds a )
does not converge to zero and since 0 ,,; I.(aa,> ;:;; 1 it follows from
the dominated convergence theorem (6.16) that there is a point
1,;, in S... for which f.( } is defined for all n and for which the se.
quence {/.(a )} does not converge to ro. Thus, the sequencc
,
which contradicts the fact that the intersection of a11 the sets F"
i = 1,2. . ... is void. Q.E.D.
XE( ....r8 ,$0 ,...,sC()
ft 1 q
21 DEFINITION. The measure space of Theorem 20 is caUed the
product 01 the measure spaces (Sa' I", 1-'.) and we write
(S, I. f-t) = P (S", I", Il,,).
a.,f
Just .as in the case of finite products the operation of forming
infinite produ ts of measure spaces is an associative operation. This
property is explicitJy formulAted in thc next lemma.
22 LEMMA. For eMh " in the sel A let (Sa. I". I-'a) be a positive
measu:re spau ",irh Pa(Sa} = I. Let A be parti1ioMd into a lamily al
-diajoim sets A,. where P rang'B over a Bet B. Tium
P(S.,1:".f-t a ) = p P (8 a ,1:".l-'a)'
ileA fjEB (leA.p
Paoo}'. We may suppose that B and A are disjoint and thus un-
ambiguously define the measure paces
(S,. I" 1-',) = P (8", I", pg}, p. B
aCAp
(8 1 , I" ',J = P (S,. I" p,).
p",
(S. I. p) = P (8., Ia' Pa)-
..A
With this notation it is required to 8how that (S, I, 1-') = (S" I" 1-',).
Clearly S = S,. For P. in B the family EP, of all sets of the form
Ep,x P S, with E" in I" i8 readily 8een to be the ,,-field generated by
'* ,
sets of the form P Ea with Ea in I" and Ea = S. except for a finite
a.A
(2) Is., I. . -lIs... E.(a . B.... . . .. aa.)P.... (ds...>!. . ,]p..(ds",,)
is defined and does not converge to zera, If we now apply to the se-
quence in (2) the argument just applied to the sequence (1) we may
establish thc existence of a point in S" for which the integraJ
. .
Is I.. .Us E.(a . a . B"" . . .. B",)p... (ds...'! . . . ] Pa,(ds a ,>
'" ....
is defined for an n but does not con'.erge to zero .as n approaches
infinity. By proceeding inductive1y in this fashion we arrive at a
sequence {S ,} with S , £ Sa.,' i = I, 2, . . ", and such that for each tl
and each m < k. the integral
(8)
f (. . . 1 1 X ds ' ..., s""", ' aa"," .., Ba )1'.. (ds a )1...) f-t. (ds.)
Sa"., Sac,. "'I -1 k.".1:" III
Exists and does not conyerge to zero as n -7 00. If we apply this state
ment with m = k,+1 it is seen from (8) that for some n > i the
number
is not zero for all Bft ,..., s . Thus for some t, In S ,' the point
"'J+l G&A .
li2. . .. .xs ". t J IS in Fn. Since Ft'lC Fl' we have
- .....J -
(4)
x... X8 :-':l j € Fj_
, .,
number of cJements of A . Hence IP' I for each Po in B. Since I, is
-clearly the ,,-field generated by the collection of all the families E '
with Po in B we have I, E. On the other hand, if"" is an arbitrary
206
III. INTEGRATION AND SET FUNCTIONS
III.ll.23
III.ll.24
PRODucT MEASURES
207
a,.
= Is 1/1:p.,(ds.)
.
= If:. Q.E.D.
24 TIl£OREM. (Mean Fubi,u-Jessen theorem) Let (S, I, p.) be
the product 01 the p<J8itroe measure 1IpOCeB (8 a , Ia' p.,), <x. A, where
p.,(8 a ) = 1. Let the linite Be!&:n in A be rdered by inclusion. Then. lor
any I in L»(8, :E, p, I) with 1 ,s; p < 00, the funrtum I". delined On 8
to the B..pace I by the lormula
I..(s, ',s".) = Is Ils n ys".)/1n(ds.J,
n
COlUoerges in the 'IOrm 01 L.{8. I. p., I) to the co""",1-! function whose
value al ea(;h point 01 8 is the integral
Is/(B)p(ds).
Furthermore the I..'!dwn In on 8 defined by
In(BnXB n ,) = f IIBn X s".)"".(ds h .)
s",
cmroerges in the norm of L.(8, l.. 1', I) to I.
PROOF. By Lemma 26 and Theorem II.l.I8 it is sufficient to
restrict our attention tu functions f in a fundamental set in
L.(8,:E, p., I). SineeIis thea-field determined by the sets E.. " P 8 a
a....
with E.. in :E.., it follows, from Lemma 8.3, that L.(8, I"1', :£) is
dense in L.(8, :E, p, I) where I 1 is the field generated by these set8,
Thus J it is sufficient to restrIct our attention to the characteristic
function of a set in:E1. By Lemma I8,:E 1 = U nL", suthatany EinI 1
has the form E = F xS", for some finite set n. and some F in :E",
Letl = Xl; and letn no' Then, since I(B) = I(s, xs.') is independent
of B.. we have
element of A, "'0 is an element of some set Ap,. Then each set of the
form EfZoX PaoF u" with EC1.tJ in D' is in EA,. and henceinEt. Since the
e<>llection of all these sets generates the a-field I, it is seen that
L G: II and thus that:E = LI'
Now,letn be a finite subset of A, and let T be a finite subset of B
such that U Ap "" Then
pn
p.,(PE a xP8,,)=p,(P(PE.x P 8 a )/.PSp)
aoE.1t o::vz" {J€t u(Aft' a Ae-Ti (kr.'
= IT,t,( PEa/. P 8a)
p UfAIf" O:I;'Ap--:'I
= IT IT p,(E.)
fjf'f f.(AfJ7I
= IT p.(E.).
Thus it follows from the uniqueness assertion in Theorem 20 that
p. = p,. Q.E.D.
23 LEMMA. Let (8 1 , :EI' p.,) alld (8., :E.. 1'.) be two p<J8itroe measure
Bpaces with p,(8,) = p.,(8.) = 1, and let (S. I, 1') be their produc/. For
each I in L , (8,:E. p, I), w""re I is a B-spou. let TI be the lundW.. on 8
deli,l£Il by the formula
(Tj)(sl's.) = f I(s,. t.)p.,(dt,,).
s,
Then. il I is in L.(B, I. p, ;E) with 1 ,s; p < 00 the Iltnetum TI is also
in L.(8,:E, P. !) and
IT/I. :;;; III..
PROOF. It follows from the Holder inequality (8.2) that
L.(S, I, p, if) is contained in L I (8, I, p, I) and thns the Fnbini
theorem (9) together with Lemma 10 shows that TI is defined p-almost
C\'er)"Where and is p-measurable. We have. by Theorem 14, and an-
other application of the HOlder inequality,
IT/I: = Is, Us,IIs,/(B,,!,,)p,(dt,,)I' p.,(ds 1 ) I p.,(ds.)
;:;; Is, Us, Is,I/(B I . !")I.p.,(dt,,)] p.,(ds,)]p.,(ds.)
= Is, Us I/(s)l.p(ds)]p.,(ds.)
In'(B) = f X"(Bn><s,,.)p.n(dsn)
s,
= Is I(s)p.(ds),
and
'h(S) f X,,(sn X s..>"n'(d.,,')
SJI' '
= I(s).
Q.E.D.
208
III. INTEGRATION AND SET FUSCTIONS
III.I1.25
I1I.n.27
PRODUCT MEASURES
2()9
25 COROLLARY. Umler the hypolksu, of Throrem 24, we have, for
erJ"y f in a dense SI<bst1 of L I (8, E, 1'). a finite set n. in A S1Uh 1M!
In = fsf(s)1'(ds), fn = f. n n..
We shaU now prove a theorem analogous to the preceding one
wIth the norm convergence of that theorem replaced by pointwise
convergence almost everywhere. For this purpose the following lemma
is needed.
! Js.... f(..... x..)p,.(ds...)I.
= fs n , 'Xc,(sn, .<....) Ifsn/(Sn,xs...)1'.;(ds.)\ p.Jds n )
= Is Xc..(Sn.tX8 )gk(82101: .:S:'t )}ln.(ds:n.)'
n,
and, since the integrand is inde pe ndent of 8 .
n,'
J f(s)I'(ds)
c,
= Is .Ifs 'XC,(B n , 'S...)gk(.... x ..),u,,(d8.,)\ 1'. (ds..J
.... "
= fc g.(B)p(ds) b,u(C.).
,
By summing on k we get
L/(s)p-(ds) 1I.u{A,).
A simimr proof may be made for the other choice of g.(B). Q.E.D.
26 LEMMA. Let (8, E,,u) be lhe producl of lhe positive .nea.run:
spaces (8., E., 1'.), n = I, 2. . . ., with p,(8.) = I. Letn. = {l. . . ., n}
and for f in LI(S, E. p,!) and. in 8 let g.(s) be either
Ifs. f(s....xSn;,)/,..;,(ds n ;.!:,
I>/'
A. = {sl sup gn(s) > b}.
l n<CJ:I
27 THEOREM. (Pointwise Fubini-Je..e-n Iheorem) Let (8, E. p)
be the producr 01 lhe positive measure spaces (8n, E.. p.), n = I, 2. . . .,
withp.(S.} = 1. Let". = {I,..., n} and fl>/' f in L 1 (S, E.p,!} and s
in S lei
ForlJ>Olet
Then
15,u(A.) < J I/(s)lp(ds).
A,
PROOF. Since the meaSures afe all pOSlbve J the norm of an Inte-
gral is at Inost equal to the integral of the norm, Thus the set A, will
not decrease if f is replaced by If(')1 and we may. and shaH, assume
that f is real and positive. Let B. be void and
and
I..;.(B) = f.....(B..XS.) = f. f{s"'xs.....)p",,!ds..)
n.
fn. = f...I..... '-:Sn) f. ,f(s... x......)p.Jds.J.
'.
Then
B. = {sl sup g,,(s} > lJ},
1':;;"$f1c
C}c = Bk-U:: Bn.
n= 1.2.....
lim f.' (B) = J f(s}.u(ds),
. s
..
Then {C.} is a sequence of dIsjoint sets with union A,. We nOW sup-
pose, for the sake of definiteness, that g,,(B} i8 the first of the two al-
ternative functions mentioned in the statement of the present lemma.
Then g..(.) is independent of sn;, and the same must therefore be true
of the characteristic function of Cft. Consequently, by the Fubini
theorem.
and
lim f. (s) = fIB),
.
n
far almasl all s in 8.
J . I(s)p(ds}
c,
= Is, Us.., 'Xcn.!s... xs..)f(sn, x s }/'.)ds.;)1 p,.!ds...>
, .
PROOF. For a given £ > O. we may. by Corollary 25. write
f = g+h where Ihl < £ and where g.... = g for all large n. If r(s} is
defined by the equation
r(s) = lim sup I/n.(')-lnm(s}1
0-+0'> m.fi>q
we have
210
Ill. INTEGRATION AN]) SET FUNCTIONS
III.12.I
III.12.I
DJ:FFEItENTIATION
21I
res) = lim SUp Ihn.(s)-hn..,!s) I ,,;; 2 sup Ihn.!s)!.
(i'-+CI> m,n>O l rz<1JC
PROOF. We first define the family {Ffl}' Let FI be chosen arbitra-
rily and suppose FI' . . ., F. already chosen. If A FI U. . . U F.,
the lemma is satisfied. Otherwise, let £. = lub ii/F), where F varies
over a]] sets F in :F satisfying
Thus, by Lemma 26,
p({slr(s) > 26}) :;,: Ihl/ii ,,;; £fii.
Since e > 0 is arbritrary we have p({sfr(s) > 26}) = 0 and since
d> 0 is arbitrary it follows that res) = 0 almost everywhere on 8.
This means that the limit I*(s) =lim,. f .ls) exists almost everywhere
onS. By Fatou'8 theorem (6.19) and the mean Fubini-.Jessen theorem
(24) we have
Is 1/*(s)-f(s)ip(ds) lim Is If..{s)-f(s!lp(ds) = 0,
fl
S(F,lJ(F))F, =.".
i = I, . . . k.
12. Differentiation
It is clear.. since S is a metric space and LJ :""'1 F, is closed., that this
collection is non-vacuous and that E;& > O. Let Fk+l be any set in :F
such that 8(F.w ii(F.+J))F, =.", i = I, . . ., k and satisfying
lJ(Fk+I) > 2"./8. We have thus defined the family {F.} by induction.
Suppose that [oJ is false for some mteger n> 1. If p" A-
-[F I u... oJ F. u U;;'_n+1 8(F., S6(F.»J, let F be a fixed set in:F
containing p with d(F) > 0 and for which S(F, lJ(F))F, =.",
i = I, . . ., n. If it can be shown that S(F, lJ(F))F. *'." for some
k > n, this will involve us in the desired contradiction. For if
S(lI',lJ(F))F. *'." for some k > n. let ko be the least such k. Then
lJ(F) < "',_1 so that <5(F..) > 2lJ(F)/8. Since ko> n, by assumption,
p is not in 8IF." 8Ii(F.,)), If q is in S(F,lJ(F»F... then
e(p, q) < 2lJ(F) < M(F..).
This implies that p" S(q, 86IF.,)) S(F.., SlJ(F..n, a contradiction.
Thus to prove that [*J holds for each n > I, it remains to prove
that under the assumptions above S(F, lJ(F) )F. #0'" for some k > n.
If this is not the case the intersection is void for every k, and by con-
struction of (Fn} we have ii(F) < s. for every k. This implies
ii(F.) > 2lJ(F)f8 > 0 for all k > I, Let {p.} be any sequence of points
in 8 such that p." F.. If i < i then S(F" lJ(F,))F, =.". Smce
.S(p" 2lJ(F)/3) S(F..lJ(F,)),
and so (6.8) t*(s) = I(s) ahuost everywhere. The other conclusion
may be proved similarly. Q.E.D.
In this section we will prove some of the fundamenta1 theorems
of the Lebesgue theory of the differentiation of set functions in Eucli-
dean spaces" and a. number of classical theorems of the form
r +=
I(s) = lim K.{s, t)/(t)dt
.-
.
"\'Vhere {Kn} is a suitable sequence of kerne]s and convergence is almost
everywhere. The first theorem. the covering theorem of Vitali, is the
basic tool for the development of the differentiation theory.
1 LEMMA. Let 8 be a compact metric .pare and A be an arbW-ary
subset 01 8. Suppose tlw.t :F is a family 01 closed subsets 01 S with 1M
properly rli.at 1M each pain! s in S there is a set F in :F at orlJitrorily
small positive diameter lJ(F) containing s. Then tlm'e exUlts a finire 07
oowmuabl<: lamily {F.} 01 disjoin! sets 01 :F such thai A U F. il
llu: lamily i$ linite, and
we have e(p" p,) > 2b(F)/8. The sequence {Pk} then clearly contains
no con\Pergent subsequence. This contradicts the compactness of S..
We conclude that 8(11', ii(F)F. ¥'." for some k> n, and thus [*J
holds for each n > 1.
Finally, since
[*J
'"
A FlU.. .UF.U U S(F..alJ(F.»)
......1
=
PI U... UF. u U S(F.. 8b(F.)) Fl U S(F., 3lJ(1I.))
k=l'I+l J:",,2
for every n. it follows that [*J holds for every n. Q,E.D.
lor <very n il the lamily i. denumeral>k.
212
III. IN'l'EGRATION AND SET FUNCTIONS
1I1.12.2
111.12.5
DIFFERENTIATION
213
2 DEnmTION. Let I' be a finite positive meaSUre defined on the
a-field of Borel sets of a compact metric space 8, A set A !: 8 is said
to be rovn-pd in tk _IBe of Virali hy a family 9F of closed s-;ts if each
FE !F has positive p-measure and there is a positive constant ct such
that each point of A is contained in 8ets 1" € 9F of arbitrarily smBll
positive diameter for which 1'(8(1", 3MF})) Ip(1") ,,;; a.
3 THEOREM, (Vitali cooering lheorpm) Let I' be a fmite positive
metuiUre tkfiwod on 1m, Bore! sefs of a compact meITk apace 8. If a family
9F of closed sds covers a set A 8 in /he sense of Vitali, then tkre ,:mills
a sequence of disjoint sets {1" fl} 9F such l!wl A - U ::'_, Fa is p-n'UU
set.
5 LEMMA. Let A be a fimb: positive measure defined on lhe Borel
subsets of tk closure of a bounded open set G of rea! Euditkat, ,
Ea. L,t 0 <'f < 00.
(B).If for each p in a set A G
A(C)
limlnf- <r,
plC) O ,uf C)
'Where C is a closed rube COlllainurg p, lhen each ""ighbofhood of A con-
lai1ls an open set Q such l!wl A-Q is a p-nu!! set and A(Q) < rp(Q),
(b) If for each p in a set A G
PROOF. By Lemma I there is B sequence { Fa} of disjoint sets in fF
such that A- U , F. U:"a+I S(F.. 3b(F.)) for eBch n. Now
. A(C)
hmsup- >T,
piC)...... pIC)
then each 'leighborhood 0/ A C07llai1l8 a Bore! Bet B Buch that A - B is a
p-"IItdJ oct am! A(B) > rp(B).
m m
1'( U S(F., 3d(F.)));;; Z ,u(8(F.,3b(F.)))
k-n+] k-n+l
;;;a f p(F.) o
i-n-H
BS 11 ->- <IJ since Z;;'., ,11(1".) ..;; p(8) < 00. Thus for each € there is
an 7l 5uch that
m
fl'
m
PROOF. To prove statemfllt (B) let U be an Brbitrary open set
such that A U G and let 9F be the family of Bll closed cubes C
contained in U 8atisfying A(C) < rp(C}. Since every cube C sBtisfies
,u(S(C, 3b(C»)) ;;; (6vn+1)flp(C). it follows that 9F covers A in the
sense of Vitali. Hence by Theo m 8 there is a sequence of closed cubes
{C.} 9F such thBt A- u:",C. is B p-null set. For each k let D. be
the interior of Cko Since the faces of a cube have zero fl-measure p
A - U:., D. is B p-null set Bnd l(D.) < rp(D.). If Q = u ;:'_, D.
then Q is open, Q (;; U, A -Q is a p-null set, and
A- U F. A- u F.!: u S(F.,8d(F.))
.t-l .t-l - lr_n",+l
and ,u( U;:'-a,+I S(F., 3b(F.))j < €. Thus A- U:;'., Ffl is a p-null
set. Q.E.D.
4 DEFlNITWN. Let A be B vector vBlued set function defined on
aU closed cubes contained in some open set G in real n-dimensional
Euclidean space Ea and let I' be Lebesgue measure in En. Then A is
said to be differenl.iah/;, Bt a point p in G if the limit
dl (p) = lim A(e)
dp p(C) O 1'( C)
exists, wbere C is B closed cube containing p. The function dljdp is
ca1led the ckrivalizJe of A.
Theorem 6 below will show that the termmology and notation
introduced in the preceding definition are consistent with those intro-
duced in the note following Theorem 10.7_
'" m
A(Q) = ! A(D,) < r! p(D,) = rp(Q),
J l _l
proving (B).
To prove (b) let U be Bn arbitrary open set such that A U G
as before. Now the family 9Ft' of closed cubes C U such that
A( C) > rp( C), covers A in the sense of Vitali. If {C.} fF I is a se-
qUfllce of disjoint cubes such that A - U;:'_, c. is a p-null set. let
B = U:=l Cko Sincf'
'"
A(B) = ZA(C.) > r!plC;) = r,u(B),
1--1. j...1
the set B satIsfies the reqUirements of (b J- Q.E.D.
214
Ill. I:STEGRA't'ION AND SET l<'UNCTIONS
111.12.6
111.12.6
DIFF:enNTIATION
215
6 THEOREM. Let}. he a linite measure <kjimd lor th£ Borel sulnds
01 an open Be! G in Tea! Ew:lidarn n-space En, and let ,; <knot.. Lebesgue
71IUJSUTf' in En. Then, for p-almost aU p in G ,
[OJ
i i
A(Q) p(QJ < (fl+e).
1 1
By applying Lemma 5(b) to the set A,R, we see there is a Borel set
B Q such that A,R- B is a p-null set and
'+1
A(B) p(B).
1
Since AfJ B U(A,,-Q) U(A,,Q B), pCB) p. Thus
(P+d > A(Q) A(B) > (i-J:-IJ P
1 1
which yields a contradiction for sufficiently small e. Thus we have
shown A is a p-null set, and it follows that the limit [oJ exists p.almost
everywhere in K
We will show now that dJ.Jdp is p-measurable. Let C(p,. a)
denote the closed cube with center p and side length a. Let
l a:+1/'ffl
Pm(P, 0:) = 2m p(C(p, fl))dP,
a+llt!...
l C1 + 1/m
A (p, 0:) = 2m A(C(p, {J))d{J.
m a+1I2m
dA .
- (p) = hm A(CJlp(C)
dp p(q.....
tX;W, where C denote8 an arbitrary closed cube zn G containing p.
lI10reIJ'fJtT
(i) dA/dp is p-ifltq,Toole;
(ii) },(BJ = JB(dJ.jdp){p)p[dp) lor et'£TY Bore/subse! Bol Gi/and
Ot.ly il A is p-oonlinu0U8;
(iil) (dAldp){p) 0 p-ulmosl everywh£re il and only if ,1 is 1'-
';flgulaT.
PROOF. Since G is the union of a denumerable family of open
cubes whose closure- is contained in G. it is clear that we can confine
our attention entirely to subsets of the interior Ko of some fixed cube
K. By decomposmg A into its real and imaginary parts, and then de-
composing each of these measures into the sum of a positive and nega-
tive measure by the Hahn decomposition theorem (4.10), it is also
clear that we need only consider the case where.Ais positive. Therefore,
we shall assume haeajl£r that ,1 is positive.
First, we shall prove the existence of the limit. Let A be the set
of points p in Ko for which
( A(C) m+J m A(C) }
A... = pllimsup --- > -.- > - > lim inf - .
.IC)-+O pIC) n n .(c)-+o pIC)
Then Am(P, a.)J/lm(P, IX) is a cuntmuous function of p for each EX.
and hence (C(v, a.))/p(C(p, a)) = lim".... Am(P, a.)I/lm(P, a.)
is Jl-measurable. Consequently,
dA (p) = hm A ( C(p, ) ) II' ( C(P, ) )
dJj n---Jo-D:> n n
is it-measurable.
It is convenient next to prove the converse assertion of (iii): if A
is p-singular then (dAld.u)(p) = 0 p-almost everywhere. For, if A is
p-,,;ingular, there is a p-null Borel8et N such that A(G N) = O. Sup-
pose that D = {pi (dAjdp(p)} > O} i8 nm a p-null set. Then since dAldp
is measurable there is an e > 0 and a Borel subset E of D-N such
that peE) > 0 and (dAldp)(p) > e, p' E. Since f-L is regular we can
suppose that E is dosed. By Lemma 5(b), every neighborhood of E
has A.measure greater than EI'(E). Since E is the intersection of a se-
quence of its neighborhoods, A(D) ;;;" 'p(D) > 0, contradicting the
fact that E is contained in the A-null set D-N. We have thus shown
p({pl(dAjd,u}(p) > O}) = O. Since,1 is non-negative, dAld,u ::2: 0, and
thus (dlldp)(p) = 0 p-almost everywhere.
. A(C) .. A(C) ,
limsup- > hmmf-
pICJ_O pIC) .(C)-+o pIC)
where C is a closed cube containing p. Let
for every non-negative integer m and positive integer n. Suppose that
A is not ap.-nullsct. Thcll since A = U: 7I_.A.-, some set AI.J is not a
p-null set. If {J =infB A pCB) where BisaBorelset, then {J> o.Now
& <J
given E > 0 and using the regularity of I' we can find an open set U
such that A;j U Ko and Jl(U) <p+e. By Lemma 5(a) there is
an open set Q U such that A;;-Q is a p-null set and
216
JII. INTEGRATION AND SET Ft:NCTIONS
III.12.7
III.I2.8
DIFFERENTIATION
217
We proceed next to prove (i) and (ii). Using the result ofthe last
paragraph and decomposing iI into the sum of a p-continuous and 1'-
singular measure by Theorem 4.14, it is clear that we can assume,
withoutloss of generality, that}, is p-continuous. Then, by the Radon-
Nikodym theorem (10.2), there exists a p-integrable function I such
that .<I(B) = IE I(p)p(dp) for p-a]most aU p. If {pl/(p) > (dNd,u){p)}
is not B p-null :set, then there exist positive constants c and e such
that
Many other families of closed sets (e.g., spheres) covering G in the
sen8e of Vita1i wonk! do as well.
In the next result we e"tend the discussion to vector valued
functions.
A = {PI/(P) > <+. > c> (1')1
is not a p-null set, and by the regu1arity of 1', there exists a closed set
n!;; A for which p(D) # o. Then it follows that .<I(D) = JDf{p)p(dp)
> (c+e)p(D). However. by Lemma 5(a), any neighborhood of D con-
tains a 8et Q such that iI(D) :::; iI(Q) < <p(Q). Since D is the inter.
8ection of a sequence of its neighborhoods. itfollows that iI(D) ;;;; <p( n).
and hence that <p(D) > «+f:)p(D), a contradiction. Thus we have
shown, using Lemma 5(a), that p({plj(p) > (d),jdl')(P)}) = O. It
follows similarly, using Lemma 5(h) that p({P!/(P) < (dA{dp)(p )})=O.
It remains to prove the direct assertion in (iii) that (dAfdp )(1') =0
for p-almost a1l I' implies). is p-singu1ar. We may write iI as the sum of
a p-singular positive measure and a p-continuous measure Az. From
the definition of the derivative it is clear that dA/dl' = rV."fdp+clAofdp,
p-almost everywhere. By the part of (iii) already proved dA.fdp = 0
I'-almost f'Yerywhere. Thus d4.ldp = 0 p-a1most everywhere. Apply-
ing (ii) to the p-continuous measure , we see that
8 THEOREM. Let I he a vector valued Lebesgu;; uaegralb lurutit...
.ulimd on an open set G in Teal n-dimensWnal Eucli.uan spa<e and let
aCE) = IE/(p)l'(dp). Then
lim - f. I/(q)-f(p)lp(dg) = 0
p(CJ O I'(C) C
lor al,n<JSI. all p in G. where C is a clo8M cube cvrdLJining p.I.. particular
th I f.
d.. (I') = Jim (C) /(q)l'(dg) f(p)
r p(CJ_O p C
lor almost all p in G.
PROOF, By Theorem 8.5 there is a ,..nuU set No and a separable
subspace.8 of 1: such that I(G-N o ) !;;.8. Let {z.} be a countable dense
subset of .8. It follows from Theorem 6 that for each n = I, 2. . , .,
Jim f. I/(q)-".II'(dg) = I/(P)-".I
ptCJ-+..p(C) C
for p In the complement of a I'-null set N.. The set N = U::'o N, is
a p-null set. Letp E G-N and e > O. Selectz.such that If(p)-".I <e.
Then
f dA,
},.(B) = - (p)p(dp) = 0
E d,u
for each Borel set B. Q.E.D.
lim sup f. If(q)-/(p)ll'(dg)
p!C)-+O pIC) C
S lim 8U P f. {1/(q)-z.I+J".-/(p)l}p(dg)
p(C)-+'O C
= I".-/(p)] +limsup f. I/(q) -..II'(dg)
p(C)-+<! p(C) C
= *.-1(1')1 < 2t.
7 COROLLARY. II I i. a i1ltegrabl£ fw1dian .uli..ed in an
open Bet G oj real Eucli4«zn n-spa<e th2n
1 f. t1 + h i tll +
Jim . . . I(s,. . . ., sn)dsl' . . .. ds n = f(I" . . ..1,,)
1H>(J h'l '.
almost everywhere in G.
Note that we are not limited to the use of cubes in Theorem 6.
Since £ is arbitrary
j/(p) - 1'( ) L,(q)p(dg): <. P ( J c I/(q)-/(p)lp(dg) -+0
as p(C) -+0 for each pEG-N. Q.E.D.
218
UI. INTEGEA.TION AND SET FUNCTIONS
111.12.9
III.I2,}o
DIFf'E.RENTtATJON
219
9 DEFINITION. Let f be a ">'ector valued Lebesgue integrable
function defined on an open set in Euclidean n-space. The set of aU
points p at which
lim f. It(q)-f(p)il'(dq) = 0
p{C) O pIC) c
is caUed the Lebesgue sel of the function f.
Clearly, the Lebesgue set off contains each point of continuity of f.
Let us suppose that f is a vector valued Lebesgue integrable
function of one real variable t. - ro < t < roo Let
S '"
lim
"_O'J -
sin'n(l-s)
) f(8)ds = f(t)
71(1-8
and
..
ri.(I) = -,
2
71- 1
It I :5: 2 ,
n- 1
1 1 1>-.
2
lim n JOo e-'U-"f(s)ds = f(t),
'10__01 t
each holding in the Lebesgue set of f.
Instead of proving Theorem 10 directly we shall consider in
Theorem II below the much more genera! question of when
lim rOo K.(s, t)f(sJds = fIt)
. Oo
=o
in the Lebesgue set of f, where the kernels K.(s, I) are not necessarily
positive or even real. Theorem IO will follow from Theorem 11 by
taking K.(s, I) = Q.(t-s).
10 THEOREM. Lei {Q.} be a sequence of non--negative real valued
fwru:tUms of lhe real variable t which satisfy
(a) Q.(I) is conlinuoUil onlherighl andisincre""ing fort :5: o and
decreasing for t ;;;; 0;
(b) lim Q.(t) = 0;
1_1-+0:0
(c) 11m Q.(I) = 0 for t #- 0;
' Oo
(d) ! e. Q.(t)dt = I.
Then if f is a Lebesgue .TiUgrahlt- function of t wilh values in a B-spm:e
I, the fvnd-Wns Q.(t-s)f(s) are inugrable in s for each 71 and t a..d
lim rOo Q.(I-s)f(s)ds = f(I)
. Oo
Theorem 8 states, in ttomewhat different notation, that
lim r", Q,(I-r)j(s)ds lim rOo f(l-s)Q,(s)ds = fIt)
._ n
for each I in the Lebesgue set of j.lt is clear thAt the integca1s above
average the va!ues of t in the neighborhoods [t-l/n, I+l/n] of the
point t. This interpretation of Theorem 8 as .a theorem about "aver-
ages" is capable of great genera!ization Consider the functions
Q (t) = ('M-"")/";". Then J",, Q:(I)dt = I, 71 I, 2, . ... The
functions Q: have the familiar "bell-8haped" graph of the Gaussian
density functions; for increasing n the peak at t = 0 becomes higher
and narrower in such a way thAtforeach £ > O. lim J::: (t)dt = 1.
' Oo
In this localizing behavior the functions Q: behave very much like the
functions QR- It is reasonable to ask whether the "weighted averages"
formed with the "density functions" Q: behe.ve like the ordinary
averages formed with the (unctions Q., i.e.. whether
n f +Oo
lim - r"u '}'/(8)ds = f(t)
,j:n: _011
in the Lebesgue set of t as before. That this is true will follow from
our Theorem 10 below. Other special consequences of Theorem 10 will
be the limit relations
for ClUh t in the Lebesgue set of f.
11 THEOREM. Let {K.}, (B.J be sequences oj scalar jv:nt1ilms de-
fined on the plane with B. real valued and IK.{s, 1)1 B.(s, t). Suppose
that for each jia:ed . we have
(a) B.(s, I) is der:TeasinglL'lafunclionojl UJhent ;;,; s, i.increasing
JDhen t :5: s and is continuous on lhe right:
(b) lim R.(s. t) = U:
111-00
( c) lhere is a constant M (s) such Ihat
220
Ill. IKTEGRAT!OK ASD SET FUNCTIONS
111.12.11
1I1.12. II
DIFFERENTIATION
221
f O+I
. I Bn(s, I)dl M(s).
f '+1
(d) Jim K.(s, t)dt = 1;
71._1;1:1 .-1
n = 1. 2 . . .;
G(w) -+ J: Ig(IJldt < <0.
Hence, letting w -+ 00 in [**1 we find that
lim r G(I)dB.(s., I) = - r B.(so. 1)lg(l}(dt.
U1_0C0 $.0 ..
(e) Jim B.(s. ,) = 0 for ea£h pair (s, I) with s 0# I. Then if f is a
.
Since G is non-negative, and smce Ru(8o,.) is decreasing so that
- Rn(s4)' .) determines a non-negative measure, an application of
Fatou's lemma (6.19) to the limit on the left shows that
J:, G(I)dB.(s., t) exists and
f oo G(I)dR.(s., I) = - f oo Bn(s., l}(g(t)ldt.
.. .0
Thus to prove [*] we need only show
[t] lim r G(t)dR.(so. t) = o.
'IJ_OII I'd
LelJugue iJ?Jegrable fr-mdion defmed for -0: < S < 00 U!ith values in a
R-spaa' :£,
! r.. K.(s, I)/(t)dt = f(s)
JIlT roery s in lhe Lebesgue stl of f.
PROOI!'. Since IKn(s, 1)1 Rn(s, I) R.ls, sJ it foUows from
Theorem 2.22 thatKn(s, t)f(t) is Lebesgue integrable for each n and s.
Choose some fixed s. in the Lebesgue set of f and let g(t) = f(t)
-lAt)f(s.) where 1= [s.-I, '0+1], In view of condition (d), Theo-
rem 11 amounts to the assertion tnat
[*]
lim r B.(s., t)lg(l)ldt = 0
'II_a:. ,g
Since au is in the Lebesgue set of I,
0= lim h- 1 f '.+h 1/(I)-/('o)ldt
h-+O Co
= Em h 1 f ,,+> Ig(t)ldt = lim h-IG(So+h),
h_O"D "-0
Thus given e > 0 we can choose > 0 such that G('o+h) < ell for
o < h ;:;;; lJ. Then, integrating by parts (Theorem 6.22). we have
f ll'd+1i f .....
G(t)dR.(so, t) :<;; E (t-so)dB.(s., I)
f. "-I<I
= e R.(so' (So+ )- )-e R.(so, t)dt.
"
Applying (b) and (e) it follows that
lim sup f ...... G(t)dR.(so' t) eM(s.).
n-+C1J
Jim f oo K.(so, t)g(t)dt = O.
ft-+OQo -0>
It is clearly sufficient to prove that
lim f m R.(s., t)lg(t)ldt = o.
lI-+CD _01
"Ve shall prove
The cOJTesponding assertion
. f: Rn(s., t)lg(tHdt = 0
may be proved in an entirely analogous manner. The essence of the
method is to integrate by parts; i.e., to rewrite the limit [*] in terms
of a Lcbesgue-Stieltjes integral (cf. the definitions and notation of
Seetion 5.)
Defining G(t) = I:.lg(r)ldr, we have, by Theorems 10.4 and 6.22,
['*] J: Rn(so, t)lg(t)ldt = G(w)Rn(s.. m-) - f: G(t)dR.(.o' t).
As w -+ co, R.(s.. w-) --+0 by (b) while
On the other hand, since Jim G(t) < co, g(t) is bounded by some con.
stant L. 'lllus f OD
J .. G(t)dR.(s., t) L f '" dR.(so' t) = LR.(s.. so+ ) --+-0
.o l!a+
as n --+ co by (e). Consequently
lim sup J'" G(t)dR.(s., t) < EM(s.).
n_CIC .0
Since E is arbitrary, fonnul& [t] IS proved. Q.E.D.
222
[II. INTEGRATION AND SET FUNCTIOr;S
III.IS,I
IILIIJ.5
EXERCISES
22S
The following special case of the pre,,"ious two theorems is often
useful.
12 COROLLARY. Let Q be a ncm--negatirw lunc/ion 01 the Tea! 'lH1rinble
I. -C) < I < 00. wilh the properlUs
(a) Qisiru;reasinglor I O, decreasing lor I ;;;; O,andisconlinuoU$
on 1M Tight;
(h) IimtQ(I) = 0;
ItJ_
(c) lim J +. Q(s)ds = 1.
l'l co -:I
II I is a Lebesgue illregrobk lunction delirud lor - 00 < t < 00 'triO.
oalues in a B-spO£e I., IMn
Q(n(l-s))/(s)
is integrable Icn cock n and I, and
5 Let h be a function of bounded variation on the interval (a, b)
and continuous on the right. Let g be Ii function defined on (a, b) such
that the Lebesgue-Stieltjes integral 1= i:g(s)dh(s) exists. Let I be a
continuous increasing function on nn open interval (c, d), with ICe }=a.
I(d) = b. Show that the Lebesgue-Stieltjes integral
J: g(/(s») dh (/(s»)
!.:. Cm Q(n(l-s»)/(s)d8 = 1(1)
lor each I in the Lebesgue set all.
PROOF. This result follows immediately on taking Q.(I) = nQ(nl)
in TheOl-em 10. Q.E.D.
exists and IS equal to I.
6 Show that .a monotone increasing function J defined on an
interval is differentiable almost everywhere with respect to Lebesgue
measure and toot I' llUly vanish almost everywhere without I being a
constant.
7 Let (S. E,I-') be the product of the regular measure spaces
(S., 1:., 1'.). Ot. A, If S is endowed with its product topology show
toot (S, E, 1-') is also regular.
S For each integer ft J let (8ft, };", Pn) be the measure space for
which S. is the set consisting of the two points 0 and 1, each of which
IS taken to bave measure 1/2, and I. is the family of all subsets of S..
Let (S, E, 1') = P .(S., E., 1-'.). Let I be the interval [0, I). Define a
mapping of I -'> S as follow8: for 0 s < I, let
13. Ex...,.,."
m 8
s=I
n-1 2 f1.
1 Let (S, 1:, 1-') be a finite measure space. Let Ot and {J be hound-
ed eountably additive functions defined on 1:. Suppose that Ot is I-'-con-
tinuous, and f3 is a.-continuous. Show that fi is It-continuous, and that
(dfJ/dp.)(s) = (dfJ/da.)(s)(da./dl')(B) l-'-alm08t everywhere.
2 Show that Theorem 10.2 fails without the hypothesis that
(S,1:, p) is a-finite.
S Construct a bounded Lebesgue measurable function I for
which JM(B)d8 is non-differentiable on a given set of measure zero.
4 If I is a function with a derivative bounded on the finite inter-
val (a, b), then I is of bounded variation, Rnd
be the unique dyadic expansion of B defined by the requirement that
£n = 0 or 1 and, f{)r infinitely many ft, we have Eft = 0, and let
<pes) = [8 10 8., 8 3 , . . ,]. Show that the a-field {'rl(E)IE c L} is the
<,-field of Rorel sets of I, and that if we put
A(r-I{E») = peE),
A is Borel-Lebesgue measure.
9 Let I be a Lebesgue integrable function defined on the unit
mterval [0,1). Put I.(s) = 2. Jr,t!'12" I{B)ds for i12. -;£B < (i-t-I)/2.,
o i ,;; 2.-1. Showtbat/.(s) --> I(B) (Lebesgue) almost everywhere.
. 10 Let I be a Lebesgue integrable function defined on the unit
interval [0, I). Put t.(B) = 2 . Z:U I /(B+j!2.) (where B+I is to he in-
terpreted as B+I-I if s+t;;;; I). Show that I.{B) i /(s)d8 for
(Lebesgue) almost all B.
f: g(s)d/{s) = J: g(s)/'(s)ds,
the integral on the left existing and the displayed formula being valid
whenever the function gl' is Lebesgue integrable.
22
111. INTEGBATIOIS AND SET FUNcnONS
IlI.1
III.14
FUNCTIONS OF A COMPLEX VARIABLE
225
DEFINITION. Let G be an open set in the space of n complex va-
riables %" . . ., z,.. (Such a 8et is often called a domain.) A funetjon I
defined on G and with values in X is said to be analytic 071 G if I is
continuous and the first partial derivatives olloz" i = I, . . -J nJ exist
at each point of G.
It is evident that if I is a vector valucd analytic function of the
complex variabJes ".t, . . ., %., then :r;*1 is a complex valued analytic
runction of ZJ' . . _, Zn for each xII' € 1:..
The theory of vector valued analytic functions, like that of com-
plex valued analytic functions, can be developed most efficiently
through the use of line integrals. These integrals may be defined as
foUows: Let I = {Ila -,;; I::;; b} be an interval of the real axis and let"
be a complex valued function whIch is defined, continuous and of
bounded variation on I. Then a. is the parametrization of a cotmnuous
recti/i(lble l'UTV£ C = a(/) in the complex plane. If a(l,) '" ,,(t.) unless
I,. = t" or .. and t" are the same as a and b. C is called a simple Jordan
curve. If <x(a) = a(b), and C is a simple Jordan curve, then C is said to
be closed.
If I is a vector valued function of a complex variable which is such
that 1(<x(I» is defined for all a ;;;; I < b and such that the Radon-
Stieltjes integral J I(a(l»da(l) is defincd. we write
J: l{a(l»d<x(I) Jcl(a)da,
and caU Jcf(<x)dot the line inl<!grol of lover (or along) the curve C. It
is easily seen that if we make .a continuous monotone change of para-
meter t = t(8), so that as 8 increases from t!:I. to hIt t increases from a
to b, we have, putting al(8) = ,,(1)8»,
J:: 1("1(s»<fa,(8) = J: h(a(l))da(t)
(cf. Theorem 10.8) In particular, if C IS a closed Jordan curve, under-
stood to be traversed in a certain direction, then Jcl(a.)da is inde-
pendent of the particular parametrization of C. and thus, as the
notation indicates, depends only on the point set C.
The fundamental theorem in the theory of complex line integrals
is the Caw;hy i7l1<!g,aJ IMorem. We may phrase this theorem as follows.
Let U be a bounded open set in the complex plane, and let B denote
the boundary of U. We suppose that B consists of a finite collection
of dis.joint closed rectifiable Jordan curves; that is, we suppose that
B can be decomposed into the union B = BI U B. U. . . U B. of dis-
joint closed sets B, in 8uch a way that each B; is a closed rectifiable
Jordan curve:
11 Let (S,1:, p) be a ,,-imite positive measure space, and
(B, PiI, A) the Borel-Lebesgue measure space on the real line B. Let
(Sl' 1: 1 , Pi) = (S.1:. p) '. (B. PiI, A). If I is a real function defined on S,
its graph is the subset P(f) = Us, 1(8)]is S} of S1" Show that f is
p-measurable if and only if its graph is a Wnull set.
12 Under the hypotheses of Exerci8e 11, let I be p-measurable
and non-negative. Show that
JS/(S)p(ds) = Pl{[8. I] £ Sl!O < I < I(s)}.
IB Let {(Sa.1:a. Po)} be a family of finite positive measure spa-
ces each of which bas Po(Sa) = I. Let (S,1:, /-I) = PaISa' Ea. P.). let
E a £1: a , and let E = p. E.. Show that E £ 1: if and omy if Ea = Sa for
all but a countable number ofindice8 <x, and that in this casep(E) can
be expressed as tbe unconditionally convergent infinite product
naP.(Ea)'
14. Function. of a Compl.x VariJllJle
In some of the cbapters to follow, and especially in Chapter VII.
we shall use extensions of certajn well-known result8 in the theory of
analytic functions of a complex variable to the case where the func-
tions Bre vector valued. It will be assumed that the reader is :familiar
with the elementary theory of complex valued analytic functions of
one complex variable and tbis theory will be applied here to obtain the
extenBiom which will be used later.
Throughout this section, J: will denote a eomplex B-space.
B,=a,(l,),
I, = {lla; ;::;; I ;::;; h,),
' e suppose in addition that the various curves B i are onented ion the
positive sense custmnary in tM IMory 01 complex ooriabk8: i.e., if the
points in U lying close to Bl are inside B" we suppose that B, is tra-
versed in the counter-clockwise direction as , goes from QJ to bi while
226
Ill. INTEGRATIOr.. AND SET FUNCTIONS
IIU4
111.14
FUNCTIONS OF A COMPLEX VARIABLE
227
( 1/'
1P/
Ai
a
/ /;zi$
all open segments of the mesh which separate two such squareSt and
all vertices of the mesh which arf' common vertices of four such
squares.) Let I be analytic in V-A. Then the second form of
Cauchy's inkgral theorem states:
II we agree to orient 1M Jordnn CUT0e6 comprising B in the polIitWe
ee1l$e cu8tommy in tM theory 01 rompleaJ variables, then J B I(a)da depends
<mly on th£ I.nuwm 1 and tM eet A, and is indRpendent 01 any particular
choia 01 th£ flI'ighhorfwod V 01 A.
In other words, the integrals I Band j 8 1 are equal provided that
Band BI bound domains U and Vi which contain the Same set of sin-
gularities of I. Here we are using the term singulmity for any point
where 1 is not defined Rnd analytic. This statement may be proyOO by
the use of linear functionals in precisely the same manner as In the
proof of the first formulation.
The same use of functionals proyes the Cauchy inlegrallormula:
if the pojnts in V lying close to B, are outside B" we suppose that B,
is traversed in the clockwise dirernon as t goes from Qj to h j (see
figure). Let 1 be a function analytic in a nejghborhood of U UB. By
I(z) = f I(a) doc.
2n1JB«-z
fB'(a)d« = o.
where 2 is a point of the bounded open set V whose boundary B con-
sists of a finite number of closed rectitmble Jordan curves oriented in
the positive sense customary in complex variable theory, and f is a
vector valued function analytic in II neighborhood of V U B. The
Cauchy integral fonnula may also be proved directly from the Cauchy
integral theorem just as in the case of complex valued analytic func-
tions.
Let VI" . ", Dn be a finite family of bounded open sets. with each
U I having boundary BJ as above, and let f be a vector valued function
of the complex variables Zl! . . ., Zn. analytic in n neighborhood of
(VI UBI)x.. .x(V, UB,). Then, by applying the Cauchy integral
formula to each of thr: variables zJ' . . ". Zn in succession, we readily
derive the Cauchy integral formula in se,,'eral variables:
h/(a)d« we understood I -I IB,f(a)doc. Then Cauchy'8 integral theo-
rem states that
The validity of this theorem for vector valued functions foJlows from
its validity for complex functIons: by Theorem 2.I9{c)
",* fB/(a)da ta:*/«J()d« = 0, a:*. 1*,
and thus, by Corollary II.8.I5, IBI{a)da = o.
Just as In the familiar classical case of complex functions. the
Cauchy integral theorem may be reworded in B somewhat more ge:ner 4
al form. To state this other form, let A be a compact set in the complex
plane and V a neighborhood of A. Then Vactually contains a neigh-
borhood V of A which is bounded by a set B consisting of a finite
number of closed Jordan curves. (To See this we may rule the complex
plane into a sufficiently fine square mesh, and let V be the union of
all open squares of the mesh whose closures intersect A, together with
( 1 ) ' J J I(a"...,cx,,)
/(ZJ'..4' Zn) ::: -. ... - _. 00 1 ., .00n'
2", B. B. «J(l-':'.)'" «J(. z.)
which is valid for ever>' [z" . . ., z.] in V, >(. . . . V..
From this fonnula it faUaws readily, as in the cla."8ical one varia-
ble case, that 1 has continuous partial derivatives of all orders in
228
DI. INTEGRATION AND SET FUNCTIONS
III.I4
III.I4
FUNCTIONS OF A COMPLEX VARIABLE
229
U u . . . U.-a Just as in the classical one variable case we can prove,
using this Cauchy integral formula in several variables, the following
ronvergence theorem of Weierstrass:
Let fft be a uniformly bounded ""'JUence of _or valtud "met ions
each tUfined and analytic on an upm .et V in 1M space 01 the compIe..
ooriablu ZI' . . ., Zn' Let V be a bounded upen subset oj V "'Mse closure is
confained in V. II fft convergu al each point 01 V to a fundinn I on U
th£n I is tNUllyric in V, and IMpilrtia! derit'tltives of f. oj arbitrarily large
order converge to 1M CO'I'I"UpONding parl;,,! tUrivaJive. oj I uniformly in V.
From this theorem. we can easily derive the useful fact that if I
is analytic in the u.rtesian product V.x.. .xV. of a collection of
open sets in the complex plane, and C is a continuous rectifiable wrve
lying wholly in V ft, then the function g defined by
g("1,.... :"'-1) = Jef(zl'..., znJdz,.
is analytic in UI) ... X V_to
If I is analytic in a neighborhood of the closure of the bounded
open set U which is bounded by a finite collection B of closed disjoint
rectifiable Jordan curves oriented in the custoD'UU")' positive sense then
it follows from the Caucby integral formula by differentiating p times
that
T = (limsup lap[I/ )-I.
.--.'"
The series converges absolutely and uniformly on any set I.-zol "
with " ,,;; T. Furthermore the series is uniquely defined by I, i.e.,
f' )("o)
a=-
pI'
p=0..1..2......
These facts, as well as the following remarks about Laurent series may
all be proved by the standard arguments used for complex functions.
A function I analytic 10 an annulu8 " < IZ-"ol < (J has a unique
Laurent expamion
I{z) = ! a.(z-"o)P,
.,__00
which converges uniformly and absolutely In every .annulus a;+E
,,;; Iz-zol (J-E with E > 0, The coefficients a. are given by the for-
mulas
1 f. II")
all = - dcx,
2.1ti C (CL-ZO)p+l
p = U, :i::l, :1:2, .. .,.
f"'{z) = f f(") do<,
2mJ.. (,,_,,)>+1
For such a function I the Taylor expansion
0> 1"("oJ
I(z) = I - ("-"oj',
""",0 p!
is va1id and the series converges absolutely and unifonnly for z in any
closed set of the form {zJlz-",,1 T) which is contained in V. This
expansion may be proved from the formula for l"'l(z} by the same
method that is used for complex functions.
Com...ersdy. any power series
ZEV.
where C is any closed rectifiable Jordan curve in the annulus
,,< Iz-",,[ < II which separates the circles Iz-".I = "and IZ-"or = II
and which is travers.ed in the counter-cIockwase direction. Conversely..
an arbitrary series I:"",-u;> ail(z-zo)Ji con'\"erges in the annulus tX
< Iz-..I < II where
« = lim sup la.I I/ .,
jp->_O>
(3 1 = lim sup la.IIi..
.--.'"
ZOE U.
Its sum I is an analytic function in this annulus and the series is the
Laurent expansion of its sum. This annu1us is the largest annulus with
center Zo in which an analytic function with the given Laurent expan-
sion can be analytic4
If I is analytic in the (degenerate) annulus 0 < IZ-201 < T, but
not analytic for Iz-""I < r, then "'0 IS said to be an i.8t1!otrd singularity
of I, The Laurent expansion of J(.) = I :"o>a.(z-",,)' wbich converg-
es. in the annulus 0 < Iz-""I < T is called the Laurent expansion of
J about "0. If an infinite number of coefficients a, with p < 0 are non-
zero, "" is said to be an eS8mtini si,lgVJarity of f. If some, but onlyI'
finite number of a JJ with p < 0 are non-zero, Zo is said to be a p6le of I.
00
flz) = ! a.(z-Uo)",
o
defines an analytic function in the open set Iz-zol < ", where T is
given by the formula
280
III I"NTEGRATIOK AXD SET F£:'NCTIOKS
IU.14
III.14
FUNCTIONS OF A COI\1PLEX V _4.RIAHLE
281
The largest number ..such thata I., F 0 is caUed the order ofthcpolc
"'0. If no as> with p < 0 JS non-zero, and if we put f("'o) = "0, then f be-
comes analytic in 12-;1 < r, so that the singularity at z = Zo is
Tl'7TIuooble. If a. = 0 for p 0, o is called a zero off; thus...o is a zero of
f if 1("'0) = O. If, in this case, a. = 0 for p < n but a. F 0, n is called
the order of the zero "'0-
We recall that a set U 10 a topological space is said to be comleCted
if it is not the union of two norry-oid disjoint sets, both open in the re-
lative topology of U. Another useful criterion for connectivity is avail-
able in the space Z of n complex variables, for a dumain U in Z i.
conncd£d il and only il every pair 01 itB poinl6lies On some simple Jor.u.n
curve crmtainm in U.
Let 1 be a function analytIc on .. domain U in the space of n
complex vro:iable8, and lct g be an analytic function defined on a do-
main V in this spac<'. Then g is said to be an analytic rontimullion 011
if V contains U properly, if g( l' . . ., '.) = 1( 1' . . _, .) for ewry point
2:1, . . ., Zn in l1 p and if every point in V can be connected to a point of
U by a continuous curve lying in V, If 1 admits no analytic continua-
tions, U is said to be the natlJ.Tal domain oj eil:istence of J.
The well known maximum modulus principle is valid for vector
valued functions_ In particu1ara the following two forms of thlS prin-
ciple will be used in the sequel
Ma:J:imum modulm principk. Let f be an analyric tunrfion defitU!rJ
on a conm'Cted domain D in thR. complex plall£ a1ltl having its mlue8 in a
rompla B-spact'I. T/uon 11( )1 does not have if8 ma;c;,num at any point
01 the domain D, unless 11(z) I is idenlirolly con8fanl.
To prove this an indirect .argument may be llsed by assuming
that, for some o in D, If("'o)1 :2: 11( )1 for ever)" z in D. If C. is a circle
of small radius T with.; as center l then
On the other hand, since
11(zo)I-lf(re;o+ 0)1 01:: 0,
we have 11("'0)1 = I/(re' +"'0)1 for almost all 6. Since 1 is continuous,
this holds for all 6. which shows that I/(z)1 = 1/("'o>! for all sufficiently
close to "'0. The proof thus far show. that the set
{ lIf( )i = 1/( o)l}
is open. Since this set is clearly dosed and since n is connected,
1t( )1 = It( o>l for all z in D.
M=imum modulus primiple lor a slrip_ Let l(tE+iy) = l(z) be
an atwlyric lunctio" ,dIll valu,," in a comple.r B-spa« I, defined and
uniformly "",,,,ded on a 8I1ip tE. ;;;; tE ,.;: tEl' - CI) < y < + 00. Suppose
that
11(tE o +iy)1 < M,
I/(a:1+iy)1 M.
so that
] i "-'
rl( .)1 ..;: - I/(re" +z,,)ldIJ,
2" 0
Then 11(tE+iy)1 ,.;: III lor "'. ;::;; '" < "'1'
To prove this we maYI without loss of generalitYI suppose that
"'0 01:: 1. Then for each. > 0, the function z l(z) is analytic and uni-
rormly bounded in the strip, tends to zero as y :f: 00, and is bounded
hy III on the edges of the strip_ Hence Iz-'f(z)illSsumes its maximum
value somewhere in the strip. By the maximum modulus principle,.
this maximum must be on one of the edges, a.nd COll!oiequently
1 'I( )i < 11-1 in the whole strip. As E approaches zero, it is seen that
!1( )i < 1IJ ev<r)'Whcre in the strip.
If 1 is analytic in a connected open set U of the complex plane and
not identically zero, U contains no point which is the limit of zeros of
1. This fact can be conduded from the com-sponding fact for complex
functions as follows: if X:l is the limit of zeros of , I then for each x* E I*,
1 is the limit ofzeros of ",.,. Hence ",., = 0 for each tE*, and by 11.8.15,
1=0.
A function 1 defmed and analytic in the whole complex plane IS
said to be entire. Liouville's theorem states that a bau1lded entire lunc.
lion is con8fa"t. To prove this, lct 1 be bounded and entire, and define
g J:>y g( ) = 1( )-I(O). Then g is bounded and entire, and g(O) = O.
For each x* E 1*, x.g is bounded and entire, and x*g(O) = O. Hence
by Liouville's theorem for the complex valued cast', ,x*g = 0, and
by 11.3.15, g = O. Thus f(') = 1(0), and I is constant.
Hence
1 J. 1( )dz ] i 2 .
1("'0) = -. - = -----: l{re'''-!-'''o)d8.
2311 C r Z-Zo 2711 0
i ..'
o tIf( 0)1-II(Te' +zo)l}d8 o.
282
Ill. INTEGRATION AND BET FUNCTIONS
111.15
111.15
NOTES AND REMARKS
288
Finally we will bave need for tbe Weiers!Tass preptlralion thRorem
which we quote here for the :reader's convenience in the form in which
we will use it.
.2j(w) = I aJt!W P '",
-"
i= I,. .., k
£ntegrals for functions with values in a locally convex topological
space were obtained by Phillips [7J and Rickart [I]. All of these inte.
grals are countably additive integrals. In Seetion IV.IO we will pre-
sent a Lebesgue type theory of integration of a scalar function with
respect to a countably additive vector valued measure. Instances in
which both the function and the measure are vector valued have also
been considered by Bochner and Taylor [1; pp. 915-917] and Go-
wurin [I] who gavc Riemann type integrals. and by Day [9], Price [I],
Rickart [I J and Bartle [8] who discussed Lebesgue integrals. For an
excellent expository account of these integrals and their relations
tbe reader 8hould refer to Hildebrandt [4]. To be added to the re-
ferences cited there are the works of Cbristian [I] and McShane [8]
dealing with integrals defined by means of order; Birkhoff [6],
Masani [I], Maslow [1] and Stewart [1] concerning multiplicative (as
contrasted with additive) integration; and Monna [6] which discusses
the integral of functions vlith range in a field with a nOfi- Archimedea.n
valuation.
A decomposition of a countably additive vector valued measure
along the lines of the Lebesgue decomposition was obtained by
Rickart [3] and Nakamura and SWlouchi [I].
Finitely additive sel /undio,,". The possibility of integrating
bounded functions with respect to a finitely additive measure was
demonstrated by Hildebrandt [3] and Fichtenholz and Kantorovitch
[I]. Such an integral has been used by other authors, usually for
bounded functions. Recently, Leader [I] has de\'eIoped n theory of L»
space8 of finitely additive meaSures. He actually discusses the indefi-
nite integrals of functions in L'J)' which avoids certa.in limiting devices.
Alexandroff [I] has given an extensive account of the theory of
bounded regular finitely additive measures on n unormalH topological
space. In particular Theort'm 5.18 is due to him (Alexandroff [I; p.
590]). Alexandroff [I; II. p. 618] has given conditions under which a
bounded regular finitely additive measure can be decomposed into the
Sum of a countably additive and a finitely additive part. His decom.
position differs from that presented in Theorem 7.8, which is due to
Yosida and Hewitt [I; p. 52].
The Vifali-IIahn-Saks fhearem. FrkI>ct [8] introduced a metric
in the space of measurable functions on [0. I] such that com"ergence
THEOREM. Ltt f(2. "') be campte", valued and analytic in 1M two
comple:r variables £, to for 2 in an open sel U, and w in a neighhurkood
I'" I < lJ, of Ihe origi... Suppose thaI f(z, 0) is not identically zera but has a
zero at some paint "" in U, and that Ihe order of this zera '" m. Thrn there
e.rU4s a neiglWorkood Vof "0' a posWvt'lJ < <5" an integer k -<::: m and an
inleger-'II, such thalfar eaeh Iwl < lJ, '" "t O,f(z, w)has exaellykdis#itld
zeras 2 1 (W). . . ., 2.(W) in V, and these zeros are gw..R by fraeti01lllI pawer
series
i.t'., by powt'T series in IV' = w 11n .
15. Nole. Bod Remark.
There are a number of expositions of the Lebe8gue theory of
integration of scalar valued functions with respect to a scalar measure.
The treatises of Lebesgue [2] nnd Carathc!odory [I. 2] are classical;
more recent treatments are found in books on the theory of real
variables nnd particularly in the treatises of Bourbaki [4], Hahn and
Rosenthal [I], Halmos [5], McShane [2, 8], Munroe [2] and Saks [I].
Since the works of Haho and Rosenthal [I] and Saks [I] contain
excellent historical notes and further references, we shall content
ourselves with n brief discussion of features of the treatment given
bere that differ from the standard approaches.
Vector inl<watimr.. In this chapter we have been concerned with
the integration of vector valued functions with respect to a scalar
valued measure. The possibility of extending the integral to this
realm was recognized by L. M. Graves [8], who discussed and npplied
the lliemnnn integral. A theory of tbe Lebesgue type WaS constructed
by Bochner [2]. The Cauchy sequence method ofthe text was used by
Dunford [4] to obtam an integral equivalent to the Bochner integral.
Somewhat more general intcgrals have been obtained for B-space Va-
lued functions by Birkboff [4], Gelfand [2], Pettis [4] and Price [I].
284
III. INTEGRATION AND SET FUNCTIONS
111.15
III,J5
:NOTES AND REMARKS
285
with :respect to the metric was equivalent to convergence in measure.
When applied to chara<.1;eristie functions, this yields the space .E(I')
studied in Section 7. This metric space was specificaUy studicd by
Aronszajn and Nikodym [7,8]; it is an important and powerful device.
Vita-Ii [2; p, 147] showed that if {In} is a sequence of Lebesgue inte
grabl functions on [0, 1] which convcrge almost everywhere to f then
f, 1 f(s}ds. lim f. '/.(s)ds
o n--Joo. 0
exist and are equal if and only if thc indefinite inregrals of the In are
continuous uniformly with respect to Lebesgue measure. (This is
essentially a special case of Theorem 6.15,) Hahn [2] proved that if
{In} is a sequence of Lebesgue inregrable functions on [0, 1] and if
lim S,d.(s)ds exists for every measurab1e set E, then the indefinite
integrals are continuous uniformly in 'n J and con1!efge to a set function
which is continuous with respect to Lebesgue measure. Another proof
of this theorem was given by Banach [6; p. 152]. The important
Theorem 7.2 is a generalization of this theorem and is due to Saks [8]
in the case of scalar meas1ll'CS, although his proof is perfect1y general.
Actually, Saks proved that the theorem holds under som hat weaker
hypotheses.
Phillips [7; p. 125] and Rickart [I; p. 502] have .observed that
essentially the same proof i8 valid when thc values of the indefinite
integrals Or the measures lie in a locally convex topologica.l lint:ar
space. Other extensions have been given by Alexiewicz [1; I. pp.
15-20]. Sec also G. Sunouchi [1]. For other reJated results see Saks
[2], Saks and Tamarkin [1], and Hahn and Rosenthal [I; pp. 56-60].
Corollary 7.8 in the ease of scalar measures is due to NikodYn'
[6] who proved it previous to the pub1jcation of Theorem 7.2.
The Rad!Jn-Nikody,n rhrora1l. In 1904, Lebesgue [2; p. 129] gave
8 necessary and sufficient condition for.a function on O, 1] to be ex
p....ssed as an indefinite mtegral. The next year, Vitali [I] character.
ized such functions as the now familiar absolutely continuous func-
tions. These results were exrended by Radon [2; p. 11149] for a Borel
measure p defined in EuC]idcan space. The general theorem is due
to Nikodym [7], IB; p. 168]. Other proofs have been given. e.g.,
Yosida [2]-see also Hahn and Rosenthal [1; p. 171] for additional
references.
An extension of the Radon-Nikody-m theorem forfimte1y adclitive
meaSlll'CS has been given by Bochncr [II] and Bochner and Phillips [1].
This theorem will be given in IV.9.I4.
Generalizations of the Radon-Nikodym theorem to the ca.", of
vector valued measures .are discussed -in Section IV.8 and additional
remarks are found in Section IV.12.
Product measures. For 8 rliscussion of measures in fimte products
see Hahn and Rosenthal [I; Section 8] and Saks [1; Chap. II], where
many references are cited. Halmos [5; Chap. 7] also discusses infinite
product measures. All of these treatments deal with seaJar ,'alued
functions.
Jessen [2] was the first to extend thc }'uhml theorem to thc case
of infinitely many factors. The same problem, without the use of
topology, waS treated by von Neumann [4]. ThroreIDS 11.24 and II.\!7
were given original1y by Jessen [1] and in the form stated here by
Dunford and Tamarkin [I]. For other remarks on infinite product
measures, see Dieudonne [12], Kakutani L 14]. and SpaITe Andersen and
Jessen [I. 2].
Dilte,<ntialion. Wc refer the reader to Hahn and Rosenthal [I;
Chap. V] and Saks [I; Chap. IV] for references ""ncerning the theory
of differentiation of seaJar valued functions.
Dillermliation in B-spates. In this chapter the theory of the
integral of a vector valued function has been considered at some
length. There is also rather extensive literature on the theory of dif-
ferentiation of a function on a linear interval to a B-spaee. We shall
not discuss these results, but refer the reader to the following papers:
Alaoglu [1], Alexiewicz [3], Alexiewicz and Orlicz [3], Birkhoff [4],
Bochner [5], Bochner and Taylor [1], Clarkson [I], Dunford and )(orse
[I]. Gelfand [2], I,. Jlf. Graves [3], Izumi [4], Munroe [3,4]. Pettis
[I, 4, 7], Phillips [7J. Sebastiao e Silva [I].
CHAPTER IV
Special Spaces
1. Introduction
For roncrete applications to analysis it is desirable to supplement
the general theory of the text with a detai1.-d investigation into the
propertie8 of special spaces. What, for eXRIllple, is the analytical fonn
of the general functional in the spoce conjugate to the Lebesgue space
L, = L1(S, E, p)? When does a sequence in Ll converge weakly? What
sets in Ll are compact, oT weakly compact"!' The answers to such
questions, and similar ones for the spaces commonly encountered in
mathematical analysis, will enhance the apphcability of the general
theory. This chapter is devoted to a 8ystematic study of such concrete
questions.
In Section 2 ,, ll be found a list of special spaces, mostly B-spaces,
which have frequent occurrence in ana1ysis. Each of these spaces is
1itudied in an attempt to solve the eight problems listed below. The
results of these studies are presented in tabular form in Section 14.
I l'Tobh:m. What is an analytical representation of the conjugate
space ;£* of the gi 'en spoce ;£?
2 Problem. When does a sequence {"'nJ in 1: have the property
that the lim a:*ir n exists for each x* in .!
3 Problem. When does a sequence converge weakly to a speci-
fied limit?
4 Problem. Is ;£ weakly complete?
5 Problem. Is 1: reflexive?
6 Probkm. Which subsets of I are weakly sequentially compaet?
7 l'robI£m. Which subsets of i( are compact in the metric topo-
logy of ;£?
8 Problem. If {x n } is a sequence in ;£ and ,f i( is the conjugate of
¥J, when is the sequence {"'.J 'ID-convergent in the sense tlult the limit
lim. "'nY eXISts for each y in ?
237
238
IV. SPECIAL SP.\CES
IV.2.I
IV.2.3
A LIST OF SPECIAL SPACES
289
During the coursc of the investigation a number of interesting
special properties of the spaces to be considered and ertain relations
between them wiU appear. These win also be incorporated in the
tabulation of Se_tion IS.
bers p with I < p < 00. It consists of ordered \'I-tuples x = ["'" ...,0:.]
of scalars :Xl' . _ .., a. n and has the norm
.
Ix[ = (! [""I'}"'.
i-1.
2. A List of SperiaI Spaces
3. The spacc I is the linear space of aU ordered n-tuples
x = [!Xl' .. .. .oj CAn] of scalars f. . .or Gtft with the norm
Ixl = sup 1",,1.
l i:;;fi
We givc bdow a list of various special B- and F-spaces. With the
one exception of Hilbert space, each of them will consist of reaL or
complex valued functions /, g defined on a specified domain S. Here,
addition and multiplication arc understood to be defmed in the-
natura] way, i.e., by the equations
4. The space I. is defined for I P < ro as the linear space of
aU sequences x = {o:.} of scalars for which the norm
(l+g)(8) = /(8J+g(8)
(0:/)(8) = o:/(s).
.
Ixl = ( ! 10001P}'lp
_1
Thus our zero vector will be the function which is identically zero_
In the list below, we will not ordinarily specify whether the spaces
are to consist of all real valued functions with the stated properties. or
of all complex valued functions with these pNperties. Unless the con-
trary is specif1ed. hoth possibilities are admiUed_ The first leads to
a real B- or F-space, the second to a complex B- or F-space. Thus, for
example, if S is a topological space, C(S) can denote either the real
B-space of all real valued bounded continuous functions on S or the
complex B-space of aU complex valued bounded continuous functions
on S. We will only make a definite choice ofthe real or of the complex
numbers when the real and the complex B-:spaces under consideration
actually require separate treatment.
The proof that a given space satisfies the requIrcd axioms will
usually be found in the section where the space in question is dIS-
cussed. The more elemental'.y of such proofs are sometimes left as
e..xercises for the reader
I The 8paee En is the linear 8pace of ordered n-tuples x
[0: 1 ,.. "J an of scalars a1'>...J an_ The norm is Ix] = <1t"l.112+. . .+
10:.1 2 )1/2. If the field of scalars is thc real number system E" is called
..-dimensional Euclidean space; if the f1eld is the field of complex
numbers En is called n-dimellsional unitary space, or n-dimellsimlal
Hilbert span'.
2 The space ': is defined for positive integers n Bnd real I1Uln-
is finite.
5. The 8pace , is the linear space of all bounded sequences
x = {"'.} of scalars. The norm is given by the equation
l.x\ =supla:..l.
fl
6. The space c is the linear space of all con'.'l rgent sequences
(f: = {cx,,} of scalars. The nonn is
l.xl = sup 10:.1.
.
7. Thc space c. is the linear spacc of all 8equences x = {o:.} con-
verging to zero. The nonn is
/.vl = sup 10:.1.
8. The space bv is the linear spllce of all sequences x = {",,} of
senIsrs for which the norm
Ix[ = 1"',1+ ! 1......1-""1
.-1
is finite.
9. Thc space b". is the linear space of all oC'Iuellces x = (a:..}
of scalars with lim a.ft = 0 and for which the norm
.
1"'1 = ! )......1-0:.1
fl_1
is finite.
240
IV. SPECIAL SPACES
IV.2.10
IV.2.18
A LIST OF SPECIAL SPACES
241
.
IXi = SUp' a.1
n i",,]
defined on the a.field!l4 of all Borel sets in S. The nonn 11'1 is the total
variation v(p, S).
18. The space L.(S, E, p) is defined for any real number p,
1 < p < 00, and any positive measure space (S, E, pl. It consists of
those p.-mea8urable scalar functions 1 on S for which the norm
1/1= Ifs I/(B)I p(a.,)Jl/'
10. The space bs is the linear sp""e of all sequences", = {cx,,} of
scalars for which the no:rm
is finite.
n. The space cs i8 the linear space of all sequence; '" = (an)
for which the series I::l an is convergent. The norm is
III = sup I/(s)[.
..s
is finite.
Remark. In Chapter III the space L.(S. E, p) was defined without
the assumption that p is non-negative. The 8pace L.(S, E, p.) is, in
any case, the 8ame as the space L.(S, E, v(u» and the variation v(u)
is non-negative. As indicated by the remarks after Corollary 111.2.5
and Theorem 111.8.5, the elements of L (S, E,I') are not actually
functions but equivalence classes of functions, two functions being
equivalent if their difference is a I-'"null function, (cf. 111.6.8), i.e., if
they are equal for p.-almost all B £ S. The same remarks apply to the
8paces L (S,E,p.) and TMCS,E,p) introduced below.
19. The space L (S, E, 1') is defined for a positive measure space
(S, I, p) and consists of all p-e8sentially bounded p.-measurable
scalar functions. (cr. Definition 111.1.11) The nonn is
I/j = p ss sup I/(s )1.
"S
Remark. In defining the follnwing four spaces the term interval
is used for a set of real numbers having anyone of the following forms:
[a.b], [a, b), (a.b], or (a, b), where a is eitherreal or -co andbiseither
real or + co. In all four cases a is called the left endpoint of the inten-al.
20. The space BV(I) is defined for an intervall and consists of
all scalar functions on I which are of bounded variation (cf. 111.5.15).
If a is the left end point of I then
Ifl I/(a+)I+v(/,I),
v(/. I) denoting, as usual, the total variation of 1 in 1. (It has beeu
shown an 111.6.21 that the limit I(a+) exists for every 1 BV(I).)
21, The space NBV(I) is defined for an interval I and consists
of those functions I in BV(I) which are nonnalized by the require-
ments that (1) 1 is continuous on the right at each anterior pomt of I
and (2) I(a+) = 0 where a is the left end point of 1. The norm is
given by the equation
Ixl = sup I <x,I.
n '-1
12. Let S be an arbitrary set. and I a field of sub.sets of S. The
space B(S. E) consists of all uniform limits of finite linear combina.
tions of characteristic functions of sets in E. The norm in B(S, E) is
given by the formula
A scalar function 1 on S is E-mt!asurabk if l l(A)£E for every Borel
set A in the range of I. It is clear that enxy bounded E-measurable
function is in B(S. E} and that such functions are dense in B(S, E).
It is evident that if we define the set function p on E by placing
pIE) = 00 if E"* P and pep) = 0, then a bounded function is
I-measurable if and only if it is totally p..measurable.
18. The space B(S) is defined for an arbitrary set S and con-
sists of all bounded scalar functions on S. The norm is given by
III = sup 11(8)1-
..5
14. The space C(S) is defined for a topological sp""" S and con-
sists of all bounded continuous scalar functions on S. The norm is
111 = sup 1/(8)[.
"s
15. Tbe space ba(S, 1.') is defined for a field I of subsets of a
set S and consists of all bounded additive scalar functions defined
on I. The norm 11'1 is the total variation of I' on S, i.e., 11'1 = v(p,S).
16. The space ca(S. I) is defined for a a-field E of subsets uf a
set S and consists of all scalar functions which are defined and count-
ably additive on E. The norm Ipl is the total variatIon v(l', S).
17. The space Tea(S) is defined for a topologIcal space Sand
consists of al1 regular countably additive scalar valued set functions
,
242
IV. SPECIAL SPACES
IV.2.22
IV.2.27
A LIST OF SPECIAL SPACES
248
.
! 1/{b,)-f(a,)1 < E
i_I
(ii) (x, x) ;';0, x€ ;
(iii) (x+y, z) = (X, "I+(y, ,,).
(iv) (ax, y) = "'(X, y). '" dP,
(V) (x,y) = (y,...);
(vi) If "'n E , n = I. 2, ..., and if lim",m-+.. ("'n-xm, xn-a;.)
= 0, then there is aJl X in ,p with lim. ("'n-"', "'n-x) = O.
The function (-, ,) is called the Bl't1lar or inner product in ,p and
("'. y) is called the 8£Illar or inner product of '" and y. The '/WT1n in .p
is 1"'1 = ("'.X)1I2.
&mark. Hilbert space has becn defined by a set of abstract
axioms. It is noteworthy that some of the concrete spac", defined ahove
satisfy these axioms, and hence are special cases of abstract Hilbert
space. Thus, for instance, the n-dirnensiona1 unitary space E is a
Hilbert space. if the inner product (x. y) of two elements '" =
[.... , , .. "'n] and y = [Ji" . . .. Pn] in E' is defined by the formula.
a;,y,z£ ;
m,y£ ;
III = v(f, I).
22. A function f E BV(I) is said to be absoluUly continuous if for
each . > 0 there exists a iJ > 0 such that
whenever ("it b i ), i = l 2, . .. n, are non.overlappmg submtervalsof
I with l Ib,-a,1 < iJ. The space AC(I) is defined for an interval I
and CQl1sists of all absolutely continuous functions on 1. If a is the left
cond point of I the nOrm is
III = I/(a+)I+v(/,I).
23. The space cn(I) is defined for a CQmpad interval I and a
positi"e integer.. as the family of those scalar functions on I having ..
bounded continuous derivative8. The nonn is
n
If I = ! sup I/'''(B)I.
1...0 ad
24. The space A{D) is defined, for an open set D of complex
numbers, as the family of those complex functions which ,Ire bounded
and continuous on the closure of D and which are .a.natytic on D.
The norm is
..
("" y) = ! ,,;p,.
'-1
In the same way, complex 10 is a Hilbert space if the scalar product
("" y) of the vectors '" = {<Xn}, y = {P.} is defined by the formula
jzl = sup I/(z)I,
..v
m _
(....y) = !0c,J3.,
n=1
The space A (D) is a complex linear space w,th no obvious real analogue.
25. A function I of the real variable t i8 said to be almost perivdic
if for each E > 0 there exists an L > 0 such that every interval of the
real axis of length at least L contains some point x such that
I/(t)-/(I+"')1 < E for -co < t < +co. The space AP is the linear
space of aU continuous almost periodic functions of 11. real variable. The
norm IS
Also the complex space 4,(8, I. p) is a Hilbert space with the scalar
product
(I. g) = fs/(s )g{B)p (ds)
I. g E 4,(8. I, f-I),
III = sup 1/(1)1.
_u><t<
T"" 1;=1 spaces on ,"" lis! are F -spau. but ..ot B-spau..
27. The space TM(S, I, p) is defined for a positive measure
spllce (S, I, pl. and consists of all totally mcoasurable functions I
defined on S (cf. IIl.2.10). The metric function in TM{S.I, p) is
elf, g) = I/-gl, where
If I = inf {a+ arctanp(S(1/1 > all},
u:>C
S<lfl > "') = {sis E S, I/(sJl > IX}
28. The space S is the spllce of aU sequences x = {<Xn} of scalars.
The metric function in S is e(;c. y) = I"'-yl where
.. I !""I
1"'1 = 2nHI<XnI '
It will be shown in Section 7 that every almost periodic function is
bounded.
26. Hilbert spaa i8 a linear ,'cctor space over the field <1> of
c::omplex numbers 2 together with a complex function (., .) defined 011
,p x,p with the following propertie8:
(i) ("'."') = 0 if and only if", = 0;
244
IV. SPECIAL SPACES
IV.B.I
IV.3.3
FINITE DIMENSIONAL SPACES
245
3. Finite Dimeusiomd Spaces
The space En, as will be seen presently, is the prototype of all
n-dimensional nonned linear spaces. and hence it should be observed
first that En is a B-8pace_ The lIIinkowski inequality (111.3.3) shows
En to be B. normed linear space. If y = [oc;j, . . ., Cl,n] £ E" I then
lex, I Iyl and hence the completeness of En follows from that of the
field q, of scalars. Thus E" is a B...pace. A bounded closed set in E" is
compact. for if y'" = [ex , . . ., "'::'] is bounded, the sequence
{ex';', m = 1,2, . . .} is bounded in q" and consequently there is a sub-
sequen e {mJ} of {m} for which the limits lim, rx.";"J = lXi' i = I, . . 'p n,
exist. Hence tl.e sequence {ym,,} converges to the vector [«1" .", 0:: 11 ]
in E .
1 LEMMA. A Jinil£ dimensional fWrmed linrar space is comp!el£
and hau:e iI is a B-spaa.
PROOF. Let {b" . . ., b.} be a Hamel basis for the finite dimen-
sional Dormed linear space E. For each point y = [(Xl' . . 'J C1 n ] jn E'\
let Ty = :r: where w = :I;-l IXibio Then T is a one-to-one continuous
map of En onto 1:. To see that I is complete. it will first be shown
tbat the inverse T-1 is continuous. If it is not continuous there is a
sequence {a;n} in and an E > 0 with m" -* 0 and .T-1,rwl 8,
" = 1,2, . . .. If ff' = (T l.x")/IT ''''"1 then IY"I = I and Y" = T-'z"
where z" -+ O. Since the sequence {yO} is in the compact set {yly' E",
Ivl = I} in E", thexe is a subsequence of {yO} converg;ng to a point
'If = [a . . " "' a ] with 111'1 = I. Since T is continuous, 0 = Tyo =
C( +." .+o:: bn' andt since the vectors ,..., b n are linearly inde-
pendent, "' = . . . = = O. Thi8 contradicts the fact that 1y"1 = 1,
and proves that T l is continuous. Thus, by Lemma 11.3.4, there is a
constant 111 with IT l"'l MI4 which shows that a Cauchy sequence
{o:"} in I maps into a Cauchy sequence V n = T-'x" in En_ If V =
lim y' then ",n = Tff' converges to TV in I and 3:: is complete. Q.E.D.
S COROLLARY. An 7l-dimerl8iona! B-apare i. equivalent ro E".
4 COROLLARY. Every linear optT/11or on a finite dimrnsional
nOTrMd linear space is cominu4JJu.
PROOF. Let {bI' , . .. b.} be a Hamel basIs for the fmite dimension-
al normed linear space so that every or in I has & unique represen-
tation in the form", = ",,-b I +. . . +""b". It was 8hown in the proof of
Lemma 1 that lXi' i = 1, . . ., fit depends continuously upon x. Thus if
U is a linear operator on I it is seen that U:£ = C1..1Ubl. +. . . +ct.1lUbfl is
also continuous in 3:. Q.E.D.
5 THEORE". A n""ned linear space is finite dimmsiona! il and
only iJ ;Is closed unit sphere is wmpad.
PROOF. Suppose that the sphere S {"'II"'I ,<:; I} in the normed
linear space I is compact. It will be shown tha.t there is 8 finite set
{", . . . ., "':} in 1* such that if "':("') 0, I ; ;;;; 1'1. then x = o.
Suppose the contrary. Then for each finite set A x*, the set
SIAl = {"'lIxl = I,.1'*(x) = 0 for x* < A}
is a non-void closed subset of S. From our assumption it follows that
any finite number of the sets SIAl has a non-void intersection. Thus.
by 1.5.6, there must exist an x common to all S(A}. This vector x has
the properties: Ixl = 1, and "'''(x) = 0 for all x*in1:*. Thiscootradicts
11.8.15 and proves the assertion. Let :1].:, i = 1, . . ., 11-) have the pro..
perty that {1! a; = 0, i = 1, . . ., 'nt implies :£ = o. Then the map
:c --)- [a1 it', .. .:r x::£] of 1 into Eft is linear, one-to.one, and has finite
dimensional range. Thus ! hAs finite dimension.
The converse statement follows from Corollary 3. Q.E.D.
6 LEMMA. A nfWmI!d linear space ha3 Jit.Ue di,no on 1'1 iJ at>d
only iJ ;u adjoint hiu dim",s;on n.
PROOF. Let {b, ,. . ., b n } be a Hamel basis for the normed linear
space I. Then the functionals b . i = 1, . . ., n, defined by
2 COROLLARY. A JiniLc dimensionallitu!ar manifold in a B-space
is dosed.
PROOF. 111is foHows from the preceding lemma and Lemma 1.6.7.
Q.E.D.
n
X = Ib (x)b" xdZ,
i-I
are, by 4, in .. Also, for any .x* in 1* we have
"
x'x = I br(",)",*(b,),
1=1
.
x* = I b x*(b,),
1=1
,
246
IV. SPECIAL SPACES
IV.S.7
IV.B.9
HILBERT SPACE
247
so that sp{bf} = :£". r\ow the vectors b:, i = I, , . ., n are linearly
indepcndent. for if I -Ipg = 0 then {j; = (L'; I fJ.br>b, = 0,
i = J, . . .. fl. Thus the dimension of if" is fl. Conversely, let the di-
mension of:£" be finite. Then the dimension of :£... is finite, and, since
I is equivalent to a subspace of iE.... (U.S.19), the dimension of:£ is
finite. Hence, from the first part of this proof. I and I" have the same
dimension. Q.E.D.
In the preceding lemma it is assumed that the spaces are normed
linear spaces,. for there are examples (see the prelimina.ry discussion in
Section IV.Il) of infinite dimensIonal F-spaces with zero dimensIonal
conjugate spaces.
The following corollary was established during the first part of
the preceding proof.
7 COROLLARY. If {f>.. . . ., b.} is a Hame! b...is 1()1' tlu! rwrme<l
Imror space:£ thEn lit< lunctionalB b:, i = J, . . ., n. dR/ined by the equa-
tions
of the functional in terms of the scalars representing it. Thus, to com.
plete the solutions of the problems listed in Section I, it will be neces-
sary to represent the conjugate spaces of Er.. 1: and l . Since EIJ = J;
the following theorem gives the desired results:
9 THEOREM. If 1 P 00 and p-I +q 1 = I, IMn tlu! mapping
",,, -<---+ [",-, .., an] determined by tlu! <quaIivr.
n
"'''''' I""P.,
.-1
'" = {P.}.I;,
i. an isome/ric isorrwrphism of (I;)" onto I;.
PROOF. It is clear that the mapping is an IsomorphIsm, To see
that it is also an isometric map we 8uppose first that 1 < p < 00.
Then, from HOlder's inequality (1II.3.2),
. n
loX""'] { I la,lv}"v{ I IP,I.p/.,
i=l '_1
..
'" = I b:(oX)b"
i-I
tV 1:,
which shows that 1"'''1 < {I::",la.IV}'lv. Nowletp. = 1",lvfa, if <X; ".. 0
and P. = 0 otherwise_ Then
farm a Harne! b...is for I".
8 COROLLARY. A finire dimmsiotw.! narmroliflroT 'paa is ullex-
ft
"''''''=II",I",
'_1
..
loXl = {I la,I(V u.}'I.
<-I
ive.
PROOF. In the notation of Corollary 7,
ft
= {II",I"}I!.,
<-I
"
","" = I b (",)",.{b,),
10",,1
ft
"," = I b:",*{b,),
'-1
which, together with the inequality 1"''''''1;;;: Ix*H4 gives
{I II",I.}'I. 1"'''1. Thus Ix*1 = {I ,I"',IV}'IV, which shows that the
mapping is isometric. These steps, with obvious changes in notation,
may be used to establish the isometry when p I or 00. Q.E.D.
and thus fora!'. in .*wehave a::**a:* =tt*a:, where a:: = .I:...l a:*.(b:}b .
Q.E.D.
From Corollary 7 it follows that wcak and strong convergence
are the same in finite dimensional spaces and from Corollary a that
a set is compact if and only if it is bounded and closed. Thus the
Problems 2, . . ., 6 listed In Section 1 are readily solved for finite
dimensional spaces.
According to Corollary 8 and Lemma 6 every finite dimensinnal
normed linear space IS equivalent to its conjugate. but this observa-
tion does not complctely solve the problem of representing the con-
jugate of a given space. What is n(leded is an expression for the norm
4. Hilbert Spa-
Of the infinite dimensional B-spaces. Hilbert space is the most
closely related, especially in its elementary geometrical aspects. to the
Euclidean or finite dimensional unitary spaces. It is not immediate
from the definition (2.26) that R Hilbert space is a B-space, but this
fact is established in the following theorem. Throughout this discus-
sion of Hilbert space the conditions (I), . . " (vi) in Definition 2.26 will
,
248
IV. SPECIAL SPACES
IV.4.1
IV.4.3
HILBERT SPACE
249
be u8ed without explicit reference and the symbol .\:1 will always be
used for a Hilbert space.
1 THEoJtE", A HUbert space .\:1 is a campl"" B-B'pa<'C and
l(x.y)I ';:: Ixliyl, x,ye!j;).
PROOF. The above inequality, known as the Schu:arz irlLtJUl1lity,
will be proved first. It foUows from the postuJates for !j;) that the
Schwarz inequality is valid if either x or y is zero. Hence suppose that
x # 0 # y. For an arbitrary complex number 0;
O ';:: (",+o;1/.x+o;1/)
= Ixl'+locl'.yl"+oc(y, xl+«("'. yl
= l"'I'+locl"11I1"+29i'(0;(y, a-»,
where the symbol B/!(J.) i8 used for the real part of J.. If oc = re' and
if 6 is cho8en properly, it follows from the above inequality that
Ixl"+r2Iyl" :;;, 2rl(a-, y)1
for every positive r. Upon placing 7 = l"'l/lyl the Schwarz inequality
follows.
To complete the proof of the theo",m it will suffice to show that
Ia-+yl ;;;: 1",1+lyl. First note that
("'. y}+(y. a-) = 29i'(a-. y) ,;:: *11111
PJ<OOF. The !dentity
1"'+yl"+Ia- !II" = *,I'+2Iyl", x,ye.\).
caUed the parallelogram WnItity, follows immediately from the axioms.
If {j = inf I",-kl the preceding identity shows that
..K
Ik,-k,12 = 2Ix-k,I"+2ja--k,I"-4Ix-(k,+k,}/21"
;;;: 21"'-k,12+21",-ktl"-43 -+ O. Q.E.D.
and hence that
8 DEFINITION. Two vectors "'. y in.\:1 are said to be orlhog,mal if
(x, y) = O. Two manifolds ID1, !J! in !j;) are orthogonal manifolds if
(ID1, !J!) = o. We write '" .L y to indicate that x and y are orthogonal,
and ID1 .L !J! to indicate that ID1 and !J! are orthogonal. The orthacom-
plementof a setA!;; istheset{"'I(""A) = O}. It is sometimes denoted
by.\:1 e A, o , if.\:1 i8 understood, by Ai.
.. 4 LEMMA, The orlIwcomplement !J! of a closed linear rI1MIifold ID1
in .\:1 is a c10liM linear .nrmifold complementary ro IDI. i.e..I) = IDI (jj !J!.
PJtOOF. It follows from the linearity and the continuity of the
scalar produd (Theorem I) that the orthocomplement of any set IDI
is a closed linear manifold. IfIDI is a closed linear manifoW and if x is
an arbitrary point in .\) there is, by Lemma 2, an m eIDI such that
Ix-ml = {j = inf m ,'\IJ1I",-m , l. It will now be shown that the element
n = ",-m is in !J!. For any complex number « and any m I in ID1 the
vector m+ocm" is in ID1 and hence Ire-(m+«m,,)1 ;?; {;, Thus
o $ 1",-(m+ocm,,)1 2 -jnI 2 = In-«m"ILlnI2
-aIm" n}-a:(n. m,J+1",12Iml'"'
Let 0; = J.(n. m 1 } where J. is an arbitrary real number. Then
o ;;;: -2J.I(n, m,,)1 2 +J. 2 1(n. m,}121m,1'
I"'+yl" = I",J'+lyI2+(X, y}+(y, x}
;;;: 1"'12+lyI2+21a:llyl
= (Jxl+lyIJ2. Q.E.D.
Remark. It 8hould be noted that the above proofs of the Schwarz
inequality and thc triangle inequality I"'+yl ,;:: Ixl+lyl do not re-
quire that be complete or that (x. a:) vanish only when", = O.
2 LEMMA. Let a: be an element of and let K be a trUbsct of !j;) with
the p"<>perty thol !lK +K} C K. Let (k i } be a uquenee in K with the
property thot
which is possible only if (n, m l ) = o. Thus n £!J!. To complete rhe
proof note thatx£IDIn!J!implieslxl = ("'.x) = o. ThusIDIn !J/=O
and = IDI (!) !J!. Q.E.D.
lim Ix k,1 = inf !", kl.
i d(
.. 5 THEOJtEM. Every yO in .1)0 uniquely determines a y in such
thaI
Then {kit is a ccmroergem ""llln!c£.
y.;r= (x.y),
a:. .
250
IV. SPECIAL SPACES
IV,40.6
IV.40.9
HILBERT SPACE
251
This map u : y* -+ y is a one-to-om isometric map 01.\;1. (>n!Q all 01.\;1 and
a(y*+.*) = "(Y*)+<T(z*), "(,,yo.) = (i<T(Y*),
PROOF. If y* = 0 let Y = O. If y* oF 0 the set!m = {"'Iy.'" = O}
is a proper closed linear nmllifold in Sj and its orthocomplement !n
contains, by Lemma 40, a vector YI oF O. Let Y = rzy, where 1i =
y*(y,)/I111I'. For an arbitrary vector", in.\;l the vector"'-(y*"'}/(Y.YI)YI
is in !m so that ("" Y) = y*"'(y" Y )/y*y, = yO"" which proves the
existence of the desired y. To see that y is unique, let y' be an element
of.\;l such that y*", = ("'. y') for every"'. . Then ("" y-y') = 0 for
every ",..\;1 and, in particular, (y-y', y-y') = 0, so y = y'. Thus <T
is well defined. Since j("', y)1 S; 1"'lIyl it follows that Iy*, S; lu(y.)I,
and since (y, y) = Iyl' it follows that ly*1 )u(y*)I. Therefore <1 is an
isometry. The remaining properties to be proved for <1 follow inuncdi-
ately from the postulated properties of the scalar product. Q.E.D.
6 COROLLARY. Th£ trpm:e o is also a Hilbert space and Sj is
.
Sj=!m!li(.pe!m)
where !m i8 an arbitrary closed linear manifold in i). If '" = y+. where
y .!m and" . Sj e !m let us define the transfonnation E in by placing
Ex = y. It is clear that E is a projection, i.e., E' = E, and that E
is an orthogonal projection. It is the uniquely detennined orthogonal
projection with E =!m, For if D is an orthogonal projection with
D =!m then ED = D and, since (I D)Sj e !m, we see that
E(I-D) = o. Thus
D = ED+E(I-D) = E.
This uniquely determined orthogonal projection E w,th ES) = jJJ/
is called the orthogonnJ -projedion on !m or sometimes simply tlu
projecti<m. on !m.
9 LEMMA. II {y,} is an ortJwrwrmal sequence and {",} is a sequence
01 scalars, then the series I",y, wnrerge8 it and only il II",I' < 00,
and in this case
PROOF. If the scalar product in .p* is defined by
(a:*, y.), = (<T(y.). "(,,,0»),
then 4t is clearly a Hilbert space. For y.o . Sjoo tbere is, according
to the theorem. an element y*..\;10 such that
II",y.1 = (II",J"}'/".
JJ7,e" i: converges, tlu series I",y, i8 i.w£pmde>,t 01 the (mur in wl,ieh irs
teTm8 are arrrnlged.
PROOF. For m > n
y..",. = (",., y.), = (u(y.), "(,,,.») = ",.y,
where y = a(y*). Q.E.D.
OV.Et>..
m m m m m WI
I! ",y,l" = (!a'lI" !a,y,) =! !a,ii,(y"y,) =! 1",1",
i=-'J ;f-h II=-n 1""'" f_1\
'1 COROLLARY. Hilbert trp= is _oldy complere and a subset is
lCCakly seqUf!ntially compact ;/ and o-nly it it is bounded.
PROOF. This follows from 6. 11.8.28, and 11./1.29. Q.E.D.
8 DEFINITION. A set A C is called an <>rlkonormal set if each
v tor in A has norm one and if every pair of dio(;'tinct vectors in A is
orthogonal. An orthononnaI set is said to be comple/2 if no non.zero
vector is orthogonal to every vector in the set, i.e., A is complete if
{OJ = e A. We recaU that a projection is a linear operator E with
E" = E. A projection E in is called an orrhogonal proiection if the
manifolds E and (I-E are orthogonal.
It has been shown in Lemma 40 that'
and so the one series converges if the other does. If, in the ahove equal
ity. one puts n = 1 and allows m to increase indefinitely. the .second
conclusion of the lemma follows. Finally let z = I -l C1.i"Yi" be a
series obtained from m = I a..y, by II. rearrangement of its terms.
Then
I"' "I' = ("" "')-("" ")-{", "')+(". "I.
and a direct computation, simi1ar to that above, shows that each of
these scalar products is ! 1".1". Thus z = "'. Q,E,D,
... 10 THEOREM. Let A be an orthonormal set in.\;l and let '" be an ar-
b;tTary vector ;n . Th£n ("" y) = 0 tor all but a counlnhle number 01 y
in A. T/U; series
E",= !("" Y)y, "'.
..A
,
252
IV. SPECIAL SPACES
[V.4.11
IV.4,I3
HILBERT SPACE
253
conIT S and i. indep€1/lknt of the order in rfflich its non-:<cro ta",s are
arranged. The operator E is the orrhogona! pro;ection on lhe closed linear
manifold ddermined by A.
PROOF', Let Yl' . . ., Y. be distinct elements of A and let Y =
I::",(", y,)y, so that (by Lemma 9), lyl" = I; ll("', y,)I" and
o I"'-yl" = 1"'1"-("'. y)-(y, ",Hlgl".
.
("" g) = I ("', y,) ("" y,) = Igl',
i l
.
(g, ",) = I ("'. g, )(",. y,) = Iyl'.
i'=1
1 !J.)l. Since A is maximal!JJ! e 2!1 = o. But by Lemma 4, !JJ! =
2!I EI> (!JJ! e 2!,), and so!JJ! = 2!r The desired conclusion now follows
from Theorem 10. Q.E.D.
13 THEOREM. For an orthonormal se! A C tJw following Blat<:.
mt:nts are equi'Vl1lenf:
(i) tJw set A is complele;
(ii) the se! A is an ort/woormal bll3is for ;
(iii) 1"'1" = E.. A 1("'. g) I', ., E .
PROOF. The equivalenee of statements (i) and (ii) is clear from
Theorem 10. That either one of these implies (ii.) follows from Theo-
rem 10 and Lemma 9. Now assume (iii) and let", be an arbitrary
"ectorin .By Lemma 4, "'= u+o whereu E8p (A)BI1dv. e sp (A).
Thus 1"'1' = luI2+lvl'. But. by Theorem 10 and Lemma 9, lul" =
E..A I(u. y}I". Hence 1"'1' = jul" and v = O. Thismeansthat sp (A) =
from which (i) follows. Q.E.D.
The next result enables U8 to define the dimension of a Hilbert
space.
14 THEOREM. All arlhorwrmal bases of a gi''i'n H.1bert space
have the Some cardinality.
PROOF. If is fmlte dimensional, the result is a well-known result
in algebra. Suppose then that is infinite dimensional, and let {u a }
and {"6} be two orthononoal bases for . We shall say that the vectors
"01: and U«f in the basis {ua:} are equivalent if there eXIsts a finite chain
Thus Iyl' 1"'1', i.e.,
.
II(x,y,)IZ < I"'j".
'-1
This shows that at most a finite number of vectors Yl' . . ., Yn. in A can
have 1("', y,)1 greater than a preassigned positive number and pro"es
that at most a countable number of the scalar products ("', y) with
y in A fail to vanish. Since
I(",.y)j" ':;: 1"'1',
...
the preceding lemma shows that the 8eries defining Ex converges and
is independent of the order of its terms.
Now it is clear that E is a linear operator with E", = '" for '" in A.
Thus Ex = '" for'" in the closed linear manifold !leI determined by A.
Also Ex = 0 if., is orthogonal to A. Thus E is the orthogonal projec.
tion on 2!1' Q.E.D.
II DEFINITION. A set A is called an orOun/onnal basis for the
linear manifold !J/ III if A is an orthonormal set contained in !J/ and if
x = I ("" y}y, '" E !J/.
..A
12 THEOREM. E,oery c/o.ed linear IIW.1Iifold in CORlains an
ortlwnormal basis for itself.
PROOF. If the orthonormal sets in the dosed linear manifold !JJ!
are ordered by inclusion, it is seen from Zorn's lemma (1.2.7) that
there is a maximal one A which determines the closed linear Inanifold
[*]
U a , VPl' "lXl'....' ulX..1.:' V p _ H1 ' u a ",
of vectors in which the scalar product of any two successive vectors
i. non-zero and in which the renos alternate between vectors in {uu}
and {v 6 }. The equivalence of two vectors "6 nud v P ' in {v 6 } is defined
similarly. It follow. immediately from Theorem 10 that any equiva-
lence class of vectors is either finite or countable. An equivalence class
U of vectors u a wiU be said to correspond to nn equivalence class Vof
vectors vtJ if there is a pair of vectors, one from U and one from V,
with a nOn-zero inner product. Suppose that U and V are correspond-
ing equivaleoce classes nnd that u a ' U. Consider an arbitrary ele-
ment v 6 in the basis {"6} for which (u a , "6) =F O. It will be shown thnt
VB IE V. Since U and JT are corresponding classes there are elements
,
254
IV. SPECIAL SPACES
IV.4.11>
IV.4.16
HILBERT SPACE
255
"a" vfJ' in U, V respectively with (u.., vJi') # o. Now since...... E U
there is a finite chain ofthe form given in [*] above in which successive
vectors have non-zero scalar products. Thus by forming the chain
vII' U al . . .,. "ct. vf!' it is seen that vfJ is equivalent to v JJ ' and thus that
rJ l1 is in V. Since {v p } is a basis, the vector ua: has .an expansion of the
form 'U;x = Iji(u(i:" v(J)v p , so that 'U« is in the closed linear manifold de-
rermmed by those v, with ("«' v,) # O. Since surhv, are in Vwe have
u«. .p [Y] and thus 81' [U]!; 81' [Y]. Similarly .p [Y]!; 81' [U]. It is thus
seen tlmt corresponding equivalence cu.sses U and V determine the
same dosed linear manifold 9Jt Hence. if one of U and V is finite. !In is
finite dimensional, and therefore the other of U and V is finite and
has the same cardinality. If neither of U and V is finite, both are
countable. Thus {u«} and {v,} break up into a disjoint union of corres.
ponding pairs U. Vof equivalence classes, each U having the same
cardinality as the corresponding V. Consequently {u.} and {v,} have
the same cardinality. Q,E.D.
tively. For each scalar function C on A with C(ot) = u for all but a
countable set of indices ot and 8uch that IIC(ot)l" < 00. let
U(I C(ot)u.) = 1 C(ot)v«.
It follows from Theorem 13 that U is an isometric isomorphism of
onto ,. Q.E.D.
This shows that for arbitrary ).
0= (U"").Uy)+(U,,,,}.Uy],
Dired SU1nIJ of Hilbert Spaces
We recall ref. 1.11) that the direct Sum
iE=iE> ... iEn
of the -.-ector space8 ,. . .,1. is the set :<:I"x. . . xl. in which
addition and scalar multip]ication are defined by the formulas
["'1"'" "'.]+[y""" Y.] = [""+y",,., "'.+Yn],
rl[a: 1 ! . . "' :en] = [oot'" . . ., OOl'n].
The space 1, is algebraically cquivalent to the subspace!In, of 1 con-
sisting of all vectors [",>, . . ., "'.] in iE with "'i = 0 for i # i. It is some-
times convenient to refer to the space iE i itself as a subspace of 1 and.
when such reference is made, it is the equivalent space ».R J that is to be
understood. The map
[:c 1 .... .,.T,..] --> [0... .,tt" '..1'0]
of I onto !In, is a projection and is sometimes called the projedion of 1
Ollto!In,. Equivalently, the map ["'" . . ., "'.] -+- m,iscalledtheprojretion
0/1 onlo I,. If each of the spaces , . . ., I. is a linear topological
space, then the direct Sum 1. with the product topology (cf. 1.8), is
also a linear topological space in which the subspace!In. is topo]ogically
as well a8 algebraically equivalent to I,. If a topology in each of
the summands I iJ i = 1, . . ., n, is given by a norm HiJ i.e.l' if
each of the spaces ;{i is a normed linear space, then the space I is a
normed linear space. Tbe norm in iE may be introduced in a variety
of ways; for example, anyone of the following nonns defines the pro-
duct topology in 1.
(i) 1["'1,..., "'.]1 = 1"'111+1",.1.+.. ,+ ".I..
(il) 1["'1,...,31.]/ = sup 1"',1.,
l i;:;;n
(iit) I [x". ... 31.]1 = (Im,t. +... + 1"'.I;)'i 2 .
15 DEFINITION. The cardinality of an arbItrary orthonormal
basis of a Hilbert space is its dimension.
16 THEOREM. Two Hillwrl spaa!s are isometrically isomorphic
if and rmly if they Mve the same dim.....ion.
Paoo>.. Let U be an isometrIc lSomorpbism of onto .\')", Then.
if a; and y are orthogonal elements of J'
IU(",+}.y)j2 = Ix+Ayl" = Ixl"+I;\I"lyl" = IU", +).Uyl"
= IU"'I"+I;\I"IUyj"+(U"" }.Uy )+(U"" AU y)
= l"'I"+1A12jYI"+(U"" AUy)+(U"" AUy).
and if we let}. = (U"" Uy) in this equation it is St'ell that (U"" Uy
= o. Thus U maps an orthonormal basis for 41, onto an orthonormal
basis for " and consequently {I, and .p" have the same dimension.
Conversely, let .\), and have the same dimension, and let
(u., a.. A) and {v«, ot. A} be orthononna] bases for 41, and.\), respec-
256
IV. SPECIAL SPACES
IV.4.17
IV.4.19
SPACES BfS.E) AND .8lSI
257
\Vhenever the direct sum of normed linear spaces is used as B normed
space, the nO!111 will be explicitly mentioned. If, however, each of the
spaces I" . . ., I is .. Hilbert sp..ce then it will alw..ys be understood.
sometimes without explicit mention. that :t is the uniquely deter.
mined Hilbert spare with sc..lar product
19 LEMMA. If { .}, E A. i. a family of Hilbert <pace<, their
dind BUm I . i. a Hilbert <pace.
PROOF. As remarked above, it only remains to prove the com-
pleteness of I .. If {x:}, n = I, 2, . . "J is a Cauchy sequence in I l..
it is dear that for fixed 1', {w:} is a Cauchy sequence in ,. converging
to some element . For Bny finite subset 1f, C A and any integer 11.,
I IX:- I' = lim I 1",:-",:,,2
n
(iv) (["'I' - . .. "'oJ, [y,.. . .. Yo]) = I ("';' y,)"
,-I
where (', '), is the scalar product in I,. Thus the norm in .. direct sum
of Hilbert spaces is always given by (in). To summarize, we state the
following definition.
17 DEFINITION. For each i = I, . -'J fi, letta, be aJIilbert space
with scalar products (-, -),. The direct sum of 1M Hilbert <pace.
s;,., . . .. .\;I. is the line.... space = -\\ @ . . . @ o in which.. sco.l.... pro-
duct is defined by (iv).
Let = -\\ @ . . . @ .\1. be the direct sum of the Hilbert spaces
, . . ...\10' Then for i '* j the manifolds , and.\;l, are orthogonal in
S,1 and the projection of onto . is the same as the orthogonal pro.
jection of.\1 onto ,. Thus, for example. the subspace @ . . . @ .\';I.
of is the orthocomplement of -\\.
The following definiti n generalizes Definition 17 to cover the
case of an infinite family of direct summands.
18 DEFINITION. For each in an index set A let . be .. Hilbert
space. The d;,.ect BUm I.\;I. of the Hilbert spaces {>. is defined to be the
family of all functions {.:c,} on A such that for each v, .:c. < . and such
that 1:.", Ix.1 2 < W.
It is clear that I.\;I. is a vector space if addition and scalar multi-
plication are defined by the formulas
a{"'.J = {ax.J. {"'.}+{Y.} = {"'. -rY.}.
Moreover. one may define an inner product in I . by the formula
({",.), {Y.}) = I.("'.. Y.).
the series converging unconditionally since
.'"
m-+m fiE'"
Iim sUp Ir",:}-{",:"}i".
m
It follows that
lim sup I.lx:-"' I' lim sup !{"':J-{"':'H' = 0
,......0:: m._
showing that { } is in I . and that {"':} converges to {",:}. Q.E.D.
We conclude this section hy listing, in the following lemma. a few
useful properties of the orthocomplement.
.. 20 LEMMA, Let B he a Bet in .\J andIDI a closed linear manifold
in . Then
(i) =IDI@(.\Je!)J!);
(ii)IDI=.\) e( e!)J!);
(Hi) BP (B) = e ( e B).
PROOF. Equation (i) is merely a restatement of Lemma 4.
Equation (ii) may be proved by replacing IDI by .\;I e IDI in equ..tion
(i). This shows that e (.\;I e IDI). as well as its closed subspace IDI,
is a complementary manifold to e!)J!. Thus IDI = e (.\) e IDI).
To prove (iii) note that for an arbitrary set B G the condition
(B. "') = 0 on an element", in .\J i8 equivalent to the condition
( sp (B),,,,) = o. Thus .\J e B = e <p (B) and (iii) follows by
placing IDI = sp (B) in (ii). Q.E.D.
I.I("'.. y.)1 1:. 1"'.1 IY.I
(1:.I"'.12)1/2(I,ly.1 2 )"2.
Properties (i)-(v) of Definition 2.26 may readily be verified.
5. The Spa"". B(S, I) and B(S)
In this section it is observed that B(S) and B(S. E) are B-spaces.
Their conjugate spaces are represented and a condition for compact-
ness is given. \Ve..k compactness and weak convergence in B{S) will
be discussed ..t the end of Section 6,
.
258
IV. SPECIAL SPACES
IV.5.l
IV.5.2
SPACES BIS,E) AND B(S,
259
It is clear that B(S) is a normed linear space, To see that it is
complete and hence a B-space, suppose that {fn} is a Cauchy sequence
in B(S). Then for each.. > 0 there is an m(e} with I/.-Iml < e for
fI, m ::;" m(£). Let I('} = limn In(') for each. in S. For each 8 in S
there is a p ;;;:; m(£) with 1/(8)-1.(')1 < s and thus
I/(')-I.(B)I ,;; 1/(8)-1.(')1+1/.(')-1.(')1 < 2£,
for j = 1, . . ., n, and put I(B) = e,e, fora e E" then If! ;;;; I, f < B(S.E),
and
n;;;:; m(e), uS.
i""'j ;;;:; I s /(')f'(d8) = 1!-t(E.)1 > II-'I-e.
Since e is arbitrary, 1.x*1 ;;;:; 1f'1. ThU8. 1.x*1 = 11-'1. To show toat every
x* < B*(S, E) is given by some f' < ba(S, E), we have only to let XE
be the characteristic function of a set E < E, and define I-'(E) = X*(XlJ.
It is toen evident that I-' is additive. that 'f'(E)1 ,;; 1.x*I, and that [*]
holds for e,'ery function f which is a linear combination of character-
istic functions of sets m E. Such functions are dense in B(S, E) and
therefore, since both sides of equation [*] are continuous in " it
follows tMt [*] holds for all f in B(S, E). Since tne linearity of the
correspondence between tc* and p. is dear. the thoorem is proved.
Q.E.D.
This shows that I. converges to I in B(S) and proves tnat B(S) is a
B-space. To see that B{S, E) is also a B-space it suffices to note that
it has been defined as tl1e closure in B{S) of the 8et of all finite linear
combinations of characteristic functions of sets in E. Thus B(S. E) is
a cIoood linear manifold in B(S) and is therefore a B-space. Since the
product of two characteristic functions of sets in I is atso a charac-
teristic function of a set in E, it follows from the definition of
B(S, E) that it contains the product of any two of its elements.
Thus B{S, E) i. a dO$Cd bra of B(S), a fact that will be
useful later.
2 DEnI<ITlON. If E is tne family of aU 8ubsets of a set S, we
abbreviate batS, E) 8S ba(S).
Since B(S) = B(S, I) if E is the family of all subsets of S. we
have the following coroUary.
[*]
x*1 = fs/(B)I-'(ds).
IJ COROLLAI<Y. There is an ..omm;,. isomorphi,,", between B*(S)
and ba(S) detcrmimd by the icknlity
x*f = J.f(B)I-'(ds), I. B(S).
Ncxt we wish to give conditIons on a subset of B(S, E) equivalent
to compactness. Since a set in 8. complete metric space is compact if
and only if it is closed and conditionally compact (1.6.15), it will be
5uffi lent and convenient for our present purposes to state conditions
for conditional compactness. The following elementary lemma is use-
ful here as well as in later discussions of compactness in other B-
spa£es.
1 THEOREM. There is an isommie """"'rphism brlween B*(S, I}
and ba(S, E), det£rmi7ll!d by the identity
Thus, for each x* in B*(S, E) there is a unique IL in ba(S, E) suck that
[*] holds; for each IL in ba{S, E) there is a unique x* such that [*] holds;
and the betmei>n x* and I-' is linear and i8vmetric.
PROOF. It is clear from the definition of a I-'-integrable function
that for any I-' < ba(S, E) we have B(S, E) (; LI(S, E.I-') and that for f
in B(S, I}
lIs f(.)I-'(ds) I S sup It(s)lv(P, S).
..s
4 LEMMA. Let {U.} be a "niformly oowllkd generalized ""'iusl",e
01 linear operaters it! the B-.pa« I. II lima U.", =.x for every .x in I,
then this limil e;rUit. uniformly on any compact ad. COlli).rsdy, if
lima Va.1r =;x uni/ot"mly JOT a; in a boundtd set K, and ii, ill addition,
U.({xlixl ;;;; I}) is oollditionally compad for each a, tlull K is condition-
ally compact.
Thus for each I-' m batS, E}, equation [*] defines a point x* in B*(S, I)
with 1"'*[ oS; 11-'1. To .ee tl1at Ix*j ::;" I,uj, let e > 0 and let EI' . . ., E.
be a partition of S into clisjoint sets in E such that I _III-'(Ef)1
> II-'I-e. Then ifwelet 0. satisfy 0 < 0; ,;; 2" and ,i.p(E,) = II-'(E,}I
260
IV. SPECIAL SPACES
IV.5,5
IV.6.I
S1>ACE CiS)
261
PROOF. Let K be compact and E > O. There is a finite set
{k:., ..., k n } of elements of K such that in! Ik-k,1 < £for every k inK
l:5;'Sn
(1.6.15). Let a. be such that IU.lc,-k,1 < E for a a. and for 1 ";; i n,
Then. if IU.I :<;: M for all a,
IU.k-kl inf ([U.(k-k,)I+IU.k.-k,I+lk,-klJ (M+2)E,
IS.Sn
for an k in K and an a ;;" GO' Thus U.k _ k unifonnJy for k in K.
ConverseJy, let E> 0, and let a be such that
iU.k-kl < E, kd('
Smce U..K is conditionaIly compaet there are elements k, e K with
inf IU .k-U,k,1 < E, k . K.
l j t>
of sets in E it is clear that there is an element "<> in A such that f. i,
constant on each set in "<>, Thus U.lD = fo for a ;;" aD' For such f D
therefore, lima U.to = f.. Since these functions are dense in B{S, E)
it follows from 11.1.18 that lim. U.I = f for every f in B(S. E). The
conc1u8ion now follows from Leml11& 4 and Theorem 3.5. Q.E.D.
6. The 5paee C(S)
In thi8 8ection, it wiU be assumed at first only that S is a normal
topological space. The space C(S) is the set of an bounded continuous
rea! or complex functions defined on S. The norm in CIS) is given by
the fonnula
If I = sup If(s)l.
...
Thus inf Ik-k,1 < 2E for every kinK. Q.E.D.
l;:5;fSft
5 COlWLLARY. If {IE,} is a b08i8 f"" 1: then lhe empansirm '" =
L::'I ".'". crmverges uniformly ''''' IE in a bounded 8e1 K if and tmly il K i.
ro,uJ;tiona1Iy compa£!.
6 THEOREM. A bounded 8el Kin B(S, E) is C(!fU!itionolly compact
iJ and tmly if for every E > 0 there is a 'inile eoIl.a:!ion {El" . .. En} oj
disjDinf sets in L with tmwn S, and' pQints 8, in E" i = 1, . . ., n, such
that
It follows from Lenuna 1.4.18 and Corollary 1.1.1 that C(S) is a B-
space. We shan begin our discussion by representing the conjugate
space, C*(S).
sup 11(8,)-f(8)1 < E.
.rrE f
feK,
i= I,. ..,n.
1 DEFINITION. If S is a topological 8pace. the space rba(S) is
the linear space of Tegular bounded additive set functiow defined
on the field generated by the closed sets. The norm 11'1 of I' is its tota]
variation, The space rba(S) is partially ordered by defining I' ;;" ,l to
mean that I'(E) ;;0; A(E) for every E in the field determined by the
c10sed sets. Similarly. the space C(S) is partiaUy ordered by defining
f gtomean thatf(s) ;;0; g(8) foraU8 inS. FinaUy, C.(S) is partiaUy
ordered by defining ",* ;;0; y. to mean that ",*f y*f for every f . C(S)
with f O.
Before representing the conjugate space C*(S) we first ohoerve
that every f in C(S) is integrable ,nth respect to every I' in .ba(S).
To see this, cover f(S) with npen sets 0 1 , . . .. G" with diameters less
than a given positive E. Let
PROOF. Let A be the set each of whose elements a = {EI' . . " E.;
8 1 , . . ., s..} con8ists of II finite eolJection {E I , . . ., En} of disjoint sets in
I with union 8. and points 8 1 , . . "I 8,. with Bt E Eft i = I" . . ., n. Let
A be ordered by defining a ;;0 a' to mean that each set in a is eo union
of sets in u'. For 1 in B(S, E) and a = {EI' . . ., E.; 8 1 , , , ., s.} in A,
let Ua! = f. where
"
/. = Lf(8')XE.'
....1
and X" is the characteristic function of E. Clearly
IUol = 110 Vo"U o = Va for a' a.
Now if fo is a finite linear combination of cbamcb:ristic functions
Ai = 01'
I-I
AJ=OI-U G "
'-1
i=2,...,71,
and.. if A j is not vOId, choose a point aJ If AJ. If A, is void, let a.j = O.
Since G, is open, f- 1 (OJ) is also open, and thus the set B, = f-I(A,)
is in the domain of 1" Then the function
,
262
IV. SPECIAL SPACES
IV.(J,2
IV.6.2
SPACF. CIS)
268
.
f.= Ia.'XBJ
,-,
is B p-simple function with sup.I/.(s)-f(o)1 < s. The function f is
therefore the uniform limit of p-simple functions and, since v(u, B)
< co. f is p.integrabIe. Since the integral Is/(s)p(ds) satisfies the in-
equality
Ifsf(s)p(ds)! s p I/(o)lv(P, B),
it i. clear that the integral i. a continuous linear functional on C(S).
The following theorem is a converse to this statement.
lIs g(s)p(ds)-,,(E)I is less than 88/4. so that Isg(s)p(ds) 0 is im-
possible.
Thus all that remains to be shown is that every continuous func-
tional :x* on C(S) can be represented in the form [*], where I' £ rba(S).
By 11.3.11. a;* can be extend d to n continuous functional y. on
B(S) and by Corollary 5.8, there cx;"ts an clement). . ba(S) such that
y*1 = Isf(s)J.(ds) for f. B(B). By the Jordan derowposition (IILI.B),
;. can be written in the form A = I.:.-J..+i()..-)..), where ).i > 0,
i = I, . . . 4 1 and so it suffices to consider the .case In which J. is non-
negative, and to find apHba(S) such that Is f(s)p(ds) = Is f(s»).(ds)
for every 1£ C(S).
Let F repre5Cnt the general closed subset, G the general open
subset. and E the general subset of S. Define set functions p, and 1',
by putting
2 THEoJU::M. II S is normal, there i. an isfW!dric isommphism
between C*(S) and rba(S) BUCh that oorrespondi:ng ehments :x. and I'
satisfy tJw identity
[*] :<*f fsf(B)fI(ds), 1 £ C(S).
F , lhi. iromm-phism pres""",,, urdu_
PRoOF. It has just been observed that every I' _ rba(B) deter-
mmes a functional:xl> £ C*(S) by the formula [*] and that 1:x.1 -;: 1,,1.
To show that 1:x*1 = 11'1, let s > 0, and let EJ' . . ., E. be disjoint sets
in the domain of p such that :E_Ilp(E,)1 IP[-E = v(u, B)-s.
Let C, be a closed suhset of E, such that v(/l, E,-C,) sf" and let
{G" ' , .. G n } be a family of disjoint open 8ets containing the disjoint
closed sets C1't. . ., C n - Since p. is regular. it is clear that we may
assume thatv(tt, G,-C,) ,,;; sin. By 1.5.2, there exists a set {I". . .,f.}
of continuous functions with 0 /,(8) ;:;:; I, and such that "(8) = 0
if 0 f G, and f,(8) = 1 if 8 £ C,. Let a." . . " "'" be complex constants of
modulus one such that ",.fI(E,) = II'(E,>I and put f. = I -J a.J,.
Then 1"'*(/.)-11'11 ;:,; 8E, so that sup Ix*(f)i = 11'1.
III'"
We next consider order. It is clear that $s/(o),,(ds) 0 if /l i. a
non-negative set function e.nd I B non negative continuous function.
Conv",,",ly, let Is /(o)p(ds) 0 for each non-negative f- C(S). If
there exists a p-measurable set E such that p(E) < -E < 0 we can
find a closed subset F !; E such that v(p, E - F) < _/2, and an open
set G E such that vIp, G- F) < sf4. If g £ C(S) is chosen by 1.5.2
to satisfy 0 -;: g(s) ,,;; 1, g(8) = 0 if s f G and g(o) = 1 if o. F, then
p}(F) = inf )'(GI. p,(E) = sup p,(F).
G2F Fs;;.E
It is clear that these set functions are non-negative and non-decreas-
ing. Let G, be open and F. he erased. Then, if G F,-G., it follows
that G, UG FI and A(G J UG) < ).(G,)+)'(G) so that p,(F.)
A(GJ)+;'(G). Since G is an arbitrary open set containing F,-G, wc
have
p,(F,) ;::;; A(GJ)+p,(F.-G J ).
If F IS a closed set it follows from this inequality, by allowmg G 1 to
range over all open sets containing FF)'t that
/l,(F.) < p,(PPI)+p,(P,-F).
If E is an arbitrary subset of S and PI nlOges over the closed subsets
of E it follows from the preceding inequality that
(i) p,{E) p,(El<')+,u,(E-F).
It will next be shown that for an arbitrarY set EmS and an acbitran-
closed set F in S we have' .
(ii)
p!(E) ?: p,IEF)+,u,IE-P).
To see this let FI and F. be disjoint clOSlu sets. Sinl.., B is normal there
are disjoint neighborhoods G 1 and G. of F, and F, respectively. If G
is an arbitrary neighborhood of FI U F. then A(G) ,:::: )'(GGI)+J.(GG,)
sO that
,
264
I"\? SPECIAL SPACES
IV.6,2
IV.6.1!
SPACE C(SJ
265
PI(F I UF.} ;;?: PI(F 1 }+f'1(F.}.
We now let E and F be arbitrary sets in S with F closed and let FI
range over the dosed subsets of EF while F. ranges over the dosed
8ubsets of E-F. The preceding inequality then proves (ii). From (i)
and (ii) we have
b, = inf/{s} ;;?: a, - ,
..G, nipi
and hence
(iii) f'2(E} = f',(EF}+p,(EF'},
E(;,S,
F closed.
n
! btJ-!IG,}+3e :::>: J I(s}p(d:i}.
-1 s
Now It is clear that f'1(F) = ",(F} = p(F) for a closed set F,
and if the open set G contains F then p(F} ,;: A(G}. Thus, since p is
regular, pIG} A(G} for G open. We therefore have
The function", is defined on the field of aU subsets of S and it follows
from (iii) that every closed set F is " ",-set in the sense of Definition
1l1.5.I. If p is the restriction of p, to the field determined by the
dosed sets. it follows from Lemma III.5.2 that P is additive on this
field. It is clear from tbe definition of f'1 and '" that f'1(F) = f'2(F}
= p(F} if F is closed and thus pIE) = 8UPF>;'" p(F). This shows
that p is regular, and since peS) < GO, we have f" Tba(S}. All that
remains to be shown is that
n n
! b;p(G,) ! b,A{G,} f I(s)l(d:i),
f_1 f l 5
and so
(iv)
JsI(s})'(d:i} = Is/(s)p(ds),
I . C(S}.
(v) Js/(s}).(ds) > fs/(s)p(d s ).
Since pIS} = lIS} it follows from (v) that
Is (I-/(s)}l(d:i) Is (I-/(s})p(d:i).
But, smce 0 I-/(s) ,;; I, the function I may be replaced by I-I
in the inequality (v) and this, together with the precedIng inequality,
shows that f(I-f)d.< = f(I-f)dp. and this proves (iv). Q.E.D.
+ II THEOREM. (Hie&; Tcprcsentalian theortJr1I) II S is a compact
Hausdorff space there is an isomerrie ;somurphism between COtS} and
Tea(S} such that tlu! corresponding ekrnerW; ",0 am:! p smis/y flu! ikmity
[*J "*1 = fs'(s)p(ds}, /. CIS).
It will clearly suffice to prove (iv) for real I and. since a real function
in C(S} is the difference of two non-negative functions in C(S}, it is
sufficient to prove (iv) for non-negative I. Finally, since every I in
C(S) is bounded, we may "nd shall restrict the proof of (iv) to the
case where 0 :=;; I(s} I.
Suppose then toot t is continuous on S "nd 0 I(s} 1. For
E > O let EJf . . _, En be a partitioning of S into disjoint sets in the
domain of p such that
n
.!atp(E,)+E ;::' f s /(8)I-'{ds),
Furlhermare, thi3 isomorphism presertV?8 c-rdtr.
PROOF. The previous proof shows that each 1-'. Tca(S) determines
an ,,*. C*(S) by the formula [*J, that 1",°1 = Ipl. and that the cor-
respondence between 2. and p is ]inear and presenres order. Thus, in
order to prove our present theorem, we have only to 8how that each
}.. Tba(S) determines ap uca(S} such that Js/(s).«ds} = Jst(s}p(ds}
for /. C(S). This, however, follows from III.5.14 and III,8.I(e}.
Q.E.D.
where a, = mf 1(8). Since p is regular, there "re closed 8ets F, (;, E,
such that .EEt
n
!a t p(F,}+2e:::>: J I(s)p(ds).
-1-1 s
It follows from the normality of S 8.I1d the continuity of I that there
.are disjoint open sets G II . . ", G n with G f F i , i = I, . . _, n and such
that
4 COROLLAl<¥.11 In, I. C(S), n = 1,2, . . ., where S i. a compact
Hausdorfl space, !hen tM S<queMe {In} converges i1Jeakly to 1;1 and only il
it is bou.nJkd and I(s} = limn/n(s} lor each s in S.
266
tV. SI'EC'IAL SPACES
IV.6.5
[V.6.8
SPACE CIS)
267
PROOF. If In -->-1 weakly then (11.3.20) sUPn Ilnl < 00. Also, for a
fi"ed . in S the number g(.) is continuous and linear in g. Thus,
In(') -->-/('} for each. in S. The converse statement follows from the
preceding theorem and the dominated convergence theorem of
Lebesgue (IlI.6.16). Q.E.D.
5 THEOREM. Let S be an arbitrary topological 8pace and K a
bounded .ubset 01 CIS}. l'hen K is eondiliondly eompact il and only if
for every £ > 0 thod. a finite collection {E" . . ., En} of sef8 with union
S, and points "i in Ea. i = I, . . ", n Buch thai
[t.(.}-t.(I)[ < £/8.
,"N,
i = 1,. .."n.
Then, for each I in K, each I in N, and some i < n,
1/(8)-/(1)1 [f(s)-I,(sJI+lf,(8)-t.(I)I+V,(t)-f(I)I <"
and so K is equicontinuous. Q.E.D.
8 COROLLARY, Let S be a compa.:! metric space andK be a bounded
.et in C(S). Then K is oonilitiorwlly compact il and only illor every
E > 0 lhere is a iJ > 0 such tJwt
8UP sup 1/(',)-/(8)1 < E,
r K E«
PROOf'. If E IS the field of all sets in S then C(S) is, by Corollary
1.7.7, a closed linear manifold in B(S, E) and the theorem follows
from Theo....m 5.6. Q.E.D.
6 DEFINITION. A subsetK!;; C(S) is said to be equiron!inU(fU8 if
to every E > 0 and every 8 e S there coITeSJ'Oods a neighborhood
N = N(s) of 8 with
i = 1.... ..n.
sup If(8}-f(I)1 < .,
!.K
e(8, I) <iJ.
sup sup If(8)-/(I)1 <..
lEX I N
An eqUIva]ent condition is as fo]]ows: if {sa} is a convergent general-
ized sequence with 'A .... 8, then f(8 A ) -->-/(8) unifonuly with respect
to f in K.
7 THEOREM. {ATZeltl-A..roli} 11 S is ",m.pacl, !hen a 8e! in C(S)
is conditiU1wlly colllpacl if and vnly il it is boumkd and equietmlinuOU8,
PROOF. Let K be an equicontinuous and bounded set in C(S) aud
let E- > o. From among the neighborhoods whose existence is asserted
in the preceding definition, choose a finite number N I , . . _, N m which
cover S. Then
PROOF. If the condition is satisfied then K is an equicontinuous
family in C(S) and, by Theorem 7, K is conditionally compact.
Conversely, let K be conditionally compact and suppose the con-
dition is not satisfied. Then there is an B > 0 and sequences
{8.}, (t,,}!;; S, {In} K with If.{8.J-I.(l n }1 > E, e(8., t,.) -->- O. Since S
and Ii are compact metric spaces, it may be supposed that the se-
quences {8.} and U.} are convergent. If fn -->- I in CIS) WId ". -->- 8,
then !. -->- 8 and. by Lemma 1.7.6, 0 = If(8}-f(8}1 ;;?: E> 0, a contra.
diction which prove8 the corollary. Q.E.D.
sup sup [/(Bi)-f(811 < £,
Id( uN.
nnd so. by Theorem 5. K is conditionally compact.
Conversely, let K be conditionally compact and hence totally
bounded (1.6,15), and bounded (II.I.8). If. > 0 there are functions
f l , . . ., fn in K such that every 1< K has distance les8 than 8/8 from onc
of the functions f" . . ., In. For. < S choosetheneighborhoodN = N(s)
of " such that
9 COROLLAR'i'. Let S be a compact BUb8el vf i2 Wpological group G
and /elK be abounded .etin C(S). ThenK is condmrmaIly compacl if and
only il for every E > 0 lhoe is a neighborhood V vi the identity in G such
that 1/(1}-/(8)1 < 8 lor every I inK and every paiT8.linSwi!h I in VB.
PROOF, If the condition is satisfied, the family K is clearly equi-
continuous and hence, by Theorem 7, conditionally compact. Converse.
ly, if K is conditionally compact then, by Theorem 7, it is equicontin-
nous and for every. > 0 and 8 e S there is a neighborhood V, of
the unit in G such that
Ii)
If(I)-f{.) I < 8/2,
'EK,
if I is a point in S with I < V.... Since the group operations are contin-
uous. there is " neighborhood V, of the unit of G such that V;llJ.
C V.. Since S is compact;, "finite set V, 8 1 _, , .. V. 8. covers S. Let
, .
V =n -l V. 'lndlet8, I< Swithle VB. Then. for some i and U J E V,
, J
and some It E U, t = us, t = ,"jSj, and
,
1!68
IV. SPECIAL SPACES
IV.6.IO
[V.6.II!
SFACE C(SJ
1!69
6 = U lUJ8J IE U-IU B 8 j C U;lU. 8J C VII 8 J -
- J' I
Thus it follows from (i) that
1/(8)-/(s,)1 < e/2, I e K.
12 COa01.LARY. A seqtU'nCt: in C(S) i. weakly oom'fTlienJ il and
<mly il it is boumkd and quasi-unilormly C011vngeut On S.
I/(t)-/(s)1 ;;; 1/(1)-1(8,)[ +1/(s,)-/(s)I,
and since t £ U 11 8j C V,,8 j , it fo]]ows that
, I
I/(t)-/(s}1 < e for / e K.
Q.E.D.
IS DEFINITION. A family F = {I} C(S) IS said to be quasi-
qui On S if 8. 'o implies that the convergence I(s.) ->-/(so)
is quasi-uniform on F. That is. given any s > 0 and «0 there exists a
finite set of indices "" e;; «0. i = I, . . ., n. such that for each /. F,
Since
10 DEFINITION. A generalized sequence {f.} of functions on a
set S is said to be qlMlSi-uni/Q1'11lly ronvergrnt on S if there exists a
function I. on S with 1,,(8) fo(') for every. in S, and such that for
every 6 > 0 and eta there exists a finite number of indices exIt. . ", O::n
e;; «0 8uch that for each 8 e S,
min If...(8)-/.(.)1 < s.
1;S':;7J
11 THEOREM. (An:eld) 1/ S is a compact Ha,mlorll space and
{j,,} i8 a generalized 8fiJ!I6= in C(S) which oom....-ges at each point of S
10 a fundum f.. then f. i. clmtinuou. if and 1111ly il {i.} oonverges qlMlSi.
unif<>rmly vn S.
PROOF. If fo . C(S), then given ",", e > 0 and any I e S, there is an
",(I) > "'" such that [f.II)(t)-lo(t)1 < e. Let N(/) = {sll/.w(s)-Io(.)]
< e}; since /0 is continuous, N(t) is an open set contaiuing t. By the
compactness of S, only a finite number of N(t) are required to cover
S, which proves the qua8i-uniform convergence of {f.}.
Conversely, suppose that {f.} converges quasi-uniformly to /..
We will show that the continuity of I. at a pomt So follows from that
of the I". For, given 8. e S, e > 0, there exists an suchthatif", e;; «0,
then 1/.(8 0 )-10(8.)1 < e. Select "'" . . ...... "'" as described iu the de.
finition of quasi-uniform convergence$ and let
N,(s.) = {sll/...(s)-I.,l.o)1 < e} for i = I, . . ., n.
Since the I. are continuous. the sets N i (..) are open: hence N(s.)
= n _I N,(..) is open and contains 8.. Now for the proper choice of i
and for any s. N(..) we have
If.(.) - fo(8.)1 < 1/0(.) - 1..(8)1+11...(8) - f...(8 0 )1+1I.,(8 0 )-/.(8 0 )1 < 3e.
Thus fo is continuous at the point 8.. Q.E.D.
min )/(8..1-/(8 0 )1 < e.
l:t':;n
W" recall that if F is a family of functions from a set S to the
-scalar field /1J, then F can be regarded as a subset of the product space
p. tS /1J under the one-to-one embedding I ..... p..s 1(8). The relative
product Wpolcgy on F is the topology generated by the neighborhoods
N(lo;A,e) = {fl/ eF , 1/(')-lo(s)1 <e,8eA}whereAisafinitesub-
"et of S, It is clear that conyergence of a generalized sequence {f.} iu
the product topology is eqUIvalent to the convergence of the scalars
(f.(s)} for each.. S. The relative product topology on F is seen to be
the weakest topology on F iu which each s . S generates a rouli....w...
functiOn S on F defined by s(l) = I(s), f. F.
The weak Wpolcgy of C(S) is the topology generated by the neigh-
borhoods N(I.; B, e) = {fll E C(8), 1"'*(/-1.)1 < e, fI)* e B} where B
is a finite 8et in C*(S), Since every point in S gives rise to a continuous
linear functional on C(S), it is clear that the product topology of C(S)
is weaker than the weak topology of C(S).
The next theorem indicates a close relation between weak se-
-quential compactness of a. set of continuous functions on a compact
Hausdorff space, compaetness in the product topology, compactness
in the weak topology. and quasi-equicontinuity.
14 THEOREM. Let S be a compact HaUiJMrflspace and I,' CiS).
Then the foUGWing conditUms are equivalent.
(I) The closure of F in the weak t"fKllogy of C(S) is weakly compact.
(I!) F is bounded and irs cl08urc in thc product tupo/tJgy is a compact
-Bel of ctmlinunus fu1u:timu in this /Qp<IIogy.
(13) F is bounded and quasi-equicontinuous on S.
(4.) F is bounded and if F. is a denwnerable .ubsel vi 1<' and
,
270
IV. SPECIAL SPACES
IV.6.14
IV.6.14
SPACE C<S,
271
{so, S.. S.' . . .} is a seqqence in S lor which f(s.) ..... f{s.), f E F., !hen
s. +- s. quasi-uniformly on F 0'
(5) F is weakly sequentially compa£l.
PROOF. If (I) holds. then, sin<'t' the product topology of C(S) is
weaker than the weak topology, the weak closure of F in C(S) is also
compact in the product topology. Also, since a continuous scalar
function on a compact set is bounded (1.5.10), the sebr* F is bounded
for each a;* in £* and thus (11.8.20) the set F is bounded in the norm
topology of iE = C(8). Hence (1) implies (2).
To see that (2) implies (8), let Ii' be the closure of F in the pro-
duct topology. Since each f < F is a continuous function, if {s.} is a
generalized sequence converging to So E S, then f(s.) ...../(so). On the
other hand, each 8 E S gives rise to B continuous function s n the com-
pact Hausdorff space F. Thus a(f) --+ so(f) for every 1< F, and since
So is continuous, it follows from Theorem II that this convergence
must be quasi-uniform on Ii'. But this implies that F is quasi-equi-
continuous in the sense of Definition IS.
Let (3) be true nnd suppose that so' SI' 8.2' . . . is 8 sequence in S
such that I(s.) --+ I(so) for f in some denumerable subset F. of F. Let
Iff. be the collection of all subsets of S which contain some set
Eft = {.., .»+1' .. .}, n = 1, 2,. . .. Clearly Iff. is a filter on S (cf. De-
finition 1.7.10); let 8 = {Ka}' (J. E A, be an ultrafilter which refines
CfJ. Then every set Ka. E C contains some point S'" with n > I, for
otherwise tfi = E 1 (J Ka E ,c, which is a contradiction. For each Ko. in
4, let t a = 8 ft , where n is such that 8n is in E 1 n K(').o If the set: A is
ordered by the requirement that" < (3 meanS that K« Kp, then it is
clear that A is a directed set. It follows from Lemma 1.7.12 that the
ultrafilter 8 converges to a unique point 10. S, and hence that the
generalized sequence {Ia} converges to I.. Thus the hypothesis in (3)
implies that the convergence of f/(I.)} to f(l,,) is quasi-uniform for
IE F and a lortiori in F., and it is readil)' seen that I(s.) = 1(10) for
fE Fo, since En E C for each n.
Now let. > 0 and 71. be given, and let "'0 be the index correspond.
ing to E. . Then by the quasi-uniformity of the convergence, there
,
exist ex l , 0 0 ., :X r a;, such that
min If(t..,)-!(t,,)[ < ., IE Fo'
1Si:;T
But t = 8r1, ,j = 1, _ . 0' T, where each nj no. Hence we have shown
a, ,
that there exi8ts ...' . . ., 71, 11. such that
min I/(sn,)-f{.oJl < E, IE Fo,
l J r
which proves the quasi.uniform convergence of f(sn) to 1(.0)' Thus {81
implies (4).
We now show that (4) implies (5). Let Fo = {II' f., . ..} be a de.
numerable set of functions in F" Let
w 1 If,(s)-I,(I)I
1'(., I) = 6. 2' 1 +I/,(.)-/;{/)I ' ., t. S.
Then e defines a metric on the set S which may identify points in S;
we denote this metric space by S . It is clear that the natural mapping
. .
of S onto S is continuous (but perhaps not one.to-one): thus 8. IS a
. .
compact metric space. By I. 6. 15, S. IS separable. Let T = {t., I., . . ,}
be a denumerable dense subset of See By a diagonal process, one can
select a subsequence {gn} of (f.) such that g. converges on T to a limit
10 defined on T.
(t will next be shown that I. bas a contiuuous extcnsion!o to all
of S and that {g,.} converges at every point of S. toJo. If {I,}!;; T and
.
1 -+ 8 in S then from ( 4 ) the converaence of every subsequence
r 0 '
of fir} is quasi-uniform on Fo. We now show that if a subsequen e
{h,} of {g.} has the pro(H"rty that II,(so) ..... L, then Io(t,) ..... L.. For If
h,(.o) --> L. then given ,> 0 there is an i. such that If . ;;; '. hen
Ih,(.o)-LI < E. Let {t } be a subsequence of {I,], so tha given
any TO there is a finite set of indices 1'1' . . "Tm To SUC l that If f E Fo
there is some index 1 with I :::;; 1 :S m such that If(t,,>-f(..)1 < E.
Since {h,} is a subsequence of {g.}, it converges on T. Thus there exists
a 10 such that if i ;;; 10 then
Ih,(I ,)-lo(t ,>: < E, 1 = 1, . . " m.
Now take a I1Xoo i ii), 10; then for some i we havc
lfo(t ,>-LI < jfo(t )-h.(I ,)I+lh,(t ,)-h.(.D)I+lh,{.o)-LI < 8,.
, { " }
This shows that every subsequence {I,} of {t,} has a subsequence t,
such that/o(I ') ..... L, which implies that fo(I,) ->- L. Now if some other
subsequence of (g.) converges at So to a limit L'. then the argument
ust given shows that 10(1,) .....L'. Therdore L' = L.
,
272
IV SPECIAL SPACES
IV.6.I5
IV.6.16
SPACE C{SJ
273
Thus we conc1ude that g.(8 0 ) converges to a limit L and that if
4 --+ s. in S. then lo(t,) --+ L. Itfollows tl1at I. has a unique continuous
extension J. to S .and that {g.} converges to!o on S.. Since the mapping
of S into S is continuous, and weak convergence of a bOlU1ded se-
.
quence in CIS) is implied by pointwise convergence, -we conclude that
F is weakly sequentially compact.
The fact that (5) implies (1) is due to Eberlein and is proved in
Chapter V (cf. V.6.1). Q.E.D.
Remnrk. It should be observed that we can require that the points
8 1 , 8., . . . in condition (4) be contained in a preassigned dense subset
of S. Thi8 fact will be used in the proof of Theorem 29.
We continue Our BURlysis of the space CIS) with a discussion of
certain important special properties remted to its strocture 88 an
algebra. One of these properties is a well known approximAtion theo-
ttm of Weierstrass" which asserts that a sca1ar function contmuous on
a compact interval of real numbers is the unifonn limit an the interval
of polynomials. Thi8 important theorem bas had n number of far-
reaching generalizations; notable among the8e is one due to M. H.
Stone which will be discussed here. We note fir8t that C(S) is an
algebra, for if 1 and g are in C(S), tben the product Ig, defined by
(/g)(s) = I(s)g(s), is also in C(S) (cf. 1.4.18). The algebra C(S) has a
unit e, i.e.. el = I for I in C(S). This unit is defined by the equation
e(s) = l,seS,A clDGtd subalgebra ofC(S)is ac1osedlinearnumifoldin
C(S) which contains the product of every pair of its elements.
15 DEFlNlTION. A 8et A in B(S) is said to distinguish be_en
1M points 01 S if for every pair s, I of distinct points of S there is a
function I in A with I(s) oF I(t).
Stone's generalization of the Weierstrass theorem may be stated
in terms of these concepts as follows:
16 TOEOREM. Lei S be a compact Hamdorlf spa<:e and CIS) be
1M algebra 01 all real rontim.unts fum:tUms on S. Let 1!! be a dosed sub-
algebra 01 C(S) which contains the unil e. Tium 1!! = C(S) il and only
i/1!! distinguishes between 1M paints 01 S.
PROOF. Let 2f = C(S) and s and I be distinct points of S. Since ..
compact Hausdorff space is nonnal (1.5.9), there is, by Urysohn's
lemma (1.5.2), a function I E I)! with I(s) = 1 and I(t) = O. To prove
the converse we define the functions I v g, I A g, and p(1) as follows:
(/ v g)(s) = max (/(s), g(s)},
(f A g)(s) = min (/(8), g(s)},
1>(f)(8) = If(s)l.
Now by the classical Weierstrass theorem there is a sequence p. of
polynomials with
11).I-Pn().)1 :;;; 11",
-n ;;;;;' :;;; n.
Thus
IIg(s)I-Pn(g)(s)j = Ilg(s)I-Pn(g(sJ)1 ;;;; 1/71,
provided that '11 :;;; g(s) :;;; n. This shows that1>(g) .1!!ifgEI1r. Since
1 v g = (l+g)/2+1>(/-g)/2,
and
I A g = (/+g)/2-1>(f-g)/2,
we see that 5l( is closed under the lattice operations v and 1\. Next. we
note that for an arbitrary F E C(S) and an arbitrary p..ir s, t. S there
is an I. .' I1r with I. ,(s) = F{s) and I. ,It) = F(I). To se<> this, let
. . ,
g E I1r and g(s) oF get). Then real numbers a. and {J may b. found so
that
ag(sJ+{J = F(s),
ag(tH{J = F(t).
Now if t E S, then for each s . S there is a neighborhood D. of s such
that I. ,(u) > F(..)-e for u. D.. Suppose that U.. ..., D. cover S
. . .
and define
I, = I. ,v... vI. ,.
1"' p
Thus It(u) > F(u)-e for u E S. Since I. t(l) = F(t), we have It(t) =
.'
F(t), and hence there is a neighborhood V t of t with
t.(u) < F{u)+s, ue V,_
Let V t ,.O'., Vi cover S, and define
. .
I = It A. . . A It .
. .
Since It (u) > F(u)-s, u E S. we have also
,
I(u) > F(u)-s, ... s.
274
IV. SPECIAL SPACES
IV.6,17
IV.6.18
SPACE C{SJ
275
On the other hand, for an arbitrary ...S, say u€ V,;, we have
feu) ;:;; f,,!u) < F(ul+E.
uous campi"" fU"dion of a crnnpl£;< t'llriabk and if f is in 2[, the" P(f)
is in 2[ and V (P(f)) = P( U (f)).
If(u)-F(u) I < E,
t.t S.
PROOF. Let S} consist of those non-zero continuous linear func-
tionals in the closed unit sphere of 2[* for which ",*(fg) = ("'*f)("'*g)
Qnd ,,,*(1) = ""'(f). Every 0 < S defines an "': < 8 1 by the equation
"';f = f(o). Clearly
and so
Since f. 'iJI. and < > 0 is arbitrary, the theorem is proved. Q.E.D.
. 17 THEOREM. Let S be a campact Hausdorff Bp<= and C(S) be
the algebra of all comp"'''' contintr0U8 on S. Let 2[ be a closed
oubalgebra of C(S) which contains tM unit e and cantu;ns, with f, its
compleuonjugatel defined I>y 1(') ,;, f(.) . Then 2[ = C(S) if and only
if 'iJI. distmguishu bdween tM points of S.
PROOF. The necessity of the condition is proved as it was in
Theorem 16. To prove the converse, let \!, consist of the real functions
in \!. Then II!,. is a closed subalgebra containing the unit of the real
algebra Cr(S) of all real continuous functions on S. If f. 'iJI. and
I = II +il. with fd. real. then f. = (/+/)/2 and f.= (/-f>/2i are in
\! and tbus in II!,.. Hence if f(o) * 1(1), then either 1.(8) if'Mt) OJ
Iz(s) if' Iz(I). This shows that II!,. distinguishes between the points of
Sif\! does. The preceding theorem gives Cr(S) = II!,.C\1I. Since every
function I in C(S) is a linear combination I = !r +if. of real functions
It, f, in Cr(S). it fol\uws that \11 = C(S). Q.E.D.
Theorem 17 Can be used to establish an intimate relation between
the space R(S) and the space of continuous functions on a certain
compact Hausdorff space. The .pace R(S) is au algebra under the
natural definition of multiplication, (/g)(8) = I(S)g(8). Also, R(S) has
Q unit e defined by e(8) = I, 8. S. As in the case of the algebras of
continuous functions, a closed of R(S) is defined to be 8
closed linear manifold in R(S) which contains the product of every
pair of its elements.
18 THEOREM. Let \11 be a clooed BUbalgebra 01 tM comple" algebra
B(S) containing the unit e as well as the comple", crmiugate 01 each of it.r
elements. TI2£n there e:rists a compacl Hausdorfl 'pace S, and an isometric
algebraic ieommphism U between tM algebras C(S.) and'iJI.. Furt1u:rrrwre,
V maps Teal functions into Teal functions, p08irive functions into poeiJive
functi<ms, and cample", coniugate functions into compk.r: conjugate lunc-
tions, i.e., VI = VI lor every fin \11. Monroer, if P is an arlJitrary contin.
(i)
sup I";fl = Iii.
.
If ",*. Sl there is an 1<\11 with a:*f '1= 0 and hence. since ",*f = a:*(fe)
= (",*f)(,,*e), it i8 seen that ",*e = 1 and 1a:*1 :2 1. If III < I then
1"'*/ln = ""*(/")1 ;:;; 1"'*1 and so 1 :::;; 1"'*1 ;:;; 1. This fact combined with
(i) gives
(ii)
sup I"'*fl = If I,
ia'.cs1.
I_ 2[.
Since
",*f Elf = {}.IA. w, IAI < 1/1}, ",* . 8 1 , 1<\11,
the topology in the product space P If taken over I £ \11 induces a rela-
tive topology in S,. Since P If i8 a compact Hausdorff spaee(L8.2,
1.8.5), Sl is also a compact Hausdorff space if it is closed (1.5.7)_ Let
A.8,; then (1.7.2) some generalized sequence {"':} S, converges to A,
This means that "':f ..... AI for I in \11. It follow8 that
),(fg) = lim x:(/g) = lim (tv:f)(x:g) = (Af)(),g).
a a
It may be shown similarly that A is linear and that WI ;:;; If I. Thus
),.8 1 and S, is compact. Define the map U : I .....1. ofm into C(Sl) by
placing I.tv* = ",*f. Then V is linear and it follows from (ii) that U is
an isometry. Clearly V2[ distinguishes between the points of S" and
since tv*e = 1 for tv* in 8 1 , VW contains the unit in C(Sl)' Since
IV/I = If I, the algebra VW is closed in CIS,). Thus Theorem 17 shows
toat VW = C{Sl)'
It is clear that V maps products into products, complex conju-
gate functions into complex conjugatc functions, and therefore real
functions into real functions. Thus 1£ CI. is a polynOlnial in two varlables
then
V(,,-(f, f» = a(Vf. Uf) .
276
IV. SPECIAL SPACES
IV.6.19
IV.6.2
Sl'ACE C{SI
277
ft
oontinIMU8 C01nple.r junction on S has a unigue enrllsWll. to a cotliinuOU8
fundWn to BI'
PROOF. Since the algebra 11! = C(B) satisfies the hypothl of
Corollary 19, the present theorem follows from that corollary if it is
shown that the one-to-one embedding of S in 8 1 is a homeomorphism.
In the notation illtroduced in the proof of Theorem 18 this means that
it wiU suffice to show that the one-to-one correspondence s :E:
between S and a subset Bo of B 1 is a topological one. Here we are using
the symbol So for the set of all points ",* in SI having the form ",* = ..:
for some s in B. Let. > 0, So . B, and It, . . ., 1ft' C(B). Then the set
{sllJ.(s)-I,(so) [ <', i = 1, . . ., n} is open and contains so' Its cor-
respondent in So is the set
{"':II"':I,-"':/,I < ., i = I, . . ., n},
which is, by definition, the general neighborhood in Bo. Thus to cOm-
plete the proof it will suffice to show that neighborhoods in S of the
fonn {'II/,(.)-t.('o!l < E. i = 1, . . ., n} form a basis for the topology
in S. This may be done by using the complete regularity of S in the
following way. Let So be in the open set G in S. Then there is a function
I in C(S) with 0 ;;0 I(s) ;;0 1, I(so) = 0, and I{s) = 1 for s in the com-
plement of G. The set
B = {sll/(s)-/(so)1 < ]/2}
is a neighborhood of So which is contained in G. This completes the
proof of the theorem. Q.E.D.
To see the remarkable nature of the preceding theorem suppose
that S is the half open interval 0 < s ;;0 1 of real numbers. The space
S is clearly a dense subset of the compact interval 0 ;;0 s ;;0 1, but the
functions sin(I/8) on S has no continuous extension to this interval.
Even in this simple case the compact space SI of the precedJng-
theorem has no simple or familiRr representation.
By the Weierstrass theorem there is a sequence {et,,} of such polyno-
mials for which ",.(A, A) converges to (J(A) uniformly for A in the rsnge
of I. Thus
P(f(.» = lim "'.(/(8), /(8»
uniformly for 8 in S. Consequently (J{/) is in fi( and U({J(IJ) = P(U(IJ).
If we consider the function (J(A) = 1.11 it is clear that U maps positive
functions into positive functions. Q.E.D.
19 COROLLARY. Suppose, in addition to the hypothese8 01 Tkote",
18. tluU the lunctiomoll1! distinguishbefween the point.s' 01 S. Then tMt,
eil'isIB a compacl Hausdurll space S. and a mu-to-cm embedding 01 S as a
dense ..-uhset 01 S, sw:h ,hat each I in \11 hn$ a unique crmtinuous
h 10 Sl' and sw:h tiult the cot1'C8pOnderu:e I ........ I. is an iso11l€ltU: iso.
murphism 01 \11 and C(S,).
PROOF. We use the notations of the proof of Theorem ]8. It is
clear that the map 8 -+:c is 8 one-to-one emh ddillg of S in 8 1 , and
to prove the corollary it will 8uffice to show that S is dense in B 1 . If
this is not the case. there exists, by 1.5.2, an f E C(B 1 ) such that
1#<0 and I(s} = 0 for s. S. If g. 11! is such that Ug = I, tben g(8)
= f1::1 = 0 for 8. S, i.e., g 0, which contradicts the fact tbat
o #< I = Ug. Q.E.D.
20 THEOREM. Let the dosed ..-uhalgebra \11 01 the teal alg,lIra B(S)
conlain the unil. Then 'here is a compad Hausflorll space s.. and an
isometric isomotphism between the teal algebras \11 and C(Sl)'
PROOF. The proof follows the lines of that of Theorem 18, except
that Theorem 16 is used in place of Theorem 17. Q.E.D.
21 DEFINITION. A topological space S is complddy tcgular if
points are dosed and, given any point 8. in S and any closed set F
not containing 8 V ' there is a function I defined and continuous On S
and satisf) ng 0;;0 I(s) -s:: ], I(so) = 0, and I(s) = I for 8 in F.
This class of spaces contains. for example, all normal and all
rompact Hausdorff spaces (cf. 1.5.2 and 1.5.9).
22 THEOREM. II S is complddy regu1m-, il is Iu>n1aJnwrphic with
a dense subset 01 a compa<1 HausflorJ/ space SI ,mch that every bounded
28 DEFINITION. A linear functional ",* on an algebra 11! will be
called multipli«>live if "'*(tg) = (",*f)(x*g) for every I and g in W.
24 LEMMA. Let '!.I be a CI08ed subalgdn-a 01 the olgebra B(S) and
let '!.I ""nwin the unil e. Then any non-zero 1nu!tiplirativ, linear lunc-
tional en 11! is ""'llinuoUIJ and has 'W1'1n one_
278
U". SFECIAL SPACES
IV.6.25
IV,6.27
SPACE CCSj
279
PROOF. Suppose that * is a multiplicative linear functional on
and that I is an element of \!! with x*1 * O. Then x*1 = x*(el) =
(x*e)(x*/) so that x*e = I and hence Ix*1 I. Next let g be an arbi-
trary eJement of \!! with Igi ;;;;; 1 and let}. be a scalar with !11 > 1.
Then the series ::-o g'fjlln+1 converges to an element h in 2.[ and
c ( If' gn+1 )
(M-g)h= --- =e,
n=O A." :"+)
For each t in T let y*(t) be the funchonal on C(S) defined by the
equation
y*(t)1 = x:Ilf. f < C(S).
Since x: and H are both multiplicative, it is cIcar that y*(t) is multi-
plicative. Thus by the preceding lemma there is a point e = h(t) in S
such that y*(t)1 = I(e). Hence
(i) (IlIHt) = f(h(t)). t. T, f _ CrS).
which 8hows that IHfl < III and pr"'..... the H is continuous. To see
that h is continuous, let N be a neighborhood of the point e. = h(Io).
By Theorems I.5.2 Rnd 1.5.9 there is a continuous function I on S
with/(eo) = 1 and/(s) = o for every e in the complement ofN. Since
f(hlt» = (Hf)(t) is continuous in t. the 8et
Thus
1 = x*e = (l-x*gJx*h.
whi h shows that :x*g #= A. Since 1 is an arbitrary scalar with IA I > 1
it follows that Ix*gl < I. Since g is an arbitrary element of ill with
Igi < 1 it follows that Ix*1 ,;;; 1. Therefore Ix*1 = I. Q.E.D.
25 LEMMA. Let S be a compact HaustkJrff space and ",* a non-=<>
mu!tiplirotive linear lunctwnal on C(8). In tM e<m>pleJ: case it is awo
assumed that x*1 = ,,*1 . Then there is a point s in S BUCh that
U = (tl/(h(t» * O}
"'*1 = f(e),
I- C(8).
is a neighborhood of to- If t is in U then I(h(t» * O. This shows that
hIt) is inN. Thus h(U) N and his continuous. If H is an isomorphism
with HC(8) = C(T) the result already proved yields a continuous
function I<,. on 8 to T with
PROOF. By the pre<:eding lemma ,,* is a point In the space 8 1 de-
fined in the proof of Theorem 18. By Theorem 22, S is homeomorphic
to a dense subset So in Sl Smce S is compact So is compact and thus
closed (1.5.7). Therefore 8 0 = 8 1 and ",* _ So' According to the defini-
tion of 8. as given in the proof of Theorem 22, this mean> that for
some 8 in S we have m*1 = f(8) for every I in C(8). Q.E.D.
(ii)
(H-1f)(S) = 1(I<,.(s»,
S S,
1£ C(T).
This, combined with (i), shows that
(iii)
1(8) = I(h(h,(e))),
s£8,
1£ C(8).
26 THEOREM. Let II be an Qlgebraic homoltwrphism 01 C(S) inlo
C(T), where 8 and T are compact Hausdorlf spaces. II tM algebras
C(8) and C(T) are over the field 01 compla numbere, it is also _umed
thai Ht = Ill . Then Il is oonlinuoU8 an<! has 1M lorm
Since there are sufficiently Illany functions in C(S) to distinguish
between points of S, itfollows that e = h(h,.(8». Similarly, t = I<,.(h(t))
for every t in T Since h and are continuous, the proof is complete.
Q.E.D.
(HI)(I) = /(h(t»,
t£T,
1.c(S).
27 COROLLARY. II 8 and Tare compact Hal18dorf/ spaces suck
that the rea! algebras C(8) and C(T) are algebraically I'fJUi-valent, IMn
the space8 Sand Tare Iwmeom"'1'hic.
Corollary 27 shows that the compact Hausdorff space 8 1 associat-
ed with 8 given completely regular space S in the Olanner described in
v
Theorem 22 is unique. It is called the 8tmlC-Cech C<1mpadi/ication of S.
We conclude this section by showing how Thcort'm 14 may be
u8ed to derive conditions for weak sequential compactBl'SS in B(S).
First, however, a few introductory remarks must be made.
whoe h i8 a amli"",,,,. map vf T into S. I/ H is an ;.omorphism 01
C(8) 01110 C(T) then h is a homeomorphi"m of T onlo 8.
PROOF. }'or each tinT define the multiplicative linear functional
"': on C(T) by the eqImtion
x:/ = I{t), f _ C(T),
280
n°. SPECIAL SPACES
IV.6.28
IV.6.80
SPACE AP
281
Let C = {Ea} be an ultrafilter of sets on the set S. and for each
a, let sa be some point in E.. If {ex} is ordered by the requirement that
ex :S: (J meanS that Ea Ep, then it is evident that {sa} is a generalized
sequence of points in S. We will say that the generalized sequence
{Ba} is gem'Tated by the ullTafilter C = {Ea}' Further, for each f £ B(S)
the generalized sequence {f(B.)} of scalars has a limit. which we will
denote hy f(C). Though it is ohvious that each ultrafilter generates
many generalized sequences) it is easily seen tbat if {s:} is any other
generalized sequence generated hy 8, then {f(s;)} also converges to
f( If), so that this notation is unambiguous.
28 DEFINITION. A set F!;; B(S) is said to be quasi-equicontin-
"ous on S if every generalized sequence {sa} in S which is generated
by an ultrafilter C has the property that f(s.) converges to f(C) quasi-
unifonnly on F. Note that in this definition we make no assumption
as to the nature of the set S. If S is a compact Hausdorff space, it Can
be proved that this definition is equivalent to the statement that
F !;; C(S) and is quasi-equicontinuous On S in the sense of Definition IS,
29 THEOREM. Let S be an arbitrary set and F!;; B(S). Then the
fQllvwing statem£nts are equimJenL
(I) F is bounded and quasi--equictmlinWJus on S.
(2) F i. bo1mded and if F. i. a demnnerable subset of F and
{Bi'S., . ..} is a Beq'/',,,,,, in S fM' which {f(sn)} corrvergea for each
f. F.. then the convergerwe is fJULlSi--tl¥liform on Fo.
(8) F is U2eakly stqt<entidly compad..
PROOF. That (1) implies (2) can be proved in a manner similar
to that used in Theorem 14 to show that condition (3) of that theorem
implies (4).
From CorolllUj' 19 it follows that S may be embedded as a dense
subset of a compaet Hansdorff space Sl in such a way that each
f . B(S) has a unique extension fl to C{Sl)' and so that the coITCSpOnd-
ence 1-<-->- A is an isometric isomorphism of C(S) with C(Sl). That
(2) implies (8) then follows hy virtue of our observation after Theorem
J4 that it is sufficient to select the sequence of points of Theorem
14(4) from a set S dense in S.. The relation between B(S) and C(Sl)
also shows that the Implication that (3) implies (1) follows from the
implication that (5) implies (8) in Theorem J4. Q.E.D.
30 LEIDoIA. Let A be a dense subset of a compad- Hausdorlf $pace
S, and suppose that a sequeru:e {fn} of continuous fu7ldions convn'ges at
efJeTY point of A to a continuous limit fo' Tkn {fn} co-nverges to f. at
every point of S if and only if {fn} and every 8I1bsequence of {fn} converges
to f. quasi-uniformly on A.
PRoOF. Theorem 11 implies that the condition is necessary. To
prove the sufficiency, suppose that fn(s.) does not converge to fo(so)'
Then there exists an eo and a subsequence {g.} such that Ig.(so)-fo(s.)1
> eo' k = I, 2. . . .. Let k:., . . ., k, be the indices corresponding to e.
and k = I guaranteed by the quasi-uniform convergence of {g.}. Then
V, = {BlIg.,(S)-f.(B)1 > co}
is an open set containing 8 0 for i = I, & . ., T. Since A is dense in S,
there exists a points E An vin...n V, for which Ig.,(B)-f.(s)I>s",
i = I.. . . "' r, contradicting the quasi-uniform convergence of {gk}.
Q.E.D.
81 THEOREM. Let S be an arlJitrary Bel. A sequerwe UA} in B(S)
converges weakly 10 fo if and only if it is bounded and.logether with every
8Ulmvurnce, cvm;erge. 10 f. fJULlSi--1J3.if",mZy on S.
PROOF. The sequence {In} in B(S) converges weakly to f. if and
only jf the ool'reSpOnding sequence of continuous functions {!ft} in
C(SI) converges weakly to f.. (See Corollary 19, which shows tha. S
may be identified with a dense subset of a compact Hausdorff space
S..) Making this identification, we can write!n(B) = fAlsI, $£ S, and
the theorem follows from Lemma 80 and Corollary 4. Q.E.D.
7. The Space AP
Harald Bohr's elegant theoI1' of almost periodic functions char-
acterizes those complex functions of a real variable which may be
uniformly approximated over the whole real number system by trigo-
nometric polynomi8Js of the form
..
s(;<) = 1: "'De.....
n 1
where a. l , .. .. 0' a.,. are arbitrary complex numbers and )'11 .. . "? ).n are
arbitrary real numbers. In other words, the theory gives an intrinsic
,
282
IV. SPECIAl. SPACES
IV.1.1
IV.7.2
SPACE AP
283
charact.erization, without reference to trigonometric polynomials, of
those complex functions I{"), - 00 <" < C() with the properly that
for every E > 0 there is a trigonometrIc polynomial s with the above
form such that
and thus any point of 8ceum.ulation of the sequence {'II} is a period
for I.
For). £ R the transfutc I. of 1 is defined by the equation hi") =
1("+).).
1/(")-8(")1 < e,
-00 < it' < 00.
2 THEOREM. (Bachnerl A lunction i1l C(R) is almnsl periodic il
and o..ly if the set 01 ils translali!s is c<mdiliollally compact.
PROOF. The proof will require the following two lemmas.
The principe,] result in Bohr's theory is that the class of such compte:=<
functions of a rea.l variable is precisely the class AP of almost periodic
functions. In this section the class AP will be define it will be shown
that AP is a B-space, and a criterion equivalent to almost-periodicity
due to Bochner will be given. Other important results of the theory
(in particular the result which identifies each function in AP with the
Ilnifonn limit of trigonoIDf'tric polynomials) will be presented later,
when some of the basic tools of speetmI theory have been developed.
1 DEFIKITION. For a complex function I defined on the dass R
of real numbers and a positive number. the set T(., f) R is defined
as
3 LEMMA. An almost paiodic JuIU'lion M bounded.
PROOF OF LEMMA 3. Since an almost periodic function / is contin-
uous, the function I/(s)1 has R maximum R on the interval 0 :S: J:
;:';; L(l). Let" be an arbitrary real number and choose ,£ T(l, f) in
the interval -" ;:';; I;:;; -,,+L(l). Thus 0 ;;; t+,,;:';; L(I) and
If(,,+t)1 ;:';;K,
1/(.xJl;:';; jf(x+t)i+I/(")-/(x+t)1 ;:';;K+1. Q.E.D.
T(., f) = {tll/("+I)-/(re>l < e,
" £R}.
4 LEMMA. An almost periodic IUII<lion is "";Iormly oo..linuous.
PitoO}' OF LEMMA 4. Since an almost periodic function I is contin-
uous. for each . > 0 there is a lJ with 0 < lJ < 1 such that
I/(s)-/(I)1 < '/3 for every pair s, I with -I ;;;; s, I :<;;: L(Ef8)+1 and
IS-II < lJ. Now suppose that re, yare arbitrary real numbcl'S with
I"-yl < lJ. Choose u £ T(e/3) satisfying -x;;;; u ;;;; -x+L(e/3).
Then 0 ;:';; ,,+u ;:;; L(e/3) and -1 < y+" < Lk/8)+1. Thus
(")-/(y)1 ;:';; (")-/(x--ru)I+lf("+")-f(Y--r")1
+If(y+''j-f(y)1 < e. Q.E.D.
PROOf' OF THEOREM 2. Using Lemma 4, for each t > 0 there is
a lJ _ 0 such that !t.<x)-I.(y)] < . for all), when Ix-yl < lJ. Thu8 it
is seen (5.8) that an arbitrary sequence {f.) contains a subsequence
{fl.'} uniformly converga>t on the interval Ixl ;:;; 1. By the same rea-
soning {f,..} contains a subsequence {fe,.} convergent umformly on the
interval l.xl 2. In this way successive subsequences are chosen so
that the limit lim'/fl,.(") exists uniformly on themtervallxi n. The
sequence {g,. = In,n. 11 = 1,2, . ..} then is a subsequence of {f,)
which converges uniformly on any finite interval. Now let E > 0
and choose 1I(e) so that
Any number I. T(., f) is caJ]ed a tran.fulion n"mhn- vi I cotrup,,,,ding
to.. When there Can be no confusion the symbol T{.) may be used in
plaeeof T(e, f). It is clear that T(E) T(lJ) if e < lJand that -t£ T(.)
whenever I £ T( E). The function 1 is said to be almOBt paiodic if it is
continuous and if for every. > 0 there is an L = L(e) > 0 such tha.t
every interval in R of length L conta.ins at least one point of T(.).
It is clear that B periodic function is almost periodic. It a1so fol-
lows irnmediate1y from the definition tha.t if I of" APt if rJ. is an ar.
bitrary complex number, and jf;' IS an arbitrary real number then the
functions defined by the expressions
«/(1), 1(1+).), fIt) , I. R,
are also in AP. Since
Ilf(I+).)I-!/(t)1I ;:';; 'j{t+J.)-/(I)1
it is clear that 1/(' >1 . AP whenever I . AP. It is also .helpful to note
that unless the almost periodic function f is actually periodic the ad.
m.ssiblenumbers L(.) are unbounded fore near zero. For if L(.) ;:';; K,
. > 0 then th...... i8 a sequence {I.} with 0 ;-;;; I. ;-;;; K and
i/(a;+t.)-/(re)i < I/n.
x€R,
,
284
IV_ SPECIAL SPACES
IV.7.5
IV.7.6
SPACES Lj'CS.Z:.p)
285
e
Ign(U;)-gm(U;)1 < -,
8
for wI n. 7n, and x with 0 u; L(e/B), and n. m ;;; nee). For every
real number iE choose aYE T(e/B, f) such that -x Y -x+L(e/8)
and note that, since g1l = I Pa for some p'm the number y is also in
T(e/B, g..) = T(e/B, f) for every n = I, 2, . . .. Thus for n, m ;;:; nee).
jg..(iE)-gm(iE!I 19,,(iE)-gn(u;+y)I+Ig,,(iE+y)-gm(u;+y)1
+lgm(x+y)-gm(a:)1 < ..
We have 8hown that an axbitrary sequence {f,,} of translates of I
contains a subsequence which is uniformly convergent on the whole
real number 8ystem R. Thus if I is an wmost pertodic function the set
{I.. A E R} is conditionally compact in C(H).
Conversely let I be a bounded continuous complex function 0"
the real number system R whose translates {I,. A E H} form a condi.
tionally compact set in C(R), The set {fA' A. R} is totally bounded
(1.6.15) and thus for every e> 0 there are numbers ;1.". . . .,).", such
that each translate IA satisfies one of the inequalities 1/,-1,,1 <.,
i = 1, 6 _", m. That is, for every AiE" Rand XE" H,
shows that I +g is an almost periodic function. Finally let {ffl} be a
uniformly convergent sequence of almost periodic functions and let f
be the limit of Ifl in C(H). Fix n" so that the function g = In satisfies
.
the inequality Ig II < ./B. Using Theorem 2 (and 1.6.15) choose
AI' . . ., Am so that for every A, Ig,-g,J < e/8 for somci m. Then for
e TJ.,
It.-f,,[ I/.-g,I+lg, g..I+lg" 1,.1 < e
for some i < m, Thus the set Vb A E H) is totally bounded in C(H)
and hence (1,6.15) is conditionally compact in C(H). Theorem 2 then
shows that I is almost periodic. Q.E.D.
I/(x+).)-/(u;+A,)1 < e
for some integer i m. Thus for every A . H and every "'. H,
I/(",)-f(x+).-).,)I < e
for some i m. If k = max IA,I it follows that any interval of length
l::;fSm
Ilk contains a point in T(e, I). Thus f is almost periodic. Q.E.D.
5 THEOREM. Tk spm:e AP of aU complu; periodic funcliom of a
Teal lJlIriable is a complex B-space under lhe norm
6 THEOREM. The spm:e AP 01 all complex almosJ periodic lurn;.
wms 01 a Tea! variable ro,oo;ns, with f, g, also the lundwRS fg arn! 1 <k.
lined by (fg)(/) = f(t)g(/), /(t) = f(/) . There is an iso_ic al€dn'aic
(i.e.. multiplication and con;Uf¥1Iion prcset'V;ng) ;SO"ItWTphism berween
AP and the allJ'bra C(S) 01 all complex N17IIinuous fundions on some
compac! Hausdm"/f spm:e S.
PROOF. It has already been ob.nved that fbelongs to AP when-
ever I does. The argument in the preceding proof which was used to
show that the sum f+g of two almost periodic functions is almost
periodic, also shows that the product fg is almost periodic. Thus the
present theorem is a corollary of Theorem 6.18. Q.E.D.
8. The Spaces L.(S. E, /1)
Ifl = sup 1/("')1.
-D'J.<Z<OI
The spaces L.(S, E, /1), 1 < p < 00, have already been studied
in Chapter III. In particular it was shown in Theorem III.6.6 that
they are B-spaces. In this section the study of these spaces will be
eontinued with a view to solving the problems listed in Section 1.
In addition we shall study the space L",(S. E, /1) of Definition 2.19.
It is clear from Corollary 111.6.14 that this space is a B-space. Since
L.(S, E,I') = L.(S.E. v(/1)) we may and shall assume throughout
the present sectivn that (By I. Jl} is a positive measure space.
The reader should note that the space I; is just the space L.(S,E,/-,)
in which S is the set of all integers, E the family of all subsets of S,
and /1(E) the number (finite or infinite) of elements of E. Thus the
PROOF. It has already been observed that the product a.1 of a
scalar a and an almost periodic function / is again almost periodic.
If f and g are both almost periodic, it is seen from Theorem 2 that any
sequence (j +g)" = fA. +g" contains a subsequence I'n = A,. such
that Up) and {gpJ axe both uniformly convergent. Thus the sequence
{(/+g)l') = {fp, +gl'J is also wrifonnly convergent and Theorem 2
,
286
IV. SPECIAL SPACES
IV.8.1
IV.8.1
SPACES LJ'(S.E.I:I
287
discussion 'If the present section covers the space I as well as the
space 4,(S. E, p),
1 THEOREM. If 1 < p < 00 and Ijp+l/q = I, lhere is an iso-
merric ioomarphism between L:(S, E, p) and L.(S, E,p) in which COr-
responding veclor8 it. and II aTe relaud by lhe identify'
.,.f = Is g{B)f(s)p(ds), f. L.(S. E, p).
PROOF. For I < P < 00 let L. = L.(S, E, p) and let III. he the
norm of f BS aTI element of LII" Let l£" E L: and assume, for the present,.
that peS) < 00. If XI!. is the chmacteristic function of the set E E E,
then, if {E,} is a disjoint sequence of measurable sub8ets of Sand
U::I E, = E., it follows from III.6.16 that I::'. XE, = XE,' the series
converging in the norm of L;o Hence a:*XE D =- .I;:1 X*XE/1 so that
.,.XI!. is a countably additive set function. Since ]xEI. -+ 0 as peE) -->- 0,
.,.XI!. is p-continuous, aod the Radon-Nikodym theorem (III.1O.2)
yields ag E L" with".XE= Jsg(B)XE;(S)p{ds). Thusforsimplefunclionsf
(i) ".f = IsII(s)f(S)p(ds).
If {I.) IS a sequence of p-integrable simple functIOns convcrgin
p-almost everywhere and in L. to f (by III.II.S, III.a.6, and III.6.U
such a sequence always exi<ts), then gl. glp-8lmost ever)
where. Since .,.(f"zl!.) converges, it is seen from the Vitali-Hahn
Saks theorem (III.7.2) that
Iim I 1I(8)/.(s)p{ds) = 0
....(£)-+-0 E
uniformly in n. Since it is assumed for the present that peS) < 00 it
is seen from Theorem III,6.15 that fg is in LI and that equation (i) is
valid for every f in L.. It will next be shown that g is in L.. For a
complex number let ",( ) = e "ih = rc", ",(0) o. Then "'(g('» is
p-measurahle hy III.6,D, so that. by III.2.IZ, III(') Ig('>1"'",(g('»
is p-measurable and hence is in LfJ. Thus
Is Ig(8)1l+ p(ds) = "'.(gl) ;;:: 1"'*llg,l.
= Ix"1 Ifs Ig(8)1,u(ds)P
From this we see that Ig(')II+1/. E LI so that the function g.(-}
= Ig(.) (I+'/"/o:(g('» is in L., and moreover,
. J '
Ig.:. = Us III(s);'+;;p(d.r) ;;
. . .
;;:: 1.,*I,+;;ip(8}".
Thus
1. 1 11. I 1
Is [g(sJIH.+.,p(ds) = "'*(112) Ix*lIg21. :::: Ix*1 +.+"p(S)...
Proceroing inductively by defining
.. .
gn(') = [g(')j'+"+-"+;;;",(g('»
it is seen that
1 1 I
(ii) Is 111(8)11+.+ .+", peds) s; 1"'*1 1 +.+--'+"p(8)",
n = I, 2, . a u
Since p > 1, I':_ol/pn = q, and Fatou'8 lemma (IIl.6.19) gives
Igi. ix*l. On the other hand, Holder's inequality (III.B.2) gives
[",.[ Ig!.. Thill< Ix*1 = Igl.. .. *
The mapping 3:* -+ g is then a one-to-one lsom trie map of L'IJ
into L.. It is c"ident from the HOlder inequality that any g £ L. deter-
mines an 3J* €- L: satisfying (i), so that the mapping m* g is a
one-tO-Dne isometric map of L: onto L(]. Since the linearity of the map
i. evident, the theorem is proved for the case peS) < 00.
Kow let (8,E,I-') be an arbitrary positive measure space, and let
E consist of those 8et. EEL' with p(E) < w. For E £ E. let L.(E)
b the closed linear manifold in Lp consisting of those functions which
* .. f * t
vanish on the complement of E. Let IX E be the restriction 0 x 0
L.(E) so that if E £ LI there is. by what we have already shown, a
gEEL.(E) with
.
= 1",*I{x.",(g)}.
1+1 I
;;:: 1"'*1 .p(S)..
"':1 = IsgE(8)f(s)p{ds), fEL.(E),
IgEI. = !x 1 ;;:: Ix*l. E EL"
lt is clear from the uniqueness of the function gE that if A, B . LI
then gAls} = IIB(8) = gAB(B) for p-almost all s in AB. Thus IgEI:
= h!gE(S)[.I'(ds) is a non-negative additive set function defined for
288
IV. SPECIAL SPACES
IV.8.2
IV.8.B
SPACES L.,CS. X.".
289
I"' .I ....SUp 1"':1;:;> 1"'.1.
EIf.I'J..
PROOF. Let X**.: (L:)*. By Theorem 1, L: is isometrically iso-
morphic to La, so that there is B functional y. £ L: such that
'1'..('1'*) = y*{g)
when /I and x. are connected. as in Theorem ], by the formula
E . 1:,. Consequently, there is a non-decreasing sequence {En} C 1:,
with
Since CEJS) = CE..,(S) 1'-a1most everywhere on E. the limit /I(s)
= lim"g" (8) exists I'-almost everywhere and vanishes on the com-
plement o'f F = U:_1 En. It follows (111.6.]7) that
1111. = lim I/lE.I. = sup 1'1':1 ;:;> 1"'*1.
n E£r[
If E .1:, and EF = f. then EE. = f for each n, and IgEVE I: =
Ig"I:+IIIE,I:- Since IgE):.... sup IgEI:. we must have IgEI ' 0 if
E<i:,
EF = f. Hence, if f 0 J.,,(E) for some E 01:" we have
rr*f = J s f(8)II(8)/l(ds),
f.L..
Applying Theorem I once more. this time to L: and L., we find there
exists an h E: L such that
'1'*/ = "':1 = JEIIE(8)f(8)I'(ds)
= JE FIIE\S)f(s)l'(ds) + JEFgE(8)f(8)/,(ds)
I" FgE-F(S)f{8)l-'lds) + I"FCEF(8)/(S)I'(dsl
= IEF IIEF (S)!(S)I'(ds).
Since CEF(s) = liE (s) p-almost everywhere in
IIEF(8) = C(8) l'.al';;o8t "'"erywhere in EF. Hence
Eo1: l ,
y*f = Is h(s)f(8)I'(ds), f. L..
Thus ",..(",.) = y*(g) = Jsg(S)h(8)I'(ds) = ",*(h); i.e., for each
"'**oL:* there is ,m hoL. such that ",**(",*) = ",*(h). Thus L. is
reflexive, Q,E.D.
8 COROLLARY, II I <. p<. 00 tlu! B'pace L.(S, 1:, 1') U weakly
e(J11lph'k.
PROOF. This follows from CorollRry 2 and Corollary 11.8.29.
Q.E.D.
EEnF = EE.,
If f 0 L.(E) for
4 COROLLARY. III <. P <. 00, a sel in L.(S, 1:, 1') is WMkly Be-
IJW!ntiaUy compact if and only il it iB bounded.
PROOF. Thi8 follows from Corollary 2 and Theorem 11.8.28. Q.E.D,
Next we consider the problem of representing the conjugate space
L: when p = ]. A result analogous to that of Theorem 1 may be ob.
tained by assumiog that (S, 1:, p) is a a-finite meaSUre space.
... 5 THEOREM. II (S.1:, 1') is a positive a-finite measure B'pace,
/herds an isometric iromorphism bebct:en Lt(S, 1:, p) and L (S. 1:, p)
in which coTTe8pOnding vectorB ",* and g are related by tlu! idtmlity
..*f = IEFg(B)f(s)p(ds) = Is g(S)f(B)[1(ds),
Since U "<I, L.(E) IS dense in L by III,8.8 and the right and left
:sides of the last equation are both continuous in I,
J:*I = Isg(s)/(B)p(ds),
foL..
",*f = I s II(B)/(B)[1(ds).
I. L 1 (S.1: , 1').
It has been shown that Igl. ;s; 1"'*1. On the other hand it follows from
Holder's inequa1ity that JX.I Iglqo Thus,x$ g is an isOmetric map
of L: into L.. The remainder of the proof is identical witb that given
above for the case peS) <. 00. Q.E.D.
2 COROLLARY. II I <. P <. 00. t/ui B'pace L.(S, 1:, I') is reflr.xitV!.
PROOF. First assume [1(S) < 00. Then the steps in the proof of
Theorem I apply without change through the point where we obtained
the inequality (ii) in that proof. For p = I tbis inequality becomes
Is Ig(s)I'p(ds) 1"'*lnp(S), n = 1,2, ....
If we let E", be the set where Ig{s)1 ;;; m, thIs shows that m.,u(Em)
,
290
IV. ,SPECIAL SPACES
IV.8.6
IV.8.7
SF ACES Lp(S, r. pJ
291
:S: 1",-lftp(S); i.e., [P(E,.)/p(S)]lIft :S: lx-11m. Letting n -+ 00, we find
that p(E m ) = 0 if m> ''''-'' Thus Iglm :S: 1"'-'. It is obvious that
1"'-1 :;; Igl"" and so 1"'-' = Iglm.
Now suppose that (S, I. p) is ,,-finite, and let Eft be an increasing
se __I}" f measurable sets of finite measure whose union is S. Using
the theorem for L.,(En) = L.,(E A , I(E.). p), we obtain a sequence
{gn) of functions in L", such that Igftl", :S: 1"'-1, gn(s) = gA+I(8) for p-
almost all 8 in Eft, and
the closed sub.pace L I (E) = 4(E, I(E), p) of L I (S, I, p) consisting
of aU functions vanishing outside E. If we can find an f L,.(E) to
which (fn) converges weakly, we will have shown that4 is weakly com-
plete. Since {fft} is a weak Cauchy sequence in LI(E) (by [J.3.11) the
whole argument may be madc in the space L I (E). Thus, without loss
of generality we may assume that (S,:E, p) is a-fmite.
By 11.8.20 the sequence {fn} is bounded in L I . Since thc charac.
u-ristic function of omy E I is in Lm(S, I, p), the number leE)
= limn '" hfA(S)p(ds) exists for each E in I. It follows from III.7.2
that). is p-continuous. Thus. by the Radon-Nikodym theorem
(111.10.2), there is a function f in L,.(S. I, 1') such that
"'.f = J gn(s)t(s)p(<I8),
E.
for every f in L} which vanishes outside En. Let g(s) = lim gn(S) so
that g is defined almost everywhere. IgJ", :S: I"'.'. and .
"'.UE f) = J g(S)XE (8)/(8)1'(<18), 1 £ 4, n 1,2. . . .,
n S n
Hm JEfA(8)p(<I8) = f"/(s)p(ds),
n '"
E I.
where XE is tbe characteristic function of the set En. Since. by III.6,16
If-x,,)I: -+ 0 as n -+ 00, it is seen that
",.f fsg(8)/(8)p(ds), f € L,..
It is then clear that 1"'-' :S: Iglo>' and since it has been shown that
Igl", ;;;; lx-I, there i8 ar! i80metric correspondence between Lt and L",.
The linearity of this correspondence being evident, the theorem is
proved. Q.E.D.
Remark. It is a matter of some importance in the study of locally
compact groUP8 that the preceding theorem remains valid if S is the
union of a (possibly uncountable) collection of disjoint subsets {S }
in I each of which i8 a-finite and such that if E I and peE) < 00,
then E has non-void intersection with at roost a countable number of
the sets Sa' and such that p(K) = 0 for every set K in I for which
p(KS a ) = 0 for all 0:. The prereding argument 8hows that a function
the uniqueness has been demonstrated for IIIIY ,,-finite space, the
uniqueness on S follows from the fact that any set of finite measnre is
contained in at most a. countable union of the Sal which is a a-finite
set.
Hence
(i)
lim fsfn(s)h(s)p(ds) = Js/(s)h(s)p(ds)
A m
for every p-simple function h. Since, hy 11.3.20, tbe sequence {f.) is a
bounded sequence in L I . it will follow from Theorem 11.1.18 that
equation (i) holds for every h in Lw as soon as it is shown that the
/A-simple functions are dense in Lo;"
Thus let E > 0 and let h be an arhitrary element of Lm' We may
suppose without loss of generality that h is bounded. Let AI' , . .. A.
be a finite coJJection of disjoint Borel sets in the field of scalars, each
with diameter less than E, and such that hIS) C UA,. Let 0:, E A"
B, = f-l(A,), and h.(8) = <1-, if S € B,. Then by 111.6.10, and IH.5,17,
h. i. a p.simple function and Ih-h.l", < E. Thus equation (i) holds for
every h in Lm and the desired conclusion foJJows from Theorem 5.
Q.E.D.
6 THEOREM. Th£ space L}(S, I, p) is weakly oompleU.
PROOF. Let {fA} be a weak Cauchy sequence in 4. By IH.8.5,
there exists a ,,-finite set E E :E such that all the functions f. belong to
7 THEOIllEM. A 8t'tjIUtICe (fft) in 4{S, I. p.) is a weak Cauchy
8equence il ami rmly if it i. bounded and IIu: limil lirn,.J,dA(s)p(<I8)
e:ri.ls for every E in I. Th£ sequenre {fA} converges weakly 10 an elemenl
fin L} (S, I, p) if and only il it is bounded and
f"ll S )p{ds) = lim f"fn(S)p.(ds),
"
E :E.
292
IV. SPECIAL SPACES
IV.8.S
IV.8.10
SPACES Lp(S.X.pJ
293
PROOF. In the final two paragraphs of the proof of Theorem 6 it
was shown that a bounded sequence in (S, I, 1') converges weakly
to an element fin LJ(S, I, 1') provided that J"fn(8)P-(ds) -7 f"f(s)P-(ds)
for every E in I. To prove the necessity of the conditions, let {In} be a
weak Cauchy sequence in (S.I, p). In view of Theorem 6, the se.
quence {In} converge> weakly to a function f in (S, 1:, 1'). Since for
each E in I the iutegral ["f.(s)p(ds) depends linearly and continuous-
ly on f, we have [Ef.(8)P-(ds) -+ ["f(8)p(ds). The boundednessof {I.}
follows from the principle of uniform boundedness (II.8.27). Q.E.D.
8 LEMMA. Let 1: be a v-field of set3,1: 1 alJUbfidd of 1: determining
Ihe u-fieW 1:, and {,u.} a ""querw<' of c""n!ably additive set jwne:ions de-
fiwed I>n 1: ."ilh values in a B-apace :E. Suppose IIuU 1M oowlWble addili.
vily of Pn is "niform in n, and that lim p.(E) exim for E .1: 1 , Then
Hm p.(E) ea:ists for E .1:. fl-+m
.....'"
lim L)(8)!-'(ds) = 0
fl
PROOF. Let 1:. be the family of aU sets E in 1: for which
lim p.(EF) exists for each F .1: 1 , and let 1:. be the family of all setsE
.....'"
is unifonn for f in K. Assume now that K is weakly sequentially com-
pact. It follows from Lemma II.8.27 that K is bounded. If the inte-
grals J ,d(8 }p( d8) are not countably additive uniformly with respect to
f in K there is a number e > 0, a decreasing sequence En .1: with a
void limit. and functions f. in K such that 'J E f.(8)P-(ds)j ;;., e for
n = 1, 2, . . .. Since K is weakly sequentially compact it may be as-
sumed that {In} is weakly convergent. The limit lim,,-+ JEfn(8)P(ds)
then exists for each E.1: and Corollary III.7.40 is contradicted.
Conversely. suppose that K is bounded and that the integraJs
h/(')p(ds) are countably additive unifonnly with respect to f in K.
Let I.' K and suppose that 1/.1 C for n = I, 2, . . .. By Lemma
III.8.5 there is a (J-finite set Sl in 1: and a sub v-field 1:. of 1:(S.) which
is generated by a denumerable field 1:0 = {En} such that the func-
tions all vanish outside of Sl and {In} C LJ(SI' 1:.. pl. We now, by the
Cantor diagonal process, choose a subsequence {g.} of {In} 8uch that
the limit
in 1:. for which EF E 1:. for each F .1:.. It is clear that if F 1 and F.
are elements of 1:., then F.F. .1:.. It is also clear that if F. . 1:., then
S-F 1 E1:., and that if Ft. FoE1:. with FiF. = r/>, then F. UF..1:..
It follows that I. is a !reld. If {F.} is a sequence of disjoint elements of
1:. with union F and if E. E 1: 1 and E E 1:.. then, by hypothesis,
lim I:_IP.(F.EE l ) = 1,.(FEEl)
A(E) = lim JEg,,(B)p(ds)
.-+
m-+
exists for every E in 1:0' By Lemma 8 the limit J.( E) exists for each E
in 1: 1 , Thus. by Theorems 6 and 7, the sequence {g,.} is weakly conver.
gent in L l (Sl.1: 1 ,P)' Since (S..Il' p) is a linear 8ubspace of
(S, 1:, p,) the sequence {g.} is weakly convergent in L,.(S, 1:, Jt).
Q.E.D.
unifonnly in n. Since lim p.(F.EEl} exists for each k. it follows by
.-+
n
IU COROUARY. If {I} i. a lamily of fu-ndtons in L l (S.1:. p)
whuh is weakly 6CtJUCRtially compact, thm the family {If(')1} is 000
weakly sequentially cDmpacl.
PROOF. First, {If(')I} is clearly a bounded set. By Theorem 9. it is
sufficient to show that if E. is a decreasing sequence of sets with void
intemrlion, then lim,, h.lf(s)lp(ds) =0 uniformly for f in the
family K = {I}. If this is not the case, then one of the statements
lim f 18i'/(8)lp(ds) = 0, unifonnly for f. K.
n-+ Ell
Lemma 1.7.6 that lim ,u..(FEE l ) exists. Thus 1:. is a a-field. Since it is
clear that I. ;;! II' we conclude that 1:.;:) 1:, from which the desired
result follows. Q.E.D.
9 THEOREM. A subset K of Ll (8, I, p) is weakly seqtID1/ially
compact if and only if it i8 bounded and the COU1IIi1hleaddilivity of tM
integraI.. fEf(s)p(ds) i. uniform ."irh respec! 10 f in K.
PROOF. The statement that the countable additivity of the inte-
grals JEf(s)p(ds) is uniform with respect to f inK means thatfor each
decreasing sequence (E.) in I with void intersection the limit
and
,
294
IV. SPECIAL SPACES
IV.S. n
IV.8.I2
SFACES Ll'IS,E,p)
295
lim J lJ'/(8)J,.(ds) = 0, uniformly for f "K
n w E.
p(E.) -+ 0 and JE.I.(8)I"(ds) ;?; E. We may and shall assume that {1ft}
is weakly cOn\'ergent and thus that the sequence {jEI.(s)p(ds)} con-
vfl'gf'S for each E in J:. Thus 111.7,2 gives the desired contradiction.
Conversely, if peS) < 00 and if the I,-continuity of the integrals
JE/(8)p(ds) is uniform for I in a bounded set K then the countable
additivity of the integrals is uniform with respect to I in K and. by
Theorem 9, K is weakly compact. Q.E.D.
is false. We may suppose, without loss of generality, that the former
does not hold. If E" E,I' K, and we define E+ = {8" EIJP/(8) ;::" O}
and E = (8" EIBi'/(s) < 0), then
I" 1Bi'/(s)l,.r ds ) = IE. Bi'!(s),.(ds) - IE"" Bi'/(s),.(ds).
Since there exists an E > 0 such that for each fl. there is some If/.. to K
such that J ".lBi'/ft(s )1/'(ds) :2: E, we can find a subset Aft of Eft such that
II...I.(s)p(ds)! ;::" ff2.
Since K is weakly sequentially compact, a subsequence of {1ft} con-
verges weakly, and it may be a8sumed without loss of generality that
{1ft} itself converges weakly. By Theorem 7, {J,dft(s),.ids)} converges
for each E" E.
Let
12 THEOREM. Let fft C01I:iJerge weakly 10 f in L1(S, J:, ,.). Tium 1ft
"""verges slrongly 10 I if and only il 'n com>erges in ,.-mI'll8I.... to I on
roery measurabk set of finite measure.
PROOf'. If Ifft-fl --+ 0 then Theorem III.3,6 shows that 1ft con-
verges to f in fl-measure. To prove the con,,"erse l observe first that
since 1ft approaches I weakly the sequence {In-I} is weakly compact
and thus the sequence W.(')-I(.)I} is, by Corollary 10. also weakly
compact. Then, by Corollary n, the ,.-continuity of the integrals
J"I/.(8)-/(s)I,.(ds) is uniform in n. Since In-I converges to zero in
p-measure on every measurable set of finite measure it follows from
Theorem III.3.6 that JEII.(s)-1(8)1,.(ds) -+0 for every set Eoffinite
.u mea.sure. Now, since the functions t, In' n = 1,2" a a ., are p-inte
grable they all vanish outside of 80me a-finite set E. Let {Em} be an
increasing sequence of sets with union E and with J-'(Em) < 00. Since
the sequence {[/.(')-f(')I} is weakly sequflltia1ly compactthcre is, for
each E> 0, an m (Theorem 9) such that
f 1/.(') - l(s)I,.(ds) < 8/2,
5-E>OJ
1(')lp(ds) -+ 0 as n -+ 00 there is an neE) with
n= 1,2,....
A,,(E) = IE I/n{S)],.(ds), A(E) =" 2 :: .
Then, since ca(S, J:) is a B-space (cf. Section III.7). A is in ca(8, E).
Since each set function J"/ft(s),.(ds) is clearly A-continuous, it follows
from 111.7.2 that !im JEI.(B),.(ds) = 0 unifonnly in n, Since En is a
A(E)_O
decreasing sequence with void intersection, .A(En) --J. 0, and since
A,. Eft, itfollows that A(A.) --+ O. Hence !im J.. fft(s),,(ds) 0 uni-
n
m_m
fonnly in n. contradIctlDg the inequality !JAj.(s),.(ds>l 8f2_
Q.E.D.
11 COROLLARY. If a sel K in L1(S, J:,,.) is weakly uqumlially
compacl lhen
Since I IM8)
Em
II. - Ii = Js-E 1/.(s) - f(S)lp(ds)
n + I I/ft(S) - 1(8)1,.(ds) < E,
En
and thus Ifft-/I-+O. Q,E.D.
n :2: n(£),
lim r I(s),.(ds) = 0,
IE1_0 a E
unifonnly /01' f inK. II p{S) < 00 thn1 conl'<'rsely Ihis condition is sulfi-
cient lor a bounded 8el K to be weakly sequmlU2Uy CVlnpad.
PROOF. LetK be a weakly sequentially compactset in Ll (8, J:, fl)'
n the p-continuity of inUgraJs JEI(s)fl(ds) is not unifonn for f in K
there is an £ > 0, a sequence {En} in J:, and a sequence {1ft} in K with
13 COROLLARY. If eN'Tg point hM lion-zero mrosurr 1M" weak and
strong convergence of sequences in L 1 (8, E,,.) are t/u; same.
PROOF. Let In converge weakly to I in 1-,,(8, E, ,.). Since /ft, I are
integrable, 'n(8) = I(s) = 0 for any point 8 with ,.({s}) = 00. If
o <1l({8}) < ro then
296
IV. SPECIAL BP ACES
IV.8.I4
IV.8.17
SPACES L,,(S.E.,.,t
297
p,(E) pIE),
E L.,
1I1.2.20(a) that IJ s /(8)A(ds}i -<:: IfII},l. Thus, equation [.] does define
an element ",.. L:'(S, E. 1') with- 1"'.1 1A1.
If E" i = 1, 2, . . ., n are disjoint sets in E , with _IIA(E,)I
> l.:tl-', let "'I' . . ., 0;" be scalars with 1",,1 = 1, ""A(E,) = I}'(E,)I,
and def"me f = I l (tiXE.' where XE is the characteristic function of
E. Then f' Lw(S, E, 1'), If I = 1 and 1"'*1 ",*f 1),1-" Thus 1"'*1
= IAI.
lt is clear that the map), --> ",* of ba(S, E " ,.,) into L:'(S,E, p}
defined by [.] is one-to-one. To seethat an arbitrary ",* in L:'(S, E,p)
is the correspondent of some}. in ba(S, E I , /101), let },(E) = X.XE for
E,E" and let f,Lw(S,E,II). Then If.-/I <., while "'.1.=
Is 1.(s)A(ds) is evident. Thus. allowing. to approach zero, Is I(s).:t(ds)
= "'*1, Q,E.D.
Next we turn to the study of compactness in L" spaces. There
are various types of criteria for compactness that can be given. First,
we give a quite general criterion based on Lemma IV.5.4, which, how-
ever, is somewhat difficult to apply to specific cases.
17 DEFINITION. Let (S. E, 1') be a positive measure space and
let II be the set of all finite collections '" = {E" . . ., En} of di8joint
sets in E with finite positive meaSure. Let II be ordered by defining
:n: $:. n: 1 to mean that every set in :n is, except for a set of measure
zero, 8. union of sets innl" For everyll = {E1.'. a.1 En} E 1I and every
function I on S which is integrable on every set of finite roeasure.
define the function In by the equations
p({s})fn(s) = I fn(s)p(dsl --> I l(s)p.(ds) = p.«sl)I(8),
j.l} t..
and so In(s) I(s) for every point 8 satisfying 0 <p({s}) < 00. Thus
(III.6.13(b» In converges in measure to f on every setoffinitemeas.
me. Tbe desired conclusion now follows from Theorem 12. Q.E.D.
14 COROLLARY. Weak and 8Irong convergence 01 se<[IU!11.Ct:8 in I.
llre the same.
15 DEFINITION. Let (S, E, p) be a positive measure 8pa.ce. Let
E. be its Lebesgue extension, and let E, be the family of all sets
E!;;" S for which AE, E. for every set A, E with pIA) < roo C]early
E) is a a-field containing E. The function PIon E) defined by the
equations
= WI E E.l-EI
i8 a countably additive extension of I' from E. to E" The space
ba(S, E, 1') i8 the space of those bounded additive functions on E
which vanish on sets of p-measure zero. The norm of .an element in
ba(S, E, 1') is its total variation.
Ihhould be IWted that if (S, I, 1') is a a-finite measure space then
(S, E.. I') = (S, E I , /101). If S is the set of integers, E the set of all
subsets of S, andp(E) the cardinality ofthe set EoE, thenL",(S,E,p) .
is simply Iw. Th theorems concerned with L", to follow therefore
apply to I w as welL
16 TUEOREM. ThEre is an ioom£lric isrmwrphimr. IJebDe£n
L:'(S. E, 1') and ba(S, I" 1',) determined by the idrntiry
[*J "'*1 = I s f(8).:t(ds), I' L",(S, E,p.).
PlIOOF. Let Ie Lw(S, E,p). Then, there exists a p-nuJl set N
such that I(S-N) is bounded. The set I(S-N) is therefore contained
in the union of disjoint Borel sets AI' . . ., A. in the field of scalars,
each of diameter less than R prescribed positive number E. By Theorem
111.6.10, the set E, = j-'(A,) is in El' If we let "',' A, and put
I.=E""XE" then If(8)-I,(s)1 < .foruS-N. Since, for},oba(SI,I " p.,),
each p,-null set is a A-null set, it follows that I is ),-measurable. Since
I is ),-essentiaJIy bounded, it is )'-integrable. It follows from Theorem
fn(8) = 0
'n(B) = p( ,J E.'(8)plds)
n
if s U E"
<-,
if 8E E j .
and let U.J = In'
18 THEOREM. I.t:! 1 ,;;;: p < 00 and let Un be the map delined in
the preceding definition. ThEn a bounded set K in 4,(S, E, p) i. c01idi-
tionally compMt if and rmly if Em,. U,j = f unilmmly on K. II
p(S) < 00 the critrrion is also valid in Lw(S, E, 1').
PROOF. Let I ;;;; p < 00, let XE be the characteristic function of
E, and let I' L.IS, E, 1'). Then for", = {EI' _ . ., En}, we have
,
298
IV. SPECIAL SPACES
IV.8.I11
IV.8.20
SPACES L (8. r.,to)
21111
.
U,j = I :p(E,) l IE I(s)p(ds)\ lE,'
i-I f
n i '
jV,j1 :;;; !f(8)lp(ds)p(Ei) 1+;.
.=1 E..
Thus. from the Hijlder inequality (III.9.2)
(a) r: If(a:+y)-f(y)I'dy=O uni/ormly for f K, and
(b) 1 f: + r If(y)i"dy = 0 uniformly for f.K
PROOF. Suppose K ;s conditionally compact, Then K is bounded.
Let. > 0 be given. By 1,6,15 and 1I1.9.8 we can find a finite set of
.u-integrable simple functions gi' . , ., gN such that for each I . K there
exists some i with !f-g,1 < E. By 111.7.1, we may 8uppose that each
g;J is a. linear C!ombination of chal'a.cteristic functions of intervals. Sup-
posing this. it follows that all the functions gl' . . .J gN vanish outside
some sufficiently large interval [-A.,+A.], so that
J: + r If(y)l"dy = L'" + C: If(y)-g,(y)I'dy
:;;; I/-g,:' :;;; .'
IV,j1 :;;; i [f If(s):'p(ds) ] II. <: Ifl.
f-I 1£,
Since V n has a finite dimensional range it maps bounded sets into
conditionally compact sets. If" = {El' . . .. E.} and f = I; llX'lE.'
then Un) = I for "1 :2: ". Thus Unl f for simple functions. Since
IV.I :;;; 1 it follows by III.8.8 that Vnf f for all f in L.(S, E.p).
Hence if 1 S P < <XJ. the theorem foUows from Lemma IV.5.4. If
peS) < <XJ a similar argument proves the desired result in Loo(S, I,p).
Q.E.D.
If S is n-dimensional Euclidean space. E the field of Borel sets in
S and I' Lebesgue measure. more applicabJe condiuons may be given.
For this purpose we need the following Ienuns.
19 LEMMA. II I' is a regular finitely addititoe set fllf4Ctwn on a
fieldIcftrrdi8et.of a normal spaceS, then, lor 1 ::;;; p < 00, the functions
in L.(S.I.p) ...hickare bmmded andct>ntinuous are dense in L.(S,E,p).
PROOF. SinCf" It-integrable simple fUJ1ctions are dense in
L.(S, E, p). (III.3.8). it suffices to prove thatthe characterist;cfunc-
tion of a set E £ Ewith v(p, E)< 00 may be approximated by bounded
continuous functions in L.(S, I, 1'). Let Fl' F. be sets in E with
PikE. PokE'. and
v(p. E-F I ) < E. v(p, E'-F.) < E.
By Crysohn's theorem (1.5.2) there IS a continuous functIon f on S
with 0 ::;;; I(s) ::;;; 1 and with f(.) = 1 for. in PI and f(.) = 0 for 8
in p.. Thus
Js It(8) - lE(s)I'v(p, ds):;;; 2". Q.E.D.
20 THEOREM. Let S be the reala>:is, 8B the field of Borel subsei3 of
S, and p the Lebesgue meLIS'!tTC of sers in 1ft. Suppose 1 s P < <XJ. Then
a subset K of L.(S, !ltJ,p) is condi!ioJlclly comp&;1 if and only if it is
bounded and
for A ;;;:; Ao, prm'ing (b).
To prove (a) we note fir8t that it IS evident that
f +"' 1 .
lim _00 X(a:+Y)-X(Y),"dy = 0
. o
if X is the characteristic funct;on of a finite interval. Thus
Iirn J.::: Ig,(a:+y) - g,(y!l'dy = 0 for each function g,; and hence
"..0
Ii p r: If(a:+Y)-f(y)I'dy :;;; Ii':,': p r: If(a:+y)-gj(a:+y)!Pdy
-t- Ii", sup r: If(y)-gj(y)j'dy
.->0
+ lim sup f +'" Ig;(a:+y)-gj(y)I'dy
:r-=.-O _00
= 2!/-g,l'
2tJl,
uniformly for f. K. Thus (a) ;s proved.
To prove the converse, we argue as follows. The measure J1 is the
unique Borel measure defil1fd by the condition p([a. b]) = b-a for
each interval [a. b]. Hence p(a:+E) = peE) for each Borel set E. It
follows by III.1O.8 that the operator T. defined by the equation
(T.f)(y) = f(y+:r) defines a map of L. into L" and that IT..!I = III.
Since lim IT.I-T.fl = 0 is evident if f is the characteristic function
.-.
800
IV. SPECIAL SPACES
IV.8-20
IV.8.21
B}>AC£8 L.IS, E*,..I
801
of a bounded interval. it foUows by 111.7.1 and 111.8.8 that
lim IT.I-T./I = 0 for all I .L . Thus. for each fixed I, T./is a cantin-
......
uous function of the real variable x. Assumption (a) states that
lim T.I = I uniformly for I in K. Let
. o
1 f +.
J.I = - T.ldy;
2a -4
Since T.T.I = T.+-I = T.T.I, it follows, from 1I1.2.19(c), that
f I f +. ] I f +.
T.J.I = T. - T.lelm = - T.\T.f)dx = J.(T.n
_2a 2a --a
then, by 111.2.20(0),
IJ.t-/I ";; sup [T.I-/I,
---A:SZS+Q
for I. Lv If , > 0 is given, we can find . so small that IT.f-/1 < 6,
for Iyl < . and I. K. Then for each fixed a> 0,
I(J.f)(x+y)- (J.f)(")1 = [{J.(T.I-f)}(x)1 = 14>:.(T.I-f)I
< <\ (2a )_l/ .
Therefore, for each a. the set offunctions J.1, I . K, is uniformly equi-
continuous.
Let e > 0 be given. Choose a so small that IJ./-/I < e for I E K.
Choore A so large that
f + f: m 1/(a:)!'elm < e, for I. K.
Then, using Theorem 6.17, and 1.6.15, choose a finite set of continuous
functions 111, . . ., gN defined on the interval [-A, + A] 8uch that
Ig,{a:)-J.1(a:)1 < eA-U' for -A ;;;., ,,;; A. Then, if we put .,,(11') =
g,(a:) for 11'. [-A, +A] and v,(w) = 0 otherwise, it is evident that
v,. L.. and that If-v,1 < 8.. Thus the conditional compactness of
K follows from 1.6.15. Q.E.D.
Theorem 20 may readily be generalizOO to Euclidean n-space.
We will state the generalization. leaving the appropriate modification
of the details of the proof of Theorem 20 to the reader.
21 TIIEOREM. Let 8 be Euclidean n-3pace, fJ6 the lield 01 Borel
8tI1Isets of 8. and I' 1M Lebesgue mea.mre 01 sets in fJ6. Then a subset K
01 L.(S, fJ6,I') is c01ldilionally compact if and only if it is IHmndtd and
1M lolWrcitl{! limits are ..nifor'" 1()1' 1 in K.
(a) lim r ...rmll(a:'+Y"""'-".-rY_)-/{y"""Y.)I'=O,
:rc -O. .z._o _aJ _G>
and
(b) lim J If(y)I'dy = 0,
.It-Jo-G> s-c.A
so that J,J -+ f uniformly for I. K as a -+ oc.
Since T.f ]s continuous in :JJJ the function h" defined by
h,,(a:) = T'.J,J for ialn ";; a: < {i+1)aln, i = 0, :1:1. :1:2,. .., con-
verges to T fJ;f unifonnly on every finite interval of :11. Hence
1 ,-+0 1 n-l
J.I = lim - J h.(,-,,)dx= lim - ! T,.I,
11-+(P 2a -0 2an 1--n -;;
where the limits are to be taken in the metric of L . By 111.8.6 and
III.6.J8, on passing to a subsequ,,"ce {n,} of I, 2, . . ., we have
1 _.-1 ( ia )
{Jot)("') = lim - ! I - + '-"
f-HP 2aJ1 1__11, n
tor p-almost all a:. If I is continuous, the limit on the right is evidently
1 f H J f o+o
- f(y+a:)dy = - t(y)dy.
2a -a 2a 3:-iJ
Thus if we define the element 1>:.E L. by putting .... (g) =
. II Y"ft Z
(1/2a>J ::g{y)dy for g. L , then by Theorem 1 14>:..1 = (2a) II , and
we have (J,J)("') = 1>:.1 for - ro < a < -t- 00, 1 continuous and be.
longing to L., and I'-almost all "'. By the preceding lemma there is a
sequence {t.} of continuous functions converging in L. to I. Then
J.1. -+ J.f and 1>:j. -+1>:.1. If we choose a subsequence by IIl,6,18,
we can also have (J./.){,-,,) -+ (J.1){a:J for almost all.,. It follows that
(J.1)('-") = 1>:.1 for almost all 11'. Since the function on the left of this
equation is only defined modulo null sets, we an take this equation to
hold for all a and x; i.e.,
(J./)(",) = <1>:.1,
-co <1l X < +00,
I.L .
wMre C" is 1M cube -A ,,;; "'I'...' w. A.
The ultimate generalization of this line of thought is the generali-
zation to arbitrary groups with invariant measures, a topic which is
discussed in Chapter XI.
302
tv.. SPECIAL SPACES
IV.8.\!2
IV.8.\!4
'sPACES L"IS. E,,o}
303
We now append some properties of the space L p which sprmg
from its natural ordering. and which will be useful later. We say that
f < L.(B, £, p) is pfXlitive and write f 0 if f(s) 0 for p-almost all
s . 8. If hand f. are two real or complex valued functions in
L.(B,£, I-')sueh thatfl-f. ;;;:; Owewritef, ;;;:; f.o r f. <::, fl' This clearly
is a partial ordering (1.2.1) in Lv We now establish completeness
(1.12) with respect to this ordenn/(,
the sequence {h.,Js)} is an increasing sequence of real numbers and we
take h(s) = limn lI,.(s). The function h is measurable and since
hIs) :s: go(s) for almost ails, it is essentially bounded. By construction
h is an upper bound for the set U a }. If it is not the least upper bound.
there is a measurable set of finite positive measure E C S. and a
= "10
measurable function h' such that for each <1., f.(s) < h'(s) < hIs)
= h n (s) for almost all s in E. But this violates the construction of
,
h. . Q.E.D.
,
Some additional results will be found in Section n. We 01>..-"..,
tbat L * has been proved in Theorem 16 to be a space of set functions.
and so by 1II.7.6 it has the property that subsets which possess upper
bounds have least upper bounds. Now Lr can be regarded as being
embedded, by the natural mapping ". in the space L *. For a later
application it is important to know that the least upper bound of a
subset in L, is the same as its least upper bound when regarded as a
subset of L *.
22 T>tEOREM. Let (B. £,1-') he a positive measure space. Th£n the
real partially ordered space L (B. £, 1-'), I :::; p < 00, is a complete
lallice.
PROOF. It is evidently sufficient to show that if Ua} is a set of
functions in Lr such that 0 < fa <::, go for some go.L 1 . then sup. U.}
exists in Lr, Further, since go is integrable it vanishes p-almost every-
where outside of a set of a-finite measure. We may t fore suppose
that (B, £, p) is "a-finite positive measure space. Now the mapping
fa -+Aa defined by A.(E) = hfa(s)!'(ds). E. £. i. a one-to-one order
presen;ng map of L 1 (B. £, p) into tne spaee ca(S, £) with its natural
ordering (III,7J. Thus if go is mapped Into Ao' ca(B, £}, then
o <::'Aa :s: ).". Using CorollaryIII.7.6,let P = sup {A.}. i.e.. pistheleast
upper bound of tbe set {Aa}' Hence v . mIS, £J and 0 <::, A. <::, p ,;; .
Since is I-'-continuous so is p and the Radon-Nikod:fm theorem
(111.10.7) implie8 that there isanh. L 1 such thah(E) = JEh(S)p(ds).
The fact that h = SUPa (fa} follow. from the relation p = sUPa {Aa} and
the order preserving cbararter of the map of L 1 into ca, Q.E.D.
24 THEOREM. Let (B, £. 1-') be a a-finite pos;tive measure spare.
If" i8/he natural isomnric isomorphimn of L 1 = Lr(B, £, 1-') ,..to L:*,
and if (/a} has an 'wper boond in the partially ordered space L I , then
" (suPa {/a}) = sUPa {,,/}.
23 TIfEOREM. If (B. £, p) is a a-finite positive measure spaee,
then the real parrihUy ordn-ed space L",(B, £, pI, is a oomplde /attire.
PROOF. Since (B,£,I-') i>; a-finite it follows that L *(S,E.I-')
= ha(B.E*.I-'), the spaee of all bounded additive functions on the
Lebesgue extension £* of £ which vanish on sets fromE* of p-meas-
uie zero. If f . L 1 . it is readily seen that "f is the set function defined
by ("/)(E) = J,d(s)p(ds), E. E*. In particular "f is countably addi-
tive and I-'-continuous, Suppose that 0 <::'/0 = sup. {/a}' Since "
preserves order it is clear that 0 S A = sup. {"fa} S "fo. the least
upper bound being taken in the partially ordered space batS, £*. 1-').
It follows that A is countably additive and I-'-continuous. so by the
Radon-Nikodym theorem there is a functiong. L,(S, £*. p) such that
A(E) = hg(s)p(ds), E. £*, Since "I; = A :s: ></0 we have g ;:;;;; fo' On
the other hand. since "fa;:;;;; "g, fa < g for each IX. Thus /. = sup fa :S: g
so that /0 = g. Q.E.D. a
We now show that the space of hnear mappings between the L.
spaces also is a partially ordered space. We say that a linear mapping
PROOF. Let S.' £ be such that p(B.) < 00, B. S...., and
8 = UB.. Let la' go < L", be such that fa <::, go. Since L",{B., E. p)
Lr(B.. E.I-') the preceding theorem Implies that there exists an
h. . L 1 (B., E.I-') such that h. is tbe supremum of {/a} regarded in
L 1 (B.,£. pl. In particular. for each <1., fa(s) ;:;;;; h.(s) < g.(s) for 1-"
almost ails < B., and so h.. L",(B., £.1-'). We may take h. to vanish
outsideS. and obtain an h.. L",(B.E.I-')' Now for p-almost alls< B,
804
IV. SPECIAL SPACES
IV.8.25
IV.9.1
SPACES OF SET FUNCTIONS
805
T : L . L. is positive and write T 0 when I E L and I 0 imply
that TI ;;;,; O. Similarly T. ;;;,; T. or T. ;:;;; T. means that T.-T. o.
It is readily seen that if T O. then T maps rea] functions mto rea]
functions.
"
I. = 2 h,.. g. = h..+h".. i = 1,2, k = 1, . . .,...
k-'
" "
SI = 2 S g,;'; 2 T .,g,
f-l i-I
for any decomposition and hence S/ :S T,J, We now show that To is
additive on positive elements. Let I. E L.(S, E, 1-')' I, ;;;,; o. j = 1,2,
Imd let I, = 2 , g,;. I. = 2;-, g" be decompositions of I, and I. into
positive functions. Then I gJj + I g2i is a decomposition of /1 +/'1.'
and 80
T.(/,+I.) .,; T.(fIJ+Tol/.).
To show the opposite inequa1ity, let 1.+1. 2:-,g. be a decompo-
sition of f. +f. into a sum with g. ;;;,; o. By the preceding lemma there
is .(I. set h Jk , i = I, 2, k = I, . . _, n, of positive elements in L (S, I, It)
'with f. = 2:-,h" and g. = h,..+h"., Thus
25 LEMMA. Let (S, E. p J be a positive measure space and let
1 :5: P :5: GO. SuP'fJOJ!€ I. +f. = 2:"lg.. where f" g. are pos;live ekmenls
in L.(S, E, pl. Then tlu?re are posUive dements h,. in L (S. E, pl.
i = 1, 2, k = 1, _ . 0, n, such 'hat
PROOF. Suppose n = 2. Since 0;:;;; f., g. < fl +gI the bounds
inf {jl' gl} and sup {II' g,} exist in L,(S,E, pl. We take flu = infUI' g.}.
hu = I.-h,." hu = gl-fIu and h., = (f.+f.)- sup U.,g,}. The 8tate-
ment follows from these choices for the h.. and the observation that
inf UI' g,} + sup {II' g,} = f. +g..
" . "
To(f.J+To(f.) '" 2 T..lh,.>+ 2 T..(h".) = 2 T..(g.),
11-1 J:=-l .t-l
and since T.(f. +1.) is the infimum of sums of the last kind, we con-
clude that
To(/,)+T.(f.) .,; T.(f. +f.).
Hence To is additive on positive functions. Imd its homogeneity with
respect to positive scalars is evident.
If ft. f., Ih, g. are positive and I.-I. = g,-g. then , , +g. = g,+f.,
Tol1+T"g. T.,g,+T,J. and ToI.-T,J. = T.g.-T.,g." Thus To may
be defined for a rea] function f by placing T,J = T ,JI-T,J. where
II' f. are positive and f = I.-f., This extended function To is a linear
map. and it is clear from the way in which it was defined that it is
the greatest lower bound of the maps T.. Q.E.D.
The statement for arbitrary choice of n follows by induction and the
resu]tforn = 2 bygrouping/,+I. = .I".=;g.+(g.+I:.+l). Q.E.D.
26 THEOREM. Let (S, E. p) 1M a positive measJl¥t' spa,," and la
I :5: P ,,;; GO and I '" q < GO. Then 1M pa1tially ordered sp(UJe of linear
mappings from tlu? Teal sp(UJe L (S, E. p) to tlu? Teal sp(UJe L.(S, E, 1-')
is a Ctm1p1ae lattice. If (S, E, I-') is a-fini"'. the result also holds if q = GO.
PROOF. It is sufficient to show that if {T.} is a set of positive
linear mappmgs, then they have a greatest lower bound To which is
also a linear mapping. We first define T. on the positive elements f of
L.(S, E, p). To do this, let f = 2;'.,,1:, be a decomposition of f into a
finite sum of positive functions g, in L (S, E. p). Set
9. Spaces of Set Function.
In this section we investigate special properties of batS, E), the
space of bounded additive scalar functions on a field of sets, and
ca(S. E}. the space of muotably additive measures defined on a a-field.
The first theorems identify the weakly compact sets of catS. E).
1 THEOREM. A setK C catS, I) i. weakly sequentially compact if
and only if it is bounded and the countable additivity 01 p. on E is uniform
with respect to I-' in K.
.
Tol = inf {2 T.,g,}
.-,
where the infimum is taken over all such finite decompositions
I = 2 g. of f and arbitrary choices of T. . i = 1, . . ., n. It is evident
.
that 0 S; T 01 ;:;;; T.J for any a. Also if S is any lower bound for {T.}.
then
I!06
IV. SPECIAL SPACES
[V.9.2
[V.G.2
SPACES ()F SET FU CTIOSS
807
PROOF. [f K is weakly sequentially compact, then H.8.27 shows
that K is bounded. If the countable additivity of I-' is not uniform for
f' in K there is a decreasing sequence of sets En in E with void mter-
section, a sequence {Pn} K. and.. number B > 0 such that
11-'.(En)I>E.
n= 1,2,....
compact and let M be a bound for the norms 11-'1 of elements I-' in K. It
ill first be shown that for each E >0 there exists a finite set 1-'1. . . "I-'n
mK and ab > 0 such that II-'(E)I < "forevel)'1-' in Kprovided that
v(I-'., E) < b. i = 1, . . ., n. [f this is not true. there is an E > 0 such
that for every 1-',' K there is a .et E,. E and a 1-'. . K such that
I
v(,u" E,) < \;, !".(E , ») ;;:; E.
There also exists a set E 2 E I and an element f.ta in K such that
I I
v(,u" E.) < ..' v(,u., E.) < ..' Il-'a(E.>! ".
[n this fashion sequences (I'.} K, (E.) E are defined for which
The functions ftn are all continuous with respect to the measure de-
fined by
1 v'.. E )
A(E) = L - v-o n> , EeE,
n-I 2 n 1 +v(,u., E)
and thus all belong to the subspace catS, E,.I.) consisting of all
A-continuous functions in oa(8. E). According to the Radon-Nikod)'111
theorem (IH.1O.2) the formula
p(E) = JEI(S).I.(th)
establishes an isometric isomorphism between ca(S.lL.I A} and
LI(S, E, A). Thus the set K' in L,(S, E, .I.) corresponding to K is se-
quentially weakly compact. Theorem K9 shows that the countable
additivity of peE) = h/(s);!(ds) is uniform with respect to I in K'
and hence uniform with respect to I-' in K.
Convenely. suppose that the 8et KC catS, E) satisfie8 the two
conditions and let 1'.' K. n = 1,2, . . .. U8ing the measure A defined
above we have functions In' L,(S, E, J.) such that
p.(E) = J,Jn(s);!(ds), 11'.1 = Ifni, n = 1,2,....
Thus (by 8.9) the sequence {f,,} has a subsequence converging weakly
in L,(S, E, A), Since the spaces catS, E,.I.) and L,(S, E, .I.) are equiva-
lent the sequence {PfI} contains a subsequence weak3y convergent in
€a(S, E. A}, and hence in w(S. E). Q.E.D.
Another useful criterion for weak sequential compactness in
w(S, E) is given in the following theorem.
2 THEOREM. A 8Ubset K C ea(S, E) is weakly sequentiaJly com-
pac! il and only if it is bounded and, lor some pos;live }. in ea(S. E), Ihe
limit lim p(E) = 0 is unilorm with respeel 10 I-' in K.
"(.£)-+0
PROOF. The sufficiency of the conditions as we]! as the necessity
of the boundedness condition follows from Theorem I. Thus let K be
I
v(,u;, E.) < .. '
II-'.+I(E.)I ;;:; ..
Since K IS weakly sequentially compact a subsequence of {!'n}
is weakly convergent. In order to simplify notation We suppose that
the 8equence {P.} itselfis weakly convergent, Let = L::, 2 'v(l"l) so
that each 1'. is Ao-continuous. Since l!'n} is weakly convergent,
lim p.(E) exists for each E in E. It follows from the Vitali-Hahn-Saks
theorem ([[[.7.2) that lim ".(E) = 0 uniformly with respect to n.
Now ..(E)....
i = 1,.. ..'11,
. n 1 l 1 1+111
"a(E.) ;:;; L ----: - + L - M < --,
;=1 2' 21'1 j...n+l 2 ' 2"
and therefore lim,.p",(E.) = o uniformly withR><pect to m = I. 2,....
But this contradicts the fact that 11'.+I{En)1 ;;0- 8 > 0 and proves the
original assertion. Now let 11" > 0 and let p. fi), . . ., p be elements of
K such that Ip(E)1 < I/n for every pinK and every E. Efor which
v(p\n). E) < .. i = 1,.. .. m n _ If ). is tJefined by
(XI m.. 1 I
j! = L L --; --. v(.u nl),
n=l i=] 2 2
it follows from Lemma [[1.4.18 that every I' in K is .I.-continuous. i.e.,
K C catS. E, A). The Radon-Nikodym theorem (III,lO.2) shows that
the fonnula
peE) = J8 / (S)A{J..)
B08
IV. SPECIAL SPACES
IV.9.B
IV.9.8
SPACES OF SET FUNCTIONS
B09
A(E) ..;: SUp IpIE)I,
p,l{
PROOF. In view of Lemma III.1.5 and the formula defining A, the
measure Af4 has the desired properties. Q.E.D.
EEI.
PROOF. Let E be an arbitrary positive number. Sinee pIS) < 00
there is at most a finite set {El' . . ., E SI } of disjoint atoms with meas-
ur greater than E. The set A = S - u :_1 E i th n contains no atoms
baving measure greater than E. It will now be shown that every
measurable subset B of A eontains a set F with 0 < p(F) E. Sup-
pose, on the contrary, that some such set B contains no set of I with
positive measure at roost to. Then B is not an atom and thus contains
a set G. in I with 0 < p(G 1 ) < p{B). The set B -G 1 also contains
no set in I with positive measure at most E, Thus there is a set G in I
.
with G.!;; B-G l and with 0 < p(G.) < p(B-G l ). Continuing induc-
tive1y we obtain a sequence {G.} of disjoint sets of positive measure.
Since II'(G,) < C1) we must have p(G.) < E for sufficiently large n.
This contradiction proves the existence of a set F B with 0 < p{F)
E.
For every set EinIlet{i(E) = supp(H) where Hvaries over a!]
measurable subsets of E With p{H) E. Then, by the preceding argu-
ment, 0 < (J(G) ..;: E for every measurable 8ubset G of A with
pIG) > O. By induction we determine a sequence {F.} of disjoint
measurable subsets of A with
estab1ishes an equiva1ence between catS, I, A) and LJ{S, I, A) and
thus the present theorem foUows from Corollary 8.11. Q.E.D.
3 COROLLARY. Under 1M hypotlu?s;s 01 Tlu?orem 2, A may be
chosen 80 that
4 THEOREM. The spcu;e ca(S,I) is weak!y oompleW.
PROOF. If {p.} is a weak Cauchy sequenee in catS, I) then the
1imit limp.IE) erists for every E in I and, by II.3.27, the sequence
-(p.} is bounded. According to Corollary III.7.4 the countab1e additivi-
ty of p,,(E) is uniform with respect to n = 1,2, . . . and thus, since
{p,.} is a weak Cauchy sequence, Theorem 1 shows that ;t is a weakly
convergent sequence, Q.E.D.
5 THEOREM. A seyrKnCl) -(p.} in catS, I) oonverges weakly (1<> 1')
if and only if it is boundea ant! 1M limit lim p.(E) wisIs (and is equal
10 p( E}) for every E in I. fl
PROOF. Let A be defined as in the proof of Theorem 1. Then
ca(S, I, A) is equivalent to 1-,,(S, E,).) and the sequence
p.(E) = fEf.(s»),{deJ, n I, 2,...
is weakly convergent in catS, E. A) (and thus in catS, I» if and only if
the sequence U.} is weakly convergent ;nLJ(S, I. A). The desired con-
clusion follows from Theorem 8.7. Q.E.D.
.
P(A - UF,) p(F....]) E,
<-]
Vi. = I, 2, . . n
Let Fo=A - U::',F, so that
.
P(Fo) {i(A - U F,) 2p{F"",), n = 1, 2, ....
'-1
6 DEFINITION. Let (S, I, p) be a measure space. A set E. I is
called an mom if pIE) oF O. and if F. I, F!;; E, then either plF)
= pIE) or p(F) = O.
It is clear that if El and E. are atoms, then either ,«EIE.) = 0
or p{E l bE.) = O. Also a finite positive measure space Can have at
mnst a countable family of disjoint atoms.
7 LEMMA. (Saka) Let (S, I. p) be a finir" positive measure spcu;e.
II c > 0 1M-n S is 1M union 01 a finir" 8eqrum<e 01 disjoin! se!.>
EJ' . . ., E.. E such that eadl E, i. either an a!om or pIE,) ,;;; e,
However Ip(F,) ';;; p(A) <: co and consequently Iimp(F.) = o.
Thus, the above inequality 8hows that (J(Fo) = o. Consequently
p(Fo) = O. Let T be an integer sueh that I:-""1P(F,) < E and let
Em+! = Fl' .. .. .., E"'H = F , and Em+r+1 = U :r+l Ft U FQo The .sets
EJ, . . .. E. with P = m+r+I satisfy the requirements of the 1emma.
Q.E.D.
The l1ext theorem is a striking improvement of the prmciple of
uniform boundednes. ;n the space catS, I).
8 TIIEOREM. (Nikoaym) 11111 is a set in catS, E) ana if for ecu;h
E in I Ihere i. an N(E) < 00 such that
310
IV. SPECIAL St'ACES
IV.9.S
IV.9.9
SPACES OF SE't' FUNCTIONS
311
Ip(E)1 <1'1(E},
then there "",ists a number 1'1 < 00 su<h that
Ip(E}1 <1'1, IHM, EEE.
PROOF. If the conclusion is false, then for each integer n there
exist measures JLo' 111 and sets Gfi' E such that Ip.(G.) I > n, Let
), . ea(S, E) be defined by
., 1 V ( " E }
)'(E}= - ,. .. EEI,
1'1=1 2- vtun' S) I
pEM,
for any E . I and all n = I, 2, . . .. The right hand side is independent
of n, contradicting the supposition that there was a set Gfi E I with
Ip.(G.}1 > n for each integer n. Q.E.D.
Next we turn to an investigation of the space ba(S. I).
.
1p,.(E)1 N(E.}+2mo(m-p)
,-,
9 THEORE"'. T 8paCe batS, E) is weakly CDmpUIe. If S i8 a
topological 8fJ<Jff, then Tba(S) i. also wrokly complrlF.
PROOF. Consider the closed subspace B(S, E) of B(S). According
to Theorems 6.18 and 6.20 there is a compact Hausdorff space S] such
that B(S, E) is equivalent to C(S.}. Theorem 5.1 shows that there is
an isometric isomorphism 11). - p between B*(S, I} and ba(S, E),
which is determined by the equation ",*1.£ = pIE}, E E E. Thus, since
B(S, E) is equivalent to qSI)' ba(S, I} is equivalent to Tca(S.)
(Theorem 6.8). But Tca(S]}, being a closed subspace of the 8pace of
countably additive mea.<I1rei on the Borel sets in SI' is weakly com-
plete by Theorem 4. Therefore ba(S, E) is also weakly complete.
Since Tba(S} 's a closed subspace of batS, E), where I is the field
generated by the closed subsets of the topological space S, Tba(S) is
weakly complete. Q.E.D.
The eS8ential tool of the proof of Theorem 9 was the Isometric
isomorphism of B(S, E} with C(S,) where S, is a particular compact
Hausdorff space. \Ve shall now investigate what properties the
existence of this isomorphism implies for 8J and investigate in more
detail the isomorphism of bu(S, E) onto Tca(S,}. This information will
be used to obtain further properties of the space batS, E). Let H
denote the isomorphism of B(S, E) onto qS]) and let E E E. We ob-
serve that if X" is the chamcteristic function of E, then H(X,,) is con-
tinuous on S, and H!x.:>' = H(x ) = H(X,,)' Thus H(xd(8 1 ) is
either zero or one for each 8, E S]' i.e., H(Z,,) is the cbaracteristic
function of a set E, S1" In view of tile continuity ofH(Z,,}, E] must
be both open and closed. One may ask whether the converse is true: If
E, is an open and closed set in S" isH I(XE ) the characteristic function
,
X" of a set E. I? Stated differently, does the existence of the
isomorphism H of B(S, E) onto C(S]) imply the existence of an
isomorphic mapping T of I onto the field I] of all open and closed
sets of SI?
That this is so will be proved in Lemma 10 below. Moreover. it
and consider the complete metric spaceE()') discussed in Section 111.7.
Let
H", (E E I(),)IIp.(E)1 ;'i, m, n = 1,2, . . .1.
so that H.. is a closed set in I()') and I()'} = U.':-I Hm' The Baire
category!h""rem (1.6.9) asserts that there exists a set B. E I(A) and
a number E> 0 such that if )'(E LI Bo) ,,;; <, then Ip.(E}1 ";; ?no for
some integer and a11 integers n = 1, 2 1 . 4 U
Let A bean atomo!)..If F A, FE I, and 0 <v{pfi,F) <v(p,.,A}
for some n, then 0 < )'(F) < A(A). Con8equently, for each n, either
v(p,., A} = 0 or A is an atom of v(!'.). If A is an atom of v(p,.) then if
F A, FE I, and p.(F) oF 0, we mU8t have v(P.. A - F) = 0, from
which it follows that p.(F) =p.(A); i.e., A is an atom of p.. Now let
E > 0 and let E., . . ., Em be a decomposition of S with respect to the
measure A as described in Lemma 7. Let E. E and F. = En E..
k = 1, . . .. m. If EI' . . ., E. are the atoms of the family {E" . . ., Em}
for which A(E,) ., then by OUr remarks above,
I!,.(F.)I ;;;; 1p,.(E.}1 < 1'1(E,), Ie = I, . . ., p.
Now ).(F.) ,,;; E for k = p+l, , , " m. Write
F, = (B. U F.) - (B. -"'.).
Since B.LI (B.u F.J = F.-B. and B.LI (B. F.) = B. n F., it
folloW1; that )'(B.LI (B.-F.» and ).(BoLl (B.UF.)) are at most
equal to ),(F.) ;;:: )'(E.) E. Consequently
Ip.(E.) I 2m", k = p+I" . ., m.
Thus
312
IV. SPECIAL SPACES
IV.9.10
IV.9.B
SPACES ()F SET FUNCTIONS
313
will be .een that Sl is totally di.connected, i.e., the open and dosed
.ets form a basis for the topology.
10 LE...IA. Let S. be a romptJd Hamdorff Bpace stu:h 1/w.1 B(8, E)
i. isometrically isomorphic with C(S.), Then 1M Bpace S. i. uniquely de.
!ermined 10 within a Iwmromorphism and is totally disctmnecred.. The
corresponrkw-e XE -+ XE establish£s an immmphism T of 1M field I' onlo
,
the fieldE, of all open and closed sels in 8" i.e., T(E UF) = T(E) U.-(F),
T(EF) = T(E)T(F), and ..(E') = T(E)' for a!l E, F £ E.
PROOF. A. before, let H be the isomorphi.m of B(S. E) onto C(SI)
given by Theorems 6.18 and 6.20, We have .hown that T(E) is open
and closed for E E E. Conversely, let E. be an}' open and closed set in
8,. We wish to show that the set E = .--I(E.) ;,; in E. Since XE ;,;
E-mcasurable, there exists a finite decomposition of S into disjoint
sets At, . . "I An in I, and scalars Cl 11 . . 0, (X11. such that IXE- -1 (XiX.Acl
< 1/4. We observe fir.t that E r;; U _, A" .ince if s belongs to
E- U _,A" then IXE(s)- ! _,a'XA.(s)1 1> 1/4. We will show
that if EA, #- .", then A, r;; E, from which it will follow that E is the
union of all the sets A, which it contain., so that E E E. Indeed, if
.. EA, forsomci, then IXE(8)- ! _,a'XA.(s)1 = 11-a,[ < 1/4. Thus
la,1 > 3/4. However. if t . Ai and XE(I) 0, then Ix,,(I) - ! _, a'XA,(t)1
= 1",,1 < 1/ 4 , which i8 impos.ible. This show. that A, r;; E, and h€Ilce
that EEI. The fact that T is an iwmorpliliim of I' onto E, follows from
the equations H(l-XE) = 1- H(X.:!' H{XEXF) = H(X.,)H(xF)' and
H(XE+XF-XEF) = H(XEJ+H(XF)-H!xE)H(XF)'
It will be shown next that S, is totally disconnected, If G I is a
non-void open set in S,Iet '-0' G. and let f, be a continuous function
such that 1.(10) = I, and I.(t) = 0 for t in G (cf. 1.5.2), As before, we
select a simple funcuong = !: l ail"" in B(S,E) where Al ""' An I,
such that Ig-H '(fl)1 < 1/4. If 111 = H(g) = I;-. "',X'IA,,' let
VI = {sl!lgl(slJI > 1/2}. Then V. is open and closed and t" E V. r;; G l .
The uniqueness of S, follows from Theorem 6.26. Q.E.D.
II LEMMA. Employi..g the rwlation of Lemma 10, let B(S, E) be
isomerTically isnmurphic Irith C(SI)'
(a) Thereis an isomm-icisomorphism T of batS, E) onto ba(S,. E.)
determined by the curre.pondmce (Tp)(E,) = ,u(..-I(E,)) for ,u in
ba(S, E) and EI in E..
(b) Each,u,. ba(S" II) has a unique emnsio" ro a.-.gular mum-
ably aJditit'f! ,u, in cu(S,. E.) WMT/! E. is the ".field genoated by
E,. Each,u, in ca(S., I.) is regulllr. The correspondence V :,u, p. i. an
isometric isomorphism of ba(SI' I.) onto ca(S., I.).
(e) If E, is in II then v(,u.. E.J = v(V(i<J.), E.) for aU 111 in
batS" E.).
PROOF. Recalling that T is an isomorphism of I onto El' it is
clear that the mapping T is an isometric ISOmorphism of ba(S, E) onto
batS" E,), .inee
n n
T,ul = .up ! I(TI-')(TE,)I = sup! 1,u(E,)1 = 11-'1,
10",,1 .-1
where {E.. ..., En} is an arbitrary partition of S. This proves (a).
Since each ,u, . batS" II) is clearly regular, it follows from Theo.
rem 111.5.13 that every ,u, in ba(S,. E,) is countably additive. Hence
by 111.5.14 every ,u, £ ba(SI' E.) has a unique regular extension to a
,u, E ca(S., I,). On the other hand the restriction of each Po . ca(SI' I,)
toE.is regular. Thus each,uo. ca(8.. E.) is regular and the mapping V
;,; an algebraic isomorphism of ba(S,. E.) onto catS" I.). We shall
show that V is isometric. By Theorem 6.3
IVPII = rup I Is f(SI)(Vp,)(dsl)l.
jtJ=1 L
f. C(S.).
Since" by Lemma 10, the field II is a basis for the topology in S1 1 it
follows from the Stone-Weierstras.< Theorem 6,16 (or 6.17) that
functions of the form I;.1 rJ.i'1E, are d.ense in C{Sl)' where lt . . ." tI
are scalars and El' . . ." En are disjoint sets in 1:'1" }\.(oreover ,
Is, {! ex'XE.(S')}(Vp,)(ds l ) = Is, {!"',XE.(s,)}i<J.(ds l ).
Thus if H is the ;,;ometric ;,;omorphism of B(S, E) onto C(S,),
IVi<J.1 = I !' I Is,!(S.),uI(ds.)1
= sup I J (H 'f)(S)(T ',u,)(ds) ]
IErJ(I)I""1 s
= IT ',u.1 = [p,1
by (a) and Theorem 5.1.
To prove (c)let,u, E ba(S., E.) and E. E,.LetA. be defined by the
814
IV. SI'ECJ:AL SPACES
IV.9.12
IV.9.IS
SPACES OF BET FU}\CTIOXS
815
equation A.(F) = f'I(EF). F. Er Then U(A.)(G) = (Up.)(GE) for
G in E.. By part (b),
v(U(p.), E) = IU( )I = IA"I = v(."., E). Q.E.D.
12 THEOREM. A subset K 01 batS, E) is weakly tteqttentiaUy rom-
pad il and only il !here eccists a non-negative tf. in batS, E) s!Uk that
Iim A(E) = 0
,..(E)-+O
quently, by Lemma Il(c), v(A", U _, E,) < 4. for each n and .I.. m
K.. Letting n ---+- 00, we find that v(A", U:, E,) ;:;;; 4e for .I.. in K..
Hencel'.(A} < "12imp lies lA,,(A}1 < 46iorA".K.,sowe have proved
Iim J.,,(E) = 0, E. E., uniformly for A". K.. Q.E.D.
112 CE )-+O
Our next lemma is .. corollary of the proof of Theorem 12.
IS COROLLARY. Let s" be a sd, E. a field of subsets of Sl' and ILt
I'., be in ba(Sl' E l }. Suppose tluzt E. is the a.field generatm by EI' and
that 1', and .I.. have counfably additive exl£YI8irms ". and .I.. to E.. TJun
A, is I'.-amtimwus il and onry if A" is ".-continuous.
PRDOF. Clearly if 1.2 is ,u2-continuous "I is PI-continuous. To prove
the converse we recall (ef. the remarks following Definition 1I1.4.I2)
that it is sufficient to show that ifv( } is vtu.)-continuous, then (A,,)
is v(l'o)-continuous. However, it follows from the last paragraph of the
proof of Theorem 12. that. given e and ,,> O. if " is such that
v(f'I, E) < lJ implies v(A l , E} < e, E. L" then v(I'" A} < {j/2 implies
v(A", A} :s;: 4e, A. E., Q.E.D.
We shall now prove a generalization, due to Bochner, of the Ra-
don-Nikodym thcorem.
14 THEOREM. Let f-' be a ""n-negative clement of batS, E}. Let
A . batS. I) be p-crmunuous. Then fM cach e > 0 there is a I'-integrable
simple funclion I. slUh that the function F defined by the equation F(E)
= J.I.(s}l'(ds}. E.I, satisfies tlu! incqualify IA-FI = v(}.-F, S) <..
PROOF. Let U and T be as in Lemma II so that V = UT is an iso-
metric isomorphism of batS, E) onto ca(S., I,). Since A is p-continuous.
Lemma Il(a} shows that TA is TI'-continuous and thus Coronary 18
shows that the function .1.,,= VA is continuous with respect to the
function!" = VI" Hence, by the Radon-Nikody.n theorem (III.IO.7).
there exists a ",-integrable function g such that
A,,(E} = fE g (SI}1'2(da l ). E. E..
If 1'. = U l"" then by Lemma 111.8.3 and Lemma II(c} there exists
a p,-integrable, simple function h. such that !A,,-F , ! < E where
FI(E) = fE h .(S.)I'.(ds.).
Let E 1 , . . OJ En be a partition of 8 1 and let lXI' . . .. n be a set of scalars
uniformly for A. K.
PROOF. Let K!;; ha(S, I} be weakly sequentially mmpaet and let
V = UT be the isometric isomorphi8m of batS, E) onto ca(S., E.).
Then VK ca(S., I,} is weakly sequentially compact. By Theorem 2
there exists a non-negative 1'2' ca(8.. I.) such that lim A.(E} = 0
II;i(E)-O
uniformly for A. . VK. It is then clear that I' = V '(.",} is a non-nega'
tive element of hatS, I} such that lim A(E} = 0 uniformly for A.K.
pIE)-o
'l'o prove the conversc, suppose there eXists a non-negative
p. batS, I) such that lim A(E} = 0 unifonnly for A in K. Then
p(E) O
1', = T(I'} is a non-negative measure in ba(S., E.) such that
lim (E}=O, E.I., uniformlyforA.€KI=T(K). Let 1'2=UI'I
(E)-+O
and K. = UK r We 8hall show that lim A,(E) = o. E.I., uniformly
pJ(£)--D
for A" € K., from which it will follow that K. is weakly sequentiall)
compact in ca(S.,I.}. whence K is weakly sequentially compact in
ba(S,I).
For A S. let A(A) = inf I::,I',(E.}. where the infimum is
ta be taken over all sequences {E,} ofsetsinI, such that Uf_l E, A.
By the umqueness assertion of Theorem 111.5.8. and by Theorem
III.5.4 and Lemma 111.5.5, A(A} = I'2(A) for A in Io' Let. > 0 be
given, and let lJ> 0 be snch that f'I(E} < ", with E. El' implies
IAI(E}I < E for all in K I , so that v(A., E) < 4E, (cf. III.I.5). Then if
A . l. and I',(A) < 6/2. there is a sequence {E,} of sets in E. such that
U ::.E, A, and I:"_.f'I(E.} <{j. Since f'I is positive, we may and
shall assume that the E i aTt: disjoint. Then, since J1.1( U ""l E.) < b
for each n. VCA l " U l E i ) < 4E for each n and each Al in K I - Conse-
816
IV.. SPECIAL SPACES
IV.9.I5
IV.9.15
SPACES UF SET FUNCTIO S
aI7
such that E,. E 1 and ex, = h.(s,) where s,' E,. Put G, = T l(E,). E
and define 1.(') = <x, for s in G,. It is evident that I. is .. p-integrable
simple function and that if
F(G) = L/.(s)p(d&), Gd:,
then FI = T(F). Since T and U are isometrics we have IA-FI < e.
Q.E.D.
This section will he concluded hy givIng one solution to Problem
1.8 in the ca8e where 1: = C$(S) and ID = C(S). The following theo-
rem is stated in R :somewhat more general form. far it applies to set
functions in barS, E) and not just to those in C$CS) = rba(S),
15 THEOREM. (Ale;rondrolt) LeI p, p.. n = I, 2, . . ., be a bounded
sequence in ba(S, E) 'Where 1: i. a lield c&t!wining 1M open .ets in the
wpological space S. In order !1ULt
lim I.I.(S)P.lds) = I.I.(s)p{ds).
n
Thus. if Ip.1 < K and jp[ -;:; K, then
IIs/(s)p.(d&) - I/(s)p(d&)1
;;;; II. (/-I.}(s)(p.-p)(ds)] + I Isl.(s)tu.-p)(ds)!
;;;; 2.K --rl !.1.(S)(p.-p)(d&)!,
Ii::: p I Is/(s)p.(ds) - Is/(s)P(ds)! ;;;; 2.K.
..nd
Ci) Is/(S)p.(ds) Is/(')p(ds),
it i. ""lfidenl that
(ii) P.(G) pCG)
lor every open set G withuCG) = p(G).lf S is normal,pis r<'g.dar, andp,
fl.", n = 1, 2, .. . . aTe tt011-negom'e. the cmuJition is al$(} t'i.tct!ssary.
PROOF. It will be sufficient to prove (i) with f real valued. Thus
suppose that -M < fCs) < 1>1, .. S, and choose a", . . ., "'m with
-It 1 =a" <",,- <a,,<... <ex m = 1>1,
I. C(S),
This proves (i),
We shall now prove the converse, assuming that S is normal, that
pis ....gular. and that all the set functions 1', P., n = 1, 2, . . " are non-
negative. Let G be a fixed open set in S with peG) = p(G). Let e > 0
and choose a closed set F and an open set H such that
FS;;GS;;GS;;H,
pCH-F) < e.
Let I, h be continuous functions with
o S; ICs), hCs) s; 1, s. S;
fCS)= { I, s.F; h(s) = ( 0, sfH;
0, tlf.G; 1, BEG.
ot';-C(i_J. <E,
i = 1. . . . m,
Then
p({sV!s) = "'I}) = 0,
i = 1, . . "I In.
p(F) ::;:; IsfCs)p(ds) <;; peG)
= JlCG) <;; Is h(s)Jl(d&) s; Jl(H).
and
This last condition may be achieved since sets of the form F. =
{slfC» = ex} are disjoint and thus there sre at most a countable num-
ber of yalues of IX for which I'CF.) oF o. If G j = {sI/Cs) < ex,}. then
G, S;; {sl/(s} -;:; "'t}, From (ii) it is seen that P.(G;) ....I'CG.) and bence
that
(iii) P.(G;-G'_l) .... p(G,-G' I)'
Let X, be the characteristic function of G;-GI-l and let f. =
!;':..I"';X,' Tben It-I.: < e and (iii) sbows that
Thus
o -;:; Is {h(s)-/(')}p(ds) ;;;; p(H-F) < ".
Consequently, we have
I s /(s)p.(d8) S; p,.(G) ;:;; I s h(8)p.(ds),
f./(s)p(ds) <;; p(G) ;:;; Ish(s)p(ds) ;:;; Is/(s)pCds)+l;,
318
IV. SPECIAL SPACES
IV.IO.l
IV.I0.2
VECTOR VALUED MEASURES
319
Thus the hypothesIS (i) shows that
limsup 1p..(G)-,u(G)1 < 6.
sequence {y;: = x: } of {x:} such that lim Y::''''k exists for all k. Since
"-+00
.
ly::'1 = I. m = 1, 2, . , ., it follows from Theorem 11.3.6 that lim Y::'x
m....'"
and this proves (ii). Q.E.D.
exists for every x I.. and, in partIcular, lim y (E) exists for each
m....'"
10. Veetor Valued Measures
E. :E1" By Corollary 111.7,4, the set {Y:'I-'} of scs.larvalued measures is
uniformly countably additive on E., which contradicts the assumption
that y:;,p(E. ) -. 6, m = I. 2, . . .. This pro,'os the first assertion.
If p. is n t A-contmuous, then for sonle Ii > 0 there is 8 sequence
{E.} in I 8uch tl",t A(E.) < Ifn and II-'(E.)I > e, n = 1, 2, .. .. Pro.
ceeding exactly as before, a sequence {Y::'} C I* is obtained such that
lim Y:'I'(E) exists for E.I, Imd Y::'I'(E.) > 6, m = 1,2,.... Since
m_
The theorems on spaces of set functIOns proved in the last section
permit us to develop a more satisfactory theory of vector valued count-
ably additive set functions (briefly, vector valued measures) than we
were able to develop in Chapter III. In particular, we will now be able
to add to the integration theory of Chapter III a satisfactory theory of
integration of 8caJar valued functions with respect to a vector valued
measure.
Throughout this section, we shaH suppose that S is a fixed set.
that I is a u.f're1d of subsets of S, and I-' is an additive 8et function de-
fined on I with values in a B--space I. We suppose in addition that I-'
is weakly ClYUnlably addinve; that is, I:', "'*/l(E,) = ",*I'( U _I E.)
for each x* in I* and each sequence of disjoint sets E. in :E.
I THEOREM. (Pet#8) A weakly coumobly aMitifJl' vector valued set
fundionl-' kfined on au-field :E is coun!ably addinJJe.ln additWn, if ),
is a tinil.e posilive measure on :E and if I-' vanishes on ).-null sets. then /l
is ),-l:cm1inuOUIJ.
PROOF. If {E.} is a sequence of sets in I. let Io be thefield genera.
ted by {E.} and let 1; be the a-fie1d generated by :Eo' By Lemma
nI.8.4, :ED is countable and so I, = sp{P (E}!E. ED} is a separable
subspace of I. We assert that I-'(F) E 1" if F. 1;. !fthis is not the case
for some F E :E" then by C0r0lIary 11.8. IS there is an ",* . I* such that
x*I-'(F) oF O. and x*I-'(E) = 0, E.:E., which contradicts the unique.
ness assertion of Corollary IV.5.9.
If I-' is not countahly additive, then for some s > 0 there exists a
decreasing sequence {E.} in I with void intersection such that
II-'(E.)I > s, n = 1,2, . . .. By Corollary 11.8.14 there is a sequence
x:.I* such that Ix:1 = 1 and "':I'(E.) = II-'(E.JI > s, n = 1,2, . . ..
Form I} and 1. as in the preceding paragraph and let {"'k} be a count-
able dense set in I". Using a Cantor diagonal procedure, there is a sub.
y;:/l(E) = 0 whenever A(E) = 0, by Lemma 111.4.18 each measure
y::'/t i. ).-continuous, and it follows from the Vitali-Hahn-Saks
theorem (111.7.2) that the A-continuity is uniform for m = 1, 2, . . ..
But this contradicts the assumpt;on thatA(E. ) < I/nm andy:;,p(E. )
> f"t m = 1, 2, _ ... This shows that P. is }.-coniinuous. and complet s
the proof, Q.E.D.
2 COROLLARY A z>nft>r m£i1S1lTt' is btn..,tkd. and the sel
{x*l-'ix*.I*. 1"*1 ,,;; I} of n,,,,,enrol meaJJUTe$ is weakly sequ<',rtiaUy
compact as a subset of ca(S, I).
PROOF. Since IX*I-'(E}[ ;;:;v(x*I-',S)foreachx* Imd E.I. itfollows
from Theorem 11.3.20 thatthere is a constant M such that 1/t(E>! ;;:;1Il.
E .:E. Since
1"'*1'1 = v(x*J.l. S) ;;:; 4 sup IX*I'(E)I ;;:; 4,)1, 1"'*1 1,
E S
the set of mC11SUreS i. bounded in catS, I). Let {E.} be a decreasing
sequence of sets in I with void intersection. Since /l is countably ad-
ditive, lim,,_ I-'(E.) = O. Thus, Iim._ x*I-'(E,) = 0 uniformly for
1"'*1 1. The desired conclusion follows from Theorem 9,1. Q.E.D.
In contrast to the case of complex valued measures, the total
variation of a yeetor valued measure (cf. Definition 111.1.4) need not
be finite. Our next step is to construct a finite positive set functjon
which CRn replace the total variation in the vector valued casc.
320
IV. SPECIAL SPACES
IV. 10.8
IV.JO.5
VECTOR VALUED MEASURES
321
8 DEFINITION. The semi-variation of the vector valued measure
p is defined by
i' k D;J D;J
I Ot'i«F,JI = I Ot,I'(E,F,>I ";: IIpll(E,),
,=1 1=1""'1 l
E.E,
so that
n
II"II(E) = sup I ",p(E,)I.
<-I
'"
Ilpll(E) ..;: 1Ii<II(E.). Q.E.D.
'_1
The next lemma is crucial for the development of the integral for
scalar functions with respect to 1"
5 LEMMA. There exisls a finite posilive measure A tkfined on E
such that
where the supremum is taken over all finite collections of sc.alars with
IOt,1 ..;: J and all partitions of E into a finite number of disjoint sets in
E.
A number of elementary properties of the semi-variation are
listed in the next lemma.
4 LEMMA. Let I' be a vtdoT valued '11I£aSUX'e. Then
(a) IIpll(E) r,,(E)1 ;;;; 0, E. E;
(b) II,'II(E) 4suplp(F)1 < 00. E.E;
F.fE
(c) II"II{F) IIpIl(E) if F E;
(d) if {E,} ;., a 8€fJU€1'C€ of eels in E IMn 111'111 U:"_I E.) .,;:
::',IIpll(E,).
&mark. Even if the sets E. in (d) are disjoint, the inequality
may be 8trict; that is. II.... II need not be an additive function. It is
easy to see that Ilpll is additive if and only if 111'11 = v(P); so that if
v(p, S) = 00, 111'11 camwt be additive,
(a) A(E) .,;: IIpll(E).
(b) lim II....II(E) = O.
.t'E)-+<I
PROOF, By Coroll&ry 2, Theorem 9.2. and Corollary 9.8, we can
find a positive measure A such that A(E) sup Ix.p{E)1 = Ip(E)I.
Iw-I=t:l
and such that lim "'.p(E) = 0 uniformly for 1"'.1 .,;: I. Thus A(E)
J.(EI-Jo-Q
IIpll(E) by Lemma 4(a), and hm 1I,uIl(E) = lim 1,u(E)] = 0 by
Lemma 4(b). Q.E.D. lIE)--+O AIE) O
Lemma 5 enables uS to prove a result, promised in Chapter 111.7,
which generalizes a theorem of Nikodym to the Case of 'Vector valued
measures.
EEE;
n n
Ilpll(E) = sup 1 Ot,....(E.)1 = sup sup I Ot",,*p(E,}1
1"",1 Iz'!::iil _1
6 THEOREM. Let {It.} be a S€fJU£n<€ of veclor oolued measurrs tk-
fined on the a-field E.lf p(E} = lim,, ..I'n(E) e;rials for each E in E,
pie a vecIM measure on E and tM counfable a4ditivity of It. ;., uniform
in It = 1, 2 , . . u
PROOF. Statements (a) and (c) are obvious. To prove (b), observe
that we have
n
::s;: sup sup IOt,lv("'.", E,) s sup v(x"p, E)
la.l:a i_I 1.;!C.1 1
PROOF. For each fZ let).", be a positive finite measure correspond-
ing to 1'. by Lemma 5. Let A be the measure defined by the formula
A(E) = i 1 An(E) .
";1 2 n 1 +J.,.(S)
Then each P. is A-contmuous. Coroll&ry 111.7.8 shows that /' IS
counlably additive. If {E...} i. a decreasing sequence of sets in E with
void intersection. limA(E...) = O. By the Vitali-Hahn-Saks theo,..,m
... '"
.,;: 4 8UP sup 1"'.p(F)j = hup Ip(F)1 < 00
1:z.1 1 F£..E F!:.E
by Corollary 1I.1I.15 and Corollary 2.
In proving (d) we .hall assume that the sets E. arc di8joint. Note
that if F I , . . .. F. is a disjoint partition of E = U::, E" then
E,F...... E,F.is a disjoint partition of E,foreach i. ThusiflOt,1 < J,
j = I, . . ., k , -we have
(111.7.2), lim ".(E..) = 0 uniformly for n = 1, 2..... Q.E.D.
.. ..
B22
IV. .sPECIAL SPACES
IV.IO.6
IV.IO.7
VECTOR VALUED MEAS RE6
828
For the rest of this sectlon J }, will be :a finite positive measure
related to p as in Lemma 5.
We now proceed to develop a theory of integration of scalar
functions with respect to the vector measure p. A p.-nullset is a subset
of a set E < E such that IIpll(E) = 0; by Lemma 5, this is the same as
a A-null sct. The term p-almvst eve1')j'l1Jh£n refers to the complement of
a p-null set, aod is hence synonymous with the tenn A-almost every-
where. The symbol E* denotes the Lebesgue extension of E, Thus
(111.5.17) E* is the a-field of union8 E UN, E e E, Nap-null set. A
scalar function I defined on S is p-mi!tJlJU1'tlblc if for every Borel set B
of scalars, I-I(B) e E*; by 111.6.9, this i8 the case if I is A'measurable,
A scalar valued function f defined on S is p.-si7nple if it is a finite linear
combmation of characteristic functions of sets in 1:*; this is evidently
the case if and only if I is A.simp". It follows from Corollaxies III.6,13
and 111.6_14 that I is p-measurable if and only if it is the limit p-almost
everywhere of a sequence of ,u-simple functions. By 111.6.14, t1)e limit
of a sequence of p-measurabJe functions converging p-Blmost every-
where 1S po-measurable.
If I is the p-simple function ;_1 rLiXE.' where E . . ., En-.are s.ets
in E, then the inugral of / over a set E < E is defined by the equatiOn
If I is an arbitrary measurable function, we define the ,u-£ssential
ropremum of I on E to be the infimum of those numbers A for which
(s. EII/(s)1 > A) is a ,u-null set. If p-ess sup 1/(8)1 < 00, we say that
..E
I is p-es8elltiaJly bauJUkd on the set E e E.
It is cll'al' that p-e.s sup [/(')1 = A-ess sup 1/(811, and that I is
n£ 'IfE
p-e8sentially bounded if and only if I i8 A-essentially bounded. Equa-
tion [*] mny be written somewhat more generally as
I IEI(s),u(ds)! ;:;:; (,u-es:.:u p I/(sJl}II,uIl(E),
if I is p-8imple.
7 DEFINITION. A scalar va1ued Ineasur.a.ble function / is said to
be inlegrablL if there exists a sequence (In} of simple functions such
that
.
I I(s),u(ds) = "'i}t(EnE.).
E i_I
lUollows just as m the case in which,u is complex valued that the
integral of I is independent of its particular representation as a linear
<:ombination of <:haractenstic functions (cf. the paragraph following
Definition JIl.2,13).
Obviously, Integration of simple functions over E is a linear
operation. Also, the integral of a simple function is a countably addi-
tive set function with values in ;1;. If I is a simple function such that
1/(.)1 ;:;:; M for each s. E, then
if I(S),u(ds)! 1 = Ii ""p(EnE,)1 = M I i ( "" ) I'(EnE') 1
E '1=1 '-1 11-1
MII,uIl(E);
(i) In(B) converges to I(s) poalmost everywhere;
(ii) the sequence {jEln(B)P(ds)} converges in the norm of I for
each EeE.
The limit of this sequence of integrals i. defined to be lhe illtegral
011 wilk respect 10 ,u over lhe .et E e E, in 8ymbols:
I EI(s)p{ds).
hence
[*]
I ' I I(s),u(ds) [ ;:;:; {sup I/(s)IJII,uIl(E).
E ,e-E
8 THEOREM. (a) II E e E and I is scalar valued and p-inkgrahle,
lhe ffitegral 01 I r.oifJo respect 10 ,u over E is an unambiglrously rklined
tilerMnl 01 ;1;;
(b) il I alld g are .calar valued and p-inUgrablL, il '" and p are sea.
lars, and il E e E, lhen
IE ("'/(.) +pg(s)}p(rk) = '" IEI(S)p(ds) +p tg(s)p(ds);
(c) ill is a ,u--nu:asurable and .calar valued fundio" which is ,u-
uB.mtiaJly bounded on E, Ikn I is p.1ntegrablc and
IfEI(S)p(ds)) ;:;:; (,u.es:,:u p I/(s)IHII,uIl(E)};
(d) ill is .calar valued and p-integrable, lhen f E/{s)p{ds) is a
oountahly aMitive lunction em E 10 ;1;;
324
IV. SPECIAL SPACES
IV.1O.8
IV.IO.9
VECTOR VALUED MEASURES
325
(e) # I is ..calar valued and p-inr<:grable. then
lim J I(s)p(ds) = 0;
11#111")....0 "
(f) il U is a bounded mu:t1T operator from :f into a BalUlCh space 1lJ,
then U JA is a _ measure ITom L to \1), and lor any JA-imegrable sealaT
I'tllued funrlion I and EeL. we have
V lJ"f(s)JA(ds») = JEf(S)Up(ds).
PROOF. To prove (a), let {In} and {gn} be two sequences of simple
functions as in DeImition 7.. \If e are required to show that the two
sequences of integrals approach the 8ame limit. We define hn(s) = 0
if s is a point at which either {In(s)} or IgnIs)} fails to converge to f(s),
and set h.(s) = fn(B)-g.(S) otherwise. It i8 evident that {h.} con-
verges to zero everywhere, and that (J"h.(s)p(ds)} converges in the
nonn of:f for E . L. We must show that thi8 sequence of integrals con-
verges to the zero element of I..
Let A be a positive measure related to p as in Lemma 5. Clearly,
since each h n is a simple function.,
(*) lim J h.(')JA(ds) = O. n = 1,2, .. .;
)'(E)--+O Ii
further the sequence of integrnls (JEh.(S),u(ds)} converges for each
EeL, so by the Vitali-Hahn-Saks theorem (111.7.2), the limit in (*)
is uniform in... Consequently, for each e > o there exists a = (e»O
such that jf A ELand A(A) < IJ then
I L h.(S)p{ds)! < e. n = 1,2. . . ..
By Egoroff's theorem (11I.e.12) there exists a set A . Lwith A(A) < IJ
such that {h,,(s)} converges to zero uniformly for s.S-A. Having
specified e and chosen I) = I)(e) as above, there exists an N = N(E)
such that if n ;?;N. then Ih.(s)1 < e for s.S-A. Hence if n ';?; N,
IJ"hn(S)p(ds): < IJE-A h,,(s)p(ds)1 + I fEn.< hn(B)p(ds)j
ell,.II(S)+e
uniformly for E. L, Thus the integral is well defined.
Statement (b) follows from i<s validity for slmplc functions and
the additivity of thc limit operntion.
To prove (c), Ict f be I,-measurable with p-essentia! bound B on
E, and let e > O. Let 10;, . . ., Fn be a covering of I(E) by disjoint
Borel sets of 8calars. and dcfine E, = f '(F;). Let "'J £ F" and define
1.(8.) = "" for s,£ F,. Then I. (modified if need be on "p-null set) is a
p-slmple funcbon, and p-ess sup 1/.(s)-/(s)1 < e. Let e. -+ O. Then
.."
Iim p ss sup II.. (s )-1 ,)s) J = O. Since we have already observed that
m,n-+O:> ..E
(c) holds for each p-simple function, we can lmmediately conclude
that
m,I :m If"I..(B)P(ds) - J"I.",<s)JA(ds)1 = 0,
so that {J" f.JB)p(dsl} converges for each E. E, and we have
J"/(B)Plds) = lim J f..(s)p(ds),
ft C'D E
EEL.
Since p-es5 sup 1/..(s) 1 B+e., the general validity of (e) now fol-
..E
lows from its validity for p-simple functions.
. We have a!ready seen that (d) and (e) are true for simple func-
bons. Let I be an arbitrary p-integrable function and {I.) be a se-
quence of 8imple functions as in Definition 1. The Vitali-Hahn-Saks
theorem (111.7.2) implies (d), and the fact that
Jim J I(s)p(ds) = 0,
A{EJ_D E
from whic!' (e) follows immediately by vu-tue of Lemma 4(a).
fJr t ertion in (f) is obvious. ,,'hile the second follows by
an eVIdent ilmltlOg argument from its validity for p-simple functions,
Q.E.D.
9 THEOREM. Let {In} be a sequtnl'e 01 JA-integrable lunt'/;ons which
converge JA-almost ev<!I'ywhere to I. Then I is JA,i il
Iim J /n(s)JA(ds} = 0
11#/lIE)....O "
unilormly lor n = I, 2, . ... In this case we have
J"/(s)p(ds) = lim J . 1.(s)JA(ds).
_-+0> E
326
IV.. SPECIAL SPACES
IV.IO.9
IV.1O.9
\-'ECTOR VALUED MEASURES
827
(8)
(4)
1J.(8)-g.(8)1 < 2--1<.
Ig.(8!1 21/.(8)1.
8£S-A kl
8 8_
lIE (f.(8)-g.(8)}p(ds)! ;;;; lIE_A, U.(8)-g.(8)}p(ds)1
+ IIEnA,t.(8)p(ds)1 + lIEn.<, g,(8)p(ds)l.
The integral over E-A. is at most 2-'l/pl/(8) by (8). Since
I/pl/(EnA.) < 15.. we have .een in (1) that the .econd term on tbe
right is at most 2--1<. To estimate the last term let ",* E 1* Ix*' 1
F E.F.1:'.andllpl/(E)<<1..Thenby(I) . -,
IIF fn (8)X*p(ds)! <2--1<,
so that by Theorem 111.2.20 and the remark following Definition
III.4.I2.
(5) IE I/n(s!lv(x*p, ds) < 4. 2 ', n = 1,2. ...,
if IIpll(E) < <1 k " Thus by (4) and (5)
IIEnA gk(8)p(ds) 1 1 = sup I I g.(s)x*p(ds)1
I: 1 .1 1 EnA It
8UP I Ig.(s)lv(x*p. ds)
I I ], EN k
";; 2sup I 1t.(8)lv(""p,ds);;;;8'2--1<.
11:.1 1 EnA.
Combining th€se statements we condude that
(6) II" {f,(8)-g.(s)}p(ds)1 2--1<{lIpll(S)+9}
which, since (J"t.<s)p(ds)} com'erges, shows that {fEgk(S)p(ds}} con-
verges, and that f is p-integrable.
To obtain the last conelusion of the theore observe that. since
{JEJ.(8)p(ds)} cam-erges, it follows by the Vitali-Hahn-Saks theorem
(111.7.2) that for each x'.I* we have lim JEt.(8)X'p(ds) =0 uni-
"( Il.E)-+G
formly in k. Thus, by Theorem 111.2.20 and the remark following
Defmition 111.4.12,
lim I" 1J.(8)lv(x*p. ds) = 0
tI(Z.JI, E)-+D
uniformly In k. It follows from Theorem 111.6.15 that
n:: x' I"J.(8)p(ds} = "" I,,/(8)p(ds)
PROOF. Let k be a positive iuteger and let <1. > 0 be sucb that if
Ed; and I/pl/(E) < <1k' then
(1) IIE f .(8)p(ds)1 < 2--1<, n = I, 2, ,. .
Evidently we may assume that 6. ;:;; 2---k. Letti, > 0 be such that
if A 1:'andA(A) < "I. then II!'II(A) < 15.. The sequence {fn} converges
A-almost everywhere, and, by an application of Egoroff's tbcorem
(111.6.12), we can seIect a set A 1:' such that A(A) <"I. and such
that the convergence of {I.} is uniform on S-A, Thus there is an N.
such that if E I and n, m > N,u we have
(2) lIE U.(8)-/m(8)}p(ds)1 ;;;; I fE-A {f.(8)-fm(8j}p(ds)1
t-IIEnA f.(8)p(ds) \ + IJEl1A fm(8)p(ds)1 < 2--1<Ulpll(8)+2}.
Bnt since k is an a.rbitrary positive Integer, this proves that the se-
quence {JEf.(8)p(ds)) converges in the norm of :E for any E E E.
We noW prove that f is p-integrable, Let <1. and "10 have the same
meaning as in the previous paragraph. Since each f. is p-integrahle it
follows from Egoroff's theorem (111.6.12) and the second paragraph of
the proof of Theorem 111.2.22 that there is a simple function g. and a
set A. 1:' with A(A,) < 'io such that
Let B, = U::. A, so that B.. 1:' and {B.} deCl"f'ase8 to the set B =
n;:lBk. Since
00 00
III'H(B,) S I 1II':I(A,) < I6, ;;;; I 2 ' = 2-(' 1).
i k '_k i-1
it follows that 1I1'1I(B} = o. Now
1/(8)-g.{8)1 ;:;; If(s)-f.(811+IMs)-g.(s)l.
If 8E S-B, then 8 .S-B, for k greater than some integer K(s), and
so (3) holds provided that k > K(s). Since f. was assumed to converge
!,-almost everywhere to I, wc conclude that the sequence {gk} conver-
ges p-almost everywhere to f.
It remains to show that the integrals {J "g.(8)p(ds)) converge
far E. 1:'. But
828
IV. SPECIAL SPACES
IV.tO.IO
IV.Il
SPACE TM(S,E.f'1
829
for each x*. :1:*. Thus x*(jEf(s)p(ds)-hm JEf.(s)p(ds» = 0 for
x* .1*, sO that by Coronary II.8.IS, .
lim f./ (s),,(ds) = J ,,J(s),,(ds). Q.E.D,
.--+
11. TheSpaceTM(S,E,p)
J f(s)p(ds) = lim J Ef.(8)p(d8),
E _m
E.E.
We shall be eonceml'd here with a set S, a a-field E of its subsets.
and a scalar valued countably additive set function I' on E. The
symbol Till(S. E, ,,) wi!! be used for the set of aJi scalar valued func-
tions on S which are totally p-measurable (ef. Definition III,2,IO).
More precisely, as in Chapter III, the elements of TM(S, E,I') arc
equivalence classes where two totally me..urable functions are defined
to be e<juivaJent if their difference is a null function. A number of
properties of TM(S. E, ,,) have bccn established in Chapter III. In
particuJar TM(S, E, p) is a linear ,.cctor space which is a metric
space under the distance function e(f, g) If-gl, the norm If I being
defined by
We now show that the theorem on dominated con'\'ergence IS
valid for vector measures.
10 THEOREM. If {f.} i. a ""'luenIT 0/ ".integroble funcfionB whi<:h
co"""rg.. ,,-almost coerywhere 10 f and if g is a p-inkgrabk funclirm
8U h lhat !f.(s)! ;;;; g(s) p-o.bnOJIt n = 1,2, . , .,Ihen f i.
".rntrgrahle and
PROOF. By the preceding theorem. it suffices to show that
lim f I.(s)p(ds) = 0
II"IHE) Q E
uniformly for n = 172,. ... Given of> 0, we may, by Theorem 8(eJ,
choose a lJ> 0 such that if E. E and III'II(E) < lJ, the"
IfEg(S)p(ds)! < s.
Hence if F \;: E, F. E, and III'II(E) < lJ, we have
IfF g (s)",*p(d8)! < e, 1"'*1;;;; J.
By III.2.20 and the remark following 111.4.12 it follows that
fEg(S)V("'-'" ds) < ole. 1""1 -;;: 1.
Consequently, if IIpll(E) < lJ, then
If f.(s)p(ds) I ;;;; sup f 1/.(o)lo(",*p, ds)
E 1 1 1 E
;;;; sup f g(s )v(",.I', ds) ;;;; 4£, n = I, 2, . . "
Iz.I"] Ii
from which the conclusion follows. Q.E.D.
II = mf arctan (O:+V-(I" S(lfl > 0:»),
0>0
where S(jfl > 0:) = {sls. s. If(s)/ > o:}. This metric space is com.
plete (111.6.5) and convergence of a sequence U..} \;: Till(S. E, ,,) is
equiva1ent to convergence in measure of the functions 1ft on Sa
It is easily seen that TM(S, E, p) is an F-£pace. To see this we
note that. in view of Lemma III.2.8(b), it suffices to prove that
limo:/=O, for each I.TM(S,E.,,). Let I. TM(S,E,,,) and let
O .
s> o. Let g, be a p-simple function such that I/(s)-g,(s)1 < e foe 8
in the complement of a set E.. E such that p(E,) < e. If M =
ess 8UP Ig,(s)l and 10:1 < e/(M +e), then 10000(s)l < s for 81 E.. Thus,
..s
by Lemma 111.2.7, lim 0:1 = O.
o--+Q
Note that lim CT.} = 0 in p-measure is not necessarily true for
o-+{)
every measurable function. For example, if S = (- 00, 00) and" is
Lebesgue measuee, let I he the function defined by f(8) = s. Then
fin does not approach zero in measure since I'(E(if/nl > 0:») = 00 for
all n = 1,2,... and all 0: > o. Thus the space lIl(S,I,,,) of all
measurable functions need not be an F-space.
The F.,space TM(S, E, p) need not admit any continuous Imeae
functionals. To See this, consider the case of Lebesgue measure Jl on
the setS = [0, I]. If 0 oF x*. TM-(S, E, ,,), i.e., if x* is a continuous
830
tv. SPECIAL SPACES
IV.ll.I
IV.n.l
SPACE TM S.E. pt
831
linear functional on T l(S, E, p) which is not identically zero, then,
since linear combinations of characteristic functions of intervals are
dense in TM(S, E, p), then; is a subinterval.-l. of [0, 1] oflcngth les8
than Iln and such that a:* does not vanish on the characteristic func-
tion x. of .-I.. Let a:*X. = 6. * 0 and let f. = X./6. so t1mt f. -+ 0
ond 3J*Jft = 1" 11. = I. 2" .. ., which is a contradiction. Thus the con-
jugat.e space of t.he space of totally measurable functions may consist
of the zero vector only a This is not always the case; for if the measure
of the set {BO} consisting of the single point BO is not zero, then f(BO)
depends linearly and continuously on f and f(B.) = g(BO) for every
pair f, g of equivalent functions,
Thus all but one of t.he problems described in Section 1 fail to have
significance for some spaces of measurable functions. The one problem
of the list which has significance in wI cases is the seventh one, i.e.,
t.o determine which subsets of TillIS, E, p) are compact in the metric
t.opology of TM(S, E, p). One answer to this question i8 contained in
the following theorem.
First suppose that A is t.otally bounded so t1mt given I: > 0
there are functions h, , . " f. in A with
inf !f,-fl < 1:/4.
l:.i/:iiv
From the definition of total measurability (III.2.10) it follows that
there are simple functions g" . , '. g. such t1mt
fEA,
Ig,-f,1 < a/4,
inf Ig,-fl < 1:/ 2 ,
l:;f cr
i = 1... '"lJ
lEA.
Thus there are sets Elf'."' Eft satisfying (i) and constants a t W ,
i = I, . . "0 fli i = 1, . . ". q with
.
g,(.) = ct,Ij}X..-(B),
;_1 I
where X..- i8 the characteristic function of E"
I
For each f in A there i8 an i for which Ig,-fl < ./2, and henL'" an
ct > 0 such that
i = 1,.. OJ g,
I THEOREM. Let p be a complex or extmiled Teal valued countobly
additive Bet funa;on on a u-fieldE of subsets of a set S. Then a Btd18d A of
TM(S, E, p) is ronditwnally compacl if and only if for eroery 8 > 0
there are Bets 1!;, . . "' En in E, a co-n8tant K, and, €orresponding tv each
f E A, a se! E, in E smh thaI
(I) EIUE.U.. .UE. = S,
(2) v*(/-" E,) < 1:,
(8) If(B}; < K,
(4) sup I/(B)-f(t)[ <..
So tdirEI
E,E,=+,
i *i;
ct+v*(p, S(jg,-fl > ct» < 8/2.
where the set S(lg,-f[ > ct) is defined by
S(lg,-fI > 0:) _ {sluS,lg,(B)-f(s)1 > ct}.
Since ct ;:;; 1:12, ,t follow8 that
S(lg,-fl > 1:/2) S(lg,-fl > ct},
v*!J', S(lg,-fl > 1:12») ;:;; 71*(/-" S(lg,-fl > 0:)) < ei 2 .
[f E, = S(!g,-fl > 812), K = 1:+ eSS suP".lg,(B}I, (2) and (3) follow
immediately. Since g,(s) = g,(!) if sand t both lie in some set E"
and since Ig,(B)-f(s)1 < el2 for sf E" (4) is also evident.
Now conversely suppose that A satisfies the conditions (I), . . .,
(4). Let I: > 0, 0: = 2 1 tan e,
-K =<>.0 <"'I <... <",.=K
fEA;
lEA,
Sf E,;
1 i ;:;;n.
PROOF. Since /-' is countably additive on the ,,-field E, the space
TM(S, E, p) of all totally measurable functions on S is a complete
metric space (111.6.5) and thus (I.6.15) 0. set A TM is conditionally
compact if and only if A is totally bounded. (It is worth noting that
the preceding argument is the only place in the proof where the count-
ab1e additivity of I' is used, i.e., the conditions of the theorem are
nCi'CSsary and sufficient for total boundedness even if E is just a field
and J1 is only an additive, not necessarily bounded function on E )
Cii-CXi-l < «
i= I,.. .,p,
and consider the set of all simple functions which axe constant on cach
of the sets El' ..' En and whose values are in the set {O:i' i=O, 1, ..., pl.
There are a finite number gl' . . .. g", of such functions, and iTl view of
SS2
IV, SPECIAL SPACES
IV.1I.2
IV.II.3
PACE TM(S,E.JlJ
333
(2). IS). Bnd (4) we have for every f in A an i < m and a set Et' E
with
v*{p, Et) < ex,
Ig,(8)-f{a)1 < ex,
a1 Et.
Let Al A. . . . be denumercibl£ Bets and for each a E Al let Tn be a
continuous linear map fr<Jm an F-spuce;£ into thesp<u:e TM{S.E.p)of
real or camp lex valued torally mea.surulJk fmlClwfia. S_ thaI
(i) for c<u:h a: in I
sup IT.{x, a)/ < OJ.
Oo!'A.
Thus
S([g, fl > ex)[;: E,
and hence
"-rv*(P, S(lg,-fl > ,,» < 2ex = tan e,
alrM'! evfT1/"l1Jhere on S; and
(ii) for cach x in a ReI deme in I
lim sup ITn{x, a)-T.(a:, 8)1 = 0,
J)- 0, biEA p
which shows that Ig,-fl < 6. This proves that every f in A is within
distance 6 of one of the functions g" . . ., gm and proves that A is
totally bounded, Q.E.D.
We know from the general theory of continuous linear maps be.
tween F-spaces 1 and IJ) that a 8equence {Tn} of such maps with the
properties that (i) {T.x} i. bounded for each x and Iii) {T.",} is con-
vergent for each IX in a dense 8et. also has the property that {T,.IX} is
convergent for each x in the domain space (8ee Theorem 11.1.18). If
the range space ID is the space Till (S. E. 1') where (S, E, p) is a positive
a-fimte measure space, there is an analogous theorem in which the DO
tions of boundedness and convergence are taken in the sense of holding
almost everywhere on S. If T is a mapping from an F-space l' into
TM{S. E.p) we shall write T(x. 8) for the value of Tx (i.e., the value
of anyone of the functions in the equivalence class determined by
Ta:) at the point a.
almost everywhere on S. Then the equation appearing in (ii) is valid for
€Very x in ;:E.
PROOF. First we observe that it is sufficient to prove the theorem
for the case of a finite measure space. For, let S = U:_ 1 S. where
{8ft} is a sequence of disjoint measurable sets of finite I'-measure. Then
if p, is the measure defined by
2 THEOREM. (Banach) Let {T.} be a sequen« of conlinwms lineur
map. jr= an F-sprM:e I into the apace TM{S, E. p) of all Teal or com.
plex totally =rab/£ fwu:tions on a positive a-finite measu.... space
(S, E,p), Suppose that for erM:h x in 1 we have sup. JT.{x, a)1 < OJ for
almost aU a in S. Suppose also that for e<u:h IX in a deme set in 1, tlu: limit
limn T.(x. s) e:cis!s for almlJSt all 8 if. S. Then for every x in 1 the limit
lim. T .(IX. 8) exists al1n08! €Verywhere on S.
We shall occasionally need a generalization of this result which is
given in the following theorem. Theorem 2 is seen to be a special case
of the next theorem hy taking the set A. to be the set of all integers
n ;;;;k.
p{ES.)
pI{E) =. 2"[I+p{S.)] '
then PI is B finite measure and its null sets are the same as those of p"
Consequently we suppose that J.t is a finite mea.sure.. and so
TM(S,E.I-') =1I/{S,E.p).
Let , D,2! . 4 . be an enumeration of the e1ements of Ai' Let the
maps W, V. V., n = 1,2. . . _ of the space ;£ into TM{S, E. p) be
defined by the equations
V.{x, a) = sup IT. (x, a)l, V(IX, 8) = sup IT o {",,8)1.
ISm:S:n 11ft G A)
W{"" s) = lim sup ,T.{",. a)-T.{"" 8)1.
JI O> G, b AJj
EEE.
i3 THEOREM. Let (S, E. p) be a a-finite p08ilive measu.... space.
It is easily seen that V. is a continuous map of I into Till{S, E. p)
satisfying 1V.{x+y)1 ;;; 1V.(x)I+IV.<Y)1 and IV.{""')I = I"V.{"')I for
every pair IX, y lfi 1 and every scalar ex, Condition (i) assures that V
maps a: into TM(S, E, p). and it follows from their definitions and the
fact just proved that I"V.{x)1 :<:; I«V(.71)I. For each .... «V{x) ->- 0 as
" .... 0 and so the set {V,{"')ln = 1, 2, . . .) is a bounded set (IL1.7) in
the space TM(S,E,p). By Lemma 11.1.18 wc conclude that
334
IV. SPECIAL SPACES
IV.ll.4
IV.II.5
SPACE PM(S.x.llt
335
PROOF. The definitions of a lattice and of a-completeness were
given near the end of Section 1.12. To prove the first statement it
suffices to observe that
5 LEMMA. Let L be a G--eomp1de laui"" in 'Which every set of ele-
menls of L 'Which i. 'Well-ordered "..der the partiol ordering of L i. at most
coun!able. Then L i. complete and every subset A of L has a least upper
bou..d ..hich i. the least upper OOw.d of a countable .ub.ef of A.
PaoOF. Let A be a suhset of L which has an upper bound and let
A1 be the collection of least upper bounds of all countable 8ubsets of A.
Consider the family TV of subsets of A1 which are well-ordered under
the ordering inherited from L. We shall order W by defining the rela-
tion a ,.; b between elements a, b in TV to mean that a C;; b and that
each eJement ., which is in b but not a is an upper bound for a. It will
first be shown that W satisfies the hypothesis of Zorn's Jemma. To do
this we let We be a totally ordered subset of TV (1.22) and let c U We.
Then, for some a. W o , c n a is not void. Let:r be the smallest eJement
of cn a and let V be any other element of e. If y. b E W o , we have either
b < a or a "; b. If b ";: a, then, since YE b. we have aJso YEa and
thus y.cnaand V :? .,. Ifa "; b and YEa then v.ena and V :? .,.
Finally, if a ..;: band Y a then V :r by the definition of the ordering
in W. Thus '" is the smallest element of c. This shows that u tV o is
well-ordered and is thus an upper bound in W for WOo Zorn's lemma
shows that W contains a maximaJ element b.,. By hypothesis, be is at
most countable and hence Yo = sup b o exists and is in A1' \Ve now
prove that y ;;;; Yo for any Y E A1' For if this were not true for some
VI E A 1 , then sup {Yo, yJ > Yo; but V. = sup {Yo, Y1} . Al> b o ";
b.U {Y2}' and so b. is not maximal. Therefore Y ,.; Yo, YEA., and smce
Yo E A. we conclude that Yo = sup ...1 1 = sup A. It may be shown in a
similar manner that the infimum of a set with a lower bound exists.
This proves that L is compJete; the final statement of the lemma
follows from the observation that Y. is the least upper bound of a
sequence from A1 and hence of a sequence from A. Q.E.D.
6 THEOJlEM. Let (S,:E, J1) be a positive G-finiu measwre sp<UJe.
Then the partially wdered space of real measurable functions en S,
rd1ne f :? g mew," that f(II) g(s) for J1-a!mes! all 8 in S, is a complete
laiiite. Furthermore 1M le<Mt "pper bound cf every bourukd lie! B in this
lattice i"M leas! bound of a ,,,'!ably cll/Nien COUlltnble subset cf B.
PROOF, Let B be a bounded set in the lattice 1I1(S,:E, p) of real
measurable functions on S. We may and shall suppose that the func-
Iim._. V n (",) = 0 uniformly for n > 1. By Corollary III.6.I3(b),
Vn(x) V(",) and so it follows that V is continuous at", = O. Since
jTV(x, 8)1 ;;;; 2V(x, II), it follows that I W{:r) I ;;;; 2JV("')1 and hence TV
is continuous at oX = o. :Sow it may be readily :shown that
ITV(x, s)-W(y, 8)1 ,.; W(",-y, s),
for almost all " and hence it follows that
IW(,,) W(y) I < IJV(x-y)I, x, y E 3:-
This proves that JV is continuous at e,'ery point of :E. By (ii), W van-
ishes on a set which is dense in 1'; consequently W vanishes idmtica.I1y.
Q.E.D.
We shall now consider s?me order properties of the space
1I1(S, E, 'L). If f is in 11-1(S. E. J1) and if f(II) :? 0 for J1-almost alls S,
we say that f is positive and wTite f :? O. If f. and f. are real or compJex
valued functions in 1I1(8,:E, J1) and if A -f. :? 0, we write f. :? f. or
f. ,.; A. This makes 111 (S, E. J1) into a partially ordered system in the
sense of Definition 1.2.1. We note that the space TM(S,:E, J1) is aJso
partially ordered by the same ordering,
4 LEMMA. If E is a field of subsels of Sand p a finitely additive
Bef fwnction, then the real spaces M(S,:E, J1) and TM(S,:E, J1) are
lattic£S. If (S,:E, 1-') is a positive measure "pace then 1M real space
M(S, E, J1) i. a G-iJOmplete lattice.
8UP U, g} = Hlj(.)+g(')I+[f(.)-g(')IJ,
inf{j,g}= Hlf(.)+g(')1 If(.)-g(.)IJ.
The ract that these functions are in M(S,E,I-') or in TM(S,E,I-')
follows from Lemmas II1.2.11 and III.2.12. It is also dear that the
value of sup U. g} at the point 8 . S is almost e,'erywhere equal to the
number sup U(s), g(8)}. The seeond statement or the lemma was
proved following Theorem III.6.1O. Q.E.D.
In order to establish another type of completeness for the space
M(S, I,I'}' it will be convenient to have a generallemIn8. on (i-com-
plete lattices.
836
IV. SPECIAL SPACES
[V.U.7
[V,12.1
FUNCTIONS OF BOUNDED VARIATION
337
tions in B are positive and bounded above by the rueasurable function
g. We shall f"n-st show that the lattice L of aJI I in 1I1(S, E, p) wit"
o I ,;;; g has the property that every well-ordered subset is count.
able. To do this let (R. E., A) be the reaUine under Lebesgue measure;
if we put (T.El' 0) = (S,E,p)X(R,E.,A) then the space (T, E., 0)
is a.finite (III.n.6). To each IE L we associate the measurable set
A(f) = {[s, r]ESx RiO ';;; r ';;; /(s)}. Note that if I.,f.-L and if II /.,
then A(f.) A(/.) and 0 < O(A(/.) - A(/.» = IsU.(s) - f.(s)}p(ds)
00. This implies that J. and f. are equaJ I,-almost everywhere if
and only if O(A(/I» and O(A(/.» are equal. Now the ,,-finite space
(T. Ell 0) can contain at most a countable number of disjoint measur-
able sets of non-zero O-measure. and so any well-ordered subset
of L can contain only a countable number of non.equivalent
functions, The theorem then follows from Lemmas 4 and 5. Q.E.D.
The natural ordering just used for functions in M(S, E.I') bas
already been employed for functions in the spaces L (S, E, fI),
I p ,;;; 00. In theorems 8.22 and 8.23 we proved that if a subset of
one of these spaces is bounded above by some function then there
exists 8. least upper bound in the same space. Each of these spaces is,
of course, a subspace of M(S, E, 1'), and it is useful to know that the
least upper bounds may be taken in either the space L.(S, E, 1') or in
M(S, E, pl. We state this result formally.
7 COROLLARY. Let (S, E, p) be a p<MiliVl' a-jim/£ measure spcu;e.
Then tM rea! spaces L.(8, E, I')' 1 ,;;; P 00, and M(S, E.I') aTe com-
plete lattU:rs and the supremum in L (S, E, 1') 01 a sel bounded in this
lattice is the same as its B'Upr m"m in 1M InttU:e ",U(S, E. p). Further.
more any sel B which is oo..>tc!ed in the laltice L (S. I p) co"tni1l3 a
cuuntl1hle subset lu,,'ing 1M sa"", supremum as R.
PROOF. It fol1ows from the fact that L.(S,E".) lIl(S,E'fI)
that M -sup" U.} ,;;; L.-sup. {t.}; sin<'C L. sup. {I.} is in the
space L (S, E, p) it follows from Theorem 1I1.2.22(b) that M -sup{f.}
is also in L.(S, E, 1') and hence the two suprema coincide. The final
statement follows from the preceding theorem. Q.E.D.
12. Function. of Bounded Variation
Let I be an intcrvaJ with end points a and b. Let E be the field of
sets in I consisting of all unions of inter"aJs (c, d], balf open on the
left unless c is the left end point a of I, and a. I, in which case we take
the closed interval [a, d]. If f. BV(I) is given, define /1,. bali, E) by
p,([a, dJ) = l(d)-/{a).J',«c, dJ) = I(d)-/(c) if c * a. It is then evi-
dent that v(p" I) = v(f, I). Thus, ba(S, E) is isometrically isomorphic
with the closed subspace BV.(I) of alii E BV{I) such thatf(a+) = O.
If N is the one.dimensional space of constant functions, it is evident
that BV(I) = BV.(I} E!J N. Thus BV(n is isometricalty isomorphic
to the direet sum of ba(I. E) and a one-dimensional space. From this,
the fol1owing theorem is evident (cf. 9.9).
1 THEOREM. The space BV(I) is a weakly complete R-spaee.
It is easily seen that the isomorphism defined above can be used
to give answers valid for the space BV(I} to many other of the ques.
tions asked in Section 1. We leave the details to the reader as an exer-
cise.
It was shown in Chapter III.s (cf. the discussion fol1owing Lemma
111.5.16) that if I is in NBV, then fI, is regular; and the converse is
equally evident. Thu8 f -+-+- fI, determines an isometric isomorphism
between NRV(I) and rha(I.E). U8ing Theorem 9.9, we obtain the
following result.
2 THEOREM. The space NBV(I) is a mrokly complde B-$pare.
Again we find that we are considering a space isometrically iso-
morphic to a space studied earlier; and again this isometric iso-
morph1sm Can be used to give answers to the problems listed in Sec-
tion 1. We leave the details to the reader as an exercise.
Finally. let I- AC(I), and suppose that I(a+) = 0, so that
I. NBV(I). Let E, be the ,,-field determined by E; i.e.. the field of all
Borel subsets of I. Let A denote Borel-Lebesgue measure, and... its
=triction to the field 1:. It is then clear that p, is A.-continuous, Con-
versely, if I.N BV(I} and p, is A.-continuous, it is clear that I . AC(I).
If ft, denotes the unique countably additive extension of 1', to
E". (which exists. according to the discussion foUowing 111.5. IO) then,
by Lemma 9.18. p, is A-continuous if and only if 1', is A.-continuous..
888
IV. SPECIAL SPACES
IV.12.3
IV.13.4
EXERCI8ES
339
fit(E) = fEg(it)dx,
g LI(I. E, A).
[al a 2t . . .] K. Show tlmt in 11' strong conditional compactness and
weak sequf:ntial compactness are the same.
4 If <.. { tin). } . k
co>p>lasequencex = i ,'.=1,2,... ISRwea
Cauchy sequence in I,. if and only if it is bounded and the limits
i = limn rI), i = 1, 2 , . . . all exist, and that such a sequence COD-
vere<"' weakJy to the element it = { i}' Show that if P = 1. the same
condition describes Co-coDveq.rence in ' 1 = 1:6 _
5 Show that no spare B(S, E) is weakly complete unless E IS
finite and that no space B(S) is weakly complete unless S is finite.
Show that batS, E) is not reflexive unless it is finite dimensional.
e Let 1./ft Lm(S,E,!t) then Iim.Is!n(s)g(S)fL(ds) =
Is I(s}g(s}p(ds) for every g in LI(S, E.fL) if and only if the sequence
{tn} is bounded in Lm(S,E,p) and
According to the Radon-Nikodym theorem (111.10.7), Pf is represent-
able as an integral in the form
Conseqnently, an arbitrary function I AC(I) Can be written in the
form
I(it) = I(a+) + f: g(y)dy,
where g is an element in L I {8, E, A). Conversely, every function lof
this form clearly belongs to AC(I}. It is readily seen that
It I = V(a+}1 + f: Ig(Y)ldy.
These facts establish the foHowmg re8ult.
S THEOREM. The spaee AC(I} is isamctricolly isamarphic U> the
direct sum of LI(I. E, A) and a one-dimenswnal space. CORSCfJlU'nJly,
AC(I) is weakly complete.
Solutions of the problems about AC(I) raised in Section 1 can
easily be given by using the isometric isofllorphism noted in Theorem
8. Details are left to the reader as exercises.
Ii:," f.1.(B)p(ds} f.t(8)fL(ds)
13. Ex"",,-
for every e in some field which dettonnines the a-field E.
7 Using 6.8, repr<sentthe spaces c and c.. (cf. ExtTcise II.4.SB).
8 Show that Co and c are not weakly complete and not reflexive.
9 A setK in c or in Co is conditiollRlly compact if and only if it is
bounded and the limit limn . exi8ts nnllonnly for", = { } in K. A set
Kin cor e. is weakly sequentially compact if and only if it is bounded
and limn /;ft exists quasi-uniFormly for '" {/; } in K.
10 Let "'n { ft!}, it = { ,} be vectors in c or in co' Then
"'n - it weakly if and only if {it n } is bounded and
A. Exercises which complete the table of Section 15.
1 Show that all possible topologies of a finite dimensional linear
topological space I are equivalent. Sl10w hence that 1\ subset of I is
conditionally compaet if and only if it is bounded. Show that if
{reJ' . . ., re..} is a basis for the n-dimensIonal linear topological 8pace I,
and {Ym} is a sequence in I, then Ym converges to an element y if and
only if a!.:) -+ am, where Ym = I l )ot!i' Y = I -l a.(llaJ;_ If I is a
B-space the sequence {Ym} is a weak Cauchy sequence if and only if
li -+Q> a ") exists" for each i, 1 i n.
2 Show that no space L,,(8, E,p) is rencxive unless it is finite-
dimensional.
S Show thl\t I\suhsetK of I., p ;:0> 1, is conditionally compact if
and only if it is bounded and lim I::-.I fl.l" = 0 uniforml)- for
ft--+m
Iimlim \ '=lim ,
n i "
lim .,) = t i ,
ft
i = 1,. , ..
The sequence {re.} is 1\ .veak Cauchy sequence if and only if Iim. t;\n)
and lim. lim., t; .1 exist.
n Show that the space bv. is i80metrlcally isomorphic to the
space l". and that bv is the direct sum of bvo and a one dimensional sub-
space. Using this isomorphism, the results obtained for I. all carry mler
to these spaces. " hat are the detailed results obtained?
12 Show that bv may be interpreted naturally as cs., and that
840
IV. SPECIAL 8PACES
IV.ll1.11!
IV.ll1.20
EX:£RI"UI.'J;'J::.
1141
bv. has a 8imilar interpretation as the conjugate of the subspace of cs
consisting of series with sum equal to zero. Use these facts to extend
Exercise 4 to fro and bv o .
13 Show that the space bs is isometricaJly isomorphic with the
space l... Show how this isomorphism can be used to solve aU the pro.
blems indicated in the tab1e for bs. What are the detai1ed fonns of the
results obtaIned Y
14 The space C$ is isometriiCaUy isomorphic with the space c. On
this basis. solve all the prohlems indicated in the table for this space.
IS Let S be a compact Hausdorff space. Show that C(S) is
weakly complete if and only if it is fimte dimensional, which is the case
if and only if S is finite. Using this result and 6.10, show that the same
statements may be made for Bny normal space.
16 Let S be a completely regular topological space. Show that
C(S) is separahle if and only if S is compact and metric.
17 Show that a 8equence {A,.} of elements of batS, E) converge
wqkly to an element A batS, L') if and only if there exists a non.
negative p batS, L'} such that lim j)..(E)1 0 uniformly in n. and
p(£)--<I
Show that a set K C batS. E) is conditionaJly compact if and only if
(i) K is bounded.
(ii) There is a non-negative pin ba{S, E) with respect to which
every A in K is continuous.
(iii) Iim.U.)=A uniformly with respect to AeK.
20 Let L' = {En} be a countable field of subsets of a set S, and
let 1.'1 be the ,,-field generated by L'. Let I' be a non-negative finite
countably additive measure defined on El' In the set A,. of ,.-measur.
able functions f with ,..ess sup It(8)1 :s;: 1 we introduce the metric
..s
e,.{t. g) = 1: I r { !(8)-g(8)}P(d8) ! .
......1 JEp.
Show that A,. is .. compact metric space. Show that.. bounded set K
in catS, E 1 ) is conditionally compact if and only if there exist8 a non-
negative p in catS, L'l) such that the continuity of
fS!(8)).(d8)
lim An(E] = l(E) for EeL'.
n"""
for f in A,. is uniform for 1 in K.
21 Show that catS, E) is reflexive only when it is finite di-
mensional.
18 Let p. E batS, L'). Then there is a p . batS, L') such that
lim J f(s)p.(d8) = J f(sJp(d8).
n s S
f B(S, L')
22 Let S be a normal topological 8pace and Yca(S) the regular
conntably additive set functions on the field of Borel sets in S. Prove
that
n "Ie,)
(U,)){e) = I - ( ) p(e;e),
i-lP e,
eeL'.
(i) Yca(S) is weakly complete.
(ii) A sequence {P.} in Yca(S) is a weak Cauchy sequence if and
only if it is bounded and the limit limnp,,(e) =p(e) exists for every
Bore] set e in which case p. £" 1'ca a.nd JJ." f.t weakly.
(iil) A subset K!:;; Fca(S) is weakly sequentially compact if and
only if it is bounded and, for some positive 1 in ua(S), the limit
liml(.I_o pie) = 0 uniformly with respect to p in K.
(iv) A set K Yca(S) is weakly sequentiAUy compact if and only
if it is bounded and the countable additivity of p(e] fore in the field of
Borel sets is uniform with respect to I' in K.
(v) rea(S) is reflexive only if it is finite dimensional.
if and only if {1p,,1} is bounded and the limit lim p,,( E) exists for every
set EeL'. ft
19 Let I' be a non-negative element of batS, L') and let ba(S,1:,I')
be the subspace of batS, L') consisting of those A which are p-con-
tinuous. For each a = (e l . . . ., e.) in the partially ordered set A de-
fined in 5_6 let the operator U. in batS, E, p) be defined by the
equation
342
IV. SPECIAL SPACES
IV.I3.2S
IV.IS.SO
EXERCISES
848
28 Let <0 > p> 1, I., I Lp[O, I] (Lebesgue measure is under-
stood). Then I. .. I weakly if and only if
surable functions on I and if the spnce !1>+Lw(l) is normed by the
equation
(i)
sup J: IWJ!Pdt < co
.
la+gl = [al+lgi = lal+ess sup Ig(B)I,
"r
then the equation
(ii)
J: J.(I)dt --->- J: I(t)dt,
O x < I.
x*1 = a/(a) -j- J,gI8)f'(B)ds,
I. AC(I)
The sequence {f.} is a weak Cauchy sequence If and only if (i) holds
and lim. I.I.{t)dt exists for each 0 '" 1.
24 Let I, f.' Lp(S, E, p) where J < p < 00, and let Eo be a
family of sets Qf finite measure whose characteristic functions form a
fundamental set in L.(S, E, 1'). Then the sequence {f.} converges to I
weakly if and only if it is bounded and
estabbshes an IsometrIc isomorphism between AC*(I) and !1>+Lw(I),
80 A bounded subset K of NBV(I) (or, BV(I)) is sequentially
weakly compact if and only if there is a g NBV (or, BV) snch that
for e > 0 we have a 6 > 0 with
lim fr,I.{8)p(ds) = JE/(B)p(ds),
.
n .
! Ig(B,)-g{t,)1 <,6 unplies ! If(B,)-/{t,)1 < e
1:_1 i-I
E.E..
for each I in K.
A sequence IfnI in BV(I) or NBV(I) conY<Tges weakly to an ele-
ment I if and only if the set {fn} is weakly sequentially compact and
we bave I.(B) -+/(B) for 8 in I.
81 A bounded subsetK of AC(I) is sequentially weakly compact
if and only if for each e > 0 there is a 6 > 0 such that
The sequence {I.} IS a weak Cauchy sequence if and only ifit is bound-
ed and lim.JEI.(B)p(ds) exists for each E.Eo'
25 Let 1.,1' L,,{S, E, 1'). Then I. "I weakly if and only if
bm. I,d.(B)p(ds) = h/(B)p(ds) for each E. E. Moreover, {I.} IS a
weak Cauchy sequence if and only iflim.Jld.(8)p(ds) exists for all
E.E.
26 Show that a bounded subset K Lw(S, E, p) is compact if
and only if for each £ > 0 there exists a partition n of S into a finite
number of measurable sets such that
. .
! 18,-t,1 < 6 implies! i/(8,)-/(t,}I < .
1=1 i...l
ess sup I/(B)-f{t)1 < £
""
t<A
tor each I in K.
A sequence {I.} in AC(I) coO\'ergt.'S weakly to an element f if and
only if {I.} is weakly sequentially compact and '.(B) -+/(B) for aU s.
32 LetK AC(I) and if 1 is not (-co. <o} let AC(I} be em-
bedded in AC« - 00, co)) by defining each I" AC(I) to be constant
outside of 1. The set K is conditionally compact in AC(I) if and only if
(i) K is bounded;
(ii) I;m.-+m v{f, I UI;;) = 0 uniformly for I in K, where I =
In. <0) and 1;; = (-oo,nJ;
(iii} lim.-+ m 1/-1.1 = 0 uniformly fori inK, whereJ.(B}=/(s+€).
38 On the closed interval I. let E be the field of sets gt'ncrated
by the family of subintervals with rational end points, and let {E.}
be an enumeration of E. Let p be Lebesgue nleasure. In the set A of
for each A £.:7l.
27 Let g,g..Lm{O, 1). Then I g,,(/)J(t)dt -+ I g(t)/(t)dt for
every I L 1 (0. J} if and only if
(i) sup css sup !g.(t)1 <0
. ,
(i;) I gn(t)dt -+ J gltldt.
28 Sbow that BV{I), NBV(I) and AC(I) are not reflexive.
29 If Lw(I) is tIle space of essentially bounded Lebesgue mea.
344
IV. SPECIAL SPACES
IV.18.34
IV.I:! 87
EXERCISES
845
11::(/) I,I(s)dg(s),
leC(I)
if and only if it is bounded and I (s) converges (to 1{J'(a» for each
s in [a, b] and each j = 0,1.. n, p.
(c) CP is not weakly complete, and not reflexive.
(d) A subset A CP is conditionally compact if and only if it is
bounded and for each e > 0 there is a {,> 0 such that Is tj < ()
implies I/,p'(a)-I<>I(t)1 < e for a, te [a, b].
(e) A subset A !;; C' is weakly sequentially compact if and only if it
is bmmded and the set {fl.,}, I e A, is quasi-equicontinuous.
37 Let D be a bounded domain, Show that a sequence of func-
tion8 In A(D) is a weak Cauchy sequence (a sequence converging
weakly to I in A(D» if and only ifit is uniformly bounded and conver-
ges at each point of the boundary of D (to f). Show that a sub8et of
A(D) is conditionaUy compact if and only if it is bounded and the
functions in it are uniformly equicontinuous. Show that a subset of
A(D) is weakly sequentiaUy compact if and only if it is bounded and
quasi-equicontinuous on the boundary of D. Show that A(D) is never
weakly complete and never reflexive. Show that A(D) is a closed sub-
space of C(D).
38 Show that AP is not weakly complete and not reflexive.
89 Show that a bounded subset K of the space AP is condi-
tionaUy compact if and only if
(i) there exists a function I. defined for e> 0 such that thc 8et
Lebesgue measurable functions such that ess sup I/(a)1 ;;;; I we intro.
duce the metri" .d
w I I f I
(2(/, g) = -;; I {f(a)-g(s)}l'(ds) ,
._12 E,.
Show that A is a compact metric space. Show that a bounded set K
in AC(I) is conditionaUy compact if and only if tbe continUIty of
J,I(s)dg(s) for I in A is uniform for I in K.
84 Under the same assumptions and with the same notation as
in the preceding exerci5e. Jet K be a bounded subset of NBV(I). Using
the notation of Exercise 20 and of Section 12, show that K is condi-
tinnaUy compact if and only if there exists a function g in N BV(I)
such that the continuity of J,h(a)l'l(ds) for h in A p . is uniform for
I in K.
85 (a) Let I be a closed interval. Show that the formula
determines an isometric isomorphism between C(l)* and NBV(I).
Show that if {gn} is a sequence of functions m N BV(I), we have
lim,, oo J,/(a)dg,.(s) = J,/(s)dg.(a) for alII in C(l) if and onJy if
(i) v(g..l) is uniformJy bounded;
(ii) g,,(s) --+ g.(s) at each poin a of contmUlty of gO'
(b) Using the relationship between BV(I) and the space ba(I, I) dis-
cussed in the first paragraph of Section 12, show how BV(I) may he
regarded as the conjugate space of the direct sum I of B(S, I) with
a one dimensional space, and give B. necessary and sufficient condition
for I-convergence of a sequence of elements in BV(I),
36 Show that the space Cora. b] is decomposable into the direct
sum of a finite dimensional space and a space isomorphic to C[a, b].
Show that
(a) every dement:£* in the conjugate space of CJlIS uniquely repre-
sentab]e in the form
M. = {tllf(a--t-t)-f(all -<: E for -00 < S -<: +00 and I in K}
has a non-void intersection with every interval of length I.;
(ii) for e,,"'1' e> 0 there is a {j > 0 such that
I/(a)-/(t)1 -<: E if Is-tl < {j and I is in K.
p-1 II I
11:*(/) = IXd"'(a) + r f1p,(s)l'(ds).
4=0 J.
40 Let S be a compact Hausdorff space. Show that a sequence
{In} e C(S) is a weak Cauchy sequence if and only if Ilnl is uniformly
bounded and lim.--+ w I.(s) exi8ts for each a. S.
41 Show that a sequence {In} of elements of AP is a weak Cau-
chy sequence if Bnd only if !In! is uniformly bounded and each sequence
{8m} of reaJ numbers contoms 8 subsequence {a",} such that
,
lim,,-.m lim'_01 In(8m,) exists. Show that a sequence {In} of elements
of AP converges weakly to I in AP if and only if each sequence
where Jl is a regular Borel measure.
(b) A sequence /. is a weak Cauchy sequence (converges weakly to f)
846
IV. SpECIAL SPACES
IV.18.42
IV.18.50
EXERCISES
847
{s.} of real numbers contains a subsequence (s..} such that
,
Jimn CD lim. In (8m) = lim,-+oc 1(8.,. ).
42 Let S be a nonnal topological space. Show that a sequence
{j..} E C(S) is a weak Cauchy sequence if and on1y if I/nl is uniformly
bounded and each sequence {s..} of points in S contains a subsequence
{s...,} such that limn_..lim. .. In(s..,) exists.
48 Show that a sequence {In} of elements of B(S, I) is a weak
Cauchy sequence if and only if Ifni is unifonnly bounded and each
sequence {8m} of points in S contains a subsequence {8m} such that
limft-+ lim,......GO J,,(sm) exists.
.
44 Show that a sequence {x.} of elements of Hilbert space is a
weak Cauchy 8equence (with weak limit x) if and only if Ix.1 is uni-
fonnly bounded and lim_eo ("'.' 11'.) exists (Iim._.. ("'.' 11'.) = (x. 11'.))
for each element 1Iu. in an orthonormal basis.
45 Let {Y.} be an orthonormal basis for Hilbert space Ii}. Show
that a bounded subset A of is conditionally compact if and only if
there exists for each E > 0, a finite collection ya." l' . . ., Yrx. of the
orthonormal basis {Y.} such that I 1(a:,1I'.>I" < e, all a: in A.
a;#a".....C\o.
46 Show that e\'ery continuous linear functional on the space 8
is of the form
of sequences coincidp in IIJ.JS, I ,p.), then e,'ery set of positive measure
in S is an atom.
(b) Show that L 1 (S, I, 1') is equivalent to 1 1 if and only if there
exists B countable collection of atoms of finite measure {En} in E such
that every measurable subset of S - U:... 1 E'f'I. is ither an atom of
infinite measure or a null set.
50 Show that no space equivalent to a space C(S) is equivalent
to a closed subspace of a space ba(S, I) unless both are finite dimen-
sional.
51 Show that no space L {S,I'I')' 1 <p < 00, is equivalent
eIther to a space CIS) or Ii space L 1 (Sl' I 1 , ,1'1)' tmless it is finite di-
mensional.
52 Show that if 3'1 is a finite dimensional subspace of R B-space
3', 1: 1 is closed, and there exists a second closed subspace 3'. of 3' such
that 3' = 3'. ffi 3'._
53 Let (S. I, 1') be a measure space which is not necessarily
positive. Let v(E) = v(p, E) for E E I. Show thatthe spaccsL.(S.E,p)
and L.(S, I, v) arc isometrically Isomorphic in a natural way for
I ::;;; P ::;;; 00. Rephrase all the theorems of Section 7 to obtain vcrsions
valid in this slightly more general setting.
54 Show that a bounded subset K of L,,(S, I, 1') IS weakly se-
quential1y compact if and only if
(i) lim JEf(8)p(S) = 0 uniformly for f 0 K;
,..(E)--?O
(ii) there exists a sequence of sets {A.}. A. £ I, p(A.) < 00,
such that
.
l(x)=Io:, ,.
<-,
where", = { .} E B, and ["':1,..., 0:.] is a finite collection of complex
numbers.
47 Show that a collection {:r 4 } = { nJ} of elements of 8 is con-
ditionally compact if and only if !.) is bounded ill 0: for each fixed i.
each fixed i.
48 Show that BV(I) is decomposed lIS the direct sum of its sub-
space NBV(I) and the subspace consisting of all functions in BIT
which vanish except for a denumerab1e set of points. Prove that this
laUer space is isometrically isomorphic to a space L-.. Use this fact and
Exercise 84 to give a characterization of the family of conditionally
compact subsets of BV(I).
limf I(s)p(ds) = 0 uniformly for loK,
n---7 S-A...
55 Let I be a B-space, anti let (S, I, 1') be a measure space.
Suppose that I : S -+ 3', and that x*/(') is p-integrable for each ",* in
1*. Show that there exists an ",** in r** such that
x*"(a:*) = Isa:*f{j)p(dt),
x* E 1:*.
B. Miscellaneous Exercises.
49 (a) Show that if strong convergence and weak convergence
56 (Gelfand). Let I be a B-space, and (S, I, 1') a meaSure space.
Let f* : S -+ 1*, and suppose that f'(')'" is p-integrable for each", in
!Ii. Show that there exists an ",* in <t* such that
848
IV. SPECIAL SPACES
IV.13.57
IV.18.6B
EXERCISES
849
w.", = fsl*(a).xp(ds), w.!:.
57 Let!: be a B-space. W1d let K be a real valued function de-
fined on:£ X [0, 1] which is linear in '" for each fixed I in [0, 1 J, and
which lies 10 L,[O, I] for each fixed a: in!: (Lebesgue measure under-
stood.) Suppose that
lim r' K.(I)dl = 0,
l:-)o-oJo
0;:;;;8;:;;; I.
measurable function defined on S X 8 1 8uch that for each 1 in
L (81.1:1' p,), the integral
g(s) = f K(s, sl)/(Sl)P,(dsJ
s,
exists p,-almost everywhere and lies in L" Show that there exists a
constant M < 00 such that Igl.;:;;; Mill..
68 If 1 and g are complex valued functions defined on the closed
interval [a, b], we say that the integral J:/(s)dg(a) exists in the IDe.
mann-StieItjes sense if for each e > 0, there exist points 8 1 " . . ., Sn in
[a, b] such that ift" . . .. !"W1d "'t,.. ., u, are two increasing sequences
.of points in [a, b], both containing aU the points 8 1 , . . 'J Sn, we have
Prove that
lim r l iK.(IWdl = 0
.-+0 Jo
if I;:;;;q< 00.
and that
hm ess sup IK,(I)I = 0
o O:ij:,:;l
58 Let:£ be a Bal1&ch space, W1d K a complex valued function
on!: X [0, 1] which is linear in '" for each fixed I in [0,1] and belongs
to NBV(O. IJ for each fixed x. Suppose that lim.-+{)KJI) = 0 for
o ;:;;; t ;:;;; L Prove that lim..-.-o v(K., [0, 1]) O.
59 Let 1 ;:;;; p S; 00 and let {...} be a sequence of complex num-
bers such that ... . converges for every ( .} in l . Then {a.} is in l "
where l/p+l/p' = 1.
60 If {...} is a sequence of complex numbers 8uch that a. .
converges for every a: = { .} in c. show that 1...1 < 00.
61 Let 1 S; P < 00, 1 < q S; co. Let (aij) be an infinite matrix
such that the .series t}, = 1 C1.uE, aU converge for every = L l' '2' . . .]
in I., and such that t} = ['11.7)., . . .J lies in I.. Show that if q < co.
there exists a constant K such that
if q= 00.
11-1 l-l
I III,)(g(tm)-g(I,» - l(u,)(g(u'+I)-g(u,))1 s; B.
pI pI
Show that if g is a function defined on [a, b] such that the integral
J:/(s)dg(s) exists in the Riemann-Stieltjes sen8e for each 1 in C[a, bJ
then g is in BV(a, bJ, and conversely.
64 Show that every continuou8 complex valued function t(8)
of the real variable 8 which satisfies f(.) = 1(8+2.1>:) can be approxi-
mated by.ll. finite linear combination of terms etA',. - OJ < 8 < + 00.
65 Show that every continuous function on the Cart.e5ian pro-
duct 8 X T of two compact Hausdorff spaces 8 and T can be approxi-
mated nniformly by finite linear combil1&tions of terms I(a) . get).
66 Let 8 be a compact Hausdorff space. "', "'n C(S), and
(a) lim ",.{a) = ",(s),
SES;
ft
(b) Ix.(s)1 S; II-! < co,
S S,
n=l,2,....
00 00
( 17),1,)1/. S; K( 1 ,1.)1!. for every = [E , ] in L
i-1 j__1
Then for every £ > 0 there is an integer tz and complex numbers ex"
i=l,...,t1,with
and if q = 00 there eXists a constant K such that
"
IX(8) - a"",(a)l < e
'.1
s£S.
00
sup 1'1'[;:;;; K{ 1 ,I')'f. for evcry = [E,J in L..
I '<<x> 1-1
67 Show that Hilbert space is isometrically equivalent to a
space L.IS, 1:, p) where 1: consists of all subsets of S and where p. is a
olIDta.bly additive function assuming the value one for each set con-
sisting of one point.
68 Let (8, L, I') be a finite measure space, and let K be a bound-
62 Let l::;;p<oo and l < q<co. Let (S,1:,!,) and
(8" L" f'1) be measure spaces, and let K be a complex valued f' xp.,-
350
IV. SJ>ECIAL SPACES
IV.13.69
IV.13.77
EXERCISES
351
ed subset of L (8, I, pl. Show that K is weakly sequentially compact
when regarded as a subset of L,,(8, I, 1').
69 Show that the family of characteristic functions of sets in I
is fundamental in L (S, I, 1').
70 The set of aU vectors '" = {'In} with 1'1.1 < Ifn in reall. is
called the Hilbert cube. Show that this set is compact in '..
71 Let (8, I, I-' ) be a measure space. Let I he a complex valued
function defined on 8 such that Ig is in L,,(8, I, ,,) for eyery g in
L,,(8. X, 1'),1 < p :0:: 00. Show that I is in Lo(8, I, 1'), where Ifp+1f
= 1. Show that if 8 is (T.finite. the same holds for p = 1.
72 An operator A in Hilbert space is said to be Hermitian if
(AlE. Y) = (x. Ay) for each IE, y in .p.
(a) Show that if A is Hermitian, A = 0 and (Ax, "'J = 0 for all
or in are equivalent.
(b) Show that if A.. i8 Hermitian for n O, Iim._ (A."" y) =
(A"x, y) for aU "'. y in .p if and only if lim"....oo (A."" ",) = (A,;r, IE)
for all x in t>.
73 A real function defined on an interval 1 belongs to BV(/) if
and only if it is the difference of two bounded monotone increasing
functions defined on I.
74 Let (8, I, 1') be a finite positive measure space. Show that
an equivalent norm in the F...pace Till(S, I, 1') is given by the for-
mula
and that f ;:; g if and only if
Js/(B)p(ds) ;:; fsg(B)p(ds) for all " > 0.
77 Introduce an ordering into Loo(8, X, l-') by putting I > g if
I(B) ;:; g(B) for ,,-almost ails in 8, and an ordering into ba(S, X 1 ,1"1)
(c£. Definition B.I5 for notation) by putting I' ;:; A if peE) :;;;).( E)
for E in X.. Show that I-' :;;; A if and only if
f.'(B)p(ds) fsf(B)A(dsl for aU I 0,
and that I g if and only if
JsI(B)p(ds) J.g(s)p{ds)
for all p ;:; o.
f V(B)I ds
III = Js 1+1/(8)1 ,4 ).
C. Summabilily EJcercI8<!S lor I ntegralB
The foUowmg exercJSeS are Ucontmuou i" .analogues of exercises
JI,4,3I - II.4.54. The reader can compare the solutions of the corres-
pooding exercises in Section 11.4 to construct solutions to the eXer-
cises in the present set. The reader should obsel"\Te that except where
oth€rwise noted Exercises 78-99 remain valid if the spaces 1Ilf)J ]Jf 1
and M 2 defin€d below are interpreted as spaces of . valued functions,
where 1 is a B-space.
78 Let R denote the positive real axis, /JI the field of Borel
subset8 of R. anel ). the Lebesgue measure of sets in /JI. Let il10
be the family of bounded ).-measurable functions I on R such that
lim. fIx) exU.ts. Sbow that Mo is a B-space, if we put
III = lub I/(x)l.
O;:;z<:o:.
79 LetK(x, y) be a.it x.il measurable function on R>-. R. Suppose
thatK(IE, yJ is A-integrable for each fixedx. Show that fO'K(;r,y)/(y)dy
is in M. whenever f is in III. if and only if
(a) folK(IE, y>ldy is bounded in "';
(b) lim f K(IE, y)dy exists for aU 0 < A < 00;
.-+
75 Let S be a topological space, I a a.field of subsets of S, and
if a B-space. Let I' be a set fonction defined on I and with vaJues in if.
Suppose that for each x* in if* the set function "'*p IS reguJar and
countably additive. Tben there exists a non-negative reguJar count-
ably additive set function v in catS. I) such that lim peE) = 0,
..(E)-+{!
76 Introduce an ordering into B(S, I) by putting I g if
1(8) :;;; g(s) for all 8 in S, and an ordering into ba(S, I) by putting
f-I .it if peE) :2: A(E) for E in X. Sbow that" :;;;). if and only if
J s /(8)/l(dsJ :;;; Js/(B)A(ds)
for a1l I > 0,
(e) For each > 0 and A> 0 there exists a b> 0 and N> 0
such that
iJ"K(""y)dY[ <e if E(;(O,A], )'(E) <b. ",>N;
852
IV SPECIAL SPACES
IV.18,80
IV 18.84
EXERCISES
853
(d) Jim f:K("" y)dy exists.
........
2", f. ..
(d) (Gauss) lim e-cz."/(y)dy = lim 1("');
O V.n 0 Qt-H"
Show thRt fv K(o:, y)f(y)dy has the same Jim,t at '" = co as 1(..1 ifand
only if we have
(b') lim f:K("" y)dy = 0 for all 0 < A <
-..
2 I. .. ( sin "'1/ ) "
(e) lim- - I(y)dy=lim/(o:).
F+03lX (I Y
Rnd
(d') lim f; K(o:, y)dy = 1.
-..
84 Let (B. E, A) be as in Exercise 78. Let M. be the space of all
bounded A-measurable functions I defined on B such that lim 1("')
exists. Putting z->1)
80 Let k be a non-negative function of a real variable which is
Lebesgue integrable over every finite interval. Put K(",) = J k(y)dy.
Show that we bave
1 I. "
lim/("') = Jim - I(y)k(y)dy
z..... _..K(",).
for all I in !If. if and only if IimK(",) = co.
-..
III = lub 1/("")1,
(I:S;;;r<
81 Let k be an increasing non-negative function of a real varia
able which is integrable over every finite interval. Put K(",)
f k(y)dy. Show tbat if lim....... k(",)/K(,.,,) 0, then
show that M I is a B-space.
85 LetK(,.", y) be a AXA measurable function on Rx R. Sup-
pose that K("" y) is A-integrable for each fixed "'. Show that
I;K("" y)f(y)dy is in !If, whenever I is in M I if and only if
(a) f:IK(""y)[dy is bounded in "';
(b) liIl\.--.o JA'K("" y)dy exists for all 0 < A < co;
(e) For each e> 0 Rnd A> 0 there exists a > 0 and N> 0
such that IJEK("" y)dyl < e if Er;; [A, co], A(E) < , and", < N;
(d) for each e> 0 there exists an M> 0 and an N> 0 such
that f:.tIK("" y)ldy < e for w < N;
(e) limIvK("'.y)dy exists.
z....
1 I. z
Jim - l(y)k("'-y)dy = lim I("'}
m OI K(m) 0 I»
for all I in Mo'
82 Let p be a non.negative measure defined for all Borel .ub.
sets of the positive real axis, Suppose that I;e-"'p(dt) = co, but that
f;e "p(dt)=N(8) < CO for.> 8., Put N(f,8)= f;e-"/(t)fI{dt) for
8 > 8. and I in M.. Show that
limN(8} lN(/, 8) = tim/("') for I in M..
...-r.o
Showthatf{",) has tbe .ame Jimitat", = 0 as JvK(""y)f(y)dy if and
only if we hAve
(b') lim fA' K("" y)dy = 0 for 0 < A < co;
.-"
(e') Jim I. K(w, y)dy = 1.
-.
86 Show that if f is in M l then
88 Show that if I is In M.
(a) (CesAro) Jim [ I(Y)dY = lim 1("');
z_o:>Ot' 0 c_
(b) if ,,> O. lim r (",_y}. I/(y)dy= limf("');
It-+OI 3fI 0 C>
(e) (Abel) lim... I;r'/(y)dy = lim/(",);
;c-+{) Ho.
I I. z
(n) lim I(y)dy = hm/l"');
;Xf) O
C1. I. .
(b) lim - ("'-Y)' '/(y)dy = lim/("');
2-'I>OafI- 0 z--+-O
(e) lim '" J. r"J(y)dy = lim I(x);
oz-o-\)
354
IV. SPECIAL SPACES
IV.18.87
IV.13.93
EXERCISES
355
2x f. '"
(d) Iim rl..../(y)dy = lim I(x);
Z_UJ "In 0 :11=_0
2 5. '" ( sin '"Y ) '
(ej Iim - - I(yJdy = 1im/(x).
_o:>nx (J Y :t->M)
87 Show that if jis in La>(R,BI,l), then. 2 Ji:' e-'" Jo/(y)dydJ:
=z JO' "--"/(y)dy, and heneethat if lim'_a> (It"'>Jo/(y)dy exists, then
Iim._o z Ja r"/(y jdy exi8ts and has the same value. Show that if I
is in L", (R.BI, A), «> 0, and lim ", (at""') Jo(",-yj' l/(yjdy exists.
then 1im:2l_o z J; f!-r;.f(y)dy exists and has the same value.
88 Show that if I is in L",(R,BI,l) and if Jim "'/("') = 0 then
(c) lim", J.(",-y)"I(yJdy = lim Jg l(yJdy,
r A_
a. o;
f. A ( sin '"Y ) ' f. A
(d) lim lim - I(y)dy = Iim I(y)dy.
z_o .A_CXI 0 try J!_:iO 0
93 If {a} is a set of indices.
(a) Pa(O) i8 uniformly bounded in 11.;
(b) v(P.. [0, 00» is uniformly bounded in 11..
Then if I is in 111"
lim Jg 1("')f!a(OJ)dJ:
A-+o>
a_a>
exists uniformly in a..
94 Let 1("') be a l-measurable function which is A-integrable
over every finite interval [0, A]. Suppose that for some complex
number Iim Jg .,--"'/(",)dJ: exists. Then
A-+o>
lim JO' .,--"'f(y)dy A if' and only if lim (11"') JI; ("'-y)/(y)dy = A,
o z-»CX'
(Hint: Compare exercise II.4.54.)
89 Let 1>1, be the set of all A-measurable functions f such that.
(a) f is .I.-integrable On each finite int"","" [0, A]
(b) lim Jg I("')rk converges.
A_o>
lim Jg e "zf(",)<Lx
A_o>
0>
Put III sup IJg/(",j<Lxl+ };I./{2'(I+I.», where 1.= J,JIf("')I<Lx.
() A<oo 7/....1
exists for 91(.') > 91(.) and is analytic in this half-plane. (Hint: use
Exercise 98).
95 If An is a. sequence of positive real numbers monotonically
approaching co, and if the series (generalized DiricWet series)
.I:-o an"'; converges for some comp1ex number ;, then the series
converge8 in the half plane 9i'(z) > 91(.,,) and i8 analytic there.
(Hint. cr. Exercises 93 and 94.)
96 If I is integrable over any fmite interval, if (11"') J 1/(/)ldt
B, and if lim...... J /(/)dt = A, then
Show that 1>1. is a separable F-space. If M. is interpreted as a space
of I-valued functions where I is a B-spacc then ifl. is 8eparable if and
only if I is separable.
90 Show that if p is a function of bounded variation defined
on R, then IP is in M. if I is in Mo'
91 Show that if P("" 'II) is a function defined on RxR such that
(a) the variation v{fJ("" '),(0, 00» is uniformly bounded;
(b) [P("" 0+)1 is uniformly bounded;
(c) lim Jg pC",. y)dy = A for each 0 < A < <X:I;
then ;Z_(:r>
8 f. 0> sin" mt
lim - -/(/)dt = A.
11:-+(» 3.mc 2 0 f3
lim lim Jt p(a;. y)/(y)dy = lim Jg I(y)dy,
;II:-+W .d"--+CIC .4-+0;>
I in 4-
97 Let K be the Laplace transform of a function g such that
g(s)/s belongs to Ll and J;;'(g(s)/sjds = 1, If I is integrable over any
finite interval. if
92 Show that if t is in Mo, then
(a) lim Jim Jt e-z'/(y)dy = lim Jt I(y)dy;
_O.d-+Qc A_
(b) lim lim Jt r(""/(y)dy = lim Jt I(y)dy;
2_0A-+(:r> A-+
fim I roo e-"/(.)dz = A,
'-+0 Jo
and if
856
IV.. SPECIAL SPACES
IV.18.98
IV.14.1 ORTHOGONAL SERIES AND AYALYTIC FUNCTIONS
857
I f: e " 1/(.>1<1. S; B,
f Hod { I f P-& } I "
(a) -O>! z I(y)dy -/(:x), dJ: = 0;
(b) lim f +'" I( f '*& (E--t-:X-Y)O-lf(Y)dy j -/(:x) I " dJ: = 0;
E--+D -00 f!I r
(c) hm J :: I{n J: e n'/(:x-yldy}-f(:xIIPdJ: = 0;
then
lim t Co. K(tz)/(z)dz = A.
t-o 10
98 Ifl is integrable over any finite interva!, if lim 'Joe "/(.)dz
.... A. and I f: e " 1/(')ldz ;;;; B. then . O
J. '" at
lim I(z)dz = A
....0 0 (tz+a)'
n '"
for a> O.
99 Let I S; P < 00 and for each 1 in Lp(R,.IB, A) let I.(:x)
= I(:x+y). Then I. is a continuous function of y with values in
Lp(R,.IB. A).
100 For every B in R, let K, be an element of L,(B..IB. A).
Suppose that
(a) J,;-IK.(a;)!dJ: ,;; M < 00. B. R;
(b) lim fA K.(a;)da: = 0, 0 < A < 00:
(d) lim f +O> I{ n_ f To. r.n')'/(3J-Yldy j -I(3J) I " d:x = 0;
71_01 _()C Vn-Q1
f +'" I ( I f +o. ( sin ny ) ' } I "
(e) lim - - 1(3J-y)dy -f{:x) dJ: = 0
fl'-+CXI -0:> 1ltt -Q!> Y
lim/. 1
101. Exadoes on OrthO!\onal Sene8 Bnd Analytic Functions
The following set of exercises is concerned with the application of
linear space methods to the theory of orthogonal series. The most
important special case of this theory is that of Fourier series in which
we consider the expansion of arbitrary functions on the interval
[0,2.n] in series of the form :arl!i . In view of the importance of
this special case, (and more out of convenience tha.n out of necessity)
we shall take [0, 2'1"] as a 8tandard interval in aU our problems. Then,
by C(" we shall mean CI"[o, 2"]; by AC and BV, AC[0,2'I"] and
BV[O, 2,,]; by Lp, I S; P < 00, the space of fW1ctions f defined
and Lebesgue measurable on tbe interval [0, 2,,] such that
j/lp (fol/(3J)I"rk;}l/. <. 00, etc. We shall also find it convenient to
use the 8ymbols co. for n:_ 1 C'n) and CBV for CnBV.
In the specific case of Fourier series it will be assumed that our
functions are periodic: i.e../(O) = 1{2,,) for 1 in C, AC, BV. or CBV;
1(1'(0) = /(1'(2,,), 0 S; k ;;;; n. for 1 E c,n" and 1"'(0) = 1("(2,,) for
all k 0 if 1 E C'''''. or course, a restriction like /(0) = 1{2'I") is
meaningless in the space Lr
I DEFINITION. By a closed orthonormal (c.o.n.) system wc
mean a two-sided sequence of functions 4>.. n = 0, I I. I2, . .. in
CCO» such that
(i) linear combinations of 4>. are dense in every space C",,
o ;<:; k < 00.
.-.'"
(c) for each e> 0 there exists an N ;;;, 0 and a K > 0 such that
J; 1K.(a:)IdJ: < E, S ;;;, N;
(d) for each E> o and A> 0 tl1ere exists all> 0 and an N> 0
such that
IfEK,(3J)da:1 < e
if E[;;; [A, 00). A(E) <lI, and S N.
For 1 S; P < 00 show that if 1 is in 4(R..IB. A). the function
I. defined by
1.(3J) = J: K.{y)f(x+y)dy
is defined A.almost everywhere for B. R, belongs to L.(R..IB, A) and
that the limit relation
.-.
holds in the norm of Lp.
101 Let 1 be Lebesgue measurable on the whole real axis, and
let e::: If(:x)["dJ: <. 00, where I S; P < 00. Show that
858
IV. 51'ECJAL SPACES
IV.I4.2
IV.14.18 ORTHOGONAL SERIES AND ANALYTIC FUNCTIONS
859
(ii)
J: 4>.(x Mm(x) dx = 0,
-."
Jo 14>.,x)!"dx = I,
n mJ
I sin{[n+(1/2)](x-y)}
E.(x,y)=- .
2" sm(I/2)(x-y)
-oo<n<oo.
for 4>.("') = €'=/ V2,,-
For f in L}O
By f.. the nth coefficient of a fundion f . L" we understand the quan-
tity fo" f(x )if>.(x) dx. By S.I, the nth partial sum of the orthogonal
expansion of f, we understand the sum Ii:-n/.if>.(x).
2 Let {4>.} be a c.o.n. system. Let };'.(x. y) = I':.4>,(X) .pi(y)'
Show that S./ is given by the formula
f. = (2n) 111 J: f(x)r'=Ik
is cal1ed the ..th Fourier voofjici<mt of f and the formal serIes
r"
(S.,)(x) = Jo E.(",. y)/(y)dy,
GO
(2n) ]j1 I lor
-GO
f: IEn(x, y)ldy ,;; -,'t!,
O;$;x ;$;2", n>O.
i" called the Fourier series 01 I,
18 Show that if {cn} is a sequence with le.l" < 00, then
there is some I in L. whose nth Fourier coefficient i8 c.. Show that,
conversely if f is in L2, and In is the nth Fourier coefficient of /,
then GO If.I' < 00.
140 The nth Fourier coefficient of a fundion in L, approaches
zero as n approal'hes infinity.
15 Show that the Fourier series of some contmuous function
fail. to converge uniformly on [0.2n]. Show that there exists a con-
tinuous function whose Fourier series diverges at o.
16 Show that there are functions in Ll whose FourIer series
diverge8 in L,.
17 Show that if IE AC and hence if , E C"', k ;;;; I, then the
Fourier series of I converges nnifnnnly on [0,2,,].
18 Show that there exists an I in AC such that I':_.'/ft€'= rails
to com-erge unifunnly.
]9 Define the operator E by
N N
E( I a,,<".') = I 0,"='
n--N ti-U
and is a projection StJ in each of the spaces Lp, BV, CRY, AC, C(J;J,
1 P 00" k = 0, I, 2, . . .t 00. Show that the range of 8n lies in
C("').
8 Show that 8ft --+ I strongly in anyone of the space. ClkJ,
k < co, AC, L., 1 ;$; p < 00 if and only if 18.1 ,;; K, where 1 8 ft I de-
notes the operator norm of 8ft in the space. Show that in Lo, 8. --+ I
strongly for all c.o.n. systems.
4, Show that for a given e.o.n. system, Sn --+ I strongly in L, if
and only if Sft --+ I strougly in C.
/; Show that S. --+ I strongly in L. if and only if Sft --+ I strongly
in L., (l/p+I/'i = 1).
6 Show that (S./)("') c;onverges to 1("') uniformly on [0,2,,] for
alii' C'.) if and only if the operator norm of 8n as an operator from
C(k) into C is uniformly bounded as n 00.
7 Show that (S./)(x) converges to fIx) uniformly on (O,2"J for
each I in AC if and only if I J E n ("" z)d.1 ,;; M for all y and a;.
8 Show that S. --+ I strongly in C if and omy if
9 Show that J '4>.("')f(a;)dx--+O as n --+ 00 for all' in L. if and
only if the .pft are uniformly bounded.
10 Show that J "'.("')f(x)dx --+ 0 for all , in L», I < p < GO,
if and only if fo"l.p.(x)I"<I.x <},f, I!p+I/'i = 1.
II Show that the functions {(2" ) "........} "' form a e.o.n. system.
12 Show that
It will he shown later that for p> I, E may be extended to be a
bounded operator from L. to Lv Deduce from this that Sft --+ I
strongly in L., 1 < p < GO.
20 Show that there are functions I in C having Fourier series
I:.-a, f.,einz such that no g in C has Fourier series "l:-o I"el .
The convergence of the partial sums Sri with respect to a given
closed orthonormal system is said to be localized if for every I in L.
860
1\'.. SPECIAL SPACES
IV.14.21
IV.14.83 ':)RTHOGONAL SERIES AND ANALYTIC FUNCTIONS
361
which anishes in a neighborhood of a point p the sequence (8../){",)
converges to zero unifo-mly for r;t in some neighborhood of p.
21 Show that if I J E.(x, ...)dzl M, then the convcrgence of
S../ for a given c.o.n. system is localized if and only if max IEn("" y)1
S; M. < co for each e> O. 10-.1;';'
22 Suppose that (8../)(",) -+ I("'} uniformly for eveI')' I in AC.
Show that there exists a finite constant K such that for I in CRY.
1(8../)("')1 K(v(l, [0,2"])+ sup 1/("')1>, 0 < x S; 2,..
1):;2":;211
23 Suppose that
(i) (8../)(x) -+ I(x) uniformly in x for I in AC,
(ii) The convergen.... of 8nl is localized. Show that for any t in
CRV, (8../)(",) -+ I(m) uniformly in x.
24 Suppose (i), (ii) of the last exercire. Show that if I is in BV
then (8../)(",) -+ I("'} at each point'" where I is continuous.
25 Suppose that (8../)(",) -+ (1/2)(/("'+ )+/("'-}) for each step
function I. Show that under bypotheses (i) and (ii) of Exercise 23,
(8../)(",) -+ (1/2)(/("'+ )+1("'-)) for every Ie BV and each "'.
26 Show that convergence of Fourier series is localized.
27 Show that for Fourier series
(a) (8../)(",) -+ 1("') uniformly in x for I in CBV.
(b) (8../)(",) -+ 1("') if I is in BVand if I is continuous at "'.
(e) (8../)(",) -+ (1/2)(/("'+ H/(x-)) for all x if I is in BV.
28 (Dini) Let c/>. be a c.o.n. system such that (8../)(",) -+ I(x)
uniformly for all I in AC. Let 0 ;,; "'. S; 2,.. Show that the condition
(y-x.) I(/(Y)-/("'.)) £ I.,. is sufficient to insure that (8../)(",.) -+ 1("'.1
if and only if there exists a finite constant M such that
IEn(x o , y)(x.-y)1 ;,; 111 for 0;'; Y < 2,..
29 Show that the Fourier series of a function in Ll con\-erges
to the value of the function at every point where the function i8
differentiable.
30 Show that if I E C"', the Fourier series of I converges abso-
lutely. Show that this is no longer the Case for each 1£ AC.
31 Sbow that not every sequence {tn, - 00 < n < oo} with
limlnl-+'" In = 0, is the sequence of Fourier coefficients of a function
in LI"
32 Lct F'n) be a sequence offunctions on [0, 2,.] with absolutely
convergent Fourier series, let g E Lr Suppose that
(i) lim Flnl(x) = g("') for all "';
ft-+'"
'" '"
(ii) F'nl(x) = I F.'nle''''' and I ]F.'nll S; K. n = 1,2, .. ..
_-tD _-'1!>
Show that then the Fourier series of 2("') converges absolutely and
that g is equivalent to a continuous {unction. (A. Beurling, "Sur les
integrates de Fourier nbsolument convergentes", 9th Scandinavian
Mathematics Congress, 1938.)
83 Let (ex, fJ) be any subinterval of [0. 2,.J. Show that not every
continuous function I on (ex. fJ) can be represented on (ex. fJ) as an
absolutely convergent Fourier series f(at) = I:'_OIcn.ein2, ex ;£ fJ,
I:::'_",lcftl < 00. (Hint: U8e Exercise 32 and the open mapping p n-
ciple to show that in the case excluded by our statement there eXIsts
s. discontinuous function with an absolutely convergent Fourier
series. )
In the following set of problems, we suppose that we have given
B summation procedure which maps convergent series into convergent
sequences (cr. Exercise 11.4.46). That is, we have a collection of real
numbers {A..n}, 1 S; m S; 00, -00 < n < +00, such that if the series
O> C conver g es to a limit C, then each of the series 2:=_cpAn.n C 'R'
.Ln__o:> 11
m = 1, . . "f converges, and we have lim I _w1mnCm = C. We make
the addItional standing hypotheses m_'"
(\) :_'" IA...I < co, m = 1.2. . . -
(ii) The c.o.n. system c/>. is uniformly bounded.
This being the case, :_",}.m,J..c/>.("') conW'tges uniformly in x for all
m> I, for each f in I.,.. (t. is the nth coefficient of I: 1ft =
fo" f("' >4>.(",) <k). We shall write the sum of this series as T,J, i.e.,
we put
+'"
{T,J)(x) = I J.m.M.(x),
m l.
....-'"
84 Show that there eXists a continuous function Kml"', y} of
two real variables such that
(T,J)(x) = J: f(y)Km("" y)dy,
m 1,/eI.,..
35 Show that T,J --+ I strongly as m --+ 00 in anyone of the
spaces C"I. AC or L. if and only ifT m maps the given space into itself
862
IV. SPECIAL SPACES
IV.I4.36
IV 14.48 ORTHOGONAL SERIES AND .\.NALYTIC FUNCTIO S
868
and ITml < K, where JTml is the operator norm of Tm regarded as an
operator in the given 8J>M<'.
86 Show that convergence of T,J in the space C or in the space
L,. is equivaJent to the statement that
f: n IKml"', ylld!! <;; lH, 0 <;; '" <;; 2n.
87 Show that if <hI"') =(2n) 1;2 aJK! if Km("" y) :2: 0 for an m.
then T m. converges in C and Lr
88 Given abounded sequence of numbers {a.}, -00<"<+00.
Under the hypotheses of Exemse 87, show that there exists I in C with
aft = fo"/(",) 9'>.("') dz if and only if the functions L:.._",A...a.9'>.("'),
m 1, are unifonnIy bounded and equicontinuou&.
89 Let {u,,}, - 00 < n < + 00, be a bounded sequence of num-
bers. Show that under the hypotheses of Exercise 87 there exists a
compJex-vaJned regular measure I-' in C' with a. = fo" P.{Y)I-' (dy)
if and onJy if fo"lI:--m A...a.<p.("')ldz < K, for aU m I. Show that
there exists an I in L, with a,. = fu n<pn(Y )/ (y )dy if and only if in addition
to the preceding hypotheses,limA!E)->O!EI};;:'__",A...u,,<p.("')Id.'v=O.
uniformly in .., E denoting a Borel 8et and iI{E) its Lebesgue
measure.
40 Let {a.}, -00 < n < +00, be a bounded sequence of
numbers and let I < p < OJ. It is assumed that the summation pro-
cedure is such that T..j converges to f in Lp for every I inL.. Show that
there exists an f. Lp such that a. = fo"/(",>P.("')d.'v if and only if
there exists an 1"1 < OJ such that
};;;:_",a.b. converges for eooh sequence {bft} of the form b. =
fo"g(",)e-'''''d.'v, with g. L..
48 Let {a..}, - 00 <.. < + OJ, be a bounded seqnence of num.
bers. Show that, under the hypotheses of Exercise 40 1 there exists
an /. Lp such that a.= Ji:'f(", )<p.(", )d.'v if and only if lim",-->",}; _",
A...a.b. exists for each sequence {b.} of the form b. = fo"P.("')g(",)d:r,
with g. L. where I/p+I/q = I.
44 (Cesaro Summability) Let
A... = l-(Inllm), ,,= 0, :i:I, :i:2".., :i:(m-I)
A... = 0, Inl m.
Find the corresponding kernels K,..(",. y). Show that for I L.,
1 m-l
T,J = -- }; S,I
m 1-0
where 8 1 and T m have their earlier mea.nings.
45 Show that if {P.} = {(2")-I/',.,,,} and {il m .} is as in Exercise
44, then
(a) K m ("" y) > 0
(b) T..j / in C and in L,.,
46 Let [40.] be any uniformly bounded c.o,n, system. For
I L,., set Ifl = fo" I(y).pn(y)dy. and set
'"
(Trj)(w) = }; TI.I/.p.I"), 0 < r < 1.
71__«'
.. '"
10 1 }; i!"..a.40.(w>i"da: < 11-1,
.,,__0:>
m :2: 1.
Find a kernel Pr(w, y) so that
(Tr/)("') = I: l(y)P r ("" y)dy.
47 (Poisson-Summability). Let {P.} = {(2n) 1/2,.",}. Show that
here the kernel of Exercise 46 is
I 1-,'
Pr("',Y) = - .
2n I+T 2 -2Tcos(",-y)
Show that T,/ -+ I in C and L."
48 For I. L. aod - 00 < 1 < + 00 define U d by the fonnula
(U.f)(",) = 1(",+1). 0 '" 2n (we definto' 1("') for w < 0 b}' perio-
dicity; i.e., by requiring that I(w) = 1(,,+21<). - 00 < '" < +00).
41 Let {a.}, - 00 < " < +00, be a bounded sequence of num-
bers and let I < p < 00. Show that there exists an f in Lp such that
u" = fo"/(",Ie-i"'dx if and only if there exist8 ao M < 00 such that
"" +m
10 1 2 a.,i""I"d:r < M, for m = 1,2, . . ..
_-m
42 Let {an}, - 00 < n < + 00, be a bonnded sequence of num-
bers. Let I < p < 00 and let I!p+I/q = I. Show that there exists an
f Lp such that a. = fo" I(",)e-'''''d:r. if and only if the series
864
IV. SPECIAL SPACES
IV.14.49
IV.14.55 ORTHOGONAL SERIES A]J}) A:NALVTlC FUNCTIONS
865
where Km(t) is Km(O, t) in the notation of Exercise 84. (Here 1 is in
L , AC, or Cln).
50 Show that in case P.("') = (2n)- lf "e'=, T..f ---" 1 in the nonn
of L. (orAC, or Clrt') for IEL. (or AC, or Clrt') if T..f_/in the norm
of C for each 1 E C. (Hint: Use Exc£cises 85 and 49.)
51 Show that if T m is the operator of Exercise 45, (T ..f)("') _/(",)
at every point of the Lebesgue set of a function / E L". Show that the
same holds for the operator Tr of Exercise 47. (Hint. Use Theorem
JII.12.n.)
52 (Hardy) Let 1(2) be analytic in 121 < 1. Show that for p :2 1.
NrU, pI = U:'If( r c"8)I.dllj1J.
(a) I(re") = f. "" F(t)Pr(t, 6)dt,
2", 0
(b) {ft'I/(re'-&)I.d8}'/. < IFI..
Show that the map: f ---" f defined in Exercise 53 maps H. In a
linear one-one manner onto the closed subspace of L consisting of
those F all of whose negative Fourier coefficients vanish.
55 Using the notations of Exercises 53 and 54, show that if
/_ H. and if (Urf}(6) = /(re"), then [Vrf-JI. -+ 0 as r -+ 1. (p> 1).
56 Using the notations of Exercises 58 and 54, show that if
IE B., p> 1, theu for [zl < I.
f(.) = f f(/;}d
2"" /;-"
1<1-1
57 Show that if we normH. hysetting III =8up{fo"l/(re"JlPdO}"..
HI' becomes a reflexive Banach space. +'<1
58 Using Exercise 19, 8how that if FE L., GEL.. I/p+l!q = 1,
then :O=-UI FftG n converges and
I f. "" m
- F(t )G(t)dt = I FiJ.
2x 0 n--(P
where Frt = (2",) 1 fo"F(t)'-"'dt, G. = (2n)-1 ft'G(t).-,.,dt.
59 Let {a.e m be a bounded sequence of numbers. Show that if
Show that if 1 E L. or AC or C'rt' (being in each case subject to the
periodicity requirements set down in the discussion preceding Defi-
nition I) V J is a vector-valued function of t (with vaiues lying in the
given space L. or AC or C( ), as the case may be) which varies con.
tinuously with t, and that IV,/I = It I.
49 Show that in case 4>.("') = (2,,) 1I>e"". the operator Tm is
given by the integral
Tmf = J: (V.I)Km(t)dt,
i. an increasing function of r, 0 ,;: r ;;;; I. (Hint. Apply the maximum
modulus principle to the vector-valued function F defined by
(F(,,»(6) = 1(""'").)
53 Let the class B. consist of all functions I(z) analytic in Izi <I
such that
u(r, 6) = I a",.I.le i "' :2 0,
r> I.
0;::;;;0<271:,
'J'I""'-CO
N(/, p) = sup N r (/, p) < co,
r<'
then there exists a positive measure p. in C* with J "-<"dl-'(t) ano
+co> 11 > -co. (Hint: cf. Exercise 89.)
60 If1'.(t, 6) is defined as in Exercise 47, and U(T, 0) and p. as in
Exercise 59, show that
u(r, 0) = 2", J:- Pr(t, O)dp.{t}, r < 1, 0 ;::;;; 8 < 2""
61 (Herglotz) Let I(z} be analytic in Izi < I and !Jl/(z) :2 0,
Show that there exists a positive measure I-' E C* and a real constant
v. such that
where N r (/, p) is defined as in Exercise 52. Assume p > 1. Show that
if I(z) = I:_.I.""EH., then there exists a function f in L. with
J."" f<O)e ..dO = 0, 11 < 0
= 2n/., n > O.
54 Suppose that F is in L. for some p > 1 and is such that
J F(6)e'.'d8 = 0, for all n < O. Let /(,,) = I:'...F.z' where
F = (lf2",)fo"F(O)..-<.8dO for 11 ;;;; O. Show that
r ef'+z
1(") = --:--- . l-'{dt)+;vD'
_0 e t -2
Izi < 1.
866
IV.. SPECIAL SPACES
IV.a.62
IV414.67 ORTHOGONAL SERIES AND AN"AL"'TrC FUNCTlOSS
867
(Hint, Use previous exercise; in Izi < 1 an analytic function is deter-
mined by its real part up to an imaginary constant.)
62 Let {/.J be B sequence of monotone increasing functions
which is uniformly bounded. Let 1 be a monotone increasing function
and assume that
lim f, "" e-'''''/.(a:IdJ: = f"" r'''''f(a:)dJ:,
Ir-+co 0 Jo
for oJ! n. Show that 1>(a: I converges w I(a: I at each point of continuity
of I in (0,2n).
63 Let (4).} be a C.O.n. sY8tem and for f in L,. set a.(f) =
J:'4>.(a:)/(a:)da:. A set E of integers is coiled p, I] la=nary if f E L. and
lfi = 0 for n E implies {f.} ", . I.. Let 1 S; P < 00 and 1 S; I] < 00.
Let p',I]' be 80 that IIp+llp' = I, 1/1]+1/1]' = 1. Show tlmt E is p, I]
lacunary if and only if whenever {"'} '" is in I., there exists an I in L".
such tlmt <X" = I. for n. E.
Let {4>.} be a unifonnly bounded c.o.n. system and let {A,.},
- 00 < n < + 00, be a sequence of numbers. Let be any of the
function spaces on [0.2n] which we have been considering. We say
that (A,.} is a lacloT-Sf'IJ'U"'l£€ 01 Iype (I!, 2/), or bridly {A,.} is (I)(, 1)(1,
if for each f E \JI there exists some 1* E \JI with r.. = A.f.- If rea = C*
denotes the spoce of regular measures, we 8ay {A.} is (rea. Teal if for
each p.£ 'lea, there exists p. in Tca with
f:- 4>.(a:)p *(da:) A. r M"If' (d.x).
64 Show that If each A" IS real. the sequence {A,.} is (L,., L..) if
and only if it is (L"" L m ), (C, C) or (rea. rea). (Hint: C eLm. Tea is the
conjugate space of C, L, C Tea, L", is the conjugate 8pace of L..,)
65 Let {A,.} be a g;ven sequence. Show that if
1 " J .-1 ( 1'1 ) I
! A, 1-1- 4>,(o: )4>,(y) dy
o J...-('"-1) n
is bounded for all n, IX, then {A,.} is a factor sequence of type (C, C).
Show that if we have l es8ro summability in C, (i.e.. if the operators
T m of Exercise 44 converge strongly to I) then the condition is also
necessary.
66 Show that a factor sequence {A,.} is in (C, C) with respect to
the system (2n) 'J'e'= if and only if there exists a regular measure f'
with A,. = fo"e-'=Jl(d.x).
Multiple FQurUr Seri
Let A denote the Cartesian product, with its product topology,
of n replicas of the interval [0, 2n]. The symbol L. will be used for
L.(A, $I, A) where $I is the field of Borel sets in A and A is the Lebes-
gue measure on f!J. In the next exercise a notion of a closed orthonor-
mal system, which is somewhat less restrictive than that introduced
in Definition I, will be used. It is g;ven m the following definition.
67 DEFINITION, By a dosed orrlwnormal (c.o.n.) system of func.
tions on A will be understood an indexed 8et {4> } of functions in C(A)
such that
(i) linear combinat ions of the f undions 4>0 are dense in C(A);
(ii) JA4> ("',.. _ ., "'n)'Mx,. . . ., ", )dJ:, . . . d.x. = 0, " ,p p;
(iii) fA 14>0("'" . - .. x.)12d.x, . . . da: = 1, for all (I..
68 Let {4>",} be a c.o.n. system on [0. 2n] (in the senSe of Defi-
nition 1). Show that the set of aU products of the form
4>...(IX,)<ft...(a:.) . . .4>m.(lX n )
fonn 8 c.o.na system of functions on A (in the sense of Definition 67).
A multiple Fourier srneB is a series whose general term is a con-
stant multiple of the function exp {i(m"x,+.. .+m lXn)}' It will be
assumed in the following exercises on multiplicatiye Fourier series
that C(A) is the space of all scalar valued continuous functions I on A
which are multiply periodic in the senSe that
1(0, ,xi' . . -, :l'fl) = !(2n, :.t'2' . . .J a.'n); . . -; /(i!J., . . ", .1:n l' 0) =
= 1("',. . . ., "' " 2n).
69 Show that the family of functions exp {i(m"x, +... -t-m,;c,.)}
with -00 < mi < 00. i = I....," is dense in C(A), as well as in
L (A) for each p with 1 < p < 0':>.
70 Let K be a continuous functIOn on A" A of the form
K(x" . . ., "'.; y,. . - ., Yfi) = K,("", YI)' . .K.<",.. YR)'
where K I ,. . ., K R are continuous functions on [0, 2"J x [0. 2,,]. Ex-
press the norm of the operator K in C(A) defined by the equation
(KIHy" . .., yfi) = JAK(YI' -. .. y ; lXI' . . .,IX.)/("',.. . ., x.)d.x,. _. da:.
in terms of the norms of the operators KI' .." K R in C[O, 2n] defined
868
IV. SPECIAL SPACES
IV.14.71
IV.14.76 ORTH()GON'AL SERIES AND ANALYTIC FUNCTIONS
869
similarly in terms of the kernels KIt. . -J Kft. How.are the correspond.
ing nonns of K and K" ..., Rn as operators in L.{A) and L.(0,2",)
related?
71 For each I in 4(A) let
1m, .. ...... = J,.t("", . - ., "'n) exp (-i(m,,"', + . . . +mn",.)}dx.. . . d.x.,
If I is in L.(A) with 1 < P < 00. then as R, ..... 00,.. ., R. ..... 00,
1= lim ( ) n ! ... I fm,...m. exp {i(""",. +... + m.",.)}
2n m.l"",-RJ. m",---R..
in the norm of L.(A). This i8 not true if p = 1.
72 With the notation introduced in Exercise 71 we have, as
Tl -+ 1, . . -J r fI. -+ 1,
than n. Regard Po as a subspace of C[ -1,1]. Let I be a linear func-
tiona1 on P n" Then there exists an it'o in P nand R measure p. in
Tca[ -1, 1] such that
(a) 1("'1 = f-l "'(t),u(dt), "'. p.;
(b) max_,,..,;;, 1"'.(/)1 = 1;
(C) if Cis the set oft in the interval-I < t < 1 where 1"'.(/)1=1,
then v(p, C') = 0,
Coru;equentIy, unless "'o(t) is a constant of absolute value 1, C is a
set of at most n+ I points -1 :5: t, ;;;; t, .. . < t. ;;;; I, and there are
constants c" . . _, c. with I -l ie,l = If I, and in tenns of which we may
write an uinterpolation formula"
( 1 ) . m
f=lim - I
2n: mt--W
m
.
1("') = I c,,,,(II),
'_1
76 Let Tn be a real polynonual of degree n. not identically con-
stant, such that
XoEPft.
I Im,........T m,I...,.I:-lexp{i{m,,""
m,,-m
+ - . . +m."'nH
whcre for each I in C(A) the limit exists in the norm of C(A) and for
each/inL.(A) with 1 :5: p < 00 the limit exists mthenorm ofL.(A).
73 With the notation introduced in Exercise 71 we have, as
Nt """* 00, . . -J Nfl. ...... 00,
IIJAX i..-.(t)I = I,
-lSi;'::5i:J
and such that 1..-.(/») takes on its maximum value 1 at n+I distinct
points. Then T7i satisfies the differential equation
. ( 1 ) . N, N. ( 1m,,1 ) ( Im.l )
I=hm - I... I 1-_ .. 1-_
2n: r/I:1--N 1 f ,.--l>IfI N 1 N n
(/'-1)(..-:(/»" = ","(..-.(t)"-I),
and is consequently identical (up to sign) with the ..th TchLbich.lf
polynomial lor the interval [-I, +1], i.e.,
r.(/) = cos (n arc cos I).
I.. ..... exp {i(m"a:, +. . . +mn"'nH
, .
where for each I in C(A) the limit exists in the nonn ofC(A) and for
each I inL.(A) with 1 ;;;;p < 00 the limit exists in the norm ofL.(A).
77 Let Pfl Bnd 1 be as in Exercise 75, and Tn be as in Exercise
76. Suppose that max".p.I I",lf("')1 is not reached when", is the
con8tant function "'{I) == 1. Tben unless there exist k pomts t, < . . .
< I., with k ::;;: '" such that the values 1("'), "'. p. are determined by
the values "'(1,), . . ., ",(I.). we have
max If("'>1 = )f(-.:.)I.
nPW'I I::;;l
78 If a..("') is the leading coefficient ofthe polynomIal", of de-
gree n, then
&tnmwl MEthods lor PolY'lOmials and Clasus E.
74 Let]: be " finite-dimensional subspace of a B-space ID, and
let I be " linear fuuctional on ]: whose norm is Itl. Then there exists
an "'. m 1:, and " linear funetional/. on ¥J, such that
(a) 1'("') = I(x), x £ 1:.
(b) 1.("'.) = 1/'1 = 1/1-
(e) 1"'.1 = I.
75 Let p. be the space of all polynomials of order not more
la.("')1 :5: 2-' lDRX Ix{/)I,
-l tSJ
870
IV. SPECIAL SPACES
IV.I4.79
IV.14.84 ORTHOGONAL SERIES AND ANALYTIC FUNCTIONS
871
and the equality is attained only by scal..,. multiples of the Tchebicheff
polynomw.l ....
79 Tne inequality
1 '(I)J ;:;:; ,," max 1"'(t)1
-l:ii':iil
( 1 f "" ) I'P ( I f "" I,p
2" . Ix'(e")'" dO ,;; n 2" . I",(e"}," dOj .
84 Let (S. I, p} be a positive measure space, and let L. =
L.(S, I, p} with p 1. Let f and g be two elements of Lp such that
II +AgI III for each scalar A. Then
Js I/(sJi" 1 sgn(f(s }}g(8}I' (ds} = 0,
where sgn z IS defined by the equatIons
holds for each x in p._
80 If n is odd, the inequality
I '(O)I ,;; n max 1 (t)1
-l:iii'::ii+l
holds for each", in p.. If n is even, the inequality
"
1""(0)1 ,;; (n-l) max 1"'(/)1
-l::iit:a+l
sgnz =j;f'
=0 , 2=0.
85 (Blaschke Product) Let p > I and let 1 be a fWJction in H.
which does not vanish identically. Then there is Ii function g in Hoo
with Ig(e")! = 1 for almost all 9 and which has the Same zeros as f in
the interior of the unit disc. (Hint: Suppose that 1(".) *' o. From
among all functions h with I(z.) = h(z.) and for which h(z) = 0 if
I(z) = 0 choose one with smallest norm,)
86 Letp, I be as in Exercise 85. Then/(e") * 0 for almost allO.
87 Let p > 1 and let I be a function in H.. Then there exists a
function g in H", such that g(e") = 1 for almost all 9,
£H., ! J=lfl'
and such that fig has no zeros.
(Hint: Generalize the argument of Exercise 85 to apply to zeros
on the boundary of the unit di8c.)
88 Show that Exercise 87 is valid even if p = 1.
89 Every function I in H. can be written as a product gh. where
/; and h are in H 2 . (Hint: Use Exercise 88,)
90 Show that Exercise8 55, 54, and 56 remain valid for p = 1.
(Hint: Use Exercise 89.)
91 (F. Riesz.M. Riesz). A Borel measure p on the interval
[0, 211:] such that
f: .''',,(dO) = 0, n 0,
15 absolutely continuous.
(Hint: Use Exercise 90 and the method of Exercise 60.)
z*o
holds for each", io p..
(Hint: The function "'. of Exercise 75 may be taken in the present
case to be odd.)
81 (Bernstein} The inequality
1''-''(1)1 ;:;:; nmax l.x(z) 1
1.1"1
holds for every polynomial of degree n.
(Hint: The function "'. of Exercise 75 is of constant m6dulus in
the present case.)
82 (H. S. Shapiro) Let fl. denote the space of polynomials of
degree n in the variable z, with the norm
I I = max 1",(z)l.
1.1:;;1
Let I be a linear functional on fl., and define a linear mapping F by
putting
F( )(C) = 1("',),
where "'c(z) = "'(C ). Then F maps fl into itself, and has norm equal
to iii. More generally, for 1 ,;; p < co and '" in fl.,
( f "" IF(x)(e'.W dol'" ;:;:; 1/11 , f "" Ix(ejSW d O j "P.
2" . j 2" .
(Hint: Find a measure like that of Exercise 75.)
83 If l;:;:;p < 00 and if", is in fl., then
372
IV. SPECIAL SPACES
IV.15
IV.16
NOTES AND REMARKS
373
15. A Tabulation of Results
16. Notes and ReQUU"L
It is a special case of the Holdennequality (III.3.2) obtained for sums
by Holder [2; p. 44] and for integral8 by F. Riesz [2; p. 456].
Lemma 40.2 is due to F. Ricsz [8; p. 36] and was also used by
Sz.-Nagy [5]. A similar argument may be applied to obtain this re8ult
in Bny uniformly convex B-space. This generalizes and abstracts a
result proved for closed linear manifolds in L,,[O, 1] by E. Fischer [2].
The fact that a linear manifold which is not dense in the entire
space has a non.zero orthogonal complement (proved in 4.4) was
proved without the assumption of separability by F. Riesz [8]. His
proof follows the lines of an argument employed by Levi [1; Sec. 7]
in a study of the Dirichlet problem.
The fact that every continuous linear functional on L.[O, 1] arises
from an element of L. was proved independently by Frechet [4]
[5: p. 439] and F. Riesz [9]. The proof of Theorem 4.5 given here is
due to F. Riesz [8]. Corollary 4.7 was proved for L.[O, 1] by F. Riesz
[2: p. 466J.
The circle of ideas in 4.9-4.18 expr<ss in abstract form the reo
suIts usually known as the Riesz-Fischer theorem, which was proved
independently by E. Fischer [1] and F, Riesz [5], although their
names are also given to the theorem asserting that L, is complere. The
equation in Theorem 4.18 is classica1ly known as "PlU'Se'\ p al'sequality,t t
and the related inequality in the proof of Theorem 4.10 is called
u:Bessel's inequality"'.
The fact that aU orthonormal bases of a Hilbert space have tbe
same cardinality was shown by Lowig [1; p. 81] and Rellich [3: p.
355]. Theorem 4.16 1S due to Lowig [1; p. 27].
The spaces B(8, E) and B(S). The results in 5.1 and 5.3 were
proved independently by Hildebrandt 3J and by Fichtenholz and
Kantorovitch [1]. (See also Yosida and Hewitt [1].) Lemma 5.4 and
Corollary 5.5 are due to Phillips [8; p. 526J. Theorem 5.6 was proved
by Veress [1], [2; p. 184]
The space C(S). Since the results in Section 6 fall into several
groupings t we will break our comments into various subheadings.
The Riesz representaMn tJwJT<m (6.1-6.8). This name is fre.
quently given to Theorems 2 and 3, since this fundamental integral
representation for a continuous linear functional on C[O,. I] was first
discm'ered by F. Riesz [7]. (Text continues on p. 380.)
In this 5ection we will give 8. summary of what is known in the
way of an answer to the eight Questions of Section 1 as applied to the
twenty-eight SJ'R""S listed in S«tion 2, The information is presented
10 Table IV.A (pp.1374-379) cross-indexing questions and spaces, and
gi\'ing references to the appropriate theorems and exercises in this
chapter, in previous chapters. or. in a sma]] number of cases, in chap-
ters to follow.
Definite H yes or non statements on the problems of weak com.
pleteness and reflexivity are made in the table: these should be under.
stood as covering the "'''general cases" of the spaces under considera-
tion. For instance t in writing uno'" in the table .as the answer to the
question "Is B{8)weakJy complete?", we bave in mind the fact. stated
in Exercise 18.5, that B(8) is weakly complete if nnd only if S is
finite,
Symbols like (F8) in parentheses refer to footnotes coHected
immediately after the ble.
Finile dimensi<>Ml and Hilbert spaces. The notion of a finite di-
mensions] space,. is of course, an a1gebraization of orrlina.tJ.. geometric-
al concepts. The a.xioms for finite dimensional Euclidean space were
stated explicitly, e.g., in Weyl [8; p.15-25]. The study of norms other
than the Euclidean norm. is primarily due to Minkowski. The spaces
I, and L" were 8tudied in detail by Hilbert and others, but the abstract
8xioIDsti:zation of Hilbert space is due to yon Neumann [8; p. 15-17],
[7] in the separable case, and LOwig [1 J and Rellich [3] in general.
Tychonoff [1; p. 769] proved that any finite dimeosional topolo.
glcal linear space is equivalent to an Euclidean space. This, in par-
t1cuJar, implies the completen...,.. Throrem 8.5, which cbaracterizes
locally compact B-spaces is due to F. Riesz [4].
The "Schwarz inequality" (Theorem 4.1) goes back vcr}' far.
For 11 = 3" it is s consequence of a well-known identity due to
Lagrange [1; p. 662-3J proved in 1778. For a finite sum, it was proved
in 1821 by Cauchy [2; p. 373J. It w..... proved for integral.s in 1859 by
Buniakowsky [I: p.4] and in 1885 by Schwarz [I: p. 251]. Of course,
IV.I5 A TABULATION OF REBULTI'i 875
374- IV. SFECIAL SPACES IV.I5
'l '\BLE IV.A (fuW...,.,j)
TABLE IV.A 1 8 .
Space 1:: 115. l 1 6 . . 1 7 . .. 00 1 9 . 00,
Spa<:< 3' II I. E" 1 2 . r- 1 3 . r", ] 4.A. '1' 1 4oBo I,
" 1 <11 < <:0 Conjugate
I Spa<:< I" 8.1(1 13.7 13.7 IS.I1 13.11
Conjugate
Spa.ce * 3.9 3.9 8.9 8.1 8.5 U"eak no no 110 yes yes
Comp1eteness 18.5 13.8 18.8 13_11 13.11
Weak yes yes yes yes yes
Completen<ss ]1.8.29 n.8.29 11.3.29 II. .29 8.6 Rcllnhity no no 110 no 110
[]43.29 13.8 13 8 13.11 IS.l1
Reflexivit) yes yes yes yes no
3.8 3.8 5.8 8.2 U .2 Strongly
c.ompact Sets 5.6 13.9 13.9 I3.I1 13.11
Strongly ui.]
Compact Sets lB.] 13.1 UtS 13.3 \\'ea'k1y
Compact Seb 6.29 13.9 13.9 13.n 15.11
Woakly
Compact Sets 11.8.28 11.8.28 11.5.28 II.3.28 18.8 \"Veak Caucl1y
Sequences 13.43 18_10 13_111 ]3_11 ]3.11
\Veak Cauchy IB.l 13.1 13.1 13.4 8.14
SeqUBlOOS (F3) (F'S) (F3) 13.24 (}'3) 13.25 (F3) \Yeak Con-
vergence to :r 6.31 18.10 111.10 III.II 13.11
VtTeak Con- 13.1 18.1 IS.1 1.3.4 8.14-
vergence to :t! 18.24 13.25 ¥J COD'-ergence meaning meanlng-
in J = . 13.6 less ..... IS.II IS.1l
'g} Conwrgence 18.11
in E - 'ID* 18.1 15.1 IB.l l3.4- 13.4- MiseelLaneous 6.18 13.n
Properties (F4) (1!'4) (}'4) 13.12 13.12
Miscellanwu.s 8.8,3.4. 3..3,3.4. 8.3, 8.4, 13.59 8.14.13.49. IS_59 13...00 (F5) (Fa)
Properties .8.6. .23.7, 3..6,8_7, 3.6.3.7, 13.61 13.59
13.1 S.9 3.9 18.70 13.60 Tabte continued
13.50 18.1 18.1 IF6) 1.8.fU
13_51 (F5)
Footnote8
(}'I) Ko COmp1ctcl)T satisfuctory" representation for tht CQI1jugate sp.\l( e of
ba(S I), m(S.,!;), Or Tca{S L'), or for the conjugate S}J8ttS ()(the "' BV(l)
and BJ;(I), which arc isometrically isomorphic to spu.oes of rm.'8SW'eS, to be
known How -er various sorts of reprt<;flltations have bcrn considered in the
literature. References aTI' gn'en in the noiR and ronuIIEnts section belo)\"
(F2) A representation for L: (8, I, It J in terms of a space of mea.sures. valid
in Ute non l'1-finitc case was given in J. Schwartz. [I).
(FS J Note that in a weakly complete space a wt'ak Cauchy sequence con-
verges weakly to sOme definite etement.
FoofnLJII!S mntinuerl
876
Space .t
Ccnjl1gate
Space :£.
Wea1c
Comp1etmess
RdI.xivity
Strongly
Compact Sels
\\'eak1y
Compact Sets
\Veak Cauchy
Sequences
\Veak Con-
vergence to a:
!> Convergence
in a: 'IJ.
Miscellanoous
Prop>rti.o;
IV. SPECIAL SF ACES
TABLE IV.A
1110. hs In. cs
18.18 13.14
no no
18.13 18.14-
no no
IS.I8 13.14
18.18 IS.14
18.13 18.14
15.13 13.14
13.13 }8.14
18.18 18.14
IS.18 13.14
1 .4) IF4)
(CrmIirIoud)
)12. B(S. I)113.
5.1
B(S) 114. C(S)
I
5.3
no no
'3.5 13.S
110 no
n.3.29 11.3.29
5.6
6_29
13.43
6.S1
meaning-
less
6.13
6.1
(F4)
13.76
5.6
6.29
13.48
6.31
meaning-
less
6.18
6.19
(F4)
IV.I5
IV,I5
877
A TABtJLATIOX OF RESULTS
TABLE IV.A ( )
6.2
6.8
17. IS.A. 18.B.
Space I. 15. bu(S, I) 16. caIS.I) Tca(S, I) L.(S,E,p) L,(S,I.I')
1 <p < co
Conjugate I
8.1 8.5
Space 1. (Fl' (Fl) (FI) (F2)
"'eak yes yes yes yes yes
Completeness. 0.9 9.4 ]8.22 IL3.29 8.6
Reflexivity no no no y.. no
13.5 13.21 13.22 8.2 13.2
Strongly 15.19 13.19 18.19 8.18 .18
Compact Sets 13.20 18.20 8.20 8.20
13.68
WeakI)' IU2 9.1 13.22 11..3.28 8.9
Compact Sets 9.2 8.n
13.54
\\'eo.k CQucby 13.17 9.5 13.22 13.23 13.25
Sequences 13.2:4
(F3) (FO) (F3) (F3) (FB)
'Weak Con- 18.17 9.5 13.22 13.23 U,I.'25
vergence to fl: 13.24
'IJ Con""'!!""C" I 19.18 meaning. 9.15 15.24 meaning-
in1:= i 1ess less
I
l\Iisce1lRnemlS 9.Il(b) , 111.7.5 (F5) 13.51, 3.22 13....9 1 8.10
Properties 111.7.5 III.7.6. 13.53. 8.26 13.51. 8.18
IlL7.6 9.8 UI.62. lI.7 IS.53, 8.14
la.50 (F5) I '3.71 (F6) 18.54.8.22
18.76 i 18.62, 8.240
, 13.77 I '5.68, 8.26
IF5) i 13.'71. 11.7
i I (F5)
no
13.15
no
IUS
6.5, e.'i,
6.8, 6.9
6.14
13.40
6.4, e.12.
e.31
meaning-
less
6.16,6.17,
6.26
V.8.8 (F4)
13.50
13.51
13.63
IS.64
18.65
18.66
I
Table crmtinuaI
CF4) 1n 8 space I: isometrically ismorphic to spact"S of rontinuous fun(:tud1s.
an interesting order relation can be introdueed, which makes into a vector
lattice of M-space t }'pe. \Ve may aho introduce a murtip1ication of functions whicll
makes I: into Q B*-a1gebra. Refeft'OCeS for these two points ore given. in the notes
and comments I!ection belo\\'.
(}.'5) Spaces of roea.suJTS, L...-spaccs, and spa.cetl isometrically isomorphic to
such spaces can all be made into vector lattices of type by the introduction
of a suitable order relation. Compare the ftrnarks in the notes and comments
section below.
(F6) The spact'51, and 4,(S.1:.IL). as Hilbert sP . have numerous special
properties. FCJomlJtu ronfinued
878 IV. SPECIAL SPACES IV.I5 IV.IS A TABtJLATI{)N Ofo RESULT!:, 879
TABLE IV.A (CmdinuafJ TABLE IV.-'\. (Continued)
11 19 ' ' I I Spa :( II 24. A(D) 125. AP 126. H bert 1 27 . I
Space Z L",(S,E,I') i 20. EV(I) J 21. NEV(I): 22. AC(I) 23. C"(l) I Spu:e T1'tl(S,E.p>: 28. !ol
ConjUgate I 8.16 18.29 Conjugate (F9) I 4.5 meanmg- meaning-
18.36 I
Space . (FI) (FI) Spo.ce . ,.... Iess(F7)
Weak no yes yes yes 110 Weak no no yes meaning4 meaning-
CQmpietenc5S V.ll.2 12.1 12.2 12.8 1.B.36 Compl 1$_37 13.88 4.7 less Iess
Reflexh.ity no 110 no no no RefI('Xivity no 110 yes meaning- mcaning-
V.11.2 nU 8 13.28 18.28 13.36 13.37 13.:38 4.6 less Iess
StroJJgIy 6.26 13.48 13.84 U-S2 18.86 Strongly 13.37 13.89 13.45 11.1 18.47
Compact Sets J.3.83 ("cunptLCt Sets
W . 19..30 13.30 13.31 13.86 \Yeakly 18.37 6.29 4.7 meaning- meaning-
Compact Sets (F8) Compact Sets less Iess
\Veak C mchy \'.11.'2 18.80 1:3-30 IS.S] 18.136 \Yeak Cauchy 13.37 13.41 15.44 mearring- meaning-
Sequenres (F3) (F8) (F3) Sequences Ie.s I....
Weak Con- V.II.2 13.30 13.30 I8.BI 15.36 \Veak Con- 13.37 18.41 ]3_44- meaning- me.ani.nJ!-
vergwmce to x vergence to ;r less less
ID Convp 13.27 IB..85(RJ 13.55(A) . meaning- mean og- ID Convergence meaning- meaning- 13.44 me3I1ing- meaning-
in = 'ID. less less. in l' = 'ID* ..... less Iess less
AJisreUaneous 11.7, V.8.n IB.48 18.B5 12.3 13.56 :UiseeUaneOII'S 7.6 4.1 4.4" 11.2
Properties IB.55, 8.23 18.63 (F5) (F5) Properties Section 4.5,4.9, 11.4-
Is.eo. 8_26 . 13.73 XI.2 4.10. 4.12, 11.6
18.77 ; (F5) (F4) US. 4.16. 11.7
18.71 (F4) I 18.67 13.74
13.70
]3.72
(F7) Note. however. the result given in ]8.46.
(F8) Using the isomorphism betwecnLf;C(S, E,]A) and Q space of continuow;
functions establi.shcd in V.S.ll, a condition for weak cornpac:t.ness can be obtained
trom ti.14 (Compare V.l1.2. where the corre5p"\ result is given lor weak con-
vergence.) Unfortunately, this condition ean only be stated in an exCtSsivc-ly
cumbersome form.
(F9) Using Theorem 7.6. we can, of rourse npresent AP'" as Tca(S). S
being the compact space of that theorem, which is $oOmtti.mcs. known as the Bahr
Cmnpadijiwlicm of tbe Tea] line. No more concrete representation of Ap. seems to
be kno-wn. The ltiult in this direction .announced by E. Hewitt (Hewitt [6]) does
not seem to be completel.)" pro\'ed.
880
IV. SPECIAL 8P ACES
IV.16
IV.16
SOTES AND REMARK
881
Earlier, however. certain representations for linear functionals on
C[O, I] had been given, butthey aU suffered from various defects, such
a8 the lack of uniqueness. For example, Hadamard [I J showed that
each ",* £ C*[O, I] has the form
"*1 = lim f: km(s}/(s)ds
_m
where k m . qo, IJ. Frechet [5; I] gave a different proof of this fact,
and observed [5; II] that the k m may be taken to vanish at 0 and I, or
may be taken to be polynomials (but not both). In particular, there
exists it double sequence of constants b mwt 0 n < m, 1 l1l < 00,
snch that
"*1 lim i bnml ( ) .
m-+oo ...-1 m
paration axiom but in which uncountable unions of open sets: are not
necessarily open, For such spaees, Alexandroff [I; II p.577J proved
Theorem 2, and related the additivity properties to the compact.
ness properties of the space [II. p, 587J and the convergence proper-
ties of the functional [II. p. 598].
There are also B number of recent papers related to this result.
For example, Halmos [5; Coop. 10], Hewitt [8] and Edward8 [IJ
consider functionals on the spaee of continuous functions on a locaUy
compact Hausdorff space which vanish outside of compaet sets.
Arens [8] discussed certain sub-algebras of continuous functions on a
topological space such that {sll/(s)l> c> O} is C<Jmpaet for each
c> o. In each of these cases the representation is effected by a regular
countably additive measure on a certain field of subsets. Glicksberg
[I] showed that if 8 is completely regular, theu ""Cl)' non-negative
functional on C(S) may be represented by means of a countahly
additive measure if and only if anyone of the following conditions
hold: (I) In . C(S), n = 0, 1,2, . . . and 'n(s) t Io(s), u8 imply that
In ..I. uniformly on 8; (2) every continuous real valued function on
S is bounded: (8) every continuous real valued function on S assumes
its maximum; (4) every bounded equicontinuous family in C(S} is
conditionaUy compaet.
Up to now we have discussed linear functionals on the ooutltkd
continuous functions. Hewitt [I] showed that if S is completely re-
gular, then a positive linear functional on the space of all continuous
functions on S may be represented by means of a countably additive
measure p defined on 8 ct'rWn a-field, and that every function is
bounded except on B p-null set. This extends a result announced for
C(- 00, co) by Wehausen [I; p. 164], In this paper, Hewitt also treat-
ed linear functionals continuous in certain topologies (e.g., compact-
open, and product topology).
An inspection of the proof of Theorem 2 indicates toot the pro-
blem of representation may be viewed as One of extending the linear
function, originally defined on C(8}, to be defined on a larger collec-
tion of functions on S such as the bounded Borel functions. Once this
-extension is achieved the measure is readily obtained, and the func-
tional represented as an integral. This is tile point of view ofthe Daniel1
[1] approach to the theory of integration, modifications of which have
Frechet gave other applications of these results.
Riesz announced his result in 1909 (F. Riesz [7)}. Since then he
has given several different proofs of this result (Riesz [3, 10, II)}.
Another proof, stiU for qO. I] was supplied by HeUy [IJ. Radon [2;
p. 18381 extended the theorem to a compact set in En, and cast it in
the dress of an integral \vith respect to a regular measure, rather than
a Stieltjes integral. See also the paper of C. A. Fischer [2]. Hilde-
brandt [8] and Hildebrandt and Schoenberg [1] showed that the re-
presentation theorem implies and is implied by the theorem of Haus-
dorff on moments. A further extension of the theorem was made, in
1987. when Banach (in Note II of Sak8 [I)) proved it for C(S), where
S is a compact metric space. In tbe same framework, the theorem was
proved by Saks [4]. In 1941. Kakutani [9; p. 1009] extended the
theorem to compact Hausdorff spaces by modifying a process used in
80me unpublished notes of von Neumann.
Somewhat earlier, in 1988, the first attempt to extend the result
to non-compact spaces was made by Markov [2J, who considered thc
bounded continuous functions on a space which satisfies the norma)
separation axiom except that points are not assumed to be closed. He
showed that positive functionals coITeSpond to positive regular finitely
additive meRSlII'eS, and considered cert.ain invariant functionals, i.e.,
such toot "*(Ig) = .,*(f), for all I. C(S). A similar iuycstigatiou was
made by Alexandraff [I] for "spaces" wl1idl satisfy the normal se-
382
IV. SPECIAL SPACES
lV.lt!
IV.16
NOTES AND REMARKS
383
been presented by Bourbaki [4 , LoomIs [1] and Stone [6]. Hewitt [2]
and Loomis [2} have appht!d this View to diS£'uss linear functionals.
The Daniell attack has been extended greatly to order preSPJ"V:ing
maps bctween ordered spaces by McShane [8] and to positive map-
pings of C(S) into ordered spaces by Christian [1].
Strmig and weak COl1lpoctness in C(S) (6.5-6.14). Ascoli [2; p. 545]
defined the notion of equicontinuity of a set of continuous functions
(of a real varmble) at 8. fixed point; this concept was also used by
Arzela [5] about the same time. Definition 6.6 merely applies his
df-finition at every point of the domain. This fundamental concept
CRn readily be extended to functions with range in a metric spact"., or
still more general functions (see Bourbaki [5; Chap. 10]).
The important Thl'Orem 4.7 is known as the ArzelA-Ascoli theo-
rem, although many authors us[' only one of these names. In the case
of C[O, 1], Ascoli [2; 545-549] UsM a construction whicb essentially
amounts to the sufficiency of the condition for compactness. Arze1iL
[2] proved the neCt'SSity of thi8 condition. Both of these papers are
phrased in gpometrical terms and it is difficult to resurrect this result
from them. However.. an extremely cleaf presentation of this and re-
lated theorems was given by Arzelit [3; p 56-60J. The extension to
a case in which the domain is a space with a notion of limit (saYt a
metric space) was done by Fre.:het [I}. It is not difficult to cxtend it
to a case where the range is taken to be a metric space instead of the
real or complex numbers a1though in this case we must also suppose
that {f(s )11 E K} is conditionally compact for each BE S.
In the CBSf' that S is not necessari.ly compact or that the range
of the functions is not necessarily B metric spsce, similar compact-
ness criteria have been established by Arens [5], Gale [1], and Myers
[I] (see also Bourbaki [5; Chap. 10] and Kelley [5 ). In these cases one
usually emplo}Ts the Ucompact-openH topology of fnnctions. A differ-
enttype of criterion for compactness in C[O, IJ was given by Izumi [2].
It is perhaps appropriate to insert .at this place a few hi to-
rical comments concerning the notion of uniform convergence-the
mode of convergence in this space. The importance of this mode of
convergence is now fully apprt"ciated, but it has not always been so.
Even the mighty Cauehy stumbled on this score and asserted, in 1821,
that the sum of a convergent series of continuous funetions is itself a
continuous function (_ Cauchy [1; p. 120]). That this waS false Was
pointed out, in 1826, by Abel [I; p. 316]. There the matter rested for
Some years. In 1847 Stokes [I; p. 562]. in 1848 Seidel [I], and in 1853
Cauchy [1; p. 30 36J independently demonstrated that unifonn eo..-
vCll:'Cflce is sufficient to assure the continuity Qf the limit function.
(It .IS mteresting that Weierstrass [I; p. 67, 70] had employed this
notIon of convergence in some unpubJished manuscripts written in
1841-he even used the tenn "gleiehmassig".) It is to Seidel's credit
that he observed that he was unable to prove the necessit), as \,,'ell;
Stokes went astray on this point, and Cauchy remained silent. Con-
ditions that are neeessary as well as sufficient were not to come for a
number of years.
The notion of the quasi-uniform conyergence of a sequence of
functions was introdnced in 1884 by Arzola [1] to whom Theorem
6.11 is due in the dassieal case of a sequence in C[O, 1]. In 1878,
howen-r, Dini [I; p. 107-109] }",d gJven necetisarJ' and sufficient
conditions for continuity of the limit function at 8 point, and an-
nounced [po 110-112] his classical theorem concerning monotone
convergence of continuous functions.
. The concept of quasi-equicontinuity (which is related to qua.si-
uniform con\"ergence in exactly the same way ordinary equicontinuity
is relnu,d to unifonn convergence) wa.s introduced by Sirvint [2, 8]
for [O, 1]. and by Bartle [2] for C(S). In the ease of C[O, 1], the
eqUl aI nce of statements (I), (2) and (S)ofTheorem 6.14 was proved
by Suvmt [2, 3; p. 76, 82] and by Bourgin [1; p. 601]. In a geneml
framework, Grothendieck [2; p. 180-182] proved the equivalence
of statements (I), (2) 8Ild (5). The general equivalence of (1). (3)
and (4) was proved by Bartle [2], to whom this proof is due. Grothen-
dieck [2] considered the relationship bctween compactness, countable
compactncs:' and sequential compactness in the case where the range
of the contmuous functions is in 8 more general topological space.
Some of Bartle's [2J results are valid in this more general ease, as well.
The Slone-Weierstrass and related tMorems (6.15-6.27). The
classical theorem on the approximation of continuous functions bv
polynomials was given by Weicrstrass L2; p. 5]. lIlany proofs of this
theorem have been given; see, e.g., L. f. Graves [1, 4], Hobson
[1; II, p. 228-234J and Widder [1; p.152-153;. (The proof in Graves
384
IV. SPECIAL SPACES
IV.I6
IV.I6
NOTES AND REMARKS
385
[4] shows that if J. Cn[O, IJ, then the polynomials may be chosen so
that aU derivatives including those of order.. converge uniformly to
the corresponding derivatives of J.)
Of the many extensions of the Weierstrass theorem for [0.1] we
mention the striking theorem of IIliintz [1] which 855<'I1:s that the 8et
{I, :rf'1, . . .,:rf'-, . . .} is fundamental in C[O. 1] if and only ifthe series
I a.;1 diverges. This theorem was sharpened and simplified by SZRsZ
[1] and Clarkson and Erdos [1].
Stone"s extension of the Weierstrass theorem for real fum.1:ioIlS
was made in Stone [I; p. 466 469], the discussion being concerned
principally with the continuous fu,;ctions as an algebra. The complex
case was treated by Gelfand and Si10v [1]. Kakutani [9] discussed a
similar question. basing his work on the lattice properties of the 8pace.
In .4], Stone considered both of these aspects and presented a com-
plete and elementary approach to this beautiful and important gener-
alization. In this latter paper. Stone investigates B number of related
a>pects of this problem, and makes many applications of this result.
A different type of proof, based on semi-group theory, was given by
Dunford and Segal [I].
In the case of real s ala.rs Stone's theorem asserts that a1gebraic
combinations of a family DC C(S) are dense in C(S) if and only if
the functions in D separate the points of S. Hewitt [4] showed that if
S is only assumed to be completely regular and not compact, then
the theorem is no longer valid. Hewitt also proved that a stronger
separation property (concerning closed 8cts rather than points)
suffices to establish the theorem in this case.
Arens [4] has given a generalization of the Stone-Weierstrass
theorem in the case where the range is in an Abelian group with cer-
tain lattice and topoJogical properties. Kaplansky [I: p. 228-233]
proved a. version of this theorem in an instance where the space S
is compact Hausdorff. but the funetions at a point 8 E S take their
values in a C.-algebra A. which depends on B. This is a ".cnon-commu-
ativeU generalization of the theorem. Even in the ordina.r): case. his
proof is different from the one presented here. Kaplansky [2J has also
presented a theoremoftheStonetype where the scalars are taken to be
in a division ring with B valuation.
All of the abstract theorems mentioned above deal with establish-
ing conditions that are sufficient to insure that a class of functions
generates the entire space. Wermer [6, 9J has given sufficient condi-
tions that two functions generate C(S) when S is the unit circle.
If I is one-to-one. or the function II),) = ),", then necessary and suffI-
cient conditions are given on a function g in order that I and g generate
C(S). This is closely related to cmssifying the closed subalgebras B
which are maximal in the 8ense that if B' is a closed 8ubalgebra of
C(S) and if B B'. then B' i8 either B or all of C(S). Additional re-
sults concerniog maximal 8ubalgebras and remted topics are found in
Wermer [10, ll], Helson and Quigley [1,2] and Rudin [1].
We now comment briefly on the Theorems 6.18-6.27. They are
essentially due, at least in the real case, to Stone [1], although his
tenninology and proofs often differ from that given here. It should be
mentioned that Theorem 6.22 was provcd independently byeech [1]
only slightly later. (See also Stone [5] for an elementary treatment.)
Lemma 6.25 was proved 01 Stone [I: p. 465J-extensions of this re-
sult are also found in Hewitt [5] and Kaplansky.
There are several theorems closely related to Theorems 6.26 and
6.27 -see for example Theorem V.8.8 where it is shown that if C(S)
is isometricaUy isomorphic with C(T), where Sand T are compact
Hausdorff space8. then Sand T are homeomorphic. The theorem just
mentioned was proved for real scalars and compact metric spaces by
Banach [1; p. 170] and for compact Hau8dorff 8paces by Stone [1;
p. 469]. (Related results have heen given by EiJenberg [I], Arens and
Kelley [1] and Hewitt [5]). It may be summarized as ossert.ing "the
Banach space C(S) clmraeterizes S." Silov [1] showed that C(S) as a
topological ring characterizes S, provided S is compact metric. Gelfand
and Kolmogoroff [I] proved the sharper theorem that if S is compact
Hausdorff, then the ring C(S) characterizes S. ThIs includes Corollary
6.27. Stone [7: II] showed that as a lattice-ordered group C(S) char-
acterizes S. FinaUy, Kaplansky [3: I] proved that merely as a lattice,
CIS) characterizes S. Hewitt [5], Nagata [I], and Shirota [1] have
ohtained some results when S is not required to be compact. Kadison
[2] has obtained results of this nature for non-commutative C*-alge-
bras.
The preceding paragraph makes it appear that any reasonable
topological or algebraic property of C(S) characterizes S, provided
86
IV. SFECIAL SPACES
IV.16
IV.I6
NOTES AND REMAltKS
87
that S is compact. That this breaks down if C(S) i8 regarded as a
topolOl.<icallinear space is demonstrated by the fact that C[O, 1] may
be mapped in a linear .and homeomorphic manner on the space
C([O,I: U 2). (See Banach [1; p. 184]).
Weak compadt1e&8 in B(S). Definition 6.27 is equivaJent to a de-
finition given by Bartle [2], to whom Theorem 6.28 is due. Lemma
6.29 is essentially due to Bourgin [1; p. 600], the proof given here and
its application to 6,80 is due to Bartle [2]. Theorem 6.30 was first
proved by Sirvint [3; p. 80], who based his proof on some related
throrems in Ban&ch [I; p. 217-225]. This throrem had been an-
nounced earlier without proof by Flchtenholz and Kantorovltch [2].
Th£ space AP. The theory of almost periodic functions was
created by Harald Bohr [1], although it has been considerablv extend-
ed by many other mathematicians. Although it is a naturaJ a d beauti-
ful generalization of the theory of periodic functions, Bohr was led
to it by the study of Dirichlet series. For a most readable expository
account of some different proofs of the principal theorems of the
theory, the reader is referred to Bohr [4]. The book of Bohr [2] gives
a very enjoyable account of the elementary theory, and that of Besi-
covitch [IJ considers certain generalizations as wen as analytic al-
most periodic functions. (See also Maak [1].)
Theorem 7.2 has been used as a definition of almost periodic
functions by Bochner [4J. This led von Neumann [9] and Bochner and
von Neumann [1] to extend the theory to an arbitrary ab.-trnct group.
They required G to be an abstract group; a function I. B(G) is said
to be right almost prrioou: ifthe set {t.la. G}, where t.("') = I(",a), is a
conditionally compact set in B( G). For an expository papcr on this
facet of the thcory, see Bohr [3]. If the strong topology is replaced
by the weak topology of B(G), then we have a weakly al1fW3l. periodic
function in the Sense of Eberlein [3J.
Certain aspects of these generalizations will be discussed in a
later chapter. The reader will find other references in Loomis [1] and
Weil [1].
The space S of Theorem 7.6 is called tI,e Bohr complJdi/ication
of the real line. Weil [2, 1; p. 124-139] has shown that a simIlAr
result may be obtained for any locally compact Abelian group and
has given applications of this fact. Anzai and Kakutani [I] showed,
among other things, that the Bohr compactification of a locally com-
pact Abelian group G may be obtained by taking the character group
(; of G, equipping {} with its discrete topology, and tben taking
the character group of this discrete group. Hewitt [6] !>as used
th.. Bohr compactification to study the adjoint space of AP.
(See also Art..menko [2] and Krein [5] for certain positive linear
functionals. )
Th£ 8pLJce L». In the case of L.[O, I], Theorem 8.1 was announced
,ndependentJy and simultaneously in 1907 by Frbohet [4] and F.
Riesz [9]. A detailed proof was gIven hy Frechet [5; III. p. 441]. The
theorem for L p [O.I], 1 <p < 00, was demonstrated by F. Rie.z
[2; p. 475]. In the case of a finite measure space the theorem waS
e.tablished by Nikodjlm [9; p. 182] and later by Dunford [I; p. 338]
by essentially the same method used here. A proof based on the prop-
erty of unifonn conv<'xity was given by Jl[cShane [1] for a completely
arbitrar)T measure spacea A different proof in this context was given
by.J. Schwartz [1]. Generalizations of this theorem to the space. of
Orlicz were obtained by Zaanen [I, 5; p_ 188].
In the case Lp[O, 1], 1 < p < 00, CorollRl'ies 8.8 and 8,4 were
proved by F. Riesz [2; p. 467].
Steinhaus [2] proved Theorem 8.5 for [0, 1], and ohtained Corol-
lary 8.6. Dunford [I; p. 888] extended 8.5 to a finite measure spoce.
An example due to T. Botts (given in .J. Schwartz [I]) show8 that this
th orem is not valid without the assumption of a-finiteness. However,
if S is locally compact and p. is a regular measure, then Lf = L . (See
Dieudonne [7; p. 88].).J. Schwartz [1] has givcn a representation of
L in the case of a general measure. Before the Steinhaus paper,
Frechet [5; III] gave.. representation for the linear functionals F on
LJ[O' IJ which are continuous m tbe sense that if In(s) ->- I(s) aJmost
everywhere, then F(fn) --->- F(t). An extension of the Steinhaus theo-
rem has been obtained by San .Juan [1].
Theorem 8.9 was proved m the case of finite measure by Dunford
[9; p. 643], and in the a-finite case by Dunford and Pettis [1; p. 876J.
If S i. locally compact and I' is a regular positive measure on the
Borel sets I, then Dieudonne [7; p, 98] has 8hown that a set K C
L,(S,I,p.) is weakly c mpact if and only if(I)K is bounded; (2) for
any £ > 0 there is a 6> 0 such that if pIE) < {j then
888
IV. S::rECIAL SPACES
IV..6
IV.W
NOTES AND REMARKS
889
JAI/(8)lp(ds) < 8, I. K: (3) for any 8 > o there is a compact setC!;; S
such that Js-c I/(s)llL(ds) < e, /. K.
Dieudonn [7] has extended these results to a certain class of
functions closely related to L 1 , but which do not form a B-space.
The reader is referred to his paper for the details,
CorolIary 8.18 is a classical result due to Schur [.]. There is a
similar theorem valid in L., 1 < p < 00, which was proved by Radon
[2: p. 1863] and F. Riesz [18].
THEonM. If I < p < <X> tlum a seque""" fin} l'Onvergeti strongly
to f in L.{S. I. 1') if and only if it converges weakly and Ifni -->-Itl.
This theorem remains valid in any unifonnly convex B-space.
Theorem 8.15 was proved independently by Hildebrandt [8; p.
875] and Fichtenholz and Kantorovitch [1; p. 76]. Earlier, Steinhaus
[2] showed that the general continuous linear fnnctionalon theessen.
tially bounded measurable functions with the 4-norm is given by an
element of L",.
Frechet [9: p. 1108] gave necessary and sufficient conclitions for a
set in I. to be compact. Similar results for L.[O, I] were given (see
Frechet [7: p. lIUJ) but they involved a preassigned orthonormal set.
Other results for L.[O. 1] were obtained by Veress [2]. Theorem 8.17
is essentially due to Kolmogoroff [2] in the case that 1 < p < co
and S is a bounded set in finite dimensional Euclidean 8pacc. The
exrension to unbounded sets was made by Tamarkin [I]. Tulajkov [.]
showed that the Tamarkin theorem was valid for p = I as well.
ilL Riesz [2] gave a different proof of this condition. Takahashi [I]
showed that the same result is valid in the generalized L. spaces of
Orlicz. The form of Theorem 8.17 presented here and its validity for
p = <X> waS given by Phillips [8; p. 527]. A different criterion was
given for L., p ;;,; 1. by Frechet [7], Nicolesco [1] has aJ80 discussed
the Kolmogoroff result. Conditio"" of the type introduced by Kolmo-
goroff were employed by Izumi [2] to find compactness criteria for
C[O,I] and T.III{S.I.iI).
Theorems 8.18 and 8.20 are due to M. Riesz [2]. An extension to
the case 0 < p < 1 was given by Tsuji [2]. Lemma 8.25 and Theorem
8.26 are due to F. Riesz [2B], who was concerned with a somewhat
more abstract situation..
Since eael) element of L is an equi,ralence class of functions, it is
natural to mquire whether bounded reprerentatives may be chosen
from these equivalence classes in such 8 manner as to preserve sums
and scaJar products. It is a striking fact. due to von Neumann [2.],
that sueh a selection can be made in L", (0, 1) so as to preserve poly-
nomw identities.
THEOREM. Let (S, I. p) be a positive finire Jneu...... Bpace 6U€h that
4(S, I, p) i. sepm-ahlc. Thffi there €ilJisl.8 a linear mapping. T f
L",(S, I, p) into B(S) ..ilh ITI 1 such that Tf and fare ""nta.ned on
the .a"'" equivalence clas8 for all I. L",(S, I. I' ).
For S = [0, I], this is a spedal case of II theorem of von Neu.
mann. A sbort proof of this result, using a theorem of Halmos and
.On Neumann [I] has been given by Dieudonne [9], who has shown
that the above result IS intimately related with some theorems to be
discussed in Seetion VI.8.
Spaces 01 se! f"'wA()7l!J, The fact that uniform countable additivity
of a set in a(SJ E) is equivalent to equi ontinuity with respect to a
fixed positive measure was proved by Dubrovskii [2]. Dubrosvkii [1]
also proved in the case of 8 compact cube in En, either assumption
plus boundedness implies that every sequence has a subsequence
which converges for each Borel set. For related results, see also
Cafiero [8, 4, 5] and Dubrovskii [8, 4. 5, 6]. A proof of Theorems
9.1-9.3 different from that found here is found in Bartle, Dunford
..nd Sehwartz [1].
Simila.r weak compactness criteria have been proved for regular
measures by Grothendicck [4; p. 146]. We cite his result.
THEOREM. Let III be locally compact 8pal:e. and let K C rca(M).
The" th£ foUowing .wtcmi:nts are N}ui'tJalenL
(I) K i3 weakly sequenuaUy compad:
( ) if {fn} i3 a uniformly boutukd 8eIJ"i:'I€i: of oontinuou.t fwu:ti<ms
on M which colWl'Tge at each point to =<I, then
lim fMfn(S){t(ds) = 0
n_m
unilormly with respect to I' in K;
(3) lor f'OW!J sequml:e {G n } 01 pairwise di8foint open sets liml'(G.)
= 0 unifoTmly fOT '" in K;
390
nt. SP C[AL SPACES
IV.lf>
IV.I6
NOTES AND REMARKS-
391
(4) (a) for every rompad Bel C M and E > 0 Ih£re rJ:;s/$ an opt'"
tlrighborhood U of C S!M:h !hat v(l-'; U C) < E for EVery p. in K,
{b} given E > 0 IMre e:£is/$ a eompact Bel C 1Il BUch that
t'v.,lIl-C} E for EVery p. inK.
In view of the Radon-Nikodym theorem, Theorem 9.5 may be
regarded as a generalization of a theorem due to Lebesgue [1; p. 57J.
Theorem 9.4 is a special ease of this result and a theorem of Nikodym
[6]. namely Theorem 111.7.3.
Theorem 9.8, which strengthens the uniform boundedncss theo-
rem in a special case, is due to Nikodym [5], The proof given here, as
well as Lemma 9.7, is due to Saks IS], where a slightly stronger version
of this result is proved. (For other results related to the atomic 8truc-
ture of a measure space, see Hahn and Rosenthal [1; pp.45-58] and
Halmos [5; pp. J65-174].)
Theorem 9,14 is due to Boclu,er [8]. Bochner and PhiJlip8 [1]
.also gave a proof of this result.
Theorem 9.15 was proved by Alexandroff [1; III. p. 182] to
whom a numher of similar results are due (cf. Alexandroff [1; III]).
The following comments are pertinent to this theorem.
Some rl!mt1rks em I.-cDnvl!Tgena ill I.. One of the problems set in
Section I of this chapter is the determination of ooP-C'Ute conditions
for l-converg61ce in 1*; i.e., to describe in terms of the spaces 1 and );*
what is meant by thestatementa:::r Ol)*ov, 0Zi If; I. Theorem 9.15 is an
instance of such .a theorem. Similar questions were considered in a
classic paper of Lebesgue [1]. Hederived several necessary and sufficient
conditions guaranteeing that
[*:
J f(s)p.(ds} 40,
I.F,
where F is a specified coJlection of ftlnctions. Here the integral may be
in the Stieltjes sense. In this connection we mention explicitly a
classical theorem due to Helly [1; p. 268] and Bray [1: p. 180].
THEOREM. II {ex,,} W a selpUnet' of functions of unilormly b",."ded
oorialirm, and if there is a functiolta. BVrO, 1] such that a.(",} 4 a(:£)
lor '" 211 a dense BUbset of [0, I] rontam;..g ° and 1 tMn
J f(s}...(ds} --'; J>(s}rx(ds), fEC[O, 1].
The condition in this theorem is sufficient, but not necessary; a
ne"""sary and sufficient condition waS gIven by Hildebrandt [9].
For other results the reader may refer to Glivenko [1: Chap. 7] or
L. 111. Graves [2; p. 281-292]. H. M. Schwartz iI] has a1so obtained
a number of results in this direction when I is not assumed to be con-
tinuous.
Dieudonne [II] considered the convergen<'<' in [0] where S is a
compact Hausdorff space, the p" are regular rnea.sures, and F is one of
the following classes: (1) continuous functions; (2) IIRiemann inte-
grable functions"; (S) 5ffili-continuous functions; (4) bounded Borel
measurable functions. Probably his most striking result is
J: f{B)<J..(s)dx 4 o.
f.F.
THEOREM. If S is compad mane and 1-'.' rcu(S), Ih£n if ,u,,{G}
-->-p(G) forevl!TY 01"nselG S, IMnp..(E} 41-'(E}for ewry Bore!Bel E.
Vector valued meaBW'e8. The important Theorem 10.1 is due to
Pettis [4; p. 283) who provro it for an indefinite integral by means
of a theorem of Orliez and Banach, although this proof is valid for
the genera] case. The following year, Pettis [6] announced the general
result. Kunisawa [1] gave the first published proof of the general
theorem. (See al80 Nakamura and Sunouehi [IJ.)
The semi-variation, as defined in 10.3, reduces in the scalar
valued cases to the ordinary total variation. In an abstract case, it
was employed by Gowurin [1] who developed it Riemann-type inte-
gration theory where the function and ml"aSure take values in two
vector spaces on the product of which there is defined a veetor valued
bilinear function.
The I"ebesgue.typc theory of integratIon of a scalar valued func.
Where the functions I and {P.} are taken to be in certain pre...signed
classes, e.g.. L", L., L«, C, BY, etc. Some of these results are weak
convergence, some 3:-convergence in ., .and some are neither. Camp
[I] extended a number of Lebesgue'8 results to several variables. An
e,,-rensive dIscussion of such conditions was given by Hahn [2], who
considered 0. wide variety of spaces.
Correspondmg problems SU{4.rest themselves for measures-that
is, to determine conditions on {P,J such that
392
IV. SPEC]AL SPACES
IV.I6
IV.I6
NOTES AND :REMARKS
893
tion with respect to a vector va]ued measure which is presented here
is the one given in Bartle, Dunford and Schwartz [1]. A similar proee.
dure has been employed by Bartle [3] to obtain a Lebesgue-type inte-
gration theory where both function and measure .are 'lector valued.
The 8pace TM(S, E, p). Although the notion of convergence in
measure was introduced in 1909 by F. Riesz [12], it was &«'het
[8; p. 199] who introduced a metric in the space of measurable func.
tions in such a waJt that metric convergence is equivalent to conver-
gence in meaSUre. Frechet [6] gave necessary and sufficient conditions
for a set of measurable functions on [0. 1] to be compact under this
metric. (Earlier, Veress [1] had given conditions assuring that a
sequence of measurable functions has a. uniformly convergent sub-
sequence.) Frechet's arguments were simplified by Hanson [1]. Some-
what different conditions have been given by Izumi [2] and Medved",'
[I]. Theorem ILl is a generalization ofFrechet's results Rnd is due to
Smulian [14]. For another generalization, see Cafiero [2].
Theorem ll,2 is a generalization of a theorem due to Banach
[8; p. 37]. In its form given here it is a generalization of a theorem of
Dunford and Miller [1; p. 542]. The proof given here is essentially that
of Mazur and Orliez [1; p. 157]. Alexiewicz [1; IV] treated polynomial
operators when the d.omain space is not assumed to be B B-space, but
satisfies certain limit conditions. For related theorems and .applica.
tions see Saks [2. 5].
We have seen that the space TM(S, E, p) is not a B-space, and
hence the existence of non-zero continuous linear functions is in doubt.
Nikodym 9; p. 141] showed that if pIS) < CXJ then a necessary and
sufficient condition that there exists a non-zero continuous linear
functional on TM(S, E, p) is th.at there exists an atom for 1-'.
FundivrnJ vi bounded variation. The concept of function of bound-
ed variation was introduced, in 1881. by Jordan [1] and that of an
absolutely continuous function, in 1905, by Vitali [1 J. While these
lasses of functions are of considerable importance in much of analysis,
their study has largely merged into the more general modern concept
of measure, This merger w,," effected principally by Radon [2].
Representations of linear functionals On BV have been given by
Hildebrandt [7] and by Artemenko [1] and Grosberg [I]. In some-
what more generality this problem Jlas been treated by Sreider [1"
but none of these re8ults are entirely natural. Adams (1 J and Adams
and Morse [J, 2] have discussed the space BVand certain of its sub-
spaces with a different metric under which it is not a B-space. They have
been able to give natural representations for the most ge.neral function-
als which are continuous and uniformly continuous under this metric.
There are a number of definitions of bounded variation and ab-
solute continuity for functions of two variables. The reJation between
these definitions and the properties of the associated notions have
been eJ<aIIrined in dctail by Adams and CJarkson [1, 2, 8, 4].
ChiJToctl'Tization vi Hilbut 8pace. Jordan and von Neumann [1]
proved that in a nonned linear space 13 of two or more dimensions
for which the "parallelogram identity"
[x+yj"+lx-yl" = 2{l x l"+lyI2)
is valid for arbitrary :£, Y E I, an inner product call be defined such
that [xl" = (x, x). Thus the parallelogram identity is characteri8tic of
inner product spaces. (See a1so Rubin and Stone [1].) The same con-
clusion has been obtained from other identities or inequalities assumed
for the norm by Birkhoff [1], Day [7], Ficken [1], James [2], Lorch
[3, 4], and Schoenberg [1].
Characterizing conditions based upon certain properties of linear
functionals, hyperpJanes, and types of orthogonality have been dis-
cussed by Birkhoff [I] and James [1, 2, 3]_
Kakutani and Mackey [I] showed that a real B-space }' can be
given an equivalent norm under which it is a real Hilbert space if there
is a mapping T -+ T* of the ring B(I) of bounded linear operators
in}' which sati8fies (TiT.)* = T:Tr, (TI+T")* = T +T:, T** = T
and T "" 0 implies that T*T oft o. They showed that the same con-
clusion is true if there is a IIlapping 9J1 -+ 9J1' of the lattice !l' of
closed linear manifolds of }' for which 9J1" = ID1, ID1' n 9J1 = 0, and
9J1 1 C ID1" implies ID1; J IDJ,;. In this case the space ID1' can be identified
with the orthogonal complement of 9J1.
Kakutani [6] proved that if}' is a normed linear space of three or
more dimensions, then the norm can be given by an inner product if
and only if every two dimensional subspace is the range of a projection
of norm 1. (See also Bohnenblust [2], Phillips [2]. Sobczyk [I].)
For a related problem, see Blumenthal [1].
894
[v. SPECIAL SPACES
IV.I6
IV.16
NOTES AND REMARKS
895
Refert'TIl:u. Aronszajn [1], Birkhoff[I], Blumenthal [I], Bohnen-
blust [2], Day [7], Ellis [1], Ficken [1], James [I, 2. 8], Jordan and
von Neumann [I], Kakutani [6], Kakutani and )\fackey [I), Lorch
[8,4], Nagumo [B], Ohira [I, 2], Phillips [2], Rubin and Stone [I],
Schoenberg [1], Sobczyk [1].
Ordned spaces. There is a vast literature dealing with vector
spaees which are RIso assumed to possess an additional structure of
order. For example, a partially .".dered vecwr 8pw:e is a vector space !B
in which tbere is defined a relation a: y for some pairs of elemenh
in !B for whicb
(i) tJ) ;:;; 0 and -tJ);:;; 0 imply x = 0:
(ii) x y and y ;;" z imply x ;;';z;
(iii) x ;:;; 0 Rnd ;j a non-negative real number imply Ax ;;;: 0;
(iv) x;;;; y implies ",+z;:;; y+z.
If. for cv<'I"Y two elements in !B there is a least upper bound", v y and
.a greatest lower bound x A y, one says that m is a t'edo,. lattice.
Frequent1y there are other relations between the ordering and the
algebraic structure (as in the case of ordered algebras) or between the
ordering and the topological or metric structures. This field lends itself
to a wide va.riety of possibilities. We will confine oUr remarks to re-
presentation theorems for abstract L- and M -spa es.
A real B-8pace is said to be an alndroct L-space if it is a vector
rattice in which
a c!)Untably additi"" 'llI'aSUTC p defilled 011 tlw B.".el field E of S such that
tlw abs!ract L-spacc is isomdTic and laII;ce isomo7phic to the real B-space
L,(S,E,p).
Kakutani [8,9] (and Bohnenblust and Kakutani [1]) define a
real B-space to be an abstr-cu:t ...41-splJN' if it is a vecl.or lattice for which
(v) t£n ;;;; Yn, ..en -- .xo Yn - Yo implies .7 0 > Yo.
(m.) "'''y = Oimphesthat I"'+y[ = I"'-yland Ixvyl =max(I"'J, lyD.
(II "';:;; 0 and y;:;; 0 imply I"'+yl = l"'I+lyl.
Such B-spaces were introduced axiomatically by G. Birkhoff [2] as
abstractions from the concrete B-spaces of Lebesgue integrable func-
tions on a measure 8pace. (See also Freudenthal [1 J, Kakutani
[3, 7, 8. 9], and Smiley [1].)
Kakutani [8] showed that every abstract L-space can be provided
with an equivalent norm which satisfies (I) and a1so the condition
(m) "'''y = 0 imphes [a:+yl = I"'-yl.
An abstract L Bpace is said to have a unit if there exists an element e
for which," > 0 implies e " '" > O. Extending a result of Freudenthal,
Kakutani [8] proved:
THEORE". Giroi:n any abstract L.space satisfying (m) alld p08Sessi''Ii
a ,,"it. there e.x;sls a totally disconneded compact topological 'pace S alld
We say that an abstract lI-'l-space has a unit if there exists an element
e for whieh c ;:;; 0, lei = 1 and Ixl ;"'; 1 implies x :s: e. Independently,
Kakutani [8 and M. and S. Krein [1, 2] showed:
THEOREM. ForanyabatractM-spacemith unit. thertt:oriBls acol1lpact
H ausdlJr/f spa,.. S such that tJu: abstract spacc is isomnr;c and Wtt;,..
isomorphic to tlw rea! B-spacc C{S).
In the case where the abstract space is not BSSUDled to possess a. unit.
a similar representation theorem can be obtained in .,yhich there may
be linear relations between the values of the functions at pa.irs of
points.
The following result is also due to Kakutani.
THEOREM. The colliugate 8p<>"" of on abstN'ct M-spau is all ab-
strad L-space. The "''''iugale of an abstrad L-space is an abstract 11[-
space ",ilk uni!.
Representation theorems for non-Ilormed spaces. similar to those::
cIted above, have been obtained by Kul1er [1].
The following is an incomplete list of works primarily conremed
with various aspects of the theory of ordered spaces. Books: Birkhoff
[8], Nakano [2], Kantorovic. Vutih and Pinsker [1]. Papers: Berri [I],
Birkboff [2], Bochner [1], Bochner and Fan [1], Bochner and
Phillips [1], Bohnenblust [1], Bohnenblust and Kakutani [1], Dieu-
donne [4, 5, 6], Freudenthal [1], Fan [1, 2], Grosberg and Krein [I],
Kadison [1], Kakutani [II, 7, 8, 9], Kantorovitch [1, 2, II], Kantorovic,
Vulih, and Pinsker [2], Krein [2, S, 4], Krein and Krein [I, 2], Krein
and Rutman [I], Mikusinsk; [I], Nachbin [2], Nakamura [1, 2],
Nakano {2,. 8, 4, 5, 6,. 14, 15, 16], Ogasawara [I. 2, 3, 4. 5, 6], Ogasa-
Wara and Maeda [I, 2], Orillai'"" [I], Pierce [I], Pinsker [I, 2, 8, 4, 5, 6,
7]. F. RI<'SZ [28], Sirohov -1], Smiley [IJ, Smnlinu [II], Sz.-Na{D' [IJ,
B96
IV. SPECIAL SPACES
1\'.16
IV.I6
NOTES AND REMARKS
897
Tagamlitzki [I], Udin [I], Vulich [1, 2, 8, 4. 5, 6, 1, 8, 9, 10, II],
Wassilkoff [I, 2, 8. 4], Yosida [I, 2].
Charad€rization oj Ll and L.. In the preceding paragraph we have
discussed the characterization of the space L 1 as a concrete :represen-
tation of the abstract L-spaces. Bohnenblust [I] has given a vel")"
interesting characterization of the L. spaces, I ;:;; p < 00. \Ve com-
ment very bricfly on his results, If!B is a partially ordered real B-
space, let thc abs6late value of x !B be defined as IIxll = x v ( -x).
Two elements x, y in !B are said to be orthogonal if 11",11 A Ilyll = o.
A 'Unit here denotes the same kind of unit as for an L-spac . For
convenience we say that !B has property P in case:
(P) if x = ""+"'., where"" and xoare orthogonal, and y y,+y.,
where Yl and Y. are orthogonal, and if
1"',1 = ly,l, 1"'.1 = IYol,
then it fol1ows that 1"'1 = Iyl.
We may now state Bohnenblust"s theorem.
THEOIlEM. Any separable, partially ord.et-ed rea! B-3pace uilh unit
"Which is a (Hompkte /atria, havify; at least three dimensions and p<JSSI'SS'
ing propn1.y P it equivalent to ane of the spaces ,;, l , lfJ' L , Lj) EB ,;,
L. eJ I., I < P < 00, or "0' Furlhn, tM isomorphism preserot!s norm
and order.
Additional conditions can be given to distinguish between the
various possibilities. Another characterization of L", related to the
work of Clarkson [2], has been given by Fullerton [5]. Another charac-
terization of L spaces has been given by Nakano [14, IS, 16].
Choracterbnt;ct. oj C. There have been many cluiracterization8 of
the space of real continuous functions. In a preceding paragraph we
have already mentioned the theorem of Kakutani [9] and M. and S.
Krein [2] reprcsenting M-spaces as C{S), for some compact Hausdorff
S. Similar results empl0,ying norm and lattice properties were obtained
by Stonc [7; II] and Yosida [1]. Stone [7; I] also gave a characteriza-
tion in tcrms of algebra. nOrm and order properties. Further re8ults
based only on algchra and nOrm properties were developed by Gelfand
[I] in the complex case and were further studied by Gelfand and Neu-
mark [I], Arells [6, 7], Arens and Kaplansky [IJ and Segal [1]. We
Vlll deal with these aspects in a subsequeut chapter on B-algebras.
Most of the characterizations arising from .algebraic considerations
are for complex scalars. The lattice and order properties generally give
rise to real C(S) "p"""". Arens [4], however, has given conditions under
which a real B-algebra is the space of quatemion valued continuous
functions on a compact Hausdorff space.
Characterization on the basis of order and linear properties were
made by Fan [2] and Kadison [1]. Kadison's work is sufficiently
general so that he is able to encompass most of the preceding theories.
Nachbin [2] employed order, norm and linear properties.
Results cha.racteri7ing C(S) among real B-spaces I have been
given by ArellS and Kelley [I], Clarkson [2], .Jerison [I] and Myers
[2, 8. 4]. These results are concerned with certain special properties
poosessed by the unit sphere of 3: or 3:*. For example, Clarkson [2;
p. 847] found that a real B-space is C(S) for some S if and only if (I)
there exists a point V, with Ivl = I, and such that any element on
{"'I 1",1 = I) may be connected with either v or -v by a line segment
lying entirely in this stnfare, and (2)thc half-coneoflines from V to every
point in the solid unit sphere has the property that the intersection
of two of its translates is itself a tran8late. See also Fullerton II, 5].
Arens and Kelley [I] showed that I is isometrically equivalent
with C(S) if and only if (1) the extremal points of the unit sphere U
of I* are contained in two 8upporting hyperplanes, and (2) any col-
lection of extremal points of U whose closure contains no antipodal
points lies entirely in some hyperplane supporting U. They gave an-
other condition which was extended by .Jerison.
Several other in eresting conditions were obtained by Myers. The
reader is referred to his papers for details-Myers [4] is an expository
article.
Abdelhay [I, 2] has used rmg and la tice properties to character-
ize co, and the space of continuous functions vanishing at a point.
.Jerison [I] has treated the lattice question purely by B-space methods.
Speeial C(S) spaces. If S is assumed to have special properties,
then they are often reflected by the space C(S), For example, M. and
S. Krein [1] showed that if S is completely regular, then C(S) is separ-
able if and only if S is compact metric. (See also Myers [31.) That the
space C(S) can be decomposed as a direct sum when and only when S
is not connected. was proved by Eilenberg [I].
898
IV. SPECIAL SPACES
IV.I6
IV.16
NOTES AND REMARKS
899
A completely regular space is etx:trrmoJJy disconneded ifthe closure
of every open set is itself open. Compact exhemally disconnected
'paces are freqnently called Stone Bpace8, since Stone [I] proved that
every complete Boolean algebr.. is isomorphic (M a Boolean algebra)
to the Boolean algebra of all open and closed sets of 8uch a spooe. Such
disconnectedness is reflected in the fact th..t the real space C(S) is a
complete lattice in the n..tuml order. (See Stone [8] for additional
results of thi8 sort.) We will see in Chapter V that the real space L..
is isometrically isomorphic to a real C(S) where S is .. Stone space.
Let S be a Stone 8pace and a: = C(S) the real continuous fUhe-
tions. Grothendieck [4; p. 168] showed that every 3Z.convergent se.
quence in :E* is actually a;**-convergent. and that if ID is a separable
B-..pace, then any operator in B(3Z, ID) IS weakly compact. Goodner
[1; p. 103] proved that the unit sphere in I is tbe closed COnvex hull
of its extremal point8. Kelley [2] completed a result of Naehbin [8]
and Goodner [1] to the effect that if 3Z = C(S) is a closed linear mani-
fold of a B-space 8, then there is a projection of norm one mapping
B onto 3Z. In addition, this property is characteristic in that any B-
space possesSIng it is isometrically equivalent to C(S) where S is a
Stone SFooe. Nachbin [3] also proved that ifID i8 a real B-space whose
unit sphere contains an extremal point and such that every collection
of spheres,. every two of which intersect bas non-void intersection,"
then ID is isometrically equivalent to C(S), S a Stone spooe.
Even more special spaces S (the h:yp£r-Stnn. lif'il'Y8) are found
to be useful in the study of algebras of operators. The reader should
refer to Dixmier [8] for a discussion of them.
Other spnial Bpau8. In addition to the spaces listed in Section 2,
there .are many other spaces which have been studied by various
authors.. Some of these are B-spaces, some on1y topological linear
spaces. We mention here only a few that have been investigated4
Day [1_ has considered the spooe L., 0 < p < I, which is a linear
space of functions on which there IS a "nann" defined which does not
satisfy the triangle inequality, although there are inequalities which
partiaUy compen8ate for this lack. In particular, Day showed that the
only continuous linear functional On this space is the zero functional.
On the other band the space L.[O. 2",] contains the subspace R, of all
functions regular in the unit circle and such that
1/1. = sup [ f. "'I/(re"!!"d6]ll' < 00.
0:;",<1 2x 0
Even though the space L SJ , 0 < p < 1, has 110 non trivial continuous
linear functions, Walters [1] has shown that R., 0 <p < 1, has suf-
ficiently many functionals to separate between functions in the space4
(See also Livingston [1] and Walters [2].)
Arens [2] h", introduced the space Lw[O' 1], which consists of
aU functions I for which Itl.. III., . . . are a1l finite. He showed that the
inclusions L C L CLare P ro p er, and although Lw is a locally con-
0:> It) .
vex topological linear algebra, the topology cannot be given by a
norm. In particular if U is a convex open set containing 0 for which
UU C U, then U = Lw' For other remarks about the spaces L.,
o < p < 1, and Lw' 8ee LaSalle [3]. .
The B-space H.. p > I, with the norm described above (or with
the norm given as a subspace of L.) has been studied by many
authors. See. in particular, the work of Taylor [4, 5, 6, 7], For the
study of integral functions, see Iyer [1]. An extonsi...e theory of """-
lytic functions from the linear space view, going back to the work of
Fantappie and VolteITa. has been developed. In this connection we
mention only the papers of Grothendieck [5], Sebastiao e Silva [2,3]
and da Silvas Dias [I], where addition referenC<'S may be found.
Spaces consisting of functions which are almost periodic in variou
sen8es have been investigated by Bohr and FlJlner [1] (see also Hart-
man and Wintner [I]).
Kothe and Toeplitz [1 j introduced a class of topological vector
spaces, called uperfect spaces" e'"vollkommene Raume").. formed by
sequences {xn} of real or complex numbers which satisfy a set of con-
ditions of the form
! laJ."1"'nl < 00.
These spaces include some of the cla.ssical sequeuCt."S spaces J admit 8
theory of duality (Kothe [1-9], Toeplitz [1]) and have application;,
to the solutions of systems of equations with infinitely many un-
knowns. Generalizations and other results concerning this type of
space (particularly the "Stufemaume" introduced by Kothe [5])
have been presented by Dieudonn [7], Dieudonn and Gomes [1],
and Dieudonn and Schwartz [I]. Dieudonne and Schwartz [1 j, see
400
IV. SPECIAL SPACES
IV.I6
IV.I6
NOTES AND REMARKS
401
also Dieudonne [III], have studied a class ohpaces which are the union
of a collection of locally convex F-spaces. the topology being defined
in a suitable manner, and have shown that many of the basic results
on B-spaces remain valid in this realm of generality. (For example,
tbe space C of continuous function on ( - 00, (0) may be considered as
a union of C[ -n, n], n = 1,2, . . ., tbe topology in C becoming
uniform convergence On compact sets.) The Same type of spaces have
been investigated independently by Mazur and Orlicz [8], who have
developed an extensive theory.
Vector spaces in which the scalars are taken from non-Archi.
medean fields have been discussed by I. S. Cohen [I] and Monna
[1- 19]. See also Fleischer [I], Ingleton [I] and Ono [I].
Birnbaum and Orliez [1], Odicz [8, 4] andZygmund [I; Chap. 4]
have discussed a generalization of the L. spaces of the fol1owing type.
We let M be a continuous. convex. function on [0" (0), vanishing only
for u = 0, and for which u-IM(u) approaches 0 and 00 with u. The
space L M ( 0, 1) is defined to bc tbe set of measurable functions I on
(0. I I for which
f: M( If(ir)I)d.x < 00.
These spaces are a class of B-spaces which include the spaces L-s;.
1 < p < c::c, and possess many analogous results. For example, there
exists a function N having the same properties as M. which plays
the role of the conjugate function. In particular if there exists a k > 0
such that 1I-1(2u) kM(u), then (L M )* is equivalent to the space LN
(see Zaanen [I], where a definition is given that incJudes the s}lliCCS
L" and LoS> as well). Conditions for conditional compactness in LM are
exactly similar to tl10se in L. (Takahashi [I]). Further conditions that
an integral operator in LM be compact are quite analogous to condi-
tions in L.. (Zaanen [2]). Tbese spaces are diseussed in detail io the
book of Zaanen [5}. See also Krasnosel'skii and Rutickii [I, 2, 8}.
For other generalizations of the Lebesgue spaces, see Ellis and
Halperin [1], Halperin [1.8,4] and Lorentz [1,2]. Spaces of Deajoy-
integrable functions have been 8tudied by Sargent [I, 2].
A function defined in a suhset E of Euclidean space for which
I II I/(ir)-f(y)1
=sup I ,. <00
s,lIEE X-YI
is said to satisfy a H(jldn condition of uplJrumt" in E, or to be Holder
continuous. It is clear that the family of all such functions, "ith the
indicated norm, forms a B.space. This B-space of functions plays an
important role in connection with the study of certain singular inte-
gral operators, particuJarly those whieh arise in the theory of partial
differential operators More detailed indications on this score are given
in the section of Notes and Remarks at the end of Chapter XI of
Part: II. For an account of the principal inequalities connecting HOlder
continuous functions and singular integral operators see Friedrichs
[II}. For an illustration of the application of this type of inequality
in a connection other than the theory of partial differential operators,
see Friedrichs [I]. Very little seems to be known about the B-space
properties of the B-space of all functions satisfying a HOlder condition
of exponent a. t and additional information on this score would be use-
fuL
An interesting variety of locally convex linear topological space
(see the next chapter for the general definition of such spaces j has
been introduced into consideration by Laurent Sch\Vartz and seems
destined to play " conspicuous part in many branches of analysis.
Let I be an open ioterva! of the real axis. and let C o (1) denote the
linear space of all complex-valued functions defined in I which are in-
finitely often differentiable and vanish outside a compact subset of
1. Let r be an arbitrary p08itivc integer, and 4>., . . ., 4>, be an arbitrary
set of T + I everywhere positive functions defined in I. Then, if we
put
N(g;4>"....4>,) =
{I £ Co(/)ilt<"(tj-g';'(t)1 < 4>,(1), t £ 1, t £ 1, i = 0,. . ., r}
for each g £ Co(/). the set of neighborhoods N(g; "'., . . .. 4>,) define a
topology for Co(/) in terms of which the linear space becomes a
(locaUy convex) linear topologica! space. The space of aU continuous
linear functjonals defined on this linear topological space, which we
shall denote by the 8ymbol D(/), is called the space of di8trib tKms de.
fined in 1. The mapping f --+ F" where
Pf(g) = tf(t)g(t)dt.
imbeds Co(/) (and evcn L.(/» mto D(l), and enables us to regard
402
IV. SPECIAL SPACES
IV.I6
IV.I6
NOTES AKD REMARKS
408
D(l) as forming a space of generalized functions. Very man)' of the
generaJized functions which have been considered from time to time
in heuristic analysis (such as the famous Dirac (I-function and its
derivatives) can then be identified with rigorously defined elements
of D(l). If a suitable weak topology is defined in D(l), it becomes
possIble to define such analytic operations as differentiation as con-
tinuous mappings in D(l), and. in this sense, to define a su.table
generalized derivative for every function in. say, 4(1). In his ground-
breaking book [5), L, Schwartz treats all these questions in detail. and
also studies the theory of Fourier expansions, integral transforms.
convolutions, etc. of distributions. In addition, he gives 8 variety of
applications of this theory to various branches of analysis. J. Djeu-
donne and L. Schwartz in [1) give a general theory of a variety of
linear topological space including the spaces C;;"(I) and D(I). We shall
reproduce parts of the theory of djstributions in Chapter XIV of
Part 11, in connection with the study of partial differentia] operators
to be made there.
E" and Em, respectively, and if e $ f denotes the set {x$ ylx. e,
y. f}, then !1'Tm(e $ f) = p.(e)/,.(f). In partIcular,
[I]
P'i-m(e EIJ £m) = p.(e).
It follows from the rotationa1 inv.ariance of Pn that /In may be re-
garded as a measure defIned intrinsically in any n-dimensional real
Hilbert pact: , without referenct: to any particular coordinate
system in that Spa<'<'. This measure will be called the Gauss fi'IeaS(U"e in
,t.. In particular, let o be such a space, and a 8ubspace of .\:1.. Let
E be the orthogonal projection of .\')0 onto .\:". Suppose that Pfh, and
P v , denote the Gauss measure in .po and t>r, re8pectively. Let e bc a
Horel subset of .\>o sueh that x . e if and only if Ex. e. Thell.t follows
easily from (I) tl1at
(2)
P V, (e.\).) JtfJo{e).
The Gau.Js- Wiener InregTal in Hilbert Space
Let En be n.dimensional (real) Euclidean space. Let P. denote
the Horel measure in E" defined by
EqLlatIon (2) enahles us to define a Gauss metUlUTl! m real Hil,,",
'pace as follows. Call a Borel 8ubset e of {I a cylinder sel if there
exists an orthot,ronal projection E nf onto a finite dimensional sub-
space " Of.\'8Uch that x. eifand only if Ex.e. If this i8 theca8e, put
(3)
p(e) = PV1( "\)'
Il.,,(e) = 1t-n}2. Ie clot,l! dx,
the integral being an n-dimensional Lebesgue mtegra), and Ixl de-
noting the norm of the vector tc in En. Since
Then (2) show8 that the left s.de of (3) .s mdependent of .\>"; i.e., that
the definition given in (3) is univalent and hence legitimate.
It follows very easily from the corresponding propertic8 of finite
dimensional Gauss measures that
(i) p is a non-negative, finitely addjtive set function defined
on the field E of cylinder sets in .j;>.
Iii) Let U be a linear mapping of into itself which is norm-
presen'ing. Then, for every e in E, UE IS also m E and p(e) = p(Ue).
This is the property of rola/ional inMriance in HUbert spare.
(iii) p(.\» = 1.
Using (1) and the general theory of Sections 111.1, III. , and
111.8, wc may now establish an integration theory (finitely additive)
for functions on . It turns out, however, that this integration theory
is not sufficiently inclusive for the customnry Bpplications of the Gauss
integral. Hence, it is well to extend this throl)r somewhat, as follows.
(a) First establish the intcgration theory of Sections 111.1, 111.2,
f +oo
--00 e " dt = vn.
p,.(E') = I. A]so, the measure Pn is easily seen to have the following
fundamental property of rota1wnal invariance:
p,.(e) = !,-.(Ue),
where U is any linear and norrn-preservhJg mapping of E' onto a1l of
itself. The spaee E"i-. may evidently be regarded as the direct sum of
En EIJ £m in the sense of Section IV.4, Then {/orlEIJ lyD" = Ixl" EIJ fyl",
and henee exp ( - (lxlEIJ Iyl )") = exp ( -Iorl") exp ( -Iy'") for all or in
En, and y in Em. It follows readi1y tlmt if e and f are Borel :sets in
404
IV. SPECIAL SPACES
IV.16
IV.16
NOTES A:ND REMARKS
405
and III.I!. which gIves among other thmgs a definition of p-measur-
able and p-integrable functions.
(b) Let C be the set of all projections E of.\1 onto its finite di.
mensional subspaces, and let If, be the set of all bounded linear maps
in .\) which have IInite dimensional ranges. Put
III = inf sup
E IE 4FtE.4.
11>0 IE-F£I<e
if this quantity is finite; otherwise put III = 00. Tben III defines a norm
on a certain linear subspace r,l) of the set of functions on . It is easy
to see that <P mcludes the space <p. of all wintegrable functions, and
that the linear functional S
f4> I/(l<'x)II'(dx)
sional Gauss measure on the real line. The space lJ' b, of course. the
space of all real sequences iI: = [iI:,] as distinct from I,. which is the
subspace of 8 determined by the condition ;::,.:c; < 00. The measure
p= is countably additive; the subset I. of 8 is of ,u=-measure zero: the
measure ,u is not countably additive. In fact, using the relation
between f'= and p. it is easy to see that t. is the union of a
countable family of p-nun sets. These relationships may be summed
up in the following heuristic formula; by passing from the full infinite
product space 8 to its subset I.. we lose countable additivity. but gain
in return an important property of rotatIonal invarmnce.
As B general reference for the above remarks, see Friedrichs [12],
pp. 52-63.
There is yct another method, mtroduced by Norbert Wiener, for
obtaining a countably additive theory at the cost of abandoning
rotational invariance. This may be described as follows. Reprcsent.\1
as the real space La( - 00, + (0). Then the mapping I --+- TI defined by
(T/)(iI:) = f:/(I)dt, I.L,(-oo, +(0),
maps La into 11 (rather "thin") subset of the spllee C of all continuous
"-
functions defined on the real axis. This enables one to define a field 1:
of subsets of t and an additive set function p on f as follows:
1: = {e. CIiI:T-1,.<P,J
p(el = fg,XT - I,("')I'(d"'I, e. i.
X II denoting the char -t.ic functIon of the set eo, as usua.l. This
measure ;;. on C is substantially the same as the measure of \Viener.
More specifically, note that every set of the form {I. tl/(l o )' eo},
where - 00 < 10 < 00 and e. IS a Borel subset of the field of scalars,
belongs to i. Let 1:. be the subfield of i generated by the famil)' oC
sets of this form. Then it may be shown that , is conntably additive
on i.. Hence. by Theorem III.5.B, p may be extended to a countably
additive measure p" on the a-field 1:", of subsets of t g<'nerated by
i.. The measure space (t, EIO' Pm) is the \Viener measure space.
The theory ofthis measure space has been studied quite eJaboratcly.
The fundamental early papers are Wiener [6] and [7], and Paley,
Wiener, and Z)'gmund [1]. Most of the subsequent progre>s is due to
S ; 1->- fg,/(i<)p(di<), I-!p.
is uniformly continuous on !p. relative to the topology induced by the
norm 111. Hence. by Theorem 1.6.17, S may be extended uniquely to
a continuous linear functional defined on all of ;Po = <PI' We say that
a function I in t,P is p-integrable in lM cmndal sense, and write
Jg,/(iI:),u(dx} for S(f} if I is in <P,. This "extended sense" theory lIas
many of the properties of ordinary finitely additive integration theory.
In addition. to these, it is l'ota.tionally invariant, i.e., if U is a litlC«t
norm-preBen:ing mapping 01 inlo itse'f, and If 1(') is in <P" then
I(U(,)) is in <PI' and
fg,/(iI:}p(dx) = f4>/(UiI:)I'(dxJ,
Suppose that.\1 is 8eparablc, and that we realize it 8S I., i.e., we
ma.p it in a one-to-one, linear and norm-preserving way on l,l (say,
by use of Theorem 4.16). Since,u is lUtrinsic to , we obtain a Gauss
measure p, in , and it is easy to see from the definitions that this
measure satisfies the equation
,u({[iI:,] d"la, iI:, b;, i = 1, . . ., n}}
I 1 ', f. ,. J '. .,2 · d
= n;-n · ... exp [-(111 +.. .+y.)]dy,... y..
Qi. o. u.
Conscquently it is ,...ery closely related witli the infinite product
measure J1.= = PI XPl A. . . defined on the infinite product s of count-
abl)" many replIcas of the real axis J p., being as above th onc-dJmen-
406
tv. SPECIAL SPACES
1\'.16
IV.16
XOTES _'l:s'D REMARKS
407
R. H. Cameron n'. T. ,}[artin, and their students. Canteron and !\lar-
till 3J, LaJ, [7], and Cameron and }'agall fl], study the effect of va-
rious sorts of mappiDg5 in (; on the mCasure flu" establishmg genCTali-
zations of the .Jacobian determinant law governmg changes of variable
in finite dimensional multiple inkgrals. Cameron and :lIartin [6] eval-
uate various \Viener intc '1"Rls by the use of a general method involv-
ing H hanges of variable'" in the space (;, and making use of certain
Sturm-Liouville differential equations. Cameron and Martin [2 J,
Cameron and Hatfield [1], l2] establish a complete orthonormal set
of uFourier-Hermite functiona1s" in L 1 CC, Etq, Pw)' and study the
thcory of expan8ion of arbItrary elements of LJ(C, Lw, "w) m these
functional>. Cameron [4] and Cameron and lIIBrtin [9] provide are.
lated theory of FourIer mtegraIs. ('ameron and :I!artin [1], [4],
Cameron and Shapiro [1], Cameron, Lindgren, and lIIMtin [1] show
how the solutIOns of <.'erbUn non-lillcar integral equations can he ex-
pre>sed "exphcitly" in tenns of Wiener integrals. Cameron [2] and
Owchar [I] study formul"" for Wiener integrals related to thc formula
I(x, I) = fGI(<p(I) + .r)l'w(d<p).
There eXISts a rorresponding \Viener-integral formula for the solution
F of the more genera] parabolic initial value prob1em.
d I '
-. I(x)d.r = fIt)
dt
a I a'
- F ( x. t ) = - - F ( x, IJ-t- V(x, t)F(x, t),
ot . 4 ax'
F(x. 0) = Ilx),
V being .a given coeffICient function. 'Illis formula is
[tt] Fix, t) = f,;/('I'(t>+x) exp If V(t-s, 9'ls) +x)dsll'w(d<p).
The authors cited above have investigated various aspects of the
relationship between the partIn} differential problem Lt] and the
formula [tt]. Cameron [3] in particular gives vcry detailed "'''"I1lts
nnder very mild analytical restrictions. It should also be remaJ'ked
that the connection of [ti and [tt] is related to a more general rela-
tionship, known from the probability theory of Markoff pro<'Csses,
betwt.-''(-n a,. .Markoff PIU{'{"ss in its "'transition probability" Rnd its
"samplc function" representations. For applications of formula [tt]
to the theory of probability, see Kae [1] and Erd08 and Kac [1].
Gelfand and Yaglom ,1] give an exrellent review of the theory of the
\Viener integral with sprcial emphasJs on formula t J.
For various other, quite different, approaches to the problem of
integration III Hilbert space, see K. Lowner [1]; E. R. Lorch L12],
[13], ,14]; Friedrichs :12]. pp. 121-132; P. Lcvy [I], pp. 209-355.
[t]
t 2' 0;
for functions of a real variable. Cameron [1] gi,\ces a "Simpson s rule"
for the numerical evaluation of \Viener integrals.
See also Kae L:2], 1\-farumaya [I], Call1(T{)n [8], Cameron and
Graves [I], Cameron [5], Wiener [8], Paley and Wiener [1], Chapter IX.
A most interesting development of the theory begins with the
thesis of the physicist Feynman [I], and conti.nues in tile 1:udies of
Kae [1] and [8], Rosenblatt [1], Tingley 1], Fortet [4], Cameron [3],
1\IontroU [1], Steinberg [1]. Tile formula
1 I +'"
[*] f(I,x) = --- -('-"'/f/(y)dy
v'ni -00
expresses, as is well-kt1ow the solution of thf' partial differential
initIal value problem 01' "heat flow"
a 1 iJ'
iJt I(x, I) = 4" ax' fix, I),
t o;
I(x,o) =/(3:).
It is eas,y to from the definition of \VJcncr's measure that tillS may
be written as
CHAPTER V
Convex Sets and Weak Topologies
In Chapter II we have .een that the continuous linear functionals
provide important tools in the study of B-spaces; the present chapter
continues these invf'stigntions in more general spaces. We begin by
studying the notion of convexity in B general linear space, and by
proving a fundamental lemma equivalent to the Hahn-Banach theo-
rem. which relates linear funutionals to convex sets. These results
are examined in Section 2 under the additional assumption that the
space is a linear topological space. In Section 8 it is shawn how certain
classes of linear functionals determine topologies in 8. linear space.
In particular for B-spaces a topology, called the weak topology. may
be introduced such that weak convergence of elements y as defined in
11.3 is equivalent to convergence in the weak topology.
Sections 4-6 continue the study of various topologies for B-
spaces determined by linear functionws. In particular. an inyestiga-
tion is made of compactness properties. relations to metric topologies,
reflexivity, bounded and unbounded ets, Rnd sequentia1 properties.
Many of these results are valid for locally convex linear topological
spares.
Sections B-I0 discuss the topics of extremal points, tangent
planes, and fixed point theorems. The ideas of these sections, while
highly interesting in themselves, will be applied much less frequently
in later chapters. Additional re8ults and examples will be found in the
exercises of Sections 7 and II.
1. Convex Set. in Linear Space.
In this section, I, t), etc. will denote linear vector spaces, and p,
q, 3:, !i, . . ., points in these :spaces. The symbols \'X, P, . . . will denote
real or complex numbers, a, b, . .., rea1 numbers.
'09
1O
V. CO!llVEX SETS .-\
D \VEAK 'j'OPOLOOIF.S
V.I.l
V.l.8
COt\VEX SETS .:s LINEAR SPACES
411
] DEFIN1TlOX. A sctK
1: IS C()lIvex if X, Y E" K, and 0
a
I,
imply ax+(I
a)y£K.
The fo]]owing lemma is an obvious consequeOI"e of Definition ].
2 LEMMA. The intersection oj an arbitrary family of COIllTZ subsets
oj the linear space.! is C01l.l'fJ'.
As examples of convex subsets of I, we note the 5ubspaN."s of I,
and the subsets of l' consisting of oue point.
LEMMA. Let .x]t . . "' x n be point:1 in the l'onve:r set K und let
U J ,..., an be rwn-negati'l)e srolars with u.+.. .+a n = I. Thrn al..J"l+
. . .+atl.T" in in K.
PROOF. If It = 2, the statcnlent is true by defimtion. Suppose
that the lemma. is true for n = m. TJ\en, setting h =
+.. .+am+I'
and
9JJ+i
alxl. = a.xl+by€K.
'-1
= {ala> 0, a-1x £ K}, and f(x) = inf a. The fundion fIx) is called
the support function of K. a <1(0)
For """",pIc, if K is the unit sphere of a B-spaee 1. then
f(x) = 14
S LEMMA. Let K be a convex set in I c01ltaining tlte origin as an
intunal point. and let f be its support func/ion. Then
(a) f(<<);:;: 0:
(b) fIx} < +00:
(c) flax) = af(x) for a ;:;: 0:
(d) if x£K, tkRn fIx) < I:
(e) f(x+y} < f(x)+f(y):
(f) the set of in"'mal poi,w of K is dtarac/tri:zd by Ihe condition
fix} < I. and the sel of baullding points by the eondition f(x) = I.
PROOF. Statement (a) is obvious. Statement (b) follows from the
fact that the origin IS an internal point of K. Statements (c) and (d)
arc self-evident. To prove (e), we note that if C > f(x)+f(y), then
c = a+b with a > f(x), b> I(y). It follows from the convexity of
K that the point
.x+y = x+y = ,:(a-1x )+b(lr-1y)
c a+h a+b
is in K, sinee a
]x and b
ly are both in K. Hen("(" f(x+y) < c.
If x is an mternal point of K, then x+£.7' = (I +,)x is in K for
some sufficiently small. > 0, so that fIx)
(J +,)
]. Conversely,
iff(x) < I. let . = I-f(a:). To complete the proof of (f) we shall sup-
pose that I is real, leaving the details of the complex case to the reader_
Let 1c5!(f(y)+f( -y» < .. Then
f(x+.5y) < (1-<)+£ = I,
irrespective of whether c5 is positive or negative, so that I . (x+c5y) =
i1: +
y £ K. Therefore, x i
an internal point of K. In the same way it
follows that f(x) > I characterizes the internal points of the comple-
ment of K. 'rhus, fIx) = I characterIZes the boundary points of K.
Q.E.D.
y = (a.Jb)x.+.. '+("mH!b).r
I'
it follows frolIi our induction hypothesis that y £ K. Since a] +b = I.
Q.E.D.
4 LEMMA. Let I be a linear apau.lj KII K 2
.! are C011'L't'X. thtn
fJK 1 and K,:!:K. are COn",x.
PROOF. If3J, y EpK 1 , wchave.r = {h!,y = py'. for some a::", y'
Kt-
Then, if 0
a
I. n.:r+(I-a)y = Pf.,...'+(l-a)y'} cfJK1' since Kl
is Convex. The .second part of the lemma may be proved in the Same
way. Q.E.D.
The proof of the following lemma employs the same idea.
5 LEMMA. If T is a linear map from x to
, and K i. a cOnvex set
in .!. then TK is convex.
6 DEF1NITIOS. It'i'J,I is a suh.'O("t of the linear spare 1:, then R
point p c 1'.1 is called an ".Iannl point of 1'>1 if, for each x £ 3.':, there
exists an £ > 0 such that p + c5x £ M for 1.5[ ;;; t. A point p £ 1 is
called a baunding point of ,'1 if P is neither an internal pomt of M nor
of the ,,,mplement of ,11.
7 DEFINITIOK. Let K be a convex
et In a linear Sj)af'1.' I and let
thc origin 0 of.r be an interD&I point of K. For rach xc.r, let Itx)
9 DEFINITION
If I is a vector space. and lJl and 1\1 are sub.ets
of 3.':, a functional f on ! is said to separate 11'1 and IV if there exists a
real constant c with £it/eM) ;;; c,
/(N) < c.
412
v. CONVEX SETH AND WEAK TOPOLOGIES
V. I.](}
V.I/.I
LINEAR TOPOLOGICAL SPACES
413
10 LElofMA. Tk linear futidirmalf8i!fJllral£s the subsets M and N
of I il and only if it separal£s Ihe subsets .'W: -N and to} 0/ I.
The proof is elementary, and is left to the reader.
In dealing with subspacesJ' it is often convenient to make use of
the following lemma:
II LEMMA. Let I be a lirwar functional on 1M vector space I, and
let'ID be a tndJsyxJa! 01 I. II 1('19) is nol 1M whole field 01 smlars, then
f(¥J) = O.
PROOF. Suppose that there exists a y. 'ID with I(y) #= o. Then
f(aY/I(y» = a, so that every scalar is in I!ID). Q.E.D.
12 THEOREM. (Basic separation tIreo1-em) Let .'W: and N be dis-
joint co"''''''' aubsets 01 a linear space I, and let hI have an i"lo7wl poinl.
Tkn thrre e:xi$/:; a non-zero linear lundinl/al I which 8Cparaf£s 111 and N.
PROOF. Suppose that I is a real vector space. If m is an internal
point of bI, then the origin 0 of I is an internal point of III -m. It j,
easily Seen that a functional separates M and N if and only if it se-
parates M -m and N -ffl. Thu8 it suffices to prove the theorem under
the additional assumption that 0 is an internal point of hI.
Let p be any point of N, so that -p is an internal point of 1'>1-."'.
and 0 an internal point ofK = 1I1-N +p. Since hI andN are disjoint,
the set JJf N does not contain 0; hence, K does not contain p. Let I
be the support function of K, so I(p) > I. If we put fv(ap) = al(p).
then 10 is a linear functional defmed on the one dimensional subspace of
I which consist8 of real multiple8 of p. 1II0reover, fv(ap) I(ap) for
all real a. since for a :2. 0 we have I.(ap) = flap), while for a < 0 we
have lo(ap) = al.(p) < 0 $;: I(ap). By the Hahn-Banach theorem
(11.3.10),1. can be extended to a linear functional/such that I(x)
f(3:) for all 3:. I. It follows that I(K) ;;; I, while I(p) ;;: 1. Thus f
separates K and {p}; by Lemma 10, f separates M -N and to}, and,
again by Lemma] 0, / separates iJ'I and N. Thus the theorem is pro\'Cd
for real Sp3('ft;.
If the space .1 is complex, we can still regard it as a vector span"
Over the subfield of real scalars. By the proof given above.. we can con.
stract a real-valued function I on 3::, such that I(x+y) = l(x)+/(y),
I(ax) = o./(x) for a real, and such that IPI) and tIN) belong to non-
overlapping intervals. Then, the function F(x) = 1(3:)-i/(ix) is a
non-zero linear functional on the complex space , which separates
the sets M and N. Q.KD.
2. Linear Topological Spaces
In this section, the results of Section I are applied to linear
topological spaces. Statements 1-6 of this section are elementary
results, Statements 7-12 are applications of the fundamental Theo-
rem 1.12.
I THEOREM. (a) Tk closure and 1M inleTior 01 a co"","", set in a
li,u:aT topological space are CI11II'£.r.
(b) An interior point 01 a set in a linear topologirol spm:e is an
inl£rnal point 01 1M set.
(c) I I a am....x sel K in a limar wpolDgirol spm:e hM al leMt <me
inter-iur point, fhton a point p is an internal paim of K if and only il if is
an interior point; it is a bou.uling point il and only il if is a boundary
point. Moreover. the interior 01 K is t!nuie in K.
PROOF. Let 3:: be a linear topological space, let K be a subset of I
and let I be the closed unit interval. Then K is convex if and only if
the mapping
"': [x,y,a] -->-a.x+(I-a)y
of x1:}II in to I, sends KxKxI intoK. But, since¥, is continuous,
and KxKxl = Kx K xl, we have
v>(KxKxl) = ",(KxKxI) !;;",(KxKxI)!;;K
whenever K is convex. Thus K is convex if K is COnvex.
Next we show that if P is an interior point of K, aad q a point in
K, then ap+(I-a)q is an interior point of K for 0 < a < I. Indeed,
there exists a neighborhood U of the origin such that p+U K, and
a point q, £ K in the neighoorhood a(a-I ) IU +q of q. Now, since K
is convex, the open 8et U, = a(p+U)+(I-a)q, lies in K. Since
(I-a)(q-ql) £ aU. ap+(1 -a)q = ap+(I-a)q, +(1 -a)(q-q,) £ U I .
and hence ap+(I-a)q is interior to K.
The second part of (a), and the last part of (e). follow immedIate-
ly from what we have just proved. Statement (b) is an immediate con-
sequence of the definition of a linear topological space. It follows from
414
v. COXVEX SE"I'S A:KD WEAK TOPOLOGIES
Y.2.2
Y.2.
J,[NRAR TOPOLOGICAL SPACES
I5
(b) that a bounding point of K is a boundary point of K; it remains to
show that if the convex set K has .at least one interior point P. an
jlJtemal point qI is an interior point) Rnd a boundary pomt q2 is a
bounding point.
Since q. is internttL the vector r -<p (I+<)ql belong< to K
for some sufficjently small positive E. It follows from the ahove that
for somc sufficiently small po<itive <, ql = T!(I+<)+,p!(I+.) is an
interior point of K. Since q2 is a bOl1nrlar}r point, it is not an internal
point of K. But we have shown that ap+(l-a)q. £ K for 0 < a < I;
hence g'2, is not an internal point of tlle complement of K. Therefore
q. is a bounding point of K. Q.E.D.
2 [)EFINI'l'ION. If A is oR subset of the linear space It the set
co (A), caUed the cont'rx hu.ll of A, is the interspction of aU onvex sets
containing A; if 3: is a linear topological space, the set co (A). called
the closed conVCd: hull of At is tbe intersection of all closed convex sets
containing A.
It is eadily seen that co(A) is the set of all linear combmations
Ii-t ueri of elements Xi E A in which 0 ;;S; at 1, and I:_IlZj = J.
Such hn ar combinatjons art' sometimes caned C01lflf'.r combinatiulls;
hence co(A} is the set of all convex combinations of points of A.
The opcratiuns co(A) and co (A) map sets mto sets. Some uf thc
elcmentary properties of these operations are giycn in Lemma ..
below. The proof of Lemma 4 rcquires the following lemma on topo-
logIcal groups.
; LE1\mA. If A and K are do8t'd sIdJsds of all addilif'i' topologirol
group G, with K campact, then A +K is closed.
PROOF. Let p e A+K For each neigbborhood U of p, let
Ku = {ki'aK, ke V-A}. Since p e A+K, eachKu is non-void. Iti,
evid ent that if Ud;;U.. then Ku,!;;Ku,. It follows that the closed
sets Ku ha,'e the finite intersechon prop["rly. \\TC call now apply
Lemma 1.5.6, and conclude that there is 8. point ko K common to all
the Ku ' Thus, if N is any neighborhood of the identity,
(N+ko) n (l\'+p-A) "Fq,.
N-N M. Thus, any neighborhood of k. intersectsp-A. Since A is
c1osed,-p-A is closed. Hence k.. p-A, and thus peA +k.!;; A +K.
Q.E.D.
Since the commutativity of the group G is not essential to the
proof, the snme result holds for non-Abelian topological group<.
LEMMA. For arlJifTary seta A, D in a lilleaT Spa<'< 3::
(i) co(exA) = ex colA), co(A+D) = co(A)+co(B).
If l' is a linear lopologieal space, Ihm
(ii) col A) = colA) ,
(iii) Co(exA) = ex co (A),
(iv) If colA) is compuCI, then co(A+B) = co( A) +co( D).
PROOF. The first part of statement (i) follows in an elementary
fashion from Lemma 1.4. Lenuna 1.4 aIso shows that ",o(A+B)
!;; co(A)+co(B). Now, if y. Band "' = :_I a.",. e coCA), then
",+y = :_. a,(ir,+y), so co(A)+y = co(A+y), and thm co(A)+B
!;;co(A+D). Tile same argument sllows that co(A)+co(B)
co(co(A)+B). Thus co(A)+co(B)!;; co(co(AJ+B)!;; co(co(A+B))
= co(A+B). This completes the proof o f (i ). To prove (ii),note that
co lA) is dosed and contains co(A). Thus co(A) co(A), By Them'ern
I, the closure of a convex set is convex; so co, A) is convex t and in-
c1ud"" A. Thus coCA) d co lA). which completes the proof of (ii).
Stntement (m) follows from (i) and (it)_ Wc now prove (iv). Statemcnt
(i) and Lemma 3 show that co( A)+ co (D) is convex and closed, so
that co (A+D) co( A) +co( D ). Now , since m+y i< a continnous
function of '" and y, Xl --i-- Y) X I + Y. for arbitrary <ubsets XI' Ylof
1'. Hence, from (i) and (ii),
Co(A+B) co(AJ+co(B) co(A)+ co( D).
This completes the proof of (iv). Q.E.D.
5 LEM>lA. Let A, B be sets in a linear lopologirol spacc. If Ille
closed conve", hulls of A and B aTe compact. Ih", co lA U D) =
co(co(A) U co (D)).
PROOF. The inclusion co (co( A) u co (B))!;; co lA u B) is clear
from the definitions involved. LetK, = co lA). K. = co( D). The map
'1': (A,p,q) --+ap+(I-a)q,
is a c:ontinuous mapping of the compact space K = [0 7 Ij xK1xK?
This means that (N --N +ko) n (p-A) "F q,.lf!II is any ncighborhood
of the identity, there is a neighborhood N of the identity stich that
416
v. CO "VEX SETS AND WEAK TOPOLOGIES
V.2.6
V.2,7
LIS-EAR TOPOLOGICAL SPACES
417
into co(K, uK.); therefore 'ilK) is compact and hence closed. Ru
A u B \;; K, UK. \;; ¥.(K). If I"(K) is also convex, then colA U B)
:;;; W(K) \;; co(K I UK.). Hut this fact is shown by the fo]Jowing ele-
mentaJ}" calculation.
If II ;:;;; a,. a., b ::£ I, then
b{u,1':1 +(I-u,)q,}+(I-b )(a.p.+(1-a,,)q.)
{ ba, (I-b)a" \
={bu,+(I-b)a.} bu,+(I-b}a. p,+ bu,+(I-b)a'p '/
{ b(I-u,)
+(b(I-u,J+(I-b)(l-a.)} b(l-a,J+(I-b)(I-a,,) q,
(I-b }(I-a.) }
+b(I-U,)+(1 b)(I-a.)q. .
Q.E.D.
.s({k".. .. kml, £/2). But then cO lA) C S({k". . " k,.}, 0). Q.E.D.
7 LEMMA. II a linear lunc/iOlwl em a linear topofugical space
separalFs two sets, <me 01 which has an inkrior point, thim the IWu:lional
is continuous.
PROOF. Let 1: be a linear topological space. and AI' A. \;; 1:. Let h
be a linear functional separating A, and A., and let p be an interior
point of A,. If I, g are the real and imaginary parts of h, then g("'}
= -/(1x), and hence, to show that h is continuous, it suffices to prove
the continuity of I. Let N be a neighborhood of the origin such that
p+N \;; AI' Then/(N) r;; I(A,)-/(p}, and I{N) is contained in a proper
subinterval [-a, c1J), or (- 00, a J, of the real axis, where a> O. Let
111 = N n (-N); then }J = -M., and M is a neighborhood of the
origin such that I(M) is containcd in the interval [ -a, a J. In this case.
l(m-'lIl) is contained in the interval [-£, £]. Since £a-'M is a
neighborhood of the origin, I is continuous at O. By Lemma 11.1.3,
I is continuous. Q.E.D.
Lemma 7 and Theorem 1.12 yield the following result.
8 THEOREM. In a lim'flr topological space. anytreo di8joinlronveJ:
sets, one oj which has an illtnior point, an be separated by a non-zero
wn1inuow linear luneti""a!.
9 DEFINITION. A linear topologIcal space is said w be l(}CaUg
convex if it possesses R base for its topology consisting of convex sets
to THEOREM. II KI and K. are disjoin! d_d caRlon subsets vI a
locaUy conve", linear topological space I, and il Kl i8 compact, Ihell thrre
e.xi8 constants c and e, E > o. and a l'ontinufJuslillt'D.T fundional f on:t..
s"ch that
6 THEOREM. (.Uao"r) Let I he a B-space, and let A r;; ! be com-
pact. Then co lA) is compad.
PROOF. As a closed subset of a complete space, the set co lA)
i8 complete. Hence, by Theorem 1.6.15, it suffices to show tnat co lA)
is totally bounded. Let £ > O. Since A is totally bounded, there is a
finite subset {zJ, . . ., z.} \;; A 8uch that A r;; S({z" . . ., z.}, </4). Let
K = co({z,,, , ", z.}). Now co lA) C S(co(A), £/4}. But if y £co(A),
y = :'1 aiYi where 11. A. ai 0 and I -l lli = 1. Let v be a func-
tion on A to {I....,,,}, such that if JJ. A. I"'-z"., 1 < </4. Then,
m m £
Iy- a,z....)1 = I a,(y,-z.,..,}1 < -.
i=l '-1 4-
and thus co lA) C S(K, £/2). Now,
"
\V: (a 1 .. . ., an, z11 . . ., Z'n) -+ :I aiz,-
&=1
9P/(K.) ::£ c-£ < c ::£ 9l/{K,).
PROOF. By Lemma 3, the set K,-K. i8 closed; by Lemma 1.4,
it is convex. Since KI-K does not contain 0, there is a convex neigh-
borhood U of o. which does not intersect KI-K.. By Theorem 8,
some continuous non-zero linear functionalj separates U andK 1 -K ir
i.e., there exists a real constant d, such that :Jt1(K, -K.) 0:: d.
!li/(U) ;:;;; d. Now, since I is non-zero, there exist8 an JJ. I with
1("') = I. It follows that f(""') = <t. On the other hand, ""'. U for <t
sufficiently small. Thus, there exists an e > 0 such that flU) contains
Tne mapping,
. "
K={klk= a,z" a, 0::0, ai=I}.
&=1 i l
is a continuous mapping of the compact set [0, IJ x. . . X [0, I] X {z,}
X. . . >. {z.} onto K. Thus K is compact, and hellce totally bounded.
There is, then, a fmite subset {kJ,.... k m } of K, such that K C
418
\". (."OI'VEX SETS AXD W1:.A).,: 'COFOI.OGIES
V.2.1I
V.S.I!
WE.<\I\: '£QPOLOGIES
419
every scalar of modulus Jess than r, Hence [ff/(KI)-.JP/(K.) =
&l/(KI-K.) d ;::,: r. so that eWl)" number in .JtJ(K 1 ) is at least r
b'l'f:'ater than any number in :/if(K 2 ). The desil'ed conclusion follows
by placing c = inf /(K1)' Q.E.D.
2 DEFINITION, Let be a linear vector space, and let r be a
total8uhspace of 3;'. Then the r wpology of 3; is the topology obtained
hy taking as base all sets of the form
N(p: A, e) = (qll/(p)-/(q)1 < e, 1 e A),
where p < 3i, A is a finite subset of r, and e > O.
The terms r-open and r.cIosed subsets of 3;, r-contmuous maps,
etc. will refer to the r topology of 3i.
The following lemma is a com;equencc of Definition 2.
3 LEMMA. II r is a lolal Unear .pa.... o/lillror IUlIl'/ionals 011 I,
I is a 10000ily C1m""", li..ear topvlogical 8ptree in its r topology.
Note that I may already be a linear topological space, possessing
notions of open and closed subsets, continuous maps, etc. 'l'hc!!ie con-
cepts have to be distinguished from the eorresponding concepts in
the r topology. Thus, if I is a B-space, J: has a natural mctric topo-
logy defined by its norm. This topology is often rereInd to as the
8traJlg. or metric, topology. When reference is made to a c]osed subset
of I. or a continuous map of I, without qualification, it.is to be under-
stood that the topology in question is the strong topology.
The r topology of a linear space J: is related to the product space
topology of Definition 1.8.1. Let 3:: be a linear space over thefieldlT>,
and let r be a total subspa", of J:'. Let IT>, = IT> for each I £ r, and let
'P = P IT>f' Let the map T on :E to 'P be defined by
f'C
.". 11 COROLLARY.l! Kl K 2 aTe di8jDint dost"d, conr_ ex Sllhsrl.s of a
locally COl11'f.'.l' li11ear f.tJpologiral3pac 1:, and if K} is compact, lhe" some
nOn-:£ru continuous linear IUlIctiQnal on :E separates Kl and K 2 .
I CoROI.I.ARY. II K is a dosed <Ont"'... subset of a locally convc..
linear tnpalogirol spnC't', and p "K, then ...lJme mm-Ct"1"fJ continuuu-s linear
lunctional "parales K and p.
I3 COROLLARY. II p and q art' disli..ct points 01 a 10000lly collvex
lill( ar topological 8p(lf: .f, there is a cOllti11UOll.S linCllT fUliditmal f d£-
lined on 3: .ach t"al/(p) # I(q).
As a. last corollary we state a result which will have important
appli ations in later sections.
14 COROLLARY. Let a li1lear spa l! I be git'Ol two locally cont'ex
lopalogies T 1 and T.. II (J:, T 1 ) amI (I, T.) "aloe Ihe sa",e.-alilinIlO'" lill,ar
jallctiOl/Ols. thell a coo""... set is clased in (J:, t 1 );1 and only il it i8 cl"""d
in (J.T.).
PROOF. Let K hc a convex set closed in (J:, Tl) and let p f K
Theorem 10 )'ields a continuous linear functiona] I on (3::, Tt) and real
numbers c and t:, with E > 0, such that
T(x) = P I(x).
f,r
Since r is total, T is a one-to-one embedding of in tp, consequently
I may be regarded us a subset of 1Jl. It is then evident, from DefinitIOn
I! and Definition 1.8.1, that the r topology of 3i is identical with tile
relative topology of:£ as a subset of the product space IJI. In the next
sedlOn this remark will enable us to prove a number of interesting
theorems on tile r topolog)" of the linear spact' I.
'fhere are two particularly important instances of locally con,'cx
topologies defined hy total sets of hnear functional.. If J: is a B-space,
or, rllorc generally, any locally convex linear topological space, and
r = I* is the set of aU contmuous linear functionals on 3i (which
exist hy CoroUary 2.IS), then the l'topology is the 3i* topology, or
the U:falr topology. of 1'. A gem'tahzed sequence {xoJ will converge to ...
&l/(K) ;;;; c < e+e ,,;; 9i/(p).
Since I is also continuous On (I, TO)' the neighborhood {...il/(x)-f(p}j
< e} ofp in (:I:, T.) does not meet K. ThusK is dosed 111 (J:, TO)' Q.E.D.
3. Weak Topoloj;ies.
Dermitions and Fundamental Properties
1 DEFINlno>,:. If 3i is a linear veetot space, J:+ is the space of
aU linear functionals on 3i.
A linear subspace r of 3i+ is eaUed Iota! (cf. 11.2.6) if I(x) = 0 for
aU 1< r implies :E = o. The space r is often called a total space I
lallciiollal:r on :E.
420
v. CONVEX SETS AND WEAK TOPOLOGIES
V.3A
V.3.9
WEAK TOPOLOGIES
4.21
in the I* topology if and only if limo "'. = '" weakJy in the sense of
Definition II.3.25. On the other hand, if I is a subspaee of 'Jt, then
each element y. ID determines tbe linear functional f. on I defined by
f.("') = "'w), ",.]i,
and the subspace r = {f.ly. Y}!;; ,e is obviously total. The r to-
pology of I is often eaIled the '[J taparagy of::£. It is dear that a genera-
lized sequence {"'.} converges to '" in this topology if and only if
lim "'.W) = "'(y) for each y . W.
The most important case of this latter type of topology for a
space of functionals occurs when ID is 8 linear topological space and
I = W*. In this ease, what is known as the ID lopology of '[J* is ob-
tained.
The n>ader will have obsenped that in certain cases a number of
different topologies have bee" defined for the same space ::£. For in-
8tanee, if I is a B...pace. there is both a metric and an ::£* topology
for]i. If '[J is a B-spare. its conjugate spare::£ = '[J* has a metric, a '[J,
and a '[J** (or I*) topo10gy. In addition, various fragmentary topolo-
gical notions such as weak sequential compactness have already been
defined in Chapter II (cf. II.8.25).
The next few sections will investigate the relatIons between the
various topologies that have been defined.
4. LEMMA. The topology of a lacully corn'f!.r space iE is stronger
tlian tlie I* topology of I.
ij COROLLARY. The mrlric Inpolagy of a B-space I i. stronger than
its weak topology.
6 LEMMA. Let I be a linear space, and let r 1 wid r. be two loInl
subspares of r. If r, r 2 , lhen the r l lopulugy of iE is U'€t1ker than the
r 2 topology of ]i.
The proof is elementary, and is left to the reader. Lemma 8
has the following important converse.
\! _THEOREM. Let I be a linear spat:#', and let r be a Mal stWspa«
of if'. Then tlie li7lffi1' fundiotla18 an I which are continurnl$ in (he r
topology are precisely the ftmctiDncls in r.
The proof of Theorem II will be based on the following lemmn,
10 LEMMA. If g, fl' , . ., fn are any n+l lillear furlClionals on a
linror S'J1<I-"" I, and if f.("') = 0 fori = I, . . ., n. implie8 g(",} = 0, then
II is a linear romhitwlion of the f..
1'1<OOF. Consider the linear map T : I En, defined by
T{",) [1.(4 . . ., fn(X)]'
On the linear subspare T(I) of En, define the mnpping 'P by
'P[T(",)] = 'PlM"'), . . ., U"')] = g(x).
The map\" is well-defined. since T(",) = T(y) implies that T(",-y)=O,
so that g(",) = g(y). It is obvious that'P is a linear functional on the
subspaee T(I) of En. By 1I.3.n, it can be extended to a linear func-
tional 'Pt on En. By IV .3. 7, \"1 has the form
n
VJJYl' . . . Yn] = a.. Yt-
i l
Hen e
n
g("') = 2."'.1.(",),
;:_1
x.I.
7 COROLLARY. If I i. a B-spau. the Ilnpology of :£* i. weaker
than the .r.. topology of :£*.
The proofs of 4. 7 are c1ementary, and are left to the reader.
H LEMMA. Let I be a lillear 8pace, alld let r be a latal subspm'e of
.J:; . Theil Ihe r topology of ]i i. the u:eakesl topology in which every
jurldional in r is continuous.
Q.E.D.
PROO1i' OF "rHEOREM 9. Every functional in r is r -continuous,
by Lemma 8.
Conversely, let g # 0 be a linear functional on I which is r-con-
tinuous. There exists a r-neighborhood N(O; f., . . ., fn; E) which is
mapped hy g into the unit sphne of /1J. For f. r let )f = {x!f("')=O}.
and supposethat"'0.n 1 \' Then"'.. N(O; It, . . ., fn' E), and hence
Ig(x4»)1 < 1. Since (1 ""l.f;111i is R linear space, it ontains 1nJ: o for every
integn m. Hence mlg(",.)! = [g(mJ'.)! < I, from which we conclude
thatg('-.) = O. That is.g(x o ) = 0, whenever f,("'.) = Ofori = I, n., n.
It follows, from Lernmn 10, that g is a linear combination of the t..
Hence II e r. Q.E.D.
422
V. CONVEX SETS AND WEAK TOPOLOGIES
V.S.1I
V..u
""EAK TOPOI.OGlES
423
II COROLLARY. Let J be a linear functional all the linear 6pa('f' ,
a1ld let r be a lotal SUhspaff 01 £'. Then the 'oll"",in{5 s!<llelllents are
equimlNlt:
Ii) I is in r;
(ii) I ;s I'-ro..li.."o"s;
(iii) " = {"'I/("') O} ;s r -dosed.
PROOF. By Theorem 9, (i) is equivalent to (II). Clearly. (ii) im-
plies (iii); we now show that (iii) implies (i). Suppose that I oF 0, anrl
kt p £ 3i be such that I(p) oF o. By Theorem 2.10, there ex;,,--!s a non-
zero linear F-contmllQllS functional g, and a real constant 1:, such that
8ig( ,) c.lly Lemma 1.1I, g(t1,) = 0; i.e., 1("') = U implies g("')=O.
It follows from Lemma 10 that g =- oct for Some nOH-zero scalar IX. B)-.
Theorem 9, g is in r; thus f is in r. Q.E.D.
12 COROLURY. Let 3i be a linear va:lor spa«, and let T be a lotal
suhJrpaee of 3Z'. A lil/eIlr ."b8paee 'ID 01 I is T-rlosed il and only if lor '"
not ;n Ihere ""isla an I ;n T wilh I('V) = 0, I(a;) = 1.
PROOF. If VI is not T-closerl, Jet x E '[J' n \1}. where the closu... is
taken in the Ttopology. By contillUlty, if ,£ T, and I("J» = 0, then
I ('iI ) = O. and thus 1("') = n. Conversely, if ID is r-closcd and a: VI.
then, by Corollary 2.-12, there is a F-continuous to and a constant c
8nch that &el.(g) ::::: c, 10("') '* o. By Lemma 1.11, Io(ID) = 0; Ly
Theorem 9, 10 £ r. Pllt I = 10IMa;), and the corollaJy is proved. Q.E.D.
18 THEOREM. A ronvex su/mer of a locally com.." linear wpalagieul
spaN' is 3;3-c1fJSed il and only il it is closed.
PROOF. This resll]t fonows from Theorem 9 and Corollary 2.14.
Q.E.D.
14 COROLLARY. II I is a B"'-paee, and {a;.} is a Sf'qu""N' 01 ere-
mruts of , emu.'erging OJY:akly to :.t', tllnl Bome Mt}URllce of ctJIzvex cmu-
binatiuns 01 the c1nnen/3 "'. ccnr>nges to a: in tlw maric fop1logy.
PROOF. Let A = co :",.}. By the theorem just proved, A is closed
in the weak topology, hence x (; A. 'Ine corollar:r now follows readily
from Lemma 2.4.(h) and Lemma 1.6.6. Q.E.D.
15 THEOREM, Let T be a IUleUr muppirlg 01 a B-spaa ! illio a
lJ-3pace . Theu T is rotllinll914.Y with r sped to the mtlric to-pologies ill
3Z a1l<1 'D ;1 aad only it il is cml/itluo"s with '..pee! 10 the _uk lopalogies_
PROOF. Suppose that T is continuous with respect to the metric
topologies. Let N(O; yf,. .,1/:. e) be a neighborhood of 7.er.. in 11).
For ea h y <1cfine x by
",:(a:) = ynTa;).
Then Ix 1 ;;; [y ! .IT[, aod so x £ 3i . If '" d"(O; xi. .. ., ..:' e) then
I",; (a:) I < e. Hence ly;(Ta:) I < E, so that T"'EN(O; yf,.... y:, e).
Thf'l't>'fore, Tisweakly continuous.at the origin, andhenceatevery point.
. \d . ] * ""*
Conversely. :s:uppose that T is wen y contmuous, am Y E tJ
Thcn y* T is a linear functional on I which is * -continuous. Hence.. by
Throl'flIl 9, y* T IE 1* for y* £ 'ID*, so that tJ* T is continuous in the
n!C'tr]c topology for y* £ ID*. Then, by Theorem 11.2.7, T is continUOUS
ill the metric topology. Q.E.D.
4. Weal< Topologies.
Compactne8S ami. Reflexivity
The following two 8<'etions arc d,,-otcd to the .tully of the 3;
topology for the conjugate 'pa('t" I* of a B-8paee. The next basic lem-
ma is nothing more than a simple consequence of TyehonofCs theorem
(1.8.5).
1 LF:MMA. Lei I be a linear spaee, and let c be a real mlued lunct;on
"It 1". Then the. set
K = {flf E I+, I/(a:)1 e(",j)
is COJIIIJocl in Ihe ! wpology ul I'.
PROOF. For each 3' < I, let 1(3') be the set of s a1a" "- such that
1"'[ ;;;e(a:), and let l=l'"f-/(a'). Ikfioe the map 1::K--+I by 1:(/)
= l'"y.f("'). Let1; have the I topology, K the rc1ative topology as a
subset ofI-I-, and 1 the produ('t topology. Then,. as is evident from the
defjnitions and the discussion rcHawing Lemma 3.8 T is a homeo-
morphism. By Theorem 1.8.5, I is compact. Hen(Oe. by Lemma
1.5.7(a), it remains to show that 1:K is a c\used subset of 1.
It is easy to \'Crif)" that 1:K is the set of all g < 1 which lie in all the
sets A(""y) = {glpr.+vg=pr,g+pr.g}, and ill all t11e sets B(""",)
424
V. CONVEX SETS AND WEAK TOPOLOGIES
V,4.2
V.4.6
WEAK TOPOLOGIES
425
= {gJo:pr:tg = prCl:tg}. Since eacb projection is 11 contmuous map eacl1
a the sets A(""y) and B(ex, x) is elooed Hence..-K=n rA ( ", y)
. :r."E'
n n..<>,.d B(ex, "') is also closed. Q.E.D.
2 THEOREM. (Alaoglu) Th£ cwsed uni! sph£re in tlw conjugale
space 1:* al the B-spact' 1: is compact ill tlw 1: topol"lfll 01 30*.
PROOF. By Definition II.<!.5, the unit sphere in :1:* is the set
fill .1:+, If("')1 Ixl}, and thus the theorem follows from Lemma 1.
Q.E.D.
X**. and constants rand B, C > 0, such that !fif(S1) c, !fi/{"'**)
2:; c+.e. By Theorenl 3.9, there is an element a;* tIE 1* such that
1("'"*) = "'** "'* for x**. "'"*. Since ,,(S) S1' it follows that
!fix*{",) c for",. S But",. S implies ax. 8 for 1"1 = I, hence
Ix*(x)1 c for x. S. Thus, Ix*1 c, and Ix**(",*)I clx**1 ,;: c,
contradicting f?.i'a.:**(a.:*) c+£. Therefore every a:** S.* is in 8l"
Q.E.D.
sup 1';'("'*11 = /"'1
III:-I£A
6 COROLl.ARY. If " is tlw natural emberlding uf a B-spacc I into
I**, thai ,,3; is I*.<h-nse in I**.
PROOF. The I*-c1osure of ,,(I) is a subspaee of I**, which, by
Theorem 5, contains the unit sphere of if**. It follows immediately
that it contains every pomt in I**. Q.E.D.
Theorems '2 and 5 lead to an important result on reflexive spaces.
7 THEOREM. A B-ap«<:e is refl£.rive if and only if its closrd unit
sphae is cO'''pacl in the u...ak tapology.
PROOF. Let I be " reflexive B-8pace, and let " be the natural
embedding of I onto 1".. Then i( and ",-1 are isometries, .and" maps
t1le c100ed unit sphere 8 of 1: onto the closed unit sphere S** of J:**.
It is dear from the definitions of the two topologie8 that" is a homeo-
morphism between S with it81:* topology, and S** with its I* topo-
logy. Theorem 2 now establishes that 8 is weakly compact.
Conversely, let the closed unit sphere 8 of I be weakly compact.
Since" is II homeomorphism between Sand ,,(S) with the "'* topology
on both Sand ,,(S), it follows that ,,(8) is compact. By Lemma 1.5,7,
,,(8) is closed in the 1* topology. By Theorem 5, ,,(S) is dense in
S*'. It follows that ,,(8) = S**. Thus ,,(I) = 1**, and I is reflexive.
Q.E.D.
8 COR01.LARY. II 1: is a B-spoce, a subset of :1:* is compact in the
I lopowgy if and only if il i. closed in the 1: tbpology, and bounded in the
f'lIRIric topology.
4 COR01.LARy.If J: fS a B-.pace, tJu>n if is ismnetrirolly isomorphic
to a closed 8Ubspaa; of the spoce C(A) of contilll"'", fundion. on 80me
compact H au.dvrll space A.
PROOF. Let A be the dosed unit sphere of I*, Then, by Tbeorem
2, A is It compact Hausdorff space in its I topology. Let " be the
natural embedding of 1: into I**. Then, by Lemma 8.8, for each
:JJ E I the U"Striction of xx = fi to A is .a continuous function On A.
Moreover.
by II.8.I5. Thus" detennines an isometric isomorphism of I with a
subspace 1: 1 of C(A). Since I is complete, I, is complete and therefore
a closed ,ubset of C(A). Q.E.D.
Since the natural embedding x : I -+ 1:** is an isometry, it maps
metrically dooed subsets of 1: onto metrically closed subsets of :1:**.
However, ifthc metric topology of 1:** is replaced by its 1:* topolog},
tbe situation is quite different, QS the next theorem shows.
5 THEOREM. (Goldstine) Lei" be tlw nahtral cmbeddillg of the
B-spacc 1: inlo its second conjugate space I** and let 8, 8** be the closed
unit sphrres in I, l*., resp€dively. Th n "S is 1:*-d£nse in S..,
PROOF. Let 8, be the 1:* closure of ,,(S). Smce S** is J:*-c1osed
(Theorem 2), S1!;;S**. Also S1 is conyex, by Throrem 2.1. It will be
shown that 8 1 = S.*. If there is an element a:'.. £. S** but not in S
I'
then, by Theorem 2.10, there eXist an *-conbnuous functionalj on
8 COROLLARY. A bounded _akly closnl sr! in a reflexive B-spoce
is ",eakEy compact. CaJlVi!Tsely, thispropertych{jraclerizeBreflexivespal'es.
s. Weak Topologies.
Metrizabilily. Uobouoded Sets
This ion continues the discussiOn of the topolog ' of the
conjugate space 1* of a B-space.
426
v. CONVEX SJ::TS AND WEAK TOPOLOGIES
V,5.t
V.5.S
\VF.AK TOPOr.QGIF..8
427
I THEOREM. If i is a B-spttee, then the I topology of the d08t'd
unit sphere S* of 1* is a metric topology if and only if I is separahlR.
PROOF. If I is separable, let {x n } be a countable dense subset of
I, and define
I l(x*-y.)"'.1
O ( x* Y * ) - -
- ,. - n7:, 2' I +I(x*-Y*)"'nl
It is easy to verify tlmt the topology of S* defined by this metric is
weaker than the I topology of S*. Hence, by Theorem 4,2 and Lemma
1.5.8, the metrie topology for S' defined by (! is the same as the I
topology of S*.
Com-ersely, if the I topology of S* is a metric topology. there is
a denumerable sequence {U:} of I-neighborhoods of the origin 0 of
1*, such that n:., U: = {OJ. We may suppose that
U: = {x*lx' E S*, 'x*(x)1 < En' X E An},
where Ayj is a fillite subset of I, and En> O. Let A = U::... 1 An; if
a:*(A) = 0 1 then a;-* £" U: for each n, and consequently a;* = o. Let
= sp (A). It follows from Lemma 11.1.17 that I, is separable, and
from Corollary II.S.t8 that 1:, = 1:. Q.E.D.
2 THEOREM. If I is a B- «, t1u:a the "'* "'poIogg of t1u: c/osro
unil sphrre of '" is a 11UJ/ric topology if and only if 1'* is separable.
PROOF. Let 1* he separable. and let >< : I --7 "'** be the natural
embedding. By Theorem I, the !* topology of the dosed unit sphere
S** ofI** is a metric topology. If Sis the closed unit sphere in!, the
mapping >< : S --7 S** is a homeomorphism of Sand >«S) in their I*
topologies. It follows from Lemma 1,6.4 that the "'* topology of S is a
metric topology.
Conver8ely, let the 1* topology of S be a metric topology. Then
there exists a sequence {Un} of I*-neighborhoods ofthc origin 0 of:E.
such t]lat every I*-neighborhood of 0 contains some neighborhood
U., Wc may suppose that
U. = {xix c S. Ix*(x)1 < En' x* < A:},
where A: is a finite subset of 3::* and C n > O.
Let A* = U:., A:, and let X = sp (A*). By Lemma II.1.17,
! is separable, and it remains to show that 1* = t.
.,,* ,,* h *"**"* Lt
If L1. /:':\'1' we can C oosc y ".:..... Y ,/a-t. C
<I = inf Iy*-xn
iEX
Then d,> 0, and, by 11.3.12 , there is an x** £ .£** with Ix**1 = lid
such tlmt xOO(Ii) = 0, x**(V*) = 1. The set V = {X!XES, Iv*("'>!
< di2} is an 1:*-n('jghborhood of O and hence V Un for some n_
Since d;c** £ S**. there is. by Theorem 4.5,. an d:] IE S such that
iX*(X,)I Itlx**(.r*)-x*(x,jl < "n- x* c A:,
d
,d-v*(x,)1 = [ll...**(y*)-y*(x,)1 <'2 .
Thus
Iv"(x,1I :> df\!;
IX*(.rl} < £"'
.1:* £. A:.
But this means that Xl £ Un. and .xl ; V. a contradiction which proves
that Xi = ;t*. Q.E.D.
The remainmg theorems in this secti.on concern convex sets whICh
are not necessarily bounded. \Ve may remark that the analogues for
the 1* topology of I of Statements 3-6 are all trivial consequenITs of
Theorem 3.13.
11 D£FI"ITIOX. Let I he R B-spaCt'. The bOlmJed I wpology. or
BX topology, for I* is the strongest topology which roincide8 with the
X topology on each set as* = {x*lx* £ X*, Ix*l;£ a}. Thus, a set
U C 1* is BX-open if and only il'UnaS* isardativcly I-open suhset
of as* for every a ;,; 0, and a set K X* is BX-c1osed if amI only if
KnaS* is I-dosed for every a ;,; O.
4 LEMMA. Let .r be a B-spaC<'. A fUllllnmetllClI system of neigh-
barh,)()ils oflhe origin 'or the bOlullkd I topology of 1* consisls of the sets
(x*I!.r*{x>! <. I, xC AI, where A = {x,} is a seq,m,U' of elemel/ts of I
(:(mterging to zero.
PROOF. Let S* be thc closed unit sphere of 3:'*. If A is R sequence
of elcmcnts converging to zero, t],en {x*;:x*(x) I < 1, ",cA}n oS*
= {, *! x*(x)1 <. I, ,r c A,}n as*, wbere A, j. the fmite .et of ele-
ments x < A of norm Ixl > tia. Thus, {x*I,.r*(J'): < I, .I < AI n oSo
is a relath.'"ely i-open su t of l1S*.
In proving the converse assertion of the lemma, tbe notation
AO = {x*1 '.:r*(x) I ;£ I, x < A} for snusets A of 3: is mnvenient. Let
j
428
Y. CONVEX SE'l'S AND ' EAK TOPOLOGIES
V.5.5
V.5.7
WEAK TOPOLOGIES
429
l.' be a BX-neighborhood of the origin. Then, by definition of the
BX topology, there is a finite set A I !:;:{ such that A nS*!:; U.
Suppose that for some integer.. we have defined a finite set A. !:; 30
such that A n IIS*!:; U. It wi1l be slmwn that there is a finite set of
elements B.!:;:£ such that IB.I;O;: 1/.. and such that (A. U B.).
n(n+I)S*i:;U.
If this is not the case, it is clear that the famIly of sets of the form
(An uB)"n (n+l)S*n U' where B i8 finite and IBI < 1/", has the
finite intersection property. Since V' is BX-closed. aU tILese sets are
;{-closed, and, since (n+ I )S* is I-compaet, by Tbeorem 4.2, it fol-
lows from 1.5.6 that there exists anx* e (I1+I)S*n U'n A such that
Ix*(x>1 ;0;: I for every x e:£ with 1"'1 < I/n. Thus 1"'*1 < n, so that
x* enS*n A n U', eontradieting the faet that nS*n A C U.
Defining A n +1 = An U Bnt we have established an inductive con..
struction of a sequence of finite sets AIJ. C I such that A n 1'IS* U,
and such that an)' enumeration of A = U: 1 Att is a sequence of cI('-
ment8 of;{ tending to zero. Hence {"'*I"'* <3;*, Ix*(x)1 < 1, "'. A} ..
a set of the desired fonn which is contained in U. Q.E.D.
The reader will bave no difficulty in appl}'ing Lemma 3 to pron
the next corollary.
IV.6.3. there is a sequence [iXo' CXIt . . .J with I:.n 1((,,1 < 00 such that
h( ) = I::', ",, , for = [ " .' . . .J . co' (cf. IV.II!.7). 'Chus
oc
6(",*) = I",.,*("';) ="'*(Io<,.r,),
i=l ,=1
x* £: .1*.
16(x*)1 ,;; 1 if Ix*("'.l1 < 1,
i = 1., 2 1 .... .
That is, 8 has the form 8(.7'*) = a::*(.x)t where:r= I;o=l i i € 1- HencE'.
by Theorem 3.9, 6 is I-continuous. Q.E.D.
7 THEOREM (Krein.Smu/ian j A co'uJI'''' set in IO is I-closed if
and anly if its intn-section with f1'I'ry posilive multIple of the clPMd "nit
spher of :£* is I. closed,
PROOF. ThIS follows from the preceding theorem and CoroUar)
2.14. Q.E.D.
8 COROLLARY. If 30 is a B-spaee, a li1lear .uwpacc Il) G; 3::* is
I-clOSNI if and only if thRre e",is/,!; an I-c1osnl hounthd subset K of ;{*
confaining a non.mid metrically rYpen subset of Il).
PROOF. If Il) is I-closed, the closed unit sphere S* of I* is I-
closed, and we may take K = Il)n S*.
Conversely, let K be a bounded I-closed 8ubset of 1lJ, and
K IlJn S*(p*, <'I}. If a> 0, the mapping x* --+ a{"'*-p*)/lI is an
.homeomorphism of I* with itself. Thus a(K-p*)/lI is I-closed.
Since IlJn lIS* G;K-p*. '[In as. i:; a(K-p*}/lI. and benee IlJn as*
= as*n a(K-p*)/lI is 3O-closed. The desired conclusion follows from
Theorem 7. Q.E.D.
9 COROLLARY. Let I be a E-sp"'" and letK be a conw", I-do.ed
subset vf I*. Let J be lhe linear Bp"Ct! opa.",ed by K. Theil Il) is closed in
1he melTic topology of I*, if and @!y if it is I-closed.
PROOF. If Il) is I-closed. then it is closed m the metric topolog}'
by Corollanes 3.5 and 3,7.
Com-elSel)', let Il) be closed in the metric topology. We sbaU
assume that I is real, leaving the details of the complex case to the
reader. Let S* be the closed unit sphere in I*, and K. = Kn ..S*.
Let K = co(K U -K). and K. = eo{K. UK.). Then K. is I-
closed bv Lemmas 2.5 and 4.3; hence. by Corollaries 3.5 and 3.7, Kn
is cI in the metric topolugy. ow each y£'g) can be written as
Y = a 61'.- l a.z- , where X , - K., Rnd all the ai are positive.
L,=. I 4,=1'. . I
5 COROLLARY. Let I he a B-Bpace. Theil :£*, with ils bounded ;{
topology, i8 a locally r01UV'.x linear topological 8pace.
Tbe next tbeorem gi'TS a fundamental property of tI,e BX topo-
logy.
6 1'UEOREM. A jUliclilJlwl () un 1* is cont.inuous in the X topology
if and only if it i8 oolltirn'uu8 in the bounded 3; topology.
PROOF. By definition the EX topology is stronger than the :\'
topology so that :an -continuous functional is BX -continuous. Con-
versely, let the linear functional 8 on I* be continuous in the BX
topology. Theil there i a sequence {.rih with limi:4:rJ 3:. = 0 such t]18t
Let T: :r* [.x*(x i )] map J'. into tIle B- pace CO' Since :c*(:ri) = o.
i I, 2, . ... implies (i(x*) = 0, the functional h(T",*) 6(",*) on
T£* is well-defined. It is clearly eontmuollS, and by II.3.ll can be c"-
tended to the B-spaee c = C(S). where S {O, 1,'''.11 ;;;; 1). Tbus, by
-ISO
v. COXVEX SETS _\XD \\'E.1.K TO}>OLOGIES
V.6.1
V.6.1
""EAK TOPOLOGIES
-131
It follows that y aX with a = I l a.; since 0 E K. aK k bK if
o a b; hence any clement y £ ID is in nK fur all sufficiently large
integers n. Smce K = U:=t K", it follows that ID -= U::=-] nK 1I . SJnce:
) is a closed subspace ofI*, itis complcte by Lemma 1.6.7. Hence, by
the Haire category tbro1"f'fD, 1.0.9. some set Kfl contains a non-vOId
metrically open subset of t). Our result now follows from Corollary R.
Q.E.D.
each elem('nt of EfJ can be extended to a linear functional on aU of I.
Taking one such extension for each element of Ho we get a denumern-
ble subset H of I..
Since A is bounded, by a diagonal profi we may extract a sub-
sequence {Y..} of {x.} such thatlim..-+«> x* Ym exists for each x*. H. B!
condition (ii) there i!'i a point Yo E. I such that every weak neighbor-
hood of Yo contains at least one Vm' Since {Y..} C .'£. and 3':. is x*-elosed,
it follow8 that Yo' 3':.. It is c1car that
6. Weak Topologie..
Weak Compadnel3s
X*Yn = lim :lJ.Ym'
m-+O>
x*EH,
We have aln-ady introduced and empJoyed the eonC<'pts of weak
sequential rompactness (II.3.25) and eompactu.... in the x* (or weak)
topology. There is at least one other type of weak compactness that is
Q('ca.:sionaUy of use. It is R remarkable and important fact that these
three concepts are equivalent.
1 THEOREM. (Eberlein.Smaliall) Let A be a ."bset of a B-space
.'£. Tlu:n the follUU!ing stolemenls art' equi''lllmt:
(i) A is ZWQkly Bet}ut:lltially cmnparl - i.e., any sequen e in A
/tas a sllbsrquence which crnnoerges u' akly tu an element vI I;
(ii) nv:ry countably infinite slI.b.¥t!t vI A lids a tL'f'o.k limit point itt
l-i.e., a point Burh that t"l't:ry Wl'llk neighhorhood t..'fJntains an dl''lnl'nt itl
the infinite subset;
(iii) Ihe elosure of A iu the .\:* tap%w.} is I*-culi/pact.
PROOF. \Ve observe first that e.ach of the three conditions Implies
that A is bounded in the mctric topology, for x*{A) is a bounded sct of
scalars for each x* 3::* and we can apply II.IJ.20. It is reudily seen
that (iii) implies (ii). The othcr implications wc desire are decidedly
non-trivial; we will complete the proof hy showing flrsUhat (Ii)implies
(i), and then that (i) implics (iii).
: Proof that condition (ii) implies (i). Let {x,,} b,' an arhitrary se.
quence in A and let Xo = sp {x.}, so that, by Lomma II.1.5, it, is sep-
arable. By Thcorem 5.1 and CAJrollary 4.2, the 1Imt SIJhere 111 x; is
\;;eparable in the :Ii) tQPolog)". Since ! is the union of a scquence of
.multlple!:; of its unit sphere,. X is s('parable in t]1C Io topology. Let Ho
be a denumerable dense set in :. Clearly Ho is a total !'>et on f() and
and it remains to show that this is true for every xi< I*. If this is not
true, there exists an a7ri f: *, an t > 0, and a subsequence {Ym,,}
such that
( I iX;lY...-Yo)1 > €, k = 1,2, . . ..
Applying condition (ii) to (YmJ we ohtain a point y . X such that
every weak neighborhood of y contains at least one Ym. . Just as above
we show that y f; 10 and
(**)
*' I . *
x Yo = nnm y,,.,,,
k_w
a:*£H.
Hence x* Yo = .1:* y for all it* E" H, and since H i total on Io, Yo = y .
But this fact and (**) contradict (.). Hence the arbitrary scquence
{ain} in A contains a weakly convergt"nt subsequence {Ym}, and so A
1S weakly sequcntially compact.
Proof llult coudition (i) implies (iii). Let A bc the closurc of A in
the :£* t-Opolog)' of I; we must show that (i) implies that A is I*-
compact. Since the natural embeddmg ,,::£ -+ 3::** is a hume -
morphism between I and ,,(I) in their I* topologies, wc have "JA)
= ,,(A) n ,,(I), and moreover A is I*-compact if and only if ,,(AI i.
I*-compact. Sincc..4 is bounded, by Corollary 4.3, ,,(..4) is x*-compact
if and only if ,,(..4) is an I*-dosed subset of 3:**. Since ,,(A) ,,(.4 j ,
the bar denoting closure in the I* topolugy. it will suffice to show that
"IA) ,,(A), but this will be true by virtue of ,,(A) = ,,(A) n ,,(J)
on.... it is shown that ,,(A) ,,(x). Let x** . .'£** be an element in tlte
I*-closure of ,,(A); we wIll show that x*.. "II)- This amonnts to
. ." hht *'** * * ..
showing that there l"XlSts an .r of: sue t a X X = x .r :r E:..\; .
432
v. COSVEX SETS AND WF;.AI{ TOPOLOGIES
V.6.1
V.6.2
WEAK TOPOLOGIES
433
First, however, we prove the weaker assertion: if {or:. . . .J' x:} is an
arbitrary finite subset of 1.. then there exists a z € A such that
oX"'. x: = x:z, i = 1, . . ., n. To see this, let m be an arbitrary integer;
since .x** is in the I*-closure of x(A), there is an element Zm E A such
that
sequence of {x n } which converges weakly to an clement x £ A. To
avoid changing notation we suppose (without loss of generality) that
the entire sequence {xnJ converges weakly tox. Now from (bl and (el
we have
Ix:(z",I-x**(xill < 11 m ,
i = I,.. .,71.
Iy:(xnll < E/4,
'11 = I, ....n.-I,
Since A is weakly sequentially compact, a subsequence uf {z..} w;n
converge weakly to an element z which is certainly in A, since the se-
quential closure of A is contained in A, and hence .x (z) = :r..(It' ),
i = I, _._,71..
The remainder of the proof is concerned with showing that
a:** £ ,,(II. By Corollary 8.11 this is true if and only if the subspace
£I of I* defined by IU = {a:* £ I*lx** ",* = O} is I-closed. If S* is the
closed miit sphere of 1:*, then, by Corollary 5.8, £I is I-closed if
£In s* is I-dosed. Thus we must show that if y is in the I-closure
of £In S*, then y .Dn S*. To do this, we choose an arbitrary
E > 0 and will construct three sequences {zn} .iI, {a: n } A, and
{V:} £In S*, in the following manner: From the remark in the pre-
ceding paragTaph there exists a z,..iI such that y (zll = "'**(Y I.
Since 2} is in the :I*-closure of A, there exists an .xl £ A such that
!yri("'l}-yri(",11 < cf4. Since yri is in the 1:-elosure of £In S*, there
exists a y £ £In s* such that IY ("'l)-yZ(a:ll' < £/4.
By induction, if elements with subscripts less than 'II have been
chosen, we select z" .A, lEft If At and y: £ On S* in such a way that
(al y':(zn) = x**(y:1 = 0, m = 0, . . ..11-1;
(bl jy':(a:n)-y':(z.11 < _/4, m = 0,...,11-1;
(c) Iy:("',) -y Ia:.J1 < £/4, i = 1, .. ,.11.
In this way we construct three sequences. From the construction we
have
(dl Iy;:' ;;;; 1, In = 1,2, . . .;
(e) y':(znl = O. m = 1,2, . . ..11-1.
Let '" = 0 in (a) and (b) and combine with (cl to get
(fl Ix"(Y I-Y:("',11 < Ell!, i = I, . . ., 11.
Since {"'.} A and A is weakly sequentially compact, there is a sub-
and hence it follows that
(gl Iv;:("'11 ;;;; £/4, In = 1,2, . . ..
By Corollary 3.14, t1lt re is a convex combmation UJ = ! =1 a,x,_
with a, 0, If-, a, = 1. such that I",-wl < '/4. In If) Ict 11 = N
so that
(hI 1"'**(vril-y1:{w)1 ;;;; If l a,lx'*(yZI-y (a:,11 < Ei2.
It follows that
Ix**(yrill Ix**(yril-V:(wll+lyZ(wl-yZ("'II+I ("'}I.
But the first term is at most Ell! by (h), the second less than E,'.J. by
{dl and the fact that Iw-"'I < '/4, and by (gl thc final term is domi-
nated by £/4. Since e was chooen arbitrarily it follows that
a:**(yri) = O.
Hence yri .IU; since S* is I-closed, yri £ £In S*. This shows that £I
is I-closed, so that x** £ ,,(I) and the proof of thc theorem is com-
plete. Q.E.D.
2 THEOREM. (Smulia1l1 A """va subSi'! K of a B-space I is
weakly campact if and only il "'-""Y ikcrl!llsi'lg sequence of ..on-void
closed co"",,'" subsets of K has a .w,,-emply i1llLTsec!icm.
PROOF. The necessity of the condition is immediate from 1.5.6.
For the sufficiency, we obseNe that the condition implies that K is
bounded. For otherwise, there exists an "'t E I* such that ",:{K) is nn
unbounded convex set of scalars, and hence there exists an x* IE 1*
such that ",*(KI contains a segment [1\1, ct:J). If Kn = {'" E Klx* or
;<:: N +1I}, then the sequence {Kn} violates the assumed condition.
Further the condition implies thatK is d for if &t n oTO' Lr. n EK,
wesetKn = Kn co{x ,IU .Tn+l'" .}. Clearly {x } = n:-'=l cofxn, ,xn+l,....}'
so the condition implies that :ro K.
To prove thatK is weakly compact take an arbitrar)' sequence {.r n}
434
\T. CONVEX SETS AND WEAK TOPOLOGtES
V.6.3
V.6,4
'WEAK TOPOLOGIES
485
and proceed as in the first part of the proof of the preceding theo-
rem to construct a subsequence f.Ym} of {xn} such that lim"._", x.Ym
exists foreachx. in theselH of that proof, LetKm = cO{ Ym, Ymw" .}
andletyCJ bea.n arbitrary point in n :"rKm" Foreacha:" 1*, we have
;X.Yo = lim x.Ym.
a;.EH.
PROOF. Lel A be a weakl)' compact subset of the B.spacc I.
Since co rA) is :f*-c1osed by Theorem 3.13, it follows from Theorem 1
that it suffices to 8how that corA) is weakly sequentially compact.
Let {Pn} be a sequence of points in co(A); then Pn is a convex combina.
tion of a finite set Bn of points of A. Let Bo = U:: I Bn, and let
10 = sp (B.); by 11.1,5, I. is separable. Let A" = A:£o; by Theorem
3.13 and I.5.7(a). A. is weakly compact. Since {Pn} co(A,,) the
theorem will he prm'ed if we show ro(A,,) is weakly compact.
By Theorem I, A. is weakly sequentially compact; by Theorem
11.3.20 there exists a constant K with ,Au I K. Further, in the rela-
tive I* topology A. is a compact Hausdorff space. Let C(A,,) be lhe
space of continuous functions on Au, and C.(An) the conjugate space
of C(A.), so from Theorem IV.6.B, C.(A.) is isometrically isomorphic
to the space of all regular measures on A". Let S* be the closed unit
sphere of C.(A.).
Define a linear map W : C*(A.) --? I by
w{f*) = f a,ut*(da),
A.
where f* < C.(Ao), aod 1-'1* is the regumr measure coll<'SpOnding to
f*. Since the set Ao is separable, and since lal ..;; K for a < A. this inte-
gral is defined (cf. III.6.9.). Define rx* for x*. iI:* as the restriction of
the linear functional x* to A". Then. by 3.8, T.x*<C(A o )' Moreover,
it is seen from the definition of W that .x*'I4. = f*T3)* for f*. C*(A.)
andx. E I., Hence, iF J is an arbitrary finite subset of 1*, V' maps the
C(A)-neighborhood N(f*; rJ, E) of f* into the I*-neighborhood
N(wf*; J, E) of '14* (cf. Definition 3.I}. Thus W : C*(A.) X is con-
tinuous if COlAo) is given its C(Ao) topology, and 3: its I* topology,
By Lemma 1.5, the set \O(S*) is convex; and by Theorem 4.2 and Lem-
nud.5.7(h), this set is I*-compact. If we put J:(g) 00 g(a) for a< A"
and g € C(A o )' then it is easily Seen that 'l'1f:) = a and hence w(S*)
;J A". Since W(S*) is closed in the metric topology by Lemma 1.5.7(c)
and Lemma 3.4, it follows that \O(S*);J co (A.). By Theorem 3.13 and
Lemma 1.5.7(a), co (A,,) is weakly compact. Q.E.D.
It should be noted that the analogue of Theorem 4 for :£-compact
subsets of ;E* follows trivially from Corollary 4.3.
'"
x. Yo € n ;r*(K".).
m-I
This fact readily imp];es that
m_w
To prove that this is true for all 3)* € 1* we proceed as in the proof of
the first part of Theorem I, replacing condition (ii) of that theorem
with Our present hypothesis. We thus conclude that K is weakl)' se.
quentially compact, but since K is a closed convex set and therefore
(3.18) :£*-closed, the preceding theorem applies to 8how that K is
;E*-compact. Q.E.D.
3 THEOREM. The ruak topology of a weaJdy compac! ...bsd A of a
stparoole B-spat:e is a mrlric topoWgy.
PnoOF. Suppose that :E = sp {x" .x._ . . .}. Construct H I* as
in the proof of Theorem 1. Let H = {x:}. The metric
'" I I x*(x- y)1
e(3), y) = ! - "
n_1 2 n I +lx:(m-y)1
defin... a topology for A which is weaker than the I* topology of A.
Hence, hy 1.5,8 these two topologies are the same on the set A. Q.E.D.
It should be noted that the analogue of Theorem 3 for the I
topology of I* follows trivially from CoroBary 4.3 and Theorem 5.1.
The analogue of Theorem 1 for the :£ topology of ;E* is not true. While
it follows immediately from Theorem 4.8 that an :£-sequcntially com-
pact subsct of I* has an iI:-compact 3:-closure, a subset of ;E* can be
I-compact without bemg I-sequentially compact. A method for Con-
structing an example of this phenomenon is given in Exercise 7 .82
As an application of Theorem I, we prove:
4 THEOREM. (Krein-Smu!ian) The d..cd co",,,,,,, hull of a U'Nlkly
compact su1net of a B-.pace is i!$elf u:ealdy compact.
486
V. CONVEX SETS A'N'D WEAK TOPOLOGIES
V.7.1
V.7.15
EX1<RClSES
4037
7. Exerrises
1 Let I be a linear vector space. Show that .!+ is a total space
of linear functionals on I.
2 If I is an infinite dimensional B-spacc then I+ *- J:*.
3 Let I be a linear topological space. Then J: bas a non--zero
continuous linear functional if a.nd only if tbe origin is interior to
some convex proper subset of I.
4 If a convex set in a linear topological space has an interior
point, it has the same interior as its closure.
5 Let F be a total set of linear functionals on the space I. Show
that if J: contains a non-void F-open bounded (11.1.7) set. then J:
must be finite dimensional.
6 Let I be a B-1!pace, and J: 1 a sub"pace of I. Show that the
J:r topology of I. is the Same as the relative 1* topology of I..
7 Let a: be a linear space. and F a total subspace of a:+. Show
that a set A f; a: is r-bounded if and only if I{A) is a bounded set of
scalars for each I E F.
8 Let 1 be a B-space. Show that a subset of 1 is I..bounded if
and only if it ,s metrically bounded, and tha a subset of 1* is 1-
bounded if and only if it is metrically bounded,
9 Show tlmt the weak and the metric topologies of the unit
sphere of a normed sp e .are the same if a.nd only if the space is finite
dimensional.
10 Let 1 be a linear space. and let FI and r. be two total sub-
spBCf'S of 1+. Show that if F, and F. determine the same topology
for 1, then F, = F..
11 Prove 11.3.28, 11.8.29, and 11.8.24 using Theorems 4.8 and 6.1.
12 Show that a B-space is separable if and only if it is isomet-
rically isomorphic to a closed subspace of C(S), where S is a compact
metric space.
18 Show that there eXIsts a contmuous mappmg of the Cantor
perfect set onto an W'bitrary compact metric space S. (Hint. Construct
a covering of S = U :1 C; by a sequence of closed sets C; such that
c;= C;:t UC;i!.t)i and such that the diameter of C;-+O as t1-? oc.
14 Show that a B-space is separable if and only if it is iso-
metrically isomorphic to a closed subspace of C( P), where P is the
Cantor perfect set.
15 If I is a separable linear topological space and A is an I-
compact sub8et of if., then the I-topology of A i. a metric topology.
16 If J: i8 a separable B-space, a convex subset A of if* is I-
closed if and only if "': £ A, and lim "':{.x) = ",*(x), .x £ 1, imply
A. n_
17 If S is a normal space and C(S) is separable, then. is a com-
pact metric space, and conversely.
18 If S is a normal space, S is homeomorphic to a subset of the
unit sphere of the conjugate of C(S) with the C(S) topology.
19 Every normal space S is homeomorphic to a dense subset Sl
of a compact Hausdorff 8pace C 1 , 8uch that every bonnded contiuuous
function on 8 1 has a unique extension to a continuous function on C t "
20 If I is a B-space, then a convex set K f; 1 i8 weakly closed
if and only if its inten;eetion with every bounded weakly closed set is
weakly closed.
21 If S is a compact Hausdorff space, and {In} is a sequence of
continuous functions on S snch that sup Ilnl < CO and In{s) I{s)
for each 8 £ S,. and J is continuous, then some sequence of convex
combinations of the In converges uniformly to I.
22 Let 1 be a B-space, and A f; I. If every separable sub.pace
of I intersects A in a weakly compact 8et, then the weak closure of A
is weakly compact.
28 Show that every neighborhood N of the identity of a linear
topological space contains a neighborhood M such that aM f; M for
lal :S; 1.
24 Show that if the linear space I is finite dimensional, K f; it
is convex, and 'P K, some functional on if separates K and 'P.
25 Find a convex set K and a point 'P K in a linear space such
that no non-zero functional separates K and 'P. (Hint. Let I be a
space with a denumerable Hamel basis {"',J, and consider the set K
of vectors of the form .I7-1 aix, with afl > 0.)
26 Find a convex set K with an internal point aud a point
P f K in a B-space such that no non-zero continuous functional sepa-
rates K and 'P'
27 Every infinite dimensional B-spa.ce is the union of two dis-
joint dense convex subsets
488
Va CONVEX SETS AND WEAK TOPOLOGIES
V.7.28
V.7.41
EX".l'JiE1I4AL FOINTS
489
28 Find two c10sed subsets A, and A. of a topological group
such that At+A. is not closed.
29 Find two closed convex sets At> AJ: in a linear topological
space such that coCA, UA.) #- co (A, UA.), and two sets B l , B. such
that CO (BI +B.) #- co( B,) + co (B.).
80 A linear homeomorphic mapping of a locally convex 8poce
onto some normed space exists if and only if some open set of the
locally convex space i bounded.
31 If K is a conVeX subset of alioear topological space, and thc
origin is an internal point of K, show that the support function of R
i!! continuous if and only if the origin is an interior point of K.
82 Show that B compact space may contain a sequence having
no convergent subsequence.
88 Show that if a subset of the conjugate :£* of a B-space :£ is
I-sequentially compact, its 1-dosure is :£-.,ompact. but that the con-
verse is not necessarily true.
34 If:£ is a linear space and r a total subspace of if'. then the
r-topology of a: is a mctric topology if and only if r has a countable
H1tlnel basis.
85 If the weak topology of the umt sphere of a B-space is a
metric topology. 1* contains a countable total set.
86 If 3:: is reflexive, and :£* contains a countable total set, :£* IS
separab1e.
87 Let S be the unit 8phere S = {xllxl < I} of the F-space
L.(O, I) where 0 < p < I. The norm in this space is given by the
equation 1"'1 = mx(t)l.dt. Show that co(S) is the whole spacP L.(O, I).
Show that there is no non-zero continuous linear functional on Lj)(O,. 1).
38 (von Ncumann) Let A be the subsrl of I. consisting of vectors
{xmnll $ m < n < co}. where the m-th coordinate of:l1rnfl is one. the
n-th coordinate is m, and all other coordinates are zero. Show that the
origin is in the weak. closure of A. but that no sequence of elements of
A converges weakly to zero.
89 Show that if a point p mI. is in the weak closure of a boundcd
set A !;; I., then p is the weak limit of a sequence of elemcnts
of A.
40 Let.8 be a dense hnear manifold of a B-space 1'. i>how that
g* and . are isometrically isomorphic, but that the isometric iso-
morphism between them is not So homeomorphism with the .8 topo-
logy of .8* and the :£ topology of 1'* unles8 a: = .8.
41 Let:£ be a local1y convex linear topological space and let ill
be a linear subspace of 1'*, Then ill is I-dense in 1'* if and only if ill
is a total set of functionals on I.
42 Let 3:: be a locally convex Imear topologiCal space, and 3:; a
subspace of 1:. Let xi £ 1:. Then there exists an element 3'* £ 1:* such
that 3:"(x l ) = xi(x l ) for "'1"3:;.
43 Let {x.} be a bounded sequence m a reflexIve B-space :£ and
let K. = co{ x.. "'.w . . .}. Then "'. _ "'0 weakly if and only if {xo}
= f):_lKuo Show that this theorem is not true if we omit the as-
sumption of reflexivity a
44 Let:£ be a complex locally convex linear topological space.
Show that the weak topology of 3:: is the same whether we take it as a
complex spa e or regard it as a vector spaC'C Over the field of real
scalars.
8. Enremal Point.
] DEl"]NITION. Let K be a subsrl of a real or complex linear
\rector space I. A non-void subset A K is said to be an e.riremol8Ub-
Eel of K if a proper Convex combination akl+(I-a)k., 0 < a < I, of
two points of K is in A only if both k. and k. are in A. An extremal sub-
set of K consisting of just one point i8 called an e.rtremal point of K.
For example, in three dimensional Euclidean space the surface
of R solid sphere is an extremal subset of the sphere, and every point
un the surface is an extremal point. The vertices. sides, and faces of a
solid cube form an extremal subset of the cube, but only the eight
vertices are extremal points of the cube the remaining points 011 the
sides and fac s are neither extremal nor internal points. A onvex set
may have no e:\.1:rema1 point at all, as in the case of an open sphere.
2 LEMMA, A non-void compact set in a locally WllVe.r Iitll'ar topo-
logical EpeCf has enremal poinls.
PIWOF. Let K be a compaet subset of the locally convex linear
topologi al space :£. Let .<I be the non-void family of closed extremal
subsets of K. Order .<I by inclusion. It is readily seen that if .<11 is a
440
\'. CONVEX SETS AND WEAK TOPOLOGIES
V.8.3
V.8.6
EXTREMAL POINTS
441
4 THEOREM. (Krein-MihMn) If K is a compact subset of a locally
COfI,oe;r linear Wpological 8p<ICe I ana; E is the set of its e",tremal points,
then co lE) -;;! K. Consequenily co lE) = co CK), and co lE) = K if K
is convex.
cover ing of Q; le t {q, + U}, i I, . . ., n, be a finite subcovering. Put
K, = co«q, +U)n Q) q.+U. Then K. is a closed. and hence a
compact, subset of co (Q). Hence
Co(Q) = co(K. U . . . UK.) = coCK, U . . . UK.),
by an easy induction on Lemma 2.5. It follows readily that p has the
form p = I l Qik., a. 0, I "'l ai = I, k. E K i ; and. since p is ex-
tr emal, that k, = P if a, > O. Hence p. U;_I K, U;_, (q.+V )
Q+U. This contradiction proves the lemma. Q.E.D.
6 LEMMA. Let if be a closed linear manifold in the B-spaCl' C(Q)
of arl real (or rompln:) «mUnu""" fu,u:l.wwt on the compat:t Hausdorff
spaN' Q. FOT each q in Q let "': in if* be defined by
"':f = f(q), Id.
Then every e:drema1 point of the eJ.os.od unit 8phere S. of if. is of the form
ax: milh 1"'1 = 1 and q in Q. If if = C(Q) the converse holds. i.e., every
element of the form ax: ",ilA 1"'1 = 1 and q in Q is an e.rtremal point S..
PROOF. Let A be the set of all points in 3::* of the form ax. with
.
1"1 = 1 and q. Q, so that A S*. Let if* have its if topology; since
S* is convex nd 3::-dosed, by V.2.4 the if-closure colA) = co lA)
!;; S*. If ",* f co(A), then by 2.12 Rnd 3.9, there is an "'. if and real
constants c and E, e > 0, with
totally ordered subfamily of -", the non-void 8et n -", is a dosed
extremal subset of K which furnishes a lower bound for d.. It follows
by Zorn's lemma tha.t $I contains a minimal element Au- Suppos("
that A., contains two distinct points p and q. Then, by 2.15, there is a
functional ",- £ 1* sucb that 91",.(p)"* 91",*(q). This implies that
A. = ("'I",.A., 91",*(",) =inf"A,91x.(y)} is a proper subset of A.. On
the other hand, if1':1and k. are points of K such that ak" +(I-a)k" . A,
for some 0 < a < I, then k" k. £ AD since AD is extremal. It follows
from the definition of Al that k l , k". A,. Hence Al is a proper closed
extremal subset of AD. This contradiction shows that At) contains
on1y one point which is therefore an extremal point of K. Q.E.D.
a LEMMA. LelK be a 8Ub8et of a linear space, kt A. be an extrema!
subsct 01 K, and A. an e.rtTemal stWsrl of A.. Then A. is an extremal
wbset of K.
The proof is eleroental"Y, and is left to the reader.
PROOF. Let k £ K and k co lE). Then, by 2.10. we can find an
",* . I. and real constants c and e, ,,> 0, such that 91x*(k) ;:;;; c,
Gi'",. (co (E» c+e. LetK, = ("'luK, Gi'",*(",) = inf..K91",.(y)}. Then
K. is a closed extremal 8ubset of K, and KIE = .p, By Lemma 3, K.
has no extremal points, but this contradicts Lemma 2. Thus the first
assertion of Theorem 4 is proved and the remaining assertions follow
trivially. Q.E.D.
5 LEMMA. Let Q be a compac! se! in a locally conve", linear wpo-
logical spoce I mhose closed oonve.. hull is compact. Then !he Qnly extrem
al poims in co( Q) are pou,ts in Q.
PROOF. Let P be an extremal point of co (Q) which is not 10 Q.
Since Q is closed, we can find a neighborhood U 0 of the origin of:le such
that (p+u.)n Q =.p, Rnd can then find a convex neIghborhood U
of the origin such that U - U!;; U.. It follows that (p+U)n (Q+U)
=.p, so that p, Q+U . Tl1e family of sets {q+U}, q. Q. is an open
Gi'",*(",) c; Bi'ax(q) < c-e, q. Q, 1"1 = I.
Hence i"'l ;;:; c-e, so that ""., > I. Thus co lA) -;;! S*, so that co lA)
= S*. It then follows from Lemma 5 and Theorem 4.2 that everv
extrema' point of S. lies in A. .
Conversely, let if = C{Q) and let q. Q be such that ",* =
,. ( ) * h . .
ay + I-a z , were 0 < a < 1 and y*, e* .S.. It WIll be shown
that y. = e* = "':. Let "'0' c(Q), 1"'01 -;: 1, and "'.(p) = 0 for p in
some neighborhood N of q. By Theorem 1.5.8. there exists a y. C(Q)
such that Iyl :;,: I, y(q) = 1, yep) = 0 for P f N. Then ay*(y)+
(l-a)z*(y) = "':{y) = I and ly*(y)1 < I, le*{y)1 ,;;; I. Hence y*(y)
= .*(y) = I. In the samc way it follows that y.(a;o+Y) = .*("'o+Y)
= I. Thus Y*('I'o) = ..("'0) = O. l"ow let "'.' C{Q), 1"'11;;:; I, and
"'1(q) = o. Then for eRch integer n there exists a neighborhood Nft of
q such that 1"',(p)1 < Iill for p' N.. Let .11ft be a neighborhood of q
442
V. CONTEX SETS AND WEAK TOPOLOGIES
V.8.7
V.8.9
EXTRE IAL POINTS
443
such that M. [;;: N n ; by Theol't'm 1.5.8, let g. C(Q) be such that
Ignl ,;;; I/n, g,,(p) = 0 for p N n . and gn(P) = "'l(P) for P Mn- Then
.T 1 -g fl -+ .7'1' loT 1 -g 7l 1 I, and :t'l-grt vanishes in J."ln_ It follows that
Y*("'l) = z*(""J = O. If x. C(Q) is such that x(q) = o. then I#nl ;;; I
for some sufficiently large integer n, so that y*(x) = z*(x) = O. Now
Lemma 8.10 can be applied to show that sea1Brs IX and p exist such that
y* = a.r:, z* = fJx:. Since y*, z* fiS., 10:1 I, IPf J. Since:£: =
(ao:+(1 -a)p)",:, 0: = P = 1. This proves that x; is an e,,1;remal point
of St:.; a similar argument shows that ax: with IIXI = I is a1so extremal.
Q.E.D.
7 LEMMA. If Q is a eompa€l Hamdmlf space, and C{Q) is the
E-space oj all Teal OT complerE ronti1'1U1JU8 fulldiOllg on Q. then the map-
ping). : q ... "'; of Q illto a suWel Ii of the enrrmal puint8 of s* is a
homromorphUmi where C*(Q) has itJJ C(Q) topology.
PROOF. The mapping A : q -->- «: is clearly one-tn-one. By Lemma
6 it sends Q into a subset of the extremal points of S*. To show that A
is continuous, let N(",;; "'0' e) = {"'*II("'*-"';)"'ol < e} be a subbasic
neighborhood of ",;. Since "'o c(Q), the setN(q) = {pll"'o(p)-",.(q)1
< e} is open in Q, and it is clear that A{N(q») [;;:N(",;; "'0' e). Hence
Q = A(Q) is compact, and A is a homeomorphism, Q.E.D,
8 THEOREM. (Banm:h-Swne) Let Q and R be compad Hausdorff
sptlCf8, and lei T be an ismnetric i80nwrphism brtween C(Q) and C(R).
Th£n therr exists a 1wmeomorpkism -r bdtJ'een Rand Q, and a funetio..
0: in C(R) with 1001r)1 = I, r£ R. sw:h that
R and a subset of EQ in these topologies {I.5.S}. From Lemtna 6, to
each r R, T*y; = o:(r)"' ,), where Io;(r) I = I and -r(r)EQ. From the
fact that T* maps E R onto EQ' and from Lemma 6, it follows that
t : y:- oX:("l maps R onto Q.. and S1II.ce T* is one-to-one, t IS also.
Thus t is a homeomorphism betw.een Rand Q. But sinc , by Lemma 7,
A : Q Q and p : R ..,. R are homeomorphisms, -r = ),-, tp is a homeo-
morphism from R to Q. Thus, for any x. C(Q) and r R, we have
(Tx)(r) = y;(T"') = (T*y;)(x) = ex(r)",':", (x) = o:(r)x(T(r)).
which is equation [*1. It remains to show that a.. is continuous. In the
fOl'mula above, substitute the function Xo E CIQ) which is identically
One. This yields 0: = Txo' C{R). Q.E.D.
Just as we were able to prove a number of interesting results
about the space C(S) by considering the extremal points of the unit
sphere of C*(S), so we shall see that consideration of the extremal
points of L: (S, 1:, p) leads to interesting facts about L (S. I, p).
9 LEMMA. Let (S, I. f-') he a p68itive measure spate. A functional
",* in L:'(S, I,p) is an e;r!remnl point of /lie ew.ed unit sphere s* of
L:'(S, 1:, p) only if it is of the form x* = o:y*, where 10:1 = I, alld wh£re
y. is naU-:FTO llnd muUiplica.tiz'C;
[*]
(T"')(r) = o:(r)",(-r(r»;
"' C(Q),
TEE.
y*(fg) = y*(l)y*(g),
where (fg)(s) = f(s)g(s) for ,u--all1WlJt all 8 in S.
PROOF. We will first show that the norm of an extremal point ",*
in S* is equal to one. Clell-rly x* "* 0 so that y* = x* f:x* I is in S* and
",* = 1"'*ly*+(I-!x*IJO.
Thus, by Defmition I. 1-[""1 = o.
By Theorem IV,8.I6. there is a A in ba(S,l."',., Pi) with IAI = 1 and
PROOF. The linear map T*: C*(R) --+ C*(Q), defined by
(T*y*)'" = y*(Ta;); y* E C*(R), x. C{Q). is readily seen to be an iso'
metric mapping. Furthel'more T* maps onto C*(Q); for given an
arbitrary functional ",*. C*(Q), let y* = ",* T I. Thus if S and SR
are the unit spheres in C*(Q) and C*(R), T*(S;) = S;. Since T* is
linear and isometric, it is clear that it maps the extremal points ET(
of S; onto the extremal points EQ of S in a one-tn.one fashion.
It is elementary to show that T* is continuous with the C(R)
topology in C*(R) and the C(Q) topology in C*(Q). Since, by Lemma
7. R is compact in the C{R) topology, T' is a homeomorphism between
",*f = Jsf(s)l(ds},
fEL",(S,I,p).
]t will next be shown that} v.ani!ilhes on at least one set in every pair
of disjoint sets in 1:'1< To see this, assume that there exist two disjOInt
sets E I , E 2 II with l(Et) "" 0 and A(E.) "F o. If ).,,(E) = A(EEI)
andA.(E) = A(E(S-E l )) for E It it is c1eartlmtl l ,;.,..ha(S, II' Pi)'
that v().", E) = VIA, EE,). and that V(A2' E) = v(i. E(S-E I » for
444,
,...-. CONVEX SETS AND WEAK TOPOLOGIES
V.8.10
V.8.1I
TANGENT FU};C1'!OKALS
U5
E e 21. Hence, 1 = 1',1 = IA,I+I'\'I. Since Al oF 0, ,\, oF 0, we may put
11 1 =AJIA 1 1 and v,=A./ll,l. Then v 1 ,v,eS*, and l=llll"t+
(I-iA,lJv.. Consequently VI = V. = A, and thus 0 oF A{E 1 ) = v,(E 1 )
= 0, which is the desired contradiction.
Since .A vanishes on one set in each complementary pair we have
where £ > O. Then, according to Lemma 9, the set
A = {x*""'*1 ;;;; 1, Ix*{/.) I s: [/ol-e}
A(E){A(S)-A{E)) = 0,
EeE 1 ,
.contains all the extremal points of the closed unihphereof L:'{S,E,p.).
On the other hand, A is evidently convex and L (S, E, p. I-closed. By
Theorem 4.2 and Theorem 4, A contain8 the entire unit sphere of
L:. That is
which shows that the function m = AjA(S) assumes only the values
o and 1. Thus
sup 1"*(/0\1 I/.I-e.
Iz.l l
(I)
m(AB) = m(A)m(B),
A,BE:E 1 ,
But. by the Hahn-Banach theorem, 1.8.15, this is impossible. Q.E.D.
II THEOREM. ul (S, E, p.) be a positive measure space. Then
then exists a eompacf Hausdorff space SI and an irometric isornurphum
A betr.van L {S, E, 1'-) and C{Sl)' The isomorphism A maps Teal fun.c-
Ii""" (i.e., lunctions r£at p.-dmost e-onywhere) into .-eal functions, posi-
tive ftmdwlIII in!u positive fw1din'18, and comple", conjugate ftmd.itJn.s
into comp/el1J conjugal<? lunclions. Moreover, A u an aJgebraic isomorph-
ism in tlu! Be_ thatil h(s) /{s)g{s)l'--dm()$j e.. Ah=AI' Ag.
11 (J i$ an arbitrary cantinuous fundion 01 a comple", varfuble, and I
isinL (S,E'Ji)' then A «(J(t)) = (J(A(t)).
PROOF. In view of Corollary 10, we may take the proof to be
word for word the same as the proof of Theorem IV.6.I8. Q.E.D.
for if either A or Bisanm.nullsetsoisAB, while ifm(A)=I=m(B)
.
then, since A - AB and B-AB are disjoint, one of them is "n m-null
set "nd m(AB) = 1.
If y* is defined by the equatl0n
y* I = Is I(s}m(ds},
for I inL", then ly*1 = Iml = 1 "nd y* = CliD* where 1"'1 = I/IA(S)I=I.
Equation (1) shows that y*Ug) = y*(f)y*(g) if 1 "nd g are both
<>h"racteristic functions of sets in E 1 . For any g in Lm the maniFold
!DI. = If II E L"" y*{fg} = y*(f)y*(g)}
is clearly a closed linear manifold in L", and it follows from the pre-
ceding remarks that!!J!. = Lm if g is a characteristic function. (It was
shown in the proof of Theorem IV.8.16 that characteristic functions
form a fundamental set in L".) This mean. that if 1 is an "rbitrary
function in L" the manifold !!J!, contains all chamcteristic functions
and thus !DI, = L". Thu. y*{fg) = y*(j)y*(g) for all I and g m Lm'
Q.E.D.
II. Tangent Funetional.
sup 1"'*(/): = III,
.C"M
I £ L (S, E, I'}'
We begin this section with a study of functional. tangent to a
convex set K. Since many of our results depend on the assumpticn
that K has an internal pomt, it is convenient to observe that p is an
internal point of K if "ad only if the origIn is an internal point of
K -po Consequently we will consider only subsets which contain the
origin as an internal point. The reader will have no difficulty in carry-
ing over our statements "nd definitions to the slightly more general
ease of sets not necessariJy containing the origin.
1 LEMMA. Let K b< u conve", set in a linear spate .f, and let the
origin be an internal poi"l 01 K. Le! f be the support lunction 01 K. Then
(f("+ay)-f[a!»!a is an incr<asing lunction 01 the pa..i/ive Teal variable
10 COROLLARY. Let (S, E, I'-) be a positive mea""re space. Let M
be the eallectwn 01 a!lllon-zero ",* in the dQsed ..nit sphne of L:'(S, E, p)
s"ch that ",*(h) = ,r*{f)"'*(g) u:henn'Cr h(s) = I{s}g(s) p.-almost every-
where. Then
PROOF. It is clear that sup.,.", 1"'*(/)1 ;;;; If I for I £ Lw(S, E, p.).
Suppose that ror some lo.L (S,E",), sup...", 1"'*(/o>! < 11.1-£,
446
V.. CONVEX SETS AND WEAK TOPOLOGIES
V.9.2
V.9.4
TANGE T FUNCTIONALS
447
a jor all x, y in I. The limil
I
T(X,y) = lim -(f(x+ay) f(x))
6.....;..0..... a
PROOF. B ' 1.8(c) and I.8(e), we have
I
- {f(x+ay)-f(x)} f(y),
a
E'.rists for each :r, y in I.
PROOF. Let a 1 "" > 0; then
1(a"x+"Ia.y) < l(a.x+a,,"ay)--t- f «a 1 -a.)x)
by 1.8(e). Thus
u 1 {I(x+a.y)-f(xH "a{I(x+a 1 y)-I(x)}
by 1.8(c), so that
1 1
- {f(a:+a.y)-I(x)} ;;;; - {1(x--t-a1y)-I(x)}.
a 2 at
Thus the function
which implies (a). Statement (b) follows from the inequalIty
a
21(x+ 2" (Y1 +Y.)) ;;;: f(x+aYl)+f(x+ay.).
Statement (c) is.. trivial. Statement (d) follows from the inequality
.-(a:. -Y)+T(a:. y) T(X, 0) = o. .-(x. y) = O.
Statement (e) is trivial. Q.E.D.
4. DEFINITION. If A is a subset of .a linear space .I, and :c is a
bounding point of A, a functionalj. I+ is said to be ttmgt'nt to A at X
if there eXists B real constant c such that
I
- {!(x+ay)-((x»
a
iitj(A) ;;;; c,
JIlj(tr) = c.
I
T(tr. y) lim - (!(x+ay)-!(xH
R---Jo{H- a
We note that if j is tangent to A at a:. so is every real multiple of
t. Conversely. if every tangent to A at x is a multiple of j, we say that
A has a unique tangt'nt at x.
Observe that if i£ is a linear topological space and A has all in-
terior point. then it follows from Lemma 2.7 that any func-tional
tangent to A IS continuous.
The next theorem gives a criterion for the e.. ce of linear
functionals tangent to a COnvex set in terms of its tangent function.
5 THEOREM. Let i£ be a linroT space, K a m.lt'''''' subaet ojl'. and
suppose that the origin ;" an i7.t£rnal poinl oj K. Let T be the tangent
function oj K. Then ij x ;" a bow/ding point oj K, a functionalj in r
roilh j(x) = I is langt'nl to A at x ij and oaly ij
-T(tr. -y) ;;;: !Jij(y) < .-(x, y) jor all y I.
Conversely, ij x is a bounding paint oj K and y is any poi..t in I jor
which
decreases as a d«=ases. Since f(a:+ay)+!(-ay) f{x),
{f(x+ay)-I(xH/a;:;;-f( -y), so that {k(x+ay)-I(.rH/a IS bounded
below. This proves the lemma. Q.E.D.
2 DEFINITION. Let K be a convex set in a linear space I and let
K caotain the origin as an internal point. If ! is the support function
of K, then the real valued function T defined for x. y I by
is called the tangellt jwU'tiolJ, of K.
.s LEMMA. Let K be a ronvex set in a linear spa«, and let the
origin be an internal po;nl oj K. Let! be the sappor! j.tndion and .- the'
langent jum!ion oj K. Then
(a) .-(x, y) I(y);
(b) T(X'YI+Y,) ;:;;.-(X'Yl)+T(X,y.);
(c) T(X, ay) = aT!a:. y) for u ;;; 0;
(d) -T(X. -y) ;:;; T(tr, y);
(e) T(X. =) = a!(x) jar a real.
-.-(X, -y) c < T(X. y),
flu?nthaeisajulU'fimuI1ftangmttoK a! x wilh jlx) = I and!Jij(y) = c.
PROUF. Iftbe functionalj is tangent toK at x and j(x) = I, then
by l.8(f), fey) < I implies !Jij(y) < I. It then follow8 readily from
448
v. COSVE..'"'{ SETS AND WEAK TOPOLOGIE S
V.9.5
V.9.6
TANGENT FUNCTIONAL8
449
f(a.x+bll);--f( -a.x) ;;;; be.
Hence fo(z)' -S; f(z) for z @i. 8y the Hahn-Banach theorem
(11.8.10),1 0 can be extended to a linear functional f defined on all of
3: such that f(lX) ;:;;; I(IX) for IX. 3:. It follows by I.8(d) that I(K) ;:;;; I,
so that f is tangent to K at IX, and f(y) = e. In the case that 3: is a
linear space over the complex numbers, the functional f(IX)-if(ix)
is the required tangent functional. Q.E.D.
6 COROLLARY. If a convex se! K in a linear spl1£e has the origin
as an inln-lInl poinl, K has a non-uro tllngalt ju.ll'Iional tU each of i/$
bounding poinfs. There is a unique tangent furu:tio.1ll1 allX if and only it
-'-(IX, y) = --.-(a:. -y) for all y 3:.
In the case of a linear topological space, we have a converse
result.
7 THEOREM. Let I be a linear topological space, and let A be a
cl08fd sub..t of I, having inlfTior points. Suppwe thai. A has a non-zen'
tangent functional. tU .fUh poinl of a dense subset of il8 00u7U!ary. The"
A is conve .
PROO\'. Denoting the interior of A by AI' we will show first that
there is no non-zero tangent to A at any point of aAl+(I-a)A. for
0< a < I. Let p AI' q A, and let IX = ap+(I-a)q where 0 < a
< I. If 1 is a functional tangent to A at IX, there is a real number c
such that atf(lX) = c, atf(A) 5: c. Since 1(3:) = af(p)+(I-a)f(q), it
follows that at/(p) = atf(q) = c. Let N be a neighborhood of the
orig;n such that p+N A, and let.1Il be a neighborhood of the origin
with MU(-M) N. Then Eftf(N+p] c, and thus atf(N);:;:; O.
Hence, 0 ;:;;; at/(II!) ;:;;; O. i.e.. Eft/(lIl) = O. from which it follows that
1=0.
Let Bl be the dense subset of the boundary B of A at which there
are non-zero functionals tangent to A. We have seen that
(aA1+(I-a)A)nB l = '" for 0 < a < I. Since aAl+(I-a)A is
open, (aA1+(I-a)A)n B = '" for 0 < a < 1. Let p Al and q A;
since p is interior to A. (I-a)p + aq is in A for all sufficiently small
positive a. If d is the least upper bound of the sct
1.8(c) that I(y) Eftf(y). Consequently, since f«1:\ = few) = I.
I I
9ft(y) = Eft - {f(x+ay)-f(x}} - {f(w+ay)-I(",)},
a a
so that {it/(y) 5: -.-(x, y). Replacing y by -y, we get -9ff(Yl 5:
T(W, -y), so that --.-(w, -y) ;:;;; {it/{y) T(IX, y). On the other hand
if f satisfies this inequality, 8(a) shows I is tangent to K at m.
To prove the converse. we regard I as a linear space over the
reals. ObseNe that the functions f and ..- are unchanged. Let y . 3:
and -..-(:c, -y) c T(W, y). Every element z of @i = sp{w, y} has
the form z = a.x+by; define f. on@i by fo(z) = a+bc. If y = dw, thcn
it follows from 8(e) that c = d; so that z = 0 implies fo(z) = O. If y
is not a multiple of w, the representation z = a.x+1Iy is unique. Thus
fo is a well defined linear funetional on @i.
We wish to show that fo(z) fez) for z @i. Since this is trivia'
when !J is a scalar multiple of x, we can assume that every Z E e has a
unique representation 2 = ax+by.
Case I. a> O. Since 10(Y) = c. it suffices to show that
b be
f(w+ - y) f.(IX)+ -;
a a
or, letting bla = a" that
f(w+a,.y)-I(x) alc.
smce I.(m) = f(w) = I. If a,. = 0 this is obvious. If a,. > 0,
f("'+a,.y)-I(w) > a,.T(:C, y) :<: a,.c by Lemma 1. If a 1 < O. put
a. = -a,., andYl = -Yo Then f(w+a,lh)-f(w) a,T(m, -y) -a
by Lemma I. so that 1(1X+a,y)-f(w) :<: ""-C in this case also.
Case 2. a -<:; O. We wish to show that
f(ax+by)-af(w) :<: be,
i.e., that
If b O, we have
f(=+by)+f(-ax) :<: f(lIy) = bf(y) :2: bT(.r, y) ;;; be
by I.8(e) and 8(a). If b < 0,
f(ax+bll)+f(-a.x);;; f{by) = -bf(-y)
;;; -b,(x, -y);;;; (-b)(-c) = be.
{aiD < a < I, (l-a)p+aq. A},
then it is seen that (I-d)p+dq B, so from the above, d = I. Conse-
quently (I-a)p+aq.A for 0 < a < I, and (I-a)A.+aA A
450
v. CONVEX BETS AND WEAK TOPOLOGIES
V.9.8
\'.D.9
'l'A:SGENT FGSCTIOY.'\LS
451
)A A . P en for O<a<l,
for 0 < a < I. Since (I-a I+a IS 0
)A A C A for 0 < a < I' therefore AIlS conveX.
(l-a ,+a ,- I . . f A d'f
Since A is-clooed, A AI' On the ther hand. I .p £ 1 an
q£A. q=lim.-+ o {(l-a)q+ap}. so A Al' The convexity of A =Al
follows from that of Al and Theorem 2.I(a). Q.E.D.
While it is clear from elementary examples that a c m.ex set
need not have a unique tangent functional at ",-e!'}' boundmg pomt.
the next theorem gives a strong result in this direction.
8 THEOREM. If a Cl)fltle<J! subset of a ..eparable B..pace I has an
. . . I . 1 L a uninue tan"""l at each poinlof a dEnse sub8et of
tnieTlor potn , 'l ,w..:s b-'.
irs boundary.
PROOF. Let K be the convex set. It win be shown that -1:«..,.y)
_ ( _y) y. I for", in a dense subset Z of 3:. The set K contam8
- T "', h ' S{O IN ) about the origin, This clearly Implies that the
.somesp ere <0 I . )
f t . . of K satisfies 1(....) N.xl. By Lemma 1.8{e ,
support unC Ion 1 _ I
Since the function
I
g(a, iE, y) = - {1(....+ay)-2l(...)+I(....-ay)}
a
IS (by Lemma 1) the Sum of two monotone increasing functions of a
,t has thIS Saine property for aU .....11£ 3:. Consequently, letting
Z" j , = I xix d. i{f("'+Yn!i)-2f{x)+f("'-Yn!iJ} < } ,
. \ I 1
[OJ
If(YI)-I(Y2>1 ';:; NIYI-Y2!>'
we have ZtI = n;:t U;:'J Z'R,i.i# If we put ZPJ.f = U:' l Z n . i . J , then
Zn.i is open in I. and Zn = n:' l Zn.t.
Ve wish to prove that Z = n:... 1 Zft = n:.... 1 n:: 1 Zn.i is dense
in I. Suppo8e that Z is not dense in I, an d that p t Z. Then Some
sphere S(p, ") does not intersect Z. If S = SIp. £/2). then SZ = "'.
Hence U:', U;:', SZ .f = S. It follows from Theorem 1.6.9 that
some set Z:. i contains .au open set, i.e." that some set Zn,.i is not
dense in}:; since Z....i Zru this implies that SOme set Zn is not dense
We will show that this is impossible.
Suppose that "', £ I, Xl t Z., then T("'. Yfi) -T(..... -Yn) for '"
in some remtive neighborhood of ....,. Thus. the function f(...., +aYfi)
has no derivative at any point a in II neighborhood of zero. But [oJ
shows that 'I'(a) = f(a: 1 +aYn) is continuou8 and of bounded variation.
Thus by the remarks preceding Theorem 111.5.17, there exists a
BoreJ-Stieltjes mea8ure p such that pIc, d) = 'I'(c)-'I'(d). Thus. from
111.11.6 ,t follows that f("'l Tay.) has II derivative almost everywhere.
This contradiction proves that Z. lS dense m I. Hence it follows that
Z is dense ill I. Since T(",", ay} = aT(...., y) for a > 0, "'" £ Z if '" £ Z
and a > O. Consequently, the continuous mapping '" _ ....If("') of
{"'. Ilx oF 0) onto thc boundary B of K maps Z into a >ubset of itself
which, since Z is dense in I, is clearly dense in B. This shows that
Z n n ,s dense in B. The present theorem now follows immediately
from Corollary 6. Q.E.D.
There .arc interesting connections between the tangents to a set
in a linear space.I and certain special convex subsets of I, called cones.
9 DEFINITION. If I is a vector space:. a convex set K I is
called a ron" with verte", p, if P +x . K implies that p +ra: . K for r O.
The CMe K with <'crle.r p genwaW by A is the intersection of aU
Also
r{x. YI)-T(a:. Y2) ::s:: T(X, YI-Y.)
::s:: f(y,-y.) ::S:: Nly,-y.l.
CODSCfjuently.
IT(X, y,)-T("', Yo)1 ,; NIYcY2:'
Thus, .f we let {Yn} be .. denumer..ble dense subset of I. and put
Z. = {"'Ix, 3::, T(..... Y.) = -r("'.-!In»'
then", £ n:", Zn is equivalent to T(X, y) = -T("'. - ) for aU y £ I.
. h f th t Z - n Z IS dense m 3::.
It remaInS to prove. t ere ore, a - ft l on
Now, Z. is defined by the condition
lim 2. {J(",+ay.)-f(",» = lim - 2. {f(....-ay") -f(a:J},
a 0---1'-11+ a
and since tbese limits exist:. Zn is the set of a: for which
1
lim - {f(....+ay.)-2f(....)+f(:r-aYn)} = o.
u-+IH- a
452
v. CONVEX SETS AND ""'"EAK TOPOLOGIES
V.9.10
V,101
FIxED POINT THEOREMS
453
cones with -.-ertex l' which contain the set A. It is easy to see that
K = {z!z = T(q-p)+1'. '1 A. T :;;:; o}, if A is convex.
10 THEOREM. If K a closed cone with ver1€x l' in a Tea! Wa1Uy
co...""" linear trrpolDgiool space :E, and K '* :E, then th£re eitisu a ?!MI-
2/'TO ctmtinuOUB linear fwrn:tiol'll1l i4ngent to K al p. If A a subset Df I,
and p is in At then there e:risls a tlOn-UTO COJzUn.uous linear fundiunoJ.
!angent to A at l' if and vnly if the cone B wilh Verf£1X l' neTaUd by A
is not denae in I.
PROOF. If '1 ,K, then, by 2.12 we can find a functional f and a
rea! constant c with fJif(K) S; c ,,;; fJif(q). Let fJi/(p) = a. Then if
z K and Bt/(z) > a, we have
fJif(z-p} :;;:; e> 0, and Btf(r(z-1')+p} :;;:; ..+a.
which contradict8 fJif(K} ;:;0 c for r sufficiently l!ll'ge. Hence fJi/(K)
;;;;; E!i1<P), which proves the first part of the theorem.
It is cIe!ll' that B and ii are cones. If ii '* ;E, then any non-zero
continuous linear functional tangent to ii at l' is a tangent to A at p.
Conversely" if / is B non-zero continuous linear functional tangent
toA at 1', then Btf(p) = c, Btf(A) < c. It follows that fJif(a(q-p}+p}
S; c for a 2: 0, 80 that fJi/(B} < c, and since ii = I Lemma 1.11
implies I(I) = 0; since I #> 0, this is impo8sible. Q.E.D.
P'<OOF. Let z K be in the boundary of K; let '1.,K, 'I. --+z.
Then, if p. K is such that 11'.-'1.' = inf..., Iz-qnl, it follows from
Theorem 1 I that there exists a non-zero functional tangent to K at 1'..
But, clearly, p. --+ z. Q.E.D.
10. Fixed Point Theorem.
12 COROLLARY. LeI I be a normed liMar spaa and K a conv<:r
8Ubset of ;E. Suppose t/wt IQT each '1 not in K there lXistB a l' in K such
that Ip-'1[ = inf"" [z-q[. Tko K has non-:::tTo rontinUOU$ limor fun-
genl fundiorwls at each point Qf a dense sub.m Qf its boundary.
1 DEFINITION. A topological space R is said to have the fiJxd
point property. if for every continuous mapping T : R --+ R, there
exists a l' R with l' = T(p).
The famous Brouwer fixed point theorem states: The dosed unit
sphere Qf Eft has the lix d point property.
This seetion is devoted to proving a striking generalization (Theo-
rem 5) of Brouwer'8 theorem. 'Ve shaU use the Brouwer theorem in
proving Theorem 5; however, since the Brouwer theorem is quite
well-known, we do not give the details of its proof in th.is section
but we refer the reader to the notes at the end of the chapter where
B proof and some additional references Are given.
The Hilbert cube C is the set in the B-space l. conSISting of all
sequences [ nj with I .I ,;; l/n, n = I, 2, . . .. It is seen that C is a
compact subset of l. (e.g. see Corollary IV.5.5),
2 LEMMA. The Hilbert cube has the li<ced poinl property.
PROOF. Let T : C --+ C be continuous Rnd let P n : C --+ C be the
map defined by
P'([ l" . ., .. n+l" , .J} = [ 1' .. .. n' 0, U,.. .j.
The set C. = p.(C) is homeomorphIc to the closed umt sphere in E".
Since the mapping PnT : C", -+ C n is continuous, the Brouwer theorem
implies that it has a fixed point Y. E C n C C, so that
ly.-T(Yn») fi l/i'.
i-7J4-1
Since C is compact, {Yn} has a convergent subsequence. The limit of
this sequence is clearly a fixed point of T. Q.E.D.
8 LEMMA. Any convelX c!os d subsel K of th£ H ilbat cube C has
the fi<ced point properly.
II THEOREM. Let;E be a .",nn£d linear spaee, and let K be a COI/va
subset 01 ;E. If there are poinu 1', '1 with l' in K, '1 no! in K, and
1'1-1'1 = inf Iq-zl,
"s
then lhere elXisu a nun-zero ccmtinuous lin ar /Jmdumal i4" l/t 10 K at p.
PROOF. Let d = 1'1-1'1 and 8 = S(q, d}. Then S is an open set
and SnK = p. By Theorem 2.8, there exists R non-zero continuous
linear functional I such that E!i/(K) ;$; [It/(S). Since pis in thc closure
of both K and S, it is evident that I is tangent to K at p. Q.E.D.
454
v. CONVEX SETS ANlJ 'WEAK TOPOLOGIES
V.IO.4
V.1O.4
FIXED FOINT THEORE)fS
455
PROOF. To each point pEe there corresponds a unique nearest
point N(p) £K. To see this, note that Lemma IV, .2 implies that if
{k.} is a 8equence in K such t t lim,-+a Ip-k.l ----: l r Ip-kl then
{k.} converges, say. toqoK. If {k,} IS another such mlmml mgs uence
converging to if oK, then IV.4.2 implies t!",t {I<" kl' k,: 1<;",..}
is also convergent, Hen.... q = q' and q is the desIred nearest pomtN(p).
Now, N(p) is a continuous function of p. For, if P. -+ p, and
N(p.) -J N(p), then siIJce K is compact, {N(p.)} has. a con el'!,'Cnt
subsequence (N(p..)}, converging to an element q In K different
from N(p). Thus
1P..-N(p.,J1 Ip.,-N(p), 1P.,-p:+lp-N(p)l;
so that lp-ql :5: Ip-N(p)l: by the fll',:t part o the-proof, this implies
Nip) = q. WenotethatN(C) K.whllepoKlmp"est!",tN(p) = p..
Now if T : K K i5 contlnuous. TN : C K 1S contmuous and b)
the receding lemma l>as a fixed point. Tills fixed point is in K; it is
therefore a fixed point of the mapping T. Q.E.D.
4 LEMMA. Let K be a oompad ('(If'''''''' subset 01 a locally 00"""'"
linear topological space iE. Let T : K -+K be /'Oll/inuaus. II K camains
at kast two pOU'Is, Ihne e;rjlIts a pruperelasfd conl'£.rsub&et KICK ..",h
that T(K I ) K I .
PROOF. We may suppose that K has the I* topology, since the
idenhty mappmg from I with its original topology to I with i.ts £*.
topology is continuous. Since a continuous and one-to one mappIng of
K is a homeomorphism, (cf. Lemma 1.5.8), changing to the 1:* topo-
logv does not affect thc hypotheses of the lemma.
. We will say that a set of continuous linear functIonals P = {f} IS
detennined by anothcr set G = {g}, If for each f 0 ]<' and, > D, t ere
exists a neighborhood l\i(0; y, Ii) = (.r;lg(x)1 < Ii, g c y), where y IS a
finite subset of G, with the properly that if p, q c K and p - 9 c N (0;)' ,Ii),
then I/(Tp)-/(Tq)1 < c. It is cle8I" that if F 1S determined by G, then
g(p) = g(q), g c G, implies that f(Tp) = f(Tq), f c F.
Each continuou linea.r functIOnal J is detennill d by some de-
numerable set of functionals G = { ,"}. For, by IV.6.0, the scalar
function J(Tp) is umfomlly contmuous on the compa.::! setK. n e
for each integer n there IS B nClghborhood N(O; }'t1., b n ) of the orlgm In
l giveI'l by a. finite et Yn of continuous linear functiona1s. and a Cj,. > 0,
such that if p,qcK and p-qcN(O,y.,Ii.), then If(Tp) f(Tq)1
< Ifn. Let G = U : I Yn: then f is determined by G. It follows that if
F is a denumerablc subset of 1*. there exists a denum fable subset
G F of I* snch that each I F is determined by G F"
We can e\.'en assert that each contmuous linear functional f can
be included in a denumerable self-<lelcrmined set G of functionals.
For, if I is determined by the denumerable set G i . let each functional
in G] be detenuinFd by the denumerable et G 2 , eseh functionat in 02
by the denumerable set G., etc. Put G = {f}u U:: I G,.
Now, suppose thatK contains two distinct points, p and q, and let
1£1:* be such that 1(P) '" I(q). Let G = {g,} be a deuumcrable self-
determined set of continuous linear funclionals containing f. Since K
:is compact, E,(K) is a bounded set of scalars for each i. and since
we can multiply g, by a Sllitable constant, we may suppose that
Ig,(K)j ;;;; Ifi. In this case, the mapping II: K -+ I" defined by
H(k) = [g,(k)]. is a contmuous mapping of K onto a compact convex
subset Ko of the Hilbert cube which eontains at least two points. Con-
sider the mapping Tv = IITH I : K. Kv: since G is self-determined,
To is single-valued. To see tJmt To is continuous, Jet ho € Ku and
o < E < 1. Choose N such that I:r.+l Ifi' < c. Then since G is self-
determined, there is a Ii> 0 and an m such that if Ig,(p)-g,(q)1 < Ii,
i = I. . . ", nI. then
[*]
ig,(Tp)-g,(Tq)1 < V .
i=I,...,N.
Thus if Ib-b.1 < Ii, and ifp and qare any points in K with b = [g,(p)]
and b. (g,(q)], then [*] holds and
IT.(b)-T.(bo)l. = IHTII-l{b)-HTH-'(b o Jl2
N .
:::; I ig,(Tp)-g,(Tq)I2+2 I I,i2 < 3e.
i l , N+l
Hence To is a continuous mappingofKo intoK(I' It fonows from Lem-
ma 3 that Tv has a fixed point ko' Thus TH '{ko) H lTo(ko)
= H '(ko}' Setting KI = H l(ko)' we note that K, IS a proper closed
subset of K, and that T(K , ) Kl' The linearity of H implies that Ki
is Convex. Thus the lemma is proved. Q.E.D.
456
V. CONVEX SETS AND WEAK TOPOLOGIES
V.I0.5
V.lO.8
EXERCISES
6 THEOREM. (Markov-Kaktdani) Let K be a <ompacl CD7liW'"
$Ubsd of a linear topologicaI space :£. Let 3 be a oorrmwtitlg family of
rorrlinUOWJ limar mappings which map K inlo i"'ell. Th£n there uiBfs
a poim p in K BUck tJw.t Tp = P far each T in 3.
PROOf'. Let n be a positive integer, and T" 3. Put Tn =
n-l(l+T+.. .+T. l). Let.:Jf' be the family of all sets T.(K) for
n 1 and T ,3. Then, each set in.:Jf' is convex by Lemma 1.5, and
compact by 1.5_7(b); since K is convex T.(K)!;;K. Since Tn and 8m
commute, it follows that T.8m(K) T.(K)nSm(K), T. s, 3. Thus
any finite subfamily of :K has a non-void interstct:ion. By 1.5.6,
there is a pen.:Jf'.
If T e 3 and Tp *- p, there is a neighborhood U of the origin of
£. such that Tp-p U. If n is an arbitrary positive integer, since
p e Tn(K). there exists a 'I' K such that p = n-l(l,T+. . .+T. I)'1.
Hence Tp-p = n- I (T"-l)'1 U. Since T"g, K. it follows that
n-I(K K) i8 not a subset of U for any positive integer n. But
K-K = rJ.(KXK), whererJ.("', y) = :<-y, and thusK-Kis compact.
But this contradicts II.l.8. Q.E.D.
Examination of the above proof will show that the on1y property
of the mappings T besides continuity that was used was the property
T(tu+(l-a)y) = aT(:<J+(l-a)Ty.
457
the origin such that if k,., k.,K and k,-k., U then <!I(kI-k,,)C V'
that is, T(k I 1<0)' V for T, <!!. ,
8 TmwREM. (K"kulalli) Let K be a compact ccmvea: BUlJs£t 0/ a
locaUy CUll""'" rillt'ar tCYJJOWgkal spa" :£, and let <!I be " group a/linear
mapping. which i. equicem!inuo".. <m K alld BUch IMt <!!(K) C K. Th£n
there e",isu a pomt p. K such tMt <!I(p) = p. -
PROOF. By Zorn's lemmaK contains a minimal non-void compact
convex sU 8et K I such that <!!Kl Kl' If KI contains just one point.
our pl'OQf IS complete. If this is not the case. the compact (11.1.2) set
K 1 -K 1 contains some point other than the origin, and, consequently,
there exists a neighborhood Vof the origin such that tl does not con-
tainKI-KI' There is a COnvex neighborhood Ji oHhe origin such that
0: Ji V for lal ;£ I. By the equicontinuity of <!! on the set K there
isaneighborhoodUloftheoriginsuchthatifk b eK andk 'b U
1 9 ""8 1 1""2 1
then <!!(k,-k.) Ji. :rut U. = co(<!IU I ), sinee <!! is a group <!IU. =U.,
and from Lemma I.4,16(d) we see that <!IU. = U.. Let (j = inf {ala>O,
aU. Kl-KJ, and U = (jU.. It follows readily that for each a with
0< a < 1 the set KI-KI is not contained in (l-e)U, while KI-Kl
(I +e)U. The family of open sets {2- I U +k}, k e K I , is a covering of
El' Let {2- 1 U +k., . . ., 2 IU +k.} be a finite subcovering and let
p = (k,. +. . . +k.)/n. If k is any point in KI' then k,-k e 2- I U for
some i between I and n. Since k,-k. (1 +a)U for 1 i ;£ nand
e> 0, we have pen- I (2- I U+(n-l)(1+a)U)+k; substituting
a = 1/4(n-l), we have p (1-I/4n)U+k for each k,KI' Now let
K. = K 1 nn_, «1-I/4n)U +k) *- rJ.. Since (l-l!4n)U does not
contain K!. - Kl' ' oF KI' The closed set K. is clearly convex_ Further,
since T(aU) aU for T e<!!, we have T(aU +k)!;; ail +Tk for T. <!!,
k e KI' Since <!I is a group and TKI K I , T. <!I, it follows that TK.
= KI for T. <!I. Thi8 implies that <!IE. K., which contradicts the
minimality of KI' Q.E.D.
5 THEOREM. (SchoudRr-Tychonofl) A compact co"","" subset 0/ a
locally 00'''''''' linear WpOlogir.al spate Iws thR. jiud point property.
PJtOOF. By Zorn's lemma there exists a minimal convex subset
KI of K with the property that TKI K.. By the previous lemma, this
minimal subset contains only one point. Q.E.D.
The importance of Theorem 5 lies in the fact that it applies to
non-linear mappings. If we consider only linear mappings, we can
prove a stronger result by more elementary means.
for :<, Y E I and 0 ;£ a 1. Mappings of E which have this property
are often called alfille IlUlppings.
7 DEFINITlO". A family <!! of linear traosforIlUltions 011 a linear
topoJogical space :£ is said to be equiamtinWJUB on a subsd K of I if for
every neighborhood Vof the origin in I there is a neighborhood U of
ll. Exerci"".
I Let C be a closed convex separable set in a B-space, and let
p be an extremal pomt of C. Let p be a positIve measure defined for the
Borel subsets of C, such that pIC) = 1. Show that if p = Jc"'p(d.1:),
then 1'(1') = I.
58
v. CONVEX SETS AND WEAK TOPOLOGIES
V.11.2
V.U.I0
EXERCISES
45
2 Let (S,.E, p) be a positive measure space. Show that
Lm(S, E, p) is not weakly complete or reflexive unless it is finite di-
mensional. Let {fn} be a 8equence in L {S,.E, p), and f. Lw(S,.E, p).
Let 111 be tbe set of all }. in batS, .E" p,) (of. Theorem IV.8.16 for
notation) which take on only the ,mues 0 and I. Show that {In} is a
weak Cauchy sequence if and only if it is wrifonnly bounded and
limn_ Ssln('»).(d.<) exists for each}. in 111. Show that Ift->-I weaklyif
and only if {In} is unifonnly bounded and limn_ Is In('»).(d.<) =
Is i(.J).(d.<) for each), in 1If.
S Show that the closed unit sphere of Co contains nO extremal
points.
Let (S, .E, p) be a v-fmite positive measure space. Show that
LI(S,.E, p) is ,sometrically isomorphic to the conjugate IE* of a
B-spacc if and only if S Can be written as a denumerable union
S =U;,:, S, of measurable subsets S,sueh that peS,) < 00, and such
that every measurable subset A of S, satisfies either pIA) = p(S,)
or pIA) = O.
5 If the closed umt sphere of an infinite dimensional B-spaee I
contains only a finite number of extremal points, then I is not iso-
metrically isomorphic to the conjugate of any B-spaee.
6 Let S be a topological space, and let C(S) be the B-spaee of
real bounded continuous functions on S. How rnany extremal points
are there in the closed unit sphere of CIS)?
7 Show tbat evcry boundary point of the closed unit sphere S
of a B-spare I is an extremal point if and only if I"'+yl "" Ixl+lyl
unl""" x and y are linearly dependent. A space with this property
is called midly crm""x. Show that I is 8trictly convex if and
only if for each z* in *, SUPZfS fJ/JJ*x is attained by at most one
:r:in S.
8 Let I = c and 'tJ = eX c, where the nonn in 'tJ is given by
![YI' Yo]1 = max ny,l, ly.I)- Show that 3:* and 'V. are isometrically
isolnorphic, but that J: and 'V are not.
9 (Klee) LetKbe the set of sequences x = [ ,J .1.,1 P < 00,
fOT which i 0, i = 1, 2,. .. Then K is B closed convex set, each
point of which is a boundary point. But K has a continuous tangent
functional at [ ,] if and only if m = 0 for some m ::0- O.
10 Calculate the tangent function of the closed unit sphere of
Hilbert sJ'll"".
U Let (8, L" p) be a positive measure space, and let p> 1.
l'nlcuIate the tangent function of the closed unit sphere of L.(8, .E, p).
Show that the closed umt sphere of L.(S,.E, p) has a unique tangent
functional at each of its boundary points. Is this true if p = I?
12 Let IE be a B-space, and let K be a weakly compact conve>.
subset of.1:. Show that K has a continuous tangent functional at each
point of a dense subset of its boundary.
IS Let I be a B-space, and letK* be a bounded x-closed convex
subset of IE.. Show that K. has a continuou8 tangent functional at
each point of a dense subset of its boundary.
14 DEFINITION. A point p of a subset A of B metric space is
caUed d;amrlral if SUP""A ,,(1', x) = SUp.,..A ,,(x, y). A subset of a
metric space lJI is said to be admissihlR if it is an intersection of
closed spheres {x[,,(x, Yo) ;:;; co}, Yo . lit, 0 < Co 00. A metric space
has normal structure if each admissible subset which contains more
than one point contains a non-diametral point.
15 A l!ompaet convex subset of a B-space has normal structure.
16 Let 111 be a compact metric 8paee, and let A be a closed 8ub-
set of Ill. Let T :]If ->-lIf be such that ,,(Tx, Ty) ;:0-, e(x, y) for
x, y.lIf. Then, if TA A, TA A, and if TA A, TA = A.
17 Show that if a metric space 1If with normal structure has at
least two points, it contains a proper subset A such that T A !: A
for every T mapping .u onto M such that ,,(Tx, Ty) < ,,(x y),
x, y. 1o-f. Show that if in addition ]If is compact then 111 contains a
point l' such that T1' = P for every T mapping Manto -1{ such thai
,,(Tx, Ty) ,; e(x, y).
18 Let M be a compact metnc SJ'll"" with normal structure.
Show that there is a point p. M such that Tp = l' for every map
T : M ->- M such that ,,(Tx, Ty) ;:0-, e(x, y), x, y < _ f.
19 Let III be a complete metric space. and let T : M ->- 111 be
sucb that e(Tx. Ty) ;::;;; a/l(x, y) for x, y < lIf, where 0 < a < 1. Show
that there is exBetly one point l' . lIf such that Tp = p.
20 Let T be .a non-linear map of the reflexive B-SI)aCe
460
".. CONVEX SETS AND .WEAK TOPOLOGIES
V.Il.21
V.12
NOTES AND REMARKS
461
12. NOles and Remarks
and an arbitrary convex set is possible, provided they are disjoint
(compare Th€Ol1'm 2.8). He also proved that a convex set K which
is compact in the It< topology of the normed linear space I. can be
separated from an arbitrary closed convex set disjoint from K (corn.
pare Theorem 2.10). Tukey observed that thi8 result implies that in
B reflexive B-space two disjoint closed convex sets, one of which is
bounded, can be separated hy a hyperplane.
Tukey demonstrated that these results cannot be extended very
far by giving examples of:
(i) Two disjoint bounded convex sets. one of which is closed,
which cannot be separated.
(ii) Tw" disjoint closed convex sets of a Hilbert space which
cannot be separated.
In this spirit, Dieudonn" [2] exhibited:
(iii) Two disjoint closed bounded convex sets in l" which cannot
be separated.
This result WaS extended by Klee [4; p. 881] as follows:
(iv) Every non-reflexive separable B-space contains two disjoint
closed hounded ronvex sets which cannot be separated.
In view of these examples. the following theorem of Tukey [I;
p.99] seems remarkable: If A and B are closed conVex sets of a normed
linear space, and if A is bounded, then the difference set A - B =
{a-bla" A, b" B} contains every 8phere in which it is dense.
Tukey showed that ev ' infinite dimensional normed linear
space! is the union of two complementary dense convex sets. That
the number 2 can be replaced by any cardinal number not greater
than the cardinality of I, was demonstrated by Klee [2]. Klee [3;
p. 454] also extended Tukey's result to a more general type of space.
Lemmas 2.4 and 2.5 Were proved in the important special case of
ubsets of a conjugate space It< taken with its topology by Krein and
Smulian [1].
Tbeorem 2.6 IS due to Mazur [2].
Weak Iopologies, The notion of weak convergence of a sequence in
L.[O, 1] was used by Hilbert, and in L.[O, 1] by F. Riesz, but the USe
of the weak neighborhoods in defining a true topology was introduced
by von Neumann [2; p. 380], who demonstrated (cf. ExerCise 7.38)
that it is not sufficient to employ sequential notions alone in using
into itself wbich is continuous with the £. topology in I. Let
liml.I IT"'I/I"'1 = O. Show that (I+T)I = J;.
21 Let S be a compact Hausdorff space. and let I-' be a finite
regular meaSure on S. Let <1> be the real or complex numbers, and let
K be an element of C(SxSx<1». Show that the non-linear integral
equation
fIB) = g(s) - Is K(B, t, g(t»l-'(dt)
has a solution g C(S) for each f C(S).
22 DEFINITION. Let G be a topological group, Then a regular
measure I-' on G is said to be left-invariant if l-'(sE)=I-'(E) for all
S E G, E E E. Such a measure is often called HaaT measuTe.
23 (Haar) Let G be a compact topological group. and let E be
the Borel sets of G. Show that there exists a regular measure on L
which is left-invariant and is not identically zero, and that any two
left-invariant measures differ only by a scalar factor. Show that a
left-invariant measure also satisfies I-'(Es) = I-'(E) andl-'(E-I)=fl(E).
Conve.r sets and !;l/£LIT topologirol Spl1£t?B. The proof of Theorem
1.12 is due essentmlly to Mazur [1; p. 78], who proved that a convex
-set with interior point in a real normed linear space can be separated
(in the sense of Definition 1.9) from any nun-interior point, This
generalized a similar resull proved for separable spaces by Asroli
[J; p. 206]. Eidelheit [1] extended this result to include the case oftwo
convex sets which have intenor points, but have no such points in
common. Simpler proofs of Eidelheit's theorem were constructed by
Kakutani [1] and Botts [1].
The first statement of Theorem I.J2 in ,ts full generality IS due to
Dieudonn.! [1], but his proof was somewhat different from ours. Dieu-
donne observed that although the hypotMsis concerning the existence
of an internal point can be weakened to the. assumption that 1Il has
an internal point relative to the least vector subspace containing ...\1,
it cannot be eliminated entirel).. Another approach to this result was
given hy Stone [2] and summarized by Klee [3; p. 455].
Tukey [I; p. 96] proved that separation of an open convex 8et
462
V. CONVEX SETS ANn WEAK TOPOLOGIES
V.I2
V.12
NOTES AND REMARKS
463
this topology. Bourgm [1; p. 608] amplified this hy exhibiting a set
which is compact in the 3:' topology of the conjugate of a B-space 1:,
a.nd whose only convergent sequenceg are constant after some index.
Wehausen [1] showed that the weak topo]ogy i8 equiva]ent to a norm
topology if and only if the :space is finite dimensional.
It may be mentioned that some authors refer to the I topo]ogy
of 3:'* as the ,"eak* (or w*) lopology of I*, but we shall not use this term.
Theorem 8.9 is due to Phillips [7; p. 116,. Dieudonne [8; p. 109]
proved 3.9 after estab1ishing Lemma 8.10 by induction. The Case of
Theorem 3.9 in which I = 't)* and r = 't). was proved in the scpa ra -
ble case by Banach I; p. 131] and in fuU genera]ity by AlaOl,>lu [1;
p. 256]. Michael [I] gave an extension of Lemma 3.10 to a rn8(' where
tinear operators are considered.
The equivalence of weak and strong closure for subs] of a
nonned linear space (a special case of Theorem 3.13) appears in
Banach [1; pp. 58, 184]. )lazur [1; p. 80] showed that a stroll/,,"yclosOO
convex set in a norm£d lipear space contains all the weak limits of
sequeIl("f"S in the set. His proof requires only minor changes to yield
Theorem 8.13. Banach and Saks [I] proved that every weakly con-
vergent sequence {:v n } ill L:p(Ot I} or lfJ' P > 1, contains a subsequence
{Yi} which is (C, I )-summable in norm; i.e.. {n- 1 I;:t y,} converg s
strongly. That this stronger version of Corollary 8.14 IS not true In
C[O, I]" waS demonstrated by a counterexample due to Schreier [1].
By studying general convex combinations, ZaIcw..-r [I] and Gille8-
pie and Hurwitz [1; p. 588] independent]y proved the validity of
Corollary 8.14 in the 8pace C[O, 1]. Kakutani [22] gaw a proof of
the BRnnch-Seks theorem valid in any uniformly convex space.
The fact that the ordinary (metric) continuity of a linear trans-
formation between B-spaces implies weak continuity was observed
by Banach [I; p. 143]. The converse implication in Theorem 8.15 was
proved by Dunford [1; p. 317]. A number of other results in this direc-
tion have been obtained by D.eudonne [3: pp. 122, 181-137].
In addition to the topologica] notions of closure which we hav.
studied, various special de£lnitjons of closure for subspaces or convex
subsets of a linear topological spa.ce have been considered. In his
treatise Banach introduced the notions of rtgular and transfinite
dnsure for linear manifolds in the conjugate of a general B-space. and
showed that these concepts are equivalent (see Banach [1; p. 121]).
Banach [I; p. 124] also pro,'ed that in the case of a separahle space
these notions coincide wIth that of closure in the I topology of I*.
Alaoglu [I; p. 256] and Kakutani [2; p. 170] independent1yestablished
the equivalence of these types of closure without any separability
a.ssumptions. In a similar vein, Krein nnd SmuIian [1] introduced a
definition of a Tq;ularly crm:tJe:r 8et in I*. It is not difficult to establish
that the reguJarly convex sets in I* are merely the convex sets which
are closed in the 3:; topology of 3:'*.
Weak IDpologiu and Tefl£.rivily. A sequential form of the important
Theorem 4.2 was demonstrated by Banach [1; p, 128] for separable
spaces; A]aoglu [1; p. 255] proved it in the fonn stated. (This theorem
bad been announced earlier in full generality 1 but without proof, by
Alaoglu [2], Bourbaki [1] and Kakutani [3: p. 63]). Theorem 4.5 is
due to Goldstine [1; p. 128]. although he expressed this result in
other terms, and gave quite a different proof. Other proofs more
closely related to the one presented here were offered by Kakutani
[2: p. In], Day [2; p. 764], and Dieudonne [3; p. 187].
Theorem 4.7 was proved for separable 8paces by Banach [1;
p. 189]1 and a number of generalizations to arbitrary spaces ha.ve been
made. The form In which we state Theorem 4.7 is the same as that
employed by Bourbaki [I: p. 1703], whose argument was not presented
in detail. The method of our proof is '-eI"Y similar to that suggested by
KaIrutani [3; p_ 64] and [2; p. 171]. This theorem was al80 proved by
Smulian [2: p. 471] independently. The stronger result that reflexivity
is equivalent to weak sequential compactness of the unit sphere of a
B-sJ>a<-'<' is due to EberleIn [I].
Let I be a linear spare, and let r be a tota] subspaet' of I*. The
notion of r-compactness is related to various other notions of com-
pactness which have been introduced for convex sets. The theorem
below, which makes use of the theory of cardinal and ordina1 numhers.
is typical of the results which have been proved in this direction. Re-
sults of this sort. which relate compactness and convexity to variou.
types of transfinite processes, are studied in Banachls treatise, but
much of the recent progeess along these lines is due to the work of
:such Russian mathematicians as Smulian [I, 5 8. 101. Gantmacher
and Smu!ian [I], and Milman [I]. See also Phillips [1].
464
v. COSVE.X SETs AND WEAK TOPOLOGIES
V.I2
V.I2
NOTES AND BEMABKS
465
THEOREM. (Smulian) Ler I be a linear .pace and let K be a c,,,,vea:
sub.et 0130. L.I rbe alota/subspace 01 1*. Thm menta (1)-(4) are
cguivalent.
(1) K is compact in the r ropology.
(2) II xI' < e, e a limil fHdinnl, i8 a tramlinirc IICC}U€IU'C in K.
r1u:n there is an x. K with
lim inf Bi/("'E) < 1("'.) :;;: lim sup :!t/(x,),
c 8 t-s
lim inf &l/{x E ) Bl/(Ii) :;;: lim sup Blj(x,). Ie r.
!-+ l-+O
Since, by (*),
limBlj(x l ) =&lIP(f) for IeF'.
1->'
inf BlI(x) ,;: &l1P(f) ,;: sup &l/("'),
_ ..K
ler
we have YtIP(j) = &lllli) far I e F', from which </J(/) = 1(1i), I. F' fol.
lows readily. IfN is a finite cardinal n. thenF' = {fl" . ., I.}. and we
Can argue os follows. The setK' = {[fl("')' . . ., I.("')]}, x £ K, is clearly
a convex subset of n.dimensional Euclidean space. The set K' is easily
seen to be closed, by (2). If we put p, = </J(f,) and p = [Pl' . . ., P.].
we see that p; K'. Thus, by Theorem 2.10, we can find scalars
a. I , . . .0 D:n and real numbers c and B E. > 0, such that
lor ler.
(S) For every I. r, sup_ &l/(x) < 00; nwTcover, each linear
jtmd:iooal <1> on r which satisfies
also salislics
. .
Bi(2«,P,) > c+c > c> Bl(2«.!,(X)),
i-I i:_]
xeK.
<1>(/) = I(x.),
ler
.
Thus 2 rJ.,f. = Ie r, and
i l
for some 3: 0 E K.
(4) II KI' < e, 8 a limit CJTd;nal, is a monotone decreasing tram.
linite scfJucTu'c of r-clased conve'" s.18, all intersecting K, Ihcn
Kn(nK,) <F</J.
Bl<t>(f) > c+c > c > BlI(",), a: e K.
which contradicts the hypothesis in (8).
Finally, (S) implies (I); for, let (S) hold. To each Xe K let there
correspond the functional <1> on r defined by
PROOF. That (1) implies (4) is clear. Statement (4) implies state-
ment (2); far if we define
KI = co (U"'.).
.<1
the closure being taken in thertopology, then K, satisfies the require-
ments of (4); and if x.' Kn (nK,), x. is clearly as desired in (2).
Now, (2) implies (8): for, assuming (2), let </J be as in (S), Sup-
pose (S) is false, and let II be the least cardinal for which there exists
a subset F' of r with cardinality II such that we do not have
</Jlf) =/{"'),
leF'
<t>(j) I(x).
It follows from (S I that K is mapped onta the set
{<t>J<t> e r+. inf Bl/(K) :;;: Bl</J(f) ;0; sup &If(K)},
This mapping is easily seen ta be a homeomorphism if hoth I and r+
are taken with their r topology. The compactne8s of K' now follows
readily from Lemma 4.1. Q.E.D.
Weak topoiogiL8 and compactness. The direct assertions in Theo-
rem 5.1 and Tbeorem 5.2 are due ta Banach [1; p. 185].
The special case of Thearem 5.7 dealing with subspaces of the
conjugate .pace of a B-space was announced by Bourbaki [I], and a
proof given by Dieudonne [8: p. 129]. The general case of Theorem 5.1
is due ta Krein and Smuhan [1].
The definition of the BX-topolagy, and the proof of Lemma 5.4.
are due ta Dieudonne [8]. For an extension of Theorem 5.7 ta more
general spaces, see Kothe [10].
for any a: K. Let 8 be the least ordinal of cardiruility N, and well-
order r' os h, E < 8. If R is infinite, 8 is a limit ordinAl. In this case
we can find a transfinite sequence {xI} of elements of K. such that
(*) t1>(/.) = I.(x,) for '1 .
Then, hy (2), we can find tteK with
466
'\'. CONVEX SETS AXD WEAK TOPOLOGIES
V.12
V.I2
NOTES AND R.Er.uRKS
467
The fundamental Theorem 6.1 developed gradually. Smulian [8]
proved that (ii} implies (i} and also that the weak sequential closure
<Jf a weakly sequentially compact set is itself weakly sequentiaIly
compact. (See Krein and Smulian [1] for the latter.) Eberlein [1]
showoo that a set IS weakly compact if and only if it is weakly closed
.and weakly sequentially compact, The proof given here is an ingenious
modification of the proofs of Smulian and Eberlein and is due to
Brace [1, 2]. Generalizations of these results to more general spaces
have been given by Grothendieck [I, 2], Collins [1], Dieudonm! and
Schwartz [1; p. 89], and Pt!k [1, 2,3].
Theorem 6.2 is due to Smu]ian [5]. Another proof was given by
Klee [4], and an extension to more general spaces by Dieudonne [15].
In tbe case of a separable B.space, Theorem 6.4 was proved by
Krein [1], and the general case by Krein and Smulian [I; p.581]; see
.also Phillips [1].
EtdrrnUll points. Theorem 8.4 is due essentially to Krein and
Mi]man [1]. An improved version of Theorem 8.4 was subsequently
proved by Milman and Rutman [1], We have given the proof of Theo-
rem 8.4 due to Kelley [1]. See also HoUa [1], Yosida and Fukamiya
[I].
Lemma 8.6 is due to Arens and Kelley [1], who used it to prove
Theorem 8.8. Milman [2, S, 4] gives related results concerning e.-rtre-
mal points. Theorem 8.8 itself is due to Banach [1; p. 173] in a specia1
case. and to Stone [1; p. 469] in the general case.
Tangellt fundiona!s. Lemmas 9.1 and 9.3 and Theorem 9.5 are
<lue to Ascoli [I; pp. 53-56, 205] in the case of a separable normed
space, and to Mazur [1; pp. 75-78] in the case of an arbitrary normed
space. Theorem 9.8 is al80 due to Mazur [1]. Moskovitz and Dine8
[1; p. 526] proved Theorem 9.7 for Hi]bertspace, buttheirproofnceds
no modification for a general space.
Other proofs that a convex set with an interior point has a tan-
gent plane at every boundary point were given by Moskovitz and
Dines [2], and KIee [1. S; p. 457], to whom 9.10-9.12 are due. Mos.
kovitz and Dines [1; p. 531], and Klee [1; p. 771], give examples to
-show that it is not possible to drop the condition that an interior
point exists and still have a tangent plane at every boundary point.
A number of other results concerning convex sets in very general
space8 are contained in KI.e [3].
F;.ced point theom1l8. A proDf of the Brouwer fixed point theorem,
using R minimum of homology theory, is given in Graves [2; p. 149].
AI.xandroff and Hopf [1: 377] give another proof of this theorem
together with a discussion of various other fixed point theorems that
can be obtained by homological methods. See al80 Hurewicz and
Wallman [1; p. 40] or Lefschetz [I; p. 318 ff], [2; p. 117].
Before we prove the Brouwer fixed point theorem) we observe
that the Case of complex :scalars is a consequence of the case of real
scalars. This follows from the fact that the complex space E" is iso-
metric with the natural space E2n) and the unit spheres in these spaces
correspond in R natural way. Thus we restrict our attention to real
Euclidean spnce. We will need the following lemma.
LEMMA. Let 1 be an irl/illitely difftTentioble /u,u:ti,m 01 n + I variabks
(:ro. . . ., "'n) with ,,,.lI«>. in En. Let D, dt:note the ddcrmifUlnt rofwst.
columns are the n partial dt:riOOtiVl?8 f. , . . ., f . , f . ... ., f - . Then
" i-I t+1 ....
n iJ
I(-I)'-D,=o.
'-0 ax,
PROOF. For every pair i, i of unequal integers between 0 and n,
let Cfj denote the determinant whose first column is f and whose
remaining columns are / . . ., /2 arranged in order f increasin g
, .
indices, and where Jr and 1:1:- are omitted from the enumeration. Clear-
, ,
ly Cij = Cft, and by the laws governing differentiation of determinanb
.and Interchange of columns in them we have
(*]
a
- iJ D,=I(-IPC,,+I(-I)HC.,.
x. i<'i 1>1:
Hence
iJ "
(-I}'" D, = I (-l)'''C,,-u(i,j),
U,xi f=O
where <I(i, i) = 1 if i < i, l1(i. i) = 0 if i = j, and <I(i, j) = -I if
i > i, Thus
n V "
I(-I)'"D,= I (-I)i+JC"I1(;.j).
1...0 (IX. l.f=O
J
468
v. CONVEX SETS AND WEAK TOPOLOGiES
V,I2
V.12
OTES AND REMARKS
469
Interchanging the dummy indices i, i in this latter expression and
using the fact that G(i. i) = -G(j, i), we see that
,
=(-l)}; ( 1);+;C"G(i,i).
..1
(x, x-4>(x») * 0, for otherwise (x. 4>(x)) = 1 and the inner product of
two vectors with length at most 1 can be equal to I only when they
are equal Thus the discriminant is ne'\'er zero for m in S. Since the
function t 112 is an infinitely differentiable function of t for t > 0, and
since Ix 4>(re II * 0, Il. 8, it follows from formula [+] that the
function a(ll) is an infinitely differentiable function of x.8. IIl0re-
over, it follows from [+J that a(x) = 0 for Ix1 = I. Now, for each reaI
number t. put I(t; "') = ",+Ia("')("'-4>("')). Then I is an infinitely dif-
ferentiable function of the n+l variables tt tel' . . ",;en. with values in
En. Since a(",) = 0 for Ixl = 1, we have I,(t; x) = 0 for Ixl = I. Also
/(0; "') = x, and from the definition of a we have 1/(1: "'II = I for all
x.8.
Denote the determinant who8e columns are the vectors I. (t; ",),
,
. . ., I. (I: "') by Do(/; "') and consider the integral
.
I(t) = J . . J Do(/; ",)d.x,. . . da:..
It is de... that I{O) is the volume of 8 and hence 1(0) * O. Since
1(1: "') satisfies the non-trivial functional depel!<lence 1/(1; x)1 = I, it
follows that the Jacobian determinant Do(l: x) is identically zero,
hence 1(1) = O. The desired contradiction will be obtained if we can
show thAt I(t) is a constant: i.e., that I'(t) = O. To prove this, differ-
entiate under the integral sign and employ [oJ to conclude that I'(t\
is a sum of mtegrals of the form
" ,
}; (-I)'+;C"G(i,i) = }; (-I)I+lC"G(i. i)
f,1-0 ."...{I
Thus all the three equal quantities in the formula just written must
be zero. and formula [*] is proved. Q.E.D.
THEOREM. (Brouwer) II 4> is a c01IliuUQU8 mapping 01 the closed
unit 8phere 8 = {"" E'lIxl S I} 01 Euditkan ..-space into itself. then
there i8 a point y in 8 BUCk thaJ 4>(y) = y.
PROOF. We have remarked that it suffices to consider real
Euclidean space. Further, the Weierstrass approximation theorem for
continuous functions of It variables implies that every continuous
map 4> of 8 into itself is the uniform limit of B sequence {4>.} of infinite-
ly differentiable mappings of S into itself. Suppose that the theorem
were proved for infinitely differentiable map'. Then, for each integer
k there is a point y.' 8 such that 4>k(Y') = y,. Since 8 is compact.
some subsequence {y ) con'\'erges to a point y in S. Since lim.,-+cv 4>k, (it')
....(:<) uniformly on S. 4>(y) = liml--> 4>. (y, ) = lim.-+.. Y. = y.
or i "
This shows that it is sufficient to consider the case that {> is infinitely
differentiable.
We suppose that {> is an infinitely differentiable map of 8 into
itself and that 4>(:<) oF x, a:. 8. Lct a = a(",) be the larger root ofthe
quadratic equation Ix+a(x-4>(x))I" = 1. so that
I = ("'+a(a: "'(x)), ",+a(Il-4>(x)))
= I x l"+2a(:<, :<-4>(x))+a"I"'-4>("'JI2.
:f: f '" f D,(/; x)d.r",.. da:..
s iJx;.
where Di(t; x) is the determinant whose columns are the vectors
c++]
[+J I"'-{>("')I"a = ("'.4>(X)-Il)
+{(x, x-{>(",)2-j-(I-I"'I')I:<-4>(IlI!'}I/".
Since Ix-4>(x)) * 0 for ",.8, the discriminant (:<, x-4>("'»'
-j-(I-I:<I')lx-4>("'JI" is positive when Ixl * I. Also if Ixl = I, then
f,(/; x), 1.,(1; :<), . . ., f.._.(I: ",). 1.,.,(/: x). " . ",1',(1; x).
Let Sf denote the unit sphere in the space of variables .xl' . . 'J Xi-I'
"'HI' ..., x.. Let "'i denote the positive square root {I-(oti +.".
+x._ +x,+ +... +a?,;)}lI',Bndx"idenotethecorrespondingnegativc
square root; let pt denote the point whose j-th coordinate is Xi if
i * i and is "'i if j = i, and let P"i denote the point whose j-th
coordinate is x; if j * i and is "'"i if j = i, Then the integral in [++]
is
By the quadratic formula
470
'". CONV.E:X SETS AND WEAK TOPOLOGIES
V,I2
V.I2
NOTES .AND REMARKS
471
:1: I. . . f D.{t; p1')dx l . . . dx'_ 1 dx'+I . . .dx.
s.
:1: I. . . f Dilt; p-;-)dx l . . . (lX'_1 dx HI . . . dx..
s;
But 'p1'1 = Ip-;-I = 1 and since ,,(t; "') = 0 for 1"'1 = I, it f01l0ws from
the definition of D i that these integrals are zero. This completes the
proof. Q.E.D.
Birkhoff and Kcllogg [I] were the first to make an extension to
infinite dimensional vector spaces. by proving that compact convex
sets in C.[O. 1] and 1.0[0, 1] have the fixed point property, and by
applying these results to differential and integral equations. Sehauder
extended this theorem, first to compact COnvex sets in a B-spaee with
a basis [1]. and then to arbitrary B-spaees [2]. It remained for Tycho-
noff [1] to make the generalization to locally convex topological linear
spoces, in which form the theorem is applicablc to the weak topologies
as well as the strong topology in B-spaces.
Of other generalizations of fixed pomt theorems, we mention the
following due to Rothe [I]; A continuous mapping of the solid unit
sphere S of a B-space I into a condItionally compact subsct of iii,
which sends the boundary {"'lIxl = I} into S, has at least one fixed
point
M08t of the papers mentioned above bave applications to differ-
ential equations. Discussions of fixed point and other abstract ap
proaches to existence theorems for differential equations can be
found in the expository' articles of L. M. Graves [1] and Leroy [1]. The
work of Miranda [1] and Niemytsky I] will also be useful; the
former is particularly recommended because of its extensive bibliog-
raphy. It might be mentioned that although fixed points and other
topological methods generally yield only existence theorems, Aronszajn
2] and Rothe [2], among others, have indicated bow uniqueness
theorems can also be obtained.
Applying Corollary 4.7, it follows that every weakly continuous
(i.e., contInuous in the weak topology) mapping of the unit sphere of
a reflexive B-space into Itself always has a fixed point. Kakutani [5]
ga've an example to show that the corre:sponding statement for strong-
ly contmuous maps if; not true t-"llen for a homeomorphism of the
sphere of Hilbert space onto itself. Dugundji [1] showed that thc unit
sphere of a B-spaee with the strong topology has the fixed point
propert)' if and or-Iy if the space is finite dimensional.
StudIes have been made of the "nature" and the "stability" of
fixed points of functions in a suitable neighborhood of a given func-
tion whose fixed points are known. For questions of this nature see
Fort [I], Kinoshita [1], and Wehaw;en 2].
Markov [1] pro.-ed Theorem 10.6 by using the Tychonoff theo-
rem. The proof gIVen here is essentially that of Kakutani [ ], who
made SEveml applications of this result, and to whom Theorem 10.8
is due, (See also Peck [1].)
The material in 11.14- n.I8 IS taken from BrodskiI and
Milman [1].
Finite diJnrnsimuJl spaces. This chapter ha.s been cOnImed to the
treatment of convex sebs in infinite dimensional spares. There is a
very extensive theory of thc special properties of convcx sets in finite
dimensional spaces. }I'Of thh:" the reader is referred to the work of
Minkowski [1] and the treatise of Bonnescn and Fenchel [1]. The
latter contains a great wea.lth of results and applications, Rnd a large
bibliography.
Locally oom'l?x spaces. \Ve have discussed only a small portion of
the very extensive theory of locally convex linear topological :;paces.
The theory of such spaces has been extended considerably further
than we havc indicated. Moreover, many results have been obta.ined
for topological linear spaces which are not assumed to have the prop-
erty of local convexity. The interesred reader should consult the
treatises of Bourbaki [2] find Nakano [I], and the expository article
of Hyers [3].
Uniform conveJ:ity and differentiability of norm.. The tangent
plane theory of Section 9 has been considerably extended in various
directions. One of the roost interesting lines of investigation is con-
cerned with the derivability of the support function II"') of a convex
body in a stronger sense than that of 9.2,
DEFINITION. Let I be the support function of a convex body con-
taining the origin as .an interior point. and let T be its tangent funL-tion.
If
472
v. CONVEX SETS AND 'WEAK .TOPOLOGIEs
V,II/
V.II/
NOTES AND REMARKS
478
I
lim _ I 1 (lea: + y) - l(a:) - .-(a:, y)} = 0,
I.I--+ Y
we say that l is slrongly difft:rrnlia!Jle at the point a:.
Banach [1; p. 168] sbowed that the norm in C[O, 1] is strong1y
differentiab1e at a: o < C[O, I] if and only if the function a: o achieves its
maximum at exactJy one point. Mazur [I; p. 78-79] proved that the
same condition holds in B(S), that the norm in L , p > 1 is strongly
differentiable at every point but tbe origin, and gave conditions for
strong differentiability of the norm in the space L,.. He also 8howed
that in the F...pace ofmeasurab1e functions on [0, I], the norm is not
differentiable at any point.
Mazur [3] proved that in a ret1exlve space in which the norm is
strongly differentiable at every non.zero point, a bounded closed
COnvex set is the intersection of all the closed spheres which contain it.
v
Smulian [4. 6. 7.' 9] proved a number of result!; concerning dif.
ferentiability and other properties. In the first two papers, necessary
and sufficient conditions for a weaker type of differentiability of the
norms in I and};. are given, together with resu1t!; relating differentia-
bility, tangent pJanes to the unit sphere. reflexivity and various other
geometrical properties.
SmuJian [7] obtains two interesting necessary and sufficient con
ditions for strong differf'ntiability of the norm.
THEOREM. In order that the norm is sfrongly diflerrnJiahle al a poinl
a: in a B-span I, it is tm:e88O.ty and sulfiri£nt that et""1l BelJIM!1U:t! 01
elements a:: .l* satis/yit!g 1":1 ;;;; 1 and a::(.,) --+ 1"1, is convergent.
THEOREM. In order that the norm is strongly difln-cntial>k at a
point.,. in the conjuga!e I* vf a B-space I, il is necessary and suffidenl
that every sequence 01 ckments a:. < I satisfying Ix.1 ;;;; 1 and .,.(a:.)
-+- Ix. i is c O l1vergent
In [7], Smulian gives resuJts reJating strong differentiability of
the norm with reflexivity, weak completeness, and uniform convexity
(see below). Smulian [9] pursues this study further, deriving condi-
tions for strong differentiability in l , c, c.' C(S) and L,., and proving
a few results concerning differentiability of norms in Banach algebras.
James [1/] applies differentiability concepts to derive a number
of results concerning a type of "orthogonality" in normed linear
spaces.
The two results of Smulian, cited above. add interest to the fol-
lowing definition, due to Clarla;on [1].
DEFINITION. A B.space 3: IS saId to be uniJormly e<nwe:l: if when-
ever "'. < 3:, Y.' I, ["'.1 ;;;; 1, ly.1 I, and IX.+Ynl --+ 2, then I"'.-Ynl
--+0.
Clarkson [I] showed that the space" L., p> I, are unifoITnly
convex (see also Boas [I]). It has been shown by Milman [1] and
Pettis [1/] (see also Kakutani [1/]) that every uniformly con-rex B-
space is reflexive, but that there are reflexive spaces which are not
equivaJcnt to any uniformly convex space (Day [3]).
Day [5] showed that unifonn convexity in the neighborhood of a
point imp1ies uniform convexity, and (Day [4,6]) demonstrated that
under certain conditions oombinations also yield uniformly convex
spaces. A duaJ notion of "uniform flattening" is reJated to that of
uniform convexity by Day [6],
For other results on uniform convexity see the papers of Smu1ian
aJready cited, and a180 Fortet [I, 1/, 3], James [2], Kra6kovskii and
Vinogradov [I], and Ruston [1].
BiU;ogr
C01WCX SCfs: Ascoli [1], Botts [I], Brodskii amI Milman [I],
Dieudonne [I. 2], Eberlein [1/], EideJheit [I], Halperin [2], Klee
[1,1/,3, 4], Krein [1], Krein and SmuJian [I], Mazur [1, 1/, 8], Mos-
kovitz and Dines [I, 2]. Schoenberg [1/], SmuJian [8, IO]. Stone [2],
TagamJitzki [1/], Tukey [1], Yosida and Fukamiya [1].
Weak wpalagies and Teflr.rivi1y: Alaoglu [1], Arens [1], Bourbaki
[1], Bourgin [1], Dieudonne [3], Dieudonne and Schwartz [1], Day
[2, 8], Eberlein [1], Gantmacher and Smulian [I, 1/], Goldstine [I],
James [4], Kakutani [2, 3], Klee [7], Krein and Smulian [I], Mackey
[1, 1/], Milman [1]. von Neumann [2], Pettis [I, 2], Phillips [I],
Ruston [4], Smulian [1-10, 12, 18], Taylor [2. 3].
Rdrcmul poinfs: Arens and Kelley [IJ, Hotta [I], Jerison [2],
Kelley [I], Krein and Milman [1], Milman [2,8,4,7], Milman and
Rutman [1], Tomita [1], Yosida and Fukamiya [1].
474
V. CONVEX SETS AND WEAK TOPOLOGIES
V.I2
Fia:ed point tMurems: Birkhoff and Kellogg [I J. Brouwer [I],
Fort [1], Hukuhara [I , Inaba I], Kakutani [4, 5] Kinoshita [I],
Krein and Smulian [I], Leroy [11, Markov [1 J, l\!iranda [1 J, Niemytsky
[1], O'Neill [I], Peck [I], Rothe [1, 2J, Schauder [I, 2], Tychonoff [1],
Wehausen [2], Yood [8].
Topalogicallinear spaas: Arens [I], Bourgin [2], Dieudonne [3],
Dieudonne and Schwartz [1], Donoghue and Smith [I], Grothendieck
[I, 2], Hyers [1, 2], Klee [3, 4], Kolomogoroff [I], Mackfy [1, 2],
von Neumann [1], Tychonoff [I], Wehausen [1].
Uniform cDnve:xity: Boas [I], Clarkson [I], Day [8, 4, 5, 6],
Fortet [1, 2, 3], .James [2], Kakutani [22], Kraekoyskii and Vinogra-
dov [I], Lovag!ia [lJ, Mihnan [I], Pettis [2], Ruston [1], Smulian
[4,6,7,9].
DijJercllJinbili!y of the norm: Banach [I], .James [2], }Iazur [1],
Smu1ian [4 6t 7, 91.
CHAPTER VI
Operator8 and Their Adjoints
This chapter continu Si the study of linear maps hetween B
spact'S begun in Chapter II. Various topologies .are introduced in the
space B(I, Ill) of bounded linear maps between the B.spaces I and \1).
The notions of adjoint operators, projection operators. weakly com-
pact operators and compact operators are introduced, and the basic
properties of these operators arc studied. Representations for various
general classes of operators in the spaces of continuous and integrable
functions are given Othersimilarrepresentation theorems are contained
in the exercises. In addition, the important conve:xity theorem of
M. Riesz is discU5SCd. Throllghout the chapter, tlu! symbols 3:, \1), .B will
<1",01. B-spaca, unless the contrary is explicitly stated.
We recall that If T is in B(I), we shan frequently say that T
is an opera.tor in I
I. The Space B( E, VJ)
A B-spet't' I has at least two important topologies: the strong,
or metric, topology and the weak, or 3:*, topology. If E is the conjugate
space of \1), there is also the 'lJ topology in :E.
The linear spa= B(3:, \1) of continuous linear mnppmgs T : I-->-\1)
has a correspondingly more comphcated set of topologies. The three
most commonly used topologies in B(:E, \1) are the ,,"ifo,m, stTo"g,
and _ok operalor ropalogics, as given in the following definitions.
I DEFINITION. Thc uniftlTm operatDT topology in B(I, \1) is thc
metric topology of B(I, \1) induced by its norm,
ITI = sup jT"'I_
1 1 1
2 DEFINITION. The strong ope,ator lopmogo in B(I, \1) is the
topology defined by the basic set of neighborhoods
475
476
VI. OPERATORS AND THEIR ADJOINt'S
VI.l.S
VI.I.4
THE SPACE B(l, ID)
477
N(T; A, e) = {RIR E B(I. ID).I(T-R)x[ < E, "'. A}
where A is an arbitrary finite subset of I, and 10 > 0 is arbitrary. Thus,
in the strong topology. a generalized sequence {Tn} converges to T if
and only if {T "",} converges to T", for every '" in I.
S DEFINITION. The 'Weak operafcr topology in B(I, W) is the topo-
logy defined by the basic set of neighborhoods
N(T; A, B, 10) = {RIB E B{I. W), ly*(T-B).r1 < 10,
strong. and the weak operator topologies in B(I, ID). It is evident
that the uniform operator topology is stronger than the strong opera-
tor topology. and that the strong operator topology is stronger than
the weak operator topology,
Witb its unifonn operator topology. B(I. W) becomes a B-space;
as such. it has a weak topology which shonld not be confused with
the weak operator topology in B(I, WI.
4 THEOREM. A linear lundimooJ on B(I. W) is conun'UfJus with
respecl to tlu: WEak opera1or topology il and only il if is coRtin"""> with
nsped to th£ stTtmg operahJr topology.
PROOF, Since the strong operator topology is stronger than the
weak operator topology. a functional continuous in the weak topoWro'
IS continuous in the strong topology. Conversely. let F be a functional
on jS = B(I, W) which is continuous in the strong topology. Then
there exists a finite subset {x,., . . .. m",} of I and an E > 0 such that
IT"'.I < E, T. jS, i = I, . . ., n implies IF(TH < l.
Consider the B-space W. = ID (j) . . . (!) ID of all n-tuples =
(y., . , "y.] with y,' ID. i = 1, . . ..11; the norm 10 ID. is I[Y1' . . .. y.]1
= max,,;,s;. ly,l. Derine H :!B ->- ID. by HT = [T"'l' . . ., T",.], and
put I{'II) = F(T) if'll.H(!B) and 'II =HT. Since jH(T)1 <li.implies
IF(T)j < li. / is well-defined and continuous on H(!B). By II.S.I1,
I has a continuous linear extension I. defined on all of ID.. It is easily
seen that any such functional must have the form
y* . B, '" E A}.
where A and B are arbitrary finite sets of elements in I and W*,
respectively. and E > 0 is arbitrary. Thus, in the weak topology. a
generalized sequence {Tn} converge8 to T if and only if {y'T.,a:} con-
verges to y*T", for every '" in I and y* in W'.
These topologies are by no means the only interesting topologies
of B(I, ID). Other topologies in B( I, W) can be introduced in such a
way that the convergenee of a generalized sequence {T.J to a limit T
means anyone of the fol1mving:
(i) for each a; in :E. the generalized sequence {T.,a:} converges
to To: uniformly for", in any compact subset of I;
Iii) for each y* in ID'. the generalized sequence {y*T.4 con-
verges to y'T'" unifonnly for 0: in any compact (or bounded) subset
of I;
(iii) the generalized sequence {T.} converges to T as defined in
<i) or (ii). with "compact" replaced by "weakly compact";
. (iv) ifW is the conjugate space of.8, then in the.8 topology of [J,
1m... T.,a: = T", for any a;. I, or the same limit holding uniformly in
compact, weakly sequentially compact, or bounded subsets of :E
As a final example, we mention the topology whose basic neigh-
borhoods are
"
I.[YI' . . .. Y.] = I Y (Y.).
'_1
..
N(T; "'1' "'.,..., .) = {RIR E B(1:, [J), II(R-T).x.1 < E}.
'-1
where c > 0 is arbitrary, and .t:'l &V,2, . . . is an arbitrary sequence of
elements in I with z::'ll"',1 < 00.
With each of these topolog1es, B(I, 'D) is a locally convex linear
topological space. In this text, interest centers in the uniform the
.
where y . ID*, i = 1. ..., n. Consequently. F(T) = ft(HT) has the
form F(T) = I _l!t.T"'., and it is then obvIous that F is continuous
in the weak operator topology. Q.E.D.
5 COROLLARY. A conce", set in H(I. 'g) has tlu: same c/a8Ure in the
'Weak operalor topology a8 it do.. in tlu: sfrong operator topology.
PROOF. This fonows immediately from Theorem 4 and CorollAry
V.2.I4. Q.E.D.
478
VI. OPERATORS AND TIIEJ:R ADJOI:OOTS
vr.2.1
V1.2.6
ADJOINTS
479
2. Adjoint><
1 DEFINITION. The adjoint T' of a linear operawr T in B(I, n
is the mapping from 1lI* to 3<:* defined by T"y' = y*T.
2 LEMMA. The mapping T -+ T* i8 an isometric isomorphism
of B(I, Ill) i..w B@", I").
PROOF. The linear functiorwJ y"T is continuous (1.4.17), and
hence T.y* E x*. The map T -+ T* is clearly linear. From 11.8.15"
ITxl = sup IY"Txl. and thus
1.,91:;;1
6 LE....A. If T is in B(I, Ill), th< s«ond adjoint T.... : I.... -+
Ill'" is an ezll'llsion of T. If I is refl£xive then T** = T.
PROOF. Let x I, y*EIlI". Then,
{T"*a:)y* = ",T*y* = (T*y*)", = y*Tw = ri'a:)y*
IT" I = sup IT"y*1 = sup sup ly*Twl
11I-J;S;l JJI'I l Irr l
= sup sup ly*T"'1 = sup ITxl = ITI,
l::tl . 1...I 1 11I:1 1.
which sl10ws that the map T -». Tfc is an isometric isomorphism.
Q.E.D.
Q.E.D.
7 LEMMA. A li..ear optTator T in B{I, Ill) hM a bounded iJlZ..rse
T l defi.U'd on all of III if and o..ly if its adjoint T* has a bounded in-
verse {T*)-l defin€d on all of if*. When t""se invers," exist, (T l)*
= (T*)-I.
PROOF. If T-I exists and is in B(IlI,3<:), then, by Lemma 4,
(TT-I)* = (T-I)'T' is the identity in 1lI* and (T lT)* = T"(T ')*
is the identity on I*. 7hus (T*) l exists. is in B(I", 1lI*). and equals
(T-I)*. Com'ersely, if (T*)-l exists and is in B{I*, 1lI*), then, by
what has already been proved, (T**)-I exists and is in B(\!J*', if").
Thus T*. is a homeomorphismi by Lemma 6, it is an extension of T.
Hence T IS one-to-onc, and TJ. is closed. It only remains to be 8hown
that TJ. = Ill. If y EIlI and Y 1 T:£, there is (1I.8.J3) a y* in Ill' with
y* #- 0, y*T = T'y. = O. This contradicts the assumption that T*
is one-to-one, and proves the Jemma. Q.E.D.
The final argument in the above proof also establishes the follow-
ing lemma.
8 LEMMA. If T is in B(!, Ill), t""n the do.",... in ID of TI is the
ee! of ,..doTe y such that y*y = 0 for each y* which .ati.fies tM i!tJIUltion
T*y* = O.
For operators in a Hilbert space, a slightly different notion of the
adjoint is customary. Let be a Hilbert space, and let T e B( ).
Then the adjoint operator T. of T is in B( *), Howcvcr, since 5;1
and * are intimately related, as is shown by TIleorem IV.4.5, it is
customary to refer to the operator T. = oT1"I, where C1 : ' -+ is
the map given by Theorem IV.4.5, as the adjoint of T, if T e B( ).
7his has the advantage that T. is in B( ) rather than in B( .).
We call T. the Hilbert space adjoint ofT. Let us give a formal definition.
9 DEFII<XTION. Let be a Hilbert space, and let T B(,\;').
There is a uniquely determined operator T* B(.\l), called the Hilbert
space adjoin! of T, which satisf.es the identity
3 LEMMA. The adjoin! T* vf an vpaawr T in B(l:, Ill) is a co,,-
tinuo"s mapping vf 1lI* illlo 3<:* if the"" 8'pf1t:e8 have the ID and 3<: lopalvgies,
respedi...ly.
The proof is trivial, and is left to the reader.
4 LEM'IA. If T is in B(3<:. \!J), and U is in B(IlI, 81, then (UT)*
= T*U*. The adjoinl of the id£ntity in B(3<:) is the idenlily in B(I*).
PROOF. For z* E:.8*, (1;* E: x*
(UT)*z* = z'UT = (U.z*)T = T*(U*z*) = (T*U*)z*,
l*x* = 3;*1 = x*.
Q.E.D.
Thus the mapping T -+ T* of the ring B(I) into the ring B(I')
is an -<anti-isomorphism.'"
" "
5 DEFXNITION. Let I, ID be the images under the natural em-
beddiog of I, \!J inw I**, ID**. respeetively. For T e B(!, ), define
- "'" "
T. B(I, ID) by the equation Tx = fJ, where y = Tx. A function U
whose domain is a set in .* contaimng £ is said to be an fJ:lension of
T. if Ua: = Tx for a: in :E. Thus the notio11 of an extension of T is
applied as though if and i were identified. Similarly, if j; = 3<:*',
the equation U = T is understood to mean that Ua: = Tx for x in i
J
480
'VI. OPERATORS AND THEIR .o\DJOJNTS
VI.2.10
VI.8.2
PROJECI'lONS
.,\81
(T"" y) = (x, T'y),
x,y.ifJ
spaces corresponding to E are EI and (1- E)I, charncterized respee-
tiveI)- by Ex = '" and Ex = o.
Some useful elementary properties of projections are summarIzed
in the following lemmns. Further properties wiU be found in the exer-
cises
Unless the contrary is explicitly stated, lhe term adjoinl. and Ihe
8!J11Iboi T', when applied 10 an operaUn' in H i/hrt Bpace, will refer 10 lhe
Hilbert Bpace adjoinl. An operator T in Hilbert space is called self-
adjoin! if T' = T.
The preceding lemmas concerning adjoints take the following
form in Hilbert space.
. 10 LEMMA. If T and V are bounded linear opt!1"ulors in Hilbert
space, tJir"
(a) (T+V}' = T'+V.;
(b) (TU)' = V'T';
(c) (o:T)' = «T';
(d) I' =1;
(e) T" = T;
(f) IT' I = IT!;
(g) it either T-' or (T') ] e",is/s and is in B( }, then the other is
also. and IT ')' = (T'} ].
These stauments follow from Lemmas 2, 4,6. and 7, Q.E.D.
3. Projection.
A projection in an arbitrary linear space I has been defined in
Section I.ll as a linear operator E for which E' = E. If I is a linear
topological space, we shall require. from this point on, that E be
continuous.
2 LEMMA. L<I E, and E. be commuting projections in a B-space I.
If!IJI, = E,I, !J1, = (I-E;}I, i = 1,2, then
(a) EIE. = E. it and only ;rifJ/. !IJII' or equit'llWnlly, it and only
it !J1, !J1,;
(b) if E = E,+E.-EIE., then E i. a pTDi€di01! milk EI
= sp{ID/,u!lJl,,) and (I-E)I = !J1,n!J1.;
(c) il E = E,E., Ihen E is a pr0edion wilh EI = IDI, n!lJl" and
(I-E)I = sp{91,u!J1,};"
(d) il E = E,-E.,lhenEisaproieclionifandon!yil E,E. = E..
In Ihis eMe EI = IDI,n!J1" (I-E}I =!J1] EIJ!IJI".
The proofs are immediate consequences of the definitlons and
are left to the reader. (cf. Exercise 1.14.6.)
3 LEMMA. II E i$ a projEdion in iE, E* is a projcclion in I* ani!
E'i£' = {"'*Ix'''' = 0, "'E (I-E}i£)
(I-E*)l' = {x*lx.", 0, XE EI}.
PROOF. Clearly E*' = E* so E' is a projection. If ., E I and
E'y* = y*, then y'x = E'y'''' = y'Ex and y'(",-Ex) = O. Con-
versely, let y*(.,-Em) = 0 for every., in I. Then y*x = y' Em. y* =
y' E, Bnd y' = E'y'. The second statement follows from the fir8t by
sub.tituting I-E" for E". Q.E.D.
There is an interesting way in which projecl1ons can be ordered.
4 DEFINITION. Two projections aTe said to be ordered in their
natural order E. ;;;; E. if E,E. = E.E, = E,.
This amounts to requiring E,I E,.I, (I-E.)I;;! (I-E.}I.
The reader will have no difficulty in proving the next lemma.
5 LEMMA, Tm natural ordering < 01 proj«limUJ salistics
Ii) E, :S': E,;
(ii) il EI :S': E. and E. ;;;; E. then E, ;;; E.;
(iii) il E, :S': E. ani! E. ;;;; E,lhen E, = E.-
1 DEFINITION. A proj«lion in I is an operator E E BII} with
E'=E.
. If E is " projection in I, then every element", can be written
uniquely as lI. sum = it l +,xa where EX I = tel' Ex" = O. Indeed.
., = Em+(I-E}x is sucb B decomposition. Conversely, given two
closed linear subspares 1. Bnd I. of I such that every '" can be
written uniquely as '" = "', +"'2' "', E I, Bnd "'. E 1". then the function
E defined by E(",} = "', is B closed, and hence. by Theorem 1I.2.4. "
bounded linear transformation of I into 3: with E' = E. Thus there
is a one-tO-Dne correspondence between projections in I and direct
SWll decompositions of I into two closed subspaces I, Bnd :f,,- The sub-
482
VI. OPERATORS AND THEIR ADJOINTS
VI.u
VI.4.S
WEAKLY COMPACT OPERATORS
488
El V E. = EI+E,-EIE"
and the greatest lower bound
Ell', E. = E1E.,
These two operations will be of fundamental importance in
Volume II where we will introduce and disrnss the conccpt of a
Boolean algebra of projections in a B-space.
We conclude this section with a few remarks on projections in
Hilbert space. Let E be a projection in Hilbert space . and let E*
be its Hilbert space adjoint. Then the identity
(Err. (I-E)y) = (Err, y)-(E*&, y)
shows that the complementary manifolds EQ and (1- E)Sj are ortho-
gonal if and only if E = E* E, or, equivalently, E = E.. Thns a self-
adjoint projection is sometimes called an orllwgonnl or 'P"rpenmrolar
projedioll. Since closed complementary manifolds 1 and ID detennine
uniquely a projection E with = if, (1- E){! = ID, the above iden-
tity shows that there is a one-to-one .correspondence between self-
adjoint projections and complementary orthogonal manifolds. It
should be recalled (IV.4o.4o) that every closed linear manifold in
determines uniquely an ortho-complement; hence every closed linear
manifoW J: in determines uniquely a self-adjoint projection E In
with E = 1.
PROOF. The symbols S, S.* will be used for the closed unit sphere;
in.IJ !**, respectively.. Note that T** is continuous with the £*, it*
topologies in ):.., cg).., respectively (cf. 2.3)4 Hence, since T*. is an
extension of T (cf. 2.6),
(i) T.*(S,) T*.(xS) = x(TS) !;; x(TS ),
,"",here 8 1 is the 1* -closure of "S, and where the bars denote closures in
the ¥J* topology. If T is weakly compact, then TS is compact in the
ID. topoJogy of ¥J and thus x( TS ) is compact and hence closed in the
ID. topology ofID... Thus if T is weakly compact. (i) yields
T**(S,) x{ TS ).
According to Theorem V.4o.5, SI S**, and so T.*S.* x( TS ),
which proves that
(ii) T'*1** 4).
Conver8ely, let the operator T E B(l, ID) satisfy (ii). Since, by
Lemma 2.8, T*. is continuous with the 1*, VJ* topologies in **,
¥J'*, respectively, and S.* is J:*-compact in J:** (Theorem V.4o.2),
it follows that T.*S'* 4) is ¥J*-compact (1.5.7). Thus the ID*'
homeomorphic image x(TS) of TS is a subset of a ID*-compact subset
of KID. Hence, the ID*-closure of x(TS) is a ¥J*-compact subset of
x'D. and the 'D*-closure of TS is a ¥J*-compact subset of ID. Q.E.D.
8 COROLLARY. If either I or ID i8 reflea:ive. rocry operator in
8(1, ID) is rN.i1kly C<lmpad.
PROOF. Let T. B(I. ID). If ID is reflexive, then
T.. I** ID*. = KID.
Thus, the famil)' of all projectlons in B(I) form a partially ordered
set. Any two commuting projections, El and E., will have the least
upper bound
01. Weakly Compact Operator.
I DEFINITION. Let T E B(1, ID), and let S he the closed unit
sphere in 1. The operator T is said to be weakly """'pac! if the weak
closure of TS is compactin the weak topology ofW. Thus, by Theorem
V.6.1, an operalor i8 weakly camp""! if and only if it maps bovnded se's
into weakly St!I}'I.Ientially camp"'" sets.
2 THEOREM. A litlear operalnr T in B(I, ID) is weakly compacl
if and only if T**l** is (;(Jnll1in.ed in the ..atural emlwdiling KID of
'D inlo W**.
and, if I is refJexive,
T.*l** = T** xJ: = "T1 xI!J.
Thus, in either case, Theorem 2 shows that T is weakly compact.
Q.E.D.
4 COROLLARY. The set of weakly campacl uperators is closed in
the uniform operalor topology of B(I, ¥J).
PROOF. If Tfi .." T in B(I, ¥J), then, by Lemma 2.2, IT:. T**I
-+ o. If Tft is weakly compact, then for each x** in 1:*., T:*.x** E xID
484
VI. OPERATORS AND THEIR ADJOINTS
VI.4.5
VI.4.8
COMPACT OpERATORS
485
(Theorem 2), and, since is closed m the metric topology of '[}",
T""," . . Hence T" I" ",1), and Theorem 2 gives the desired
conclusion. Q.E.D.
5 THEOREM. Linear cumhinations of tJJI!akly Wlnpact l} raWT$ are
weakly compact. The prodtU:1 of a 'Weakly compM! linear operator and a
bounded linear op<rator is 'Weakly compact.
PROOF. Let T, U . B(I, W), W. B('[},.8). V. B(.8. I). Ct, {h W.
and let T, U be weakly compact. The following inclusions then follow
from Theorem 2, Lemma 2.2 and Lemma 2.3.
(o:T+PU)"3!" = (o:T..+pu..)I.. ,
(TV)"g*' T"V"S" T**I.' !;; ,
(WT)**I" = W"T"I"!;; W" = W'[) ".8.
Theorem 5 follows from these inclusions and Theorem 2. Q.E.D.
8 THEOREM, (Ganlmocher) An I>pUtIIor in B(I, W) i8 weakly
compact if and cmly if il8 adjmn! i8 weakly compM!.
PROOF. Let T be weakly compact. Since the closed unit spbere
S' of 'ID' is W--compact (VA.2), it follows from Lemma 7 and Lemma
1.5,7 that T'S' is compact in the ;E" topology of };'. Hence T' is
weakly compact.
Conversely. if T' is weakly compact, it follows from Lemma 7
that T.* i8 continuous relative to the I', '[}... topologies in I",
'[}.', respectively. If S, S" are the closed unit spheres in };, ;E**,
respectively, and if" is the natural embedding of I into X", then by
Theorem V.4.5, ItS is I'.dense in S", and so. from the continuity of
T" we see that T"S'* is contained in the 'ID'**.closure of T"xS
= "TS. According to Theorem V .8.13 the W**'.closure of the COnvex
set -xTS is the same as its strong closure. Thus T**S** "1Jt and
Theorem 2 gives the desired conclusion. Q.E.D.
6 COROLLARY. In the unifwm operalor topology of B(X), the
VJi!akly .ompM! rrperotma form a .I08ed ttro-aUkd i<kaJ,
We have already observed (2.8) that the adjoint T* of any T
in B(I, \\I) is continuous relative to the I, 'ID topologies in I*, '[}*,
respectively. The following result shows that, if T is weakly compact,
its adjoint T' has a stronger continuity property.
5. Compact Operato1'8
1 DEFINITION. Let T B(I, ), and let S be the dosed unit
sphere in I. The operator T is said to be compact if the 8trong closure
of TS is compact in the strong topology of '[}.
7 LEMMA. An operator on B{a;, 'VI is weakly etYmpcct if and only
if ils adjm..! is ronJimMJuswi!h rupeello IheX", g) !opolcgie8 in X', 'ID*.
respedivdy.
PROOF. Let T be weakly compact. By Theorem 2. for each ,,*'
in 1:**. there is a 11 in with
""(T'y*) = (T""'.)y' = y*y, y. 'ID*.
Thus, if y: ___ y' in the 'V-topology of '[)', then T'y: ___ T*y* in the
I" topology of 1*, Hence T' lw-s the stated continuity property
(1.7.4). Conversely, let T' be continuous relative to the X*., '[} topo-
logies in X', 'ID', respectively and let ,, . X**. If y:y --- y'y, y. 'l),
then :r:!' *T' y, * = T""" Y ' ___ T*''''** Y * Thus T'."," in m.. is a
o a () 0: (}. () 'tJ
continuous linear functional on 'ID* with its topology. Theorem V.8.9
shows that T""' " ,,'l), so T"I" C ,,'[}. The desired condusion
follows from Theorem 2. Q.E.D.
2 THEOREM. (Schauder) An I>pUtIIor in B(I, W) is OOlllpcct if and
only if ils adjoint is oompaeI.
PROOF. Let S, S' be the closed umt spheres in 1;, ID', rcspectively.
Let T be compact, and let {y:} be an arbitrary sequence in S'. Since
Iy:y- zl ::;:; Iy-zl, n = 1, 2, ' . .. it follows, from Theorem IV.6.7,
that some subsequence y converges uniformly for y in the compact
- ,
set TS. Hence y:,T'" = (T'Y:.I'" convergt's uniformly for", in S. It
follows that T' converges in the strong topology of I', Thus T'
.
is compa t.
Conversely. let T' be compact. Then, by the pomt just proved,
T" is compact; hence if S** is the closed unit sphere in X*., T"S"
is totally bounded (1.6.15). Thus, since "TS T'*S", "TS is totany
bounded; hence TS is totally bounded. Therefore TS is compact.
(1.6.15) and T is compact. Q.E.D.
486
VI. OPERATORS AND THEIR ADJOIS'TS
V1.5.3
VI.6.1
OPERATORS WITH CLOSED RANGE
487
3 LEMMA. The B<t of compact operarors is closed in the uniform
operator t(}pology of B(3:, ID).
PROOF. Let S be the closed unit sphere in 3:, let Tn be compact,
and let ITn-TI _ O. Then,fors> O. there is ann with ITn-TI < £f3.
Since Tn is rompact there are, by Theorem 1.6.15, points a:J . . .. xJI
in S, with
in S. Hence. by IV.6.6, the condition is equivalent to the statement
t1w.t T(S) i8 an equicontinnous subset of C(S*). It follows from
Theorem IV.6.7, that T(S) is conditionally compact in the metric of
ID if and only if the condition is satisfied. Q.E.D.
inf ITn"'-Tnx,1 < cIS,
l i:;tI
",.S.
6. O,e.alol'8 wilh Closed Range
It was observed in Lemma 2.8 that the closure of the range of an
operator V. B(3:, ID) consists of those vectors y such that y.ViI:: = 0
implies y.y = O. Or, in other words t
V3: = fyIV.y. = 0 implies y.y = O}.
The dual of this theorem states the fullowing: if V. B(!. ID), then
V*ID. = {"'*IV", = 0 implies ",.", = O},
and this statement is, in general, false. This will be seen in an exercise.
However the dual statement is true if the range Vii:: is closed, in
which case the range VoW. is also closed. Dually, if V.ID. is closed,
so is UI. These result:) are contained in the next two theorems. Addi-
tional information along these lines is to be found in the set of
exercises in Section R
It follows t1w.t
inf IT",-T",.I < £,
1",';:;S;
Thus TS is totally bounded, and TS is compact (1.6.15). Q.E.D.
m.s.
4 THEOREM. LineaT CV7nmnali.>rIB of compacllinem- 0l"'raturs are
"""'pad operat,/" , and any p..oo..d of a colllpaclli 0l"'TaloT and a
bounded limar opt'Talor is a compact liMar operatOT.
PROOF. The conclusions of Theorem 4 follow readily from the
fact that B set in 8 metric space is compact if .and only if it is sequen-
tially compact (1.6.181. Q,E.D.
5 COROLLARY. In the uniform operator Wpology of B(iI::), the COllI--
pacl opt'Talors form a dosed two- id£d ideal.
PROOF. This corollary follows I1IUnediately from 3 and 4. Q.E.D.
The reader will observe the analogy between Lemma 4.7 and the
next result.
6 THEOREM. An operator in B(iI::, ID) is oompacl if and only if its
adjoint sends bo,,,,ded generalk£d sequenffS whiM converge in the
topology of ID. into ger""alized whic" converge in lhe mnric
of :E*.
PROOF. Let S and S. denote the unit spheres of if and ID.,
respectively, and let T. B(I, ID), We recall t1w.t a generalized se-
quence in 3:. converges in the metric of I. if and only if it converges
uniformly on S. It is seen from the proof of V.4.4 that T(SJ is isometric
to a oounded subset of C(S*), where S. has the ID topology. The stated
conditio" is equivalent to the assertion t1w.t if {y:J is bounded and
!I: ->- y in the ID topology, then y:(T",) ->- y (T",), uniformly for '"
I LEMMA. If the range of an operator V in B(I, ID) is d<,srd, there
is a CD,..wnt K such that to cae" y in Vii:: corresponds an '" with V", = Y
and 1"'1 < KlyJ.
PROOF. It is 8een from the interior mapping principle, (1I.2.1),
that the unit sphere S in maps onto a set US which contains some
remtive sphere {yly' Vii::, Iyl < t5} with t5 > O. Thus, for 0 0/= y. VI,
the vector t5yl2lyl i8 the image under V of a vector z with Izl ;;; I.
Hence, if", = 2Iyl%/t5, we have Vx = y, and 1"'1;;; (2ft5)lyl. Q.E.D.
2 THEOREM. If the range of tM operator V in B(I, Ill) is closed.
then tM range of its adjoint is tM sel of ",* in 3:. such that Vm = 0
implies m*", = O.
PROOF. Let m* satisfy this condition, and define a (posSIbly d,s-
continuous) linear functional yri on IDo = Vii:: hy the formum y (U",)
= 31.(x). Because of the condition imposed on .1:*1 this defines yci
uniquely. By the preceding lemlTIR, there exists a constant K such
488
VI. OPERATORS AND THEIR ADJOINTS
VI.6.S
VI.6,5
REPRESENTATION OF OPERATOI\S IN C(S)
489
that to each y Wo there corresponds an 31 with 1311 Klyl, U31 = y.
Hence, IY6(y)1 :5: KI31*lIyl. It follows from Theorem 11.8.11 that y:
can be extended to a continuous linear functional y" on all of J, and
now V.y. = x..
It follows from the definition of U. that every element in its
range !3stisfies the stated condition. Q.E.D.
since the range of U* is c1osed ,1:* = V.y. for some y. £ *. If z. is
the restriction of y. to.8, then;z* = U:z*. Hence. the range of U is
also closed. It follows from the previous lemma that U;£. = UI = B.
Hence, U has a closed range. Q.E.D,
3 LEMMA. If tJu: adjoint of an <>perawT U in B(i'£, W) is o",,-to-eme
and hlJ3 a clo..d range, !hen Ui'£ = W.
PROOF. Let 0 ;6 y Wand define
r = {y*ly* ., y.y = O},
Then r is W-closed in *,
Suppose, for the moment, that u*r is I-closed and different
from U*1)*. From Corollary V.8.I2 it is seen that there is an ;v I
with.fU*'[J*;6 O,tiJu*r= o. This means that U31 ;6 O.andy*U31 = O.
for pvcry y. r. By Lemma V.B.IO, for some non-zero sc.ala.r tt,
U31 = "-y. Therefore y. UI and UI = W as desired.
It remains to be shown that U* r is I-closed, but not equal to
U*W*. Sincey * 0, ris a proper 8ubsetof *. Hence, sinceV* has an
inverse, u*r is a proper subset of V*W*. Finally, to show that v*r
is i'£-closed, it suffices, in view of Theorem V .5. 7 (or V.5.8), to show
that (u*r)ns* is I-closed, where S* is the closed unit sphere in I*.
By Lemma I, (V*)-',S* is bounded. Thus, (V*J'S* is contained in
some multiple 08: of the closed unit sphere S of '[1*. Theorem V.4.2
shows that ns:' is compact in the '[I-topology of '[)*. Since, by Lemma
2.8, V* is a continuous mapping from '[)* with its '[I-topology to if*
with its i'£-topology, the image under U* of the compact set rnnS:
is closed. Hence (u*r)ns* = S*n u*(rnnS ) is i'£-closed. Q.E.D.
4 THEOREM. If the adjoint "f an operator V in B(I, 1) has a
closed range, then the Tange of U is c!o ed and comists of those Netor. y
in ID for which V*y* = 0 implies y*y = O.
PROOF. Consider the map U I from if to .8 = VII), defined by
U.(31) = U(31). Then, since V. has a dense range, U; is one-to-one. If
x*£1:* is in the closure of Vis*, then 3.:* -= lim,. g:, U:Z:, where z: .8..
If y: is an extension to ID of z: (IL8.Il) then a:* = Jimft...,. U*Y:, and.
5 THEOREM. If U is in B(I, WJ and map. lwunded clGsed .e18
onto cwaed sets, then U has a closed range.
PROOF. Let Y = limn U31 n be a point in the closure of UI, and let
!m = {"'IU31 = OJ. Let d. be the distance hetween 31. and ID1. and let
UJ. .!m be such that
d n IXn-wni 2d,."
If the sequence {31.-W.} contains a bounded subsequence {31. -w.}.
. .
then, by hypothesis. the closure of this subsequence is mapped onto B
closed set containing 'IJ = lim, U(31. -w.), and so 'IJ' UI. Thus. to
. .
complete the proof. it will be sufficient to show tbat the assumption
1:C'J-wnl -to- CO leads to B contradiction.
H IlIXn-wnl -fro 00, then) since U(a:R-w n ) -fro Y, we have
V(("'n-w.)/I;v.-wnl! -+- 0, and hence, by hypothesis. !m contains a
point w of the closure of the bounded sequence {(31.-w.)/I31.-w.I}.
If n is fixed so that
[ "'.-Wn I 1
-tv < - JI
131.-w.1 8
then
1;v.-UJ.-wl31.-u...I!< 11;v.-w.1 < fd.,
which contradicts the definition of d.. Q.E.D.
6 COROLLARY. If V is in B(;!;) and map. bountkd closed.e18 emto
closed .ets, tM Tunga of all its iJoo1es are closed.
7. Representation of Operators in C(S)
A detailed knowledge of the specific analytical form of the most
general compact or weakly compact linear map between a given pair
of B-spaces is often useful in applying the theorems of Sections 4 and
5. In certain cases fairly complete information is easily obtained. It
will be seen in this section that this is so if the range of the operator
490
VI.. OPEJtATORS AND THEIR A1J'}OlNTS
V1.7.1
V1.7.1
REPRESENTATI()N OF OPERATORS iN C(S)
491
d f. 1
(s) = - K(8, t)/(t)dt,
rU v
i8 continuous with the I topology in I', then equation (I) clearly
defines a linear map from 1 into C(S) whose norm is
IT I = sup sup 1-r(s)"1
1<1"'1 ..s
- sup sup 1-r(8)x1
.5 rzl '
- sup 1-r(8)1.
..s
is in a. space of continuous functions. In some other cases very little
is known. For example. while it is easy to See that the general conti-
nuous linear map from L.[O,IJ, p> 1. to L.[O.IJ has the form
no satisfactory expression for the norm of T is known. No conditions
on K(8, t) are known which are equivalent to the compactness of T.
Of course, conditions on K(B. t) which are suflicienJ to insure the com-
pactness of T may be given. Such conditions will be found in the
exercises.
The present section, which is concerned with 8 compact Haus-
dorff space S, is divided into two parts. We first consider operators
with range in C(S) and then operators defined on C(S).
This completes the proof of the first part of the theorem.
If T is weakly compact, Lemma 4.7 implies that T* is continuous
with the C(S) topology in C*(S) and the 1** topology in I, so the
asserted continuity of 't is guaranteed. Conversely, if y is continuom:
in the I.* topology, and if s. 80 in S, then -r(s.) -r(80) in the 1**
topology of 1*. Now-r(s.) and -r(s.) are in C(B.), where B. is the solid
unit sphere in 1** endowed with its 1* topology. By Arzela's theorem
(1V.6.11) the convergence is quasi-uniform on B.and hence on B. the
unit sphere in I. From this fact and equation (I) we conelude that the
bounded set T(B) is a quasi-eqmcontinuous collection of functions in
C(S). It follows from Theorem IV.6.I4 that T(B) is conditionally
weakly compact, so that T is a weakly compact operator. This com-
pletes the proof of the assertion concerning weakly compact operators.
Finally if T is compact, then it follows from 5.6 and the fact that
",,(S) is bounded in C'(S) that -r is continuous with the norm topology
in 1*. Conversely, let T be continuous with the norm topology in
I*, Then given € > 0 and 8. . S, there is a neighborhood N of 8 0 such
that if 8. N then
sup ITtc(8)-Tx(so)1 = 1-r(8)-7("0)1 < E.
..B
I THEo1<E)I. Let S be a compact Hamdorff space and let T be a
bound€d linear rrperalvr from a B-space I into C(S). Then there ui.!s a
mtrpping -r : S 1* which is oontinuous with the I topology in 1* such
that
(1) Tx(s) = -r(s)x, x£I, 8£S;
(2) ITI = sup 1-r(8)1.
..s
CUlII'ff8ely, i/ such a map -r is given, then the operator T deji.1ed by (1)
i8 a boumled linear rrperalvr from I into C(S) with norm given by (2).
The rrperalor T is 'tJJ£akly compact i/ and only if -r is conti:n:uous with the
1** trrpology in 1*. The UfJI'J"llWr T is rompad if and <mly i/ -r is con-
tinuous with the norm topology in I*.
PROOF. Let T be a bounded linear map of I into C(S). Its con-
jugate T* maps C*(S) into I.. Furthermore tbe map"': S C*{S),
defined by the equation
"'(8)(/) = /(8),
f. C(S),
8.S
Hence if s is in N, then IT.x(8)-T.x(8 0 ) I < £ for all '" in B. It follows
from Definition 1V.6.6 that T(B) is an cquicontinuous set in ('(S).
Since T(B) is bounded, it is a consequence of Theorem IV.6.7 that it is
conditionally strongly compact. Thus T is a compact operator and the
thl'Orem is proved. Q.E.D.
The theorem just proved yields rather complete information con-
cerning operators with range in C(S). We now turn to the question
of representing operators T defined on ('(S). lotivated by the Riesz
representation theo....m (IV.6.8) for linear functionals On C{S), we
is a homeomorphism of S into a compact 8ubset of C*(S) in the C(S)
topology (see V.8.7). By Lemma 2.8, T* is continuous with the
C(S) topo10gy in COtS) and the I topology in 1* so the map -r : S ->1*
defined by -r = T*", is continuous with the I topology in 3:*. Equa-
tions (1) and (2) are easily seen to be valid. Conversely if -r : S 1*
492
VI. OPERATORS AND THEIR ADJOIKTS
VI.7.2
VI.7.S
REPRESENTATION OF OPERATORS IN C(S)
498
aTe led to hope that the Tcpresentation of operators will be effected
by 8 vector measure whose values lie in 1,. This turns out to be the
case for weakly compact operators; for the general operator the mea-
sure has its values in 1**.
In the following, f!iJ denotes the field of Borel sets in S, i.e., the
v-field generated by the closed sets of S. If p is a function on f!iJ with
values in a B-space, then as in Defmition IV.IO.8, the symbollll-'II(E)
denotes the semi-variation of p over E E !!8 and is defined as
Conve.rsely, if (a) and (b) are satisfied for the mapping which
sends "'. into "(0)"", then it follows that for each fixed I_ C(S) the
mapping
III-'II(E) = sup Ila"u(E,)j.
'-I
'where the supremum is taken over all finite collections of disjoint
Borel sets in E and all finite sets of scalars "'-, . . ., IX" with 1".1 ,;;; 1.
We are now prepered to Tepresent the general operator.
2 THEOREM. Let S be a compact HausMrIl space and Ie! T be an
opt;raUJr on C(S) to 1£. Then thr:re e.rists a unique se! fundiDn p, defimd
on tM Borel .e!s in S and having values in 1£**, su<:h thaI
(a) "(.),,,* is in rca(S) lor each ",. in i£*;
(b) the mapping "'* --+ p(' )",* 01 1£. i..to rca(S) is continuo"" wilh
the 1£ and C(S) topologies in tMae spaces respt'Ctively;
( ) ",*TI = Js/(s)p(ds)",*, f _ C(S), "'. E i£*;
(d) ITI= III-'II(S).
Conversely, ilp is a set/uncliD" on the Borel sels in S to i£** which
satisfies (a) and (b), tlwn eqrwrion ( ) defines a linenr map T of C(S)
;nJo I rohose 110rm is gWen by (d), and su<:h that T*",* = p(')"".
PROOF. If E E f!iJ, let 'he be the element in C**{S), the second ad-
joint of C(S), defined by
PE(A) = A(E), A_ rca(S).
Define the set function p : f!iJ .... i£*. by the equation
peE) = T**(4),,), E _ f!iJ.
It follows from the Riesz representation theorem (IV.6.3) that T*",*
is a meaSUTe A.' _ rca(S). Since
1..(E) = 4>,,(A..) = 4>"(T*,,,*) = T**4>,,(x*) = "(E),,,.,
it fo\Jows that (a) and (c) are valid. This equation also shows that
T*",* = 1'(.)",' from which (b) fo\Jows. Equality (d) is readily checked.
x. -+ fs/(s)l-'(ds)"'*
is continuous in the}; topology of};o. and therefore (V.8.9) is generated
by some element "', . 1£. Thus the mapping T : I --+ xI defined by (c) is
a \ineRT mapping of C(S) into 1£. It is easy to verify that it is bounded
and has the stated properties. Q.E.D.
In the case of a weakly compact operator the measure takes its
values in 1:, and not merely in :I**.
:J THEOREM. Let S be a compact Hausdorlf space and leI T be a
weakly eompacl operator Irom C{S) to 1£. TMn tMr, exisls a veelor mea-
BUre " cklimd on tM Borel sels in S and having values in 1£ such thaI
(a) "'." i. in rea{S), ",* _ i£o.;
(b) Tf = Is f(s)p(ds).
(c) ITI IJpll(S),
I' C(S);
Id) T*",* "'*'" "'* . 1£*.
Crmvertlt:ly il " is a vedOT measure on tM Borel sels in S to the
B-space }; which solioli.. (a) 1M" tM operator T defi.1ed by (b) is a
T1Xt1kly compact operoior Irom C(S) to I who.e norm is given by (c) and
whose adjo;..t is given by (d).
PROOF. If T is weakly compact, then by Theorem 4.2, T'. maps
C*.(S) into ,,(I), the natural embedding of 1£ into 1£**. Hence by the
construction in Theorem 2, I-' is defined on the Borel sets I nnd has its
values in ,,(I). Thus we may and sha\J Tegard p as a mapping into i£.
Since "'*P is in rca{S) for every "'* in 1£., it fo\Jows from Theorem IV.
10.1 that P is a strongly countably additive vector measure. Thns
from Theorem IV.10.S(e) the integral in equation (b) exists nnd is in
};. From equation (c) in Theorem 2 we conclude that
Tf = Jsl(s),,{ds),
I_CIS).
The validity of equations (c) and (d) RTe consequences of the cor.
responding Tesults in Theorem 2.
494
VI. OPERATORS AND THEIR ADJOINTS
VI.7.4
VI.7.6
REPRESENTATWN OF O:PERATOIlS IN C(SJ
495
Converse]y let p be an -v.aiued measure defined on the Borel
sets in S with the property that x*f-' is in rea(S) for every x* in ..
It is clear that the operator T, defined by (b), is a bounded linear
operator on C{S) to whose adjomt T* is given by (d). From IV,10.2
we conclude that T* maps the unit sphere of * into a conditionally
weakly compact set of rea(S), and therefore T* is a weakly compact
operator. By Theorem 4.8 this Implies that T is a weakly compact
operator. Q.E.D.
given hy Theorem 2. To prove the theorem it will, by Theorem B.
8uffice to show that f'(E) is in ,,( ) for every Borel set E.
Let£ii' be the Borel sets in S. Then the space B(S, £ii') (cr. IV.2.12)
is the space of bounded Borel measurable functions on S. We let !B.
be the intersection of aU linear manifolds !B B(S, £ii') with the two
properties:
(i) C{S) !B,
Tin = L!n(s)f-'Id.),
n = 0, 1, 2, . . ..
(ii) if {In} is a umformly bounded sequence In !B and if lis) =
lim.-+", In(s) for every . in S, then I !B.
It is evident that !B. J""'sesseB these two properties. lYe now
prove that !B. is an algebra under the natural product (fg)(s) =
I(s)g(s), s, S. To see this, let h be a fixed element of C{S) and let
!B(h) = {I' !B.llh. !B.}. Evidently !B(h) !B., and it is clear that
!B(h) satisfies properties (i) and (ii) above so that !B(h) = !B o ' This
proves that if h, C(S) and I' !B., then Ih . !B.. Now let I be a fixed
element of !B.o and let !B(t) = {g, !B.I/g . !B.}. We have just pm"""
that C(S) !B(t), and it is clear that (ii) is satisfied. As hefore. this
shows that !B. = !B(t), so that !B. is an algebra.
Denoting the characteristic function of a set E by b:, we Ict
IJIJ o = {E. IJIJb:". !B.}. Since !B. is an algebra and 8ati8fies condition
(ii), it is readily seen that£ii'. is ao.field contained in £ii'. We now show
that £ii'o = IJIJ by proving that £ii'o contains aU the closed Set8.
Let F be an arbitrary closed set in S, Since S is aS8umed to be a
compact m tric space, there is .an increasing sequence of open sets
{G n } inS with F' = U:' I G n and Gn nF = r/>. By the UrY80hn theo-
rem (1.5.2) there is an In' C(S) with 1 1,,1 = 1 and such thatln(F) = I,
In( G,, ) = O. Clearly In(s) .b('), s, S, and so XF' 58 0 ,
We now show that p(E), for E £ii'. Consider the collection
!B I of all I' B(S, £ii') such that
4 THEOREM. II T is a uoeaJdy rompad operaJor Irom C(S) t<J ,
then T send. weak Cauchy sequences into strongly con'/JfTgent sequences.
CO'f!St:f}UfflUy, T maps rorulitimwlly Wi!akly rompact subseIs 01 C(S) into
crmdUionully strongly ccnnpac! subsets 01 I.
PROOF. If {In} is a weak Cauchy sequence in CIS), it is (11.3.20)
bounded. Clearly the limit I.(s) = lim I,,(s) exists for each., S.
Although the limit function I. may not be in C(S), it is certainly
bounded and measurable. Let f-' be the vector measure corresponding
to T as in the preceding theort'm. Then
Thus by Theorem IV.IO.IO it fo]]ows that {TIn) is a convergent 8e-
quence .and this proves the first .assertion. The second conclusion
follows immediately from the first. Q.E.D.
5 COROLLARY. Tlui produd of two 'U!fflkly compact operators in
C(S) is compact; in parlicular, the equaTe 01 a UJeakly compact 9pcrator
in C(S) i. compact.
PROOF. This fact follow8 directly from Theorem 4. Q.E.D.
It was proved in Corollary 4.3 that an arbitrary bounded operator
with range in a reflexive B-space is weakly compact. The next theorem
asserts that this remains true for a weakly complcte space provided
the domain is C(S).
6 THEOREM. An arbitrary lJoumkd limaT opcrahJr from C(S}
inlo a UJ€akly romplele B-spaa: J:: is Wffikly c01npaet.
PROOF. We shall first prove the theorem under the assumption
that S is a compact metric spaec. In this case let p be the set function
Is/(s)p(ds) .1'.
The set !B I fonns a linear maoifold which contains C(S). That 58 1
satisfies (ii) follows from the relation
UsI(s)f-'(d.») ",* = ':::1;* Is I.('),u(d.),
Ol'* E *
496
VJ. O.!"ERAYOnS AN)) THEIR AD.10INTS
VI.7.7
VI.7.7
REPRESENTATJON OF OPERATORs IN C{8}
497
and the weak completeness of I. Hence !8.!;; 18 1 , Since
pIE) = f"x(alu(ds)d;
for E" = !lio' it follows tbat p maps 91 into I. This proves the
theorem under the additional assumption that 8 is a compact metric
space.
To complete the proof, let 8 be a compact Hausdorff space. Let
U.} be an arbitrary sequence in the unit sphere of C(S). Let 8. be the
set of equivalence classes of S under the relation: a a' if and only if
I.(a) = I.(a'), n = 1. 2. . ... We make S. into a metric space by
defining the metric
.
Icr.,p(E,).
i=1
where the {E,} are disjoint and 1...1 < J. is a totally bounded set in 3::.
Let" > 0 be given and let M be the semi-variation of p on S. Sclect a
set {PI' . . ., P.} of complex numbers with !Pil ..;; 1 such that if 1cr.1 I
then there exists a p, = P(<<) with IP(cr.)-«1 < ,,/2]1.[. Let !li be the
Borel sets in 8 and let {FI' . . ., F.} C!J# be such that if E ,,91, there
is an F. = F(E) with Ip(F(E))-p(E}i < r/2p. Then from the defi-
nition of the semi-variation
. . .
I I cr.",(E,) - I P(cr.,)p(E,)1 = I I (cr., - P(<<,)}p(E,)f
a-1 '-1 p]
e(a, I) = I 2 .lt.(a)-I.(t)l,
_I
8,t SfJ.
E E
:::;;;-M=-.
2M 2
Now I:'_IP(ot,)p(E,} Can be written as a sum If-,P,p(Ej), with
{Ej} a disjoint family in 91. Thus
Let n : 6' -> 8 0 he the canonical map of a pomt into its equivalence
class. From the continuity of the In we see that is continuous. Con.
sequently. So is a compact metric space, Consider the space C(So);
we note that if 'I' £ C(So) then the function I defined by I(a) = p(n(a))
is in C(S), and we define To; C(S.) -+1 by T.", = TI. Clearly T. is a
linear map and IT.I ITI. We also note that each I. gives a weH-
defined function 'l'." C(S.} such that I.(a) = 'I'.(..(a)). Now from the
first part of the proof we bave that T. is weakly compact, so there is 8
subsequence {'I'..} such that {TP..} converges weakly in 3::. Since
TI. Top., we conclude that the subsequence {TI..} converges weak-
ly, 80 that T is weakly compact, as was to be proved, Q,E,D.
Since a compact operator is wealdy compact, it may be represented
by it vector measure.as in Theorem 3. As would be expected this mea.-
:sure has a special nature.
. . .
1 I P,p(Ej)- I lI,p(F(Ej»1 I 1,,(Ej) - p(F(Ej))i
,-1 1-1 jo..-J
E E
<p'-= ,
2p 2
Thu8 it bas been shown that each element in K can be approximated
within an arbitrary positive distanee E by sums of the form
'2:.f_,fJ,p(F.,)' This proves thatK is totally bounded. Hence the opera-
tor T given by
TI = fs,(a)p(ds),
I C(S}
7 THEOREM. An <1pC1'alor T : C(S} -+ 3:: is cmnpacl il tlnd only il
the vector me=re p :!JI -+ 3:: corrCBp,mding to it lU in Theorem 3 takes
ifs ""lues in a compact BUbse! of !.
PROOF. If T is compact, then it follows from Theorems 4.2 and
5.2 tbat T** is a compact operator from C**(S) to 3::. and it foHows
from the construction of" that it bas its values in a compact set of!.
To prove the eonverse, it is evidently sufficient to show that the
set K of all sums of the form
is compact. Q.E.D.
We have already seen (IV.6.18, IV,7.6 and V.8.1I) that the
spaces B(S), (B(S, E), AP, and L (S. E, p) are isometrically iso-
morphic to a spacc C(Sz) where SI is some compact Hausdorff space.
The same is true (IV.6.22) for the space of bounded continuous func.
tions on a completely regular space. and for the spaces c and I"" Con-
sequently any operator with one of these spaces as domain and with
range in a weakly complete space is automatically weakly compact.
Further, any weakly compact operator defined 011 olle of these spaces
498
VI. OPERATORS AND TREIR ADJOIN'lS
VI,8.l
VI.8.2
OPERATORS ljo; A LEBESGUE SPACE
499
maps a weak Cauchy sequence into B strongl}? convergent sequence.
and the square of .su h .an operator in these spaces is compact.
Additional information and special cases will be foul1d il1 the
-exercises of Section 9.
then statements (i) and (ii) are immediate, By Theorems III.2.20(a)
and III 1.5, we have., for each E in ,
8. The Re tion of O.eralo.... in a LehCSWIc Space
Ix*(E)1 = sup I",*(E)"I :;;;: sup J I(T"'){8)lv(l', cis)
111:]::;1 rzr l s
= ITI = sup V("'*(')", S)
Izl;:$;l
;;;; 4 sup sup Ix*(E)x! = 4- sup I"'*(E>!.
r :;:l Ed: EEl:
Conversely. if ",*{.) on E to * has the property stated in (i). then the
operator T defined by (ii) (cf. the note following Theorem III.IO.7) is
clearly linoear. To see that it is continuous it will therefore suffice to
show that it i8 closed (II.2.4). If "'n -.. '" and T",. -.. f, then, for each
EinI,
JEf(8)I'(ds) = lim JE (T"'n)(8)I'(ds)
n
= lim"'*(E)xn = ",*(E)", = JE (T"')(8)f'(ds).
.
This section parallels the preeeding one. At first the general
operator and the weakly compact operator from an arbitrary B-space
to an L" .pace are represented. Then the problem of representing an
operator whose domain is an space is considered. The compact and
weakly compact operators are given a kernel representation and the
topologi.cal properties of the operator are stated in equivalent fonn in
terms of the kernel. The property of mnpping a weakly convergent
sequence into a strongly convergent sequence, which is enjoyed by
the weakly compact operators on C(S) (Tbeorem 7.4), i8 a property
a.lso shared by the weakly compact operators on Ll.
1 THEOREM. Let (S.1:, 1') be a maI/""" 8p""e and let T be a con-
tinuous lineae map of the B-8pnce l into LI (S, 1:, 1'). Then there is a
uniquely deln-mi"",d fw/dion "'" (.) on E to * BUch that
(i) for ea<:k a: in;r th£ 8el fUndion a:"(')x i8 ,,-continuous and
£ountably additi"" on E, and
d,x*(-)x
(ii)T",=-,
d"
"'. ,
which shows that TaJ = f and proves that T is closed and thus contin-
uous. To prove the final statement of the theorem consider the sub-
space ca(S, 1:, 1') of catS. E\ which consists of all f'-continuous func.
tions in catS, E). By the general Radon-Nikodym theorem (III.1O.7).
and Theorem III.2.20(a), the space ca(S,E,f') is equivalent to the
space LI(S, E.I')' Under this equivalence T determines the operator
'" --+- ",*(.)", on to catS, E. 1'). Thus T is weakly compact if and only
ifthe set of all set functions "'*(')x with 1"'1 ;:;;; lis conditionally weakly
compact in ca(S.1:, 1'). According to Theorem IV.9.1 this is the cas
if and only ifthe countable additivity of ",* (. )JJi8 uniform with respect
to 1"'1 ;:;;; I. Thus T is weakly compact if and only if ",*(.) is countably
additive in the 8trong topology of *. Q.E.D.
2 TIUWEEM. Let (S, E,I') be a (J-finit. positi"" "..asuee 'pace
and let T be a ro,,'inuous linear map of LI(S.E, f') into a linmr Iopolog-
iea! &p""e .:E. Let T 'I/"P the c1",cd unit .ph£.. in L I (S, 1:. 1') onlo a 8et
whose closure K is compact and has a cnu..labl£ base. Tb£.. there i8 a
fundion ",(.) on S to K such that aJ*"'(') is inL (S.1:,f') for ea<:k x* in
* and BUch that
Th£ norm of T 8a!isfies th£ relutiOnB
(m) sup I",*(E)I :;;;: ITI :;;;: 4 sup Ix'(E);,
EEl: EEl:
Conversely, if ",*(.) on E to .:E* satiBfies (i) then (ii) tUfi"",. an operalor
T on ;E to L,,(S.1:. 1') w/wse YUmn 8atisfies (Hi).
Furthhmore T i. weakly eompa<:t if and only if ",*(. \ is roU7dably
additive on 1: in tb£ 8/rong wpalogy of .:E*.
PROOF. If. fDr Eil1E, the functiDnal",*(E) in * is defined by the
equation
""'(E)", = f E (T;r}(8)f'(cI8),
Js",*",(s)f(8)f'(ds) = ",.Tf.
/- LJ(S, 1:, 1').
500
\'1. OPERATORS AND THEIR ADJOINTS
VI.8.a
VI.8.4
OPERA"fORS IN A LEBESGtT1::. SPACE
501
The theorem will first be proved under the assumption that
,.(8) < 00. The proof will be based upon the following hree lem as
whose stat m('nts require the introduction of the followmg notation:
If 7< = {E" .. ., En} and ",' = (F" . . ., F",} are two partitions nf 8
into disjoint sets in I of positive measure we write -n: n if and only
if for each F,.;r;' there is an E..:n such that p(F,-E.) = O. It is
straightforward to verify that the collection of partitions of 8 fo ms
a directed set (1.7.1) under this ordering. If:lt = {El"'" En} IS a
partition of Sand h is a bounded measurable function on 8, we define
the function It" by
hn(l) = i ( r h(B}p(ds) l x.,(/).
1=1 p(E,»).,
_ TU.,} t
"'n(t) - (E ) X.) ).
""l P I
3 LEMMA, Let (S, 1:. 1') be a finite positive meUS!lre space and I£t
II be a boundw met1BWi'able f1mdinn on 8. Then given e > 0, there is a
parhti"" :no of S nu:1I that if :n "0' IMn
Ihn(B)-h(B)1 < e
fur all . ?lOt <orI1Rimd in a null Bet E(:n) dq>ending on ".
PROOF. Let the range of h be written as the union of disjoint Borel
sets AI' . . ., A. of diameter less than B. At least one of the subsets
G, = h-'(A i ), i = I, . . ., k of S has positive measure, and we suppose
it to be Gto The sets Elt. . "7 E'I'I of the partition no are obtained as
follows. We adjoin to G;1 those sets G i of measure zero. obtaining E 1 -
The remaining sets G f of positive measure are the sets Ez, - . ", En-
Thus there is a null set E. such that
Ih(B)-h(t)1 < B, S, t. E,-E.. i = 1...., n.
Nmvif", :<: :n",:n = (1'" . . .. 1"...), there is anull set F. depending onn
such that each of the sets F ,- F CJ is contained in some one of the sets
E,. Thus for . EoUF.
I '
[hn(s)-h(s») = ---' f I lh(s)-h(/)}p(dt) 1
,,(F,) I F,
1 ' f I
= : {h(/) - h(s)}p(dt} 1 < B.
p(E,nF,)' .,nr,
We define
4 LE....A.If 1M compact Hamdurff sp""e S has a cUlmtable base
the space C(S) i. separable.
PROOF. By Theorems 1.6.19 and 1.6.12. S is a separable metric
space. If !I(x, y} is a metric in S let fn(x) = !I(x, x n ) where (xn) is a
denumerable dense set in S. By 1.5.10 ffl is a bounded function and
hence an element of C(8). By IV.6.I6 (or IV.6.17) the closed a1gebra
generated by the denumerable set {In} is all of CIS). Thus CIS) is
sepm-able. Q.E.D.
Let U be the closed unit sphere in Ll(S, 1:, 1'). Then, by the pre-
ceding lemma, since K = TU is compact and has a countable base the
space C(K) is separable. Since a subspace of a separable metric space
is separable (1.6.12) there is a sequence {", } k 1* such that for any
oX. in 1* and {: > 0
(I)
Ix*(k)-",:(k)1 < B,
k.K,
for some intOb'tT j.
Since we are assuming that pIS) < 00, the set function ro*TXT<
is, for each or. in 1*, p-continuous and thus, by Theorem III.Io.2.
there is a function «(-, ",*) in L l (S.1:, 1') such that
(ii)
ro*TXE = f E ex(/, ro*)p(dt},
E.1:.
Since ;x*X is a continuous linear functional On (S.I,,u) we have
I,,'TXEI ;;; I",*TII'(E),
E.1:
from which It follows that «(', ",*) is p-essentially bOWlded. Thus
fs «(I, ",*)f(/}p(dt) and ro*Tf are both defined and continuous for f in
L l (8,1:, 1'). Since they are equal, by (ii), for characteristic functions
they must coincide everywhere on L,.(S.1:. 1'), i.e.,
(iii)
",*Tf = fs«(/. ",*)f(/)p(dt),
f. L,(S, 1:,,").
5 LEMMA. There i. a seque1.CB {:nn} of partitions of 8 inliJ Bets 01
positive mt"astATe and a. null set Eo such that
hm", xn,,(t) = ex(/. x J, i = 1,2,...,
n_
Q.E.D.
unifonnly fvr I in S-E..
PROOF_ We first observe that for any partition 1t = {E t ) . . n En}
502
VI. OPERATORS AND THEIR ADJOINTS
\'1.8.5
VL8.6
OPERATORS IN A LEBESGUE SPACE
508
"",(I, x*) = i r - (E I ) f IX(S, X*)p(ds)l XE,(t)
1=1 L# j JE J IJ
. x*T(X,d .
= ' Xs (f) = ",*x.\f).
'_1 I-'(E.) J
The partition n. will be chosen by induction. By Lemma 8 there
is a partition ""- and a set El with p(E.) = 0 such that
I",:,,,,...(t)-«(t. "':')1 < 1, IoS-E l .
Now suppose that for i :,; k the partition n, and the set E, with
pIE,) = 0 have been ch"","n in such a manner that
I",:x..(t) -ex(l. x:)1 < , 1 ";; i:'; k, IoS - El.
By applying Lemma 3 in turn w each of the function8 «(t. x:).
i = 1...., k+l, with 8 replaced by l/(k+l) a partition n:'+l :<: ".
is obtained such that
Since x*x(. ) is the uniform limit of bounded measurable functions ,t is
hounded and measurable. Moreover, if If I < 1, then
Ix*Tf - Is x*"'(I)J(t)l'(dt)1
:::: Ix*TJ-x;Tfl + Is l.1:*x(t) - x;x(I)IIJ(t)lp(dt)
* 1
IX:-".",.(t) -ex(I, x, )] < k+l ' I ';; i :S. k + I, 10 S - E.w
<2t:,
which proves the theorem under the assumption that 1-'(8) < 00.
In case S = U: , 8. where 1-'(8.) < 00 and S. C 8.", we may
apply the nesult already proved to the space 4(8., E., 1-') where E.
consists of those sets in }; which are subsets of 8.. The function x(. )
on 8 to K is defined in the natural way as the limit of the sequence
.1'.(') obtained for (8., E.. I-' ). Q.E.D.
In the following we shall give several applications of Theorem 2.
The first makes use of the compactness Theorem V.4.3 to give the
generlll form of a mapping from L l (8,E,I-') w the conjugate of a
separable spa.ce.
6 THEOREM. Let (8. E. 1-') be a a-finite p".itive melUure 8plWe and
let T be aronJin1UJuslinmrmap of [.,(8, E.p) into the ",,,,jugate I* of a
'"pilrablR B-"f1l1u I. Then there is a p-i!SBi'ntially "..iqUR funeti'>n .1'*(' )
on 8 10 I* suek that m*(')x isp-i!ssenlinlly MUI/ded for each x in I and
[*J (Tf)x= Isx*(s)xJ(s)p(ds), loL.(8,E,p), ",do.
MorffJI'h", ITI = ess sup Ix*(s)l. Ctmversely, iJ x*(.) is any juru:tion on
..s
for SOme p-nullset EMI' The conclusion of the lemma then follows by
letting E. = u;_, E._ Q.E.D.
PROOF OF THEOREM 2. We note that for each I" III 8 the sequence
{",,,.<I,,J} lie8 in K. Since K is a compact Hausdorff space with a
countable base it is a metric space (I.6.19) and thus a subsequence
converges w a vector x(le) inK (1.6.13). Let x(t) be arbitrarily defined
for each tin S as the limit of such a subsequence. Then for i = l 2, . . .
we have
lim x*x . (t) = oo;(t. a; ) = .1':*).
. .
....
US-E.,
S ro I* such Ihat x*(.)x is ml'arurable for eaeh x in I, and such lluzt
ess sup 1",*(s)1 = M < <:1),
..s
1.8.
then 'gllation ['J delines a co..unuous IiI/ear map T oj L,(8. E.p) inlo
i£* ",hose norm is 111.
PROOF. If T IS a bounded operator from L1(S, E, p) to 1'* and
V is the unit sphcrc of L.(8, E.I-')' then K = TV is compact in thc l'
topology (V.4.3) and has a countable base in this wpology (V.5.1).
By Theorem 2 there is a map s ->- "'*(s) of 8 into K C 1'* such that
['J holds, and where )",(s)! ;;;; ITI. On the other hand it follows from
[*J that ITI ;;;; ess sup 1",*(s)l, so IT! = ess sup 1""(s)l. We now prove
so that the functions x:x(.) are bounded and measurable and
",:Tf = r xrx(l)f(t)l'(dt),
. s
i = 1, 2, . .,
10 L 1 (8, E,p).
Since x(8) K we see from (i) that for every x*
E > 0 there is an integer i such that
Ix*x(t)-..;..,(t)1 < £,
in 3::* and O\'el)'
5Q4
VI. OPERATORS AND THEIR ADJ"OINTS
VI.8.7
VI.B.9
OPBRATORS IK A LEBESGUE SPACE
505
thel-'-essential uniqueness of the funetion ",*(s).1£ ",*(s)",. L",(S, L, p)
for each x 0 I and J",*(s)"'f(s)l-'(ds) = 0 for eacb '" £3:: and
f . L" (S, L, l-'), then hy the uniqueness part of IV.8.5, there exists, for
each a E 1', a measurable set Ell of measure zero :such that a:*(8).1' = 0
for s. S, B t E., Let XI be a countable dense subset of :t, and let
E =0 X E . Then it i8 clear that x*(s)", = 0 for",.I, B'S, at E
". .
Hence ",*(s) = 0 for", t E.
Conversely, let ",*(.) be a map ofS into I* such that ess sup 1"'*(8)1
= III < GO and ",*(. )'" is measurable for each", . I. Define T on L" hy
[*]. Since IlT!)"'1 MlfII"'l, it is evident that Tf. 1*, Hence
T. B(L,(S, L,p),I*). The statement concerning the norm of T
follows from the first part of the theorem. Q.E.D.
7 COROLLARY. Tlu!orem 6 remains valid if the hypothesis that I*
IS the conjugate 8p""e of a Bf!]Jtlrable "PaJ:e is repl""ed by the hypothesis
Ih.ai I* is the conitlgate 8J1""e of an arbitrary B aJ:' a.nd T Iu1s a separa-
ble rang..
The proof of the corollary will reqmre, besides Theorem 6, the
following lemma.
s LEM"A'A. L.t I* be the conjugate "P"'" of a B'8J1""e 1:. L.I!IR I*
be a uparable linear manifold, TIu!n there e",isls a closed aeparable sub-
spac. ID of I BUch that!IR is equivalent to a mbspace of ID*-
PROOF. Let {"':} be a countable dense subset of!IR, and let {"'m.},
m, n = 1,2, . . ., belong to 1: and satisfy the relations I"'..nl = I and
1..:(.....)1 ( 1 -;) Ix:l.
If ID = Sp {x a .), then 'ID is separable. The mapping V: I* -+ IDe de-
fined by
separable subspace '[J of I. By Theorem 6 there is a l-'-essentially
unique function ",*(.) on S to!IR with ITI = ess sup 1",*(a)1 and such
that for each m in 'D the function m*(')'" is p-measurable and
(i) Js"'*(B)xf(s)p(ds) = (T!)x, foL 1 {S,L,p).
To complete the proof of the corollary it must be shown that for an
arbitrary x in 3i the function ",*(.)x is p-measurable and equation (i)
holds. Consequently, let "'0 be a fixed element of I and let 'ID. be a closed
subspace spanned by"'. and ID. Then. as before. there is a l-'-essentiaUy
bounded function (.) on S to!IR such that mt(.)m is p-measurahle for
every m in . and for 8uch m
(ii) Lx:(s)mf(s)p(ds) = {Tf)""
Thus, since ID o, it is seen from (i) that
f" {x (s)-x*(s)}"'jt(ds) = 0, E. E
for x m . Thus there is al-'-null set Es su h that "' (8)m = m*(s)x for
m in ID and 8 1 Es. Since'ID is separable there is a I-'-null set E such that
foraUmin
f £ L,,(S, L, pl.
{x;:(S)-x*{sj}", = 0,
st E.
satisfies IVI 1. However, since
IV"':I sup I"':(xmn>l = 1"':1.
n= 1,2,...,
Since the only vector in!IR which vanishes on 'ID is the zero vector and
since m (s)-m*(s) is in!IR, it follows from the P ....-!;11g equation that
X (8) = m*(s) for p-almost aU sin S. Equation (ii) holds for "'. and
therefore equation (i) does likewise. Q.E.D.
In the following theorem it is shown that if the range of an opera.
tor on L,{S,L,p) is another L, space we may give a specific scalar
kernel representation of T rather than represent it by means of a
vector valued integral. In the statement of this theorem the deriva-
tive notation dJ./djt introduced in connection with the Radon-Niko-
dym theorem (111.10.1) is used. We recaU that for Ii p-continuous
omplex valued measure }. there is a unique p-integrable function
dA/dp. with
v",*(y) = x*(y),
y.ID, "'*01*
m
}.(E) = 1: (:) (s)p(ds),
9 COROLLARY. Let (S, L, p) be a a-tinire posiiWe 11I<'asure space
and kl.1. be a positi e regular measure on the Bo1'el sets fJ4 in the compac'
E.L.
the mapping V defines an i80metric mapping of!IR into *. Q.E.D.
PROOF of COROLLARY '1. LetIDC be the closure of the range of T.
By the lemma,!IR is equivalent to a sub.pace of the conjugate 'V* of a
506
VI. OPERATORS AND THEIR ADJOINTS
VI,8.9
VI.8.1O
OPERATORS IN A LEBEI:'GUE SPACE
507
Hous,]"rJf space W. Let T be a continuous linear map of Li(S, E,p) into
L i (1V, f16, A). It is assumro tlwt eillm- (a), W is a mdric BpaN', or (b), T
hU$ a separable range, Thm Ih£re is a Bcalar 'undion K on f!iJ X S wUh
the foU<>rDing PTopmiCB.
(i) For each 8 in S. K('.8) is a regular measure on f16 ",Uk
ess 8UP v(K(', 8), S) = M < 00.
.
may be noted that the next th€orem applies to every continUOUS linear
map of Li(S,E,p) into a separable reflexive space.
10 THEOREM. Let (S, E,p) be a a-Jinite po8itive rn<'U8UT< spa«,
and let T be a rrcaklycompact op<:ratoronL,,(S, E, 1') too separable8ub-
se! oj the B-spcu:t' 3Z. Then there exists a p-essentially unique bounded
measurable tunctim. xl') on S W a weakly compact subset oj I such that
Tf = J>(S)f(8)p(cU),
JeLi(S, E, 1')'
[OJ Tf = fsxrs)f(S)p(ds). J.Li(S,E"u),
and ITI = ess sup I"'(s )!.
Com'CTSc/Y, if x(.) is a tnffl1S1U'l1b1e, p.-csMntiolly bounded function
on S wilh al11loat all oj ils values in a 'Wel1kly compact subset oj 3Z, then
ffjUl1lion [oJ deJines a 'W£l1kly compact mapping of Li(S, E, 1') inJu 3Z
71'ith separable range.
PROOF. Let U be the closed unit sphere of Li(S, E.p). If T is
weakly compact and has a separable range, the existence of a function
x(') On Ssuch that all the values ",(s) lie in the separable weakly COm-
pact set T(U) follows from V,6.8 and Theorem 2. By III.6.1l, ",(s) is
measurable, so that [oJ holds. Since ",(s). TU , we have sup. 1"'(8):
;;; ITI. On the other hand, [oJ shows that ITI -;: ess sUP.lx(8)1 so
ITI = ess sup 1"'(8)1.
Under the hypoth.....s of the Converse part of our theorem it is
clear we can assume without loss of genera1ity there is a weakly
compact set K such that ",(s) e K for s e S. Let
K i = co (KU-KUiKu-iKI.
Then, by V.6.4, KI is weakly compact. Since it is easily seen that
Tf . K i whenever J is a finitely-valued function in Li(S, E,p) such
that IJI 1, it follows readily that TU K. Thus T is weakly compact.
By III.6.n, there exists a separable subspace 3Z i of I Rnd a null set
F. I such that ",(s). 3: i if 8 e S-F. Since Tf e II for finitely valued
functions T, T has a separable range. Finally, the uniqueness of ",(.)
follows immediately from Lemma III.6.8. Q.E.D.
Since every COIDpal-t. operator is weakly compact and has a sep.
arable rnnge, Theorem IO yields the following corollary.
11 COROLLARV. The operator T of Theo,"Jn 10 is compact iJ and
(ii) For em:h E in f16. K(E, .) u a meo.surnble function on S.
(iii) For em:h A in 1: with p.(A) < 00 the "",a81U"C JAK(E, s)p(ds)
th>Jincd for E in f16 is rEgular and A-continuous.
. d i
(IV) TJ = - K(', s)f(s)p(ds),
dJ. s
(v) ITI = N.
Conversely, iJ the Jundicn K tm 91 xS salis/ies (i), (ii), and (Hi)
Ihffl (iv) dejincs QCOntinllOfISUnel11' map oJ L,,(S, E, 1') into Li(JV, f16, A)
whose nmm is given by (v).
f. Li(S,I, 1').
PROOF. Let I = C( TV) so that 3Z* is tbe space of regular measures
on W (Theorem IV .6.3). The 8pace L i (W, f!iJ, A) i8 isometrically iso-
morph.ic to the :set of regular measures which are .A-continuous (ct
IrI.IO." and III.2.20(a)). Thus L I ( W, 91, A) may be regarded as a
subspace of :r o . If condition (a) is satisfied I = C(W) is separable
hy Lemma 4 and We may apply Thron'ill 6 to ohtain the function K.
In the case of condition (b) we apply Corollary 7. Q.E.D.
\Ve return uow to the case where the range of T is in an arbitrary
B-srace. It will be shown that if T is weakly compact and has "-
separable range its integral representation may be accomplished by a
vector valued kernel which has many properties not enjoyed by the
kernels of Theorems 2. 6, and 7. In this case, the kernel is a bounded
p-measurable fnnction x(.) and thus the vector fnnction x(.)J(.) i8
p-integrable for every f in L,,(S. 1:,1')' The n'presentation of T in this
situation is
which is easily stated without the use of functionals x* in if.. Since
bounded sets in a reflexive space are weakly sequentialJy compact it
508
VJ. OPERATORS AND THEIR ADJOINTS
VI.8.12
VI,8.12
OPERAToRS IN A LEBESGUE SPACE
509
only il tllere is a p-rrnll.et E and a compacl6e!K inI withx(s) inK lor
every 8 in the complement of E.
PROOF. Let V be tl1e unit sphere of L,(S, E, 1-'). Tl1en if T is com-
pact, K = TV is a compact set in the separable 8pace T(Ll) ' nnd it
follows from tl1e proof of Theorem 10 tl1at .70(8)' TV for 8. S.
Conversely.letK be compact and let E be a subset of S of measure
-..:ero such tbat x(.) . K for 8 E. It follows from the proof of Theorem
10 that
X(8)' TU co(KU-KUiKU -iK).
Hence, it follows from V.2.6 that T is compact. Q.E.D.
Re>nark. The following statement follows readily from Theorem
10 if we use Theorem IIl.n.17.
Let (S. E, 1-') and SI' E,. PI) be a-fimte positive measure spaces.
Let T be a weakly compact mapping of 1.,(S. E, 1-') into a separable
subspaceof L,(S" El' pd. Then there exists ap XI-',-essentiRllyunique,
pxp,measurable function K defined on SxS,. such that
wesssup f IK(8. 81)IPI(ds l ) < 00
s.
the resteictiol1 p, of P to 1.'1 has the property that the measure space
(SI' E" PI) is a.finite and the space L,(S,. E" f11) is a separable sub.
"pace of L,(S, E, p) which contains the sequence U.}. Tbus, by Theo-
rem 10, there is p,-measurable. PI-essentially bounded function x(.)
<In S, to the separable closed linear manifold spanned by the set
TL,(SI' 1.'.. f11) and such that
Tin = fs x(8)1.(8)f11(ds).
.
Let (".J be dense in I, and let
BI = 8(",. e),
.-,
B. = S(z., e) - UBi'
' l
k> I.
(TI)(sl) = I,K(., '.)f(8)p(ds).
Ioreover we have
p-esssup J IK(s. 8,>lPI(ds l ) = ITI,
s.
On the basis of Thcorem 7.4 it was observed at the end of the
preceding section that a weakly compact operator on any of the spaces
B(S), B(S. E), AP. C(S), or L (S, 1.'.1-') maps every weak Cauchy
sequence into B strongly convergent :sequence. The next theorem
shows that the Lebesgue spaces L,(S. E, p) also have this property.
I. L,(S. E, p).
Then the sets A. = ;r1(B.) are disjoint and the fUllction x,(.) defined
by the equation x,(s) = Zk for x in Ak lrns the properly that
(i) Ix,(8)-x(8)1 < e, s.SI'
For each k = 1, 2,..., we letx.(s) = "',(8) for sin A 1 U ... UA.. and
",.(s) 0 elsewhere. By Theorem 111.6.10 the sets A. are in the Le-
besgue extension Ei of EI' We may and shall assume that Ei = 1.', so
that the functions ;2:. and :Ck are p.-measurable. Now
(ii) If,. (",.(S)-x,(s»)/n(8)p,(ds)1
= [fe,.. x,(s)/.(s)p,(ds)1
:5;. M f. If.(s)IPI(ds).
Cjr+)
where III = ess sup Ix(s)1 and C. = U;:'.A.. Since L,(SI' E"I-'I} is
weakly complete (IV.B.6) the sequence {I.} is weakly compact and
thus the sequence (iI.(' )I} is also weakly compact (IV.8.9). Hence
Theorem IV.8.8 shows that
and
12 THEOREM. Let (S, E, 1-') be a pos;tWe measure space and let T
be a weakly compact linear map 01 1-.(8. L. p) into a B-3pace. Then T
mo.ps weak Camhy sequences into 8/7ongly t ""'1"""IT8. Con-
sequenlly, T maps ronditlotwUy ",eakly compact sets into condi!ionaUy
strongly compact sets.
PROOF. Let {I.} be a weak Cauchy sequence in L,(S. E,I-')' By
Lemma 111.8.5 there is a set 8, . E and a ,,-field Z',!;; E(SI) such that
lim f. 1/.(8)lfll(ds) = 0
,,_CD C a + J
'Uniformly with respect to n = 1, 2, . . .. From (ii) it follows that
(Hi) lim I, ",.(s}/.(8)fl.(ds) = I "'.(8)/fl{8)I-'I(ds),
1:-+0:> 1 5.1
'1lJliformly in n = 1, 2, . . .. Since {f n} is weakly convergent, the limit
lim. h/.(s)PI(ds) exists for each E in E, and thus for the simple
510
VI. OPERATORS AND THEIR ADJOISTS
VI.8.13
VI.9.I
EXERCISES
51I
lim Is "'.(8)f.(sJI'-1(ds), 8 > 0
OI J.
exists. Since {f.} is bounded (11.8.27) the inequality (i) shows that
lim f "'.(s)f.(s)l'-1(ds) = Is "'(8)f.(B)I'-1(da)
.- s.
uniformly with respect to n = 1,2..... Thus Lemma 1.7.6 may be
applied again to yield the existence of the limit
lim J ",(s)fn(s)I'-1(da) = lim TI.. Q.E.D.
fi 51 "
13 COROLLARY. Let (8, E.It) be a posilive I1IffiIIwre 8pa«!. Then
the product oJ two Wiiakly rompac! "PeralOTs in L,(8, E, It) is compac!.
In particulm, the square of a weakly compact operator in L,(8, E.It) is.
compact.
It should be observed that the only place in the preceding proof
where the hypothesis of weak compactness is used is to show that the
operator Thas the form Js",(s)f(s),t{ds) where ",(.) isWmeasurableand
bounded. The fact that the kernel ",(.) representing a weakly compact
operator has its values in a weakly compact set was not used. Thus
the preceding proof has also demonstrated the following theorem.
14 THEOREM. Let (S, E, pI be a p<1Bilivt' mea.mTe spMe and let IV
be a It-measurable bo"",:I£d funetic", on S to the B-spoce I. Then the
opaalor
Chapter IV or mdicated in the exercises of Se.,tion IV.II!. Thus Theo-
rem 12 and Corollary 18 are true if the space L, is replaced by any OIlC
of the spaces I" bo, bv., batS. E), Tba(S, 1:), catS, E), rea(S. 1:), BV(I),
or AC(I). These spaces together with tho8c 8paces which are equiva-
lent modulo a finite dimensional space to 8paces C(S) of continuous
functions. and for whjch it is known that ThcoTem 12 is true (7.4),
practically exhaust the list in Section IV.2. In fact the only remaining
B-space on the list besides the reflexive spaces.v, If" L'P' 1 < p < oc,
is the spact' A(D) of analytic functions.
functions fC ll the limIts
lim J "'.(8)f.(s)....(da), k = 1, 2, . . -
. s,
exi8t. Since the limit in (iii) is uniform in n = 1, 2, _ . ., Lemma J.7.6
shows that the limit
O}. ExerciB..
Tf = Is ",(s)f(s)jl(ds),
f.L,(S.E,p.),
1 The space B(I, ID) is algebraiCally isomorphic to a subspare
oftheproductP ..31W" whercIDz=ID. undeT the mapping T P ..3'.Ta;.
Show that the strong topology of operators in B(I, ID) is identical
with the usual product topology where the strong topology is taken
in each W" and that the weak operator topology i8 that where each
factor is taken to have the W. topology.
\! A set A C B(3i, ID) is wmpact in the weak operator topology
if and only if it is closed in the weak operator topology and the weak
closure of Ax is weakly compact for each m . I. A set A C B(I, ID) is
compact in the strong operator topology if and only if it is closed in
the strong operator topology and Am is wnditionaUy compaet for
each ",.I.
8 Let A C B(I. W). Then If A is compact in the weak operator
topology, 80 is the weak operator closure of co(A). If A i8 compact in
the strong operator topology, so is the strong opeTator closure of
corA).
4 If a 8et A C B(3i, ) is sequentially compact in the weak
operator topology, its weak operator closure is compact in the weak
operator topology. If A is sequentially compact in the strong operatoT
topology. then its strong operator closure is compact in the strong
operator topology.
5 If U is a subset of a topological space, let iJ be the set of all
sequential limit points of U. If I is separable. a set A B(!. 'g) is
sequentially compact ill the strong operator topology If and only if .4
maps weak Cauchy sequences into 8/rongly coII.-.rgml _tq",,"ees.
It has been mentioned in Section IV.16 that the abstrll-ct L-
spaces are equivalent to the concrete L-spaces and 80 Theorem 12 and
Corollary 18' remam valid for these spaces. The equivalence needed
to prove this statement for each of the L-spaces on the list in Section
IV.2 may readily be made on the basis of the analysis presented in
512
vI. OPERATORS AND THEIR ADJOJNTS
VI.II.6
VI.9.12
EXERCISES
513
{TIT E B(I, 1lI).ly;T"';1 < E,
i = 1. 2, . . .}..
topology, but that {A.A } does not converge to zero in this to-
pology even though {A An} CODV<'I"gCS to zero in the strong operator
topology_
12 If 1S a Hilbert space, the mapping T ..; T* of B( ) into
it.e1f is continuous with either the unifonn or weak operator topology.
By considering the sequence {An} defined in Exercise 11, show that
this mapping is not continuous in the strong operator topology.
13 If U : 'g)* -+ 1:* is a linear mapping whieh 1S continuous with
the W topology in 1lI* and the 1: topology in 1:*. then there exist. a
bounded linear operator T : 1: -+ III such that T* = U.
14 Let T be a linear, but not nece8sarily eontinuous, mapping
between B-space I and 'g). Let T* be defined on the set (T*) of those
y* E 1lI* for which y*Ta: is eontinuous in a: by setting T*y* = y*T.
Then the following statement8 are equivalent.
(i) T* is defined on all of 1lI*.
(ii) T is eontinuous with the strong topologies in I and 'g).
(Hi) Tis eontinuous with the 1* and 1lI* topologies in I and 'g).
15 Let I, III be B-8paces, and U a continuous linear operator
from I to Ill.
(i) If U has a contmuoU8 inverse, the range of U is closed.
(ii) The range of U i8 cl08ed if there exists a constant K such
that for any y in the range there exists a solution of " = Ua: such that
1",1 Klyl. .
(iii) U is one-to-one if the range of U* is dense in I*.
(iv) U* is one-to-one if and only if the range of U is dense in 'g).
(v) If U maps onto 'g), then U. hns a eontinuous inverse.
(vi) If U. maps onto I.*, then U has B cont.inuous inverse.
16 If'g) is a closed subspace of a B-space and W is a finite di-
mensional subspace, then III 111 !n is a closed subspace. If III 111 !n is a
dosed 8ubspace, and !n is finite dimensional. it does not follow that
III is dosed.
17 Let I be a B-space and suppose that I = ID 1I1!n, where
ID is closed and W is finite dimensional. Let T : I -+.8 be a bounded
linear operator mapping into a second B-space. Then T(I) is dosed if
and only if T(ID) is closed.
18 Every non-null, fimte dimensional. proper subspace of a
B-space has infinitely man,y projections mapping onto it.
is compact in the strong operator topology. If III is also separable. A
sequentially compact in the weak operator topology if and only if A
is compact in the weak operator topology.
6 If III is reflexive. then the closed unit sphere of B(I, 'ID) is
compact in the weak operator topology. Conversely, if the elosed unit
sphere of B(I, 'ID) is compact in tbe weak operator topology, III is
reflexive.
7 Define the BWO topology for B(I, Ill) to be the strongest
topology whieh COlncides with the weak topology on eveI')' positive
multiple as of the dosed unit sphere S of B(I, Ill). Show by the
method of proof of V.5.4 that if III is reflexive then a fundamental 8et
of neighborhoods of zero in the BWO topology is given by the sets
where Y: E .., and !t -+ 0; Lei E I.. and :x, -+ o.
8 Let g) be reflexive. Show that a continuous linear functional
on B(I.IlI) whieh we take with .It. BWO topology must bave the form
T -+ II< Y "'T", where { a. } is an absolutel y convergent series of
.Li-O l, I' &
scalars. (y:J is a bounded sequenee in 1lI*, and {",,} B bounded sequence
in 1:. Conversely, show that a funetional on B(1:, Ill) with the given
fonn is eontinuous in the BWO topology.
9 Define the BSO topology of B(I, ID) to be the strongest topo-
logy which eoincides with the strong operator topology on each posi-
tive multiple as of the unit sphere S of B(I, Ill). Show that a eonvex
subset of B(1:. ID) is BWO-closed if and only if it is BSO-closed and
that a linear fnnctional is BSO-continuous if and only if it is BWO-
continuous.
10 Show that every BWO-continuous linear function on B(I.IlI)
is continuous in the weak operator topology if and only if either I
or III is finite dimensional.
11 Let A, BE B(I). Then the mapping (A, B) -+ AB is a con-
tinuous function in e""h variable separately when B(I) is taken to
bave the unifonn, strong or we&k topologies, This mapping is eon-
tinuous in both variables with the uniform topology. and also in the
strong topology provided that A is restricted to a bounded set in
B(1:). If 1: = I" and {A.} is defined by An["'l' ..., "'n' ...J = ["'n+1'" .J,
show that both {An} and {A:} eonverge to zero in the weak operator
514
VI. OPERATORS ANn THEIR ADJOINTS
VI.D.ID
VI.D.28
EXERCiSES
515
19 If E is a projection with n dimensional range, then E* is a
projectIOn with n dImensional range..
20 A projection has finite dimensional range if and only if it is
compact.
21 A linear mapping E such that E' = E is a projection (i.e.,
is bounded) if and only if the ranges of E and 1 - E arc closed.
22 Let E be a projection in the B-space I, and let !m = E(I)
and m = (I-E)(:E). Let !m-'- = {"'*I"'.'" = 0, "'E!m} and similarly
for m-'-. Show that 3i* =!m-'- Ej) m-'- and tbat E*(I*) = m-'-,
(I-E)*(!*) =!m-'-.
23 Tbe lcttcrs!m and m have the same meaning for a projection
as in the preceding exercise.
(i) If E 1 and E. arc projections, EIE.= E.ifand only if!Dlo !D1,.
Also E.EI = E. if and only ,f m l m..
(ii) If tbe E, are perpendicular projections in Hilbert space, tben
EIE. = 0 if and only if E,E, = o.
(iii) If EI' . . ., E. are projections, tben E = EI +. . . +E. is a
projection if E,E, = 0 for i "* j. In this case !m = 9RI Ej) .. . ffi ID/.
and m=m,n ...n9!".
(iv) If the projections in (Hi) are perpendicular projections in a
Hilbert space, E is a projection if and only if E,E, = 0 for i oft j.
24 (i) E = EI -E. is a projection if and only if EIE. = E,EI
= E.. In this case 9R = 9RI n!Jl" and m = m l Ej)!JR..
(ii) EIE, is a projection if and only if EI(ffiI,) !JR. EI) m,n!Jl".
(iii) If E = EIE. = E.EI' then E is a projection and 9R =
!llI1 n !m., m = sp {m. Um.}. which i8 therefore closed.
(iv) EIE, = E.EI if and only if 9R" = !JR.n9R 1 EI) !JR.nm l and
m. = m.n!m l EI) !JI"nm l ,
(v) If EIE. = E.EI' then EI+E.-EIE. is a projection with
range sp{mIu!JI,,} and null manifold m 1 n!Jl".
25 A weakly compact projection in a space C(S) or a 8pace
B(S) has a finite dimensional range.
26 Show that a linear operator T m a finite dimensional space
may be represented as a matrix.. In terms of this matrix, what is the
representation of the adjoint T.Y
27 In tblS exercise let I be n.dimensional Euclidean space and
let el . . " en be the basis of coordinate vectors
(i) If E is a perpendicular projection. show that its matrix
representation is (a,-;) = (I _]PtkPlk)" where gk = .I?=lPill't'k' k = I.
. . .. T i. any orthonormal basis of!m = E(I).
(ii) Let 9R and m have bases {a",.... a,.} and [b l ,.... b }.
respectively. Let T be the transformation defined by
Te,=a ij
Ter+r = b ,
i = 1, . 'f r;
i = 1, _ ., n-r.
If T = (t,,) and T I = (.,,), show t1mt E = (I';"',.,.,.,).
28 Define the trace of a matrix A = (ail) by tr(A) = I::"la".
Show tlIat tr(A,B) = tr(A)+tr(B) and tr(AB) = tr{BA). If E
is a projection in Euclidean 8pace, show iliat tr(E) = dim(!D1).
29 Let Ej, . ., Ep be projections in II finite dimensional Eucli-
dean spacc. If E = EI +.. .+E is a projection, show that tile mani.
folds {!D1,} arc linearly indepcndent, tbat!m =!m, Ej) . . . E9 9R p , and
tbat E,E, = 0 for i"* j. (Hint: Use Exercise 28.)
30 If T. B(I, ID) i. compact tben it maps every weakly con-
vergent sequence onto a strongly convergent sequence in 'lJ. If 3i is
reflexive. this property implies iliat T is a compact operator
81 Let T. B(:E) be compact and), oft o. Tben the equation
(ll - T)x = 11 has a unique solution for every 11 in ID if and only if tbe
equation (ll-T)", = 0 has no solution other than '" = o.
82 If 'lJ has a basls, every compact operator in B(I, 'ID) is the
limit in tbe unifonn operator topology of a sequence of operators with
finite dimensional ranges.
33 If (8, E. p) is a positive measure space, weakly compact pro.
jections in L,,(S, E, 1-') have finite dimensional ranges.
34 A continuou8 linear mapping from a reflexive space to l" is
compact.
35 A continuous linear mapping from c to a weakly complete
space is compact.
86 Let 4> be a function mapping a set 8 mto Itself. If T i. the
hounded linear operator in B(S) defined by T/(.) = 1("'(.»), represent
tbe adjoint T*.
87 Let'" be a continuous function defmed on a compact Haus.
dorff space 8 to S. Let T be the bounded linear operator In C(S) de.
fined by TI(s} = I("'(s». Represent the adjoint T*.
516
VI. OPERATORS AND THEIR ADJOINTS
VI.9.38
VI.9.46
EXERCIsEs
517
38 (Markov) Let 8 be a non-void set and f a function on 8 to 8.
A function I' defined on the family of subsets of 8 is said to be "'-in-
variant in case pIE) =p.(f IE), EC8, where ",-IE = [sl4>..E].
Show that there is a non-negative bounded additive function I' defined
for wl subsets of 8 which is not identically zero and is "'-invariant.
89 Let 8 be a compact Hausdorff space and '" a continuous
function on S to S. Show that there is a regular countably additive
non-negative measure p defined for all Borel sets in 8 with the prop
erties that I' is not identically zero and I' is 4>-invariant.
40 Let 8 be a non-void set and G a family of functions'" on 8
to 8. Suppose that ""(f,(s» = 1>.(""(8)), 8 E 8, "",1>. E G. Show that
there is a non-negative additive set function I' defined for all subsets of
8 and with the properties that I' is not identically zero and p is f-
invariant for every ",. G.
41 Let 8 be a compact Hausdorff space and G a family of contin-
uous functions '" on 8 to 8 with "',"'.. = M', B. 8, "',' 1>.' G.
Show that there is a cOWltably additive non-negative measure defined
on the Borel sets of 8 which is not identically zero and is "'-invariant
for every ",. G.
42 Show that in Exercise 38 the set function p IS unique up to a
positive constant factor if and only if ., 1 ! :U(""i(B» converges
uniformly to a constant for each f. B(8).
43 Show that in Exercise 89 the measure p is unique up to a
po8itive constant factor if and only if .,-1 I:;::"lf(""'(s» converges
uniformly to a constant for each f E C(8),
44 Let 8 be a compact metric space. and'" : 8 1:/ a mapping
such that p("'(",), "'(y» p("', y). Suppose that there exists an s.
in 8 such that the set {"'"B.ln ;;" 0), is dense. Show that there exists a
unique reguJar measure I' defined for the Borel subsets of 8 such that
fL("' I(E» = piE) for each Borel subset of 8, and such that 1'(8) = 1.
(Hint, Use Exercise 43 and the fact that only constant f\lnctions can
satisfy the equation I(""(B» = I(B).)
45 Let S be B compact Hausdorff .space, K be a continuous
function on Sx8, and I' E rca(8). Define the operator 11= Tf by
g(s) = IsK(B, t)f(t)p.(dt).
Show that T is a compact operator on C(8) to C(8) and that its ad-
joint is represented by the formuJa
T*",*(E) = IE [IsK(s, t)"'*(ds)]p(dt),
for every Borel 8et E.
46 Lct C = C[O, IJ and T. B(C, C). Then there is a scalar
function K on [0, I] X [0, 1] sueh that
(i) For each s . [0, I] the function K(8, .) is a normalized func-
tion of bounded variation on [0, 1];
(ii) T(I, s) = JtJ(t)K(B, dl), O :s: B 1, I. C;
(iii) K(B, 1) and J K(s, t)dl are continuous in s for eacb rE O,lj;
(iv) sup var K(s, t) = M < 00;
II C)St l
(v) III = ITI.
Conversely if K is a function satisfying (i), (iii), and (iv) then (ii)
defines an operator T E B(C, C) whose norm is given by (v).
47 Stale and prove theorems similar to that of the preceding
exercise for the representation of the general linea.r operators in
B(L., C), B(B(8), C), B(e, C), and B(C, e) where C = C[O, 1] and
L. = L.[O,IJ.
48 Represent the general compact operator in B(Lp, C).
B(B(8), C), B(e. C) where C = C[O. I] and L. = L.[O, 1J.
49 Show that the adjoint of the operator T in Exercise 46 lS
given by the formuJa
T*(g.t) = I: K(s, t)dg(s), g. NBV[O, I],
50 Let 1 :s: p, q < 00 and let T. B(L.[O, I], L.[O, I]). Show
that there is a function K on [0. I] X [0,1] such that
TU, s) = !!.. J. 1 K(s, 1)/(t)dt, I. L.[O, IJ.
ds 0
51 Let (8, E, 1') be a positive measure space, and K a measUr-
able function on 8 to the B-8pace X. Let
Us [K(sW'p(ds)Y'" = M < <0,
where 1 < p < 00 and (l/pJ+(l/p') = I. Then the operator T on
L.(S,E,p) to if defmcd by
TI = Is 1((s)/(s)ds
is compact and has norm at most M.
418
VI. OPERATORS AND THEIR ADJOINTS
VI.9.52
VI.9.56
EXERCISES
519
Us Us IK(E, 1)I"p(ds»)""Vp(dt)t p ' = M < 00.
Let g = Tj be defined by
g(s) = r K(a, t)f(l)dt.
.s
Then T is a compact operator In Lp(S, I, I') whose norm IS at most iU_
5S Let 1 < P < 00, (l/p)+(1/p') = I, and let (8,1:,1') be a
positive finite measure space. Let K be a measurable function on S X S
with
56 Let (8, 1:, 1') be a finite measure space whose space 8 is a
compact Hausdorff space. If 1 < p < a;J, show that any continuous
linear operator from L.(8, 1:, 1') into C(8) is a compact operator when
it is regarded as mapping into L.(8, 1:, 1').
57 Let (8, 1:, 1') be a positive finite measure space and let
K(s, I) be bounded and measurable on 8x8. Let T in B{LI(8,1:,p»)
be defined by
52 Let I < p < 00, (lfp)+IIfp') = 1. Let (8,1:,1') be a POSI-
tive measure space and K 8 scalar yalued measurable function on
S X S which satisfies the condition
T(j, a) = fsK(s, IJf(I)J«dt).
8UP J IK(s, '>1"' dt < 00.
. s
Then the operator g = Tf defined by
g(s) = fsK(s, t)f(l)dt
is a compact operator in Lp(S, 1:, p).
54 Let (8,1:, p) be a positive measure space, Lv = Lv(8, 1:. p),
1
P
co, and K a measurable function on 8 y 8 with
Show that T* in L",(8, 1:, p) is given by
T*(g, I) = Isg(s)K(E, I)J4ds).
Show that the operator T, when regarded as acting in L",(8, E, pI,
is weakly compact and that its square is compact.
58 Let (8, E, p) be a (>Csitive finite measure space and K an
essentially bounded measurable function on 8 x8. Let v be a bounded
additive function on I which vanishes on sets of p-measure zero.
Show that
A(E) = Is [IER(s, I)p(ds)] v(dt)
ess sup Is IK(s. 1)lp(dt)
M,
.
ess sup Is IK(s. t)IJL(ds) < M.
.
Then the operator g = Tf defined by
g(s) = IsK{S, I)f{t)dt
is a continuous linear map of L. into L
and ITI
M.
55 Let K be a Lebesgue measurable scalar function with period
2", and
is countably ac1ditive for E E E. If the measure space is a-finite in-
stead of finite, what restrict.ions On K are equivalent to the countable
additivity of .1.1
59 Let (8,1:,1') and (S', E', 1") be positive a-finite measure
spaces. Let L = L{8, E, 1') and L.=L.(8',E',I")' If p> 1 and T i8
s separable bounded linear map of L into L F there is a scalar function
K on 8xS' measurable with respect to ExE' and such that
(i) T(j. s) = fsK(s, I)f{s}p(ds), f £ L;
(ii) ess sup <Is' IK(s, t)IDp'{ds»)lID = M < 00;
.
IKI = f; jK(a)lds < 00.
Then for 1
P < 00 the operator g = Tf defined by
(..
g(s) = Jo K(s - t)f(l)dt
is a compact linear operator in LIJ(O' 211:) whose norm is at most IKI.
(iii) ITI=M.
ConverseJy, if K is a measurable function satisfying (ii) then (i) de-
fines an operator T £ B(L. L.) whose norm is given by (Hi).
60 Let L be the space of Lebesgue integrable functions on [0, 1],
Represent the general linear operators in B{L, L}, B(L, lI)' B(lI' L).
and B(l.., l..). In each case give the nonn of the operator in terms of
the kernel.
520
VI. OI"'ERATORS AND THEIR ADJUIN'I'S
VI.lO.l
VI.1O.4
THE RIESZ CONVEXIT\" TUEOBEM
521
10. The Riesz (:onvexilY Theorem
In this section we prove the deep and important convexity
theorem of M. Riesz by the method due to G. O. Thorin. The proof is
a particularly beautiful instance of the applicatIon of complex variable
theory to a seemingly unrelated problem in the theory of linear spaces.
Throughout this section !ro denotes a compkx B.space, and E'
denotes k-dimensional Teal Eudidean space. The reader should observe
that the same letter 111 is repeatedly used for different functions. each
eXplicitly defined in the statement of a given theorem or in its proof.
1 DEFINITION. Let C be a convex subset of Ek, and let M be a
function defined on C and having values which are either real num-
ber8 or + 00. We say that M is COIWt'a: if for any", v . C,
M(oc",+(l-oclvl ccM{u)+(I-",)M(v),
whenever 0 a. S; 1.
2 LEMMA. Let {M K ) be a family of rom",... functions defined on a
co""," set C!;; E'. Tllen the fundio.. M defined by
M(",) = sup M.(",)
e"'M(b) rnax{""'M(a),e"M(c)}.
We now choose r such that """M(a) = c"M(c); that is.
log M(c) - log M(a)
r= .
a-c
Substituting this value of T into
rb+ log M(b) re -rlog M(c)
and using the fact that c-b = -o:(a-c), we find after 8implification
tho.t
log 1I1(b) a. log 1I1(a)+(I-a.) log M(c).
Thus log lIf(",) is convex lIS stated. Q.E.D.
We now extend this result to k variables.
is a "'''IV'''' fwu:tWn.
K
4 C080LLARY. Let f be a bounded analytic fvm:tion oj the complex
Vl1Tioble8 2'1" . . ., 2.t. 2j = aJ i +i1l1' which is dejiru:d lor 3: = [Xlt ". ", 3'J n ]
lyi..g in a 'onvea; set C E' and y = [y" . . ., y.] Uf1rC8trided. Suppose
f has tHIl..es in !ffi, and let 111 be defirn:d an C by
11-1(",) = sup {If(",+iy)ll- 00 < y, < 00, i = I, . . ., k}.
Th£n log 111(",) i. a convex ftmchon oj the vector variable '" inC.
PROOF. Let ",',:J!' £ C be held f,xed, and let y = (y" . . ., y.] be
arbItrary. Let A = '" +ip be a complex variable, and define g by
g(A) = I(M' +(I-A).<" +iy) = j(u" . .., u.),
PROOF" For each n we have
lIl K (a.u+(I-",)v) :$ 0:1I:l.(")+(I-a.)M.(v).
whenever u, v E C, and 0 ::;: « l Taking the supremum over all n,
we have the desired assertion. Q.E.D.
The next result is sometimes called the "three lines theorem".
where
Mt",) = sup 1/(",+iy)l.
-0;><",-<0'>
", = ""';+(I-")X;' +i[jix;+(I-fJ)",;' +y,], j = I, . . _, k.
We now apply Theorem 8 to the function g on the strip 0 ::;:: 0: :-<=; 1,
- CO < fJ < + 00, obtaining
log Ig{o:) I ::;:: log {sup Ig(a.+i{J)I}
p
S; 0: Jog {sup Ig(I +i{J)I}+(I -a.) log {sup Ig(O+i{JJI}
p p
:-<=; 0: log 111(",')+(1-",) log 1I1(x").
We have shown that for arbitrary choice of y = (y,. . . ., 11,].
log If("",'+(I-a.).<"+iy)1 = log Ig{ot)/
:$ 0: log M("")+(I-o:) log 111(",").
3 THEOREM. La I be an a:nalytit: functiv.. vj a compk", 'UWiabk
Z = oJ: +iy rbitll 1'al..es in !ro. Suppose thaI f i8 defined and """"lied in the
81rip "'0 ::;:: '" < "'1' - 00 < y < + 00. Let 111 be defined for Xo '" XI
by
Then log 1I1{x) ;s a canvex juntIWn of the real ""riable "'.
PROOF. Let "'0::;:: a ::;:: c < "'1 and let b = aa+{I-a)c for some a.
with 0 CL :$ 1. For any reoJ number r, the function e'"/(z) is analytic
and bounded in the strip a '" c. By the maximum modulus prin-
ciple .for a strip (cr, 111.14), we have
522
VI. OPERATORS AND 'l'HEIR ADJOINTS
VUO.5
vr.lO.8
THE RIESZ COS-VEX1TY THEOREz.r
5'lB
Takmg the supremum over aU choices of y we conclude that
logM("""'+(l a)x") ,,; ",log 1I1(x')+(1-a}log M(,,,"),
which proves the statement. Q.E.D,
DEFINITION. If .8 is a complex vector space, a function
G :.8 -+ !ffi is said to be analytic if G(A.z, +. . .+1.":<.) is an analytic
function of the complex variables All _ . _, Ap in the sense of Section
III.I4 for every finite collection {ZI' ..., z;}C8. If 8,.,....8, are com-
plex vector 8paces. let .8 be their direct sum (cf. I.U); then the
definition just given also gives a concept of ana]yticity for a function
G: 8 8,. Gi .. . EII.8, -+ fill.
To facilitate the statement of the next result it will be con-
venient to introduce tbe following notation.
6 DEFINITION, Let (S" :E" 1',) be a positive measure space for
e""h i = I, . . ., k, Let .8, be the space of aU complex valued prin-
tegrab!e simple functions on S,. If a [ , . . ., a.] e E' and a, > 0,
we define A(a) = A( ,. .., a,) to be the set of aU collections
f = Ul" ... f.] with J, c.8J and
[*] Js,IJ.(8)I"a'pJ(ds) ,,; I, i = I, . . ., k.
If a; = 0, then condition [*] is replaced by the requirement that
1MB)! :::;; 1 pralmost e"Verywhere,
for that value of i.
7 LEMMA. Wilh the lnmirwlol!Jl oj !he preuding de/inilions, let
G be an analytic fulldion on.8 = 8. Ell . . . Ell .8. wilh t-alue3 in fill. Let
lI-I(a) = sup IG(J)I
A( )
Tkn log 1I1(a) is a convex june/ion of a = [a,., . . ., a.] Jor a, ;;;; 0,
i = J. .. ., k.
PROOF. Let A+(l) denote the set of all / = U l , ' . ., J.] in
A(I, .. ., J) such that each J; O. Let a = [ . .. ., a.) with a, ;;;; 0,
then if JcA+(I) and geA(O) =A(O,.. .,0), the collection
J"g = Ui%, . . " /.'g.]
is an element of A{a), It is readily seen that an arbitrary element of
A(a) can be obtained in this way. Further, if b = [b I ,. . ., b.] £ E'is
arbitrary then
/a+"g = Ui'+;"gl' ..., f:r....gk]
is in A(a). Consequently,
M(a) = sup IG(J"g)1 = sup sup IG(Ja+;'g)1
A+UI.A(O} " ..4+(1I.A(O)
sup sup IG(Ja+;'gJl.
.4:+(I),A(O) 1I
Letl, = as+ib;;t DJ 0; then.since /;and gf are simple fUH()tions,
tigj can be written as a sum I:t.. fn.Zjmt where 2'im IE" Zj and Plm is a.
positive real number. Since G is assumed to be analytic. it follows that
G(fg) = G(fa+"g) is an analytIc function of the complex variables
A = [A.,. . ., I..], and is bounded on each 8trip 0 :::;; &i(A;) < c, < OJ,
j = I, . . ., k. By Corollary 4, Lemma 2t and the increasing nature
of the logarithm we conclude that
log 1I/(a) = sup log {sup IG<r-"'g)l}
A+(1).AlOt b
is a convex function of the vector a = [ ,., ..a.) for a, > 0. Q.E.D.
8 THEOREM. Let (S. E, 1<) be a ptJSitive measure space ana: La the
space oj aU p-",ugrable simple jundimui. Let T be a linear mapping 01
L" inlo a comple", B-.pace I. IJ T can be e.rtended to a bounded linear
Iransformalion oj L (S. :E, 1') into I, let ITI b" the norm of thi8 e.rfnI8ion;
iJ rw such e:ctension e:ris/s, leI ITI = + 00. Tkn log ITII/u is a COIWI':1J
Junction oj a for 0 ;;;; a -<;; I.
PROOF. Since L. is dense in L.(S,:E. pI for I :::;; p < OJ, it is clear
that if 0 <a::;:;l,
[*] IT]ll" = sup {iT/II/ e L o ' III,," s;: I}.
It is also evident that
ITI > sup {IT/III d., )/I -<;; J}.
Thus. if M(a), 0 < a -<;; I, denotes the supremum in [*] and ]I{ is
defined by N(O) = ITI , N(a) = 0 for 0 < a ;;;; 1, then ITlt!u =
max {M(a), N(a)}. Since a linear mapping is obviously analytic. the
theorem foHows from Lemmas 7 and 2 and the observation that the
logarithm of the maximum is the maximum of the logarithms.
Q.E.D.
620:1
VI. ORBATORS AND THEIl\. ADJOINTS
VI.I0.11
VI.lO.1l
THE RIESZ CONVEXITY THEOREM
525
II LEMMA. Let IS. I. 1') be a poBWve measure sp<u:e, and leI I
bea p 1e lut1dion delined on S.II I £ LpIS, I. 1'), leI Illp denole
its norm a" an element 01 this sp<u:e; otherwise pal III. = + 00. Tlu:n
log I/lv. is a c.nvex fut.ction 01 a, 0 ;;;; a ;;;; I.
PROOF. If III.,. = +00 for aU a. 0 < a ,;; 1, the conclusIon is
trivial, so we suppose that I. L..(S.I, p) for some Po' By Lemma
III.8.t>, we may suppose that S is a-finite. Let L" denote the class of
p-integrabl.. simple functions and gEL", then HOlder's inequality
IIII.8.2) implies that fg is p-integrable. Let
MIa) = sup Ii JsI(S)gI8)p(da)jl gEL", IgII/l ';; 11.
If I is in Lv.IS, I, 1'), then the Holder inequality asserts that
M(a) < Ifll/.' Conversely, we shall show that ,f M(a) < oo,O<a<l,
then I is in LI,.(S, I, 1') and Iflv. ;;;; "'I1la). Thi8 will prove the lenuna,
since ifweputN(I) = I/I"N(O) = Ifl .N(a) = Of orO < a < 1 then
IIII/o max {Mla),Nla)} and the conclu8ion follows from Lemmas
7 and 2.
Suppose that MIa) < 00 for some a E (0. 1). Since Lo is dense in
LII,_(S. I. p). it follows that
",.(g) = J. /(s)g(s)p(da)
can be extended to be a contmuous Imear functional of norm MIa) On
all of L1/l_' By Theorem IV.S.l. there exists an i E LIJ.(S. I. !') such
that lil Il . = 1I1(a) and
Is I(s)g(s)plda) = JJIs)gls)plda), g. Lo'
In particular. if pIE) < 00, then
I"/(s)p(da) = J"/(s)plds).
By Lemma III.6.S, it follows that fls) = lIs) p-almost everywhere on
each set in Iof finite measure. Since we have taken S to be a.fmite,
f(s) =l(s) p-almost e,'erywhere. Hence I.LI/.(S.I. p ) and
1/11'. MIa). Q.E.D.
The next theorem is a companion result to Theorem 8.
10 THEOREM. Let IS. I, 1') be a positive 111<'O-SUTe sp<u:e. let I be a
complea: B-space and leI M = ,'l-IIS, 1:,1') be t sp<u:e 01 all <omplex
valued p-measu,-aMe fuoctil!ns defined on S. Lei T be a linear mapping
011: into 11-1.11 T is a bounded linear m«ppmg 01]; into L.{S, I, pI, let
ITI. be the twrm of thi.$ operahJr, othetmise let ITI. = +ro. Tlum
log ITllIa is a C<m1!elC IUflctirm 01 a for 0 ;;;; a ;;;; 1.
PROOF, If "'. 1:. the precedilJg lemma shows that log ITa:I IJ . is
a convex function of a, 0 :;;; a < 1. It follows from Lemma 2 that
log ITII}. = log sup IT"'lv. = sup log IT",llI a
1.1'" 1*;;'
is also a convex function of a in this rangea Q.E.D.
... n THEon!!:",. (Riesz crwWI'.l:ity throrem) Let (S" II''''') and
IS., I., 1-'2) be poBilive measure sp<u:es. Let L" be tlu: set of all CIJ111f1l=
valued p,-inlegrahle simple fundions, let M be the set of all m"'fJkz
valued p,.mrosuroble functions, and let T be a linear mapping of L. inro
M. II for a given pair (p, '1), T has an e:runsion to a bounded limar
mapping of L,(SI' 1:",..,) inJo L.(Sz, I., 1-'2). let ITI.,. denote th£ norm
01 thi. f:ZtIrn8;on; if no su<h exle11.rion ea:isfs, let ITI.,. = +00. Then
log ITI"..". i. a conv= lund;on of la, b) in the redm'l5le 0 ;;;; a. b ;;;; 1.
PROOF. If ITI.. = + 00 for Ip, q) in the range 1 ,;; P ;;;; co,
l ;;;; '1 ;;;; 00. then the assertion follows from Theorem 8 with 1: =
L (S.,..:.. p,). Hellce we may suppose that there is some pair (Po, '10)
in this range with ITI..... filJite. Hellce if I, E LJ,') = L", T/I is in 80me
space L..IS., I., p,). It follows from Holder's inequality, that if I. is
any function in the space L ') of alll-'2-integrable simple functions.
then the integral
[.] G(/I' f.) = f (Tf,)ls)/.($)"'lds)
s,
exists. Thus, under the assumption that there is Some ITI lloo which
is finite. then the integral in [0] exists for any /, £ L ') and any
I.. LJ,'I.
Let a = lip, b = 1/'1. 11'1+1/'1' = 1, and put M(a. b) =
sup IG(/I.I.)I, where the supremum i.taken over all II . LJ,I), 1f,1. < I,
and over alii, E LJ,'i. 1f.1., < I. It is clear that M(a, b) ;;;; ITlp,'
Conversely, suppose that 0 < a, b < 1 and M(a, b) < ::0. We
shall show that ITI. . ;;;; MIa. b). To see this. observe that for each
It £ L '), equation [oj determines a linear functional on a den8e subset
of L.,(S., I., 1-'2) with bound at most equal to MIa. b)Jt.I... Consequent-
.
526
VI. OPERATORS AND THEIR ADJOINTS
V1.10.I2
VI.l1.I
VY'FR('J6)f.$ ON INEQUALITIES
521
11. Exercises on lne.[ualitie8
A. l1!li(jW1lilu,s obrainabk Irom com_ilg rhevrem and k1l<J'l1iledge
oj ewernL.' cases.
I Let (S, I, p) be a positive measure space. Show, using a con
vexity argument. that the mapping [j, g] h defined by h(s) =
I(s)g(s) is a continuous map from L.(S,I,p) xL.(S, E,p) to 4{S,!:,p),
whcre l!p+Ilq = Ilr, and that Ihl. 1/1.lgl., thereby obtaining
Holder's inequality as the special case IIp+lfq = I. (p, '1," ;:;, I.)
2 Generalize Exercise I to 8how that if hIs) = I.(s). ../fl(s),
l,eL.,(S,E,p), and I _11fp, = If.., then h is in L.(S,I,p) and
Ihl. ;:;;; Iftl... . . [ffl[" . (p" .. ., P.. r ;:;, I.)
3 Let (S" E" P,) and (5., E., ",,) be two positive measure
spaees. Let K be a P, x".-measurable function defined on SI X 5., and
suppose that !s,IK(sl' s.III-'1(<I8 I ) < M , < <1) for p,.almost all s. in S.'
and !s,IK(sl' s.II",,(<I8.) < M, < w for l-'1.almost wI s, in 5,. Show
that if / is in L.(S., I., 1'.). then the integral
I K(s" s.)/(s.)p(d3.)
s,
exists for J.l1-almost aU 8 1 , and defines a function in Lj:I{Sl' Xl' Ilt) of
norm at most M /'111 -I/'IfI.. (I ;:;;; p w)
4 Let (51' L" 1-'1) and (5., E., ",,) be two positive measure spaces.
Let K be a 1-'1 X ",,-measurable function defined on 5, X 5., and suppose
that fs.IK(al' a.)I"'p,(d3,) ;:;;; M. < w for l-'1-aImost all aI' and
Is.IK(s" S,II"'Pl(d3,) < M, < <1) for ".-almost all s.. Show that for
each f in L.(S., I., ".), the integral
I K(sl' s.)/(s.)p,(<I8.)
s,
exists for l-'1-almost all s" and defines a function in 4(S" E"Jl1) of
nonn .at most
ItI.MiI/.,H..r..,1 ""'l /'.
Here I PI' p, <1), I!p,+l/q, = I, Ifp+I/'1 = I, 1 < '1 :5; '1., and
r = PPI(P-p,) I.
5 Let (5"I"p,) and (S"I.,,,.) be two positive measure spaces.
Let K be a p, X ",,-measurahle function defined on 5, X S., and suppose
that
ly. it can be uniquely extended to aU of L." and by Theorem IV.8.1
th«e is age L.(S., I" 1',) with Igi. 1I1(a. b)l/ll. such that
f (TI1)(a)f,(s)".(<I8) = I g(s)f.(s)",,(<I8}, I, € L 11, f.- L 2}.
Sol 5",
Applying Lemmas 111.6.8 and 111.8.5, we conclude that TfIle) = g(8.
",,-almost everywhere; hence TI,' L.(S" E., ",,) and
IT/II. Mia, b}lfll..
Since thi8 holds on the dense 8ubset Ll,IJ of L,(Sl' E"I-'1), T may be
extended to a mapping of this space into L.(S., I., p,) with norm at
most M(a, b). Hence ITI.,. M(a, b).
Now the function G is a complex valued bilinear function de-
fined on L 'I xLl,2), and so is analytic. By Lemma 7, log M(a, b) is a
convex function on the rectangle. In addition we have shown that
M(a, b) ITI I '.,I1b for all a. b and that if 0 < a, b < I, then
"U(a, b) = ITllI..1'" Let N be defined on the rectangle by N(a, b)
= ITI'/.,lIo if either a or b is equal to 0 01" 1 and N(a, b) = 0 for all
other pail'S. Theorems 8 and 10 imply that log N{a, b) is a convex
function. Since ITl:u a .I1o = max {M(a, b),N(a, b)], the conclusion of
the theorem follows from Lemma 2. Q.E.D.
We conclude this section by giving a very simple application of
the Riesz convexity theorem which will be used later.
12 COROLLARY. Let (S, I,,u) b a positWe mt'aBUT space and let
T be a linear mllp'liifig which 8ends each eompk., L.(S, I, p} space ink>
itself, 1 P <1). If T ia known 10 be oo1lti1./WUS for p = I and p = <1),
with .wnn alma'" C, tlum T : L. L. i. .tmt.nuous for all p. I p W,
and has norm at moat C.
The proof of this statement follows readily from Theorem 11 and
will be left to the reader.
The convexity methods de'\"eloped in the previous section, if
taken together with a few elementary devices, can be used to derive a
large number of the most familiar and important inequalities of
analysis. In the present section, we shall give a connected series of
exerciseti on inequalities, designed to illustrate this statement.
f . [I IK(a" a.)I"',u,(d3.W'I'1(<I8,) = 111 1 < <1),
:!it S..
Is. [Is, IK(a" s.)jo'Pl(<I8,W'P.(<I8.) = M. < <1).
.
528
VI. OPERATORS AND THEIR ADJOINTS
VI.1I.6
VI.n.1I
EXERCISES ON INEQUALITIES
529
Show that for each f E Lo(S., E., /l2),
f K(s" s.)f(s.)/l2(ds.)
s.
eXIst, for PI-almost all s" and defines a function in L,(SI' E"PI) of
norm at most Ifloj1.1'Xlf'Ii1J.M l-o;)I"2;Pa. Here q is between q2 and
r iF.(r iF. -I )-1,
qriP.-q-riP.
a=
q-qr,
exists for almost all w, and defines a funchon h In L.. liT =
!::'IP,l_ n + l . Moreover, Ihl r ;:;;; Iftl.," .Ifnl ..
II (Hausdorff-Young) Let k be an integer I, and let p =
(2k+ I )/2k. Let f be in L., Show that the multiple integral
h(ll) = r: . .. r: f(W-yl)f(ycy.)...f(yn-2-y.....I)/(yn-l)dyl...dyn 1
exists for almost all w, and defines a function in L.. Show that
Ihl.;:;;; III:.
10 Show that if {a.} and {b n } are (two-sided) sequences of com-
plex numbers such that !;;=-w 1a,.1 < co and !;;:_m IbnjP converge,
p 1, tben Cft = :_o-a bm is defined for each n., and
and
71B1Pl
1=
a(pl +r 1 s l )+r l s,pl-r 1 s,
Simil..,. inequalities might easily be given for multilinear forms
of the type
f ... f K(s1"'" Sn)fr(sl)' . ,Tn(s.),u,(ds l ). . .p.(ds n ),
5[ 5..
but we leave the development of tills line of thonght to the reader.
In VIII.I.24 we will show that if f is a function on the real line
which is Lebesgue mea8urable, the function g of two real variables
defined by
+m + +G
( ! Ic.I"}l/. ! ja,.l{ ! IbniPPI..
71=-1;1)
__w
n__CD
II Let fa,.} and (b n } be (two-sided) sequences of complex
numbers such that :-OJ lanll' < W, !::-o:. [bftl"" < 00, 1 P < oo
I ;:;;; r < 00, where l/p+I/r ;?; I. Show that c. = L;t:-m a_b m is
defined for all n, and that
+0'> f-o;. -to;.
{ ! Ic.I'}II' < ( ! la.I }'J'{ ! Ibnlr}I/r.
g(w, y) = f('"-y)
is measurable with respect to two dimensional Lebesgue measure. In
the following exercises On integrals of the "convolution n type, free use
may be made of this fact. (In the next four exercises. L. denotes the
L. space fonned with respect to the Lebesgue measure on the real line. )
6 Let f be in L.. g be in L p , p 1. Then the integra) h(w) =
J :f(,"-y)g(y)dy exists for almost all w, and defines a function in L..
Moreover, Ihl ;:;;; Igl.I/II'
7 Let f be in L.. and g be in £,., where Ijp+I/r ;?; I, P I,
and T I. Show that the integral h('"J = J :f(,"-y)g(y)dy exists
for almost all x and defines a function in Ls, where g-l = T-I+p-l_1.
Moreover, jhl. < II/./glr.
8 Let If be in L." Pi Z I, i = I. . . ., 11 1 and suppose that
! ll/pj ;?; n-I. Show that the integral
'"+()CI .+(;1:\
h(x) = Lw ... Lo> t,(x y,)f'(y'-Y2)" .f t(Y""'2-Y.-I)f.(Yn l)
dy,. . . dYn_1
_-0>
tt__u>
fi=-O;>
where l/r+ljp = (1/6)+1.
12 Let {a )}, -co <n < +co. i I, ..., k+l, be a family of
sequences (two-sided) of complex numbers, such that r,:_O)ta j)ISI.
< co, p, I, i = I. . ... k+l, and ! _1 lip, ;?; n-1. Show that
the multiple series
+1» +0:.
c n = ... a(l) all!) a(k) a(k+1)
-' tI- n...-tI;... m--m., mot
"".--CQ "',1:--01
con absolutely for each n, and that
+00:1 .1:+1 +m
{ ! le.!'}'lr <::: II { ! la )I.,}ll".
1'1=-0' '=1 fl=-
B. Generatizatiom of Holder's and MinkOW8ki's inequditieB.
Often a familiar inequality, when applied to vector valued func-
tions l will take on an interesting, but less familiar form. Minkowskils
inequality leads immediately to the formula
is If(s)Ii'(ds) IJ s f(8),u(ds)1
II
580
VI. OPERATOItS AND THEIR ADJOINTS
VI.ll.I8
VI.ll.I8
EXERCISES ON INEQUALITIES
531
I fs, [fs,IK(B I , 8.W p,,(ds.Jr' f-'I(ds,)II/'
;;: US, [Is, IK(8 1 , s.)I' f-'I(dsIJJ" ",,(ds.)II/'.
'"
I I fsKft(B)L.(sJp(ds)[
.....
s; [fs {1.IK.(8J1"}I"P(ds)] [fs {ft! IL.(8)IV}"Vp(ds)],
the series on the left beIng well-defined and ..bsolutely convergent
whenever the quantities on the right are finite,
18 Let f and g be Lebesgue measurable functions of two real
variables. Let p ;;: I, l/p+I/'1 = I. Show that
IJ : [r: I r: I(x, y-z)g(x, Z)a..ld", r dul 'l -
U : r: Ig(x. Y)IPd",duJI" r: [r: I/(x, yJI°d", ]1'" dy.
the quantity on the left being defined if the quantities On the right
are finite. (Hint. This is the vector form of Exercise 6,)
C. ImqunIi!ies of Hardy-Hi!berl Iype.
The next .set of inequalities are all variations on the elementary
theme given in Exercise 15, whi h lends itself to surprisingly manifold
ramifications. As an introductory example, we give:
19 Let f be a Lebesgue-measurable function defined on the real
axis. and let f be in Lp. Define the mapping T, : Lp -+ Lp by putting
(T J)(x) = I(x-I). Show that T J is .. continuous function of I with
values in Lp for each f in L., and that IT,tl=lfl. Show thatifg is in L I ,
(f : (T,!)g(t)dt) (x) = r: f(x-t)g(t)dt
for functions with values In the B-space L . In more analytical terms,
we obtain the following inequalities:
13 Let (8 1 , E " f-'I) and (S" Eo,p.) be positive measure Space8,
and letK be a f-'Ixp,-integrable function On S. xS.. Then, for p ;;:; 1,
fs, Us,IK(8" 8.)IPp,,(ds.)jI,P p,(ds,)
;;:; Us, [Js,IK(8 I , 8 0 )!!'1(ds I Jr p,,(ds.)IIIP.
14 (Jessen) Under the hypotheses of Exercise 13. if T :2: 8 > 0,
(Hint. Put l' = Tis in Exercise 18.)
In the same way, Holder's lllequality, when applied to vector
valued functions, may lead to unfanriliar looking inequalities.
IS Let (S, E, pJ be a positive measure space. I and Y) B-spaces,
fa p-measurable function with values in :£1 gap-measurable function
with values in B(I, Y». Show that if p, '1 ;;: I, l/p+I/'1 = 1 and
I" 4,(S, I, p, I), g" L.(S, I, p, B(I, Y»), then the function h de-
fined by hIs) = g(8)/(8) is in LI(S,I,/-" Y»). and we have Ihl, :s; 1/1.lgl..
16 Let (S" II'!'1) and (S., E" p,) be positive measure spaces.
Let KI and K. be PI X p,-measurable functions defined on S, X So' Sup-
pose that p" Po ;:0; 1, I{1',+I/'11 = I, 1/1',+1/'10 = 1. Show that if
Ifs, [fs,IK I (8 1 . s.)I"'p,(ds l )]"'" p,,(ds.)jll., = 111, < co,
J J KI(8I' s.)K,(sl' s.)f-'I(dsI)",,(ds.}
51 s.
for almost alIa:, and hence derive the re8ult of Exercise 6 from Exer-
cise 15. (Or from the consideration mentioned at the beginning of B. J
In the following exercises we deal once more with Lebesgue
measure. this time on the positive real axis. By p we will always de-
note a quantity between 1 and 00.
20 (Hardy-Littlewood-Polya) Let K be Lebesgue measurable.
Show that the map T defined by
f, '" 1 1 '"
(T!)(x) = K(yJ/(xy)dy = - K(II/x)/(II)dy,
o x 0
:1:>0.
anrl
Ifs, [fs,IE.(s" s,)I'" f-'I(ds I )] aol'" p,(ds.)!"'" = M. < 00,
then
exists, and is in ab80lute value nO greater than M,M..
17 Let (S, I,p) be a meaSure space, letp ;;:; 1 and I/p+l/fJ = I,
and let {K.} and {L.} be sequences of p-measurable functions defined
on S. Show that
is a map of L.(O, 00) into itself of norm at most J.\"IK(y)ly 1/Pdy.
Show that if K(x) :2: 0 for almost all x, this gives the exact norm.
582
VI. OPERATORS ..6,.ND THEI1t ADJOIXTS
VI.Il.21
VI.I1.25
RCJSES ON INI!:.QUALITIES
588
21 Show that the map T defined by
1 I. "
(a) (Hardy) ITj)(",) = - fly)dy
x 0
is a map in L.(O, co) of norm 1'1(1'-1), p> 1,
(b) (Hilbert. Schur, Hardy, !II. Riesz)
(Tf)(x) = I. m j(y t dy
o x+1I
is a map in L..(O, co) of norm ",(sin "'Ip) ', p> 1,
(c) (Hardy, Littlewood, Polya)
(Tf)(x) = f. f(y) dy
o max (x. y)
is a map in L..(O, co) of norm 1"(p-I ) ', l' > I.
22 Show that the mapping T : {a.} _ {b.} of sequences defined
(b) (Hardy) Show that the map S : {a.} --->- {b.} defined by
b. = }; a./k
.....
is a map in I. of norm p.
25 Let K be a function of " real vlU"mbles defined for positive
values of tJ,U these variAbles and measurable with respect to n-dimen-
sional Lebesgue measure. Let Pi It i = 1, . . 'J '1'1, and q I. Let
q-I = I -, 1',1. Suppose that
J: . . . J: [Klx 1 , . . ., x.)lx,'I., . . . x;;I,..&, . . . &. = C < 00.
Show that if I. is in L..(O. co). the integral
I(m) = J: ' . . J: K(y,/x, . . "y.!m)ft(y,I, . . I.(y.)dy, ' , . dyo
by
exists for almost all x 2: 0, and that we have
(a)
1 .
b.=-Ia.
fl.1t_l
{1 m ] 1 I . } 11'
o m" I(x) & olhl., . . . 1/.1...
is a map in I.. of norm p!(P-I), l' > 1.
°1
Ib) b. = I ------;
1-1 "+1
is a map in I.. of norm n(sinnIP) ', p> I,
Ie) b = i a J
IJ 1_l max (j. n)
is a map in I. of nOrm p'(p_I}-I, p> 1.
28 LetK be Lebesgue measurable, and let J IK(y>ly l/.dy< co.
Let P 2: I, IIp+llq = 1. Show that the adjoint of the map T:
L.IO. co) --->- L.IO, co) of Exercise 20 is the map S: L.IO. co) --->-
L.(O, co) defined by the formula
(Sg)I"') = J: K(xly)gly)y- 1 dy.
If Klx) 2: 0 for all x. what is the nOrm of Sf
24- la) (Hardy) Show that the map S defioed by
(Sf)(x) = J: Ily)y 'dy
is a map in L..(O, (0) of norm p.
Show that if K is non-negative. the constant c ,n this meqUAlity IS the
best possible.
26 Let , and . be Hilbert spaces. Let T 1 map a dense subset
D, of , into {J., and let T, map a dense subset D. of into {Jl' Sup-
pose that TI and T, are adjoint in the sense that (TIm. y) = lx, T"y)
for m in D, and y in D" Show that T" TIT" T.Tl' and TI are all
extendable to everywhere defined bounded operators if anyone of
them is. How are the norms of the extensions related?
27 (Hardy) Consider the map T defined by
(Tf)I"') = J: e--«'j(t)dt.
Show that T is a bounded operator in L,,(O. co), of norm Vn, and that
TT* is given by the formula
(TT*f){m) = J: /(t)(m+t) ldt.
Show that if 1 -s;. P;;; 2, IIp+I!q = I, then IT II. -s;. n'/'I/I. for fin
L,,(O. co).
28 Show that the map T which sends the Lehesgue integrable
534
VI. OPERATORS AND THEIR ADJOINTB
VI.H.29
VI.H.30
£XERC'lSES ()N INEQUALITIES
585
a,
b=""
n ,_on+j+I
Show that T has norm Vn. Show that the rrmp S of 4(0, 1) into it8e1f
defined by
30 If co;;';p,;:';:p ;::" P.>O, and I is III L.,(S,E.!')n
L.,(S, E, pI, then I is in L»(S, E, p), and log III. is a continuous con-
vex function of IIp. (Hint. Prove the equivalent fact that p . log III.
is a continuous convex function of p.)
31 If pIS) = 1 then L.,(8,1,", p) is contained in L.,(S. E. p) if
o < p, ;;;; P., and If I. is an increasing function of p.
82 Suppose that I is in L.(S, E, p) for some p > o. Show that
unless f vanishes outside a certain set E in E such that pIE) ;:;; 1,
Itl. co as p .... o. Show that in the contrary case, Itl. is a decreasing
function converging to
function I defined on the interval Co, 1) into the sequence (an) defined
by
an = f: :r"/(:r)d.x, n ;::.. O.
is a bounded map of L. into I" such that TT* is the map (an) .... {b.}
defined by
(Sf)(:r) = I: l(y)(I_:ry) ldy
exp (f ,,log If(:r)lp(d.x)j = Iflo.
33 Suppose that pIS) = {, Show that the set 4,(S, E. p) of
all functions I such that
has norm :no
29 Let K be a Lebesgue measurable function defined on the
positive real axis. Show that the map T defined hy
(T/)(:r) = I: K(:ry)y'2j'J-1/(y)dy
is a map in L.(O, co) of norm at most J:: IK(:r)I:rUJ»I-Id.x, ....d that
this is the exactnonn ifK(:r) ;::.. 0 for all:r > o. Show that the adjoint
map is
-a;J ;:;; Is log 1/("')ip(d.x) < co
(T*!)(:r) ",'2/.1- 1 I: K(:ry)/(y)dy.
(Hint. Put 11 = 1/1 1 .)
form a linear space, and the result of Exercise 31 holds in the extended
range 0 ";; p;;;; co.
34 (Inequality of arithmetic and geometric means) If ",. . . ., an
are complex numbers show that
D. Gi!1UTal properties 01 L. Norms.
In thi8 set of problems, let (S. E, p) be a positive measure space.
and let L.(S, E. p) be defined for 0 < p < co as the set of p-
measurable functions satisfying the requirement:
,,,,... a.I I }. ,,;; (Ifn)(la,1 + ... + 1a,.1).
35 Assume ,,(S) = 1. Put
exp Ifs log I/(s)IJl(da») J/lo
for I in 4,(S, E, p). Show that if I and g arc non -negative functions
in Lo(S. E, p), then [f+glo Iflo+)gl.. (Hint. Use EXJ'rcise 111.9.29.)
36 Let (S, E, p) and (S., E 1 . PI) be positive measure spa<:es.
Assume pIS) = 1, Show that if K is a pXPt-measurable function
defined on SxS 1 .
Is, exp Us log )K(8, SI»)P(da)jl',(da 1 )
;:;; exp Ifs [log Us.IK(S, s,)IPt(ds,))] p(ds)j.
(Hint. Use Exercise 14.)
37 (a) Show that if f and K are Lebesgue measurable functions
Itl. = Ifs l/(s)IP,,(ds)j1/P < co.
Lm(S, I,p) has a known meaning; in the course of this section we
will also see how to define Lo(S, E, pJ.
For 1 ;:;; P ;:;; co, L. is a B-space, but for 0 < p < 1, L. is merely
an F-spa<:e (cf. Exercise I1I.9.30, where. however, the symbol III. has
a slightly different meaning for 0 < p < 1). Nevertheless, there are
certain interesting properties of the function Ifl which hold in the
extended range 0 < p ,,;; 00.
536
VI. OPERATORS AND THEIR AD.JOINTS
VI.l U!8
VLl1.41
EXERCISES ON INEQUALITIES
537
defined on tbe positive real axis. Rnd if K is non-negative and has
J:K{a:)dz = 1, then
J: exp If: K(a:) log 1!(a:Y)ldzj dy
< exp (- J: K(a:)loga:dzl' J: I/(y)ldy.
(b) (Knopp) Show that if 1 1S a Lebesgue integrable function
defined on the positive real axis, then
max ",<.<+", log IT(x+iy)IIIo, II. is a convex function of [x, a, b] in
the region c, ,,;; '" ,,;; c.' 0 ,,;; a ;;;; 1, 0 ;;;; b ;;;; I.
41 Let (S.. E,.....) and (S., E., 1'.) be positive measure spaces,
and K " non-negative ....XJ-lo-measurable function defined S,xS..
Suppose that JE,JE,K(s" ...)....(d8 I )J-lo(ds.) < 00 if E, is in I" i = 1. 2
and I'/(E,) < 00, i = I, 2. Show that the nonn nf the map T of
L.(S., I.. ",,) ->- L.(S., I"....) defined by the fonnula
r exp {;J: log If(y)ldy}dz '';; e r 1/(y)ldy,
the constant e being the best possible.
(c) (Carleman) Show that !::'-ll",-... a.I I /8 ;;;; e !::'-1 la.1 for
each sequence {a,.}, the constant e being the best possible.
[*]
(Tf)(s,) = 1 (K(sl' ".)}"/(s.)J-lo(d8.)
S,
E. E.rlensions 01 the exmOOllity theorem.
88 Let (S, I,I') be a ,,-finite measure space, and let / be a
p-measurable full£tion defined on S with values in a B-space $:, and
suppose that! is p-iutegrable over every set E in I 8uch that pIE)
< 00. Show that if I ,;: P :-;; 00 then I is in L.IS. I, p, I) if and only if
[*J IJsg(S)!(..),u(ds}1 < 00, gEl], !gl. ";; I,
where 11 IS the subspace of p-slmple functions in L.IS, E,,u, a:*} and
l!p+l!q = 1. Show that in this case. III. is equal to the supremum in
[*],
89 Sbow that Lenuna 10.7, Theorem 10.8, Lemma 10.9. Theo-
rem 10.10, and Theorem 1O.n all hold even if the spaces of complex
valued functions are replaced by the rorr<sponding 8paceS of vector
valued functions (i.e.. if L.(S, E, p, I) replaces L.(S, E, ,u), etc.).
40 Let (S" I" Pt.) and (S., E., J-lo) be positive measure spaccs.
Let z = x+iy be a complex parameter anging over a strip "'- ;;;; a:
;;;; c.. Suppose that for each z. T(z) is a linear mapping ofthe space LCl'
of all P1-integrable simple functions into the space VO) of aU ""-
measurable functions integrable over every set of finite measure.. and
that for each /. in V ll and E in E. such that }lIE) < 00,
JE (T(Z)/l)(S)",,(d8) is analytic and unifonn]y bounded. Let IT(')I...
be defined for each z as in the 8tatement of Theorem 11. Show that
(in the sense that the integral is to exist ....-almost everywhere for
each 1 in L.(S., E., J-lo) and lie in L.{S., I" P:t» is a convex function
of "'. lip, I/q. (Of course, if [*] does not define a bounded map of
L. ->- L., we put the nonn equal to + 00).
42 Let I be Lebesgue mftJSlll'llble on (0, 00), p > I, 0 :-;; ), ;;;; I,
and l{p+l{q = 1. Show that if f is in L./r-.(O. 00), the integral
J./(a:)/{x+y)'clx exists for almost aU y, and detennines a function in
L./.(O, 00). Give an upper bound for the nonn of this function.
F. Inequalities from the theory 01 orl/wrwrl1U1l. 8erk8.
In the next set of exercises, we adopt the notIon and definitLOns
of IV.14 and in particular, of Definition I of that section.
43 Let {4>.}, - 00 <.. < +00 be a uniformly hounded c.o.n.
system and let 1 ,,;; p ";; 2. Show that if I £ L.,anda. = fo"/(x} 4>.("')clx ,
then !=:: 1a,.lq < 00, where l!p+l/q = I.
44 Let {4>.}. -00 < n < +00, be a uniformly bounded c.o.n.
system_ Suppose that I;;;; p :-;; 2, IIp+l/q = I, and !=:la.I.< 00.
Show that there exists an I in L. such that a,. = fo"/(x} q,.(x)clx .
45 Show, under the hypotheses of Exercise 48. and the addi-
tional assumption that {ftft} is R sequence of complex numbers such
that : 1.6.1 < 00, that :: 1.6.I' 'Ia"I. < 00 for all / in L..
46 Let T. be the operator defined in the paragraph preeeding
Exercise IV.a.1I4. Show that if T./ ->- f in the norm of C for every
1 £ C, then T./ ->-/ in the norm of L. fnr CYery 1 £ Lv
47 Let {An} be a rea] factor 8equence wllich is of type (C. C) in
the sense of the definition preceding Exercise IV.14.64. Show that
{A,,} is also of type (L., L.) for 1 ,,;; P ;;;; 00.
.
588
V-J. OPERATORS AND THEIR _.o\.DJOINTS
VI.n.48
VI.12
SOTES AND REMARKS
589
G. So"", miscfilaneowJ romxrity iru:qr;aJ;ti"".
48 (Hadamard three CIrcles theorem) Let I be an analytic func-
tion defined in the annular domAin a < Iz! < b and having va1ues in
a B-space I. Show that if M(r) = max 1/(:<)1. log M(r) is a convex
function of log r, a < r < b. I_I-r
49 (Hardy) Letlbe a complex-valued aIJ.Rlytic function defined
in the annular domain a < Iz[ < b. Let I P < 00. Show that if
M.(r) = {ft'I/(rei.Wd8}.t.. log M.(r) is a convex function of log r.
a < r < b, (Hint. Apply EXfl'Cise 48 to the function F(z) defined by
(F(z»(O) = I(Z"-o)}.
50 Let I be a complex valued analytic functlOn defined in an
annular domain a < 1:<1 < b. Let 0 < '" < I, and let
lI-f.(r) = max 1/(:<,)-/(",,)1 .
I"I-I-,I-r 1""-,,,,1.
Show that log 1I-1.(r) is a convex function of log r, a < r < b.
12. Note. and Remark.
operator and its importance was clearly reroguized by E. Schmidt [I],
to whom the geometrical terminology in linear space theory is due.
COTItplld o1ld weakly compact opetarors. The concept of a compact
(or complctely continuous) operator is essentially due to Ililbert [1;
IV] where it was defined for bilinear forms in 10. In terms of operators,
Hilbert require8 the operator to map weakly co"''''.-gent sequences
into strongly convergent sequences. In reflexive spaces this is equiv-
alent to Definition 5.1, which is due to F. Riesz [4] who made a pen-
etrating study of these operator8.
The study of weakly compact (or weakly completely continuous)
operators was initiated by Kakutani [18] and Yosida [4] in connec-
tion with ergodic thf'Ory. Gantmaeher [1] proved Theorem 4.8. and
also Theorems 4.2 Rnd 4.7 for separable spaces. These facts are proved
without the assumption of separability by Nakamura [8].
Theorem 5.2 is due to Schauder [6] and a sequential fonn of
Theorem 5.6, valid in separable spaces to c"lfand [2; p. 269]. Kaku-
tani [11] has given a symmetric proof of Theorem 5.2; a .imilar treat-
ment for weakly compact operators is found in Bartle 2].
Operators with dnSI'd range. Some particular rases of these theo-
rems were proved by Hellinger and Toeplitz [I] for I. and by F. Riesz
[2, 6] for Lp, I p , P > 1. Related abstractly-phrased results were
obtained by Hahn [3]. In the form presented they are eS8entially due
to Banach [4; p. 284-9, I; p. 145-152] although his proofs are
different. For additional results of this nature the reader may consult
Hausdorff [3] and Dieudonne [3].
&presentation ot operauns in C. The representallon of the
general operator with domain and range in qo, 1] was given by
Radon [1]. Both C. Fischer [I] and Radon [1! treated the compact
operator from qo, 1] to itself. c"lfand :2] represented the general
and compact operators with range in C[O, 1] but domain an arbitrary
B-space. Sirvint [2, 3] gave a similar representation for weakly com-
pact operators mapping I into qo, I]. Hartle [2] showed that thIS
8ame representation is valid for any of these three types of operators
mapping if into the B-space of bounded continuous functions on an
arhitrary topological space.
In the ease that C[O, I] is the domain and if the range, Gelfand
[2] represented by means of Stieltjes integrals both the compact
TopologieB, adfninh and projectimu;. The strong and weak opera-
tor topologies for bounded operators on Hilbert space were introduced
and employed systematically by von Neumann [2]. The notions of
strong and weak con' ergence of sequences of operators had been used
earlier, however, (see Hilbert [1J, Riesz [6; pp. 107, Ill]). The final
topology mentioned in Section I is sometimes called. the l"strongest ll
operator topology, and was introduced by von Neumann [5]. The
question of finding the form of the linear functionals on B( ) which
are continuous in these and other topologies was considered by
Dixmier [2]. He proved Theorem 1.4 for this case; the general form is
due to Bade [8]. Related results were obtained by Michael (1].
The formal concept of the adjoint operator goes back to matrix
theory and to the thf'Ories of differential and integral equations. In the
spaces L , p > 1, and I., Riesz [2: p, 478. 6; p. 85] made use of this
notion and proved the validity of Lemma 2.2. Banach [4: p. 235] intro-
duced the adjoint operator in a general B-..pace and proved Lemmas
2.7 and 2.8 in this context. The fundamental idea of a projection
540
VI. OPERATORS AND THEIR ADJOINTS
VI.I2
VI.12
NOTES AND REMARKS
541
operator and the operator mapping into a weakly complete space a;.
Weakly compact operators from C[O. 1] to 3:: were treated by Sirvint
[8]. A very incisive discussjon of weakly comp""t operators with
domain CIS) was given by Grothenweck [40] who proved Theorems
7.4-7.6 hy other means. Grothendieck showed there is a one-to'one
correspondence between weakly compact operators On CIS) to 3! and
certain vector measures but did not use this correspondence to re-
present them. This integral representation WaS employed by Bartle,
Dunford and Schwartz [1] to prove these theorems essentially as
discu8sed here.
In Section 7 and Section 8, it is shown that an arbitrary weakly
compact operator on a B-space 3:: to a B-space ¥J has the property that
it sends weakly convergent sequences into strongly convergent se
quences, provided that I is C or or one of the many spaces isometri-
cally equivalent to a Cor Lz space. An abstract study of this property
of the space I was made independently by Brace [1] and Grothendjeck
[4.]. Brace employed the following condition on a B-space ;E, if ("'.)
converges weakly to "'0 and {"':} converges weakly to "' then (",:",,)
converges to "' "'0' Brace [1; p, 18] proved that if this condition is
sati8fied in 3::. then every weakly compact operator T , 3:: -+- ¥J maps
weakly convergent sequences in I into strongly convergent sequences
in ¥J. The converse of this statement was proved by Grothendieck
[4; p. laB]. For other related results consult these two works,
Repres£ntatwn oj OpeTakJr8 in a Lebesgue space. The form of the
representation in Theorem RI for the general operator was given by
Kantorovitch and Vulich [I; p, 138]. The bound for norm of the
operator was found in the case that I = L D by Fullerton [8]. Related
throrems have been obtained by Bochner and Taylor [I: p. 941-943].
The general operator from Lz[O, 1] to a uniformly convex space
:f, or a space with a certain kind of basis was represented by Dunford
8]; he also treated general and compact operators from L 1 [0, 1] to
LD[O, 1). In a similar vein, Gelfand [2] represented the compact
operator from L,[O,l] to a general B-space, and also the general
operator from L 1 [0, I] to a space which is reflexive or a separable COll-
Jugate space. These last results were extended by Dunford and Pettis
[1] to the ca8e of a measure space. When Ii is a finite or mfinite
Euclidean interval, they gave a concrete representation for the weakly
compact and compact operators from L,(S) to an arbitrary spaee ;E,
Phillips [8] treated the same ease for an arbitrary a-finite measure
space .I obtaining a representation of the general operator as an in-
tegral with respect to a Lipsehitzean vector measure, and obtaining
kernel representations for the weakly compact and strongly compact
operators, See also Phillips [1].
Sirvint [1] gave an example of a (weakly compact) operator in
L 1 [O, 1 J which is not compact but whose square is compact. An almost
exactly similar example was given by Yosida, 1\1imura and Kakutani
[1]. If S is Euclidean, Dunford and Pettis [1] showed that the square
of any weakly compact operator in Lz(S) is strongly compact. This
waS proved for a measure space by Phillips [a].
Closely related to the problem of representing operators on L 1 (S)
is the vector form of the Radon-Nikodym theorem. Dunford and
Pcttis [I] showed that if (8, I, 0:) is a a.f"mite positive measure space
and if I' is a measure on I with values in a separable conjugate space
;E such that II'{E) [ Ka(E), E E I, then there exists a measurable
function '" on 8 to 3:: such that ess sup 1"'(8)1 K and I'(E) =
IE "'(8)0:(ds). A similar theorem is due to Phillips [I] where 3:: is now
an arbitrary B-space and the set
{f'(E)fo:(E)IE £ I, 0 < o:(E) < oo}
is weakly compact. Dieudonne [9, 10, 14] has given other .wnsions
of the Dunford-Pettis theorem. A more general Radon.NikodYm
theorem is due to Rickart [2]; in his case the function to be inte-
grated is not single-valued, in general.
RW82 convexity theorem. The principal result in this section is due
to M. Riesz [I], and has a number of important applications (see, for
example, Hardy, Littlewood and Polya [1; Chapter VIII] and
Zygmund [1; Chapter IX]). The proof given here is essentially due to
Thorin [I], although his discussion is principally concerned with the
spaces lD." Calderon and Zygmund [1,2] have e.. ended this theorem
to the strip 0 ;:;;; a ;:;;; 1, 0 ;:;;; b < 00, thereby including the spaces L D ,
o < p < 1, and enabling them to make some applications to the
spaces H D' The theorem may also be extended to multilinear functions.
In addition to the above references, the reader will find other
proofs (sometimes only for I.,.) and applications in Paley [1, 2] (com-
542
VI.I2
VU2
VI. OPERATORS AND TI-IEIR AD.JOJNTS
pIeted by Zygmund [1]), Salem [1], Salem and Zygmund [1], Ta-
rnArkin and Zygmund [1], and Young [1].
\Ve hs,\.re discussed the case of complex !Spaces. In the .real case,
the convexity is only valid in the triangle 0 ,;;; a. b I, a-t-b ;;;; 1.
The reader should consult the above references, e.g. Thorin [1] for a
discussion of this case.
As is indicated in the Section II of exercises, many of the most
important inequalities of analysis may be readily derived from the
Riesz convexity theorem .and from a. ff"w elementary ideas on vector
functions. There is a class of deeper inequalities which will be discussed
in the text of Chapter XI and in the section of N ole. and Rerrw.rk.
appended to that chapter.
Repres...taI.ion of linear opnulms. In the application of the
abstract theory of linear operators to concrete spaces it is of some
importance to know the form of the operator in terms of the proper-
ties of the domain and range spaces. For the spaces C and Lt, concrete
representations were given in Sections 7 -8. For the convenience of
the reader, we have tabulated here references to the literature where
such repl'fSentation theorems are explicitly stated. There are four
tables; one for the general operator, one fOT each of the compact and
weakly compact operators, and one for representations conrerning
various order properties.
In a sense the results may be regarded as complete for a given
space when the form of the operator mapping an arbitrary B-space
into that space, W1d the form of the operator mapping that space into
an unrestricted B-space are both known. Actually, however, it fre-
quently happens that when it is a question of two specific spaces,
these general results may be improved or phra.ed in terms more
easily verified.
The user of these tables wiU find some duplications and different
sets of conditions. Sometimes, for example, more detatlcd information
is available under the assnmptions of separability, renexivity, etc.;
such instances are noted. o attempt has been made to distinguish
between theorems stated for L.[O, 1] and L.(S), where S is a a-finite
or an arbitrary measure space, for example, although not aU of these
results stated for [0, I] generalize.
Further in most of the spaces thtTe are other notions of conver-
TABLE VI
NOTES AND REM:ARK:S
543
Representation of Op rat(trs
Legend
The rows denote a axed domain space p and the columns denote a fixed
range space. The papers listed below are entered into the btbles by their code
letters and u!;ually the page numbe-r for a particular theorem is noted unless
the paper is short. The following abbreviations ate used:
b .... some ba<!ois restriction,
c = conjuga.te (Space.
p = positive operator.
r = renexive space.
[A] A. AWsiewic. [2].
[B] R- G. Bartle [2].
[BDS] R. G. Bartle. N. Dunford. and
.I. Schwam [1].
[BT] S.BoohnerandA.E.Taylor[I].
[Ch] I!-. R. Christian [I].
(C] L. W. Cohen [I).
[CD] L. 'V. Cohen and N. Dunford
[I].
[D] N. Dunlord [8].
[DP] N.DunfordandlJ.J.Pettis [1].
(E) I. A. E.rohi [1).
[F)
[F;]
[FK]
[Fs)
[Ft]
[Fu)
[Ful]
(G)
[Go)
[Ge]
G. Fichteobobi [3).
G. _Ix [2].
G. F1chtenholz and L. Kan-
torovitch [I).
C. A. Fischer [1].
R. E. FuIkrlon [2 J.
R. E. F\tllerton [3}.
R. E. FuDerton [4].
I. Gelfand [2).
M. Gowurin [1].
A. Grothendieck [4].
8 = separable space,
u = wlifonnly convex spa.ce p
w = weakly complete 6poce.
[HT] E.HilIeand.J.D.Tamarkin[2].
[IS] S. Izumi and G. Sunouchi [1 j.
[K) L. Kantorovitch [3]-
(Ka) L. Kantoroviteh [4J-
[KVJ L. Kantorovit...h and B. Vulich
[I].
[Ka V] L. Kantoanitch Bnd B. Vu1ich
[2).
[L] G. Lorentz [4]
[M) I. Madda.us [2].
[0] W. Orlicz [5].
[Pel B. .I. Prl1ll; [1].
[P] R. S. Phillips [3J.
[PhJ R. S. Phillips [I].
,Ra]
[RJ
[8J
[SmJ
.1. Radon [1).
C. E- Ri.kart [2].
G. Sinint :3J.
1< . Smithies i2].
[VJ
[Vu]
[Vh)
B. VuUch [I2J.
B. Vulieh [13].
B. Vulieh [14!.
544 VI. OP'£RATORS AND THEIR ADJOINTS VI.I2 VI.12 NOTES AND REMARKS 545
TABLE VI.A TABLE VI.A I CfmIimwJ)
ReprestmtAl)On of General Linea.r Operator i I,
L I, I c
Genero1 B-space C L, L. i 1 <p <:0 !
1 <p < C1J ,
I [CD,689]b [E)b General [BT;1J42.8] i [E] [KV,l28] [E] [IS, [E]
General [B] [ISJ [BT;9403) [BT:04lJ B-8pa e [G;279] [CD,698Jb [p:5Sl] [IS] [IS]
B-space [BT;948]s [KV;18S] [KV:l.8J [G;27I] [Pe:424]r [KV;128'
, (G:287J ;15] [1',581]
C [BDS] [BDS] [5;95] C
[G;280 w [F] [F]p (DP: 848-50] [D:486J
[P,58I] [Ha] L, [D:486]
[G:279] [Vu.42]
L, [D;-4oB2,5]b [G,275]r [V;279] [D:488] [D:485.5] [Ful] [V;288]
[D;482]u [G;276]f.iC [DP;358] [DP;S47] [KaV] L.
[DP;B69]r [PE;428]r [KV;I46] [DP;36'O] [K:264] [Pe:425] [KV;IS]
[DP;M5-6]sc [H;65] [V;288] [DP;379] [Vb] l<p<oo
[F"I] I
L
L. [D,476] [G;267] [D;488] , [D:48.] I [CD;697]
1 <p...:.: co [D;482]b [Fu] I [FuIJ I, [G,270J
[I',528J [FulJ I [K;275J [L;85]
[Vh] I. [CD;699] [K;272J
L [D;482Jb [FK;",,] [D;483J [D;488] I <p < 00 [Pe:425J [Vh]
[K;238J :
,
;1':528] , [C;334'
[A:146]
c
I, [EJ
[G;270J <. [CD;699]
[P;530] B(8)
[V;1IOOJ
I. [EJ
1 "p < OJ [P;630] B(8,I) [V;800J
I [P;580]
Tabu rontinued
, I [EJ
[G;27BJ
c, [Gr;l68]*
B(8) ! [A;146] [FK;90J [V;300J
, [Ge] [V;295]
I [K,288]
I
B(8,I) I [A;146J [FK;OOJ iV;300]
[Ge] [V;295)
.. -.-
546 VI. OPERATORS AND "rHEIR ADJOINTS VI.12 VI.12
TABLE VLA (C<nIIimI<dJ
B(B) B(B,E) BV C'
NOTES AND BJ::MARKS
TABLE VLB
Representation of Compact Operat<n'
547
Genernl [8] [Ft;270]
B pa.ce [IS] [ 't 2]r
[P,53B]
C
L, [V;2'8] [DP;352'7] [V;2'9] [Ft;2"]
[G;278]
[K;262]
[Ka;I06]
L. (Ft;277]
Lo
I, [Ft:274]
I. fFt;2'4]
1 <p < 00
10
c [Ft;2'4]
..
B(B) [V ;296]
B(B.E) [V;294] [v;296]
General
B-space
c
L,
I L.
l<p<oo
Lo
Genel'al
B-'Sp8C<'
C
L,
[ClJ:693]b
rM]b
[BDS]
[G;2 2]
[P;5371
[DP;369]c
[DP;369]
[G;277]
[P:529]
[P;584]
[P;536]
:B'
[G:267J
[BDS]
[F'J
[Ra]
[DP;370]
[DP;379]
[G;278]
L. [DP;383] [G;298] [D:487]
l<.P<cO [Pi 529 ] [DP;384]
[Pi S36 ]
L [P:529] [0:487]
rp;537]
I, [G;270]
[P;530]
[P:.36]
I. [P;580]
1 <p < 0::> [P:586]
10 P;530]
rP:536]
c
c,
[D;490]
[DP:369.70]
[DP:879-80]
[G;278]
[D;487]
,DP;884]
[HT;446]
iSm]
iDi 487 ]
[Sm]
[DP;370]
[DP;379]
[DP;S81]
[D;4.92]
[DP;384]
Table continued
548
VI. OPERATORS AND TI{EIR ADJOINT5
\'1.12
VI.12
NOTES AND REMARKS
549
TABLE VI.E (Continued]
TABLE VI.l.'
I,
I J < '<" I' I
<
'.
I BV I c.
Rep1"e5eDtation of Wt'akly Compact Operator
Genera.t. (G;271. [P;551] (G,284) [Pt:272]
(P:53':
IPe;424:r i
C I
L, {CD;700] [CD:700) [Ft:281J]
L. IPe;425 J [Sm) [Ft;280]
l<p<oo
L ,
I
I, [C;327-9) [C:327] [CD;697) !
(G;27I) [CD:697] ,
[L:S5]
I. [C:S27 -8] i
. [Ft:275]
I<p<oo [CD:694.5] I
[Sm) ,
I
, I
I
< . [l.'D;6921 [l.':320] [Ft;275]
,
t. I
I
G...........
B- pace
c
L,
L
I
General [13]
B-spo.ce :8;87] !
C [BDS] :I3DS] [5;93)
[GI';187-8]. .5:881
[Gr:173]O
rS:98]s
L, [DP:868-0) :S; 8 [DP:S78] [DP;38J)
[DP:875].
[P;554]
[Ph;JSl]
L [Gr:140]-
[Gr;155J.
I, [DP:368] [S:88]
550 VI, OPERATORS. AND THEIR ADJOINTS VI.I2 VI.12 NOTES AND REMARKS 551
TABLE VI.D TABLE VI.D (ConHnrud)
Representation (){ Qrder..continuou!l Linea.r Opera.tars I I I
I I Lw I, Il<P <OO B(S) BV
General Ordered C L, I I,.
B-spare Spare 1 <p < a:;
I Ordered lKV;Ui7} [KV;I28]
Ordered [KV:13S-0] [IS] Space- [KV;158) [KV;180)
, [KV;I£I)
Space [KV;I38-0)
[KV;151). C [KV:le3) ,KV:133] [KV:183:
C [ChIp [KV;154) :KV;1541] L, [K:258 ] [K;262]
[K;2 41 .J Ka:105] [V;279)
r., Ka;I03] [KV:l54] K;259] -K;259] L, [KV:162: [K';1061
(K;2.55-6] KV;IM] K;2M]
...KV;t40] ;286] ........p<C7J
L, [K;273) [KV;I55) [K;275) L Fi;218)
[K;245]
1 <p < co [K.;I04] [KV;153] [KV;158)
Lw [A;147] [K.;I04] .K;252--1!] [Ki 252 ] [0;76;
[K;247) I KV;I48) I,
[K;250]
I, [Ka;102. I, [KV;182) [K:27 2 )
1 <p < co [KV;132]
I. [K:269] BIS) K;245]
1<11 < co [Ka;102J
B(S) [A;147] [K;237] B(S,E)
[K;254]
I
B(S,E) [A;147] [K;237) I
--
gence , such as pointwise convergence:t convergence in measure, etc.
the final table refers to theorems which represent operators enjoying
various order properties
While some care has been exercised in the compilation of these
tables, the authors are aware that they are not complete and not
entirely accurate; the authors welcome additions and corr<>ctions.
Of particular importance are the expressions of the nonn of the
operator in tenns of the objects used in the representation. The user
wiJ] observe that this representation of thc norm is not always known.
552
VI. OPERATORS AND THEIR ADJO[ TS
VI.12
VI.I2
NOTES AND REMARKS
558
ADDITIONAL REMARKS.
L A quest.ion related to the representation of linear operators is
that dealing with the representation of linear functions defined on
certain spaces with va1ues in .a B-space. Gowurin gave a representa-
tion for the general bounded Jinear functional on tbe space of conti-
nuous functions on [u, b] with values in 3:'. Bochner and Taylor treated
this space Bnd also similar spaces corresponding to L , 1 s:: P < co.
2. The paper of Grothendieck is not specifically concerned with
representation; however, he proves B number of deep theorems con-
cerning weakly compact operators on C and L .
8. Izumi and Sunouchi represent operators mapping an arbi-
trar.y B-space into a B-.pace of functions satisfying specified condi-
tions.
4 Maddaus gave conditions which are sufficient for a compact
operator to be the limit of a sequence of operators with finite-dimen-
.sional range.
5. The explicit expre.sion of the norm is difficult to obtain for
maps between L spaces. A lower bound for this quantity has been
obtained by Fullerton [4].
Bilillea7 fundiona!8. It is easily seen that the colJeetion of all
scalar valued biljnear functions on a product l' X 'iJ oftwo B.spaces is
in onekt.o-one corresponden.ce with the collection of linear mappings
of 3:' into 'iJ. (or of'iJ into 3:'.). In this way problems concerning linear
operators can be replaced in terms of bilinear functioIlBls, Rnd con-
ver8e1y.
A concrete representation for bilinear functionals on C "" C was
given many years ago by Frechet [10]. Recently, :\Iorse and Tran8ue
have made a comprehensive study of bilinear functions on very general
function spaces, including c, C, 19 L7}1 I P < oo and others. (We
refer only to their papers [I, 2, 8]; additional references may be found
in lIIorse [I] and Morse and Tran8ue [4].) It is seen in lIforse and
Transue [2; IJ that under certain conditions the bilinear functionals
can be represented in a canonical manner by repeated Lebesgue-
Stieltjes integrals.
In their later papers extensive applications are made, among
other things, to tbe convergence of double Fourier series.
Ideals of operatork. Let:£ be a B-space. Let g:!;; B(3:') be the set
of all operators with finite dimensional range, let 1:1: !;; B(l) be the set
of compact operators, !ID the set of weakly compact operators, and $
the operators which map weakly convergent sequences into strongly
convergent sequences. All of these four classes are seen to be two sided
ideals; that G: and !ID are closed in the uniform topology of B(I) was
established in Corollaries 5.4 and 4.6, and the reader can easily show
that $ is also closed, It is always true that
g: I:1:!;;$,
\3'!;;I!!;; !ID.
In a finite dimensional space all these sets coincide with B(3:'). In a
reflexive space, I! $ and !ID = B(l). In Hilbert space, or a B-space
with" basis, tr i8 the cl08ure of \3'. Calkin [I; p. 841] has shown that
in Hilbert space is a maximal two-sided ideal. We have seen in
Theorems 7.4 and 8.12 that in the spaces C and L"
g:C C!ID $.
Grothcndieck [4; p. 153] proved that in C, the ideals !ID and $ coin-
cide. This is not the case in LJ' however, for since LJ is not reflexive
there exist subsets which are bounded but not weakly compact. The
fact that !ID C $ follow8 from this observation and Theorems 8.10
and 8.14.
Another Ideal closely related to the compact operators was intro-
duced by Kleinccke [I] and is briefly discussed in VII.ll.4.
Comp/o11£nts and pToiections. Two linear manifolds !In and 91 in
a B-8pace 3:' are said to be campkmroWry in case !Inn 91 = 0, !In e 91
= 1'. Either one is said to be a cornplrment of the other. We have com-
mented on the relation between cla8ed complements and the existence
of bounded projections. In the Case offinitedimensional submanifolds
there are always infinitely many projections, and hence c10sed com-
plements. In the case of infinite dimensional subspaces this is not al-
ways true, as was shown by :Murray [I] for certain subspaces oft"
I < p oF 2. Other suhspaces which have no complements have been
constructed hy Komatuzaki [I, 2], Phillips [8] and Sobczyk [1, 2];
see also the exercises in Section 9.
If we reqUire only that !In e 'in be dense in :£, then we say that 91
is a qtUI.'Ji-compkmmt of !In. In this case the "projection" on!In is not
" bounded operator. That every closed subspace has (infinitely many)
554
VI.. OPERATO:n.s A1"D THEIR ADJOINT8
VI.12
quasi-complements was shown by MUlTay [2] when I is a separable
reflexive space, and by Mackey [3] without the assumption of re-
flexivity.
References. Bohnenblust [8, 4], Dunford [2]. Goodner [1].
Kober [1], Komatuzaki [1,2], Lorch [2], Mackey [3], MUlTay [1, 2).
Phillips [8], Sobczyk [1, 2. 8J.
0/ Li'1lear Trans/ormation. Taylor [I J studied conditions
under which the extension of linear functionals will be a uniquely
defined operation. Kakutani [6] showed that this operation is linear
and isoIIletrie for each closed linear manifold if and only ifthe space
is a Hilbert space.
It is clear that the closed subspace 10 C I has the property that
every bounded operator T : 1:0 --+ h has an extension (with the same
norm) T : I --+ Wr if and only if there i8 a projection (of norm 1)
from 1: onto 1:0' Thus Kakutani [6] proved that I is a Hilbert space if
and only if an arbitrary bounded operator defined on a subspace of J:
has an exten8ion to all of 1: with the same norm.
By allowing the range space to increase, Phillips [8J and Sobczyk
[8J showed that it is always possible to find an extension without in-
creasing the norm. Sobczyk [8] proved that if 3io is closed in I and
T is a one-to-one bounded linear operator from Xo to ft, then there
exists a space !IE J J: and an exten8ion T : J: --+!IE which is also
one-to one and has the same norm 8S T.
Kelley [2] has considered a reciprocal problem of characterizing
real B-spaces J: with the property that a bounded linear operator on
a closed subspace of any B"'pace W to I has a norm-preserving ex-
tension to all of W. He shows that I is equivalent to CIS), where S
is an extremallydisconnected compact Hausdorff space. This extends
a previous result of Nachbin [8J and Goodner [1].
References. Akilov [1, 2J, Goodner [1], Kakutani [6], Kelley [2],
Nachbin [3J, Phillips [3J, Sobczyk [8), Taylor [1 J,
CHAPTER VII
General Spectral Theory
In the first section of this chapter we shall see that a study of the
polynomia1s in an operator on a finite dimen.sional unitary space
leads to a rather complete description of the analytic behavior of the
operator and, at the same time furnishes a cleat: geometric picture of
the manner in which the operator transforms the unitary space upon
which it operates. In attempting to make a corresponding study of an
operator T on an infinite dimensional complex B-space, one is imme-
diately confronted with the necessity of introducing an algebra lar r
than that consisting of the polynomials in T. The development of the
theory in B finite dimensional space suggests that a. useful definition
of a function /(T) of an operator T is given by the Cauchy formula
I(T) = i /(J.) <1).,
2nt cJ.-T
in wbich / is an analytic scalar function and C is an appropriately
chosen contour. In giving 8 meaning to this formula we are natura]]y
led to the study of questions conceming the existence of, and proper-
ties of the function (}J - T)-l. It will be seen that (}J - T) I is defined
and analytic everywhere in the J.-plane except for J. in a certain com-
pact set, which is known as the ap<drotn of T. The general concepts
I'nd method8 introduced in this chapter all center around the concept
of the spectrum of an operator. It is for this reason that the term
"spectral theoryU is used in the title of the chapter.
The present chapter is a. fundamental turning point in our in-
vestigations. Until now our study has been directed towards the topo'
logical aspect of operator theory. The function-theoretic and algebraic
mechanisms introduced here will make possible OUT future detailed
analyses of operators.
:555
556
VII. GENERAL S"ECTRAL THEORY
VII.I.l
VII.l.40
SPECTRAL THEORY IN FINITE SPACE
557
1. Spectral Theory in a Finite Dimensional Space
Throughout this section. 1: will denote a finite dimensional com-
plex B-spaee, and T a linear operator in B(1:), Onr aim is to study the
algebraic and topological properties of T. This is achieved, here and
in the more general theory of the next sections, by studying a class of
functions of the operator T. The symbol 1 will denote the identity
operator in I; we will interpret T" as 1.
zero polynomial SI such that Sl(T).r1 = O. In the same way. there
exist non-zero polynomials S" i = 2, ' . ., k such that S,(T)"" = O.
If R = Sl . S.' . . S., then R(T)"" = 0, and consequently R(T)", = 0
for all '" E I. Thus a non-zero polynomial R exists 8uch that R(T) = O.
LetR be factored as R(A) = PII::1(A-A.>a'.IfA, ja(T), then (T -A,I)x
= 0 implies'" = O. Consequently. the product R, of all the factors
(A-A,)"' in R such thaH,. a(T), still8atisfies R,(T) = O. In the same
way, the product R. of all the factors (A-A/) ', where p, =
min ("" v(A,», satisfies R.(T) = O. Since any polynomial P having a
zero of order vIA) at each A. a(T) is divisible by R,., any such poly-
nomial satisfies PIT) = O.
To prove the converse statement, suppose that PIT) = 0, where
PIA) = P rr::.,(A-A,)a.. By the argument used in the first part of the
theorem we may suppose each A,' aCT). We now show aCT) =
{ . . . " A.}. For if A. E a(T), then Ty = AoY for some vector y T- O.
Then P(T)y = P(A,,)y, and. 8ince PIT) = 0, it follows that P(A,,) O.
To prove that "1 (A,), we suppose on the contrary that ex; < v(A 1 ),
so that there exists an "'I T- 0 with (T -A 1 1'f'+'"" = 0 and Y1 =
(T-A,I)a''''l T- o. Let PIA) = (A-A,)aIQ{A), where Q( ) ,.. o. Since
TYI = A'YI' P(T)x 1 = Q(T)y, = Q(A')Y1 * 0, contradicting the fact
PIT) = O. Similarly "" vIA,), i = 2, . . ., p, so that P has a root
of order vIA) for each A. aCT). Q.E.D.
1 DEFJNITION. If PIA) = ! o")" is a polynomial with complex
coefficients, then by PIT) is meant the sum !;:""",T' = rx"T"+...
+''IT+rxJ.
Our first task is to discover when two polynomials determme the
same function of T.
2 DEFlNITION. The sprdrum a[T) of an operator T in a finite
dimensional B-space is the set of complex numbers A such that AI - T
is not one-to-one. The inde", v(A) of a complex number A is the smallest
non-negative integer v such that (M-T)'''' = 0 for every vector", for
which (M-T)'+l", = O.
It foUows that If Ao E a[T), there eXIsts an "'0 T- 0 such that
(T -;"I)x. = O. The number A" is frequently called an nvalue of T,
and any corresponding "'0 is caUed an cigerwtdor.
For each non-negative integer n and complex number J.. defme
the linear manifold!R = {"'I(T-AI)"", = OJ. Then the index vIA) is
the least integer v such that !Ri'"1 = !R . Obsel've that !R = !R.("
for n vIA). Since I has finite dimension, there can be proper in-
dusion for at most a finite number of terms in the sequence
9-r,> !R1 !R . . ., and thus ..(A) < dim I for every A, We note that
A. a(T) if and only if vIA) > O. For example, the operator T in two
dimensional space given by the matrix (g ) has aCT; = {OJ and
v[O) =2.
3 THEOREM. If P and Q arc polynomials, !her. PIT) = Q[T) if
and only if P-Q a zero of order vIA) at each poinl i. in afT).
PROOF. It is dearly sufficient to consider the case Q = O. Let
1: be k.dimensional, with basis {xl' _ . ., "'.}' Then the k+ I vectors
"'1' T"'l' . . ., Tk"" must be linearly dependent. so there exists a non-
40 COROLLARY. The ectrum of an operator in a finate dimen-
sional ace is a ?wn-void finite sel of points.
PnooF. ThIS follows from Theorem 3. We have seen that T always
satisfies a non-zero polynomial equation PIT) = 0, where the roots of
PIA) are the spectral points of T. Q.E.D.
Theorem II enables us to define the operator I(T) for I in a class
of functions larger than that consisting of the polynomial functions.
Let jO[T) be the dass of all functions of the complex variable A which
are analytic in some open set containing a[T). The open set need not
be connected, and can vary with the function in jO(T). If I' jO(T),
let P be a polynomial such that f'm){i.) = p'm'(A), m 0;; >(A)-I. for
each A E aCT). We define I(T) = PIT). Itfollows from Theorem II that
this definition of tIT) is unambiguous. The following theorem follows
immediately from the corresponding results for polynomial functions.
558
VII. GENERAL SpECTRAL THEORY
VII.I.5
VII.l.8
SPECTRAL THEORY IN FINITE SPACE
559
5 THEOREM. II I, g are in (T) and ex, (J are complex """,bers,
thm:
(n) exJ+{Jg i.. in (T) and (o;J+{Jg)(T) = ex/(T)+{Jg(T);
(b) I' g i.. in (T) and (f. g}(T) = I(T}' geT):
(c) il I(A} = I: o 0:,.1.. then I(T) = I:::'" o;.T.:
(d) I(T} = 0 i' and cm!y il
l'ml(A) =0, A a(T), O;;;m ";; v(A}-I.
Note that (b) implies f(T}g(T) = g(T)/(T) for aU f, g (T).
If;" is a complex number, let e..(A) be identically equal to one in
a neighborhood of lo, and identically equal to zero in " neighborhood
of each point of a(T)n {lo},. Put E(},,} = e..(T). The next theorem
follows immediately from Theorem 5.
PROOF. The preceding paragraph demonstrated that if A a(T),
then (.ill-T)'(A)E(A) = O. This shoW!! that E(A)I 91;(A). Since
a(TJE(A) = I, to show the reverse inclusion it is sufficient to prove
that 91. 1 ') n 91:,.1 = {O}, for A *- p., J., p. u,(T).
Suppose that there is an '" *- 0 with "' 9I;1"n!1l;!'). Let ex,O ,,;;
0; < {A}, be the greaust integer such that z = (T-.ill)"", * O. Then
Tz = Az, so (T-p.lylp)2 = (A-p.)'{.lz * o. On the other hand,
(T-p.l)"')Z = (T_p.l)".I(T-.ill)"'" = (T-.ill)"(T-p.l)"I.I", = 0,
since LV € 9r.{p). Hence :x must be zero. Q.E.D.
The projectIOns E(J.) define a very useful direct sum decomposi-
tion of .!, and permit us to give a simple analytical expression for
functions of T.
6 THEOREM. (a) E(;") * 0 il and nly if AD is in aCT).
(b) E(J. o )' = E{lo) and E(lo)E(J.,} = 0 I r Aa *;...
(c) I = I E(A).
ho-(TJ
Let {A" . . ., A.} be an enumerahon of aCT), and let I, = E(J.,):£.
It follows from (b) and (c) of Theorem 6 that
I=I,E!J...ElJI..
Moreover, 8ince TE(A,) = E(A,)T, it follows that TI i I.. i = I, ,. "
k. Thus. to the decomposition of the spectrum aCT) mto k points there
corresponds a direct sum decomposition of i into k 8ubspaces , each of
which is mapped into itself hy the operator T. Thus the study of the
action of T on I may be reduced to the study of the acuon nf T on
each of the subspaces :f,. Since (J.,-J.Y''''' e..,(A} has a zero of nrder
(l) at each point J. in a(T), the operator (;',1 T)"'.IE(A,) = o.
Thus, in each space i' the operator T is the sum of a scalar multJple
J.,l of the identity and a nilpotent operator T -Ail. Such a direct sum
decomposition of :£ can be enormously advantageous in many in-
vestigations of the properties of T. Theorem 7 cmifies the relation
between the index J'(A) of a point in aCT) and the corresponding pro-
jection E(J.).
8 THEOREM. II I is in (T), then
'[')-1 (T -.ill)'
fIT) = I I ., I'" (J.)E(J.).
kD(T) (...{I I.
PROOF. This formula follows immediately from Theorem 5, since
I and the function g (T) defined by
'[')-1 ( A)'
g<ftl = I I 1"'(A}.,(p.)
llEa!TI i:-o z!
satisfy the relations I'm'(J.} = glml(A), m;;; (A)-l, for A ,,(T).
Q.E.D.
Theorem 8 gives us a powerful method for explicit calculation of
functions of Tt and has a number of interesting theoretical implica-
tions.
7 THEOREM, If A i8 in oCT), then
E(J.)I = 91.") = {"'I(T-.ill)'''I", = oJ.
9 THEOREM. Let f. be in (T). Then {/.(T)} C(J1I1v:rgt:B if and
only il thueqUl!n.ees {/ ml(A)}. 0 ;;; m S (A)-l, converge lor Ain ,,(T).
If I i8 in (T), tkn f.(T) --+ I(T) i/ and only il I::-'J(A) --+l'm)(J.),
o ,,;; m ;;; (A}-I, I r J. in afT).
PROOF. The sufficiency of the first condition follows immediately
from Theorem 8. Conversely, suppose that {,.(T)} converges, and let
A£a(T). Since (T-}J)"'HE(A) * 0, we can find an., such that
(T-}J)"'I--'E(A)", * o. Let y = E(J.)"" and y, = (T-.ill)'y, for
0;;; k;;; (A)-l. Put v(A)-1 = T. Then I.(T)YT = I.(A)YT' so that
<t.(A)} converges. In the same way, I.(T)YT-l = I.(J.)YH +/:(A)yTO so
560
Vll. GENERAL SPECTRAL THEORY
VII.I.lO
VII.2.1
EXERCISES
561
that (/:V.)} converge.. Proceeding in thjg inductive fashion. we
establish that {f ml (A)} converges for each Tn < v(A) 1. The second
statement is proved in the same manner. Q.E.D.
1 fl-l
lim pt?, i, i = 1,2,..",52.
w n ,,=Q
There are 52 different ways in which the card originally in the i-th
place may transfer to the j-th place in two shuffles; it may go to first
place after the first shuffle and then from first place to the j.th place.
or it may go to second place and then to j.th place, etc. Thus
10 THEom:J\l. Let I in $<"(T) be analytic in a domain containing
the clOtJUTt: 01 an opt'n $el U co-ntaining aCT), and $Uppose thai the bound-
ary B 01 u CCYll8iols 01 a linite numhr 01 dO&?d redifiabl. Jordan ctU'VC$,
orimfftl in lhe po8itive 8ense cueWmary in the theory 01 complex variables.
Then I(T) may be expressed as a Rinnann corduur inJegml over B
by the lollowing lormula:
I(T) = 2-, f I(A)(M-T) I.u.
27rt B
PROOF. Let A f aCT) = {AI' . . .. A.J, and let r( ) = (A-n '. Then.
by Theorems 5 and 8.
· .I;"H (T-A 1)"
(M-T)-l=r(T}=I I ' E(A,).
1-1 ..-0 (A-lj}"+t
Thus. if I. $<"(T).
1 i · '(;"H II')(A )
- I(A)(M T} ].u = I I (T-A,l)" E(A,) = I(T).
2n:i B J-1 ._0 ....!
Q.E.D.
..
p = I PilPJk"
0-'
A :!!imilar inductive argument shows that p ll = I:1P J'PkJ for
n = 0, 11 . . .. The matrix P = (Ptj) defines a linear transformativn in
E" whose n.th power is pn (1'\1). Since 0 s: pijl I. we have
P'ln -+ O. The preceding example shows that n 1 I::"Jp ) converges.
(c) For an arbitrary 8calar t. the function e" is entire in A. and
hence belongs to $<"(T). Furthennore.
dn "'(""_"" d n
lim - - - (k"), n = 0, 1.2. . . ..
A--+<J .un h dil n
Thus, by Theorem 9. (dld!)e'. = Ae'. for all matrices A in E"', Since
e"" A etA = I. the columns of the matrix e'A form a set of m linearly
independent solutions of the equation dy!dt = Ay.
(d) If T is such that 1'(A) = 1 for A. u(T). Theorem 8 yields
.
I(T) = I/(A,)E(A,).
.
A few examples will illustrate applications of the preceding theo-
rems.
(a) Pnt In(A) = n 1 I::,j, Am and gn(A) = An!n. Then {fn(AJ} con-
verges if and only if III < I. while if j> 0, (f )(A)} converges if and
only if IAI < 1. It is apparent that the restrictions on A in order that
gn(A) -+ O. and g )(A) -+ O. for j > O. are exactly the Same. Hence. it
follows from Theorem 9 that {n l I:;:; Tm} converges if and only if
(Tn!n) converges to O. and that this is the case if and only if lo(T)I ::::: 1
and 1'(l,,) = 1 for those Ao' a(T) with 1101 = I.
(b) Let a machine shuffle a deck of cards m such a way that there
is a definite probability p" that a card originaBy in the i-th place be
found in tbe j-th place after the shuffle. Suppose that this probability
Pn is independent of the preceding- shuffles. Let p:jl be the probability
that the card originally in the i-th place be found in the j-th place
after n shuffles. and let pi ) = iJ.,. We show the existence of the limit
We shall show that ,,(A) = 1 for A' oCT). if T is all Hermitian
matrix in the finite dimensional Hilbert space En; i.e. if T satisfies
the identity (T",. y) = (x. Ty) for x, Y' E'\ For, if T is Hermitian,
and (T-M)x = 0 for some x oF 0, then (T." x) A(x, x). Since
(Tx, a:) = (a:, Ta:) = ( T.,.x ). it foBows that A is real; hence a(T) is
a subset of the real axis, Now let A.a(T). and let (T-M)2y = O.
Since A is real, ((T-M)2y. y) = «T-M)y, (T-M)y) = I(T-Mjyl'
= 0, so that (T-M)y = O. Consequently. 1'(A) = I, for any A. aCT).
2. Exercises
1 Let T be a matrix, and let LI (A) be the determinant of the
matrix M - T. Show that A . oCT) if and only if A is a root ofthe poly-
562
VII. GENERAL SPEC1'R.\.L THEORY
VIl,2,2
VII.2.10
EXERCISES
563
nomial equation L1(A) = O. The polynomial LIlA) is called the charac-
reristU:
of the matrix T.
2 If T is a linear operator in B finite dimensional space, show
that any two matrix representations of T have the same characteristic
polynomial. This will pennit us to speak without ambiguity of the
characteristic polynomial of a linear operator.
S If T is a linear operator in a finite dimensional space and
}IE <tIT), let T
be the restriction of T to the subspace m;r'l. Let
LI
(A) be the characteristic polynomial of T
. Show that
(a) LI
IA) = IA-I')"
). where ..(1') = dim m;I.);
(b) >'(}-') ;;;; ..(fI);
(c) LI(A)
IT L1 p (A).
crIT)
'" (Hamilton-Cayley) Show that any linear tnmsformation T
in a finite dimensional space satisf"'1eS its characteristic equation, i.e...
LIlT) = O.
5 Let
( 1 0
T= 2 I
o 0
D.
10 Let f. :F(T). g. :F(f(T)). and F(,) = g(flm. Then
F. :FIT). and FIT) = g(f(T)).
11 Letf.:F(T)andletf{A) = 1:::
",.A'.Findconditionswhich
are necessary and sufficient in order that fIT) = 1:::_o...Tn.
12 If, for some real number T < 2, the elements of the matrix
Ar(M-T)-1 are bounded in some deleted neighborhood 0 '" Jll < e
of the origin, what can be said about the existence of the limit
lim,\-+o A{ll _T)-I?
13 The .pectra <tIT) and <tIT") are identical. Moreover f(T.)
= I(T)* for I' :FIT).
14 An operator T in the finite-dimensional Hilbert .pace i. .aid
to be normal if TT* = T*T, where T* is the Hilbert 'pace adjoint
defined by the identity (T:r.!!) = (:r, TOy). Show that, if T is nonna!,
then >'(A) = 1 for A.<tIT).
15 If A" <t(T), the domain of {ll - T)-l is I.
16 Let I have dimension ... If T satisfies Tn = O. show that
there is a basis {Xl' . . ., xn} for 1, and a set of integers 110, . . ., nit'
1 < no < 1l]. < . . . < fl,l; = 11, such that Ta: i = a'i+l unless i is one
of the integers nj, in which case Ta:. = O.
17 (Jordan) Let I have dimensIon n. Show that there is a basis
{l.C 1 , . . ", an} for .1, 8. set of integers TltI, _ . _, t1;1.::, such that 0 = no < n
< _. . < n. = n. and an enumeration (with possible repetitions)
AI' . . ., A. of u(T), such that Ta:, = Ap,+:r1+1 for nJ
I < i < "J,
Ta: n = Ap, .
, ,
18 Let B be the Boolean algebra of sets ill the complex plane
and let Bl be the Boolean algebra of projections generated by the
projections E(A,,), . _ .. E{.i!,,). Let a map E : B --+ BI be defined by
placing EI<t) = 0 if un <tIT) is void and otherwise defining E(<t) lIS the
sum of aU E{A,) with A,. <t. Show that
(i) E is a homomorphism and EI<t(T)) = I;
Iii) Elu)T = TE{<t). <t.B;
(iii) the spectrum of T when considered as anoperatorinEI<t)];
is contained in a.
In addition. show that no other map E of B into B , satisfies the
conditions (i). (ii), and liii).
Find matrices A and B for which
A' = 7",
m Bn
T = 1:-.
n-o n!
How many matrices can you find!
6 Let <tIT) = (AI' . . ., .i!,,). Show that if >'IA,) = I. i = I, . _ .. k,
and I. :FIT). then
fIT) =:i IIA,) IT (T-l,I),
'_1 m' IA,) ,...
where mlA) = (A-A,). . .(
-A..),
7 Put!1!l = {:rI(T -ll)i:r = O}. Show that I
ml eo (T -MY];
if and only if i
>'Il) or i = O.
8 If E = limn ..-1 1:
:-JT' show that E'
E, ET = TE, that
E(I) is the set {a:!.,. I, Ta: = :r}. and that (I -E)(I) is the set
{a:I"'. I.:r = (I-T)y).
1/ Show that I(A i,,)lW T)
ll
is bounded in 11 neighborhood of i" if and only if i
.(i,,).
56
VII.. GENERAL SPECTRAL THEOR'I{
VII.2.19
VII.2.25
l:X:E.RClSES
565
(d/dt) [det yet») = [dot Yet») [tr A (t»)
yet) is non-singumr everywhere on I if it is non-singular at one pomt
on I.
25 Let yet) be a solution matrix of dY/dt = A(t)Y which is
non-singular. Show that the set of all non-singular matrix .olutions
are precisely the matrices Y(t)C where C is any n xn constant, non-
singular matrix.
26 Let A(t) have perIOd p > 0; that is, A(t+p) = A{t) for aU
ton - co < t < co. If Y(/) is a non-singular solution matrix of dY/dt
= A(t)Y then show that Y(t+p) = Y(t)C for some non-singular
constant matrix C. Show that the conespondence y(/) .....y(t+p) de-
fines a non-singular linear transformation T of the solution space of
dy/dt = A(t)y onto itself and that the matrix of T, relative to the
basis formed by the columns of Y(t), is just C.
27 Let A, Y, and GbeasinExercise26. Show that X(t) is a non-
singular solution matrix of dXfdt = KX if and only if Yet) = P(t)X(t)
is a non-singular solution matrix of dYjdt = A{t)Y; where pet) = Yet)
exp (-tfp log C) and A{t) have period p > 0, K = p
' log C, and C
is the constant period-shift matrix for Yet). Show that the real parts
of the points in u(K) are independent of the determination of log C.
These values .'Jt'G(K) are called the characteristic exponents of A(t).
Show that the system dyfdt
A(t)y is stable if and only if the
ch8l'8Cteristic exponents of A(t) are non-positive while those pure
imaginary Aeu(K) have vIA) = 1. Also every solution yet) -..0 if and
only if the characteristic exponents of A(t) are aU negative.
28 Suppose A(/) is continuous and sup la,;(/)1 < B for all
a < t < c:o and some constant B. Show that for every solution
vector Yilt) of dyfdt - A(t)y, lim sup.....o> t
llog ly,(tJl = A.. IA,I < Bn.
The real numbers Ai which arise in this way are called the generalized
characteristic exponents of A(t). Show that there are at most n dis-
tinct generalized characteristic exponents and that the differential
system is stable whenever all the l's are negative.
29 If A(t) is either a constant or a periodic matrix show that the
real parts of a(A) or the characteristic exponents of A(t), respcctivel)",
are precisely the generalized characteristic exponents of A(t).
19 Find the most general solullon of the differential equation
y' = Ty where T is the matrix of Exercise 5.
The next ten exm:ises refer to the stability theory ofsystems of
n linear homogeneous differential equations, dy(t)fdt = A(t)y. Here
A(/) = (a,,(I)) is an n:< n complex valued matrix, continuous in the
real variable hI: - CO ;:;; oc < t < P :5 +co, and a solution is a
complex valued (column) vector y(l) £ En, differentiable and satis-
fying the differential system for each I £ I. The theory of differential
equations assures us that for eacb fa E I and each '110 E En there exists a
unique solution y(I) such that y(t.) = Y..
20 Show that the solutions of dYldl = A(t)y form an n-dimen-
siona1 complex linear vector space.
21 Consider the matrix differential equation dYjdt = A(t)Y
where a solution is anxn complex valued matrix Y(t), differentiable
and satisl)ing the differential equation for each t £ I. Show that for
eaeh lo £ I and each complex (constant) matrix Y. there exists a unique
solution matrix Yet) such that Ylt.) = Y.. Show that a set of solution
vectors y,(/), . . ., Yn(t) of dyfdt = A(t)y form a basis for the solution
space if and only if they form the columns of a solution matrix Yet)
of dY fdt = A(t)Y which corresponds to a non-singular initial matrix Y."
22 Show thatif J'..A(s)ds and A(t) commute for each I £I, then
the matrix solution of dy/dt = A(t)Y with Y(lo) = Y. is Yet) =
[exp J
A(s)ds]Y.. Sbow that if A(I) is either constant or diagonal
(i.e. all entries off the principal diagonal are zero). then the above
formula for yet) is conect..
23 The differential system dy/dl = A(t)y, wbere 0: < t < P
= 00.. is caUed 81.able if every solution remains bounded as t -+ co;
that is, lim SUPi
o> ly(t)1 < co. Show that, if A(t) = A is constant, the
system is stable if and only if no points of alA) have positive real
parts, while all pure imaginary A £ a(A) have
(A) = 1. Sbow that
lim sUP,
o> [y(t)1 = 0 for e..ery solution if and only if .'Jt'G(A) < O.
24 Let Yet) be a solution matrix of dYfdt=A(t)Y and show
tbat
at each point t e I where Y(/) is non-singular and tr A(t) is the sum
of the entries on the principal diagonaL Show that a solution matrix
,
566
VII. GENERAL SPECTRAL TIIEORY
VII.S.l
VII.S.4
FUNCTIONS OF AN OPERATOR
567
3. Functions of an Operator
Throughout the remainder of this chapter, J: will denote a com-
plex B-space, and T a bounded linear operator in::E. IVe eJrlude the
trivial CMe I = {O}.
If 1. is infimte dimensional, T need not satisfy any non-trivial
polynomial equation PIT) = o. Nevertheless, the procedure suggested
by Theorem 1.10 will enable us to generalize many of the results of
Section I to the infinite dimensional case. We begin by studying the
function (M-T)-l.
1
IR(A; T)I
d(A) , A. e(T).
Thw jR(A; T)[
00 as deAl ..... 0, and the Tesolvent Bet is fk natural
domain of tn1AJytU:ity 01 R(A; T).
PROOF. We have seen in the proof of Lemma 2 that if 1,.1 <
[R(A; T)I-" then A+,.. e(T). Hence deAl
IR(A; T)I-', from ....hich
the statements follow. Q.E.D.
.. 4 LEMMA. The ./nsed aet aCT) is bounded and non.void. Moreover
sup I,,(T)I = lim n _", VITnl ,,;; ITI. For IAI> sup I,,(T)I the series
R(A; T) = 1:."-0 TnlA n +' cunvergeB in 1M uniform operatGr topology.
PROOF. Let I(A) = I;:,.fJT"fAn+'. From 111.14 it is seen that the
series I(A) has domain of convergence D = {AIIAI > limsup VITnl} .
ft_"
1 DEFlN1TION. The TUOl:ve1l1 act e(T) of T is the set of complex
numbers A, for which (M _T)-l exists as a bounded operator with
domain I. The BpCdrum a(T) of T is the complement of e(T). The
funclion R(A; T) = (ll-T)
', defined on e(T), is called the Tesolvent
frmcticm of T, or simply the resoh1en, of T.
.. 2 LEMMA. The re.rolvent set e(T) is open. Th£ jwJdion R(A; T)
ia cmalytW in e(T).
PROOF. Let A be a fixed point in e(T), and let I' be any complex
number with II'I < IR(A; T)I-'. It will be shown that A+I" e(T).
Heuristic considerations. based upon an analogy with geometric series,.
suggest that if {A+I')l -T = pJ +(ll T) has an inverse, it is given
by the series
'" '"
B(,.) = 1 (-I')k(M-T)-Ik+11 = 1 (-I')kR(A; T)k+'.
k-I) 1:=0
As in the proof of Lemma 2, we verify that I(A)(M - T) = (M - T)f(A)
= I, for A . D, so that e(T)
D, and consequently aCT) is bounded.
Since e(T) is the natural domain of analyticity of R(A; T) by Corollary
S, the Laurent series for R(A; T) will have the domain of convergence
IAI > sup lu(T)f. Thus sup la(T)1 = limsup VIT"I . It will next be
shown that sup lu(T)1 ,,;; lim inf VIT"I . Note that if A is an arbitrary
point of ,,(T), then Aft . a(Tn); for the factorization
(A.I-Tn) = (M-T)P.(T) = P.(T)(ll-T)
shows that if (AnI_Tn) has a bounded inverse, so will (M-T). Thus
IAI"
ITnl, and hence
sup I,,(T)I ,,;; ITnl'ln.
It remains to show that the spectrum is not void. If ,,(T) = </>, then
R(A; T) is entire, and, since R(A; T) is readily seen from its Laurent
expansion to be analytic at infinity, it follows from Liouville's theo-
rem (111.14) that R(A; T) is a constant. Hence, the coefficient of A-I
in the Laurent expansion of R(A; T) vanishes, so that I = 0, which
contradicts the assumption I oF {O}. Q.E.D.
5 DEFlN'T10N. The quantity
TIT) = sup I,,(T)I = lim VITn)
Since I.uR(A; T)I < 1, this series converges. Since B(.u) commutes with
T, and
«A+p)I-T)S(.u) = (M-T)S(j.)+I'S(I')
'"
= l: {( -I'R(A; T))"-( -I'R(A; T))"+')
k_D
=1,
it follows that A+I" e(T), and that R(A+I': T) = S(,.) is analytic
at the point I' = o. Q.E.D.
II CORoLLARY. II deAl is the distallCi! Irom A to tM spectrum oCT),
then
......'"
is called the spedrnl Tadius of T.
568
VlI. GENERAL SPECTRAL THEORY
VII.B.6
VII.S.n
FUNCTIONS OF AN OPERATOR
569
6 LEMMA. The /oUrnDing identity, knCIWn as the rcsoh.."t tqualion,
is valid lor every pa.ir A, p. in (I(T);
R(A; TJ-R(u; T) = (.u-A)R()'; T)R(!,; T).
PROOF. The lemma follows by multiplying both sides of the equa-
tion
(.ul-T)(AI-T){R(A: T)-R(u; T)} = (fll-T)-(M -T)
= (fl-A)l
suppose that U1UB,!;;; U.. Suppose also that U.UB. is contained in
a common region of analyticity of I and g. Then
I(T)g(T) = -
. (fn/(A)R(A: T!<v.) {t. g(u)R(u; T)dp)
= -
/ f I{A)g(u)R(A; T)R(fl; TJdpdA
4n: JB 1 BJ.
1 I, f I(A)g(,u)(R(A; T)-R(u; T))
=-- dl'dA
4",' B, ", (fl-A)
= -
f I{A)R(A; T) {I, g(,u) dp } dA
4n 2 Bl B./l--),
+ 2, I, g(fl)R(u; T) {f I(l) dl J dp
4.11: B 2 BIp-l
=
f I(A)g(A)R(A; T)dA
21rIJBI.
= (I' gIlT).
by R(A; T)R(u; T). Q.E.D.
7 LEMMA. The .-pectnun 0/ the adjoint T- 2S idenliml with the
spectrum 01 T. Farther, R(A; T*) = R(A; T)- lor Ain (I(T) = (I(T*).
PROOF. ThIS follows immediately from VI.2.7. Q.E.D.
8 DEFiNITiON. By JF(T). we denote the family of aU functions I
which are analytic on s<>me neighborhood of aCT). (The neighborhood
need not be connected, and can depend on 'e JF(T).)
9 DEFINiTiON. Let Ie JF(T), and let U be an open set whose
boundary B consists of a finite number of rectilIable Jordan curves.
oriented in the positive sense customary in the theory of complex
variables. Suppose tbat U
aCT), and that U u B is contained in the
domain of analyticity of I. Then the operator I(T) is defined by the
equation
I(T) = _1 . f I(A)R(A; T)d.<.
23nJB
It follows from Lemma 2, and from the Cauchy integral theorem,
that I(T) depends only on the function I, and not on the domain U.
.... 10 THEORE'L III, g aTe in JF(T), and ex, fJ aTe complex numbenr,
Ihen
(a) exl+fJg is in JF(T) and ex/(T)+fJg(T) = (exl+fJg)(T);
(b) I' g is in JF(T) and I(T) . g(T) = (I . gIlT);
(c) ill has the pat£'l!T stria c.rpansirm I(A) = !:-o a..J!, valid in a
migkborlwcd 01 a(T), then I(T) = !:;'..o "",T';
(d) I is in JF(T*) and I(T*) = I(T)*.
PROOF. Statement (a) is obvious. It is clear that I' g. JF(T);
let U 1 and U. be two neighborhoods of aCT) whose boundaries RI
and B. consist of a finite numbcr of rectifiable Jordan curves, and
by Lemma 6 and the Cauchy integra1 formuJa. This proves (b). To
prove (c), we note that the power series !.:'.oa"A' converges uniformly
on the circle C = {AI [AI <;: r(T)+c} for c sufficiently small. Conse-
quently,
I(T) =
f { . h.,lk } R(A; T)dA
2x'l Jc k
O
1 m i
= _. ! cx, A'R(A: T)dl
23z1 lr-O C
1 0> f. m
= _. ! ex. A' { ! T; fA H '} dJ.
2;rr
lr
O C j=<J
0>
= Iu.JcT",
k=O
by Lemma 4 and Cauchy's integral formula. Statement (d) follows
immediately from Lemnm 7. Q.E.D.
.... n THEOREM. (Sped"'/ m<1pping /heo,.,.",.) II I is in JF(T), then
f(a(T)) = G{/{T))_
570
VI1. GENERAL SPECTRAL THEORY
VII.3.12
VII.S.IS
FUNC'rIOS$ OF AN OPERATOR
571
PROOF. Let A . ,,(T), and define the function g in the donmin of
definition of I by
g(
) = W.)-/(m/(A-
).
By Theorem 10, I(A}I-/(T) = (ll-T)g{T). Hence, if I(A)I-/(T)
had a bounded everywhere defined inverse A then g(T)A would be a
bounded everywhere defined inverse for }J -T. Consequently
I(A). "(/(T}).
Conversely, let I" ,,(f(T», and suppose that,. f1(,,(T». Then
the funetion h(
) = (/(n-,.)-l belongs to F(T). By Theorem 10,
h(T)(f(T}-,uI) = 1, which contradicts tbe assumption that
,. E ,,(fIT»
. Q.E.D.
10 and 12 will be used in the rest of this chapter without explicit re-
ference to these theorems.
13 LEMMA. Let In be in F(T), n = 1, . . ., and BUppOJIe Ihat all
1M functWns In are analytic in a fiazd neighhOThood Vol ,,(T). Then. il
In ronvergea unilormly to I on V. I.(T) ctm'O€Tges '0 I(T) in 1M unilorm
tcpology 01 operafors.
PROOF. Let U be a neighborhood of ,,(T) whose boundary B con-
sists of a finite number of rectifiable Jordan ares, and such that
U U B f V. Then In -+ I uniformly on B, and consequently
.... 12 THEOREM. Let I be in $>(T), g be in F(/(T», and F(
)
= g(f(m. TMn F is in F(T), ami F(T) = g(/(T».
hOOF. The statement FE F(T) foHows immediately from
Theorem n. Let U be a neighborhood of ,,(f(T» whose boundary B
consists of a finite nmnber of rectifiable Jordan arcs, and suppose that
UUB is contained in tbe donmin of analyticity of g. Let V be a
neighborhood of aCT) whose boundary C consists of a finite numher of
rectifiable Jordan arcs, and suppose that Vu C is contained in the
domain of analyticity of I. Suppose, moreover, that I(VuC) f U.
By Theorem 10, the operator
1 f. R(
; T)
A(A) = 2,,; c A-/(!;)
satisfies the equations (}J-/(T»A(A) = A(A)()J-/(T» = 1. Thus
A(A) = R(A; I(T». Consequently,
g{f(T» = 2... r g(A)R(A; I(T))dA
27t.J8
1 i 1 g(A)B(E; T)
= - - dEdJ.
"",2 B C ).-f(
)
= 2... 1 B(!;; T)g(f(m
=F(T),
2.1U C
f In(A)R(A; T)dJ.
2]f1JB
converges in the uniform topology of operators to
r I(A)R(A;T)dA.
2:lnJB
The I}ext lemma Can be proved in the same way.
14 LEMMA. Let V be a ..eighbarhood of <I(T), and let U be an rYpffi
se! in 1M campi"", plane. Suppose llurt f is an analytic lunction 01 the
two complea: mriables A, ,.Ior [A,,.] in Vx U. Then I(T,,.) is a B(}')-
tlalu-rd function which is alwlytic lor I-' E U.
Q.E.D.
by CauchY'8 integral formula. Q.E.D,
The elementary algebraic rules of operation given by Theorems
15 DEFINITION. A point A" £ ,,(T) is 8aid to be an isolared point
of ,,(T), if there is a neighborhood U of J." 8uch that o{T)n U = (J.,,).
An i80lated point J." of ,,(T) is called a pole 01 T, or simply a pole, if
B(A; T) has .. pole at J.". By the order '-(A,,) of a pole J." is meant the
order of Ao as a pole of R(A; T).
The following theorem, which IS thc analogue of Theorem 1.3,
takes on .a somewhat different form in the general case,
16 THEOREM, (lliinimal equation) Let f, g be m F(T). Thm
I(T) = g(T) if and only ill(A) = g(A) idenlimlly on an open sel includ-
ing all of ,,(T) excepl lor a linire number 01 poles (A., . . " )..}, and lor
each i with 1 < i
k, f-g has a zero 01 order a! least
()..) at At.
PROOF. It is dearly sufficient to consider the case g = O. Let I
vanish identically on an open set V containing all of ,,(T) but the poles
AI' . . .,;... Then it is dear from Definition 9 that
.
572
VIla GENERAL SPECTRAL THEORY
VII.3.17
VII.3.18
FUNCTIONS OF AN OPERATOR
578
I(T) = i . J. I(A)R(l; T)d?,
f-l 2:ni CII'
where C. is a sufficiently small circle about A.. If I(l) has a zero of
order at least (A;) at A = A" then, since R(l; T) has a pole of order
(A;) at A = A" it follows that I(A)R(A; T) is regular inside Ck' Thus.
by Cauchy's integral formula, I(T) = o.
Conversely, let I(T) = 0; then, by Theorem II, 1(<t(T» = o.
Let I be analytic on a neighborhood U of <tIT). For each 0.. <tIT),
there is an .(0.) > 0 such that the sphere 8(1X, .(0.» r;; U. Since <tIT) is
compact. a finite set of spheres 8{"'I' '(IX I ». . . ., 8(1X., f(rx,.» will cover
<tIT). If some sphere 8(0." '(0.,» contains an infinite number of points
of <tIT), it follows from the theory of complex variables that I vanishes
identieally on 8(0." '(IX,».
Thus, if U I is the union nf those spheres 8(0.., f(o.,» which
contain an infinite number of points of a(T), then I vanishes identi-
cally on U I . Hence, U I contains all but a finite number of isolated
pOlnts of aCT), which we suppose to be the points {AI' , , ., },,}.
Suppose that I does not vanish identically in any neighborhood of
).,.. Then, since l(a(T» = O. Ibns a zero of finite order n at).,.. Conse-
quently, the function CI' defined by CI(.!") = (J.,-f;)nfl(/;). is analytic
ia a neighborhood of J.,. Let e be a function identically one in a neigh-
borhood of Al and identically zero in a neighborhood of every other
point of aIT), and let g = Cle. Then (l.I T)ne(T) = I(T)g(T) = 0.
The Laurent expansion of R(f;; T) in a neighborhood ° < 1/;-)",1 < .
is given by w
R(/;; T) = Arn(J.,-l;)m,
It is evident tbat the spectral sets form a Boolean algebra of
subsets of a(T). If a is a spectral set, there is a function f. :F(T)
which is identieally one on <t and which vQlushes on the rest of a(T).
We put E(a; T) = fIT). If the operator T is understood, we may
write E(a; T) simply as E(a). It is clear from Theorem HI that E(<t)
depends on1y on a, and not nn the particular I e :F(T) chosen to de-
fine it. If the spectral set a consists of the single point l, the 8ymbol
E(l; T) may sometimes be used instead of E({A}; T). It will occasion-
ally be convenient to use the symbol E(a) for any set a of complex
numbers for which un a(T) is a sp<rlral set. In this case, we put
E(a) = E(unu(T».
Thus E(u) = 0 if unu(T) is void.
A comparison of Theorem 16 witb Theorem 1.3 suggests that
there is B relationsbip between the order of a pole and its index as
defined in Definition 1.2. The following tbeorem gives such a relation-
ship. Though the notion of index was defined for operators in a finite
dimensional space, the definition given has a general application.
18 THEORE>f. If l is a pole of T of order P, thm A has imf£", P.
Furlherowre, an i30latro paint J. in the spectrum of T is a pale of order "
if and ollly if
(AI -T»E(A; T) = 0, (M T»-Il!:(A; T) oF 0.
PROOF. It was shown during the course of the proof of Theorem
16 that tbe Laurent expansion of R(,; T), in the neighborhood
o < 1/;-.1.1 < . of an isolated point J., is given by
where
_-w
w
R(/;; T) = A.(l-"n,
A.... = - . f. (AI _/;)m-l R(/;; T)d; = - (llI - T)m-Ie(T),
27ft C.I.
and where C I is a small circleaboutA r ThuSA-ern+ll = -(AII-T)me(T)
= 0 for m n, and therefore II is a pole of order at most n. In the
same way we see that either f vanishes identically in a neighborhood
of A" i = 2, . . ., r. or A, is a pole of u{T) and f has a zero of order at
least (l,) at A,. Q.E.D.
17 DEFINITION. A subset of aiT) which is both open and closed
in a(T) is caUed a ..pe<tra! set.
-
with
A_. rn + u = -(M-T)rnE(A; T).
Thus A IS a pole of order .' if and only if
(M T)'E(l; T) = 0, (ll-T)'-IE(A; T) if' 0.
To prove the first conclusion of the tbeorem let A be a pole of order ".
Then there is a vector Of: with
(ll-T)'", = 0. (ll-T)'-I",if'O,
574
'VII. GENERAL SpECTRAL THEORV
VII.3,19
VII.3.21
FUNCTIONS OF AN UPERATOR
575
which shows that the index of A is at least v, Now, suppose that n is
the index of A. Then for some x, {AI-T)n", = 0, (M-T)n-I x oF O.
Since
(M-T)'
R(E; T) = - 1: . " IA-EI > IAI -TI,
;.... (A-E)'+
as is seen by multiplying both sides of this equation by (EI -T)
= {E-A)l +(M T), the function
PROOF. Let A Hr. and suppose that A,. oCT.). Then there eXIsts a
bounded linear operator A in the space ;f. such that (M - T)Aa:
= A (M - T)", = '" for '" x.. Let the function g be equal to zero for
f' in a neighborhood of a, and equal to (A_p) I for f' in a neighbor.
hood oftheremainingpointsofa(T). Then g{T)(M-T) =(M -T)g(T)
= I E(a). If we define AI:! ! by A,,,, = AE(a)"" then
(M T)(A I +g(T)) = (AI +g(T»(M -T) = I.
0-1 (}J -T)''''
R(E; TI", = -, (A-E)J+l
is ngular over the entire plane, except perhaps at the point E = A.
ThU8, if K i8 any reetifmb!e contour surrounding o(T), and C is a
small circle about A,
'" = f R(E; T).x = 2.. f. R(E; T)x e(T)x.
2n JK 23t1 c
This shows that (AI - T)'", = (AI T)'e(T)x = 0, and proves that the
index n ;S;; v. Q.E.D.
19 THEOREM. Let f be in 9'"(T), anlllet T be a spedral sel of I(T).
Tium a(T)nf-](T) is a spedral sel 01 T, and
E(T; fIT)) = E(f ](T); T).
Consequently A (T), contradicting A E a. This 8hows that a a(T.).
Conversely, let A,. a. Then define h to be equal to (A-I')-] for f'
in a neighborhood of a not containing ).. and to be identically zero in ..
neighborhood of the remainder of aCT). We have h(T)(AI T)
= (AI T)h(T) = E(o), Consequently, the restriction hIT). of hIT)
to Xu satisfies h(T).(AI.-T.) = (AI. T.)h(T). = I., so that
).,. o(T.). This proves that a(T.} a, and that R(A; T.) = R(A; T)..
If f E 9'"(T). let U be .. neighborhood of oCT) whose boundary
B consists of a finite number of reetifiab!e Jordan arcs, and such that
U U B is included in the domain of analyticity of f. Then
PROOF. Let e.(p) = 1 for f' in a neighborhood of T, and let
e.(p) = 0 for pinaneighborhoodoftherestofa(f(T», Thene.(j(T»
= E(T; f(T». If -c' i8 the complement of T in a(f(T», Theorem 11
shows that aCT} is the union of the disjoint sets f-'{T} and I-](T').
Since f is continuous. these two sets are both open and closed. It
follows that a = a(T)n I ](T) is a spectral set of T. If e.(A) = e.(/(A»,
tllen E(a; T) = e.(T). and Theorem 12 shows that
E(T; fIT» = E{o; T) = E(f l(T); T). Q.E.D.
For any set 0 for which E{a) is defined we place ;f. = E(o)I.
Then TI.!;;" x.' and tile restriction of T to I. will be denoted bv T..
t(T)d 2.. {f I(A)R(A; Tldl } .
2nt B
= 2.. i I(J.)R{A; T).d}.
2m B
= i I{A)R(A; T.)d}. = fIT.).
2n1 B
By Theorem 18, J. is a pole of order v for T if and only if
(AI-T)"E(A) = 0,
(M -T)'-IE(A) oF o.
Since A" a we have E(A)E(o) = E(A) and thus
(AI-T)mE(A) = (AI.-T.)mE(A),
m = I, 2, . . n
Hence). is a pole of T of order v if and only If it is a pole of T. of order
v. Q.E.D.
20 THEOREM:. Let 0 be a Itpet:tr-al set 01 aCT). Then a(T.) = a. If
f is in 9'(T), then I is in 9'"(To), anll I(T}. = f(T.). A point}. in a
is a pore of T 01 order v il and only il it is a pole of To of order v.
21 COROLLARY. The 7TU1p (J --+ E(o) is an isomorphism of the
Boolean algebra 01 spectral sels onto the Roolean algebra 01 all projections
of the lorm E( 0), with a a spectra! 8et.
576
VII. GENERAL sF£CTRAL THEORY
VII.a.22
VII.4.1
SPECTRAL THEORY OF COMPACT OPERATORS
577
22 THEOREM. Let A", . . "' }.k be poles of T, let P" . . ", P k be their
oroers, and let u = {A". . . "' }.kJ. Then. for f in ff(T),
. ,,
1 f'm)(A )
f(TJE{u) = }; L
{T-A.I)mE(A.).
i
lm-O ml
(ii) !.
{"I(T-,U)'x = OJ.
Also if (T-'ut" = 0 then, by (I),
0= (T-,U)' {E(}.)x+E(al)x} = (T-,U)' E(u,)x.
Since by Theorem 20, (T -,U) is one-to-one on !a it follows that
,
E(u,)x = 0 and thus that E(}').x = x. This proves that {xl(T-'u)'x
= O} (:;:£, which, when comhined w;th (ii). completes the proof of the
theorem. Q.E.D.
PROOF. It follows from Theorem 10 that the map 0 --+ E(u) is a
homeomorphism. To yerify that it is an isomorphism, it will suffice to
show that E(u) = 0 only when u is the void set"'. Now if E(a) = 0,
then Ie = (OJ and aCTa) = t/>. It follows from Theorem 20 that
a = aCTa) =",. Q.E.D.
PROOF. If
4. Spectral Theory of ComPJl"t Operators
. ',-I f,m)(}.,)
g(}.) =! L ----. (}._}.,)m,
....1171.=11 m.
ft
«
It has been observed in some of the exercises in Section VI.9 that
8 number of linear operators of importance in analysis either are COIn-
paet, or have compact squares. The structure of the spectrum of such
an operator is particularly simple. The spectral theory of compact
operators,. as presented in this section, was initiated by F. Riesz, and
constitutes a generalization of some of the work of Fredholm on the
theory of lineaf integral equations.
1 LEMMA, Let T be a cumpaet uperatf1T, and let). be a "",,-zero
oorn.pl£.x mlmher. If'u T is one-to-one, the ra1U?,e of ,U - T is closed.
PROOF. Let Y = lirn.
m Yn, where Yft = (,U - T)x.. If the sequence
{,xn} contains .a bounded subsequence, then, since T maps bounded
sets into conditionally compact sets, {:en} contains a sequence {xV/.}
such that {T;r. } converges. Since "'n = (y +T.., )1 :1 { X } conver g :s
{ { n, fit:' ft.
to some element x. I, and y = (M -T)x.
If {x.} contains no bounded subsequence, then Ix./ --+ 00. Put
%.
x./I".I, so that (,U - T)z.
0 and )'.1 = 1. Since T is compact,
there exists a subsequence {z..l of {z.} such that {Tz.} converges.
Since 2: n , -l-lTz n , ---> O. it follows that {.t n ,.} converges. Let % = lim zn,.
Then Izl = I, and (,U - T)z = 0; consequently, contral)' to hypothe-
sis. 'u-T is not one-to-one. Q.E.D.
2 COROLLARY. Let T be a compact operator, and leI 0 * A be in
,,(T). Then there e<risls either a non-zoo x in ! BUch that Tx = J.x.
Qr a non-::ero x'* in 3:. such that T*.x* = Ax..
PROOF. If U T is one-to-one, and if (,U - T)I i. dense in 30, then,
it follows that glm,(}..) = flm,(}..), for 1 ;;;; i ,;;: k and 0;;;; m < Pi' Thus
the equation f(T)E(a) = giT)E(o) follows from Theorem 16. Q.E.D.
28 COROLLARY. Let the f""clions f, foo n = I, 2, , . ., be in ff(T)
and assume that fn(T)
to fiT) in the wcak operator topology.
Then, for every pale A of T of arder
we ha:re
flrn)(A) = lirnf
ml(A), 0 < m < P.
PROOF. If T,IS the restriction of T to E(}.)!, then, by Theorem
20,}. is a pole of order
for T" Theorem 18 shows that T. has index P.
Thus the corollary follows from Theorem 22 by the same argument
used to derive Theorem 1.9 from Theorem 1.8. Q.E.D.
24 THEOREM. Let A be a pole of order P for T a"d let 0, be the
camp[R,"ent in u(T) of the set {A}. Then
30, = {"I(T-'u)'x = Of,
and
Ie, = (T-H)'I.
PROOF. By Theorem 20, iT-H)'!a, = f o ," By Theorem 18,
Ii) {T-iJ)"I, = 0,
and thus
(T-U)'I = (T-}J)'{I, e;!e} =.Ie'
. ,
In view of (i) we have
578
Vll GENERAL SPECTILAL THEORY
VII.4.3
VII.4.5
SPECTRAL THEOR'\' OF COMPACT OPERATORS
579
by Lemma I, (M T)I = I, and M T has an everJ'Where defined in-
verse. By Theorem II.2.2, this inverse is bounded; therefore A E e(T),
contradicting the assumption that AEn(T). It follows that (M-T)I
is not dense in I. By Corollary 11.2.18. there is an ",* "" 0 in I* with
",*(ll -T)I = O. Hence (Ax" T"",")I = 0, and Ax" = T*OJ*. Q.E.D.
It will follow from Theorem 5 of tlus 8ection that if 0 "" A E <tIT),
neither the operator (ll - T) nor the operator (ll - T*) is one-to-one.
3 LEMMA. Let and ffi be closed s-ubspMes of I, and suppose that
is a proper subspMe of ffi. Then. fCH every e > 0, there is a Y in ffi, wilh
Iyl = 1 and !"'-yl > l-e, fCH eMh '" in .
PROOF. Let bE ffi, b f , and 6 = inf Ib-al. Since is closed,
/j> 0, and there is an "'E with Ib-...I < 6(1+e). If b. = b-...,
then
3, there is a Yn in n with jYnl = 1 and /Yn-a:1 > 1/2 for", in 11[n_1'
The vector Yn i8 ofthe form "'IX , +. , . +"''''no so that (T-J..I)yu E n-l'
Thus, if n > m, the vectorz... = (Yu-A;:'TYn) +J.;;;ITYm is in w.. l' and
therefore
,T G y,) - T C y ) 1 = IYn - zn,...1 > .
n m
Ify = b,/lb 1 I, then [yl = I, and
Iy-al = I - a I = !... l lbca'l
Ib.1 Ib 1
1 I
> Ib,-a'i ;?; - > I-e.
6(I+e) I+e
4 LEMMA. Let T be a tampaet ap"rator, {An} a 8I!quenct: of distinet
scalars, and {"'n} a _nee of non-<:ero veetCHs sueh that (T -J..I)"'n = 0
for eaeh n = 1, 2, . ... Thm J.. approaehu UTa.
PROOF. If J.. does not approach zero, there is an e > 0 and a sub-
sequence {J..,} with 1).",1 e. We may sup ose that J.., = A,. Let
11[.. = sp {"'1' .. ., "'n}. By Corollary IV.B.2 w.. IS a closed subspace of I.
To verify that w.. is properly contained in " it will be shown that
for any n the vectors Xl' . . A' '" are linearly independent. Suppose
that "'., . . .. "' 1 are linearly independent, but that "'n = "'lOJ. +. . .
+"' 1"' 1' Then
0= (T-A,.I)m. = "',(A.-J..)"" +... +"' l(J..-I-J..)"'H'
and, since A.-A", -::F 0 for i #-11, we have !It = 0, i = It. . ", n-l,
and "'« = 0, "eontradiction. Thus ')!. C \!!n+l properly, and, by Lemma
Q.E.D.
Hence no subsequence of {T(y./J..)} conwrges. Since [Y./A.I l!E,
this contradicts the eompactness of T. Q.E.D.
..... 5 THEOREM. If T is a compact OpaalOT, its spedrum is at most
denumernbie and hM no po;nl of aeeu:mulatitm in tM compkx p!<1ne
e.ocept possibly A = O. &erg Mn-zero number in a(T) is a pale of T and
has fin;1£ po3ilnoe indu,. For such a number A, 1M projection E(A) has a
non-zero finil£ dimt7ls;onal range given by tlu: !ormu!<1
E(A)I = {.xI(T-ll)"x = O}
whn-c " is the artln- of tM pate.
PROOF. Since u(T) is compact) the conclusions stated in the first
sentence of the tbeo.-effi will follow as soon as it is known that every
non-zero A e a(T) is isolated. But. if A "" 0 is not isoJated. we Can find
a sequence of distinet pornts An e a(T), 8uch that An ->- A. By Lemma 4.
only a finite number of the maps AnI - T are not one-to-one. TheIl, by
Corollary 2, only .a finite number of the maps ).111* .T* are one-to-one.
However, T* is compact (by VI.5.2), and Lemma 4, applied to T*,
yields a contradiction. This proves that every non-zero A E nIT) is
isolated.
Let T. be the restriction of T to I. = E(A)I. It is seen from
Theorem 3.20 that 0 # A = a(T.), and, hence, that T. has a bounded
im<erse. Thus if S is the closed unit sphere in I.. then Ti'S is bounded,
and. since T, is compact. S = T,TA'S is compact. Theorem IV.8.5
then shows that E(A)I is finite dimensional. According to Theorem
1.8. tnere is an integer" with (T,-M,)' = o. By Theomn 8.18, A is
B pole ofT" and by Theorem 3.20, A is B poleofT. Thus Theorem 8.18
shows that the index of A is a positive finite number. The final con-
clusion follows from Tht'OreIIl 8.24. Q.E.D.
6 THEOREM. All of tM condusil>ns 0/7'heorem 5 remain valid if it
is 08aumed only that 7'" is compact for B()1J't positive integer fl.
(1+E) inflb,-al = (l+E)05 > Ibll.
..<].I
.
580
VII. GENERAL S}>ECTRAL TJIEORY
VII.5.1
VIl.5.4
EXERCISE8
581
PROOF. By Theorem 3.11, (a(T)}n = a(T") and so Theorem 5
shows that u(Tn) is either finite or else a denumerable sequence con-
verging to zero. Let A * 0 be a point in afT) and let , . . ., A, be the
set of all points in ,,(T) for which A = An. By Theorem 8.19
.
E(An; T') = I E(A,; T)
'_1
5. Exercises
the space of 011 continuous functions on [0, I] which vanish at o!
4 Let Y = Ta: be the operator in C[O. I] defined by y(l) = l.1:(t).
Determine a,(T), a (T), ae(T). Find I(T) for I. $"(T).
5 Let tot,} be a bounded sequence of complex numbers. Let T
be the map in I. defined by T[E.] = [ot, .J. Find ,, (T), ae(T), and
",(T).
6 Show that any compact set in the plane can be the spectrum
of an operator
7 Let T be the map in I . 1 :;;; P < 00, defined byT[C"I' 2" ..]
[ 2' 3' . . .J. Find ap(T), a.(T), a,(T).
8 If E is a projection operator, find the resolvent R{A; E) ex-
plicitly in term8 of E and A. What is the spectrum atE)! Find I(E) for
I. $"(E).
9 For any bounded linear operator T show that
a,(T) k a.(T*) a.(T) Ua (T).
10 If there is a number A on the circle IAI = ITI which is in the
point spectrum of T, then A is also in the point spectrum of T*.
11 Show that if T, and T. In B{1:) satisfy T,T. = T.TI' then
r(T, +T.) :;;; r(T,)+r(T.), but that if T,T. * T.T" this need not be
the Case even if is two-dimensional.
12 DEFINITION. The operator T is called quasi-nilpotent if
limn_ VIT'I = O.
13 Show that T is qImsi-nilpotent if and only if afT) = (OJ.
14 Let" {An} be a denumerable compact set in the complex
pmne such that iI. --+ O. Show that there eXists a compact operator T
in some B-8pace witb afT) ".
15 Let (S, E, p) be a positive a-finite measure space and h be
p.essentially bounded on S. In L (S, E, p), I :S: P :S: 00, let T be the
Inmsfonnation defined by Ta:(t) = h(t).z(t). Show that oCT) is the set
of all points each of whose neighborhoods :r.f sati.nes the inequality
p(h l(M») > o. Find I(T) for I. $"(T).
16 Show that ,!-T is a differentiable operator valued function
of the real variable t. and that
!! ,!-T = Tee.
d!
Let y. 1:. Solve the differential eqImtion
which shows that
E(A; T)I ElAn; Tn)£.
By Theorem 5, E(An; Tn) has a finite dimensiona1 range and the above
inclusion shows that E(A; T) also bas a finite dimensional range. The
proof of Theorem 6 may now be completed by the reasoning used in
the proof of Theorem 5. Q.E.D.
The weakly compact operators in tbe spaces C{S), AP, B(S).
L 1 (S), rea(S). ca(S), ba(S), Tba(S) etc. which have been discussed in
Sections 7 and 8 of Chapter VI provide instances of operators to
which Theorem 6 may be applied even though Theorem 5 is not always
applicable.
It is convenient for many purposes to introduce a rough classi-
fication of the points of a(T).
I DEFINITION. (a) The set of A £a(T) such that M T is not
one-to-one is called the point spedrum of T, and is denoted by ".(T).
Thus, }.. u.(T) if and only if Tit = A.x for some non-zero a; £ 1:.
(b) The set of all A. aCT) for which ill T is one-to-one, and
(M-T)£ is dense in :E. but such that (iIl-T)I * I is called the
spectrum of T, and denoted a,(T).
(c) The set of all A. afT) for which M-T is one-to-one, but such
that (M-T)I is not dense in I is called the reaiilual speclrum of T,
and is denoted by a,(T).
2 Prove that ",(T), oe(T), and a.(T) are disjoint and ofT)
= o,(T)uo,(T)ua.(T).
S Determine the pOJnt. residual, and continuous spectra for the
operator y = Ta: in qo, I] defined by y(s) = 1.a:(t)dt. Does your
answer change if T is regarded as an operator in L[O. 1], or in C.[O, I],
582
VII.. GENERAL SPECTRAL THEORY
VII.5.17
VII.5.26
EXERCISES
588
dy(t) = Ty{t),
dt
y(O)=y,
26 Let A € o,(T).
(a) Show there exists a sequence {",,} such that 'x_I = 1 and
I(Al T)x.1 -+ O.
(b) If 0 is a spectral set and A € <I show that for the sequence in
(a),
and show that the solution is unique.
17 The operator T satisfies a non-trivial polynomial equation
PIT) = 0 if and only if o(T) consists of a fjnite set of poles.
18 Let IX be a spectral8ubset of a(T). Then <I.(T,) = «no (T),
<I,(T.} = «n<l,(T), (T,(T.) = IXno,(T).
19 Let I. F(T}, and let (T be a spectral subset of u(T). Let
IX = a(T}nu', and let I be non-zero on o. If f(T)x = 0 for80mex€I,
then x is in I..
20 Let A be a pole of (T(T). Then
I = (M-T)'!EB {"'Ix do, (M 7"fx = O)
if and only if k :;:. vIA).
21 Let I. .fI'(T) and p be a complex number, and suppose that
l l(p)na(T) is finite. Show that p is a pole of a(f(T)) if and only if
each point of I '(p)n o{T} is a pole of u(T).
22 Let I€ F(T), and suppose that f '(O)n<l(T) is a finite 8et
{A:., . . ., A.} of complex numbers. Show that the following 8tatements
are equivalent:
(a) I(T)! is closed and I = I(T)I EB {xix .1:, f{T)", = O}.
(b) Each point Ai' i = I, . . ., k, is a pole of (T(T) of order less
than the order of Ai as a zero of f.
(e) The set (T = {A., . . ., A.} is a spectral set, fIT)! =
E«(T(T)no'}I. and {"'Iu 1:, f(T)x = OJ = E(o)I.
23 Let T be an operator in the B-spa<'C I, and let T* be its
adjoint. Let 0, and <I. be disjoint spectral sets of T. Shmv that "'i (x,)=O
for4EI: and .1:1£1"0.
. ,
24 (Ricsz and Sz.-Nagy) If ITI ;;; T' < T and if I is analytic for
IAI ;;; T and I/(A) I :'::: R on IAI = T, show that
TR
If(T)I;;;-.
r-r'
lim 1",.-E(o)x.1 = o.
-
27 Let I = C[O, 1] and let T be the operator in 1: defined by
Tx(t} = J;a:(B)ds.
Calculate R(A; T) and show that the differential equation
x,.!(t) + orl.-])(t) +... +o.",(t) = y(t),
;r(0) = ",'(0) = . . . = ",. I(O) = 0
has the solution
1 f A'R(A; T)ydA
x = 2"d d + A +... +a..il"
where C is a circle about the origin excluding the roots of the deno-
minator, or (setting z 1/.1.)
I i ' f. &,u-., dz
;r(/) = ----: y(s)ds
'2n:1 0 KZ'ft+ l+...+afi
where K encloses the roots of the denominator.
28 Let G(T) lie in the half plane 91'(.1.) < o. Show that
I f HW
exp ( T) = lim -. R(A; T)dA. > O.
10_0: 2nl -iw
25 (Riesz and Sz.-Kagy) Let a be a spectral set of T lying inside
the circle IA-Aol = T. Let a(T)nG' lie outside the circle. Shuw that
or .1:. if and only if
limsup 1( _T)'xll/' <T.
.-+
29 Assuming that G(T} lies in 91'(.1.) < O. show that
R(A; T) = J: ,,--A' exp ( T)d ,
where the integral converges for 91'(,,) > O'
30 Show
1
sup 9I'(A) = lim - log I exp ( T)I.
o,T) f"-+w
81 Let T be an operator in the B-space 3:, and suppose that
G(T) does not intersect the ray Te", r > O. If IR(re'''; T)J = O(T 'I'''')
584
VII. GENERAL .sPECTRAL THEOR'Y
VIL5.82
VII.6,2
PERTURBATION THEORY
585
for some <' > 0 as T -+ 0, show that there IS a sequence {f } C ff(T}
and an operator U such that f.(T} -+ U and U' = T.
82 Let f. £ ff(T}, and suppose that fo(T) converges in the
uniform topology of operators. Then 10 converges uniformly on arT}.
88 Let U be an open set in the complex pmne, Suppose that
f(A, .} <' ff(T) for each A € U and that f(A, T} is an analytic function
with values in B(I). Then f(A, 1-') is an analytic function of A for each
pEa(T),
84 If a is a spectral subset of arT) such that In is finite-dimen-
8ionBl then (J is a finite set of poles.
85 If A £ arT) is isolated and II is finite-dimensional. then
(}.I-T»I is the set of xEI such that y'(x) = 0 for every Y'EIo
8atisfying (}.Io-T*}'y> = 0, and (}.I'-TO}'I' is the set of x> E E'
such that ",> (y) = 0 for every y E I satisfying (}.I - TY'y = o. The
sets {xix E E, (}.I -T}>x = O} and {",>["" <' E', (}.I>-T'»x- = O}have
the same dimension.
SB = BS = [l-(I-B}]S = L(l-B)"- L(l-B}O =1,
tt=O n=1.
it follows that {Bill-B) < I} C G. Now let A <' G, and let IA-BI
< IA IH. Then II-BA-11 = I(A-B}A-1) < I; hence. by what has
just been proved, BA l has an inWl'OO in B(E}, given by the series
'"
L (I BA-1)0 = L [(A B}A-1]".
111=0 n=O
Thus B has an inverse in B(I}, given by the formula as stated in the
lemma. This formum 8hows that
IB '-A-II = 1A-1 I [(A-B)A-1]01";; IA-II'IA-BI
0-<1 -I-IA-BIIA II'
from which it follow8 that the map B -+ B-1 of G onto G is a homeo-
morphism. Q.E.D.
2 COROLLARV. Let T, T, be in B(I), A be in e(T} and IT T.I
< IB(A; TJI I. Then A is in e(T I ), and
6, Perturbation Theory
B(A: T I ) B(A; T} L [(TI-T)B(A; T}]".
...0
8 LEMMA. Let T be in B(E), and leI s > O. Then there is a Ii > 0
8u<:hthat ifT, is in B(I) and ITI-TI < Ii, thena(T I ) S(a(T), s)and
IB(A; TI)-B(A; T)I < s. A StolT), s).
PROOF. By Lemma 1.
lim IB(}'; T}I = lim IA-I ( I _ ) I I = 0,
A--.a:I ),-+ODI ;.
and so IB(A; T)I -<::; N. for). in the complement of SCotT), £). Thus, by
Corollaty 2, if 1\ = N;I > ITI-TI, we have a(T.) C SCotT), s). Also.
by Corollary 2,
IB(}.; T,)-B(A; T)I < ITI-TI < s
I-lT.-TIN,
if ITI-TI < "" = s/( +<,N,). The desired conclusion thus follows
by defining lJ to be the smal!er of Ii. and Ii,. Q.E.D.
4 LEMMA. Let T(}t) be an analyrit: opcralnT valued fundio,. defined
for II'/ < y, where }' > 0, and let U be an open 3et with U C e(T(O)).
Letl-' --->- T(}t) be an operator valued function of a complex para-
meter I-' which is continuous (or analytic) in the uniform operator
topology. The purpose of this ""ction is to investigate how the spec-
trum and the resolvent operator change with a SIDAII change in 1-" The
basic result of this section is a theorem. essentially due to Rellich,
describing how certain isolated points of the spectrum of T(O) vary
when T(}t) depends analytically on 1-"
I LEMMA. TIu: set G 01 elemtnt3 in B(E) which have inVf:r388 in
B(I) is an open set in tlu: lmiflfrm topology of B(I), conraining with an
operatcr A tlu: 3phn-c {BIIA-BI < IA-11 I}. II B is in !his sphere, its
inverse is given hy the JJ£ries
B l = A-I I [(A_B)A I]O.
.,...1)
Furthermore, tlu: map A -+ A I of G onto G is a homeomvrphism in the
uniform operot'" topology.
PROOF. Let II-BI < 1, SO that the senes S = I: (I-B)"
converges. Since
.
586
VII. GENERAL SPECTRAL THEORY
VII.6.S
VII.6.1
PER7URBATJON THEORY
587
00
Lemmas 4 and 6 can be considerably improved in the important
case in which C/(T(O») contains an isolated point such that
E( ; T(O»I is finite-dimensional. To study this situation, we first
need a lemma on projections.
1 LEMMA. Let E, EI be two projections in I such that IE-Ell
< min (IEI I, IEll-I).lf 01>£ of tM proiedions has a finite dimemnoru:U
range then so does tM other and
dim EI = dim E l '&:.
PROOF. Consider the map EEl E restricted to EI. Since E is the
identity in EX and since, by hypothesis. IEEIE-EI < 1. it is seen
from Lemma 1 that EEIE is a one-to-one map of EX onto all of it:sell
and thus that EE.EI = EI. Hence EI EE;J: EEIEI = EI.
and therefore E! = EEl'&:' This shows that dim El'&: > dim E£.
Similarly, dim EI > dim E;J: and thus dim EI = dim Ell. Q.E.D.
8 LEMMA. Let E(}l) be an analy!!c proja:tion valued furu:lion de-
fined for 1,,1 < y, whne y > 0, and wt E(O)I hare the finite dime>I8Wn
m. TMn there um a () > 0 such that, if {ltl' . . ., "'m} i. a bOlli. for
E(o)I, thR Bet {E("lxI' . . .. E(I-'I"'m} i. a bOlli. for E(p)I whm II'/ < {).
PROOF. It is readily seen that there exists a {) with 0 < {) :::;;: y,
such that
IE(O)-E(}l)1 < min (IE(OJl-l, IE(}l)I-I), 11-'1 < {).
From the proof ofLernma 7, we know that the dimension of E(}l)E(O)I
is equal to m. Since the vectors {"'I'" ., "'m} span E(O}I, the set
{E(}lPl" . ., E(}l)xm} spans the m-dimensional space E(}l)E(O)I.
Hence these vectors are linearly independent. and form a basis for
E(}l)I. which is an m-dimensional sub8pace by Lemma 7. Q.E.D.
9 THEOREM. Let y > 0 and let T(,,) be a B(I) IJilhud function
defined and analylic for )1-'1 < y. Let .1.0 be an isolo.ted poin1 of ,,(T(O)).
and suppose that 1M s-ubspace E( ; T{O))I ho.oi finite di'1If1"I8wn m. Let
V be an open set with UnC/(T(O» { }. Then there i. a posilive
li < y, an mli!ger k m, and an inl'l'.'" n, such that for 11-'1 < ()
UnC/(T(}l») is a finite set (A 1 (}l), . . ., A.(,,)}. Each fundion }..(}l) de-
pend" arwlytically an the principal Niue of the fractional power 1'1)"
of 1', and sati.fies .1..(0) = . lIforeuver, the projections E(A,(}l); T(}l))
can be e:rpanded in fraclional power Law-ent series
Then there €.l:i81B a" > 0 such that if 1,,1 < {), tMn U C e(T(}l» and
R(A; T(,u» is an anolytic function of ,u for each A C V.
PROOF. By Lemma 8, there is a "1 such that if 11-'1 < <\' then
U C e(T(}l». Let lJ lJ 1 be chosen Sllch that IT(O)-T(I-'H <
inf IR(A; T{0))1-1 whenever l,ul < {). It follows from Corollary 2 that
l£U
[Oo] R{A; T(}l» = R(A; T(O» [(R(}l)-T(O»)R(A; T(O))]".
'11=0
Since the series converges absolutely and uniformly for Ittl < ()J and
T(}l) is analytic, it follows from the general theory of analytic func.
tions (cf. III.14) that RI}.; T(}l») is an analytic function ofp, 11-'1 < li,
for each A. V. Q.E.D.
5 LEMMA. Lei T be in B(I), f be in S"(T), and e > O. TMn there
is a {) > 0 Buch that if Tl i. in B(I) and ITI-TI < (), thRn f i. in
S"{T I ) and If(T)-f(TI)J < e.
PROOF. Let V be a neighborhood of v(T) on which f is analytic.
Lct VI be a neighborhood of v(T) whose boundary B consists of a
finite number of rectifiable .Jordan arcs, and such that U. u B C U.
Then, by Lemma 8, there is a ()I > 0 such that C/(T I ) C VI for
ITI-TI < <\. Consequently f. S"(T I ) for iT I -TI < <\. Also. by
Lemma 8, R(}'; T l ) is near to R(A; T) uniformly for}. in B if ITl-TI
is small. Thus. for some positive () lJ I ,
I/(TI)-f(T)1 = :" ILf(A){R(A; TI)-R(}'; T)}dJ.1 < e, Q.E.D.
6 LEMMA. Let f be in S"(T(O», whoc T(p) i. an OJwl:ytic opera-
tor valued funetion, tkfi1!Cd for 11'1 < y. where y > O. Then there i. a
positive lJ less than y such thai f is in S"(T(I-')). and suck that feTe,,) is
an arwlyti<: operator valued funetio" of 1', for 11'1 < {).
PROOF. Let B be chosen as in the proof of Lemma 5. By Lemma
4. {) may be found such that the series [*] used in the proof of that
lemma com'crges absolutely and unifonnly for A on B. Thu8
f(T(p)) = I . f f(A)[T(}l) - T(O)]"[R(A, T(o))]n+ld...
n=<O 2JttJB
the series converging to an analytic function of 1" Q.E.D.
588
VIla GENERAL SPECTRAL THEORY
VII.6.9
VII.6.9
PERTURBATION THEORY
589
E(A.(.u); T(.u» = ! A"I"!n,
f"",,-N
Ipl <6,
.,
A,(.u) = ! al.".jn
.....
"'Mre A'I are ()P"alOTB in B(I).
PaooF. For 8implicity of notation we shaH write a(.u) for
Una(T(p». It is seen from Lemma 6 that, for small p, a(,u) is a
spectral set of T(p). The symbol E(p) will be used for E(a(.u); T(.u»).
It follows from Lemma 6 that E(.u) depends analyticaHy upon p. If
{Xl' . . ., a:..} is a basis for E(O)I then, by Lemma 8. there is a positive
number <II 8uch that for Ipl < 6 1 the set {E(.u)x.,..., E(.u)x m } is a
basis for E(.u)I.
Let the functions I., be defined by the equations
of the principal value of p.'l .
Let E,(.u) = E(A,{!,); T(.u», for 0 < II'I < (j and 1 < i :0;;: k. It
remains to show that each E,(.u) Ims a Laurent expansion about
p = 0 in terms of pl}n. Let q(A) = II _2(A-A,(.u»", rIA) = l/q(A),
and
p(A) = i rl'I( (.u» (A-A,.!!,))'.
1-0 ,1
Consider the polynomial
..
seA) =p(A)q(A).
T(.u)E(plx. = ! !jj(,u)E(.u)x,. i = I,.. ., m.
-1
\Ve first 8bow that the I" are analytic functions if p is sufficiently
small. Let "': .a;* be such that ",:(a:,)=<lkj, k = I",., m. The first
of the above equations yields m equations,
By the Leibnitz rule
,
BIn(A) = I ( )pl'J(A)qll-4>(A).
i O
..
The form of q sbows that for 0 < Ipl < 0,
B(iJ(A,(.u» = 0, j = 0,..., m-I, i = 2,.. _, k.
Moreover;,
",:T(,.)E(f')x, = II"(,u)",:E(.u}a:,, k = 1,..., m.
'-1
Since "': E(O)"" = a::"' = 6." the determinant LI(I') of the matrix
(",:E(I')x,) equals one for f' = 0, and is therefore bounded away from
zero for II'I < 0. < 6 1 , Consequently, it is possible to solve for the I",
and obtain in each case the quotient of an analytic function by LI (1').
Since, for 11'1 < 6., the function ,1 (I') o. its reciprocal. and therefore
each !", is analytic. Thus the !" are analytic for 11'1 < 0..
If T.(,u) denotes the restriction of T(I') to the m dimensional
space E(f')I for II'I < 6., then the spectrum of T. (f') consists of the
roots of tbe equation
[*] d(A, 1') = dct (M,,-I,,(I'» = o.
By Theorem 8,20. a(l') = a(T.(,.». The function d(A.I') IS a poly-
nomial of degree m in A, whose coefficients are analytic functions of 1';
for I' = 0, equation [*] has only the m-fold root A =).". By the
Weierstrass preparation theorem (111,14) there exists a positive 6 ;;; 05",
an integer k -<:; m and an integer n such that if 11'1 < 6.1' 0# 0, d(A.,.)
has exactly k distinct zeros Al(I'),..., A.(.u), and these zeros are
analytic in J." being given by fractional power series
pUl(}.,,(I'» = fliJ{}.,,(.u»,
i=O,. ,m.
Thus
s"'(}.,,(,u» = I Wqli iJ(}.,,(,u»plil(A.(I'»)
t=O
I
= I ({)qli ;)(Al(l'»rlil(A.(,u»
i=O
= [q(A)r(A)]IJI(}.,,(.u»,
Since q(A)r(A) = I, we have
sli)(Al (.u» = 0,
B(}.,,(,,)) = 1.
Consequently, by Theorem 1.8
E.(I') = B(T(,u»E(.u).
Since the coefficients of the polynomial B have Laurent expan-
sions in pN" about l' = 0, which contain only a. finite number of negative
exponents, the projection EI(p) bas a Laurent expansion with the
0<11-'1 <<I.
l;£j;£m,
.
590
vn. GENERAL SPECTRAL THEORY
VII,(!,IO
VII.6.1I
PERTURBATION THEORY
591
same property. The projections Eitu), i = 2, .", k arc treated simi-
larly. Q.E.D.
The next theorem gives an extenslOn of Taylor's theorem to func-
t,iuns of an operator.
DO
V = RfA; S)n+1N"
=0
converges uniformly for A in any set C whose mlmmum distance
from 0(8) is greater than e, Since Sand N commute, it is 8een. by
direct multiplication, that V(Al S N) = (Al-S-N)V = I. Thus
if A has distance greater than" from a(S) then A is in the resolvent set
of S+N and
10 THEOREM. Let Sand N he commuting l>fJl'Tarors. Let f he a
function a.wlytw i.. a domain D, i..cluding tM sp<drom 0(8) of Sand
every point wilhin a diskmce of a(S) not greaw- tlw.n some po8itive
..umber e. Suppose that the sp«tntm a(N) of N lies within tM open
eirew of radius e about the origin. TMn f is analytic on a neighh<JrMod of
a(S+N), and
..
R(A; S+N) = RfA; S)"+Wn.
"_0
DO f'nl(S)N"
f(S+N) =
1P-O n!
Thus the function f of Theorem 10 is aUJllytic on a neighborhood of
0(8+N) as 8tated.
Now let C denote the union of a finite collection C 1 . , , .. C" of
disjoint closed rectifiable Jordan contours wruch bound a region D
containing every point whose distance from u(T) is less thuD Et and
wruch lie. together with D, entirely in the domain of aUJltyticity of f,
Suppose, moreover, that the contours C f are oriented in the positive
sense customary in the theory of contour integration. Then
tM serics COnveTgU.g in the .....iform topoWgy of opiTaWrs.
We begin the proof of Theorem 10 by proving the following
lelIlIIlB.
II LEMMA. Let C be a set whose minimum distance from tM
sp€drum afT) of an OptTO.t1>T T u greatn- than some positive number E.
Thetl IMr. is a constant K such tool
IR(A, T)"I < KE , n > 0, A £ C.
PROOF. Let the open set U contain oCT) Rnd have a boundary
which consists of a finite number of rectifiableJ"ordan curves. Suppose
also that for ewry A in C and every a in UUB we have IA-aj > e.
Then
f(S +N) = . I. f(A)R(A; S +N)dA
2nt c
= . }: I. /(A)(RfA; 8»n+W"dA.
2:nz. n_tJ C
On the ether hand, it is seen from the resolvent relation
KE.-h.
Q.E.D.
R(A,,; 8)-R(A,,; S) = (A'-A,,)R(A,,; SIRe),,; S),
that (d{dA)R(A; S) = -(R(A; S»", and, mductivcly, that
'd ) "
(dA R(A;S) = (-I)"n!(R(A;S»)"i- 1 .
IR(A; T)nl = I i In (l-a)-n R(a; T)d 1
PROOF OF THEOREM 10. Let lJ = sup IAI so that, by hypothesIs,
.A£a!N1
Hence
This inequality, together with Lemma II, shows that the series
I. f(A)(R(A;S»"+Id). = (-I)" I. f(A) ( d\ " R(A;S)dA.
C n! c ill
Integrating 11 times by parts we find that
fJ(A)(R(A; SJ)n+ld). = ;! L ( (:J " f(A») R(A; S)dA,
So that
lJ < e. Choose 0 < I so that lJ < Oe < E and let B be the circle
{AIIAI OE}. Then
IN"I = I . ( A"R(A;N)dA I < K(OE)"+" 11 = 0, I,....
2:i't JB
.
592
VII. G£NERAL SPECTRAL THEORY
VII.6.I2
VII.7.1
TAUBERIAN THEORY
593
I(S+N) = I { f. f( I(A)R(A;S)dl } N.
n-o 2x c
'" I"(S)N.
=1 .
n=-O nl
and Theorem 10 is proved. Q.E.D.
12 COROLLARY. II a(N) = (OJ where N is an operalor etnl!'J1/.llling
wilh an operalor S, and il I i. a function mwlyt«: on a neighborhood 01
a(S), then I is annlytie on a neighborhood of a(S +N), and
'" f(.'(S)Nn
f(S+N) =1 I '
tp.-O n.
the seri.. eonverging in the '!mifo,,", topowgy oloperaW78.
We conclude this section with the following lemma which will
be needed in Chapter VIII.
18 !.EMMA. If A --+ T(A) is an analytic operator oo/ued fUtldion
tklined on a domain D. then the function A _ T 'rA) i. tkfined on an
open sulJ8et 01 D and isanaly!ic there. II T(A) is compact for each A in D
and il D is aJm!£Cted. then eiJher 1- T(A) hM a bounded inm-oe for no
point in D or else this inveToe mists except at a eowntohlc number of
isolated poinls.
PROOF. If A" E D is sueh that T-1(A D ) exists, then it follows from
Lemma 6 that for A sufficiently near A" the inverse T-1(,-) exists and is
an analytic function of A in a neighborhood of AD' To prove the second
part of the lemma we suppose that there is a numher '-D in D and a
sequence {'-".} C D such that 1 E a(T('-".», m;;;: 0; Am..... '-D; and
'-". '1= A", m> O. It will be shown that 1 E a(T('-» for every '-. D.
By Theorems 4.5 and 0, for'- sufficiently near AD the points of <T(T('-»
in some neighborhood of the point <I. = I are gi\'en by the fractional
power series
('-".) CD satisfYing I E "(T('-,,.», m 0; Am --+ '-D; and'-". =ft '-D' m > o.
We ha\'e shown abo\'e that A is open; since it is also closed in D and
D is connected, it follows that either A = '" Or A = D. This completes
the proof of the lemma. Q.E.D,
7. Tauberian Theory
Let {I.} be a sequence of functions in $W(T), where T. B(1:),
and suppose that the sequence (In(T)} converges in B(1:). If 'E $W(T),
it is clear that (f(T)/n(T)} converges. We are intcteSted in the con-
verse problem: under what conditions on I, 1ft and T does the conver.
gence of {I(T)/n(T)} imply the converg1'l1ce of {I.(T)}? Theorems
describing this situation are in the nature of Tauberian theorems. The
prototype of these theorems is the ergodic theorem which ari8es when
I(A) = 1-'- and In('-) = ",-1 I,:O' A'. In this case, one determines
conditions under which the convergence of n-1T" implies the conver-
gence of the av n-'(I+.. .+T 1).
We first consider this converse problem for convergence in the
uniform operator topology and later discuss the same question when
B(!) has the weak or the strong nperator topologies.
Note that if 1('-) =ft 0 for '- E a(T), then I(T) has a bounded in-
verse, and hence In(T) = U(T)]-l/(T)f.(T) converges. However, it is
not obvious that the convergence of (fn(T)} can be deduced if I
vanishes at certain points of <T(T). The next theorem is concerned with
this possibility.
00 '"
la,(A-A,,);'.,.. .,l€;('--A,,)J}n.
j-D 1-",,0
Since I . ,,(T(A m ) for m 0, one of these series assumes the \'alue
unity infinitely many times near A" and hence is identically equal to
unity. Thus for A sufficiently near A", IE ,,(T(A». Now let A denote
the set of points A" in D with the property that there is a sequence
I THEOREM. Lrl f. In be in ....(T). and let (f(T)fn(T)} CQlI
to =0 in the unilorm "'P"oror topology, Lei f vanish a! a finiU set oj
poles 01 R('-; T). Suppose that each root '-D 01 I on ,,(T) hM liniU order
a(A,,), that the setJllLf'C'!s {f "'I(,-.)} €Orw#ge lor 0 < m < <I.(A,,), and tJw.t
Iim_oo I.(A,,) =ft o. Then the seqtWl1« {In(TJ} eonnerges in the unilorm
"'P"ator topology.
PROOF. Let ;,., . . ., A. denote thc roots of I on ,,(T), and let ai'
and "I' i = I, . . ., k, be the order of A.: as a root of /. and as a pole of
RIA; T), respectively.
Wefirst show thah, <I.,. Letg n = 1'1.; then (g.(T)} converges
to zero in the uniform operator topology. By Corollary 8.23, {g ml (Ai)}
594
\'11. GENERAL sPECTRAL THEORY
VII.7.2
VII.7.8
TAUBEIt(AN THEOR\;"
595
conyerges to zero for 0 m < "',,0 If a. < 'J'i<o put m = ai" Then since
A, is a root of f of order Cl. we have
lI a'!(A;) = ia'!(A;)fn(A,) -->- o.
Since l'a"(A,) ¥' 0, we conclude that In(A,) --+ 0, contradictmg OUT
hypothesis. Hence 'Vi a.."
Now let U I be the complement in aCT) of the set {A" . . ., ;"}.
By TheOl'em 8.22,
. ..-1 IV) (A )
['J 'n(T) = f.(T)E(a]) + 1: I ¥ (T-An E(A,).
1=1 I O ,.
Since f does not vanish on u 1 ' there is an h %(T) 8uch that fh is
identically one on u 1 ' and identically zero on {A"..., A.}. Thus
f(T)h(T) = E(a l ), so that f.(T)E(uI) converges in the unifmm topo-
logy of operators. It follows from ['J that {fn(T)} will converge in the
uniform topology if U "I(A,)} converges for m < v" 1 S i s k. Since
v. so:. the theorem is P roved. Q.KD.
_ s.
analogues of Theorem 1 for the weak and strong topology, which we
study next.
3 THEOREM. LeI I, fn be in .!F(T), and let {f(T)f.(T)} oo,u'ffge to
zero in Ibr Walk opt'raw, topology. Suppose that {fn(T)",} is rNakly se-
quentially compact for each x in :£, and Ihat I vanishr.. at a linif£ 8<1 of
points 01 u(T). II ruch rool has lin;f£ orw o:( ). if the MtjIU'1U't"s
(f m)( )} rom-rrgt" la' 0 < m < o:( ), and il lim n ->-", fn( ) oF 0,
Ihm {f.(T)} ctmvergt8 in the weak operator topology. MGl'OOfJ1'r,
In(T)E(u l ) = E(u,)fn(T) = h(T)f(T)/n(T) --+ O.
:£ = f(T):£ e {xlm.:£. I(T)", = OJ.
PROOF. Let "'I = f(T)!, x 2 = {mix I. f(7')x = OJ, and 7£:
= {x'lx' . "",/(T')x" = OJ. If an operator U in B(:£) leaves "'2 in-
variant, we let U 2 denote the restriction of U to x 2 .
It will first be shown tbat, for each non-zero m in £.' the sequence
{fn(T)",} converges to a non-zero element of I". Since f(T) commutes
with R(A: T), A e(T), we have R(A: T)I,,!;; I", and, consequently,
R(A: T)2 = R(A: T.). and u(T,)!;; u(T). I<'urthermore, Definition 3.9
.hows that g(T.) = g(T.). for g £ .!F(T). Smce f(T.) = 0, it follows
from Theorem 3.16 that u(T 2 ) {AI' . . ., ;..}, the set of zeros of f. and
that the order vIA,) oU, as a pole of R(A: T 2 ) docs not exceed the order
O:(A,) of A, as a zero of f. Let g be a function in %(T 2 ), such that
g,m'(A,) = ]imn->-wf m)(A,}, for 1;:;;; i;:;;; k and 0 < m< .-(A,). By Theorem
8.22, {tn(T 2 )} converges to g(T.) in the strong operator topology of
I", Since g(u(T 2 }) does not contain the point 0, the operator g(T 2 ) has
an inverse on the space I". Thus, for each non-zero m in I", {fn(T)",}
converges to a non-zero element in I2 We an prove J in the same way,.
that for each non-zero ;r* in 1': I f/n(T*)x*} converges to a non-zero
element in r..
We next prove that X,n"'2 = to}. Since U.(T)x} is weakly se-
quentially compact for each m in :£, it follows from 1I.<J.27 and 11.3.21,
that the sequence {)I.(T)II is bounded. Since we have assumed that
{fn(T)",} converges weakly to zero for m f(T):£, Theorem 11.8.6 im-
plies that {fn(T)",} converges weakly to zero for m. £1" But, since
{fn(T)",} converges strongly to a non-zero element for each non-zero
'" £ "'., we conclude that Xl n "'. = {OJ.
It will next be shown that {tfi(T)",} converges in the weak topo-
2 COROLLARY. LeI ITnl = 0 (n), and let A =] be a pole of
R(A; T) of order one. Thrn {n- 1 1:i:JT'} com'Crges in the uniform
topology to E(I).
PROOF. Let fn(A) = n-'(I+A+.. .+A I), and let f(A) = I-A.
Then f(A)f.(A) = n l(l-An), and f(T)fn(T) = n- 1 (1 Tfi). Since
IT'I = 0 (n), it follows that f(T)ffi(T) .. O. It follows readily from
Theorem 1 that {n- I I::JTJ} converges in the uniform operator
topology.
Let u, be the complement in u(T) ofthe set {II, and let h. .!F(T)
be equal to (I_A)-1 in a ne,ghborhood of u1' and be identieally zero in
a neighborhood of A = L Then h(T)f(T) = E(a l ). Since f(T)fn(T) --+0,
we have
From equation [* of Theorem 1,
f.(T) = f.(T)E(u,)-t-fn(I)E(l),
so that f.(T) -->- E(I) in the uniform topology. Q.E.D.
The central hypothesis in TheoTem I is the assumption that eacb
zero of f is a pole of R(A: T). This assumption is not required for the
.
596
vn. GENERAL SPECTRAL THEORY
VII.7.40
VIJ.7 .5
EXERCISES
597
logy for each II: I, If not, since {f.(T)>:} is wea1dy sequentially com.
P act, we can extract two sequences {f. (T).,) and {fm (T)",), such that
, ,
!im fA (T)., = y" lim fm (T)., = y" II, oF II"
, ,
i_tv '-+0;1
{fACT)} convt'Tges in 1M Blrong operaWr topology. JJ!OTroru,
I = fCT)H {ltlu I, fCT)., = o}.
", (y,) = lim (f.,(T)x) = lim ",.jCfm,(T)",) = ",.r(y,I,
i-+cu '-+Cc
PROOF. All parts of Theorem 40 but the strong convergence of
U (T)} follow immediately from Theorem 8. The proof of Theorem 8
shows tllSt {f.(T)x} converges for '" I", and that the sequence
{I/.CT)I} is bounded. Since we have assumed that {f.(T)m} converges
for '" f(T)I, it follows from II.8.6 that {f.(T)"'} converges for II:
= I(T)I. Our result now follows from the decomposition I = EIJ I".
Q.E.D.
We conclude this section with an a.pplication of Theorem 4.11 some-
what different from the ergodic theorem proved in Corollary 2. Further
applications will be found in the exercises of Section 8. In the follow-
ing chapter, Theorems 8 and 40 will fonn the basis for a comprehensive
discussion of ergodic theory.
both limits being III the weak topology. Since f(T)f.(T} converges to
zero in the weak operator topology, f(T)(y,-y,) = O. Thus y,-II, I",
and 1I1-1I,1 . It follows from II.8.IS that there exists an "'6 I.
such that m6'( ) = 0, and m6'(y,-II.) oF O. Since f(T)I , we see
that ",:(f(T)I) = 0, so that f(T).",: = I(T.)": = 0; i.e., 1I:.r d::.
It was remarked above that {f.(T.),x.} converges strongly for each
u;* 3::' Thus lim m.!(f.(T)",) = lim (fn(T.)>::)C"') exists for each
lC E 1:, and 'fI_U' n-+OQ
contradictiug the inequality",: WI-Y') *- O. This proves that
{f.(T),x} converges in the weak topology for each '" 3:.
To prove the final statement of the theorem, let
T,p:=limfn(T)x,
.--+
5 COROLLARV. Let i£ be , let;'" be a 8elpJeT!ce in e(T)
which rnnverges '" zero, and kt sup. IA,.R(J..; T)I < 00. T"""
I = Tit' EIJ {"'I'" £ I, T", = OJ,
and 1M 8eg""""e {;"'R(A,.; T)} converge8 in t he 8!ron g operator "'pology
'" the projection E, whose null manifold is T3:, and who8e range i.
{"'IT'" = OJ.
PROOF. Let I.(J.) = J..(J.,.-J.) l. and let I{J.) = J.. Then f(T)f.(T)
= A,.TR(;"'; T) = J.;;R(;"'; T)-A,.I; &0 f(T)/.(T) ..,. 0 in the uniform
operator topology. Since I is reflexive, it follows from 11.8.28 that for
every'" ill I the sequence U.(T)",,} is weakly 8equentially compact.
As fn(O) = 1 for all n. Theorem 40 shows that lim_eo ;"'R(A,.; T)
exists in the strong topology, and I has the decomposition above.
Examination of the proof of Theorem 8 shows lim_..;"'R(J..; T) = E.
Q.E.D.
the limit being in the weak topology. Then. by II.8.2I and 11.8.27,
T. £ B(I). Moreover, T,p: = g(T,)'" for '" in I". Since geT,) has an
inverse on I", geT,):£' = i£" and T.1, I". Sinrllarly TtI* IE:'. But
T .J(T) = f(T)To = 0, so T.1, I" and T.,i£, = O. Thus the operator
E, defined by EiIJ = g(T.)-lT,p:, '" 3:, is a projection whose range is
I". Since we know that (1 I" = 0, in order to prove I EIJ I", it
i. sufficient to show that Ex = 0 implies '" E . If E", = 0, then
T If& = 0, so (1'63:*)", = O. But {"'*I"'.( ) = O} = T:I., so
"'*11: = 0 for ",. £ IE:'. It foJlows from II.B.IB and from the definition
of , that II: £ ; SO (I E)I = . Q.E.D.
The corresponding result for the strong operator topology follows
from what we have just proved.
40 THEOREM. Let f, f. be in $>(T), and kt {f(T)/n(T» converge w
zero in the mung operator topology. Suppose that U.(T)a:} is weaJcly
ly eompaet for eaeh", in I. and that f vanishes at a finite Bet 01
pointa of aCT). If eaeh root.. has finit£ OTder a(}.,,), if the Bequences
If.m)(J.,,)} rorrcerge for 0 :iO m < a(}.,,), and if limft--+ IftC}.,,) oF 0, then
8. Exerci..s
1 If T., T E B(3:), T. ..,.T and 0 £ p(T.), n = 1, 2,..., then
O£e(T) if and only if sup.l7';lj < 00.
.
59B
"D. GENERAL SJ>ECTRAL THEORY
VII.8.2
VII.B.IO
UNEOUNDED CLOSED OPERATORS
599
2 Let g. e :F(T), n = 1,2, , . .. Suppose that g.(T) converges
in tbe uniform operator topology to a compact operator. Let A e ,,(T),
and Jim._ w g.(A) oF O. Show that A is a pole of afT), and that
E(A; T t has a positive finite dimen8ion. (Hint. See Exercise
VII.5.35, )
3 Show that if g. e :F(T}, n = 1,2, . . ., and (g.(T}) converges
to a projection E in the uniform operator topology, then there exists a
spectral subset ", of ,,(T) such that E = E(",). {Hint. See Exercise
VII.5.32. }
4 Let T. B(J:}, T. e B{I), n = 1,2, . ... Suppose that Tn T
in the unifoml topology of operators. Let A e afT) be an isolated point
sueh that E{A; T)I is one dimensional. Let U be a neighborhood of A
sueh that U n,,(T) = {A}. Show that for n sufficiently large,
Un ,,(Tn) contains just one pointA,., thatA. --+A. and that E(A.; Tn)
E(A; T} in the uniform operator topology.
Ii Let T(,u) be an analytic function with values in B(J:} dermed
for 11-'1 < s. Suppose that A e ,,(T(O» is an isolated point such that
E(A; T(O»I is one dimensional. Let U be a neighborhoud of A such
that Un,,(T(O» = {A}. Show that there exists a positive lJ less than
s such that Una(T(,u» consists of a single point A(,u) for 11-'1 < lJ, and
that A(I-') and E(A(,u); T(p)} are analytic functions of I-' for 11-'1 < s.
6 Let ITI 1, and let T be weakly compact. Then the limit
lim n _ w n-'(.I +.. .+T.-I} = E exists in the strong topology ofoper-
ators, The operator E is a projection of I onto {"'I"'. iE, Tx = x}.
7 Let A = 0 be a pole of R(A; T). Suppose that there exist real
constants K and s such that
10 Let (S, E, p) be a positive finite measure sp . Let « : S
-+ S be a mapping such that e e E if and only if «(e) is in E, and
pIe) = p(<<{e». If / e Lp(S, E,I-'} for p ;?, I, and we put I.(S) =
..-1 L;:-t!(".'(s)} for n = I, 2,..., then l.eLp(S,E,p), "nd lim/.
exists. 11-+00
11 Let iE, be " closed subspaee of a B-space I such that
T.I, 3:, for eacb operator Tn in" sequence {Tn. n = 1,2,...} of
commuting operators in B{iE). Let U. be the restriction of T. to I,
and let V. : III, --+ iElI, be the map defined by
V.(x+I,) = T."'+I" a: e J:, n ;:;" 1.
Let U. converge weakly to zero and V. converge weakly to an opera-
tor Vsucb thatO, ,,(V). Fmal\y let {T.",} be weakly sequential\ycom-
pact for each", in I. Show that (a), the sequence {Tn} converges in the
weak operator topology, and (b). the space J: can be written as a
direct sum 3: = I, !IJ J:., where T.io I" for al\ n ;:;" 1. (Hint. Show
first that the sequence {T.) has one a.nd only oae accumumtion point in
the weak operator topology. Compare with the proof of Theorem 7.8.)
12 Assume in addition to the hypothesis of ExCl'ClSC II that
(U.} and {V.} converge in the strong operator topology. Show that
(T.) converges in the strong operator topology.
IS Letx.. I,,, = I, 2. .... Suppose that ITa:.-itx.1 --+ O. Show
that I/(T)x.-f{A)x.1 0 for each f e :F(T).
IAR(A; T)I ;;;; K for 0 < IAI < E.
Then lim. D AR(i.; T} = E({O}} in the uniform topology of oper-
ators.
8 Let S be a compact metric space, and let ex : S -+ S be such
that eta:, y} = e(=, «y) for "', yeS. Show that (n ' L::J I("';"')} con-
verges for IE C(S}, uniformly for", e S.
9 Let t be an irrational real number, and il) be the fractional
part of nt. If 1 is a subinterv"l of [0, I}, let N. be the number of
It" . . ., I.} which lie in 1. Show that lim f;;-'N. exists and is equal to
the length of 1. 1<--+ '"
9. An Opn-aticmal Calculus for Unbounded Clooed Operators
We 8han now 8how that many of the results of the operational
calculus for a bounded operator may be extended to the case of" closed
operator T with non-empty resolvent set.
We recall that a linear transfonnation T whose domain is a linear
manifold (T) is said to be closed if its graph is closed. Equivalently,
if a:.e (T),.. = 1, 2,..., a:. --+x, and Tx. y, then xESD(T) and
Tx = y. If T is closed and everywhere defined it is in B(iE) (II.2.4);
hence we shan supp08e tllat its domain SD(T) is a proper subset of I.
This important case occurs for many differential operators in various
function spaces.
As in the case when T is in B(iE), we define the ,esolvent set e(T)
of T to be the set of complex numbers A such that (M - T)-' is in
.
600
VII. GENERAL sPECTRAL THEORY
VII.9.1
VII.9.8
VNBOUNDED CLOSED OPERATORS
601
B(I). and the sp«tTum arT) of T to be the complement of e(T). A:.
before, (d. Definition 5,1), the spectrum IS divided into three disjoint
sets: the point spectrum, continuous spectrum and residual spectrum..
It is seen from LemnIa 2 below thAt the spectrum is a closed set. But.
in eontrast to the case where T is a bounded operator, the spectrum
may be a bouDded set. an unbounded set, the void set. or even the
whole plane. This is observed in Exercise 10.1. We exclude the last
possibility, and suppose throughout thi8 section that e(T) is not void,
We nOW show how the development of an operational calculus
for T IllIlY be based on the calculu8 already obtained for an operator
in B(I).
1 DEFINITION. By $'(T) we denote the family of all functions
I which are analytic on Borne neighborhood of arT) and at infinity.
A:. in the case of a bounded operator (Definition 8.9), the neigh.
borhood need not be connected, and can depend on I. $'(T).
Let 0: be a fixed point of e(T), and define
A = (T-o:.l)-l = -R(o:; T).
Then A defines a one.to-one mapping of I onto (T), and
TAo11 = «.b+x, ",.I,
AT", = o:Ax+w, "'. SD{T).
Our objective is to define an operational calculu8 for T in terms o£that
already obtained in Section 8 for the bounded operator A.
If K denotes the complex sphere, with its usual topology, we let
<l>:K --+K be the homeomorphism defined by
p. = <l>(A) = (A_«) l, <l>( 00) = 0, <l>(o:) = 00.
2 LEMMA. II 0: is in e(T), tMn <l>(a(T)U{ co}) = alA). and !he
relation
But we also have
(T-«I){T-Al) 1 =A {(T-o:l) -n I
= ) i8 analytic on U. Since qJ(O) = f( co) and O. alA), we have
from [*], Definition 3.9, and the fact that dA = -dILI,,2
. r f(.<I)R(A, T)dA = i (IL)[-IL-II+R(IL; A)]dJL
23Zl J r 21r1 C
= 9'(A)-qJ(O)1 = f(T)-f(oo)1. Q.E.D.
Throrem 4. with Theorems 3.10. 3.1l, and 3.12. now yields
5 THEOREM. If f and g aTe in #(T), IMn
(a) (f+g)(T) = f(T)+g(T);
(b) (fg)(T) = f(T)g(T);
(c) a(f(T» = f(a(T)Uloo});
(d) if f is in F(T), g is in :F(f(T)). alld F(E) = g(/(E)). then
F is in :F(T) and PIT) = g(f(T)).
For a comprehensive operational calrolus for T, it is important
to include a tbeory of polynomials in T (which will be defined only on
proper subsets of I), and to have rolf'S relating them to the operators
f(T). The domain of a polynomial in T is defined in the natural way
in the following definition.
6 DEFIKITIO . For n = 0, J.. . . . the uperator Tn is defined in
duetively by the relations T' = I, T' = T, and
(Tfl) = {"'Ia;. (T" l), Tn-'a; . (T)}
Tna; = T(Tfl-l",), a;. (Tfl).
III some of the proofs to follow we shall (!ollsider the intersection
Then, under the transformation <1>, PIA) goes into JL.....p(JL) where
(*)
fl
p(",} = !,bk",k.
>_0
If ",. (Tfl), p(A),.. {Tn), since for any '/, A' maps (Tfl) onto
(Tfl-t-'). Also
P(T)", = (T-o;l}"P(A)x = p(A)(T-cd) x, x. (Tfl).
Now let "'r' (Tfl). a;r x, P(T}x r y. We must show that", is in
(T"), and that P{T)x = y. The operator (T-cd)" is closed. as it is
the jnverseorthe bounded operator A", Thus. sincep(A).r n p(A).x,
p(A)x. (Tfl}. To see that x is in (Tfl), we write
p(A)x bo"'+bJA.x+.. .+bflA"""
b.if"0.
and note that. since A1: = (T), all terms except possibly b,x are
in (T). Thus", is in (T). We proceed by induction. Suppo,e that
'" £ (Tm), where I ;;; m < n. Then
(T-cd)"'l'(A)x = b,(T-cd)m",+b1(T-,.,J)m-t",+. ,.+b"A" x.
By the same argument. (T-cd)m.T£'1;(T), and hence .x£ (T'"+').
Thus. by induction, '" £ (T"). Thi8 completes the proof. Q.E.D.
8 TIIEOREM. Let P be a pol1f'l0m;al of tUgr"" n, and let thr fundi,,,,
f in :F{T) have a ""TO 01 orMr m, ° $; m OS; 00, at infinity.
(a) If'" is in (Tn). then I{T);}) is in (Tm-t-"), mIIae m+n = co
if m = co. mill P(T)f{T)x = f{T)P(T)x.
(b) If 0 < 'II ;;;;; m. and g(;.) = P(.<I)f(;.), then g is in :F(T), and
g{T) = P{T)f(T).
n'1;(T"),
n=l
wllich we will denote by the convenient if not qmte ngorous symbol
(T ). If PIA) = 2:_0"';" is a polynomial of degree 'II the 8ymbol
PIT) will denote the operator !,:=<>o;,T' with domain (Tfl).
\V c now prove an important result.
7 THEOREM. 1/ T is a closed lint'ar opt'ratur with ROn-vuid t"e-
solvent sa. and P is a polynomial, then PIT) is a dost'd operator.
PROOF. Suppose tbat the degree of P is positive. Let 0; ,,,(T).
.and write
.
P(A) = !,bk(;.-o;)"---".
k=O
PROOF. Let q = m, if m is finite, or any positive integer, if m = 00.
Let 0; £ ,,(T), and (u) = f(.<I), (A-o;)f' = 1. By defining pep) =
,,-<vr(u) when" if" ° and P{O)=limp_o"-"V'(u)' it is seen thatp is in
:F(A) and thatA'p(A) = 9'(A) = f(T). Thus f(T)! A"I = (T').
Now let "" (Tfl). Then '" = A"y for some y in 1:, and f(T)x =
A"HP(A)y, (T"H), proving the first part of (a). To prove the see-
ond statement. write.x = A"y, and define l'tu) by formula (*) of the
preceding theorem. Then,
604.
VII.. GENERAL SPECTRAL THEOny
VII.9.9
VII.IO.2
EXERCl8ES
605
P(T)j(T)x = P(T)A"qJ(A)y
= p(A)p(A)y
= '1'(A)P(A)y
= f(T)p(A)(T-cd)"x
= f(T)P(T)",.
(a) StI(T) = {"'Ix € C[O, 1]. ",(0) = O} (no spectrum).
(b) StI(T) = {"'I"'" qo, In (no resolvent set).
(e) StI(T) = (:cl"'" qo, I], ",(0) = :c(I)}
(a.(T) = {2nin. n = 0, :1:1. :1:2... .}, a.(T) = t/>, a,(T) = tf>,.
2 In tbe spaces L.( -:1<, :>t) I s: P s: 00 on the unit eirele. let
T be the differentiation operator (T:c}(I) = :C'(I) with domain StI(T)
= {:c)", is absolutely continuous and ,,;, €L.( -:>t, ",/}. ShowthatTisa
closed unbounded operator whose domain is dense for p < 00, whose
spectrum is the set {:l:in}, n=0,1,2,.... and that a(T)=a.(T).
3 In the spaces L.( - 00, 00). 1 s: p 00, let T be the operator
(Tx)(t) = aI(t) with domain StI(T) = {"'Ix is absolutely continuous
on each finite interval, ",' € L (- 00, oo/}. Show that (a) T is a closed
unbounded linear operator whose domain is dense for p < 00. and
(b) the spectrum of T is the imaginary axis, and
R(l; T)("" I) f: e-"x(I+ ) , Ol(l) > o.
= e", e-"x(I+ )d , Bi!(l) < o.
4. It is known (Bade [1; p. 278]) that a functionf is analytic on
the imaginary axis and at inf"mity if and only if it has the representa-
tion
Finally, for (h), let 1'(1') = gel). Then y has a removable 8ingu-
larity at l' = O. and YVI) = 1' "p(,u)'P(,u). Now A";'(A)=p(A)p(A).
and thus A"g(T) = p(A)f(T). By operating on both 8ides by (T _cd)".
we obtain P{T)f(T) = geT). Q.E.D.
9 THEOREM. If f is in JI'"(T). and I ha$ no "","os in u(T), but a
zero uf finile order n at inlinily, then (f(T)} l exists and ha$ domain
StI(T").
PROOF. We let gel) = (.I.-a)"f(l). ex € e(T). Then g and l/g are
in .F(T), and fIT) = A"g(T). Thus f(T)I StI(T"), and [f(T)]-l
= [g(T)] l(T-cJ)". Q.E.D.
As a final result, we extend the spectral mapping theorem to
polynomials in T.
10 Tm:OIl-EM, If P is a polynomial.
P(u(T)) = a(P(T».
with
f{A) = [", ,,--'<G{ )d
G( ) = Fl( )'
=F.( ),
>O.
s: 0,
PROoF. Let P be of degree n, and suppose l P(a(T». If
g( ) = [l_P( )]-l, g is in JI'"(T), with no ZCrOSOD a(T), and a zero of
order n at infinity. Then, by Theorems 8 and 9, [g(T)]-l = J.I - PIT)
with domain StI(T'). Thus l; a[P(T)). and u(P(T» P(u(T». To
prove the converse inclusion. let Q be the polynomial defined by
P(l)-P( ) = (J.-E)Q(E). If P(l);u(P(T», then P(l)-P(T) =
(J.I -T)Q(T), has a bounded inverse R, and hence (ll _T) l = Q(T)R
is a closed everywhere defined operator. Thus .I.; u(T). Q.E.D.
Further results on closed operators wi1I be found in the exercises.
10. Exnrises
1 Let 1= C[O, I]. (T:c)(t) = ""(I). Show that T is a closed
operator and determine the spectrum when
where PI and F:e Rre entire functions such that for some constant
c > 0, IF,(,,» = O(e,I.I). i = 1,2, and
Fl( ) = 0(..---«) .... +co.
F.( ) = O(c,'I) .... -co.
For the operator T of Exercise 8 show that if f € .'F(T) then
I(T)("" I) = J:", G( ).x(I- )d .
5 Let A be a bounded operator and J.,,€a,(A) or a.(A). Then
(A_J."I)-l is a closed operator and u«A_J."I)-I) = fllA =(J.,,_ )-l.
Ecu(A».
6 Let T be a closed operator with non-ernpty resolvent set.
.
606
VII. GENE1tAL SPECTRAL THEORY
VII.IU.7
VII.ll
NOTES A:SD REMARKS
607
11. Note. aDd Remark.
smoke in a toba co-leaf.n We will not adhere to his terminology. The
term "sp('t:tnun n is due to Hilbert.
Polynomials of a matrix were used almost from the beginnmg of
the theory. and by 1867 Laguerre [I] had considered infinite power
series in a matrix in constructing the exponential function of a matrix.
Sylvester [1. 2] constructed arbitrary functions of a matrix with
distinct eigenvalues by means of the Lagrange interpolation formula.
Ris method was generalized by Buchheim [1] for the case of multiple
eigenvalues, although Buchheim did not expn>ss his result as in Theo-
rem 1.8. This form i8 found first in Giorgi [1]. Even hefore Sylvester,
Frobenius [I; p. 54, 2] had obtained expansions lor the resolvent
(J.l- T)-l in the neighborhood of a pole.
A special case of Theorem 1.9 is due to Weyr [I], and in full
generality it was proved by Hensel [1].
In regard to Theorem 1.10, Frobenius [3; p. 11] stated that If I
is analytic. then I(T) can be obtained as the sum of the residues of
(J.l-T)-If(A) with respect to all the eigenvalues of T. He a>sertcd
that this notion had bcen used in the dissertation of L. Stiekelberger
(1881), but Frobenius did not develop a pn-cise calculus. The fIrst to
make a clear use of thi8 device was Poincare [1] who employed it
where all the roots are distinct. In the case of multiple roots a for-
mula equivalent to Theorem 1.10 was derived by Fantappie [3] on
the ba:tis of certain requirements including the relations in Theorem
1.5, that would be expected for a '"'reasonable" operational calculus.
The fonnula in Theorem 1.10 was used as a definition for I(T) by
Giorgi [I] at the sugg<o;tion of E. Cartan, who was undoubtedly
familiar with Poincar 's use.
For other related remarks. see MacDuffee [I: Chaps. 9, 10]. An
interesting account of vanou.!J function!!. of a. matrix is given in
Rinehart [1].
Fund;<m'J 01 an <>pn'alOr. The results of Sections 8 and 4 may be
regarded as being a unification of two historical developments. On the
one band, these results are a genen,lization of those in the theory of
matrices, and secondly they are an abstraction of results in the tbcory
of integral equations. Consequently it is hardly possible to give
complete and accurate credit of referfnces to many of these
notions. For example the resolvent operator, its functional equation
Show that if A e(T), 11- is any complex number. and if il isin (T').
then
n (T -cxI)'il (T -cxI)'+1
R(A: T)il = I -- + R(A; T).r.
,_0 (A_I1-)Hl ()._a)n+l
7 Let T be as in the preceding problem and let I in $""(T) have
a zero of order n at ). = 00 and no zero on a(T). Show that [f(T)]-1
bas the domain (T') and the representation
1 i (T-aI)'+1
[/(T)]-lil = 2ni r 1()')(A-a)'+1 R(A. T).rdJ.
where il (T') and r is a 8uitab1e contour.
8 Let T satisfy the hypotheses of Exercise 6 and be unbounded.
Show that there exists no polynomial of degree n, n 1, not
identically zero. such that P(T)", 0 for all '" in (T')_
Genernl reluenas. For a general discussion of the theory in and
related to this chapter, the reader is referred to the expository articles
of Dunford [6] and Taylor [10]. Additional results may he found in
the treati8es of Rille [I; Chap, 5]. Riesz and Sz.-Nagy [I; Chap. ll]
aud Stone [8: Chap, 4], the latter dealing with Hilbert space theory.
Fillite dimen..w.wl space. Spectral theory in finite dimensional
spaces is a portion of matrix theory. For the many other questions in
this theory which we do not discuss the reader should consult IIIac-
Duffee [1] or Wedderburn [1] - the former is particularly recommend-
ed for its copious references to the literature. The books of Ralmos [7J.
Hamburger and Grimshaw [1], and Schwerdtfeger [I] are close in
spirit to the treatment in this section and will be found useful. We
will confine our remarks principally to Theorem8 1.8-1.10.
A number)" is called (1.2) an eigenvalue of the linear operator
T if there exists an .To *- 0 such that Ta: o = lcxo. The terms "proper
value...., ucharacteristic value"', usecu1arvalue H and "Iatent-valuenor
Ulatent root" are sometimes used by other authors. The latter term
is due to Sylvester [2] because such numbers are "latent in a some-
what similar sense as vapour may be said to be latent in water or
.
608
VII. GE:S-EItAL SPECTRAL THEORY
VILn
VII.l1
NOTES AND REMARKS
609
and expansion, were employed in both of these theories.
Considerablc credit 8hould be conferred upon Hilbert [1] and
E. H. Moore [I, 2] for perceiving and establishing this unification.
However, it seems fair to state that it was F, Riesz who most fully
revealcd and developed it along the lines presented here. Thc reader
of his book (F. Riesz [3], particularly Secs. 71-82) will find many
of these concepts aud Tesults cxp<>sed witb an approach that is strik.
ingly "modem". Although he dealt principally with compact opera-
tors in '", he established that the resolvent set is open, that the resolvent
operator is analytic and indicated that. at least in the case of a pole,
the Cauchy integral theorem could be employed to obtain a projection
operator commuting with the operator.
In the case of a bounded or unbounded nonual operator in 8
Hilbert space, many of the results of this section becomc simpler and
can be proved more directly by other methods. With these hypotheses
considerable extension js possib1e. For an elaboration of these reo
marks, we refer the reader to Volume II of this book or to the books
of Stone [3], Halmos [6] or Rie8z and Sz.-Nagy [I]. Our remarks will
deal only with the B-space case.
The expansion for the resolveut is due to NeullU!.nn [1] who esta.
blished it in potential theory. In a more general context it is due to
Hilb [I],
The fact that a closed linear operator on an arbitrary complex
B-space has non-void spectrum was proved by Taylor [12]. A special
case of the fact that rnax la(T)1 = lim,,-+o> IT"lll" was proved by
Beurling [I], and the general case by Gelfand (1].
In 1923 Wiener [2] observed that Caucby's integral theorem and
Taylor's theorem remain valid for anaJytic complex B-space valued
functions of a complex variable. It is perhaps surprising that not much
application was made of this fact for about a dozen years when a
number of researchers independently found it useful. In 1936, Na-
gumo [1] studied B-algebras from a function-theoretic standpoint
and proved, among other things, some theorems due to Riesz for
compact operators. Later, Taylor [13] studied certain abstract ana-
lytic functions, and Hille [2] applied similar methods in the study of
semi-groups, In 1941, the famous paper of Gelfand [I] appeared
which, although it partially overlapped with Nagumo's work, devel-
oped the ideal theory of B-aJgebras. In addition, Gelfand used the
contour integral to obtain idempotents in B-algebras. Independently,
Lorch [6] employed thc same device and initiated a study of "spectral
sets n .
Theorem 8.10 is due to Gelfand [I]. Theorems 8.n, 3.16 and 1J.19
are found in Dunford [7], where there is 80me additional material.
Spectral IMDry of oompad operaWTS. AI< we bave observed. this
theory generalizes the work of Fredholm [I] on a type of integral
equations. Fredholm t 6 original approach was by means of expansions
in detenninants which. while intricate, gives detailed representation
of the resolvent as the quotient of two entire functions. (See Hellinger
and Toeplitz [3; Sees. 9-10] and Chapter XI of the present work
for further references.) Of several other methods, we mention the one
due to E. Schmidt [2] depending on the possibility (in Hilbert space)
of approximating the compact operator by operators with finite
dimensIonal ranges.
Probably the most ingenious and elementary approach is due to
F. Riesz [4] and is valid for an arbitrary real or complex B-<space.
Certcin of Riesz's results concerning the adjomt operator were not
eompJetely general, but were completed by Hildebrandt [6] and
Schauder [6]. For an exposition of this method, see Riesz and Sz,-
Nagy [1; Chap. 4] or Zaanen [5; Chap, 11], A similar treatment is
given by Banach [1; Chap, 10],
The line of argument given here is closer to Nagumo [1] and is a
speciaJ case of some results of Dunford [7; p. 208].
The results of this section have been generalized to locally convex
topological linear spaces over the complex numbers by Leray [2] by
using a deep theorem on the invariance of domain.. Other extensions
to spaces more general than B-spaces have been given by Altman
{8. 5]. Hyers [2], Marinesen [1] and Williamson [3]-
The following theorem, called the Fredholm A/!i!rnnlive, IS a con-
sequence of the theorems in this section.
THEOREM..Ld T beacDmpactoperafurina cDmpkx B-8paceI, and let
). be a fixed mm-zerD cDmpkx number. Thm 1M nonhmrwgC1leOU8 equnJinn.r
(NJ
(N')
(U-Tp = y,
(M-TOp' = y'
.
610
VIl. GENERAL SPECTRAL THEORY
VII.n
vII.n
NOTES AND REMARKS
611
have unique wlutWns for any y in I or y" in I* il and only if tM
homogeneous <fJIUJlions
(H) (U-T)x = 0,
(H") (U- T*)x* = 0
have only 1M zero solutions. Furlhennon if <me of t1u: humogeneom equa-
liol18 has a 1Wn-zerO roltdion, IIu:n lhey both have t1u: same linile number of
linearly independent solutions. In this eMe t1u: eqU4lions (N) and (N")
haveBO!ulWll8 if andtmly if yandy"areorlJwgunalloallt1u:solutionsof
(B.) and (H), y. Moreover 1M general BOl1dUm for (N) is found
by wlding a particular roltdion of (N) 10 t1u: general8fJhdWn vI (B).
The results of Fredholm pertaining to the representation of the
resolvent or the determinental approach has been discussed by Alt.
man [5], R. Graves [I], LeZlmski [I, 2], Michal and Martin [I].
Ruston [2,3,5,6], Sikorski [I,2],and Smithies [1]. See also Groth-
cndieck (3] and Zaanen [5; Chap. 9].
For the purposes of applications it is important to be able to
compute the eigenvalues of an operator; this is partIcularly true for
self adjoint compact operators in Hilbert space. We refer the reader to
the work of Aronszajn (3, 40 J and Collatz [1] for these questions. Also
of considerable importance is knowledge concerning the distribution
of eigenvalues. In the case of integral operators the reader should
consult Hille and Tamarkin [1] and Chang [I]. For related results in
ab8tract spaces see Fan [3, 5], Horn lI], Silberstein [I], Visser and
Zaanen [I], Weinberger [1, 2J, and Weyl [I].
It is a consequence of Theorem 4.5 that ifT is compact and a( T) con-
tains at least one non-zero number,. then T has a.n invariant subspace,
that is, there exists a proper closed linear manifold I D C I such that
T(I D ) I D . It i8 an interesting and non-trivial fact that this is true in
general. Thefollowingtheorem was proved by Aronszajn and Smith [I].
THEOREM. Any eompact linear operaler in a B-space has a proper
invariant subspace.
y ood [2] has investigated ctrtain properties of an operator that
are unchanged upon adding a compact operator, .and obtained results
related to those in this section. Atkinson [2], Gohberg [I, 2, 3]
and Taldykin [I] have also considered similar questions. Using their
methods, Kleinecke [I] has proved the following theorem.
THEOREM. Let 3Z be a B-space, and leI ffi B(}:) be t1u: interuction
of an ma.ximal one-sided ideal. in B(3Z) oomaining all uniform limits of
operalor. with finite dimm.wnal range. TIu:n t1u: speclrum of any opera-
tM in m is a eountable Be! of isolaled eige"")(Jlues of jiniIe """"'plicity
with no limit points excepl possibly}. = O. Further ffi contains any other
ideal in B(I) whose opn-aWr8 ho.ve specfra of t1u: nature just specified.
[n certain 8paces, e.g. C or 4, we have seen that there exist
operators which Are not compact but whose spectra are the same as
that of a compact operator. This is not true for normal operators in
Hilbert space (see Sz.-Nagy [3; p. 55]). Similarly von Neumann
[6; p. 16] has shown that if a (not necessarily bounded) self adjoint
operator T in L.( - co, co) bas a countable set of isolated eigenvalues
of finite multiplicity with A = 0 as the only limit point of a(T), then
T is unitarily equivalent to an integral operator of a certain classical
(Carleman) type.
L. M. Graves [6] has extended some of the results of the Riesz
theory to mappings of the form E+ T, whereE ruaps a B-space3Z onto a
B-space ID, and T : I 'ID is compact. See also L. Schwartz [4] where
some of these results are proved for locally convex spaces.
For additional information concerning compact operators. the
readerisreferred to Atkinson [2,8,4], Audin [I]. Gohberg [I, 2, 8. 4],
Gol'dman and Krackovskii [1], Hamburger [4], Harazov [1, 2, 8],
Keldys [1], KraCkovskii [I, 2], KraCkovskii and Gol'dman [I, 2,8],
Krein and KrasDosel'skii [I], Liv ic [2, 3], Nikol'skii [2], Sz.-Nagy
[12, 13] aDd Zaanen [6. 9].
Pertu>'b<IIimI t1u:ory. The questions of perturbation theory go back
to the work of Lord Rayleigh and E. SehrOdinger, but it is Rellich
who developed the theory along the lines presented here. (For an
expository paper on this theory, see Rellich [I].) The principal result
of this section is an extension of a theorem of Rellich [2; I] to a situa.
tion admitting elementary divisors. The mode of proof is essentially
the same .as in Rellich.
In a series of five papers, Rellich [2] considered the nature of the
spectrum of the perturbed operator, principally in the neighborhood
of an isolated eigenvalue of the unperturbed operator. In his first note,
Rellich [2; I] treats bounded self adjoint operators III Hilbert space,
and in his third note the hypothesis of boundedness is dropped; in
612
VII. GENERAL SPECTRAL THEORY
VII.n
both cases the perturhation depends analytically on a single para.
meter. Sz.-Nagy [2. 4] gave different proofs for some of these results
and extended some to B-spaces; further results in this general setting
were obtained by Kato [1. 2] and Wolf [IJ.
In his second paper Rellich [2; II] discuSl!C<:l continuoUB pertur-
bation of unbounded self adjoint operators; these results were com-
pleted by Heinz [1]. See also Newburgh [1, 2].
Most of these results pertain to the point spectrum, The con-
tinuous spectrum is much more difficult to handle. but has been dis-
cussed by Friedrichs [1. 2].
Une:qJected phenomena can take place under perturbation. For
example. Weyl [2] showed that if T is a self adjoint operator (which
may have void point spectrum) on a separable Hilbert space, then a
self adjoint cnmpact operator K may be fnund such that T +K has
enough eigenvectors to span the entire space. This result was extended
to unbounded T by von Neumann [6; p. 11] who showed that the
norm of K may be arbitrarily small.
Perturbation theory finds particumrly fruitful application to
differential equations. .and is frequently studied in that context.
Particular reference is made to the papers of Titchmarsh [2] and
Mooer [1].
Theorem 6.10 i8 due to J. Schwartz [8].
In addition to the papers mentioned above, the reader is referred
to Gavurin [1, 2], Holder [1]. Jamison [I. 2], Kato [3, 4], KIein£-cke
[2. 3], H. P. Kramer [1]. V.A.Kramer [1]. Krein [8], Lifsic [1. 2,3, 4J,
Phillips (6), Rabinovic [1], Rosenbloom [2J. Schafke [3]. Schroder
[1], Smulian [17]. and Solomyak [1].
Taub£rian thecry and unboundrd oper_s. The results of Section
7 are found in Dunford [7] and have application in ergodic theory,
We will cite some references to the pertinent literature of ergodic
theory in the notes to Chapter VIII.
The results in Section 9 are due to Taylor [11]. who describrd the
method given here of ba8ing the theory of the unboundcd operator on
that of the bounded, and also developed a theory for the unbounded
operator direct1y. A somewhat more detailed calculus for a restricted
class of unbounded operators was given by Hille [1; Chap. 15, Sec. IJ.
A 8imimr program was carried out by Bade [1 J.
CHAPTER VIII
Applications
1. Semi-woop8 of Operators
It .s well known that the exponential functIon I(t) = exp(ta) is
the most general continuous real (or complex) function I of the non-
negative real variable t which satisfies the functional eqU&tions
1(0) = 1, I(t+u) = l(t)/(u). A corresponding problem is to determine
the most general continuous operator valued functions defined on the
range t :2: 0, which satisfy the equations
(i) T(t+u) T(t}T(u). T(O) = I. t, u ;;; O.
An operator valued function T(t) satisfying these equations is caUed
.. semi-group of operator8. In this section will be found the salient
features of the nnalytical theory of these semi-groups os developed
by E. Hille. R. S. Phillips. nnd K. Yosida. By annlogy with thescamr
case we could expect that a semi-group T(I> is, in some senge, an ex-
ponential function. If we ossume that T(t) is continuous in the uni-
form operator topology, then, as shown in Theorem 2 below, there
exists a bounded operator A 8uch that T(t) = eM. If it is merely
assumed that T(t) is continuou8 in the strongoperator topology,then
the problem becomes more difficult to handle. Still. it will be seen that
T(t) can be regarded, in an appropriate sense, as e'A. where now A is
an unbounded operator, called the infinitesimal generator of the serni-
group. We 8ha11 also study the important problem of determining
which unbounded dosed operators are infinitesimal generators of
strongly continuous semi-groups. The solution of this problem to be
giyen in the discussion below will enable us to discuss the "abstr t
Cauchy problem": to find for a given clOSEd unbounded operator A.
a function defined for t 0, with each of its values belonging to the
domain of A. which satisfies the equations
(ii)
dir
-=A.x,
dt
x(O) = xo
Gig
,
614
VIU. APPLICA"I'IONS
VIII.l.I
VIIl.l.2
vIU. BEMI-GROU:PS OF OPERA.'I'OBB
615
where ... is 8 given vector. The theory wi1l be illustrated by solving
the abstract Cauchy problem for the special case of an integro-differ-
ential operator of the fonn
PROOF. Since T(O) = I, it follows by VII.fi.fi that there exists an
,,> 0 such that U(t) = log (T(t)) is defined and continuous for
O .s: t e. If 111 < e. then
(A..)(a) = .."(a) + h(a);r{a) + f: K(a, u}x{u)du,
U(lIl) = log (T(t)") = n log (T(t)) = nU(t).
Thus, (lln)U{t) = U(lln) for each I with 0 <;; t e, and consequently
This amounts to solving the ordinary Cauchy problem for a partial
integro-differential equation of the fonn
iJ.. iJ2.. f. '"
ilt = ils" + h(8)" + 0 K(a. u)..(u, I)du,
"'{8,0) = ".(8),
m
- U(t) = mU{tln) = U(mtln)
n
where h. K, and "'. are given functions, The general theory could he
used similarly to solve many other Cauchy problems for partial dif-
ferential and integro.differential equations.
Throughout this section, i wilI denote a complex B-space. and
{T(/)} a strongly continuous semi-group of operators in i; i.e., a
family of operators 8atisfying the conditions of the following definitjon.
for each rational number mln with 0 .s: mfn .s: 1, and each t in the
interval 0 ;,;; I e. in partil'Ular, (mln)U(e) = U(emln), so that, by
continuity, IU{e) = U(el) for 0 ;;;; I I, and U(/) = (1Ie)U(e) for
o < t < e. If we put A = (l/e)U(e), we have
[oJ T(t) = <fA
for 0 .s: t .s: e. If t > 0 is arbitrary then tIn < e for some sufficiently
large integer n. and so we have <fA = {<f/....)ft = (T(tln)}ft = T(t),
Thus [0] holds for 0;';; t < co. Since liml>->O (""-I )/h--+% uniformly in
any bounded set of the ",.plane, the Corrnula for A follows immediately
from VlI.8,IS,
In the same way we see that (dldt)T(t) = AT(/) for all I :=:: O. and
consequently T(t) is continuous and has a continuous derivative.
Since T(t) = (tA)ftlnl it is seen that
IT{t)l .s: e AI.
Thus, for &itA) > IAI, the integral IO'e---"T(t)dt exists. Since a bounded
linear operator commutes with the integral, (111.2.19(c)), we have
(ll -A) f: c"T(t)dt f: (ll -A)e-"e'" dt
f. 'd
_ _ (e >'elA)dt
adt
=1-e-J.,e"'.
Since Bi'(A) ;;, [A I it is seen that J",.£'A I ;,;; eH+1AI}. 0 as a --+ co,
and thus, by the dominated convergence theorem (III.6.1fi). we have
(ll-A) f: c"T(/)dt = 1.
Thus, since (ll-A)-> exists for IAI> IAI by VII.3.4. we have
1 DEFINITION. A family {T(t)}, 0 I < co, of bounded linear
operators in i will be called a atrongly continwms 8emi-group if
(i) T(s+/) T(8)T(/), 8, I ;;;; 0;
(ii) T(O) =.1;
(iii) For each ",£1'. T(/'" is continuous in I on [0, co].
If, in additjon, the map I -+ T(t) is continuous in the uniform
operator topology, the flUDily {T(t), t :e: O} is called a uniformly con.
tinuous semi-group in B(i).
It is clear from the operational calculus develop.,.} in VII.S that.
for any A in B(1'), <fA i. a uniformly continuous 8emi-group. The
following theorem shows that every such semi-group is of this form.
2 THEOREM. Let {T(/)} be a uniformly continuous semi-group.
Then there exi.rts a bounded operafur A stU:h tJw.t T(t) = tf4 for t :e: o.
Tm, operator A i. given by tm, formula A = limA-><) (T(h)-.1)lh, For
Bi'(A) sufficienOy l4rge, tM rnKJIvent of A can be upresS£d in terms of the
semi-group by the formula
R(A; A) = f: "-"T(/)dt.
.
ti16
VIII. APPLICA TIO S
VIlI.1.8
VIII.1.8
SEMI...OROUPS OF OPERATORS
617
(M-A)-' = J: r"T(t)d!,
&itA) > IAI.
To complde the proof of the second pnrt of the lemma we will
show that if T(')x is measurable on (U, co) for each",. J:, then IT(')/
is bounded on each interval [Ci, II"], Ci > O. We first show
(i) if "'0 . J:, then there is a separable clO5Cd linear manifold Io of
I containing "'0 and a null 8et Eo of (0. co) such tJmt if I t Eo then
T(t)x . Io whenc...er ",.10.
By Lemma 111.6.9 there is a nuU set Fo such that {T(t)xolt, Fo}
is .eparable. Thu. Io = 8p {"'O' T(t)x o ' I, Fo} is a S<"pW"Rble closed
linear 8ub8pace of I. and there is a sequence {t.} with t., F..
n = 1,2, . . ., .uch that the set {"'o' T{t.)x o ' n = 1,2, . . ,} is funda.
mentaJ (11.1.4) in II!' Now if I, Fo and t+t. t F.. n = 1,2, , . " then
T(t)x o and T(t)[T(t.)",o] = T{t+t,.)x o belong to II!' Let Eo =
Fou U _l(T-t.), .0 that Eo is a null .et. It foUows from the
boundedness of the operator T(I) tJmt if t, Eo, then T(t)I. (;; Io,
which proves (i).
Suppose that there is an interval [15,1/15] on which IT{')I is not
bounded. Then there exists 8.' [15,1/15] and "'.. iE, Ix.1 = 1 such that
IT(8.)x.1 > n. n = 1,2, . . .. Applying (i) for each n. there is a se-
parable subspace J:. containing "'. and a null set E. with T(t)I. (;; I.
for t, E.. Define Im = sp( I., n = 1,2". ,} and Em = U;:"E.. It
is clear that x m is separable. Em is a null set, and T(t)J: m J: m for
t, Em' For each t. set
Q.E.D.
The remaining part of the present section will be devoted pr<-
mariJy to a study of strongly continuous semi-groups. Theorems 10
and 11 to follow show the counterpart of Theorem 2 in this case.
I! LEMMA. Let (T(t)} be a lamily 01 bounded opt'rators delined on
a linite dosed i1II£rMl [11.. P] su<>h that T(t)'" is conlinwJUs in t lor each
",.J:; then IT(')I is mt!I18«roble and bounded on [o:,P]. Com.....sely, il
(T(t), 0 ;>; t} i. a Sl!mi-group 01 bounded linear operolor8 in J: and il
T(')x is mcasurobU: on (0, 00) for ea<:h "'. x, rIum T(')x i8 continuous
01 every point in (0, <XJ).
PROOF. Since T(-)oX IS continuous for each 0; in.!, it is bounded on
[0:. P]. TIlUS the boundedne8s of IT(." foUows from the uniform bound-
edness principle 1I.1.11. To see that IT(')I is measurable let Ci > 0
and U = {tIIT(t)1 > 151}. If 10' U we can find an '" with 1"'1 = I and
jT(t)xl > 15 for every t in an interval containing ' 0 - Thus U is open in
fa, PJ and the first statement foHows from Theorem 111.6.10.
Next we show that if (T(t». 0 :>: t < ct), is a .emi-group, if
T(.)x is measurable on (0, 00) for each x. I, Qnd if IT(')I is bounded
on each interval [15. 1/15], Ci > 0, then T(.)x is continuous at every
point 10 > 0, for any '" E I. To do this, let 0 < 0: < P < 10 and take
a 15 > 0 such that 2 is Jess than 1, a, Io-P, and (t,,+1)-1. Since
T(Io)x = T(t)[T(Io-t)x], t < to, and .ince the right side is independ-
ent of t, it is integrable over [0:, Pl. If lei < Ci, we have
(P-o:)[T(to+e)-T(r"I]x = f: T(t){T(Io+ e - t J-T(t o -t]]", dt.
By hypothesis there exists an M> 0 such that IT(t)1 <M for tE [o:.PJ;
further i[T(to+e-tl-T(t,,-t)]"'1 is a bounded me..urable function
for t. [0:, P]. Hence
(fJ-a)I[T(r,,+e)-T(t,,)]xl < M J: I[T(to+e-t)-T(Io-t)]"'ldt
= 11-1 r" o I[T(s+r)-T(8)]xlds.
J'n-fJ
It follows from Theorem IV.8.20, or may be verified directly, that as
e -->- 0 the last integral approaches zero. and hence T(.)x is continuous
att=lo.
IT(t)l' = sup {IT{t)x[. XE Im' 1"'1 ;>; I};
since "'. . x m we have IT(8 n !l' > n. n = 1, 2, . . .. Let {z.} be a count-
able set which is dense on the unit sphere of £m; since IT(- )znl is a
measurable real valued function, it follows (111.6.101 that IT('!I'
= sup.IT(')z.1 is also measurable. Also iff., EM' then for any",.1 m .
T(r..)x.1m and IT(t.)xl < IT(t.)I'lxI- Hence we SeC that
IT(t,+r..>I' = sup {[T(t1)[T(t.}xJIx.J:",.I"'1 ;>; I}
<;; sup {IT(t,)ylly. X m , Iyl <;; IT(r..)j'}
< IT{t,!!'IT(t,,>I'.
provided t", Em' We now define w on (0, 00) by w(t) = log IT(t)I'.
From the above we know that OJ is 8. measurable function which never
takes the value +00, that w(t,+t,,) < ru(t,)+w(t.) provided at Jeast
one of the points t, , Em' and thatW{8.) > log n wherethes. are pomts
618
VlII. ",-PFUCATIONS
VIIJ.1.4
VIIU..5
SEMI BOUPS OF OPERATORS
619
in f". II"]. That this is a contradiction follows from the statement
(ii) ifm is a measurable extended real valued function on (0. OJ),
if m(l) < OJ for each t> 0, and if m(,>+t,,) s;: m(,»+m(t,,) for one of
the t i not in a null set E, then m is bounded above in eaeh finite closed
interval
To see this. let a > 0 and let A = mea). Then if,>+1" = a and
t" I E, it follows that A = w(a) s;: w(ft)+w(t,,). Thus if F (tl
o < t < a. met) > A/2} and if a-F is the set of all points of the
form a t with hF, then EuFU(a-F) [0, a]. Consequently,
p(F)+p(a-F) a where l' denotes Lebesgue measure. Since p(F)
= pea-F) we have p(F) a/2. This shows that if Bft is a point of a
finite interval [«. (J] at which W(B.) ;;;, 2n. then the set {till. < t < (J,
m(l) n} has measure atleast «/2. Hence if m is not l>oundedaboveon
[«. (J] it follows that m(l) = OJ on a set with measure at least «/2, but
this contradicts the hypothesis that met) < 00 for h (O, 00). This
completes the proof of the lemma. Q.E.D.
Our next task is to determine the behavior of IT(I)I as t approach-
es +<0. For this we will require the following lemma on BUbaddilive
!urwtilJtlB, i.e. functions w such that m(,> +1,,) :;:; me,» +w(I,,).
4 LEMMA, Let w be a BUbadditive funcrion rkjined on [0, 00),
and ooundnl above on eO£h linire BUbinteroal. Then w. = inf w(t)lt is
jinife or egual$ w, and '>0
. wet)
w.o=hm -
t--> I
PROOF. Given any number i! > w. there i8 " point r" such that
wCr,,) <6.
10
Foranylwe write I = n(I)Io+r, wheren(l) is an integer and 0 s;: r<l".
Then
Thus
. wet) «>(10)
IWlSUP- s;: - <".
t-->m t - 10
Since Wo s;: lim infw(t)/t, we see limw(t)/I exists and equals wo'
s-.oc t-+IXI
5 COROLLARY, The limil w. = hm'_m{logIT(t)l)(le.nm. For eO£h
Ii> w. lhere is a eQtlB!ant M. nu:h that IT(I)I < M.t!' lor I ;;;, O.
PI\OOF. Define wet) log IT(t)I, I ;;;' o. Since w(,.+t.,,)
log IT(,.+t,,)1 s;: log (IT(,.)IIT(t,,)j) =w(t,,)-t-<n(t,,), m i8 subadditive.
The result now follows from Lemmas 8 and 4. Q.E.D.
6 DEFINITION. For h> 0 the linear operator A. is defined by
the formula
T(h)",-",
A,x = h ' ",,,:£.
Let 5D(A) be the set of all '" in 30 for which the limit. lim A,,,,. exists and
.....
define the operator A with domain 5D(A) by the formula
A", = lim A.",. u 5D(A).
.....
w(/) w(n(t)I,,} mer)
-;:;; +-
tit
n(l)w(lo) mer)
s;: --+-
t t
w('o) w(r)
=- -+-.
Ig +rln(t) t
The operator A with domain 5D(A) is called the inliniftBimal
generatcr of the semi-group T(').
7 LEMMA. (a) These!5D(A) is a linear manifold and A is linear
on 5l1(A).
(b) II '" is in 5l1(A), then T(t)", is in 5D(A). 0 s;: t < w. and
(d{dt)T(t)x = AT(t)x = T(t)Ax.
(c) II a: is in 5l1(A), tl1m [T(/)-T(s)]'" = J;T(u)A",du, lor
O ';; s<t<oo.
(d) If t ;;;, 0 and 11 i8 a Lebesg,"" imegrnhle function continuous
at t then
I f '+'
lim- g(uIT(u)xdu = g(t)T(t)x.
,,_ok,
PROOF. Statement (a) is clear from the definitions. To prove (b)
let k>O, 1 ;;:" 0, and a:e5l1(A). Then T(t)A,,,,=A.T(t),,,, so that
lim A."T(t):r = lim T(t)A,a', and hence T(/).:r .-5D(A). By definition
a--o "_0
.
620
VIII. APPLlCA.TIONS
VIII.l.8
VIII.l.9
6EMI-GRQUPS OF OPERATORS
621
A(T{t)x) = lim A,T(t)x.
....0
Thus T(t):.!.r = AT(t)x for x. (A). If t> 0 and h> 0 then
lim { Tlt).x-T(t-h)X _ T(t)A.r)
11--+0 h
= lim T(t-h)(A.",-Ax) + Jim [T(t-h)-T(t)]A",
1I.--Jo-1} A-o
smee lim T(a)A",. = T{s)yo uniformly in [0, t]. Thus
. m
lim A,x o = lim C' T(s)ycP = Yo
t_D .._0 t Jo
by Lemma 7Id). Consequently "'o. (A) and Axo = Yo, i.e., A is
closed. Q.E.D.
=0
by Definition 1 (Hi) and Lemma S, On the other hand,
Tlt+h)",-T(t).r = T(t)A,x --+ T(t)A",.
h
so that (dldt)T(t)x = T(t)Ax is established for", . (A).
Statement (c) follows by applying linear functionals to both
sides of (b) and integrating. For (d), see Theorem III.I2.8. Q.E.D.
8 LEMMA. The linmr manifold 1J(A) is dense in and A is
dosed on (A).
PROOF. Let x be any vector in . Then if t, h> O.
A. C' T(sJxds r'IT{h+s)x-Tla)x)ds
Jo h Jo
= f Hh T(s)xds- f ' T{s)xds
h. .ho
f l+' T(a)xds - r" T(s)xds --+T(t)x-",
h , hJo
as h -+0 by Lemma 7(d}. Thus J T(s)xds. (A). However, x=
lim(I/t) J TIs).rds,so that 1J(A) is dense in I. To see that A is clOlred,
'_0
g COROLLAB.Y. A aem;./I1'aup has a bmmded infinilesimal genera-
tVT il and only il it is uniformly c<mtinuous.
PROOF. If T(.) i. a uniformly continuous semi-group then. by
Theorem 2, it has a bounded. infinitesimal generator. Conversely,. sup-
pose that T(') has a bounded generator A. It follows from the pre-
ceding lemma that A is everywhere defined. Thus Lemma 8 and the
principle of uniform boundedne.s (II.S.2I(ii» show that
sup IA.I = J( < co.
O A l
By Lemma S we have, for each s 0, R constant M. with
ITlt)! < 111..
o ;$ t. It-sl;$ 1.
Now
Tlt)-Tls) = T(s)[T(I-a)-/].
= -Tlt)[T(s-t)-/].
1>8,
a> t.
Thus
IT(t)-T(s)[ ,,;; M. .J( . [t-sl.
o t, It-al < 1.
which proves that T(') is a uniformly continuous semi-group. Q.E.D.
suppose tt'li £ (A), n = 1, 2, . . _, lim:J: n = a'D'
Using Lemma 7(c) we have ._m
T(I)xo-x o = lim T(t)xn-x.
and lim Ax" = yO"
. c
10 THEOREM. LeI T(t). I ::>- 0, be a strongly €on(inuQUs semi-group
01 optTVlors and let A. = (T(h)-/)/h. Then
T(t)x = lim eM.",. x. 1,
. "
. m
unilvrmly Ivr t in any linite inkrval.
PB.OOF. \Ve note first that we may write
e ' ''' = ,-'I' e('/.)TI'I = ,-'JA i tnT(nh )..
n=O n!h"
= lim C'T(s)Ax.ds
fi_CCJO
= J; T(s)yods,
If {} > w., then by Corollary 5
.
622
VJJJ. APPLICATIONS
VIIU.Il
VI1U.I2
SEMI-GROUPS OF OPERATORS
628
m t'"e"'1
1....1;:;; e-""M.!-
_ nlh
(il
If we can show
Ill-AIR(AI'" = 0:,
x I.
= M. exp He" h 1)).
(ii) B(A)(ll -A)", = 0:. lEE SD(A),
then R(A) = R(}.; A). Thus, in view of (i), it remains to prove
R(A)A", = AR(}.)o:, x £ SD(A). However. if x SD(A). then T(t)", E s!)(A)
for t ;::: 0 and AT(t)", = T(I)Ao: by Lemma 7. Consequently, Theorem
111.6.20 shows R(}.):HSD(A) and
A f: '-"T(t)o:dt = f: ,,-"T(t)A;xdt. Q.E.D.
Our next step is to find sufficient conditions on an unbounded
operator A that it be the infinitesimal generator of a semi-group.
12 LEMMA. Let A be a closed operalor with dense domain U!/wse
speclrnm lies in the half plane BI'(A) ;:;; w. Let S(I), t :;;, 0, be strongly
comnuuus in t and ealwly the relatimu
Consequently there is a constant K. such that
Ie....' ;:;; K.. 0;:;; B ;;;: t. 0 < h ;;;: I. If O:ES!)(A) and t ;;;: 10, then
(cf. Lemma 7)
IT(t)'" - ",A'xl 11' (i....JA.T(B).v)d.t1
= II: el....JA.T{B)(h-A.X)dsl
;;;: IoK..M.....IAo: - A."'I .... 0
as h ....0. Since S!)(A) is dense in I by Lemma 8, the conclusion follows
from Theorem 11.8.6. Q.E.D.
This theorem and the following one together give the analogue of
Theorem 2 for strongly continuous semi-groups,
IS(t) I ;:;; Me.',
R(}.; A);x = f: .-"S(t);xdt,
t ;:::0,
;x 3:'.
Then
AEe(A) and
n THEOREM. If W. = lim (log IT(t>l>/t and BI'().} > w., Ihro
....'"
IR("; A)"i ;:;; M(BI'(,,)---w)-n,
PROOF. We first establish the formula
tt= 1,2,.....
R("; A)", = f: e-.liT(t)",dt,
"'E1.
I f. '"
R(}'; A)nx - e.J.'t"-lS(t);xdt,
(n-I)! 0
It follows from the resolvent formula (cf. VII.a.6) that
[*]
BI'(") > w.
PROOF. Suppose that Wo < lJ < BI'(}'). By Corollary 5 there is B
constant M. such that IT(t)l;::; M. t, I :;;' O. Thus the integral'
JO' .-'-'T(I).vdt exists if BI'(}.) > wDand defines a bounded operator. Let
R(}.)<t = f: e.J.'T(I};xdt, ",£3::. BI'(}') > w..
I f. '" I f. '"
A.R(}').v = - .-'-'T(I+h);xdt - - .-'-'T(t).vdt
h D h 0
(e»- I) f. '" e»- f. "
= e.J.'T(I)",dt - - r"T(I);xdt
h . h 0
....}.R(")"' o:
as h -+0 by Lemma 7(d). Thus R(}.)x£S!)(A) and
R(A; A)-R(}<; A) = (,u-A)R().; A)R(,u; AI
by letting }. -+ p, that
d
d}. R(";A) = -W(}';A),
and inductively, tlmt
d"
dAft R(}'; A) = (-I)"n!R(}';A)H+1.
Now suppose co < lJ <BI'(}'),9i'(}<), If
I(".,u, t) = le.J.t-e "')(}._p)-l
}.E(!(A}.
Then
then
624
VIII. APPLICATIONS
VIII.I.lS
VIIU.IS
SEMI-CItOUPS OF OPERATORS
625
If{A, 1', 1)1 = Ir"' f: r''-'')' dsl
lpU r' fA--ub d8
- )0
< tc"',
(A>t)'R(A' A)"
tl B , = r'" I I '
"...0 n.
we have
I O.
(A't)"
[e'B'1 < Me " I
- -" n!(A-w)"
(/wA)'
<MI
,-0 n!(A-w)'
= M exp [/wA(A W)-I].
If WI > W then for A sufficiently large wA(A-w ) 1 < WI' Thus
[*] le1811 < Me'wl
for large values of A.
We next 8how that lim B,,,, = A"" ",.SD(A). If ",.SD(A),
' m
Consequently,
If(A,p, l)tnS(t).r1 :5: lIII"'ltn+lr"' w)'.
It follows from Corollary III.6.16 that we may let A approach 1';
i.e., we may differentiate
f: r"tnS(t)",dJ
under the integral sign, and obtain
d 1 0> 1 0>
- e I'I"S(t)xdt = - r"'t"+1S(t);rdt,
dA 0 0
Thus, inductively, we find
&teA) > w.
M f. '"
IR(A; A)nl :5: tn I,,(<it")-"dt
(n-l)! .
M
(&t(A)-W)'
Q.E.D.
IAR(A; A}x-xl = IR(A; A}AxI ;;:; lIfIAxl(A-w)-1 -+ 0
as A -+ 00. Since [AR(A; A)I ;:;; MA(A-W)-l < 2M forlarge A, we con-
clude (cf. II.S.6) that AR(A; A)x -+x, x. I as A -+ 00. Therefore
B,x = AR(A; A )Ax -+ Ax for x in SD(A).
Now define.s.(t) = e 'Bl . For any I' and A we have B,B. = B.B..
The series formula S.(t) = I::'-tJ tnB;:ln! shows B.s.{t) = Sl(I)B..
Consequently, if x. SD(A) we have (cf. Lemma 7(b»
Sl(t)X-S.(t)x = i ' [S.(t-8)S.(8)X]ds
ods
= i ' S (t-sHB, B.)S,(s)xds
o ·
= I: S.(t-8)S,(8)(B,-B.).xds.
d n f.
- B(A;A).r = ..-"(-t)"S(t)xdt.
dAn 0
Combin,ing this formula with the one above. we obtain formula [*],
Finally if &teA) > w, it is seen from [*] and the assumptions on
Set) thai
IS THEOREM. (Hille-Yosida-Phillips) A net:t!SSl1T!J and BUffieim!
,o..dition that a dotied linear optraror A milk dense domain be the infinite-
simal generator of a strongly oonJ./mums semi-group i& that thoe exist
real numbers 111 and w such that for every real A > w, A is in e(A) and
IR(A; A)"I ;;:; M{A-w)-",
n = 1,.2,.....
Csmg [.J we obtam
IS.(t)x-S.(t)xl < r-Ie'm1IB,x-B,.xI,
for large values of A andp. Thu8 S.(t)x converges to a limit uniformly
in each finite interval. Since SD(A) is dense in I it follows from the
inequality [*] and Theorem II.8.6 that there is a bounded operator
T(/) such that lim S,(I)x = T(I)x, if:.:I:. lIIoreover IT(tJl <
, W
PROOF. The necessily of the condition foJlows from Corollary 5,
Theorem 11, and Lemma 12. To prove the sufficiency let B A =
-A[I-AR(A; A)], A> w. We shall construct the semi-group T(t) as
the strong limit as 1 -+ 00 of the semi-groups e fB ).. Since
626
VIn. APPLICATIONS
VIII.I.U,
VIII.1.I6
8EMI-GRO"CPS OF OFERATORS
627
lirn inf IS.(t)1 ,:; e'''. The continuity in t of T(t)", follows from the
k+0>
unifonnity of the convergence. Since S.(t) is a semi-group it now fol-
lows easily that T(t) is a semi-group. Due to the inequality
/a,(I)B.",-T(tIA"'1 :5: IS.(/)(B.",-AiI:)I+I(S.(/)-T(t»A"'1
:5: Me''' IB.iI:-Ail:1 + 2Me'''IAil:1
valid for II' € 5D{A), we may take the limit as A --+ ro (cf. Corollary
III.6.16) on both sides of the equation 8.(/).2:-... = Ji,S.(B)B..rda
to obtain
Thus if B is the infinitesimal generator of TIs).
I i '
B.-. = lim - T(s)Ail:M = Ail:,
t--+D t D
Consequently, 5D(B);25D(A) and B is an extension of A. However,
for large A, Aee(A)ne(B) and the equations (AI-A)5D(A) = I
= (JJ-B)5D(A), (AI-B)5D(BI=I. imply 5D(BI=5D(A). Thus
B = A. Q,E,D.
II' € 5D(A I.
PROOF. Suppose that the equation holds for !Il(A) ;;:" w. Put
A(t) = r""f(/l, so that fl € 1..(0. co) and Jtft(t)e-J:dt = 0 for
&lIA) o. We make the change of variable u = e '. Thent = -logu.
and JorA'f.(tldt = fou'g(u)du. where g(u) = u-I(-logu) is in
L1[O, I} by Lemma IILI0.B. Hence J u"g(u)du = 0, n = 0, 1, 2, . ...
Consequently, by the Weiers1:r8.ss approximation theorem, and
Corollary III.lO.6,
0= f; h(u)g(u)du = f: h(u)G(du). h.-qO,I),
where G(E) = Jd(u)du. Since Lebesgue measure is regulHr so is G
and thus, by the Riesz representation theorem (IV.6.8), JEg(u)du = 0
for cvexy measurable set E. Thus g( u) = 0 almost everywhere
(III.6.8). Consequently II and thus f vanishes almost everywhere.
Q.E.D.
T(t)iI:-.r = f; T(s)Ail:ds.
14 CoROJ.LARY. A flecell8ary and sufficietlt condition tJuu a closed
/i'1fflr operator A 'Wilh dense domain (!€""oU a lJ1ro..gly e,mlinuous Bemi-
group T(/) of bounded operators BUCh lOOt IT(t)/ :5: e'"' for Bome ..eal
..umber CQ is tJuu
[*) IR{A; A)I :5: (A-W)-1; A> CQ.
PROOF. The fonnula R(A; A).2: = $3' e..a'T(t)ii:dt, ... €;E, shows
the necessity of the inequality [.J above, Clearly [*J implies that
IR(A; ...1)1- :5: (A-CQ)-. A > CQ.and thus by Theorem 18, (withM =1)
A is the generator of a Bemi-group T(t). It was shown in the proof of
Theorem 18 that IT(/)I :5: Me'''' for each ""t > w. Thus IT{t)/ :5: e'.,
t ;;:; o. Q.E.D.
The next corollary will require the following lemma.
15 b::anu.. Let 1 be in 1..(0. ro) and
f: e-"/(t)dI = 0
for a'(A) ""ffit:knily large. Thefl fIt) = 0 al1TWsl everywhere.
16 COROLLARY. A 'IO£C£SSary and '''ffieient ermdit;"n tlwl It
dOBrd upi"TUfm A with dense domain sho"ld be the infinitRsimal gcl'U'raim
01 a strongly ctmlintwus semi-group is tlwl lhere ea:ist a slrtmgly eon-
linlu"u family 8(/), 1 :2: 0, of bounded linear operatorB .atisfyirq:
S(O) = I, la(t)1 ,,;, M"..' for ..eal nurnlie7's 111 and w, and Buch tlwl
R(A; A)x I: rA'S(/J.rdt, A> CQ.
Then Set) is the Bl'mi-group 'Wilh inlinilesimal gfflRralm A.
PROOF. By Lemma 12, [R(A; A)"I ;;;; M(A-w) -. A> w. Thus
by Theorem 13, A is the infinitesimal generator of a semi-group T(t)
and IT(/)I;;;; Me.'. By Theorem n, R(A; Alx = Jo e-"T(t).2:dI,
:£ €. I, ). > (J). Now if ;r,* £ 1* we have
J: r"","(T(t)x-8(/)x)dt = 0
for A> w. Setting f(t) = e-'m""x*(T(t)x - S(t).2:) we have
J8' rAt f(I)& = 0 for A > 0. It follows from Lemma 15 that x*T(/)x
= ",*S(t)x for almost all I. By continuity this equation holds for all
t ;;; 0, and thus (cf. II.8.14) T(t) = Set), t ;;;; O. Q.E.D.
We now consider the question of when a strongly continuous
semi-group of operators defined on [0, co) may be extended to a
group T(/) of operators defined on (- co, co). Such an extension is
628
VlII. APPLICATIONS
VIII.1.17
VilLI ,17
SEMI-GROUPS OF OPERATORS
629
clearly unique if it exists, and the family S(/) = T( -I), 1 0, is a
strongly continuous semi-group. Since. if 0 < 1 < I,
S(I)",-",
t
-T(-2)[T(2-t)",-T(2)",]
-t
pies, use the notatIon (T"')(8J or T(",,8) for the value of Tx at the
point 8. Of course if 1 is a space. such as an L'J) space, whose elements
are equivalence classes of functions, then these symbols refer to one of
the functions in the equivalence class T",. Some of the simplest and
most important eX&mples of 8emi-groups of bounded operators arise
from the operation of translation T(/)(X,8) = "'(1+8) in the spaces
L (O, co) and C[o, co]. Throughout this discussion C[O, co] is the
space of all continuous functions on the compact extended non-
negative real number system. i.e.. the space of all function8 '" of a
non-negative real number for which the limit ",( co) lim x(s) exists.
o--->m
it is clear that the infinitesima1 generator of S(/) is the closed operator
- A, SD(-A) = SD(A). We shall call the operator A the inlin;',es;.mal
genera1<Jr of the group and A will be said to generah T(/), - co < t
< co. The question of whether T(t), t 0, may he extended to a
group may be answered in terms of the infinitesimal generator A.
17 COROLLARY. A meeNsury and sufficiEnt cond;uon that a
closed linear operator A 'With tkme domain generat£B a strongly conlin-
'U0U8 group 01 boulUled operators on (- co, 00) is tluzt there e",ist Tea!
"umbers M > 0 and (JJ :::>- 0 BUCk thtd
[*] IR(A; A)"I ,,;; 1I1(jAI-O) , A> 0) and A < -0).
Lf A generoUs T(t), -co < t < co, then IT(tli :;; lIfe.. ld ,
PROOF. The neces8ity of the inequality [*] follows from the reo
marks above, Theorem IB, and the relations R(A; -A) = -R( -A; A}
and a( -A) = -alA) (ef. VII.9_10). On the other hand if [*J is satis-
fied, hoth A and - A satisfy the condition of Theorem 13 and generate
semi-groups T +(/) and T _(t) respectively. One shows easily that the
approximating semi-groups stet) and SA(t) (of the proof of Theorem
13) commute, and hence T+(t) and T_(t) likewise commute. Thu8
Wet) = T+ (t}T _(t) is also a semi-group defined on [0, (0). However if
",.SD(A) = SD(-A).
W(t)m-", [ T +(t)"'-"' ] T _(*-'"
= T_(t) +
t t t
-+Aov+(-Am) = 0
as I -+ O. Thus dW(/}"'ldt = 0, and consequently W(I)", = "', for
",.5D(A). Since SD(A) is dense in 32, it follows that T (/) = T+(t) l.
Therefore if we define T(/) = T .(/), I 0 and T(/) = T (/), I ,,;; 0,
T(t) is a strongly continuous group of linear operators with infinite-
simal generator A. The inequality IT(t)I ";; lIfe )'1 is clear. Q.E.D.
EaoaI7rples. If T is an operator in a space 1 whose elements are
functions defined for each 8 in a set S, we shall. in the foUowing exam-
Similarly C[ - co, co] is the space of all continuous functions of a real
variable for which both limits "'(00) and "'(-00) = limx(8) exist.
_-m
The infmitesimal generator in these cases is the operator of differen-
tiation A = dldt. We shall verify this and find a(A) for the case of the
space C[(), 00]. It is easily seen from the uniform continuity of the
functions in C[O, co] that T(t) is a strongly continuous semi-group,
and moreover IT(t)1 = I, t :::>- o. Let", £SD(A) and y = Am, then
. [ "'(t+h)-X!/) ( )] 0
hm -yt =
h_O h
uniformly in t. It follows that y = ",' d.xldt. On the other hand let x
be a function in C[O, co] such that ",' . C[O, 00]. Then
] ",(t+ h 1- X (t) -""(/») if"lx'(8)-X'(t)lds
which approaches zero uniformly in t as h -+ 0 due to the uniform con-
tinuity of x'. Thus
SD(A) = {xl"" . C[O, oo]}
and A = dldt. It follows from the general theory that A is closed.
For A to helong to the resolvent set of A it is required that the differ-
ential equation Ay-y' = x should have a unique solution in C[O, 00]
for each",. C[O, 0:>]. In this case y = R(A; A)x. Consideration of the
general solution of this differential equation shows a(A) is the half
plane m(A) ,,;; 0, and
R(l.; A)(x. t) = J: .--"",(t+s)ds, meA) > o.
630
VII[. APPLICATIONS
VIII.1.18
VIII.1.I9
SEMI-GROUPS OF OPERATORS
6S1
The foregoing discussIOn applies with minor changes to the case of
the space C[ -00, 00]. Here T(t)("" s) = ",(t+s) defines a strongly
continuous group on (-co. co). Again A = dldt with domain SD(A)
= f"'I"" E C[-oo. oo]}. In this case o(A) is the imaginary axi8 and
(iii) The con8tantsK, in (ii) may be chosen so that JAK. rUexists
and is finite.
R(l; A)",(t) = f: r""'(t+s)ds,
= - f ", r"",(t+s)ds.
9I'(A) > 0
19 THEOREM. Let T(t), t 0, "" a 8Irrmgly continuous semi.
group of bounded opera1<Jrs in 3; with injinikttimal genera1<Jr A. If
P E9'(A) tlwn the opera1<Jr A+P deJimd 011 SD(A), is dOled and is tlw
injinitesimaJ genera1<Jr oj a semi-group T(t; A +P). FurIMr
91'(1) < o.
'"
The reader will have little difficulty extending the discussion above
to the case of tbe spaces L.(O. (0) and L.( - 00, co), 1 P < co.
A8 before A = dlrU. with SD(A) consisting ofthe absolutely continuous
functions 3:J in Lp for which :x' L.. The spectrum and reso]vent for-
mulas remain the same as for the spaces C. We shall return to these
examples to illustrate the later theory.
As III&Y be expected from the attention we have devoted to
Theorem 13, Corollary 14, and Corollary 16, it is important in the
present theory to discover when a closed. operator A is the generator
of a strongly continuous semi-group. Theorem 18 gives necessary .and
sufficient conditions, but these conditions are often difficult to verify.
in concrete analytical cases of interest. Consequently, we shall devote
the rest of this section to an elucidation of the problem of semi-group
generation from the point of view of perturbation theory. Our guiding
idea will be the following: if A is a semi-group generator, and if P is
not too irregular relative to A. then A+P i8 a semi-group generator.
A precise, though rather :)pecial case of this somewhat imprecise
principle is the following result, which is a particular case of Theorem
19 below: If A is a semi-group generator. and P is a bounded operator.
A+P is a semi-group generator.
The exact range of operators covered by our perturbation prin-
ciple is singled out in the following definition.
18 DEFINITION. If A is the infinitesilIl&l generator of a strongly
continuous semi-group T(I) we denote by 9'(A) the class of closed
operator8 P 8atisfying the conditions
(i) SD(P);;!SD(A);
(ii) For each t> O. there exists R constant K, < 00 snch tbat
IFT(I)"'I K,["'I for uSD(A);
T(I;A+P) = Sft(t).
_0
t o.
where S.(I) = T(t) and Sn(t)", = J T(t-S)PSft 1(8)"'ds for '" I 4nd
n I. tlw series being absolutely convergent. uniformly wtlh respecl to
t in each finite interval, Fer eaIJh nand"" tlwjundion Sft(/"" ..contin-
uous lor t O.
We will build up the proof of Theorem 19 through a series of
lemlIl&s. Throughout the remainder of this section. we shall use the
notations of Definition 18 and Tbeorem 19.
20 LEM1oIA. If P E 9'(A), th£n
(D) SD(P) U.>oT(t)I;
(b) The mnpping '" --+ PT(/)"" '" SD(A). has a unilfUl' extension
w a hourukd opera1<Jr (which we shall write PT(/» dejimd 011 all of I;
(e) PT(/)", is etmtmoous in t jor I> 0 4nd each", E I. If "'0
= lim (log IT(/m/l, lhen lim sup (log IPT(/)I)/t "'.;
t-HJ> t......o>
(d) if 91'(1) > "'D' Ih£n
PR(A; A)", = f: e-"PT(t)",dl. "'EI.
PROOF. Since SD(A) is dense in 1, by Lemma 9, statement (b)
clearly follows from (ii) of Definition 18 by virtue of 1.6.11.
Let "'0 E 1, "'0 = lim "'., where "'ft E SD(A). Then T(tj.r. --+ T(t)",o'
ft-+..
and PT(t)",. --+ {PT(t»",o' Since P is closed, T(/"". SD(P) and
P{T(t):>;,} = {PT(t»",.. This proves (a). To prove (c) let 0 < li < t.
The equation PT(/"" = PT(li)T(t-li)", shows PT(tj.r is continuous.
Since
log IPT(/)! log IPT(li)l+ log jT(t-li)l.
it is seen that
.
632
VU[. APPLICATIONS
VIII.I.21
VIIU.22
SEIdl-GROUPS OF OPERATOJl.S
688
Jim log IPT(/)I . log IPT(<5)1 . log IT(/-")I
sup :£ hm + hm = w..
C-+ , ,-+ t t-!>-D.> t
Thus (c) is proved, Statement (d) follows from Theorem III.6.20.
Q,E.D.
21 LEMMA. Lei f be a continuous function defined fur I > 0 wifh
values in if and suppose Ihat IbIf(t)ldt < co, If g(/) = JAT(t-B)f(s)ds.
lhen g(t) is in stI(P).
Pg(/) = S; PT(/-8)f(s)ds,
and g and Pg are conlintwus fum rms of 1 for t > O.
PaOOF. The integral defining g exists for each 1 ::2: 0 sincc IT(/)I
is bounded on each finite interval (Lemma 8). For each s < 1 the
vector T(/-8)/(s) is in stI(P) by Lemma 20. Thus Theorem III.6.20
wiU show that g(/) £ stI(P) and also establish the formula given for
Pg(/) ... soon... it is shown that the function B .... PT(/-s)f(s) is
integrable over the interval [0, I]. It follows from Lemma 20(b) and
the principle of uniform boundedness (11.8.21) that IPT(' )1 is bounded
on any interval not containing the origin. Let 0 < t" < I so that the
functions....IPT(/-B)1 is bounded and If(')1 is integrableon the interval
o ;;;; B :<;; t", while /1(')1 is bounded and B ....jPT(/-B)1 is, by Lemma 8
and Definition 18(iii), integrable on the interval t" :<;; s ;;;; I.
To see that Pg is continuous for 1 > 0, let 0 < 2 < 10 and let
M. = sup IPT(B)I for 10-2<1 ";; B ;;;; to+ ' Then IPT(/-B)/(s)1
:<;; lIf,lf(B)1 if II-I"I :<;; 11. Consequently, by Corollary IIL6.16.
lim f" PT(/-B)f(s)ds = J . PT(/.-B)f(s)ds.
f-Io-",Jo 0
22 LEMMA. Let f be a continuous /undiDn defined for t > 0 rDifh
values in I and supp""e that I: .-/f(B) Ids < co for some w. Let
w. = lim (log IT(/)!>II and F(A) = I::' .-A'f(s)ds Then, for Bi'(A)
, '"
> maxIm, w.),
(i) R(A; A)F(A) = S: c" S; T(t-s)f(B)dsdt,
and
Now
(ii) PR()'; A)F(A) = I.'" c lt P S: T(/-s)f(B)dsdt.
PROOF. Suppose that el().) > max(w, w o )' To prove (i) we have
R(A; A)F(A) = f: .-"T(/) If: . "f(s)dsl dt
by Theorem II. The function .--""+"T(/)f(B) is continuous on the
product (0. co) X (0. co) and hence measurable on the product. By
Tonelli's theorem (III.II.15) we have
R(A; A)F(.iI) = f: c" f: c"T(tll(s)dtds.
Now for each s we roake the substitution 1 .... (I-B) in the second
integral and interchange the order of integration again. Thus
R(A; A)F(.iI) = f: r c"T(t-s)f(B)dtds
= f: . " S T(t-B)/(B)dsdt.
Statenlent (ii) now follows from (i), Lemma 21, and Theorem In.6.20.
Q.E.D.
The last bit of information we need to be able to prove Theorem
19 concerns integmL; of a certain type important in other branches of
lIIRthematics as well. We collect this information in the next definition
and lemma.
f: PT(t-SI/(B)ds = f:' PT(.)f(t-s)x(O,t-oI] (.)ds.
and if M. = sup If(B)1 for 11 :<;; 8 ;;;; Io+ , the norm of the integral on
the right is bounded by M.IPT(s»). Thus
lim f' PT(/-a)f(B)ds = fto PT(I,,-s)f(B)ds.
t_ J" JlI
Combining this result with the limit above it is seen that Pg is con-
tinuous at the arbitrary point I. > O. The result just proved. if applied
to the case where P = I, shows that g is continuous. Q.E.D.
28 1JEFImTI0N. Let F and G bc Lebesgue me"-'urable scalar
functions defined on (- <JO, co ). We define the function F. G by
putting
(1<'. G}{I) = rQ F(/--s)GlB)ds
for all values of 1 for which the integral exists. The function F . G is
called the convolutitm of F and G.
634
VIII. APPUCATIONS
VIII.l.24
VIII.I.25
SEMI-GROuPS OF OPERATORS
635
We remark that if F and G vanish for B < 0, then the formula
for F * G takes the form
r: I(F * G)(/Jldt = r: I r: F(I-a)G(a)dsl dl
< r= r: IF(t-B)G(B)ldsdt
= r: r: JF(t-s)IiG(s)ldtds
= JFII r: IG(s )Ida
= IFIIIGi"
from which (a) follows. The proof of (b) is elementary. Stntement (c)
follows from (a) since
f: I(F* G)(tJldt = f: I(F, * GJ)(tJ/dt.
where Fl(/) = F(t) and G,(t) = G(t) for 0 < t < p. and Ft(t) =G,{t)
= 0 for I > P and t :S: O. Q.E.D.
25 LEMMA. (a) IfF and G are Lebesgue ""a.mroble ju,u:tions
tkfined on tM Teal line, !hl'n F * G = G * F,
(b) If F,G and H belong to 1.,(-00. +(0). then (F*G)*H
= F*(G*H).
PROOF. Part (a) follows immediately from the equations
(F*G)(t) = r: F{t-s)G(s)da = r: F(s)G(t -s)ds = (G* F)(t).
Part (b) follows from the equation
«F * G) * H)(T) = r: (f : F(a)G(t-s)dsj H(T-t)dt
= r: r: G(t-s)Ji'(a)H(T-t)dadt
= r: (f : O{t-s)H(T-t)dtl F(s)ds
= r: If : G(t)H(T-s-t)dtj F(a)da
= (F*(G*H»(T),
which holds for almost all T by (a), and by Tonelli's theorem (IILn.
14), since
(F * O)(t) = f: F(t-s)G(a)ds.
In the next two lemmas are proved certain basic properties of
the convolution whjch will be used in this section .and the next.
24 LEMMA. (a) If F and 0 belmrg to Ll(-oo, (0) (w;thT/?spedro
Lebesg1U measure), /hen F * 0 is tkfined for almost all t. i$ a fUIlction
in 1.,(-00, (0). and IF * Gil IFhIGlt.
(b) If F is in L,(-oo, 00) and 10(t)1 :S: M, th£n I(F * G)(t)1
< 1I11FIr
(c) Let F and 0 be tkfi=d for t > 0 and be BgU£ inregrable over
each finire interrol. Th£n (F * O)(t) = J F(t-s)G(a)ds is Lebesg1U
intl'gTable over each finite inleroal.
PROOF. To prove statement (a) we first show that the function
[s, I] -+ O(t-s) defined on the plane (-00, oo)X(-oo, (0) is measur-
able with respect to two-dimensional Lebesgue measure.
lf E is a subset of the real axis, let p( E) be the 8ubset of the plane
defined by pIE) = {[s, t]ls-t E}. Then p( U::' I E;) = U::'lp(E,),
pIE') (p(E»)', and p("') =.". Since pIE) is open if E is open, it
follows immediately that pIE) is a Borel set if E is n Borel set, Now
let E be a Borel set of measure zero. By Fubini's theorem (III,n.9),
we have
r: r: XplEJ (s, t)dsdt = r: r: XE (s-t)dsdt
= r: If : XE (s-t)dsj III
= f +oo O. dt = O.
_00
Thus, pIE) has measure zero if E has measure zero. It follows that if
E is in the Lebesgue completion of the a-field of Borel subsets of the
line, pIE) is in the Lebesgue extension of the a-field of Bore I subsets of
the plnne. Let U be an open set of complex numbers, E = {tIG(t) E U},
and D = ([s, t])O(I-s) £ U}. Then D = pIE), and now the measura-
bility of the funcbon O(t-s) follows immediately from 111.6.10.
Now let F, 0 1.,. Then, hy Tone1li's theorem (IILn.14),
J oo [" roo jO(/-s)F(s)H(T-t)ldrdtds
= IHIIIOIIJFh < 00
636
VIII. APJ'LICATIONS
VIII.1.25
VIII.I.25
SEMI-GROUPS OF OPERA"J:'ORS
637
and since the measurability of all our functions was proved as the
first part of the proof of Lenuna 24. Q.E.D.
Finally. we give the proof of Theorem 19.
PRoOF OF THEOREM 19, Let X(/) = IT(/)I and 'P(/) = IPT{/)I.
Then X and '" are measurable (cf. Lemma II). If en i. any constant
greater than en. = li""--.m log IT(/)II'. then there e,asto an Me < CO
such thatX(t) :;; lUe' ' forI :2: O. By Lemma /I and Definition 18(iii),
I€'P(t)dt < co for each (J> o. Put ",(1) = "'. and. inductively,
'P'o' = 'Plo- tJ * 'P' By Lemmo 24(c), we see inductively that an the
functions 'PI.' are Lebesgue integrable over every finite interval of the
positive real oxi.. Put X IO ) = X, x'.' = X * 'PI.'. By Lemma 24(c),
X 1ft ) is integrable over every finite interval of the positive real axis.
Let So(/) = T(/) and define
[*] S.(I)'" = f; Tlt 8)PS._l{8)xd8, for '" 6 if,
inductively. We shall show that this inductive construction is legiti-
mate by proving tha
(i) S.(t)X6 (P)
(ii) B.(t)x i. continuous in I for t > 0,
(iii) 18.(/)1 XI.'(/);
(iv) PS.{/)", i. continuous in 1 for t > 0,
(v) IPS"I/}I :;; 1jJ<n+ 1 J(t).
For n = 0, all tlUs is either obvious or follow. from Lemmas 20
and 21. Suppose that (i), . . ., (v) are known to hold for n = m. Then
it is clear from (i), (iv) and (v) that the integral in [*] exist8 for all
I> o. and may be used to define S_I' Statement. Ii), (ii) and (iv) for
the case n = m+l then follow from Lemma 21. We have
1 8 m+tl t )xl = ! f; TI/-8)P8 m {8).21d..!
< 1"'1 f; X(/-s)",lm+u(s)d..
= l"'IxIm+U(/).
which proves (iii) and Iv) for the case n = m+l. Consequently,
(i)" . ., (v) ore proved inductively for aU n.
\Ve now obtain an e.timate for the series I::'- OXI.'(/) which
majorizes I:' 018.(tll,
By Lemma 201c), for each en> en. there exists a constant
M", < co such that W(/) = IPT{/)I < M",."" for sufficiently large I.
On the other hand. we have seen that'P i8 integrable over every finite
interval of the positive real oxis, Thus, if we choose w. sufficiently
large,
:J:E i
f: ,,--w"'P(t)dJ < co.
Consequently. by 111.6.16.
lim f,'" '-"'PI/)dl = lim f'" rl'-w.II{, w"1jJI/)}dJ = 0;
J.__m 0 A-+oc 0
so that:!' if w > wl is chosen large enough, we will have
I: ,,--m'1jJ{/)dJ =" < I,
We w,1I now show. inductively, that
xl.)(/) :;; M e"'y..
This is clearly the case if n = O. Suppose that it is true for a given val-
Ue of n. Then, by Lemma 25(h),
XI-+1I II) = I: Xl.) (t-8)Y;(S)d..
;:;;: M",""". I: "--W'1jJ(8)d8
:5: Mo£\>eQl y'fi+l,
t>o.
:'£.E1,
t> 0;
3:£1;
Clearly lim S.{t) I in the strong operator topology. Since
.--..
By Lemma 21,
IPSm+l(t)xl = II: PT(t-s)P8 m {8)xd..1
:;; 1"'1 f:1jJ(I-s)y;,m+l'ls)d8
= 1.rlopIM2)(/),
x<.'(t) = I: X(/-8)",I.'(s)d.. :;; Mw' W ' f: '-.'op<.)(s)d...
it is clear that x'.Jlt) -+ 0 as I -+ 0 for n 1. Thus, since 18.(t)1
;:;;:: Xlo'{t), B.(t) -+ 0 for n 1. Hence, if we put 8.(0) = I, B.(O) = 0
for n O. 8.(/)x wiI!, for each .r in if. be continuous in I for I O.
Morecver, we will clearly have IS.I/)I -;; Mw.m'y.fort Oandn O.
It now follows that the series I::' oS.(t) converges absolutely,
uniformly in each finite interval [0, {fJ, and that
688
VIII. APPLICATIONS
VIII.1.25
VIII.1.25
SEMI-GROUPS O OFERATORS
639
w
[**) I ISn(I)1 ,,;; (I-y) lllfwewf.
_-0
We write S(l) = I::'- OSn(I), I;;; O. Since each of the terms of this
series is strongly continuous for t 0, it follows that the same is true
of S(I). Further IS(I)I ,,;; (I_y)-lllf w e"".
It remains to show that S{I), I ;;; 0, is a semi-group of bounded
operators with infinitesimal generator A+P, (A+P) = (A). To
see this note first that, by [**] and III,6.16. we have
f c"'S(s)",d" = i f'" e-"Sn(s):xd". :xdZ, .'1i!(l) > co.
Jo .....0 Jo
By Lemffi6. 22(i)
I: e-"'Sn(s):xd" = R(l; A) I: e "PSn_I(S):Xd".
Now repeated application of Lemma 22(ii) gives
I: ",-"Sn(S)"'d" = R(l; A)PR(A; A) f: .,.-"'PSn_,(s)xds
. . . = R(l; A)[PR(l; A}]n",.
Consequently,
fO> "-"S(s),,,<18 = i R{A; A)rPR(l; A)]n"" Bi(A) > w.
Jo oM>
By Lemma 20(d), and 18(;)
IPR(l; A)I ;';; f: e-G'tp(s)ds = y < I, Bi{A) > w.
Thus the senes I:.o[PR(},; A)]n converges absolutely. Let (A +P)
= (A). Recalling that R(A; A)! = (A) we have
Thus }'[-A-P with domain (A) has the bounded inverse
R(A; A) I::'-o [PR(A; A)]n. Con8equently A+P is closed Bnd
o,
R(A; A) I [PR(A; A}]n = R(A; A+B).
-0
The conclusion of Theorem III now follows from Coronary 16. Q.E.D.
&le. In order to illustrate the application of Theorem III we
consider the space C( - co, <0] and the group of translations {T(t)}
defined by T(I)("" s) = "'(I+s); this group has the infinitesimal
generator A = dlds (ct the examples following Coroltary 17). Con-
sider the operator A' = d:'lds' whose domain (cf. VII.II.6) consists of
all functions '" in C[ - co, <0] for which X and ai' belong to C[ - co, co].
That A' is closed was shown in Theorem VII.II.7. It is easily seen that
(A') is dense. Since alA) has been observftl to be the ;ffi6.ginary
axis, alA') is the negative real axis (ct VII.II.IO). If A > 0, then in
view of Theorem VII.9.5
R(A; A') -R(Vi; A)R( -Vi; A).
Consequently IR(A; A"U ,,;; A l, A> 0, and it follows from Corollary
14 that A' generates a strongly continuous semi-group T(t; A') satis.
fying IT(!; A')I ,.;: I,
We shall obtain an explicit expressIOn for T(I; A')... By Theorem
VII.9.4 and Theorem VII.9.5
R(A; A")(oT, s) = f. . R(I-'; A)("" s)dl-' , - co < a < <0,
2ni C,+C. (J-I-vA)(,u+vA)
(Al-A-P)R(A: A) I PRe},; A)J:
n-U
where C 1 and C 2 are small positively oriented circles about the points
I' = -VA and I' = VA respectively. On making the substitution
R(I-'; A)("" s) = f: e .''''(1+8Idt, 9i'(,u1 > 0,
= - r e-P'a:(t+a)dt. Bi{J-I) < 0,
and calculating residues, we obtain the formula
f o, e IIIv'1
R(A; A')(a:, s) = - x(s+tldt,
- 2V A
oo < B < 00.
0>
= I [PR(A; A)]na:- I [PR(A; A)] x = a:. a: e I.
ft=O 71=1
Moreover, if "'e (A),
o,
R(A; A){ I [PR(A: A)] }(Al-A-P)..
U
= ",+R(A; A) I [PR(A; A)]n Pa:
O
o,
-R(A; A) I [PR(A; A)]np", = "'.
=f)
We now substitute
640
VIII. APPLICATIONS
VIII.l.25
VIII.2
FUNCTIONS OF AN INFIN:I'r SIMAL CENERATOR
641
e I'Iv'A. f. 1);> rlf"e-t"/4r
-= dr
VA 0 VW
and invert the order of integration using Tonelli's theorem (III.ll.14)
obtaining
R(A:A")("" 8) = f. m e-"' ( I_ 1 m "-""''''(B+I)dt } dr.
o 2Vw _m
a ()2 <J
/l) ai Y(8. t) = as" Y(8, I) + h(8) as Y(8. I),
(2) limY{B, I) = "'.(B) unifonnly in 8.
0--.0
It is clear that the same method would establish the existence of
a solution to many other initial value problems such as. for example,
the one mentioned in the introduction to the chapter (provided that
the kernel K defines a bounded linear operator) or the problem ex-
pressed by the equations
However, we know from Theorem 11 thai
R(A; A")("', 8) = f: e-"T(T: A")(",. B)dr,
and thus it follows from Lemma 15 that
(1')
a ()2 a
ai Y(B, t) = <J8' Y(B, I) + "'{B) <J. Y(8. I) + h,,(8)Y(8. I).
1 J
T(T: A")("" B) = r"W"'(B+I)dt,
2Vm- -m
Now let hE C( -co. 00]. and let P be the (unbounded) operator
defined as follows:
(a) The domain of P coru;ists of all '" E C[ - co, co] such that '"
has 8 continuous derivative in a neighborhood of each point Iu for
which h(Io) *0, and 8uch that h(/)""(I) is io C(-co, co]:
(b) For "'ESD(P), (P",)(/) = h(I)""(/).
The operator P is easily seen to be closed.
We shall now verify the conditions of Definition 18, to show by
Theorem 19 that A2+P with domain SD(A2) is the gcnerator of a semi-
group. Clearly SD(A') SD(P). If '" E SD(A2) and I> 0. then
IPT(I: A2)("" B)I :0;; Ihll Tel: A")("" B)I
= Ihl l -1 J ( -B)e ('-J'/""'( )d$ 1
4IV,,' -
:0;; 1"'lIhl f. e--o!')" d = 1"'lIh] .
- 2/0i1 0 V"j
T>O.
(2') lim Y(B, I) = "'.(B) uniformly in 8,
' o
for any"', h" E C( - co, co] and "'. E'II(A").
2. Function. of an Inf'mite.imal Generator
Thus conditions (ii) and (Hi) are satisfied also. In view of Lemma 7(b),
for each "'0 E'II(A"), the function
Y(8. I) = T(t: A"+P}(",.. B)
is a solution of the initial value problem
It was shown III SectIOn 9 of Chapter VII how an operational cal-
culus could be constructed for an unbounded closed operator A with
non-void resolvent set. Specifically, to each function J analytic on
alA) and at infinity we assigned a bounded operator I(A) such that
mapping J -+ I(A) was a homomorphism. In this section we suppose
A is the infinitesimal generator of a strongly continuous group of
operators T(I), - CO < I < co. and show in this case how bounded
operators may be assigned to each of a larger class of functions. This
class will include functions which are analytic on alA), but not neces-
sarily analytic at infinity. The functions to be considered are bilateral
Laplace.Stieltjes transforms. \Ve also discuss the inversion of these
operators by limits of polynomials in A.
Throughout this section, we let T(/), - 00 < t < co, be a strongly
continuous group of bounded operators in a complex B-space ;E, and
A its infinitesimal generator. We recall (cf. 1.17) that there exist
positive constants M and w such that IT(t)1 :0;; Me ld, and s\lch that
the spectrum of the infinitesimal generator A lies in the vertical strip
-ru < ().} < ru. Moreover,
.
642
VIII. APPLICATIONS
VII1.2.1
VIII.2.8 FUNCTIONS OF AN INFlNlTEBIMAL GENERATOR
648
R(A; A)x = J: .-"T(I)xdt,
= - J: '->'T(t)zdt,
a(A»w
a'(A) < -w
III e.....,)I,1 S; Ke,...,I,I. -00 < 1< 00.
Thus, since {3£Y(A),
f: e.-."Itlv(pl ', dt) = f: el.....'ItIIt) vCP, dt)
S; K f: ",_IIt1 v (p. dt) < 00.
and (J' '" yeA).
Since 1' "'-e-"II,u-}.I 1 IIIO"....JltI for I (A)I < ro+E and
I (A)I < W+E. we have. by III.6.16 and 111.10.6.
. f(A)-f(P) . 1 m r" -e "'
Urn = l.m P(dt)
p....A ),-1' p-+A -. A-I'
We begin our analysis with a discussion of bilateral Laplace-
St.eltjes transforms.
1 DEFINITION. We denote by YeA) the family of all finite
complex valued measures p defined on the Borel sets in (- 00, (0)
and such that
J:-. O'...+<IIt! vIP; dt) < 00,
where e is a positive number (which may vary with (!). The function
t(A) = f:. e-"{!(dt). -(w+e) < alA) < w+.
is called the bilaUral Laplace-Slidrjes translorm of p. We denote by
'Y (A) the family of bilateral Laplace transforms of measure P" 09' (A).
If {3 in YeA) is continuous with re8pect to Lebesgue-Stieltjes meas-
ure and if F is the function in L,.(-oo, 00) given by the Radon-
Nikodyro theorem (III.1O.2) such that PIE) = J £F(s)ds the function
teA) = Cm'-" F(/)dt
is called the bilateral Lapl.tw£ tra....farm of F.
We now prove certain basic facts con ermng Laplace-Stie1tjes
transforms.
= C (-/)e-"P(dt)
= C. ,->'P(1) (dt), la(),)1 < W+E.
Thus' is analytic in lat{A)1 < ro+... and
df (A) = f'{A) = f . e-"{J'I1 (dt), lat(A)1 < W+E.
d..1
It is clear that an inductive repetition of the argument just given will
show that
2 LEMMA. Iff is in 'Y(A). and II),} = f:,..-"{J(dt). lhen I i.
analytic in a strip -(w+d) < &t{A) < (w+d). The 11U:asures defined
for each Borel Bel E by
(J'ft'(E) = f E (-I)"{J(dt). n = 0, 1,2, . . '.
belong 10 YeA) and
d n , f .
- (A) = I''''(}.) = trA'{J''''(dt)
dAft -0:>
= J ", (-I)"trA/P(dt), -(W+5) < a(A) < w+e.
PROOF. For eachn and each 5, < 5 there is aconstantK such that
I (A)I < ro+e.
Q,E.D.
8 DEFIN1TION. If a. (J are in YeA) let ax{3 be the product
measure defined on (- 00, (0) X (- 00, 00) (ef. Section 111.11), It
was shown at the beginning of the proof of LeIlUIlA 1.25 that if E is B
:Borel subset of the real line, the set PIE) = {(a:. y)I"'+y £ E} is a
:Borel subset of the plane. Fot each Borel subset E of the real line let
,,(E) = (ax{3}{P(E)}, We call" the amvoluliLm of a and {3 and write
'Y = a * {J. It is dear that V is a Borel measure Bnd a * (! = P . a.
Now let E:.. . . _. Eft be disjoint Borel sets so that
f''''(),) = C ..-"{JI )(dt).
ft ft ft
L Ir(E.)1 = L!(aX{J)(P(E,»I S; Lv{aXp. E,).
t-l 1-1 '_1
It follows from tlUs inequality and Lemma 111.11.11 that
vIr, E) v(a)Xv(p)(P{E» = v(a). v({J)(E)
644
VIU. APPLICATIONS
VIII,2.4
VIII.2 6 FUNCTIONS OF AN INFINITESIMAL GENERATOR
645
for every BoreJ set E on the real line. By UI.lO.B(b) and Theorem
IU.Il,1S, we have
[oJ r F(r)y(dr} = r r F{s+t)a.(ds),6(dt)
if F IS )'-integrable.
FilUllIy, we remark toot by Fubini's theorem
y(E) = r r XE(S+t)a.(M){J(dt)
= r a(E-t){J{dt).
I/{A}I <;; M r emh1v(a.; dt).
Thus I{A} is bounded. We note that for each 10 the function f,P,)
= ..... is in ,v(A), being the transform of the measure which assigns
the value one to the point t = -10 and vanishes on each Borel set not
containing -t.. Moreover, f..fA} = T(t,,). If 19l{).)1 > w then the
function fd defined by fd().} = (a_).) l is in ,vIA) since
1 f.
-= r"tf"dt,
a-A 0
9l(a) < 91(A),
4, LEMMA. Let a and,6 be metJ8UTl!sin 9'(A) with bilaWralLapku:e-
Stieltjes transforms I and g. Then y a.,6 is in 9'(A) and
= - J o clitf""dtJ
-oo
9l(a) > 9l(A).
Moreover.
r.. r''r(dt) = f(A)g(A),
-(w+e) < ai(A) < w+e.
'4{A} = - J: ""T( -t)dt = J: ."""'T(t)dt
= R(IX;A). ai(a.) > w,
PROOF. Since the variations of y. a, and,6 are related by v(y, E)
vIa) . v(j!) (E),
S:oo .'.1(_' v (1', dr) <;; f: f:", .,..+.)I...lo(IX, M)o(,6, dt)
,:;a; U:ooe...H>I,Tv(IX.M») U:Oo.,..HJhTv{{J,dl))
by Fubini's theorem, and thus y IS In 9'(A J. If . is 8ufficiently small.
it is seen, from formula [oJ toot, for lai(A)/ < ru+e. we have
rOo e-"y(dt) = Do, ro, e I"MIX(dt),6(M)
= Ir r"a(dl») II.: .--",6(M»)
= f(A)g(A), Q.E.D.
and .similarly
fd{A} = R(a: A), ai(a) < -co,
6 THEOREM, If f and g are in ,vIA) then aI, I+g and Ig are in
,vIA) and
(a) (af){A) = a/{A}:
(b) (/+g){A) = f{A}+g{A}:
(c) (fg){A) = I{A}g{A}.
PROOF. Statements (a) and (b) are clear from the linearity of the
formula defining the operator I{A}. To prove (c) we observe thAt for
each linear functional :xo. .
5 DEFINITION. Let I. ,vIA), and
f(A) = f:oo '-"a(dt), -(co+e) < 91(A) < co+e
whcre a. 9'(A), If A is the infinitesimal generator of the strongly
continuous group T{t) we define the operator I{A} by the formula
I{A)", = r T(-t):xa.(dt), :xd.
Since IT(t)1 < lUemt.1 the above formula shows that
:x'/{A}g{A}", =:x' ro, T( -s)g{A}.xa(M)
=;x. roo T( -s) rm T( -tj"'P{dtJ..(M)
= S:mr :x'T(-s !):xP(dt)..(M)
= f:m '" * T( -r):xy(dr)
where y = a * (J. By Lemma 4, (fg)(A} = J ..e-Ity(dt). Thus I{A}gfA}
= (/g){A). Q.E.D.
For I in ,vIA) and u: in SD(A2) we shall obtain, in the ncxt two
646
VIII. APPLICATIONS
VIII.2.7
VIII 2.8 FUNCTIONS OF AN INFINITESIMAL GENERATOR
647
lemmas, a formula for f{A}a:. This formula will enable us to relate the
present operational calculus for A to that constructed in Section
VIL9 and will be used in the diseussion of the inversion of convolution
transforms to follow.
It is convenient to begin by making a convention with regard to
contour int£ogra.ls. If c is a real number. then Fe wiJI denote the in..
finite contour consisting of two vertical lines: the line .A = c +iT,
- co <... < co, directed upward. and the line l = -c+i-r, - CO <...
< co , directed downwards.
Then, successive substitution in the identity
-:r (aI-A)RVt;A)a:
R(,u;A)a: = - +-
rx.-p rx.-p
7 LEMMA. Let rx. be a complea: number and c be a rea! number
chosen BUCh lhat (J) < c < lot(rx.)!. Thm. fot a: in (A').
[ * J _ 2:... r e'R(A; A)(aI -A)'a:d..\
T(I)a: - 2niJr. (rx.-A)"
PROOF. First we note that since R(A; A) = JO' e-"T(I)dt.
IR(l; A)I KJoel--Il"'I'dt for ot(A) > w, so that IR(A; A)I is uni-
formly bounded in each half plane ot(A) > w+c. Similarly, IR(A; A)I
is uniformly bounded in each half plane ot(A) < -(J)-C. Thus the
integrand in [*] is of the order of IAI-4I as IAI --+ co. so that the integral
in [*J is well-defined. Let:r E (A') and let B(t)", denote the integral
in equation [*1 above. Suppose first that t ;;>: O. Then if ot(,.) > c,
f. 0 1 i R(A' A)(aI-A)' 1
,-p' B(t)",dt = ---: ' a: ,('-P)' dId,.
o 2,,,,, r. (rx.-A)' 0
l r R(A; A)(aI -A)'a:d..\
= 2",d r. (,.-l)("'-A)'
The integrand in the last integral is O(lll--S) as III --+ 00 in the half
plane ot(l) c, and also in the half plane ot(A) ;;;; -c. Thus, using
Cauchy's throrem, we may replace the contour r, by two small nega-
tively oriented circles about A = a. and A = p respectively alld cal-
CIliate the residues to obtain
shows that
f; c P ' B(/)"'d.t = R(,u; A)", = f; ""'T(I)"'d.t,
On applying linear functioTmIs to both sides. it follows, by Lemma
1.15, that B(I)'" = T(I)a:, '" E (A'), I ;;>: o.
Applying the same reasoning to the 8emigroup T( -I), which has
the infinites.imal generator -A, we see that
_ 1 i e'R(A; -A)(aI-A)'redA
T(-I)'" - -. ( A)' I O.
2JtJ. ra 1%.-
Substituting -A for l, and remembering that B( -A; -A) =
-R(A; A), we find that
1 r e--A'R(A; A)(aI+A)'a:dA
T(-t)'" = 2niJ r, ("'+A)' I O.
f. 0 RVt; A)(aI-A)":r R{rx.; A)(aI-A)'.,
c"' B(I)",dt = -
o (rx.-pl' (rx.-p)"
R(a.; A)'(aI-A)'a: -0; (aI-A)a: R(P; A)(aI-A)'o;
- =- - + .
"'-I-' "' P (rx.-I-')' ("'_1')'
If we put -C( for a and -t for t l we obtain
1 i e' R(A; A){aI -A),.,dA
T(e)a:=-
2ni r. (",-l)'
Thus T(/)a: = B(I)a: for all real I, Q.E.D.
8 LEMMA. If f i. in reA) and lal(",)! > C > w. IMn
I i I(A)
f{A}a: = -. - R(A; A)(aI -A )":rdl, u S\)(A'),
2m r. (",-l)2
..here the number c is such lhat w < c < lot(a.) I and BUCh lhal f is
analytic on the conlour r,.
PROOF. Since f(A) = J:>",e--"{I(dt) for some P in .9'(A) by Lemma
7, we have
. r f(A)R(A; A)(aI-A)"",dl
2n,Jr. (a.-A)"
= f oo { r C"R(A;A)(od-A)".vd..\ } (I(dt)
2",i _ Jr. (rx.-A)'
1 f '"
= -. T( t)"'P(dt) = f{A}",.
2m -co
I :5: 0,
648
VIII. APPLICATIONS
VIII.2.9
VIII.2.11 FUSCTIONS OF AN INFINITESIMAL GENERATOR
649
Fubini's theorem is applicable here since J::"e( t<)ltlv(ti,dt)< 00 for
e > 0, and, as was shown in the first paragraph of the proof of
Lemma 7, IR(A; All is uniformly bounded on r,. Thus there is a
constant K < 00 such that
1 "--" R(A; A)(ed-A)"", I I <:;; Kcl'I(IAI+I)-2.
(a-A)"
Q.E.D.
graud isO{IAI ") as IAI 00 with JBI'(A)I ;?; c. Thus we may replace the
contour C. +C, in the displayed integral by the contour re' It follows
from Lemma 8 that I(A)x=I{A}x for "'c (A'). By Lemma 9,
(A') is dense in 3Z, and since the operators I(A) and I{ A} are bounded,
we conclude that I(A) = I{A}. Q.E.D.
We consider now the problem of inverting an operator of the
form I{A}. The problem is complicated by the fact that the inverse
transformation, if it exists, is onti.narily unbounded, and cannot be
constructed directly by the operational calculus given so far. However,
if a sequence of polynomials A can befound such thatJim P.(A )f(A} = I
9 LEMMA. If C is a closed uperolor wilh dense dumain and non-
void 1/i8olrJent set, thnl (C') is deme in if for each porilive integer n,
PROOF. If a. c e(C), then (C') = S!J«ed C)n) = (R(a.; C))nif.
Thus if ",*(SD(C')} = 0, then [(R(a.; C))n]*",* = [R(a.; C)*Jn",* = O.
The equation R(a.; C)*y* = 0 implies that y*(SD(C» = 0, and since
(C) is dense, it follows that y* = O. Hence (R(a.; C)*)n",* = 0 im-
plies ",* = O. The desired conclusion follows from the Hahn.Banach
theorem. Q.E.D.
fi OO
suitably on <T(A), It is to he expected that lim p.(A )/{A]x = '" for
n OO
10 THEOREM. If I is in 7""(A) and is analytic at inlinity, then f{A}
is equal to the operator I(A) of Delinition VII.9.S.
PROOF. Let I belong to 7""(A), so that I is analytic in a strip
JBI'(A}I <:;; «>+c, and let f be analytic at infinity. Then the singularities
of I form two bounded sets HI and H. in the right and left half plane
respectively. Choose a. such that BI'(a.) > «>+e and let C I and C. be
two simple closed negatively oriented Jordan curves such that C I con-
tains HI u{a}. C.contains H 2 , and C I and C.do not intersect the lines
BI'(A) = ::I:(<<>+c), 0 < c < d.
We recall that the operator g{A) is given by the formula. (cf.
Theorem lfII.9. )
g(A) = g(00)1 + . f. g(A)R().; A)dA.
2,n:1 c,:t-c.
Let g(A) = f(A)(a.-A)-2. Then, if x e (A2), it is seen by using the
operational calculus of Section VII.9 (cf. Theorem VII,!I.5), that
f(A}x = I(A)R'(a.; A)(ed-A)"",
= i /(A)R(l; A)(ed-A)'''' dJ..
2",; c,+c, (a._A)'
Since f i8 bounded in a neighborhood of infinity, the displayed mte.
every o'V In 1. Theorem 13 below gives sufficient conditions for the
validity of an inversion fannuls. of this type.
II LEMMA. Let p be a polyrwmial in A 01 degree m and leI I and
pI both bolong to 7""{A). Th£n f{A}3Z (A"') and p(A)I{A}.x =
(pf){A}.x for x in I.
PROOF. First suppose that x is in (Am+2). By Theorem 6. Theo-
rem 10, and Lemma 8,
I i p( A )f( A ) R ( A' A )( ed-A ) ''''
Jlm(o:; A)(pf){A}x = -. ' dJ..
2",. r, (a_).)m+2
Writing p(A) = I7_oa.(a-).)' and using Theorem 6, Theorem 10,
and Lemma 8 again, we have
I i ( '" a. }
Jlm(a.;A)(pf){A}",=-. L '. R(A;A)(o:I-A)".rdJ.
2:n:z T" .,,,,,0 (a_;')flH2-
{ m . . } ] i /(A)R(A;A)(ed-A)''''
= }; aRrn '(a'A) - dJ.
,-0 . '2ni r, (o;-A)2
m
= (Rm(a.;A) };a,(o:I-A)'}p(A)f{A}x
._0
= Rrn(a.; A)p(A)f{A}x.
Consequeotly, (pf){A}x = p(A)f{A}x for.xc S!J(A"'+2). Now let "'eI
and let "'. . SD(Am+2) with "'n '" (cf. Lemma 9). Then I{A}x. -+ f{A}x
and p(A)/{A}x. = (pf){A}",. -+ (pf){A}x. Since p(A) is closed on
650
VIII. APPLICATIONS
VIII.2.12
VIII.2.14 FUNCTIONS OF AN INFINITESIMAL GENERATOR
651
5D(Am) (Theorem VII,9.7), it follows that f{A}il€5D(Am) and
p(A)f{A}.. = (Pf){A}",. SinceSD(Am) is den8e (Lemma 1.8 and Lemma
9) this equation holds for all '" in I. Q.E.D.
12 DEFINITION. A sequence of polynomials p.(A) will be called
an i1werriflg sequeru:e for a function IE r(A) if
(a) The functions {p,J} belong to rIA);
(b) Ip.(A)f(A)1 ,;; M and lim p.(A)/(A) = I in a strip 19l(A)1
s: CO+E; fi OO
(c) I(p,J)fA}/ ';; M, n = 1,2.....
18 THEOREM. If {P.} u an im>erting 8equeru:e for a furu:tion f in
rIA), t1um
operator f{A} il and only if '" is in 5D(p.(A» for ecu:h n and flu: sequence
{P.(A)",} i8 /Jo1nuW.
PROOF. We know from the previous theorem that if", = I{A}y
then lim p.(A).x = y 80 the sequence {P.(A)y} is bounded. To prove
.-
lim p.(A)f{A}", = "'.
_co
",.I.
the converse 8tatement, let {p.(A)",} be bounded. Since I is reflexive
we may 8elect a subsequence of integers in,} and " vector y such that
"'''p.,(A)", --+"'''y for each a;" E I" (cf. IL8.28). We shall show that
'" = I{A}y.
We have
a;"f{A}p.,(A)", = f{A}"m"p.,(A 1m --+ "'''f{A}y,
However, if lu5D(p.,(A», then T(t)mE5D(P..{A» for - ro <t < +ro.
by 1.7, and
f{A}p.,(A)", = f: T( -t)1'., (A)"",(dl)
= p..<A) f: T(-t).M(dl) = p.,(A)/{A}",
by Theorem 111.6.20. Thus p.,(AI/fA}", --+ '" by Theorem 18. so that
"'''/{A}y = a:*a: for ",* E I*, and m = f{A}y. Q.E.D.
Erampks.Let I be one of the spaces C[-ro, ro} or L.(-ro. rol,
I ;:;; P < ro discussed as examples in Section I, and let T(t) be the
group of translations T(t)(a;, 8) = ",(t+s), with infinitesimal generator
A = dldt. We recall that alA) is the imaginary "xis. If I(A) =
J:,.,,-uP(dt) E rIA), then the transformation I{A} takes the familiar
'''convolution'' form
PROOF. "First let a; E SD(AS). By Lemmas 8 and II,
["] p.(A)f{A}", = (p.f){A}.x = J r. P.(A}f(A) ;s(rxl A)S", ell
Cor w < c < 19l(<<)1 and c-w sufficiently small depending On n. We
have assumed that Ip.(A)f(A)1 ,;; M in a strip /9l(A)1 < W+8. where
8 is independent of n. In the first paragraph of the proof of Lemma 7 it
was seen that IR(A. ..1)1 is uniformly bounded in any ha1f plane
Bi'(A) > w+eandinanyhalfplane&l'(A) < -(w+8).HenceCauchy's
integral theorem shows that we may take c in Cormula ["] to be any
real con8tant between wand 1&1'(<<)/, provided that c <w+e. Thus.
we need not, and sball not. allow c to depend on ...
Applying Corollmy III,6.16 it is Seen that
I 1 R(A;A)(rxl A)''''
lim p.(..1)f{A}", = -----: , ell = "'.
R--+OO 2m r. (et-A)
since (Lemma 8) the integral on the right is g{..1)'" where g is identi-
cally equal to one. Since the trnnsformations (p,J){A) are assumed
to be uniformly bounded and 5D(A') is dense in I, the theorem now
follows from Theorem II.I.I8. Q.E.D.
The following corolJary shows that when J: is reflexive, an in-
verting sequence characterizes the range of f{A} in a simple way.
14 COROLLARY. Let I be re/lc<rive and {P.} be an inverling se-
quence fur a fu'1ldion f in rIA). Then a veclm- '" is in flu: range of the
U{A}",](t) = f: a;(I-s)fi(ds).
In particular, if P is continuous with respect to Lebesgue measure, so
thatp(E) = JEF(I)dtCorsomeFin (-ro. 00), thenfisthebilateral
Laplace transfonn of F and
U{A}",](t) = f: F(t-a)"'(8)ds.
The Stieltjes transform
I f co (1-8)
yet) = - sech - ",(a)ds
"" -00 2
652
VIII. APPLICATIONS
VIII.2.14
VIII.a,I
EXERCISES
653
provides an example for the inversion Theorem 18. In this case,
3. Exenioes
I f I
I(A) = - .,->, scch dl = [C05 :nA]-l.
:n 2
n ( A2 )
Vn(A) = II 1 - 2 .
0-' (k _ )
I Let T(t) be a semi-group of bounded operators in I such that
",*T(/)'" is continuous on [0, 00) for each",. I and ",*. I.. Prove that
T(/) is 8trongly continuous on [0. 00).
In Exercise 2-9 below T(/) is a strongly continuous semi-group
of bounded operators defined on the interval [0, 00). The operator A
is the infinitesilIUll generator of T(t).
2 Suppose lim,_o t l[T(/)"'-x] =y weakly. Prove that
1im,_ot l[T(t)"' "'] =y strongly, and thus y. (A).
8 Prove that n:;"_1 (An) is dense in S. (Hint. Let X denote
the class nffunctions K in C (O, 00) each vanishing outside a compact
subset of (0,00). Prove that if ID {yly = J;;'K(/)T(t)",.K .X,
",.J}, then ID is dense in J and ID n::'_I (An).)
4 (a) Prove thatlim AR(A; A).x = '" if IAI 00. larg AI < ,,/2.
._
Since
( J.. )
cos:nA=.TI 1- (k- r '
we choose
The functions v.(A)/(A) have the representation
Vn(A}/(A) = J.:" r"G.(/)dt
where it ma.y be shown that the kernels G n are positive. Thus
(b) Prove that if "'. (An), then
l(p./}(A)J ;0; J: Gn(/)dt = (P.f)(O) = 1,
Consequently
n = 1, 2, . . n
{ -> AO", }
lim An+1R(A;A}",- _ = An",
A_co 1-0 },k+l
d'
lim IT ( 1 - ( dt" r ) f sech (t-8) "'(8)ds = "'(I)
"-+00 k-l k- 71. _OJ 2
2
in tbe norm of any of the 'paces L p ( - 00. + 00), I P < 00. or
C( - 00, 00]. A function y . L p ( - 00, (0), 1 ,.; V < 00, has the repre-
sentation
as IAI --+ 00, Illl"g AI < :n:12.
5 Prove that if / > 0 and c > OJ, where OJ = Iim(log IT(/)lJII.
then ,.......cc
T(/)X = lim f r [ 1 _ ITI ] e,.H." R(c+iT; A).xdT.
r""'co 2x -r T
3! 1".
1 f (/-8)
yet} = - .ech - "'(8)ds,
n _00 2
X E" L'D( -00, co),
uniformly in each interval [e, lIe]. e> O. Show that at 1=0 one
obtains the limit "'12.
6 (a) Show tbal
if and only ifthe sequence {Pn(dldt)y(t)} is bounded in norm. Reference
to anal .ticaJ details and further applications will be found in the
notes at the end of the chapter.
kA", 1 f. '+' AO
(AR(A; A}]"", ="'+- +-. R(I';A)A 2 .xd.u
A 2". , , I"(A-.u)"
for :E . (A2) and A > c > OJ, where w is as in the previous exercise.
(b) Prove that if I > O. then
[ k ( k )J "
T(/)'" = ':: t R t; A .x,
x.I.
654
VIU. APPLICATIONS
VIII.s.7
VIII.8.1S
EXERCISES
655
7 Prove that if t > 0 and", E SD(A"), then
.,.-1 t1< 1 J, '
T(t)a: = - A"", + - (t-B) ]T(B}A"",ds.
._0 kl (n-l)! 0
8 Prove that if '" E SD(A"), then
lim t-. [ T(I)X _ ".i t" A."' J = A".x .
, o .-0 k! n!
9 Defining the differences
.1:T(t) = h-» ._o(-I)" . <:) T(t+kh),
show tlmt if I :;-: B. then
1 f " (l-e ')x(8+ )
T(t)(", s) = - ,
2n -.1-2e- t cas E +e- 2l
defines a strongly continuous semi-group on [0, 00). Equivalently,
mE J
T(t)("" 8) = .--1.10 "'"e""
--cc
if
:r(a) I it!:n e1n3 ,
-00
1 f .
"'" = - "'(B)..--'''''d.t.
2 ...-.
(t-B)"
T(t)x = Jim -o - .1 T(B)X,
._0 n!
feEl,
18 Let 3: = L,( --no n), 1 ..,; p < 00. Show that the family of
operators defined by the formula
1 f "
T(t)(.x, s) = - II. (s-f, t)x(f) .
2n _
mE!:>
t:;-: 0,
the limit existing unifonnly for t in any finite interval.
10 Let E:;. be the set of points 8 [B1' . . ., s..] in Euclidean
n space whose coordinates t!( are non-negative. Let T(a). 8 be 8
family of bounded operators 8atisfying
T(8+1)=T(s)T(I), T(O) =1, IimT(s}a:=T(t)a:, u3:. B,teE';..
. I
where 8.(B, t) = 1 +2 _I e ' cos ...., is a strongly continuous semi-
group on [0, 00). E<Juivalently, T(t)(.x, s) = !:""'ne 't+'" if .x(8)
"'. Show that the infinitesimal generator of the semi-
group T(t) is the operator A whose domain SD(A) consists of all
periodic functions I of period 2n witl. absolutely continuous first deri-
vatives and second derivatives r lying in L... and which is defined by
AI =,. for I eSD(A).
14 Let 3: = L,( 00,00), I;:;; P < co. Show that the family
of operators defined by the formula
t f '" "'(s- )dE
T(t)(.x, B) =;; _ f"+L' ' "'E 3:,
Let h, = (0. . . ., 0, h. U, . . .. 0) be the vector in E:;' wIth h> 0 In the
i.th place and zeros elsewhere, Let A(h. i} = h ][T(h;)-l] and
SD(A,) be the domain of the operator defined by
A,,,, = Jim A (h. i)a:
. O
where this limit exists. Prove that n '-1 SD(A,) is dense in 3: and
..
T(8)X = lim II ""AI"') "',
A-+O i-I
"'E 3:.
is a strongly continuous semi-group on [0. co).
15 Let 30 = L.( - co, co), 1 P < co. Show that the family of
operators defined by the formula
1 f -r'
T(t)(OI', s) = "'(s- )e' ,
v'm
a::E "
11 (Weierstraos) Let '" be a continuous complex valued function
defined on a compact subset K of Euclidean n-space. Then", is the
unifonn limit of polynomials in the n variables. (Hint. Let I be the
B-space of all functions uniformly continuous on En with the uniform
norm and suppose K E:;'. Define T(t)(",. 8) = ",(t+8) for tEE:;. and
apply Exercise 9.)
12 Let I = L,( -n, n), 1 ,::; p < 00. Show that the family of
operators defined by the formula
is a strongly continuous semi-group on [0, CJ). Show that the infini-
tesimal generator of the semi-group T(t) is the operator A wbose
domain SD(A) consists of all functions f e L, with .absolutely contin-
uous first derivatives and with second derivatives r lying in L., and
wbich is defined by AI = f ', I. SD(A).
16 Let 3:=L.(O, 00), l p<CJ). Let T{t)(X,B) = ",(t+s),
656
VIII. APPLICATIONS
VIII.8.17
VIII,4
ERGODIC THEORV
657
'" E I. Show T(t) is a strongly continuous semi-group whose infinite-
simal generator is A = dlds. Show c(A) = {AISl(A) ,;; O} and o(T(1})
= {AIIAI ';; I} if I> O.
17 Let A and B be closed linear operators in a complex B-<;pace
I with non-void resolvent sets.
(a) If)",. etA) and B()",; A) is compaet (weakly compact), then
R(A; A) is compact (weakly compact) for each A. etA).
(b) 1fS!)(B) !;; S!)(A) and iffor some A. etA), B()",; A) is compact
(weakly compact). then B(,u; B) is compact (weakly compact) for
every p.e(B),
18 Let A be the infinitesimal generator of a stmngly contin-
uous semi-group on [0.00). If BE B(I) and R(A; A) is compact
(weakly compact) for some A E e(A), then B(p; A +B) is compact
(weakly compact) for every p< e(A-'--B).
19 Show that the partial differential equation
il.x(s, I) (1'>;(8, t) f. '"
- = -,,- + .-u'",(u.l)du,
ill .." 0
lim "'(8,1) = ",o(s),
'_0
has a solution for every function .xo. C[O, 00] for which x E C[O, co].
20 Show that the partial differential equation
(I",(s, I) (I''''(s, t) . (I f '" x(u. I)d"
- = +e-' -f£ ( S t ) +
(II (I,' ils' _'" 1 +(s-u)"'
lim x(s, t) = "o(s),
<->(j
has a solution for every function xl) E" C[ - 00. co] for which
a: . E C[ COy ooJ.
21 Let :£ = C[-oo, 00] and A = dlds with S!)(A) =
{X!f£'(I) < C[ - 00, con. Show that the closed operator A' is not the
infinitesimal generator of 8 strongly continuous semi-group of bound-
ed operators.
4. Ergodic Theory
A fundamental mathematical question in the statistical mechan-
ics of Gibbs and Boltzmann concerns the existence of certain types of
time averages. The problem may be formulated in abstract terms as
follows: The momentary state of a mechanical system is de.cribed by
specifying a point in a "phase space" S. The mecbanirn.l system is
assumed to be governed by the classical Hamiltonian equations and
so is subject to a principle of scientific determinism whereby it is
known that an initial state :r will, after t seconds have elapsed, have
passed into a uniquely detennined new state 'If. Since 'If is uniquely
determined by x and t. a function .". on S to S is defined by the equa-
tion 'II = "',(",). The flow"'. is assumed to have the property that
<i)
"'.«/>,(",)) = ""-H("')'
for aU points f£ in phase space and for all times sand j, The identity (i)
may be proved for certain mechamcal systems and in particular it is
easy to verify if the Hamiltonian function is independent of the time.
Now any numerical quantity determined by the momentary state of
the mechamcal system (for instance, the force exerted by the given
syt>-tem. assumed to be a large collection of gas molecules contained in
a vessel) will be given as a real function I defined on S. If the initial
8tate of the 8ystem is specified by the point", in S, the value of the
quantity / at time I will be 1("',(Il!)). The quantity 1("',("')) will ordinari-
ly fluctuate very rapidly with I. as. for instance, in the case where we
consider the force exerted by gas molecules on the wall of a container;
since the force depends upon the number of molecules recoiling from
the wall at any given instant. What is significant, and measurable in
the laboratory, is not the quantity /(<I>.(x)) but its average value
I i T
T 0 /(.". (,,»)dt
(ii)
computed over a certain time interval 0 t $: T. Ordinarily, the
quantity T, which is dctermined by the inertial character oruma-
croscopic" instruments, such 8.S pressure gauges, thermometers, etc..
is very large compared to the natural rate of evolution of the mechan-
icalsystem under consideration. This may be expected to be the case,
for example) with a gas in a ve;sel where. in each second. the molecules
658
VIIJ.. APPLICATIONS
VIIU
VIII.4
ERGODIC THEOR'\'
659
travel thousands of feet and recoil from the waIl nlillions of times.
Thus. from the physical point of view, the time T involved in the
experiment is large enough to give a good value for the limit
1 i T
Em - t(</>. (;e»)dt,
T-+eo T ()
lim { i T (Ud)dtl (;e).
T-+co To'
(iii)
and we shall show, following J. von Neumann and F. Riesz. that this
limit exists in the norm of L.(S, E, 1'), and also, following G. D. Birk-
hoff, that the limit exists for almost all points in the phase space S.
Actually, our discussion will treat a semi-group of operators which
has a considerably more general form than the one defined by equa-
tion (vi).
However, in order to explain the main concepts, it is convenient
to avoid certain technical difficulties by first treating the discrete case
rather than the continuous caSe. For example, instead of studying a
continuous flow </>, we study the discrete flow 1>., where r/>.HO> = r/>.r/>...
Since r/>. = r/> , we shall be studying averages of the form
1 N-l
N n?;/(r/> (x)),
tEL.(S,E,p),
which, in physical theories. is assumed to exist.
Thus. the mathematjcian is led to the problem of determining
whether or not the limit (iii) exists. The next four sections are devoted
to a study of this problem and various of its generalizations which
arise in the theory of stochastic process<:s.
It should be observed that this problem is one of interest pri-
marily to the mathematician. To the chemist or physicist the main
question. and one which is still in need of a. satisfactory discussi'IJn, is
that of determining when the limit in (iii) is the constant space
average
Is/(')p(ds)
peS)
taken with respect to ordinary Lebesgue measure p in the phase space
S. When a mechanical system has this property it is saiel to be ergodic.
From the time of Boltzmann various physical assumptions known as
ergodic hypot1lue8 have been made in order to insure that the system
is ergodic. In what follows we shall ob8erve that systems which are
metrically transitive, in the sense of G. D. Birkhoff, are ergodic but
we shall not endeavor to discus8 the difficult and important problem
of determining which mechanical systems are metrically transitive.
One key observation in the limit theory to follow is the theorem of
Liouville which asserts that, in 8 conservative mechanical system, the
measure p has the invariance property expressed by the equation
(v) p(r/>,'(E» = p(E), E E E,
where E is the a-field of all measurable sets in S. If, for each !. we
define the linear transformation V, by the equation
(vi) (V,t)(x) = 1(4). (;e)), I. L,(S, E, p},
then equations (i) and (v) 8how that {V,} is a semi-group of unitary
(norm preserving) transformations in L,(S,:E, ,,). The limit in (iii)
may be expressed in terms of U, as
(iv)
where r/>, is a mapping of S into itself.
In probability theory an important class of operators. called
laTkov pracesses, in a natural manner. Let P be a non negative
function defined on S :<.E satisfying th.. conditions
(a) for each E.:E, Ph E) is a measurable function on S;
(fJ) for each s. S, P(.. -) i8 a countably additive measure on E:
(1') pes, S) = I. ..S.
We may regard the number P(" E) as bemg the probability that the
process sends the point s into the set E after the elapse of one unit of
time. With P we may associate the operator T defined by
(Tf)(.) = Is f(t)P(., dt),
where f belongs to a suitable class of functions on S. The reader will
observe tlmt the family of such operators certainly includes those of
the form f(') -+ I(r/>(')). It wiU be seen that the discussion which we
give in the sequel includes the operators arising from a Markov pro-
cess as a special case.
A word about the organization of the following sections. In Sec-
tion 5) we obtain results in the discrete case concerning convetg\:nce in
the mea14 and in Section 6 the pointwise convergence is treated for the
660
VIII. APPLlCAT10NS
VIII.5
VIII.5
MEAY ERGODIC THEOREMS
661
discrete ctt.se. These results are applied to obtain in Section 7, cor.
responding mean and pointwise convergence theorems for the contin-
uous case. Sectlon 8 is concerned with a certain c1ass of operators T
for which the sequence of average. {N-l ! :t Tn} converges in the
uniform topology of operators. Finally, in Section 9, many applica-
tions and jllustrations of the theory are given in the form of exercises.
Theorem 9, and Corollary 10 below, the space (S, 1:, 1') is assumed to hc
a finite measure sp""e. This is done only to avoid technical complica.
tions and the changes needed to give similar results for a. general
measure sp""e will be found in the exercises.
The symbol A(n) will be used for the averages
1 7.1-1
A(n) = - 1: Tm, n I.
11 ",_0
5. Mean Ergodic Theorems
In this and the following three sections we sball discuss the
behavior of the averages of the iterates of a linear operator and thus
attempt to throw Some light upon the problems of statistical mechan-
ics and probability theory which were presented in the preceding
section. However. it wj]] not be necessary to restri.ct our attention to
operators associated with the flows arising in statistica.lll1echanics or
tbe Markov operators of probability theory. In the present section
conditions on an operator T in an arbitrary complex B-space :£ will
be given which are necessary Bnd sufficient for the convergence in I
of the averages
1 _1
A(n)=- ! Tm
n IJ_f)
It is desirable, at times. to emphasize the dependence of A(n) upon
T and, 0;> these occasion8, we shall use the symbol A(T, n) instead of
A(,,).
I THEOREM. Let the averages A(,,) of the males of the opera!ar T
in the B-space :£ be blJUnded. Then the set of those paints;J; in 1: fOT UJhU:h
the Bi'fJ'Ioi'TU% {A(n)",} is is a closed lineaT manifold consisting
01 aU vectorS;J; for which the set {A(n),,} .. weakly BffjUmlially compact
and Tnxfn converges to ?eTa.
PROOF. This theorem is essentially a corollary of Theorem VII.1.4.
We shall apply VII.7.4 with f(A) = I-A. fn(A) = (! :p')/n, and
with I replaced by the set Io of allm in 1: for which the sequence
{A(n)x} = {fn(T)",} is weakly sequentially compact and Tnxln -+ O.
Since {A(n)} is bounded, Lemma II,3,30 shows tlw.t the set of those
;J; for which {A(n),,} is weakly sequentially romp""t is a dosed linear
numifold. The identity
Tn n-I
- = A(n) - - A(n-I)
n n
(*)
of the iterates of T. These general conditions will then be interpreted
for operators in a Lebesgue space L.(S, 1:.1') which have the form that
is encountered in .statistical mechanics. In the present section only the
strong cOn\'ergetlce of the averages A(n) is discussed. Questions con-
cerned with the almost everywhere pointwise behavior of A (n)f for a
function I III Lp are postponed until the next section.
For simplicity of statement. we will ""sume throughout the re-
mainder of this chapter that we are dealing with complex B-spaces.
In Sections 5, 6 and 7 below, this restriction is not rea1Jy essential,
and the reader will see readily that a slight rewording of the proofs
given (if, indeed, any is needed) will establish the results of these
s('ctions for real B-spaces also. Only in Section 8 wi]) the restriction
to complex B-spaces play an)' important role.
In the later sections the measure space (S. I, 1') will be an arbi-
trary one but in the mean ergodic theorems as given in Corollary .5.
shows that {Tnln} is bounded and hence, by 11.1.18, the set of;J; for
which T'xln --->- 0 i8 a closed linear manifold. Thu8 3::. is a closed linear
manifold and, since a continuous linear operator maps weakly con-
vergent sequences into weakly convergent sequences. we have
T.I. I.. Hence, we may apply VII.7.4 to the re8triction of T to the
B-space:£.. The identity f(T)fn(T) = (1 - Tn)ln show8 thatthe hypoth-
esis, f(T)/,(T)x --->- 0, of Theorem VII.7.4 holds for x in X.. Since f
has only the simple root A = I and since I,(I) = I, it follows from
VII.7.4 that {A(n)x} ronyerges for every IE in :£.. Conversely, if, for
somc 3: in I, the sequence {A(n)",} is convergent. then it is weakl)'
compact and the identity (*) shows that Tn.xln -+ O. Q.E.D.
662
VIII. APPLICATIONS
VIII.5,2
VIII.5.6
JI.IE:.A ERGODIC THEOREMS
663
2 COROLLARY. When 1M BIrong limit E=limfiA(n) "",.618 it isa
projulion 01 I upon 1M manifold {xlTx = x} ollixed po;nu 01 T. TM
romplrmenwry projmicn has the closure 01 (I -T)I lar irs ra .
PROOF. Since (I-T)A(n) = (I-Tfi)/n, the identity (*) shows
that TE = E and thus that A(n)E = E and E2 = E. Hence E is
a projection upon the fixed points. Since E{I-T) = o the range E'I
of the complement E' of E contains (I T)I. Now let re* be a linear
functional with ",*(I-T) = O. Then ",* = ",*T=",*A(n)=",*E and
so re*E' = O. It follows from Corollary II.S.la that E';£ is contained
in the closme of (I-T)I. Q.E.D.
a COROLLARY. 111M {A(n)} is lJou"dallhen it romJ£Tge8
in 1M strong opeTator topology il and only il T'xJn ""''''''''ges 10 "eTO
lorreina JundameNllllset and the srqu£7lC£ {A(n)x} is weakly sequentiaUy
compacl lar x in a juru1nmcnlol set.
PROOF. It was shown at the beginning of the proof of Theorem 1
that the set of", for which TnxJn -->- 0 is a closed linear manifold and
also that the set of a: for which the sequence {A(n)",} is weakly se-
quentially compact is a closed linear manifold. Thus these sets are
both;£ and Theorem 1 shows that {A(n)x} is convergent for every x
in I. Q.E.D.
4 COROLLARY. 11;£ is reflr.r:i:v€ lhen the sequt'f!C" {A(n)} COnt0£rg£8
in the strong opmdor /npJlogy il and only if il is bounded and {TnxJn}
Ctmtvrges to %eTO lor each x in a fundamenra! set.
PROOF. This follows from Corollary a ;md Theorem n.3.28.
Q.E.D.
by Corollary IV.S.ll, weakly sequentially compact as a sequence in
L,,(S, E, p). The desired conclusion follows from Corollary a. Q.E.D.
The prereding general results will now be applied to the case
of an operator in Lp(S, E.I') having the special form TI = Irp, i.e..
the form (Tj)(s) = 1('P(s)), where I is in L.(S, E.p). and where '1' is a
map of S into itself. Throughout the l'emainder of this section it is
assumed that (S, E, 1') is a linite positive measure space. In order to
apply Corollaries 4 and 5 to the operator T we must first discover
conditions on tp which are sufficient to insure that the operator T
maps L.{S. E,p) into L.(S. E.p) and has the corresponding sequence
(A(n)} bounded. Since the points in L.(S, E, ,,) are not functions but
classes of equivalent functions) it is .seen that T may not be regarded
as being defined on L.(S. E, ,,) unless I(rp(s)) = g('P(s» almost every-
where whenever I(s) = g(s) almost everywhere. The following lemma
will give conditions on rp which will insure this and .also allow us to
infer the p-measurability of TI from that of I. This lemma and some of
the theorems to follow will apply to functions in a class somewhat
more general than L (S, E.p). Fnr thi8 reason it is convenient to de-
fine the operator T as the mapping in the class of all functions with
domain S which is given by the equation
(i)
(Tj)(s) 1(9'('»'
..S.
Thus if f is a fonction on S so is TI and the range of Tt is contained
in the range of I.
6 LEMMA. Let I * 0 be a comple", B-space, (S, E.p) a linite
posil"'" measure space and rp a map 01 S inlo irsell which sutislies tM
conditi(}n&
5 COROLLARV. Let (S, E,p) be a lini!e I7!£tJ8W'C space and let T
be a linear opeTator in L,,(S. E, 1') whieh maps essenJially bourukd
IUflctions inlo eS8€ntially bounded junctions. Let tM llN'f'ages A(n) be
unilormly bouwkd as opeTa!orsin Loo(S. E, ,,) as well as inL,,(S, E,p).
Then/Mse t1T:f3Y1ges are strongly convergent in L,(S, E.p) il and only il
Tnlln oon1v;rges to:no in L,(S, E, 1') lor t:VeT!J I in ""me lundamenm!
eet in L,(S, E.,,).
(ii) 'r'(e). E. p('r1(a» = o. il a. e. E and p(a) = O.
For evn-y lunefion I on S 10 3:' leI TI be delined on S by the equation (i).
T""n T maps p-meOBUrabk lunctions into p-meamrable lunctions and
p-equivalent /undio,,", into p--equivalent Jundi01l8. Furthn7nore T is a
<'Onlinuous linear map 01 1M F-space lIf(S) = M(S, E,p. X) 01 all 3:'-
valued p--measurable lundWns iflto irsell.
PROOF. Since ,,(S) < co, every ,,-measurable function is totally
p-measurable (Definition IJI.2_1O) and thus. as WaS shown at the
beginning of Section IV.H. the spaee M(S) is an F-spaee. The Con-
PROOF. If f is the characteristic function of a set in E then, since
the sequence (A(n)/} is bounded as a sequence in L (S, 2', 1'). it is,
664
VIII. APPLICATIONS
VII1.5.7
VIII.5,7
M AN ERGODIC THEOREMS
665
dition Iii) shows that T maps p-equivalent functIOns wto ".eqUlvalent
functions, i.e., 1(9'(8» = g(9'(s» for p-almost all s if lIs} = g(s) for
,,-almost ails. Thus T may be regarded as a linear map in the F-space
M(S) provided that TI is p-measurable whenever I is p-measurable.
To see that T has this property we recall (111.5.18) that the Lebesgue
extension X* of I consists of all sets of the form e* = eUa where e
is in E and a is a subset of a set b in E with I'(b) = o. Thus. by (ii),
r 1 (e"} = 9' l(e)U9'-l(a),
where 9'-l(e) is in E and rl(a) is a subset of the set 9' I(b) in E
with p(9'-I(b» = o. Thus .r 1 (e*). E* and hence
(iii) 9'-I(E") E*.
Now let I be a I'-measumble function and let G be an open set in .:E.
Then, by Lemma 111.6.9, r 1 (G) is in E* and hence, by (iii),
U<p)--l(G) = 9'- 1 U- 1 (G» .E".
Also, since I is ,,-essentially separably valued, conditions (ii) show that
TI is likewise I'.essentially separably valued. Thus, by LelllIlUl 111.6.9,
TI is p-measurable for <:;very I'-measurable function I on S to .:E. and
T is " linear map of M (S) into itself. It remains to be shown that T
is a continuous linear map in M(S). To do this we shall use the closed
graph theorem (11.2.4). If Ifl I and Tlfl -+ g in .M(S) then. by
111.6,18. there is a subsequence (f..) with I..(s) -+ I(s) and 1.(9'(s»
-+ g(s) for every 8 in S except for those s in a ,,-null set e. Thus
1.(9'ls)) -+ 1(9'(s» exceptfors in theset9'-l(e). ItfolJows from hypoth-
e8is Iii) that 1'(9'- l le» = 0 and so g(8) = /19'(8» for p-almost all s
in S and thus TI = g, which shows that T is closed. The closed graph
theorem now yields the continuity of T. Q.E.D.
The next lemma will g;ve an additional restriction On 9' which
will insure that T maps L (S, E. p, X) into itself.
7 LEMMA. Let J: *- 0 be a cample", B-space. (S, E, p) a linire
positive mal.OUre sp= and q; a map vi S into ilsdl lor which 9'-I(E) 1:.
Then, lor 1 :<;;; p < 00, the operator T, defined by equation (i), maps
L (S, E, 1', ;{) into ilsell if and only il
1'(9' I(e»
(iv) sup = M < 00.
..x pee)
F'urlhermure, wlu:n this condition is satisfied T is a CQ1ltinuous linEtlT
map in L,IS, E, ".!) whose norm ITI is equal to MI/p.
PROOF. First suppose that T maps L, = L (S, E, p. 3Z) Into
itself. It will be shown that T is closed and hence (11.2.4) continuous.
Since T is defined on L , it maps p-equiva1ent functions into p-equiv-
alent functions. Now let a*-O be a fixed vector in J: and let e be
a ,,-null 8et in E, Tben T(aX.)=aX.-I'd =0 in Lv Thus9'--l(e} is
a ,,-null set in E and the conditions (ii) of Lemma 6 are satisfied. Since
convergence In Lt} implies convergence in measure (111.8.6), Lemma
6 shows that TI. -->- TI in measure if Ifl I in L.. Thus if I. -->- I in
Lp and TI. -+ g in L. then TI = g and T is closed. By the closed graph
theorem (II.2.4) T is continuous and thus (II.8.4) bounded. If a*,O
is a vector in I Bnd e is a set in E then
lal"(9' lle»'/. = IT(al'.)1 ;-;; ITlJalp(e)l/p,
",(,,,-l(e)) :<;;; ITI'p(e),
which 8hows that M ,;; ITlp < 00. Thus if T maps L. mto Lp .t is
continuous and (iv) holds.
Conversely, let q; have the property (iv). Let I be a p-integrable
simple function assuming its values aI' . . 'J 0:.... on the disjoint sets
e lt . . ., en of positive . Then Tf has the va.lues «:1, . . ." IX" on
the sets 9'-I(e 1 ), . . ., q; lle.) and
fl
ITII = [1: la,I'Jl{9' I(e,})]I1.
'-1
fi
;-;; lIP/' [lla,I.",(e,}]'/p
':-1
=111 1 /'1/1.
Since the ",-integrable simple functions are dense in Lp (111.3.8), this
shows that T is continuous on a dense set in L'IJ and thus has a unique
continuous extensIOn l' defined on all of Lp and with norm 11'1 :<;;; MI/,.
Now if I. -->- I in L p then Ifl -+ I in p-measure and Lemma 6 shows that
TI. -+ TI in measure. Since TI. -+;PI in L. we have (1\/)(s) = (T/)(s)
for p-almost all 8 in S and hence T = T is a continuous linear map in
Lp with norm [TI;:;;; MI/'. On the other hand it is clear from the
definition of 111 that ITI 11£1/". Q.E.D.
666
VIIL APPLICATIONS
VIII.5.8
VIIB,9
MEAN ERGODIC THEOREMS
661
8. LEMMA. La (S, E....) be a finite 71U'asun space, and
'I' a map of Sima iuelj fo-r which '1'-' (E) E. Suppose that there is a
connan! M lor which
:;:: log IA(n)I /> < log MIl>,
and so
(vi)
IA(n)Jp 5: llPI',
n= 1,.2,......
(v)
1 I
- ! ...(<p j(e» :;:: Mp(e),
n,=o
eE 1: , t1 = 1,2, . ....
Conversely, suppose that T maps Ll into Ll and that IA(n)I, :;:: M
for n :;:", I, Thrn for e in E,
lft-' 1 1ft '
- ! p(<p---1(e) = -! X 'e.) (s)p(ds)
21:1=0 Snj-{I
Then jar every p with I < p < 00 the operator T dcjfwd by equation
(i) maps Lp(S, E, p) inlo ilselj, and the averages A(n) are unilormly
bountled as vpaawrs in Lp(S, E, pl. Conversely, il the operalor T
dejined by (i) maps L,(S, E, p), inlo ;tsell, and il the averages A(n)
are unijormly bounded as operatGrs in Ll (8, E, p), then there e",i.!.
a connanlllI in terms oj which (v) holds.
PROOF. The symbols ITlp, IA(n)lp will be used for the norms of T,
A(n) respectively when they are considered QS operating in L.
= Lp(8, E, I')' Likewise for a ,u-measurab1e function I, tbe symbol
I/lp is used for (fsl/(s)lpp(ds»l/p whether or not this is finite, We shall
first prove the sufficirncy of the condition (v). Using (v), with n = 2,
it is seen that IL(<p I(e» ,s; (2M I)p(e) for every ein E. and thus, by
Lemma 7, ITlp < OJ for each p with I P < OJ. This inequality also
shows that p(ep-I(e» = 0 if pee) = 0 and thu8
= IA(n)r..1 5: Mp(e),
n= 1,2, .....,
which completes the proof of the lemma. Q.E.D.
&mark. It is worth noting that the final inequality and the
inequality (**) taken together 8how that
I I
IA(n!!, = sup - ! p(rr' (e)JIIL(e).
8EE n j_O
(*)
ITI",, I.
9 THEOREM. (Mean ergcdic theorem) Let (S, E, I') be a linite
positive mea#tU'e spoce and let 'P be a mapping 01 8 into iuell with the
'f'TOPI'rliEs that <p-1(E) E and
171-1
- ! p(<p j(e») 5: Mp(e), HE," = 1, 2, _..,
nj-D
Now let I be a p-integrable sImple functIon which assumes tbe values
all. . .. ale On the disjoint sets ell'. ", f!k respectivel)", Then
I _1 k I PI-I
- ! T'I = ! "-r-! X..-'(,,)'
n J""'O II_I n 1_0
and so. using (v),
I T'/I ,s; M J, 1,,-,11'(1:;) ,;;; 1111/11'
(.*)
IA(nlll < M.
where M is a COllstant intkpl'7ldenl 01 e and n. Then, lor every p with
I < p < OJ, the transloT1lW1ion T defined by the equation (TI)(o) = 1('1'(0»)
ua continuous lil1Lar .nap in L. L.{S, E, I') and the averages A(n)
are strongly canvtTgenl in L.,
PROOF. By Lemma 8 the sequence A(n) is bounded. Also if
1/(811 < K for 0 in S then ITn(j, o)lln ;;;; Kin and so the throrem fol-
lows from Corollaries 4 and 5. Q.E.D.
It should be oOOen'ed that a measure pTl'seroillg lranslO1'mntion 'I'
(i.e., One for which p(<p I(e)) = p(e) for ""<T)0 e in E) satisfies the hy-
pothesis of the preceding theorem. It has been mentioned earlier that
it is exactly this type of transformation which arises in the study of
conservative mechanical systems. The transformation rp is metrically
tranrilive if, for some e in E, l'(eJ<p-'e) 0 then either I'(e) = 0
or p(e') = O.
and thus
The Riesz convexity theorem (VI.IO.Il) and the inequalities (*) and
(**) now give
log IA{n)lp (I - ) log IA(nJl"" + log IA(")11
fJ68
VIII. APPLICATIONS
VIII.5.IO
VIII.6.1
POINTWISE ERGODIC THEOREMS
669
10 COROLLARY. I I, in addit"'" to the: conditions 01 t& preceding
lheorem, it is assUmffl tMt rp is mea&ure preserving and 1I1dricaUy
transitive rhet., jar each j in L.(S,I, p), tkelimillim n A(n)j is almosl
egual to t& constaJIt space average J s I(s)p(ds)/p(8).
PROOF. Let g = limn A(n)j so that. by Corollary 2. Tg = g. Thus.
for every Borel 8et E We have. modulo p-null sets,
6, Pointwise Ergodic Theorems
This norm IS defined by the equation ITlp = sup ITlip where the su-
premum is taken over all I in the domain of T with I/lp ;:;;; 1. If
ITI II < CD and l' < co then T has 8. unique continuous extension to
L. and the same symbol T wIll be used for the extended operator.
Most of the results of this section are concerned with an operator T for
which ITI, ;:;;; I and IT[", 1. It follows from the Riesz convexity
theorem that ITI. I for I :s;;: p co, so that T is.a continuous linear
map in each space L., 1 ;:;;; p < w. It should be noted that the map
J -+ /q;, discussed in Section 50, whkh arises from a measure preserving
transformation 8 -+ fjJs in 8, comes into this category. Another example
is that of a Markov process; still another is an operator of the fonn
J ....a(.)/(VJ(.)) where the multiplier a is a measurable function with
lal", ;:;;; 1. Our principal objectives wi!\ be to demonstrate the almost
everywhere convergence of {A(n)!} and to obtain estimates On tbe
function sup. JA(n)/].
1 LEMMA. (Hopf) Let P be a poIIitive operator in L"" wirh
!PI", s: 1. Let (e"} be a decreanng 8equrnce 01 cI1maetRristic fundicnt8
..ilk.. zero lor k > n. Then there is a 8"'JU1"'CC' {g., 0 ;:;;; k} in L= such
tMt ij i :2: o. then
(i) 0 ;:;;; g, ;:;;; g,ef+l;
(ii) 0 ;:;;; e'+'(II<+1-g,);
(iii) e'+1 = e'+l(g,+PgHI+P'gH'+" .).
PitOOF. Let g, = 0 for i ;;;:; n, aod. for i < n. define g, by down-
ward induction from the equation
(slg(8) E} = {slg(q>s) e E},
so that p«(g-IE)A(q> lg lE») = O. Hence, it follows from the deli-
tion of metric transitivity that either p(g IE) = 0 or pIg-IE) p(8).
For an arbitrary e > 0 there is. since g is almost separably valued
(III.6,IO), R sequence {En} of disjointBorel8ets each of mameterIess
than 8 and such thatg(a) EUEfl for almost a!lain S. Thus for 8ome"
we have p(g-IEn) = pIS) which means that Ig(s)-g(t)1 < e for all
sand t in the complement of a null set. Therefore, for almost all s,
g(s) = g, a constant. Since VJ is measure preserving Jsl(s)p(ds) =
Js{A(n)j(8)}p(ds) = Jsg(s)p(ds) = gp(8), which completes the proof
of the corollary. Q.E.D.
The B-space 1: of the prereding section wi!! now be replaced by
a space L.=L.(8,I,p.) where (S,I,p) is an arbitrary positive
measure space. For an operator Tin L. and a point I in L. the symbols
(Tf)(s) and T(f, a) will be used for the value at the place s of one of
the functions in the equivalence elms TI. As before, the symbol A(n)
will denote the a-verage n- l Tm and sometimes, when it is de-
sirablc to show the dependence of A(n) upon T, the symbol A(T, n)
will be used instead of A (n). As usual the 8ymbol III. will be used for
the p norm
I/lp = (J 1/(8)I.p(ds)r'P,
= C8S sup I/(s)l,
..s
(I)
Then clearly
(2) e HI = e i +1(g,+Pg'+I+' . .),
which proves (Iii). We shall next show that
(3) g,+Pgl-t1 +P'g,+.=+... ;:;;; 1,
g, = e'+l(I_Pg'+I_P'g,+._.. .),
O;:;;;i <no
0::;:; i,
0;:;;; i.
I < p<oo,
This is clear for, :2: n while for i < n it may he proved bydownward
induction as follows: since (I ei+I )g, = 0 we have, by the induction
hypothesis.
(I-e'+I)(g,+Pg'+t+.. ,) = (I-ei+I)P(g'+I+Pg,...+...)
s: (I-eHI)PI < I-e'+1,
p= 00,
of a. measurable function on S. At times it will be convenient to use
the notion of the p norm 01 an op<TalDr T whose Mmain is deme in Ll'
670
VIII. APPLICATIONS
VIII.6)!
VIII.6.S
POINTWISE ERGODIC THEOREMS
671
which. when combined with (2), proves (8). From (I) and (8) it IS
seen that
_l
e, I P;I ;;;; 0,
j=m
m <i.
e H1 g, = g, = e i + 1 [1-P(g'+I+Pg'+2+" .)] ;:;; o.
which proves (i). To prove (ii) we shall first prove, by induction down-
wards. that
Upon adding these inequalities we get
(1)
' I
I Ie,P;1 = Ie H1 P;1 > 0,
i>mJ-m 1;:71'1
O m.
(4)
(g,+Pg'+I+" .)-(g'+I+PgH'+" ,);;;; o.
o i.
The preceding lemma .s nOW applied to the adjoint operator p. in L
so that there are functions g, E L , 0 i. with the properties (i). (ii)
of that lemma and also with the property
(jjj') e' = e'(&. + p.g,+p.'g.+.. .).
Let g_1 = 0 so that from (1) and (iil we have
o :S I e""+l(gm-gm--I) I e'+'P;f = I I e'+I(g..-g,, ,)P'f
m0:1.0 f "" m;;:O f;:JI'l
,
= I I (1!..-g"_I)e'+lP;f = II!;e'+IP;t = Ig,P;I.
I U om-iJ I O 1;;:0
Consequently
o J (I I!,Pi/)(s)p(ds) = f I (P"g;)(s)/(s)p(ds).
s i O S I O
Since p.' g, > 0 and I = Ii is negative on S-Er;;; S-E. we see there-
fore that
Suppose that (4) holds for i> j. Then, by (2) and (8),
(5) e'+l(g;+Pg'+I+" .-gm-Pgm-.' ,)
= eH1 e;+l(g'+I+PI!H.+...) ::2: O.
Also. since (I_e'+l )g; (1-e'+1 )g;+I = O. we see from the indue.
tion hypothesis that
(6) (1-e'+l)(g,+Pg;+l+" .-gm-Pgi+'-" ,)
= (I_e H1 )P(g;+.+Pg;+I!+'" -gi+,-Pgl+'-"') ;:;;0.
Thus (4) follows by adding (5) and (6). Since e<+'.'+l = e'+2 we see
from (I) and (4) that
e'+'(g"'I-g,) = e>+'P(g'+I+Pg.+.+.. .-gH.-PI!H'-"') ;:;; 0,
which proves (ii). Q.E.D.
2 LEMMA. (Hvpf)LeIPbeapusiti.V!opnalorinL.",.th !PI, I.
Then, Ivr wtTg real I in LJ and ""ery positive inte{!P' n, we have
fE/(s)p(tIs) ;:;; 0 where E = (sl sup A(P, k)(t.s) ;:;; O},
l;:;;k 7I
PROOF. For i > n let E, be void and for 1 :;:; i < n let
o J I (p.' g,)(s)f(s)J-l(ds).
BI O
Since e 1 i8 the characterIstic functIOn of E it follows from (iil') that
2;"0 (p., g,)(s) = I for S in E. Thus f"f(s)p(ds) ;:;; O. Q.E.D.
S LEIIMA. Let A be a boundro subset of L with r<A r;;; A for
lexl = 1. Then sup 1/(')1 = sup !Jtl_
ffA r A
E, = (8IA(i)(f, 8) ::2: 0; A(j)(f. s) < 0; j < i),
where A(n) = A(P. n). Let E' = E,UE'+lU ... so that El = E
and let e, and e' be the characteristic functions of E, and E' respec-
tively_ Then
i-I
e, IP'f;:;; 0,
j=O
..-I
e.IP;/ S: o,
1=0
m <i
PROOF. The suprema are taken in the lattice ordering of L , Let
gl = sup 1ft. )1, g. = sup !Jtf. Then, sincel/{')1 ;:;; !Jtf, we have g, z g.,
/E.A f A
nence. to prove the lemma. it will suffice to show that I!. ;:;; 1/(.)1 for
every I in A. If thi8 is false, there is an I in A. an " > 0, and a measur-
able set e of positive measure such that If(s)l ;:;; g2(S)+" for s III e.
LetN bea positive integer with 41/1 :n < Ne. Since 0 ;:;;; arg I(s) < 2n
there is an integer i N and a measurable subset Ii of e with positive
so that
1J72
VIII. APPI.ICATIONS
VIII.IJ.4
VIII.6.4
POINT1VISE E GODIC THEOREMS
673
2"1/1"" e
IBi/(o)-f(o)1 ,;;; 11(0) sin arg f(o)1 ,;;; < Ii' 0 HI'
real scalars" and real funcbons! In L"nL"". For an arbitrary fin
L,nL"" we let Pf = P9if+iP /f. It is evidentthat P is additive and
that p"J = "Pf for" real. Thus to see that P i8 linear it suffices to
note that iPf = Pif, i.e., that P9f(itl+iP/(if) = i(P9iI+iP/f)
for each f in L, n L"".
To see that IPI"" ,;;; ITI"" we note that PBif = [JtPf and thus. by
Lemma 8,
measure and such that 2ni/N ,;;; arg f(s) < 2Jt(i+l)!N for 0 in e1"
Since e-""'IN f 8 A we may and shall assume that 0:':;: Brg f(s) < 2Jt/N
for S' in el. Then
Bnd hence 9f1 ;;;; g.+e/2 for s in el which contradicts the definition of
g. and proves the lemma. Q.E.D.
I(T"/)(-)I ,;;; pn(lf(-)j),
l $n. f8L1"
I(PfU.)] = 8UP :iiP"f = sup PBi,,!
1«]-1 Icd-l
,;;; Plf(')1 = sup I(Tg)(.)I ,;;; ITI..I!I",,"
1.(.)1"'11(.)1
for 18 LlnL"". which proves that IPI"" ,;;; ITI"".
To prove that IPI, ,;;; ITI I we apply the method used above ro
the adjoint operator T*, which i8 defined in L: = L... In this way we
construct aD operator PI in LtxJ with
4. LEMMA. Let (8,:E. 1') be a a.finife me<1$IU"I' opace and let T be
a bom,ded Zinear opt'TalJJr in L, wltose L"" nvrm i8 also finite. Then !Mre
i. a poritWe ZitlUll' aperator P in L" wlto.. L, and L"" norms do '/Wt ex.
ceed those 01 T and which is IJ'!{,8h that
PROOF. Using the completeness of the lattice L"" (Theorem IV.
8.23), we define PI for 0 $ f e L" n L.. as sup [JtTg where g varies
over aU elements in L.. with Ig(')1 ,;;; f. Thus. by the pl'<'Ceding lemma,
PI = sup 9fTg = sup I(Tg)HI. 0 $ f e L"".
I,I.U';I I.HI';1
It is clear that PI ;;;; 0 if 0 ;:;; f 8 LI n L"". Also, if Igk II ,;;; II 8 L 1 n L""
and Ig,(.)J ';;; f.eL"nL"", then BiTg,+BiTg.=9fT(gl+g.);:;;
P(I.+I.) from which it follows that P/,+Pf. ';;; P(!I+I.) if 0 ';;; I"
f.eLlnL"". Now let 1..f.,heL"nL"" with 1.,1.;;:;0 aod with
Ih(.)1 :.:;: 1.+1. and define h" = 1,-11, where h,(G) = 0 if h(G) = 0 and
h(o)
11,(0) = Ih(o)1 Uh(s)I"/,(s)],
otherwise. Then clearly 111,(')1;:;; f.. 111,(')1 $ I., so that 9fTh =
!1lTh,-r9fTh. ';; P/I+PI. which proves that P(f.+I.) < PI1+Pf.
and establishes the equation
(IJ P, ;;;; o. !P.I",,:,:;: jT'I"" = ITI,.
I(T*f}(')1 ;:;; Pllf(')1 = sup ITg(.)!, 0 ,;;; fE L"".
I,HISI/{.II
Let 0 I e L"". geL,. and let" be the natural embedding of L 1 into
L:* Then
P(f.+f.) = PI.+Pf.,
o ,;; It. I. e L,nL"".
f s /(G)(BtTg)(8)p(ds) = 9i fs / (8)(Tg)(8)p(ds)
$1 fS ' (8)(Tg)(s)p(ds)[ = Ifs (T*f)(s)g(G)p(ds)1
;;;; fs I(T'f}(s)lIg(8)[p(ds) ';;; fs (PJ)(s)lg(s)I,u(ds) = "I,
where I' = J'i"lg(')I. Since (8,:E.p) is a-finite the element" in L':.,
may be represented as a bounded additive 8et function (IV.8.16)
whose value on a set e in I is "(Xot) wh re Ze is the characteristic func-
tion of e. In the preceding inequality we shall replace I by the charac-
teristic function of a set e in :E and write 1'( e) instead of vf. Thus, by
the precediug inequality.
If. (Tg)(8)p(ds}1 ,;; .(e), geL" ee L.
The set function file) = J.(Tg)(8)p(ds) therefore has its variation
v(fJ. e) $ .(e). Thus, by Lemma 111.2.15, J. j(Tg)(s)lp(ds) = v(,B. e)
;:;; ,'(e), which shows that
If I.. f., g., g. are non-negative elements of L 1 nL"" with fl-I. =
g.-g, then/.+g, = I.+g, so that Ph TPg. = PI.+Pg 1 and Pit-PI.
= PgI-Pg.. This shows that PI may be defined for an arbitrary real
element in L"nL"" by the equation PI = P/,-PI. where f l and f.are
non-negative functions with f = fl-I.. It is dear that P"-I = "PI for
674
VIII. APpLICATIONS
VIII.6.4
VIII.6.5
POINTWISE ERGODIC THEOREMS
675
[2]
"lrTg)(')1 J1"lg(')I.
g 'L..
equality holds for alii. Ll' It follows by induction that pn+'!/(')1
;;; PI(Tn/)('>I > I(Tn+lf)(')I. Q.E.D.
5 LEMMA, Let (S, E, p) be a a-linite 'I>ICGStlTe space and let T be a
linear vperalor in Ll with ITI"" 1 and ITll 1. Then lor I P < cD
and I in L (S, E, p) we hat", sup IA(T, n)(/, $)1 < cD lor "lmost all
B in S. 1;S;1'I;:5;;ct)
If 1. is a non-negative measurable function with h < I_ L1nL""
then 1. is also in both L. and L"". Thus an element defined by an ex-
prESSion of the form sup 11.( - >I will be the same whether the supremum
..A
is taken in the complete lattice Ll or the complete lattice L"" provided
only that tbere is an element I in L.nL= with 11.(')1;;:; I for every 1.
in A. Similarly. if 0 ,,;; I_ Ll' '1" L:., and 0 ;;:; 'I' ;;:; "I then the set
function 'I' is p-continuous and hence belongs to >eLl" Thus (cf. IV.8.
24), for a set A inL. for which there exists a non-negative I in L. such
that Ih(')1 ;;:; I for h in A. we have "sup 11.(')1 = 8UP "Ih(.)j. Finally
kA IlleA
PROOF. We may and shall assume that I > O. Let a' be the com-
plement of the set " = (el/(e) ;;; I}. Since I_ L it follows that
1'( a) < 00 and thus I is the sum of a summable function Ix. and a
bounded function Ix.,. Now, since IT/",, :-;;; I, we have IA(n)gl", ";; Igl""
for a bounded function g in L . Thus in proving the lemma it may
be assumed that I is in Ll' In view of Lemma 4 it may also be assumed
that T is positive. Let
''''' = {el sup A(T, k)(f, HI cDJ.
I'"
Since p is a-finite on S it will suffice to prove that pree oo ) = 0 for
every set. in E with p.(e) < cD. Let g be the characteristic function
of eo oo where pee) < cD. If ot > 0 and Lemma 2 is applied to the func-
tion l-rJg it is seen that
(*) cxp(ee""c) ,,;; fs/{s)p(ds)
wbere C = (HI 8UP A(T,k)(f-cr.g, s) ;;; OJ. Since JA(T,k)loo ";; liUol-
ISle:;';"
we observe that a bounded set A in Loo and the characteristic function
X. of a set . in I satisfy the relation sup X.h = X. sup h.
1I£JI. MA
Using the observations of the pre<'eding paragraph and formula
[2] it is seen that for 0 < I_ LlnLooandeEEwithl'(') < cD we have
"X. PI = "Z. sup ITg(')1
1.1.)1'"
=" sup X.I(Tg)(')1
1.1-11;;'
= sup "[x.I(Tg)(' JIJ
1_(.11'"
= 8UP "1(Tg)(')1 sup P "lg(')1
1.(.11;;' 1.(.)1",
= pi "I.
Thus. for each set e in E with pIe) < cD, we have JsX.(s)(Pj){e)p(ds)
;;:; IPi"/l. Now, from [11, it is seen that !Pil = !Pll"" ITI1' and so
Js(PlJ(s).u(ds) ,,;; IT111"/1 = ITI.IIII for every non-negative I in
LlnLoo' Since, as shown earlier, I(PI)(-)I::;:: PI/(.)I, we have
Jsl(P/J(H)lp(ds) ;;:; ITllllh for alii in LlnL . Thus jPII ";; ITI I , and
P has a unique extension to an operator (which we still call P) defined
on aU of L..
By definition.
PI/(.)I = sup I(Tg)(')I :2: I(T!)(.)], j_ nL"".
1.('11"11(.)1
Since Ll nL is dense in L. and jPlI has been proved finite, this in-
lows that 0 ';:; A(T, k)a.g ;;:; ot, and thus c;;) e. where en = {sl
sup A(T. k)(f, s) ;;; ot]. The inequality (*] then gives
t::;k:iin
"'I,(ee.) ";; fs/(s)p(ds), n = 1, 2,. _",
and, since en e"", we have ot,lt(ee oo ) ,,;; Js/(s)l'(ds). Since this holds
for every ot > 0 it follows that I'(ee oo ) = 0, Q,E,D.
6 THEOREM. (Poimmjse ergodic theorem) Let (S, E, 1') be a posi-
tive measure space and let T be a lineaT ooperatlJr in L1(S, I, p) with
ITI ;;:; 1 and ITh 1. TNn, lOT every p with 1 <;; p < cD and evcry
functimz j in L (S, I, 1'), tN limit
1 n_1
lim - I (TmlJ(s)
"'_00'1/..",.--0
.",isls lor "lmost all s in S,
676
VIII. A}>PLICATIONB
VIn.6.7
VIII.6.7
POlNTWISE ERGODIC TII:EOREMS
677
PROOF. Since the funct,ions Tnl. fl = O. J,. . . ., all vanish on the
complement of a c-finite set we may and shall assume that (S, E, p)
is c-finite. Since ITI", ,,;; 1 and ITI, ,;;; I it follows from the lliesz con-
vexity theorem that ITI ,;;: 1. For 1 < p < 00, L is l'f'flexive (IV.
8.2) and thus, from Corollary 5.4, it follows that A(T. n)1 converges
in L" for every I in L". The d.ecompositiun given in Corollary 5.2 then
shows that vectors oftheformh = f+(l-T)g, with I, ge L , TI = I,
and g bounded are dense in L . For such a vector h we have A(T, n)h
= 1+(I Tn)gln. and thus. for almost all s in S, we have
g(s) = I(s) if I(s) > ct and g(s) = 0 otherwise, Then I ';;: g+ct.
f-2rt. ,;;: g-ct. and, since ITI"" ,;;: I, we have
A(n)/-2,,- < A(n)(f-2«) ;::;; A(n)(g-«).
This shows that e"(2ct) (;; B (;; C, where
B = {_I sup A(n)(f-2,,-, s) OJ,
1 fI
C = {_'sup A(n)(g «.8);:;; OJ.
':>n
IA(T, n){h, s)-f(8)1 ;::;; 2lgl""ln -+ O.
By Lemma 2, Ie (g-ct){8),u(d$) ;;.- 0, and so
rt.,u(e"(2ct)) ,;;: "-p(C) ,;;: Ie g (8),u(d$).
If s is a point such that g(_) .p 0 then 0 < g(B)-« = A(l)(g-«, 8)
and thus B is in C. This means that g vanishes on the complement of
C and hence
This shows that A(T. n)h converges almost everywhere for every h
in a dense sctin L aod. by Lemma 5, sup IA(T, n)l(h, s) < 00 almost
everywhere for every h in L,.. Thus, by Theorem IV.n.\!, the sequence
A (T, n)h converges almost everywhere for every h in L . Since L. is
dense in £" we may apply Lemma 5 and ThCQrem IV.n.2 again to see
that the sequence A(T, n)1 converges almost everywhere for every
I in £", Q,E,D,
It is seen from the preceding theorem and from Corollary 5.4
that for 1 < p < 00 and for f in L. the sequence {A(n)f} of averag1's
not only converges in L. but also converges almost everywhere on S-
It will next be 8hown that this sequence of averages is bounded by a
function in L.. The proof of this is based upon the next lemma whose
statement refers tn the following notation; A(n) = A(T. n), I*(B)
= sup lA(n)(/, _)1, e"(<<) = {sl/*(s) > ct}, e(<<) = {BII/(s)1 > «}.
«p(e"(2,,-)) ;::;; J g(s)p(d$) = J I(s),u(d$).
S .11%)
This proves the lemma under the additional assumption that peS)
< 00. We nOW allow (8, ];,p) to be an arbitrary positive measure
space. Since all of the functions A(n)1 vanish on the complement of
Some a-finite set, we may and shall assume that S is (J-finite. Let
{S,,.} be an increas.ing sequence of sets whose union is S and with
p(S.) < 00. Let Tn = BnTB. where B. is the operation of multi-
pJication by the characteristic function nf 8n. Let
e*(m, «) = {sl sup A(k)(f, 8) > ctJ,
l:;k:iirn
and
ap(e.(2",» ;::;; J Iffs)lp(d$).
...(a)
e*(n, m. ctJ = {BI sup AfT., k)(f, B) > «J,
l;S;kSIn.
Then. by what has already been proved,
(*) ap(e*(n. m, 2,,-)) ;::;; J f(B)p(d$).
5....(01)>
Since Tn -+ T in the strong L. topology, the function sup A(T.. k)1
l l: m
7 LEMMA, Let T be an opercztor in £" with ITI"" :;;; I, ITI, ;;;;: 1.
and let 1 ;::;; p < 00. Then, lor every fundion I in L. and every positive
nll31lber ct. roe have
PROOF. The lemma will first be proved under the assumption that
1-'(8) < 00. If P is the positive operator associated with T as in
Lemma 4, then e*(ct) (;; {al sUh,;;. A(P, n){I/(' )1,8) > ct} from which
it fo\lows that we may, without loss of generality, assume that T is a
positive operator and that I is a non-negative function III L". Let
approaches sup A(k)1 in the norm of L. as n -+ 00. On the otber hand,
l l::;;m
since I;:;; 0 and since Tn increases with n, the sequence (sup A(T.,k)
l .t '"
(f.8)} is lOcreasing in n. ThIS shows that the 8equence {e*(n, m, "-)}
inCl'f'ases with n and bas the limit e*(m, «). By letting n -+ co in the
e78
VIII. AI'FLICATIONS
VIII.e.8
VIII.e.9
POINTWISE ERGODIC THEOREMS
679
8 THEOll.EM. Ld T b. an opcratm in L. with ITlco 0;;: 1 and
ITI, ;:;;; 1. FOT each I in L kt
1*(8) = sup I 1: ( Tm /)(8) 1 .
1;S;.,. nm-o
I.I>(s)p(&) = Is If:'(o) dal p(&)
= IsJ:' X."[O) (s)p(&)da
= I: p(.*(a»da ;:;;; 2f'(S) + r ,,(e*(a»da.
inequality (') one obtains. therefore, the inequality «p(.'{m.2«»
;;: I.[o]/(.)p(ds), from which the desired inequality follows by letting
m ce. Q,E.D.
TMn. il 1 < I' < 00, me MViJ
and
f co ,,(.>(a»)da < 2 f a-' I f I(s)p(ds)\ da
! 2 e1012] I
= 2 I a 1 J f l(s)p(ds) 1 da
I } e(a.)
= 2 I Is a l/(s)X.(ol (s)l'(ds)da
= 21./(8) If;"' [1,1[')) a-Ida) ,,(ds)
= 2 L/(8) log+/(s),,(ds).
Q.E.D.
r I*(a)"p(ds) 0;;: 2"1' r 1/(8)I"p(ds),
Js p-d.
while i/ I' = 1 and peS) < 00 we have
I. /*(a)p(ds) 0;;: 2("P(S) + I. It(a)llog+!/(B)lp(ds»).
Note: The symbollog+a is defined for a > 0 to be the larger of
log.. and o.
{} THEOREM. Let Tit i = I. . . ., k. be linear optTaWr8 in Lr with
IT,I", ;;: 1 and IT,ll ,;:; I, i = I. .. " k. Then, lor elJfJry / in L. with
I' > 1, the multiple seqtli'1'I£e
'11..-1 11.-1
(1) (.,.. . .no)-I L ... L (T;;'>,., T:"f)(s)
""o m,.,=-O
P1l00F. In view of Lemma 4 we may and shall assume that T
and I are both non-negative. The case I < p will be treated first by
using the preceding lemma as follows:
I.'*(8)'p(ds) = pIs U:'(a) a' lda)p(ds)
= p I.fo'" a.- l x."[o) (s)Jl(ds)da
= p fo'" a" ll'(e*(a»da
0;;: 2p f, "" a" ' lf I(B)I'(ds) ] da
o .(aJ2)
= 21' fJ.m a' ./(s)x,(ol') (s)p(ds)da
= 21' f./(B) If:") aHda) peds)
= 2'" i
- I(s)'p(ds).
1'-1 .
Tbe case p = I is treated .imila.rly as follows:
i. convergent (as .,., . . " n_ CD inkpendenrly) alnwst roaywhere on
S, as well 1M in tM nonn 01 L.. F"rlh",.,,,ort', this murtiple 8e'JU""'"' i8
domina1ed hy a fulll;t;V1I in L..
PROOF. Let V(.,.,..., no) = A(T o , n.). . .A(T I , fIt), .0 that
V(",-, . . ., 1I.)(f, 8) is the multiple sequence (I). Since IT,loo;:;;; 1 and
IT,ll < 1 it follow8 from thc Riesz convexity theorem (IV.IO.n i that
IT,I. < 1 and thus that
(2) IA(T" n,») :s;; I, W(n l , . . ., n.)1 :s;; 1,
where here, and throughout the remaining part of the proof, Ule norm
without a .ubscript refers to the L. nonn. By Corollaries 5.2 and 5.4,
there are projection operators E. with
(3)
lim A(T" n)1 = Ed.
f L'JI' i = I. . . _. k.
ft
From (2) Bnd (3) it follows immediately that
(4) Jim V(.,.,. . ., n_)1 = Eo.. .EJ,
f£LJ1;
680
VIII. APPLICATIVNS
VIII.6.9
VIII.6.10
POINTWISE ERe-ODIC THEOREMS
681
for indeed Buppose this fact has been established for k -1 operat.ors
T:e,..', Tk and note that
IA(T.. n.). .. A (T i , ni)/ E.... EJI
:;;: IA(T., n.).. . A(T., ""HA(T" nJ)-E.)/1
+ I{A(T., n.J.. .A(T., "")-E.,.. E.) /I
:;;: I{A(TI' n,J-E.}fI+I{A(T.. ",,).. . A (T" "")-E....E.)E i /l
approaches zero br the induction hypothesis. By Corollary 5.2, E,
projects L. onto the manifold !II, of those I in L. for which T ,I = I and
the complementary projection E; = I E, projects L. onto the clo-
sure of the manifold (1- T,)L.. Thus, if we let!m, denote the set of
functions of the form (I-Ti)1 with f bounded, we have
(5) !m.+W. is dense in L., I ,;: i ,;: k,
a fact which will be needed later. Now Ict g = (I-T.)fe!m J with
II(a)I -:5 K. Then A(TI' n)(g, B) n-IU(8)-T (I, a)] and thus
!V(":1, . . ., ...)(g, a)1 ;:;0 2KIn" for almost all a. This shows that. for
almost all 8 in S,
IV(":1' . . .. n.)(f. B)I ;:;0 A(P., ...). . . A(PI' ":1)(g, a).
Thus, in proving that V( ":1. . . ., ...)f is dominated by a function in L.
we may aod 8hall assume that I 0 and that T, 0, i = I, . . _, k.
By Theorem B there are functions fl' . . ., f. in L. with
A(T I . n)f ,;: fl'
A(T., ",,)A(T., n,,)f ;:;;; A{T., n.)t. ,;: f., n l ,
A(T., n.}. . . A (TI' ",,}I ,;: f"
":1 I,
",, I,
11t, 0 a_7 ft lt .:?:: 1,
(6) Hm V(":1, . .., ...)(g, B) = 0, g e!m l ,
For a function I in !Ill we have TI(I, B) = fIB) for almost all a in 8 and
thus A(T" n)(I, 8) = I(a) for almost all a and all m = 1,2, . . .. Since
the theorem is true for k = I (Theorem 6), we 8hall apply induction
and asSUme that it has been proved for the case of k-I transforma-
tions T., _ _ _, T.. The induction hypothesis yields then for I in !II J the
convergence almost everywhere of the multiple sequence
which proves that the multiple sequence V("", . . ., ...)1 is dominated
by 8 function in Lv We may nOW deduce the almost everywhere con-
vergence of this sequence from Theorem IV.n.s. In that theorem let
A. be the set of a1l k.tuples a = En}, . . ., ",] of integers with n, p,
i = If . . "J k, and, for a = [ . . . "J n.J in All Jet the operator Ts of
Theorem IV.n.S be replaced by V(":1" _ .. ...). The bypothe8es of
Theorem IV.n.S have all been verified and by that theorem we then
conclude that the multiple sequence V(":1,.... ...)(/. a) converges
almost everywhere on 8 for every f in L . Q.E.D.
The preceding theorem is not true if p = I. but there is a k.para.
meter analogue of Lemma 5, This will be found at the end of the next
section.
The con'''ergence theorems of this section have assumed an opera-
tor T with IT!. ,;: I and ITI= ,;: 1. In some cases, however, they may
be applied to prove the convergence almost everywhere of the aver-
ages A(n)(/, s) even when ITI} > I and indeed when IA(n!!, -->- cD.
We sha1l conclude this section with two such theorems whose proofs
will use the following lemmas.
V(":1, . . ., ...)(/. a) = A(T., n.), , ,A(T., ",,)(1, 8).
This fact combined with (5) and (6) shows that the sequence
V(n", . . .. ",)(/, a) converges almost everywhere on 8 for every f in
a set dense in L.. It will next be shown that for every I in L. the se.
quence (I) is dominated by a function in L . To prove this we first use
Lemma 4- to find positive operators Pi. i = I, . . 'J k with IPiioo < I,
JP,II ;:;0 I and such that
JA(T" n)(/, ')1;:;;; A(P" "IIV(')/), I < i :;;: k, I -:5 ...
If g(a) = If(s)1 then it follows that IA(TI' ",)(f, a)1 ,;: A(P" n})(g, a)
for almost a1l a in 8 and hence that
10 LEMMA. Let (8, E, p) be a linite pasilive measure apace. A
bounded 8 """ (IL.) i.. the B.s-pace of IL-oontinuous real or rompla
cu!ditive sel functions on E i8 'lJ'eokly sequentially compacl procided toot
lim lim sup Ip.(e») = O.
,...(e)=O ft_OG
PROOF. The a.field I is a complete metric space E(,u) under the
distance function e(a, b) = p(aL1b) and the functions p. are continu-
ous on E(p} (see Section 111.7). Thus, for e > 0, the sets
C, = (ele. E(,u), Ip.(e)1 ,;: E, n k}
682
VIlla APPLICATIONS
VIII.6.n
VIII.6.J8
POINTWISE ERGODIC THEOREMS
688
are closed in E(P) and, by hypothesi.. their union contains a .phere
in E(P). Thus (1.6.1, 1.6.9) there is a set a E E, a number T > 0, Bnd
an integer k such that e E C. if p(aLle) < T. Fix b in E with p(b) < T
and let b J = a+b, b. = a-b. Then b = b J -b., p(aLlb J ) < T. Bnd
p(aLlb.) < T. Thus b J . b. E C. and hence Ip,.(b)1 < 2. for all n k.
There is a positive number TI T such that Ip,.(b II ,;;; sCar J ,;;; n ;:;; k
provided tlmt p(b) < TI and this proves that the functions 1'.,
n = 1, 2, . . . are uniformly I'-continuous. The conclusion of the lem-
ma now follows from Theorem IV.9.1.
from Lemma JO and Corollary 5.8 that the limit m = lim p. eXISts m
ca(E,p). By CoroUary 5.2, m(q:>-I e ) = m(e). 80 that the map T :/(.)
.... /(q:>('» as an operator in the space Lz{S.E, m) has its norm ITI, = I
(Lemma 5.1). Now let I be a bounded p-measurable function on S.
Then I is m-measurable, m-integrable. and, by Theorem 6. the limit
I n-l
gee) = lim I I(q:>qe)
n-+-QQ 'It m=O
exists for m-Blmost all points in S. (It should be noted that the only
way in which the requirement that / be bounded is used, is to insure
the m-integrability of I. In other words the following proof shows the
existence of the limit g(s) for p-almost alls in S provided that I is m-
integrable.) Let eo = (sl(dm/dp)(s) '1= O} so that a 8ubset of eo is a
p.null set if and only if it is an m-null set. Thus the limit g(.) exists
for p-ahnost all points in '0 and the proof of the existence of g(s) will
be complete if it is shown that for p-almost all points s in e we have
q:>"s E eo for all sufficiently large m. To see this let b be a subset of e
which :remains in e under all iterates of rp, i.e. t rpmb e for m o.
Then b 'r"'e and pCb) < p.(e ) .... m(e ) = o. Thus p-almost all
points in e map, under .some iterate of !PI into eO" It remains to be
8hown that for p-almost all 8 in eo we have q:>s also in eo; which thus
wi1l show that p-alrnost all points in e eventually become and remain
points of eo' Let a eo and 'l'a e . Then a!;;; 'r'e and thus m( a)
,;;; m(q:>-'e ) = m(e ) = O. Since a!;;; e. we also have pia) = o. Thus
g(.) exists for p-almost all points in S. Q.E.D.
It is natural to ask when the pre<:eding thoorem is valid for every
It.integrable function I. An answer is given in the following theorem
of C. Ryll-Nardzewski [1; I].
JS THEOREM, Let (S,E,p) be D lini'e measuTe space and'l'D mapol
S into i!seli with <p l1: E and with p( rr'e) = 0 lor eury p-nuUsete. Then,
lor ct>cry I in Lz(S, 1:, 1') there is a gin LJ(S, E, 1') lor which the limit
1 n-l
(I) g(s) = !im - I I{<pffls)
n-+OO n m=O
11 LEMMA. A positive linear map P in LJ is ronlinuoU$.
PROOF. If not, there are positive elements lfi in LJ with Itn.1 = I,
and lPi.1 > n".Let I =EI.ln" so that lPil :2 JP I;' 1./n"1 = ZlPi.l/n"
:2 m for each m :2 1, which is a contradiction. Q.E.D.
The final two theorems to be discussed return to the type of
operato:r arising in classical statistical mechanics. They are concerned
with a finite positive measure space (S, E. p) and a map 'I' of S into S.
We reca]] (Lemm" 5.6) that ifq:>-'E E (i.e., 'I'-'e E Efore EE) and if
p('I'-le} = 0 if pee) = 0, then the map T : I.... /('1') is a continuous
linear map in the space 11-1(8) of all I,-measurable functions.
J2 THEOHEM, Let (S, E, p) be a linite positive measure space and
let 'I' be a map 01 S into i!sell ",ilk tM propertiEs
(1) q:> 'E E and ",(q:>-I e ) = 0 il pee) = 0;
1-'
(2) lim lim sup - I I'(<p-me) = O.
U(II!I) O ft OO n m=O
ThRn. lor every bound£d fRCfJ3urable IIJ11dion I on 8. thR limit
1-1
lim - I 1(q:>mB)
fi-HIO n tn=Q
exists lor almost oJl s in S.
PROOF. We shall apply Lemma 10 to the set functIons
1 ____I
p.(e) = - I p(q:> "e). eEE, n :2 I.
n ....
exists lor almost all s in S, il and only illor Bome tonsUltIt K,
By Lemma I1I.4.18 these set functions are in the B-space cafE, 1') of
p-continuous additive set fnnctions on E. Since 11'.1 ,;;; II'I it follows
(2)
I n-1
lim sup - I p('I''"'''e) ;:;; Kp{e),
n-+oo n In=!)
eEL.
.
6840
VIII. APPLICATIONS
VIII.7
VIII.7
ERGODIC THEORY OF CONT1NUOUS FLOWS
685
PROOF. If the limIt g exists and if g is in LI then, by Lemma II.
the map I -7 g is continuous and thus there is a constant K with
Igh ;0:;; Kl/ir Let I be the cb&racteristic function of a set e in I; then
the convergence in (l) is bounded and hence in the norm of Ll' Thus
i 1 " I 1 _I
- }; I(cpms)p(ds} = - }; p(rrme)
snrn...o nm-1)
-7 Igi ;0:;; Kill = K",(e),
which proves (2). Now conversely if (2) holds then the set function m
in tbe proof of the preceding theorem satisfies the inequality m(e)
:$ K",(e) and thus the p-integrab!e function I is also m.integrable, It
waS observed in the preceding proof that the limit g(s) exists for "'-
almost all s and hence it only remains to be shown that g IS ",-integra-
ble. It was observed in the preceding proof that m(cp le) = m(e) for
e in I and thus the mean ergodic theorem (5.9) shows that g is in
L,(S. I, m}. Sincegcp = g, sets of the form e = {sla < g(s) ;0:;; b} have
cp Ie = e. Thus, for such sets, m(e) = ",(e) which proves that
Jg(s)m{ds) = Jg(s)p(ds). Q.E.D.
In order to be able to assIgn 8 meanmg to the averages
1 1 "
A(a) = - T(I)dt,
a 0
which are to be our basIc concern in this section. it will be desirable
to supplement the algebraic condition (i) by a condition concerning
the aJU!.lytical dependence of the semi-group upon the parameter I.
We recall tlmt the semi-group {T(I), 0 < t} is said to be sfTongly con-
tinwus if its dependence upon t is continuous in the strong operator
topo1ogy, i.e., if lim IT(I)",-T(u)"'1 = 0 for each ;v in 3: and each
<-+.
(ii)
o .
7. Tbe Ergodic Theory of Continuous Flows
u ;,;;; O. The semi.group is said to be strongly mmsurab/e if, for each '"
in 3:, the function T(' ).r is measurable, with respect to Lebesgue meas-
ure. on the infinite interval 0 < t. It was observed in Lemma 1.3
that a strongly measurable semi-group is strongly continuous except
possibly at the origin I = o. A related concept is that of strong inte-
grability. The semi-group is said to be strongly inkgrahk over every
linite interval if, for eacb " in 3: the function T(.)", is integrable with
respect to Lebesgue measure on every finite interval 0 ,,; t :$ a, If
the semi-group is strongly integrable on every finite interval we ma.y I-
for each" ::2: 0, define a bounded linear operator A(a) called tk 4verage
01 {T(t}, 0 ,,; I} on 1M i'llteruol 0 ::;:: I :;:: a. The operator A(a) is defined
for a = 0 as A(O) 1 and for a> 0 by the equation A(a}" =
a- 1 J T(I)"d1. To see that A(",) is a bounded operator we note first
that the map '" -7 T(').r of 3i into the space L" of 3: valued Lebesgue
integrable functions on [0,,,) is closed: indeed if ". -7" and T(. )"'.
. I in LI then, for some subsequence {"'n,), T(I)",., -7/(1) for almost all
I in [0, a]. Since T(t}",. -7 T(I)'" for every I we have T(I}" /(1) for
almost alii which proves that the map'" -->- T(.)", is closed and thus
(11.2.4) continuous. It fullows immediately that A(a) is a continuous
linear operator in the space . It is in this sense that the integral
appearing in equation (ii) is defined.
This notion of the average A(a) is 8ufficient for the statement of
the first few results for they are concerned with strong limits of the
type lim A(a}". In most of the section, ho 't'r, the B-space 3i is a
"
In Section 40 it was shown how the rrgodie hypothesis in classical
statistical mechanics has led to questions involving averages of B
particular one parameter semi-group of unitary operators. In this
section we sha1l study such que8tions and show how they may be
resolved by a reduction to the study of the averages of the iterates
of a single operator It win not be necessary to restrict the discussion
to the type of semi-group arising in classical statistical mechanics as
the results to be described are valid in a situation having the same
degree of generality enjoyed by the discrctc 8emi-group {T",O < 'II}
discussed in the preceding section
The basic notion underlying the present discussion is that of .a
one parameter 8 rm-gr(jup oj boundnL linear operators in a real or COIh-
pIe", B-.poce. We recall that such a semi-group is a set {T(I), 0 ..;; I)
of bounded linear operators in a B-space :£ for which
(i)
T(O) = I, T(t+u) = T(t)T(u),
o tIU.
space L = L.(S, I, ",) where (S, I, p) is a positive measure space
and we shall be concerned with the ..Imost everywhere convergence
686
VIII. APPLICATIONS
VlII.7
Vlll.7.1
ERGODIC THEORY OF CONTINUOUS FLOWS
687
and the almost everywhere boundedness of the averages A(",)I for a
particular function I in Lv Since the point I. = A(ex)1 in L. is a class
of equivalent functions W1d two functions I. and go represent the
same point if I.{B) = goes) except on a ".null set E. which may vary
with a., it is imperative to define more explicitly what is to be mcant
by the averages A(ex)!!, s) of I at a point s in S. To make such a defi-
nition we suppose that the semi-group (T(/), 0 -<;: I} is strongly in-
tegrable on every finite interval and that it operates in Lv Then. by
Lemma 1.8. for each f in L. the set of all vectors T(/)/, I ;:" 0, is a sep-
arable 8ubset of L. and hence. by Lemma III.8.5, these vectors aU
vanish on the complement of a ,,-finite subset of S. Thus we may and
shall, when defining the o"emge A(ex)U, s), assume that the measure
space (8, E,p) is ".finite. Then. by Theorem III.ll.I7 there is for
each fin L., a scalar representation T(t)!!, s) of T(t)! which is measur-
able in [I, s] (i.e., measurable with respect to the product of Lebesgue
measure Bud p) and such a measurable representation is unique ex
cept on a set of points [t, s] whose product measure is zero, Also-
Theorem III.ll.I7 shows that there is a null set E(f) which may de-
pend upon f but which is independent of! and is such that T(')U. s1
is integrable on every finite I-interval for every s not in EU), Further-
more, by Theorem III.ll.17, for each ex> 0 the integral
(iv)
f'(s) = sup IA(exH/, s)1
V<tI:<w
is the same as sup..-" IA(ex)(f, s)1 wbere R is the denumerable set of
positive rational numbers. In view of Theorem rv.1I.6 it follows that
f' is 0.180 the [east upper bound of the set {IA(a.)(f, ')1, 0 < a.} when it
is regarded as a 8et of elements in the lattice of real p-measurable
functions. Thus if {JA(ex){!. ')1. 0 < ex} is a bounded set in this lattice,
its supremum
M
f' = sup IA(ex)!!.')1
0<.
(iii)
1 1 '
A(ex)!f. s) = - T(/}(!. s)dt,
ex °
o <ex. s E(f),
taken in the lattice ordering is represented by the scalar function (iv)
so that no confusion co-neeming the int"pretation of least upper
bounds can arise. Similar remarks are valid in the situation discussed
in Theorem 10 where averages of the product of k different semi-
groups are considered.
We shaH when convenient J continue to use the notation lUISI'
which was introduced at the beginning of the last section. for the L.
norm of an operator U. We recall that IUI» = sup IUfl. where f varies
over all elements in the domain of U with !/I. -<;: I. We 8hall begin by
a discussion of the strong convergence of the averages A(ex) as ex ... 0:>
and for this it will not be necessary to restrict the B-..pace upon which
the semi-group act8.
is a scalar representation of the vector A(a.)! in L . If we had started
with another [t, s]-measurable representation K(t, s) of T(/}I then,
since for almost aU s. K(/, s) = T(t}{/, s} fo almost aliI, it is seen that
for almost all B. ex- 1 J K(t, s)dt = A(ex)(f, s) for all a., Thus for almost.
ails in S the average A(ex)(f. B) as given in equation (iii) is uniquely
defined for aU positive values of 0: and furthermore furnishes an.
[ex. B ]-measurable scalar representation of the vector A(ex)1 as defined
in equation (ii).
This uniquely defined average A(ex}{!, B) is no. only a measur-
able function of (ex, s) but, for every s not in the null set EU}. it is
continuous in rJ. on the interval 0 < a. < co. This continuity in tL
shows that, for almost all B in S, the nnmber f'(s) defmed by the
equation
I THEOREM. For a. ;:" 0 lei A(ex) be the average on the lntervnl
[0, ex] of tM one parameter semi-group (T(t), 0 ;;;; t} which is assumed
10 be strongly i<l1egrabk on e:very finite intervaL Suppose also that
T(n)
(I) lim -t£=0,
ft-+oo n
a;E i
(2) IA(exJl -<;: K, O;£a.;
(3) for each t£ in a fundnmmtnl set in l' tM set {A (ex}"" 0 < a.) is
weakly Bet]/JAmtially compact.
Then the averages A(a.) ctmneTge. as a. ... 0:>, in tM strong operater
topology.
PROOF. The proof will be based upon the following identity which
will serve to reduce the present theorem to the discrete case already
088
VIII. APPLICATIONS
VIII.7.2
VIII.7.13
ERGODIC THEORY OF CONTINUOUS FLOWS
689
discussed. Let n = [aj so that a = n+T with 0 ;;;; T < I. Then. for
a. I,
. T(n)
bm - TA(T)'" = 0
tt-+oo n
the 8emi-group. Smce E'{T{u)-I) = T(u)-I. the range of E' con-
tains the union of the ranges of all the operators T(u) 1. If ",* is a
functional v8Jlishing on the ranges of all the operators T(u)-I then
x* = x*T(u) = x'A(u) = x'E 8Jld thus x' varushes on the range of
E'. The desired conclusion follows from Corollary II.II.la. Q.E.D.
II COROLLARY. In a relk",ive space, IIu: average> A(a) aTe slTongly
amvergent if they aTe bounded and if T(n )In ctmvergea 10 "ero strongly.
PROOF. This follows from Theorem I and Theorem 11.8.28. Q.E.D.
4 COROLLARY. LeI (S, E, p) he a fini'-" po.titive 'lMa8t<re space and
(T(I),O ;;;; I) a semi-group of operators in Li(S, E, 1') which i81ih'ungly
irdegrahle on every finite mtmJal. It is /lJ8Umed that lOT SIm1-e oonBtant K
IA(a)II ;;;;K, IT(tll= '5:. K, 0 <a.t,
and that T(n)/n converges to "ero slTongly in L,,(S, I,p), Then the
averages "'''''-'erf!'' Iih'<mgly in Li(S, I, pI.
PROOF. If I is in L={S. I,p) then, for all a and almost all s,
IA(a)(f, s)1 '5:. Klfl= and itfollows (IV,8,!!) that the set {A (a)/. 0 '5:. a}
is weakly sequentially compact. in Li(S. E. p). The conclusion now
follows from Theorem 1. Q.E.D.
The remaining part of the section will be concerned exclu8ively
with the case where the semi-group operates in a space L D = LD(S,E,}-l).
The basic assumption in the theorems to follow are that the semi.
group (T(t). 0 '5:. t} is a strongly measurable semi-group in L" for which
IT(tli l '5:. I and IT(tll '5:. I. There are two immediate conclusions that
nmy be drawn from these assumptions 8Jld which will be used repeat-
edly without further explicit mention of them. The first ofthese is that
IT(tli. '5:. I for all p I. This follows from the Riesz convexity theo-
rem (VI.IO.Il). Thus for each p ;;:> I the semi-group {T(t;, O ;;;; t} is
a semi-group of bounded linear operators in L D = L.(S, E./,). The
second consequence of the assumptions which we wish to mention here
is that, as a semi-group of operators in L. with I s: P < 00, {T(t),
o -<::: t} is strongly integrable on every finite interval and thus the
averagesA(a) are defined forO '" < 00 ""linear operators in L D and
havenonns IA(a)l. < I. To see this letf. L,,(lL. so that T(t)(/. s) is
[I. B)-measurable and, IT(!)/I. ;;;; If I.. It follows from Lemma III.II.IO
that the L.-valued function T(')f is measurable. Since I < 'P < a),
l i ft I f n+.
A(a) = - T(t)dl + - T(t)d!
Ct 0 a n
I n_l f - I I f n+,
= - I T(t)dl + - T{I)dl
1Xm-o 'f'I'I a; n
I , 1 1 I i '
=- I T(t+m)dl+- T{t+n)dt.
ctm-o () a. 0
nnd so
n [ I I T(n) J
(vi) A(",) = - - I T{m)A(I) + - yA(.-) .
a. n ",-0 n
For a fixed:r, rA(r).x is continuous in r Bnd thus the set of all vectors
rA(y)", with 0 < r s: I is compact. It follows from hypothesis (I)
and from Lemma IV.5.4 that
uniformly on 0 ;;;; y '5:. 1 and thus hypothesis (3) and the identity (vi)
show that the sequence {n l T(m)XJ is weakly sequentially com-
pact for each x in a set fundamental in the closure of the range of
A(I). Since T(m) = 7""(1), Theorem 4.1 nmy now be appJied to the
operator T(I) on the space A{I)! to give the strong convergence of
A(a). Q.E.D.
2 COROLLARY. Under the h of the thoorem tlu: limit
E", = Jim. A(a)", pr&jec18 I onlo tlu: manifold {"'IT(t)", = "', 0 ;;;;t} of
/irzed poinl8 of the semi-group and tlu: compkmmlat-y projection E' =
1- E projects! onto tlu: closed lineaT manifold determined fly tlu: ranges
of all 0/ tlu: operafors 1- T(t) wilh t ;;:> O.
PROOF. Clearly Ex = '" if '" is a fixed pornt. Now the identity
T(u)A(a) = J T(t+u)dt = [f T(t)dl- f T(t)dl + f ' T{I)dl ]
shows that j(T(u)-I)A(a)l;;;; 2w;c', from which it follows that
T( u)E = E. Thus every x in the range space of E is a fixed point of
690
VIII. API"LJCATIONS
VIII.7.5
VIII.7.6
ERGODIc THEDII.'\'" OF CONTINUOUS FLOWS
691
L,. n Lp is dense in L., and thus the semi-group is strongly measurable
when regarded as operating in L,.. Since IT(t)lp ,;: 1 it is also strongly
integrable over every finite intervsJ and therefore A(oc) is a bounded
operator in L. with 'A(oc)l. ,;: 1. In what follows the symbol Lp will
always be used for the space Lp(S,L,p).
5 THEOREM-II {T(t). 0 ,;: t} i8 a fdrangly meaBUrabl< .emi-group
in L", 'With IT{t)l, ,;: 1 and IT(t)I= ';: 1, tM... lor every I in Lp with
1 ;:;;; p < co, the averages A(oc)(f,8) ronverge almost here as
.0: co.
IgJ: = Is <Is U: IT(t)(/, 8)jdtY
,;: Is <Is I: IT(t)(f, · W dt = I: IT(t)fl: dt ,;: Ifl:,
f* = sup 8UP IA(oc)(I., . )i.
",cU 0<0:
and A(oc) = OC I I: T(t)dt. Thm
oc,u(e*(2oc}) ,;: f 1(8)P.(<Is),
ot!(a)
PROOF. By Theorem III.Il.I7 there is, for each u in U, a null set
E(u) for which the averages A (oc)(f.. .) e"ist for all non-negative oc, all
u in U, and all. not in the null set E(u). By Lemma 1.3 the operator
T(t) is strongly continuous in I at every point t > 0 and thus, since
IT(t)l. ,;: I, it follows that, for each" in the set R of non-negative
rational nUmbers
I ..'-' ( m )
A(")I. = lim - ! T - f.,
ft-+cc cxn! m...{J n!
U8ing Corollary 111.6.13, Theorem III.1I.I7, and the Cantor diagonal
p we may find, for each u in U. a sequence {n,a depending upon
u and such that
,,>0.
PROOF. Let 1 ;:;;; p < co. f. L., and let g(.) = J IT(t)U, ')Idt.
By Theorem III.ll.17 the number g(8) is finite for every. not in a
null set E(/) and, for such '. we have IrA(r)(f. ')1 ;:;;; g(.) for every r
in the interval 0 ;:;;; r ,;: 1. Furthermore, since
Uc:U, cxeR.
I T' P'
--;:;- rA(r)U, ')1 ,;: --;- (g,.) 0
. I .','-' ( m )
A(oc)(fuo 8) = hm, ! T - (f.,')
i-+oo aUi o ,,"-0 nil
for every ocin R and every B not in a null set E I (u):::1 E(u). Foru in U
and 8 f EI(U) let
I I · I '
r..(U,8) = sup - I T ( m ) (fu, ') 1
0<11:<0;) I k -m-O n!
so that for u" lJ. oc e R, S f E. (u), and c > 0 there is an integer
N(u, ",8, t) with
it is seen that g is in L . By Lemma 6.4 there is a positive operator
PinL"with IPII ';: I, ,PI",,;;;;I, and IT"U,')I ';: P"W('!I.'), n=
I, 2, . .._ By the Riesz convexity theorem we have also IPlp 1,
nn since p,. = pm- -1 pm, it is seen from Theorem lt5 that
almost everywhere on S and uniformly on the interval 0 ;:;;; r ,;: 1.
The desired conclusion now follows from the identity (vi) Ilnd Theo-
rem 5.5. Q.E.D.
6 LEMMA. Let (8. L.p) be a posiW.v: measuu space and for t > 0
let T(t) be an operator in L, wilh IT(t)I,;:;;; 1 and IT(t)loo ,;: 1. It is
assumed tlutt either {T(/), 0 < I} i. a ./rrmgly mt:USW'abIe .emi-group
in 4. or that 1M operator. T(/) are p<mtive, 8!rangly eonlinuoU$ in t.
and 8alisly the i7lefJIMllity T(t)T(v) ;;;; T(t+v). Len ,;: p < co and for
ea.:h u in a Bet U let I. be an ckTl/Rnt 01 L. sueh that the latrice supremum
1= sup.,u Ilti(" )[i8 also in L". For oc> 0 let e(oc) = {'11(8) > ct} and
e*(,,) = {slf*(') > oc} ...here
r..(u, 8) 2: IA(,,)U., 8)1-C.
n .2: N(u, fX. s, e).
and therefore
Urn inf r..(u. s) > jA(")(f., 8)1,
ft-+OO
""U. oc.R, 8fEI(U).
Now if. f E.(u) then 8 E(,,) and since, for such 8, A(,,)(f.,.) is Con-
tinuous in a on the interval 0 < ex < 00, we bave
sup IA(")(f.. ')1 = sup IA{ex)(f., 8)1
O<a<QC aER
and thus
lim inf r..(u,.) > sup [A(oc)(I., ')1,
,"-co O<a<;oa
neU, 8f E I (<<).
692
VIII. APPLICATIONS
VIII.7.6
VIU.7.7
ERGODIC THEORY OF CONT{NUOUS FLOWS
698
ti
Thi8 proves the following theorem.
7 THEOREM. ut {T(I), 0 ;;:;; I} be a Blrongly m£a8Urable 8emi-
group in 4 mith IT(t)11 ::;; I and IT(I)I", ::;; I. For each u in a 8et U
let lti be an e!emrntof L.llUChlluJliMlatticernpremum I =suP..u 1/.('»)
i. also in L.. II P = 1 il u also assumed 11uJ! peS) < co and tJw.1
1 5 /(8) 10g+/{a)p(ds) <; co. Then 1M function
1* = sup sup IA(at)(fti, ')1
,."u O<a<co
Let
I*(u, 8) = sup IA(at}(/ti, a)/,
O<a<oo
so that
1* = sup/*(u. '),
and for every fl, in U
Hm inf I:(u. 8) ;;" I"(u. 8),
n
for almost aU 8 in S. Now let Pen) be the positive operawr associated
with TU/nl) as in Lemma 6.4 so tlmt
Ii]. T( :I) (fti. .)1 i]' P(n)"'I, u. U, 1 k.
is in L. and
Let
1/"1. ::;; 2 p J/PI/I.' 1 <p < co,
::;; 2[,u(S) + J5 1(8) log+/(8)p(ds)], p = I.
11;-1
1:= sup P(nY"f
km=D
so that I: :e: 1:(", .) for every u in U and thus
Hm mf I: ;;:>. 1"(", .),
...U.
The final two theorems in the present section are concerned with
generalizations of Theorems 5 and 7 to the case of k-parameter semi.
groups. We slmll first define the basic concepts associated with such
semi.groups and their averages.
S DEFINITION. A strungIy measurable k-paromeUr 8emi-group of
operawrs in a real or complex B.space 1: is a set {T(,.. . . ., I.,)
,., . . ., t. > O} of bounded linear operators in a; with the properties
(a) T(,., . . .. t.)T(..... , ., Uk) = T(I" +U.. . . ., I.+u.);
(b) T(I",..., I.)", is Lebesgue measurable in [I", . . .. t k ] for each
a: 1D 1:.
9 LEMMA. II T(I", . .., I.) u a Iitrong/u measurable k-partml<Ur
semi-group in a B-space a; Ih£n, lor each", in a;, T(I", . . " t.)", u conlin.
..<>us 00 1M dumain ,., . . ., I. > 0,
PROOF. The case k = 1 was proved in Lemma 1.3 and an exam.
ination of tlmt proof shows that it is valid also in the general case
of Lemma 9. Q.E.D.
If, besides being strongly measurable. the semi-group is strongly
integrable on every set determined by inequalities of the form
o < 1", . . " t. ::;; a then the averages
A{a) =!. r".. . [ T(I", ..., I.Jdt"... dt.
a,kJo . 0
n-+
It follows tlmt
(.) lim inf I: ;;;; sup f*(u, .) = I".
- .
Thus. if e:(ex)= (Slt:(8) > at}, we have €.(at)!;;limlnfne:(",),Lemma
6.7 and Fatou's lemma (111.6.19) show that
"'p(e.(2",» ::;; lim inf exp( (2a» ;;:;; J. I(s)p(ds). Q.E.D.
ft-+fXj _ta;)
Similarly the inequality lim inf. I: ;;" 1*, together with Fawu's
lemma and Theorem 6.8 show that
J I.(s»,,(ds) ::;; J lim infl:(8)'p(ds)
S S n-+CO
;;:;; lim inf J f:(8)"I'(ds)
R-+.cx. S
::;; 2.p r f(s).p(ds), I < p < 00,
p-ds
;;:;; 2fp(S) + Js f(8) Iog+f(s)p(ds)]. p = 1.
694
VJII. I\PPLICATIONS
VIII.7.1O
VIII. 7.10
ERGODIC TI{EORY OF CONTINUOUS FLOWS
695
are defined for fJ. > 0 in a manner similar to that used in the one
parameter case. In particular, A(a) is a bounded linear operator in I.
Also, as in the one parameter case, we see that if £ is the space
L.(S, E, It) and if T(I:.. . . ., I.)U...) is a scalar representation of the
"edor T(/., . . ., t.)1 which is measurable as a function of 1:., . . ., I.
and .. then
I f. " f. "
A(<<)(/, s) = - .. _ T(I:., ...,1.)(1, s)d!,.... dt.
fT. 0 0
on the interval (0, a) then the multiple sequence (I) may be written
as V(a.,. . ., a.)(/. s) where
(2) V(a., . . ., a;.) = A.(a.) . . . A.(a I ).
Since IT,(/)I"" S; 1 and IT(/)II S; 1 it follows from the Riesz convexity
theorem (IV.IO.n) that [T,(t)l. I and thus that
(8) [A,(a)1 ;:;; I, W(al' . . ., a.>I I, I i k,
where here, and throughout the proof, the norm without a subscript
refers to the L. nOrm.
According to Theorem I the limits
is a scalar representation of the vector A(a)1 and is, for almost all sin
S, continuous in (t. This observ.ation shows that the function '*(8)
= sup IA(a)U. 8)1 is the same as the function sup IA(a)U, 8)1, where
o< R
(4)
EJ = lim A,(a)/,
jIEL'IJ'
I < i k,
a ""
R is the set of positive ratiQnal numbers. Thus j* is u-measurable and,
indeed. is the same as the supremum ofthe 8et {IA(a)(/, . >I, 0 < a} in
the lattice of p-measurable fill1ctions on S.
Actually, in the following theorem. which is a generalization of
Theorem 7, the situation discU88ed IS somewhat more general than
that of a k-parameter semi-group for here we are dealing with the
averages of the form
exist in the strong L. topology. From (8) and ('I.) it follows that
(5) Ek'" E,f = lim V(a.. .. ., «,)1: f < L.
in the norm of L.. To see this we use (4) induetively and suppose that
(5) has been proved for the productofk-l f""tors A k (",,), . .., A.(a,,).
Then
a,I . . . ",:;1 J: .. . J: Tk(t k ) . . . TI(/,)d!,. . . . dt k
where T I (;), . . ., T.(/.) are one parameter 8emi-groups. The mterest
here lies in the fact that these one parameter semi-groups need not
eommute, for if they do commute then T(I:.,. . ., I.} = T.(I.). . .T,{I:.)
is a k-parameter semi-group.
[V("l" . " "'.)/-E k ' , , EJI < IA.(ak) .. . A.(a,,){A.(a.)-E,}fl
+1{A.(a.) . .. A.(",,)-E. . . . E.}E,fl
I{A,(al)-E,}/I+j{Ak(a.),.. A.{ex,,)-E.... E.}EJI
approaches zero hy the inductIon hypothesis and establishes (5). It
will next be shown that the functions (I) are dominated by a funetion
in Lt) whi<!h is independent of the parameters exi. . . ., txk' The preceding
theorem shows that this is the ease if k = I. Let us suppose that it
has now been established in the case of k-l semi-groups TIt "t T k-I
so that the function
10 THEOREM. Let lhe .-emi-groups {T,{/), 0 t}. i = I, . . ., k,
be 6Irongly metJSUrtlbk semi.groups in L, with IT,(t)11 S; I and
IT,(/)]"" I. Then, lor every I in L. with I < p < 00, lhe func/ions
I f. '. f. ',
.. . T.(/.) . . . T.(I:.)(f, s)dt i . . . dl,
fX.1... 0 0
(1)
g = sup IAk I(a;. I) . . . A,(a.)(f, ')1
(I<czt. .... 0:.1_1 <00
is in L.. In the preceding theorem let u = (a., . . ., a'_I) he a point in
k-I dimensional Euclidean space and let I. = A._I(a._ I )... Al("',)/.
It follows then, from that theorem, that
sup sup IA(a.)(f.,' )1.
u O<CI,t,<OO
which dommates all the functions (1), is in L..
Finally it will be proved that the functions (1) converge almost
approt1£h a limit almost t:N'T"JfllJMTe on S as IX l -+ COt . . " IX k -+ ro inde-
peru1n.tly. The limi/ also e.rists in the rwrm 01 L. and lhe I"nc/ions (I)
are, lor a,. . . ., a, > 0, all dmni1UJ.ted by a fundion in L .
PaooP. If A,(IX) is the average of the semi-group {T,(I), 0 I}
696
VIII. APPLICATIONS
VIII:r.IO
VIII,7.U
ERGODIC THEORY of CONTI,,"UOUS FLOWS
697
everywhere on 8 as "", . . ., a... .... CO independentJy. If k = I this
folIows from Theorem 5 and we suppose that it has been established
in the case of k 1 semi-groups T., . . ., T.. By CorolIary 2, functions
of the form
U LE....A. Let (S, E,1') be a positive measure sp e and let
{T(t,., . . '. t.), t" . . .. t. > O} be a Btrongly measurable Berni-group 01
operatars in LI(S, E, /-I) ",ith ,T(t" . . ., t.)I. I. IT(t",. . .. t.)' S; I.
Let 1 P < CO, I € L., and I"(s} = sup IA(aHt. s)1 where
O<a:<oa
ft
h = f+ }; [I-T.(t,)]g,
'-I
with TI(t}t = f. 0 t, and with g,. Loon L. are dense in L.. Thu.,
since
AI(a}(I-T,(u)) = [I TI(t)dt -f._o T(t)dt].
A(a) = I. f. " .., f. " T(t", . . ., t.)dJ" . . . dt..
". 0
Then tkr. is an absolute constant c., uohi£h is independent 01 the semi.
group and indep<ruJenl 011, such tluzl
p(t"(fJ)) -<;; fJf It(B)lp(ds}, fJ > O.
Ci tCA,II)
where t*(fJ) = {slt"(s) >fJ} and .(fJ) = {sllt(')1 >fJ}.
The proof of Lemma n will be an inductive one based upon its
special case k = I which has been establisbed in Lemma 6, Since the
proof is a rather circuitous one, based upon three auxiliary lemmas.
it will perhaps be ofsome help if we make a schematic display of the
major logical implications involved in proving Lemme. 11 from Lem-
ma 6. To make such a diagram we will use the symbol C. for Lemma
II and D. for its discrete analogue. (D. is stated explicitJy in Lemma
16). Then C I is Lemma 6 and DI is Lemma 6.7. The symbol CPo will
be used for C. with the additIOnal hypothesis that the operators in the
semi-group Bre positive and DP k wi1l stand for the discrete analogue
of CP.. The lemmas designated by CPo and DP.are stated explicitJy
in Lemmas IS and 14 respectively. In terms of these symbols the
Jogical structure of the proof of Lemma II is as follows: C 1 _ CPo
- DP k => Dk CI:" The first implication in this sequence, i e., the
reduction of CPo to C 1 is obtained by a transformation which reduces
a 2k-parameter semi-group to a k-parameter semi-group. The device
is based upon the observation that if a family {IP., 0 < u} of functions
form .a. semi-group under onvolution, i.e... tI · rp" = q;U+tll and if
IP.("') = 0 for '" 0, then the transformation
8("'1...., ",.}
= f: ... f.' IP.,<t,,}IP.,(t,,>9'..(t.)'I'..(/.} ... IP..(t.._ 1 >9'..(t".)T(t" . . ., t"ddt l ... dt..
reduces the 2k-parameter senu-group T(t l , . . ., t".} to the k-parameter
semi-group 8("'1' . . ., ",,), '1'0 be sure that the semi-group 8("'1' . . .. ",,)
we have, for such a function h,
ft
V(a l . . . .. a.)h = A.la.1 . . , A.(",,}/+ }; h,
'-1
where Ih,l -<;; 2t,lg,I",laI' The induction hypothesis then shows that
Vh .... E.. . .E,j almost everywhere on 8. To complete the proof we
may apply Theorem IV.n.S. We shall let Ap be the set of all elements
a = [ , . _ .. ([ok] with !Xi rational and !Xl :2: p, i = 1, . . ., k, and let
To = Veal = V("",.. ., a.). We note that since, for almost all s,
V("", , , .. ex.)(f, s) is continuous for 0 < "", . . ., a... we have
sup jV(a)(f. s)- V(b)(/. ')1 sup [V(a)(f. s)- V(b}(f. s)l.
a.r.II :A. .fiJ-=p
where. in the second supremum , . ., /31.: vary over .all real numbers
greater than or equal to p. Thus, by Theorem IV.n.S,
lim sup !V(a)(/, s)- V(b}(!. s)1 o.
oo a ,p,i:ofJ
so that V(a)(/. s) converges for almost aU s in 8 as aI' . . ., a... .... CO
independently. Q.E.D.
If P 1 the preceding theorem is no longer true because (even
if k = I) the averages need not be bounded by a summabJe function.
However the averages of a k-parameter 8trongJy measurable semi-
group {T(t", . . ., I.}, t", . . ., I. > O} in LI(S, E, p} with IT(", .. ..I.}II
-<;; 1, JT(",..., t.}!", -<;; I do. when operating on a function in
LJeS, I, P,), converge almost everywhere_ This result, which will be
proved by induction on k, is based upon the following key lemma
which genera1izes Lemma 6 to the case of B k-parameter semi-group.
698
VIII. APPLICA.TIONS
VIII.7.I2
VIII.7.18
ERGODIC THEORY OF COSTJSUOUS FLOWS
699
bas the desired properties the functions 9'. must be chosen with care.
The following lemma defines these functions and states the properties
we shall use.
12 LEMMA. Fur U> ° let 9'.("') = u ("",--2) where
1
'1'(iX) = _1t-l/ta:-.I'e /.:e1
2
I f 1
A = .. e-" do = - vn.
2_00 2
.,>0
Therefore
1 f. e-ll'"' e- V ' f. - ( _!.....-V.,).
- dx = - a:-Slie z,jz dx
2Vn 0 ",31' 2v:n 0
2e V' f. '" vI _ ( V' _. ) '
= - -e 2" dy
vn 0 2y' .
2e- V '
=-- A =e- V '.
vn
= OJ'
", S;: o.
Then 9'. *9'. = 9'0+, and J m9'("')dz = I.
PROOF. We have
f '" 9'(",)dz = 2-1:n 11' roo :r'I'e-l/" dz
- Jo
= 2-1:rr;-I/2 loCO y-1/2e f.dy = n-]/ Jv oo ov- 1 / 2 e-4tJ.r
= :n ll' r(I/2) 1.
To prove that 9'. * 9'. = 9"H it will suffice to show that
(*)
f: 9'(.,)e "' dz = e- V ',
t> 0.
which proves (*) and completes the proof of the lemma, Q.E.D.
We shall now state and prove the lemma referred to as CPl' For
technical reasons occurring later the following lemma is stated for
what might be called a positive sub-semi-group rather than for a
positive semi-group. The proof of this lemma is the most involved of
all the steps in the proof of Lemma 11 ..... outlined in the diagram:
C I ,.. CP. ,.. DP.,.. D.,.. C.. The proof of the implication CP I ,.. DP I
which is the proof of Lemma 14 is very similar to the proof of the
following lemma but considerably easier in details and thus the reader
may prefer- to read the proof of Lemma 14 before that of Lemma 13.
13 LEMMA. Let (S, E, 1'-) he a positive measure sp<ICi! and for
t",.. ..1. > 0 let P(t",..., t.) he a tivr QJXTa/or in LICS, E.p)
with IP(t",. . ., t,)11 s;: 1, jPCt",.. ., t,)I ;;; 1 and
PCt I , . . ., t.JP(u", . . ., Uk) ;;:;; P(t" +u", . . .. t.+u,).
It is as.mmed that the opt"ra/or oolu,ro fwwtitm P is 8/TrJ1lgly crmtinuoU8
em the domain 1;.,..., t, > 0. Let 1 ;;; p < 00, f L , and f* =
sup A (O;)!f(' )1 where
0<0
For, if C*) is known, then
S "" 9'.(.,j.-"'dz = f '" 9'(",)e-"dz = e-"V',
--00 _'"
and thus, by Lemma 2.4, we have
f: C9'. *'I'.)(.,)e-'tJ.x = e- I "+"'''' = f: 9'.+" (",)e-'dz.
t>o,.
1>0,
which, in "View of Lemma I.15 t proves that 'flu. q; = fP +". To estab-
lish the equation C*) let A = Jg'e ('I.--tiI'du for cx> o. Then, by
pl.cing u = If v we find that
f. OO" - ( -. ) "
A = -e. d".
o u'
Upon adding the two formulae for A it is seen that
1 f. , f. "
A(cx) = - ... PCt., . .., t,)dt l . .. dt..
a. k t) 0
A = f. "' ( 1 + ) e-(;-) " du,
2 0 u'J
and thus. by putting cx/u-u = v, that
Then there is an absolute crJ1lstnnt c l , which is indepl'ndent of the opera-
tors PIt" . . ., t,) and indepl'nrlRnl of f, such that
p(e*{fJ)} < I p f. 1/(s)Ji«d.!), p> 0,
Cot 1'(IJ.tll
,vhere e*(fi) = (slt*(s) > fJ} and e(fJ) = {sIVCs)1 > fJ}.
700
VIII. APPLICATIONS
VIII.7.I8
VIII.7.18
ERGODIC THEOn OF CONTINUOUS FLOWS
701
PROOF. We observe that if I ;;; m s:: k and if T(t", . . ., 1m) =
P(t", . . ., I.) then
I i " i " I i " i .
- ... T(t",..., 'm)dt".. th m = -. ... P(t"...,I.)dll"..dt..
am 0 0 a 0 0
This shows that if the lemma is known to be true for an integer k it
is also true for any integer m < k. Thus, to prove the lemma) it will
8nffice to show that it is true if k is even. If k = I the lemma has al-
ready been proved (Lenuna 6). We shall thus suppose that the lemma
has been proved for the integer n and shall conclude its validity for
the integer k = 2n. Let 9'., 9' be the functions defined in Lemma 12
and let
where
p{BI/*.(B) > {f} s:: I R f. I/(B)lp(d.9),
c,.p e(c,JIJ
p>o,
I f " f "
1*. = sup ----;; ... 8("'1'...' "'.)I/(.)!tk 1 " .tk..
0<0: a 0 4)
S("'l'" .."'.)
= f"...Jo 'P.,(t,)<I',.,(I.)9'o,(I.)9'.,(/.).. .qo..(l.-l)'P..(I.}P(t",..., 1.)d4....dt..
To complete the proof of the lemma it is therefore 8ufficient to estab-
liBh the existence of an absolute constant d. such that 1*. ::?: d,j*.
For this it will suffice to show that for each lit > 0 there is an "t =
"t(IIt) > 0 such that
[*J A (8, "t)1 = i .... . i "' 8("'10 . . .. /);.)/tk l . . . tk.
«1 0 0
d. i " .. . i " P(t", . . ., 1.)/dt, . . . dt.,
a: 0 0
By Lemma 12 we have
L . _.1. 00 9'.,(t,,)'I'..(t,,)... 9'..(/k--1!<P...(/.)dt".. . dt. = (f" rp(/)dt). = I,
and. since rp(I) > 0, it follows that S("'I' . . '. "'.) is a positive operator
with 18("'1...., "'.)11 s:: 1 and IS("'l,..., "'.1100 ;;; l. Moreover, since
'P("') = 0 for", < 0, we have by Lemma 12, for 0 s:: f E LI(S, I, 1'),
for every non-negative function I in L". Since
A(S,"t)1
2-k,, '" f:... J: h("t, t", t")h(",,fo, I.).. .h(a" 1. ,.t.)P(t".. .,t.)/dt,.. ,dt.,
where
8("", . . ., "'.JS(y., . . ., y.)1
= {""... {"" 'l'. (t,,) ''''l'. (/.)9', (u.)... 'l'. (",)P(t", ..., I.)P(u,., ..., u.)/dt, ...du. .
Jo Jo I. ... 1 to.
J .. .J ",,'P.,(t,,).. .'Po.(I.)'P,,(u,.}.. .rp..(u.)P(t,,+u,.,..., I.+u,)fdt".. .du.
f"" .. . J "" 'Po (V 1 -"'1)9'.,("'1)" ''P..!v.-w')'I'w.(w.)P(v 1 , ..., v.)fdv 1 ... rho.
J-ac -co I
= f"" ... J "" 'P. +> (VI)" .'P. +> (v.)P(v 1 ,..., v.)fdv 1 ... dt.,
J-t'O -00 11ft .
= S(""+y,,...,",.+y.)f.
h(a1' I, v) = !.. f " 'P.(I)'I'.(v)du
"t 0
I i "' ..(.!+!. )
= (tv)-3/2 u 2 e tr fit du)
a1 0
Thus 8(x" . . ., "'.) satisfies the hypotheSIs of Lemma 13 and so by
our inductive hypothesis there is 8 constant C n such that
it is clearly sufficient to show that h(a 1 , I, v) "fa.' for all I, v s:: a;
for then [.J will follow with d. = (fJ/4n)k". This will be verified for
the function a 1 a. lJ ', i.e., we sball show that
(t,.fo) " f' .h -u, (. . + . ) du > lI, t", '" ;;; a. .
By placing u = IItJV, t" = c?,SI' I. = a B, this inequahty t",nsforms into
f t . (l +.!... )
(B18.) 21' 0 v 2 e \4;, '" dv > fl. 0 < B 1 . 8. "'" I.
Let G(a) = fov..........dv so that we wish to show
102
'\"111. APPLICATIONS
VIII.7.I4
VIII.7.!4.
ERGODIC THEORY OF CONTINUOUS }'LOWS
708
['.J
(SIS,)-8'OC ( 2.. + 2.. ) > ,
48 1 48 2
o < Sl' 8 2 < 1.
we see that IS("",.. ., "'.)1, ;;;; 1, IS(x",..., "'.)1= :;;; I, and thus, by
the Riesz convexity theorem. that IS("", . , ., "'0)1» ;;;; 1. It is clear also
that S(x 1 , . . , oZ'k) is a positive operator in L". Also
Since G 1S positIve and continuous It suffiC!es to prove r..] in the case
where either 8J or 8 2 is near zero. 'Ve have
i l . f. 1
CIa) = . tJ"'-- °dv = 0 u"oc,odu
S(I1:,. . . ., "'o)S(y" . . ., Y.)
!7>'. ""i..ft. dJ"
-, ...-.", ...y.
=e- Z +II.+.._+Z.+"t) . . I .1 . , P(iJ.'." ",i k ) P(jl'.."' i,,}
1,1.. .1.... .1.... .1..
xfl . .. y:.t
e-(Z +lIl.n+%t+y.t) I _ I . 1 P(i.+i J ...., "'.I.:+i,.;}.
".. ..10'
a-Bf2 i o
= - V 1 / 2 tr" dv.
2 .
and so. for some positive k. C( a) ;?; ka--"'l for all sufficiently large
values of a. Thus
where E is taken over all non-negative integers . . . ., i k , iI' . ... ik.
Thus
(SIS.)-8'2C ( + ) > Sk(s, +s.)-8"
43 1 43 2
if either 8} or 8 2 is near zero. This establishes [**] and completes: tile
proof of the lemma. Q.E.D.
14 LEMMA. Let (S, E, p) be a positive mearnre space and lor
every Bet 01 k wm-n..ga6ve inl£gers i" . . ., i.let P(,., . . ., i.) be a positWe
V'fJ"Nltor in L.(S, E, p) with !P(i" . . ., i.)11 ;;a; 1, IP(i". . ., i.)I"" ;;; 1,
and P(,., . . ., i.)P(i" . . ., i.) ;?; P(i, +1" . . ., ,.+i.). For I in L. let
I' = supA(nJlf(')f where
S(",., . . ., x.)S(y" . . ., y.J
"" T(m"..., m.)
;e, e-".+>1+...+..t-o.) L ... '" r , (x,+y.)""...(I1:.+y.)m l
flt-J-o f'llc-1) mJ.... m lr .
S(I1:. +Yl' . . .. "'o+Y.).
and so it is seen that the operators S(x., . . ., "'.) satisfy the require-
ment8 of the preceding lemma. Consequeotly, if
n
1 i " i "
f'. = suP. ... S("'...... x.)I/(')ldr.... dr..
O<a. f'.J.. 0 0
I 71-1 .._1
A(n) =. I ". I P(i"..., '.J.
n "1:"",,0 ',1:-0
Then too, is a constant c., indep€/"/tkm 01 Ih£ operator. P( iI' . . ., i k )
and the funetwn f, B=h that
where I e L», then
p({sl/'(s) > jJ}) ::o 1 p f I/(s)ll-'(ds),
C" elr'iPl
PROOF. For 3: 1 , . . ... a;J: > 0 define the operator
0:> 00 Xil...X'"
S( - ) - D-"'+",+X.' 1 · P ( i . . i .) .
...J'....'''''k -L- .IIt.t... L ., . I ...
f.l...{l :i.-=D i l _... k'
P> o.
p({s!/"(s) > jJ}) ;;a; f 1!(s)lp(ds),
cJ1 e\c )
Thus the present lemma will be proved if we establish the existence of
an absolute constant d. with I.' ;?; d,j'. This inequality will follow
from the statement that for 0 ::;; 1 e L. and for n ;;;; 0 there is an
0: = o:(n,l) such that
P>o.
Since the sum of the coefficients in this series is
[.J
1 J. " i "
- . . . S(",., . . ., x.)/d.x 1 . . . <Lv.
a. k 0 0
d k _1 11-1. .
;e, . I... L P(",....l.)/.
n '1=0 fk"",O
00 a;......xi'"
e-( J+...+%.t) "L"'... ] k = I,
.. ...., . I
'1...0 jol: 'l:t... .1k-
.
704
VIJJ. APPLICATIONS
VIII.7.I5
VIII.7.I6
ERGODIC THEORY OF CONTINUOUS FLOWS
705
I 1 " 1 "
- . . . S("'1' , . ., ",.)<k l . . . da:.
a.rc 0 D
1 fa-I 'fI-l
.1(71) = -. :! ... :! T;'... T ',
n -o f..,-O
Then theT. is a £"lUItanl £., ioukpendmt 01 lhe operalOTa T" . . ., T. and
eM lundi"" I, """h /hal
p({al'*(a) > (f}) ,.;; f. II(B)II-'(ds).
£Jl .!.,P)
PROOF. Using the notation P(T) introduced in Lemma 15 we
shaU define, for each set , . . "J iic On non-negative integers, the opera-
tors P( , . . ., i.) = P(T '. . . T '). Then, by Lemmas 6.4 and IS, the
operators P( , . . ., i.) satisfy the hypothesis of Lemma 14. Hence.
for Some constant £k
Since
"" 00
= :! .,. :! e"(",),,, ei.(")P( '. . ., i.),
",-0 f,t-D
where e (") = ,,--, Joe-.",mda:Jm!, to prove [..] it suffices to show that
there exists a b > 0 and. for each n. an "'(71) > 0 such that cm{",(n»
{jfn for m < 71; for then [.] wiU hold with d. = li". This last state-
ment will be verified for a(n) = n. i,e., we shall show that, for some
fJ > o. r. "-o,,,mda:Jm! fJ for all m < n. It thus suffices to show that
lim inf [;r/,.{",}<k > 0 where Im("') = e ",mlml. Since I;'{a;) 0 and
..-+00
l:.(a;) ;:;; 0 on the interval m-ym ,.;; 31 ;:;; m we have
1 m f. '" I
Im(31)<k Im(",)<k Ii ym !",(m)
o m-v_
[..]
1'((1.*(8) > fJH;:;; I li f. If(B)II-'(ds),
c k .,(cJ3)
fJ> o.
where
e
- ,\/,& '
1 tt-l 1:1-1
I.. = suP.. :! --. :! P( ...., i.)/f(.)!.
R l n '1-0 i:.Ii-()
But. by Lemma 6.4.
f." sup I I. 1 ... "i I T ... T '(f, .)1 = f*,
,,;:1 n 1,/.-0 ".-0
Hence (8Jf*"(B) > (f};;) (8If'(8) > Pi which, in view of [oJ, proves the
lemma. Q.E.D.
We are now prepared to give the proof of Lemma n. This lemma
will first be proved under the slight additional assumption that the
semi-group T(t", . . ., I.) is defined for all Ii O. To simplify the no-
tation the proof will he given for the case k = 2 but it will be clear
that the method is satisfactory for an arbitrary positive integer k.
By Theorem I1I.n.17 there is a p-null set E for which the averages
1 e-mmm+lm-J/2
2 m!
by Stirling's fannula. Q.E.D.
In proving the implication DP. "'" D. we shall need tbe following
lemma.
IS LEMMA. Far every bou,nded operalor T in LI' for which
ITJoo < co let peT) be lhe pomtiu: operator as80ciafed ",itA T as in
Lemma 6,4. Then P(TI)P(T.) P(TIT.).
PnooF, We recall that, for 0;:;; f LInLOO
P(T)f = sup IT{g. ')i.
1.(.)1'"
Let Ig(')i s;. f so that, by Lemma 6.4,
JT,T.(g, .)i s;. P(TI)IT.(g, .)i s;. P(T.)P(T.)I€(.)I ,.;; P(T.)P{T.)f.
Thus P(TIT.)f ;:;; P(T,)P(T.)f for every non.negative function 1 in
L"nL"". A continuity argument shows that this same inequality is
valid for all positive 1 in L.. Q.E.D.
16 LEMMA. Let T I , . . .. T. b. commuling operal<>ra in L 1 willi
IT,ll' IT,loo < I Jor i = I,..., k. For f. Lp let fO = sup IA(n)(f, ')1,
where n;;:1
1 1 " 1 "
A(",){f, 8J = - T(t".to)(f. s)cU,dl"
«2 0 fI
exist for all 8 not in E. Thu8, for a {E, A(",)(f, 8) is continuous for
'" > O. By Lemma 9 the semi-group {T(t".to) '1' 10 OJ is strongly
continuous at every point t" > 0, 10 > 0, and thus. since iT("-,IoHp
,.;; I, it follows that for each a in the set R of non-negative rational
numbers,
706
VIII. APJ>1.ICATIONS
VIII.7.16
VIII.7.16
ERGODIC THEORY OF CONTINUOUS FLOWS
707
1 a.1J!-1 II.n!-1 . _
A(rx)f=lim - I I8 1 (n)"S.(nJ"f,
<IJ_ ( n!) it=;() i.l O
This proves Lemma 11 under the additional assumption that the
semi-group is defined for all'"..., I. > o. Now 8uppose that
(Sit" . . .. '_). '" . . ., I. > O} is a semi-group which satisfies the hypo-
thesis of Lemma 11 and, for E> O. let T(E; t" . . ., ,_) = I if I, = I"
= . . . = I_ = 0 and otherwise let T(E; '" . . ., '.) = 8(t, +EU:.,. . .,
I.+w.), where u j = 1,+.. '+"_'+"+1+" .+1_. Then we may apply
the result just proved to the semi-group {T(E; I".. .,I.},,,,.. ..'. O}.
For f in L we let
where 8,(n) = T(Iin!, 0), S.(n) = T(O. Ifn!). Using Corollary 111.6.
18, Theorem III.ll.17, and the Cantor diagonal process. we may find
a sequence {nj} such that
A(rx)(/, s} = lim o.f' onfl S,(n j )"8.(n j )"(/, s)
j CQ (o:njI)2 '1.-0 '2",,0
for each a m R and each s not in a null set E I 2 E. For 8 E, let
II .-, ' 1 I
f:(s) = sup 1 --:2 I I S,(n}"'S.(n)"'(j, s) ,
1St k m.=O "'t-O
I: = sup IA(E, a)(/, ')1,
0"0
1* = sup IA(rx)(/, ')1.
.<0
where
so that if a. £ R J 8 f. EJ' and E> 0, there is an integer N(a., SJ B) with
1 L " L "
A(E. rx) = ----. ... T(s; t" . . ". I.)di" . . . dJ.
a. 0
If:(s)1 ;::" IA(a)(/, s)l-e,
n N(rx.s,e).
and
lim infr.(s) > IA(rx)(/, s)l.
rxeR, s E,.
1 L " L o
A(rx) = . ... 8(1,. . , '. t")di,, . . . dJ..
rx 0 .
Therefore
"
Thus it has been proved that
Now if s E, then sf E and hence for Sf E, the avn'age A(a)(f, s) i8
continuous in a. on the interval 0 < tX. < OJ. Thus
[*]
p({sll:(s) > PH :5: f Ij(s)lp(ds),
cA;P .11:,.13)
E,P>O.
lim infr.(s) ;::" I*(s) = sup IA(rx)(j, s}I,
n-Jo'w O<a:
Sf E,.
It is seen from the Lehesgue dominated convergence theorem (III.6.
16) and from Lemma 9 that for each I in L we have, for a > 0,
limNoA(e, rxJI = A (rx}1 in the norm of L., Thus, hyTheoremIII.8.6,
A(E, rx)1 -+ A(rx)! in measure and hence. by Corollary 111.6.18 and
the Cantor diagonal process, we can find a sequence ei -)0. 0 such that
A(e" a)(/, s) -+A(rx)(j. s) forp-almostallsinS and for all rxin the set
R of positive rational numbers. It follows that Iim inf. = I:.(s)
IA(rx)(j, 8)1 for a]most all s in 8 and all rx in R. Since, for almost all s
in S, A(rx)(j. s) is continuous for 0 < a. we have
Tb"" tor P > 0 we have lim inf h Xh X where Xn and X are the charac-
teristic functions of {slr.(s) > fJ} and {s *(s) > P) respectively. Con-
sequently, by Fatou"s lemma and Lemrrw. 16, we have
p{{slf*(s) > PH = J s X(s)l'(ds}
:5: Iim inf J s X.(s)l'(ds)
h
= lim inf p{sjj: (s» P)
h
I*(s) = sup IA(rx)(/, a)1 ::;:; lim inf I:.(s)
at"R '-+00
:5: lim inf 2.. f If(s)lp(ds)
ft_ao CIt;{1 III( 1:")
= 2.. f 1!(S)JfL(ds).
CkfJ .(c,ft,
almost everywhere on S, If e*(P) = {alj'(s) > {J} and e:'({i} =
{slf.;(s) > fJ} then, modulo a null set, lim inf, "" e:'({i} 2 e*(fi) and
so [*] and Fatou's lemma yield
.
70B
""III. APPLICATIONS
VIII.7.17
VIII.B.1
UNIFORM ERGODIC THEORY
709
I"{e*(fi» I " J I/(s)ll"(ds).
ckP drtfJ)
This completes the proof of Lemma 11 and prepares us for the
fol1owing basic result on the almost everywhere convergence of the
averages of a k-paramder semi-group in L,(8, E,I").
17 THEOREM, Let IS, :E,I") be a positive measure space and let
{T(r",. . ., td. r". . ... t. OJ be a BIrongly rnetlSUTalh k-parameter
semi-group 01 operiWJr8 in L,,(S, :E. 1") with jT(r",.... 1.)11 ,.;;: I and
IT(r", . . ., 1.)1= I. Then, lor etoery I in L,,(S.:E, 1"), 1M limit
lim I. i '... i " T(r", . .., I.}(/. s)dt,. . . . dt.
ct-HJQ a. 0 0
e:rists lor olmost all 8 in S.
PROOF. Let
lems in the theory of Markov processes, although we shall only sketch
these applications.
I LE.....A. Let T be an operator in a B-sp<we I and w.ppose that
{n-'Tn) oonverges 10 zero in 1M weak opera"'r lopology as n approaches
infinity. Then 1M spectrum 01 T is a subset 01 1M unit disk {z[lzl ,.;;: 1),
and any pole A 01 T with 1.1.1 = I has order rm£.
I i " i "
A(a) = ----. ,., T(t", . . ., I.)dt, . . . dt..
a 0 0
For p > I the set LpnL 1 is dense in L" and for I in L p nL 1 it is seen
from Theorem 10 that the limit lim....= A (a )(/, 8) exists for almost a1l s
in S. In view of Lemma n we may apply Theorem IV.n.S. with
A p = the set of all rational numbers a ;;:; p, to conclude that for every
I in L"
PROOF. The hypothesis and the uniform boundedness theorem
imply that ITnfnl K, n = 0, I, 2. . .., for Some K, and so
lim suPn_= ITnl11n 1. It fol1ows from Lemma VII.8.4 that la(T)j ,.;;: 1.
If A is a pole of T and [AI = I. then I is a pole of TI = TfA and
T; fn ->- 0 in the weak operator topology, Hence to prove the second
8tatement it suffices to treat the case that 1 is a pole of T. Suppose
that the order nf the pole I is at least two. It follows from Theorem
VII.a.IB that there exists an "0' E(I; T)3:: such that (I-T)x. *' 0,
but (1- T)'xo o. Now apply Theorem VII.a.22 to the fundion I
defined by I(A) = Anln, to obtain
I I
Tn",o = "'o+(I-T)xo.
n n
Iin, sup IA{a)(f, s)-A({i)(/. 8)1 = 0
II a,PEA"
Letting n -+ 00, we conclude that ",*(I-T)",o = 0 for any ",*. :£*,
which is a contradiction. Hence the only poles of T which lie on the
unit circle are simple poles. Q.E.D.
We now give a condition which implies that if ja(T)I ,.;;: I. then
the only spectral points A with 1.1.1 = I are isolated and the carre.
sponding projections have finite dimensional ranges.
for almost all $ in S. Hut since, for almost all 8, A (a )(f, 8) is continuous
in a, this means that the limit Ii""...'" A(a)(f, s) exi8ts almost every-
where on 8. Q.E.D.
8, Uniform Ergodic Theory
2 LEMMA. Let T be a baunded linear operator whose specfrum i8
contained in 1M unit disk and kt ITn-KI < I for 80me positive integer
n and so"", compact operator K. TMn every spectral poW A 01 T wifh
IAI" > ITn-KI is isolated and 1M corresponding projection E{A; T) ho.s
a linite dimensional range.
PROOF. Let.. be as in the hypothesis and let w be a primitive
n-th root of unity. It fol1ows from Theorem VII.8.II that if A £ aCT)
and IAI = I. then
E(A; T)+E(Aw; TH.. .+E(Awn l; T) = E(.1.n; Tn).
In this section we obtain conditions On a bounded linear operator
Tin R complex B-space which are sufficient to insure that the averages
on-I !;= TJ converge in the unifonn topology of operators. A special
study will be made for certain operators on C(S) and L,,{S, E, 1")
where a rather complete decomposition of the space S is possible. The
results of this section can be advantageously applied to some prob-
710
VIII. APl'LICATIONS
VIII.8.2
VIII.8.8
UNIFOIU4 ERGODIC THEORY
711
By Corollary VII.S.21 we have E{}.w"; T)E(W; T) = 0, P '1= 9., and
so if E()'"; Tn) has a finite dimensional range, so does E(A; T). Also
by Theorem VII.S.ll, if I. ft is an iso1ated point of a(T") = [aCT)]".
then}. is sn isolated point of aCT). Hence it suffices to prove the lemma
under the a..'L"mmption that n = I. which we now make.
Let V = T-K. It wi1l first be shown that if II'I > IVI and if
(1,- R (I-'; V)K)-t exists then R (p; T) exi8t. and equa1s
(/-R(P; V)K)-1R(P; V). This follows from the identity
R(I-'; V)(.uI T) = R(I-'; V)(.uI-V-K) =I-R(p; V)K.
E(A; T) = 2... f. 1/(1'; T)dp
2m c
= f. R(P; V)K(/-R(I-'; V)K) IR(P; V) dl-"
2m c
Since K i. compact, the integrand is a compact operator for each f'
on C. By the definition of the integral and Lemma VL5.3, we conclude
that E()'; T) is also a compact operator, But E(}'; T) is the identity
operator on the sub.pace E(A; T)I and by virtue of Theorem IV.8.5,
this implies that E(I.; T)I is finite dimensiona1. Q.E.D.
8 THEOREM. Let T be BUch Ihat T"!n ronverges 10 "ero in tM weak
Iop<JIngy, and let ITft-KI < 1 t... some positive i1itegern and some c""'.
pad operal... K. Then there are al most a Jinik number ot poinls A., . . ..
J... of unil 11J()du/us in the spntncm of T. Each point A, is a simple pole and
E(}.,; T)I is tinire dimensi01wl.
PROOF. Let ).. e afT) and IA,I = 1. By Lemma 2, E(A,; T)I is
finite dimensional and so the operator T restricted to this subspace is
compact. It follows from Theorem. VII.4,5 and VILS.20 that )., is a
pole of T. By Lemma 1 it must be a simple pole. Q.E.D.
4 COROLLARY. If T Biltisfies tM hypothnis of 1M throrem, then
n- 1 I;.: Ti converges to tM proimion E(l; T) in 1M uniform lopology
0/ operurors.
PROOF. Let A(n) = n- I Tm, let a be that portion of aCT)
in the open set IAI < I, and let if = a(T)-a. Then, by Lemma VII.S.
18. we have A(n)E(a) --+0. By Theorem VII.3.20 the points A., .. .,}."
are simple poles of the restriction Tu of T to E(d')I. Thus, since
21- 1 I::. J.;' --+ 0 for each At '1= I, we see. from Theorem VII.8.22, that
A(n)E{a')--+E({I}). Since A(n)=A(n)E(a)+A(n)E(O") the corollary
is proved. Q.E.D.
We now turn to an examInation of certain operators T which
are defined in C(S), where S is a compact Hausdorff space. We say
thatT is posilire if (Tf)(s) ::2: 0,8£ S, whenever/is such that/(s) 0,
8 E S. It will now be seen thn.tif Tis posItive and satisfies the conditions
imposed in Theorem 3, then the points of a(T) of unit modulus are
all roots of unity.
5 LEMMA. Let T be a posilire liMar operafur in C(S) such lha
and the calculations
[(I-R(I-'; V)K) 1R(I-'; V)]IJd-T] =I:
f.ul-T][(I R(p.; V)K)-IR(P: V)]
= (pI-V)R(P; V)(I-'I-T)(/-R(I-'; VJK)-1R(I-'; V)
= (.uI-VJ(I-R(P: V)K)(/-R(P; V)K)-IR(I-': V) =1.
Now by VI.5.4 the operator R(P; VJK is compact for each I-' in the
domain 11-'1 > IVI and it evidently depends analytically on p. Since
IR(P; V)I --+ 0 as 11-'1 --+ 00, it follows that for II'I 8ufficiently large
IR(P; V)KI < 1. By Lemma VIl.3.4 we conclude that if II'I is suffi-
ciently large, then the number 1 is not in the spectrum of R(P; V)K.
It follows from Lemma VIl.6.1S that (1- R(P; V)K) 1 exists and is
an analytic funetion of 1', for 11-'1 > lVI, except at countably many
isolatOO points in this domain. By the remark. above tbis shows that
R(P; T) exists for II'I > IVI ""rept at a countable nwnber of isolated
points.
Let A e aCT} snd IAI > IV); it remains to show that E(}'; T) has
finite dimensional range. To do this, let C be a circle with center at A
and radius small enough so tbat C lies entirely in the domain IIlI > IVI
and does not contain in its interior any point except A at which
{I -R(p; V)K)-I fail8 to cxi5t. For fl-'Ilarge, the Laurent expansion
leads to the identity
(I-R(P; V]K)-I =I+R(I-'; V)K{/-R(P: V)K)-1,
and so by analytic continuation this holds on C as well. Consequently,
R(P; T) = R(P; VJ+R(P; V)K(/-R(,..: V)K)-lR(I-': V).
Now,. since R(P; V) is analytic on C, we have
.
712
VI1I. APPLICATIONS
VIII.8.5
VIII.8.6
UNIFORPr( ERGODIC THEORY
718
Tntn ctJ1Wl?7ges 10 =0 m IIw weak opn-ulDr topology and let ITn-KI < 1
lor some positive inte(!p' n and some compire! operalor K. Tlwn Iwe a.isls
aninUger N <mehlha!il A",. . ., A. are tlwpoint.s01 <T(T) oluni! modulus,
Iken Ai: = I, k = I. . . ., q.
PROOF. Let A 0# I be in aCT} with IAI = 1 and let f 0# 0 be in the
range of E(A) so that TI = Af. Let s. be a pOInt of S at which If(' II
attains its maximum. Since E(A)C(S) is a linear manifold we may
suppose that I(s.) = I. Let IJ be the linear functional on C(S) defined
by IJg = g(s.}, g. C(S). Then (T*)"b is a non-negative linear fune-
tio",,! on C(S) and so by Theorem IV.6.3 there i8 a non-negative
measure 7t n in rca(S) such that
(Tng)(so) = Isg(s)nn(ds), gEC(S).
Since An/(so) = (T'f)(s.) = JsI(s)n,(ds), and I/(s)l;;;; 1(.0) = 1 it
follows that ".(S) ;;;; I, n = I, 2, . . ..
We now show that for each n, the open 8et A, {. E SI).-n/(s)
:f=. I} has .1tn measure zero. Since T"/ = Aft'. we have
1 n-1 ]
o S; ,,(A;) = lim - ",(A;} = lim - = o.
___co fl f-D ft__OC n
Therefore ,,(A') = ,,(A;) = O. Since A and A' are complemen-
tary sets, wc conclude that 0 = n(A)+n(A') = ,,(S) I. This con-
tradiction proves that the sets {A;} cannot be pairwise disjoint.
We have shown that there exist distinct integers m and n such
that .(.A contains a point sr Consequently ).--></(8]) = 1 = J. m/(a,)
and so J..- = I. But J. was any point of O'(T) with III = I, and since
there are only a fimte number of such points. the existence of the in-
teger N described in the statement i8 proved. Q,E,D.
We now collect the results already obtained.
6 THEOREM. Le! T be a positive lim'tlr operator in C(S) such thai
T.!n OO1Ivergea to zero in tlw weak operator topology arn! leIIT'-KI < 1
lor 80"", positive integer n and a."", compact operator K. Then O'(T) may
be decomp68ed into tlw union vI a closed set 0', which lies inside a circre
Izi < '" < I, and 01 a linite number of simple pores eOn;'., ",We e. i-a
Taiimwl, k = I, . . ., q. II we pul E. = E(cOn;'.), ED E(O') arn!
D = TED' tlwn cach E. has linite dimena«mal range. TIw it£Ta!e8 01 T
are given by the formula
o = f(S.}-A n(Tnf)(8.) = Is {I_). n/(.)}",(ds),
and. taking rea.1 p8rts
0= Is {1-9I'().-n/(a))}n,,(ds).
Since 19I'(A--></(s»1 ;;;; 1/(')1 S; I, the integrand just written is non-
negative. Since "n i8 non-negative, it follows from 1I1.2.20(d) and
111.6.8 that if Bn denotes the set Bn = {BE SI9I'(). /(B» 0# I}, then
"n(Bn} = O. Since I/(B)I S; I(Bo) = I, it is easily seen that Bn An
and hence "n(A.} = o.
It will now be shown that the complements A = S-A.,
n = 0, I, 2, . . ., cannot be pairwise disjoint. Applying Corollary 4,
we define a measure " by the formula
I _1 1 n--l
,,=lim - ",=Iim - (T*FIJ.
ft-+OJ n :1-0 CX) n 1...0
Since ",(8) ;;;:; I, we have ,,(S);;;; I. Let A = n oA,; since A A"
we have ",(A) = 0 for i = 0, I, 2, . .. and therefore >t(A) = O.
Let A' = U:':.A;, so that A' = S-A. If the sets A , k = 0, I, 2, .. .,
are pairwise disjoint then :n:J(A ) = 0 for j -# k and so
.
Tm = I el:l" m E k +Df7I.
.-,
Fur/lwr, twe exists a positive number M such that
ID"'[ ;;;; Mcr."',
m;;;;l.
m l.
PJ<OOF. Only the last two statements remain to he proved. Since
the points e"lni. 8 k are simple poles of T, the expression for is aD im-
mediate consequence of Theorem VII.8.22. Finally D = T. on
E(O')C(S) and vanishes On (I E(a»C(S) so <T(D) = O'(T.}U{O}.
By Theorem VII.8.20, O'(D) = aU{O} and so <T(D) is contained in the
disk Izi < '" for some cr. < 1. By Lcmma VII.I!.4 this implies that
fun suP..-oo IDml'/m< cr., from which itfollows that IDml;;;; Mcr. m , m I,
for some positive number 1.1. Q.E.D.
7 THEOREM. Let T 8atisfy the hypo!lwsis 01 tIw prooed:iug tJu?omn
and leI Ep = ,E.. Then the suhspare C p = Ep[C(S}] is linite
dimelUlional, and il CD = ED[C(S)], then C(S) iB the direct sllln of C,.
and CD' Both 81J.bspirees C,. and CD are invariant ..tuler T, and
.
714
vnl APPLICATIONS
VIII.8.8
VIII.8.8
UNIFORM ERGODIC THEORY
715
(a) there exislsa 'jJOBiiiveinreger N such that T'111 = 111, for I11E Cpo
(b) Tn", -+ 0 eI11p6lU!7lrinlly fast. for '" . CD'
Moreover, the IrUbspMes C p and CD are uniquely tkfined by 'JlTf'P"!ies
(a) and (b). napoctit'ely.
PROOF. It follows from its definition that E p is a projection, that
EpEo = EoEp = 0, and that I = Ep+ED- Further T commutes
with E p and ED so this direct sum decomposition is into subspaces
invariant under T. Statements (a) and (b) follow from the formula for
T'" given in Theorem 6. To prove the final assertion, let,", C(S} be
such that T"", o. Then 111 = '"P+'"D' where JJ p = Er. C p and
I11 D = ED'" . CD- It follows that T n l11 p -+ 0 and Tn"'D -+ 0; but sinee
{Tn",,,} has infinitely many tel111S equal to '"p. it follows that '"p = o.
Hence CD = {"'. C(S)iT"", OJ. Similarly if '". C(S} is such that
Tn", = ",forsomen;;:; I,itfollowsthat",. Cpandso C p = {or. c(S)1
Tn", = 111. for some p ;0.. I}. Q.E.D.
The conclusions of Theorem S are valid for any B-space J and in
particular for the space 1.:.(S, E, 1')' However. it is not evident that thc
more complete decompositions obtained in Theort'DlS 6 a)1d 7 for C(S)
ean be derived for any other spaces, We now prov that for the space
1.:.(S, E. p} such a derivation is possible due to the fact that its con-
jugate space may be represented as a. space of continuous functions.
If T is an operator in the space L 1 (S, E, p), we say that T is posititoe if
(Tf}(s) ;0.. 0 I"almost everywhere on S, whenever f(s) ;0.. 0 p-almost
everywhere.
8 THEOREM. Let (S.E,p) be a a-finire measure spMe.
Suppose that T is a positive linror operotor in 4(S, E, p) such thoJ
T"/n tXmVl!rges to zero in the weak operator topology and let IT"-KI < I
for some positit'e integer n and some campa£! operator K. Then the con-
cl-usians of Theorems 6 and 7 hold ;/ C(S) is TeplMed by 1.:.(S. E, p).
PROOF. We consider the adjoint operator T* in the space
L=(S. E, p). It is easily seen thatsince T is positive. T* is also positive.
Further, if Tn = K + V, where K is compact and VI < 1 then
(T*)n = K*+V* and K* is compact, by Theorem VI.5.2, while
IV*I < I. by Lemma VI.2.2. Now by hyPOthesis Tn/n 0 in the
weak operator topology. An argument similar to that in the proof of
Corollary 4 shows that the sequence {T" In} converges to zero in the
uoiform operator topology of B(L 1 }, By Lemma VI,2.2 this implies
that {T'"/n} converges in the uniform operator topology of B(L",,),
and therefore in the weak operator topology of this space. Thus we
have shown that the properties assumed for T are also valid for T*.
Now Theorem V.8.11 asserts that there is a compact Hausdorff
space 8 1 such that L",,(S, E, p) is isometncally isomorphic with the
space C(S]), and that the isomorphism preserws the notion ofpositiv.
ity. Thus it is seen from Theorem 5 that all the points of a(T'} of
unit modulus are roots of unity, and by Lemma VII.8.7 the 8ame
holds for a(T). The remaining conclusions in Theorems 6 and 7 are
then provided exact1y as before, since no special property of the space
C(S} was used to establish them. Q.E.D.
We sball conclude thi8 section with a brief indication of how the
results already obtained can be applied to the theory of Markov
processes, The exposition here i8 not complete; the reader should refer
to the paper of K. Yosida and S. Kakutani [2] for details. Actually
the procedure they employ is not exactly the one we will describe but
it does not differ in an essential way.
Let (St E, It) be a. fInite positive measure space and consider a
real valued function P defined on S 'Y- E. The function P is called the
transition probability function, and we regard the number pet. e) as
giving the probability that, after the elapse of a unit time. the point
t. S will be in the set e _ E. Let B(S, E) denote the space of bounded
E-measurable complex valued functions on S with the norm If I
= sup..s 1/(8 )1. f. B(S, E). By ca(S,.E) we denote the 8pace of count.
ably additive complex valued measures defined on the a.field Eo We
.assume
(a) P(', e}. B(S, E},
(p) P(t,.}. catS, 1:),
(y) P(t.e) ;0.. 0,
(eI) P(t,S) = I,
eE"E;
tES:
t.S, e.E:
t.S.
Under these assumptions it is readily seen that the probability that
t e point t . S will be in the set c E 1: after an elapse of n unit times. is
gIven by the recurrence
pln'(t,.) = fsP'-"(I,ds)P(s,c) = Lp(t.ds)P(" 1I(S,c}, n=2,3,...,
716
VIII. APPLICATIONS
VIII.8.g
VIII.9. I
E.XERCISES ON ERGODIc THEORY
717
where P(U = P. The problem of Markov is to investigate the asymp-
totic behavior of the sequence {p(nJ(t, ej} and the means
n-' !;:: pilI (I, e), where P(O'(t.e) = 7..(1).
In this way one is naturally lead to the study of two linear map
pings
.can be further S p lit into Bfinite Dumber of dis J 'oint Borel sets eil e . .
....., ..'
where k, is a divisor of the integer N of Theorem 7, and !f.., k,
= dim E.[B(S, I)]. The sets e", i = 1, . .., k, are called the Bub-
ergodic kerml3 belonging to e" they are determined up to ,,-null sets,
and ej = U: l CHo Further, putting e',kt:+ 1 = e nl we have
P(t. e.,Hi} = I.. t £ eijl
so that the process transfers (with probability one) the points of an
ergodic kernel cyclically through the sub-ergodic kernels which belong
to it.
t --+ Tt = f s t(8)P(', ds), t < B(S, I),
p---->-T'p= fs,,(ds)P(8,.), ,,<ca(S,I).
which act in the spaces B(S, E) and catS, I) respectively. It is readily
seen that the operator T Bnd its iterates are positive and have nonns
equal to One. Also the function identically equal to one is left fixed
by T, so 1 < aCT). In the study of such processes one makes additional
hypotheses on P which will guorantee that there exists an integer n
and a compnet operator K in B(S, I) such that ITR-KI < I.
Recalling Theorem IV.6.1g, we note that the space B(S..1:) is
isometrically isomorphic with the space C(S,). where S, is some com-
pact HausdorlI space. Since the isomorphism preserv.. norms ond
positivity, it is seen that the results of Theorems 6 and 7 are valid
for the operator T in the space B(S, I}. It is possible to decompose the
transition probability function of P in a way corresponding to the
decomposition of the space B(S, E) established in Theorems 6 and 7_
Perhaps somewhat more surprising is the decomposition of the space
that can be obtained. Indeed, if g is the dimension of E(I; T)B(S, I).
it is possible to decompose S into g mutually disjoint Borel sets e"
i = 1.. . ., g. which are called the ergodic kerne18 and are determined
up to wmeasure zero, and into the complementary portion L1 =
S - U :_1 e" caUed the di8Sipative part of S. These sets have the proper-
ty that
9. Exercises on Ergodic Theory
1 Show that Theorem 5.9 ond Corollary 5.5 remain valid if
p > 1, even jf (8., I, 1') is an infinite measure space.
2 Show that if the measure space (S, E, p) in Theorem 5.9 is not
finite, the necf'Ssa.ry and sufficient condition that the theorem contin 4
ue to hold in the case p = I is that for each e > 0 and each e < I
,"uch that pee) < 00. there exist an a < I such that pea) < 00 and
.,-1 I;:- ,u("' i(e)-a) < e.
8 Let {T,} be a strongly measurable positivity presening semi-
.group of operator8 in L, such that IT(tll l :;:: I, IT(t)/..;;;; 1. t> o.
Show that for each t < L., P ::;; 1, there exists a measurable function
J* which is finite almost everywhere such that
f: I(T J)(B)lfi(l)dt :;:: /*(B) J: fi(t)d!
pet, e,) = I,
sup P("'(t, .II) < Ma",
«,
toE e i .
Jor every positive ond decreasing fuuction {i. Show that if / < L.,
P > I, we Can take I' < L..
4 Let (T(t,. . . ., '.)} be a strongly measurable positivity pre-
-serving k-parameter semi-group of operators in Ll such that
IX{t" . . ., '.)1, :;:: I, IT(t,...., '.)1= :;:: 1, " > 0. Show that for each
J E L. there exists a measurable function /' which is finite almost
everywhere such that for almost all 8
o < ex < I" n = 1, 2, . . u
These relations may be int.etpreted as saying that if t < e.. then it is
transferred by the process T (with probability one) into the same
ergodic kernel e" and that as time increases the dissipative part is
evacuated. Moreover, the kernels e i cannot be decomposed into small-
er sets with the first mentioned property. However, each kernel e,
J: . .. J: IT(t" . . ., '.)(/, 8)lfi(t,. . . ., t.)dt l . . . dt.
;;;; /'(8) f: ... J: fi(t", . . ., t.Jd!, . . . dt.
718
VIII. APPLICATIONS
VIII.9.5
VIII.9,10
EXERCISES ON ERGODIC THEORY
719
provided one of the following conditions is satisfied:
(a) p > 1 and ,8( ... .,I E ) =y( +... + ) whereyisapositive
and decreasing function, or
(b) p> I and ,8( , . . ., t,J = rr:".y,(t.) where y,(t,) is positive
and decreasing for t, > 0, i = 1, . . .. _, k.
Show that if p > 1 we can take 1* .L .
5 Let,8 be a p08itive, even, integrable function of the real
variable", which is decreasing for", > O. Let ,8("'} Iy("')!, and let y
be measurable nnd f :y("')d.x = 1. Then for I in L. we have
hm I J: y(t("'-Y»/(y)dy = I("'}
,
for a.lmost all m.
6 Let,8 be a positIve mtegrahle function ofthe real "ariables "'I'
. . ., "'A which has the fonn {J("'], . . ., "'.) = {J](a{+. . .+"';), where,8.
is decreasing. Let ,8("']' . . ., "'.} ;;" Iy("'., . . " "'.)1, and let y be meas-
urable and have f .. . f!:y("']. . . ., "'A)d.x r . .d.x. = 1. Then for
I in L, we have
lim t. f +oo ... J +OO y(t{.:v] -YI)' .. ., t(",. -y.»f(YI' , .., y.)dyl' ' ,dy.
'_00 -00 - 00
=/(""".. .,.:v.J
for almost all "'.
7 (Hardy-Littlewood) Let h be R hannonic function defined in
the circle ",' +y' < 1, and let 1 < p < 00. Suppose that
fo" lh(re"Wdll 5:. K, 0< r< 1. Let h*(I9) = max,,«<1 h(re"). Show that
there exists an absolute constant C such that fo" Ih*(I9)f o dll 5:. C.,K
Show that Ii ] h(re") exists almost everywhere. Hint. Cf. Exereise
IV.14.eO.
8 Let h be a harmonic function defined in the sphere ! -Ix'i < 1
in Euclidean n-space. Let 1 < p < 00, 0 < K < 00. Suppose that for
each r, O<r<l, the integral of the function [h(r",) I' over the surface
of the tmit sphere is 5:. K. Puttingh*("'J =suPo«<llh(r"')1 for 1"'1 = I,
show that there exists an absolute constant C.,» such that the integral
of h *. over the surface of the unit sphere is at most C.,.,K. Show that
lim.--..I h(r.:v) exists for almost aU '" on the surface of the unit sphere.
9 Let h be an infinitely differentiable function of the 2" real
variables a'l"'" nr Yt. . . -, Yn defined in the region +!ii < 1,
i = 1, . . ., n. Suppose that for each i = 1, .. ., n we have o'hloX:+
o'h/oil. = O. Suppose that p > 1, and that for 0 < r < 1
Jo" ... J: I/(r cos 19], r cos 19.. . . ., r sin 0.) IpdIJ]. . . dlJ A 5:. K.
Show that Iim fer. cos 19], . . ., r sm 19.) exists for almost all
rl l....r...-rl
0 1 ", ..On-
10 Let h be a hannonie function as in Exercise 7. Show that for
almost all II, lim h(2.J exists, provided that larg (1-2,'-")1 5:. K <n/2.
cr+f.tf)
Hint. use the method of Exercise 7 with a modifiEd kernel.
11 Let I be a measurable function of the real variable "'. let
1 5:. P 5:. 00, and let I L . Sho,w that for alm08t all '" we have
(a) lim 1/t/n r: ,-"'-r>' l(y)dy = f("');
.
(b) limt r: e,cc-"f(y)dy = 1("');
, OO
(c) lim (:nt) ' f + ( Sin I -Y) ) ' l(y)dy = I(.:v);
"1--+00 _00 tJ) Y
f +OO I
(d) lim (e/n) ' +( _ ) ./(y}dy 1("').
1I...-K1+ --<10 E 11: Y
12 Letfbeameasurablefunct.ionofthereal variables Xl' 6. .,..Tn'
let 1 ;;;; P ;;;; 00, and let I Lp. Show that 1(""" . . ., "'.) is, for almost a1l
x.l 1 . . ., .t':n' equal to
( t ) .I' f +OO f +
(8) lim - .... e-C{{;Z:l-tfIl +...+I Jt--.,..)1I1/{Y.tI'" ., Yn)dYl ° .... dYn;
'-+1:10 jf, -00 -t)Q
. 1 f +<O f +OO ( sint("',-YI)...sint("'.-YA) j '
(b) hm - ( ) . . . . J(YI"'" y.)dy1''' dy .
, ",,:nt _ _ ("'I-y')"'("'.-YA)
13 Show that, by applying Theorems 7.5 and 7.7 directly to
the semigroup IS,} defined by
(S./)(",,-,.. ""'.)
J +oO I . . }
- t"'n J' .-' ,.,-0,1 +...+('.-0.) I(y Y ) d y du
--co .It..". 1'1 1-.' .," I
an mcquaIity strong eno,ugh to, yield the result (a) of the previous
exercise can be obtained. Prove that thi8 implies the Lebesgue theo-
rem 'Which asserts that for an integrable fun<:tion I,
720
VIII. APpLICATIONS
VIII.9.14
VIII.9.19
EXERCISES ON ERGODIC THEORY
721
lim h--l"+'.. .1"+"/(Y" . . ., y.)dy, . . - dy. = l(x I , . - ., x.)
11.....0+ 2'1
almost everywhere. Also 8how that this Lebesgue theorem implies
the result (b) of the previous exercise.
14 Let I be as in ExeIrise 12, and suppose p> I. Show that m
this case /(:£1" . . '1 oX,.) is" for almost aU :ell' .. ., a: n . equal to
[ +00 f +oo
--00 ... --00 1/("'1"'" ",.)1(1+ 10g+lj("'I"'" "'.J[)d.r p ., d.r. < 00
. ( . ,,'. ) I J +OO J +OO ." .
(a) 11m --;;- .., exp(-.!I,(",,-y,) )jUh,...,y.)dy,...dy..
:n: _CQ -co ._1
. I J +OO J +OO ( . 8int,(X,-y,» ) "
(b) hm ( ). ... IT /lYI,....y.)dyl...dy.;
t} . . . 'n n: -W' -co i_I Xi.-Yi
(C) lim (I!:,... hn)-I 1=1+-. ...1:+" I(Y". .., y.)dYI'" dy.,
where the limits are taken with respect to . .. . "' In ....,. CO and , . "' h n
O+. (Part (c) is a result ofSaks, Zygmund ane! Marcinkiewicz.)
15 Let (S, 1:, /-,) be a finite positive measure space. and T
an operator in L:,(S, 1:, /-,) with ITI, I, ITloo ";; I. Put 1*
sup IA(n)(j. .)1 for each 1£ L I . Show that
I".
is then 8uffident to guarantee the validity of the results of Exercise 14.
19 Let S be a separable metric space. Let !JI be the field of Borel
sets of S, and p a ".finite measure defined on !JI, every open subset of
S having positive p-measure. Let {T.J be a sequence of bounded opera-
tors in L:,(S.!JI. p) of the form
(T.f)(s) = IsK.(s. t)j(t)}l(<U).
(a) if 1£ L:" 1 0 £ Lp{S. 1:. p} for each p, 0 < p < I;
(b) if Is 1/(s)I(I+log+I/(s)l)tp(ds) < 00, then
Is 1/*(s)I(I+ 10g I/O(s)J» lp(ds) < 00.
Establish the corresponding results for a strongly measurable n-
parameter semi-group of operators.
16 Show that the convergence almost everywhere in Theorem
6.9 remains valid if (S, 1:. p) is a finite measure space and
Is Ij(a)I(I+log+I/(a)i)'-lp(ds)< 00. Establish thecorrespondinggen-
era.lization of Theorem 7.10.
17 Show that ExerciBe 9 remains ,'alid if
Suppose tlmt
(i) K.Ca.l) is a bounded uniformly continuous function of a and
t for each.. I; lim K.Cs, t) = K.(s., I) uniformly for ,£ S, for each
n L .-+'"
(ii) If U is an arbitrary neighborhood of B, K.(s, ,) converges
uniformly as n -+ 00 on S U.
(iii) lim. (T,J)(s) exists p-almost everywhere for each
I_ L:,(S, !II. p).
Show that for each "E ca(!JI), 1im,._ IsK.(;r, y),,(dy} exists p-
almost everywhere. (Hint, Decompose" into its p.continuous and /-'-
singular parts. Using the method of Banach's theorem IV.1I.2 and
the C(S).density of L.(S,!JI,jt) in caC!II), show tlmt for .>0 there
exists a lJ > 0 such that
/-' I sup I f K.(s, I)V{<U) ! > . ) <.
l::i;ft<oo S
ifl!(".S) <lJ.)
20 Show tlmt if the function (J in Exercise 5 is continuou8. and l'
is Borel-measurable. then, for every regular and finite Borel measure
v. the limit
I;.., I;/jCHoSOI,....rsinO.)I(1 +log+I/(rcos 0 1 ,,, .,rsinO.II> .dOl... dO.
lim I J -o-oo 1'(t(;r-y)}v(dy)
,_co -t:O
is finite. Establish a corresponding generalization of Exercise 14.
18 Suppose that I!:" . , ., h. 0 in such a way that Ih,{h,1 re-
mains bounded for 1 i, i n., and n.+ 1 i, i n. Show that the
condition
exists (Lebesgue) almost everywhere. Establish the corresponding
generalization of Exercises 6, 7. 8. 10, II, 12, and lR
21 Let (S, 1:, p) be a measure space. Let A be a closed unbound-
ed operator with dense domron in (S, 1:./-,), such that R(l; A} exists
for l > 0, and IR(l; A)I, I, IR(}.; A)loo ";; 1 for}. > O. Show that
722
vJn. APPLICATIONS
VIIl,9.22
VIII.9.26
EXERCISES ON ERGODIC TImORY
723
Iim,+DO (AR(A; A)f){s) exists almost everywhere for I€L., 1 :;::; p < co.
Show that if S is a topological spaee, and if, for each}, > 0, R(A; A)I
is continuous if I is continuous, then for 1 P < 00 and I E L. the
limit lim,...., (AR(A; A)f)(s) exists almost everywhere.
22 Let T be a trwu;fonnation in , T 0, ITI I :;::; I, and
A(..) = A(T, ..). Show that if I is real. I€ , and sUPo,,"RA(n)/ :2: 0
almost everywhere, and info.... A (.. )/ :;::; 0 almost everywhere, then '=0.
28 (Hopf) Let T be a positive linear mapping of (S,:E:, p) into
itself with IT II I. Let I E , and g EL,; let g(a) > 0 almost every-
where. Show that
(a) rp .:E: if eE:E:;
(b) pee) = 0 implies p(p-'e) = O.
Let v € ea(S, :E:), let Vl n ) (e) = j'_ov(9' ;e), and Pln)(e) = i !'(9'-le).
Show that
dv I
lim (a)
n-+OO dplrd
l(a)+(TI)(a)+ . . . + (TR/)(a)
sup < 0:>
..... g(a)+(Tg)(a)+ . . . +(TRg)(a)
exists p-almost cyerywhere. (Hint. Use the preceding exercise.)
26 Let (S,:E:, p), 'P, "', and T be as in Exerci8e 24. Let g. L"
g(a) > 0 almost everywhere. and let I be uon-negative and p-measur-
able. Show that
. A(T, ..){f, a)
11m -
n A(T, n)(g. 8)
ahuost everywhere. Show from this that
lim I(a)+.. _+(T"/)(a)
.._ g(e)+. ..+(T"g)(8)
either converges or diverges to + 00 for p-almost all 8 . S. Show in
particular that if", = I, and peS) < 00, then for each non-negative
p-measurable function I the limit lim.._ (A(T, ..)/)(..) exists or
divergt'S to + 00 almost everywhere.
27 Let (S,:E:, 1') be a finite positive measure space, let 0
;>; f. L.(S,:E:,p), and let rp satisfy the conditions of Lemma 5.8. Show
that
exists almost everywhere on the set {81 o (T"g)(e) < oo}.
24 (Halmos ergodic theorem) Let (S.:E:.p) be a positive meas-
ure space, 'I' : S -+ S, and suppose that 'I' le E:E: if e E:E:. Let <0 be a
non-negative measurable function defined on S. Suppose that the
mapping T defined for each p-measurable function 1 by (Tf)(8)
= "'(8)/(9'("}) maps (S,:E:, 1') into itself, and that ITII :;::; 1. Show
that if I is a real function in Lxi there exists no set e of positive measure
such that
lim (/{e)I('I'8).. ./{V'''..»'-/"
" ""
Jim sup A(T, n)(t, 8) > O.
ft-+co
lim inf A(T. ")<1,") < o.
ft_
exists p-almost everywhere.
28 Show that if {pR} is a bounded sequence of elements of
en(S,:E:) which is such that
lim lim sup Ip"(em)1 0
m-+oo n_oo
. A(T,..)(f,..)
hm
ft-+co A(T...)(g, 8)
for each decreasing sequenee (em) of sets in :E: with ne m = 'P, then
{!'R} is weakly compact.
29 Show that the converse of Theorem 6.12 is also valid.
30 Show that Lemma 6.10 holds as well for finitely additive set
functions as for countably additive set functions.
81 (Y. N. Dowker) Let 9' be a mapping of a set S into itself, and
let :E: be a ,,-fieW of subsets of S such that 9' 'e E:E: if e .:E:. A non-
negative element m . ea(S,:E:) is said to be potentially 'P-invariant if
there exists a non-negative element p' ca(S,:E:) such that p(9'-l e )
for B€ e. Show from this that if I. , it. , and g(..) > Op-almost
everywhere. then
exists Jl-almost everywhere.
25 (Hurewicz-Oxtoby) Let (8,:E:, pJ be a posltlve ,,-finite
measure space. and let V' : S -+ S have the following properties:
724
VIII. APPLICATIONS
VIILII.31!
\'111.9,37
EXERCISES ON ERGODIC THEORY
72.'i
= pIe) and I-'(e) = \) .mplies m(e) = O. Show that m IS potentially
invariant ifand only if the limit m(e) = I DQn l .I .:;}m(qr'e) exists
for each e E E, and that m is an element of catS, E) satisfying m(9' le)
= m(e). Hint. Consider the 'pace of allp-continuous elements of
ca(S,E).
32 (Y. N. Dowker) Let S, E, '/', m be liS in the preceding
exercisf'. Show that m is potentially invariant if and only if
lim._ n- 1 .Ii-l I(qh) exists m-almost e''-et"}'where for every
f.L (S,E,m).
83 (Dunford-JllilJer) Let S, E, m, 9'. be as in Exercise 81. Show
thAt limft-+DQ n l .I;:-U(9"s) converges in the mean of L,(S,E, m) for
every f. L,(S, E. m) only if there exists a con.tantK < 00 such that
1 I
lim sup - .I plr'e) ;,; Kplc)
7I_0g n J-O
1 fi-l
- .I m(9' 'c' :;; Km(e),
n,,_o
n= 0, I......
for each set c of finite I-'-measure. (Hint. Consider the map I(s)
- ;I:..(a)/(9'$) for each A E E with I-'(A) <. 00.)
87 Let (S, E, 1-') be a positive measure 'pace, and T a non-nega-
tive linear tnmsfonnation of LI(S. E.p) into it8elf. Suppose that
ITI I <. 1 and that there eXists aconstantK such thAt IA(T, n)l= :;; K.
Show that limn_= (A(T, n)/)(s) exists p-almo.t everywhere for each
IEL., I <' p<.co.
38 Let S be a compact metric 8pace. and let (S, E, 1-') be a reg.
uJar finite measure space, Let 'P be a mapping of S into itself such
that the set {9"} of ""'ppings is equicontinuous. Show thAt 9' is met-
rically transitive if and only if (9"",) IS dense in 8 for some point "'.
89 (Weyl) Let ["'t, . . .. "'.J be a point in n-dimensional Eucli-
dean space whose coordinates are independent over the fie1d of l'a-
tional numbers. Put "".::' = [,......J. where [yJ denotes the greatest
integer in the real number y. Show that if C is a rectangular subset of
the unit cube {["'I' . . ., "'.JIO :;; a:, < I}, and vIm) denotes the number
of IUdices k ;,; m for which [a: ", . . ., :1,,'1] E C, then Iim.._= m Ic(m)
is the volume of C.
40 Let (S, E.I-') be a finite positive measure space, and let
(S, EO. v) be the product measure space of (S. E, p) with an infinite
number of replicas of itself. Show thAt the map 9' : S 8 defined by
\V(slxs.X...) = saX... is metrica1ly transitive.
41 Show that for almost a11 real numbers a:, the digIt 7 occurs
with limiting frequency 0.1 in the decima1 expansioo of if, i.e., thAt
lim,._= n IN(n) = 0.1. where N(n) is the number of 7's occurring
among the first n digits of the decima1 expansion of a:.
42 Let'P be a metrically transitive mapping of a finite positive
measure space (8, E,p) into itself and suppose that p(\V-'e) = I,(e)
for e. E. Show thAt if I is non-negative, p-measurable, but not ,,-
integrable,
34 (Y. N. Dowker) LetS, E. 'P, m be as in Exercise 81. Show thAt
if for Some P. 1 P < 00, the limit limn oo n- 1 I:;: f('PiB) exists in
the mean of L.(S,E,m) for each I.L , then lim,._=n l .Ii /(\V's)
exists m-almost everywhere for each I. L..
85 (Dunford-Miller) Let (S. E, 1') be a finite measure space,
and, for "'.,.. ., a:.:> 0, let 9'.......... be a mapping of S into itself.
Suppose thAt A denotes the Borel-Lebesgue measure ofsubsetsofthe
set {"'t. . . "' "'.1"', :> 0). Let 'P..,...,... hAve the following properties:
(a) {"'I'.""' "'., al9'....... r. (s). c} is A XJL.measurab1e for each
e':Lj
(b) there exists a constant K < co such that
I-nfo... J p{81'P..._..... (a) a}"",. _. "". :;; Kp(c) for 0 < I < co.
Show thAt for each I. L.(S. E, 1"), 1 :;; p < 00,
Jim ,-. f: ... f: 1(9'r.....,.. a)""l'" "".
.-=
exists In the mean of L Bnd a1so exists ,u-almost everywhere. Hint.
Use the '''change of measure'" method of the last four exercises.
36 (Ryll-Nardzewski) Let (S. E, 1") be a positive measure space,
and 9' aInapping of S ....8 .uch that 9' le E Eif c. Eandp(9'-Ie) = 0
if p(c) = O. Show that the sequence n l : /(9"s) converges p-a1-
most everywhere to a function i in L, for each I. L] if and only if
1 1
lim - 1(9'1 a) = co, p-almost everywhere.
f1.__(10 n 1...0
43 Show that 9' is a metrically transitive mapping of a fimte
positive measure space (S, E, 1-') into itself if and only if no non-
726
VIII. APPLICATIONS
VIII.9.44
VIII.10
NOTES _4.ND MABKS
727
eonsumt ,u.measurable function / can satisfy lI'Ps) = f(a) ".almost
everywhere, and that in this case, any p measurable function g satis-
fying g(ps) = 4(a) ,u-almost everywhere, where IAI = 1, satisfies
Ig(a)1 = II'-almost everywhere. Show that if h(ps) = Ah(s) I'-almost
everywhere .al o, then h = cx.g,.
44 (Random ergodic theorem) Let (S, 1:, 1') be a a.finite
measure space. Let To,..., TII be ten operators in Ll! each satisfying
jT,11 ,.;; 1, IT,lco 1. For each decimal '" = 0""1.... .. such that
0<", < 1, put
10. Notes and Remarks
seen in Hille [1; p. 162] that if the mapping t.... T(/) is measurable in
the uniform operator topology for I in (0, w), and if T(/+s) =
T(/)T(a}, t, a> 0, then it is al80 continuous in this topology fort>o.
However, th conditions do not imply the existence of lim,_o T(t)
or the differentiability of T(/} for t > 0, and so the conclusions of
Theorem 2 fail.
It was shown by von Neumann [10] that if U(t). - 00 < I < 00,
is a one parameter group of unitary operators on Hilbert space tt
and if (U(I)x, y) is measurable for all"" ye.\), then U(I)x i8 continuous
on 1.( - 00, w) for an '" e .\). This was extended by Dunford [12], who
showed that if T(I), I > 0, is a semi-group of bounded linear operators
in a B-space, if ",*T(-);r is measurable on (0, w) for any .r* e ;£*,
",,!, if IT(t)1 < M fortin Some interval (0, a) andif{T(t)xlt. (0, 00J)
is separable for each .r £!, then T(.) is strongly continuous on the
right. It follows from Dunford's argument, see also HiDe [I; p. 184],
that if T(') is such that T(')x is measurable on (0, co) and if T(') is
bounded on every finite interval of (0, co). then T(.)x is continuous on
(0, w), The fact that this boundedness assumption is unnecessary
was proved by Phillips [8] by means ofthe ingenious device reproduced
in the present chapter (cf. 1.0). However, the condition of the
measurability of a;*T(. )x 9 :v* E 1*, OJ of:£, alone is not suffieient to
imply the strong continuity. Semi-groups with this weak meastllcability
property have been studied by Jo'eller [1].
The proof of Theorem 10 given here is found in Dunford and Segal
[I]. Somewhat mnre general results of this nature are found in Hille
[I; p. 187-9]. The first conditions that a closed linear operator gener-
ate a 8trongly continuous semi-group were given independently by
Hille [I;p.238] and Yosida [8]. The complete characterization of the
infinitesimal generator given in Theorem 13 was obtained almost
simultaneously by Feller [2], Miyadera [1] and Phillips [6], For other
results in this direction, see Hille [I] and Phillips [10].
The results concerning tne perturbation of semi-group generators
are due to Phillips [6]. See also Phillips [10].
Fundions 0/ an in/il!it".;mal generator. Hille [1; Chap. IS]
established an operational calculus for the infinitesimal generator of
.a semi-group for functions which are Laplace-Stieltjes transfoTIns and
are analytic on the spectrum of the generator. A- somewhat different
1- 1
A(l!, a) = - T..T. ... T...
n,£. -., ;-1. -..
;_0
Show that If 1£ L.(S, 1:, 1'), 1 :<::: P < co, lirn,. A(l!, a)/ exists
almost everywhere for (Lebesgue) almost all a. Show that If p> I,
lirn,. coA(n, a)/ exists in the mean of order p, and that the same
h01d8 if ,u(S) < 00 for p = 1. (Hint. Consider a suitable operator J
of the fonn
(J/)(a, <x) = (T",/Ha, '1'1%).)
S.mi-groups 01 operatora. The theory of semi-groups of linear
operators is of rather recent origin, the first results in this direction
being obtained by M. IL Stone [10], in 1930, who discussed the case
of a group of unitary operators in Hilbert 8pace. Since that time a
considerable development has taken place, largely due to the efforts
of E. Hille. whose treatise [1] gives an extended account of the ab-
stract theory and many Ji,pplications to concrete mathematical prob-
lems. We refer the reader to this book (and its forthcoming revision)
for further results as we1l as for references. In addition, the reader
should consult the expository article by R. S. FhilJjps [9] for some
recent developments. We mention here references for the small por-
tion of the theory presented in Section 1. and do not go beyond these
results.
The representation of uniformly continuous groups of operators
as an exponential Was dcmonstrated independent1y by Nathan [1;
p. 525] and by Nagumo [1; p, 72] and Yosida [7; p. 24]; in fact,
Nagumo and Y osida treated the case of a group on a B-algebra. It is
728
VIII.. APPLICATIONS
VIII.IO
VIII.IO
NOTES AND REMARKS
729
treatment was given by Phillips [5]. Bade [I] showed that for the
infinitesimal generator of a group, it is possible to extend the class
of functions to include polynomials and other functions with sjrnilar
growth conditions. The treatment in Section 2 follows his work most
closely. Theorem 18 generalizes certain theorems of Pollard [1],
Widder [2] and Widder and Hirschman [I, 8] on the inversion of con-
volution transforms by differential operators of infinite order. There
is an extensive literature on this problem---porticularly on the difficult
question oethe pointwise convergence of {p.(D)j(D):v(t)} to ",(t), where
I(D) is a convolution tnmsfonn and {p.(D)} is an inverting sequence.
References to further discussions of this problem may be found in the
cited papers and the book of Hirschman and Widder [1]. See also
the expository articles of Schoenberg [3] and Widder [8]. The fonn
of Theorem 18 given here is due to Bade [1]. Corollary 14 is a result
of Widder and Hirsc1I1nan [2].
Ergodw theory. Although the development of ergodic theory has
taken place principally since 1981, there is considerable literature on
the subject. Fortunately, the excellent monograph of Hopf [I] treats
the early developments, and the expository articles of Halmos [4],
Kakutani [10] and Oxtoby [1] discuss rather completely .e,-era! dif-
ferent facets of the theory and contain many references to the litera-
ture. (See also F. Riesz (18],) Therefore, it is not necessary for us to
give an extended account or bibliography of this theory. However, we
do wish to make a few observations that may be found of interest.
restricting our discussion to the material in the text.
II/can ergodic theorem. The first proof of the mean ergodic theorem
was given by van Neumann [UJ after it was observed by Koopman
[I] that measure preserving mappings in a measure space S give rise
to unitary operators in £,(8). Van Neumann's proof was based on the
spectral theory of unitary operators in Hilbert space. Many exten.
sions llI1d generalizations of this ergodic theorem have been given,
both to mOre general B-spaces and to more general operators. The
papers of Visser [lj, F. Riesz [15, 17], Yosida 4], Kakutani [18],
Lorch [8] and Yosida and Kakutani [2J are based on various weak
compactness properties. A geometrical proof for operators in Hilbert
space, based upon the fact that there is a shortest distance from a
point to a com'ex set. was given by Wiener [8]. Shorter geometrical
proofs, valid in uniformly convex spaces. Were given by G. Birkhoff
[7] and F. Riesz [16. 18]. Another proof, based on the interesting fact
that a fixed point for a contraction in Hilbert space is also a fixed
point for its adjoint. was given by Rie8z and Sz.-Nagy [2]. Theorems
for absuact vector lattices were proved by G. Birkhoff [2], Kakutani
[7, 8], and F. Riesz [17].
Several generalizations of the mean ergodic theorem to groups or
semi.groups of operators more general than the discrete semi-group
{Tn,,,, = 0, 1, 2, . ..J have been presented in the papers of Alaoglu
and Birkhoff [1, 2], G. Birkhoff [8], Day [8, 10], Dunford [9, 11],
Eberlein [3, 4], and Wiener [3].
Ergodic theorems of the mean type, but in which other methods
of summation replace the (C, I)-method ordinarily used, are proved
by Coben [2J, Hille [1; Chap. 14] and Phillip' [4].
Poi1'l1:wi8e ergodic theorem. Thi. theorem was established by G.
D. Birkhoff [1 J, who discussed measure presen;ng homeomorphisms
of manifolds. The case of a finite measure space was treated by
Khintchine [1] and the case of an infinite measure space by Stepanoff
[IJ. Some other generalizations have been given by Doob [I], Dowker
[2.3], Dunford and Miller [I], HaImos [8], Hurewicz [I], Khintohine
[2], Oxtoby [2], Riesz [19], Ryll-Nardzcwski [I], Wiener [8] and
Wiener and Wintner [1],
One extension of the pointwise theorem (Theorem 6.8), called the
dominalRd ergodic theorem is due to Wiener [8]. Other proofs of the
dominated theorem were given by Yosida and Kakutani [I] and
Fukamiya [1]. An important lemma in the proof of either the pomt-
wise or the dominated ergodic theore_ is the maximal ergodic theo-
rem (Lemma 6.7). A proof of this result WaS given by Yosida and
Kakutani [I J, although a similar result W&i established in the paper
of G. D. Birkhoff. The key to the treatment given here. i.e., the gener-
alization of the maximal ergodic theorem to Markov processes (es-
sentially Lemma 6.2) is due to E. Hopf [2]. Other discussIOns of the
maximal ergodic theorem are due to Caratheodory [3], Dowker [2],
Hopf [8], Pitt [1], and Riesz [18]. P. Hartman [1] proved the maximal
ergodic theorem for the case of a flow.
A pointwise ergodic theorem for an n-parameter group of measure
presel'Vinj( transformations was given by Wieoer [8]. The nOn-com-
.
730
vrI1a APPLICATIONS
VULlO
mutative case was discussed by Dunford [3] and Zygmund [2]. A
generalization to a CW.8 of abstract groups WaS given by Calderon [1].
The theory of Markov processes is a generalization of the theory
of point transfonnations. The ergodic theory of such processes lIDs been
treated by Doob [2,3], Kakutani [16], Yosida [9]. Vosida and Kaku-
tani [2], and most recently by E. Hopf [2], \Ve refer the reader also
to the recent treatise of Doob [4].
Uniform ergodic throrem. This result is due to Y osids and Kaku-
tani; See their paper [2]. where it is applied to the theory of Markov
proct'SSCS to obtain results previously obtained by Doeblin, Doob.
Frechet, and KryJoff and Bogoliouboff. For a more detailed probabil-
istic discussion of Markov proces.... we refer the reader to Dooh [4].
It may be remarked that such pro<'esse8 are important in the theory
of card shuffling.
REFERENCES
Thillist indades "q fw Pay! 11 WI wrU as Part :I oj this oolume
Abdelha:r, J.
I. CcmxtlriMllkm de l'tspG« de lkmtlt-h tk toutes les.sWttit de nombrts ri. /8
ktldont verB urQ. C. R. Acad. Sci. Paris 229, 1111-]112 (Ul4.9).
2. On a 1Re07t':m oJupTQJt'Blalion. Eu]L Amer. :}'[atn. Soc. 55. 408--417 (1949).
Abel. N. H.
I. UnteT8tJditmgm 'Ubt,. dIe Reine:
m m'(m-1) m (m-I).(m-2)
1+-z+ ;r1+ +... u.s.w.
1 12 1.23
.T. Reine Angew. Math. I. 311-339 (1826)_
Achieser, N. I (see Ahie:ter).
Ada...., C, R.
I. The I!pace vI fllRCtJ"O'US oj bot1 mrffltion and cerlain general spaces.
Tra.ns Amer. Math. Soc. 40, 421-488 (1'Q36).
Adams, C R... and C1arkson. J. A
1. On dRfin.itions oJ bounded varialiim Jor jim£tifJm oj two oo:rioblts. Trans.
Amer 'Math. Soc. 35 j 824.--854 (1933).
2. Prop£r1ies oj /unaUms/(x.y) 6J tJounckd Mt'illtivn. Trans. Amer. :}lath.
Soc. 36, 711-780 (1934). Errata. ibid. 46, 468 (1959).
8. On in mrialiOR. BulL Amer :Moth. Soc. 40. 418-4]7 (1994).
4. Tm rypc of lY!rtuin BOTd sers in 6 N'Q' Bfl1IlJ h $pacu Trans. Amer.
Math. Soc. 45, 322--384 (1989).
Adams. C. R., and Morse. A. P.
]. On th $p (BV). Trans. Amer. Math. Soc. 42. 194-205 (1937).
2. Continuow a.ddib..L'f: jv:ndionn1g OR I'h£ spaCf: (BF) and mmin .
Trans. Amer. Math. 800. 48. 82-100 (1940).
Agtnon, S. (aee Mandelbrojt. S.)
Agnew, R. P.
1. LiRl!l1J" Jlm£Iilmob satisfying p rxnuIitirms. Duke Math. .Y. 4., 55-77
(1988).
Agnew. R. P., and Morse. A. P.
I. E:rlmsicms oj linffff',functicru:lls. with opplirotitms to limils, udrgmb.
"""'""""', and dens;,;".. Ann. of Math. (2) 89, 20-30 (1938).
Ahiezer. N I.
1. Infinite Jacobi flICJiJ'iao6 and the probkm oj mommt.s. Uspehi l\fftt. Kauk 9.
12&-156 (11141).
Ahiezer (Achieser), N. I., and GlAzman (Glasmann). L M.
1. The theory oj limar ope:mtms on Hi1her. spac . Gosudarst..... Izdat. Tehn.-
Teor. Lit.. Moscow-Lenil1grad. 1950. German translatIon. Akademie-
Ver1ag. Bedin. 1954.
AhJfor:s, L. V.
1 CrnapIn: CUifdysis. McGra,,'-Hill, :'tJew York (1953).
731
.
782
REFERENCES
REFERENCES
783
Aki1{)v, G P.
1. On fh< ...teMon .J 1t1l<aT opeTalions. Doldady AkBd. Nauk SSSR (N.!>.)
57, 64_6 (1947). (Russian) Math. Rev. 9, 241 (1948).
2. Necessary ootIditimas far lhe uten8i oJ Iimu,. opnutions. DQkJady Akad.
Nauk SSSR (N.S.) 59, 417-418 (1948). (Russian) Math. Rev. 9, 858 (1948).
.\IuogIu. L.
I. W€ak topologies oJ nQTfflld rimar -Ipzr:e3. Ann.. or Math. (2) 41, 252--267
(1940).
2. Wt.'ak amvergmce oj linear jum:IiDwals (abtd:ract). BuD. Arne.... 1\o:lnth. Soc.
44. 100 (1988).
AIaogIu. L.. and Birkhoff, G.
1. General trgodi£ theorem. Proc. Nat. ACad. Sci. U.S.A. 25. 628--630 (193'9).
2, Gmeral ergodic theorems. Ann. of Math. (2) 41. :2II3---3JD (1040).
Albrycht. .T.
I. On a rkeorem oj Saka lOT abatro.cr PQ1YJ1.fllniats. Studia Man., 14 (1953),
79--31 (1954).
Alexandroff. A. D.
I. Additive Bet in ab,trad 'paces, I-III.
I. I\l&t. Shornik N.S. 8 (50), 807--M8 (1940).
II. ibid. 9 (51), 5684128 (1941).
III. ibid. 18 (55), 169-288 (1943).
AlexandrofC. P.. and Hopt, H.
1. Topologif.', I. .J. Springer, Berlin, UJ35. Reprinted by Edwards Bros.,
Ann Arbor.
Alexiewicz. A.
1. On sequemt8 oJ rJpnalions I-IV.
I. Studia Math. 11. t---sO (1950).
II. ibid. 11, 200-286 (1950).
Ill. ibid. ]2, 84.-92 (1951).
IV. ibid. 12, 9:>--101 (1951).
2. Linear vpemI.ions among boundui tnta$uMblr: ftmctiIJmJ. I, II.
I. Ann, Soc. Polon. Math. 19, 1_161 (1946).
II. ibid. 19, 161-164 (1946).
3. On diJ1erentiolWn .J vedot"- ftuu'tioz"" Stndia Math. II, 185-196
(1950).
4. CO'f/tmuity vJ vtdor;xduedJi.tnctilms oj baumlt'd variation. :stll.dja Math. 12,
185 142 (1951).
5. On BOrne th£mnntt DJ S. BokiJ. Studia ).!ath. 13, 18-29 (1'953..
6. A theQrem on Ih sfTu.cture oJ limar opaa!ionJ. Studia Math. J4 (1953),
1-12 (1954).
Alexiewicz, A'J and Orlicz, '"V.
1. Remarks on Riemann-inttgmIiJmoJ .nalut!.dfunclirms. Studia)lath. 12,
125 132 (1951).
'2. On analytic JUrJChons oJ a Trol varinbU. Studia Math. 12.
lOS-Ill (1951).
3. On 1M diHr:rmtWl3 in Banach 8pac S. Ann. Soc. Polon. Math. 25 (1952),
95-99 (1953).
4. A:halytic operatiOtb in Teal Banach 8plJ€-ts. Studla Math. }.j. (19531. 57-78
(1954).
Altman (Al'tman" I. S.
1, On bas" in Hilbert space. Doklady Akad. Nank SSSR (S.s.) 69. 488-485
(11149). (Ru..i.n) Math. Rev. II, 525 (1950).
2. On -con<>l ........ Doklady A""d. Sank SSSR (N.S.) 67, 413-416
(1949). (Russian) Math. Rev. 11, U4 (1950).
8. On linear Junctional equatiQtls in locally convu BpCUes. Studia Math. 13t
1940-207 (195S).
4. It.fean ngo.d:iL; theorem in locally ronlJe.z lUuqr kIpoIogical space,. Studia.
Math. 18. 1_193 (1953).
5. Th. Frn/iwlm fh<q,y .J Ii"""" equati.... in Woolly COIW<Z I sp"'''.
Bull. Acad. Polan. Sci. Cl. III. 2, 267-289 (1954).
Ambrose, W.
1. Strv.dure theorems 1m' a sptcial class 8} 8afKlJ:h algebras. Trans. Amer.
Math. Soc. 57, 3640-386 (1945).
2. leasur'e:I on IQcally compad Wpowgical groups. Trans.. Amel". Math. Soc. 61,
106-121 (11147).
8. Direct sum. theorem lor Haar ftUa..it.m:.Y. Trans. Amer. i\'lath. Soc. 61.
122-127 (1947).
4. Spe&ulusoltdirm of QUp'oJunita':!l opmuon. Duke Math. J. II, 589-595
(1944).
Anzai, H.. and Kakutani, S.
1. Bohr compadijiazti.0n.8 vI a locally Qmpacl abelian group. I. II.
I. Proc. Imp. Acad. Tokyo 19, 476---480 (1943).
II. ibid_ 19, S311-539 (1945).
Arens. R. F.
I. Duality on linmr spaa'B. Duke J.\.Iath J. 14, 781-794 (11147).
2. T& spact LOJ and Clmvt'4' kpological rings. B1Jll. Amer. Math. Soc. 52,
981-985 (1946).
8. oJ[tmdimIolsby inUgm/s. DnkeMath..J.17.499-506 (1950).
4. Appnxrimation in. and npr oj. UTtain Baoolh aJt,ebmt. Amer.
.J. Math. 71. 768-790 (1949).
D. A Wpology for spaces oj tranRf8t'"t1lLItilms. Ann. of Math. (2) 47,480-495
(1\146).
t3. On a thmrem. of lJ(md and NeumarIr. Proe. Nat. Acad. Sei. U.S.A. 32.
257 239 (1946).
7. &1" ""tiM oj Banach .-aIgmms. Dttke Math. .Y. 14, 269--282 (1947).
8. Lin ar dWisitm algebras. Bull. Amer. (\.latb. Soo. 53, 628--630
(1947).
9. A genmzhZtlti01l of flormtd rings. Pacific .t. l\lath. 2, 455-411 (1952).
Areru;, R. F.. and Kaplansky, I.
1. Topalogiazl tqJrtsrnlation ()J lllgetwas. Trans. Amer. :Math. Soc. 63, 457-481
(1948).
Arens. R. F., and Kelley. J. L.
1. Charadtri2Otions oj the SpU£t oJ conlirnwus JunL:ti.on.s over a compaclilaus-
doTII s'}HJCt. Trans. Amer. Mfath. Soc. 82, 499-508 (1941).
Amous, E.
1. SUr' Its groupes t:onlinU8 de trrmBJomvItirms "nitaim de l',spcu:e de RilIwrt.
Comment. [a.th. Helv. 19. 50--60 (UJ46).
784.
REFERENCES
RE::FER:E:NCES
735
ArOnszajn? N.
1. 0f1 mttrigue de l'espace: de Hilbert, des e:spau8 Dedoritli e:E de
rertains- groupes '1lJttriqves. C. R. Acad. BCI. Paris 201, 811-818. 873-875
(1985).
2. Le ""''''F''''ulant fapoItJgique de. l'uniciri dam la 'IlIJorie de$ iguations
difI-n... Ann. of Math. (2) 45, 78(1-738 (1942).
3. Apprarimaliorz 'I1U:lluxh/or oJ romplddy .continuous 81Jmmdric
Dpua!oTs. Proceedings of the SympoSioOi on Spt'Cb'a1 Theory and Differen-
tial PJobJem&.. 179-202 (1951). Oklahoma Agricuttural and Mechanical
College. Stillwater,. Oklahcma.
4. Tht Rayltigh-Rilz and A.. W,nnslnfl 71U!lb.Qd$/Q7' {Zppro.rimafim oJ ei&en-
1.JallU'S. II. Proc. Nat. Acad Sci. U.S.A. 84, 474-480, 594-601 (1948).
5. Sur quelqtKs prvblimu1 concnnar1t Ils espaug th Mit1k(1tCski If:! Us esptJt:t!s
1Jl'I'tarids gI:nhma. AtU Accad. Naz,. Lincei. Rend. CI. SeL Fis. Mat. Nat.
(6) 26, 874-376 (1D37).
Aronszajn. N., and Smitl1, K. T.
I. Invariant subspaces (;/ oomplndy ccmtinoow 0JN,alDrs. Ann. of .Math. (2)
00, 84.5-350 (11.154.).
Arternenko. A.
J. La forme d'une /onctismJulle /inEalTt' dan$ l'e8 e ,us f d
""nation IwTm!t. Mat. Sb<Jrnik N. 5. 6 (48), 215-220 (1939). (Rru;sian.
French summary) Math. }Iev_ I. 239 (1'940}.
2. On linear jtm.ttUm.a.b in Ou! If.Pact of fllJIIVSI pwiOOic fuoctiqn.s oj
H. Bohr. Ccmm. Inst. Sci.. Math. Mc. Univ. Kharkotf [Zllpiski Inst. Milt.
Mech.J (4) 16, III-II4 (1940). (Russian. Engliw summary) Math. Rev. 8,
207 (1942).
AnclA, C.
1. InWr'no aUa cvntiRuitd della somma di itifinite Junzitmi rontiAtu!. Rend.
dell'AiCcad. R ,delle Sci.. deU'Istituto di Bologna., 79--84 (1888-1884).
2. .Ftmzinm di linu. Atti della R. Accad. dei LinceL Rend. CI. Sei. Fis. :Mat.
Nat. (4) 5" 842--M8 (1889).
S. 8ulle Juruirmi di lime. Mem. Acead. Sei. 1st. Bologna Cl. Sci. Fis. Mot. (5)
5. 55-74 (1895).
4. Sulk aerie di f , t, II.
I. Memorie dells. R. Accad. delle Sci.. dell'lstituto di Bologna Sci. Fis. e
Mat. (5) 8. 8-58 (1899).
II. ihid. (5) 8, 91-134 (1899).
5. Un" OS8a'tIa.:Wne mJomo aUe serie di jrmtioni. Rend. dell' Accad. R. delle
Sci. deU'Istituto di Bologna, 142-159 (188'2-1883).
A>ooli. G.
1. Su,gli spo.zi linwri metrici Ie low Dll7'idii Unmri. Ann. Mat. Pun Appl. (4.)
10, 83---81, 208-282 (1952).
2. Le ct.I:1"t'( lirniti di una OOTidd duta di wrot. AUi. dena R. Accad. dei Lincei
Memorie della CI. SeL. Fis l\lat. Nat. (8) 18, 521-586 (1883-1884).
Atkinson, F. V.
1. Symmetric limar upnatora on (J Btmnt'h spaa. Mona.Ig,)). Math. 53, 278-297
(1949).
2. The normal solubihty oj linmr equatiom in nOTmed BfKlUs. J\lat. SlJornik
N. S. 28 (70), 5-14 (1951). (R........) Math. Rev. 13. 4<1 (1952).
3. A >pfffml problem lor rornpkl<ly eon1i"""", <pm4ors. Acts Math. Acad.
Sci. Hungar. 8, 53-60 (1952). (RUBsian l'ioummary)
4. On re/alirdy Ttgtdar operator.. Acts Sci. Math. Szeged IS. 38-56 (1953).
5. On the second-vrder lintar fJSCiIlalJJr. Univ. Nac. Tucuman. Revista A. 8.
71-87 (t951).
Audin, lt1.
L SUT cert.al1US Bingulmilis des tmmJfJTJf«llJorulliniailn btmJiu. C. R. Acad.
Sei.. RriS 238, 2221-2222 (1954).
Babenko., K. I.
I. On ton jugal< /""""""'. Duklady Akad. Nauk SSSR (N. S.) 62, 157 100
(1948). (Russian) Math. Rev. 10. 249 (1949)
Bade. W. G.
1. An operatWaal mlculus lOT OfJfTlllor8 with speclJ'Um in a .strip. Pacific J.
Math. 3, 257 290 (1953).
2. VnOOuncled (lpc"alurs. Pacific J. Math.. 4. 878---892 (1954).
3. Weak ands!.TonglimiUo! $ptdr'l'J.loptrolors. Pacific.J. Math.4, 893-4.]3 fI954).
4. On Booltan a1.groras oj projecJions and algebras oj operolorB. Trans. Amer.
Math. Soe. 80, .345-360 iI955).
Bade, \V. G., and S{'hw&1'tz. ..I.
1. On ali:strott eigenJunakm t:r . P1'OO. Nat. Acad. Sci., U.S.A. 42,
519--525 (1956).
Baker. H. F.
1. On mlLgmlinn vf linear difff!r't'l'lfinllYJUlllWns. Proc. LondOQ Math.
Soc. (I) 35. :135-578 (1905).
Bsnsch, S.
1. du opbntions lifllain-.s. ,Monografje Matematyczne. Warsaw, 1932.
2. Ubcr di Bait 'SCm Kar.egOTi FrmlrJi(JRf!flJ1Wf1gera. Studia I\tath_ S.
174-179 (1931).
3. Sur lea ophations dans lea enaemblu abBttaits et leur applicGfion aw:
i"rPgmko. Fowd. Iath. 8, 18!J.-I8I (1922)
4.. Sur lt8 fonai lle$ linL.ai:us. I, II.
I Studia Math. 1, £1l-216 (1 29).
n. ibid. I, (1929).
5. VIm Ioomogme Pvly>omo< in (T.')_ Studia Math 7, 86-44 (1938).
6. Tfflf'ja . War:sQw. ID81. (Poli8h).
7. iIbe!' mdr'iJ>ch< GruJ11Un. Studia Math. 8, ICl 1I8 (1931).
8. Sur Ia Ctnlf. 'gt...rt' presque partout de jonctiCJf'l1'l£lks Ufiiaius. Bull. Sci.
Math. (2) 50, 27--'12. 3t1--43 (1926).
Banach, S., and Mazur, S.
1. Zur TheorU dtr lintaun Dtrne1uwta. Studia Math. 4, 100-112 (1933).
Bonacb" S., and S.aks, S.
1. SU71a rom'ergl'luT furk dang lea champs £fJ. Studill. Math. 2, 51-57 (1930).
Banach, S., and Steinhaus, H.
1. Sur l principe de fa amdensatirm de rirlgulari:lis. FWid. Math. 9. 50-61
(ID27).
Barankin, E. \V.
1. 801Lru/$ Pn C'haractrri.slic valu s. BulL Amer. Math. Soc. 54, 728-785 (1948).
2. Bounds [Qr chamcr T-;sPic 70Q1$ vJ a nwtrix. BulL Amer. M.ath. Soc. 51.
767-770 (1945).
'1'86
REFERENCES
REFEBESCES
737
Barenbla.tt, G. I.
1. On a method GJ solution oJ the equation oj hUll condKdioJI.. Doklady Akad.
Nauk SSSR (N. S.) 72. 667--870 (19501. (Russian) Math. Rev. 12, 183
(1951).
Bari (Baxy), N. K.
L 1J sylIUm8 (lnd bas in Hilkrl lJpau. Moskov. Goo. Univ.
Ucenye Zapiski 14.8, :Matematika 4, 69-1V7 (1 51). (Russian) Math. Rev.
14, 289 (1958).
2. Sur la sfabiliti de fa pTopritft d'&-e un sysrbne campfd .u/onctkms. Dokla.dy
Akad. Nauk SSSR (N. S.) 87, 83---87 (11.42).
Bargman, V.
1. RmwrM on the ddn'minafion oj a cmrral fidd oJ !Mce 1rom the elasHe
attJtteting phaat limits. Phys. Rev. 75. 801-803 (I949).
Barry, J. Y.
1. On the corwngenu oJ orckred $efI pJ projrdirms. Proc. Amer. :&lath. Soc. 5,
818-314 (1954).
Bartle, R. G.
1. Sir>gul<zT p.nn/4 of j\m<IWml tqU<!lions. Trans. Arner. Math. Soc. 75,
8611-884 (195S).
2. On txnnpt;1J:tMB8 in fImd:ional analysis. Trans. Amer. Math. Soc. 79,
85-57 (1955).
8. A g.........aI bilin= vector inl<gral. Studia Slath. IS, 357--352 (1958).
4. Implicil Jun<:tiom and BOltItion.t vJ in graups. :Math. .ze.t. e2.
885--M6 (1955).
5. Nerokm". method in Banw:h Bpacu. Proc. Amer. Math. Soc. 6. 827-831
(1955).
Bartle. R. G., Dunford.. N... and Schwartz, .I.
1. W.eak campaclnus and vedlJT melJSUTe$. Canadian J. Ma.th. '1. 289-305
(1955).
Bartle, R. G.. and Graves, L. 1\1.
I. Mopping. belrve<n}'lmdWn spil«s. Tram. Amer. Slath. Soc. 72, 400--418
(1952).
EB88ali. W. A. (Stt Stevenson, A. F.)
]JeU, R. P. <I'
1. Eigtnoolue.t mid oigenfunctiooaf.., 1M o.perolor dr. -I"" Philos. Mag. 85.
385-588 (1944).
Bellman. R
I. A ...rvey of 0.. o..my of 0.. bound<dm8., .labilily and "'Y"'pwti< behavior of
swutiom oj lirJeQT and non-limar diJltTentitll and diJJt.TeRCe eguafions.
Office or Naval Research Washington, D. C., 194.9.
2. Slability o..ory of differential <guali<ma. McGraw-Hill Co., New York, 1953.
Bennett. A. A.
1. 1Vewkm's method in smaal analysis. Proc. Nat. Acad. Sei. U.S.A. 2.
592-598 (1916).
J!erezanski!. Yu. III.
1. On 1M unigumess oj t.ht: 4eter.minarion oj SChTlJdl'nf,N'S eguation from its
opec".1 furoctwn. Doklady Alrnd. Nauk SS.5R (N. S.) 98. 591-594 (1053).
(Russian) Math. Ra.'. 15. 797 (19640).
2. On hypercompla ttyfJrems f:omfructed Irrnn a Sturm-LiQuvilk equa!Wn on [I
.eml-em... DokIady Akad. Nauk SSSR (N, S.) 91, 1245-1248 (1953).
(RtJ&sian) Math. Jtev. 15. 'rn7 fItJ54).
Berkowitz,. J.
I. On 1M dmetnl.e3$ oj 1M spectra oJ Sturm- operl'IIOr.f. Dissertation.
New York University. I'OSI.
Bem, R.
). An inve8tigati<m oj tM QJ ektnen" in a parlially f.l1YleTed apace.
Mat. Sbomik N. S. 23 (65), 411J-44O (1'048). (Russia.n) Mil-tn. Rev. 10,
880 (1949).
Besioovitch. A. S.
I. Almost ptrlodic ftu'adit:m.s. Cambridge Unn'. Press, Cambridge, 1932.
Reprinted by Dover Pub. Co.. New York.
Bethe, H. A.
1. ThImy oj «:tive image in nuctear.scan.tring. Phys. Rev. 76, 38-50 (194.0).
Beurling.. A.
I. Stl:rk8inti.grak3&FfJUri.n t.rkur6pplimtUmf}um
'ransJormatit:m J . Proc. IX Congre!J de Math. SeandinlLves,
Hdsingfon. 845--3&\ (loeS).
2_ Un tUorbM .MIl' In Jondiom OOrnies et uniforrnbnrnl amtlnues sur l'aze
hl. Auta. .Math. '77, 127-136 (11)45).
8. On 0.. sp«fml of Ixmntkd Juroctiooa. Acta Math. 81. 225 288
(1949).
4. On two problnM (.'OfiCeming lim«r transformatio1u in Hilbert space. Acta.
Math. 81, 239--255 (IR49).
-'L.
). Ldrbuch fkr FurJctionmthrorit. Vo1. I.. Fourth Ed., 1934; vol. II Second
Ed., 1981. Twbner. Leipzig. Reprinted by Chelsea. Pub. Co.. New York.
Birkhoff, G. (see BlBo Alaoglu, L.)
1. in. l1JU!4T metric 8pm:u. Duke lto:[atb J. 1.. 169-1'12 (1935).
2. Depend<nl probabiHIiu and 0.. 'pac< (L). Proc. Nat. Acad. Sci. U.S.A. ....
154-159 (1988).
8. Latl:iu Uteo1y. Amer. Math. Soc. Coll. Publ. 25. New York. 1940.
... .1flkgrancm of fuwdi(m8 with IJfJiIIftl in a llafJaC.h 8pae . Tl'l\ns_ ArneI'. IUath.
Soc. 88, 857--37S (1985).
5. .A flak tm fopologiwl groups. Compositio Math. 8, 427-430 (1986).
6. On produd ifllqraliCJfl. J. 1\fath. and Phya. Mass. Inst. Tech. 16, 104-132
(1937).
7. Th< mum "I1odi< 0....,..... Duke Math. .T. 5, 19--20 (1939).
8. .An ergodic thMrtm for gentTal semi-groups. Proc. Nat. Acad. Soi. U.s.A. 25.
625----627 (1989).
Birkhoft, G.. IUld Mac>Lo.ne. S.
t. A 8u:roey oj modem a(gdlra. MacmiD.an Co.. New York. 1941.
]J;rkhol!, G. D.
1. ProoJoJlN:ugodktheornn.Proc.Nat.Acad.Sci. U.s.A. 17.656-660 (19S1)
2. On 1m asymploti.c charada oj the BO!tAticmB oj certain linear differential
operati.an.s containing a pamnukT. Trans. Amer. Math. Soc. 9.. 219-231
(1008).
738
REFERENCES
REFEIlENCES
789
8. Bourulary value and on problnns vJ ordi:na1Y linear diJfamJiai
. Tram. Amer. Math. Soc. , 373--895 (1908).
4. and o9tillativn tht(Jttm$ [M' a c"rain boundary vahu' problem.
Trans. Amer. Math. Soc. 10, 259-270 (1009).
5. Quan'um nwdianus and mympWfic .erics. B'U11. Amer. Math.. Soc. 39,
681-700 (1933).
f5. NlJtt;onl11eupamivnoJth£GTee-n sfuwdicm.1tlath. Ann. 72, 292-294 (1912).
? Note on the expansion problems oj ordinary lmoor diff l ftJUCltWns.
Rend. Cire. Mat. Pa1enno 86 U5-126 (uns).
Birkhoff. G. D., and KdJogg, O. D.
I. Itmariampoin13 inJunctionspace. Trans. AmeT.Math. Soc. 28. 96-115 (1922).
Birkhoff. G. D., and Langer. R. £.
L The oo-undaryproo't1'ff4 ana wi1.h a system oj otdinarJJ
diffrrrmtial eguali0n9 oJ the fita, order. Proc. Arne1'. Aca.d. Arts Sci. (2) 58.
51-128 (1925).
Binnan. M. S.
1. On 1m tMory {lJ fI lf-adjoint (JfpnsiJint! tkfinite Vptro,lhrs. Doklad'y
Akad. Nauk SSSR (N. S.) 91, 189--191 (19531. (Russian) Math. Rev. IS,
826 (1954)
Birnbaum. Z. W. p and Orlicz. \V.
1. Ow die V w,s &griffrs w" """,,,,,.,f,o, Koojug......
Po"""". Stndia Math. 8. 1-67 (193]).
Bliss, G. A.
1. A boundary va!... pToblem 10' a "Y'- of otWra>y ,"-' mlf<'Uftlia/
rquat.ions. Trans. Amer. :Math. Soc. 28. .561---589 (1 26..
Block, H. D.
1. Linear transJonnatiOflS on (IT onto a Banach space. Proc. Amer. Math. SOC. S,
12/1--128 (1952).
Blumenthal, L. M.
1. Chneraliud Eudidemt sp(J£ in tmns oJ a guasi-itmn produ.ct. Amer. J.
Math. 72, 686-698 (19501.
BORS 1\1. L.. Bow;. fl. p . and Levinson, N.
]. The 15",,,,111 of of a differffltWltqtJLJlioo. Duke Math. .I. 9, 847--853
(1942).
Boas, R. P.. Jr.
l Some unifmmly mnT.Jr.I' tpaffB. Bull. Amer. Math. Soe 406. 8f.»---SII (1940).
:2. Ezptmsions oj analytk jMncfiDns. Trans. Amer. .Math. Soc. 48, 467--487
(1940).
"B6cher. ¥.
1. On ,. poinl$ of linear difft:.Tt!'Mlial tf)UlZtinnv (Jf the s crmd order
whose ooeffi£irnls are not necessa-rily analytic. Trans. Amer. Math. Soc 1.
40-52 (1900).
2. Green's JllJIIdiorts in Bpaces oj O1'le dimension. Bull. Amer. 1\J8th. Soc. 7.
297 2.9 (]Do]).
3. Boundary problems and Green's fu'J'ldicr&sfor linror diJJerentil21 and diUf.TeJ1(X
rquati",,-.. Ann. of Math. (2) 13, 71--88 (1911).
4. Appl flnd itnlWlIS oJ the crmcept oj adjoinl $ytdt1n. Trans.
Amer. lllath. Soc. 14, 403-420 (I9t8).
5. Lefons sur les mifhfxf€s de ShuwI. Gauthier-\!ilIars, Pari!;. Hit?
Bochner. S.
I. Completely tnonokme I in partially ordered ttpaCt. Duke Math. .J. 9 J
51tHi26 (I 42).
2. :In titm vtm Funktkmm. derm Werle die Ekmer1te. anes Vectorrwme.s
rind. Fund. lII..h. 20. 26\'--270 (1038).
8. AddiIire sel "'_ "" group.. Ann. Math. (2) 40, 769-799 (]9SD).
4. B<ilr e ou, TheorU drt I Funktioram. Math. Ann. 96.
n....]47 (1927).
5. AbsolUl-D4ditio< _Ie M""iI<"furik/itm<n. Fund. Math. 21, 2n 2t8
(]953).
6. VOtl<lungen iJb<r FourietBdoe Lti/qTaZ.. Akad. Verlag., Leipoig. 1032.
Reprlnt.d by Ch...... Pub. Co., New York.
7. S lirwttn Schar umtarrr Opn-atoren p S.-B. Preuss..
Akad. Wis... 8'11--876 (1988).
8. :Inwr.non Icrrmula and unitary tr'an8Jonnalions- Ann. (J( Math. (2) 35,
ln n5 (1984).
Boo1mer, 8" and Fan, K.
1. Di.JlTibutive mder-pTur:rving operatitms in p4Tliallg or d vecJw eel8_
Ann. 01 Math. (2) 48. 168-170 (1947).
BOchner. S., and von Neumann, ..I.
I. Amw,l functWns in gr01AP'. II. Trans. ArneI'. Math. &tc. 8'1.
2I-lIo (1985).
Bochner, S., and Phillips, R. S.
I. Additi.. sel ",...tWo. """ vec/o1' /attic"". Ann. 01 Math. (2) 42. 8t 24
(1041).
2. Absvr..-t.Jy cCJnt7(1"grnt Fourier £iXPansWn.r f(JT normed
ring.. Ann. or Math. (2) 48, 409-418 (1942).
Bochner, S., and Taylor, A. E.
I. Limar JUtKtion4l8 on certain spac fl oj fumticm. Ann. of
Math. (2) 89, 918-944 (1938).
BohnenbIust, H. F.
I. .A"azUnnatkcharQt; HonoJ L.-apaces. Duke Math. . 6 , 621--840 (1940)
2. A oj complu Hilbert Bpaces. Portugaliae Math. 8. IOB-I09
(1942).
8. Suhspaus oj J.. tt spacu. Amer. ..T. Math. 63. 64,-12 (1941).
.... Coove.r Tegions and proj«tions in MinkorvBki ttpMU. Ann. of Math. (2) 39.
301--808 (] 88).
BohDenblust, H. F., and Kakutani. S.
J. Concrete Tqrresentations oj (M)-3pacu. Ann. of Math. (2) 42, 1025-1028
(]04I).
BohnenbJust, H. F., and Sobczyk, A.
1. E:demions vJ jtmdi£mals (H'i. comp!Q lima, Bp0U8. Bun. Amer. Math. Soc.
44, 91--'18 (]058).
Bohr, H.
]. Zur Th«n'i< d<T lasJpericdisc/Im Funktionen. I-III.
I. ACIA Math. 45. 29--127 (I 25).
II. ibid. 46, I01 2]4 (I 2'1.
III. ibid. 47. 257-281 (1926).
740
REF£RENCES
REFERENCES
741
2. FOGfp€rioolSche Fv.nA"tiOItUl. Ergebnisse dcr Math. und iltter Grenzgebiete
I 5 J. Springer. Berlin. 1982. EnR'li h translation,. Chelsea Pub. Co.,
Sew York, 1(}47.
3. On llltnDSf pafodk [unctirms and the thnuy oj gnmpff. Amer. J\J.ath. Month!y
56, 595-609 (1949).
4. A i1un'ty pJ 1110:: difftJTlii proofs oj the mum thff1J't'f1ls in iht: Uirory oj almOfil
prrjodJ.cJvnl'liuns. Pree. Int.em.ational Congo lath.. Cambridge, I. 339--34.8
(1950).
Bohr. Ho. Bnd FDlner. E.
I. 011 type» oJ spatf'f. A ccmrnbutiQn to rhe IhcQry oj alrrum
periodic JIlfu:rfMi. Acta Math. 76. 31-155 (10440).
Ikll1n 8t>n. T., and FrneJwl, V{.
1. Throf'i drr lrolWt'.l'eIJ K(Jrper. Ergebnisse der Math. und ihrer Grenzgebiete.
III I. ..1. Springer, Berlin. ]{J34.
1kms.aD, F. F.
I. A 120fe (In 5rdx.rdditWeJundionnls..I. London l\lath. Soc. 29. 125--126 (1054).
Bore], E.
I. BUT l"iquatitm. adjvinlt!. d .FUr cntaIns lIgmtmes d'tqualions difJtTmtielles.
Ann_ SeL Ecole Sorm. Sup. (8) D. f53-90 (1892)_
Borg, G.
I. Vbtr du SllIbildat gnt:lsser Klasgen von lilletD'm DiJJm:ntitJJglefehlJ.1ll!Pi.
Ark. Mat. Astr. Fys. 3lA j no_ I (111'44).
2. Eine UmMhTvng de:r ShJ.l11I-Libu'OfllU€hm Ei fgube Bt$I.immll.rtg
der lJiff<rmtial{/lddJung durch dU: E . Acta !\lath. 78,1--96 (1946).
S. .lnvt'1'U p7'VUema in the tkeary oJ mararlnistk ooJues oJ dijJeren!ial gystems.
C. R. Djxi tnC CongMi I\futh. Scandinaves, Copen.baf:'en. 1946.
4. On Ihe compl£tmess oj li'mne sels oj ftlndi(ftt$. Acta Math. BIt 266-283
(1949).
5. On a Lwpa.nnff crimi"" of ._lily. Amer. J. !\lath. 71, 67-70 (1949).
6. Oller die Ablrittmg der S-FtAMktion. Math. Ann. 122, 326---831 (1950-1951)_
7. On.he point spedra of II"' + ( --q("'» y fl. Amer. J. Math. 78, 122-126
(19M),
Bott.c;, Truman
J. On COftiIU sets in liflMr.,.,orm d8))€l£tll. RuH. Amer. )fath. Soc. 48.150-152
(1942).
2. Crm.n-,z srls. Amer. l\lnth. )'Ionthly 49, 527-531 19"2).
Bourbaki, N.
I Sur lea ftpaaR de Bfmf1Ch. C. n. Acad. Sci. Pa.ri!'! 206, ]701-1704 (19SS).
2. Elbrtc?m detmllhtmatiqUf', Li[l'f(" V. Espm:nt:tdoriels topologiqut'-B. Herman11
et Cic. Act. Sci. et. Ind. 1189, 1229. Pari!). 1953, 1955.
5. Sur «r1nins f'BfXIL'£B rw'.lorids topvltlgiqtu:s. Ann. lost. Fourier Grenoble 2.
5-16 (1950).
4 Elimalls de malhem4fiqur. Livre VI.lntigmtio-n. Hnmann d Ci<e. Act. Sri.
et Ind. 1175. Parj$. J tI,52.
5. £1€TH.enls de J1WIhhwl , Lnn Ill, TopolDgie l!fnhu1 . H et Cie..
Act. Sci. et Ind.. nos. 858, 916. 1029. 10"5, 1084, Pwis. 1940-1949.
llourgin, D. G.
I. SOt'H(' prtpnfies o} BaRl1L'h spaces. Amer. .J. :\lntll.. fi.... 5'97-612 (1942).
2. Linwr IUPQlvgical spaces. ..<\rner. J Math. 65. 637-649 (1943).
Brace, .J. \V.
I. TrcmsJarIRatlf1l1S on Banm:h spaces. Dissertation. Comt'll University (U.l5S)_
2 Crmtpacmess in 'he flJeak topolagy. :Math. Ma.g. 28. 12,5-134 (lU55).
Bram. ..I.
1. SuInJmmal opauIo1o. Duke M.ili. J. 22, 75 1J4 (1955).
Bray, H. E.
1. ElemnoJuTy propmint oflhe Sti<lfi<s inlL[J,ml. Ann. ofM.th. (2) 20, 177-186
(1918-1919).
Brauer, A.
1. Limits J(Yf' Ihe rliU"l't.1l"kruhr roots oj a tnatri.r. Duke Math. . IS. .387-4i94
(1946).
Brmouin. L.
I. La micaniqut- VQdulut k Sc"rlJdi.nger; une mAthvde glnirtJ.le dt T6olution
par appmzim.tdimu tIeR. C. R. Aco.d. Sci. Paris 183, 24-26 (1 26).
Brodskii, M. S., and Milman, D. P.
1. On the unler I)} a 00I'I[IIf0l' set. Doklady .Akad_ Nflqk SSSR (N. S.) 59. 887-840
(1948). (]I..,..;,m) M.th. Rev. 9, 448 (1948).
Brouwer, L. E. .T.
I. t)bereiruint1evtige. stetige TramfDTrrlatiOlUTJ von Fliif::hM insich. Math. Ann
69, 176 180 (191U).
Browder. F E.
L The Dirichl pl'Oblnn Jor linrn,. elliptic D} arbiETary rven Droo-
with ttl.I1"ilIlJle roefficlmts. Proc. Nat. Acad. Sci U-5_A 58. 230-235 (1052).
2. Th Dirichld and vibration problems Jor 1ilUtJ:r l'lliptit:. dignmliiil '9lLations
of mbitmry order. Proc. Nat. Acad. Sci. U.S.A. 38, 741-747 (1(52)
8. .Aasunlption oj bounda'Y values tmd ,he Green.s funrtWn in the Diridlkt
problem JOT tJu: gemrallimar elliptic equQlicm. Proc. Nat, Acad. Sci. (..l.S.A.
29, 179-]84 (1053).
4. l.inm,. parabolic diJJneRtial ""JUl.IIiom' oj arbitmry orderj gneral boundary-
00_ probl.tmlr Jor elliplk n]uativns. Proc. Nat. A . Sci. U_S-A. 39.
185---190 (1958).
5. 6/:7mJgly f"lliplic sy.tenu ()! diJlert>nJ.inl6JlUdions. Contributions tG the theo1).
of partial differentia] equations, 15-51. Ann. of I\-Iath. Studie:s. no. 83
Princeton, 1054,
6. On Ihe and 'IUS ojrheunerallfnenrelliptic diHermtial
GpeTutor. Proc. Nat. Acad. Sci. 89. 433-439 (1953).
7. The eigenjul1ctiott apaRSicm throrem f()r tM tpu'-rlll sc'1-adjOl'nt singulf1,.
elliptic partial differt'fJliaJ opnulor. I. Th£ onalytiooJ jowuInJitm. Proc.
Nat. Acad. Se;. U.S.A. 40, 454-459 (1954).
8. Ei[J,mfUtOdion...-pansUmN Jor a_tar dlipti<: opaalor's. II. Th< Hillier'
space argument; parabolic 01i open mmaifold3. Proc. Nut, Acad.
Sei. U.s.A. 010, 459--4113 (1954).
Brown. A.
1. On a class oj operalors. Proc. Amer. Math. Soc. 4. 728-728 (1953).
2. The unitary knce oj biJUR"J7'lLll oprraltlrs. AmeT. J". Math. 76, 414---434
(19541.
Browne, E. T.
t. Limits 10 UIf: dtarcu:tcrmic roolI1 oj a maJrU. Amer. '-1ath. Monthly 46.
252 265 (1989).
742
REFEllENCEg
REFERENCES
746
l!u<bheiro, A.
J. .An.r.rfenlrion of a tMMtm. oJ ProJft8DT SyIruIu's ulatiftg ttJ maIl'iuJl.
Phil. Mag. (5) 22. 173-174 (1886).
Buniaknw8ky. V.
1. SUT quelques iRIgaliIis emanl lt8 inIiguJIt1s ordina;f'tS el its intigralu
ou.x diJfbmU3 Jinies. M m. Acad. St. Petersburg (7) I. no. 9 (1859).
Burgst. P.
1. .RistJlubVft$d p aTLilJ limm au moyen de trruJNfrJt"1IIH1im1s ftnu:I:iun
nelk. Dissertation. UniwTsitk de NeuchAtel, Lausanne, ]950.
2. llLsdtdicn de prOOlbnes aux limiJu au moyen de tronsJcmnrrliom JOndbm-
mae.. Z. Angew. Math. PhY"ik 4, 146--152 (1953).
Burkhardt. H.
I. &t lu foncticms de Green Ttlatiu'.s a une domaine d'U1U dimension. BuU.
Soc. Math. France 22. 71-'75 1894).
Burnett. D.
1. The db;tributirm oJ vdncitie8 in a 8lidrfly tWi-uniJarm f.lJ$. Proc. London
Math. Soc. (2) 59, 385-430 (19351.
Burton, L. P.
1. Oscillativn thtfrf'fTJ1.S for Ihe BOlutitmS vJ linear. non- , stcond vrdn
mff"",,MI "1I$uma. Pacilic .J. Math. 2, 28I 289 (1952).
Butler. ..J. B.
1. Pnfu.7fJalion series fen eigmvaltfe8 of f'.egukJT tiQJFsWmndric uperatqn
'Tecbnica.! Report no. 8 to the Office of 0rdinaJx.e RestaTch, Univ. or
California, Berkeley (1956).
Cafiero, F.
1. Criteri dieompaUma p /e cmidif Wn:i tRaDUri
limitaln., I. II.
I. AttiAccad. a:z..Lincei.Rend.Cl.Sci.Fi5.Marh.Nat. (8), 305--311 (1950).
II. ibid. (8) 8, 450-457 (1950).
2. Bugtiinsiemi amtpaItidiftJRZicmi m.isumbil:i. m-glispazi astratIi, Rend. Sem.
Mat. Uruv. Padova. 20, 48-58 (1951).
8. Sulle ft',mIiglie di Junzi01ti additiK rrinsinne. tmijormemmle cun1iJwe. AttJ
Accad. Naz. Lincel. nd. Cl. Sci. Fi . Mat. Nat. (8) 12. 155-1(12 (1952).
4. SuI passaggin 1Il1imire Botto if 8t"gM trinltgralt di SfWljt.8. n li
8pil2; astmtti, Clm masse 'Daf'iabili con gli intqp'mtdi, I. II.
J. Atti Accad. Naz. Lincei. Rend. CI. Sci. Fis. Mat. Nat. (8) 14. 4088-4941
(i953).
II. Rend. SernA lat. 1.:niv. Padova 2'2, :223-245 (1953).
5. StJ.lle Jamfglie r:cm.ptJlle di furdmri adttititle di iwrimtl.' aslratto. Atti del
Quarto Congre$so dell nione IUat. Italip,na, "('aQrmin. 1951, vol. II..
pp. 1}-4{). Casa Editrice P JTeIlB. Rome, 1 tJ.53.
Calderon. A. P.
I. A general ergodic 'MOTtm. ..'\nn. of Math. (2) 58. 182-ltll (1053).
Calderon, A. P., and Zygnmnd. A.
I. A nol.e tm Ole iNtrpolaIion oj linMT . Studia Matb. 12, 1tJ4-204
(1951).
2. On tlJe lheou'm oj HawdorJf-Young and ils applirot;OfI8. Contrilmtjons to
Fourier- Ann1y8is, 166-188. Ann. of Math. Studies, No. 25. Princeton Univ.
Press (1950).
3. A note on the oj 8Ublimar Pn8. Amer. J. Math. 78,
282-288 (1956).
4. On Iu uis:ence oj certain sirlguklr . Acta Math. 88, 85-139 (1952).
5. On ringufar integmls. Am.... J. 1\1ath. 78, 289--309 (1956).
6. Algebras of mtuin. ri optrralm"lI. Amer. ..T. Math. 78, 31o-a20 (ltJ56).
CalJdn, J. W.
I. AfIBtrart ttymUU.'tric bouncrory an&di.tions. Trans. Amer. Math. Soc. 45,
309-442 (1939).
2. Two Bidal iddilI and in the rin.g of bouniUd opemJorB in HilbeTt
apa«. Ann. 01 Iath. (2) 42, 889--873 (IMI).
8. Syro.odri£ 1nm3f""""'""'" in Hilbort __e. Duke .J. Math. 7, 504-508
(1940).
C"meron, R. H.
1. A 'Simp3"n'tl Bute" JOT the numnirol evallUltiQn oj "Timer's integrals in.
Ju.ncti{lft 3pace. Duke Matb. .1. J8 JJl-I80 (UJ51).
2. Tkr. first umiat.ima. of an i1Jkfinite lYitner inltgroJ. Proc. Amer. l\otath.
Soc. 2, 914-924 (1951).
8. The gm.tJ'Ulized heat flow t ualion and a cvnespvnding P ,cm /ormukl.
Ann. 0( Math. (2) 59. 4.34.---462 (1954).
4. Smne ,..mrn (}J Fouritr-Wiener tranq .oj analytic j"Bndionols. Duke
Math. .J. 12, 485-488 (1945).
5. The tTatI.3laIion paU:w1qw oj WI-mer space. D ke I\Iath_ J. 21., 628--627
(1954)_
Cameron. R. H., and Fagan, R. E.
1. N01I-linear t1fm..forma1icnu oJ V ()UeTTa type in 'YiDJfT space. T1'8ns. Am.er.
Math. Soc. 75. 552-575 (1958).
Cameron R. H., and Graves. R. E.
1. Additive jwacIionals on a Bpat"(' oj continuous jun£ticm. I. Trans. Amer.
Math. Soc. 70. 160--176 (1951).
Cameron. R. H.. and Hatfield, C.
I. 8tmmw1nli1lf.J mf<rin m1hogonal dro.r.p......'" oj ROI1-1iatar fundionals.
BulL Amer. Math. Soc. 55, 180--145 (IM9).
2. Summability of «rlain smea lor 1:f flOn-linear fxnctirmab. Proc.
Amer. Math. Soc. 4., 375---387 (11153).
Cameron, R. R.. I...indgI'en,. B. W.. and Martin, \\'. T.
I. Lineari:a:dirm of urlain non-linear fundionaI equaticms. Proc. Amer.
Math. &e. 3, 138-143 (1952).
Cameron. R. B.. and Martin, W. T.
1. An e:tpnssion for the oJ a class oj integral onr.
Amer. J. Math. 66. 281-298 (ItJ44).
2. TM ort1wgonal drot!lopmmt oJ non-lineaT ita ames oj FourieT-
Ham; fimcli""""'. Ann. I Math. (2) 48. 385-1192 (1947).
S. The I:rol&sJarmtJticnt oj JViener integTals by non-liaear tranaformtltion".
TraIlJl. Amer. Math. Soc. 66, 253-288 (1949).
4. Non--lin=r iwhgrol quntions. Ann. of Math. (2) 51, 629-642 (1950).
5. Transformntitms oj Wiener integu:ll8 under a general class ()J linear tram.
formations. Trans. Amer. Math.. Soc. 58, ]84-219 (194.5).
6. EvaltJatinn of IJcni.ous Wimer inJ4rtlls by Il.Yt' oj Sturm-L.iouvilIL! diHerential
quations. Bull. Amer. Math. Soc. 51. 73-90 (1945).
744
REl'EREXCES
REFERENCES
745
7. TmrujorrnnflOtllJ oJ IVimn inl€gmh undtT tmnsbztimu. Ann. of r.tath. (2)
45, 386--:196 (1944).
8. The Jriena meaBare oJ Hilbert nrigbborhoods in 'M space 0] 'ftal conliJ1&wU$
fv.n.dkms. ..I. Math. Phys. Iass_ In!';t. Tech. 23, 195-209 (1944).
9. F rif'T-Jf!iener /omu of t'lnGltJtic functhmals. Duke Math. J. 12.
489-507 (1945).
CameroTl. 'L B.. and Shapiro. .Y. M.
I. Noh..Jit1ear inU'pal ftj1Iotions. Ann. or Matb. (2) 62. 472-497 (1955).
Camp. n. H.
I. Singular 7ftNltipk intq!mlR. Q.Jilh applimti01UJ In sma. Trans. Amer. !datl:a.
Soc. 14 j 42-64 IID18).
Caratlreodory. C.
1. Vorlesungen 'UbeT rulle .Fvudrtionrn. Second Ed-. Teubner, Lei}:Wg. 1027.
2. J'orlesuf"lgt:lJ ii t1" rWlr Fvwktirmna. Teubner, R lin and Uipzig, 1918.
Reprinted by CheIs:e9. Pub. Co., New York.
3. &1tnkungt'n :z:ur RieB% FiNCilt'nlchtn Satz und 2UT ErRodenO«orie- Abh.
l\lath. Sem. Hansi&>hen Unjv. 14. 351-889 (IS)4-1).
CarlemaD, T.
1. Sur les imigmles siwgll.riiTn a wyau Tid el1>ym . Almquist
and "WikseUs. Uppsala, 1923.
2. ZUTThe9TiederlifW;(l,rtn <nJqJru.lgkimaJl#r1.l\fath. Zt."it. 9. 196---217 (1921).
3. Vber dk Oll Vatdlung do Ei partidI£R Differenlial-
gli'.it'hrmgm. Ber. Vern. Sachs. Akad-. \Yisa. Leipzig. l\lath.. at. RI. 88.
119-132 (1936).
Cartan. E.
I. Sut fa me.sure de Haar. C. R. Acad. Sci. Paris 211. 759-762 (1940).
Cartan. H., and G:Kkment. R.
I. Thtori#: de fa dutdilt et al1L1lyRe hLlnncmiqur dans les grooJ'1'f?i/ abil ns locale-
mnd cmnpads. Ann. Eoo]e Norm. Sup. 64.. 79---09 (1947).
Cauchy. A.
1. 0euI0ra. seer. I, t. 12. Gauthier.Vi1lars Paris. 1900.
2_ . ser. n. t. 3. Ga.uthier-Vinal'S, Paris. 1900.
(';..,11. E.
I. On _pac! opaC<fl. Ann. 01 :\Iatl1. (21 38. (1937).
Chal1g. 8. H.
I. On flu distribtltitm oJ the c oaluf'.S lmd singular I'l1lues oj lintar
inkgrol tvpmtions. Trans. Amer. :Math. Soc. 67. 851-367 (1949).
2. Gau>mlizalion oj a t1Irorem oJ Laksro. J. London Math. Soc. 22'. 185-189
(1947).
Charz -ns.ki. z.
1. SUT les tromJormutions Uomitriques tUS t:Bpflfts du type (F). Studia !atll.
18. _121 (1953).
ChevaJle-y, C.
1. Theory vJ Lu f,TQUP$. J. Princeton Cniv_ Press, Princeton. 1'946.
2. Thturir des groupn de Lie. II. Hnmaqn et Cre.. Act. Sci. d Ind. 115'2,
Paris, 1951.
Chian", T. P.
I. A thronm on the JWI'JTi.Oky oj romplndy contin operators. Adn Sri.
Math. S.."..J. 14, 188-196 (19521.
Christian. R. R_
1. On integratltm urith Tf'sp«l to aJinitdy additiiJe measure w1wse values lie in a
Dnfd.indrompldl: partWlly ordnedVf'l'!or spaa.Dissert.. Yale Univ. (1954).
Clarkson. J. A. (see also Adams, C. R.)
1. VniJorRIIJj rot'iI'U space.s. Trans. Amer. Math. S()C. 40. 396-414 (1036).
2. A ch<InJ<1eri%<diOR oj C-IIp"""'. Ann. 01 Math. (2) 48. 845--350 (1947).
Clarkson. J. A.. and Erdos, P.
I. Appro..ri7aalkm by polynomials. Duke Math. . 10, 5-11 (1943).
Clifford. A. H. (see Michal, A. D.)
Coddington., E. A.
1. On 1M specfml Wn oj ordinary selJ-.adjoinl dilfeuntial opt'MlfmJ.
Proc. Nat. Acad. ScL 38. 732-797 (1952).
2. The spa/nll .-.p_ oj orr1iwry selJ-adjoi", differmJWl "Perale...
Ann. of Math. ('2) eo. 192-211 (1954).
3. A a.a'-on oj ordinary selJ-<1djoinl diJfemrlinl syotnRs (abst....t).
Bull. Amer. l\olath. Soc. 58, 42 (1952).
4. The sp«trnl rnafr"ix and GTe(.n's ftuu'tion fM singular S 'lj-adjoiRt bmmdmy
",,1= probUms. Canadian .I. M.tl1. 6, 169-185 (1954).
Coddingtoo. E. A.. and Levinson. )l.
1. Theory oj dilfn'mlial azuatWm. McGraw-Hill. New Yor1(.. J955_
2. On the nahu'e oj 1he sprdrum oj singular sewnd order linear difftrt:nrial
opemkh8. Canadian .I. Math. 3, 555-338 (1951).
3. Perhtrbaticms oj lirlfflT sysI£1m with constant CfJ£/1it:i.rn.ts possessing periodie
scllllions. Contribution to tbe theory Qf non 1inear oscillations II. 111-35,
Princeton. 1952.
Cohen. I. S.
1. On 1Km-ATChimfilwn rwrnu'd spaces. NederL Akad. \Vetmsch.. proc. 51.
69:>-698 (1948).
Cohen L. W.
I. 7'Ttmsfomtation.son spact8()finfinitdynumy dimensions. Ann. of&Iath. (2)
87, 826---335 (1936).
2. On 1M. mean ngodic 11womrt. Ann. of Math. (2) 41. 505-500 (IG40 .
Cohen, L. \V.. and DlIDford, N.
t. Trtmsjonnations en .sequexa spaces. Duke [ath. J. 3. 689-70J. (193'n.
CoJ1atz, L.
I. 'E mbI,.""r und wre tluntri«.he. &MndlU1l/!.. Akademischer Vertag,
Leipdg. t 45. Reprinted Chelsea Pub. Co.. New York, 1'948.
Collif1s, H. S_
I. Complde'iUs rm.d compodr'wsB in linear topoIogirol 8pattIJ. Trans. Amer.
Moth. Sot-. 79. 256-2$0 (1055).
Cooke, R. G.
I. Li1N'al' operators. Macmillan, London. 1958.
CooJX:r. ..). L. )J
I. The sp«trol analysis oj seU'-adJOita operators. Quart. J. Math. (Oxford) 16,
81--48 (1945).
2. Sym,mnri operators in Hilbert space Proc. London Math. Soc_ (2) 50.
11---55 (IG48).
3_ Otu-paroradn Nl'bIi-gmup. oj i. omf'fri£ upnalOTS in llilber' space. Ann. of
Math. (2) 48. 827-.842 {UJ47).
746
REFERENCES
REFERENCES
7407
C<>rdes, H. O.
1.. 8epamrwn des VarwtJlm 'In Hilbn1sdJ£n RlJu.mffl.. Math. Ann. 125. 4.01-434
(Iti58).
2. Der EnJ:oi<k"'_", mxh ProduJdm bei.;
pmfid/er DiJJ<TmIiD/{!leidnmgFn, die d.reh &pao-aWm ""Jallen. Nacl1r.
AJrnd. Wi... Math.-Phys.-KI. lti54, 51---<19 (Iti54).
(A)tlar M.
I. On a tMarcm oJ BruriingandKap/amky. PacilicJ. Math. 4,459---465 (Iti54).
C()tJa1' M.. and Ricabarra R. A.
I. On lm.RsfonlttIlw"., oJ Beff and Koopman's operalor!l. Revista Uni6n Mat.
Argentina 14. 2112--254 (19501. (Spanish) Math. Rev. 12, 719 (1951).
Cmrrant. R. p and Hilbert, D.
I. Melhodm aer physik. I, II..J. Sprih.get". Berlin, U 24. 1937.
2. Jt.felhod8 oJ 'lllalhnnatiwi phyms. I. Inter&cience Pub., ew York, U}53.
Courant, R., and Lax. A.
I. &maTks on Om<htl. problem JOT hypm>Gli< partial diJfennNal <quaticns
roir.h I wefficU:nts in several indeperut.ent variables. Comm. Pure Appl.
Math. 8, 497-50. (Iti55).
Cronin, J.
1. Bramh points oj solutions oj ions in Banach span. 'I':rans. Amer. Ma.th.
Soc. 69, 105---181 (Iti50).
2. Bran€h poinu of 8ultdinns of tqUatiom in Banach BPQU, II. Trans. Amer.
:Math. Soc. 76. 207-222 (195"').
8_ A dqinitivn oJ degru Jor cerklin mappings in HilbcrlspfHe. Amer. J. Ma.th.
78, 763-772 (1951).
4. Analyti< fumtiooaJ . Anu. cf I\lath. (2) 58. 175-181 (1958).
Daniell. P. J.
I. A IImeTaI Jqrm oJ iniegrlll. Ann. 01 Math. (2) lti, 279-2'" (1917-1918).
van Dant7.ig D.
1. ZUT tnpolDgiuhm A/JJdJra, I. Math. Ann. 107. 587--626 (1982).
2. EmiJIe Bdiu flber Grupp"". Jb.... Deutsch. fatb. Verein. 41.
42-44 (193').
Davies. H.
1. E:rpansi0n8 in 1/I£rit>1J oj rigenfu'lK'tWm. Industr. Math. 4,
9--16 (t058).
Davis. H. T.
1. The. tM&ry oJ litlffl1" opnnltml. Principi.. Fregs. Bloomington. Indiana, 1936.
D y, M. M.
1. TIu! spael! Lp with V < p < 1. BuH. Amer. Math. Soc. 40.. 8]6-828 (1940).
2. A prapmy oJ Banach apacts. Duke Math. J. 6, 768 770 (1"'1).
3. &Jlcrive Banaeh spac s nol iMnnmphU: ,,, untJoroIly convex 8pQCt8. Bull.
Am". I\f th. Soc. 47, 818-817 (1941).
4. S mort unifurmly CQ1ivez lJ]Ja£ s. Bull. Amer. Math. 500:. 4.7. 5f»-517
(1941).
5. Uniform ronvuity. III. Bull. Arne.-. Math. Soc. 49. 745-700 (1943).
6. Uniform C'01I'Ve.ri inlac/C1' and «mjugcle ttpaus. Ann. of Math. 45, 375-385
(1944).
7. Some durrot:u:ri:ations oJ innn'- prOduct 8. '1'11105. Amer. Itfath. Soc. 62.
320-837 (1947).
8. Means Jor lhe bounded fumtioos ami eT/iOfHd'y oJ the bounded I't'pT<'_rntUms
oJ . Tram. Amer. Math. Soc. 69. 276---291 (1950)_
9. Operotions in Banach spa££s. Trans. Amer. Math. Soc. 5]. 583--608 (19402).
10. ETgooic theorems IQT abelian semi-group3'o Trans. Amer. Matll. Soc. 51,
899--412 (1942).
11. Strict and sawofhness oj normtd irpw:u. Trans. Amer. l\latb. Soc.
78, 516-528 (I955).
de Sz.-Nng)'; B. (J>ee under Sz.-Nagy)
Devinatz, A.. Nussbaum, A. E.. BOO von Neumann, J.
1. On lhe pnnoutaMlify oJ Be/f-<>4ioW ope1'fJWB. Ann. 01 Math. (2' 62, 199-203
(ItiS5).
Dielldonne.. .I.
I. SUT Ie thioreme lU Hahn.Bl.&1t(Wh. Rev. Sei. 79. 642--6403 (1941).
2. Sur W siparation de.I ensem.blt3 .conuuu dam Un UJHU:t fh Banach. Rev_
Sci. 81. 277-278 (1943).
8. La dualiJi dans r.u espacu 1I. Ann. Sei. £cole Nann.
Sup. (8) 69. 107-189 (m42).
4. Sur Ie 'hearl"" de Leb<sg..-NikDdfIm. Ann. of Math. (2' 42, 547--"55 (Iti41).
5. Sur Ie 1hi0Trnu: de Lehugue-Ni1wc1ym., II. Bull. Soc. Math. France 12.
198-239 (1_); ......ta, ibid., 74, 66-68 (1946).
6. C 8fr1taUt'e8 on rial Banach spaus. Proc. Amer. Math. Soc. 8,
162-164 (Iti52).
7. Sur UI upaces. rl£ KiJIM. .I. Analyse Math. I. 81-115 (1951).
8. Na!uml hcmom in Banach l1paces. Proc. Amer.lt1ath. Soc. 1, 54-59
(1950).
9. SUT h IhCrnlnu de Lebesgue-NilwdJ}m.. IV. 3. Indian :I\fath. Soc. (N. S.) 1.5,
77-86 (1951).
10. Bu, k IhImmv-deLehe8g...NikIxfton. V. Canadian J.M th.3, I29 I39 (1951).
11. BUT la con'Vtr,gtntt 4k3 &mires de 7mSU'i"e.8 de Rn.dtm. ADaia Acad. BrasH. Cia
28, 2I-S8. 277-282 (1951).
12. Sur un thtorhm de .Jessen. Fund. Math. 87, 242-248 (U 50).
18. Recenl devt:lapmenl.$ in 1M theory oj locally convu vecloT S]Jace3. Bull. ArneI'.
M.th. Soc. 59. 495---512 (ItiS.).
14. SUT Ie thiOTtmt de LdJesgtu-NikodYm.III. Ann. Il18t. Fourier Grenoble 23.
25-58 (I947 I948). .
15. SUT tm rhiarl"", de _ A,-ch. I\lath. 8. 48&-440 (I952).
16. On bi syswns. Michif!an Math. .I. 2, 7-20 (19M).
17. Sur Ie produit de .comporition. Compositio Ma.th. 12 17-a4 (1954).
18. Bournle<l Bel. in (F)-spacts. Proc. Amer. Math. Soc. 6. 729-751 (1955).
19. B., la d'"ne a1g11n'e d'opira1rors. PorttJgaliae Math. 14.
35---88 (1955).
20. B.. la rhiarie spuIJ'ak. .I. M.th. Pur.. Appl. (9) 85, 175-187 (1956).
21. ChamP3 de VUkuT3 ROn localemen triviaU%. Archiv des Math. 7.6-10 (1956).
J., and Gumes, A. P.
1. SUT etTtaim Mpa£.t8 'Vf'.€toriel8 . C. R. Acad. Sci. P&m 230.
1129-1130 (1950).
Die:udonne. .I.. Bod Schwarb. L.
I. La dualiu dam k$ 8paces (F) d (LF). Ann. JI}.st. Fourier, Grenoble I.
61-101 (1950).
748
REFERENCES
REFERENCES
749
Dines, L. L. see Moskovitz, D.)
Dini, U.
I. FunalJU'nll. per la IImria:z delle Junzioni di tKITicMli rwli. Piss. (IS7S).
Dirac, P. A. M.
J. The principk$ oj qw.utfum JTIIChn.nia. Oxford Press, London. 1935
Ditlc.in. V. A.
I. On 1M sfrodure. oJ idmls in UTttd-n normed rings. UCnt)"C Zapislo:i MOskov.
Gos. Vniv. Matematllm 30. 83---180 (1939). (Russian, English summary)
)lath. Rev. I. 336 (11)>0).
DixmIer, .I.
I. Les moyennes i1lt'ClJ"ianl£s dans les smti-groupes ellr:UTS appllCdiQl'J8. Acta
Sei. Math. Szeged }2 PaI'$ A. 213--227 (1950).
2, Lot fOAd.Wnnt!Ua lirlfflirn sur "ensmt1;h de3 ophatnrrs bornis dOtm f$pQ«
<k HifUrr. Ann. of Math. (2) 51, 887--408 (1950).
3. Sur «rluitw tBpat.'ftJ oo'Uddires pal lU. H. Stone. Summa Brasil. l\lnth. 2,
151-182 (1951).
4. Sur un rhJDn.mf' tlt B6nacA_ Duke :\rath. .T. 15. 1057-1071 (1948).
5. Les algt!bres d'nptmteuTs dans fupace hilberfien. Gauthiers-ViUaTS, Paris.
11)57.
6. Sur 'UfU ;71igcdiil de ll. Rein._ J\.lath. Ann.. 126, 75-78 (1953).
7. SUT M'iU orthotlM'mlllei dans us a:pat'i's prlhilbntieras. Acta Sci. Math.
&.god 15, 29-30 (1953).
Dixon, A. C
I. On Cl class vJ l! in oscillating flJ.nctiut/il. Proc. London Moth. Soc.
(2) 3. 83-108 (1005).
Donoghue, 'V. F. p and Smith. K. T.
I. On the symmdry and bvrtrrckd dot.'RJT oj locIllly coPlI-'l'it Bpt1£t!S. Trans. Amer.
Math. Soc. 7B 821-344 (1052).
Doob. ..I. L. (see 0.1so Koopman, B. 0.)
I. The law oj large num.ben/fvTcon!inuous BIochasti£ processes. Duke Math. J. (5,
200-{j06 (1940).
2. StodJtJStit1 x tl)ilh an inrtgral-valutd pt1Mmeln. Trans. Amer. "Iatb.
Soc. 44. 87-150 (1088).
3. .Asympfotic properties oj .,HomO transition ]JnJbabilitin. Trans_ Amer.
Moth. Soc. C3, S1J3-421 (1948).
..... Stvd!D8tk prott'ue&. \\o'iJey, ew York. 1953.
Dorodnicv14 A.
I. ..isympl.dic laws oJ distri1Julion oJ the dfomderi.stic oohItR for crrtain Bptrial
flHVUJ of diJ/Ot!Tdiul r:qIWtioDB oj stwnd otder. Uspchi Natfill. Nauk (X. S.)
7, no. 6 (521, 5-06 (1952). (Russian) Math. Rev. 14, 877 (1953).
Doubro"uy. V. :M_ (see Dubl'O'\."tdai)
Doyle, T. C.
1. .Invariant throry of rlll ordinary. linear. honwgoIttJta. s cond order
diflnmdiaI boundary probl<m.!. Duke Math. .J. 17, 249-261 (1950).
Dowker. Y. .N.
1. Finite and (J.Jinite i'm'tJ'rirml . Ann. of Math. (2. M, 595---608 (10.51)
2. A new proof oj th€ eral rE(}dic tll ortm. Acta &i. lAth. Szc ed 12 Pars
B, 162-166 (1950).
3. A nore (111 the ergodic thoornlt. BulL ."mer. 1\1&0. Soc. 55. .3jg-3 S (1949).
Dresden. A.
1. Sohd tmtllgtit:ol and dttmnloonfs. H. Halt Co., Sew York, 1930.
Dubronkil: (Doubrovsk,Y), V. M.
I. On some properties vJ CQ1n-pf,er.ely addi itw lief/unctions and ,lIIir llpplimtion
W izm.iDn of a lhtOTtm oj . Mat. Sbornik N. S. 20 (62),
317 2. (U147). (Russian, English sumnuuy) Math. Rev. 9. 19 (11148).
2. On the baBiR oj a family 01 rornpUUty Qddilive Jtmrfinns (JJ .sets and on 1M
propnl,in vJ wrilorm adlliliuily and efjai-rntltillkity. Doklady Akad. Natlk
SSSR (N. S.) 58. 787- 40 (U147). (Russian) Math. Rev. 9, 275 (1948).
S. On proptrfin oj obsolute wntimriIy and f'tJUi nuity. Doklady Akad.
:Sauk SSSR (N.S.) 63. 483--486 (1948). (llUESian) Math. Rev. 10,361 (1949).
40. On tltJUi fundiCJ'TU and on the proptrfin (JJ uniJOMfI, adtlitivi1y and
e(jUi-conlinuity (JJ a jamfly 0/ oompldely addi1iw sel JunclifWUJ. Izvestiyn
AkBd.. Sauk SSSR. Ser. Mat. 13, 341-356 (H j.g). (Russian) )\fath_ Rev. II.
90 (1950).
5. On'I>< property 01 nuUy of a lamily 01 rompldt'/yaddilire 8<1
Jum.tiOOR with wsp«t to proper and improper rosa. Doklady Akad.. Nauk
SSSR (:S. S.) 76, 3IJ3--jjS6 (1951). (Russian) Math. Rev. 12, 598 (1951).
6. On a properly 01 a leNnu", of NifrtxfY... DokIad). Akad. Nauk SSSR (1'0. S.)
85 7 693--69£1 (1052). (Russian) :MBth. Rev. 14" 456 (1 53).
7. On mtain oonditimu (JJ rompacbwls. Izvemiya Akad. auk SSSR. Ser.
Math. 12, 897--410 (1948). (Rusgian) !ath. Rev. 10. 108 (19'.).
Dugundji, J.
1_ An ro:tnMitm. of Tietze's thmTma. Parif"IC J. Math. l 353-367 (U51).
Dunford, N. (see also Bartle. R. G., and Cohen, L. W.)
L Uniformity in linmr sptl€n. Trans. Amer. Math. Soc. 44. 305---358 f1938).
2. Dirrel deroIJIpvsitiom vJ .&mClcIl 8pU«If_ BoL Soc. I\Iat. J.\[exicMa. 8, 1-12
(1946).
B. An indicidual ergad.ic thmem Jor non...oonuJ'iltMtitY tran8.formatUms. Acta
Soi. Math. Sug<d 14, 1---40 (1951).
4. Inlegmtivn in gennat a1JlJ1"m$. Trans. Amer. Math. S<.Jc. 37. 441-453
(1935).
5. On «mtinuous mnppffigs. Ann. of Math.. (2) 41. 639-661 (1940).
f5. Sp«trollheory. Bull. Amer. Math. Soc. 49, 637 Sl (1943).
7. Spedml theQry I. (' tQ prQjfrlimas. Trans. Arner. Math. Soc. 54,
185-217 (1943).
8. Itlugrotion. lInd lirwar opera1ions. Trans. Amer. Math.. Soc. 40. 47,f......4.94
(1986).
Q. A 7nean rrgodic theorem. Duke Math. ..T. 5, 635-646 (1939).
)fJ. On a tMorem 61 Pkssrur. Bun. Arner. Math. Soc. 41. 856-358 (1035).
11. An e1'fJVdit' lhe(JTemfM n-paramdtT group8. Proc. Nat. Acad. Sci. U.S.A. 25.
195-196 (1939).
12. 011 one parameter grWP8 6} linrar tmnlJlormt1.l:itms. Ann. of Math. (2) 89,
569-573 (I 88).
13. ResduJima. oj 1M it1£ntity [or .commldatil'e -algbras (JJ operators. Acta Sei.
Math. Szeged 12 Pars B, 51-56 (1950).
14. Spedml theory in nbst1'act llpac:cs and BanadI ulgdJro8. Proc. Symposium
on Spectral Theory ond Differentia.l ProblfiT1s. 1-65 (IDSI). Oklahoma
.t\gricultural ond l'tlecbanical College StiUwatcr, OkIaboma.
750
REFERENCES
REFERENCES
751
.i5. SprclTallkmy. Proc. S:rmposium on Spectra! TheOTY etc., 203-208 (IDS1).
16. TIw. 1Wltu1ion problem. in .sprrh'al lhemy. Froe. Intematiol1Al Congress
Ma.th., Cambridge, l\[o.ss., U50. Vol. 2, 11,5.-1:22.
17. 8p_aI theury. II. &soh<lions oJ the ;rrem;Iy.I'Bcif"K" J. Math. 2, 559---<>14
(1952).
18. Spec:tml opeTalors. PDdrtc .Y. Math. 4. 321-854 (1954).
Dunford. N.. and Miller, D. S.
I. On ergodic Ou:O'TMn. Tram. Amer. Math. Soc. 60. 538-5409 (1946).
Dunford, N., and Morse. A. P.
1. Remarks on 1m pretDh7lg papu oj .Jttmt$ A. Cla-rksun. Trans. Amer.
Math. Soc. 40. 415-420 (1936)
DUDford. N., Rnd Pettis. B. J.
1. Linear op"arions on 8Ummablt: fundl'OIIS. Trans. Amer. Math. Soc. 47,
823--392 (19<0).
Dunford. N.. and Segal. I. E.
1. Semi-groups oJ opf'Tafurs and the JVrier3tmss thwrt:r1l. Bull. Amer. Math.
Soc. 52, 9I1 14 (1946).
Dunford, N., and Schwartz, J.
1. C aim"'" oJ up<TOtor am-op;es. PrO<!. Nat. Acad. Sci..
U.S.A. 41, 229---231 (1955).
2. Conrergeme almost evetyWMre oj operalnr UUf!mgn. .T. Ilational Mech. and
Anal. 5. 129---178 (1956).
Dunford. N., and StQne. (1,[. H.
1. On rh rtpre.tentalion IRrorr:m for Boo/fa'll algebras. Revista CL. Lima 48,
447---458 (1941).
Dilllford. N.. and Tamarkin, J. D.
1. A principle of Jr:;(!(7J and gmcrnl .FubUd thtorems. Duke Math. J. 8,
743 749 (1941).
Dunham, J. L.
I The JVmtul.Brillou K mdhod oJ BOlz1ing the wave Phys.
Rev. 41. 713--720 (1932).
2. The energy Imtls oj .a rolatinC vibrator. Phy.s. Ilev. 41, 721-731 (1932}.
Dvoretzky, A., and Rogers, C. A.
1. ond #J'JOOf1dilional eorwergm«' in normrd linetlY 8p(JJ;e8. Proc. Nat.
Acad. 8<i. U.S.A. 38, 192-197 (1950).
Eberlein, W. F.
1. JVeal.: rompadDas in Banach spmes. I. Proc. Nat. Acad.. Sei.. U.S.A. 33.
51--53 (11147).
2. . canverity. and lintarily in Bllf1(1.ch 8paa!J. Ann. of Math. (2) 47.
e58-703 (1946).
8. ANtrmt ergodic rheoTem.s and rvtak almost periodk. J . Trans. Amer.
Matn. SO<!. 87, 217 240 (1949).
4. Abstract eTBodil: t1U!(lTtm8. Proc. Nat:. Acad. Sci. U.S.A. 34, 43-47
(1948).
5. A fiOle on 'he 8pecfTal th ()7rn1. BuU. Amer. Ma.th. Soc. 52, 828-331
(1948).
Eckart, C.
1. The pn2dration oj a PQknfial bamt1' by electnm3. PbY$. Re..... 35, 1803-1309
(1980).
Edwards. R. E.
1. A therrry 01 RD.don mt'a8Urt8 on lac.aily eomp«r tlpacM. Acta Math. 89.
188-164 (1953).
2. Mullipliqltive 011 Banada algebras. Proc. Cambridge PhiJos. Soc. 47,
475--474 (1951).
Eidelheit, M.
).. Zur The dtT Meng in lirat'W'f!71 ftQrmicrten Rdunun. Studia
Math. 6, 1M-Ill (19M).
Eide1heit, 1\1.. and Mazur, S.
1. Eiru: Berm:rkung ilber du Raume VcmI- Typu.s (F). Studia. I\1ath. 7. 159-161
(193.).
Eilenberg. S.
I. Banach e melh0d3 in topology. Ann. of Matb. (2) 48. 568-579 (1942).
Elcorrin. V. (.see Micbal. A. D.)
EUiott, J.
1. The bfJUndary value pToolems and semi--groops associaWl wirh cerlain
diffuerdial operators. Trans. Amer. Math. Soc. '16, 300--331 (1954).
2. E;/!<flfwu"tion <"'Pa...;.... with singular diJ1<rmtia1 <p<rnlfJrs.
Tran.. Amer. Mat1>. Soc. 78, 406-425 (1955).
Ellis, D.
I. A rruxtifiro/ioIo oJ the paraIl<!;;gram law oJ Hil/Je" spa",.
Math. Zeit. 59, 94--98 tI953),
Ems. H. W.. and Halperin. I.
I. Ftmmon spaces _ by a leoeIIing l<ngthftmdi<m. Canadian.J. Math.
5, 578-592 (1958).
Erdo._ P. (see Clarkson. .I. A.)
ErdOs. p . and Ka.c.. M.
1. On cerlaif'llimit tMorems oJ the tJuwy oj probability. Bull. Amer. Math. Soc.
52, 292---302 (1948).
Esclangon, E.
I. Nmwdks sur usJ quasi-pbiodiquu. Ann. Ob.s. Bordea.ux
16, 51 26 (1917).
Esser, M.
I Analyticity in Hilbert. space ;md sdf--tJtljaint Amer. ..T.
Math. 69, 825-836 (1947). .
Ezrohi. t. A.
1. Tm gennul Jcrm o/linNT operations- i" tJpClUQ witlf q CQtlf1lable ba$1:s.
Doklady Almd. NBuk SSSR (N. S.) 59. 1537 1540 (1948). (Ru..;an) lIlath.
Rev. 9, 4.4.8 (1948).
Fagan, R. E. (see CIImeItm, R. H.)
Fage. M. K.
I. On _mmy atal oJinJb<m«ftm<tion<. Mat.Sbomik N.S.
32 (74), 345-852 (1953). (Russian) lIlath. Rev. 14, 1088 (1953).
2. Tm c1wmt:lr:ristic Jundion oj a one.poinl boundary problem for an ordinary
linea1' diJferffirtal tqfUlfion oj ucOJ'Ul (n'der. Doklady Akad. Nauk SSSR
(N. S.) 96, 92IJ--0O2 (1954). (Russian) Math. Rev. 16, 382 (1955).
Fan.. K. (see also Bochner. S.)
I. U prokmgeme1Jt des lorKti.onml.Us cmlinues sur un apace semt-cmImml.
Rev. 8<,. 52, 131-139 (1944).
';52
REFERENCES
REFERENCES
756
2. P(1rri.al'y mtftol't'd adtb."ive groups of amtin&wuS Ju»dirms. Atm. ()f Math. (2)
51, 4{) --427 (IDao..
2. ..."Iaximum proper1ies and ifU:fJlUllifks JQr the t"igmvalNf'S oJ compkhly
oontin opt:TCllcl'x. ,Proc. Nat. Acad. Sci. lJ.S.A. .37. 760-766 (1951).
4. us functions difinia-positi'C'ts el la jcm.aions compliYltvnt monoIDJ1£S.
Gauthier-Villars, Paris, 1950.
5. On a fhWTf:1lt oJ JVtyl aJIJI.Cft"7ting cigemJolue8 oj lmMr trnrnformatWm I,
}>roc. Nnt. Acad. Sei.. U.S.A. 35, 652-655 (1949).11. ibid. 36, BI-B5 (1950).
FaDtappi , L.
1. La leIRia dti.fa.cm;Umali unolifki. It. sue app/im::ioni £ i BUm pOBSibUi
indiri%Zi. Reale Accadcmia d'IUlia. F()ndazion Ale5!)8ndro Volta, Atti dei
Cunvegni. IJ. 223.---2'7ti (1930). Rome. 1943.
2. L'tlnalMi fan:zim'uJlp ne.l campo compPuso € i mwt'i mdodi d'inUgrazione delk
equa:ioni a 4erivare pur.:iali. Rivista :Mat. Un i'\!. Parma. 1.. 117-120 (1950).
3. Le calml des lfUltrius. C. R .Acad. Sc.-i. Pa.ris 186, GUJ--{)21 (1(128 J.
FarneU. A.. E.
1. Limits for the thirradnwic TOols oJ a BlalTiz. Bu11. Amer. :n-Jath. Soc. 50,
78 -794 (1944).
Fell. J. M. G.. and KcIJy, J. L.
L An a1gebra oj UAbou)Ufed rJptTt'durs. Proc. Nat. Acad. Sci. U.s.A. S8.
592-598 (1 52).
FeUer. "V.
1. Semi-poup$ oj tm. fU17l'KdirJWI in gffieml weak wpolngin. Ann. of Math. (2)
57, 287-308 (1953).
2 On the getlDfIlion oj tmbormdro semi-groups oj bountkd linf'tlT operatDTs.
Ann. 011\lath. (2) 58, 166-174 (ID55).
3. On posf.tWity p anni.groups oj tra?iqonnat.iou em C[rt.1"2]' Ann.
Soc. Po]on. Math. 25 (1952), 85-940 (ItI53..
4. DifJruion protYSSl',lj in vne dimrnsion. Trans. Arner. Math. Soc. 77, 1-31
(1954).
.5 TIlL pcwuhoIic diff rr.ntiQr equot1oo and tM- o3BOCiated 8Emi-group of trans.
'ftrmllliOM. Ann. of Math. (2. 55, 468-519 (1052).
6. On U'COfId order diJfrrmtial operalbrs. Ann. of Math. (2) 61, 00-10.5 (1955).
7. On di//ermtitlJ opnatcrTs and botuadaTy mndilions. Comm. Pure AppJ.
1\Inth. 8, 203-216 (1955). .
Fenchel, \V. (se-e Bonnesen. T.)
Feynman, R. P.
I. Spau..firrfe. approoch W DOrM'datWisfic qvaRirlm ma:hani.c8. Rev. M()d.
Phys. 20. no, 2, 367-387 (1948).
Fichtenholz, G.
I. SUT les !onctiOf1ndles liniaiTU, conti'UJI!.$ au Rem giniraIi.si4 :Mo.t. Sbornik
(N. S.) 4 ( 6), 193-214 (1938).
2. Sur uht classe d'optrotiowJfrmc1.ionl'N!1l£s liniaira. :\1at. Sbomik (N. S.) 4.
(46), 215-226 (1938).
3. Sur les OptmtiORS limaires dans l'npaa des Jom:tirms cantinue... BuJI. Acad.
Roy. Belg. 22, 26-"3 (1956).
Firhtpnholz, G.. and Kantoroviteh. L. V.
1. SUT Its opiratwnsliniGiTes dans '.espna desJonctions bonties. Studja. Math.
5. 69-98 41934).
2. Qwelqt/e3 thiori:n&es 8U1 les joncfwlJutdlts Ullemrt:lr. Doklady Akad. NBUk
SSSR (N. S.) 3. 307-312 (1934). (Russian nnd French).
Ficken. F. A.
I. Narc. on the <£xisIence oJ scalar products in normt.d ItrIM,. 8pa£ s. Ann ()r
Moth. (2) 45, 362-066 (1944).
Fischer. C. A.
1. Naessary and svJJirient. nm4ilion.s that a lint'a,. tmmJormation be: complddy
l:ontiflUQU8 Bu.]). Amer. Math. Soc. 27. 10-17 (1920).
2. Linrar fiu><ti<mals oj N-.prrods. Ann. or Math. (2) 19,37-43 (1917-1918).
Fischer, E.
I. Sur fa en . C. R. A d. SeL Paris 144, 1022-1024.
(1007).
2. ApplU:alVms d'un fhifJTtme Bur f.a IA,Jr.-.. .f(% en JROlJf:l'lfW. C. R. Aca.d. Sci.
Paris 144, U48-1I5I (1907).
Fishfl, B.
I. Th oontintmU8 spectra oJ certain differmtiDl equati'OJl.S. J. London Math.
Soc. 21', 175 180 (1952).
Fieisohor, I.
I. SUT Ie! qJaJ:f$ 9WmIes n . Nederl. Akad. Wetensch. Proe.
Ser. A. 57, 16,>-168 (1954).
Feiner. E. (see Bohr, H.)
Ford. G. C. (see Mishoe, L. I.)
Fort. M. K . Jr.
I. Essrntinl and aljiHdpoinrs. Amer.J.l\olath. 72. 815-322 (1950).
Fortet R.
1. llemar'qua' sur les espccu t'niJumriwtenl C. R. Acad. Sci. Paris 210.
497-4 (1940).
2. SUT les espaus u.niJormimenI. . Bull. Soc. Math. France
69, 25-46 (1941).
8. Les d.tq ti?lmirrs dam 1M apaus um"Jormhaenl corzreres.
C. R_ Acad. Sci. Paris 211. 422-423 (1940).
4. Lea funtti()t1S ala:doi.res du type 1rlaTkoJI d fY!71niRl';8 iquaticnB
linttlins auzdtritlia parlidlesdu lypepmdXJliqru:. J. Math. Pnres Appl. 22_
177 243 (1943).
Fri:<het, 1\1.
I. Sur points du calcul fmu:tWtmeL Rend. Clre. l\1a.t. Palermo 22_
1-74 (1906'.
2. us f'sptl«B OO$J.rails ' G/fines. Acta Math. 47, 25--52 (U)26).
S_ us esptre s tlbstmilB. Gauthier-Villars. Paris, 1928.
4. Sur Its ensemble! de Jom:Iions et les oplrations U'I1iaiTC$. C. R. Acad. ScJ.
Paris 144. 1414-1416 (1907).
5. Sur les opbations linini'rt$. 1.111.
I. Trans. Amer. Math. Soc. 5_ 493--499 (1904).
n. ibid. 6, 184-140 (1905).
III. ibid. 8, 433--446 (1907)_
6. Sur leI' ensembles (,Ofnpac- tk /11ndions mcsuroblu. FW1d. l\otath. 9. 25-32
(1927).
7. .sur le.s f'f18e7fIble.s l:ompttCl$ de fundiom de wtt/s svml'1llJbks. Acta SeL
:\I.to. Szegro 8, II6-126 (1937).
754
REFERENCES
REFERENCES
755
8. Sur mtIeTB m0de8 de convergence d'um suite de loncnons d'une variable. Bun.
Calcotta Math. Soc. II, 187---206 (19I I920).
9. Euai de glutnl.trU d tme infinilt de . Nuuvelles Ann.
de Math. (4) 8, 97 II6, 289-317 (1908).
10. SUT res j'rmctirJflZld.h:s biUnlalres. Trans. Amer.. Mat Soc. 16. 215-234
(1915).
Fredh()lm I.
I. Sur un, class< d'ilJlUlti<m3 fomtWnndles. Acta Math. 'ZT, 365-390 (190S).
Freudenthal. H.
I. Tt'ilwdse ,gtMdfU It:lodul:n. Neded. Akad. Wetensch. Proc. 39 641--651
(1686).
2. EinigeSdtu rib" topGIogisrh, Grupprn. Ann. of Math. (2) 37, 46-56 (1600).
8- Vl><rdi< FIi_ _ Henni_ Op"a-
toren. NederJ. Akad. Wetensch. Proc. 89, S32-883 0'1180).
Friedman, B.o and l\olishoe, L. I.
1. Eigrnfunctirm upanriom associated wi", a -mm-seU a4j0int diJ1ermtinl
oqunIWn. Poci!;c .J. Math. 6. 249--270 (1958).
Friedman, .ft.J. D.
I. Ddmninati<>n of wing a IIrnffaliud Lapl""" .rtJRS/<mn. .J. Appl.
Phy:s. 21, 1883--1387 (1950).
Friedrlms, K. O.
1. VbeT die ng eims nugraloperol,tws. Math. Ann. 115, 249-272
(1988).
2. On tM pmwbaticm oJ continWJUI 3p«lTa. Comm. Pure Appl.. Matb. I,
861---406 (1948).
3. SpdcIralfheorU Operotmm. I-III.
I. Math. Ann. 109. 465--487 (1984).
n. ibid. 109:. 685--713 (1934).
III. ibid. no. 777 779 (1935).
4. Beitrdge ZUT Theorie tltr ktralsrlin:r. Math. Ann. lID. !W.---62 (1985).
5. V1m' die in du Spe1dm/llIrori< der ha/bbe.
-. mffemltialopcrJlqrm "",ril<T Ordnung. Math.
Ann. H2, 1-25 (1955).
6. On diJ1erential operators inHiCbertapm:e. Amer4.J4 Math. 61. 523--544 (1989).
7. SptIrtraltkcri.limarer Di/1eren Jber. Deutsch. 1'tlath. Venin.
.... 181-198 (1985).
8. DieW1ita1rnJmxJrianten OptJlfknt71 imHirhertschen &urn.
Jber. Deutsch. Math. Verein. 45, '19-82 (1935).
9, The i.-ry of"""" an4 strong e:d<nsimu of di!/errnlial operalaT3. Trans.
Arner. Math. 800. 55. 182--151 (11)104).
10. CriJeria for were" 8p<dra. Comm. Pore Appl. Math. 8, 431>--M9 (1650).
11. Functional amdym and uppliaJticms. lost. I\"Jath. Sei., New York Univ..
Ntw York. 1056.
12. Critnia lor IN iliscrf"le haratt.er oJ 1M spectra oj urdinary difff1Tntial
opeTak1rs. Courant Anniversary Volume. 145-180. Interscience Pub.. ]9"8.
13. Spec'ral oj limar ope7ators. Inst. .Math. Sci.. New York
Univ., 195$.
14. Symmetric hype:rbolic linear digetrnlial. t'tpJLJfion.t. Comm. Pure Appl
'ath. 7. 84iH192 (1954).
IS. Diff"""'iobilily vJ so/uIiom vJ lin=r dliplic difft:rmJ.ial op.rolqro. Camm.
Pure Appl. Math. 6. 209-326 (1953)
J6. MaI.hmwtkal asputs oj 1M quantum theory 6} Jielda4 In Pub..
New York and London, 1953.
Frink, 0.. Jr.
1. Berks l':rpansions in liRnIT IW'foT sp4Us. Amer. .I. Math. 63. 87-100 (1941).
FrobeniU!5. G.
I. Vbe-r lint'Ll."l'£ Su1Jldi.hIJ;Of'/L"J'a «114 bilirJ«l1'e Forrmn. J. Reine Angew. l'tfath.
64, I £8 (I87S).
2. lJ°1Jer die srhUfe .lnvarianu ana bUbt.eaTm oder Furrnen.
..I. Reine Angew. A'Iath. 86. 44-71 (1879).
8. V".,. di< Tmusformnlion<n du bilinromJ Formrn. Silzungs-
berjchte der K. Preuss. Akad. der \Viss. zu lIedin. 7-16 (1896).
Fuch!5. J....
I. l}beT Rdatiotum, wekhe .fUr die Z'WiscIJm i zwei Pun/den er-
_ Inlegro/< <kr Liisungen Ii-=< Diff_algleid,,_lIfaff/inden.
..I. Reine Angew. !\:lath. 76. 171-218 (1873).
Foglede. B.
1. A COOItmdativUy ,htJmnnjQf normal upnatorB. Proc. Nat. Acad. Sci. U.S.A.
80, 85--40 (1950).
Fukami)"R. M. (see also Yosida. K.)
I. On dllllllnaled ergodic Uu:OTems in L. (p J). Toholm Math. J. 46. 15()-153
(1939).
2. On B.o.GlgdJros. Proc. .Japan Acad. 27. 321--827 (1951).
3. On a thnJnm oJ Ge1jand and Neumnrk and the B*.olllgrbm. Kumamoto.J_ Sei.
Ser. A. 1. no. I. 17-22 (1952).
F1llIertoo. R. E.
J. On a Bem1,gTOUp oj BUl.rstfs (JJ a litltta space. Proc. Amer. Math. Soc. I.
440-442 (1950).
2. Lirwhr oprrulors mith range in a BpQce QJ diJJerenIiobIt> fundiLms. Duke
Math. .J. 13, 261>--280 (IM6).
3. The an o/liAffiJ'opeTalors/rmn L"wL. Proc.AmeT :Math. Soc. 5,
689-699 (IG54).
4. An Wquality f(N linear operaWT8 bdwern LJI spacts. Proc. Amer. Math. Soc.
6, 186-190 (1855).
5. A C'liaroderizaIion oj L sptlff-ll. Fund. Math. 88. 127-136 (1051).
Gagaev. B
1. Onl'OO ih Banach spares. tJepehi Mat. Nauk 3, no. 5 (27),171-173
(1948). (Russian) Math. Rev4 10. 255 (1'949).
Gal. I. S.
1. SUT la miOwde lk n'Bonarwe ct sur un Uliorbne c.mactr'nant. des de
Iype (B). Ann. Inst. Fourier Grenoble S, 23-30 (1951J.
2. Th< principl, of _ion of 8inguJarilies. Duke Math. .1_ 20, 27---35
(1958).
3. em lOtIJVtn«k vJ vperot1OfJR 1Q complel£ 'Vector spaces. Amer. Math. Monthly
60, 527-538 (1955).
Galbraith. A. S. and \\"Bl'SI"hawskt. S. E.
1. Th£ Wnl!f:7gen« of e:tpqnsiotl3 Te81dJ /T()m a selj-adjoint btn.ntImy
probk... Duke Math. .J. £, 31S 340 (U'4<I).
756
REFERENCES
REFER:E:.NCES
757
Gale, D_
1. Compt2d sets oJ Jundi0Jf3 and IUru::UQR rings. Proc. Amer. Math. Soc. 1.
80S-808 (1050).
Gantmacher, V.
J. Vber f;I:/arod>£ I.mlstdige Opnaiorm. Mat. Sbornik N. S. 7 (40), 5m-308
(1940)
Gantmaeher. V_.. Rnd rrmlian. V.
1. SUT ks npl1£t8 litlla:irn donI fa sp" re unit,.aire ul faibILmniJ oompacl8.
DokJady Akad. :\Jauk SSSR (N. s.) 17, OJ-04 (J087).
2. lJber st:/ruIat:he Kompa7cthrit in :IJtmadItrlInt Raum. l\!at. Sbornik S. S. 8
(50), 480-492 (1t)40). (Russian. Gennan 8UJ11J11BI'Y).
P.R.
1. The dtJsyu L.. and rrmft"lJ"mlll . Tra.ns. Amer. Math. Soc. 69.
392--415 (1050).
G8l'8bedian. 1'. R.t and Shiffman. M.
1. On IItIIutWn oj partial dVlemdWl by 0." Hahn-Banach The""",.
Tmns. Amer. Math. Soc, 76. '288-299 lll ).
Gbding, L.
1. Linear hgpnbolic partUll diJJt.rmlial ftjUflIiom u'il.h CQ1Jsfant mtifru:ir1lJtJ.
Acta Math. 85, 2 2 (1050).
2. DirichIeI', pn>b/<>It Jor r;...a.. ellipM partiul difJnmtiol eqrJrdions. l\Iath.
Scand. ). 55-72 (1958).
8. Le problhnt: de Dirich1d pOUT US itp.wiiom au dirivlcs parIielkii tIlipliques
linlairn dans des domaims lxlrnes_ C. R. Acad. Set. Paris 233, 1554-1556
(1051).
4. DiridlldB proolem and me vibmti.on probleta fur linror elliptic pamal
difJerenlial qrm1ions wilh rondeml <:vefJi<i<nU. Proc. Sympo'iUffi Spectral
Theory and Diftamtial PrQb1ems. 201-801. Oklahoma Agricultural and
:Mechanical t Stillw1d.er. Oklahoma, 1951.
5. .11;nfgclili d< Frifflrichs .1 Leroy pour 1<, tq",,/i<m9 /i"-re.
d M'dre suphU1n'. C. R. Aca.d. Sci. Paris. 239, 849---850 (t954.).
6. AppN<tJti<ms oj 0." !heo,)! DJ dired DJ HUb"" spa= fo som' inkgml
and diH rin1 vph'lIIm'S. Inst. Fluid Dyrtamics. Univ. of JI4aryhmd.
c., Park, 1054.
Ga'\I'UJ'iD M. K.
1. Onfttimak-s/or Ihe tlkt1ibtr8 andvn:Wrs oJ aperruTbed operaror.
Dokl.dy Alrnd. N"uk SSSR (N. S.) 76. 769-770 (1051). (Rwtiian) Math.
Rev. 12, 617 (19511.
2. On estimalu lOT rigen-t'Cllw8 and ctors vJ a pet'hltbed opnoJor. Dokla.dy
Akad. Nauk SSSR (N. S.) 06, 1093-1 95 (1954). (Ru"ian) Math. Rev. 16,
2M (1955).
S. On the -.as oj ",<tho,," DJJinding DJ i
operalors. Doklady Aka<!. Nornk SSSR (N. S.) 07.13-15 (1954). (Rm,ian)
Math. Rev. 16, 264 (1955).
Gelbaul1'. B. R.
1. Eapansion..f in BafUlCh spacu. Duke Motl). .t. 1'2". 187-196 (1950).
2. A b JUTHilb"Ispaa.Proc.Amer.1tI.ath.Soc.2.72()'-721(11)51..
Gelfand (GePland), t. !\I.
I. J\lormitrle Ringe. )18t. Sbornik N. S. 11 (5J). 8-24. (1941).
2. A_ Funktw.... un<! Iinffln, . Mat. Sbornik N. S. 4 (46),
285-286 (1038).
B. .lc:kale undprimiJre.ldeGll inrlormiakR Ringen. Mat. Sbormk N. S. I) (51).
41-48 (1041).
4. ZUT T dn ChamIrIen der Abelschen f()pologis;dIen Groppen. ::\ll\t.
SbornLk N. S. 9 (51), 49-50 (1941).
5. Ober abriuf konverg.r1lU he Reihe:n und .lnlfgrale. Mat.
Sbo,nik N. S. 9 (511, 51-<16 (1041).
6. Rnnnrkon 1M-work oJN.K. Ban ' BiDrIhr>gonal sySInns and bases in Hilbm
spau." Moskov. Gas. Univ. Ulenye Zapi'3ki 14.8. Matematika 4. 224--225
(1951). (RUS'ian) Math. Rev. 14, 289 (1053)_
Gelfand. I. M. and Kolmogoroff. A. N.
1. On rings D/ anrtinuous furu:l:iCJ1lS on a tvpr;logiool 3pfl€e. DokIady Akad.
Nauk SSSR (N. S.) 22, 1l 15 (1030).
Gelfand, I. M., and Kostyufenko, A. G
1. E:qKmsims in rigmfvriclW1u oJ diffen:nlial and orher oprraWrs. Doklady
Akad-. Nauk SSSR (N. S.. 103. 349-352 (1955). (Russian) Math. Rev. 17.
8B8 (1036).
Gelfand, I. M., and Levitan. B. M.
I. On th ddnuinalwn of a di/funlial equatWn from its BpecIffll.fvnctWn
bvestiya. Ako.d. N'auk SSSR 15,309-360 (tG51). (Russian) Amer. Math.
Soc. Trluudation, (2) 1, 253--ID4 (I053).
2. On a simpk 'identity fr:rr the t'CtueB oj a diffcrerdial fJpe.ralor
of SIfiJIId vrdu. DokIady Ak&d. NQU\': SSSR (N. S.) 88. 593-596 flDS3).
(RtlSsian) IlIath. Rev. IS. 38 (1054).
Gelfand (GeI"rand). I. :M.. and .Neumark (NaimarkJ. M. A_
I. On Ihe im1JMditl{! of hOr1Md ri'V:8 into the ring iJJ upt¥'tJlDT1I in Hilbert spac .
IlIat. Sbornik N. S. 12 (54), 107-218 (1948).
2. Nonned rings urith inoolution and tfuoir Tepn'smtaliorUl. Izvest.iya Akad.
Nauk SSSR 12 4J.5-480 (11148). (Russian) Math. Rev. 10. 199 (1949).
Gelfand, I. M.. and Raikov. D. A.
I. On tlu: IhwTy oJ cliam<t<Ts oj ev,,".um_ topalO/liool groups. Dvldad). Alrnd.
Nauk SSSR (N. S.) 28, 105-108 (1040).
2. .Inw1MciblL unitary upre.sntlalimu oj lomlly bicompacl gJ"fJUps. Mat. Sbom.ik
N. S. 18 (55), 301--S16 (1043).
Gelfand. I., Bnd ilov. G.
1. Vber VCTscI1iffleae ltlethoden der Ei.nJtihrurtg <kr Topolagu' 'In die J."denge thy
marimalm .ltkale dfles norntit.Ttm. Ringu. Mat. Sbornik N. S. 9 (51)
25--40 (1941). (German, flussian 8UIDIIlBI')T).
GE>1fand. I. M.. and Yag1om, A. M.
I. nkgrnIWn i.. J_mwI 8pat:es and il8 app/ioolWn in guan/UnI physia.
UspdU Mat. Nauk (N.S.) 11, 77 1l4 (1056).
Gillespie, D. C.. and Hurwitz, W. A.
I. On s oJ oontinuvus [unctivm haring aHlJimwus limit.s. Trans. Amer.
Math. Soc. 32, 527 M3 (1080).
GiOt'gi. G.
1. Nuove VSBtT'DllZivni _lk fUm:1011i ddle mnlrici. Atti ..-\£cad a7.. Lincei.
Rend. Cl. Sei. Fis. !\la.t. Kat. (6) B, 3-8 (1928).
758
REFERENCES
REFERENCES
7511
GIauwm, I. M. (",e aloo Ahiezer, K. I.)
I. On rho "'lory oj .;tI{IUl<udi/feovdial_. U.pehiMa.. Nauk (N.S.) 5,
no. 6 (40). 102-185 (1950). (Russian) Math. Rev. IS, 254 "052). Amer.
Math. Soc. Translation no. 96 (1'953).
2. On "" dIf indrz oj di/f......ool oP<Tafon. DokJady Akad. Nauk
BBSR (K. S.) 64. I5t-154 (11149). ) Math. Rev. 10. 53S (1949).
3. On the spednm oj li, digeren1ial opeTalorS_ Doklady Akad. Nauk
SSSR (N. S.) 80, 153-156 (1051). (Russian) Math. Rev. 18, 654 (1052).
4. On the charcu:.t.tr oj Bp«tra oj one mwl singular baundary value
prolllems. DokJady Akad. Nauk SSSR (N. S.) 87, 5-8 (1052). (Russian)
Malh. -Rev. 14. 1088 I1P58).
Glicksberg. I.
I. T/u np,....ltotUm oj jiau:ti<>oolo bs i_gruls. Du!.;. Ia'h. J. 10, 253-261
(IP52).
Code1. K.
1. TIlL ronsi8ttnql vJ lht amtim.wm. . ArID. of Math. Studies, no. 3.
Princetoo Univ. Press. Princeton, 1940.
2, 'Vffl formal ttnnIt£chridbare SiJt%e de,. .Pri1u:ipia falhematica'UndVL'n'IlUl'l(fln
, I. Monat.!Ih. fur Math. u. Physik 38. 173-198 (1931).
Godernent J R. (see .a1sc Canan. H..)
1. Thiori:mes tauUriemr et thior'-h sp«tra/L. Ann. Sci. cole Norm. Sup. (3) 64,
IIP---I88 (1047).
2. Lu flJt1Ctkms lk type posit"! d la tNori£ des groupes. Trans. Amer. Math.
Soc. 63, 1-84 (1948).
3. Sur la thioric des rqwIsmlGtimu unitairfs. Ann. of Math. (2) 53 68---)24
(1051).
4. Mitttoirt' sur la thiorit &s d.tm8 ks groupt'S locarement compads
tmimc.dulaireB. J. Math.. Pure" Appt. SO. 1-1I0 (1951)_
5. SU'r une d'un thiorhne de StOfU. C. R. Acad. SCL. Paris 218.
POl-90S (IP44).
Gohberg, I. C.
I. On limaTrquatioRsin HifbertBpaJ:€. Doklady Akad.NBUk SSSR ( . 8_)76.
9-12 (IP51). (RnWan) Math. Rev. 13, 46 (IP52).
2. On linnlr equatitmR in faO"l'Tf&ed spac . DokJady Akad. Nauk SSSR (N. S.)
76. 477-480 (1'951). (Russio.n) Matb. Rev. lB. 4.6 (IQ52)_
3. On lUu>er ppt1'afoTs tkpeOOi.ng anaJytiMlly an a fJllI'i1'MttT. Doklady Akad.
Nauk SSSR (:'J.B.) 78. I!2\HJ3O! (1051). (Rus.ian) I..h. Rev. 13, 46
(IP52).
4. (h, 1m indtx aJ an ndtd nperatur.l\fat. Sbornik N. S. 33 (75). 19&--'98
(1053). (R",,,iaa) Math. Rev. IS, 293 (IP54).
Gol'dman. M. A. (see a1so K'rOCkovslui. S. N.)
Gol'dman, 1\1. A., and KralIrovt3kii. S. N.
1. On Ihe aJ a linear operator in its Fredlwlm region. Doklady
Akad. Nauk SSSR (N. B.) 86.15-17 (1952). (Ru.sian) Math. Rev. 14.478
(IP53).
Goldstine, H. H.
1. Weakly compld. BunndI .pac... Duke Math. J_ 4, 125 151 (IP38).
2. Till o.rom.. oj Hildd>randl. Studia Math. 7. 157-(;;8 (1088).
Gomes, A. P. (see Dieudonn . J.t
Goodner, D. B.
1. Projections i1l nonned llnear spaces. Trans. Amer. Math. Soc. 69. 89-108
(1050).
Gowurin. M.
1. l)ber die lnllgr'tlti.rm abSlrakteT FtmkfWtlm. Fund. Math. 27,
255--268 (IP36).
Graft, A. A.
I. On th therny oJ sysum& of linear diJlrnztial rqru:dWns in a
dotllLUn I. II.
I. Ma.. SOOrnik N. S. 18 (60), 805--928 (UJ46).
I1 ibid. 21 (63), 148-159 (IB47). (Russian. English swnmary) )'[ath.
Rev. 8. 74 (IM7) and 8, 186 (IP48).
Graves L. M. (see also Bartle. R. G., and Hildebrandt. T. H.t
I, Topica in the /1n1dional Mkulu.. Bun. Amer I\Iath. Soc. 41, 641-662
(IB85). E1't1'I.ta, ibid. 42, BI---382 (IQao).
2. TIu:. theoryolfKndinns oJT al vtJl'iDbIn. McGraw-Hili Company. New York.
1946.
3, :Rift'JW.mJ. inlf'#tdion and Taylr:rr'8l1et'c1rem. in geqnal arKJlysis. Traw. Amer.
Math. Soc. 29, 163-177 (1927).
4, Bomegmeral appro.rimatitm theorems. Ann. of Math. (2) 42. 281-2Q2 i194.1).
5. 80m. mopping thIo1-ems. Duke Math. J. 17, Ul 114 (1950).
8, A gmemI icm CJJ the Rinz. fh my oj CV1JIplt'tdy cQ1I.!inuQus tramfonnati.c1m.
Trans. Amer. Math. Soc. 79. 14]-149 (105$).
7 RernllTlal on singular pai'l1l8 oj [tmmonall'tjllations. Trans. Amer. Math. Soc.
70, 150-157 (IP55).
Gravcs, R. E. (t; Cmnt.'IUIl. R. H.)
Graves, R. L.
1. Tht F-redhvlm thtQTY in Bmwdl. spaa.'l. Dbt6ertatJ.On, Harvanl. Umversity
(UJ511_ Abs.tract. Bull_ ArneI'. Math. Soc. 58. 479 (19521.
Greco. D.
1. Bulla convergenm tWgIi suiluppi in serie di autosoluziani lJS80Cimi ad un
problnna ai limik rdatiro ad un"equaxicme diJf ordinaria dd
s candf} OTdi'l1 . Rend. Ace. Sci. Fis. Mo.t. Napoli (4) 17, J71-189 (1950).
Grinblyum (Grunblum), .M. M.
1. Cntains thlorima sur fa ba$e dans un e8pace du 'ype (B) DokIady Akad.
Nauk SSSR (N. S.) 81, 428--432 (1041).
2. B 18flSllros in &",,,<1. spacc..DoIdarly Akad. Nauk SSSR (N. S.)
47, 75-78 (IP45).
3. SUT la fl<itJrie tUS sysl£rn€s biorIhogmlmtL DokIady Aka.d. 8uk SSSR
(N. B.) 55. 287 290 (1947).
4. On a1""':l""'1!loJ a ba8i8. Doklad}.Akad.NaukSSSR (N.S.)50,P-II (1948).
(Russian) Ma",. Rev. IV. 807 (1949).
5. Spectmlmrnsllrt'. Doklady Akad. auk SSSR ( S.) 81. 315--348 (ID51).
(Russian) Math. Rev. 13, 4.70 (1952).
6. Opnarioool i..tqval in a Btmat-k <po". Doklady Akad. "auk s.<;SR (N.S.)
71, 5--8 (1950). (Ru.siaa) f.th_ R".. II, 601 (IPSO).
Gro5berg .T.. ond in. !ti.
1. Sur la dtirotftposition tks 1000000001WllL en ('flmpoNnnk$ ]1QSiiWes. Doklady
Akad. Nauk SSSR (X. 8.) 25, 723-726 (1939).
760
REFERENCES
REFERENCES
761
Gro8berg Yu. I.
1. On liPWT Jtuu1icma18 on the 3}Jace oJJunrli{m.Qf bouRdWvariaJion. NaukO\/i
Za.pi::;ki Kdvkogo Pedinstutu 2, 17-23 (1939). (Ukrainia.n).
Grothendieck, A.
I. C'riJtTes girli:raw: de dans l npa«s lJIft10Tiels lemr1U .
PaIhoWgie des ntpU("e3 (LF). C. R_ Aead. Sci. Paris 231 (140-941 {19S0t.
2. Crilhn de (:(17npUClti dans les U]KKV"S /ondionnds . Amer. J.
Math. 74, 168-186 (1952)
8. .PTOduits tensorids t.opologi./}llR8 tl espana nvcllLrintJ. f'.lemoirs Amer. Math.
Soc. no. 16. 1955.
4. SUt k. app/imli.... lintaites f- rompt1<lu d'espaas du typ, C(K).
Canadian J. Math. 5, 1'D-17 (1958).
5. Sur cerlaim ettpOClS de JOI'1dii:m8 hdomruphnJ, I. tI.
I. ..J. Reine Angew. I.\lath. 192. 85-64 (19.53).
II. ibid. 19', 77-D5 (1958).
Grunblum. 1\1. It!. (see GrinbJ:yum)
Gurevit. I., A.
I. On uuamditifPWi bases. Uspehi Mat. Nauk (X. S.) 8, 1\0. 5 (57), 153-J56
(1953). (RulSsiarJ.) Math.. ev. 15. 631 (1954).
Saar. A.
1. Der 1!'1cmAx:griHin der Throne deTktmtinuinlil'htn GnIppnt_ AIm. ofl\1at11.
(2) a4. 147-160 (1988).
2. Ober die ltlu1tipliktrliotudalJf'lk d T . Math.
Zeit. 41, 761)-798 (1930).
8. Z"r TIJf:Qrie dtr fll'lh;gDrwlnI Funkhonm I. II.
I. Math. Ann. 6D, 31 71 (IDIO).
II. i id. 71. 88-!i8 (1911).
Hadam.a.rd J.
1. Su-rklloptm1irm.8Joo.ctiOfU1f'lks.C R. Acad. Sci. Paris 1.86, B51-a54 (1003).
Hahn. H.
I. iJbn' die Dar'Bltllung FtmkIirmnl .w."'CIt Bingulare Inkgrale, II.
Denksduiften der K. Akad. Wien. Math..Naturwiss. kl. 93. 657--692
(1916).
2. Dba Folgen linear" Opmv;rtitmt'R. l\lonabl1. fUr Math. nnd Physik 32t
!HI8 (ItI2.).
8. Vber liFWf.lU Cl,.;rll1m .68fIBlm! in linrorm Rii.tnnen. ..T. Reine Angew.
Math. ]57, 214-229 (11}27).
4. Rrelle FtmktUmm.. Almd. Vetlag. t Lftpzig. 1932. Reprinted by Chelsea.
Pub. Coo, New York.
5. Obe, die InkgmW d R-errn Hdlinger «n4 dle lirmarinnterJ dcr
qtUlllmti.sthtn Forme» IJQfl u diidJ t"icb V rlichen. .Monahh. fur
Moth. und Physik 23, 161 22' (IDI2).
Hahn t H., and Rosenthal, A.
1. Set jiJ,hditnl8. Univ. of New MexICO Press, Albuquerque. IIJ.J8.
Halrnos, P. R.
t. NQTT1UlI dilarnms and t:dm3ions oj opnYltct'S. Summa Brasil. Math. 2.
125-t84 (IDSO).
.. A "1JGdU' fhromn. Trans. Amer. Malh. Soc. 66, 284-288
(16.6).
3 CtJJJt.mutalit'iJy tJljd Rpft."l1'aI propn,ies of nVM1lal nperalon. Acta Sci. Math.
SzegW 12 Pa.. B, 153-156 (ID50).
4 ......,lmsurable tmn.form.afimu. BuH. Amer. Math. Soc. 55. 1015-1034. (1949J.
.5 ....yeasuft Theory. D. Van Nostrand, New York. 1950.
f5. .lntTOdudiOfi 10 HilbeTt space and the tlu!my oj sptrlml "'NUiplicity. CheJs.ea,
ew York, UJ51.
7. Finit£ dimt'A8icmal vtclor spaus. Ann. of Math. Stud. No.7. Prmcduo
L'niv. Press, Princeton, 1942.
B. An t:rgvdic theorem. Proc. Nat. Acad. ScL U.S.A. 32: 156-161 (1046).
9. Sp«tnl cmd .sp«ITul manifolds. Ann. Soc. Po'on. I\latb. 25. 43-49 (1952).
10. ColfIJ1H&tutoI'3 oj optTtJIon, I. II
1. Arner. J. Math. 74, 237-240 (IDS2).
II. ibid. 76, IDI-198 (ID54).
Halmos. P. R., and Lunter.. G.
1. Square roots oj opemltJ1'B. II. PrlJoC. Arne('". :!tia.th. Soc. 5. 589-595 (11154).
Halmos, P. R.? Lumer. G., "nd &hii.fffi", .T. J.
I. Sqtulre roo!B vj opemwrtJ. Ptoc. Amer. Math.. Soc. 4. 142-140 (1953).
1-Ia.Imos;. P. R," Qnd van r.;'eumann. J.
1. Operator mdhodB in classical medJonicf1 II. Ann. of Math. (2) 43. 882---.350
(19'2).
Halperin, I. (see also Ellis, H. "".)
1. Ftmrtitm 8pa£es. Canadian .J. .l\-lath. 5, 273--288 (UI5S)_
2. COllft'Z sel.s in liRWr lopolvgiml s. Trans. Roy. Soc. Canada Sec. III
47, I (1953).
3. UtdfOTm oonue.r1ly infvnt:tWn spaces. Duke Math. J. :21, 195-2040 (IY54).
4. Rej'la.icity in 1M V. Jv.ndirm space:;. Duke IUatk ..J. 21. 205-208 (IY54.).
5. Closures and Gdjoinb of tin«u diffUf'fitinl opnators. Ann. of Math. (2) 38.
880-012 (1937).
Hamburger, H. L.
I. Fiw notts on a grn,erolizaJwn GJ qU4S1.rp.(pvleRl t:nm.sfortl'u:ltiom in Hilbert
SPM(:. Proc. London .Math. Soc. (3) I. 494---512 (1951).
2. On a fleW ,.ha oj selj-aLfjoint di/Jeren,itJI opcraJ.ors in Ole Hilbert
space La. Proc. Symposium on Spectral. Theory and Ditfnen.tial Problems.
22P-247 (1951 J. Oklahoma A.. .and M. CoUege. Stillwht.er. Oklahoma.
3 RemCITkR (In 6 lJ-mljoift1 diffnDflinl operalt»'B. Proo. London !\Ia.th. Soc. (3
3, ....6-463 (1653).
4. Dber die Zalegung des Hi n. Raumu cfg1"di uo&trlige IirtM1 Trans-
lormaticmt'n. Math. :N'achr. 4., 56-69 (1951).
5. Ccmtribulim18 la the thr.ory oj c£osed HnrlUlian tmnsJornwtiOllS oj dtficiency
i._ (m, mI. Ann. 01 Math. (2) 45, 5D-69 (1944).
b. COdtributions 10 ,h.e theory oj closed HmnitiaA hYm.'lJorwwtiU'1U oJ dl[i£iency.
index (m, m). Quart. J. .:\tath. Oxford Ser. IS.. 117-128 (1t)42..
'i. IltrmiJian transJurotllliO'M oj dPjkient:y-indn' (II I). .1w:ob1 maIri«.. and
nde!omined moment problem3. Amer. J. Math. 66, 489-522 (1944).
is. On a claJS oj Hnmuian frangj'Cf1'7JI(lJion.s cQnlt1ining sdJ-adjoint diJferenlial
. Ann. 01 l\Ioth. (') 47. OO7-<!67 (1946).
Hamburg€r, H. L., tLt\d Grimshaw. M. E.
1. Linror 'ranaJom.aticms in fi-diJRmsiOltal tmtn' Bpact:. Cambrid Cniv.
1951.
762
REFERENCES
REFEJtENCES
763
Hamel, G.
1. Coo linrore DifJeTttJfiolgleidungen zweitu Ordnung mil pniodisthen
Korffrdentm. Iath. Ann. 75, 371-412 (1918).
Hanson, E. H.
1. A "ok on compadPael's. BuU. Arner. Math. Soe. 89, 897-4.00 (1933).
Harazov, D_ F.
I. On a cla.ts oJ linAlJ'" ffJUl.Ilicms in Hitberl spCUl:s. SooMCeniya. Akad. Nauk
Gruzin. SSR 18, 65-72 (1952). (Russian) Math. Rev.. 14. 900 (195S).
2. On a elass oJ liRroT eqtUItirms wi!h symrndriz.iJble operalcr8. Doklady Akad.
Nauk SSSR (N. S., 91, ]023-1026 (1958). (Russian) Math. Rev. 15,
881 (1954).
3. On the theory oj BJIfflmrlri:nb/£ 01''''.10'' wilh poI Up'" a
puramder. Doklady Abc!. Nauk SSSR (N. S.) 91, 1285--]287 (1958).
(Russian) Math. Rev. 15. 881 (1954).
Hardy. G. H.., and Littlewood. J.
1. Some p1'fJ'JJerlies oj fMl:Iio1aal intq?rOls. I, II.
I. Math. Zeit. 27. 565--606 (1028).
II. ibid. 84, 408--439 (1932).
Hardy, G. H.. Littlewood :I. E., and Polya.. G.
1. .lncgualitin. Cambridge Uuiv. Press, 1984.
Hartman, P.
I. On lhe l'I'gOdic , . Amer. J. l\lath. 69, 193-199 (1947).
2. On the naenool sputra of symmelrit operators in Hilbert 8pacr. Amer.
.... fath. 75, 229-24<1 (]053).
S. Tht LI.-svIutiO'lU (1) tint:ar diJferenlial equrrticmR oj second mder. Duke Math.
.... 14, 823-326 (19<7).
4. UMmrid.u1. solutirm fields oJ almost 8eparable. diffl!rt'nlilll . Tram.
Amer. MatlJ.. Soc. ti3, 560-580 (1948).
5. On diJ/mmtitJl f:'fJIUI1iORS with ncm-rJSCillalory dgenftJ.1Jdimi,.,. Duke Math.
.... 15, 697 709 (1948).
6_ On the Ii""", /oglriIkm rliJJemuibl "J'WI-ion oj Ih, II<roJId
order. Amer. .J. Pr!ath. 70, 7M-779 (1'Q4S).
7. On thf 8p«t1'd of slighJly disrurbtd linmr oscillatcm;. Amer. J. Math.. 71,
7I 79 (1040).
8. A oJtht sptdru oj th one-dil'lUlUionalw vquaIinn. Amer.
..1. Math. 71 915-920 (1949).
9_ TII< """"'" oj L,--aoIutimu oj "," +q(t),< - O. Amer. .... Math_7B. 635-<345
(1051).
10. On bounded Green's Mr'mls fen' second «riler linMT differt'l1tial. .
Amer. .I. Math. 73, 646--656 (1951).
II. On th, ri/1<m>alues oj difJem>Iial .Amer.....Matb. 73,657 62(I051).
12. Oq limaT sccond order difJerenlial f'tJ1U1li0tV with small . Amer.
J. Math. 78, 955-962 (1951).
IS. Some eaumpln in Ik therny oj Bingular lH>undary valut problems. Amer. J.
fath. '1'4, ]07-]26 (1952).
14. On nan-oscillaWry linear diJlt:renIiol oj I«:t1IUl OT . Amtr.
J. Math. 74, 380-400 (1952)_
15. On the tlerioolires oJ SDlutitm.t oj linear IW'OJ'1d order diJJertRlial equations.
Amer. .). 1\Ittth. 75, 173-177 1'958).
16. Onthe....ntial6pft'U'<1 oJOJ'dintuy diJI.......oot l'fJU'lli<nu. Am.-r. J. Math. 76,
831-888 (1954).
Hartman. Po, and Putnam. C.
J.. The hast clwteT poim Df rht aptCITvm oJ boundary rahu probkms. Amer.
J. Math. 70, 847-855 (1948).
2. Tlu gaps in the usenlial spedm of wave «JIUllitms. Amer. J. Math. 72,
849-862 (1050).
Hartm n. p _0 and Wintner A.
1. Tht (L2)-8pQce oJ rdaftve metlStlr'f'. Proc. Nat. Acad.Sci. U.S.A.S3.128-182
(1947'.
2. An oscillDticna theurem /M oontint.rovs . Proc. Xat. Acad. Sci. U.S.A.
33, 376---379 (1947).
8. The osymptotit aTCIUl oo"o.tll.m of solutioftB oJ real litu:aT diUeTeNtial t'QUlI-fiont
oj IItC01id emler. Amer. J. Math. 70. 1-10 (1948).
4. Crikria Jor the rwn-c:k£e1ln«y of lhf! wave equaUon. Amer. .L Mrath. 70.
295-308 (]IJ48).
5. On the err1mllItiuno/unikrkralsp«lTa. Amer..J. Math. 70. 309--816 (1948).
6. On ntm [Ie linffn" mclltalnn vJ Ww /r€qtUncy. Amer. J. Math. 70.
529-539 (1948).
7. A hitnion Jvr the rwn vJ fhe wave npmJiOJ'l. Amer. J. :Math. 71,
206 215 (]949).
S, On the location oj spn'h'a oJ'tlJtlm Amer..J.:Math. 71, 214---217 (1949).
9. On II>< Lt:Iplaa>-Fouri.-r . Amer,.T. Iath. 71, 367-372 (]940).
10, Oscillalmy and Uatory I;nnu diffwmtiul eguntilJrut. Amer. J. .Math.
71, 627--<1408 (1949).
11. A ft'Plll'OIicm theoremJM .continllOK$ speetra. Amer..J. Math. 71. 650-662
(1949).
12. On the dnimativu of 1M soItaions oj the ont-di al tcatte cqlUllion.
Amer. .J. Math. 72. 148-155 (1950).
18. On the nt;al spectra oj .rin(!ular ri probleml. Amer. .I. Math. 72.
545--552 (1050).
14. On an ost'illatimt crilmon oj LiapOImoff. Amer.J.l\lath. 78, 885-890 (1951).
15. On perl:urbati.tm8- vI the CQntil1uQUS oj flu! hannuuu: osciUalQnL
Amer. J. Matb. 74, ?Q-B5 (1952).
16. An Uwqtwiily for the amplitudes and GTCUS in Rbmtion dw.grams oj ti1m-
dqmu1enl Jr"lu<ncy. Quart. Appl. Iath. 10. 175-176 (1952)_
17. On non-&dllatory liflorr difJ 1Itial6JllutiC/fl.S. Amer. . Math. 75, 717-730
(1053).
18. On curves defined by binary non-amstmm'ir>e differential systems. _4.mer.
J. Math. 76. 497--501 (1954).
10. On lhe tJ8Bigamem vJ l1.8JP1lpl<Jtic values JOT the sdution oj liltMT diffn't!OOal
tquatiooB oj 8€cond emler. Amer. .I. Math. 77. 475-488 (1955).
20. On limar secrmd tmler diHema1ialt.tJl.lDlinns in 'he unit circle. Trans. .Amer.
Math. Soc. '1'8, 492-500 (lOSS).
21. On non-tJfilCillakny lWar diUerrntial ft}I.l(ltions tt'irh 1f'I01I0t0ne' roefJicim4
Amer. .Y_ Math.. 76. 207-210 (1954).
Bartman, S.
1. Quelg1u1J propn'it£s ergotfiqu-es des /radinns crmti ut$. Studia :\[ath. 12,
27I 278 (]9M).
764
REFEltENCES
REFERENCES
765
Bartman, S., M E., and Ryll-Kardzcw . C.
1. Thiorhntsergodiqve3d leuTSappliadionN. C()lIoq. :Math. 2, 109-123 (19.51).
Hartogs, F'J and Rosenthal. A.
I. Vb" F./gm anaIyW;t:hn Fu1Iktiomn. Iatb. Ann. 104, 6OIHIIO (1051).
Hatfie1d C. (see CameroD., R. H.)
Haupt. O.
1. ()ber lirutl7'e lKrmognu: Difftrenrio.lgrrichungen %'Weiler Qrdnu"I: mil ptriodi-
schtn K . .Math. Ann. 79. 278-285 (loQI8}.
Hausdorll. F.
I. GnIJwzige der lilmgroltllrf!. Verlag von Veit. Lcipzig. 1914. Reprinted by
Chelsea Pub_ Co., New Yl{Jrk.
2. r,,1 ngrnlehve CDriue Auf1age). \V. de Gru)"1.er, Berlin and Lcipzig. 1935.
Reprinted by Dover Publications, New 'York.
3. Zur Thwr der liR«lTftI. 'JRdriB('hm Rdumt. .1. Reine Angew. Math. 167,
294--311 (1932).
Heim .. £O.
1_ Beilrdge%urSt duSpelrt . 'Math. Ann. 123.415-4.38
(1051).
2. Ein v_ Nrumarrn8€ht:r Satz iWtr be&c'hrnnkle OptrataTm im Hilbrrl8Chm
Raurn. Nachr. Akad. \ViS8. GottingrI.'m. Math..Pbys. KL 1952. 5-6
(1052).
8. ZUT Thtviie drT H en rh:s Rilkrtschrn RmuIIt'8. aehr.
Akad. Wiss. Gottingen.. l\Jath..Phys. KI. 1951. no. 2. 4 pp. (It(51).
4. On an int'1fJUlllity for linear opaafunr in a llilbert Npacf Report on Operator
Theory and Group R tations. Pub. no. 387 Nat. Aca.d. Sci. U.S.A..
pp. 27-29 (1955).
.5. ZUT Fragt der DiJjnmz:intJarfreit der S-FunlrtiQn. Math. Ann. 122. 832-833.
(1050).
Hellinger. E.
1. Neue B nd.ug der Tlwrrie 'lfJildrotisclter Fwmm VQn unmdl.ichvidt:n
V('tij dnli£M:n. .J Reine Angew. Math. 1':36, 210--271 (t909).
Hellin.ger. E.. and TiJeplitz. O.
I. Grundlagrn far nnt' Themie dtr umndlidlen lUatrizeR. Math. Ann. 69.
289--830 (1010).
2. Gtundlagm fur rifle Theori der endlichen Mu.b'Y.zn,. aehr. Akad. " iss.
Gbttin l.l.. Math.-Phys_ I{t. 1006, 8.51-355 (1906).
3. .l1ikgrulgleicll-.ngm und GleiMungm mil unen.dlidmif.'1rn [rnbe .
ncyklopBdie der Matheme.tisclLen \nssenschaften 11 C18. 1.835-]0]6
(1928). Reprinted by Chelsea. Pub. C().. New York.
Helly, E.
1. Vber Famlr:tintIolopt!mIitmeti. S.-H. K. Akad. '\.Vis!i1. '''ien .Math.-
Naturwi<:ss. KL 121. IIa. 265--2m' (1912).
2. Vber Sysft1M linm:n:r Gleicliungrn mil uJ'U"l'ltllidl viden Unbtkannlen.
l\Ionatsh. fUT Math. u. Phys. 3). f)I}-U1 (1921).
Heh()n. 1:1.
]. SpHtrnl synthesis oj oounded !1lf1nirms. Ark. for l\lat. 1. 497--502 (1951).
Helson. H.. and Quigley. F. D.
1. .r.-lo:rimal l11,grbrQ.$ vJ ronlinuotts ftuu:tions. Proc. Arner. "lath. Soc.. 8.
UI-1I4 (1957).
2. Ea:iMcR« oj marimtll idMIS in ul oj mntinuoU8 fu.ndlrnu. )'roc.
Amer. Ia.th.. Soc.. 8. 115-119 (1957).
Hen. ]. K
I. t bcr Potm::nilw:n.tJon.iUatrben. . ReineAngew.Math.155.1()7-110 (1926).
Herglotz, G.
1. ()ber Poten:zrrihen mit posilivC'm, rrdlem Teil im Ei7ihdWaris. S.-B. Sachs.
Akad. \Viss. 63, 501-511 (1911).
2. Vbel' die Integmtion linearer. ller DiJlermtialglrii:1l.ungrn mil ktm.
8tanten K X-IV.
[ S.-B. sachs. Ak.d. Wi". 78. 3-126 (1026).
n. ibid. 78, 287 I8 (1926).
III. ibid. 80, 69 Il4 (1028).
IV. Abh.. !\'lath. Sem. Univ. Hamburg (). 189-Un 1'IJ2S).
Hewitt, E. (see also Yosida. K.)
1. Linear frmdionals on spaces oJ contiJlUlJU3 . Fund. Math. 87.
161 189 (1950).
2. Integral tFprrSf7l.tlJfi()l1 oJ certain li'iiear flmdioJu:Jb. Ark. fol' Mat. 2. 269---282
(1952).
S. .1nkgratitm on locally amr.pad spaces, I. Univ. of \V88hington Pub. in
Math. 3. 71-75 (1052).
4. Ca,lIin generalizations £If the Weierstrass apprarimation 1N:urem. Duke
.1IatlJ. J. 14, 419-427 (IQ47).
5. Rmgs oJ f'eakJaltwd amti1UWU3 jundiO'lUJ. I. Trans. Amer. Math. Soc. 64,
45-99 (10481_
6. LinMr JIAn£tWnuls rm nlmVld pmiodicflfRdi(.l"Q. Trans. Amer. Math. Soc. 74.
3OIHJ22 (1053).
7. -4 probum con«min,g finitely oddili:Df rmas'Ures. Mat. Tidsskr. B ItJ51.
81-94 (1951).
Heywood, P.
1 On the UlIYfflptnli£ diBlrlbulion (JJ dgn.MhIa. Proc. London Math. Soc. {3) 4,
456-470 (1954).
Hilb, E.
1. l1b r dk Aa/l&tf tJon GkichvRgen mil vnencllich nf.'lffl. VNb€kanntm.
S.-B. I'hy,..Med. Soz. , 84--89 (1908).
2. Obtr 11l'eprnl miUlrarlicher Funktimtn&. !t1ath. Ann. 66. 1---66
(1909).
B. i ber Rdh Mnrrdd.Ylu.ng tulrh thn EigenjunlrfiOVlrrf linmrer DiJJnrntial-
g/f'idungn 2ter OTdnung. Math. Ann. 71, 76-87 (1911).
4, Oller grr.OOh",icht- DiJ!ermIialglNhu gm mit Singultm.'Idlm. und die
dBzugf.'hiiri;gen EIlhDidrdw.ngeq u'illkiirlid.fT FunJrtiOf1€n. :\fath. Ann. 7ti.
833--339 (1915).
Bilb. E., and Szasz. O.
1. Altg€m€'im Rrilimmtmidrlunwn. I£l1cyklop&die dcr )Iath. 'Vis!';. lie]],
1229-1276 (1922).
Hilbert, D. (see also Courant, R.)
L Gnmd:i:iigf: eifler allgemdnm ThtQrie der lint'tm':n InlegralglridlHng:II, I-VI.
1- NachT. Akad. \Vis!!. Gottingrn. Math.-Ph}'s. ({I.. 49-91 (1904).
II. ibjd., 218-259 (lg05).
III. ibid., 807-338 (UK15)
766
]tEFERENCES
REFERE:NCES
767
IV. ibid., 157 227 (1906).
V. ibid., 439-480 (19061.
VI. ibid.. 355--417 (1010).
(Published in book form by Teubner. Lei(Jzig. ]912. Reprinted b)
Chelsea Pub. Co, p New York, )tl52}.
Hildebrandt. T. H.
J. On utl.COtUfiti.otl in t1ormu11JectoT spaces. Bull. Amer. fath.
Soc. 46, 959-962 (1940).
2. On uniform limitcdmss oJ sets oj ftmdif./I'WJl opnalUn18. Bull. Amcr'. Matlt.
80c. 29. 309--315 (1023).
3. On lJQuncUdfunttio-nal ope1'tJIimas. Trans.Amer.Math.Soc.86,868-87S (1934).
4. I7IIqJraIion in aII8trad spac",. BulL Amer. Math. Soc. 59, 111-139 (1955).
5. Lebe iRtegratV.m in general R7WJly8is. (Abstraet)_ Bull. Amer. Math.
Soc. 33, 646 (1027).
6. t)/Jer V<IilBI<fi,ge Uru>are 'hmasfornlLllionni. Acta Math. 51, 3II 3I8 (1928).
7. Linear opero.tions on fundwms oj bounded r:aricticm.. null. Arner. Math.
Soc. 44, 75 (I03S).
8 On th lJUJfJIU!J2t problem faT a.J'iniU inIn'ool. Bull. Amer. Math. Soc. B8.
200-270 (1952).
9. Convergtnce oj SC'qI«7'iCeB oJ lineaT oprratioRs. Bu1L Amer. 1\Iath. Soc. 28,
5&--58 (1022).
lIildebrandt, T. H.. and Graves.. L. M.
:L .lmplidl.fwu:tions and their differentials in gentral mtalyris. Trans. Amer.
Math. Soc. 29. I27 I53 (1927).
HHdeb-randt. 'J:'. H.. and Schoenberg. t. .Y.
I. On linear fundint1a1 and lh. mcnunl problem/err ajinik iulerval
in one f)1' lIf!l1f"ml di1'Re1lSimu. Ann. of Math. (2) 84. 1317-828 (IP33}.
Hilding. S.
1. On mm oj Paley-WilJTU!T type. Ann. oOf l\tath. (2) 49.
95&--954 (1948).
2. On the closure oj dUturted C1f"thonormal sets in Hilbert spcu:e. Ark. Ma.t. Astr.
Fys. 32B, no. 7 (1046), 8 pp.
Hille, E.
1. Ftmdional anal:yi.is and Bmii-groups. Amer. Math. Soc. Colloq. Pub. vol.
31, New York (1948).
2. Notes on li1Ka7' trrlnk . fL AftL1lytiri.fy uJ umi-gmups. Ann. of
Math. (2) 40, 1---47 (19SU).
8. On Ole oJ semi-groups and tht thtQry oj conj'4galt lunctibns. PrQc.
Roy. Physiog. Soc. Lwul 21, 1-13 (1951).
.... N()n--f}Scillnlion tneQrem,s. Trans. Arner. I\:lath. Soc. (W.. 234-252 (lfi48).
5. Th< "b.ttroct Caudly problLm "nd Cauchy's prOOlnn for pmt1btJIU: diffmnlilll
<q!UJtitnlS. .I. d'Analys' Math. 8, 81-196 (1953).
HilJc E.. and Tamarkin. J. D.
I. On 1M. rharaderiBlic values oj liRnn- integral t'qUlliions. Acta ).lath. 51.
1 76 (1951).
2. On the theory DJ linmr inkgrol equations, II. Ann. of Math. (2.35.445-455
(193')
Hir8c.>hman. I. I.. and \Vidder. D. V. (see also Widder and Hirschman..
1. The ammlution Ira7lsform P'rineetoD Univ. Press, Princeton. 1055.
Hobson. E. tV.
I. TM theary uf /Wld1ons oj q real 0tJ1'iaWe. (Two volumes) Second edition,
Cambridge Univ. Press, 11321. UJ26.
2. On (l gem1'fll Ih€orem. cnd lhe thewy oj Ore vI a
fWl<liml by a serks oj ........41 furu:twru. P1-oc. Lonoon Math. Soc. (21 6.
849-395 (1006).
Bolder, E.
1. Vlw:r dU J?ulfacMeikn gesIdrter Eig,mwertL Math. Ann. 118. 82G-62S
(1936).
2. Vbcr eimn Mittdwert.st:rl2. .saehr. Akad. Wiss. GOttingen. Math.-Phys.
KI. 1889, 38--47 (18S9).
Holmgren. E.
1. Vber Sy8In1Ie votI li'lltal'"eA parfiellm DiUnm Olvera.
Kongl. Vetens.-Akad. Fork. 58, 91-103 (1901).
Hopf.
1. .Ergodtnthevri.e. Ergebnisse del I\lath. V 2. ". Springet. Berlin. 11337.
Reprinted by Chelsea Pub. Co., New York, 1948.
2. The gtTfnTIl fmlpomlly discrrtt> Markov PTOCe.ss. .I. Rational Mech. and
Anal. 3. 18--45 (ID5').
3. Vber citlt U tIer 1!Jrgotlm . S.-B. !tlath.- at. KI. Bayet'.
Akad. 'Yiss.. 171-1'76 (194.40).
Horn. A.
1. On th si...lar valv.t8 oj a product J completely OO1ilinuous opera1m8. Proc.
Nat. Acad. Sci. U.S.A. 86, 374--875 (1950).
Hotta, J.
1. A fmIIaTk on regularly wmY:l' fiets. K dai Math. Sem.Rep. 1951,37--40 (1951..
lluknharn, I.
1. Sur l' des poiuts inooritrtl.g d'une tmnsfurmntion dll1lS t'upt:ree
/mactiannd. Jap. J. Math. 20. 1-4 (1950).
Hull, T. E. (see Infeld, L.)
HultMn. L.
L On the Shur1t.-LimmiDe Probkm 00t1f1f!CU(f wir.h a rontinUDU8 spntrImt. Ark
l\Iat. Astr. Fys. S$A. no. 25 (1949). 25 pp.
Hurewicz. W.
I. Ergodic withord irmnrinnf mft16I.I7'e'. Ann. of Math. ('2) 45. 192-206
(1944).
Hurewicz. W.. and Wallman, H.
I. on v,eory. Princeton Univ. Press. Princeton, 1 4L
Hurwitz. \\-T. A. (6ee Gillespie, D. C..
Hyers, D. H.
L .f'snrdo.normed linear fiptlUS and abt/i.cm groups. Duke 1\lath. .J. 5, 628--634-
(1939).
. Locally lKmnded litJ,m,. IQPfJlogirol spaces. -iHt.o. Ci., Lima 41. 555-574
(1939).
3. LUwar IopoWgiool $paces. Bull. Amer. :Math. Soc. 51. 1-21 (11145).
4. A note on li'licar al spacef>. Bull. Arner. J\Jath. Soc. 44 , 76-80 «1938).
Inaba. M.
I. A ,h,eQ'f'tm on fixed points and its application to the throry oj diJJtTt':ntial
equa'ifl11li. Kumamoto J. Sci. Ser. A. I. no. 1. 13-16 (1952).
768
REJ."ERESCES
REFERENCES
769
Infeld, L.
1. On a new f:TwInu;11l oj !lome rigewoorue. problems. Phys. Rev. (2) 59. 731-747
(1941).
Infeld L.t pnd Hull, T. E.
1. The factDrization 7Mlhod. Rev. :Mod. Phys. 23. 21-68. (1951)
Inglrtoo, A. \\'.
1. Tile llflhn.Barro h tntorlJ'lll Jor non-Ar£himtdcan f,'almd fitlib. Proc.
Cambridge Philos. Soc. 48 41-45 (1952).
lonc:5cu Tulcea. C. T., and l\larmescu. G.
I. Therrrie pour deB clas8t$ d'opiratil)flS non com r aJfU'inues.
Ann. of Math. (2) 52. 140--147 (1950).
Iwata. G.
I. Non-hermitian operator and eigma/uncf;im f'apunsivns. Progre8 Theoret
Phys. 6. 21&-226 (ID5I)
Iyer, V. G.
1. On lhi! space oj inkgmJ fundi()l1B. I-III.
I. .I. Indian Math. Soc. (2) 12, 13-50 (1948).
II. Quart..J. Math. (()J<fmd) (2) I. 86--96 (1950).
III. Proc. Amer. Math. Soc. B. 874---883 (1952).
Izumi S.
I. On the bili"",," fundiOl1L1lo. Tbhoku Math. J. 42, 195-209 (1986).
2. On 1m cmn -BIi vJ a dm9 oj juJu'ticnw. Ptoc. Imp. Acad. Tokyo 15.
nI n8 (1989).
3. Lcbt6gue inh'gml in ,he abstrtUI rpat:e. J"ap. J. ltltlf11. IS, 501-513 (1986).
4. NGUS on Banach space, I. DijJotnliatifJt'i vJ t1bstmd j'tmc:titm3. J>roc. Imp.
Acad. Tokyo 18, 127-180 (1942).
Izumi, S , :and Sunouchi, G.
1. Nares on Banach space (VI): Ab$tract ffi and linear opemfiom. Prot':.
Imp. Acad. Tokyo 19 ]69--178 (1948).
.Jackson, D.
1. Algr.brat£ proputie3 oJ stlJ-l2djoinl $Ys!ems. Trans. Amer. l\[ntb... Soc. 17.
418--424 (1916).
..JacObson, N.
I. LectuTfH in ab8lrad afWlnt1. J. Bane Coru'f'P'IS.
11. Limar a1;gebrm-. D. van ostr nd, New Ycrk. IDS). 1958.
James, R. C.
1. Orfhogonnlily in normed li-mar 8paces_ Duke .Math...J. ]2, 291-302 (1'945).
2_ 0rt.hctgvtWli1y and linear juncti.orwls in nunned liIImr Sp6UJI. Tl'8ns. Amer.
Math. Soc. 61. 265-292 (1947).
:so Inner produds in normed Iimar spaus. Bull. .A.meT. Math. Soc. 58, 559--566
(1947).
40 B(lJl(s and uJILriuity oj Banach BpCWfS. Ann. of Math. (2) 52, 518-527
(1950).
5. A non-Te/kriot Banach spou iamnetri tvirh its Sf'l'ORd ronjugalr space.
Proc. Nat. Acad. Sd. U.S.A. 87, 174-177 (1051).
Jami!ion, S. L.
1. p oJ normal operokJn. Proc_ Arner. Math.. Soc. 5, 103-110
(1954).
2. On ana normal operat07s. Proc. Amer. Math. Soc. 5, 288-290 (1954).
Jerigon. M.
1. C1wmcttnzatwns oj cerrain spaces oJ l'<lntim.c.ou$ ftmc.t.irms. Trans. Amer.
Ma.th.. Soc. 70, 103-118 (1951).
2. A pmpntg OJ t..Xlr'nne poinbl oj C011t.pad ront'U! Bets. Proc. Amer. .Mat.h. Soc_
5, 782-783 (I954).
.Josscn, B.
1. Th thLory of in OR in a space oj an itl/ini t1um.btT oj dtmeruicmtJ.
Aota Math. 63, 249-323 (10M).
2. Bidrog til megmlte.vrim lQr FunJrtivlJLT aJ fl'llendlig ma e Vmiable.
, 1930.
Joltn, F.
I. The fun4am<7olal smmon oj linror elliptic dilTerrnMl <YJU<dWm with analytic
ooejJidnIbJ. ComlTl. Pitre Appl. Math. 8. 273--804 fUJ50).
2. Grncral s vJ oj linear elliptic pmtial diDerrntial "'JUOIions.
PrOO. Symposium Spectral TheQry and Differential Problems. 113-175.
Oklahoma A.gricu1tunl and :\lechanical College, Stillwa.ter, Oklahoma.
1051.
Jordan. G.
1. Sur I.a abi£ de FG'UrUr. C. R_ Acad. Sel. Pari 92, 228-230 (1881 \-
Jorda.n. P., and von Newnann. J.
]. On inner proc1u.t;* it) lillf'UJ', m.t.tri£ Rpl.IaS_ Ann. of Math. (2) 86. 719-728
(1935).
.Jost, R. (see also Nev.'ton, R. G. J
1. Bernerkungen ZUT mathmlanlf'.1jt!Jt T ckr Zl1hler. lIffvet:ica Ph ,
Acta 20. 178---182 (1947).
Jost. B., and Kohn, w_
I. Cma.sb'ltCtioa oj a potentialfrom aphaBeshiJt. Phys. Rev. 87, 077---992 (1952).
.Jost, R.. and Pa.is, A.
1. On 1M: 8Caltn"i 01 a parhde by a 8latu- potmlial. Phys. Rev. 82, 840-851
(1951).
JuHa., G.
]. SUT us racims carrh1r IUTmiti,...na d'un op/:ratt;vr hennitim pGBiti[ donnf.
C, It. Aco.d. Sei. Paris 222. '701-709 (1946).
2. sur Its mcina cQrTlea hermUiennes d'un ophalnn- hctntitim
poritiJ bomi_ C. R, Acado 8<:i. Paris 222, 82G-882 (1946)_
S. Su.r la s efts rnrints herm.ititnneR d'un optrateur
hmnilu.n pmdlif dim"'. C. R. Acad. Sci. Faris 222, )()19--1022 (UI46).
4, Sur la -racines tarriu selj-6djoit1t d'un optmtnJ.r self-adjoint posiriJ non
borni. C. R. Acad. SCI. Paris 222, 1061-1068 (UJ46).
5, Sur Us racines ",if",'!'> htTmilientl.ta d'un oplra1t>ur hermitien donnl. C. I{.
Acad.. Sci. PQris '222. 1465-1468 (]946).
6. DilnminatWn de bdts lu f'OCint:8 carrks d'un 6p ruhTJ.T hrnnitien bornt
qudc&nq'1U, I, II.
I. C. R. Acad. Sc;. Pari. 227, 792-794 (1948).
U. ibid. 227, 931---933 (1948).
7. .Ifilmdut:IWn malhimLJtilJfU aux thloriu gtMmliqrus. Paris, 1938.
){ac. 1\1. (see aha ErdOs. Po)
1. On oj terrain lJ'iliffieT jM'ACtionGls. Trans. Amer. )Iath_ Soc. 65.
I-IS (1949).
770
REFERENCES
REFERENCES
771
2. On 1M avera.gr oJ a cerlain Wienn- /Undicmal and (I relatnf limit thwrem in
tht eclcultt.9 01 probability. Trans. Amer. M.at1\. Soc. 59, 401-414 (1046).
3. On some COflneclWns between probability thef1l'1J and diflerenfW.1 and inIr.gral
rquatWns. Proc. Second Berkeley Symposiwn :Math. Statirtics and Prob.,
189-215 (1951).
KaC%m9.I"7., S., and Steinhaus, H.
1. Theur1.e de Orthf.Jgoa.ahdhm. .Mouvgra.fje ,Matematyczne, vol. 6, ,"Yarsaw.
1935. Reprinted by Chelsea Pub. Co... New York, J951.
Kadison, R. V.
1. A represrntatwn thwry 1M' annmUlafWt pologu:al al,gebTa. 'Memoirs Amer.
Math. Soc. no. 7, 1951.
2. .J af operalO1' (l1grbms. Ann. of Math. (2) 54.. 325-838 (1951).
Kakutani, S. (see 8180 Anza.i. H., Bohnenblu8t, H. F.. and Yosida. K.)
1. Ein Bewei.r des Satze$ vcm ft-l. Eit'k11leU iiber konvexe A-lengm. Proc. Imp.
Acad. Tokyo 18. 93-94 (1987).
,. W Qk lnpal(Jgyand uj Bnnurbspaces. Proc. Imp. Aead. Tokyo 15.
169-178 (1989).
8. Weak topology. bkompad Beland IMprincipk oj duality. Proc. Imp. Aca.d.
Tokyo 16, 63-67 (1940).
4, Two Jioud-poiRt IIwnrr:rns oonaminc hirxmlpad rnnDr.lJ ts. Proc. Imp. Acad.
Tokyo 14, 242---245 (1958).
5. T(}}XJlqfiool prvperfi.n oj the unit sphere oJ a Hilber spau. Proc. Imp.
Acad. Tokyo 19, 269-271 (1948).
6. Srmu: vJ Eutlidt:an 4pacu. .Jap. . Math. 10,.08-97 (11139).
7. Mmn ergodic thrortm,s in abstrad. (L}-qJaas. Proc.lmp. Acad. Tokyo 15,
121-128 (1959).
8. CImcr:tk TqJreBmtati(1l'J 01 ab$tr t (L and the mean ETgfldic IheOTem.
Ann. or lII.th. (2) 42, 523---587 (1901).
9. ..,.,._fation oj abotmd (JI-l)--spa<:fS. (A cllmnaeri.zalWn oj 1M
spa<:' oj conful...... lunctirms.) Ann. ollllath. (2) 42. 994--1024 (19401).
JO. Ergodic thl!DfY. Proc. Internati.onal Co Math_, Cambridge, l\lass. 2,
128 142 (1950).
n. A prooJ oj Scha1J.>kT's t"""""" J. Math. Soc. Japan 8, 228--281 (1951).
12. VbeTdi< 1'1cfriaatWn<kT Grupprn. Proc. Imp. A.ad. Tokyo 12.
82-84 (1986).
U. .1rnatian oj linMT opemti07l8 in compla BatUl£h spllUB. Pr<'IC. Imp. Acad.
Tokyo 14. 295--300 (IDS8).
14. NfiFu on inJiQ.f product mta8Ure spaces, I. II.
L Proc. Imp. Acad. Tokyo 19, 148 151 (1943).
II. ibid. 19, 184--188 (1948).
15. An uzmtplr concernin,g uniJonn oj sptdrol11U'.G!UUM. Pacific
.I. Math. 4, 86S--372 (1954).
Ie. Ergodic l1tecu7M and 1M. Markoff proUS$ with a st.uhle disiribtdir.m. Proe.
Imp. Acad. Tokyo 16, 49-54 (19-10).
17. Ontheuniqvent-ss vJ HaaT'smea8Ur('.Proc.lmp. d. Tokyo 14,2'7-31 (1938).
IS A proof oj the BS of Haar's :PJIf'aSV'I"e. Ann. of ,Math. (2) 49, 225-226
(1948).
Ut On the uni/ann. ergodiC' tht'(}1'em concemiug rtallimar oprrmkms. Jap. .
!\lath. 17, 5 12 (1940).
20. Some 'I"f'Afl11s Tn the vpcrawr-tJlftJJ'tt tn:ahrt€nt oJ the lUarkofl prot'f'ss.
Proc. Irnp. Acad. Tok)"D lli, 260--264 (1939).
21. SimullrmeoWl UkJlSion. oj iCi9nti1iU fundions ronsideTed as a posilir:e
linmr operalica. .tap. J. It1ath. 17. 1-4 (1040).
22. Weak ev.1.... ;Jt...ce in unijlJTJllly amvt' spnoe:J. T6hoku l\loth. J. 4,!j.. ]88-193
(IP3S).
23. Rings oJ analytic ftuutions. Lectures on functions of a complex ,'ariabJe,
pp. 71-.83, Ann Arbor, 1955.
Kaklltllm. S.. and Kod8.im. K.
I. Cber da3 Haarache JUass in dt'r lokal bilwtJapakltn Gn.pfW. Proc. Imp.
Acad. Tokyo 20, 444-450 (IV....).
Kakutanl, S., and Mackey. G. \'\'.
I. TIt'v dlal"lJt"lnizatifJfu oj Teal Hilbrrl SfJfJff. Ann. of Math. (2) 4.5, 5()...-5H
(IV....).
Kamke, E.
1. .I'tltrtgn1./t'hu. \\'. de GroJo'tf"r, Herlm .and LeI(Jzig, 1928.
2. ':l'fl.rory oJ stls. Translation of Second Gennan f"dition.. Dover Pub. Co.,
::\rew York.
8. Xt:U Herleitung der Chqill4ti fUT die linmren s lbsIadjug Jf,
Rartdu>cr1aulf,<1ben =rikT Ordnu"ll. }Iath. Zeit. 44, IJSS---658 (1938).
van Kamprl1. E. R.
I. Locally birompact groups and thei'l' dJnmcter grOUP$_ Anll. ("If !.\:mth. (2) 36,
448-468 (1935).
KantOJ'O'\itch (Ksntonnil), L. V. (see also Ficbknhob, G.)
t. LiJW«rc ha Raume. rtLt. Sbornik fo;. S. 2 (44), 121-168 (1937).
2. The mRtIwd oj llUCa"..ssilY appmwnmatirms for jlmclirmal t¥JI1alirms- Acta
Iath. 71, 63-97 (1939).
. Linear opt'rrdions in umi-ordeud spaces, I. Mat. Soornik N. S. '1 (49),
210.-284 (IQ40)_
4. Al1gmeit1e Formtn gewisur Kla5sm vcm lihf!4n'n Oper-atiU1WR. Doklady
Al<ad. Nauk SSSR (N. S.) 12, 101-106 (1986).
Kantorovitcn (Kantorovic), L. V., and Vwich (VuUh) D. Z.
I. Su.,.la ivn des vphalirms liniaius. Compositio :\lallL S. 119-]65
(1938).
2. Sur un Ih£,ori:m.e de ..."1. N. Dun.ford. Coruposibu1.lat11. 5,4."10-432 (1938).
Ka.ntorovitch (KnnWro\ ), L. V., Vu1'ih, R. Z_ and Pinsker, .-\. G.
I. Ftl7ldintiallll4n1!1riIr in partially onkud spaces. Gosudarstr. boot. Tehn.-
Teor. Lit. l\Ioscow-Uningrad, 1950. (RUBSian).
2. Partially ordered groups and linear partially tJrdntd spaas. Uspehi :\latem.
au:k (s. S.) 6, £10.3 (43), 31-98 (IO;;I). (Rnssnm) t\Iath_ He,'. ]3, 361
(]9d:t).
K JJ1all!Sky, I. (1'iee aL,") Arens. R.)
1. Tlie slrur:t re oj certam oJ1t'1'flIor algdmu. Trans. Amer. Math. Soc. "70,
219-255 (1951).
2. Tile .rnC1Srrass theorem inftelds 'Ii'ith oolootivJL!. Proc. Amer. :\lath. Soco. I.
356-357 (1950).
3. Lo.Ib'cu oJ cvnliruious fUllctions, I, II.
I. Bull. Amer. ')Iath. Soc. 53. til7---623 (UJ47).
II. AmEr. J. J,[ath. 70, G-'"¥'......GM (U)48).
772
REFEltENCES
REFERENCES
773
4. Topological rings. Bun. Amer. :I\:latl1. Soc. 54. 809-826 (1948).
s. Pri:mmy itkal.! in gwup algt'bms. Proc. at. Acad. Sci. U.S.A. 35. 183-]:3(1
(ID4D).
6. Prodtu1JJ oj nQnnal opeTarors. Duke J\'Jath. J. 20, 257-2tW (10!>3).
7. A throrem. on riRgfJ oj f11N.Talon. Pacific J. 1!ttath. 1. 227-232 (1951).
Karaseva, T. 1\1.
I. On 'h.e iRutr8e Slurm-Liovclll prOOl£m Jor a non-Hermitian nptTHlnr. Mat.
Sbornik N. S. 82 (74). 477-484 (1953). (Russian) Math. Re1. . 14. 1088
('D58).
Karlin.. S.
1. Unronditional n in Banach $ptliY8. Bull. Amer. :Math. Soc. 54 ,
I48 152 (1948).
2. B in Banuch 8pact:y. Duke MaUL. .J. 15. 971----985 {Itl4B).
Kitto, T.
1. On IIu; oJ Ihe per!u1baIitm mdhod, I, H.
I. Progress Theoret. Physics 4, 514-523 (U 49).
II. ibid. 5. G6-101. 207-:212 (1950}.
2. On Ih I)J'he perturbationmerhod..Y. Fac. Sei. Univ. Tokyo Sect.
I. 6, 145-226 ('951).
8. Perlurbarim throry oJ Bf.'1lIi-bounded operutors. )la.th. Ann. 125, 485-447
(ID53).
4. On the pt'rltatIation Ihrory of closed linLllr ...J. Math. Soc. .Japan 4,
323--337 (1952).
5. Nukscrn 80'JI'u 'fUJIPlaNt1tsfQ7linmr .Math.Ann.125. 208-212(1952).
6. On B()f1I(' appro.riltmtt "Intrhods CVftttrning the operators T*T. .Math. Ann.
126, 253-262 (1955).
7. On !he .....i-groups gmemkd by Kolmcguroff. diff_al equations.
J. Math. Soc. .J.opan 6. 1-15 (11154).
8. On Ihe upper and lm«r botmd Q1 rigt>nvallltS. .I. Phys. Soc. .Japan 4.
354--j!5D (11149).
]{a.y. I.
I. TJte fnntta:e SIt:llllhing probUm. Div. E)ectromog. Res.. lust. :\obtb. Sci..
New York Univ., 1955.
Kay, I.. and Moses. H. E.
I. The innJion v/ tlu! pnkt1tirll lu}'m the spet.1rnl BIIm3UTt'
junction, I. II Nuovo Cimento (10) 2. 917-961 (1955}.
2. The determination oj the U'attning poIenliaJ jr&m the I'i'j1Htral mrosure
,{1mctirm. I-III. Div. cf Elcctromae:. Res., lost. !ath. SeL, New York
Univ.. 1055.
Ka7.. I.
I. On llilbn1 spaus g£MTakd by pGJfive Hermitian ma1ri.x Junl'tions. Zapi ki
aulno.llmIffi. lost. Jat. )Ie)J. i Ha-r'kmro Mat. Obsc. 22 (1950).
Keldy , M. V_
I_ On the dlmat:t£ri.tti£. roI and dlnrarlerislic IU'MJiUllS oj certain classes oJ
flf,Wl-8elf..a4jui711 equations. Doklady Akad. :Sauk SSSR (N. S.) 77, 11-14
('951). (I\U>Sian) Math. Rev. 12, 835 (195').
Kelley. .L I . (see also Arens. R.)
J_ Nole on a thenrem ofKnin and lilibtwn. J. Osaka [mt. S i. Tech. PaTt 1_ 3.
1-2 (1951).
2. Banad 8pacCS with the QR. properly. Tram,. Amer. Math. Soc. 72.
:!23--326 (ID52).
3. The TydIonofJ product tMrn'em implies 11 axiom oj choice. Fund. Mat11. 87.
75-76 (1950).
4. C in ropology. Duke Math. .T. 17. 277-283 U95{).
5. GencGI topology. D. van Nostrand. New York. 1955.
6. Com',udtditte cperuk1r algdnus. Pruc. Nat. Acad. Sci. U.S.A. 88, 598-005
(1952).
Kelley. ..J. L., and Vought.. R. L.
1. The positiR cone in Banach algebras. Trans. Amer. Math. Soc. 74, 44-55
('953).
Kellogg. O. D. (see Birkhoff. G. D.J
Kemble. E. C.
I. A cmlr'ihtJt.ion-lo the tJuO'ry{lIthe B.JJ'.K. method. Phys. Rev. 48, 549-581
(1935).
2. Note (In thr S'uTm.Liour:ilk rige.1a:aluR-eiRm/1nu:tUm probln71 mith ttiPJguklr
endp<>;nts. Proc. Nat. Aead. Sel. U.S.A. ID, 710-714 (1933)_
3. The JU1ldn11lnlln1 prind.pleB {If quantum malumit:s. New Y()Tk, 1937.
Kerner. M.
1. Abtdract diJlamfitJl gtometTy. Compositio Math.. 4, 308-&1.1 (11)37).
2. Die Diffrrmliale in der aU,ge1m:im'n AnalysiB. Ann. of Ma.th. (2) 34. 564--512
(1983).
Khintchine. A..
1. Zu Birlrhof/s L(jsungdes Ergotlmprob1emr. Math. Ann. 107.485--488 (1983).
2_ Fmt.ri kf:4Ji Id1lg8 nmr Bahn 'il.n Pha.sermnmt. .&Iat. Sbomik 41,
1->-16 (1934).
Kilpi, Y.
1. Ober linean: JWnRale TmnsJormationm im Hi.lberIst:hm Raum. Ann. Acad.
Sci. Fennicae. Ser. A I, no. 154. 88 pp. (1958).
Kinoshita, S.
I. On £BSft'Itial romponm {}} the sttoJliz" poinfs. Osaka. Math...J. 4. 19-22
(1052)
Kite. V. L.. .JI".
1. Tm BIIpport pmpnly o} a {'OO:I)Q: Bel in a lintdr twrmm 8JK1C't'. Duke :\{at1l_
J. IS, ?'67 772 (1948).
2. 1Jen8 r.s. Duke Math. J. 16. 351-354 194D).
3. C sera in linear . Duke .Math...J. 18,4.4.1-466 (1951).
4. Comtu sell in linear BjJfUfll. II. Duke Math. -'. 18, 875-883 (1051).
5. .llWClriant e.rknsi01l3 oj linear ftmdionabl. Pacific J. Math. 4. 37--46 (1954).
6. .l'llDlIrianl1lll'lrin in groups (Svlutiun vI a problem (1/ Banach). Proc. Amer.
M.tl1. Soc. 3. 484-487('952).
7. Somc tm$ oj "[leziuity. Revista Ci., Lima 52, 15 23 (1950).
8. ('(J'IJOU bodUs and periodic horraromor;phisms in Hilbnt qJace. Trans. Amer.
Math. Soc. 74, 10-43 (1953).
Kleioecke, D. C.
I. A gt'nrrali=ation oj comptet £oorinuity. Technical Report 00. 8. to the
Office ()f Ordina fles.earch. University of California, Berkeley (1954).
2. INgennme perturbations. T hniCtll Report no. 1 to the Orfic."e' or Ordinance
R rch. Ulliversity or California. IWrkfoley (1953).
,
774
Rl:J.'ERENCES
REFERENCES
775
3. Finite prr1u.roalums and the f'J1«rdml rpectnJm. TeclI..nit-sr Repcrt no. 4 to
the orr of Ordinance h. University ofCa1ifornia Berkeley (1954).
KI1e r,A.
1. VnlrTsUdlll7l,gt'n 1l.bf'r dir V'cdm Nv.lbWlrn del' .lnkgmk hnt'tlrf'T DiJlert.n
tialRkidJlJJl#n_ l\l.ath. Ann. 42, 409-435 (189a).
2. L'nltTsudungen iibn' die IJarstdltDIg wUl/.'utUcht'r Furllrtivnl!n in de,.
muilftDWtisrhen Ph.rp;ik. )lath. Ann. 58, 81-147 (1904).
3. Britni:!e ZIIT Thmn"e du ShlrJJI-LiQf.lt'flhtfhm Dame/lung UJillkurlidlO'
Fvnktionen. :l\tath. Ann. on. 402-42:i (1005).
4. Die Thftnie der .lnt lcichlmRf'n 'Und die Ilung R,illlrit.rlu,hn
Funkl ll in drr ".tdhmwh hen Physik, II. Nachr. Akad. 'Viss. Gouin-
gen. l\Iuth.-Phys. Kl. 1906. 2]3.-252 (1900)
KJJ.opp, K.
1. ThrorJ! oj !unf.1i9J1S, I. II. Dover Publif atjonsJ e\.\' York, 19405, 1947
Kober. H. A.
I. A throTt:m on &nat'l, IIp<<£tJt. Compositio l\lath. 7, Iti5-1oW (1939).
Kodamt. K. (see alYoO Kakutani, S.)
I. On urdinary diJICR'nlial t'f}lMIions oj any t'tVn vrdIT and the NJJTnptmdiHf!,
rigrnfaJ1clWn t!Zpal1lJion.s. Amer. .J. :Math. 72. 502-544 (ID50).
2. On some.Jwtdt:rmf1ttnl tM8tems in 1M tJwory ofopf':rat(Jrs. in lli rpq«.
Proc. Imp. Acad. Tokyo 15. :207-210 (1939).
3. ()b r die Brzidn.j %Wischm den .,-'lassen und den Ttlpologim in riner
Gruppe.. m.... PhY8.- f8th. Soc_ .Japan (.8) 23, 67-]]9 (1941).
4. The f"ipnftlI pmblmt J())" ordinary dijJttmtial rqua''-om uf the Sff'fJRd rndt!'r
and .llt:isrnbng'1J IMory oj 8-motrins. .4.mer. .J. Math. 71, 021---Q45 (1M!]).
5_ On Bingular MVl.timaN vI &frond order diUcrf7llial opnatorff, I, 1I
I. Sugaku 7, In-1m (1"48).
II. ibid. 2, IIS-I8" (1"48). (.Japon<''''')'
KohJl. \\' (see Jost R.)
Ko rf, A. (see also Ifand. I.)
1. Zur Ntmtfinbarhil. einn alJgt-Mrinm isch£a lllHYlJ'lTl Rau .
Studia Matn. 5, 29----aa (1"34).
2. 'ObO'R(1mpaktlwit der Fmlktionrn.JJlntg€n bei d€r Kmn::ergen::: im ]Uittd.
Nnchr. Gbo. Gottin n Math.-Phys. KL, 60--68 (1931).
Komatuzaki., H.
I. SUT res projn:ti01UJ dans cn1ains r.apace8 du type (B). Proe. Imp. Acad.
Tokyo 16, 274-279 (1940).
2. Vne Tt'Manjtie sur lea projections dan:\" (:.e'rtaw.3 r8pfK'f'8 du type (B). Proc.
Imp. Acad. Tokyo 17, 238-240 (1941).
Koopman, B. O.
I. H(lmilloniall and IfflusjomlllJ;oT13 in Hilbcrl ¥Cl« Pmc. I"at
Acad. Sci. U.S.A. 17, 515-318 (ms1).
Koopman. B. 0.. and Doob 7 J. L.
I. On unalyti !"rlrtions u';tlt po:c.tn'f' ilffUJlirwry 'Parts. DuU. AmCT. :\Jath.
Soc. 40, e01 (1934)
Kostyucr-nko, A. G. (see Gelfand. J. M.)
KOJ;tyuc:enko, A'7 and Skorohod. A.
1. On a tlwurn'n (if .U. K. Ban. Uspt"h! Mate-m. Nauk ( . S.) 8. nil. 5 (57).
1435-166 {IUS3). (RlbSiaD) Math. Rev. 15, 682 (1954).
Kothe, G.
1. Die Teilrciumc eincs lirrftlTeJJ KoordintJl£nruu",u. Math. Ann. 114, 99-125
(1937).
2. .l.MbukrifsbtxlingtlRgf"n Jilr GleI.t:hungm mir ta1endlich lJU!tnl; U ".
.1. Reine Angew. Matn. 178. I93-2In (1938).
3. Irrung van Linnufurtktirm.t!n in lim'llren RiJtmtm. l\lath. Ann. 116,
719-732 (193").
4. Die QrIOIimtn"lMme f?ina lilt£crcn vorlkommezwn Rriu1lln. }:(a.th. Z. 51.
]7---lJ5 (lV4.7).
5. Die Stu/trlriJUfM, eine einft«Jw. KIU.'fs 1i.n#Qrf'T oolllrontmen.m Rc'i:ame.
Math. Z. 51. 817-."145 (1948).
6_ Eine axinmati&dJe KmnzriM1IIlrfg der linttl:1'rn Raunu> oon Typu m. Math.
Ann. 120, (1949).
7. Vb« die Vollsttmdigkdl einer Kbwr lokulkcmzoayr Rdwne. Math, Z. 52,
627--1J30 (1950).
8. Vb" 2'INi Stine van &mad. Math. Z. 53, 203-209 (1950).
o N ubtgrUndttng de" Thron"e der 'L'Olu..TJD'fwrel'lt:71 Rdlwu'. )lath. N81'hr. 4.
76-410 (1"51).
10. Vber:o::u:ri Sat;x '("On Banuch.. )'l8.th. Z. 53, 203-209 (19.50).
11. FunktionalanaIY8;s71nl t"JQsJomlUtiO'lUA. Naturforschung und I\[edizin
in DeUbW>hI.and I93'D--I{j46, Band 2, 85--DK Dieter'icb'sche Verlagsbuch-
ha.ndlung, \Vie baden, 1948
Knthe. G.. and. Toeplitz. O.
I. LiuLan' Roome mil ",JUTJL1Ii,.hr!irlnt. l\.oordiwuen. J. Reine Angcw. Math
l?I, 100-226 (1934).
Kowalewski. G.
1. EinflJ.hrung in di,f DrlenainanJelllh£tni . Set.'Ond cd., \V. de Gt1l)"te....
Berlin and LeipziK, 1025.
K07.10"', V. Ya.
I. On bast', in the space L.III[O,I]. Mat. Sbomik N. S. 26 {fiS}, 85-102 {1'950}.
(Russian) .Math. Rev. 11. 602 (1950).
2. On a fptnilliZLlliQn of 11/( wm:epf uf basis Doklacly Akad. auk SSSR
(N. K) 73 7 fl43--646 (UJ5fl). (Ruseia.n) .1Iath. Rev. 12, no {IDS1).
Km.&ovskji. S. N. (:see also Gol'dman. .M A.)
1. Canrmirnl Tf'pTf'SfTlfnlivn oJ ?lull clcmf'lls vJ a liJ&ror operaJur in i18 li'rf'dhnlm
Tegion. Doklady Akad. N.uuk SSSR ( . S.) 138, 201-2fI4, (1953). (Russian)
.Math. Rev. ]4. 1095 (1953).
2 On propnti.t!1t of a linear oprmlor CtlnRftYd with its enemlized 'rMhollll
.-.ginn. Doklml)< Akad.NankS8SR (N. S.) I, 1011-1013 (IDS.'). (Ra......)
:Math. Rev. 1.5. 437 (1954).
. On the extended rqion oj singularity oj lh operator Tl = E - AA. DQklady
Akad. Nauk 8SSII (:\'. S.) "6, 1l01 II04 (1"54). (Ru.",..n) Math. Rev. 16,
263 (195.:;).
Kra&o,"8Iai 7 5. :\1'., and Gol'dman, 1. A.
1. On lli principal parr oJ a wmplt:ldy conlihULJltS vpe.rtllor. Doklady Akad.
NaltkSSSR (N.S.)70, .....-948 (1950). (Russian) Math. R.".1I,600 (1"50).
2. Null tkmenJs and nuN JWI tiuunls of CfmIptt:tdy CQl'ltilluOllS operalcrs.
Lah-iJa.."i PSR Zinalnu -"karl. Vestls 1950 no. 6 (35), 87-100 (19.50)
4Rus.sian. Latvian 51..ttIU'1Uiry) )lath. Rev. ]3, 251 (1952).
776
REFERENCES
REFERENCES
777
3. Somcpropa1i :iQJ oamrp1rteI.llwtltimrousCJperafortnHilkrl space. Lat'\1ja&
J'SR Zinatnu Ab.d. V stis IP50 no. 10 (30). 93--106 (III-50). (Russian.
Latvian summary) Math. ReY ]5. 4.4.0 (10M).
Kra ? S. N., and Vinogradov, A. A_
I. On a crimioa oJ ttniJcmn ronoeriltl .oj a space oj t!fPt! B. Uspehi
l\olatem. Nauk 7. no. 8 (4g) 131-134 (1952). (Russian) Math. Rev. 14?
S5 (1953).
Kramer.. H. P.
1. pf"f"fu:dJatiot oJ diJJerestial operaI'(If'8. DisstTtation. Umv. of California at
Berkeley, 1954.
Kra.mer.. V.. A.
1.. .lvwntigatiQ1l8 'In asymptot/£ peTtu'1f1ation urKS. Dissertation, Univ. or
CalifOT11ia at BerkPIey, 19540.
2. AsyrttpIdic i'notr3c series. Pro ArneI'. Math. Soc. 7, 429-437 (1956).
Kramers. H. A.
1. JVtlkn:ml'f;hanik bM hallnahlige Qu.cmtisU:ncng. Zeitscbrift fi:ir Phys. .89,
828-M6 (1926).
2_ Das rrn in rirWimensiVJll11 perilJtli.tthrn KTaJtfe1dt. PhJ'Sica 2.
483--490 (1985).
K tskij. M. A. ( e also Krein, .M.)
I. On certain types DJ e:dt'R.!iom vI Hermilirm opemtm'S_ Ukram. Mat. 1. 2.
no. 2. 74-83 (1950). (Russian) l\lath. Rev. 18, 47 (1952).
2. On selJ..adjoird I7In1sWnt of Hermitian . Ukrain. Mat. 1. 1 DO. I.
21-88 (1IJ49). (Russian) 'Math. Rev. 13. 954 (1052).
S. On lhe deficiency numoos vJ ckmnl vperu!or"s. Doklady Akad. Nook S8SR
(N.S.) , 559-561 (194.7). (RuMian) M.tb. Rev. 9, 242 (1948).
4. On 1M ion of Hermitian o]JfTlltors wlth G JIOR.deRx dt.mwin of drJiniliml.
DoklOOy Akad. Nauk SSSR (N. S.) 50, 18-16 (1048). (R......n) !\Iatb.
Rev. 9, 447 (1948).
Krasnosel"lIkii, M. A., and Rutickii. Va. B.
I. On !h. Ih,.ry oj OrIia spaWi. DokIady Akad. Nauk SSSR (N. S.) 81,
497..,;00 (1951). (Russian) Math. Eev. 13, 357 (19521.
2 Lmmr inkgral operalor,s in Orlit;. . Doklady Akad. Nauk gSSR
(N. S.I 85, 33-86 (1952). (Russian I Math. Eev. 14, 57 (1953).
8. Di ty oj twfl-linm:l' inkgrar vperaIorR in Orlic'Z spank. DokJaiI)'
Akad. Nauk 8SSR ( . S.) 89 601-fJ04 (UI53). (Rm.sian) l\.fat"h. Rev. 15,
137 (1954).
Krein (Krein). AI. G.
I. Sur quesfWns tk la giomttrie d s tvm.1t..«8 BiJuiM dam un
e:rpoa IiniGire rwrmt er wmpld. Doklady Akad. Nauk SSSR (S. S.) H,
5--7 (1937).
2. Sur le$ oplratimu: liniaiMi tnmsformant un certai. msemble ooniqK en
,......£m.. Doklady Akad. Nank 88SR (N. S.) 23, 749--752 (t939).
3. Propri.at'J JUftdantmtall'8 d 8 rnsernbln roaiqllRs rI dans "esptl«' de
Bmmch. Dokl.dv Akad. Nauk SSSR (:-.T. S.) 28, 13-17 (1940).
4. Sur la diooM on minimal d'un f lI li11ioire en rompmardt'8
posiri.... Doklady Akad. Nauk SSSR (X. S.) 28, 18 22 (t94<).
5. On pmntiK fU1ictional& on alnw8! prriodic [unctirms. Do'klady Akoo. NstJk
SSSR (S. S.) 30, 9-12 (1941).
6. SUT uriC Ifnbalisalion du theoreme de PI'lJU"had au cas des iBlLgrak(l de
FC!urUr 8U?' lLs grQUpes f.8 CV1AT1Iufati[S. Doldady Akad. Nauk
8SSR (N. S.) 30, 484-488 (19411.
'T. Infinite J-rootTicnf and a mlllrV RWIJIfTlt problem. Duklady Akad. Nau"
SSSR ("- S.) 69. 125--128 (1949). (RllSSian) Malb. Rev. n, 670 (1950).
8. On the 'rate junnldo. in perftrr'bation 'hrcny. Mat. Sbomik N. S. 33 (75).
597--t!26 (1953). (Ru.siaa) Math. Rev. 15. 720 (1954).
9. Th Ihwry oJ !lc{f-adj<Jint QIuts;On3 oJ M'mi mN.d Hmnitian O alors and
its applimlirm.s, I. II.
I. Mat. Soornik N. S. 20 (62), 481-495 (19407).
n. ilJid. 21 (63),365---MI> (194.7). (Russi. ) Math. Rev. 9, 515--516 (1948).
10. SUT us foodi<rrw ae Gm:n non-symilriques OIlCillaloira dts cphauun
diJIiunlii1b otdinoo..s. Doklady Ak.d. Nauk SSSR (N. S.) 25, 643-M6
(1939).
II. On a gemTal mdhod oJ docomposing Hl!nnik-paBittt RUClei inta d m.ffll4ry
prod_cis. Doklady Ak.d. Nauk 88SR (N. S.) 58, (19461.
12. On Ilt'mlitWH. opet'Clt!Jn llnd diRding f . Akad. N"auk Ukrain.
RSR. Zbir.nik Prac. Mat. Inst. 10. 83-106 (1048).
13. 0" a cme-dimms1'ORaf singvlllr tmmdmy value problcn C!J f!Vtn order in tlu!
mtm>al (6,co). Doklad). Aka<!. Nouk SSSR (N.S.) 74, 9 12 (1950).
(Russian. .Math. Rev. 12. .502 (UI51).
14. Solution {JJ the inmse Sturm-LiO'Mcillt pt:r;Ihm. Doklady Akad. Nauk
SSSR (N. S.) 76, 2I 24 (1951). (Russian) Math. Rev. 12, 618 (1951).
15. On mtain prolJlf'1IU on th maa-il'lUUR and minimum oj maraderi.dk vaJ1UB
emd on tM Lyapunoo 2:ones of stabib.'ty. Akad. Nauk SSSR. Prikl. Mat. Meh.
15,323-348 ilfJ:U.. (Russian) Math. Rev. 18, 348 (11l52)
16. On ,he iJUrk case oj the Sturm-Limmille boundary prOOlnlt in t.he
intn'Ml (0. aJ ).lzvt.stiyu. Akad_ Nauk SSSR Ser. Mat. 1£, 2QS-324 (1952).
(Russian) fatb. Rev. 14, 558 (1953).
17. On s<nne cases oJ Jfedive tlder1n.inatitm {JJ the demUy of an inh
<o,d from i.. sp«fIol ftmcti<m. Dokl.dy Akad. Nauk SSSR (N. S.) 93,
61? 20 (1953). (Rwo.ian) Math. Rev. IS. 796 (1954).
18. On a mdhvd of eJJedi.ne 8CItllion oj an iJU"f'TlJe boundary probln1l. Doklady
Akad. :-.Tauk SSSR (N. S.) 94, 987--990 (1954). (Russian) fath. Rev. 16.
BS (11155).
19_ Detaminnlitm oj lI1t densily oJ a l'IVJ1hom rous sgrmRetrlc cord by its
frequency sp«tr'um. DoIdndy Akad. Nauk SSSR (N. S.) 76. 34.5-.'UB
(1951)_ (Rn.'.'..m) }Iath. Eev. 13, 48 (1952).
Krein, 1\1'9 and Krasoose['skii. AI. A.
1. SrobiJily oJ the in oj an unbounded fJpnatf)T. Mat. Sbornik . S. 30 (72),
'219-224 (1952). (Russjan) (\.[ath. Rev. IS. 849 (11152).
2. FtmdurnnItnllhrorems on the exft'DstOrl oj Hermitian opnatcrs and 8tnne 01
,hdT app1iMti to rh t.'1ucny f)J l polyIIDmiall and 1M 1nmnent
problem. Uspe'hi l\.[atem. NQuk 2, no. 3 (UI), 60-]07 (1947). (Russian)
Math. He-v. 10, 198 (1949).
KreIn. :M. G.. K:msnosel'skli, M. A., and !\tilma.n. D. P.
1. On fh ckjidency itJdicn of lint-aT opt'TClot'$ in Banach spt1«8 and some
grotndriuzr f}Ilwions. Sbo(nik Trudov In t. Akad. Ruk Ulkr. SSR ] 1.
97 tI2 11948). (Rn......n).
7711
REFERENCES
REFERE CES
779
KreIn, Mo. .and Krein. S.
1. On an infln' thamderistic {If the tiel oj all C:Qnlinuou.s JUnctiVDS drJi"lUMl on 0
Inrompatf HavwWrff space. Doklady Akad. Nauk SSSH (K. S.} 21, 421--430
(1940).
2. Sur Cf!BpOCe &S joncticmfl rorUwurs dtfinirs sur un tJimmparl de HuusdarJJ
er Be. .rrmimfmlJ2iB. .Mat. Sb<Jmik N.S. ]S (55), 1--37
(194S).
Krein, Mo. rmd :r.1iIman. D.
1. On crI7rme. pal,ds oj n:galarty t'QtlVf;f t;tfs. Studia l\'lath. '9. 188-138
(1940).
Krein., 1\1.. Milman. Do. and Rutman, M.
1. A note on bam in Banmh B]Jar:r. CommA In t. Sd. Mot.h. l\I c. Univ.
Khllrkoff [Zapiski Inst. l\lat. Mech.j (4) 16. 106-1I0 (1940). (Russian.
EngIiodl SUD:IIIUn)T) l\'lath. Rev. 3, 49 (1942).
Krein, Mo. and Rutman. 1\1. A.
1. Lin.ta7 opnaIurs 1£uring irlDlll'Kml a ct.mc in a BarJQch 8J1flff. Uspehi Matern.
Nauk 3. no. 1 (23). 3--95 (19.&8). Amer. Math. Soc. Translation no. 26
(1950). .
Kt'ein, .M_. and muliaD. V.
I. On regulurly CCJ'RKX Bets in 1M space (:DHjUguk to a &rtm:h . Ann. of
M th. 41. 556--51i3 (I!).l.()J.
KuUer. R. C.
1. Locally 00IWf':l' tQP()lngicol tw:lDr laltkrs and their repJ'f: tinnfj. Disserta-
tion. Univ. of Michigan, 1'9;;5_
}(unisa:,,,,a, K.
I. Some IbroJ'fflUi on abstmdly-t'fllutdjimditmS in an abtdract spac . PrQc. Imp.
Acod. Tokyo 16, 68 72 (1940).
J{\1Tatow!!iki, C.
]. SUT la propriitJ de Baire dans les /.?'OUpI's ntttriqtfCIC. Studia. l\lath. 4.
38-40 (1933).
KUT91.:hak, J.
1. Vber LiRll'llbildu tJnd rzllgmcit/.t' KtJrpt!rlhffJrie. .t. Reine A cw. !Hath.
142, 2II 255 (l912}.
1...aaRonu:1, P.
I. U1Jer die NtJhrnulEsliJsu.rtgnJ d{q' Stu.TIIt-LilJlA"iU,rim Ei ufgabt..
Proo'. XII S<Bnd. Malh. eongr..s Lund, 1955, 176-182 (1954).
1I e, J. L.
I. Oeu:vTl'B, t. 3. G"uthier-' Paris, 1869.
2. Oeuvres. t. I. Gauthit"T.Vjnar J Paris, 1867.
Laguerre, E. .
1. Sur h mind des sPJStfmes hniaires. Reprinted in . t. I. 221-'267
(1898).
LanLqm. K. \"
1. A general implicit Junt'lion fhe rem with n appliwlum '0 probInns oj
rehdWe mfllil1/ll. Amer. J. :lath. 42, 243-256 (]( 20).
LHndulI. E.
1. i!ber rine-n Kon :\jachr. Akad. 'Viss. Gottjngen. Math.-Ph:) .
I{!. IIa 1907. 25-27 (1907).
2. Vher' rinnl 8aiz ....'On H 1'Tn EBdangms. 1ath. Ann. 102, 177-188 (1929).
Langer, R. E. (8ee also Blrkhof1,. G. D.)
1. On the roIIlI£rtiim JormulruJ and the svluti.om oj the wat't' equation. Phys.
R",.-. 51, 669-676 (1987).
2. On ,he 'Imr1e t!tJualion wilh BntalllJ1Ul1lllflf'l numbers. Phys. Re'\". 75. 1573-1078
(1949).
3. The e.zpansWn prob/I'm '(1"j. the f/lnJry 6J O1'clinary difff'rr7Itial systnna 6J lite
8U(md order. Tra.ns. Amu. Math. Soc. 81. S6H--'IIOG {I92U}.
LaS9.lle .J. P_
I. Pstudn-nOJWJW lilU'UT Bpar:C:1. Duke Math. J. 8, 131-185 (104.1)_
2. Application of 'he pMlI.do-no,.m '0 the. study oj linf'flr topological SfJah'.s.
Revista Ci.. I,ima 47. 545-.Sti3 (1945).
3. Singular mrosurahle :retx mid linear functiono.bi. Math.. Mag. 22, 67..72
(11)48).
l..at. h w. V. V.
I. The. al#bM 61 serJ'd.djolnt bou ry-lVllue problnn.. Bull. Amer. Math.
Soc. 89. 969-978 (l!l3.1).
uurikainen, K. V.
1. Asymptotic ei lutiotJJr f.JI tlit raddfll detdn(Jh f'qufltinm... Ann. Acad. Sci.
Fennicae Set'. A. I. no. 180 (1Q52). 10 pp.
Lavrerltieff., 1\1.
I. Snr us fUlfdifJW: d'u'fll 'fOClTic,ble romplt>.rf' rrpTf'SCRtables paT tlf'S serif'S de
polgnornt'-S. Act. S...i. Ind. 441. Paris, 1936.
Lax, A. (see Courant, R.)
I..ax, P. D.
J. 011 ,he t':dsILRre of Grt:eu's fltnclion. ProC. Amt'r. '\Iath. SlJ('. :So ..26---5.").]
(1052). Et"rIltA., ibid. 3. 9'.13 (1952).
:2 SymmdTiZLIDle linNir traN,,/urmulimu. Cornm. Pure AppJ. :Hath. 7, 633--647
(1954).
3_ Reciprocal r.rtrf'mal probl"ms znfundwn '1u!R'1I. COlntn. Pure .'-PI)). :\Iath. 8
4"7-453 (1955).
Lax. P. D., 81'1I1 :\lilgntm, A. X.
1. Paro.hQlic f'(j1fati0tt3. Contri1m.tums to the tJre.ory of partial dlff{'£("ntia1
equations, 167-I!W. Ann. uf !\13th. Studief;. no. 33, Princeton 1954.
Leader. S.
1. Tl lheary of LfJ-.spat:€J> f()T fil/itely arIdllmr 'et fU1.cti(lIIS. ;\11I1_ )Iath- (2)
58, 5 (195-').
LebeswJe. H.
1 Sur leg integrales singulii" . .Ann. rle Toulouse (a) I, 117 (1909).
2. Ltrf<ms SUT Cintigmtion d In Techerdle des !o1irli(lns printjtii CS. Gauthier.
Villars. Paris I!M)J.. Second edition 1928.
L f!5chetz. S.
L Algebraic IDpology. Anwr. :\Jath. SIN'. Colloquium Pub. \-at. 27, Xew Y()rk.
1942.
2 Intmdudion to trpfJlo y. Princeton Uni\"{'J"jit.y P,.ill(Tton.. 1940.
Leighton, \V.
I. Bowmls for the solutions 6/ a urond order lin{'ar dlJfermtwl ('f}uuri(m.
Proc. .at. Acad. S<,i. U.S.A. .s5, 190-103 (1049).
2 On sclf.adj(lilU dijfermliul tfJuatutta (If llle s«ond ()r r. Pro£>. Xat. A('a.d.
ScL {J.S.A. 35. (J56--G57 U'9..t,9).
780
REFERENCES
REFERENCES
781
8. On the drtn:tiun oj rht! oscilllilicm oj a order lint:ar dljJnential U]rmrion.
Duke Math. .J. 17, 57--62 (1950).
4. On sdJ-adjoint tliJltTmtial f'(}tIllliom oj 8tcond vrthr. J _ London Math.
Soc. 27, 33--47 (11),52).
Leja. F.
1. SUT la PfJIiDn du groupe 00stmi1 'opol _ Fund. Math. 9. 37-44
(1927).
Lengyel, B. A.
1. On the spearal ihromn oj 8elJ juint uptmlnrs. Acta Sei. l\latb. Szcged 9.
174--186 (1959).
2. nv..ndOO "elf-adjmn v ratvr8 and the problmt oj ml'mUTJts. Bull. Amer.
Math. Soc. 45, 3WI-306 (1939).
Lengyel. B. A.. and Stone, 1\J. IL
1. Elementary proof vJ 'hI! sp«trul thmn:m. Ann. of I\.lath. (2) 37. 853-864
(10361.
Leroy, .f.
1_ La Ulrorie des pOints fLuB f't ses applirolUm$ t'n an,.. Proc. IntErnational
C""I!f= Iath., Cambridge, Maos. ., 202-208 (1950).
2. J7ahu,.B propm: el "' propm d'un mdomorphimlt'oomplitmient
OOfttinu d'un t!8J1l1« tY:dorid a ooiail1t1p8 co _ Acta Sci. Mat1l. 8zeged
12 Pars B, 177-186 (IPSO).
3_ 7'QpoIogit d s espaffs abstrails de 1_ Btmwh. C. R. Acad. ScL Paris 200.
]082--1084 (1935).
4. Lnl.un:s on hgpnfJolic ttptClrirms with UJnublt' I'Oifficirnts. Imt. Ad\.'.
Studies. Princeton. 1952.
Levi. B.
.. Su.l prindpio di Diri£hld. Rend. del Circolo Matern. di Palenno 22.
29:HJ60 (1906).
Leviruion. N. (see also Boas, ItL L.. and Coddington, E. A_)
1. Gap and dnuily tNornM Amcr. Math Soc_ Colloquium Pub. '"01. 26,
)lcw York, 1040.
2. Criteria/or 'he limit-pain' case Jer SffOnd ordtr linear diffnentiQl opn'CltfJn.
l:asopis. Pdt. Mat. Fys. 74, 17-20 (1949).
3. On OU! 1Rtiqu.nJei3 oJ ptlInItWl in a &hrodinger .equa,ion JOT a il'm asymp-
totic p . Danske Vid. SdodL .Mat.-Fys. l'ttedd. 25 no. 9, 25 pp.
(1949).
4. The i-nlJ rse Sfurm-TAuuvilk prOOlmL Mat. Tidsskr. B. If)4D. 2.J---."IO
(1949).
5. .A simpli/iM prool (JJ th upanaion throtna for singular &«m1d order linear
diJJnmlial ffll«flimls. Duke Math. .T. 18. 57-71 (1051).
6 AdllrNdm:lrl 10 ".4 IltRlpliJim proof oj 'he e;rptU&SioA IhffJrml 1M sin-
euFar s cand 6rdtr diJfnrnfiul t'qfU1fil;Jas:. Duke :r.-Iath. J. 18, 710-722
(1951}.
7. Th L-clQStl.re oJ ageRJuncliom CWJIf.Icial£d with st.1f-adjCJinr boundary t,YJlue
prob1nn<. Duke }!ath. .J. 19, 23-26 (1952).
13. CrJ'tain nlationship8 beht'ten phase shifts and scatrering potential. Ph)'s.
Rev_ 89. 755-757 (1953).
9. Tilt e;rpansinn rhrortm IQr Slngv.laT seU-adjoil1.llinear differ€hlial operGloTs.
Ann. 01 Math. 12) 59, 800--'115 (19541.
Levitan, B. M. (see a1so Gelfa.nd, I. M.)
I. Th, app/irofi<m oj groemIized displm:t:menl op=lm. '" _ di/lm:ntial
npwtiQIIII oJ the suond qrd". Uspehi Ma.tern. NBUk (N. S.) 4. 00.1 (29).
3-112 (1949). (Rus5ia.n) Math. Rev. n. 116 (1050). Amer. Matb. Soc.
Tnm.Iation no. 59 (1951).
2. in £Mmdm8tU /uncti(ffl$ f differential eguatiom oJ the second
order. Gosudll.rstv. Izdat. Tehn..Teot. Lit.. Moscow-LaUngrad. 1050.
8. On a dn:c&tposiUon throma for dlaraderisIU: furn:li01l3 oj di/l'""tinl
f<[U<dirms oj second order. Doklady Akad. NBUk SSSR (N. S.) 71, 605-<308
(1950). (RU$!;ian) Math. Rev. H. 720 (1050).
4. Proof !I} 1M theorem on th npmuitm in dgm.funcdom oJ 8tU*a4joinl
diff<mttinl ""..,.-.. Doklady Akad. NBUk SSSR (N. S.) 73, 651--654
(19501. (Russian) Math. Rev. 12. 502 (1851).
5. 0.. a u-r.. of H. 1¥eyl. DokIarly Akad. Nauk SSSR (N. S.) 82, 673--676
(1952). (Russian) Math. Rev. 13. 8440 (1952).
e. On the cr;mpleknniB oj Ihe BqUaTC3 oj func:tions. Doklady Akad.
Nauk SSSR (N. S.) 58. 84D-852 (1952)_ (R...,,;,..,) Math. Rev. 14. In
(19531.
7. On tM asymproti£ behavior oj a Bp«Jrol ftmt:tWn and on expansion in t'igen-
functions oj a sdJ joint diHtT€1Itial t'fPUIlicm oj second ordeT. I, II.
I. In-estiya Akad-. Nauk SSSR. Ser. Mot. 17. 331-864 (1958).
n. ibid. 19, 88-58 (1955). (Rusaian) Math. Rev. 15, 816 (1954) and 16.
1027 (1955).
Levy, P.
L PrdJlhno 00Dl'ft't8 d'a1Ullys fundinranelk. A c un cmnplhnent BUT l
JOOcliumfi!Un anulytiqUe3 paT F. P UqJrino. Gauthier-ViUa.rs. Pa.ris.
&oond edition 484 (1951).
2_ Lepms d'am:&Iyse jf1'fl.Ctionndle. Gauthier-Villars, Pam. 1922.
Leia6.ski, T.
1. The Fredholm ' rny oj li7U'.lJ,f' f'fjIUltioltS in Banach spact.,rr. Studia. Math. 13.
244---276 (1958).
2. Sur 1<. f....a;onndln multip/irotiveB. Sludia MatI>. 14 (1953). 18--28 (1954).
Lichtenstein, L
L Zur Analysis der une1ldlicflf1m.rn Ymiable1a., I. Enlwicklungssiitu del'
Tmm gewiJhnlichu linearer DiJfermtial/!,lddnuagrn rwd/D' Ordntmg. Rend.
Cire. .Mat. I?alenno 88. 113-166 (1914).
Lidskii, V. B.
L On the :number I)J 8tJlufimIB with i square oJ the system oJ diIJert.ntinl
<qIUlti<ms. -1f'+P(I)y ly. DokIady Akad. Nauk SSSR (N.S.) 95,
217-220 (1954). (Russian) MatI>. aev. 15. 957 (1954).
LifSic, L .M.
1. em the lheory oj regular perlKrlJations. DokIady Akad. Nauk SSSR (N. S.)
48, 79-51 (1945).
2. On regulnF pn<url>olWns, I, n.
I. Akad. Nook SSSR Zhurnal Ek&per_ Teoret_ Fi2.. 17,1017-1025 (1947)_
n. ibid. 17, 1076-1089 (1947). (R........) Math. Rev. 9, a58 (1948).
8. On !he problem oJ !he th=y of perhnf>tdions 001I7I<Ck4 wi!h quantum .tali.-
tk8_ U!5pehi Matern. Niluk (N. S.) 7. no. I (47). 171 180 (1952). (Russian)
Math. Rev. 14, 185 (1958).
782
REFERE CES
REFERENCES
783
40. On 1' gJlrfJT pertu.roatio," £1/ an operolhr mith a qum>i-nm,itnunu; sptdnDn.
Ulenyf:: Zl\pWd ltar'kov. Gos. 1.:niv. 28. Zapiski Nnul:no-Issled. Inst.Mat.
.Mch. i Hst7Jmv_ Mat. ObAc. (4) 20. 77-82 (1950). (Russian),l\1ath. Rev. 14,
565 (1953).
Lindgren, D. 'V. «(;e-e Cl;J.meron R. H.)
Liouville, .1.
I. Sur u dadoppenmt tks Jrmdirmt; €n l>inc dant ley divCT,y tcmu':r SQnt
llRBUjf1iea a satisfain d une mbn lquatirnt dJ.lIin!nridl du st!rond vrdTf
.conte1wnr ,m ptnTlBIdn I I-III.
I. J. !\lath. Pures Appl. (1) 1. 253-265 (I_I.
II. ibid. (I) 2, 16-.37 (1837).
III. ibid. (1) 2. 418-436 (18371-
2. D'uJi. tJ/iQrmrL du a 1J.l. Sturm et ulatif aunt: dasse de fORrlions tmnscm-
dntI".. J. !\lath. Pures AppJ. (I) ], __277 (1856).
Littlewood. .T. (see also IIH.rdY. G. H.)
Littlnwod, .1., and Paley. R.E.A_C.
1. TIwoTems on Foun&" serit:s and pO'llJeT 8eries, I.. II.
I. .J. London .Math. SOC'. 6, 230-233 (1931).
II. Proc. London )'Iath. Soc. (2) 42. 52----89 (l9.n)_
Livingston. A. E.
1. Tm spm:e H". 0 < p < I. is not RtmlIabl,.. Pacific .T. Math. 3 613-616
(19531.
Lhisic.. M. S.
1. .Isomd'rie operalrws with equal dfjif"lf7kY I.tidiU1:, tpWki-unitary upnt110TS.
Mat. Sbornik N. S. 26 (68), 247-264 (1950). (Russian) Math. Rev. 11.
669 (1950).
2. On the rWluti6R vJ a 1mem' mm-HermiJ.ion UjJB'UIor 10 "iTinng:ula7 ' form.
Doldady Akad.. Nauk SSSR ( . S.) 84.. 87S-----S76 (IS)52). (Russia.n) Math.
Rl:v. 14 184 (19.53)
3. On the TtSQWent oj a linoor mmsYJfum1.J'U: opeTaifIT. DoJ;.:I00.}' Akarl_ Nauk
SSSR (N. S.) 84. 1l I-U34 (11152), (.fLus5ian) :\!ath. Rev. 14, 185 (IQ53).
4_ On spt'f"lral do:rntIpvsition oj linMr H6hulfad;'oinr opna1nrs. Mat. Sbornik
N. S. 34 (76), 145 199 (1954). (Ru..oan) Math. Rev. ]6, 48 (1955).
5. On !he fMcTy oJ Be!f-adjoift' <y<""" oJ diJlermtial eqwdi..... DoklRdy Akad.
Nauk SSSR (N. S.) 72.. 1013-1016 (1950). (RUfO'jl3n) Math. Rev. IS, 747
(1952).
Liv ic M. S., and Potapov, V. P.
1. A thn#mt on ,he mv/tiplicab01l oj ".hmu1t'J"istic mum,}' junrtirms. Doklady
Akad. ::VII-UK SSSR (N. S.) 72, 625-628 (1950). (Rwssjan) Math. Rev. 11,
669 (1950).
Loomis, L. H.
1. An intrvdfu:tioR to dJslTad harnonle tmcrlyNiJf, D. '\'an K05trand Co. Kew
Ymk, IQ53.
2. Line4T luhditmD.u ana con/mI. Amer. J. Iath. 76, 168-182 (1954).
3. Ab8tmct and 1M tl:nifJUDWSs oj Haar mro6lrU. Ann, or Math. (2)
46, 348-355 (1945).
4. HaaT 1R0000rt in unifQ'rm $trkdrJ...e. . Duke !\1nth. J'. 16. Ig.'J- .WS (1940).
5. On me Tf'prt'fDJJn1iQJ1 0] G-amt}llele Bavl€'llR algebras. BulJ, Amer. Math.
Soc. 53, 757-'760 (J94-7).
Lo E. H. (S€e a1so Riesz. F.)
I. lJirontinuow linw:r tmnsjfJ17lVllions in ctTfain vector $]XJ«B. Bull. Amer.
Math. Soc. 45, 5m-569 (1959).
2. On a cukulu oJ optJ'al,on in ref1£zivf: fl«/or .plK'd. Trans. Amer. Math.
Soc. 45. 217-23-J. (J939).
S. The Cmu:hy-Srh.-arz ilUflrullily and #If-Cldpwt space . Ann. of Math. (2)
40, 468--473 (1945).
4. On €ertain implicatirm3 'l.vhich cItamderiu Hilbert space. Ann. of Math. (2)
49. 523-532 (1948).
5. lleturn to 'he self-fldjfJinl ImnsJonootion. Acta Sci. Math. Szeged 12 Par5
B, 137-]44 (1950).
6. The m oJ liru!ar trnnsJormcltKwt.. Trans. Amer. Math. Soc. 52.. 23H-248
(1942).
7. The i1lkgm1 uplU('nlation of wroklg almosr.p€ri.t:kIic t7etnlJJormanuns in
uflerirw. vector 8JN1LE-1Il. Trans. Amer. Math. Soc, 49, 18--40 (1941).
8. .1J.ll't1tu1 oJ iteruled ttuJ1Jrjmmnhons in reJle:cive vector ttpQ«tf. J.lull. Amer.
lnth. SIK-. 45, 945-957 (1939).
9. The m-udvre oj fWITJIf'd abelilJR rinp. Bull. Amer. Math. Soc. 50. 447--463
(1944).
10. 7'he thoory oj aruJ.lyric J"'kltiB in nnrmnJ abdiun. vector ri<n8s. Trans. Amer.
Iath. __ 54, 414--425 (1943).
11. FNnctUMs £)J st:lJ-adjoint InlRs/oJ"1l&fftkms in HilbeTt space. Acta Sci. Math.
Su-gro 7, 186-146 (1 :W).
12. Differmti.abl£ irlffJullli,i€S and lhe throry ()J 00Rf1l':r bodieg. Trans. Amer.
I:\-Iath. Soc. 71, 24.'l-UG (IP51).
13_ Su cerle ,,-i tkl di RJlu.m. _ Rend. Ace. Naz_ LiDcei (8) 16.
25-2" (1954).
14. On the ooluJ1U" oj smooth cmn.'U' bodi£B in Hilberl spau. Iath. Zeit. 61,
391-407 (1955).
Lorentz, G. G_
I. On 1M th«Jry ()J span's A. Pac1fic .J. ,Math. I, 411-4,29 (1951).
2. 8orm: flew funcliurwl spaces. Ann. <Jr :Math. (2) 51. 87-55 (IDro),
3. Opemticms in linco.r mL'lric spt.UY8. Duke I\lQ.th. J. 15. 755-761
(1948).
4. .Ftt.nl...,iona/ und Operalinrltrl in den Rinmtrn deT ZahlenJoign. DokIady
Ak.d. Nauk SSSR (100. S.) I. 81-85 (1955}.
Lovaglia. A.. R.
1. LvrnIly uuifurmIy MhN!;t! Bmaac.h ..ptJ£U. Trans. Amer. :\.fath. Sfi.e. 78.
225-258 (ItI5o').
LOW1g H.
I. K(Jmpl 1e eul..lidin-M Riiume UDI'l bt.liffiigEr ndJlrher oda U1lendlicher
Dimnw.'onr..ahl. Acta ScL .Math. 7.1---.."3 (H)M).
Lowncr, K.
1. GnmrMgt' €'iner IOOlllls/eliTc 1m llilb£rlsrhfon RallllK'. Ann. of Math. ( ) 40,
8]6-833 (1939).
LukoIn!lkh, T. I.
I. On tile tlit!OTY (JJ matrix f'tprl'gen'aUcms oj ,mbOimded fielJ-adJOln' O mtf)T3.
Doklwy Akad. !'auk SSSR ( , S.) 7(). :i77....."fi9 (UJ!){)). (Hus51an) Jath..
Be\.... II. mi9 OD5ll).
784
REFERENCES
REFERENCES
785
Lumer G. (see HaJmos. P. R.)
Ma. S. T.
1. On a gennal oondUion oj 11nserdJtTg JOT ,he S-flUltriJ:. PhY8. Rev. 71..
195-200 (11!4.7).
Maak.. W.
I. FOBtperiodischc FunktiC1l1£n. SpriDger, Berlin, 1'950.
MoclJuf!re, C. C.
1. The th my oJ . E ebnisse der Math. und ihrer Crenz.gebiete, voL 2,
Berlin. 1938. Reprinted CbeJsa. Pub. Co., New York, 1946.
McEwen. W. H-
I_ Spedrall1u!qry and its rrpplimll.'rm.lo diffl!'f't'nliol. _ Arne,..
Moth. Monthly 110, 223--238 (1953).
Macmtyre, A. .Jo. and Rogosinski. W. w.
I. _ probkms in !h, fhrory oJ analyti' fundWns. Acta Math. 82.
275-.'!25 (1951J).
Mackey, G. W. (see also Kakutani, S.)
1. On eonva' IopolQgialt limar spaces. Trans. Amer. :Matb. Soc. 60, 519-587
(11146).
2. On infinilt: dirneJlSirmallinear spaces. Trans. Amer. b1ath. Soc. 57, 155-207
(11!4.5).
3. Nole on a tAeQTem J JUurray. Bull. Amer. Math. Soc. 52. S22-325 (1946).
4. Cormnutativr: Banach algeb1'as. Mimeogt'aphed h;cture notes. Hanat'd
Univrn;ity.. lE52.
5. F'1u1t:tUms on locally compacr groups. Bu1L Amer. Math. Soc. .56, 385-412
(1050).
J\lact'hai1. M. S.
1. Ab80luuanrf unoon4i1i0l'Ull (OIU'tljg( . Bull. Amer. Mdh. Soc. 58, 121-12$
(1947).
l\k-Sbane. E. J.
1. Liru:ar fuudUmals on verIo.iB Bannch Bpac f/. Proe. Amer. .Math. &Ie. 1.
402-408 (1951J).
2. .l'J'lkgralion. Princrlon University Press,. Princeton, 1'944.
3. Orrkr-............... ";',g map$arnl inkgmtionproce:sse& Arm. ofl\latb. Studies, no.
81, Princeton Univ. Press, ID53.
4. .Images oj sell satisfying the OO1Il1itioa oJ Boire. Ann. cf Math. (2), 51.
380-586 (1950).
1\1add&U8. I.. .Jr
I On typu oj "u.'fflk"' in linMr nmmed NJKIl'rIJ.. Ann. of Math. (2)
42, 229-246 (1I!4.I).
2. On completely t'fmtiR'UOtl3linear l:1"tms[fJITJKlliom. Bul1. Amer. 1\1ath. Soc. 44,
2711--282 (1988).
!\obeda. F. (see aJso Ogas&W81"B. T.)
1. Vnitary equirraknte 0/ Belf nt ope'J't1Iors and ronsMn oJ 'hIOtion..
.f. SeL IDrosbima Univ. A. 6. 283-200 (1936).
Maharam. D.
I. The rr:pm.enttmon oj ab8trad ftmrtitms. Trans. Amer. Math. Soc.
65, 279-330 (11149).
2. The 1e8mltrliV7J of abstmd Iflkgmls. Trans. Amer. :Math. Soc. 75.
154-184 0958).
8. On Irernd rrpr vI linear optrarcrs.. Trans. Arner. Math. Soc. 79.
229 255 (1955).
l\1akai. E.
I. ABymprotisth AbocIuJbJung <kr Eigerm;m< gewis.", DiJJermlWlgkidilm&ffl
%Weiler 0rdmaIg. Ann. Scuola Nonn. Sup. Pisa (2) 10, 123--126 (1941).
Mandelbrojt, S.
}. Un l/Wren.. de !<rmefuTe. C. R- Acad. &i. Paris 231, 16--18 (1951J).
2. 'l'himbnu &lninua d, Jrnn<fI<T<. C. R. Acad. &i. Pam 232, 284-286
(IQ51).
3. 7'hivTbnes d'appmril1UlliOit el prvbIi:ma lhs moments. C. R. Acad. Sei. Pari$
232, 1054-1058 (1951).
4. General lheQTtmS oj t"tosuu. Rice Inst. Pamphlet. Homton, 1951.
5. Qut'lques Ulif'l1imes d'waicilt. Proe. Internationa.l Congo Math., Cambridge,
M..,. I. 841H155 (1050).
6. glnirn= d, fe-rmmw.. J. An8l).... Math. 1, 180-208 (105').
(Hehrew 8UIIlIDQ1'Y).
7. Qu.elque3 nouveauz thtorbnu cU Je'I'1mlUre. Ann. Soc. Polon. Math. 25
(1052), 24I 25I (1053).
Mandelbrojt. S_. and Agmon. S.
1. Un ginbrJJi.satii: du thiorinu taubtritn de Wimer. C. R. Acad. Sei. Pari$
228, 1894-18116 (III4Q). (ef. Math. Rev. II, IX! (1950)).
2. UVIt: gbItmli.satiofI da tht!oreme Iaubtrit:n de Wimer. Acta Sci. Math. Szeged
12 1 Pars B. 167-176 (1950).
Martenko, V. A.
I. Conammg the theQry oJ a diJ/erenJial oprra1CJr D/ second order. Doklady
Aka<!. Nauk SSSR (N. S.) 72, 457-4060 (I951J). (Russian) Math. Rev. 12.
183 (19511.
2. On II", trnnsJortMtiua formulas by a /&ta)r diJJeTnllial op<ralol' oJ
_ lYIder. DoIdad Akad. Nauk SSSR (N. S.) 74, 657-flOO (1950).
(RwHan) 5lath. Rev. 12. ?07 (1951).
Marcinkiewicz. .J.
1. Sur les IfWltipliet1Jaln tk 8irin iU Fourier-. Studia. Math. 8, 78-DI (1989).
Marines.cu. G. (see also Ionescu Tulcea, C. T.)
1. Optmtions R'laJ::ir.emrn! annpltlnn€Dl rontimus.. Aoead. Repub. Pop.
RomAne. Stud. Cere. Mat. 2, 107-194 (1'951). ( o . Russian ond
French 81lII1I'1UUies) Math. Rev. 16. 487 (1955).
:Markoucbevitch, A.
1. SUT lea baus (au Seml large) dam leg up es liBlains. Doklady Akad.
Nauk SS8R (N. S.) 41, 227 229 (1943).
2. Sur Ia _Ikure app_. DokIady Akad. Nauk SSSR (N.S.) 44,
262-264 (1944).
3. Sur une ginlralisatitm d'u1I thitni:m£ de Menc1l.(jJI. .Mat. Sbornik N. S. 15
(57), 433-4.36 (1944). (N.UB8ian. :French summary) l\1Pth. Rev. 6. 274-
(1945).
l\Iad:ov (MarkoCC), A.
1. Qrulquu sur les l'1I3t"f1Ibks abiliens. Doklady Akad. Nauk SSSR
(:\I. S.) 10, 811--314 (1936).
2. On mean val s and exterWr densiries. Ma.t. Sbomik N. S. 4 (46). 165-191
(19S").
786
REFERENCES
REl'ERENCES
787
Yartin R. S. tsee Michal, A. D.}
:Mar1:in \V. T. (see CaJIK"I'Of1, R. 11.)
Mnru:pl.lIla, G.
1. Nores on Wiener inlrgmls. K6dai Math. Sem. Rep. 1950.41-44 (1950).
l\lasani.. P. H
J. MurliplirotirY Rift7laJIh intqp't11km in ring$. Tr'IlJIS. .-'\mer. Math.
S()c. 61, 147-192 (1947).
Masl0\0\. A.
1. A 'noleon BiTk1wJ/'s l'rod /. Leningrad State Uni,,', Annals Uche-
n)"eZaplskr 83 [l\fath.Ser.12j,42-56(1941.. (RUBSian. summary)
Math. Rev. 7, 455 (1946).
Mautner, :F. I.
1. On ri#RJUlJdIQtI . :Proc. Nat. A arJ. U.S.A. 39. 49-.53 (1953J.
Mazur, S. (Fie-e aka Ranacl1. S., and Eiddhcit. M.)
1. l}ber ktml'f'.ze M in liJl:l'C1Tm IWnnierle Riiu.mm. Studia l\lath.. 4. 'm---&-I,
(1933).
2. Vher die kldn.sl(',. ..."'l (. rin f 1ronIpakIt' ",UeR# mthidI.
Studi9. Math. 2. 7-9 (1030).
8. Vber Kont'fT'gt7i% in den Rdumcn (L:I'). Studia Iath. 4, 128-133
(19331.
4. lIne umu'V'"' sur I'hnmlnrmwpbie rks chnmp8 jfnlL'fiol'/nrl$_ Studia Mp.ta. J.
I<3--S5 (1Q29).
$. Sur les t/UI'lt'tlWr lifliai7u. C. R. Aced.. Sri. Paris 207. )V25-1027 (1938).
Mazur. 8_. "od Odicz. \V.
I. VbeT FvYJt:R rinnIUr Operalimzen.. Studja Math. 4, 152-157 (1933).
2. Gnmdkgrnde ElfP'St'hnfun der poIynt>lIIischEn Operatj""",. 1, fl.
I. Studio Math. 5, 50- (1_).
II. ibid. 5 179-189 (19M).
S. Sur In l1p{lUlf mitriykes lintai.,.es. I, II.
I. Studia l\lath. 10, ]84-208 (1948).
fl. ibid. 13, I37 179 (19531.
Mazur, S., nnd Ulam. S.
I. Sur les tronsJrJttItatitJft& i&Jm.iI:riques d't'oIrj)U« nrlorir1s 'IUJJ71Iis. C. R. Aca"
Sea. Pari 194, 946-948 (1982).
I\Iedvedev. YlL T.
I. Two crirma oJ compartRess oj JumiliLI DJ /_ndi()#js. Doklady Akad. RU"
SSSR (N. S.) 00. 837-340 (1953). (Russian) Math. Rev. 14, 1072 (958).
I _ S. No
I. 0" the T(,pm£ntatfun vJ fu1u:tions by uries oj polynomiLlls en clost:tl sa..
Doklady Akad. N'auk SSSR (:S-. S_) 78, (W5I). (R.......n) lath
Rev. 13. 23 (1s)52). Arner_ Mat1l. Soc. TranoJatIon, J1(}. 85.
2. Uniform approzimatitrns to jWldions oj a campleJ! rorinbI . Uspchi lat('m
Nouk ( . S.) 7. flU. 2 (48), 31-122 (1952). (Rtl sian) Math. Rev 14,
547 (1953). Amer. )13th. Soc. Translation, no. 101.
.Miehat.:l, R.
1 7'rcvuj'ormoJion.9 from a linwr I>:pau fl'ill, 'iCtok lopology. PrrJIC. Amer.
Math.. Soc. 3, 671-ti76 (1952).
2. I..nt:aUy multfplicatirt!ly--wnt'fX lopologirnl a/.1!cbms. Memoirs Amer. :Math
Soc. no. 11, 19 2.
Mi.-hal. A D.
I Gmaal diJftTffltial t,rometl'i s and ulaJ.nJ topi . B1JIL Amer. )'lath Soc. 45.
529-563 (19391.
"Helml, A. D I and Clifford. A. II.
1. FonC'lWm analytiquu implidt.es dans tks rtpffC('S '-'«loriels absl:1'ti,Ug.
C. R. Acac:L Sci. Paris 197, 7a5-737 (1933).
Michal, A. D., and ElNInin, V.
1. f'mnplntl.1f intrgtubk diffomtiul nJUL1Iirm. ill ttbKtffld spoa$. Arta )Iatk tiS,
71-107 (1937).
Mi('hal. A D.. and Martin. R. S.
1. Some t'iEJK1J1S1'OIUJ in vecror sfKK-? T. fath Pures et Appl. (9) 13, 6!l--91
(1934).
!'I1ichlin pUWin), C. G
1 On the coIl'tlr J'fcc: oj thc FTnlIwlm stria. Doklady Akad. Kauk SSSR
(N. S.) 42, 278-876 (1944).
1\hkusinski. .T. G
1. SUT cnto.ms t:lipa«8 absJrnils. Fund. Math. 36, 1 5-1.30 0(1t)4.0).
:Miller, U. S. (see Dunford, S.)
Mjllet, K. S.
l A Slurm.LiauviUe problmI associated with itnutive tN#'l1iods Ann. ot Ma.th,
(2) 53, 5 (1951).
'2. Crmstrudion oJ the. Gre.eu's fanction oJ « liwal' difft:n:nh'a1 8J1. /fflL lath.
Iag. 26, 1-8 (1952).
t;.. SelJ-llIijalnl diJ/rrmfial rystem:J. Quart. J". l\Iath Oxford (2) 3, 175-178
(1952),
Miller. K. S., arId S...hiffer.. M. 1\1.
t. On the Green?s JunctWn oj (Jrdinl1ry differmJial Kg!de.m,s. Proc Amer. Math
Soc. 3, ol33-44I (1952).
2. lcmolcm;e. pmpDlie8 of the Gf'en,'s ficracli01l. Proc Amer. IHath. Soe 3
!J48---D5Ii (19!;2)
Milman (Mil"man), D. p (see aJso Brodskii? M. S , and Krein, M.)
1 On some critmafQr the ngularity ()J spaces oj the. type (B). Doklady Akad.
Nauk SSSR (I'. S.) 20. 234 (1938).
2. Characrtris11CB oj n.1rnnt11 pvlnts oj gula1f1l WRvt'Z sets. Dokladv Akad.
Nau'k SSSR (N. S.) 57, 111)-122 (11J47). (Russian) M.ath. Rev: 9, ]1)2
(1948).
8. A("('f'ssihk poinfq oj a juru:tirJRul romptH'l sel. lJoklady Akad. N'aqk s.."\SR
(X. S.) 59, 1045-1048 (1948}. (Russia.n) Mo.t11. Rev. D. 449 (1048).
4. lBUlftdry and €.rtmRal point . Dokla.dy Akad. :Nauk SSSR ( . S.) 59,
1241-1244 (UJ.t.8). (Rl1I6iHn) rllth. I{",'. '9, 516 (1048)
5. lttul1imdn.c '"fIn«':I. AntdJPJis 6} the invariant sub8ds of a mulli,.,nmed
hiiYnNpad pace under a stmigroup oj nonincrrosing operators. ()oklady
Akad Xauk SSSR ( . S ) 67, 27-30 (1'949). (Ru.qsian) :\18th. Rc" 11,
117 (1950).
6. &1r-nnal poim8 and center8 oj birumpac18. U'Tt'hi Mat('m. auk
(X.S.) 4, no. 5 (:1:1),179--181 (1949). (Ru. ial1) lath. Rev.II.H? (191j(J)
7. Tile J(l( illl 3#rUmttT (If a CURCcr lJirontpt:ld. space and inkgral tkrompmiliung
ojtlll'Uml. finkhuJ)' AktLd.N'lluk s.. R (X. 8.)83.357-360 (1952) (Russian)
Math. Re'\-". 13. stS (11J.'i2).
.
788
REFERENCES
REFERENCES
789
8. Sur rme dassijimtiCin des poiRts du SfJffhY d'un o-peratekr liniD.i-n. Doklady
Akad. !>;suk 88SR (N. S.) 33, 279-287 (1941).
l\IiIman (Mil'man). n. p", and Rutman, !\L A.
]. On a more pret:iBr t1!£Drcm alJIiUl (he romplLlfflt8S oj Ole wJpttrm vJ r.dr't>nwl
points of regulaTly convex .-b. DokJady Akarl. Xaljk SSSR (N. S.) 60,
25-27 (1948). (R.......u) )'ath. Rev. 9, 448 (1948).
Milne, 'V. E.
1. The llf'harior oj a botmdary value problmt as the iRinTaI bacmles infinite.
Trans. Amer. Math. Soc. W. 797-802 (1928).
2. On tJu oj oj eapt1nMQnS in fin inJillik ittlt71-l(J/. Trans.
Amer. :Math. Soc. 81. 00&-9]8 (ID29).
8. Th.e 7IU11I£riral detmniflllfion vJ chnrncleristiC' numbt-rs. Phys. Rev. 35,
865 887 (1950).
Mimura. Y. (see aIM "'Yosida. K.)
I. COO, Funkti'onen von Funktiat1al in nmtll. Hil.hfff1J£h,e" Raunl.
Jap. .1. Math. 18, n9-I28 (1986).
Minkowski,. H.
I. Abhandlungen. Vol. II. Teubner, Berlin. lOll.
Nimnda. C.
1_ Pr/JUuni di uiJIIm:zKJ in cmuhri /unzillllole. Litngndia TM'l'hi. pjsa, 1949.
2. Sul principiQ di Diri€Met per I ftmr';PI1i annoni€ht. Atti Accad. :N'az.
Lincei. Rend. Cl. Sci. Fis. :Mat. :Sat. (8) 8. 55-59 (1947).
I\UrkiJ, H.
1. T/lt! work oj Silov on .commlllu1ive semi-.rimp Banach algebr'm. Techmcal
Report, Contract 218(00), Office of Naval Re.seardl.
Mishoe. L. I. (!!see alS() B.)
I. On the up.Mien of an 6rbilTary fv- in Unn' of 11M ri.gn>futu:rions of
tlVlotI-sdj-adjoint diJ1t:reRti6l system. D&.er1:., New ¥tJrk University, 1953.
Mishoe.. L. I., ond Ford.. G. C.
I. Studies in the eWnfuracli&n series assodlUUf with a 1J-lldjuird differtn--
tiat 81Jstem. Tech. Report N'at. Sci. Foundation, 1955.
:2. OnDttvniJOTm rJfacrT!ain 9RBn'i,a. Pa.citicJ. Math.
6, 271 278 (1956).
Miyadera. I.
1. Gmerafi.on oj a Bfrongly wntimwus semi-RrQup of opemIors. T6hoku Math.
.1. 4 (2), 109 IJ4 (1952).
l\lohr, E.
1 DU KrmsIruklion der Grun3t:hm Fu:II1rtUm im £1Wdtn1m Sinne. ..T. Reme
Angew. l>Iath. 189. 129-140 {I95I).
J\.ldlanov, A. M.
1. On cOflditions for d oj Ihe spedrum oJ Mlf-ndjuint diJJnen1inJ.
nptalions oj second order. Trudy Moskov. .Mat. OliSC. 2, 1£9-199 (1953).
(Russian) Math. :Rev. 15, 2U-S (1954).
Monna, A. F.
1. On a lim:ar P.adic qKJCL Xederl. Akad. 'Yetensch. Verslagcn, Afd. Katuur.
kunde 52. 74-jj2 (1943) (Dutch, Engl..h S1JIJJlIIa')').
2. On weak and Slron.c C'tJnVtTgfflCe in a P-adic Banat;h tJpaCe. Nederl. Akad.
\Vdensch. Verslagt=n. Afd. Natuurkunde 52. 207-211 (1943). (Dutch.
English summary).
3. On non--Archimedam liru:ar spaces. :S-ederJ. Akad. \Veten5ch. V n.
Aid. l\atl1urkWlde 52. 808-321 (194.3). (Dutch. English sununary).
4. l:.inear ftmdiunal in non.An:bimtdMn Banach . Nellerl.
Akad. Wetm!iiCh. Verslagcn, Ald. NBtuurkllnde 52. fi54.-661 (1943).
(Dutch. E li5b liurnmary).
5. On ordered groups and linear BpaJ:ts. Nedet!. Akad. Wetenseh. V Jogen.
Afd. ro;atuurkund 53. 178-182 (1944). (Dutch. EI1gIi8h summary).
£. On the inbpal oj aJuru1irm m valUl3 are elem,ents oJ a non-An:him£dmn.
'OO/1UtI field. r.;'ederL Akad. \\'etensch. Verslagen. Afd. 8tmnkunde 53.
381>-399 (11144). (Dutch. EngH.h SUIImUDy).
7. Sur fes Wl]1ll£eS linlai'l'u norrnh. I-VI.
I. N.derl. Akad. \V_h., Proc. 49. 1045-to55 (19461.
II. ibid. 1056-1062 (1946).
lIl. ibid. 1134--1141 (1946}.
IV. ibid. 1142-1152 (1946).
V. ibid. 51. I97 210 (1048).
VI. ibid. 52. I51 I60 (1949).
8. E8pa£f!s I:iniQiru d vue mfinitt deoonabmbh- de €OCi'I'C!r»Inh. Nederl_ Akad.
Wetensch.. Proc. 58, 1548-1559 (1050)_
9. SUTURe cla88e d't8pon.liRiairt'.S 1Iorntoh. Nederl. Akad. \Vett"nscJ.. Proc. 55,
513-525 (1952).
Montroll. E. \V.
L hllJ1'1rof1chains. JViene7 i . and quaxIzmIlheary_ CoIT1JI1. Pure Appl.
l>Iath. 5, 415-453 (1952).
Moore. E. H.
1. .lntrod.ut:tion to a form (JJ g.tnt:nrl rmnlyBi8_ The New Haven lUath_ Collo-
Quium of the Amer. Math. Soc., UOlt
2. cll " I. II Mem. Amer. Philo!S. Soc., Philadelphia, 1935,
1939.
Moore, R. L.
1. FoundationB 6/ pciRI Be! Ihtory. Amer. Math. Soc. Colloquium Puhlif)ations.
vol. 13, New York, 1932.
Morse, A. P. (.Bee also Adams.,. C. R.. Agnew, R. Po, and DunfOl1l. N.)
I. A theory oj I:Overing and dJU . Trans. Amer. Math. Soc. 55,
20.'<-235 (1944).
Morse, fl...
I. Bilin«lr ftmdimwls Duer C X C. Acta Sci. Math. Su-...red ]2. Pars. B.
41-48 (1950).
MOrsc, M., and Transue, \V.
1. FanditmalB oj boun(kd Frhhd uarialion. Canadian J. )Iath. I, 153-165
(19-49).
2. hnclionab:F bilinear over the product A X B oJ two pseudrJ.n(mn d
utdOt . I. IL
I. Ann. r Math. (2) 50. 777--815 (19-49).
II. ibid (2) 51, 576-<114 (1950).
$. Lnkgm/ 'Tep1Uf!l'dalicnfJ vJ lriUfiear JWJCIimmis. Proc. Xat. .\cad. Sei. U.S.A.
85. 136-145 (1949).
4. The Unaali:utl Frichtt variation and Rksz-}'llU .HQWJdQrJJt!Jpe .
Rehd. Cire. 1\Iot. Palermo (2) 2, 5--35 (1953).
79Q
REFERENCES
ItEFF.RE CES
791
Moser J.
1. StOril" 1£ des konhn.ilTlit.'hen SpeklTU'B'&S JUT 1idte DiJjnrnrinl-
glei.dm,gt''' ::.wrila Ordrwng. Math. Ann. 125. aG6--S9.'I (IPSB).
M05(' H. E. (see Kay I.)
MosJtcn.ib., D., and Dines, L. L.
I. C ly in a linear spoc€ TriM an iJiner product. Duke I\latb..1. 5, 5
(J089).
2. On the mpporlirrg-plant pmP£f1Y oj (J rortt"t.I:' body. Bull. Arner. Math. Soc.
46, 48"..---41!9 (II'40).
MUill'(le. M. E.
1. Ab8om und l.d'lrotulitirmal oCOlIl't' in lltmudt Bpan1l_ Duke Math. J. 13,
351 65 (1946).
2. .Introduction to rnm.sun' and intwation. Addison \Vesley. Cambridge,
Mass.. 1953.
3. A nolt' en 'lNtlJ." di[ftw'l1tioUlity ()f Pttti, ihlt-pnls. Dllll. Amer. Math. Sor. $2..
167-174 (1946).
4_ A M'Wtld "Gte (111 rorok difftTadiability vJ Pt:UiB inugrols. BuH. Amer.
:Muth. Soe. 52, £68-670 (1946).
Miintz, Ch. IL
I. Ober dtn Appmrima sat: van Wl'i . Math. Abhandlungt>n H. A.
Schwarz gewidmet. .Berlin, 12 (1f114).
1\Iut't'a.y, F_ J.
I. On amlplfJUnlcJ.ry manifolds and proj«tions in 8'pt1aS L,. and I". TrAns.
Amer. Math. Soc. 4\, )88-152 (1937).
2. QIJU8i-amr.plemmts and closrd proj«lions in".fl BQftQCh ¥JRVf'3. Trons:.
Amer. Math. Soc. 58? 77--95 (1945).
3. The a oJ linear 'nJm!ormatU:mR. RuU. AmeT. Math. Soc. 48. 76-93
(1942).
4. Linear trtmsJotma1i.oltt lxfuHtl Hilbut sptlf'f7 and th o.pplicution oJ 'his
throry to limar partial diDermtlal rf'tJI'atiOM. Trans. Amer. !\lath. Soc.'. 37.
301 58 (1005).
S .1...inmr trt.m.sf in L:p. P > 1. Tram _ Amer. :}'Iatll. Soc_ 39, 83-100
(1936).
6. Bilinear trrrmformati9fls in Hilbert spact. Tn,r1.<5. Amer. Math. Soc. 45.
474-507 (1""9).
7. An 171trOOaditm fa lirlfflJ' l:ro1Is.fu'rtrlatiaml in l/i/berl. spar: . Ann. or )'\.latl1.
Studies. no. 4. Princeton. 1941.
Murray. F. J.. and von e'.&manll. J.
I On ri"lJl' .J oJl<"Ult#>, I, U, IV.
I. Ann..1 Math. (2) 87, 116-229 (1936).
U. Trans. Amer. :r.1ath. Soc. 41. 208-24K (1'937).
IV. Ann. of )lath. (2} 44. 7]6-SOK (1048).
M Tno.. S. B.
1. Equ.kcmtinlJOUs Bets o} mappings. Ann. of Math. (2) 47, 496-502 (1'946).
2. lJanaeh Ii.patTfl GJ CORIi'nuFIW' /UfJdiCMS. Ann. of Math. (2) 49. 132-148
(1948).
:3. Spa«8oJl'OO'inIUJ'MSJundiutd. Hun. Arncr.l\lath. Soe. 55,402-407 (194rJ).
4. l\()T71Ied linear span!S oJ continuous fn'K1icm!. HuH. Amer. l\Jath. ()('. .1'6,
233-2-U (::t950).
Sachblll. L.
1. On t.he o.xiom oJ'he flQ gt"Ut. ces in Qme linfflr lnpolngiCYll R]'1Qa>.
HE'Vista UniOn Mat. Argmtina 12, 129-150 (1947). (Sp8ni h. Freu.:h
summary).
:0::. A dtaruderi:aliQn ()J '"11(; lIormed I1reWr ardt7UlJpaces oj ronn1/.UQU$ ftaJdWlCl
(1f'f7 f1. COlftpad space. Amet4 .To. Math. 71, 701-7US (1949).
:3 A thnwvrr oj rhe Rahn-lJo.nam lype Jar 1iRi't1r 'rlJR.s!cTmalions. Trans. Amer.
Matb. So<-. 68, 2I<--4G (1950).
Nagata. J.
I. On lultices oj !Id&ctiat'ui un t.opalugiooJ Gpaa!t and of fuUdioos on unijoTfA
. Osaka MaUL J. I. ]66-]81 (]949).
XagW11o M.
I. EiR U o.70cdytische Vnkrsw:;hungen in linmR'n mrl.risclwn RillJ!Oi. Jap..J.
Mat11. 13. 61---80 (. 36).
2. INWU vI mo.pping in 001Itv:;r lillftlr to irol3plKes. Amer. J. l'tIath. 73.
497-5II (1951).
3. ChafflClniskrv. dcr lJl lntta kklidiaden RliUrne. durch ine Postulate
fur Sdnm-fYUnA-tP. Jap. J. Matb. 12, 128-]28 11936).
XSJQ.'. B. von Sz. - (see under Sz.-l'agy).
Naimu.rk. 1-1. A. (see IQIlder Kemnark)..
Xakamura, 1\1.
I. ...'\'ofes on lJaMch tqIlJ('f:. X. Vitali-HIl1&n-Suf.',,,. theurnN and K-spaces.
T6hoku Math. J. (2) 1. I I-108 (1949).
2. Noles on Bant.lClJ space. XI. Bo.nflt"h lathot'! mi1h pasi!ivr: btbeli. T6hoku
Math. J. (2) 2, 135-141 (1950).
R COf1lpktt wnlinuilio oJ li"wr operulrm.. Proc. Japan Acad. 27. 7
(IB51).
Nakamura, l\I.? an.d Sunouchi. S.
I. .Note on lkmoch spaff (IV). On a Wrn1ll.JKlfttian oj additive sd!lI.lIcfiom.
Proc. Imp. ..\cafl. Tokyo 18. 333-335 (1942).
akamura l\L and Umegaki II.
L A t'tmLlrk on tkrot'OHli ()J Slvne and Badtt&et'. Proc. .Japan Acad. 27. 506-atri
(1051).
Nakano, H.
I. Top61og" and linenr lLrpoItipical spatT . i\lan17.en Co.. Tokyo? 1951.
2A ...'Uoo,daTfil sotli-tWdt>R'tl linear spllCf's. I\laruzcn Co.. Tok} I. 1950.
:-1. Ri€xz-Fiulterscher Sa!z im normle1it'1i kilwei<re Jfadul. Prop.
IIf1(J. Acad. Tokyo 18. 350--353 (U)4.2)_
4. ("ber Envl1lntlngrn t'fIQ llllgtmein Uilweia! ,;'tlodulu, I. Proc.
Imp. AcaoL T. -o 18, (1942).
5. iJber EnveiteruRgf'n I.'em allgemefn kihDeise gt'OI"drukn lItodv.ln. II. Proc.
Imp. Acad. Tokyo IV. 138-]43 (1943).
u. . lodu./b;tffi lin aT kJlUL'€B...J. Fac. SeL Lnn.-. "O. Sect. I. 6, 85-131 (19S0).
7. Zur EigenU"el'"tthfarie flof'1IIakT OpnaIoun. Proc. Phys.-l\1ath. Soc. Japar.t
(3) 21, 315--339 (1939).
H. t"bcr Abelsche Ringe von ProjddiQll3flperul(W('t1. Prof:. Ph 's.- :lath. Soc.
Japan (8) 21. 357-575 (1059).
O. UniMrirmarianlt: h1flKTll'arimale normale Oprmloren.. Ann. of Math. (2) 42.
ti57-664 (194]).
792
REFERENCES
REFERENCES
793
10. Unildrint'lf21'innkn in «l1gMnrinen EuklUhw:hen llaum. .Math. Ann. 118"
112-133 (1941).
II. F.nktivnen hypnmarimalw tim"r1takr Operatvrm. Froc. Phys.-
)'lath. s.K". ..Japan (3) 21,. 713-728 (1939).
12 lUodern sp«fral tbtt>ry. faruzen CC). TQkyo, 1950.
IS. Spedml theory in the Elitbat apa«. ..Japan Soc. fetr I"romotion of SeL,
TokJ-o, 1953.
14_ Ober 1ID1'm lriIwrifle MtJduha. Proc. Imp. Acad. Tokyo 17.
811-317 (1941).
15. Strtigt! Fvm.k.tWnaU auJ dun geOf'dntk Vodul. ..Y. Fae. Sci.
Imp. Univ. Tok).... 4. 201-382 (1942).
16. Owein lin«rre FunIditmal #lUJ den teilrveisr gmrdndm ..'t1odu/. Proc. Imp.
Acad. Tokyo 18, 5408-552 (1942).
1'1. Vbu tkn Bnreis des Strmt'Schen Satus. Ann. of A1ath. (2) 42, 665-667
(1941).
18. RedIldi01'l oj Bochner's tht!owm to StQf1e'S theorem. Ann. of Matl1. (2) 49.
271>--280 (1948).
Nakayama. T. (see Yo.sida. K.).
Nathan.. D. S.
J. Ont>-parometer grotlpS oj tm:I:uljormntiorlB in GbsIrod vedm space.'. Duke
MBth, J. I, 518-500 (1935).
Ne'igauz, M. C.
I. 011 the drlemtioorim oj lhe ""havi", oj a ftm£lion q("') by the
properti<'B oj Ill< "1'eTaWr --11' + q("')y. DoIdody Akod. Na k SSSH (N. S.)
102, 25-28 (1955). (Russian) Math. Rev. 17, 370 (1956).
"eimark. F. A.
1. ErtmsKm oJ a Hermilian operatqr ro one rmllrtJble with a given Humitian
<>]J<'akJr. Doklody Akad. NBUk SSSR (N. S.) 66, 9-12 (1949). (Russian)
Moth. Rev. II, 371 (1950).
NemyBW. V. (see NiemyIzki).
Neumann c.
1. Unkrsud.i.1Jf'J#n i1her da3logo:rilhlniM find N Puknlinl. Teubner
Leip>jg, 1877.
von Neumann. J. (liee also Bochner.. K. 1Jevinatz, A.. Balmos t P. R., ..Jordan. P..
and !\(urray, F. J.).
I. On Icpofogitul spacu4 Trans. Amer Math. Soc. .37, 1-20
(1935).
2. ZUT Algebra der i.onrn und Thef1Tie 4er Nortfttllrn Optra-
I()Tt n. Matn. Ann. 102. 870-427 (192G-I030).
S. Eine Spdrtmlth!&rk jur allgemeine Operatoren rims uniliirrn .
tath. Nachr. 4. 258-281 (IDS!).
4. .Functional operators, I. Annals or Matb. Stltdies no. 21 , Princeton Univer-
sity Press, Princeton, 1950.
5. On a cerl4in tvpvlogyfor rings ofojHralOTS4 Ann. otMath. ('2) 37, UI-1l5
(1936).
6. ChamJ."teririrnnrl!. des Spektrums dnt$ Intt>gmlapau1nTs. Act. Sd. et Ind.
229, Pam, 1935.
7. Allgemeine Eigenmntthcorn: Hermiletrchf.T Funkti01tl1.Ioperalortn. )Iath.
Ann. 102, 49-131 41929-1930).
8. Ma1helnalisdu: I1<grlJmhmg del" Qrumlmmeot:hnnik. Nacllr. Ge.eU. Wi...
Gottiogen. l\tr.th..Phys. K1., 1-57 (1927).
9. .4lmod periodic ful1diORS> in a group, I. Trans. Amer. Math. Soc. 86,
445-492 (1934).
10. ObeT dneu Sal% vim Berm :1. H. SW . Ann. or Math. (2) 33, 567-573
(1932).
11. PTooJ oJ the lJuasi-ergodic h . Proc. Nat. Acad. Sci. U.S.A. 18,
7!>-82 (1932).
12. Zum HQ(ll'$c1u!n ltlfl&s in WpoIogisdIm Gt1qJ Compo Ma.th.. I, 106-114.
(1934).
13. 011 ring, oJ ope7flI<Jr8, III. Ann. 01 Math. (2) 41, 94---161 (1940).
14. On B/mle I!J of ope1'alor rings. Ann.. of Math. (2) 44,
709 715 (1943).
IS. On rings oj oprratrn-s. R€dJtdi<m 1lI<0ry. Ann. 01 Moth. (2) 50, 401-485
(1949).
16. V".,. ""j",, F.mktionalopendmm. Ann. of Moth. (2) 33, 294--310
(1932).
17. The UlWJKDU'B8 oj HOaT's measure. Mat. Sbornik S. S. 1 (43). 721-734
(1936).
18. Vber Funlrtionn: van Fimkti.oollloptl'tl.loren. Ann. of Math. (2) 32, 191-226
(1931).
19. EiniAe S(Jtze abu .AbbiltfuRgrn. Ann. or :'1at11.. (21 83. 574--586
(1932).
20. XUT Opemtort in dt-r Jcl.asRi.sdIn M«hanik. Ann. of Math. (2) 88,
587-6402,781>--791 (1932).
21. AlgdmIiBche Repriisadanlen der Punlttioom .'w auf ei" lttnlg vom MfMse
Null.II..T. Reine Angew. Math. 165. 109-115 (1081).
22. On an /IffieI'OlizatiDII oJ .he qwmh<m mechoniall JOT11IQI- I.
Iat. Soornik 1 (43), 415-482 (1936).
23. ltlathnnalische Gnmdlagm 4er l'Itedl.a1J.ik. .I.. Springer, Berlin. 1932.
EDgIish translation, Princeton UniV'. Press, Princeton, 1955.
24.. Appmrimalim oj matr'i.t'e8 oj high finite order. Port. Math. 3,
1--62 (1942).
NeumaTk (Nai'rnad:). 1\1- A. (flee 8180 Gelfand. I.)
I. Poritit1t tkfitliU opnaror [unctions on a romrrwltJlioe group. Izvestiya Aknd.
NBuk SSSR 7, 237-244 (1943).
2. RI'. oJ op€rntors in llillKrt space. Uspehi Mat. Nank (N. S.) 4, no. 4. (82)
B3---14.7 (1049). (Russian) .Math. Rev. II, 186 (1950). German translation
in '.Sov.jetiscl\e Arb€iten zur Funktional-analy5is " VerlHg Kultur und
Fortsc:h.ritt, Berlin. 1954.
3, On a nwtif#l. oJ additive tpen:ilor sel Jum:fi.ong. Doklad,:,- Akad. Nauk
SSSH (S. S.) 41, 85 61 (1943).
4. On,he dLficinu:y inde.r oj linear diJferm1ial opt'f'(ll.t'Jn. Dokla.dy Akad.
Nouk SSSH (S. S.) 82, 517-520 (1952). (H.........) fath. He\'. 14, 277
(1953).
5. LinMr diJf 6peramD. Gosuda.rstr. Izdat. Tehn..-Tec>. Lit,. Moscow,
19.54.
(I.. On '1I 6f{'£Q1T fJJo. closed synmlelric op r(1tar. Doldad ' Aknd. Xauk SSSR
fX. S.) 26, ROft---870 (1 40t ibid. 28, o7-2i'8 (I9 O).
794
REFERENCES
lU:.-FBItENCES
795
7. Selj-tldjoinl f'OI."ktI.SiOnB of tJ a;et'V1Uf kind vJ a :rymmelIV operator. Iz ya
Akad. Xauk SSSR 4, 53-]04 (1'94(J). (RmMan. English !iummary) Math.
ev. 2, 104 (1941).
8. Spn:tml/undion.<: oJ a symm-rw 6ptTClttJr. IzV't.'StiYB Akad. Xauk SSSR
pl. S.) 4, 277-318 (1940). (Rmsum. Engfu;h ,,,,,,,,,,,,,'j Math. ev. 2,
105 (1941).
9. On Ih spednfrl, ollJi"IRldar no-u-seU-adjoin, d;gerf'nlifll operatntll oj the
Bff'OIK! order. Doklady Akad. Nauk SSSR (N. S.) .85. 41--44 (I ). (Russjan)
1Jath. Rev. 14. 473 (1953).
HI. :J1I'NStigqtirm oj 1M sptrlrllm and expansion in eiUuJundJom oJ singular
non-rlf-udjmnt difff"n'I'Jtiol QpeTGIo vIOle second order. Uspehi Matern.
N'auk (X. S.) 8. no 4. (56). 174-175 (1953). (H Il) !\Jath. Rev. 15.530
(1954).
II. On e;rpansion in IC4arucIn1w fvm1wn£ vJ JloJt-selj-adjomr sittgllll11' difft:TeA-
rial tI tT1IOt"s tJf "w OTd T. Doklady Aka-a. Sauk SSSR (N. S.) 89.
213.--216 (1953). (Rus!Iian) Math. ev. 15. 83 (1954).
12_ IIft oj 'he sp«lntm aud the upaRstOO in eig€hJ.nttiOWi oj a non-
8elf-tu1jtrin. opnmor oj t} fft'rond Qrder on a 3tmi..a.ris. Trudy MOiIkov.
:\lat.Oblit. 3, 181-270 (1054). (Russian) .Math. R . 15, 959 (1954).
Kewton. R. G.. and Jost. R.
1. Th Qn vJ potmtialE from ,lu: S-'liUJm:r for sgsIt'JIU oj diffrnmJ.ial
rqUlJIi&n.t. 11 Nuovo Cinwnto (10) 1. 500--622 (1'955).
Xiroltsnl. M.
I. On the <criterion vJ rom]HJdnl>ss oj A. KD/mogorw. A....ad. Repub. Fop_
ROmane. Du1. 8tL &or. ?iotat. Fj . Chim. 2. 401-41.5 (1950). (Rouma.nian.
RU8Sian.and French summaries). 1Uath. Rev. 13 357 (1952).
Xiem)'1:zki {Nem)"tlai), V.
1. The rttdIIod oj fWd points in mKJ/yttiJI. l:'spchi I\Intem. .r\auk I, 141-174
(1936). (Russian).
2. Prohlnru oj the qvoUtnrive thtuty oj diffr.re.nJiui f!qualiQH$. Vmnik M()skov.
U",jv. Ser. Fil':.-.:\Iat. :&rt:.e5t. 'lauk ]9.52, no. 8.. 1 ---,:J9 (1952). (ilussian)
Math. Rev. 14" 758 (1953).
Xikodym, O. 1\1.
I. llDrtarquu sur 1£. intigroles de Stiellj s ». rnnnt'orion m-a= ce fk Jt,l1U.
lfDLlo" d Frtdid. Ann. Soc. Polon. }Iath. ]8, 12-24 (1945).
2. Sut ler,johdirmn£'lleslir.lIfaiTet;;. C. R. Acad. Set Paris 229, 16-18, 1£9-171,
288-289 (1949).
3. R€l1KlTt[I«3 Bur la psnu1D-IO}JQlogie et sllr US jvnttimltlellcs lineaires. C. R.
Acad. Sci. Faris 229. 863---865 (1'949).
4. Un tU.lUf-,...l appt#ril matJuilaahqu.f' pour la des fJIlClnta. Ann. Inst.
H. Poincare 11. 49-112 1949).
5. Sur le.'l Jt.lFRilks bornffs dt fUfldiun:J parfllWIIIE'nr additif'U d'l:'WItmble
ab&tmit. \Ionatsh. fur }Iath- u. Phys. 40, 41 (1933).
G. Sur ks 1iudes amtVrgentes de fonttinrw pa"Jait lnnIt addllive. d' mble
aWrait. )Jonatsh. fur Math. u. Ph}oo;. 40, 421-----432 (1933).
I. SUT lesfow:ti0n3 d'e11It07lbln. C()'IIlptes Rendus du I Congre..; de;;. Iatlt. des
Pays Slaves, "-arsa\.\.. .304--313 (1929).
S. SilT nile ghriraIiaution dt's IlJligmlt'8 de 111. .1. Radun. Fund. Math. 15,
131-179 (1950).
9. Cuklribution Ii la thmric des Jnnrticmnellts lil2m;rflI en c(jn iUII avec 14
t"- m la 1IIf"-'lUr'- dell erl$('mbla ah:dmits. Mathematica, Cluj, 5. 180-141
(1931).
10. Sur I R optmkun nomullu ma.ximauz datu; l'e.spGce hilbrrlien #Jipamble d
l'-omple.t, r, II.
T. C. R. Acml. Sci. Paris 288, 1878-1375 (1954).
fl. ibid. 238, 1467-1469 {19541
ikol'skJ.i, V. N.
I. 11...81 appm.rimulion and ba!ri'l in a Frkhd spat:e. Doklady Akad. auk
SSSR ( . S.) 59. fi3'9---G4.2 (1948). (Rm;sian) Math. Rev 10. 128 (1949).
2 Lin«n' etpudWras in nomtf'd linenr spac s. 1z\.'t'5tiya Akad. al1k SSSR 7.
147-166 (1943). (Rrn;sian. Eng1ish 8UIIlfDBI)') I\lath. Rev. 5, 187 (1944).
:Sikovic. I. A.
I. On 'he Fredholm series. lloklady Aka<!. :Suuk SSS}{ (N. K) .:iD. 4.23---.125"
(1948). (Hmsianl ntatb. ev. 9, 92 (1948).
jren1Jerg, L.
I. Remurlc,; on nrvngly dliphC parf'-al diffffelltial np.urti . COITIIIl. Pure-
App1. Math. 8. 648-674 (1955).
It.s baum. A. E. (see Devinatl':. A.)
Nyman, B.
I. On the one-dimffl8irmal h'uhJtdioll gmuJJ flnd N"Mi-group i n certain/unction
s. ti()n. University of Cppsala (1950). :\'Iat],. Rev. 12, 108
(195J.).
Oga."W.wara. T.
1. Compact mt'lric BooUaJl mgronlil and t'I(. IrJr lattiN#:. L .sci. Hit'O,,-irna lJniv.
Ser. A. 11. 125-1 (1942).
2. On PI'u.hd lnllic"., I. J. St.;. Hiro irna Uniy. 8('('. A. 12. '235-248 (1943).
(.Japafil"'s€) "lath. Rn'. 10, 544 (1949).
::3. Rmmrfur on a untOT lattiu VJith a mt'lrU.- funclion...T. Sei. Hiroghima L'ni.v.
Ser. A. 13, 317-325 (1944). (Japanese) .:\iath. Rev. 10, 54.4. (1940).
4. Commutmimty of A-nhif1l detlH Sf'mi-ardnl>d gnlUps_ .L Sci. Hirosima ITniv.
Ser. A. 12. 24Y---254 (1943). (.JalJaDesf") Math. Rev. 10, 544 (1949).
5. Thl'Ol1J oJ r«tor lattins, I, II.
I. J. Sci. HlI'osima Univ. Ser. A. 12, 17-35 (1942),
II. ibid. 12. 217-234 (1943). (.Tapanest') Math. Rev. ]0. 3-L.'i (1949).
6. Some un ral throrntls and ron.L Iheornns it! t"frlnT laltitc.oIO. .1. Sei.
HiOO$Wma Univ. Ser. A. 14, 14-25 (IMO).
7. (J'1 the intt'prat repJTBCJJ.tatiCM oJ rtnOOul'idetl self-adJvint transfol'mcrtiIJ1I-'Il.
J. Sci. Hiroshima. Univ. Scr. A. 6. 279-2131 (1'936).
Ugasawara. T., and Maeda, I".
1 Representation lJ/f.lU:btTia1l.iees. J. Sci. Hiroshima IJniv. Scr. A. 12, 1'1-33
(1942). (J.apafil"'se) M.Jtth. Rev. 10, 544 (1949).
2. RmtlJ:t"k$ un T p1l'st:1l1ali.oa ofvetWr lattm. .T. SCI.lIll'Os1,ima t"niv. Set". A.
12, 2]7-284 (1934). (Japanese) Math. Rev. w, 59-1. (1949).
Ohira. K.
I. (hJ a cntnin cQ-mplete. sepnrable ,wd rPldric 'iputY. :\Iem. Fac. Sd. Kylisyil
Uni",. A. 6, 9-15 (19:il).
2. 0tJ smne c:hmacfoiootion1l of aIMtnJrt F.uclitft>an spaces by propt'TtU's (I
ity. Kumatnoto J. 8(=i. Ser. A. I, no. I, 23- 6 (195Z).
796
REFERENCES
REFERENCES
7g7
O eill. B.
1. Esst:Rtial sers andJi.rrd points. l\.Iner..J. Ma.th. 75, 497-509 (1953).
On<>, T.
I. A gtmemlizaIion oj the IJa1m-Bunach tIteo1rm. Nagoya Math. J. 6, 171-176
(1953).
Orihara 1\1.
1. On 'he fTgUlar veclor laUice. Proc.lmp. Acad. Tok,)'o 18. 525-.529 (194 n.
OrliC%. \V. (see also Alexiewic J A.. .and l\Iaz;ur. S.}
1. Vber "nbtding! K in Funktimml.urr . It II.
I. Studio fath. 4, 3&-37 (1933).
II. ibid, 4, 41--47 (1933).
2. Vb... k<mjucint< &l'o",..;tmforg",. Studla Iath. 3, 200--2II (19311.
3. Ober rim gewisst Klas$t von Raumm uon TypU3 11. BldJ. Int. Acad. Polan.
Sci. 8er. A" 2()7-220 (1932).
4. Ein SuIz r1.bu di El"'ltXilt.Tlmg [.'011 linroren Opemtima.m. Studia Math. 5,
127 14<) (1934).
5. SUT Us opimtions lmiaires datt8 l',..spua tk3 I bornks. Studia
"ath. IV. 60 89 (1948).
6. Linftu vpwtltlQWJ in Saks spaces (I}. Studia Math. 11, 237-272 (1950).
7. Vber Fo1gm liltPa:ru Opemti die tlQI1 eincm Parameter ab/u'inwn.
Studia Math. 5, 16(}-I70 (1934).
8. 'BritrtJ.D zur Throrit der 0rth0g01UllenJmicl,:lunt,rn. I-VI.
I. Studia. Math. I, 1-39 (1029).
II. ibid. 1, 241-255 (1929).
III. BuJJ. Int_ Acad. Poloo.. Sci. &r. A. 8-9, 22Q-238 (11132).
IV. Studio Math. 5, 1-14 (lOa.).
V. ibid. 6. 20--"8 (IOa6).
VI. i"id. 8, 141-147 (1 39).
Orlov. S. A.
1. On thr index oj liRoor diJJ niial opnl1tms. Doklady Akad.
Nauk SSSR (N. S.) 92, 463--486 (1933). (Ru.-oian) Math. Rev. IS. 802
(1954).
Owchar. M.
l. Wiener ihtLgmls #]} nwltiple varia.,iQn3. Proe. Amer. Math. So£>. ::t. 459-470
(1952).
Oxt<Jby, J. C
I. Ergodic 8tl8. Bull. Amer. :Math. Sor. 58, 116-136 (UI52).
2. On the ergodic theorrm 6J Rur.ewicz. Ann. of Math. (2) 49, 872---884 (UI48)
3. .Invariant mt'a8t.UY"& in J1rrMPS mhich au not locally compact. Trans. Amer.
Iath. Soc. 60. 215--287 (19406).
4. The cat oTY and BQrd da.'iS 01 r.erlain ()J L,,_ BuH. Amer. Math. Soc.
43, 245--2<8 (1937).
(h:toby. J. C.. and L:la.m. S-
1. On 'lie rorislma 01 a ftc£'fI8UU' lnva-rian, tltukr a trorntllJt'matuDL Ann. of
Mati_ (2) 40, -"'00-566 (1939).
Pais, A. (see .Jost, R.)
Paley. R. E. A. C. (see also Littl ood.. .T.)
1. A proof oJ a ,I,C'Q7em (in bilinulr fomls. .J. London 11ath. oc. 0, 22fi.-230
(1931).
2. A fiO on bilinea7 jOT'7M. Bull. Amer. ,Math" Soc. 39, 259-200 (1933).
8. Some Ihrorans on urIhogonal Studia Math. 3, 226--236 (1931).
Paley, R. E. A. C., and Wiener, N.
1. Fourin in tM. rornplM doIaain" Amer. Math. Soc. Colloquium.
Pub. 110. lfi. New York. 19M.
Paley, R. E. A. C., \\'iener, S.. and Zygmund, A.
L NQ 3 on mndom: Juncthnu.. Math. Zeit. 37, 647--006 (1933).
Parker, \V. V.
1. Lintils to Ihe l'hamdnistU: roots (JJ a ....atri.r. Duke }Iath. .J. 10, 470-482
(1943).
Pauli. \V.
1. f son 11u!ory oj nuclear !C1rCU. Interscience Pub., Sew York, 1046_
Pea.no, G.
1. Ink per sene chllt i diJfere'll2iali linearL Atti R. Ace. Sci.
Totino 22, 298--802 (11387}. German tmndation in rwlatb. Anl1. 32. 45{)....456
(1888).
Peck, J. E. L.
1. An r:rgodic I}umrem fqr a tatWe semi-group oJ Ufuar Operat0T8.
Proc. Amer. Math. Soco. 2. 414--421 (1951).
Pete:r. F., and 'Vey). H.
1. Die V(iltstdndiglreit tier pruJtuiv£n l1w11teUwtgen einer /?f!SChlosserwn kana
'inuimklwn Grnppe. M.o.th. Ann. 97. 737-755 (1927J.
Pettis. ll. J. (see also Dunford. N.)
1. A nok' on regular Ban<u:h tip(:l1tt-s. Bull. Amer. lI-lath. Soc. 44, 42{)......428 (UJSS).
2_ A proof that every uniJurmly CVIWl"..1' space is r£jlaitx.. Duke Math. . 5,
24D-253 (ID89).
3. Rnru:uIts on a thecrmt. oJ E. J. McShane.. Proc. Amer. Math. Soc. 2. 1186-171
(1931).
4. On iflIqmtiun in vtclQr 1pact"S. Trans. Amer. )1ath. Soc. 44, 277-304 (1938).
5. On oontmu.ily and ;kg of hmrtvm.orphisms in tvpQ/ Ml gmtlpR. Ann_
of lath. (2) 52, 29&-308 (1950).
6. Absolulelg amlinuO'Us ftuu:ti0fUJ in V€clor 1pOU8. (Abstract} BulL Amcr.
rnth. Soc. 45, 677 (1939).
"1. Din ali01l in But'U1Ch . Dukt ,Math. ..I. 5. 2M-269 (1939).
8. Linear IrmdiOfl(lls and comp/PtFly addI'hrot' sel fandionf;. Duke Math. .T. 4,
[i5 (1938).
Phillips, R. S. {see also nochner S J
I. On 'itWlkly rot'IIplNt svhsdR oJ (1 BllflhC'h tptlff. Am r. .1. futh. 65, 108-136
(1943).
2. A oJ ElIditkan space3. Dull. Amer. Math. oc. 46, 930-933
(1940).
3_ On Iwror tmns[OTIJIllJimu. Trans. Amer. Ma.th. Soc. 48. 516-541 (UI40).
4. A note vn ergodi£ thefJry. Proc. Amer. Math. Soc. 2. 662-4169 (1951).
5. Sprdral fltecry for semi-groups of limar operators. Trans. Amer. [atb..
SOC':. 7]. ag3-4I5 (ltJ51).
6. PlT'tUrbatioo tlu!(Jry 1m semJ.-groupr oj linear opnaItJt'S. Tran . Amer. :\rnth.
Soc. 74, 199-221 (1953).
7. Inll!grnJUm in a CORlT.t' linear tfJpoItJgical space_ TmJ1!J.. Amet'. 11"tl1.. Soc. 407.
))01.-145 (1940).
.
798
REFERENCES
REFEREXCES
799
8. On one parruneln Sl'mi..,,-oup3 oJ linear inmsJorJR.azicns. PrO(!. Amer. :Math.
Soc. 2 234---237 (1951).
9 Settti-graUJNI of 6pn-aton;. DuH. Amer. Math. Soc. 61. 16-33 (1955).
10. An illtJeT.nM formula Jor Laplna fransfOl'1f'lB and semi-groupg oj t;ftffir
opemk>n. A n. or Iath. (2) 59, (1954).
1J. The adjoint semi-group. Facifie .J. Math. ii, 269-288 (UiS5).
12. A dn-omposition oj addiritoe Bel funtJ;oJU_ :Hull. Amer. Math. Soc. 46.
274--277 (1940).
13. Linear rmIinnry diHfff'1Itild rJ} the xrontJ onkr. Di,-. EleI:-tTomsg.
Res_. Inst. Math.. Sci.. New York Univ.. 1952.
Picone. M.
L Sui valuri l!m:Zimaii di un paramdnJ da cui dipoJde un'f'IjIUl::i01U' diJ/ ren-
zialeddarror.ufvvrdi'lle.Ann.R. ScuolaNorm. Sup. Pi (I) 11,1-141 (IDlO).
Pierce. R.
I. Conn and the duumposilinn o} lunctiooals. Math. Mag. 24, t 17-122 (1951).
Pincherte. S.
1. PunktionalUJN7a1irmen NRd -Gteic1run ,.". EnrykIO] de:r Math. \VIBS.
II A n. 761-817 (1'905}. }'rench tran 1alion: iol1s d vpirot;ons
J<mctitlfmdks. Ene. de.. IK"iem:es math.., II, Vn!.. 5, lase. t, DO. 20, ]-86.
Pinsker, A. (see also Kantornvitch. L. V..
I.. OnadaBSlJJopt'1V1iunsinK-spIU'l'\'I'i..Doklady Akad. aI1k.sssR (S.. 8.) 36.
227-230 (1942).
2. On nrmedl{-3fKllYJS..Dok1ady Akad. Nauk SSSR (N4 S..) 23,12.,,14 (1941).
3. UnWen>a1 K--8pUffE. Doklady Akod. Nau" SS8R (N. S.) 49, 8-11 (1945).
4. On Ole dectmipodtion oJ K into ('lemodary spans. Doklody .Akad.
::IIauk SS8R (:'ol. S.) 49, I6B-171 (1945).
5. On 8f'pardik J<.-ttpf«'fs. Doklad)' Akad. Nauk SS..<liiR (:"IJ".. S.) 49, 818-819
(1945).
I). (.'ompleldy linear [1lJU'tiontIk in K-spaa..,. Doklad)' Akad. Sauk sssk
(N_ S.) 55. 299-302 (1947).
7. On rontTrlf' upramtatimt8 {If lilll'aT semi nkred spaas. DokJady Akad.
Xauk SSSR (N. S.) i;5, 37G-38I (1'947).
IYrtt. H. R..
I. SrHIf.e genrrali¥llifPJ.$ vI the ergodk throrem. Proc. Cambridge Phil. Soc. 88,
325--343 (1042).
PlanchereI, M.
I.. In lrJ"""1l'lh"'.grn 'Imllktlrliche:r Fank'lifJWn. :\Iath. Ann. 67, .5]1}---.534.
(11'09).
Plr.'iSDcr, A. I.
1. Coo halbuni/iiN Opern1oren. UokJady Akad. :Sau'k SSSR (X. S., 25,
710-712 (1989).
2. SpnIrallk&Jty of linear f) , I.. Uspchi Mat. Xauk 9. 3-125 (1941)..
(Russian) Math. Rev.. 3, 210 (1942).
Pl€S!111er, A. I... and Rohlin, v. A.
L lIpertraltlworyvjlinearo]H!raWrs,I1.. Uspehil\-tat. aukf .. S..) 1 {1l}, no. 1..
71-Un (1946). IRusgjan) :Math. Rev. 9, 43 (1948).
Poirw."IU'(', H.
1. Sur les grvapes> ccmtiRI4S.. Cambridge Phil Trans.. 18, :t2O-255 (1699)..
Reprint<-d in OeuV'J't"s 3. 173-212.
2. Sur Its €'loolions de la p/l1J$tIP1e mCItlWnwhqw. Rend. CII'C. l\-tot. Palermo 8.
57-156 (18!J4)..
Pollard, H.
1. .Inkgral fmnsjorms. Duloe 1\JHt11. .J. 18. 301-330 (1946).
P6hra., (;.
1.. RrIIUlTk on Weyl's nole "I1iLVjtU1hh£s bdwem the tu.'O kinds oJ t'iperrMlUt"l oJ
a linarr 1rclns/0f"f7I6ticn.... Proc. at. Acad. SCl. U.S..'\.. 36. 49-51 (1950).
Pontrjagin.. L.
I. Topol groUpR. [trans1a.ted by E. J:..E.hmR] Princeton Umw-rsrty
Press, Princeton. It:139.
Poole. E. G. C.
1.. Introdudima to the throty of linf'flT difJt'n:»liul fY}tuzhons.. Oxford Univ. .
]936..
P0t3.PllV, V. P. (see LivAic, M. S.)
Potter R. L.
1. On seIJ-adjrJinl rliffetmtiol equal.cnt3 oJ flu serond order. Pacific..l.. Math. S.
467--491 (1953).
Po r, A.
1. On.'l(Rlf.r applimtif1ll8 vf a dass oj llihrl spatT-s oj functiotUl. Doklady
Akad. :'olauk SSSR (N. S.) 74, 13-W (1950). (Russian) Matb. Rev. 12,
343 (1951).
2. On the spmmofbcurnkdft<ncr;ons. Doklady Akad. Nauk SSSR (N. S.) 57,
755---758 (1947). (Russian) l\lath. Rev. 9, 236 (1048).
3. On the }J«1Ta vJ bottndffi fuJ'ldims and the LapIn« lnmsfoma. l)Qklady
Akad. Kauk S8SR IN.. 8.1 57. 871-874 (19471. (Russian) Math.. Re-v.9.
236 (1948).
4. On same #Rwal iNl'trXiot1 'MltnnS of PlntKhm:ellype. Doldady Akad. Nauk
SSSR (S. S.) 57, 123-125 (1947). (R....w.) Math. Rev. 9, 193 (1948).
5. Sur les €yuah'VftB du type de St«rm.LivllUille et des ftuidWn& patitiLY'R_
])<>kIudv Aknd_ Nauk S88R (N. S.) 43. 867--371 (1944).
6. On rfifi etpJaliuna oj Btu.rm-LifJUl'illt' type on a halj-arfs.. Mat,
8bomik X. S. 23 (65), 3-52 (1948). (RlJE>!iun) Math. Rev. 10,299 (1949).
Amer. l\-1ath. Soc. Translation no. 5. 1950..
7.. On the JtU',hod oj dirming fll.ndionnls 01 f.. G. Krein. Zapi8ki aulno.
IssJe-d. Ins!.. .:\Iot. Ieh. i Har'kov.. Mat. ObSt:. (4) 20, 43-52 (1950).
8. On tM diffnen.lialtflft 0] the ttp«trol frmdivn oj the SC'h1ik1ivlpa eqrwliClf'l..
DokIatly Atwtl. Nattk SSSR (:\'".8.) 79, HIS-IDa lIDSl). (Russian) l'tfath.
Rev. IS, 241 (I952).
Price, n. B.
1. TIlt Ih«wy oj ird ;oR. Trans:. Amer. Math. Soc. 47. 1-50 (1040).
Priifer. If.
I. Neue I/CTlrihltq! dCT Slkna-Lioucille.het'i nhI'idl."t'lu1lf!, stelif!T
Fu1l.ktiOllm. Matb. Ann. 95, 499-518 (Ul26J..
Ptak, V.
1. On comp1ete topdugicallirtror spaces. C't"hoslOV3Ck. Ist. . 3 (78). :1.01-864
(1953). (R"",""". EngIll<h 8ummary) bIath. Rev. 16, 262 (195.,).
2. On (I theurnn oj W. P. _no Studia lath. 14, 276-284 (1954).
3. Weak CQ'l1lpacbl:(" :; in roIItT.£' 'npolDgicallinE'(lr pacr8. Cehoslovack. l\Iat.
2. 4 (79), ]7ii-186 (l1Hi4). (Russum Ithlm.a.ry).
800
REFERENCES
REFERENCES
801
Putnam. C. H. (see also Hartman, P.)
1. On JWnnal oprratDrs in Hilbert fJ . Amer. .}. :MfLtb. 73. 357-362 (1951).
2. On rs oj bounded "*'11rit:e3. Amer. .J. ]'fath.. 73, 127-181 (1951).
S. On the :tpedrn oj commt4lWr8. Proc. Amer. l\lath. Soc. 5. 929-931 (1954.).
4. An application oj spec/ral thwry to a singular Mlcu1ftS oj l)uriatiQM prOOlem.
Amer. J. Math. 70, 78(}-.808 (1948).
S. The dustn spl!c ra oJ lwunded potmtjals. Amer. . Math. 71, 612-620
(1949).
6. An &dUattcm. mtmon irlflOloing a J"J'Iinim"m J17Vx'ipk. Duke J..lath. J. 16.
633---636 (1949).
7. On the. "pedro oj bQurnJury varue problems. Amer. J. Math. 71,
lOB-ill (1949).
8. an isvIakd rigmJandiom aswriataI lrith bGuftdpd . Amer. J. Math.
72, 135 147 (1950).
9. The oomparison oj speclra ng to poImtialf with a bounded d;gt:U'rW.
Duke ]\Jath. J. 18, 261-273 (1951).
10. On the least ltu oj Hilrs equation. Quart. Appt Math. 9. 310-814-
(1951).
n. The Bpf'Ltra oJ (J1WtItu.m-mn:1Jtmiml operators. Amer. J. Math. 74. 311--388
(1952).
12. On '1M unboKlI oj 'he essenUal sptclrUtn. Amer...J. Math. 74.578--585
(1952).
18. A.../firilim ron4iti<mJ&ran ;nfinil< msaet£ 8p<d7um. Quart. AppL Math.
II, 484-486 (1958).
14. On Ih gap in the spectrum oJ the Ilill equation. Quart. AppL I\tatn. Il.
49<H.98 (1958).
15. .Integrable potrntiaI;s and halj-liTl#!. $pt.Ctrn. Proc. Amer. Math. Soc. 6,
2403-246 (1955).
16. On the mntinuQUtl spn:tru oJ Ii.ngtJlor boundnry rolUl' pmblnns. Canadian
J. Math. 6, 426--426 (1954).
17. Note on a limiJ-ptJUil criterion. .Y. LondoI') lttath. Soc. 29. 126-128
(1954).
1£1. NetUsary and liUf/icimt oon4lIicms far the uistmtt oj A:p clra.
Quart. AppL Math. 18, 335--337 (1955).
Quig1ey. F. D. (see Helson, H.)
Rabinovil:. Yu. L.
I. On tM. contin.t.wu..! ikpemknce upon a portl1nder ojlh£ pecrnlJn vJ a k
lineaTirtUgral npUalcr. Moskov. Coso Univ. Ufenye ZapisId 148, Matemau-
1m 4. I8I I91 (1951). (Russian) I>Jath. Bev. 14, 289 (1955).
Radon. J.
1. 000 Um...e rmE1I und F,mk,;OJUI1gINhungen. S.-B.
Akad. \Viss. Wien 128. 1083-1121 (1919).
2. Theorie nml A thr _ addirm.on lIIengenfunkff"""". S.-B.
Akad. Wias. \VieD 122, 1295-1438 (1913).
Ral1cov (Raikov). D. A. ( e also Celrand. I. 1\[.)
I. lIarmcmic anal}ptis on commutatiur groups with 1M Haar JllULSUr£ and the
Ikory of charaders. Trav. Inst. Math. Steklov 14. 5-86 (1945). (Russmn.)
Math. Rev. 8. ]83 (1947). [GennaQ. traJbda.tion in "Sowjetische Arbeiten
ZIIT Funktio .. Ver1ag Kultur ..nd FOTtschritt. BerJin r 1954.]
2. A tat'W proof oj 111£ oj the llaars 1II.erlSUre. Dukbldy Akad. Nauk
SSSR (N. S.) 34, 211-214 (1942).
3. Porilhn: definite Jllndioml on anrmpdafive groups with an iIwariant measure.
Doklady J\kad. Nauk SSSR (N. S.) 28, 200--300 (1940).
Ramoswmni, V.
1. Normed .algebmw. ilKmlorphism and 'he v pvstulak. J. Indian l\fath.
Soc. (N. S.) 14, 47_ (195Q).
Re.poport, I. M.
1. On BirtguZar boundary prol:;lenu lor ordinary linear diffnmtial «jULJli£m.R.
Doklady Akad.NaukSSSR (N. S.) 79, 2I 24(I951). (R....ian) Math.Rev.
13. 558 (1952).
2. On eatinaalion oJ rifprDalMes oj Hnmili6n O])Utllorll. DokJsdy Akad.
Nauk SSSR (N. S.) loa. 199--202 (1955). (Russian) Math. Rev. 17, 388
(1956).
Reid, W. T.
1. S ly continl.U".llUi lilU'tZ7' tmnsjormctfjons in Hilbert apMt.
Duke Math. J. 18, 41-56 (1951).
2. E;rpansi&n problems with a oJ linear integml f:fJUldions.
Trans. Amer. Math. Soc. sa) 475--485 (1931).
3. A nt"W elas.! oJ se1j-adjoint lJoumftuy value problems. Trans. Amer. Math.
Soc. 62, 881-4025 (1942).
Reiter.. it .I.
I. .lttlJtfdigt4ion. in analJpiB. Trans. Amer. Math. Soo. 73, 401--4.27
(1952).
2. On a UTfain class oj iikals in 'he Ll-6lgdmJ 0/ a locally rompad Gbd;an
group. Trans. Amer. Math. 800. 75. 5G5--.509 {1953)_
ReUich, F.
1. 81f1fw1gRhtorie fUT Spe1rtrob:er1C/!,ung. Proc. Intttnat. Congress of Math. 1
CalIlbridge, Mas.. I, 606---613 (1950).
2. thrS _. I V.
I. Math. Ann. 115, 6OO 619 (1956).
II. ibid. 113, 677--685 (19Be).
III. ibid. II6, 555-570 (1939)_
IV. ibid. 117. 35fJ.-.382 (1940-1941).
V. ibid 118, 482484 (1941-1943).
8. in ni£h/SqKlrr1brln Rdomm. Math. Ann. IIO, (1935).
4. me mll8lrig<n ng<n bei ckn .;n "..... E;_rlprOOl<no'"
d... Phyrik. Math. Zeit. 49, 70'l-728 (19....).
5. Die Eindrotigk£ils8atzjur die LOsangen qaanf€Rm«haniscl1e J7 mau.st:.hu1l8S-
rdalicme1s. Nachr. Akad. Wiss. GOttingen. l.\lath.-Phys. Kl. 1946. 107-115
(1946).
6. H__ g<wMnl;. Di pemtmen mve;l<T atdnung. Math.
Ann. 122, 24:HIfi8 (1951).
7. SP«fmllhemy oj a vrder ordinary differential equation. Inst. 1:Iath.
Sci. New York University. 1951.
Rey Pastor, .J.
la F..rn:Iitmal analysts and the general theory oJ jUndwns. Reale Academia
d.ltalia. Fondezione Allesandro Volta. Atti dei Coovegni. 9. 389-372
(1939), Rome .943 (Spani b).
802
REFERENCES
RE.FEREXICES
803
Ricl<att, C. E.
1. Integrotion in a CORUe..1: linw.r toJKilol:iml space. Trans. Amer.Math. Soc. 52,
498-521 (IB42).
2. An ab8tnu.1 Radcm-NilaxIJm. thLOf"em. 'l'rans.. Amer. Math. Soc. 56. 50-66
{1B44).
3. DA.-omposilWR oJ additive 8d.fIutd.Wn.'l. Duke :ttlath. J. 10 6S3--(i65. (1943).
4. The siflgldaJ' oj (J Banach algebra. IkIke }-[ath. J. 14. J.063-1077
(1947).
5. l.romorphiI: groupr of linfXlT transjornwlions. Amer. .J :Math. 72, 451-464-
(lB50).
fj Banach lIlgrbms u,ith un adjoint opmmtm. Ann. of '-latb. (2) 47, 52H-55n
(1946).
7. The 'UniqUf."fU:SB 01 norm problem in BD.JUlt:'h al/{f'bms. Ann. orn-lath. (2) 51,
615--628 (1950).
8. Repr€amILltiun of tntnin Banarh algebras on 11iIlwri space. Duke Math.
J. 18, 27--39 (lB5I).
'9. On I r1Wl'lUNCe lor l.'f.Tfain &1u:J£h algrlwwl. Proc. Amer. Math
Soc. 4. 101-196 (1953).
10. Theory oj Banach u (forthooming book).
Riesz F.
L S!effglrtiP:begriU utUl a.lMmkk lJlmgenlt:hre. Atti del IV Congresgo Intern.
dei Matern.. Bologna. 2. 18--24 (1908)_
2. Untersuchungen wer Syglnlte iR Funktionelt. l'tJuth. Ann. 60,
449-497 (I9W).
3. Sur EY'rlLl.i'll$ 8illgUlifTS d'iquatums inkgroks. Ann. coIe N'()TTTl.
Sup. (3) 28. 3.'HI2 (IBU).
4. VlieT linum: Fuflktionalgkid1.urrgm. Ada :lfath. 41. 71-98 (1018).
5. Sur le$ 3]JSItmes orthogooauz de jORdioruJ. C. R. Acad. Sci Paris 144. 4U5-
619 (1007).
6. us 6gstJn&n d'itpations liniam:iJ ,u une infinite d';lU:IJRl?UeS. Gauthier-
Villan. Paris U}JB
7. SUI' leg opinltiom /vndlunnt"lles linrnms. C. R. Acad. SCI. Pa.r18 149. 974-
977 (IB09).
B. Zur Theorie des Hilbwtsd£a Rasuna. Acta S"l. J.Iath. Suged 7, 34.---38
(IB34).
D. SUT 'Um" esphf de (jlUrlytiqv.es des deformirms som1Jflfbh1i._
C. R. Acad. SeL Paris 144. 1409-1411 (1907J.
]0. lJiRwnstratio» fWtQIf'lh d'un thitJrl!m tmlUrllLJ.rd ks ophalivns [ouctionrlf'lles
,iniairrll. Ann. l cole Norm.. Sup. (8) 81. 9--14 (1914).
11. Sur la 'Tiprrsen.tmiou tks operations fCMCtimJruUes liRirures par dr1i. integm".
de Sti£hjes. Free. Roy. Ph}-siog. Soc. Lund 21, no. 16. 145-151 (1952).
12. SUT les lfitts 4efondirms mf'sl.lmbies. C. R. Acad. Sci. Paris 148 1303-130;'i
(1909).
13. Sur fa C()TltJeT en vwyrnnr, I, II.
I. Ada Soi. III.t1. _god 4, 5S---M ('B28-I929).
fl. ibid. 4, 182 I85 (19"-8-1929).
14. ClMr di" linroren 'l"ronsJ(Jf"fflIlfw"en des kamplLun llillKrkMn R(lumes.
Acta Sd. Math. Szfged 5, 23-M (1980-1932).
15. Some mean ergc.dic UIWTf't1tS. J. London Math. Sor: 13. 274-278 (UI38).
16. A:wlller proof oj the moon ,..rgodiL lheornn. Acta Sci. Math. Szt-ged 10. 75-76
(194'-1943).
17. Sur la thiririr Wfpdiqm: des t"spac-r.s abstrails. Acta Sci. Math. Szeged 10,
1 20 (1941-1945).
lB. Sur la Ihiorie agodiqU£. Comment. .:\Iath. Helv. 17, 221-239 (1945).
]9. On a I't:'a'nl JJenemlu:nl;9f1 oj G. D. Rirkhofrs rrgvdi(" tJzrorem. Acta Sci.
Math. Szegffi 11, 1""-"00 (IB46-1948).
20. Ober qllfJdTahde Forwtffl mm uJ1erJdlicfj Nlen Vn-nndnlid1t-n. Xachr.
Akad \Vi!iW.. GOttingen Uath.-Phyt'l;. KI. ID()-195 (1910).
21. Sur lu, Jmu:ti0n3 £ks: ormalio1U h£rrRitinuws dn'Ml'espace ck llilbm.
Acta Sci. .Math. Szebtffl. 7. 147-159 (1935).
22. t.. rm' S'lb:e van Stone tmd Bochner. Ac Sci. Math. Suged 6, 184.---198
(1933).
23. b'UT qtU'lqaes tH)tirms f91U/LJmenml€s dans la 'IiIiuri.. ginhYde des optruJ:iJm,s
tiniairrs. Ann. of Math. (2) 41, 174---206 (1940).
Rifosz. F.. and LordJ. E. R.
I. The integral repre1ff7jtotirm oj unl10lthdrd 8e1J-adjoi1l1 lransJC1lTf1atUms in
llifberl 8]'10££. Tro.m.. Amer. r.fnth. Soc. 39, 831--840 (1936).
Riesz F_. a.nd Sz.-Xagy, B.
L Urons d'unalyse jondionncUe. Akadknia.i KiadO. Budaptst. 1952.
2 Coo Kontmktivnen d Hi n Rnumt's. Acta Sci. Math. SzegOO 10.
202-205 rlB4I I943).
Rie:sz.l\-I.
1. SUT US IriIaz'-ma des forma bilintaire& et Akr les fmutWnndJu liniaires.
Acta. Matb. 49. 465-497 (1926).
2_ Sur us l'nsernbltl com de ftmdiOflS 5lJlll'lnurbl€8. Acta Sei. ).[ath. Szeged 6.
1311-142 (lB'3).
S. Sar les funtlions f'firIjl1gtes. Ma.th. Zeit. 21, 218-244, (1927).
4. L intigrak de Rinuann-Liom.,.lle er Ie prnlJUmt' ck Caudy. Acta l\lath. 81,
1-223 (1949).
Rinehart. R. F.
1. The efJuil:alena oj dejiAitiotv pf a ntdril'jHnl"tion. Amer.l\lnth. Monthly 62
895--414 (J055)
Riss, J.
J. TnmgjvrnudUm tk FOUTi€T des rJiJdn7Julions:. C. R. Acad. Sci. Paris 229.
12-14 (IB49).
Roher!.. U. J)
1. On the j!.eOml!lry oj .'rod redor sptlU&. Tohoku 1\Intll. J a9, 42-59 (1934).
Robison, G. B.
L lmvuillJlt inttgrals over a lass of BmUK'h spun.. Pai.cifico.Y. )[a1lt. 4, 123-150
(1954).
Rogers, C. A. (... DvureUky, A.)
Rogosjmki, \V. "-. (see Macintyre, A. J.)
ROg05inski, ,v. ''''., and Shapiro, H. S.
1 On ('rrtail1 e.rlrentam probkms Jor tmtdgtic /U1fctinm. Acta .Math. 90,
287--318 (195').
Rohlil1. V. A. (see aha Pl t A. }.)
I. On tf2fknllarplli'ln of compact mmmldUtiue grwp", Izvesti.>'a Akad. nuk
SSSR Ser. Mot. la. 32D--3-W (1949). (Russian) )[ath. Rev. 11.40 (1950).
804
REFERENCES
REFERENCES
805
2. &1f'Ckd IQPI' s lrom the mdric I/wflTy of dyraamiml sys m,.,. IJspehi }lat m.
Nauk (K. S.) 4, no. 2 (80). 57-128 (1949). (Russian) Math. Rev. 11 40
(1950).
S. On the drcomposltion oj a i4'al8Y8Iem into lnmsiliw COrnpormt,m. Mat.
SbOl'nik r\. S. 25 (67), 23:}...z,s'9 (194-9). (RtlBfIian) Math. Rev. 11. 373
(1050).
Rosenblatt, 1\1.
1. On a elms oj lUarlwil prot'.U8f'fj. Trans. Amer. .})ath. Soc. '11, 120-135
(lD5])
.ltosen1:Jloorn, P. C.
I. Elemrntv oj mufhematirnl lugit:. J)over Publications, Sew York, 1950.
2. P /I vI linear oprrrdonl in Bimoch spaces. Arch. Math. e, 89-101
(1055).
Rosenthal. A. (see Hahn, H" and Hartogs. F.)
Rosser,.T. H.
1. Logic for nwthrmuticiuns. McGra.w-Hill Co., New York. 1953.
RQta. G. C.
J. EnnaBimt ,Mary oJ ordinary limaT diJJt7eUIia! opemtors. Di tion.
Yale University, 1956_
Rothe. E. l-I_
I. Zur ThMrie tkr ,opolagisr'Itrn Ordnung und der VeklnrJdder in Bmmwschm
Baumert. Cornposito Math. 5. J77-196 (I037-IG38).
2. Thpvlogiwl pTQafs of IlniqzwnrSS in rM thaJry 0/ differenlial and
i'llf'gml rquations. ButL Amer. Math. Soc. 45, 606-613 (1939)_
8. Crirkal poirtls l1nd grodindfiW1s GJ smlan ill Hilbert 'Pac . Acta P,[ath. 135.
7a- 8 (1951}.
4. Gmdirnl mappings. Bull. Amer. Math. 800. 59. S-IO (1953).
5. Compk 1y rontimwus scalars and varioJicmal methods. Ann_ or Math. (2)
47, 58o-S 2 (1946).
6. Gmdiml mappings and mwmo in BMtOC'h 8pf1£I!8. Duke :Math. J. J 5.
421-481 (1 48}.
7. Japping tkgrn in &nat:h spaces and sprelml . Math. Z. 63. 195-218
(1955).
Rubin. H.. and Stone, M. H.
I. Pmttdtr.Us 1M geaf'Tlllizahom oj HUbal pc1«. Proc. Amer. J\-lalh. SOC'. 4,
611-616 (ID03).
Rudin, \V.
I. ArJUlytirity, and .he tlllUhrl'UTif modulus principll. Duke :\lath. J. 20,
449-457 (1953).
R1u.ton, A. .....
J. A 'lQre vn t!/ in Btmad spaus. Proc. CambridgC" Philos. Soc. 45.
157-159 (1949).
2. On the Frn1JHJlm throry oj inkgrolefjualiom fOT oplrcllMS bdnngmg tf) the
ITcrlT class vJ a Bannch 1rpllt.t!. Proc>. London Math. SOl:. (2) 53,
109-] 24 (IU51).
S. DiTed prothu:Is oj h spa«_ and linear Jundional equativns. Pruf'.
London I\lath. Soc. (3) I. 327-884 (1951).
4. A short proof ()J a Ihffirrm on rQli":ri . Proc. Cambridge Plulos. Soc.
4.5. 674 (1949).
5. 1" ormulae oJ J.'rt:dholJR Iypr- [Of' cOmpal!'f linctlr operation.. 071 a glneral
Banach spare. Proc. LondoD tath. Soc (3) 8. 368-377 (1953).
f1. OpnaJors 'With a FFetlhoim lhMTy..T. London Math. Soc. 29 318--a26 (1954).
RuticklI, Ya.. B. (see KraJ;J"osel':skli. M. A..)
Rutman. 1\1. (see I(rein. M.. and Milman. D. P.)
Ruto\rit2.. D.
1. On the L'D...comrrgmoc f)J eit,enJKndion expansiOflS. Quart. J. Math. Oxford
(2) 7. 24-38 (19M).
Ryll.Na.ru-c""ki, C.
1. On the f"q,otlk thaPnns. 1. II.
I. G-nu!roli%«l ugu.dCc Ihnmmllt. Stu.dia l\'Iath. 12, 65--73 (1951).
II. Ergodk theory vJ MlllifUdd . ibid. 12, 74-79 (1951).
Saks. S. (see a]so Banach, S.)
1. TMOry 6J the intlgm/. &cond cd. Monografje I\fa -ezne, '''01. 7.
\Varsaw. J.937. Reprinted St.ecIwrt.Hafner Pllb. Co.. New Yor'K;.
2. On Borne fldU:tionnls. I. H.
I. Trans. Amer. Math. Soc. 35. 549-556 (19.'13).
II. ibid. 41, 1110-170 (1937).
3_ Addition In t. nok on same fll.nctiunnJs. Trans. Amer. Math. Soc. 85,
967---974 (1933).
4 .InlqJmtion in absIrud 1IIdric spaces. Duke Math. J. 4, 408-411 (1938).
5. SU-T le-s jonctimJl'Jdkl ck ....\1. Ea h d kun> l"l1Q" dtoefnppe1l1mts
de Jundioo.. Fund. _Math. 10. 189--106 (1028).
Saks. S.. and Tamadcin. .T. D.
1. On a fhwrmt ()J llahn-Skinhaus. Ann. of Math. (2) 34. 595-601 (1933).
Salem. R.
1. Sur unt t.rtmsion du de t.'Oflf'f!Zit£ d£ M. It-Jarcel Ria:t. Colloq.
!>laIn. I, 6--8 (1947).
Salemi R., and Zygmund, A
1. A £'OR(If!Z;fy thf"f1U1R. Proc. Nat. Acad. Sci. U.S.A. B4, 443---447 (1948)_
San ..Juan, R.
1. Gmendizmicm ()J a thu1nrA. oj Skinhnus ()n linear /NIKtionais. Las CienciHs.
!>lad rid 17, DO. 2. 2(15.-208 (1952). (Spanish) !>Ialli. Rev. 14.657 (1953).
Sa.-gent, 'V. L. C.
1. On lil1£(lr /u1tdimlahr in spactS ()J ccmdi.timw.lly intq?rable funt:l1.om. Quart.
J. Math.. Oxlot"d. Set". (2) I, 288-298 (1950).
2. On 80me rheOTtm8 oj Hllhu. h and Steit'llitnu. J. London Math. Soc.
28. 438--451 (1953).
8cbaBf, H. I.
1. Sur l'fUliL:ite des m,efUU8 ilffllUf'ianks. C. R. Acad. SeL Patis 22". 1053-1055
(1949). Errata, 230, 795 (1050).
2. SUT l'vnicilt! de la mataI: deHaar.C.R.Acad.St.-i.Pa.ris229,1112-1113(19491.
SchaCf'er, J. J. (see also Halmos, P. R.)
1. On Ilftirory dilatifJIIB oJ amiracticms. Proc. AlTIer. )Iath. Soc. 6, 322 (195 ).
2. On .tOr1It' problems Mfl.tYTRing operato1s in llilbert space. Anais Acad. Bra..-ril.
CiA 25. 87-90 (1953).
Scharktc". F. W".
1. Vbtr ritliU .m?1UlIiL:hL linmn Gku:hv. sI£mR. }lath.. achr_ 8, 4{)--58
(1049).
.
806
REFERF.N('E5
REFERENCES
807
2. Vas K.rikrium van Pal€y IUId JVinuT in BcmaC'h3cI/.en llau", )Jath. achr.
a, 59-61 (1949).
3_ Cber EigmttETtprOOlemt mil W1l:i Pu . :\:lath. Xachr. 6, 109-]24
(1951).
&-hatten. R.
1. A theury fll a'DID-t;p(J.cr . Ann. of Math. Studies. Xo. 26, Princelon Unjver_
sity Press, Princeton, 1 50.
Sehau(!er. J
I. ZUT Throrie srdlger Abbildu n in 1<'lmlrtiIJ1Ul.IFiiIl'l1l(ll. l\I"-t11. Z. 26,
47-65, 417-431 (1927).
2. Der FixpunktJJat:. in Funktionalro.umnt. Studla :\Jath. 2. 171-180 (1930).
3 1!:i71l! RignuLltafl des Ho'(J,TfI(:hetf, yYkJM . )Ia.th. Z. 23, 317-320
(lfI'>-").
4. .In'l'Cl1"ian:: dts Groides in FURkt.iaurlmumm. Studia Matb. I. 123-189 (1929).
5. Ober den ZmsalRmmlKmg ;;:W;K#wn drr E["de tigl...tU und L&barkrit
partiell",. Diffamtia'glridau.rtgnI zzaitt'r Ordnliftg ellipliSt'hen Typus.
]lJath. Ann. 106. 661 721 (1932)
6. Cber lineare. tJolb/di# FU11"..ttOnalopnalionen. Studia ,Math. 2. ]83-196
(1930).
7. L'''Jt( die Utnkehrtlng lin££l,R'f" df1.i#r FURI..-timw'oprm1;mtER.. tudia l\Lo.tlL
2. 1-6 (1930).
SdUffur, ]II. M. (see Miller, I{. S.)
Sehme.idler" 'V.
I. I'l'itegrtJ1g1rlrnurwn tIlllAnwenmrngtJ'/ tn PhYSIk ""d Tf't'hnik. Akadftmschc
Verla llschaft. Leipzig. 1950.
Sehmidt, E_
I. "t"btt di Au./llwtJne liDftJRT GkI'Nn.l"UR mlt ulWndfidl "l'idrn UnbeknN7Iteu.
Rend. del Cirt>oIo Ma1ematico di Palermo. 25, 53-77 (1008).
2. AufMnmg. dcr aIlgnReint'R IiRnlrtn .ln g,roIElridnmp'. .Math. Ann. 64.
161 174 (1007).
Schoenberg, I. .I. (see also Hildebrandt, T. H.)
I. A TfT1#.aTk on M. .l.W. DrQ/B C'haMCtDizntion oj innnpl'fJdurt Bpacts and a
omfrrture oJ L. 1. Blum.tntMl. Proc. Arner. }la.th. Soc. 3, 961--$64 (1952).
2. On local mnz..aity in Hilbe.rt Spaa'. null, Amezo. ):lath. Soc. 48. 432---S3ft
(1942).
3. On 8fmXJthing opem1ions and their ng functIOns. Rull. Amer. :Math,
SOC. 59. 199-230 (1953).
Schreiber. M.
I. Gt:rlerazll::nJ Bp€'ClTa1 re8tJluti()ll fvr operators in 1I,lberl spa.ce. llisse-rtation,
Cnivenrlty of Chicago, IDS-i.
Sc>hreier. .I.
1. Ein GegtTlbeispitl .2:ur TI,eoTle der sehttvI,.hen Kuncrl'gprz. Studia )Jath. 2,
2. 58--62 (1930).
Sc-hmer. O.
I. Abstmkte kon/fntunfidw Gruppen. ..'\Lhand. Math. t"m. Hamburgischen
Uni,". 4, 15-32 (1926).
SC' r.J.
I. Fehle ng.tR 2:ur StiJrIm/!,.ff>£.MUtIf! Wi lilU'llml Eigf!n'l1'fl1prtJlJkMell
mitOperatoTrn rifles llilbertsda€ft, RaUm€8. Ma.th. achr. IO 113-128 (UJ53).
Schrooinger, E.
I. QmlRlisitTung al roblrnt. Annalen der Ph k (4) 80, 437-490
(1926).
2. Vft'"lll(1SMkn1e Eigl'llrtTfMp«fTI1. S. B. Preussidten Akad. Wiss.. 1929.
668-682 (1920)_
Schur. A.
1. Zur Entwidrehmg wilDrii:rlicfiw Funll:tUmm rureh LiJsu.ngen VQn Systenu;n
lin<tlTlT DiJf<mltioJglrichu"l'P'. Math. Ann. 82. 213-239 (1921).
Schur, I.
1. l b r die dJamktrristJ'scht:fl Wvndn einer linrorm Substitt&tiott mil einer
All'lfIe1U!ung auf dir T6tlJt& der IRtegrr1.lgkichu1I/!!-'R. Math. Ann. 66,
438-510 (1900).
Schur, ..I.
1. Vber linMre Tmnafurtnaliunm in 4e:r TIreorie ckr unendl.iden Rdh£A.
J. Reine Angew. .Math. 151. 79-111 (1920)_
SC'hwartz H. M.
1. &qvhU%s of SlU./tjes in1q!ra/o, I-III.
I. Bull. Amer. A-Iath. 800. 47, D4.7---055 (1941).
II. Duke Math. J. 10, 13 22 (1\143).
III. ihid. 10, d95--{;1O (I9 ).
Schw8rtz J. (see also Bade. \V. G_. Bartle, R. G., and Dunford. N.)
1. A 1'lClle on 1M space L:. Proc. Amer. Math. SQC_ 2. '270---275 (1951).
2. Pertwrhations vJ sp«trol oper:lIloTs, and applimtions. I. Pacifie J. .Math_ 4.
415---458 (1954).
3. Two pn1urlJtllion formulae. Comm. Pure Appl. Math. 8. 871-.a76 (1955).
Schwartz. L. (see also Dieudonne. .T.)
I. hlUlyu d S!Jl'It6tBt: harrJwrliqrus dam US f'sptlffS de dhtribuJiong. Canadian
J. J'\.lath. 2. 503---512 (I051)
2. Sur 1tkt' propritti de sytIthhrt- spectral dans les f,1()upes non rontpillU.
C. R. Acad. Sci. Pari . 424-426 (UI48).
9. TWork plmle tk. Jondims rlIoycnh . Ann. of Ma.th. (:2) 48.
857 929 (1947).
4. 1ioRlomorphilmtn el applications l'Dmpletemrnl Wlltinun. C. R. Ac8fl. SeL
Paris. 2S6. 2472--2473 (IPS:!).
5. Tf;rorie des di'ilributUm.s, I. II. Act. Sei. Ind., 1091. 1122, JIermann et
Cie., Paris (1951).
Seh""""" Ii. A-
I. GesalJlUlldk lJlatlwrrfalische AbhandlaJl#1r. Band I. .J. Sprint.,oer, Berlin.
1890.
ScJlwcrdtfeger. H.
I. Lt" frmdi()'fJJr de matrices. Ad. Sd. rl Ind., 4li9. Humann et Cie.. Paris,
1958.
Scars D. H.
I. O"fJ tile so/utirms nf a linrar 8f'('f)1Id "rdrt' rlaffrrential equaliou v.;1I;ch are oJ
inlq:mblt: BfJWlIY. J. London .:\:lath. Sm-. 24, 207 -21.'1 (1949).
2. Nole on the ttniqu-tn('JIS of Green's function.'! flSqJ('ialed u:ith arluin differential
eguatior.s. Canadian .T, l\latl}. 2. 31.1.-325 (lu.iOJ.
S. 011 the _peel",1II oj a certain dilf€Tmti(ll t'fJlrolion. J. 1.ol1d0l1 )fath. Soc. 26,
2O. 210 (ID51).
.
808
REFERE1"CES
REFERENCES
809
4, Al1 e.qx.r:nrion in t! j'IJJtctiom. Proc. London Math. Soc. (2) 53. 30fJ--t.21
(1051).
!i Some propnties oJ a diUrrtnlial rqualirm. J. London 'fatll. Soc_ 27. 18(}-188
(1052).
e .lnttgml trmu.forms and ei nfu1ll.'f;on throry. Quart. .J. Math. Oxford (2) 5,
47---58 (1954).
7. Some properliC'tI. of a tllfff'.Tt!1ltial tqtU1tian. ..I. London Math. Soc. 29. 35-Ir--3OO
(1054).
SeaTS t D. B.. and "I'Itcbmarsh. E. CoO
I. Srnne rigmfvnt:tiOli form,ulae. Quart. J. hIDth. OxrOTd (2) I. U 5-17.5
(1950).
ebastmo e Silva. ..L
I. Inrqranon and dniration in Bamtdl tqX1£'I!B. Uni".. I i!\'boa. Revista Fac. Ci.
A. Ci. .\lat. (2) J, ))7-166 (1950). Errata 4OI 402 (105t}. (Portugu...)
Math. Rev. 1.8. 43 (1952).
2. Anallfl fUJU"lions and JunctiotUll. a1ffllysU. Portuga&e Math. O. 1-180
(1950). (Portuguese. French. 6l,munary) Math. Rev. II, .524 (ID50).
S. Sui Jondammri ckllo lftJria dri juns:ionali analitici. P4Jrtugoliae Mat"h. 12.
1--47 (1953).
&gaI. I. E. (see also Dunford, N.)
I. PoJtulatu Jor :m: mtrhnnics. Ann. o[ l\Iath. {2) 48. 93()-..9.j,8
(1947).
2. T group algebra oj a locally rom.pact group. Trnlls. Amer. .Math. Soc. 61.
6 105 (1947).
8. The span oj the tTcttIlntilJ1LY oJ a /utlmOt1 in a .Ltbe5gw 3pClct'. Proc. ;-Jat.
A ad. Sci. U.S.A. 80, 165-169 (1944}.
4. An nttnsiun oj P/.anchenl'sJonnula to separoble tm:inwdulnr ps_ Ann. of
IIIBth. (2) 52, 272 292 (1950).
5. .lkcomJXJBiticms cJ vperaloT . I, 11. Mf'noirs Amer_ Math. Soc. no. 9
1951.
6. .l1UYlf'imd meastl1ft on lomlly cum-pac! _.I. Indian 'Math. Soc. (1\'. S.)
18, I05 I30 (1949)
Seidel. Ph. L.
I. Note fWn tine Eilf,NiUhaft der Reihrn, mclt;he disrorJfinuinlicht; Ftrnl'fiOflcn
dar8tellen. Abhandlungen der JJayerischen Akad. der ,",'iss. Munc]len li
I!71HI98 (1847-1848).
Seirert. G.
1_ A ,hird order boondary value pTQblnn ariml1g in UPrOtIasti€ wing Ihfnry.
Quart. Appl. IIIBth. 9, 21!>--218 (1951).
2. A lhird order inrguillf hotmdary miue prOOlem and the associaUd serif's.
Paeific .T. Math. 2. 895-406 (1952).
Seitz, F.
I. The rttodt1n Oleory oJ solids. Xcw York. ID4H.
Shah. S. M.
L Note on d/!PIfundion upa1i8ions. J. London .l\fath. 21. 58--fU
(1052).
Shapiro. II. S. (!SoC also Rogosinski, ".. 'V.)
L F2trrnurl problnII$ Jm poIlJ1hAffials (2nd prnctr series. [)i lion JIass.
Inst. Tech.. ]{15'2.
2. Applicatirm.s oj tlotmrd lint:ar Spa£f!8 to Jundl.(JfI..fheordlc e:t'ln:mat problems.
Lectun:s of functiuns of a .complex ,,-ariable. 39'9-4D4... Univ. of Michigan
Pres5, Ann Arbor. UJ55.
ShI:Ipiro. J. M. (see Cameron., R. H.)
Shiffman. M. (see Garabedian, P. R.)
Shirota, T.
L A gmnaliMtim& oJ a thl':orem oj L KnpIansky. Osaka. .Math.. J. 4. 121-182
(1952).
Shohnt. J. A . and Ta.ma.rkin,. J. D.
l.. Tht problem (1J fs. l\Il1th. Surw-y . 110 l Amer. .M:l1th. Soc. New
York, 1943.
Sikor.ski. R.
1. On mulliplicatWn oj d(krminanb ir Banach s. Bull. Acad. Polan.
Sci. CI. III. 19 219-221 (1'(153).
2.. On Lucubki.'s de:te.rorina:nI (1J lint!ar ft}Wdions in BUJUlf'h 8p4C _ Studia
III tJl. 14 (1053), 24-48 (1954).
Siloo.tein, J P. O.
I On dge1walun and singulLrr t:alkt. of cmnpad fiJU'.(Jr operalars in Hilbert
spact:. Proc. Cambridge Philos. Soc. 49, 201-212 (UJ58).
:Silov, G. (see also Gdfand. I.)
L Ideals and 8ubrings of ring oj rxmtinucrcs Jun.dirm:J Doklady Akad.
f'; uk SSSR (N. S.) 22, 7 10 (1939).
2 Sur la thffnk des idimu; dans lu mmetJlr.J' rwrm.h de joncrions. Doklady
M.d. Nauk SSSR pol. S_) 27, 900-903 (1940)
8. On not'nUd rings 1I8ing one generat{Jf'. L\[at Sbornik N. S. 21 (63).
25-47 (1947). (RussiaJ1. English summary) I\la.th. Rev. 9 445 (1948).
4. On rt'gumr IWmIm rings. Trav. lost. Iath. Ste-klov 21, 118 pp. (1947).
(RUAAian. English BtlIIlmary) Math. Rev. 9. 596 (1948).
5 On the uIl>nsian oj rntuimaf idMt.. DokIady Akad. :Nsuk SSSR (N.S.) 29.
83 84 (1940).
da SiIv3s Dias. C. l..
I. To l 'l"«lm- lJptIcDJ and tlwir applicati.on In 6nalyfic frnu:1imwl sptI£tS_
Bol. Sue. Mat. Sac Paulo 5 (1950). 1-li8 (1952). (Portuguese) I\lath_ Elev.
18, 249 (1952).
SiJverman R. J.
1. Inmrimd linml' Juncllons. Trans. Amer. Math. Soc. 81. 4U-424 (1956)
Sil1. D.
1. On quU8i--diff....mol upmdrn-. in Hilbert gp<u:<. Doklady Akael. Nauk SSSR
(N. S.) 18, 523--526 (193S).
2_ (lb<r di< limtNgrIl einer quari-DiffenminIgIPidm.'11 d£r n--tm Orduung.
M t. Shomik N. S. 7 (49), 479-532 (1940).
3. Quasi-diffen:ntinl oprraIrlrs in Hilbert spact. lUst. Sbum.ik (S. S.) 18 (55),
89 70 (1f!4:J). (Russian) Math. Rev. 6. 179 (1945).
Sil1j!'er. I. M.. and ".enner. J.
I. lkrir-'f1lim'uJ un rommutalil-'e fiormW algdJras. r.lath. Ann. 129 2GO-264-
(1955).
Sirohov r 1\1. F_
l. 1<'undiQJ}1l 01 I'lnftmts oj paTlial ordem:f spt1Cf't;. Dokll1.dy Akl1.d. X$I.tk
SSSR (N'.. S.) 74. 1057-")60 (]()30). (Russian) Iath.. Rev_ 12.341 (1951)
8ID
REFERENCES
REFERENCES
8Il
Sirvmt. G. (or J.)
I. Sur lC3 fruna!Qr17U1liOlU i1iligmhs ck l' spure L. DokJady Akad. Nauk S:SSR
(N. S.) lE 256-257 (1938).
2. SchUKJl'he Kmnpakthri/ in den &J'U1l.'h3cMn RaKmnt. Doklady Akad. )Jauk
SSSR (N. 8.) 28, 199-202 (1940).
8. U't:ak ctRftpodness in Banach fiJJIlffS- Studia 1I1ath. n. 7]-'94 (1950).
SkorolJod, A. ( Kostyutt-nko. A.)
Slobndyanskir. 1\1. G.
L On ,.timates far 'he f'igmool f's vJ a self-adjoinl operalor'. AIrnd. Nauk 8SSR.
Prikl. Mat. Me!;. 10, 295-314 (1955). (II"",",,") Math. lIev. 17. 286
(1956).
Smney. 1\1. F.
1- A 'R'1IUH'k on S. Kmtulafti'sc1uJrunn1¥l1ion GJ (L)-span>s. Ann. of ath. (2)
43, 52H-521> (1942).
SmitJl. K. T. (see also AronszaJII. "N.. and Donoghue, \V. F.)
I. Sur Ie thiorbne sp«tro1. C. }{. Arad ScL Paris 234, 1024r---:(025 (1952).
Smithies, F.
I. TIlt! Fredholnm lh O'!'!J ()Jinlq:rul . Duke Matb. J. 8, 107-130 (Ui41).
2 A 1Wle on rompl£tdS cxmlirrurnu IIYlJU/ormmirJn$. Ann. of Math. (2) 38,
626--"30 (1937).
Smu1ian. V. L. ( ml1l Y<'-Il. Yu. L. J(see also Gantmacher, V.. and KreiI4 .M.)
1. Sur u.s 'ligu1j en' fumes er Jaiblemrnl CfmIpad! dans l'esp<1l:t:
du type (B). DokJady Akad. Nauk 8SS11 (N.8.) 18, 40:>-407 (1938).
2. Unmr tupol.vgirol l'f'S and their mnn«tion rvUh .he Ba1UHh paaB.
DokJa<!y Aka<!. I'<Ruk 8S8R (N. S.) 22. 471---473 (1939).
3_ SUT le8 topoltJgie8 diffml1Vs dans l'espan de 1i. Doklady Akad.
Nauk S8811 (K. 8.) 23, 81--334 (1939).
4. On MJf1I gwmdnwl pmJWrlil's (}J th sphnr in a sp«e. of 11M type (R).
Dokfady Akad. Nauk 8SSH (N. S.) 24, 648--<152 (1939).
5. On tlJ principlf" €Jj indamon in the spa« oj the IJITW (B). Mat_ Sbornik X. s.
5 (47), 317-328 (1939). (Ru.-Nan. ng1i. b summary) Math. Rev. ], 335
(1940).
{L 0'1 som gromeIriroJ pmpnfiu oj tM unil sp/I.I!U En the pace QJ the type (BJ.
l\Iat. Shormk X. S. 6 (48). 77--94 (1939). (Rrn;gian. English summary)
IIIatl>. II"". I, 242 (1940).
7. SUT la dIrioobiliti tk La 7WnR£ dons I'npatr de Banach. Doklady Akad.
NRuk SSSI! (N.8.) 27, 6-l:!--648 (1940).
8. t.Jbt71i7lrQre tfJporogiHChe Rl11i1'I'ie.lIat. Stlornik:S. S.? (49J.425-448 (1940).
O. SUT la strt«:lure de la sphert unilairf' dan.$l'e$p t de Banach. :Mal. SboTnik
X.8. 9 (51), 5-1.:>---001 (1941).
10. SUT les t!lpQas lintalrt:, mpolog;qun. II. .Mat. Sbornik S. S. 9 (5]), 727-730
(1941).
J J. Sur fJUe1qut"8 prQpriitu girmrilTiques th la splirre dam les espuu:s lin{air s
&nfIi-mdonn6 de Banach. Doklady .o\.kad. .Nauk SSSR (r\'. S.) 50, 394-398
(m41).
12. On ..me p mB oj 'lie fU1U:tumal tJ.fJL1Iyris. Doklw;ly Akad. f\o:auk SSSR
(N. S.) 3S, 157-150 (1943)_
]::1. S"r les nJsembles compnd 4!t J'"bkmt:1U ctanpads daas l'eBpl1N' du type (B).
118t. Sbomik X. b. ]2 (54). 91-{)5 (194."1).
14. Ou com]JUct Rds in the spaf't' (JJ mmsumblt- jlutdlrm.$. .Mat. Sbomik N. S.
15 (57). (In,"). (Ru.s ian. English summar}") rath. Rev. 6. 276
(11145).
15. lromdric 9pCmI.OTS with infinite dejirif'1K1J 'Indiu. aml their
en£k:liOl'Uf_ DokJady Akad... KlIuk SSSR (N. S.) 87, ]]-14 U95'2). (Russian)
Iath. Re,, . 14, 8S2 (1958).
16. Opncrlon with lWrale dmroderistic llJ.n(;h."6 . Doklad)' Akad. .xrallk
S88R (N. S.) 03, 985-988 (1955). (llussian) IRtb. lIev. IS, 803 (1954).
17.. Complth'ly lxmtitaunus ptrlarbutiOAS DJ vperaWrB. Dok!ady .Akad. allk
SS8R ( . s.) 101. "18 (1055). (RlW;mn) Math. Rev. 16, 933 (J955).
Snol, E.
L Bt"hazVor GJ eigmju.ndinm flnd 'he sprclnfm Df Stkrm-Li0Uf.'111r opera/ors.
(}spehi Mat. Nauk (N. S.) I!, no. -4 (62), 113---132 (1934). (RuSlillm) Math.
.N.ev. 16, 824 (1955)
Sobczyk. A. (s("r- also Bohnenblust, H F.)
I. Prajectinns in MinkrnrsJ.i and Bunuch sptl(.n. Duke .\lath. .J. 8. 78-100
(1941).
2. PTOj "tifJfI oJ the space (m) on its subapnn (ee)' BId]. Amer. MaUl. 80(". 47,
93'<-1>47 (1041).
3. On the t'nrttsima t)J linea.r transjormaiicm:J. Tram;. AIrl£'r. .Math. Soc. 55.
153-169 (1944).
Sobolev. S. L_
1. Th fiJuCItions QJ malhemaiioolphys;c.._2d d.C.osuda...st.\..lzdat Tehn..TeOr.
Lit.. I\JClscow-Leningr 1950 (RlUisIant_
2. On q th('f)f'ftft oj !fJ.twtio1l.lll analysis. }i;at. Sbomik X.8. 4 f46). 47]--4.97
(1938).
SQlomyak. 1\-1. z.
I. On charaderlstic vo.lu 1I and hnMLktistic I'ft"ton oj a pnlurlnl opntltnr.
Dokhtdy Akad. Nauk 8&<;1{ {:N. S.I 90. 21>-->12 (1953). (Russian) Math.
Hev. 15, 196 (1954).
Sonirlc. :s.
J. Rrch€TCbu Bur ItfJ IQncllOIlS cyliudriqua et Ie Iuppemt'nl des fVRd;om
I'ot1tlnlieR en sbiLs. Math. Ann. 16, 1-80 (1880).
Soukhom1inoff. G. A
1. lJbtr FrntselZtlng l'UJi lirwaTnl Funkb.'fNWl in linl'Urf'n J.."(}ltjplrrn>n R4umen
unc11il'Jellrt:nQunlUhiom-tiamm. Mat. Soomik1'\'. S. 3 (45). 853--358 (1'938).
(Russnm. German summary-)_ ZbL f. !\lath. 10. 169 (1938-]939).
Sparre Andersen, E., and J . B.
I. Soml limit thtQTan. (.In i11.ttgrals in iln ab'Jirad ¥rl. Dan::;ke \"id. Sdsk.
Matl1.-Fys. lttedd. 22. No. 14 (]946).
2'. On the irltmdudi.cm vf U.T£8 in infihik product 8ds. Danske Yid. SE-Isk..
l\Iath.-F}-s. 1!edd. 25. :Xo. 4. (]048).
Sp , W. H.
1. On series oJ WaZs/, eigenJuru:liQIl8. Proc. Amer. :\latll. SoC". 2. 2112-204
(1951).
rddu, Yu. A.
1. The ctruchlrf" oj ma.nmal idMls in rmg8 of IIIM.YU7("S Ivilli ('(J11vol"tw1I. \Jat.
Sbornik 1\".8. 27 (69), 2[17-318 (1950). (ltlL'lSiant )'I th. R \.. 12.420
(1951). Amer. ltith. SetC'. Tr.tuJ..o;la.bon no 81 (lD53).
J
812
REl?ERESCES
REFEREKCES
Ins
Stas..-.bya, V. V. . . .
1 On inverse prOOImuI of sp«tml aJluly,d.s for a dass vJ differenll.al rum8.
. Doklady Akad. Sauk SSSR (N. S.) 93, 409-401I (!P5S). (R.......) Uatl1,
Re>. IS. 873 (1954).
Steinhaus. IL (see also Banach? S.. alld Kt1cmarz. S.) . ,
I. Sur Ie! divrlnppcm n" orlhogonaux. Bull. Int. Acad. Polon.. SCI. Ser.A.
11---39 (1926).
2. Addil und stdige Funkticmalopt:rutivnen.. Math. Z. .5, 181>-2".n (UUO).
SUkID V. . M'..
1. SUI' la u:pm.swns llS'JIRIptvlUjUt8 d£ C'£lttriJlt'S jlJ1fCtioml J mu aT. s
eq difJirenriftlls lifliaires du mu vr Te.. et IruT pphca!-rom
au pmbli1rJ£ du dttrewppemenl d'uue JcmctWn arlJ'ilnIu.,. l'n senl'B procirJntd
6uivunlles diks /rmctivns. Comm. Soc. Math. Kha.rko'W (2) to (2-6), 97-1'09
(1007-1009). Rev. Sem. Publ. J.fe.tb. 21, 117 (Una).
Stcpanoff. ,\,\'. . . qo 01_
I. Sur tJne t.rlmsioR du lhWriure rFgf)d; . CQmposltIo I\.lath. 8. 289--...iJ3
(1956).
Steinberg, H. . _
1. Dif/utdrm pl'lX.'f:3Sf'-8 f£'ilh obsorplion. Thesis. Yale UrllVel"!!ilty. 190.1.
Stevenson. A. F., and . ,"V. A.. .
I. On the pwribk forms vJ diffnnliio.l f!fJ ilrion w/ril'1t t:an be !ndorized by 'he
Schrvdi-nger-InJrld MnhDd.. Canadian J". Math. 4, 385-39,::, (1952).
Ste\\'art, F. 1\1. .
1. Inlt;grolion in nVflromnthMive sy:dt'ms. Trans. ArneY. l\IaUI. .:soc>. 68,
7&--1()4 (1050).
Stieltjes, T. .f. _
1. llet;hnrhes SUT les fractions amlifillft. Ann. Fac. SCJ. 'I'm1louse (1) 8. J". 1-22
(1894).
Stokf'8, G. G_ _ _
L On 'Ile critical mlua oj Ole NUmB oj periodi£ Krif?B. Trans. Cambridge Phd_
Soc. R, (1849).
Ston , }t. H. (r;;ee also Dunford, .t u.r.gyeI, B.. and Rubin. H.)
I. Applil'ations oj the fheary oj BooIffm ring8 to #7If?mllopolDgy. Trans. Amer.
)Iatl1. Soc. 41, 875--481 (1937).
2 ContlUity. :Mimeographed lecture notes, The Unh.,.mitJrofChica .194n.
S Linear lTtrn8formnlinnoJ in Hilbert pcCf' and Ihtir applittlrions 10 ant1lysu..
Atnf.'1". MQth. Soc. CoUoquium Pub. vol. IS, Sew York. 10:12.
4 Thegt7ln'Cllized JVritnlnus appro.nmation thoorem.l\Iath.l\Jag. 21, 167-184,
237-254 (1947-1948).
5. On the l'Of'IIpn£tifimtioo (Jf lupoWgicul g. Ann. de 1& So . Polonaise de
)Inth. 21, 153-160 (1048).
r. Notn on integration. I-IY.
I. Proe. l"at. Acad. Sci. L.S.A. 84, 336--342 (1948).
II. ibid. 84. 44.7-455 (1948).
III. ibid. 84, 485--490 (1948).
IV. ibid. 35, 50-58 (1940).
7. A general theQry oj 1l}Jedm, I II.
I. Proe. Xat. Acad. Sei. U.S.A. 26, 280-283 (1940).
11. ibid. 27. 83--87 (1941).
8. BoundMn,. propertUs in fkhcl;on-laU;t:n.. Canadia.n.t. SI th. I, 176-186
(1949).
fL The theory ()/ iVQfor BoolOO1l a/gffnus. Trans. .:\mer. ra.th. So("
40, 37 nl (1936).
10. Linror tnmsfornvdions in llilbert space, I-III.
I. Proc. Nat. Acad. Sci. l:.S.A. 15, 198-200 (1929).
U. ibid. 15. 428--425 (1929).
III. ibid. 16, 172-175 (lfj30..
11. On the thwre:m of G iJand.Mt1Zkr. Ann. Soc. Polon. Ma.th. 25 (1952),
238--240 (1955).
12. On the jcnnu1ations 0/ hnnnrmic wudysi<l. Proc. Roy. Ph}"!iQnn. Soc. I.und 21.
no. 17. 152--172 (1952).
13. On UJibounded optf'Q1orB in Hilberl &pIUY. J. Indian Math. Soc. (X. K) 15
(1951), 155-192 (1952).
]4. On a tMfJ'7eTn of P6lya. J4 India.f"I lath. Soc. (N. S.) 12, 1-7 (1948).
15. Th.t oJharmonieahalysiR.J\.lath. Student 17, 81-92 (1949).
16. On cnu--paromdn unito.ry groups in Hilbt!rl:pace. Ann. of Math. (2) 83.
fl43--6<II (1932).
17. Ct'rlLrin i1llegm.UannMgoRsto Fourirrirlkgrnlr.Math.Zeit.28,6U-fi'76(1928).
18. An 1mU8tUl1 type oj e.rpansion pmblmf. Trans. Amer. Math. Soc. 26,
_5 (1924).
10. A cvmparison of the seriu 01 FoKrin and Birklw.ff. Tfflll$. Amer. Math. Soc.
28, 695-761 (1926).
20 breguJar a;grrmtiGl systems oj l"JtJkr Imo and the rekited f?.l'lW1SiUR proWmr.
Trans. Amer. .MQtlL Soc. 29, 23-53 (1Ir".l7).
21. The upansime. problfTn8 ll$sociakd with r rhllernttial 81P/D1U1 oj tht:
8fTOI1d order. Trans. Amet4 .Math. Soc. 29, 826-844 (1927).
traus, A. V.
I. On the themy oj fll, gmemHud resolrvnt oj a syr1UAdTic operator. Dok1ady
Akad. Na1Jk SSSR (N. S.) 78, 217-220 (IG51). (Russian) Math. Rev. 12,
837 (1951).
2. On , properlies oj gmemH..,} r<sob1mts. Doklady Akad. Souk
SSSR (N. S.) 82, 209-212 (1952). (Ru.'<Sion) Math. Rev. 18, 755 (1952).
3. OnlhdheoryojHennilinnopemJurs. IJokJady Akad. Nank 8SSR (N. 8.)67,
611 I4 (1949). (Russian) Math. Rev. 1I, 186 (1950).
4. On 8",,,,,,,,liud rwokmts oj a symm<fri, up<mtor. DokIady Akad. Nauk
SSSR (N. S.) 71. 24I 244 (1950). (Ru-..ian) Math. Rev. 11, 600 (1950).
fi. Genrtuli::M nts oJ syrnmrlTit: operators. Izvt'stiyn Akad. Nauk SSSR
Ser. lat. 18. 51--S8 (19M). (Russian) latb. Rev. 18. 48 (1955).
Strutt, M. J. ().
L LmMfs,chR. Malbil!tl«he und -oenrondte hnlrtitmCJ in Pli.ysik und T«hnik.
Ergebnisse der Math., I 3, J. Springer, Berlin. 1032.
2. Rrelk Ei/!!=«T1eVl!r HilUehrr Jgabrn 2. Ordo"og.
Latb. Zeit. 49, 593--643 (1943-1944).
Sturm, C.
1. SliT Its kjuatima.s diffboWt:lles du second o-rdn. :1. Math. Pures Appt. (1) 1,
IUG-136 (1836).
2. SUT unt! t:Uzsse d'6Juaticms a din parliel1e,<;. J. :\latl1. Pures Appl. (1) I,
373--444 (1836).
814
REFERENCE
RElfERES'CES
815
Sunouc'hi. G. ( a180 JZl1ml, S.)
1_ em. the sequrna of Cldditiur set fu.nctions. ..t. Iath. Soc. Japan 3, 290-295
(1951).
Sunouc1li. H.
1. On inlt'groJ rt'prtlltttlallOm vf bUi"Brar JU1JctiQnals. Proc. Japa.n Acad. 27,
159-161 (1951).
Sunouchi,. S. (5ee Nakarnura? ).%.)
Syl...ter. J. J.
I. On the fTjfUZtion to the uculat- irn:qualiJia in the. pfmIettlry IlIrory. PhiL Mag.
16. 267-269 (1883). Reprinted in ColledftJ Papers 4, lIO-IU
2. Sur lfCs pUi.B3t1r"' 8 et les roriru:s de trUbstilunow linimns. C. II.
Acad. Sci. Paris '94, 55-59 (1882). J:{eprinted in Colleded Papers 3.
5re-564.
SU!'iZ, O. (see plSQ Htlb. E.)
). t)bet die Appmn'mulir;m Rtdigu FrmJrli.tmell durrh lmear are urn
PoieA::rn.. Math. Ann. 77, 4B"J-4OO (19t5---1916).
Sz__l"\agy, B. von (see also Hies:!;, I'.)
I. SUf' res lnllis/iTltairrs tk dimemitmJinie. Corom. Math. Rei", 17,209---213
(1945).
2. p des rmns,{crtn.Q'ians lirWai.7U. fl'n'll«s. Arla Sci. l\lath. Szcged
14. 125-137 (1951).
3. SptkrmldaTsk>llung liJUan.'r TransJormatioRrn des Hi 'Rt.mmnL
Ergebnisse der Math.. V 5 J Sprinb-er Berlin. 1 42. Reprinted Edward
Bros., Ann Arbor, l\Iich , 1 47.
4. Pertrn1Kdioos des transformations autoadjoin!e.s .d4ns l'espacf! de HiltJert,
Cotnment. Math. H.Jv. 19, 347-366 (1946--1947).
5. On the se! oj positi fUndUms in L!_ Anl1. of .!\Iath. (2) 39, 1-18
(1938).
n. On semi l'fJII.p" oJ Btlj-adjoint ln1n1if()rnlalions in Hilberl . Proc at.
Acad. Sci. U.S.A. 24, 559 60 (1938).
7. On uniJormly oounded Unror trrmsformarinns i» Hilber, space. Acta Sei.
Math. n, I52 I57 (1947).
13. Sur I", cmdmd.Wns de "upm:t: de Hilbert. Acta Sci. }lath_ Szeged 15, 87---02
(1953).
D. A m f probkm fOT self-adjoint opuators. Acta -'Iatb. AI-ad,. Sci. 1-J ,ng&r.
3, 285-293 (11)52).
10. Tmn,gJurtnIl Ik "t'spaL'f! de HiUJert,jcmct.ic;nfii de t!.fP'- pOfitij sur un groupe.
Acta Sd. Math. s...g1'd 15, 104-114 (1954).
1I PmIongmt'nt.s des lrunxJonnafiom de r de Ililber1. qui 80Ttmf de eel
npaa Akad. Kiado, Budapest. I!J55. (Appendix for Hiesz and Sz.-NajQ'
,I]).
12. On a sp«lTal pl'OtJ.1£m v/ Arki11..*tJni. -\.cta :\lath. Acad. Sci. Hllllgar. R. 61-66
(1952). (RnssiaQ summar r).
13. On thl' slability of the inckx oj urWoum!ed liftftlr 'rrm,'if9rmnJ;.on, _ .\ctli. }Jath.
Acnd. Sri. Hungar. 8, 4D--ii2 (195'2.. (Rw!>jan sllmmalJ").
14. ilber lJK"83bare lJursff'llu»gnI Liesclie:r Gruppen. 1'ath.. Anll, 112, 286-296
(1936).
15. E.rplJ1lXirm thromtt& of Puley.Wimer i!Jp€. Duike J.at1J. J. 14. pr.5-978
(m-i7).
Tagamlit'Zkl, Y
1. Sur qu€lfJUf?3 applirotiOh1l de la Ihlcrrif! gir.erale du tspa,as V«fol'ids par.
tirU6ftn<t urdtmna, Annuaire GodiSQjk] Fac. Sci.. Phys. [a.th., Univ.
SoCi8. Ljvre I, Partie II. 45. 263-286 (1949) (Bl.dgaritu1.. French sl1mmary)
Math. Rev. 12, 420 (IDS1).
2, Zf,.!1' eres. Kegd m drn llitberlsclen RtiuJIU'R. Annuaire [Godisnik]
Fac. Sei. Phys. :Math. Uni"\-'. Sofin. Livre I. Partic II. 47. 85-107 (ID52)
(Bulgarian. Russian and German summarir:;.) Math. Re\.'. 15 135 (1954).
Takahaw, T.
1. On ,he mnrpactness of the fvndi01'lt-Srl by the CfNtt't'rgrncc in irlf'LIR oj gDU?ral
t.ype Studia. .1\Ja.th 5. 141-1 0 (ID340).
Taldykio, A. T.
1. On linnu eq"at QrU J» Hilbert space. .Mat. Sbornik :'\l. S. 29 (71), 529-550
(1'Q51). Errata so (72). 463 (1952). (Russian) Math. Rev. 13,564 (1952).
Tamarkin, .I. D. (see also Dunford, _. Hille, E., Saks, S.. Sh.ohat. .J. A.. and
Stone, 1\( H.)
I. On rorJt aJthe I-"JKlCe I 4p . BulL Amer. Math Soc. 38, 79-84 (1932).
2. Sur qltl£lqua poinl8' de la I1I.iorie des iqa,ali0R.8 difJirrnJi,,/In liTlmlres
ordiMins d sur fa ghIimlisation ck la IlLri,. d Fourln-. Rend. Cire. Mat.
Palermo 24. 341>-382 (1912)
3. S(flfl gt!1JRT(J1 pmblt'fRS aJ thf! tlwrny vJ m-du'lary liR«U' differt'1lhal eqNQtif"J1lJl
and uprlr1.nous oj an adAtnJry fun.t:titltI in a series -vI ftmdmRnltnl fu.ndiDns.
MatJJ. Zeit. 27, 1-.54 (IS27).
Tamarkifl J. D.. tmd ZY UJ)d. A.
1. Proo} oj a theuren& oj Thnrin. Bull. Amer Matb SIte. 50 279--282 (1(J.U).
Taylor, A. E. {see also Bochner, S.)
1. Th t'XWl$iun. oj 1i'li a7 [u.ndilJfW.ls. Duke Math. J. 5. 588-547 (1939).
2. T'Jt r«dr topolugin vI Bcmacli ttp('JCa.l{evista Ci., Lima 42. 355 -366 (1940):
43. 465-474 (11141); 44, 45-63 (1D42)
3. The weak IeJpvlogies oj Banach spaus Proc. Nat. Aca.d_ Sci. U..S.A. 2..";,
438-440 (1939).
4. On cntnin lluJUlit"h. spaatr whose e/(w!ents ar QYfalgtu: JUJ?ctwns. Act.....
Aca.d. Ci. Lima 12, :U---43 (11I4D).
5. Weak ron in the space lIp Duke Math J. 17, 409--418 (19501.
6. New proQfs oJ svme thrormlS oJ Ilardy by HanMA spau MeIIwd."I. lath.
Mag. 23. 115 124 (1950).
7. Banach spaces aJ /lJ.nrt;ons analylic in tM unit cin:-k. I. II.
I. Studia. .l\lBth. II. 145--170 (1950).
.n. ibid. 12. 25-00 (1951).
8. Conjugalion.<r Qf oompk.;r linea, 8pt1C't'" Univ. California PubL )Iath. (X. S.)
2, 65-102 (1 44).
D. Spec:tT¥11 theory oj IlnOOlU'Id€d rltlSff! operaiJml_ Pr()c. Symposium on Spectral
Theor.y and D.ffer-ential Problem!'!. 267-275 (1 51). Oklahoma. Agri-
cultural and Mec:>haniea.I ('ollr lf". Stillwater. Oklahoma.
10. AnalJPis ill compl .x Banadt. spaces. null Amer'. 1ath_ Soc. 49. 052-009
(IU>3).
II. Spu:lml th or.'l/oJrllJa!ddi:rtr;lrulll'e(JperatQJ's.Aet&:\Iath. 84 189-224 (ID51).
12, The "t oJ a dmu1lra4:1jormall6n. HuU.. Ame... h..t1I. 80(", 44. 70-74
(193").
816
REFERE:\1CES
REFERENCES
817
13. Lillear operarimi.S rdllCh deperpl tlnalyW:qUg upon a . Ann. of
:\Iatl<. (2) 39, 574--593 (1958).
14. A note un vlll'81lllititnUll ctmIugenu. Studia Math. 8. 148-158 (1930).
Teichmiiller, O.
1. Bruuc:hl der Atgtfnaikl!T da8 A ? Deutsche Math. 4. 567-.';77
(1939).
2. Opnarorm un JVnchssekm Raunt.J. ReineAngew.l\lath.174. 73-124 (19:15).
Temple. G.
1. The wmpuiutiurl DJ t'hanldaisUc nlullbrts cmd cluuatfnilJtic Jund.irms
Proc. London Math. Soc. (2) 29.. 257-280 (1'929).
ThohUl.9, .1'.
1. U " 1ih<r dO$ Ei_lpmbIrm
(U("') : ) + 19(",)y - o. J: A(",)y(x).tr - f: B(xly(x)th = o.
Math. Nachr. 6, 229-261 (1951).
Thor}n, G. O.
I. C thNJrtmtJ_ Camm.. Sem. Math. Univ. Lund no. 9.. 19408.
2. An .rtrnsion oj (I OOIfCUity thecrem due to ft.l. Ria%. Comm. Sem. Math.
Univ. Lund no. 4. 1980.
Tingley, A. J.
1. A grntTllli::.ation J the P8ismn formula lor the soluticm oj the heal Jlr>w
Et}IUdimL Dis!;ertation, Univ. or Minnesota, 1952.
Titmmarsh, E. C. (see abw Se,p:rs. D. B.)
1. The Ul.t!Ory oJ Clarendon Press.. O-"foOO. ]932.
2. Some rheorems on perturOOlion theory. I-IV.
J. Proc. Roy. Soc. London, Ser. A., 200. 84-46 (1949).
II ibid. 201, 47a--479 (1950).
IH. ibid. 207, 821-$28 (1951).
IV. ibid. 210, 80--47 (1951).
3. .In.trrKluction to the theory GJ Fourier integral$.. Oxtord Univ. Press, ItJ91.
4. Weber tI inkgrallhnm'm. Proc. London Math. S<le. (2) 22. 15-'28 (1923).
5. On r in eigenrohus l I-VIII.
[. Proc. London I\lath. Soc. 14, 274-2'78 (1939).
II Quart. J. Math. Oxforo n 12D-I40 (1940).
IU. ibid. 11, 14.1-145 (1'Q40).
IV. il>id. 12. 8:\---50 (1941).
V. il>id. 12, 89-107 (1041).
VI. ibid. 12, 154-166 (1 41).
vu. ibid. 16. 103-114 (1'Q45).
VIII.ibid. 16. 115-128 (1'945).
ti. An eip,enfunction problem Ol:t'JI.rring in quantum mochanics. Quart...1. :Mat'h
Oxfotd 13, I IO (1042).
7. On the eI (iJ diffennrlal UJa«tio»s. J. London :.\-lath. 80('. }9,
66--<!8 (1944).
B. On the disudeness oJ the 8pft'frwm llJiSOCiaUtf rvith cUMin differentlal
ftJIUllion.<t. Ann. }Jat. PU1"a AppL (4) 28. 141-141 (1'949).
9. On Ilie uui'lue7lns oj Grttn'S functirm assocurled It'ith a secQnd order differen-
tial v]JeralfJr. Canadian J. Mat1J. I, 191-198 (11)>9).
10. Eigm.ftmdirm probll'BIS 'l1,'ith pr:riodic pot.t11tinLJ. Proc. Roy. Soc. London,
Ser. A.. 203. 501-514 (1950).
11. On Uu: d oj spectra of diDermtial equawmtt_ Acta Sd. l\fo.tl1.
Szrgrd 12 Pars B, 16 18 (1950).
IZ. On 1M. summabiliry ()J rigenJunctivn e.rpt.D"ISIOm'. Quart. .T. :1Jatll. Oxford
(2) 2, 250-268 (1951).
18. Trarou.:r mmtx Bur la 1lI6me deJJfolldWn8 charudiristigues. Bull. Soc. Roy.
Sci. Liege 20. 543-561 (1'051).
14. On Ole C'OrfC'<c fI:.>.a: oj ripenJu.ncb..oo upamions. Quart. J. Math.. Oxford
(2) 3, I39 I44 (1052).
15. S{J propnties of eigenjundiOl1 upansi.tms. Quart. .J. Math. Oxford (2) 5.
59-70 (1054).
16. Eigt:nJund:ion upanrions aawciated with uroruJ...onkr differential <<IN<d;ons
Oxford Univ. Pre!;;s wndon 1946.
Titm.., N. S.
]. On different kinds of on&.gt.I.oe oj ele:mmIs and linear operators in Banach
apIICU. Doklady Mad. Nauk SSSR (N. S.) 52. 500-572 (1046).
2. COIU'f1't'I&tg 'OOTiomr 1fJJ"1Wi, n} of rlnntmts OT lil'lUlJ'" uperalors in
BUfUl£h spm:es. Uspehi Ma.tern. Nauk II no. 5-6 (15-16) 228-229 (1946).
(RuBSi.n) Math. Rev. 10, 307 (1940).
Toeplitz. O. (see aIso Hellinger, E. and Kothe G.)
1. Die oollknmmetU71 Ri.iumr tkr FrualdiotItht.orit. Comment. Math.
Helv. 28. 222-242 (1949)
2. VbfT aIlgemrint: tin-eare lJfitkllJildungrn. Pmce :Math.-Fiz. 22. 113-11D
(1911).
Tomita. M_
I. On the ugulnrly ronVe.z' hull oJ a set in a ronjlJ8Gle Ikl1llJdt spa.ee. Math. J.
Okayama Univ. 3. ]4S-145 (1954..
Tornhejrn. L.
I. Nmmedfields 01Jet the r-eal and oontp/afklds. Michigan Math..T. 1. 6I--tl8
(1052).
Transue. \V. (see blul'Se. M.)
Tseng, Y. Y.
I. On bWrIhOJP1al e:tpan.tions in 'RILtrit; and unitary spllI:£8. Proc.
Nat. Acad. Sci. U.S.A. 28, 170-175 (1042).
2. lk1sualizal inue1'Sl:S oj J'lded betwun ltcJo unitary spaccs.
DokIady Akad. Nauk SSSR (X. S.) 67,431-434 (1049). (Russian) MatJl.
Rev. 11, 115 (1950).
8. ProJWrlies and classijiwtitm oJ gt:nn'tlli'Z6l i'lff.lrl'S('s oJ closed operators.
Dok!&dy Akad. :>Iauk SSSR (X S.) 67, 607 10 /l04D). (Russ;,m) Math.
Rev. 11, lIS (1050).
Tsuji, M.
1. On t1u inkgral TqJMIDilatitm OJUllilary and sclJ-adJOinl nperotorg in Hilbert
$pact. Jap. J. Math. 19. 287-297 (ItJ48).
2. On the cumpat::bu:ft GJ $pacc LP (p>O) and ill> applirotioA to integral eqt.Ul.
ticm. KMai Math. s.m. Rep., 85-36 (1051).
Tukey. J. \V.
1. 8fJme noks on the srpamlion oj (.'QR('&f" Sd3. Portl1o<YJl.1iae :\Iat.h. 3, 95-102
(1942).
BIB
REFERE CES
REFERENCES
BI9
TuJajkov p A.
1. Z1Jr KQmpaktJ,t:il im Raum L p jur p_I. Nf:u: nr. Ge . \\"j!OS. Gottml!;E'n.,
l\Iath. Ph}.s. KL 167-170 (19M).
Tychonoff A.
1. Ein F )fath. Ann. Ill. 767-776 (1935J.
L'din. A. I.
I. SomI! grorndrie (jUf'slicms ill the lheary oj Iirum' snni-crdned spl1u . I.l'nlng_
grad State Univ. Annals [Ul:en)"C Zapiski] Math. SerA l(]. 64-83 (19-IOJ.
(Russian) Ma.th. Rev. 2. 314 (1$141).
Ulam, S. (see l\lazur, So. and Oxtoby. .J. C.)
Umegaki. H. (see Nakamura M.)
van Danb;.iR. D. (see under DantziK)
van Kampen, E. R. (Eee under Kampen)
van der Waerden, D. L. (see under \\"aerden)
Vaught, R. L. (see Kelley, J. L.)
Veblen. O.
1. .ItTOllrianu oj quadrol;" diJft'Tmtialforms. Cambridge Urnv. Pn>s!.. London.
1933.
"'eress, P.
1. lJbn kompnltte FunkrimuTmr.mlfpJ und Ba1.rtM4e l(lassfn. FUI1d. )[ath. 7,
244---249 (1925).
2. Vber Funlititmenmengen.. Acta l\lath. Sci. Suged 3, 177-192 (1927).
Vidav. I.
I. Uber tine JI'rTJ'TfUltmg lJon Kaplanslry. Math. Z_ 62, 3OO (UHi5)_
Vinogradov, A. A. (see Kralko,-skii. S. .s.)
Vinokurov, \'. G.
1. On bitJrlhvgonol. sy Jem$ i'l1g a givcn subNpaa-. Doklarly Akad. Nauk
SSSR (N. S.) 85, 68!H!87 (1952). (Rus,ian) Math. Rev. 14, 183 (1953).
Vi!iik. .M. I.
J. LilUar oj Q])QCIlvrB and buundary coruIition.s. Dokla.d)' \kad.
.auk SSSR (N. S.) 65,438-486 (1049). (Russian) 1\Ip.tb. Rev. II,
(1950).
2. On lineaT bvvRda7y p-'fOT r1ifferrnJkJl equ<>tKm.I. Doklady Akad. Nauk
SSSR (N. S.) 65, 785 788 (1949). (Russian) Math. Rev. II, 39 (1956).
3. On a geueral form lJj wlNbk problems for hnmogenmru and JW)1-
/Itnnt>gffl<o1Ul elliplic r1il1emtJiol operaloni. DokJady Akad. Nauk SSSR
(N. S.) 82, 181-184 (1952). (Ru"ian) Math. Rev. 14. 279 (1953).
4. The tlll'lliod oj fJrlhog<mal and di.red da.vmptJltition in tht- ory oj eaiptic
r1iJJ.-.oo1 fij1UIIWRs. Mat. SOOmik N. S. 25 (67), 189-234 (1949). (RUBSianl
Math. Rev. II, 520 (1950).
5. On stnmgly elliptic syskms 6J diJJemmql . Mat. Sbornik . S.
29 (n), 6I!H!76 (HI5I). (R....sian) )fath. Rev. 14, 174 (1953).
Visser, C.
1. On the iteraticm oj lim:ar Qpnatioru in a llilbert space. eder. Akad.
W.-..,h. Proc. 41, 487--495 (1938).
2. Note on linMT f'lpt:mJcrs. )J"edcr. Akad. ',,"etfonBeh. Proc. 40, 2'iO-272 (1937).
'Vi$ser, C.. and Zaanen, A. C.
I. On tht. n nr:ahw.. vJ (;Qmpact lmoor trnnsforllUlhony. Xed ["l. Akad.
\y . Proc. SeT. A. 55, 71-78 (1952).
Vitali, G.
1 Sul& Jun:z;iLmi itllq:mli. Atti R. AffiLd. deUe SeL d.i Torino 40, '153-766
(1905).
2 SuU'ifl 1)(:1' Bme. Rend. del CirooIo Ma.t. di Palermo 23, 137-155
(1907).
VQlterra, V.
I. TMqry oj jundionc.ls. Blackie and Sons, London a.nd Glasgow. 1930.
,"On Neumann. .I. (15« under Newnann)
yon Sz.-No.gy. B. (see under Sz.-Nagy)
Vulich (Vulih), B. Z. (see a1so Kantorovitch, L. V.)
I. Une definition r1u produil r1a1l31<s eJlpaus Iioilaius. Doklady
Akar1. Nauk sssn (N. S.) 26. 850-854 (I\J40).
2. BUT US propriLtis du produ.it d rk IWl:mtnt ;J'lV£J"Se dam les upacu semi-
OTcforml.linlaireB. Doklady Akad. Nauk SSSR (N. S.) 26. 855--1159 (I\J40).
S. Limar SPQCe3 wi1h giN;n CQ1i.VffgenCt.. Leningrad State University .Annals
[Ulenye ZRpiski] Math. Ser. 10, 4G-83 (1940). (Russian) Math. Rev. 1.
818 (I\J40).
4. SUT rintigmle ck StUlIjes dt. /mu:lil11l8, dont lu valt.ut... d un
e.,-pace Bemi-cn.JonnL Leningrad State Univ.Annals [Ul.enye Zapiski] Math.
Ser. 1'2, 8--29 (lo.n). (Ru.asian. French swmnary) Math. Rev. 8. 80 (1947).
5. BUT l tl foru1ionnrlles limaires dans ks espacel! 8e11Ii orckmnis tmtain:s.
Doklady Akad. Nauk SSSR (N. S.) 52. 95--98 (1946).
6. Sur U8 o linlai.,.cs multipliootive3. Doklady Akad. Nauk SSSR
(N. S.) 52, 8811---386 (11!46).
7. Sur quelqtuS opimtions non-liniaim; dans Its e.spaces $emi-ordQrmu
fintaiT<S. Doklady Akar1. Nauk SSSR (N. S.) 52. 476-478 (1946).
B. Crmc1'l!k oj linear partially OTdered tlpact3. Doklady Akad.
Nauk SSSR (N. S.) 58, 733-786 (1947). (Russian) Math. Rev. 9, 290
(1948).
9. Tile product in liA£ar pmtially ordued spaces and its appliootion to the
lhemyoJ opemti""-,,, I. Mat. Sbomik N. S. 22 (64), 27-78 (1948). (R....ian)
?Iath. Rev. 10, 46 (1949).
10. The prod;ad in liturlr parti4Uy ordered gpaus and its appli«Ition to the
1"''''1J .J .perotiom, II. l\Iat. Sbcmik N. S. 22 (64), 267--317 (1948).
(R....ian) Math. Rev. 10, 46 (t949),
ll. On flu toncT.ere oj partially ottkred lint!als. DQkll;ldy Akl\d.
Nauk SSSR (N. S.) 78, 189-192 (1951). (Russian) Math. Rev. 18. 140
(1952).
12. SuT l s formes ghtiraks & arlaiDl!B opbati0n3 l:PUoirn. Mat. Sbornik N. S.
2 (44), 275--1105 (1987).
18. Sur Iu 6pbations linhzi1ft oom fespace des j'ohctim&g s.ommables. Mathe.
matica, ClvJ. 13 40-54 (1937).
14., On a notion oJ coover genre in a Bfl1Ill{:h 8pau. Ann. or Math. (2)
88, 156--174 (1937).
15. Some guuliOfl8 oj Ilu' theory oj linear partiaUy ordered Bets. ya. Akad.
Nauk SSSR SeT. Mat. 17, 36<HJ88 (1958). (Russian) Math. Rev. 14.
828 (1954).
van del Waerd.en B. L.
t. Modeme Algebra, I. II. Springer, Berlin, 11180, 193].
820
REFERENCES
R:&FERENCES
821
Wallach. S.
I. On Ihe _on OJ BP"'tra oj diIJ<reJ1ti<>j <q1UJri...... Amer. J. Math. 70,
838-341 (1043).
2. TM speclra oj periodi< polffitiala. ADler. J. Math. 70. 842----843 (1048).
'Walsh, J. L.
I. On Ihe ...-.vergence oj 1M Sturm--LWuoiIk sm.,. Ann. 0' Math. (21 24,
IOII-I2Q (11128).
2. Ubcr dit title; analJjti8chen Funktion rw:h .PoIyrnmIen.
Math. Ann. 06, 430-486 (1026).
3. 0&<7 die einer Fua1rIi<m einer ktmoP'= V<rtifId<rIidlffl nach
Po/yn<>mcl. Math, Ann, 06, 437-450 (1926).
4. I ""d byTalional/unctionsin Ihe."",p!ezdmnain.
AInu. Math. Soc. Colloquium Publication, vol. 20. New York. 1935.
Walters. S. S.
1. Tht I1pllCt Hp with () < p < 1. Proc. ArneI'. Math. Soc. l, 800-805 (1950).
2. 1lnJwrks on Iht, space H . Pacific J. Math. 1, 455--471 (1951).
V{ard, L. E.
I. A third order irrtgular boundary val1U prOOlem and 'he associated series.
Trans. Amer. Math. Soc. 84. 417-4S4. (1982).
W....chaw.ki, S. It, (.ee G.lh"uth, A. 13.)
\Vassilkolf, D.
1. Partially vrdend linear syslems, Banach spaces and 'JI8lmu oj
Dok1ady Akad. N"uk SSSR 85, 185-137 (1....2).
2. CIa.tsiJ'i<atUm oj ord<ringB oj lUIItJT sy./Rms. Doklady Akad. N.mk SSSR
(N. S.) 89, 167-169 (1M3).
8. On the theory oj partially ordertd linear IIJI-stnnf and /:i.J1wr $pace$. Ann.. of
Math. ". .580-609 (1943). [:see Math. Rev. ti, 186 (l )].
4. Orderings oj abstract st'Lt and lineaT sysrema. Izvestiya Akad. Nauk SSSR
Ser. lolat. 7. 203--286 (]9481. (Rwoian. Engli.h .UlllInBry) l\!ath. Rev. 6.
180 (1045).
Waiew.ski.. T.
1. Sur "_ du donwin< d'uiskna de3 Ivndivns imp/iril<B dans f< cas
de3 up""" al>strai,.. Fund. Math. S1, (>-24, (IP50).
Wecken, F. d.
1. &r Th<om """""" aperatoren. Math. Ann. no, 722--125 (1085).
2. sdheIadjugimn- Operator.... Math. Ann. no. 422---455
(1059).
WedderburD. J. H. PtL
1. Lutu-ru 1m mll' Jf. Amer. Math. Soc. Colloquium Pub. 17. New York.
1084.
Wehausen, J. V.
1. TronsJonna.tion:J in linmr topological spaces. Duke Math. .I. 4. ]57-]69
(1058).
2. TTanslonna.tion:J in mdm 8paces and' o-rdinary dignmtial .
BuU, Ame<. Math. So<:, 81. U3--n9 (I0405).
Weien.trass, K.
1. Mathem4lisdIe Werke, Band 1. Mayer und Miiller, Berlin, 18Q4..
2. Ma0aem4ti8c1le Woke. Band 8, Mayer und l\Jiiller. Berlin, 1908.
Weil, A.
l L'i dans ks groupu t,t 8M appIitaticn8. Hennann et
Cie" Act. Sci. et Ind. 869, Paris, ]940.
2. Sur lu lonctUnl3 prcsque plrWdique.s de van Neumann. C. R. Acad. Sci.
P.;ris 200, 38-40 (1085).
3. 8ur la groupes ropologiquu ellu groupa mesures. C. R. Acad. Sei. Paris
202, Il41-n49 (1086).
Weinberger, H. F.
I. An"""""" prolJ in IIIe Weinstein tII<Ihod lor e!genvalu<.. Pacific J.
Math. 2. 418-418 (1952).
2. ENM mimalion in OM: Wrinstein met1w4 lor Proc. Amer.
Math, Soc, 8, 643---646 (IP52).
8. An UlenaUm oj the cla3mal Sturm-limmilU theory. Duke Math. .I. 22,
1 I4 (1055).
Weinstein, A.
I. Quanti wur.1wd8 in Sturm-L.iot.miIJe 1htMy. Proc. Symposium on Spec-
tral Theory and DiflC1'eJ1tial Problems (1051). Oklahoma AgricuItmaI and
Mechanical College. Stillwater. OkJahoma.
\Ventze1, G.
I. Eint V"'''III."..;ntN.lng der flJ.r d.. Zweek< der
WrlImrn«Iumik. Zeit. fUr Physik 88, 5I1!-529 (1926).
Wenner. J (see also Singer, I. M.)
l TM ezi8rm.ce oj i1J.varian s. Duke Math. ..T. ]9, 015-622 (11'52).
2. .lnvaricnt 8Ub8pact8 CJ} bounded operators. Proc. XlI Sca.nd. Math.. Congress,
Lund (1058).
8. Commuting sputral measuru on Hilbert apau. Pacific J. Math. 4. 855-36]
(1054),
4. On invariant .subspacu oj normal operator.. Proc. Amer. Math. Soc. 8,
270-277 (1052).
5. On restriction& oJ operaWrs. Proc. Amer. Mqth. Soc. 4, 860-865 (]D53)
6. On.,!gebras oj -fuowti..... Proc.Amer.Math.Soe.4,866-1369(1055).
7. On a cla&s oj fW'rfMd rings. Arkiv. Cor Mat. 2, 587-.551 {1958J.
8. .ldt4lsina class oJoommutatiu: Banacha{g . Duke Mat"h...T. 20,278-278
(1058).
I!. ATgWrak 1Vi!h """ generators. Arner. J. Math. 76. 858-359 (1954).
]0. SuhalgeMlJ3 0/ the (J ebra DJ all.conlintwtU complt.o.Mxzbu4 fUneODm on the
circle. Amer. J. MaUl.. 78 , 225-242 (1 58).
II. Polynomuu app on an arc in CS. Ann. vf Math. (2) 62. 269-270
(IPSS).
Westfall, .J.
I. ZUT Theari.e der .I Dissertation G<5ttingen. 1005.
Weyl, H. (oec oIso Perer, F.)
.. IntquOIilhs betweenllle .... kind8 01 dgenvalu<. 01 a linear fmnsjoTm<Ition.
Pro<:. Nat. Acad. Sd. U.s.A. 35, 4OS--4n (1049).
2. Vb<r bm/m1nkf< quadroIi3die Formen. deren lJifIerenz voll8letig ..I, Rend.
Cm. Mat. Palermo 27, 373-892 (1000).
3. Raum l Zeit, MaterU. Vierte Aufl.. .I. Springer, Berlin, 1921.
4. llI::mrij'icatiom, (}ld and mw. oj the eigenrJahu problem. Bull. Amer. I.\[att..
Soc. 56, IIS-I39 (IP50).
.
822
REFERENCES
REFERENCES
828
5. tJbeT gewMn&M mi' Singu!aritdJen ..nd die EU-
geMrigen wiUki),/i<ha F'Mnk!ionen. I\fath. Ann. 68. 22(}-269
(19101.
o. Almo:r£ pMO il'JOOrian:t vecWr Bets in a metric vector space. Amer. J. Math.
71, 178-205 (11)49).
7. Vber gewNu>Iithe Ii"",,, DiU...."'iolgkidllmgon w.;' singKlmTn Sf</Ien urn!
ill1't: E Nachr Akad. Woo. GOtIingon. jl,lath.-Phy.. KL
1909, 87-M (1909).
8. lJber Diff..-..ti41gl..d"mgen mit riwgularrn S,<l1en und ihre
Eig<n Nachr. Akad. Wiss. GotdngeoJ. Math..Phys. 10. 1910.
"'2467 (IGW).
9. Tk me.thod vj m11wgmw.' i poUnliallherny. Duke Math. .1. 7.
4U--4440 (1940).
Wey<, E.
I. Note BUr fa theme au guantitts oomplemr1J [armies QtIlC Ii unitis principalu.
Bull. Sc;. Math. (2) ll, 205-.15 (1887).
Whitn<y, H.
I. On iMals vj di/J""em;aIi1< flmdions. Arner. 3. I\fath. 70, 655-658 (11)48)
Whyburn, G. T.
I. Analytic topology. Amer. "Iatb. Soc. CoUoq. Pub. vol. 28, New V(l1'k, 1942.
2. Open mappings on lot:ally mm.pad spaces. Mern. Amer. I\fath_ Soc. no. I,
New Ycrk. 1950.
Whybum, W. M.
I. DiU....min1 "'fUllHans wilh general _ndary ron4itiom. Bull. Arner. Math.
Soc. 48, 69Z-704 (1942).
'\Vidder, D. V. (.see also Hirscl1rnan, I. I.)
1. The Lapf,a(;e fran:ifarm. PrincetQn UQiv. Press, Princeton, 1941.
2. .lnverri'onjormulaJJJorronooltJtion fmf'I3/unrul. Duke I\.lath. J. 14, 217-249
(1967).
S. TM "......,"""'. Bull. Amer. Math. Soc. 110. 4044-456 (195'),
Widder, D. V., and HirschmAn, I. I.
1. The invmrion oj a general claM oj transfQrnl.fJ. Trans. Amer
Malh. Soc. 86. 185-201 (1949).
2. A theory for a gemml class 01 convolution transjorm.s. Trans.
Amer. Matb. Soc. 67, 69 97 (I....).
3. Conool:utirm transf01TfU tclth t:tnnp d1 kermls. Pacific.T. Math. 1. 211-225
(1051).
\Viegma.nnt N. A.
1. A nofe on infinite flonnal matrUu. Duke :J\:lath. .T. 16.. 535-588 (1949).
\Vie1andt. :a.
1. NatLnforschung und Medizin in Deutsch1and 19SQ-lfJ40.
Band 2, 85-98. Dieterich.llche Verlagsbucl1l1andluDg, Wiesbaden. 1948.
2. llbeT di£ IkTDperawren tk, Qwm Matl1. Ann.
1'1, 21 (1"'9).
\VieJ1er t N. (see Ql Palty R. E. A. C.)
I. Limit in krms oj oontiiUW1l$ tramJurmati.vn. Bull. de Is SQc.l\.lath. de Frnncc
50, 119-184 (19221.
2. Nw. on a pap.,. vJ M. Banadl. Fund. 1lath. 4, IS6-I45 (I92S).
3. The ergodic theomn. Duke Matn. A. .5, 1-18 (11}39).
4. T Fourier integral and certain oJ its opplicntions. Cambridge Univ. Press..
1939. Reprinted by Dover Pub., Sew York.
5. Tau1>erian 1he<n'<:m3. Ann. 01 I\fatb. (2) 83, I IOO (193').
6. hn.rmonic analysis. Acta bfuth. .55, 117-285 (1030).
7. The 6Vtrtlge ooltu oJ a junctional. Proc. London Math. Soc. (2) 22,
454-487 (1924).
8. DiU<renIiaJ space. J. Mat1l. Phys. MM'. Inst. Tech. 2. 181-174 (19'3).
Wiener., N., and WiDtner. A.
1. HOI'1RanU analysis and ergodic theory. Amer. .T. Math. 68. 415-426 (1941).
WiIansky, A.
1. The basis ifl BanaM 1lplIU-. Duke Math...T. 18, 795-798 (IOn).
2. An appri£ation DJ Banm:h linear Junclionala 10 summabilily. Trans. Amer.
Math. Soc. 67. 5H8 (1949).
Wilder, C. E.
I. &pan.rion p1'oblemlt of &rdinaty linea, dif1<m>tio-l "JWliotl8 with aw-ilimy
conditim'13 at mort' than two points. Trans. Amer. Math. SO!!. 18, 4.15-44.2
(1917).
2. P,oblem8 in /he lheory oj OI'dina'1llinw, diU<renIiaJ <_Hans with aw;ilimy
conditions t1l tnON) than two points. Trans. Amer. Ma.th. Soc. IfJ. 1 1-t86
(IBI8).
Wilder, R. L.
1. l to t1u: JQUnda.ti.tJn8 of f7JtJfhematm. Wiley, New York, 1052.
Wilkins., .T. E.. Jr.
I. Definifdy "!J a4j<>inl integl'a1 "'fUllHans. Duke Math. 3. II,
155 I66 (1944).
WillliuD8()n, .T. H.
t. Spt.ctrd oj linear transjrmnalitms in (I). Proc. Ca.mbridge
Philo.. Soc. 47. 461-472 (1951).
2. Linmr tmns[ormafion.s In arbitrary linear 8paCU. J. London Math. Soc. 28
203-210 (19,3).
S. Compad limar l'Iperalm'3 in linUlT topDI.ogilxd SJN1U3..T. London Ma.th. Soc.
29. 1411-156 (1954).
4. On!opo/clliBing lk<ji£14 C(I). Proc. Amer. M.t1l, Soc. 5, 7'9 784 (I9'4).
Windsu, W.
I. VbeT linem-e Di/ferentialglddltmgen vietin' Ordmmg mil ....gur.;rilaIm tlnd
die Dandelhmgcn II>iIIkiJF#idie FImktivnm. Matb. Ann. 88.
2.6-279 (1921).
Wintner A. (see also Hartman. P. and Wiener, N.)
1. der tmendlichm It-Ialriun. !linel. Leipzig, 1929.
2. Z.., TheorU: tier BilbI£mform<1l.l\fath. Z. 30. 228 289 (1929).
S, The vj "",trieu. Physical Rev. 71,
788-739 (1947).
4. (L.}-cot1Judions betwun the kindic and potential energies oj linear BJPk'ms.
Amer. J. Math. flU, 5-18 (1947).
5. On the Laplace-Fourier occurring in rnafhematirol -phyrirs.
Amer. 3. Math. 89. 87 98 (1947).
6. Asymplr>tic QR8 oJ ,he a4iaba!ic osciIlaIor. Amer. 3. Math. 69,
251-272 (1947).
7. SlabiHly and high . 3. Appl. Physies 18. 9'1--tJ42 (1947).
824
REFERENCES
REFERENCES
825
8_ Stobility Jnd '" in the wave wurhonkB vJ laUicu. Phys. Rev. 72
81--82 (1947). '
9. On the oj chtn aciQist ic diJJu nti4b in nmti7l1UlUS B]JtctTa.
Phys. Rev. 72, 516-517 (1947).
10. On the oj rnuJW 8 tra. Amer. J. I\lath. 70, 22-80 (1948).
n. _4symp/Dtic -inI.t'gm1ions oj 1M t14iaIxdic arillatm- in it.! range.
Duke Math. J. IS, 5$-67 (1948).
]2. On l'Jirae'8 the-my ()J wntiRhOUS spedra. Phys. Rev. 78" 781-785 (1948).
13. A n"" c:riI<ricn I'" non-=il1nImy dill "'JU'ltiQfl3. Quart. Appl
Math. 6, 188-185 (1948).
14. A <riJ<ri... oJ oscillatory slafJiHty. Quart. Appl. Math. 7. n5 n7 (194.).
15. A priori Laplan Imnsfcwmurirm oJ linNT diJfrrent.ia1 equalions. Amer. .T.
Mnth. 71, 587 94 (194.).
16. On almo.rt free limar motions. Amer. .I. Ma.th. 71.. 505--802 (11149).
17. On the smallnes oj isolated . Amer. J. Math. 71 , 603---8n
(11148).
18. A crikrionlorth< oJL,-80/_oJa diflemtIWl
£quation. J. London Math. Soc. 25, M7-a51 (1950).
Ie. 0'1 oj ronjv.gole points. Amer. J. Math. 73, 888-380 (1951).
20. On linear _lily. Quart. Appl. Math. 18. 182--185 (I855).
\Virtinger, W.
I. lkifrlJgf E" lIiemarm'. I /ii, 1iyp<1OO1Uc'" DifI...minl-
g/£Uh""fpJ, ..'1<1 d<Trn A........wngm auJ Br:Irrr1ingruogB<mII. lIfath.
Ann. 48, 865-389 (1887).
1Vitticb. H.
I. O/>er d<u Anwa<hsrn der LDsungen Ii"",", Dill . Math.
Ann. 124. 277-288 (1952).
Wolf,F.
1. Analytic pn1urbation oj operators in Banach spa;;e8. MI'd:h. Ann. 124
817-888 (1952).
2. Simplicity nf tpectra in g ld . (Abstract) Bull. Amer. Math.
Soe. 60. 845 (1954).
\Vo1fson, K.
I. On th, 'Pmrmn oJ a boundary val.. p,oblem witk two Biugula' rndp&i.....
Arner. J. Math. 71!, 713 719 (1850).
2. On Ihe separation oj spectra. Proc. Amer. Math. Soc..f, 4.08-409 (1953)
Wrlgbt, F. B. ,.
I. A"""",,, va!md alg,'''''', Proc. Nat. Acad. Sei. U.S.A. 89, 1J3{HJ82 (1953).
Yaglorn, A. M. (see Gelfand, I. M.)
Yamabe, H.
I. On a ultnsion oJ Belly's tMarem. Osaka Math. J. 2, 15-1'1 (1950).
Yood, B.
1. Banach algebras oj ronfinu.ou.s/rmtfiom. Amer..J. Mrdh. 78. SO--42 (1951).
2. Propertit:s oj linear t::trms[orma.tions VRdt1- addition oj a roMpltUJy
,confiuU0U8 trmJ.sformati011. Duke Math. .J. 18. 599---612 (IDS)).
8. Onlizedpoint.t[(JT'setni--grvKpaoJlinearoperotors. Proc.Amer.l\omth. Soc. 2.
22$-285 (1951).
4. Tmmft.rrmatWm between Banach spaces in the unifr:mn topo gy_ Ann. .of
Math. (2) 50. 486-508 (1949).
5. Additioe groups and linear nwnifotcls of tmns[QmWi(WJIJ. b...b1Jem Banac.h
spacu. Amer. J. Math. 71, 663-677 (1949)
6. Diffm:nA' a oj linetU' 1.7tJn.<if0J'11&l1li0ns on a Banad. spaa. Pacific
J. Math. 4, 615-686 (1954).
Yosida. K.
1. On vecltJr laUicu wi!h a ..mil. Proc. Imp. Acad. Tokyo 17.. 121-124 (1941).
2, Yulor lattices and addiliM It! lumtiom. Proc. Imp. Acad. 'Tokyo 17,
228 232 (1941).
8. On the unitary i1l grmeraZ Euclidean apaa,. Proc. Japan Acad.
22. 242--245 (1948).
4. Mean ergodic theorem in B(lM.Ch spaces. Proc. Imp. Acad. Tokyo 14,.
292--294 (1838).
5. E'godi< 1/1wmn3 01 BirkMfl'KJoimdIim'. typ,. Jap. J. Math. 17, 31 6
(1940).
6. An abstrad treatment oj the in4Widual ergodic tlwn' . Proc. Imp. Aca.d.
Tokyo 16, 280--284 (1940).
'1. On th< group mnbeddtd .n th< metrical romp!./< riT!JI. Jap. J. Math. 13.
7-26 (1986).
8. On Ihe diflaentiabilify and th< repmmtation oJ one- .emi-groupB
01 fimar _am.. J. lIfath. Soc. Japan I. 15-21 (18481.
9. The Mcn-Iroff process with. a srahle distribution. Proc. Imp. Acad. Tokyo 16.
4S---48 (1940).
10. On 7'itdma.a:Tsh-Kodaim' formula Weyl-Stont'8 eigfmJunt.tWn
eapansion. Nagoya. Math. . I, 49--158 (1950). Errata, ibid. 6. 187-188
(11153).
n. On th< theory oJ .peclra. Proc. Imp. Acad. Tokyo 16. 378-388 (1940).
12. Ncmned rings and' sp«fral tMorl!fflS. I-VI.
L Proe. Imp. Acad. Tokyo 19, 856-359 (1943).
II. ibid. 19, 466-470 (1943).
III. ibid. 20. 71-75 (1_).
IV. ibid. 20. 188-185 (194.4)_
V. ibid. 20. 269--278 (1_).
VI. ibid, 20, 451--4.58 (1_).
Yosida.. K. and Fukamiya. M.
1. On rrgularly convu fiers. Proo. Imp. Acad. Tokyo 17, 49-52 ()941).
Yosida, K.. and Hewitt, E.
I. Fin./<Iy addilioJ< m=ru. Trans. Amer. Iath. See, 72. 46--66 (1952).
Yosida, K., and Kakutani, S.
1.. BirkJwff'B ergodic tMOTeTn ood 1M ntarimal ergodU 'Moreni-. Proc. Imp.
Aoad. Tokyo 15. 165 168 (1839).
2. treatment DJ Marko//proCU8 and an Dgoolc.lheCJrem.
Ann. 01 lIfath. (2) 42, 188-228 (11'41).
Yosida. K.., Mimura. Y., and Kakttt.a.W. S.
1. lntf:grul vperaYA with bounded kernel. Proc. Imp. Acad. Tokyo 1.... 59-362
(1938).
Yosida. K.. and Nakayama, '1'.
1. On the serni-otdered ri"8 and it.t appli.catiota to 1M spectral theorem. I. II.
I. Proc. Imp. Acad. Tokyo 18, 55$-560 (1942).
II. ibid. 18. 144--147 (1948).
826
REFERENCES
Young, L. C.
{, On n irnqwlily OJ Mar«1 }l;..",. Ann. 01 MaUl. (2) 40. 567--574 (IG89).
Zaanen, A. C. (see also Visser. C.)
I On a eerlain c148s ()J Banach sprue'. Ann. or Math. (2) 47.. 654--668 (1946).
2. .InlqJrol tromfurmati.0'4s and their Te30wents in Orlicz and Bpacu.
Cotnpcsitio Msth. 10. 56-(H, (1952).
8. NIJf'f1U1liulble tnmsformaUons in Hilbert space and sys!em3 oJ linear in al
.quati<m.. Acta Math. 83. I97 248 (IG50).
4. NQle on Q. cmain elMs oj Baooch 8pac . Nederl. Akad.. Weteasclt. Froc. 52.
4088--499 (IG49).
5. Limar analyris. P. Noordhoff, Groningen, and Inter8cience Pub., New
York, 1953.
6. {if a ceTCain elms ()J linear trun4furmations il1 IIn UTmfrary
Banach apau. Nederl. Aka<!. We'tensch. Proc. Sere A. 54, .87-$3 (1951).
7. Vber ooUstetig, und symmetriBierf>a1< ()p<mtcu>o. Nieuw Arch.
Wi.lrunde (2) 22. 57-/!O (1943).
8. On th. ory oj 1i'lUaT inf al r.quatinns, I. Neder]. Akad. Wetell.'!ch.
Proe. 49, {94--204 (to'G).
9. On linear fImcIU>n<>l e<J1IllliDm. Nieuw Arch. Wi,kunde (21 22. 269-282
(1948).
,Z.
1. SU1' unt' pmprilti du champ des /f)'I1dirms ronlimu:B. StudiB !flath. 2. 68-67
(lG30).
_.... E,
I. Bewei.t, dassjedt 7J.lt.tI8t 'WOAlgtordntJ wtrden kann. Math. Ann. .59. 514-516
(1904).
2. Neuer Beweis JiiT die MiJglichkeit eimT JVvhlonflllmg. J\>Jath. Ann. e5
107-128 (1908).
ZimrneIberg. IL J.
1. On normalCuble tmmformatiDtI8 in Hilbert lIpace. Acta }:lath. 86, 85-88
(1951).
2. Dtfini'" iJ1tq!rtd .yst...... Duke !\lath. J. 15, 871---388 (1948).
Zorn, M.
1. A Temark vn rMthod in transfinire aJwbra. Bull. Amer. lI-la.th. Soc. 401.
667-"70 (1935).
ZwahJen, R.
1. Ein u neuu " Eigerr.wertprOOlnn. Actes Soc. He1v. Sci. Nat. 133, 60-65
(1954).
Zygmund, A. (see also Calderon, A. P., Paley, R. E. A. C., Salem, R., Bnd
Tamarkin., .T. D.)
1. l St:rie.3. Monogral'je Matematyczne, ,"VBrs&W" 1935. Re.
printed Dover Bnd Chelsea. Pub. Co.. New York.
2. An indicidual ngcdic tht(J1'ml Ivr :non-.commtJtalivt rransfOTmllli01l!l. Acta
Sei. Math. S.egOO 14, 10a-IIO ({951).
8. On a fh«ITem oJ Pal<y. Proe. Cambridge Phil. Soc. M. 125-133 (1038).
4. On tht CtAo4t:,.g£JoU and 8IJmmabili1y oj power s s on tlu cinle of
(1). Fund. Math. M, I7I I96 (1958).
NOTATION DIDEX
(a, bl, etc. (4)
A (a) (522)
A(ab . . ., ak) (522)
A (a) (685)
A. (619)
A (D) (242)
A(n) (661)
A(T, n) (661)
AC(I) (242)
AP (H2)
A (11)
batS, 2:)
barS, 1:, E)
bs (240)
bv (239)
boo (239)
B(S) (240)
B(S, 2:) (240)
BV(I) (241)
B(E, W) (61)
(240)
(160)
C (289)
Co (239)
catS, 1:) (240)
catS, 2:, E) (161)
coCA) (414)
Co(A) (414)
cs (240)
C'(l) (242)
C(S) (240)
d>. (182)
d,.
!I)(T")
(T )
(602)
(602)
E" (238)
E(I r I > a) (101)
E(>.) (558)
E(g) = E(g; T) (573)
HAJ (644)
f(T) (557), (568), (601)
f . g (683)
F(S) or F(S, 2:, p, E) (103)
!f (T) (557), (568). (600)
glb A (3)
ha (85)
(242)
inr A (3)
,q(z) (4)
f (410)
I p (230)
1m (239)
r;. (238)
I" (239)
li11l/(a>_.u(a] (26)
lim inffl_cu n (4J
lim inf A (4)
lim iof_mE. (126)
lim_ E. (126)
lim inf_ol(x) (4)
827
828
lim inr. . + I(x)
Jim sup A (4)
lim sup._ a" (4)
lim sup__ E. (I!W)
lim sup._.f(x) (4)
lim sup._o + f(x) (4)
lub A (S)
L,(S, 2:,1')
L (S, 2:, 1')
LiS, 2:.1'. I)
L;(S, 2:, 1', I)
E(A) (64i1:)
(241)
(241)
(Ii1:I)
(ll9)
M(S) or M(S, 2:,1', if)
NBV(/) (241)
91;: (556)
0, () (27)
pry! (9)
PA.orP..xA. (9)
<P(A) (680)
7(T) (567)
rba(S) (261)
rba(S, 2:, 3:) (161)
7ca(S) (240)
rca(S. 2:, if) (161)
R(A; T) (566)
m(..) (4)
B (248)
speRl (50)
sp (B) (50)
sup A (8)
(S. 2:, 1') (I26)
sex, E) (19)
SeA, E) (10)
T(f, .) (668)
Tb-/(S) or TM(S, 2;, 1'.
TM(S. 2:,1') (243)
NOTATION INDEX
(4)
(106)
(106)
I'll') or vu., E) (97)
I!!(A) (642)
:r*. J*
x**, .1**
i,f
if+
J/iII
(61)
(66)
(66)
(418)
(38)
AUTHOR INDEX
At!delhay, .J.,. 897
Abel. N. H., 76, 352, B88
Adams. C. R.. 393
Agnew, R. P., 81
Ahlton. L. V," 48
Akilov. G. Po. 5M
Alaoglu, L" 235. 424, 462, 4.63. 729
A1ex.a.ndroff, A. D., 188, 283. 816,
380-881. 390
Alexandroft. Po. 41, 467
Alexiewia. A' I 82,. 83, 234, 285. 392,.
M3
Altman, M. S... m. 600. 610
An:r.e.i, Ho, 886
Aren8, R. Fo. 881, 882, 88'. 385,
8116-897, 899. 466
Aronszajn. No. 87, 91, 2M. 3D4, 610
A.rtemenko, A., 887. 892
Arzelit., C., 286, 268, 882, 888
Ascoli. Go. 266.. 882. 460. 468
Atkinson, F. V" 610, OIl
Audin. M.. 611
a * (3 (643)
. (1)
" (66)
XR (S)
,..-t-, 1'- (98), (180)
1'* (99)
II I' II (820)
fJ (184)
.(A)
9("" Y)
u(T)
u.(T)
up(T)
u,(T)
2:(1')
T (446)
t/> (I)
4> (49)
w. (619)
(5,56)
(18)
(556), (566)
(580)
(580)
(580)
(156)
BlI.benko K. I.. 9"
&de. W. G., 538. 612, 728
Bam-. R." 20
Banach. S., 69. 62. 7S. 80, 81. 82.84,
85. 86.. 89. 91.98. 94... 284., 832,
8 OI 88.5.886, 892, 442, 462:-463.
46,5-466, 472, 538, 530. 609
Bari, N. K.. 94
Bartle, R. Go. 85. 92. 288. 883. 886,
889.. 892. 539.54rO. 543
Bennett, A. A" 65
Bernstein. F., 48
Berri, R., BPS
Besirovitch, A. S., 886
Beurling, A," 861
Bieber'bach. L., 48
Birkhoff, G., 48, 00. 93. 232. 285.
893-394, 395.. '729
Birkhoff, G. D., 410. 658-659. 720
(2)
1. (7£), (249)
LI (96)
e (249)
E9 (87), (256)
Bimb&un, Z. W. o 400
Blumenthal, L. N., 893
BGa3, R. Po. 94. 473
Bochner. S., 232-288, 235. 2:88. 815.
886. 890. 89S, 54(J. 548, M2
N., 780
Bohn nblustl H. P.. 86, '94" lJD3, 894,
895-396, 654
Bohr. Ho o 281. 886-387. 399
Boltzmann, L., 657
BOnne8en, T., 471
BonsaU, F. F.. 88
Borel, E.,. 182. 189, 142
Bo..uk, K.. 91
Botts, T., 887. 460
Bourbaki, N.. 4.7. 80, £12. 84., 282,
882, 463, 465. 471
Bourgin, D. G., 888. "62
Bra . .I. W. o 4.66
Bray, H. E., 891
Brodskii M. S.,. 47]
Buchheim, A" 6(YT
Bunlakowsky, V., 872
Cafiero, F., 889, 892
Calderon, A. P.. 541.780
Calkin, J. W.. S53
Cameron" R. H." 406. 407
Camp, B. H., 390
Caratheodory, C' P 48. 1M, 282, 129
Ca:rleman. T.. 566
Cartan, ." 60T
Canan, H., 80
Cauchy, A'J 372. 882.883
Cech, E.. 279. 885
Cesaro, E., 75, 352. 368
Chang, S. H., 610
01arzyi1.ski, Z.,. 91
Chev&lley, C., 79
Olristian. R. R.. 233, 882. 543
Clarkson. J. A., 285, 884, S93, 898,
S97, 476
829
830
AUTHOR INDEX
AuTHOR INDEX
881
Clift'on1, A. H., 92
f:,()hen, I. S., 400
Cchen, L. W., 648. 729
Colla.tz, L., 610
Collins. H. S., 466
Cooke. R. G.. 80
Cronin, J., 92
Daniell, P. J., 381-382
Dantzig, D. va.n, '19. 91
Davis.. H. T OJ 80
Da '. M. M., 82. 238, 898.394., 898.
463, 729
Dieudun . J. A.t 82, .84. 94. 285,
887-388. .BS9, .s91, 395. 899-400,
402, 460, 462-463, 46 , 466, 539.
54l
Djne8, L. L.. 466
Dim, D., 360.. 883
Dirac, P. A.M., 402
DixmiM-. J.. 94, 398,538
Doeblin. W., 730
Doob, J. L.t )'29-730
Dowker, Y. N., 723--7240, 729
DuhrowJa1, V. M.. SSg
Dugundji, J.. 470
Dunford. N.. 82. 84, '93, 232. 285, 384.
887. 889, 392, 462, 540-5.101, 54.3,
554,606,600,612.724..727.729-180
Dvoretaky, A" 93
F.berIein. Vi. F.. d8. 886, 430. 468,
4t56,729
Edwards, R. E.. 881
Egoroff. D. T., 149
Eide1heit. M.. 91, 460
Eilenberg. S., 885. 397
Elamin. V'.J 92
Ellis, D.. 394.
Ellis, H. W., 4.00
Erd&, P.. S84. 407
Ezrohi, I. A., 548
Fagan, R. E., 406
Fan, K.. 395. 897. 61C
Fantappi . L.. 899. 607
Fatou. P.. 152
Feller. W.. 727
Fenchel. W_. 471
Feynman. R. P.. 406
Fichtenholz. G., B3. 233, 873. 386.
ass. 548
Ficken. F. A" 393. 894
Fischer. C. A., 880. 539, 548
Fischer. E., 37S
Fleischer. I.. 88. 400
F.01ner, E.. 399
Fort, M. K., 471
Fortet. R.. 9a, 406. 473
Fr8:het. N., 79. 238. 873, 380, 882.
387-888. 302, 730
Fredholm, 1_, 7g. 009
Freudenthal, H.. 84, 394. 305
Frirddchs. K. 0.. 4001. 405,401. 612
Frink, 0.. 'It4
Frobenius, G.. 001
Fubini. G.. U O. 207. 209
Fukaroiyo.. M.. 466, 729
Fullerton. R. E., 396. 897. 540. 548.
552
Gm.ve:s. R. L.. 61Q.
Grimshaw. M. E.. 606
Grinblyum. M. M.. 94
GI"08berg, .. 895
Grosberg. Y.. B92
Grothendieck. A.. 00. .BBa. 889, 398.
899. 466. 540, 54.8, 552, 553. 610
G , L. A., D4
Hadamard. .T.. 880. 538
Hahn, H., 48, 62, 80, B5,. 86. 88. 129.
186, 158. 232.. 233.. 284-235. 890..
539
Halmos. P. R.. 48. 80. 282. 235, 381,
889, 890. 606, 608, 722. 728. 729
Halperin, I.. 400 J 478
Hamburger, H. L., 606. 611
II&oson. E. H.. 392
Harazov. D. F., 611
Hardy. G. B.. 78.. 864. 581-.533. 538,.
541. 718
Hartman, P., 899, '129
Ha.tfield, C.. 406
Hausdorff. F., e, 47-4.8. 79, 89. ]74,
880. 529. 639
Heinz.. }!:.. 612
He1lir1ger. E.. 79. 80. 85, 539. 009
Belly, E.. 81, 86, 280, 391
Helson. H , 385
Hensel, K..I 607
Herglotz. G.. 365
Hewitt. E.. 233. 873. 379, 381-382.
884-885. 887
Hilb, E.. 808
Hilbert, D.. '79-80. 372. 461. 531-582,
538-539, 608
Hildebrandt. T. H.. 81, 85.. 92-93.
288. 878. 880, 388. 891. 302, 609
Hille. E., 80, 92J 543. 806. 608. £10,
612, £24, 726-727. 729
Hirschman, :r. :r.. 728
Hobson. E. W.. 1S83
Holder, E.. 110, 378, 612
EWpf, E., e69, 670. 722. 728. 729
Hopf, H.. 47. 4.61
Horn, A.. 610
Hotta. J_. 466
Uukuhara, M., 474
Hurewicz:. \V.. 467, 722. 729
Gagaev, B., 93
GaI.. I. S., 80. 82
Gale. D., 382
Gantmacher. V., 463. 485, 589
GambedJan, P. R., 88
Gavurin. M. K... 612
Gelbaum, B. R.. 94
Gelfand, I. M... 79, 94, 232. 235, 34.7.
.384, 385. 806. 407. 539. .540, 543.
6GS, 609
Gibbs, J. W., 657
GiIJespU-. D. C., 462
Giorgi. G.. 607
Glicksberg, I.. SSI
GJivenko, V . a9]
Godt), K.. 47-
Gohberg, I. C... 610, 611
Gol'dman, 1\-1. A.. 611
Goldstine. H. H., Ell. 424. 463
eom.., A. P., 899
Goodner.. D. Bo. 898. 554
Gowurin, 1\1., 2a3, 891, 543, 552
Grave:s. L. M.. 48, 85. 92. 232, 235.
883, 391. 467, 61 J
Graves, R. E_. 406
Hurwitz. \V. A., 462
Hyen, D H.. 92,. 471. 009
Inaba. N.. 474
Ingle ton, A. W., 88. 400
Iyer. V. G.. 399
Izumi. S... 235, 882. 888. 892. 548.1 552
Jacobson. N.. 48
Jam . R. C., 88. 93. 94. 898.894,
472 478
.Jamison. S. L.. 612
Jenson. M_. 897.. 478
Jessen. B.. 207. 209, 235. 530
Jordan. C... DB. 392
Jordan, P., 893-394.
Kac, M.. 406.. 407
Kaczrnarz. S.. 94
Ks.diSQn. R. V., 885. 395, 307
Ka.kutani. S.. 86, EO, 235, 80, 884.
386. 893-394, 895, S9a. 456-457.
460, 462.1 463. 471, 478. 539, 541.
554, 'i15. '128-'780
Kamke. E., 47
Kantonwitch. L. V.. 283.. 873, 386.
888. 895, 540, 543
Kaplansky, I.. 384-385. 3'96
Karlin, S., G3. 94
Kato. T.. -612
KeLly!, M. V., till
Kelley. J. L.. 47-48, 382. 385.. 307..
898. 466. 554
Kellogg. O. D.. 470
Kerner. M.. {l2
Khintchine. A.. '120
Kinoshita, A., 471
Klee, V. L... 87, 00. 460-4.61. 466
1f1Pi 1ao. D. C., 553. 610, 612
KnoPP. K.. 48, 5S0
Kober, H. A.. 554
Kolmogvroff, A., 91, 885, 888
Komatnz.aki 554
Koopman. B. 0.. 728
yuttnko, A., 94
Kothe, G.. 84, 899, 465
Kozlov. V.. tJ4
Kra6kovskii. S. :S., 47S. 611
832
AU'tROR J;NDEX
AUTHOR INDEX
833
Krnmer, H. P., 612
Kramer, V. A.t 612
Kmsnosel Bk.ii, M. A," 400. 611
Krein, M., 94. 887. 895, 800, 897.
4.29. 434. 440. 461. 463. 465-466,
611. 612
Kreio, S., 895, 1W6. 397
KryJoft, N., 730
Koller. R. G' t 895
Kunisawa, K., 891
Kuratowski. Co. 88
Kti<SChllk, J., 79
Lagrange. J. L.. 372
Laguerre. E. N.. 607
Lamson. K. 1-V" 85
Landau, E.. 80
Lasalle, J. P., 01, 399
Ltt.x 1 P. D., 88
Leader, S., 283
Lebesgue. H.t 130. 12.... 182, 148, 151.
218. 282. 234. ROO
LefseheU. S., 47. 467
Lejs. K. 79
Lera.y, J' t . 470, 609
Levi. B., S7S
Levy, P.. 407
LezaI'1$ki. T., 610
Lie. S.. 79
LifSi 1 I. M., 612
Lindelof. Eo. 12
Lindgren, B. W., 406
Littlew()od, J. E., 78, 531-532, 541.
718
Livingston. A. E.. 399
Liv i<:, 1\01. S., 611
Loomis. L. H.. 79, 382, 386
I..orch. E. R. , 88. 94, 398-3940. 407,
554, 600, 728
Lcrentz. G. G., 84. 400. 548
Lo'Wig. H.t 372, 373
L6wner. }{., 407
Maak, \-V., 386
NacDufJee, C. C.. ti06. 607
MacIrey. G. \V., 393-394. 554
MscLane. S., 48
Iacphail, I'tl. S.. 93
McShano, E. J., 84. 282-233, 382. 387
1\1addaus, I., 98, 54$. 552
Maeda, F., 395
Marcinkiewic:t. .. 720
Marinescu. G., 609
Markouchevitch. A.. 94
MBrk()v, A.. 880, 456, 471
Martin, R. S., 79, 010
Martin.. W. T., 400
MarumaYB, G., 406
MaSlilli, P. R_. 288
Maslow, A.. 288
Mazur, S., 80, 81-82, 83. 91-92, 892,
400. 418. 460, 461-462. 466, 472
Mdvedev. Yu. T.. 892
:Mertens. F., 71
:Micbael. E., 462. S38
Michal. A. D., 79, 02, 61()
Mikusiiuiki, .J. G., 395
Miller, D. S.. 392, 724, 729
Milman. D. P _, W. 440, 463, 466, 471,
473
Mimura, Y., 541
Minkowski, H.jo 120, 372. 4.71
Mimnda, C.. 88, 470
Miyadera, I., 721
MOnn8. A. F., 283, 400
Montroll. E. W... 406
Moore. E. H., 28. 80. 608
Moore, R. L., 48
Morse. A. P., 87. 235. .393
.Moser. .l., 612
Moskovitz, D., 466
Munroe, M. E., 93. 232. 235
Muntz, C. R.. 384-
Murray, F. J.. 554
Iyers, S. B.. 382, 397
Neumark, M.. 896
Newburgb. J. D.. 612
N-.. M.. 388
NJemytsky, V.. 470
Nikodfm, O. M., 98, 160, 176, 181-182,
284-285. 309, .381. 390, 892
Nikol"skil. V. N., 94, 611
Norlund, N. E., 75
Ogasawara. T., 395
Ohira. K.. 894-
O'Neill, B., 474-
Ono, T., 88. 400
Orihara, M.. 895
Orliez. \'Y., 50, 81-82. 83, 93. 94, 235,
E87, 888. 391-392, 4.00, 543
Owcha.r. M., 406
Oxtoby, J. C.. 722. 728. 729
Paley, R. E. A. C.. 405. 406) 541
Peck, J. E. L., 471. 474.
B. J.. 81, 83-84, 88, 232, 235,
318. 387, 891. 473, 540-S..... 543
Phillips. R. .. 233. 234- 5. 373. 388,
390, S9S. 395, 4062. 463, 466, 541,
543, 553-554, 61'2. 6240. 726.728.
729
Pierce, R., 395
Pin-cherle, S., 80
Pinsker. A. G., ass
Pitt, H.R., 0;29
Poincare. H., -607
Foi!ison, S. D.. 363
Pollard. H., 728
Pdya, G., 531, 532. 54.1
PontTjagin., L.. 47, 7Q
:Price.. G. B., 232-233
Ptik:, V., 84, 466
Nacbbin, L., 98, 395, 397, 398, .554
Nagata) .J., 5
Nagumo. M.. 79. 84.. 3940, 608. 609,
726
Nakamura, M., 233, S91. 395. 589
Nakano, H.. 80. 895, 471
Kathan, D. S., 726
NeurnalUl, C., 608
Neumann, .T. von, 80. 85, 88, 235,
72. 380, 386, 389. 31)8.3g.I. 438,
461. 538, 611, (j.J2. 650. 727, 728
Quigle)', F. D_, 385
RabinoVlc., '-'u. L., 612-
\ladon. J.. 142. 176, 181-182. 234,
380, 888, 892. .539, 543
Rayleigh., Lord, 611
flellich. F., 372, 37.9. 611-612
Rk>ko.rt:. C. E.. 233, 234, 541, 5.J.3
Rie5z. F., 79. 80-81, 8 .86. 88. 265,
872-378. 880. 881. 888, 892. 895.
538, 589, 606, 608.. 609. 659. 728-7:W
Riesz. )1., 388. 525, 532, 54.1
Rinohart. R. F., 607
Roberts, B. D.. 93
Rogers, C. A.. 98
Rosenblatt, M.. 4()6
Ro&enbloom. P. C.. 47, 612
Rosentha.I, A.. 282, 284.295, 390
Ros!Ier. J. B.. 47-1J.8
Rotho, E. M_. 92, 470
Rubin, fl., 893
audio, 'V., 385
R1lSton. A. F.. 473, 610
Ruticltii, Va. B., 400
Rutman, 1\1., 94, 395, 466
Ryll-NQrdu:wski. C., 683. 724. 729
Sa.kis. S.. 80, 82. 158, 232. 233-235,
308. 880, 390. 892, 462. 720
Sa.lem. It_. 5402
San .Juan. R., 38'1
W. L. C.. 81, 400
SebiiI1re, F. W.. 94, 612
Schatt.en. R., gO
Schauder. .I.. 83, 84. 98-94. 456. 470,
485, 539. 609
Schmidt, E., 79. 88_ 539. 609
Schoenberg, I. J.. 380_ , 728
Sehteier, D., 79. 462
SchrOder, J., 612
SchrOdinger. E., 611
Schur. I., 582
Schur. .J' I 77. 388
Schwart:t. H. l\1., 391
Schwart7., .)., 375. 387. 389, 892, 540,
543, 612
Schwartz, I... 82. 84, 899. 401, 402,
466. 611
8chwar7.. H. A.. 248, 372
Schwerdtfeger, H., 606
Sebastiao e Silva, .I.. 235. 399
Segal, I. E.. 884., 727
Seidel, P. L., 388
Shapiro, .r. M.. 406
Sh1ffman. 1., 88
Sikorski, R., 1510
Silberstein, J. P.O.. 610
8340
AUTHOR INDEX
AUTHoR INDEX
835
Silov. G. 884, 885
Silvas Dias, C. L. da, 899
Silverman, L. L.. 7,5
Sirohov. M. F., 3'95
Sirvint. G., 288.386,589-340.541,54.3
Skorohod, A.. 94-
Smiley, M. F., 894, 395
Smith, K. T.. 61V
Smithies. F.. .543, 610
Smu1ian, V. L., 392. 895, 429, 480,
483, 434.. 461, !l68-464, 465-466,
472-473, 612
Sobczyk, A.. 86, 393-894, 558-554
Solomyak. M. Z., 612
Soukhom)jnoff, G. A., 86
Sparre Andersen, E., 285
S...der. Y., 392
Steinhaus.. H., 80-81. 94, 387-888
Stepanorr. \V," 729
Stewart. F. M., 233
SticlreJbeqer, L., 607
Stieltjes, T. ..J., 13'2, 142
Stokes, G. G_. 8S3
Stone, M. }J.. 41, 48. 80, 85. '272. 791
82. 883-J185, 398, 896, 898. 442.
.&eO, 466, 606, 608. 726
Sunoucbi, G. p 233, 234, 89:1. !i4S. 552
Sylvester, ..Y. J.. 606-607
Sz.-Nagy, B. vOn, 80, 873. 895, 606,
608, 609, 611, 612. 729
&asz. 0_. 884
Tngamlitzld.. Y., 896. 473
Takahashi, T., S88, 400
'Tatdykin, A. T... 610
"I'amarkin J. D., 80 284-285, S88,
542. 543, 610
Tarski, A.. 8
Tauber, A., 78
Taylor, A. £. 92. 233, 399, 540, 543.
552, 554. 606, 608, 612
Teiclm:riiller, D., 48
Thorin, G. 0., 541
Tietze, H., 15
TingIey, A. .I., 406
Titcbmanh. E. C., 48, 612
Titov, N. S., 03
Toeplitz. 0., 'i . 79, 80. 85. H99, 539,
609
Tomita, M., 473
ToneHi, L., 194.
Tseng, Y. Y., D...
Tsuji, M., 888
Tukey, J. W., 460-461
TuJ.,jkov, A., 888
Tychonof'f. A., 32, 872. 458. 470
Yood. B., 474, 610
\:"O£lda. K., 233. 234, 373, 898. 466.
539.541,624,715,726.727,728-730
YOUI1g, L. C., 542
Young. \V. H.. 52g
Udin, A. J., 396
Ula.m. S- 9l
Urysohn. P., 15 24
Veress, P_, 873. 388, 392
'Vinkurov, V. G., 9'
Vinogmdov, A. A... 473
V"IS8eC. C., 810. 728
Vitali G., 122, 150. 158, 212 283-234,
892
Volterra. V., 79, 80, 399
V:ulich. H. Z.. 9S. 8D6, 54.0, 543
Wallman. H., 467
\Valtel"s. S. S.. 399
Wassilkoft. D.. 896
Wedderburn,..J. H. 1\1., 006
Wehausen. J. V.. 83, 91, 381. 462,
471
\Velerstrass. K., 228, 232, 272-27.3,
383.884
\V<'11. A. 79. 386
Weinberger. H. F.. 610
,"Vermer, .1., 385
Weyl. H. , 372, 610. 812, 725
Weyr, E., 607
Wl1yburn, G. T., 84
\"idder.. D. V.. S8S. 728
WieneJ' " 85. 402, 405. 406. 008.
7.28.729
\\'Dansky. A., 94
Wilder, R. L., 41
Willmmson, J. H., 609
'Vintner. A., 899. 729
\Volf. F.. 612
Yaglom. A. M., 407
Yamak. H.. 87
Zaanen, .0\. C. 80, 387, 400.609,610.
6lt
ZalcwBS!ItT. Z., 462
Zermelo. E.. 7, 48
Zorn, !\.I.. 6. 48
Zygmund. A_. 400. 405. 541, 720 730
SUBJECT INDEX
StditJn numbers cu Jollrnctd by page numbers in paR7llftf!8tB.
A
Abel l!Iummability. of 8enes. 11.4.42
(76)
Abelian group, (S4)
Absolutely continuous functions. <!rfi.
nition, IV.2.22 (242)
6et function. (See CunliRuous BlI
ft"",1Inn and 8<1 j'wnM",,)
6paoe of, additional properties"
IV.I5 (378)
def'mJtion. IV.2.22 (242)
remarks concerning. (392)
study 01, IV.12.3 (338)
Ab601ute convergence, in a B..space.
( 3)
Accumulation. point of, IA.l. (10)
Additive set function. (See Set [unt:-
ticm)
Adjoint element J In an algebra with
involution, (4IJ). (See also
Adjoinl sp<><e)
AdjQint of an operator, between
B..spac 8, VI.'2
C<J1TIpact opemtor. VI.5.2 (485),
VI.5.6. (486), VIIA.2 (577)
continuity .of .operation,. VI.9.12
(513)
criterion for, VL9.13-14 (513)
in Hilbert space. \'1.2.9 (479).
VI.2.m (480)
remarks on. (588)
resolvent of. VII.3.7 (568)
spectra of, VII.8.7 (568), VII.3.9-10
(5S1), VII.5.23 (582)
weakly compact operator, VI.4.7
(484-485)
Adjoint "pace. definition, JI.3.7 (61)
representation for 8.peci:al spact'S.
IV.15
.e. (h, AI..... I
Affine mapping. dft'anltion. (4.56)
fixed points of, V.l0.6 (456)
AIexandroft' theorem, em countable
additivity of regular !iiet fune-
tiOIDi un compact tlpaces.
][1.5.1. (188)
on C(S) COD ce or bounded
additive .set t\uJctioJ18. JV.9.15
(316)
Algebra, a]gebraic PftIimiDaries.
1.10-13
Boolean. (See al&o Field oj sets:)
definition, (43)
representation of. (44)
definition (40)
quotient, (40)
of £lets. (See Fkld oj sets)
Almost everywhere (orp-almost every-
where) def"mition for additive
sa.lar set functions, 111.1.11
(100)
definitjon for vector-valued Bet
functions, IV.IO.6 (.22)
Almost prriodic functions.. delinitione
IV.2.25 (242)
F.p8tt of. additional properties,
IV.I5 (879)
definition, IV.2.25 (242)
remarks conc>eming. (S86-887)
stlJdy of. IV.7
Almost unifonn (()r p-unifom1 con-
) def'mition, ][1.6.1
(145). (See also c of
fundi"",,)
Analytic oontinuatioQ, (280)
Analytic function {vt'CWr-vatued,.
betw n complex vector spaces,
VI.IO.J (522)
def'mition, (224)
properties, 1II.l4
83i
838
SUBJECT INDEX
SUBJECT INDEX
839
space of, dermition. IV.2.24 (242)
properties. IV.I5
Annihilator of a set, 11.4.17 (72)
Arzela theon.'UI. on continuity of limit
functJon,. IV.6.11 (268)
H'IDBI'ks concerning, (383)
Ascoli-Arzel8. theorem, on OOhJpact.
ness of continuous functions.
IV.6.7 (266)
rem"..b . (882)
Atom, in a measun> space, IV.9.6 (SOB)
AutQrnorphisms, in groups, (35)
B
B-space (or Banach spare). bRsic
pwpert.ie of. Chap. II
definitioI4 11.8.2 (59)
integration, Chap. III
Bpecial B-spaces. Chap_ IV
propnties, IV.IS
Baire cakgOry theorem, 1.6.9 (20)
Banach limits, existence and pro-
perties, II.-L2Z-23 (73)
&nsch theorem, un cOQV£TgE'I\Ce of
measurable functions,lV.II.2-3
(332-334)
Baruu.h-Stuoe theorem. on eq'Uiva.loence
01 C.......... V.8.8 ("'21
remarks on. (896-397. 466)
Base for a topology, criterion for,
1.4.7 (111
definition, 1.4.6 (10)
Theorems concerning countable
bases, 1.4.14 (12). [.6.12 21},
I.e.IO (24)
Base (or basi,,). (See olso Ham,d base)
in 8 B_spatt. <':riterion 'or om-
pactness with. 1\'.5..5 (200)
definition, 11.4.7 (71)
properties, II.4.8-12 (71)
remarks on (93--940)
in a linear !SopacE'. (See HlUIIel baBe)
orthogonal and m1iHmormal bases
in Hilbert spa.ce derirJition
IV.4.n (252)
existence of IV.4.12 (252)
Basic liepa.ration the()rem concerning
convex sets. V.I.12 (412)
BeJDStein the<n-em. t'OlK"PITIing cardi-
nal numbeI'S J.14.2 (46)
BiJ..QterWLaplace and Laplace-Stieltjes
b-aruJ'fJD118" dftinitions. VIII.2.1
(642)
Biline., funct 11.4.4 (70)
BiorthogonaJ system. In a .8-spa.ce
II.4.II (71)
Booleanalgebrn. (Seeals.oBmkanring)
definitioD j (43)
prop<'l1io<;, (...)
representation of. (44)
1:Ioolean ring, definition, (40)
representation of. 1.12.1 (41)
Borel field of sets, definition, 11I.5.IV
(137)
Borel I"IIIeIIsure (or Burel-Lebesgue
measure), OODStmction of. (189)
III.I3.8 (225)
Borel-Stieltjes rnea.sure. (142)
Bound.. of un operatoT. 11.8.5 (00)
in a partially mdcred Bet. 1.2.3 (4)
jn tbe (cxtended) rea.l number
S)"Strm. (3)
BounWu,.. of a set. 1.4.9 (11)
Bounded, ia]JY(O!Jl-essmti8:UY.,
definition l III.I.ll (100)
iOperator, definition l 11.8:.5 (.fW}
set in a linear topu1ogical space.
11.1.7 (51)
criterjon for boundedness in 0.
B-space. II.3.. (59)
relTlarks on, (80)
totally bounded set l defjnition.
U.14 (22)
Bounded function space, additional
properties, IV.1S
dofitUt...., IV.2.13 (240)
rema.rks concerning. (373)
sludy of. IV.5
Bounded sets. in linear 6]J8I."t"S., V.?a
(43a), V.7.7. (436), V.7.8 (436)
Bounded \."81'1&tlOn of B function.
additional properties, 1\'.15
(3781
LTitenon to be. IV.13."i'3 (350)
ddinition. 111.5.15 fl40.
generating Borel-StieJtjes measure,
(1421
integral with re.sped to. IV.18.68
(3'.)
integration by parts, 11:1.6,22 (J54)
reman.. on, (392-4103)
ri,ght- and len-band limits (Jf.
In.5.16 (140), In.6.2I (154)
set function, criteria for. 111.4.4-5
fI27-128). (See aho Varia-
tion)
det'"uUtion, nU.4 (97)
study of. IV.12
Bounded strong operator topology-.
defimtion and properties,
VI.9.9 (5U!)
Bounded weak operator topology.
definition and properties,
VLO.7-10 (512)
Bounded X topology, rontinuous
Ijn<ear funclionaIB. V.5.6 (428)
system of neighborhoods for. V.5.4
(4271
Boundedness, of an almost Pf'Iiodic
function, IV.'l.3 (283.
of a continuous function 011 a com-
pa.et set, 1.5.10 (18)
cf a rmite countably additi.ve set
function, 111.4.4-7 f127-128)
principle of 'Uniform boundednes.s,
in B-Sf"""'S, n.5.20-21 (66),
(80-82)
in F . 11.1.11 (52)
Bounding point of 0. 8d. criteria for.
V.L8 (411), V.2.I (418)
definition. V.l.6 (410)
Brouwer fi::(:ed point theo proof m.
(467)
8tatement (453)
C
Ca.lculu8. operational. fSu OperatiOfUlI
t:aku1Its )
C.ntm dmgontJ. p""-"",,, (23)
CfJ,ntor perfe t set, V.'2.13-14 (436)
Carath odory theorem. oo
(luter measures 111.5.4 (1&4)
l:ardina.l numbers? Bernstein theorem.
1.14.2 (46)
compllrab1llty theorem 1.3.5 (8)
Carle:<iian product of seb, definition.
1.3.II (9)
propertj("5 1..8.12-14 (9.
Carte dan »roduct of t.opological
spaces. 1.6
Category theorem, of Baire. 1.6.9
(20)
Cauchy integral formula. (227)
for functions ()f tm operator. in a
finite dimensional pace.
Vn.I.IO (5601
in general space, VII.3.'G (568)
remarks (In, (607-609). (612)
for unbonnded closed operators.
VII.9.4 (601)
Cauchy integral tl1eorem. (225)
Caucht problem. (018-614) (639---64])
Cauchy l'iequence. generalized. (28)
in 8 metric space. 1.6,5. (UJ-20)
weak. in a B-8pa 1£.8_25 (67-68)
criterion for in various spaces.,
IV.I5
Cech compoctjr.:2f.tion theorem,
IV.6.22 (276)
IQf 8 completely regular space. (279)
Ce.'!aro summability. (If Fourier !!'oeries.
IV.14.... (36S1
01 series, JI.4.37 (75)
Change of variables. fQr (unction!:!.
HI.18.4.--5 (222--223)
for """'""""', IJI.I0.8 (182)
Olaraderistic function. (3)
Characteristic polynomud. definition,
VIT.2.1 (561)
properties, VII.2.1--4 {561-562).
VII.5.17 (582). VIUO-8 (606)
Characteristic ,-alue. (600.
Chamderizations. of Hilbert .space.
(395-394)
01 L" (3<14-'!00 1
of the fipace of eontinllOU:i functions,
(3o.H197)
Closed curve. positive orientation of.
(225)
Closed graph theorem. 11.2.4 (57)
remarks on. (83-85)
Closed linear manifold tl;panned by B
set, IU.4 (50)
C1IY-Sed (lpemtor. defin.ition. 11.2.3 (57)
540
SUnJECT INDEX
SUBJECT INDEX
841
Clo d orthonormal system. definibon.
IV.14.1 (.57)
study or IV.14
CI05t'd set. definition, L4.3 (10)
properties, 1.4.40-5 (I()
Closed "P11.... II.4.1 (70)
Closed unit :sphere. 11.3.1 {59)
Closure of a set. criterion to be in.
1.7.2 (27)
definition. 1.4.D (11 I
properties of the closure operation,
1.4.10-11 (11 12)
Cluster pelot. or a set, 1.7.8 (29)
C«;.mpact ()peratot in C,. VI.OA5 (516)
criteria for and properties Clf,
VI.D"0 55 (515)
d.lirntioD. VI.5.1 (485)
elementary VI.S
id..1s <>f, (552-558)
in L., VL'D.51-57 (517-519)
remarks conce.-ning. (589).(609-611)
representation of, (547--551.
into C(S), VI.7.I (490)
on C(S), VI.7.7 (496)
on Ln VI.S.lI (501)
spectral theory cr, VII.4. VlI.5.35
(584), VII.8.2 (59 )
Compact space, conditional compact-
ness,. 1.5.5 (1'1)
criteria for LS.6 (17).
1.7.9 (29), 1.7.12 (80)
def'initic>n, 1.5.5 (17)
mc1;:t'ic spwx's, 1.6.18 (21-22).
1.6.18-1" (2<)
pr0pcrbe8, 1.5.6-10 (17-18)
sequential compactness, definition
1.6.11} (21)
weak sequent.ial compa.ctness, con
ditions fQr in special B-spaces.
IV.15
definition. 11.8.25 (67)
in refJexive spaces, II.S.28 (68)
eo.mplement, orthooomplement,IV.4..8
(2<9)
or1bcgtmaI. II.4.I7 (72)
Ilnd projections, «553-554)
of a set, (2)
Complemented laltice, «43)
Complete and a.complete lattice. (43)
Complete metric !Space. compact,
1.6.15 (22)
definition, I.{J..5 (19)
properties, 1.6.7 (20), 1.6.9 (20)
Complete nonned linear space. (See
B-spaff)
Complete orthononnaI set, In Hilbert
space, IV.4.8 (250)
Canplete part.ia1ly ordered spa.ce.
definition. 1.3.11 (8)
Completeness, weak. See Weak £Om
pI-)
Completely :regular space, compactifi-
catjOD of. IV.6.22 (270.
defimtwn. IV.6.21 (276)
Completion or a normed linear space,
(89)
Complex numbers. extended. (a)
Complex vector space, (88). (49)
ConditionaJ. compactness. derwition.
1.5.5. (17). (Se. aloo Campud)
Cone, definition, V.P.9 (451)
Conjugate space, defjnition, U.8.7 (61)
representation for space-s,
IV.15
Conjugations, in groups, (35)
Connecl:.ed tI in rHlpBce. (280)
Connected apace, L4.12 (12)
Contirwity of functionah and
topology, V".8-9 (426--421).
V .8.11-12 (422)
in bounded X topology. V.5.6 (428)
mteria (or or continuous
linear funct.ionaIs. V.7...3 (4.86)
non xistence in L.., 0 < p < I"
V.7.S7 (438)
Continuous functions.. CSee also Ab-
BDlrddli a>nlin-.s fundion)
as a B-space. additional p
IV.15
deljrution. IV.2.I4 (240)
remarks ronenning. (873-386)
study of. IV.6
£'hara.cterizations of C-space. (89G-
397)
on H compact space... L5.8 US).
I.5.1C (18)
critel'ia and properties of. 1.4.16-15
(13-1<), 1.6.6 (20), 1.7.4 (27)
criteria for the limit to be con.
tinuous, 1.7.7 (29), IV.6.n
(268)
deruDtion. 1.4.15 (18)
del1sRy in TJt.t and L,#, lII.O.17
(170), IV.8.19 (298)
existence or non-differentia.bJe ron.
tinoou. functiono. 1.9.6 (88)
existence un a norma.l space. 1.5.2
(IS)
extension of 1.5.8-4 (15-17), L6.17
(28)
representation as A C-space. almost
periodicfunct.iomo, IV.7.8 (285)
bounded functions. IV..6.18-22
(27<0-277)
op<ciaI C-space., (897 398)
uniform continuity, 1.6.16-18 (28-
2<)
of almost periodic functions,
IV.7.4 (283)
Continuous (Ot p-oontinuous set func
tions), criterion for. 111..4.]$
(131)
definition, 1I1.4.12 (131)
derivative of. 111.12.6 (214)
relation with absolutely oontinuous.
functions. (838)
relation with integrable f\Inctions.
IIUO
Co of functions, IV.15
almost everyv,:hete, criteria for,
1l1.6.12-18 (149-150)
def'uDtion. llU.ll (100)
propertie.. III.6.1<O-17 (150-151)
in L , criteria fOF. 111.8.6---7 (122-
124), Ill.6.15 (ISO), III.9.5
(169), IV.8.12-I4 (2D5-200),
(.88)
10 IIX"$W'C (or in /.Nneasure).
counter examples -concerning.
III.9.4 (169), lII.D"5 (171)
definitIOn. 111.2.6 (IV4,)
P"'P"rtie., III.2.7 8 (IO<--W5).
1l1.6.2-3 (145), III.6.13 (ISO)
flua.si-uniform. definition. IV.6.10
(268)
properties, IV.6.II-I'2 (268-269).
IV.6.30-31 (281)
p-unifon-n. criteria for. JU.6.2-3
(1<.5), 111.6.12 (149)
definition. 111.6.1 «145)
unifonn. definition. 1.7.1 (26- 1)
properties, 1.7.6-7 (2&-29)
Convergence of filters. 1.7..10 (30)
Converge.nceofsequences.
I.7.1 7 (26-29)
in a metric space, 1.6.5 (19)
in special spaces. IV.IS
weak convergence in a B-Bpace,
II.3.25 (67)
Convergence of rie.s in a B-space,
Bboolute. (GB)
unoonditional, (G2)
Convergence of sets. ddinition {126-
127)
measurable sets in !:(p), IIL7.1
(158)
properties, III.GAS (174)
lSet functions. lJl:7.2-4. (158-100),
IV.8.8 (2G2), IV.G.<O-5 (808),
IV.D.15 (816), IV.I().6 (321),
IV.I5
remarks on, (889-392)
Convergence theorems. IV.15
Alexandroff theore.monoonvergenoe
o(Jf measures. IV.9.15 (816)
Arz.elil theof'(:m on continuous limits
IV.6.11 (268)
Banach theorem for operators into
space of measumIJJe functions.
IV.ll.2-3 (832-883)
Egoroff theorem cn a.e. and p-uni-
formconvergencc.III.6.12(149)
Faton theorem on limits or integrals,
III.6.IG (152), I11.9.S5 (172)
for functions of an operator.
examples of, VIJ.8
in finite dimensional spaces,
VII.l." (55"). (SeeBoo E,g..
die 'hlorems)
in general spaees. VII.S.IS
(571). VII.!!.23 (576).
Vll.5.82 (584)
by in....-ung ""Ju.nee..
VIII.2.13 (650)
study 01, VI1.7
forkemels,IILI2.IO-12 (219-222)
842
SUBJ"ECT INnEX
SUBJECT INDEX
813
Lebesgue dominated convergence
theorem, III. .7 (1'24).111.6.16
(151), IV.to.tO (328)
for linear operators in F- and
B pace$. 11.1.17-18 (54--55),
II.3.6 (60), (80-82)
Moore theolTt'ft on intuchange of
Iimils, 1.7.6 (23)
Vitali theorem for integmIs. 111..8.6
(t22), 111.6.15 (150), III.9.45
(173), IV.to.9 (325)
VitaJi-Hahn-Sub theorem for meas-
ures, 11].7_2--4 (158-160)
\Vrierstr8ss theorem on analytic
CuncI.,.., ('28)
C()DvexoCombinatioh, V.2.2 (414). See
also Conl'f'.1' hull, CMDf'Z Itd,
C...........!p<K'<)
Convex function. definition. VI.lU.I
(520)
study of, VI.lO
(''''''''''' hull, V.2.2 (414)
Convex ..., IU.l (70)
definition, V.L> (410)
study of, Vrl-2
Convex spQf!e,locDIIy. V .2.9(417), (471)
strictly. V.n.7 (458)
unifonnIy, dd"med. IU.27 ('74)
..emarks on. (471--474.)
Convexity theorem of 1\1. Riesz..
VI.IO.lI (525)
applica.tions of, VI.1l
Convolution of functions. definition.
VIlI.I.23 (655)
inequa1itiB'l «Jncerning, VI.ll 6-12
(528-529)
properties. VIIU.24--25 (684--<!35)
Convolution of rneasurt's.. VIII.2..8
(648)
OJrrespondence. (See F.ndion)
Co,et, def"miOOn, (35)
CountabJy additive set runctron. (See
also Set Furu:tion)
iCOunt.able additivity ()f the integral.
III.6.18 (t52), IV_IO.8 (323)
definition. 111.4.1 (126)
extnWon of. 111.5
integration with to. 111.6.
IV.IO
properties, IV.9, IV.15
spaces of, ]11.7, IV.2.16-17 (2J.O)
stud). of. 111.4
uniform countable additivity.
III.7.2 (158), 111.7.4 (U'O),
IV..!!.8-9 (292-295), IV.9.1
(305)
weak countable additivity.. defi-
nition, (818)
equiV31E>nce with strong. IV.10
(318)
Covering of 8 topologica.l spact"
definition. 1..5.5 (17)
Heine.BoreI covering theorem, (17)
LindeIOf covering tbeot' m, (12)
in tbe sense of Vitali, definition.
III.12.2 (212)
Vita1i cmumg theorem. 111.12..3
(212)
Cross product. See PJ'odUd')
Cube, Hilbert. (See Hilbert cube)
Curve. (See Jordan curu, J'f'Ctijlabk
cu )
Density of the natural mbedding of
JL B-spa.ce X into X" in theX.
topo1ogy, V A.a"';; (424--425)
Derivative,chainru1cfor.III.lS.1 (222)
exmene<: of, III.12.6 (214)
of Cunction.... ][1.12.7--8 (216--217),
111.13.8 (222), III.I3.6 (223)
properties, IV.15
of Radon- mwdym. (182)
rel'erences for differentiation, {235}
of 8 $e1: function. 111.12.4 (212)
of differentiable functions J
IV.2.23 (242)
Determinant. dcfilution. (44-45)
elementary properties of, 1.13
Diagunal pro«.'SS, (23)
Diameter of a set. def'mition, 1.6.1 {19}
Diamctra1 point, V.11.14 (459)
Differt'lltiability of the norm, remarks
on, (471--47a), (474)
}]iIferential calculU8. (See also INri[Jtl-
,;".)
in a B pace. (92-93)
Frechet. dirfe1'(:ntial. ( 2)
Differential equations, Mlutions or SYSa
terns 01, (561), VII.2.19 (564),
VII.5.16 (581), VII.5.27 (583)
.ta1)ilily of, VIL2.2I>-2U (5 65)
Differentiation VIIUI.13-14
(719-720). (See also Dt:rivuIftJ<)
Dimeru,ion ('If Hilbert spaoe. as a
criterion for isometric isomor a
phism, IV A.I6 (254)
def"mition, IVA.I5 (254)
invminnce of. IV.4.14. (253)
DiJnengion or a linear space. m a
B-,_ (9I--Jj2)
definition, (36)
in of, 1.14.2 (46)
Direct product, of B-spa.ces, (89-90}
Direct EilJm. of D-spaces, (89-90)
of Hilbert spu . JV.4.17 (200)
of linear Tnanifold., in a linear
space. (37)
of linear spa.ces. (37)
IJm.octed .... defini.Km. 1.7.1 (26)
Disconoect.ed,. extrema.U .. (anH)
totally, (41). (See nlso CDRRf'dofd)
Disjoint famiJ) of sets, defmition, ('2)
D
JJt>compoa}tion('lfm andt;pPCt'8.
Hnhn deoo tion, 111.4.10
(129)
Jordan decompo5ition, for finitely
additive Ed functions. IILI.7
(98)
for measures, 111.4.7 (128).
111.4.11 (180)
Lebesgue decomposition. [11.4.14
(182)
Saks deoompo.sition. JV.9.7 (308)
Yosida..Hewitt dctvrnposition.(283)
De l\'lorgan. ru]es of, (2)
Dense COftvex sets. V.7.27 (43'1)
Dense line11r mtwifolds V.7.40--41
( ..s8--4S1I)
Dense set, definition. I.G.II (21)
d.ensity of simple functions in L..
1 ;;;; p < 00, IlI.3.8 (125)
d.ensit)' of continOOll functiolU> in
rM and L., IIU.17 (170),
IV.8.IV (2"8)
I)(mhcre dn....e !<d. 1.6.11 (21)
h between points. dct'II1ilion.
IV.6.15 (272)
Domain, of a function, (2)
in complex variables, (2240)
Dominated con theorem.
III.S.7 (124), III-O.W (151),
IV.to.IO (328)
Dmninated ergodic t1lt C)rem. k-pam-
meter continuous ca.ooe in L p .
I < p < 00, VIII.7.to (694)
k.p;muneter discrete case. VIII.6.9
(679)
one.para.meter oontinuous case.
VIII.7.7 (693)
one--pararndu discrete <."Wie.
VIII.6.8 (673)
remarks on, (729)
Dual space (or conjugate space).
definition, 11.3.7 (fli J
E
Ebedein-$OluJian theorem on vn;:ak
compactness, V.6.1 (430)
remarks on. (466)
Eguroff 1heore on almost every-
where and -unif()rm con.
verge'IJre. 111.6.12 (149)
Eigenvalue, eigenvector definitions.
VILl.2 (556) (606)
Embedding. natural, of a D-space into
its. second conjugate, 11..3.18
(66)
End point, ot' an mtet'val, 111.5.15 (140)
Entire function, definibon.. (231)
Liouville's theorem on. (231)
Equicontimdty. and compu.ct:ness.
IV.G.O ( ). IV.6.7--9 (266-
267)
defmltion. IV.6.6 (266)
prin('iple of, 11.1.11 (52)
q ...equicoontjnuity. and (."Ompact-
[}(':Ii;I!I;. IV.6.14 (269). [V.(j.29
(280)
dermitlOn. IV.G.13 ( 69). IV.C3.28
(280)
.Equicontinuous famll,y of linear ttans-
f()rmalions, deCimtioll. V.1O.7
(45ti)
844
SUBJECT INDEX
.sUBJECT INDEX
845
fixed point of. V.IU-6 (4.57)
Equn-olence of normed linear fipaceS,
def"1I1itioo. n.S.17 (65)
Ergodic toooret'O:!:i. VIJ.7, VII.6.8-10
(598-5.9), VIII.4-S. (See aloo
Dominated throrelru. Maximal
IhOOR'Jl&3,. Mean lheorems. Point-
wise 'hromns. Uwi:form ergodic
1/,1'0......)
rernarl<s on, (728-730)
E&,;,entia:J least upper bound, definition
III.I.ll (106-101)
Essent.ialsinguIarity. definition, (229)
Esst-ntia1 supremum, definition..
IH.I.ll (106-101)
Es.-sentially bounded. definition.
III.I.ll (106-101)
E8stmially sepanWly valued, deftni-
tiQn. 111.1.11 (100-101)
Euclidean t;pacc. dff"mibon. IV.2.1
(288)
further properties, IV.15 (874)
study of, 111..3
Extended real and complex numbeT8.
definitions. (3)
topology of. (11)
Extension ofa fun.ct:ion" by continuity,
I.e.17 (23)
definition, (3)
'I'ietze"s theorem, 1.5.34 (15-]7)
ion of IDeHSUI'£'8 to arbitrary
sets, III.1.S-1O (90-100)
to a a-field. ]11.5
Lebe'gue, IlI.5.17-I8 (I42 143)
EuensioI'l$ of linea.r operators, \'1.2..5
(478), (554)
Extremal pointand subset, definitions
V.8.1 (439)
examples and pro}*rt.ies, V.ll.l-(1
(457--458)
remarks 00. (466). (407S)
study cr, V.8
ExtrernaIly di8COnnected (B98)
F
F.sp.ace. basic prope:rties) 11.1-2
definition.. 11.1.10 (51)
examples of.. IV.2.27-2S (243)
FllCtor group, dprmition, (85)
Factor 6f:quence, (366)
Factor space. in vr..-w:r .spaces,. (8S.
in F - and B-spaccs, defjnition,
II.4.I3 (71)
propertie,. II.4.13 20 (71-72)
remark on J (88 J
Fatou theorem, on limits and integrnls,
111.6.19 (152), 111.9.85 (172)
Field. in a.1gebraic 5ense, (36)
of subsets of a set J Borel field.
I1I.5.10 (137)
definition, 111.1.8 (96)
determined by B collection of (jets.
111.5.6 (185)
u-fieJd,III.4.2 (126), III.5.e (185)
Lebesgtle exI.en9ion cf au-field..
I1L5.IS (1<18)
restriction of a set functiOn to.
(166)
Filter, definition and properties
1.7.10--12 (80-4111
Finite dim.elNonal spaces.. additional
p'op<Tties, IV.I5 (8741
definitions. IV.2.1-$ (288---289)
study of, IV.3
Finite inter8cction property, as
criterion fOT compPCt
I.5.e (17)
defi.nition., 1.5.5 (17)
Finite meo.sUl'e (space), criterion for
aDd properties. 111.4.4.---0 (127-
129)
definition. 111.4.3 (J26)
o-finite meagure. IJl.5.7 (136). (See
also S t juru:timt, Jtleasu.rt"
spac )
Saks deC()mposilion ot IV.9.7 (308)
Finitely additive set function. (See
also S t jundioo)
dd;mnon. IIU.2 (96)
study of, III.I
Fixed point property. definition
V.10.1 (453)
exercises, V.ll.I6-23 (459--460)
rema.rkg on. (467-470). (474)
theorems, V.I0
Fourier coefficients., dermition,
IV.14.12 (35S)
Fourier serin.. convugt'nce of,
1V.14.27 (360), IV.14.20-3a
(_1)
definition. IV.14.12 (358)
localization of. [V.14.26 (360)
multip1c series, IV.14.GB (367)
study of. IV.14.69-73 (367-368)
study of. IV.14. esp. IV.14.12-20
( .)
Fredholm alternative. (609--610)
Frechet rllfferential. dcl'inition. (92)
theory for compact operator&, V[I.4
.-'llbil)i Utrorem. for general finite
11K'3"mTC sp;i(X'S, III.ll.IS {UI3)
for positive a-finite mea.sure spaces..
11[.11-'9 (190)
Fubini-..Jessen theorems, mea.n,
IIUI.24 (207)
pointwbe. IlI.ll.21 (200)
Function. a'b mlutcly continuous,
IV.2.22 (242)
additive set. (See Set .funt'dms)
fLtmoot periodic. tV.2.'25 (242), IV.7
anal}-tio, III.14
between oomplex ,-ector spaces.
VI.IO.5 (522)
Borel..stirltjcs Inf'8SUre of, 111.5.17
(142)
£Jfbounded va.rmtion. 111.5.15 (140)
dJalaetA:ristic, (a)
ontinuous. ].4.15 (13)
om.-ex, VI.IO.l (520)
definition, (3)
doma.in of, (2-3)
entire. (281)
t'SSf'ntial bound or I!uprenmm of.
IIU.n (100)
. nol, (8)
hom..omotpJu.m. 1..0.15 (18)
homomol'phism, (35), (89), (-to),
(44)
integrable. 111.2.17 (II:!!). IV.IO.7
(823)
imTniI.'.. (3)
isometry. 11.3.17 (65)
isomor,phis.m, (35). (88). (89)
linear functiona1 J (88)
linear operator, (86)
measumblf'. 111.'2.10 (106). 111.2.22
(117).. 3".l' )
metric. 1.6.1 (18)
null, III.2.8 (103)
onc.ta-one, (3)
ope-rotor. (36)
of an operator. (See Calotlws)
orthonorma) system uf, IV.I4.1
(357)
projection. 1.3.14 (9), (37), IV_4.8
(250)
ranae of, (8 J
representation of "«-lor valued.
1I1.1I.15 (194)
resolv nt.. VII.3.1 (566)
restriction or, (3)
"t. 111.1.1 (95)
!Simp1t, 111.2.9 (105). (822)
suba.dditive. (618)
support, V.I.7 (410)
tangent, V.O.2 (446)
total variation of, 111.5.15 (140)
wtally moasmable, If 1.2.10 (106).
(See also Jl.f«l3aroble ftmdion)
uniformly continuous. 1.6.\6 (23)
Functional(s), bilinear, 11.4.4 (70)
in bounded 3' tupology, V.5.6 (428)
onti""UUU8. 11.8.7 (61)
('xistPJIDe of.. 11_3_12---140 (64.----65)
extenBion of, 11.3.10-11 (62-63)
non-existence of. (329-330), (392)
for rep tation in special
spaces, IV.iS
dj.!,continuous.. existence ()C. 1.3.7
(8)
linear, (38)
multiplicative, IV.6.23 (277)
of L . V.S.9 (443)
in th unit 5phere of C*. V..8.6
(441)
separating. "-".1.0 (4lJ)
tangent, V.D.4 (447)
total""""" 01. V.a.l (418)
in weak and strong opetalO(
topologies. VI_1.4 (47'1)
FundamentAl fan ily of neighborhoods,
definition. IA.6 (to-Il)
Funda.mel1ul !l;et. in a linear Wpoto.
lica.1 !!pa.ce. 11.1.4 (50)
846
SUBJECT INDEX
SUBJECT INDEX
847
G
GenuaIizcd sequence. definition and
properties, J.7.1-"1 (26-29)
Generator, infinite:siJna1 of a semi-
gJ'Otlp of operators. VIII.I.e
(619)
Grapb. dosed graph theorem, 11.'2.4
(57)
cl on oper.ator, II.2-8 (57)
Group, basic properties. J.I0
_on, (B4)
metri..ble. (90)
topolcgical. II.l.l (49)
H
Haar measure on a compact group.
V.n.2 3 (460)
Radama.rd three ircles theorem.
Vl.n.48 (588)
Hahn-Banach thecrem. II.3.IO (62)
disrus;ion 01, (8!H18)
Hahn decomposition theorem, III..4.10
(129)
Hahn extension theorem, IlI.5.-8 (136)
JIamel base or basis. definition. (86)
fot general vector spaces, 1.1....2 ( )
for real numbers. 1.8.7 (8)
Hardy-Hilbert type inequ.a.tities.
VI.n.11l--2D (531-."34)
Hausdorff y 1.2.6
(6)
lJausdvrft «-measure. 111.'9.47 (174)
Hausdotff space, criterim1 fOl". 1.'1.9
(27)
definition, 1.5.1 (15)
Heine.Borel theorem, {17)
Hermitian matrix. definition, (561)
Hermitian operator, definition.
IV.J8.72 (550)
Hilbert cube. (See also Hilbert spactJ
definition andcompa.ctncss,IV.18.70
(350), (453)
as tl fixed point in £pnce V.I0.2-3
(455-454)
Hilbert space, adjoint of an operator.
VL2.9--10 (479-480)
finite rnmtnsionQl. IV.2.1 (238).
IV..
general. additional plopertle!i. IV ..15
(379)
haractffii'.atiom of. (393-394)
definition. IV.2.2tJ (242.
remarks (In, (872-313)
study of, IV.4
Hille.Yosida.Phillips theo.. m on the
generation or semi-groups.
VnI.I.I5 (624)
Holder inequatit)", III.3.2 (U91
ns for equality in, UJ.9A2
(175)
genera.lizations of. VI.ll.1-2 (527),
VI.U.I8---I8 (530-581)
condition for, 1.5.8
(18)
definition. 1.4.15 (13)
Homomorphism. between algebras.
(40)
between Boolea.n algebrasjo (4S-44)
between ups, (35)
between rings. (39)
!;Iatural. between linear spaces, (38)
of II semi-group of operators.
definition, VIII.I.O (fU9)
functions of. VIII.2
pertud:mtion of. VIII.t1.I9 (fl31)
!Study cl'. VIII:1
Inner product in B HiJbert s.pace.
IV.2.26 (242)
Integrable function. condibQn!50 for
integr.ability, fII.2.22 (JJ7),
III.>!, nI.6, IV.8, IV.1O.9-IO
(325-528)
definitJ.On, 111.2.17 (112), IV.IO.T
(323)
properties, IIL2.t8-22 (1I.-1I7),
IV.tV.S (823)
simple function, definition. 111.2.]3
(108)
p<op<rt;e., 11I.2.I....18 (lOB JJ3)
Integral. change (Jf variables, 111.10.8
(182)
countable additive case, I1I.6
extension to positive Jnea'!iUrable
filnctions. tIl8-119)
finitely odditine case. 111.2-3. esp.
III.2.J7 (112)
inu,gration by parts, 11I.(S.22 (154)
line integral. (2'25)
8urnmabiJity of, IV.13.'18-1V} (851-
356)
with vector valued measure. IV.IO.7
(523)
Interi01' mapping principle. 11.2.1 (55)
discussion of. (63-85)
Interior point. 1.4.1 (10)
Interior of a. set. 1.4.1 (10)
Internal point, definition, V.L6 (410)
IntervalB. defmitions, (4). (11.5.1.5
(140)
Invariant mea.!!.ures, V.IL22 (460).
VI.9..8-44 (SI6)
Invariant metric. in a group, (9Q.-91)
in II linear spa , 11.1.10 (51)
Invaria.nt set, (3.
Invariant subgroup. (35)
}nverse function and inverse image. (3)
Invel"!5e of an opt'ratot a.nd adj<lints,
VI.2.7 (479)
exi:stenoe and continuity of. "11.6.1
(584)
I
Ideal(S), In on a1,gebra.. (4.0)
existence of ma.ximal, (89)
01 operator.. (552 553), (6U)
in a ring. (38)
Idempotent element. definition, (40)
Idempotent operator or projection,
dd"mition, (87)
Imaginary part of B complex number.
dermitM>n, (4)
Independent. linearly, (56)
IQdex, definition. VII.I.2 (558)
ludexed :set (8)
Inequa.lities. remarks on, (541)
1\1. Bien convexity theorem.
VI.lo.n (5251
8JJPlica.tions to other inequalitiel.
VI.II (526)
Infimum. limit inferior of 8 sequence
vf !Sets, (126)
limit infnior of a set or sequence of
real numbers, (4)
of B set of real munben.;, (3)
IDf"I.fiit£simal generator, of a group.
(627-628)
Inverting sequence of p(1).nomia1s.
V1I1.2.12 (650)
Involution, in an algebra, (40)
Isolated spectral point, VII..3.15 (.571.
Isometry, discuss-ion of. (91 2)
embedding of B B-space into its
second conjuga.u space,
n".18-1D (66)
momorphism and eQu[\la1ence
I1.8.J7 (65)
IsomOlprusm.
(See nlso H hi$m)
topological. (See Homemrwrphism)
.J
.Jessen. (See Fubini.Jesscn Uawrems)
.Jordan c:l.nonica.l form for a matrix,
VII.2.17 (G03)
.Jordan <'UTVe. (225)
.Jordan deoomposition, of an additive
real set function, III.l_S ({:I8)
of a rrw;'a$UI'e, [1].4.7 (l28). 111.40.11
(J20)
K
Kakutaa1i. (See MmkoP-KaA:wani
Ihrorem )
Kernel. of 8 homomorpl1i6m. (39),
IV.JBC, IV.J4
COnvergence of. 111.12.10-12 (219-
222), IV.13C, IV.14
Krein.Milman on extremal
points, V..6.4 (440)
Krein.!;;mulia.n theorem. on convex
c10sure of a weakly compact:.
set, V.6.4 (434)
on ! closed IXlfivex set!!. in 3:...
V.5.7 (429)
L
Lacunary series, definition, IV.14.63
(866)
Laplace and Laplace-Stieltj trans.
form, VII1.2.1 (642)
Lattice. definitions. (43)
84.8
SUBJECT INDEX
SUBJECT INDEX
849
Laurent expansion, (229.
Lea.st upper bound, essential III.LIt
(100)
in a partially ordered set, J.2..3 (4)
in the real numbers. (3)
Lebesgue. decomposition theorem
IIl.4.14 (18'1, ('33)
domina.tt>d comrergence theorem.
lII.8.7 (1241, III.6.16 (151),
IV.lO.lO (828)
n theorem. 11I.5.17-1B
(142-148)
measure. on an interval, (143)
in n--dirnensional space, 111.]].6
(188)
set, III.I2.11 (218)
pace:s_ (See L,, lJ)
Lebef.gue-Stieltjes measure on an
interval, 14a)
Limit. (See also CQf'l )
Banach, 11.4.22-23 (78)
inferior (or .superior), I()f a set lOr
sequence or real numbers (8)
ma liequence of sets. 111.....8 (12(1)
point of a set, 1.4.1 lO)
weak, definition. 11.8.25 (67)
__, fI.3.'6--27 (68)
in special I'.ipaces, IV.15
LindelOf theorem, 1.4.14, (12)
Line integral. definition. (225)
Linear di nJ (Dl)
Linear functional, (88). (See a1so
Fundi<mal)
Linear manit0k4 (.30.. tSee also
.Manifold)
Linear space, 1.11
normed, 11..8.1 (5'9). (See also
B-sp(J£ )
topologi<al, II.I.I (49)
Lillearopcmtor, (36). (See also B-J.pan)
L1D("ar tmnsfonJ1l!tion, (86) (See .nIsi)
Operator)
LinearI)' jndependent, (86)
LiouviUe theorem, (231).
L,I(S, I:..}l), 0 < p < 1. definition,
111.9.29 (171)
properties. Jn 'lt29-31 1171)
L,,{S, :E. 14), 1 P < 00, claa:racteriza
tions of, (394-396)
completeness of, JII 6.6 (1-46),
111.9.10 (169)
criteria tor convergence in, nr.S.6-7
n'2-I24). 111.6. IS (150), IV.15
(S88)
definition. III..aA (121
remarks on, {387--388)
tiepaiable manifolds in. 111.8.5 (168),
111.1>.6 (169)
study of, 111.3, 111.6, ]V.S, IV.IS
Loo(S,I:.,u), definition, IV.2.19 (2-i1)
study (If, IV.8, IV.15
I...ocaliUltion of serie!'i. definition. (859)
Locally compact space, definition.
1.5.5 (17)
wca.lly wnvex 1IJIftoCe, definitIOn,
V.2.11 (417)
local COD'\--exity. of r and weak
topologies, V.3.3 (41DI
of X. in the bounded 1: topology,
V.5.5 (428)
separallon of convex sets in,
V.2.IU-18 (417-418)
nonnaJ., "VII 2.14 (563)
of a projechon. VI.Y.27 (514)
stud)' of. VII.l
trace of. VI.D.28 (515)
Maximal element. Hau'!dorff ma.xi-
ma1it3- theorem, 1.2.6 (6)
in a partially ordered space, 1.2.4
(4J
Maximal ergodic lemma, discrrle caS<',
VIII.6.7 (676)
k.paTameter case, VIII.7.H (697)
one-parameter continuous case,
VIII.7.0 (6'.1<1)
........m. on, (721))
.Maximal ideal, definition and existen-
ce in a ring, (39)
Maximum mQdu.lus.tbeorem, (230-231)
Mazur t . on the COnvex hull of
a compact set. V.2.6 (416)
Mean ergodic tbrorem, (728-=)
continuous case in B-s;pace.
VIIU.I-8 (687-<1811)
in L" VIII.7A (68D)
in L.. VIIL7 IO (694)
diBerde Case in B-space. \"111.5.1--4
(661-£62)
in L" VIII.5.S (662)
in 4,. V11I.5.D (667)
MeanFubini-..Jessen theorem,llI.ll.24.
(207)
Measurable fWlction. conditions for
(total) mea8urability. 111_'2.21
(116), 111.6.1>-11 (147-149).
111.6.14 (150), III.D.II (169),
In.II.II (169), In.9.18 (170),
11[.11.24 (171), 111.9.37 (172),
III.D.44 (175), III.15.U (224)
definition, [11.2.10 {10ft)
exk11Biom of the ootion of mea sura-
blilY, (1I8-IIII), (8221
properties, lII.2.11 12 (100)
space of (totally), criterion for
oomp/eten.... 11I.6.5 (146)
delinition, 111.2.10 (106), IV.2.27
(243)
propertie., IIU.ll 12 (106)
remarks concerning, (392)
I: measurable function. 1\'.2.12
(2<0)
1\1
Manifold. closed linear. spanned by Ii
set. 1I.1.4 (50)
in a litJeaf . (36). (See also
Li1tetIT mcmifold)
ort11Ogona1. in Hilbert space IV.4.3
(2<9)
Mapping. (See 0180 Fultdiora)
interior principle, 11.2.1 (55
"""""" on, (83-85)
I\b.rkov-Kaku.tani tllOOIftn. on fb.:.f'd
points of affine maps, V.10.6
(456)
Markov process. application of
uniform ftgodic theory to.
VIII.tI
definition. (65'9)
1latrix, (44)
characteristic polynomia1 of,
VIU:J-4 (561-562)
t'Xercises on. VII.2
Jlermitian. (561)
Jordan canonical form fOT, VIL2.17
(568)
study of T...U. ]V.11, (V.1S
as 8 topQlogrcal linear Space.
111.1>.7 (1691, III.D.28 (171)
Measurable set. definition. III.4o.S
(126)
Measure. (See also Sr.t function)
Hore] or Borel-ubesgue. (189)
]Jon,1--S1idt.je., (142J
demrnposition 01. (See Dfcflm_
altitm}
detennjned IJ}- a function, (142).
(144)
difrenonti:ation of, 111.12
defimtion. 111.4.3 (126)
Haar, V.II.22--28 (460)
Hauododf -. III.9A7 (174)
In,-ariant. VI.9.88--44 (516)
Lebe5.gue and Lebesgue-Stieltjes.
(143)
Lebesgue exfAurion of, 111_5.18
(14.8)
.preserviDg transfonnation, (667)
outer. 111.5.8 (133)
product, 111.11
Radon, (142J
regu1an-ector-valued. IV.18.75 (350)
""'-riction 01. (166)
Bpaee. of. 111.7. IV.2.15-17 (24.0).
IV", IV.15, (_1)
'reCtor-valued. study of, IV.IO (391)
:Measure SfJ€l.ee. decomposition of. (See
Decomposilinn )
definition, 11[.4.3 (126)
finite. ]11.4.3 (126)
Lrbesgue exte.usion of [1I.5.18
(143)
as a metric 8pacC. 11l.7 1 (158),
111.11.6 (169)
positive, 111.4.3 (126)
product, of finite number of finite
............, 'pac<". III.II.S (186)
of finite number of a-finite
measure tipaces, (188)
of infinite number of fiOlte
measure spans. 111.11.21 (2{)5)
c1-finite. IIL'i.7 (13fi)
Metric(.), 1.6.1 (18)
invariant. in a hnf'ar "pace, 11.1.10
(51)
850
SUBJECT tN]JEX
SCBJECT INDEX
851
In a group, (90-r>1)
topoloJ!}T in normed linear space.
II.3.1 (59). (4]9)
l\letric complete. 1.6.5 (19)
defiwtJon, 1.6.1 (18)
propertiPs. 1.6
1\letricallj" transitive Iransfurmation,
(e67)
l\Ietrizability. (See ulslI IIJt'tri i()JI)
ond dimensionality, V.7.D (436).
V.7.3-H15 (438}
and separabiht.:r, V.5.1-2 (426),
V",.. (434), V.7.I5 (437)
Metriza.tion. of (L meaSUfi: spaee.
III.7.] (]58)
of a regular spaee, 1.6.]9 (24)
of the 5et of aU functions, 111.2.1
(102)
)Ii1man. (See KreiR-.'Uilman Ihtt;Irnn)
l\tinkrm.-ski inequality. 111.8.11 (120)
conditiuDS for equality. 1I1.9AS
(173)
gcncralr ations of, VI.ll.13--18
(531)--531)
Moore theorem, ro inter-
change 01 limits, ].7.6 (28)
Mu1tiplicative linear fW1ctional..
IV.6.23 (277). (See also Funt.
1Wmll)
!<;
Xatufal domain of exbtence. or an
analytic 'unction. (280)
l'o.tl1rat embedding of a H-!S eJ
II".18 (66)
Natural hommnorphism onto fnctor
space. (38), (39)
)Jeighborhood. E-. in D. metric spare.
I.e.1 (18)
fundamental family 0', 1.4.6 (10)
('If a po1nt ot' set J 1.4.1 (10)
XikQdyrn. (See alSQ Radrm Nilrodi'm
theorem)
boundedness theorem. IV. ..B (309)
Nilp4Jtent e1ement, (40)
Kon-singula.r linear fDsnsrormati()n
(45)
Norm, in It B.-space. II.3.1 (59)
in a conjug-dte SImcoe, 11.8.5 (60)
diff rentiabihty of. (471-473),(474)
il"xmence of, (01)
in fin ""-space, 11.1.10 {51)
In Hilbert slJa(,..... IV. .26 (242)
inequalities. on L&I-norms. "[.11..30-
37 (,;35--536)
of an opt-mtor, 11.3.5 (60)
in special spaces, IV.2
topo1og)", 11.3.1 (SO)
Xormal opern.tor, in II. finite dimen-
sional space, VJI.2.14 (563)
XorInal structurt". dcfjrntion, V.ll.14
(459)
propertI.es. V.U.15-i8 (459)
Normal subgroup, (35)
Normal wpo1ogical 1!!JIBl"e. compat1.
Ha1.l$dorff s.pacc. 1.5.9 (181
definition. 1.5.1 (15)
metric !Space. 1.6.3 (1 )
propertiEs, 1.5.2-4 (15-17)
regula.r space with countable ba.se.
(24)
ormed (nonncd linear spa.cc). (See
also B....pai'tj
definition, II.S.l (59)
stud)" of.. II.2
l'\owhere dense. 1_6_11 (21)
:SuU function.. (See also Null 8et)
criterion for. III.G.B (147)
defiIJition, 111.2..3 (103)
}.lull set. (See o1so ...Vull fundii'm)
addltion.al vroperties of.. IIJ.9.2
(169), HI-9.8 (169), U[.9.le
(170)
criterion for. 111.6.7 (14TJ
definition.. 111.1.11 (100)
fot' tU)II(Mlndl:d closed operators"
nl.9.:; (6m)
Operator.. adjoint of. VI.2
bound of, 11.3.5 (CO)
clos.ed. 11.2.8 (57)
compact, deflniti<m. VL;.I (485)
sotndy of, VI.5. VITA
continuit.y of in R p ces. IL'.4
(59)
discu n «Jf, (82-83)
in F . U.1.14-16 (54)
dffinition, (36)
extensions of. VVl.5 (47 ), (5';;4.)
in a finite dimensional . (44)
functinnfi of. (See Calculw)
grapl_ vf. 11.2.3 (57)
Hermitian. IV.lS..72 (350). (561)
ideals m, (552-553), (611)
identit)', (37)
limits of. in B-spaces. U.JJ.6 (60)
in J.'-spaoes, 11.1.17-18 (M-55)
matrix of, (44)
non-sjngular. (45)
ll(JTm ()f. n..8 (60)
nOTmal. VII.2.14 (!i6S)
(lerturbation of, VII.6
pol,"llOmiBJ..! in, VII..I..! (356)
product of, (37)
projection. (57), VI.5.I (480)
&tudy of.. VI..3
qUMi-nilpoteot. VU.5.12 (581)
range of, VI.2.8 (479)
with closed range, VI.6
representa.tion of. in Cl' VI..7
in Ll' VI.8
in other spaces. (542-552)
resolv.ent. VII..'!).! (566)
study of. VU..S
spectrnI radius of, VU.3.5 (567)
spectrum o VU...I (566)
sum of, (37)
unbounded.. VII.9
weakly compaet, definition. VI.4.1
(482)
study of,. VI.4
zero, (37)
(Jperator topologies, VI.I
bounded .w-mg. VI.9.9 (512)
bounded weak. VI.9.7-IO (512)
o
OJ)en tJ ,.iterion for. 1.4-.2 (10)
definition, 1.4.1 (to)
Operational calculus, jn finite dimen-
lOiohal pace. VII.I.5 (558)
for (unctions of an inf"mitftimal
generator.. VIII.2.6 (645)
in genera' cmnpleJC B-8pace.
VJI.3.1() (568}
remarks on, (607--609)
("ont[nuou linear functioIUll" in.
VI..I..... (477)
properties, YL9.1-12 (511-513)
on. (:iSH)
rtrong, n.,-" (475)
stron(!"St, (538)
uniform. VI.I.t (47.5)
liveak, V1.1.3 (470)
OnIrr of a po1e, (280)
of an operator. VII..3 13 (57)
OrdlT of a zero. (230)
Ordered set. definition. 1..2.2 (4)
directed set.. 1.7.1 (26)
partiaIly, 1.2.1 (4)
study of. ].2
totaIl)., 1.2.2 (4)
well, 1.2.8 (7)
Orientation. of a dosed curve, (225)
Origin. vf 8 linear a.cc. 11.8..1 (59)
Orthoromp1cment of a set in Hilbert
space. definition, IVA_B (24.9)
properties,IV.4.4 (249},IV.4..18 (256)
() nal complement of a set in a
normed space.. 11.40..17 (72)
t'tIIladcl on. (93)
Orthogonal elements and manifolds in
Hilbert spa<'<', IV.4.. (249)
()rthogonal projectiom in Hilbert
8paces. IV.4o.S (2.50)
O nal series, on.
VUL.&3--47 (5371
study of. IV.I4
Orthonormal set in Hilbert space,
oIo.od set, IV.IU (357)
complete sct l IVA.8 (250)
definition. IV.4o.8 (250)
Jlropertiefl., IV.4.9-16 (251-254)
Orthonormal basis in Hilbert space.
IV.4.1I (252)
cardinality of, IV.4.14 (253}
criteria for. IV 4.13 (253)
t:Xistence of. IV.4.12 (252)
Outer measure. 111.5..3 (J33)
p
Parallelogram.. identity, {249)
Partially ordered set, bounds in,
[.2.. (4)
852
SUBJECT INDEX
sUBJECT INDEX
853
completely ordered 1.3.9 (8)
dd"mition. 1.2.1 (4)
directed set. 1.7.1 (26)
fundamental theorem 00. 1.2..5 (.5)
study of, 1.2
totally orden'd, 1.2.2 (4)
well ordered, 1.2.8 (7)
Perio<bcCunctian (aIJDOIItperiodicfunc-
tion). dermitton, IV.2.25 (242)
multiply, IV.14.68 (367)
slud)' of. IV.7
Pertl,lr1Jation or oounded linear opera4
toni, remaoo on, «(ln 12)
study of, VII.6. VII.8.1-2 (597-
598), VIUI.4-5 (598)
Perturbation()finfinitesimal generator
of a. semigroup. (63{}-(}.3Q)
Phillips' perturbabon theorem,
nn.I.19 (6311
Hille-Yosida-Phillip&' tMoreII"4
VIII.U5 (624)
Pointwise ergodic thoo k-pa.ra-
meter ntinuou8 QSe in LJ.>
Vln.7.I7 (708)
k-parameter continuous case In L."
I < p < "', VIII.7.IO (694)
k-pa.rameter di8nete .ea5f'. VIIl.6.
(679)
one-parameter !COntlnuQus case,
VII1.7.5 (690)
one-parameter discrete case.
VIII.6.6 (675)
remarks on.. (729-130)
Pointwise Fubini...Jessen toeoJ'eD1,
llLU.27 (209) .
Poi8o;on fSUmTtHIbility, IV.14.47 (863)
Pole, of an onaIytic fundion, (229)
of an operator criteria for. VII.B.18
(573), VII.8..0 (574)
definition, VII.B.15 (571)
PoI)"DOmiaI in an operator, charac.
teristic, VII.2.I (561), VII.5.17
(582), VII.IO.ti (606)
in a finite dimensional :spaee t
VII.I.1 (556)
in a. genera1 8pac:e VU.S.I0 (568).
VII.5.17 (582)
Pol.ynomial or an l.mbounded closed
operator, VII.9.6-lC (602 04)
Preparation tl1eorem of ""e J'Strnss,
(252)
:Product., of B-spaces, {89-90.
C of lIlt'asgre YpaCa,III.l1
(285)
of sets, 1.3.11 (i})
cf spaces, 1.8
topoJogy, U.I (821
Tychonofl t.heorem. 1.8.5 (32)
intersection of sets. (2)
QI Qperaton. (87)
sealar, in a Hilbert space. IV.2.26
(2421
Projection. and complements, (553)
der;rution, (87), VI.8.1 (480)
exercises on t VI.tI.18-25 .513---514).
VU.27-29 (514-515)
and extensions. (554.)
natural order for, VI..8-4 (481)
orthogonal or perpendicu1ar t IV.4.8
(250), (482)
study of. VI.3
Projection mapping in pro.
ducts, .continuity and Openness t
1.8.8 (32)
def"mition. :r.8_14 (9)
Proper ,'we, de!milion, (606)
Radon m a$ure. definition, (142)
Radon-Nikodym the<Jrem, for bound.
ed additive t. functions.
IV.9.I4 (815)
counterexample. 111.13.2 (222)
general case, 111.10.7 181)
PQsitwe CWjc, 111.10.2 (176)
remarks on, (2M)
Flange of an operator VI.2.8 (479)
closed, criterion for, VII.4.1 (577)
study 01, VI.6, VI.9.I5 (518),
VI.P.17 (5181
remarl<s on, (5391
Real numbers. extended, (S)
lopology of, (n)
Rcal part. of 0 complex number t (4)
Real VK'tor space, (88) (49)
Rectif"l8ble curve, 225.
Ref1exivity, alternate pl'QOf. V.7.U
(436)
criterion Cor, V.4.7 (425)
definition. 11.3.22 (66)
discussion, (88.
examples of reflexive spaces, IV 15
properties, IL3.23--'24 (67), 11.3.28-
29 (6 -69)
remarks f)n, (468), (4.73)
.fI.egular B-!Sp8C'e. (See J
Regular clo mre. (462--463)
Regular com"t"xity, (462-463)
Regular e1t'ment in a ring (40)
IWguIor method uf fiummability.
11.4.35 (75)
Regular set function. (See also Set
Junmon)
additional pt<lJ)erties, III.D.IO-22
(170)
countable addlti ity and regularity,
111.5.13 (188)
defmltion, 111.5.11 (137)
extension 01, 111.5.14 (138)
products of. IlI.IS.7 (223)
regularity of varjatioJl5. 111.5.12
(187)
'"l'rtA;Jr-vaJued measures. IV.13.'i5
(B5u)
Regular topological sptLC'C'. -completelj'
regular, \.'1.6.21-22 (276)
definition, 1.5.1 (15)
Q
Qua.9i quicont.inuity for bounded
functions, IV. .28 (280)
for continuous functions, rV 6.13
(269)
and weak rompact.ne.Iw, IV.6.14
(269), IV.6.29 (280)
Quasi-nilpotent operatm', definition,
VII.5.I2 (581)
Quasi-unifonn oConvcJReDC.'e, as a
criterion for continuous limit,
IV.6.ll (268)
deri1lition, IV.e.l0 (268)
properties, IV.tU2 (260). IV.G_30-
81 (281)
Quotient, group, (8S). (See also Factor.
space, (381
R
Radius, spectral, VII..3"",'; (567)
normality of, with CQunt.a.ble base.
(24)
Relative topology definition, 1.4.12
(I')
RepresentatIDn, ff)r Boolean al2ebras.
(44)
for Boolean rings with unit, 1.12.]
(41)
for conjL1gate spaces, IV.15
(;If finitely additive set functions,
IV.I!.l(}-1l (SI2), IV.9.18(815)
of opemtors, in C, VI.'1, (539-540)
in L;.p \1'1.8, (540-541)
in other spaces, (512---552)
8'" a 8pr8.Ce of oontinuous functions,
IV.6.I8-2. (274-276), IV.7.6
(285), (894-897)
RS 0 space of integrable functlOn....,
(894-896)
of a 1-reto.....valued function, (1116)
tor 'Tdor-vaJued integrals. (11.11.17
(lP8)
Resolvent, dtiinitiol4 VII.S.I (566)
equation VII.3.6 (566)
tiel, VILs.I (560.
:study of, VII..3
Ri sz convexity theorem, VI.IO
VUO.ll (525)
app1ications and extemions, VI ll
remarks on. (541-542)
J;Ung (algebraic), Boolean. (40)
def"mi1ion, (85)
properties, (40-44)
study of, 1.11-]2
Rout nalim i )
s
Saks d mposition, of a nleasure
space t IV.D.7 (308)
Sealer prodUoCt in a Hilbert space.
IV.2.26 (242)
Scalar>, (861
Schwa.rz inequaJity, 1\-'.4.1 (248)
Semi.group cf operat.ors, definit.ion,
Vlfl.I.1 (614)
infinitl"!Sima1 gmcrator of VIII.).f;
(619)
A'-pkn-.met.er. VIII.7.8 (693)
851
SUBJECT ISDEX
St:BJECT INDEX
85':;
:perturbution theory of (6SD-G3V)
"itrorIgly ()ntinuous, (685}
rtrongly measunble. (ti85)
stud,), of. VIII.L3
St:ml-vanation of a vector- 'alued
measqre. defiJ1ition. IV.IO.3
(320)
properties. IV.IO.4 (320)
SelJaubility and compact sets, V.7.15-
16 (437)
of C. V.7.17 (437)
criterion C()r. V.7.S6 (438)
Separability and embedding, V.7.12
(436), V.7.14 (430)
Separability and metru.alJility.
V..5.1-2 (426)
Separable sm. 1_6.11 (21). (See also
&potable linear manifolds)
SPparablc linear mani£oJds. 11.1.5 (SO J.
(See aoo &:pamhll! " 18)
in C. IV.IS.lf) (840)
in L., Ifl.8.5 (168), III.9.6 (169)
Separab1y-valued. 111.1.11 (11m)
Sepat"ation of convex sets, counter
CKamp1es, V.7.25-28 (4-37)
in finite dil))(:nsi.Qnal spaces. V.7.24
(437)
m linear spaces. V.I.12 {412}
10 linear topologIca.1 spa.ce:i. V.2.7-
I" (417--418)
SequellC€'. (See also Conl'fT#Jl«)
Cauchy, 1.6.5 (19)
generali7.Crl. 1.7.4 (28)
_, H.S.25 ( 7)
convergent. ].6.5 (]9)
factor. (366)
gmemhRd, 1.7.1 (26)
generated by an ultrafilter. (280)
of sets. non-increasing and limits of.
HIA.. (126)
spaces of, fk.fmitions, 1\'".2.4-]1
(239 2'0). IV.2.28 (243)
properties, 1"".15
Se(llJ ntial compactness. definition,
1.6.10 (21)
rtlatioru; with other compactnt:'s'i in
metric spaces. 1.6.18 (21).
1.6.15 (22)
".- p,.k. ddil)ihon. 11.3.25 (67)
in reflexive . 11.3.28 1£8)
in SJX'C19.i :spaCf'S. IV.13
SerLes. (See al..o Cmll )
lacunar:-' 1\-'.14.63 (366)
ortlUJgnna1. 1\,'.14
f;mmnalJ.ility ()f. 11.4.81-:>4 (74-78)
Sel.(a). Borel, 111.5.10 (137) conver.
gencevr I26-I27), 1l1.9ABI174)
field vf, 111.1.5 (96)
},.,.et, 111.5.1 (183)
Lcl . 111.12.9 (218)
open. (See Open)
a.fleld of. IJI.4-.2 (126)
in :E(I'). III.7.1 (156)
Set funL'tlon. additive. 111.1.2 (96)
botll1ded ,'ariation of, 111.1.4 ( 7)
contmulty of. 111.4_12 (131).111.10
CQnvergrncem.llI.7.2-4 (15M-lOO).
IV.9, IV.15
countable additi,,'-e, 111.4.1 (126)
study of. "1.4
decomposrt.ion" cf. IlJ.L7 (98).
llU.7-14 (128 132), (233)
d-eiimtlOn, '11.1.1 (1Hi)
difrem1tia.tlOn of. 111.12
eJ(t:enSions. of, 111.5
to arbitrary seb, 1I1.1.D-1O rD9-
100)
non-uniqueness of, 111.9.12 (UJG)
to a a.(a.eld, 111.5
measure, IIIA_S (126)
positrve, 111.1.1 (05)
guIar, defmition. 111.5.11 (137)
propertieS, 111.5.12-14 (137-138).
III.9.1tl--22 (170). IV..13.'i5
(350), IV.6.I-3 (261-263)
rclativiza.tion or res.trictiom of.
IU.8
a.fjnite. 111.5:1 (136)
!ii 1T\J.1ar, 11].4.12 (131)
!o1pa.ces of. as conjugate
IV.5.1 (258), IV.5" (259),
IV.6.2-5 (262--264), IV.8.16
(296)
defjnitiom. (lfiO---I62).l\ .2.15-17
(240), IV.IU (261)
on, (389-390)
study of, 111.7. IV.O,"IO. 1\.'.15
'I.-ariation of III.L4 (tJ7)
Simple funclion(s), definition, 111.2.9
(105)
density in £J" 1;5 P < O'J of,
111.3.8 (125), 111.8.3 (167).
111.9..6 (174)
Simple Jordan mrve, (225)
Si lar elem{>nt in a ring, (40)
non-singular operator. (45}
Singular sd function, definition,
11104.12 (181)
derhratives of 111.12.6 (214)
I..eIJesguc d mpo!Oition theorem,
111.4.14 (132)
Singularity of an onalytic function,
(229)
SmuliaQ. criterion for r-compactness.
(464)
criterion for weak comp.actne.w.
V.6.2 (433)
and Eberlein theorem (In weak
cornpo.ctn-ess, V.6.l (430)
and Krein. (See Kf'rin-Smulian
01.........)
Space, Chap. ]V
B- and F-, oe1cmcntary properties
ofJ Chap. II
list cf speclal ;spaces, IV.2
study 01, Chap. IV
Banach. iSee B )
h compa.ctification of. IV.6.27
(279)
compact, 1.5.5 (17)
complete. 1.6.5 (19)
complete normed linea.r. (See B-
pa£f)
completeJy regular.. IV .6_ 1 (276)
compkx. linear, (38). (49)
con ate. 11.8.7 tel)
CVIUK'ctro, 1.4.12 (12)
dimension of. (86)
direct sum (Jr. (38)
extremaIIy disconnectro, (398)
F 5pace, 11.1.10 (51)
facto<. (88)
fixed point property of, \ .1O.1
(453)
HaU5dorff. ..5.1 (15)
Jjnear topoJogin&l. 11.1.1 (49)
locally C'{Jmpact. [.5.5 (17)
Iom.Uy ( JftVCX topol al lineAr.
V.2.9 (417)
rneasu . 111.4,3 (126)
rnctrjc, 1.6.1 (18)
normal. 1..5.1 (15)
Donna1 stf\K"tllre of. V..11.14 (4;')9)
J\Ormed or normed linea1' 11..8.]
PO)
product. 1.8.1 (32)
real linear. (88), (.j.S)
("t:'flexive. 11..8.22 (66)
regular. 1.5.1 (15)
'Separable, 1.6.11 (21)
subspace. (36.
sub_"" opunned, (S6)
topological, 1.4.1 (10)
total. of fUIl(.-tjn1mls. V.3.1 (418)
_y . (41)
Span t in a linear space, (36), 11.1.4-
(SO)
Spectml radius, dcl"mition. VII.8.5
(567)
properties. vII.a.' (567). VII.5.1I
13 (581)
Spectral set. definition. VII.3.1'l
(572)
propertieo, VII".IP-21 (574-575)
SpectmI theury. for compact oper.
o.tors. VIlA,
in a finite tlimeotdonal space, VII.)
Spcbum" continuous, VII.5.1 (580)
in 0. finite dimensionoJ. spaet>,
VII.l.2 (556.
in .a general 8pace. Vll.3.1 (.566)
isolated pOint of. VII.S.la (571)
point, VII.5.I (580)
residual. VII.5.1 (580)
of 8pecial bounded opt'mtors.
VII.5.2 15 (580-581)
of special I1nbounded (Jpers,t.or8.
VII.IO.I-3 (61J.HlO5)
of an unbounded operator, (5-911)
Sphere, closed, 11.4.1 (70)
closed unit. 11.3.1 (59)
in a rnctric . [.6.1 (19)
StabIlity cf a K}-st("IU of differentIal
equations, VII.2.23 (564}
Stom'. and Banach. {Sr--e Bllrwtll SI()f1t;
tlleOrtl1l)
856
SUBJECT INDEX
SUBJECT INDEX
857
-CEdI compactificatinn theorem,
IV.B.22 (276)
remarks on. (385)
space, definition, i39S)
theorems. on represen\a.tion of
Boolean rings and algebras.
1.12.1 (41), (44)
-".eierstrass theorem, IV.6.16
(272)
com})1ex case, IV.6.1'1 (274.)
remarks on, (383---885)
StrictJ)' oonvex B- pace. definition,
V.n.7 (458)
Strong operator topology, dermition.
VI.1.2 (475)
properties. VI.D.I--5 (511). VI.9.11-
12 (512--513)
Strong topology.. in 8 Donned space.
I1".1 (59), (416)
Subadditive fu.nction.. definition, (618)
Subba.se for 8 topology, 1.4.6 (10)
criterion for, 1.4.8 Ill)
Subspace. of a linear pacel (36).
(S.. ..1>0 MallijOOJ)
Summability, of Fourier aeries.
IV.I4.84--5I (861--36-<)
or IV.I8.78 101 (851-
356)
regular nIL'tJwds, IU.85 (75)
of ,:,erie$. 11.....31-54 (74-78)
..,...mJ types 01, A!Jel, I1.4.42 (76)
C.saro, IU.S7 (75), I1A.39 (76).
IV.I4.44 (868)
Norlund. 11.4.88 (75)
Poi...,n. IV.14.47 (363)
Support function, dermition. V.I.?
(410)
Supremum, limit SUperioT o[ a se-
quence of sets. (126)
limit superior of 8 set of real
numbers. (4)
of Q se-t of real numbel"lil, (3)
Symmetric difference, (41), (OO)
T
Tong...t IUII<.'tion. dermition, V.9.2
(446)
examples, V.lI.D-IS (458-459)
pro""rti.., V.9.I (445), V.9" (_),
V.II.lO-tI (459)
Tangent functionals. definition. V.R4
(447)
Ta1'Skj fiud-IJOint theorem. 1..3.10 (8)
Taylor expansion fOf analytk- func-
tions, (22S)
Tc!rebichdI pdynomjal, (869)
Tiet extension theorem. 1..5.3-4
(I5 17)
Tonelli theorem. III.11.14 (194)
Topology, base and subbase for. 1.4.6
(10)
basic definitions. 1.4.1 (10)
bounded :t wvolo!lY, V.5.8 (427)
functionalor r topology. V.-9.2(419)
study of, V.8
in linear spaces. (See Operator
kpQl<>gy)
metric. definition, J.6.I (18)
metric or strong, in Q B-space, (419)
IIItudy of, 1.6
norm or strong. in B normed linear
.1'..., 11.8.1 (59)
product, dd"mition, 1.6.1 (82)
of real numbers (11)
study of. 1.4---8
Wpolog>caI group, ddinitioo, I1.I.I
(49)
kIpologico.l 'Space. ddlnition. 1.4.1
(10)
study of. 1.4-8
wea'k. in a B-spa.ce. (419)
weak + topology. (46'2)
a: and I.. topologies in :£*. (41(})
Tatal boundednesg. in :n mclric space,
1.6.14 (22)
Total differential. (02)
Total (41)
Total fnrniIy 01 fwrlions, 11.2.6 (58)
Total measumbility, definition.
fII.2.10 (100). (See ..Iso M.a-
""rabl, JUR<'IivnJ
Total space of funetiona's. dt>f'mrbon,
V.S.I (418)
Tota1 varia.tivn of a function, 111.5.15
(140)
01.. set l<m<tion, IILI.4 (97). Is..
also Variafion)
TotaU . ordered set. 1.2.2 (4)
Tru('e of a matrix.. definition, '"1.1).28
(515)
Transfimte closure ora marufold. (462)
'l'ransformation. (See also Qpnat(JT)
mea ure (667)
metrically b1msit:iw. (667)
Translate of IL lunct.iOD, Mmrtion.
(283)
Tmn lation number, IV.7.2 (282)
Tl'am>JatiOD by a vector, (86)
T)-("bonoff theorem. on fixed pOints,
V.IO.5 (456), (470)
on product spaces, 1.8.5 (32)
1.1
Ultro/Ute<, derll1lbon. 1.7.10 (80)
pro""rties. I.7.Il 12 (.01
Unbounded operators. on.
VII.I0
remarks on. (612)
study 01, VILp
Unconditional con ufo series,
(92)
Uniform boundedness principle, in
B-{'jpaces. 11.5.'20-21 (66)
ctisffission of, (80--82)
in F-spaces, (LI.ll (52)
lor """""""". IV.9.s (309)
Uniform oontirmity, of an a1most
periodic function. IV.7'.4 (283)
criterion for, 1.6.18 (24)
d..r-mition, 1.6.16 (28)
extension of Q function. 1.6.17 (23)
Uniform convergence. as 0. riterion
tor Jimit interchange. 1.7.6 (28)
dermilion, 1.7.1 (26)
remarks concerning, {382---S8S:)
p-uniform convergence, criteria for,
111.6.2-8 (145), 1I1.6.I2 (149)
definiOOn. III.6.1 (145)
1!nifonn convexity, definition, 11.4.27
(74)
properties. IU.28 29 (74)
...-.arb on, (471--474)
CnJfonn countable additivit). (See
C'mmlnbly additive)
Uniform ergodic theory VIII.S
ttm8J"ks on, (730)
Unifonn operator topology? deCinition
VB.I (475)
properties. V].9.11-12 {512-518)
Unit,. uf a group. (84)
Unit sphere in 8 nOl'med space. com-
pactness and finite dimen-
oionali1y of. IV.8.5 (245)
definition, 11.3.1 (59)
Ur')"SOhn the metriz.ation. 1.6.19
(24)
fOr J'lormal spa.ces. 1.5.2 (15)
v
Variation. of a rountably additive 8et
function. IIIA.7 (128)
of 8 lunetIDn, III.5.15 (140). (S..
also BOII.ndul ooriQtion T()lal
variatiQl1)
of a p-CQntjrnlOus set function, (131)
of a regular set function. 11].5.]2
(187)
semi.varia.tion uf Ii. wrtor-valued
""'""""'. IV.IO.8 (820)
of 8 set function, 111.1.4--7 (9,.---t}8
Vector space. definition. (86)
dinIeosion of, (36)
elementary properties. I.ll
real or oompk-x., (49)
Vitali-Hahn-Saks 111.7.2-4
(158-1110). IV.1O.6 (321)
Vitali theorems, on convergence £If
int.grals, III.8.6 (122).III.6.U
(150). III.OAS, IV.IO.9 (825)
covering theorem, III.12.2 (212)
w
\\'eak Caoohy 8equenee. C2it.eria for in
special spr.cL'S. IV.15
definition, 11.3.25 (67)
\Veak comp1dcne!SoS, definition, 11.3.25
(67)
cquivBlence of weak and strong
convergence in L i . IV.8.1S-14
(295-296)
or reflexive spaces. 11.8.29 (69)
of special S I IV.15
858
8l-:'BJECT IXDEX
Weak conv
C{'. definition, 1I.
.'2;j
(67)
properties, 11.3.26-27 (08)
in
pccial
. IV.fa
\Venk countable addttivit:y, definition.
(318)
and strong. IV.tO.1 (318)
"'eak limjt, definitiun. 11.3.25 (£7)
\Veak
equenttal com
defini-
tion, 11.3.25 (07)
in rcnexiye I!>paccs. II.3
(68)
in
spaces, JV.l
\Veak to]xtlogy in a B
spa.cel (419)
bounded X topoIoJo- in 1*, \-'.5.3
(427)
reJatiom with reflexivity, VA
relatioru with separability and
metrizability. V.5
study of fundamenta.l lJroperties.
V..
weak compactness. V.6
w
ak operator topolof::o-. delirUtion.
VU.8 (476)
properties. VI.IU-12 (511-5t.S)
weak * topolo
)'. (462)
\\-eakJy compact o}.d81or. In C,
VI.7.I (490), VI.7....6 (493
496)
delirution. VU.I (482)
in Lt. V1.8.1 (49B" Vl.
.IO-U,
{5U7-5101
in LOQ, VLO.57 (310)
J'tmarl.s on, (539), P4I)
reprrsenWwn of, (3409)
spt'{'Iral throry of. in cerLulJ)
p
I"(-S,
VII.4.6 (580)
study of, VI.4
Weient.ra."I!Sw aplJ1OXlnrntloo theorem..
IV.6.I6 (1!72)
comTrgt'nce tbCQreDl for a..Ua1
tic
functions. (228)
preparotinn theomn, (=)
\VeU-Qrdercd set. definition, I.2.M (7)
well.onkring t11eorcm, 1.2.9 (7)
Wiener measure space. (400S;
y
YO!ilida. (See lliile-PJdUips-'l'"fJliid6.
Utmrem)
z
Zennelo theorem, (:IQ well-ord.etl!\g,
1.2.0 (7)
Zero. of an analybt: functilm. (230)
or B group, (34)
Zero opemtor. (37)
7.orn, IPmIl'" 01, 1.2.7 (6)
..
TO
.lId
n. Bllaic: Pribclll
rOTB
1IJ.1 m.n.IIUt
NiE&llIroeTbrar:y
IV.1.2 Lialof
SpecLaI Spllte!-
Boull
td
FuDdion.
c_
-
.........
SP'
IV.I SNt'Uoof
St:t'"Func1iOM
1\'.10 Vector V.lued
.._
Openlo!"llw1tla
CIoMd "-ntiE
INTElIDEPENDENCE TJUILE
LEGEND:
(8) A aection Ia dependent only on thooc aectiono to which it is eonnected
by 8 __ of riIirW Iinao. e:J:cept that
(b) A _on dependent on 8 tIotte4 oeotion is aIao dependent on any
_ on which the do-' aection Ia dependent,..- though the ooneoponding
Ning W- &Ie not obown in the taNo.
--
r-----
--------1
: "1.2 AdJoiDl
t-.
=---------------_: -----........
v.i---i;k;
;I----;
______
n
____J
..
T
alli!
II. Da
c PriodJ)k:&
forB...J"ICft
111.1 nUt.IIUt
Menure Theory
1\'.1.1 Lwltll
S.fW81 Spaee:I
lkIund...d
Fultlctiool
Operalor
TopOlOIi
""""""""
.........
Adjoiatl
ubtolglle
...-
IV.O
ICI'IOr
St:tF'unttiom:
IY.10 V«!:or"\'.aluM.
MCa
lll"t'
i:"tremIlL
Poiol.!!
VU WII'Dklv
Compllel Op;ratora
\11-1 OpeT'lltOI"lOO
CoDlinUQ\lBFutw:lio1l1
VIIUI Unifonn
F.rsooi.c ThrtJr:y
:ivi--
be-s!;e---1/
,": :SpliCes.
I'
-
-
--
-------,
..
.
Et'JOCIicntOl'1!ml
...----------------.
J1VjI
ur i,.......
,.. Sel Fundioa, .
/...---------------'
I :i"v.Ii"-.t;;.;;
;b
--t..........
'. Fuodlun!l'
..---------------.1
VIU Ffnile Dim.
&IIsto llo3l Openlor5
VIII.. &J!odiI:
Theo1")"lntroduttion