Author: Хилл Ф.
Tags: компьютерные технологии программирование компьютерная графика
ISBN: 5-318-00219-6
Year: 2002
Text
I» *
О
made by Dickobraz, May-2004
ВТОРОЕ ИЗДАНИЕ
Francis S. Hill
Computer Graphics
Using
OpenGL
Second Edition
ppj Prentice HaH PTR
ртр lipper Seddie River, New Jersey 07458
. _www.phptr.com
Френсис Хилл
"П НО' ПВОАС^МОШ-ВЛП
да •* да - л . * » , <
OPENGL
Программирование
компьютерной
ГРАФИКИ
Второе издание
{^ППТЕР
Москва Санкт-Петербург Нижний Новгород Воронеж
Ростов-на-Дону • Екатеринбург • Самара
Киев - Харьков Минск
2002
Френсис Хилл
OpenGL. Программирование компьютерной графики
Для профессионалов
Второе издание
Перевела с английского А. Шкадова
Главный редактор
Заведующий редакцией
Руководитель проекта
Научный редактор
Литературный редактор
Художник
Иллюстрации
Корректор
Верстка
Е. Строганова
И. Корнеев
А. Васильев
А. Шкадова
Е. Ваулина
Н. Биржаков
В. Шендерова
В. Листова
Р. Гришанов
ББК 32.973-018.3
УДК 681.327.1
Хилл Ф.
Х45 OpenGL. Программирование компьютерной графики. Для профессионалов. — СПб.: Питер, 2002. — 1088 с.: ил.
ISBN 5-318-00219-6
Эта книга — введение в мир программирования компьютерной графики. Графические системы становятся лучше, быстрее
и дешевле. Каждый год изобретается множество новых технических приемов, однако основные принципы и подходы к програм-
мированию по-прежнему остаются неизменными. Автор написал в высшей степени практичный и доступный для восприятия текст,
отличающийся основательным и интегрированным подходом. Понятия тщательно определены; их математические основы разъ-
яснены, доказана важность каждого рассмотренного понятия. Книга показывает читателю, как переводить математические пред-
ставления в программный код, и демонстрирует результат. Предлагаемое новое издание предоставляет самую современную инфор-
мацию в области компьютерной графики.
© Prentice Hall, 2001
© Перевод на русский язык, ЗАО Издательский дом «Питер», 2002
© Издание на русском языке, оформление, ЗАО Издательский дом «Питер», 2002
Права на издание получены по соглашению с Prentice Hall, Inc.
Все права защищены. Никакая часть данной книги не может быть воспроизведена в какой бы то ни было форме без письменного
разрешения владельцев авторских прав.
Информация, содержащаяся в данной книге, получена из источников, рассматриваемых издательством как надежные. Тем не менее,
имея в виду возможные человеческие или технические ошибки, издательство не может гарантировать абсолютную точность и полноту
приводимых сведений и не несет ответственность за возможные ошибки, связанные с использованием книги.
ISBN 5-318-00219-6
ISBN 0-02-354856-8 (англ.)
ООО «Питер Принт». 196105, Санкт-Петербург, ул. Благодатная, д. 67.
Лицензия ИД № 05784 от 07.09.01.
Налоговая льгота — общероссийский классификатор продукции ОК 005-93, том 2; 953005 — литература учебная.
Подписано в печать 06.07.02. Формат 84х108'/|6. Усл. п. л. 114,24. Тираж 4000 экз. Заказ № 815.
Отпечатано с диапозитивов в ФГУП «Печатный двор» им. А. М. Горького
Министерства РФ по делам печати, телерадиовещания и средств массовых коммуникаций.
197110, Санкт-Петербург, Чкаловский пр., 15.
Краткое содержание
Введение................................................................... 18
Глава 1. Введение в компьютерную графику................................... 28
Глава 2. Начальная стадия: рисование фигур................................. 67
Глава 3. Дополнительные инструменты для рисования......................... 118
Глава 4. Векторные инструменты для графики................................ 192
Глава 5. Преобразования объектов.......................................... 263
Глава 6. Моделирование поверхностей полигональными сетками................ 350
Глава 7. Трехмерный просмотр.............................................. 426
Глава 8. Визуализация граней для усиления реалистичности.................. 481
Глава 9. Приближение к бесконечности...................................... 551
Глава 10. Средства для растровой графики.................................. 617
Глава 11. Создание кривых и поверхностей.................................. 689
Глава 12. Теория цвета.................................................... 770
Глава 13. Удаление невидимых поверхностей................................. 799
Глава 14. Введение в трассировку лучей.................................... 838
Приложение А. Графический инструментарий: получение OpenGL............. 939
Приложение Б. Немного математики для компьютерной графики ................ 941
Приложение В. Некоторые полезные классы и служебные подпрограммы ......... 956
Приложение Г. Введение в PostScript®......................................1001
Приложение Д. Введение в SDL...............................................1038
Литература.................................................................1046
Список терминов............................................................1058
Алфавитный указатель.......................................................1065
Содержание
Введение.........................................................................................18
Предполагаемая аудитория..................................................................... 18
Необходимая математическая подготовка ................................................... 18
Необходимая подготовка по программированию............................................... 19
Философия книги.............................................................................. 19
Упражнения и задачи...................................................................... 19
Использование OpenGL..................................................................... 20
Использование C++ в качестве языка программирования...................................... 20
Акцент на трехмерной компьютерной графике................................................ 21
Описание ЗО-сцен с помощью языка проектирования сцен..................................... 21
Дополнительное использование PostScript.................................................. 21
Структура книги и планы курса................................................................ 21
Краткий обзор глав....................................................................... 22
Рекомендуемые последовательности изучения глав книги..................................... 25
Возможные планы курса.................................................................... 25
Дополнения................................................................................... 25
Благодарности................................................................................ 25
Примечание для читателя: как смотреть стереоскопические изображения.......................... 27
Об авторе.................................................................................... 27
От издательства.............................................................................. 27
Глава 1. Введение в компьютерную графику.........................................................28
1.1. Что такое компьютерная графика?......................................................... 28
1.2. Где используются изображения, создаваемые компьютером................................... 30
1.2.1. Искусство, развлечения и издательское дело........................................ 30
1.2.2. Компьютерная графика и обработка изображений...................................... 31
1.2.3. Управление процессом.............................................................. 32
1.2.4. Отображение имитаций.............................................................. 33
1.2.5. Автоматизированное проектирование................................................. 34
1.2.6. Научный анализ и наглядность...................................................... 36
1.3. Элементы изображений, создаваемых в компьютерной графике................................ 37
1.3.1. Ломаные линии..................................................................... 38
1.3.2. Текст............................................................................. 40
1.3.3. Закрашенные области .............................................................. 42
1.3.4. Растровое изображение............................................................. 43
1.3.5. Представление оттенков серого и других цветов в растровых изображениях............ 47
1.4. Графические устройства отображения...................................................... 50
1.4.1. Графические дисплеи............................................................... 51
Содержание
7
1.4.2. Растровые отображающие устройства................................................. 52
1.4.3. Индексированный цвет и кодовая таблица............................................ 56
1.4.4. Другие устройства растрового отображения.......................................... 58
1.4.5. Растровые устройства для изготовления твердых копий............................... 59
1.5. Входные графические примитивы и устройства.............................................. 61
1.5.1. Типы входных графических примитивов............................................... 61
1.5.2. Типы физических входных устройств................................................. 62
1.6. Заключение.............................................................................. 65
1.7. Дополнительная литература............................................................... 66
Глава 2. Начальная стадия: рисование фигур.......................................................67
2.1. Начальная стадия создания изображения................................................... 68
2.1.1. Аппаратно-независимое программирование и OpenGL................................... 69
2.1.2. Оконное программирование.......................................................... 70
2.1.3. Открытие окна для рисования....................................................... 72
2.2. Рисование основных графических примитивов............................................... 73
2.2.1. Рисование созвездия точек......................................................... 78
2.3. Создание рисунков из линий.............................................................. 83
2.3.1. Рисование ломаных линий и полигонов............................................... 86
2.3.2. Рисование линий с использованием movetoQ и linetof)............................... 91
2.3.3. Рисование выровненных прямоугольников............................................. 92
2.3.4. Форматное соотношение выровненного прямоугольника................................. 94
2.3.5. Закрашивание полигонов............................................................ 96
2.3.6. Другие графические примитивы в OpenGL............................................. 97
2.4. Простое взаимодействие с помощью мыши и клавиатуры...................................... 98
2.4.1. Взаимодействие с помощью мыши..................................................... 98
2.4.2. Взаимодействие с помощью клавиатуры.............................................. 102
2.5. Резюме................................................................................. 103
2.6. Тематические задания................................................................... 103
Тематическое задание 2.1. Псевдослучайные облака из точек .............................. 104
Тематическое задание 2.2. Введение в систему итерируемых функций........................ 106
Тематическое задание 2.3. Золотое отношение и другие жемчужины.......................... 109
Тематическое задание 2.4. Создание и применение файлов для ломаных линий................ 112
Тематическое задание 2.5. Рисование линий и многоугольников пунктиром.................... ИЗ
Тематическое задание 2.6. Редактор ломаных линий........................................ 114
Тематическое задание 2.7. Построение и запуск лабиринтов................................ 115
2.7. Дополнительная литература.............................................................. 117
Глава 3. Дополнительные инструменты для рисования...............................................118
3.1. Введение............................................................................... 119
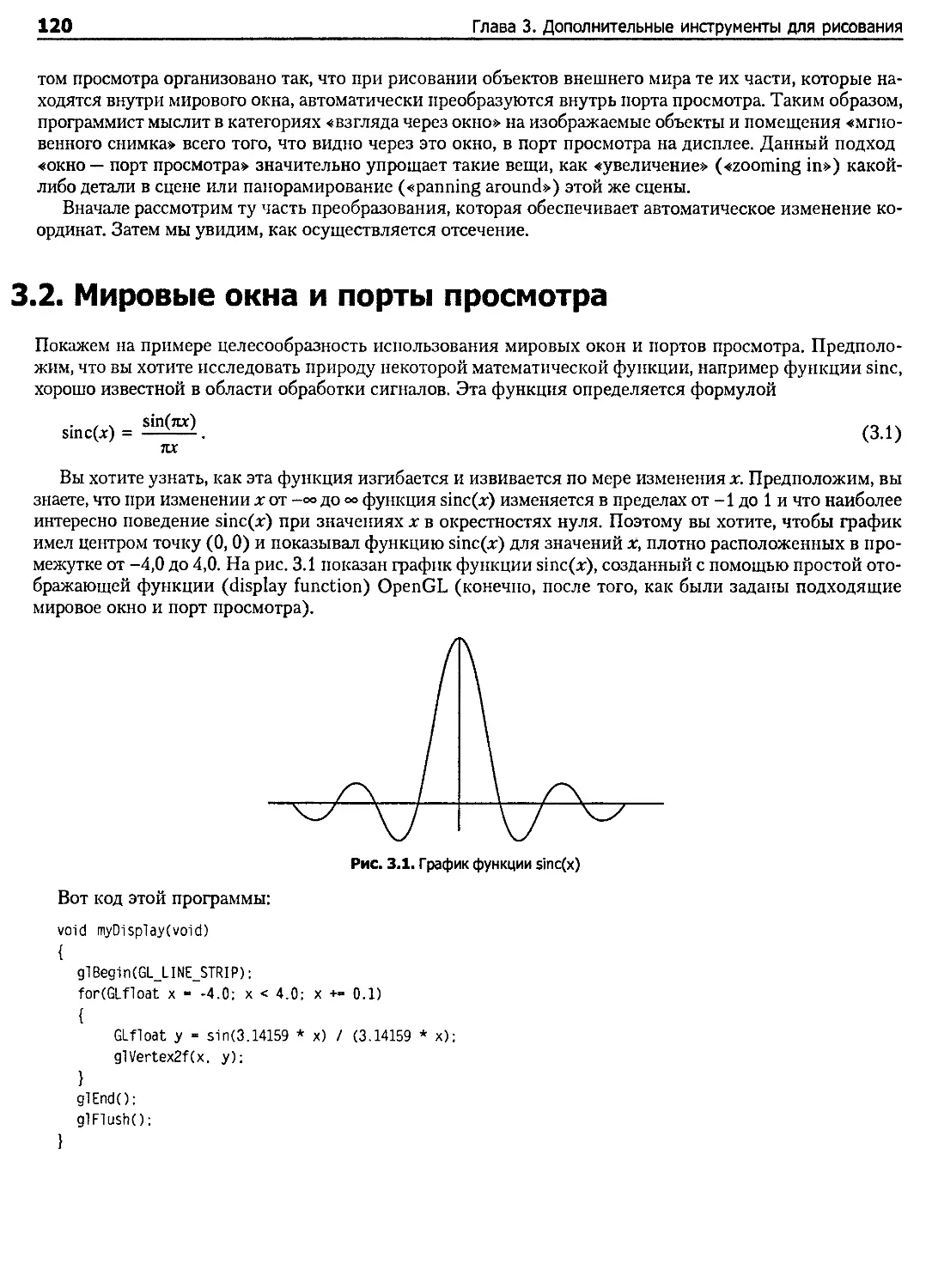
3.2. Мировые окна и порты просмотра......................................................... 120
3.2.1. Преобразование из мирового окна в порт просмотра................................. 121
3.2.2. Автоматическая установка окна и порта просмотра.................................. 132
3.3. Отсечение линий........................................................................ 135
3.3.1. Отсечение прямой................................................................. 135
3.3.2. Алгоритм отсечения Кохена-Сазерленда............................................. 136
3.4. Разработка класса Canvas .............................................................. 140
3.4.1. Несколько полезных вспомогательных классов....................................... 141
3.4.2. Реализация класса Canvas......................................................... 144
3.5. Относительное рисование................................................................ 146
3.5.1. Разработка moveRel() и lineRelQ.................................................. 146
3.5.2. Черепашья графика................................................................ 148
3.6. Фигуры на основе правильных многоугольников ........................................... 153
3.6.1. Правильные многоугольники........................................................ 153
3.6.2. Вариации п-угольников............................................................ 155
3.7. Рисование окружностей и дуг............................................................ 159
3.7.1. Рисование дуг.................................................................... 159
8
Содержание
3.8. Применение параметрического задания кривой............................................... 164
3.8.1. Параметрические формы для кривых................................................... 165
3.8.2. Вычерчивание кривых, заданных параметрически....................................... 167
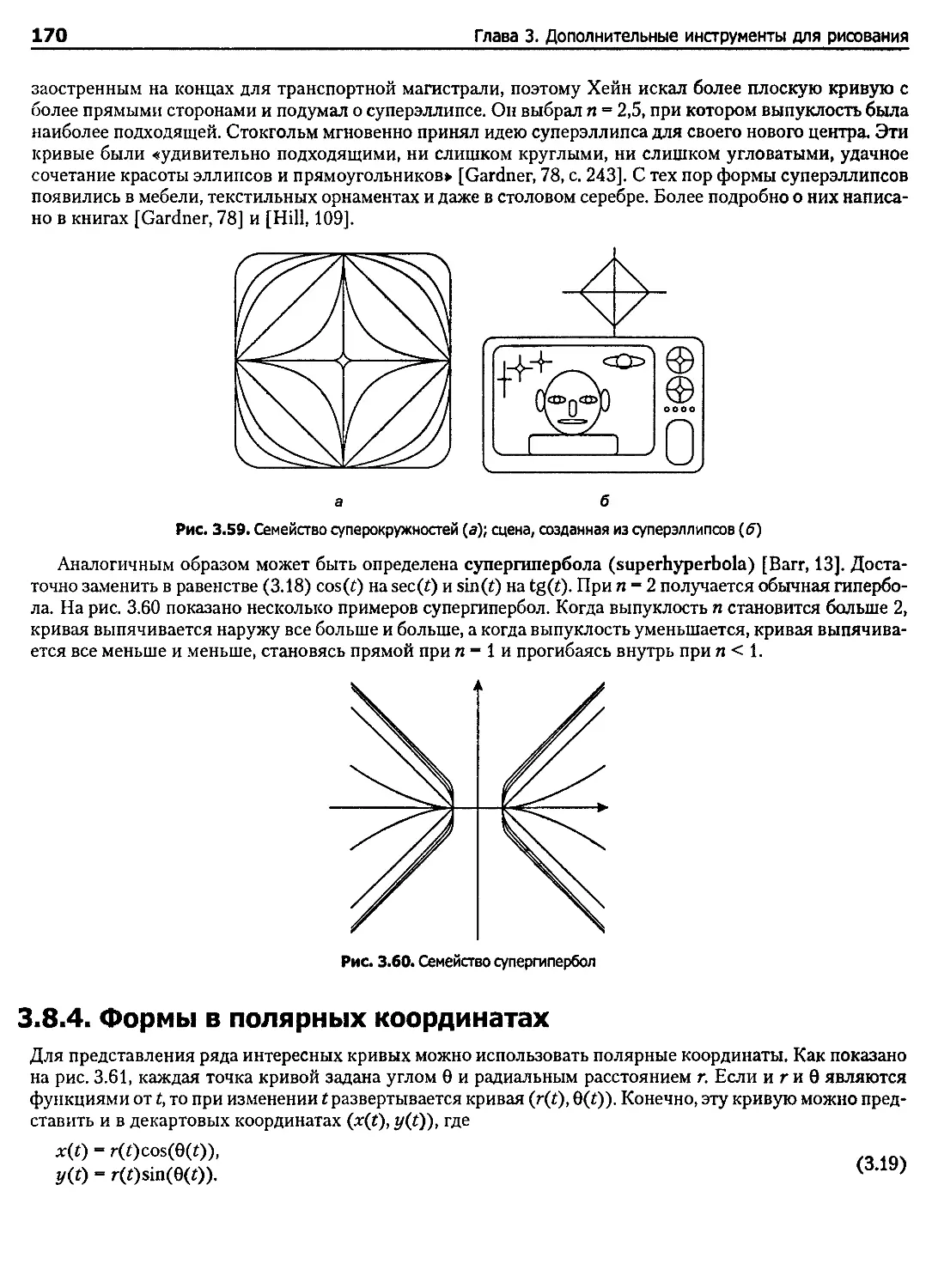
3.8.3. Суперэллипсы....................................................................... 169
3.8.4. Формы в полярных координатах....................................................... 170
3.8.5. Трехмерные кривые.................................................................. 172
3.9. Резюме................................................................................... 174
3.10. Тематические задания.................................................................... 175
Тематическое задание 3.1. Изучение логистического преобразования и имитация хаоса......... 175
Тематическое задание 3.2. Реализация отсекателя Кохена—Сазерленда на С или C++............ 177
Тематическое задание 3.3. Реализация Canvas на Turbo C++.................................. 179
Тематическоезадание 3.4. Рисование арок................................................... 182
Тематическое задание 3.5. Некоторые рисунки, используемые в физике и технике.............. 183
Тематическое задание 3.6. Мозаики......................................................... 186
Тематическое задание 3.7. Веселые вариации на тему........................................ 187
Тематическое задание 3.8. Окружности, вращающиеся вокруг окружностей...................... 189
Тематическое задание 3.9. Суперэллипсы.................................................... 190
3.11. Дополнительная литература................................................................ 191
Глава 4. Векторные инструменты для графики........................................................192
4.1. Введение................................................................................. 193
4.2. Обзор векторов........................................................................... 195
4.2.1. Операции с векторами............................................................... 197
4.2.2. Линейные комбинации векторов....................................................... 198
4.2.3. Модуль вектора; единичные векторы.................................................. 200
4.3. Скалярное произведение................................................................... 201
4.3.1. Свойства скалярного произведения................................................... 201
4.3.2. Угол между двумя векторами......................................................... 202
4.3.3. Знак b • с и перпендикулярность.................................................... 203
4.3.4. Двумерный «перп» вектор............................................................ 204
4.3.5. Ортогональные проекции и расстояние от точки до прямой............................. 206
4.3.6. Приложения проекции: отражения..................................................... 208
4.4. Векторное произведение двух векторов..................................................... 209
4.4.1. Геометрическая интерпретация векторного произведения............................... 210
4.4.2. Нахождение нормали к плоскости..................................................... 211
4.5. Отображение ключевых геометрических объектов............................................. 212
4.5.1. Системы координат и координатные фреймы............................................ 213
4.5.2. Аффинные комбинации точек.......................................................... 216
4.5.3. Линейная интерполяция двух точек................................................... 219
4.5.4. Твининг в искусстве и анимации..................................................... 219
4.5.5. Обзор: квадратичный и кубический твининг и кривые Безье............................ 222
4.5.6. Представление прямых и плоскостей.................................................. 222
4.6. Определение точки пересечения двух отрезков прямой....................................... 231
4.6.1. Приложение пересечения прямых: окружность, проходящая через три заданные точки..... 234
4.7. Пересечения прямых с плоскостями; отсечение.............................................. 236
4.8. Задачи о пересечениях многоугольников.................................................... 238
4.8.1. Работа с выпуклыми полигонами и полиэдрами......................................... 239
4.8.2. Пересечение с лучами и отсечение для выпуклых полигонов............................ 240
4.8.3. Алгоритм Сайруса—Бека.............................................................. 243
4.8.4. Отсечение границами произвольных полигонов......................................... 246
4.8.5. Более сложное отсечение............................................................ 248
4.9. Резюме................................................................................... 249
4.10. Тематические задания..................................................................... 250
Тематическое задание 4.1. Анимация с твинингом............................................ 250
Тематическое задание 4.2. Разные окружности .............................................. 250
Тематическое задание 4.3. Находится ли точка Q внутри выпуклого полигона Р?............... 252
Тематическое задание 4.4. Отражения в комнате (двумерная трассировка луча)................ 253
Тематическое задание 4.5. Отсечение Сайруса—Бека.......................................... 254
Содержание
9
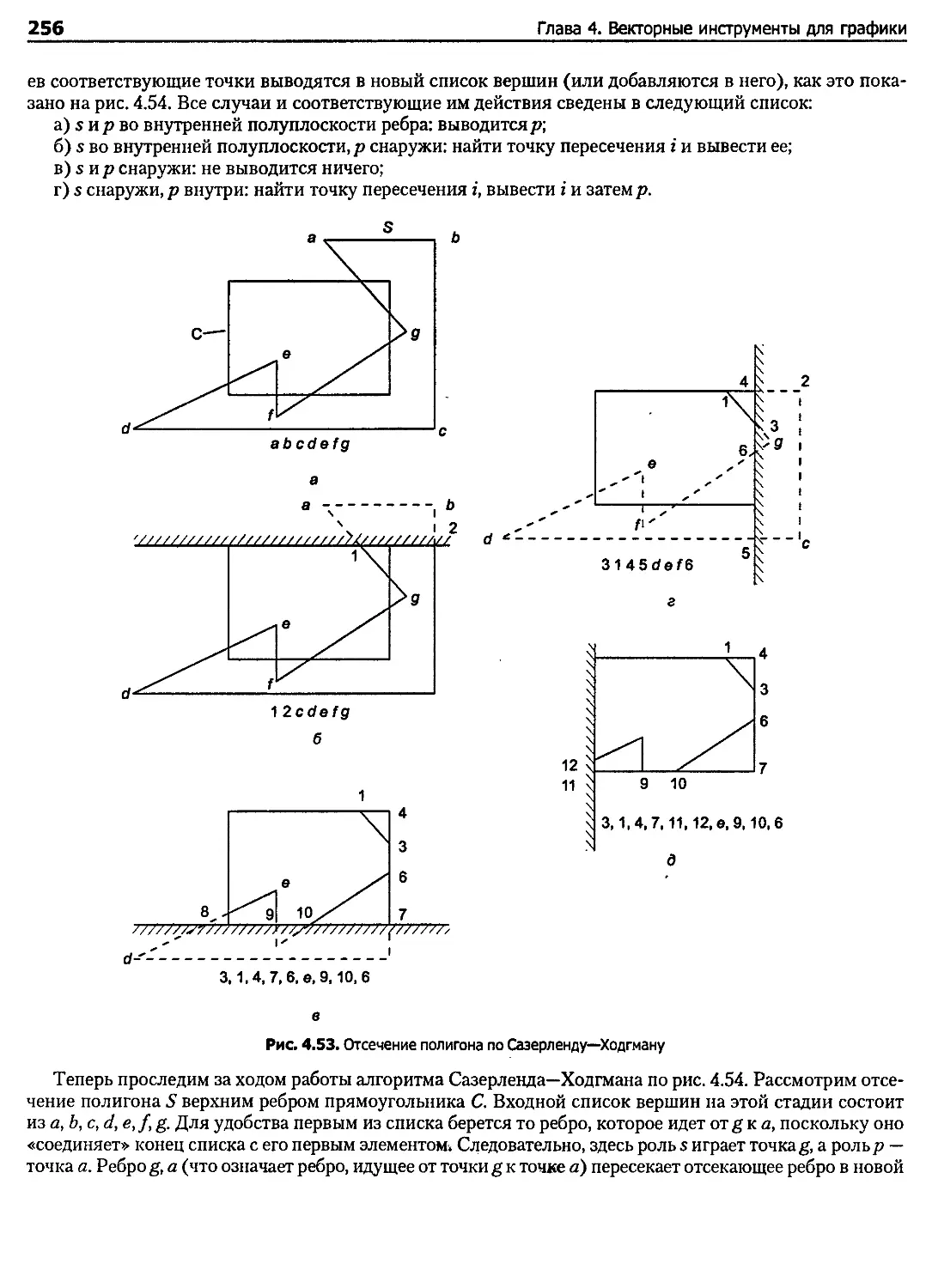
Тематическое задание 4.6. Отсечение полигона границами выпуклого полигона: отсечение
Сазерленда—Ходгмана................................................................. 254
Тематическое задание 4.7. Отсечение одного полигона границами другого: отсечение
Бейлера—Азертона.................................................................... 257
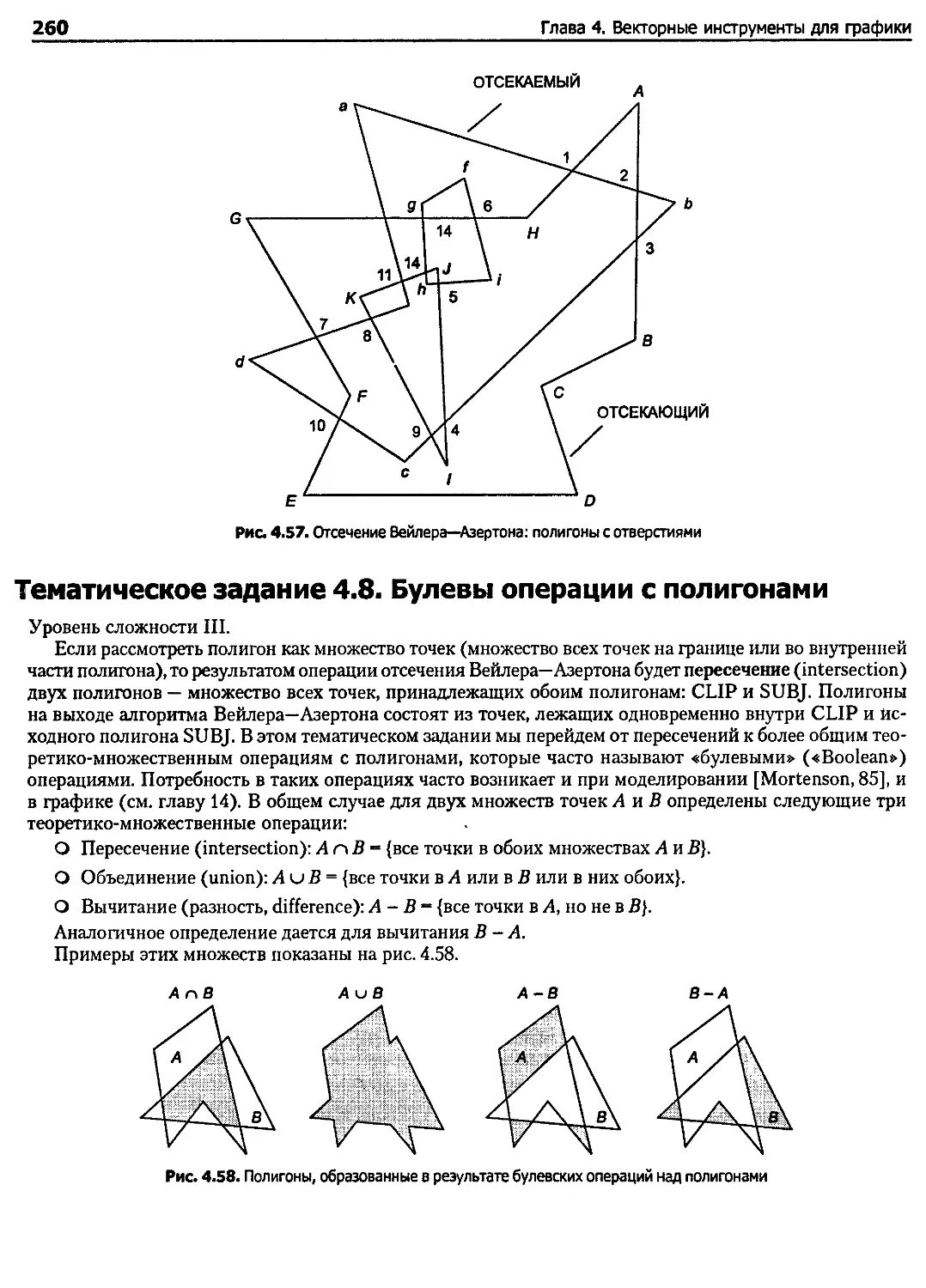
Тематическое задание 4.8. Булевы операции с полигонами ............................... 260
4.11. Дополнительная литература............................................................. 262
Глава 5. Преобразования объектов...............................................................263
5.1. Введение.............................................................................. 264
5.2. Введение в преобразования............................................................. 265
5.2.1. Преобразование точек и объектов................................................ 268
5.2.2. Аффинные преобразования........................................................ 270
5.2.3. Геометрические эффекты элементарных двумерных аффинных преобразований.......... 271
5.2.4. Инвертирование аффинного преобразования........................................ 276
5.2.5. Композиция аффинных преобразований............................................. 278
5.2.6. Примеры композиции двумерных преобразований ................................... 279
5.2.7. Некоторые полезные свойства аффинных преобразований............................ 284
5.3. Трехмерные аффинные преобразования.................................................... 289
5.3.1. Элементарные трехмерные преобразования......................................... 289
5.3.2. Компонование трехмерных аффинных преобразований................................ 293
5.3.3. Комбинирование поворотов....................................................... 294
5.3.4. Краткое изложение свойств трехмерных аффинных преобразований................... 299
5.4. Изменения систем координат............................................................ 300
5.5. Использование аффинных преобразований в программах.................................... 303
5.5.1. Сохранение СТ для дальнейшего использования.................................... 311
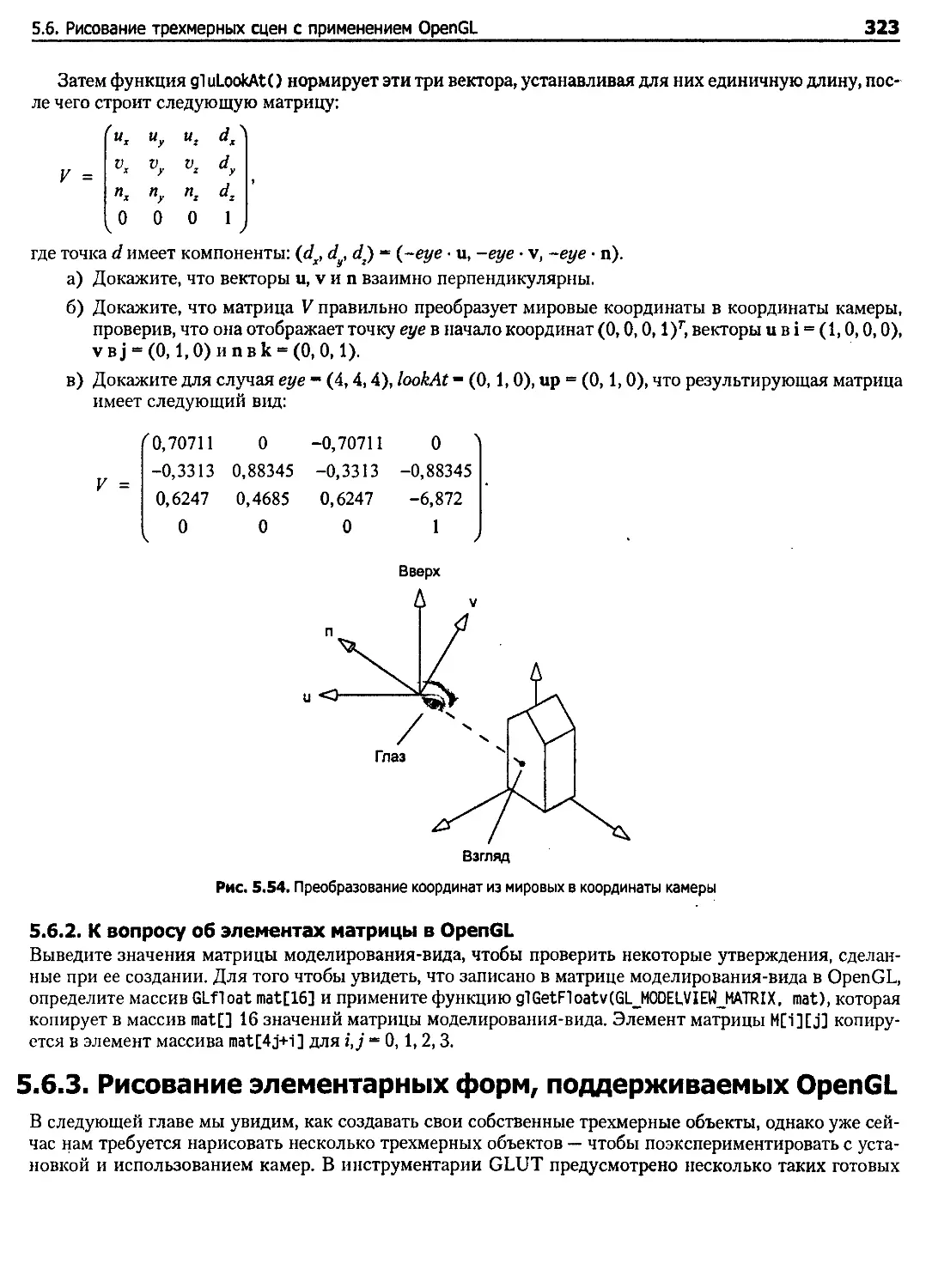
5.6. Рисование трехмерных сцен с применением OpenGL........................................ 316
5.6.1. Знакомство с процессом визуального отображения и графическим конвейером........ 316
5.6.2. Некоторые инструменты OpenGL для моделирования и вида.......................... 320
5.6.3. Рисование элементарных форм, поддерживаемых OpenGL............................. 323
5.7. Резюме................................................................................ 338
5.8. Тематические задания.................................................................. 339
Тематическое задание 5.1. Выполнение вашего собственного преобразования с помощью
СТ в классе Canvas.................................................................. 339
Тематическое задание 5.2. Рисование звезды с рисунка 5.39 с помощью многократных поворотов. 340
Тематическое задание 5.3. Разложение двумерного аффинного преобразования.............. 340
Тематическое задание 5.4. Обобщенные трехмерные сдвиги ............................... 344
Тематическое задание 5.5. Вращение вокруг оси: конструктивный подход.................. 346
Тематическое задание 5.6. Разложение трехмерных аффинных преобразований............... 347
Тематическое задание 5.7. Рисование трехмерных сцен, описанных на языке SDL........... 349
5.9. Дополнительная литература............................................................. 349
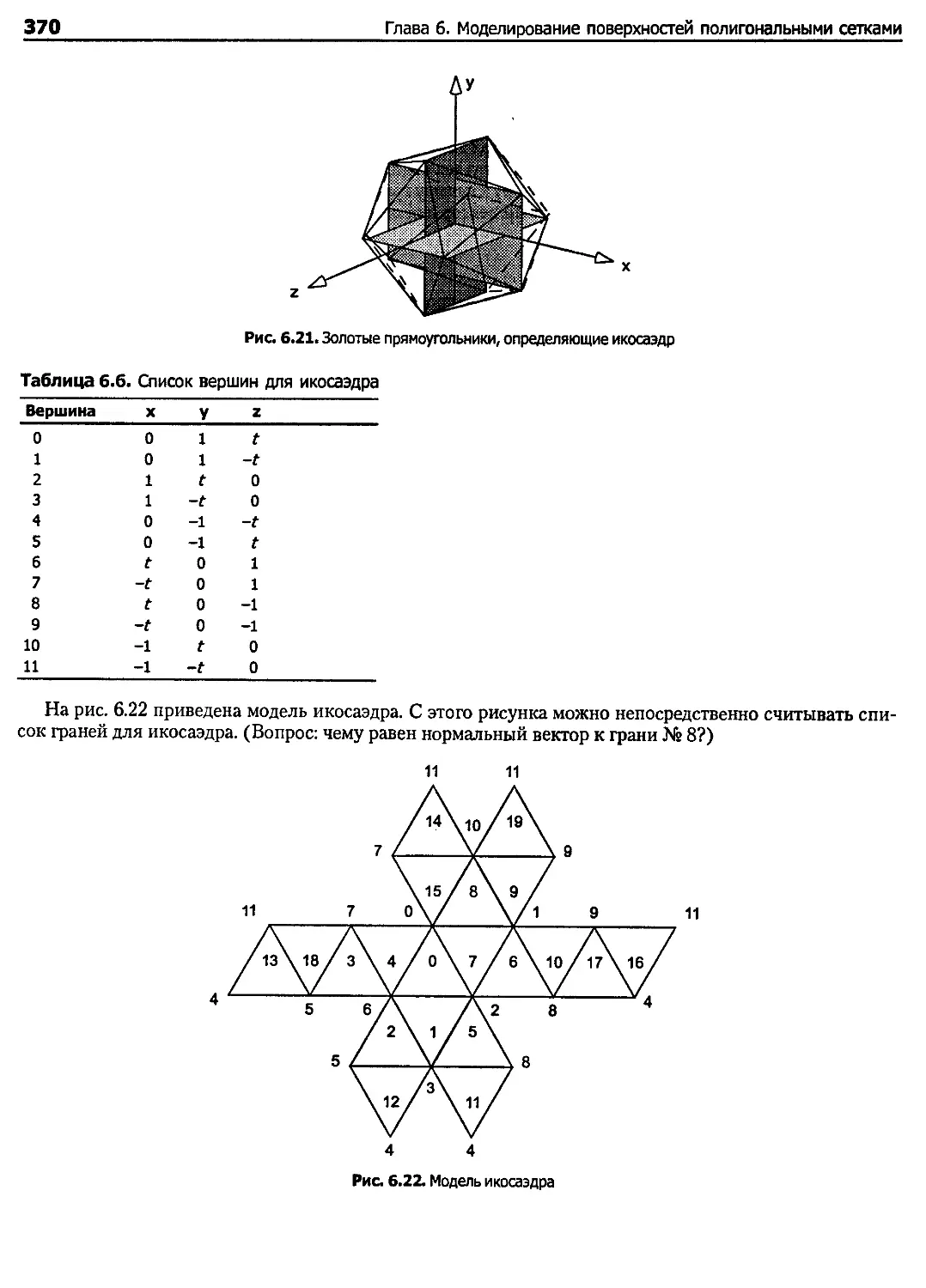
Глава 6. Моделирование поверхностей полигональными сетками ....................................350
6.1. Введение.............................................................................. 351
6.2. Введение в трехмерное моделирование полигональными сетками............................ 351
6.2.1. Определение полигональной сетки................................................ 353
6.2.2. Нахождение нормальных векторов................................................. 355
6.2.3. Свойства сеток................................................................. 357
6.2.4. Каркасные модели для немонолитных объектов..................................... 358
6.2.5. Работа с сетками в программе................................................... 359
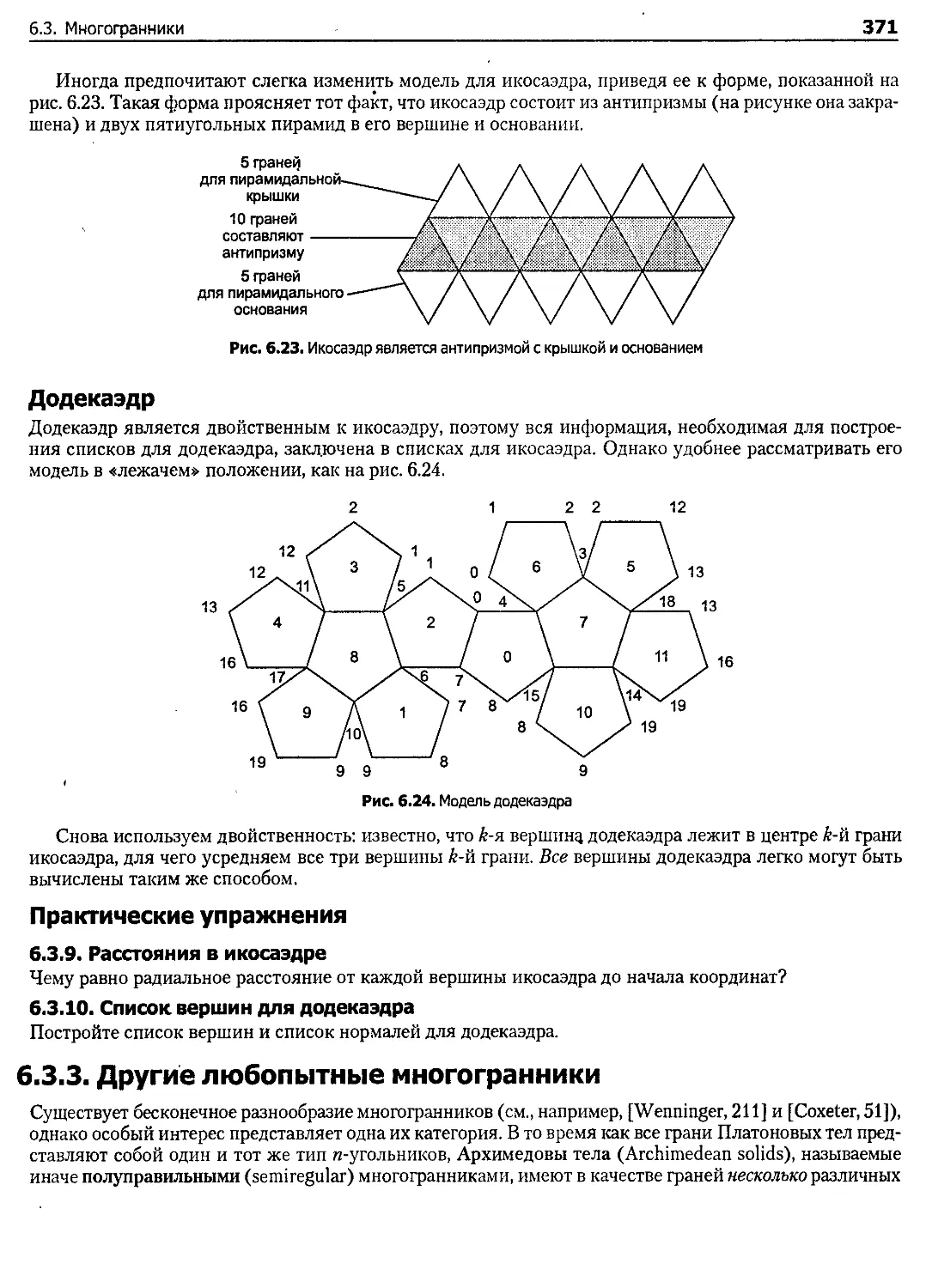
6.3. Многогранники......................................................................... 363
6.3.1. Призмы и антипризмы............................................................ 365
6.3.2. Платоновы тела................................................................. 366
6.3.3. Другие любопытные многогранники................................................ 371
6.4. Экструзивные формы.................................................................... 375
6.4.1. Создание призм................................................................. 375
6.4.2. Совокупности экструзивных призм: «кирпичная кладка»............................ 376
6.4.3. Экструзии с «поворотом»........................................................ 378
6.4.4. Создание сегментированных экструзий: трубки и змейки........................... 379
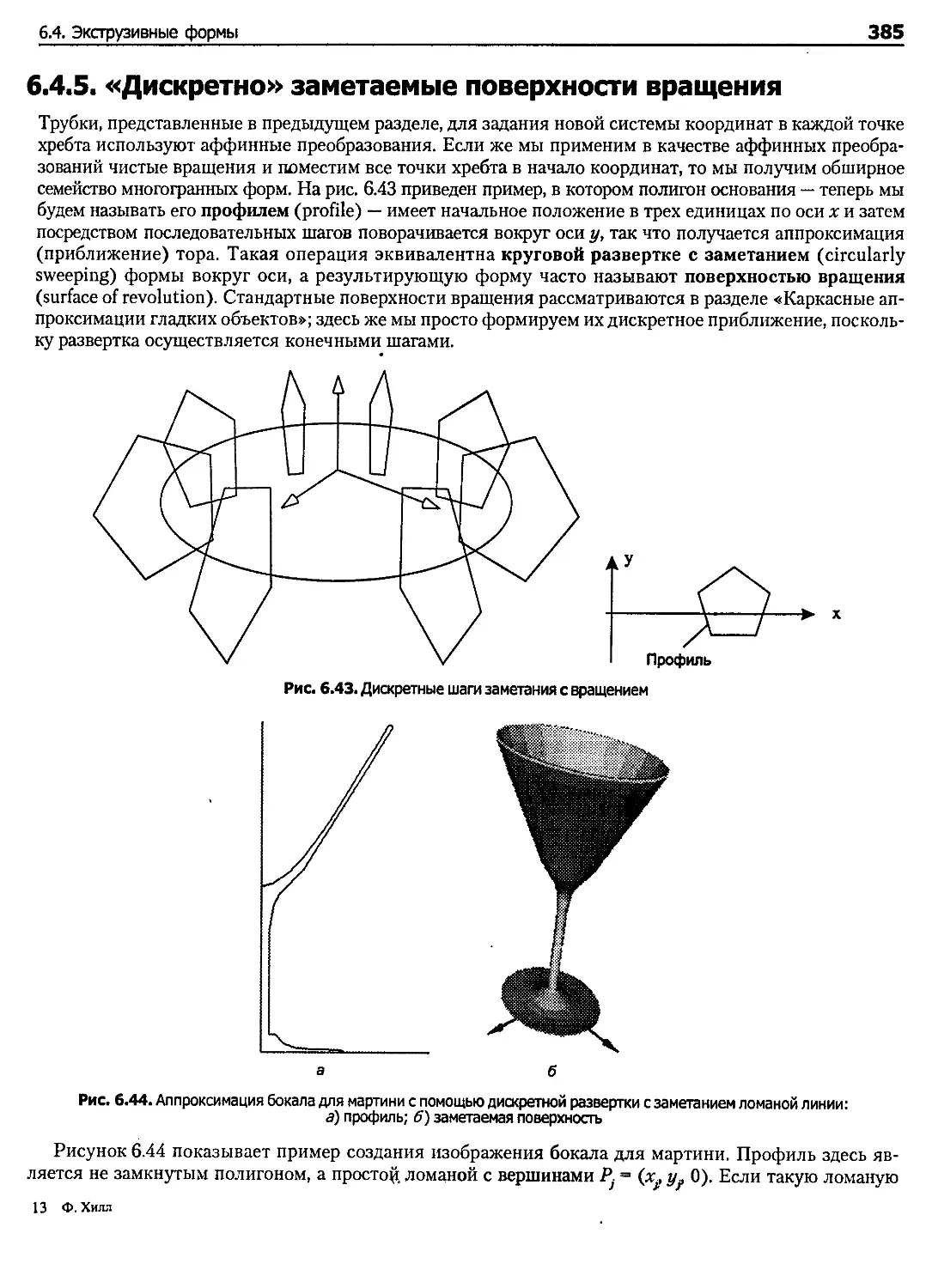
6.4.5. «Дискретно» заметаемые поверхности вращения.................................... 385
10
Содержание
6.5. Каркасные аппроксимации гладких объектов................................................... 386
6.5.1. Представления поверхностей.......................................................... 386
6.5.2. Нормальный вектор к поверхности..................................................... 388
6.5.3. Влияние аффинного преобразования.................................................... 389
6.5.4. Три «базовые» формы: сфера, цилиндр и конус.................................... 391
6.5.5. Формирование полигональной сетки для криволинейной поверхности...................... 394
6.5.6. Линейчатые поверхности.............................................................. 396
6.5.7. Поверхности вращения................................................................ 402
6.5.8. Поверхности второго порядка......................................................... 404
6.5.9. Суперквадрики....................................................................... 408
6.5.10. Трубки на базе трехмерных кривых................................................... 409
6.5.11. Поверхности на базе явных функций двух переменных.................................. 410
6.6. Заключение................................................................................. 411
6.7. Тематические задания .
Тематическое задание
Тематическое задание
Тематическое задание
Тематическое задание
Тематическое задание
Тематическое задание
Тематическое задание
Тематическое задание
Тематическое задание
6.1. Сетки, записанные в файл ........................................
6.2. Вывод метода Ньюэлла.............................................
6.3. Призма...........................................................
6.4. Совокупность призм и экструдированные полосы из четырехугольников ...
6.5. Трубки и змейки на базе параметрической кривой...................
б.б. Построение поверхностей вращения с дискретными шагами............
6.7. Списки ребер и каркасные модели .................................
6.8. Сводчатые потолки................................................
6.9. О Платоновых телах...............................................
412
412
414
416
417
418
419
419
420
420
Тематическое задание 6.10. Об Архимедовых телах............................................ 420
Тематическое задание 6.11. Алгебраическая форма поверхностей второго порядка............... 420
Тематическое задание 6.12. Сцены с супеквадриками........................................ 422
Тематическое задание 6.13. Рисование гладких параметрических поверхностей.................. 422
Тематическое задание 6.14. Сузить, закрутить, изогнуть и расплющить........................ 423
6.8. Дополнительная литература ................................................................. 425
Глава 7. Трехмерный просмотр..................................................................425
7.1. Введение............................................................................. 427
7.2. Снова о камере....................................................................... 427
7.2.1. Установка отображаемого объема................................................ 428
7.2.2. Позиционирование и ориентирование камеры...................................... 429
7.3. Встраивание камеры в программу....................................................... 434
7.3.1. «Пилотирование» камеры........................................................ 436
7.4. Перспективные проекции трехмерных объектов........................................... 440
7.4.1. Перспективная проекция точки.................................................. 441
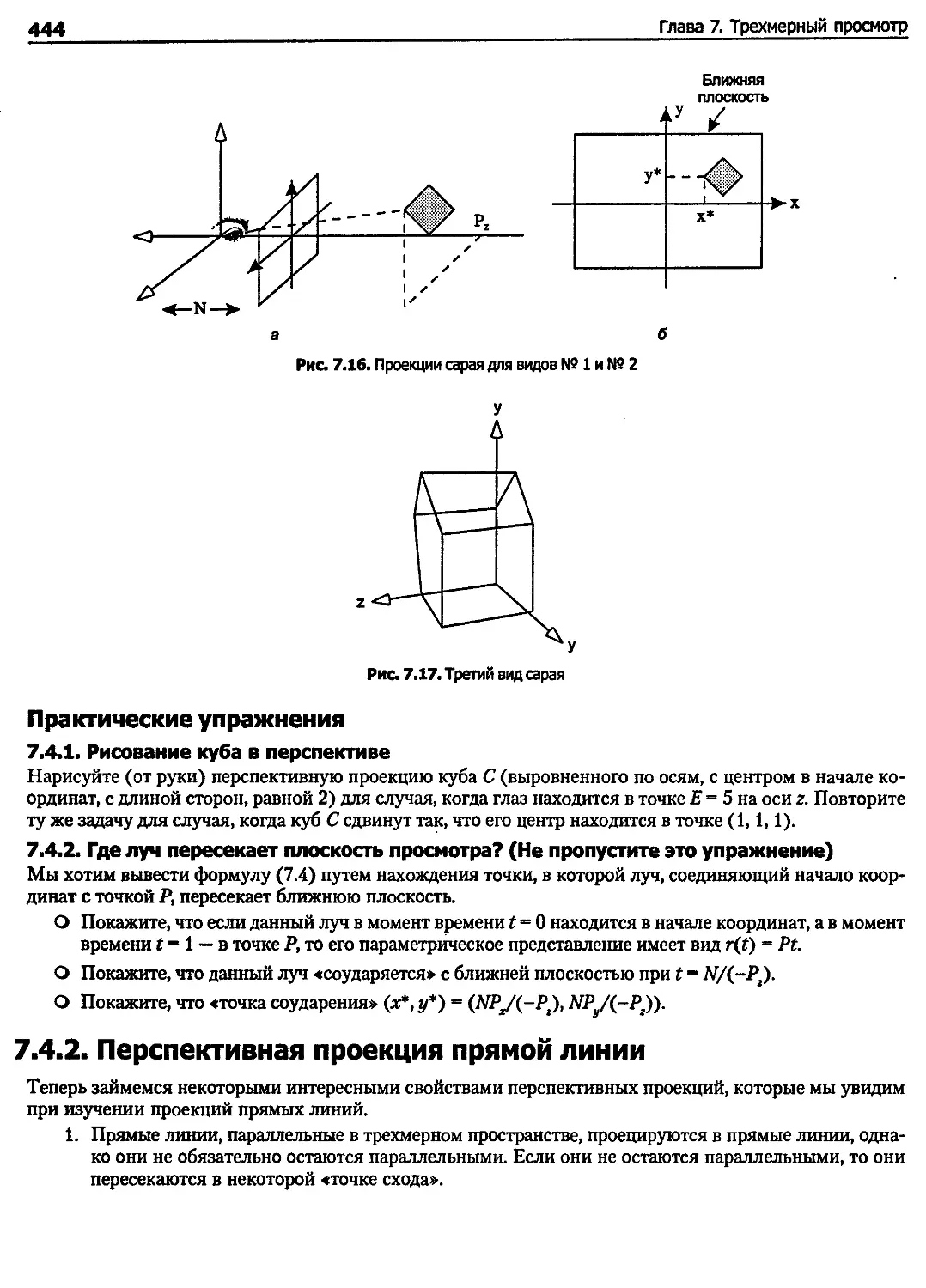
7.4.2. Перспективная проекция прямой линии........................................... 444
7.4.3. Включение перспективы в графический конвейер.................................. 449
7.4.4. Отсечение граней границами отображаемого объема............................... 456
7.5. Создание стереоизображений .......................................................... 463
7.6. Классификация проекций............................................................... 465
7.6.1. Одно-, двух-и трехточечные перспективы........................................ 465
7.6.2. Параллельные проекции......................................................... 470
7.7. Резюме............................................................................... 477
7.8. Тематические задания................................................................. 477
Тематическое задание 7.1. «Пилотирование» камеры по сцене............................ 477
Тематическое задание 7.2. Стереоизображения.......................................... 478
Тематическое задание 7.3. Создание параллельных проекций ............................ 478
Тематическое задание 7.4. Самодельное проецирование (если бы OpenGL был недоступен).. 479
Тематическое задание 7.5. Удаление невидимых граней для большей эффективности........ 479
7.9. Дополнительная литература............................................................ 480
Глава 8. Визуализация граней для усиления реалистичности......................................481
8.1. Введение............................................................................. 482
8.2. Введение в модели закрашивания....................................................... 486
8.2.1. Геометрические составляющие для нахождения отраженного света.................. 487
Содержание
11
8.2.2. Вычисление диффузной составляющей ............................................... 488
8.2.3. Зеркальное отражение............................................................. 489
8.2.4. Роль фонового света.............................................................. 492
8.2.5. Комбинирование компонентов освещения............................................. 493
8.2.6. Добавление цвета................................................................. 494
8.2.7. Закраска и графический конвейер ................................................. 496
8.2.8. Использование источников света в OpenGL.......................................... 497
8.2.9. Работа со свойствами материалов в OpenGL......................................... 503
8.2.10. Закраска сцен, заданных с помощью SDL............................................ 503
8.3. Плоское и плавное закрашивание.......................................................... 504
8.3.1. Плоское закрашивание............................................................. 506
8.3.2. Плавное закрашивание ............................................................ 507
8.4. Удаление невидимых поверхностей......................................................... 511
8.4.1. Использование буфера глубины..................................................... 511
8.5. Добавление текстуры к граням............................................................ 514
8.5.1. Наложение текстуры на плоскую поверхность........................................ 517
8.5.2. Визуализация текстуры ........................................................... 519
8.5.3. Что регулирует текстура?......................................................... 526
8.5.4. Пример текстурирования с использованием OpenGL................................... 528
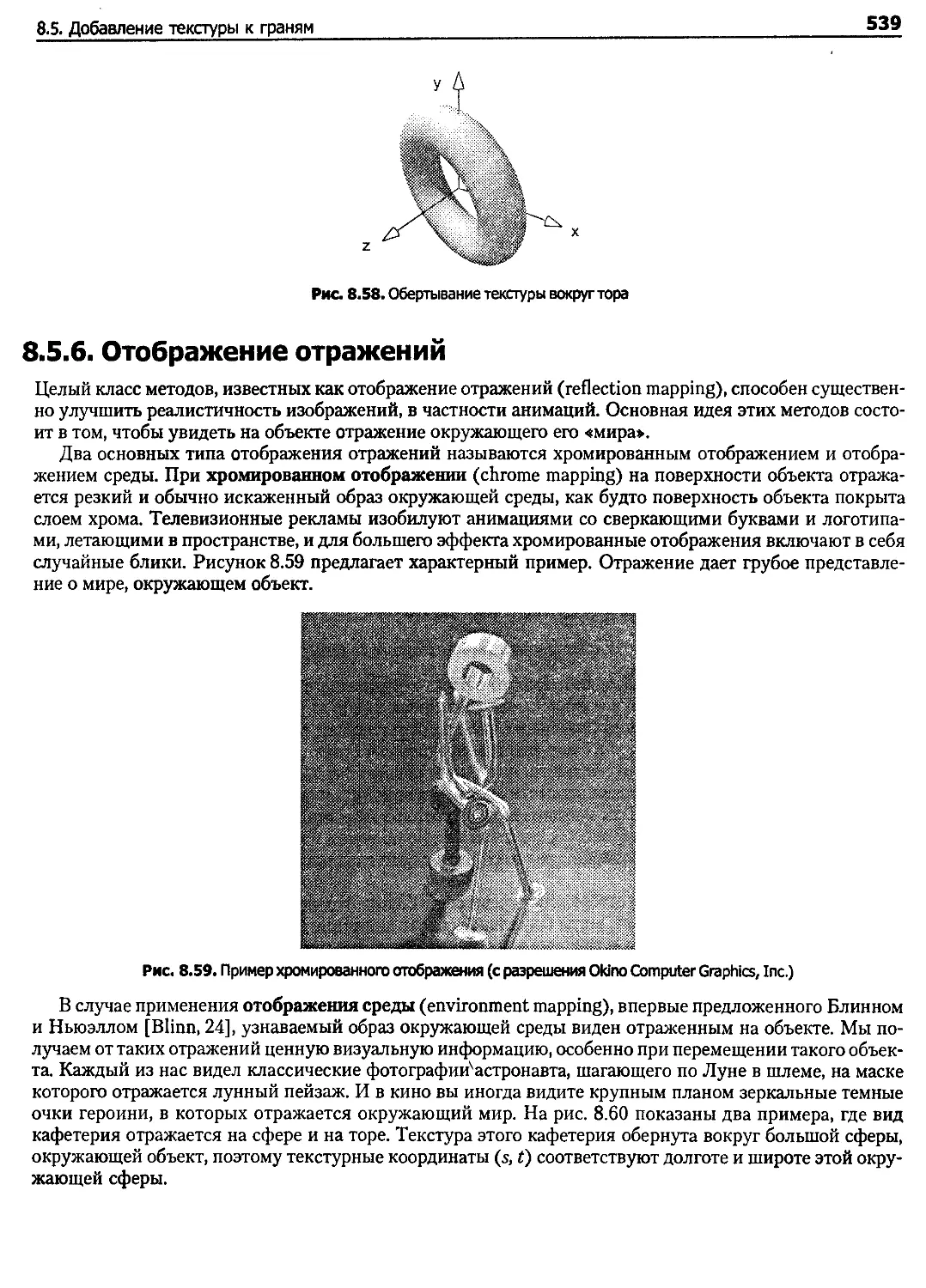
8.5.5. Обертывание текстуры вокруг криволинейных поверхностей........................... 534
8.5.6. Отображение отражений............................................................ 539
8.6. Добавление теней объектов............................................................... 542
8.6.1. Тени как текстура ............................................................... 543
8.6.2. Создание теней с помощью буфера теней............................................ 544
8.7. Заключение.............................................................................. 546
8.8. Тематические задания.................................................................... 547
Тематическое задание 8.1. Создание закрашенных объектов с использованием OpenGL......... 547
Тематическое задание 8.2. Самодельный графический конвейер.............................. 548
Тематическое задание 8.3. Добавление закраски полигонов и удаления невидимых поверхностей
при помощи буфера глубины............................................................. 548
Тематическое задание 8.4. Визуализация текстуры......................................... 548
Тематическое задание 8.5. Применение процедурных 30-текстур............................. 548
Тематическое задание 8.6. Рисование теней............................................... 549
Тематическое задание 8.7. Расширение SDL с целью включения текстурирования.............. 549
8.9. Дополнительная литература .............................................................. 550
Глава 9. Приближение к бесконечности........................................................... 551
9.1. Введение................................................................................ 552
9.2. Фракталы и самоподобие.................................................................. 552
9.2.1. Последовательное усложнение кривых............................................... 553
9.2.2. Рисование кривых и снежинок Коха................................................. 554
9.2.3. Дробная размерность.............................................................. 556
9.3. Создание строк и кривые Пеано........................................................... 557
9.3.1. Рекурсивная генерация строк и рисование в программе.............................. 559
9.3.2. Разрешение ветвления............................................................. 562
9.3.3. Добавление случайности и сужения................................................. 565
9.4. Замощение плоскости..................................................................... 565
9.4.1. Моноэдрические мозаики........................................................... 566
9.4.2. Диэдральные мозаичные размещения................................................. 568
9.4.3. Рисование мозаик ................................................................ 571
9.4.4. Рептилии......................................................................... 571
9.5. Создание изображений с использованием системы итерируемых функций ...................... 574
9.5.1. Экспериментальный копир.......................................................... 574
9.5.2. Теоретические основы процесса копирования........................................ 576
9.5.3. Рисование k-й итерации........................................................... 577
9.5.4. «Игра в Хаос».................................................................... 579
9.5.5. Нахождение системы IFS; фрактальное сжатие изображений........................... 582
9.6. Множество Мандельброта.................................................................. 586
9.6.1. Множества Мандельброта и системы итерируемых функций............................. 586
12
Содержание
9.6.2. Определение множества Мандельброта............................................... 590
9.6.3. Определение того, находится ли точка с в пределах множества Мандельброта......... 592
9.6.4. Рисование множества Мандельброта ................................................ 593
9.6.5. Некоторые замечания по поводу множества Мандельброта............................. 595
9.7. Множества Жюлиа......................................................................... 595
9.7.1. Плотное множество Жюлиа Кс....................................................... 596
9.7.2. Рисование плотных множеств Жюлиа................................................. 596
9.7.3. Некоторые замечания относительно неподвижных точек и бассейнов притяжения........ 596
9.7.4. Множество Жюлиа Jc............................................................... 599
9.8. Случайные фракталы...................................................................... 602
9.8.1. Фрактализация отрезка............................................................ 602
9.8.2. Контроль за спектральной плотностью фрактальной кривой........................... 604
9.9. Резюме.................................................................................. 606
9.10. Тематические задания.................................................................... 607
Тематическое задание 9.1. Рисование по генерации строк.................................. 607
Тематическое задание 9.2. Рисование снежинок и рептилий................................. 608
Тематическое задание 9.3. «Игра в Хаос» ................................................ 610
Тематическое задание 9.4. Рисование орбит внутри множества Мандельброта................. 611
Тематическое задание 9.5. Создание изображений множества Мандельброта................... 612
Тематическое задание 9.6. Создание изображений множеств Жюлиа........................... 612
Тематическое задание 9.7. Непериодические мозаики; мозаики Пенроуза..................... 612
Тематическое задание 9.8. Фрактализация кривых.......................................... 614
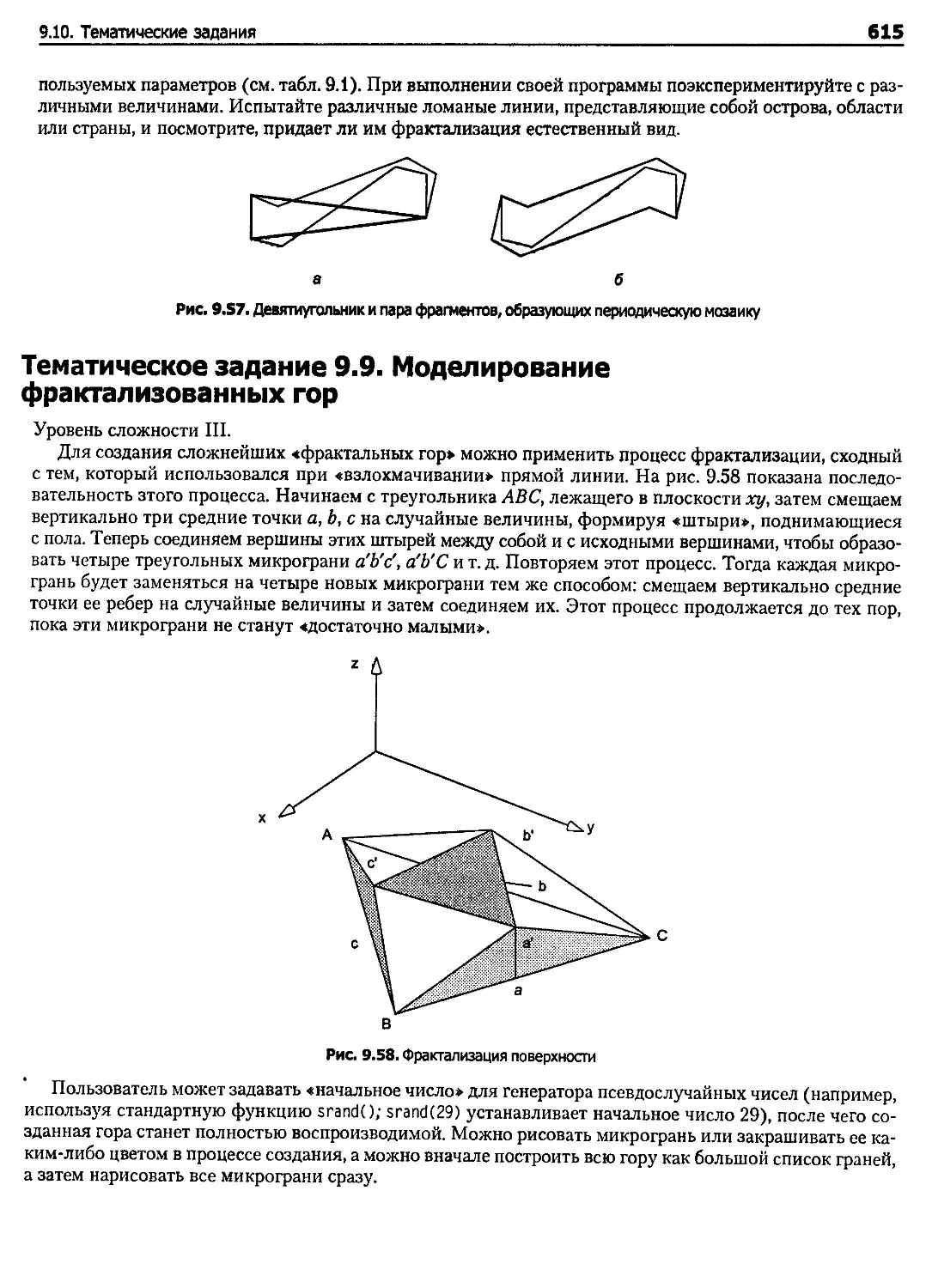
Тематическое задание 9.9. Моделирование фрактализованных гор............................ 615
9.11. Дополнительная литература............................................................... 616
Глава 10. Средства для растровой графики.................................................... 617
10.1. Введение............................................................................... 618
10.2. Управление пиксельными картами......................................................... 619
10.2.1. Важные операции с пиксельными картами........................................... 619
10.2.2. Типы данных, используемые для пиксельных карт................................... 620
10.2.3. Масштабирование и поворот изображений........................................... 627
10.3. Объединение пиксельных карт............................................................ 630
10.3.1. Цикл «чтение — модификация-запись».............................................. 631
10.3.2. Альфа-канал и смешивание изображений............................................ 632
10.3.3. Логические комбинации пиксельных карт........................................... 636
10.3.4. Операция BitBLT................................................................. 640
10.4. Рисование прямых своими силами: алгоритм Брезенхема.................................... 641
10.4.1. Алгоритм Брезенхема для рисования прямых линий.................................. 642
10.5. Определение и заполнение областей из пикселов.......................................... 648
10.5.1. Задание областей................................................................ 648
10.5.2. Пиксельно-определенные области.................................................. 649
10.5.3. Рекурсивный алгоритм заливки.................................................... 650
10.5.4. Заполнение областей узорами .................................................... 652
10.5.5. Использование связности: заполнение области на основе серий пикселов............ 653
10.6. Манипулирование символически-определенными областями................................... 655
10.6.1. Области, описываемые прямоугольниками........................................... 655
10.6.2. Области, заданные контуром...................................................... 657
10.7. Заполнение полигонально-определенных областей.......................................... 658
10.7.1. Какие пикселы ребра принадлежат полигону?....................................... 659
10.7.2. Повышение эффективности алгоритма............................................... 662
10.8. Ступенчатость; технологии сглаживания.................................................. 666
10.8.1. Технологии сглаживания.......................................................... 667
10.8.2. Сглаживание текстуры............................................................ 672
10.8.3. Сглаживание с применением OpenGL................................................ 675
10.9. Увеличение количества цветов и оттенков................................................ 676
10.9.1. Упорядоченное размытие.......................................................... 678
10.9.2. Рассеивание ошибок.............................................................. 682
10.10. Резюме................................................................................. 684
Содержание
13
10.11. Тематические задания.................................................................... 685
Тематическое задание 10.1. Чтение и просмотр BMP-файлов изображений...................... 685
Тематическое задание 10.2. Растворение одной пиксельной карты в другой с помощью OpenGL.. 686
Тематическое задание 10.3. Заполнение области на основе серий............................ 686
Тематическое задание 10.4. Работа со структурой данных «формы»........................... 686
Тематическое задание 10.5. Цепное кодирование форм....................................... 687
Тематическое задание 10.6. Заполнение «горизонтально-выпуклых» полигонов................. 687
Тематическое задание 10.7. Заполнение полигона общего вида............................... 688
Тематическое задание 10.8. Рассеивание ошибок............................................ 688
10.12. Дополнительная литература .............................................................. 688
Глава 11. Создание кривых и поверхностей..........................................................689
11.1. Введение................................................................................ 690
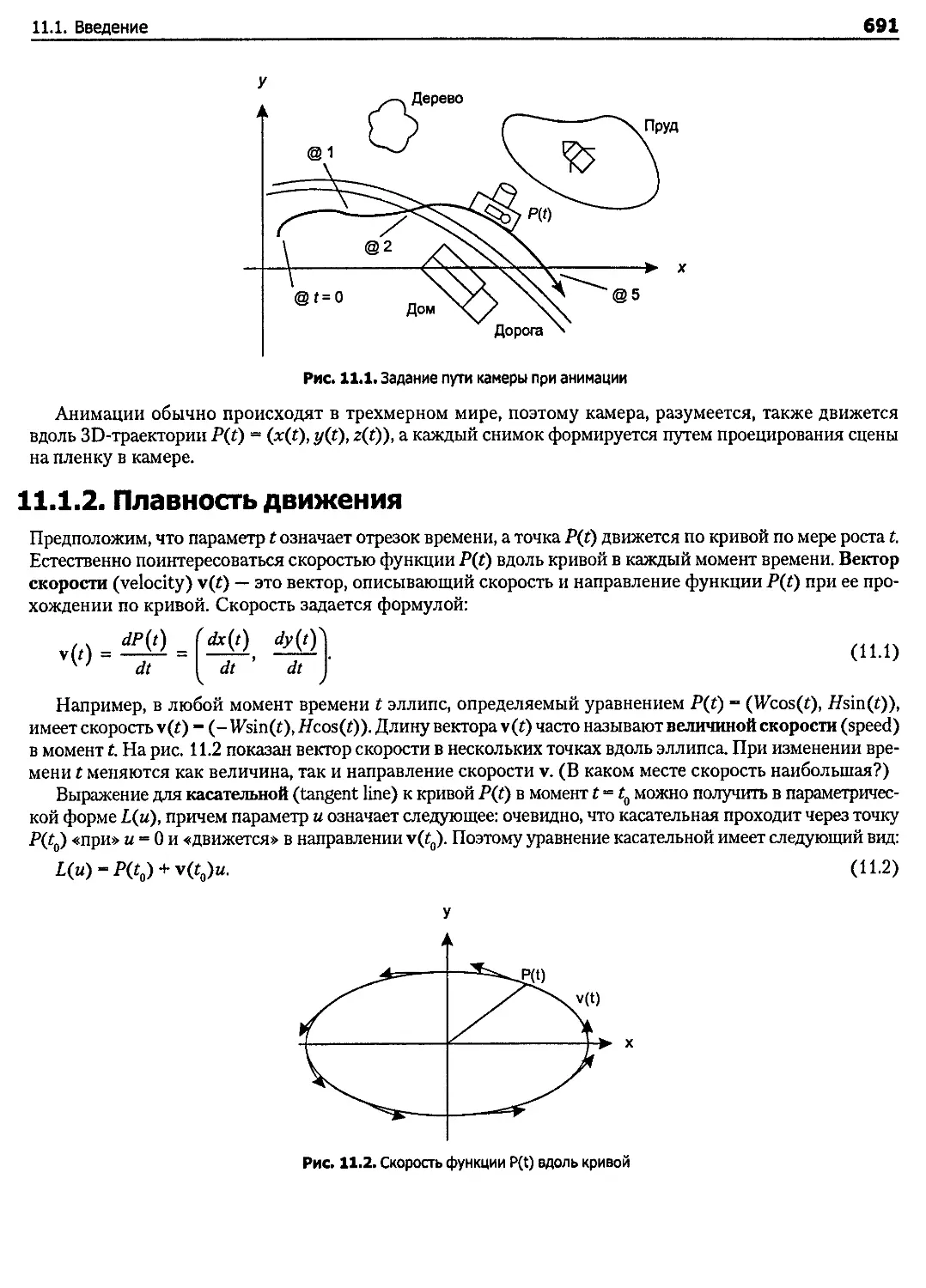
11.1.1. Параметрические кривые как траектории............................................ 690
11.1.2. Плавность движения............................................................... 691
11.2. Описание кривых полиномами.............................................................. 695
11.3. Интерактивное конструирование кривых ................................................... 700
11.4. Применение кривых Безье для построения кривых........................................... 702
11.4.1. Алгоритм де Кастельо............................................................. 702
11.5. Свойства кривых Безье .................................................................. 707
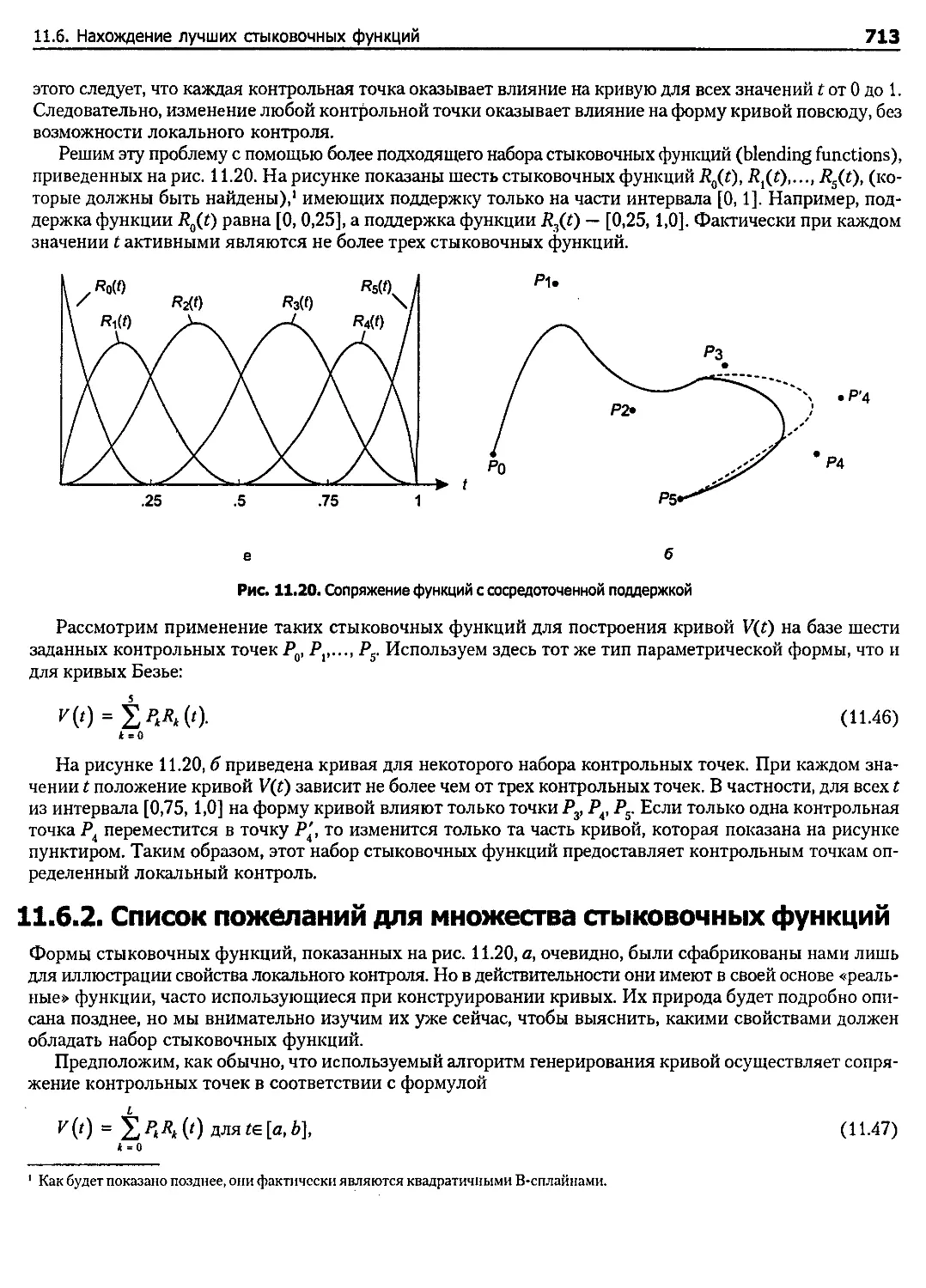
11.6. Нахождение лучших стыковочных функций................................................... 712
11.6.1. Проблема локального контроля .................................................... 712
11.6.2. Список пожеланий для множества стыковочных функций............................... 713
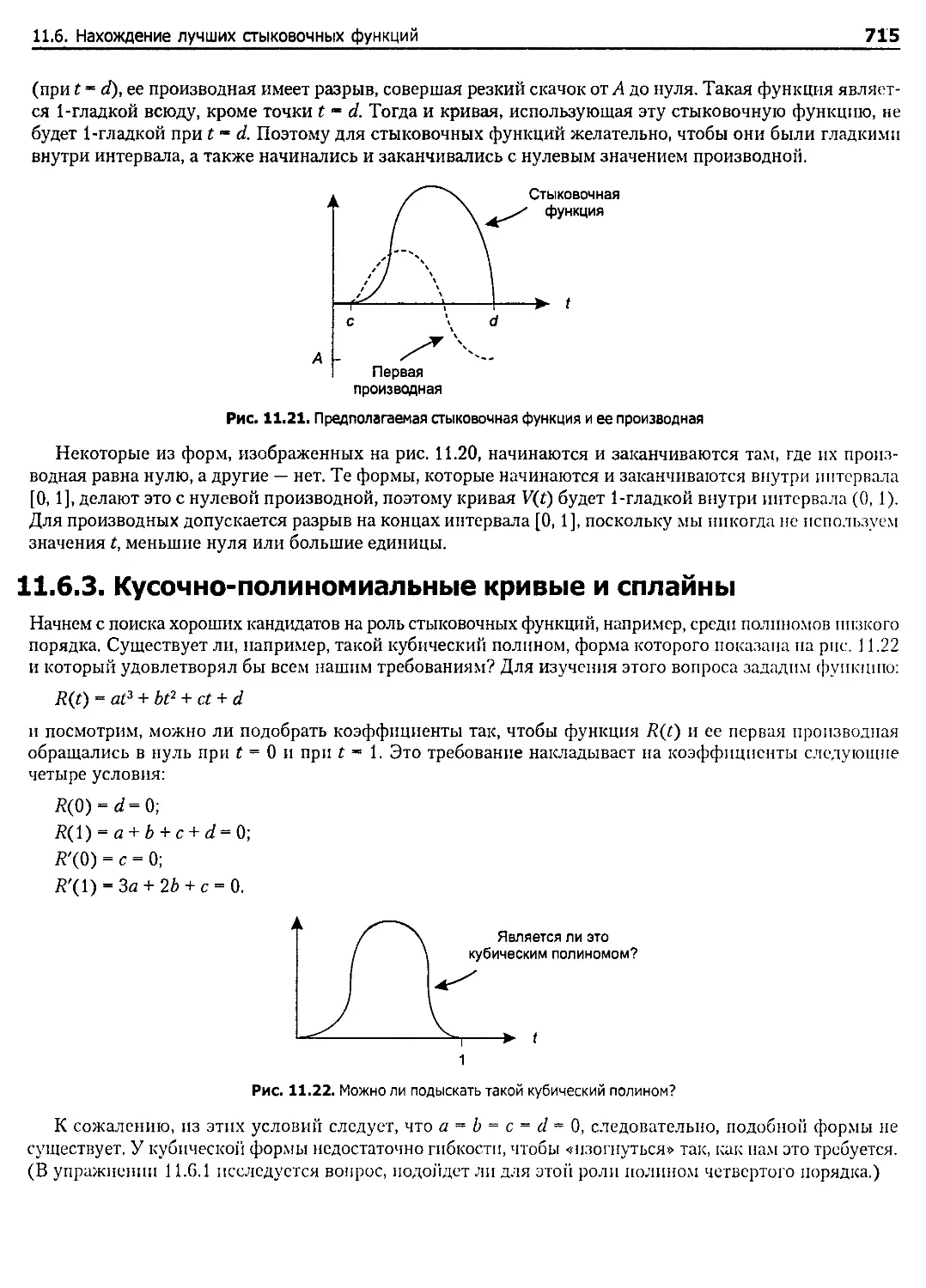
11.6.3. Кусочно-полиномиальные кривые и сплайны ......................................... 715
11.6.4. Построение из g(t) множества стыковочных функций................................. 717
11.6.5. Сплайны и базисные функции ...................................................... 720
11.7. Базисные функции В-сплайнов............................................................. 721
11.7.1. Определение В-сплайн функций..................................................... 721
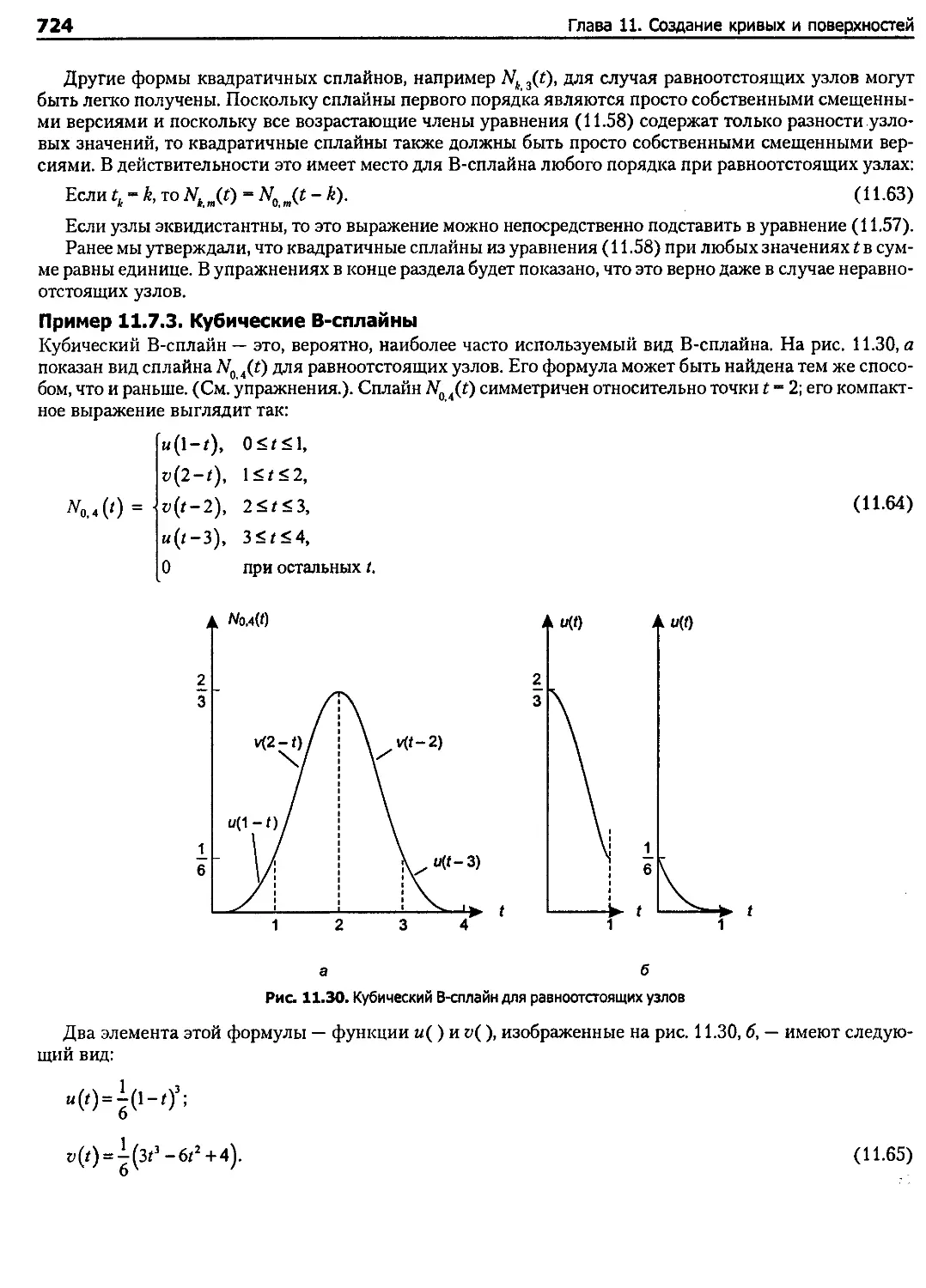
11.7.2. Использование кратных узлов в узловом векторе.................................... 726
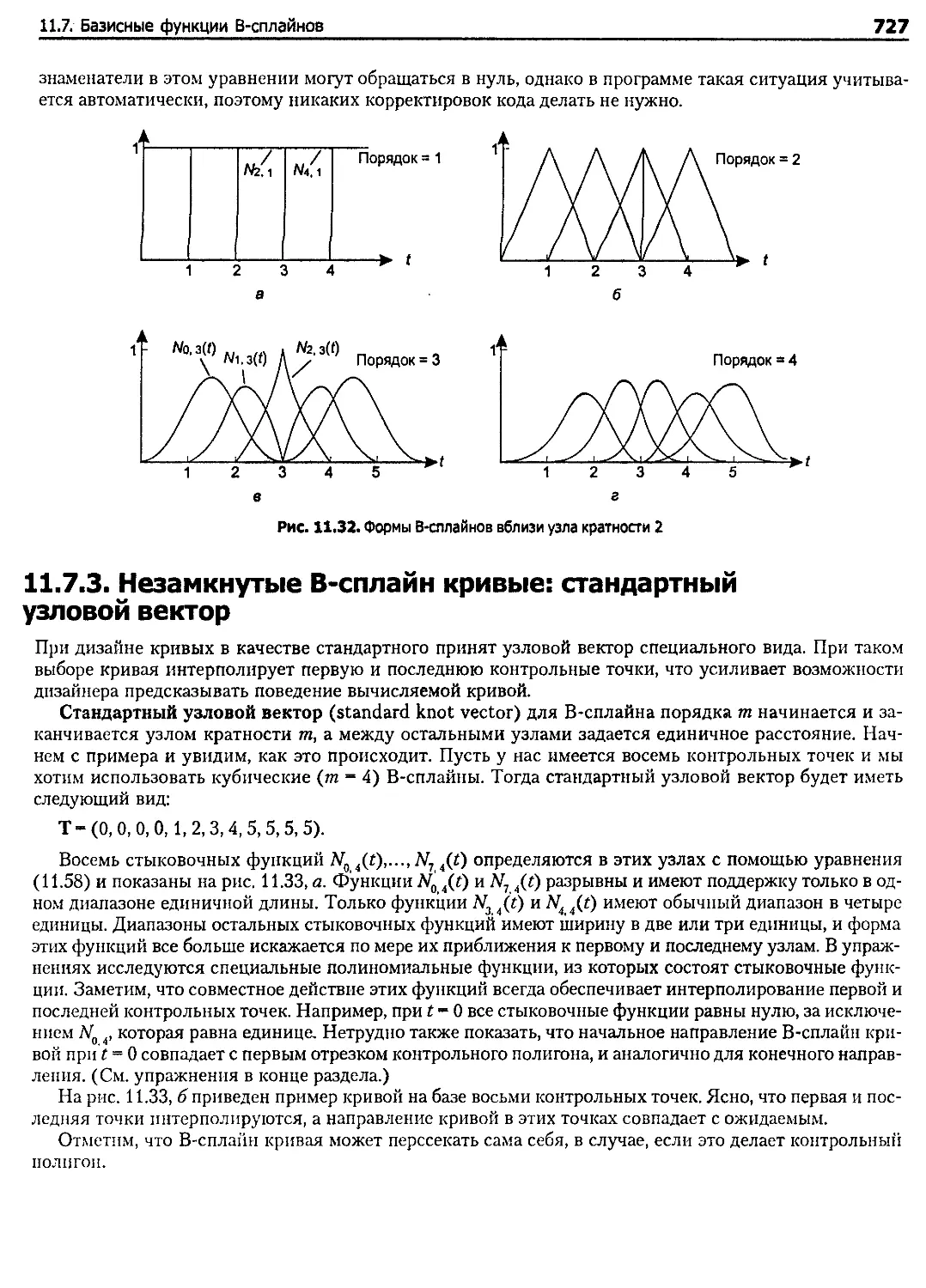
11.7.3. Незамкнутые В-сплайн кривые: стандартный узловой вектор.......................... 727
11.8. Полезные для дизайна свойства В-сплайн кривых........................................... 730
11.8.1. Использование кратных контрольных точек.......................................... 732
11.9. Рациональные сплайны и NURBS-кривые..................................................... 733
11.10. Краткое знакомство с интерполяцией...................................................... 737
11.10.1. Интерполяция посредством кусочных кубических полиномов.......................... 737
11.10.2. Эрмитова интерполяция........................................................... 739
11.10.3. Естественные кубические сплайны................................................. 742
11.10.4. Вычисление наклонов при кубической интерполяции ................................ 743
11.10.5. Интерактивное задание касательных векторов ..................................... 748
11.11. Моделирование криволинейных поверхностей................................................ 748
11.11.1. Линейчатые поверхности на базе В-сплайнов....................................... 748
11.11.2. Поверхности вращения на базе В-сплайнов......................................... 749
11.11.3. Лоскуты Безье................................................................... 751
11.11.4. Сшивание лоскутов Безье......................................................... 752
11.11.5. В-сплайн лоскуты................................................................ 754
11.11.6. NURBS-поверхности............................................................... 755
11.12. Резюме.................................................................................. 757
11.13. Тематические задания.................................................................... 759
Тематическое задание 11.1. Попурри из интересных параметрических кривых................... 759
Тематическое задание 11.2. «Эллиптипул»................................................... 760
Тематическое задание 11.3. Кривые Безье................................................... 762
Тематическое задание 11.4. Генератор квадратичной сплайн-кривой .......................... 762
Тематическое задание 11.5. Создание редактора сплайн-кривых............................... 762
Тематическое задание 11.6. Интерполяция контрольных точек В-сплайнами..................... 763
Тематическое задание 11.7. Интерполяция кубическими полиномами............................ 765
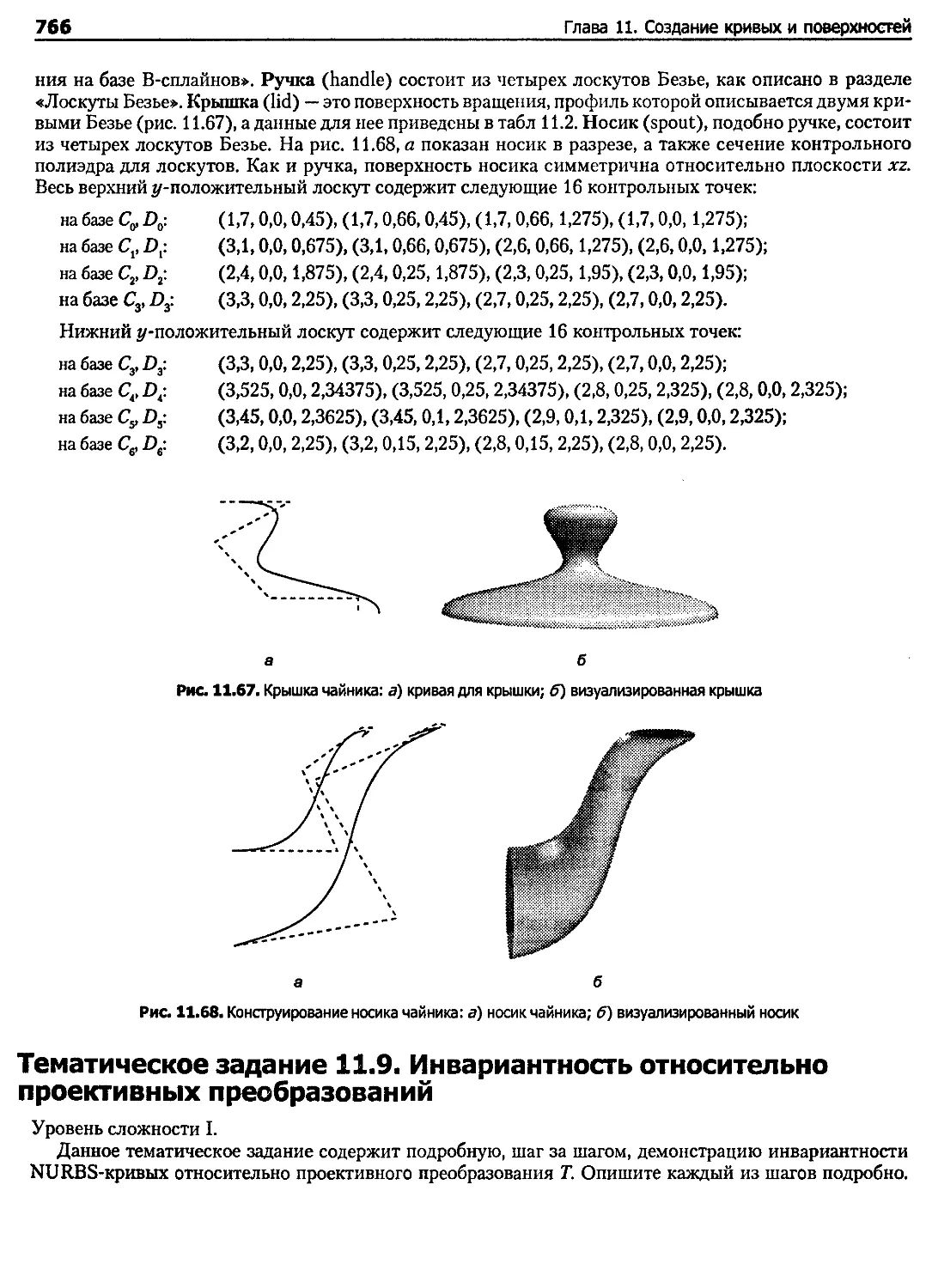
Тематическое задание 11.8. Многоуважаемый чайник.......................................... 765
Тематическое задание 11.9. Инвариантность относительно проективных преобразований......... 766
Тематическое задание 11.10. Рисование NURBS-лоскутов..................................... 767
11.14. Дополнительная литература .............................................................. 769
14
Содержание
Глава 12. Теория цвета...........................................................................770
12.1. Введение............................................................................... 770
12.2. Описания цветов........................................................................ 772
12.2.1. Доминантная длина волны.......................................................... 773
12.2.2. Подбор цветов.................................................................... 774
12.3. Международная комиссия по стандартам освещенности...................................... 777
12.3.1. Построение С1Е-диаграммы ........................................................ 778
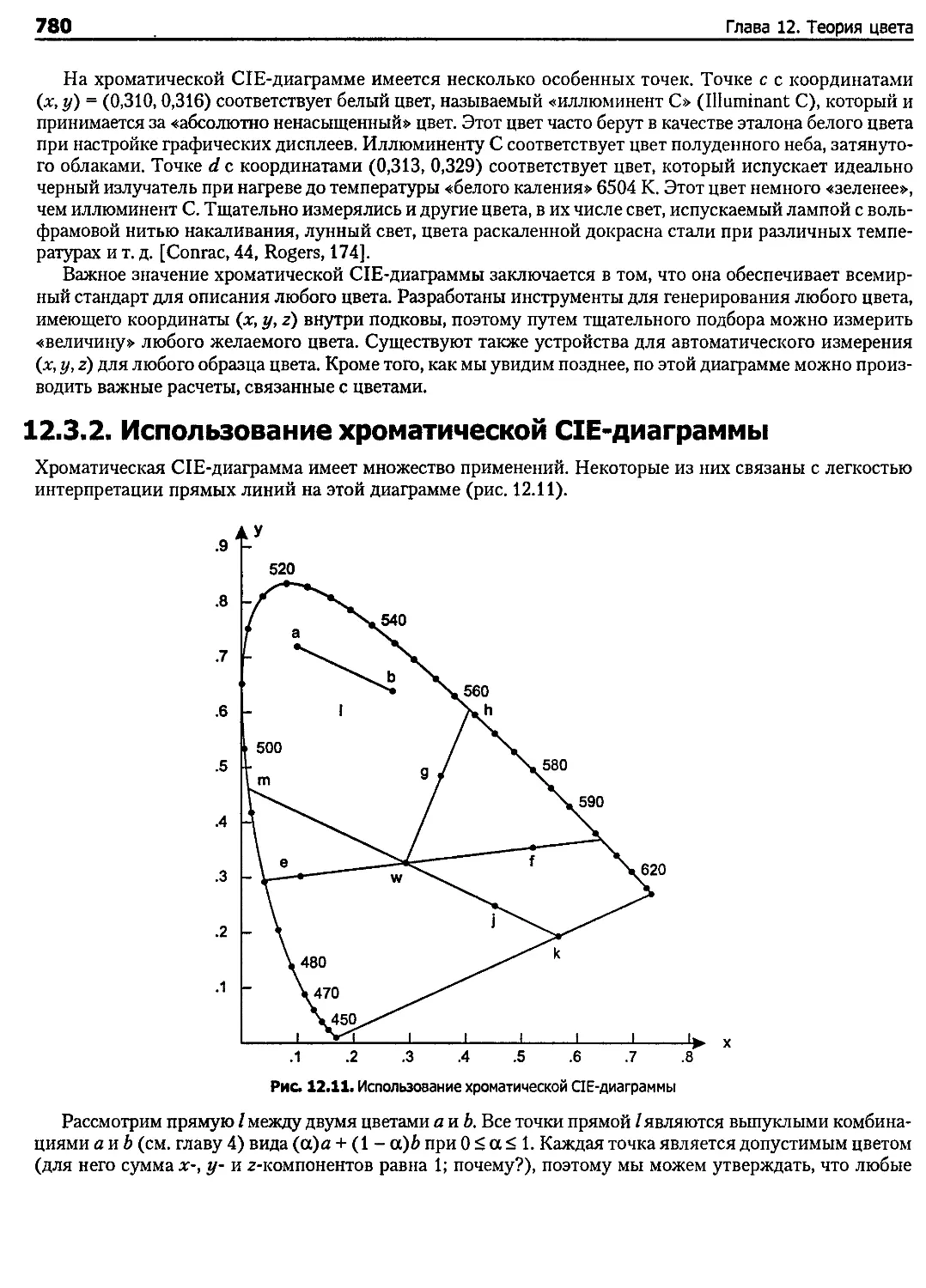
12.3.2. Использование хроматической С1Е-диаграммы........................................ 780
12.3.3. Цветовые охваты.................................................................. 781
12.4. Цветовые пространства.................................................................. 782
12.4.1. Цветовые пространства RGB и CMY.................................................. 782
12.4.2. Аддитивные и субтрактивные цветовые системы...................................... 783
12.4.3. Цветовая модель HLS.............................................................. 785
12.5. Квантование цвета...................................................................... 787
12.5.1. Квантование с постоянным шагом................................................... 789
12.5.2. Алгоритм популярности............................................................ 791
12.5.3. Алгоритм медианного сечения...................................................... 791
12.5.4. Octree-квантование............................................................... 792
12.6. Резюме................................................................................. 795
12.7. Тематические задания................................................................... 795
Тематическое задание 12.1. Рисование С1Е-диаграммы....................................... 795
Тематическое задание 12.2. Рисование RGB-пространства.................................... 795
Тематическое задание 12.3. Из HSV в RGB.................................................. 796
Тематическое задание 12.4. Однородное квантование цвета.................................. 796
Тематическое задание 12.5. Квантование цвета по популярности............................. 796
Тематическое задание 12.6. Квантование цвета методом медианного сечения.................. 796
Тематическое задание 12.7. Квантование цвета методом октодерева ......................... 796
12.8. Дополнительная литература.............................................................. 798
Глава 13. Удаление невидимых поверхностей .......................................................799
13.1. Введение............................................................................... 800
13.1.1. Два подхода: «точность по объекту» и «точность по изображению»................... 802
13.1.2. Описание данных для полигональных сеток.......................................... 802
13.2. Снова об алгоритме буфера глубины...................................................... 805
13.3. HSR-методы со списками приоритетов..................................................... 806
13.3.1. Алгоритм беспечного художника ................................................... 807
13.3.2. HSR с использованием деревьев двоичного разбиения пространства................... 808
13.3.3. Алгоритм сортировки по глубине................................................... 812
13.4. HSR-метод построчного сканирования..................................................... 816
13.5. Методы разбиения области .............................................................. 818
13.5.1. Квадрантное разбиение............................................................ 819
13.5.2. Другие определения простой области............................................... 822
13.6. О методах удаления невидимых линий..................................................... 825
13.6.1. Геометрическое тестирование в подпрограмме edgeTest()............................ 828
13.7. HSR-методы для криволинейных поверхностей.............................................. 829
13.8. Резюме................................................................................. 832
13.9. Тематические задания................................................................... 834
Тематическое задание 13.1. Проверка алгоритма художника.................................. 834
Тематическое задание 13.2. Тест и разбиение.............................................. 834
Тематическое задание 13.3. Удаление невидимых поверхностей с использованием BSP-деревьев.. 835
Тематическое задание 13.4. HSR с использованием сортировки по глубине.................... 836
Тематическое задание 13.5. Использование HSR-метода построчного сканирования............. 836
Тематическое задание 13.6. Рисование при помощи алгоритма Варнока........................ 837
Тематическое задание 13.7. HLR с помощью алгоритма стека ребер........................... 837
13.10. Дополнительная литература............................................................. 837
Содержание
15
Глава 14. Введение в трассировку лучей...........................................................838
14.1. Введение............................................................................... 839
14.2. Построение геометрии трассировки лучей................................................. 840
14.3. Обзор процесса трассировки луча ....................................................... 842
14.4. Пересечение луча с объектом............................................................ 844
14.4.1. Пересечение луча с базовой плоскостью........................................... 845
14.4.2. Пересечение с базовой сферой.................................................... 845
14.4.3. Пересечение луча с преобразованными объектами................................... 846
14.5. Организация трассировщика луча в приложении............................................ 848
14.5.1. Подпрограмма для вычисления пересечений луча со сферой.......................... 855
14.5.2. Полный трассировщик лучей для сцен с излучающей сферой.......................... 857
14.6. Пересечение лучей с другими примитивами................................................ 858
14.6.1. Пересечение с квадратом......................................................... 858
14.6.2. Пересечение с коническим цилиндром.............................................. 860
14.6.3. Пересечение с кубом (или с любым другим выпуклым полиэдром)..................... 864
14.6.4. Добавление новых примитивов..................................................... 871
14.7. Рисование закрашенных изображений сцен ................................................ 872
14.7.1. Нахождение нормали в точке соударения........................................... 873
14.7.2. Раскраска объектов в соответствии с материалами поверхностей.................... 874
14.7.3. Физически обоснованные модели закраски: закрашивание Кука—Торренса.............. 877
14.8. Наложение текстуры на поверхности...................................................... 883
14.8.1. Текстура твердого тела.......................................................... 884
14.8.2. Наложение изображений на поверхности............................................ 894
14.8.3. Сглаживающая трассировка лучей.................................................. 896
14.9. Использование экстентов................................................................ 897
14.9.1. Боксы и сферические экстенты.................................................... 899
14.9.2. Использование проекционных экстентов............................................ 904
14.10. Добавление теней для большей реалистичности............................................ 907
14.11. Отражения и прозрачность............................................................... 910
14.11.1. Преломление света.............................................................. 913
14.11.2. Обработка преломления методом shade().......................................... 918
14.12. Составные объекты: логические операции с объектами..................................... 921
14.12.1. Трассировка лучей для CSG-объектов............................................. 922
14.12.2. Структура данных для Булевых объектов.......................................... 924
14.12.3. Пересечения лучей с Булевыми объектами......................................... 927
14.12.4. Построение и использование экстентов для CGG-объектов.......................... 933
14.13. Резюме................................................................................. 935
14.14. Тематические задания................................................................... 936
Тематическое задание 14.1. Эмиссионный трассировщик..................................... 936
Тематическое задание 14.2. Усовершенствованный трассировщик лучей....................... 936
Тематическое задание 14.3. Реализация теней при трассировке лучей ...................... 937
Тематическое задание 14.4. Использование экстентов для ускорения трассировки лучей......... 937
Тематическое задание 14.5. Трассировка лучей с ЗО-текстурами............................... 937
Тематическое задание 14.6. Сглаживание..................................................... 937
Тематическое задание 14.7. Трассировкалучей для других примитивов.......................... 937
Тематическое задание 14.8. Двумерный трассировщик лучей для работы с преломлением. 938
Тематическое задание 14.9. Отраженный и преломленный свет......................... 938
Тематическое задание 14.10. Трассировка Булевых комбинаций объектов............... 938
14.15. Дополнительная литература ...................................................... 938
Приложение А. Графический инструментарий: получение OpenGL................................939
Al. Получение и инсталляция OpenGL ................................................... 939
Приложение Б. Немного математики для компьютерной графики.................................941
Б1. Некоторые основные определения, относящиеся к матрицам и операциям над ними....... 941
Б1.1. Действия с матрицами ....................................................... 942
Б1.2. Умножение двух матриц....................................................... 943
16
Содержание
Б1.3. Разбиение матрицы на блоки .................................................... 944
Б1.4. Определитель матрицы........................................................... 945
Б1.5. Обращение матрицы.............................................................. 946
Б2. Некоторые свойства векторов и операции над ними...................................... 948
Б2.1. Перп вектора; перп-скалярное произведение...................................... 948
Б2.2. Смешанное произведение..........................>.............................. 949
Б2.3. Двойное векторное произведение................................................. 950
БЗ. Арифметика комплексных чисел......................................................... 950
Б4. Сферические координаты и направляющие косинусы....................................... 953
Приложение В. Некоторые полезные классы и служебные подпрограммы ... 956
В1. Классы для двумерной графики......................................................... 957
В2. RGBPixmap CLASS...................................................................... 961
ВЗ. Класс SCENE и сопутствующие классы................................................... 966
В4. Класс NOISE.......................................................................... 995
В5. Некоторые классы, полезные при трассировке лучей..................................... 998
Приложение Г. Введение в PostScript®...................................................... 1001
Г1.0 языке PostScript................................................................... 1002
Г1.1. Некоторые предварительные замечания........................................... 1002
Г1.2. PostScript основан на стеке................................................... 1003
Г1.3. Некоторые операции со стеком: pop, dup, exch, clear........................... 1004
Г1.4. Более сложные операторы работы со стеком...................................... 1005
Г1.5. Некоторые арифметические операторы............................................ 1005
Г2. Графические операторы в PostScript.................................................. 1008
Г2.1. Системы координат и преобразования............................................ 1008
Г2.2. Команды создания контура...................................................... 1009
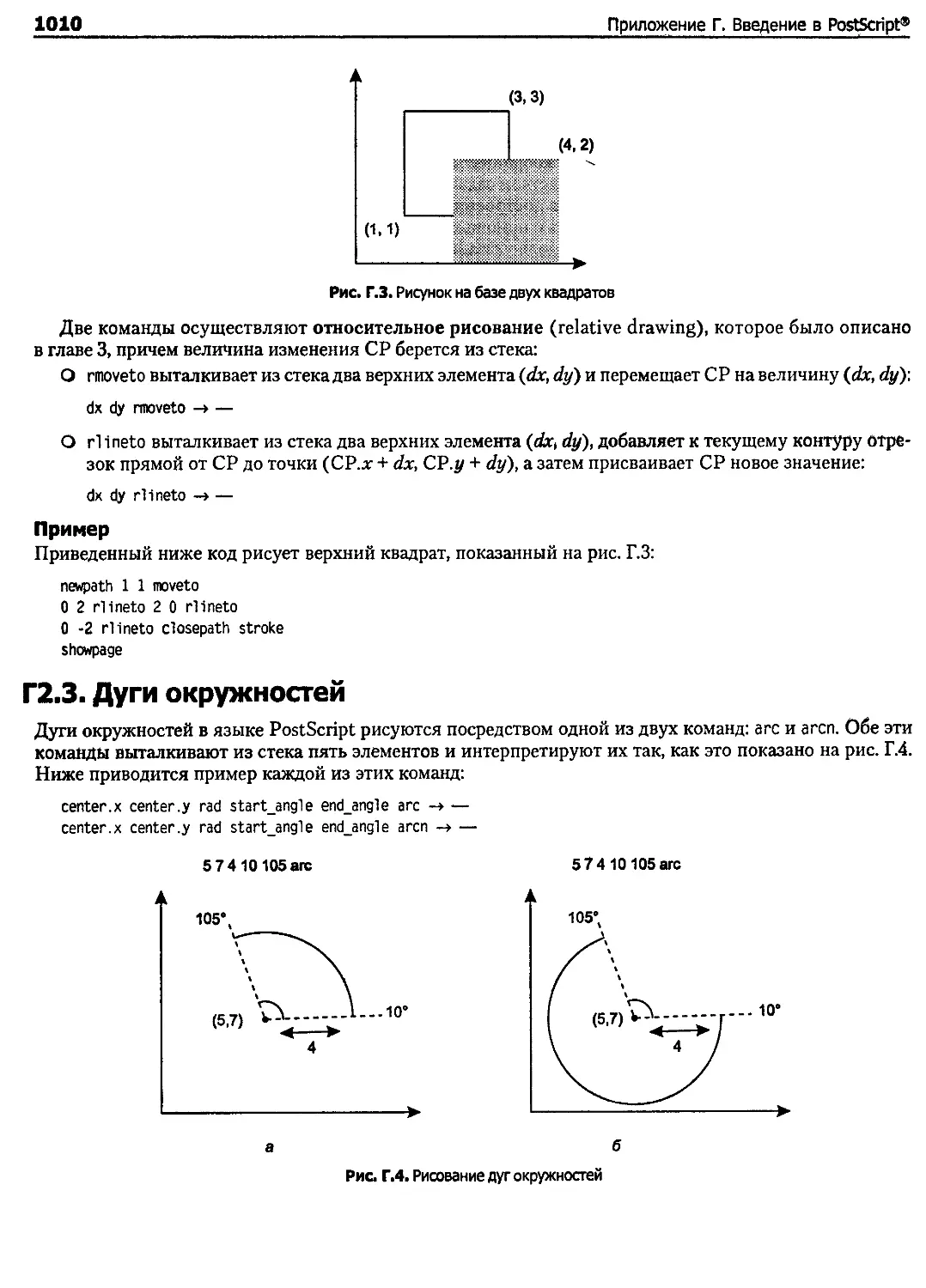
Г2.3. Дуги окружностей.............................................................. 1010
Г2.4. Использование операторов закрашивания......................................... 1011
Г2.5. Преобразования координат...................................................... 1012
Г2.6. Операторы графического состояния.............................................. 1016
ГЗ. Рисование текста в PostScript....................................................... 1019
Г4. Определение новых переменных и процедур............................................. 1019
Г4.1. Определение переменных........................................................ 1020
Г4.2. Определение процедур.......................................................... 1020
Г4.3. Простейшая форма итерации с использованием оператора repeat................... 1024
Г5. Команды решений и итераций.......................................................... 1026
Г5.1. Команды, принимающие логические величины в качестве аргументов................ 1027
Г5.2. Принятие решений.............................................................. 1027
Г5.3. Итерация...................................................................... 1029
Гб. Печать численных значений........................................................... 1034
Г7. Рисование полутоновых изображений................................................... 1035
Приложение Д. Введение в SDL.............................................................. 1038
Д1. Синтаксис SDL....................................................................... 1039
Д2. Макросы в SDL....................................................................... 1043
ДЗ. Расширение SDL...................................................................... 1044
Литература................................................................................ 1046
Список терминов.............................................................................1058
Алфавитный указатель.................................................................... 1065
Посвящается Мерили, а также Грете, Джесси и Рози
Введение
В этой книге содержится введение в компьютерную графику для тех студентов, которые желают изу-
чить основные принципы и технические приемы в этой области и, кроме того, намерены сами писать
солидные графические приложения. Сфера компьютерной графики по-прежнему обладает невероят-
ной живучестью и продолжает стремительно развиваться. Использование возможностей графики во
все возрастающем числе полнометражных анимационных фильмов производит головокружительное
впечатление, а широкий доступ к ней через компьютерные игры и Интернет побуждает людей учиться
применять эти возможности самим.
Графические системы становятся лучше, быстрее и дешевле с невероятной скоростью. Каждый год
исследователи и практики всего мира изобретают множество новых технических приемов, однако
основные принципы и подходы по-прежнему составляют неизменный и логически последовательный
стержень знания компьютерной графики. Большинство этих сведений может быть получено в резуль-
тате изучения одного курса графики, и в этой книге делается попытка систематизировать идеи и мето-
ды так, чтобы даже начинающий читатель со скромным опытом программирования смог придумывать
и писать серьезные графические программы.
Предполагаемая аудитория
Эта книга предназначается в качестве одно- или двухсеместрового курса для студентов-старшекурсни-
ков или аспирантов первого года обучения. Она может быть также использована для самообучения.
Книга преимущественно нацелена на студентов, специализирующихся в компьютерной теории или
практике, но подойдет и студентам других областей знания, таких как физика или математика.
Необходимая математическая подготовка
Читателю желательно обладать знанием математики в объеме одного года колледжа; предполагается
также знание элементарной алгебры, геометрии, тригонометрии и основных вычислительных методов.
Полезным было бы некоторое представление о векторах и матрицах, но не обязательно глубокое, по-
скольку векторные и матричные технологии вводятся в контекст графиков по мере необходимости; кро-
ме того, ключевые идеи резюмируются в приложении.
В компьютерной графике используется много математики для выражения геометрических соотно-
шений между линиями, поверхностями и взглядом на них наблюдателя. Хотя ни одно математическое
понятие не является сложным по своей сути, общее количество необходимых инструментальных
средств может показаться устрашающим. В книге делается особый акцент на обосновании причин, по
Философия книги
19
которым следует использовать тот или иной технический прием, и на том, как правильно описывать
в программе нужные графические объекты с помощью объектов математических.
Необходимая подготовка по программированию
Вообще говоря, читателю следовало бы иметь по меньшей мере опыт одного семестра написания ком-
пьютерных программ на языках С, C++ или Java. Значительная часть программирования графики сво-
дится к непосредственному переводу геометрических соотношений в код и, следовательно, непосред-
ственно использует переменные, функции, массивы, циклы и тестирование, что является общим для
всех языков. На протяжении всей книги используется C++, однако большая часть материала будет близ-
ка и тем, кто знаком только с С.
Читателю очень поможет опыт работы со структурами (structs) на С или с классами на C++. Они
используются для охвата достаточно сложной структуры некоторых графических объектов, участвую-
щих в сцене, когда объект (скажем, замок или самолет) состоит из множества частей, которые, в свою
очередь, сами состоят из сложных элементов. Желателен (но не обязателен) также некоторый опыт ра-
боты с элементарными связными структурами данных, такими как связные списки (linked lists) или
деревья.
Читателю, знающему С, но не C++, придется познакомиться с основами объектно-ориентированного
программирования. Мы определим несколько полезных классов, таких как Window (окно), Mesh (сетка),
Scene (сцена), Camera (видеокамера) и Texture (текстура), и покажем, почему они являются столь удоб-
ными и полезными. Некоторые признаки объектно-ориентированного программирования, как, напри-
мер, наследование и полиморфизм, используются лишь для того, чтобы облегчить работу программис-
та, однако мы не уделяем чисто объектно-ориентированному подходу слишком большого внимания.
Философия книги
После выхода первого издания книга была полностью реорганизована и переписана заново, однако при
этом была сохранена ее основная философия: изучать компьютерную графику — значит создавать ее:
чтобы полностью постичь то, что происходит, необходимо писать и прогонять реальные программы.
Главная задача книги состоит в том, чтобы показать читателям, как преобразовать отдельную проект-
ную «задачу» сначала в основные геометрические компоненты, затем найти для выбранных объектов
соответствующее математическое представление и, наконец, перевести это представление в надлежа-
щий алгоритм и программный код. Читатели начинают с изучения того, как разрабатывать простые
подпрограммы для создания изображений; затем шаг за шагом показываются методы визуализации
(rendering) рисунков или более сложных объектов.
Упражнения и задачи
На протяжении всей книги предлагается более 440 практических упражнений. Большинство из них
относятся к типу «остановись и подумай», не требующему программирования и позволяющему читате-
лям самим проверить понимание материала. Некоторые упражнения побуждают студента воплотить
новые идеи в программном коде.
Кроме того, в конце каждой главы приводятся тематические задания («case studies») по пройденно-
му материалу, общим числом около ста. Эти задания представляют собой обычные программистские
задачи для домашнего задания, в диапазоне от простых до сверхсложных. Они основаны на материале
соответствующих глав и зачастую развивают высказанные идеи в новых направлениях. Но независимо
от того, выполняются ли эти контрольные задания студентами до конца, они должны изучаться как
неотъемлемая часть главы.
Для каждого тематического задания приведен предполагаемый «уровень сложности», чтобы обозна-
чить, сколько примерно времени может понадобиться студенту для выполнения данного задания. Про-
20
Введение
граммирование — это непредсказуемое занятие, к тому же возможности студентов различны, однако
в первом приближении нужно руководствовать^предложенным ниже разбиением.
Уровни сложности.
1. Простой проект, который может быть реализован за один вечер, его можно сделать к очередно-
му занятию в классе.
2. Более сложный проект, на который нужно отвести около недели, так что студент должен иметь
время на разработку программы и достаточно времени для многократного (и иногда тщетного)
тестирования и процесса отладки, в котором проекты, похоже, нуждаются всегда.
3. Крупный проект, который может потребовать до трех недель для разработки и реализации. Та-
кой проект требует солидной работы по проектированию и тщательной компоновке програм-
мы, а его выполнение будет заслуженно рассматриваться студентом как значительный успех.
Использование OpenGL
Когда человек впервые начинает совершенствоваться в области компьютерной графики, зачастую кам-
нем преткновения является начальное создание изображений. Не так уж трудно написать программу,
однако должен быть базовый инструмент, который, в конечном счете, рисует на экране линии и кривые.
К счастью, такой инструмент имеется и легко доступен. OpenGL был разработан в 1992 году фирмой
Silicon Graphics, Inc и превратился в широко используемый интерфейс прикладных графических про-
грамм (graphics application programming interface — API). В нем представлены инструменты рисования,
действующие с помощью целого набора функций, которые вызываются внутри приложения. Как опи-
сано в приложении А, этот интерфейс доступен (обычно его скачивают из Интернета) для всех типов
компьютерных систем, встречающихся в колледжах, университетах и в промышленности. OpenGL
прост в установке и изучении, и его долговечность в качестве стандартного API поддерживается экс-
пертной комиссией по архитектуре OpenGL (OpenGL Architecture Review Board — ARB) — промыш-
ленным консорциумом, ответственным за направление развития программного обеспечения.
Еще одним аспектом OpenGL, который делает его столь удобным для использования в курсе компь-
ютерной графики, является его «независимость от устройства», или мобильность. Компьютерные ла-
боратории многих университетов имеют множество различных компьютеров. Студент может разраба-
тывать и запускать свою программу на любом доступном ему компьютере. Затем эта программа может
быть запущена на другом компьютере, например, для тестирования или оценки, и графика на этих двух
машинах будет одинаковой.
OpenGL предлагает обширный и чрезвычайно удобный набор API-функций для 2В-графики и об-
работки изображений, но его истинная мощь проявляется в SD-графике. Используя OpenGL, студенты
могут быстро развивать свое умение и изготавливать великолепные анимации уже после курса, прочи-
танного за один семестр.
Использование C++ в качестве языка программирования
В настоящее время язык C++ достаточно хорошо знаком большинству студентов, как в технической
области, так и в вычислительной технике, из начального курса программирования, поэтому естестве-
нен выбор этого языка для дальнейшего использования. Он имеет ряд преимуществ по сравнению с С,
таких как передача параметров функции посредством ссылки, что уменьшает необходимость в явных
указателях и упрощает чтение кода. Файловый ввод-вывод также стал значительно проще с примене-
нием потоков, и вообще синтаксис всех видов ввода-вывода в C++ прозрачнее, чем в С. Проще говоря,
в C++ не делается ударения на исполняющих операторах.
Более того, в C++ легко разрабатываются полезные прикладные классы: точка на плоскости и в про-
странстве, линия, окно или цвет, что делает код более простым и ясным. Студенты видят преимущества
инкапсуляции деталей геометрического объекта внутри самого объекта и наделения этого объекта спо-
собностью делать такие вещи, как рисование самого себя или проверку на пересечение с другим объек-
том. Класс Canvas (полотно), введенный в главе 3, является хорошим примером этого, так как он под-
Структура книги и планы курса
21
держивает свое собственное понятие окна, порта просмотра (viewport) и текущих координат; кроме
того, он может рисовать основные фигуры при минимуме усилий со стороны программиста.
Акцент на трехмерной компьютерной графике
Поскольку игры на персональном компьютере стали очень популярными, а в фильмах появилось ог-
ромное количество великолепной анимации, студенты особенно интересуются разработкой приложе-
ний с ЗО-графикой. По этой причине несколько глав из первого издания было переписано заново, а их
расположение было изменено таким образом, чтобы как можно быстрее перейти к темам по ЗО-графи-
ке. В ряде случаев новые понятия вводятся для случаев 2D- и ЗО-графики одновременно, что помогает
уяснить различия между ними.
Описание ЗО-сцен с помощью языка проектирования сцен
Было бы весьма затруднительным и неэкономным с точки зрения времени проектировать сцены, содер-
жащие много ЗО-объектов, с помощью «сырых» команд OpenGL. Поэтому в главе 5 вводится (а в при-
ложении полностью определяется) простой язык проектирования сцен (Scene Design Language — SDL)1.
Используя этот язык, студенты могут описывать сцены в привычных терминах, таких как «куб», «сфе-
ра», «повернуть», и создавать файлы, состоящие из инструкций, которые будут считываться в их про-
грамму во время выполнения. В приложении (и на сайте книги) имеется код интерпретатора, способ-
ного читать SDL-файл и создавать список объектов, описанных в этом файле. По этому списку объектов
нарисовать сцену с помощью OpenGL уже несложно.
Те же самые язык и интерпретатор успешно применяются в главе 14, где разрабатывается код для
трассировки луча (ray trace) по сцене, описанной с помощью SDL. Студенты могут разрабатывать и
создавать с помощью трассировки луча значительно более сложные и интересные сцены, чем это было
возможно без SDL.
Дополнительное использование PostScript
В последние годы язык описания страниц PostScript фактически стал стандартным языком для размет-
ки страниц (page-layout), поскольку он предлагает богатый набор операторов для аппаратно-независи-
мого рисования текста и графики. Обычно PostScript работает незаметно внутри лазерного принтера,
получая команды от текстового процессора или программы разметки и преобразуя их в линии, точки и
символы. Однако можно подготовить «сценарий» (script) из команд PostScript и направить их принтеру,
после чего встроенный в принтер интерпретатор PostScript создаст желаемую графику. Таким спосо-
бом может быть создана прекрасная графика. Поэтому PostScript является блестящим примером крат-
кого и мощного языка для 2О-графики, с теми же возможностями выполнения преобразований и визуа-
лизации, что и OpenGL.
Язык PostScript помещен в приложении, где студентам, заинтересованным в таком подходе к графи-
ке, демонстрируется, как создавать интересные сценарии, которые создадут симпатичные картинки.
Кроме того, в приложении показано, как загружать язык GhostScript и как работать с этим языком,
в котором содержится экранный интерпретатор PostScript, позволяющий легко просматривать и отла-
живать картинки во время их разработки.
Структура книги и планы курса
В книге намного больше материала, чем может вместить курс в один и даже в два семестра. Книга орга-
низована так, что преподаватель может выбрать различную последовательность глав для подробного
изучения — в зависимости от длительности курса, а также от интересов и подготовленности студентов
' В приложении 5 этот язык называется языком описания сцен (Scene Description Language — SDL). — Примеч. nep.
22
Введение
группы. Ниже, после перечисления основных тем каждой главы, приведено несколько возможных по-
следовательностей глав, выбранных из всей книги.
Краткий обзор глав
О Глава 1. В этой главе дается обзор всех областей применения компьютерной графики с примера-
ми того, как используется графика в разных областях. Описаны различные виды имеющихся си-
стем графического отображения, а также типы «примитивов» — полигоны (многоугольники),
текст, изображения, — которые отображает данная графическая система. Кроме того, в данной
главе описываются некоторые из многих широко применяющихся входных устройств: мышь,
планшет (tablet), информационная перчатка (data glove) и т. д.
О Глава 2. В этой главе студенты начинают писать графические приложения. Описано программи-
рование с помощью OpenGL, приведено несколько законченных приложений для вычерчивания
линий, в том числе популярного «ковра Серпинского» («Sierpinsky gasket»). Обсуждаются техни-
ческие приемы использования OpenGL для рисования различных примитивов, таких как лома-
ные линии и полигоны, а также применение мыши и клавиатуры в интерактивных графических
приложениях. Практические примеры в конце главы содержат интересные программные проек-
ты, помогающие студентам получить четкое начальное представление о том, как создается гра-
фическое приложение.
О Глава 3. В этой главе вводится центральное понятие отображения окна в порт просмотра (window-
to-viewport mapping) для задания размеров и расположения изображений на экране. Обсуждает-
ся управление окнами и портами просмотра по принципу «сделай сам» («do-it-yourself»), а также
использование OpenGL для проработки деталей. Разрабатывается первый алгоритм отсечения
графического изображения границами области (clipping). Кроме того, описываются задание мас-
штабов (zooming), панорамирование (panning), наклон (tilting) с целью получения интересных
визуальных эффектов, а также простейшая анимация рисунков. Разработан класс Canvas, вклю-
чающий в себя все эти инструменты. Здесь же обсуждается рисование кругов, дуг, сложных фи-
гур из многоугольников, а также представление двумерных и трехмерных кривых в параметри-
ческой форме.
О Глава 4. В этой главе дается обзор векторов и основных операций с ними, а также демонстриру-
ется большое преимущество применения в графике векторных инструментов. Студенты, знако-
мые с векторами, могут только просмотреть эту главу, обращая внимание на то, как с помощью
векторов описываются соотношения между геометрическими объектами, которыми они манипу-
лируют в своих программах. Там, где это возможно, векторные операции рассматриваются без
указания на размерность пространства, но в трехмерном случае уделено специальное внимание
применению векторного произведения (cross product).
В четвертой главе введено понятие системы координат и показано, как такие системы делают ес-
тественной работу с однородными координатами. Для прояснения различия между векторами и
точками обсуждаются аффинные комбинации точек (чтобы помочь обойти обычный подводный
камень при написании графических приложений). В некоторые приложения включены интерпо-
ляция, простейшие кривые Безье (Bezier curves) и пересечения линий. Детально разработан фун-
даментальный алгоритм отсечения прямой границами выпуклого многоугольника, а более слож-
ные алгоритмы отсечения приведены в практических упражнениях по теме. (В одном из таких
упражнений предложен интересный проект «Двумерная трассировка луча».)
О Глава 5. Преобразования занимают центральное место в компьютерной графике, но студенты
иногда испытывают затруднения при работе с ними, особенно с трехмерными преобразования-
ми. В этой главе излагается базовая теория преобразований фигур и систем координат с исполь-
зованием аффинных преобразований для двумерных и трехмерных случаев. С самого начала для
описания преобразований применяются однородные координаты. Специальное внимание уделе-
но трехмерным поворотам, поскольку общеизвестна трудность их визуализации. К инструмен-
Структура книги и планы курса
23
там класса Canvas, введенным в главе 3, добавляются средства для сдвига (shift), масштабирования
(scale) и поворота (rotate) фигур посредством «текущего преобразования» («current transformation»),
причем для осуществления этих функций привлечены матричные операции OpenGL Далее при-
водится обзор конвейера просмотра OpenGL (viewing pipeline), а также описывается значение пре-
образований моделирования-вида (modelview), проекции (projection) и порта просмотра. Рассмот-
рено рисование трехмерных объектов с помощью инструментов OpenGL Впервые применен язык
описания сцен (SDL), а также показано, как использовать интерпретатор SDL для чтения описа-
ния трехмерной сцены из файла и рисования объектов, представленных в этом файле.
О Глава 6. В этой главе рассматриваются средства моделирования и рисования сложных каркас-
ных (mesh) объектов. Приводятся примеры каркасных объектов, в том числе многогранников,
таких как додекаэдр и усеченный икосаэдр (buckyball), а также более сложных форм, таких как
арки (arches), купола (domes), трубки (tubes), извивающиеся в пространстве, и поверхности вра-
щения (surfaces of revolution). Рассмотрена техника визуализации этих объектов с различными
способами закрашивания (shading) их поверхностей: плоским (flat) и плавным (smooth).
О Глава 7. В этой главе рассматриваются средства для гибкого (flexible) просмотра трехмерных
сцен. Задается «искусственная камера» («synthetic camera»), формирующая объемные представ-
ления, и обсуждается ее связь с имеющимися в OpenGL средствами просмотра низкого уровня
(low-level viewing). Создан удобный класс Camera, инкапсулирующий в себе детали управления
камерой и упрощающий пилотирование камеры по сцене в процессе анимации.
Подробно рассмотрен математический аппарат построения перспективных проекций (аксоно-
метрического представления объемных объектов на плоскости) наряду с обсуждением вопроса о
создании в рамках OpenGL перспективных проекций с использованием матричных преобразо-
ваний. Подробно рассмотрен алгоритм отсечения, действующий в однородном координатном
пространстве (он используется и в OpenGL). Описываются методы создания объемных изобра-
жений. В конце главы проведена классификация множества видов проекций, используемых в ис-
кусстве, архитектуре, инженерном деле, и показано, как включать каждый из них в программы.
О Глава 8. В этой главе намечаются способы усиления реалистичности изображения трехмерных
сцен. Разработаны модели закрашивания (shading models), вычисляющие различные световые
компоненты, которые отражаются от объектов, залитых светом. Описаны методы OpenGL для
настройки источников света и изменения свойств материала поверхностей объектов. Подробно
описан метод буферизации глубины (depth-buffer) OpenGL, предназначенный для удаления неви-
димых поверхностей. Вводятся приемы наложения текстуры на поверхность объекта для прида-
ния ему большей реалистичности, причем «раскрашиваются» как промежуточные, так и готовые
изображения. Наконец, представлены методы добавления к изображениям простых теней.
О Глава 9. Эта глава погружает нас в восхитительный мир фракталов (fractals) и описывает спосо-
бы создания изображений из них. Представлены методы усложнения (refining) формы кривых
для придания им «самоподобия» («self-similarity»), что в предельном случае и создает фрактал.
Кроме того, представлены методы рисования очень сложных кривых, основанные на небольшом
своде правил «замещения строк». Описывается замощение плоскости с использованием неболь-
шого набора форм, включая класс рекурсивной мозаики, называемый «рептилиями».
Описаны методы рисования сложных изображений, известных как «странные аттракторы»
(«strange attractors»). В этих методах используется многократное применение нескольких видов
аффинных преобразований. Приведено решение и обратной задачи — как найти ту последова-
тельность аффинных преобразований, аттрактором которых является данное изображение. Это
приводит к обсуждению фрактального сжатия изображений, которое используется в данной тех-
нологии. Вводятся знаменитые множества Мандельброта (Mandelbrot) и Жюлиа (Julia), а также
инструменты для их рисования.
О Глава 10. В этой главе рассматриваются мощные графические методы для обработки изображе-
ний, созданных на растровом дисплее (raster display).
24
Введение
Повторно рассматривается пиксельная карта изображения (pix map) как фундаментальный
объект для хранения изображений и манипулирования ими; приводится ряд операторов для
манипулирования пиксельными картами. Детально описан классический алгоритм Брезенхэма
(Bresenham) для рисования линий. Излагаются способы описания «областей» («regions») в карте эле-
ментов и заполнения их цветом или узором. Особое внимание уделяется заливке многоугольной
области. Обсуждаются явления ступенчатости (aliasing) изображения, являющиеся головной бо-
лью программистов, работающих с графикой, и приводятся некоторые способы уменьшения сту-
пенек. Описаны методы размытия (dithering) и рассеивания ошибок (error diffusion), что приво-
дит к эффекту большего количества цветов, чем физически может отобразить устройство вывода.
О Глава И. Эта глава посвящена разработке и рисованию «гладких» кривых и поверхностей. Опи-
сана теория кривых Безье (Bezier) и В-сплайн (B-spline) кривых, а также приложение этойтеории
к рациональным В-сплайнам, что приводит к обсуждению NURBS-кривых (non-unifomrrational
B-spline — неравномерный рациональный В-сплайн). Представлено интерактивное проектиро-
вание кривых, когда разработчик при помощи мыши задает набор «контрольных точек» и исполь-
зует алгоритм генерации кривых для предварительного просмотра кривой, построенной по этим
точкам. Кривая может либо интерполировать эти точки, либо только приближаться к ним.
Изложены также методы создания сложных поверхностей с применением метода Безье, В-сплайнов
и NURBS-лоскутов (patches), причем решается задача бесшовного соединения двух лоскутов.
О Глава 12. В этой главе исследуются некоторые сложности системы восприятия цвета человеком
и решается проблема цифрового представления цвета. Описывается хроматическая диаграмма
стандарта CIE, а также различные способы использования ее при расчетах цвета. Кроме того, об-
суждаются цветовые охваты различных устройств, разнообразные цветовые пространства и пре-
образование цвета между ними. Рассматривается задача эффективного квантования цвета, кото-
рая сводится к уменьшению количества различных цветов в изображении без ухудшения его
зрительного восприятия.
О Глава 13. В этой главе рассматривается несколько способов корректного удаления невидимых
поверхностей (hidden surface removal — HSR) в изображениях трехмерных сцен. Обсуждается
различие между «точностью изображения» («image-precision») и «точностью объекта» («object-
precision»), а также способы предварительной обработки граней многогранника (polygonal faces)
в сцене для ускорения HSR. Более детально исследуется введенный в главе 8 метод буферизации
глубины.
Описываются также некоторые HSR-методы, основывающиеся на сортировке списка граней для
обеспечения быстрой визуализации, в том числе принцип двоичного разделения пространства
(binary space partition). Рассматривается HSR-метод построчного сканирования (scan-line) и опи-
сываются его преимущества перед методом буферизации глубины. Кроме того, обсуждаются до-
полнительные HSR-методы, основанные на принципе разделения («divide-and-conquer» — раз-
деляй и властвуй).
О Глава 14. В этой главе вводится эффективный метод трассировки лучей (ray-tracing) для визуали-
зации трехмерных сцен с высокой степенью реализма. Работая над этой главой, студент вначале
может создать исходный простой трассировщик луча (ray tracer) и затем наращивать его воз-
можности, чтобы в конечном счете получить полноценный трассировщик, способный генериро-
вать великолепные изображения. Обсуждаются методы пересечения лучей с различными фор-
мами, а также способы визуализации объектов с применением разных моделей закрашивания.
Для использования в методике трассирующего луча предлагается физически обоснованная мо-
дель отражения (reflection model) Кука—Торренса (Cook—Torrance), не поддерживаемая OpenGL.
Подробно обсуждаются методы наложения текстуры на поверхности, созданные трассирующим
лучом: трехмерные текстуры, такие как мраморная (marble), и текстуры, основанные на изобра-
жении (image-based texture). Рассматриваются методы ускорения работы трассирующего луча с ис-
пользованием экстентов (bounding box).
Благодарности
25
Значительное преимущество метода трассировки лучей заключается в том, что он автоматиче-
ски выполняет HSR и упрощает создание точных теней объектов. Кроме того, он позволяет ими-
тировать отражение света от блестящих поверхностей, а также преломление (рефракцию) света
внутри прозрачных объектов. Описываются методы достижения каждой из этих целей. Глава за-
канчивается подробным обсуждением метода трассировки лучей для сложных объектов, создан-
ных с применением «конструктивной стереометрии» («constructive solid geometry»).
Рекомендуемые последовательности изучения глав книги
Все предлагаемые последовательности включают в себя главы с 1 по 5 как фундаментальные, хотя гла-
ва 4 теми студентами, которые хорошо знакомы с векторами, может изучаться самостоятельно. После
главы 5 можно браться за главу 9, так же как и за главу 10, без потери связности. Разделы главы 11, по-
священные двумерной графике, также могут изучаться после главы 5.
Возможные планы курса
О Для односеместрового студенческого курса с особой ориентацией на трехмерную графику: главы
с 1 по 5, частично главы 6,7 и 9.
О При расширении данного материала до двухсеместрового курса добавьте остальную часть гла-
вы 7 и частично главы 8, 10 и И.
О Для односеместрового студенческого курса с особой ориентацией на двумерную и растровую графи-
ку: главы с 1 по 3, далее приложение PostScript и частично главы 4 и 5. Кроме того, включите главу 9.
О При расширении данного материала до двухсеместрового курса добавьте частично главы 7 и 8 и
включите главы 10 и И, а также частично главу 12.
О Для односеместрового аспирантского курса с особой ориентацией на трехмерную графику: главы
с 1 по 7, а также частично главы 8 и 9.
О При расширении данного материала до двухсеместрового курса добавьте остальную часть гла-
вы 10 и все главы с И по 14.
О Для односеместрового аспирантского курса с особой ориентацией на двумерную и растровую гра-
фику: главы с 1 по 3, далее приложение PostScript и частично главы с 4 по 8. Кроме того, включи-
те главы 9 и 10.
О При расширении данного материала до двухсеместрового курса добавьте главы 11 и 12 и частично
главы 13 и 14.
Дополнения
Разъяснения и листинги к законченным демонстрационным программам для технологий, рассматрива-
емых в тексте, доступны на сайте данной книги в Интернете: http://www.prenhall.com/hill.
Кроме того, там имеется множество примеров кода и библиотек утилит, а также изображений и тек-
стур. Все это может быть использовано бесплатно.
Благодарности
Данная книга и ее первое издание возникли из записей, использованных в тех курсах, которые я вел в
Массачусетсском университете в продолжение последних 19 лет. В течение этого времени множество
студентов оказывали мне помощь в разработке демонстрационных программ и вносили свои предло-
жения по совершенствованию курсов. Кроме того, они создали много изящных графических примеров,
26
Введение
часть которых приведена здесь. Вот имена некоторых студентов, которые особенно помогли мне в вы-
пуске первого и второго изданий книги: Тарик Абу-Райа (Tarik Abou-Raya), Эрл Биллингсли (Earl
Billingsley), Деннис Чен (Dennis Chen), Дэниел Ди (Daniel Dee), Бретт Даймонд (Brett Diamond), Джей
Греко (Jay Greco), Том Копек (Тот Корее), Адам Лавин (Adam Lavine), Рассел Тёрнер (Russell Turner),
Билл Верте (Bill Verts), Шел Уолкер (Shel Walker), Ноэл Ллопис (Noel Llopis), Рассел Сван (Russell
Swan), А. Чандрашехара (A. Chandrashekhara), Эммануил Агу (Emmanuel Agu), Том Ларами (Тот
Laramee), Чанг Су (Chang Su), Ксионджи Ли (Xiongzi Li), Юнг-Яо Хуанг (Jung-Yao Huang), Анджул
Шривастава (Anjul Srivastava), Стив Морин (Steve Morin) и Элвуд Андерсон (Elwood Anderson). Про-
шу прощения, если я кого-нибудь случайно пропустил.
Некоторые мои коллеги вдохновляли и направляли меня в период зарождения этой книги. Я осо-
бенно благодарен Чарли Хатчинсону (Charles Hutchinson) за его поддержку в начальной стадии моей
работы в области графики в университете, Майклу Возни (Michael Wozny) за его энтузиазм и ободрение
в продвижении этой работы, а также Чарли Раппу (Charle Rupp) за множество конструктивных идей
по графике, которые он мне предложил. Я хотел бы особо поблагодарить Дэниела Бергерона (Daniel
Bergeron), который внес значительный вклад в связность и читабельность первого издания книги.
Я хотел бы поблагодарить персонально перечисленных ниже, а также многих из тех, кто не упомянут
по имени, за их совет и помощь.
О Эдвард Хэммерэнд, Государственный университет Арканзаса (Edward Hammerand, Arkansas State
University);
О Дебора Уолтерс, Государственный университет Нью-Йорка в Буффало (Deborah Walters, SUNY at
Buffalo);
О Сюзанна M. Леа, университет Северной Каролины в Гринсборо (Suzanne М. Lea, University of North
Carolina at Greensboro);
О Джон Нейтзке, Государственный университет Северо-восточного Миссури (John Neitzke, Northeast
Missouri State University);
О Норман Хосей, университет Нью-Хэйвена (Norman Hosay, University of New Haven);
О Дэвид E. Мак-Эллистер, Государственный университет Северной Каролины (David Е. McAllister,
North Carolina State University);
О Джон Де Катрель, Государственный университет Флориды (John DeCatrel, Florida State University);
О Стив Каннинхем, Государственный университет Калифорнии в Станислаусе (Steve Cunningham,
California State University, Stanislaus);
О Поль Хекберт, Карнеги Меллон университет (Paul Heckbert, Carnegie Mellon University);
О Анджело Ифантис, университет Невады (Angelo Yfantis, University of Nevada);
О Ли X. Тиченор, университет Восточного Иллинойса (Lee Н. Tichenor, Western Illinois University);
О Норман Уитгелс, Уорчестерский политехнический институт (Norman Wittels, Worcester Polytechnic
Institute);
О Эдвард Энджел, университет Нью-Мексико (Edward Angel, University of New Mexico);
О Мэттью Уорд, Уорчестерский политехнический институт (Matthew Ward, Worcester Polytechnic
Institute);
О Ричард E. Неаполитан, университет Северо-восточного Иллинойса (Richard Е. Neapolitan, Northeastern
Illinois University);
О Джек Е. Бресенхэм, университет Уинтропа (Jack Е. Bresenham, Winthrop University);
О Майкл Госс, Государственный университет Колорадо (Michael Goss, Colorado State University);
О Бикаш Сабата, Государственный университет Уэйна (Bikash Sabata, Wayne State University);
О Поль T. Бэрхэм, Государственный университет Северной Каролины (Paul Т. Barham, North Carolina
State University).
От издательства
27
Некоторые части этой книги были написаны, когда я работал с доктором Германном Мауэром
(Hermann Maurer) в Институте информационных процессов и компьютерной медиа-поддержки при
Техническом университете Грац в австрийском городе Грац во время годичного отпуска для научной
работы. Другие части были написаны, когда я был стипендиатом Фулбрайта (Fulbright grant) в Индий-
ском научном институте в Бангалоре. Я весьма признателен за поощрение и поддержку, полученные
мною во время этих поездок.
Мои особые благодарности менеджеру этого проекта Ане Ариас Терри (Ana Arias Terry) за ее руко-
водство и ободрение во время подготовки книги и Ирвину Цукеру (Irwin Zucker), выпускающему редак-
тору, чья внимательность при просмотре книги значительно ее улучшила. И, наконец, благодарю своих
родителей, жену Мэрили (Merilee), а также Грету (Greta), Джесси (Jessie) и Рози (Rosy) за терпение и
поддержку, проявленные ими, пока книга мед ленно приобретала нужную форму.
Примечание для читателя: как смотреть
стереоскопические изображения
Для наглядности изложения материала по трехмерной графике в книге помещено несколько стереоско-
пических рисунков. Они приведены в виде пары почти одинаковых изображений, помещенных рядом.
Чтобы увидеть эти изображения как одно целое, необходимо заставить левый глаз смотреть только на
левую картинку, а правый глаз — только на правую. Это может потребовать определенной практики:
некоторые люди осваивают это быстро, другие — только после многих безуспешных попыток, а некоторые —
никогда. Впрочем, эти рисунки поясняют изложение даже тогда, когда стереоэффект не достигнут.
Один из способов научиться видеть эти картинки — держать указательные пальцы вертикально перед
собой, на расстоянии примерно двух дюймов (пяти сантиметров), и пристально глядеть «сквозь них»
на голую стену вдали. Естественно, каждый глаз видит оба пальца, однако в середине они совмещаются.
Такое совмещение — это именно то, что нужно для просмотра стереорисунков: каждый глаз видит два
рисунка (итого четыре), однако «средние рисунки» полностью совмещаются. Когда «средние пальцы»
сливаются подобным же образом, мозг составляет из них одну трехмерную картинку. Некоторым людям
помогает кусок белого картона, который они помещают между рисунками и прислоняют к нему свой
нос. Барьер из картона не дает каждому глазу видеть изображение, предназначенное для другого глаза.
Об авторе
Ф. С. Хилл (F. S. Hill) является профессором в области электроники и вычислительной техники Массачусетс-
ского университета, Amherst. Он получил степень доктора философии Йельского университета в 1968 году,
три года работал в области цифровой передачи данных в телефонных лабораториях Белла (Bell Telephone
Laboratories), а в 1970 году поступил работать в университет. Хилл является автором многочисленных
статей по обработке сигналов, по технике связи и компьютерной графике. Он был редактором и соредак-
тором журнала IEEE Communications Society Magazine. Он также является членом IEEE (Institute of
Electrical and Electronics Engineers — Институт инженеров по электротехнике и электронике). Хилл — соав-
тор книги «Введение в инженерное дело» и лауреат нескольких премий как выдающийся преподаватель.
От издательства
Ваши замечания, предложения, вопросы отправляйте по адресу электронной почты comp@piter.com (из-
дательство «Питер», компьютерная редакция).
Мы будем рады узнать ваше мнение!
Все исходные тексты, приведенные в книге, вы можете найти по адресу http://www.piter.com/download.
На web-сайте издательства http://www.piter.com вы найдете подробную информацию о наших книгах.
1 Введение в компьютерную
графику
□ Обзор областей применения компьютерной графики.
□ Описание основных устройств для ввода и вывода графики.
«Начните с самого начала, — резко сказал Король, — и продолжайте до самого конца; затем остановитесь».
Льюис Кэрролл. Алиса в стране чудес
Машина не изолирует человека от великих проблем природы, а глубже погружает его в пих.
Антуан де Сент-Экзюпери
Раздел 1.1 «Что такое компьютерная графика?» является введением в область компьютерной графики,
в разделе 1.2 «Где используются изображения, создаваемые компьютером» приводятся примеры исполь-
зования компьютерной графики в настоящее время. В разделе 1.3 «Элементы изображений, создавае-
мых в компьютерной графике» дано обозрение примитивов, создающих компьютерную картинку;
в частности, в разделе 1.3.4 «Растровое изображение» дано понятие растрового изображения, которое
используется на протяжении всей книги. В разделе 1.4 «Графические устройства отображения» мы
рассмотрим некоторые из наиболее часто используемых устройств вывода графической информации,
а в разделе 1.5 «Входные графические примитивы и устройства» дается обзор различных входных
устройств, применяемых в приложениях «интерактивной графики».
1.1. Что такое компьютерная графика?
Любая достаточно передовая технология неотличима от магии.
Артур Кларк
Хороший вопрос! Люди используют термин «компьютерная графика» в различных контекстах, имея в
виду разные вещи. Самое простое: компьютерная графика есть картинки, созданные компьютером. Куда
бы вы ни взглянули, всюду найдете примеры, особенно в журналах и на телевидении. Данная книга была
набрана с помощью компьютера, каждый символ (даже этот: G) был «срисован» из библиотеки начер-
таний символов, хранящейся в памяти компьютера. Книги и журналы пестрят изображениями, создан-
ными на компьютере. Некоторые из них выглядят настолько естественно, что вы не сможете отличить
их от фотографий «реальных» сцен. Другие производят впечатление искусственных или сюрреалиста-
1.1. Что такое компьютерная графика?
29
ческих, что сделано специально для достижения некоторого визуального эффекта. И в фильмах сегод-
ня часто показывают сцены, которые никогда не существовали в действительности, но были ловко смон-
тированы компьютером, смешавшим реальное с воображаемым.
Под словами «компьютерная графика» также понимают и инструментальные средства, используе-
мые для создания таких изображений. Цель данной книги состоит в том, чтобы показать, что это за сред-
ства и как их использовать. Существуют как аппаратные, так и программные средства. Аппаратные
средства включают в себя видеомониторы и принтеры, отображающие графику, а также входные уст-
ройства, такие как мышь или трекбол (шариковый манипулятор), позволяющие пользователю отме-
чать отдельные элементы и рисовать картинки. Компьютер в целом, вместе со своими специальными
устройствами, разумеется, тоже является аппаратным средством вывода графической информации и
ввода изображения.
Что касается программных инструментальных средств, то вы уже знакомы с основными из них: опера-
ционная система компьютера, редактор, компилятор, отладчик, имеющиеся в любой среде программиро-
вания. Для графики должен также существовать целый набор «графических подпрограмм», создающих
сами изображения. Например, все графические библиотеки имеют функции для рисования простой
линии или круга (или символов, таких как G). Некоторые библиотеки делают гораздо большее: они
включают в себя функции для рисования окоп и управления ими с помощью раскрывающихся меню
и диалоговых окон или устанавливают «камеру» в трехмерной системе координат для выполнения
«снимков» объектов, записанных в некоторой базе данных.
В этой книге мы показываем, как писать программы, использующие такие графические библиотеки,
и как добавлять к таким программам другие функциональные возможности. Еще недавно программисты
были вынуждены использовать в высшей степени «аппаратно-зависимые» («device-dependent») библио-
теки, предназначенные для работы в компьютерной системе определенного типа и на дисплее определен-
ного типа. Было весьма затруднительно «переносить» программу в другую компьютерную систему или
использовать эту программу на другом устройстве. Обычно программист был вынужден делать существен-
ные изменения в программе, чтобы заставить ее работать, этот процесс занимал много времени и сопровож-
дался ошибками. К счастью, в настоящее время ситуация значительно улучшилась: стали общедоступ-
ными аппаратно-независимые графические библиотеки, что позволяет программистам использовать в
рамках приложения общий набор функций и использовать одно и то же приложение для различных
систем и дисплеев. Одной из таких библиотек является OpenGL — основной инструментарий, который
мы будем использовать в этой книге. Создание графики с помощью OpenGL широко используется как
в университетах, так и в промышленности. Подробное обсуждение OpenGL мы начнем в главе 2.
И наконец, под словами «компьютерная графика» понимают всю область науки, которая вклю-
чает в себя как эти инструменты, так и изображения, которые они создают. Эта область науки, как
принято считать, зародилась в начале 1960-х с изысканий Ивана Сазерленда (Ivan Sutherland), MIT
(Massachussets Institute of Technlogies — Массачусетсский технологический институт) в его доктор-
ской диссертации под названием «Альбом» («Sketchpad»). Интерес к графике стремительно возрастал
как в самой науке, так и в промышленности, вследствие чего происходил быстрый прогресс в техноло-
гии получения изображений и в алгоритмах, используемых для обработки графической информации.
В 1969 году была создана SIGGRAPH1 (Special-Interest Group) — группа людей, объединенная общими
интересами в графике, и в настоящее время она ведет активную деятельность во всем мире (в ежегод-
ном обязательном собрании SIGGRAPH принимает участие 30 000 человек). Подробнее об этом мож-
но узнать на сайте http://www.siggraph.org. Сегодня во всем мире существуют сотни компаний, использую-
щих какой-либо аспект компьютерной графики среди своих основных источников дохода, и предмет с
названием «компьютерная графика» изучается в большинстве колледжей или университетов, которые
имеют факультеты теории вычислительных машин и систем или электротехники.
Компьютерная графика является чрезвычайно привлекательным предметом для изучения. Вы охот-
нее учитесь писать программы для создания изображений, чем программы с потоками текста или цифр
на выходе. Люди лучше реагируют на графическую информацию и способны усвоить гораздо больше
1 SIGGRAPH является группой людей, объединенных общими интересами, созданной при ACM (Association for Computing Mach-
inery — Ассоциация вычислительных машин). — Здесь и далее примеч. авт.
30
Глава 1. Введение в компьютерную графику
информации из изображений, чем из набора цифр. Наша зрительно-мозговая система в высшей степе-
ни приспособлена к распознаванию зрительных образов. Чтение текста тоже, конечно, является фор-
мой распознавания образов: мы мгновенно распознаем символы, формируем из них слова и осмысляем
их значение. Но мы еще более сообразительны при взгляде на картинку. То, что в виде текста могло бы
выглядеть как бессмысленный набор чисел, в графическом представлении имеет мгновенно узнавае-
мую форму. Количество информации в изображении может быть невероятно большим. Мы не только
понимаем, «что нарисовано», но также собираем бездну информации из тончайших деталей изображе-
ния и текстуры.
Люди изучают компьютерную графику по разным причинам. Одни хотят приобрести лучший на-
бор инструментов для рисования кривых и представления данных, которые они получили на других
стадиях своей работы. Другие хотят писать игры с компьютерной анимацией, а третьи ищут новый спо-
соб художественного выражения. Каждый хочет работать более продуктивно и реализовывать свои
идеи более эффективно, и компьютерная графика может быть для них большим подспорьем.
Существует еще аспект «ввода». Программа генерирует «выход» — изображений или чего-нибудь
другого — при помощи комбинации алгоритмов, выполняемых внутри нее, а также данных, которые
пользователь вводит в программу. Некоторые программы принимают исходные данные в необработан-
ном виде, как символы и цифры, вводимые с клавиатуры. С другой стороны, графические программы
придают особое значение более привычным формам ввода: перемещению мыши по рабочему столу,
рисованию пером на графическом планшете или движению головы и рук пользователя в установках
виртуальной реальности. В этой книге мы сравниваем между собой различные приемы «интерактив-
ной компьютерной графики», то есть мы сочетаем технологии естественного ввода данных пользовате-
лем с технологиями вывода графической информации.
1.2. Где используются изображения,
создаваемые компьютером
С помощью компьютерной графики можно создавать изображения существующих объектов с потряса-
ющим реализмом. Но возможно также рисовать вещи, которые не существовали или в принципе не
могут существовать. Программист описывает в программе интересующий его объект с помощью неко-
торого алгоритма, а программа по этой модели генерирует изображение.
В этом разделе будет сделан краткий обзор некоторых приложений, использующих компьютерную
графику, чтобы продемонстрировать диапазон тех ситуаций, в которых применение графики является
полезным. Позже мы детально разберем некоторые из этих ситуаций в тематических заданиях.
1.2.1. Искусство, развлечения и издательское дело
Компьютерная графика широко применяется при создании фильмов, телевизионных программ, книг и
журналов. Стоимость графических систем существенно уменьшилась за последние годы, и для исполь-
зования таких систем разработаны мощные программные средства. Талантливые дизайнеры имеют те-
перь возможность повседневно использовать компьютеры для создания специальных эффектов, ани-
мации и публикаций высокого качества.
Производство фильмов, анимация и специальные эффекты
Мы регулярно можем видеть по телевизору рекламу с компьютерной анимацией, и весьма впечатляю-
щая анимация иногда встраивается в игровые фильмы.
Мультфильмы создаются посредством записи последовательных изображений на кино- или видео-
пленку, причем каждое изображение лишь слегка отличается от предыдущего. Когда кино- или видео-
пленку воспроизводят с частотой от 20 до 30 кадров в секунду, человеческий глаз соединяет эти изобра-
жения и видит плавное движение.
1.2. Где используются изображения, создаваемые компьютером
31
Компьютерные игры
Игрок двигает джойстиком и нажимает спуск, на что незамедлительно реагирует компьютерное изоб-
ражение. Для увеличения скорости создания последовательных изображений часто используются
специальные аппаратные средства. Игры из галереи автоматов представляют собой самую сложную
задачу для программистов графики, так как движение должно быть реалистичным и в то же время очень
быстрым.
Просмотр Всемирной паутины (World Wide Web)
Мы живем в мире, объединенном в сеть, и многие из нас регулярно «плавают по волнам» WWW. Иллюст-
рация 4 демонстрирует пример изображения из web-браузера. Пользователь перемещает мышь к опреде-
ленному месту на экране и щелкает на нем, выбирая для посещения следующий web-сайт, после чего из
Интернета присылается страница информации. Браузер должен быстро интерпретировать данные этой
страницы и изобразить их на экране в виде высококачественной текстовой и графической информации.
Разработка слайдов, книг и журналов
Программа компоновки страницы (page layout) используется для разработки окончательного «вида»
каждой страницы книги или журнала. Пользователь может в интерактивном (диалоговом) режиме
перемещать текст и иллюстрации по странице, чтобы выбрать то расположение, которое ему нравится.
Существует другая форма публикаций, называемая иногда «графикой презентаций» («presentation
graphics»). На коммерческих предприятиях изготавливаются высококачественные слайды для показа
группам клиентов или руководству. Часто такие слайды содержат столбчатые или круговые диаграм-
мы, которые резюмируют сложную информацию и представляют ее в готовой для понимания форме.
Такие графики должны быть высокого качества и иметь внешнюю привлекательность, чтобы достичь
определенной цели.
Другим инструментальным средством для создания изображений на компьютере является система
рисования (paint system). Пользователи формируют изображение посредством его вычерчивания —
часто при помощи планшета или светового пера — и выбора цвета или узора для получения желаемых
эффектов. На рис. 1.1 показана система рисования в действии. В системе предусмотрен богатый набор
инструментов: визуализированные (rendered) ранее изображения могут быть извлечены из запомина-
ющего устройства большой емкости (mass storage) и объединены с новыми изображениями; может быть
осуществлен показ и применение «палитр» различных цветов; с помощью несложных команд может
быть создано множество различных текстур. Такие системы часто используются для создания страниц,
с которыми вы можете встретиться во Всемирной паутине.
Еще одной формой публикации является изготовление географических карт. Создание карт являет-
ся сложной работой, поскольку необходимо с большой точностью свести воедино огромное количество
подробной информации.
1.2.2. Компьютерная графика и обработка изображений
Области компьютерной графики и обработки изображений (image processing) год от года все больше
сливаются вместе, поэтому становится все более трудным (и менее важным) провести границу между
ними. В этой книге мы фокусируемся на компьютерной графике, но попутно описываем большое коли-
чество технологий, которые исторически можно было бы отнести к области обработки изображений.
Главная задача компьютерной графики состоит в создании картинок (pictures) и изображений
(images), то есть в синтезе их внутри компьютера на основе некоторого описания или модели. С другой
стороны, главная задача обработки изображений заключается в том, чтобы улучшить или изменить образы,
созданные где-то в другом месте, возможно, оцифрованные с фотографий или записанные с помощью
видеомагнитофона. Обработка может убрать с изображения «пятна» помех, улучшить его контрастность,
очертить контуры (sharpen edges), настроить цвета. Можно использовать специальные подпрограммы
для выделения определенных черт изображения, чтобы сделать более заметными или более понятными.
32
Глава 1. Введение в компьютерную графику
Рис. 1.1. Создание пользователем изображения с помощью системы рисования
(Интерфейс ZBrush. С разрешения OferAlon.www.pixologic.com)
На рис. 1.2, а показано изображение, полученное цифровым сканированием фотографии. На рис. 1.2, б
приведено то же изображение после того, как была улучшена его контрастность, удалены помехи и очер-
чены контуры.
б
Рис. 1.2. Улучшение изображения: а) исходное; б) улучшенное
Иллюстрация 9 демонстрирует причудливое смешение графики и обработки изображений.
1.2.3. Управление процессом
Системы высокой сложности, такие как фабрики, электростанции, системы управления воздушным
движением, подлежат тщательному контролю. В ряде случаев в данную систему должен быть обяза-
тельно включен человек — для выявления угрожающих ситуаций. Такой оператор должен снабжаться
информацией на специальном индикаторе состояния (status display), причем эта информация должна
1.2. Где используются изображения, создаваемые компьютером
33
быть оперативной и должна интерпретироваться немедленно. Измерения в системе высокой сложнос-
ти совершаются один раз в секунду или около того, и эти данные передаются на управляющую станцию
(monitoring station) для преобразования в графическую информацию и представления оператору.
Для примера на рис. 1.3 показано устройство отображения производственного процесса. Пользо-
ватель видит схематическое представление процесса, дающее полную картину при одном взгляде.
Различные пиктограммы (icons) могут мигать или менять свой цвет, чтобы предупредить пользователя
о тех изменениях обстановки, которые требуют его внимания.
Рис. 1.3. Мониторинг производственного процесса (с разрешения Dataviews Corporation)
1.2.4. Отображение имитаций
Одни из графически отображаемых систем действительно существуют и могут оцениваться в реальном
времени. Другие никогда не были или не могут быть созданы и существуют только внутри компьютера
в виде уравнений и алгоритмов. Тем не менее они могут быть проверены и «подвергнуты испытанию»,
как если бы они существовали, и таким способом может быть получена ценная информация. Компью-
терная графика может отображать объекты так, как будто они уже существуют физически, в то время
как в действительности они всего лишь модели внутри компьютера.
Моделирование целого ряда систем может принести пользу: движения робота во время спуска по
склону действующего вулкана, реакции человеческого тела на введение чужеродного тела, эффекта гло-
бального потепления вследствие возрастания концентрации углеводородов. Классическим примером
является имитатор полета (flight simulator). Система представляет собой самолет с заданной формой и
летательными характеристиками, а также некий соответствующим образом смоделированный «мир»,
состоящий из посадочной площадки, гор, других самолетов и, конечно, «воздуха». В имитаторе полета
динамика движения самолета моделируется на компьютере. Во время имитационного полета в соот-
ветствии с тем, как пилот управляет приборами, компьютер вычисляет новые координаты и скорость
имитируемого самолета. Вокруг кабины пилот видит имитируемый пейзаж. Программы имитации поле-
та относятся к наиболее ответственным и трудным для написания графическим приложениям, поскольку
они должны иметь очень высокую скорость реакции.
Еще одна форма имитации стала популярной совсем недавно: имитация «виртуальных миров». Рису-
нок 1.4 изображает женщину, взаимодействующую с виртуальным миром с использованием дисплея-оч-
ков (head-mounted display) и информационных перчаток (data gloves). Когда она поворачивает голову,
графический дисплей показывает различные виды мира, созданного в компьютере, и она может двигать
своими «виртуальными руками», чтобы касаться различных предметов этого мира. Она видит изобра-
жение своих «рук» в этом мире, и когда она «хватает» какой-нибудь предмет, то она видит, как он пере-
мещается и реагирует на движения ее рук.
2 Ф. Хилл
34
Глава 1. Введение в компьютерную графику
Представте себя сидящим за терминальным устройством и взаимодействующим с миром, расположен-
ным на удаленных компьютерах во Всемирной паутине. Для продвижения в этом мире вы используете
мышь и «болтаете» («chat») с другими встреченными вами людьми посредством набора сообщений.
Эти люди являются графическими представлениями других пользователей, они видят ваше представ-
ление и отвечают вам.
Рис. 1.4. Женщина, надевшая дисплей-очки (head-mounted display) и информационные перчатки (data gloves)
для взаимодействия с виртуальным миром (с разрешения NASA)
1.2.5. Автоматизированное проектирование
Многие дисциплины широко используют интерактивную компьютерную графику для облегчения проек-
тирования какой-либо системы или изделия. Компьютер хранит в памяти модель устройства, и пользо-
вателю для изучения выдается изображение, построенное на основе этой модели. Дизайнер может по-
ворачивать объект и увеличивать его для более детального рассмотрения, причем для осуществления
этих манипуляций он может использовать трекбол или «информационную перчатку». Для ускорения
визуализации применяется каркасное черчение (wire-frame drawing), при котором форма объекта
задается сеткой из соединенных линий.
Досконально исследовав текущую модель, дизайнер, вероятно, осуществит определенные измене-
ния в ее форме, после чего модель будет усовершенствована и визуализирована заново. Когда форма
становится соответствующей проекту, пользователь запрашивает ее более реалистичное изображение.
Создание такого изображения может занять больше времени, потому что алгоритмы, обеспечивающие
полноцветный рендеринг с тенями, бликами и мелкими деталями изображения, могут быть очень слож-
ными.
Здесь также могут быть использованы анализ и имитация. Форма паяльника может обрести желае-
мый внешний вид, однако, если корпус оказался недостаточно прочным, слишком тяжелым или неудоб-
ным, можно применить к модели алгоритмы, анализирующие ее вес и массу, а также проверить, будет
ли внутреннее содержимое паяльника должным образом размещаться внутри такого корпуса. С помощью
других алгоритмов можно проверить, не будет ли данная форма слишком дорогостоящей при изготов-
лении ее из стали или алюминия, и даже смогут ли внутренние части быть правильно скомпонованы во
время процесса окончательной сборки! На протяжении всего процесса проектирования и изготовления
компьютер может быть мощным союзником. В этой книге основной акцент будет сделан на создании
таких изображений объекта, которые предоставляют дизайнерам нужную информацию.
1.2. Где используются изображения, создаваемые компьютером
Автоматизированный архитектурный дизайн
Компьютерная графика может также помочь архитекторам в проектировании зданий. Здесь модель
может быть архитектурным планом (floor plan) дома. Архитектор вносит изменения в архитектурный
план, передвигая стену здесь или прилаживая окно там (разумеется, с помощью мыши), и затем просмат-
ривает полную визуализированную версию того, как будет выглядеть такой дом. Можно испробовать
различные текстуры, такие как кирпич или штукатурка. Работая в интерактивном режиме, архитектор
может даже «совершить экскурсию» по дому и показать клиенту, как он или она будут чувствовать себя
в этом доме, когда он будет построен.
Проектирование электрических схем
Рисунок 1.5 являет собой пример еще одной области, где компьютерное проектирование предоставляет ог-
ромные выгоды. Здесь показана модель символического описания электрической схемы, которая может
быть частью нового компьютера. Проектировщик добавляет в схему новые элементы (называемые «венти-
лями» — «gates»), выбирая их из меню иконок (это маленькие картинки, изображающие элементы) и «пе-
ретаскивая» («dragging») иконку на нужное место в схеме. Посредством таких простых помечающих дей-
ствий проектировщик добавляет, удаляет и соединяет «вентили». После этого имитирующее программное
обеспечение может протестировать, как будет работать реальная версия данной электрической схемы.
Основываясь на результатах этой имитации, проектировщик корректирует схему и тестирует ее вновь.
Serial
CLK2
А>В
А=В
А<В
АЗ
85 А2
АО
ВЗ
В2
В1
ВО
A>Bin
A=Bin
A<Bin
1
К
11
9
f
Reset Receiver
iHassasEi
11
3
+5V
АЗ
А2
А1
АО
85
ВЗ
В2
В1
ВО
A>Bin
A=Bin
A<Bin
А>В
А=В
5
6
7
5
L
I
Рис. 1.5. Приложение цифрового логического проектирования (с разрешения Chris Vadnais
and Capilano Computing Systems, Ltd.)
36
Глава 1. Введение в компьютерную графику
1.2.6. Научный анализ и наглядность
Научные данные часто бывают сложными, и соотношения между различными переменными в экспери-
менте иногда трудно представить зрительно. Графика является превосходным средством для представ-
ления научной информации в форме, обеспечивающей наглядное восприятие. Когда данные представ-
лены должным образом, вы нередко по-новому понимаете суть исследуемого процесса. Кроме того, при
правильной демонстрации данных вы можете эффективнее передавать свои идеи коллегам.
Рисунок 1.6 является примером графического представления сложных научных данных. На рисун-
ке показана поверхность, прогибы которой могут мгновенно восприниматься глазом. Высота поверхно-
сти отображает одну величину (например, температуру или вязкость) в зависимости от двух других
величин, что и создает трехмерный график. Подчеркнем, что если бы эти данные были представлены в
виде всего лишь числовой таблицы, то для получения той же самой информации эту таблицу пришлось
бы долго изучать.
Рис. 1.6. Изображение сложных научных данных
Необычна структура сложной молекулы «фуллерина» — вещества, названного в честь Бакминстера
Фуллера (Buckminster Fuller). Молекула состоит из 60 атомов углерода, расположенных в виде специ-
фического геометрического узора, и представляет собой третью стабильную форму углерода (наряду
с графитом и алмазом). (Мы будем изучать ее форму далее в главе 6.) Это геометрическое расположение
сделано непосредственно видимым с помощью компьютерной графики. Изображение данной молекулы
представлено не только ясным и удобным для понимания, но и красивым.
Помимо облегчения понимания человеком измеренных данных, компьютерная графика прекрасно
приспособлена для проникновения в суть сложных математических идей. Недавно был разработан ряд
мощных программ (таких, как Mathematica, MatLab, MathCad и т. д.), которые позволяют пользователю
вводить уравнения и «соотношения», связывающие различные величины, и сразу же видеть результи-
рующие объекты, изображенные в какой-либо форме. Например, на рис. 1.7, а показана поверхность,
заданная математической формулой. Эта поверхность рисуется с помощью программы Mathematica,
если написать единственную команду
ParametricPlot3D[t.u.Sin[t u]}(t.0.3}.(u.0.3}]
В графической форме все сложности формулы хорошо видны с первого взгляда, и пользователь мо-
жет варьировать некоторые параметры, чтобы исследовать получившуюся поверхность с различных
1.3. Элементы изображений, создаваемых в компьютерной графике
37
точек зрения. На рис. 1.7, б показано применение той же программы Mathematica для построения слож-
ного трехмерного объекта (звездчатого икосаэдра), чтобы помочь пользователю в изучении структуры
этого многогранника.
Рис. 1.7. Mathematica демонстрирует: а) сложную математическую поверхность;
б) математически заданный трехмерный объект
Минимальные поверхности (minimal surfaces') — это целый класс математически определяемых поверх-
ностей со специальными свойствами. Замечено, что, например, куски мыла иногда самоорганизуются
как минимальная поверхность. Многим известно компьютерное изображение новой минимальной
поверхности, открытой недавно профессором Дэвидом Хоффманом (David Hoffman) и его коллегами.
Интуитивные предположения исследователей о возможности существования этой специфической
поверхности привели к цели с помощью компьютерной графики.
Иллюстрация 18 демонстрирует фрагмент занимательного множества Мандельброта (Mandelbrot set),
которое названо «самым сложным объектом в математике». Это множество будет изучаться в главе 9.
1.3. Элементы изображений, создаваемых
в компьютерной графике
Из чего состоит компьютерное изображение? Основные (базовые) объекты, из которых компонуются
такие изображения, называются графическими примитивами (output primitives). Вот одна из полез-
ных классификаций примитивов:
О ломаные линии (polylines);
О текст;
О закрашенные области (filled regions);
О растровые изображения (raster images).
Мы увидим в дальнейшем, что эти типы частично пересекаются между собой, однако для начала
достаточно будет такой терминологии. Мы поочередно опишем каждый тип примитивов и покажем
типовые подпрограммы для их рисования. Конечно, в последующих главах об этих инструментах будет
рассказано подробнее. Атрибутами (attributes) графического примитива называются характеристики,
определяющие его вид, например цвет и толщину.
38
Глава 1. Введение в компьютерную графику
1.3.1. Ломаные линии
Ломаная линия, или просто ломаная (polyline), представляет собой последовательность соединенных
между собой прямых линий. Каждый из примеров на рис. 1.8 содержит в себе несколько ломаных:
а) одна ломаная тянется от носа динозавра к его хвосту;
б) график математической функции представляет собой одну ломаную линию;
в) «каркасное» представление шахматной пешки содержит множество ломаных, очерчивающих ее
контур.
Рис. 1.8. Рисунок динозавра из ломаных линий (С разрешения Сюзанны Вербек (Susan Verbeck))(a);
график математической функции; каркасное представление трехмерного объекта (б)
Отметим, что ломаная может выглядеть как гладкая кривая. На рис. 1.9 показано увеличение (blowup)
кривой, обнаруживающее составляющие ее короткие отрезки прямых. Глаз воспринимает ее как совер-
шенно плавную кривую.
Рис. 1.9. Гладкая кривая, составленная из отрезков прямых
Изображения, составленные из ломаных, иногда называют линейными рисунками (line drawings).
Некоторые устройства, такие как перьевой графопостроитель (pen plotter), специально предназначены
для создания линейных рисунков.
Простейшая ломаная представляет собой единственный отрезок прямой. Отрезок прямой опреде-
ляется его двумя концевыми точками, например (xv и (х2, у2). Подпрограмма рисования прямой
может выглядеть следующим образом:
drawLine(xl, у]. х2. у2):
Эта подпрограмма рисует прямую линию между двумя концевыми точками. Позже мы разработаем
такой инструмент и покажем множество примеров его применения. А сейчас мы определим, в каком
виде задаются координаты xt и прочие (целыми или вещественными числами) и как в программе можно
представить цвета.
1.3. Элементы изображений, создаваемых в компьютерной графике 39
Особый случай возникает, когда отрезок прямой вырождается в единственную точку и рисуется в
виде «точки» («dot»). Даже скромная точка, как мы увидим позднее, имеет важное значение в компью-
терной графике. Рисование точки может быть запрограммировано при помощи подпрограммы
drawDot(xl. yl);
Если ломаная состоит из нескольких прямых, то каждая из них называется ребром (edge), а две
смежные прямые встречаются в вершине (vertex). Ребра ломаной могут пересекаться, как показано на
рис. 1.8. Ломаные задаются списком своих вершин, каждой из которых соответствует пара координат:
(х0, г/0), (х,, г/(), (х2, (х, уп).
(1.1)
5 10
Рис. 1.10. Пример ломаной линии
Например, ломаная, показанная на рис. 1.10, задана такой последовательностью:
(2,4), (2, И), (6, 14), (12, И), (12,4) ...
(Как задаются остальные вершины этой ломаной?)
Для рисования ломаных линий нам потребуется инструмент, представляющий собой подпрограм-
му типа
drawPolyl1ne(poly);
где переменная poly — список, содержащий все концевые точки (х, у) в какой-либо форме. Существу-
ют различные способы введения такого списка в программу, и каждый из них имеет свои достоинства и
недостатки.
Ломаная линия не обязана образовывать замкнутую фигуру, но если первая и последняя точки со-
единяются ребром, то такая ломаная линия становится многоугольником, или полигоном (polygon).
Если, кроме того, никакие два ребра не пересекаются, то такой полигон называется простым (simple).
На рис. 1.11 представлено несколько интересных полигонов: из них только а) и г) являются простыми.
Полигоны являются фундаментальными примитивами компьютерной графики, отчасти потому, что их
легко задавать. Многие алгоритмы рисования и рендеринга были специально настроены на оптималь-
ную работу с полигонами. В главе 3 производится глубокий анализ полигонов.
Атрибуты прямых и ломаных линий
Важными атрибутами ломаной являются цвет и толщина ее ребер, способ начертания ребер и способ,
которым жирные (thick) ребра соединяются в концевых точках. Обычно всем ребрам ломаной линии
задаются одинаковые атрибуты.
Две первые ломаные линии на рис. 1.12 отличаются друг от друга атрибутом «толщина линии» (line-
thickness). Третья ломаная нарисована при помощи штриховых отрезков.
Когда линия является жирной, то ее концы имеют свои очертания и пользователь должен решить,
каким образом «соединить» два смежных ребра. Рисунок 1.13 показывает, какие имеются возможно-
40
Глава 1. Введение в компьютерную графику
сти. Случай а) показывает линии, соединенные «встык» («butt-end»), при таком соединении остается
неподобающая выемка. В случае б) концы линий скруглены, поэтому они соединяются плавно. Слу-
чай в) демонстрирует угловое соединение (mitered joint), а случай г) — усеченное угловое соединение
(trimmed mitered joint). Программные средства в ряде пакетов позволяют пользователю выбирать тип
соединения. Некоторые методы требуют значительных вычислений.
Рис. 1.12. Ломаные линии с различными атрибутами
а
г
Рис. 1.13. Некоторые способы соединения двух жирных линий в ломаную
Атрибуты ломаной иногда устанавливаются посредством вызова подпрограмм типа
setDash(dash7) или setL1neThickness(thickness).
1.3.2. Текст
Некоторые графические устройства имеют два различных режима визуального отображения: тексто-
вый (text mode) и графический (graphics mode). Текстовый режим применяется для простого ввода
и вывода символов при управлении операционной системой или редактировании программного кода.
Текст, отображаемый в этом режиме, использует встроенный генератор символов, который способен
рисовать буквенные, цифровые символы, знаки пунктуации, а также набор специальных символов,
таких как «V», «?», «А». Обычно такие символы не могут быть помещены в произвольное место экрана,
а только в строку и столбец встроенной сетки.
1.3. Элементы изображений, создаваемых в компьютерной графике
41
Графический режим предлагает более богатый набор форм символов, нежели текстовый режим,
к тому же символы могут помещаться в произвольное место экрана. На рисунке 1.14 приведены примеры
текста, нарисованного графически.
Крупный текст
Мелкий текст
Затененный текст
Повернутый текст КикЕшуршвый ТИКСТГ
МАЛЕНЬКИЕ ЗАГЛАВНЫЕ БУКВЫ
Рис. 1.14. Примеры текста, нарисованного в графическом режиме
Подпрограмма для рисования строки символов может выглядеть следующим образом:
drawString х. у. string:
Эта подпрограмма помещает начальную точку строки в позицию (х, у) и рисует последовательность
символов, записанных в переменной string.
Атрибуты текста
Существует множество атрибутов текста, наиболее важными из которых являются тип шрифта (font)
текста, или его начертание (typeface), его цвет, размер, интервал (spacing) и ориентация.
Font — тип шрифта, или начертание, — это набор форм символов определенного стиля и размера.
На рис. 1.15 показаны различные шрифты.
Helvetica
Helvetica bold
_ Helvetica italic
Times
Times bold
Times italic
Courier
Courier bold
Courier italic
Рис. 1.15. Некоторые примеры шрифтов
Форма каждого символа может быть задана с помощью ломаной линии (или более сложных кри-
вых, таких как кривые Безье (Besier), см. главу И), как показано на рис. 1.16,6. Графические пакеты
поступают с набором определенных шрифтов, а дополнительные шрифты могут быть приобретены
в фирмах, специализирующихся на их разработке.
Символы также можно рисовать наклоненными в каком-нибудь направлении. Наклонные строки
часто используют для комментариев к частям графика.
Графическое представление текста высокого качества является сложной задачей. Едва заметные раз-
личия в деталях способны превратить приятный текст в безобразный. Действительно, просматривая в
повседневной жизни горы печатного материала, мы подсознательно ожидаем, что символы должны
иметь определенную форму, разделяться определенными интервалами и сочетаться друг с другом.
42
Глава 1. Введение в компьютерную графику
Рис. 1.16. Начертание символа, заданное: а) ломаной линией; б) комбинацией точек
1.3.3. Закрашенные области
Примитив «закрашенная область» (filled-region) (иногда его называют «fill area» — закрашенная пло-
щадь) — это некоторая форма, заполненная каким-либо цветом или узором. Границей закрашенной
области часто является полигон (хотя в главе 10 рассматриваются более сложные области). На рис. 1.17
показано несколько закрашенных полигонов. Полигон а) закрашен так, что его стороны остаются види-
мыми, в то время как б) закрашен таким образом, что его граница не прорисована. Полигоны в) и г) не
являются простыми. Полигон г) даже содержит в себе еще один полигон. Такие формы также могут
быть закрашены, однако необходимо точно определить, что подразумевается под «внутренностью» по-
лигона, поскольку в зависимости от этого определения алгоритмы закрашивания будут различными.
Алгоритмы для выполнения операции закрашивания обсуждаются в главе 10.
Рис. 1.17. Примеры закрашенных полигонов
Чтобы нарисовать закрашенный многоугольник, следует использовать подпрограмму вида
fillPolygonCpoly. pattern):
где переменная poly содержит данные полигона — список такого же вида, как и для ломаной линии, —
а переменная pattern содержит описание того узора, которым будет осуществляться заполнение.
1.3. Элементы изображений, создаваемых в компьютерной графике
43
На рис. 1.18 показано использование закрашенных областей для тонирования различных граней
трехмерного объекта. Каждая многоугольная грань объекта закрашена определенным оттенком серого
цвета, соответствующего количеству света, отражающегося от данной грани. Такая комбинация тонов
создает эффект освещения объекта светом, падающим с определенной стороны. Тонирование трехмер-
ных объектов обсуждается в главе 8.
Атрибуты закрашенной области включают в себя атрибуты границы, очерчивающей область, а так-
же узор и цвет заполнения.
Рис. 1.18. Закрашивание многоугольных граней трехмерных объектов для создания нужного тонирования
1.3.4. Растровое изображение
На рис. 1.19, а показано растровое изображение (raster image) шахматной фигуры. Это изображение
составлено из множества маленьких «клеточек», заполненных различными оттенками серого цвета, как
показано при увеличении на рис. 1.19, б. Отдельные клеточки часто называют «пикселами» («pixels» —
сокращение от «picture elements»). В обычных условиях наш глаз не способен видеть отдельные клетки:
вместо этого он сливает их вместе и синтезирует общую картину.
а б
Рис. 1.19. Растровое изображение шахматной фигуры (а); увеличение изображения
(Трассировка луча. С разрешения Эндрю Слатера (Andrew Slater)) (б)
Растровое изображение хранится в компьютере в виде массива числовых величин. Предполагается,
что этот массив является прямоугольным, с определенных числом строк и столбцов. Каждая числовая
величина представляет значение пиксела, записанного в этом месте. Этот массив в целом часто называ-
ют «пиксельной картой» («pixel map»). Используется также термин «побитовое отображение», или
44
Глава 1. Введение в компьютерную графику
«битовая карта» («bitmap»), хотя многие полагают, что этот термин следовало бы зарезервировать для
таких пиксельных карт, где каждый пиксел представлен одним битом, имеющим значение 0 или 1.
а
22222222
22222227
2 2 2 2 2 7 7 1
2 2 2 2 7 1 1 1
2 2 2 7 1 1 1 1
2 2 2 7 1 1 7 7
б
Рис. 1.20. Простой рисунок, представленный в виде битовой карты
Рисунок 1.20, а показывает простой пример изображения, представленного в виде массива размером
18 на 19 клеток (18 строк и 19 столбцов), причем клетки имеют три оттенка серого цвета. Пусть эти три
оттенка серого закодированы величинами 1,2 и 7. На рис. 1.20, б показаны числовые значения пиксель-
ной карты для левой верхней части изображения размером 6 па 8.
Как создаются растровые изображения? Вот три их основных источника.
Изображения, созданные вручную
При этом способе дизайнер вычисляет, какие значения требуются для каждой клетки, и заносит их в
память. Иногда для автоматизации этого процесса можно использовать программу раскрашивания.
Дизайнер может рисовать и манипулировать различными графическими формами, наблюдая при этом
за процессом. Когда результат удовлетворяет дизайнера, он записывает все в файл. Значок на рис. 1.20
был создан именно таким способом.
Компьютерные изображения
Согласно этой методике, для визуализации сцены, которая может быть абстрактно смоделирована в па-
мяти компьютера, используется особый алгоритм. В простейшем случае сцена может состоять из одной
желтой гладкой сферы, освещенной источником оранжевого цвета. Такая модель содержит описания
размера и положения сферы, расположение источника света, а также гипотетической камеры, которая
должна заснять эту картину. Растровое изображение играет роль пленки в этой камере. Чтобы создать
растровое изображение, алгоритм должен вычислить цвет луча света, падающего на каждый пиксел
изображения в камере. Таким методом «трассировки луча» (ray-traced) создаются изображения, подоб-
ные шахматной фигуре на рис. 1.19 (см. главу 14).
Растровые изображения зачастую содержат изображения прямых линий. Линия в изображении созда-
ется путем установки пикселов нужного цвета на очертание линии. Однако для определения последо-
вательности пикселов, которые «наилучшим образом» представляют идеальную линию между двумя
заданными концевыми точками, требуется некоторое количество вычислений. Алгоритм Брезенхема
(Bresenham, см. главу 10) обеспечивает весьма эффективное приближение для определения этих пикселов.
Рисунок 1.21, а демонстрирует растровое изображение, включающее в себя несколько прямых линий,
дугу окружности и текстовые символы. На рис. 1.21, б показано увеличение части этого растрового
изображения, при котором становятся видимыми отдельные пикселы, находящиеся якобы «на» прямых.
Для горизонтальной и вертикальной линий черные квадратные пикселы выровнены хорошо, образуя
1.3. Элементы изображений, создаваемых в компьютерной графике
45
четкую прямую. Однако для остальных линий и для дуги «наилучший» набор пикселов дает только
приближение к нужной «истинной» линии. Кроме того, увеличение высвечивает ужасные «ступеньки»
(«jaggies»), являющиеся неотъемлемой частью растровых изображений.
Контрольный образец
а б
Рис. 1.21. Совокупность линий и текста (а); увеличение части а, показывающее «ступеньки» (5)
Сканированные изображения
Фотография телевизионного изображения может быть преобразована в цифровую форму (оцифрована).
На практике поверх исходного изображения помещается сетка, и в каждой точке этой сетки специаль-
ный цифровой преобразователь (digitizer — цифратор) передает в память «ближайший» цвет из своего
ассортимента. Созданная таким образом битовая карта записывается в файл для дальнейшего исполь-
зования. Изображение котенка на рис. 1.22 было сформировано именно таким способом.
Рис. 1.22. Сканированное изображение
Поскольку растровые изображения являются обычными числовыми массивами, они могут быть
впоследствии обработаны на компьютере для их улучшения. Например, на рис. 1.23 приведены три по-
следовательных укрупнения изображения котенка с рис. 1.22. Эти укрупнения были осуществлены
с помощью «повторения пикселов» (pixel replication, подробно это обсуждается в главе 10). Каждый
пиксел был повторен в каждом направлении: 3 раза в случае а), 6 раз в случае б) и 12 раз в случае в).
Рассмотрим еще один пример. Пусть требуется «улучшить» (clean up) сканированное изображение.
На рис. 1.24, а показано изображение котенка с рис. 1.22, причем оттенки серого цвета были изменены
с целью увеличить контрастность и сделать детали более явными (evident), а на рис. 1.24, б отображен
эффект от «выделения контуров» («edge enhancement»), которое было произведено одним из способов
фильтрования изображения.
46
Глава 1. Введение в компьютерную графику
а б в
Рис. 1.23. Три последовательных увеличения изображения котенка с рис. 1.22: а) трехкратное увеличение;
б) шестикратное увеличение; а) двенадцатикратное увеличение
Рис. 1.24. Примеры улучшения изображения
Рисунок 1.25 представляет два примера редактирования изображения для достижения определен-
ного визуального эффекта. Часть а) рисунка демонстрирует «рельефное» («embossed») изображение
котенка, в то время как на фрагменте б) это изображение подвергнуто геометрическому искажению.
Рис. 1.25. Примеры изменения изображения для достижения визуального эффекта
1.3. Элементы изображений, создаваемых в компьютерной графике
47
1.3.5. Представление оттенков серого и других цветов
в растровых изображениях
Важным аспектом растрового изображения является способ, которым оттенки серого и других цветов
представляются в его битовой карте. Сделаем краткий обзор наиболее употребительных способов.
Полутоновые (gray-scale) растровые изображения
Если в растровом изображении имеются пикселы только с двумя значениями, то такое изображение
называется двухуровневым (bi-level), или черно-белым. На рис. 1.26, а показано простое двухуровне-
вое изображение, представляющее собой всем известный курсор в форме стрелки, который мы часто
видим на экране компьютера.
1 0 0 0 0 0 0 0
1 1 0 0 0 0 0 0
1 1 1 0 0 0 0 0
1 1 1 1 0 0 0 0
1 1 1 1 1 0 0 0
1 1 1 1 1 1 0 0
1 1 1 1 1 1 1 0
1 1 1 1 1 1 1 1
1 1 1 1 0 0 0
1 0 1 1 1 0 0 0
1 0 0 0 1 1 0 0
0 0 0 0 1 1 0 0
0 0 0 0 0 1 1 0
0 0 0 0 0 1 1 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
б
Рис. 1.26. Двухуровневое изображение курсора (а); битовая карта изображения (£)
Растр этого изображения состоит из 16 рядов по 8 пикселов в каждом. Рисунок 1.26, б показывает
битовую карту этого изображения в форме массива, состоящего из единиц и нулей. Изображение слева
связывает черный цвет с единицей, а белый — с нулем, однако это соответствие легко может быть ин-
вертировано. Так как для различения двух величин достаточно одного бита информации, двухуровне-
вое изображение часто называют изображением «один бит на пиксел» («one-bit-per-pixel»).
Если пикселы полутонового изображения могут принимать более двух значений, то каждый пиксел
требует для представления в памяти больше одного бита. Полутоновые изображения часто классифи-
цируются с применением термина «глубина пиксела» («pixel depth»), которая равна числу бит, необ-
ходимых для представления уровней их полутонов (оттенков серого). Поскольку n-битовая величина
имеет 2п возможных значений, то в изображении с глубиной пикселов, равной п, может быть 2" оттен-
ков серого. Чаще всего используются такие величины:
О Два бита на пиксел обеспечивают 4 оттенка серого.
О Четыре бита на пиксел обеспечивают 16 оттенков серого.
О Восемь бит на пиксел обеспечивают 256 оттенков серого.
Рисунок 1.27 показывает 16 оттенков серого, расположенных от черного к белому цвету. Каждое из
16 возможных значений пиксела соответствует двоичной тетраде (quadruple) — структуре из четырех
элементов, например ОНО или 1110. Здесь значению 0000 соответствует черный цвет, 1111 означает
белый, а остальные 14 значений отображают различные уровни интенсивности (яркости) серого цвета
в промежутке.
48
Глава 1. Введение в компьютерную графику
0000 0001 0010
1110
1111
Яркость
Черный
Белый
Рис 1.27. Шестнадцать уровней яркости серого цвета
Многие полутоновые изображения1 используют 256 уровней яркости, поскольку именно такое число
обеспечивает сканированное изображение приемлемого качества. Каждый пиксел отображается некото-
рой восьмибитовой величиной, например 01101110. Обычно значение пиксела обозначает «яркость»,
причем значению 00000000 соответствует черный цвет, 11111111 — белый, а серому цвету средней интен-
сивности соответствует число 10000000. Рисунок 1.22 создан с использованием 256 оттенков серого.
Влияние глубины пикселей: квантование уровней яркости
Бывает так, что изображение, в котором вначале использовалось восемь бит на пиксел, изменяется так,
что используется меньшее число бит на пиксел. Это может быть вызвано неспособностью дисплея ото-
бражать 256 уровней или связано с тем, что полное изображение занимает слишком много памяти. Рисун-
ки 1.28—1.30 показывают, как влияет на изображение котенка с рис. 1.22 простое усечение значений
пикселов до меньшего числа бит. Потеря точности едва заметна на рис. 1.28, где используются шесть и
пять бит на пиксел (что обеспечивает соответственно 64 и 32 различных оттенков серого).
б
Рис. 1.28. Изображение с рис. 1.22: а) с уменьшением числа бит на пиксел до шести и б) до пяти
а
Потеря качества на изображениях рис. 1.29 уже значительна. Часть а) рисунка показывает влияние
усечения величины каждого пиксела до 4 бит, вследствие чего в нем возможно всего 16 уровней ярко-
сти. Например, величина пиксела 01110100 заменена на 0111. В части б) рисунка четко видны все 8
возможных оттенков серого. Отметим, что некоторые области рисунка, где на исходном изображении
(см. рис. 1.22) имелись различные оттенки, теперь представляют собой «озера» однотонного серого цвета.
Этот эффект часто называют сегментацией (banding), поскольку те области, в которых должно про-
исходить постепенное смещение уровней яркости, теперь являют собой последовательность однотон-
ных серых зон — «сегментов».
1 Тысячи таких изображений доступны в Интернете; их форматы обычно gif, jpg, tif.
13. Элементы изображений, создаваемых в компьютерной графике
49
Рис. 1.29. Изображение с рис. 1.22: а) с уменьшением числа бит на пиксел до четырех и б) до трех
Рис. 1.30. Изображение с рис 1.22: а) с уменьшением числа бит на пиксел до двух и б) до одного
Рисунок 1.30 показывает случаи двух и одного бита на пиксел. В части а) четко видны четыре уров-
ня и имеется значительное количество сегментов. В части б) остались только черный и белый цвета,
вследствие чего большая часть информации об изображении оказалась потерянной. В главе 10 мы про-
демонстрируем некоторые приемы, такие как размытие (dithering), для улучшения качества изображе-
ния, в котором используется слишком мало бит на пиксел.
Цветные растровые изображения
Все же мы предпочитаем цветные изображения, поскольку они больше, чем серые полутоновые изображе-
ния, соответствуют нашему повседневному жизненному опыту. Цветные растровые изображения стали в
последние годы более доступными, поскольку резко упала стоимость высококачественных цветных дис-
плеев. Стоимость сканеров, способных оцифровывать цветные фотографии, также стала приемлемой.
Каждый пиксел цветного изображения имеет свой «код цвета» («color value») — числовое значение,
которое каким-либо образом представляет цвет. Существует много способов связывать между собой
числа и цвета (за подробностями обращайтесь в главу 12), однако чаще всего цвет описывается комбина-
50 Глава 1. Введение в компьютерную графику
цией величин красного, зеленого и синего цветов. Значение каждого пиксела представляет собой упо-
рядоченную тройку (ordered triple), например (23,14,51), которая описывает интенсивности красной,
зеленой и синей составляющих — в указанном порядке.
Число бит, используемых для представления цвета каждого пиксела, часто называют глубиной цве-
та (color depth), или цветовой насыщенностью пиксела. Каждая величина в тройке (красный, зеленый,
синий) занимает определенное число бит, а глубина цвета является суммой этих трех величин. Глубина
цвета, равная трем, позволяет использовать по одному биту на каждый компонент. Например, вели-
чина пиксела, равная (0,1,1), означает, что красная составляющая «выключена», то есть отсутствует,
а зеленая и синяя — «включены» (присутствуют). На большинстве дисплеев все составляющие склады-
ваются (исключения см. в главе 12), так что (0,1,1) означает сочетание зеленого и синего, воспринима-
емое как голубой цвет (cyan). Поскольку каждый компонент может быть включен или выключен, то
существует восемь возможных цветов, как показано в табл. 1.1. Как и ожидалось, одинаковые количе-
ства красного, зеленого и синего цветов (1,1,1) образуют белый цвет.
Таблица 1.1. Простое соответствие между кодом цвета и воспринимаемым цветом
Код цвета Изображение
0,0,0 Черный
0,0,1 Синий
0,1,0 Зеленый
0,1,1 Голубой
1,0,0 Красный
1,0,1 Пурпурный
1,1,0 Желтый
1,1,1 Белый
Глубина цвета, равная трем, редко предоставляет достаточную точность для задания значения каж-
дого компонента цвета, поэтому используются большие глубины цвета. Поскольку на компьютере столь
естественно иметь дело с байтами, то многие изображения имеют глубину цвета, равную восьми. В этом
случае каждый пиксел имеет один из 256 возможных цветов. В простейшем случае по три бита отво-
дится под красную и зеленую составляющие и два бита — под синюю. Однако чаще соответствие каж-
дого байта определенному цвету имеет более сложный характер, и применяется так называемая «кодо-
вая таблица цветов» («color look-up table»), которая будет обсуждаться в следующем разделе.
Изображения наивысшего качества, обеспечивающие «реалистичное цветовоспроизведение», называ-
ются полноцветными изображениями (true color). Они имеют глубину цвета 2м и используют, таким
образом, по одному байту для каждой составляющей. Похоже, достигнуто самое лучшее воспроизведе-
ние цвета, какое может воспринять глаз: увеличение числа бит уже не улучшают изображения. Однако
такое изображение требует огромного количества памяти: три байта на каждый пиксел. Высококаче-
ственное изображение размером 1080 на 1024 пиксела требует более трех миллионов байт!
На рис. 19—21 приведены цветные растровые изображения с различной глубиной цвета. На рис. 19
показано полноцветное изображение с глубиной цвета 24 бита. На рис. 20 показано ухудшение этого
изображения, происходящее при уменьшении глубины цвета до 8 посредством простого усечения крас-
ной и зеленой составляющих до 3 бит на каждую, а синей — до 2 бит. Изображение на рис. 21 также
имеет глубину цвета, равную 8, так что его пикселы содержат только 256 цветов, однако отдельные ис-
пользуемые в нем цвета были тщательно отобраны для лучшей цветопередачи. Методы такого выбора
мы рассмотрим в главе 12.
1.4. Графические устройства отображения
В данном разделю мы предлагаем обзор ряда аппаратных устройств, используемых для отображения
компьютерной {рафики. Список устройств включает в себя видеомониторы, графопостроители (плотте-
ры) и принтеры. За последние 30 лет было разработано огромное количество разнообразных графиче-
1.4, Графические устройства отображения
51
ских дисплеев, и продолжают появляться все новые и новые. Задача заключается в отображении как
можно более высококачественных картинок, которые как можно более точно передавали бы замысел
художника или инженера. Ниже мы кратко рассмотрим, какие типы изображений производятся сегод-
ня, как они применяются и какие типы устройств используются для их отображения. Одновременно
мы рассмотрим способы измерения «качества» изображения и покажем, какие из многочисленных ти-
пов устройств отображения соответствуют этому качеству.
1.4.1. Графические дисплеи
Некоторые устройства способны только вычерчивать линии (line-drawing devices). В силу ограничен-
ности технологии того времени большинство ранних компьютерных графиков было создано именно на
таких устройствах. Классическим примером такого устройства является перьевой графопостроитель
(плоттер) (pen plotter), перо которого перемещается над листом бумаги к определенному месту, зада-
ваемому компьютером, затем опускается и перемещается к другому месту, оставляя след чернил како-
го-либо цвета. В некоторых плоттерах имеется карусельный механизм с несколькими перьями, кото-
рые могут меняться автоматически согласно программе и таким образом чертить линии разных цветов.
Обыкновенно выбор различных цветов весьма ограничен, так как для каждого цвета нужно использо-
вать отдельное перо. «Качество» вычерчивания линии зависит от точности, с которой позиционирует-
ся перо, и от тонкости рисуемых линий.
Существуют различные виды перьевых графопостроителей. Планшетные графопостроители (flatbed
plotters) перемещают перо в двух направлениях относительно неподвижного листа бумаги. В барабан-
ных графопостроителях (drum plotters) бумага перемещается взад и вперед с помощью барабана, обес-
печивая таким образом одно направление движения, в то время как перо в вершине барабана движется
вправо и влево, что создает второе направление.
Рис. 1.31. Пример барабанного графопостроителя (предоставлено компанией
Hewlett Packard. Воспроизводится с разрешения)
На рис. 1.31 приводится образец барабанного графопостроителя. Для вычерчивания линий приме-
няются также видеодисплеи, называемые «векторными» («vector») дисплеями, дисплеями «случайной раз-
вертки» («random-scan») или «каллиграфическими» («calligraphic») дисплеями. Такие устройства име-
ют встроенные схемы, специально предназначенные для развертки электронного луча, оставляющего
светящийся след, от точки к точке экрана катодно-лучевой трубки. Поскольку каждый отрезок линии,
подлежащий отображению, требует очень мало памяти (две концевых точки и, возможно, цвет), век-
торные дисплеи могут рисовать изображение очень быстро (сотни или тысячи векторов в секунду).
Однако векторные дисплеи не могут отображать плавно закрашенные области или сканированные
изображения. Закрашивание области обычно имитируется штриховкой (cross-hatching) с различны-
ми узорами линий, как предлагается на рис. 1.32. Сегодня векторные дисплеи в большинстве случаев
вытеснены растровыми, за исключением узкоспециализированных приложений.
52
Глава 1. Введение в компьютерную графику
Рис. 1.32. Штриховка области для имитации его заполнения
1.4.2. Растровые отображающие устройства
В настоящее время большинство устройств, используемых для компьютерной графики, являются рас-
тровыми. Наиболее известными из растровых отображающих устройств (дисплеев) являются: видео-
монитор (video monitor), соединенный с персональными компьютерами или рабочими станциями
(рис. 1.33, а), и индикаторная панель (flat-panel), применяемая в портативных персональных компьютерах
(рис. 1.33, б). Широко используются устройства, создающие твердую копию (hard сору) изображения:
лазерный принтер (laser printer), матричный принтер (dot matrix printer), струйный плоттер (ink-jet
plotter) и устройство записи на пленку (film recorder).
б
Рис. 1.33. Видеомониторы как часть персональных компьютеров (а); индикаторная панель (5)
Растровые устройства имеют поверхность отображения (display surface), на которой располагает-
ся изображение. У этой поверхности определенное количество пикселов, которое она может показать, —
например 480 строк, каждая из которых содержит 640 пикселов. То есть такая поверхность изображе-
ния может одновременно показывать 480 х 640 ~ 307 000 пикселов. Во всех растровых дисплеях имеет-
ся встроенная система координат, которая устанавливает соответствие между заданным пикселом на
изображении и физическими координатами на поверхности отображения. Пример этого приведен на
рис. 1.34. Горизонтальная координата sx возрастает слева направо, а вертикальная sy — сверху вниз.
Такая «перевернутая» система координат типична для растровых дисплеев.
1.4. Графические устройства отображения
53
Рис. 1.34. Встроенная система координат для поверхности отображения растрового дисплея
Растровые дисплеи всегда тем или иным образом соединены с буфером кадров (frame buffer), обла-
стью памяти, достаточно большой, чтобы хранить все значения пикселов для дисплея (то есть хранить
битовую карту изображения). Буфер кадров может быть физической памятью внутри дисплея или мо-
жет храниться в главном (host) компьютере. Например, видеокарта (graphics card — графическая кар-
та), установленная в персональном компьютере, фактически содержит всю память, необходимую для
буфера кадров.
На рис. 1.35 показано, как изображение создается и отображается на дисплее. Графическая програм-
ма помещается в системную память и последовательно, инструкция за инструкцией, выполняется цен-
тральным процессором (central processing unit — CPU). Программа вычисляет значения для каждого пик-
села генерируемой картинки и загружает эти значения в буфер кадров. (Этот процесс мы подробно
обсудим позднее, когда будем создавать программные средства для записи «правильных» значений пик-
селов в буфер кадров.) Текущий процесс отображения контролируется «контроллером развертки»
(«scan controller»), работающим автономно (что предпочтительнее, чем под управлением программы)
и делающим то же самое, пиксел за пикселом. Контроллер развертки заставляет буфер кадров «про-
пускать» каждый пиксел через конвертор для преобразования его в соответствующее физическое
пятно (spot) на поверхности отображения. Конвертор считывает значение пиксела, например 01001011,
и преобразует его в соответствующую величину, которая создает цветовое пятно на дисплее.
Системная шина
Рис. 1.35. Блок-схема компьютера с растровым дисплеем
Процесс развертки
На рис. 1.36 приведено больше деталей процесса развертки (scanning process). Главная проблема состоит
в том, чтобы «послать» каждое значение пиксела из буфера кадров в нужное место поверхности отобра-
жения. Предположим, что каждый из пикселов в буфере кадров имеет двумерный адрес (х, у). Для каж-
дого адреса, например (136, 252), имеется определенная ячейка памяти, где хранится значение нужного
пиксела. Обозначим эту ячейку тет[13б][252].
54
Глава 1. Введение в компьютерную графику
Рис. 1.36. Развертка изображения из буфера кадров на отображаемую поверхность
Контроллер развертки посылает логический адрес (136,252) в буфер кадров, который задает значе-
ние тет[136][252]. Одновременно контроллер фиксирует физическую (точнее, геометрическую) пози-
цию (136, 252) на поверхности отображения. Позиция (136, 252) соответствует определенному физи-
ческому расстоянию в 136 единиц по горизонтали и 252 единицы по вертикали от левого верхнего угла
поверхности отображения. Различные растровые дисплеи используют различные единицы.
Величина mem[136][252] преобразуется в соответствующую интенсивность или цвет в соответствии с
заданным преобразованием, и эта интенсивность или цвет пересылаются в нужную физическую пози-
цию, а именно (136, 252), на поверхности отображения. Чтобы развернуть изображение всего буфера
кадров, каждая величина пиксела используется только один раз, а соответствующее ему пятно на по-
верхности отображения «возбуждается» нужной интенсивностью или цветом. В некоторых устройствах
такая развертка должна повторяться много раз в секунду для «регенерации» картинки. Видеомонито-
ры, к которым мы сейчас переходим, относятся как раз к таким устройствам.
Видеомониторы
Основным элементом видеомонитора является катодно-лучевая трубка (cathode-ray tube — CRT), по-
добная трубке телевизионных приемников. Рисунок 1.37 добавляет некоторые подробности к приве-
денному ранее обобщенному описанию систем, использующих в качестве устройства отображения ви-
деомонитор. В частности, на рисунке показан процесс преобразования значения пиксела в «световое
пятно». Изображенное там устройство имеет шестибитовую глубину цвета; поэтому буфер кадров также
имеет шесть битовых «плоскостей». Каждый пиксел использует по одному биту из каждой плоскости.
Таблица 1.2. Входные/выходные характеристики двухбитового АЦП
Ввод Напр яжение/яркость
00 0 * Мах
01 0,333 * Мах
10 0,666 * Мах
11 1 * Мах
Красная, зеленая и синяя составляющие пиксела занимают по паре битов каждая. Эти пары передают-
ся трем цифроаналоговым преобразователям — ЦАП (digit-to-analog converters — DACs), которые
преобразуют логические величины типа 01 в физическое напряжение. Соответствие между цифровыми
величинами на входе и напряжением на выходе показано в табл. 1.2, где под Мах понимается наибольший
уровень напряжения, который может задавать ЦАП.
1.4. Графические устройства отображения
55
Bvcbeo кадров Цифроаналоговые пушки Катушки
(6 плоскостей) преобразователи(ЦАП) Д™°™°нения
Рис. 1.37. Работа отображающей системы с цветным видеомонитором
Три уровня напряжений управляют тремя «пушками» внутри электронно-лучевой трубки, которые
поочередно возбуждают три потока электронов с интенсивностями, пропорциональными напряжени-
ям. Катушки отклоняющей системы отклоняют эти три луча таким образом, что они возбуждают три
крошечные фосфорные точки в нужном месте с координатами (х, у) на внутренней поверхности катод-
но-лучевой трубки. В зависимости от используемых фосфорных составов одна точка светится при воз-
буждении красным светом, другая — зеленым, а третья — синим. Эти точки расположены столь близко
друг к другу, что глаз человека видит одну составную точку и воспринимает цвет, являющийся суммой
трех цветовых составляющих. Таким образом, составную точку можно заставить светиться 4 х 4 х 4 = 64
различными цветами.
Как было описано ранее, контроллер развертки передает одно значение пиксела mem[x][y] в буфер
кадров и одновременно «передает» одну позицию (х, у) на внутреннюю поверхность электронно-лучевой
трубки CRT посредством посылки нужного сигнала катушкам отклоняющей системы. Поскольку свечение
фосфорной точки быстро тускнеет после прекращения сигнала, изображение в CRT необходимо быстро
обновлять (refresh) (обычно 60 раз в секунду), чтобы избежать неприятного мерцания (flicker) изоб-
ражения. Во время каждого «периода регенерации» контроллер развертки быстро сканирует всю па-
мять буфера кадров, отправляя каждое значение пиксела на его законное место на поверхности экрана.
Сканирование происходит строка за строкой по всему буферу кадров, причем каждая строка снаб-
жает значениями пикселов одну строку развертки (scan line) на внутренней поверхности CRT. Поря-
док сканирования обычно осуществляется слева направо вдоль строки развертки и сверху вниз самой
строкой развертки. (Историки говорят, что термин «строка развертки» произошел вследствие услов-
ных обозначений, а порядок нумерации строки развертки сверху вниз, при нулевом значении наверху,
есть результат перевернутой системы координат.)
Ряд более сложных и дорогих систем имеют буфер кадров, поддерживающий 24 плоскости памя-
ти. В каждый ЦАП может входить восемь бит, следовательно, имеется 256 уровней красного цвета,
256 уровней зеленого и 256 уровней синего, то есть всего 224 = 16 миллионов цветов.
Другим предельным случаем являются монохромные видеодисплеи, которые отображают единствен-
ный цвет различных уровней интенсивности. Единственный ЦАП преобразует значения пикселов в
буфере кадров в уровни напряжений, которые управляют единственной электронно-лучевой пушкой.
Трубка CRT содержит только один тип фосфора, так что он может выдавать различные интенсивности
только одного цвета. Отметим, что шесть плоскостей памяти в буфере кадров дают 26 = 64 оттенка серо-
го цвета.
Цветной дисплей на рис. 1.37 имеет фиксированную связь с отображаемым цветом. Например, значение
пиксела 001101 посылает 00 в «красный ЦАП», 11 в «зеленый ЦАП» и 01 в «синий ЦАП», выдавая смесь
яркого зеленого и темного синего цветов — голубовато-зеленый цвет. Аналогичным образом 110011
отображается как ярко-пурпурный цвет (bright magenta), а 000010 — как синий цвет средней яркости.
56
Глава!. Введение в компьютерную графику
1.4.3. Индексированный цвет и кодовая таблица
В некоторых системах используется альтернативный метод связи значений пикселов с цветами — кодовая
таблица цветов (color lookup table — LUT), которая предлагает программируемую связь между значени-
ем пиксела и результирующим отображаемым цветом. На рис. 1.38 дан простой пример такой связи.
Рис. 1.38. Устройство цветного дисплея со встроенной LUT
Глубина цвета по-прежнему равна шести, однако эти 6 бит, записанные в каждом пикселе, проходят
еще один промежуточный этап перед тем, как управлять электронно-лучевой трубкой. Эти биты ис-
пользуются как индекс в таблице из 64 элементов, обозначаемых как LUT[0]..LUT[63]. (Почему в этой LUT
ровно 64 элемента?) Например, если значение пиксела равно 39, то для управления ЦАП используются
величины, записанные в LUT[39], в отличие от той схемы, которая использует для ЦАП саму величи-
ну 39. Как показано на рис. 1.40, элемент таблицы LUT[39] содержит 15-битовую величину 01010 11001
10010. Первые пять бит (01010) направляются для запуска «красного ЦАП», следующие пять — для за-
пуска «зеленого ЦАП», а оставшиеся пять — для запуска «синего ЦАП».
Каждый из элементов таблицы LUT[ ] может быть заполнен программно, с помощью какой-нибудь
системной подпрограммы вроде setPaletteO. Например, команда
setPalette(39. 17. 25. 4):
установила бы в элемент LUT[39] 15-битовую величину 10001 11001 00100 (поскольку 17 в двоичной
системе равно 10001,25— 11001, а 4 — 00100).
Для того чтобы заставить определенный пиксел — скажем, тот, который находится в точке с коорди-
натами (х, у) = (479,532), — светиться заданным цветом, в буфер кадров необходимо записать величи-
ну 39 при помощи описанной раньше подпрограммы drawDotC):
drawDot(479. 532. 39):
// set pixel at (479, 532) to value 39
// устанавливаем пиксел с координатами (479, 532)
// значение 39
Каждый раз, когда буфер кадров «сканируется» для отображения, этот пиксел прочитывается как
величина, равная 39, вследствие чего значение, записанное в элементе таблицы LUT[39], посылается в
ЦАП. Такая программируемость предоставляет большую гибкость в выборе цветов, однако за все при-
ходится платить: программа (или программист) должны вычислять, какие цвета следует использовать!
Мы рассмотрим эту дилемму позже, в главе 10.
1.4. Графические устройства отображения
57
Какие возможности имеет данная схема отображения цветов? В системе, изображенной рис. 1.40,
каждый элемент таблицы LUT состоит из 15 бит, так что каждый цвет может быть выбран из 215 = 32 Кбайт =
- 32768 возможных. Набор из 215 предусмотренных системой цветов называют ее палитрой (palette),
поэтому мы говорим: данный дисплей «имеет палитру из 32 Кбайт цветов».
Проблема заключается в том, что значение каждого пиксела находится в пределах от 0 до 63, вследствие
чего одновременно в таблице LUT может быть записано только 64 различных цвета. Поэтому данная схе-
ма может отображать одновременно не более 64 различных цветов — «одновременно» означает время
одного сканирования всего буфера кадров, то есть примерно 1/60 секунды. Содержимое таблицы LUT не
может меняться посреди цикла развертки изображения, так что одна полная развертка использует фик-
сированный набор из 64 цветов палитры. Как правило, содержимое LUT остается неизменным на протя-
жении многих циклов развертки, хотя программа может изменить содержимое маленькой таблицы LUT
во время короткого периода «бездействия» (dormant) между двумя последовательными развертками.
Обобщая сказанное выше, представим себе систему растрового дисплея, которая имеет глубину цве-
та Ь бит (в этом случае в ее буфере кадров имеется Ь плоскостей), а каждый элемент кодовой таблицы
цветов LUT имеет размер w бит. В этом случае система может отображать 2® цветов, из них одновре-
менно 2Ь цветов.
1. Система с Ь - 8 битовыми плоскостями и шириной LUT w - 12 может отображать 4096 цветов,
из них любые 256 цветов одновременно.
2. Система с b - 8 битовыми плоскостями и шириной LUT w = 24 может отображать 224 - 16 777 216
цветов, из них любые 256 цветов одновременно.
3. Если b - 12 и w - 18, то такая система может отображать 256К - 262 144 цвета, из них 4096 одно-
временно.
Между числом битовых плоскостей b и шириной w таблицы LUT не устанавливается никакой жест-
кой зависимости. Обычно w кратно трем и, следовательно, равное число бит (®/3) управляет каждым
из трех ЦАП. Кроме того, Ь никогда не превышает w, вследствие чего размер палитры по меньшей мере
равен числу цветов, которое может быть отображено одновременно. (Почему никогда не создавалась
система с w < 6?)
Отметим, что LUT сама по себе требует очень мало памяти — всего 2Ь слов по w бит в каждом. Напри-
мер, если b ~ 12, a w “ 18, то LUT занимает всего 9216 байт памяти. Для чего вообще нужна LUT в системах
с растровым дисплеем? Обычно она используется в тех случаях, когда требуется уменьшить занимае-
мую память. Увеличение b значительно увеличивает размер памяти, необходимой для буфера кадров,
главным образом из-за большого количества пикселов. Устрашающий размер необходимой для этого
памяти способен значительно поднять стоимость всей системы.
Сравним стоимость двух систем с таблицей LUT и без нее. На рис. 1.39 приведен пример двух диспле-
ев размером 1024 на 1280 пикселов (таким образом, каждый из них поддерживает около 1,3 миллиона
пикселов). Обе эти системы позволяют задавать цвета с точностью до 24 бит, то есть обеспечивают «ре-
алистичное воспроизведение» полноцветного изображения («true color»).
1-я система (дорогая). Первая система имеет буфер кадров с 24 битами на пиксел и не имеет табли-
цы LUT, вследствие чего каждому из 1,3 миллиона пикселов может быть присвоено любое значение из
224 цветов. Каждый ЦАП управляется восемью битами. (Цифра «8» и косая черта «/», пересекающая
линию, ведущую к каждому ЦАП, указывают на наличие восьми битовых путей в ЦАП.) Объем памя-
ти, необходимый для буфера кадров данной системы, составляет 1024 х 1280 х 24 бита, что соответству-
ет почти четырем мегабайтам.
2-я система (недорогая). Вторая система имеет буфер кадров с 8 бит на пиксел, а также таблицу LUT
шириной 24 бита. Такая система может отображать 224 различных цветов, но не более 256 одновремен-
но. Объем памяти, необходимый для буфера кадров, составляет 1024 х 1280 х 8, то есть около одного
мегабайта. (Таблице LUT требуется всего лишь 768 байт памяти.) При значительной стоимости мегабайта
памяти вторая система значительно дешевле первой.
Помещение LUT в недорогую систему призвано компенсировать небольшое число допускаемых ею
различных значений пикселов. LUT позволяет программисту создавать полный набор цветов, хотя и це-
ной того, что конкретное изображение может содержать лишь усеченный их набор.
58
Глава 1. Введение в компьютерную графику
Дорогой (буфер кадров требует » 4 Мбайта)
1,3 миллиона пикселов
Недорогой (буфер кадров требует «1 Мбайт)
Рис. 1.39. Сравнение двух систем с растровыми дисплеями
В настоящее время дисплеи с LUT все еще широко применяются, потому что стоимость памяти оста-
ется высокой. Однако ситуация быстро меняется, поскольку стоимость памяти быстро падает. В настоя-
щее время многие персональные компьютеры приемлемой стоимости имеют 24-битовые буферы кадров.
Практические упражнения
1.4.1. Почему нельзя всегда иметь LUT?
Если LUT стоит недорого и дает много возможностей, то почему бы не иметь LUT и в системах с 24 би-
тами на пиксел?
1.4.2. Конфигурация системы
Сконфигурируйте свою систему для каждой из нижеперечисленных систем.
1. Нарисуйте блок-схему, подобную схеме на рис. 1.41.
2. Отметьте количество бит, связанных с буфером кадров, цифроаналоговыми преобразователя-
ми и с таблицей LUT (если она есть).
3. Вычислите (в байтах) объем памяти, необходимый для буфера кадров и таблицы LUT (если она
есть).
1. b - 15, LUT отсутствует;
2. 6 = 15, ® = 24;
3. Ь = 15,®= 18;
4. 6 = 12, LUT отсутствует.
1.4.4. Другие устройства растрового отображения
Видеомониторы — не единственные устройства растрового отображения; недавно были разработаны и
другие их виды. В состав портативных («laptop») компьютеров часто входят дисплеи типа «индика-
торная панель» (flat-panel), как показано на рис. 1.40. Каждый пиксел расположен на пересечении го-
ризонтальной и вертикальной проволочной сетки (grid wire). Для «включения» пиксела соответствую-
1.4. Графические устройства отображения
59
щие горизонтальная и вертикальная проволочки сетки возбуждаются, что порождает электрическое
поле в месте нахождения пиксела. Вследствие этого изменяется яркость в нужной точке.
Точный механизм преобразования электрического поля в видимую точку зависит от используемой
технологии. В случае жидкокристаллического дисплея (liquid crystal display — LCD) электрическое
поле изменяет поляризацию длинных кристаллических молекул внутри материала LCD. Это измене-
ние поля либо позволяет свету пройти сквозь панель, либо препятствует этому прохождению. Панели с
активной матрицей (active matrix panels) — это такие LCD-панели, в которых в месте расположения
каждого пиксела находится мельчайший транзистор. Этот транзистор реагирует на электрическое поле
и изменяет количество соответствующих жидких кристаллов пропорционально величине поля, обес-
печивая тем самым отображение различных уровней яркости. Кроме того, в этих транзисторах имеется
своя «память», которая сохраняет кристаллы в их настроенном виде, так что этот дисплей не нуждается
в регенерации. Такая схема резко увеличивает яркость дисплея. Цветные LCD-панели обеспечивают
разрешение от 800 до 1000 пикселов.
Вертикальные
проволочные
сетки
Рис. 1.40. Дисплеи типа «индикаторная панель»
Дисплей с плазменной панелью (plasma panel display) имеет геометрическую форму, подобную
изображенной на рис. 1.40, однако в материале пластины на месте каждого пиксела находятся мельчай-
шие неоновые лампочки. Такая лампочка включается и выключается с помощью электрического поля.
Подобно дисплею с активной матрицей, плазменная панель не нуждается в регенерации.
Еще некоторые типы растровых дисплеев рассматриваются в ссылках на других авторов (например,
Foley, 64).
1.4= 5. Растровые устройства для изготовления твердых копий
Зачастую желательно иметь постоянную версию изображения, обычно на бумаге или на пленке. Суще-
ствуют растровые устройства, изготавливающие твердую копию (hard сору) растрового изображения.
Каждое из них рисует картинки посредством передачи информации из буфера кадров, точка за точкой,
на носитель изображения.
О Устройства для записи на пленку. В устройстве записи на пленку (film recorder) «экраном» яв-
ляется полоска фотопленки, а электронный луч экспонирует пленку, пробегая (однократно) над
ней в соответствии с растровым рисунком. Иногда устройства записи на пленку являются от-
дельными устройствами со своими собственными буферами кадров, а иногда это просто камеры,
вмонтированные прямо в CRT-дисплей. Устройства записи на пленку часто используются для
изготовления кинофильмов или высококачественных 35-миллиметровых слайдов. Кроме того,
существуют видеомагнитофоны, делающие твердую электронную копию любого изображения,
записанного в их буфере кадров, которые затем могут быть показаны на экране телевизора.
60
Глава 1. Введение в компьютерную графику
О Лазерный принтер. Лазерные принтеры (laser printers) также развертывают растровые рисунки
из внутреннего буфера кадров путем быстрого сканирования внутренней поверхности отображе-
ния лазерным лучом. В точках, над которыми проходит луч, поверхность получает электриче-
ский заряд, что вызывает притяжение красящего порошка (тонера) к этим точкам. Затем тонер
переходит на бумагу и таким образом создает изображение. Лазерные принтеры обеспечивают
значительно большее разрешение, чем матричные, вследствие огромной точности, с которой мо-
жет быть позиционирован луч лазера.
О Струйный плоттер (принтер). Струйные плоттеры (inkjet plotters) делают твердые копии рас-
тровых изображений в цвете. Над листом бумаги быстро проходит мельчайшее сопло и разбрыз-
гивает чернила нужного цвета в каждую «позицию пиксела».
Рисунок 1.41, а показывает текст и графику, отпечатанную на матричном принтере, чаще всего
используемом с персональными компьютерами, а на рис. 1.14, б изображена печать, полученная с
помощью лазерного принтера. Матричные принтеры печатают точки с плотностью около 70 точек
на дюйм (dots per inch — dpi). С другой стороны, лазерные принтеры могут осуществлять печать
с плотностью 600 dpi или более, вследствие чего они могут производить графику очень высокого
качества.
displayed,
at we needn
to exclude
version tak
implificati
ssident campus
: programs to t
te course to ea
ard a degree la
rtes. This flexib
а б
Рис. 1.41. Увеличенные фрагменты изображений, отпечатанных на матричном (а) и лазерном принтерах {б)
Еще более высокая плотность печати может быть достигнута с помощью принтеров, используе-
мых в полиграфической промышленности. Например, наборная машина Linotronics осуществ-
ляет печать с плотностью 2540 dpi. Именно на таком устройстве был напечатан оригинальный
тираж этой книги.
Многие современные принтеры оборудованы встроенным микропроцессором с интерпретатором
языка описания страниц (page description language) PostScript1, который может генерировать
на печатаемой странице высококачественный текст и графику. На рис. 1.42 приведен короткий
«сценарий» (script), написанный на языке PostScript. При выводе файла с этим описанием на
печать встроенный интерпретатор PostScript создает изображение, показанное на рис. 1.42, б.
PostScript является аппаратно-независимым (device-independent) языком, поэтому одни и те же
команды можно посылать на различные принтеры, и, если не принимать во внимание различие в
качестве, все они напечатают одну и ту же основную страницу. (На принтерах, которые обладают
большей плотностью точек, тонкость линий, текста и рисунков заметно выше.) PostScript широ-
ко используется для лазерных принтеров, и мы неоднократно будем возвращаться к нему в рам-
ках этой книги.
1 PostScript является торговой маркой Adobe Systems, Inc.
1.5. Входные графические примитивы и устройства
61
200 300 moveto
200 300 200 60 0 аге
closepath
.7 setgray fill
showpage
Рис. 1.42. Сценарий на языке PostScript (а) и результирующее изображение (5)
PostScript можно использовать в качестве мощного языка программирования для создания гра-
фических изображений. Приложение Г знакомит нас с языком PostScript; там же показывается,
как писать небольшие сценарии, которые, будучи переданными на принтер, позволяют напеча-
тать запрограммированные в них графические изображения.
1.5. Входные графические примитивы и устройства
Многие устройства ввода позволяют пользователю управлять компьютером. Можно рассматривать ус-
тройство ввода с двух точек зрения: что это устройство представляет собой и что оно делает. Физиче-
ски каждое устройство — это некоторый механизм, например мышь, клавиатура или трекбол. Устрой-
ство определенным образом подогнано под руку пользователя, и пользователю удобно управлять им.
Устройство считывает манипуляции пользователя и посылает соответствующую цифровую информа-
цию обратно в графическую программу.
Посмотрим сначала, что делают устройства ввода, для этого исследуем типы данных, которые
каждое из них посылает в программу. Затем рассмотрим ряд устройств, наиболее часто применяемых
сегодня.
1.5.1. Типы входных графических примитивов
Каждое устройство передает в программу данные определенного вида (например, число, строку симво-
лов или координаты — position). Различные типы данных называются входными примитивами (input
primitives). Два устройства ввода, различающиеся физически, могут передавать данные одного и того
же типа; поэтому они логически генерируют одинаковые графические примитивы.
Важнейшими графическими примитивами являются:
О строка;
О вариант;
О валюатор;
О локатор;
О выбор.
Строка. Строка (string) является наиболее известным входным примитивом, создающим строку
символов и тем самым моделирующим работу клавиатуры. Когда приложение запрашивает строку,
работа программы приостанавливается до тех пор, пока пользователь вводит эту строку, отмечая ее ко-
62
Глава 1. Введение в компьютерную графику
нец знаком окончания (termination character). Затем введенная строка записывается в память и про-
грамма возобновляет работу.
Вариант. Вариант (choice) уведомляет о варианте выбора (selection) одного из пунктов заданного
перечня. Программист моделирует эту ситуацию с помощью блока кнопок или с помощью набора кно-
пок мыши.
Валюатор (ввод значения). Валюатор (valuator) генерирует вещественную величину в диапазоне от
0,0 до 1,0, которую можно использовать для задания длины строки, скорости действия или размера изоб-
ражения. Его моделью в представлении программиста является рукоятка (knob), которую можно плав-
но повернуть от 0 до 1.
Локатор. Основным требованием интерактивной графики является предоставление пользователю
возможности указывать местоположение на дисплее. Эту функцию выполняет входной примитив ло-
катор (locator), дающий на выходе пару координат (х, у). Пользователь манипулирует с устройством
ввода (обычно это мышь) для установления позиции видимого курсора на определенное место и дает
сигнал (triggers) для подтверждения своего выбора. Это действие возвращает в приложение величины
х и у, а также величину сигнала.
Выбор. Входной примитив «выбор* (pick) используется для указания на часть изображения, пред-
назначенную для добавочной обработки. В некоторых графических пакетах разрешается определять
картинку в терминах «сегментов* (segments), которые являются группами связанных между собой
изображений (например, отрезков прямых). В таких пакетах имеются средства для определения сег-
ментов и присвоения им идентификационных имен. При использовании функции pickO пользователь
«указывает* на часть картинки с помощью какого-нибудь физического устройства ввода, а пакет вы-
числяет, какой сегмент был выделен. Затем примитив pickO возвращает в приложение имя сегмента,
что позволяет пользователю манипулировать с этим сегментом: стереть его, переместить или сделать с
ним что-либо иное.
Перед запуском приложения графическая рабочая станция (автоматизированное рабочее место про-
ектировщика) устанавливается в исходное состояние. Помимо всего прочего, каждый логический вход-
ной примитив связан с одним из установленных физических устройств.
1.5.2. Типы физических входных устройств
Рассмотрим теперь входные устройства с другой точки зрения: как физический механизм, присоединя-
емый к компьютеру или рабочей станции.
Клавиатура. В состав всех рабочих станций обязательно входит клавиатура (keyboard), которая
по запросу посылает в приложение строки символов. Следовательно, клавиатуру обычно используют
для получения входного примитива string. В некоторых клавиатурах имеются клавиши управления
курсором или функциональные клавиши, часто используемые для генерирования входных примити-
вов choice.
Кнопки. Иногда на рабочей станции установлен отдельный блок кнопок (buttons). Пользователь
нажимает одну из этих кнопок, выполняя тем самым входную функцию choice.
Мышь. Компьютерная мышь (mouse) — это, вероятно, наиболее известное входное устройство, по-
скольку она проста и удобна в работе. Когда пользователь плащи перемещает мышь по поверхности
стола, мышь посылает в рабочую станцию информацию об изменении своей позиции. Программное
обеспечение рабочей станции отслеживает позицию мыши и соответственно ей перемещает по экрану
графический курсор (graphic cursor) — маленькую точку или крестик. Чаще всего мышь используется
для выполнения входных функций locate или pick. Как правило, на корпусе мыши имеется несколько
кнопок, которые пользователь может нажимать для запуска желаемой операции.
Планшет. Подобно мыши, планшет (tablet) используется для генерации входных примитивов locate
или pick. Как показано на рис. 1.43, у планшета имеется некоторая плоскость, по которой пользователь
может скользить пером (stylus). На конце этого пера имеется микропереключатель. С помощью нажа-
тия пером на планшет пользователь может запускать необходимую ему логическую функцию.
1.5. Входные графические примитивы и устройства
63
Рис. 1.43. Графический планшет
Планшет особенно удобен для оцифровки рисунков. Пользователь может с помощью скотча при-
крепить на поверхность планшета картинку и затем перемещать перо по ней, посылая путем нажатия
пером на поверхность планшета информацию о каждой новой точке, выбранной им для рабочей стан-
ции. Иногда меню отпечатано прямо на планшете, в этом случае пользователь просто выбирает (picks)
нужный пункт меню, нажимая пером на соответствующий ему прямоугольник. Программное обеспече-
ние преобразует каждый прямоугольник в нужную функцию выполняемого в данный момент прило-
жения.
Джойстик и трекбол
На рис. 1.44 изображены два похожих входных устройства, предназначенных для управления пози-
цией курсора на экране дисплея. Джойстик (joystick) на рис. 1.44, а представляет собой изогнутый
(arkade-style) рычаг, который можно повернуть в любом направлении для указания позиции. Трекбол
(trackball) на рис. 1.44, б снабжен крупным шаром, который можно вращать большим пальцем руки в
любом направлении для изменения позиции курсора. Внутренняя схема каждого из этих устройств
преобразует физическое перемещение в электрические сигналы, аналогично тому, как это делается в
мыши. Эти устройства используются преимущественно для функций locator и valuator.
Рис. 1.44. Джойстик (а) и трекбол (5)
Рукоятки. На рис. 1.45 показан блок рукояток (knobs), которые пользователь может поворачи-
вать, чтобы «набрать» какую-либо величину. Каждая рукоятка выполняет логическую функцию valuator.
64
Глава 1. Введение в компьютерную графику
Блоки рукояток, подобные приведенному на рисунке, часто входят в состав рабочей станции, использу-
емой для интерактивного проектирования трехмерных объектов. Пользователь может вращать отобра-
жаемый объект в трех направлениях, изменяя положение трех независимых рукояток. Кроме того, две
рукоятки можно использовать для установления курсора на экране в положение х и у. Таким образом,
с помощью этих рукояток можно выполнять функции locator, stroke и pick.
Рис. 1.45. Блок рукояток (с разрешения Tektronix, Inc.)
Спейсбол и информационная перчатка. Спейсбол (space ball) и информационная перчатка (data
glove), изображенные на рис. 1.46, являются сравнительно новыми входными устройствами. Оба они
предназначены для того, чтобы предоставить пользователю полный и одновременный контроль над
несколькими переменными посредством движений руки или пальцев. Сенсоры внутри каждого из этих
устройств воспринимают тончайшие движения руки, преобразуют их в значения функции val uator,
которые возвращаются в приложение. Эти устройства особенно удобны в тех ситуациях, когда сами движе-
ния руки имеют смысл в контексте программы (например, когда пользователь управляет рукой виртуаль-
ного робота), а эффект от этих движений имитируется на экране, за которым наблюдает пользователь.
Рис. 1.46. Спейсбол (с разрешения Logical 3D, Logitech Company) (а) и информационная перчатка
(с разрешения NASA Headquarters) (5)
1.6. Заключение
65
Оцифровка трехмерных объектов и запись движения
Рисунок 1.47 показывает устройство, которое может измерять положение точек в пространстве, позво-
ляя фиксировать трехмерные очертания предметов. В то время как луч лазера сканирует трехмерный
объект, создавая плоский растровый рисунок с координатами х, у, записывается информация о рассто-
янии до этого объекта. На рис. 1.48 показано аналогичное устройство, способное следить за положени-
ем нескольких точек на движущемся теле, что позволяет, например, подробно записывать движения
танцора.
Рис. 1.47. Оцифровка трехмерной формы (с разрешения Digiboties, Inc.)
Рис. 1.48. Запись движений танцора (с разрешения Motion Analysis, Inc.)
Раньше употреблялись и другие устройства, такие как световое перо (light реп), координатный ма-
нипулятор (thumbwheel), пульт ручного управления (paddle) и т. д. (Полное описание подобных уст-
ройств можно найти в таких книгах, как Foley, 64 и Rogers, 175).
1.6. Заключение
В этой главе мы ознакомились с предметом компьютерной графики и рассмотрели различные области
применения компьютерной графики при создании изображений. Нами было описано много видов гра-
фических устройств, из которых чаще всего используются растровый видеомонитор и лазерный прин-
тер. Кроме того, мы определили главные выходные примитивы (output primitives) — ломаные линии,
текст, закрашенные области и растровые изображения — и описали атрибуты, которые обычно связаны
с каждым из этих примитивов. Особое внимание было уделено растровому изображению — в силу его
важности как средства создания картинок, а также как внутреннего механизма устройств отображения.
Главным свойством растрового изображения является то, что оно состоит из набора чисел, причем каж-
дое число может принимать только определенное множество значений, что делает растровое изображе-
3 Ф. Хилл
66
Глава 1. Введение в компьютерную графику
ние дискретным как в двух пространственных направлениях, так и в измерении цвет-яркость. Столь же
важным является естественная связь между значениями пикселов и их расположением в памяти компью-
тера; и мы будем многократно использовать эту связь на протяжении всей книги.
Мы описали различные типы графических входных устройств, используемых в интерактивной ком-
пьютерной графике; кроме того, обсудили входные примитивы (input primitives), создаваемые при по-
мощи этих входных устройств.
1.7. Дополнительная литература
Многие книги предоставляют отличное введение в предмет компьютерной графики. Херн и Бейкер
(Hearn and Baker, [Hearn, 101]) дают обстоятельный и интересный обзор этого предмета с множеством
примеров. Фолей и Ван Дам (Foley and Van Dam, [Foley, 65]), а также Дэвид Роджерс (David Rogers,
[Rogers, 174]) предлагают дополнительные технические подробности о многих типах графических вход-
ных и выходных устройств. Превосходная серия из пяти книг, известная как «Графические самоцветы»
(«Graphics Gems», [Gems]), впервые опубликованная в 1990 году, содержит в себе множество новых
идей, почерпнутых у исследователей и практиков, работающих в области графики во всем мире.
Существует также целый ряд газет и журналов, которые дают хороший обзор новых технологий в
области компьютерной графики. Самым доступным из них является журнал «Компьютерная графика
и ее приложения» («Computer Graphics and Applications»), выпускаемый Институтом инженеров по элект-
ротехнике и электронике (Institute of Electrical and Electronic Engineer — IEEE), в котором часто публи-
куются обзоры новых идей в области графики. Классическим собранием новых результатов в области
графики являются ежегодные Труды SIGGRAPH (Proceedings of SIGGRAPH, [SIGGRAPH]), а также
журнал Ассоциации вычислительного оборудования (Association for Computing Machinery) «Новости
графики» (ACM’s Transactions on Graphics, [TOGS]). Следует также упомянуть сравнительно недавно
появившийся «Журнал графических средств» (Journal of Graphs Tools, [JGT]).
2 Начальная стадия:
рисование фигур
□ Первые программы, создающие картинки.
□ Знакомство с основными компонентами, имеющимися в любой
программе с OpenGL.
□ Разработка нескольких элементарных графических инструментов
для рисования прямых линий, ломаных линий и полигонов.
□ Разработка инструментария, позволяющего пользователю
управлять программой при помощи мыши и клавиатуры.
Машины существуют; так давайте использовать их, чтобы создавать красоту, современную красоту,
пока мы сами занимаемся этим. Ведь мы живем в двадцатом веке.
Олдос Хаксли (Aldous Huxley)
В разделе 2.1 «Начальная стадия создания изображения» рассматриваются основы написания про-
грамм, выполняющих простые рисунки. Обсуждается важность аппаратно-независимого програм-
мирования, описаны особенности оконных программ, а также программ, управляемых событиями.
Раздел 2.2 «Рисование основных графических примитивов» знакомит с использованием OpenGL как с
аппаратно-независимым интерфейсом прикладного программирования (Application Programming
Interface — API), что подчеркивается на протяжении всей книги; а также показывает, как рисовать
различные графические примитивы. Использование OpenGL иллюстрируется примерами рисунков,
таких как созвездие Большой Медведицы, ковер Серпинского (Sierpinski gasket), а также график
математической функции. В разделе 2.3 «Создание рисунков из линий» показано, как создавать изобра-
жения на базе ломаных линий и полигонов; а также начинается построение персональной библиотеки
графических утилит. Раздел 2.4 «Простое взаимодействие с помощью мыши и клавиатуры» посвящен
интерактивному графическому программированию, когда пользователь может указывать положения
точек на экране с помощью мыши или управлять работой программы нажатием клавиш на клавиатуре.
Глава заканчивается тематическими заданиями, которые иллюстрируют высказанные ранее идеи и глуб-
же погружают нас в основные темы главы.
68
Глава 2. Начальная стадия: рисование фигур
2.1. Начальная стадия создания изображения
Как и в случае многих других дисциплин, компьютерная графика изучается быстрее всего в процессе ее
создания: при кодировании и тестировании программ, воспроизводящих различные изображения. Луч- '
ше всего начинать с простейших задач. Когда вы их изучите, можете попытаться написать их различ-
ные варианты, чтобы посмотреть, что получится, и таким образом, продвигаться к рисованию более
сложных сцен.
Для того чтобы начать работать, вам необходима программная среда, которая позволит вам писать и
исполнять программы. Что касается графики, то эта среда должна включать в себя как аппаратные сред-
ства для отображения графики (обычно это CRT-дисплей, который мы в дальнейшем будем называть
«экраном»), так и библиотеку инструментов, которую ваши программы смогут использовать для фак-
тического рисования графических примитивов.
Каждая графическая программа начинает работу с задания некоторых начальных условий, которые
включают в себя установку желаемого режима дисплея, выбор системы координат для задания точек,
линий и т. д. На рис. 2.1 показан ряд вариантов, которые могут встретиться. На рис. 2.1, а для рисования
используется весь экран. Инициализация дисплея заключается в переключении его в «графический
режим», а система координат установлена так, как показано на рисунке. Координаты х и у измеряются
в пикселах, причем х возрастает вправо, а у — вниз.
Рис. 2.1. Некоторые часто встречающиеся варианты форматов дисплея
На рис. 2.1, б изображена более современная система, так называемая «оконная» («window-based»).
Такая система может одновременно поддерживать на экране дисплея несколько различных прямоуголь-
ных окон. Ее инициализация включает создание и «открытие» нового графического окна (мы будем
называть его «экранным окном»1 («screen window»), В графических командах используется система
координат, привязанная к этому окну: обычно х возрастает вправо, а у — вниз. На рис. 2.1, в показан
вариант, в котором использована начальная система координат «вправо-вверх»2, где у возрастает при
движении вверх3.
Обычно в каждой системе имеется несколько элементарных графических инструментов, с помо-
щью которых пользователь может начать работу. Самый главный из них имеет название типа
setPixel (х.у.color) и предназначен для присвоения отдельному пикселу с координатами (х,у) значе-
ния цвета, задаваемого переменной color. Иногда этот инструмент имеет другое имя, например
putPixel(), setPixel О или drawPointO. Наряду с setPixelO почти всегда имеется еще один инструмент
для рисования прямой линии, например Iine(xl,yl,x2.y2), который рисует прямую между точками с
1 Слово «окно» («window») в графике употребляется чрезмерно часто; мы будем стараться выделять различные варианты использо-
вания этого термина.
2 Некоторые системы представляют собой рабочие станции UNIX, работающие с X Windows, компьютер IBM PC с системой
Windows 95 под API, атакже компьютер Apple Macintosh, использующий встроенную библиотеку QuickDraw.
3 Пример такой системы координат — любая «оконная» система, работающая с OpenGL.
2.1. Начальная стадия создания изображения
69
координатами (xl.yl) и (х2,у2). В других системах этот инструмент может называться drawLineO или
LineO. Группа команд
linedOO. 50. 150. 80);
line(150. 80. 0. 290);
нарисует в каждой из систем изображения, приведенные на рис. 2.1. Другие системы могут не иметь
команды 11 пе(), а вместо нее для рисования прямых пользоваться командами moveto(x, у) и 1 ineto(x, у).
Можно провести аналогию между этими командами и перьевым плоттером, перо которого имеет неко-
торые «текущие координаты» («current position»). Предполагается, что команда moveto(x, у) переме-
щает перо над бумагой в положение (х, у), устанавливая тем самым текущие координаты (г, у); команда
11 neto(x, у) рисует линию от текущих координат до координат (х,у), после чего текущие координаты
устанавливаются в этой точке (х,у). Каждая из этих команд перемещает перо из его текущих коорди-
нат в новые координаты. Затем эти новые координаты становятся текущими. Картинки на рис. 2.1 мож-
но было нарисовать с помощью группы команд
movetoClOO, 50):
lineto(150. 80):
UnetoCO. 290);
Получив такую систему в свое распоряжение, энергичный программист может разработать целый
инструментарий сложнейших функций, использующих эти элементарные команды, и тем самым со-
здать мощную библиотеку графических подпрограмм. Тогда законченные графические приложения
могут писаться с применением этой персональной библиотеки.
Очевидная проблема состоит в том, что каждый графический дисплей использует для своей работы
различные основные команды, а каждая программная среда имеет различные наборы инструментов для
создания графических примитивов. Такое разнообразие делает затруднительным перенос программы
из одной программной среды в другую (рано или поздно каждый сталкивается с необходимостью передел-
ки программы под новую среду), следовательно, программист должен создавать все необходимые инстру-
менты для новой программной среды. Необходимость подобной реконструкции может потребовать суще-
ственных изменений всей структуры библиотеки или приложения и большой работы программиста.
2.1.1. Аппаратно-независимое программирование и OpenGL
Приятно, когда возможен одинаковый подход к написанию графических приложений, когда, например,
одна и та же программа может быть скомпилирована и запущена в различных графических средах, ког-
да есть гарантия, что на любом дисплее будет получено примерно одинаковое изображение. Такой под-
ход и называется аппаратно-независимым графическим программированием. В OpenGL предлагается
программное средство, при котором перенос графической программы требует только установки соот-
ветствующих библиотек OpenGL на новой машине, а само приложение не требует никаких изменений
и вызывает из новой библиотеки те же самые функции с теми же параметрами. В результате получают-
ся те же графические результаты. Метод создания графики в Open L был принят большим количе-
ством компаний, и библиотеки OpenGL существуют для всех значимых графических сред1.
OpenGL часто называют «интерфейсом прикладного программирования» (Application Programming
Interface — API), Он представляет собой набор подпрограмм, которые может вызывать программист,
и примеры того, как эти подпрограммы работают, создавая графику. Программист «видит» только ин-
терфейс и поэтому избавлен от необходимости вникать в специфику оборудования и в особенности
программного обеспечения установленной графической системы.
OpenGL наиболее ярко проявляет свои возможности при рисовании изображений сложных трех-
мерных (3D) сцен. Эти возможности могли бы показаться даже чрезмерными при рисовании простых
двумерных (2D) объектов. Однако OpenGL прекрасно работает и при 2О-рисовании, обеспечивая тем
самым унифицированный подход к созданию изображений. Мы начинаем наше знакомство с OpenGL
1 В приложении А показано, как организовывать и начинать работу с OpenGL в различных программных средах.
70
Глава 2. Начальная стадия: рисование фигур
с применения более простых его конструкций, используя многие опции по умолчанию. Позже, при на-
писании программ для создания сложной ЗП-графики, мы изучим более мощные инструменты OpenGL.
Хотя мы будем разрабатывать большинство наших графических средств на базе возможностей OpenGL,
мы тем не менее «приоткроем завесу» и посмотрим, как работают классические графические алгорит-
мы. Важно понять, как реализовывать такие программные средства, даже если вы используете в боль-
шинстве своих приложений уже готовые версии OpenGL. При особых обстоятельствах вам может по-
требоваться для какой-либо задачи альтернативный алгоритм, или вы можете встретить новую задачу,
которую OpenGL не умеет решать. Кроме того, вам может понадобиться разработать графическое при-
ложение, вовсе не использующее OpenGL.
2.1.2. Оконное программирование
Как уже упоминалось, многие современные графические системы являются оконными (windows based)
и показывают на экране несколько перекрывающихся окон одновременно. Пользователь с помощью
мыши может перемещать окна по экрану, а также изменять их размер. При работе с OpenGL мы будем
рисовать в одном из таких окон, как мы уже видели на рис. 2.1, в.
Программирование управляемости событиями
Другим свойством, которым обладает большая часть оконных программ, является их управляемость
событиями (event driven). Это означает, что программы реагируют на различные события, такие как
щелчок мышью, нажатие на клавишу клавиатуры или изменение размеров окна на экране. Система авто-
матически устанавливает очередь событий (event queue), которая получает сообщения о том, что произош-
ло некоторое событие, и обслуживает их по принципу «первым пришел — первым обслужен». Про-
граммист организует свою программу как набор функций обратного вызова (callback functions), которые
выполняются, когда происходят события. Функция обратного вызова создается для каждого типа со-
бытий, которые могут произойти. Когда система удаляет событие из очереди, оно просто выполняет
функцию обратного вызова, связанную с данным типом событий. Тем программистам, которые при-
выкли делать программы по принципу «сделай то, затем сделай это...», потребуется некоторое перео-
смысление. Новая структура программ может быть передана словами «не делай ничего, пока не произой-
дет какое-нибудь событие, а затем сделай определенную вещь».
Метод связи функции обратного вызова с определенным типом события часто полностью зависит
от системы. Однако вместе с OpenGL поставляется набор утилит (Utility Toolkit) (см. приложение А),
в котором предусмотрены программные средства для того, чтобы помочь в организации управления со-
бытиями. Например, команда
gl utMouseFunc(myMouse):
// register the mouse action function
// функция для регистрации действий мыши
регистрирует функцию myMouseO в качестве функции, подлежащей выполнению при возникновении
события «мышь». Префикс «glut» показывает, что данная функция является частью OpenGL Utility
Toolkit. Программист размещает в myMouseO код для обработки всех возможных действий мыши, кото-
рые представляют для него интерес.
В листинге 2.1 приведен скелет примерной функции mainO для программы, управляемой события-
ми. Большинство наших программ в данной книге будут основываться на этой структуре. Существует
четыре основных типа событий, с которыми мы будем работать, а «gluU-функции доступны каждому.
Листинг 2.1. Структура управляемой событиями программы, использующей OpenLG
void mainO
{
initialize things1
1 Замечания, выделенные курсивом внутри фрагментов исходного кода, представляют собой скорее псевдокод, чем настоящий про-
граммный код. Эти замечания предполагают действия, которые должен выполнять в этом месте подразумеваемый реальный код.
2.1. Начальная стадия создания изображения
71
// инициализируем все. что необходимо
create a screen window
11 создаем экранное окно
glutDIsplayFunc(myDisplay);
// register the redraw function
// регистрируем функцию обновления окна
glutReshapeFunc(myReshape):
// register the reshape function
// регистрируем функцию изменения формы
glutMouseFunc(myMouse);
// register the mouse action function
// регистрируем функцию реакции на действия мыши
glutKeyboardFunc(myKeyhoard);
// register the keyboard action function
// регистрируем функцию реакции на действия
// клавиатуры
perhaps initialise other things
И при необходимости инициализируем что-то еще
glutMainLoopO:
// enter the unending main loop
// входим в бесконечный главный цикл
}
all of the callback functions are defined here
// здесь определены все функции обратного вызова
О glutDisplayFuncCmyDisplay). Когда система решает, что какое-нибудь окно на экране подлежит пе-
рерисовке, она создает событие «redraw» (обновить). Это имеет место при первом открытии окна,
а также когда окно вновь становится видимым, когда другое окно перестало его заслонять. В дан-
ном случае функция myDi spl ay С) зарегистрирована в качестве функции обратного вызова для со-
бытия обновления.
О gl utReshapeFunc(myReshape). Форма экранного окна может быть изменена (reshape) пользователем,
обычно путем захвата мышью угла окна и смещения его с помощью мыши (простое перемещение
окна не приводит к событию «изменение формы».) В данном случае функция myReshapeO зареги-
стрирована с событием изменения формы окна. Как мы увидим дальше, функции myReshapeO ав-
томатически передаются аргументы, информирующие о новой ширине и высоте изменившего
свою форму окна.
О glutMouseFunc(myMouse). Когда нажимают или отпускают одну из кнопок мыши, то возникает со-
бытие «мышь» (mouse). В данном случае функция myMouseO зарегистрирована в качестве функции,
которая будет вызываться всякий раз, когда произойдет событие «мышь». Функции myMouseO
автоматически передаются аргументы, описывающие местоположение мыши, а также вид дей-
ствия, вызываемого нажатием кнопки мыши.
О glutKeyboardFunc(myKeyboard). Эта команда регистрирует функцию myKeyboardO для события,
заключающегося в нажатии или отпускании какой-либо клавиши на клавиатуре. Функции
myKeyboardO автоматически передаются аргументы, сообщающие, какая клавиша была нажата.
Для удобства этой функции также передается информация о положении мыши в момент нажа-
тия клавиши.
Если в какой-либо программе мышь не используется, то соответствующую функцию обратного вы-
зова не нужно писать или регистрировать. В этом случае щелчок мыши не окажет на программу ника-
кого действия. Это же верно для программ, не использующих клавиатуру.
Последняя функция, использованная в листинге2.1, — это glutMainLoopO. Когда выполняется эта
инструкция, программа рисует начальную картину и входит в бесконечный цикл, находясь в котором
72
Глава 2. Начальная стадия: рисование фигур
она просто ждет наступления событий. (Нормальное завершение работы любой программы осуществ-
ляется щелчком мыши по прямоугольнику «выход» (go away), который имеется в каждом окне.)
2.1.3. Открытие окна для рисования
Первая задача при создании изображений заключается в открытии экранного окна для рисования. Эта
работа является достаточно сложной и зависит от системы. Поскольку функции OpenGL являются ап-
паратно-независимыми, то в них не предусмотрено поддержки управления окнами определенных сис-
тем. Однако в OpenGL Utility Toolkit включены функции для открытия окна в любой используемой
вами системе.
Листинг 2.2. Программный код, использующий OpenGL Utility Toolkit для открытия начального окна для рисования
// appropriate includes до here - see Appendix 1
// здесь должны стоять соответствующие операторы
// включения includes - см.приложение А
void maindnt argc. char** argv)
{
glutlnit(&argc. argv);
// initialize the toolkit
// инициализируем инструментарий
glut!nitDisplayMode(GLUT_SINGLE | GLUT_RGB);
// set the display mode
// устанавливаем режим дисплея
glutIn i tWindowS i ze(640,480);
// set window size
// устанавливаем размер окна
glutInitWindowPosition(100,150):
// set the window position on screen
// устанавливаем положение окна на экране
glutCreateWindowC'my first attempt"):
//"my first attemptмоя первая попытка"
// open the screen window
// открываем экранное окно
// register the callback functions
// регистрируем функции обратного вызова
glutDisplayFunc(myDIsplay);
glutReshapeFunc(myReshape):
glutMouseFunc(myMouse);
glutKeyboardFunc(myKeyboard);
mylnitO:
// additional initializations as necessary
// дополнительные инициализации при необходимости
glutMainLoopO:
// go into perpetual loop
// входим в бесконечный цикл
Листинг 2.2 конкретизирует структуру листинга 2.1, показывая целиком функцию mainO на при-
мере программы, рисующей графики в экранном окне. Первые пять вызовов функции используют
OpenGL Utility Toolkit для открытия окна для рисования. В своих первых графических программах вы
можете просто скопировать отсюда эти функции; позднее мы увидим, какой смысл имеют различные
2.2. Рисование основных графических примитивов
73
аргументы и как заменить некоторые из них для достижения определенных эффектов. Первые пять
функций инициализируют и отображают экранное окно, в котором наша программа будет работать с
графикой. Дадим короткое описание того, что делает каждая из этих функций:
О glutlnitC&argc.argv). Эта функция инициализирует OpenGL Utility Toolkit. Ее аргументы для пере-
дачи информации о командной строке являются стандартными; здесь мы не будем их использовать.
О glutInitDisplayMode(GLUT_SINGLE|GLUT_RGB). Эта функция определяет, как должен быть инициали-
зирован дисплей. Встроенные в нее константы GLUT_SINGLE и GLUT_RGB с оператором OR (или) меж-
ду ними показывают, что следует выделить один дисплейный буфер и что цвета задаются с помо-
щью сочетаний красного, зеленого и синего цветов. Позднее мы будем изменять эти аргументы.
Например, для плавной анимации мы будем использовать двойную буферизацию.
О glutlnitWindowSize(640,480). Эта функция устанавливает, что экранное окно при инициализации
должно иметь 640 пикселов в ширину и 480 пикселов в высоту. Во время выполнения программы
пользователь может изменять размер этого окна по своему желанию.
О glutInitWindowPosition(100,150). Эта функция устанавливает, что верхний левый угол данного
окна должен находиться в 100 пикселах от левого края и в 150 пикселах от верхнего края. Во вре-
мя выполнения программы пользователь может перемещать это окно, куда пожелает.
О glutCreateWindow("my first attempt"). Эта функция фактически открывает и отображает экранное окно,
помещая текст заголовка «ту first attempt» (моя первая попытка) в строку заголовка (title bar) окна.
Остальные функции в mainO регистрируют функции обратного вызова, как уже описывалось ранее,
выполняют все инициализации, специфические для данной программы, после чего запускают на вы-
полнение главный событийный цикл (event loop). Программист (вы!) должен реализовывать каждую
из функций обратного вызова аналогично mylnitO.
2.2. Рисование основных графических примитивов
Мы намерены рассмотреть технику программирования для рисования большого числа геометрических
форм, которые составляют интересные картины. Команды рисования будут помещаться в функцию
обратного вызова, связанную с событием redraw (обновление), например, в функцию myDisplayO.
Прежде всего мы должны определить систему координат, в которой будем описывать графические
объекты, и назначить, где они будут появляться в экранном окне. Похоже, что программирование ком-
пьютерной графики вовлекает нас с бесконечную борьбу с заданием различных систем координат и
управлением ими. Поэтому мы будем двигаться от простых случаев к более сложным.
Рис. 2.2. Начальная система координат для рисования
74
Глава 2. Начальная стадия: рисование фигур
Начнем с интуитивной системы координат, которая привязана непосредственно к системе коорди-
нат экранного окна (см. рис. 2.1, в) и измеряет расстояния в пикселах. Наше первое шаблонное экран-
ное окно, показанное на рис. 2.2, имеет 640 пикселов в ширину и 480 пикселов в высоту. Координата х
изменяется от 0 на левом крае до 639 на правом крае. Координата у изменяется от 0 на нижнем крае до
479 на верхнем крае. Мы определим данную систему координат позже, после изучения нескольких ос-
новных примитивов.
OpenGL предоставляет средства для рисования всех выходных примитивов, описанных в главе 1.
Большинство из них, такие как точки, линии, ломаные, полигоны, задаются одной или несколькими
вершинами (vertices). Для рисования таких объектов в OpenGL необходимо передать ему список вер-
шин. Этот список возникает между двумя вызовами OpenGL-функций: glBeginOn glEndO. Аргумент в
glBeginO определяет, какой объект рисуется. Например, на рис. 2.3 приведены три точки, нарисован-
ные в окне шириной в 640 пикселов и высотой в 480 пикселов. Эти точки рисуются с помощью следую-
щей последовательности команд:
glBegin(GL_POINTS):
glVertex2i(100.50):
glVertex2i(100.130);
glVertex21(150.130);
glEndO;
Рис. 2.3. Рисование трех точек
GL_POINTS является встроенной константой OpenGL. Для рисования других примитивов следует за-
менить GL_POINTS на GL_LINES, GL_POLIGON и т. д. Каждая из этих констант будет введена в свое время.
Как мы увидим позже, эти команды посылают информацию о вершине в «графический конвейер»
(«graphics pipeline»), в котором она проходит ряд преобразований. Для наших целей достаточно счи-
тать, что эта информация направляется более или менее прямо в систему координат экранного окна.
Многие функции в OpenGL, такие как glVertex2i(), имеют несколько вариантов, различающихся
между собой числом и типом аргументов, передаваемых в функцию. Рисунок 2.4 показывает, какой
формат имеют вызовы таких функций.
glVertex2i(...)
/ / tx
Библиотека gl Основная Число Тип
команда аргументов аргумента
Рис. 2.4. Формат команд в OpenGL
2,2. Рисование основных графических примитивов
75
Префикс «д!» указывает, что функция взята из библиотеки OpenGL (в отличие от префикса «glut»
у функций из GL Utility Toolkit). Затем идет основная часть команды, за ней следует число аргументов,
пересылаемых в функцию (чаще всего 3 и 4), и, наконец, тип аргумента (i для целых величин, f или d для
величин с плавающей точкой и т. д., так как у нас всего лишь краткое описание). Если мы захотим сослаться
на основную команду, не уточняя специфику ее аргументов, то будем использовать звездочку: gl Vertex*().
Для создания той же картинки из трех точек, изображенной на рис 2.3, вы могли бы, например, пере-
дать функции вещественные величины вместо целых, используя для этого следующие команды:
glBegin(GL_POINTS):
glVertex2d(100.0,50.0):
glVertex2d(100.0,130.0):
glVertex2d(150.0.130.0):
glEndO:
Типы данных OpenGL
OpenGL работает с определенными типами данных. Например, функции вроде glVertex2i() требуют
целых величин определенного размера (32 бита). Хорошо известно, что в некоторых системах тип дан-
ных int из С или C++ является 16-битным, в то время как в других системах он 32-битный. Не суще-
ствует также стандартного размера для типов float и double. Для гарантии того, что OpenGL-функции
получают нужные типы данных, полезно использовать для типов OpenGL встроенные имена, такие как
GLint или GLfl oat. Список типов OpenGL приведен в табл. 2.1. С некоторыми из этих типов мы столк-
немся лишь позднее.
Таблица 2.1. Суффиксы команд и типы данных аргументов
Суффикс Тип данных Обычный тип С или C++ Название типа в OpenGL
b 8-битное целое (символ со знаком) signed char Glbyte
S 16-битное целое (короткое целое) short Glshort
I 32-битное целое (длинное целое) int или long GLint, GLsizei
f 32-битное вещественное (с плавающей точкой) float GLfloat, GLclampf
d 64-битное вещественное (двойной точности) double GLdouble, GLclampd
ub 8-битное число без знака (символ без знака) unsigned char DLubyte, GLboolean
us 16-битное число без знака (короткое целое без знака) unsigned short GLushort
ut 32-битное число без знака (целое без знака или длинное целое без знака) unsigned int или unsigned long GLuint, GLenum, GLbitfield
Пусть, к примеру, функция с суффиксом 1 «ожидает» 32-битное целое, а ваша система может пере-
дать int как 16-битное целое. Тогда если бы вы захотели инкапсулировать команды OpenGL для рисо-
вания точки в базовую функцию вроде drawDott), то было бы соблазнительно использовать такой код:
void drawDotdnt х. int у)
<- danger: passes ints
<- опасность: передает целые (int)
{
// draw dot at Integer point(x.y)
// рисуем точку с целыми координатами (х.у)
glBegin(GL_POINTS):
glVertex2i(х.у):
glEndO:
1
Этот код передает ints в функцию glVertex2i(). Это сработает в системах, использующих 32-битный
тип ints, однако в тех системах, где ints — 16-битный, могут возникнуть проблемы. Надежнее писать
76
Глава 2. Начальная стадия: рисование фигур
функцию drawingDotO1 так, как приведено в листинге 2.3, а также использовать в своих программах тип
GLints. Когда вы перекомпилируете свои программы в новой системе, типы GLint, GLfloat и т. д. будут
связываться с соответствующими типами C++ (в заголовочном файле GL.h OpenGL — см. приложе-
ние А) для этой системы, и эти типы будут использоваться постоянно во всей программе.
Листинг 2.3. Подробности инкапсуляции OpenGL в базовой функции drawDotO
void drawDot(GLint х. GLint у):
{
// draw dot at integer point (x. y)
// рисуем точку с целыми координатами (х. у)
glBegin(GL_POINTS):
glVertext2i(х, у);
glEndO:
}
«Состояние» OpenGL
OpenGL отслеживает множество переменных состояния (state variables)-, текущий размер точки, теку-
щий цвет рисования, текущий цвет фона и т. д. Значение любой переменной состояния остается неиз-
менным до тех пор, пока не получено новое значение. Размер точки может быть установлен с помощью
функции glPointSizeO, принимающей один вещественный аргумент. Если этот аргумент равен 3.0, то
точка обычно рисуется как квадратик со стороной в три пиксела. (Если вы хотите узнать дополнитель-
ные подробности об этой или о других функциях OpenGL, то вам следует обратиться к соответствую-
щей документации по OpenGL, часть из которой доступна в он-лайновом режиме в Интернете; см. при-
ложение А). Цвет для рисования (color of a drawing) может быть задан с помощью функции
glColor3f(red. green, blue):
где значения переменных red, green и blue изменяются от 0,0 до 1,0. Например, некоторые из цветов,
перечисленных в табл. 1.1, можно задать с помощью такой группы командных строк:
glColor3f(1.0, 0.0. 0.0):
// set drawing color to red
// устанавливаем красный цвет рисования
glColor3f(0.0. 0.0. 0.0):
// set drawing color to black
// устанавливаем черный цвет рисования
glColor3f(1.0. 1.0. 1.0):
// set drawing color to white
// устанавливаем белый цвет рисования
glColor3f(1.0. 1.0, 0.0);
// set drawing color to yellow
// устанавливаем желтый цвет рисования
Цвет фона (background color) устанавливается с помощью функции gl Cl earCol or (red. green, blue, alpha),
где переменная al pha определяет степень прозрачности и будет рассматриваться позднее. (Пока задавай-
те alpha=0.0.) Для очистки всего окна до цвета фона следует использовать функцию glClear(GL_ COLOR_
BUFFERJ3IT). Аргумент GL_COLOR_BUFFER_BIT представляет собой еще одну встроенную в OpenGL константу.
Установка системы координат
Наш метод установки начальной системы координат может сейчас показаться неясным, однако он ста-
нет более понятным в следующей главе, где мы рассмотрим окна, окна проекции и отсечение (clipping).
Пока что примем несколько команд на веру. Функция mylni t () на рис. 2.9 представляется хорошим сред-
1 Использование этой функции вместо соответствующих команд OpenGL придает программе большую читабельность. Не является
необычным создание из таких подпрограмм персональной коллекции.
2.2. Рисование основных графических примитивов
77
ством назначения системы координат. Как мы увидим позже, OpenGL регулярно производит большое
число преобразований. Для этого используются матрицы, и команды в mylnitO также оперируют опре-
деленными матрицами для достижения своей цели. Подпрограмма glu0rtho2D() производит нужное нам
преобразование для экранного окна размером 640 пикселов в ширину и 480 пикселов в длину.
Листинг 2.4. Установка простой системы координат
void mylnitfvoid)
glMatrixMode(GL_PROJECTION);
glLoadldentityO;
gluOrtho2D(0. 640.0, 0. 480.0):
}
Соберем все это вместе. Законченная программа на OpenGL
В листинге 2.5 приведена законченная программа, рисующая три непритязательные точки из рис. 2.3.
Как мы увидим, эту программу нетрудно изменить так, чтобы она рисовала более интересные объекты.
Инициализация функции mylnitO задает систему координат, размер точки, цвет фона и цвет рисова-
ния. Само рисование инкапсулировано в функции обратного вызова myDi spl ау(). Поскольку данная про-
грамма не является интерактивной, не используется никаких других функций обратного вызова. Функ-
ция glFlushO вызывается после того, как точки нарисованы, чтобы убедиться, что все данные были
должным образом обработаны и отправлены на дисплей. Это важно для некоторых систем, работаю-
щих с сетью. Данные буферизуются на хост-машине (host-machine) и пересылаются на удаленный дис-
плей только при переполнении буфера или при выполнении команды glFlushO.
Листинг 2.5. Законченная OpenGL-программа рисования трех точек
#include<windows.h)
// use as needed for your system
// используем, как нужно для вашей системы
#include<gl/Gl,h>
#include<gl/glut.h>
//«««««« my I nit »»»»»
void mylnit(void)
glClearColor(1.0.1.0.1.0.0.0);
// set white background color;
// устанавливаем белый цвет фона
glColor3f(0.0f. 0.0f, O.Of):
// set the drawing color
// устанавливаем цвет рисования
glPointSize(4.0);
// a 'dot' is 4 by 4 pixels
// "точка" размером 4 на 4 пиксела
glMatrixMode(GL_PROJECTION);
glLoadldentityO;
glu0rtho2D(0.0. 640.0. 0.0. 480.0);
}
//«««««« myDispl ay »»»»>
void myDisplay(void)
gl Cl ear(GL_COLOR_BUFFER_BIT);
// clear the screen
// очищаем экран
продолжение^
78
Глава 2. Начальная стадия: рисование фигур
Листинг 2.5 (продолжение)
glBegin(GL_PDINTS):
gl Vertex21(100. 50):
// draw three points
// рисуем три точки
glVertex21(100, 130):
glVertex2i(1506 130):
glEndO:
gl Flush»;
// send all output to display
//отправляем весь вывод на дисплей
}
//«««««« main »»»»»>
void mainCint argc. char** argv)
{
glutlnit(&argc, argv);
// initialize the toolkit
// инициализируем инструментарий
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
// set display mode
// устанавливаем режим отображения
glut!nitWindowSize(640.480):
// set window size
// устанавливаем размер окна
glutlnitWindowPositiondOO, 150):
// set window position on screen
// устанавливаем положение окна на экране
glutCreateWindow(“my first attempt”):
// open the screen window
// открываем экранное окно
glutDisplayFunc(myDisplay):
// register redraw function
// регистрируем функцию обновления
mylnitO;
glutMalnLoopO:
// go into a perpetual loop
// входим в бесконечный цикл
}
2.2.1. Рисование созвездия точек
Созвездие точек — это некий узор, составленный из точек (dots or points). Мы рассмотрим несколько
интересных примеров созвездий точек, которые легко получить при помощи основной программы, при-
веденной в листинге 2.5. В каждом случае соответствующая функция объявляется в glutDisplayFuncO
как функция обратного вызова для события обновления. Мы настоятельно рекомендуем вам реализо-
вать и протестировать каждый пример для приобретения некоторого опыта в графике.
Пример 2.2.1. Большая Медведица
На рис. 2.5 изображен узор из восьми точек, представляющих собой Большую Медведицу — привыч-
ное созвездие на ночном небе.
Названия и местоположения этих восьми звезд Большой Медведицы (при одном определенном виде
ночного неба) — Дубхе, Мерак, Фекда, Мегрец, Алиот, Мицар, Алькор, Бенетнаш (Алькаид) — задают-
2.2. Рисование основных графических примитивов
79
ся посредством следующих упорядоченных троек: {Dubhe, 289,190}, {Merak, 320,128}, {Phecda, 239,67},
{Megrez, 194,101}, {Alioth, 129,83}, [Mizar, 75,73}, {Alcor, 74, 74}, {Alkaid, 20,10}. Поскольку данных для
точек очень мало, проще внести их в явный список или «вмонтировать» («hardwire») в код. (Если тре-
буется нарисовать много точек, то удобнее записать их в файл и заставить программу читать их из фай-
ла и рисовать; позже в данной главе мы проделаем это.) Эти точки могут заменить собой те три точки,
которые задавались в листинге 2.5. Полезно поэкспериментировать с этим созвездием точек, задавая
различные размеры точек, цвет фона и линий.
У
Моя первая попытка
Рис. 2.5. Простое созвездие точек
Пример 2.2.2. Рисование ковра Серпинского (Sierpinski gasket)
На рис. 2.6 изображен ковер Серпинского1. Совокупность точек для него генерируется процедорно. Это
означает, что каждая последующая точка определяется некоторым процедурным правилом. Хотя этот за-
кон в данном случае весьма прост, результирующий орнамент является фракталом (fractal) (см. главу 9).
Сначала выведем правило построения ковра Серпинского чисто интуитивным путем. В тематическом
задании 2.2 мы увидим еще один образец системц итерироемцр фонкций (iterated function system).
Рис. 2.6. Ковер Серпинского
Ковер Серпинского рисуется посредством многократного вызова функции drawDotO с координата-
ми точек (хй, уй), (xvyf, (х2,у2)..., задаваемых с помощью простого алгоритма. Обозначим k-ю точку
РГ {хк’Ук)- Каждая следующая точка зависит от предыдущей точки pk_v Процедура вычисления точек
заключается в следующем:
1. Выбираем три фиксированные точки Го, Гр Г2, так чтобы они составили некоторый треуголь-
ник, как показано на рис. 2.7, а.
2. Выбираем в качестве начальной точки для рисования рй одну из точек Го, Гр Т2 случайным образом.
1 В математической литературе прошлых лет эта фамилия переводится как Серпиньский. — Примеч. пер.
80
Глава 2. Начальная стадия: рисование фигур
Теперь будем выполнять итерационный процесс до тех пор, пока поле рисунка не будет заполнено
в достаточной степени.
1. Выберем случайным образом одну из точек То, 1\, Г, и обозначим ее Т.
2. Вычислим следующую точку pk как середину1 отрезка между точкой Т и найденной ранее точ-
кой pk V Это означает, что pk является серединой отрезка, соединяющего точки pk l и Т.
3. Рисуем точку рк с помощью функции drawDotO.
т т°
'о я
Л
/
Л \
/ \ / .₽3
т/--------------'• т‘ т'-‘'.......................
а б
Рис. 2.7. Построение ковра Серпинского
Рисунок 2.7, б отображает несколько итераций описанной процедуры. Пусть начальной точкой бу-
дет То, а следующей выбрана точка 7’1. В этом случае точка pt ляжет посередине между pt и ТГ Пусть
далее выбрана точка Т2, так чтор2 ляжет посередине между р{ и Т2 Пусть далее опять выбрана точка Tv
так что р3 будет вычислена по приведенной схеме и т. д. Данный процесс продолжает создавать и ри-
совать точки (теоретически бесконечно), и на экране быстро появляется орнамент ковра Серпинского.
Представляется удобным определить простой класс GlintPoint, описывающий точку с целыми коор-
динатами2:
class GlintPoint:
public:
Glint x. у:
Теперь создадим и инициализируем массив из трех точек Т[0], Т[1] и Т[2] для хранения в нем трех
углов треугольника, используя
GlintPoint Т[3]"{(Ю.Ю). (300.30). (200.300)}
Нет необходимости запоминать каждую точку pk последовательности по мере ее возникновения, по-
скольку мы просто хотим нарисовать ее и затем идти дальше. Поэтому зададим переменную point для
хранения этой переменной точки. На каждой итерации point заменяется новым значением.
Для случайного выбора одной из точек T[i] используем выражение i=random(3). Функция random(3)
возвращает с одинаковой вероятностью одно из значений: 0,1,2. Она определяется следующим образом3:
int random (int m)
{
return randOXm;
)
1 Для того чтобы найти среднюю точку между двумя точками, например (3,12) и (5,37), нужно просто вычислить среднее ариф-
метическое каждой пары координат* и у, сложив их и разделив на два. Таким образом, средняя точка между (3,12) и (5,37) =
= ((3+5)/2, (12+37)/2) - (4,24).
2 Если используется С, а не C++, то здесь подойдет простая структура typedef struct Glint х,у:} GlintPoint:.
3 Напомним, что стандартная функция rand () возвращает псевдослучайную величину в диапазоне от 0 до 32767. Функция пересче-
та по модулю уменьшает этот диапазон до уровня от 0 до 2.
2.2. Рисование основных графических примитивов
81
В листинге 2.6 приведены остальные детали алгоритма, который генерирует 1000 точек ковра бер-
линского.
Листинг 2.6. Генерирование ковра Серпинского
void Sierpinski(void)
{
GLintPoint T[3]'[[10,10}.(300.300.(200.300)}:
int index = random(3);
// 0. 1 or 2 equally likely
//0. 1 или 2 равновероятны
GLintPoint point - T[index]:
// Initial point
// начальная точка
drawOot(point.x. point.у):
// draw initial point
// рисуем начальную точку
fordnt 1 — 0: i < 1000: i++)
// draw 1000 dots
// рисуем 1000 точек
index ' random(3);
point.x = (point.x + T[index].x) / 2;
point.у = (point.у + T[index].y) / 2:
d rawDot(poi nt.x.poi nt.у):
glFlushO;
}
Пример 2.2.3. Простейшие «точечные рисунки» («Dot Plots»)
Предположим, что вы хотите изучить поведение некоторой математической функции /(х) от перемен-
ной х. Например, как изменяется
/(х) - e*xcos(2n х)
при изменении аргумента х от 0 до 4? Многое может прояснить быстрый график, построенный в осях
/(х) и х, подобный приведенному на рис. 2.8.
Рис. 2.8. «Точечный график» зависимости функции f(х) = e-xcos(2nx) от аргумента х
82
Глава 2. Начальная стадия: рисование фигур
Для построения графика данной функции просто подсчитаем ее значения при равноудаленных зна-
чениях аргументах и нарисуем точки для каждой координатной пары (х,/(х.)). Выберем какой-нибудь
подходящий шаг между двумя последовательными значениями аргумента х, например 0,005, и тогда
процесс в общих чертах пойдет так:
glBegin(GL_POINTS):
forCGLdouble х = 0: х<4.0 ; х+= 0.005)
glVertex2d(x. f(x)):
glEndO;
glFlushO:
Имеется, однако, одна проблема. Получившийся график будет недопустимо маленьким, так как зна-
чения х от 0 до 4 преобразуются в четыре первых пиксела в левом нижнем углу экрана. Более того, от-
рицательные значения f(.) будут размещаться ниже окна и будут невидимы. Поэтому нам необходимо
масштабировать и позиционировать величины, подлежащие рисованию, таким образом, чтобы они пра-
вильно располагались в экранном окне. Здесь мы делаем это волевым усилием, в сущности, выбирая
несколько значений так, чтобы график адекватно вырисовывался на экране. Позже мы создадим общую
процедуру, которая будет сама осуществлять эту подгонку; она называется процедурой преобразова-
ния координат из мировых (world coordinates) к оконным (window coordinates).
Масштабирование х. Допустим, мы хотим, чтобы диапазон от 0 до 4 был преобразован так, чтобы он
размещался по всей ширине экранного окна, заданного в пикселах величиной screenwidth. В таком слу-
чае нам нужно всего лишь перемасштабировать все значения х в screenWidth/4 раза, используя:
sx = х * screenwidth /4.0;
Величина sx равна 0 при х = 0 и screenwidth при х = 4.0, к чему мы и стремились.
Масштабирование и смещение у. Значения функции /(х) лежат между -1,0 и 1,0, следовательно, мы
должны их тоже перемасштабировать и сдвинуть. Пусть мы задали экранное окно высотой в screenHeight
пикселов. Тогда, чтобы поместить график в центре окна, умножим все значения у на screenHeight/2 и
сместим их вверх на screenHeight/2:
sy = (у + 1.0) * screenHeight / 2.0;
Как нам и нужно, это преобразование выдает 0 при у = -1,0 и screenHeight при у = 1,0.
Отметим, что преобразования от х к sx и от у к sy имеют следующий вид:
sx = Ах + В;
sy = Су + D (2.1)
для должным образом выбранных значений констант А, В, С и D. А и С выполняют масштабирование,
а В и D — смещение. Операции масштабирования и смещения являются, в сущности, вариантом «аф-
финного преобразования» («affine transformation»). Мы будем подробно изучать аффинные преобра-
зования в главе 5; они предоставляют более состоятельный метод отображения любого заданного диа-
пазона величин х и у в экранное окно.
Нам необходимо только правильно установить значения А, В, С и D и начертить точечный график с
помощью следующего кода:
GLdouble А. В. С. D, х;
А = screenwidth / 4.0;
В = 0.0:
С = screenHeight / 2.0:
D = С:
glBegin(GL_POINTS):
for(x =0; х < 4.0: х += 0.005)
glVertex2d(A * х + В. С * f(x) + D):
glEndO:
glFlushO:
2.3. Создание рисунков из линий
83
В листинге 2.7 программа для рисования точечного графика приведена полностью для демонстра-
ции того, как соединяются вместе ее различные блоки. Начальные установки похожи на те, которые
были в программе рисования трех точек в листинге 2.5. Заметим, что ширина и высота экранного окна
задаются как константы и используются внутри кода по мере необходимости.
Практическое упражнение
2.2.1. Точечные графики для произвольной функции f()
Рассмотрим рисование точечного графика функции f(.) аналогично тому, который приведен в приме-
ре 2.3, если известно, что при изменении х от x|ow дохы h/(x) принимает значения otz/Iow до z/high. Найдите
необходимые коэффициенты масштабирования и сдвига из уравнения 2.1, так чтобы точки всегда рас-
полагались в пределах экранного окна шириной W и высотой Н пикселов.
2.3. Создание рисунков из линий
Гамлет: Видите вы вон то облако в форме верблюда?
Полоний: Ей-богу, вижу, и действительно, ни дать ни взять — верблюд.
Гамлет: По-моему, оно смахивает на хорька.
Уильям Шекспир, Гамлет (пер. Б. Пастернака, действие 3, картина 2)
Как уже говорилось в главе 1, рисование линий является основой компьютерной графики, и почти в
каждой графической системе имеются «драйверные» подпрограммы для рисования прямых линий.
OpenGL упрощает рисование линий: воспользуйтесь GL_LINES как аргументом для функции glBeginO и
передайте в нее две концевые точки в качестве вершин. Тогда для рисования прямой линии между точ-
ками (40, 100) и (202, 96) можно использовать следующий код:
glBegin (GL_LINES):
// use constant GL_LZNES here
// используем здесь константу GL_LZNES
glVertex2i(40. 100):
glVertex2i(202. 96);
gl EndO:
Листинг 2.7. Полный текст программы вычерчивания «точечного графика» функции
#include<windows.h>
// use proper includes for your system
// используйте допустимые для вашей системы
// включаемые файлы
#include<math.h>
#1 nclude<gl/Gl.h>
#include<gl/glut.h>
const int screenwidth = 640:
// width of screen window in pixels
// ширина экранного окна в пикселах
const int screenHeight = 4B0:
// height of screen window in pixels
// высота экранного окна в пикселах
GLdouble А. В. С. D:
// values used for scaling and shifting
// величины, используемые для масштабирования и сдвига
//«««««« mylnit »»»»»
void mylnit(void)
{
продолжение^
84
Глава 2. Начальная стадия: рисование фигур
Листинг 2.7 (продолжение)
glClearColord.0.1.0.1.0.0.0):
// background color Is white
// цвет фона - белый
glColor3f(0.Of. 0.0f. O.Of):
// drawing color is black
// цвет для рисования - черный
gIPointSize(2.0);
// a ’dot' is 2 by 2 pixels
// «точка» является квадратом 2 на 2 пиксела
glMatrixMode(GL_PROJECTION);
// set "camera shape”
// устанавливаем «форму камеры»
glLoadldenity():
glu0rtho2D(0.0. (GLdouble)screenWidth. 0.0. (GLdouble) screenHeight):
A = screenwidth /4.0:
// set values used for scaling and shifting
// задаем величины, используемые для масштабирования
// и сдвига
В = 0.0:
С = D = screenHeight / 2.0:
//«««««« myDisplay »»»»>
void myDisplay(void)
{
glClear(GL_COLOR_BUFFER_BIT):
// clear the screen
// очищаем экран
glBegin(GL_POINTS):
for(GLdouble x - 0: x < 4.0; x += 0.005)
{
GLdouble func = exp(-x) * cos(2 * 3.14159265 * x):
glVertex2d(A * x + В. C * func + D):
glEndO:
glFlushO:
// send all output to display
// отправляем весь вывод для отображения
}
//«««««« main »»»»>»
void maintint argc. char** argv)
{
glutlnit(&argc, argv}:
// initialize the toolkit
// инициализируем инструментарий
glut!nitDisplayMode(GLUT_SINGLE | GLUT_RGB):
// set display mode
// устанавливаем режим дисплея
glut!nitWindowSize(screenWidth, screenHeight):
// set window size
// задаем размер окна
glutlnitWindowPositiondOO. 150):
// set window position on screen
// устанавливаем положение окна на экране
2.3. Создание рисунков из линий
85
glutCreateWindow(”Dot Plot of a Function"):
// open the screen window
// открываем экранное окно
glutDisplayFunc(myDisplay):
// register redraw function
// регистрируем функцию перерисовки (обновления)
mylnitO;
gl utMainLoopO:
// go into a perpetual loop
// входим в бесконечный цикл
Данный код можно было бы для удобства инкапсулировать в подпрограмму drawLinelnt:
void drawLine!nt(GLint xl. GLint yl. GLint x2. GLint y2)
{
glBegin(GL_LINES):
glVertex2i(xl. yl):
glVertex2i(x2. y2);
glEndO:
Альтернативную подпрограмму, drawLineFloatO, можно было бы реализовать аналогично. (Как?)
а б в
Рис. 2.9. Простое изображение, построенное из четырех линий: а) тонкие линии;
б) утолщенные линии; в) пунктирные линии
Если между командами glBegin(GL_LINES) и glEndO задано больше двух вершин, то они принимаются
парами и каждая пара соединяется отдельным отрезком прямой. Поле для игры в «крестики-нолики»
(tic-tac-toe board), приведенное на рис. 2.9, а, можно было бы нарисовать с помощью следующих команд:
glBegin(GL_LINES):
glVertex2i(10. 20):
// first horizontal line
// первая горизонтальная линия
glVertex2i(40. 20)
glVertex2i(20. 10):
// first vertical line
// первая вертикальная линия
glVertex2i(20, 40):
four more calls to glVertex2i() here for the other two lines
// здесь еще четыре вызова glVertex2i() для двух
// оставшихся прямых
glEndO:
glFlushO:
OpenGL предлагает средства для задания атрибутов линий. Цвет линии устанавливается точно так
же, как и для точек, с использованием функции glColor3f(). На рис. 2.9, б показано применение утол-
щенных линий, они установлены с помощью команды glLineWidth(4.0). По умолчанию толщина рав-
на 1,0. На рис. 2.9, в показаны пунктирные линии (из точек или из штрихов). Подробности штрихова-
ния приведены в тематическом задании 2.5 в конце данной главы.
86
Глава 2. Начальная стадия: рисование фигур
2.3.1. Рисование ломаных линий и полигонов
Напомним (из главы 1), что ломаной линией (polyline) называется совокупность отрезков прямых, со-
единенных своими концами. Ломаная описывается упорядоченным списком точек, как в равенстве:
Ро = <хо- Уо>’ Pi“ (*i> УгУ'-’Рп = (*„- У „)• <2-2)
В OpenGL ломаная называется «полосой линий» («line strip») и рисуется посредством задания вер-
шин в нужном порядке, между командами glBegin(GL_LINE_STRIP) и glEndO. К примеру, код
glBegin(GL_LINE_STRIP);
// draw an open polyline
// рисуем открытую ломаную
glVertex2i(20. 10);
glVertex2i(50. 10);
glVertex2i(20. 80):
glVertex2i(50. 80):
glEndO;
glFlushO:
генерирует ломаную, изображенную на рис. 2.10, а. Такие атрибуты, как цвет, толщина и штриховка,
могут быть заданы для ломаных линий таким же способом, как это было для одиночных прямых линий.
Если нужно соединить последнюю точку с первой, чтобы ломаная линия превратилась в полигон, дос-
таточно просто заменить GL_LINE_STRIP на GL_LINE_LOOP. Полученный полигон изображен на рис. 2.10, б.
a б
Рис. 2.10. Ломаная линия и полигон
Полигоны, нарисованные с помощью GL_LINE_LOOP, нельзя заполнять цветом или узором. Для рисо-
вания закрашенных полигонов следует использовать команду glBegin(GL_POLYGON), которую мы будем
рассматривать позднее.
Пример 2.3.1. Рисование линейных графиков
В примере 2.2.3 мы рассматривали построение точечного графика функции в осях f(x) — х из последо-
вательности точек с координатами (х, /(х)). Линейный график является непосредственным расшире-
нием этого подхода: эти же самые точки попросту соединены отрезками прямой, то есть получается
ломаная линия. Рисунок 2.11 представляет собой пример такого построения для функции
/(х) = 300-100 cos(2n х/100) + 30 cos(4n х/100) + 6 cos(6n х/100),
где х изменяется в шагах от 3 до 100 шагов. При увеличении этого рисунка была бы видна последова-
тельность соединенных между собой отрезков прямой; в изображении же нормального размера они
сливаются вместе и выглядят как плавно изменяющаяся кривая.
Процесс вычерчивания графика функции с помощью отрезков прямой почти идентичен созданию
точечного рисунка, так что можно использовать (с небольшими изменениями) программу из листин-
га 2.7. Нам следует произвести масштабирование и сдвиг начерченных прямых, чтобы правильно раз-
местить их в окне. Это требует вычисления констант Л, В, Си D аналогично тому, как это делалось нами
раньше (см. уравнение 2.1). В листинге 2.8 показаны те изменения, которые следует внести во внутрен-
ний цикл рисования в функции myDispl ау():
2.3. Создание рисунков из линий
87
Листинг 2.8. Вычерчивание линейного графика функции
glBegin(GL_LINE_STRIP);
for(Gldouble х = 0; х < 4.0: х += 0.005)
{
define func // задаем функцию
glVertex2d(A * х + В. С * func + D);
}
glEndO:
gl Flush:
Рис. 2.11. График математической формулы
Пример 2.3.2. Рисование ломаных линий, заданных в файле
Наиболее интересные изображения, которые можно создать из ломаных линий, содержат значительное
количество отрезков прямых. Описание этих ломаных удобно записывать в файл, чтобы при желании
изображение можно было бы нарисовать снова. (Ряд интересных примеров можно найти в Интернете;
см. введение к данной книге.)
Рис. 2.12. Рисование ломаных линий, записанных в файле
Не составляет труда написать подпрограмму, рисующую ломаные, записанные в файл. Рису-
нок 2.12 — это пример изображения, которое можно нарисовать таким способом.
Рассмотрим файл dino.dat, содержащий набор ломаных в следующем формате (комментарии не яв-
ляются частью файла).
21
// number of polylines in the file
// число ломаных в файле
4
// number of points in the first polyline
// число точек в первой ломаной
169 118
88
Глава 2. Начальная стадия: рисование фигур
// first point of first polyline
// первая точка первой ломаной
174 120
// second point of first polyline
// вторая точка первой ломаной
179 124
178 126
5
// number of points in the second polyline
// число точек во второй ломаной
298 86
// first point of second polyline
// первая точка второй ломаной
304 92
310 104
314 114
314 119
29
32 435
10 439
и т.д.
(Полностью данный файл доступен на web-сайте к этой книге. См. введение.) В листинге 2.9 приве-
дена подпрограмма на C++, которая открывает такой файл и затем рисует все ломаные линии, которые
тот содержит. Читается файл с именем, содержащимся в строке fileName, после чего рисуется каждая
ломаная линия. Данную подпрограмму можно использовать вместо myDisplayO в листинге 2.7 в каче-
стве функции обратного вызова на событие перерисовки redraw. Величины A,B,CnD следует выбрать
так, чтобы ломаные линии имели нормальный масштаб. Мы изложим общие принципы такого выбора
в главе 3.
Вариант функции drawPolyLineFileO, приведенный в листинге 2.9, имеет очень слабый уровень кон-
троля ошибок. Если файл нельзя открыть — возможно, потому, что в функцию передано неверное имя, —
подпрограмма просто возвращает управление в главную программу. Если файл содержит неверные дан-
ные, например вместо целых чисел стоят вещественные, — результаты будут непредсказуемы. Очевид-
но, что данную подпрограмму следует рассматривать только как точку отсчета для разработки более
адекватной версии.
Листинг 2.9. Вычерчивание ломаных линий, записанных в файле
#include <fstream.h>
void drawPolyLineFile(char * fileName)
{
fstream inStream;
inStream.open(fileName, ios ::in);
// open the file
// открываем файл
if(inStream.fail О)
return:
glClear(GL_COLOR_BUFFER_BIT);
// clear the screen
// очищаем экран
GLint numpolys. numLines. x, y;
inStream » numpolys:
// read the number of polylines
// читаем число ломаных
2.3. Создание рисунков из линий
89
for(int j = 0: j < numpolys: j++)
// read each polyline
// читаем каждую ломаную
{
inStream » numLines:
glBegin(GL_LINE_STRIP):
// draw the next polyline
// чертим очередную ломаную
for (int 1 = 0; 1 < numLines; i++)
{
inStream » x » y:
// read the next x, у pair
// читаем очередную пару x. у
glVertex2i(x, у);
glEndO:
}
glFlushO;
inStream.closeO;
Пример 2.3.3. Параметризация рисунков
На рис. 2.13 изображен простой домик, состоящий из нескольких ломаных. Его можно нарисовать с
использованием кода, частично приведенного в листинге 2.10. (Какой код понадобится для рисования
двери и окна?)
Листинг 2.10. Рисование домика с «вмонтированными» размерами
void hardwirededHouse()
{
glBegin(GL_LINE_LOOP);
glVertex2i(40. 40):
// draw the shell of house
// рисуем остов домика
glVertex2i(40. 90):
glVertex2i(70, 120);
glVertex2i(100. 90):
glVertex2i(100, 40):
glEndO:
glBegin(GL_LINE_STRIP);
glVertex2i(50. 100):
продолжение^
90
Глава 2. Начальная стадия: рисование фигур
Листинг 2.10 (продолжение)
// draw the chimney
// рисуем трубу
glVertex2i(50. 120):
glVertex2i(60. 120);
glVertex2i(60. 110);
glEndO:
// draw the door
// рисуем дверь
// draw the window
// рисуем окно
}
Данный подход не является достаточно гибким. Координаты каждой концевой точки «вмонтирова-
ны» внутрь кода, вследствие чего функция hardwirededHouseO может рисовать только единственный до-
мик одного размера, размещенный единственным образом. Большей гибкости можно достигнуть, если
параметризовать этот рисунок и передавать значения этих параметров в подпрограмму. Таким спосо-
бом мы можем рисовать семейства объектов, отличающихся различными значениями параметров. Ли-
стинг 2.11 демонстрирует такой подход. Параметры задают расположение верха крыши, а также шири-
ну и высоту домика. Такие детали, как рисование трубы, двери и окна, оставлены для вас в качестве
упражнения.
Листинг 2.11. Рисование параметризованного домика
void parameterizedHouse(GLintPoint peak. Glint width. GLint height)
// the top of house is at the peak;
// верхняя точка домика;
// the size of house
// is given by the height and width
// размер домика задается его высотой и шириной
{
glBegin(GL_LINE_LOOP):
glVertex2i(peak.x. peak.y):
// draw shell of house
// рисуем каркас домика
glVertex2i(peak.x + width / 2. peak.y - 3 * height /8):
glVertex2i(peak.x + width / 2. peak.y - height);
glVertex2i(peak.x - width / 2. peak.y - height);
glVertex2i(peak.x - width / 2. peak.y - 3 * height /8):
glEndO;
draw the chimney in ihe same fashion
11 рисуем трубу таким же способом
draw the door
II рисуем дверь
draw the window
11 рисуем окно
}
Данная подпрограмма может быть использована для того, чтобы нарисовать целую «деревню», как
это показано на рис. 2.14, посредством последовательных вызовов функции parameterizedHouseO с раз-
личными значениями параметров. (Каким образом один из домиков оказался «перевернутым»? Все ли
домики с этого рисунка можно нарисовать с помощью данной подпрограммы?)
2.3. Создание рисунков из линий
91
Рис. 2.14. «Деревня» из домиков, нарисованных с помощью подпрограммы parameterizedHouse()
Пример 2.3.4. Создание рисовальщика ломаных
Как мы увидим, некоторые приложения вычисляют и сохраняют вершины ломаных линий в списке.
Поэтому естественно добавить к нашему растущему инструментарию функцию, которая принимает
такой список в качестве параметра и строит соответствующую ломаную. Список должен иметь форму
массива или связного списка. Здесь мы используем форму массива и определим класс для его инкапсу-
ляции, как показано в листинге 2.12.
Листинг 2.12. Тип данных для связного списка вершин
class Gl 1 ntPolntArray(
const int MAX_NUM = 100;
public:
int num;
GLintPoint pt[MAX_NUM]:
В листинге 2.13 показана возможная реализация подпрограммы для рисования ломаных линий. Эта
подпрограмма имеет, помимо прочих, параметр closed. Если closed не равен нулю, то последняя верши-
на ломаной соединяется с первой. Значение closed устанавливает аргумент для glBeginO. Эта подпро-
грамма просто посылает каждую из вершин ломаной в OpenGL.
Листинг 2.13. Тип данных «связный список» и рисование ломаной линии или полигона
void drawPolyLine(GlintPointArray poly, int closed)
{
glBegin(closed ? GL_LINE_LOOP; GL_LINE_STRIP);
forCint 1=0: I < poly.num: I++)
glVertex2i(poly.pt[I].x.poly.pt[I].y);
glEndO:
glFlushO;
2.3.2e Рисование линий с использованием movetoO и linetoQ
Как мы уже отмечали ранее, многие графические системы имеют инструменты для рисования линий на
базе функций movetoO и 1 inetoO. Эти функции используются столь часто, что представляется важным
поближе познакомиться с их использованием. Мы приспособим свои собственные функции movetoO и
1 inetoO, которые действуют при вызове инструментов OpenGL. Кроме того, в главе 3 мы «приоткроем
завесу» и покажем, как бы вы создавали функции movetoO и 1 inetoO, исходя из базовых принципов,
если бы мощная библиотека типа OpenGL не была доступна.
Напомним, что функции movetoO и 1 inetoO управляют гипотетическим пером, позиция которого
называется текущими координатами (current position), или СР. Мы можем объединить действия обе-
их этих функций следующим образом:
92
Глава 2. Начальная стадия: рисование фигур
moveto(x, у): устанавливаем СР в (х, у),
Hneto(x, у): рисуем прямую линию от СР до (х, у) и затем присваиваем СР значение (х, у).
Таким образом, прямая линия из точки (хр у() до точки (х2, у2) может быть нарисована посредством
двух вызовов: moveto(xl, yl) и 11neto(x2, у2). Ломаная линия на базе списка точек (х0, у0), (хр г/,),...,
(хл-р^л-1) легко вычерчивается с помощью такого кода:
moveto(x[0]. y[OJ):
fordnt 1=1: 1 < n: 1++)
lineto(x[i], y[i]);
Нетрудно построить функции movetoO и linetoO в среде OpenGL. Чтобы осуществить это, нам не-
обходимо определить и поддерживать свое собственное СР. Для случая целых координат проделать
этот фокус могла бы реализация, приведенная в листинге 2.14.
Листинг 2.14. Определение moveto() и lineto() в OpenGL
GLintPoint СР:
// global current position
// глобальные текущие координаты (СР)
//<«««««« moveto »»»>»»
void moveto(GLint х, GLint у)
{
СР.х = х: СР.у = у:
// update the СР
// обновляем СР
)
/ /««««« 11 net о »»»»»
void lineto(GLint х. GLint у)
{
glBegin(GL_LINES);
// draw the line
// рисуем линию
glVertex2i(CP.x. СР.у);
glVertex2i(x. у):
glEndO:
gIFlushO:
СР.х = x: СР.у = у;
// update the CP
// обновляем CP
)
2.3.3. Рисование выровненных прямоугольников
Особым случаем полигона является выровненный прямоугольник (aligned rectangle), названный так
потому, что его стороны выровнены параллельно осям координат. Мы могли бы создать свою собствен-
ную функцию для рисования выровненного прямоугольника (как?), однако в OpenGL предусмотрена
готовая функция
glRecti(GLint xl. GLint yl. GLint x2. GLint y2):
// draw a rectangle with opposite corners
//(xl. yl) and (x2. y2):
// чертим прямоугольник с противоположными углами
// (xl. yl) и (х2. у2);
// fill rhe rectangle with the current color;
// заполняем начерченный прямоугольник текущим цветом
2.3. Создание рисунков из линий
93
Рис. 2.15. Два выровненных прямоугольника, закрашенных разными цветами
Эта команда рисует выровненный прямоугольник по двум заданным точкам. Кроме того, этот
прямоугольник закрашивается текущим цветом. На рис. 2.15 показано, что рисуется при выполнении
следующего кода:
glClearColord.0.1.0.1.0.0.0):
// white background
// цвет фона белый
glClear(GL_COLOR_BUFFER_BIT);
// clear the window
// очищаем окно
glColor3f(0.6.0.6.0.6);
// bright gray
// светло-серый цвет
glRecti(20.20.100.70):
glColor3f(0.2,0.2,0.2);
// dark gray
// темно-серый цвет
glRecti(70. 50. 150. 130);
glFlushO;
Отметим, что второй прямоугольник «перекрывает» первый. Другие режимы рисования мы будем
изучать в главе 10.
Два следующих примера показаны на рис. 2.16. Рисунок 2.16, а изображает «шквал» выбранных слу-
чайным образом, выровненных прямоугольников, которые можно начертить с помощью такого кода1:
void drawFlurry(int num. int numColors. int Width, int Height)
// draw num random rectangles in a Width
// by Height rectangle
// рисуем num случайных прямоугольников размером
// не больше чем Width на Height
for (int i - 0: i < num; i++)
{
GLint xl = random(Width);
// place corner randomly
// помещаем угол случайным образом
GLint yl = random(Height);
GLint x2 = random(Width);
// pick the size so it fits
// выбираем подходящий размер
GLint y2 = random(Height);
GLfloat lev = random(10)/10.0;
// random value, in range 0 to 1
' Напомним из примера 2.3.2: random(N) возвращает случайно выбранную величину между 0 и N-1.
94
Глава 2. Начальная стадия: рисование фигур
// случайная величина в диапазоне от 0 до 1
glColor3f(1ev,lev.lev):
// set the gray level
// устанавливаем уровень яркости серого цвета
glRectKxl, yl. х2. у2);
// draw the rectangle
// рисуем прямоугольник
}
glFlushO;
}
а б
Рис. 2.16. Случайный «шквал» прямоугольников (а); шахматная доска (5)
Рисунок 2.16, б представляет собой знакомую шахматную доску с чередующимися оттенками серо-
го цвета. В практическом упражнении 2.3.1 вам предлагается запрограммировать этот рисунок.
2.3.4. Форматное соотношение выравненного прямоугольника
Важнейшими свойствами выровненного прямоугольника являются его размер, положение, цвет и фор-
ма. Его форма определяется форматным соотношением (aspect ratio), и мы будем ссылаться на фор-
матные соотношения прямоугольников на протяжении всей книги. Форматным соотношением прямо-
угольника называется отношение его ширины к высоте1:
, ширина
форматное отношение =---
высота
(2.3)
Прямоугольники с различными форматными соотношениями изображены на рис. 2.17.
а
1178,5
Альбомная
страница
Квадрат
fl
В,5711
Книжная
страница
в Золотой'
прямоугольник
(Ф-золотое
сечшив) I
Обратное
золотое
сечение
е
Рис. 2.17. Примеры форматных соотношений выровненных прямоугольников: а) альбомная страница; б) телеэкран;
s) золотой прямоугольник; г) квадрат; д') книжная страница; е) обратное золотое сечение
1 Будьте внимательны: ряд авторов определяют его как отношение высоты к ширине.
2.3. Создание рисунков из линий
95
Прямоугольник А имеет форму листа бумаги размером 8,5 на 11 дюймов с так называемой альбом-
ной (landscape — пейзаж) ориентацией (то есть ширина листа больше его высоты). Форматное соотно-
шение прямоугольника А равно 1,294. Прямоугольник Б имеет форматное соотношение телевизионно-
го экрана, 4/3, а В является знаменитым золотым прямоугольником (golden rectangle), описанным в
тематическом задании 2.3. Его форматное соотношение близко к золотому сечению ф = 1,618034. Прямо-
угольник Г представляет собой квадрат с форматным соотношением, равным 1, а Д имеет форму стандар-
тного листа бумаги с книжной (portrait — портрет) ориентацией, с форматным соотношением, равным
0,7727. И, наконец, прямоугольник Е, высокий и худой, имеет форматное соотношение, равное 1 /ф (обрат-
ное золотое сечение).
Практические упражнения
2.3.1. Рисование шахматной доски
(Попробуйте свои силы в этом упражнении, прежде чем заглянуть в ответы.) Напишите подпрограмму
checkerboard^nt size), которая рисует шахматную доску, изображенную па рис. 2.15, б. Расположите
левый нижний угол шахматной доски в позицию (0,0). Каждая из 64 квадратных клеток имеет в длину
size пикселов. Выберите для клеток два симпатичных вам цвета.
Решение: ij-я клетка располагается своим нижним левым углом в позиции (i * size, j * size) для
i = 0,...,7 и; = 0.7. Цвет должен быть сделан чередующимся между (rp gp Z>() и (r2, g2, /?2) посредством
следующего кода:
if((i + j)«2 =-0)
// if i + j is even
// если i + j четное
glColor3f( rl. gl. bl);
else
glColor3f(r2. g2. b2);
2.3.2. Альтернативные способы задания прямоугольника
Выровненный прямоугольник может быть описан другими способами, кроме задания двух противопо-
ложных углов. В двух таких способах задаются:
О его центральная точка, высота и ширина, или
О его верхний левый угол, ширина и форматное соотношение.
Напишите функции drawRectangl eCenter О и drawRectangleCornerSizeO, передающие эти альтернатив-
ные параметры, и нарисуйте прямоугольник с помощью функции glRectiO.
2.3.3. Различные форматные соотношения
Напишите подпрограмму, рисующую закрашенный прямоугольник с форматным соотношением R.
Пусть дисплей имеет пространство рисования 400 на 400. Выберите размер вашего прямоугольника
наибольшим из всех возможных. Это значит, что при R > 1 прямоугольник заполняет все пространство
рисования, в то время как при R < 1 он вытянут сверху вниз.
2.3.4. Рисование параметризованного домика
Добавьте деталей в функцию parametrizedHouseO из листинга 2.11 — так, чтобы дверь, окно и труба ри-
совались в тех же пропорциях при заданных величинах height и width. Выберите приятные для глаз раз-
меры и положения для различных форм.
2.3.5. Масштабирование и позиционирование фигуры с помощью параметров
Напишите функцию void drawDiamond(GLintPoint center, int d), рисующую простой ромб, изображен-
ный на рис. 2.18, размером d с центром в center. Используйте эту функцию для рисования «шквала»
ромбов, как предлагается на рис. 2.19.
96
Глава 2. Начальная стадия: рисование фигур
Рис 2.18. Простой ромб
Рис. 2.19. «Шквал» ромбов
2.3.5. Закрашивание полигонов
Мы уже умеем рисовать в OpenGL незакрашенные полигоны, а также выровненные прямоугольники,
заполненные одним сплошным цветом. Однако OpenGL поддерживает заполнение цветом или узором
полигонов и более общего вида. Ограничение только одно — полигоны должны быть выпуклыми (convex).
Определение. Полигон называется выпуклым, если прямая, соединяющая две его любые точки, це-
ликом лежит внутри него.
Рис 2.20. Выпуклые и невыпуклые полигоны
На рис. 2.20 показано несколько полигонов. Из них только полигоны Г,Дм.Еявляются выпуклыми.
(Проверьте для надежности, что каждый из этих полигонов удовлетворяет определению выпуклости).
Г несомненно выпуклый: все треугольники являются таковыми. А не является даже простым (вспомни-
те главу 1), поэтому он не может быть выпуклым. Б и В в некоторых точках «изогнуты внутрь». (Най-
дите две такие точки полигона Б, что прямая, соединяющая их, не лежит целиком внутри Б.)
Для рисования выпуклого полигона по его вершинам (х0, г/0), (хр yj,..., (хп, уп) используйте обыч-
ный список вершин, однако поместите его между командами glBegin(GL_POLYGON) и glEndO:
glBegin(GL_POLYGON);
glVertex2f(xO. уО):
glVertex2f(xl. yl);
glVertex2f(xn. yn):
glEndO:
Нарисованный полигон будет закрашен текущим цветом. Его также можно заполнить штриховым
узором (stipple pattern) (см. тематическое задание 2.5). Позднее мы научимся вставлять внутрь полиго-
нов изображения — это один из способов нанесения текстуры.
2.3. Создание рисунков из линий
На рис. 2.21 показано несколько заполненных выпуклых полигонов. В главе 10 мы будем изучать
алгоритм заполнения произвольных полигонов, выпуклых и невыпуклых.
Рис. 2.21. Несколько заполненных выпуклых многоугольников
2.3.6. Другие графические примитивы в OpenGL
OpenGL поддерживает рисование еще пяти объектов. На рис. 2.22 показаны примеры каждого из них.
Для рисования какого-нибудь из них необходимо использовать в команде glBeginO константу, изобра-
женную рядом с ним.
GL_TRIANGLES
GL_TRIANGLE_FAN
Рис. 2.22. Другие типы геометрических примитивов
Следующий список объясняет назначение каждой из этих пяти констант:
О GL_TRIANGLES: берет вершины из списка по три за один прием и рисует для каждой тройки
отдельный треугольник.
О GL_QUADS: берет вершины по четыре за один прием и рисует для каждой четверки отдельный
четырехугольник.
О GL_TRIANGLE_STRIP: (полоса из треугольников) рисует последовательность треугольников,
опирающихся на тройки вершин: п0, v2, затем v2, v{, v3, затем v2, v3, v4 и т. д. (порядок следования
такой, что все треугольники «кладутся поперек» в одном направлении, например, против часо-
вой стрелки).
О GL_TRIANGLE_FAN: (веер из треугольников) рисует последовательность соединенных между
собой треугольников, опирающихся на тройки вершин: vn, v., v,, затем vn, vv v,, затем vn, v.„ v. и т. д.
v 1 Z v Z v U О 4
4 Ф. Хилл
98
Глава 2. Начальная стадия: рисование фигур
Q GL_QUAD_STRIP: (полоса из четырехугольников) рисует последовательность четырехуголь-
ников, опирающихся на четверки вершин: вначале vv v3, v2, затем v2, v3, v5, vt, затем vt, vy vv v6
и т. д. (порядок следования такой, что все четырехугольники «кладутся поперек» в одном направ-
лении, например против часовой стрелки).
2.4. Простое взаимодействие с помощью
мыши и клавиатуры
Интерактивные графические приложения дают пользователю возможность управлять ходом програм-
мы с помощью естественных для человека движений: манипулированием и щелчками мышью, нажати-
ем на различные клавиши клавиатуры. Положение мыши во время щелчка или нажатие конкретной
клавиши фиксируются программой приложения и обрабатываются нужным образом.
Напомним, что когда пользователь нажимает или отпускает кнопку мыши, перемещает мышь или
нажимает на клавишу клавиатуры, происходит некоторое событие. С помощью инструментария OpenGL
Utility Toolkit (GLUT) программист может связать с каждым из этих событий функцию обратного вы-
зова. Это делается посредством следующих команд:
О glutMouseFunc(myMouse) — связывает myMouseO с событием, возникающим при нажатии или отпус-
кании кнопки мыши;
О glutMotionFunc(myMovedMouse) — связывает myMovedMouseO с событием, возникающим при переме-
щении мыши, когда одна из ее кнопок нажата;
О glutKeyboardFunc(myKeyboard) — связывает KeyBoardO с событием, возникающим при нажатии лю-
бой клавиши клавиатуры.
Вскоре мы увидим, как использовать каждую из этих функций.
2.4.1. Взаимодействие с помощью мыши
Как информация, относящаяся к мыши, передается в приложение? Вы должны предусмотреть четыре
параметра у функции обратного вызова myMouseO, так чтобы она имела следующий прототип:
void myMousednt button, int state, int x, int y);
Когда происходит событие «мышь», система вызывает связанную с ним функцию и присваивает
параметрам определенные значения. Параметр button должен принять одно из следующих значений:
GLUT_LEFT_BUTTON. GLUT_MIDDLE_BUTTON. GLUT_RIGHT_BUTTON.
причем смысл этих значений очевиден (левая кнопка, средняя кнопка, правая кнопка). Параметр state
должен быть равен GLUTJJP или GLUT_DOWN (вверх или вниз). Значения х и у сообщают о положении мыши
в момент события. Но будьте внимательны: величина х, как и следовало ожидать, равна числу пикселов
от левого края окна, в то время как величина у равна числу пикселов вниз от верха окна!
Пример 2.4.1. Размещение точек с помощью мыши
Начнем с элементарного, но важного примера. Каждый раз, когда пользователь нажимает левую кноп-
ку мыши, на экране рисуется точка в месте нахождения мыши. Если же пользователь нажимает правую
кнопку, программа прекращает работу. Эту работу выполняет показанная ниже версия функции myMouse ().
Заметим, что поскольку у-координата мыши равна числу пикселов от верха экранного окна, мы рисуем
точку с координатами не (х, у),а(х, screenHeight-у), где screenHeight — высота окна в пикселах:
void myMouse (int button, int state, int x. int yi
{
if(button — GLUT_LEFT_BUTTON && state — GLUT_DOWN)
drawDot(x, screenHeight -y);
2.4. Простое взаимодействие с помощью мыши и клавиатуры
99
else if(button == GLUT_RIGHT_BUTTON && state — GLUT_DOWN)
exit(-l):
}
Аргумент -1 стандартной функции exitO просто возвращает -1 операционной системе; обычно эту
величину игнорируют.
Пример 2.4.2. Задание прямоугольника с помощью мыши
В этом примере мы хотим, чтобы пользователь мог рисовать прямоугольники, размеры которого вво-
дятся с помощью мыши. Пользователь отмечает мышью две точки, задающие противоположные углы
выровненного прямоугольника, и по ним рисуется прямоугольник. Данные для каждого прямоуголь-
ника не требуется сохранять: каждый новый прямоугольник заменяет предыдущий. Пользователь мо-
жет очищать экран нажатием правой кнопки мыши.
Листинг 2.15. Подпрограмма обратного вызова для рисования прямоугольников, вводимых с помощью мыши
void myMousetint button, int state, int x, int y)
{
static GLintPoint corner[2J;
static int numCorners =0;
// initial value is 0
// начальное значение равно 0
if(button == GLUT_LEFT_BUTTON && state == GLUT_DOWN)
{
corner[numCorners].x = x:
corner[numCorners] .y = screenHeight - y:
// flip у coordinate
// зеркально отражаем координату у
numCorners++;
// have another point
// имеем другую точку
if (numCorners == 2)
{
glRecti(corner[0].x. corner[0].y. corner[l].x. corner[l].y):
numCorners =0:
// back to 0 corners
// назад к corners » 0
else if(button == GLUT_RIGHT && state == GLUT_DOWN)
g!Clear(GL_COLOR_BUFFER_BIT);
// clear the window
// очищаем окно
glFlushO:
Подпрограмма, приведенная в листинге 2.15, сохраняет угловые точки в статическом (static) масси-
ве согпег[], который сделан статическим с тем, чтобы значения хранились в нем между последователь-
ными вызовами подпрограммы. Переменная numCorners хранит информацию о том, сколько углов на
данный момент обработано; как только это число достигает двух, прямоугольник рисуется, a numCorners
сбрасывается в нуль.
При другом методе задания прямоугольника используется резиновый прямоугольник (rubber
rectangle), размеры которого увеличиваются и уменьшаются по мере того, как пользователь пере-
мещает мышь. Подробнее это рассматривается в разделе «Логические комбинации пиксельных карт»
главы 10.
100
Глава 2. Начальная стадия: рисование фигур
Пример 2.4.3. Управление «ковром Серпинского» с помощью мыши
Нетрудно расширить возможности описанной ранее подпрограммы «ковер Серпинского» так, чтобы
пользователь мог задавать все три вершины исходного треугольника с помощью мыши. Используем ту
же схему, что и в предыдущем примере: поместим три точки в массив corners[] (углы) и затем, имея в
наличии эти три точки, нарисуем ковер Серпинского. Тогда ядро подпрограммы myMouse() будет выгля-
деть следующим образом:
static GlintPoint corners[3J:
static int numCorners - 0;
if(button ~ GLUT LEFT BUTTON && state — GLUT DOWN)
{
corner[numCorners].x » x;
cornertnumCorners].y - screenHeight - y:
// flip у coordinate
// зеркально отражаем координату у
if(++numCorners — 3)
{
Sierpinski(corners):
// draw the gasket
// рисуем ковер
numCorners - 0:
// back to 0 corners
// назад к нулевому значению corners
}
}
Здесь подпрограмма Sierpinski () та же самая, что и в листинге 2.6, за исключением того, что три вер-
шины треугольника передаются в качестве параметров.
Пример 2.4.4. Создание ломаной линии с помощью мыши
На рис. 2.23 показано создание ломаной линии посредством нажатия кнопки мыши. Теперь вместо того,
чтобы замещать каждой новой точкой старую, мы будем сохранять все отмеченные точки для дальнейшего
использования. Пользователь вводит с помощью мыши последовательность точек, и каждая из этих точек
записывается в следующую имеющуюся в распоряжении ячейку массива. Если массив заполнен целиком,
то следующие точки не принимаются. После каждого щелчка мышью окно очищается и вся текущая
ломаная линия перерисовывается заново. При нажатии правой кнопки мыши вся ломаная уничтожается.
Рис. 2.23. Интерактивное создание ломаной линии
Листинг 2.16 иллюстрирует одну возможную реализацию этой процедуры. Отметим, что перемен-
ная last хранит последнее значение индекса, использованного в массиве List[]; она увеличивается на
единицу всякий раз, когда отмечается новая точка, и устанавливается в -1 при сбросе списков. Если
желательно разрешить использование точек в List вне подпрограммы myMouse[], то переменную List
можно сделать глобальной.
2.4. Простое взаимодействие с помощью мыши и клавиатуры
101
Листинг 2.16. Рисовальщик ломаной с помощью щелчков мышью
void myMouse(int button, Int state, int x. int y)
{
#define NUM 20
static GLintPoint List [NUM]:
static int last = -1 ;
// last index used so far
// последний использованный индекс
// test for mouse button as well as for a full array
// тест для кнопки мыши и для заполненности массива
if (button == GLUT_LEFT_BUTTON && state == GLUT_DOWN && last < (NUM -1))
(
List[++1ast].x = x;
// add new point to list
// добавляем в список новую точку
List[ last],у = screenHeight - у;
glClear(GL_COLOR_BUFFER_BIT):
// clear the screen
// очищаем экран
gl Begin(GL_LINE_STRIP);
// redraw the polyline
// перерисовываем ломаную
forCint i = 0; i <= last: i++)
glVertex2i(List[i].x. List[i].y):
glEndO:
glFlushO:
else if(button =- GLUT_RIGHT_BUTTON && state " GLUT_DOWN)
last = -1:
// reset the list to empty
// обнуляем список
Движение мыши
Когда мышь перемещается (на расстояние, превышающее некоторое минимальное), а одна из кнопок
удерживается в нажатом положении, происходит событие другого типа. Функция обратного вызова —
назовем ее myMovedMouseC) — связывается с данным событием посредством подпрограммы
glutMotionFunc(myMovedMouse):
Данная функция обратного вызова должна иметь два параметра, ее прототип myMovedMouseC int х, int у):
значения х и у, разумеется, представляют собой позицию мыши в тот момент, когда рассматриваемое
событие происходит.
Пример 2.4.5. Черчение «от руки» толстой кистью
Допустим, что мы хотим создать кривую посредством плавного перемещения мыши вдоль некоторой
траектории с нажатой кнопкой. Кроме того, мы хотим, чтобы эта «кисть» для рисования имела форму
квадрата. Это можно осуществить, если разработать функцию myMovedMouseC), которая будет рисовать
квадрат в текущей позиции мыши:
void myMovedMouse(int mouseX. int mouseY)
{
GLint x = mouseX;
102
Глава 2. Начальная стадия: рисование фигур
// grab the mouse position
// перехватываем позицию мыши
GLint у - screenHeight - mouseY;
// flip it as usual
// как обычно, зеркально отражаем координату у
GLint brushSize - 20:
glRecti(х.у. х + brushSize. у + brushSize);
glFlushO;
}
2.4.2. Взаимодействие с помощью клавиатуры
Как уже указывалось ранее, нажатие клавиши на клавиатуре вызывает событие клавиатуры (keyboard
event). Функция обратного вызова myKeyboardO регистрируется с данным типом события посредством
подпрограммы glutKeyboardFunc(myKeyboard), которая должна иметь примерно следующий вид:
void myKeyboard(unsigned int key. int x. int y);
Величина key определяется ASCII-кодом* нажатой клавиши. Величины х и у сообщают позицию
мыши в момент возникновения события. (Как и раньше, у измеряется числом пикселов вниз относи-
тельно верхней стороны окна.)
Программист в любой точке программы может воспользоваться наличием многих клавиш на клавиа-
туре, с тем чтобы предоставить пользователю больший выбор. Большинство реализаций функции
myKeyboardO (клавиатура) состоит из длинного оператора switch (переключатель) с описанием case (ре-
гистра) для каждой клавиши, представляющей интерес. В листинге 2.17 приведен один из возможных
вариантов. Нажатие клавиши р рисует точку в позиции мыши; нажатие клавиши «стрелка влево» до-
бавляет точку в некоторый (глобальный) список, но не рисует ее1 2; нажатие клавиши Е вызывает выход
из программы. Отметим, что если пользователь нажимает клавишу р и держит ее, одновременно пере-
мещая мышь, то генерируется быстрая последовательность точек, составляющая «чертеж от руки».
Листинг 2.17. Пример функции обратного вызова для клавиатуры
void myKeyboard(unsigned char, int mouseX, int mouseY)
Glint x - mouseX;
Glint у - screenHeight - mouseY;
// flip the у value as always
// как всегда, зеркально отражаем координату у
switch theKey)
case 'р':
drawDot(x. у);
// draw a dot at the mouse position
// рисуем точку в позиции мыши
break:
case GLUT_KEY_LEFT: List[++last].x - x;
// add a point
// добавляем точку
1 Аббревиатура «ASCII» означает «American Standard Code for Information Interchange» («Американский стандартный код для об-
мена информацией»). Таблицы величин ASCII всегда доступны в Интернете. Смотрите также файл asci i. html на web-сайте книги.
2 Названия различных «специальных» клавиш на клавиатуре, таких как функциональные клавиши, клавиши со стрелками, клави-
шу «home», можно найти во включаемом файле gl ut. h.
2.6. Тематические задания
103
List [ last].у = у;
break;
case ’Е’:
exit (-1):
// terminate the program
// прекращаем работу программы
default;
break:
// do nothing
// не делаем ничего
}
2.5. Резюме
Самое трудное в написании графических приложений — это начало: необходимо собрать вместе аппа-
ратные и программные ингредиенты в единую программу, которая нарисовала бы несколько первых
картинок. Интерфейс прикладного программирования (API) OpenGL оказывается при этом чрезвы-
чайно полезным, предоставляя мощный и вместе с тем сравнительно простой набор подпрограмм для
создания графиков. Одним из самых больших достоинств API является его аппаратная независимость,
что дает возможность писать программы для одной графической среды и без каких-либо изменений
использовать ту же самую программу в другой среде.
Большинство современных графических приложений пишется для оконной графической среды.
Программа открывает на экране окно, которое пользователь в любое время может перемещать или из-
менять его размеры и которое реагирует на щелчки мышью и нажатие клавиш. Мы ознакомились с тем,
как использовать функции OpenGL для облегчения создания подобной программы.
Мы рассмотрели применение подпрограмм рисования примитивов для создания изображений, со-
стоящих из точек, прямых линий, ломаных линий и полигонов. Затем мы скомпоновали их в более мощ-
ные подпрограммы, которые формируют основу персонального графического инструментария пользо-
вателя. Мы проиллюстрировали на нескольких примерах применение этих инструментальных средств
и описали методы взаимодействия с программой посредством клавиатуры и мыши. В приводимых ниже
тематических заданиях предлагаются дополнительные примеры программирования, которые позволят
глубже исследовать как уже рассматривавшиеся темы, так и не менее интересные ответвления от них.
2.6. Тематические задания
При использовании данного текста лучше всего практически осуществлять новые идеи по мере их по-
явления, чтобы закрепить усвоение. Это особенно верно относительно нескольких начальных глав, по-
скольку первые графические программы зачастую представляют собой барьер, который необходимо
преодолеть. Чтобы подчеркнуть важность этого момента, каждая глава завершается некоторым количе-
ством тематических заданий (case studies), в которых описываются программные проекты, интерес-
ные сами по себе и концентрирующие в себе идеи, рассмотренные в текущей главе.
Некоторые из этих тематических заданий требуют просто конкретизировать приводимый в тексте
псевдокод и запустить программу пошаговым методом. Другие являются значительно более сложными
и могут стать основой главного программного проекта за весь курс. Всегда трудно определить, сколько
времени понадобится кому-либо для выполнения какого-либо проекта. «Уровень сложности» («level of
effort»), необходимый для выполнения каждого тематического задания, — это в лучшем случае грубая
приблизительная оценка этого времени.
104
Глава 2. Начальная стадия: рисование фигур
Существует три уровня сложности тематических заданий:
1. Простое задание. Оно может быть сделано к следующему занятию.
2. Среднее задание. Его выполнение, вероятно, займет несколько дней1.
3. Сложное задание. Вероятно, может занять около двух недель.
Тематическое задание 2.1. Псевдослучайные облака из точек
Уровень сложности II. Генератор случайных чисел (ГСЧ) random(N) (см. пример 2.2.2) выдает при каж-
дом вызове величину от 0 до Л1- 1. Для генерирования своих величин он использует стандартную фун-
кцию C++ randO. Создается впечатление, что каждая величина выбирается случайно и не зависит от
предыдущих величин.
В действительности последовательные числа на выходе randO генерируются с помощью вовсе не
случайного, а скорее весьма систематического механизма, где каждое число и. получается из своего пред-
шественника nt i с помощью специальной формулы. Типичная формула такой зависимости:
и, ” [п. _, Л + В] mod N, (2.4)
где Л, В и У — надлежащим образом выбранные константы. Довольно хорошо работает данный генератор
при А - 1 103 515 245, В - 12 345 и N - 32 767. Умножение п.., на Л и добавление к результату В дает
большую величину, после чего операция деления по модулю приводит ее к диапазону от 0 до У - 1. Этот
процесс начинается с некоторого начального (seed — «порождающего») числа, выбранного в качестве п0.
Поскольку эти числа дают только видимость случайности, они носят название псевдослучайных чисел.
Выбор значений для Л, В и У очень важен, и небольшое различие в величинах приводит к весьма отлича-
ющимся характеристикам последовательности чисел. Более подробно об этом говорится в [Кнут, 124].
Графики рассеяния
Некоторые эксперименты дают результаты, состоящие из множества пар чисел (Л;, ВД, и задача заклю-
чается в том, чтобы наглядно показать, как соотносятся между собой a-величины и 6-величины. Напри-
мер, существуют результаты обмера большого количества людей и кто-то хочет узнать, существует ли
сильная корреляция между весом и ростом индивидуума.
Рис. 2.24. График рассеяния роста человека и его веса
Для наглядного представления данных используют график рассеяния. Для каждого индивидуума
данные рисуются в виде точки с координатами (рост, вес), следовательно, нам понадобится только ин-
струмент drawDotO. Рисунок 2.24 дает пример такого графика. Он наводит на мысль, что рост и вес че-
ловека приблизительно линейно зависят один от другого, хотя некоторые из людей (например, А) име-
ют индивидуальные особенности и весят мало, хотя достаточно высоки.
Понятие «день программирования» означает несколько двухчасовых «сеансов» с массой времени для размышлений (и отдыха)
между этими сеансами. Кроме того, подразумевается достаточно искусный программист (с опытом не менее двух семестров про-
граммирования), хорошо знакомый с особенностями используемого языка и платформы программирования. В этот «день» не вхо-
дятте ужасные часы, столь хорошо известные нам, когда мы сталкиваемся с какой-нибудь скрытой ошибкой, которая выставляет
перед нами кирпичную стену разочарований до тех пор, пока эта ошибка не будет выловлена и раздавлена.
2.6. Тематические задания
105
В данном случае мы используем график рассеяния для визуальной оценки качества генератора слу-
чайных чисел. Каждый раз при вызове функции random(N) она возвращает величину из промежутка
О ... ./V- 1, которая претендует на то, что она выбрана случайно и не зависит от величин, возвращенных
ранее. Однако являются ли эти последовательные величины действительно независимыми?
Одна из простейших проверочных программ строит график рассеяния, исходя из пары последова-
тельных величин, возвращаемых функцией random(N). Эта программа вызывает random(N) два раза подряд
и строит вторую величину как функцию первой:
for(int 1-0: I < num; 1++)
drawDot(random(N). random(N));
В «сыром» (raw) OpenGL мы можем поместить цикл for между командами glBegin и glEnd:
glBegin(GL_POINTS):
for(int i = 0; 1 < num: i++);
H do it num times
// выполняем цикл num раз
glVertex2i(random N. random(N)):
glEnd:
Второй способ более эффективен, так как позволяет избежать непроизводительных издержек, свя-
занных с многократными вызовами glBegin и glEnd.
Рис. 2.25. Множество из 500 случайных точек
На рис. 2.25 показан типичный график, который может получиться в результате такого построения.
Только «однородная» плотность точек на всем пространстве квадрата сможет убедить вас в том, что
величины в диапазоне 0 ... N- 1 появляются примерно с одинаковой вероятностью и что не существует
видимой зависимости между одной величиной и другой, следующей за ней.
Рис. 2.26. Графики рассеяния, построенные плохими генераторами случайных чисел
Рисунок 2.26 показывает, что может произойти, если ГСЧ плохой. На графике а) наблюдается слиш-
ком высокая плотность некоторых величин, так что распределение в промежутке 0 ... N - 1 неодинаково.
В случае б) имеет место сильная корреляция между соседними числами последовательности. Когда
одно из чисел велико, то следующее имеет тенденцию быть маленьким. Наконец, случай в) показывает,
вероятно, худшую ситуацию из всех: после того как сгенерировано несколько дюжин величин, узор по-
вторяется, а новые величины больше не генерируются!
106
Глава 2. Начальная стадия: рисование фигур
Рисование подобных совокупностей точек дает возможность грубой проверки генерируемых чисел
на равномерность. Этот тест, однако, далек от совершенства [Кнут, 123].
Напишите программу для создания графиков случайных точек, используя несколько различных ГСЧ
для формирования пар (х, у). Испробуйте различные константы А, В и Nb основном ГСЧ и оцените, как
это повлияет на совокупности точек. Внимание! Если созвездие точек внезапно «застыло» и не появляет-
ся никаких новых точек, это может означать, что комбинация чисел просто повторяется.
Тематическое задание 2.2. Введение в систему
итерируемых функций
Из его рая нас никто не изгонит.
Дэвид Гильберт (David Hilbert), защищающий теорию множеств Кантора
Уровень сложности II.
Повторяющаяся операция рисования ковра Серпинского является одним из примеров системы ите-
рируемых функций (iterated function system — IFS), с которой мы будем сталкиваться на протяжении
всей этой книги удивительно часто. Многие интересные компьютерные рисунки (фракталы, множество
Мандельброта и т. д.) построены на вариантах этой IFS.
Поэкспериментировать с простой IFS можно с помощью карманного калькулятора. Введите любое
(положительное) число пит и нажмите кнопку «квадратный корень». Результатом будет новое число,
у!пит. Нажмите кнопку «квадратный корень» еще раз, чтобы вычислить квадратный корень из ново-
го числа, а именно yj jnum Повторяйте это, пока не надоест. Посредством данной операции вы ите-
рируете функцию квадратный корень, причем каждый результат используется как входные данные для
следующего квадратного корня. При начальном значении пит = 64 генерируется последовательность:
64, 8, 2,8284, 1,68179.(Существует ли величина, к которой эта последовательность сходится?)
На рис. 2.27 приведена схема этой системы итерируемых функций, показывающая, что каждое зна-
чение на выходе вводится обратно для получения квадратного корня, снова и снова.
Начальное значение: num
а — это число
Рис. 2.27. Повторное вычисление квадратного корня
В данном примере итерируемой функцией является f(x) - Jx или символически /(.) = •/., так на-
зываемый «извлекатель квадратного корня» («square rooter»). В качестве функции/(.) могут выступать
и другие функции, например такие:
О /(.) - 2 (.) — «дубликатор» («doubler»), удваивает свой аргумент.
° /(•) = cos(.) — «косинусатор» («cosiner»).
О /(.) - 4(.)(1 - (.)) — «логистическая» («logistic») функция, используется в теории хаоса (см. главу 9).
О /(.) = (.)2 + с — для константы с используется для определения множества Мандельброта (см. главу 9).
Иногда полезно давать имя каждому числу, появляющемуся из IFS. Назовем k-e число dk и предпо-
ложим, что процесс начинается с k = 0 «введением» в систему начального значения. Тогда последова-
тельность значений, создаваемых с помощью IFS, будет иметь вид:
2.6. Тематические задания
107
d„
d^f(da),
d2 “f(f(d0)),
d3-f(f(f(dQ))),
(2.6)
так что d3 формируется путем трехкратного применения функции /(.). Это называется третьей итера-
цией функции /(), приложенной к начальному значению dQ. Короче говоря, мы можем обозначить к-ю
итерацию/() как
dk-f[kW, (2.5)
что означает величину, получившуюся после того, как функция /(.) будет k раз применена к d0. (Заме-
чание: это не означает, что f(d^) возведено в k-ю степень.) Мы можем также использовать рекурсивную
форму и записать
dk=‘f(dk {) для k - 1,2, 3,..., для заданной величины d3.
Последовательность величин Jo, dv d2, d3, dv... называется «орбитой rf0> («orbit of Jo») для данной
системы.
Пример. Орбитой 64 для функции/(.) - является последовательность 64,8,2,8284,1,68179,....
а орбитой 10 000 — 10 000, 100,10,3,162278,1,77828,... (Чему равна орбита 0? Чему равна орбита 0,1?)
Пример. Орбита 7 для функции «дубликатора»/(.) - 2(.) равна 7, 14, 28, 56, 112,..., k-й итерацией
является 7 * 2\
Пример. Орбита 1 для функции/(.) - sin(.) может быть вычислена при помощи карманного кальку-
лятора: результаты составляют последовательность 1, .8414, .7456, .6784, ....которая очень медленно схо-
дится к 0. (Чему равна орбита 1 для cos(.)? В частности, к какой величине сходится эта орбита?)
Проект 1. Вычерчивание последовательности
«градин» (Hailstone Sequence)
Рассмотрим процесс итерации не вполне тривиальной функции, которую назовем «град»:
{х/2, если х-четное:
Зх +1, если х - нечетное.
Четные аргументы делятся пополам, в то время как нечетные увеличиваются. Например, орбита 17
для этой функции равна последовательности 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1,... Как только дос-
тигается величина два, последовательность падает «как градина» до единицы, после чего оказывается
в коротком повторяющемся цикле (каком?), то есть скачет подобно градине по земле. Теперь рассмот-
рим вопрос, на который у математики пет ответа.
Вопрос без ответа. Всякая ли орбита падает до единицы?
Иными словами, существует ли положительное целое число, которое при использовании его в каче-
стве начальной точки итерации для данной функции «град» не обязательно падает до единицы? Никто
не знает этого, хотя особенности этой последовательности подробно исследовались (см. [Hayes, 100]
или многочисленные источники в Интернете, например www.cecm.sfu.ca/organics/papers/lagarias/).
Напишите программу, которая вычерчивает функциональную зависимость членов последователь-
ности ук = /М1(.УП) °т k. Пользователь задает начальную величину yQ в интервале от 1 до 4 000 000 000
(числа такого размера поддерживаются типом unsigned longs — длинные целые без знака). Каждое зна-
чение^ изображается на графике точкой с координатами (k, yk). Построение каждого графика продол-
жается до тех пор, пока ук не достигнет единицы (если это вообще произойдет).
Поскольку последовательность «градин» может быть очень длинной, а величины yk могут быть очень
большими, необходимо масштабировать эти величины перед их отображением на экране. Напомним
108
Глава 2. Начальная стадия: рисование фигур
(раздел «Рисование основных графических примитивов»), что подходящие значения А, В, С и D зада-
ются так, что когда точка (k, ук) отображается с экранными координатами
sx - (А*к + В)
sy - (C*yt + 0).
то вся последовательность помещается на экране.
Отметим, что вы не знаете заранее, какой длины будет данная последовательность или какого значе-
ния достигнут величины yk, — до тех пор, пока не будет сгенерирована вся последовательность. Самое
простое решение заключается в том, чтобы сначала запустить последовательность без рисования, най-
ти максимальную величину, которой достигает yk (назовем ее yBiggest), а также общее число итераций,
kBiggest, необходимое для того, чтобы последовательность достигла единицы. Эти величины использу-
ются далее для определения коэффициентов А, В, С, D. После этого последовательность запускается
повторно с рисованием. Для получения окончательного вида графика проделаем следующее:
О Начертим горизонтальные и вертикальные оси.
О Вместо yk нанесем на график логарифм yk.
Вопрос для любознательных. Каковы наибольшие yBiggest и kBiggest для произвольной последова-
тельности «градин» со стартовой величиной от 1 до 1 000 000?
Итерация с помощью функций, генерирующих точки
Процесс итерации чисел с помощью какой-нибудь функции /(.) достаточно интересен, однако итера-
ция точек с помощью функции еще интереснее, так как мы можем использовать drawDotO для создания
узоров из появляющихся точек. Итак, рассмотрим функцию /(/?), которая принимает на входе точку
р(х, у) и выдает на выходе другую точку. Каждая вновь получившая точка подается опять в ту же самую
функцию для создания следующей точки, как показано на рис. 2.28. Здесь точкаpk l используется для
k-й итерации рк - /W(PO)>затем она направляется обратно для создания р4+1 и т. д.
По аналогии назовем последовательность точек рй, р{, р2 орбитой точки р0.
Рк = (Xfe Ук) — ЭТО точка
Рис. 2.28. Генератор последовательности итерируемых функций для точек
Отступление. Взгляд на ковер Серпинского как как IFS
В терминологии IFS k-я точка ковра Серпинского, pk, получается из предыдущей точки pkпо следую-
щей формуле:
((Pk-t+ r[random(3)])/2,
причем ясно, что составляющие х и у следует формировать отдельно. Тогда итерируемая функция имеет
вид:
/()“(() + Т [random(3)])/2.
Проект 2. Пряничный человечек
Показанный на рис. 2.29 «пряничный человечек» («gingerbread man») создан на основе другой IFS и
может быть нарисован в виде группы точек. Эта фигура стала известным существом в теории хаоса
2.6. Тематические задания
109
[Peitgen, 88, Gleick, 87, Schroeder, 91], поскольку она является формой «странного аттрактора» («strange
attractor»): последовательные точки «притягиваются» («аге attracted») в область, напоминающую пря-
ничного человечка с любопытными шестиугольными отверстиями.
Рис. 2.29. Типичный пряничный человечек (gingerbread man)
В процессе, генерирующем пряничного человечка, нет никакой хаотичности: каждая последующая
точка q получается из предыдущей точки р согласно следующим двум правилам:
qjc = М( 1 + 2L) - р.у + \рл - LM |;
q.y^pjc. (2.7)
Заметим, что константы М и L тщательно подобраны для масштабирования и позиционирования
пряничного человечка на экране дисплея. (Значения М = 40 и L = 3 являются хорошим выбором для
экрана 640 на 480 пикселов.)
Напишите программу, которая позволяет пользователю выбрать с помощью мыши начальную точ-
ку итерации, а затем рисует точки для пряничного человечка. (Если мыши нет, то одной из неплохих
начальных точек будет (115,121).) Зафиксируйте в программе подходящие значения Ми L, но поэкспе-
риментируйте также и с другими значениями.
Вы увидите, что для заданной начальной точки появляется только определенное число точек, после
чего узор повторяется (то есть картина перестает меняться). Различные стартовые точки приводят
к различным узорам. Модернизируйте свою программу так, чтобы можно было добавлять к картинке
точки, вводя мышью дополнительные стартовые точки.
Практическое упражнение
2.6.1. Неподвижная точка в пряничном человечке
Покажите, что процесс, заданный уравнениями (2.7), имеет «неподвижную точку» ((1 + L)M, (1 + L)M).
То есть результатом введения этой точки в данный процесс будет та же самая точка. (Это была бы весь-
ма неинтересная начальная точка для генерирования пряничного человечка!)
Тематическое задание 2.3. Золотое отношение
и другие жемчужины
Уровень сложности I.
Форматное соотношение прямоугольника является его важным атрибутом. В течение столетий одно
форматное соотношение было особенно знаменито из-за своих приятных пропорций в произведениях
искусства — это «золотой прямоугольник». Золотой прямоугольник считается лучшим из всех прямоу-
гольников — про него не скажешь, что он слишком узкий или слишком широкий. Он встречается в гре-
ческом Парфеноне (рис. 2.30), в «Моне Лизе» Леонардо да Винчи, в «Таинстве последней вечери» Саль-
вадора Дали, а также во многих работах Эшера (М. С. Escher).
110
Глава 2. Начальная стадия: рисование фигур
Рис. 2.30. Греческий Парфенон, вписанный в золотой прямоугольник
Золотой прямоугольник основан на замечательной величине: золотом отношении ф - 1,618033989...
Величина ф появляется в удивительно многих областях компьютерной графики.
На рис. 2.31 изображен золотой прямоугольник с длинами сторон ф и 1. Такая форма обладает од-
ним замечательным свойством: если из прямоугольника удалить квадрат, то оставшиеся части снова
образуют золотой прямоугольник! Какую величину должно иметь ф для реализации этого свойства?
Из рисунка видно, что меньший прямоугольник имеет высоту, равную единице, поэтому, чтобы быть
золотым, он должен иметь ширину, равную 1/ф. Следовательно,
0-1+ 1/0, (2.8)
откуда легко вычислить
1 +
0 = -у- - 1,618033989... (2.9)
Это приблизительно соответствует форматному соотношению 3 на 5 учетной карточки (index card).
Мы также видим из уравнения (2.8), что
0 - 1 - 1/0 - .618033989... Эта величина является форматным соотношением золотого прямоугольника,
стоящего на своей короткой стороне.
1 1/ф
◄----------ф----------►
Рис. 2.31. Золотой прямоугольник
Число 0 знаменито в математике во многих отношениях, вот два самых известных примера:
(2-10)
2.6. Тематические задания
111
И ф = 1 + -—:--
! + гг^
1 +...
(2.И)
Обе эти формулы легко доказываются (как?) и демонстрируют замечательную простоту использо-
вания единственной цифры 1.
То обстоятельство, что золотой прямоугольник содержит в себе уменьшенную копию себя самого,
предполагает вид «бесконечной регрессии» фигур внутри фигур внутри фигур и далее до бесконечнос-
ти. Рисунок 2.32 демонстрирует такую регрессию. Мы просто удаляем квадраты из каждого последую-
щего золотого прямоугольника.
Рис. 2.32. Бесконечные приближения к золотому прямоугольнику
Напишите приложение, которое рисует регрессию золотых прямоугольников в центре экранного
окна размером 600 пикселов в ширину и 400 пикселов в высоту. Вначале определите, где и какого раз-
мера будет наибольший золотой прямоугольник, который поместится в этом окне. Ваше изображение
должно регрессировать до тех пор, пока меньший прямоугольник не достигнет размера в один пиксел.
О золотом отношении можно рассказать еще много интересного, много связанных с ним развлече-
ний можно найти в [Gardner, 75; Hill, 108; Huntley, ИЗ; Ogilvy, 148]. Например, в следующей главе мы
рассмотрим золотые пентаграммы, а в главе 6 увидим, что два из Платоновых тел, додекаэдр и икосаэдр,
содержат три взаимно перпендикулярных золотых прямоугольника!
Практические упражнения
2.6.2. Другие золотые вещи
Уравнение (2.10) представляет ф в форме повторяющегося квадратного корня с участием единицы.
Чему равна величина
W = ^k + ylk + y[k + y/k + ... .
2.6.3. О ф и золотых прямоугольниках
О Докажите, что равенства (2.10) и (2.11) верны.
О Найдите точку, в которой пересекаются две штриховые диагонали, показанные на рис. 2.32,
и докажите, что это и есть точка, к которой сходится последовательность золотых прямоуголь-
ников.
О Используйте равенство (2.8) для вывода следующего соотношения:
Ф2 + 4 = 3. (2.12)
Ф
112
Глава 2. Начальная стадия: рисование фигур
2.6.4. Золотые орбиты
Исследование уравнений (2.10) и (2.11) показывает, что золотое отношение ф является предельной вели-
чиной при многократном применении некоторых функций. Первая из таких функций: f (.) = ^/1 + (.).
А что представляет собой вторая функция? Рассматривая эти выражения в терминах итерируемых функ-
ций, можно заметить, что ф — это число, к которому сходятся орбиты при некоторых начальных значе-
ниях. (Начальное значение скрывается в многоточии выражения.) Выясните с помощью карманного
калькулятора, какие начальные значения можно использовать, чтобы процесс продолжал сходиться к ф.
Тематическое задание 2.4. Создание и применение
файлов для ломаных линий
Уровень сложности II.
Сложные изображения, подобные рис. 2.11, составлены из большого количества ломаных линий. Данные
для таких ломаных обычно записывают в файл, так что изображение может быть воссоздано позднее
посредством чтения этих ломаных в программу и повторного вычерчивания каждой из них. В разделе
«Рисование ломаных линий и полигонов» был описан походящий формат для такого файла и подпрог-
рамма drawPolyLineFileO, осуществляющая рисование.
Файл dino.dat, хранящий в себе динозавра с рис. 2.11, можно найти под именем dino.dat на web-сай-
те этой книги (см. предисловие). Там же доступны и другие файлы с ломаными линиями.
О Напишите программу, которая читает данные о ломаных из файла и рисует каждую ломаную по
очереди. Создайте по меньшей мере один собственный интересный файл ломаных в текстовом
редакторе, после чего нарисуйте с помощью вашей программы изображение на базе данных из
этого файла.
О Расширьте возможности программы из предыдущего пункта, чтобы она воспринимала некото-
рые другие форматы. Например, заставьте вашу программу работать с х- и //-координатами, за-
данными в приращениях (differentially coded). В этом формате первая точка (хр у^ каждой
ломаной кодируется как и прежде, однако все последующие точки (х, у) кодируются после
вычитания из них предыдущей. Таким образом, в файле содержится (х - х ,, у( - у,^)- В ряде
случаев в разностях содержится меньше значащих цифр, чем в исходных координатах точек, что
позволяет получить более компактные файлы. Поэкспериментируйте с этим форматом и создайте
несколько файлов данных, использующих его.
О Измените вышеописанный формат так, чтобы с каждой ломаной был связан некоторый «код цве-
та». Этот код цвета должен появляться в файле на той же строке, что и число точек соответству-
ющей ломаной. Поэкспериментируйте с этим форматом и создайте несколько файлов данных,
использующих его.
О Измените подпрограмму рисования ломаных так, чтобы она рисовала замкнутый полигон в слу-
чае, если числу точек ломаной предшествует знак минус. Так, в файле
-3 отрицательное, значит, это полигон
0 0 первая точка этого полигона
35 3 вторая точка этого полигона
57 8 соединяем ее с первой точкой полигона
5 положительное, значит, оставляем ломаную незамкнутой
0 1
12 21
23 34
первая ломаная линия рисуется как треугольник, причем ее последняя точка соединяется с первой.
Поэкспериментируйте с этим форматом и создайте для него несколько файлов данных.
2.6. Тематические задания
113
Тематическое задание 2.5. Рисование линий
и многоугольников пунктиром
Уровень сложности II.
Часто бывает необходимо провести линию штрих-пунктиром (dot-dash pattern) или заполнить много-
угольник узором, представляющим собой некоторое изображение. OpenGL предоставляет для этого
удобные инструменты.
Штриховые линии
Нетрудно задать штриховой шаблон (stipple pattern) для рисования линии. Если шаблон задан, он бу-
дет применяться для вычерчивания линии после активизации с помощью команды
glEnable(GL_LINE_STIPPLE):
и до тех пор, пока его активизация не будет отменена командой
glDisable(GL_LINE_STIPPLE);
Функция
glLineStipple(GLint factor. GLushort pattern):
задает шаблон штриховки. Величина pattern (которая имеет тип GLushort, 16-битное число без знака)
представляет собой последовательность нулей и единиц, которая определяет, какие точки будут ри-
соваться вдоль линии. 1 означает, что точка рисуется, 0 — что нет. Эта комбинация бит просматривает-
ся от младшего бита до старшего. Данный шаблон повторяется столько раз, сколько необходимо для
рисования нужной линии. В табл. 2.2 приведено несколько примеров. Для компактности битовый
шаблон записывается в шестнадцатеричной системе. Например, комбинация ОхЕЕСС задает битовый
шаблон 1110111011001100. Переменная factor (множитель) задает степень «расширения» шаблона:
каждый бит шаблона повторяется factor раз. Например, шаблон ОхЕЕСС с множителем 2 выглядит как
11111100111111001111000011110000. При рисовании штриховой линии с помощью подпрограммы:
glBegin(GL_LINE_STRIP): glVertex* О: glVertex* (); glVertex* О:...glEndO;
шаблон повторяется от конца одного отрезка линии до начала следующего, пока не встреп ггся команда gl End ().
Таблица 2.2. Примеры шаблонов штриховки
Шаблон Множитель Результирующая штриховка
OxFFOO 1 ...........................................
ОхЕЕОО 2 ....... ............. .............
0x5555 1 ..................................
0x3333 2 ......................................
0x7733 1 ..................................
Напишите программу, которая позволяет пользователю задавать битовый шаблон pattern (в шест-
надцатеричной кодировке) и значение множителя factor, после чего рисует штриховые линии по вер-
шинам, определяемым мышью.
Штриховка полигонов
Нетрудно также задать шаблон штриховки для заполнения полигона, однако здесь необходимо учесть
больше тонкостей. Если шаблон задан, он применяется к заполнению следующего полигона после ак-
тивизации с помощью команды
glDi sablе(GL_POLYGON_STIPPLE)
и до тех пор, пока он не будет деактивирован командой
glD1sable(GL_P0LYG0N_STIPPLE),
114
Глава 2. Начальная стадия: рисование фигур
Функция
glPolygonStipple(const GLubyte * mask);
применяет шаблон штриховки к последующим рисуемым полигонам на основе 128-байтного массива
nask[]. Эти 128 байт поставляют биты для битовой маски размером 32 на 32 бита. Шаблон «выкладыва-
ется мозаикой» по всему полигону, рисование которого задается обычными командами
glBegin(GL_POLYGON) glVertex* О; ... rglEndO;
Шаблон задается посредством определения массива
GLubyte mask[]-{0xff, Oxfe. 0x34. ... );
Первые четыре байта задают 32 бита нижнего ряда, слева направо; следующие четыре байта задают
следующий ряд, расположенный выше и т.д. На рис. 2.33 показан результат заполнения определенного
полигона узором «муха», который взят из «красной книги» OpenGL [Woo, 215].
Рис. 2.33. Пример заштрихованного полигона
Напишите программу, которая задает интересный шаблон штриховки для полигона и затем позво-
ляет пользователю разместить с помощью мыши последовательность выпуклых многоугольников, каж-
дый из которых заполнен этой штриховкой.
Тематическое задание 2.6. Редактор ломаных линий
Уровень сложности III.
Программы для рисования часто предоставляют возможность заходить на ломаные линии с помощью
мыши и затем редактировать эти ломаные, пока они не составят нужное изображение. На рис. 2.34, а
показан процесс рисования домика. Пользователь только что щелкнул мышью в месте, показанном на
рисунке, и предыдущая точка соединилась с точкой, отмеченной мышью, прямой линией.
Рис. 2.34. Создание и редактирование ломаных линий: а) добавление точек; 5) перемещение точки; в) удаление точки
Рисунок 2.34, б иллюстрирует процесс перемещения точки. Пользователь устанавливает курсор ря-
дом с вершиной ломаной линии, нажимает кнопку мыши и «перетаскивает» («drags») выбранную точ-
ку в какое-нибудь новое положение, не отпуская кнопку мыши. После отпускания кнопки старые пря-
мые линии, связанные с этой точкой, исчезнут и будут нарисованы новые.
2.6. Тематические задания
115
На рис. 2.34, в показано, как из ломаной линии удаляется точка. Пользователь щелкает мышью ря-
дом с вершиной какой-нибудь ломаной, после чего исчезают два отрезка прямой, связанные с этой вер-
шиной. Затем два других конца только что стертых отрезков соединяются отрезком прямой.
Напишите программу, предоставляющую пользователю возможность входить в картинки, состоя-
щие из 60 ломаных линий, и редактировать их. Пользователь взаимодействует с экраном посредством
нажатия клавиш на клавиатуре, а также указывая и щелкая мышью. Функциональные возможности
программы должны включать в себя следующие «действия»:
О begin — ('b'(создание новой ломаной);
О delete — ('d ‘): (удаление следующей точки, на которую указано);
О move — ('пГ): (перетаскивание указанной точки в новое положение);
О refresh — (' г'): (очистка экрана и перерисовка всех ломаных);
О quit—Cq'): (выход из программы).
Список ломаных может храниться в массиве BHflaGLintPointArray polys[60]. Команда begin, запуска-
емая нажатием клавиши ' b', позволяет пользователю создавать новую ломаную линию, которая запи-
сывается в первую доступную «ячейку» («slot») массива polys. При применении команды delete
предполагается, что программа определит, какая точка какой ломаной находится ближе всего к точке,
отмеченной в данный момент мышью. Когда эта точка определена, тем самым найдены «предыдущая»
и «последующая» вершины выбранной ломаной. Два отрезка прямой, связанные с выбранной верши-
ной, стираются, а предыдущая и последующая вершины соединяются отрезком прямой. Команда move
находит вершину, ближайшую к отмеченной в настоящий момент точке, и ожидает повторного щелчка
мышью, после чего данная вершина перемещается в эту новую, определенную щелчком точку.
Какие еще функции вы хотели бы иметь в редакторе ломаных линий? Обдумайте, каким образом
можно записывать массив ломаных в файл и впоследствии читать его. Также обдумайте, с помощью
какого рационального механизма можно было бы добавлять в ломаную новую точку.
Тематическое задание 2.7. Построение и запуск лабиринтов
Уровень сложности III.
Задача нахождения пути через лабиринт (maze) будет, вероятно, привлекательной всегда [Ball, 8].
Вы можете создать на компьютере замысловатый лабиринт и с помощью графики следить за его про-
хождением. На рис. 2.35 показан прямоугольный лабиринт размером 100 строк на 150 столбцов. Цель
состоит в том, чтобы найти путь от выхода на левом краю к такому же выходу на правом краю. Хотя и
возможно пройти данный лабиринт вручную методом проб и ошибок, все же интереснее разработать
алгоритм для автоматического прохождения лабиринта.
Рис. 2.35. Лабиринт
116
Глава 2. Начальная стадия: рисование фигур
Напишите и апробируйте программу, которая:
О создает и отображает прямоугольный лабиринт из R строк и С столбцов;
О находит (и отображает) путь через этот лабиринт от начала до конца.
Программа создает лабиринт случайным образом, однако он должен быть правильным: это означа-
ет, что каждая его ячейка с координатами (R, С) должна соединяться с любой другой ячейкой един-
ственным, хотя и извилистым путем. Подумайте о лабиринте как о графе, как предлагается на рис. 2.36.
Каждый путь представлен ветвью графа; а каждой из ячеек, в которой либо путь заканчивается, либо
встречаются два пути, соответствует узел графа. Следовательно, узел существует для каждой ячейки,
которая предоставляет выбор вариантов дальнейшего пути. Например, при достижении ячейки Q су-
ществует три варианта, в то время как из ячейки М их только два.
Рис. 2.36. Простой лабиринт и его граф
Как следует изображать лабиринт? Один из способов заключается в том, чтобы указывать для каждой
ячейки, есть ли у нее сплошная северная степа и сплошная восточная стена, с помощью данных следую-
щей структуры:
char northWall[R][C], eastWal1[R][C]:
Если northWallравно 1, то это означает, что ячейка [z,j] имеет сплошную стену сверху; в про-
тивном случае данная стена отсутствует. Нулевая строка является фиктивной строкой из ячеек, нахо-
дящихся под лабиринтом, причем ее северные стены формируют нижний край лабиринта. Подобным
же образом посредством eastWal 1 [i] [0] задаются любые проходы на левом краю лабиринта.
Создание лабиринта. Задайте сначала все стены сплошными, так чтобы лабиринт имел вид простой
сетки из горизонтальных и вертикальных прямых линий. Программа нарисует эту сетку. Затем в про-
извольно выбранную ячейку помещается некая невидимая «мышь», чья работа заключается в том, что-
бы «прогрызать» стены для соединения смежных ячеек. Эта мышь проверяет четыре соседних ячейки
(верхнюю, нижнюю, левую и правую) и для каждой из них выясняет, все ли четыре стены у нее сплош-
ные. Если это не так, то данный элемент ранее уже посещался и, следовательно, уже находится на
каком-то пути. Может случиться так, что мышь найдет несколько вариантов ячеек, которые еще не
посещались. Она выбирает одну из них случайным образом и прогрызает стену, соединяющую ее с
этим элементом, а координаты других вариантов записываются в стек. Прогрызенная стена стирается,
а мышь повторяет указанный процесс. Когда мышь попадает в тупик — в окружение посещенных яче-
ек, — она выталкивает из стека непосещенную ячейку и продолжает свое дело. Если стек пуст, то все
ячейки лабиринта уже посещены. «Начальная» и «конечная» ячейки выбираются произвольно, наибо-
лее вероятно на одном краю лабиринта. Очень интересно следить за динамикой создаваемого лабирин-
та, когда мышь прогрызает его стены. (Вопрос: Не лучше ли для записи вариантов ячеек использовать
очередь (queue) вместо стека? Как это повлияет на порядок, в котором создаются последующие пути?)
2.7. Дополнительная литература
117
Работа с лабиринтом. Для прохождения лабиринта мы использовали алгоритм с отходом («back-
tracking» algorithm — «поиск с возвратом»). На каждом шаге мышь пытается двигаться в случайном
направлении. Если стена отсутствует, мышь записывает ее координаты в стек и перемещается в следу-
ющую ячейку. Ячейку, где находится мышь, можно отметить красной точкой. Когда мышь попадает в
тупик, она может изменить цвет ячейки на синий и вернуться назад, вытолкнув данные из стека. Мышь
может даже построить стену, чтобы больше никогда не пытаться пройти в тупиковую ячейку.
Дополнение. Правильные лабиринты не являются слишком сложными, поскольку их всегда можно
пройти с помощью правила «плечо к стене» (shoulder-to-the-wall), когда вы отмечаете свой путь, при-
жимаясь плечом к левой стене. В тупике вы разворачиваетесь и идете тем же путем, постоянно сохра-
няя контакт со стеной. Поскольку лабиринт является «деревом», вы в конце концов достигнете цели.
В действительности, даже при наличии циклов в графе, вы всегда доберетесь до конца, поскольку и
начальная, и конечная ячейки находятся на внешних границах лабиринта. (Почему?) Чтобы сделать
задачу еще более интересной, поместите начальную и конечную ячейки внутрь лабиринта и заодно раз-
решите мыши прогрызть несколько дополнительных стен (например, случайным образом одну из 20).
В этом случае может возникнуть несколько циклов, окружающих конечную ячейку, и метод «плечо к
стене» не принесет успеха.
2.7. Дополнительная литература
В целом ряде книг имеется введение в OpenGL. Существует отличный курс «The OpenGL Programming
Guide», написанный By, Нидером и Дэвисом (Woo, Neider, Davis) [Woo, 215]. Кроме того, масса информа-
ции доступна в Интернете. (Обратитесь, например, в хранилище OpenGL по адресу http://www.opengl.org/
и к полному руководству по OpenGL по адресу http://www.sgi.com/software/opengl/manuaLhtmL)
3 Дополнительные инструменты
для рисования
□ Понятия порта просмотра и отсечения.
□ Осуществление преобразования из окна в порт просмотра.
□ Изложение классического алгоритма отсечения.
□ Создание инструментов для рисования в мировых координатах.
□ Разработка класса C++ для инкапсуляции подпрограмм рисования.
□ Рассмотрение способов выбора окон и портов просмотра
для оптимального визуального отображения.
□ Создание сложных изображений с использованием относительного
(relative) рисования и черепашьей (turtle) графики.
□ Построить фигуры из правильных многоугольников и их потомков.
□ Начертить дуги и круги.
□ Описать параметрически заданные кривые и рассмотреть способы
их вычерчивания.
Компьютеры бесполезны. Они могут только давать вам ответы.
Пабло Пикассо
Даже если вы на верной дороге, вас задавят, если вы просто сидите на ней.
Уилл Роджерс (Will Rogers)
В разделе 3.1 «Введение» вводятся понятия мировых координат (world coordinates) и мирового окна
(world window).
В разделе 3.2 «Мировые окна и порты просмотра» описывается преобразование из окна в порт про-
смотра. Такое преобразование делает графические приложения проще, так как позволяет программис-
ту работать в удобной системе координат, имея в то же время возможность отображать нужным обра-
зом все картинки на экране. В этом разделе также рассматривается вопрос, как программисту (или
пользователю) следует выбирать окно и порт просмотра для получения желаемых рисунков. Основное
правило: форматные соотношения окна и порта просмотра должны быть одинаковыми, иначе возмож-
но искажение результатов. Некоторые способы выбора могут быть автоматизированы.
3.1. Введение
119
В разделе 3.3 «Отсечение линий» строится классический алгоритм отсечения (clipping algorithm),
который удаляет все части изображения, выходящие за пределы мирового окна.
В разделе 3.4 «Разработка класса Canvas» вводится полезный класс C++ под названием Canvas (по-
лотно), который инкапсулирует множество деталей инициализации и обработки переменных, необхо-
димых для программы рисования. Рассмотрена его реализация в среде OpenGL. Программист может
использовать инструменты Canvas, чтобы создавать сложные изображения и быть уверенным в том, что
основные данные защищены от случайной порчи.
В разделе 3.5 «Относительное рисование» рассматриваются подпрограммы относительного рисова-
ния и так называемая «черепашья графика», которая добавляет к инструментарию программиста ряд
удобных методов. В разделе 3.6 «Фигуры на основе правильных многоугольников» исследуется рисо-
вание некоторых любопытных рисунков на базе правильных многоугольников, а раздел 3.7 «Рисование
окружностей и дуг» посвящен рисованию дуг и окружностей. В конце главы приведено несколько прак-
тических упражнений, включающих, в частности, разработку класса Canvas для программных сред, от-
личных от OpenGL, в которых все детали метода отсечений и преобразования из окна в порт просмотра
должны быть сконструированы в явном виде.
В разделе 3.8 «Применение параметрического задания кривой» описываются различные способы
задания кривых и излагается чрезвычайно полезная параметрическая форма, которая Позволяет легко
рисовать сложные кривые. Рассматриваются плоские и трехмерные кривые.
3.1. Введение
Хорошо сказать о предмете столь же интересно и столь же трудно, как нарисовать его.
Винсент Ван Гог
В главе 2 наши рисунки выполнялись в основной системе координат экранного окна. Эти координаты
измеряются преимущественно в пикселах и изменяются от нуля до некоторой величины screenWidth-1
пог и от нуля до величины screenHeight-1 по у. Это означает, что мы можем использовать только поло-
жительные величины х и у и эти величины должны иметь значительный диапазон (до нескольких со-
тен пикселов), если мы рассчитываем получить рисунок приемлемого размера.
Однако при решении какой-нибудь задачи мы можем не захотеть мыслить в терминах пикселов.
Было бы гораздо естественнее, если бы хизменялся, скажем, от -1 до 1, а у — от -100,0 до 20,0. (Напом-
ним, как непросто было масштабировать и сдвигать данные в программе создания точечного графика в
листинге 2.7.) Ясно, что мы должны различать величины, используемые нами в программе для описа-
ния геометрических объектов, и размер и расположение изображений этих объектов на экране дисплея.
В данной главе мы рассматриваем методы, позволяющие программисту или пользователю описы-
вать свои объекты в той системе координат, которые наилучшим образом способствуют решению каж-
дой отдельной задачи, а затем автоматически масштабировать и сдвигать изображение объекта так, что-
бы оно «вписывалось» в экранное окно. Пространство, в котором описываются объекты, называется
мировыми координатами (world coordinates) — это обычные декартовы координаты (х, у), используе-
мые в математике, причем в любых удобных единицах.
В мировых координатах мы определяем прямоугольное мировое окно’ (world window). Мировое
окно устанавливает, какую часть «внешнего мира» следует нарисовать. Смысл мирового окна в следую-
щем: все, что находится внутри этого окна, должно быть нарисовано, а все, что находится вне его, долж-
но быть отсечено и не должно рисоваться.
Кроме этого, внутри экранного окна (screen window) мы задаем прямоугольный порт просмотра
(viewport)2. Преобразование (состоящее из масштабирования и сдвига) между мировым окном и пор-
1 Как уже отмечалось, слово «окно» («window») имеет в графике множество различных значений, что зачастую приводит к неразбери-
хе. Мы будем стараться при необходимости подчеркивать различие смысла между словами «мировое окно», «экранное окно» И т. д.
2 В некоторых источниках переводится как «демонстрационное окно» или «окно вывода». — Примеч. пер.
120
Глава 3. Дополнительные инструменты для рисования
том просмотра организовано так, что при рисовании объектов внешнего мира те их части, которые на-
ходятся внутри мирового окна, автоматически преобразуются внутрь порта просмотра. Таким образом,
программист мыслит в категориях «взгляда через окно» на изображаемые объекты и помещения «мгно-
венного снимка» всего того, что видно через это окно, в порт просмотра на дисплее. Данный подход
«окно — порт просмотра» значительно упрощает такие вещи, как «увеличение» («zooming in») какой-
либо детали в сцене или панорамирование («panning around») этой же сцены.
Вначале рассмотрим ту часть преобразования, которая обеспечивает автоматическое изменение ко-
ординат. Затем мы увидим, как осуществляется отсечение.
3.2. Мировые окна и порты просмотра
Покажем на примере целесообразность использования мировых окон и портов просмотра. Предполо-
жим, что вы хотите исследовать природу некоторой математической функции, например функции sine,
хорошо известной в области обработки сигналов. Эта функция определяется формулой
. . . sin(iDc)
sinc(x) = ——-
тис
(3.1)
Вы хотите узнать, как эта функция изгибается и извивается по мере изменения х. Предположим, вы
знаете, что при изменении х от -о» до °° функция sinc(r) изменяется в пределах от -1 до 1 и что наиболее
интересно поведение sinc(r) при значениях х в окрестностях нуля. Поэтому вы хотите, чтобы график
имел центром точку (0, 0) и показывал функцию sinc(r) для значений X, плотно расположенных в про-
межутке от -4,0 до 4,0. На рис. 3.1 показан график функции sinc(r), созданный с помощью простой ото-
бражающей функции (display function) OpenGL (конечно, после того, как были заданы подходящие
мировое окно и порт просмотра).
Рис. 3.1. График функции sinc(x)
Вот код этой программы:
void myDisplay(void)
{
glBegin(GL_LINE_STRIP);
forCGLfloat x - -4.0; x < 4.0; x +- 0.1)
{
GLfloat у - sin(3.14159 * x) / (3.14159 * x);
glVertex2f(x. y);
}
glEndO:
glFlushO:
3.2. Мировые окна и порты просмотра
121
Заметим, что в этом коде используется естественная система координат для решения данной зада-
чи: задан маленький шаг по г в диапазоне от -4,0 до 4,0. Главный вопрос заключается в том, каким обра-
зом следует масштабировать и сдвигать различные величины (г, у), чтобы изображение должным обра-
зом размещалось в экранном окне.
Необходимые масштабирование и сдвиг осуществляются посредством установки мирового окна
и порта просмотра и задания соответствующего преобразования между ними. Как мировое окно, так
и порт просмотра являются выровненными прямоугольниками, задаваемыми программистом. Миро-
вое окно выражается мировыми координатами. Порт просмотра является частью экранного окна.
На рис. 3.2 приведен пример мирового окна и порта просмотра. Идея заключается в следующем: все,
что находится внутри мирового окна, масштабируется и сдвигается так, чтобы оно правильно отобра-
жалось в порту просмотра; все остальное отсекается и не отображается.
а б
Рис. 3.2. Мировое окно (а) и порт просмотра (5)
Мы хотим описать не только то, как осуществлять операции масштабирования и сдвига в OpenGL,
что очень просто, но также и то, как организованы процессы масштабирования и сдвига, чтобы вы смогли
разобраться в используемых в них алгоритмах низкого уровня. Здесь мы работаем только с 2О-верси-
ей, однако позднее мы увидим, что эти идеи естественным образом распространяются и на ЗО-«миры»,
обозреваемые с помощью «камеры».
3.2.1. Преобразование из мирового окна в порт просмотра
На рис. 3.3 более детально показаны мировое окно и порт просмотра. Мировое окно описывается свои-
ми левой (left), верхней (top), правой (right) и нижней (bottom) границами, или W.l, W.t, W.r и W.bl соот-
ветственно. Порт просмотра описывается подобным же образом в системе координат экранного окна
(открытого в каком-либо месте на экране) посредством координат V.l, V.t, V.r и V.b, которые измеряют-
ся в пикселах.
Мировое окно может иметь любой размер, форму и положение, оставаясь при этом выровненным
прямоугольником. Подобным же образом порт просмотра может быть любым выровненным прямо-
угольником, хотя, конечно, обычно его выбирают так, чтобы он целиком находился внутри экранного
окна. Более того, мировое окно и порт просмотра не обязаны иметь одно и то же форматное соотноше-
ние, хотя различие форматных соотношений приводит к искажению. Как показано на рис. 3.4, искаже-
ние возникает из-за того, что рисунок в окне необходимо растянуть, чтобы он вписался в порт просмот-
ра. Позднее мы узнаем, как устанавливать для порта просмотра форматное соотношение, которое будет
всегда соответствовать форматному соотношению экранного окна, даже если пользователь изменяет
размеры последнего.
1 Для краткости мы используем в математических формулах I вместо left, t вместо top и т. д.
122
Глава 3. Дополнительные инструменты для рисования
Рис. 3.3. Задание мирового окна (а) и порта просмотра (£)
окно окно
Рис. 3.4. Картинка, преобразованная из мирового окна в порт просмотра. Здесь возникает некоторое искажение
Имея описание мирового окна и порта просмотра, мы производим преобразование (mapping), или
трансформацию (transformation), называемые также преобразованием мировое окно — порт просмот-
ра (window-to-viewport mapping). Это преобразование основывается на формуле, которая вычисляет
точку (sx, sy) в координатах экранного окна для любой заданной точки (х, у) мирового окна. Мы хотим,
чтобы это преобразование было «пропорциональным» в том смысле, что если х составляет, например,
40 % всего расстояния от левого края мирового окна, то sx должен составлять 40 % всего расстояния от
левого края порта просмотра. Подобным же образом, если у составляет некоторую долю f от высоты
мирового окна, считая от его нижней границы, то sy должен составлять ту же самую долю/, отсчитыва-
емую от нижней границы порта просмотра.
Из пропорциональности следует линейная форма преобразования:
sx - Ах + С,
D ’ (3.2)
sx - By + D, v '
с некоторыми константами А, В, С и D. Константы Ли В изменяют масштаб координат х и у, а С и D
сдвигают (или переносят) (translate) их.
х зх
_J--------I------------1---> _I---------1-----------1---->
W.l W.r V.l V.r
Рис. 3.5. Пропорциональность в преобразовании х в sx
3.2. Мировые окна и порты просмотра
123
Как определить А, В, Си D? Сначала рассмотрим преобразование для х. Как видно из рис. 3.5, про-
порциональность требует, чтобы разность (sx-Vl) составляла ту же долю от разности (V.r-V.l), кото-
рая составляет величина (x-WJ) от величины (W.r-W.l), следовательно:
sx-V.1 _ x-W.1
V.r-VJ ~ W.r-WJ
или
У.г-У.1 ( У.г-У.1
IVx-WJ Wx-WJ J
Обозначив множитель при x буквой А, а свободный член — буквой С, получим:
А _ Ух-VI
Wx-W.l
и
С = VJ - AWJ.
Подобным же образом пропорциональность для у означает, что
sy - V.b _ у — W.b
Ул-Vb ~ Wj-W.b ’
а запись sy в виде By + D требует соотношений
Vt-Vb
В = j -о D = Vb_BWbt
Wi-W.b
В результате мы имеем следующие формулы преобразования мирового окна в порт просмотра:
sx = Ах + С
и
sy = By + D,
где
У.г-У.I
Wx-Wj'
C-V.l-AW.1
(3.3)
и
в = УЛ — УЬ
№Л-№Ь’
D = V.b-BWb.
Это преобразование можно использовать для любой точки (х, у) внутри или вне окна. Точки внутри окна
преобразуются во внутренние точки порта просмотра, а точки вне окна — в точки вне порта просмотра.
Следует тщательно сверить следующие свойства этого преобразования, используя равенства (3.3):
1. Если х находится на левом краю окна (х = W.I), то sx находится на левом краю порта просмотра
(sx = V.I);
2. Если х — на правом краю окна, то sx — на правом краю порта просмотра.
3. Если х составляет /-ю часть от ширины окна, то sx является f-и частью от ширины порта просмотра.
4. Если х находится вне окна слева от него (х < W.I), то sx также находится вне порта просмотра
слева (sx < V.I), и аналогично в случае, когда х вне окна справа от него.
Проверьте аналогичные свойства для преобразования у esy.
124
Глава 3. Дополнительные инструменты для рисования
Пример 3.2.1
Рассмотрим окно и порт просмотра, изображенные на рис. 3.6. Окно имеет размеры (W.l, W.r, W.b,
W.r) = (0,2,0, 0,1,0), а порт просмотра — (V.l, V.r, V.b, V.r) - (40, 400, 60, 300).
300
60
400
40
а б
Рис. 3.6. Пример окна (а) и порта просмотра (£)
Используя формулы в уравнении (3.3), получим:
А = 180, С = 40, В = 240, D = 60.
Тогда для нашего примера преобразование окно — порт просмотра примет вид:
sx= 180х + 40;
sy - 340г/ + 60.
Проверим, что данное преобразование правильно переводит различные характерные точки, например:
О Каждый угол окна действительно переводится в соответствующий угол порта просмотра. Напри-
мер, (2,0,1,0) преобразуется в (400,300).
О Центр окна, то есть (1,0,0,5), преобразуется в центр порта просмотра (220, 180).
Практическое упражнение
3.2.1. Построение преобразования
Найдите величины А, В, С и D для перевода мирового окна (-10,0, 10,0, -6,0, 6,0) в порт просмотра
(0, 600,0, 400).
Как выполнить это в OpenGL?
В рамках OpenGL перевод из окна в порт просмотра очень прост, он автоматически осуществляет
для каждой задаваемой вершины (ломаной линии) нужную последовательность преобразований с по-
мощью команды gl Vertex2 * О. Кроме того, OpenGL автоматически отсекает части объекта, находящи-
еся за пределами мирового окна. Все, что от нас требуется, — это правильно назначить преобразования,
а все остальное делает OpenGL.
Для двумерного случая мировое окно устанавливается с помощью функции gl uOrtho2D(), а порт про-
смотра — функцией gl Viewport(). Эти функции имеют следующие прототипы:
функция
void glu0rtho2D(GLdouble left. GLdouble right.
GLdouble bottom. GLdouble top);
устанавливает для окна левый нижний угол (1 eft, bottom) и правый верхний угол (right. top), а функция
void gIViewport(GLint х, GLint у.
GLint width. GLint height):
устанавливает для порта просмотра нижний левый угол (х, у) и верхний правый угол (х + width,
у + height).
3.2. Мировые окна и порты просмотра
125
По умолчанию порт просмотра является полным экранным окном: если ширина и высота экранного
окна равны соответственно W и Н, то порт просмотра по умолчанию имеет левый нижний угол (0, 0) и
верхний правый угол (W. Н). •
Поскольку в OpenGL для настройки всех его преобразований используются матрицы, то до вызова
функций glu0rtho2D()1 необходимо вызвать две «установочные» функции: glMatrixMode(GL_PROJECTION) и
glLoadldentityO. (В главе 5 мы рассмотрим более подробно, что при этом происходит за сценой.)
Таким образом, для настройки окна и порта просмотра из примера 3.2.1 нам следует использовать
следующий код:
glMatrixMode(GL_PROJECTION):
glLoadldentityO;
glu0rtho2D(0.0, 2.0. 0.0. 1.0):
// sets the window
// устанавливает окно
glViewport(40. 60. 360. 240):
// sets the viewport
// устанавливает порт просмотра
В дальнейшем каждая точка, отправленная в OpenGL посредством функции glVertex2*(x, у), под-
вергается преобразованию согласно уравнениям (3.3), а края автоматически отсекаются границами
окна. (В главе 7 мы подробно рассмотрим, как это происходит в трехмерном случае; в процессе этого
рассмотрения также станет понятно, что двумерный вариант является всего лишь частным случаем
трехмерного.)
Мы сделаем программы более читабельными, если инкапсулируем все настраивающие окно коман-
ды внутрь функции setWindowO, как показано в листинге 3.1. В листинге показана также функция
setViewportO, внутрь которой упрятаны все детали OpenGL-функции glViewport(. .). Для простоты
использования функции setViewport ее параметры слегка перегруппированы, чтобы соответствовать
параметрам setWindowO, так что теперь в обеих функциях они идут в таком порядке: left, right, bottom,
top (левый, правый, нижний, верхний).
Листинг 3.1. Полезные функции для настройки окна и порта просмотра
// ........-........ setwindow .........................
void setW1ndow(float left, float right, float bottom, float top)
{
glMatrixMode(GL_PROJECTION):
glLoadldentityO;
glu0rtho2D(left, right, bottom, top):
}
// ............... setViewport .......................
void setViewportGnt left, int right, int bottom, int top)
{
glViewport(left, bottom, right - left, top - bottom):
}
Отметим, что для удобства мы используем для параметров функции setWindowO тип float. Парамет-
ры 1 eft, ri ght и т. д. автоматически преобразуются к типу GLDoubl е при передаче их функции gl u0rtho2D(),
как указано в прототипе этой функции. Подобным же образом мы используем тип int для парамет-
ров функции setViewportO, зная, что тип аргументов функции glViewportO также будет правильно
преобразован.
1 Корень «ortho» появляется потому, что настройка окна таким способом фактически устанавливает так называемую ортогональ-
ную проекцию (orthographic projection) для трехмерного случая, как мы увидим в главе 7.
126
Глава 3. Дополнительные инструменты для рисования
Стоит вернуться назад и посмотреть, что мы использовали для окна и порта просмотра в наших ран-
них программах на OpenGL в главе 2. В листинге 2.5 и на рис. 2.8 в программах использовались такие
команды:
1. Команды, устанавливающие размер экранного окна 640 на 480.
В main О:
glutInitWindowS1ze(640, 480)
// set screen window size
// устанавливаем размер окна
Величина порта просмотра принималась по умолчанию, поскольку еще не было команды
gIViewportO; а по умолчанию порт просмотра — это экранное окно целиком.
2. Набор команд
в mylnitO:
glMatrixMode(GL_PROJECTION):
glLoadldentityO;
glu0rtho2D(0.0. 640.0. 0.0. 480.0):
Эти команды устанавливают мировое окно в выровненный прямоугольник с углами (0,0) и (640,0,
480,0), как раз в соответствии с размером порта просмотра, так что основное преобразование
окно — порт просмотра ничего не изменило. Такой выбор представляется разумным для первых
программ.
Пример 3.2.2. Снова построение графика функции sine
Собрав вместе предшествующие компоненты, можно увидеть, как вычертить форму графика функции
sinc() с рис. 3.1. При использовании OpenGL достаточно задать окно и порт просмотра. В листинге 3.2
приведен код, отображающий график этой функции для значений х с малым шагом в промежутке от
-4 до 4 в порт просмотра шириной 640 и высотой 480. (Окно сделано несколько шире, чем диапазон
графика, для того чтобы оставить вокруг графика некоторое пространство для красоты.)
Листинг 3.2. Построение графика функции sine
void myDisplay(void)
// plot the sine function, using world coordinates
// строим график функции sine, используя мировые координаты
{
setWindow(-5.0, 5.0. -0.3. 1.0):
// set the window
// устанавливаем окно
setViewport(0, 640. 0. 480):
// set the viewport
// устанавливаем порт просмотра
glBegin(GL_LINE_STRIP);
for(GLfloat x - -4.0; x < 4.0: x += 0.1)
// draw the plot
// рисуем график
glVertex2f(x. sin(3.14159 * x) / (3.14159 * x)):
glEndO;
glFlushO;
}
Пример 3.2.3. Рисование ломаных линий из файла
В главе 2 мы нарисовали динозавра, изображенного на рис. 3.7, с помощью стандартной подпрограммы
drawPolylineF11e( "dino.dat") из листинга 2.9. Данные о ломаных линиях, необходимые для этого рисун-
3.2. Мировые окна и порты просмотра
127
ка, хранились в файле "dino.dat”. Мировое окно и порт просмотра в эту подпрограмму еще не вводи-
лись, так что мы принимали ряд вещей на веру или по умолчанию, но, к счастью, все же получили рису-
нок динозавра.
Теперь мы можем понять, почему все сработало. Использованное нами мировое окно охватывало
все данные по динозавру (см. практическое упражнение 2.4). Все ломаные в dino.dat располагались
внутри прямоугольника с углами (0,0) и (640,480), так что при таком выборе окна отсекать было нечего.
Вооружившись средствами для установки окна и порта просмотра, мы можем лучше контролиро-
вать ситуацию. Следующие два примера являются чисто иллюстративными.
Рис. 3.7. Динозавр внутри своего мирового окна
Пример 3.2.4. Покрытие экранного окна мозаикой из динозавров
Чтобы сделать экран немного интереснее, можно украсить его копиями динозавра в виде некоторого
узора. Укладывание вплотную множества копий одного и того же рисунка с целью заполнения всего
экранного окна называется мозаичным покрытием (tiling) этого окна. Изображение, которое копиру-
ется в разных положениях, называется мотивом (motif). Мозаичное покрытие экранного окна легко
осуществить, если использовать индивидуальный порт просмотра для каждого экземпляра аппликации.
На рис. 3.8, а показано мозаичное покрытие, использующее 25 копий мотива. Эта мозаика была выпол-
нена с помощью следующего кода:
setWindow(0, 640.0. 0. 440.0):
// set a fixed window
// задаем постоянное окно
for(int i=0: i < 5: i++)
// for each column
// для каждого столбца
for(int j-0: j < 5: j++)
// for each row
// для каждой строки
glViewports * 64. J * 44 . 64 . 44):
// set the next viewport
// устанавливаем следующий порт просмотра
drawPolyli neFileC“dino.dat”):
// draw it again
// рисуем динозавра снова
}
(Здесь проще использовать gl ViewportO, чем set Viewport О. Какие аргументы следовало бы взять для
setViewportO, если бы мы все-таки использовали эту функцию?) Отметим, что каждая копия рисуется в
порте просмотра размером 64 на 44 пиксела с форматным соотношением (64/44), что совпадает с фор-
матным соотношением мирового окна. Поэтому каждый динозавр нарисован без искажений.
Рисунок 3.8, б изображает другое мозаичное покрытие, здесь каждый второй мотив перевернут вверх
ногами для создания любопытного эффекта. Это было сделано с помощью зеркального отражения
128
Глава 3. Дополнительные инструменты для рисования
каждого второго окна сверху вниз, а именно изменением порядка параметров top и bottom в функции
setWindowO1. (Удостоверьтесь, что такое зеркальное отражение окна правильно влияет на значения BhD
в уравнении 3.13, описывающем преобразование окно — порт просмотра; это преобразование и являет-
ся нашим инструментом зеркального отражения картинки в порте просмотра). Затем код для двойного
цикла был изменен следующим образом:
fordnt i - 0; i < 5: i++)
for(int j = 0: j < 5; j++)
(
if((i+j) % 2 == 0)
// if (i+j) is even
// для четного (i+j)
setWindow(0.0, 640.0. 0.0, 440.0);
// right-side-up window
// правое верхнее окно
else
setWindow(0.0. 640.0, 440.0. 0.0):
// upside-down window
// перевернутое окно
glViewport(i * 64. j * 44. 64. 44);
// set the next viewport
// устанавливаем следующий порт просмотра
drawPolylineFile("dino.dat");
// draw it again
// рисуем динозавра снова
}
а б
Рис. 3.8. Мозаичное покрытие дисплея копиями динозавра
Пример 3.2.5. Отсечение частей рисунка
Изображение также может быть отсечено посредством соответствующей установки окна. OpenGL
автоматически отсекает части объекта, расположенные за пределами мирового окна. Крайнее левое
изображение на рис. 3.9 состоит из множества шестиугольников разных размеров, каждый из которых
слегка повернут по отношению к соседнему. Предположим, что эти шестиугольники нарисованы в ре-
зультате выполнения некоторой функции hexSwirl () (завихрение гексагонов). (В разделе «Фигуры на
основе правильных многоугольников» мы увидим, как написать функцию hexSwirl ().) На рисунке по-
казаны два наложенных на шестиугольники квадрата, которые демонстрируют различные способы вы-
бора окна. Среднее и правое изображения на рис. 3.9 показывают, что будет нарисовано, если эти квад-
1 Казалось бы, проще инвертировать порт просмотра, однако в OpenGL не разрешается использовать порт просмотра с отрицатель-
ной высотой.
3.2. Мировые окна и порты просмотра
129
раты взять в качестве мировых окон. Важно иметь в виду, что если использовать следующий код, то в
каждом случае будет нарисован тот же самый целый объект:
setWindow(...):
// the window is changed for each picture
// окно изменяется для каждого изображения
setViewport(...
// use the same viewport for each picture
// для каждого изображения используем тот же самый
// порт просмотра
hexSwi г 1 ():
// the same function is called
// вызывается та же самая функция
С другой стороны, что именно будет изображено, зависит от установки окна.
Рис. 3.9. Использование окна для отсечения частей рисунка
Изменение масштаба изображения и блуждание
Пример на рис. 3.8 показывает, что изменение окна может вызывать полезные эффекты. Уменьшение
окна напоминает приближение (zooming in) объекта с помощью кинокамеры (камера «наезжает» на
объект). Все, что находится внутри окна, должно точно соответствовать фиксированному размеру порта
просмотра, поэтому, когда окно уменьшается, его содержимое увеличивается. Аналогично увеличение
окна эквивалентно отодвиганию (zooming out) объекта (камера удаляется от объекта).-(Представьте
себе мысленно, как бы выглядел динозавр, если бы окно увеличилось вдвое по сравнению с изображен-
ным на рис. 3.7.) Кроме того, камера может блуждать (roam) по сцене (иногда это называют «панора-
мированием» — «рап»), снимая в различные моменты времени различные участки сцены. Это легко
достигается сдвигом окна в новое положение.
Пример 3.2.6. Увеличение масштаба рисунка в анимации
Рассмотрим пример составления движущегося изображения, полученного при приближении камеры к
какой-либо части шестиугольников с рис. 3.9. Для решения этой задачи мы создаем серию изображе-
ний, часто называемых кадрами (frames), каждое из которых использует окно, чуть меньшее, чем пре-
дыдущее. Когда эти кадры выводятся на экран с большой скоростью, визуально это выглядит как каме-
ра, наезжающая на объект.
На рис. 3.10 показаны некоторые из использованных окон; все они являются концентрическими и
имеют фиксированное форматное соотношение, но с каждым последующим кадром их размер умень-
шается. Представьте мысленно, что нарисовано в порте просмотра для каждого из этих окон.
Скелет программы, позволяющей достичь этого эффекта приближения, показан в листинге 3.3. Для
каждого нового кадра экран очищается, окно делается все меньше (с фиксированными центром и фор-
матным соотношением), а рисунок внутри окна рисуется в постоянном порту просмотра.
5 Ф. Хилл
130
Глава 3. Дополнительные инструменты для рисования
Листинг 3.3. Создание анимации
float сх - 0.3, су - 0.2;
// center of the window
// центр окна
float Н. W - 1.2. aspect - 0.7;
// window properties
// свойства окна
set the viewport
// устанавливаем порт просмотра
for(int frame - 0: frame < NumFrames: frame++)
{
// for each frame
// для каждого кадра
clear the screen
// очищаем экран
// erase the previous figure
// удаляем предыдущий рисунок
W *- 0.7:
// reduce the window width
// уменьшаем ширину окна
H - W * aspect;
// maintain the same aspect ratio
// сохраняем прежнее форматное соотношение
setWindow(cx - W, сх + W. су - H. су + Н);
//set the next window
// устанавливаем следующее окно
hexSwi rl();
// draw the object
// рисуем объект
}
Рис. 3.10. Приближение к завихряющимся шестиугольникам
Получение плавной анимации
Предыдущее приближение не является вполне удовлетворительным, поскольку рисование новой фи-
гуры занимает определенное время. Все, что видит пользователь, — это повторяющийся цикл из следу-
ющих двух действий:
О А. Мгновенное стирание текущей фигуры.
О Б. (Как можно более) медленное рисование новой фигуры.
3.2. Мировые окна и порты просмотра
131
Проблема заключается в том, что пользователь видит создание нового кадра строка за строкой, что
может отвлекать внимание. А пользователь скорее хотел бы видеть такой повторяющийся цикл:
О А. Постоянный показ текущей фигуры.
О Б. Мгновенное замещение текущей фигуры законченной новой фигурой.
Хитрость заключается в том, чтобы нарисовать новую фигуру «где-нибудь в другом месте» в то вре-
мя, пока пользователь разглядывает текущую фигуру, а затем мгновенно переместить готовую новую
фигуру на дисплей пользователя. OpenGL предлагает для решения этой задачи двойную буферизацию
(double buffering). Выделяется память для дополнительного экранного окна, которое невидимо на дей-
ствующем дисплее, и все рисование выполняется в этом окне, называемом буфером. (Использование
такой «внеэкранной памяти» («off-screen memory») рассматривается более полно в главе 10.) Затем с по-
мощью команды glutSwapBuffersO изображение из буфера передается в экранное окно и становится
видимым для пользователя.
Для того чтобы OpenGL зарезервировал для этой цели отдельный буфер, в подпрограмме, которая
используется в тэтп() для инициализации режима работы дисплея, вместо команды GLUT_SINGLE нужно
применить команду GLUT_DOUBLE:
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB):
Команду glutSwapBuffersO нужно расположить сразу после hexSwirl О в коде из листинга 3.3. В этом
случае, даже если на рисование ломаной линии уходит заметное время, в процессе анимации изображе-
ние будет быстро меняться от одной картинки к другой, что обеспечивает более плавное движение и
производит приятный для глаз эффект.
Практическое упражнение
3.2.2. Вращающиеся вихри
Рисунок 3.11, а представляет еще один пример отсечения и мозаичного покрытия. На нем показано завих-
рение шестиугольников с рис. 3.10 с выделением некоторого окна. В этом примере окно остается неизмен-
ным, а порт просмотра изменяется от рисунка к рисунку. На рис. 3.11, б показано несколько копий этого
рисунка, составленных вместе и покрывающих дисплей мозаикой. Попробуйте выделить отдельные вихри.
(Некоторые из этих вихрей были зеркально отражены. Какие именно?) Получившийся результат слепит
глаза, отчасти в силу склонности наших глаз складывать множество мелких элементов в единый узор.
Приведенный ниже код создает узор рис. 3.11, б, за исключением зеркального отражения. Функция
myDisplayO устанавливает окно один раз и затем рисует отсекаемые вихри снова и снова в различные
порты просмотра. Вот этот код:
void myDisplay(void)
{
clear the screen
// очищаем экран
setWindow(-0.6. 0.6. -0.6. 0.6):
// the portion of the swirl to draw
// часть вихря для рисования
for(int 1=0; i < 5; 1++)
// make a pattern of 5-by-4 copies
// создаем узор из 5x4 копий
fordnt j - 0: j < 4: j++)
{
int L - 80:
// the amount to shift each viewport
// количество для сдвига каждого порта просмотра
geViewportd * L. L + i * L. L. L):
hexSwi rl():
132
Глава 3. Дополнительные инструменты для рисования
а б
Рис. 3.11. Заверяющиеся шестиугольники в фиксированном окне (а); мозаика, сформированная
с использованием многих портов просмотра (б)
Наберите этот код в среде OpenGL и поэкспериментируйте с рисунками, которые он создаст. Поза-
имствовав идею из предыдущего примера, определите, как перевернуть вверх ногами каждый второй
рисунок.
3.2.2. Автоматическая установка окна и порта просмотра
Давайте посмотрим, как выбирать окно и порт просмотра, чтобы получить нужные изображения сцены.
В ряде случаев программист (или, возможно, пользователь во время выполнения программы) может
ввести спецификации для окна и порта просмотра для получения необходимого эффекта; в других слу-
чаях одна или обе эти спецификации устанавливаются автоматически, согласно некоторым требовани-
ям к изображению. В данном разделе мы рассмотрим несколько вариантов выбора.
Установка окна
Зачастую программист не знает, где располагается интересующий его объект или каковы его размеры в
мировых координатах. Подобно рассмотренному ранее динозавру, этот объект может храниться в фай-
ле или может генерироваться процедурно согласно какому-либо алгоритму, детали которого неизвест-
ны. В любом случае выбор окна удобно предоставить самому приложению.
Обычно стремятся найти окно, в которое объект помещается целиком. Для этого необходимо найти
обрамление данного объекта, называемое экстентом (extent). Экстент, или ограничивающий прямо-
угольник (bounding box) объекта — это выровненный прямоугольник, в точности покрывающий данный
объект. На рис. 3.12 приведен чертеж, составленный из нескольких отрезков прямых. Экстент данной
фигуры, показанный штриховой линией, равен (left, right, bottom, up) = (0,36, 3,44, -0,51,1,75).
Рис. 3.12. Использование экстента в качестве окна
3.2. Мировые окна и порты просмотра
133
Как вычислить экстент для заданного объекта? Если все конечные точки линий, из которых состоит
объект, хранятся в массиве pt[i], где i = 0,2,..., п - 1, то экстент можно определить, найдя экстремаль-
ные значениях и у в данном массиве. Например, левая сторона экстента равна минимуму из всех значе-
ний pt[i] .х. После того как экстент найден, окно можно положить равным ему.
Если же объект задан процедурно, то не представляется возможным заранее определить его экстент.
В этом случае можно прощать рисующую данный объект подпрограмму дважды, но по-разному:
1 прогон. Выполнить подпрограмму рисования, но фактически не рисовать, а только вычислять
экстент. Затем установить окно.
2 прогон. Снова выполнить подпрограмму, уже с рисованием.
Автоматическая установка порта просмотра
с сохранением форматного соотношения
Предположим, вы хотите нарисовать фигуру наибольшего размера, которая без искажений поместится
в экранном окне. Для того чтобы сделать это, необходимо задать порт просмотра с тем же форматным
соотношением, какое имеет мировое окно. Обычно выбирают наибольший из портов просмотра, кото-
рый поместится внутри экранного окна на дисплее.
Предположим, что форматное соотношение мирового окна известно и равно R, а экранное окно име-
ет ширину W и высоту Н. Теперь следует рассмотреть отдельно два случая: мировое окно может иметь
большее форматное соотношение, чем экранное окно (R > W/Н), или, наоборот, меньшее форматное
соотношение (R < W/Н). Оба этих случая показаны на рис. 3.13. Мы рассмотрим их поочередно.
R> W/H
Мировое окно
Форматное
соотношение: R
Порт Экранное
Рис. 3.13. Возможные форматные соотношения для мирового и экранного окон: a) R > W/Н; б) R < W/H
Случай a)-. R > W/Н. Здесь мировое окно короче и толще, чем экранное окно, следовательно, порт
просмотра с таким же форматным соотношением R целиком поместится по ширине экранного окна,
однако вверху и/или внизу останется некоторое неиспользованное пространство. Поэтому наибольший
порт просмотра будет иметь ширину W и высоту W/R и его можно задать с помощью следующей ко-
манды (убедитесь, что этот порт просмотра действительно имеет форматное соотношение R):
setViewportCO. W. 0. W/R);
Случай б): R< W/H. Здесь мировое окно выше и уже, чем экранное окно, следовательно, порт про-
смотра с таким же форматным соотношением R расположится сверху донизу экранного окна, однако
справа и/или слева останется неиспользованное пространство. Поэтому наибольший порт просмотра
будет иметь высоту Н, а длину HR; это устанавливается следующей командой:
setViewportCO. Н * R. 0. Н);
Пример 3.2.7. Высокое окно
Пусть форматное соотношение окна составляет R = 1,6, а экранное окно имеет высоту Н = 200 и ширину
W= 360, отсюда W/H= 1,8. Следовательно, имеем случай б), и порту просмотра назначается высота
200 пикселов и ширина 320 пикселов.
134
Глава 3. Дополнительные инструменты для рисования
Пример 3.2.8. Короткое окно
Пусть R » 2, а экранное окно такое же, как и в предыдущем примере. Тогда имеем случай а), и порту
просмотра назначается высота 180 пикселов и ширина 320 пикселов.
Изменение размеров экранного окна; событие Resize
В оконной системе пользователь может изменять размеры экранного окна динамически, обычно про-
таскиванием мышью одного из углов окна. Это действие генерирует событие resize (изменение разме-
ров), на которое система может реагировать. Функция glutReshapeFuncO из инструментария OpenGL
специфицирует функцию myReshape, вызываемую при возникновении данного события:
glutReshapeFunc(myReshape)
// specifies the function called on a resize event
// задает функцию, вызываемую no событию resize
(Данный оператор появляется в mainO наряду с другими вызовами, определяющими функции об-
ратного вызова.) Кроме того, эта зарегистрированная функция вызывается, когда окно открывается
впервые, и должна иметь следующий прототип:
void myReshape(GLsizei W. GLsizei H):
При выполнении данной функции система автоматически передает в нее новую ширину и высоту
того экранного окна, которое эта функция может затем использовать в своих вычислениях. (Glsizei яв-
ляется 32-битным целым; см. табл. 2.1.)
Что должна делать myReshapeO? Если пользователь увеличивает экранное окно, можно использовать
прежний порт просмотра (почему?), однако пользователь может захотеть увеличить порт просмотра,
чтобы использовать преимущества увеличенного размера окна. Если же пользователь уменьшает свое
экранное окно, пересекая при этом одну из границ порта просмотра, то он почти наверняка захочет пе-
ресчитать новый порт просмотра.
Создание согласованного порта просмотра
Обычно требуется найти новый порт просмотра так, чтобы он вписался в новое экранное окно и имел
такое же форматное соотношение, что и мировое окно. Согласование форматных соотношений порта
просмотра и мирового окна позволит избежать искажений в новом изображении. В листинге 3.4 приве-
ден вариант функции myReshapeO, осуществляющей желаемое согласование: она находит максимальный
порт просмотра с тем же форматным соотношением, как у окна, который впишется в новое экранное
окно. Эта подпрограмма получает ширину и высоту нового экранного окна через свои параметры. Ее
код является просто выражением результата с рис. 3.13.
Листинг 3.4. Использование функции изменения формы (reshape) для задания наибольшего согласованного порта просмотра
при обработке события resize
void myReshape(GLsizei W. GLsizei H)
if(R > W/H)
// use (global) window aspect ratio
// используем форматное соотношение (глобального) окна
setViewport(0. W. 0. W/R):
else
setViewport(0. H * R. 0. H):
}
Практические упражнения
3.2.3. Найти ограничивающий прямоугольник для ломаной линии
Напишите подпрограмму, которая вычисляет экстент ломаной линии, записанной в массиве точек pt[i ],
для i = 0,2,.... п - 1.
3.3. Отсечение линий
135
3.2.4. Согласование порта просмотра
Найдите согласованный порт просмотра для окна с форматным соотношением 0,75, если экранное окно
имеет ширину 640 и высоту 480.
3.2.5. Центрирование порта просмотра (не пропускайте этот пример!)
Измените подпрограмму myReshapeO из листинга 3.4 так, чтобы порт просмотра размещался не в левом
верхнем углу дисплея, а в центре экранного окна — как по горизонтали, так и по вертикали.
3.2.6. Как расплющить домик
Выберите окно и порт просмотра так, чтобы изображение расплющилось до половины его настоящей
высоты. Чему равны в этом случае коэффициенты А, В, Си D?
3.2.7. Вычисление преобразования
Найдите коэффициенты А, В, С и D для преобразования окно — порт просмотра для окна с координата-
ми (-600, 235, -500, 125) и порта просмотра с координатами (20, 140, 30, 260). Будут ли искажены фи-
гуры, нарисованные в мировом окне? Измените правую границу порта просмотра так, чтобы исправить
это искажение.
3.3. Отсечение линий
Отсечение (clipping) является одной из основных задач графики и применяется для того, чтобы пре-
дотвратить рисование тех частей объекта, которые размещаются вне заданной области. Разработано
большое количество алгоритмов отсечения. В среде OpenGL каждый объект автоматически отсекается
в мировом окне с использованием особого алгоритма (в главе 7 мы подробнее рассмотрим этот алго-
ритм для дву- и трехмерных объектов).
Поскольку OpenGL осуществляет отсечение за вас, то может возникнуть соблазн вообще пропус-
тить изучение этого процесса. Однако принципы, использованные при разработке отсекателя (clipper),
являются фундаментальными и пригодятся в различных ситуациях. В следующих главах мы будем рас-
сматривать целый ряд подходов к отсечению. (Кроме того, полезно знать, как должным образом осуще-
ствить отсечение, если не использовать средства, подобные OpenGL.)
В этом разделе мы разрабатываем алгоритм, отсекающий выступающие части каждого переданного
ему отрезка прямой. Этот алгоритм можно включить в подпрограмму рисования прямых, если мы не
можем воспользоваться отсечением, производимым OpenGL. В практическом упражнении 3.3 разраба-
тывается реализация класса алгоритмов, рисующих отсеченные прямые.
3.3.1. Отсечение прямой
В этом разделе описывается классический алгоритм отсечения прямых — отсекатель Кохена—Сазерленда
(Cohen—Sutherland clipper), который вычисляет, какая часть отрезка прямой с концевыми точками pl и
р2 лежит (и лежит ли вообще) внутри мирового окна, и возвращает концевые точки такой части отрезка.
Мы разработаем подпрограмму clipSegmentCpl, р2. window), которая принимает в качестве парамет-
ров две 2Э-точки (на плоскости) и выровненный прямоугольник, после чего отсекает границами окна
window отрезок прямой, определяемый конечными точками pl и р2. Если хоть какая-то часть данной пря-
мой остается в границах окна, то в переменные pl и р2 помещаются новые значения концевых точек и
функция возвращает единицу (информируя тем самым, что некоторая часть отрезка видима). Если же
прямая отсечена полностью, то функция возвращает величину 0 (никакая часть отрезка не видима).
На рис. 3.14 показана типичная ситуация, включающая в себя многие из возможных действий отсе-
кателя. Функция clipSegmentO совершает с каждым отрезком прямой одно из четырех действий.
О Если прямая целиком лежит внутри окна (как, например, отрезок CD), то функция возвращает
величину 1.
О Если прямая целиком лежит вне окна (как, например, отрезок АВ), то функция возвращает вели-
чину 0.
136
Глава 3. Дополнительные инструменты для рисования
О Если одна концевая точка находится внутри окна, а вторая — вне его (как, например, отрезок ED),
то функция отсекает часть отрезка, лежащую вне окна, и возвращает величину 1.
О Если обе концевые точки расположены вне окна, но тем не менее часть отрезка проходит сквозь
него (как, например, отрезок ЛЕ), то функция отсекает оба конца и возвращает величину 1.
Рис. 3.14. Отсечение прямых границами окна
Существует много возможных расположений отрезка прямой по отношению к окну. Этот отрезок
может находиться слева, справа, над и под окном; он может пересекать любую границу окна (или две)
и т. д. Поэтому нам необходим систематизированный и эффективный метод, который идентифициро-
вал бы существующую ситуацию и вычислял бы новые концевые точки для отсеченного отрезка. Эф-
фективность здесь важна, поскольку в типичном изображении содержатся тысячи отрезков прямой,
каждый из которых необходимо отсекать границами окна. Алгоритм Кохена-Сазерленда применяет к
задаче быстрый метод «разделения» («divide-and-conquer» — разделяй и властвуй). Другие методы от-
сечения будут обсуждаться в главе 4.
3.3.2. Алгоритм отсечения Кохена-Сазерленда
Алгоритм Кохена-Сазерленда быстро выявляет и отбрасывает два распространенных случая, называе-
мых «тривиальный прием» («trivial accept») и «тривиальное отклонение» («trivial reject»). Как показа-
но на рис. 3.15, обе концевые точки отрезка АВ расположены внутри окна IV, и поэтому весь отрезок АВ
должен располагаться внутри W. Следовательно, отрезок АВ может быть тривиально принят: он не нуж-
дается в отсечении. Такая ситуация часто возникает при использовании большого окна, охватывающе-
го большинство отрезков прямых. С другой стороны, обе концевые точки CnD лежат целиком по одну
сторону от окна W, поэтому отрезок CD должен располагаться целиком вне W. Следовательно, CD три-
виально отклоняется и не рисуется ничего. Такая ситуация часто возникает, когда маленькое окно ис-
пользуется для плотного изображения, многие из отрезков которого находятся вне этого окна.
Проверка на тривиальный прием и тривиальное отклонение
Мы хотим быстро выявлять такие случаи, когда отрезок прямой может быть тривиально принят или
тривиально отклонен. С целью облегчения этой задачи для каждой концевой точки отрезка вычисляет-
ся «кодовое слово внутри/вне» («inside-outside code word»). Рисунок 3.16 показывает, как происходит
3.3. Отсечение линий
137
это вычисление. Точка Р находится левее и выше окна W. Эти два обстоятельства записываются в кодо-
вое слово для Р. Буква Т (TRUE) указывается для двух полей: «слева» от окна и «выше». Буква F (FALSE)
указывается для двух остальных полей: «справа» от окна и «ниже».
Окно (W)
Находится ли Р слева от W?
Находится ли Р перед W?
\ Находится ли Р ниже W?
Код для Р: | Т | Т | F | F
Находится ли Р справа от W?
Рис. 3.16. Кодирование расположения точки Р относительно окна
Пусть, например, точка Р находится внутри окна, тогда ее код равен FFFF. Если Р ниже, но ни слева,
ни справа от окна, то ее код равен FFFT. На рис. 3.17 показаны все девять возможных расположений с
кодом для каждого из них.
TTFF FTFF FTTF
TFFF FFFF окно FFTF
TFFT FFFT FFTT
Рис. 3.17. Коды вне/внутри для точки
Мы формируем кодовое слово для каждой концевой точки тестируемого отрезка прямой. Условия
тривиальных приема и отклонения легко связываются с этими кодовыми словами:
О тривиальный прием-, оба кодовых слова равны FFFF;
О тривиальное отклонение-, кодовые слова имеют Т в одном и том же месте, то есть обе точки нахо-
дятся слева от окна или обе — справа и т. д.
Наделе формирование кодовых слов и тестирование может быть эффективно реализовано в С/С++
с использованием характерных для этих языков манипуляций с битами; мы покажем это в тематичес-
ком задании 3.3.
Разделение отрезка в случае, когда не имеет места ни тривиальный
прием, ни тривиальное отклонение
Алгоритм Кохена—Сазерленда использует стратегию «разделяй и властвуй». Если отрезок не может
быть ни тривиально принят, ни тривиально отклонен, он разделяется на две части по разные стороны
одной из границ окна. Одна его часть располагается вне окна и отбрасывается. Вторая часть является
потенциально видимой, поэтому весь процесс повторяется с оставшимся отрезком относительно дру-
гих границ окна. Вся эта процедура приводит к следующей стратегии:
do {
form the code words for pl and p2
11 формируем кодовые слова для pl и р2
if (.trivial accept} return 1;
// если (тривиальный прием), возвращаем 1
if (trivial reject} return 0:
// если (тривиальное отклонение), возвращаем 0
138
Глава 3. Дополнительные инструменты для рисования
chop the line at the "next” window border:
discard the "outside" part:
// разделяем прямую у «следующей» границы окна:
И отбрасываем «внешнюю» часть
} whiled);
Алгоритм прекращает работу, пройдя данный цикл не более четырех раз, так как в каждой итерации
мы оставляем только ту часть отрезка, которая «выдержала» тестирование относительно предыдущей
границы окна, а таких границ всего четыре. Поэтому после максимум четырех итераций обеспечивает-
ся тривиальный прием или тривиальное отклонение.
Как осуществляется разделение на каждой границе? На рис. 3.18 показан пример, относящийся
к правой границе окна.
Рис, 3.18. Отсечение отрезка относительно границы
Положение точки А необходимо вычислить. Ее х-координата равна, очевидно, W.right - координате
правой границы окна. Для определения ее г/-координаты необходимо найти pl.y с помощью поправки d,
как указано на рисунке. Однако из подобия треугольников
d _ е
dely delx ’
где е равно pl.x - pl.right, а равенства
delx - р2.х - pl.x:
. . ~ - (3.4)
dely = р2.у - pl.y:
задают приращения координат для этой пары концевых точек. Следовательно, d легко определить
и новое значение pl.y находится путем добавления приращения к старому значению:
pl.y += (W. right - pl.x) * dely / delx (3.5)
Аналогичные рассуждения используются при отсечении на остальных трех границах окна.
В некоторых наших вычислениях встречается выражение del x/dely, а в других del у/delx. Следует
всегда следить, чтобы не было деления на нуль, помня о том, что delx равен нулю для вертикальной
прямой, a dely равен нулю для горизонтальной. Однако, как показано в упражнениях, при равенстве
нулю знаменателя эти рискованные строки кода никогда не выполняются, и поэтому деление на нуль
не производится.
Все высказанные ранее идеи собраны вместе в подпрограмме clipSegmentО, приведенной в лис-
тинге 3.5. Концевые точки отрезков передаются по ссылке, поскольку изменения в концевых точках,
сделанные подпрограммой clipSegmentО, должны быть явными для вызывающей программы. (Тип
Point2 содержит двумерную точку, а тип RealRect — выровненный прямоугольник. Оба этих типа пол-
ностью описаны в разделе «Разработка класса Canvas».)
3.3. Отсечение линий
139
Листинг 3.5. Отсекатель линий Кохена-Сазерленда (псевдокод)
int clipSegment(Point2& pl. Point2& p2 . RealRect W)
do{
if (.trivial accept) return 1:
// some portion survives
// некоторая часть выдерживает тест
if (trivial reject) return 0:
//no portion survives
// ни одна часть не выдерживает тест
if (pl is outside) И если pl снаружи
if {pl is to the left) chop against the left edge
11 если pl слева, разделяем через левую границу
else if (pl is to the right) chop against the right edge
// иначе если pl справа, разделяем через правую границу
else if {pl is below) chop against the bottom edge
// иначе если pl снизу, разделяем через нижнюю границу
else if (pl is above) chop against the top edge
11 иначе если pl сверху, разделяем через верхнюю границу
}
else
// р2 is outside
// р2 вне окна
if (р2 is to the left) chop against the left edge
11 если p2 слева, разделяем через левую границу
else if (р2 is to the right) chop against the right edge
// иначе если p2 справа, разделяем через правую границу
else if (р2 is below) chop against the bottom edge
// иначе если p2 снизу, разделяем через нижнюю границу
else if (р2 is above) chop against the top edge
// иначе если pl сверху, разделяем через верхнюю границу
}
}while(l):
}
Каждый раз, когда выполняется цикл do, код для каждой концевой точки вычисляется заново и тес-
тируется. Когда возникает случай тривиального приема и тривиального отклонения, алгоритм прове-
ряет, находится ли точка pl вне окна, и если находится, то этот конец отрезка отсекается границей окна.
Если же pl находится внутри окна, тогда р2 должна быть снаружи (почему?), следовательно, точка р2
отсекается границей окна.
Данный вариант алгоритма отсекает по порядку сначала слева, затем справа, затем снизу и затем
сверху. Выбор порядка несущественен, если отрезки с одинаковой вероятностью размещаются в экран-
ном окне. На рис. 3.19 показан случай, когда требуются все четыре отсечения. Первое отсечение пре-
вращает pl в А; второе меняет р2 на В, третье обнаруживает, что pl все еще вне окна и под ним, поэтому
изменяет А на С; последнее отсечение изменяет р2 на D. При любом выборе порядка тестов на разделе-
ние всегда встречается ситуация, когда необходимы все четыре отсечения.
Отсечение является фундаментальной операцией, которая в течение многих лет привлекала к себе
повышенное внимание. Попутно были разработаны некоторые другие подходы. Некоторые из них мы
изучим в тематических заданиях в конце этой главы и в главе 4.
140
Глава 3. Дополнительные инструменты для рисования
Рис. 3.19. Отрезок, которому требуются четыре отсечения
Практическое упражнение
3.3.1. Ручная имитация dipSegment()
Пройдем вручную процедуру отсечения для случая окна с координатами {left, right, bottom, top) = (30,
220,50,240) и следующими отрезками прямых:
1. pl » (40,140), р2 = (100,200);
2. pl = (10,270),р2- (300,0);
3. pl - (20,10),р2 - (20,200);
4. pl - (0,0),р2 = (250,250).
Для каждого случая определите конечные точки отсекаемых отрезков и для визуальной проверки
сделайте эскиз всей ситуации на миллиметровке.
3.4. Разработка класса Canvas
Не следует думать, что чувства — это все. Искусство без формы — ничто.
Гюстав Флобер
Работа в мировых координатах предоставляет значительную свободу, если есть гарантия, что примити-
вы будут должным образом отсечены и преобразованы из окна в порт просмотра. Однако этой свобо-
дой нужно правильно пользоваться. Существует такое множество взаимодействующих ингредиентов
(точек, прямоугольников, отображений и т. д.) в этом «вареве», что следует инкапсулировать их и огра-
ничить к ним доступ для разработчика приложений во избежание трудноуловимых ошибок. Следует
также убедиться, что различные ингредиенты правильно инициализированы.
Представляется естественным применять классы и пользоваться теми возможностями, которые они
предоставляют для сокрытия данных. Поэтому мы разработаем класс, называемый Canvas (полотно),
который обеспечивает удобную графическую канву для рисования прямых, многоугольников и прочих
интересующих нас вещей. Этот класс предоставляет простые методы создания желаемого экранного
окна, установки мирового окна и порта просмотра; кроме того, класс гарантирует правильное преобра-
зование из окна в порт просмотра. В нем предлагаются подпрограммы moveToO и ИпеТоО, нравящиеся
многим программистам, а также полезные подпрограммы «черепашьей графики», которые мы рассмот-
рим позднее в этой главе.
Существует много способов определить класс Canvas. Вариант, представленный здесь, следует рас-
сматривать лишь как отправную точку для вашей собственной версии. В данном разделе мы реализуем
этот класс с помощью OpenGL, используя все операции, которые OpenGL делает автоматически (такие,
как отсечение). В то же время в тематическом задании 3.4 мы описываем совершенно иную реализацию
3.4. Разработка класса Canvas
141
(на основе Turbo C++ в среде DOS), которую нам придется снабдить всеми инструментальными сред-
ствами. В частности, там используется реализация отсекателя Кохена—Сазерленда.
3.4.1. Несколько полезных вспомогательных классов
Полезно иметь несколько общих типов данных, доступных для использования в классе Canvas и других
классах. Мы определяем их здесь как классы1 и демонстрируем простые конструкторы и другие функ-
ции для обработки объектов каждого типа. В некоторых из этих классов также имеется функция draw,
которая облегчает рисование экземпляров данного класса. По мере необходимости будут добавляться
другие функции (методы). Некоторые методы реализуются непосредственно в определениях класса;
реализация других предлагается в качестве упражнения, и тогда дано только определение метода.
class PointZ. Точка с вещественными координатами
Первый вспомогательный класс включает в себя единственную точку, описанную координатами с пла-
вающей запятой. Он представлен двумя конструкторами: функцией set() для присвоения координатам
нужных значений и двумя функциями для определения текущих значений координат. Вот код для это-
го класса:
class Point2
{
public:
Point2() {x = у = O.Of:}
// constructor!
// конструктор 1
Point2(float xx. float yy) {x = xx; у = yy;}
// constructor
// конструктор 2
void setlfloat xx. float yy) {x xx: у • yy:}
float getXO {return x;}
float getYO {return y:}
void draw(void) { glBegin(GL_POINTS):
// draw this point
// рисуем эту точку
glVertex2f((GLfloat)x. (GLfloat)y):
glEndO:}
private:
float x. y:
}:
Отметим, что когда вызывается gl Vertex2f (), величины x и у приводятся к типу GLfloat. Чаще всего
в этом нет необходимости, поскольку тип GLfloat определен в большинстве систем как float.
class IntRect. Выровненный прямоугольник с целыми координатами
При описании порта просмотра нам необходим выровненный прямоугольник, имеющий целые коор-
динаты. Класс IntRect предоставляет эту функциональность в следующем коде;
class IntRect
{
public:
IntRectO {1=0: г = 100; b = 0: t = 100: }
// constructors
// конструкторы
1 Студенты, предпочитающие писать па С, могут определить подобные типы с помощью конструкции struct.
142
Глава 3. Дополнительные инструменты для рисования
IntRectdnt left, Int right, int bottom, int top)
(1 ’ left; r = right; b = bottom; t = top:}
void set(int left, int right, int bottom, int top)
{1 - left: r - right; b - bottom; t - top:}
void draw(void);
// draw this rectangle using OpenGL
// рисуем данный прямоугольник с использованием OpenGL
private:
int 1. r, b, t:
class RealRect. Выровненный прямоугольник
с вещественными координатами
Мировому окну необходим выровненный прямоугольник, указывающий свои границы в вещественных
числах. (Данный класс настолько похож на IntRect, что некоторые программисты предпочли бы по дан-
ному образцу определить класс, который содержал бы как целые, так и вещественные координаты.) Код
класса следующий:
class RealRect
{
same as IntRect except use float instead of int
}
// такой же. как IntRect, только испопьзует float вместо
И int
Практические упражнения
3.4.1. Реализация классов
Расширьте приведенные выше классы, добавив в них другие, полезные на ваш взгляд, функции, а также
реализовав некоторые уже объявленные ранее функции, такие как draw() для класса IntRect.
3.4.2. Объявление класса Canvas
Мы объявляем интерфейс класса Canvas в заголовочном файле Canvas. h, как показано в листинге 3.6.
Элементы данных файла Canvas. h включают в себя текущую позицию, окно, порт просмотра и преобра-
зование окно — порт просмотра.
Листинг 3.6. Заголовочный файл Canvas.h
class Canvas {
public:
Canvas(int width, int height, char* windowTitle);
// constructor
// конструктор
void setWindow(float 1. float r. float b. float t);
void setViewport(int 1. int r. int b. int t):
IntRect getViewport(void);
// divulge the viewport data
// раскрываем данные порта просмотра
RealRect getWindow(void):
// divulge the window data
// раскрываем данные окна
fl oat getWi ndowAspectRati о(void);
void clearScreenO;
void setBackgroundColor(float r. float g. float b);
void setColor(float r. float g. float b);
3.4. Разработка класса Canvas
143
void lineTo(float x. float y):
void lineTo(Point2 p):
void moveTo(float x. float y):
void moveTo(Point2 p):
others later
// остальные - позже
private:
Point2 CP :
// current position in the world
// текущая позиция в мировых координатах
IntRect viewport;
// the current window
// текущее окно
RealRect window;
// the current viewport
// текущий порт просмотра
others later
11 остальные - позже
}
Конструктор класса Canvas берет в качестве аргументов ширину и высоту экранного окна, а также
строку имени окна и создает нужное окно, производя при этом все необходимые инициализации. Кро-
ме того, в Canvas также включены функции для установки и возвращения размеров окна и порта про-
смотра, а также для управления цветами рисования и фона. Заметим, что в этой версии класса нет явно-
го упоминания о данных для преобразования окно — порт просмотра, поскольку это преобразование
осуществляется «молча» самим OpenGL. В тематическом задании 3.4 мы добавим элементы данных для
поддержки данного преобразования в средах, нуждающихся в этом. Остальные представленные функ-
ции— это варианты ИпеТоО и moveToO, фактически осуществляющие рисование (разумеется, в миро-
вых координатах). В следующем разделе мы добавим еще «средства относительного рисования».
В листинге 3.7 показано, как класс Canvas обычно используется в приложениях. Создается единствен-
ный глобальный объект cvs, который инициализирует и открывает требуемое экранное окно. Данный
объект сделан глобальным с той целью, чтобы его могли «видеть» функции обратного вызова, напри-
мер displayO. (Мы не можем передавать в такие функции cvs в качестве параметра, поскольку прототи-
пы этих функций зафиксированы в правилах OpenGL Utility Toolkit.) Функция displayO устанавли-
вает здесь окно и порт просмотра, а затем рисует прямую линию с помощью функций-членов класса
Canvas. Тогда прямоугольник создается и рисуется посредством собственной функции-члена.
Листинг 3.7. Типичное использование класса Canvas
Canvas cvs(640. 480, "try out Canvas"):
// global canvas object
// глобальный объект класса canvas
//«««<<«<«« display »»»»»>
void display(void)
{
cvs.clearScreenO;
// clear screen
// очистка экрана
cvs.setWindow(-10.0, 10.0. -10.0, 10.0);
cvs.setViewport(10, 460. 10. 460);
cvs.moveTo(0, -10.0):
// draw a line
// рисуем линию
cvs.lineTo(0, 10.0): ,
продолжение#
144
Глава 3. Дополнительные инструменты для рисования
Листинг 3.7 (продолжение)
RealRect Ьох( -2.0. 2.0. -1.0. 1.0):
// construct a box
// создаем прямоугольник
box.drawO:
// draw the box
// рисуем прямоугольник
}
I/«««««<«« main »»»»»>
void main(void)
{
// the window is opened in the Canvas constructor
// это окно открывается в конструкторе Canvas
cvs.setBackgroundCol or(1.0. 1.0. 1.0):
// background is white
// цвет фона белый
cvs.setColor(0.0, 0.0, 0.0):
// set drawing color
// устанавливаем цвет рисования
glutDisplayFunc(display):
glutMainLoopO:
}
Подпрограмма mainO не совершает никакой инициализации: все уже было сделано в конструкторе
Canvas. Подпрограмма mainO просто устанавливает цвета рисования и фона, регистрирует функцию
displayO и входит в главный цикл событий. (Могли бы эти специфические для OpenGL функции быть
«упрятаны» среди функций-членов класса Canvas?)
3.4.2. Реализация класса Canvas
Покажем теперь некоторые подробности реализации класса Canvas для случая, когда OpenGL доступен.
(В тематическом задании 3.4 рассматривается альтернативная реализация.) Конструктор, приведенный
в листинге 3.8, передает желаемые ширину и высоту (в пикселах) функции glutlnitWindowSizeO. а нуж-
ную титульную строку в glutCreateWindowO. Несколько обеспокоить может передача функции glutlnitO
нужных параметров, несмотря на то, что они здесь никак не используются. Обычно mainO передает в
glutlnitO аргументы командной строки, как мы видели раньше. Здесь этого сделать нельзя, поскольку
используется глобальный объект класса Canvas cvs, который создается раньше, чем вызывается mainO.
Листинг 3.8. Конструктор OpenGL-версии класса Canvas
//«««««< Canvas constructor »»»»
Canvas:: Canvas(int width, int height, char* windowTitle)
{
char* argvCIJ:
// dummy argument list for glutlnitO
// фиктивный список аргументов для glutlnitO
char dummyString[8];
argv[0] - dummystring;
// hook up the pointer
// подключаем указатель
int argc -1:
// to satisfy glutlnitO
// для соответствия требованиям glutlnitO
3.4. Разработка класса Canvas
145
glutlnit(&argc. argv):
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB):
glut!nitWindowSize(width. height):
glut!nitWindowPosition(20. 20);
glutCreateWindow(windowTitle):
// open the screen window
// открываем экранное окно
setWindow(0. (float)width, 0. (float)height):
// default world window
// мировое окно по умоляанию
setViewport(0. width. 0. height):
// default viewport
// порт просмотра по умолчанию
CP.set(O.Of. O.Of);
// initialize the CP to (0. 0)
// инициализируем СР в (0. 0)
}
В листинге 3.9 показана реализация некоторых из оставшихся функций-членов класса Canvas (другие
функции отрабатываются в упражнениях). Функция moveToO просто обновляет СР (current position —
текущие координаты); 11 пеТо() посылает СР в качестве первой вершины и новую точку (х, у) в качестве
второй. Отметим, что нам здесь не требуется явно использовать преобразование окно — порт просмот-
ра, поскольку OpenGL автоматически применяет его. Функция setWindowO передает свои аргументы
функции gl u0rtho2D() (после необходимого приведения их типов) и загружает их в window класса Canvas.
Листинг 3.9. Реализация некоторых функций-членов класса Canvas
//«««««« moveTo »»»»»»
void Canvas:: moveTo(float x. float y)
{
CP.set(x. y);
}
//«««««« 1 i neTo »»»»»»
void Canvas:: lineTo(float x. float y)
{
glBegin (GL_LINES):
glVertex2f ((GLfloat) CP.x. (GLfloat) CP.y):
glVertex2f ((GLfloat) x. (GLfloat) y):
// draw the line
// рисуем линию
glEndO:
CP.set (x. y):
// update the CP
// обновляем текущие координаты
glFlushO:
}
//«««««« set Window »»»»»»
void Canvas:: setWindow (float 1. float r. float b. float t)
{
glMatrixMode (GL_PROJECTION):
glLoadldentityO:
glu0rtho2D ((GLdouble)l. (GLdouble)r. (GLdouble)b. (GLdouble)t):
window.set (1. r. b, t);
}
146
Глава 3. Дополнительные инструменты для рисования
Практические упражнения
3.4.3. Конкретизируйте каждую из следующих функций-членов
a) void setViewportdnt 1. int г. int b. int t);
6) IntRect getViewport(void);
в) RealRect getWindow(void);
r) void clearScreen(void);
д) void setBackgroundColor(float r. float g. float b):
e) void setColor(float r. float g. float b);
ж) void lineTo(Point2 p):
3) void moveTo(Point2 p):
и) float getWindowAspectRatio(void):
3.4.4. Использование Canvas для имитации: числа Фибоначчи
Увеличение числа популяции кроликов может быть смоделировано следующим уравнением:
где ук — число кроликов в £-м поколении. Согласно этой модели, численность особей в данном поко-
лении есть сумма численностей особей в двух предыдущих поколениях. Начальные популяции равны
у0 = 1 и ” 1. Последующие величины ук формируются путем подстановки более ранних значений, и
полученная последовательность представляет собой хорошо известную последовательность Фибонач-
чи: 1,1,2,3,5,8,13,... График зависимости ук от k показывает природу этой формы роста. Используйте
класс Canvas для написания программы, рисующей график этой последовательности длиной N. Задай-
те размер графика, соответствующий различным N. (Эта последовательность растет очень быстро, по-
этому вместо этого вы можете захотеть нарисовать график зависимости логарифма^ от k.) Кроме того,
нарисуйте график последовательности отношений рк = ук/ук_{ и проследите, как быстро рк сходится к
золотому отношению.
3.4.5. Еще одна имитация: синусоидальные последовательности
Синусоидальная последовательность генерируется с помощью следующего уравнения в конечных раз-
ностях:
Ук = аУк-ГУк-2 Для&= 1,2,...
Здесь а — константа между 0 и 2,ук= 0 при k < 0, ау0= 1. В общем случае, если положить а = 2соз(2л/5),
то один цикл будет состоять из 5 точек. Хороший график получается при 5 = 40. Напишите подпрог-
рамму, рисующую последовательности, сгенерированные таким образом, и протестируйте ее при раз-
личных значениях 5.
3.5. Относительное рисование
Если мы добавим еще несколько средств рисования в наш инструментарий (которым является рожда-
ющийся класс Canvas), то некоторые изобразительные задачи значительно упростятся. Часто удобно
начинать рисование в текущих координатах и описывать другие позиции относительно СР. Поэтому
мы разрабатываем функции, параметры которых обозначают изменения координат. Программист ука-
зывает, сколь далеко нужно перемещаться вдоль каждой координаты для достижения следующей жела-
емой точки.
3.5.1. Разработка moveRelQ и lineRelQ
Вот две новые подпрограммы — moveRel О и UneRelO. Функция moveRelO проста: она всего лишь «пере-
мещает» СР на расстояние (dx, dy). Функция lineRel (float dx, float dy) делает то же самое, но сначала
рисует прямую линию от старых СР до новых. Обе эти функции приведены в листинге 3.10.
3.5. Относительное рисование
147
Листинг 3.10. Функции moveRelQ и lineRel()
void Canvas :: moveRel(float dx. float dy)
{
CP.set(CP.x + +dx, CP.y + dy):
}
void Canvas :: lineRel(float dx, float dy)
{
float x - CP.x +dx. у=CP.у + dy;
lineTo(x. y):
CP.set(x. y);
}
Пример 3.5.1. Стрелочный маркер
Маркеры различной формы предназначены для размещения в разных местах рисунка для придания
изображению выразительности. На рис. 3.20 показано, как маркеры в форме пентаграммы (пятиконеч-
ной звезды) использованы для выделения экспериментальных точек на линейном графике.
Рис. 3.20. Расстановка маркеров для выразительности
Поскольку одна и та же фигура рисуется в нескольких различных точках, то удобнее просто напи-
сать drawMarker О и получить рисунок данной фигуры в точке СР. Тогда линейный график рис. 3.20 мож-
но нарисовать вместе с маркерами, используя код, подсказанный следующим псевдокодом:
moveTo(first data point):
drawMarkerO:
// draw a marker there
// рисуем маркер здесь
for(each remaining data point)
// для каждой остающейся экспериментальной точки
{
lineTo(the next point);
// draw the next line segment
// рисуем следующий отрезок прямой
drawMarkerO;
// draws it at the CP
// рисует маркер в точке СР
}
На рис. 3.21 изображен маркер в форме стрелки, нарисованный с помощью подпрограммы из лис-
тинга 3.11. Текущие координаты этой стрелки расположены в ее самой верхней точке. Для большей гиб-
кости стрелка задана четырьмя параметрами f,h,tn w, как показано на рисунке. Функция arrow() исполь-
148
Глава 3. Дополнительные инструменты для рисования
зует только lineRelO, причем нет ни одной ссылки на абсолютные координаты. Отметим, что хотя СР
изменяются в процессе рисования, в конце они снова возвращаются к своему исходному состоянию.
Следовательно, данная подпрограмма не дает никаких «побочных эффектов» (кроме самого рисования).
W t W
Рис. 3.21. Схема стрелки
Листинг 3.11. Рисование стрелки посредством относительных перемещений и рисований
void arrow(float f. float h. float t. float w)
{
// assumes global Canvas object: cvs
// предполагаем существование cvs -
// глобального объекта класса Canvas
cvs.lineRel(-w - t/2. -f):
// down the left side
// вниз по левой стороне
cvs.lineReKw, 0);
cvs.lineReKO. -h);
cvs.lineRel(t. 0);
// across
// поперек
cvs.lineReKO. h);
// back up
// назад
cvs.lineReKw. 0);
cvs.lineReK-w - t/2. f):
}
3.5.2. Черепашья графика
Последний инструмент, который мы добавляем здесь, чрезвычайно удобен. Он не только отслеживает с
помощью СР, «где мы находимся», но и «направление, в котором нас ведут». Это — разновидность че-
репашьей графики, которая считается естественной в графическом программировании1. Идея состоит
в том, что «черепаха», подобная перу перьевого плоттера, перемещается по странице, оставляя за собой
след в виде отрезка прямой линии. Черепаха помещается в СР, указывая определенное направление.
Оно называется текущим направлением (current direction — CD) и отсчитывается в градусах от по-
ложительного направления оси х против часовой стрелки (counterclockwise — CCW).
Легко добавить к классу Canvas функциональность, которая будет «управлять черепахой». Сначала
к числу частных (private) элементов данных добавляется CD. Затем добавим три функции:
1. turnToffloat angle). Эта функция задает текущее направление черепахи, равное заданному углу
(angle); реализация функции имеет вид
void Canvas:: turnTo(float angle) {CD=angle:}
1 Черепашья графика была введена Сеймором Папертом (Seymour Papert) в MIT (Massachussets Institute of Technologies — Масса-
чусетсский технологический институт) как часть языка LOGO для обучения детей программированию.
3.5. Относительное рисование
149
2. turnffloat angle). Эта подпрограмма поворачивает черепаху на angle градусов против часовой
стрелки; реализация функции имеет вид
void Canvas:: turnCanglе){CD += angle:}
Для поворота вправо используется отрицательный аргумент. Отметим, что turn обеспечивает относи-
тельные изменения направления; мы задаем не направление, а только изменение направления. Это про-
стое отличие предоставляет огромные возможности при рисовании сложных фигур с помощью черепахи.
3. forward (float dist. int isVisible). Эта команда перемещает черепаху вперед по прямой из теку-
щей позиции СР на расстояние dist в текущем направлении CD, после чего обновляет СР. Если isVisible
не равно нулю, то рисуется видимая прямая линия; в противном случае не рисуется ничего.
Новые мировые
координаты СР
Старые мировые
координаты СР
Рис. 3.22. Результат действия подпрограммы forward()
Из рис. 3.22 видно, что, двигаясь вперед в направлении CD, черепаха перемещается в направлении х
на расстояние dist х cos(n х CD/180) и в направлении у на расстояние dist х sin(n х CD/180), поэтому
forward О реализуется следующим образом:
void Canvas:: forward(float dist. Int IsVisible)
const float RadPerDeg=O.017453393:
// radians per degree
// радиан в градусе
float x = СР.х + dist * cos(RadPerDeg * CD);
float у = СР.у + dist * sin(RadPerDeg * CD):
1f(1sVisible)
11neTo(x, y):
else
moveTo(x. y):
Черепашья графика упрощает создание сложных фигур из более простых, как мы увидим в следую-
щих двух примерах.
Пример 3.5.2. Создание фигуры из мотива крючка
Стилизованный «крючок» из трех частей, показанный на рис. 3.23, а, можно нарисовать с помощью сле-
дующих команд:
forward(3 * L. 1);
// L Is the length of the short sides
// L - это длина коротких участков
150
Глава 3. Дополнительные инструменты для рисования
turn(90):
forward(L. 1):
turn(90);
forwardd, 1);
turn(90):
где параметром является длина коротких отрезков L. Пусть все эти команды инкапсулированы в про-
цедуре hookO. Тогда фигура на рис. 3.23, б будет начерчена путем четырехкратного повторения hookO.
Этот рисунок можно как угодно размещать и ориентировать посредством выбора начальных значений
СР и CD.
Мотив
а б
Рис. 3.23. Построение рисунка, состоящего из нескольких движений черепахи
Пример 3.5.3. Полиспирали
С помощью черепашьей графики легко генерировать большое семейство симпатичных фигур, называе-
мых полиспиралями (polyspirals). Полиспиралью называется ломаная линия, каждый последующий от-
резок которой больше (или меньше) предыдущего на постоянную величину, причем этот последующий
отрезок повернут по отношению к предыдущему на некоторый постоянный угол. Полиспираль форми-
руется с помощью следующего псевдокода:
for(some number of iterations)
// для некоторого количества итераций
{
forward(length.l);
// draw a line In the current direction
// рисуем отрезок в текущем направлении
turn(angl е):
// turn through angle degrees
// поворачиваем на angle градусов
length += increment:
// Increment the line length
// увеличиваем длину прямой на increment
}
Каждый раз при рисовании прямой увеличиваются и длина, и угол поворота. Если i ncrement равен
нулю, то фигура ни растет, ни сжимается. На рис. 3.24 изображено несколько полиспиралей. Реализа-
ция приведенной выше подпрограммы предлагается в виде упражнения.
Практические упражнения
3.5.1. Рисование фигур с помощью черепахи
Напишите подпрограммы, использующие движения черепахи для рисования следующих трех фигур,
изображенных на рис. 3.25. Может ли черепаха нарисовать форму на рис. 3.25, в без «подъема пера» и
без повторного рисования хотя бы одной прямой?
3.5. Относительное рисование
151
Рис. 3.24. Примеры полиспиралей. Углы (angle) составляют: а) 60°; б) 89,5°; в) -144°; г) 170°
Рис. 3.25. Другие простые черепашьи рисунки
3.5.2. Рисование хорошо известного логотипа
Напишите подпрограмму, в которой черепаха рисует контур логотипа, показанного на рис. 3.26. (Вашей
подпрограмме не следует закрашивать полигоны.)
Рис. 3.26. Знаменитый логотип
3.5.3. Управление черепахой посредством строк
Для описания фигуры можно использовать сокращенную систему обозначений. Пусть
F означает forward (d . 1): (для некоторого расстояния d).
L означает turn(60): (левый поворот на 60 градусов).
a R означает turn(-60) (правый поворот на 60 градусов).
Какое действие произведет такая последовательность команд?
FLFLFLFRFLFLFLFRFLFLFLFR.
(См. главу 9, где эта последовательность обобщена для рисования фракталов!)
152
Глава 3. Дополнительные инструменты для рисования
3.5.4. Рисование меандров (орнаментов)
Меандр1 — это орнамент типа того, который изображен на рис. 3.27, а; он часто представляет собой
длинную линию, извивающуюся вдоль некоторой траектории. Меандры можно часто видеть на грече-
ских вазах, китайских блюдцах или на плитках пола в различных странах. Мотив меандра, изображен-
ного на рис. 3.27, а, показан на рис. 3.27, б. После рисования каждого мотива черепаха поворачивается
(на сколько градусов?), чтобы приготовиться к рисованию следующего мотива.
Рис. 3.27. Пример меандра
Напишите подпрограмму, рисующую показанный выше мотив, а затем подпрограмму, рисующую
весь меандр. (Меандры получаются наиболее красивыми, если графический пакет, которым вы распола-
гаете, поддерживает управление толщиной линий — как это делает OpenGL, — так, что команда forwardO
рисует толстые линии.) Можно создать изумительное разнообразие более сложных меандров, как это
предлагается в последующих упражнениях.
3.5.5. Другие типы меандров
На рис. 3.28 изображены еще два типа меандров. Напишите подпрограммы, использующие для рисова-
ния этих меандров черепашью графику.
Рис. 3.28. Дополнительные рисунки меандров
3.5.6. Рисование сложных меандров
На рис. 3.29 приведен ряд более сложных мотивов для меандров. Напишите подпрограммы, рисующие
меандры для каждого из этих трех мотивов. Как выглядит следующий, самый сложный мотив из этой
последовательности и каков общий принцип, положенный в основу конструирования этих мотивов?
Рис. 3.29. Иерархия мотивов для меандров
3.5.7. Реализация полиспирали
Напишите подпрограмму polyspiral (float length, float angle, float incr, int num), рисующую поли-
спираль, состоящую из num отрезков, первый из которых имеет длину length. После рисования каждого
из отрезков length увеличивается на incr, а черепаха поворачивается на угол angle.
3.5.8. Является ли полиспираль IFS?
Можно ли описать спираль в категориях IFS (iterated function system — система итерируемых функ-
ций), введенных в главе 2? Задайте функцию, итерируемую черепахой на каждой итерации.
3.5.9. Рекурсивная форма для polyspiralQ
Перепишите подпрограмму polyspiral О в рекурсивной форме, так чтобы polyspiral О с аргументом dist
вызывала polyspiral О с аргументом dist+inc. Включите в программу подходящий критерий остановки.
1 Происходит от слова Maeander (в современном звучании Menderes — Мендерес), извилистой реки в Турции.
3.6. Фигуры на основе правильных многоугольников
153
3.6. Фигуры на основе правильных многоугольников
Обобщать — значит быть идиотом.
Уильям Блейк
Пчелы... в силу своей геометрической предусмотрительности... знают, что шестиугольник больше,
чем квадрат или треугольник, и в нем поместится больше меда при равном расходе материала.
Паппус из Александрии (Pappus of Alexandria)
Правильные многоугольники (полигоны) составляют обширное и важное семейство форм, часто встре-
чающееся в компьютерной графике. Нам нужны эффективные методы для их рисования. В этом разде-
ле мы выясним, как это делать и как создавать различные фигуры, являющиеся вариациями правиль-
ного многоугольника.
3.6.1. Правильные многоугольники
Вначале дадим определение правильного многоугольника.
Определение. Многоугольник называется правильным, если он является простым, если все его сто-
роны имеют равную длину и если его смежные стороны образуют равные внутренние углы.
Как уже обсуждалось в главе 1, многоугольник является простым (simple), если никакие две его
стороны не пересекаются (точнее, только смежные стороны могут соприкасаться и только в их общей
концевой точке). Назовем «-угольником правильный многоугольник, имеющий п сторон. Типичными
примерами и-угольников являются 4-угольник (квадрат), 5-угольник (правильный пятиугольник, или
Пентагон), 8-угольник (правильный восьмиугольник, или октагон) и т. д. 3-угольник это то же самое,
что равносторонний треугольник. На рис. 3.30 приведены различные примеры. Если число сторон
n-угольника велико, то этот многоугольник по внешнему виду стремится к окружности. Фактически
позже мы это применим как один из способов реализации рисования окружности.
п: 3 4 5 6 40
Рис. 3.30. Примеры п-угольников
Вершины «-угольника лежат на так называемой порождающей окружности (parent circle) данного
n-угольника, и их расположение легко вычисляется. Случай шестиугольника (гексагона) показан на
рис. 3.31; его вершины расположены на одинаковом расстоянии через каждые 60° по окружности. Центр
порождающей окружности радиуса R (на рисунке она не показана) находится в начале координат,
а первая вершина Ро лежит на положительной части оси х. Другие вершины располагаются следующим
образом: Р.= (Rcos(za), R sm(ia)), для i = 1,..., 5, где а = л/3 радиан. Аналогично вершины «-угольника
общего вида располагаются так:
Р.= (Ясоз(2л//и), R sin(2лг/«)), для i = 0,..., п-1. (3.6)
Данный и-угольник легко модифицировать. Для того чтобы его центр имел координаты (сх, су), необ-
ходимо только добавить сх и су к координатам х и у соответственно. Для масштабирования «-угольни-
ка в 5 раз необходимо просто умножить R на 5. Для поворота на угол А необходимо просто прибавить А
к аргументу при cos( ) и sin( ). Более общие методы осуществления геометрических преобразований
рассматриваются в главе 5.
Легко реализовать подпрограмму, рисующую и-угольник, как это показано в листинге 3.12. Здесь
«-угольник нарисован с центром в (сх, су), его радиус равен radius, он повернут на rotAngle градусов.
154
Глава 3. Дополнительные инструменты для рисования
Рис. 3.31. Нахождение вершин 6-угольника
Листинг 3.12. Построение n-угольника в памяти
void ngon(int п. float сх. float су. float radius, float rotAngle)
{
// assumes global Canvas object, cvs
// принимает глобальный объект класса Canvas - cvs
if(n < 3) return;
// bad number of sides
// недопустимое число сторон
double angle - rotAngle * 3.14159265 / 180;
// Initial angle
// начальный угол
double angleinc - 2 * 3.14159265 /n;
// angle increment
// увеличение угла
cvs.moveTotradius * cos(angle) + ex.radius * sin(angle) + cy):
for(int k - 0: k < n; k++)
// repeat n times
// повторяем n раз
{
angle +- angleinc:
cvs.lineToCradius * cos(angle) + ex. radius * sin(angle) + cy);
} }
Пример 3.6.1. Рисование п-угольника с помощью черепахи
Столь же просто рисовать п -угольник с использованием черепашьей графики. На рис. 3.32 показа-
но, как рисовать правильный шестиугольник. Начальные позиция и направление отмечены малень-
ким треугольником. Черепаха просто движется вперед (forward) шесть раз, делая CCW-поворот
(то есть против часовой стрелки) на 60° после каждого перемещения. Соответствующий код выгля-
дит так:
for (i - 0; i < 6; 1++)
{
cvs.forward(L, 1):
cvs.turn(60);
}
Одна вершина расположена в начальной СР, причем как СР, так и CD остаются неизменными на протя-
жении всего процесса. Рисование n-угольника общего вида, а также некоторых его вариантов, рассмат-
риваются в упражнениях.
3.6. Фигуры на основе правильных многоугольников
155
Рис. 3.32. Рисование б-угольника
3.6.2. Вариации п-угольников
На базе вершин n-угольника можно нарисовать также интересные вариации. Эти вершины можно соеди-
нять различными способами, в результате чего образуется целый ряд фигур, как показано на рис. 3.33.
На рис. 3.33, а нарисован стандартный и-угольник: соединены его смежные вершины, а на рис. 3.33, б изоб-
ражена звездчатая форма (stellation) (или звездообразная фигура), получающаяся путем соединения
каждой второй вершины. На рис. 3.33, в показана любопытная розетка (rosette), полученная путем со-
единения каждой вершины со всеми остальными вершинами. Сейчас мы обсудим розетку; остальные
фигуры описаны в упражнениях.
a б в
Рис. 3.33. Правильный семиугольник и его потомки: а) 7-угольник; б) звездчатая форма; в) 7-розетка
Пример 3.6.2. Розетка и золотая 5-розетка
Розеткой называется и-угольник, у которого каждая вершина соединена со всеми остальными вершина-
ми. На рис. 3.34 показаны 5-, 11- и 17-розетки. Иногда розетку используют в качестве тестового узора для
устройств компьютерной графики. Ее правильная форма сразу показывает любые искажения, а разре-
шающую способность тестируемого устройства можно определить, фиксируя количество «уплотнений»
(crowding) и размытий (blurring), демонстрируемых пучками линий, сходящихся в каждой вершине.
Рис. 3.34. 5-, 11- и 17-розетки
Рисовать розетки легко — просто соедините каждую вершину со всеми остальными. Псевдокод для
рисования розетки выглядит так:
void Rosettednt N. float radius)
{
Point2 enough value for largest rosette]:
// величина, достаточно большая для наибольшей из розеток
156
Глава 3. Дополнительные инструменты для рисования
generate the vertices pt [0]......pt[N-l]. as in Figure 3.43
генерируем вершины pt [0]......pt[N-l], как в листинге 3.13
fordnt 1 - 0; 1 < N - 1; 1++)
for(int j - i + 1; j < N; j++)
{
cvs.moveTo(pt[i]):
// connect all the vertices
// соединяем все вершины
cvs.1ineTo(pt[j]):
}
5-розетка особенно интересна, поскольку в ней многократно воплощается золотое отношение ф
(см. главу 2). На рис. 3.35, а показана 5-розетка, состоящая из наружного Пентагона и внутренней пен-
таграммы. Древние греки видели в этой фигуре некий мистический смысл. Ее отрезки находятся в
интересном соотношении: каждый отрезок в ф раз длиннее, чем следующий меньший отрезок (см.
упражнения). Кроме того, поскольку ребра пентаграммы составляют внутренний Пентагон, возможна
бесконечная регрессия пентаграмм, как это показано на рис. 3.35, б.
Рис. 3.35.5-розетка и бесконечная регрессия пентагонов и пентаграмм
Пример 3.6.3. Фигуры, основанные на двух концентрических п-угольниках
На рис. 3.36 изображено несколько форм, построенных на двух концентрических порождающих окруж-
ностях: внешней с радиусом R и внутренней с радиусом fR, где f — некоторая дробь. В каждой фигуре
используется разновидность n-угольника, величина радиуса которого находится между внутренним и
внешним радиусами. Части а) и б) рисунка представляют собой известные логотипы компаний на базе
6-угольника и 10-угольника. Фигура в) построена на 14-угольнике, а на рисунке г) показан в явном виде
вписанный круг.
Рис. 3.36. Семейство знаменитых логотипов
3.6. Фигуры на основе правильных многоугольников
157
Практические упражнения
3.6.1. Звездчатые формы и розетки
Пентаграмма рисуется путем соединения каждой второй точки при обходе Пентагона. Обобщите дан-
ную схему на произвольный и-угольник с нечетным числом сторон и разработайте подпрограмму, ри-
сующую этот так называемый «звездчатый многоугольник». Можно ли осуществить такую процедуру,
используя единственную начальную команду moveToO, за которой следуют только команды lineToO
(то есть без единого «поднятия пера»)? Что произойдет, если п четное?
3.6.2. Сколько ребер в hl-розетке?
Докажите, что у розетки на базе М-угольника (М-розетки) Af(N - 1 )/2 ребер. Данное число совпадает с
числом «звяканий», которые можно услышать, если каждый из Nчеловек, сидящих за столом, чокнется
бокалом со всеми остальными.
3.6.3. Розетки с простым числом сторон
Если у М-розетки простое число сторон, то ее можно нарисовать без «поднятия пера», то есть с помо-
щью одной команды lineToO. Начнем с вершины vQ и будем вести линию к каждой из остальных вер-
шин в таком порядке: v2, vy .... до тех пор, пока снова не встретится vQ и многоугольник не будет замк-
нут. Затем пойдем снова по кругу рисовать линии, однако будем каждый раз пропускать одну вершину,
то есть будем увеличивать индекс на два: v2, г4, г6,..., г0. Для этого потребуется обойти круг дважды и
снова вернуться к v0. (Над индексами совершается операция деления по модулю (modulo), так что их зна-
чения остаются в диапазоне от 0 до АГ- 1). Затем повторим эту процедуру, увеличивая индекс на три: vy
vff vy ..., v0. В процессе каждого повтора рисуется ровно АГлиний. Поскольку всего должно быть АГ(АГ- 1)/2
линий, то этот процесс рисования повторяется (N - 1 )/2 раз. Кроме того, так как число вершин — про-
стое число, ни одна конфигурация не повторится до конца рисования. Разработайте и протестируйте
подпрограмму, рисующую розетки с простым числом сторон приведенным выше способом.
3.6.4. Розетки с нечетным числом сторон
Если п — простое число, то мы уже знаем, что н-розетку можно нарисовать как одну ломаную линию
без «поднятия пера». Кроме того, для любого нечетного п розетку также можно нарисовать как единую
ломаную. Придумайте способ осуществления этого.
3.6.5. Геометрия пятиконечной звезды
Покажите, что длина каждого отрезка 5-розетки находится в золотом отношении к следующему мень-
шему отрезку. Один из способов решения этой задачи — убедиться в том, что треугольники в пятико-
нечной звезде (star pentagram) являются «золотыми треугольниками» с внутренним углом л/5 радиан.
Покажите, что 2cos(n/5) = ф, a 2cos(2n/5) = 1/ф. При другом подходе используются два семейства подоб-
ных треугольников из пентаграммы и уравнение ф3 = 2ф + 1, которому удовлетворяет ф (см. рис. 3.35, а).
3.6.6. Построение треугольников на сторонах п-угольника
Напишите подпрограмму, рисующую фигуры наподобие логотипа на рис. 3.34, а для произвольного
значения /, положительного или отрицательного. Какая может быть разумная геометрическая интер-
претация отрицательного /?
3.6.7. Вычерчивание звезды с помощью относительных перемещений
без рисования и с рисованием
Напишите подпрограмму, вычерчивающую пентаграмму с использованием исключительно относитель-
ных перемещений «по воздуху» и с рисованием, причем центр этой звезды должен быть в точке СР.
3.6.8. Рисование узора из звезд
Напишите подпрограмму рисования узора из 21 звезды, показанного на рис. 3.37. Маленькие звезды
расположены в вершинах правильных многоугольников.
3.6.9. Новые точки на «7-грамме»
На рис. 3.38 изображена фигура, построенная на семи точках 7-угольника с центром в начале коорди-
нат. Первая точка имеет координаты (R, 0). Вместо соединения последовательных точек по окружно-
158
Глава 3. Дополнительные инструменты для рисования
сти 7-угольника две промежуточные точки пропускаются. (Это еще один вариант «звездчатой формы»
и-угольника.) Найдите координаты точки Р пересечения двух сторон.
3.6.10. Рисование n-угольника с помощью черепахи
Напишите функцию turtleNgon(int numSides, float length), использующую черепашью графику для
рисования и-угольника с numSides сторонами длиной length.
3.6.11. Многоугольники с одной общей стороной
Напишите подпрограмму, рисующую и-угольники, для п - 3.12 с общей стороной, как это показано
на рис. 3.39.
Рис. 3.39. n-угольники с общей стороной
3.6.12. Более замысловатая фигура
Напишите подпрограмму, которая формирует фигуру с рис. 3.40 путем вычерчивания повторяющихся
шестиугольников, повернутых относительно друг друга.
Рис. 3.40. Повторное использование команд для черепахи
3.6.13. Рисование знаменитого логотипа
Глубокоуважаемый логотип, изображенный на рис. 3.41, состоит из трех экземпляров мотива, поверну-
тых на определенный угол относительно друг друга. Напишите подпрограмму, рисующую данную фор-
му с помощью черепашьей графики.
3.7. Рисование окружностей и дуг
159
Рис. 3.41. Логотип университета штата Массачусетс
3.6.14. Вращающиеся пентаграммы: анимация
На рис. 3.42 изображена пентаграмма, повернутая на некоторый угол относительно Пентагона, причем
соответствующие их вершины соединены. Напишите программу, анимирующую эту фигуру. Данная
композиция нарисована с использованием некоторого начального угла А поворота пентаграммы. После
короткой паузы эта пентаграмма стирается, а затем снова рисуется с немного большим углом А. Процесс
повторяется до нажатия любой клавиши.
Рис. 3.42. Вращающиеся пентафигуры
3.7. Рисование окружностей и дуг
Рисование окружности эквивалентно рисованию и-угольника с большим числом вершин. Этот n-уголь-
ник напоминает окружность (если его не изучать слишком пристально). Подпрограмма drawCi rcleO,
представленная в листинге 3.13, рисует правильный 50-угольник методом простой передачи своих па-
раметров в ngonO. Было бы более целесообразно написать drawCi rcleO с нуля, основываясь на коде ли-
стинга 3.11.
Листинг 3.13. Рисование круга на базе 50-угольника
void drawCirclе(Polnt2 center, float radius)
{
const int numVerts = 50;
ngon(numVerts. center.getXO. center.getYO. radius. 0);
}
3.7.1. Рисование дуг
Множество фигур в искусстве, архитектуре и науке включают в себя дуги окружностей, расположен-
ных согласно требованиям эстетики или целесообразности. Дугу удобно описывать положением цент-
ра с и радиусом R «порождающей» ее окружности, а также начальным углом а и углом ее развертки Ь.
На рис. 3.43 показана такая дуга. Мы считаем, что при положительном b дуга развертывается, начиная
160
Глава 3. Дополнительные инструменты для рисования
с а, против часовой стрелки (CCW); если же b отрицательно, то дуга развертывается по часовой стрелке
(CW). Окружность есть частный случай дуги с углом развертки 360°.
Нам нужна подпрограмма drawArcO, рисующая дугу окружности. Функция, приведенная в листин-
ге 3.14, аппроксимирует дугу как часть n-угольника с использованием команд moveToO и lineToO. Пос-
ледовательные точки дуги находятся вычислением cos( ) и sin( ) каждый раз внутри главного цикла.
Если величина sweep отрицательна, то угол автоматически убывает.
Листинг 3.14. Рисование дуги окружности
void drawArc(Point2 center, float radius, float startAngle, float sweep)
{
// startAngle and sweep are in degrees
// startAngle и sweep измеряются в градусах
const int n - 30:
// number of intermediate segments in arc
// число промежуточных отрезков дуги
float angle - startAngle * 3.14159265 / 180:
// initial angle in radians
// начальный угол в радианах
float angleinc - sweep * 3.14159265 /(180 * n);
// angle increment
// увеличение угла
float ex — center.getXO. cy - center.getYO:
cvs.moveTo(cx + radius * cos(angle), cy + radius * sin(angle)):
ford nt k - 1: k < n: k++. angle +- angleinc)
cvs.lineTo(cx + radius * cos(angle), cy + radius * sin(angle)):
}
СР остается в последней точке дуги. В ряде случаев предпочитают опускать начальную команду
moveToO по направлению к первой точке дуги, чтобы соединить дугу с той фигурой, которая была нари-
сована к моменту вызова drawArcO.
Значительно более быстрая подпрограмма рисования дуги, которая рассматривается в главе 5, не
проделывает многократно повторяющихся вычислений функций sin( ) и cos( ). Вместо приведенной
здесь процедуры можно с успехом использовать ту подпрограмму.
Располагая функцией drawArcO, нетрудно написать подпрограмму drawCircle(Point2 center, float
radius), рисующую окружность целиком. (Как?)
Подпрограмма drawCircleO вызывается спецификацией центра (center) и радиуса (radius), однако
существуют другие способы описания окружности, которые имеют широкое применение в интерактив-
ной графике и автоматизированном проектировании. Вот два самых известных из них.
3.7. Рисование окружностей и дуг
161
1. Задаются центр и точка на окружности. В этом случае подпрограмму drawCi rcleO можно исполь-
зовать, если известен радиус. Если с — центр, ар — заданная точка на окружности, то радиус
просто равен расстоянию от с до р, которое легко найти с помощью обычной теоремы Пифагора.
2. Заданы три точки, через которые должна пройти окружность. Известно, что через три точки,
не лежащие на одной прямой, проходит единственная окружность. В главе 4 обсуждается, как
определить центр и радиус этой окружности.
Пример 3.7.1. Плавное сопряжение дуг
Используя две касающиеся друг друга окружности, мы можем получить более сложные формы. Рис-
унок 3.41 иллюстрирует основной принцип. Две окружности касаются друг друга в точке А и имеют
в ней общую касательную L. В силу этого две дуги, выделенные жирной линией, плавно сопрягаются
друг с другом, и в точке А не видно никакого шва, разрыва или излома. Подобным же образом дуга
окружности может быть плавно сопряжена с произвольной касательной, как это видно в точке В.
Рис. 3.44. Плавное сопряжение дуг с помощью касающихся окружностей
Практические упражнения
3.7.1. Философский смысл кругов
В китайской философии и религии два принципа — инь и янь — взаимодействуют, влияя на судьбу всех
живых существ. На рис. 3.45 показан изысканный символ инь-янь. Его темная часть — инь — символи-
зирует женское начало, а светлая часть — янь — мужское. Подробно опишите геометрию этого символа,
предположив, что он находится в начале некоторой системы координат.
Рис. 3.45. Символ инь-янь
3.7.2. Семь монет
Опишите конфигурацию на рис. 3.46, где шесть монет компактно размещены вокруг седьмой, централь-
ной. Исходя из соображений симметрии, объясните причину этой компактности — почему каждая внеш-
няя монета в точности касается своих трех соседей.
3.7.3. Знаменитый логотип
На рис. 3.47 изображен знаменитый автомобильный логотип, созданный путем помещения треуголь-
ников внутрь равностороннего треугольника, причем вокруг внешнего (не показанного) треугольника
6 Ф. Хилл
162
Глава 3. Дополнительные инструменты для рисования
описаны две концентрические окружности. Определив «правильное» расположение трех внутренних
точек, напишите подпрограмму для рисования этого логотипа.
Рис. 3.46. Семь окружностей
Рис. 3.47. Знаменитый логотип
3.7.4. Рисование часов и подобных им фигур
Окружности и прямые можно заставить касаться друг друга различными способами, чтобы получились
симпатичные гладкие кривые, как на рис. 3.48, а. На рис. 3.48, б показаны основные прямые и окружно-
сти. Напишите подпрограмму, рисующую такую форму, специфическую для часов.
Рис. 3.48. Сопряжение дуг для создания плавных кривых
3.7.5. Рисование скругленных прямоугольников
На рис. 3.49 изображен выровненный прямоугольник со скругленными углами. Этот прямоугольник
имеет ширину W и форматное соотношение R, а каждый его угол обрисовывается четвертью окружно-
сти радиуса г = gW, где g — некоторая дробь. Напишите подпрограмму drawRoundRectCfloat W. float R,
float g), рисующую этот прямоугольник с центром в СР, который должны перейти в начало координат
после завершения работы подпрограммы.
W
Рис. 3.49. Скругленный прямоугольник
3.7.6. Формы, содержащие дуги
На рис. 3.50 показаны две интересные формы, включающие в себя окружности или дуги. Одна из них
похожа на символ комиссии по атомной энергии (Atomic Energy Commission). (Чем она отличается от
оригинала?) Напишите и протестируйте две подпрограммы, рисующие эти фигуры.
3.7. Рисование окружностей и дуг
163
3.7.7. Капля
На рис. 3.51, а изображена каплевидная форма, используемая во многих орнаментах. Как показано
в части б) этого же рисунка, эта фигура состоит из окружности заданного радиуса R, устроившейся в
углу ф. Чему равны координаты центра С окружности для заданных R и ф ? Чему равны начальный угол
дуги и ее развертка? Разработайте подпрограмму рисования капли для произвольного расположения и
ориентации.
Рис. 3.50. Формы на основе дуг
а б
Рис. 3.51. Капля и ее конструкция
На рис. 3.52 показаны некоторые варианты использования капли. Напишите подпрограммы, рису-
ющие каждый из этих рисунков.
Рис. 3.52. Некоторые фигуры, построенные из капель
3.7.8. Круговые диаграммы
Сектор формируется путем соединения концов дуги с центром окружности. Известная секторная (кру-
говая) диаграмма (pie chart) образуется посредством рисования нескольких секторов. Ее типичный
пример приведен на рис. 3.53. Секторные диаграммы употребляют для иллюстрации того, как целое
делится на части, аналогично тому, как пирог (pie) разделяют на части перед тем, как раздать по тарел-
кам. Глаз быстро оценивает размер каждого «ломтика» по отношению к другим. Часто бывает, что один
или несколько ломтей «вырваны» из комплекта, как показано на рисунке. Вырванные секторы просто
слегка отодвинуты от центра пирога в соответствующем направлении.
164
Глава 3. Дополнительные инструменты для рисования
Рис. 3.53. Круговая диаграмма
Для того чтобы нарисовать круговую диаграмму, нужно знать относительные размеры кусков.
Напишите и протестируйте подпрограмму, которая принимает данные от пользователя и рисует со-
ответствующую круговую диаграмму. Пользователь вводит часть пирога, которую представляет
каждый кусок, а также букву е (exploded) в том случае, если данный кусок выдвинут, и п (not) — в про-
тивном случае.
3.8. Применение параметрического задания кривой
Существует два основных способа описания формы кривой линии: неявный и параметрический.
Неявный способ описывает кривую функцией F(x, г/), в которой содержится зависимость между
координатами х и у. Точка (х, у) находится на кривой тогда и только тогда, когда она удовлетворяет
уравнению
F(x,z/) = 0. (3.7)
Например, прямая линия, проходящая через точки А и В, имеет неявную форму:
F(x, у) - (у - A^B-AJ — (х — Ах)(Ву - Ау), (3.8)
а окружность радиуса R с центром в начале координат выражается в неявном виде с помощью функции:
F(x,y)-x2 + y2-R2. (3.9)
Преимущество записи в неявной форме состоит в том, что можно легко проверить, лежит ли задан-
ная точка на кривой: для этого достаточно вычислить F(x, у) в рассматриваемой точке. Для целого клас-
са кривых имеет смысл понятие «внутренности» или «внешности» кривой; в этих случаях функция
F(x,y) называется также «внутренне-внешней функцией» (inside-outside function), причем имеется в
виду следующее:
F(x, у) - 0 для всех (х, у) на кривой,
F{x, у)>0 для всех (х, у) вне кривой, (3.10)
F(x, у) < 0 для всех (х, у) внутри кривой.
(Является ли F(x, у) из равенства (3.9) полноценной «внутренне-внешняя функцией» для окружности?)
Некоторые функции являются однозначными (single valued) относительно х, тогда существует та-
кая функция g(.), что все точки кривой удовлетворяют равенству у = g(x). Для таких кривых неявная
форма может быть записана в виде F(x, у) = у - g(x). (Чему равна функция g(.) для линии из равенства
(3.8)?) Другие кривые однозначны относительно у, поэтому для них существует такая функция Л(.),
что все точки кривой удовлетворяют равенству х= h(y). А некоторые кривые вообще не являются одно-
значными: равенство F(x, у) - 0 не может быть преобразовано ни в форму у = g(x), ни в форму х = Л(у).
Окружность, например, можно выразить равенством
y = +^R2-x2. (3.11)
Однако здесь содержится две функции, а не одна.
3.8. Применение параметрического задания кривой
165
3.8.1. Параметрические формы для кривых
Параметрическая форма для кривой генерирует различные точки этой кривой в зависимости от значе-
ния параметра. Параметрические формы можно вывести для широкого класса кривых, и такие формы
имеют много преимуществ, особенно в тех случаях, когда требуется начертить или проанализировать
кривую. Параметрическая форма напоминает движение точки во времени, которое мы можем преобра-
зовать в движение пера, рисующего кривую. Траектория движения материальной точки вдоль кривой
фиксируется двумя функциями, х( ) и у{ ), и мы можем говорить о паре (x(t), y{t)) как о текущих коор-
динатах материальной точки в момент времени t. Сама кривая представляет собой совокупность точек,
«посещенных» материальной точкой в течение некоторого интервала времени t. Таким образом, если
нам удастся придумать подходящие для кривой функции х( ) и у{ ), то они будут представлять эту кри-
вую кратко и точно.
Известная игрушка «Волшебный экран» («Etch-a-Sketch»1 — «сделай набросок»), приведенная на
рис. 3.54, может служить живой аналогией параметрического представления кривой. При поворотах
рукояток скрытое внутри коробки перо процарапывает на экране тонкую видимую линию. Одна руко-
ятка управляет горизонтальным положением пера, а вторая — вертикальным. Если эти рукоятки пово-
рачивать в соответствии с функциями x(t) и y(t), то будет вычерчена параметрическая кривая. (Слож-
ные кривые требуют значительной сноровки.)
Рис. 3.54. Рисование параметрических кривых с помощью «Волшебного экрана» (рисунок Сюзанны Касиелло (Suzanne Casiello))
Примеры. Прямая и эллипс
Прямая линия из равенства (3.8) проходит через точки А и В. Выбираем такую параметрическую фор-
му, которая «посетит» точку А при t = 0 и точку В — при t- 1. Имеем:
x{t)-A^{B-Ax)t,
y(t)=Ay+(By-Ay)t.
(3.12)
Тогда при изменении t от 0 до 1 точка P(t) = (x(t), y(t)) пробежит все точки прямой между точка-
ми Л и В. (Проверьте это!)
Еще один классический пример — эллипс, небольшое обобщение круга. Параметрически эллипс опи-
сывается следующим образом:
x(t) = W cos(t),
y(t) = Н sin(£) для 0 < t < 2л.
(3.13)
1 Etch-a-Sketch является торговой маркой фирмы Ohio Art.
166
Глава 3. Дополнительные инструменты для рисования
где W—.«полуширина» (большая полуось), а Я— «полувысота» (малая полуось) эллипса. Некоторые
геометрические свойства эллипса исследуются в упражнениях. Если W равно Я, то эллипс превращает-
ся в круг радиуса W. На рис. 3.55 показан эллипс, а также координатные функции х(.) и у(.).
t
Рис. 3.55. Эллипс, заданный параметрически
Когда t изменяется от 0 до 2л, точка Р(£) - (х(Т), у(0) обходит эллипс один раз, начиная (и заканчи-
вая) свое движение в точке ( W, 0). На рисунке показано, где находится эта точка при различных зна-
чениях t. Полезно наглядно представить процесс рисования эллипса на «Волшебном экране». Нужно
волнообразно поворачивать рукоятки взад и вперед, чтобы одна из этих рукояток имитировала cos(f),
а вторая — sin(t). (Это удивительно трудно проделать вручную.)
Преобразование параметрической формы в неявную
Предположим, мы хотим убедиться в том, что параметрическая форма из уравнения (3.13) действительно
представляет эллипс. Как мы сможем извлечь неявную форму из параметрической? Первый шаг состоит
в объединении двух уравнений для х(?) и y(t), чтобы каким-то образом исключить переменную t. Резуль-
татом этого преобразования будет соотношение, которое должно выполняться для ecext. Не всегда очевид-
но, как сделать это, поскольку не существует простых правил, применимых для всех параметрических
форм. В случае эллипса, например, мы можем возвести в квадрат оба отношения х/ W и у/Н и использо-
вать известное тождество cos(f)2 + sin(r)2 = 1, чтобы в результате получить знакомое уравнение эллипса:
В последующих упражнениях исследуются свойства эллипса и других «классических кривых». В них
даются полезные сведения о конических сечениях (conic sections) — сведения, которые будут исполь-
зованы позднее. Прочтите упражнения до конца, даже если вы не собираетесь решать каждое из них.
Практические упражнения
3.8.1.0 геометрии эллипса
Эллипс является множеством всех точек, сумма расстояний от которых до двух фокусов есть величина
постоянная. Точка (с, 0) на рис. 3.52 образует одни фокус, а точка (-с, 0) — второй. Покажите, что Н, W
и с связаны соотношением: 172 = Я2 + с2.
3.8. Применение параметрического задания кривой
167
3.8.2. Как эксцентрично!
Эксцентриситет (eccentricity) эллипса е - c/W — это мера отклонения эллипса от кругообразности,
причем для точной окружности эксцентриситет равен 0. Интересным примером являются планеты
Солнечной системы: они имеют орбиты, очень близкие к круговым, для них е изменяется от 1/143 (Ве-
нера) до 1/4 (Плутон). Орбита Земли имеет эксцентриситет е = 1/60. Когда эксцентриситет достигает
единицы, эллипс расплющивается в прямую линию. Каково соотношение Н/W высоты к ширине для
эллипса, имеющего е = 0,99?
3.8.3. Другие конические сечения
Эллипс является одним из трех конических сечений, то есть кривых, образующихся при пересечении
(«сечении») кругового конуса плоскостью, как показано на рис. 3.56. Конические сечения бывают сле-
дующих видов:
О Эллипс: плоскость пересекает одну полость конуса.
О Парабола: плоскость параллельна образующей конуса.
О Гипербола: плоскость пересекает обе полости конуса.
Парабола и гипербола имеют интересные и полезные геометрические свойства. Обе они имеют про-
стые неявные и параметрические представления.
Рис. 3.56. Классические конические сечения
Покажите, что следующие параметрические представления соответствуют приведенным неявным формам.
О Парабола. Неявная форма: у2 - 4ах = 0.
x(t) = at2, y(t) = 2at. (3.15)
О Гипербола. Неявная форма: (х/а)2- (y/b)2 = 1.
x(t) = a sec(t),y(t) = b tg(t). (3.16)
Каким должен быть промежуток изменения параметра t, чтобы пройти всю гиперболу? Замечание-.
гипербола определяется как геометрическое место точек, разность расстояний от которых до двух фо-
кусов есть величина постоянная. Покажите, что если фокусы имеют координаты (-с, 0) и (+с, 0), то а
и b должны быть связаны соотношением с2 ~ а2 + Ь2.
3.8.2. Вычерчивание кривых, заданных параметрически
Кривая, заданная параметрически, рисуется непосредственно. В этом состоит главное преимуще-
ство параметрической формы перед неявной. Допустим, что кривая С имеет параметрическое задание
P(t) - (x(t), z/(t)), где t изменяется от 0 до Г (см. рис. 3.54, а). Предположим далее, что мы хотим нарисо-
вать хорошее приближение к кривой, используя только прямые линии. Тогда нам следует взять замеры
168
Глава 3. Дополнительные инструменты для рисования
P(t) для близких значений параметра. Таким образом, будет выбрана последовательность моментов време-
ни {Л}, и для каждого вычислена текущая координата на кривой Р.= Р(£) = (x(t), z/(t)). Затем кривая P(t)
аппроксимируется ломаной линией на базе этой последовательности точек Р, как показано на рис. 3.57, б.
а б
Рис. 3.57. Аппроксимация кривой с помощью ломаной линии
В листинге 3.15 приведен фрагмент кода, рисующего кривую у(С)) на базе массива замеров вре-
мени ф]:
Листинг 3.15. Рисование эллипса с помощью точек, равноудаленных по t
// draw the curve (x(t). y(t)) using
// the array t[0]...t[n-l] of "sample-times’
// рисуем кривую (x(t). y(t)). используя
// массив t[0]...t[n-l] «замеров времени»
glBegin(GL_LINES):
for(1nt 1 - 0: 1 < n: 1++)
glVertex2f(x(t[1]). y(t[i])):
glEndO:
Если эти замеры расположены достаточно близко друг от друга, то глаз естественным образом со-
единит отрезки прямых вместе, и мы увидим гладкую кривую. Замеры должны быть расположены осо-
бенно близко в тех промежутках t, где кривая быстро «извивается», и могут быть взяты пореже в тех
местах, где кривая имеет слабую волнистость. Требуемая «близость» или «качество» аппроксимации
зависят от обстоятельств.
Код может быть зачастую упрощен, если он нужен только для определенной кривой. Эллипс из урав-
нения 3.13 можно нарисовать, задавая п равноотстоящих значений t, посредством следующего кода:
tfdefine TWOPI 2 * 3.14159265
glBegin(GL_LINES);
for(double t - 0; t <- TWOPI: t +- TWOPI/n)
glVertex2f(W * cos(t), H * sin(t)):
glEndO:
В случае рисования кривых, заданных параметрически, легко обходятся все затруднения, встречающие-
ся при явной и неявной формах задания. Кривые могут быть многозначны, они могут самопересекаться
любое число раз. Вертикальность не представляет особой проблемы: просто x(t) остается постоянным
на протяжении некоторого интервала t. Позднее мы увидим, что рисование кривых, расположенных
в трехмерном пространстве, столь же просто: используются три функции от t, а точка на кривой в мо-
мент t имеет координаты (x(t), y(f), z(f)).
Практические упражнения
3.8.4. Пример кривой
Вычислите и постройте вручную точки, которые были бы нарисованы с помощью вышеприведенного
фрагмента кода при W= 2 и Н - 1, при пяти значениях t = 2ni/9, где i = 0,1,..., 4.
3.8. Применение параметрического задания кривой
169
3.8.5. Рисование логотипа
Широко известный логотип, изображенный на рис. 3.58, состоит из концентрических окружностей и
эллипсов. Предположим, что имеется подпрограмма drawEHipse(W, Н, color), которая рисует эллипс,
заданный формулой 3.13, закрашенный цветом color. (Принимается, что когда используется выбранный
цвет, он полностью подавляет любой предыдущий нарисованный цвет.) Выберите подходящие размеры
для этих эллипсов и напишите последовательность команд, необходимых для рисования данного логотипа.
Рис. 3.58. Знакомый «глаз», построенный из кругов и эллипсов
Некоторые кривые, используемые в компьютерной графике, помогут закрепить идеи, изложенные в
данном разделе.
3.8.3. Суперэллипсы
Особой разновидностью эллипса является суперэллипс (superellipse) — семейство эллипсоподобных
форм, которые во многих ситуациях, возникающих при рисовании, дают замечательные эффекты. Не-
явная формула для суперэллипса имеет вид:
(3.17)
(ifJ (я;
где п — параметр, называемый выпуклостью {bulge — горб). Сравнивая эту формулу с соответствующей
формулой для эллипса (равенство 3.14), можно видеть, что при п = 2 суперэллипс становится обычным
эллипсом. Параметрическое представление суперэллипса
x(t) = Wcos(£)|cos(£)2/n“1)|,
y(t) = Н sin(t) | sin(r)2/n-1|,
(3.18)
для 0 < t < 2л. Показатели степени при sin( ) и cos( ) на самом деле равны 2/п, а данная специфическая
форма записи использована для того, чтобы избежать возведения отрицательного числа в дробную сте-
пень. Убедитесь, что приведенная форма записи должным образом сводится к уравнению эллипса при
п - 2. Проверьте также, что параметрическая форма суперэллипса соответствует его уравнению в неяв-
ной форме.
На рис. 3.59, а показано семейство суперокружностей (supercircles), частного случая суперэллип-
сов при W - Н. На рис. 3.59, б приведена сцена, полностью составленная из суперэллипсов и демонст-
рирующая диапазон их возможных форм.
При п > 1 выпуклость направлена наружу, а при п < 1 — вовнутрь. Когда и = 1, суперокружность пре-
вращается в квадрат. (В главе 6 мы рассмотрим трехмерные «суперквадрики» (superquadrics) — поверх-
ности, которые иногда используют в системах автоматического проектирования для моделирования
объемных тел.)
Суперэллипсы были впервые исследованы в 1818 году французским физиком Габриэлем Ламэ
(Gabriel Larne). Позже, 1959 году, выдающийся изобретатель Пит Хайн (Piet Hein) (больше всего изве-
стный как создатель куба Soma и игры Hex) решал задачу проектирования кольцевой транспортной
развязки (traffic circle) в Стокгольме. Окружность кольцевой трассы должна была вписаться в прямо-
угольник (с отношением сторон W/H = 6/5), который определялся другими дорогами, и должна была
обеспечить плавный транспортный поток, а также быть приятной для глаз. Эллипс получался слишком
170
Глава 3. Дополнительные инструменты для рисования
заостренным на концах для транспортной магистрали, поэтому Хейн искал более плоскую кривую с
более прямыми сторонами и подумал о суперэллипсе. Оп выбрал п = 2,5, при котором выпуклость была
наиболее подходящей. Стокгольм мгновенно принял идею суперэллипса для своего нового центра. Эти
кривые были «удивительно подходящими, ни слишком круглыми, ни слишком угловатыми, удачное
сочетание красоты эллипсов и прямоугольников» [Gardner, 78, с. 243]. С тех пор формы суперэллипсов
появились в мебели, текстильных орнаментах и даже в столовом серебре. Более подробно о них написа-
но в книгах [Gardner, 78] и [Hill, 109].
а б
Рис. 3.59. Семейство суперокружностей (а); сцена, созданная из суперэллипсов {б)
Аналогичным образом может быть определена супергипербола (superhyperbola) [Barr, 13]. Доста-
точно заменить в равенстве (3.18) cos(i) на sec(t) и sin(t) на tg(t). При п = 2 получается обычная гипербо-
ла. На рис. 3.60 показано несколько примеров супергипербол. Когда выпуклость п становится больше 2,
кривая выпячивается наружу все больше и больше, а когда выпуклость уменьшается, кривая выпячива-
ется все меньше и меньше, становясь прямой при п = 1 и прогибаясь внутрь при п < 1.
Рис. 3.60. Семейство супергипербол
3.8.4. Формы в полярных координатах
Для представления ряда интересных кривых можно использовать полярные координаты. Как показано
на рис. 3.61, каждая точка кривой задана углом 0 и радиальным расстоянием г. Если и г и 0 являются
функциями от t, то при изменении t развертывается кривая (r(t), 0(0). Конечно, эту кривую можно пред-
ставить и в декартовых координатах (х(Г), y(t)), где
х(Г) = r(0cos(0(0),
y(t) - r(0sin(0(0).
3.8. Применение параметрического задания кривой
171
Рис. 3.61. Полярные координаты
Однако для большинства замечательных кривых возможно упрощение. В этих случаях радиус г выра-
жается явной функцией от 0, причем параметром, пробегающим всю кривую, является сам угол 0. Для
каждой точки (г, 0) соответствующая точка в декартовых координатах (х, у) вычисляется по формулам:
х ”/(0)cos(0),
У =/(0)sin(0).
(3.20)
Кривые в полярных координатах можно создавать и рисовать так же просто, как и любые другие.
Параметром является угод 0, который должен изменяться в промежутке, соответствующем данной фор-
ме. Простейшим примером является круг радиуса К (то есть /(0) - К). Формула /(0) - 2Kcos(0) пред-
ставляет другую простую кривую (какую?). На рис. 3.62 изображено несколько кривых, имеющих в
полярных координатах простые выражения. Вот некоторые из них.
О Кардиоида: /(0) - К(1 + соз(0)).
О Розы: /(0) - Kcos(n0)), где п определяет число лепестков розы. Показано два варианта.
О Спираль Архимеда: /(0) - Кв.
В каждом из этих случаев константа К определяет общий размер кривой. Поскольку кардиоида яв-
ляется периодической функцией, она может быть нарисована при изменении 0 от 0 до 2л. Розы являют-
ся периодическими при целом п, а спираль Архимеда непрерывно растет цо мере увеличения 0 от нуля.
Форма этой спирали широко применяется в качестве эксцентрика для преобразования кругового дви-
жения в линейное (см. [Yates, 217] и [Seggem, 182]).
Рис. 3.62. Примеры кривых, задающихся простыми формулами в полярных координатах
Конические сечения (эллипс, парабола и гипербола) имеют общую полярную форму записи:
/(0) = ------------,
1 ± ecos(0)
(3.21)
где е — эксцентриситет сечения. При в = 1 кривая является параболой, при 0 < е < 1 — эллипсом, а при
е>1 — гиперболой.
172
Глава 3. Дополнительные инструменты для рисования
Логарифмическая спираль
Логарифмическая спираль (logarithmic spiral) (она же изогональная спираль) /(0) = Ке,л, график кото-
рой приведен на рис. 3.63, а, также представляет определенный интерес [Coxeter, 51]. Эта кривая пере-
секает все радиальные линии под постоянным углом а, причем а = ctg(a). Логарифмическая спираль —
это единственная из спиралей, которая сохраняет свою форму при любом изменении масштаба: увеличь-
те фотографию логарифмической спирали в любое число раз, и увеличенная спираль в точности совпа-
дет (после поворота) с исходной кривой. Подобным же образом, если вы будете вращать изображение
изогональной спирали, вам будет казаться, что она становится больше или меньше [Steinhaus, 191]1. Такая
неизменяемость формы используется некоторыми животными, например моллюском, известным под
именем наутилус помпилиус («chambered nautilus»), или просто кораблик (см. рис. 3.63, б). По мере
роста моллюска его раковина также растет по логарифмической спирали, обеспечивая тем самым домик
постоянной формы [Gardner, 76].
Рис. 3.63. Логарифмическая спираль (а); моллюск наутилус {б)
б
В упражнениях и тематических заданиях рассматриваются некоторые другие семейства кривых, а ис-
черпывающий список и описание интересных кривых дано в работах [Yates, 217, Seggern, 182, Shikin, 185].
3.8.5. Трехмерные кривые
Кривые, которые изгибаются в трехмерном пространстве, также могут быть представлены параметри-
чески и будут подробно рассмотрены в последующих главах. Для построения параметрической формы
трехмерной кривой придумаем три функции х(.), г/(.) и z(.) и предположим, что эта кривая находится
«в точке» P(t) - (x(t), y(t), z(ty) в момент времени t. Рассмотрим несколько примеров.
Винтовая линия (геликоид)
Винтовая линия (circular helix) задается параметрически следующим образом:
x(t) - cos(t),
z/(t) = sin(t), (3.22)
z(t) - bt,
где b — некоторая константа. Эта кривая показана на рис. 3.64 в виде стереопары. (Инструкции по про-
смотру стереопар смотрите в предисловии.) Если такое представление покажется вам слишком громоз-
дким, сосредоточьтесь на одном из рисунков.
1 Эта кривая впервые была описана Декартом (Descartes) в 1638 году. А Якобу Бернулли (Jacob Bernoulli) эта спираль нравилась
настолько, что она была выгравирована на его надгробном памятнике в Базеле, Швейцария, вместе с надписью «Eadem mutata
resurgo», что означает «Измененная, я остаюсь прежней».
3.8. Применение параметрического задания кривой
173
Рис. 3.64. Винтовая линия, изображенная в виде стереопары
Существует много разновидностей винтовой линии, например эллиптическая винтовая линия
(elliptical helix), заданная формулой P(t) = (IVcos(t), 7/sin(r), bt), коническая винтовая линия (conical
helix), описываемая равенством P(t) = (tcos(t), tsin(t), bt). (Нарисуйте их схематически.) Вообще гово-
ря, любую двумерную кривую вида (x(t), y(t)) можно превратить в винтовую линию путем добавления
z(t) - bt или какой-нибудь другой зависимости для z(t).
Тороидальная спираль
Тороидальная спираль (toroidal spiral), заданная формулой
x(t) - (asin(ct) + 6)cos(t),
y(t) - (asin(ct) + b) sin(t), (3.23)
z(t) - acos(ct),
может быть образована нитью, намотанной на тор (трехмерное тело в форме баранки). На рис. 3.65
представлен случай с - 10, то есть нить делает 10 оборотов вокруг тора. В главе 6 мы будем рассматри-
вать трубы, образованные такой спиралью.
Рис. 3.65. Тороидальная спираль, изображенная в виде стереопары
Практические упражнения
3.8.6. Рисование суперэллипсов
Напишите подпрограмму drawSuperEl lipse(...), которая рисует суперэллипс. Эта подпрограмма имеет
следующие параметры: с — центр суперэллипса; ширина W и высота Н; кривизна и; число «замеров»
кривой для применения аппроксимации ломаными.
3.8.7. Рисование кривых, заданных полярными координатами
Напишите подпрограммы для рисования и-лепестковой розы и изогональной спирали.
3.8.8. Золотые сечения
Найдите особую логарифмическую спираль, которая генерирует «золотые сечения», пересекаясь с бес-
конечной регрессией золотых прямоугольников, как показано на рис. 3.66. (Вспомните главу 2.) Как
составить алгоритм рисования такой картины?
174
Глава 3. Дополнительные инструменты для рисования
Рис. 3.66. Спираль и золотой прямоугольник
3.8.9. Полезная неявная форма функции
Найдите соответствующую неявную форму для розы, которая ранее задавалась в полярных координа-
тах с помощью равенства /(0) - Kcos(nO).
3.8.10. Внутренне-внешние функции для кривых в полярных координатах
Обдумайте, существует ли единственный способ, дающий соответствующую внутренне-внешнюю функ-
цию для любой кривой, заданной в полярных координатах, как, например, в равенстве (3.20). Приведи-
те примеры или контрпримеры.
3.9. Резюме
В этой главе мы разработали несколько инструментов, которые позволяют разработчику приложений
работать над задачей непосредственно в наиболее удобной «мировой» («world») системе координат.
Объекты задаются («моделируются») с использованием высокоточных вещественных координат, без
забот о том, где и какого размера будет изображение моделируемого объекта на экране. Эти вопросы
решаются путем последующего выбора окна и порта просмотра (вручную или автоматически), кото-
рые и определяют, какого размера будет данный объект и как он расположится на экране. Такой подход
отделяет стадию моделирования от стадии просмотра, позволяя программисту или пользователю скон-
центрироваться на важных аспектах каждой из фаз, не отвлекаясь на детали устройства отображения.
Использование окон делает возможным «приблизить» или «отодвинуть» («zoom») сцену, а также
«блуждать» («гоаш») по различным ее участкам. Подобные действия хорошо знакомы нам из ежедневно-
го общения с кино- или фотокамерой. Мы рассмотрели также использование портов просмотра, кото-
рые позволяют программисту размещать картинку или несколько картинок в нужных местах дисплея,
чтобы скомпоновать итоговое изображение. Мы также обсудили различные методы, обеспечивающие
во избежание искажений одинаковое форматное соотношение окна и порта просмотра.
Отсечение (clipping) является фундаментальной технологией в графике, поэтому мы изложили клас-
сический алгоритм отсечения отрезков прямой относительно мирового окна. Этот алгоритм дает програм-
мисту возможность определять, какая часть изображения будет фактически визуализирована (rendered):
те части, которые находятся за пределами окна, отсекаются. OpenGL осуществляет отсечение автома-
тически, однако в других программных средах «отсекатель» должен содержаться в явном виде.
Мы разработали класс Canvas для инкапсуляции многих основных деталей и тем самым предоста-
вили программисту единый и единообразный инструмент для создания графических программ. Canvas
3.10. Тематические задания
175
прячет детали OpenGL внутри удобных подпрограмм, таких как setWindowO, setViewportO, moveToO,
lineToO и forwardO, а также гарантирует, что будут произведены все необходимые инициализации.
В тематических заданиях мы будем реализовывать Canvas в обобщенной программной среде, без OpenGL,
где подпрограммы отсечения и преобразования «окно — порт просмотра» должны иметься в явном виде.
В такой среде значение инкапсуляции данных внутри класса Canvas становится даже более очевидным.
Разработан целый ряд вспомогательных инструментов для выполнения относительного рисования
и черепашьей графики, а также для создания рисунков, содержащих правильные многоугольники, дуги
и окружности. Была введена параметрическая форма задания кривых и показано, что она является наи-
более естественной при описании любой кривой. Параметрическая форма упрощает рисование кри-
вых, даже многозначных, самопересекающихся или имеющих вертикальные участки.
3.10. Тематические задания
Один из симптомов приближающегося нервного срыва — это вера в то, что твоя работа чертовски важна.
Бертран Рассел (Bertrand Russell)
Тематическое задание 3.1. Изучение логистического
преобразования и имитация хаоса
Уровень сложности И.
В конце главы 2 рассматривались системы итерируемых функций (IFS). Рассмотрим IFS, которая дает
возможность по-новому взглянуть на мир хаоса и требует корректной установки окна и порта просмот-
ра. Последовательность величин генерируется посредством повторяющегося применения функции/(.),
именуемой логистическим преобразованием (logistic map). Эта функция описывает параболу с помо-
щью следующего уравнения:
/(х) - 4Хх( 1-х), (3.24)
где Л — некоторая константа, выбранная из промежутка от 0 до 1. При итеративном применении функ-
ции /(.), начиная с заданной точки х0 (также из промежутка от 0 до 1), генерируется орбита (orbit)
(вспомните определение этого термина в главе 2):
Как ведет себя эта последовательность? Здесь таится много сложностей. Поведение данной после-
довательности можно сделать более наглядным, если определенным образом отобразить его графиче-
ски. На рис. 3.67 показана парабола у - 4Лх(1 - х) для А, - 0,7 при изменении х от 0 до 1.
Рис. 3.67. Логистическое преобразование для А = 0,7
176
Глава 3. Дополнительные инструменты для рисования
Здесь выбрана начальная точка х0 = 0,1, и в этой точке проведена вертикальная линия до параболы,
что дало величину /(х0) “ 0,252. Далее нам следует применить рассматриваемую функцию к новой ве-
личине х, - 0,252. Это наглядно демонстрируется с помощью горизонтального движения до прямой у - х,
как показано на рисунке. Затем, чтобы выяснить значение функции/( ) в этой новой точке, снова про-
водим вертикальную линию до параболы. Данный процесс повторяется бесконечно, как у всякой систе-
мы итерируемых функций. Из предыдущей точки с координатами (xt ,, xt) проводится горизонтальная
линия к точке (xt, xt), откуда проводится вертикальная линия к точке (xj6,xj6+1). Из рисунка видно, что
при Л - 0,7 эти величины быстро сходятся к постоянному «аттрактору» — фиксированной точке, в ко-
торой /(х) - х. (Каково значение этой точки при А, - 0,7?) Заметим, что этот аттрактор не зависит от
начальной точки: последовательность всегда быстро сходится к конечной величине.
Исследуем, как можно управлять этим процессом, задавая различные значения параметра Л, то есть
покрутим «А-рукоятку». Если Л мало, то процедура будет даже проще: единственный аттрактор обнару-
жится при х = 0. Однако когда значение «А-рукоятки» увеличивается, начинает твориться что-то стран-
ное. На рис. 3.68, а показано, что происходит при А = 0,85. «Орбита», представляющая нашу после-
довательность, превращается в бесконечно повторяющийся цикл, никогда не сходящийся к конечной
величине. Здесь имеется несколько аттракторов, по одному на каждой вертикальной линии в предель-
ном цикле, показанном на рисунке. А когда А становится больше критического значения А = 0,892486418...,
процесс становится воистину хаотическим.
Рис. 3.68. Логистическое преобразование для а) А = 0,85 и 6} А = 0,9
Случай А - 0,9 приведен на рис. 3.68, б. Для большинства начальных точек орбита еще остается пе-
риодической, однако количество орбит, наблюдаемых между повторами, теперь очень велико. Другие
начальные точки приводят к действительно апериодическому движению, и небольшие изменения на-
чальной точки могут повлечь за собой существенные различия в поведении. До того, как этот воистину
замечательный феномен был впервые обнаружен Митчеллом Фейгенбаумом (Mitchell Feigenbaum) в
1975 году, большинство исследователей были уверены, что малые изменения в системе должны приво-
дить к соответственно малым изменениям в ее поведении и что простые системы, подобные этой, не
могут демонстрировать сколь угодно сложное поведение. Работа Фейгенбаума породила новую область
исследования природы сложных нелинейных систем, известную как теория хаоса. Чрезвычайно инте-
ресно поэкспериментировать с этим логистическим преобразованием.
Напишите и выполните программу, позволяющую пользователю изучать поведение повторяющих-
ся итераций логистического преобразования, как показано на рис. 3.68. Установите подходящие окно и
порт просмотра — так, чтобы все логистическое преобразование было хорошо видно. Пользователь за-
дает значения х0 и А, а программа рисует предельные циклы, создаваемые системой
3.10. Тематические задания
177
Тематическое задание 3.2. Реализация отсекателя
Кохена-Сазерленда на С или C++
Уровень сложности II.
Основы алгоритма Кохена-Сазерленда (Cohen—Sutherland) были приведены в разделе «Алгоритм
отсечения Кохена-Сазерленда». В данном тематическом задании мы конкретизируем некоторые под-
робности его реализации на языках С или C++ в силу эффективности поддерживаемого этими языка-
ми низкоуровневого управления битами.
Прежде всего нам необходимо сформировать кодовые слова «внутри/вне», определяющие, как точ-
ка Р расположена относительно окна (см. рис. 3.15). Для этого достаточно единственного восьмибито-
вого слова code: четыре его бита используются для записи четырех элементов информации. Точка Р по-
очередно проверяется относительно каждой границы окна; если Р расположена вне этой границы, то
соответствующий бит в слове code устанавливается в 1, что означает TRUE.
В листинге 3.16 показано, как можно провести такую проверку. Сначала code устанавливается в 0,
а затем его отдельные биты устанавливаются в нужные значения с помощью побитовой операции OR.
Величины 8, 4, 2 и 1 являются простыми масками. Например, поскольку 8 в двоичной форме равно
00001000, побитовая операция логического сложения с 8 установит четвертый бит с правого конца в 1.
Листинг 3.16. Установка битов кодового слова «внутри/вне» для точки Р
unsigned char code - 0:
// initially all bits are 0
// вначале все биты равны 0
...if(P.x < window.l) code |- 8:
// set bit 3
// устанавливаем бит 3
if(P.y < window.t) code |- 4:
// set bit 2
// устанавливаем бит 2
if(P.x < window.r) code |= 2:
// set bit 1
// устанавливаем бит 1
if(P.y < window.b) code |- 1:
// set bit 0
// устанавливаем бит О
В отсекателе обе конечные точки — Р1 и Р2 (см. рис. 3.17) — проверяются относительно окна, и фор-
мируются их кодовые слова codel и code2. Затем мы должны проверить их на «тривиальный прием» и
«тривиальное отклонение».
О Тривиальный прием. Обе конечные точки находятся внутри окна, поэтому и codel, и code2 равны 0.
В С и C++ это легко определяется с помощью побитовой операции OR: тривиальный прием име-
ет место при равенстве нулю (codel | code2).
О Тривиальное отклонение. Случай тривиального отклонения возникает, если обе конечные точ-
ки расположены вне окна по одну и ту же сторону от него: обе слева от окна, обе выше, обе ниже
или обе справа. Это условие эквивалентно следующему: коды этих точек имеют по крайней мере
одну единицу в той же битовой позиции. Пусть, например, codel - 0110, a code2 - 0100, тогда Р1
находится выше и правее окна, в то время как Р2 лежит выше окна, но ни правее, ни левее его.
Поскольку обе точки располагаются выше окна, ни один отрезок прямой не может находиться
внутри окна. Тривиальное отклонение легко проверяется с помощью побитовой операции AND
над codel и code2; если каждая из них имеет 1 в той же самой позиции, то (codel & code2) будет
отлична от нуля.
178
Глава 3. Дополнительные инструменты для рисования
Разделение отрезка в случаях, отличных от тривиального
приема и тривиального отклонения
На рис. 3.18 приведена еще одна реализация эффективного отсекания той части отрезка прямой, кото-
рая расположена вне окна. Пусть известно, что точка Р с кодовым словом code расположена вне окна.
Тогда отдельные биты слова code можно проверить для выяснения того, с какой стороны окна располо-
жена точка Р, и тогда произвести разделение согласно уравнению (3.5). В листинге 3.17 приведена под-
программа разделения, которая находит новую точку (такую, как точка А на рис. 3.18) и замещает ею
точку Р. В этой подпрограмме используется побитовая операция логического умножения AND над сло-
вом code с маской, определяющей, где относительно окна расположена точка Р.
Листинг 3.17. Разделение отрезка, расположенного вне окна
ChopLine(Point2 &Р. unsigned char code)
{
if(code & 8){
// to the Left
// слева
P.y +- (window.! - P.x) * dely / delx:
P.x - window.!:
}
else if(code & 2){
11 to the Right
// справа
P.y +- (window.r - P.x) * dely / delx:
P.x - window.r:
}
else if(code & 1){
// below
// ниже
P.x +- (window.b - P.y) * delx / dely:
P.y - window.b:
}
else if(code & 4){
// above
// выше
P.x +- (window.t - P.y) * delx / dely:
P.y - window.t;
}
}
Напишите полную реализацию алгоритма Кохена—Сазерленда, собрав вместе части, описанные здесь,
с частями, которые приведены в разделе «Алгоритм отсечения Кохена—Сазерленда». Если вы делаете это
в контексте реализации класса Canvas, как рассматривается в следующем тематическом задании, то обду-
майте, как наилучшим образом предоставить данной подпрограмме доступ к частным элементам данных,
связанных с окном и участвующими в процессе точками, и разрабатывайте свой код в соответствии с этим.
Проверьте данный алгоритм, нарисовав окно с большим разнообразием случайно расположенных
линий: Пусть программа окрасит в красный цвет те их части, которые расположены внутри окна, и в
черный цвет — те, которые расположены вне его.
Практические упражнения
3.10.1. Почему никогда не произойдет «деление на нуль»?
Рассмотрим вертикальный отрезок прямой, для которого delx равен нулю. Почему же никогда не появ-
ляется код Р. у+= (window. 1 - P.x) * dely/delх, который вызвал бы деление на нуль? Объясните также,
почему не появляется ни один из четырех операторов, где вычисляется delx/dely или del y/del х, если его
знаменатель равен нулю.
3.10. Тематические задания
179
3.10.2. Выполняются ли два разделения во время одной итерации?
На первый взгляд кажется, что кодировку алгоритма Кохена-Сазерленда можно было бы улучшить,
если заменить в нем такие строки, как else 1f (code & 2) на if (code & 2) и попытаться выполнить два
«разделения» отрезка подряд. Тем не менее покажите, что такой подход приводит к вычислению оши-
бочных конечных точек и, как следствие, к катастрофе.
Тематическое задание 3.3. Реализация Canvas на Turbo C++
Уровень сложности III.
Представляется интересным разработать класс для рисования такого типа, как Canvas, в котором про-
работаны все детали, чтобы посмотреть, как многие его составляющие могут работать вместе. Иногда
это делать даже необходимо, когда, например, недоступна библиотека поддержки, такая как OpenGL
Здесь мы создадим класс Canvas для популярной графической платформы, использующей Turbo C++
фирмы Borland.
Мы хотим иметь реализацию класса Canvas, которая в основном имеет такой же интерфейс, как в
листинге 3.6. В листинге 3.18 показана версия, разрабатываемая нами здесь (фрагменты, совпадающие
с листингом 3.6, опущены). Конструктор берет нужную ширину и высоту, но не заголовок, поскольку
Turbo C++ не поддерживает экранных окон с заголовками. Несколько новых частных элементов дан-
ных осуществляют внутреннее управление отсечением и преобразованием «окно — порт просмотра».
Листинг 3.18. Интерфейс для класса Canvas на Turbo C++
class Canvas {
public:
Canvas(int width, int height):
// constructor
// конструктор
setUindowf).setViewportO. 1 ineTof).etc.. as before
// setWindowO.setViewportO.lineToO и т.д.. как и раньше
private:
Point2 СР;
// current position in the world
// текущая позиция в мировых координатах
IntRect viewport;
// the current window
// текущее окно
RealRect window:
// the current viewport
// текущий порт просмотра
float mapA, mapB. mapC. mapD:
// data for the window-to-viewport mapping
// данные для преобразования «окно-порт просмотра»
void makeMap(void):
// builds the map
// выполняет преобразование
int screenwidth. screenHeight:
float delx.dely:
11 increments for clipper
// добавления для отсекателя
char codel. code2:
// outside codes for clipper
// внешние коды для отсекателя
void ChopLine(tPoint2 &p. char c):
int clipSegment(tPoint2 &pl, tPoint2 &p2);
}
180
Глава 3. Дополнительные инструменты для рисования
Реализация класса Canvas
Здесь мы покажем некоторые из функций-членов класса Canvas, чтобы проиллюстрировать, что нужно
делать для управления преобразованием «окно — порт просмотра» и отсечением.
Конструктор Canvas
В первую очередь в конструктор передаются нужные ширина и высота экрана. Затем Turbo C++ пере-
ходит в графический режим с самым высоким разрешением, которое поддерживается используемой
графической системой. Проверяются действующие ширина и высота экрана; и если хотя бы одна из
них меньше, чем было запрошено, то программа прекращает работу. Наконец, устанавливаются по
умолчанию окно и порт просмотра, после чего выполняется преобразование «окно — порт просмотра»
(внутри функции SetViewportO). Имеем следующий код:
Canvas:: Canvasdnt width, int height)
{
int gdriver - DETECT, gmode;
//Turbo C++: use best resolution screen
//Turbo C++: используем наилучшее разрешение экрана
initgrapht&gdriver, &gmode. :
П go to "graphics” mode
// переходим в «графический» режим
screenWidth - getmaxxO +1:
// size of available screen
// размер имеющегося экрана
screenHeight - getmaxyO + 1:
assert(screenWidth >- width):
// as wide as asked for?
// достаточна ли ширина по сравнению с запрошенной?
assert(screenHeight >- height):
// as high as asked for?
// достаточна ли высота no сравнению с запрошенной?
CP.setCO.O, 0.0):
window.set(-l.0.1.0.-1.0.1.0):
// default window
// окно по умолчанию
setViewportCO. screenWidth. 0. screenHeight):
// sets default map. too
// устанавливается также преобразование по умолчанию
}
Установка окна, порта просмотра и преобразования
Когда бы ни были установлены окно или порт просмотра, преобразование «окно — порт просмотра»
всегда обновляется для гарантии того, что оно является текущим. Вырожденное окно нулевой высоты
вызывает ошибку. Преобразование использует данные об окне и порте просмотра для вычисления че-
тырех необходимых коэффициентов А, В, С и D. Ниже приведен код, выполняющий эти операции:
//«««««« set Window »»»»»
//«««««« установка окна »»»»»
void Canvas:: setWindow(f1 oat 1. float r. float b. float t)
{
window.set(l. r, b. t);
assert(t !- b);
//degenerate !
// вырожденное!
makeMapO:
3.10. Тематические задания
181
// update the mapping
// обновляем преобразование
}
//««««« set Viewport »»»»»
//««««« установка порта просмотра »»»»»
void Canvas:: setViewportdnt 1, int r. int b. int t)
{
viewport.set(l. r. b. t):
makeMapO:
// update the mapping
// обновляем преобразование
}
//«««« make Map »»»>»»
ц«««« преобразование »»»»»>
void Canvas:: makeMap(void)
// set mapping from window to viewport
// устанавливаем преобразование «окно-порт просмотра»
IntRect vp = getViewportO;
// local copy of viewport
// локальная копия порта просмотра
RealRect win = getWindowO:
// local copy of window
// локальная копия окна
float winWid - win.r - win.l:
float winHt = win.t - win.b;
assertCwinWid !- 0.0): assert(winHt !- 0.0):
// degenerate!
// вырожденный случай!
mapA = (vp.r - vp.1)/winWid:
// fill in mapping values
// заполнение величин для преобразования
mapC = vp.l - map.A * win.l;
map8 = (vp.t - vp.b)/winHt:
mapD = vp.b - map.В * win.b:
}
moveToQ и lineTo() с отсечением
Подпрограмма moveToO преобразует точку из мировых координат в экранные и затем вызывает специ-
альную подпрограмму Turbo C++ movetoO для обновления внутренних текущих координат, поддержи-
ваемых программной средой. Кроме того, moveToO одновременно обновляет и СР в мировых координа-
тах класса Canvas. Подпрограмма 1 ineToO работает аналогично, однако она сначала должна определить,
какая часть отрезка прямой расположена внутри окна (и расположена ли вообще). Для того чтобы вы-
полнить это, она использует функцию clipSegmentO, описанную в разделе «Отсечение линий» и в тема-
тическом задании 3.2, которая возвращает концевые точки fi rst и second лежащей внутри окна части
отрезка прямой. Если какая-то часть отрезка расположена в окне, то происходит перемещение к first и
рисование прямой до second. clipSegmentO заканчивает свою работу командой movetoO, для гарантии
того, что СР класса Canvas и внутренние СР Turbo C++ будут текущими.
В приведенном ниже коде ChopLine и cl ipSegment такие же, как в тематическом задании 3.2:
//«<««««« moveTo »>»»»
void Canvas:: moveTo(float x. float y)
182
Глава 3. Дополнительные инструменты для рисования
int sx = (int)CmapA * х + mapC):
int sy = (int)(mapB * у + mapD);
moveto(sx. sy);
// a Turbo C++ routine
// подпрограмма Turbo C++
CP.set(x, y):
}
//««««« lineTo »»»
void Canvas:: lineToffloat x. float y)
{
// Draw a line from CP to (x.y). clipped to the window
// Рисуем линию от СР до (х.у). отсеченным по окну
Point2 first = СР;
// initial value of first
// начальное значение first
Point2 second(x, y):
// initial value of second
// начальное значение second
if(clipSegment(first. second))
// any part inside?
// находится ли какая-нибудь часть внутри окна?
{
moveTotfirst.x. first.у):
// to world СР
// для внешних СР
int sx = (intHmapA * second.х + mapC):
int sy = (intKmapB * second.у + mapD);
lineto(sx.sy):
// a Turbo C++ routine
// подпрограмма Turbo C++
}
moveTo(x. y):
// update CP
// обновляем CP
}
Напишите полную реализацию класса Canvas на Turbo C++ (или в подобной программной сре-
де, которая требует от вас реализовывать отсечение и преобразование). Разберитесь должным образом
с установкой цветов рисования и фона (данная операция обычно сильно зависит от системы). Про-
тестируйте свой класс, использовав его в приложении, которое рисует полиспирали, задаваемые пользо-
вателем.
Тематическое задание 3.4. Рисование арок
Уровень сложности II.
Арки использовались в архитектурных композициях на протяжении всей истории строительства.
Их структурная прочность и декоративная простота делают их чрезвычайно важными элементами
структурного проектирования, поэтому большое разнообразие подобных форм входят в состав церквей,
мостов, порталов и т. д.
На рис. 3.69 показаны две основные формы арок. Арка на рис. 3.69, а с центром в начале координат
имеет ширину 2 W. Эта арка начинается на высоте Я над основанием. Ее основным элементом является
полукруг с радиусом R = W. Отношение Н/W может быть задано по желанию. Например, Н/W может
быть связано с золотым отношением.
3.10. Тематические задания
183
Рис. 3.69. Две основные арочные формы: а) закругленная арка; б) стрельчатая арка
На рис. 3.69, б показан идеализированный вариант второй из широко известных арочных форм, на-
зываемой «стрельчатой» («pointed»), или «равнобочной» («equilateral»), аркой, которую часто можно
видеть в соборах*. Здесь два арки радиуса R - 2 W сходятся точно над центром. (Чему равен угол раз-
вертки каждой арки?)
Арка под названием «гусек»1 2 (или «килевидная» — «keel») показана на рис. 3.70. Такая арка впер-
вые появилась около 1300 года н. э. и была популярным архитектурным элементом на протяжении все-
го позднего средневековья. В верхней части полукруглой арки радиуса R располагаются два круга ра-
диуса fR, где f — некоторая дробь. Такая структура определяет положение этих двух кругов. (Какие
координаты имеет точка С?) На каждой стороне обе дуги сопрягаются вместе, образуя плавную остро-
конечную вершину. Интересно определить параметры различных арок в терминах Wnf.
Разработайте подпрограммы, с помощью которых можно рисовать каждый из вышеописанных ти-
пов арок. Кроме того, напишите приложение, рисующее интересное сочетание арок в церкви, мечети
или мосте вашей разработки.
Тематическое задание 3.5. Некоторые рисунки,
используемые в физике и технике
Уровень сложности II.
В данном тематическом задании мы имеем дело со множеством интересных рисунков, которые появ-
ляются в определенных разделах физики и техники. Первый такой рисунок иллюстрирует физический
1 Словарь архитектуры (J. Fleming, Н. Honour, N. Pevsner. Dictionary of Architecture. London: Penguin Books, 1980).
2 Архитектурный термин «гусек» («ogee») происходит от старофранцузского ogive, означающего S-образную кривую.
184
Глава 3. Дополнительные инструменты для рисования
принцип пересечения окружностей под прямым углом; во втором создается график, который можно
использовать при изучении электромагнитных явлений; на третьем рисунке показаны некоторые симво-
лы, применяемые в конструировании цифровых систем.
Электростатические поля
Узор из окружностей, приведенный на рис. 3.71, изучается в физике и электротехнике и изображает
линии электростатического поля, окружающего электрически заряженные проводники. Узор такого же
вида появляется и в математике при исследовании аналитических функций комплексной переменной.
Здесь же мы рассматриваем этот узор просто как элегантный набор окружностей и обсуждаем, как на-
рисовать их.
Рис. 3.71. Семейства ортогональных окружностей
Существует два семейства окружностей, которые мы будем называть «двухточечными» («two-
pointers») и «охватывающими» («surrounders»). Семейство двухточечных состоит из окружностей, про-
ходящих через две заданные точки. Пусть эти точки имеют координаты (-а, 0) и (а, 0). Двухточечные
окружности можно задавать с помощью некоторого параметра т, причем для каждого значения т гене-
рируются две различные окружности. Центры и радиусы каждой из этих окружностей будут соответ-
ственно равны
center = (о, ± a\lm2 -1 j и radius = ат,
где т изменяется от 1 до бесконечности.
Окружности семейства охватывающих «окружают» одну из точек: (-а, 0) и (а, 0). Центры и радиу-
сы охватывающих окружностей задаются параметром п и соответственно имеют вид:
center = (± ап, 0) и radius - а\}п2 -1,
где п изменяется от 1 до бесконечности. Охватывающие окружности называют также «окружностями
Аполлона», они возникают в задачах преследования (pursuit) [Ball, 8]. Расстояния от любой точки на
окружности Аполлона до точек (-а, 0) и (а, 0) имеют постоянное отношение. (Чему равно это отноше-
ние в терминах а и и?)
Семейство охватывающих окружностей тесно связано с семейством двухточечных окружностей:
каждая охватывающая окружность «пересекает» каждую двухточечную окружность под прямым углом.
Поэтому эти два семейства окружностей называют ортогональными (orthogonal) друг другу.
Напишите и выполните программу, рисующую эти два семейства ортогональных окружностей. Выбе-
рите такие сочетания значений тип, чтобы изображение было гармоничным и приятным на вид.
3.10. Тематические задания
185
Диаграммы Смита
Диаграммы Смита (Smith charts), представляющие собой еще один вид узора из окружностей, извест-
ны в электротехнике в связи с силовыми линиями электромагнитного поля. На рис. 3.70 изображено
два ортогональных семейства из диаграмм Смита. Здесь все члены этих семейств проходят через об-
щую точку (1,0). Окружности семейства А имеют центр в точках (1 - т, 0) и радиусы т, а окружности
семейства В имеют центры в точках (1, ±и) и радиусы п, где т и п изменяются от 0 до л. Напишите и
выполните программу, рисующую эти семейства окружностей.
Рис. 3.72. Диаграмма Смита
Логические вентили для цифровых цепей
Логические вентили (logic gates) хорошо известны ученым и инженерам, занимающимся основными
электронными цепями для компьютеров. Каждый тип вентилей обозначается в схеме цепи символом
определенной формы, некоторые из них построены из дуг окружностей. На рис. 3.73, а изображен
так называемый вентиль НЕ-И (NAND-gate) в соответствии с мировым стандартом*. В основе вентиля
НЕ-И лежит полукруглая арка, повернутая на бок. Единственная используемая здесь дуга имеет ра-
диус 13 единиц относительно других элементов, поэтому весь вентиль НЕ-И должен иметь в высоту
26 единиц.
а б
Рис. 3.73. Стандартные графические обозначения для вентилей: (а) НЕ-И и (б) НЕ-ИЛИ
На рис. 3.73, б показано стандартное обозначение для вентиля HE-ИЛИ (NOR gate). Он напоми-
нает повернутую набок стрельчатую арку. Здесь используются три дуги, каждая из которых имеет
радиус 26 единиц. (Опубликованный стандарт, показанный здесь, содержит ошибку, которая делает
невозможным соединение некоторых элементов. В чем состоит эта ошибка?)
Напишите программу, которая может рисовать оба типа вентилей любого размера и расположения
в мировых координатах. (Для вентиля HE-ИЛИ найдите и реализуйте корректное исправление ошиб-
’ Institute of Electrical and Electronic Engineers (IEEE) публикует много работ, в том числе стандарты по терминологии и графиче-
ским формам элементов схем. Эти рисунки взяты из сборника стандартов IEEE Std. 91-1984.
186
Глава 3. Дополнительные инструменты для рисования
ки, показанной на рис. 3.73, б.) Кроме того, усовершенствуйте свою программу так, чтобы она могла
рисовать эти вентили повернутыми на 90°, 180° или 270°.
Тематическое задание 3.6. Мозаики
Уровень сложности II.
В компьютерной графике имеются мощные инструменты для создания замечательных картин, составлен-
ных из геометрических объектов. Одна из наиболее увлекательных видов картин кажется бесконечно
повторяющейся во всех направлениях. Такие картины называются мозаиками (tilings), или повторяю-
щимися узорами (repeat patterns).
Основные мозаики
На рис. 3.74 показана элементарная мозаика. Мотив (motif)> в данном случае четыре четверти окруж-
ностей в несложном сочетании, помещен в квадратную область мировых координат. Для того чтобы
составить из этого мотива мозаичное покрытие плоскости, нужно создать множество портов просмот-
ра, прилегающих сторона к стороне и покрывающих поверхность дисплея, причем мотив в каждом пор-
те просмотра рисуется один раз.
Рис 3.74. Мотив и результирующее мозаичное покрытие
Напишите программу, которая:
О выбирает в мировых координатах квадратное окно и рисует в нем какой-нибудь интересный мо-
тив (возможно, отсекая его части, как это сделано на рис. 3.11);
О последовательно рисует картину во множестве портов просмотра, которые примыкают друг к дру-
гу и покрывают поверхность дисплея.
Выполните свою программу по крайней мере для двух мотивов.
Мозаики Труше
Небольшая вариация метода из части 1 заключается в том, что последовательность мотивов выби-
рается случайным образом из «пула» (pool — накопитель) мотивов-кандидатов. На рис. 3.75, а пока-
зана известная мозаика Труше (Truchet tiles)1, основанная на двух четвертях окружностей с центра-
ми в противоположных углах квадрата. Элементы мозаики 0 и 1 отличаются друг от друга только
поворотом на 90е.
Напишите приложение, которое рисует мозаику Труше по всей поверхности порта просмотра. Каж-
дый последовательный элемент мозаики использует мотивы 0 или 1, выбранные случайно.
Кроме дуг используются и другие кривые, такие, например, как на рис. 3.76. Какие ограничения долж-
ны быть наложены на тот угол, под которым каждая кривая подходит к краю элемента, чтобы избежать
изломов в общей кривой? Это условие также может быть распространено на более чем два мотива.
* С. Smith, «The Tiling Patterns of Sebastian Truchet and the Topology of Structural Hierarchy,» Leonardo, 20:4, pp. 373—385,1987.
3.10. Тематические задания
187
Рис 3.75. Мозаика Труше: а) два мотива; б) узор Труше
Рис. 3.76. Расширение мозаики Трачета
Усовершенствуйте предыдущую программу так, чтобы в ней осуществлялся случайный выбор из
двух или более мотивов, и выполните эту программу для разработанных вами мотивов. Убедитесь, что
вы разработали мотивы, корректно сопрягающиеся между собой.
Тематическое задание 3.7. Веселые вариации на тему
Уровень сложности II.
В разделе «Применение параметрического задания кривой» мы изучали, как рисовать кривую, задан-
ную параметрически с помощью функции Р(Г): следует взять последовательность моментов времени {Г}
и соединить прямыми линиями последовательные «замеры» (х(Г), y(ty). Изменяя способ выполнения
этих замеров, можно получить широкий диапазон изображений. Рассмотрим несколько возможностей.
Для каждого из методов, описанных ниже для выполнения замеров по t, напишите программу для
рисования следующих четырех форм:
О эллипс;
О гипербола;
О логарифмическая спираль;
О пятилепестковая роза.
Неравномерно взятые значения t
Вместо постоянного приращения между значениями t при взятии замеров функций х( ) и у{ ) будем
использовать переменное приращение. Интересно поэкспериментировать с различными способами и
посмотреть, какие визуальные эффекты достигаются при этом. Вот некоторые варианты для последо-
188
Глава 3. Дополнительные инструменты для рисования
вательности из п + 1 значения t в диапазоне от 0 до Г (выбранные в зависимости от формы рассматрива-
емой кривой):
О t^T\[17п : замеры группируются все ближе и ближе друг к другу по мере роста г.
О t. = Г(г/и)2: замеры распространяются шире по мере роста i.
О rf - T(i/ri) + .Asin(£?7«): замеры циклически собираются вместе или отдаляются друг от друга. С
помощью констант А и k регулируются величина и скорость изменения.
Значения t, выбираемые случайно
Значения t можно выбирать случайно, если создать для этого функцию
L = randChoose(0, Г),
которая при каждом вызове возвращает случайно выбранную величину в диапазоне от 0 до Т.
На рис. 3.77 показана созданная таким способом ломаная линия для точек, находящихся на эллипсе.
Интересно наблюдать за развитием такой картины на дисплее. Вначале появляется шквал кажущихся
независимыми линий, однако вскоре глаз обнаруживает некоторый порядок в этом хаосе и видит эл-
липтическое «обрамление», проступающее по границе облака линий.
Рис. 3.77. Случайная эллиптическая ломаная линия
В качестве альтернативы можно взять последовательность возрастающих значений t, создаваемых с
помощью функции
t. = t._t + randChoose(0, г),
где г — малая положительная величина.
Соединение вершин в разном порядке
В популярной детской игре в доску втыкаются булавки в виде некоторого узора, затем вокруг этих бу-
лавок в каком-либо порядке обвивается кусок нити. Здесь значения t задают позиции булавок на доске,
а функция LineToO играет роль нити.
Замеры Р(Г) предварительно записываются в соответствующий массив Р[1], 1 = 0 .1.п. Лома-
ная линия рисуется путем прохождения последовательности значений 1 каким-либо интересным путем.
Это означает, что последовательность г0, i,,... компонуется из значений от 0 до п, причем для каждого
индекса ik осуществляется вызов функции worldL1neTo(P[ik]). Возможны следующие варианты:
О «Случайная раздача»: последовательность i0, i(,... представляет собой случайную перестановку
величин 0, 1,..., п, аналогично раздаче заданного количества карт из перетасованной колоды.
О Каждая пара точек соединяется прямой линией. Поэтому каждая пара значений в диапазоне О,
1......п появляется на соседних местах где-нибудь в последовательности i0, i,.Одним из приме-
ров того, как рисуются линии посредством соединения каждой точки со всеми остальными, явля-
ется простая розетка.
3.10. Тематические задания
189
О Можно также рисовать «паутины», как предлагается на рис. 3.78. Здесь индекс многократно цик-
лически принимает все возможные значения, пропуская каждый раз некоторое число М. Это мо-
жет быть легко сделано, если последующий индекс формировать из предыдущего по формуле
i = (i + М) mod(n + 1).
Рис. 3.78. Добавление «паутин» к кривой
Тематическое задание 3.8. Окружности,
вращающиеся вокруг окружностей
Уровень сложности II.
Еще одно большое семейство интересных кривых, которые могут быть использованы в графике. Рассмот-
рим путь, который проходит точка, жестко закрепленная на окружности, в то время как эта окружность
вращается вокруг другой зафиксированной окружности. Кривые, являющиеся траекториями таких
точек, называются трохоидами (trochoids), и на рис. 3.79 показано, как они образуются. Точка, пред-
назначенная для трассировки, прикрепляется к вращающейся окружности (радиуса Ь) на конец стерж-
ня на расстоянии k единиц от центра окружности. Радиус зафиксированной окружности составляет а
единиц. Существует два основных вида трохоид: когда окружность вращается по наружной стороне
зафиксированной окружности (см. рис. 3.79, а), то получается эпитрохоида (epitrochoid); если же по
внутренней стороне (см. рис. 3.79, б), то получается гипотрохоида (hypotrochoid). Известным инстру-
ментом для рисования трохоид является детская игра «Спирограф» (Spirograph)1. С ее помощью можно
начертить трохоиды, имеющие следующие параметрические формы.
Эпитрохоида:
(
x(t) = (a+b)cos(2itt)-kcos 2 л
(а +
b
(
y(t) = (a+b)sin(2nt)-к sin 2я
Гипотрохоида:
( (a-b)ty
x(t) = (a-b)cos(2nf) + kcos 2л----— •
b
(a-b)t
y(t) = (a-i)sin(2nt) -k sin 2n----—
Гипоциклоида превращается в эллипс при а = 2Ь для любого k.
1 Торговая марка фирмы Kenner Products.
(3.25)
(3.26)
b
190
Глава 3. Дополнительные инструменты для рисования
Рис 3.79. Окружности, вращающиеся вокруг окружностей
Когда трассирующая точка лежит на вращающейся окружности (k - b), то описываемые ею кривые
называются циклоидами (cycloids). Известны некоторые особые случаи циклоид, например эпицикло-
иды и гипоциклоиды.
Эпициклоиды:
О Кардиоида (cardioid): b - а.
О Нефроида (nephroid): 2b - а.
Гипоциклоиды:
О Отрезок прямой: 2Ь - а.
О Дельтоида (deltoid): 3b - а.
О Астроида (astroid)’: 4b - а.
Некоторые из этих кривых приведены на рис. 3.80. Напишите программу, способную рисовать и эпит-
рохоиды, и гипотрохоиды. Пользователь может выбирать, какой тип семейства он хочет нарисовать,
а также вводить нужные параметры. Выполните эту программу для каждого частного случая из списка.
Рис 3.80. Примеры циклоид: а) нефроида; б) а/b = 10; в) дельтоида; г) астроида
Тематическое задание 3.9. Суперэллипсы
Уровень сложности I.
Напишите и выполните программу для рисования суперэллипсов. Чтобы нарисовать каждый суперэл-
липс, пользователь назначает противоположные углы ограничивающего прямоугольника и набирает
значение выпуклости (bulge), после чего рисуется заданный суперэллипс.
1 Отметим, что астроида является в то же время и суперэллипсом! Ее кривизна равна 2/3.
3.11. Дополнительная литература
191
(Факультативно.) Усовершенствуйте свою программу таким образом, чтобы она могла рисовать по-
вернутые суперэллипсы. Пользователь набирает значение угла после ввода выпуклости.
3.11. Дополнительная литература
В начале работы с графикой большое удовольствие доставляет писать приложения, дающие на выходе
замечательные кривые и орнаменты. Это приводит вас к пониманию глубокой взаимосвязи между ма-
тематикой и изобразительным искусством. Имеется множество книг, готовых предложить вам руко-
водство и мириады примеров. Книга Мак-Грегора и Уоттса «Искусство графики для IBM PC* (Mc-
Gregor and Watt's. The Art of Graphics for the IBM PC [Mcgregor, 138]) предлагает множество алгоритмов
для создания интересных орнаментов. Вот еще несколько заслуживающих особого внимания книг
о кривых и геометрии: Джей Каппраффс «Соединения» (Jay Kappraff Connections [Kappraff, 121]),
А. К. Дьюдни «Мир кресел» (А. К. Dewdney. The Armchair Universe [Dewdney, 58]), Стен Огилви «Экскур-
сии в геометрию» (Stan Ogilvy Excursions in Geometry [Ogilvy, 148]), Д. Педо «Геометрия и изобразитель-
ное искусство» (D. Pedoe Geometry and the Visual Arts [Pedoe, 155]), Роджер Шеперд «Взгляды разума»
(Roger Sheperd Mind Sights [Sheperd, 184]), а также целый ряд книг о математических путешествиях
Мартина Гарднера (Martin Gardner), такие как «Путешествие во времени» (Time Travel [Gardner, 77])
и «Мозаики Пенроуза для шифровых замков» Penrose Tiles to Trapdoor Ciphers [Gardner, 78]). Коксетером
(Coxeter) написаны элегантные книги по геометрии, в том числе «Введение в геометрию» (Introduction
to Geometry [Coxeter, 51]). В книгах «Математические развлечения и эссе» (Mathematical Recreations and
Essays [Ball, 8]) и «Математика для компьютерной графики» Хоггара (Hoggar. Mathematics for Computer
Graphics [Hoggar, 112]) рассматриваются многие свойства IFS.
с J
Векторные инструменты
для графики
□ Обзор арифметики векторов и обоснование причисления векторов
к объектам, представляющим интерес для графики.
□ Соотнесение геометрических понятий с их алгебраическими
представлениями.
□ Описание параметрических прямых линий и плоскостей.
□ Обозначение четкого различия между точками и векторами.
□ Применение к графике скалярного произведения.
□ Разработка инструментов для работы с объектами в трехмерном
пространстве, включающих в себя векторное произведение
двух векторов.
Знание, к которому стремится геометрия, — это знание о вечном, а не о смертном и преходящем.
Платон
Для нас, чьи плечи гнутся под тяжестью наследия мысли древних греков, чьи пути проторены
героями Возрождения, цивилизация без математики немыслима.
Андре Вейль (Andre Weil)
Давайте согласимся, что занятие математикой — это прекрасное безумие человеческого разума.
Альфред Норт Уайтхед (Alfred North Whitehead)
Все, что находится за пределами геометрии, находится за пределами нашего понимания.
Блез Паскаль (Blaise Pascal)
В данной главе разрабатывается много полезных инструментов для работы с геометрическими объекта-
ми, встречающимися в компьютерной графике. В разделе 4.1 «Введение» мотивируется использование
векторов в графике и описываются основные графические системы координат. В разделе 4.2 «Обзор
векторов» дается обзор основных идей, относящихся к векторам, и описываются ключевые операции
над векторами. Хотя большая часть полученных результатов применима к любому числу измерений,
делается акцент на 2D- и 3 D-векторах. В разделе 4.3 «Скалярное произведение» рассматривается мощная
операция скалярного произведения и ее применение ко многим геометрическим задачам, таким как
4.1. Введение
193
выполнение ортогональных проекций, нахождение расстояния от точки до прямой и определение направ-
ления луча, «отраженного» от блестящей поверхности. В разделе 4.4 «Векторное произведение двух
векторов» описывается векторное произведение двух векторов и обсуждаются его важные приложения
к трехмерной графике.
В разделе 4.5 «Отображение ключевых геометрических объектов» вводятся понятия координатного
фрейма (coordinate frame) и однородных координат (homogeneous coordinates); делается акцент на том,
что между точками и векторами как геометрическими объектами есть существенные различия. Кроме
того, в этом разделе рассказывается о двух важных математических понятиях — прямой и плоскости —
с указанием того, где используется каждое из них. Вводится понятие аффинных преобразований точек,
а также описывается интересный тип анимации, известный как «твининг» («tweening» — построение
промежуточных отображений), в котором применяются кривые Безье (Bezier curves).
В разделе 4.6 «Определение точки пересечения двух отрезков прямой» исследуется важная проблема
нахождения точки пересечения двух отрезков прямых, которая значительно упрощается с применением
векторов. В этом разделе также обсуждается задача нахождения единственной окружности, проходя-
щей через три заданные точки. В разделе 4.7 «Пересечения прямых с плоскостями; отсечение» исследу-
ется вопрос о том, где «луч» пересекает прямую или плоскость, причем используются понятия, связан-
ные с проблемой отсечения. Раздел 4.8 «Задачи о пересечениях многоугольников» посвящен отсечению
прямых границами выпуклых многоугольников и многогранников; в связи с этим излагается мощный
алгоритм отсечения Сайруса—Бека (Cyrus—Beck).
Глава заканчивается тематическими заданиями, в которых расширяется инструментарий средств,
рассмотренных в основном тексте, а также предоставляется возможность обогатить свои навыки в гра-
фическом программировании. Задания включают в себя обработку многоугольников, эксперименты с
«трассировкой лучей» на плоскости, скругление углов на фигурах, получение анимации при помощи
твининга, а также совершенствование методов отсечения.
4.1. Введение
В компьютерной графике мы работаем с объектами, заданными в трехмерном мире (двумерные объек-
ты и миры являются лишь его частными случаями). Все подлежащие рисованию объекты, а также «ка-
меры», используемые для их рисования, имеют форму, положение и ориентацию. Мы должны писать
компьютерные программы, которые каким-либо образом описывают эти объекты и отражение ими па-
дающего на них света, с тем чтобы вычислить результирующие значения пикселов на дисплее. Пред-
ставьте себе мультфильм, где камера летит по неровной сцене, содержащей различные здания, деревья,
дороги и автомобили. Что же «видит» камера? Все, что бы она ни увидела, необходимо в конечном сче-
те перевести в цифры. Это нелегкая задача.
Нашей работе в графике помогут две фундаментальные математические дисциплины: векторный
анализ и преобразования. Изучая тонкости этих дисциплин, мы разработаем методы описания различ-
ных геометрических объектов, с которыми мы столкнемся, а также научимся переводить геометричес-
кие идеи в цифры. Результатом этого явится набор важных алгоритмов, к которым мы сможем обра-
щаться в графических программах.
В дайной главе мы изучим фундаментальные операции векторной алгебры и их применение в гра-
фике, а преобразования будут рассмотрены в главе 5. Мы начнем с самого начала и разработаем ряд
важных инструментов и методов, которые будут встречаться нам снова и снова на протяжении всей
книги. Если вы уже изучали векторы раньше, многое в этой главе будет вам знакомо, однако многочис-
ленные приложения векторного анализа к геометрическим ситуациям все же следовало бы тщательно
рассмотреть. Данная глава может показаться вам выпадающей из общей картины из-за обилия матема-
тического текста. Однако нам представляется весьма полезным иметь всю информацию, содержащую-
ся в ней, собранной в одном месте и отнесенной к реальным проблемам, встречающимся в графике.
7 Ф. Хилл
194
Глава 4. Векторные инструменты для графики
Почему векторы столь важны?
Обзор некоторых ситуаций, в которых на помощь приходит векторный анализ, может доказать необхо-
димость изучения векторов. На рис. 4.1 приведены три геометрические задачи, возникающие в графи-
ке. Можно было бы привести много других примеров.
а бе
Рис. 4.1. Три примера геометрических задач, легко решаемых с помощью векторного анализа
На рис. 4.1, а представлена задача компьютерного проектирования: пользователь пометил мышью
три точки на дисплее и хочет, чтобы была нарисована та единственная окружность, которая проходит
через эти три точки. (Вы можете представить себе эту окружность?) Где находится центр этой окруж-
ности при заданных координатах точек? В разделе «Определение точки пересечения двух отрезков пря-
мой» мы увидим, что без векторов эта задача имеет громоздкое решение, однако при использовании
векторных инструментов является почти тривиальной.
На рис. 4.1, б показана камера, помещенная в сцену, содержащую рождественскую елку. Камера
должна сформировать изображение этой елки в своей «плоскости обзора» (подобно киноэкрану для
настоящей камеры), и это изображение должно быть передано на экранное окно дисплея пользователя.
Где в этой плоскости появится изображение дерева и какова его точная форма? Чтобы ответить на эти
вопросы, нам потребуется подробно изучить перспективные проекции, чему в огромной степени будет
способствовать применение векторных инструментов. Если это покажется вам слишком простым, то
представьте себе, что вы работаете над анимацией сферы и что камера приближается к этой сфере по
некоторой траектории, поворачиваясь при этом. Попробуйте написать программу, генерирующую всю
последовательность изображений!
На рис. 4.1, в изображен блестящий конус, на поверхности которого можно видеть отражение куба.
Как определить, имея координаты конуса, куба и камеры, где в точности будет находиться отраженное
изображение, каковы будут его цвет и форма? Изучая трассировку луча в главе 14, мы будем активно
применять векторы и увидим, что эта задача вполне разрешима.
Основные положения
Все точки и векторы, с которыми мы работаем, заданы относительно какой-нибудь системы координат.
Рисунок 4.2 показывает обычно употребляемые системы координат. Каждая из этих систем имеет начало
отсчета (origin), обозначаемое б, и несколько осей, исходящих из точки б. Эти оси обычно направлены
под прямым углом друг к другу. Вдоль каждой оси нанесен масштаб, и любая точка имеет координаты
в соответствии с тем, насколько далеко она расположена вдоль каждой оси. На рис. 4.2, а приведена
обычная двумерная система координат. На рис. 4.2, б показана правая трехмерная система координат, а
на рис. 4.2, в — левая трехмерная система координат.
В случае правой системы, если вы поворачиваете свою правую руку вокруг оси z от положительного
направления оси х к положительному направлению оси у, как показано на рисунке, то ваш большой
4.2. Обзор векторов
195
палец будет иметь то же направление, что ось z. В случае же левой системы вам необходимо проделать
все это левой, рукой, чтобы ее большой палец был направлен вдоль положительного направления оси z.
Правые системы координат являются более привычными, и именно они обычно применяются в мате-
матике, физике и технике. В данной книге при моделировании объектов мы также используем правую
систему. Однако левые системы координат также широко применяются в графике при работе с систе-
мами просмотра и с «камерами».
Рис. 4.2. Известные двух- и трехмерные системы координат
Прежде всего мы рассмотрим основные понятия, связанные с векторами, и увидим, как они исполь-
зуются в графике. В разделе «Отображение ключевых геометрических объектов» мы вернемся к осно-
вам и продемонстрируем важное различие между точками и векторами, при игнорировании которого в
графических программах могут возникать большие трудности.
4.2. Обзор векторов
Не только законы Ньютона, но и другие законы физики, которые известны нам на сегодняшний день,
имеют два свойства, которые мы называем инвариантностью относительно переноса и поворота осей.
Эти свойства настолько важны, что был разработан математический метод, помогающий записывать
и использовать физические законы... называемый векторным анализом.
Ричард Фейнман (Richard Feynman)
В векторной арифметике имеется стандартный способ алгебраического выражения геометрических идей.
В графике мы имеем дело с векторами двух, трех и четырех измерений, однако некоторые выводы доста-
точно сделать один раз, и они применимы к векторам любой размерности. Эта широкая применимость
дает возможность сводить различные случаи в графике в единое выражение, которое затем можно
применять в различных задачах.
С геометрической точки зрения векторы — это объекты, имеющие длину и направление. Они пред-
ставляют различные физические категории, такие как сила, перемещение и скорость. Векторы часто
рисуют в виде стрелки определенной длины, указывающей определенное направление. Полезно мыс-
лить геометрически о векторе как о перемещении от одной точки к другой.
На рис. 4.3 векторы использованы для того, чтобы показать, как звезды Большой Медведицы
движутся во времени [Kerrod, 122]. Текущее положение каждой звезды показано точкой, а вектор пока-
зывает скорость каждой из них. «Наконечник» каждой стрелки указывает на ту точку, в которой соот-
ветствующая звезда будет находиться через 50 000 лет, что приведет, конечно, к совершенно другой
Большой Медведице!
196
Глава 4. Векторные инструменты для графики
На рис. 4.4, а показаны в двумерной системе координат две точки: Р = (1,3) и Q = (4,1). Перемеще-
ние от точки Р к точке Q1 есть вектор v с компонентами (3, -2), которые вычислены путем почленного
вычитания координат соответствующих точек. Для «перехода» от точки Р к точке Q мы перемещаемся
на 2 единицы вниз и на 3 вправо. Поскольку вектор — это перемещение, он имеет размер и направление,
но не присущее ему положение; две стрелки, обозначенные на рисунке буквой V, фактически представ-
ляют собой один и тот же вектор. На рис. 4.4, б показана аналогичная ситуация в трех измерениях: v —
это вектор перемещения от точки Р к точке Q. Часто говорят, что вектор — это разность между двумя
точками: v - Q - Р.
Рис. 4.3. Большая Медведица сейчас и в 50 000 году н. э.
Рис. 4.4. Вектор как перемещение
Сформулируем обратное высказывание: точка Q получена путем перемещения точки Р на вектор v;
говорят, что v «перемещает» Р для создания Q. Тогда в алгебраических терминах Q — это сумма:
Q = Р + v. Кроме того, сумма точки и вектора есть точка: Р + v = Q.
С этой точки зрения мы представляем вектор списком его компонентов; и-мерный вектор задается
посредством его п-кортежа (n-tuple):
w = (w{, w2,..., wn). (4.1)
Большей частью мы будем интересоваться двумерными векторами, такими как г = (3,4, -7,78), и
трехмерными, например, t = (33, 142,7, 89,1). Позднее, когда это понадобится, мы исследуем различие
между вектором и его представлением и будем применять слегка расширенную систему записи для
представления векторов (и точек). Запись вектора в форме матрицы-строки (row matrix) вида t = (33,
142,7, 89,1) выглядит красиво на странице, однако иногда, когда это имеет значение, мы будем вместо
этого писать векторы в виде матриц-столбцов (column matrices), например:
( 33
142,7
89,1
Это имеет значение, когда нам нужно умножить точку или вектор на матрицу, как мы увидим в главе 5.
Для точек обычно используются большие буквы, а для векторов — маленькие жирные.
4.2. Обзор векторов
197
4.2.1. Операции с векторами
С векторами можно проделывать две основные операции: их можно складывать и умножать на скаля-
ры (scalars) (вещественные числа)’. Итак, если а и b — два вектора, as — скаляр, то будут иметь смысл
следующие выражения: а + b и $а. Если, например, а » (2,5, 6), а b = (-2, 7,1), то мы можем построить
следующие два вектора:
а + Ь = (0,12, 7)
и
6а = (12, 30, 36),
причем все эти операции всегда выполняются покомпонентно (componentwise).
Рис. 4.5. Сумма двух векторов
На рис. 4.5 показан пример сложения двумерных векторов а = (1, -1) и b = (2,1). Графически сло-
жение двух векторов можно представить двумя способами. На рис. 4.5, а оба вектора показаны «исхо-
дящими» из одной и той же точки и образующими таким образом две стороны параллелограмма. Тогда
сумма этих векторов равна диагонали параллелограмма — той диагонали, которая исходит из общего
начала этих векторов. Этот рисунок — так называемое «правило параллелограмма» для сложения век-
торов — является обычной картиной сложения сил, действующих в точке; тогда диагональ будет ре-
зультирующей силой.
С другой стороны, на рис. 4.5, б показан случай, когда один вектор (Ь) начинается из конца другого
(а), а их сумма изображена соединяющей начало вектора а с концом вектора Ь. Суммарный вектор замы-
кает треугольник, который представляет собой обыкновенное сложение одного перемещения с другим.
Ясно, что компоненты суммы равны сумме компонентов ее слагаемых, как и предписывает алгебра.
Рис. 4.6. Масштабирование векторов
На рис. 4.6 показан эффект масштабирования векторов. Для s = 2,5 вектор $а имеет то же направле-
ние, что и а, но в 2,5 раза длиннее. При отрицательном $ направление $а противоположно направлению а.
На рисунке приведен случай $ = -1.
Вычитание легко выводится из понятий сложения и масштабирования: а - с есть просто а + (-с). Рису-
нок 4.7 показывает геометрическую интерпретацию этой операции, представляя разность векторов а и
с как сумму а и -с (см. рис. 4.7, б). По правилу параллелограмма эта сумма равна вектору, исходящему
Существуют такие системы, в которых скаляры могут быть комплексными, однако здесь они нам не понадобятся.
198
Глава 4. Векторные инструменты для графики
из конца вектора с и заканчивающемуся в конце вектора а (см. рис. 4.7, в). Этот вектор равен одной из
диагоналей параллелограмма, образованного векторами а и с. Отметим, что вторая диагональ этого па-
раллелограмма представляет собой сумму а + с.
Рис. 4.7. Вычитание векторов
4.2.2. Линейные комбинации векторов
После введения правил сложения и масштабирования векторов мы можем определить линейную ком-
бинацию (linear combination) векторов. Для того чтобы составить линейную комбинацию двух векто-
ров v и w (одной и той же размерности), нужно масштабировать каждый из них с помощью скаляров,
например а и Ь, и сложить эти взвешенные величины для создания нового вектора av + iw. Дадим более
общее определение линейной комбинации т векторов.
Определение. Линейной комбинацией т векторов vp v2,..., vra называется вектор вида
w » a.v. + a,v, + ... + a v , (4.2)
1 1 £ £ ГП ГП 4 z
где ap а2,..., ат — скаляры.
Например, линейная комбинация двух векторов 2(3,4, -1) + 6(-1,0, 2) образует вектор (0,8,10).
В последующих главах мы будем оперировать с довольно сложными линейными комбинациями векто-
ров, особенно когда будем искать представление кривых и поверхностей с помощью сплайн-функций.
Аффинные комбинации векторов
Линейная комбинация векторов называется аффинной комбинацией (affine combination), если сумма
коэффициентов av а2..ат равна единице. Таким образом, линейная комбинация в равенстве (4.2) яв-
ляется аффинной, если
fll + o2+... + an-1. (4.3)
Например, За + 2Ь - 4с является аффинной комбинацией векторов а, Ь и с, в то время как За + b - 4с
таковой не является. Коэффициенты линейной комбинации двух векторов а и b часто искусственно
приводят к тому, чтобы их сумма равнялась единице, умножая один вектор на некий скаляр t, а вто-
рой — на (1 - t), как показано ниже:
(l-t)a + (t)b. (4.4)
Аффинные комбинации векторов появляются в различных контекстах, так же как и аффинные пре-
образования точек, как мы увидим позднее.
Выпуклые комбинации векторов
Выпуклые комбинации занимают важное место в математике и в многочисленных графических прило-
жениях. Выпуклая комбинация (convex combination) возникает как дальнейшее ограничение аффин-
ной комбинации: не только сумма коэффициентов линейной комбинации должна равняться единице,
но каждый коэффициент, кроме того, должен быть неотрицательным. Таким образом, линейная комби-
нация из равенства (4.3) является выпуклой, если
4.2. Обзор векторов
199
aj + a2+...+аи“ 1 (4.5)
и
at> 0 для i -
Следовательно, все должны находиться между 0 и 1. (Почему?)
Таким образом, 0,3а + 0,7b является выпуклой комбинацией векторов а и Ь, в то время как 1,8а - 0,8b —
нет. Совокупность коэффициентов ava2,...,am иногда называют разбиением единицы (partition of unity),
подразумевая под этим, что единичное количество «материала» разбивается на части. Выпуклые ком-
бинации зачастую возникают в приложениях, где кто-то составляет единичное количество некоторой
«смеси» и может комбинировать только положительные количества различных ингредиентов. Такие
комбинации появляются в самых неожиданных контекстах. Например, мы увидим в главе И, что
сплайн-кривые фактически являются выпуклыми комбинациями некоторых векторов, а в наших ис-
следованиях цвета (в главе 12) узнаем, что любой цвет единичной яркости можно представить в виде
выпуклой комбинации трех простых цветов!
Нам представляется полезным понятие «множество всех выпуклых комбинаций» некоторого набо-
ра векторов. Для двух векторов vt и v2 множество всех выпуклых комбинаций представляет собой мно-
жество всех векторов вида
v = (1 - a)v( + av2, (4.6)
где параметр а может изменяться от 0 до 1. (Почему?) Что это за множество? Преобразуя равенство
(4.6), получим:
v = v(+a(v2-v(). (4.7)
Рис. 4.8. Множество векторов, представимых выпуклыми комбинациями
На рис. 4.8, а показан вектор V, равный сумме V, и некоторой части от v2- vp причем конец вектора v
расположен на прямой, соединяющей v( и v2. Так как а изменяется от 0 до 1, конец v может занимать
положения, совпадающие со всеми точками отрезка прямой, соединяющего концы V, и v2, и только эти
положения.
На рис. 4.8, б показано множество всех выпуклых комбинаций трех векторов. Мы выбираем два па-
раметра — а, и а2, — оба лежащие в промежутке между 0 и 1, и составляем линейную комбинацию:
q = alvl + a2v2+(l-al-a2)v3, (4.8)
в которой также необходимо, чтобы сумма at и а2 не превышала единицы. Вектор v является выпуклой
комбинацией, так как ни один из его коэффициентов не отрицателен, а в сумме они составляют едини-
цу. Рисунок 4.8, б показывает три радиус-вектора V, = (2,6), v2 = (3,3) и v3 = (7,4). Соответствующим
подбором а{ и а2 можно выразить любой вектор, оканчивающийся внутри затененного треугольника,
а пи один из векторов, оканчивающийся вне этого треугольника, таким способом выражен быть не
200
Глава 4. Векторные инструменты для графики
может. Показано, например, как представить вектор b = 0,2у( + 0,5v2 + 0,3v3 в виде векторной суммы
трех взвешенных компонентов. Заметим, что он построен из «долей» трех составляющих векторов.
Таким образом, множество всех выпуклых комбинаций этих трех векторов «охватывает» затененный
треугольник. (Доказательство этого утверждения предлагается в качестве одного из упражнений.)
Если а2 = 0, то соответствующим подбором можно «добиться» выражения любого вектора, состав-
ленного из v, и v3 и оканчивающегося на прямой L, Например, вектор, оканчивающийся на 20 % рассто-
яния между V, и v3 вдоль L, задается выражением 0,8V, + 0v2 + 0,2v3.
4.2.3. Модуль вектора; единичные векторы
Если вектор w представлен с помощью n-кортежа (дар w2,..., wn), то как определить и вычислить его мо-
дуль (или, что то же самое, какова его длина, или величина)? Обозначим модуль вектора символом |w| и
определим его как расстояние от начала до конца вектора. Согласно теореме Пифагора получаем:
|w| = yjwf+wl +...+W* . (4.9)
Например, модуль вектора w = (4, -2) равен >/20, а модуль вектора w = (1, -3,2) равен ->/14. Вектор
нулевой длины обозначается 0. Отметим, что если w — вектор, идущий от точки А к точке В, то |w| будет
равен расстоянию от А до В. (Почему?)
Часто бывает полезно масштабировать вектор так, чтобы результирующий вектор имел единичную
длину. Такой способ масштабирования называется нормированием (normalizing) вектора, а нормиро-
ванный вектор носит название единичного вектора (unit vector), или орта. Для примера создадим нор-
мированный вариант вектора а, обозначаемый а, масштабируя а величиной 1/|а|:
й = (4.Ю)
1а1
Очевидно, что |а| = 1 (почему?) и а является единичным вектором, имеющим то же направление,
что и а. Если, например, а = (3, -4), то |а| = 5, а его нормированный вектор а = (|, у). Иногда единич-
ный вектор называют направлением (direction). Отметим, что любой вектор может быть записан в виде
его модуля, умноженного на направление: если а — орт вектора а, то вектор а всегда можно записать
так: а = |а| а.
Практические упражнения
4.2.1. Представление векторов в форме линейных комбинаций
Обратимся к рис. 4.8. Какие величины или диапазон величин для а{ и а2 создают следующие мно-
жества:
О v,.
О Прямая, соединяющая vt и v2.
О Вектор, проходящий посередине между v2 и v3.
О Центроид (центр тяжести) треугольника.
4.2.2. Множество всех выпуклых комбинаций
Докажите, что множество всех выпуклых комбинаций трех векторов vp v2, и v3 — это множество векто-
ров, концы которых расположены в «треугольнике», образованном концами этих трех векторов. Под-
сказка: каждая точка этого треугольника является комбинацией вектора v( и какой-нибудь точки, лежа-
щей между векторами v2 и v3.
4.2.3. Вынесение скаляра за скобки
Покажите, как масштабирование вектора v скаляром $ изменяет длину v. Иными словами, докажите,
что [sv| = |s| |v|. Отметим двойственное применение знака модуля 11: один раз для скаляра, а другой раз —
для вектора.
4.3. Скалярное произведение
201
4.2.4. Нормирование векторов
Нормируйте каждый из следующих векторов:
О (1,-2, 5).
О (8,6).
О (4,3).
4.3. Скалярное произведение
Имеются еще два мощных инструмента для работы с векторами — это скалярное произведение и век-
торное произведение. Результатом скалярного произведения является скаляр; векторное произведение
имеет дело только с трехмерными векторами и его результатом является также вектор. В этом разделе
дается обзор основных свойств скалярного произведения, главным образом рассматривается понятие
перпендикулярности. Затем мы используем скалярное произведение для решения ряда важных геомет-
рических задач графики. После этого вводится векторное произведение и также используется для ре-
шения ряда трехмерных геометрических задач.
Скалярное произведение (dot product) двух векторов легко определить и легко вычислить. Для дву-
мерных векторов (а,, а2) и (6р Ь2~) это просто скаляр, величина которого равна + а2Ь2. Таким обра-
зом, для того чтобы вычислить скалярное произведение, надо перемножить соответствующие компо-
ненты двух векторов и сложить результаты. Например, скалярное произведение векторов (3, 4) и (1, 6)
равно 27, а для векторов (2,3) и (9, -6) оно равно 0.
Определение скалярного произведения легко обобщается на п измерений.
Определение скалярного произведения. Скалярное произведение двух «-мерных векторов v = (vv v2 vn)
и w = (wv w2,..., wn) обозначается v • w и имеет величину:
d = v-w= (4.И)
i = I
Пример 4.3.1
О Скалярное произведение (2, 3, 1) и (0, 4, -1) равно 11.
О (2, 2, 2, 2) • (4, 1,2, 1,1) = 16,2.
О (1,0,1,0, 1) • (0,1,0,1,0) = 0.
О (169,0, 43) • (0,375,3, 0) = 0.
4.3.1. Свойства скалярного произведения
Скалярное произведение обладает четырьмя главными свойствами, которые мы часто используем и
которые с очевидностью следуют из его основного определения:
1. Симметрия (коммутативность): а • b = Ь • а.
2. Линейность (дистрибутивность): (а + с) • Ь = а • Ь + с • Ь.
3. Однородность (ассоциативность): (sa) b = s(a • Ь).
4. |Ь|2 = Ь • Ь.
Первое свойство означает, что порядок, в котором следуют два вектора, не играет роли: скалярное
произведение коммутативно (commutative). Из двух следующих свойств следует, что скалярное произ-
ведение линейно (linear): скалярное произведение суммы векторов можно выразить как сумму отдель-
ных скалярных произведений, а масштабирование любого вектора масштабирует и величину скаляр-
202
Глава 4. Векторные инструменты для графики
ного произведения. В последнем свойстве утверждается, что скалярное произведение вектора на тот же
вектор равно квадрату длины этого вектора. Это свойство часто записывают в форме: |b| = Vb • Ь.
Выкладки примера 4.3.2 показывают, как вышеприведенные свойства могут быть применены для
упрощения выражений, содержащих скалярное произведение. Результаты будут непосредственно ис-
пользованы в следующем разделе.
Пример 4.3.2. Упрощение выражения | а - b 12
Упростить выражение для квадрата длины разности двух векторов а и Ь для получения равенства:
|a-b|2 - |a|2-2a-b+|b|2. (4.12)
Вывод этого соотношения делается так: обозначим буквой С выражение |а—Ь|2. Тогда, согласно чет-
вертому свойству, С является скалярным произведением:
С = |a-b|2 = (а-Ь)-(а-Ь).
Используя дистрибутивность, то есть раскрывая первые скобки, получим: С = а • (а - b) - b • (а - Ь).
Исходя из свойств симметрии и линейности, упростим это выражение дальше: C = a- a-2a-b + b-b.
Наконец, из четвертого свойства получаем С = |а|2 - 2а • Ь + |Ь|2, это и есть искомый результат.
Заменив в равенстве (4.12) знак минус на плюс, получим аналогичное полезное соотношение:
|а + Ь|2 = |а|2 + 2а • Ь + |Ь|2. (4.13)
4.3.2. Угол между двумя векторами
Наиболее важным применением скалярного произведения является нахождение угла между двумя
векторами или между двумя пересекающимися прямыми. На рис. 4.9 приводится двумерный случай,
когда векторы Ь и с расположены соответственно под углами и относительно оси х. Из элементар-
ной тригонометрии известно, что
b = (|b|cos0A, |b|sin0A); с - (|c|cos0c, |c|sin0e).
Рис. 4.9. Нахождение угла между двумя векторами
Таким образом, скалярное произведение векторов Ь и с равно
Ь • с = |b||c|cos0ccos0ft + Ibllcisin^sin^ = |b[|c|cos(0c - 0ft),
следовательно, для любых двух векторов b и с получаем
b с = |b||c[cos(0), (4.14)
где 0 — угол между векторами b и с. Отсюда следует, что b • с изменяется пропорционально косинусу
угла между b и с. Этот же результат справедлив для трех, четырех и любого другого числа измерений.
Чтобы получить более компактную форму, разделим обе части равенства на |Ь||с|, а также использу-
ем запись единичного вектора в виде b = b/|b|. Тогда получим:
cos(0) = b • с. (4.15)
4.3. Скалярное произведение
203
Это и есть желаемый результат: косинус угла между двумя векторами Ь и с равен скалярному произ-
ведению нормированных векторов.
Пример 4.3.3
Найдите угол между векторами Ь = (3,4) и с = (5,2).
Решение.
Вычислим |Ь] = 5 и |с| = 5,385, следовательно, b = (3/5,4/5) и с = (0,9285,0,3714). Скалярное произ-
ведение Ь • с = 0,85422 = cos(O), отсюда 0 = 31,326°. Этот результат можно проверить, если нарисовать
эти два вектора на миллиметровке и измерить угол между ними.
4.3.3. Знак b • с и перпендикулярность
Напомним, что cos(0) положителен, если |0| меньше 90°, равен нулю при |0| = 90° и отрицателен, если |0|
превышает 90°. В силу того, что скалярное произведение двух векторов пропорционально косинусу угла
между ними, мы можем сразу определить, что угол между двумя векторами (любой длины, отличной от
нуля) составляет:
менее 90°, если Ь • с > 0;
ровно 90°, если Ь • с = 0; (4.16)
более 90°, если Ь • с < 0.
Все эти результаты приведены на рис. 4.10. Знак скалярного произведения используется во многих
алгоритмических тестах.
Ь«с>0 Ь»с=0 Ь»с<0
Рис. 4.10. Знак скалярного произведения
Особенно важным является случай, когда векторы расположены под углом 90°, то есть перпендикулярны.
Определение. Векторы Ь и с называются перпендикулярными, если
Ь-с = 0. (4.17)
Иногда вместо слова «перпендикулярны» употребляют синонимы: ортогональны (orthogonal) и
нормальны (normal), и мы будем пользоваться всеми этими тремя словами попеременно. Вектор, пер-
пендикулярный прямой или плоскости, также иногда будем называть нормалью.
Наиболее известными примерами ортогональных векторов являются те, которые расположены вдоль
осей дву- и трехмерных систем координат, как показано на рис. 4.11. На рис. 4.11, а двумерные векто-
ры (1,0) и (0,1) являются взаимно перпендикулярными единичными векторами. Трехмерные анало-
ги этих векторов употребляются столь часто, что их называют «стандартными единичными векто-
рами» (координатными ортами) и обозначают буквами i, j, k.
Определение. Координатными ортами в трехмерном случае называются векторы, имеющие следую-
щие компоненты:
i = (1,0,0), j = (0,1, 0), к = (0,0,1). (4.18)
На рис. 4.11, б показаны эти три орта в правосторонней системе координат, а на рис. 4.11, в — в лево-
сторонней системе. Отметим, что к всегда указывает на положительное направление оси г.
С помощью приведенных определений можно записать любой трехмерный вектор (а, Ь, с) в альтер-
нативной форме:
(a, b, с) = ai + bj + ck. (4.19)
204
Глава 4. Векторные инструменты для графики
Пример 4.3.4
Заметим, что v = (2,5, -1) — это то же самое, что 2(1,0,0) + 5(0,1,0) - 1(0,0,1), или 2i + 5j - k.
Форма записи, использованная в равенстве (4.19), представляет вектор в виде суммы отдельных эле-
ментарных составляющих векторов, что упрощает различные вычисления с помощью карандаша и бу-
маги. Эта форма записи особенно удобна при операциях с векторным произведением, к рассмотрению
которого мы перейдем в разделе «Векторное произведение двух векторов».
Практические упражнения
4.3.1. Еще одно доказательство тождества b • с = | b| |с|cosQ
Отметим, что векторы Ь и с образуют две стороны треугольника, а его третья сторона равна Ь - с. Пред-
ставьте, используя формулу косинусов, квадрат длины Ь - с через длины векторов Ь и с и косинус угла 0.
Сравните свой ответ с равенством (4.12).
4.3.2. Нахождение угла
Вычислите угол между векторами (2, 3) и (-3,1) и проверьте результат графически, с помощью милли-
метровки. Затем вычислите угол между трехмерными векторами (1,3, -2) и (3,3,1).
4.3.3. Проверка на перпендикулярность
Какие пары из перечисленных ниже векторов перпендикулярны друг другу:
(3,4,1), (2,1,1), (-3, -4,1), (0,0,0), (1, -2,0), (4,4,4), (0, -1,4) и (2,2,1)?
4.3.4. Теорема Пифагора
Обратимся к равенствам (4.12) и (4.13). В случае перпендикулярности векторов а и Ь оба этих выраже-
ния — квадраты суммы и разности векторов — имеют одинаковую величину, что на первый взгляд не
имеет геометрического смысла. Докажите, что все вычислено правильно, и примените полученный ре-
зультат к теореме Пифагора.
4.3.4. Двумерный «перп» вектор
Пусть двумерный вектор а имеет компоненты (ах, ау). Какие векторы перпендикулярны к а? Один из
способов получения такого вектора состоит в том, чтобы поменять местами х- и ^-компоненты и сме-
нить у одного из них знак*. Пусть Ь = (-а , ах). В таком случае скалярное произведение а • Ь = 0, поэтому
а и Ь действительно перпендикулярны. Если, к примеру, а = (4,7), то вектор Ь = (-7,4) является нор-
1 Это равносильно известному факту, что перпендикулярные прямые имеют взаимно обратные и различающиеся знаком угловые
коэффициенты (к, “ -1/к2). В главе 5 мы увидим, что операция «переставить и сменить знак» («interchange and negate») есте-
ственным образом появляется в связи с поворотом на 90°.
4.3. Скалярное произведение
205
мальным к вектору а. Существует бесчисленное множество векторов, нормальных к любому вектору а,
так как любое скалярное кратное (scalar multiple) вектору Ь, то есть вектор Ь, умноженный на скаляр,
например (-21,12) и (7, -4), тоже нормально к а. (Нарисуйте на бумаге несколько таких векторов для
заданного а.)
Удобно иметь символ для одного исключительного вектора, нормального к заданному двумерному
вектору а. Для этой цели мы будем использовать символ «1» («регр», произносится «перп»).
Определение. Пусть а = (ах, ау). Тогда
а^(-а,ах) (4.20)
называется перпендикулярным против часовой стрелки (counterclockwise perpendicular) к а.
Рис. 4.12. Вектор а1, перпендикулярный к а
Отметим, что а и а1 имеют одну и ту же длину: |а| = |ах|. На рис. 4.12, а показаны произвольный век-
тор а и результирующий вектор а1. Отметим, что движение от направления а к направлению а1 требует
левого поворота. (Правый поворот эквивалентен повороту в направлении к -а1.)
В следующем разделе мы покажем, как лучше всего использовать это обозначение. На рис. 4.12, б
показано, что в случае трех измерений не существует единственного вектора, перпендикулярного к за-
данному трехмерному вектору а, поскольку таковым является любой вектор, расположенный в плос-
кости, перпендикулярной к а. В то же время для работы с такими векторами существует простой инст-
румент — векторное произведение, к которому мы обратимся позже.
Практические упражнения
4.3.5. Некоторые замечательные свойства а1
В ряде случаев полезно рассматривать символ «перп» (1) как оператор, выполняющий над своим аргу-
ментом операцию «левый поворот на 90°», и в этом случае а1 является вектором, полученным в результа-
те применения оператора ± к вектору а, подобно тому как 4х есть величина, полученная в результате
применения к х оператора «квадратный корень». Рассматривая оператор 1 с этой точки зрения, пока-
жите, что он обладает следующими свойствами:
О Линейность: (а + Ь)1 = а1 + Ь\ и для любого скаляра А (Ла)1 = Ла1.
О а1-1 = (а1)1 —а (два перпа осуществляют реверсирование, то есть изменение направления на об-
ратное).
4.3.6. «Перп-скалярное» произведение
Любопытные вещи происходят при вычислении скалярного произведения перпа некоторого вектора
на другой вектор, то есть а1 • Ь. Назовем такую операцию «перп-скалярным произведением» («регр dot
product») [Hill, 95]. Докажите, используя основное определение а1, что
a±-b = aZ> - а b
х у ух
а1 • а = 0
|ах]2 = |а|2
а1- Ь = -Ь1 • а
(величина перп-скалярного произведения),
(а1перпендикулярен к а),
(а1 и а имеют одинаковую длину),
(а1 антисимметричен).
(4-21)
206
Глава 4. Векторные инструменты для графики
Четвертое утверждение означает, что перп-скалярное произведение является антисимметричным:
перемещение знака ± от одного вектора к другому изменяет знак скалярного произведения. Другие по-
лезные свойства перп-скалярного произведения мы будем рассматривать по мере необходимости.
4.3.7. Вычисление перп-скалярного произведения
Вычислите а • b и ах • b для векторов а - (3,4) и Ь = (2,1).
4.3.8. Определитель
Покажите, что а1 • Ь можно записать в виде определителя
(Определения матриц и определителей приведены в приложении Б.)
4.3.9. Разные задачи
О Докажите, что (а1 • Ь)2 + (а • Ь)2 = |а[2|Ь|2.
О Докажите, что если а + Ь + с = 0, то а1 • Ь = Ьх • с - с1 • а.
4.3.5. Ортогональные проекции и расстояние от точки до прямой
В графических приложениях часто возникают три геометрические задачи: проецирование (projecting)
вектора на данный вектор, разложение (resolving) вектора на составляющие в одном и другом направ-
лении, а также определение расстояния между точкой и прямой. Все эти три задачи упрощаются при
использовании перп-вектора и перп-скалярного произведения.
Рис. 4.13. Разложение вектора на два ортогональных вектора
На рис. 4.13, а проиллюстрированы основные проблемы. Нам даны две точки А и С, а также вектор V.
Возникают следующие вопросы:
О На каком расстоянии находится точка С от прямой L, проходящей через точку А в направлении
вектора V?
О Если мы опустим перпендикуляр из точки С на прямую L, то в каком месте он пересечет L?
О Как разложить вектор с - С - А на составляющие вдоль прямой L и в направлении, перпендику-
лярном к L?
На рис. 4.13, б введен ряд дополнительных величин: вектор vL — это вектор v, повернутый на 90°
против часовой стрелки. Опустив перпендикуляр из точки С на прямую L, мы говорим, что вектор с
разложен на составляющую Kv вдоль v и составляющую Mv1 перпендикулярно к v, где К и М — некото-
рые константы, подлежащие определению. Тогда имеем:
с = Kv +MvL. (4.22)
Зная с и v, можно определить К и М. После того как они найдены, мы говорим, что ортогональная
проекция (orthogonal projection) вектора с на вектор v есть Kv и что расстояние от точки С до прямой
равно |Л/ух].
4.3. Скалярное произведение
207
На рис. 4.13, в показана ситуация, в которой могут возникнуть все три вопроса. Мы хотим про-
анализировать, как на груз, показанный на рисунке, действует вектор силы тяжести G, стремящийся
столкнуть его вниз по наклонной плоскости. Чтобы проделать это, нам нужно разложить силу тяжести
G на силу F, действующую вдоль наклонной плоскости, и силу В, действующую перпендикулярно этой
плоскости. Это означает, что мы ищем F и В такие, чтобы G = F + В. (Правильно ли изображены на
рисунке В и F?)
Уравнение (4.22) на самом деле содержит два уравнения: правая и левая его части должны удовлет-
воряться как для х-, так и для ^-составляющих. Имеется две неизвестных величины: К и М. Таким об-
разом, мы имеем два уравнения с двумя неизвестными и можно применить правило Крамера. Однако
кто помнит правило Крамера? Мы используем один прием, который легко запомнить и который сразу
приводит к результату; он эквивалентен правилу Крамера, однако проще в употреблении.
Наш способ решения двух уравнений с двумя неизвестными состоит в том, чтобы исключить одну
из переменных. Для этого построим скалярное произведение, умножив обе части уравнения (4.22) на
вектор v:
с • v = Ку • v + MvL V. (4.23)
К счастью, слагаемое v1 • v обращается в нуль (почему?), и тогда получаем:
С- V
К- ----
V-V
Аналогично скалярно умножим обе части уравнения (4.22) на вектор v1 и получим:
М =
причем мы использовали третье свойство из равенств (4.21). Собирая все воедино, имеем:
(разложение с на v и v1).
(4-24)
Данное равенство применимо для любых векторов с и v. Та часть вектора, которая направлена вдоль v,
носит название ортогональной проекции (orthogonal projection) вектора с на вектор v. Второй член в
явном и компактном виде представляет «разностный член»; его модуль равен расстоянию от точки С до
прямой:
(Убедитесь сами, что второе выражение действительно равно первому.) Возвращаясь к рис. 4.13, б, мы
можем сказать, что расстояние от точки С до прямой, проходящей через точку А в направлении v, равно:
distance -J-----г—:------
v
(4.25)
Пример 4.3.5
Найдите ортогональную проекцию вектора с = (6,4) на вектор а = (1, 2). (Нарисуйте соответствующие
векторы.)
Решение
Вычислите первый член равенства (4.24) и получите вектор (14, 28)/5.
Пример 4.3.6
На каком расстоянии находится точка С = (6,4) от прямой, проходящей через точки (1,1) и (4,9)?
208
Глава 4. Векторные инструменты для графики
Решение
Задайте точку Л = (1,1), возьмите вектор v = (4,9) - (1,1) = (3,8) и вычислите distance (расстояние)
по формуле (4.25): результат должен быть таким: distance = 31/V73 .
Практические упражнения
4.3.10. Разложение
Представьте вектор g = (4,7) в виде линейной комбинации векторов Ь = (3,5) и Ь\ На каком расстоя-
нии находится вектор (4,2) + g от прямой, проходящей через точку (4,2) в направлении вектора Ь?
4.3.11. Блок, спускаемый по наклонной плоскости
Блок покоится на наклонной плоскости, наклоненной под 30° относительно горизонтали. На блок дей-
ствует сила тяжести величиной в один ньютон. Какова величина составляющей силы тяжести, движу-
щей этот блок вдоль наклонной плоскости?
4.3.12. Расстояние от прямой до точки
На каком расстоянии от прямой, проходящей через точки (2,5) и (4, -1), расположена точка (6,11)?
Проверьте полученный результат на миллиметровке.
4.3.6. Приложения проекции: отражения
Для того чтобы отобразить на дисплее отражение света от зеркала или поведение соударяющихся би-
льярдных шаров, нам необходимо найти то направление, которое получает объект после отражения от
заданной поверхности. В тематическом задании, находящемся в конце данной главы, описывается при-
ложение, которое прослеживает путь луча света, когда тот отражается от различных точек внутренней
поверхности комнаты, или путь бильярдного шара при его отскакивании от бортов стола. Как будет
показано в данном разделе, при каждом отражении луч света или бильярдный шар движутся в новом
направлении.
Известно, что когда луч света отражается от зеркала, угол отражения должен равняться углу паде-
ния. Позднее мы покажем, как использовать векторы и проекции для вычисления направления, в кото-
ром отражается свет. Для простоты мы можем рассуждать в терминах двумерных векторов, но посколь-
ку при выводе размерности векторов не фигурируют явно, полученный результат будет верен и для
случая трех измерений при отражении от поверхности.
а б
Рис. 4.14. Отражение луча от поверхности
Луч, изображенный на рис. 4.14 а, движется в направлении а, попадает на прямую L и отражается в
направлении г, которое пока неизвестно. Вектор п перпендикулярен прямой. Угол 0( должен быть ра-
вен углу 02. Как связан вектор г с векторами а и п? На рис. 4.14, б показано разложение вектора а на две
составляющие: ш, параллельную п, и е, перпендикулярную п. Вследствие симметрии вектор г имеет
4.4. Векторное произведение двух векторов
209
такой же компонент е, ортогональный к п, но противоположно направленный компонент, параллель-
ный п, следовательно, г = е - т. Из равенства е = а - m следует, что г = а - 2m. Поскольку m является
ортогональной проекцией а на п, из уравнения (4.24) следует:
m = —-?гп = (а-п)п. (4.26)
п
(Напомним, что п — это единичный вектор в направлении п.) Таким образом, мы получаем следую-
щий результат:
г “ а - 2(а- n ) п (направление отраженного луча). (4.27)
В трехмерном случае, как того требует физика, направление отраженного луча г лежит в плоскости,
построенной на векторах п и а. Равенство (4.27) удовлетворяет этому требованию, как мы впоследствии
покажем в главе 5.
Пример 4.3.7
Пусть а = (4, -2) и Ь = (О,3). В этом случае из равенства (4.27) следует, что г = (4,2), как и следовало
ожидать. И угол падения, и угол отражения равны arctg2.
Практические упражнения
4.3.13. Направление отражения
Найти направление отражения для векторов а = (2,3) и п - (-2,1).
4.3.14. Длины векторов падения и отражения
Используя равенство (4.27) и свойства скалярного произведения, докажите, что |г| = |а|.
4.4. Векторное произведение двух векторов
Векторное произведение (cross product, или vector product) двух векторов — это тоже вектор. Оно име-
ет много полезных свойств, но здесь мы чаще всего будем использовать то, что оно перпендикулярно к
обоим исходным векторам. Векторное произведение определено только для трехмерных векторов.
Для трехмерных векторов а = (ах, ау, ах) и Ь = (Ь^ Ьу, Ьг) векторное произведение обозначается а х Ь.
В терминах стандартных единичных векторов i, j и к (см. равенство 4.18) оно записывается так:
а х b = (ayb2 - aby)i + (abx - axb2)j + (axby - ауЬх)к. (4.28)
(На самом деле векторное произведение может быть выведено из более фундаментальных принци-
пов, как это делается в упражнениях.) Поскольку вышеприведенная форма достаточно трудна для за-
поминания, векторное произведение часто записывают в виде легко запоминаемого определителя:
i j k
(4.29)
(В приложении Б приведен обзор определителей.) Таким образом, для запоминания структуры век-
торного произведения достаточно запомнить, как сформирован этот определитель.
Пример 4.4.1
Непосредственное вычисление векторного произведения векторов а = (3, 0, 2) и Ь = (4,1,8) дает а х Ь =
= -2i - 16j + 3k. Чему равно Ь х а?
210
Глава 4. Векторные инструменты для графики
Из равенства (4.29) можно легко увидеть, что векторное произведение обладает следующими алгеб-
раическими свойствами:
1. ixj = k; j хк - i; к xi = j.
2. а х b = -Ь х а. (антисимметрия).
3. ax(b + c) = axb + axc (линейность). (4.30)
4. (5а) х b = 5(а х Ь) (однородность).
Все эти равенства справедливы как для левосторонней, так и для правосторонней систем координат.
Отметим последовательный (по алфавиту) порядок следования векторов в выражении i х j = к, в котором
содержится удобный мнемонический прием для запоминания направления векторных произведений.
Практические упражнения
4.4.1. Демонстрация четырех свойств
Проверьте каждое из четырех вышеприведенных свойств векторного произведения.
4.4.2. Выведение векторного произведения
Форма векторного произведения, приведенная в равенстве (4.28) в качестве его определения, на самом
деле может быть выведена из более общих соображений. Мы должны только предположить, что:
О Операция векторного произведения линейна.
О Векторное произведение вектора на самого себя равно нулю.
О ixj = k, j хк - i, и кхi = j.
Представив векторы в форме а - axi + ayj + ajc и b = bxi + + Z>2k, примените сделанные допуще-
ния для вывода представления а х b в форме (4.28) или (4.29).
4.4.3. Перпендикулярность а х b и а
Докажите, что векторное произведение векторов а и b действительно перпендикулярно вектору а.
4.4.4. Векторные произведения
Найдите вектор b = (bx, b , Ь2), удовлетворяющий соотношению векторного произведения а х b = с, где
а = (2,1,3) и с = (2, -4,0)\ Является ли этот вектор единственным?
4.4.5. Неассоциативность векторного произведения
Докажите, что векторное произведение не является ассоциативным. Иными словами, докажите, что
а х (Ь х с) не обязательно равно (а х Ь) х с.
4.4.6. Еще один полезный факт
Докажите с помощью непосредственного вычисления в компонентах, что длина векторного произведе-
ния имеет вид:
а х b = ^|a|2|b|2 -(а-Ь)2.
4.4.1. Геометрическая интерпретация векторного произведения
По определению векторное произведение двух векторов а х b также является вектором, однако как оно
выглядит геометрически и почему оно вообще представляет интерес? Рисунок 4.15 дает нам ответ на
это. Векторное произведение а х b имеет следующие полезные свойства (их проверка вынесена в уп-
ражнения по данному разделу).
1. а х b перпендикулярно (ортогонально) обоим векторам а и Ь.
2. Длина вектора а х b равна площади параллелограмма, построенного на векторах а и Ь. Эта пло-
щадь равна:
|а х b| = |a|[b|sin (0), (4.31)
4.4. Векторное произведение двух векторов
211
где 0 — угол между векторами а и Ь, измеренный от а к Ь или от Ь к а, в зависимости от того,
какой из этих углов меньше 180°. Особый случай, а х Ь = 0, имеет место тогда и только тогда,
когда а и Ь имеют одинаковое или противоположное направление или нулевую длину. Чему
равен модуль векторного произведения, если векторы а и Ь — взаимно перпендикулярны?
3. При работе в правосторонней системе координат смысл а х Ь можно лучше уяснить при помо-
щи «правила правой руки». Поверните пальцы правой руки, например, от а к Ь, тогда направле-
ние а х Ь будет указано направлением вашего большого пальца. (Если вы работаете в лево-
сторонней системе координат, то используйте левую руку.) Отметим, что равенство i х j = к
подтверждает зто свойство.
Рис. 4.15. Интерпретация векторного произведения
Пример 4.4.2
Пусть а = (1,0,1), а Ь = (1,0,0). Эти векторы легко изобразить, так как оба они расположены в плоско-
сти х — г. (Нарисуйте их.) Площадь параллелограмма, заданного векторами а и Ь, очевидно, равна еди-
нице. Поскольку вектор а х Ь ортогонален обоим векторам а и Ь, он должен быть параллельным оси у и,
следовательно, пропорциональным ±j. Как в правосторонней, так и в левосторонней системе коорди-
нат при повороте пальцев соответствующей руки от а к Ь большой палец указывает положительное на-
правление оси у. Непосредственное вычисление согласно равенству (4.28) подтверждает правильность
этих выводов, так как в данном случае а х b = j.
Практическое упражнение
4.4.7. Доказательство свойств
Докажите три приведенные выше свойства векторного произведения.
4.4.2. Нахождение нормали к плоскости
Как мы увидим в следующем разделе, иногда возникает необходимость вычислять компоненты векто-
ра п, нормального к плоскости. Если известно, что эта плоскость проходит через три заданные точки, то
эту задачу можно решить с помощью векторного произведения. Любые три точки Рр Р2 и Р3 определяют
единственную плоскость, если они не находятся на одной прямой. Это показано на рис. 4.16.
Для нахождения нормали к данной плоскости построим два вектора: а = Р2 - Р1 и b = Р3 - Pv Их век-
торное произведение должно быть нормальным к векторам а и Ь, следовательно, оно нормально к каж-
дой прямой, расположенной в этой плоскости. (Почему?) Поэтому это и есть искомый нормальный век-
тор. (Что произойдет, если все три точки лежат на одной прямой?) Произведение этого векторного
произведения на любой скаляр также является нормальным вектором, в частности вектор b х а, имею-
щий направление, противоположное направлению а х Ь.
212
Глава 4. Векторные инструменты для графики
Рис. 4.16. Нахождение плоскости по трем заданным точкам
Пример 4.4.3
Найдите вектор, нормальный к плоскости, проходящей через точки (1,0,2), (2,3,0) и (1,2,4).
Решение
Непосредственным вычислением получаем: а = (2,3,0) - (1,0,2) = (1,3, -2), b = (1,2,4) - (1,0, 2) =
- (0,2,2), откуда их векторное произведение п = (10, -2,2).
Ввиду того, что векторное произведение сводится к вычитанию различных величин (см. равен-
ство 4.28), данный метод нахождения вектора п является чувствительным к погрешностям вычисле-
ний, особенно когда угол между а и b мал. Позднее мы рассмотрим более устойчивый метод для прак-
тического нахождения нормальных векторов.
Практические упражнения
4.4.8. Значение выбора точек
Получится ли та же самая плоскость, как в примере 4.4.3, если мы возьмем те же точки в другом поряд-
ке, например: а = (1,0,2) - (2,3,0) и b = (1,2,4) - (2,3,0)? Докажите, что в результате получится та же
самая плоскость.
4.4.9. Нахождение плоскостей
Для каждой тройки точек найдите нормальный вектор (если он существует) к плоскости, проходящей
через эту тройку:
О Pt = (1,1,1), Р2 = (1,2,1), Р3 - (3,0,4).
О Р, = (8,9,7), Р2 - (-8, -9, -7), Р3 - (1,2,1).
О Р, = (6,3, -4), Р2 - (0,0,0), Р3 = (2,1, -1).
О Р, = (0,0,0), Р2 = (1,1,1), Р3» (2,2,2).
4.4.10. Нахождение нормальных векторов
Вычислите нормальные векторы к каждой грани двух объектов, изображенных на рис. 4.17. Куб имеет вер-
шины в точках (±1, ±1, ±1), а вершины тетраэдра расположены в точках (0,0,0), (0,0,1), (1,0,0) и (0,1,0).
4.5. Отображение ключевых геометрических объектов
В предыдущих разделах мы обсуждали некоторые основные положения теории векторов и их прило-
жения к важным геометрическим проблемам, возникающим в графике. Теперь мы рассмотрим ряд фун-
даментальных идей, облегчающих работу с прямыми и плоскостями, являющимися центральными
объектами в графике, поскольку их «прямизна» и «плоскостность» обеспечивает простоту их отобра-
жения и работу с ними.
4.5. Отображение ключевых геометрических объектов
213
Рис. 4.17. Нахождение нормальных векторов к граням
Что означает «представить» прямую или плоскость и почему это важно? Задача состоит в том, что-
бы получить формулу или уравнение, с помощью которого можно определять, какие точки лежат на
прямой, а какие — нет. Это могло бы быть уравнение, которому удовлетворяют все точки данной пря-
мой, и только они. Или это могла бы быть функция, возвращающая различные точки прямой при изме-
нении некоторого параметра этой функции. Такое представление позволяет ответить на следующие
вопросы: Находится ли точка Р на прямой? Где пересекается данная прямая с другой прямой или с ка-
ким-нибудь другим объектом? Так как прямая, лежащая в плоскости, делит эту плоскость на две части,
часто нам необходимо выяснить, по какую сторону от этой прямой находится точка Р.
Для корректной работы с прямыми и плоскостями мы должны вернуться к основам и вспомнить,
чем отличаются друг от друга точки и векторы и каким образом представляется каждый из этих объек-
тов. Необходимость в данном обзоре возникает потому, что для представления прямой или плоскости
нам требуется «складывать точки» и «масштабировать точки», то есть выполнять операции, которые
фактически не имеют смысла для точек. Для того чтобы увидеть, что в действительности происходит,
введем понятие координатного фрейма (coordinate frame), которое проясняет существенную разницу
между точкой и вектором и которое придает смысл операции «сложения точек». Использование коор-
динатных фреймов приводит в конечном счете к понятию «однородных координат» («homogeneous
coordinates»), являющимся основным инструментом компьютерной графики и значительно упрощаю-
щим многие алгоритмы. Мы будем использовать координатные фреймы явно лишь в нескольких мес-
тах книги, преимущественно при изменении системы координат и при «полете» камеры вокруг сцены1
(см. главы 5, 6 и 7). Но даже если основной координатный фрейм явно не виден, он тем не менее будет
присутствовать в каждой ситуации.
4.5.1. Системы координат и координатные фреймы
Нельзя открыть новых земель, не потеряв из виду берег на очень долгое время.
Андре Жид (Andre Gide)
Рассматривая векторы в предыдущих разделах, мы говорили о векторе, например, о векторе v = (3,2,7),
как об упорядоченной тройке. То же самое мы можем сказать и о точке, например: Р= (5,3,1). Вслед-
ствие этого может показаться, что точки и векторы — это одно и то же. Однако на самом деле точки и
векторы сильно различаются: точки имеют местоположение, но не имеют размера и направления, в то
время как у векторов есть размер и направление, но нет местоположения.
Что мы имеем в виду, говоря о векторе v = (3,2,7)? Разумеется, то, что вектор v имеет компоненты
(3,2,7) в основной системе координат. Подобным же образом, Р= (5,3,1) означает, что точка Р имеет
координаты (5,3,1) в основной системе координат. При обычных обстоятельствах эта путаница между
объектом и его отображением проблем не создает. Проблема возникает, когда присутствует более чем
1 А именно в этой области программистам-графикам часто приходится туго: их программы создают такие изображения, которые вы-
глядят хорошо в простых ситуациях, однако непостижимым образом становятся удивительно плохими, когда ситуация усложняется.
214
Глава 4. Векторные инструменты для графики
одна система координат (очень частое явление в графике) и когда происходит преобразование точки
или вектора из одной системы в другую.
Обычно мы представляем себе систему координат как три оси, исходящие из начала отсчета, как
было показано на рис. 4.2, б. Однако на самом деле система координат «расположена» где-нибудь
«в мире» (in «the world») и ее оси лучше всего описываются тремя взаимно перпендикулярными векто-
рами. В частности, важно явно задавать «местоположение» системы координат, поэтому мы расширяем
понятие трехмерной системы координат1 до понятия трехмерного координатного «фрейма». Коорди-
натный фрейм (coordinate frame) состоит из заданной точки б, называемой началом отсчета {origin),
и трех взаимно перпендикулярных единичных векторов2: а, Ь и с.
На рис. 4.18 показан координатный фрейм, «находящийся» в некоторой точке 5 «в мире», с вектора-
ми а, Ь и с, изображенными так, что они исходят из точки 5 в качестве осей.
Рис. 4.18. Координатный фрейм, расположенный «в мире»
Теперь для того, чтобы представить вектор v, мы должны найти такие три числа (vt, v2, v3), что
v = v{a + n2b + г>3с, (4.32)
и сказать, что вектор v имеет в данной системе отображение (vt, v2, v3).
С другой стороны, чтобы представить точку Р, мы рассматриваем ее местоположение как смещение
на определенную величину относительно начала координат. Мы представляем вектор Р - О посред-
ством нахождения трех чисел (р1,р2,р3) следующим образом:
Р - О = р,а + р2Ь + р3с,
и тогда, соответственно, саму точку Р запишем в виде:
Р = 5 + р,а + р2Ь + р3с. (4.33)
Такое отображение точки Р является не просто тройкой, а тройкой вместе с началом отсчета. Р нахо-
дится в месте, которое смещено относительно начала отсчета на р{& + р2Ь + р3с. Основная идея состоит
в том, чтобы сделать начало отсчета системы координат явным. Это приобретает значение только в том
случае, когда имеется более одного координатного фрейма и при преобразовании из одного фрейма в
другой.
Отметим, что когда мы ранее определяли стандартные единичные векторы i, j и к как (1,0,0), (0,1,0)
и (0,0,1) соответственно, мы фактически определили их представления в основной системе координат.
1 Для двумерной системы суть изложенных идей в основном та же.
2 Вообще говоря, эти векторы не обязаны быть взаимно перпендикулярными, а только «линейно независимыми» (то есть ни один из
них не должен быть линейной комбинацией двух других). Однако координатные фреймы, с которыми мы будем работать, будут
всегда иметь взаимно перпендикулярные векторы осей.
4.5. Отображение ключевых геометрических объектов
215
Так как, согласно уравнению (4.32), i = la + Ob + Ос, вектор i фактически равен самому а! Это вопрос
наименования: говорим мы о векторе или о его представлении в координатном фрейме. Обычно мы не
различаем эти два понятия.
Отметим, что нельзя определенно утверждать, где находится или точно указать направления а, b
и с. Для того чтобы сделать это, необходимо иметь другой координатный фрейм, чтобы представить в
нем данный фрейм. В терминах своего собственного координатного фрейма О имеет представление
(0,0,0), представление вектора а равно (1,0,0) и т. д.
Однородное представление точки и вектора
Полезно представлять точки и векторы с помощью одного и того же набора основных базовых объектов
(а, Ь, с, О). Из равенств (4.32) и (4.33) следует, что вектору v = vta + r>2b + г>3с требуется четыре коэф-
фициента (vt, v2, v3, 0), в то время как точке Р = рга + /?2Ь + р3с требуется четыре таких коэффициента:
(рх,р2,р3,1). Четвертый компонент показывает, входит ли в состав объекта начало отсчета Ь. Формаль-
но мы можем записать любые v и Р, используя умножение матриц (умножение вектора-строки на век-
тор-столбец, как указано в приложении Б):
v = (а,Ь,с,О)
Р = (а,Ь,с,О)
v3
Р2
Р3
(4.34)
(4.35)
Здесь матрица-строка определяет природу координатного фрейма, а вектор-столбец является пред-
ставлением конкретного интересующего нас объекта. Таким образом, векторы и точки имеют различное
представление: векторы имеют четвертым компонентом 0, а точки 1. Уравнения (4.34) и (4.35) являются
примерами однородного представления (homogeneous representation) векторов и точек1. Использование
однородных координат является одним из признаков компьютерной графики, так как это помогает,
с одной стороны, сохранять различие между точками и векторами, а с другой стороны, предоставляет
компактную запись при работе с аффинными преобразованиями. Весьма удобно в компьютерных про-
граммах представлять точки и векторы в однородных координатах в форме упорядоченных четверок
(тетрад) путем добавления 1 или 0 в качестве четвертого компонента2. Это особенно полезно, когда мы
должны проделать преобразование из одного координатного фрейма, где имеются представления точек
и векторов, в другой.
Нетрудно преобразовать «обычное» представление точки или вектора (как упорядоченную тройку
в случае трехмерных объектов и упорядоченную пару — в случае двумерных) в однородную форму.
Для перехода от обычных координат к однородным необходимо:
Если объект является точкой, то добавить 1.
Если объект — вектор, то добавить 0.
Для перехода от однородных координат к обычным необходимо:
Если объект — вектор, то его последняя координата равна 0. Удалить этот 0.
Если объект — точка, то ее последняя координата равна 1. Удалить эту 1.
1 На самом деле мы прошли лишь часть пути при рассмотрении этого вопроса. Как мы увидим в главе 7, где мы будем изучать про-
екции, однородные координаты предоставят там возможность дополнительной операции, которая сделает их действительно одно-
родными. Однако до изучения проекций нам нет необходимости вводить эту операцию.
2 В случае двух измерений точки являются тройками вида (prp2, 1), а векторы — тройками вида (vt, v2,0).
216
Глава 4. Векторные инструменты дляграфики
OpenGL использует четырехмерные однородные координаты для всех вершин своих объектов. Если
вы посылаете в OpenGL тройку в виде (х, у, г), она немедленно преобразуется к виду (х, у, z, 1), Если
же вы посылаете в него двумерную точку (х, у), то он первым делом добавит 0 в качестве z-компонента,
а затем 1, в результате чего получится (х, у, 0, 1). Все вычисления внутри OpenGL производятся в че-
тырехмерных однородных координатах.
Линейные комбинации векторов
Многие действия можно успешно производить в однородных координатах путем покоординатного опе-
рирования с векторами. Все определения и операции сохраняются.
О Разность двух точек (х, у, z, 1) и (и, v, w, 1) равна (х - и, у - v, z - w, 0), то есть, как и ожидалось,
является вектором.
О Сумма точки (х, у, z, 1) и вектора (d, e,f, 0) равна (х + d, у + е, z +f, 1), то есть другой точке.
О Два вектора можно складывать: (d, e,f, 0) + (т, n,r,0) = (d+m,e + n,f+ г, 0), в результате получа-
ется другой вектор.
О Имеет смысл масштабирование вектора: 3(d, e,f, 0) = (3d, Зе, 3f, 0).
О Имеет смысл создание любой линейной комбинации векторов. Рассмотрим два вектора: v =
= (v(, v2, v3, 0) и w = (w{, w2, w3,0). Тогда для произвольных скаляров а и b имеем av + bw = (avt +
+ bwy av2 + bw2, av3 + bw3,0), что действительно является вектором.
Формирование линейной комбинации векторов четко определено, однако имеет ли это смысл для
точек? Ответ является отрицательным, за исключением одного особого случая, который мы рассмот-
рим позже.
4.5.2. Аффинные комбинации точек
Рассмотрим формирование линейной комбинации двух точек: Р = (Р,, Р2, Р3,1) и R = (Rt, R2, R3,1) со
скалярами fug:
fP + gR-(fPi + gRyfP2 + gR2,fP3 + gR3,f + g).
Мы знаем, что результат является истинным вектором, если f+g = 0. Однако мы увидим, что резуль-
тат не является истинной точкой, если только не выполняется равенство f + g = 1! Вспомним равенство
(4.3): когда сумма коэффициентов линейной комбинации равна единице, это равенство называется «аф-
финной» комбинацией. Таким образом, мы видим, что единственная истинная линейная комбинация
точек — это аффинная комбинация. Например, объект 0,ЗР + 0,7/? является истинной точкой, равно как
и 2,7Р - 1,77? и точка 0,5Р + 0,57?, однако Р + R точкой не является. Для трех точек, Р, R и Q можно
сформировать истинную точку 0,ЗР + 0,97? - 0,2Q, но не Р + Q - ОДД. Таким образом, любая аффинная
комбинация точек является истинной точкой.
Но что же является неправильным с точки зрения геометрии при формировании произвольной линей-
ной комбинации двух точек, например, таких:
E=fP + gR,
когда сумма f + g отлична от единицы? Неправильно то, что возникает проблема при смещении начала
отсчета системы координат [Goldman, 85]. Пусть начало отсчета смещено на вектор и, тогда точка Р
смещена на Р + и, а точка R смещена на R + и. Если Е является истинной точкой, то она также должна
быть смещена в новую точку Е' = Е + и. Однако вместо этого мы имеем:
E'=fP + gR + (f + g)u,
что не равно Е + и, несмотря на то, что f + g = 1.
4.5. Отображение ключевых геометрических объектов
217
Рис. 4.19. Сложение точек — недопустимая операция
Неудачный исход простой операции суммирования Р1 + Р2, которая не приводит к тому, чтобы резуль-
тат также был точкой, проиллюстрирован на рис. 4.19. Точки Р, и Р2 показаны в двух системах коорди-
нат, одна из которых смещена относительно другой. Рассматривая каждую точку как конец вектора,
исходящего из начала координат, мы видим, что сумма Р{ + Р2 дает в двух системах координат различ-
ные точки. Следовательно, Pt + Р2 зависит от выбора системы координат. Отметим для контраста, что
аффинная комбинация 0,5(Pt + Р2) не зависит от такого выбора.
Точка плюс вектор — аффинная комбинация точек
Существует другой способ изучения аффинных сумм точек, который интересен и сам по себе, а еще
потому, что из него получается полезный инструмент для графики. Этот способ не требует использова-
ния однородных координат.
Рассмотрим формирование точки как смещение точки А на вектор v, масштабированный скаля-
ром V. А + tv. Данное выражение представляет собой сумму точки и вектора, поэтому оно является ис-
тинной точкой. Если мы возьмем в качестве вектора v разность между некоторой точкой В и А (то есть
v = В - А), то мы получим точку
P = A + t(B-A), (4.36)
которая также является истинной точкой. Теперь с помощью алгебраических преобразований перепи-
шем уравнение (4.36) в виде равенства
P=tB + (\-t)A, (4.37)
правая часть которого является аффинной комбинацией точек. (Почему?) Это придает смысл написа-
нию аффинных сумм точек: в сущности, любая аффинная сумма может быть записана как точка плюс
вектор (см. упражнения 4.5.1,4.5.2). Если вы еще не привыкли писать аффинную сумму точек в форме
(4.37) (а мы будем часто ее использовать), то просто примите к сведению, что эта сумма означает точку,
заданную уравнением (4.36).
Пример 4.5.1. Центроид треугольника
Рассмотрим треугольник Тс вершинами D,EnF, показанный на рис. 4.20. Воспользуемся приведенны-
ми выше идеями для доказательства того, что три медианы треугольника Т пересекаются в точке, рас-
положенной на двух третях расстояния вдоль каждой медианы. Эта точка называется центроидом (цен-
тром тяжести)1 треугольника Т.
Упоминание о тяжести возникло потому, что если топкую пластину вырезать в форме треугольника Ти подвесить за нить, при-
крепленную в центроиде, то пластина удержит равновесие. Сила тяжести действует во все стороны относительно центроида оди-
наково, поэтому пластина сбалансирована.
218
Глава 4. Векторные инструменты для графики
Центроид С
Рис. 4.20. Центр треугольника как аффинная комбинация
По определению, медиана из точки D есть прямая, проведенная из вершины D в середину противо-
положной стороны. Тогда G = (Е + F)/2. Прежде всего выясним, где находится точка, отмеряющая две
трети расстояния от D до G. Применяя параметрическую форму, мы видим, что искомая точка должна
иметь вид D + (G - D)t, где t - 2/3, что приводит к следующей аффинной комбинации:
D + E + F
3
(Проверьте это!) Это — замечательное деление [Pedoe, 70]: поскольку результат симметричен отно-
сительно точек D, Е и F, то он должен также составлять две трети длины медианы, считая от Е, и две
трети длины медианы, считая от F. Следовательно, в точке С встречаются три медианы, и эта точка
является центроидом.
Данный результат имеет красивое обобщение для правильного N-стороннего многоугольника: его
центр является просто средним значением местоположений всех его N вершин, иначе говоря, аффин-
ной комбинацией. Для произвольного многоугольника центроид имеет более сложную формулу.
Практические упражнения
4.5.1. Любая аффинная комбинация точек — истинная точка
Рассмотрим три скаляра: а, b и с, которые в сумме равны единице, и три точки: А, В и С. Аффинная
комбинация аА + ЬВ + сС является истинной точкой, так как, приняв с = 1 - а - Ь, мы видим, что данное
выражение равно aA + bB + (l-a-b)C=* С+ а(А - 0 + Ь(В - 0, то есть сумме точки и двух векторов.
(Проверьте это!) Для обобщения покажите для данной аффинной комбинации точек wtAt + + ... +
®пАя, где wl + w2 + ... + wn = 1, что она может быть записана в форме суммы точки и вектора и поэтому
является истинной точкой.
4.5.2. Смещение системы координат
Рассмотрим общий случай составления линейной комбинации из m точек [Goldman, 85]:
Зададимся вопросом, является ли Е точкой, вектором или ни тем, ни другим? Считая, что каждая
точка Р. переместилась на вектор и, покажите, что Е «переместилась» в Е' = Е + 5и, где
является суммой коэффициентов. Кроме того, покажите, что
О Е является точкой, если 5=1.
О Е является вектором, если 5 = 0.
О £ не имеет смысла при других значениях 5.
4.5. Отображение ключевых геометрических объектов 219
4.5.3. Линейная интерполяция двух точек
Аффинная комбинация точек, выраженная уравнением (4.36), а именно:
Р = А(1 -t) + Bt,
выполняет линейную интерполяцию между точками А и В. Иными словами, х-компонент Px(t) гене-
рирует величину, которая составляет t-ю часть расстояния между точками Ах и Вх; аналогично для
^-компонента (в трехмерном случае и для z-компонента). Эта операция заслуживает присвоения
имени, и для случая линейной интерполяции (linear interpolation) часто употребляется название 1егр().
Для одного измерения функция lerp(a, b, t) возвращает число, являющееся Г-й частью на пути от а до Ь.
В листинге 4.1 представлена простая реализация функции 1 егр():
Листинг 4.1. Линейная интерполяция, осуществленная функцией 1егр()
float lerpffloat a, float b. float t)
{
return a + (b - a) * t:
// return a float
// возвращаем вещественное число
1
Подобным образом часто вычисляется точка P(t), которая является Г-й частью на пути по прямой
линии от А и В. Такую точку часто называют «твином» («tween» от слова «in-between» — промежуток)
точек А и В в (момент) t. Каждый компонент результирующей точки формируется как 1егр() соответ-
ствующих компонентов точек А и В. Для выполнения «твининга» («tweening») легко может быть на-
писана (как?) процедура
Po1nt2 Canvas:: Tween(Point2 A. Point2 В. float t)
// tween A and В
// твин А и В
Трехмерная версия почти не отличается от этой.
Пример 4.5.2
Пусть А = (4, 9) и В = (3, 7). В этом случае функция TweenCA, В. t) возвращает точку (4-t, 9-2t),
aTweenCA. В. 0.4) возвращает (3.6, 8.2). (Проверьте это на миллиметровке.)
4.5.4. Твининг в искусстве и анимации
Можно создать интересную анимацию, которая показывает, как одна фигура совершает «твин-пре-
образование» в другую. Эта процедура наиболее проста в том случае, если обе эти фигуры являются
ломаными линиями (или семействами ломаных) и состоят из одного и того же числа точек. Предпо-
ложим, что первая фигура, которую мы обозначим А, состоит из ломаной линии с множеством точек А;,
а вторая фигура В — из ломаной с множеством точек В., где г = 0,..., n - 1. В этом случае мы можем
создать ломаную P(t), называемую «твином в Г», состоящую из точек:
P(t) - (1 - t)A(.+ tBt.
Если мы посмотрим на последовательность значений t между 0 и 1, скажем, t = 0, 0,1,0,2.0,9,1,0,
то увидим, что эта ломаная начинается с формы А и заканчивается формой В, а в промежутке является
переходной между этими двумя формами. При малых значениях t она похожа на А, однако по мере ро-
ста t форма этой ломаной плавно деформируется в сторону формы, близкой к В. К примеру, при t - 0,25
точка Р/0,25) твина находится в 25 % пути от А к В.
На рис. 4.21 показан простой пример, в котором ломаная А имеет форму домика, а ломаная В имеет
форму буквы Т. Точка R на домике соответствует точке S на букве Т. Различные твины точки R на доми-
ке и точки S на букве Т расположены на прямой между R и 5. Твин для t = 1/2 расположен в средней
точке отрезка RS. Промежуточные ломаные показывают формы твинов для t = 0, 0,25, 0,25,0,75,1,0.
220
Глава 4. Векторные инструменты для графики
Рис. 4.21. Превращение буквы Т в домик
Листинг 4.2. Твининг двух ломаных
void Canvas:: drawTween(Point2 А[]. Point2 В[]. int n. float t)
{
// draw the tween at time t between polylines A and В
// рисуем твин в момент t между ломаными А и В
for(int i - 0: i < n: i++)
{
Point2 P;
P » Tween(A[i]. B[i]. t):
if(i — 0) moveTo(P.x. P.y):
else lineTo(P.x. P.y):
Листинг 4.2 представляет собой подпрограмму drawTweenO, рисующую твин двух ломаных Л и В, каж-
дая из которых имеет п вершин, для заданного значения t.
Подпрограмму drawTweenO можно использовать в цикле анимации, осуществляющем твининг Л и В
назад и вперед, вначале с возрастанием t от 0 до 1, а затем с убыванием t обратно до 0 и т. д. Для перехо-
да от одного отображенного твина к следующему мгновенному твину применяется двойная буфериза-
ция, которая рассматривалась в главе 3. Код для этой операции имеет такой вид:
for(t - 0.0. delT -0.1: : t +- delT)
// tween back and forth forever
// осуществляем бесконечный твин взад-вперед
{
clear the buffer
И зачищаем буфер
drawTween(A. В. n. t):
glutSwapBuffersO;
if( t >- 1.0 || t <- 0.0) delT - - delT;
// reverse the flow of t
// реверсируем направление изменения t
На рис. 4.22 показано искусное использование этой техники, основанной на двух множествах лома-
ных линий. Показаны три твина (какие значения t взяты?) Поскольку эти два набора ломаных нарисо-
ваны достаточно далеко друг от друга, остается место, чтобы нарисовать между ними твины без пере-
крытия, так что все пять изображений отлично помещаются в одном кадре.
Сьюзан Е. Бренман из корпорации Хьюлетт Паккард в Пало-Альто, Калифорния (Susan Е. Brennan
of Hewlett Packard Corporation in Palo Alto, California), опубликовала сделанные с помощью этого мето-
да карикатуры знаменитых личностей (см. [Dewdney, 58].) На рис. 4.23 приведен пример такой карика-
туры. Второй и четвертый рисунки сделаны на основе оцифрованных портретов Элизабет Тейлор и
Джона Ф. Кеннеди. Третий рисунок является твином, а остальные три сделаны методом экстраполя-
ции (extrapolation). Иными словами, использованы значения t, большие 1, так что член (1-0 становится
отрицательным. С помощью экстраполяции получаются карикатурные искажения, в некотором смыс-
4.5. Отображение ключевых геометрических объектов
221
ле «переход по другую сторону» ломаной В относительно ломаной А. На рисунке также использованы
значения t, меныппе 0, что дает аналогичный эффект.
Рис. 4.22. От мужчины к женщине. (С разрешения Марка Инфилда (Marc Infield))
Рис. 4.23. Карикатуры из лиц: твининг и экстраполяция. (С разрешения Сюзанны Бреннан (Susan Brennan)
Твининг используется в киноиндустрии для уменьшения стоимости производства мультипликаци-
онных фильмов. Раньше художник должен был рисовать по 24 рисунка на каждую секунду фильма, так
как фильмы показывают 24 кадра в секунду. Теперь же художнику нужно нарисовать в определенном
порядке только начальный и конечный рисунки, называемые ключевыми кадрами (key frames), и пре-
доставить компьютеру автоматическое генерирование всех остальных кадров. Например, если персо-
нажи не движутся слишком быстро в течение какого-нибудь полусекундного фрагмента мультфильма,
то художник может нарисовать и оцифровать первый и последний кадры этого фрагмента, а компью-
тер создаст 10 твинов с помощью линейной интерполяции, сэкономив тем самым художнику огромное
количество времени (см. тематическое задание в конце этой главы, где приводится проект программ,
осуществляющий эти эффекты).
Практические упражнения
4.5.3. Предельный случай твининга
Какой будет эффект твининга в случае, когда все точки А. ломаной А одни и тс же? Как искажается вид
ломаной В в каждом твине?
4.5.4. Экстраполяция
Пусть ломаная Л является квадратом с вершинами (1,1), (-1,1), (-1, -1) и (1, -1), а ломаная В — клином
с вершинами (5, -2), (4,3), (4,0) и (3, -2). Нарисуйте (от руки) форму P(t) для t = -1, -0,5, 0,5 и 1,5.
4.5.5. Экстраполяция и твининг
Пусть рядом изображены пять рисунков из ломаных линий. Произведя тщательные вычисления, вы
обнаружили, что три средних рисунка являются промежуточными между первым и последним, а также
вычислили использованные при этом значения t. Но кто-то утверждает, что на самом деле последний
рисунок является экстраполяцией первого и четвертого. Существует ли какой-нибудь способ выяснить,
так ли это на самом деле? Если это экстраполяция, то можно ли вычислить, какое значение t использо-
валось при этом? Если можно, то чему оно равно?
222
Глава 4. Векторные инструменты для графики
4.5.5. Обзор: квадратичный и кубический твининг и кривые Безье
В главе 11 мы будем заниматься вопросами проектирования сложных форм, называемых кривыми Бе-
зье (Bezier curves). Основная идея заключается в обычном твининге между множеством точек. В случае
линейной интерполяции мы «разбиваем единицу» на части (1 -t) и t и используем эти части в качестве
«весовых коэффициентов» для точек А и В. Мы можем распространить этот прием на квадратичную
интерполяцию, разбивая единицу на три части. Написав следующее выражение:
1-((1-0 + Г)2,
мы обобщаем нашу формулу на случай трех частей (1 - 02,2(1 - t)t и t2. Очевидно, что их сумма равна
единице, поэтому эти части можно использовать для формирования аффинной комбинации точек А, В и С:
P(t) - (1 - t)2A + 2t( 1 - t)B + t2C. (4.38)
Рис. 4.24. Кривые Безье как твининг
Это и есть кривая Безье для точек А, В и С. На рис. 4.24, а показана форма P(t) при изменении t от 0 до 1.
Данная кривая плавно переходит от Л к С. (Обратите внимание, что кривая пропускает среднюю точ-
ку.) Продвигаясь дальше, можно разбить 1 - ((1 -1) + i)3 на четыре части (какие?), которые могут быть
использованы для «кубической интерполяции» между точками А, В, С и D, как показано на рис. 4.24, б.
Практическое упражнение
4.5.6. Рисование ломаной линии
Нарисуйте на миллиметровке три точки: А, В и С. Для каждого значения t" 0,0,1,0,2,..., 0,9,1 вычисли-
те положение P(t) из уравнения (4.38) и нарисуйте ломаную линию, проходящую через эти точки. Всегда
ли это парабола?
4.5.6. Представление прямых и плоскостей
Обратимся теперь к разработке главных математических форм, которые представляют прямые и плос-
кости. Вполне естественно найти внутри графической программы такие структуры данных, с помощью
которых можно выразить прямую или плоскость.
Прямые в двумерном и трехмерном пространстве
Прямая (line) определяется двумя точками, например Си В (рис. 4.25, а). Она не ограничена по длине, про-
ходит через эти точки и бесконечно продолжается в обоих направлениях. Отрезок прямой (line segment)
(для краткости — просто отрезок (segment)) также определяется двумя точками, а именно своими конце-
выми точками (endpoints), однако продолжается только от одной концевой точки до другой (рис. 4.25, б).
Порождающая (parent) этот отрезок линия является бесконечной прямой, проходящей через его конце-
вые точки. Луч (ray) является «полубесконечным» («semi-infinite»). Он определяется точкой и направле-
нием, начинаясь в данной точке и простираясь бесконечно далеко в заданном направлении (рис. 4.25, в).
4.5. Отображение ключевых геометрических объектов
223
Рис. 4.25. Прямые, отрезки и лучи: а) прямая; б) отрезок прямой; в) луч
Эти объекты очень хорошо знакомы, тем не менее полезно собрать их важные представления и свой-
ства в одном месте. Кроме того, мы опишем самое важное в компьютерной графике представление пря-
мой: параметрическое представление (parametric representation).
Параметрическое представление прямой
Структура, представленная в равенствах (4.36) и (4.37), очень полезна, поскольку по мере изменения
параметра t точка Р проходит через все точки прямой линии, определяемой точками С и В. Следова-
тельно, такая структура дает возможность указывать и вычислять любую точку прямой. Это делается с
помощью параметра t, который отличает каждую точку прямой от другой точки. Пусть прямая обозна-
чается L, тогда через L(t) обозначим положение точки на прямой, соответствующее t. Используя вектор
Ь - В - С, получим:
Z(O-=C+b£. (4.39)
Рис. 4.26. Параметрическое представление прямой L(t)
По мере изменения t положение точки L(t) перемещается вдоль прямой. Часто под параметром t под-
разумевают время и используют для описания различных частей прямой такую терминологию: «в мо-
мент времени 0», «с течением времени» или «позднее». На рис. 4.26 показаны вектор b и прямая L, про-
ходящие через точки Си В (проиллюстрирован двумерный случай, однако в трехмерном используются
те же понятия). Отметим, где располагается положение точки L(t) для различных значений t. При
t - 0 положение L(t) соответствует точке С, поэтому мы говорим, что при t = 0 мы находимся «в точ-
ке» С. При Г=11(1) = С+(В-С) = В. По мере изменения t мы добавляем к точке С большее или
меньшее значение вектора Ь, получая в результате новую точку вдоль прямой. Если t больше 1, то новая
точка располагается где-нибудь за точкой В относительно С; если же t меньше 0, то новая точка распо-
лагается на прямой за точкой С относительно В.
Для фиксированного значения t, например t - 0,6, равенство (4.39) дает формулу для ровно одной
точки прямой, проходящей от С к В, а именно точки 1(0,6). Таким образом, данное равенство описыва-
ет точку. Но в силу того, что это равенство можно рассматривать как функцию от t, генерирующую ко-
ординаты каждой точки на прямой L по мере изменения t, это равенство называется параметрическим
представлением прямой L.
224
Глава 4. Векторные инструменты для графики
Прямая, луч и отрезок на рис. 4.25 могут быть представлены с помощью той же функции £(Г) из ра-
венства (4.39). Эти объекты отличаются друг от друга только промежутком изменения входящего в ра-
венство параметра t.
для отрезка прямой 0 < t < 1;
для луча 0 < t < оо; (4.40)
ДЛЯ ПрЯМОЙ ЛИНИИ -оо < t < оо.
Луч «начинается» в точке С при t - 0, проходит через точку В при t = 1 и затем продолжается до бес-
конечности по мере роста t. Точку С обычно называют «начальной точкой» такого луча.
Весьма полезным является тот факт, что L(t) располагается на «Г-й» части пути между точками С и В,
когда значение t находится между 0 и 1. Например, при t - 1/2 точка £(0,5) является средней точкой
(midpoint) между точками С и В, а когда Г = 0,3, то точка £(0,3) находится в 30 % пути от С к В. Это с очевид-
ностью следует из равенства (4.39), поскольку |£(t) - С\ - |Ь||ф а |В - С| = |Ь|, откуда следует, что значение
|t| является отношением расстояний |£(0 - С| и |В - С\, что и требовалось доказать.
Можно также говорить о «скорости», с которой точка £(t) «движется» по прямой £. В силу того, что
точка «преодолевает» расстояние |b||ij за время t, она движется с постоянной скоростью |Ь|.
Пример 4.5.3. 20-прямая (прямая на плоскости)
Найдите параметрическую форму прямой, проходящей через точки С - (3, 5) и В - (2,7).
Решение
Введем вектор b = В - С - (-1,2) и получим параметрическую форму £(0 - (3 -1, 5 + 2t).
Пример 4.5.4. ЗО-прямая (прямая в пространстве)
Найдите параметрическую форму прямой, проходящей через точки С - (3,5,6) и В = (2,7,3).
Решение
Строим вектор Ь = В - С- (-1,2, -3) и получаем параметрическую форму £(0 - (3 -1,5 + 2t, 6 - 30.
Возможны и другие способы параметризации прямой линии, однако они используются редко. Напри-
мер, точка
W)”=C + bt3
также «пробегает» через любую точку прямой £. Она находится в точке С при t = 0 и достигает точки В
при t = 1. Однако в отличие от £(0 W(t) «ускоряется» по мере продвижения от точки С к точке В.
Точечная нормальная форма для уравнения прямой (неявная форма)
Эта форма уравнения прямой лучше отражает основную геометрию прямой. Известное уравнение пря-
мой на плоскости имеет вид:
/x + gy=l, (4.41)
где/и g — константы. Смысл в том, что каждая точка (х, у), удовлетворяющая этому уравнению, лежит
на прямой, следовательно, это уравнение обеспечивает условие расположения точки на прямой. Это
справедливо только для 2 D-прямой; для SD-прямой требуются два уравнения. Таким образом, в отличие
от параметрической формы, прекрасно работающей как в двух, так и в трех измерениях, точечная нор-
мальная форма применима только для двумерных прямых.
Уравнение (4.41) может быть записано с помощью скалярного произведения: (f,g) (х,у) = 1. Таким
образом, для каждой точки прямой указанное скалярное произведение должно быть постоянным. Мы
рассмотрим геометрическую интерпретацию «вектора» (/, g) и попутно усовершенствуем точечную
нормальную форму прямой. Эта форма очень полезна в таких задачах, как отсечение, удаление скры-
тых линий и трассировка лучей. Формально в точечной нормальной форме ничего не сказано о числе
измерений: в двумерном пространстве точечную нормальную форму имеет прямая, а в трехмерном про-
странстве ее имеет плоскость.
Пусть нам известно, что прямая £ проходит через точки Си В, как показано на рис. 4.27. Что такое
точечная нормальная форма прямой £? Если мы найдем вектор п, перпендикулярный к £, то для любой
4.5. Отображение ключевых геометрических объектов
225
точки R = (х, у), лежащей на прямой L, вектор R- С должен быть перпендикулярен к вектору п, поэто-
му для R справедливо следующее условие:
п • (R - С) = 0 (точечная нормальная форма).
(4.42)
Это называется точечным нормальным (point normal) уравнением для прямой; оно выражает тот
факт, что указанное скалярное произведение должно быть равно нулю для любой точки R, лежащей на
прямой. Это должно выполняться для любой точки, расположенной на прямой, и любого вектора, нор-
мального к этой прямой.
С
Рис. 4.27. Нахождение точечной нормальной формы для прямой
Мы должны найти подходящий вектор п. Обозначим буквой b = В - С вектор, соединяющий точки
С и В. Тогда вектор Ь1 (перп Ь) может служить в качестве искомого вектора п. Для построения точечной
нормальной формы в качестве вектора п может выступать любое скалярное кратное от Ь1 (то есть лю-
бой вектор, полученный из Ь1 умножением на скаляр).
Пример 4.5.5. Найдите точечную нормальную форму
Пусть прямая L проходит через точки С = (3,4) и В = (5, -2). Тогда b = В - С = (2, -6) и Ь1 = (6,2) (изоб-
разите Ь1). В качестве точки, принадлежащей прямой, выберем С, тогда получим точечную нормальную
форму: (6,2) • ((х, у) - (3,4)) = 0, или 6х + 2у = 26. При желании обе части этого уравнения можно раз-
делить на 26 (или другое число, отличное от нуля).
Столь же просто найти нормаль к прямой, заданной точечным уравнением, например fx + gy = 1.
Преобразовав это уравнение к виду (/,g) • (х, у) = 1, мы обнаружим, что нормаль п равна просто (/, g)
(или любому скалярному кратному этого). Например, прямая, заданная уравнением 5х -2у = 1, имеет
нормальный вектор (5, -2), или в более общем виде К(5, -2) для любого К, отличного от нуля.
Столь же нетрудно получить параметрическую форму прямой, если задана ее точечная нормальная
форма. Допустим, нам известно, что прямая L имеет точечную нормальную форму п • (Р - С) = 0, где п
и С заданы в явном виде. В этом случае параметрическая форма имеет вид: L(f) = С + n11. (Почему?)
Вы можете также получить параметрическую форму прямой, если задано уравнение этой прямой, сле-
дующим образом:
1. Найти нормаль п, как это делалось в предыдущем параграфе.
2. Найти на прямой точку (Сх, CJ), произвольно выбрав Сх.
3. С помощью уравнения найти соответствующее Су.
Переход от одного представления к другому
Нами было описано три различных способа описания прямой. Каждое представление использует опре-
деленные данные, отличающие одну прямую от другой. Эти данные можно было бы записывать внутри
программы в соответствующей структуре данных, чтобы хранить константы любой прямой, представ-
ляющей интерес. Например, данные, связанные с представлением прямой, заданной в параметрической
форме С + bt, — это информация о точке С и направлении Ь. Иначе говоря, данные об этой прямой мо-
гут выглядеть так: {С, Ь}.
Ниже приведены три представления прямой и их данные:
О двухточечная форма: С и В; datum = {С, В}.
О параметрическая форма: С + ЪТ; datum = {С, Ь}.
О точечная нормальная (неявная) форма (только для 2Э-прямых): п • (Р - С) = 0; datum = {С, п}.
8 Ф. Хилл
226
Глава 4. Векторные инструменты для графики
Отметим, что точка С, лежащая на прямой, является общей для всех трех форм. На рис. 4.28 показа-
но, как данные для каждого из представлений могут быть получены из данных для других представле-
ний. Например, имея {С, Ь} для параметрической формы, нормаль п для точечной нормальной формы
получается просто как Ь1.
{С.Ь}
Рис. 4.28. Переход между представлениями прямой
Практическое упражнение
4.5.7. Нахождение точечной нормальной формы
Найдите точечную нормальную форму для прямой, проходящей через точки (-3,4) и (6, -1). Нарисуй-
те на миллиметровке эту прямую и нормальный к ней вектор.
Плоскости в трехмерном пространстве
Поскольку в трехмерной графике интенсивно используются многоугольники, кажется, что плоскости
появляются всюду. Многоугольник («грань» объекта) располагается в плоскости своего «родителя»,
и нам часто приходится отсекать объекты относительно плоскостей или находить плоскость, в которой
располагается определенная грань.
Подобно прямым, плоскость имеет три основные формы: трехточечную форму, параметрическое
представление и точечную нормальную форму. Мы уже рассматривали трехточечную форму в разделе
«Нахождение нормали к плоскости».
Параметрическое представление плоскости
Параметрическая форма для плоскости построена из трех составляющих: одной из ее точек, С, и из двух
(непараллельных) векторов, а и Ь, расположенных в данной плоскости, как показано на рис. 4.29. Если
нам даны три (неколлинеарные) точки А,Ви С плоскости, то в качестве векторов можно взять а = А - С
и Ь = В -С.
Для построения параметрической формы для этой плоскости отметим, что любая точка на данной
плоскости может быть представлена с помощью следующей векторной суммы: точка С плюс некото-
рое скалярное кратное вектору а плюс некоторое скалярное кратное вектору Ь. Используя для обо-
значения этих скалярных кратных параметры $ и t, имеем С + $а + rb. Из этого следует требуемая пара-
метрическая форма:
P(s, t) = С + as + bf. (4.43)
4.5. Отображение ключевых геометрических объектов
227
Задаваясь любыми значениями s и t, мы можем идентифицировать соответствующую точку на плос-
кости. К примеру, положение s = t - 0 есть сама точка С, а значениям $ = 1 и t = -2 соответствует точка
Р(1,-2) = С + а - 26.
Рис. 4.29. Параметрическое задание плоскости
Заметим, что в параметрическое выражение поверхности включены два параметра, в то время как
для кривой требуется только один параметр. И действительно, если один из параметров зафиксирован
(скажем, $ = 3), то Р(3, 0 уже является функцией одной переменной и представляет прямую линию:
Р(3,0 = (С + За) + bi.
Иногда удобнее преобразовать параметрическую форму к виду, где ее «компоненты» будут явными.
Мы можем сделать это путем расписывания уравнения (4.43) по проекциям:
P(s,t) = (Сх + axs + bt, Су + as + bt, Сг + as + bt). (4.44)
Можно также переписать параметрическую форму в уравнении (4.43) в явном виде в терминах за-
данных точек А, В и С. Используем определения векторов а и b для получения
Р($, 0 = С + $(Л — С) + t(B — С),
что может быть перегруппировано в аффинную комбинацию точек:
Р($, 0 = + tB + (1 - s - 0С.
(4.45)
Пример 4.5.6. Нахождение параметрической формы по трем точкам плоскости
Рассмотрим плоскость, проходящую через точки А = (3,3,3), В = (5,5,7) и С= (1,2,4). Из равенства (4.43)
следует, что данная плоскость имеет параметрическую форму P(s, 0 = (1, 2,4) + (2, 1, -l)s + (4, 3,3)Г.
Это равенство можно перегруппировать в компонентную форму: P(s, 0 = (1 + 2s + 40i + (2 + s + 30j +
+ (4 - s + 30k или в аффинную комбинацию P(s, 0 =s(3,3,3) + Г(5,5,7) + (1 - s - 0(1,2,4).
Точечная нормальная форма для плоскости
Плоскости также могут быть представлены в точечной нормальной форме, откуда легко выводится
классическое уравнение для плоскости.
2Д
х У
Рис. 4.30. Определение уравнения для плоскости
228
Глава 4. Векторные инструменты для графики
На рис. 4.30 показана часть плоскости Р в трех измерениях. Плоскость полностью определяется с
помощью
О одной точки В “ (Ьх, Ьг), лежащей на ней.
О направлением п - (пх, пу, пг), нормальным к этой плоскости.
Подобно тому, как вектор, нормальный к прямой в двух измерениях, указывает ее направление, нор-
маль к плоскости указывает ориентацию этой плоскости в пространстве.
Известно, что нормаль п перпендикулярна любой прямой, расположенной в плоскости. Для произ-
вольной точки R = (х, у, г) плоскости вектор, проведенный из точки R к точке В, должен быть перпенди-
кулярен к нормали п, откуда
п(Я-В)-0. (4.46)
Это и есть точечное нормальное уравнение для плоскости. По форме оно идентично точечному нор-
мальному уравнению для прямой: множество скалярных произведений равно 0. Все точки на плоско-
сти образуют с точкой В векторы, составляющие аналогичное скалярное произведение с нормальным
вектором. Раскрывая скалярное произведение и используя выражение п - (пх, пу, п), мы видим, что точеч-
ная нормальная форма преобразовалась в традиционное (общее) уравнение для плоскости, а именно:
пхх + пг/ + пг2“ D, (4.47)
где D = п • (В - 0). Например, имея уравнение плоскости вида 5х - 2у + 8z = 2, можно сразу определить,
что нормалью к этой плоскости является вектор (5, -2,8) или любое скалярное, кратное ему. (А как опре-
делить точку, лежащую на плоскости?)
Пример 4.5.7. Нахождение точечной нормальной формы
Пусть плоскость Р проходит через точку (1,2,3) с нормальным вектором (2,-1, -2). Точечная нормаль-
ная форма для этой плоскости имеет вид: (2, -1, -2) • ((х, у, z) - (1,2,3)) = 0. Уравнение для данной
плоскости можно записать в форме: 2х - у - 2z = -6.
Пример 4.5.8. Нахождение параметрической формы по уравнению плоскости
Найти параметрическую форму для плоскости 2х - у + 3z - 8.
Решение
По виду уравнения легко выяснить координаты нормали к плоскости: (2,-1,3). Существует много
вариантов параметризации, нам нужно найти только один из них. В качестве С возьмем любую точку,
удовлетворяющую уравнению плоскости, например, С - (4,0,0). Найдем два (неколлинеарных) векто-
ра, скалярное произведение которых с нормалью (2, -1,3) равняется 0; после некоторого поиска нахо-
дим подходящие векторы: а - (1,5,1), Ь-=(0, 3, 1). Таким образом, параметрическая форма для данной
плоскости имеет вид: P(s, 0 - (4,0,0) + (1,5,l)s + (0,3, l)t.
Пример 4.5.9. Нахождение двух неколлинеарных векторов
Как, имея нормаль п к плоскости, проще всего найти два неколлинеарных вектора а и Ь, оба из которых
перпендикулярны п? В предыдущем упражнении мы подобрали два подходящих вектора; здесь же мы ис-
пользуем то обстоятельство, что векторное произведение любого вектора на п нормально к п. Поэтому выбе-
рем простейший вектор, например (0,0,1), и построим а как векторное произведение этого вектора на п:
а = (0,0,1) х п = (-пу, пх, 0).
(Действительно ли этот вектор нормален к п?) Мы можем использовать эту же идею для формиро-
вания вектора Ь, нормального к векторам п и а:
b = п х а = (-цд, "V»’ ”*2 +
(Проверьте, что действительно b ± а и b ± п.) Тогда вектор Ъ несомненно неколлинеарен вектору а.
Применим этот метод к плоскости (3,2,5) • (R - (2,7,0)) = 0. Зададим векторы а = (0,0,1) х п = (-2,3,0)
и Ь = (-15, -10,13). Тогда параметрическая форма плоскости будет иметь вид:
P(s, 0 = (2 - 2s - 15f, 7 + 3s - lOt, 130.
4.5. Отображение ключевых геометрических объектов
229
Проверка. Действительно ли вектор P(s, t) - С= (-2s - 15t, -3s - lOt, 13t) нормален к n при любых
значениях s и t?
Практическое упражнение
4.5.8. Нахождение плоскости
Найдите параметрическую форму для плоскости, совпадающей с плоскостью у, z.
Переход от одного представления к другому
Как и в случае прямых, представляется полезным уметь осуществлять переходы между тремя представ-
лениями плоскости и переводить данные, описывающие плоскость, в форму, наиболее подходящую для
данной задачи.
Ниже приведены три формы представления плоскости вместе с их данными:
О трехточечная форма, например С, В и Л; datum = {С, В, А}.
О параметрическая форма С + as + bt; datum = {С, а, b}.
О точечная нормальная (неявная) форма п • (Р - С) = 0; datum = {С, п}.
Рис. 4.31. Переход между представлениями плоскости
Точка С па плоскости является общей для всех трех форм. На рис. 4.31 показано, как данные для
каждого представления могут быть получены из данных для других представлений. Тщательно прове-
рим каждое преобразование. Большинство подобных случаев уже подробно рассматривалось в разделе
«Нахождение нормали к плоскости» и в данном разделе. Некоторые из них предлагались в качестве
упражнений. Самым сложным является, вероятно, вычисление в примере 4.5.9. Еще один случай, за-
служивающий некоторого пояснения, — это нахождение трех точек плоскости, заданной в нормальной
точечной форме. Одна точка, С, уже известна. Оставшиеся две находим при помощи конкретных значе-
ний самой точечной нормальной формы, являющейся уравнением: пхх+ пуу + nz = п • С. Выберем для
удобства А = (0, 0, «,) и используем это уравнение для нахождения аг = п • С/пг. Аналогичным обра-
зом выберем В = (0, Ьу, 0) и снова применим это же уравнение для нахождения Ьу = п • С/пу.
Плоские лоскуты
Подобно тому, как мы можем ограничить область изменения параметра t в представлении прямой ли-
нии для получения луча или отрезка, мы можем ограничить диапазоны изменения параметров s и t в
представлении плоскости.
230
Глава 4. Векторные инструменты для графики
В параметрической форме уравнения (4.43) значения s и t могут изменяться от до °®, поэтому плос-
кость может простираться неограниченно. В ряде случаев мы хотим иметь дело только с «куском» плос-
кости, например, с расположенным в этой плоскости параллелограммом. Такой кусок носит название
плоского лоскута (planar patch), этот термин позволяет вообразить плоскость в виде лоскутного одея-
ла (quilt), сшитого из множества соединенных вместе кусочков. Позднее мы будем изучать криволи-
нейные поверхности, сшитые из лоскутов, которые не обязательно будут плоскими. Большая часть
практического моделирования объемных тел сводится к собиранию в одно целое лоскутов различной
формы для создания поверхности объекта.
Пространство
а
Рис. 4.32. Преобразование из одного пространства в другое для определения плоского лоскута
Плоский лоскут формируется посредством ограничения диапазона допустимых значений пара-
метров sat. Например, часто требуют, чтобы s и t изменялись только от 0 до 1. Лоскут позициониру-
ется и ориентируется в пространстве с помощью соответствующего подбора векторов а, Ь и точки С.
На рис. 4.32, а показана область допустимых значений $ и t в виде квадрата в пространстве параметров
(parameter space), а на рис. 4.32, б показан лоскут, который получается при таком ограничении в про-
странстве объекта (object space).
Каждой точке (s, t) в пространстве параметров соответствует одна трехмерная точка на лоскуте
P(s, t) = С + as + bi. Такой лоскут является параллелограммом, углы которого соответствуют четырем
углам в пространстве параметров и расположены следующим образом:
Р(0,0) - С,
Р(1,0)*=С + а, (4.48)
Р(0,1) = С + Ь,
Р(1,1)-=С + а + Ь.
Векторы а и b определяют размер и ориентацию лоскута. Если векторы а и b взаимно перпенди-
кулярны, то сетка становится прямоугольной. Если, кроме того, а и b имеют одинаковую длину, то сет-
ка становится квадратной. Изменение точки С просто сдвигает лоскут без изменения ее формы и ори-
ентации.
Пример 4.5.10. Построение лоскута
Пусть С = (1, 3, 2), а - (1,1, 0), b - (1,4, 2). Найдите углы плоского лоскута.
Решение
Из формул (4.48) получим четыре угла
Р(0,0) - (1, 3,2), Р(0,1) = (2,7,4), Р(1,0) - (2,4,2), Р(1,1) - (3,8,4).
Пример 4.5.11. Описание лоскута
Найдите значения векторов а, b и точки С, образующие квадратный лоскут со стороной 4, с центром в
начале отсчета и параллельную плоскости х, г.
4.6. Определение точки пересечения двух отрезков прямой
231
Решение
Углы этого лоскута равны соответственно (2,0,2), (2, 0, -2), (-2,0, 2) и (-2, 0, -2). В качестве точ-
ки С выбираем любой угол, например (2,0, -2). Тогда каждый из векторов а и b имеет длину 4 и парал-
лелен одной из осей х или г. Выбираем в качестве вектора а = (-4,0,0), а в качестве вектора b = (0,0,4).
Практическое упражнение
4.5.9. Нахождение лоскута
Найдите точку С и векторы а и Ь, образующие лоскут, четыре угла которого равны соответственно
(-4,2,1), (1,7,4), (-2, -2,2) и (3,3,5).
4.6. Определение точки пересечения
двух отрезков прямой
Часто возникает необходимость вычислить точку, в которой пересекаются два отрезка прямой в дву-
мерном пространстве (то есть на плоскости). Иногда такое вычисление необходимо для решения дру-
гой, связанной с этой задачи, например, чтобы выяснить, является ли полигон простым. Определение
точки пересечения двух отрезков иллюстрирует мощность параметрического представления отрезков
и скалярного произведения.
Задача: даны два отрезка прямой; требуется определить, пересекаются ли они, и если пересекаются,
то найти точку их пересечения.
г д
Рис. 4.33. Различные случаи для двух отрезков прямой
Решение. Пусть один отрезок имеет концевые точки Л и В, а другой — концевые точки С и D. Как
показано на рис. 4.33, два эти отрезка могут быть расположены различными способами: они могут во-
все не пересекаться (рисунки а и б), иметь одну общую точку (в и г) или даже перекрываться в некоторой
области (е). Они могут быть или не быть параллельны. Требуется единый подход, охватывающий все
эти случаи.
Каждый отрезок имеет порождающую прямую (parent line) — бесконечную прямую линию, частью
которой он является. Если две порождающие прямые не параллельны, то они пересекаются в некото-
рой точке. Вначале определим эту точку.
Введем параметрические представления для каждого из исследуемых отрезков. Пусть АВ — отрезок
от точки А до точки В. Тогда
4B(0-4 + bt, (4.49)
232
Глава 4. Векторные инструменты для графики
где для удобства мы ввели вектор b - В - А. При изменении Г от 0 до 1 пробегаются все точки данного
конечного отрезка прямой. Если же разрешить t изменяться от -<» до то будет пройдена вся порожда-
ющая прямая линия.
Аналогичным образом дадим параметрическое представление отрезка CD (с применением нового
параметра и):
CD(u)~C + du, (4.50)
где d - D - С. Мы используем для двух прямых различные параметры: для одной — t, а для другой — и,
чтобы можно было независимо описывать различные точки этих прямых (если бы использовался один
и тот же параметр, то точки этих двух прямых оказались бы связанными между собой).
В случае пересечения порождающих прямых должны существовать определенные значения t и и, при
которых правые части уравнений (4.49) и (4.50) будут одинаковыми:
А + bt = С + du.
Введем для удобства вектор с = С - А и запишем это условие в терминах трех известных векторов и
двух (неизвестных) параметров:
bt = c + da. (4.51)
Подобно уравнению (4.22), уравнение (4.51) в двумерном случае содержит в себе два уравнения с
двумя неизвестными. Решим его тем же способом: скалярно умножим обе его части на d1, чтобы исклю-
чить члены с d, тогда получим d1 • bt - d1 • с. Теперь рассмотрим два основных случая, когда d1 • bt равно
или не равно нулю.
Случай 1. Произведение d1 * b отлично от нуля
В этом случае мы можем решить последнее уравнение относительно t:
d1 • с
d • b
Аналогичным способом, используя одно из дополнительных свойств перп-скалярного произведения
(какое именно?), скалярно умножим обе части уравнения (4.51) на Ь1, после чего получим:
Ь1 • с
и =—;---.
d • b
(4.52)
(4.53)
Теперь мы знаем, что две порождающие прямые пересекаются, и мы знаем где. Однако это не означает,
что пересекаются заданные отрезки этих прямых. Если t расположено вне интервала [0,1], то отрезок
АВ не «достанет» другой отрезок; то же можно сказать в случае, если и расположено вне интервала [0,1].
Если же t и и расположены между 0 и 1, то данные отрезки прямой должны пересечься в некоторой точ-
ке I, положение которой легко найти подстановкой значения t в уравнение (4.49):
1 = А +
d1 • с
d< b
lb (точка пересечения).
(4.54)
Пример 4.6.1
Имея концевые точки А - (0,6), В = (6,1), С - (1,3) и D = (5,5), найдите точку пересечения отрезков АВ
и CD, если таковая существует.
Решение
d1 • d = -32, откуда t - 7/16 и и - 13/32, то есть значения обоих параметров располагаются между 0 и 1.
Следовательно, данные отрезки пересекаются. Точка пересечения имеет координаты (х, у) - (21/8,61/16).
Полученный результат можно подтвердить визуально, если построить отрезки на миллиметровке и оп-
ределить координаты искомой точки пересечения.
4.6. Определение точки пересечения двух отрезков прямой
233
Случай 2. Произведение d1- b равно нулю
В этом случае нам известно, что векторы d и b параллельны. (Почему?) Отрезки тем не менее могут
перекрываться, однако это может произойти только в том случае, если параллельные порождаю-
щие прямые идентичны. Проверка этого условия рассматривается в одном из приведенных ниже
упражнений.
Практические упражнения
В этих упражнениях рассматривается разработка подпрограммы, которая выполняет полное тестиро-
вание двух отрезков прямых на пересечение.
4.6.1. Случай перекрывающихся порождающих прямых
Рассмотрим случай 2 этого раздела, когда произведение d1 • b = 0, то есть порождающие прямые парал-
лельны. Нам необходимо выяснить, являются ли порождающие прямые идентичными, и если являют-
ся, то перекрывают ли отрезки друг друга.
Чтобы проверить, являются ли порождающие прямые одной и той же прямой, посмотрим, распола-
гается ли точка С на порождающей прямой, проходящей через Ап В.
1. Сначала докажите, что уравнением для порождающей прямой является Ьх(у - Ах) - Ьу(х - Ау) = 0.
Затем подставьте Сх вместо х и С вместо у и посмотрите, является ли левая часть уравнения
достаточно близкой к нулю (то есть является ли ее значение меньшим некоторого допуска вро-
де 10~8). Если нет, то порождающие прямые не совпадают и пересечения нет.
2. Если порождающие прямые совпадают, то нужно проверить, перекрываются ли данные отрезки
прямых. Для выполнения этой проверки покажите, как найти такие два значения te и td, при
которых прямая, проходящая через точки Ап В, достигает соответственно точек С и D. Посколь-
ку порождающие прямые идентичны, то можно использовать только х-компонент. Отрезок АВ
начинается в 0 и заканчивается в 1; тогда, последовательно подставляя четыре значения пара-
метра: 0, 1, tc и td, можно без труда определить относительное положение этих двух отрезков.
3. Теперь покажите, что перекрытие имеет место, за исключением случаев, когда tc и td оба меньше
нуля или оба больше единицы. Если перекрытие существует, то его концевые точки легко найти
по значениям t и t..
с а
4. В заключение по заданным концевым точкам А = (0,6), В = (6,2), С = (3,4) и D - (9,0) опреде-
лите виды возможных пересечений.
4.6.2. Алгоритм определения пересечения
Напишите подпрограмму seglntersectO, которую можно было бы использовать в таком контексте:
1f(segIntersect(A. В. С. D. InterPt)) <do something*
Такая подпрограмма принимает четыре точки, определяющие два отрезка, и возвращает 0, если эти
отрезки не пересекаются, и 1, если пересекаются. Если отрезки пересекаются, то расположение точки
пересечения помещается в InterPt. Подпрограмма возвращает -1 в случае, если порождающие прямые
идентичны.
4.6.3. Тестирование полигона на простоту
Напомним, что полигон Р является простым, если в нем нет пересечений ребер, за исключением конце-
вых точек смежных ребер. Напишите подпрограмму int isSimpleCPolygon Р), которая решает задачу
«в лоб»: проверяет, пересекаются ли какие-нибудь пары ребер, заданные списком вершин полигона, и
возвращает 0, если это так, и 1, если нет. (Polygon — это соответствующий класс для описания полигона.)
Это простой, но не самый эффективный алгоритм. (Более сложные проверки со специальной сорти-
ровкой ребер по х и по у описаны в [Moret, 142] и [Preparata, 172].)
234
Глава 4. Векторные инструменты для графики
4.6.4. Пересечения отрезков прямых
Для каждой из следующих пар отрезков АВ и CD определите, пересекаются ли они, и если да, то где:
1. Л = (1,4), В-(7,1/2), С = (7/2,5/2), £> = (7,5).
2. А = (1,4), В = (7,1/2), С = (5,0), D = (0,7).
3. А = (0, 7), В - (7,0), С= (8, -1), D - (10, -3).
4.6.1. Приложение пересечения прямых: окружность,
проходящая через три заданные точки
Предположим, что дизайнер хочет иметь инструмент для рисования единственной окружности, прохо-
дящей через три заданные точки. Пользователь задает мышью на дисплее три точки А, В и С, например,
как на рис. 4.34, а, и окружность рисуется автоматически, как показано на рис. 4.34, б. Единственная
окружность, проходящая через три точки, носит название описанной окружности (circumscribed circle),
или вневписанной окружности (excircle), около треугольника, определяемого этими точками. Что это
за окружность? Нам необходима подпрограмма, которая может вычислять ее центр и радиус.
В В в
a б в
Рис. 4.34. Нахождение описанной окружности: а) какая окружность? б) она выглядит так; в) так находится ее центр
Рисунок 4.35, в показывает, как найти описанную окружность. Центр S искомой окружности дол-
жен быть равноудален от всех трех вершин, поэтому он должен располагаться на срединном перпенди-
куляре (perpendicular bisector) каждой из сторон треугольника АВС (срединный перпендикуляр — это
множество всех точек, равноудаленных от двух заданных точек). Таким образом, мы можем определить
центр окружности S, если вычислим точку пересечения двух срединных перпендикуляров.
Рис. 4.35. Срединный перпендикуляр для отрезка прямой
Вначале покажем, как найти параметрическое представление срединного перпендикуляра для
отрезка прямой. На рис. 4.35 показан отрезок S с концевыми точками Ап В. Его срединный перпенди-
куляр L является бесконечной прямой, которая проходит через середину М отрезка S перпендикулярно
4.6. Определение точки пересечения двух отрезков прямой
235
к нему. Однако нам известно, что средняя точка Мопределяется выражением (Л + В)/2 и что направле-
ние нормали задается выражением (В - А)1, поэтому параметрическая форма срединного перпендику-
ляра имеет вид:
L(t) = (Л + В) + (В - А)Ч (срединный перпендикуляр для АВ). (4.55)
Теперь мы можем вычислить описанную окружность по трем точкам. Возвращаясь к рис. 4.33, в, най-
дем точку пересечения S срединных перпендикуляров для АВ и АС. Для удобства введем следующие
векторы:
а = В - Л;
Ь = С-В; (4.56)
с = А- С.
Для того чтобы найти срединный перпендикуляр отрезка АВ, нам нужна середина отрезка АВ и на-
правление перпендикуляра к АВ. Средняя точка АВ равна А + а/2. (Почему?) Направление перпенди-
куляра к отрезку АВ задается вектором а1. Таким образом, параметрическая форма для срединного
перпендикуляра имеет вид: А + а/2 + аЧ. Аналогично срединный перпендикуляр отрезка АС имеет
вид: А - с/2 + cLu, где используется параметр и. Точка S расположена в точке пересечения срединных
перпендикуляров, которая может быть получена из решения следующего уравнения:
аЧ - Ь/2 + с1и
(где использован тот факт, что а + b + с - 0, что следует из определения этих векторов). Чтобы исклю-
чить член, содержащий параметр и, умножим скалярно обе части этого уравнения на с, откуда t - (1/2) х
х (Ь • с)/(а± • с). Для нахождения S используем это значение t в формуле для срединного перпендикуля-
ра. Тогда получим А + а/2 + аЧ, откуда следует простая явная форма':
1 f b * с
S = J + - а + —:—а1 (центр описанной окружности). (4.57)
2^ а -с j
Радиус описанной окружности равен расстоянию от S до любой из трех вершин — иными словами,
|5-А|. Поэтому мы должны просто вычислить длину вектора, входящего в правую часть уравнения (4.57).
После некоторых преобразований (проверьте их) получим:
|al if b-c Y
radius = — J —:— + 1 (радиус описанной окружности). (4.58)
2 у^а -сJ
А когда S и радиус известны, мы можем использовать подпрограмму drawCi rcleO из главы 3 для вы-
черчивания описанной окружности.
Пример 4.6.2
Найдите срединный перпендикуляр L для отрезка S, имеющего концевые точки А = (3, 5) и В - (9,3).
Решение
Непосредственным вычислением находим середину отрезка М = (6,4) и вектор (В - А)1 = (2, 6), тог-
да представление L будет иметь вид: L(t) = (6 + 2t, 4 + 6t). Чтобы увидеть этот результат, полезно начер-
тить S и L.
Каждый треугольник имеет также вписанную окружность (inscribed circle), которую иногда требу-
ется вычислить в контексте автоматизированного проектирования. В тематическом задании в конце
этой главы мы покажем, как это делается, а также рассмотрим любопытную девятиточечную окруж-
ность (nine-point circle).
1 Другие аналитические выражения для 5уже появлялись ранее (например, в [Goldman, 84].
236
Глава 4. Векторные инструменты для графики
Практическое упражнение
4.6.5. Срединный перпендикуляр
Найдите параметрическое выражение срединного перпендикуляра для отрезка с концевыми точками
А = (0,6) и В = (4,0). Начертите отрезок и перпендикуляр.
4.7. Пересечения прямых с плоскостями; отсечение
Задача нахождения точек пересечения прямой линии с другой прямой или с плоскостью возникает в
графике в удивительно разнообразных ситуациях. Мы уже имели дело в предыдущем разделе с одним
таким подходом, когда определяется точка пересечения двух отрезков прямых. В том методе использо-
вались параметрические представления обоих отрезков и совместно решались два уравнения.
В данном разделе мы рассмотрим другой метод, который годится как для прямых, так и для плоско-
стей. В нем пересекающая прямая представляется параметрически, а пересекаемая прямая или плос-
кость — в точечной нормальной форме. Этот метод является непосредственным и в нем ясно видна суть
происходящего. Мы разработаем его один раз, а затем применим его результаты к задаче отсечения пря-
мой линии границами выпуклого двумерного многоугольника или выпуклого трехмерного многогран-
ника. В главе 7 мы увидим, что такая техника пересечения является важнейшим этапом при отображе-
нии трехмерных объектов. В главе 14 мы используем ту же технику пересечения при выполнении
трассировки лучей.
Если в двумерном пространстве мы находили точку пересечения прямой с другой прямой, в трех-
мерном пространстве обычно нам необходимо найти точку пересечения прямой с плоскостью. Обе эти
задачи можно решить за один прием, поскольку задача формулируется в терминах скалярных произве-
дений, вследствие чего одни и те же выражения описывают двумерные и трехмерные векторы. (Задача
о пересечении двух плоскостей будет рассматриваться в упражнениях в конце главы; ее решение также
основано на скалярном произведении.)
а
Рис. 4.36. Где луч пересекает прямую или плоскость?
Рассмотрим прямую, которая параметрически описывается формулой R(f) = А + ct. Будем называть
ее также лучом (ray). Мы хотим определить, где этот луч пересекает объект, заданный в точечной нор-
мальной форме п(Р - В) = 0. В двумерном пространстве этот объект является прямой линией, а в трех-
мерном — плоскостью. В любом случае точка В расположена на этом объекте, а вектор п — нормален к
нему. На рис. 4.36, а показан луч, падающий на прямую, а на рис. 4.36, б — на плоскость. Мы хотим най-
ти положение «точки соударения».
Допустим, что соударение происходит при t = ?hit, в «момент соударения». При этом значении t пря-
мая и луч должны иметь одинаковые координаты, поэтому А + cthjt должно удовлетворять уравнению
точечной нормальной формы для прямой или плоскости. Подставим эту неизвестную «точку соударе-
ния» в точечное нормальное уравнение и получим следующее условие для £hit:
п(Л + c£hit- В) - 0.
4.7. Пересечения прямых с плоскостями; отсечение
237
Данное уравнение может быть переписано в следующем виде:
п(Л - В) + п • c(hit = О,
которое является линейным относительно thit. Вот его решение:
th = —d) (время соударения, для двух и трех измерений). (4.59)
ПС
Как всегда в случаях с дробями, следует иметь в виду возможность обращения знаменателя форму-
лы для £hit в нуль. Такой случай имеет место при п • с == 0, то есть когда луч параллелен плоскости, и
тогда соударения нет вообще1.
Когда время соударения вычислено, легко определить положение точки соударения — просто под-
ставим £hit в формулу для луча и получим;
Phjt = А + cthjt (точка соударения, случаи двух и трех измерений). (4.60)
Рис. 4.37. Луч: а) сонаправленный с нормалью п и б) противоположно направленный к ней
В практических упражнениях в конце этого раздела нам также нужно будет определить, в каком направ-
лении луч падает на прямую или плоскость: сонаправленно с нормалью п или противоположно направлен-
но. (Эта ориентация будет важна по той причине, что нам понадобится знать, уходит луч от объекта или
входит в пего.) На рис. 4.37 показаны два возможных случая соударения луча с прямой. На рис. 4.37, а угол
между направлением с луча и нормалью п меньше 90°, поэтому мы говорим, что луч сонаправлен с п.
На рис. 4.37, б угол превышает 90°, поэтому луч противоположно направлен с нормалью п.
Легко проверить, какая из этих возможностей имеет место, поскольку знак скалярного произведе-
ния п • с сразу говорит о том, меньше или больше 90° угол между п и с. Сведя воедино все сказанное
выше, имеем три следующие возможности:
если п • с > 0, то луч сонаправлен с нормалью;
если п • с = 0, то луч параллелен прямой; (4.61)
если п • с < 0, то луч противоположно направлен с нормалью.
Практические упражнения
4.7.1. Пересечение луча с прямыми и плоскостями
Найдите, где и когда луч А + ct соударяется с объектом п(Р - В) в 0 (с прямой для двух измерений,
с плоскостью для трех измерений):
1. А = (2, 3), с = (4, -4), п - (6,8), В = (7, 7).
2. А = (2, -4,3), с = (4,0, -4), п - (6,9,9), В = (-7,2,7).
3. А = (2,0), с = (0, -4), п - (0,8), В - (7,0).
4. А = (2,4, 3), с = (4,4, -4), п = (6,4,8), В - (7,4, 7).
Если же числитель также равен пулю, то луч целиком лежит в рассматриваемой прямой (для двумерного случая) или плоскости
(в трехмерном случае). Почему?
238
Глава 4. Векторные инструменты для графики
4.7.2. Соударение луча с плоскостью
Найдите точку, в которой луч (1,5,2) + (5, -2,6)t соударяется с плоскостью 2х - 4г/ + z = 8.
4.7.3. Чем является пересечение двух плоскостей?
Из геометрии мы знаем, что две плоскости пересекаются по прямой линии. Однако что это за прямая?
Рассмотрим две плоскости, заданные уравнениями п • (Р - Л) = 0 и m • (Р - В) = 0. Найдите параметри-
ческую форму прямой, по которой они пересекаются. Возможно, наиболее простой вам покажется
такая процедура.
1. Сначала запишите в параметрической форме одну из плоскостей, например вторую плоскость:
В + as + bt.
2. Затем подставьте это выражение в точечную нормальную форму для первой плоскости и таким
образом получите уравнение, связывающее параметры s и t.
3. Выразите из этого равенства s как функцию от t, например, s = Е + Ft. (Найдите выражения для Е и F.)
4. Запишите искомую прямую в виде В + а(Е + Ft) + bt.
4.8. Задачи о пересечениях многоугольников
Многоугольники (полигоны) являются основными объектами, используемыми как в двумерной, так и
в трехмерной графике. В случае двумерной графики описывать и рисовать полигоны просто, так как
они имеют прямые ребра. В трехмерной графике объект часто моделируется в виде «сетки» из полиго-
нов — множества примыкающих друг к другу многоугольников, образующих «оболочку» («skin») объек-
та. Если эта оболочка образует замкнутую поверхность, ограничивающую некоторую часть простран-
ства, то такая сетка называется многогранником, или полиэдром (polyhedron). Мы будем подробно изучать
сетки и полиэдры в главе 6.
а б
Рис. 4.38. Задачи пересечения прямой с полигональными объектами
На рис. 4.38 показаны двумерный полигон и трехмерный полиэдр, которые нам, возможно, нужно
будет анализировать или визуализировать в графическом приложении. В связи с такими объектами
возникают три следующих важных вопроса.
О Находится ли данная точка Р внутри или вне объекта?
О В каком месте данный луч R первый раз пересечет объект?
О Какая часть данной прямой L лежит внутри объекта, а какая — вне его?
4.8. Задачи о пересечениях многоугольников
239
Вот простой пример: какая часть (или части) прямой Зу - 2х - 6 лежит внутри полигона с вершина-
ми (0,3), (-2, -2), (-5,0), (0, -7), (1,1)?
4.8.1. Работа с выпуклыми полигонами и полиэдрами
Общий случай пересечения прямой с произвольным полигоном или полиэдром достаточно сложен,
поэтому оставим его до раздела «Отсечение границами произвольных полигонов». Задача становится
намного проще, когда полигон или полиэдр являются выпуклым, поскольку выпуклый полигон полно-
стью описывается набором «ограничивающих прямых»; в трехмерном случае выпуклый полиэдр пол-
ностью описывается набором «ограничивающих плоскостей». Поэтому нам необходимо только прове-
рить эту прямую на предмет пересечения с совокупностью неограниченных прямых или плоскостей.
Рисунок 4.39 иллюстрирует двумерный случай. На рис. 4.39, а показан выпуклый Пентагон (пяти-
угольник), на рис. 4.39, б — прямые La, Lt и т. д., ограничивающие этот Пентагон. Каждая ограничиваю-
щая прямая определяет два полупространства: внутреннее полупространство, которое содержит
данный полигон, и внешнее полупространство, не имеющее с полигоном общих точек. Рисунок 4.39, в
показывает часть внешнего полупространства, соответствующую ограничивающей прямой L2.
Внешнее
полупространство
б
Рис. 4.39. Выпуклые полигоны и полиэдры
Пример 4.8.1. Определение ограничивающих прямых
На рис. 4.40, а показан единичный квадрат; четыре ограничивающих его прямых описываются уравне-
ниями х = 1, х= -1, у = 1, у = -1. Кроме того, для каждой ограничивающей прямой мы можем указать
внешний нормальный вектор, который направлен во внешнее полупространство, соответствующее дан-
ной ограничивающей прямой. Внешней нормалью для прямой у = 1 является, конечно, п = (0,1). (Чему
равны остальные три внешние нормальные вектора?)
Треугольник на рис. 4.40, б имеет три ограничивающих прямые. (Какое уравнение имеет каждая из
этих прямых?) Точечные нормальные формы этих трех прямых имеют следующий вид:
(-1,0)(Р-(0,0)) = 0;
(0,-1)(Р-(0,0))-0;
(1,1)(Р -(1,0)) = 0.
Отметим, что в каждом случае используется внешняя нормаль.
Большое преимущество работы с выпуклыми полигонами состоит в том, что проверка на пересече-
ние выполняется только относительно бесконечных прямых, и нет необходимости проверять, располо-
жена ли точка пересечения «по другую сторону» от концевой точки. (Вспомните сложность тестов на
пересечение в предыдущем разделе.) Кроме того, в случае выпуклых полигонов можно использовать
точечную нормальную форму, что упрощает вычисления.
Для выпуклого полиэдра в трехмерном пространстве каждая плоскость имеет внутреннее и внешнее
полупространство и внешний нормальный вектор. Полиэдр является пересечением всех внутренних
240
Глава 4. Векторные инструменты для графики
полупространств (множеством всех точек, одновременно находящихся во внутренних полупростран-
ствах каждой ограничивающей плоскости).
Рис. 4.40. Примеры выпуклых полигонов
4.8.2. Пересечение с лучами и отсечение
для выпуклых полигонов
В разделе «Пересечения прямых с плоскостями; отсечение» мы разработали метод нахождения точки
соударения луча с отдельной прямой линией или плоскостью. Мы можем использовать этот метод для
нахождения точки соударения луча с выпуклым полигоном или полиэдром.
Задача пересечения
На рис. 4.41 показан луч А + ct, пересекающийся с выпуклым полигоном Р. Мы хотим узнать все точки
пересечения этого луча с Р. Поскольку полигон Р — выпуклый, то луч пересекает его ровно два раза:
один раз на входе и один раз на выходе. Обозначим те значения параметра t, при которых луч входит
в полигон и выходит из него, соответственно t.п и tout. Теперь задача сводится к вычислению значений ?jn
и £out. Если будут известны эти моменты времени, мы узнаем и сами точки пересечения:
Входная точка пересечения = А + ci.n.
Выходная точка пересечения = А + ctout. (4.62)
Луч находится внутри полигона Р для всех t из интервала [tn, tout].
Рис. 4.41. Луч А + ct, пересекающий выпуклый полигон
4.8. Задачи о пересечениях многоугольников
241
Отметим, что нахождение tjn и tout решает не только задачу пересечения, но и задачу отсечения: если
нам известны tin и toul, то мы знаем, какая часть прямой А + ct расположена внутри полигона Р. Обычно
задача отсечения ставится так: какая часть отрезка прямой АС для заданных точек А и С расположена
внутри Р? Исследуем эту задачу подробно.
Задача отсечения
На рис. 4.42 показаны некоторые аспекты задачи отсечения. На рис. 4.42, а показан случай, когда обе
точки А и С расположены вне Р, но часть отрезка АС находится внутри Р. Если рассматривать отрезок
АС как часть луча, задаваемого выражением А + ct, где вектор с = С - А, тогда точка А соответствует
точке этого луча в момент времени t = 0, а точка С соответствует точке луча при t = 1. Эти «моменты
времени луча» («гау times») отмечены на рисунке. Для того чтобы найти отсеченный отрезок, вычис-
лим tin и tout только что описанным способом. Отрезок, подвергнутый отсечению, имеет концевые точки
А + ctin и А + ctoul. На рис. 4.42, б точка С расположена внутри Р, следовательно, значение tout больше
единицы. Отсеченный отрезок имеет концевые точки А + ctin и С. На рис. 4.42, в и А, и С расположены
внутри Р, хмагктку отсеченный отрезок равен АС.
Рис. 4.42. Отрезок, отсеченный полигоном
В общем случае мы вычисляем tin и сравниваем его с нулем. Большая из величин tin и нуль использу-
ется в качестве «времени» для первой концевой точки отсеченного отрезка. Меньшая же из двух вели-
чин: единицы и tout — используется для нахождения второй концевой точки. Таким образом, концевые
точки отсеченного отрезка равны:
А' - А + с max(0, tin) (4.63)
и
С' = С + с min(tout, 1).
Но как вычислять t.n и fout? Мы должны рассмотреть каждую из ограничивающих полигон Р прямых
поочередно и найти, в каком месте луч А + ct пересекает эту прямую. Мы предполагаем, что каждая
ограничивающая прямая записана в точечной нормальной форме в виде пары {В, п}, где В — некоторая
точка данной прямой, ап— внешняя нормаль для этой же прямой; это означает, что п указывает на-
правление наружу от полигона. Так как это направление от полигона, проверка по уравнению (4.61)
приводит к следующим трем условиям:
если п • с > 0, то луч покидает Р;
если п • с - 0, то луч параллелен прямой; (4.64)
если п • с < 0, то луч входит в Р.
Для каждой из ограничивающих прямых находим:
О время соударения луча с ограничивающей прямой (используется уравнение (4.59));
О входит ли луч в полигон или выходит из него (используется уравнение (4.64)).
242
Глава 4. Векторные инструменты для графики
Если луч входит в полигон, то мы знаем, что момент времени, в который луч войдет в полигон (если
войдет вообще), не может быть более ранним, чем момент пересечения ihit, найденный другим способом.
Нам нужно определить t.m как самое раннее из возможных времен входа. Для каждого момента пересе-
чения при входе thil заменим tn на max(tin, ilnt). Аналогично мы отслеживаем £out — самое позднее из воз-
можных времен выхода, и для каждого момента пересечения при выходе заменяем tout на min(£out, ihit).
Здесь луч
находится вне Р
Возможный
интервал
Здесь луч
находится внв Р
tout
Рис. 4.43. Возможный интервал для пересечения
Полезно представлять себе интервал времени [tjn, tout] как возможный интервал (candidate interval)
времени t — такой интервале t, в пределах которого луч может находиться внутри объекта. На рис. 4.43
приведен пример задачи отсечения. Мы знаем, что точка А + ct не может находиться внутри Р ни в какой
момент времени t вне возможного интервала. По мере проверки каждой ограничивающей прямой воз-
можный интервал сокращается, так как £jn увеличивается, a tout уменьшается: части этого интервала как
бы «отсекаются». В начале решения задачи отсечения мы устанавливаем tin равным нулю, a tout — едини-
це, следовательно, возможный интервал равен [0,1]. Алгоритм вычисления следующий:
1. Инициализируем возможный интервал [0, 1]*.
2. Для каждой ограничивающей прямой применяем уравнение (4.59) для нахождения времени
пересечения thjt и определения того, произошло данное пересечение на входе или на выходе:
• Если ibjt — пересечение на входе, то устанавливаем iin - max(tin, rhit).
• Если ilnt — пересечение на выходе, то устанавливаем tout - min(tout, thit).
Если в какой-либо точке tin становится больше, чем t^, то луч вообще не пересекает Р и проверка
прекращается.
3. Если возможный интервал не является пустым (нулевым), то, согласно уравнению (4.63), отре-
зок от А + сГ.п до А + с£ои[ расположен внутри Р. Для задачи отсечения прямых эти точки являют-
ся конечными точками отсеченной прямой. Для задачи пересечения лучом они являются соот-
ветственно входной и выходной точками луча.
Отметим, что мы прекращаем проверку, как только возможный интервал обращается в нуль. Это
называется досрочным выходом (early out): если мы до окончания процесса проверки устанавливаем,
что луч находится вне полигона, то для экономии времени мы немедленно выходим из проверки.
На рис. 4.44 показан типичный пример отсечения: мы ищем часть отрезка АС, расположенную внут-
ри полигона Р. Начальное значение времени £.п устанавливаем в нуль, a i — в единицу. Луч «стартует» из
точки А в момент t = 0 и движется к точке С, достигая ее при t = 1. Мы проверяем луч относительно каж-
дой ограничивающей прямой Ео, Ер... поочередно, причем t.m и fout при необходимости обновляются.
Предположим, что при проверке луча относительно Ео мы обнаруживаем при t - 0,83 пересечение на
выходе. Тогда tout устанавливается в 0,83 и возможный интервал становится равным [0,0,83]. Затем луч
проверяется относительно Е( и обнаруживается пересечение на выходе при t = 0,66. Это уменьшает воз-
можный интервал до [0,0,66]. Проверка относительно L2 выявляет пересечение на выходе при t = 3,4.
Это не дает нам ничего нового: мы уже знаем, что луч находится вне полигона при t > 0,66. Тест относи-
тельно Е3 показывает пересечение на входе при t = -4,7, то есть в более ранний момент, чем текущее
значение t.m. Тест относительно Li указывает на пересечение на входе при t = 0,2, поэтому t.n обновляется
до 0,2. И, наконец, проверка относительно L5 выявляет пересечение на входе при t = 0,28, и на этом про-
' В задаче о пересечении луча, когда луч неограниченно распространяется в обоих направлениях, мы полагаем tm - и toul = «>.
На практике tin присваивается какое-либо большое по модулю отрицательное значение, a tml — большое положительное значение.
4.8. Задачи о пересечениях многоугольников
243
верка завершается: возможный интервал составляет [0,28, 0,66]. И действительно, луч находится внут-
ри Рдля всех t от 0,28 до 0,66.
Рис. 4.44. Проверка нахождения луча внутри выпуклого полигона
Таблица 4.1. Обновления значений tm и tout
L(прямая) ^>ut
0 0 0,83
1 0 О,бб
2 0 0,66
3 0 0,66
4 0,2 0,66
5 0,28 0,66
В табл. 4.1 показана последовательность обновлений значений tin и toul, которые происходили при
тестировании относительно каждой из описанных выше прямых.
4.8.3. Алгоритм Сайруса—Бека
Давайте теперь применим только что изложенные идеи к созданию подпрограммы, осуществляющей
отсечение отрезка прямой границами произвольного выпуклого полигона. Впервые этот метод был со-
здан Сайрусом и Беком (Cyrus, Beck) [Cyrus, 78]. Позднее высокоэффективный отсекатель для прямо-
угольных окон, основанный на аналогичных идеях, был разработан Лиангом и Барски (Liang, Barsky)
[Liang, 84]. Последний алгоритм будет рассматриваться в тематическом задании в конце главы.
Подпрограмма, реализующая отсекатель Сайруса—Бека, имеет следующий интерфейс:
int CyrusBeckClip(Line& seg, LineList& L);
Параметрами являются отрезок прямой seg, подлежащий отсечению (он содержит первую и вторую
концевые точки, именуемые соответственно seg.first и seg.second), а также список прямых, ограничи-
вающих полигон. Подпрограмма производит отсечение seg относительно каждой прямой из списка L,
как описано в разделе «Пересечение с лучами и отсечение для выпуклых полигонов’», и помещает отсе-
ченный отрезок обратно в seg (поэтому seg должен передаваться по ссылке). Подпрограмма возвращает
следующие значения:
О 0, если никакая часть отрезка не располагается в Р (возможный интервал пуст);
О 1, если некоторая часть отрезка располагается в Р.
244
Глава 4. Векторные инструменты для графики
Листинг 4.3. Псевдокод отсекателя Сайруса-Бека для выпуклого полигона, двумерный случай
int CyrusBeckClip(LineSegment& seg, LineList L)
{
double numer. denom:
// used to find hit time for each line
// используются для нахождения времени соударения
//с каждой прямой
double tin -0.0. tOut -1.0:
Vector2 c. tmp:
form vector: c - seg. second - seg.first
11 формируем вектор: с - seg.second - seg.first
for(int i - 0: i < L.num: i++)
// chop at each bounding line
// отсекаем на каждой ограничивающей прямой
{
form vector tmp - L.line[i].pt - first
// формируем вектор tmp - L.line[i].pt - first
numer - dot(L.line[i].norm. tmp):
denom - dot(L.line[i].norm. c);
if(ichopCKtln, tOut numer. denom.)) return 0;
// early out
// досрочный выход
}
// adjust the endpoints of the segment; do second one 1st.
// корректируем концевые точки отрезка:
// сначала делаем второй
if (tout < 1.0 )
// second endpoint was altered
// вторая концевая точка была изменена
{
seg.second.х - seg.first.х + c.x * tout:
seg.second.у - seg.first.у + c.y * tout:
}
if (tin > 0.0)
// first endpoint was altered
// первая концевая точка была изменена
{
seg.first.х - seg.first.х + c.x * tin:
seg.first.у - seg.first.у + c.y * tin:
}
return 1:
// some segment survives
// какой-то отрезок остается
}
В листинге 4.3 приведен псевдокод алгоритма Сайруса-Бека. Типы LineSegment, LineList и Vector2
являются типами данных, удобными для хранения используемых величин (см. упражнения в конце это-
го раздела). Переменные numer и denom содержат соответственно числитель и знаменатель выражения
для £hit из уравнения (4.59):
numer = п • (В - А);
denom = п • с. (4.65)
Отметим, что значение seg. second обновляется первым, поскольку нам приходится использовать ста-
рое значение seg.first для обновления как seg.first, так и seg.second.
4.8. Задачи о пересечениях многоугольников
245
Листинг 4.4. Отсечение относительно одной ограничивающей прямой
int chopCI(doublе& tin, doubles tOut. double numer. double denom)
{
double tHit:
if(denom < 0)
// ray is entering
// луч входит
{
tHit - numer / denom:
ifCtHit > tOut) return 0;
// early out
// досрочный выход
else 1f(tHit > tin) tin = tHit:
// take larger t
// берем большее t
else if(denom > 0)
// ray is exiting
// луч выходит
{
tHit = numer / denom;
if(tHit < tin) return 0;
// early out
// досрочный выход
if(tHit < tOut) tOut - tHit:
// take smaller t
// берем меньшее t
else
// denom is 0: ray is parallel
// denom (знаменатель) равен нулю: луч параллелен
if(numer <= 0) return 0;
// missed the line
// прошел мимо прямой
return 1;
// CI is still non-empty
// возможный интервал по-прежнему не пуст
Подпрограмма chopCI () приведена в листинге 4.4. Для вычисления момента соударения луча с огра-
ничивающей прямой в ней используются numer и denom из уравнения (4.65), а уравнение (4.64) исполь-
зуется для определения того, входит луч в полигон или выходит из него. Подпрограмма «отсекает» ту
часть возможного интервала CI, про которую выяснено, что она находится вне полигона.
Если луч параллелен прямой, то он может целиком располагаться или во внутреннем полупростран-
стве этой прямой, или целиком во внешнем полупространстве. Из этого следует, что numer = п(В - А)
является именно той величиной, которая определяет, какой из этих случаев имеет место (см. упражне-
ния ниже).
Трехмерный случай. Отсечение прямой границами выпуклого многогранника
Алгоритм отсечения Сайруса—Бека работает в трех измерениях точно так же, как и в двух. В трехмер-
ном случае ребрами окна становятся плоскости, ограничивающие выпуклый многогранник, а отрезок
прямой при этом висит в пространстве. В подпрограмме ChopCI () не требуется вообще никаких измене-
ний (поскольку она использует только значения скалярных произведений через переменные numer и
denom). Типы данных в подпрограмме CyrusBeckClipO должны быть, конечно, расширены до трехмерных
типов, а при задании концевых точек прямой необходимо задавать дополнительно z-компонент.
246
Глава 4. Векторные инструменты для графики
Практические упражнения
4.8.1. Типы данных для переменных в отсекателе Сайруса—Бека
Дайте подходящие определения для типов данных, таких как структуры или классы, для переменных
LineSegment, LineLi st и Vector2, используемых в алгоритме отсечения Сайруса—Бека.
4.8.2. Что делает numer<=0?
Нарисуйте эскизы векторов, связанных со значениями numer в подпрограмме chopCI О, и покажите, что
когда луч А + ct движется параллельно ограничивающей прямой п • (Р - В) = 0, то он располагается
целиком во внутреннем полупространстве этой прямой тогда и только тогда, когда numer > 0.
4.8.3. Нахождение отсеченной прямой
Определите, какая часть отрезка прямой с концевыми точками (2,4) и (20,8) расположена внутри че-
тырехугольного окна с углами (0,7), (9,9), (14,4) и (2,2).
4.8.4. Отсечение границами произвольных полигонов
В предыдущем разделе мы видели, как осуществляется отсечение отрезка прямой границами выпукло-
го полигона. Расширим эту процедуру до метода отсечения отрезка границами любого полигона.
Рис. 4.45. Когда луч находится внутри произвольного полигона Р?
Основная задача состоит в том, чтобы найти, когда луч А + ct расположен внутри полигона Р, задан-
ного списком вершин Ро, Pv..., PN_V Пример приведен на рис. 4.45.
Ясно, что в общем случае луч может входить в полигон Р и выходить из него много раз и что резуль-
тат отсечения отрезка границами Р может привести не к одному отрезку, а к целому списку отрезков.
Кроме того, полигон Р более не описывается набором бесконечных ограничивающих прямых в точеч-
ной нормальной форме; мы вынуждены работать с Оконечными отрезками типа Р3Р4, из которых фор-
мируются его ребра.
Данная задача близка к той, с которой мы уже имели дело в разделе «Пересечения прямых с плоско-
стями; отсечение»: нахождение пересечения двух отрезков прямой. Теперь мы пересекаем один отрезок
прямой последовательностью отрезков прямой, связанных с полигоном Р.
Мы будем представлять каждое ребро Р параметрически (а не в точечной нормальной форме). Напри-
мер, ребро Р3Р4 представляется в виде: Р3+ е3ы, где е3 = Р4 - Р3 — вектор ребра (edge vector), связанный с
вершиной Р3. В общем случае г-е ребро задается в виде Р.+ ей, где и изменяется в интервале [0,1];
г = 0,1,...,2V - 1; а вектор е. = Р.+, - Р(, причем, как всегда, PN отождествляется с Ро.
Напомним из раздела «Пересечения прямых с плоскостями; отсечение», что луч А + ct пересекает i-e
ребро, когда t и и имеют значения, удовлетворяющие равенству А + ct = Р + ей. Вводя вектор Ь. = Р - А,
ищем решение следующего уравнения относительно t и и:
ct = К + ел.
4.8. Задачи о пересечениях многоугольников
247
Уравнения (4.52) и (4.53) содержат нужные ответы. Выражая их с помощью введенных ранее обо-
значений, получаем:
е1 • Ь,
и = -у-----.
е, • с
Если вектор е,1 равен нулю, то г-е ребро параллельно направлению с луча, и, следовательно, пересечения
пет. Истинное пересечение с г-м ребром происходит только в том случае, если и попадает в интервал [0,1].
Нам необходимо найти все истинные пересечения луча с ребрами полигона Р и поместить их в спи-
сок моментов соударения. Назовем этот список hitList. Тогда псевдокод для такого процесса будет вы-
глядеть примерно так:
Initialize hitList to empty
for(int i - 0; 1 < N: i++)
// for each edge of P
// для каждого ребра полигона Р
{
build bi. ei for the i-th edge
// строки bi. ei для-1-го ребра
solve for t. u
// решаем относительно t. u x
if(u lies in [0.1])
// если u расположено в интервале [0. 1]
add t to the hitList
// добавляем t к списку hitList
Что мы будем делать дальше с этим списком, зависит от стоящей перед нами задачи.
Задача пересечения лучом
Где луч впервые сталкивается с полигоном Р? Ответить на этот вопрос можно, найдя наименьшее зна-
чение t в hitList. Назовем это значение t .. В таком случае точка соударения, как всегда, равна А + ctmjn.
Задача отсечения прямой
Для решения данной задачи нам требуется последовательность интервалов времени t, в течение кото-
рых луч находится внутри полигона Р. Поэтому необходимо отсортировать hitList по возрастанию t и
затем взять значения t попарно. Луч входит в полигон Рв первый момент времени каждой пары и выхо-
дит из Р во второй момент времени каждой пары.
Пример 4.8.2. Отсечение отрезка прямой АВ границами полигона Р
Пусть АВ — прямая, подлежащая отсечению, как показано на рис. 4.46, где А = (1,1), В = (8, 2). Поли-
гон Р задан списком вершин: (3, 2), (2,0), (6, -1), (4,1). Рассматривая каждое ребро поочередно, полу-
чаем при пересечениях следующие значения t и и.
Ребро U t
0 0,3846 0,2308
1 -0,727 -0,2727
2 0,9048 0,7142
3 0,4 0,6
4 0,375 0,375
248
Глава 4. Векторные инструменты для графики
Соударение с ребром 1 происходит при значении t, находящемся вне промежутка [0,1], поэтому
оно отбрасывается. Проведем сортировку (по возрастанию) оставшихся значений t и получим следую-
щий отсортированный список соударений: {0,2308, 0,375, 0,6, 0,7142}. Таким образом, луч входит в Р
при t = 0,2308, выходит из него при t = 0,375, снова входит при t = 0,6 и выходит из него в последний раз
при t = 0,7142.
Практическое упражнение
4.8.4. Произвести отсечение прямой
Найдите те части прямой от точки А = (1,3,5) до точки В = (9,3,5), которые находятся внутри полиго-
на со списком вершин (2,4), (3,1), (4,4), (3,3).
4.8.5. Более сложное отсечение
Алгоритмы отсечения являются основой компьютерной графики, в связи с чем было разработано боль-
шое количество эффективных алгоритмов такого рода. До сих пор мы исследовали два подхода: алгоритм
отсечения Кохена—Сазерленда (Cohen—Sutherland), описанный в главе 2, отсекает прямые граница-
ми выровненного прямоугольника; отсекатель Сайруса—Бека (Cyrus—Beck) обобщает первый алго-
ритм на отсечение прямой границами любого выпуклого многоугольника или многогранника. Однако
возникают ситуации, когда необходимо более сложное отсечение. Здесь мы коснемся двух таких мето-
дов, однако их детали рассмотрим в тематических заданиях в конце главы.
Отсекатель Сазерленда—Ходгмана (Sutherland—Hodgman) напоминает метод Сайруса—Бека, выпол-
няющий отсечение границами выпуклого полигона. Однако вместо того, чтобы отсекать один отрезок
прямой, он отсекает целый полигон (который не обязан быть выпуклым) границами выпуклого поли-
гона. Самое важное при этом, что на выходе он снова дает полигон (или несколько полигонов). Иногда
бывает необходимо сохранять полигональную структуру во время отсечения, так как отсеченные поли-
гоны, возможно, требуется заполнить каким-нибудь узором или цветом. А этого нельзя сделать, если
вершины полигона отсекаются по отдельности.
Алгоритм отсечения Уейлера—Азертона (Weiler—Atherton) отсекает любой полигон Р граница-
ми любого другого полигона W, как выпуклого, так и не выпуклого. Этот алгоритм может выдавать
на выходе ту часть полигона Р, которая располагается внутри W (внутреннее отсечение — interior
clipping), или часть Р, расположенную вне W (внешнее отсечение — exterior clipping). Кроме того,
внутри обоих полигонов — Ри W — могут содержаться отверстия («дыры»). Как и следовало ожи-
дать, данный алгоритм является более сложным, чем все другие, изученные до сих пор, однако бла-
годаря своей мощности он оказывается прекрасным дополнением к инструментарию для многих
приложений.
4.9. Резюме
249
4.9. Резюме
Векторы представляют собой удобный способ выражения многих геометрических соотношений, а опе-
рации, производимые над векторами, являются мощным средством алгебраического управления гео-
метрическими объектами. Многие алгоритмы компьютерной графики упрощаются и становятся более
эффективными благодаря использованию векторов. Поскольку большинство векторных операций вы-
ражаются одинаково, независимо от размерности их базового пространства, можно получать результа-
ты, одинаково верные для двумерного и для трехмерного пространства.
Скалярное (внутреннее) произведение двух векторов является фундаментальной величиной, упро-
щающей нахождение длины вектора и угла между двумя векторами. Оно может быть также использо-
вано для нахождения таких величин, как ортогональная проекция одного вектора на другой, располо-
жение центра окружности, проходящей через три заданные точки, а также направление отраженного
луча. Скалярное произведение часто используют для проверки ортогональности двух векторов друг
другу и в более общем случае для проверки того, является ли угол между двумя векторами острым или
тупым. Оно также применяется при работе с двумерным вектором а1 (перпом), который получается из
заданного вектора а с помощью левого поворота на 90°. В частности, скалярное произведение а1 • Ь
(перп-скалярное произведение) дает важную информацию о том, как векторы а и Ъ расположены отно-
сительно друг друга.
Векторное (внешнее) произведение двух векторов также дает информацию об угле между двумя век-
торами в трехмерном пространстве и, кроме того, задает вектор, перпендикулярный к ним обоим. Его
часто используют для определения вектора, нормального к плоскости.
При разработке алгоритма важно иметь компактное представление участвующих в нем графиче-
ских объектов. Двумя основными формами такого представления являются параметрическое пред-
ставление и неявная форма. Параметрическое представление «посещает» каждую точку объекта по мере
изменения параметра, так что этот параметр «указывает» на различные точки объекта.. Неявная форма
представляет собой уравнение, которому должны удовлетворять все точки объекта, и только они. Обыч-
но она имеет вид/(х, у) = 0 для двух измерений и /(х, у, г) = 0 для трех измерений, где /( ) — некоторая
функция. Значение /( ) дает информацию не только о том, находится или нет заданная точка на объек-
те, знак/( ) может указывать, на какой стороне от объекта расположена заданная точка. В данной главе
мы нашли представления для двух фундаментальных «плоских» объектов графики: прямых и плоско-
стей. Для этих объектов и параметрическая, и неявная формы являются линейными относительно сво-
их аргументов. Неявная форма может быть наглядно записана в виде скалярного произведения нор-
мального вектора и вектора, расположенного внутри объекта.
Произвольные линейные комбинации можно создавать из векторов, но не из точек. Для точек допу-
стимы только аффинные комбинации, в противном случае при изменении используемых систем коор-
динат, что часто случается в графике, возникнет хаос. Исключительно полезными в графике являются
аффинные комбинации точек, и мы показали, что они составляют основу «твининга» (построения про-
межуточных отображений) для анимации и для кривых Безье.
Параметрическая форма прямой линии или луча особенно удобна в таких задачах, как определение
точки пересечения двух прямых или точки пересечения луча с многоугольником или с многогранни-
ком. Эти задачи важны сами по себе, но они также лежат в основе алгоритмов отсечения, которые явля-
ются важнейшими в графике. Отсекатель Сайруса—Бека, который определяет, где прямая, заданная в
параметрической форме, попадает в ту же точку пространства, что и неявно заданные прямая или плос-
кость, может решать больший класс задач, чем отсекатель Кохена—Сазерленда из главы 2. Далее в этой
книге мы рассмотрим отсекатель Сайруса—Бека в других контекстах.
В представленных ниже тематических заданиях векторные инструменты применяются в различ-
ных интересных ситуациях, возникающих в графике, что еще нагляднее демонстрирует их мощность.
Вне зависимости от того, собираетесь вы доводить до конца программную реализацию этих мини-
проектов или нет, полезно будет прочитать их и представить себе, какой путь вы бы избрали для их
осуществления.
250
Глава 4. Векторные инструменты для графики
4.10. Тематические задания
Тематическое задание 4.1. Анимация с твикингом
Уровень сложности II.
Придумайте две интересные ломаные линии, подобных ломаным А и В, которые изображены на
рис. 4.47. Позаботьтесь о том, чтобы ломаные Л и В имели одинаковое число вершин, а при необходи-
мости искусственно добавьте дополнительную вершину, например, в верхний отрезок ломаной В.
1. Разработайте подпрограмму, подобную drawTween (А, В, n, t) из листинга 4.2, которая рисует
твин, соответствующий моменту t для ломаных А и В.
2. Разработайте подпрограмму, рисующую последовательность промежуточных изображений
(твинов) между АиВ при изменении параметра t от 0 до 1, и поэкспериментируйте с этой под-
программой. В качестве средства обеспечения плавности анимации примените двойную буфе-
ризацию, предлагаемую OpenGL.
3. Усовершенствуйте данную подпрограмму так, чтобы после постепенного изменения параметра
t от 0 до 1 он плавно уменьшался бы обратно до 0 и затем повторял все снова, вследствие чего
анимация будет многократно показывать превращение Л в В и обратно. Это чередование долж-
но повторяться до нажатия какой-либо клавиши.
4. Разработайте подпрограмму, позволяющую пользователю вводить с помощью мыши две лома-
ных, после чего будет осуществляться твининг этих ломаных. Пользователь нажимает клавишу
«А» и начинает отмечать точки для создания ломаной А; затем он нажимает клавишу «В» и от-
мечает точки для ломаной В. Нажатие клавиши «Т» прерывает этот процесс и начинает тви-
нинг, который продолжается до тех пор, пока пользователь не нажмет клавишу (quit). Пре-
дусмотрите случаи, когда пользователь вводит для А а В различное количество вершин: ваша
программа должна автоматически создать необходимое число дополнительных вершин вдоль
отрезков прямой (возможно, в их средних точках) на той ломаной, у которой точек меньше.
Рис. 4.47. Твининг двух ломаных
Тематическое задание 4.2. Разные окружности
Уровень сложности II.
Напишите приложение, которое позволяет пользователю вводить посредством мыши вершины тре-
угольника. Затем эта программа будет рисовать этот треугольник вместе с его вписанной, описанной и
девятиточечной окружностями, причем каждый объект должен иметь свой цвет. Постройте подпро-
грамму так, чтобы пользователь мог затем перемещать с помощью мыши вершины треугольника на но-
вые места, после чего этот новый треугольник вместе со своими тремя окружностями должен перерисо-
вываться заново.
251
4.10. Тематические задания
Мы видели в разделе «Приложение пересечения прямых: окружность, проходящая через три задан-
ные точки», как рисовать описанную окружность. Здесь мы покажем, как находить вписанную и девя-
титочечную окружности.
Вписанная окружность
Это окружность, которая «устроилась» внутри заданного треугольника и касается всех трех его сто-
рон1. На рис. 4.48, а показан треугольник АВС вместе с вписанной в него окружностью. Как было и
в случае с описанной окружностью, труднее всего найти центр вписанной окружности. Прямой метод2
основывается на том, что окружность, вписанная в треугольник АВС, является описанной окружностью
для другого треугольника, RST, вершины которого показаны на рисунке.
Рис. 4.48. Окружность, вписанная в треугольник АВС, является описанной окружностью для треугольника RST
Нам достаточно найти координаты точек R, S и Г и затем применить метод описанной окружности из
«Приложение пересечения прямых: окружность, проходящая через три заданные точки». На рис. 4.48, б
показаны расстояния от точек R, S и Тдо точек Л, В и С. В силу симметрии окружности расстояния |В - 7?|
и |В - 5| должны быть равны друг другу, и существует еще две пары отрезков, имеющих одинаковую
длину. Используя определения векторов а, Ь и с, согласно уравнению (4.56), имеем:
|а| = L. + L , |Ь| = L, + L, |с| = L + L,
откуда с помощью перегруппировки можно выразить La и
2Za = |а| + |с| - ]Ь|; 2Lb = ]а| + |Ь| - |с|.
Зная La и Lb, находим:
R = A+L±
1а1
S = В + Lb Д,
|Ь|
т = с + 4Д.
|с|
(Проверьте эти выражения!)
(4.66)
1 Отметим, что нахождение вписанной окружности попутно решает задачу нахождения единственной окружности, касательной
к трем неколлипеарным прямым на плоскости.
2 Предложен Расселом Сваном (Russell Swan).
252
Глава 4. Векторные инструменты для графики
Мы можем инкапсулировать вычисление точек R, S и Гпо точкам А, Ви Св простой подпрограмме
getTangentPoints(A, В, С, R. S. Т). Преимущество такого подхода состоит в том, что если у нас есть
подпрограмма excircleO, вычисляющая по трем точкам центр и радиус определяемой этими точками
описанной окружности, то можно использовать ту же самую подпрограмму для вписанной окружно-
сти. Поэкспериментируйте с этими инструментами.
Девятиточечная окружность
В каждом треугольнике имеется девять замечательных точек:
О середины трех сторон;
О основания трех высот;
О середины отрезков, соединяющих ортоцентр треугольника (точка пересечения трех высот) с его
вершинами.
Рис. 4.49. Девятиточечная окружность
Примечательно, что через все девять точек проходит единственная окружность! На рис. 4.49 показа-
на девятиточечная окружность1 для произвольного треугольника. Такую девятиточечную окружность,
наверно, проще всего нарисовать как окружность, проходящую через середины сторон треугольника.
Тематическое задание 4.3. Находится ли точка Q
внутри выпуклого полигона Р?
Уровень сложности II.
Задан выпуклый многоугольник Р. Пусть требуется определить, находится заданная точка Q внутри
полигона Р или нет. Однако во время изучения выпуклых полигонов в разделе «Работа с выпуклыми
полигонами и полиэдрами» мы выяснили, что этот вопрос равносилен вопросу о том, расположена ли
точка Q во внутреннем полупространстве каждой ограничивающей полигон Р прямой. Для каждой ог-
раничивающей прямой L. от нас требуется только проверить, составляет ли вектор Q - Р. с внешней
нормалью угол больше 90°. Другими словами:
Qрасположена внутри Р, если (Q - Р) • п.< 0 для i - 0,1,..., N- 1. (4.67)
Рисунок 4.50 иллюстрирует такую проверку для конкретной ограничивающей прямой, проходящей
через вершины Р, и Р2. Для точки Q, расположенной внутри Р, угол с вектором п( тупой (больше 90°).
Для точки Q', расположенной вне Р, этот угол острый (меньше 90°).
Напишите и протестируйте программу, позволяющую пользователю выполнять следующие действия:
1. Задавать с помощью мыши вершины выпуклого полигона Р.
2. Последовательно задавать с помощью мыши проверяемые точки Q.
1 «Эта окружность — первое, что по-настоящему поражает в любом курсе элементарной геометрии», — писал Дэниел Педо в своей
книге «Окружности» (Daniel Pedoe, Circles. New York: Pergamon Press, 1957).
4.10. Тематические задания
253
3. Печатать слова «внутри» или «снаружи» в зависимости от того, находится данная точка Q внут-
ри полигона Р или нет.
Рис. 4.50. Находится ли точка Q внутри полигона Р?
Тематическое задание 4.4. Отражения в комнате
(двумерная трассировка луча)
Уровень сложности II.
В данном тематическом задании используются некоторые идеи и инструменты, описанные в этой
главе, для осуществления замечательной, но в то же время простой имитации. Эта имитация выполня-
ет своего рода трассировку луча, причем для простоты иллюстрации в двумерном пространстве. Трех-
мерная трассировка луча подробно рассматривается в главе 14.
В этой модели прослеживается путь одного маленького шарика, когда он рикошетирует от различ-
ных стен внутри некоторой «комнаты». На рис. 4.51, а показано поперечное сечение выпуклой комна-
ты W, имеющей шесть стен и содержащей три выпуклых «колонны». Шарик начинает свой путь из точ-
ки 5 и движется по прямой линии в направлении с до тех пор, пока не ударится о препятствие, после
чего он «отражается» от этого барьера и движется в новом направлении, снова по прямой. Это движе-
ние продолжается вечно. На рис. 4.51, б показан пример пути в виде ломаной линии, которую описыва-
ет луч, представляющий этот шарик.
Рис. 4.51. Эксперимент с двумерной трассировкой луча
Для любого заданного начального положения луча S и его направления с трассировка его пути тре-
бует выполнения следующих двух операций.
О Нахождение первой стены «комнаты», о которую ударяется шарик.
О Нахождение нового направления, которое получит луч после отражения от этой первой стены.
254
Глава 4. Векторные инструменты для графики
Обе эти операции уже обсуждались в этой главе. Отметим, что при создании каждого нового луча
его начальная точка всегда находится на какой-нибудь стене, в «точке соударения» с этой стеной.
Мы описываем комнату списком выпуклых полигонов: колоннаО, колонна!,..., и располагаем их так,
что колоннаО и есть та «комната», внутри которой происходит все действие. Информация о колоннах
хранится в соответствующих массивах точек. Для каждого луча, начинающегося в положении 5 и дви-
гающегося в направлении с, просматривается весь массив колонн для определения пересечений этою
луча с каждой из колонн. Эта проверка осуществляется с использованием алгоритма Сайруса—Бека из
раздела «Алгоритм Сайруса—Бека». Если происходит соударение с колонной, то в качестве «момента
соударения» берется время «входа» луча в колонну. Инкапсулируем этот тест в подпрограмму
int rayH1t(Ray thisRay. int which, double& tHit)
вычисляющую время удара tHit луча thisRay о колонну номер which (pillarwhich) и возвращающую 1,
если луч ударяется о колонну, и 0, если луч проходит мимо. Подходящим типом для Ray является
struct{Point2 startPt; Vector2 dir;} или соответствующий класс; эта структура содержит стартовую
точку луча 5 и его направление с.
Мы хотим знать, с какой колонной луч столкнется в первый раз. Ответ на этот вопрос можно полу-
чить, если зафиксировать самое раннее время соударения при просмотре списка колонн. Следует учи-
тывать только положительные значения времени соударения: отрицательные моменты соударения со-
ответствуют соударениям с точками, лежащими на противоположном направлении пути луча. Когда
это самое раннее время соударения найдено, от точки 5 в эту точку рисуется отрезок прямой.
Необходимо найти направление отраженного луча во время его движения от точки соударения. Это
направление с' отраженного луча выражается через направление с падающего луча с помощью уравне-
ния (4.27) и имеет следующий вид:
с' = с - 2(с' • п ) п, (4.68)
где п — единичный вектор нормали к той стене комнаты, с которой происходит соударение. Если со-
ударение происходит с колонной внутри комнаты, то используется внешняя нормаль; если же удар при-
ходится на стену самой комнаты, то используется внутренняя нормаль.
Напишите и запустите программу, рисующую путь луча, отражающегося от внутренних стен комна-
ты W и от стенок выпуклых колонн внутри этой комнаты. Составьте ее так, чтобы пользователь мог
читать список колонн из внешнего файла. Кроме того, пользователь должен задавать начальное поло-
жение луча и его направление. (См. в главе И двумерную трассировку луча в эллиптической комнате.)
Тематическое задание 4.5. Отсечение Сайруса—Бека
Уровень сложности II.
Напишите и запустите программу, выполняющую отсечение последовательности отрезков граница-
ми выпуклого полигона. Пользователь задает полигон, отмечая мышью последовательность точек (пос-
ле нажатия клавиши «С» полигон считается законченным и начинается отсечение). Затем генерирует-
ся последовательность отрезков со случайно выбираемыми концевыми точками.
Сначала каждый отрезок рисуется полностью красным цветом, а затем та его часть, которая распо-
ложена внутри полигона, окрашивается в синий цвет.
Тематическое задание 4.6. Отсечение полигона границами
выпуклого полигона: отсечение Сазерленда—Ходгмана
Уровень сложности III.
До сих пор изучаемые нами алгоритмы отсечения отсекали отдельные отрезки прямых границами
полигона. Однако когда производится отсечение полигона границами окна, этот полигон можно разбить
в процессе отсечения на несколько других полигонов, как предложено на рис. 4.52, а. Возможно, этот
4.10. Тематические задания
255
полигон требуется заполнить цветом или узором, а это означает, что этот узор должен окрашивать каж-
дый из отсеченных фрагментов, как показано на рис. 4.52, б. Следовательно, алгоритм отсечения дол-
жен рисовать ребра ab, cd и т. д. и должен сформировать новый полигон (или несколько полигонов) из
исходного полигона. Важно, что алгоритм не сохраняет ненужные ребра, такие как Ьс, в качестве эле-
ментов нового полигона, и такие ребра не будут нарисованы, так как в действительности они должны
быть невидимыми.
Рис. 4.52. Отсечение полигона границами полигона
Назовем тот полигон, который подлежит отсечению, отсекаемым {subject) полигоном S. Тот поли-
гон, границами которого отсекается полигон S, будем называть отсекающим (clip) полигоном С. Как же
нам произвести отсечение полигона S, представленного списком вершин, границами полигона С, чтобы
создать совокупность списков вершин, правильно представляющую множество отсеченных полигонов?
Здесь мы используем алгоритм отсечения Сазерленда—Ходгмана, который достаточно прост и от-
секает любой полигон (выпуклый или нет) границами выпуклого отсекающего полигона. Этот алго-
ритм может оставлять ненужные ребра, которые в дальнейшем необходимо удалить.
В силу того, что может возникнуть множество различных вариантов, нам необходим организован-
ный метод слежения за ходом процесса отсечения. В алгоритме Сазерленда—Ходгмана используется
метод «разделяй и властвуй»: сложная задача разбивается на несколько простых. Этот метод основан
на подходе Сайруса—Бека, однако в данном случае он должен работать со списком вершин, представля-
ющих полигон, а не просто с парой вершин.
Подобно алгоритму Сайруса—Бека, алгоритм Сазерленда—Ходгмана отсекает полигон 5 относитель-
но каждой ограничивающей полигон С прямой поочередно, оставляя только ту часть, которая находит-
ся внутри С. После того как все ребра полигона С будут обработаны таким способом, полигон 5 будет
отсечен границами полигона С, как и требовалось. На рис. 4.53 показано применение этого алгоритма
к отсекаемому семиугольнику 5 и отсекающему прямоугольнику С. В этом примере мы будем описы-
вать каждый шаг процесса. Полигон S описывается списком вершин a, b, с, d, e,f, g. S отсекается относи-
тельно верхнего, правого, нижнего и левого ребер С поочередно, и на каждой стадии из старого списка
вершин генерируется новый список. Этот список описывает один или несколько полигонов и выступа-
ет в качестве отсекаемого полигона для отсечения относительно следующего ребра полигона С.
Таким образом, основная операция состоит в отсечении полигона(ов), описанных посредством вход-
ного списка вершин, относительно текущего ребра полигона Сив создании выходного списка вершин.
Чтобы проделать это, мы просматриваем входной список, формируя последовательные ребра из смеж-
ных пар вершин. Каждое такое ребро Е имеет первую и вторую концевые точки, которые мы назовем
соответственно $ и р. Существует четыре возможных ситуации для точек $ и р: они могут обе распола-
гаться во внутренней полуплоскости отсекающего ребра, обе быть в его внешней полуплоскости, одна
из них может быть по одну, а другая — по другую сторону от ребра, и наоборот. В каждом из этих случа-
256
Глава 4. Векторные инструменты для графики
ев соответствующие точки выводятся в новый список вершин (или добавляются в него), как это пока-
зано на рис. 4.54. Все случаи и соответствующие им действия сведены в следующий список:
а) $ и р во внутренней полуплоскости ребра: выводится р\
б) s во внутренней полуплоскости, р снаружи: найти точку пересечения i и вывести ее;
в) s и р снаружи: не выводится ничего;
г) s снаружи, р внутри: найти точку пересечения г, вывести i и затем р.
Рис. 4.53. Отсечение полигона по Сазерленду—Ходгману
Теперь проследим за ходом работы алгоритма Сазерленда—Ходгмана по рис. 4.54. Рассмотрим отсе-
чение полигона 5 верхним ребром прямоугольника С. Входной список вершин на этой стадии состоит
из а, Ь, с, d, e,f, g. Для удобства первым из списка берется то ребро, которое идет от g к а, поскольку оно
«соединяет» конец списка с его первым элементом^ Следовательно, здесь роль s играет точка g, а роль р —
точка а. Ребро g, а (что означает ребро, идущее от точки g к точке а) пересекает отсекающее ребро в новой
4.10. Тематические задания
257
точке «1», которая выводится в новый список. (Список вывода на каждой стадии алгоритма показан
под соответствующим чертежом на рис. 4.54.) Следующим ребром во входном списке является а, Ь.
Поскольку обе конечные точки находятся выше отсекающего ребра, не выводится ничего. Третье ребро,
Ь, с, дает на выходе сразу две точки, 2 и с, а четвертое ребро, с, d, выводит точку d. Этот процесс продол-
жается до тех пор, пока не проверено последнее ребро, /, g, которое выводит точку g. Таким образом,
новый список вершин для следующей стадии отсечения имеет вид: 1,2, с, d, е, f, g. Весьма полезно тща-
тельно проработать пример на рис. 4.53 полностью, чтобы увидеть, как работает данный алгоритм.
Внутри L Снаружи
г
Рис. 4.54. Четыре случая для каждого ребра полигона S
Отметим, что образовались ненужные ребра (3,6 и 9,10), соединяющие три фрагмента полигона,
созданные алгоритмом отсечения. Такие ребра могут вызвать проблемы в некоторых алгоритмах,
осуществляющих заполнение полигонов. Удалить эти досаждающие ребра возможно, хотя и непросто
[Sutherland, 193].
Реализуйте алгоритм отсечения Сазерленда—Ходгмана и протестируйте его на различных приме-
рах полигонов. Пользователь с помощью мыши намечает выпуклый полигон С и затем таким же обра-
зом создает отсекаемый полигон S. Каждый из них в момент создания рисуется красным цветом. Затем
производится отсечение, и все отсеченные полигоны окрашиваются в синий цвет.
Тематическое задание 4.7. Отсечение одного полигона
границами другого: отсечение Вейлера—Азертона
Уровень сложности III.
Отсечение Вейлера—Азертона является наиболее общим механизмом отсечения из всех, которые мы
изучали. Оно отсекает произвольный полигон границами любого (возможно, невыпуклого) отсекаю-
щего полигона. Эти полигоны могут даже содержать отверстия.
9 Ф. Хилл
258
Глава 4. Векторные инструменты для графики
Елгоритм Сазерленда—Ходгмана, который мы изучали в тематическом задании 4.6, использует
выпуклость отсекающего полигона в том смысле, что применяются внутреннее и внешнее полупрост-
ранства. Однако в некоторых приложениях, таких как удаление невидимых поверхностей или визуали-
зация теней, приходится отсекать один невыпуклый полигон границами другого. В таких случаях отсе-
чение становится более сложным. Метод Вейлера—Ефертона отсекает любой полигон границами любого
другого, даже если в них содержатся отверстия. Он также позволяет применять теоретико-множествен-
ные понятия: объкдинкник (union), пкркскчкник (intersection) и ремносчь (difference) к двум полиго-
нам, которые мы будем рассматривать в тематическом задании 4.8.
Начнем с простого примера, показанного на рис. 4.55. Мдесь два невыпуклых полигона, обозначен-
ных SUBJ и CLIP, задаются списками вершин (a, b, с, d) и (А, В, С, D) соответственно. Примем согла-
шение располагать вершины в списке таким образом, чтобы внутренняя часть полигона находилась
справа от каждого ребра, когда мы обходим полигон от вершины к вершине согласно этому списку. На-
пример, внутренняя часть полигона SUBJ располагается справа от ребра, идущего от с к d, и справа от
ребра, идущего от d к а. Это аналогично перечислению вершин «по часовой стрелке».
Все точки пересечения двух данных полигонов определяются и помещаются в специальный список
(см. ниже). В данном примере таких пересечений шесть. Для отсечения полигона SUBJ границами по-
лигона СЫР будем идти по SUBJ в прямом направлении (так, чтобы его внутренняя часть была спра-
ва) до тех пор, пока не будет обнаружено «входящее» пересечение, то есть точка, являющаяся границей
перехода полигона SUBJ из внешней части полигона СЫР в его внутреннюю часть. Так мы находим
точку 1, и она заносится в выходной список, где записываются данные отсеченного полигона(ов).
Этот процесс легко изобразить геометрически: движемся вдоль SUBJ, отрезок за отрезком, до мо-
мента пересечения (точка 2 в примере). Теперь имеет смысл прекратить движение по SUBJ и вместо
этого перейти к обходу СЫР. Существует два способа перехода на отсекаемый полигон. Во-первых,
можно повернуться так, что СЫР будет обходиться в своем прямом направлении. При этом внутрен-
ние части обоих полигонов SUBJ и СЫР будут оставаться справа. Матем, найдя пересечение, снова по-
вернемся и проследуем вдоль SUBJ в его прямом направлении и т. д. Каждая обнаруженная вершина
или точка пересечения вносится в список вывода. Повторим процесс «повернуть и перескочить на дру-
гой полигон», обходя каждый из полигонов в его прямом направлении, до тех пор, пока не придем снова
к первой вершине. В этот момент список вывода состоит из (1, Ь, 2, В).
Теперь проверим, нет ли еще каких-либо пересечений с полигоном SUBJ. Обнаружена точка 3, и этот
процесс повторяется, в результате чего составляется следующий список вывода: (3,4,5,6). Дальнейшие
проверки пересечений показывают, что все они уже встречались, поэтому процесс отсечения прерывается,
4.10. Тематические задания
259
и в результате остаются два полигона (1, Ь, 2, В) и (3,4,5,6). Систематизированный способ реализации
процесса «следуй прямо и перескакивай» состоит в том, чтобы путем обхода каждого из полигонов (так,
чтобы его внутренняя часть была справа) и попутной записи вершин и точек пересечения (в том порядке,
в которым они обнаружены) создать следующие два списка:
SUBJLIST: а, 1, Ь, 2, с, 3,4, d, 5,6,
CLIPLIST: А, 6,3, 2, В, 1, С, D, 4,5.
(Как будут выглядеть эти списки, если между двумя полигонами не будет обнаружено пересечений?)
Таким образом, обход полигонов равносилен просматриванию списка, а перескакивание на другой по-
лигон равносильно переходу к другому списку.
Отметим, что когда составлены эти списки, в процессе остается очень мало геометрии — только тест
«находится ли точка вне полигона?», чтобы правильно идентифицировать входящую в список верши-
ну. Правильное направление, в котором нужно обходить каждый полигон, задается порядком следова-
ния элементов его списка. Ход выполнения этого алгоритма показан применительно к вышеприведен-
ному примеру на рис. 4.56.
a
SUBJJST: о
CLIPJ.IST: о
А
Запуск Перезапуск
Осмотрено Осмотрено
• = выводим эту точку
Рис. 4.56. Приложение метода Вейлера—Азертона
Пример более сложных полигонов, содержащих отверстия, показан на рис. 4.57. Те вершины, которые
описывают отверстия, также вносятся в список в таком порядке, чтобы внутренняя часть полигона распо-
лагалась справа от ребра. (В случае отверстий это можно назвать порядком «против часовой стрелки».)
Применяется то же правило, что и раньше: поворот и обход другого полигона в его прямом направле-
нии. Если начать с регистрации точки пересечения 1, то образуется полигон (1, 2, 3,4, 5, i, 6, Я). Затем,
начиная с регистрации точки пересечения 7, создаем полигон (7,8,9, с, 10, F). Какое входное пересечение
нужно использовать для создания третьего полигона? Это хорошее упражнение для построения спис-
ков SUBJLIST и CLIPLIST и для прослеживания операций алгоритма отсечения Вейлера—Азертона.
Как и во многих других алгоритмах, в основе которых лежат пересечения, нам требуется проверить,
как данный алгоритм работает в случаях, когда ребра полигонов CLIP и SUBJ параллельны и совпада-
ют на некотором конечном отрезке. Для того чтобы выполнить такую проверку, создадим такие поли-
гоны CLIP и SUBJ — в файлах или разрешив пользователю задавать их с помощью мыши. В этой реа-
лизации мы тщательно рассмотрим, как будет вести себя алгоритм в следующих ситуациях:
О Некоторые ребра SUBJ и CLIP параллельны и совпадают на некотором конечном отрезке.
О SUBJ или CLIP или они оба являются полигонами с особенностями.
О Некоторые ребра SUBJ и CLIP совпадают только в своих концевых точках.
О CLIP и SUBJ не пересекаются.
О SUBJ целиком лежит внутри отверстия CLIP.
260
Глава 4. Векторные инструменты для графики
Рис. 4.57. Отсечение Вейлера—Азертона: полигоны с отверстиями
Тематическое задание 4.8. Булевы операции с полигонами
Уровень сложности III.
Если рассмотреть полигон как множество точек (множество всех точек на границе или во внутренней
части полигона), то результатом операции отсечения Вейлера—Азертона будет пересечение (intersection)
двух полигонов — множество всех точек, принадлежащих обоим полигонам: CLIP и SUBJ. Полигоны
на выходе алгоритма Вейлера—Азертона состоят из точек, лежащих одновременно внутри CLIP и Ис-
ходного полигона SUBJ. В этом тематическом задании мы перейдем от пересечений к более общим тео-
ретико-множественным операциям с полигонами, которые часто называют «булевыми» («Boolean»)
операциями. Потребность в таких операциях часто возникает и при моделировании [Mortenson, 85], и
в графике (см. главу 14). В общем случае для двух множеств точек А и В определены следующие три
теоретико-множественные операции:
О Пересечение (intersection): А л В - {все точки в обоих множествах А и В}.
О Объединение (union): А и В = {все точки в А или в В или в них обоих}.
О Вычитание (разность, difference): А - В - {все точки в А, но не в В}.
Аналогичное определение дается для вычитания В - А.
Примеры этих множеств показаны на рис. 4.58.
Рис. 4.58. Полигоны, образованные в результате булевских операций над полигонами
4.10. Тематические задания
261
Нетрудно приспособить метод Вейлера—Азертона, который уже выполняет пересечение, к выпол-
нению операций объединения и разности полигонов А и В.
1. Вычисление объединения полигонов А и В. Для настройки этой операции будем обходить полигон А
в прямом направлении до тех пор, пока не обнаружим выходную точку пересечения — такую
точку, при переходе через которую полигон А из внутренней области полигона В становится его
наружной областью. Мы записываем эту точку пересечения и продолжаем обходить А до обна-
ружения следующего его пересечения с В. Затем мы переходим к обходу В в его прямом направ-
лении. При каждом последующем пересечении мы записываем вершину и переходим к обходу
другого полигона в его прямом направлении. Вернувшись к исходной вершине, ищем другие
выходные пересечения, в которых мы еще не побывали.
2. Вычисление разности полигонов А и В (внешнее отсечение — outside clipping). Поскольку нахож-
дение пересечения двух полигонов дает в результате отсечение одного из них границами друго-
го, операция вычитания «заслоняет» один полигон другим. Это означает, что разность двух по-
лигонов SUBJ - CLIP состоит из тех частей полигона SUBJ, которые располагаются вне CLIP.
Не подлежит рисованию ни одна часть SUBJ, расположенная внутри границы CLIP, так что
область, заданная полигоном CLIP, надежно защищена, или заслонена.
Для реализации этого алгоритма мы будем обходить полигон А до обнаружения его входной точки
пересечения с полигоном В. Затем переходим к В и обходим в его обратном направлении — так, чтобы
внутренняя часть В оставалась слева. После достижения следующей точки пересечения снова переска-
киваем на А. При достижении каждой точки пересечения мы перескакиваем на другой полигон и всегда
обходим полигон А в прямом направлении, а В — в обратном. Ряд примеров по образованию объедине-
ния и разности двух полигонов приведен на рис. 4.59. Применение операций объединения и вычитания
формирует следующие полигоны:
POLYA U POLYB
4. 5, g. h (отверстие)
8. В. С. D. 1. Ь. с. d
2, 3. 1. j (отверстие)
6, Н. Е. F. 7. ^отверстие)
d с
Рис. 4.59. Формирование объединения и разности двух полигонов
262
Глава 4. Векторные инструменты для графики
POLYA-POLYB
4. 5, 6. Н. Е. F. 7, е, В. В. С, D. 1. а
2. 3. к
POLYB-POLYA
1. Ь. с. d. 8. 5. g. h. 4. А. 3. i. j. 2
7. f. 6. G
Отметьте, как нужно правильно обрабатывать отверстия в полигонах (Е, F, G, Н) и (k, i, j) и убеди-
тесь в том, что алгоритм генерирует отверстия должным образом. (Отверстия являются полигонами,
которые заносятся в список «против часовой стрелки».)
Усовершенствуйте метод Вейлера—Азертона так, чтобы он мог формировать объединение и разность
двух полигонов, и отработайте полученные подпрограммы на различных полигонах. Для облегчения
тестирования формируйте полигоны А и В в файлах или с помощью алгоритмов. Рисуйте исходные
полигоны AvB двумя различными цветами, а результат операции — третьим цветом.
4.11. Дополнительная литература
Введение в векторную алгебру подробно описывается во многих книгах. Лучшей из них является книга
Хоффмана «О векторах» (Hoffmann. About Vectors). Серия книг «Графические драгоценности» (Graphics
Gems series [Gems]) предоставляет новые подходы и результаты алгоритмизации арифметики и гео-
метрии векторов и предназначается для профессионалов в области компьютерной графики. Выделим
три превосходных статьи: Алана Паета «Использование для вычислений тождества, содержащего по-
ловинный угол: очарование тангенса половинного угла» (Alan Paeth. «А Half-Angle Identity for Digital
Computation: The Joys of the Half Tangent»), Рона Голдмана «Треугольники» (Ron Goldman. «Triangles»),
а также Лопеца-Лопеца «Снова о треугольниках» (Lopez-Lopez. «Triangles Revisited» [Lopez, 133]). Реко-
мендуем также две книги, которые глубже других проникают в природу геометрических алгоритмов —
Морет и Шапиро «Алгоритмы от Р до NP* (Moret and Shapiro. Algorithms From P to NP [Moret, 142])
и Препараты и Шамоса «Компьютерная геометрия, введение» (Preparata and Shamos. Computational
Geometry, an Introduction [Preparata, 172]).
Преобразования объектов
□ Разработка инструментальных средств для преобразования одного
изображения в другое.
□ Знакомство с основными концепциями аффинных преобразований,
осуществляющих повороты, масштабирования и сдвиги
в различных сочетаниях.
□ Разработка функций, использующих аффинные преобразования
объектов в компьютерных программах.
□ Разработка инструментов для преобразования координатных
фреймов.
□ Демонстрация установки камеры для визуализации трехмерной
сцены с использованием OpenGL.
□ Разработка сцен с помощью Scene Design language (SDL) — языка
проектирования сцен, и написание программ, способных читать
SDL-файлы и рисовать описанные в них сцены.
Минус на минус дает плюс, и причина этого не обсуждается.
В. X. Оден (W.H. Auden)
«Если я съем пирожок, — подумала она, — обязательно что-нибудь случится с моим ростом...»
Она проглотила один пирожок и с радостью заметила, что росту в ней поубавилось.
Льюис Кэрролл (Lewis Carroll) Алиса в стране чудес
(пер. Н. Демуровой)
Множество ярких мозаичных стен и полов в Альхамбре (Испания) доказывает нам, что мавры
были великие мастера в заполнении плоскостей одинаковыми фигурами, прилегающими друг
к другу без зазоров. Как жаль, что их религия запрещает им рисовать картины!
М. К. Эшер (М. С. Escher)
Главная цель настоящей главы — разработка технологий для работы с особенно мощным семейством
преобразований — аффинными преобразованиями (affine transformations) — как с карандашом в руках,
так и в компьютерной программе, как с пспользованйем, так и без использования OpenGL. В разделе 5.1
«Введение» доказывается необходимость применения в компьютерной графике двумерных и трехмерных
264
Глава 5. Преобразования объектов
аффинных преобразований, а также даются некоторые основные определения. В разделе 5.2 «Введение
в преобразования» даются определения двумерных аффинных преобразований, в частности, в терминах
матриц. Для облегчения понимания того, какие объекты подвергаются изменениям и каким образом,
используется понятие координатных фреймов. Кроме того, в этом разделе показано, как элементарные
аффинные преобразования могут производить масштабирование, поворот, перенос и сдвиг. В подраз-
деле 5.2.5 «Композиция афинных преобразований» показано, что можно комбинировать сколько угод-
но аффинных преобразований и в результате получить другое аффинное преобразование, также опи-
сываемое матрицей. В подразделе 5.2.7 «Некоторые полезные свойства афинных преобразований»
рассматриваются ключевые свойства всех аффинных преобразований — особенно важно, что после
этих преобразований сохраняются прямые линии, плоскости и параллельность, — и показывается, по-
чему такие преобразования столь распространены в компьютерной графике.
В разделе 5.3 «Трехмерные аффинные преобразования» идеи раздела 5.2 «Введение в преобразова-
ния» распространяются на трехмерные аффинные преобразования; здесь показано, что все основные
свойства, имевшие место для двух измерений, сохраняются и для трех. Однако трехмерные преобразо-
вания — особенно трехмерные повороты — более сложны, чем их двумерные аналоги, и их труднее пред-
ставить наглядно, поэтому особое внимание уделено описанию и сочетанию различных поворотов.
В разделе 5.4 «Изменения систем координат» обсуждается взаимосвязь между преобразованием то-
чек и преобразованием систем координат. В разделе 5.5 «Использование аффинных преобразований
в программах» показано, как управлять аффинными преобразованиями в программах, если доступен
OpenGL, а также насколько упрощаются многие операции, необходимые в графических программах,
с применением этих преобразований. Моделирующие преобразования и использование «текущего пре-
образования» проиллюстрированы целым рядом примеров. В разделе 5.6 «Рисование трехмерных сцен
с применением OpenGL» рассматривается моделирование трехмерных сцен и их рисование при помо-
щи OpenGL. Определено понятие «камеры», которая устанавливается и ориентируется так, чтобы она
сделала нужный моментальный снимок сцены. В разделе также рассматривается использование преоб-
разований для изменения размеров и расположения объектов согласно задуманной сцене. Моделиро-
вание и визуализация трехмерных сцен показана на нескольких примерах, приведен необходимый для
этого программный код. Кроме того, в данном разделе вводится язык описания сцен (Scene Description
Language — SDL) и показывается, как писать приложения, которые могут нарисовать любую сцену, опи-
санную на этом языке. Такое воспроизведение требует разработки ряда классов для поддержки чтения
и анализа SDL-файлов, а также для создания списков объектов, подлежащих визуализации. Эти клас-
сы доступны на web-сайте данной книги.
В конце главы дано несколько тематических заданий для развития ее основных концепций, которые
предоставляют возможность поработать с аффинными преобразованиями в графических программах.
В одном из таких заданий вас просят разработать подпрограммы, выполняющие преобразования при
отсутствии OpenGL. Описываются также способы разложения аффинного преобразования на элемен-
тарные операции и разработки быстрой подпрограммы для рисования дуг окружностей, основанной на
эквивалентности поворота трем последовательным сдвигам.
5.1. Введение
Аффинные преобразования {affine transformations) являются краеугольным камнем всей компьютер-
ной графики и составляют основу OpenGL, так же как и большинства других графических систем. Од-
нако они являются проблемой для многих программистов, потому что их правильное применение час-
то вызывает затруднения. Особенно сложной сферой стала путаница понятий точек и векторов. Те и
другие выглядят очень похоже и часто выражаются в программах одним и тем же типом данных: как
правило, списком из трех чисел вроде (3,0, 2,5, -1,145). Однако подобная практика может привести к
5.2. Введение в преобразования
265
неприятностям в виде серьезных ошибок (bugs), которые крайне сложно выявить при отладке, в основ-
ном из-за того, что точки и векторы не преобразуются одинаковым образом. Но нам необходим метод
проведения правильных преобразований, и этого можно достичь, используя координатные фреймы
{coordinate frames) и соответствующие однородные координаты, как было описано в главе 4.
5.2. Введение в преобразования
Вселенная наполнена разными волшебными вещами, терпеливо
дожидающимися, пока мы станем более сообразительными.
Е. Филлпоттс (Е. Phillpotts)
Мы уже рассмотрели несколько примеров преобразований, по крайней мере в двух измерениях. Напри-
мер, в главе 3 преобразование «окно — порт просмотра» использовалось для масштабирования и переме-
щения в порт просмотра объектов, расположенных в мировом окне, к их окончательному размеру и рас-
положению.
Мы хотим расширить эти понятия и получить более гибкий способ управления размерами, ориен-
тацией и расположением интересующих нас объектов. В последующих разделах мы разработаем нуж-
ные инструменты, основанные на мощном аффинном преобразовании (affine transformation), которое
является главным элементом компьютерной графики. Мы будем оперировать с ним как в двух, так и в
трех измерениях.
На рис. 5.1, а приведены рисунки двух вариантов простейшего домика, полученные до и после того,
как была преобразована каждая из его точек. В данном случае домик был уменьшен в размерах, немного
повернут, а затем передвинут вверх и вправо. Суммарное преобразование является комбинацией трех
элементарных преобразований: масштабирования, поворота и перемещения. На рис. 5.1, б изображен
трехмерный домик до и после такого же преобразования: каждая трехмерная точка этого домика под-
вергнута масштабированию, повороту и перемещению.
Рис. 5.1. Рисунки объектов до и после их преобразования
Преобразования очень полезны в таких ситуациях.
1. Мы можем составить «сцену» из нескольких объектов, как это показано на рис. 5.2. Каждый
объект, например арку, легче всего разработать (одну для всех экземпляров) в своей собствен-
ной «основной» системе координат. Затем сцена составляется посредством помещения несколь-
ких «экземпляров» этой арки различного размера в различные места, с использованием нужно-
го преобразования каждого экземпляра. На рис. 5.3 приведен трехмерный пример, в котором
сцена составлена из множества экземпляров куба; в результате пх масштабирования и позицио-
нирования создан целый «город».
266
Глава 5. Преобразования объектов
Рис. 5.2. Составление картинки из одинаковых объектов простой формы
Рис. 5.3. Составление трехмерной сцены из примитивов
2. Некоторые объекты, как, например, снежинка на рис. 5.4, имеют определенную симметрию. Мож-
но разработать один «мотив» и затем составить всю форму с помощью отражений, поворотов и
переносов данного мотива.
Рис. 5.4. Использование «мотива» для создания рисунка
3. Дизайнеру может понадобиться рассмотреть свой объект с различных точек наблюдения и по-
лучить изображения с каждой из них. Можно поворачивать сцену и осматривать ее одной и той
же неподвижной камерой, однако, как это показано на рис. 5.5, естественнее оставить сцену в
покое и передвигать камеру, ориентируя и позиционируя ее для каждого снимка. Подобное пе-
ремещение и ориентирование камеры может быть осуществлено с помощью трехмерных аффин-
ных преобразований.
4. В компьютерной анимации несколько объектов должны от кадра к кадру двигаться один отно-
сительно другого. Такой эффект может быть достигнут путем сдвига и поворота отдельной ло-
кальной системы координат каждого объекта в процессе анимации. Рисунок 5.6 дает пример
такой анимации.
5.2. Введение в преобразования
267
Рис. 5.5. Просмотр сцены с различных точек наблюдения
Рис. 5.6. Анимация посредством преобразования форм
С чего мы начнем? Использование преобразований с OpenGL
В нескольких начальных разделах данной главы были представлены основные концепции аффинных
преобразований и показано, как они приводят к определенным геометрическим эффектам, таким как
масштабирование, повороты и сдвиги, — как в двумерном, так и в трехмерном пространстве. Разумеет-
ся, конечная цель состоит в создании изображений объектов, преобразованных до необходимого разме-
ра, ориентации и положения, с тем чтобы они составили желаемую сцену. В целом ряде графических
платформ, в том числе и в OpenGL, предусмотрен так называемый «графический конвейер» («graphics
pipeline») или, иными словами, последовательность операций, применяемых ко всем точкам, которые
«пропускаются» через такой конвейер. Рисунок создается путем обработки каждой точки.
На рис. 5.7 показан упрощенный вид графического конвейера OpenGL. Приложение посылает на
конвейер последовательность точек Р2, Ру... посредством уже известных нам команд:
glBegin(GL_LINES);
glVertex3f(...):
// send Pl through the pipeline
// посылаем на конвейер точку Pl
glVertex3f(...):
// send P2 through the pipeline
// посылаем на конвейер точку Р2
glVertex3f(...);
// send P3 through the pipeline
// посылаем на конвейер точку РЗ
glEndO:
Как показано на рис. 5.7, все эти точки вначале подвергаются преобразованию, которое называется
«текущим преобразованием» («current transformation» — СТ) и изменяет их значения, генерируя дру-
268
Глава 5. Преобразования объектов
гую последовательность точек, например Q2, Q3...Если исходные точки Р. описывают некоторый
геометрический объект, то точки будут описывать преобразованный вариант того же самого объек-
та. Эти точки затем посылаются на следующие этапы преобразования и в конечном счете используются
для рисования окончательного изображения на дисплее.
Рис. 5.7. «Конвейер» OpenGL
Таким образом, СТ является ключевым инструментом управления графическими объектами, и для про-
граммиста приложения жизненно необходимо знать, как настроить СТ именно таким образом, чтобы были
произведены все желаемые преобразования. После изложения основной теории аффинных преобразова-
ний в разделе «Использование аффинных преобразований в программах» мы покажем, как это делается.
Преобразования объектов в сравнении с преобразованиями координат
Можно рассматривать преобразование с двух сторон: преобразование объекта (object transformation)
и преобразование координат (coordinate transformation). При преобразовании объекта координаты
каждой его точки изменяются в соответствии с некоторыми законами, а соответствующая система ко-
ординат остается неизменной. При преобразовании координат старая система координат преобразует-
ся в новую, и все точки объекта получают представление в этой новой системе координат. Эти два под-
хода тесно связаны между собой, каждый из них имеет свои преимущества, однако реализуются они
по-разному. Вначале мы рассмотрим основные идеи в терминах преобразований объекта, а затем при-
ложим их к преобразованиям координат.
5.2.1. Преобразование точек и объектов
Рассмотрим сначала общую идею преобразования, а затем частный случай аффинного преобразования.
Любое преобразование переводит каждую точку Р в пространстве (двумерном или трехмерном)
в новую точку Q согласно заданной формуле или алгоритму. На рис. 5.8 показаны примеры для двух и
трех измерений.
Как показано на рисунке, произвольная точка Рна плоскости отображена (is mapped) в другую точку Q.
Тогда мы говорим, что точка Q является образом (image) точки Р при отображении Т. На рис. 5.8, а
показана двумерная точка Р, отображаемая в новую точку Q, на рис. 5.8, б показана трехмерная точка Р,
отображаемая в новую точку Q. Преобразование всего объекта осуществляется посредством преобра-
зования каждой из его точек, причем для каждой точки используется, разумеется, та же самая функ-
ция Т{). Можно отображать за один раз целые совокупности точек. Такой совокупностью могут быть
все точки прямой или все точки окружности. Например, образ прямой L при преобразовании Тсостоит
из образов всех отдельных точек прямой Z1.
* Более строго: если S — множество точек, то его образ Г(5) является множеством всех точек Т(Р), где Р — некоторая точка из
множества S.
5.2. Введение в преобразования
269
Рис. 5.8. Отображение точек в новые точки
Рис. 5.9. Сложное преобразование фигуры
Большинство интересующих нас преобразований непрерывны, поэтому образ прямой линии есть
также связная линия некоторой формы, однако не обязательно прямая. При аффинных преобразованиях
тем не менее прямые линии сохраняются. Как мы увидим в дальнейшем, образ прямой линии после
аффинного преобразования Т также есть прямая линия. Большая часть этой главы будет посвящена
аффинным преобразованиям, однако для создания специальных эффектов могут быть использованы и
другие виды преобразований. Например, на рис. 5.9 показано сложное преобразование фигуры, которое
не может быть достигнуто ее аффинным преобразованием. Примененное здесь преобразование может быть
использовано для создания визуального эффекта или для того, чтобы подчеркнуть особенности объекта.
Чтобы сохранить прямые линии, при выполнении преобразований мы используем явный коорди-
натный фрейм. Напомним из главы 4, что координатный фрейм состоит из специальной точки Ь, назы-
ваемой началом координат, и нескольких взаимно перпендикулярных векторов (в двумерном случае
их обозначают i и j, а в трехмерном — i, j и к), которые служат осями этого координатного фрейма.
Рассмотрим вначале двумерный случай, поскольку он более нагляден. Какой бы координатный
фрейм мы ни использовали, точки Р и Q имеют следующие представления:
и
Р =
fa
Q =
а
1
270
Глава 5. Преобразования объектов
соответственно. Напомним: это означает, что точка Р находится в положении Р = Pi + PJ + f>, анало-
гичное выражение можно написать и для точки Q. Рг и Р# обычно называют координатами точки Р. Пре-
образование воздействует на это представление точки Р и на выходе дает представление точки Q в соот-
ветствии с некоторой функцией Т(); то есть:
'QA (р/
Qy =т ру
id Id
или, более кратко:
Q-P(P).
(5.1)
(5.2)
Сама функция Т() может быть сложной, например:
cos(Px)e^
1 + P,2
1
к У
и такие преобразования могут привести к интересным геометрическим эффектам, однако мы ограни-
чимся более простыми семействами функций: линейными относительно Р. и Р. Именно это свойство
характеризует аффинные преобразования.
5.2.2. Аффинные преобразования
Короче, что такое алгебра? Это вон те треугольные штуки?
Дж. М. Бэрри (J. М. Barrie)
Аффинные преобразования наиболее часто используются в компьютерной графике. Помимо всего про-
чего, они упрощают масштабирование, поворот и перестановку изображений. Последовательность аф-
финных преобразований легко может быть преобразована в простое суммарное аффинное преобразо-
вание; кроме того, аффинные преобразования допускают компактное матричное представление.
Форма аффинных преобразований проста: координаты точки Q являются линейными комбинация-
ми соответствующих координат точки Р. В матричной записи это выглядит так:
'QA +
Qy = т21Р.+т22Ру+т23
(5-3)
где тп, ш12,... — шесть известных констант. Компонент Q состоит из долей Рх и Ру, то же касается и Qy-
Такое «перекрестное опыление» компонентов х и у вызывает повороты и сдвиги.
Аффинное преобразование равенства (5.3) имеет удобное матричное представление, которое помо-
гает уяснить суть дела1:
fa)
Qy
т\2 тЧ ( Рх '
т22 т23 Ру
(5.4)
Непосредственное перемножение членов правой части этого равенства показывает, что оно совпада-
ет с равенством (5.3). В частности, отметим, что третья строка матрицы обеспечивает равенство едини-
Обзор матриц дан в приложении 2.
5.2. Введениевпреобразования
271
це третьему компоненту Q. Для любого аффинного преобразования третья строка матрицы всегда рав-
няется (0,0, 1).
Векторы могут быть преобразованы так же, как и точки. Напомним, что если координаты вектора V
равны V и V, то его представление в координатах фрейма является вектором-столбцом с нулевым тре-
тьим компонентом. Действие на вектор того же аффинного преобразования, какое применялось в ра-
венстве (5.4) для точек, имеет следующий вид:
'"’ll
ти2|
о
ТИ,2
О
7П|3'
(5.5)
причем ясно, что исходный вектор превращается в другой вектор: его третий компонент всегда равен
нулю.
Практическое упражнение
5.2.1. Применить преобразование
Аффинное преобразование задано следующей матрицей:
' 3 0 5'
-212.
<° ° и
Найдите образ Q точки Р - (1,2).
Решение
'8'
2
' 3 0 5VT
-2122
5.2.3. Геометрические эффекты элементарных двумерных
аффинных преобразований
Аффинные преобразования осуществляют комбинации из четырех элементарных преобразований: пе-
ремещение, масштабирование, поворот и сдвиг.
На рис. 5.10 показан пример действия каждого типа преобразований, примененного в отдельности.
Перемещение
Часто требуется переместить изображение в другое положение на дисплее. Часть аффинного преобра-
зования, отвечающая за перемещение, располагается в третьем столбце преобразующей матрицы:
(5.6)
0
0
или просто
(р.+^
Qy = Ру + W23
Тогда в обычных координатах имеем Q = Р + d, где d = (ти13, т23) — «вектор перемещения».
Глава 5. Преобразования объектов
272
,.„А.....
Рис 5.10. Преобразование географической карты: а) перемещение; б) масштабирование; в) поворот; г) сдвиг
Если, например, вектор перемещения равен (2,3), то каждая точка будет перенесена в новую точку,
которая на две единицы правее и на три единицы выше исходной точки. В этом случае точка (1, -5)
преобразуется в точку (3, -2), а точка (0,0) — в точку (2,3).
Масштабирование
Масштабирование изменяет размер изображения и использует два масштабных множителя — Sx и Sy
для координат х и у соответственно:
(QX,Q,)-(5A>W-
Тогда матрица для масштабирования в и Sy раз соответственно в координатных направлениях х и
у имеет следующий простой вид:
'Sx 0 (Г
о S, о
0 0 1
к /
(5.7)
Более строго такой способ масштабирования называется масштабированием относительно начала
отсчета (scaling about the origin), поскольку каждая точка Р передвигается в раз дальше от начала отсчета
в направлении х и в Sy раз дальше от начала отсчета в направлении у. Если масштабный множитель
отрицателен, то происходит также отражение (reflection) относительно координатных осей. На рис. 5.11
показан пример, в котором масштабирование (Sx, Sy) “ (-1,2) применено к совокупности точек. Каждая точ-
ка отражается относительно оси у и одновременно масштабируется в 2 раза в ^-направлении.
Существуют также «чистые» отражения, при которых каждый из масштабных множителей равен +1
или -1. Пример такого отражения:
т(рх,ру)-(-рх,р,),
(5.8)
в результате которого происходит зеркальное отражение картинки посредством «переворота» ее по го-
ризонтали относительно оси у, причем каждое значение координаты х заменяется на -х. (Как выглядит
матрица этого преобразования?)
5.2. Введение в преобразования
273
Рис. 5.11. Масштабирование и отражение
Если оба масштабных множителя одинаковы (Sx=* Sy= S), то такое преобразование называется рав-
номерным масштабированием (uniform scaling) или увеличением (magnification) относительно начала
отсчета, с кратностью увеличения |5|. Если S отрицательно, то происходят отражения относительно обе-
их осей. Точка отодвигается от начала отсчета в |5| раз дальше. Если |5| < 1, то точки будут придвигаться
ближе к началу отсчета, что приводит к уменьшению (или «антиувеличению» — «demagnification»)
изображения. Если же масштабные множители различны, то такое масштабирование называется диф-
ференцированным масштабированием (differential scaling).
Практическое упражнение
5.2.2. Нарисуйте эффект масштабирования
Аффинное преобразование, состоящее из чистого масштабирования, использует масштабные мно-
жители Sx = 3 и Sy = -2. Определите и нарисуйте изображения каждого из трех объектов, показанных
на рис. 5.12, после такого преобразования. (Используйте то обстоятельство (оно будет проверено
позже), что аффинные преобразования переводят прямые линии в прямые линии, а эллипсы — в эл-
липсы.)
Рис 5.12. Объекты для масштабирования
Поворот
Одной из основных операций в графике является поворот изображения относительно заданной точки
на некоторый угол. На рис. 5.13 показано множество точек, которое поворачивается относительно на-
чала отсчета на угол 0 = 60°.
В том случае, когда Т( ) является поворотом относительно начала отсчета, вектор перемещения d
равен нулю и уравнение Q = Т(Р) имеет следующий вид:
Qx~ Pxcos(0) - P^sin^),
Q,-Pxsin(0) + P,cos(0). (5.9)
274
Глава 5. Преобразования объектов
Как будет показано ниже, при положительных значениях угла 0 поворот осуществляется против
часовой стрелки (CCW rotation). В матричной форме чистый поворот относительно начала отсчета
имеет вид:
<cos(0) -sin(0) 0^
sin(0) cos(0) 0
0 0 1
\ 7
(5.10)
Пример 5.2.1
Найти преобразованную точку Q, полученную при повороте точки Р - (3,5) относительно начала от-
счета на угол 60°.
Решение
Для угла 60° cos(0) = 0,5 и sin(0) - 0,866, тогда из уравнения (5.9) следует:
Qx= (3)(0,5) - (5)(0,866) - -2,83
и
(3)(0,866) + (5)(0,5) - 5,098.
Проверьте полученный результат на миллиметровке, для чего проведите из точки (3, 5) дугу в 60° и
прочитайте координаты отображенной точки. Кроме того, проверьте численно, что точки Q и Р нахо-
дятся на одинаковом расстоянии от начала отсчета. (Чему равно это расстояние?)
Рис. 5.14. Вывод преобразования поворота
Вывод преобразования поворота
Мы хотим продемонстрировать, что уравнение (5.9) верно. На рис. 5.14 показано, как найти коор-
динаты точки Q, полученной в результате поворота точки Р относительно начала отсчета на угол 0.
Если точка Р находится на расстоянии R от начала отсчета под некоторым углом ф (к оси ОХ), то
5.2. Введение в преобразования
275
Р “ (Pcos(0), .Rsin(ф)). Точка Q должна отстоять от начала координат на такое же расстояние, что и Р,
но под углом 0 + ф (к оси ОХ). После тригонометрических преобразований получим, что координаты
точки Q равны:
Qx= Pcos(0 + ф),
Qy~ Rsin(Q + ф).
Подставим в это уравнение два известных тригонометрических соотношения:
cos(0 + ф) - cos(0)cos(0) - sin(0)sin(0),
sin(0 + ф) = sin(0)cos(0) + cos(0)sin(0)
и после замены Рх= Pcos(0) и Р - Psin(0) получим уравнение (5.9).
Практическое упражнение
5.2.3. Поверните точку
Примените уравнение (5.9) для нахождения образа каждой из следующих точек после поворота отно-
сительно начала отсчета:
а) (2,3) на угол -45°;
б) (1,1) на угол -180°;
в) (60,61) на угол 4°.
В каждом случае проверьте результат на миллиметровке и численно сравните расстояния исходной
точки и ее образа от начала отсчета.
Решение
а) (3,5355,0,7071);
б) (-1,-1);
в) (55,5987, 65,0368).
Сдвиг
На рис. 5.15 ггриведен пример сдвига «в х-направлении» (или «вдоль х»), В этом случае координата у
каждой точки остается неизменной, а каждая координата х перемещается на величину, которая линей-
но возрастает с ростом у. Сдвиг в х-направлении описывается следующими формулами:
Рх+ hPy,
Q ~Р,
^У У
где коэффициент h определяет, какая доля координаты у точки Р должна быть добавлена к координа-
те х. Значение h может быть положительным или отрицательным. Матрица, соответствующая такому
типу сдвига, имеет вид:
'1 Л О'
0 1 0
(5.И)
0 0 1
к /
Сдвиг иногда используют для создания курсивных (italic) букв из стандартных (regular). Можно
осуществлять сдвиг «вдоль у», для которого Рх и Qy= gPx + Ру для некоторой величины g, в таком
случае матрица преобразования имеет вид:
'10 0'
g 1 о
0 0 1
к 7
(5.12)
276
Глава 5. Преобразования объектов
Пример 5.2.2
В какую точку произойдет сдвиг точки (3,4), если в уравнении (5.11) h = 0,3?
Решение
Q = (3 + (0,3)4,4) = (4,2,4).
Пример 5.2.3
Пусть в уравнении (5.12) g = 0,2. В какую точку отображается точка (6, -2)?
Решение
Q = (6,0,2 • 6 - 2) = (6, -0,8).
Более общий вид сдвига «вдоль» произвольной прямой линии рассматривается в тематическом за-
дании в конце этой главы. Важной особенностью сдвига является то, что определитель его матрицы равен
единице. Как мы увидим позднее, из этого следует, что площадь фигуры при сдвиге не изменяется.
Практическое упражнение
5.2.4. Сдвиг прямых линий
Рассмотрим сдвиг, для которого g = 0,4 и h = 0. Поэкспериментируйте с различными множествами из
трех коллинеарных точек, чтобы убедиться, что после сдвига точки остаются коллинеарными. Затем,
исходя из того, что прямые после сдвига остаются прямыми, определите, в какие объекты превратятся
после сдвига следующие отрезки прямых:
а) горизонтальный отрезок прямой между точкой (-3, 4) и точкой (2,4);
б) горизонтальный отрезок прямой между точкой (-3, -4) и точкой (2, -4);
в) вертикальный отрезок прямой между точкой (-2, 5) и точкой (-2, -1);
г) вертикальный отрезок прямой между точкой (2,5) и точкой (2, -1);
д) отрезок прямой между точкой (-1, -2) и точкой (3, 2).
5.2.4. Инвертирование аффинного преобразования
Большинство представляющих интерес аффинных преобразований являются неособенными (nonsingular);
это означает, что определитель т матрицы М из равенства (5.4), равный1
detM = mnm22-m12m21, (5.13)
отличен от нуля. Отметим, что третий столбец матрицы М, содержащий величину перемещения, не вли-
яет на величину определителя, так как в третьей строке матрицы М стоят два нуля. В тех редких случа-
ях, когда будут использоваться особенные преобразования, мы будем отмечать это особо.
1 Обзор определителей дается в приложении 2.
5.2. Введение в преобразования
277
Полезно иметь возможность отменять результат преобразования. Это особенно просто делать с не-
особенными аффинными преобразованиями. Если точка Р преобразована в точку Q в соответствии с урав-
нением Q = МР, то мы просто умножаем слева обе части этого уравнения на матрицу, обратную к М,
которая обозначается Л/*1, и пишем:
P = MlQ. (5.14)
Матрица, обратная к М, имеет вид1:
detAf I -т21 тп
Используем эту формулу для получения матриц элементарных обратных преобразований:
О Масштабирование [матрица М получена из матрицы (5.7)]:
О Поворот [матрица М получена из матрицы (5.10)]:
' cos(0)
-sin(0)
0
к
М~х
sin(0) О
cos(9) 0
0 1
7
О Сдвиг [матрица М получена из матрицы (5.11)]:
'1 -Л
М'1 = 0 1
О'
о
1° 0 ч
О Перемещение (при обратном преобразовании перемещение просто вычитается, а не прибавляется):
о
1
о
0
0
к
М~х =
~т\Ч
-Щ23
Практические упражнения
5.2.5. Что является обратным преобразованием для поворота?
Докажите, что обратным преобразованием для поворота на угол 0 является поворот на угол -0. Обо-
снованно ли это геометрически? Почему?
5.2.6. Обращение сдвига
Является ли обращение сдвига тоже сдвигом? Докажите, почему да или почему нет.
1 Обзор обратных матриц дается в приложении 2.
278
Глава 5. Преобразования объектов
5.2.7. Обратная матрица
Вычислите матрицу, обратную к данной:
5.2.5. Композиция аффинных преобразований
Прогресс — это неплохо — один раз, но он продолжается слишком долго.
Огден Нэш (Ogden Nash)
Не так уж часто мы выполняем только одно элементарное преобразование; обычно в приложении тре-
буется, чтобы мы создали сложное преобразование из нескольких элементарных. Например, нам может
понадобиться:
О переместить на вектор (3, -4),
О затем повернуть на 30°,
О затем масштабировать с помощью множителя (2, -1),
О затем переместить на (0, 1,5),
О и, наконец, повернуть на -30°.
Как эти отдельные преобразования объединяются в одно суммарное преобразование? Процесс по-
следовательного применения нескольких преобразований с целью формирования единого суммарного
преобразования называется компоновкой, или композицией (composing), этих преобразований; иногда
употребляется еще более сложный термин: конкатенация (concatenating). Как мы увидим, при компо-
новке двух аффинных преобразований результирующее преобразование является (к счастью) тоже
аффинным.
Рис. 5.16. Композиция двух преобразований
Посмотрим, что происходит, когда компонуются два двумерных преобразования, Т(( ) и Т2( ).
Как показано на рис. 5.16, ) преобразует точку Р в точку Q, а Г2( ) преобразует точку Q в точку IT.
Какое преобразование Т( ) преобразует точку Р сразу в точку W? Иными словами, какова сущность
w- т2(0) = т2(1\(Р))?
Пусть эти два преобразования представлены матрицами и М2. Тогда точка Р вначале преобразу-
ется в точку М{Р, которая затем преобразуется в М2(МХР). В силу свойства ассоциативности последнее
выражение равно (M^f^P, тогда мы имеем:
W=MP, (5.16)
где суммарное преобразование представлено одной матрицей
M-M2Mt. (5.17)
5.2. Введение в преобразования
279
При использовании однородных координат аффинные преобразования компонуются посредством
простого умножения матриц. Отметим, что матрицы расположены в порядке, обратном по отношению
к тому, в котором эти преобразования применяются. Если мы сначала применяем преобразование с
матрицей М(, а затем к результату применяем преобразование Т2 с матрицей М2, то матрица суммарного
преобразования равна М2Ме то есть вторая матрица в произведении стоит первой, если читать слева
направо. (При преобразовании систем координат мы увидим как раз противоположный порядок.)
Рассуждая аналогично, любое количество аффинных преобразований может быть скомпоновано
простым умножением соответствующих им матриц. Таким образом могут быть сформированы и за-
ключены в одну матрицу преобразования, содержащие любую последовательность поворотов, масшта-
бирований, сдвигов и переносов.
Пример 5.2.4. Построение композиции
Постройте преобразование, которое:
а) поворачивает на 45°,
б) затем масштабирует вдоль х на 1,5 и вдоль у на -2,
в) и, наконец, перемещает на вектор (3, 5).
Решение
Постройте три матрицы и перемножьте их в нужном порядке (первая идет последней и т. д.):
О
-2
О
OV 0,707
0 0,707
-0,707 О'! f 1,06 -1,06 3'
0,707 0 = -1,414 -1,414 5
0 1 0 0 1
7 4 7
Теперь, чтобы преобразовать точку (1,2), расширим ее до тройки (1,2,1), затем умножим ее на ком-
позитную матрицу и в результате получим тройку (1,94,0,758,1). Затем отбросим 1, чтобы увидеть ото-
браженную точку (1,94, 0,758). Полезно на миллиметровке произвести все эти преобразования пооче-
редно, чтобы увидеть, как отображается исходная точка (1,2).
5.2.6. Примеры композиции двумерных преобразований
Искусство — это задание схемы переживания, и наше эстетическое
наслаждение заключается в принятии этой схемы.
Алфред Норт Уайтхед (Alfred North Whitehead)
В данном разделе мы разберем несколько важных примеров компоновки двумерных преобразований и
посмотрим, как они себя ведут.
Пример 5.2.5. Поворот относительно произвольной точки
До сих пор все рассмотренные нами повороты были относительно начала отсчета. Но предположим,
что вместо этого мы хотим поворачивать точки относительно какой-либо другой точки на плоскости.
Как предложено на рис. 5.17, наша «опорная» точка — это точка V- (17,J7,), и мы хотим повернуть точ-
ку Р на угол 0 до совпадения ее с точкой Q. Чтобы проделать это, нам нужно свести поворот относитель-
но точки V к известному повороту относительно начала отсчета.
На рисунке показано, что если мы вначале преобразуем все точки так, чтобы точка V совпала с нача-
лом отсчета, то затем можно будет применить поворот относительно начала отсчета (преобразующий
точку Р' в точку Q'). После завершения этого поворота вся плоскость перемещается обратно, чтобы
установить точку V в прежнее положение. Таким образом, поворот состоит из следующих трех элемен-
тарных преобразований:
1. Переместить точку Р посредством вектора v = (-17, - V ).
2. Повернуть относительно начала отсчета на угол 0.
3. Переместить точку Р обратно посредством вектора V.
280
Глава 5. Преобразования объектов
Рис. 5.17. Поворот относительно точки
Создание матрицы для каждого элементарного преобразования и умножение этих матриц приводит
к следующему:
'1 О
О 1
о о
cos (0)
Vy sin(0)
1Д 0
-sin(O) OV1
cos(0) 0 0
0 1 0
J \
О -К/
1 -Vy
0 1J
^cos^O) -sin(O) df
sin(0) cos(0) dy
0 0 1
где компоненты суммарного преобразования равны:
dx—cos(0)V + sin(0)V + Vx,
Jy--sin(0)Vx-cos(0)Vy+ Vx.
Поскольку в полученном результате фигурируют те же самые члены cos(0) и sin(0), что и при поворо-
те относительно начала отсчета, мы видим, что поворот относительно произвольной точки эквивалентен
повороту относительно начала отсчета, за которым следует сложное перемещение с помощью {dx, dy).
В качестве характерного примера найдем преобразование, которое поворачивает точки на 30° отно-
сительно точки (-2, 3), и определим, в какую точку преобразуется точка (1, 2). При повороте на 30°
используются величины cos(0) = 0,866 и sin(0) = 0,5. В этом случае вектор перемещения равен (1,232,
1,402), тогда преобразование, которое нужно применить к произвольной точке (Рх, Ру), равно:
Qx=0,866P-0,5Р + 1,232,
(^=0,5Р+0.866Р + 1,402.
Применение этого преобразования к точке (1,2) дает в результате (1,098,3,634). Этот результат явля-
ется правильным, что может быть проверено путем вычерчивания на миллиметровке. (Проделайте это!)
Пример 5.2.6. Масштабирование и сдвиг относительно произвольных «опорных точек»
Подобно тому, как это было сделано в примере 5.2.5, часто бывает необходимо масштабировать все точ-
ки относительно некоторой опорной точки, отличной от начала отсчета. Поскольку элементарная опе-
рация масштабирования из равенства (5.7) производит масштабирование относительно начала отсче-
та, нужно проделать ту же последовательность операций «перемещение — преобразование — обратное
перемещение», что мы проделывали для поворотов. Такое масштабирование и обобщение операции
сдвига рассматриваются в упражнениях в конце данного раздела.
Пример 5.2.7. Отражения относительно наклонной прямой
Рассмотрим прямую линию, проходящую через начало отсчета и составляющую с осью х угол ₽, как
показано на рис. 5.18. Точка А отражается в точку В, а каждый из показанных на рисунке домиков отра-
жается в другой домик. Мы хотим создать преобразование, которое отражает любую точку Р относи-
тельно прямой, называемой осью отражения {axis of reflection), в данную точку Q. Является ли это пре-
образование аффинным?
Чтобы показать, что это аффинное преобразование, построим его из трех частей:
О поворот на угол ₽ (так, чтобы ось отражения совпала с осью х);
О отражение относительно оси х,
О обратный поворот на угол ₽, «восстанавливающий» ось отражения.
5.2. Введение в преобразования
281
Рис. 5.18. Отражение точки относительно наклонной оси
Каждое из этих преобразований представлено матрицей, и суммарное преобразование получается
посредством умножения трех матриц, откуда следует, что суммарное преобразование является аффин-
ным. Убедитесь в том, что каждый из этих этапов правильно представлен тремя приведенными ниже
матрицами и что их произведение вычислено верно:
' с
-s
О
s 0V1 О
с 0 0 -1
О lj[o о
'с1 - s2 —2cs О'
-2cs s2 — с2 О
О 0 1
к 7
О A f с -s О'
О s с О
Ф 0 \
Здесь буквой с обозначено cos(-0), а буквой 5 — sin(-0). Используя тригонометрические тождества,
напишем окончательный вид матрицы (проверьте это!):
^005(20) sin (20)
sin (20) -cos(20)
О О
О
О {отражение относительно оси под углом 0}
1
(5.18)
Общий вид этой матрицы напоминает матрицу поворота, за исключением того, что угол поворота
удвоен, а во второй столбец вкрался минус. Однако в действительности — это матрица отражения отно-
сительно оси, наклоненной под углом 0.
Практические упражнения
5.2.8. Классика: преобразование «окно — порт просмотра»
Мы уже рассматривали это преобразование в главе 3. Перепишем уравнение (3.2) в текущих обозначениях:
О С'
В D
О 1.
где компоненты A,B,CnD зависят от окна и порта просмотра и приведены в уравнении (3.3). Покажи-
те, что данное преобразование составлено из:
О перемещения посредством вектора (-W.I, - W.b) для совмещения левого нижнего угла окна с на-
чалом отсчета,
О масштабирования с параметрами (Л, В) для задания размеров изображаемых объектов,
О перемещения посредством вектора (У./, V.b) для переноса порта просмотра в желаемую позицию.
5.2.9. Формирование поворота относительно точки
Докажите, что преобразование на рис. 5.17 может быть записано в виде:
£= cos(6)(Pr- УД - sin(0)(P#- УД + Уд,
= sin(0)(Px- УД + cos(0)(Py- У) + У.
282
Глава 5. Преобразования объектов
Эта форма записи ясно показывает, что точка сначала перемещена посредством (-V*, затем
повернута и, наконец, снова перемещена посредством (Vx, V ).
5.2.10. Результирующая точка
Где будет находиться точка (8,9) после того, как ее повернули на 50° относительно точки (3,1)? Найди-
те соответствующую матрицу М.
5.2.11. Два способа рассмотрения
Отметьте на миллиметровке точку Р - (4, 7) и точку Q как результат поворота точки Р относительно
точки V - (5,4) на 45°. Теперь поверните точку Р относительно начала отсчета на 45°, в результате чего
получится точка Q', которая явно не совпадает с точкой Q. Разность между точками Q и Q' равна V- VM.
Покажите на графике точку V - VM и проверьте, что Q - Q' “ V- VM.
5.2.12. Случай, когда ось проходит через начало отсчета
Найдите такое аффинное преобразование, которое производит отражение относительно прямой, задан-
ной в параметрическом виде L(t) - А + bt. Докажите, что это преобразование сводится к уравнению.
(5.18) в случае, когда Л + bt проходит через начало отсчета. Как связаны между собой b и Р?
5.2.13. Отражение относительно прямой х = у
Докажите, что отражение относительно прямой х = у эквивалентно отражению относительно х и после-
дующему повороту на 90°.
5.2.14. Масштабирование относительно произвольной точки
Сформируйте аффинное преобразование, которое масштабирует точки относительно опорной точки
( V, V). Проверьте суммарное преобразование на нескольких точках, чтобы убедиться в правильности
работы операции масштабирования. Сравните это преобразование с преобразованием поворота отно-
сительно опорной точки.
5.2.15. Сдвиг относительно наклонной оси
Сформируйте преобразование, которое сдвигает точку вдоль оси, описываемой вектором и, наклонен-
ным на угол 0, как показано на рис. 5.19. Точка Р сдвигается вдоль вектора и на величину, являющуюся
частью f расстояния d между точкой Р и указанной осью.
Рис. 5.19. Сдвиг вдоль наклонной оси
5.2.16. Преобразование трех точек
Любое аффинное преобразование полностью определяется указанием того, что оно делает с тремя точ-
ками. Для иллюстрации этого утверждения найдите аффинное преобразование, которое превращает
треугольник С с вершинами (-3, 3), (0,3) и (0,5) в равносторонний треугольник D с вершинами (0,0),
(2,0) и (1, >/3 ), как показано на рис. 5.20. Для решения этой задачи используйте следующую последова-
тельность трех элементарных преобразований.
1. Переместить точку С вниз на 3 и вправо на 3, после чего вершина с превратится в с'.
2. Масштабировать по х в 2/3 раз и по у в -Уз/2 раз, чтобы треугольник D совпал с треугольником
С по ширине и по высоте.
3. Осуществить сдвиг на -1/V3 в направлении х, чтобы верхняя вершина треугольника С совпала
с соответствующей вершиной треугольника D.
5.2. Введение в преобразования
283
Рис 5.20. Превращение одного треугольника в другой
Убедитесь, что данное преобразование действительно преобразует треугольник С в треугольник D.
Теперь найдите преобразование, обратное к этому, и покажите, что оно превращает треугольник D об-
ратно в треугольник С.
5.2.17. Неподвижные точки аффинного преобразования
Точка F называется неподвижной {fixed) точкой аффинного преобразования Т{р) - Мр, если T(F) - F;
иными словами, если точка F удовлетворяет уравнению MF= F.
а) Докажите, что когда третий столбец матрицы М равен (0, 0, 1), так что перемещения нет, то на-
чало отсчета всегда является неподвижной точкой преобразования Т.
б) Докажите, что если F— неподвижная точка преобразования Т, то для любой точки Р справедли-
во равенство Т(Р) - М(Р - F) + F.
в) Что является неподвижной точкой при повороте относительно точки V? Докажите, что эта точ-
ка удовлетворяет условиям из пункта б).
г) Что является неподвижной точкой при масштабировании с масштабными множителями 5х и
относительно точки V?
д) Рассмотрите «пятую итерацию» Т{ ), приложенную к точке Р, задаваемую формулой
Т(Т(Т(Т(Т(Р))))).
(Вспомните системы итерируемых функций, описанные в конце главы 2). Используйте резуль-
тат пункта б), чтобы показать простую форму вывода точки R в терминах неподвижной точки F
преобразования Т{ ), а именно R - М5(Р -F) + Е
5.2.18. Нахождение матриц
Напишите явную форму матрицы размером три на три, представляющую каждое из следующих преоб-
разований:
а) Масштабирование с множителем 2 в х-направлении с последующим поворотом относительно
точки (2,1).
б) Масштабирование на (2, 3) с последующим перемещением на (1,1).
в) Сдвиг на 30 % по х, масштабирование в 2 раза в х-направлении с последующим поворотом отно-
сительно (1, 1) на 30°.
5.2.19. Нормирование прямоугольника
Найдите аффинное преобразование, которое отображает прямоугольник с вершинами (0,0), (2,1), (0,5)
и (-2,4) в квадрат с вершинами (0, 0) (1, 0), (1,1) и (0,1). Нарисуйте эти фигуры.
284
Глава 5. Преобразования объектов
5.2.20. Коммутативность некоторых преобразований
Докажите, что равномерное масштабирование коммутативно с поворотом в том смысле, что результи-
рующее преобразование не зависит от порядка, в котором применяются отдельные преобразования.
Покажите также, что два перемещения коммутативны, так же как и два масштабирования. Наконец,
докажите, что дифференцированное масштабирование не коммутативно с поворотом.
5.2.21. Отражение плюс поворот
Докажите, что отражение относительно х с последующим отражением относительно у эквивалентно
повороту на 180°.
5.2.22. Два последовательных поворота
Пусть 7?(0) обозначает преобразование, производящее поворот на угол 0. Докажите, что последователь-
ное применение 7?(0() и Т?(02) эквивалентно применению одного поворота Т?(04 + 02). Иными словами,
покажите, что последовательные повороты являются аддитивными.
5.2.23. Последовательность сдвигов
Скомпонуйте преобразование нз чистого сдвига вдоль оси х и следующего за ним чистого сдвига вдоль
оси у. Является ли оно по-прежнему сдвигом? Нарисуйте от руки пример того, что произойдет с квад-
ратом, имеющим центр в начале отсчета, если его подвергнуть, в одном случае, одновременному сдвигу,
а в другом — последовательности сдвигов вдоль двух осей.
5.2.7. Некоторые полезные свойства
аффинных преобразований
Мы уже видели, как представить двумерные аффинные преобразования в виде матриц, как составлять
сложные преобразования из последовательности элементарных преобразований, а также какой геомет-
рический эффект имеют различные двумерные аффинные преобразования. Прежде чем перейти к трех-
мерным преобразованиям, полезно резюмировать ряд общих свойств аффинных преобразований. Эти
свойства легко формулируются, а так как размерность преобразуемых объектов специально не огова-
ривается, то они применимы и к трехмерным аффинным преобразованиям. Единственное, что нам сей-
час следует знать о трехмерных преобразованиях, это то, что они, подобно своим двумерным аналогам,
могут быть представлены в однородных координатах в матричной форме.
При аффинных преобразованиях сохраняются
аффинные комбинации точек
Известно, что аффинной комбинацией двух точек Р, и Р2 является точка
IV= atPt + а2Р2,
для которой а( + а= 1. Что произойдет, если применить к такой точке Wаффинное преобразование Т( )?
Мы утверждаем, что Т(1Г) является той же самой аффинной комбинацией преобразованных точек;
то есть
Т(а^ + агР2) = Я1Т(Р4) + а2Т(Р2). (5.19)
Например, Г(0,7(2, 9) + 0,3(1, 6)) = 0,7Т((2,9)) + 0,ЗГ((1,6)).
Доказательство этого утверждения в общем виде основано на его линейности. При использовании
однородных координат мы видим, что точка P(W) есть MW, откуда из линейности произведения мат-
риц следует:
MW- M(atPt + а2Р2) - а{МРх + й2МР2,
что в обычных координатах и есть а(Т(Р1) + й2Т(Р2), что и требовалось доказать. Свойство аффинных
преобразований, состоящее в том, что аффинные комбинации точек сохраняются в результате аффинных
преобразований, выгладит элементарным и абстрактным, однако оно является основой всей мощи аффин-
ных преобразований. Иногда это свойство берется в качестве определения аффинного преобразования.
5.2. Введение в преобразования 185
При аффинных преобразованиях сохраняются прямые линии и плоскости
При аффинных преобразованиях сохраняются коллинеарность и «плоскостность», поэтому образом
прямой линии является также прямая линия. Чтобы убедиться в этом, напомним, что параметрическое
представление L(t) прямой, проходящей через точки А и В, само является аффинной комбинацией А и В:
L(t) = (1 - t)A + tB.
Это равенство представляет собой аффинную комбинацию точек, поэтому из предыдущего резуль-
тата следует, что образ L(t) является той же самой аффинной комбинацией образов точек А и В:
Q(t) - (1 - 0Т(Л) + tT(B). (5.20)
Эта формула является уравнением другой прямой линии, проходящей через точки Т(А) и Т(В).
Использование этого обстоятельства в компьютерной графике значительно упрощает рисование пре-
образованных отрезков прямой: достаточно просто вычислить две преобразованные концевые точки
Т(Л) и Т(В) и затем провести между ними прямую линию! Это избавляет от необходимости преобразо-
вывать каждую точку вдоль этой прямой, что совершенно невозможно.
С помощью тех же аргументов можно доказать, что плоскость преобразуется в другую плоскость.
Вспомним уравнение (4.45), где было дано параметрическое представление плоскости как аффинная
комбинация точек:
P(s, t) = sA + tB + (Д - s - t)C.
После преобразования каждой точки это уравнение примет следующий вид:
T(P(s, t)) - бТ(Л) + tT(B) + (1 - s - t)T(C),
что, очевидно, также является параметрическим представлением некоторой плоскости.
Сохранение коллинеарности и «плоскостности» гарантирует, что полигоны будут преобразовывать-
ся в полигоны, а плоские полигоны (planar polygons) (все вершины которых лежат в одной плоскости)
будут преобразовываться также в плоские полигоны. В частности, треугольники будут преобразовы-
ваться в треугольники.
Параллельность прямых и плоскостей сохраняется
Если две прямые или плоскости параллельны, то их образы после аффинного преобразования также
являются параллельными. Это легко доказать. Сначала сделаем это для прямых. Возьмем произволь-
ную прямую А + bt, имеющую направляющий вектор Ь. Эта прямая преобразуется в другую прямую,
задаваемую в однородных координатах уравнением М(А + bt) = МА + (Afb)t и имеющую направляю-
щий вектор Mb. Это новое направление не зависит от точки А. Следовательно, две различные прямые:
At + bt и А2+ bt, имеющие одно и то же направление, будут преобразованы в две прямые линии с одним
и тем же направлением Mb, то есть эти прямые параллельны. Важным следствием этого свойства явля-
ется то, что параллелограммы отображаются в другие параллелограммы.
Такое же доказательство применяется и к плоскости: ее направляющие векторы (см. уравнение 4.43)
преобразуются в новые направляющие векторы, значения которых не зависят от расположения этой
плоскости. Следствие этого свойства: параллелепипеды1 отображаются в другие параллелепипеды.
Пример 5.2.8. Преобразование сетки
Поскольку аффинные преобразования отображают параллелограммы в параллелограммы, они могут
менять форму геометрических объектов в достаточно ограниченных пределах. Для иллюстрации этого
ограничения применим произвольное двумерное аффинное преобразование Т к единичной квадратной
сетке, как показано на рис. 5.21. Поскольку сетка состоит из двух семейств параллельных прямых, пре-
образование Т отображает квадратную сетку в другую сетку, также состоящую из двух семейств парал-
лельных прямых. Чтобы получить представление о том, каким образом искажаются объекты в резуль-
1 Как мы увидим позже, параллелепипед является трехмерным аналогом параллелограмма: шесть его сторон являются попарно па-
раллельными гранями.
286
Глава 5. Преобразования объектов
тате преобразования, будем рассматривать сетку как «несущую с собой» любые объекты, которые в ней
определены. Это все, что способно сделать аффинное преобразование: исказить рисунки в той же мере,
в какой одна сетка преображается в другую. Новые прямые могут быть наклонены под любым углом,
они могут отстоять друг от друга на любое (одинаковое) расстояние, и две новые координатные оси не
обязаны оставаться перпендикулярными. И, конечно, вся сетка может быть расположена в любом месте
плоскости. Тот же результат имеет место и для трех измерений: все, что может сделать трехмерное аф-
финное преобразование, — это отобразить кубическую сетку в сетку из параллелепипедов.
Рис 5.21. Преобразованная сетка
'«п
«2!
О
«а
О
/и|3
«23
М =
Столбцы матрицы показывают преобразованный координатный фрейм
Полезно подробно изучить столбцы матрицы М аффинного преобразования, поскольку они показыва-
ют, как преобразуется координатный фрейм. Пусть матрица М имеет следующий вид:
а(ш,: ш2: пц), (5.21)
X >
так что столбцы этой матрицы равны соответственно ш,, т2 и т3. Первые два столбца являются вектора-
ми (их третий компонент равен нулю), в то время как последний столбец является точкой (его третий
компонент равен единице). Как всегда, интересующий нас координатный фрейм задается началом от-
счета 6 и базисными векторами i и j, которые имеют следующие представления:
Рис 5.22. Преобразование формирует новый координатный фрейм
Отметим, что вектор i преобразуется в вектор т( (проверьте это) согласно уравнению
m, - Mi,
5.2. Введение в преобразования
287
аналогично вектор j отображается в вектор ш2, а начало отсчета # отображается в точку ти3. Эти
отображения проиллюстрированы на рис. 5.22, а. Координатный фрейм (i, j, О) преобразуется в коор-
динатный фрейм (Шр т2, ?и3), и эти новые объекты в точности являются столбцами матрицы преобразо-
вания.
Оси этого нового координатного фрейма не обязательно перпендикулярны, не обязаны они иметь и
единичную длину. (Они сохраняют перпендикулярность, если преобразование включает в себя толь-
ко повороты и равномерные масштабирования.) Любая точка Р - Pvi + Pyj + 6 преобразуется в точ-
ку Q = Pxmt + P#m2 + т3. Иногда очень полезно взглянуть на матрицу аффинного преобразования с этой
точки зрения.
Пример 5.2.9. Поворот вокруг точки
Преобразование, которое уже изучалось в примере 5.2.5, состоит из поворота на 30° относительно точ-
ки (-2, 3) и имеет следующую матрицу:
'0,866 -0,5 1,232'
0,5 0,866 1,402 .
0 0 1
к 7
Как показано на рис. 5.22, б, в этом случае координатный фрейм преобразуется в новый координат-
ный фрейм с началом отсчета (1,232,1,402,1) и координатными осями, задаваемыми векторами (0,866,
0,5,0) и (-0,5,0,866,0). Отметим, что эти оси остаются перпендикулярными, поскольку осуществлялся
только поворот.
Относительные пропорции сохраняются
Аффинные преобразования имеют еще одно полезное свойство. Рассмотрим точку Р, расположенную
на части t расстояния между двумя заданными точками А и В, как показано на рис. 5.23. Применим аффин-
ное преобразование Т( ) к точкам А, В и Р. Мы утверждаем, что преобразованная точка Т(Р) также рас-
полагается на той же части t расстояния между образами точек Т(А) и Т(В). Это нетрудно показать.
(См. упражнения в конце данного раздела.)
Рис. 5.23. Относительные пропорции сохраняются
В частности, середины отрезков преобразуются также в середины отрезков. Это свойство приводит
к замечательному геометрическому результату: диагонали любого параллелограмма делят друг друга
пополам. (Доказательство. Любой параллелограмм является аффинно-преобразованным квадратом
(почему?), а поскольку диагонали квадрата при пересечении делятся пополам, то и диагонали парал-
лелограмма также делят друг друга пополам.) То же самое относится и к трехмерному пространству:
диагонали любого параллелепипеда делят друг друга пополам.
Заметим, в качестве любопытного отступления, что кроме сохранения прямых, параллельности и
относительных пропорций аффинные преобразования сохраняют эллипсы и эллипсоиды, как мы уви-
дим в главе 6.
288
Глава 5. Преобразования объектов
(5.22)
= detAf.
Влияние преобразований на площади фигур
В приложениях по тематике автоматизированного проектирования (computer-aided design — CAD) часто
возникает необходимость вычислить площадь или объем объекта. Например, как изменяется площадь
полигона, когда все его вершины подвергаются аффинному преобразованию? Геометрически понятно,
что ни перемещения, ни повороты никак не влияют на площадь фигуры, однако масштабирования точ-
но влияют, а может ли повлиять сдвиг, пока неясно.
Приводимый ниже простой результат исследуется в упражнениях: когда к объекту применяется дву-
мерное преобразование с матрицей М, то его площадь умножается на модуль определителя матрицы М:
площадь после преобразования
площадь до преобразования
Для двух измерений определитель матрицы М, согласно уравнению (5.4), равен т{1тп - т12т211. Следова-
тельно, для чистого масштабирования, согласно уравнению (5.7), новая площадь отличается от исходной
в SxSy раз, в то время как при сдвиге вдоль одной оси новая площадь остается той же самой, что и исходная!
А уравнение (5.10) подтверждает, что поворот не изменяет площадь фигуры, поскольку cos2(0) + sin2(0) = 1.
Для трех измерений можно применить аналогичное доказательство и сделать вывод, что объем 3D-
объекта, подвергаемого трехмерному преобразованию с матрицей М, изменяется в |detM| раз.
Пример 5.2.10. Площадь эллипса
Чему равна площадь эллипса, вписанного в прямоугольник шириной 2 IT и высотой 2Н?
Решение
Данный эллипс можно сформировать посредством масштабирования единичного круга х2 + у2 = 1
с масштабными множителями 5х= IVи Sy= Н. Матрица такого преобразования имеет определитель WH.
Известно, что площадь единичного круга равна л, поэтому площадь эллипса равна п WH.
Любое аффинное преобразование составлено из элементарных операций
Мы уже знаем, что компоновкой нескольких элементарных преобразований можно создать сложное
аффинное преобразование. Интересно поставить обратный вопрос: из каких элементарных преобразо-
ваний составлено данное аффинное преобразование?
Вообще говоря, матрица М может быть представлена в виде произведения элементарных матриц
различными способами. Один из возможных путей разложения матрицы М связан с двумерным аф-
финным преобразованием (см. тематическое задание 5.3) и приводит к следующему результату:
М = (перемещение) (сдвиг) (масштабирование) (поворот).
Это означает, что любая матрица М размером три на три, представляющая двумерное аффинное
преобразование, может быть записана в виде произведения (читается справа налево) матрицы поворо-
та, матрицы масштабирования, матрицы сдвига и матрицы перемещения. Особенности компонентов
каждой входящей матрицы даны в упомянутом тематическом задании.
В случае трех измерений дела обстоят несколько сложнее. Матрица М размером четыре на четыре,
представляющая трехмерное аффинное преобразование, может быть записана в виде:
М = (перемещение) (масштабирование) (поворот) (сдвиг() (сдвиг2),
то есть как произведение (читается справа налево) матрицы сдвига, еще одной матрицы сдвига, матрицы
поворота, матрицы масштабирования и матрицы перемещения. Этот результат рассмотрен в темати-
ческом задании 5.6.
Практические упражнения
5.2.24. Обобщение аргумента
Докажите, что если W— аффинная комбинация из Nточек Pt, i = 1,..., N, а Г( ) — аффинное преобразо-
вание, то Т( W) является той же самой аффинной комбинацией Nточек: Т(Р.), i = 1,..., N.
1 Эта величина может быть отрицательной. Приведите пример, когда это происходит.
5.3. Трехмерные аффинные преобразования
289
5.2.25. Доказательство сохранения относительных пропорций
Рассмотрим точку Р, заданную уравнением А + bt, где b = В - А. Найдите расстояния |Р - Л| и |Р - В|
соответственно от точки Р до точки А и от точки Р до точки В и докажите, что они относятся друг к
ДРУГУ,как t к 1 -1. Будет ли это верно, если t выходит за пределы промежутка от 0 до 1? Проделайте то
же самое для расстояний \Т(Р) - Т(Л)| и |Т(Р) - Т(В)|.
5.2.26. Влияние на площадь
Докажите, что двумерное аффинное преобразование приводит к умножению площади фигуры на мно-
житель из уравнения (5.22). {Подсказка: представьте, что геометрическая фигура состоит из множества
маленьких квадратиков, каждый из которых преобразуется в параллелограмм, и затем найдите площадь
этого параллелограмма.)
5.3. Трехмерные аффинные преобразования
К трехмерным аффинным преобразованиям применимы те же идеи, что и к двумерным аффинным пре-
образованиям, однако выражения будут, конечно, более сложными, к тому же наглядно представить
эффект трехмерного преобразования значительно труднее.
Снова будем использовать координатные фреймы и предположим, что у нас есть начало отсчета & и
три взаимно перпендикулярных оси в направлениях i, j и к (см. рис. 4.18). Точка Р в таком фрейме зада-
ется уравнением Р = б + Pri + + Pk, и, следовательно, имеет представление;
Пусть теперь Т( ) является аффинным преобразованием, которое преобразует точку Р в точку Q.
Тогда, аналогично случаю двух измерений, преобразование Т{ ) отображается матрицей М, размер-
ность которой теперь равна 4 на 4, а именно:
'"*11 ^12 ™13
м = m2I т22 т23
т3{ т32 т33
О О О
поэтому можно сказать, что отображение точки Q можно найти, умножив точку Р (справа) на мат-
рицу М:
/и24
1
(5.23)
Отметим еще раз, что последняя строка матрицы аффинного преобразования состоит из ряда нулей,
заканчивающегося одной единицей. (Это уже не будет выполняться, когда мы перейдем к проективным
матрицам в главе 7.)
5.3.1. Элементарные трехмерные преобразования
В этом разделе мы рассмотрим природу каждого из элементарных трехмерных преобразований, после
чего составим из них трехмерные аффинные преобразования общего вида.
10 Ф. Хилл
290
Глава 5. Преобразования объектов
Перемещение
В случае чистого перемещения матрица М имеет простую форму:
'10 0 /и,/
0 1 0 /я24
0 0 1 т}4
ООО 1
Проверьте, что Q = МР означает простое смещение точки Q на вектор m = (ml4, mw т^).
Масштабирование
Трехмерное масштабирование является прямым расширением двумерного и его матрица равна:
'Sx ООО''
° ^ ° ° , (5.25)
о о sx о
.° 0 0 I
где три константы 5х, Sy и S2 определяют масштабирование по соответствующим координатам. Как
и в двумерном случае, масштабирование производится относительно начала отсчета. На рис. 5.24 пока-
зан эффект масштабирования в z-направлении с множителем 0,5 и в х-направлении с множителем 2.
Отметим, что на рисунке показаны различные прямые до и после преобразования; здесь используется
то важное обстоятельство, что прямые преобразуются в прямые.
Рис. 5.24. Масштабирование базового сарая
(5.26)
Сдвиг
Трехмерные сдвиги отличаются большим разнообразием, чем их двумерные аналоги. Матрица про-
стейшего элементарного сдвига является единичной матрицей, в которой один нуль заменен некото-
рой величиной /:
'10 0
f 1 0
0 0 1
0 0 0
\
Отсюда Q = (Рх, fPx + Ру, Р2); то есть Ру смещено на некоторую величину, пропорциональную Рх, а ос-
тальные компоненты остались неизменными. Это вызывает эффект, подобный показанному на рис. 5.15
для двумерного случая. Голдманом [Goldman, 84] рассмотрен намного более общий случай трехмерно-
го сдвига, который мы будем рассматривать в тематическом задании 5.4.
5,3. Трехмерные аффинные преобразования
291
Повороты
Повороты в трех измерениях являются обычным делом в графике, поскольку нам часто требуется по-
вернуть объект или камеру с целью получения различных видов. Разнообразие поворотов в трех изме-
рениях значительно больше, чем в двух, поскольку в 3D мы должны задавать ось, вокруг которой осу-
ществляется вращение, а не только одну точку. Одним из плодотворных подходов является разложение
поворота на последовательность более простых поворотов.
Элементарные повороты относительно оси координат. Простейшим поворотом является поворот
относительно одной из координатных осей. Назовем поворот вокруг оси х — «х-вращением», поворот
вокруг оси у — «г/-вращением», а поворот вокруг оси z — «z-вращением». Представим по отдельности
матрицы, осуществляющие х-вращение, г/-вращение и z-вращение. В каждом случае поворот осуществ-
ляется на угол Р относительно заданной оси. Положительные углы определяются с помощью правила,
называемого «взгляд вовнутрь»: положительные значения угла /3 вызывают вращение против часовой
стрелки (CCW) относительно оси, если наблюдатель смотрит внутрь, по направлению к началу отсче-
та, с точки, находящейся на положительном направлении оси.
Рис. 5.25. Положительные повороты относительно трех координатных осей
Три основных положительных поворота приведены на рис. 5.251.
Такая формулировка совместима также с нашим пониманием двумерных поворотов: положитель-
ный двумерный поворот эквивалентен z-вращению, если смотреть на плоскость ху из точки на положи-
тельной оси z.
Отметим, что происходит в рамках этого соглашения для частного случая поворота на 90°:
О при z-вращении ось х поворачивается в сторону оси у,
О при х-вращении ось у поворачивается в сторону оси z;
О при г/-вращении ось z поворачивается в сторону оси х.
Ниже приведены три матрицы, представляющие преобразования поворота точек на угол р относи-
тельно координатной оси. Здесь мы используем естественную запись ), ) и Rz( ) для обозначения
соответственно х-, у- и z-вращений; параметром является угол в радианах, на который поворачиваются
точки; кроме того, введены обозначения с для cos(P) и s для sin(P):
1. х-вращение:
W =
1 о о
0 с -s
0 s с
ООО
О'
0
0
(5.27)
1 В левосторонней системе координат поворот на положительный угол Р против часовой стрелки будет при взгляде наружу вдоль
положительной оси из начала отсчета. Такая формулировка используется рядом авторов.
292
Глава 5. Преобразования объектов
2. //-вращение:
'с 0 з
О 1 О
я'(» "-.Ос
ООО
3. z-вращение:
'с -з О
О'
0
0
1
(5.28)
О'
0
0
1
(5.29)
ООО
Отметим, что 12 элементов каждой матрицы являются нулями и единицами из единичной матрицы.
Они находятся в последней строке и последнем столбце, а также в строке и столбце, соответствующих
оси, вокруг которой производится вращение (например, для х-вращения это первая строка и первый
столбец). Эти элементы гарантируют, что соответствующая координата преобразуемой точки не будет
изменяться. Элементы с и s занимают оставшиеся места и всегда образуют вершины квадрата.
Отметим также, что элемент -s появляется в верхней строке квадрата для х-вращения и z-вращения,
но в нижней строке квадрата для ^-вращения. Имеет ли ^-вращение какое-то существенное отличие?
Этот вопрос исследуется в упражнениях.
Пример 5.3.1. Повороты сарая
На рис. 5.26 нарисован «сарай» в его исходной ориентации (а), а также после х-вращения на -70° (б),
^-вращения на 30° (в) и z-вращения на -90° (г).
Рис. 5.26. Повороты базового сарая: а) сарай; б) х-вращение на -70°; в) у-вращение на 30°; г) z-вращение на 90'
5.3. Трехмерные аффинные преобразования
293
Пример 5.3.2
Поверните точку Р = (3,1,4) на 30° вокруг оси у.
Решение
Используя уравнение (5.28) при значениях с = 0,866 и s = 0,5, преобразуем точку Р в
'с 0 5 О' '3' ' 4,6 '
0 1 0 0 1 1
Q = -S 0 с 0 4 = 1,964
0 к 0 0 < 1 J
Как и ожидалось, координата у этой точки не изменилась.
Практические упражнения
5.3.1. Наглядное представление поворотов на 90°
Нарисуйте правостороннюю трехмерную систему координат и убедитесь в том, что поворот на 90° (против
часовой стрелки, если смотреть в сторону начала координат) вокруг каждой оси помещает каждую из
оставшихся осей на место другой. Каков будет эффект от вращения точки на оси х вокруг самой оси х?
5.3.2. Поворот стандартного сарая
Нарисуйте стандартный сарай после того, как каждая его вершина подверглась х-вращению на 45°.
Повторите рисунок для случаев //-вращения и 2-вращения.
5.3.3. Выполнение поворота
Найдите образ Q точки Р = (1, 2, -1) после //-вращения на 45°. Нарисуйте точки Р и Q в трехмерной
системе координат и покажите правильность полученного результата.
5.3.4. Проверка поворотов осей на 90°
В данном упражнении содержится полезный прием для запоминания структуры матриц поворота. При-
мените каждую из трех матриц поворота на 90° к каждому из стандартных единичных координатных
векторов i, j и к. В каждом случае исследуйте эффект преобразования единичного вектора.
5.3.5. Действительно ли у-вращение является особенным?
Кажется, что знак минус в уравнении (5.28) стоит не на месте: перед нижней буквой $, а не перед верх-
ней. Докажите, что в действительности уравнения (5.27)-(5.29) непротиворечивы, а все дело в порядке
следования осей. Рассмотрим три оси х, у и z в циклическом порядке: х—»//—>2 —»х—>//,... ит. д. Если
мы исследуем вращение вокруг какой-нибудь «текущей» (current) оси (х, у или z), то мы можем указать
«предыдущую» (previous) и «последующую» (next) оси. Если, например, текущей является ось х, то
предыдущая — 2, а следующая — у. Докажите, что при такой системе названий во всех трех видах
поворотов используются одни и те же уравнения: Qcurr- Purr, Qnext = cPnext- sPfKV и Qprcv = sPncxt + cP .
Напишите эти уравнения для каждой из трех возможных «текущих» осей.
5.3.2. Компонование трехмерных аффинных преобразований
Нет ничего неожиданного в том, что из трехмерных аффинных преобразований можно составлять ком-
позиции и в результате получать новое трехмерное аффинное преобразование. Ход рассуждений ана-
логичен тому, что привел нас к уравнению (5.17) для двумерного случая. Матрица, представляющая
суммарное преобразование, является произведением отдельных матриц и М2, выполняющих два
преобразования, причем умножение идет в обратном порядке: М2 является первым сомножителем, то
есть умножается на М, слева:
M=M2MV . (5.30)
Таким способом можно компоновать любое количество аффинных преобразований, и в результате
получится одна матрица, представляющая суммарное преобразование.
294
Глава 5. Преобразования объектов
Рис. 5.27. Компонование трехмерных аффинных преобразований
На рис. 5.27 показан пример, в котором сарай сначала преобразуется с помощью некоторой матри-
цы после чего преобразованный сарай снова преобразуется с использованием матрицы М2. Резуль-
тат совпадает с тем, который получится при одном преобразовании этого сарая с матрицей M2MV
5.3.3. Комбинирование поворотов
Результаты! Ну, конечно, я получил кучу результатов. Теперь я знаю тысячи вещей, которые не будут работать.
Томас А. Эдисон (Thomas A. Edison)
Одно из самых важных различий между двумерными и трехмерными преобразованиями заключается в
способе сложения поворотов. В двумерном случае два поворота, например /?(₽,) и /?(Р2), при сложении
дают /?(Р, + Р2), причем порядок, в котором складываются эти повороты, значения не имеет. В случае
трех измерений дело обстоит намного сложнее, поскольку повороты могут происходить вокруг различ-
ных осей. Порядок, в котором осуществляются два поворота вокруг различных осей, имеет значение:
трехмерные матрицы поворота некоммутативны. В этом разделе мы исследуем некоторые свойства
трехмерных поворотов, изучим различные способы представления поворота и посмотрим, как созда-
вать повороты для решения конкретной задачи.
Поворот в трех измерениях обычно строят как композицию трех элементарных поворотов: вначале
х-вращение, затем у-вращение и, наконец, z-вращение. Используя для каждого отдельного вращения
обозначения, принятые в уравнениях (5.27)-(5.29), получим выражение для суммарного вращения:
м - ад) ад) ад). (5.31)
В этом контексте углы Рр Р2 и Р3 часто называют углами Эйлера1 (Euler angles). Одна формулировка
теоремы Эйлера гласит, что любой трехмерный поворот может быть получен тремя вращениями вокруг
осей х, у и z, и поэтому любое вращение может быть записано в виде специфического произведения пяти
матриц при соответствующем выборе углов Эйлера (см. ниже). Из этого утверждения следует, что для
полного задания поворота требуется три величины.
Пример 5.3.3
Какая матрица соответствует х-вращению на 45°, следующему за ним у-вращению на 30° и последую-
щему z-вращению на 60°? Непосредственное умножение трех составляющих матриц (обязательно в
«обратном» порядке) дает следующий результат:
' 0,5 -0,866 0 О' '0,866 0 0,5 О' ;i 0 0 О' '0,433 -0,436 0,789 О'
0,866 0,5 0 0 0 1 0 0 0 0,707 -0,707 0 0,75 0,66 -0,047 0
0 0 1 0 -0,5 0 0,866 0 0 0,707 0,707 0 -0,5 0,612 0,612 0
1 0 0 0 1 0 0 0 и 1° 0 0 1 1 0 0 0 1
1 В честь Леонарда Эйлера (1707-1783), швейцарского математика необычайных способностей, внесшего неоценимый вклад во все
разделы математики.
5.3. Трехмерные аффинные преобразования
295
Иногда используют для создания сложного поворота другой порядок «вращений». Можно, напри-
мер, выразить поворот в форме /2 (|31) /?г(|32) вначале х-вращение, затем 2-вращение и затем
//-вращение. В силу некоммутативности трехмерных поворотов для того, чтобы получить тот же самый
поворот, для данного преобразования требуются другие углы Эйлера Р,, Р2 и Р3. Всего существует 12 воз-
можных порядков следования трех отдельных вращений, и в каждом из них используются различные
величины Р(, Р2 и Р3.
Повороты вокруг произвольной оси
При использовании углов Эйлера мы выполняем последовательность х-, у- и z-вращений, то есть вра-
щений вокруг координатных осей. Однако работать с поворотами было бы намного проще, если бы у
нас была возможность осуществлять повороты вокруг произвольно направленной оси. Представьте себе
Землю или игрушечный волчок, вращающиеся вокруг наклонной оси. В действительности в теореме
Эйлера утверждается, что каждый поворот может быть представлен в такой форме.
Теорема Эйлера. Любой поворот (или последовательность поворотов) вокруг произвольной точки
эквивалентен однократному повороту вокруг некоторой оси, проходящей через эту точку*.
Что же представляет собой матрица такого поворота и будет ли удобно с ней работать?
На рис. 5.28 показана ось, представленная вектором и, и произвольная точка Р, которая после пово-
рота на угол Р вокруг оси и должна перейти в точку Q. Поскольку вектор и может иметь любое направ-
ление, то на первый взгляд было бы затруднительно найти ту единственную матрицу, которая описыва-
ет такой поворот. Однако в действительности такая матрица может быть найдена двумя различными
методами, так называемыми классическим (classic) и конструктивным (constructive).
Классический способ. Разбиваем искомый поворот на последовательность знакомых шагов:
1. Выполним два поворота таким образом, чтобы вектор и совместился с осью х.
2. Выполним z-вращение на угол р.
3. Аннулируем два совмещающих поворота для восстановления исходного направления вектора и.
Рис. 5.28. Поворот вокруг оси, проходящей через начало координат
Этот метод напоминает поворот вокруг точки в двух измерениях. Первый шаг подготавливает
условия для более простой и знакомой операции, затем эта простая операция выполняется, и, наконец,
подготовительный этап аннулируется. Результат для трехмерного случая (он рассматривается в упраж-
1 Эта теорема иногда формулируется так: «Если заданы две прямоугольные системы координат с общим началом и произвольными
направлениями осей, то всегда существует такая прямая, проходящая через начало координат, что одна система координат может
быть совмещена с другой посредством поворота вокруг этой прямой».
296
Глава 5. Преобразования объектов
нениях в конце раздела) заключается в том, что нужное преобразование требует перемножения пяти
матриц:
*„(₽) - Rv(-e)R^)R(₽)/?2(-0)/?у(е). (5.32)
Каждое умножение является поворотом вокруг одной из координатных осей. Такое преобразование
является громоздким для выполнения вручную, однако удобно для воплощения в компьютерной про-
грамме. В то же время раскрытие произведения дает мало представления о том, как эти «ингредиенты»
работают совместно.
Конструктивный способ. Используя некоторые векторные инструменты, можно получить более на-
глядное выражение для матрицы 7?и(Р). В последнее время этот подход стал весьма популярен, и раз-
личные его варианты описаны несколькими авторами в GEMS I [Glassner, 5]. Мы используем вывод
Мэйлота [Maillot, 135].
На рис. 5.29 показана ось вращения и, и нам нужно написать выражение для операции перехода
точки Р в точку Q с помощью поворота на угол р. В данном методе, подробно описанном в тематичес-
ком задании 5.5, в плоскости вращения устанавливается двумерная система координат, как показано на
рисунке. В этой системе координат два ортогональных вектора а и b располагаются в данной плоскости,
и, как показано на рис. 5.29, б, точка Q выражается линейной комбинацией этих двух векторов. Выра-
жение для Q включает в себя скалярные и векторные произведения различных «ингредиентов», завися-
щих от специфики задачи. Однако, поскольку каждый член линеен относительно координат точки Р,
он может быть записан как произведение матрицы на Р.
Рис. 5.29. Точка Р переходит в точку Q в плоскости вращения
Окончательным результатом является матрица
с + (1—с)а2 (1-с)ауа,-su, (\-c')u2ux+suy (Г
(l-c)axav + зи2 с + (1—с)а2 (1-с)агау-зих О
(1-с)ала2-$ал (\-с)иуих + зих с + (1-с)а2 О
I ° 0 0 U
(5.33)
где с - cos(P), s = sin(P), а (их, и*, иг) — компоненты единичного вектора и. Эта матрица кажется более
сложной, чем она есть на самом деле. В действительности, как мы увидим позже, структура элементов
этой матрицы позволяет для любой заданной матрицы поворота определить ось и угол, которые обес-
печивают требуемый поворот (что доказывает теорему Эйлера).
5.3. Трехмерные аффинные преобразования
297
В дальнейшем мы также узнаем, что в OpenGL имеется функция для осуществления поворота вок-
руг произвольной оси:
glRotated(angle. их. иу. uz);
Пример 5.3.4. Поверните вокруг оси
Найдите матрицу, осуществляющую поворот на 45° вокруг оси и = (1,1,1)/л/з = (0,577,0,577,0,577).
Решение
При повороте на 45° с = s = 0,707. Подставив их в уравнение (5.33), получаем:
'0,8047 -0,31 0,5058 О'
0,5058 0,8047 -0,31 0
7?и(45 °) = .
“ -0,31 0,5058 0,8047 0
; 0 0 0 J
Определитель этой матрицы, как и следовало ожидать, равен единице. На рис. 5.30 показан базовый
сарай, смещенный относительно начала координат, до поворота (ближняя фигура), после поворота
на 22,5° (средняя) и после поворота на 45° (дальняя).
Рис. 5.30. Базовой сарай, поворачивающийся вокруг оси и
Определение оси и угла поворота
Согласно теореме Эйлера любой поворот эквивалентен повороту вокруг некоторой оси на некоторый
угол. Если поворот задан с помощью матрицы, часто бывает полезно определить характерные для дан-
ного поворота ось и угол. Попытаемся извлечь из элементов тп~ матрицы поворота
ти12 mI3 0
ЯИ(Р) = m2I т22 «23 0
m3I т22 m33 0
(° 0 0 1
характерные угол Р и орт и. Это удивительно легко сделать, если обратиться к уравнению (5.33)
[Watt, 138]. Заметим, что след (trace) матрицы 7?и(Р), что в данном случае означает сумму трех элемен-
тов ее главной диагонали, равен Зс + (1 - с)(и2 + и2+ и2) = 1 + 2cos(P). Выразим отсюда cos(P):
cos(P) = 1/2(щп+ т22+ т^) - 1.
298
Глава 5. Преобразования объектов
Найдем арккосинус этой величины для получения угла Р, который используем для вычисления
s - sin(P). Тогда мы увидим, что элементы матрицы поворота попарно входят в выражение каждого ком-
понента вектора и:
и = ^32-^23
2sin(P)
у 2sin(p)
t = /Н21 ~^12
1 2sin(P)
(5.34)
Пример 5.3.5. Найдите ось и угол
Сделайте вид, что вам неизвестны характерные ось и угол для матрицы поворота из примера (5.3.4) и
вычислите их. След равен 2,414, откуда cos(P) - 0,707, Р - 45°, следовательно, sin(P) = 0,707. Далее вычис-
лим все компоненты вектора поворота из уравнений (5.34); все они получатся равными 0,577, поэтому
и-(1,1,1)/ч/з , как и следовало ожидать.
Практические упражнения
5.3.6. Какое преобразование коммутативно?
Рассмотрим два аффинных преобразования Т\ и Т2. Является ли преобразование Т{Т2 идентичным Т2Т\, если
а) оба они являются чистыми перемещениями;
б) оба они являются масштабированиями;
в) оба они являются сдвигами;
г) одно из них является поворотом, а другое перемещением;
д) одно из них является поворотом, а другое масштабированием;
е) одно из них является масштабированием, а другое сдвигом.
5.3.7. Частные случаи поворота вокруг произвольной оси и
Всегда полезно выяснить, как сложный результат в частных случаях сводится к известным. Проверьте,
что произойдет с уравнением (5.33), если ось и является:
а) осьюх, i;
б) осью у, j;
в) осью 2, к.
5.3.8. Классический подход к повороту вокруг оси
В этом упражнении мы предлагаем способ нахождения поворотов, в результате которых ось и совмес-
тится с осью 2. (В приложении Б приведен обзор сферических координат.) Пусть направление и задано
в сферических координатах углами ф и 0, как показано на рис. 5.28. Совместим и с осью х посредством
у-вращения на угол 0; в результате и перейдет в плоскость ху и создаст новую ось и'. (Нарисуйте эту
ось.) Найдите /?^(0) из уравнения (5.28). Завершим процесс совмещения осей посредством 2-вращения
на угол -ф. Поскольку теперь вектор и совпадает с осью х, выполним желаемое х-вращение на угол Р,
используя уравнение (5.27). После этого следует аннулировать повороты совмещения, чтобы восстано-
вить исходное направление оси. Для выполнения этого используйте матрицы, обратные к 7^(0) и Дг(-0),
которые равны соответственно /?^(-0) и К2(ф). Сначала аннулируйте 2-вращение и затем у-вращение.
В заключение перемножьте эти пять элементарных поворотов, чтобы получить уравнение (5.32). Выпол-
ните все эти вычисления и примените результаты к определению матрицы М, которая выполняет пово-
5.3. Трехмерные аффинные преобразования
299
рот на угол 35° вокруг оси, заданной сферическими координатами 0 = 30° и ф - 45°. Покажите, что окон-
чательный результат имеет вид:
' 0,877 -0,366 0,281 О'
0,445 0,842 -0,306 0
М =
-0,124 0,396 0,910 0
/О 0 0 1J
5.3.9. Ортогональные матрицы
Матрица называется ортогональной (orthogonal), если ее столбцы являются взаимно ортогональными
векторами единичной длины. Докажите, что каждая из трех матриц поворота, заданных равенствами
(5.27)-(5.29), ортогональна. Чему равен определитель ортогональной матрицы? Ортогональная мат-
рица обладает замечательным свойством: ее обращение равносильно ее транспонированию (см. также
приложение Б). Докажите, что это свойство матрицы следует из ортогональности ее столбцов. Найди-
те обратные матрицы к каждой из трех упомянутых матриц и докажите, что обращение (инверсия) по-
ворота — это просто поворот в противоположном направлении.
5.3.10. Матрица является ортогональной
Докажите, что сложная матрица поворота из равенства (5.33) является ортогональной.
5.3.11. Структура матрицы поворота -
Докажите, что у матрицы поворота М размером 3 на 3 все три строки попарно ортогональны, а третья
является векторным произведением первых двух.
5.3.12. Ось поворота не проходит через начало отсчета?
Если ось вращения не проходит через начало отсчета, а вместо этого задана в виде S + ut, где S — некото-
рая точка, то необходимо вначале произвести перемещение в начало отсчета посредством -5, проделать
нужный поворот и затем произвести обратное перемещение посредством S. Напишите суммарную мат-
рицу, описывающую эти действия.
5.3.4. Краткое изложение свойств трехмерных
аффинных преобразований
Свойства, отмеченные в разделе 5.2.7 для аффинных преобразований, конечно, применимы и к трех-
мерным аффинным преобразованиям. В терминах произвольного трехмерного аффинного преобразо-
вания Т(.) с матрицей М эти свойства имеют вид:
О При аффинных преобразованиях аффинные комбинации точек сохраняются. Если а + b = 1,
то аР + bQ — полноправная трехмерная точка, и Т(аР + bQ) = аТ(Р) + bT(Q).
О При аффинных преобразованиях прямые линии и плоскости сохраняются. «Прямизна» сохра-
няется: образ T(L) прямой L в трехмерном пространстве также является прямой; образ Т( W) плос-
кости W в трехмерном пространстве также является плоскостью.
О Сохраняется параллельность прямых и плоскостей. Если 17и Z — параллельные прямые (или
плоскости), то их образы T(W) и T(Z) также параллельны.
О Столбцы матрицы показывают преобразованный координатный фрейм. Если столбцами мат-
рицы М являются векторы т); т2, т3 и точка тп(, то преобразование отображает фрейм из (i, j, k, 0)
в (m,, m2, m3, m4).
О Относительные пропорции сохраняются. Если Р находится на части /расстояния от точки А до
точки В, то Т(Р) находится на части/расстояния от точки 7'(Л) до точки Г(В).
300
Глава 5. Преобразования объектов
О Влияние преобразований на объемы объектов. Если трехмерный объект D имеет объем V, то его
образ T(D) имеет объем |detA/| V, где |detM| — абсолютная величина определителя матрицы М.
О Каждое аффинное преобразование состоит из элементарных операций. Трехмерное аффинное
преобразование может быть разложено на элементарные преобразования, причем несколькими
способами.
5.4. Изменения систем координат
Можно рассматривать аффинные преобразования с другой точки зрения. В случае моделирования сцен
это во многих отношениях более естественный подход. Вместо того чтобы рассматривать аффинное
преобразование как создание новой точки в неизменной системе координат, рассмотрим его как созда-
ние новой системы координат, в которой нужно отобразить точки.
Несколько слов об обозначениях. Для того чтобы запись лучше помещалась на странице книги, мы
иногда будем писать (Рх, Р, 1)г вместо
Ру (см. также приложение Б).
Надстрочное Т означает транспонировать (transpose), так что мы просто записываем вектор-стол-
бец в виде транспонированного вектора-строки.
Рис. 5.31. Преобразование координатного фрейма
Допустим далее, что у нас имеется двумерный координатный фрейм № 1, как показано на рис. 5.31,
с началом отсчета v и осями i и j. Пусть, далее, мы имеем аффинное преобразование Т(.), представлен-
ное матрицей М. Тогда Т(.) преобразует координатный фрейм № 1 в координатный фрейм № 2 с новым
началом отсчета б' = Т(б)и новыми осями i' = T(i) и j' = T(j).
Пусть (с, d, 1 )г — представление точки Рв новой системе № 2. Чему равны значения а и b в представ-
лении (а, Ь, 1)гэтой же точки Р в исходной системе № 1? Для ответа на этот вопрос достаточно умно-
жить М (слева) на (с, d, 1)г:
(5.35)
5.4. Изменения систем координат
301
Обобщая эти рассуждения, сформулируем следующую «теорему». Предположим, что система коор-
динат № 2 получена из системы координат № 1 посредством аффинного преобразования М. Предполо-
жим далее, что (Рх, Р, 1) — это координаты точки Р в системе координат № 2. Тогда координаты точ-
ки Р в системе № 1 равны МР.
Данная «теорема» может показаться некоторым читателям слишком очевидной, но для тех, кто с
этим не согласен, ее доказательство рассматривается в упражнениях в конце раздела. Разумеется, этот
результат справедлив и для трехмерных систем, и мы будем широко использовать его при вычислении
преобразования трехмерных точек, когда они проходят через графический «конвейер».
Пример 5.4.1. Поворот системы координат
Вновь рассмотрим преобразование из примера 5.2.5, где осуществляется поворот точек на 30° относительно
точки (-2,3) (см. рис. 5.22, б.) Это преобразование отображает начало отсчета О и оси i и j в систему № 2,
как показано на рисунке. Рассмотрим теперь точку Р с координатами (Рх, Р, 1)г в новой системе координат.
Чему равны координаты этой точки в системе координат № 1? Ответ прост: МР. Например, точка (1,2,1)г
в новой системе соответствует точке М{\, 2,1)г - (1,098,3,634,1)г в исходной системе. (Нарисуйте это на
бумаге.) Отметим, что точка (-2,3,1)г— центр вращения данного преобразования — является неподвиж-
ной точкой преобразования: ЛД-2,3,1)г- (-2,3,1)г. Поэтому, если мы возьмем точку Р - (-2,3,1)гв но-
вой системе, то она представляется в новой системе тоже как (-2, 3,1)г. (Проверьте это графически.)
Последовательные изменения координатного фрейма
Рассмотрим теперь формирование преобразования, состоящего из двух последовательных изменений
системы координат. Каков будет суммарный эффект? Как показано на рис. 5.32, система № 1 переходит в
систему № 2 посредством преобразования 7'1(-), а система № 2 трансформируется затем в систему № 3
посредством преобразования Т2(.). Отметим, что система № 3 трансформируется относительно № 2.
Рис. 5.32. Двукратное преобразование системы координат
Вопрос снова ставится так: если представление точки Р равно (е,/, 1)гв системе № 3, то чему равны
координаты (а, Ь, 1)гэтой же точки Рв системе № 1? Для того чтобы ответить на этот вопрос, вернемся
назад и соберем вместе эффекты от каждого преобразования. В системе № 2 точка Р имеет координаты
(с, d, iy = M2(e,f, 1)г. А в системе № 1 координаты точки (с, d, 1)гравны (a, b, 1)г= М^с, d, 1)г. Объеди-
нение этих фактов приводит к равенству:
(5.36)
302
Глава 5. Преобразования объектов
Существенным является то обстоятельство, что при определении координат (а, Ь, 1)г из (е,/, 1)г первым
применяется преобразование М2, а затем Mv то есть в обратном порядке по сравнению с тем, когда мы
рассматривали применение преобразований к точкам. Обобщим вышесказанное на случай трех последо-
вательных преобразований (после этого результат может быть обобщен на любое число преобразований).
Преобразование точек. Для того чтобы применить последовательность преобразований Г/.), 7'2(.), Т3(.)
(в указанном порядке) к точке Р, сформируем матрицу:
М~ М3хМ2хМ{.
Затем Р преобразуется в МР. Для составления каждого последующего преобразования Mj нужно
умножить на него М. слева.
Преобразование системы координат. Для того чтобы применить последовательность преобразова-
ний !}(.), Т2(.), Т3(.) (в указанном порядке) к точке Р, сформируем матрицу:
М~ М{х М2х М3.
Таким образом, точка Р, выраженная в преобразованной системе, имеет в этой системе координаты МР.
Для подключения каждого дополнительного преобразования М. матрицу следует умножить на М. справа.
Как работает OpenGL
В следующем разделе мы увидим, что в OpenGL имеются инструменты для последовательного приме-
нения преобразований и создания из них суммарного «текущего преобразования». Фактически OpenGL
устроен так, что умножает справа каждую новую матрицу преобразования при компоновке их в сум-
марное преобразование. Поэтому разработчику модели часто представляется более естественным рас-
суждать в терминах последовательного преобразования системы координат, так как порядок, в котором
эти преобразования выполняются, mom же, что и порядок, в котором их выполняет OpenGL.
Практические упражнения
5.4.1. Связь между преобразованием системы координат и преобразованием точки
Мы хотим проверить уравнение (5.35). Для того чтобы сделать это, докажите каждый из следующих
пунктов:
а) Покажите, что точка Р с координатами (с, d, 1)г в системе № 2 имеет представление ci' + c?j' + О'.
б) Мы хотим выяснить, где располагается точка Рв системе № 1. Покажите, что представление
(в системе № 1) вектора i' равно М(1,0,0)г, вектора j' — Л/(0,1,0)г, а точки О' — М(0,0,1).
в) Покажите, что представление точки ci' + dj' + О' равно сМ(1, 0, 0)г + dM(0, 1, 0)г + М(0, 0,1)г.
г) Покажите, что представление из пункта в) то же самое, что М(с, 0, 0)г + М(0, d, 0)г + Л/(0, О, 1)г,
и что оно равно М(с, d, 1)г, как утверждалось выше.
5.4.2. Использование элементарных примеров
На рис. 5.33 показано действие четырех элементарных преобразований системы координат. В каждом
случае исходная система с осями х и у преобразуется в новую систему с осями х' и у'.
а) На рис. 5.33, а показан результат перемещения на (т, п). Покажите, что точка (е,/) в новой сис-
теме имеет координаты (е + m,f + п) в исходной системе.
б) На рис. 5.33, б показан результат поворота относительно начала координат на угол А градусов.
Покажите, что точка (e,f) в новой системе имеет в старой системе координаты (ecos(a) -/sin(a),
esin(a) + /cos(a)), где a - лД/180 радиан.
в) На рис. 5.33, в показан результат масштабирования осей на (3,2). Для наглядности новые и ста-
рые оси изображены слегка смещенными. Докажите, что точка (e,f) в новой системе имеет в ста-
рой системе координаты (Зе, 2/).
г) На рис. 5.33, г показан специальный случай масштабирования: отражение относительно оси х.
Докажите, что точка (е, /) имеет в старой системе координаты (е, -/).
5.5. Использование аффинных преобразований в программах
303
з э
в г
Рис. 5.33. Элементарные преобразования между системами координат: а) перемещение (т, п); б) поворот (а);
в) масштабирование с множителем (3, 2); г) масштабирование с множителем (1, -1)
5.5. Использование аффинных
преобразований в программах
Мы хотим узнать, как теория аффинных преобразований применяется в программах при осуществле-
нии масштабирования, поворота и перемещения графических объектов. Мы также исследуем, как это
делается при использовании OpenGL. Сначала мы разберем двумерные примеры, так как они более на-
глядны. Затем мы перейдем к трехмерным примерам.
На данном этапе предположим, что мы имеем подпрограмму houseO, которая рисует домик № 1 на
рис. 5.34. Пусть вместо этого домика вы хотите нарисовать домик № 2, повернутый на -30° и затем пе-
ремещенный на (32, 25). Подобная ситуация встречается очень часто: имеется заданный объект подхо-
дящего размера и расположения, однако нам нужно нарисовать его (и, возможно, много раз) с другими
размерами, ориентацией и расположением.
Как уже рассматривалось в главе 3, подпрограмма houseO будет рисовать различные ломаные линии
этой фигуры (домика). Если бы эта подпрограмма была написана на «голом» OpenGL, то она могла бы
состоять из большого числа кусков такого вида:
glBeg1n(GL_LINES):
glVertex2d(V[0].x. V[O].y):
glVertex2d(V[l].х. V[l].y):
glVertex2d(V[2].x. V[2].y):
// the remaining points
// остальные точки-
glEndO:
304
Глава 5. Преобразования объектов
Рис. 5.34. Рисование домика с поворотом и перемещением
Данный код мог бы использовать некоторый массив точек V[J. Если использовать класс Canvas, рас-
смотренный в главе 3 (а также глобальный объект класса Canvas cvs), то программа будет содержать
многократные вызовы функций moveToO и lineToO такого вида:
cvs.moveTo(V[0]):
cvs.lineTo(V[l]):
cvs.11neTo(V[2]):
// the remaining points
// остальные точки
В любом случае нам придется задать мировое окно и порт просмотра с помощью следующих вызовов:
cvs.setW1ndow(..
cvs.setV1ewport(..
После этого мы можем быть уверены, что все координаты вершин V[i] «молча» преобразованы из
мировых координат в экранное окно посредством базового преобразования «окно — порт просмотра».
Однако как все это сделать, если нам нужно нарисовать домик № 2? Для этого существуют два пути:
сложный и простой.
Сложный путь
При этом подходе мы создаем матрицу М нужного преобразования, а также подпрограмму с названием,
например, transform2D(), которая преобразует одну точку в другую:
Q - transform2D(M. Р);
Эта подпрограмма дает на выходе Q = МР. Для того чтобы применить это преобразование к каждой
точке V[i] в подпрограмме houseO, мы должны изменить приведенный ранее исходный код следующим
образом:
cvs.moveTo(transform2D(M. V[0]));
// move to the transformed point
// перемещаемся к преобразованной точке
cvs.lineTo(transform2D(M. V[l]));
cvs.lineTo(transform2D(M. V[2]));
Теперь в подпрограммы moveToO и 11пеТо()передаются преобразованные точки. Такой способ исправ-
ления возможен, если доступен исходный код подпрограммы houseO. Однако этот способ является
в высшей степени громоздким и невозможен вовсе, если исходный код для houseO недоступен. Кроме
того, нам в первую очередь нужны средства для создания матрицы М.
5.5. Использование аффинных преобразований в программах
305
Простой путь
Сделаем так, чтобы нужное преобразование применялось к каждой вершине автоматически. Так как
мы знаем, что отображение «окно — порт просмотра» применяется к каждой вершине «молча», как часть
работы функций moveToO и ИпеТоО, то можно сделать, чтобы дополнительное преобразование приме-
нялось также «молча». С таким преобразованием мы уже сталкивались раньше под названием текущее
преобразование (current transformation — СТ). Усовершенствуем функции moveToO и ИпеТоО в классе
Canvas таким образом, чтобы они вначале молча применяли к вершине-аргументу текущее преобразо-
вание СТ, а затем преобразование «окно — порт просмотра». (Кроме того, также производится отсече-
ние границами мирового окна.)
На рис. 5.35 показано небольшое усовершенствование графического конвейера, который мы впер-
вые ввели на рис. 5.7. При вызове функции gl Vertex2d() с аргументом V вершина Vвначале преобразу-
ется при помощи СТ в точку Q, которая затем подвергается отображению «окно — порт просмотра»,
после чего превращается в точку 5 экранного окна. (Как мы увидим позднее, «внутри» последнего про-
цесса отображения также выполняется отсечение.)
окно
Рис. 5.35. Текущее преобразование, применяемое к вершинам
Как же должны быть расширены функции moveToO и ИпеТоО, чтобы они молча выполняли это до-
полнительное преобразование? (Иными словами, как переписать эти функции в классе Canvas?) Если
вы работаете без OpenGL, то вам придется самим написать код, фактически осуществляющий это
преобразование; такой код описывается в тематическом задании 5.1. Если же вы используете OpenGL,
то преобразование выполняется автоматически! В OpenGL содержится так называемая матрица мо-
делирования-вида (modelview matrix), на которую умножается каждая вершина, проходящая через
графический конвейер. Нам остается только настроить данную матрицу на выполнение нужного
преобразования.
OpenGL всегда работает в трех измерениях, поэтому его матрица моделирования-вида осуществля-
ет SD-преобразования. В данном случае мы работаем с матрицей моделирования-вида, ограничиваясь
частным случаем двумерных преобразований. В дальнейшем мы будем использовать ее на полную
мощность. На рис. 5.36 показано, как ограничить трехмерные преобразования так, чтобы получить не-
обходимые нам двумерные преобразования. Основная идея заключается в том, что двумерное рисова-
ние производится в плоскости ху. Предполагается, что координата z равна нулю. Поэтому при преобра-
зовании двумерных точек та часть основного трехмерного преобразования, которая воздействует на
координату z, настраивается так, чтобы это воздействие полностью отсутствовало. Например, враще-
ние вокруг начала координат в двух измерениях эквивалентно повороту вокруг оси z в трех измере-
ниях, как это показано на рисунке. Далее, поскольку у трехмерного масштабирования имеется три масш-
табных множителя Sx, Sy, и S2 для масштабирования соответственно в направлениях х, у и z, мы задаем
масштабный множитель 5-1.
306
Глава 5. Преобразования объектов
Рис. 5.36. Двумерное рисование, осуществляемое в плоскости ху
Основными подпрограммами для поддержки матрицы моделирования-вида являются gl Rotated О1,
glScaledO и glTranslatedO. Они не устанавливают СТ прямо. Вместо этого в каждой из них матрица
моделирования-вида СТ умножается справа на заданную матрицу, например М, после чего результат
помещается обратно в СТ. Таким образом, в каждой из этих подпрограмм создается матрица М, необхо-
димая для нового преобразования, и выполняется следующая операция:
СТ = СТ*М. (5.37)
Порядок следования здесь имеет значение: как мы уже видели ранее, применение преобразования
СТ*Л/к точке означает, что выполняется преобразование, задаваемое матрицей М, а затем преобразова-
ние, диктуемое прежним значением СТ. Если же рассуждать в терминах преобразования системы коор-
динат, то все это эквивалентно выполнению одного дополнительного преобразования текущей систе-
мы координат.
Ниже приведены подпрограммы OpenGL для преобразования в случае двух измерений:
О glSealed(sx. sy, 1.0): умножает СТ справа на матрицу, выполняющую масштабирование на вели-
чину sx по оси х и на величину sy по оси у, результат помещается обратно в СТ. По оси z никакого
масштабирования не производится.
О glTranslated(dx, dy, 0); умножает СТ справа на матрицу, выполняющую перемещение на dx по
оси х и на dy по оси у, результат помещается обратно в СТ. По оси z никакого перемещения не
производится.
О gl Rotated (angle, 0, 0, 1): умножает СТ справа на матрицу, выполняющую поворот на angle гра-
дусов вокруг оси z (она обозначена (0,0,1))2; результат помещается обратно в СТ.
Поскольку эти подпрограммы только компонуют преобразование с СТ, то для начала процесса нам
необходимо инициировать СТ для тождественного преобразования. Для этого в OpenGL содержится
подпрограмма glLoadldentityO. Поскольку все перечисленные функции могут быть настроены для ра-
боты с любой из поддерживаемых в OpenGL матриц, мы должны информировать OpenGL о том, какую
матрицу мы изменяем. Это осуществляется посредством функции glMatr1xMode(GL_M0DELVIEW).
Листинг 5.1. Подпрограммы для поддержки СТ в случае двумерных преобразований
//«««««««« initCT >»»»»>»»»»
void Canvas:: initCT(void)
{
glMatrixMode(GL_MODELVIEW);
glLoadldentityO;
1 Суффикс «d» означает, что аргументы данной функции имеют двойную точность (doubl е). Существует также версия gl Rotatef(),
принимающая аргументы типа float.
2 Здесь, как всегда, положительные углы означают повороты против часовой стрелки.
5.5. Использование аффинных преобразований в программах
307
// set СТ to the Identity matrix
// устанавливаем СТ в матрицу тождественного преобразования
}
//««««««« scale2D »»»»»»»»»»
void Canvas:: seale2D(double sx, double sy)
{
glMatrixMode(GL_MODELVIEW):
glScaled(sx. sy, 1.0):
П set CT to CT * (2D scaling)
// устанавливаем CT - CT * (двумерное масштабирование)
11«««««««< translate2D »»»»»»»»
void Canvas:: translate2D(double dx. double dy)
{
glMatr1xMode(GL_M0DELVIEW):
glTranslated(dx, dy. 0):
// set CT to CT * (2D translation)
// устанавливаем CT - CT * (двумерное перемещение)
11«««««««« rotate2D »»»»»»»»»»
void Canvas:: rotate2D(double angle)
{
glMatr;xMode(GL_MODELVIEW):
glRotated(angle. 0.0. 0.0. 1.0):
// set CT to CT * (2D rotation)
// устанавливаем CT - CT * (двумерный поворот)
В листинге 5.1 приведены соответствующие определения четырех новых методов класса Canvas для
управления текущим преобразованием, которые позволяют построить любые сложные двумерные пре-
образования. Столь приятная их простота связана с тем, что всю черновую работу выполняет OpenGL.
Теперь мы готовы к применению двумерных преобразований. Возвращаясь к рисованию домика № 2
с рис. 5.34, приведем код, который сначала поворачивает этот домик на -30° и затем перемещает его на
вектор (32, 25). Отметим, что для получения прямого порядка следования этих операций они вызыва-
ются в порядке, обратном тому, в котором они применяются: сначала операция перемещения, а затем
операция поворота.
cvs.setW1ndow(...):
cvs.setV1ewport(..):
// set the window to viewport mapping
// настраиваем преобразование окно-порт просмотра
cvs.initCTO:
// get started with the identity transformation
// начинаем с тождественного преобразования
houseO:
// draw the untransformed house first
// вначале рисуем непреобразованный домик
cvs.translate2D(32. 25):
// CT now includes translation
// теперь СТ включает в себя перемещение
cvs.rotate2D(-30.0):
// СТ now includes translation and rotation
//теперь СТ включает в себя перемещение и поворот
houseO:
// draw the transformed house
// рисуем преобразованный домик
308
Глава 5. Преобразования объектов
Отметим, что домик можно любым образом масштабировать, поворачивать и перемещать и при этом
нет никакой необходимости «влезать внутрь» подпрограммы houseO или изменять ее. (Более того, ис-
ходный код ИоизеОнам и не понадобится.)
Рис. 5.37. То же самое преобразование, рассматриваемое как последовательность изменений систем координат
Некоторые авторы находят более естественным рассуждать в терминах преобразования системы
координат, а не самого домика. Как показано на рис. 5.37, первое перемещение системы координат на
(32, 25) образует систему № 2, а затем поворот этой системы на -30° превращает ее в систему № 3. По-
скольку OpenGL применяет преобразования в том же порядке, в каком изменяются системы коорди-
нат, код, выполняющий такое суммарное преобразование, вызовет вначале cvs.translate2D(32, 25) и за-
тем cvs. rotate2D( -30.0). Разумеется, это идентично коду, выполняющему данное преобразование другим
способом, однако мы пришли к нему, рассуждая иным путем.
Далее приводятся несколько примеров, демонстрирующих, насколько просто управлять текущим
преобразованием СТ для произведения различных эффектов.
Пример 5.5.1. Использование осевой симметрии
На рис. 5.38, а показана звезда, созданная из полосок, которые выглядят переплетенными друг с дру-
гом. Такая фигура легко может быть нарисована с помощью подпрограммы rotate2D(). Пусть подпрог-
рамма starMotifO рисует часть данной звезды — полигон, показанный на рис. 5.38, б. (Определение
положения вершин этого полигона достаточно сложно и вынесено в тематическое задание 5.2.) Теперь
для того, чтобы нарисовать звезду целиком, мы просто рисуем данный мотив пять раз, каждый раз
поворачивая его на 72°.
for(1nt count = 0; count < 5; count++)
{
starMotifO ;
cvs.rotate2D(72.0):
// concatenate another rotation
// присоединяем другой поворот
Изобразите на бумаге, что происходит после каждого из этих шагов.
Пример 5.5.2. Рисование снежинок
Красота снежинки в значительной степени проистекает из высокого уровня ее симметрии. Снежинка
состоит из шести одинаковых спиц (так называются линии, идущие от центра круга к его периферии),
отстоящих на 60° одна от другой, причем каждая спица симметрична относительно своей собственной
оси. Нетрудно построить сложную снежинку, если разработать одну половину спицы и затем нарисовать
ее 12 раз. На рис. 5.39, а приведена снежинка, созданная из мотива, показанного на рис. 5.39, б. Этот
мотив является ломаной линией, которая расположена выше положительной части оси х. (Чтобы избежать
перекрытия с другими частями снежинки, эта ломаная не поднимается выше показанной на рисунке
прямой, наклоненной под углом 30° к оси х.) Пусть этот мотив рисуется подпрограммой flakeMotifO.
5.5. Использование аффинных преобразований в программах
309
Рис. 5.38. Применение последовательных поворотов системы координат
а б
Рис. 5.39. Проектирование снежинки
Каждая спица снежинки является комбинацией мотива и его же отраженной версии. Отражение
относительно оси х осуществляется с помощью подпрограммы scale2D(l. -1) (почему?), так что мотив
в совокупности со своим отражением можно нарисовать посредством следующего кода:
flakeMotifO;
// draw the top half
// рисуем верхнюю половинку
cvs.seale2D(1.0.-1.0):
// flip It vertically
// зеркально отображаем ее по вертикали
flakeMotifO:
// draw the bottom half
// рисуем нижнюю половинку
cvs.scale2D(1.0.-1.0):
// restore the original axis
// восстанавливаем исходную ось
Для того чтобы нарисовать всю снежинку, нужно просто выполнить этот код шесть раз, с промежу-
точным поворотом на 60°:
void drawFlakeO
for(int count ‘ 0: count < 6: count++)
// draw a snowflake
// рисуем снежинку
{
310
Глава 5. Преобразования объектов
//
//
flakeMotifO:
cvs.seale2D(1.0. -1.0):
flakeMotifO:
cvs.scale2D(1.0. -1.0):
cvs.rotate2D(60.0):
concatenate a 60-degree rotation
добавляем поворот на 60 градусов
Пример 5.5.3. Шквал из снежинок
Шквал из снежинок, подобный приведенному на рис. 5.40, можно создать посредством многократного
рисования снежинки в случайных позициях. Вот соответствующий код на OpenGL:
while(!bored)
cvs.initCTO:
cvs.translate2D(randan amount, random amount):
// (аргументами являются два случайных числа)
drawFlakeO:
Отметим, что СТ необходимо инициализировать каждый раз во избежание концентрации снежи-
нок в одном месте.
Рис. 5.40. Шквал из снежинок
Пример 5.5.4. Создание узоров из мотива
На рис. 5.41 показаны две конфигурации из мотивов динозавра. В обоих вариантах динозавры распре-
делены вокруг окружности, по в одном случае каждый динозавр повернут так, что его ноги направлены
к началу координат, а во втором случае все динозавры расположены вертикально. В обоих случаях для
создания узора используется комбинация поворотов и перемещений. Интересно посмотреть, как на
получающуюся картину влияет порядок операций.
Допустим, что подпрограмма drawDinoO рисует вертикального динозавра, помещенного в начало
координат. На рис. 5.41, а система координат для каждого мотива вначале поворачивается вокруг начала
на нужный угол, а затем перемещается вдоль своей оси у на Н единиц. Ниже приведен код, выполняющий
эти операции. Отметим, что СТ заново инициализируется на каждом шаге цикла, так что экземпляры
не концентрируются в одном месте. Подумайте, какие преобразования вы использовали бы, если бы
захотели создавать этот узор путем преобразования точек самого мотива.
const int numMotifs - 12:
for(int i - 0: i < numMotifs: i++)
{
5.5. Использование аффинных преобразований в программах
311
cvs.initCTO;
// init СТ at each iteration
// инициализируем СТ при каждой итерации
cvs.rotate2D(i * 360 / numMotifs):
// rotate
// поворачиваем
cvs.translate2D(0.0. Н):
// shift along the y-axis
// смещаемся вдоль оси у
drawDinoO;
}
а б
Рис. 5.41. Два узора на основе одного мотива: а) каждый мотив повернут автономно;
б) все мотивы расположены вертикально
Простой способ удержать мотивы в вертикальном положении, как это показано на рис. 5.41, б, за-
ключается в том, чтобы поворачивать каждый мотив до его перемещения. Например, если какой-либо
мотив должен в конечном счете расположиться под углом 120°, то он сначала поворачивается (когда
еще находится в начале координат) на -120°, затем перемещается вверх на Н единиц и затем поворачи-
вается на 120°. Какие изменения в вышеприведенном коде приведут к'этому эффекту?
5.5.1. Сохранение СТ для дальнейшего использования
Программа может включать в себя весьма длинные последовательности вызовов функций rotate2D(),
scale2D() и translate2D(). Эти функции вносят «дополнительные» или «относительные» изменения в
СТ, но иногда нам может понадобиться «вернуться» к какому-нибудь предшествующему СТ, чтобы сле-
довать по другому пути преобразований для следующего экземпляра рисунка. Для того чтобы «запом-
нить» желаемое СТ, нужно сделать его копию и записать ее в удобном месте. Тогда в дальнейшем мы
сможем восстановить это СТ и быстро вернуться к преобразованию, которое имело место в тот момент.
Мы даже можем хранить целую коллекцию прежних СТ и возвращаться к любым из них в нужные момен-
ты. Для того чтобы осуществить это, можно работать со стеком преобразований (stack of transformations),
как это предлагается на рис. 5.42.
Верхняя матрица в стеке — это фактическое СТ, и операции вида rotate2D() компонуют с ним свои
преобразования описанным ранее способом. Для того чтобы сохранить это СТ для дальнейшего исполь-
зования, делается его копия и «вталкивается» в стек с помощью подпрограммы pushCTO. После этого
два верхних элемента стека становятся идентичными. Теперь верхний элемент может быть изменен с по-
мощью дополнительных вызовов seal e2D() и подобных ей подпрограмм. Для того чтобы вернуться к преж-
нему СТ, верхний элемент просто «выталкивается» из стека с помощью подпрограммы рорСТО и затем
отбрасывается. Таким способом можно вернуться к самому последнему СТ, затем к следующему самому
последнему СТ и т. д., в порядке «последним вошел, первым вышел» («last-in, first-out»).
312
Глава 5. Преобразования объектов
а б в г
Рис. 5.42. Управление стеком СТ: а) до преобразованией; б) после pushCT(); а) после rotate2D(); г) после рорСТ()
Реализация подпрограмм pushCTO и рорСТО с использованием OpenGL проста, так как в нем имеют-
ся подпрограммы glPushMatrixO и glPopMatrixO, управляющие различными стеками из матриц. В лис-
тинге 5.2 приведены нужные функции. Отметим, что каждая из них должна информировать OpenGL
о том, в каком из матричных стеков происходят изменения.
Листинг 5.2. Подпрограммы для сохранения и восстановления преобразований СТ
void Canvas:: pushCT(void)
{
glMatrixMode(GL_MODELVIEW):
glPushMatrixO;
// push a copy of the top matrix
// вталкиваем в стек копию верхней матрицы
}
void Canvas:: popCTCvoid)
{
glMatrixMode(GL_MODELVIEW):
gl PopMatrixO:
// pop the top matrix from the stack
// выталкиваем верхнюю матрицу из стека
Пример 5.5.5. Простой способ выкладывания мозаики
Множество красивых узоров, называемых мозаикой (tiling), украшают стены, посуду и ткани. Они
основываются на повторении основного мотива — как по горизонтали, так и по вертикали. Рассмотрим
мозаичное выкладывание окна каким-нибудь мотивом, как предложено на рис. 5.43. Мотив нарисован
в центре своей системы координат, как показано на рис. 5.43, а, с помощью некоторой подпрограммы
motif (). Копии этого мотива рисуются с отступом в L единиц в направлении х и в D единиц в направле-
нии у, как показано на рис. 5.43, б.
В листинге 5.3 показано, как просто можно манипулировать системой координат в двойном цикле
при рисовании этой мозаики. После прорисовки каждого ряда преобразование СТ восстанавливается
таким образом, что оно возвращается в начало этого ряда, готовое подняться наверх для начала следую-
щего ряда. Кроме того, весь блок кода заключен между подпрограммами pushCTO и рорСТО, поэтому пос-
ле завершения всей мозаики СТ возвращается к своему начальному значению — на тот случай, если
понадобится рисовать еще.
Листинг 5.3. Рисование шестиугольной мозаики
cvs. pushCTO:
// so we can return here
// вталкиваем в стек, чтобы сюда можно было вернуться
cvs.translate2D(W. Н);
5.5. Использование аффинных преобразований в программах
313
// position for the first motif
// положение первого мотива
for(row - 0; row < 3: row++)
// draw each row
// рисуем каждый ряд
{
cvs.pushCTO:
for (col - 0: col <4: col++)
// draw the next row of motifs
// рисуем очередной ряд мотивов
{
motifO;
cvs.translate2D(L. 0):
// move to the right
// перемещаемся вправо
cvs.popCTO;
// back to the start of this row
// обратно к началу этого ряда
cvs.translate2D(0. D):
// move up to the next row
// перемещаемся вверх на следующий ряд
cvs.popCTO:
// back to where we started
// назад к тому месту, откуда мы начинали
а
б
Рис. 5.43. Мозаика, выложенная одним мотивом: а) мотив; б) мозаика
Пример 5.5.6. Использование преобразований моделирования в программе
автоматизированного проектирования (CAD)
В некоторых программах требуется рисовать много экземпляров нескольких форм. На рис. 5.44 пока-
зан пример программы автоматизированного проектирования (computer-aided design — CAD),
в которой анализируется схема соединения цифровых логических вентилей. Пользователь может
314
Глава 5. Преобразования объектов
конструировать схему посредством «выбора и размещения» («picking and placing») различных венти-
лей, возможно, разного размера и разной ориентации, в нужные места рабочей зоны. Каждое изображе-
ние объекта на этой сцене называется экземпляром (instance) данного объекта. Определение объекта
дается один раз, в системе координат, удобной для работы с формой данного конкретного объекта, и
носит название локальной системы координат (master coordinate system). Преобразование, которое пе-
реносит объект иэ его локальной системы координат в мировые координаты для создания экземпляра,
часто называют преобразованием моделирования (modeling transformation).
Создать
Соединить
Удалить
Имитировать
Выйти
Рис. 5.44. Создание экземпляров в приложении с «выбором и размещением»
На рис. 5.45 показаны два логических вентиля, каждый из которых определен один раз в своей
собственной локальной системе координат. При создании пользователем каждого экземпляра одного
из этих вентилей генерируется соответствующее преобразование моделирования, которое ориентирует
и позиционирует данный рисунок. Это преобразование может быть сохранено просто как набор пара-
метров, например: S, A, dx и dy, — что отражает тот факт, что преобразование моделирования всегда
должно состоять из следующих операций:
1) масштабирование с множителем 5,
2) поворот на угол А,
3) перемещение на (dx, dy),
выполняемых именно в этом порядке. Список всех вентилей схемы хранится вместе с параметрами пре-
образований для каждого из них.
Рис. 5.45. Каждый тип вентиля определяется в своей собственной системе координат
Всякий раз, когда рисунок должен быть обновлен, каждый экземпляр рисуется поочередно с примене-
нием соответствующего преобразования моделирования. Код этого обновления выглядит примерно так:
clear the screen
// очищаем экран
for(i - 0; 1 < numberOfGates: i++)
5.5. Использование аффинных преобразований в программах
315
// for each gate
// для каждого вентиля
{
pushCTO:
// remember the СТ
// запоминаем СТ
trans!ate2D(dx[1]. dy[i]):
// apply the transformation
// применяем преобразование
rotate2D(A[1]);
scale2D(S[1]. S[1J);
drawGate(type[1]):
// draw one of the two types
// рисуем один из двух типов
рорСТ():
// restore the СТ
// восстанавливаем СТ
}
Текущее преобразование СТ вталкивается в стек перед рисованием каждого экземпляра, поэтому
оно может быть восстановлено после того, как этот экземпляр нарисован. Преобразование моделирова-
ния экземпляра определяется его параметрами, после чего рисуется один из двух типов вентилей. Необ-
ходимый для этого код организован просто, поскольку рутина масштабирования, ориентации и позицио-
нирования каждого экземпляра выполняется соответствующими инструментами, которые управляют
СТ и его стеком.
Практические упражнения
5.5.1. Разработка преобразований
В предположении, что OpenGL недоступен, детально опишите следующие подпрограммы, выполняю-
щие элементарные изменения системы координат:
void scale2D(double sx. double sy):
void translate2D(double dx. double dy);
5.5.2. Реализация «вталкивания» и «выталкивания» в стеке преобразований
Определите, при отсутствии OpenGL, соответствующие типы данных для стека преобразований и на-
пишите подпрограммы pushCTO and рорСТО.
5.5.3. Мозаика из шестиугольников
Гексагональный узор предлагает богатый набор мозаик, поскольку правильные шестиугольники точно
совмещаются друг с другом, как в пчелиных сотах. На рис. 5.46 показано девять столбцов упакованных
шестиугольников. Эти шестиугольники начерчены пустыми, однако внутри них можно рисовать различ-
ные интересные фигуры.
О Докажите, что длина каждого ребра шестиугольника радиуса R такл?е равна R.
О Докажите, что центры соседних шестиугольников в столбце отстоят друг от друга по вертикали
на R х/з и что соседние столбцы отстоят друг от друга по горизонтали на 3R/2.
О Используя подпрограммы pushCTO, рорСТ и соответствующие преобразования для отслеживания
начала каждой строки и каждого столбца, разработайте код, осуществляющий рисование шести-
угольной мозаики, показанной на рисунке.
316
Глава 5. Преобразования объектов
Рис. 5.46. Простая мозаика из шестиугольников
5.6. Рисование трехмерных сцен с применением OpenGL
В главе 3 мы уже познакомились с рисованием двумерных объектов, разработав при этом простой класс
Canvas. Этот класс поддерживает функции, которые устанавливают окно и порт просмотра и которые
рисуют прямые линии с помощью функций moveToO и ИпеТоО. Помимо этого в данной главе мы доба-
вили понятие текущего преобразования СТ и ввели функции, осуществляющие двумерные повороты,
масштабирования и перемещения. Такие двумерные преобразования в действительности являются ча-
стными случаями трехмерных преобразований, а именно тех, которые игнорируют третье измерение.
В данном разделе мы рассмотрим, как трехмерные преобразования используются в программах, ос-
нованных на OpenGL. Основное ударение делается на преобразовании объектов для ориентирования и
позиционирования их в трехмерной сцене. Неудивительно, что вся эта работа выполняется с помощью
матриц и OpenGL поддерживает необходимые функции для построения нужных матриц. Кроме того,
OpenGL поддерживает матричный стек, который дает возможность проделать преобразования над од-
ним объектом и затем вернуться к предыдущему преобразованию и подготовить преобразование друго-
го объекта.
Было бы неплохо создать программу, рисующую различные сцены с помощью набора трехмерных
преобразований. Кроме того, экспериментирование с подобной программой дает вам дополнительную
возможность увидеть, что делают различные трехмерные преобразования. OpenGL упрощает установ-
ку «камеры», которая делает «снимок» сцены из заданной точки. Подобная камера также создается с
помощью матрицы, и в главе 7 мы будем подробно изучать, как это делается. Здесь же мы просто вос-
пользуемся средствами OpenGL для установки подходящей камеры, при этом наше внимание будет
сосредоточено на преобразовании объектов. Несмотря на то что мы используем программное средство
до того, как разобрались в его операциях, выигрыш велик: вы сможете создавать впечатляющие изобра-
жения трехмерных сцен посредством лишь небольшого числа вызовов функций OpenGL.
5.6.1. Знакомство с процессом визуального отображения
и графическим конвейером
Все двумерные рисунки, выполненные нами до сих пор, фактически использовали частный случай трех-
мерного визуального отображения, основанный на простой «параллельной проекции». Мы использо-
вали «камеру», подобную той, что показана на рис. 5.47. «Глаз», который наблюдает сцену, смотрит
вдоль оси z на «окно», представляющее собой прямоугольник, расположенный в плоскости ху. Отобра-
жаемый объем (view volume) камеры — это прямоугольный параллелепипед, четыре боковые грани
которого определяются границами окна, а две оставшиеся грани определяются ближней плоскостью
(near plane) и дальней плоскостью (far plane). Точки, располагающиеся внутри отображаемого объема,
проецируются на окно вдоль прямых, параллельных оси z. Это эквивалентно простому игнорированию
5.6. Рисование трехмерных сцен с применением OpenGL
317
z-компонентов таких точек, так что трехмерная точка (хр z/p zj проецируется в точку (xv yv 0). Точки,
располагающиеся за пределами отображаемого объема, отсекаются. Отдельное преобразование в порт
просмотра (viewport transformation) отображает проецируемые точки из окна в порт просмотра на уст-
ройстве отображения.
Рис. 5.47. Простое визуальное отображение, используемое в OpenGL для двумерного рисования
Обратимся теперь к трехмерной графике и разместим трехмерные объекты на сцене. В приведенных
здесь примерах мы продолжаем использовать параллельную проекцию. (Более реалистичная перспек-
тивная проекция, в которой удаленные объекты имеют меньший размер, чем близкие объекты, описы-
вается в главе 7.) Поэтому мы будем применять такую же камеру, как на рис. 5.47, однако предоставим
ей большую свободу положения и ориентации на трехмерной сцене, — с тем, чтобы получить лучший
обзор сцены.
На рис. 5.48 изображена такая камера, внедренная в сцену. Эта сцена состоит из параллелепипеда,
часть которого располагается за пределами отображаемого объема. На рисунке также показано изобра-
жение, создаваемое камерой.
Рис. 5.48. Камера, создающая параллельные виды сцены
Плоскость
проекции
Создаваемое
изображение
В предыдущем разделе мы видели, что в OpenGL содержится три функции glSealedC...), glRotatedC...)
и glTranslated(...), предназначенные для применения к форме моделирующих преобразований. Парал-
лелепипед на рис. 5.48 в действительности представляет собой куб, который был растянут, повернут и
смещен до состояния, показанного на рисунке. Кроме того, в OpenGL содержатся функции для задания
отображаемого объема и его положения на сцене.
Графический конвейер, реализованный в OpenGL, выполняет основную работу посредством мат-
ричных преобразований, поэтому мы прежде всего должны разобраться в том, что делает каждая мат-
рица этого конвейера. На данном этапе нам важно только понять основной принцип работы каждой
матрицы, а в главе 7 будет дан детальный разбор. На рис. 5.49 показан такой конвейер (в слегка
упрощенном виде). Каждая вершина объекта пропускается через конвейер посредством вызова функ-
ции типа gl Vertex3d(x, у, z). Эта вершина умножается на различные матрицы, показанные па рисунке,
318
Глава 5. Преобразования объектов
при необходимости производится отсечение; и если вершина пережила это отсечение, то в конечном счете
она отображается в порт просмотра. Каждая вершина встречается со следующими тремя матрицами:
О матрица моделирования-вида;
О проекционная матрица;
О матрица порта просмотра.
Проекционная
Матрица
порта просмотра
Матрица
моделирования-вида
Рис. 5.49. Конвейер OpenGL (упрощенный)
Матрица моделирования-вида в основном занимается тем, что мы называли СТ (текущее преобра-
зование). Она компонует два действия: последовательность моделирующих преобразований, применя-
емых к объектам, и преобразование, ориентирующее и позиционирующее камеру в пространстве (от-
сюда и ее название — моделирование и вид). Хотя матрица моделирования-вида является единственной
в каждом действующем конвейере, проще представлять ее в виде произведения двух матриц: матрицы
моделирования М и матрицы вида (просмотра) V. Сначала применяется матрица моделирования, а затем
матрица вида, так что матрица моделирования-вида фактически является произведением матриц VM.
(Почему?)
Рис. 5.50. Эффект применения матрицы моделирования-вида в графическом конвейере: а) до преобразований; б) после
преобразования моделирования; в) после преобразований моделирования и вида
На рис. 5.50 показано, что делают матрицы М и Удля того же случая, который показан на рис. 5.49,
где камера «смотрит вниз» на сцену, состоящую из параллелепипеда. На рис. 5.50, а показан единич-
ный куб с центром в начале координат. Преобразование моделирования с матрицей М масштабирует,
поворачивает и перемещает этот куб, превращая его в параллелепипед, изображенный на рис. 5.50, б, на
котором показано также относительное положение отображаемого объема камеры. Затем применяется
матрица V, которая поворачивает и перемещает параллелепипед в новое положение. Специфика преоб-
разования заключается в том, что оно как бы переносит камеру из положения на сцене в ее «исходное»
положение, когда глаз находится в начале координат и отображаемый объем выровнен по оси г, как
5.6. Рисование трехмерных сцен с применением OpenGL
319
показано на рис. 5.50, в. Вершины параллелепипеда теперь позиционированы (это означает, что их ко-
ординаты имеют правильные значения), так что их проецирование на ближнюю плоскость дает пра-
вильные значения для отображения проецируемого образа. Следовательно, матрица V фактически вы-
зывает преобразование координат вершин сцены в систему координат камеры. Координаты камеры
иногда называют также координатами наблюдателя (глаза) (eye coordinates). В системе координат ка-
меры ребра отображаемого объема параллельны осям х, у и z. Отображаемый объем заключен по оси х
между величинами left (левая) и right (правая), по оси у между bottom (нижняя) и top (верхняя), и по оси
z между -near (ближняя) и -far (дальняя). (Ниже мы вкратце обсудим смысл знаков «минус» перед
near и far.) После того как вершины исходного куба обработаны всей матрицей моделирования-вида,
они располагаются так, как показано на рис. 5.50, в.
Проекционная матрица масштабирует и перемещает каждую вершину особым способом, так что все
те вершины, которые располагаются внутри отображаемого объема, будут располагаться внутри стан-
дартного куба, расположенного в промежутках от -1 до 1 по каждому измерению1. (При использова-
нии перспективных проекций эта матрица делает еще кое-что, как мы увидим в главе 7.) Проекционная
матрица эффективно преобразует отображаемый объем в куб с центром в начале координат, что явля-
ется наиболее удобным геометрическим телом, границами которого производится отсечение объектов.
Такое масштабирование параллелепипеда может сильно исказить его, однако это искажение будет ском-
пенсировано при преобразовании в порт просмотра. Кроме того, проекционная матрица инвертирует
ось z в том смысле, что возрастающие значения z теперь означают большее удаление (глубину) точки от
наблюдателя. Рисунок 5.51 демонстрирует, как исходный параллелепипед с помощью такого преобра-
зования превращается в другой параллелепипед. (Отметим, что сам отображаемый объем камеры ни-
когда не нужно создавать как объект; он определен только как специальная форма, которую проекцион-
ная матрица преобразует в стандартный куб!)
Р
Рис. 5.51. Действие проекционной матрицы (для параллельных проекций)
Далее выполняется отсечение, которое отбрасывает ту часть параллелепипеда, которая лежит за пре-
делами стандартного куба. И, наконец, матрица порта просмотра отображает «выжившую» часть па-
раллелепипеда в «трехмерный порт просмотра». Эта матрица отображает стандартный куб в паралле-
лепипед такой формы, величины которой х и у соответствуют размерам порта просмотра (в экранных
координатах), а его z-компонент изменяется от 0 до 1 и содержит в себе глубину точки (расстояние от
точки до глаза камеры), как показано на рис. 5.52.
В этом обзоре было вкратце обрисовано, как работает весь графический конвейер OpenGL, причем
было показано, что главным его элементом являются преобразования. Каждая вершина объекта под-
вергается последовательности преобразований, которые переносят ее из мировых координат в коор-
динаты наблюдателя, в нейтральную систему, специально разработанную для отсечения, и, наконец,
в систему координат, служащую для правильного отображения. Каждое преобразование осуществляет-
ся путем умножения матриц. Отметим, что в этом первом обзоре нами были пропущены некоторые важ-
ные подробности работы конвейера. При использовании перспективных проекций нам потребуется
включить так называемое «перспективное деление» («perspective division»), которое использует свой-
Координаты в такой системе иногда называют нормированными приборными координатами (normalizeddevice coordinates).
320
Глава 5. Преобразования объектов
ства однородных координат. И, конечно, множество интересных деталей раскрываются на последнем
этапе фактической визуализации образа, такие как вычисление цветов пикселов «в промежутке» меж-
ду вершинами и контроль правильности удаления невидимых поверхностей. Рассмотрение всех этих
деталей отнесено в следующие главы.
Рис. 5.52. Действие преобразования в порт просмотра
5.6.2. Некоторые инструменты OpenGL для моделирования и вида
Рассмотрим теперь, какие функции предусмотрены в OpenGL для моделирования и установки камеры.
Три функции, используемые для установки преобразований
моделирования и вида
Ниже приводятся функции, обычно используемые для модификации матрицы моделирования-вида,
которая вначале сделана «текущей» посредством вызова функции glMatrixMode(GL_MODELVIEW):
О glSealed(sx. sy. sz); умножает справа текущую матрицу на матрицу, выполняющую масштаби-
рование на величину sx по оси х, на sy по оси у и на sz по оси z. Результат помещается обратно в
текущую матрицу.
О glTranslated(dx, dy, dz); умножает справа текущую матрицу на матрицу, которая выполняет пе-
ремещение на dx по оси х, на dy по оси у и на dz по оси z. Результат помещается обратно в теку-
щую матрицу.
О glRotated (angle, их. иу, uz): умножает справа текущую матрицу на матрицу, которая выпол-
няет поворот на angle градусов вокруг оси, которая проходит через начало координат и точку
(их, иу, uz)1. Результат помещается обратно в текущую матрицу. Для выполнения поворота
используется матрица иэ уравнения (5.33).
Установка камеры в OpenGL (для случая параллельной проекции)
Функция glOrtho(left, right, bott, top, near, far): устанавливает в качестве отображаемого объема
параллелепипед, располагающийся от21 eft до right по оси х, от bott до top по оси у и от -near до -far по
оси z. (Так как это определение работает в координатах наблюдателя, объектив камеры находится в на-
чале координат и направлен вдоль отрицательной части оси z в сторону уменьшения значений z, то
есть в сторону увеличения абсолютных величин.) Эта функция создает матрицу и умножает на нее спра-
ва текущую матрицу. (В главе 7 мы точно укажем, какие величины содержит эта новая матрица.)
1 Положительные значения угла angle соответствуют повороту против часовой стрелки при взгляде вдоль оси поворота со стороны
точки (их, иу, uz) в сторону начала координат.
2 Все параметры функции glOrthoO имеют тип GLdouble.
5.6. Рисование трехмерных сцен с применением OpenGL
321
Поясним знак «минус» перед величинами near и far. Так как по умолчанию камера расположена в
начале координат и смотрит вдоль отрицательных значений оси г, использование для near значения 2
означает помещение ближней плоскости в z = -2, то есть на расстояние в две единицы перед глазом.
Аналогично, использование 20 для far помещает дальнюю плоскость в 20 единицах перед глазом.
Установка проекционной матрицы осуществляется с помощью следующего кода:
glMatrixMode(GL_PROJECTION);
// make the projection matrix current
// делаем текущей проекционную матрицу
glLoadldentityO:
// set it to the identity matrix
// устанавливаем ее в единичную матрицу
glOrtho(left, right, bottom, top. near, far):
// multiply it by the new matrix
// умножаем ее на новую матрицу
Позиционирование и нацеливание камеры
В OpenGL предлагается функция, которая упрощает установку основной камеры:
gluLookAt(eye.x. eye.у. eye.z. look.x. look.y. look.z. up.x. up.y. up.z):
Эта функция создает матрицу просмотра и умножает на нее справа текущую матрицу. Функция при-
нимает в качестве параметров: eye — положение наблюдателя (камеры) и точку, на которую направлен
взгляд — look. Кроме того, она принимает параметр up — приблизительное направление вверх. Посколь-
ку программисту известно, где расположена интересующая его часть сцены, обычно нетрудно выбрать
соответствующие значения eye и look для обеспечения хорошего первого взгляда. При этом параметр up
чаще всего принимается равным (0, 1, 0) для того, чтобы направление вверх было параллельно оси у.
Позднее мы разработаем более мощные инструменты для установки камеры и интерактивного «пило-
тирования» ее в процессе анимации.
Мы хотим, чтобы эта функция установила часть V матрицы моделирования-вида VM. Поэтому она
запускается до того, как добавлены какие-либо преобразования моделирования, поскольку последую-
щие преобразования будут умножаться на матрицу моделирования-вида справа. Поэтому для исполь-
зования функции gluLookAtO необходимо применить такую последовательность команд:
glMatrixMode(GL_MODELVIEW);
// make the modelview matrix current
// делаем текущей матрицу моделирования
glLoadidentity():
// start with a unit matrix
// начинаем с единичной матрицы
gluLookAtCeye.x. eye.у. eye.z.
// the eye position
// положение наблюдателя
look.x. look.y. look.z,
// the "look at” point
// точка направления взгляда
up.x. up.y. up.z):
// the upwards direction
// направление вверх
Работа этой функции рассматривается в главе 7, там же мы разработаем более гибкие средства для
установки камеры. Тем, кого интересует, какие конкретно величины функция gluLookAtO помещает в
матрицу моделирования-вида, следует обратиться к упражнениям в конце раздела.
11 Ф. Хилл
322
Глава 5. Преобразования объектов
Пример 5.6.1. Установка типичной камеры
Камеры часто устанавливают так, чтобы они смотрели «вниз» на сцену с какой-либо ближней позиции.
На рис. 5.53 показана камера, объектив которой расположен в точке eye - (4, 4, 4) и смотрит в начало
координат, причем значение параметра look (0,1,0). Направление вверх установлено параметром
up=(0,1,0). Предположим, нам нужно, чтобы отображаемый объем имел ширину 6,4 и высоту 4,8 (при
этом форматное соотношение равно 640/480), а также чтобы near = 1 и far = 50. В этом случае камеру
можно установить посредством следующего кода:
glMatixMode(GL_PROJECTION):
// set the view volume
// устанавливаем отображаемый объем
glLoadldentity():
g!0rtho(-3.2. 3.2. -2.4. 2.4. 1. 50);
glMatrixMode(GL_MODELVIEW);
// place and aim the camera
// размещаем и нацеливаем камеру
glLoadldentity();
gluLookAt(4, 4. 4, 0. 1. 0. 0, 1. 0);
Рис. 5.S3. Установка камеры посредством функции gluLookAtO
В упражнениях показаны конкретные величины, которые при этом помещаются в матрицу модели-
рования-вида.
Практические упражнения
5.6.1. Что делает функция gluLookAtO?
Нам уже известно, что функция gluLookAtO строит матрицу, которая преобразует мировые координаты
в координаты наблюдателя. На рис. 5.54 показана камера в качестве системы координат, подвешен-
ной в пространстве. Ее начало координат находится в точке eye и она ориентирована с помощью своих
трех взаимно перпендикулярных ортов u, v и п. Глаз камеры «смотрит» в направлении (-п). Функция
gluLookAtO использует параметры eye, look и вектор up для того, чтобы сформировать векторы u, v, п в
соответствии со следующими соотношениями:
n = eye - look,
u = up х n, (5.38)
v = nxu.
5.6. Рисование трехмерных сцен с применением OpenGL
323
Затем функция gl uLookAtC) нормирует эти три вектора, устанавливая для них единичную длину, пос-
ле чего строит следующую матрицу:
'и, иу иг dx'
v v v d
у = х ^у "z
Пу Пг dz
0 0 0 1
\ /
где точка d имеет компоненты: (dx, dy, d2) = {-eye • u, -eye • v, -eye • n).
а) Докажите, что векторы u, v и n взаимно перпендикулярны.
б) Докажите, что матрица V правильно преобразует мировые координаты в координаты камеры,
проверив, что она отображает точку eye в начало координат (0,0,0,1)г, векторы и в i = (1,0,0,0),
v в j = (0,1,0) и п в к = (0, 0,1).
в) Докажите для случая eye - (4,4,4), lookAt - (0,1,0), up = (0,1,0), что результирующая матрица
имеет следующий вид:
'0,70711 0 -0,70711 0 '
V = -0,3313 0,88345 -0,3313 -0,88345
0,6247 0,4685 0,6247 -6,872
t 0 0 0 1 ,
Рис. 5.54. Преобразование координат из мировых в координаты камеры
5.6.2. К вопросу об элементах матрицы в OpenGL
Выведите значения матрицы моделирования-вида, чтобы проверить некоторые утверждения, сделан-
ные при ее создании. Для того чтобы увидеть, что записано в матрице моделирования-вида в OpenGL,
определите массив GLfloat mat[16] и примените функцию glGetFloatv(GL_MODELVIEW_MATRIX, mat), которая
копирует в массив mat[] 16 значений матрицы моделирования-вида. Элемент матрицы копиру-
ется в элемент массива mat[4j+i ] для i,j = 0,1,2,3.
5.6.3. Рисование элементарных форм, поддерживаемых OpenGL
В следующей главе мы увидим, как создавать свои собственные трехмерные объекты, однако уже сей-
час нам требуется нарисовать несколько трехмерных объектов — чтобы поэкспериментировать с уста-
новкой и использованием камер. В инструментарии GLUT предусмотрено несколько таких готовых
324
Глава 5. Преобразования объектов
объектов, включая сферу, конус, тор, пять Платоновых тел (обсуждаемых в главе 6), а также небезызвест-
ный чайник. Каждый такой объект доступен в виде каркасной модели и в виде объемной модели с гра-
нями, которые могут быть закрашены. Ниже приводится список, показывающий, какие функции ис-
пользуются для рисования некоторых из этих объектов:
О куб: glutWireCubeCGLdouble size); каждая сторона имеет длину size;
О сфера: glutWireSphere(GLdouble radius, GLint nSlices, GLint nStacks);
О тор: glutWireTorus(GLdouble inRad, GLdouble outRad, GLint nSlices. GLint nStacks);
О чайник: glutWireTeapot(GLdouble size).
Существуют также функции glutSolidCubeO, glutSolidSphereO и другие, которые мы будем исполь-
зовать позднее. Форма тора задается с помощью внутреннего радиуса inRad и внешнего радиуса
outRad. Сфера и тор аппроксимируются полигональными гранями, поэтому путем изменения парамет-
ров nSlices и nStacks можно устанавливать, сколько граней будет использовано в аппроксимации. Пара-
метр nSlices — это число «долек» вокруг оси z, a nStacks — число «ломтиков» вдоль оси z, как если бы
данная форма была стопкой из множества nStacks дисков.
Для визуализации четырех из Платоновых тел (пятым является куб, который уже был представлен)
используются следующие функции;
О тетраэдр: glutWireTetrahedronO;
О октаэдр: glutWireOctahedronO;
О додекаэдр: glutWireDodecahedronO;
О икосаэдр: glutWire!cosahedron().
Все вышеприведенные формы имеют центр в начале координат. Кроме них, имеются еще следую-
щие тела:
О конус: glutWireCone(GLdouble baseRad, GLdouble height. GLint nSlices, GLint nStacks);
О усеченный конус (конический цилиндр): gluCylinder(GLUquadricObj * qobj, GLdouble baseRad,
GLdouble topRad, GLdouble height, GLint nSlices, GLint nStacks).
Оси конуса и усеченного конуса совпадают с осью z. Их основания находятся в плоскости z = 0 и
простираются вдоль оси z до плоскости z = height. Радиусы конуса и усеченного конуса при z = 0 зада-
ются переменной baseRad, Радиус усеченного конуса при z = height равен topRad.
В действительности усеченный конус является целым семейством форм, различающихся значени-
ем параметра topRad. При topRad = 1 сужение отсутствует, и мы имеем классический прямой круговой
цилиндр (right circular cylinder). Если topRad = 0, то усеченный конус идентичен конусу.
Отметим, что рисование усеченного конуса в OpenGL требует некоторой дополнительной работы,
поскольку он является частным случаем поверхности второго порядка, как мы увидим в главе 6. Для
того чтобы нарисовать его, необходимо
1) определить новый квадратичный объект;
2) задать стиль рисования (GLUJ.INE для каркасной модели, GLU_FILL для объемной визуализации);
3) нарисовать объект.
Код в листинге 5.4 делает все вышеперечисленное.
Листинг 5.4. Формы, доступные в GLU
GLUquadricObj * qobj - gluNewQuadricO;
// make a quadric object
// создаем квадратичный объект
gluQuadricDrawStyle(qobj.GLU.LINE);
// set style to wireframe
// устанавливаем стиль каркасной модели
5.6. Рисование трехмерных сцен с применением OpenGL
325
gluCylinderCqobJ. baseRad. topRad. height. nSlices. nStacks):
// draw the cylinder
// рисуем цилиндр
Впоследствии мы применим некоторые из вышеупомянутых форм в двух фундаментальных приме-
рах, в которых основное внимание уделяется использованию аффинных преобразований при модели-
ровании и визуализации трехмерной сцены. Там же приведена законченная программа для рисования
каждой из заданных сцен. Вы серьезно продвинетесь в понимании сути этих программ, если введете их
в компьютер, создадите эти фигуры и затем понаблюдаете за их изменением путем варьирования пара-
метров, входящих в этот код.
Пример 5.6.2. Сцена, составленная из каркасных объектов
На рис. 5.55 показана сцена с несколькими объектами, расположенными в углах единичного куба, один
угол которого совпадает с началом координат. В различных углах этого куба расположено семь объек-
тов, причем все они изображены в каркасной форме.
Рис. 5.55. Каркасное изображение различных примитивных форм
Камера имеет отображаемый объем с форматным соотношением 640/480, располагающийся в про-
межутке от -2 до 2 по оси у. Ближняя плоскость определяется значением N= 0,1, дальняя плоскость —
значением F = 100. Это достигается посредством вызова функции
gl0rtho(-2.0* aspect, 2.0* aspect. -2.0. 2.0. 0.1. 100);
Камера позиционируется с параметрами eye - (2,2,2), look - (0,0,0) и up = (0,1,0) (параллельно оси
у) посредством вызова функции
glutookAt(2.0. 2.0, 2.0. 0.0. 0.0. 0.0. 0.0, 1.0, 0.0):
Листинг 5.5. Полная программа для создания рис. 5.55 с использованием OpenGL
#include <windows.h>
//suitable when using Windows 95/98/NT
//применимо при использовании Windows 95/98/NT
#include <gl/Gl.h>
#include <gl/Glu.h>
#include <gl/glut.h>
//««««« axis »»»»»»»
void axis(double length)
продолжением
326
Глава 5. Преобразования объектов
Листинг 5.5 (продолжение)
// draw a z-axis. with cone at end
// рисуем ось z с конусом на конце стрелки
glPushMatrixO;
glBegin(GL_LINES):
glVertex3d(0. 0. 0); glVertex3d(0.0,length);
// along the z-axis
// вдоль оси z
glEndO:
glTranslated(O. 0.length - 0.2):
glutWireCone(0.04. 0.2. 12. 9):
glPopMatrixO;
}
//«««««<««<««««««« displayWire »»»»»»»
void displayWire(void)
{
glMatrixMode(GL_PROJECTION):
// set the view volume shape
// устанавливаем форму отображаемого объема
glLoadldentityO:
g!0rtho(-2.0*64/4B.0. 2.0*64/48.0. -2.0. 2.0. 0.1. 100):
glMatrixMode(GL_MODELVIEW):
// position and aim the camera
// позиционируем и нацеливаем камеру
glLoadldentityO:
gluLookAt(2.0. 2.0. 2.0. 0.0. 0.0. 0.0. 0.0. 1.0. 0.0);
glClear(GL_COLOR_BUFFER_BIT);
// clear the screen
// очищаем экран
glColor3d(0.0.0)
// draw black lines
// рисуем черные линии
axis(0.5):
// z-axis
// ось z
glPushMatrixO:
glRotated(90. 0. 1.0. 0):
axis(0.5);
// y-axis
// ось у
glRotated(-90.0. 1. 0. 0);
axi s(0.5);
// z-axis
// ось z
glPopMatrixO:
glPushMatrixO;
glTranslated(0.5. 0.5. 0.5):
// big cube at (0.5, 0.5. 0.5)
// большой куб в точке (0.5. 0.5. 0.5)
glutWireCube(l.O):
glPopMatrixO:
5.6. Рисование трехмерных сцен с применением OpenGL
327
glPushMatrixO:
glTranslatedfl.0.1.0.0);
// sphere at (1.1,0)
// сфера в точке (1,1,0)
glutWireSphere(0.25. 10. 8):
glPopMatrixO:
glPushMatrixO:
glTranslated(l.O.O.l.O):
// cone at (1.0.1)
// конус в точке (1.0.1)
glutWireCone(0.2. 0.5. 10. 8):
glPopMatrixO; .
glPushMatrixO:
glTranslated(l.l.l):
glutWireTeapot(0.2);
// teapot at (1.1,1)
// чайник в точке (1.1.1)
glPopMatrixO:
glPushMatrixO;
glTranslated(0, 1.0 ,0):
// torus at (0.1,0)
// тор в точке (0,1,0)
glRotated(90.0. 1.0. 0):
glutWireTorus (0.1. 0.3. 10.10):
glPopMatrixO:
glPushMatrixO:
glTranslatedd.O. 0 .0):
// dodecahedron at (1.0,0)
// додекаэдр в точке (1,0.0)
glScaled(0.15. 0.15. 0.15):
glutWi reDodecahedron();
glPopMatrixO:
glPushMatrixO:
glTranslated(0, 1.0 .1.0):
// small cube at (0,1.1)
// малый куб в точке (0,1.1)
glutWireCube(0.25):
glPopMatrixO;
glPushMatrixO;
glTranslated(0. 0. 1.0);
// cylinder at (0.0,1)
// цилиндр в точке (0.0,1)
GLUquadricObj * qobj:
qobj - gluNewQuadricO;
gluQuadri cDrawSty1e(qobj.GLU_LINE);
gluCylinder(qobj. 0.2. 0.2. 0.4. 8,8);
продолжение-^
328
Глава 5. Преобразования объектов
Листинг 5.5 (продолжение)
glPopMatriх():
glFlushO;
//<<<<<<<<<<<<<<<<<< main »»»»»»»»»»
void main(int argc, char **argv)
{
glutlnit(&argc. argv):
glut!nitDisplayMode(GLUT_SINGLE | GLUT_RGB );
glutInitWindowSizeC640.480);
glutlnitWindowPositiondOO. 100);
glutCreateWindowCTransformation testbed - wire frames");
// "Испытательный стенд для преобразований
// каркасных моделей"
gl utDisplayFuncCdisplayWire):
glClearColorQ.Of. l.Of. l.Of. O.Of):
// background is white
// фон белый
glViewportCO, 0. 640. 480):
glutMainLoopО:
}
В листинге 5.5 приведена полная программа для выполнения этого рисунка. Подпрограмма mainO
инициализирует экранное окно размером 640 на 480 пикселов, устанавливает порт просмотра и цвет
фона, а также указывает функцию displayWireO в качестве отображающей функции, вызываемой для
выполнения рисунка, В displayWireO вначале устанавливаются форма и положение камеры. Затем каж-
дый из объектов рисуется поочередно. Для большинства объектов требуется их собственная матрица
моделирования, чтобы повернуть и позиционировать их должным образом. Перед установкой каждого
преобразования моделирования для запоминания текущего преобразования используется функция
glPushMatrixO. После того как объект нарисован, текущее преобразование восстанавливается посред-
ством вызова функции glPopMatrixO. Поэтому код для рисования каждого объекта заключен внутри
«скобок», образуемых парой функций glPushMatrixO и glPopMatrixO, Внимательно проверяйте, чтобы
каждое преобразование помещало свой объект в нужное место.
В листинге также приведены оси х, у, z, нарисованные с коническими наконечниками стрелок. Изоб-
ражение основной системы координат может помочь наблюдателю сориентироваться. Для рисования
оси х ось z поворачивается на 90° относительно оси у, чтобы создать повернутую систему координат,
и ось х рисуется заново при этой новой ориентации. Отметим, что эта ось рисуется без заключения ее в
«скобки» glPushMatrixO и glPopMatrixO, так что следующий поворот для создания оси у осуществляется
в уже повернутой системе координат. Убедитесь, что этот поворот правильный.
Отметим, что стороны большого куба, параллельные в трехмерном пространстве, изображаются так-
же параллельными — это результат использования параллельной проекции. Данный куб выглядит не-
сколько неестественным, потому что мы привыкли видеть мир в перспективной проекции. Как мы уви-
дим в главе 7, если вместо параллельной проекции использовать перспективную, то параллельные ребра
не будут нарисованы параллельными.
Пример 5.6.3. Визуализация трехмерной сцены с затенением
В этом примере мы разработаем немного более сложную сцену, чтобы проиллюстрировать дальнейшее
использование моделирующих преобразований. Мы также покажем, как OpenGL обеспечивает созда-
ние гораздо более реалистичных изображений трехмерных объектов с помощью добавления теней и
корректного удаления невидимых поверхностей.
На рис. 5.56 показаны два вида одной сцены. В обоих случаях используется камера, установленная
функцией
gluLookAt(2.3. 1.3, 2, 0. 0.25. 0, 0.0, 1.0, 0.0).
5.6. Рисование трехмерных сцен с применением OpenGL
329
а б
Рис. 5.56. Простая трехмерная сцена: а) использование большого отображаемого объема;
б) использование малого отображаемого объема
На рис. 5.56, а используется большой отображаемый объем, заключающий в себе всю сцену; на
рис. 5.56, б используется маленький отображаемый объем, заключающий в себе только малую часть этой
же сцены, что обеспечивает изображение крупным планом.
Сцена содержит в себе три объекта, лежащих на столе в углу «комнаты». Каждая из трех стен созда-
на путем сплющивания куба в тонкий лист и перемещения его в нужную позицию. (Эти стены тоже
выглядят несколько неестественно из-за использования параллельной проекции.) Переключатель (jack)
составлен из трех вытянутых сфер, ориентированных под прямыми углами друг к другу, и шести ма-
леньких сфер на их концах. Стол состоит из столешницы и четырех ножек. Каждая из этих пяти частей
стола представляет собой куб, масштабированный до нужного размера и формы. Чертеж этого стола
показан на рис. 5.57; он зависит от четырех параметров, характеризующих размер его частей: topWidth (ши-
рина столешницы), topThick (толщина столешницы), legLen (высота ножки) и legThick (толщина ножки).
Подпрограмма tab!eLeg() рисует ножку и вызывается четыре раза внутри подпрограммы tab!е() для рисо-
вания ножек в четырех различных местах. Использование различных параметров внутри tabl eLeg() обес-
печивает вызов различных преобразований моделирования. Как обычно, функции моделирования за-
ключены в скобки gl PushMatrd х(), gl PopMatrl х() для изоляции преобразований, которые они проделывают.
столешницы
Рис. 5.57. Проектирование стола
Полный код этой программы приведен в листинге 5.6. Отметим, что в ней использован сплошной
(solid), а не каркасный вариант каждой формы, например glutSol 1dSphere(). Проверьте соответствую-
щие преобразования, примененные для ориентации и позиционирования каждого объекта в сцене. От-
330
Глава 5. Преобразования объектов
дельно проверьте модель переключателя. Этот пример был разработан с целью разжечь ваш аппетит,
чтобы вы попробовали составить свои сцены, экспериментируя с преобразованиями.
Приведенный код демонстрирует также различные операции, которые необходимо проделать для
создания изображений с тенями. Нужно указать положение и свойства источника света, а также специ-
альные свойства поверхностей объектов, которые описывают, как эти поверхности отражают свет. Так
как процессы затенения рассматриваются в главе 8, сейчас мы только покажем различные вызовы функ-
ций; а использование их в соответствии с данным образцом и создаст затенение.
Листинг 5.6. Полная программа для рисования сцены с затенением
linclude «windows.h>
linclude <iostream.h>
include <gl/Gl.h>
linclude <gl/Glu.h>
linclude <gl/glut.h>
//<<<«««««« wall »»»»»»»»
void walKdouble thickness)
{
H draw thin wall with top - xz-plane.corner at origin
И рисуем тонкую стенку e верхней плоскостью xz
//ис углом в начале координат
glPushMatrixO:
glTranslated(0.5. 0.5 * thickness. 0.5):
glScaledCl.0. thickness. 1.0):
glutSolidCube(1.0):
glPopMatrixO:
}
//««<«««««<« tab!eLeg >»»»»»»»»»
void tableLeg(double thick, double len)
{
glPushMatrixO:
glTranslated(0. len/2. 0):
glScaled(thick. len, thick):
glutSolidCube(l.O):
glPopMatrixO:
}
II<<<<<<<<<<<<<<<<<<<<< jack part »»»»»>»
void jackPartO
{
// draw one axis of the unit jack - a stretched sphere
// рисуем одну ось единичного переключателя - вытянутую сферу
glPushMatrixO:
glScaled(0.2.0.2.1.0):
gl utSol 1dSphere(1.15.15):
glPopMatrixO:
glPushMatrixO;
glTranslated(0.0.1.2):
// ball on one end
// шарик на одном конце
gl utSolidSphere(0.2.15.15):
glTranslated(0.0. -2.4):
glutSolidSphere(0.2.15.15)://ball on the other end
gl PopMatrixO:
}
5.6. Рисование трехмерных сцен с применением OpenGL
331
//<«««««<<««« jack »»>»»»»>»»»
void jackO
{
// draw a unit jack out of spheroids
// рисуем единичный переключатель из сфероидов
• glPushMatrixO;
jackPartO;
glRotated(90.0. 0. 1. 0):
jackPartO;
glRotated(90.0, 1,0.0);
jackPartO:
glPopMatrixO;
}
//<<<<<<<<<<<<<<<<<<<<<<< table »>»»>»»»»»»
void tableCdouble topWid. double topThick, double legThick. double legLen)
// draw the table - a top and four legs
// рисуем стол - столешницу и четыре ножки
glPushMatrixO;
// draw the table top
// рисуем столешницу
glTranslatedCO. legLen. 0);
glScaledCtopWid. topThick. topWid):
glutSolidCube(l.O);
glPopMatrixO;
double dist - 0.95 * topWid/2.0 - legThick / 2.0:
glPushMatrixO;
glTranslatedCdist. 0. dist):
tableLegClegThick. legLen);
glTranslated(0, 0. -2 * dist);
tableLegClegThick. legLen);
glTranslated(-2 * dist. 0. 2*dist):
tableLegClegThick. legLen);
glTranslatedCO, 0. -2*dist):
tableLegClegThick. legLen);
glPopMatrixO;
}
//<<<<<<<<<<<<<<<<<<<<< displaySolid »»»»»»»»»»»
void displaySolid(void)
// set properties of the surface material
// задаем свойства материала поверхности
GLfloat mat_ambient[] - {0.7f.0.7f,0.7f.1.Of}:
// gray
// серый
GLfloat mat_diffuse[] = {0.6f.0.6f.0.6f.1.Of}:
GLfloat mat_specular[] = {l.Of.l.Of.l.Of.l.Of};
GLfloat mat_shininess[] = {50.Of};
glMateri alfv(GL_FRONT.GL_AMBIENT,mat_ambi ent):
glMateria 1fv(GL_FRONT.GL_DIFFUSE.mat_di ffuse);
glMateri alfv(GL_FRONT.GL_SPECULAR.mat_specular);
glMaterialfv(GL_FRONT,GL_SHININESS.mat_shininess):
продолжение &
332
Глава 5. Преобразования объектов
Листинг 5.6 (продолжение)
// set the light source properties
// задаем свойства источника света
GLfloat lightIntensity:] - {0.7f.0.7f,0.7f,1.0f}:
GLfloat light_position[] - {2.Of.6.Of.3.Of.0.Of}:
glLightfv(GL_LIGHTO. GL_POSITION, light_position);
glLightfv(GL_LIGHTO. GL_DIFFUSE. lightintensity);
// set the camera
// устанавливаем камеру
glMatrixMode(GL_PROJECTION):
glLoadldentityO;
double winHt -1.0;
// half-height of the window
// половина высоты окна
gl0rtho(-winHt*64/48.0. winHt*64/48.0. -winHt. winHt. 0.1. 100.0);
glMatrixMode(GL_MODELVIEW);
glLoadldentityO:
gluLookAt(2.3. 1.3. 2. 0. 0.25. 0. 0.0. 1.0. 0.0):
// start drawing
// начинаем рисовать
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT):
// clear the screen
// очищаем экран
glPushMatrixO:
glTranslated(0.4. 0.4. 0.6):
glRotated(45.0.0.1):
glScaled(0.08. 0.08. 0.08);
jack!);
// draw the jack
// рисуем переключатель
glPopMatrixO;
glPushMatrixO:
glTranslated!0.6. 0.38, 0.5);
glRotated(30.0.1.0):
glutSolidTeapot(0.08):
// draw the teapot
// рисуем чайник
glPopMatrixO;
glPushMatrixO;
glTranslated!0.25. 0.42. 0.35):
// draw the sphere
// рисуем сферу
glutSolidSphere(0.1. 15. 15):
glPopMatrixO:
glPushMatrixO;
glTranslated(0.4. 0. 0.4):
table(0.6. 0.02. 0.02. 0.3):
// draw the table
// рисуем стол
glPopMatrixO:
wall(0.02):
// wall #l:in xz-plane
// стена #1: в плоскости xz
glPushMatrixO;
5.6. Рисование трехмерных сцен с применением OpenGL
333
ф Rotated(90.0. 0.0. 0.0. 1.0):
wall(0.02):
// wall #2:in yz-plane
// стена #2: в плоскости yz
glPopMatrixO:
glPushMatrixO:
glRotated(-90.0. 1.0, 0.0. 0.0):
wall(0.02):
// wall #3:in xy-plane
// стена #3: в плоскости xy
glPopMatrixO;
glFlushO;
}
//«<«««««<«««« main »»»»»»»»»»»»»»»>
void maindnt argc. char **argv)
glutlnit(&argc. argv);
glut!nitDisplayMode(GLUT_SINGLE | GLUT_RGB | GLUTJDEPTH):
glut!nitWindowSize(640,480):
glutlnitWindowPositiondOO. 100):
glutCreateWindowC'shaded example -3D scene"):
// «пример с затенением - трехмерная сцена»
glutDisplayFunc(displaySolid):
glEnable(GL_LIGHTING);
// enable the light source
// включаем источник света
glEnable(GL_LIGHT0);
glShadeModel(GL_SMOOTH);
glEnable(GL_DEPTH_TEST):
// for removal of hidden surfaces
// для удаления невидимых поверхностей
glEnable(GL_NORMALIZE);
// normalize vectors for proper shading
// нормируем векторы для правильного затенения
glClearColor(0.If.0.If.0.If.O.Of);
// background is light gray
// фон светло-серый
glViewport(0. 0. 640. 480):
glutMainLoopO;
}
Практические упражнения
5.6.3. Настройка сцены
Какие изменения должны быть сделаны в листинге 5.6, чтобы положить переключатель на пол, а сферу
водрузить на чайник?
5.6.4. Чтение описания сцены из файла
Во всех предыдущих примерах сцена описывалась посредством специальных вызовов OpenGL, кото-
рые преобразуют и рисуют каждый объект, как в следующем коде:
glTranslated(0.25.0.42.0.35):
glutSolidSphere(0.1.15.15);
// draw a sphere
// рисуем сферу
334
Глава 5. Преобразования объектов
В силу этого все объекты на сцене жестко «зашиты» в программу. Такой способ задания сцены явля-
ется громоздким и подвержен ошибкам. Замечательно, когда разработчик имеет возможность задавать
объекты в сцене с помощью простого языка и помещать описание сцены в файл. Тогда программа рисо-
вания становится гораздо более простой универсальной программой: она читает файл, описывающий
сцену, во время выполнения (динамически) и рисует любые объекты, встречающиеся в таком файле.
Такое средство предоставляется языком описания сцен (Scene Description Language — SDL), который
представлен в приложении Д. Мы определяем класс Scene (он также описан в приложении В и доступен
на web-сайте книги), который поддерживает чтение из SDL-файлов и рисование объектов, описанных
в этом файле. Использование класса Scene в приложениях очень просто. Вначале создается глобальный
объект класса Scene посредством следующего кода:
Scene sen;
// create a scene object
// создаем объект класса scene
Для чтения файлов сцены вызывается метод readO данного класса посредством функции
scn.readCsimple.dat ");
// read the scene file & build an object list
// читаем файл сцены и строим список объектов
На рис. 5.58 приведена структура данных для объекта sen, созданного путем чтения следующего про-
стого SDL-файла:
! simple.dat:a simple scene having one light and four shapes
! simple.dat: простая сцена с одним источником света и четырьмя формами
background 001
! give the scene a blue background
! придаем сцене синий фон
light 2 9 8 1 1 1
! put a white light at (9.9.9)
! помещаем белый источник света в точку (9.9.9)
diffuse .9 .1 .1
! make the following objects reddish
! придаем следующим объектам красноватый цвет
translate 35-2 sphere
! put a sphere at 3 5 -2
! помещаем сферу в точку 3 5-2
translate -4 -б 8 cone
! put a cone in the scene
1 помещаем на сцену конус
translate 111 cube
! add a cube
! добавляем куб
5.6. Рисование трехмерных сцен с применением OpenGL
335
. diffuse 0 10
! make the following objects green
! делаем следующие объекты зелеными
translate 40 5 2 scale .2 .2 .2 sphere
! add a tiny sphere
! добавляем маленькую сферу
Первая строка является комментарием, каждый комментарий продолжается до конца строки. Дан-
ная сцена имеет ярко-синий цвет фона (red, green, blue) - (0, 0, 1), ярко-белый источник света, распо-
ложенный в точке (2,9,8), и четыре объекта: две сферы, конус и куб. Поле light указывает на список
источников света, а поле obj — на список объектов. Каждый объект определенной формы имеет свое
собственное аффинное преобразование М, описывающее, как он масштабирован, повернут и позицио-
нирован на сцене. Кроме того, каждый из перечисленных объектов имеет различные поля данных (data
fields), задающие свойства его материала, существенные для реалистичной визуализации объекта (этот
вопрос рассматривается в главе 8). На рисунке показано только диффузное (diffuse), то есть рассеиваю-
щее луч поле.
После того как созданы списки источников света и объектов, приложение может приступить к визуа-
лизации сцены посредством следующего кода:
sen.makeLi ghtsOpenGL():
sen.drawSceneOpenGL():
// render the scene using OpenGL
// визуализируем сцену с использованием OpenGL
Первая команда передает в OpenGL описание источников света. Вторая команда использует метод
drawSceneOpenGL() для рисования каждого объекта из списка объектов. Код этого метода очень прост:
void Scene :: drawSceneOpenGLО
forCGeomObj* р * obj: р : р =p->next)
p->drawOpenGL():
// draw it
// рисуем зто
Листинг 5.7. Методы drawOpenGL() для двух форм
void Sphere :: drawOpenGLO
tel1MaterialsGLО:
// pass material data to OpenGL
// передаем в DpenGL данные по материалу
glPushMatrixO;
glMultMatrixf(transf.m):
// load this object's matrix
// загружаем матрицу данного объекта
glutSol1dSpherе(1.0.10.12):
// draw a sphere
// рисуем сферу
glPopMatrixO:
}
void Cone :: drawOpenGLO
tellMaterialsGLO:
// pass material data to OpenGL
// передаем в OPenGL данные по материалу
продолжение^
336
Глава 5. Преобразования объектов
Листинг 5.7 (продолжение)
glPushMatrixO:
glMuitMatri xf(transf.m);
// load this object's matrix
// загружаем матрицу данного объекта
gl utSol idConed. 0.1.0.10.12):
// draw a cone
// рисуем конус
glPopMatrixO:
}
Эта функция перемещает по списку объектов указатель и вызывает метод drawOpenGLO для каждого
объекта поочередно. Это хороший пример применения полиморфизма, который является краеуголь-
ным камнем объектно-ориентированного программирования: каждая форма «знает», как нарисовать
саму себя; она имеет метод drawOpenGLO, который вызывает соответствующую подпрограмму для этой
формы. Поэтому когда указатель р указывает на сферу, то автоматически вызывается подпрограмма
drawOpenGLO для сферы, а когда р указывает на конус, то вызывается подпрограмма drawOpenGLO для
конуса и т. д. В листинге 5.7 приведены такие методы для классов Sphere и Cone; они отличаются друг
от друга только вызываемой в конце OpenGL-подпрограммой рисования. Каждый метод вначале пере-
дает в OpenGL свойства материала объекта и затем обновляет матрицу моделирования-вида с помо-
щью специфического для данного объекта аффинного преобразования. Исходная матрица моделиро-
вания-вида вталкивается в стек и впоследствии восстанавливается для защиты ее от изменений после
окончания рисования объекта.
Листинг 5.8. Рисование сцены, прочитанной из SDL-файла
include "SDL.h”
//ШШШШШШШ GLOBALS ШШШШШШ
Scene sen;
// construct the scene object
// создаем объект scene
II<<<<<<<<<<<<<<<<<<<<<<< displaySDL »»»»»»»»»»»»»
void displaySDL(void)
glMatrixMode(GL_PROJECTIDN):
// set the camera
// устанавливаем камеру
glLoadldentityO;
double winHt - 1.0:
// half-height of the window
// половина высоты окна
g!0rtho(-winHt*64/48.0. winHt*64/48.0. -winHt, winHt, 0.1. 100.0);
glMatrixMode(GL_MODELVIEW):
glLoadldentityO:
gluLookAt(2.3. 1.3. 2. 0. 0.25. 0. 0.0.1.0.0.0):
glClear(GL_COLDR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT):
// clear screen
// очищаем экран
sen.drawSceneOpenGLC):
}
// end of display
// конец отображения
5.6. Рисование трехмерных сцен с применением OpenGL
337
II<<<<<<<<<<<<<<<<<<<<<< main »»»»»»»»>»»»»»»»
void main(int argc. char **argv)
glutlnit(&argc. argv):
glut!nitDisplayMode(GLUT_RGB | GLUT_DEPTH):
glut!nitWindowSize(640. 480):
glutlnitWindowPositiondOO. 100):
glutCreateWindowdread and draw an SDL scene"):
// «читаем и рисуем SDL-сцену»
glutDi splayFunc(di splaySDL):
glShadeModel(GL_SMOOTH):
glEnable(GL_DEPTH_TEST):
glEnable(GL_NORMALIZE);
glViewportCO. 0. 640. 480);
sen.read("myScenel.dat”);
// read the SDL file and build the objects
// читаем SDL-файл и создаем объекты
glEnable(GL_LIGHTING):
scn.makeLightsOpenGLO:
// scan the light list and make OpenGL lights
// просматриваем список источников света
// и создаем источники света OpenGL
glutMainLoopO:
}
В листинге 5.8 приведена программа, которая читает SDL-файл и рисует сцену. Программа эта очень
короткая (но кроме нее, разумеется, должен быть загружен код для классов Scene, Shape и т. д.). Эта про-
грамма читает специальный SDL-файл myScenel.dat, который вновь рисует ту же сцену, что изображена
на рис. 5.56. Отметим, что путем простой замены читаемого SDL-файла данная программа способна
нарисовать любую сцену, описанную на языке SDL, без каких-либо изменений в ее коде.
Листинг 5.9. SDL-файл для создания сцены с рис. 5.56
l-myScenel.dat
light 20 60 30 .7 .7 .7
! put a light at (20.60.30). color:(.7..7..7)
I помещаем источник света в точку (20.60.30). цвет: (.7..7..7)
ambient .7 .7 .7
! set material properties for all of the objects
! задаем свойства материала для всех объектов
diffuse .6 .6 .6
specular 111
specularExponent 50
def jackPart{ push scale .2 .2 1 sphere pop
push translate 0 0 1.2 scale .2 .2 .2 sphere pop
push translate 0 0 -1.2 scale .2 .2 .2 sphere pop
}
def jack{ push use jackpart
rotate 90 0 1 0 use jackpart
rotate 90 1 0 0 use jackPart pop
}
продолжение &
338
Глава 5. Преобразования объектов
Листинг 5.9 (продолжение)
def wall{push translate 1 .01 1 scale 1 .02 1 cube pop}
def leg {push translate 0 .15 0 scale .01 .15 .01 cube pop}
def table{
push translate 0 .3 0 scale .3 .01 .3 cube pop
.'table top
! верх стола
push
translate .275 0 .275 use leg
translate 0 0 -.55 use leg
translate -.55 0 .55 use leg
translate 0 0 -.55 use leg pop
}
! now add the objects themselves
! теперь добавляем сами объекты
push translate .4 .4 .6 rotate 45 0 0 1 scale .08 .08 .08 use jack pop
push translate .25 .42 .35 scale .1 .1 .1 sphere pop
push translate .6 .38 .5 rotate 30 0 1 0 scale .08 .08 .08 teapot pop
push translate 0.4 0 0.4 use table pop
use wall
push rotate 90 0 0 1 use wall pop
push rotate -90 1 0 0 use wall pop
SDL-файл, описывающий сцену с рис. 5.56, приведен в листинге 5.9. Этот файл задает форму пере-
ключателя, состоящего из девяти сфер, следующим образом: вначале определяет jackPart (часть пере-
ключателя) и затем использует ее трижды, как объясняется в приложении Д. Ножка стола тоже внача-
ле определяется как элемент (модуль) и затем используется четыре раза.
Теперь, когда доступны язык описания сцен (типа SDL), а также инструменты для чтения и анализа
этих описаний, разработчик может сосредоточиться на создании сложных сцен, без необходимости ра-
ботать на уровне кода приложений. Сцена в процессе разработки может редактироваться и тестиро-
ваться снова и снова, до полной ее готовности. Разработчик кода вкладывает основное усилие в разра-
ботку приложения, способного визуализировать любую сцену, которая может быть описана на SDL.
5.7. Резюме
Аффинные преобразования являются главным элементом компьютерной графики, поскольку они
являются универсальным средством управления графическими объектами в важнейших направлени-
ях. Разработчику всегда требуется масштабировать, ориентировать и позиционировать объекты, чтобы
скомпоновать сцену и получить ее вид с нужной точки. Аффинные преобразования позволяют доста-
точно легко осуществить все это программным способом.
Аффинные преобразования конвертируют один координатный фрейм в другой, и при использова-
нии однородных координат аффинные преобразования выражаются в единой матричной форме. По-
следовательность таких преобразований может быть скомпонована в единое преобразование, матрица
которого является произведением матриц отдельных преобразований. Важно, что аффинные преобра-
зования сохраняют прямизну, так что образ прямой линии остается прямой линией, а образ плоско-
сти — плоскостью. Такая инвариантность значительно упрощает работу с прямыми и плоскостями в
программе: можно извлечь большую выгоду из простоты представления прямой (двумя конечными точ-
ками) и плоскости (тремя точками или четырьмя коэффициентами). Вдобавок сохраняется параллель-
ность, так что параллелограммы отображаются в параллелограммы, а трехмерные параллелепипеды —
5.8. Тематические задания
339
в параллелепипеды. Помимо этого, такая инвариантность упрощает визуализацию геометрических эф-
фектов, производимых аффинными преобразованиями.
Трехмерные аффинные преобразования намного сложнее своего двумерного аналога, особенно ког-
да нужно представить себе комбинацию поворотов. Заданный поворот можно рассматривать как три
элементарных поворота на углы Эйлера, или как поворот вокруг некоторой оси, или просто как матри-
цу с некоторыми специальными свойствами (ее столбцы являются ортогональными единичными век-
торами). Часто бывает важно чередовать эти три формы представления поворотов.
OpenGL и другие графические пакеты предлагают мощные инструменты для применения преобра-
зований и управления ими. В OpenGL все точки подвергаются лишь нескольким видам преобразова-
ний, и программист может использовать это обстоятельство при установке «камеры» и манипулирова-
нии ею, а также при задании размеров и расположения различных объектов на сцене. Два вида матриц,
используемых в OpenGL (матрицы преобразований моделирования-вида и порта просмотра), задают
аффинные преобразования, в то время как проекционная матрица обычно задает перспективное преоб-
‘разование, которое будет подробно изучаться в главе 7. OpenGL также поддерживает стек преобразова-
ний, упрощающий контроль за положением одного объекта относительно другого, и создание объектов,
составленных из нескольких похожих частей.
Язык SDL наряду с классами Scene и Shape значительно упрощает разделение задач программирова-
ния и задач проектирования сцен. Программист создает приложение, способное рисовать любые сце-
ны, описанные с помощью списка источников света и списка геометрических объектов. Это приложе-
ние может использоваться снова и снова с различными файлами описания сцен. Ключевой задачей
в процессе разработки сцен является применение к каждому объекту правильных геометрических пре-
образований. Поскольку обычно делается известное количество проб и ошибок, весьма удобно иметь
возможность выражать эти преобразования в компактной и читабельной форме.
Тематические задания, к которым мы переходим, конкретизируют основные идеи данной главы и пред-
лагают способы попрактиковаться с аффинными преобразованиями в графических программах. В этих'
упражнениях представлен широкий диапазон: от глубокого погружения в теорию преобразований до
фактического моделирования и визуализации таких объектов, как электронные схемы CAD и роботы.
5.8. Тематические задания
Тематическое задание 5.1. Выполнение вашего собственного
преобразования с помощью СТ в классе Canvas
Уровень сложности II.
Легко представить себе ситуации, в которых вам придется реализовать сам механизм преобразова-
ний, а не полагаться в этом на OpenGL. В этом тематическом задании вам предстоит добавить в класс
Canvas поддержку текущего преобразования СТ для случая двумерного рисования. Это предполагает
написание нескольких функций для инициализации и изменения самого СТ:
void Canvas:: initCT(void):
// init CT to unit transformation
// инициализируем СТ в единичное преобразование
void Canvas:: scale2D(double sx, double sy):
void Canvas:: translate2D(double dx. double dy):
void Canvas:: rotate2D(double angle):
Вам придется также написать другие функции, включаемые в состав функций moveToO и lineToO
таким образом, чтобы все посылаемые туда точки «молча» преобразовывались бы до их применения.
В качестве дополнительного усовершенствования добавьте стековый механизм для СТ наряду с функ-
циями pushCTO и рорСТО. Примените свои новые инструменты для каких-нибудь интересных примеров
двумерного моделирования и рисования.
340
Глава 5. Преобразования объектов
Тематическое задание 5.2. Рисование звезды с рисунка 5.39
с помощью многократных поворотов
Уровень сложности I.
Разработайте функцию, которая рисует полигон, изображенный на рис. 5.39, б, являющийся одной
пятой частью звезды с рис. 5.39, а. Используйте этот полигон и преобразования поворота для того, что-
бы нарисовать целую звезду.
Тематическое задание 5.3. Разложение двумерного
аффинного преобразования
Уровень сложности II.
Как мы уже видели, некоторые аффинные преобразования могут быть представлены в виде комби-
нации других аффинных преобразований. Здесь мы «разложим» произвольное аффинное преобразо-
вание на комбинацию из масштабирований, поворотов и перемещений. Мы также покажем, что пово-
рот может быть выполнен посредством трех последовательных сдвигов, что приводит нас к очень
быстрой подпрограмме рисования дуг. Кроме того, здесь рассматриваются некоторые скрытые особен-
ности каждого трехмерного аффинного преобразования.
Поскольку аффинное преобразование является линейным преобразованием с последующим смеще-
нием, опустим ту часть аффинного преобразования, которая отвечает за перемещение, и сосредоточимся
на его линейности. Таким образом, мы будем использовать упрощенные матрицы размерностью два на два.
Два двумерных линейных преобразования
Рассмотрим матрицу М размерностью два на два, представляющую двумерное линейное преобразова-
ние. Матрицу М всегда можно разложить на множители поворота, масштабирования и сдвига. Обозна-
чим для краткости четыре элемента матрицы М буквами a, b, с, d. Убедитесь с помощью непосредствен-
ного умножения, что М является произведением следующих трех матриц [Martin, 137]:
° V Я
1 О
'а
с
b'
' 1
ac + bd
(5.39)
где R = Va2 + b2. Легко видеть, что крайняя матрица слева является сдвигом, средняя — масштабирова-
нием, а крайняя справа — поворотом. (Почему?) Следовательно, любое двумерное аффинное преобра-
зование является поворотом, за которым следует масштабирование, а затем перемещение. Альтерна-
тивный вариант разложения рассматривается в тематическом задании 5.6.
Пример 5.8.1
Разложите матрицу М = на произведение матриц сдвига, масштабирования и поворота.
^2 7 J
Решение
Проверьте следующее выражение, полученное прямой подстановкой в уравнение (5.39):
4 -3^ _ Г 1 Оу5 0 у4/5 -3/5'
2 7J “ [-13/25 lj[o 34/5 Дз/5 4/5
Двумерный поворот эквивалентен трем сдвигам
Матрицы могут быть разложены различными способами. Фактически матрицу поворота можно запи-
сать в виде произведения трех матриц сдвига [Paeth, 152]. Из этого следует особенно быстрый способ
для выполнения серий поворотов.
5.8. Тематические задания
341
Рассмотрим уравнение:
cos (a) sin (а) А _ f 1 tg(a/2)
-sin(a) cos(a)
О 1
1 0V1 tg(a/2^
-sin(a) lj[o
(5.40)
1
представляющее поворот в виде трех последовательных сдвигов. Данное уравнение можно прове-
рить непосредственным умножением. Оно показывает, что поворот является сдвигом вдоль оси у,
за которым следует сдвиг по оси х, а затем повторение первого сдвига. Обозначьте Т= tg(a/2), S = sin(s)
и покажите, что последовательность операций поворота точки (х, у) может быть записана следующим
образом1:
х' = Т*у + х, (первый сдвиг)
У' = У>
х" “ х', (второй сдвиг)
y"~y'-s*x':,
х' “ Т*у" + х', (третий сдвиг)
У'" = У",
где штрихи использованы для того, чтобы отличить новые значения от старых. Однако операции
вида х" “ х'? не делают ничего, поэтому штрихи здесь не нужны, и последовательность равенств выгля-
дит короче:
х = х + Т*у,
у=*у - 5*х, (фактические операции для выполнения трех сдвигов)
х = х+.Г*у.
Если нам нужно выполнить только один поворот, то этот способ не дает выигрыша. Процесс, одна-
ко, становится более эффективным, если нам требуется выполнить целую последовательность поворо-
тов на один и тот же угол. Это может понадобиться нам в двух типичных случаях:
1. При вычислении вершин n-угольника, которые являются точками, расположенными на равных
расстояниях по окружности.
2. При вычислении точки вдоль дуги окружности.
Разработайте программу для вычисления положений п точек по окружности. Эта программа загру-
жает последовательные значения (cos(2ni/n + b), sin(2m/n + b)) в массив точек р[].
Листинг 5.10. Программа быстрого рисования дуги
void drawArc2(RealPoint с. double R.
double startangle, double sweep)
// in degrees
// в градусах
{
#define n 30
#define RadPerDeg .01745329
double delang - RadPerDeg * sweep / n:
double T - tan(delang/2):
// tan.of half angle
// тангенс половинного угла
double S - 2 *T/(1 +T * T):
' Отметим, что sin(a) можно легко найти из tg(a/2) с помощью одного умножения и одного деления: 5 - (2Г)/( 1 + Т2).
продолжение#
342
Глава 5. Преобразования объектов
Листинг 5.10 (продолжение)
// sine of half angle
// синус половинного угла
double snR =R * sintRadPerDeg * startangle);
double csR =R * costRadPerDeg * startangle);
moveTo(c.x + csR. c.y + snR);
for(int i - 1; i < n; 1++)
{
snR +- T * csR;
// build next snR. csR pair
// создаем следующую пару snR. csR
csR -= S * snR;
snR += T * csR;
lineTotc.x + csR. c.y + snR):
}
}
В листинге 5.10 показано, как использовать сдвиги для создания программы быстрого рисования
дуг. Она делает ту же самую работу, что функция drawArcO из главы 3, однако является значитель-
но более эффективной, поскольку в ней нет повторных вычислений sin( ) и cos( ). Разработайте тесто-
вую программу, использующую эту подпрограмму для рисования дуг. Сравните эффективность вашей
программы с теми «рисовальщиками дуг», в которых каждая вершина вычисляется с помощью три-
гонометрии.
Является ли сдвиг «фундаментальным» преобразованием?
Иногда в литературе по графике можно прочитать, что фундаментальными элементарными преобразо-
ваниями являются поворот, масштабирование и перемещение; а сдвиги относятся к «гражданам второ-
го сорта». В основе такого отношения лежит то обстоятельство, что любой сдвиг может быть разложен
на комбинацию поворотов и масштабирований. Приводимое ниже равенство может быть проверено
путем перемножения трех матриц правой части [Greene, 94]:
10 1 fl -д') (а 0 V а 1
1___
+ д2
(5.41)
Средняя матрица является масштабированием, а обе крайние матрицы (вместе со своими мас-
штабными множителями) у поворотами. Для левой матрицы поворота примем величину 1/Vl + a2 равной
косинусу, а величину -а/х/1 + аг — синусу некоторого угла а. Тогда tg(a) = -а. Для правой матрицы
поворота также сопоставим аналогичные выражения с косинусом и синусом некоторого угла р, тогда
tg(P) = 1/a. Заметим, что углы а и Р связаны соотношением: 3 = a + л/2. (Почему?)
Используя разложение равенства (5.41)* запишите сдвиг в виде поворота, за которым следует мас-
штабирование, а за ними — вновь поворот, чтобы убедиться в следующем:
Произвольное двумерное аффинное преобразование - Перемещение х Поворот х
х Масштабирование х Поворот х Масштабирование х Поворот. (5.42)
Практические упражнения
5.8.1. «Золотое» разложение
Рассмотрим частный случай «единичного сдвига», где элемент а - 1/а равенства (5.41) равен единице.
Чему должно быть равно а? Определите два угла а и Р, связанные с этими поворотами.
5.8. Тематические задания
343
Решение.
Поскольку число а должно удовлетворять уравнению а =* 1 + 1/а, оно является золотым соотноше-
нием ф! Тогда
А
1
О') Г cos (а)
и Lsin(a)
-sin(a)'l (ф
cos (a) J (О
0 'j Г cos(p) sin(p)>
1/0J [-sin (р) cos(p)
(5.43)
где a = tg-‘(0) = 58,28° и 0 = tg~‘( 1/0) - 31,72°.
5.8.2. Единичные сдвиги
Докажите, что любой сдвиг содержит в себе единичный сдвиг. Разложите сдвиг, заданный матрицей
А (А
Ь и’
на Произведение масштабирования, единичного сдвига и другого масштабирования.
5.8.3. Рисование вручную
В соответствии с рассуждениями из упражнения 5.8.1 нарисуйте на миллиметровке прямоугольник,
поверните его на -58,28°, масштабируйте его с множителями (0,1/0) и, наконец, поверните его на 31,72°.
Изобразите каждый промежуточный результат и покажите, что окончательный результат является тем
же самым параллелограммом, что и исходный прямоугольник после единичного сдвига.
5.8.4. Разложение преобразования
Разложите следующее преобразование:
Qx=3Px-2Py+5,
Q =4Р +Р -6
на произведение поворотов, масштабирований и перемещений.
5.8.5. Одно отражение может быть всегда от оси х
Докажите, что поворот на угол А вокруг начала координат всегда приводит к тому же эффекту, что
и отражение от оси х с последующим отражением от прямой линии под углом А/1.
5.8.6. Изометрии
Изометрии (isometries — «та же мера») являются отдельным важным семейством аффинных преобра-
зований при исследовании симметрии, поскольку они не изменяют расстояние между двумя точками и
их образами. Если преобразование Т( ) является изометрией, то для двух произвольных точек Р и Q
расстояние \Т(Р) - Т(Q)| равно расстоянию |Р- Q\. Докажите, что если Т( ) — аффинное преобразование
с матрицей М, то Тявляется изометрией тогда и только тогда, когда первые две строки матрицы М, рас-
сматриваемые в качестве векторов, имеют единичную длину и ортогональны друг другу.
Решение
Введем вектор г - Р - Q. Тогда |Т(Р) - Т(Q)| = |Л/г| = |(гхти + rymi2, гхттг21 + ?уи22)|. Равенство выраже-
ний 1Л/г]2 и |г[2 требует, чтобы выполнялись соотношения т2 + m2 = 1, т2 + m2 = 1, яг„т„ = 0, что
и требовалось доказать.
5.8.7. Эллипсы инвариантны
Докажите, что эллипсы инвариантны относительно аффинного преобразования. Это означает, что если
Е — эллипс, а Т — аффинное преобразование, то образ Т(Е) из точек эллипса Е также является эллипсом.
Ключ к решению
Любое аффинное преобразование является комбинацией из поворотов и масштабирований. Очевид-
но, что после поворота эллипс остается эллипсом, поэтому испортить этот эллипс могут только нерав-
номерные масштабирования. Поэтому достаточно доказать, что эллипс, подвергнутый неравномерно-
му масштабированию, остается эллипсом.
344
Глава 5. Преобразования объектов
5.8.8. Другие инвариантные формы
Рассмотрим, какой класс форм (возможно, более широкий, чем эллипсы) является инвариантным отно-
сительно аффинных преобразований. В предположении, что некоторая форма описывается уравнени-
ем f(x, у) = 0, докажите, что после преобразования Т новая форма описывается множеством всех точек,
удовлетворяющих уравнению g(x, у) = у)) = 0. После этого опишите детали этой формы в слу-
чае, когда Т— аффинное преобразование. И, наконец, попробуйте описать наиболее общий класс форм,
сохраняющихся под воздействием аффинных преобразований.
Тематическое задание 5.4. Обобщенные трехмерные сдвиги
Уровень сложности II
Сдвиг может иметь более общий вид, чем тот, который рассматривался в разделе «Элементарные
трехмерные преобразования». Как предложил Голдман [Goldman, 84], сдвиг состоит из:
О плоскости, проходящей через начало координат и имеющей единичную нормаль т;
О единичного вектора V, лежащего в этой плоскости (и поэтому перпендикулярного вектору т);
О углаф.
Рис. 5.59. Определение трехмерного сдвига
Тогда, как показано на рис. 5.59, сдвиг точки Р в точку Q осуществляется посредством ее перемеще-
ния на нужную величину в направлении V. Эта величина пропорциональна расстоянию, на которое точ-
ка Р отстоит от плоскости, а также тангенсу угла ф. Голдман доказал, что такой сдвиг имеет следующее
матричное представление:
/ \ mxvx mxvy mxvx
М = I + tg(0) myvx myvy myvx mxvx mxvy mxvX' (5.44)
где I — единичная матрица размерностью три на три. Некоторые детали вывода уравнения (5.44) при-
водятся ниже.
Пример 5.8.2
Найдите сдвиг, соответствующий плоскости, имеющей единичную нормаль m = (1,1,1)/>/з “ (0,577,
0,577, 0,577), единичному вектору v - (0,0,707, -0,707) и углу ф“30°.
Решение
Заметим, что вектор v, как и требуется, лежит в данной плоскости. (Почему?) Используя равенство
(5.44), получим: '0 0,408 -0,408' '1 0,235 -0,235'
M = I + 0,577 0 0,408 -0,408 = 0 1,235 -0,235
0 0,408 -0,408 0,235 0,764 ,
5.8. 'Тематические задания
345
Выведем теперь матрицу сдвига. Мы хотим выразить точку Q с рис. 5.60 через точку Р и «компонен-
ты» сдвига. Расстояние (с учетом знака) от точки Рдо плоскости определяется выражением Р • m (если
рассматривать точку Р как радиус-вектор, исходящий из начала координат). Собирая вместе все ком-
поненты, получим:
Q = Р + (Р • m) tg( ф) V. (5.45)
Отметим, что точки «по другую сторону плоскости» сдвигаются в противоположном направлении,
как и ожидалось.
Теперь нам требуется найти второй член, представляющий собой произведение Р на некоторую мат-
рицу. Известно, что Р • m = PmT (см. приложение Б), откуда Q = P(I + tg(0) mTv). Теперь покажем, что
матрица сдвига равна (Z+ tg(0) mTv), где член mTv имеет следующий вид:
' mxvx mxvy
т m v = ту = myvx tnyvy mxvx mxvy myvx mxvx^ (5.46)
Это выражение носит название внешнего произведения (outer product) или тензорного произведе-
ния (tensor product) вектора ш на вектор v.
Практические упражнения
5.8.9. Связь с простым сдвигом
Напишите выражение для сдвига, определяемого направлением v = (1, 0, 0) и плоскостью, имеющей
нормальный вектор (0,1, 0). Докажите, что для любого угла ф это выражение совпадает с элементарной
матрицей сдвига из уравнения (5.45).
5.8.10. Нахождение сдвига
Вычислите матрицу сдвига для сдвига, имеющего нормальный вектор ш = 0,577(1, 1, 0) и угол ф = 45°.
Нарисуйте все участвующие векторы и плоскость. Кроме того, нарисуйте, как этот сдвиг повлияет на
куб с центром в начале координат и с ребрами, выровненными вдоль координатных осей.
5.8.11. Чем трехмерный сдвиг напоминает двумерное перемещение в однородных
координатах?
Рассмотрим конкретный сдвиг:
fl 0 t 0А
1° ° ° 1J
под действием которого трехмерная точка Р сдвигается вдоль оси х, отдаляясь от оси z на величину Г, и
вдоль оси у, отдаляясь от той же оси z на величину s. Докажите, что точка Р, расположенная в плоскости
z = 1 и имеющая координаты Р = (Рх, Р, 1), преобразуется в точку (Рх + Г, Ру + s, 1). Иными словами, эта
точка просто перемещается вдоль оси х на величину t и вдоль оси у на величину s. Докажите также, что
для произвольной точки в плоскости z=l такой сдвиг эквивалентен перемещению. И, наконец, дока-
жите, что левый верхний минор размерностью три на три, вырезанный из матрицы (5.47), идентичен
формуле чистого двумерного перемещения в однородных координатах. Осознание этой идентичности
углубит понимание того, как работают однородные координаты.
346
Глава 5. Преобразования объектов
Тематическое задание 5.5. Вращение вокруг оси:
конструктивный подход
Уровень сложности II.
В данном тематическом задании вас попросят заполнить пробелы в выводе уравнения (5.33) для
матрицы поворота /?И(Р). Примем для простоты, что вектор и является ортом: |и| - 1. Обозначим через р
радиус-вектор, заканчивающийся точкой Р, так что р - Р - О, где О — начало данной системы коорди-
нат. Теперь спроектируем вектор р на вектор и для получения вектора h, как показано на рис. 5.29, а.
а) Докажите, что вектор h имеет форму (р • u)u. Определите два перпендикулярных вектора а - р - h
и Ь - и • а, лежащие в плоскости поворота.
б) Докажите, что векторы а и Ь взаимно перпендикулярны, имеют одинаковую длину, оба располо-
жены в плоскости вращения, а также что выражение b - и • (р - h) можно упростить до и • р.
Таким методом можно эффективно задавать двумерную систему координат в плоскости вра-
щения. Посмотрите теперь на плоскость вращения, приведенную на рис. 5.29, б. Операция по-
ворота поворачивает вектор а в а' - acos0 + bsinP, следовательно, повернутая точка имеет вид:
Q - h + acosp + bsinP,
или, используя вышеприведенные выражения для векторов а и Ь, получаем:
Q - pcosP + (1 - cosP)(p • u)u + sinP (u x p). (5.48)
Это довольно общий результат, показывающий, как повернутая точка Q может быть разложена
на части вдоль вектора h и вдоль двух ортогональных осей, лежащих в плоскости вращения.
В представлении точки Q, приведенном в уравнении (5.48), с трудом можно узнать произведе-
ние точки Р на некоторую матрицу, однако это так, поскольку каждый из трех слагаемых про-
порционален вектору р. Преобразуем каждый из членов этого уравнения в нужную нам форму
следующим образом:
в) Заменим вектор р на Р, откуда сразу получим p(cos0) - Z(cosP)P, где I— единичная матрица
размерностью три на три.
г) Используем тот факт (см. приложение Б), что скалярное произведение двух векторов р • и может
быть записано в форме произведения точки Р на матрицу: (итР) и покажем, что (р • u)u - итиР,
где uru — тензорное произведение, аналогичное приведенному в равенстве (5.46).
д) Используем утверждение из приложения Б, что векторное произведение двух векторов и х р
может быть также записано в форме произведения Р на некоторую матрицу, и покажем, что
и х р = Cross (u)P, где матрица Cross(u) имеет следующий вид:
' о иг -иу
Cross (и) = -и, 0 Ux
k иу 0
(5.49)
е) Собирая эти члены вместе, получим матрицу*
М “ cos01 + (1 - cosP) uru + sinP Cross(u), (5.50) .
следовательно, M является суммой трех взвешенных матриц, что, несомненно, проще постро-
ить, чем произведение пяти матриц, как это было при классическом выводе.
ж) Выведите равенство (5.33) из равенства (5.50).
1 В работе Голдмана [Goldman, 83] приводится та же форма для матрицы Ми даются компактные результаты для нескольких других
сложных преобразований.
5.8, Тематические задания
347
Тематическое задание 5.6. Разложение трехмерных аффинных
преобразований
Уровень сложности III.
В данном тематическом задании рассматривается несколько обширных семейств аффинных преоб-
разований.
Что такое трехмерное аффинное преобразование?
Мы вновь игнорируем связанную с перемещением часть аффинного преобразования и сосредоточимся
на той его линейной части, которая представлена матрицей М размерностью три на три. Что же за пре-
образование «вложено» в М? Голдман [Goldman, 83] показал, что каждая такая матрица Л/является про-
изведением масштабирования S, поворота R и двух сдвигов Ht и Н2, а именно:
M = SRHlH2. (5.51)
Тогда каждое трехмерное аффинное преобразование может рассматриваться как последовательность
элементарных операций, за которыми следует перемещение. В данном тематическом задании мы ис-
следуем, какой математический аппарат применяется в равенстве (5.51), и в результате увидим, как на
деле осуществляется это разложение.
Полезные классы преобразований
Полезно распределить аффинные преобразования по категориям в соответствии с тем, влияют они или
не влияют на определенные свойства объекта, подвергающегося этим преобразованиям. Нам уже изве-
стно, что при таких преобразованиях всегда сохраняется параллельность ребер объекта, но какие пре-
образования сохраняют также длину каждого ребра, а какие из них сохраняют углы между каждой па-
рой ребер?
Движения жесткой конструкции. Интуитивно понятно, что перемещение объекта или его поворот
не изменяют его форму и размер. Кроме того, отражение объекта относительно плоскости также не вли-
яет на его форму или размер. Поскольку ни одно из перечисленных преобразований по отдельности не
влияет на форму объекта, то не влияет на нее и их любая композиция. Обозначим через
Г d = {повороты, отражения, перемещения}
множество всех аффинных преобразований, состоящих из произвольной последовательности поворо-
тов, отражений и перемещений. Эти действия известны как движения жесткой конструкции (rigid-body
motions), поскольку в этом случае из одной позиции и ориентации в другие перемещается жесткий
объект. Такие преобразования имеют в однородных координатах ортогональные матрицы, то есть мат-
рицы, для которых инверсия равносильна транспонированию:
ЛГ1 = МТ.
Конформные преобразования (преобразования, сохраняющие углы). Равномерное масштабирование
(у которого масштабные множители одинаковы: 5Л = 5у= 5) раздвигает или сжимает объект, но делает
это равномерно, так что в форме объекта не происходит никаких изменений. В этом случае угол между
двумя ребрами остается неизменным. Обозначим такой класс преобразований так:
Т. |(! = {повороты, отражения, перемещения, равномерные масштабирования}.
Этот класс шире класса движений жесткой конструкции, поскольку он включает в себя равномер-
ное масштабирование. Он также является важным классом, поскольку, как мы увидим в главе 8, вычис-
ления освещенности и затенения зависят от скалярных произведений различных векторов. Если дан-
ное преобразование не изменяет углы, то оно не изменяет и скалярные произведения, и в этом случае
вычисления освещенности можно осуществлять как в преобразованном, так и в непреобразованном
пространстве.
348
Глава 5. Преобразования объектов
Разложение трехмерного аффинного преобразования. Для заданного трехмерного аффинного преоб-
разования {М, d} мы хотим знать, из какой последовательности элементарных преобразований оно со-
ставлено. Проделаем вслед за Голдманом [Goldman, 83] все шаги, требующиеся для разложения матри-
цы М размерностью три на три в произведение масштабирования S, поворота R и двух сдвигов Ht и Н2
(уравнение (5.51)).
Вам предлагается проверить каждый шаг на этом пути и разработать подпрограмму, создающую
матрицы 5, R, Hi и Н2 по отдельности.
Пусть имеется матрица М со строками u, v, w, каждая из которых представляет собой трехмерный
вектор:
М = v .
<WJ
Подход Голдмана основывается на классической процедуре ортогонализации Грама—Шмидта (Gram-
Schmidt), посредством которой строки матрицы М комбинируются таким образом, что они становятся
взаимно ортогональными и имеющими единичную длину. Следовательно, матрица, состоящая из та-
ких строк, является ортогональной и поэтому представляет вращение (или вращение с отражением).
Голдман показал, что процесс ортогонализации по существу представляет собой два сдвига. Осталь-
ное — уже детали. Тщательно выполните каждый из следующих шагов (по Голдману), а также все зада-
ния, заключенные в круглые скобки.
1. Нормируйте вектор ubu* = u/5t, где 5t -,|и|.
2. Вычтите часть вектора и* из вектора v так, чтобы остаток был ортогонален и*. Пусть Ь v - du*,
rued^v • и*. (Покажите, что b • и* - 0.)
3. Нормируйте вектор Ь, для чего задайте вектор v* = b/S2, где S2 - |b|. __
4. Введите некоторые промежуточные величины: m - w • и*, и - w • v*, e-^Jm2 +п2, а также
г - (mu* + nv*)/e.
5. Вычтите из вектора w часть вектора г так, чтобы оставшаяся часть стала ортогональной векто-
рам и* и v*. Обозначьте с = w - er. (Докажите, что с • и* = с • v* = 0.)
6. Нормируйте вектор с, для чего задайте вектор w‘ - c/S3, где 53 - |с|.
7. Таким образом, матрица
является ортогональной и поэтому представляет вращение. (Вычислите ее определитель: если
он равен -1, то просто замените w* на -w*.)
8.
Определите матрицу сдвига Н{ = I +
ведение векторов v* и и*.
(v*®u*), где (v*®u*) - (v*)ru* — тензорное произ-
9.
10.
Определите матрицу сдвига Н2 = I +
(w*®r *), где (w*®r*) - (w*)rr*.
Докажите, что u*Hl = u*, v*Ht = v* + du*/S2 - v/S2 и w*H, = w*. Сначала докажите следующее
свойство тензорного произведения: для любых векторов а, Ь, с справедливо равенство а(Ь®с) =
- (а • Ь)с. Затем примените это свойство и факт ортогональности векторов u*, v*, w* для доказа-
тельства истинности первых трех соотношений.
5.9. Дополнительная литература
349
И. Докажите, что и*Н2 = u*, v*H2 = v* и w*H2 = w* + er/S3 = w/53.
12. Объедините все промежуточные результаты и покажите, что М = SRH{H2,
где S =
О
О
О О'
S2 О
О s3>
Отметим, что такое разложение не является единственным, поскольку векторы u, v и w можно было
бы ортогонализировать в другом порядке. Например, мы могли вначале сформировать вектор w* = w/
|w|, затем вычесть часть v из w* и получить вектор, ортогональный к вектору w*, а затем вычитанием
вектора из и получить вектор, ортогональный к двум остальным.
Напишите подпрограмму
void decomposeCDBL ш [3][3]. DBL S [3][3]. DBL R [3][3], DBL Hl [3][3].DBL H2 [3][3]).
которая принимает матрицу M и вычисляет матрицы 5, R, и Н2 методом 12 шагов, как это описано у
Голдмана. Величина DBL определена как double.
Известны и другие способы разложения трехмерного преобразования — см., например, работы Томаса
[Thomas, 195] и Шумейка [Shoemake, 186].
Тематическое задание 5.7. Рисование трехмерных сцен,
описанных на языке SDL
Уровень сложности II.
Разработайте закопченное приложение, которое использует классы типа Scene, Shape, Affine4 и под-
держивает чтение и рисование сцепы, описанной в SDL-файле. Для упрощения работы используйте
классы, содержащиеся на web-сайте книги. Конкретизируйте любые методы drawOpenGLO, которые вам
потребуются. Разработайте файл описания сцены, содержащий описания переключателя, деревянного
стула н нескольких стен.
5.9. Дополнительная литература
Среди нескольких превосходных книг о преобразованиях, которые дополнят приведенные здесь сведе-
ния, отметим роскошную книгу Джорджа Мартина «Геометрия преобразований» (George Martin. Trans-
formation Geometry [Martin, 137]) и книгу Яглома «Геометрические преобразования» (Yaglom. Geometric
Transformations [Yaglom, 216]). Прекрасная глава, посвященная векторам и преобразованиям, имеется
у Хоггара [Hoggar, 112]. Несколько блестящих статей Блиина в его сборнике «Путешествие по графи-
ческому конвейеру» (Jim Blinn’s Corner: A Trip down the Graphics Pipeline [Blinn, 31]) содержат замеча-
тельное исследование однородных координат и преобразований в компьютерной графике.
Моделирование
поверхностей
полигональными сетками
□ Разработка инструментов для работы с объектами в трехмерном
пространстве.
□ Представление трехмерных объектов полигональными сетками.
□ Рисование простых видов каркасных объектов.
Постарайтесь узнать обо всем понемногу и все о немногом.
Т. X. Хаксли (Т. Н. Huxley)
В этой главе мы исследуем способы описания трехмерных объектов с помощью полигональных сеток.
В разделе 6.1 «Введение» дается обзор процесса трехмерного моделирования. В разделе 6.2 «Введе-
ние в трехмерное моделирование полигональными сетками» описываются полигональные сетки, позво-
ляющие описывать форму сложных трехмерных объектов с помощью простых структур данных. Пере-
числены свойства таких сеток и приведены алгоритмы для просмотра представленных ими объектов.
В разделе 6.3 «Многогранники» описываются семейства интересных трехмерных форм, таких как
платоновы тела, усеченный икосаэдр (бакибол), геодезические купола и призмы. В разделе 6.4 «Экст-
рузивные формы» исследуются семейства экструзивных и «заметаемых» форм и показывается, как
создавать трехмерные буквы для логотипов, трубки, извивающиеся в пространстве кривые («змеи»),
а также поверхности вращения.
В разделе 6.5 «Каркасные аппроксимации гладких объектов» обсуждается построение сеток для мо-
делирования объемных тел, имеющих плавно изгибающиеся поверхности. Сетки аппроксимируют не-
которую гладкую «истинную» поверхность. Ключевым моментом является вычисление нормального
вектора к истинной поверхности в любой точке. Рассматривается несколько интересных семейств глад-
ких тел, в том числе поверхности второго порядка (квадрики) и суперквадрики, линейчатые поверхно-
сти и лоскуты Кунса (Coons patches), явные функции двух переменных и поверхности вращения.
В тематических заданиях в конце главы многие вопросы изучаются углубленно и для их проверки
предлагается разработка приложений. Некоторые тематические задания являются по своей природе
теоретическими, например вывод формулы Ньювелла для вычисления нормального вектора или ис-
следование алгебраической формулы поверхностей второго порядка. Другие задания в большей степе-
ни практические — например, чтение из файла данных для сеток или создание красивых трехмерных
форм типа трубок и арок.
6.2. Введение в трехмерное моделирование полигональными сетками
351
6.1. Введение
Полигональные сетки (Polygonal meshes) являются просто набором полигонов, или «граней», которые в
совокупности формируют «оболочку» (skin) объекта. Сетки в графике являются стандартным спосо-
бом представления широкого класса объемных форм. Мы уже видели несколько примеров, таких как
куб и икосаэдр, а также аппроксимацию гладких поверхностей, подобных сфере, цилиндру и конусу.
В этой главе мы рассмотрим значительно больше примеров. Популярность полигональных сеток в гра-
фике основана на простоте использования полигонов: их легко представлять (последовательностью
вершин) и преобразовывать, у них простые свойства (единственный нормальный вектор, четко опреде-
ляемые внутренняя и внешняя области и т. д.); кроме того, их просто рисовать (с помощью подпро-
граммы закрашивания полигонов или наложения текстуры на полигон).
Многие системы визуализации, в том числе OpenGL, основаны на изображении объектов посред-
ством рисования последовательности полигонов. Каждая грань полигона посылается в графический
конвейер, где ее вершины подвергаются различным преобразованиям, и та часть грани, которая оста-
лась после отсечения, закрашивается или «затеняется» и демонстрируется на устройстве отображения.
Мы рассмотрим, как конструировать сложные трехмерные формы, задавая совокупность граней.
Одни объекты могут быть точно представлены полигональной сеткой, а другие только аппроксимиру-
ются ею. Например, сарай на рис. 6.1, а действительно имеет плоские грани, и при визуализации ребра
между гранями должны быть видны. Однако цилиндр на рис. 6.1, б должен иметь гладкую боковую по-
верхность. Такая закругленность не может быть достигнута только с помощью полигонов: отдельные
плоские поверхности вполне различимы, так же как и ребра между ними. Существуют, однако, техно-
логии визуализации, с помощью которых подобная сетка выглядит гладкой, как на рис. 6.1, в. Детали
так называемого закрашивания Гуро (Gouraud shading) будут рассматриваться в главе 8.
Мы начнем с описания полигональных сеток в довольно общем виде и увидим, как задавать их и управ-
лять ими в программе (с использованием OpenGL или без него). Далее мы применим эти идеи к модели-
рованию многогранников, которым свойственны плоские грани, и изучим несколько интересных семейств
полиэдров. Затем мы перейдем к задаче использования сетки для аппроксимации гладких криволиней-
ных поверхностей и разработаем необходимые инструменты для создания и обработки таких моделей.
6.2. Введение в трехмерное моделирование
полигональными сетками
Я никогда не забываю ни одного лица, но в вашем случае я сделаю исключение.
Гручо Маркс (Groucho Marx)
Мы будем использовать сетки для моделирования как монолитных (сплошных) форм, так и тонких
оболочек. Объект считается монолитным (solid), если его полигональные грани плотно примыкают друг
к другу и ограничивают некоторое пространство. В других случаях грани объекта совмещаются без ог-
352
Глава 6. Моделирование поверхностей полигональными сетками
раничения пространства, тогда они представляют собой поверхность бесконечно малой толщины.
В обоих случаях назовем эту совокупность полигонов полигональной сеткой (poligonal mesh) или про-
сто сеткой (mesh).
Полигональная сетка задается списком полигонов и информацией о направлении, куда «обращен»
каждый полигон. Информация о направлении часто задается в виде нормали к плоскости его грани.
Эта информация используется при закрашивании объекта для определения того, сколько света от источ-
ника рассеивается на этой грани. На рис. 6.2 показаны нормальные векторы к различным граням сарая.
При детальном изучении этого вопроса в главе 8 мы увидим, что одна из составляющих яркости повер-
хности берется пропорциональной косинусу угла (угол 0 на рисунке для боковой стенки сарая) между
нормалью к поверхности и вектором, указывающим на источник света. Таким образом, ориентация по-
верхности по отношению к источнику света играет существенную роль в окончательном изображении.
Нормальный вектор
к передней стене
Рис. 6.2. Нормальное направление к грани определяет ее яркость
Нормали в вершинах и нормали к поверхностям
Оказывается, выгоднее связывать нормальный вектор с каждой вершиной грани, чем задавать одну нор-
маль для целой грани. Как мы увидим, подобная практика упрощает процесс отсечения и процесс за-
крашивания для гладких криволинейных форм. Для плоских поверхностей, вроде стенки сарая, каждая
из вершин V2, V3, V4, определяющих боковые стенки сарая, будет ассоциирована с одной и той же
нормалью Пр которая является нормальным вектором для всей стенки (рис. 6.3, а). Однако вершины
передней стенки, такие как У5, будут использовать нормаль п2. (Отметим, что вершины Vt и V. располо-
жены в одной и той же точке пространства, но используют разные нормали.)
Рис. 6.3. Связывание нормалей с каждой вершиной каждой грани
6.2. Введение в трехмерное моделирование полигональными сетками
353
Для гладких криволинейных поверхностей, таких как цилиндр на рис. 6.3, б, используется другой
подход, делающий возможным закрашивание, которое придает поверхности гладкий вид. Обе верши-
ны — Vt с грани Ft и V2 с грани F2 — используют одну и ту же нормаль п, являющуюся вектором, перпен-
дикулярным к будущей гладкой поверхности. В разделе «Нахождение нормальных векторов» мы уви-
дим, как удобнее вычислять этот вектор.
6.2.1. Определение полигональной сетки
Полигональная сетка — это совокупность полигонов вместе с нормальными векторами, связанными с
каждой вершиной этих полигонов. Начнем с примера.
Пример 6.2.1. «Базовый сарай»
На рис. 6.4 показана простая форма, которую мы называем «базовым сараем» («basic barn»). Он имеет
семь полигональных граней и 10 вершин (каждая из которых одновременно принадлежит трем граням).
Пусть для удобства сарай имеет квадратный пол с единичной стороной (перед помещением на сцену
этот сарай можно как угодно масштабировать и ориентировать). Поскольку стены сарая плоские, име-
ется всего семь различных нормальных векторов: по одной на каждую грань, как показано иа рисунке.
Рис. 6.4. Представление «базового сарая»
Существует много различных способов хранения информации о сетке в файле или в программе. Для
данного сарая можно использовать список из семи полигонов и для каждого из них список, содержа-
щий вершины полигона и нормали в каждой из этих верщин (всего 30 вершин и 30 нормалей). Однако
такая структура была бы избыточной и громоздкой, поскольку у нас всего 10 различных вершин и семь
различных нормалей.
Более эффективным является подход, при котором используются три отдельных списка: список вер-
шин, список нормалей и список граней. В списке вершин содержатся координаты различных вершин
сетки. В списке нормалей описываются направления различных нормальных векторов, которые име-
ются в данной модели. Список граней является просто индексом для остальных двух списков. Как мы
увидим позднее, наш сарай записывается с помощью 10 вершин, семи нормалей и списком из семи про-
стых дескрипторов граней.
Все три списка работают совместно: список вершин содержит информацию об их координатах, или
геометрии; список нормалей содержит информацию об ориентации; а список граней содержит инфор-
мацию о связности, или топологии.
12 Ф. Хилл
354
Глава 6. Моделирование поверхностей полигональными сетками
Таблица 6.1. Список вершин для стандартного сарая
Вершина X У Z
0 0 0 0
1 1 0 0
2 1 1 0
3 0,5 1,5 0
4 0 1 0
5 0 0 1
6 1 0 1
7 1 1 1
8 0,5 1,5 1
9 0 1 1
Таблица 6.2. Список различных встречающихся нормалей
Нормаль пх пу nz
0 -1 0 0
1 -0,707 0,707 0
2 0,707 0,707 0
3 1 0 0
4 0 -1 0
5 0 0 1
6 0 0 -1
Список вершин для нашего сарая приведен в табл. 6.1. Список из семи различных нормалей приве-
ден в табл. 6.2. Индексы вершин изменяются от 0 до 9, а индексы нормалей — от 0 до 6. Все векторы,
приведенные в этом списке, уже нормированы, поскольку для большинства алгоритмов закраски тре-
буются единичные векторы. (Напомним, что косинус угла между векторами равен скалярному произ-
ведению двух соответствующих ортов.)
Таблица 6.3. Список граней для стандартного сарая
Грань Вершины Ассоциированная нормаль
0 (левая) 0, 5,9,4 0, 0, 0, 0
1 (крыша левая) 3,4,9,8 1, 1, 1, 1
2 (крыша правая) 2,3,8, 7 2, 2, 2, 2
3(правая) 1, 2, 7, 6 3, 3, 3, 3
4 (нижняя) 0, 1, 6, 5 4,4,4,4
5(передняя) 5,6, 7, 8, 9 5, 5, 5, 5, 5
6 (задняя) 0,4, 3, 2,1 6, 6,6,6, 6
В табл. 6.3 приведен список граней сарая: у каждой грани имеется свой список вершин и нор-
мальный вектор, ассоциированный с каждой вершиной. Для экономии пространства вместо вершин и
нормалей используются только индексы. (Поскольку каждая поверхность плоская, всем вершинам
одной грани соответствует одна и та же нормаль.) Список вершин для каждой грани начинается с ка-
кой-либо вершины на этой грани и обходи! эту грань от вершины к вершине до тех пор, пока не будет
пройден полный круг. Существует два способа обхода полигона: по и против часовой стрелки. Напри-
мер, грань № 5 может быть внесена в список как (5,6,7,8,9) или как (9,8,7,6,5). Можно использовать
любое направление, однако мы следуем соглашению, которое принято на практике: обходим полигон
против часовой стрелки, если смотреть на объект снаружи.
6.2. Введение в трехмерное моделирование полигональными сетками
355
Если в таком порядке вы проходите грань от вершины к вершине, идя по внешней поверхности, то
часть плоскости, содержащая эту грань (внутренность грани), находится слева от вас. Позднее мы раз-
работаем 'алгоритмы, которые применяют именно такой порядок и поэтому легко различают «перед-
нюю» и «заднюю» стороны грани.
Наш сарай является примером «интенсивной по данным» (data-intensive) модели, в которой пере-
рабатывается большое количество данных, причем координаты каждой вершины вводятся разработчи-
ком (может быть, вручную). Позднее мы увидим ряд моделей, которые в отличие от них генерируются
алгоритмически. Разобраться с вершинами для стандартного сарая не составляет большого труда: ди-
зайнер выбрал в качестве пола простой единичный квадрат, решил поместить один угол сарая в начало
координат и выбрал высоту кровли в полторы единицы. Путем соответствующего масштабирования
эти размеры в дальнейшем можно изменять (хотя отношение высоты стены сарая к его максимальной
высоте, равное 1:1,5, зафиксировано навечно).
6.2.2. Нахождение нормальных векторов
Координаты вершин можно задавать вручную, однако не столь просто вычислить нормальные векто-
ры. В общем случае у каждой грани имеется три или более вершин, и разработчику будет весьма слож-
но записывать нормальные векторы. Лучше предоставить вычисление нормальных векторов компью-
теру во время создания каркасной модели.
Если грань считается плоской, как в случае сарая, то нам требуется только найти нормальный век-
тор к самой грани и связать его с каждой из вершин этой грани. Одним из прямых способов нахожде-
ния нормали является использование векторного произведения, как показано на рис. 4.16. Возьмем на
грани три соседних точки — Vt, V2, V3 и вычислим нормаль как векторное произведение m = (- V2) х
х (V3 - V2). После этого нормальный вектор можно нормировать до единичной длины.
При этом простом подходе могут возникнуть две проблемы: во-первых, если векторы V} - V2 и V3 - V2
почти параллельны, то векторное произведение будет очень малым (почему?) и результат может иметь
большие погрешности вычисления. Во-вторых, как мы увидим позднее, может случиться так, что поли-
гон не является полностью плоским, то есть не все его вершины лежат в одной плоскости. Поэтому по-
верхность, представляемая этими вершинами, не может быть действительно плоской. В этом случае нам
придется использовать для нормали к полигону некоторую «усредненную» величину, которая учиты-
вает все рассматриваемые вершины.
Один из устойчивых методов, решающих обе эти проблемы, был разработан Мартином Е1ьюэллом
(Martin Newell). Этот метод вычисляет компоненты тх, ту, тг нормального вектора m по следующим
формулам:
W-I
= EU -Ле«(,))(г/ + Zn.ext(,)) ’
|=0
ту = - Znext(,) +Xnex.(,) ) - (6Л)
OTz=X(XI-Xnext(())U+^t(/))>
где N — число вершин грани, (х, ур z) — координаты г-й вершины, next(j) = (j + l)modN— индекс
«следующей» после j-й вершины при обходе грани. Эта формула обеспечивает «круговой» переход от
(N - 1)-й вершины к нулевой. При таком алгоритме для каждого ребра требуется только одно умножение
на каждый компонент нормали, причем не нужно никакой проверки на коллинеарность. Этот резуль-
тат выводится в тематическом задании 6.2 и там же приведен его код на C++. Вектор ш, вычисленный
но методу Ньюэлла, может быть направлен внутрь полигона или наружу от него. Кроме того, в этом
тематическом задании доказывается, что если вершины полигона обходятся (с ростом г) против часовой
стрелки при взгляде на полигон снаружи, то вектор m указывает направление наружу от этой грани.
356
Глава 6. Моделирование поверхностей полигональными сетками
Пример 6.2.2
Дан полигон с вершинами Ро = (6,1,4), = (7,0,9) и Р2 = (1, 1, 2). Найдите нормаль к этому полигону
по методу Ньюэлла.
Решение
Прямое использование векторного произведения дает следующее:
((7,0,9) - (6,1,4)) х ((1,1,2) - (6,1,4)) = (2, -23, -5).
Применение метода Ньюэлла дает тот же самый результат: (2, -23, -5).
Практические упражнения
6.2.1. Использование метода Ньюэлла
Для трех вершин (6, 1, 4), (2, 0, 5) и (7, 0, 9) сравните нормаль, полученную по методу Ньюэлла, и ту,
которая получается с помощью обычного векторного произведения. Затем с помощью метода Ньюэлла
найдите (пх, пу, пг) для полигона с вершинами (1,1,2), (2,0,5), (5,1,4) и (6,0,7). Является ли этот поли-
гон плоским? Если да, то найдите его истинную нормаль, используя векторное произведение, и сравни-
те эту истинную нормаль с результатом метода Ньюэлла.
6.2.2. Случай неплоского полигона
Рассмотрим четырехугольник, изображенный на рис. 6.5, с вершинами (0,0,0), (1,0,0), (0,0,1) и (1, а, 1).
Если а отлично от нуля, то данный четырехугольник является неплоским полигоном. Найдите «нор-
маль» к этому полигону с помощью метода Ньюэлла и исследуйте, насколько хороша эта ее оценка для
различных значений параметра а.
Рис. 6.5. Неплоский полигон
6.2.3. Представление «базового куба»
Составьте списки вершин, нормалей и граней для «базового куба» с центром в начале координат, ребра
которого длиной в две единицы выровнены по координатным осям. В этом случае восемь его вершин
располагаются в точках с восемью возможными комбинациями знаков «+» и «-» в списке (±1, ±1, ±1).
6.2.4. Грани с отверстиями
На рис. 6.6 показано, каким образом можно записать в список грань, содержащую отверстие. Как видно
из рисунка, нужно добавить пару фиктивных ребер, которые соединяют разрыв между контуром грани
и отверстием.
Обход грани производится так (если двигаться по внешней поверхности), что «внутренность» грани
располагается слева. Тогда отверстие обходится по часовой стрелке. Предполагая, что мы смотрим на
грань с ее внешней стороны, получим следующий список вершин: 5,4,3,8,9,6,7,8,3,2,1. Нарисуйте эту
рань с еще одним отверстием и составьте список ее вершин. Какие нормали будут связаны с каждой
вершиной?
6.2. Введение в трехмерное моделирование полигональными сетками
357
Рис. 6.6. Грань, содержащая отверстие
6.2.3. Свойства сеток
Имея сетку, заданную списками вершин, нормалей и граней, мы можем поинтересоваться, что за объект
представляет эта сетка. Вот некоторые любопытные свойства сетки.
О Монолитность (Solidity). Как уже упоминалось, сетка представляет монолитный объект, если
совокупность его граней заключает в себе некоторое конечное пространство.
О Связность (Connectedness). Сетка называется связной, если между любыми двумя вершинами
существует непрерывный путь вдоль ребер полигона. (Если сетка не является связной, то обычно
она представляет более одного объекта.)
О Простота (Simplicity). Сетка называется простой, если отображаемый ею объект является моно-
литным и не содержит отверстий. Это означает, что объект может быть деформирован в сферу,
не подвергаясь разрезанию. (Отметим, что термин «простой» использован здесь совсем не в том
смысле, как он применялся к полигону.)
О Плоскостность (Planarity). Сетка называется плоской, если каждая грань представляемого ею
объекта является плоским полигоном; то есть вершины каждой грани лежат в одной плоскости.
Если грань плоская, то многие графические алгоритмы работают значительно более эффектив-
но. Треугольники являются плоскими по определению. Некоторые моделирующие программы
используют это обстоятельство и работают только с треугольниками. В отличие от треугольни-
ков четырехугольники могут быть плоскими, а могут и не быть. Например, четырехугольник,
изображенный на рис. 6.5, является плоским тогда и только тогда, когда а = 0.
О Выпуклость (Convexity). Сетка представляет выпуклый объект, если прямая, соединяющая лю-
бые две точки внутри этого объекта, целиком лежит внутри него. Впервые выпуклость рассмат-
ривалась в разделе «Другие графические примитивы в OpenGL» главы 2 в связи с полигонами.
На рис. 6.7 показано несколько выпуклых и несколько невыпуклых объектов. Для каждого невы-
пуклого объекта показан пример прямой, концевые точки которой лежат внутри объекта, однако
сама прямая полностью не находится внутри этого объекта.
Наш базовый сарай обладает всеми перечисленными свойствами. (Убедитесь в этом!) Для заданной
сетки некоторые из этих свойств легко могут быть определены программно — в том смысле, что суще-
ствует простой алгоритм, выполняющий эту работу. (Позднее мы рассмотрим некоторые из таких ал-
горитмов.) Другие свойства, например монолитность, определить значительно сложнее.
Полигональные сетки, выбранные нами для моделирования объектов в графике, могут обладать неко-
торыми или даже всеми вышеперечисленными свойствами: все зависит от того, для какой цели эта сетка
используется. Если сетка будет представлять физический объект, сделанный из какого-либо материала, на-
пример, для определения его массы или центра тяжести, то мы можем потребовать, чтобы сетка была по
крайней мере связной и монолитной. Если же мы просто хотим нарисовать объект, то у нас значитель-
но больше свободы, так как целый ряд даже «нефизических» объектов тем не менее можно нарисовать.
358
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.7. Примеры выпуклых и невыпуклых трехмерных объектов
На рис. 6.8 показано несколько объектов, которые могут быть изображены в виде сеток. ПИРАМИДА
состоит из треугольных граней, которые всегда являются плоскими. Пирамида является не только вы-
пуклой; фактически она обладает всеми перечисленными свойствами. КОЛЬЦО является связным и
монолитным, однако не является ни простым (в нем имеется отверстие), ни выпуклым. Две его грани
сами содержат отверстия. Имея в распоряжении только рисунок, невозможно определить, являются ли
грани кольца плоскими полигонами. Позднее мы дадим алгоритм для определения плоскостности, ис-
ходя из списков граней и вершин.
Невозможное
Кольцо
Рис. 6.8. Примеры монолитных тел, которые нужно описать с помощью сеток
Объект НЕВОЗМОЖНОЕ не может существовать'в пространстве. Можно ли его представить сет-
кой? Кажется, что САРАЙ состоит из двух частей, однако его можно заключить в одну сетку. Будет ли
эта сетка связной, зависит от того, как были определены грани в месте стыка между силосной башней и
главным зданием. Кроме того, САРАЙ иллюстрирует ситуацию, часто встречающуюся в графике: к сет-
ке добавляются несколько граней, изображающих окна и двери, чтобы объект имел «текстуру». Напри-
мер, стена сарая представляет собой прямоугольник без отверстий, но к сетке добавлены два квадрата
для изображения окон. Эти квадраты располагаются в той же плоскости, что и стена сарая. В этом слу-
чае сетка не является связной, но она по-прежнему может быть отображена на графическом устройстве.
6.2.4. Каркасные модели для немонолитных объектов
На рис. 6.9 приведены примеры других объектов, которые могут быть описаны с помощью полигональ-
ных сеток. Все эти объекты являются поверхностями и лучше всего считать их бесконечно тонкими
«оболочками».
6.2. Введение в трехмерное моделирование полигональными сетками
359
Рис. 6.9. Некоторые поверхности, описываемые с помощью сеток: а) коробка; б) структура;
в) (с разрешения University of Utah) лицо
Объект КОРОБКА — это открытая коробка с поднятой крышкой. В контексте графики мы могли
бы раскрасить, например, внешнюю поверхность шести ее граней синим цветом, а внутреннюю — зеле-
ным. (Что получится, если мы удалим одну грань у ПИРАМИДЫ с рис. 6.8?)
На рис. 6.9 также приведены две сложные поверхности: СТРУКТУРА и ЛИЦО. В этих примерах
полигональные грани используются для аппроксимации гладкой истинной поверхности. В ряде случа-
ев сетка — это все, что известно о данном объекте, например, при оцифровке точек лица человека. Если
каждую грань сетки изобразить в виде закрашенного полигона, то изображение будет выглядеть неесте-
ственным, как и наблюдается в случае объекта ЛИЦО. В дальнейшем мы изучим инструменты, с помощью
которых можно попытаться нарисовать истинную поверхность только на базе каркасной модели.
Многие программные пакеты геометрического моделирования конструируют модель некоторого
объекта — тела или поверхности, — которая должна описывать истинную форму объекта с помощью
полигональной сетки. Задача составления списков вершин, нормалей и граней может оказаться труд-
ной. В качестве примера рассмотрим составление алгоритма, генерирующего списки вершин и граней
для аппроксимации формы блока двигателя, протеза конечности или здания. При использовании дос-
таточного числа граней сетка может аппроксимировать «истинную поверхность» с любой желаемой
степенью точности. Свойство полноты (completeness) делает полигональные сетки гибким средством
моделирования.
6.2.5. Работа с сетками в программе
Нам нужен эффективный способ программного описания сетки, упрощающий создание и рисование
объекта, представляемого этой сеткой. Поскольку данные по сетке часто сохраняются в файле, нам нуж-
ны также простые способы чтения и записи «сеточных файлов». Тогда естественно определить класс
Mesh и наделить его желаемыми функциональными возможностями.
Листинг 6.1. Примерный тип данных для сетки
1 1 II II H II II II II II tl II II II II и II It II 1/л_4.л..ТП » » » II II It It ч II II ч И II п и п II
//mmmmmt VertexID //////////////////оо////////
class VertexID{
public:
int vertIndex;
// index of this vertex in the vertex list
// индекс этой вершины в списке вершин
int normlndex:
// index of this vertex's normal
// индекс нормали этой вершины
}:
продолжение
360
Глава 6. Моделирование поверхностей полигональными сетками
Листинг 6.1 (продолжение)
Face ШШШШ1111Ш
class Face{
public:
int nVerts:
// number of vertices In this face
// число вершин этой грани
VertexID *vert:
// the list of vertex and normal Indices
// список индексов вершин и нормалей
FaceO{nVerts -0: vert -NULL:}
// constructor
// конструктор
-FaceO {del ete[] vert: nVerts =0:}
// destructor
// деструктор
}:
//#ИИИМШ^ Mesh ##################;
class Mesh{
private:
int numVerts:
// number of vertices in the mesh
// число вершин в сетке
Point3* pt;
// array of 3D vertices
// массив трехмерных вершин
int numNormals:
// number of normal vectors for the mesh
// число нормальных векторов сетки
Vector3 *norm:
// array of normals
// массив нормалей
int numFaces:
// number of faces in the mesh
// число граней в сетке
Face*face;
// array of face data
// массив данных граней
//...others to be added later
//... другие, которые будут добавлены позже
public:
MeshO:
// constructor
// конструктор
-MeshO;
// destructor
// деструктор
int readFile(char * fileName):
>/ to read in a filed mesh
// для чтения сетки из файла
..others ..
Другие ..
6.2. Введение в трехмерное моделирование полигональными сетками
361
В листинге 6.1 приведено определение класса Mesh, а также двух простых вспомогательных классов:
VertexID и Face1. Объект Mesh содержит список вершин, список нормалей и список граней, которые пред-
ставлены соответственно массивами pt, norm и face. Эти массивы размещаются динамически во время
выполнения, когда уже известны их размеры. Их длины записываются в переменные numVerts, numNormal s
и numFaces соответственно. Позже можно добавить дополнительные поля данных для описания различ-
ных физических свойств объекта, таких как вес объекта и тип материала, из которого он сделан.
Тип данных Face — это, по существу, список вершин и нормальный вектор, связанный с каждой
вершиной грани. Здесь этот тип данных организован как массив пар индексов: v-я вершина f-й грани
имеет координаты pt[face[f].[vert[v].vertlndex], а ее нормальный вектор — norm[face[f].[vert[v].
normindex]. Такой формат на первый взгляд выглядит громоздким, однако схема индексирования явля-
ется вполне упорядоченной и простой в управлении, а также весьма эффективной, так как обеспечива-
ет быструю индексную адресацию «случайного доступа» в массив pt[].
Пример 6.2.3. Данные для тетраэдра
На рис. 6.10 показан тетраэдр с вершинами в точках (0,0,0), (1,0,0), (0,1,0), (0,0,1) и представляющие
его данные. Проверьте величины, приведенные в каждом поле. (Способы нахождения нормальных
векторов мы рассмотрим позднее.)
Рис. 6.10. Тетраэдр и представляющие его данные
Вначале нужно разработать метод рисования такого каркасного объекта. Речь идет, разумеется,
о рисовании каждой из его граней. Реализация метода Mesh: :draw() на базе OpenGL должна просматри-
вать массив граней каркасного объекта и посылать в графический конвейер массив вершин и нормалей
каждой грани. В OpenGL предусмотрено, что последовательные вершины ассоциируются с нормаль-
ным вектором m посредством выполнения процедуры glNormal3f(m.x, m.y, m.z)2. Тогда основное дей-
ствие метода Mesh::drawl) выглядит так:
for(each face f In the mesh)
// каждая грань f в сетке
{
glBegin (GL_POLYGON):
for(each vertex v in face f)
// каждая вершина v грани f
{
1 Определения основных классов Point3 и Vertex3 были даны ранее, а также приводятся в приложении В.
2 Для правильного затенения нормальные векторы должны быть нормированы. Или поместите в функцию initO подпрограмму:
gl Enable(GL_NORMALIZE), которая требует, чтобы OpenGL автоматически нормировал все нормальные векторы.
362
Глава 6. Моделирование поверхностей полигональными сетками
glNorma!3f(normal at vertex v):
// нормаль в вершине v
glVertex3f(position of vertex v):
// координаты вершины v
}
glEndO:
}
Реализация данного алгоритма приведена в листинге 6.2.
Листинг 6.2. Метод для рисования сетки с использованием OpenGL
void Mesh:: drawO
// use OpenGL to draw this mesh
// для рисования этой сетки используем OpenGL
{
for (int f =0: f < numfaces: f++)
// draw each face
// рисуем каждую грань
{
glBegin (GL_POLYGON);
for (int v =0: v < face[f],nVerts: v++)
// for each one..
// для каждой...
{
int in = face[f].vert[v],normindex;
// index of this normal
// индекс данной нормали
int iv = face[f].vert[v].vertlndex:
// index of this vertex
// индекс данной вершины
glNormal3f(norm[in].x, norm[in].y, norm[in].z):
glVertex3f(pt[iv].x. pt[iv].y. pt[iv].z):
glEndO:
}
}
Нам также нужны методы для построения нужной сетки и чтения заданной сетки из файла в па-
мять. Затем мы перейдем к исследованию различных семейств интересных форм, которые могут быть
записаны в виде сетки, а также увидим, как создавать эти формы. (В тематическом задании 6.1 мы рас-
смотрим чтение сеток из файла и запись их в файл.)
Использование SDL для создания и рисования каркасных объектов
В графических приложениях удобно читать описания сеток, используя язык SDL, с которым мы позна-
комились в главе 5. Чтобы осуществить это, нужно образовать из класса Shape производный класс Mesh и
добавить метод drawOpenGLO. Поэтому дополним программу из листинга 6.4 следующим кодом:
class Mesh : public Shape {
// same as in Figure 6.13
// то же. что и на рис. 6.13
virtual void drawOpenGLO
{
tel 1 MaterialsGL(); glPushMatrix():
// load properties
// загружаем свойства
6.3. Многогранники
363
glMultMatrix f(transf.m):
draw():
// draw the mesh
// рисуем сетку
glPopMatrixO:
// end of Mesh class
// конец класса Mesh
Теперь класс Scene, способный читать SDL-файлы, настроен для восприятия ключевого слова mesh,
за которым следует имя файла, содержащего описание сетки. Следовательно, для создания и прорисов-
ки шахматной пешки с необходимым перемещением и масштабированием можно использовать следу-
ющую команду:
push translate 3 5 4 scale 3 3 3 mesh pawn.3vn pop
(Ряд таких файлов с суффиксом 3vn доступен на web-сайте данной книги.)
6.3. Многогранники
Часто бывает удобно ограничить данные в сетке так, чтобы она изображала многогранник (полиэдр).
Огромное число интересных объемных объектов в действительности являются полиэдрами; кроме того,
алгоритмы вычисления сетки могут быть значительно упрощены, если нам требуются только сетки,
представляющие многогранники.
В различных контекстах используются несколько различающиеся определения полиэдра [Coxeter, 50,
Hilbert, 107, Foley, 64], однако мы будем применять следующее.
Определение. Полиэдром называется связная сетка из простых плоских полигонов, которая ограни-
чивает конечный объем пространства.
Итак, согласно данному определению, полиэдр представляет собой единый монолитный объект. Из
этого следует, что:
О каждое ребро принадлежит ровно двум граням;
О в каждой вершине встречается не менее трех ребер;
О грани не являются взаимопроникающими (interpenetrate): две грани или не имеют общих точек,
или пересекаются только вдоль их общего ребра.
На рис. 6.8 объект ПИРАМИДА безусловно является полиэдром. Очевидно, что КОЛЬЦО ограни-
чивает некоторое пространство, поэтому оно является полиэдром, но только если его грани плоские.
Однако это не простой полиэдр, поскольку в нем имеется отверстие. Кроме того, две его грани сами
содержат отверстия. Является ли полиэдром объект НЕВОЗМОЖНОЕ? Почему? Если не принимать
во внимание текстуру граней, то САРАЙ можно смоделировать как два полиэдра — один для главного
здания и второй для силосной башни.
Формула Эйлера
Формула Эйлера (она легко доказывается; см., например, [Courant, 49]) устанавливает фундаменталь-
ное соотношение между количеством граней, ребер и вершин (соответственно F, Е, V) простого много-
гранника:
V+F-E-2.
Например, для куба V= 8, F= 6, Е= 12.
364
Глава 6. Моделирование поверхностей полигональными сетками
Обобщение этой формулы на непростой полиэдр [Foley, 64] выглядит так:
V+F-E = 2 + H-2G,
(6.2)
где Н — общее число отверстий, имеющихся в гранях, a G — число отверстий в самом полиэдре. На рис.
6.11, а изображен параллелепипед, содержащий отверстие в форме другого параллелепипеда. Две его
торцевые грани выдвинуты из основного параллелепипеда. Для этого объекта V = 16, F= 16, Е = 32,
Н = О, G = 1. На рис. 6.11, б изображен полиэдр с частично проникающим в него отверстием А и сквоз-
ным отверстием В. Здесь У= 24, F= 15, Е = 36, Н = 3, G = 1. Обе совокупности величин удовлетворяют
формуле Эйлера.
а б
Рис. 6.11. Полиэдр с отверстиями
«Структуру» полиэдра удобно описывать с помощью диаграммы Шлегеля (Schlegel diagram), кото-
рая основана на взгляде на полиэдр из точки, расположенной на некотором расстоянии от центра одной
из его граней, как предлагается на рис. 6.12, а. Такой способ рассмотрения куба приводит к диаграмме
Шлегеля, приведенной на рис. 6.12, б. Передняя грань представляется как большой полигон, окружаю-
щий остальные грани.
Рис. 6.12. Диаграммы Шлегеля для куба
Еще несколько примеров приведено на рис. 6.13. Рисунок 6.13, а — это диаграмма Шлегеля для
объекта ПИРАМИДА с рис. 6.8, б, а на рис. 6.13, б и 6.13, в показаны две различные диаграммы для ба-
зового сарая. (Какие грани являются ближайшими для наблюдателя?)
Рис. 6.13. Диаграммы Шлегеля для ПИРАМИДЫ и базового сарая
6.3. Многогранники
365
6.3.1. Призмы и антипризмы
Призма — это частный случай полиэдра. Она обладает некоторой симметрией и поэтому довольно про-
ста в описании. Как показано на рис. 6.14, призма получается в результате заметания (sweeping), или
выдавливания (extruding — экструзия), полигона вдоль прямой линии, что превращает двумерный по-
лигон в трехмерный полиэдр. На рис. 6.14, а полигон Р перемещается вдоль вектора d, в результате чего
формируется полиэдр, приведенный на рис. 6.14, в. Если вектор d перпендикулярен к плоскости Р, то
призма называется прямой призмой (right prism). На рис. 6.14, в показано несколько печатных букв
алфавита, превращенных в призмы.
Рис. 6.14. Формирование призмы
Будем называть правильной (regular) такую призму, которая имеет в основании правильный поли-
гон, а в качестве боковых граней — квадраты1. На рис. 6.15, а показана шестиугольная правильная при-
зма. Некоторым отклонением от правильной призмы является антипризма (antiprism), показанная на
рис. 6.15, б. Она не является «выдавленным» объектом: вместо этого верхний n-угольник повернут на
180/п градусов и соединен с нижним n-угольником таким образом, что получаются грани в виде рав-
носторонних треугольников. (Сколько получается таких треугольных граней?) Правильная призма
и антипризма являются примерами так называемых «полуправильных» («semiregular») многогранни-
ков, которые мы будем изучать в дальнейшем.
л-гон
Равносторонний
треугольник
а 6
Рис. 6.15. Правильная призма и антипризма
Практические упражнения
6.3.1. Составление списка для призмы
Составьте списки вершин, нормалей и граней для призмы, приведенной на рис. 6.16. Пусть основание
этой призмы (грань № 4) лежит в плоскости ху, а вершина 2 — на оси z при z = 4. Предположим далее,
что вершина 5 располагается в трех единицах вдоль оси х и что основание призмы — равносторонний
треугольник.
1 В отечественной литературе — правильная призма имеет в качестве боковых граней прямоугольники. — Примеч. пер.
366
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.16. Пример многогранного объекта
6.3.2. Приподнятый куб
Составьте списки вершин, нормалей и граней для куба, одна из вершин которого располагается в точке
(0,0, 0), а вершина, противоположная ей, — в точке (1,1,1).
6.3.3. Антипризма
Постройте списки вершин, нормалей и граней для антипризмы, верхним полигоном которой является
квадрат.
6.3.4. Определение связности сетки
Является ли связной сетка, определенная следующим списком граней: (4,1,3), (4,7,2,1), (2,7,5), (3,4,
8, 7,9)? Попытайтесь нарисовать эскиз этого объекта, выбрав для его девяти вершин произвольные по-
ложения. Какой алгоритм можно использовать для проверки этого списка граней на связность?
6.3.5. Создание сеток
Пронумеруйте каждую вершину объектов КОЛЬЦО, НЕВОЗМОЖНОЕ и САРАЙ с рис. 6.8 и затем
напишите для них списки граней.
6.3.6. Диаграммы Шлегеля
Нарисуйте диаграммы Шлегеля для призм с рис. 6.15 и 6.16.
6.3.2. Платоновы тела
Если все грани полиэдра одинаковы и каждая из них является правильным многоугольником, то такой
объект называется правильным многогранником (regular polyhedron). Требование данной симметрии
является настолько жестким, что существует всего пять таких объектов: это Платоновы тела1, изображен-
ные на рис. 6.17 [Coxeter, 50]. Платоновы тела обладают высокой степенью симметрии, а также целым
набором замечательных свойств. Они являются прекрасными объектами для упражнений в компью-
терной графике и часто фигурируют при объемном моделировании в приложениях по автоматизиро-
ванному проектированию (CAD).
Таблица 6.4. Описания Платоновых тел
Тело V F Е Символ Шлефли
Тетраэдр 4 4 6 (3,3)
Гексаэдр 8 6 12 (4,3)
Октаэдр б 8 12 (3,4)
Икосаэдр 12 20 30 (3, 5)
Додекаэдр 20 12 30 (5,3)
1 Названы в честь Платона (427-347 годы до н. э.), упоминавшего эти тела в своих Timaeus. Однако они были известны и до Плато-
на: игрушечный додекаэдр, найденный близ развалин Падуи, датируется 500 годом до н. э.
6.3. Многогранники
367
Рис. 6.17. Пять Платоновых тел
Додекаэдр
Гранями трех Платоновых тел являются равносторонние треугольники, одно обладает квадратны-
ми гранями, а грани додекаэдра представляют собой пентагоны (пятиугольники). Куб является пра-
вильной призмой, а октаэдр — антипризмой. (Почему?) Значения величин V, F, Е для каждого из Пла-
тоновых тел приведены в табл. 6.4. Кроме того, там приводится и символ Шлефли* (р, q) для каждого
тела; он означает, что каждая грань является р-угольником и что q из них сходятся в каждой вершине.
Нетрудно построить сеточные списки для куба и октаэдра (см. упражнения 6.3.7,6.3.8). В этих упражне-
ниях даются примеры списков вершин и граней для тетраэдра и икосаэдра и рассматривается способ со-
ставления списков нормалей. Кроме того, там показано, как вывести списки для додекаэдра из списков
для икосаэдра, воспользовавшись «двойственностью» этих тел (это понятие мы также определим позднее).
Двойственные многогранники
Каждому Платонову телу Р соответствует двойственный (dual) многогранник D. Вершинами полиэд-
ра D являются центры граней полиэдра Р, так что ребра полиэдра D соединяют средние точки смежных
граней полиэдра Р. На рис. 6.18 для каждого Платонова тела изображено вписанное в него двойствен-
ное тело. Ниже приводится список некоторых тел, являющихся двойственными.
О Двойственным для тетраэдра является также тетраэдр.
О Куб и октаэдр являются двойственными.
О Икосаэдр и додекаэдр также являются двойственными.
Двойственные многогранники имеют то же число ребер Е, а параметр V для одного из них является
параметром Едля другого. Кроме того, если (р, q) — символ Шлефли для одного из двойственных тел,
то для второго символ Шлефли будет равен (q,p).
Если известен список вершин для одного Платонова тела Р, то легко создать такой же список для
двойственного ему тела D, поскольку вершина k полиэдра D располагается в центре грани k полиэдра Р.
Такой способ построения полиэдра D фактически создает многогранник, вписанный в многогранник Р.
Для того чтобы следить за нумерацией вершин и граней, мы используем модель (развертку), обра-
зуемую путем разрезания полиэдра вдоль определенных ребер и «разворачивания» его в плоскую фи-
гуру таким образом, что все его грани видны с внешней стороны. Модели трех Платоновых тел показа-
ны на рис. 6.19.
Рассмотрим двойственную пару куб — октаэдр. Грань 4 куба окружена вершинами 1,5,6,2. Тогда из
двойственности следует, что вершина 4 октаэдра окружена гранями 1, 5, 6, 2. Отметим, что поскольку
тетраэдр является двойственным самому себе, то для него список вершин, окружающих k-ю грань, со-
впадает со списком граней, окружающих k-ю вершину.
' Названо по имени швейцарского математика Л. Шлефли (L. Schlafli, 1814-1895).
368
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.18. Двойственные Платоновы тела
Рис. 6.19. Развертки: а) тетраэдр; б) куб; а) октаэдр
Вершина 4 октаэдра является центром грани 4 куба. Напомним из главы 4, что координаты центра
грани вычисляются как среднее арифметическое координат всех вершин, принадлежащих этой грани.
Следовательно, если нам известны вершины V5, V6, V2 для грани 4 куба, то мы сразу же получим:
К, = + к5 + к6 + к2).
(6.3)
Практические упражнения
6.3.7. Октаэдр
Рассмотрим октаэдр, являющийся двойственным телом для куба. Постройте списки вершин и граней
для октаэдра.
6.3.8. Проверка двойственности
Исходя из списков граней и вершин октаэдра из предыдущего упражнения, найдите двойственный ему
многогранник и убедитесь, что он является кубом.
6.3. Многогранники
369
Нормальные векторы к Платоновым телам
Если мы хотим построить сетки для Платоновых тел, то мы должны вычислить для каждой грани нор-
мальный вектор. Это можно сделать обычным способом с использованием метода Ньюэлла, однако
высокая степень симметричности Платоновых тел допускает гораздо более простой подход. Пусть тело
центрировано относительно начала координат, тогда мы видим, что нормальный вектор к каждой грани —
это вектор из начала координат (радиус-вектор) к центру грани, представляющему собой среднее значе-
ние вершин. На рис. 6.20 показан нормальный вектор для октаэдра; нормаль к грани равна просто
(Заметим, что этот вектор совпадает с вектором, проведенным из начала координат к соответствую-
щей вершине двойственного к данному Платонову телу.)
Центр грани
Рис. 6.20. Использование симметрии для нахождения нормали к грани
Тетраэдр
Список вершин тетраэдра зависит, разумеется, от положения тетраэдра, его ориентации и размера.
Интересно, что тетраэдр можно вписать в куб (так, что четыре его вершины располагаются в углах куба,
а четыре его ребра лежат на гранях куба). Рассмотрим единичный куб с вершинами (±1, ±1, ±1) и выбе-
рем тетраэдр так, чтобы одна его вершина находилась в точке (1,1,1). Тогда этот тетраэдр будет описы-
ваться списками вершин и граней, приведенными в табл. 6.5 [Blinn, 30].
Таблица 6.5. Список вершин и список граней для тетраэдра
Список вершин Список граней
Вершина X У Z Номер грани Вершины
0 1 1 1 0 1,2,3
1 1 -1 -1 1 0,3,2
2 1 -1 1 2 0,1,3
3 -1 1 -1 3 0,2,1
Икосаэдр
Список вершин икосаэдра более сложен, однако его можно упростить, если использовать одно замеча-
тельное обстоятельство. Рисунок 6.21 показывает вписанные в икосаэдр три взаимно перпендикуляр-
ных золотых прямоугольника, поэтому список вершин икосаэдра можно непосредственно прочитать с
этого рисунка. Совместим каждый золотой прямоугольник с одной из координатных осей. Для удоб-
ства масштабируем эти прямоугольники так, чтобы их длинные ребра простирались от -1 до 1 вдоль
соответствующих осей. Тогда короткое ребро каждого прямоугольника будет находиться в пределах от
-тдо т, где т = (>/5-1)^2 = 0,618... — величина, обратная золотому отношению ф. Отсюда легко полу-
чить координаты вершин для списка, который приведен в табл. 6.6.
370
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.21. Золотые прямоугольники, определяющие икосаэдр
Таблица 6.6. Список вершин для икосаэдра
Вершина X У z
0 0 1 t
1 0 1 -t
2 1 t 0
3 1 -t 0
4 0 -1 -t
5 0 -1 t
6 t 0 1
7 -t 0 1
8 t 0 -1
9 -t 0 -1
10 -1 t 0
11 -1 -t 0
На рис. 6.22 приведена модель икосаэдра. С этого рисунка можно непосредственно считывать спи-
сок граней для икосаэдра. (Вопрос: чему равен нормальный вектор к грани № 8?)
Рис. 6.22. Модель икосаэдра
6.3. Многогранники
371
Иногда предпочитают слегка изменить модель для икосаэдра, приведя ее к форме, показанной на
рис. 6.23. Такая форма проясняет тот факт, что икосаэдр состоит из антипризмы (на рисунке она закра-
шена) и двух пятиугольных пирамид в его вершине и основании.
5 граней
для пирамидальной
крышки
10 граней
составляют----
антипризму
5 граней
для пирамидального
основания
Рис. 6.23. Икосаэдр является антипризмой с крышкой и основанием
Додекаэдр
Додекаэдр является двойственным к икосаэдру, поэтому вся информация, необходимая для построе-
ния списков для додекаэдра, заключена в списках для икосаэдра. Однако удобнее рассматривать его
модель в «лежачем» положении, как на рис. 6.24.
Рис. 6.24. Модель додекаэдра
Снова используем двойственность: известно, что k-я вершину додекаэдра лежит в центре k-ii грани
икосаэдра, для чего усредняем все три вершины k-й грани. Все вершины додекаэдра легко могут быть
вычислены таким же способом.
Практические упражнения
6.3.9. Расстояния в икосаэдре
Чему равно радиальное расстояние от каждой вершины икосаэдра до начала координат?
6.3.10. Список вершин для додекаэдра
Постройте список вершин и список нормалей для додекаэдра.
6.3.3. Другие любопытные многогранники
Существует бесконечное разнообразие многогранников (см., например, [Wenninger, 211] и [Coxeter, 51]),
однако особый интерес представляет одна их категория. В то время как все грани Платоновых тел пред-
ставляют собой один и тот же тип и-угольников, Архимедовы тела (Archimedean solids), называемые
иначе полуправильными (semiregular) многогранниками, имеют в качестве граней несколько различных
372
Глава 6. Моделирование поверхностей полигональными сетками
типов правильных многоугольников. Кроме того, для полуправильности многогранника требуется, чтобы
каждая его вершина была окружена одной и той же совокупностью полигонов в одном и том же порядке.
Рис. 6.25. Усеченный куб
Например, изображенный на рис. 6.25, а «усеченный куб» имеет в качестве граней 8-угольники и
3-угольники, причем вокруг каждой вершины расположены один треугольник и два восьмиугольника.
Эти два свойства данного тела описываются символом 3-8-8.
Усеченный куб сформирован путем «срезания» каждого угла куба под одним и тем же углом.
Модель усеченного куба, показанная на рис. 6.25, б, получена из модели основного куба. Каждое ребро
куба разделено на три части, средняя из которых имеет длину А = 1/(1 + V2) (рис. 6.25, в), и средняя
часть каждого ребра соединена со средними частями соседних ребер. Таким образом, если концевые
точки ребра куба равны С и D, то две дополнительные вершины, V и W, могут быть получены с помо-
щью аффинных комбинаций:
F = + ——D
2 2
и
(6.5)
1F = —С +
2
2
Исходя из этого уравнения, нетрудно построить списки вершин и граней для усеченного куба
(см. упражнения в конце раздела, а также тематическое задание 6.10).
Требование того, что все грани должны быть правильными полигонами и окружать каждую верши-
ну в одном и том же порядке, ограничивает число полуправильных многогранников до 13 возможных1.
Они будут рассмотрены позднее, в тематическом задании 6.10. Архимедовы тела все еще обладают дос-
таточной симметрией, так что нормальный вектор к каждой грани может быть найден с использовани-
ем координат середины этой грани.
На рис. 6.26 изображено одно из Архимедовых тел, представляющее особый интерес: оно является
усеченным икосаэдром 5 • 62 и состоит из правильных гексагонов и пентагонов. Этот многогранник
известен во всем мире, так как именно такую форму имеет футбольный мяч. В последнее время усе-
ченный икосаэдр получил новое название — бакибол (buckyball) — в честь Бакминстера Фуллера
(Buckminster Fuller) — из-за его интереса к подобным геодезическим структурам. Недавно кристалло-
графы обнаружили, что 60 атомов углерода могут располагаться в вершинах усеченного икосаэдра, об-
разуя новый вид молекулы углерода, отличный от графита и алмаза. Этот материал обладает многими
’ Четырнадцатый полуправильный многогранник (псевдоромбокубооктаэдр) был открыт в 1957 году советским математиком
В. Г. Ашкинузе, хотя западные ученые чаще приписывают это открытие югославскому математику С. Билинскому (публикация
1960 года). Псевдоромбокубооктаэдр получается из ромбокубооктаэдра поворотом «крышек» на 45° вокруг оси симметрии всего
тела. — Поимеч. пер.
6.3. Многогранники
373
замечательными свойствами, например, устойчивостью к высоким температурам и сверхпроводимос-
тью [Browne, 36]; неудивительно, что он получил имя фуллерин (fullerene).
Рис. 6.26. Бакибол
Весьма интересно моделировать бакибол и отображать его на графическом дисплее. Чтобы постро-
ить для него списки вершин и граней, нарисуем модель икосаэдра, изображенного на рис. 6.27, после
чего разделим каждое ребро на три равные части. Вследствие этого на каждом ребре появятся две но-
вые вершины, координаты которых могут быть легко вычислены. Пронумеруем 60 новых вершин, со-
образуясь со своим вкусом, чтобы построить для бакибола список вершин. На рис. 6.27 приведена часть
развертки икосаэдра с новыми вершинами, соединенными ребрами. Отметим, что каждая старая грань
икосаэдра становится шестиугольником, а каждая старая вершина икосаэдра «срезается» и превращается
в пятиугольную грань. Построение списка граней сводится к простому перечислению их согласно мо-
дели. В тематическом задании 6.10 проводится дальнейшее исследование Архимедовых тел.
Геодезические купола
Труднее всего примириться с хорошим примером.
Марк Твен (Mark Twain)
Хотя Бакминстер был пионером во многих направлениях, более всего он знаменит введением понятия
геодезических куполов [Fuller, 71]. Эти тела составляют интересный класс полиэдров, обладающих
многими полезными свойствами. В частности, геодезический купол, созданный из реальных материа-
лов, чрезвычайно прочен для своего веса.
Геодезический купол может принимать множество различных форм, но все они расположением сво-
их граней, обычно треугольных, аппроксимируют сферу. Когда сфера аппроксимирована такими гра-
нями, ее нижняя половина удаляется, и оставшаяся верхняя половина образует знакомую купольную
форму. На рис. 6.28 показан пример, основанный на икосаэдре.
Для определения граней каждое ребро икосаэдра разбивается на ЗГравных частей,- где величина F—
введенная Фуллером частота (frequency) купола. В данном примере F = 3, так что каждое ребро икоса-
эдра разделено на три части для образования девяти меньших треугольных граней (рис. 6.29, а).
374
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.28. Геодезический купол
а
Рис. 6.29. Построение новых вершин для купола
Эти грани, однако, не располагаются в той же плоскости, что и исходные грани. Во-первых, новые
вершины «проецируются наружу» на описанную сферу. На рис. 6.29, б показан процесс проецирования
в сечении. Например, ребро между V, и Vg при разбиении образует две точки: Wlg и W81. Первая точка
задается следующей формулой:
^,0= + |^8-
(А как задать Wgl?) Проецирование W18 на описанную сферу радиуса R является простым масшта-
бированием:
(6.6)
(6-7)
lwis|
где wlg — радиус-вектор, связанный с точкой 1У18. Старые и новые вершины соединяются между со-
бой отрезками прямых и образуют девять треугольных граней на каждую грань икосаэдра. (Почему
геодезический купол не является новым Платоновым телом?) Чему равны значения Е, F, V для этого
полиэдра? Намного больше сведений о геодезических куполах можно найти в работах [Fuller, 72] и
[Kappraff, 121].
Практические упражнения
6.3.11. Списки для усеченного икосаэдра
Напишите списки вершин, нормалей и граней для усеченного икосаэдра.
6.3.12. Списки для бакибола
Создайте списки вершин, нормалей и граней для бакибола. Поскольку вычислять 60 вершин утоми-
тельно, то, наверно, проще написать небольшую подпрограмму для формирования каждой новой вер-
шины по списку вершин для икосаэдра с рис. 6.24.
6.4. Экструзивные формы
375
6.3.13. Построение списков для геодезического купола
Составьте списки вершин, нормалей и граней для геодезического купола с частотой 3.
6.4. Экструзивные формы
Обширный класс форм может быть создан путем выдавливания (экструзии) или заметания двумер-
ной формы в пространстве. Призма, показанная на рис. 6.14, является примером формы, образованной
посредством «линейной экструзии», то есть по прямой линии. Как мы увидим, тетраэдр и октаэдр с
рис. 6.17 также представляют собой примеры экструзии формы в пространство определенным спосо-
бом. Поверхности вращения также могут быть аппроксимированы путем «вытеснения» полигона в про-
странство, если мы слегка расширим определение экструзии.
В данном разделе мы изучим способы создания сеток путем пошаговой дискретной экструзии поли-
гонов. В разделе «Каркасные аппроксимации гладких объектов» мы разработаем аналогичные инстру-
менты для построения сеток, которые позволят аппроксимировать непрерывно заметаемые формы.
6.4.1. Создание призм
Начнем с призмы, сформированной путем экструзии полигона вдоль прямой линии. На рис. 6.30, а
приведена призма на базе полигона Р, расположенного в плоскости ху. Полигон Р протянут на рас-
стояние Н вдоль оси z, в результате чего образовалась призма СТРЕЛКА, изображенная на рис. 6.30, б.
(В более общем случае экструзия может производиться вдоль вектора d, как показано на рис. 6.14.)
В результате протягивания полигона Р из каждой его вершины образуется ребро в z-направлении. Этот
процесс приводит к возникновению еще 7 вершин, так что у полученной призмы всего 14 вершин. Они
появляются парами: если (х, yt, 0) — одна из вершин полигона основания Р, то у призмы еще имеется
вершина (х(, yit Н).
Р протягивается в направлении z
Рис. 6.30. Пример призмы: а) полигон основания; <5) Р заметается в направлении z; в) модель для призмы СТРЕЛКА
376
Глава 6. Моделирование поверхностей полигональными сетками
Как выглядит список граней, описывающий призму СТРЕЛКА? Эту призму можно «развернуть» в
модель, показанную на рис. 6.30, в, чтобы были видны все ее девять наружных граней. Призма имеет
семь прямоугольных боковых граней, а также основание (base) Р и крышку (cap). Например, грань 2
определяется вершинами 2, 9,10,3.
Поскольку данная призма имеет плоские грани, мы связываем с каждой вершиной грани один и тот
же нормальный вектор, то есть нормальный вектор к самой грани.
Построение сетки для призмы
Желательно иметь инструмент, создающий сетку для призмы на основе произвольного полигона. Пусть
основанием призмы является полигон с N вершинами {xityt}. Занумеруем вершины основания числами
0,..., N- 1, а вершины крышки числами N,..., 2N- 1, так чтобы ребро соединяло вершины с номерами г
и i + N, как показано на рис. 6.33. В этом случае список вершин строится просто и содержит точки (х, у? 0)
и (х,yt, Н) для i - 0,1.
Список граней построить также несложно. Запишем вначале «боковые» грани, или «стены», а затем
добавим основание и крышку. Для j-й стенки (j - 0,..., N - 1) создадим грань с четырьмя вершинами,
имеющими индексы j,j + N, next(j) + N, next(j), где next(j) - j + 1, за исключением j, равного N- 1, для
которого next(j) - 0. Это условие обеспечивает «циклический возврат» от (N - 1)-й вершины к нуле-
вой. Тогда имеем:
next(j) - (J + l)modM (6.8)
или, на языке программного кода, next - (j < (N-l)) ? (j + 1) : 0. Каждая грань добавляется в список
граней по мере ее создания. Нормальный вектор к каждой грани легко находится методом Ньюэлла,
описанным ранее. Затем мы создаем основание и крышку и добавляем их в список граней. Более под-
робно о создании каркасных моделей для призм рассказывается в тематическом задании 6.3.
6.4.2. Совокупности экструзивных призм: «кирпичная кладка»
Некоторые инструменты визуализации, подобно OpenGL, могут надежно рисовать только выпуклые
полигоны. Они могут неправильно нарисовать, например, стрелку с рис. 6.30. Если ваше программное
обеспечение относится к такому же типу, то вы можете разбить невыпуклый полигон основания на со-
вокупность выпуклых полигонов и экструдировать каждый из них. На рис. 6.31 дается несколько при-
меров, в том числе выдавленные буквы алфавита.
Рис. 6.31. Экструзивные объекты, составленные из выпуклых призм
6.4. Экструзивные формы
377
Объекты, подобные приведенным на рисунке, составляются из совокупности выпуклых призм. Не-
которые из составляющих призм примыкают друг к другу и поэтому могут иметь общие стены — цели-
ком или частично. Но поскольку координаты вершин вычисляются с большой точностью, граница меж-
ду двумя стенами обычно невидима.
Для данного семейства форм нам нужен метод, строящий сетку по данным совокупности призм, на-
пример:
void Mesh:: makePrismArrayt...)
который принимает в качестве аргументов соответствующий список (выпуклых) полигонов основания
(расположенных в плоскости ху), а также, возможно, вектор d, описывающий направление и величину
экструзии. Список вершин должен содержать вершины полигонов основания и крышки каждой при-
змы, а сами стенки и основания каждой призмы должны находиться в списке граней. Рисование такой
сетки включает в себя много лишней работы, потому что граничащие стенки будут рисоваться (причем
дважды) даже тогда, когда они в конечном счете невидимы.
Частный случай: экструзия полос из четырехугольников
Существует простое, но очень интересное семейство призм, которое очень легко строится и эффектив-
но управляется. Это призмы, полигон основания которых может быть представлен в виде полосы четы-
рехугольников {quad-strip), то есть совокупности четырехугольников, соединенных в цепочку (подобно
кирпичам, выложенным в ряд) таким образом, что их соседние грани полностью совпадают, как показано
на рис. 6.32, а. Вспомним рис. 2.21, где указывается, что полоса четырехугольников является графическим
примитивом OpenGL. Полоса четырехугольников описывается последовательностью своих вершин:
quad-strip = {pvpvp2,...,puA}- (6.9)
Предполагается, что вершины берутся парами, причем нечетные вершины формируют одно «ребро»
полосы четырехугольников, а четные — другое ребро. Не каждый полигон можно представить в виде поло-
сы четырехугольников. (Какие из полигонов, изображенных на рис. 6.31, не являются полосами четырех-
угольников? Какие печатные буквы алфавита могут быть нарисованы как полосы четырехугольников?)
Рис. 6.32. Полосы четырехугольников и призмы, построенные на них
Когда сетка сформирована как экструзивная полоса четырехугольников, в список вершин помещается
только 2М вершин, а в список граней помещаются только «внешние стенки». Всего имеется 2М - 2 гра-
ней. (Почему?) Следовательно, при визуализации сетки лишние стенки вообще не рисуются. Метод
создания сетки для экструзивных полос четырехугольников будет принимать в качестве параметров
массив двумерных точек и вектор экструзии:
void Mesh:: makeExtrudedQuadStrip(Point2 р[]. int numPts. Vectors d):
На рис. 6.33 показан пример интересной экструзивной полосы четырехугольников. В тематическом
задании 6.4 способы создания таких сеток рассматриваются более детально.
378
Глава 6. Моделирование поверхностей полигональными сетками
6.4.3. Экструзии с «поворотом»
До сих пор экструзия только передвигала полигон основания в новое положение, определяющее поли-
гон крышки. Легко обобщить эту концепцию так, чтобы получить значительно более широкое семей-
ство форм. Для этого в качестве полигона крышки можно взять увеличенный или уменьшенный, а воз-
можно, и повернутый полигон основания. В частности, если полигон основания Р задан вершинами {р0,
р,..PN~t}> то полигон крышки Р' будет задан следующим образом:
P'={MpQ,Mp1..Мр^}, (6.10)
где М — некоторая матрица четыре на четыре, соответствующая аффинному преобразованию. На рис. 6.34
приведено несколько примеров. На рисунках 6.34, аиб показаны усеченные пирамиды, или коничес-
кие цилиндры (усеченные конусы), крышки которых являются уменьшенными версиями основания.
Матрица преобразования для объектов такого типа имеет вид:
'0,7 0 О О'
0 0,7 0 0
м =
0 0 1 Я
.° 0 0 h
Рис. 6.33. Экструзивная полоса четырехугольников, образующая арку
Эта матрица содержит только масштабный множитель 0,7 и перемещение на Я единиц вдоль оси г.
На рис. 6.34, в показан конический цилиндр, крышка которого перед перемещением была повернута
вокруг оси z на угол 0. Такое преобразование описывается матрицей:
' cos(0) sin(0) 0 0
м = -sin(0) cos(0) 0 0
0 0 1 я
0 k 0 0 1
Рисунок 6.34, г демонстрирует в разрезе, как повернуть крышку Р' на нужный угол перед ее переме-
щением в желаемую позицию.
Призмы, подобные этим, столь же просто создавать, как и те, для которых в матрице М используется
только перемещение: список граней для такой призмы тот же, что и у исходной; изменяются только
координаты вершин и значения нормальных векторов.
6.4. Экструзивные формы
379
Рис. 6.34. Пирамиды и повернутые призмы
Практические упражнения
6.4.1. Конический цилиндр
Составьте детальное описание того, как составить списки вершин, нормалей и граней для усеченной
пирамиды, основания которой представляют собой правильные пентагоны, причем верхнее основание
в два раза меньше нижнего.
6.4.2. Тетраэдр как усеченный конус
Опишите моделирование тетраэдра как конического цилиндра с треугольным основанием. Является
ли этот способ эффективным при вычислении сетки для тетраэдра?
6.4.3. Антипризма
Обдумайте, как создать антипризму, изображенную на рис. 6.15, б. Можно ли ее смоделировать как вид
экструзии?
6.4.4. Создание сегментированных экструзий: трубки и змейки
Еще одно обширное семейство объектов может быть создано путем применения последовательности
экструзий, каждая со своим собственным преобразованием, и укладкой их непрерывной цепью в форме
трубки. На рис. 6.35, а показана трубка, созданная путем трехкратной экструзии квадрата Р в различных
направлениях с различными сужениями и поворотами. Первый сегмент имеет концевые полигоны МйР
и М\Р, где начальная матрица Мо позиционирует и ориентирует начальный конец трубы. Второй сег-
мент имеет концевые полигоны М{Р и М2Р и т. д. Различающиеся преобразованные полигоны мы будем
называть «перетяжками» («waists») трубы. В нашем примере список вершин сетки содержит 16 вер-
шин: Мйрй, Мйр{, Мор2, Мйр3, М{рй, Mtpt, М{р2, М'Р3,...,М£>0, M3pv М3р2, М3р3. На рис. 6.35, б показана
«змейка» («snake»), названная так потому, что матрицы ЛЕ заставляют трубу расширяться или сжимать-
ся, чтобы изобразить тело и голову змеи.
380
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.35. Трубка, созданная путем последовательной экструзии полигона
Конструирование трубок на базе трехмерных кривых
Как конструировать интересные и полезные трубки и змейки? Можно создавать все матрицы Л/, вруч-
ную, однако это выглядит по меньшей мере странно. Намного проще представить трубу, окружающую
некоторую кривую, которую мы будем называть хребтом (spine) трубы и которая изгибается в простран-
стве определенным заданным образом*. Мы будем представлять эту кривую параметрически в виде C(t).
Например, винтовая линия (см. раздел «Применение параметрического задания кривой»), стереоско-
пически показанная на рис. 6.36, а, имеет следующее параметрическое представление:
C(t) == (cos(r), sin(r), bt), (6.И)
где b — некоторая константа.
Рис. 6.36. Стереорисунок спирали
Для формирования различных перетяжек трубы вычислим C(t) для множества значений параметра
(t0, ip...} и построим преобразованный полигон в каждой точке C(tt) в плоскости, перпендикулярной к
кривой, как показано на рис. 6.37. Это равносильно созданию локальной системы координат в каждой
выбранной точке вдоль хребта: локальная «ось 2» показывает направление вдоль кривой, а локальные
«оси хи у» направлены перпендикулярно к оси г (и перпендикулярно друг другу). Полигон перетяжки
при этом располагается в локальной ху-плоскости. Все, что нам нужно, — это задать вершины каждой
перетяжки.
Удобнее всего предоставить самой кривой C(t) определять локальную систему координат. В широко
известном методе дифференциальной геометрии в каждой точке вдоль хребта создается базис (репер)
1 Язык моделирования VRML 2.0 включает в себя узел «экструзии», работающий аналогичным образом: разработчик может вы-
брать «хребет», вдоль которого размещаются полигоны, каждый со своим собственным преобразованием.
6.4. Экструзивные формы
381
Френе (Frenet frame) [Gray, 91]. При каждом интересующем нас значении t вычисляется касательный
к кривой вектор T(t). Затем вычисляются два вектора N(t.) и B(t), перпендикулярные к вектору T(t) и
друг к другу. Эти три вектора и образуют базис Френе, соответствующий значению
Рис. 6.37. Создание локальных систем координат вдоль хребтовой кривой
Когда базис Френе вычислен, нетрудно найти матрицу преобразования М, которая переводит поли-
гон основания трубки в его новую позицию и ориентацию в данном базисе. Эта матрица преобразова-
ния переводит мировую систему координат в новую систему. (Приводимые здесь рассуждения напо-
минают те, которые использовались в практическом упражнении 5.6.1 при преобразовании системы
координат камеры в мировую систему координат.) Матрица ЛГ должна переводить векторы i, j, к соот-
ветственно в векторы N(t ), B(t), Т(Л) и должна перемещать начало координат из мировой точки в точ-
ку хребта C(t). Поэтому матрица содержит столбцы, представляющие собой векторы N(t ), В(Г ), Т(?.) и
точку C(t), выраженные в однородных координатах: '
М. = (N(Q I B(t;) | Т(Г.) | ОД). (6.12)
Формирование базиса Френе
Базис Френе в каждой точке вдоль кривой зависит от того, как эта кривая изгибается и закручивается.
Этот базис выводится из соответствующих производных определяющей кривую функции C(t), так что
он легко может быть сформирован после вычисления этих производных.
В частности, если выражение для кривой C(t) является дифференцируемой функцией, то можно
взять ее производные и сформировать вектор С(г), касательный к кривой в каждой ее точке. Если ком-
поненты кривой С(Г) равны Cx(t), Cy(t), C2(t), то вектор производных C(r) = (CJ(r),C>(r),CI(z)). Вектор
С(г) указывает направление, куда «держит курс» кривая при каждом значении t; иными словами, в на-
правлении касательной к кривой. Единичный касательный вектор (unit tangent vector) в точке t получа-
ется путем нормирования вектора С(г), то есть приведения его к единичной длине. Например, единич-
ный касательный вектор для винтовой линии из уравнения (6.11) определяется формулой:
T(r) = -^=l=(-sin(r),cos(r),Z>). 1 (6.13)
Этот касательный орт для различных значений t показан на рис. 6.38, а.
Если мы векторпо умножим вектор из формулы (6.13) на любой неколлинеарный вектор, то мы долж-
ны получить вектор, перпендикулярный вектору Т(Г) и, следовательно, перпендикулярный хребту кри-
вой. (Почему?) Особенно удачным выбором является ускорение (acceleration), представляющее собой
вторую производную С(г). Сформируем векторное произведение С(г)хС(г), и поскольку именно оно
382
Глава 6. Моделирование поверхностей полигональными сетками
будет использоваться в качестве оси системы координат, нормируем его и получим «единичный вектор
бинормали» («unit binormal vector»):
B(0 =
|С(г)хС(г)|‘
(6.14)
Рис. 6.38. Касательные к спирали (а); показан базис Френе при различных значениях t вдоль спирали (5)
Затем с помощью нового векторного произведения получим вектор, перпендикулярный к векторам
T(t) и В(г):
N(t)-B(t)xT(t). (6.15)
Убедитесь сами, что эти три вектора являются взаимно перпендикулярными и имеют единичную
длину, поэтому они составляют локальный базис Френе для кривой C(t). Кроме того, проверьте, что
для винтовой линии базисные векторы задаются формулами:
В(/) =
1
y/l + b2
(b sin (z), —b cos (z), 1)
N(t) - (-cos(Z), -sin(t), 0).
(6.16)
Численное определение базиса Френе
Если формула кривой C(t) сложна, то вычисление ее последовательных производных в аналитической
форме (чтобы формулы для векторов T(Z), B(z) и N(z) могли быть «зашиты» в программу) может ока-
заться затруднительным. В качестве альтернативы возможна численная аппроксимация этих производ-
ных по формулам:
C(z + e)-C(z-e)
2e
C(z) = c(f-e)~2C(f) + c(f + £). (6Л7)
'' е2
Вычисление по этим формулам обычно дает приемлемые направления векторов T(t), B(t) и N(t),
хотя пользователю следует отдавать себе отчет в том, что численное дифференцирование — изначально
неустойчивый процесс [Burden, 37].
На рис. 6.39 показан результат «нанизывания» десятиугольника на винтовую линию с использо-
ванием базиса Френе. Винтовая линия была построена по 30 замерам (фиксированным значениям
6.4. Экструзивные формы
383
параметра), в каждом из замеров был построен базис Френе, после чего десятиугольник строился в но-
вом базисе.
Рис 6.39. Труба, нанизанная на винтовую линию
На рис. 6.40 представлены два других интересных примера, основанные на тороидальной спирали
(впервые мы встречались с ней в разделе «Применение параметрического задания кривой») [Gray, 91].
Ребра отдельных граней нарисованы для наглядности, чтобы было видно, как поворачивается труба по
мере своей протяженности. Рисование ребер ее сетки рассматривается в тематическом задании 6.7. Торо-
идальная спираль получается путем оборачивания линии вокруг тора. (Попробуйте вообразить не види-
мый на рисунке оборачиваемый тор.) Тороидальная спираль задается формулой:
C(t) - ((а + fecos(<jt))cos(p0, (а + fecos(<yt))sin(p0, csin(^r)) (6.18)
для определенных значений констант а, Ь, с, р, д. На рис. 6.40, а параметры pvtq равны соответствен-
но 2 и 5, а на рисунке 6.40, б они равны 1 и 7.
Рис. 6.40. Трубы на базе тороидальных спиралей
На рис. 6.41 показана «морская раковина», полученная «надеванием» на спираль трубы с возрастаю-
щим радиусом. Для этого матрица из равенства (6.12) была умножена на матрицу масштабирования.
м' = м 'g(t) ООО' 0 g(Z) 0 0 0 0 10 0 0 0 1 k 7
Масштабные множители в матрице зависят от t. Здесь принято g(t) = t. Можно также добавить к
матрице поворот, и тогда труба будет закручиваться еще сильнее, если смотреть вдоль ее хребта.
384
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.41. «Морская раковина»
Одна из сложностей, связанных с использованием базисов Френе для прохождения кривых, заключа-
ется в том, что локальный базис иногда закручивается так, что на поверхности появляются нежелатель-
ные «узелки». В последних исследованиях, таких как работа Вонга [Wang, 206], найдены альтернативы
базису Френе, которые создают менее закручивающиеся и, следовательно, более изящные поверхности.
Практические упражнения
6.4.4. Что такое N(t)? 2
Покажите, что вектор N(t) параллелен вектору С (?) - (с(г) • С (z))c(z)/|c(z)|2 и поэтому указывает в
направлении ускорения, если скорость и ускорение в точке t перпендикулярны.
6.4.5. Базис для винтовой линии
Рассмотрим круговую спираль, упоминавшуюся в тексте. Докажите правильность формул для единич-
ных векторов касательной, нормали и бинормали. Покажите также, что эти векторы имеют единичную
длину и взаимно перпендикулярны. Мысленно представьте себе, как ориентируется локальная система
координат по мере продвижения вдоль кривой.
а б
Рис. 6.42. Гексагон, нанизанный на эллипс и образующий эллиптический тор (а);
гептагон (7-угольник), нанизанный на фигуру Лиссажу (б)
На рис. 6.42 приведено еще два примера. На рис. 6.42, а показан гексагон, скользящий вдоль эллип-
тического хребта и образующий своего рода эллиптический тор, а на рис. 6.42, б — составленная из ча-
стей обернутая семиугольником фигура Лиссажу (Lissajous), которая описывается формулой
С(0 = (rcos(Mt + 0), 0, rsin(№)), (6.19)
где М - 2, N = 3, ф = 0.
В тематическом задании 6.5 рассматриваются дополнительные подробности построения сеток, мо-
делирующих трубки на основе параметрически заданной кривой.
6.4. Экструзивные формы
385
6.4.5. «Дискретно» заметаемые поверхности вращения
Трубки, представленные в предыдущем разделе, для задания новой системы координат в каждой точке
хребта используют аффинные преобразования. Если же мы применим в качестве аффинных преобра-
зований чистые вращения и поместим все точки хребта в начало координат, то мы получим обширное
семейство многогранных форм. На рис. 6.43 приведен пример, в котором полигон основания — теперь мы
будем называть его профилем (profile) — имеет начальное положение в трех единицах по оси х и затем
посредством последовательных шагов поворачивается вокруг оси у, так что получается аппроксимация
(приближение) тора. Такая операция эквивалентна круговой развертке с заметанием (circularly
sweeping) формы вокруг оси, а результирующую форму часто называют поверхностью вращения
(surface of revolution). Стандартные поверхности вращения рассматриваются в разделе «Каркасные ап-
проксимации гладких объектов»; здесь же мы просто формируем их дискретное приближение, посколь-
ку развертка осуществляется конечными шагами.
Рис. 6.43. Дискретные шаги заметания с вращением
Рис. 6.44. Аппроксимация бокала для мартини с помощью дискретной развертки с заметанием ломаной линии:
а} профиль; 6} заметаемая поверхность
Рисунок 6.44 показывает пример создания изображения бокала для мартини. Профиль здесь яв-
ляется не замкнутым полигоном, а простой, ломаной с вершинами Р} - (х? y.f 0). Если такую ломаную
13 Ф. Хилл
386
Глава 6. Моделирование поверхностей полигональными сетками
поместить под К равноотстоящих углами относительно оси у, то преобразования будут описываться
матрицами:
'005(6,) 0 sin (О, ) О'
,, 0 10 0
М, = , . , . >
-sin(0,) 0 cos(0,) 0
0 0 0 1
к 7
где угол (Э - 2ni/K, i = 0,1,..., К - 1. Отметим, что здесь отсутствует перемещение. Данное преобразова-
ние достаточно просто для того, чтобы мы смогли непосредственно выписать координаты вершин. По-
ворот устанавливает точки i-й «перетяжки» ломаной в виде
(x;cos(6(), у., x;sin(0;.)). (6.20)
Построение сеток, моделирующих поверхности вращения, будет рассматриваться позднее, в тема-
тическом задании 6.6.
6.5. Каркасные аппроксимации гладких объектов
До сих пор мы строили сетки для отображения полиэдров, в которых каждая форма представляет со-
бой множество плоских полигональных граней. Такие сетки в основном являются «интенсивными по
данным» («data intensive»), то есть определяются списками вершин для каждой отдельной грани. Те-
перь же мы хотим строить такие сетки, которые будут аппроксимировать гладкие поверхности, подоб-
ные сфере или тору. Такие формы чаще задаются формулами, а не набором данных. Кроме того, мы
хотим сделать так, чтобы используемые нами сетки можно было плавно закрашивать. Даже в тех случа-
ях, когда эти сетки представляют собой, как и прежде, множество плоских граней, соответствующий
алгоритм (закрашивание Гуро — Gouraud shading) рисует их с плавными градациями цветов, причем
отдельные грани вообще не видны (вспомните рис. 6.1.) Все, что нужно для этого, — это правильно оп-
ределить нормальный вектор в каждой вершине каждой грани. В частности, мы вычисляем нормаль-
ный вектор основной гладкой поверхности. Алгоритм закрашивания Гуро рассматривается в главе 8.
Основной подход для каждого типа поверхности заключается в том, чтобы «полигонизировать»
(«polygonalize») ее, или разбить на ячейки (tesselate), представив ее в виде множества плоских граней.
Если эти грани достаточно малы и переход от одной грани к другой достаточно плавный, то получен-
ная сетка даст хорошее приближение исходной поверхности. Вершины этих граней определяются вы-
числением значений параметрического представления поверхности в дискретных точках. Сетка созда-
ется путем обычного построения списков вершин и нормалей, за исключением того, что вершины здесь
вычисляются по формулам. То же касается и нормалей в вершинах: они вычисляются по формулам
нормали к поверхности в дискретных точках.
6.5.1. Представления поверхностей
Сначала вспомним, что в разделе «Обзор: квадратичный и кубический твининг и кривые Безье» мы
рассматривали плоский лоскут (patch), заданный в параметрической форме:
Р(и, v) = С + au + bz>, (6.21)
где С — точка, а а и b — векторы. Диапазон значений для параметров и и v обычно ограничен отрезком
[0, 1], и в этом случае лоскут является ЗО-параллелограммом с угловыми вершинами С, С + а, С + Ь,
С + а + b (см. рис. 4.23).
6.5. Каркасные аппроксимации гладких объектов
387
Распространим теперь наши интересы на нелинейные формы, чтобы выразить поверхности более общего
вида. Введем три функции Х( ), У( ), Z{ ), тогда поверхность в точечной форме будет иметь представление:
Р(и, v) = (X(w, ц), У(а, V), Z(u,»)), • (6.22)
где и и v имеют свои диапазоны изменения. Различные поверхности характеризуются различными фун-
кциями X, У, Z. Будем считать, что поверхность находится «в точке» (Х(0, 0), У(0, 0), Z(0,0)), когда и = 0,
v = 0, и в точке (Х(1,0), У(1,0), Z(l, 0)), когда и = 1, v = 0 и т. д. Помните, что для представления поверхно-
сти требуется два параметра, в то время как для трехмерной кривой — только один. Изменение парамет-
ра и при постоянном значении v образует кривую, называемую ^-контуром (^-contour). А изменение v
при постоянном значении и Ьбразует и-контур.
Неявная форма поверхности
Хотя мы в основном имели дело с параметрическими представлениями различных поверхностей, по-
лезно ознакомиться и с другим способом описания поверхностей: через ее неявную форму (implicit
form). Напомним из раздела «Применение параметрического задания кривой», что двумерная кривая
имеет неявную форму F(x,y), которая должна равняться нулю тогда и только тогда, когда точки (х, у)
лежат на этой кривой. Для трехмерных поверхностей существует аналогичная функция F(x,y, z), кото-
рая равна нулю тогда и только тогда, когда точка (х, у, z) находится на этой поверхности. Таким обра-
зом, поверхность выражается неявным уравнением (implicit equation):
Р(х,у,г) = 0, (6.23)
которое удовлетворяется для всех точек данной поверхности и только для них. Это уравнение указывает,
как должны быть связаны величины х, г/, z для точки (х, y.z'), принадлежащей поверхности. Вспомним,
например (из главы 4), что плоскость, проходящая через точку В и имеющая нормальный вектор п, опи-
сывается уравнением пхх + пуу + nzz- D (где D = п • В), откуда неявная форма этой плоскости имеет вид:
F(x, у, z) = пхх + ПуУ + nz - D. Иногда удобнее считать F функцией от точки Р, а не от трех переменных х,
у, z; в этом случае уравнение F(Р) = 0 описывает все точки, лежащие на данной поверхности. Например, для
описываемой здесь плоскости можно определить функцию F(P) = п • (Р - В) и утверждать, что точка Р
лежит в данной плоскости тогда и только тогда, когда F(P) = п • (Р - В) равно нулю. Если мы хотим рабо-
тать с координатными фреймами (вспомните раздел «Отображение ключевых геометрических объек-
тов»), то точка Р будет представляться четверкой Р = (x,y,z,l) , а неявная форма для плоскости будет
выглядеть еще проще, а именно F(P) = п-Р, где величина n = (nx,ny,nz, - содержит и нормальный
вектор, и величину -D.
Не всегда просто найти функцию F(x, у, z), или F(P) из заданной параметрической формы. (И об-
ратно, по заданной функции Г(х, у, г) не всегда можно определить параметрическую форму.) Однако
если известны и параметрическая, и неявная формы, то легко определить, описывают ли они одну и ту
же поверхность. Просто подставьте в уравнение F(x, у, z) вместо х, у, z соответственно Х(и, v), Y(u, v),
Z(u, v) и проверьте, равняется ли Г нулю для всех интересующих нас значений параметров и и V.
Для некоторых поверхностей (например, для сферы), заключающих в себе часть пространства, важно
определить внутреннюю и внешнюю области. Другие поверхности, например плоскость, несомненно,
тоже разделяют трехмерное пространство на две области, однако вопрос о том, какое полупространство
является внешним, а какое — внутренним, зависит от контекста приложения. Кроме того, существует
много поверхностей, таких как бантик из плоской конфеты, когда мало смысла определять внешнюю и
внутреннюю области.
В тех случаях, когда имеет смысл выяснять внутреннюю и внешнюю стороны поверхности, неявная
форма этой поверхности F(x, у, г) носит также название «внутренне-внешней» функции (inside-outside
function). Говорят, что точка (х, у, z) находится
внутри поверхности, если F(x, у, z) < 0,
на поверхности, если F(x, у, z) = 0, (6.24)
вне поверхности, если F(x, у, z) > 0.
388
Глава 6. Моделирование поверхностей полигональными сетками
Данная совокупность условий обеспечивает быструю и простую проверку расположения заданной
точки (%', уг') относительно поверхности: нужно просто вычислить Fix', у', г') и проверить, является
эта величина положительной, отрицательной или равна нулю. Этот тест полезен в алгоритмах удале-
ния невидимых линий и невидимых поверхностей (см. главу 13); в главе 14 он используется в алгорит-
мах трассировки луча. В последнее время было предпринято множество попыток визуализации по-
верхностей непосредственно из их неявной формы (см. [Bloomenthal, 33]).
6.5.2. Нормальный вектор к поверхности
Как уже упоминалось ранее, нам требуется определять направление вектора нормали к поверхности в
любой точке. В этом разделе предлагаются способы для этого: один — исходя из параметрического урав-
нения поверхности и другой — исходя из ее неявной формы. При дальнейшем исследовании каждого
типа задания поверхности мы выведем соответствующие выражения для ее нормального вектора в лю-
бой точке.
Чтобы определить направление, нормальное к поверхности в лежащей на ней точке Р(ы0, о0), нужно
рассмотреть малую часть поверхности вокруг этой точки. Если эта область достаточно мала и поверх-
ность в окрестности точки изменяется «плавно», то данная область будет почти плоской. Следователь-
но, она локально ведет себя как маленький плоский фрагмент, у которого имеется вполне определенное
нормальное направление. На рис. 6.45 показана часть поверхности с нарисованными в различных точ-
ках нормальными векторами. Видно, что направление нормального вектора в различных точках повер-
хности также различно.
Обозначим n(w, и) нормаль в точке при данных значениях параметров (и, v). Рассмотрим теперь, как
ее можно вычислить.
Нормальный вектор к поверхности, заданной параметрически
Как и следовало ожидать, вектор п(ы0, о0) имеет форму векторного произведения двух векторов, лежа-
щих на малой плоской части в окрестности точки (ы0, v0). Будучи векторным произведением, он заве-
домо перпендикулярен к обоим векторам. Эти два вектора на плоскости (на рис. 6.45 они обозначены
как tu и tc) являются касательными к ней векторами. В дальнейшем мы увидим, что они связаны с част-
ными производными вектора р(ы, v) (это вектор от начала координат до точки Р(и, v) на поверхности)1,
вычисленными в искомой точке [Thomas, 194]. Следовательно, выражение для нормального вектора
имеет вид:
/ ч f Эр
n(«o.vo) = ЧТ
I ди
(6.25)
1 Поскольку вектор р(и, v) является разностью Р(и, v) - (0,0,0), то частная производная от р() будет такая же, как от Р().
6.5. Каркасные аппроксимации гладких объектов
389
где вертикальная черта означает, что производные* вычислены при и = и0 и v = v0. Полученный таким
способом вектор n(w(), vg) не является единичным вектором автоматически, однако при желании его
можно нормировать.
Пример 6.5.1. Применимо ли уравнение (6.25) к случаю плоскости?
Рассмотрим плоскость, заданную параметрически: Р(и, v) = С + au + by. Частная производная Р по и
равна вектору а, а по v — вектору Ь. Тогда, в соответствии с равенством (6.25), n(w, v) = а х Ь; нетрудно
видеть, что этот результат правильный.
Вообще говоря, частные производные от вектора р(н, v) существуют й тех случаях, когда поверхность
является «достаточно гладкой». Большинство интересующих нас при моделировании сцен поверхнос-
тей обладают необходимой гладкостью и описываются достаточно простыми математическими выра-
жениями, поэтому нахождение необходимых частных производных не составляет труда. Поскольку
р(н, v) = Х(и, v)i + У(н, r>)j + Z(u, 0k, то частная производная вектора р является вектором, компоненты
которого суть частные производные его компонентов:
Эр(и,г>) fdX(u,v) dY(u,v) dZ(u,vY
ди ди ’ ди ди
к >
В дальнейшем мы будем применять эти формулы ко всем типам исследуемых поверхностей.
(6.26)
Нормальный вектор к поверхности, заданной неявно
Для поверхности, заданной в неявной форме, F(x, у, z) = 0, применяется другое выражение. Нормальное
направление в точке (х, у, z) поверхности может быть найдено с помощью градиента (gradient) от F,
который обозначается VF и определяется следующим образом [Thomas, 53]:
п(хо>Л.го) = Мото
'dF_ dF dF'
дх’ ду’ dz
(6.27)
х=хо > < 2~2о
где каждая частная производная вычислена в нужной точке (х0, у0, z0). Если точка (х0, у0, z0) исследу-
емой поверхности соответствует точке Р(и0, v0) ее параметрической формы, то вектор n(x0, ya, za) имеет
то же направление, что и вектор п(н0, v0) в уравнении (6.25), однако их длины могут различаться. Одна-
ко при желании его также можно нормировать.
Пример 6.5.2. Снова плоскость
Рассмотрим еще раз плоскость с нормалью п, проходящей через точку А. Пусть уравнение этой плоско-
сти задано неявно выражением F(x, y,z~) = n- ((г, у, z) - А) = 0 или в виде: пхх + пуу + nz - п А = 0.
Эта плоскость, как и следовало ожидать, имеет градиент VF = п.
Отметим, что в формуле для нормального вектора, использующей градиент, нормаль рассматрива-
ется как функция от х, у, z, а не от и, v. Иногда нам известны для поверхности сразу ее внешне-внутрен-
няя функция F(x,y, z) и параметрическая форма р(и, v) = Х(и, v)i + Y(u, v)j + Z(u, 0k. В таких случаях
параметрическую форму нормального вектора n(w, v) в точке (w, v) проще всего найти в два этапа:
1. Нормаль в точке (г, у, г) выразить из уравнения (6.27) через х, у, г.
2. Подставить вместо х, у, г известные функции Х(и, v), Y(u, v), Z(u, v).
Этот способ будет проиллюстрирован в некоторых из последующих примеров.
6.5.3. Влияние аффинного преобразования
Иногда нам придется работать с неявной и параметрической формами задания поверхности после того,
как эта поверхность подверглась аффинному преобразованию. Нам также понадобится узнать, какое
воздействие аффинное преобразование оказывает на нормаль.
Пусть это преобразование представлено в виде матрицы М размерностью четыре на четыре, а исход-
ная поверхность задана в неявной форме (в терминах точек в однородных координатах) F (Р) и в парамет-
390
Глава 6. Моделирование поверхностей полигональными сетками
рической форме P(u,v) = (X (u,v),Y(u,v),Z(u,v)X) . Тогда параметрическая форма преобразованной по-
верхности, очевидно, примет вид MP(u,v). (Почему?) Также нетрудно показать (см. ниже приведен-
ные упражнения), что неявная форма преобразованной поверхности имеет вид:
Далее, если исходная поверхность имеет нормальный вектор n(w, v), то преобразованная поверхность
будет иметь нормаль, равную М~тп(и, v).
Предположим для примера, что мы преобразуем описанную выше плоскость, заданную уравнением
F(p\ = n-P, где n-^n1,ny,n1,-D>j. Преобразованная плоскость будет иметь следующую неявную фор-
му: F'(p) = n‘(M~lP\. Последнее выражение можно записать (см. упражнения ниже) в виде ^М~тп)-Р,
так что нормальный вектор преобразованной плоскости включает в себя обратную транспонирован-
ную матрицу, что согласуется с формулой для нормали к поверхности общего вида.
Практические упражнения
6.5.1. Неявная форма преобразованной поверхности
Предположим, что все точки поверхности удовлетворяют уравнению F(P) = 0, а матрица М преобразу-
ет Р в Q, то есть Q = МР. Докажите, что любая точка Q преобразованной поверхности соответствует
точке M~'Q и что все такие точки удовлетворяют уравнению F\M~'Q^ - 0. Далее покажите, что из это-
го утверждения следует, что неявная форма преобразованной поверхности имеет вид F(£>) = f(m~'Q) .
6.5.2. Как изменяются нормальные векторы?
Пусть вектор п = (пх,пу, л2,0) нормален к поверхности в точке Р и пусть вектор v — любой вектор, каса-
тельный к данной поверхности в точке Р. Тогда вектор п должен быть перпендикулярен к вектору v,
и можно записать: п • v = 0.
О Покажите, что это скалярное произведение можно записать как произведение матриц nrv = 0.
(См. приложение Б.)
О Покажите, что скалярное произведение п • v по-прежнему остается равным нулю при добавле-
нии произведения матриц М~*М; иначе говоря, докажите, что птМ~*Му = 0.
О Покажите, что выражение птМ~1Му - 0 можно записать в форме: (М~гп) (Му) - 0, откуда следует,
что вектор М~тп перпендикулярен вектору Му.
Теперь, поскольку касательный вектор у преобразуется в Му, который является касательным к
преобразованной поверхности, докажите, что вектор М~тп должен быть нормален к преобразо-
ванной поверхности, что и требуется доказать.
О Нормаль к поверхности задается также в виде градиента неявной формы, поэтому нормаль к преоб-
разованной поверхности в точке Р должна быть градиентом от Р(ЛГ‘Р). Докажите с помощью последо-
вательных вычислений, что градиент последней функции равен М~т, умноженной на градиент от F( ).
6.5.3. Плоскость, касательная к преобразованной поверхности
В процессе выяснения того, как преобразуются нормальные векторы, мы можем также выяснить, каким
образом плоскость, касательная к поверхности, преобразуется в касательную плоскость к преобразо-
ванной поверхности. Пусть касательная плоскость к исходной поверхности в точке Р имеет параметри-
ческое представление Р + аи + Ьг>, где а и Ь — два вектора, лежащих в плоскости.
О Докажите, что параметрическое представление преобразованной плоскости имеет вид МР + Маи +
+ Mbv и что эта плоскость имеет нормаль п' - (Ма) х (МЬ).
О Докажите со ссылкой на приложение Б, что имеет место тождество:
(Ма) х (АЛ») - (detAf) М~т(а х Ь).
Это равенство связывает векторное произведение преобразованных векторов с векторным про-
изведением самих этих векторов.
О Докажите, что из этого тождества следует, что вектор п' параллелен вектору М~тп.
6.5. Каркасные аппроксимации гладких объектов
391
6.5.4. Три «базовые» формы: сфера, цилиндр и конус
В этом разделе мы начнем с трех классических объектов — «базовых» («generic») версий сферы, цилин-
дра и конуса. Для каждого из этих объектов рассматриваются его неявная и параметрическая форма,
а также способы создания сеток для их аппроксимации. Мы выведем формулы для определения нормаль-
ного направления в каждой точке данного объекта. Отметим, что в главе 5 для рисования таких форм
уже использовались функции OpenGL. Однако добавление своих собственных инструментов имеет два
преимущества: во-первых, мы достигаем значительно более строгого контроля за деталями структуры
создаваемой формы, а во-вторых, мы фактически получаем объект в виде сетки и можем применять к
нему методы класса Mesh.
Базовая сфера
Назовем сферу единичного радиуса с центром в начале координат «базовой сферой» (см. рис. 6.46, а).
Она является основой для всех остальных используемых нами сфероподобных форм. Неявная форма
для такой сферы хорошо известна:
F(x,y, z) = х2 + у2 + z2 - 1. (6.28)
При альтернативном способе записи F(P) мы получаем более элегантное выражение: F(P) = |Р|2 - 1.
(Как изменятся эти формулы, если радиус сферы будет равен /??)
Северный
полюс
а б в
Рис. 6.46. Базовая сфера (<?); параметрическая форма (б); параллели и меридианы (в)
Параметрическое описание этой сферы непосредственно вытекает из стандартного описания точки
в сферических координатах (см. приложение Б.) Пусть величина и соответствует долготе (азимуту),
a v — широте. Тогда произвольная точка на сфере Р = (х, у, z) выражается в сферических координатах как
(cos (г?) cos (и), cos (г?) sin(w), sin (г?)) (см. рис. 6.46, б}. Для того чтобы охватить все точки на сфере, и долж-
но изменяться в диапазоне (0,2п), a v — в диапазоне (-п/2, п/2)1. Поэтому параметрическая форма сфе-
ры имеет вид:
Р(и, v) = (cos(a) cos(w), cos(a) sin(w), sin(a))- (6.29)
Легко проверить, что эта форма согласуется с неявной: просто подставим члены уравнения (6.29)
в соответствующие члены уравнения (6.28) и увидим, что для любых значений ии v равенство нулю
сохраняется.
Какую параметрическую форму имеет сфера с радиусом R и центром в точке (а, Ь, с)?
Из географии известно, что определенные контуры на сфере имеют общепринятые названия: м-кон-
туры называются меридианами (meridians), а ^-контуры — параллелями (parallels), как показано на
рис. 6.46, в. (Отметим, что из-за классического определения сферических координат, параллелей и
1 Чтобы охватить все точки на сфере, промежуток изменения и должен быть полуоткрытым: [0, 2л), а промежуток изменения v —
замкнутым: [-л/2, л/2]. — Примеч. пер.
392
Глава 6. Моделирование поверхностей полигональными сетками
меридианов сфера вынуждена лежать на боку. Это связано с привычкой рисовать трехмерные фигуры
с осью у, указывающей вверх.)
Для данной фигуры возможны различные параметрические представления. Альтернативная пара-
метрическая форма для сферы исследуется в упражнениях в конце раздела.
Что же представляет собой нормальное направление n(w, v) к поверхности сферы в точке, определяе-
мой парой параметров (и, V)? Интуитивно можно предположить, что данный нормальный вектор всегда
направлен «по радиусу наружу», так что он должен быть параллелен радиус-вектору из начала координат
в данную точку. Это подтверждается и уравнением (6.28): градиент равен 2(х, у, z), то есть пропорциона-
лен Р. Применяя параметрическую форму, получим из уравнения (6.29): n(w, v) = -cos(v) p(w, v), отку-
да следует, что вектор n(w, v), как и ожидалось, параллелен p(w, и). Масштабный множитель, равный
-cos(a), исчезнет при нормировании вектора п. Мы должны удостовериться, что в качестве нормали нужно
использовать вектор p(w, v), а не -p(w, v), чтобы этот вектор действительно указывал по радиусу наружу.
Базовый цилиндр
Назовем «базовым» такой цилиндр, у которого ось совпадает с осью z, поперечное сечение является
окружностью единичного радиуса, а сам цилиндр простирается вдоль оси z от 0 до 1, как показано на
рис. 6.47, а. Удобно рассматривать такой цилиндр в качестве представителя большого семейства кони-
ческих цилиндров (tapered cylinders), как это уже делалось в главе 5. На рис. 6.47, б показан «базовый»
конический цилиндр, «меньший радиус» которого составляет s при z - 1.
а б
Рис. 6.47. Базовый цилиндр и конический цилиндр
Базовый цилиндр является частным случаем конического цилиндра при $ = 1. Далее, базовый конус,
который мы будем изучать следующим, также является частным случаем конического цилиндра при
$ - 0. Мы выведем формулы для конического цилиндра при произвольном значении параметра s, а по-
ложив $ равным соответственно 1 или 0, из них можно будет получить формулы для базовых цилиндра
и конуса.
Если рассматривать конический цилиндр как тонкую пустотелую «оболочку», то его боковая поверх-
ность, или стенка (wall), будет задаваться неявной формой:
F(x,у, z) -х2 + у2 - (1 + (s - l)z)2 при 0 < z < 1 (6.30)
и параметрической формой:
Р(и, v) - ((1 + (s - 1)г>) cos(w), (1 + (s - 1)г>) sin(w), v) (6.31)
для соответствующих диапазонов изменения и и v. (Каких именно?) Какой вид примут эти выражения
для базового цилиндра при s - 1?
Если нужно представить конический цилиндр как монолитный объект, на его концы добавляют два
круглых диска — основание (base) и крышку (cap).
Крышка представляет собой круг на плоскости z - 1, описываемый неравенством х2 + у2 < s2, или в
параметрической форме: P(w, v) - (v cos(w), v sin(w), 1) для v из диапазона [0, s], (Каково параметриче-
ское представление основания?)
6.5. Каркасные аппроксимации гладких объектов 393
Нормальный вектор к боковой поверхности конического цилиндра может быть найден из уравне-
ния (6.27) (обязательно проверьте это) и равен
п(х, у, z) = (х, у, - (s - 1) (1 + (s - l)z)),
(6.32)
или, в параметрической форме: n(w, v) - (cos(w), sin(w), 1 - s). Нормаль для базового цилиндра равна
просто (cos(w), sin(w), 0). Такое представление совпадает с интуитивным: эта нормаль направлена по
радиусу в сторону от оси цилиндра. В случае конического цилиндра она также направлена по радиусу,
однако сдвинута на постоянный z-компонент. (Чему равны нормали к крышке и основанию?)
Базовый конус
Определим «базовый» конус как конус, у которого ось совпадает с осью z, максимальный радиус круго-
вого поперечного сечения равен 1, а располагается он вдоль оси z от 0 до 1; такой конус изображен на
рис. 6.48. Базовый конус фактически является коническим цилиндром с меньшим радиусом $ = 0. Тогда
неявная форма его стенки имеет вид:
Г(х, у, z) = х2 + у2 - (1 - г)2 = 0 для 0 < z < 1,
(6.33)
а параметрическая: Р(и, v) = ((1 - v) cos(w), (1 - v) sin(w), v) для и в диапазоне [0, 2л] и г в диапазо-
не [0,1]. Снова используя результаты для конического цилиндра, получим выражение для нормально-
го вектора к стенке конуса: (х, у, 1 - z). Как это выражение будет выглядеть в параметрической форме?
Рис. 6.48. Базовый конус
Для удобства ссылок в табл 6.7 приведены нормальные векторы ко всем рассмотренным базовым
поверхностям.
Таблица 6.7. Нормальные векторы к базовым поверхностям
Поверхность
n(u, у) в точке p(u, v) F(x, у, z)
Сфера р(г/, к)
Конический цилиндр (cos(rz), sin(r/), 1-s)
Цилиндр (cos(r/), sin(r/), 0)
Конус (COS(tf), sin(tf), 1)
(х, у, Z)
(х, у, -(S- 1) (1 + (s- l)z))
(X, у, 0)
(X.K1-Z)
Практические упражнения
6.5.4. Альтернативное представление для базовой сферы
Можно придать параметрам uhv другой геометрический смысл и получить для сферы другую пара-
метрическую форму. Пусть параметр и по-прежнему означает долготу, а v теперь означает высоту точки
над плоскостью ху. Все точки на высоте v лежат на окружности радиуса VI - V2, поэтому альтернативная
параметрическая форма имеет вид:
Р2 (и, v) = f л/1-й2 cos (и ), л/1-^2 sin (и), v
(6.34)
для и изменяется в промежутке [0, 2л], a v в промежутке [-1, 1]. Докажите, что поверхность Р2 находит-
ся на единичном расстоянии от начала координат для всех входящих unv.
394
Глава 6. Моделирование поверхностей полигональными сетками
6.5.5. Определение вида поверхности
Пусть А — фиксированная точка с радиус-вектором а, а Р — произвольная точка с радиус-вектором р.
Опишите на словах и нарисуйте поверхность, определенную уравнением:
О р • а = 0;
□ р • а = |а|;
О |рха|-|а|;
О р • а - р • р;
О р • а = |а| |р|/2.
6.5.6. Нахождение нормального вектора к базовому цилиндру и конусу
Выведите формулу нормального вектора для базового конического цилиндра и базового конуса двумя
способами:
О С использованием параметрического представления.
О С использованием неявной формы и последующим представлением результата в параметричес-
кой форме. '
6.5.7. Преобразованные сферы
Найдите неявную форму для базовой сферы, которая была масштабирована вдоль оси х с множите-
лем 2 и вдоль оси у с множителем 3 и затем повернута на 30° вокруг оси z.
6.5.5. Формирование полигональной сетки для криволинейной
поверхности
Исследуем теперь, как создать каркасный объект, аппроксимирующий гладкую поверхность, такую как сфе-
ра, цилиндр или конус. Процесс создания такой сетки называется «полигонализацией» («polygonalization»)
или, более строго, разбиением на ячейки (tesselation); он означает замену поверхности совокупностью
треугольников или четырехугольников. Вершины этих полигонов лежат на самой поверхности и со-
единяются прямыми ребрами (которые, как правило, не лежат на данной поверхности). Затем выбира-
ется множество значений а и о и в этих значениях вычисляется параметрическая форма поверхности
(«берутся замеры» формы при выбранных значениях параметров), в результате чего получается сово-
купность вершин. Затем эти вершины помещаются в список вершин. После этого создается список гра-
ней: каждая грань описывается тремя или четырьмя индексами, указывающими на соответствующие
вершины в списке вершин. С каждой вершиной грани связывается нормальный вектор к поверхности.
Этот нормальный вектор является в каждой вершине нормалью к истинной основной поверхности.
(Отметим, что эта нормаль отличается от той, которая использовалась при отображении полиэдров с
плоскими гранями: там вершина каждой грани ассоциировалась с нормалью к этой грани.)
На рис. 6.49 показано, как эта процедура работает для базовой сферы. Мы хотим разрезать сферу по
линиям долготы и широты. Используя термины OpenGL — «дольки» («slices») и «ломтиких» («stacks»)
(см. раздел «Рисование элементарных форм, поддерживаемых OpenGL»), — мы разрезаем сферу на
nSlice долек по экватору и nStacks ломтиков от южного полюса к северному. В примере на рисунке
12 долек и 8 ломтиков. Чем больше значения nSlice и nStacks, тем лучше сетка аппроксимирует истин-
ную сферу.
Для получения долек нам необходимо nSlice значений и в диапазоне от 0 до 2л. Обычно эти значе-
ния выбираются с постоянным шагом: ut - 2ni/nSl ice, i - 0,1 nSl ice - 1. Что же касается слоев, то мы
выбираем половину из них над экватором, а половину — под ним. Верхний и нижний слои будут состо-
ять из треугольников, а все остальные — из четырехугольников. Это означает, что мы должны задать
(nStacks + 1) широты: vt = п/2 - лу/nStacks, где у = 0,1,..., nStacks.
Теперь можно создавать список вершин. На рисунке показано, как можно нумеровать вершины (по-
рядок нумерации — это дело удобства): северный полюс помещаем в pt[O], нижние точки верхних сло-
ев — в следующие 12 вершин и т. д. При 12 дольках и 8 ломтиках всего будет 98 точек. (Почему?)
6.5. Каркасные аппроксимации гладких объектов
395
Рис. 6.49. Каркасная аппроксимация базовой сферы (а); нумерация вершин (б)
Столь же легко может быть создан список нормалей: в norm[k] будет храниться нормаль к сфере в
вершине pt [к]. Элемент погш[к] вычисляется посредством подстановки в параметрическую форму век-
тора п(и, и) тех значений (и, и), которые были использованы для точек. Для случая сферы такое вычис-
ление особенно просто, поскольку norm[k] — это то же самое, что pt [к].
Список граней будет содержать 96 граней, из которых 24 являются треугольниками. Можно помес-
тить верхние треугольники в первые 12 граней, 12 четырехугольников следующего слоя в следующие
12 граней и т. д. Первые несколько граней будут содержать следующие данные:
Число вершин: 3
Индексы вершин: 012
Индексы нормалей: 012
3 3
023 034
023 034
Отметим, что normindex всегда совпадает с vert Index для всех сеток, которые стремятся изображать
гладкие формы, поэтому структура данных содержит избыточную информацию. (По этой причине
можно было бы использовать для таких сеток более подходящую структуру данных. Какой она могла
бы быть?) Такой способ «полигонизации» для сферы прост, однако для более сложных форм он может
быть весьма хитроумным. (Дальнейшие обсуждения этой темы можно найти в литературе.)
В конечном счете нам нужен метод типа makeSurfaceMeshO, который генерирует такие сетки для за-
данной поверхности Р(и, v). Реализация функции, выполняющей такую работу, будет рассматриваться
в тематическом задании 6.13.
Отметим, что некоторые графические пакеты содержат подпрограммы, которые в высшей степени
оптимизированы, если они работают с треугольниками. Для того чтобы использовать такие подпро-
граммы, можно «полигонизировать» сферу в совокупность треугольников, разбив каждый четырехуголь-
ник на два треугольника.
Проще всего было бы использовать те же вершины, что и раньше, но изменить список граней, заме-
няя каждый четырехугольник двумя треугольниками. Например, грань с вершинами 2, 3, 15,14 можно
было бы разбить на два треугольника с вершинами 2, 3, 15 и 2, 15,14.
Сфера является частным случаем поверхности вращения, которые мы рассматриваем в разделе «По-
верхности вращения» Конический цилиндр также является поверхностью вращения. Нетрудно разра-
ботать каркасную модель для конического цилиндра. На рис. 6.50 показан конический цилиндр, апп-
роксимированный при nSlices = 10 и nStacks = 1. В качестве крышки и основания использован октагон
(восьмиугольник). Если вы предпочитаете использовать в сетке только треугольники, то стенки, крыш-
ка и основание должны быть разбиты на треугольники. (Как?).
396 Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.50. Каркасная аппроксимация конического цилиндра
Практические упражнения
6.5.8. Сетка для заданной сферы
Выбрав удобную схему нумерации, составьте списки вершин, нормалей и граней для сферы при
nSlices = 6 и nStacks = 4.
6.5.9. Ограничение сетки треугольными гранями
Откорректируйте все списки из предыдущего упражнения для случая, когда все грани являются тре-
угольниками.
6.5.10. Сетка для цилиндра и конуса
Напишите списки вершин, нормалей и граней для базового цилиндра при nSlices = 4 и nStacks - 2.
6.5.6. Линейчатые поверхности
В этом разделе мы продолжаем изучение криволинейных поверхностей и переходим к семейству ли-
нейчатых поверхностей (ruled surfaces). Это семейство описывается просто, однако оно содержит боль-
шое разнообразие полезных и интересных форм. Мы исследуем, как описывать такие формы, «полиго-
низировать» их и вычислять нормальный вектор к ним в любой точке.
Линейчатые поверхности (их также называют поднятыми, или навесными поверхностями — lofted
surfaces) образуются посредством перемещения прямой линии по определенной траектории. Они со-
стоят из множества прямых линий в соответствии с приведенным ниже определением.
Определение. Поверхность называется линейчатой, если через каждую ее точку проходит хотя бы
одна прямая, целиком лежащая на этой поверхности.
Поскольку в основе линейчатых поверхностей лежит семейство прямых линий, неудивительно, что
в ее параметрическом представлении содержится что-то похожее на параметрическое представление
прямой: P(v) = (1 - v)PQ+ vP{, где PQ и Р, — точки, a v — единственный параметр. Однако для линейчатых
поверхностей точки Ро и Р, становятся функциями второго параметра и: Ро становится P0(w) и Р( становится
P,(w). Тогда параметрическая форма исследуемых нами линейчатых поверхностей будет иметь вид:
Р(и, V) “ (1 - u)P0(w) + uP((w).
(6.35)
Функции po(w) и Рх(и) определяют кривые, располагающиеся в трехмерном пространстве. Каждая
из них описывается тремя функциями-компонентами, так что P0(w) = (Ха(и), YQ(u), Za{u)). Обе эти функ-
ции — P0(w) и P,(w) — определены в одном и том же интервале и (обычно от 0 до 1). Линейчатая поверх-
ность состоит из прямых линий, соединяющих каждую пару соответствующих точек P0(w') и Р/ы'), для
каждого и' из интервала (0,1), как показано на рис. 6.51. При v = 0 поверхность находится «в точке» Р0(м'),
а при v - 1 — в точке Pf(w'). Прямую линию для и = и' часто называют образующей (ruling) в точке и’.
6.5. Каркасные аппроксимации гладких объектов
397
Рис. 6.51. Линейчатая поверхность как семейство прямых линий
Для конкретного фиксированного значения и' г/-контур является аффинной комбинацией двух кри-
вых PQ{u) и P/w), причем первая из них имеет вес (1 - xf), а вторая — вес v'. Если xf близко к нулю, то
форма ^'-контура определяется в основном кривой P0(w), а при v', близком к единице, большее влияние
оказывает кривая P,(w).
Если ограничить диапазон изменения г» от 0 до 1, то в поверхности будет фигурировать только отре-
зок прямой между соответствующими точками на кривых. С другой стороны, если v ничем не ограни-
чено, то каждая прямая будет неограниченно продолжаться в обоих направлениях, и поверхность будет
напоминать неограниченный криволинейный «лист». Линейчатый лоскут (ruled patch) формируется
посредством ограничения обоих величин — и uv — некоторыми значениями, например от 0 до 1.
Линейчатая поверхность может быть легко «полигонизирована» обычным способом: выбирается
множество значений и. и гл и для каждого из них вычисляется точка P(w;, гл) и нормаль п(м, V.). После
этого формируются списки, как это делалось раньше.
В некоторых частных случаях линейчатых поверхностей проявляется как их общая природа, так и
разнообразие. Мы рассмотрим три важных семейства линейчатых поверхностей: конус, цилиндр и би-
линейный лоскут (bilinear patch).
Конусы
Конус — это такая линейчатая поверхность, одна из кривых которой, Р0(и), представляет собой един-
ственную точку, а именно вершину конуса, как показано на рис. 6.52. При таком ограничении из урав-
нения (6.35) получается следующее уравнение:
Р(и, v) = (1 - v) Ро + vP^u) (конус общего вида), (6.36)
где точка Ро и есть вершина. При такой параметризации все прямые проходят через точку Ро при v = 0 и
через точку Р^и) при v = 1. Хорошо известны частные случаи: круговой конус получается, если P,(w)
представляет собой.окружность; круговой конус становится прямым, когда эта окружность лежит в
плоскости, перпендикулярной к прямой, соединяющей центр окружности с вершиной Ро. У конуса, по-
казанного на рис. 6.52, принято P((w) == (r(w) cosw, r(w) sinw, 1), причем «радиус» кривой r(w) изменяется
синусоидально согласно уравнению r(w) = 0,5 + 0,2cos(5w).
Цилиндры
Цилиндр — это линейчатая поверхность, у которой кривая P,(w) представляет собой просто смещен-
ную кривую P0(w): Р/м) = P0(w) + d, где d — некоторый вектор, как показано на рис. 6.53, а. Иногда это
называют «разверткой» прямой с концевыми точками P0(w) и P0(w) + d (которую называют генератором,
или образующей) вдоль кривой P0(w) {направляющей кривой) без изменения направления прямой.
В результате такого процесса получается цилиндр.
Поэтому параметрическая форма цилиндра имеет вид:
P(w, v) = P0(w) + d?7. (6.37)
Для создания обычного цилиндра необходимо, чтобы кривая P0(w) располагалась только на плоско-
сти. Если Р» является окружностью, то цилиндр является круговым цилиндром (circular cylinder).
398
Глава 6. Моделирование поверхностей полигональными сетками
Вообще говоря, не требуется, чтобы направление d было перпендикулярно к данной плоскости, однако
если это имеет место, то данная поверхность называется прямым цилиндром (right cylinder). К этой кате-
гории принадлежит и базовый цилиндр. На рис. 6.53, б показан «ленточный» цилиндр, у которого кри-
вая P0(w) изгибается взад и вперед подобно ленте. Такая ленточная форма исследуется в упражнениях в
конце раздела.
Рис, 6.53. Цилиндр (а); «ленточный» цилиндр (5)
Билинейные лоскуты
Билинейный лоскут получается в случае, когда обе кривые — P0(w) и P((w) — являются отрезками пря-
мых линий из одного и того же интервала для и, например от 0 до 1. Обозначим концевые точки кривой
Р0(и) через Роо и Р01 (в этом случае P0(w) имеет вид (1-w) Роо+ wP01), а концевые точки кривой P((w) —
через Р10 и Ри. Тогда из равенства (6.35) следует, что данный лоскут имеет следующую параметриче-
скую форму:
P(w, а) = (1 -*>)(! - w)PM + (1 - v) uPOi + v(l - w)P10 + uvPlv (6.38)
Такая поверхность называется билинейной, потому что она линейно зависит от и и и. Билиней-
ные лоскуты не обязаны быть плоскими; в действительности они являются плоскими, только если
прямые P0(w) и P,(w) располагаются в одной и той же плоскости (см. упражнения ниже). В противном
случае поверхность должна изгибаться по мере того, как мы перемещаемся от одной определяющей
прямой к другой.
6.5. Каркасные аппроксимации гладких объектов
399
Пример неплоского билинейного лоскута приведен на рис. 6.54. Прямая Р0(н) идет от точки (2, -2, 2)
до точки (2, 2, -2), а прямая Pt(u) — от точки (-2, -2, -2) до точки (-2, 2, 2).
Эти прямые не являются компланарными; на рисунке показаны некоторые м-контуры, по которым
ясно видно, как изгибается лоскут.
Нормальный вектор к билинейному лоскуту легко найти из уравнения (6.25). Если лоскут является
плоским, то направление его нормали постоянно, однако ее длина может изменяться с изменением и и г?.
Если же лоскут не является плоским, то и величина, и направление его нормального вектора зависят от
его расположения. __
Другие линейчатые поверхности
Существует много других интересных линейчатых поверхностей. На рис. 6.55, а приведена двойная спи-
раль, которая образуется тогда, когда кривые PQ(u) и P/w) являются спиралями, обвивающимися одна
относительно другой. На рис. 6.55, б показана поразительная лента Мёбиуса (Mobius strip), которая
имеет всего одно ребро. Параметрические представления этих поверхностей исследуются в упражнени-
ях. На рис. 6.55, в изображен сводчатый купол, составленный из четырех линейчатых поверхностей.
В тематическом задании 6.8 рассматривается моделирование таких сводчатых куполов для соборов.
Билинейно сопряженные поверхности: лоскуты Кунса
Интересным и полезным обобщением линейчатой поверхности, интерполирующей две граничные кривые
P0(w) и P,(w), является билинейно сопряженный лоскут, интерполирующий четыре граничные кривые.
Впервые семейство таких лоскутов было исследовано Стивеном Кунсом (Steven Coons — [Coons, 48])
и поэтому иногда его называют лоскутом Кунса (Coons patch).
На рис. 6.56 изображены четыре примыкающие граничные кривые, обозначенные ри0, ри{, pQv, ph.
Эти кривые пересекаются в углах изображенного лоскута (где uiiv принимают значения 0 или 1), а при
других значениях параметров эти кривые могут иметь любую форму. Следовательно, данный пример
является обобщением билинейного лоскута, границы которого являются прямыми линиями. Выведем
формулу для поверхности Р(и, v), осуществляющей плавный переход от одной граничной кривой к другой
по мере изменения значений и и v.
В первую очередь естественно попытаться скомбинировать линейчатый лоскут, построенный изрий(и)
и /?и1(н), с линейчатым лоскутом, построенным из pQv(v) и ри(о). Однако простое сложение этих поверхно-
стей не дает результата: не удается правильно интерполировать четыре кривые (кроме того, эта опера-
ция некорректна, поскольку дает пеаффинную комбинацию точек!). Хитрость заключается в том, чтобы
сложить эти поверхности, а затем вычесть билинейный лоскут, построенные! на четырех углах гранич-
ных кривых. На рис. 6.57 наглядно показано, как это делается [Heckbert, 106].
400
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.55. Двойная спираль (а); лента Мебиуса (<5); сводчатый купол (в)
Рис. 6.56. Четыре граничных кривые, определяющие лоскут Кунса
Рис. 6.57. Комбинирование лоскутов для создания лоскута Кунса
6.5. Каркасные аппроксимации гладких объектов
401
Тогда формула для данного лоскута имеет виД:
Р(и, v) = [pte(o) (1 - w) +plt,(o)w] + [p„0(w) (1 - v) +pB1(w)o] -
- [(1 - w) (1 - 0pte(O) + w(l - o)plt,(0)w +pOv(l)o(l - w) +plt,(l)wo]. (6.39)
Отметим, что для каждой пары (и, v) данное равенство по-прежнему представляет собой аффинную
комбинацию точек, как мы и требовали: при (и, V) = (0,0) его правая часть равна ри0(0), и аналогичным
образом она совпадает с тремя остальными углами при соответствующих граничных значениях и и ».
На рис. 6.58 показан пример лоскута Кунса, ограниченного кривыми, описывающими синусоидальные
колебания.
Рис. 6.58. Пример лоскута Кунса
Практические упражнения
6.5.11. Пирамида — это конус
Какую форму будет иметь кривая Р((ы) для создания линейчатой поверхности, представляющей собой
пирамиду с квадратным основанием? Получите такие выражения для кривой и точки Ро, чтобы квад-
ратное основание пирамиды располагалось в плоскости xz, имело центр в начале координат и длины
его сторон равнялись 2. Высота данной пирамиды должна равняться 1,5.
6.5.12. Ленточные цилиндры
Найдите параметрическую форму кривой Р0(ы), обеспечивающей хорошую аппроксимацию ленточного
цилиндра, приведенного на рис. 6.53, б. Представьте, что эта лента обернута вокруг последовательности
смежных круговых цилиндров единичного радиуса. Сентр i-ro цилиндра располагается в точке (х, у;) =
(i2d, ± г), где плюсы и минусы чередуются и d2 = 1 - г2. Выберите какое-либо значение г между 0 и 1.
6.5.13. Двойная спираль
Параметрическая форма спирали: (cos(t), sin(t), t). Найдите выражения для двух спиралей, Р0(ы) и Р/м),
каждая из которых вращается вокруг оси г, со сдвигом по фазе на 180°, так что они обвиваются относи-
тельно друг друга. Напишите параметрическую форму линейчатой поверхности, образованной с помо-
щью этих двух кривых.
6.5.14. Лента Мёбиуса
Найдите параметрическую форму для ленты Зёбиуса, изображенной на рис. 6.55, б. (Подсказка. Повер-
ните прямую вокруг оси г и при этом перекрутите ее во время поворота прямой.) Описывается ли лента
Зёбиуса парой уравнений Р0(ы) = (cos(2pw), sin(2pw), и) и P,(w) = (cos(2pw), sin(2pw), 1 - и)?
6.5.15. Является ли комбинация аффинной?
Докажите, что лоскут Кунса из уравнения (6.39) составлен из аффинных комбинаций точек.
402
Глава б. Моделирование поверхностей полигональными сетками
6.5.16, Действительно ли происходит интерполяция?
Проверьте и убедитесь, что кривая Р(и, о) из уравнения (6.39) интерполирует каждую из четырех гра-
ничных кривых и поэтому интерполирует каждый из четырех углов.
6.5.7. Поверхности вращения
Как уже описывалось ранее, поверхность вращения образуется посредством вращательной развертки с
заметанием (rotational sweep) профильной кривой С вокруг некоторой оси. Пусть мы поместили этот
профиль в плоскость хг и задали его параметрически следующим образом: С(о) = (Х(о), Z(v)). Для созда-
ния поверхности вращения мы поворачиваем этот профиль вокруг оси г, изменяя параметр и, где и опре-
деляет угол, под которым каждая точка повернута относительно оси. Как и прежде, различные положения
кривой С вокруг оси называются меридианами. Когда точка (Х(о), О, Z(^)) поворачивается на и радиан,
она становится точкой (X(v) cos(w), X(v) sin(w), Z(v)). Полный поворот кривой образует полный круг,
следовательно, контуры при постоянном v являются окружностями, которые называются параллелями
этой поверхности1. Параллель для каждого значения V имеет радиус X(v) и располагается на высоте
Z(v) над плоскостью ху. Тогда произвольная точка поверхности задается выражением:
Р(и, v) = (X(v) cos(w), X(v) sin(w), Z(v)). (6.40)
Базовые сфера, конический цилиндр и конус являются известными частными случаями поверхнос-
ти вращения. (Что представляют собой их профили?)
Нормальный вектор к поверхности вращения легко может быть найден простой подстановкой урав-
нения (6.40) в уравнение (6.25) (см. упражнения в конце раздела). Отсюда следует:
п(и,г?) = Z(n)(z(??)cos(i<),Z(0)sin(i<), -X(v)j, (6.41)
где точка означает первую производную функции. Масштабный множитель X(v) исчезает после норми-
рования вектора. Этот результат относится к формам, которые мы нашли для простых базовых поверх-
ностей (см. упражнения ниже).
а б
Рис. 6.59. Тор
Например, тор (torus) получается путем развертки смещенной окружности вокруг оси г, как показа-
но на рис. 6.59, а. Эта окружность имеет радиус А и смещена вдоль оси х на расстояние Р следовательно,
ее профиль C(v) = (D + Acos(0,4sin(0). Тогда формула для тора (рис. 6.59, б) имеет следующий вид:
Р(и, v) - ((D + Лсоз(п)) cos(m), (D + Лсо$(»)) sin(w), Xsin(&)). (6.42)
Нормальный вектор выводится в упражнениях.
1 Более строго меридианом называется пересечение поверхности с плоскостью, содержащей ось вращения этой поверхности, а па-
раллелью — пересечение поверхности с плоскостью, перпендикулярной оси вращения.
6.5. Каркасные аппроксимации гладких объектов
403
Обычно мы развертываем кривую, располагающуюся в некоторой плоскости, вокруг оси, лежащей в этой
же плоскости. Однако поверхность вращения можно получить и поворотом вокруг любой другой оси.
Выбор различных осей при заданном профиле может привести к интересным семействам поверхностей.
Общая формула Р(и, v) для поверхности вращения вокруг произвольной оси выводится в упражнениях.
Сетка для поверхности вращения строится в программе обычным способом. Мы выбираем множе-
ства значений и и v, обозначаемые как {ut} и {v\, и вычисляем вершину для каждой комбинации этих
значений параметров, используя формулу для P(up Vj) и нормального вектора п(г/ , & ). Полигональные
грани строятся путем соединения четырех смежных вершин прямыми линиями. Метод для выполне-
ния этого процесса рассматривается в тематическом задании 6.13.
в
а
Рис. 6.60. Поверхность вращения — купол Тадж Махала
На рис. 6.60, а приведен пример, в котором сделана попытка моделирования купола изящного храма
Тадж Махал (Taj Mahal) в Агре, Индия. На рис. 6.60, б изображена профильная кривая в плоскости xz,
а на рис. 6.60, в показана результирующая поверхность вращения. Этот профиль описывается множе-
ством точек данных Ct - (X, Z), поскольку не нашлось ни одной подходящей параметрической форму-
лы. (Мы исправим этот недостаток в главе Ии применим В-сплайн (B-spline) для создания гладкой
параметрической кривой на базе множества точек данных.)
Для того чтобы построить поверхность вращения в случае профиля, заданного дискретными точка-
ми, будем определять у-ю вершину из равенства (6.40) в слегка измененной форме:
Pr(X/coS(M.),X?in(Mj),Z>).
Практические упражнения
6.5.17. Базовые формы как поверхности вращения
Опишите в параметрической форме профили для базовых сферы, цилиндра и конуса, а затем выразите
их как поверхности вращения.
6.5.18. Вращение вокруг других осей
Рассмотрим профильную кривую C(v) = (X(v), Z(o)), лежащую в плоскости xz, и произвольную ось,
проходящую через начало координат и заданную единичным вектором г. Из уравнения (5.33) мы зна-
ем, что матрица Д.(0) осуществляет поворот точки на 0 радиан вокруг оси г:
а) покажите, что поверхность вращения, полученная посредством развертки кривой C(v) вокруг
оси г, имеет вид:
404
Глава б. Моделирование поверхностей полигональными сетками
б) проверьте это равенство для частного случая вращения вокруг оси г;
в) повторите пункт б) для вращений вокруг оси х и вокруг оси у.
6.5.19. Нахождение нормальных векторов
Примените равенство (6.40) к равенству (6.25) для вывода формулы нормали к поверхности вращения
в равенстве (6.41).
Используйте результат пункта а) для нахождения нормалей к базовым сфере, цилиндру и конусу,
после чего покажите, что эти результаты согласуются с полученными в разделе «Три „базовые" формы:
сфера, цилиндр и конус». Докажите, что нормальный вектор к тору имеет вид:
n(w, v) = (cos(a) cos(w), cos(o) sin(w), sin(o)) (D + Acos(o)).
Кроме того, найдите для тора внешне-внутреннюю функцию и вычислите нормаль с использовани-
ем градиента этой функции.
6.5.20. Эллиптический тор
Найдите параметрическое представление для следующих двух поверхностей вращения:
О поверхность, которая получается, когда эллипс вида (acos(0,6sin(o)) сначала смещается на R еди-
ниц вдоль оси х, а затем поворачивается вокруг оси у;
О поверхность, которая получается, когда тот же самый эллипс поворачивается вокруг оси х.
6.5.21. «Фигура вращения Лиссажу»
Нарисуйте, как будет выглядеть поверхность, образованная вращением фигуры Лиссажу из равенства (6.19)
вокруг оси у при М = 2, N = 3, 0 = 0.
6.5.22. Вращение п-угольников
Нарисуйте поверхность, образующуюся при вращении квадрата с вершинами (1,0,0), (0,1, 0), (-1, 0, 0),
(0,-1, 0) вокруг оси у. Выполните аналогичную процедуру для Пентагона и гексагона.
6.5.8. Поверхности второго порядка
Важное семейство поверхностей — поверхности второго порядка, или квадрики — являются трехмер-
ными аналогами конических сечений, или коник (эллипса, параболы и гиперболы, которые мы рассмат-
ривали в главе 3). Некоторые из поверхностей второго порядка обладают красивой формой и могут
найти широкое применение в графике.
На рис. 6.61 приведено шесть поверхностей второго порядка. Нам требуется охарактеризовать толь-
ко «базовые» варианты этих форм, ибо все интересующие нас изменения можно получить посредством
масштабирования, поворота и смещения соответствующих обобщенных форм. Известно, например, что
внешне-внутренняя функция для эллипсоида имеет вид:
F(x,y,z) =
причем данный эллипсоид располагается: по х от -а до а, по у от -Ь до b, по z от -с до с. Эта поверхность
может быть получена из формулы базовой сферы путем ее масштабирования вдоль осей х, у, z соответ-
ственно с множителями а, Ь, с, как мы уже вкратце описывали. Аналогично могут быть получены повер-
нутые варианты эллипсоида.
Таблица 6.8 описывает шесть базовых квадрик, задавая и неявную, и параметрическую форму каж-
дой из них. Позднее мы рассмотрим некоторые любопытные свойства каждой из этих поверхностей.
Легко убедиться, что каждая из этих параметрических форм согласуется с соответствующей неяв-
ной формой: достаточно просто подставить параметрические выражения в компоненты по х, у и z, пос-
ле чего с помощью тригонометрических тождеств убедиться в том, что получается нуль.
6.5. Каркасные аппроксимации гладких объектов
405
Рис. 6.61. Шесть поверхностей второго порядка: а) эллипсоид; б) однополостями гиперболоид; в) двуполостный
гиперболоид; г) эллиптический конус; д) эллиптический параболоид; е) гиперболический параболоид
Таблица 6.8. Характеристика шести «базовых» квадрик
Название квадрики Неявная форма Параметрическая форма Интервал изменения no v и по u
Эллипсоид х2 + у2 + z2 - 1 (cos(v) cos(u), cos(v) sin(u), sin(v)) (-л/2, л/2), (-л, л)
Однополостный гиперболоид x2 + y2-z2-l (sec(v) cos(u), sec(v) sin(u), tg(v)) (-л/2, л/2), (—л, л)
Двуполостный гиперболоид х2 - у2 - z2 - 1 (sec(v) cos(u), sec(v) tg(u), tg(v)) (-л/2, л/2)1
. Эллиптический конус х2 + у2 - z2 (vcos(u), vsin(u), v) Любые вещ. числа, (-л, л)
Эллиптический параболоид х2 + у2 + z (vcos(u), vsin(u), v2) v > 0, (- л, л)
Гиперболический параболоид -х2 + у2 - z (vtg(u), vsec(u), v2) v > 0, (- л, л)
Отметим, что перемена знака одного из членов внешне-внутренней функции приводит к замене
cos( ) на sec( ) и sin( ) на tg( ) в параметрических формах. Функции sec( ) п tg( ) неограниченно возра-
1 Диапазон по v для полости № 1 составляет (~л/2, л/2), а для полости № 2 — (-л/2, Зл/2).
406
Глава б. Моделирование поверхностей полигональными сетками
стают при стремлении их аргументов к л/2, поэтому при рисовании и-контуров и ^-контуров соответ-
ствующий параметр следует ограничивать меньшим диапазоном.
Некоторые замечания о поверхностях второго порядка
Резюмируем кратко некоторые важнейшие свойства каждой из поверхностей второго порядка. Одним
из таких свойств является природа следов поверхности. След (trace) — это кривая, образующаяся при
пересечении поверхности плоскостью. Все следы поверхности второго порядка являются коническими
сечениями (см. упражнения в конце раздела). Главные следы (principal traces) — это кривые, образую-
щиеся в случае, когда секущие плоскости выровнены вдоль осей. Эти секущие плоскости задаются урав-
нениями z - k, у = k, х = k, где k — константа.
В дальнейших исследованиях мы будем предполагать, что базовые поверхности были промасштабиро-
ваны вдоль осей х, у, г масштабными множителями а, Ь, с соответственно, чтобы проще было судить о
размерах поверхностей и определять, какая поверхность является поверхностью вращения, а какая — нет.
Эллипсоид. Вспомним из главы 3 неявную и параметрическую формы для эллипса и сравним, как
они расширяются при переходе от двумерного эллипса к трехмерному эллипсоиду. Параметры а, Ь, с
характеризуют протяженность эллипсоида вдоль каждой оси. Если два из этих параметров равны друг
другу, то эллипсоид является поверхностью вращения. (Где находится ось вращения при а = Ъ?) Если
все три параметра а, b и с одинаковы, то эллипсоид превращается в сферу. Все следы эллипсоида явля-
ются эллипсами.
Однополостный гиперболоид. Если а = Ъ, то такой гиперболоид становится поверхностью вращения,
образованной посредством вращения гиперболы вокруг оси. Главные следы для плоскостей z = k явля-
ются эллипсами, а для плоскостей x*knyak- гиперболами. Однополостный гиперболоид особенно
интересен тем, что он является линейчатой поверхностью, как показано на рис. 6.62, а. Такая поверх-
ность может получиться, если переплести нитью два параллельных эллипса так, как показано на рисун-
ке. Формулы для образующих «нитей» рассматриваются в упражнениях.
а б
Рис. 6.62. Две линейчатые поверхности второго порядка
Двуполостный гиперболоид. В диапазоне от х = -а до х = а не находится никакой части данной повер-
хности. (Почему?) При а = b эта поверхность становится поверхностью вращения. Следы для плоско-
стей х = k при \k\ > а являются эллипсами, а остальные главные следы — гиперболы.
Эллиптический конус. Эллиптический конус является частным случаем конуса общего вида, рас-
смотренного ранее: его генератор вычерчивает эллипс. Такой конус, разумеется, является линейчатой
поверхностью, и его главные следы для плоскостей z = k — эллипсы. (Какой вид имеют следы для плос-
костей, содержащих осьа?) При а = Ь данная поверхность второго порядка является поверхностью вра-
щения: она превращается в прямой круговой конус.
Эллиптический параболоид. Следы эллиптического параболоида для плоскостей z = k > 0 являются
эллипсами, а другие главные следы — параболы. При а = b данная фигура становится поверхностью
вращения.
6.5. Каркасные аппроксимации гладких объектов
407
Гиперболический параболоид. Гиперболический параболоид иногда называют также седлообразной
(saddle-shaped) поверхностью. Следы для плоскостей z = k (k * 0) являются гиперболами, а для плоско-
стей х = k или у - k — параболами. (Какой вид имеет пересечение этой поверхности с плоскостью z - О?)
Гиперболический параболоид также является линейчатой поверхностью (рис. 6.62, б).
Нормальные векторы к поверхностям второго порядка
Поскольку неявная форма для каждой поверхности второго порядка обладает квадратичной зависимо-
стью относительно х, у, z, получение градиента для нахождения нормалей не является проблемой. Кро-
ме того, поскольку каждый компонент вектора градиента является линейным или даже постоянным
относительно своей собственной переменной, нетрудно написать градиент в параметрической форме:
достаточно просто подставить Х(и, v) вместо х и т. д. Например, градиент от Г(х,у, г) для эллипсоида
имеет вид:
F - (2г, 2у, 2z),
откуда, переходя к параметрической форме и деля на 2, получим выражение для нормали:
п(и, v) = (cos(n) cos(w), cos(o) sin(w), sin(0). , (6.44)
Нормали для других поверхностей второго порядка могут быть получены столь же просто, поэтому
нет необходимости приводить их таблицу.
Практические упражнения
6.5.23. Гиперболоид — это линейчатая поверхность
Покажите, что неявная форма однополостного гиперболоида может быть записана в виде: (х + z) (х - z) =
= (1 - у) (1 + у). Покажите также, что из этого следует, что на данной поверхности располагаются два
семейства прямых: семейство х - z =* А(1 - у) м. семейство А(х + z) = 1 + у, где А — константа. Нарисуйте
эти семейства при различных значениях А. Исследуйте аналогичные образующие для гиперболичес-
кого параболоида.
6.5.24. Однополостный гиперболоид
Докажите, что альтернативная параметрическая форма для однополостного гиперболоида имеет вид:
р(и, v) = (ch(n) cos(w), ch(n) sin(w), sh(0).
6.5.25. Следы квадрик — коники
Рассмотрим любые три неколлинеарные точки, лежащие на какой-либо поверхности второго порядка.
Они определяют плоскость, которая пересекает эту поверхность, образуя кривую следа. Докажите, что
эта кривая всегда является параболой, эллипсом или гиперболой.
6.5.26. Нахождение нормалей к поверхностям второго порядка
Найдите в параметрической форме нормальные векторы для каждой из шести поверхностей второго
порядка.
6.5.27. Гиперболоид как линейчатая поверхность
Пусть (х0, у0, 0) — точка на поверхности однополостного гиперболоида. Докажите, что вектор
R(t) = (xo + yot,yo-xot,t)
описывает прямую линию, полностью лежащую на гиперболоиде и проходящую через точку (х0, у0,0).
Является ли это свойство достаточным для того, чтобы поверхность была линейчатой? Почему да или
почему нет [Apostol, 4]?
6.5.28. Гиперболический параболоид как линейчатая поверхность
Покажите, что любая плоскость, параллельная прямой у = ±х, пересекает гиперболический параболоид
по прямой линии.
408
Глава б. Моделирование поверхностей полигональными сетками
6.5.9. Суперквадрики
Исходя из работы Алана Барра [Вагг, 12], можно расширить семейство поверхностей второго порядка
(квадрик) в значительно большее семейство, аналогично тому, как мы расширили эллипс до суперэл-
липса в главе 3. Это предоставит нам дополнительные интересные формы поверхностей, которые мож-
но использовать в качестве моделей для приложений.
Барр определяет следующие четыре суперквадратичных тела: суперэллипсоид, однополостный супер-
гиперболоид, двуполостный супергиперболоид, которые являются расширением первых трех квадрик,
и супертороид (supertoroid), расширяющий понятие тора. Эти расширения вводят два «показателя выпук-
лости» («bulge factors») т и п, в которые возводятся различные члены. Показатели выпуклости влияют
на данные поверхности примерно так же, как показатель п влияет на суперэллипс. Когда оба этих показа-
теля равны 2, то первые три суперквадрики превращаются в обычные квадрики. На рис. 6.63 показаны
четыре примера суперквадрик. В табл. 6.9 приведены их неявные и параметрические формы1.
Рис. 6.63. Примеры четырех суперквадрик. Значения п, и п,равны (слева направо):
10,2,1,11,0,77,0,514 (с разрешения Jay Greco)
Таблица 6.9. Характеристики четырех суперквадрик
Название суперквадрики Неявная форма Параметрическая форма Промежутки изменения v и u
Суперэллипсоид (л"+ /')"’/" + zm-1 (COS2/'”( k) COS^'Xt/), COS2/m(u) sin^tf), Sin2/'”(k’)) [-я/2, я/2], [-я, я]
Однополостный супергиперболоид (x/7+ 1 (sec2/'”(n) cos^^t/), sec2"”^) sin^t/), tg2"”^)) (~я/2, я/2), [-я, я]
Двуполостный супергиперболоид yriyn/n—. gm—, 1 (sec2"”^) sec^t/), sec2"”^) tg^t/), tg2"”^)) (-я/2, я/2)
Супертороид ((xn- y»)v»_ d)m+ zm-1 ((</+ COS2"”^)) COS2/n(t/), (</+ COS2/m(k’)) sin^t/), sin2"”^)) [-я, я), [-я, я)
Все суперквадрики, перечисленные в этом списке, являются «базовыми» в том смысле, что их центр
находится в начале координат, они выровнены по координатным осям и имеют единичные размеры.
Подобно другим формам, их можно по желанию масштабировать, поворачивать и перемещать, исполь-
зуя текущее преобразование для должной их подготовки для сцены.
1 Имейте в виду, что недопустимо возводить в дробную степень отрицательную величину. Поэтому выражения вида cos2/”(&) будут
вычисляться как cos(T,)|cos(&)|2/m’1 и т. п.
6.5. Каркасные аппроксимации гладких объектов
409
Нормали к суперэллипсоиду и к супертороиду
Нормальный вектор n(w, v) для каждой суперквадрики можно вычислить обычными способами.
Для суперэллипсоида и супертороида нормальные векторы одни и те же:
n(w, v) = (cos2~2/m(o) cos2'2/,l(w), cos2"2/m(y) sin2"2/n(w), sin2“2/m(t’)). (6.45)
(Как эти векторы могут быть одними и теми же? Ведь эти две поверхности определенно имеют раз-
ную форму.)
Однополостный супергиперболоид
Нормальный вектор для однополостного супергиперболоида такой же, как для суперэллипсоида, за
исключением того, что все cos(n) заменяются на sec(??), a sin(??) — на tg(&). Не заменяйте cos(w), sin(zz)
или какие-либо другие члены.
Двухполостный гиперболоид
Для двуполостного супергиперболоида заменяются тригонометрические функции как от v, так и от и.
Мы заменяем все cos(o) на sec(^), sin(r>) на tg(0, cos(w) на зес(м), sin(w) на tg(w).
Практические упражнения
6.5.29. Размеры суперквадрик
Чему равны максимальные значения х, у, г, достигаемые суперэллипсоидом и супертороидом?
6.5.30. Поверхности вращения
Определите значения показателей выпуклости т и п, при которых каждая из суперквадрик является
поверхностью вращения, и найдите ось вращения. Опишите другие оси симметрии этих поверхностей.
6.5.31. Вывод нормальных векторов
Выведите формулу нормального вектора для каждой суперквадрики.
6.5.10. Трубки на базе трехмерных кривых
В разделе «Создание сегментированных экструзий: трубки и змейки» мы рассматривали трубки, осно-
ванные на «хребтовой» кривой С(£), извивающейся в трехмерном пространстве. Для каждой выбран-
ной точки хребта устанавливался полигон, ориентированный в соответствии с базисом Френе, вычис-
ленном в этой точке. Затем соответствующие точки смежных полигонов соединялись и образовывали
вдоль хребта плоскогранную трубку.
Здесь мы поступим так же, за исключением того, что нормаль к поверхности будем вычислять в каж-
дой вершине, чтобы можно было осуществить плавное закрашивание. На рис. 6.64 показана трубка,
надетая на спиральную форму. Сравните эту форму с рис. 6.39.
Рис. 6.64. Спиральная трубка, изгибающаяся в пространстве
410
Глава 6. Моделирование поверхностей полигональными сетками
Если мы хотим нанизать окружность, заданную выражением (cos(w), sin(u), 0), на хребет C(t), то ре-
зультирующая поверхность будет иметь следующее параметрическое представление:
Р(и, v) = C(v) + cos(w) N(o) + sin(w) B(r), (6.46)
где нормальный вектор N(£) и бинормальный вектор B(t) задаются соответственно равенствами (6.15) и
(6.14). Теперь для такой трубки можно обычным способом построить сетку: «взять замеры» Р(и, о) при
различных unv, составить списки вершин, нормалей и граней и т. д. (Что бы изменилось, если бы мы
вместо окружности надели на хребет циклоиду — см. рис. 3.80?)
6.5.11. Поверхности на базе явных функций двух переменных
Многие формы поверхности однозначны в одном измерении, так что их положение может быть выра-
жено явной функцией двух независимых переменных. Например, в каждой точке (х, г) может быть толь-
ко одно значение «высоты» поверхности над плоскостью xz, как предлагается на рис. 6.65. Тогда можно
сказать, что высота поверхности в точке (х, z) есть некоторая функция f(x, z). Такую функцию иногда
называют полем высот (height field) [Bloomenthal, 33] и задают в виде формулы следующего типа:
f(x,z) = e~^~k2 (6.47)
(здесь а и b — заданные константы) или в виде «sino-функции с круговой симметрией (см. равенство
(3.1) в главе 3):
sin (7^ + Д’2)
/(*.*) = <б.48>
<jx+y
Рис. 6.65. Однозначная область высот над плоскостью xz
Сравните эту поверхность с поверхностями типа сферы, у которой с каждой точкой (х, г) связано более
одного значения у. Для однозначных функций допускается следующая простая параметрическая форма:
Р(и, o) = (w,/(w, г), о), (6.49)
а их нормальный вектор имеет следующий вид:
/ *42* ПТ* \
n(w,c) = ——, 1, —— . (Проверьте это.)
ди dvj
Следовательно, величины unv могут быть непосредственно использованы в качестве зависимых пере-
менных для данной функции. Поэтому ц-контуры располагаются в плоскостях с постоянным х, а п-кон-
б.б. Заключение
411
туры — в плоскостях с постоянным z. На рис. 6.66, а показана поверхность, описываемая уравнением (6.47),
а на рис. 6.66, б — уравнением (6.48). Каждая линия является следом пересечения поверхности плоско-
стью х в k или z e k при некотором значении k. Подобные рисунки могут помочь при иллюстрации по-
ведения математической функции.
а
Рис. 6.66. Два поля высот: а) гауссиана; б) гармоническая sinc-функция
Практическое упражнение
6.5.32. Квадрики как явные функции
Эллиптический параболоид можно записать в виде функции z**f(x, у), тогда его параметрическая фор-
ма будет иметь вид: (w, v,f(u, v)). Чему равна функция /( )? В каких случаях удобна такая форма запи-
си? Какие другие квадрики могут быть представлены таким способом? Можно ли написать аналогич-
ные явные представления для каких-нибудь суперквадрик?
6.6. Заключение
Эта глава посвящена моделированию и рисованию разнообразных поверхностей трехмерных объектов.
Для осуществления этого нужно находить математические описания поверхностей различных форм и
создавать эффективные структуры данных, в которых содержится описание поверхности, достаточно
подробное для ее визуализации. Мы разработали класс Mesh (сетка), поля данных которого содержат
три списка: список вершин, список нормалей и список граней. Такая структура может эффективно со-
хранять все необходимые геометрические данные об объектах с плоскими гранями, такими как много-
гранник; и может хранить данные, достаточные для моделирования полигональной «оболочки», ап-
проксимирующей гладкие криволинейные поверхности.
Мы показали, что когда структура данных для сетки построена, ее нетрудно визуализировать в про-
граммной среде OpenGL. Столь же просто записать данные о сетке в файл и считывать его в программу.
Современные алгоритмы закрашивания используют нормальный вектор в каждой вершине каждой гра-
ни, чтобы можно было определить, насколько светлыми или темными должны быть изображены раз-
личные точки грани. Если грань должна быть нарисована плоской, то для каждой вершины использует-
ся один и тот же нормальный вектор, а именно вектор, нормальный к самой этой грани. Если сетка
создается для приближенного представления гладкой криволинейной поверхности, то нормальный век-
тор в каждой вершине полагается равным нормали к истинной поверхности в этой точке, а алгоритмы
визуализации для передачи плавно изменяющихся теней изображения используют формулу интерпо-
412
Глава 6. Моделирование поверхностей полигональными сетками
ляции (это будет рассмотрено в главе 8). Таким образом, выбор нормального вектора для записи в дан-
ные сетки зависит от того, каким разработчик хочет видеть свой объект.
Исследовано большое количество полиэдрических форм, встречающихся в популярных приложе-
ниях, и разработана техника построения сеток для некоторых семейств полиэдров. Особое внимание
было уделено установке нормали к грани в каждой вершине этой грани. Мы также изучили большие
семейства плавно меняющихся объектов, в том числе классические поверхности второго порядка, ци-
линдры и конусы, и обсудили, как вычислять направление нормального вектора в каждой точке путем
определения соответствующих производных от параметрической формы поверхности.
Тематические задания в следующем разделе развивают некоторые из этих идей, поэтому их не сле-
дует пропускать. В некоторых из этих тематических заданий углубляется теория вопроса. Рассматри-
ваются основные положения метода вычисления нормального вектора Ньюэлла, причем вам предлага-
ется заполнить некоторые пробелы в изложении вывода этого метода. Показано, что семейство квадрик
имеет унифицированную матрицу, содержащую его основную структуру; описывается соответствую-
щий метод преобразования квадрик. В остальных тематических заданиях вам предлагается разработать
методы или приложения для создания и рисования сеток для наиболее интересных классов форм.
6.7. Тематические задания
Тематическое задание 6.1. Сетки, записанные в файл
Уровень сложности II.
Нам нужно, чтобы класс Mesh поддерживал запись объектов класса Mesh в файл и чтение этих каркас-
ных объектов из файла в программу. Выберем для таких файлов простой формат. Пусть в первой стро-
ке списка содержится число вершин, число нормалей и число граней сетки. Затем каждая вершина сет-
ки указывается в виде тройки чисел с плавающей запятой: (х., у., z). В каждой строке располагается
несколько вершин. Затем указываются все нормальные векторы, также в виде тройки вещественных
чисел. И наконец, перечисляется каждая грань в следующем формате:
О число вершин текущей грани;
О список индексов списка вершин для вершин текущей грани;
О список индексов списка нормалей для вершин текущей грани.
Например, простой сарай с рис. 6.4 будет записан в следующем виде:
10 7 7
ООО 1 0 0 1 1 0 0.5 1.5 0 0 1 0
0 0 1 10 1 111 0.5 1.5 1 0 11
-100 -0.707 0.707 0 0.707 0.707 0
100 0-10 001 00-1
4 0 5 9 4 0 0 0 0
4 3 4 9 8 1 1 1 1
4 2387 2222
4 1276 3333
4 0165 4444
5 56789 55555
5 04321 66666
В этом списке первая грань является четырехугольником, вершины которого имеют номера 0,5,9,4;
а две последние грани являются пятиугольниками.
Листинг 6.3. Чтение сетки из файла в память
int Mesh:: readFile (char * fileName)
{
6.7. Тематические задания
413
fstream infile;
infile.open (fileName, ios::in):
if(infile.fail())return -1;
// error-can't open file
// ошибка - не можем открыть^файл
ifdnfile.eofO)return -1;
// error-empty file
// ошибка - файл пустой
infile » numVerts » numNorms » numFaces:
pt = new Point3[numVerts] ;
norm = new Vector3[numNorms] :
face - new FaceLnumFaces] :
// check that enough memory was found:
// проверяем, имеется ли достаточно памяти
if(!pt || 'norm || !face)return -1;
// out of шелюгу
// недостаточно памяти
for(int p - 0: p < numVerts: p++)
// read the vertices
// читаем вершины
infile » pt[p].x » pt[p].y » ptLpJ.z:
for(int n - 0: n < numNorms: n++)
// read the normals
// читаем нормали
infile » norm[n].x » norm[n].y » norm[n].z:
ford nt f - 0: f < numFaces; f++)
// read the faces
// читаем грани
{
infile » face[f].nVerts:
face[f].vert - new VertexIdL face[f].nVerts]:
fordnt i = 0: i < face[f].nVerts; i++)
infile » face[f].vert[i].vertlndex
» face[f].vert[i].normindex:
}
return 0:
// success
// успешное окончание
}
О Для чтения сетки из файла в программу можно применить код подпрограммы из листинга 6.3.
Приняв имя файла, подпрограмма открывает и читает файл с этим именем в существующий
объект класса Mesh и при успешном завершении операции возвращает нуль. При возникновении
ошибки возвращается ненулевое значение: если, например, заданный файл не может быть найден.
Подпрограмма должна выполнять дополнительную проверку на ошибки формата, вроде получе-
ния вещественного числа там, где ожидается целое. Отметим, что поскольку информация о тре-
буемом размере сетки недоступна до того момента, пока считываются величины numVerts, numNorms
и numFaces, то массивы, содержащие вершины, нормали и грани, размещаются с нужными разме-
рами динамически во время выполнения программы.
На Интернет-сайте этой книги имеется много файлов в вышеприведенном формате. (Они имеют
расширение .3vn.) Кроме того, нетрудно конвертировать в этот формат объекты IndexedFace из библио-
теки VRML 2.0. Столь же легко настроить подпрограмму int Mesh:: writeFile(char* fileName), которая
записывает каркасный объект в файл.
414
Глава 6. Моделирование поверхностей полигональными сетками
Напишите приложение, которое читает каркасные объекты из файлов и рисует эти объекты. Пусть
эта программа позволяет пользователю записывать каркасный объект в файл. Начните работу своего
приложения с создания сеток для тетраэдра и простого сарая.
Тематическое задание 6.2. Вывод метода Ньюэлла
Уровень сложности II.
В этом задании излагается теория, на которой основан метод Ньюэлла (Newell method), предназна-
ченный для вычисления нормалей к полигону, заданному своими вершинами. По ходу изложения про-
делываются необходимые математические выкладки. Вы должны получить несколько промежуточных
результатов. Мы будем работать с полигональной гранью
Р-{Р0.Л...PN-J. (6.50)
заданной своими N трехмерными вершинами. Мы хотим показать, почему формулы в равенстве (6.1)
обеспечивают точное вычисление нормального вектора m = (тх, т ,тг) к грани Р в случае, когда Р являет-
ся плоской; и предлагают хорошее направление для «усредненной» нормали, когда Р — неплоская грань.
Рис. 6.67. Использование спроецированных областей для нахождения нормального вектора
А. Вначале рассмотрим рис. 6.67, на котором показана грань Р, ортогонально (то есть вдоль главных
осей) спроецированная на каждую из главных плоскостей, а именно на плоскости х = 0, у = 0, z = 0.
Каждая проекция является двумерным полигоном. Прежде всего покажем, что компоненты век-
тора m пропорциональны соответственно площадям Ах, Ау, Аг этих спроецированных полигонов.
Для простоты рассмотрим случай, когда Р является треугольником, как показано на рис. 6.68.
Обозначим этот треугольник Т, а его единичный нормальный вектор — т. Пусть, далее, Т' является
проекцией треугольника Т на плоскость с единичной нормалью п. Покажем, что площадь Т',
обозначенная Агеа(Т^), является определенной частью от площади всего треугольника Т, обо-
значенной Агеа(7), и что эта часть является скалярным произведением:
Агеа(Т^) = (т • п) Агеа(Т).
Предположим теперь, что ребра треугольника Т представляют собой два вектора v и w, как по-
казано на рисунке.
1. Докажите, что Агеа(Т’) = l/2|w х v| и что v х w = 2Агеа(Т) т.
Далее рассмотрим проекцию треугольника Т на плоскость с нормальным вектором п. Эта про-
екция Т" задается проекциями векторов Vх и w7; а его площадь составляет Агеа(Т’) =l/2|wx х v'|,
откуда vxxw' = 2Агеа(7’) п. Теперь вычислим w' и v' и найдем выражение для Агеа(Т').
6.7. Тематические задания
415
Рис. 6.68. Влияние ортогональной проекции на площадь
2. Используя идеи главы 4, покажите, что вектор v проецируется в вектор v' = v - (v • n) n и что,
аналогично, w' = w - (w • n) n.
Таким образом, задача сводится к сравнению длин двух векторных произведений.
3. С помощью формул для Vх и докажите, что
v' х w' = v х w - (w • n) (v x n) + (v • n) (w x n) + (w • n) (v • n) (n x n) и объясните, почему
последний член равен нулю. Тогда получим:
2 Агеа(Г') n = v х w - (w • n) (v x n) + (v • n) (w x n).
4. Умножьте скалярно обе части предыдущего уравнения на вектор п и покажите, что два послед-
них члена исчезают, в результате чего получим 2 Агеа(Т') = v х w • п = 2Агеа (Т) m • п, что и тре-
бовалось доказать.
5. Докажите, что предыдущий результат обобщается на площадь любого плоского полигона Р и
площадь его проекции Р'.
6. Исходя из того, что скалярное произведение пропорционально косинусу угла, докажите, что
Area (Г') = Агеа(Т’) cos(0), и найдите выражение для угла ф.
7. Докажите, что площади Ах, Ау, Аг, определенные выше, равны соответственно Ктх, Кту, Ктг, где
К — некоторая константа. Отсюда следует, что площади Ах, Ау, Аг пропорциональны тх, ту, тг.
Б. Теперь, чтобы найти вектор т, нужно просто вычислить вектор (Ах, Ау, Аг) и нормировать его к
единичной длине. Далее мы покажем, как вычислить площадь проекции полигона Р из равен-
ства (6.50) на плоскость ху, непосредственно используя вершины полигона Р. Две другие спрое-
цированные площади находятся аналогично.
Каждая трехмерная вершина Р. = (х, yt, г) проецируется на плоскость ху как V. = (х., уг). На
рис. 6.69 приведен пример спроецированного полигона Д'. Каждое ребро полигона Д' определя-
ет трапециевидную область, лежащую между этим ребром и осью х.
8. Покажите, что площадь этой трапеции равна произведению длины ее основания на высоту сред-
ней точки ребра. Например, площадь Ао на рисунке равна Ао = О,5(хо - х,) (г/0 + г/1). Эта величина
отрицательна, если х0 лежит левее хр и положительна в противном случае. Применим эту фор-
мулу к остальным ребрам. Тогда для i-ro ребра имеем:
где next(i) равно 0 при i = N- 1 и равно i + 1 в остальных случаях.
416
Глава 6. Моделирование поверхностей полигональными сетками
Рис. 6.69. Вычисление площади полигона
9. Докажите, что если два смежных ребра полигона коллинеарны (что обратит их векторное про-
изведение в нуль), то площадь, находящаяся между этими ребрами, по-прежнему вычисляется
правильно.
10. Докажите, что А. равно либо площади полигона, либо этой площади со знаком минус.
Теперь рассмотрим вопрос, какое из двух основных направлений вектора m указывает вовнутрь.
Иначе говоря, если вы поворачиваете пальцы правой руки вокруг вершин полигона, двигаясь от
Ро к Рр затем к Р2 и т. д. (то есть в направлении стрелки на рис. 6.70), то куда указывает вектор
m — вдоль вашего большого пальца или в противоположном направлении?
11. Докажите, что вектор m действительно направлен так, как показано на рис. 6.70. Таким обра-
зом, для сетки, у которой внешняя и внутренняя стороны четко определены, можно утверждать,
что вектор m является «внешней» нормалью, при условии, что вершины пронумерованы против
часовой стрелки, если смотреть снаружи.
Тематическое задание 6.3. Призма
Уровень сложности III.
Напишите приложение, позволяющее пользователю задавать полигональное основание призмы с
помощью мыши. Затем эта программа должна создавать списки вершин, нормалей и граней для этой
призмы и отображать последнюю на дисплее.
Рисунок 6.71, а показывает «область рисования» пользователя — прямоугольник на экране. Пользо-
ватель задает мышью последовательность точек внутри этого прямоугольника, прерывая этот процесс
нажатием правой кнопки мыши.
В трехмерном пространстве область рисования считается единичным квадратом, лежащим в плос-
кости ху, как показано на рис. 6.71, б, а основание призмы находится внутри этого квадрата. Так уста-
6.7. Тематические задания
417
навливается размер основания в трехмерном «мире». Призма представляет собой полигон основания,
протянутый (экструдированный) на единичное расстояние вдоль оси z. Выполните эту программу для
нескольких призм, вводимых пользователем. Посмотрите, правильно ли ваша реализация OpenGL рису-
ет невыпуклые полигоны основания.
Рис. 6.71. Разработка и построение сетки для призмы
Тематическое задание 6.4. Совокупность призм
и экструдированные полосы из четырехугольников
Уровень сложности III.
Напишите две подпрограммы, описанные в разделе «Совокупности экструзивных призм: „кирпич-
ная кладка"», которые создают сетки для совокупности призм и для экструдированной полосы из четы-
рехугольников (extruded quad-strip):
void Mesh:: makePrismArray(...):
void Mesh:: makeExtrudedQuadStrip(...):
1. Совокупности призм. Выберите подходящий тип данных для представления совокупности
призм. Заметим, что подпрограмма makePrismArrayO аналогична подпрограмме, формирующей
сетку для единичной призмы. Выполните эту подпрограмму хотя бы для печатных букв К и IV.
(Если хотите, то сделайте еще букву D.)
2. Экструзивные полосы из четырехугольников, используемые для создания труб. Процесс по-
строения списков вершин, нормалей и граней сетки фактически сводится к правильной обра-
ботке множества индексов этих массивов. Для облегчения разработки подпрограммы, осуще-
ствляющей это, в качестве основания рассмотрим полосу из четырехугольников, описываемую
своими вершинами с помощью равенства (6.9):
quad-strip = {р0,рР...,рм^}.
Здесь Р; = (х., у,, 0) лежит в плоскости ху, как показано на рис. 6.72, а. После экструзии каждая после-
дующая пара вершин образует «перетяжку» («waist») трубки, как показано на рис. 6.72, б. Трубка со-
стоит из num = М/2 - 1 сегментов.
Нулевая перетяжка определяется вершинами р0, р(, р, + d, р0 + d, где d — вектор экструзии. Эти вер-
шины добавляются в список вершин следующим образом:
pt[4i] - p2l. pt[4i + 1] - р21<1.
pt[4i + 2] = р21Ч + d. pt[4i + 3] = р2( + d
где i = 0,..., num, как показано на рис. 6.72, б.
Теперь возьмемся за список граней. Вначале добавим все «внешние стенки» каждого сегмента труб-
ки. Затем добавляем «концевые стенки» (то есть первая концевая стенка использует вершины первой
14 Ф. Хилл
418
Глава 6. Моделирование поверхностей полигональными сетками
перетяжки). У каждого из num сегментов имеется четыре стенки. Для каждой стенки в список вносятся
четыре вершины в порядке против часовой стрелки, если смотреть с внешней стороны. В порядке сле-
дования индексов имеются закономерности, однако они сложны. Проверьте, что следующие индексы
вершин правильно описывают каждую из четырех стенок k-ro сегмента: вершины j-й стенки k-ro сег-
мента имеют индексы iQ, i(, i2, i3, где
i0-4A+y,
i1-i0 + 4,
i3 - ik + (j + 3) mod4,
i2-i3 + 4>
дляА-0,1,...,питиу -0,1,2,3.
Чему равны индексы двух концевых граней трубки?
Рис 6.72. Построение сетки на базе полосы из четырехугольников: а) полоса из четырехугольников
в плоскости ху; б) четыре экструзивных отрезка
Каждая грань имеет нормаль, определяемую по методу Ньюэлла, и ее нетрудно вычислить, когда
индексы вершин помещаются в список граней. Все нормали вершин одной грани используют один и
тот же нормальный вектор: face[L].nornrindex = {L, L, L, L}, для каждого L.
Поэкспериментируйте с подпрограммой makeExtrudedQuadStripO, моделируя и рисуя арки вроде той,
которая показана на рис. 6.31, а также несколько печатных букв, в которых в качестве основания ис-
пользуются полосы четырехугольников.
Тематическое задание 6.5. Трубки и змейки на базе
параметрической кривой
Уровень сложности III.
Напишите и протестируйте подпрограмму:
void Mesh:: makeTube(Point2 Р[], int numPts. float t[], int numTimes)
которая строит плоскогранные сетки путем нанизывания полигона с вершинами Ро, Pt.PN_t на хреб-
товую кривую C(t). Перетяжки получающейся трубки формируются на хребте при дискретных значе-
ниях параметра t0, t,,..., tM_{, и в каждой точке C(t.) строится базис Френе. Функция C(t) «зашита» в код
программы как формула, а ее производные формируются численно.
Поэкспериментируйте со своей подпрограммой, нанизывая на хребет полигоны из примера 3.6.3,
содержащие внутри себя линию, скачущую взад-вперед между двумя концентрическими окружностя-
ми. В качестве хребтовых кривых испытайте по меньшей .мере спираль и фигуру Лиссажу.
6.7. Тематические задания
419
Тематическое задание 6.6. Построение поверхностей вращения
с дискретными шагами
Уровень сложности III.
Напишите приложение, которое позволит пользователю задавать мышью «профиль» объекта, как
показано на рис. 6.73. Затем эта программа должна создавать сетку для поверхности вращения и рисо-
вать эту сетку. Кроме того, программа должна записывать данные по сетке в файл в формате, описан-
ном в тематическом задании 6.1.
Рис. 6.73. Проектирование профиля для поверхности вращения
На рис. 6.73 показана «область рисования» пользователя, представляющая собой квадрат на экране.
Пользователь отмечает мышью последовательность точек внутри этого квадрата. В трехмерном про-
странстве этому квадрату соответствует единичный квадрат, лежащий в плоскости ху. Это устанавли-
вает размер профиля в трехмерном «мире». Поверхность вращения формируется при поворачивании
профиля вокруг оси z с числом шагов, определяемым пользователем.
Прогоните свою программу для нескольких поверхностей вращения, вводимых пользователем.
Тематическое задание 6.7. Списки ребер и каркасные модели
Уровень сложности II.
Каркасный вариант сетки можно визуализировать, проводя прямую линию на месте каждого ребра
сетки. Напишите подпрограмму void Mesh:: drawEdges(void), которая осуществляет это для любой за-
данной сетки. Подпрограмма должна обходить каждую грань, соединяя прямой линией соседние вер-
шины. При этом каждая прямая рисуется дважды. (Почему?) В условиях дефицита времени подобная
неэффективность может оказаться неприемлемой. В этом случае можно построить список ребер (edge
list), содержащий каждую вершину сетки только один раз. Такой список ребер представляет собой мас-
сив из пар индексов, где два индекса обозначают две концевые точки каждого ребра. Опишите алго-
ритм построения списка ребер для произвольной сетки. Такой алгоритм обходит каждую грань сетки,
отмечая каждое проходимое ребро, однако в список ребер оно будет добавлено только в том случае, если
его там еще нет.
Отметим, что обычно невозможно построить список граней по списку ребер и списку вершин. Рису-
нок 6.74 являет классический пример этого. Исходя из одного списка ребер, невозможно сказать, где
находятся грани. Даже каркасная модель куба может представлять собой или закрытую, или открытую
коробку. Следовательно, список граней содержит больше информации, нежели список ребер.
Рис. 6.74. Неоднозначный объект
420
Глава 6. Моделирование поверхностей полигональными сетками
Тематическое задание 6.8. Сводчатые потолки
Уровень сложности III.
Многие классические здания имеют куполовидные потолки или крыши в форме свода (vault).
На рис. 6.75, <з приведен «сомкнутый свод», построенный на квадратном основании. Четыре «переборки»,
каждая из которых является линейчатой поверхностью, натянуты на дискретные «шаги» круговой развертки
некоторой кривой и встречаются в вершине. Форма арки представляет собой «гусек» (ogee), приведен-
ный на рис. 3.70. На рис. 6.75, б изображен сомкнутый свод, построенный на восьмиугольнике и имеющий
восемь стенок. Эта арка является стрельчатой аркой, показанной на рис. 3.69. Напишите функцию, ко-
торая создает каркасную модель сводчатых куполов, построенных на квадрате и на октагоне.
Рис. 6.75. Примеры сводчатых потолков
Тематическое задание 6.9.0 Платоновых телах
Уровень сложности II.
Создайте файлы (в формате, описанном в тематическом задании 6.1) для каждого Платонова тела.
Поэкспериментируйте с чтением каждого файла в приложение и с рисованием соответствующего объекта.
Тематическое задание 6.10. Об Архимедовых телах
Уровень сложности II.
Изображения всех 13 Архимедовых тел можно найти во многих источниках (например, [Kappraff, 121]
и [Wenninger, 211]). Каждое Архимедово тело может быть сформировано посредством усечения одного
из Платоновых тел, как это описано в разделе «Другие любопытные многогранники». Создайте файлы
(в формате, описанном в тематическом задании 6.3) для каждого из следующих полиэдров:
О бакибол;
О усеченный куб;
О кубооктаэдр (cuboctahedron) — усеченный куб, новые вершины которого получены из середин
его ребер.
Проверьте полученные файлы путем чтения каждого объекта в приложение и рисования прочитан-
ного объекта.
Тематическое задание 6.11. Алгебраическая форма
поверхностей второго порядка
Уровень сложности I.
Неявные уравнения для поверхностей второго порядка можно записать в компактной и полез-
ной матричной форме. Например, неявная форма F(x, у, z) для базовой сферы имеет вид: х2 + у2 + г2 - 1.
Данное уравнение может быть записано в виде квадратичной формы (quadratic form):
6.7. Тематические задания
421
или более компактно, с использованием однородного представления точки (х, у, z) в форме Рг= (х, у, z, 1):
E(x,z/,z) = Pr/?sphereP, (6.52)
где Psphcre — матрица четыре на четыре, приведенная в равенстве (6.51). Если функция F равна нулю, то
точка (х, у, z) находится на эллипсоиде. Неявные формы для других квадрик имеют такой же вид; раз-
личаются только матрицы R. Например, определяющие матрицы для двуполостного гиперболоида и
для эллиптического параболоида имеют следующий вид:
'1 0 0 0' '10 0 o'
0 10 0
0-100
^hyperboloids 0 0-10 • 7? = * ^ellipticParab 0 0 0 (6.53)
0 0 0 -1, .0 0 -i °.
О Какой вид имеют матрицы для трех остальных форм?
Теперь вспомним из раздела «Влияние аффинного преобразования», что когда аффинное преоб-
разование с матрицей М применяется к поверхности с неявной функцией F(P), неявная функция
преобразованной поверхности равна F(M~lP).
О Покажите, что после операции преобразования квадрики ее неявная функция становится равной
С(Р) = (М‘Р)ГР(М*1Р), после чего ее нетрудно преобразовать (см. приложение Б) к виду
С(Р) = Р'(М~ХКМ~Х)Р. Таким образом, преобразованная поверхность также является поверхнос-
тью второго порядка с другой определяющей матрицей, которая зависит как от исходного вида
квадрики, так и от произведенного преобразования.
Например, для того чтобы превратить базовую сферу в эллипсоид, простирающийся по х от -а
до а, по у от -Ь до b, по z от -с до с, достаточно применить матрицу масштабирования:
'а О О О'
О b О О
М =
О 0 с О
? 0 0 U
Q Найдите обратную матрицу ЛР1 и докажите, что матрица эллипсоида равна
2 0 0 0
a
0 1 0 0
M~TRM~' = b2
0 0 1 2 0
c
0 0 0 1
Напишите неявную форму для эллипсоида.
422
Глава 6. Моделирование поверхностей полигональными сетками
О Найдите определяющую матрицу для эллиптического конуса после того, как он масштабирован
с множителем 2 в направлении х и с множителем 3 в направлении у, а затем повернут на 30° во-
круг оси у.
О Покажите, что матрица R в неявной функции F(Р) = PTRP для поверхности второго порядка все-
гда может быть сделана симметричной. (Подсказка. Запишите матрицу R в виде суммы симмет-
ричной и антисимметричной частей и докажите, что антисимметричная часть не оказывает ни-
какого влияния на форму этой поверхности.)
Тематическое задание 6.12. Сцены с супеквадриками
Уровень сложности III.
Напишите приложение, которое может создавать базовые суперквадратичные поверхности с зада-
ваемыми пользователем множителями выпуклости и помещать на сцену эти суперквадрики с различ-
ными размерами и различной ориентацией.
Тематическое задание 6.13. Рисование гладких
параметрических поверхностей
Уровень сложности III.
Разработайте функцию, которая создает каркасную модель произвольной, удобной для анализа глад-
кой поверхности, заданной в виде Р(и, v) = (Х(и, о), У(и, о), Z(u, о)). Эта функция задает выборочные
точки поверхности в numVal uesU равноотстоящих значениях и между uMi п и иМах, а также в numVal uesV зна-
чениях о между vMin и vMax. Функции Х( ), У( ), Z( ), а также функции компонентов нормали должны
быть «зашиты» в подпрограмму, которая строит на базе этих выборочных значений список вершин и
список нормалей и создает список граней, состоящий из четырехугольников. Единственная трудность
заключается в том, чтобы правильно писать индексы вершин для каждой грани в списке граней. Может
оказаться полезным скелет программы, приведенный в листинге 6.4.
Листинг 6.4. Скелет подпрограммы создания каркасной модели для гладкой поверхности
void Mesh:: makeSurfaceMeshО
{
int 1. j. numValsU - 40. numValsV -40:
// set these
// задаем эти величины
double u, v. uMin - -10.0. vMin --10.0. uMax -10.0. vMax -10.0;
double delU -(uMax - uMin)/(numValsU - 1);
double delV -(vMax - vMin)/(numValsV - 1):
numVerts - numValsU * numValsV + 1:
// total # of vertices
// общее количество вершин
numFaces - (numValsU - 1) * (numValsV - 1):
// #of faces
// количество граней
numNorms - numVerts:
// for smooth shading -one normal per vertex
// для гладкого закрашивания - одна нормаль на вершину
pt - new Point3[numVerts]; assertCpt !- NULL):
// make space
// выделяем пространство
face -new Face[numFaces]; assert(face !- NULL);
norm -new Vector3[numNorms]: assert(norm !- NULL):
6.7. Тематические задания
423
ford - 0, u - uMin; 1 < numValsU; i++, u +- delU)
for(j - 0. v - vMin; j < nutnValsV: j++. v +- delV)
{
int whichVert - i * numValsV + j:
// index of the vertex and normal
// индекс вершины и нормали
// set this vertex: use functions X.Y.and Z
// устанавливаем эту вершину: используем функции X. Y. Z
pt[whichVert].set(X(u. v). Y(u. v), Z(u. v));
// set the normal at this vertex: use functions nx.ny.nz
// задаем нормаль в этой вершине: используем функции X, Y. Z
norm[whichVert].set(nx(u. v). ny(u. v). nz(u. v)):
norma1i ze(norm[wh i chVert]):
// make quadrilateral
// создаем четырехугольник
if(i > 0 && j > 0)
// when to compute next face
// когда вычислять следующую грань
{
int whichFace - (i - 1) * (numValsV - 1) + (j - 1):
face[whichFace].vert - new Vertex!D[4];
assert(face[whichFace].vert !- NULL);
face[whichFace].nVerts - 4;
face[whichFace].vert[0].vertlndex -
11 same as norm index
// тот же самый индекс, что и у нормали
face[whichFace].vert[O].normindex - whichVert:
fасе Ewh i ch Face].ve rt Е1].ve rtIndex -
face[whichFace].vert[l].normindex - whichVert - 1:
faceEwhichFace].vertE2].vertlndex -
faceEwhichFace],vertE2].normindex - whichVert - numValsV - 1;
face[whichFace].vert[3].vertlndex -
face[whichFace].vert[3J.normindex - whichVert - numValsV;
}
}
}
Примените полученную вами функцию к задаче построения какой-либо интересной поверхности
вращения и поля высот.
Тематическое задание 6.14. Сузить, закрутить,
изогнуть и расплющить
Уровень сложности III.
Полезно иметь метод управляемого деформирования (deforming) трехмерного объекта. Например,
при анимации видно, как прыгающий резиновый мячик деформируется при ударе об пол и затем вос-
станавливает свою сферическую форму, когда подпрыгивает вновь. Или кусочек желе изгибается и дро-
жит, или флаг развевается от ветра. В таких случаях важно, чтобы эти деформации выглядели есте-
ственно, то есть подчинялись законам физики: закону сохранения массы, закону упругости и т. д.
Моделирование, базирующееся на физике (physically based modeling), которое пытается воспроизвес-
ти поведение реальных объектов под действием различных сил, является необозримым и заворажива-
ющим предметом, которому посвящены многие книги и статьи, например, [Watt, 138, Bloomenthal, 33].
424
Глава 6. Моделирование поверхностей полигональными сетками
Можно также производить чисто геометрические деформации [Вагг, 13], которые дизайнеры при-
меняют для визуального эффекта. Например, нетрудно изменять поперечное сечение (taper) объекта
вдоль оси, как показано на рис. 6.76. Это достигается масштабированием всех точек в направлениях х и
у на величины, зависящие от z, в соответствии с некоторой профильной функцией, например g(z). Та-
кая функция определяет (неаффинное) преобразование, которое можно записать в форме матрицы масш-
табирования
( g(z)
М = О
О
О О'
g(z) О
0 U
(6.54)
Если поверхность до преобразования имеет параметрическое представление Р(и, v) = (Х(и, о), У(м, о),
Z(u, v)), то его деформация, заданная равенством (6.54), преобразует его в форму:
Р\и, v) = (Х(м, v) g(Z(u, v)), Y(u, v) g(Z(u, v)), Z(u, v)). (6.55)
Рис. 6.76. Пешка до и после суживания
Для того чтобы получить рис. 6.76, вначале была создана сетка для пешки, затем каждая вершина
этой сетки (х, у, z) была преобразована в (xF, yF, z), где функция F - 1 - 0,04(z + 6). (Отметим, что эта
пешка простирается по оси z от 0 до -12.)
Еще одним полезным видом деформации является закручивание (twisting). Например, для закручи-
вания объекта вокруг оси z нужно повернуть все точки объекта вокруг этой оси на угол, зависящий от z,
используя матрицу:
M =
' cos (g(z)) sin (g(z))
—sin(g(z))
cos (g(z))
o'
0
1
(6.56)
0
0
На рис. 6.77 показана пешка после того, как к ней было применено линейно возрастающее закручи-
вание. Пешка является поверхностью вращения вокруг оси z, поэтому нет особого смысла закручивать
ее относительно этой оси. Вместо этого закручивание здесь производилось вокруг оси# с помощью фун-
кции g(z) = 0,02л |z + б|.
Примените эти деформации к нескольким каркасным моделям, в том числе к тору. Имейте в виду,
что ни для одной из деформаций вам не удастся использовать матрицу моделирования-вида OpenGL,
поскольку преобразования в данном случае не являются аффинными. Нужно преобразовывать верши-
ны из текущего списка вершин. Изгиб (bending) — это еще одна деформация, примененная Барром.
Обратитесь к его работе [Вагг, 13] и поэкспериментируйте с деформацией изгиба.
6.8. Дополнительная литература
425
Рис. 6.77. Пешка после закручивания
6.8. Дополнительная литература
Определение и создание поверхностей и монолитных тел описывается во многих книгах. В книге Род-
жерса и Адамса «Математические основы компьютерной графики» (Rogers and Adams. Mathematical
Elements for Computer Graphics [Rogers, 174]), а также в работе Фокса и Пратта «Вычислительная геометрия
для проектирования и производства» (Faux and Pratt. Computational Geometry for Design and Manufacture
[Faux, 61]) содержится блестящее введение в вопросы кривых и поверхностей. В книге Грея «Совре-
менная дифференциальная геометрия кривых и поверхностей и Mathematica» (Gray. Modem Differential
Geometry of Curves and Surfaces with Mathematica [Gray, 91]) предлагается строгое математическое описание
кривых и поверхностей различной формы, а также предлагается код пакета Mathematica для их рисования.
Книга Мортенсона «Геометрическое моделирование» (Mortenson. Geometric Modeling [Mortenson, ИЗ])
представляет собой великолепную интерпретацию объемного моделирования для автоматизированного
проектирования.
TF Трехмерный просмотр
□ Разработка инструментов для создания «камеры», воспроизводящей
изображения трехмерной сцены, и управления ею.
□ Интерактивное «пилотирование» камеры по сцене и анимация.
□ Изучение математического аппарата, описывающего различные
виды проекций.
□ Рассмотрение работы каждой операции графического конвейера
OpenGL и целей ее использования.
□ Создание мощного алгоритма отсечения для трехмерных объектов.
□ Разработка средства для получения трехмерных изображений
объектов.
Я — камера с открытым затвором, совершенно пассивная, записывающая, не думающая.
Кристофер Айшервуд (Christopher Isherwood). Берлинский дневник
В этой главе изучается трехмерная графика как с использованием OpenGL, так и без него. В разделе 7.1
«Введение» дается обзор дополнительных инструментов, необходимых для построения приложения,
обеспечивающего «пилотирование» камеры по сцене. В разделе 7.2 «Снова о камере» дано определе-
ние камеры, дающей изображения с перспективой, и показано, как создать такую камеру с помощью
OpenGL. Для описания способов управления камерой используется авиационная терминология. В этом
разделе приводятся некоторые сведения из математической теории матриц, необходимые для описа-
ния ориентации камеры. В разделе 7.3 «Встраивание камеры в программу» дано определение класса
Camera, предназначенного для инкапсуляции информации о камере и содержащего методы, создающие
и настраивающие камеру в приложении.
В разделе 7.4 «Перспективные проекции трехмерных объектов» исследуется геометрическая приро-
да перспективной проекции и применение математических средств для описания перспективы. Здесь
описывается, как включить перспективные проекции в графический конвейер — как с OpenGL, так и
без него. Для упрощения изложения вводится дополнительное свойство однородных координат. В этом
разделе также излагается мощный алгоритм отсечения, работающий в пространстве однородных коор-
динат; эффективность этого алгоритма является результатом применения к точкам нужных преобразо-
ваний до начала отсечения. Приведен код отсекателя для тех программистов, которые хотят разрабо-
тать свой собственный графический конвейер.
7.2. Снова о камере 427
В разделе 7.5 «Создание стереоизображений» показано, как создавать стереоизображения сцен с це-
лью сделать их более наглядными. В разделе 7.6 «Классификация проекций» приводится классифика-
ция различных видов проекций, используемых в изобразительном искусстве, архитектуре и технике,
а также показано, как создать в программе каждый вид проекции. Глава заканчивается рядом темати-
ческих заданий, в которых разрабатываются приложения, проверяющие изложенную методику.
7.1. Введение
Мы уже подготовились к созданию изображений сложных трехмерных объектов. Как мы уже видели в
главе 5, в OpenGL имеются инструменты для установки камеры на сцене, для проецирования этой сце-
ны в плоскость просмотра камеры, а также для передачи этой проекции в порт просмотра. Пока наша
камера производит только параллельные проекции. В главе 6 мы описали несколько классов любопыт-
ных трехмерных форм, которые могут быть использованы для моделирования нужных нам объектов
сцены, а с помощью класса Mesh мы получили возможности для рисования любых таких объектов с соот-
ветствующим закрашиванием.
Что же еще осталось сделать? Для большего реализма мы хотим создать камеру для получения пер-
спективных проекций и управлять ею. Нам также нужны методы усиления контроля над положением и
ориентацией камеры — чтобы пользователь мог «пилотировать» камеру в процессе анимации. Это, од-
нако, требует разработки более точного контроля, чем может предоставить OpenGL. Нам требуется точ-
но контролировать отображаемый объем камеры, который в случае перспективных проекций опреде-
ляется так же, как и для параллельных проекций, с помощью определенного вида матрицы. Поскольку
теперь нам потребуется более глубокое использование однородных координат, чем до сих пор, мы разбе-
рем с самого начала математику перспективных проекций и посмотрим, как она применяется в графичес-
ком конвейере OpenGL. Мы также рассмотрим, как осуществляется отсечение границами отображаемого
объема камеры, что опять^се потребует более глубоко осознанного применения однородных координат.
Таким образом, мы увидим, как проделываются все операции, от начала до конца! Наше исследование
сопровождается и основными теоретическими сведениями — для тех программистов, которым нужно
разрабатывать математическое обеспечение трехмерной графики без использования OpenGL.
7.2. Снова о камере
Это добавляет остроту зрения.
Вильям Шекспир
В главе 5 мы использовали камеру, которая осуществляет параллельные проекции. Ее отображаемый
объем — это параллелепипед, ограниченный шестью стенками, включая ближнюю плоскость и дальнюю
плоскость. Кроме этого, OpenGL поддерживает работу камеры, создающей перспективные виды трех-
мерных сцен. Во многих отношениях это похоже на камеру, использованную нами раньше, за исключе-
нием того, что ее отображаемый объем имеет другую форму.
На рис. 7.1 показан общий вид такой камеры. Она имеет глаз (eye), расположенный в некоторой
точке пространства, а ее отображаемый объем (view volume) представляет собой часть четырехуголь-
ной пирамиды, вершина которой совпадает с глазом. Раствор (opening) этой пирамиды задается углом
зрения (viewangle) 0 (см. рис. 7.1, б). Перпендикулярно к оси пирамиды определены две плоскости:
ближняя плоскость (near plane) и дальняя плоскость (far plane). Там, где эти две плоскости пересекают
пирамиду, они образуют прямоугольные окна. Эти окна имеют определенное форматное соотношение
(aspect ratio), которое может задаваться программно. OpenGL отсекает все те части сцены, которые рас-
полагаются вне отображаемого объема. Точки, лежащие внутри отображаемого объема, проециру-
ются на плоскость просмотра (viewplane) в соответствующую точку Р', как показано на рис. 7.1, в.
(В дальнейшем мы увидим, что не имеет значения, какая плоскость используется в качестве плоскости
просмотра, однако сейчас пусть она совпадает с ближней плоскостью.) При использовании перепек-
428
Глава 7. Трехмерный просмотр
тивной проекции точка Р' задается как точка пересечения прямой, соединяющей глаз с точкой Р, с плос-
костью просмотра. (Сравните это с работой параллельной проекции.) Наконец, изображение, получен-
ное в плоскости просмотра, преобразуется в порт просмотра, как показано на рис. 7.1, в, после чего оно
становится видимым на устройстве отображения.
7.2.1. Установка отображаемого объема
На рис. 7.2 показана камера в исходной позиции, когда глаз находится в начале координат, а ось пира-
миды выровнена вдоль оси 2. Глаз смотрит в сторону отрицательных значений оси 2.
В OpenGL предусмотрен простой способ программной установки отображаемого объема. Вспомним,
что форма отображаемого объема камеры записана в проекционной матрице (projection matrix), посту-
пающей в графический конвейер. Эта проекционная матрица устанавливается с помощью функции
gluPerspectiveO с четырьмя параметрами. Применяется такая последовательность:
glMatrixMode(GL_PROJECTION);
// make the projection matrix current
// делаем текущей проекционную матрицу
gl LoadldentityO:
// start with a unit matrix
// начинаем с единичной матрицы
gluPerspective(viewAngle, aspectRatio. N. F):
// load the appropriate values
// загружаем соответствующие значения
Параметр viewAngle, показанный на рисунке как угол 0, задается в градусах и определяет угол между
верхней и нижней стенками пирамиды. Параметр aspectRatio устанавливает форматное соотношение
любого окна, параллельного плоскости ху. Величина N — это расстояние от глаза до ближней плоскости,
a F — расстояние от глаза до дальней плоскости. N и F должны быть положительными. Например, вызов
gluPerspective(60.0, 1.5 , 0.3 , 50.0) устанавливает отображаемый объем с вертикальным раствором 60° и
окном с форматным соотношением 1,5. Ближняя плоскость имеет координату г = -0,3, а для дальней плос-
кости г = -50,0. Позднее мы узнаем точно, какие величины эта функция помещает в проекционную матрицу.
7.2. Снова о камере
429
7.2.2. Позиционирование и ориентирование камеры
Для того чтобы получить нужный вид сцены, передвинем камеру из исходной позиции, показанной на
рис. 7.2, и по^рнем ее в определенном направлении. Это делается посредством перемещения и поворо-
та, а эти преобразования являются частями матрицы моделирования-вида (modelview matrix), как было
показано в разделе «Рисование трехмерных сцен с применением OpenGL».
Установим позицию и ориентацию камеры в точности так, как это делалось для камеры с парал-
лельной проекцией. (Все различие между камерами с параллельной и перспективной проекциями за-
ключается в проекционной матрице, которая определяет форму отображаемого объема.) Проще всего
вновь использовать функцию gluLookAtO в такой последовательности:
glMatrixMode(GL_MODELVIEW):
// make the modelview matrix current
// делаем текущей матрицу моделирования-вида
glLoadldentityO:
// start with a unit matrix
// начинаем с единичной матрицы
gluLookAt(eye.x. eye.у, eye.z. look.x. look.y. look.z. up.x. up.y. up.z):
Как и прежде, в результате выполнения этого кода камера передвинется так, что ее глаз расположится
в точке eye и будет направлен в интересующую нас точку look. Направление «вверх» обычно задается векто-
ром up, который чаще всего равен (0,1,0). Эти параметры и весь процесс установки камеры почти цели-
ком взяты из главы 5. В этой главе мы копнем глубже, чтобы лучше увидеть процесс установки камеры
и лучше управлять им. Мы также разработаем инструменты для осуществления относительных изме-
нений в направлении камеры, таких как легкий поворот влево, наклон вверх или скольжение вперед.
Камера общего вида с произвольной ориентацией и позицией
Положение и ориентация камеры на сцене могут быть любыми. Представим себе преобразование, кото-
рое берет камеру на рис. 7.3, перемещает ее куда-нибудь в пространстве, а затем поворачивает, чтобы
нацелить в желаемом направлении. Необходимо найти способ точного описания такого преобразова-
ния, а также определить вид результирующей матрицы моделирования-вида.
Полезно будет прикрепить явную систему координат прямо к камере, как предложено на рис. 7.3.
У этой системы координат имеется начало, расположенное в точке глаза, и три оси, обозначаемые буква-
ми и, v, п, что определяет их ориентацию. Оси указывают в направлениях, задаваемых векторами u, V, п,
как показано на рисунке. Поскольку по умолчанию камера смотрит в сторону отрицательных значений г,
то считается, что камера смотрит и в сторону отрицательных значений оси п, то есть в направлении -п.
Направление и показывает «вправо» от камеры, а направление v — «вверх». Давайте думать об осях и, v,
п как о двойниках осей х, у, z с рис. 7.2, которые перемещаются и поворачиваются при установке камеры
в нужную позицию.
430
Глава 7. Трехмерный просмотр
Рис. 7.3. Прикрепление к камере системы координат
Положение камеры описывается легко, чего нельзя сказать об ориентации. Поможет задание ориен-
тации в авиационных терминах — курс (heading), тангаж (pitch), крен (roll) и рыскание (yaw), как пред-
лагается на рис. 7.4. Курс (heading) аэроплана — это то направление, куда указывает его головная часть.
Тангаж аэроплана — это угол, который его продольная ось (идущая от хвоста к носу и имеющая направ-
ление —п) составляет с горизонтальной плоскостью. Аэроплан кренится, поворачиваясь вокруг своей
продольной оси; а крен — это величина поворота относительно горизонтали. Кроме того, мы будем исполь-
зовать термины азимут (azimuth) и пеленг (bearing). Для нахождения курса и тангажа, определяемых
вектором п, нужно просто выразить -п в сферических координатах, как показано на рис. 7.5 (обзор сфери-
ческих координат приведен в приложении Б). Долгота и широта вектора -п задаются соответственно
углами 0 и ф. Курс аэроплана определяется долготой вектора -п, а тангаж — широтой вектора -п. Форму-
лы для крена, тангажа и курса в терминах векторов и и п выводятся в упражнениях в конце раздела.
Рис 7.4. Ориентация самолета по отношению к «миру»: а) тангаж; б) крен; в) рыскание
Английские слова тангаж (pitch) и крен (roll) являются одновременно существительными и глаголами.
Если их употреблять как глаголы, то они описывают изменение ориентации аэроплана. Можно сказать,
что аэроплан «тангажирует вверх», если он увеличивает тангаж (поворот вокруг оси и); словом «кренит-
ся» можно описать поворот аэроплана вокруг оси п. Общеупотребительным термином для изменения
курса является рыскание: чтобы рыскать влево или вправо, аэроплан поворачивается вокруг оси v1.
Рис. 7.5. Курс и тангаж самолета
1 На рис. 7.4, в на конце вертикальной оси должны находиться стрелка и буква V. — Примеч. перев.
7.2. Снова о камере
431
Рис. 7.6. Различные ориентации камеры: а) ориентация камеры; б) с креном; в) без крена
Те же самые рассуждения можно применить и к камере. На рис. 7.6, а показана камера с такой же
прикрепленной к ней системой координат: у нее имеются и-, &-, п-оси, ее начало координат находится
в позиции глаза. У камеры на рис. 7.6, б крен отличен от нуля, а у камеры на рис. 7.6, в крен нулевой.
Обычно камеру устанавливают с нулевым креном и называют ее камерой «без крена» («по-roll»). Ось и
камеры без крена является горизонтальной — иначе говоря, она перпендикулярна оси у «мировых»
координат. Отметим, что камера без крена может по-прежнему иметь произвольное направление п,
поэтому она может иметь любые тангаж и курс.
Как же управлять креном, тангажом и курсом камеры? Функция gluLookAtO удобна для установки
исходной камеры, поскольку обычно у нас имеются четкие представления о выборе eye и look. Труднее
зрительно представить выбор вектора up для получения определенного крена и еще более трудно осу-
ществлять относительные настройки для камеры в дальнейшем, используя только gluLookAtO. (Функ-
ция gluLookAtO работает с декартовыми координатами, в то время как ориентация имеет дело с углами
и поворотами вокруг осей.) В OpenGL нет прямого доступа к направлениям u, V, п, поэтому мы своими
силами введем их в программу. Это значительно упростит описание и настройку камеры.
Что делает gluLookAt(): некоторое математическое обоснование
Какими же будут направления u, v, п при выполнении функции gluLookAtO для заданных значений eye,
look и up? Давайте разберемся, что делает gluLookAtO и почему она делает именно это.
Как показано на рис. 7.7, а, нам известны положения eye и look, а также направление up. Тогда сразу
ясно, что вектор п должен быть параллелен вектору eye-look, как показано на рис. 7.7, б, поэтому уста-
навливаем п = eye - look (нормирование п и других векторов мы можем произвести позднее.)
Вверх
Взгляд
Рис. 7.7. Построение векторов u, v и п
Теперь нам нужно найти векторы и и V, которые перпендикулярны вектору п и друг другу. Направ-
ление и указывает «от» камеры, поэтому вполне естественно сделать его перпендикулярным к векто-
ру up, который пользователь назначил направлением «вверх». Такое допущение делается в функции
gluLookAtO в любом случае, поэтому направление и перпендикулярно к п и к up. Верный способ постро-
ить вектор, перпендикулярный к двум заданным, — это вычислить их векторное произведение, поэтому
положим u = up х п. (Пользователь не должен выбирать направление up параллельным п, поскольку в
таком случае длина вектора и будет равна нулю. Почему?) Мы выбираем u = up х п, а не n х up, чтобы
вектор и указывал «вправо» при взгляде по направлению -п.
432
Глава 7. Трехмерный просмотр
Имея векторы и и п, легко построить вектор v: он должен быть перпендикулярен векторам и и п,
поэтому снова используем векторное произведение: v =пх и. Заметим, что вектор V, как правило, не
расположен на одной линии с вектором up: вектор v должен быть перпендикулярен к п, поскольку
пользователь использует up для указания «направления вверх», и единственное используемое свойство
вектора up — то, что он векторно перемножается с п.
Резюмируем эти рассуждения. По заданным величинам eye, look, up мы назначаем:
п - eye - look,
u - up х n, (7.1)
V = n X u,
после чего нормализуем все три вектора к единичной длине.
Обратите внимание, как эта схема работает в обычном случае, когда up = (0,1,0). Убедитесь, что
в этом случае и = (пг, 0, -пх), a v = (.-пхпу> п* + п2г, -пп^). Заметим, что у-компонент вектора и действи-
тельно равен нулю, то есть он «горизонтален». Кроме того, у-компонент вектора v положителен, то есть
он направлен более или менее «вверх».
Пример 7.2.1. Нахождение системы координат камеры
Рассмотрим камеру с eye = (4,4,4), смотрящую «вниз» на точку look = (0,1, 0). Пусть вектор up имеет
координаты (0, 1, 0). Найдите векторы u, V, п. Повторите это для up = (2,1,0).
Решение
Из уравнения (7.1) находим векторы и = (4,0, -4), v = (-12,32, -12), п = (4,3,4), каждый из которых
легко привести к единичной длине. (Начертите все векторы.) Отметим, что вектор и действительно гори-
зонтален. Проверьте, что все эти векторы взаимно перпендикулярны. Для случая up = (2,1,0) (попробуй-
те до арифметических вычислений мысленно представить себе эту камеру) и - (4, -8,2), v = (38,8, -44),
п = (4,3,4). Начертите эти векторы. Проверьте, что все векторы взаимно перпендикулярны.
Пример 7.2.2. Разработка пространственного воображения с помощью камер
Чтобы помочь развитию пространственного воображения (геометрической интуиции) при установке
камеры, на рис. 7.8 приведены две камеры, каждая из которых изображена как система координат с
отображаемым объемом. Эти камеры расположены над мировой системой координат, которая для на-
глядности нарисована с сеткой в плоскости xz. Отображаемый объем обеих камер имеет форматное со-
отношение 2. Одна камера установлена с eye = (-2,2,0), look = (0,0,0), up = (0,1,0). Для этой камеры из
формулы (7.1) находим п = (-2,2,0), и = (0,0,2), v = (4,4,0). Все эти векторы, а также вектор up пока-
заны на рисунке. У второй камеры eye = (2,2,0), look = (0,0,0), up = (0,0,1). В этом случае и - (-2,2,0),
v = (0, 0, 8). Здесь направление вектора v параллельно up. Отметим, что эта камера лежит «на боку».
(Проверьте, что все эти векторы сориентированы в нужных направлениях.)
В заключение посмотрим, какие величины функция gluLookAtO заносит в матрицу моделирования-
вида. Из главы 5 мы знаем, что матрица моделирования-вида является произведением двух матриц:
матрицы V, ответственной за преобразование точек из мировых координат в координаты камеры, и мат-
рицы М, осуществляющей все преобразования моделирования, применяемые к этим точкам. Функция
gluLookAtO строит матрицу Vи умножает ее справа на текущую матрицу. Поскольку задача матрицы V
заключается в преобразовании мировых координат в координаты камеры, она должна преобразовывать
систему координат камеры в исходную позицию камеры, как показано на рис. 7.9. Это означает, что
матрица V должна преобразовать точку eye в начало координат, вектор и в вектор i, v в j, п в к. Имеется
несколько способов получения матрицы V, однако проще убедиться, что подойдет такая матрица:
'ux uy иг dx'
V= . (7.2)
«х ПУ Пг dx
0 0 0 0 ,
7.2. Снова о камере
433
Здесь (dx, dj d2) - (-eye • u, -eye • v, -eye n)‘. Проверьте, что
как и должно быть, где точка eye расширена до однородных координат. Проверьте также, что
и что матрица Vпреобразует вектор v в (0,1,0,0)г, а вектор п — в (0,0,1,0)г. Матрица Vсоздается функ-
цией gluLookAtO и умножает ее справа на текущую матрицу. У нас будет возможность произвести такую
операцию позднее, когда мы встроим в программу нашу собственную камеру.
Рис. 7.8. Два примера установки камеры
Рис. 7.9. Преобразования, осуществляемые функцией gluLookAtO
1 Ввиду того, что нельзя скалярно перемножать точку и вектор, вместо точки eye нужно взять вектор eye - (0,0,0).
434
Глава 7. Трехмерный просмотр
Практические упражнения
7.2.1. Нахождение крена, тангажа и курса по заданным векторам u, v, п
Пусть камера задана системой координат, образованной ортами u, V, п. Курс и тангаж камеры определя-
ются путем выражения вектора -п в сферических координатах. Используя приложение Б, покажите, что
курс = arctg(-/22, -пх),
а
тангаж = siir^-fQ.
Далее, крен камеры — это угол между осью и и горизонтом. Для определения крена построим гори-
зонтальный вектор Ь, лежащий в плоскости uv. Покажите, что b = j х п удовлетворяет этим требовани-
ям. Кроме того, покажите, что угол между векторами b и и определяется формулой:
крен = cos
ихпг -игпх
пгх + п2у
7.2.2. Использование up дает наилучшее приближение к up вектором v
Покажите, что использование up из уравнения (7.1) для задания векторов и и v эквивалентно тому, что
вектор v — ближайший к up вектор из всех, перпендикулярных к вектору п. Выполните следующие этапы:
О Покажите, что v = nx (up х п).
О Используйте следующее свойство двойного векторного произведения:
а х (Ь • с) = (а • с) b - (а • Ь) с.
О Покажите, что тогда вектор v является проекцией вектора up на плоскость с нормалью п (см. гла-
ву 4), откуда следует, что v — ближайший к up вектор в этой плоскости.
7.3. Встраивание камеры в программу
Хорошо сказать о предмете столь же интересно и столь же трудно, как нарисовать его.
Винсент ван Гог (Vincent van Gogh)
Для того чтобы осуществлять наилучший контроль за передвижениями камеры, создадим в программе
собственную камеру и будем управлять ею. После каждого изменения, произведенного с этой камерой,
она сама «сообщает» OpenGL, что она теперь собой представляет.
Мы создаем класс Camera, который «знает», как делать все то, что делает камера. Сделать это очень
просто, и выигрыш получается значительный. Создадим в программе объект класса Camera, например
cam, и настроим его с помощью таких функций:
cam.set(eye. look, up);
// initialize the camera
// инициализируем камеру
cam.slide(-l. 0. -2):
// slide the camera forward and to the left
// перемещаем камеру вперед и вверх
cam.roll(30);
//roll it through 30°
// накреняем камеру на 30е
cam.yaw(20);
// yaw it through 20°
// рыскаем камерой на 20°
etc.
// и так далее
7.3. Встраивание камеры в программу
435
Листинг 7.1. Определение класса Camera
class Camera{
private:
Points eye:
Vectors u. v. n:
double viewAngle. aspect. nearDist.yfarDist:
view volume shape
форма отображаемого обьема
void setModelViewMatrixO:
tell OpenGL where the camera is
сообщаем OpenGL. где находится камера
//
//
//
//
public:
CameraO:
// default constructor
// конструктор по умолчанию
void set(Points eye. Points look. Vectors up):
// like gluLookAtO
// подобно gluLookAtO
void roll(float angle):
// roll it
// накреняем камеру
void pitch(float angle):
// increase the pitch
// увеличиваем тангаж камеры
void yaw(float angle):
// yaw it
// рыскаем камерой
void slide(float delU. float delV. float delN):
// slide it
// передвигаем камеру (скользим)
void setShape(float vAng. float asp. float nearD, float farD);
}:
В листинге 7.1 приведено основное определение класса Camera. В этом определении содержатся поля
для точки eye и направлений u, v, n. Point3 и Vector3 — это базовые типы данных, определенные в прило-
жении В. Кроме того, там имеются поля для описания формы отображаемого объема: viewAngle, aspect,
nearDist, farDist.
Листинг 7.2. Служебные подпрограммы set() и setModelViewMatrixO
void Camera :: setModelViewMatrix(void)
// load model view matrix with existing camera values
// загружаем матрицу моделирования-вида
// существующими для камеры величинами
float m[16 ]:
Vectors eVec(eye.x. eye.у, eye.z):
// a vector version of eye
// векторная форма eye
m[0] - u.x: m[4] - u.y; m[8] - u.z; m[12] --eVec.dot(u);
m[l] - v.x: m[5] - v.y: m[9] - v.z: m[13] --eVec.dot(v):
m[2] - n.x: m[6] - n.y: m[10] - n.z; m[14] eVec.dot(n):
m[3] - 0: m[7] - 0: m[ll] “ 0: m[15] - 1.0;
продолжение^
436
Глава 7. Трехмерный просмотр
Листинг 7.2 (продолжение)
glMatrixMode(GL_MODELVIEW):
glLoadMatrixf(m):
// load OpenGL’s model view matrix
// загружаем матрицу моделирования-вида OpenGL
}
void Camera:: set(Point3 Eye. Point3 look. Vector3 up)
{
// create a model view matrix and send it to OpenGL
// создаем матрицу моделирования-вида
// и отправляем ее в OpenGL
eye.set(Eye):
// store the given eye position
// записываем полученную позицию eye
n.set(eye.x - look.x. eye.у - look.у, eye.z - look.z):
//make n
// устанавливаем n
u.set(up.cross(n));
// make u -up X n
// устанавливаем u -up X n
n.normalizeO; u. normalized:
//make them unit length
// нормируем n и u
v.set(n.cross(u)):
// make v =n X u
// устанавливаем v =n X u
setModelV i ewMatri x():
// tell OpenGL
// сообщаем OpenGL
}
Служебная подпрограмма setModelViewMatrixO связывает матрицу моделирования-вида с OpenGL.
Она используется только функциями-членами данного класса и ее нужно вызывать после каждого из-
менения в положении или ориентации камеры. Листинг 7.2 показывает возможную реализацию этой
подпрограммы. Она вычисляет матрицу (7.2) на базе текущих значений eye, u, v, п и загружает ее непо-
средственно в матрицу моделирования-вида с помощью функции glLoadMatrixfO.
Метод set() работает подобно gluLookAtO: он использует значения eye, look, up для вычисления век-
торов u, v, п по формулам (7.1). Затем метод set() помещает эту информацию в поля камеры и сообща-
ет ее в OpenGL.
Подпрограмма setShapeO еще проще: она помещает значения своих четырех аргументов в соот-
ветствующие поля камеры и после этого вызывает подпрограмму gluPerspective(viewangle, aspect.
nearDist, farDist) (наряду c glMatrixMode(GL_PROJECTION) и glLoadldentityO) для установки проекцион-
ной матрицы.
Главные функции камеры — это slideO, roll О, yaw(), pitchO, которые выполняют относительные
изменения положения и ориентации камеры. (Главная причина, по которой в структуре данных класса
Camera отводятся поля для eye, u, v, п, заключается в том, чтобы иметь запись «текущей» камеры и затем
изменять ее.) В следующем разделе мы рассмотрим работу методов камеры.
7.3.1. «Пилотирование» камеры
Пользователь интерактивно «пилотирует» камеру по сцене, нажимая клавиши или кнопки мыши. На-
пример, нажатие клавиши «ы» могло бы вызвать скольжение камеры «вверх», нажатие «г/» — рыскание
влево, а нажатие «/» — скольжение вперед. Пользователь может посмотреть, как выглядит сцена с одной
7.3. Встраивание камеры в программу
437
точки наблюдения, затем изменить положение камеры на лучший наблюдательный пункт и направле-
ние и получить новое изображение. Или же пользователь может «пилотировать» камеру по сцене, де-
лая различные снимки. Если эти кадры сохранить и затем просмотреть в быстром темпе, то получится
анимация камеры, летающей по сцене.
Всего существует шесть степеней свободы для настройки камеры: она может «скользить» («slide») в
трех направлениях и может быть повернута вокруг любой из трех координатных осей. Сначала разра-
ботаем функцию slideO.
Скольжение камеры
Скольжение камеры означает ее перемещение без поворотов вдоль одной из ее собственных осей —
то есть в направлении u, v или п. Поскольку камера смотрит в сторону отрицательной части оси п, дви-
жение вдоль оси п означает «вперед» или «назад». Аналогично движение вдоль оси и означает «влево»
или «вправо», а вдоль оси v — «вверх» или «вниз».
Перемещать камеру вдоль одной из ее осей просто. Для того чтобы переместить ее на расстояние D
вдоль оси и, нужно положить eye равным eye + Du. Для удобства можно объединить три возможных
перемещения в одной функции: siideCdelU. delV. delN) перемещает камеру на delU вдоль оси и, на delV
вдоль оси v, на del N вдоль оси п. Код этой функции выглядит так:
void Camera:: slide(float delU. float delV, float delN)
{
eye.x +- delU * u.x + delV * v.x + delN * n.x;
eye.у +- delU * u.y + delV * v.y + delN * n.y;
eye.z +- delU * u.z + delV * v.z + delN * n.z:
setModelViewMatrix();
Поворот камеры
хотим иметь возможность накренять (roll) камеру, тангажировать (pitch) или рыскать (yaw) ею.
Каждая из этих операций предполагает поворот камеры вокруг одной из ее собственных осей. Мы рас-
смотрим подробно операцию крена; два других вида поворота аналогичны.
Накренить камеру означает повернуть ее вокруг ее собственной оси п. Это подразумевает, что долж-
ны быть повернуты оба направления — и и V, как показано на рис. 7.10. Образуются две новых оси и' и v',
которые лежат в той же плоскости, что и и v, однако они повернуты на угол а радиан.
►
Рис. 7.10. Крен камеры
Итак, нам требуется только представить векторы и' и v' в виде линейных комбинаций и и v:
и' - cos(a) и + sin(a) v;
Vх = -sin(a) и + cos(a) v;
(7.3)
438
Глава 7. Трехмерный просмотр
Теперь новые оси и' и v' займут в камере место старых осей — соответственно и и V. Реализовать
функцию крена несложно. Для удобства углы в ней измеряются в градусах.
void Camera :: roll(float angle)
{
// roll the camera through angle degrees
// накреняем камеру на angle градусов
float cs “ cos(3.14159265/180 * angle):
float sn - sin(3.14159265/180 * angle):
Vector3 t - u:
// remember old u
// запоминаем старое значение u
u.set(cs*t.x - sn*v.x, cs*t.y - sn*v.y. cs*t.z - sn*v.z):
v.set(sn*t.x + cs*v.x. sn*t.y + cs*v.y. sn*t.z + cs*v.z):
setModelViewMatrixO:
}
Функции pitchO и yaw() реализуются аналогично (см. упражнения в конце раздела).
Соберем их все вместе
Листинг 7.3. Приложение для пилотирования камеры вокруг чайника
// the usual includes
// обычные включения
#include "camera.h"
Camera cam:
// global camera object
// глобальный объект класса camera
//<<<<<<<<<<<<<<<<<<<<<<<< my Key boa rd »>»»»»>»»»»»
void myKeyboardCunsigned char key. int x. int y)
{
switch(key)
{
// controls for the camera
// средства управления камерой
case 'F': cam.slide(0. 0. 0.2); break:
// slide camera forward
// скольжение камеры вперед
case 'F'-64: cam.slide(0, 0. -0.2): break:
// slide camera back
// скольжение камеры назад
// add up/down and left/right controls
// добавляем управление вверх/вниз и влево/вправо
case ’Р’: cam.pitch(-l.O): break:
case 'P’-64: cam.pitchd.0); break:
// add roll and yaw controls
// добавляем управление креном и рысканием
}
glutPostRedisplay():
// draw it again
// перерисовываем заново
}
I/<«««««««««<<« myDisplay »»»»»»»»»»»»»
void myDisplay(void)
7.3. Встраивание камеры в программу
439
glClear(GL_COLOR_BUFFER_BIT||GL_DEPTH_BUFFER_BIT):
gl utWIreTeapotd. 0);
// draw the teapot
// рисуем чайник
glFlushO:
.glutSwapBuffersO:
// display the screen just made
// отображаем только что сделанный экран
}
//<<<<<<<<<<<<<<<<<<<<<< main »>»»»»»>»»»>»»»»»
void maindnt argc. char **argv)
{
glutlnit(&argc. argv):
glutInitD1splayMode(GLUT_DOUBLE | GLUT_RGB):
// double buffering
// двойная буферизация
glutInitWindowSize(640, 480):
glutInitWindowPosition(50. 50):
glutCreateWindowCfly a camera around a teapot”):
// надпись: «пилотирование камеры вокруг чайника»
glutKeyboardFunc(myKeyboard):
glutDi splayFunc(myDi splay):
glClearColor(l.Of.l.Of.l.Of.l.Of):
// background is white
// фон белый
glColor3f(0.Of.0.Of.0.Of):
// set color of stuff
// задаем цвет материала
glViewport(0, 0. 640. 480):
cam.set(4. 4. 4. 0. 0. 0. 0. 1. 0):
// make the initial camera
// задаем начальную камеру
cam.setShape(30.Of, 64.0f/48.0f. 0.5f. 50.Of):
glutMainLoopO:
}
В листинге 7.3 показано, как можно использовать класс Camera и OpenGL для «пилотирования» ка-
меры по сцене. Данная сцена состоит из единственного чайника. Камера — это глобальный объект, он
устанавливается в подпрограмме mainO при выборе подходящего стартового вида и формы. При нажа-
тии какой-либо клавиши вызывается подпрограмма myKeyboardO, и камера скользит или поворачивает-
ся — в зависимости от того, какая клавиша нажата. Если, например, нажата «Р», то камера тангажирует
вверх на один градус. Если нажато сочетание «CTRL F»1 (клавиша «Р» нажимается при удерживании
клавиши CTRL в нажатом состоянии), то камера тангажирует на один градус вниз. После выполнения
нажатия на клавишу подпрограмма glutPostRedisplayO вновь вызывает функцию myDi splay О для рисо-
вания нового изображения.
Обратите внимание на вызов подпрограммы glutSwapBuffersO2. В нашем приложении для быстрого и
плавного перехода от одного изображения к другому применяется двойная буферизация (double buffering).
Для хранения созданных изображений используются два буфера памяти. Устройство отображения (дис-
плей) переключается с показа одного буфера на показ второго с помощью функции glutSwapBuffersO.
1 На большинстве клавиатур нажатие CTRL и клавиши буквы возвращает значение ASCII-кода на 64 единицы меньше, чем ASCII-
код, возвращаемый самой этой буквой.
2 Для задействования двойной буферизации функция gl utlnitDi spl ay О должна иметь в качестве аргумента GLUT_DOUBLE.
440
Глава 7. Трехмерный просмотр
Каждое новое изображение рисуется в невидимом буфере, а после завершения рисования дисплей
переключается на него. Таким образом, зритель не видит, как экран очищается и как новая картинка
медленно появляется строка за строкой, что очень раздражает. Вместо этого «старая» картинка отобра-
жается все время, пока «новая» картинка создается «за экраном», после чего дисплей очень быстро пе-
реключается на вновь нарисованное изображение.
Рисование SDL с помощью камеры
Нетрудно встроить камеру в приложение, которое читает SDL-файлы, как описывалось в главе 5. Тог-
да там фигурируют два глобальных объекта, а именно:
Camera cam:
Scene sen:
и в подпрограмме mainO SDL-файл читается и анализируется посредством функции sen.read ("myScene.
dat”). И, наконец, в подпрограмме myDisplay(void) следует просто заменить glutWireTeapot(1.0) на
sen.drawSceneOpenGLC).
Практические упражнения
7.3.1. Реализация pitch() и yaw()
Напишите функции void Camera:: pitch(float angle) и void Camera:: yaw(float angle), которые осуще-
ствляют соответственно тангаж и рыскание камеры. Сделайте так, чтобы положительное значение ры-
скания поворачивало камеру «влево», а положительное значение тангажа поворачивало камеру «вверх».
7.3.2. Создание универсальной функции поворота rotate()
Напишите функцию void Camera:: rotate(Vector3 axis, float angle), которая поворачивает камеру на
угол angle градусов вокруг оси axis. Эта функция должна осуществлять поворот всех трех осей — u, v, п —
вокруг точки наблюдения (eye).
7.4. Перспективные проекции трехмерных объектов
Трактуйте их в терминах цилиндра, сферы, конуса, причем всех в перспективе.
Поговорка Ашанти (Ashanti)
Располагая классом Camera, мы можем передвигаться по трехмерным сценам и уже готовы создавать кар-
тины. С помощью OpenGL мы создаем каждую картину посредством передачи вершин объектов (вроде
сеток, представляющих чайник или шахматную фигуру) в графический конвейер, как это описывалось
в главе 5. На рис. 7.11 демонстрируется графический конвейер, но с одним новым элементом.
Матрица Проекционная
моделирования-просмотра матрица
Разделение (тип) Матрица
перспективы порта
просмотра
Рис. 7.11. Снова графический конвейер
Напомним, что каждая вершина v умножается на матрицу моделирования-вида (VM). Моделирую-
щая часть этой матрицы (М) осуществляет все преобразования моделирования объекта; видовая часть
матрицы ( V) предназначена для преобразования, задаваемого положением и ориентацией камеры. После
выхода из этой матрицы вершина имеет координаты наблюдателя (eye coordinates) — то есть коорди-
7 А. Перспективные проекции трехмерных объектов
441
наты в системе координат глаза (eye). На рис. 7.12 показана система, в которой глаз находится в начале
координат, а ближняя плоскость перпендикулярна оси z и расположена в z = -У. Вершина, расположен-
ная в точке Р в координатах наблюдателя, проходит через следующие этапы конвейера, где она (опреде-
ленным образом) проецируется в определенную точку (х*, у*) ближней плоскости, проходит отсечение,
и, наконец, пережившие эту процедуру вершины отображаются в порт просмотра дисплея.
Рис. 7.12. Перспективная проекция вершин, выраженных в координатах наблюдателя
Сейчас самое время заглянуть поглубже в процесс построения перспективных проекций. Нам нуж-
ны ответы на целый ряд вопросов: какие операции участвуют в формировании перспективной проек-
ции и как графический конвейер осуществляет эти операции? Каково соотношение между перспектив-
ными проекциями и матрицами? Как эта проекция преобразует отображаемый объем в «канонический
отображаемый объем» для отсечения? Как производится отсечение? Как участвуют в этом процессе
однородные координаты? Каким образом сохраняется «глубина» точки относительно наблюдателя, так
чтобы невидимые поверхности могли быть должным образом удалены?
Начнем с исследования природы перспективной проекции, независимо от отдельных этапов обра-
ботки на графическом конвейере. Затем мы увидим, как для получения числовых значений, необходи-
мых для перспективной проекции, тщательно прорабатываются все этапы работы конвейера.
7.4.1. Перспективная проекция точки
Фундаментальной операцией при перспективной проекции является проецирование трехмерной точ-
ки в двумерную точку на плоскости. Рисунок 7.13 является продолжением рис. 7.12 и показывает точку
Р = (Рх, Р, Рг), которая проецируется на ближнюю плоскость камеры в точку (х*, у*). Создадим на ближ-
ней плоскости локальную систему координат, начало координат которой находится на оси z камеры.
Тогда будет иметь смысл говорить, что данная точка отстоит нах* единиц вправо от этого начала коор-
динат и на у* единиц вверх от него.
Рис. 7.13. Нахождение проекции точки Р в координатах наблюдателя
Ближняя
442
Глава 7. Трехмерный просмотр
Тогда первый вопрос состоит в том, чему равны х* и у*? Проще всего использовать подобие тре-
угольников и убедиться в том, что х* так же относится к Рх, как расстояние Nк расстоянию |Рг|. Поскольку
Рг отрицательно, можно утверждать, что
х* N
рх -рх
откуда х* = JVP^-Pj). Аналогично, у* = NPy/(-Pt). Тогда точка Р проецируется в точку
Гр Р А
(х*,у*) = N-Z-, N-+-
v z ' -Р -Р
*9 *9
(проекция точки Р)
(7.4)
на плоскость просмотра. Альтернативный (аналитический) метод получения этих же результатов при-
веден в упражнениях в конце раздела.
Пример 7.4.1
В каком месте точка Р = (1, 0,5, -1,5) располагается на плоскости просмотра камеры, ближняя плос-
кость которой N = 1?
Решение
Непосредственное применение формулы (7.4) дает (х*, у*) = (0,666,0,333).
Можно сделать некоторые предварительные замечания о том, как проецируются точки.
1. Обратим внимание на знаменатель -Р, в формуле (7.4). Его значение больше для более удаленных
точек (тех, которые находятся дальше на отрицательной части оси г), что уменьшает соответствую-
щие величины х* и у*. Это обеспечивает перспективное укорачивание (perspective foreshortening),
при котором удаленные части объекта выглядят меньше, чем более близкие части.
2. Знаменатели имеют отвратительную привычку обращаться в нуль, и Рг становится равным
нулю, когда точка Р располагается «в той же плоскости», что и глаз: в плоскости z = 0. Обычно
мы используем отсечение для удаления таких «вредных» точек до попытки проецировать их.
3. Если точка Р располагается «сзади от наблюдателя», то знак Рг изменяется на обратный. Как мы
увидим позднее, это является причиной дальнейших неприятностей. Такие точки также обыч-
но удаляются при отсечении.
4. Влияние расстояния N от ближней плоскости заключается в простом масштабировании изобра-
жения. (И х*, и у* пропорциональны N.) Поэтому если мы выберем в качестве плоскости про-
смотра какую-нибудь другую плоскость (тоже параллельную ближней плоскости), то проекция
на нее будет отличаться от проекции на ближнюю плоскость только размерами. Поскольку в
конечном счете мы отображаем эту проекцию в порт просмотра дисплея, имеющий фиксиро-
ванные размеры, размер проецируемого изображения не имеет значения. Это доказывает, что
любая плоскость просмотра, параллельная ближней плоскости, в равной степени годится для
проецирования, в силу чего мы можем использовать саму ближнюю плоскость.
5. Прямые линии проецируются в прямые линии. На рис. 7.14 приводится простейшее доказатель-
ство. Рассмотрим в трехмерном пространстве прямую, проходящую через точки А и В. Точка А
проецируется в А', а В — в В'. Однако проецируются ли точки между Ан В в точки прямой меж-
ду А' и В*? Ответ будет положительным: просто рассмотрим плоскость, проходящую через точ-
ки А, В и начало координат. Поскольку любые две плоскости пересекаются по прямой линии,
данная плоскость пересекает ближнюю плоскость также по прямой. Таким образом, отрезок
прямой АВ проецируется в отрезок прямой А'В'.
Пример 7.4.2. Три проекции сарая
Требуется весьма развитое пространственное воображение для того, чтобы представить себе, как раз-
личные камеры видят даже простой объект. В данном примере мы исследуем, как ребра сарая, опреде-
ление которого давалось в главе 6 и теперь повторено на рис. 7.15, проецируются на три различные ка-
меры. Сарай имеет 10 вершин, 15 ребер и 7 граней.
7.4. Перспективные проекции трехмерных объектов
443
Рис. 7.14. Доказательство того, что прямая линия проецируется в прямую линию
Вид № 1. Вначале установим «глаз» камеры eye = (0,0, 2) и заставим ее смотреть вдоль отрицатель-
ной оси г, причем u = (1,0,0), а и = (-1,0,0). Ближнюю плоскость установим на единичном расстоянии
от глаза. (В этом случае ближняя плоскость совпадет с ближней гранью сарая.) В координатах камеры
все точки передней стенки сарая будут иметь Pz - -1, а все точки задней стенки сарая — Р = -2. Тогда,
согласно формуле (7.4), произвольная точка (Рх, Ру, Рг) на ближней стенке будет проецироваться в
Р' - (Рх, Ру) (проекция точки ближней стенки),
а любая точка на задней стенке будет проецироваться в
Р' = (Рх/2, Ру/2) (проекция точки задней стенки).
Укорачивающий множитель (foreshortening factor) для точек задней стенки равен 2.
Рис. 7.15. Снова базовый сарай
На рис. 7.16, а показана проекция сарая для этого вида. Отметим, что ребра задней стенки проециру-
ются в половину их истинной длины, а также что реально параллельные друг другу в пространстве реб-
ра сарая не обязаны быть параллельными в проекции. (В дальнейшем мы увидим, что если параллельные
ребра параллельны плоскости просмотра, то они и проецируются параллельными, а параллельные реб-
ра, не параллельные плоскости просмотра, перестают быть параллельными: они пересекаются в так на-
зываемой «точке схода» — «vanishing-point».)
Вид № 2. Здесь камера была перемещена так, что eye = (0,5, 0, 2), однако векторы и и п те же, что
и в виде № 1. Рисунок 7.15, б показывает соответствующую проекцию.
Вид № 3. В этом случае используется камера с eye - (2, 5, 2) и look = (0, 0, 0). Результат приведен
на рис. 7.17. Для наглядности на рисунке показаны мировые оси. Данная проекция показывает сарай
с информативной точки зрения. В каркасной модели нелегко различить, где какие грани.
444
Глава 7. Трехмерный просмотр
Рис. 7.16. Проекции сарая для видов № 1 и № 2
Ближняя
Рис. 7.17. Третий вид сарая
б
Практические упражнения
7.4.1. Рисование куба в перспективе
Нарисуйте (от руки) перспективную проекцию куба С (выровненного по осям, с центром в начале ко-
ординат, с длиной сторон, равной 2) для случая, когда глаз находится в точке £ = 5 на оси z. Повторите
ту же задачу для случая, когда куб С сдвинут так, что его центр находится в точке (1,1,1).
7.4.2. Где луч пересекает плоскость просмотра? (Не пропустите это упражнение)
Мы хотим вывести формулу (7.4) путем нахождения точки, в которой луч, соединяющий начало коор-
динат с точкой Р, пересекает ближнюю плоскость.
О Покажите, что если данный луч в момент времени t = 0 находится в начале координат, а в момент
времени t “ 1 — в точке Р, то его параметрическое представление имеет вид r(t) = Pt.
О Покажите, что данный луч «соударяется» с ближней плоскостью при t - N/(-Pt).
О Покажите, что «точка соударения» (х*, у*) = (M®/(-Pt), NP^-P^).
7.4.2. Перспективная проекция прямой линии
Теперь займемся некоторыми интересными свойствами перспективных проекций, которые мы увидим
при изучении проекций прямых линий.
1. Прямые линии, параллельные в трехмерном пространстве, проецируются в прямые линии, одна-
ко они не обязательно остаются параллельными. Если они не остаются параллельными, то они
пересекаются в некоторой «точке схода».
7.4. Перспективные проекции трехмерных объектов
445
2. Прямые, проходящие за «глазом» камеры, вызывают катастрофическое «прохождение через бес-
конечность». (Такие прямые должны быть отсечены.)
3. Перспективные проекции обычно передают геометрически правдоподобные изображения. Одна-
ко этот реализм ограничен для очень длинных прямых, параллельных плоскости просмотра.
Проецирование параллельных прямых
Пусть прямая линия в трехмерном пространстве проходит (в системе координат камеры) через точку
А = (A., Ау, Л2) с направляющим вектором с = (сл, с, сг). Тогда эта прямая имеет параметрическую форму:
P(t) = А + ct. Подстановка этого выражения в формулу (7.4) даст параметрическую форму для проек-
ции прямой:
Р(0 =
\A15L хАу+су(}
(7.5)
(Может быть, это и не похоже на параметрическую форму прямой линии, но тем не менее это так;
см. упражнения.) Таким образом, трехмерная точка Л проецируется в точку р(0), и по мере изменения
параметра t проецируемая точка p(t) перемещается по экрану (по прямой). Некоторые важные свой-
ства можно извлечь непосредственно из этой формулы.
Пусть прямая А + ct параллельна плоскости просмотра. Тогда с2 = 0 и проецируемая прямая имеет вид:
Р(0 = “v(A+cx. Ау+Су)'
Это параметрическая форма прямой с наклоном (угловым коэффициентом) су/сх. Наклон не зависит
от положения прямой; скорее, он является функцией только направляющего вектора с. Таким образом,
все трехмерные прямые, имеющие направление с, будут проецироваться с этим же наклоном, поэтому
их проекции будут параллельны. Мы приходим к выводу, что если две трехмерные прямые параллельны
друг другу, а также плоскости просмотра, то они проецируются в две параллельные прямые.
Теперь рассмотрим случай, когда направление с не параллельно плоскости просмотра. Предполо-
жим для удобства, что сг < 0, так что с ростом параметра t эта прямая удаляется все дальше и дальше от
глаза. Для очень больших значений t формула (7.5) принимает вид:
(7.6)
Значение этого выражения называется точкой схода данной прямой; это точка, к которой стремится про-
ецируемая прямая по мере увеличения t. Отметим, что эта точка зависит только от направления с прямой и не
зависит от положения этой прямой (которое определяется величиной Л). Таким образом, все параллельные
прямые имеют одну и ту же точку схода. В частности, они могут проецироваться в непараллельные прямые.
Рис. 7.18. Точка схода параллельных прямых
446
Глава 7. Трехмерный просмотр
Рисунок. 7.18 делает последнее утверждение более наглядным — на примере куба. Некоторые ребра
куба параллельны: среди них есть горизонтальные, есть вертикальные, а есть такие, которые удаляются
от глаза. Изображение снималось камерой, ориентированной так, что ее ближняя плоскость была парал-
лельна ближней грани куба. Тогда в системе координат камеры компонент z вектора с для горизонталь-
ных и вертикальных ребер равен нулю. Поэтому горизонтальные и вертикальные ребра проецируются
в параллельные прямые. Однако удаляющиеся ребра не параллельны плоскости просмотра и поэтому
пересекаются в точке схода (vanishing-point, VP). Художники часто рисуют объекты именно таким спо-
собом, выбрав точку схода и рисуя параллельные прямые так, что они стремятся к VP. Позднее мы об-
судим точки схода более подробно.
Рис. 7.19. Геометрическая интерпретация точки схода
На рис. 7.19 предлагается геометрическая интерпретация точки схода. При взгляде сверху вниз на
плоскость xz в системе координат камеры мы видим различные точки прямой АВ. Точка А проецирует-
ся в А', В — в В’ и т. д. Очень удаленные точки этой прямой проецируются в VP, как показано на рисун-
ке. Сама точка VP расположена так, что прямая, проведенная от глаза и проходящая через нее, парал-
лельна прямой АВ. (Почему?)
Прямые, проходящие за глазом
Мы уже видели, что попытка спроецировать точку, располагающуюся в плоскости глаза (в координа-
тах глаза z = 0) приводит к тому, что знаменатель обращается в нуль, что несомненно приведет к непри-
ятностям, если мы попытаемся спроецировать эту точку. Рассмотрим теперь проекцию отрезка прямой,
одна концевая точка которого располагается перед глазом, а вторая — за ним.
Рисунок 7.20 вновь показывает вид на камеру сверху. Точка А находится впереди глаза и проециру-
ется в А’ без всяких проблем. С другой стороны, точка В располагается позади глаза и проецируется в
точку В', и кажется, что она находится не на той стороне плоскости просмотра! Рассмотрим точку С,
которая движется от А к В, и нарисуем, как будет перемещаться ее проекция. По мере того как точка С
движется назад к плоскости глаза, ее проекция скользит все дальше и дальше вправо по плоскости про-
смотра. Когда точка С достигает плоскости просмотра, ее проекция резко уходит в бесконечность, и по
мере перемещения точки С позади глаза, ее проекция вновь появляется издалека в левой части плоско-
сти просмотра. Можно сказать, что проекция «обернулась вокруг бесконечности» и вернулась с проти-
воположного направления [Blinn, 26]. Если бы мы попытались нарисовать такую прямую, то это вызва-
7А. Перспективные проекции трехмерных объектов
447
ло бы полную неразбериху. Поэтому все части прямой, которые находятся на меньшем расстоянии к
глазу, чем ближняя плоскость, отсекаются до того, как осуществляется проецирование прямой.
Рис. 7.20. Геометрия точки схода
Пример 7.4.3. Классическая горизонтальная плоскость в перспективе
Пониманию сути точек схода способствует рассмотрение перспективы сетки из прямых, как показано
на рис. 7.21.
Рис. 7.21. Проецирование отрезка прямой АВ, точка В которого находится «позади глаза»
Линии сетки в данном случае лежат в плоскости xz и отстоят одна от другой на единичном расстоянии.
Глаз находится на единичном расстоянии над плоскостью xz в точке (0,1,0) и смотрит вдоль векто-
ра —п, где п = (0,0,1). Как обычно, мы принимаем up - (0,1,0). Величина Nтакже выбрана равной единице.
В системе координат глаза линии сетки при постоянном значении х имеют параметрическую форму
(г, -1, -t), где i принимает значения от -М до Мдля некоторого М, a t изменяется от нуля до бесконечно-
сти. Согласно равенству (7.4) i-я прямая проецируется в прямую (i/t, -1/Г), проходящую через точку
схода (0,0), так что все эти линии сходятся в одной и той же точке, как и ожидалось.
448
Глава 7. Трехмерный просмотр
Линии сетки при постоянном значении z имеют вид (t, -1, -i), где i = 1, 2,..., N для некоторого N,at
изменяется от минус бесконечности до плюс бесконечности. Такие линии сетки проецируются в гори-
зонтальные прямые линии вида (t/i, -1/i). (Проверьте это.) Проекции этих линий являются параллель-
ными, поскольку сами линии сетки параллельны плоскости просмотра. Самые дальние из них (при
больших значениях i) располагаются близко друг к другу, представляя собой наглядный пример перс-
пективного укорачивания. Многие удаленные контуры на рисунке отсутствуют, поскольку они стано-
вятся столь частыми, что отдельно нарисовать их невозможно. Их совокупность изображена как Об-
ласть серого цвета. Горизонт (horizon) состоит из всех контуров, значение z для которых очень велико и
отрицательно; горизонт расположен при у = 0.
Аномалия при рассматривании длинных параллельных прямых
Перспективные проекции представляются хорошей моделью того, как мы видим. Однако имеются не-
которые аномалии, связанные в основном с тем, что в наших глазах нет плоских «экранов просмотра».
Одна такая проблема возникает при рассматривании очень длинных объектов. Рассмотрим для приме-
ра эксперимент, в котором мы будем созерцать пару параллельных телефонных проводов, как предла-
гается на рис. 7.22, а.
Параллельные телефонные провода
а
б
а
Рис. 7.22. Рассматривание очень длинных параллельных проводов
Мы знаем, что если сориентировать плоскость просмотра параллельно проводам, то в случае перс-
пективной проекции изображением будут две параллельные прямые, как на рис. 7.22, б. Однако то, что
мы видим фактически, сильно отличается от этого: провода кажутся изогнутыми к «точкам схода» в
обоих направлениях — см. рис. 7.22, е! На практике эта аномалия едва заметна, поскольку окно или наш
глаз ограничивают поле зрения разумной областью. (Для того чтобы увидеть различные части этих
проводов, нам приходится вращать глазами вверх и вниз, что, разумеется, поворачивает и наши «плос-
кости просмотра».)
Практические упражнения
7.4.3. Прямые линии проецируются как прямые линии: параметрическая форма
Покажите, что параметрическая форма уравнения (7.5) является параметрической формой прямой линии.
Подсказка:, для х-компонента, разделив знаменатель на числитель, получите -AxN/At + Rg(t), где R
зависит только от х-компонентов величин А и с и не зависит от их ^-компонентов, a g(t) — это некото-
7.4. Перспективные проекции трехмерных объектов
449
рая функция от t, не зависящая ни от х-, ни от г/-компонентов Лис. Повторите это для у-компонента,
чтобы получить -AN/Az + 5g(t) с аналогичными свойствами. Покажите, что полученное выражение
является параметрическим представлением прямой линии (хотя бы одной, для которой по мере изме-
нения t точка не движется с постоянной скоростью).
7.4.4. Выведите результаты для горизонтальных линий сетки
Выведите параметрические формы для спроецированных линий сетки из примера 7.4.3.
7.4.3. Включение перспективы в графический конвейер
Только глупец проверяет глубину реки обеими ногами.
Поль Сезанн (Paul Сегапп), 1925
Мы хотим, чтобы графический конвейер проецировал вершины трехмерных объектов на ближнюю
плоскость и затем отображал их в порт просмотра. После прохождения через матрицу моделирова-
ния-вида вершины выражаются в системе координат камеры, и из уравнения (7.4) видно, какие
величины необходимо вычислить для получения нужной проекции. Кроме того, мы должны произ-
вести отсечение и затем отобразить оставшиеся вершины в порт просмотра. Однако нам нужно кое-
что еще.
Добавление псевдоглубины
При проецировании отбрасывается информация о глубине; это означает, что мы теряем информацию о
том, насколько далеко от глаза находится данная точка. Однако не следует отбрасывать эту информа-
цию навсегда, иначе впоследствии нам не удастся удалить невидимые поверхности.
Рис. 7.23. Какая точка ближе: Р, или Р2?
Действительное расстояние точки Р от глаза в системе координат камеры равно ^Р* + Р? + Рг2 . Эта
формула слишком громоздка и медленна, чтобы применять ее для каждой интересующей нас точки.
Все, что нам в действительности нужно, — это некоторая оценка расстояния, которая при проецирова-
нии двух точек в одну и ту же точку ближней плоскости сообщала бы нам, какая из этих двух точ-
ек ближе. На рис. 7.23 показаны точки Р, и Р2, обе располагающиеся на прямой, исходящей от глаза,
и поэтому проецирующиеся в одну и ту же точку. Мы должны иметь возможность проверить, то ли точ-
ка Р( заслоняет собой Р2, то ли наоборот. Поэтому для каждой точки Р, которую мы проецируем, мы
будем вычислять величину, называемую псевдоглубиной (pseudodepth), которая является оценкой глу-
бины для точки Р. Тогда мы можем сказать, что точка Р проецируется в точку (х*, г/*, г*), где (х*, у*) —
величина, полученная из уравнения (7.4), а г* — псевдоглубина точки Р.
Как лучше выбрать функцию для псевдоглубины? Заметим, что если две точки проецируются в одну
и ту же точку, то более дальней из них всегда соответствует большее по модулю отрицательное значе-
ние Рг, поэтому мы можем взять в качестве псевдоглубины саму величину Рг. Однако красивее и эф-
15 Ф. Хилл
450
Глава 7. Трехмерный просмотр
фективнее выбрать функцию с тем же знаменателем (-Р2), что и у величин х* и у*. Итак, возьмем функ-
цию с таким знаменателем и числителем, пропорциональным Р2, тогда точка Р «проецируется» в точку
(x*,y*,z*)
I -р, -Рг -р, )
(7.7)
где а и b — некоторые константы. Хотя подошли бы многие другие значения а и Ь, мы выберем их так,
чтобы псевдоглубина изменялась в пределах от -1 до 1. (Позже мы увидим, почему такой выбор явля-
ется удачным.). Так как глубина увеличивается по мере того, как точка перемещается дальше вдоль
отрицательной оси z, мы назначаем псевдоглубину равной -1 при Рг = -N и +1 при Рг - -F. Имея два
этих условия, легко вычислить а и Ь:
F + N , -2FN
«ь ~~
F-N F-N
(7.8)
Рис. 7.24. Псевдоглубина растет по мере роста модуля отрицательных значений Рг
На рис. 7.24 начерчен график зависимости псевдоглубины от (-Р ). Как мы уже установили, она
растет от -1 для точки на ближней плоскости до 1 для точки на дальней плоскости. Когда Рг при-
ближается к нулю (так что точка находится прямо перед глазом), псевдоглубина стремится к минус
бесконечности. Для точки, находящейся непосредственно позади глаза, псевдоглубина большая и поло-
жительная. Однако мы будем отсекать точки, располагающиеся ближе ближней плоскости, поэтому
такое катастрофическое поведение нам никогда не встретится.
Отметим, что значения псевдоглубины сгущаются по мере того, как -Рг становится ближе к F. В силу
конечной точности компьютерной арифметики такое сгущение может вызвать проблему, например, при
удалении невидимых поверхностей, когда нужно будет различить псевдоглубины двух точек. Факти-
ческие глубины точек относительно глаза могут быть различны, однако их псевдоглубины окажутся
одинаковыми!
Отметим, что определение псевдоглубины согласно уравнению (7.7) приводит к росту ее поло-
жительных значений по мере роста отрицательных значений Р2. Такое поведение представляется есте-
ственным, поскольку расстояние от глаза растет по мере того, как Р перемещается дальше вдоль отри-
цательной оси z.
7.4. Перспективные проекции трехмерных объектов 451
Пример 7.4.4. Псевдоглубина изменяется медленно, когда -Pz стремится к F
Пусть JV- 1 и F= 100. Тогда а - -101/99, b = -200/99, следовательно, мы имеем:
. ,1 101^+200
псевдоглубина pseudodepth\N *, F = 1М = —.
Эта функция обращается в -1 при P=-N и в 1 при P=-F. Однако по мере приближения к -F она
изменяется очень медленно с изменением -Рг. Например, для значений -Р=$1,98 и 99 значения функ-
ции равны соответственно 0,9993752, 0,9995877, 0,9997959.
Небольшие алгебраические выкладки (см. упражнения в конце раздела) показывают, что когда N
значительно меньше, чем F (а так оно обычно и бывает), псевдоглубина может быть приближенно запи-
сана в виде:
2N
псевдоглубина pseudodepth = 1 + -. (7.9)
Д
Эта функция тоже изменяется все более и более медленно, когда -Рг приближается к F. Однако ее
изменение возрастает с увеличением значений N. Тогда N следовало бы установить сколь угодно боль-
шим, но, разумеется, не настолько, чтобы ближайшие к камере объекты были бы отсечены!
Использование однородных координат
Почему было принято решение использовать во всех членах уравнения (7.7) один и тот же знамена-
тель? Как мы сейчас покажем, наличие одного и того же знаменателя делает возможным представлять
все этапы графического конвейера в виде произведения матриц, что делает этот процесс эффективным
и однотипным. (Микросхемы некоторых графических карт могут аппаратно умножать матрицу на точ-
ку, поэтому эта операция выполняется предельно быстро!) Кроме того, единый знаменатель позволит
нам подготовиться к высоко эффективному и надежному этапу отсечения.
Этот новый подход требует, чтобы мы представляли точки в однородных координатах. Мы уже дела-
ли это раньше, поскольку такое представление упрощает преобразование вершин с помощью матрицы
моделирования-вида. Однако мы собираемся расширить понятие представления в однородных коор-
динатах за пределы того, что мы делали до сих пор, и тем самым обретем новые возможности. В частно-
сти, с помощью матрицы можно будет выполнять не только аффинное преобразование, но также и «пер-
спективное преобразование».
До сих пор мы говорили, что точка Р = (Рх, Ру, Рг) выражается в однородных координатах как (Рх, Ру,
Рг, 1), а вектор v - («х, v , v2) — как («х, v, ог, 0). Иными словами, мы просто добавили 1 к исходному
представлению точки и б к представлению вектора. Это сделало возможным использовать координат-
ные фреймы как основу для представления интересующих нас точек и векторов и позволило нам выра-
жать аффинное преобразование с помощью матрицы.
Теперь разовьем эту мысль и заявим, что точка Р = (Рх, Р, Рг) имеет целое семейство однородных
представлений вида (®PX, wP, wP2, w) для любого ненулевого значения w. Например, точка (1,2,3) имеет
представления (1, 2, 3, 1), (2* 4, 6, 2), (0,003, 0,006, 0,009, 0,001), (-1, -2, -3, -1) и т. д. Если вам дадут
точку в таком виде — скажем, (3, 6, 2, 3), — и спросят, что это за точка, то достаточно разделить все ее
компоненты на последний, получить (1,2, 2/3, 1) и затем удалить последний компонент: такая точка в
«обычных» координатах имеет вид 1(, 2, 2/3). Таким образом:
О для преобразования точки из обычных координат в однородные координаты добавьте I1;
О для преобразования точки из однородных координат в обычные координаты разделите все ком-
поненты на последний компонент и отбросьте четвертый компонент.
Дополнительная возможность масштабировать все компоненты точки без изменения самой точки и
послужила основанием назвать эти координаты «однородными». До сих пор мы имели дело только с
частным случаем, когда последний компонент равен 1.
1 И при желании умножьте все четыре компонента на любую ненулевую величину.
452
Глава 7. Трехмерный просмотр
Мы будем изучать однородные координаты более подробно в упражнениях в конце раздела, а теперь
сконцентрируем свое внимание на том, как они действуют при преобразовании точек. Аффинные пре-
образования при использовании однородных координат работают прекрасно. Напомним, что матрица
аффинного преобразования всегда имеет четвертой строкой (0, 0, 0, 1). Следовательно, если мы умно-
жим такую матрицу М на точку Р в ее однородном представлении для формирования матрицы МР = Q
(вспомните уравнение (5.24)):
г2 -1 3 1 'wPxy
6 0,5 1 4 wPy wQy
0 4 2 -3 wPz
1° 0 0 <w , < w ,
то последний компонент Q никогда не изменится и будет всегда равен w. Следовательно, можно преоб-
разовать Q обратно в обычные координаты обычным способом.
Однако произойдет нечто новое, если четвертая строка будет отличаться от значения (0,0,0,1). Рас-
смотрим важный пример:
N О
О N
О О
О О
О (Г
О О
а b
-1 о.
(проекционная матрица, версия 1).
(7.Ю)
Четвертая строка этой матрицы равна (0,0, -1,0) для любых значений N, а, Ь. Это похоже на то, что
позднее мы назовем «проекционной матрицей». Если мы умножим эту матрицу на точку, выраженную
в однородных координатах с любым значением w, то есть:
'N 0 0 0" 'wPxy ' wNPx '
0 N 0 0 wPy wNPy
0 0 a b wPx w(aPx+b')
1° 0 -1 °, <w , < У
то получим обычную точку. Но какую именно? Чтобы выяснить это, разделим все на четвертый компо-
нент и отбросим ее. Тогда получим
(нА. „А.
I -г: -р; -р,)'
Это именно то, что нам нужно, согласно формуле (7.7). Таким образом, однородные координаты
позволяют нам создавать перспективу при помощи умножения матриц! Однако для достижения такого
результата мы должны всегда делить все компоненты на четвертый компонент. Этот этап называется
перспективным делением (perspective division).
Матрица, четвертая строка которой не равна (0, 0, 0, 1), производит неаффинное преобразование.
Вместо этого она выполняет преобразование более общего класса, называемое перспективным преоб-
разованием (perspective transformation). Отметим, что это именно преобразование, а не проекция; ведь
проекция уменьшает размерность точки до упорядоченной тройки или пары, в то время как перспек-
тивное преобразование принимает четверку и возвращает тоже четверку.
Рассмотрим алгебраический смысл внесения ненулевых величин (А, В, С, D) в четвертую строку
матрицы. Когда мы умножаем матрицу на (Рг, Р, Рг, 1) (или на что-нибудь в этом роде), четвертый член
получающейся в результате точки приобретает вид АРг + ВРу + СР2 + D, то есть линейно зависит от каждо-
го компонента точки Р. После перспективного деления этот член появляется в знаменателе этой точки.
Именно такой знаменатель необходим для получения геометрического эффекта перспективной проек-
ции на главной плоскости, что мы покажем в упражнениях.
7.4. Перспективные проекции трехмерных объектов
453
Следовательно, перспективное преобразование переносит трехмерную точку Р в другую трехмер-
ную точку Р' в соответствии с отображением
(перспективное преобразование).
(7.И)
Когда вступает в игру эта проекция? Далее по конвейеру первые два компонента этой точки исполь-
зуются при рисовании, чтобы отметить в экранных координатах положение изображаемой точки. Тре-
тий компонент «отщепляется» для будущей проверки глубины. Пока нас интересует только положение
точки на экране, игнорирование третьего компонента эквивалентно замене его на нуль, то есть
дг дг QPz+b
-Р/ -Р/ -л J
—> N—N-Z-, 0 (проекция).
< ~Р* ~Рг ,
(7.12)
Это как раз то, что мы делали в главе 5 при ортографическом проецировании точки (перпендику-
лярно к плоскости просмотра), когда устанавливали камеру в наших первых опытах просмотра трех-
мерной сцены. Все подробности ортографических проекций мы будем изучать позднее. На данный мо-
мент можно сделать следующий вывод:
(перспективная проекция) - (перспективное преобразование) +
+ (ортографическое преобразование).
Такое разложение перспективной проекции на частное преобразование, за которым следует (триви-
альная) проекция, будет весьма плодотворным как для написания алгоритмов, так и для лучшего пони-
мания того, что конкретно происходит с каждой точкой по мере ее прохождения через графический
конвейер. В OpenGL этап преобразования отделен от этапа проецирования; фактически он включает в
себя отсечение, перспективное деление и одно дополнительное преобразование между ними. Теперь
рассмотрим более подробно часть процесса, относящуюся к преобразованию.
Геометрическая природа перспективного преобразования
Перспективное преобразование превращает трехмерную точку Р в другую трехмерную точку в соответ-
ствии с уравнением (7.11), чтобы «подготовить» эту точку к проецированию. Полезно трактовать это
преобразование как «деформирование» трехмерного пространства и посмотреть, как оно переводит
одну форму в другую. Очень важно, что при этом преобразовании сохраняются прямолинейность и
плоскостность, так что прямые линии преобразуются в прямые линии, плоскости — в плоскости, а по-
лигональные грани — в другие полигональные грани. Кроме того, сохраняется и «промежуточность»
(«in-between-ness»), так что если точка находится внутри объекта, то преобразованная точка будет так-
же находиться внутри преобразованного объекта. (Наш выбор функции псевдоглубины был обуслов-
лен необходимостью сохранить эти свойства, что будет доказано в упражнениях.)
Особый интерес вызывает то, как перспективное преобразование преобразует отображаемый
объем камеры, поскольку если мы собираемся производить отсечение в деформированном про-
странстве, то мы будем отсекать границами деформированного отображаемого объема. Преобразова-
ние блестяще справляется с этой проблемой: форма деформированного отображаемого объема пре-
красно подходит для простого и эффективного отсечения! На рис. 7.25 показано, как преобразуются
отображаемый объем и другие формы. Ближняя плоскость W, имеющая уравнение z —N, отобража-
ется в плоскость W', заданную уравнением z = -1, а дальняя плоскость отображается в плоскость z = +1.
Верхняя стенка Р «разворачивается» в горизонтальную плоскость Т', так что последняя становится
параллельной оси г. Нижняя стенка S становится горизонтальной плоскостью S', а две боковые стенки
становятся также параллельными оси г. Таким образом, отображаемый объем камеры преобразуется
в параллелепипед!
454
Глава 7. Трехмерный просмотр
Рис. 7.25. Деформирование отображаемого объема перспективным преобразованием
Легко доказать, что все эти плоскости преобразуются именно таким образом, поскольку все входя-
щие в них прямые линии либо параллельны ближней плоскости, либо проходят через глаз. Вниматель-
но проверьте следующие утверждения.
Утверждение. Прямые, проходящие через глаз, преобразуются в прямые, параллельные оси г.
Доказательство. Все точки прямой, проходящей через глаз, проецируются в одну и ту же точку, на-
пример (х*, у*) на плоскости просмотра. Тогда все точки, принадлежащие этой прямой, преобразуются
во все точки (х, у, z), где х - х*, у - у*, а z принимает все значения псевдоглубины между -1 и 1.
Утверждение. Прямые, перпендикулярные оси г, преобразуются в прямые, перпендикулярные оси г.
Доказательство. Все точки этой прямой имеют одну и ту же координату г, поэтому все они преобра-
зуются в точки с одним и тем же значением псевдоглубины.
Используя эти утверждения, нетрудно вывести точную форму и размеры деформированного ото-
бражаемого объема.
Данное преобразование деформирует также и другие объекты. На рис. 7.25, б показан параллеле-
пипед, проецируемый на ближнюю плоскость. Предположим, что верхнее ребро ближней грани парал-
лелепипеда проецируется в прямую у - 2, а верхнее ребро задней грани проецируется в прямую у - 1.
Тогда после преобразования данный параллелепипед становится усеченной пирамидой: верхнее ребро
ее ближней грани лежит на прямой у = 2, а верхнее ребро ее задней грани — на прямой у - 1. Предметы,
находящиеся ближе к глазу, чем ближняя плоскость, становятся больше, а предметы за ближней плос-
костью — меньше. Преобразованный объект на заднем плане меньше, чем на ближнем, поскольку ис-
ходный объект проецируется именно таким способом. Координаты х и у преобразованного объекта яв-
ляются соответственно координатами х и у проекции исходного объекта — это те координаты, которые
вы получили бы при ортографической проекции преобразованного объекта. Короче говоря, перепек-
7.4, Перспективные проекции трехмерных объектов
455
тивное преобразование «деформирует» объекты так, что при их просмотре в ортографической проек-
ции они выглядят такими же, как выглядели бы исходные объекты при их просмотре в перспективной
проекции.
Таким образом, все объекты деформируются в укороченные формы в соответствии с законами пер-
спективной проекции. После этого их можно рассмотреть в ортографической проекции и получить пра-
вильную картину.
Рассмотрим теперь подробнее частные случаи форм и размеров преобразованного отображаемого
объекта.
Подробно о преобразованном отображаемом объеме; преобразование
в канонический отображаемый объем
Присвоим численные значения размерам отображаемого объема до и после его деформирования. Рас-
смотрим верхнюю плоскость: пусть она проходит через точку {left, top, -N) при z = -N, как показано на
рис. 7.26. Поскольку она составлена из прямых, проходящих через глаз и через точки ближней плоско-
сти, для которых г/-координата равна top, верхняя плоскость должна преобразоваться в плоскость у = top.
Подобным же образом:
О нижняя плоскость преобразуется в плоскость у = bott;
О левая плоскость преобразуется в плоскость х = left;
О правая плоскость преобразуется в плоскость х = right.
Рис. 7.26. Подробности перспективного преобразования
Теперь мы в точности знаем, что представляет собой преобразованный отображаемый объем: это
параллелепипед с размерами, связанными очень простыми соотношениями с атрибутами камеры. Как
мы увидим, это превосходная форма для отсечения, поскольку ее стенки параллельны координатным
плоскостям. Однако для целей отсечения было бы даже лучше, если бы размеры этой формы не зависе-
ли от свойств конкретной камеры. В OpenGL перспективное преобразование компонуется с другим ото-
бражением, которое масштабирует и смещает данный параллелепипед в канонический отображаемый
объем (canonical view volume CVV) — куб, простирающийся от -1 до 1 в каждом измерении. Посколь-
ку это отображение масштабирует предметы в направлениях х и у по-разному, «втискивая» сцену в за-
данный объем, оно вносит некоторое искажение, однако это искажение будет устранено в заключитель-
ном преобразовании в порт просмотра.
Преобразованный отображаемый объем уже простирается от -1 до 1 по оси z, так что требуется
промасштабировать его в двух других измерениях. Поэтому для преобразования параллелепипеда в ка-
нонический отображаемый объем мы вводим масштабирование и смещение по г и по у. Вначале мы
смещаем этот параллелепипед на -{right + left)/2 по х и на -{top + bott)/2 по у. Затем масштабируем его
456
Глава 7. Трехмерный просмотр
с множителями 2/(right - left) по х и с 2/{top - bott) по у. После выполнения матричных умножений
(см. упражнения) мы получим окончательную матрицу:
( 2N 0 right+left right-left 0
right-left
о 2W top+bott о
R = top-bott top-bott (проекционная матрица). (7.13)
о 0 -(F+N) -2FN
F-N F-N
< 0 0 -1 0 )
Такая матрица, называемая проекционной матрицей (projection matrix), выполняет перспективное
преобразование плюс масштабирование и перенос для преобразования отображаемого объема камеры
в канонический отображаемый объем. Это точно такая же матрица, какую создает OpenGL (и на какую
умножается текущая матрица) при выполнении подпрограммы glFrustum(left, right, bott. top, N, F).
Напомним, что вместо этой подпрограммы обычно используется другая подпрограмма: gluPerspective
(viewAngle, aspect, N, F), поскольку у нее более наглядные параметры. Функция gluPerspective задает
такую же матрицу, предварительно вычислив значения top, bott и так далее по следующим формулам:
( я 1
top = Ntg I -^vietl)Anglel2 I,
bott** -top, right - top x aspect, left - -rig/it.
7.4.4. Отсечение граней границами отображаемого объема
Напомним рис. 7.11, где отсечение выполнялось после того, как вершины прошли сквозь проекцион-
ную матрицу. Отсечение производится в уже деформированном пространстве, поскольку каноничес-
кий отображаемый объем особенно хорошо приспособлен для эффективного отсечения. Ниже мы по-
кажем, как использовать это свойство, и разработаем детали алгоритма отсечения.
Рис. 7.27. Отсечение границами канонического отображаемого объема (CW)
Отсечение в деформированном пространстве проводить можно, поскольку точка находится внутри
отображаемого объема камеры тогда и только тогда, когда ее преобразованная версия лежит внутри ка-
нонического отображаемого объема. На рис. 7.27, а приведен пример действия процедуры отсечения.
Треугольник имеет вершины vv v2, v3, последняя из которых лежит вне канонического отображаемого
объема CW. Отсекатель действует на ребра: вначале он берет ребро vtv2 и обнаруживает, что оно целиком
располагается внутри CW. Затем он отсекает ребро г?2г?3 и записывает новую вершину а, образовав-
шуюся в месте выхода ребра из CW. Наконец, он отсекает ребро v3vt и записывает новую вершину —
7.4. Перспективные проекции трехмерных объектов
457
в точке выхода этого ребра из CW. К концу процесса исходный треугольник становится четырехуголь-
ником с вершинами v^ab. (Позднее мы увидим, что, кроме определения положения новых вершин, гра-
фический конвейер вычисляет также новый цвет и параметры текстуры этих новых вершин.)
Задача отсечения — это в основном задача отсечения отрезка прямой границами CW. Мы уже изуча-
ли подобный алгоритм в разделе «Алгоритм Сайруса—Бека» главы 4, — это отсекатель Сайруса—Бека.
Тот отсекатель, который мы разрабатываем здесь, аналогичен упомянутому алгоритму, но работает он,
разумеется, в трехмерном, а не в двумерном пространстве.
А фактически он работает в четырех измерениях: мы будем отсекать в однородном четырехмер-
ном координатном пространстве, которое на рис. 7.11 названо «координатами отсечения» («clip
coordinates»). Делается это проще, чем может показаться вначале, и отсекатель прекрасно отличает точ-
ки, находящиеся перед глазом, от точек за глазом.
Пусть нам нужно отсечь отрезок прямой АС, показанный на рис. 7.27, б, границами CVV. Это озна-
чает, что нам даны две точки в однородных координатах: А - (ах, ау, аг, aw) и С - (сх, су, сг, cw); и мы хотим
определить, какая часть этого отрезка располагается внутри CVV. Если при этом отрезок пересекает
границу CW, то нам потребуется вычислить точку пересечения I = (/х, 1у, 1г, Iw).
Как и в случае алгоритма Сайруса—Бека, мы представляем CW в виде шести бесконечных плоско-
стей и определяем, где находится заданное ребро по отношению к каждой плоскости поочередно. Отсе-
каемое ребро можно представить параметрически в виде А + (С - A)t. Оно находится в точке А при t = О
и в точке С при t - 1. Для каждой стенки CVV мы вначале проверяем, располагаются ли точки А и С по
одну и ту же сторону стенки. Если это так, то вычислять пересечение ребра со стенкой не нужно. Если
они лежат по разные стороны стенки, мы определяем точку пересечения и отсекаем ту часть ребра, ко-
торая лежит на внешней стороне стенки.
Следовательно, мы должны иметь возможность проверять, находится ли точка «снаружи» или
«внутри» по отношению к стенке. Рассмотрим, например, плоскость х = -1, которая является одной из
стенок CVV. Точка А находится справа от плоскости («внутри»), если
— > -1, или ах > -aw, или (aw + ах) > 0. (7.14)
я»
(При умножении обеих частей неравенства на отрицательный множитель необходимо изменить знак
неравенства на противоположный. Однако здесь мы имеем дело только с положительными значения-
ми аи; см. упражнения.) Аналогично, точка А находится с внутренней стороны плоскости х = 1, если
— < 1, или (aw - ах) > 0.
Таблица 7.1. Граничные коды, вычисляемые для каждой конечной точки ребра
Координата границы Однородная величина Плоскость отсечения
вс0 W+ X х=-1
ВС, W-X х= 1
ВС, W+ у К=-1
вс3 w-y К=1
вс4 W+ Z z=-l
вс5 w-z z= 1
Блинн [Blinn, 26] называет эти величины «граничными координатами» («boundary coordinates» — ВС)
точки А и перечисляет шесть таких величин, список которых приводится в табл. 7.1. Эти шесть величин
вычисляются сначала для точки А и затем повторно для точки С. Если все шесть величин положительны,
то точка располагается внутри CVV. Если хотя бы одна из них отрицательна, то точка располагается
снаружи. Если обе точки располагаются внутри, то имеет место тот самый случай тривиального приема,
458
Глава 7. Трехмерный просмотр
который рассматривался в разделе «Отсечение линий» главы 3 для отсекателя Кохена—Сазерленда. Если
точки А и С располагаются вне одной и той же стороны CW (соответствующие ВС отрицательны), то
ребро должно целиком располагаться вне CW. Таким образом, имеет место следующий критерий.
Тривиальный прием. Обе концевые точки лежат внутри CVV. (Все 12 ВС положительны).
Тривиальное отклонение. Обе концевые точки лежат вне одной и той же плоскости CW.
Если ни одно из этих условий не выполняется, то нам придется отсекать отрезок АС относительно
каждой плоскости отдельно. Как и в случае отсекателя Сайруса—Бека, мы должны отслеживать возмож-
ный интервал (candidate interval — CI) (см. рис. 4.43) — отрезок времени, в течение которого ребро мо-
жет все еще находиться внутри CW. По существу, нам известно и обратное условие: если t находится
вне пределов CI, то ребро не находится внутри CW. Отметим, что CI простирается от t = £jn до t = fout.
Мы проверяем это ребро поочередно относительно каждой стенки. Если соответствующие гранич-
ные коды имеют разные знаки, то ребро пересекается с плоскостью в некоторый момент времени fhit,
который мы в этом случае вычисляем. Если ребро «входит» в плоскость (то есть движется «внутрь» нее
извне) по мере увеличения t, то мы обновляем значение tin = max(old tm, thit), поскольку ребро не могло
войти в более раннее время, чем fhit. Аналогично, если ребро выходит изнутри плоскости, то мы обнов-
ляем tout» min(old tOTt, fhit). Если в какой-то момент времени CI уменьшится до пустого интервала (то есть
toM станет больше, чем tin), то ребро будет отсечено целиком и мы будем иметь так называемый «досроч-
ный выход», избавляющий нас от ненужных вычислений.
Нетрудно вычислить момент пересечения ребра с плоскостью. Запишем ребро в параметрической
форме в однородных координатах:
edge (t) - (ах + (сх - ax)t, ау + (су - ay)t, аг + (сг - az)t, aw + (си - ajt).
Например, ребро пересекается с плоскостью х- 1, когда координатах выражения А + (С- A)f равна 1,
то есть:
ах + (cx-ax)t = !
Решая это уравнение относительно t, получим:
Отметим, что thit зависит только от двух граничных координат. Пересечения с другими плоскостями
дают аналогичные формулы.
Все вышеприведенные формулы легко перевести в программный код, как показано в листинге 7.4.
В своей основе это алгоритм Лианга—Барски (Liang—Barsky — [Liang, 131]) с некоторыми тонкостями,
предложенными Блинном [Blinn, 30].
Листинг 7.4. Отсекатель ребер (усовершенствованный Блинном)
int clipEdge(Point4& A, Point4& С)
double tin = 0.0. tOut - 1.0. tHit:
double aBC[6], cBC[6J;
int aOutcode = 0. cOutcode = 0;
.. find BC's for A and C ..
// .. нахождение ВС для А и С ..
.. form outcodes for A and C ..
U .. формирование выходных кодов для А и С ..
iff(aOutcode & cOutcode) != 0)
// trivial reject
// тривиальное отклонение
return 0:
7.4, Перспективные проекции трехмерных объектов
459
if((aOutcode | cOutcode) — 0)
// trivial accept
// тривиальный прием
return 1;
forCint i = 0; i < 6: i++)
// clip against each plane
// отсекаем относительно каждой плоскости
{
if(cBC[i] < 0)
// exits:C is outside
// выходит: С находится снаружи
{
tHit - aBC[1]/(aBC[i] - cBC[i]):
tOut - MINCtOut. tHit):
}
else if(aBC[i] < 0)
// enters:A is outside
// входит: А находится снаружи
{
tHit - aBC[i]/(aBC[1] - cBC[i]):
tin - MAX(tIn. tHit):
}
if(tln > tout) return 0:
// CI is empty:early out
// CI пуст: досрочный выход
}
// update the endpoints as necessary
// обновляем конечные точки
Point4 tmp:
if(aOutcode != 0)
// A is out: tin has changed
// А выходит: tin изменено
{
// find updated A, (but don't change A yet)
// находим обновленную А (однако пока не меняем А)
tmp.x - А.х + tin * (C.x - А.х):
tmp.у - А.у + tin * (C.y - А.у);
tmp.z - A.z + tin * (C.z - A.z);
tmp.w - A.w + tin * (C.w - A.w):
}
1f(c0utcode != 0)
// C is out: tout has changed
// С выходит: tOut изменен
{
// update C (using original value of A)
// обновляем С (используя исходное значение A)
C.x - А.х + tOut * (C.x - A.x):
C.y - A.у + tOut * (C.y - A.y);
C.z - A.z + tOut * (C.z - A.z):
C.w = A.w + tOut * (C.w - A.w):
}
продолжение^
460
Глава 7. Трехмерный просмотр
Листинг 7.4 (продолжение)
A =tmp:
// now update А
// теперь обновляем А
return 1:
// some of the edge lies inside the CVV
// часть ребра лежит внутри CVV
}
Подпрограмма clipEdge(Point4& A. Point4& С) принимает две точки в однородных координатах (с по-
лями х, у, 2, w) и возвращает 0, если ни одна часть отрезка АС не располагается в CVV, и 1 в противном
случае. Она также изменяет значения Ли С так, что по окончании работы подпрограммы они становят-
ся концевыми точками отсеченного ребра.
Эта подпрограмма находит шесть граничных координат для каждой концевой точки и записывает их
в массивы аВС[] и сВС[]. Для большей эффективности она также создает для каждой точки выходной код
(outcode), в котором хранятся знаки всех шести граничных кодов этой точки. В г-м бите выходного кода
точки А находится 0, если аВС[1 ] > 0 (то есть А — внутри i-й стенки), и 1 в противном случае. Ситуация
тривиального приема возникает, когда оба выходных кода — aOutcode и cOutcode — равны нулю. Тривиаль-
ное отклонение возникает тогда, когда побитовое произведение AND обоих выходных кодов не равно нулю.
В цикле проверки ребра относительно каждой плоскости может быть не более одной отрицательной
граничной координаты ВС. (Почему?) Если точка А имеет отрицательную ВС, то ребро в точке соударе-
ния должно входить в плоскость; если отрицательная ВС имеется у точки С, то ребро в точке соударения
должно выходить. (Почему?) (Блинн использует несколько более быстрый метод проверки с помощью
введения маски, тестирующей один бит выходного кода.) Каждый раз значения tin или tOut обновля-
ются, а в случае, когда tin становится больше, чем tOut, происходит досрочный выход.
После проверки всех плоскостей одно или оба значения tin и tOut оказываются измененными. (По-
чему?) Точка А обновляется на А + (i - A) tin, если было изменено значение tin, а точка С обновляется
на А + (С - A) tOut, если было изменено значение tOut.
Блинн предлагает предварительно вычислять все ВС и выходные коды для каждой обрабатываемой
точки. Это устраняет необходимость заново вычислять эти значения, когда вершина является конце-
вой точкой более чем одного ребра, что случается часто.
Почему мы отсекаем границами канонического отображаемого объема?
Теперь, когда мы уже видели, как просто осуществлять отсечение границами канонического отобража-
емого объема, мы сможем понять значение преобразования всех интересующих нас объектов до их от-
сечения. Здесь важны два обстоятельства.
1. CW не имеет параметров. Алгоритму не требуется никакой дополнительной информации для
описания объема отсечения; в нем всегда используются только -1 и 1. Поэтому сам код может
быть сделан максимально эффективным.
2. Плоскости CW выровнены по координатным осям (после выполнения перспективного преоб-
разования). Это означает, что по единственной координате (как при ах > - 1) мы можем опреде-
лить, с какой стороны плоскости располагается точка. Если бы плоскости не были выровнены,
то потребовалось бы отнимающее много ресурсов скалярное произведение.
Почему мы производили отсечение в однородных координатах,
а не после этапа перспективного деления?
Отсечение не обязательно производить в однородных координатах, однако это делает алгоритм отсече-
ния прозрачным, быстрым и простым. На этапе перспективного деления часть информации теряется:
если у вас есть в явном виде значения ах и ат, то вы, разумеется, знаете и знаки каждого из них. Но если
вы получаете отношение ах/аи, то вы можете только сказать, имеют ах и aw один и тот же знак или про-
тивоположные знаки. Хранение данных в однородных координатах и отсечение точек, более близких к
7.4. Перспективные проекции трехмерных объектов
461
глазу, чем ближняя плоскость, автоматически удаляют точки, располагающиеся позади глаза (напри-
мер, точка В на рис. 7.20).
В литературе описывались некоторые «неправильные» ситуации, для которых отсечение в однород-
ных координатах является обязательным [Blinn, 30, Foley, 64]. Эти ситуации включают в себя случаи
специальных преобразований объектов или конструирование определенного вида поверхностей, для
которых исходная точка (ах, ау, а2, aw) имеет отрицательный четвертый компонент, несмотря на то что
она находится перед глазом. Но ни один из объектов, моделирование которых мы рассматриваем здесь,
не относится к этой категории. Мы делаем вывод, что хотя отсечение в однородных координатах, как
правило, не обязательно, оно почти без всяких затрат делает алгоритм более быстрым и простым.
Вслед за операцией отсечения выполняется, наконец, перспективное деление (perspective division)
(как показано на рис. 7.11), после чего упорядоченная тройка (х, y,z) пропускается через преобразова-
ние в порт просмотра. Позднее мы увидим, что это преобразование сдвигает и изменяет размеры ком-
понентов х и у так, чтобы они правильно разместились в порту просмотра, а также осуществляет не-
значительные изменения з-компонента (отвечающего за псевдоглубину), чтобы он стал удобнее для
определения глубины.
Преобразование в порт просмотра
Как мы уже видели, перспективное преобразование «втискивает» сцену в канонический куб, как по-
казано на рис. 7.28. Если форматное соотношение отображаемого объема камеры (то есть форматное
соотношение окна на ближней плоскости) равно 1,5, то, очевидно, что происходит искажение, когда пер-
спективное преобразование масштабирует объекты в окно с форматным соотношением 1. Однако пре-
образование в порт просмотра может аннулировать это искажение, отобразив квадрат в порт просмот-
ра с форматным соотношением 1,5. Обычно форматное соотношение порта просмотра устанавливается
таким же, как у отображаемого объема.
Форматное
соотношение 1,0
Рис. 7.28. Преобразование в порт просмотра восстанавливает форматное соотношение объекта
Мы уже неоднократно встречались с функцией OpenGL glViewport(x, у, wid, ht). Она устанавли-
вает порт просмотра левым верхним углом в точку (х, у) (в экранных координатах) и будет иметь wid
пикселов в ширину и ht пикселов в высоту. Кроме того, эта функция преобразовывает диапазон псевдо-
глубины из (-1,1) в (0,1).
Вернемся к рис. 7.11, на котором изображен весь графический конвейер. Каждая точка V(являющая-
ся обычно вершиной полигона) проходит через следующие этапы:
О Точка V расширяется до четверки однородных координат путем добавления 1.
О На эту четверку умножается матрица моделирования-вида, в результате чего получается четвер-
ка, задающая положение точки в координатах глаза.
О Далее на эту точку умножается проекционная матрица, в результате чего получается четверка
в координатах отсечения.
О Ребро, содержащее спроецированную точку в качестве концевой, отсекается.
462
Глава 7. Трехмерный просмотр
О Выполняется перспективное деление, возвращающее упорядоченную триаду.
О Преобразование в порт просмотра умножает на эту тройку матрицу; результат умножения (sx,
sy, dz) используется для рисования и для вычислений глубины. Точка (sx, sy) отображается в эк-
ранных координатах; величина dz является мерой расстояния (глубины) исходной точки от гла-
за камеры.
Практические упражнения
7.4.5. Куда проецируется точка Р?
Пусть плоскость просмотра задана в координатах камеры уравнением Ах + By + Cz - D. Покажите, что лю-
бая точка Р проецируется на данную плоскость в точку, заданную в однородных координатах уравнением
Р' - (DPX, DPy, DP2, APx + ВРу + СР).
При доказательстве используйте следующие этапы:
О Покажите, что спроецированная точка является точкой, в которой луч между глазом и точкой Р
пересекает заданную плоскость.
О Покажите, что этот луч задается произведением Pt и попадает на заданную плоскость в момент
времени
t* - D/(APx + ВРу + СР).
О Покажите, что спроецированная точка (точка соударения) правильно описывается выражением
для точки Р'.
О В заключение покажите, что для ближней плоскости мы получаем координаты (х*, у*), опреде-
ленные равенством (7.4).
7.4.6. Вывод приближенной формулы для псевдоглубины
Покажите, что псевдоглубина, равная а + Ь/(-Р), где а и b определяются равенствами (7.8), хорошо
аппроксимируется формулой (7.9), когда N много меньше, чем F.
7А.7. Бесконечные точки в однородных координатах
Рассмотрим поведение точки в однородных координатах (х, у, z, w) по мере уменьшения w. При w = 0,01
точка равна (ЮОх, 100г/, 100z), при w = 0,0001 — уже (ЮОООх, 10000г/, lOOOOz) и т. д. Точка стремится
«к бесконечности» в направлении (х, у, z). Точка (х, у, г, 0) фактически может быть названа «бесконеч-
ной точкой». Одно из преимуществ однородных координат заключается в том, что подобная идеализи-
рованная точка имеет точное конечное представление, что снимает многие сложные особые случаи в
некоторых математических выводах. Например, две прямые линии всегда пересекутся, даже если они
параллельны [Ayers, 7; Semple, 183]. Однако другие вещи не работают столь хорошо. Чему, например,
равна разность двух точек в однородных координатах?
7.4.8. Как влияет перспективное преобразование на прямые и плоскости?
Требуется показать, что перспективное преобразование сохраняет плоскостность и промежуточность.
О Аргументируйте, что для этого достаточно доказать, что точка Р, лежащая на отрезке прямой меж-
ду точками А и В, преобразуется в точку Р', лежащую между преобразованными версиями А и В.
О Покажите, что перспективное преобразование действительно генерирует точку Р' с указанным
свойством.
О Покажите, что любая плоскость, проходящая через глаз, преобразуется в плоскость, параллель-
ную оси z.
О Покажите, что любая плоскость, перпендикулярная оси z, преобразуется в плоскость, также пер-
пендикулярную OCIIZ.
О Покажите, что относительная глубина сохраняется.
7.5. Создание стереоизображений
463
7.4.9. Более подробно о преобразованном отображаемом объеме
Покажите, что деформированный отображаемый объем имеет размеры, приведенные в подразделе
«Подробно о преобразованном отображаемом объеме». Используйте информацию, полученную в пре-
дыдущем упражнении.
7.4.10. Покажите окончательную форму проекционной матрицы
Основой проекционной матрицы является матрица из уравнения (7.10), которую следует умножить
справа на матрицы перемещения и масштабирования. Обозначив матрицу из уравнения за М, матрицу
смещения за Т, а матрицу масштабирования за S, покажите, что произведение этих матриц STM совпа-
дает с тем, что приведено в уравнении (7.13).
7.4.11. Что происходит с точками позади глаза?
Если перспективное преобразование перемещает глаз в минус бесконечность, то что происходит с точ-
ками, находящимися позади глаза? Рассмотрим прямую P(t), которая начинается в точке перед глазом
при t - 0 и доходит до точки за глазом при t - 1.
О Найдите параметрическую форму этой прямой в однородных координатах.
О Найдите параметрическое представление после того, как эта прямая подверглась перспективно-
му преобразованию.
О Интерпретируйте эту ситуацию геометрически. В частности, объясните геометрический смысл
четвертой однородной координаты. Полезное обсуждение этого явления приводится у Блинна
[Blinn, 30].
7.5. Создание стереоизображений
Позволим себе краткое отступление и рассмотрим использование разработанных ранее средств управ-
ления камерой для создания стереоизображений (stereo views) сцены. Стереоизображение помогает
сделать картину гораздо более понятной: правильное стереоизображение создает эффект глубины, что
уменьшает неоднозначность двумерного изображения. Все стереоскопические рисунки в этой книге
были выполнены с помощью технологии, к описанию которой мы приступаем.
Можно было бы назвать применяемую до сих пор камеру «циклоповой», по имени легендарного од-
ноглазого монстра. Чтобы прочувствовать ее ограниченность, попробуйте с одним закрытым глазом
прогуляться по комнате и выполнить простейшие задания. Наша естественная стереоскопическая систе-
ма «глаз—мозг» предоставляет нам огромный объем информации через вырабатываемый ею видимый
эффект глубины. Мы хотим придать такую же возможность изображениям компьютерной графики.
Для того чтобы создать стереоизображение, нужно сделать два изображения — «левым глазом» и
«правым глазом» — с помощью двух слегка различающихся камер, как показано на рис. 7.29. Эти каме-
ры построены с использованием одной и той же точки взгляда LookAt, однако с различными позициями
глаза. На экране рядом создаются два порта просмотра, как показано на рис. 7.29, б. Изображение для
левого глаза отображается в левом порту просмотра, а изображение для правого глаза — в правом порту
просмотра. Для просмотра стереоизображения нужно, чтобы ваш левый глаз смотрел на левую картин-
ку, а правый глаз — на правую картинку. Если все сделано правильно, то оба изображения сольются в
единое изображение с кажущейся глубиной. (Процедура просмотра таких изображений может потре-
бовать некоторой практики; в предисловии описывается, как обучиться этому.)
На рис. 7.30 показано стереоизображение каркаса бакибола, описанного в главе 6. Две картинки выг-
лядят совсем разными, и при рассмотрении только одной из них имеет место значительная визуальная
неоднозначность: неясно, какие ребра находятся впереди, а какие — сзади. Стереоизображение, однако,
устраняет эту неоднозначность ребер, делая картинку предельно ясной.
464
Глава 7. Трехмерный просмотр
глаз
Ваш левый Ваш правый
глаз смотрит сюда глаз смотрит сюда
Рис. 7.29. Создание стереоизображений
а
б
Рис. 7.30. Стереоизображение бакибола
На рис. 7.31 показаны стереоизображения сарая. На рис. 7.31, а камера повернута на 40°. Отметим, что
при такой ориентации сарая изображение трудно понять без стереоэффекта. Рисунок 7.31, б изображает
крупный план одного из углов сарая, при этом отчетливо видно сильное искажение, вызванное перспективой.
Рис. 7.31. Изображения сарая крупным планом
При создании двух камер, необходимых для стереоскопического просмотра, нужно решить, куда по-
местить левый глаз, а куда — правый. Простейший подход состоит в том, чтобы начать со стандартной
камеры, нацеленной на одну точку LookAt и одного начального «циклопова глаза», как предложено на
рис. 7.32. Вместе с назначенным вектором up эти два параметра определяют «циклопову камеру» с
направлениями u, v, п.
7.6. Классификация проекций
465
Рис. 7.32. Установка двух позиций глаза для стереоскопического просмотра
Левый глаз и правый глаз определены с небольшим отклонением от «циклопова глаза» — на некотором
расстоянии D в направлениях соответственно -и и и. Выбор D зависит от единиц измерения, используемых
в приложении. Если все длины и расстояния измеряются в дюймах, то пользователь, скорее всего, устано-
вит камеру на расстоянии в несколько дюймов от точки lookAt. Глаза у человека отстоят один от другого
примерно на 3 дюйма, поэтому для D хорошим начальным приближением было бы 1,5. Если же вы измеря-
ете все в метрах, то следует измерять в метрах и расстояние между глаз. В тех случаях, когда сцена сложна
и в ней нет характерного масштаба, то для достижения желаемого визуального эффекта может потребовать-
ся несколько экспериментов. В тематическом задании 7.2 предлагается план создания стереоизображений.
7.6. Классификация проекций
Как прихотливы линии любви!
Две могут пересечься под любым углом;
Но наши с тобой — явно параллельны,
и иначе как в бесконечности,
встретиться не могут никогда.
Эндрю Марвелл (Andrew Marwell). Определение любви
До сих пор мы изучали основные идеи «плоских проекций», где точки тем или иным способом проеци-
руются на плоскость. В главе 5 мы рассматривали параллельные проекции, а в этой главе изучали пер-
спективные проекции. Многие частные случаи таких проекций используются в изобразительном ис-
кусстве, архитектуре, техническом черчении, поэтому теперь посмотрим на их характеристики и на то,
как они соотносятся друг с другом.
Плоские проекции образуют древовидную структуру, приведенную на рис. 7.33. Каждый потомок
определенного типа проекций представляет собой частный случай своего родителя в дереве. Первое
фундаментальное разветвление имеет место между параллельной и перспективной проекциями. Нач-
нем с исследования последнего класса.
7.6.1. Одно-, двух- и трехточечные перспективы
Перспективные проекции обычно разделяются на три класса: одноточечные, двухточечные и трехто-
чечные проекции, отличающиеся ориентацией камеры относительно мировой системы координат. Их
названия произошли от различных видов рассматривания единичного куба, показанного на рис. 7.341.
' Рису нок 7.34 неточен: левое переднее нижнее ребро куба должно заканчиваться на оси г, а не пересекать ее и продолжаться даль-
ше. — Примеч. перев.
466
Глава 7. Трехмерный просмотр
Этот единичный куб расположен в октанте с положительными значениями х, у, z, причем один угол
куба совпадает с началом координат. Особенно важно, что его ребра выровнены по мировым коорди-
натным осям, которые здесь называются главными осями (principal axes), заданными направлениями
ортов i, j, к. Три плоскости х = 0, г/ -0, г-0 называются главными плоскостями (principal planes), и шесть
граней куба выровнены по ним.
Плоские проекции
Параллельная Перспективная
Рис. 7.33. Классификация общераспространенных проекций
Рис. 7.34. Единичный куб, главные оси и главные плоскости
Относительно данной системы координат камера может быть ориентирована бесконечным числом
способов. Для некоторых из этих способов ось п камеры перпендикулярна той или иной главной оси.
Традиционно принято разделять перспективные проекции по категориям в зависимости от числа ко-
нечных точек схода (finite vanishing points), образуемых главными осями. Напомним, что если прямая
перпендикулярна вектору п, то ее точка схода равна бесконечности; в противном случае ее точка схода
конечна. Можно также сосчитать число главных осей, не перпендикулярных к п. Это число совпадает с
количеством главных осей, пересекающих плоскость просмотра камеры. (Почему?)
Одноточечная перспективная проекция
При одноточечной перспективной проекции одна и только одна главная ось имеет конечную точку схо-
да. Поэтому вектор п не перпендикулярен одному из трех направлений i, j, к и перпендикулярен к двум
7.6. Классификация проекций
467
другим направлениям; а это значит, что он перпендикулярен к одной из главных плоскостей,
трех компонентов вектора п = (пх, пу, п:) должны равняться нулю.
а б
Рис. 7.35. Одноточечные перспективные проекции
На рис. 7.35, а показана одноточечная перспективная проекция, при которой камера была ори-
ентирована так, что ее плоскость просмотра параллельна плоскости ху. Удаляющиеся продолжения
ребер куба пересекаются в конечной точке схода (VP). Здесь для камеры п = (0, 0, 1). В координатах
камеры эти прямые сходятся в направлении с - (0, 0,-1), тогда из уравнения (7.6) координаты точки
схода равны (0,0). С другой стороны, у прямых, параллельных осям х и у, точки схода расположены
«в бесконечности».
Вернемся к рис. 7.21, на котором показаны две совокупности линий сетки на горизонтальной
плоскости. Эти линии сетки идут параллельно главным осям (в мировой системе координат). Вторая
совокупность линий сетки, не показанная на рисунке, шла бы вертикально, параллельно мировой оси у.
Этот рисунок выглядит как одноточечная перспектива, поскольку в нем есть единственная конеч-
ная точка схода на горизонте. В то же время камера могла бы быть направлена «вниз», что создало бы
двухточечную перспективу, которую мы будем рассматривать позднее. Вы просто не сможете отличить
их по одному рисунку. (Если вам сказано, что горизонт проецируется в у = 0, тогда можно сделать
вывод, что камера расположена горизонтально и тогда рисунок, несомненно, является одноточечной
перспективой.)
Двухточечная перспективная проекция
В случае двухточечной перспективной проекции конечными точками схода обладают две главных оси.
Поэтому направление п камеры не перпендикулярно двум этим осям; оно перпендикулярно только од-
ной из них. Следовательно, один из трех компонентов вектора п должен равняться нулю.
На рис. 7.36, а показан куб в двухточечной перспективной проекции; на рисунке имеются две конеч-
ные точки схода, поскольку обе оси ink пересекают плоскость просмотра. Камера была установлена
так, как показано на рис. 7.36, б: ее направление п составляет угол 0 с осью г, тогда n = (sin(0), 0, cos(0)).
Здесь вектор п перпендикулярен к j, поэтому вертикальная главная ось имеет бесконечную точку схода.
Нетрудно вычислить, где расположены конечные точки схода (см. упражнения в конце раздела).
Интересно посмотреть, что получится, если мы будем рассматривать в двухточечной перспективе
сцену с бесконечной сеткой, с которой мы впервые встречались на рис. 7.21. На рис. 7.37 показан слу-
чай, когда глаз по-прежнему находится в у - 1 и смотрит горизонтально, однако камера повернута вле-
во, так что п = (0,74,0,0,67). Теперь обе совокупности прямых сходятся к горизонту, образуя две далеко
отстоящие точки схода. (Каковы численные значения этих точек схода?) Многие из наиболее удален-
ных прямых на рисунке не показаны, так как они становятся настолько близкими одна к другой, что их
невозможно различить.
468
Глава 7. Трехмерный просмотр
Трехточечная перспективная проекция
При трехточечной перспективной проекции все три главных оси имеют конечные точки схода и все три
оси пересекают плоскость просмотра. Вектор п не перпендикулярен ни одной из осей, так что все его
компоненты — ненулевые.
На рис. 7.38 показан куб в трехточечной перспективной проекции. Видны все три конечные точки
схода.
Художники часто используют точки схода при рисовании перспективы, с целью выделить опреде-
ленные свойства или усилить впечатление от рисунка. Блестящая литография М К. Эшера (М. С. Escher)
на рис. 7.39 передает ощущение пространства, полученное с помощью трехточечной перспективы. (Где
на этом рисунке расположены три точки схода?)
Практические упражнения
7.6.1. Задание одноточечной перспективной проекции
Для установки нужной камеры мы выбираем в приложении eye и look, а вектор п определяется как раз-
ность eye - look. Дайте три примера сочетания eye и look, которые дадут интересные одноточечные про-
екции единичного куба.
7.6. Классификация проекций
469
Рис. 7.38. Трехточечная перспективная проекция
Рис. 7.39. Работа М. К. Эшера «Восхождение и спуск»: трехточечная перспективная проекция
(© 1988 М. С. Escher Heirs/Cordon Art-Baam-Holland. Использовано с разрешения)
7.6.2. Положение точки схода
Нарисуйте от руки единичный куб и мировые координатные оси в одноточечной перспективной про-
екции для камеры с eye = (2,3,4).
7.6.3. Вычисление точек схода
Найдите положения двух точек схода на рис. 7.36, а для произвольного значения угла 0.
7.6.4. Создание двухточечных перспективных проекций
Приведите три примера сочетания eye и 1 оок для камеры, создающей интересные двухточечные перспектив-
ные проекции единичного куба. Для каждого примера вычислите фактические положения точек схода.
470
Глава 7. Трехмерный просмотр
7.6.2. Параллельные проекции
Ниже исследуются различные типы параллельных проекций. В главе 5 мы ввели понятие параллельных
проекций в качестве простого способа просмотра объектов. Для задания отображаемого объема была
использована функция glOrthoO, a OpenGL делал все остальное. Теперь мы взглянем несколько присталь-
нее на природу параллельной проекции и разграничим ее различные типы, используемые на практике.
Известно, что в случае перспективной проекции все точки Р сцены проецируются на плоскость про-
смотра с помощью проецирующих лучей (projectors), сходящихся в точке глаза: каждый проецирую-
щий луч определяется точкой Р и глазом, и все эти лучи имеют различные направления. Для парал-
лельных проекций, напротив, все проецирующие лучи имеют одно и то же направление, назовем его d.
На рис. 7.40 показано проецирование двух произвольных точек: точка Р проецируется в р на плоскости
просмотра, а точка Q — в q, причем обе точки — в направлении вектора d.
Плоскость
просмотра
Рис. 7.40. Параллельные проекции
Немного теории касательно параллельных проекций
В какую точку р проецируется точка Р? Рассмотрим плоскость с нормалью п, проходящую через неко-
торую точку В. Тогда точка р расположена в этой плоскости в месте пересечения плоскости и луча, ис-
ходящего из точки Р по направлению d. Ранее мы уже неоднократно производили такое вычисление.
Если параметрическая форма этого луча Р + dt, то мы подставляем это выражение вместо Q в уравне-
ние плоскости п • (Q - В) - 0 и решаем его относительно t. Для получения точки соударения подставля-
ем это значение t в выражение Р + dft
p = P+dn^B~PY (7.16)
n-d
Это выражение сильно отличается от того, которое мы использовали при перспективной проекции.
В частности, здесь отсутствует уменьшение расстояния; это означает, что в знаменателе отсутствует
член, зависящий от Р. (Отметим вдобавок, что замена направления d на на -d не окажет никакого вли-
яния на результирующую проекцию.)
Чтобы понять смысл формулы (7.16), используем обычную камеру. Мы будем работать в системе
координат камеры, тогда вектор п - (0,0,1). Проецировать будем на плоскость ху, для которой точка
В = (0, 0, 0). (Это немного проще, чем проецирование на ближнюю плоскость.) Тогда
( Р Р У
p=\px-dx-± Py-dy-f, 0
I d> J
(7.17)
(Проверьте эту формулу!) Параллельные проекции подразделяются на два основных типа, как по-
казано на рис. 7.41.
1. Косоугольная-, направление проекции d не параллельно вектору п.
2. Ортографическая-. направление проекции d параллельно вектору п.
7.6. Классификация проекций
471
Рис. 7.41. Параллельные проекции при работе в системе координат камеры:
а) общий случаи направления d; б) d параллельно п
На рис. 7.41, а показан общий случай направления вектора d, не обязательно параллельного вектору п.
(Разумеется, мы не будем выбирать его так, чтобы dz было равно нулю.) Рисунок 7.41, б демонстрирует
случай, когда векторы d и п параллельны, так что dx и dy равны нулю. Рассмотрим каждый из этих типов
поочередно.
Ортографические проекции
При ортографических проекциях два компонента dx и dy равны нулю. Тогда точка р становится равной
р = (Рх, Р, 0). Таким образом, ортографическое проецирование сводится к простому отбрасыванию тре-
тьего компонента точки Р в координатах камеры.
Интересно посмотреть, как OpenGL выполняет ортографическую проекцию. Напомним, что OpenGL
для описания отображаемого объема камеры использует проекционную матрицу. Проекционная матри-
ца, в частности, определяет, как преобразовывать вершины, чтобы «втиснуть» их в канонический отобра-
жаемый объем (CVV). Пусть фактический отображаемый объем простирается от I до г (сокращения от
left — левый и right — правый) по оси х, от А до i (bottom — нижний и top — верхний) по оси у, от -п до
-/ (near — ближний и far — дальний) по оси z. Для преобразования параллелепипеда, сформированного
таким образом внутри CW, мы должны произвести перемещение и масштабирование так, чтобы CW
простирался от -1 до 1 в каждом измерении. Легко убедиться (см. упражнения), что матрица
( 2 о 0 г+/
г-1 г-1
п 2 п t+b
t-b > t-b
0 0 -2 f + n
f~n -f-n
0 0 0 1
(7.18)
(проекционная матрица OpenGL для ортографической проекции) действительно преобразует отобра-
жаемый объем в CVV. Такая матрица формируется функцией glOrthoO. Если на нее умножить точку Р
(выраженную в однородных координатах), то получим именно ту точку р, которую предоставляет
OpenGL для отсечения и отображения в порт просмотра. Отметим, что OpenGL не устанавливает
z-компонент в нуль, как это делали мы; он производит преобразование, а не проецирование. В конце
операции он все-таки осуществляет проецирование, отделяя z-компонент; компоненты х и у в экранных
координатах используются при рисовании, а компонент z — для оценки глубины.
Типы ортографических проекций
Существуют различные типы ортографических проекций, отличающихся друг от друга ориентацией
камеры в мировой системе координат. Эти проекции названы в соответствии с тем, как расположено
относительно мировых координатных осей направление камеры п.
472
Глава 7. Трехмерный просмотр
Многовидовые ортографические проекции. Они представляют традиционные виды объекта сверху,
спереди и сбоку. Вектор п поочередно устанавливается параллельным векторам k, i, j, и интересующий
нас объект рисуется в каждом случае. На рис. 7.42 показан пример таких проекций. Многовидовые
ортографические проекции специально приспособлены для технического черчения, так как размеры
объекта можно определить непосредственно, особенно если он «кубовидный» и различные его грани
выровнены относительно мировых осей.
Рис. 7.42. Многовидовое ортографическое черчение
Аксонометрические проекции. В аксонометрических проекциях вектор п выбирается так, чтобы наи-
лучшим образом передать трехмерную «суть» формы объекта. При такой проекции вектор п обычно не
параллелен ни одной из главных осей; скорее, он ориентируется так, чтобы были видны три смежные
грани (кубовидного) объекта. Выбор тех граней, которые делаются видимыми, зависит от того, какие
грани объекта важны и должны быть выделены особо. Кроме того, одна из главных осей обычно делает-
ся вертикальной. Параллельные прямые такого объекта, разумеется, и видны как параллельные, однако
если прямая удаляется от наблюдателя, то она укорачивается с некоторым коэффициентом. На рисун-
ке 7.43 показан случай, когда вектор п составляет угол а с осью х.
Прямая единичной длины, составляющая угол а радиан с нормалью к плоскости просмотра, имеет
видимую длину sin(a); именно эта величина и называется коэффициентом укорачивания (foreshortening
factor).
7.6. Классификация проекций
473
Аксонометрические проекции подразделяются на три класса — в зависимости от того, сколько глав-
ных осей укорачиваются одинаково.
1. Изометрическая («одинаковая мера»): все три главных оси укорачиваются одинаково.
2. Диметрическая («две меры»): две главных оси укорачиваются одинаково.
3. Триметрическая («три меры»): все три главных оси укорачиваются по-разному.
Изометрические проекции. Изометрическая (isometric) проекция куба показана на рис. 7.44, а —
в направлении вдоль одной из восьми диагоналей куба. Все три оси укорачиваются с одним и тем же
коэффициентом. Как видно из рис. 7.44, б, изометрическая проекция прозрачного куба представляет
собой правильный шестиугольник с тремя диагоналями.
а б
Рис. 7.44. Изометрическая проекция куба
Условие изометрической проекции: пх = ±пу = ±пг. При изометрической проекции углы между про-
екциями главных осей одинаковы. Длина любой прямой, лежащей в главной плоскости, может быть оп-
ределена непосредственно из чертежа, после чего эту длину следует масштабировать с постоянным ко-
эффициентом (каким именно?), чтобы получить истинную длину этой прямой.
Диметрические проекции. Если только две оси составляют одинаковый угол с нормалью п, то такая
проекция называется диметрической (dimetric). При диметрической проекции два направляющих ко-
синуса должны быть равны по модулю, то есть пх = +пу, пх=±пг или пу - ±пг. На рис. 7.45 приведен ряд
диметрических проекций; третья из них — почти изометрическая. Для каждой проекции пх = пу, причем
оба отрицательны. (Чему равно приближенное значение п на первом рисунке? На последнем?) На каж-
дой проекции отмеченные углы равные между собой. Различные ориентации особо выделяют различ-
ные грани.
а бе
Рис. 7.45. Несколько диметрических проекций куба
Триметрические проекции. Если, наконец, все три оси составляют различные углы с нормалью п,
то такая проекция называется триметрической (trimetric). На рис. 7.46 приведен пример, в котором
осуществлена почти полная свобода выбора компонентов вектора п. Если эта ориентация выбрана
удачно, то триметрическая проекция может выглядеть наиболее естественно.
474
Глава 7. Трехмерный просмотр
Рис 7.46. Тримегрическая проекция
Косоугольные проекции
При ортографических проекциях сохраняется точная форма одной из граней объекта, однако они недоста-
точно хорошо передают трехмерную природу объекта. С другой стороны, аксонометрические проек-
ции передают трехмерную сущность объекта, но не показывают точную форму ни одной грани объекта.
При косоугольных проекциях предпринимается попытка сочетать полезные свойства как ортографи-
ческих, так и аксонометрических проекций. При этом обычно показывается точная форма одной грани
объекта (наиболее важной грани) и одновременно передается общий трехмерный вид объекта.
Равенство (7.17) определяет, где проекция любой точки Р сцены появляется в плоскости просмотра.
Если компонент dx отличен от нуля, то х изменяется в соответствии с коэффициентом, пропорциональ-
ным Р2. Напомним, что изменение одной координаты на величину, пропорциональную другой коорди-
нате, называется сдвигом (shear). Тогда действие «косоугольности» проекции заключается в сдвиге
изображения, который делает видимыми другие грани кубовидного объекта.
Запишем равенство (7.17) в матричной форме:
На сдвиг указывают два элемента матрицы, расположенные вне диагонали. На рис. 7.47 показан
пример вида сарая при косоугольной проекции. На верхней части рисунка показан точный вид сарая
сверху, а плоскость просмотра совпадает с задней стенкой сарая. Для показанного на рисунке вектора d
точка А проецируется в а, точка В — в b и т. д. Разумеется, точки на задней стенке сарая проецируются
сами в себя. Эта проекция эквивалентна сдвигу сарая по оси х, описываемому углом 0, где tg(0) - dx/d2.
На нижней части рисунка показано спроецированное изображение сарая при виде спереди. Ближняя
стенка сарая воспроизводится в точности, а благодаря сдвигу видна и часть боковой стенки. Обратите
внимание на длины г и s. Ширина сарая равна г единиц, что сохраняется на его изображении. Но, вдоба-
вок к ней, благодаря сдвигу стала видна и боковая стенка сарая. Ее видимая часть имеет длину s.
На рисунке 7.48 показано несколько проекций куба, полученных при различных значениях векто-
ра d. Наиболее популярны первая и последняя проекции, они даже имеют отдельные названия. Первая
из них называется косоаксонометрической (cavalier) проекцией; для нее dx = dy - d2, поэтому в результате
сдвига проекции боковой и верхней граней куба имеют ту же длину, что и передняя грань. Последняя
проекция носит название кабинетной (cabinet) проекции; для нее dx“dy“ djl, поэтому длины боковой
и верхней граней равны половине длины передней грани. Некоторым кажется, что косоаксонометричес-
7.6. Классификация проекций
475
кая проекция выглядит слишком удлиненной, а кабинетная — несколько укороченной, но, несмотря на
это, простота вычислений таких проекций обеспечивает их популярность.
Рис 7.48. Несколько косоугольных проекций куба
OpenGL не поддерживает напрямую создание косоугольных проекций. Подпрограмма gl Ortho О за-
дает только ортографическую проекцию, но тем не менее мы можем создавать косоугольные проекции,
самостоятельно производя сдвиг.
Нам нужно сначала произвести сдвиг объекта, а затем отобразить его в канонический отображае-
мый объем. Зададим поэтому начальную проекционную матрицу в форме (7.18) с помощью подпро-
граммы gl Ortho () и умножим на нее матрицу сдвига. Поскольку этими действиями мы фактически оп-
ределяем камеру, то имеет смысл добавить соответствующую функцию в класс Camera — назовем ее
setObliqueO. Эта функция в качестве параметров принимает шесть параметров (left, top ит. д.), необ-
ходимых для функции glOrthoC), а также вектор d, определяющий направление проецирующих лучей.
Если вектор d = (0,0,1), камера произведет обычные ортографические проекции. Можно использовать
следующий код:
void Camera:: setOblique(Vector3 d...others..)
// остальные
{
// establish camera for oblique projections
// устанавливаем камеру для косоугольных проекций
476
Глава 7. Трехмерный просмотр
glMatrixMode(GL_PROJECTION);
glLoadldentityО;
glOrthod. r. b, t. n. f);
// set the projection matrix
// задаем проекционную матрицу
if(d.z == 0.0) return: у
// for orthographic projections
// для ортографических проекций
float m[16];
// space for a 4-by-4 matrix
// место для матрицы 4 на 4
for(int i - 0: i < 16: i++)
// start with identity matrix
// начинаем с единичной матрицы
m[i] - (i«5 == 0)? 1.0 : 0.0:
// identity matrix
// единичная матрица
m[8] = -d.x/d.z:
// add the shear terms
// добавляем коэффициенты сдвига
m[9] = -d.y/d.z:
glMultMatrixf(m):
// postmultiply it by m
// умножаем ее справа на m
}
Эта подпрограмма с помощью glOrthoO инициализирует проекционную матрицу для параллельной
проекции и затем умножает получившуюся матрицу справа на матрицу сдвига. Что касается последней
матрицы, то в программе используется слегка модифицированный вариант матрицы (7.19), где 0 на
пересечении третьей строки и третьего столбца заменен на 1. Такой подход более совместим с OpenGL
и сохраняет информацию о глубине, чтобы OpenGL смог затем произвести удаление невидимых поверх-
ностей. В тематическом задании 7.3 предоставляется возможность поэкспериментировать с созданием
косоугольных проекций.
Практические упражнения
7.6.5. Анализ проекционной матрицы
Покажите, что равенство (7.18) правильно описывает проекционную матрицу, используемую в OpenGL.
Иначе говоря, покажите, что эта матрица преобразует каждый угол отображаемого объема в нужный
угол канонического отображаемого объема.
7.6.6. Нахождение вектора п
Определите компоненты вектора п, которые задают коэффициенты укорачивания (foreshortening ratios)
по осям х, у, г, соответственно равные 0,6, 0,4, 0,7. При скольких различных направлениях вектора п
можно получить такие коэффициенты укорачивания?
7.6.7. Вектор п в сферических координатах
Определите три коэффициента укорачивания для вектора п, имеющего широту 60° и долготу 125°.
7.6.8. Нарисуйте куб
Нарисуйте от руки последовательность диметрических проекций куба, для которых пу = -пг, а пх возра-
стает от 0 до 1.
7.6.9. Камера в сферических координатах
Какие значения могут принимать широта и долгота вектора п при изометрической проекции?
7.8. Тематические задания 477
7.7. Резюме
В данной главе мы увидели, как определять «систему просмотра» и как управлять ею в программе, что-
бы пользователь мог создавать изображения того, как «выглядит» трехмерная сцена с различных точек
зрения, а также «пилотировать» камеру по сцене в процессе анимации. Камера моделируется как глаз,
а отображаемый объем находится в собственной системе координат камеры. Она в общих чертах напо-
минает «камеру-обскуру» и проецирует точки на плоскость просмотра. Точки, лежащие внутри ото-
бражаемого объема, проецируются на плоскость просмотра, а точки, лежащие вне его, отсекаются.
Значительная часть математических вычислений при процессе просмотра связана с геометрически-
ми преобразованиями, задающими координаты точек в различных пространствах. Графический кон-
вейер, применяемый в OpenGL и многих других системах, производит последовательность преобразо-
ваний подаваемых в него вершин. Каждое преобразование включает в себя отдельные свойства камеры
и механизм проецирования. Благодаря использованию однородных координат все эти преобразования
могут быть осуществлены путем умножения матриц. Точки в конце концов отображаются в специаль-
ное пространство, которое идеально приспособлено для эффективного отсечения ребер; кроме того, при
использовании такого пространства для любой камеры можно применять единый алгоритм отсечения.
Геометрия перспективных проекций в основном является геометрией подобия, и к счастью, в ней
сохраняется «плоскостность» и «промежуточность», так что проекция всей прямой линии может быть
вычислена проецированием только двух точек этой прямой. Главное преобразование, которому подвер-
гается точка в процессе проецирования, включает в себя деление на глубину этой точки, что позволяет
более удаленным объектам выглядеть меньше. Такое деление пространственных координат на общий
делитель делает более удобным представление данного преобразования в однородных координатах, где
четвертой координатой является этот делитель. В этом случае преобразование может быть проделано с
помощью матричного умножения, за которым следует этап деления, так что геометрические подробно-
сти, отличающие одну проекцию от другой, просто определяют параметры этой матрицы.
Теперь весь графический конвейер можно представить в виде матричного умножения, за которым
следует операция отсечения, затем этап перспективного деления и, наконец, матричное^умножение для
перехода в экранные координаты. Первую матрицу часто разделяют на матрицу моделирования-вида и
проекционную матрицу, так как это позволяет задавать ориентацию и положение камеры независимо
от ее отображаемого объема. Ранее мы показали, что матрица моделирования-вида сочетает в себе два
преобразования: одно преобразование помещает объект нужного размера в нужное положение на сце-
не; второе отражает положение и ориентацию на сцене самой камеры.
Представляется полезным разделить по категориям различные виды проекций, применяемых на
практике. Основным является различие между перспективными и параллельными проекциями, каж-
дая из которых обладает теми или иными преимуществами для решения различных задач. Перспектив-
ные проекции очень хорошо отражают то, что мы видим в обычной жизни. Посредством ориентирова-
ния плоскости просмотра камеры относительно объекта можно получить одно-, двух- и трехточечные
перспективные проекции, каждая из которых обеспечивает присущий ей визуальный эффект. Парал-
лельные проекции полезны, когда важно сохранить точную форму какой-либо грани. Такие проекции
часто используются в задачах автоматического проектирования (CAD), когда измерения должны де-
латься прямо с чертежа.
7.8. Тематические задания
Тематическое задание 7.1. «Пилотирование» камеры по сцене
Уровень сложности II.
Напишите приложение, позволяющее пользователю «пилотировать» камеру по какой-нибудь сцене.
(Если вы ранее разрабатывали программу просмотра сеток, такую как в главе 5, то в ней достаточно
заменить функции просмотра функциями из класса Camera.) Для управления камерой пользователь
478
Глава 7. Трехмерный просмотр
нажимает клавиши. При каждом нажатии клавиши камера скользит в одном из трех направлений или
поворачивается вокруг одной из своих осей (путем вызовов функций, аналогичных используемым в
листинге 7.3), после чего сцена перерисовывается с точки зрения новой камеры. Кроме того, предо-
ставьте пользователю возможность изменять угол зрения и форматное соотношение камеры посредством
нажатия других клавиш.
Работа с камерой может быть сделана намного более наглядной, если заполнить горизонтальную
плоскость совокупностью линий сетки (grid lines), как показано на рис. 7.21. Это легко сделать, напри-
мер, в таком цикле:
fordnt х - -100; х < 100; х++)
{
glBegin(GL_LINES);
glVertex3d(х.0.100): glVertex3d(x.0.-100):
glEndO:
}
в результате работы которого будет нарисовано множество из 200 х-контуров. Аналогичный цикл рисует
z-контуры. Добавьте сюда управление с помощью клавиш, чтобы пользователь мог убирать линии сетки
или ставить их обратно.
В OpenGL существуют примитивы, которые можно использовать для моделирования интересных
сцен. Используйте для создания сцены некоторые из объектов, описанных в главе 5: сферы, конусы,
додекаэдры, а также чайник. Выберите каркасные или сплошные версии этих объектов. Если вы выбе-
рете сплошные версии, то установите источник света и задайте объектам свойства материала. В каче-
стве руководства используйте примеры из главы 5.
Тематическое задание 7.2. Стереоизображения
Уровень сложности II.
Усовершенствуйте свою программу просмотра сеток так, чтобы она могла создавать стереоизобра-
жения объектов, как показано на рис. 7.29. Создаются три объекта класса Camera. Вначале в качестве
постоянной камеры создается «циклопова камера», а затем с использованием хранящейся в ней инфор-
мации (значений eye, направления и и т. д.) конструируются камеры левого и правого глаза.
Изображения, созданные этими двумя камерами, помещаются рядом в два порта просмотра в экран-
ном окне. Попрактикуйтесь с перемещением своих глаз так, чтобы увидеть стереоэффект.
Обеспечьте пользователю возможность перемещать камеры правого и левого глава (сцепленные
вместе) по сцене для получения хороших изображений. Поэкспериментируйте, чтобы подобрать
наиболее подходящее расстояние между камерами как для объектов, близких к камерам, так и для
далеких от них.
Тематическое задание 7.3. Создание параллельных проекций
Уровень сложности II.
Добавьте к классу Camera функцию setObl iqueО, рассмотренную в разделе «Параллельные проекции»,
для получения ортографических и косоугольных проекций объектов. Поэкспериментируйте с этой ка-
мерой, используя сцену, составленную из линий сетки, описанную в тематическом задании 7.1, а также
из нескольких кубов, расположенных на горизонтальной плоскости и над ней. Имейте в виду, что эти
линии сетки проецируются как параллельные линии и у них нет (конечных) точек схода. Предоставьте
пользователю возможность перемещать камеру по сцене и посмотрите, как выглядят при различных
положениях камеры параллельные ребра куба.
Позвольте пользователю посредством нажатия клавиш увеличивать и уменьшать отношения dx/dz и
dy/dj что даст возможность создавать различные косоугольные проекции. Определите, когда получает-
ся кабинетная проекция и когда — косоаксонометрическая.
7.8. Тематические задания
479
Тематическое задание 7.4. Самодельное проецирование
(если бы OpenGL был недоступен)
Уровень сложности III.
Напишите приложение, осуществляющее перспективные проекции трехмерных объектов с исполь-
зованием вашего собственного графического конвейера вместо конвейера OpenGL. Эта задача проще,
чем может показаться вначале; требуется только сформировать собственную матрицу моделирования-
вида (modViewMat[16]), проекционную матрицу (projMat[16]) и подпрограмму отсечения (для нее можно
использовать код из листинга 7.4).
Для текущей визуализации вы можете все же использовать OpenGL (если, конечно, он вам досту-
пен). Для отключения матрицы моделирования-вида и проекционной матрицы OpenGL загрузите в них
единичные матрицы. OpenGL будет по-прежнему выполнять отсечение границами канонического ото-
бражаемого объема. Запустите свою программу на полет вокруг различных каркасных объектов и сквозь
них наблюдайте эффект отсечения.
Тематическое задание 7.5. Удаление невидимых граней
для большей эффективности
Уровень сложности II.
При визуализации каркасного объекта каждая из его граней посылается в графический конвейер, ее
вершины подвергаются преобразованиям, и затем грань визуализируется. Однако при любой ориента-
ции объекта существует много граней, «скрытых» от наблюдателя. Поэтому они носят название неви-
димых граней (back faces) и нет необходимости пропускать их через графический конвейер, поскольку
их не будет видно. Какая-либо грань находится ближе к глазу и поэтому заслоняет их. На рис. 7.49
показан классический базовый сарай, наблюдаемый некоторой камерой. Для любой позиции камеры
некоторые из граней этого сарая будут нелицевыми; две из них отмечены на рисунке.
Рис. 7.49. Нелицевые грани сарая (а); определение нелицевой грани {б)
Мы называем нелицевой такую грань, внешняя поверхность которой скрыта от глаза. Это означает,
что ее направленный наружу нормальный вектор, допустим ш, указывает в направлении, отличающем-
ся менее чем на 90° от вектора, проходящего через глаз и любую точку Р на этой грани (см. рис.7.49, б).
Если угол между двумя векторами меньше 90°, то их скалярное произведение положительно. Поэтому
проверка того, является ли данная грань нелицевой, выглядит так:
Грань Т7 является нелицевой, если (Р - eye) • ш > 0.
Этот тест не занимает много ресурсов. Следовательно, проверка грани на невидимость и игнорирова-
ние ее при положительном ответе могли бы заметно ускорить рисование сложных каркасных объектов.
Приведенный ниже код является слегка измененной подпрограммой Mesh :: draw() из листинга 6.2.
Эта функция рисует только лицевые (видимые) грани каркасных объектов, игнорируя те грани, кото-
рые она определила как невидимые с помощью теста 1 f (1 sBackFaceC f....)) continue. Напишите код для
функции int isBackFaceO, которая возвращает 1, если грань/является нелицевой, и 0 в противном слу-
чае. Предупреждаем, однако, что вершины каркасных объектов всегда преобразуются с помощью мат-
480
Глава 7. Трехмерный просмотр
рицы моделирования-вида, поэтому вам следует определиться, работать ли (и как) в мировых коорди-
натах, координатах глаза или в каких-нибудь еще. Вот этот код:
void Mesh:: drawFrontFacesO
// use OpenGL to draw this mesh
// для рисования этой сетки используем OpenGL
{
for(int f - 0: f < numFaces: f++) // draw each face
{
if(isBackFace(f,...)) continue:
glBegin(GL_POLYGON):
for(int v - 0: v < facetfJ.nVerts: v++)
// for each one...
// для каждой из них...
{
int in = facetf].vert[v].normindex :
// index of this normal
// индекс этой нормали
int iv - face[f].vert[v].vertlndex :
// index of this vertex
// индекс этой вершины
glNormal3f(norm[in].x, norm[in].y, norm[in].z);
glVertex3f(pt[iv].x. pt[iv].y. pt[iv].z):
}
glEndO;
}
}
Разработайте приложение, которое рисует сетки для произвольной камеры, и проверьте скорость
работы вашей программы с удалением и без удаления нелицевых граней.
7.9. Дополнительная литература
Как уже упоминалось на протяжении данной главы, в книге «OpenGL. Руководство программиста»
(OpenGL Programming Guide [Woo, 215]) предлагается хорошо изложенное введение в установку систе-
мы просмотра и управления этой системой в трехмерной графике. Фоли и другие авторы [Foley, 17]
рассматривают дополнительные подробности. В ранней статье Карлбома и Пасиорека (Carlbom and
Paciorek [Carlbom, 39]) содержатся разработки идей по различным типам параллельных и перспективных
проекций. Кроме того, в нескольких статьях Блинна в его работе «Уголок Джима Блинна: Путешествие по
графическому конвейеру» (Jim Blinn’s Comer: A Trip down the Graphics Pipeline [Blinn, 31]) предлагаются
понятные и занимательные описания проекций, преобразований изображений и методов отсечения.
8 Визуализация граней
для усиления реалистичности
□ Добавление реалистичности в изображения трехмерных сцен.
□ Изучение способов исследования отражения света от поверхностей.
□ Визуализация полигональных сеток, освещенных источником.
□ Рассмотрение способов получения гладкой полигональной сетки.
□ Удаление невидимых поверхностей с помощью буфера глубины.
□ Разработка методов наложения текстур на поверхности объектов.
□ Добавление в сцену тени объектов.
В данной главе мы рассмотрим объекты, разработанные в предыдущей главе, и попытаемся сделать их
зрительно более интересными и реалистичными. В разделе 8.1 «Введение» объясняется необходимость
усиления реалистичности изображений трехмерных объектов. Раздел 8.2 «Введение в модели закраши-
вания» знакомит с различными моделями закрашивания (затенения), используемыми в компьютерной
графике; там же разрабатываются инструменты для вычисления главных компонентов цвета объекта:
фонового (ambient), диффузного (diffuse) и зеркального (specular). В этом разделе также описывается,
как задавать источники света в OpenGL, как характеризовать свойства материала поверхностей, а как
при визуализации полигональных сеток работает графический конвейер OpenGL.
В разделе 8.3 «Плоское и плавное закрашивание» основное внимание уделяется визуализации объек-
тов, смоделированных в виде полигональных сеток. Исследуется плоское закрашивание, а также
закраска Гуро и Фонга (Gouraud and Phong). В разделе 8.4 «Удаление невидимых поверхностей» рас-
сматривается простая технология удаления невидимых поверхностей, использующая буфер глубины.
Корректное удаление невидимых поверхностей значительно усиливает реалистичность изображений.
В разделе 8.5 «Добавление текстуры к граням» изучаются методы «раскрашивания» поверхностей
объекта текстурой, в результате которого они выглядят сделанными из настоящего материала типа кир-
пича или дерева, и методы «наклеивания» на объекты ярлыков или фотографий друзей. Описываются
подпрограммы создания текстур. Подробно исследуется трудная задача правильной интерполяции тек-
стуры. Кроме того, в этом разделе:
1) представлена законченная программа наложения текстуры на объекты с использованием OpenGL;
2) исследуется наложение текстуры на криволинейные поверхности, отображение выпуклостей,
отображение окружающей среды;
3) предлагаются новые инструменты для придания реалистичности трехмерной сцене.
16 Ф. Хилл
482
Глава 8. Визуализация граней для усиления реалистичности
В разделе 8.6 «Добавление теней объектов» описываются две технологии добавления теней к изоб-
ражениям. Глава заканчивается несколькими тематическими заданиями, в которых углубленно изуча-
ются некоторые из этих тем и которые побуждают читателя поэкспериментировать с ними.
8.1. Введение
В предшествующих главах мы разработали инструменты для моделирования каркасных объектов и для
управления камерой, которая рассматривает их и создает их изображения. В этой главе мы хотим доба-
вить инструменты, которые сделают эти и другие объекты более интересными или реалистичными, или
и то и другое вместе. В некоторых примерах главы 5 осуществлялся вызов многих функций OpenGL
для создания блестящих чайников и сфер, залитых светом, однако не была рассмотрена ни одна теория,
объясняющая, как это делается. Здесь мы восполним этот недостаток и разработаем теорию визуализа-
ции (rendering) изображения интересующих нас объектов. Как должен выглядеть каждый пиксел изоб-
ражения, определяется с помощью расчета. В значительной мере визуализация определяется моделью
закрашивания (shading model), которая призвана смоделировать, каким образом свет, исходящий из
источников, будет взаимодействовать с объектами сцены. На практике обычно никто не пытается сыми-
тировать все физические принципы, лежащие в основе рассеяния и отражения света. Эти принципы
достаточно сложны, и их реализация привела бы к очень медленным алгоритмам. Однако придумано
множество моделей, использующих аппроксимацию и тем не менее хорошо представляющих различ-
ные уровни реалистичности.
Мы начнем с описания иерархии технологий, обеспечивающих возрастающие уровни реалистично-
сти, чтобы показать основные возникающие при этом проблемы. Затем рассмотрим, как включать каж-
дую из этих технологий в приложение, а также как использовать OpenGL, чтобы он выполнил за нас
большую часть самой трудной работы.
На нижней ступени этой иерархии находится каркасная (wire-frame) визуализация, обеспечивающая
низший уровень реалистичности. На рис. 8.1 показан «шквал» из 540 кубов в виде каркасных структур.
Нарисованы только ребра каждого из объектов, поэтому можно смотреть скозь каждый куб. При исполь-
зовании этой технологии трудно понять, что есть что. (Немного помогло бы стереоизображение.)
Рис. 8.1. Каркасная визуализация сцены
Рисунок 8.2 демонстрирует значительное улучшение: не рисуется ни одно ребро, лежащее позади
грани. Эту технологию можно назвать «каркасной визуализацией с удалением невидимых поверхнос-
тей». Несмотря на то что рисуются только ребра, объекты теперь выглядят объемными и уже нетрудно
определить, где заканчивается один объект и где начинается следующий. Отметим, что некоторые реб-
ра заканчиваются внезапно, так как они уходят за грань. Для любознательных: этот рисунок был вы-
полнен при помощи OpenGL при подключении его буфера глубины. Для каждого каркасного объекта
8.1. Введение
483
грани были нарисованы белым цветом с помощью подпрограммы drawMeshO, а затем ребра были нари-
сованы черным цветом посредством подпрограммы drawEdgesO. Обе эти подпрограммы были рассмот-
рены в главе 6.
Рис. 8.2. Каркасная визуализация с удалением невидимых поверхностей
На следующей ступени иерархии генерируются изображения, в которых объекты располагаются «на
сцене», освещенной источниками света. Различные части объекта отражают различное количество све-
та, в зависимости от свойств изображенных поверхностей, положения источников света и «глаза» ка-
меры. Этот эффект требует вычисления яркости или цвета каждого фрагмента, а не выбора их пользова-
телем. При этом вычислении используется модель закрашивания, которая определяет, какое количество
света отражается от каждого фрагмента.
На рисунке 8.3 показана сцена, смоделированная полигональными сетками: бакибол покоится на
двух цилиндрах (верхний является коническим), а переключатель (jack) лежит на столе. На рис. 8.3, а
показана каркасная версия, а на рис. 8.3, б — закрашенная версия сцены (с удалением невидимых по-
верхностей). Грани, обращенные к источнику света, выглядят ярче тех, которые повернуты от источни-
ка. Такое изображение называется плоским, или постоянным закрашиванием (flat shading): вычисле-
ние количества света, отражаемого каждой гранью, производится в ее единственной точке, вследствие
чего все точки грани визуализируются с одним и тем же оттенком серого. Следующим шагом является,
конечно, использование цвета.
а б
Рис. 8.3. Закрашивание каркасной модели: а) вид каркасной модели; б) плоское закрашивание
484
Глава 8. Визуализация граней для усиления реалистичности
В главе 6 мы рассматривали построение каркасной аппроксимации гладкого криволинейного объек-
та. Изображение такого объекта должно отражать его гладкость, показывая «истинную поверхность»,
а не отдельные полигоны, составляющие объект. На рис. 8.4 изображена сцена с рис. 8.3, на этот раз
визуализированная с использованием гладкого закрашивания (smooth shading), то есть с плавными
цветовыми переходами. На этих рисунках различные точки грани изображены с различными уровня-
ми яркости, найденными по схеме интерполяции, известной как закрашивание Гуро (Gouraud shading).
Изменение уровней яркости серого цвета здесь намного более плавное, чем на рис. 8.3, б, при этом
ребра полигонов исчезают, создавая впечатление ровной, а не ограненной поверхности. Закрашивание
Гуро изучается в разделе 8.3.
Рис. 8.4. Сцена с рис. 8.3, визуализированная с помощью гладкого закрашивания
Для того чтобы объект выглядел блестящим, можно добавить блики. На рис. 8.5 показана сцена
с рис. 8.4 с добавленными компонентами зеркального (отражающего) света (specular light). Чем более
блестящим является объект, тем более локализованы его блики, из-за которых объект часто выглядит
сделанным из пластмассы.
Рис. 8.5. Добавление отраженных бликов
Еще одним эффектом, увеличивающим реалистичность изображения, является добавление теней.
На рис. 8.6 показана та же сцена, что и на рис. 8.5, однако на ней соответствующим образом визуализи-
рованы тени. (Один объект отбрасывает тень на соседний объект.) В разделе «Добавление теней объек-
тов» мы изучим, как это делается.
8.1. Введение
485
Рис. 8.6. Та же сцена, визуализированная стенями
Добавление к объекту текстуры представляет собой большой шаг на пути к реалистичности. На рис. 8.7
показана сцена с рис. 8.6, однако теперь все поверхности «раскрашены» различными текстурами.
При применении этих текстур различные поверхности могут казаться сделанными из каких-нибудь
материалов, например из дерева, мрамора или меди. Кроме того, изображение можно наносить на
объект, как переводную картинку.
Рис. 8.7. Наложение текстур на поверхности
Существуют и другие технологии, усиливающие реалистичность. В главе 14 мы будем подробно изу-
чать трассировку лучей. Этот подход является дорогостоящим с вычислительной точки зрения, однако
трассировка лучей несложна для программирования и создает изображения с правильными тенями,
зеркальными отражениями и прохождением света сквозь прозрачные объекты.
В этой главе мы изложим несколько методов визуализации сцен с еще большей реалистичностью.
Вначале мы рассмотрим классические модели освещения, используемые в компьютерной графике, которые
создают вид объекта, освещенного несколькими источниками. Мы увидим, как следует рисовать полиго-
нальную сетку, чтобы она выглядела как гладкая криволинейная поверхность. Затем мы будем изучать
особый метод удаления невидимых поверхностей — технологию, используемую внутри OpenGL, — и уви-
дим, как она встраивается в процесс визуализации. (В главе 13 исследуется ряд других методов удаления
невидимых поверхностей.) Далее мы будем изучать технологии изображения теней, которые один объект
отбрасывает на другой, наложения текстуры на поверхность, чтобы она выглядела сделанной из какого-
нибудь определенного материала, или нанесения на нее какого-либо рисунка. Кроме того, мы рассмотрим
хромированное отображение (chrome mapping) и отображение окружающей среды (environment mapping)
и увидим, как в результате их применения локальная сцена кажется вложенной в более общую сцену.
486
Глава 8. Визуализация граней для усиления реалистичности
8.2. Введение в модели закрашивания
Механизм отражения света от текущей поверхности очень сложен и зависит от многих факторов. Не-
которые из них являются геометрическими — например, относительные направления источника света,
глаза наблюдателя и нормали к поверхности. Другие факторы относятся к характеристикам поверхно-
сти, таким как шероховатость, и к цвету этой поверхности.
Модель закрашивания определяет, как свет рассеивается по поверхности или отражается от нее. Мы
будем изучать некоторые простые модели закрашивания, в особенности ахроматическое (achromatic)
освещение, у которого есть только яркость, но не цвет. Ахроматическое освещение дает только оттенки
серого цвета, и поэтому оно описывается единственной величиной: его интенсивностью. Мы увидим,
как вычислять интенсивность света, направленного в глаз камеры от каждой части объекта. В дальней-
шем мы расширим эти идеи на случаи цветного освещения и цветных объектов. Эти вычисления почти
идентичны вычислениям для случая ахроматического освещения, за исключением того, что интенсив-
ности красного, зеленого и синего компонентов освещения вычисляются отдельно.В модели закраши-
вания, часто используемой в графике, предполагается, что объекты сцены освещаются двумя типами
источников: точечными источниками света и фоновым светом (ambient light). Эти источники света
«сверкают» на различных поверхностях объектов, и падающий свет взаимодействует с поверхностью
одним из трех возможных способов:
О некоторая часть поглощается поверхностью и превращается в тепло;
О некоторая часть отражается от поверхности;
О некоторая часть проходит внутрь объекта, как в случае куска стекла.
Если весь падающий свет поглощается, то данный объект воспринимается как черный, поэтому его
называют абсолютно черным телом (blackbody). Если весь свет проходит сквозь объект, то он виден
только в результате эффекта рефракции, который мы будем рассматривать в главе 14.
Здесь мы сосредоточимся на той составляющей света, которая отражается от поверхности или
рассеивается ею. Некоторая часть этого отраженного света движется как раз в таком направлении,
чтобы достигнуть глаза, вследствие чего объект становится виден. Количество света, попадающее в глаз,
прежде всего определяется геометрией окружения. Мы будем различать два типа отражения падаю-
щего света:
О диффузное рассеяние (diffuse scattering) происходит, когда часть падающего света слегка про-
никает внутрь поверхности и излучается обратно равномерно по всем направлениям. Рассеян-
ный свет сильно взаимодействует с поверхностью, поэтому его цвет обычно зависит от природы
материала, из которого сделана эта поверхность;
О зеркальные отражения (specular reflections) больше похожи на зеркало и имеют ярко выражен-
ную направленность: падающий свет не поглощается объектом, а отражается прямо от его наруж-
ной поверхности. Это порождает блики, и поверхность выглядит блестящей. В простейшей мо-
дели зеркального света отраженный свет имеет такой же цвет, что и падающий свет, что делает
материал похожим на пластмассу. В более сложной модели цвет отраженного света пробегает
интервал бликов, что дает лучшее приближение металлических поверхностей. Мы рассмотрим
обе модели зеркального отражения.
Большинство поверхностей сочетают в себе оба типа отражения; это зависит от характеристик са-
мих поверхностей, таких как шероховатость и тип материала, из которого сделаны эти поверхности.
Считается, что суммарное количество света, отраженного от поверхности в определенном направлении,
складывается из диффузного и зеркального компонентов. Для каждой интересующей нас точки поверх-
ности вычисляется величина каждого компонента, достигающего глаза. Эта задача решается при помо-
щи алгоритмов, рассматриваемых ниже.
8.2. Введение в модели закрашивания
487
8.2.1. Геометрические составляющие для нахождения
отраженного света
С внешней стороны растет мех, а с внутренней стороны растет кожа;
Так что мех — это внешность, а кожа — внутренность.
Герберт Джордж Понтинг (Herbert George Ponting).
Спящий мешок (The Sleeping Bag)
Для того чтобы вычислить диффузный и зеркальный компоненты света, нам необходимо найти три
вектора. На рис. 8.8 показаны три главных вектора, необходимых для нахождения количества света,
попадающего в глаз из точки Р:
О нормаль m к поверхности в точке Р;
О вектор v, соединяющий точку Р с глазом наблюдателя;
О вектор s, соединяющий точку Р с источником света.
Углы между этими тремя векторами составляют основу для вычисления интенсивностей освеще-
ния. Обычно эти углы вычисляются в мировых координатах, поскольку при некоторых преобразовани-
ях (таких, как перспективное преобразование) углы не сохраняются.
Рис. 8.8. Основные направления, используемые при вычислении отраженного света
Каждая грань каркасного объекта имеет две стороны. Если объект является объемным, то одна сто-
рона обычно является «внутренней», а другая — «внешней» для этого объекта. Глаз видит только внеш-
нюю сторону (если только сам глаз не находится внутри объекта!), так что именно для этой стороны
нужно вычислять компоненты освещенности. Однако для некоторых объектов, вроде открытой короб-
ки с рис. 8.9, глаз может увидеть и внутреннюю сторону крышки. Это зависит от угла между нормалью т2
к этой стороне и вектором v направления к глазу. Если этот угол меньше 90°, то эта сторона является
видимой. Так как косинус этого угла пропорционален скалярному произведению v • m2, глаз может ви-
деть эту сторону только при v • т2 > 0.
Рис. 8.9. Вычисления освещенности производятся для одной стороны каждой грани
488
Глава 8. Визуализация граней для усиления реалистичности
Мы будем разрабатывать модель закрашивания для заданной стороны грани. Если такая сторона
«отвернута» от глаза наблюдателя, то обычно она не вносит своего вклада в освещенность. Алгоритму
визуализации в текущем приложении должно быть сообщено, вычислять составляющие освещенности
только для одной стороны заданной поверхности или для обеих сразу. Мы увидим, что OpenGL под-
держивает такое сообщение.
8.2.2. Вычисление диффузной составляющей
Предположим, что свет падает от точечного источника на одну сторону микрограни (facet) поверхнос-
ти. Какая-то доля света с этой стороны микрограни диффузно переизлучается во всех направлениях.
А какая-то часть этой переизлучаемой доли достигает глаза с интенсивностью, обозначаемой Id. Как
зависит Id от направлений m, v, и s?
Поскольку рассеяние одинаково во всех направлениях, ориентация микрограни относительно глаза
не имеет значения. Поэтому Id не зависит от угла между векторами m и v (кроме случая v • m < 0, тогда
Id = 0). С другой стороны, количество света, освещающего данную микрогрань, зависит от ориентации
микрограни по отношению к источнику света: оно пропорционально «наблюдаемой» источником пло-
щади этой микрограни, то есть видимой площади микрограни.
ч1/ ч1/
Рис. 8.10. Яркость зависит от видимой площади
На рис. 8.10, а в сечении показан точечный источник, освещающий микрогрань 5, для случая, когда
вектор m параллелен вектору s. На рис. 8.10, б микрогрань отвернута в сторону от источника света на
угол 0. Теперь видимая площадь составляет только долю, равную cos(O), от той, что была раньше, так
что яркость микрограни 5 уменьшится во столько же раз. Это соотношение между яркостью и ориентаци-
ей поверхности часто называют законом Ламберта (Lambert). Отметим, что для малых углов 0 яркость
слабо зависит от угла, поскольку косинус в окрестности нуля изменяется медленно. Однако при при-
ближении угла 0 к 90° яркость быстро снижается до нуля.
Далее, нам известно, что cos(0) является скалярным произведением ортов s и т. Тогда можно полу-
чить следующее выражение для интенсивности диффузного компонента:
где 7 — интенсивность источника света, a pd — коэффициент диффузного отражения (diffuse reflection
coefficient). Отметим, что если микрогрань направлена в сторону от глаза, то это скалярное произведе-
ние отрицательно, и в этом случае мы принимаем Id - 0. Следовательно, более точная формула для диф-
фузного компонента имеет вид:
-5L5L, 0 .
Isllml ,
Л = Л^тах
(8-1)
8.2. Введение в модели закрашивания
489
Последнее выражение можно реализовать в виде кода (с помощью методов класса Vector3: dot О и
length О; см. приложение В) следующим образом:
double tmp = s.dot(m):
// form the dot product
// формируем скалярное произведение
double value = (tmp<0) ? 0 : tmp/ (s.lengthO * m.lengthO);
На рис. 8.11 показано, как выглядит сфера, отражающая диффузный свет, для шести значений коэффи-
циента отражения: 0,0,2,0,4,0,6, 0,8,1. Для каждого случая исходная интенсивность равна 1,0, а интен-
сивность фона установлена равной 0,4. Отметим, что при prf = 0,0 сфера является полностью черной, а тень
в ее нижней половине (когда скалярное произведение в уравнении (8.1) отрицательно) также черная.
Рис. 8.11. Сферы с различными коэффициентами отражения, затененные с помощью диффузного света
На самом деле механизм диффузного отражения намного сложнее, чем принятая нами здесь упро-
щенная модель. Коэффициент отражения pd зависит от длины волны (то есть цвета) падающего света,
от угла 6, и от различных физических свойств поверхности. Однако для простоты и для уменьшения
времени вычислений при визуализации изображений эти влияния обычно игнорируются. Для каждой
поверхности «разумное» значение коэффициента pd выбирается исходя из реалистичности результи-
рующего изображения, иногда методом проб и ошибок.
В некоторых моделях затенения учитывается влияние расстояния, хотя это спорно. Известно, что ин-
тенсивность света, падающего на микрогрань 5 от точечного источника (рис. 8.10), обратно пропорциональ-
на квадрату расстояния между 5 и источником. Однако эксперименты показали, что применение этого
закона приводит к картинам с преувеличенным влиянием глубины. Более того, иногда удобно создавать
модель источника света так, как будто он расположен «в бесконечности». Применение в этом случае зако-
на обратных квадратов погасило бы свет полностью! Вероятно, проблема заключается в самой модели:
для простоты источники света моделируются как точечные, однако сцены в действительности, как прави-
ло, освещены дополнительными отражениями от окружающих предметов, что смоделировать трудно (эти
влияния сосредоточены в фоновом компоненте света). Неудивительно, что строгое соблюдение физичес-
кого закона, основанного на нереалистической модели, может привести к нереалистическим результатам.
Реалистичность большинства изображений при введении члена, зависящего от расстояния, увеличи-
вается лишь незначительно. При некоторых подходах интенсивность принимается обратно пропорцио-
нальной расстоянию между глазом и объектом, однако эта зависимость не имеет физического обоснования.
Интересно поэкспериментировать с такими моделями, причем OpenGL предоставляет возможность
контролировать это влияние, как мы увидим в разделе «Работа со свойствами материалов в OpenGL»;
однако в ближайших разработках член зависимости от расстояния будет игнорироваться.
8.2.3. Зеркальное отражение
Реальные объекты не рассеивают свет равномерно во всех направлениях, поэтому к модели закраски
добавляется зеркальный компонент. Зеркальное отражение порождает блики, которые могут суще-
ственно увеличить реалистичность изображения, заставив объекты блестеть. В данном разделе мы рас-
490
Глава 8. Визуализация граней для усиления реалистичности
смотрим простую модель поведения отраженного света по Фонгу [Phong, 162]. Эта модель легко реали-
зуется, и OpenGL поддерживает хорошее приближение к ней. Блики, создаваемые отраженным светом
по Фонгу, придают объекту вид сделанного из пластмассы, поэтому модель Фонга хороша, когда пред-
назначается для объектов, выполненных из блестящего пластика или стекла. С объектами, имеющими
блестящую металлическую поверхность, данная модель работает хуже, однако, как мы увидим, путем
тщательного подбора параметров цвета с помощью OpenGL аппроксимация по-прежнему возможна.
Разработаны более современные модели отражения света, которые лучше работают с блестящими метал-
лами. Поскольку такие модели не поддерживаются впрямую в рамках процесса визуализации OpenGL,
мы отложим их обсуждение до главы 14, где рассматривается трассировка лучей.
На рис. 8.12, а показана ситуация, в которой свет от источника попадает на поверхность и отража-
ется в различных направлениях. Согласно модели Фонга, количество отраженного света имеет наи-
большую величину в направлении абсолютного зеркального отражения (вектор г), когда угол отраже-
ния равен углу падения. Именно в этом направлении отразился бы весь свет, если бы поверхность была
абсолютным зеркалом. При других углах, близких к этому, количество отраженного света быстро убыва-
ет, о чем свидетельствуют относительные длины векторов отражения. На рис. 8.12, б это распределение
показано в виде «пучка лучей», известного специалистам по радарам. Расстояние от точки Р до огибаю-
щей пучка лучей показывает относительную силу света, рассеянного в данном направлении.
Рис. 8.12. Зеркальное отражение от блестящей поверхности
На рис. 8.12, в показано, как оценить влияние пучка. Из главы 4 нам известно, что направление г
полного отражения зависит от вектора s и нормали m к поверхности следующим образом:
(s.m)
r = -s + 2-—ш (направление зеркального отражения). (8.2)
|ш|
Для блестящих поверхностей, не являющихся абсолютно зеркальными, количество отраженного света
убывает с ростом модуля угла ф между векторами г и v. Истинное количество этого убывания является
сложной функцией от ф, однако в модели Фонга данная зависимость предполагается равной некоторой
степени f от косинуса ф, то есть соз^ф), где значение f подбирается экспериментально и обычно лежит в
пределах от 1 до 200. На рис. 8.13 показан график изменения функции интенсивности в зависимости от
угла фдля различных значений/. С ростом параметра/отражение становится все более зеркальным и все
более концентрируется вдоль направления г. При/= °° можно было бы смоделировать абсолютное зер-
кало, однако чистые отражения обычно обрабатывают другим способом, как описано в главе 14.
Используя тот факт, что cos(0) равен скалярному произведению векторов г и v (после их нормиро-
вания), можно смоделировать вклад Z в зеркальное отражение следующим образом:
(8-3)
где множитель ps называется коэффициентом зеркального отражения (specular reflection coefficient).
Подобно большинству других коэффициентов в модели закрашивания, он обычно определяется экспе-
8,2. Введение в модели закрашивания
491
рименталыю. (Как и в случае диффузного члена, при отрицательном скалярном произведении г v зна-
чение Z устанавливается равным нулю).
Рис. 8.13. Уменьшение отраженного света с ростом абсолютной величины угла
Повышение эффективности с помощью -«промежуточного вектора». Вычисление члена уравне-
ния (8.3), соответствующего зеркальному отражению, может оказаться слишком дорогостоящим, посколь-
ку при этом требуется вначале найти вектор г, а затем нормировать его. На практике для ускорения
вычислений используется альтернативный член зеркального отражения, который, вероятно, впервые
был описан Блинном [Blinn, 24] и используется для ускорения вычислений. Вместо косинуса угла меж-
ду векторами г и v ищется промежуточный (halfway) вектор между s и V, то есть h = s + v, как показано на
рис. 8.14. Если бы нормаль к поверхности была направлена вдоль вектора h, то наблюдатель увидел бы
наиболее яркий зеркальный блик. Поэтому угол Р между векторами m и h можно использовать для из-
мерения спада интенсивности зеркального отражения, которую видит наблюдатель. Угол Р не совпада-
ет с углом ф (на самом деле угол Р вдвое больше, чем ф, если все векторы компланарны; см. упражнения),
однако это различие может быть компенсировано использованием другого значения показателя/. (Зер-
кальный член никоим образом не основывается на физических принципах, поэтому по меньшей мере
приятно, что такая его коррекция дает приемлемые результаты.) Обычно принято при вычислении зер-
кального члена исходить из cos(P), используя при этом скалярное произведение векторов h и ш:
(скорректированный зеркальный член).
(8-4)
Рис. 8.14. Промежуточный вектор
Отметим, что при такой коррекции нет необходимости находить вектор отражения г, что экономит
время вычисления. Кроме того, если и источник света, и наблюдатель очень удалены, то векторы s и v
одинаковы для различных граней объекта, поэтому вектор Ь понадобится вычислить всего один раз.
492
Глава 8. Визуализация граней для усиления реалистичности
Рис. 8.15. Зеркальное отражение от блестящей поверхности
На рис. 8.15 показана сфера, отражающая различные количества зеркального света. Коэффициент
отражения ps изменяется сверху вниз следующим образом: 0,25,0,50 и 0,75, а показатель степени f изме-
няется слева направо: 3, 6, 9, 25, 200. (Коэффициенты фонового и диффузного отражения одинаковы
для всех сфер и равны соответственно 0,1 и 0,4.)
На самом деле физический механизм зеркального отражения света намного сложнее, чем предлага-
ется в модели Фонга. В более реалистичной модели коэффициент зеркального отражения зависит от
длины волны Л (то есть от цвета), от угла падения света 0 (то есть от угла между векторами s и ш на
рис. 8.10), и тогда этот коэффициент превращается в «коэффициент Френеля* («Fresnel term*), который
описывает физические характеристики отражения света от поверхностей из материалов определенного
класса. Как уже упоминалось, OpenGL не приспособлен для учета подобных эффектов, поэтому мы от-
ложим их рассмотрение до главы 14 (трассировка лучей), где будем вычислять цвета каждой точки, не-
посредственно применяя модель закрашивания.
Практические упражнения
8.2.1. Рисование пучков лучей
Нарисуйте пучки лучей, подобные приведенным на рис. 8.12, для случаев f - 1,/- 10,/- 100.
8.2.2. Промежуточный вектор
Пользуясь геометрическими соотношениями рис. 8.14, покажите, что угол Р “ 20, если все векторы ком-
планарны. Покажите, что это не так, если векторы некомпланарны. (См. также [Fisher, 63].)
8.2.3. Ускорение зеркального отражения
Шлик [Schlick, 178] предложил альтернативу степенному закону при вычислении зеркального члена.
Пусть скалярное произведение в уравнении (8.3) равно D:
d = ггА-
И м
Шлик предлагает заменить на D/(f - fD + D), что вычисляется быстрее. Нарисуйте графики обе-
их функций для значений D в промежутке [0,1] для различных значений/ и сравните их. Особое внима-
ние уделите значениям D, близким к единице, поскольку именно там зеркальные блики наиболее яркие.
8.2.4. Роль фонового света
Диффузный и зеркальный компоненты отраженного света находятся путем упрощения «правил*, по
которым физический свет отражается от физических поверхностей. Включение зависимости этих ком-
понентов от относительных положений глаза, объекта и источников света значительно улучшает реа-
листичность изображения при визуализациях, которые просто заполняют каркасную модель тенями.
Однако наше стремление иметь простую модель отражения весьма сильно расходится с качественной
8.2. Введение в модели закрашивания
493
визуализацией сцены. Тени, например, кажутся нееестественно резкими и глубокими. Для смягчения
этих теней мы можем добавить еще один, третий компонент света, называемый «фоновым светом»
(«ambient light»).
Если использовать только диффузное и зеркальное отражения, то любые части поверхности, засло-
ненные от точечного источника, вообще не получают света и поэтому рисуются черным цветом! Одна-
ко это противоречит нашему повседневному опыту; сцены, которые мы наблюдаем вокруг себя, всегда
кажутся освещенными каким-то мягким светом, не имеющим определенного направления. Этот свет
приходит после многочисленных отражений от различных окружающих нар объектов, а также от
источников света, заполняющих окружающую среду, таких как свет в окне, люминесцентные лам-
пы и т. п. Однако точно моделировать такой свет стоило бы слишком дорого с вычислительной точки
зрения.
Фоновые источники и фоновые отражения
Для того чтобы преодолеть трудности, связанные со сплошными черными тенями, давайте представим
себе, что в окружающей среде существует равномерное «свечение фона», называемое фоновым светом
(ambient light). Источник фонового света не располагается в каком-либо определенном месте, и этот
свет распространяется во всех направлениях одинаково. Этот источник характеризуется интенсивнос-
тью 1а. Каждой грани в данной модели соответствует определенное значение коэффициента фонового
отражения (ambient reflection coefficient) ра (часто он совпадает с коэффициентом диффузного отраже-
ния pd), а член 1ара просто добавляется к тому диффузному и зеркальному свету, который попадает в
глаз из каждой точки Р на этой грани. Значения 1а и ра обычно подбираются экспериментально путем
варьирования различных величин и выбора наиболее подходящих. Недостаток фонового света делает
тени слишком глубокими и резкими; избыток же его делает изображение размытым и мягким.
Рис. 8.16. Влияние фонового света
На рис. 8.16 показано влияние добавления некоторого количества фонового света к диффузному
свету, отражаемому сферой. В каждом случае интенсивности диффузного и фонового источников све-
та равны 1,0, а коэффициент диффузного отражения равен 0,04. На изображениях слева направо значе-
ния коэффициента фонового отражения принимают значения соответственно 0,0, 0,1, 0,3, 0,5, 0,7. Уже
при небольшом количестве фонового света резкие тени на нижней части сферы смягчаются и выглядят
более реалистичными. С другой стороны, избыток фонового света чрезмерно подавляет тени.
8.2.5. Комбинирование компонентов освещения
Теперь мы можем сложить три компонента освещения — диффузный, зеркальный и фоновый, чтобы
получить суммарное количество света /, которое попадает в глаз из точки Р, а именно:
1 = !аРа + hPd х lambert + /рр5 х phong< (8.5)
где введены величины:
lambert = max 0,
sm
ИН,
и phong = max 0,
(8-6)
h m
lhllml,
Величина I зависит от различных интенсивностей источников и коэффициентов отражения объекта,
а также от соотношения положений точки Р, глаза и точечного источника света. Здесь интенсивности
494
Глава 8. Визуализация граней для усиления реалистичности
диффузного Id и зеркального Zsp компонентов обозначены различными буквами, поскольку в OpenGL
предоставляется возможность задавать их раздельно, как мы увидим позднее. На практике обе эти ин-
тенсивности обычно имеют одну и ту же величину.
Рассмотрим несколько подробнее изменение интенсивности I в зависимости от положения точки Р,
для чего снова вернемся к рис. 8.12. Интенсивность I вычисляется для различных точек Р рассматрива-
емой микрограни. Фоновый компонент не претерпевает никаких изменений в пределах микрограни;
вектор m одинаков для всех точек Р микрограни, но направления векторов s и v зависят от Р. (Пусть,
например, s - 5 - Р, где 5 — расположение источника света. Как значение вектора v зависит от точки Р и
глаза?) Если источник света достаточно удален (это типичный случай), то вектор s при изменении точ-
ки Р меняется незначительно; так что и диффузный компонент также будет незначительно изменяться
для различных точек Р. Это особенно верно, когда векторы вит почти параллельны, так как для малых
углов косинус изменяется медленно. Для удаленных источников света изменение направления проме-
жуточного вектора h также слабо зависит от изменения точки Р. С другой стороны, если источник света
расположен близко к микрограни, то по мере изменения точки Р векторы s и h могут сильно изменять-
ся. В этом случае зеркальный компонент может сильно изменяться в пределах микрограни, поэтому
яркий блик может быть локализован в ее малой области. Этот эффект усиливается, когда глаз также
расположен близко к микрограни, вызывая сильные изменения в направлении v, и когда показатель
степени f очень велик.
Практическое упражнение
8.2.4. Эффект расстояния от глаза до микрограни
Опишите, насколько сильно изменяются составляющие освещения по мере изменения точки Р на мик-
рограни, когда:
О глаз находится далеко от микрограни;
О глаз находится вблизи микрограни.
8.2.6. Добавление цвета
Нетрудно расширить рассматриваемую модель закраски на случай отражения цветного освещения от
цветных поверхностей. Вновь более общая модель является аппроксимацией, порожденной стремлени-
ем к простоте, однако она дает приемлемые результаты и вполне работоспособна.
В главе 12 содержится более детальное рассмотрение природы цвета, однако, как мы уже видели ра-
нее, свет любого цвета может быть синтезирован путем сложения определенных количеств красного,
зеленого и синего цветов. При работе с цветными источниками и цветными поверхностями мы вычис-
ляем каждый компонент цвета отдельно и затем просто складываем их, чтобы получить окончательный
цвет отраженного света. Тогда для вычисления красного, зеленого и синего компонентов отраженного
света необходимо трижды применить уравнение (8.5):
4 “ ArPar+ 7drPdrх lambert + Zsprpsr х phong<
4 = АЛ + 4gPdg х lambert + Zspgpsg х phong< (8.7)
h “ АьРаЬ + JdbPdbx lambert + Zspbpsb x phong/.
(Величины lambert и phong заданы уравнением (8.6).)
Отметим, что мы предполагаем наличие у источника света трех «типов» цвета:
ambient = (1м, I , Zab) (фоновый),
diffuse = (/dr, Zdg, Zdb) (диффузный),
specular - (Z,pr, Z,pg, Zspb) (зеркальный).
8.2. Введение в модели закрашивания
495
Обычно цвета диффузного и зеркального освещения одинаковы. Кроме того, отметим, что перемен-
ные lambert и phong не зависят от того, компонент какого цвета вычисляется, так что их нужно вычис-
лить только один раз. Развивая этот подход, следует определить девять коэффициентов отражения:
ambient reflection coefficients: р^, р^, р^ (коэффициенты фонового отражения);
diffuse reflection coefficients: pdr, pdg, pdb (коэффициенты диффузнбго отражения);
specular reflection coefficients: psr, psg, psb (коэффициенты зеркального отражения).
Коэффициенты фонового и диффузного отражения определяются цветом самой поверхности. Под
«цветом» поверхности мы имеем в виду тот цвет, который отражается от нее при освещении ее белым
светом. Поэтому поверхность является красной, если она выглядит красной при освещении белым цве-
том. Если же поверхность освещается каким-либо другим цветом, то она может продемонстрировать
совершенно иной цвет. Приводимые ниже примеры иллюстрируют эту относительность цвета.
Пример 8.2.1. Цвет объекта
Если говорится, что цвет сферы на 30 % красный, на 45 % зеленый и на 25 % синий, то это означает, что
для этой сферы нужно задать следующие коэффициенты фонового и диффузного отражения: (0,ЗХ,
0,45А?, 0,25Х), где К — некоторый масштабный коэффициент, определяющий общую долю падающего
света, который отражается от сферы. Так что если сфера освещается белым цветом, имеющим равные
компоненты красного, зеленого и синего цветов (7, - - 1Л - Г), а интенсивности отдельных диффузных
компонентов составляют Ir - 0,3X7, Ig - 0,45X7,1Ь - 0,25X7, то в результате мы, как и следовало ожидать,
увидим цвет, состоящий из 30 % красного, 45 % зеленого и 25 % синего цветов.
Пример 8.2.2. Красноватый объект, освещенный зеленоватым цветом
Пусть коэффициенты фонового и диффузного отражения сферы равны (0,8, 0,2,0,1), так что при осве-
щении сферы белым светом она выглядит в основном красной. Осветим эту сферу зеленоватым светом
с интенсивностью Is - (0,15, 0,7, 0,15). Тогда интенсивность отраженного света будет равна (0,12, 0,14,
0,015), что( представляет собой почти равную смесь красного и зеленого цветов. В этом случае наша сфе-
ра будет выглядеть желтоватой.
Цвет зеркального света
В силу своего названия зеркальный компонент часто имеет такой же цвет, что и источник света. Напри-
мер, из опыта известно, что блик, видимый на гладком красном яблоке, освещенном желтым цветом,
имеет скорее желтый, чем красный цвет. Такой же эффект можно наблюдать с блестящими предмета-
ми, изготовленными из материала типа пластика. Для создания на пластмассовой поверхности отража-
ющих бликов нужно придать коэффициентам зеркального отражения psr, psg, psb, используемым в урав-
нении (8.7), одно и то же значение ps, так чтобы коэффициенты отражения стали по своей природе
«серыми» и не изменяли цвет падающего света. Дизайнеру следует выбрать для слабо блестящей пласт-
массовой поверхности ps - 0,5, а для сильно блестящей — ps - 0,9.
Объекты, сделанные из различных материалов
Тщательным подбором коэффициентов отражения можно добиться того, чтобы объект выглядел — по
меньшей мере приближенно — сделанным из нужного материала, например меди, золота, олова. МакРей-
нолдс и Блайт [McReynolds, 139] предложили использовать коэффициенты отражения, приведенные
в табл. 8.1. Отметим, что коэффициенты зеркального отражения имеют различные компоненты красного,
зеленого и синего цветов, так что цвет зеркального света, вообще говоря, не будет совпадать с цветом
падающего света. Однако МакРейнолдс и Блайт предупреждают пользователей, что, поскольку алгоритм
закраски OpenGL использует зеркальный компонент Фонга, видимые эффекты не являются полностью
реалистичными. Мы вернемся к этому вопросу в главе 14 и опишем там более реалистичный метод закра-
шивания Кука—Торранса (Cook—Torrance).
496
Глава 8. Визуализация граней для усиления реалистичности
Таблица 8.1. Параметры для часто используемых материалов
Материал степени f Фоновое: р„, РЧ,Р.Ь Диффузное: Pdr, Pds,Pdb Зеркальное: р„, p4,prt Показатель
черная пластмасса 0.0 0.0 0.0 0.01 0.01 0.01 0.50 0.50 0.50 32
Латунь 0.329412 0.223529 0.027451 0.780392 0.568627 0.113725 0.992157 0.941176 0.807843 27.8974
Бронза 0.2125 0.1275 0.054 0.714 0.4284 0.18144 0.393548 0.271906 0.166721 25.6
Хром 0.25 0.25 0.25 0.4 0.4 0.4 0.774597 0.774597 0.774597 76.8
Медь 0.19125 0.0735 0.0225 0.7038 0.27048 0.0828 0.256777 0.137622 0.086014 12.8
Золото 0.24725 0.1995 0.0745 0.75164 0.60648 0.22648 0.6282810.555802 0.366065 51.2
Олово 0.10588 0.058824 0.113725 0.4274510.470588 0.541176 0.3333 0.3333 0.521569 9.84615
Серебро 0.19225 0.19225 0.19225 0.50754 0.50754 0.50754 0.508273 0.508273 0.508273 51.2
Полированное серебро 0.23125 0.23125 0.23125 0.2775 0.2775 0.2775 0.7739110.7739110.773911 89.6
8.2.7. Закраска и графический конвейер
На каком этапе работы графического конвейера выполняется закраска? И как это делается? На рис. 8.17
вновь приводится этот конвейер. Основная идея состоит в том, что вершины сетки посылаются в кон-
вейер вместе со связанными с ними нормалями, и все вычисления по закраске осуществляются именно
с вершинами. (Напомним, что подпрограмма draw() класса Mesh с каждой вершиной передает нормаль,
как показано в листинге 6.2.)
vi, гщ
V2, ГП2
vo, mo „
Закрашивание
происходит здесь
Рис. 8.17. Снова графический конвейер
На рис. 8.17 показан процесс визуализации треугольника с вершинами г>0, vv v2. С каждой вершиной vt
связана нормаль пт. Эти величины пересылаются в конвейер с помощью следующих вызовов:
g1Begin(GL_POLYGON):
for(int 1 "0; i <3: 1++)
{
glNormal3f(norm[i].x. norm[i].y. norm[i].z):
glVertex3f(pt[i].x, pt[i].y. pt[i].z);
}
glEndO:
Вызов подпрограммы glNormal3f О устанавливает «текущую нормаль», которая применяется ко всем
вершинам, последовательно пересылаемым в конвейер с помощью glVertex3f(). Эта нормаль остается
текущей вплоть до ее изменения при следующем вызове glNorma!3f(). В вышеприведенном коде с каж-
дой вершиной связывается новая нормаль.
Вершины преобразуются с помощью матрицы моделирования-вида М, которая эффективно перево-
дит их в координаты камеры (глаза). Нормали тоже подвергаются преобразованиям, однако векторы
преобразуются не так, как точки. Как показано в разделе «Влияние аффинного преобразования» гла-
вы 6, при преобразовании точек поверхности посредством матрицы М нормаль m в каждой точке пре-
8.2. Введение в модели закрашивания
497
вращается в нормаль М"7т на преобразованной поверхности, где М~т— транспонированная обратная к
матрице М матрица. OpenGL выполняет эти вычисления нормалей автоматически.
Как уже рассматривалось в предыдущем разделе, OpenGL предоставляет возможность задавать раз-
личные источники света и их расположение. Источники света тоже являются объектами, и координаты
источников света также преобразуются посредством матрицы моделирования-вида.
Таким образом, после преобразования моделирования-вида все величины будут выражены в коор-
динатах камеры. С этой точки зрения применима модель из уравнения (8.7), причем к каждой вершине
«привязан» цвет. Вычисление этого цвета требует знания векторов m, s, v, однако все они в этот момент
доступны в конвейере. (Убедитесь в этом сами.)
По мере дальнейшего продвижения по конвейеру создается член, содержащий псевдоглубину, после
чего вершины подвергаются перспективному преобразованию. К каждой вершине прикреплена инфор-
мация о цвете. Затем выполняется этап отсечения в однородных координатах описанным ранее обра-
зом. Этот этап может изменить некоторые вершины. На рис. 8.18 показан случай, когда вершина о, тре-
угольника отсекается, а вместо нее создаются две новые вершины а и Ь. Треугольник превращается в
четырехугольник. Нужно вычислить цвет каждой новой вершины, поскольку он понадобится на этапе
текущей визуализации.
Рис. 8.18. Отсечение полигона границами (деформированного) отображаемого объема
Обычно цвет каждой новой вершины определяется с помощью интерполяции. Пусть, например, цвет
вершины vQ равен (r0, g0, й0), а цвет вершины v{ — (rp fe,). Если точка а находится в 40 % расстояния от
вершины v0 к у,, то цвет, связанный с вершиной а, представляет собой смесь 60 % цвета (r0, gQ, й0) и 40 %
цвета (г,, gv bt). Это соотношение выражается следующей формулой:
цвет в точке а - (1егр(г0, гр 0,4), lerp(g0, gp 0,4), lerp (b0, bv 0,4)), (8.8)
где используется удобная функция 1егр( ) (это сокращение от «linear interpolation» — линейная интер-
поляция; вспомните «твининг» из раздела «Твининг в искусстве и анимации» главы 4), которая опре-
деляется следующим образом:
leip(G,H,f)-G + (H- G)f. (8.9)
Значение этой функции располагается на части f пути от G к Я1.
Наконец, вершины проходят через преобразование порта просмотра, где они преобразуются в экран-
ные координаты (наряду с псевдоглубиной, которая теперь изменяется от 0 до 1). Затем осуществляет-
ся визуализация этого четырехугольника (с удалением невидимых поверхностей), как показано на
рис. 8.18. Об этапе текущей визуализации намного подробнее будет рассказано в следующих разделах.
8.2.8. Использование источников света в OpenGL
В OpenGL содержится целый ряд функций для установки и использования источников света, а также
для придания поверхности свойств определенного материала. Довольно трудно охватить все их возмож-
ные варианты и детали, поэтому здесь мы остановимся лишь на основных функциях. В данном разделе
мы рассмотрим, как устанавливать на сцене различные виды источников света. В следующем разделе
мы обсудим способы описания отражающих свойств поверхностей объекта.
1 В разделе «Добавление текстуры к граням» данной главы рассматривается замена линейной интерполяции «гиперболической ин-
терполяцией», так как она более точно генерирует цвета новых вершин, появившихся в результате отсечения.
498
Глава 8. Визуализация граней для усиления реалистичности
Создание источника света
OpenGL позволяет задать до восьми источников с именами GL_LIGHT0, GL_LIGHT1 и т. д. Каждый источник
обладает различными свойствами и должен быть задействован (включен). У каждого его свойства
имеется значение по умолчанию. Например, для создания источника, расположенного в точке (3, 6,5)
в мировых координатах, следует выполнить следующий код1:
GLfloat rnyLightPosition[] » {3.0. 6.0. 5.0. 1.0};
glLightfv(GL_LIGHTO. GL_POSITION. nyLightPosition);
glEnable(GL_LIGHTING): ~
// enable
// включаем (свет)
glEnable(GL_LIGHTO);
// enable this particular source
// включаем этот конкретный источник
Массив myLightPosition[] (имя можно использовать любое) определяет положение источника света
и передается в функцию glLightfvO вместе с именем источника GLJ-IGHT0, для того чтобы связать его с
конкретным источником, обозначенным именем GL_LIGHT0.
Некоторые источники, такие как настольная лампа, находятся «внутри» сцены, в то время как другие,
например солнце, бесконечно удалены от сцены. OpenGL позволяет создавать источники света обоих
типов посредством задания положения источника в однородных координатах.
Тогда мы имеем
(х, у, z, 1): локальный источник света в положении (х, у, г)
и
(х, у, z, 0): вектор к бесконечно удаленному источнику света в направлении (х, у, г).
Рис. 8.19. Локальный и бесконечно удаленный источники света
На рис. 8.19 показан локальный источник света в положении (0, 3, 3, 1) и удаленный источник,
«расположенный» вдоль вектора (3, 3, 0, 0). Бесконечно удаленные источники света часто называют
«направленными» (directional). Существуют определенные вычислительные преимущества в исполь-
зовании направленных источников света, поскольку направление s при вычислении диффузного и зер-
кального отражений одинаково для всех вершин данной сцены. Однако направленные источники света
не всегда являются наилучшим выбором: некоторые визуальные эффекты достигаются должным обра-
зом только тогда, когда источник света расположен близко к объекту.
Можно также разложить источник света на различные цвета. OpenGL позволяет присвоить различ-
ный цвет каждому из трех типов света, испускаемого источником: фоновому, диффузному и зеркально-
му. Может показаться странным, что источник испускает фоновый свет. Однако этот тип освещения
по-прежнему рассматривается как в равенстве (8.7): глобальный всенаправленный свет, полностью зали-
вающий сцену. Преимущество привязки фонового света к источнику заключается в том, что его можно
включать и выключать во время работы приложения. (Кроме этого, OpenGL снабжен истинно фоновым
1 Здесь и всюду тип данных fl oat будет, вероятно, работать не хуже, чем тип GLfl oat. Однако использование типа GLf 1 oat сделает
ваш код более совместимым с другими программными средами OpenGL.
8.2. Введение в модели закрашивания
499
светом, не связанным ни с каким источником, однако его мы рассмотрим позднее, в связи с «моделями
освещения».)
С помощью приведенного ниже кода определяются массивы для хранения цветов, испускаемых ис-
точниками света. Эти массивы затем передаются в функцию glLightfvO:
GLfloat ambO[] - {0.2. 0.4. 0.6. 1.0};
// define some colors
// определяем некоторые цвета
GLfloat diffOt] - {0.8. 0.9. 0.5. 1.0};
GLfloat spec0[] = {1.0. 0.8. 1.0. 1.0};
glLightfv(GL_LIGHTO. GL_AMBIENT, ambO):
// attach them to LIGHT0
// привязываем их к LIGHTO
glLightfv(GL_LIGHTO. GL_DIFFUSE. diffO);
glLightfv(GL_LIGHTO. GL_SPECULAR. specO);
Цвета задаются в так называемом формате RGBA, что означает; Red (красный), Green (зеленый),
Blue (синий) и «Alpha» (альфа). Величина alpha иногда используется для смешения двух цветов на эк-
ране; это будет рассматриваться в главе 10. Для наших целей здесь alpha = 1,0.
Источники света имеют различные значения по умолчанию.
Для всех источников:
default ambient - (0, 0, 0, 1); фоновый по умолчанию,
(dimmest possible = black); наименьшая яркость — черный.
Для источника света LIGHTO:
* default diffuse = (1, 1, 1, 1) диффузный по умолчанию,
(brightest possible - white) наибольшая яркость — белый
и
default specular = (1, 1,1,1) зеркальный по умолчанию,
(brightest possible - white) наибольшая яркость — белый.
Для других источников света значения диффузного и зеркального компонентов по умолчанию уста-
новлены в черный цвет.
Прожекторы
Источники света по умолчанию являются точечными источниками (point sources). Это означает, что они
излучают свет равномерно по всем направлениям. Однако OpenGL позволяет превратить их в прожек-
торы, так чтобы они излучали свет в ограниченном числе направлений. На рис. 8.20 показан прожек-
тор, нацеленный в направлении d с «углом пропускания» («cutoff angle») а.
Рис 8.20. Свойства прожектора
В точках, лежащих вне конуса пропускания, свет не виден вообще. Для таких вершин, как Р, кото-
рые лежат внутри этого конуса, количество света, достигающего точки Р, пропорционально множите-
лю cosE(P), где Р — угол между вектором d и прямой, соединяющей источник с точкой Р. Показатель
500
Глава 8. Визуализация граней для усиления реалистичности
степени е выбирается пользователем так, чтобы обеспечить нужное уменьшение интенсивности света в
зависимости от угла.
Параметры прожектора устанавливаются следующим образом: с помощью функции glLightfO зада-
ется его единственный параметр, а с помощью функции glLightfvO — вектор:
g1Lightf(GL_LIGHT0. GL_SPOT_CUTOFF. 45.0);
// a cutoff angle of 45°
// угол пропускания равен 45°
glLightf(GL_LIGHTO. GL_SPOT_EXPONENT. 4.0):
// eps =4.0
GLfloat dir[] = {2.0. 1.0, -4.0}:
// the spotlight’s direction
// направление прожектора
glLightfv(GL_LIGHTO. GL_SPOT_DIRECTION, dir):
По умолчанию установлены следующие значения этих параметров: d - (0,0, -1), а - 180°; е - 0, что
соответствует действующему во всех направлениях точечному источнику света.
Ослабление света с расстоянием
OpenGL также дает возможность задавать скорость ослабевания света при удалении от источника. Хотя
мы и приуменьшали важность этой зависимости, представляется интересным поэкспериментировать с
различными скоростями уменьшения света и точнее отрегулировать изображение. В OpenGL преду-
смотрено ослабление силы позиционного1 источника света с помощью так называемого коэффициента
ослабления (attenuation factor):
1
(8.10)
atten = ------------7,
kc+k,D + kqD2
где kc, kh kq — коэффициенты, a D — расстояние между точкой расположения источника света и рас-
сматриваемой вершиной. Это выражение является достаточно гибким, чтобы позволить смоделировать
любую комбинацию постоянной, линейной и квадратичной (точнее, обратно-квадратичной) зависимо-
сти от расстояния до источника. Параметры управляются с помощью вызовов функции
g1Lightf(GL_LIGHT0. GL_CONSTANT_ATTENLIATION. 2.0):
и подобным же образом для GL_LINEAR_ATTENUATION и GL_QUADRATIC_ATTENUATION. Значения по умолчанию
составляют k = l, k. = O,k =0, что исключает какое-либо ослабление света.
Модель освещения
OpenGL предусматривает задание трех параметров, определяющих общие законы применения модели
освещения. Эти параметры передаются в функцию glLightModel и некоторые ее модификации.
Цвет глобального фонового света. Для любой заданной сцены можно установить глобальный фоно-
вый свет, не зависимый ни от какого определенного источника. Для создания такого освещения следует
задать его цвет с помощью следующих команд:
GLfloat amb[] = {0.2. 0.3. 0.1. 1.0};
glLightModelfv(GL_LIGHT_MODEL_AMBIENT. amb):
Этот код придает источнику фонового света цвет (0,2, 0,3, 0,1). Значение по умолчанию составляет
(0,2, 0,2, 0,2, 1,0), так что фоновый свет присутствует всегда, если только вы умышленно не измените
его. Задание фоновому источнику ненулевого значения обеспечивает видимость объектов сцены, даже
если вы не активизировали ни одной функции освещения.
Является ли точка наблюдения локальной или удаленной? OpenGL вычисляет зеркальные отражения
с помощью «промежуточного вектора» h = s + v, описанного в разделе «Зеркальное отражение» данной
1 Коэффициент ослабления отключен в случае источников направленного света, поскольку они находятся бесконечно далеко.
8.2. Введение в модели закрашивания
501
главы. Истинные направления s и v, вообще говоря, различаются для каждой вершины сетки. (Визуа-
лизируйте такую конфигурацию!) Если источник света является направленным, то вектор s — величи-
на постоянная, a v все же изменяется от вершины к вершине. Скорость визуализации возрастет, если
сделать и вектор v постоянным для всех вершин. По умолчанию OpenGL использует значение v - (0,0,1),
при этом вектор v указывает в сторону положительной оси z в координатах камеры. В то же время мож-
но принудительно заставить графический конвейер вычислять истинное значение вектора v для каж-
дой вершины с помощью выполнения оператора:
glLightModeli(GL_LIGHT_MODEL_LOCAL_VIEWER. GL.TRUE):
Правильно ли происходит закрашивание обеих сторон полигона? Каждая полигональная грань моде-
ли имеет две стороны. При моделировании мы привыкли называть эти стороны «внутренней» и «внеш-
ней» поверхностями. Принято заносить эти вершины в список против часовой стрелки, если смотреть с
внешней стороны объекта. Большинство каркасных объектов представляют сплошные тела, ограничи-
вающие некоторое пространство, так что четко определены понятия внешней и внутренней стороны.
Для таких объектов камера может наблюдать только внешнюю поверхность каждой грани (если, конеч-
но, сама камера не находится внутри объекта!). При правильном удалении невидимых поверхностей
внутренняя поверхность каждой грани скрыта от глаза какой-нибудь более близкой гранью.
а б
Рис. 8.21. Определение лицевой грани в OpenGL
В OpenGL нет понятия «внутри» и «снаружи», он может различать только «лицевые грани» и «не-
лицевые грани». Грань является лицевой (front face), если ее вершины расположены в списке против
часовой стрелки, в том порядке, каком их видит глаз*. На рис. 8.21, а показан куб — таким, каким
его видит глаз, если принято соглашение о нумерации против часовой стрелки. Стрелками показан тот
порядок, в каком вершины каждой грани передаются в OpenGL (в блоке glBegin(GL_POLYGON); ...;
glEndO). Для объекта, ограничивающего некоторое пространство, все грани, которые видит глаз, явля-
ются лицевыми, и OpenGL правильно рисует и закрашивает их. Нелицевые грани1 2 также рисуются в
OpenGL, но в конце концов они скрываются за более близкими лицевыми гранями.
Иначе обстоит дело на рис. 8.21, б, где показан параллелепипед с одной удаленной гранью. Как и
раньше, стрелками показан порядок, в котором вершины каждой грани пересылаются в графический
конвейер. Три из видимых граней являются нелицевыми. По умолчанию OpenGL не может правильно
закрасить эти грани. Для правильного закрашивания нелицевых граней нужно проинструктировать
OpenGL с пом.ощью оператора
glLIghtModel1(GL_LIGHT_MODEL_TWO_SIDE. GL.TRUE):
При выполнении этой команды OpenGL изменяет направления нормалей всех нелицевых граней
таким образом, чтобы они указывали на наблюдателя, после чего закрашивание осуществляется кор-
ректно. Замена величины GL_TRUE на GL_FALSE (принятой по умолчанию) отключает эту опцию. {Замеча-
ние. Грани, нарисованные с помощью OpenGL, не отбрасывают теней, поэтому все нелицевые грани
1 Можно заменить этот порядок на обратный с помощью подпрограммы gl FrontFace(GL_CW), в которой обусловлено, что грань яв-
ляется лицевой только в том случае, если ее вершины занесены в список в порядке по часовой стрелке. По умолчанию принято
glFrontFace(GL_CCW).
2 Можно ускорить работу компьютера, если запретить OpenGL визуализацию нелицевых граней. При этом используется следую-
щий код: glCullFace(GL_BACK); glEnable(GL_CULL_FACE):.
502
Глава 8. Визуализация граней для усиления реалистичности
получают от источника такой же свет, даже если между ними и источником света находится какая-ни-
будь другая грань.)
Перемещение источников света
Напомним, что источники света проходят через матрицу моделирования-вида наряду с вершинами.
Следовательно, источники света могут быть перемещены с помощью соответствующих вызовов функ-
ций glRotatedO и glTranslatedO. Массив position, заданный подпрограммой glLightfv(GL_LIGHTO,
GL_POSITION. position), изменяется с помощью матрицы моделирования-вида, что происходит в момент
вызова функции glLightfvO. Поэтому для изменения положения источника света с помощью преобра-
зований и для независимого перемещения камеры команду позиционирования источника нужно вста-
вить внутрь стековых скобок «push-pop», как это сделано в следующем коде:
void displayO
{
GLfloat positiont] - {2. 1. 3. 1};
// initial light position
// начальное положение источника света
clear the color and depth buffers
// зачищаем буферы цвета и глубины
glMatrixMode(GL_MODELVIEW):
glLoadidentity():
glPushMatrix():
glRotated(...);
// move the light
// перемещаем источник света
glTranslated(...):
glLightfv(GL_LIGHTO. GL_POSITIDN, position);
glPopMatrixO;
gluLookAt(...):
// set the camera position
// задаем положение камеры
draw the object
// рисуем объект
glutSwapBuffersO:
}
С другой стороны, для того чтобы источник света перемещался вместе с камерой, необходимо ис-
пользовать следующий код:
GLfloat post] - {0. 0. 0. 1}:
glMatrixMode(GL_MODELVIEW);
glLoadldentity();
glLightfv(GL_LIGHTO. GL_POSITION. position):
// light at (0. 0. 0)
// источник света в положении (0. 0. 0)
gluLookAt(...):
// move the light and the camera
// перемещаем источник света и камеру
draw the object
// рисуем объект
Этот код устанавливает источник света прямо в глаз (подобно шахтерской лампе), и тогда свет пере-
мещается вместе с камерой.
8.2. Введение в модели закрашивания
503
8.2.9. Работа со свойствами материалов в OpenGL
Влияние источника света можно увидеть только при отражении света от поверхности объекта. В OpenGL
предусмотрены возможности задания различных коэффициентов отражения, фигурирующих в равен-
стве (8.7). Эти коэффициенты устанавливаются с помощью различных версий функции glMaterial, при-
чем коэффициенты можно установить отдельно для лицевых и нелицевых граней. (Вспомним обсуж-
дение рис. 8.21.) Например, следующий код
GLfloat myDiffuse[] = {0.8. 0.2. 0.0. 1.0};
glMaterialfv(GL_FRONT. GL_DIFFUSE, myDiffuse);
присваивает коэффициенту диффузного отражения (pdr, pdg, pdb) значение (0,8, 0,2, 0,0) для всех по-
следовательно заданных лицевых граней. Коэффициенты отражения задаются в формате RBGA в виде
четверки, аналогично заданию цвета. Первый параметр функции glMaterialfvO может принимать сле-
дующие значения:
О GL_FRONT: задается коэффициент отражения для лицевых граней.
О GL_BACK: задается коэффициент отражения для нелицевых граней.
О GL_FRONT_AND_BACK: задается коэффициент отражения и для лицевых, и для нелицевых граней.
Второй параметр может принимать следующие значения:
О GL_AMBIENT: задаются коэффициенты фонового отражения.
О GLJHFFUSE: задаются коэффициенты диффузного отражения.
О GL_SPECULAR: задаются коэффициенты зеркального отражения.
О GL_AMBIENT_AND_DIFFUSE: коэффициенты фонового и диффузного отражения устанавливаются рав-
ными одному и тому же значению. Такая установка сделана для удобства, поскольку коэффици-
енты фонового и диффузного отражения часто выбираются одинаковыми.
О GL_EMISSION: устанавливается эмиссионный цвет поверхности.
В последнем случае устанавливается эмиссионный цвет (emissive color) для грани, вследствие чего
она начинает «светиться» заданным цветом, независимо ни от какого источника света.
Собирая все вместе
Расширим теперь уравнение (8.7) так, чтобы оно включало в себя вклады дополнительных величин,
вычисляемых OpenGL. Полный компонент красного цвета задается выражением:
4 = ег + /тграг + Xatten. х spot. х (4ри + 4Р* х lambert,. + /'prPsr х phongf ). (8.11)
i
Выражения для зеленого и синего компонентов задаются аналогично. Слагаемое ег означает эмиссион-
ный свет, a Zmr — глобальный фоновый свет, введенный в модель освещения. Знак суммы означает, что
для всех источников суммируются вклады фонового, диффузного и зеркального света. Для i-ro источника
atten; является коэффициентом ослабления света, как в уравнении (8.10); spot,. — это коэффициент про-
жектора (см. рис. 8.20), a lambert; и phong,. — уже известные нам скалярные произведения сответственно для
диффузного и зеркального отражения. Все эти члены должны вычисляться заново для каждого источ-
ника света. (Замечание. Если в результате вычислений 1г получается больше, чем 1,0, то OpenGL уреза-
ет его до этого значения: известно, что максимальная яркость любого компонента света составляет 1,0.)
8.2.10. Закраска сцен, заданных с помощью SDL
В языке описания сцен SDL, представленном в главе 5, поддерживается загрузка в объекты свойств ма-
териала для корректного проведения их закраски. Например, такой код:
light 3 4 5 .8 .8 .8
! bright white light at (3. 4. 5)
! ярко-белый свет в точке (3. 4. 5)
504
Глава 8. Визуализация граней для усиления реалистичности
background 111
! white background
! белый фон
globalAmbient .2 .2 .2
! a dark gray global ambient light
1 темно-серый глобальный фоновый свет
ambient .2 .6 О
diffuse .8 .2. 1
! red material
! красный материал
specular 111
! bright specular spots - the color of the source
! яркие зеркальные блики - с цветом источника
specularExponent 20
Iset the Phong exponent
! устанавливаем показатель Фонга
scale 4 4 4 sphere
описывает сцену, содержащую сферу со следующими свойствами материала (см. равенство (8.7)):
О коэффициенты фонового отражения: (раг, р^, раЬ) - (0,2, 0,6,0);
О коэффициенты диффузного отражения: (pdr, pdg, pdb) - (0,8, 0,2,1,0);
О коэффициенты зеркального отражения: (psr, psg, psb) = (1,0,1,0,1,0);
О показатель Фонга: /=20.
Для диффузного и зеркального компонентов источника света установлен цвет (0,8,0,8,0,8). Глобаль-
ный фоновый член равен (/аг, 1^, 1^) = (0,2,0,2,0,2).
Текущие свойства материала загружаются в поле mtrl каждого объекта в момент создания этого
объекта (см. заключительные строки описания функции Scene :: getObjectO в файле SDL.cpp в прило-
жении В). Когда объект рисуется с помощью подпрограммы drawOpenGLO, он сначала передает в OpenGL
свои свойства материала (см. описание Shape:: tellMaterialsGLO). Тогда в момент фактического рисо-
вания объекта OpenGL уже будет иметь эти свойства материала в текущем состоянии объекта.
В главе 14 при исследовании трассировки лучей мы аналогичным образом будем использовать поле
свойств материала каждого объекта, чтобы запрашивать эти свойства материала для правильного за-
крашивания.
8.3. Плоское и плавное закрашивание
Для различных объектов требуются различные оттеночные эффекты. В главе 6 мы моделировали раз-
личные формы с применением полигональных сеток. Для некоторых из них, вроде сарая и бакибола,
мы хотим увидеть на картинке отдельные грани, а для других, типа сферы или шахматной пешки, мы
предпочитаем видеть «истинную» поверхность, которую эти грани аппроксимируют.
В процессе моделирования мы «привязывали» к каждой вершине каждой грани нормаль к этой гра-
ни. Если поверхность является полигоном, то ко всем ее вершинам привязывается одна и та же нор-
маль; эта нормаль выбирается так, чтобы она указывала нормальное направление к плоскости этой гра-
ни. С другой стороны, если эта грань является приближением к истинной поверхности, то к каждой
вершине мы привязываем нормаль к истинной поверхности в этой точке.
Посмотрим теперь, как при выполнении разлйчного рода закрашиваний используется информация,
полученная от нормали в каждой вершине. Главное различие между методами закрашивания заключает-
ся в том, что при одном из них (плоское закрашивание — flat shading) отдельные полигоны выделяются,
а при другом (плавное закрашивание — smooth shading) происходит плавный переход между гранями и
8.3. Плоское и плавное закрашивание
505
стирание ребер между ними. Мы будем рассматривать два вида плавного закрашивания: закраску Гуро
и закраску Фонга.
При обоих видах закраски вершины пропускаются через графический конвейер, выполняются вы-
числения для привязки цвета к каждой вершине, и, наконец, вершины каждой грани преобразуются в
экранные координаты, и грань «раскрашивается» соответствующим цветом — пиксел за пикселом.
Раскраска грани
Раскраска грани производится с помощью подпрограммы заполнения полигонов. Закрасить полигон
очень просто, хотя точная настройка алгоритма заполнения для достижения наивысшей эффективнос-
ти может оказаться сложной (см. главу 10). Здесь мы займемся только основами и сфокусируем свое
внимание на том, как задается цвет каждого пиксела.
Подпрограмму закраски полигона иногда называют «плиточником» (tiler), поскольку она проходит
полигон пиксел за пикселом, раскрашивая каждый пиксел нужным цветом, подобно тому, как выкла-
дывается мозаика паркетного пола. Пикселы полигона посещаются в порядке очереди, обычно по стро-
кам развертки слева направо, снизу вверх по полигону.
Мы предполагаем, что интересующие нас полигоны являются выпуклыми. Плиточник, предназна-
ченный для заполнения только выпуклых полигонов, может быть сделан очень эффективным, посколь-
ку для каждой строки развертки существует только один неразрывный «ряд» пикселов, лежащий внут-
ри данного полигона. В большинстве реализаций OpenGL используется это обстоятельство, и выпуклые
полигоны всегда закрашиваются правильно; с другой стороны, корректная закраска невыпуклых поли-
гонов не гарантируется (см. в упражнениях дополнительные соображения о выпуклости).
Рис. 8.22. Заполнение полигональной грани цветом
На рис. 8.22 показан выпуклый четырехугольник, грань которого заполняется цветом. На рисунке
отмечены экранные координаты каждой вершины. Ординаты самой нижней и самой верхней точек гра-
ни обозначены соответственно и у . Плиточник вначале закрашивает ряд при у = z/bott (в данном
случае это единственная точка), затем при + 1 и т. д. Для каждой строки развертки, скажем ys на
рисунке, существует крайняя левая точка x|cft и крайняя правая точка xright. Плиточник движется отхЫ|.
к х^, помещая нужный цвет в каждый пиксел. Таким образом, плиточник реализуется в виде обычного
двойного цикла:
for (int у - ybott : у <= ytop : у++)
// for each scan line
// для каждой строки развертки
{
find xleft and xright
// НахОДИН Xleft И Xright
for (Int X - xleft: x <- Xright; X++)
// fill across the scan line
// заполняем строку развертки от края до края
506
Глава 8. Визуализация граней для усиления реалистичности
{
find the color с for this pixel
// находим цвет с для этого пиксела
put с into the pixel at (x. у)
И помещаем цвет с в пиксел с координатами (х, у)
(Позже мы увидим, как с помощью двойного цикла можно также легко удалять невидимые поверх-
ности.) Принципиальное различие между плоским и плавным способом закрашивания заключается в
методе определения цвета с для каждого пиксела.
8.3.1. Плоское закрашивание
Если грань является плоской (как крыша сарая) и источники света достаточно удалены, то диффузный
компонент освещения мало отличается для различных точек крыши. (Член lambert в уравнении (8.6)
практически одинаков для каждой вершины грани.) В таких случаях целесообразно использовать один
и тот же цвет для каждого пиксела, «покрываемого» данной гранью. В OpenGL предусмотрен режим
визуализации, при котором вся грань рисуется одним и тем же цветом. Хотя цвет передается в конвей-
ер как часть каждой вершины грани, в данном режиме алгоритм раскраски использует только одно зна-
чение цвета (обычно это цвет первой вершины грани). Поэтому команда fl nd the color c for this pixel
в вышеприведенном коде не находится внутри циклов, а появляется до входа в эти циклы, назначая
переменную с равной цвету одной из вершин. (Использование одинакового цвета для всех пикселов
делает плоское закрашивание довольно быстрым.)
Плоское закрашивание устанавливается в OpenGL с помощью команды
glShadeModel(GL_FLAT);
На рис. 8.23 показаны бакибол и сфера, визуализированные с помощью постоянного закрашивания.
На обоих объектах четко видны отдельные грани. Сфера смоделирована как гладкий объект, однако
при визуализации не производилось никакого сглаживания, поскольку цвет всей грани задан таким же,
как цвет одной вершины.
Рис. 8.23. Две сетки, визуализированные с использованием плоского закрашивания
Ребра между гранями явно выглядят более выраженными, чем они были бы на истинном физичес-
ком объекте, — это происходит в силу зрительного эффекта, известного как «боковое торможение»
(lateral inhibition) и описанного впервые Эрнстом Махом (Ernst Mach)1. Если на объекте имеется раз-
рыв интенсивности, то при созерцании этого разрыва в глазу возникает так называемая полоса Маха
(Mach band), в результате чего просматривается четкое ребро. Эта зона преувеличивает полигональ-
ный «вид» каркасных объектов, визуализируемых с помощью плоского закрашивания.
1 Эрнст Мах (1838-1916) — австрийский физик, чьи ранние работы оказали сильное влияние на появление теории относительности.
8.3. Плоское и плавное закрашивание
507
Зеркальные блики плохо визуализируются в рамках плоского закрашивания, опять же вследствие
того, что вся грань заполняется тем цветом, который был вычислен только для одной вершины. Если
случится так, что у этой репрезентативной вершины имеется значительный зеркальный компонент, то
вся грань будет окрашена с этой яркостью. Если же зеркальный блик не выпадает на репрезентативную
точку, то он полностью игнорируется. По этой причине в вычислительный процесс закраски мало смыс-
ла включать компонент зеркального отражения.
8.3.2. Плавное закрашивание
При плавном закрашивании делается попытка затушевать ребра между гранями — путем вычисления
цветов в большем числе точек каждой грани. Существует два основных типа плавного закрашивания:
закраска Гуро [Gouraud, 90] и закраска Фонга [Phong, 162]. В OpenGL выполняется только закраска
Гуро, однако мы опишем оба варианта.
Закраска Гуро
При закрашивании Гуро (Gouraud shading) для каждого пиксела вычисляется отдельное значение цве-
та с. Для строки развертки при ys на рис. 8.22 цвет крайнего левого пикселя co/orleft определяется посред-
ством линейной интерполяции цветов на верхнем и нижнем концах левого ребра полигона*. Для этой
строки развертки «верхний» цвет равен color1, а «нижний» — colorр так что colorkk можно вычислить по
формуле (вспомните уравнение (8.9)):
colorleft = lerp(colort, color4,/), (8.12)
где дробь
у = X -Л’ьоп
Л-Лои
изменяется от 0 до 1 при изменении уг от у^ до yt. Отметим, что равенство (8.12) подразумевает три
вычисления, поскольку каждое значение цвета содержит компоненты красного, зеленого и синего цветов.
Подобным же образом вычисляется цвет colorright — путем интерполяции цветов в верхнем и нижнем
концах правого ребра. Затем плиточник заполняет строку развертки, линейно интерполируя между
цветами colorkft и colorrjght для получения цвета пикселах
с(х) = lerp colorleft, colorrighl,
Xrighf ~ •’'left
(8.13)
Для повышения эффективности заполнения этот цвет вычисляется в приращениях для каждого пик-
села. То есть между цветами с(х + 1) и с(х) разность постоянна, так что
, а. 1Л / \ л. C010rrigh.-C0l0rien
с(х + 1) = с(х) +--------------5------------
-^righf ~ •’'left
(8.14)
Приращение вычисляется только один раз за пределами самого внутреннего цикла. Код при этом
выглядит примерно так:
for (int у - ybott ; у <= ytop ; у++)
// for each scan line
// для каждой строки развертки
{
find xleft end xright
1 Позже мы увидим, что хотя цвета обычно интерполируют линейно, как мы делаем это здесь, лучшие результаты могут быть достиг-
нуты с помощью так называемой гиперболической интерполяции. Для закрашивания Гуро различие этих видов интерполяции не-
существенно; однако при отображении текстуры оно становится критическим.
508
Глава 8. Визуализация граней для усиления реалистичности
// нахОДИН Xleft И Xright
find colorleft and colorright
// находим colorleft И colorright
Colorinc - (Colorright - COlODeft ) / (xright - Xleft ):
for (Int X - Xleft . C - Colorleft ; X <- Xright : X++. С+“С010Г1пс )
put c Into the pixel at (x. y)
// помещаем цвет с в пиксел (х, у)
}
С вычислительной точки зрения закраска Гуро обходится ненамного дороже, чем плоское закраши-
вание. Закраска Гуро устанавливается в OpenGL с помощью функции:
glShadeModel(GL_SMOOTH):
На рис. 8.24 показаны бакибол и сфера, визуализированные с помощью закраски Гуро. Бакибол выг-
лядит так же, как в случае визуализации с плоским закрашиванием (см. рис. 8.23), поскольку с каждой
вершиной грани связан один и тот же цвет, поэтому интерполяция ничего не меняет. Однако сфера выг-
лядит гораздо более гладкой: отсутствуют резкие скачки цвета между соседними гранями, а ребра между
гранями (полосы Маха) исчезли, уступив место плавному изменению цвета по поверхности объекта.
В то же время вдоль силуэта еще можно видеть ребра, ограничивающие отдельные грани.
Рис. 8.24. Две сетки, визуализированные с помощью плавного закрашивания
Почему же исчезают ребра при использовании этой техники? На рис. 8.25, а изображены две грани,
Ги F', имеющие общее ребро. При визуализации грани F используются цвета cL и cR , а при визуализа-
ции грани F’ — цвета с/ и с'. Но поскольку цвета cR и c'L одинаковы, резкое изменение цвета на ребре
вдоль строки развертки отсутствует.
а
Рис. 8.25. Непрерывность цвета, пересекающего ребро полигона
На рис. 8.25, б показано, как при закраске Гуро проступает «истинная» поверхность, аппроксими-
рованная сеткой. В поперечном сечении показана полигональная поверхность с отмеченными верши-
нами: V2 и т. д. Кроме того, показана и воображаемая гладкая поверхность, которую предположи-
тельно представляет данная сетка. Правильно вычисленные нормали в этих вершинах (тр т, ит. д.)
направлены перпендикулярно к этой воображаемой поверхности, так что в каждой вершине будет ис-
8.3. Плоское и плавное закрашивание
509
пользоваться нормаль для «корректного» закрашивания и цвет, найденный таким способом, будет вер-
ным. Затем в промежутке между вершинами производится плавное изменение цвета, не подчиняюще-
еся никакому физическому закону, но вместо этого следующее простому математическому.
Поскольку цвета скорее формируются как результат интерполяции, чем вычисляются для каждого
пиксела, закраска Гуро не может полноценно отобразить блики. Поэтому при использовании закраски
Гуро зеркальный компонент интенсивности в равенстве (8.11) обычно подавляется. Блики лучше вос-
производятся при использовании закраски Фонга, к изучению которой мы и переходим.
Закраска Фонга
Можно достигнуть намного большей реалистичности, особенно в случае бликов на блестящих объек-
тах, если добиться лучшей аппроксимации нормали к поверхности для каждого пиксела. Такой тип за-
краски называется закрашиванием Фонга (Phong shading), по имени его создателя Фонга Буи-туонга
(Phong Bui-tuong) [Phong, 162].
При работе с закрашиванием Фонга мы находим нормальный вектор для каждой точки на грани
объекта, и для нахождения цвета в ней применяем модель закраски. Вычисление нормали для каждого
пиксела осуществляется путем интерполяции нормальных векторов в вершинах полигона.
Рис. 8.26. Интерполирование нормалей
На рис. 8.26 показана проекция грани, а также нормали т,, т2, т3, т4 в ее четырех вершинах. Для
строки развертки ys векторы m|cft и mright находятся посредством линейной интерполяции. Например:
mien = lerp[m4,m3> Л Л .
I Уз~У*)
Полученный таким образом интерполированный вектор необходимо нормировать к единичной дли-
не, прежде чем использовать его в формуле закрашивания. Поскольку нормали m|eft и mright известны, то
посредством их интерполяции можно получить нормальный вектор для каждой точки х вдоль строки
развертки. Такой вектор после нормировки используется при закраске для вычисления цвета каждого
интересующего нас пиксела.
На рис. 8.27 изображен объект, визуализированный с использованием закраски Гуро, и тот же объект,
визуализированный с использованием закраски Фонга. Поскольку при закраске Фонга направление
нормали изменяется плавно от точки к точке и более точно аппроксимирует нормаль истинной глад-
кой поверхности, зеркальные блики в этом случае воспроизводятся намного правдоподобнее, чем при
закраске Гуро, и поэтому визуализация обладает большей реалистичностью. Основным недостатком
закраски Фонга является его относительно малая скорость: для каждого пиксела требуется намного
больше вычислений, поэтому закраска Фонга занимает в шесть — восемь раз больше времени, чем за-
краска Гуро. Предпринималось множество попыток ускорить этот процесс [Bishop, 23; Claussen, 43].
510
Глава 8. Визуализация граней для усиления реалистичности
Рис. 8.27. Сравнение моделей закраски Гуро и Фонга (с разрешения Bishop and Weimar [Bishop, 23]) \
OpenGL не приспособлен для выполнения закраски Фонга, поскольку в нем модель закрашивания
для каждой вершины применяется только один раз — после преобразования моделирования-вида, а так-
же потому, что информация о нормалях не передается на этап визуализации, происходящий после пер-
спективного преобразования и деления. Однако в разделе «Добавление текстуры к граням» мы увидим,
что приближение к закрашиванию Фонга может быть осуществлено посредством отображения на
объект текстуры «блика» с использованием техники отображения окружающей среды.
Практические упражнения
8.3.1. Закраска грани
Рассмотрите подробно, как работает алгоритм закраски полигона на примере полигона с вершинами
(х, У) ~ (23,137), (120,204), (200,100), (100,25) для следующих строк развертки: у - 136, у = 137, у - 138.
В частности, для каждого случая напишите значения x|eft и xright.
8.3.2. Выпуклые полигоны после отсечения остаются выпуклыми
Покажите, что если выпуклый полигон отсекается границами отображаемого объема камеры, то отсе-
ченный полигон по-прежнему остается выпуклым.
8.3.3. Сохранение ребер при закрашивании Гуро
В ряде случаев нам может потребоваться показать на модели отдельные ребра и границы. Обдумайте,
как можно управлять этим свойством с помощью выбора нормалей в вершинах. Какие, например, долж-
ны быть нормали, чтобы сохранилось ребро между гранями Ги F' на рис. 8.25? Некоторые другие при-
емы и проблемы можно найти в литературе: например, [Rogers, 105].
8.3.4. Ускорение работы закраски Фонга с помощью граничного закрашивания
Для увеличения скорости закраски Фонга Беренс [Behrens, 16] предлагает интерполировать нормали
между вершинами для получения векторов т£ и тя на каждой строке развертки обычным способом,
однако затем вычислять цвета только для этих левого и правого пикселей, а затем интерполировать их
вдоль строки развертки, как это делается при закраске Гуро. Это так называемое граничное закрашива-
ние (fence shading) поразительно ускоряет визуализацию, однако визуализация бликов осуществляет-
ся хуже, чем при истинной закраске Фонга. Укажите основные направления для нормалей тр т2, т3, т4
в вершинах, чтобы
О ограниченное закрашивание производило такие же блики, как и закраска Фонга;
О ограниченное закрашивание производило блики, значительно отличающиеся от тех, которые
получаются при закраске Фонга.
8.3.5. Алгоритм закрашивания Фонга
Произведите необходимые изменения в коде «плиточника» для включения в него закраски Фонга. При
этом должно подразумеваться, что для каждой грани известны нормальные векторы в вершинах. Кроме
того, обдумайте, как можно аппроксимировать закраску Фонга с помощью алгоритма плавного закра-
шивания OpenGL. (Подсказка. Увеличьте число граней в модели.)
8.4. Удаление невидимых поверхностей
511
8.4. Удаление невидимых поверхностей
Очень просто включить в процесс визуализации удаление невидимых поверхностей, описанный в пре-
дыдущем разделе, если имеется достаточно памяти для поддержки «буфера глубины», иначе называе-
мого г-буфером («depth buffer», «г-buffer»). Поскольку такой буфер легко встраивается в обсуждаемый
нами механизм визуализации, мы сейчас же его и рассмотрим. Другие алгоритмы для удаления неви-
димых поверхностей (более эффективные и требующие меньше памяти) описываются в главе 13.
8.4.1. Использование буфера глубины
Алгоритм буфера глубины (или г-буфера) является одним из наиболее простых и легко реализуемых
методов удаления невидимых поверхностей. Его основные ограничения заключаются в том, что он тре-
бует большого объема памяти и часто визуализирует объект, который затем заслоняется другим объек-
том (таким образом, время, затраченное на визуализацию первого объекта, тратится впустую.)
b битов
Рис 8.28. Концептуальное представление буфера глубины
На рис. 8.29 изображен буфер глубины, связанный с буфером кадров (frame buffer). Для каждого
пиксела p[i][j] на дисплее в буфере глубины хранится величина гф'][;] размером b бит. Значение b обыч-
но находится в пределах от 12 до 30 бит. Во время процесса визуализации значение буфера глубины
содержит псевдоглубину ближайшего (на данный момент) объекта для пиксела p[i][j]. Когда
плиточник проходит пиксел за пикселом вдоль строки развертки, закрашивая текущую грань, он про-
веряет, является ли псевдоглубина этой грани меньшей величиной, чем глубина J[i][j], записанная в
буфере для данной точки. Если это так, то вместо цвета р [г] [j] записывается цвет ближайшей поверхнос-
ти, а в элемент буфера d[i] [/] вместо старого значения записывается эта меньшая псевдоглубина. Грани
могут рисоваться в любом порядке. Если первой рисуется более удаленная грань, то цвета некоторых
пикселов этой грани будут впоследствии замещены цветами пикселов более близкой грани. Следова-
тельно, время, затраченное на визуализацию более удаленной грани, будет затрачено впустую. Отме-
тим, что данный алгоритм работает для объектов любой формы, включая криволинейные поверхности,
поскольку он находит ближайшую поверхность, проводя поточечную проверку.
Изначально массив d[ ][ ] заполняется значениями 1,0, что соответствует максимально возможной
псевдоглубине. Буфер кадров изначально заполняется цветом фона.
Нахождение псевдоглубины для каждого пиксела
Нам необходимо найти быстрый способ вычисления псевдоглубины для каждого пиксела. Напомним,
что каждая вершина Р - (Рх, Ру, Р2) любой грани пересылается в графический конвейер и подвергается
там различным преобразованиям. Информация, доступная для каждой вершины после преобразова-
ния порта просмотра, представляет собой значение упорядоченной тройки, которая после масштабиро-
вания и сдвига определяется формулой:
(x,y,z) =
Рх Ру аРх + Ь
-Рг ’ -Рг ’ -Рг
512
Глава 8. Визуализация граней для усиления реалистичности
(См. также равенство (7.11).) Третий компонент этой тройки и есть псевдоглубина. Константы а и b
выбраны так, чтобы третий компонент обращался в нуль, если вершина Р лежит на ближней плоскости,
и в единицу, если Р лежит на дальней плоскости. Для большей эффективности псевдоглубину каждого
пиксела желательно вычислять в приращениях (инкрементно), что предполагает использование линей- *
ной интерполяции, как это делалось для цвета в равенстве (8.14).
Рис 8.29. Инкрементное вычисление псевдоглубины
На рис. 8.29 изображена грань, закрашиваемая вдоль строки развертки у. На рисунке отмечены зна-
чения псевдоглубины в различных точках. Известны псевдоглубины dit d2, d3, d4 для вершин. Нам тре-
буется вычислить dtcft для строки развертки ys как lerp(Jp dvf) для части f-(ys- y^/ty^ - yt) и анало-
гично J как lerp(d2, d3, h) для соответствующего А. Кроме того, нам нужно найти псевдоглубину d для
каждого пиксела (х, у) вдоль строки развертки как lerp(</left, Jright, А) для соответствующего А. (Чему равны
значения А и А?) Вопрос заключается в том, получается ли в результате этих вычислений «истинная» псев-
доглубина соответствующей точки на трехмерной грани. Ответ на этот вопрос будет положительным: это
вычисление работает правильно. Докажем мы это позднее, после привлечения дополнительной алгебраи-
ческой «артиллерии», но ключевая идея этого доказательства состоит в следующем: исходная трехмерная
грань является плоской, при перспективном преобразовании плоскостность сохраняется, поэтому псев-
доглубина имеет линейную зависимость от спроецированных координат х и у. (См. упражнение 8.5.2.)
Листинг 8.1. Инкрементные вычисления глубины
for(int у - ybott: у <- ytop: у++)
// for each scan-line
// для каждой строки развертки
{
find xleft and xright
И находим xleft и xright
find dleft and dright. and dine
11 находим dleft. dright и dine
find colorleft and colorright, and colorinc
// находим colorleft, colorright и colorinc
for (int x - xleft. c - colorleft, d - dleft; x <- xright: x++. c+-colorinc, d+= dine)
if(d < d[x][yj)
{
put c into the pixel at (x. y)
// помещаем цвет с в пиксел (х. у)
d[x][y] - d;
// update the closest depth
// обновляем ближайшую глубину
}
}
8.4. Удаление невидимых поверхностей
513
В листинге 8.1 показаны почти тривиальные дополнения к алгоритму плиточника с закраской Гуро,
предназначенные для удаления невидимых поверхностей. Значения псевдоглубин и Jright вычисля-
ются (инкрементно) для каждой строки развертки наряду со значением di!K, которое используется в са-
мом внутреннем цикле. Для каждого пиксела находится псевдоглубина d, производится одно сравне-
ние, после чего элемент J[i] [J] обновляется — в случае, если обнаружилось, что текущая грань является
ближайшей к наблюдателю.
Сокращение глубины для больших расстояний
Напомним из примера 7.4.4, что псевдоглубина точки не имеет линейной зависимости от истинной глу-
бины этой точки (расстояния до глаза), а вместо этого приближается к некоторой асимптоте. Это озна-
чает, что при больших глубинах малые изменения истинной глубины преобразуются в чрезвычайно
малые изменения псевдоглубины. Поскольку для представления псевдоглубины используется только
ограниченное количество бит, то два близких значения глубины могут с легкостью превратиться в одно
и то же значение, что может привести к ошибкам при операции сравнения d<d[x][у]. Использование
большего количества бит для представления псевдоглубины помогает, однако требует больше памяти.
Может помочь также размещение ближней плоскости как можно дальше от глаза.
OpenGL поддерживает буфер глубины и использует для удаления невидимых поверхностей алго-
ритм, приведенный в листинге 8.1. Следует указать OpenGL на необходимость создания буфера глуби-
ны в момент инициализации режима дисплея. Это делается посредством команды:
glut!nitDisplayMode(GLUT_DEPTH | GLUT_RGB):
Проверка глубины включается с помощью вызова функции
glEnable(GL_DEPTH_TEST):
Затем каждый раз при создании нового изображения следует инициализировать буфер глубины
с помощью функции:
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT):
Практические упражнения
8.4.1. Приращения
Покажите подробно, как определяются </ight и d по известным значениям псевдоглубины в верши-
нах полигона.
8.4.2 Кодирование значений глубины
Пусть для каждого элемента буфера глубины выделено b бит. При помощи этих b бит предстоит запи-
сывать значения псевдоглубины, лежащие в диапазоне от 0 до 1. Величину от 0 до 1 можно представить
в двоичной форме d{d2d2 db, где принимают значения 0 или 1. Например, псевдоглубина 0,75 кодиру-
ется как 1100000000. Хорошо ли использованы эти b бит? Обдумайте другие варианты.
8.4.3. Уменьшение размера буфера глубины
Если недостаточно памяти для реализации полного буфера глубины, то имеется возможность созда-
вать изображение по частям. В рамках этой технологии буфер глубины создается только для некоторой
части строк развертки, после чего алгоритм повторяется для каждой из частей. Например, для дисплея
512 на 512 пикселов можно выделить память для буфера глубины из расчета только 64 строк развертки
и выполнить вычисления по алгоритму восемь раз. Каждый раз просматривается весь список граней,
вычисляются глубины для тех граней, которые покрывают используемые строки развертки, и выполня-
ются сравнения с преобладающими глубинами. Необходимость восьмикратного просмотра списка гра-
ней, разумеется, уменьшает скорость работы алгоритма. Пусть на сцене имеется Fграней и каждая грань
покрывает в среднем L строк развертки. Оцените, насколько больше времени займет применение мето-
да буфера глубины в случае, когда память выделена только для nRows/N строк развертки.
17 Ф. Хилл
514
Глава 8. Визуализация граней для усиления реалистичности
8.4.4. Буфер глубины для одной строки развертки
Фрагментация буфера кадров из предыдущего упражнения может быть доведена до предела, когда в
буфер глубины записываются глубины только для одной строки развертки. Очевидно, что такой подход
требует большего количества вычислений, так как каждая грань .«обновляется» многократно, один раз
для каждой строки развертки. Обдумайте, как модифицировать вышеприведенный алгоритм для обра-
ботки единственной строки развертки, и оцените, во сколько раз дольше работает новый алгоритм по
сравнению со старым, имеющим полноэкранный буфер глубины.
8.5. Добавление текстуры к граням
Я застал Рим городом из кирпича, а оставил его городом из мрамора.
Август Цезарь-Светоний
Реалистичность изображения значительно возрастает при наложении на грани каркасного объекта
текстуры поверхности. На рис. 8.30 показано несколько примеров. На рис. 8.30, а на каждую из гра-
ней коробки «наклеены» картинки. На рис. 8.30, б вокруг цилиндрической банки обернута наклейка,
а стена на заднем плане выглядит сделанной из кирпича.
Основной метод работы с текстурами заключается в том, что вначале задается некоторая текстурная
функция texture(s, t) в так называемом «текстурном пространстве» («texture space»), которое принято
обозначать параметрами s и t. Функция texture(s, t) генерирует значение цвета или яркости для каж-
дого значения s и t в диапазоне от 0 до 1. На рис. 8.31 приведены два примера текстурных функций,
где значение функции texture(s, t) изменяется от 0 (темный) до 1 (светлый). На рис. 8.30, а изоб-
ражена растровая (bit-шар) текстура, а на рис. 8.30, б — процедурная текстура, которая будет рассмот-
рена ниже.
Существует множество источников текстур. Чаще всего используются растровые отображения и
вычисляемые функции.
Растровые текстуры
Текстуры часто формируются из растровых представлений изображения (таких, как оцифрованная
фотография, графический фрагмент (clip art) или изображение, полученное заранее в результате рабо-
ты какой-нибудь программы). Такое представление состоит из массива значений цвета (обозначим его
txtr[c][r]), которые часто называют текселями (texels — от слов TEXture ELement (элемент текстуры)).
8.5. Добавление текстуры к граням
515
Если этот массив содержит С столбцов и R строк, то индексы с и t изменяются соответственно от 0 до
С-1иот0до7?-1.В простейшем случае функция texture(s, t) обращается к элементам этого массива
таким образом:
' Color3 texture(float s. float t)
{
return txtr[(int)(s * C)][(int)(t * R)];
}
где Color3 содержит RGB-тройку. Если, например, R = 400 и С = 600, то вызов texture(0,261,0,783) ука-
зывает на элемент массива txtr[156] [313] (так как 0,261 • 600 = 156,6; 0,783 • 400 - 313,2). Отметим, что
изменению параметра s от 0 до 1 соответствует 600 пикселов, в то время как такому же изменению пара-
метра t соответствует 400 пикселов. Чтобы избежать искажения во время визуализации, эта текстура
должна быть отображена на прямоугольник с форматным соотношением 6/4.
Рис 8.31. Примеры текстур: а) текстура в виде изображения; б) процедурная текстура
Процедурные текстуры
Текстуру можно также определить с помощью математической функции или процедуры. Например,
сферическая форма, изображенная на рис. 8.31, б, может быть генерирована с помощью следующей
функции:
float fakeSphereCfloat s. float t)
{
float r - sqrt((s-0.5)*(s-0.5)+(t-0.5)*(t-0.5));
if(r < 0.3) return 1 - r/0.3;
// sphere intensity
// яркость сферы
else return 0.2:
// dark background
// черный фон
}
516
Глава 8. Визуализация граней для усиления реалистичности
Эта функция изменяется от 1 (белый цвет) в центре до 0 (черный) по кромке видимой части сферы.
Другой пример, напоминающий шахматную доску, рассматривается в упражнениях, приводимых ниже.
Все, что может быть вычислено, может быть сделано текстурой: плавные переходы и вихри цвета, мно-
жество Мандельброта, каркасные изображения объемных тел и т. д.
Позднее мы увидим, что значение функции texture(s, t) может быть использовано различными спо-
собами: как цвет самой грани, когда она «ярко светится», как коэффициент отражения для «регулиро-
вания» количества света, отраженного от этой поверхности, а также как способ изменения нормали к
поверхности для придания ей «бугристого» вида.
Практическое упражнение
8.5.1. Текстура классической шахматной доски
На рис. 8.32 показана шахматная доска размером 5 на 5, состоящая из квадратов с уровнями ярко-
сти, принимающими значения 0 (для черного цвета) и 1 (для белого).
О Напишите функцию float texture (float s. float t) для данной текстуры. (См. также упражне-
ние 2.3.1.)
О Напишите функцию textured для случая доски, состоящей из Мстрок и Wстолбцов.
Рис. 8.32. Узор классической шахматной доски
Следующим этапом после задания текстурной функции является ее правильное отображение на
нужную поверхность и затем просмотр ее с помощью камеры. На рис. 8.33 приводится пример, ил-
люстрирующий эту задачу в целом. Один и тот же образец текстуры отображается на три различных
объекта: на плоский полигон, цилиндр и сферу. Для каждого объекта имеется некоторое преобразова-
ние, например Ttw («texture to world» — «текстура в мировые координаты»), которое переводит значе-
ния текстуры (s, t) в точки (х, у, z) на поверхности данного объекта. Камера осуществляет снимок этой
сцены под некоторым углом, получая вид, приведенный на рисунке. Мы вызываем преобразование
точек трехмерного пространства в точки экрана («from world to screen» — «из мировых координат в экран-
ные»), поэтому точка (х, у, z) поверхности «видна» на месте пиксела с координатами (sx, sy) = Тт(х, у, г).
Таким образом, значение (s*, t*) текстуры в результате помещается в пиксел (sr, sy) = ТТО(Т№(5*, t*)).
Рис. 8.33. Наложение текстуры на объекты различной формы
8.5. Добавление текстуры к граням
517
Фактически же процесс визуализации идет иначе: для каждого пиксела (sx, sy) мы отвечаем на та-
кую последовательность вопросов.
1. Какая ближайшая поверхность «видна» в точке (sx, sy)? Ответ на этот вопрос определяет, ка-
кую текстуру следует наложить.
2. Какой точке на поверхности (х, у, г) соответствует точка (sx, sy)?
3. Какой паре текстурных координат (s, t) соответствует точка (х, у, г)?
Таким образом, нам требуется обратное преобразование, что-нибудь типа (s, t) = Т(ч1~1(Тт~'(5х, sy)),
которое по пиксельным координатам генерирует текстурные координаты (s, t). В зависимости от фор-
мы поверхности получить такое обратное преобразование бывает или трудно, или легко.
8.5.1. Наложение текстуры на плоскую поверхность
Исследуем вначале наиболее важный случай: отображение текстуры на плоскую поверхность. Это за-
дача моделирования. В следующем разделе мы будем решать задачу просмотра, чтобы увидеть теку-
щую визуализацию текстуры. А затем исследуем отображение текстур на более сложные формы поверх-
ностей.
Наложение текстуры на плоскую поверхность
Поскольку пространство самой текстуры является плоским, то проще всего наложить текстуру на
плоскую поверхность. На рис. 8.34 показано текстурное изображение, отображенное на область плос-
кого полигона F. Мы должны указать, как связывать точки текстуры с точками области F. В OpenGL
для связи точки текстурного пространства Р. = (s., t;) с каждой вершиной У( на грани используется фун-
кция glTexCoord2fO. Функция glTexCoord2f(s, t) присваивает «текущим текстурным координатам» зна-
чение (s, t), и они привязываются к последовательно определяемым вершинам. Обычно каждому вызо-
ву функции glVertex3f () предшествует вызов функции glTexCoord2f(), так что каждая вершина получает
новую пару текстурных координат. Например, для того чтобы определить четырехугольную грань и
наложить на нее текстуру, мы посылаем в OpenGL четыре текстурные координаты и четыре трехмер-
ные точки, а именно:
glBegin(GL_QUADS): // define a quadrilateral face
glTexCoord2f(0.0. 0.0): glVertex3f(1.0, 2.5. 1.5);
glTexCoord2f(0.0. 0.6): glVertex3f(1.0. 3.7. 1.5):
glTexCoord2f(0.8. 0.6): glVertex3f(2.0. 3.7. 1.5):
glTexCoord2f(0.8. 0.0): glVertex3f(2.0. 2.5. 1.5):
glEndO;
Рис. 8.34. Отображение текстуры на плоский полигон
Привязывание Р. к каждой V. эквивалентно описанию в текстурном пространстве полигона Р с тем
же числом вершин, что имеет F. Обычно полигон Р имеет и ту же форму, что F; тогда часть текстуры,
лежащая внутри полигона Р, без искажений накладывается на весь полигон F. В тех случаях, когда по-
518
Глава 8. Визуализация граней для усиления реалистичности
лигоны PvlF имеют одну и ту же форму, преобразование, несомненно, является аффинным: это масш-
табирование, возможно, сопровождающееся поворотом и смещением.
На рис. 8.35 показан общий случай, когда четыре угла текстурного квадрата связываются с четырь-
мя углами прямоугольника. (На ЗЭ-грани отмечены текстурные координаты (s, t), связанные с каж-
дым углом.) В данном примере текстура является растровым изображением размером 640 на 480 пик-
селов, и она накладывается на прямоугольник с форматным соотношением 640/480, вследствие чего
рисунок не искажается. (Отметим, что текстурные координаты s и t по-прежнему изменяются от 0 до 1.)
На рис. 8.36 показано использование текстурных координат, при котором из текстуры делается моза-
ика — путем повторения этой текстуры. Для этого используются текстурные координаты, лежащие вне
интервала [0,1]. Когда в подпрограмме визуализации встречаются значения s и t, лежащие вне единич-
ного квадрата, например s - 2,67, то подпрограмма игнорирует целую часть и использует только дроб-
ную часть: 0,67. Например, в точку грани с координатами (s, t) = (2,6,3,77) отображается точка текстуры с
координатами (0,6,0,77). По умолчанию OpenGL именно так выкладывает мозаику из текстуры; однако
при необходимости вместо этого можно «зафиксировать» данные текстуры. (См. упражнения.)
1
а
б
Рис. 8.35. Отображение квадрата на прямоугольник
Таким образом, пара координат (s, t) посылается в графический конвейер вместе с каждой вер-
шиной грани. Как мы увидим в следующем разделе, идея заключается в том, что точки внутри F будут
заполняться значениями текстуры, лежащими внутри Р, причем промежуточные значения координат
(s, t) будут определяться с использованием интерполяции. Процесс такой интерполяции описан в сле-
дующем разделе.
Рис. 8.36. Создание повторяющихся текстур
Добавление текстурных координат к каркасным объектам
Напомним из листинга 6.1, что каркасный объект имеет три списка: список вершин, список нормалей и
список граней. Следует добавить к этим спискам еще один: список «текстурных координат», в котором
хранятся координаты (sf, ?.), связанные с различными вершинами. Можно добавить массив элементов
следующего типа:
class Txtrtoord{public: float s. t:).
8.5. Добавление текстуры к граням
519
в котором будут храниться все нужные координатные пары для сетки. Существует несколько различ-
ных способов представления текстуры объекта, и каждый из них имеет свой метод организации инфор-
мации о текстуре. Следующие два способа являются наиболее важными.
1. Каркасный объект состоит из небольшого числа плоских граней, причем на каждую из них бу-
дет наложена своя текстура. В этом случае каждая грань имеет только одну нормаль, но свой
собственный список текстурных координат. Тогда с каждой гранью будут связаны следующие
данные:
• количество вершин грани;
• индекс нормального вектора к грани;
• список индексов вершин;
• список индексов текстурных координат.
2. Сетка представляет гладкий объект, причем вокруг этого объекта «обертывается» одна текстура
(или часть ее). В этом случае с каждой вершиной будет связан нормальный вектор и соответ-
ствующая пара текстурных координат. Для каждой вершины используется единый индекс в
списках вершин, нормальных векторов и текстуры. Тогда с каждой вершиной будут связаны
следующие данные:
• количество вершин грани;
• список индексов вершин.
В упражнениях в конце следующего раздела дается более подробное описание необходимых струк-
тур данных для таких типов сеток.
8.5.2. Визуализация текстуры
Визуализация текстуры на грани F напоминает закраску Гуро: она осуществляется пиксел за пикселом
по всей грани. Для каждого пиксела нужно определить соответствующие текстурные координаты (s, t),
получить значение текстуры и придать пикселу нужный цвет, заданный этой текстурой. Мы увидим,
что нахождение координат (s, Г) следует производить очень аккуратно.
На рис. 8.37 показана камера, делающая снимок грани F с наклеенной на нее текстурой, а также сам
процесс визуализации. Строка развертки у заполняется от точки x|eft до точки rright. Для каждого значе-
ния х вдоль строки развертки мы должны правильно вычислить положение на грани (на рисунке оно
обозначено Р(х, у)) и уже из него получить нужные текстурные координаты (s*, t*).
Рис. 8.37. Визуализация грани, сфотографированной камерой
Если мы определили отображение «текстура-объект», то нам известны текстурные координаты для
каждой вершины области F, как показано на рис. 8.38. В таком случае естественно вычислить координаты
(S|cft, tkh) и (sright, для каждой строки развертки быстрым инкрементным методом (методом прираще-
ний), азатем, двигаясь вдоль строки развертки, интерполировать между этими значениями. Однако нам
следует быть внимательными: обычные приращения от skft до sright при прохождении строки развертки у
520
Глава 8. Визуализация граней для усиления реалистичности
отxteh доxight использовать нельзя, поскольку равные шаги по спроецированной грани не соответству-
ют равным шагам по трехмерной грани.
Рис. 8.38. Инкрементное вычисление текстурных координат
Рисунок 8.39 иллюстрирует эту задачу. На рис. 8.39, а показана грань F, рассматриваемая из такой
точки, что ее левое ребро находится ближе к наблюдателю, чем правое. На рис. 8.39, б показана проек-
ция этой грани F' на экран. Отметим для строки развертки у = 170 равноотстоящие точки на проекции F',
подразумевая последовательные пикселы на грани. Соответствующее расположение этих отметок на те-
кущей грани показано на рис. 8.39, а. Видно, что на дальнем конце грани F эти отметки располагаются
ближе друг к другу, что является следствием обычного перспективного укорачивания.
Рис. 8.39. Задание промежутков с помощью линейной интерполяции
Если для вычисления текстурных координат мы применим простую линейную интерполяцию с рав-
номерными шагами по s и по t, то мы «возьмем образцы» текстуры в неверных точках и исказим резуль-
тирующее изображение. На рис. 8.40 показано, что происходит с обычной шахматной текстурой, ото-
браженной на прямоугольник. На рис. 8.40, а использована линейная интерполяция, что привело к
ощутимому искажению текстуры. Такое искажение особенно недопустимо при анимации, когда по-
лигон вращается, поскольку текстура будет перекашиваться и удлиняться при движении. На рис. 8.40, б
использована корректная интерполяция, и в результате шахматная доска выглядит как положено.
При анимации эта текстура будет выглядеть прочно приклеенной к перемещающейся или вращаю-
щейся грани.
В литературе появилось несколько работ, развивающих метод корректной интерполяции. Хекберт
и Мортон (Heckbert and Moreton [Heckbert, 105]), а также Блинн [Blinn, 24] приводят элегантную раз-
работку метода, основанного на общей природе аффинного и проективного преобразований. В работе
Сегала и других авторов [Segal, 97] тот же результат получен путем алгебраических выкладок, связан-
ных с параметрическим представлением отрезка прямой линии. Здесь применяется последний подход.
Попытаемся проанализировать ситуацию, представленную на рис. 8.41. Мы знаем, что при аффин-
ных и проективных преобразованиях прямолинейность сохраняется, поэтому прямая линия Le из про-
странства глаза проецируется в прямую Ls в пространстве экрана; аналогичным образом, те тексели,
которые нам нужно нарисовать на прямой Ls, лежат на прямой Lt текстурного пространства, которая
8.5. Добавление текстуры к граням
521
отображается в прямую Le. Основной вопрос заключается в следующем: если мы перемещаемся с рав-
номерным шагом вдоль прямой Ls на экране, то какой шаг будет по текселям вдоль прямой Lt в текстур-
ном пространстве? Ниже делается вывод для общего случая, который показывает действие интерполяции:
все дело в эффекте перспективного деления. Затем мы применим этот общий результат к преобразова-
ниям, которые выполняются в графическом конвейере, и четко увидим, откуда нужно брать дополни-
тельные шаги для правильного отображения текстуры.
Рис. 8.40. Изображения, полученные при линейной интерполяции и при корректной интерполяции:
а) линейная интерполяция; б) корректная интерполяция
Рис. 8.41. Отображение прямых из одного пространства в другое: а) текстурное пространство;
б) пространство глаза; в) пространство экрана
На рис. 8.42 приведена прямая АВ в трехмерном пространстве, преобразуемая в ЗВ-прямую ab с по-
мощью матрицы М. (Матрица М может представлять аффинное преобразование или, в более общем
случае, перспективное преобразование.) Точка А преобразуется в а, а точка В — вЬ. Рассмотрим точку
R(g), лежащую на части g расстояния от А до В. Эта точка отображается в некоторую точку г(/), лежа-
щую на части/расстояния от а до Ь. Как мы увидим, части f ng не равны между собой. Как же изменя-
ется g при изменении /от 0 до 1? Иными словами, как связаны между собой движение по прямой ab и
движение по прямой АВ?
Рис. 8.42. Как работает перемещение вдоль соответственных прямых?
522
Глава 8. Визуализация граней для усиления реалистичности
Вывод соотношения между g и f
Пусть однородные координаты точки а имеют вид: а = (ар а2, а3, а4). (Мы используем нижние индексы
1, 2, 3, 4 вместо х, у, г, w во избежание неоднозначности, поскольку существует так много различных
пространств с обозначением «х,г/,и».) Поэтому точка а получается из точки а после перспективного
деления: а = (а{/а3, а2/а3, а3/а^. Поскольку матрица М отображает точку А • (Ар А2, А3) в точку а, то
а = М(А, 1)г, где М(А, 1)г — вектор-столбец с компонентами (Ар А2, А3,1). Аналогично точка b = М(В, 1)г.
(Тщательно проверьте каждое из этих соотношений.) Теперь, используя для краткости обозначение
функции 1егр( ), определим выражение R(g) = lerp (A, B,g), откуда следует: Л/(1егр(А, B,g), 1)г= 1егр( а,
b ,g) = (lerp(apZ>pg), lerp(a2, b2,g), lerp(a2,Z>3,g),lerp(a4, b3,g)). (Проверьте и это.) Последнее равенство
представляет собой выражение точки г(/) в однородных координатах, которое мы обозначим ?(/).
Восстановим истинные компоненты г(/) с помощью перспективного деления. Для простоты напишем
только его первый компонент:
r( f ч lerp(a„l>pg)
lerp(a4,Z>4,g)
Но поскольку по определению r(/) = lerp(a, b,f), у нас имеется и другое выражение для первого
компонента:
(8.15)
rt(f) = lerp [
1°4 Ь4
(8. Гб)
Аналогично могут быть получены выражения для г (/) и r3(f). (Чему они равны?) Приравниваем
эти две формулы для rt(/) и после алгебраических преобразований получаем нужное соотношение меж-
ду величинами fvtg: •
(8.17)
g =
1егр ^-,1,/
Следовательно, точка R(g) отображается в точку г(/), однако g и f не являются одними и теми же
долями. Доля g совпадает с / при / = 0 и при / = 1, однако рост g с ростом f определяется знаменателем,
зависящим от отношения Ъ3/а3. Если же а3 и Ь3 равны между собой, то g совпадает с /. (Проверьте это.)
На рис. 8.43 показана зависимость gmf для различных значений Ь3/а3.
Рис. 8.43. Зависимость g от f
8.5. Добавление текстуры к граням
523
Теперь мы можем сделать заключительный шаг и показать, где расположена точка R(g), отображае-
мая в точку г(/) на трехмерной грани: просто применим равенство (8.17) для R(g) = А(1 - g) + Bg и
после алгебраического упрощения (проверьте это!) получим для первого компонента:
1 Г 4 в> /-"I
lerp
----\а^—j (8.18)
leipl
<«4 b4 J
Аналогичные результаты получаются для компонентов Т?2 и R3 (у них тот же самый знаменатель,
что у Rt). Это и есть искомый результат; он говорит о том, какая трехмерная точка (Rt, R2, R3) соответ-
ствует (в координатах глаза) заданной точке, лежащей на части /пути между заданными точками а и b
в экранных координатах. Таким образом, любая величина (например, текстура), «привязанная» к вер-
шинам трехмерной грани и изменяющаяся линейно между этими вершинами, будет вести себя таким
же образом.
Имеются два интересных случая преобразования с матрицей М:
О Преобразование является аффинным.
О Преобразование является перспективным преобразованием.
Рассмотрим каждый из этих случаев поочередно.
Когда данное преобразование является аффинным, компоненты а4 и й4 равны единице (почему?),
следовательно, вышеприведенные формулы сразу упрощаются. Теперь части / ng становятся идентичны-
ми, a R{ превращается в 1егр(А1, Bvf). Итог такому развитию событий подводит приведенный ниже факт.
Факт: если матрица М является аффинной, то равные шаги по прямой ab соответствуют равным
шагам по прямой АВ.
Если же матрица М представляет собой перспективное преобразование из координат глаза в коор-
динаты отсечения, то четвертые компоненты а4 и bt уже не равны единице. Такая матрицам рассматри-
валась в главе 7; ее основная форма, заданная равенством (7.10), имеет вид:
'N 0 0 О'
0 N 0 0
м ~ 0 0 с d ’
? 0 -1 °J
где end — константы, отвечающие за правильную псевдоглубину. Чему же равно выражение М(А, 1)г
для этой матрицы? Оно равно а = (№4р NA2, сА3 + d, -v43), и главное состоит в том, что а4 - -А3. Это и
есть координата точки вдоль оси z в координатах камеры, иначе говоря, глубина этой точки по отно-
шению к глазу.
Таким образом, относительные размеры а4 и Z>4 лежат в основе перспективного укорачивания от-
резка прямой: они несут информацию о глубинах точек Ап В вдоль нормали к плоскости просмотра
камеры. Если точки А и В имеют одинаковую глубину (то есть лежат в плоскости, параллельной
плоскости просмотра камеры), то искажение перспективы вдоль этого отрезка отсутствует и части g
и /действительно совпадают. На рис. 8.44 показано в разрезе, как лучи от глаза, проходящие через
равноотстоящие точки (с равными приращениями по /) па плоскости просмотра, попадают в уже
неравноотстояшие точки на исходной трехмерной грани. На рисунке показан случай, когда точка А бли-
же точки В, откуда следует, что а4 < Ьд, поэтому приращения по g возрастают по мере обхода грани
от А к В.
524
Глава 8. Визуализация граней для усиления реалистичности
Рис. 8.44. Значения а4 и Ь4 зависят от глубин точек
Инкрементная визуализация изображений
Соединим теперь все вышеизложенное вместе и найдем соответствующие текстурные координаты (s, t)
в каждой точке визуализируемой грани. На рис. 8.45 показана грань сарая. Концевые точки левого реб-
ра спроецированной грани равны а и Ь. Данная грань простирается от xlcft до х ht вдоль строки разверт-
ки у. Нам нужно найти соответствующие текстурные координаты (s|eft, T|cft) и (s ht, tright) для привязыва-
ния их соответственно к точкам отх|(Л до xright, которые мы затем сможем интерполировать вдоль строки
развертки. Рассмотрим нахождение s|eft(Z/) — значения s|eft вдоль строки развертки у. Мы знаем, что тек-
стурная координата sA привязана к точке a, a sB привязана к точке Ь, поскольку эти величины передают-
ся через графический конвейер вместе с вершинами А и В. Если строка развертки у является частью f
расстояния между у^ и у^ так что/= (у - y^/{ylov - #ьоД т0 из равенства (8.18) следует, что соответ-
ствующая текстурная координата равна:
(8.19)
аналогично может быть получено выражение для f|eft. Отметим, что s|cft и ileft имеют один и тот же зна-
менатель: линейная интерполяция между значениями 1/а4 и 1/Z>4. Числители являются линейными
интерполяциями текстурных координат, деленных на ai и Z>4. Эту технику иногда называют «линейной
рациональной» визуализацией [Heckbert, 105] или «гиперболической интерполяцией» [Blinn, 24]. Для
эффективного вычисления координат (s, t) по мере роста f необходимо сохранять значения sA/av sB/b^,
tja^ tB/bA, l/a4, 1/64, так как они остаются постоянными от пиксела к пикселу. Числитель и знамена-
тель могут быть найдены в приращениях для каждого у, в точности так, как мы это делали в закрашива-
нии Гуро. (См. уравнение (8.14).) Однако для нахождения slcft и t|eft нам все же придется выполнить яв-
ное деление каждого значения у.
Рис. 8.45. Визуализация текстуры на грани
8.5. Добавление текстуры к граням
525
Пара координат (s.ght, £ight) вычисляется аналогично. Знаменатели этих двух компонентов содержат
величины а' и /?', которые получаются из проецированных точек а' и Ь'.
После нахождения (slcft, £|eft) и (srig]it, £ight) данную строку развертки можно закрашивать. Для каждого
х от x|eft до xright находятся координаты snt— снова посредством гиперболической интерполяции.
(Какое выражение имеет s в зависимости отх?)
Включение в графический конвейер
Как подключить нужное применение гиперболической интерполяции для правильной визуализации
текстуры? И нужно ли при этом уточнять этап отсечения? Как мы сейчас увидим, мы должны посылать
в графический конвейер дополнительную информацию и вычислять несколько иные значения, чем мы
полагали до сих пор.
На рис. 8.46 приведена детализированная схема графического конвейера. На этой схеме отмечены
некоторые точки и показано, какая информация содержится в каждой такой точке. Каждая верши-
на V связана с парой текстурных координат (s, £), а также с нормалью в этой вершине. Вершина преоб-
разуется с помощью матрицы моделирования-вида (а соответствующая нормаль умножается на обрат-
ную транспонированную матрицу), в результате чего получаются вершина А = (Лр А2, А3) и нормаль п'
в координатах глаза. Эта нормаль используется в вычислениях закрашивания, в результате чего полу-
чается цвет с = (cr, cg, сь). К вершине А по-прежнему привязаны текстурные координаты (хл, tA) (совпа-
дающие с координатами (s, £)). После этого вершина А подвергается перспективному преобразованию,
в результате чего получается а = (av а2, а3, cQ. Текстурные координаты и цвет с не изменяются.
Рис. 8.46. Детализация графического конвейера, включающего гиперболическую интерполяцию
Затем производится отсечение границами отображаемого объема, как рассматривалось в главе 7. Как
показано на рисунке, в результате отсечения некоторые вершины могут исчезнуть и могут появиться
новые. При создании новой вершины D необходимо задать ее координаты (й?р d2, d3, d3) и привязать к
ней соответствующие цвет и точку текстуры. В силу особенностей алгоритма отсечения компоненты
координат d. формируются посредством линейной интерполяции: dt - 1егр(аР bit t) для i = 1,..., 4 и некото-
рого t. Отметим, что четвертый компонент dt также формируется таким способом. Поэтому естествен-
но использовать линейную интерполяцию для формирования и компонентов цвета, и текстурных ко-
ординат. (Обоснование этого рассматривается в упражнениях в конце раздела.) Тогда после отсечения
рассматриваемая грань по-прежнему состоит из определенного количества вершин, к каждой из кото-
рых привязаны цвет и точка текстуры. Для точки А информация сохраняется в массиве (at, а2, а3, sA,
tA, с, 1). Добавленная в конце массива единица будет использоваться на следующем этапе.
Далее выполняется перспективное деление. Поскольку для гиперболической интерполяции нам не-
обходимы члены типа sA/aA и 1/а4 (см. равенство (8.19)), мы разделим на а4 каждый элемент массива,
который мы собираемся использовать при гиперболической интерполяции, в результате чего получим
следующий массив: (х, у, z, 1, $А/<\, tA/a3, с, 1/а4). (Можно также разделить и все компоненты цвета с
целью получения несколько более реалистичного закрашивания Гуро — см. упражнения.) Первые три
компонента массива — (х, у, z) - (а,/а4, а2/а4, а3/а4) определяют положение точки в нормированных
526
Глава 8. Визуализация граней для усиления реалистичности
координатах устройства (дисплея). (Третий компонент — это псевдоглубина, а первые два масштаби-
рованы и смещены в результате преобразования в порт просмотра.) Для упрощения записи мы будем и
дальше обозначать экранные координаты точки (х, у, z).
Таким образом, подпрограмма визуализации получает массив {х, y,z,\, sA/av tA/aA, с, 1/а4) для каж-
дой вершины грани, подлежащей визуализации. Теперь можно легко визуализировать текстуры, исполь-
зуя гиперболическую интерполяцию-согласно равенству (8.19): необходимые величины sA/aA и 1/а4
имеются в наличии для каждой вершины.
Практические упражнения
8.5.2. Структуры данных для каркасных моделей с текстурами
Рассмотрим специальные типы данных, необходимые для представления каркасных объектов в следу-
ющих двух случаях:
О на каждую грань будет наложена своя текстура;
О вокруг всей сетки «обертывается» одна и та же текстура.
Нарисуйте образцы для этих двух типов данных и для каждого из них покажите, какие данные нахо-
дятся в массивах, если каркасный объект представляет собой куб.
8.5.3. Правильность вычислений псевдоглубины
Докажите правильность утверждения раздела «Удаление невидимых поверхностей» о том, что при опре-
делении псевдоглубины точки можно использовать линейную (а не гиперболическую) интерполяцию.
Пусть точка А проецируется в а, а точка В — в Ь. При линейной интерполяции псевдоглубина спроециро-
ванной точки вычисляется по формуле lerp(a, b,f) как третий компонент этой точки. Это будет правиль-
но только при условии, что результирующая величина равна истинной псевдоглубине точки, в которую
проецируется точка 1егр(Л, В, g) (для соответствующего значения g). Покажите, что это действительно
так. {Подсказка. Примените равенства (8.15) и (8.16) для третьего компонента проецируемой точки.)
8.5.4. Обертывание и наклеивание текстур в OpenGL
Для того чтобы заставить узор «обернуться» или выложиться мозаикой в направлении s, следует исполь-
зовать подпрограмму glTexParameten(GL_TEXTURE_2D. GL_TEXTURE_WRAP_S, GL_REPEAT). Соответственно для
заворачивания в направлении t используется параметр GL_TEXTURE_WRAP_T. На самом деле это принято
по умолчанию, поэтому нет необходимости делать что-либо явно. Для отключения режима мозаики
следует заменить параметр GL_REPEAT на GL_CLAMP. Поищите дальнейшие подробности в документации по
OpenGL, а также поэкспериментируйте с различными установкаи OpenGL для выяснения их действия.
8.5.5. Обоснование линейной интерполяции текстуры при отсечении
При отсечении грани границами отображаемого объема часто создаются новые вершины. В этом случае
мы должны приписать каждой из этих вершин текстурные координаты. Пусть на части f пути от верши-
ны Л к вершине В на грани возникла новая вершина V. Предположим далее, что вершине А соответствуют
текстурные координаты (хл, tA), а вершине В — (sB, tB). Докажите, что если текстура будет «наклеиваться»
на плоскую грань, то вершине Уесть смысл приписать текстурные координаты (1егр(хл, sB,f), lerp{tA,
8.5.6. Затраты вычислительных ресурсов на гиперболическую интерполяцию
Сравните объем вычислений, требующийся для гиперболической и линейной интерполяции текстур-
ных координат. Считайте при этом, что умножение и деление требует в 10 раз больше времени, чем
сложение и вычитание.
8.5.3. Что регулирует текстура?
Как величины текстурного отображения применяются при вычислении визуализации? Мы рассмот-
рим три типичных способа использования этих величин для достижения различных визуальных эф-
фектов. Мы проделаем это для простого случая вычисления яркости серого цвета из равенства (8.5).
Если же изображение цветное, то такие вычисления выполняются раздельно для красного, зеленого и
синего компонентов.
8.5. Добавление текстуры к граням
527
Создание светящегося объекта
Этот метод наиболее прост с вычислительной точки зрения. Видимая интенсивность I устанавливается
равной значению текстуры в каждой точке (с точностью до постоянного множителя):
I - texture (s, t).
В этом случае кажется, что объект испускает свет, или светится. Меньшие значения текстуры испус-
кают меньше света, а большие — больше света. Никаких дополнительных вычислений освещения не
требуется. Для цветного света компоненты красного, зеленого и синего цветов вычисляются отдельно;
например, красный компонент Ir = texturer(s, t). Для текстурирования такого типа в OpenGL предус-
мотрена следующая команда1:
glTexEnvf(GL_TEXTURE_ENV, GL_TEXTURE_ENV_MODE. GL_REPLACE):
Раскраска текстуры путем модулирования коэффициента отражения
Мы уже отмечали ранее, что цвет объекта — это цвет его компонента диффузного освещения (когда этот
объект освещается белым светом). Тогда путем варьирования коэффициента диффузного отражения
(и, возможно, также коэффициента фонового отражения) можно сделать так, чтобы текстура казалась
нарисованной на поверхности объекта. В таком случае говорят, что текстурная функция «модулирует»
значение коэффициента отражения от точки к точке. Тогда равенство (8.5) заменяется равенством
I = texture(s, t) [Iapa + Idpd x lambert] + x phongz
для соответствующих значений s и t. Поскольку по Фонгу зеркальные отражения имеют скорее цвет
источника, а не объекта, то блики не зависят от текстуры. Для выполнения в OpenGL такого вида тек-
стурирования нужно задать
glTexEnvf(GL_TEXTURE_ENV. GL_TEXTURE_ENV_MODE. GL_MODULATE);
Имитация изрытости посредством отображения неровностей
Отображение неровностей (bump mapping) — это технология, разработанная Блинном [Blinn, 24] для
придания поверхности морщинистого (как у изюма) или изрытого (как у апельсина) вида без необхо-
димости моделировать каждую ямку в отдельности. Используется текстурная функция, которая произ-
водит «возмущение» нормали к поверхности, что, в свою очередь, вызывает изменения в величинах
диффузного и зеркального отражения. На рис. 8.47 приводится пример. Одна из проблем, связанных
с применением отображения неровностей на поверхность типа чайника, заключается в том, что посколь-
ку в самой модели эти неровности отсутствуют, то силуэт объекта не показывает этих неровностей,
а представляет собой совершенно гладкую поверхность вдоль каждой грани.
Рис. 8.47. Кажущаяся изрытой поверхность, полученная посредством отображения неровностей
(с разрешения Okino Computer Graphics, Inc. Визуализировано с помощью программы Okino NuGraf)
1 В качестве последнего параметра следует использовать GL_REPLACE или GL_DECAL.
528
Глава 8. Визуализация граней для усиления реалистичности
Нам нужно заставить скалярную функцию texture(s, t) возмущать нормаль контролируемым обра-
зом. Кроме того, это возмущение должно зависеть только от формы поверхности и от самой текстуры,
но не от ориентации объекта или его положения относительно глаза. Если бы изменение нормали зави-
село от ориентации, то ямки изменяли бы свой вид при движении объекта в анимации, что противоре-
чило бы желаемому эффекту.
m'(u, v)
P(u, v) P(u, v)
a 6
Рис. 8.48. Природа отображения неровностей
На рис. 8.48 в поперечном сечении показано действие отображения неровностей. Пусть поверхность
представлена в параметрической форме функцией Р(и, о), а ее единичный нормальный вектор равен
m(w, о). Предположим далее, что SD-точка с координатами (и*, о*) соответствует текстуре в (и*, о*).
По методу Блинна имитируется изменение положения истинной поверхности в направлении нормаль-
ного вектора на величину, пропорциональную texture(zz*, о*), то есть:
Р'(ы*, о*) - Р(ы*, о*) + texture(w*, о*) ш(ы*, о*). (8.20)
На рис. 8.48, а показано, как согласно этой технологии на поверхность добавляются изгибы и склад-
ки. В каждой точке «возмущенной» поверхности появляется новый нормальный вектор m'(w*, о*). Идея
метода заключается в том, чтобы использовать эту возмущенную нормаль так, как будто она «привяза-
на» в каждой точке к исходной невозмущенной поверхности, как показано на рис. 8.48, б. Блинн пока-
зал, что хорошее приближение для вектора ш'(ы*, о*) (до нормирования) задается формулой:
ш'(ы*, о*) - т(ы*, v*) + <1(ы*, о*), (8.21)
где вектор возмущения d определяется по формуле:
d(w*, о*) - (ш х Рг) textureB - (m х Рв) texture^,
где textureB и texture^ — частные производные текстурной функции по и и v соответственно. Далее, Рви
Рг — это частные производные функции Р(м*, о*) по и и о соответственно. Все эти функции вычисляют-
ся в точке (и*, v*). Вывод этой формулы можно найти также в работах Уатта [Watt, 138] и Миллера
[Miller, 141]. Отметим, что возмущающая функция зависит только от частных производных функции
texture( ), но не зависит от самой функции texture( ).
Если известно математическое выражение для функции texture ( ), то можно найти и аналитические
выражения для ее частных производных. Например, texture( ) может изменяться волноообразно в двух
направлениях вследствие комбинирования двух синусоидальных волн: texture (и, v) - sin(aw) sin(Zw), где
а и Ь — некоторые константы. Если же функция текстуры получена в виде массива точек изображения,
то ее вычисление в точке (и*, v*) производится с помощью линейной интерполяции, а аппроксимация
частных производных осуществляется в конечных разностях.
8.5.4. Пример текстурирования с использованием OpenGL
Для того чтобы проиллюстрировать вызов средств текстурирования, предлагаемых OpenGL, покажем
приложение, которое отображает вращающийся куб с различными узорами, нарисованными па его ше-
сти сторонах. На рис. 8.49 показан один кадр анимации, создаваемой этой программой.
8.5. Добавление текстуры к граням
529
Рис. 8.49. Текстурированный куб, генерируемый программой-примером
Код данного приложения приведен в листинге 8.2. В нем используется несколько функций OpenCL —
для задания шести текстур и для прикрепления их к граням куба.
Листинг 8.2. Приложение, осуществляющее вращение текстурированного куба
#include "RGBpixmap.h”
//1111НШНШШШ11ШН globals ш1111штшшш11ш
RGBpixmap pix[6]:
// make six (empty) pixmaps
// создаем шесть (пустых) пиксельных карт
float xSpeed - 0. ySpeed - 0. xAngle - 0.0, yAngle = 0.0;
//«««««««««««<<<<< myinit »»»»»»»»»»»»»>
void mylnit(void)
{
gl Cl earCol ord. Of. l.Of. l.Of. l.Of);
// background is white
11 фон белый
glEnable(GL_DEPTH_TEST);
glEnable(GL_TEXTURE_2D);
pix[0],makeCheckerboard():
11 make pixmap procedurally
// создаем пиксельную карту процедурно
piх[0].setTexture(2001);
// create texture
// создаем текстуру
pi x[l].readBMPFi1e("Mandri11.bmp"):
// make pixmap from image
// создаем пиксельную карту из изображения
piх[1].setTexture(2002);
// create texture
// создаем текстуру
...similarly for other four textures ...
// аналогично для остальных четырех структур
glViewport(0. 0. 640. 480);
// set up the viewing system
продолжение
530
Глава 8. Визуализация граней для усиления реалистичности
Листинг 8.2 (продолжение)
// устанавливаем систему просмотра
glMatrixMode(GL_PROJECTION):
glLoadidentity();
gluPerspective(60.0. 640.0/ 480. 1.0. 30.0):
// set camera shape
11 задаем форму камеры
glMatrixMode(GL_MODELVIEW);
glLoadldentityO:
glTranslated(O.O. 0.0, -4):
// move camera back
// двигаем камеру назад
}
11 <<<<<<<<<<<<<<<<<<<<<<.<<<<< display »»»»»»»»»»»
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);
glTexEnvf(GL_TEXTURE_ENV. GL_TEXTURE_ENV_MODE. GL_DECAL):
glPushMatrixO;
glRotatedlxAngle. 1.0.0.0,0.0): glRotatedlyAngle. 0.0.1.0.0.0);
// rotate
// поворачиваем
glBindTexture(GL_TEXTURE_2D.2001):
// top face: ’fake’ checkerboard
// верхняя грань: «фальшивая» шахматная доска
glBegin(GL_QUADS);
glTexCoord2f(-1.0. -1.0): glVertex3f(-1.0f. l.Of. -l.Of):
glTexCoord2f(-1.0. 2.0): glVertex3f(-1.0f, l.Of, l.Of):
glTexCoord2f(2.0, 2.0): glVertex3f( l.Of. l.Of. l.Of):
glTexCoord2f(2.0, -1.0): glVertex3f( l.Of. l.Of. -l.Of):
glEndO;
gl Bi ndTexture(GL_TEXTURE_2D.2002);
// right face: mandrill
// правая грань; мандрил (обезьяна)
glBegin(GL_QUADS);
glTexCoord2f(0.0, 0.0); glVertex3f(1.0f. -l.Of. l.Of);
glTexCoord2f(0.0, 2.0); glVertex3f(1.0f, -l.Of. -l.Of):
glTexCoord2f(2.0. 2.0); glVertex3f(1.0f, l.Of. -l.Of):
glTexCoord2f(2.0, 0.0); glVertex3f(1.0f. l.Of. l.Of);
glEndO:
... similarly for other four faces ...
// аналогично для остальных четырех граней
glFlushO;
glPopMatrixO:
gl utSwapBuffersO:
}
/ /<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< spi nner »»»»»»»»»»>
void spinner(void)
{
// alter angles by small amount
8.5. Добавление текстуры к граням
531
// изменяем углы на малую величину
xAngle +- xSpeed: yAngle +- ySpeed:
displayC):
)
I/««<«<««««««« main >»»»»>»»»»»>»»»»»
void main(int argc, char **argv)
{
glutln1t(&argc. argv);
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH);
glutInitWindowSize(640.480):
glutIn1tW1ndowPosition(10, 10):
glutCreateWindowC rotating textured cube”):
// «вращающийся текстурированный куб»
glutDisplayFunc(display):
mylnitO:
glutldleFunc(spinner);
glutMainLoopO:
}
Для отображения текстуры можно применять различные вариации показанных здесь параметров.
Приведенная версия программы работает хорошо, однако тщательной настройкой некоторых парамет-
ров (руководствуясь документацией по OpenGL) можно улучшить качество изображений или повы-
сить эффективность алгоритма. Мы рассмотрим только суть основных подпрограмм.
При добавлении текстуры к изображению одной из первых задач является создание «пиксельной
карты» (pixmap) этой текстуры в памяти. Подробно пиксельные карты рассматриваются в главе 10, там
же определяется класс RGBpixmap, который предоставляет инструменты для создания пиксельных карт и
управления ими. Здесь же мы будем рассматривать пиксельную карту как простой массив значений
пикселов, каждый элемент которого является тройкой байт для хранения значений красного, зеленого
и синего цветов:
class RGB{
// holds a color triple-each with 256 possible values
// хранит цветовую тройку - каждая с 256 допустимыми значениями
public: unsigned char r.g.b:
}:
Класс RGBpixmap хранит количество строк и стобцов пиксельной карты, а также адрес первого пиксела
в памяти:
class RGBpixmap{
public:
int nRows.nCols:
// dimensions of the pixmap
// размерности пиксельной карты
RGB* pixel;
// array of pixels
// массив пикселов
int readBMPFile(char * fname):
// read BMP file into this pixmap
// читаем BMP-файл в данную пиксельную карту
void makeCheckerboardO:
void setTexture(GLuint textureName):
}:
Здесь приведены только три метода данного класса, которые нам понадобятся для отображения
текстур. Остальные методы и прочие детали обсуждаются в главе 10. Функция readBMPFileO читает
532
Глава 8. Визуализация граней для усиления реалистичности
BMP-файл1 и записывает значения пикселей в свой объект типа pixmap. Эта функция детально описы-
вается в приложении В. Остальные два метода рассматриваются ниже.
В нашем примере приложения OpenGL будет использовано шесть текстур. Для их создания мы вна-
чале построим для каждой текстуры объект класса RGBpixmap посредством следующей функции:
RGBpixmap pix[6]:
// create six (empty) pixmaps
// создаем шесть (пустых) пиксельных карт
и затем загрузим в каждый такой объект нужное текстурное изображение. После этого для определения
текстуры передадим каждый объект в OpenGL.
Создание процедурной текстуры
Создадим для начала шахматную текстуру с помощью метода makeCheckerboardO. Узор шахматной дос-
ки хорошо известен и прост для создания, а его геометрическая правильность делает его подходящей
текстурой для проверочных целей. Данное приложение генерирует пиксельную карту шахматной дос-
ки в pix[0] с помощью вызова метода:
pi х[0] .makeCheckerboardO.
Сам метод имеет следующий вид:
void RGBpixmap:: makeCheckerboardO
{
// make checkerboard pattern
// создаем шахматный узор
nRows - nCols - 64:
pixel = new RGB[3 * nRows * nCols]:
if(!pixel) {cout « "out of memory!";return;}
// «выход за пределы памяти!»
long count - 0:
for(int i - 0: i < nRows: i++)
for(int j * 0: j < nCols: j++)
{
int c - (((1/8) + (j/8)) %2) * 255:2
pixel[count], r = c:
// red
// красный
pixel[countl.g - c:
// green
// зеленый
pixel[count++].b - 0;
// blue
// синий
}
}
В данной подпрограмме создается пиксельный массив размерностью 64 на 64, где каждый пиксел
является RGB-тройкой. В OpenGL требуется, чтобы и ширина, и высота текстурных пиксельных карт
составляла степень двойки. Пиксельная карта размещена в памяти как единый длинный байтовый массив,
заполняемый строка за строкой снизу вверх, а также слева направо в пределах строки. Вместе с каждым
1 Это стандартный аппаратно-независимый формат файлов изображений, предложенный фирмой Microsoft. Из Интернета можно
получить множество файлов в формате BMP, а также готовых инструментов для преобразования других графических форматов
в ВМР-файлы.
2 Более быстрый способ с использованием побитовых операторов C++выглядит так: С “ ((i&8)A(j&8))*255;.
8.5. Добавление текстуры к граням
533
пикселом загружается величина (с, с, 0), где с принимает значения вперед и назад от 0 до 255 через каж-
дые 8 пикселов. (Сходный «метод чередования» был использован в упражнении 2.3.1.) Здесь у шахмат-
ной доски имеется два цвета — черный и желтый, имеющие коды соответственно (0,0,0) и (255,255,0).
Функция makeCheckerboard возвращает адрес первого пиксела пиксельной карты, который впоследствии
передается в подпрограмму glTexImageO для создания текущей текстуры в OpenGL.
Когда пиксельная карта сформирована, необходимо связать ее с уникальным целочисленным «име-
нем», чтобы однозначно ссылаться на него в OpenGL. В нашем примере шести структурам назначены
следующие произвольные имена: 2001, 2002,..., 20061. Текстура создается посредством определенных
вызовов OpenGL, которые мы инкапсулируем внутри следующего метода:
void RGBpixmap :: setTexture(GLuint textureName)
{
glBi ndTexture(GL_TEXTURE_2D.textureName):
glTexParameteri(GL_TEXTURE_2D.
GL_TEXTURE_MAG_FILTER.GL_NEAREST):
glTexParameteri(GL_TEXTURE_2D.
GL_TEXTURE_MIN_FILTER.GL_NEAREST);
glTex!mage2D(GL TEXTURE 2D. 0. GL_RGB.nCols.nRows.O. GL_RGB.GL_UNSIGNED_BYTE, pixel):
}
Вызов подпрограммы glBindTextureO связывает заданное имя с формируемой текстурой. Если же
такой вызов будет произведен позднее, то, как мы увидим, он сделает данную текстуру «активной».
Вызовы подпрограммы glTexParameteri О указывают, что пиксел должен быть закрашен тем тексе-
лем, координаты которого ближе всего к центру данного пиксела, всякий раз, когда данную текстуру
требуется увеличить или уменьшить в размерах. Эта подпрограмма работает быстро, однако может при-
водить к ступенчатости изображения (aliasing). Вопросы фильтрации изображений и пх сглаживание
будут рассмотрены позднее, в главе 10. Наконец, вызов подпрограммы glTex!mage2D() связывает пик-
сельную карту с текущей текстурой. Этот вызов описывает текстуру как двумерную и состоящую из
байтовых RGB-троек, задает ей ширину, высоту и адрес в памяти (pixel) первого байта битовой карты.
Создание текстуры из сохраненного изображения
В OpenGL отсутствует поддержка чтения файла изображения и создания в памяти пиксельной карты.
Метод readBMPFileO, приведенный в приложении В, предлагает простой способ чтения ВМР-изображе-
ния в пиксельную карту. Например, оператор
pi х[1].readBMPFi1е("mandri11.bmp");
читает файл mandrill .bmp и создает пиксельную карту в элементе pix[l].
После создания пиксельной карты метод pix[l].setTexture() используется для передачи этой карты
в OpenGL для создания текстуры.
Кроме того, отображение текстур должно происходить посредством вызова glEnable(GL_TEXTURE_2D).
В дополнение к этому подпрограмма glHint(GL_PERSPECTIVE_CORRECTION_HINT,GL_NICEST) используется для
запроса о том, правильно ли OpenGL визуализирует данную текстуру (с применением гиперболичес-
кой интерполяции), чтобы она была хорошо прикреплена к граням даже в тех случаях, если грань при
анимации поворачивается по отношению к наблюдателю.
Создание текстуры, ее запуск и связывание требуется выполнить только один раз, в подпрограмме
инициализации. Затем эта текстура применяется всякий раз, когда вызывается подпрограмма отобра-
жения. В подпрограмме display!) куб поворачивается на углы xAngle nyAngle, после чего рисуется шесть
1 Во избежание совпадения (целых) имен в тех приложениях, где используется много текстур, лучше всего позволить OpenGL при-
сваивать текстурам уникальные имена с помощью функции glGenTexturesC). Если нам требуется шесть уникальных имен, мы
можем создать массив GLuint name[6] для хранения этих имен и затем вызвать glGenTexturesC6.name). OpenGLпомещает шесть
не использованных ранее целых чисел в элементы массива name[0]. name[5], после чего в дальнейшем можно ссылаться
на i-ю текстуру по имени name[i].
534
Глава 8. Визуализация граней для усиления реалистичности
граней этого куба. Для этого требуется только, чтобы соответствующая текстура была прикреплена к
грани и чтобы между операторными скобками glBeginO и glEndO были заданы текстурные координаты
и трехмерные координаты вершин грани, как это показано в вышеприведенном коде.
Как только процесс визуализации куба (за экраном) завершен, вызывается подпрограмма
glutSwapBuffersO, чтобы сделать видимым новый кадр. Анимация контролируется с помощью функции
обратного вызова spinnerO в качестве «функции ожидания». Когда система находится в режиме ожи-
дания — иначе говоря, когда она не реагирует на команды пользователя, — автоматически вызывается
spinner. Эта подпрограмма слегка изменяет углы поворота куба и вновь вызывает функцию displayO.
В результате получается эффект непрерывной анимации: куб выглядит вращающимся, так что его
различные грани попадают в поле зрения и выходят из него — снова и снова.
8.5.5. Обертывание текстуры вокруг криволинейных
поверхностей
Теперь, когда мы уже видели, как наклеивать текстуру на плоскую поверхность, мы можем рассмотреть,
как обертывать текстуру вокруг криволинейной поверхности, вроде банки для пива или шахматной
фигуры. Как и ранее, мы предполагаем, что объект смоделирован в виде сетки, то есть состоит из боль-
шого числа маленьких плоских граней. Как уже обсуждалось в конце раздела «Наклеивание текстуры
на плоскую поверхность», с каждой вершиной сетки связана пара текстурных координат (v, t(). Основ-
ная задача состоит в нахождении правильных текстурных координат (s, t) для каждой вершины сетки.
Приводимые здесь четыре примера показывают, как отображать текстуры на «цилиндроподобные» и
«шароподобные» объекты; в них обсуждается, что должен делать разработчик модели в каждом случае.
Пример 8.5.1. Обертывание этикетки вокруг консервной банки
Предположим, что мы хотим обернуть этикетку вокруг кругового цилиндра, как показано на рис. 8.50, а.
Естественно рассуждать в терминах цилиндрических координат. Этикетка должна простираться от угла
0а до 0А по азимуту и от za до zb вдоль оси z. Цилиндр смоделирован как полигональная сетка, поэтому
его стенки являются прямоугольными полосками, как показано на рис. 8.50, б. Для вершины V. каждой
грани необходимо найти подходящие текстурные координаты (s, £.), так чтобы на эту грань отобража-
лась нужная «часть» текстуры.
Рис. 8.50. Обертывание этикетки вокруг цилиндра
8.5. Добавление текстуры к граням
535
(8.22)
, 1
Геометрия достаточно проста, и решение не вызывает затруднений. Существует прямая линейная
зависимость между текстурными координатами (s, t) и парой азимут-высота (0, z) для точки на поверх-
ности цилиндра:
д_ в"6* f_ z~z°
0/>-0а’ zd-z£
Таким образом, если боковая поверхность цилиндра состоит из N граней, то левое ребро i-й грани
п 2тй
имеет азимут 0 = —, а текстурные координаты его верхней левой вершины равны
N
, ч <2л//ЛГ-0
($,,л) = —------1
k [ 0*-0а
Аналогично находятся текстурные координаты и остальных трех вершин грани. Связь между коор-
динатами (s, 0 и вершинами каждой грани нетрудно включить в цикл подпрограммы моделирования
(см. упражнения в конце раздела).
Сложнее обстоят дела в тех случаях, когда объект не является простым цилиндром. Ниже мы уви-
дим, как отображать текстуру на поверхности вращения более общего вида.
Пример 8.5.2. «Обертывание со сжатием» этикетки вокруг поверхности вращения
Напомним из главы 6, что поверхность вращения задается с помощью профильной кривой (х(п), z(n)),1
как показано на рис. 8.51, а, и имеет следующую параметрическую форму: Р(м, и) - (x(0cosw,x(»)sinzz, z(d)).
Форма — в данном случае это ваза — смоделирована в виде совокупности граней, стороны которых рас-
полагаются вдоль контуров с постоянными мио (рис. 8.51, б).
а б в
Рис. 8.51. Обертывание этикетки вокруг вазы: а) профиль вазы; б) грань вазы; в) четыре угла
Тогда заданная поверхность F имеет четыре вершины: Р(м;, г/), Р(м<+1, г/), Р(мр о.+1), Р(им, о1+1). Требу-
ется найти для каждой из этих вершин соответствующие координаты (s t).
Естественно было бы поступать так же, как раньше, и считать $ и v линейно зависящими от и и v, как
в уравнении (8.22). Это эквивалентно оборачиванию текстуры вокруг воображаемого резинового ци-
линдра, заключающего в себе вазу (рис. 8.52, а), а затем сжатию цилиндра, вследствие чего каждая точ-
ка текстуры перемещается радиально (и горизонтально) до тех пор, пока не достигнет поверхности вазы.
Такой метод называется «обертыванием со сжатием» («shrink-wrapping»), его авторами являются Бир
и Слоун (Bier and Sloane — [Bier, 20]), которые изобрели несколько способов отображения текстуры на
различные классы форм. Эти авторы рассматривают обертывание со сжатием в терминах воображае-
мого нормального вектора (рис. 8.52, б): точка текстуры Р связана с точкой объекта Vit расположенной
на внутренней нормали к образующей цилиндра, проходящей через Р. Метод обертывания со сжатием
хорошо работает для цилиндроподобных объектов, однако узор текстуры будет искажен, если профиль-
ная кривая имеет сложную форму.
1 Мы возвращаемся к обозначениям параметров и и v в параметрическом представлении формы, поскольку s и t заняты для текстур-
ных координат.
536
Глава 8. Визуализация граней для усиления реалистичности
Воображаемый цилиндр,
несущий текстуру
•——.Охватывающий
цилиндр
а б
Рис. 8.52. Обертывание со сжатием текстуры на вазу
Бир и Слоун предлагают некоторые альтернативные способы связывания точек текстуры на вообра-
жаемом цилиндре с вершинами объекта. На рис. 8.53 показаны две такие возможности. На рис. 8.53, а
проводится прямая из центра тяжести объекта С через вершину до ее пересечения с цилиндром в
точке Ре На рис. 8.53, б используется нормальный вектор к поверхности объекта в точке V:. Р( является
точкой пересечения этой нормали из точки Vf с цилиндром. Отметим, что три вышеприведенных способа
связывания точек текстуры с точками объекта могут привести к весьма различным результатам, зави-
сящим от формы объекта (см. упражнения в конце раздела). Разработчику следует выбрать наиболее
подходящий метод, исходя из формы объекта и характера отображаемого текстурного изображения.
(Какой из этих методов подошел бы для шахматной пешки?)
Рис. 8.53. Альтернативные отображения с воображаемого цилиндра на объект
Пример 8.5.3. Отображение текстуры на сферу
С точки зрения топологии вокруг цилиндра легко обернуть текстурный прямоугольник: цилиндр мож-
но разрезать и развернуть на плоскости без искажения. Иначе обстоит дело со сферой: как известно
всем картографам, не существует способа показать точные детали всего глобуса па плоском листе бума-
ги. При разрезании сферы и ее распрямлении некоторые части всегда подвергаются существенному
растяжению. (Попытайтесь представить себе шахматную доску, обернутую вокруг всей сферы!)
В то же время нетрудно наклеить прямоугольную текстуру на часть сферы. Для того чтобы отобра-
зить текстурный квадрат на часть сферы, лежащую между углами от 0а до 0А по долготе (азимуту) и от
фа до фь по широте, просто выполним линейное отображение согласно уравнению (8.22). Если коорди-
наты вершины V. равны (0(, ф), то мы свяжем их с текстурными координатами
(S., Г.) = ((0. - 0о)/(0А - 0О), (ф, - фа)/(фь - фа)).
На рис. 8.54, а показано наклеивание изображения на полосу, опоясывающую сферу. Наблюдается
лишь незначительное искажение. На рис. 8.54, б показано, как можно покрыть текстурой всю сферу:
просто отобразите восемь текстурных треугольников на восемь октантов сферы.
8.5. Добавление текстуры к граням
537
Рис. 8.54. Отображение текстуры на сферу
Пример 8.5.4. Отображение текстуры на шароподобные объекты
Некоторые объекты больше напоминают сферы, чем цилиндры. На рис. 8.55, а показан бакибол, граня-
ми которого являются пентагоны и гексагоны. Можно придумать целый набор пентагональных и гекса-
гональных текстур и вручную наклеить их на каждую грань, однако в некоторых сценах может быть
желательно обернуть весь бакибол единой текстурой.
Рис. 8.55. Шароподобные объекты
а
Естественно окружить шароподобный объект воображаемой сферой (а не цилиндром) с наложен-
ной на нее текстурой и использовать один из обсуждавшихся выше методов связи. На рис. 8.55, б изоб-
ражен в поперечном сечении наш бакибол вместе с окружающей его сферой. Схематически показаны
три способа ассоциирования точек текстуры с вершинами объекта
О центр тяжести объекта: Р. находится на прямой, соединяющей центр тяжести С с вершиной V.;
О нормаль к объекту: Р является точкой пересечения со сферой луча из точки V. в направлении
нормали к грани;
О нормаль к сфере: V. является точкой пересечения со сферой луча от Р. в направлении нормали к
сфере в точке Рг
Интересно, дают ли одинаковые результаты метод «центра тяжести ооъекта» и метод «нормали к
сфере» в том случае, если центр тяжести объекта совпадает с центром сферы? Метод «центра тяжести
объекта», вероятно, лучше остальных и прост в реализации. Как показали Бир и Слоун, другие два ме-
тода обычно приводят к неприемлемым результатам на стадии окончательной визуализации.
Кроме того, у Бира и Слоуна также рассмотрено окружение исследуемого объекта воображаемым
параллелепипедом вместо сферы. На рис. 8.56, а изображены шесть граней развертки куба с изобра-
жением текстуры, а на рис. 8.56, б показана та же текстура, но обернутая вокруг куба, который, в свою
очередь, заключает в себе некоторый объект. Вершины объекта можно связывать с точками текстуры
538
Глава 8. Визуализация граней для усиления реалистичности
любым из трех вышеописанных способов; лучшие результаты дают методы «центра тяжести объекта»
и «нормали к кубу».
а
б
Рис. 8.56. Использование охватывающего параллелепипеда
Практические упражнения
8.5.7. Как связать точки Pi и Vi?
Поверхность вращения, изображенная на рис. 8.57, состоит из сферы, покоящейся на цилиндре. Объект
окружен воображаемым цилиндром, на который наложена шахматная текстура. Нарисуйте, как будет вы-
глядеть эта текстура для каждого из нижеперечисленных методов связи точек текстуры с вершинами:
О обертывание со сжатием;
О центр тяжести объекта;
О нормаль к объекту.
Воображаемый цилиндр
с текстурой
Рис. 8.57. Поверхность вращения, окруженная воображаемым цилиндром
8.5.8. Обертывание текстуры вокруг тора
Тор можно рассматривать как цилиндр, который согнули по кругу и замкнули на себя. Параметричес-
кое представление тора, изображенного на рис. 8,58, имеет вид:
Р(и, v) = ((D + 4cos(o))cos(m), (D + 4cos(o))sin(u), 4sin(a))-
Допустим, что вы решили «полигонизировать» этот тор, взяв вершины в точках поверхности при
w.= 2ni/N и V. = 2nj/M, после чего обернули вокруг этого тора некоторую текстуру из единичного текстур-
ного пространства. Напишите для каждой грани код, генерирующий каждую ее вершину и связанные
с ней текстурные координаты (s, t).
8.5. Добавление текстуры к граням
539
Рис. 8.58. Обертывание текстуры вокруг тора
8.5.6. Отображение отражений
Целый класс методов, известных как отображение отражений (reflection mapping), способен существен-
но улучшить реалистичность изображений, в частности анимаций. Основная идея этих методов состо-
ит в том, чтобы увидеть на объекте отражение окружающего его «мира».
Два основных типа отображения отражений называются хромированным отображением и отобра-
жением среды. При хромированном отображении (chrome mapping) на поверхности объекта отража-
ется резкий и обычно искаженный образ окружающей среды, как будто поверхность объекта покрыта
слоем хрома. Телевизионные рекламы изобилуют анимациями со сверкающими буквами и логотипа-
ми, летающими в пространстве, и для большего эффекта хромированные отображения включают в себя
случайные блики. Рисунок 8.59 предлагает характерный пример. Отражение дает грубое представле-
ние о мире, окружающем объект.
Рис. 8.59. Пример хромированного отображения (с разрешения Okino Computer Graphics, Inc.)
В случае применения отображения среды (environment mapping), впервые предложенного Блинном
и Ньюэллом [Blinn, 24], узнаваемый образ окружающей среды виден отраженным на объекте. Мы по-
лучаем от таких отражений ценную визуальную информацию, особенно при перемещении такого объек-
та. Каждый из нас видел классические фотографий'астронавта, шагающего по Луне в шлеме, на маске
которого отражается лунный пейзаж. И в кино вы иногда видите крупным планом зеркальные темные
очки героини, в которых отражается окружающий мир. На рис. 8.60 показаны два примера, где вид
кафетерия отражается на сфере и на торе. Текстура этого кафетерия обернута вокруг большой сферы,
окружающей объект, поэтому текстурные координаты (s, t) соответствуют долготе и широте этой окру-
жающей сферы.
540
Глава 8. Визуализация граней для усиления реалистичности
Рис. 8.60. Пример отображения окружающей среды (с разрешения Haeberli, Segal [Haeberli, 97])
Рис. 8.61. Отображение среды с помощью охватывающего куба (с разрешения Yoshihiro Mizutani, Kurt Reindel, Tom Dawson)
На рис. 8.61 показано использование вместо сферы окружающего куба. На рис. 8.61, а показано
отображение, состоящее из шести изображений различных видов внутренних стен, пола и потолка
комнаты. На рис. 8.61, б изображен блестящий чайник, отражающий различные части этой комнаты.
Использование охватывающего куба было впервые предложено Грином [Greene, 92] и в общем случае
приводит к менее искаженным отражениям, чем окружающая сфера. Эти шесть отображений могут
быть созданы посредством визуализации шести отдельных видов с точки наблюдения объекта (при этом
сам объект, разумеется, изъят). Для каждого вида задаются воображаемая камера и соответствующее
окно. Возможен и альтернативный способ: текстуры можно получать посредством оцифровки фотогра-
фий, сделанных настоящей камерой, которая смотрит в шести главных направлениях изнутри настоя-
щей комнаты или сцены.
Хромированное отображение и отображение среды еще в большей степени отличаются от обычного ото-
бражения текстуры при анимациях, когда блестящий объект движется. Отраженное изображение будет
«течь» над движущимся объектом, в то время как обычное текстурное отображение приклеено к объекту
и движется вместе с ним. И если блестящая сфера вращается вокруг неподвижной точки, то обычное тек-
стурное отображение вращается вместе со сферой, а отраженное изображение остается неподвижным.
Как же осуществляется отображение среды? То, что вы видите в точке Р блестящего объекта, прихо-
дит в эту точку из окружающей среды как раз в том направлении, чтобы отразиться в ваш глаз. Для того
чтобы определить это направление, проследите за лучом от глаза до точки Р и определите направление
отраженного луча. Проследите далее за этим лучом до точки его пересечения с текстурой (на окружаю-
щем кубе или сфере). На рис. 8.62 показан луч, исходящий из глаза в точку Р. Если обозначить направ-
ление этого луча за и, а единичную нормаль в точке Р за ш, то, согласно уравнению (8.2), направление
отраженного луча будет равно г = и - 2(и • m) ш. Отраженный луч продолжается в этом направлении
до пересечения с гипотетической поверхностью, которая содержит текстуру. С вычислительной точки
зрения проще всего предположить, что блестящий объект находится в центре и по размерам намного
8.5. Добавление текстуры к граням
541
меньше окружающего его куба или сферы. Тогда отраженный луч исходит приблизительно из центра
объекта и его направление г может быть непосредствено использовано для указания на текстуру.
Рис. 8.62. Нахождение направления отраженного луча
В OpenGL содержится подпрограмма для выполнения приближенного отображения среды для слу-
чая, когда текстура находится на большой окружающей сфере. Эта подпрограмма запускается посред-
ством задания режима отображения для обеих текстурных координат 5 и t с помощью следующего кода:
glTexGenf(GL_S.GL_TEXTURE_GEN_MODE, GL_SPHERE_MAP);
glTexGenf(GL_T.GL_TEXTURE_GEN_MODE. GL_SPHERE_MAP);
glEnable(GL_TEXTURE_GEN_S):
gl Enable(GLJEXTURE_GEN_T);
Когда вершина P вместе с ее единичной нормалью m посылается в графический конвейер, OpenGL
вычисляет пару текстурных координат (s, t), которые можно использовать для указания на текстуру,
находящуюся на окружающей сфере. Такое вычисление выполняется для каждой вершины грани объек-
та, и эта грань рисуется, как обычно, при помощи интерполированных значений текстурных координат
(5, t) — для точек, находящихся между вершинами.
Рис. 8.63. Вычисление текстурных координат в OpenGL
Каким образом OpenGL быстро вычисляет нужную пару текстурных координат (5, Г)? Как показано
на рис. 8.63, а, сначала он находит (в координатах глаза) направление отражения г (с помощью выше-
приведенной формулы), где и — единичный вектор (также в координатах глаза), направленный от гла-
за к вершине V объекта, ат — нормаль в вершине V. Затем он просто использует выражение:
(8.23)
где р = ^гх2 + Гу + (г, +1)2 — малопонятный масштабный множитель. (Вывод этой формулы приводится
далее в упражнениях.) Для осуществления этой процедуры нам необходимо предварительно вычислить
текстуру, которая показывает, что бы мы увидели из окружающей среды в абсолютно отражающей сфе-
ре из точки наблюдения, находящейся вдали от этой сферы [Haeberli, 97]. Эта процедура отображает
часть среды, лежащую в полусфере позади глаза, в окружность в середине текстуры, а ту часть среды,
которая находится в полусфере перед глазом, — в плоское кольцо, охватывающее эту окружность.
542
Глава 8. Визуализация граней для усиления реалистичности
(Представьте себе эту конфигурацию.) При изменении положения глаза текстура должна быть пере-
считана заново. Изображения на рис. 8.60 были сделаны с использованием этого метода.
Имитация бликов средствами отображения среды
Отображение отражений можно использовать в OpenGL для создания на поверхности зеркальных бли-
ков. Создается текстурное отображение, имеющее интенсивное, концентрированное яркое пятно. Метод
отображения отражений «рисует» этот блик на поверхности, чтобы он выглядел как настоящий источ-
ник света, находящийся в окружающей среде. Блик, созданный таким способом, может быть более кон-
центрированным и подробным, чем блики, сделанные с помощью зеркальной составляющей Фонга при
закраске Гуро. Вспомним, что составляющая Фонга вычисляется только в вершинах грани, поэтому
легко «пропустить» зеркальный блик, оказавшийся между двух вершин. При отображении отражений
текстурные координаты (s, 4) формируются в каждой вершине и затем интерполируются в промежут-
ках. Поэтому если текстурные координаты, на которые указывают вершины, окружают яркую точку, то
такая точка будет правильно визуализирована на грани.
Практическое упражнение
8.5.9. Вычисление текстурных координат для отображения среды в OpenGL
Выведем уравнение (8.23). На рис. 8.63, б показаны (в разрезе) используемые векторы в координатах
глаза. Глаз смотрит с удаленной позиции в направлении (0, 0, 1). Сфера единичного радиуса располо-
жена с отрицательной стороны оси z. Предположим, что свет поступает в направлении г и встречается
со сферой в точке (х, у, z). Нормаль к этой сфере в точке (х, у, z) должна быть направлена так, чтобы
свет, поступающий в направлении г, отражался в направлении (0,0,1). Это означает, что нормаль долж-
на находиться посередине между вектором г и вектором (0, 0, 1); иначе говоря, она должна быть про-
порциональна сумме этих векторов: (х, y,z) = К (rx, г, г + 1) для некоторого К.
О Покажите, что нормальный вектор имеет единичную длину, если К = 1/р, гцер определяется урав-
нением (8.23).
О Покажите, что отсюда следует: (х, у) - (jx/p, гу/р).
О Предположим на минутку, что изображение текстуры простирается от -1 до 1 по х и от -1 до 1 по у.
Покажите, что в точке (х, у, z) должно отражаться значение текстурного изображения в точке (х, у).
О Покажите, что если координаты текстуры изменяются от 0 до 1 по х и по у — как это принято в
OpenGL, — то мы хотим видеть в точке (х, у) образ текстурных координат (5,4), определяемых
уравнением (8.23).
8.6. Добавление теней объектов
Тени придают изображению значительно большую реалистичность. Из каждодневного опыта нам извест-
но, что особенности отбрасывания тени одним объектом на другой предоставляют важную зрительную
информацию о том, как эти два объекта расположены по отношению друг к другу. На рис. 8.64 приведены
два изображения, состоящие из куба и сферы, подвешенных над плоскостью. На рис. 8.64, а тени отсутству-
ют, поэтому невозможно понять, на какой высоте над плоскостью парят куб и сфера. А на рис. 8.64, б тени
видны, и они дают полезную подсказку о расположении этих объектов. Тень передает большое количество
информации; вы словно бросаете и второй взгляд на объект (из местонахождения источника света).
В этом разделе мы рассмотрим два метода вычисления теней; один из них основывается на «раскра-
шивании» теней, как если бы они были текстурой, а другой использует буфер глубины, применяемый
для удаления невидимых поверхностей. В главе 14 мы увидим, что существует и третий метод, есте-
ственным образом возникающий при трассировке лучей. Существует еще много других технологий,
подробный обзор которых дается в работах [Watt, 138, Crow, 52, Woo, 214, Bergeron, 17].
8.6. Добавление теней объектов
543
8.6.1. Тени как текстура
Технология «наложения» теней как текстуры годится для теней, которые отбрасываются на плоскую
поверхность точечным источником света. Задача заключается в правильном вычислении формы тени.
На рис. 8.65, а показан параллелепипед, отбрасывающий тень на пол. Форма тени определяется про-
екциями каждой грани параллелепипеда на плоскость пола, когда источник света является центром проек-
ций. В действительности тень является объединением1 проекций шести граней. Рисунок 8.65, б иллюс-
трирует суперпозицию проекций двух граней: верхняя грань top проецируется в грань top', а передняя
грань front проецируется в front?. (Нарисуйте проекции остальных четырех граней и проверьте, что их
объединение действительно является искомой тенью2.)
Передняя
а б
Рис. 8.65. Вычисление формы тени
Это дает ключ к рисованию тени. После того как плоскость нарисована с использованием фоновой,
диффузной и зеркальной составляющих света, рисуются шесть проекций граней параллелепипеда на
плоскость с использованием только фонового света. Тени, нарисованые по этой технологии, обладают
правильной формой и цветом. Последним рисуется сам параллелепипед. (Если параллелепипед нахо-
дится близко к плоскости, то он может частично заслонить тень.)
1 Мы имеем в виду теоретико-множественное объединение: точка принадлежит тени, если она находится в одной или в большем
числе проекций.
2 Вам потребуется составить объединение только трех «передних» граней — тех, которые обращены к источнику света. (Почему?)
544
Глава 8. Визуализация граней для усиления реалистичности
Построение «спроецированной» грани
Для создания новой грани F' из исходной Гмы проецируем каждую вершину грани F на рассматривае-
мую плоскость. Нам нужен метод вычисления координат этих вершин на плоскости. Допустим, что,
как на рис. 8.65, а, плоскость проходит через точку А и имеет нормальный вектор п. Рассмотрим про-
ецирование вершины V, в результате чего образуется точка V'. Математическая сторона этого процесса
хорошо знакома: V — это та точка, в которой луч от источника света S, проходящий через точку V, пере-
секает плоскость. Как показано в упражнениях, эта точка задается формулой:
r's+(,,'s)7(F^)' <824)
В упражнениях показано, как записать это уравнение в однородных координатах в виде произведе-
ния Vна матрицу, применяемую в машинах визуализации типа OpenGL, который поддерживает умно-
жение нужных матриц.
Практические упражнения
8.6.1. Формы теней
Предположим, что куб парит над плоскостью. Какую форму имеет тень этого куба, если точечный ис-
точник света находится:
О непосредственно над верхней гранью;
О в направлении главной диагонали куба (как при изометрической проекции)?
Нарисуйте тени для сферы и для цилиндра, парящих над плоскостью, при различных положениях
источника света.
8.6.2. Создание «теневой» грани
О Покажите, что луч, идущий от точечного источника света S через вершину V, соударяется с плос-
костью п • (Р - Л) = 0 в точке t* = [п • (Л - 5)]/[п • (V- 5)].
О Покажите, что выражение, полученное согласно первому пункту, определяет точку V', удовлет-
воряющую уравнению (8.24).
8.6.3. Эквивалент умножению матриц
О Покажите, что выражение для V' в уравнении (8.24) может быть записано в форме матричного
умножения: V' = M(Vx, V, V2,1)г, где М— матрица размерностью четыре на четыре.
О Выразите элементы матрицы М в терминах Л, S и п.
8.6.2. Создание теней с помощью буфера теней
В другом методе рисования теней, радикально отличающемся от рассмотренного, используется буфер
глубины, предназначенный для удаления невидимых поверхностей. В рамках этого метода для каждого
источника света создается второй (дополнительный) буфер глубины, именуемый буфером теней
(shadow buffer). Этот подход требует большого количества памяти, однако он не ограничивается теня-
ми, отбрасываемыми на плоские поверхности.
В основе данного метода лежит принцип, согласно которому любые точки на сцене, «скрытые»
от источника света, должны находиться в тени. С другой стороны, если между точкой и источником
света не раположен никакой объект, то эта точка не находится в тени. Буфер теней содержит «картину
глубин» («depth picture») всей сцены с точки наблюдения, совпадающей с источником света: каждый
элемент буфера записывает расстояние от источника света до ближайшего объекта в соответствующем
направлении.
8.6. Добавление теней объектов
545
Визуализация при этом выполняется в две стадии.
1. Загрузка буфера теней.
При инициализации все элементы буфера теней содержат значения 1,0, то есть максимально воз-
можную псевдоглубину. Затем посредством помещения камеры в источник света производится расте-
ризация всех граней на сцене, однако проверяется только псевдоглубина точки на грани. Каждый эле-
мент буфера теней отслеживает наименьшую псевдоглубину, встретившуюся на данный момент.
Источник
Для большей наглядности на рис. 8.66 показана сцена, рассматриваемая обычной «камерой-глазом»
и «камерой-источником», расположенной в источнике света. Предположим, что точка Р находится на
луче, выходящем из источника света и проходящим через «пиксел» с/[г][у] буфера теней, и пусть точка
В на пирамиде также находится на этом луче. Если пирамида присутствует, то пиксел d[i][у] содержит
псевдоглубину до точки В; если же пирамида отсутствует, то пиксел J[z][у] будет содержать псевдоглу-
бину до точки Р.
Отметим, что вычисление буфера теней не зависит от положения глаза, поэтому при анимации,
в которой перемещается только глаз, буфер теней загружается всего один раз. Однако когда объекты
перемещаются относительно источника света, буфер теней нужно пересчитывать каждый раз заново.
2. Визуализация сцены.
Визуализация каждой грани на сцене с использованием камеры-глаза производится как обычно.
Пусть эта камера «видит» точку Р через пиксел р[с][г]. Тогда при визуализации пиксела/фс][г] нужно
найти1:
О псевдоглубину D от источника до точки Р;
О местонахождение в буфере теней индекса [i][y] подлежащего проверке элемента;
О значение этого элемента с/[г][у], записанного в буфере теней.
Если d[i][у] меньше D, то точка Р находится в тени и р[с][г] задается только фоновым светом.
В противном случае точка Р не лежит в тени и/?[с][г] устанавливается с использованием фоново-
го, диффузного и зеркального компонентов.
Как выполняются эти этапы? Как показано в приведенных ниже упражнениях, каждой точке на
плоскости просмотра камеры-глаза соответствует точка на плоскости просмотра камеры-источника2.
Для этого соответствия для каждого пиксела на экране нужно найти псевдоглубину от источника до
точки Р, а также индекс [г][у], указывающий на псевдоглубину, хранящуюся в буфере теней.
1 Разумеется, данный тест проделывается только в том случае, если точка Р расположена ближе к глазу, чем величина, записанная в
обычном буфере глубины камеры-глаза.
2 Помните, что это SD-точки: они содержат две координаты плоскости просмотра, а роль третьей координаты выполняет
псевдоглубина.
18 Ф. Хилл
546
Глава 8. Визуализация граней для усиления реалистичности
Практические упражнения
8.6.4. Нахождение псевдоглубины относительно источника света
Пусть матрицы М и Ms отображают точку Р на сцене в определенные SD-точки на плоскостях просмот-
ра соответственно камеры-глаза и камеры-источника.
О Опишите, как устанавливать «камеру-источник» и как находить результирующую матрицу Л/.
О Найдите преобразование, которое по заданным координатам (х, у) на плоскости просмотра каме-
ры-глаза вычисляет координаты (г, у) и псевдоглубину на плоскости просмотра камеры-источника.
О Как по известным (г,у) определить индекс буфера теней [i][/J и псевдоглубину точки Р для каме-
ры-источника?
8.6.5. Протяженные источники света
В данной главе мы рассматривали только точечные источники света. Однако при моделировании протя-
женных источников света достигается большая реалистичность изображения. Как видно на рис. 8.67, а,
такие источники отбрасывают более сложные тени: полную тень (umbra), внутрь которой свет от источ-
ника не попадает вообще, и более светлую полутень (penumbra), внутри которой видна часть источника
света. На рис. 8.67, б светящаяся сфера радиуса 2 испускает свет на единичный куб, вследствие чего на
стену W отбрасывается тень. Сделайте аккуратный эскиз тени и полутени, которые наблюдаются на
стене. Как и следовало ожидать, алгоритмы для визуализации теней в случае протяженных источников
света весьма сложны. (Исчерпывающее решение для этого случая можно найти в работе [Watt, 138].)
а б
Рис. 8.67. Полная тень и полутень для протяженных источников света
8.7. Заключение
С момента зарождения компьютерной графики не прекращались попытки достижения большей реали-
стичности при визуализации трехмерных сцен. Каркасные представления объектов можно нарисовать
очень быстро, однако они трудны для восприятия, особенно когда несколько объектов на сцене пере-
крывают друг друга. Реалистичность значительно возрастает, если грани объектов раскрашиваются ка-
ким-либо цветом, а поверхности, которые не должны быть видны, удаляются. Однако изображения,
визуализированные таким способом, все же не создают впечатления объектов, расположенных на сце-
не, освещенной источниками света.
Возникает потребность в модели затенения, которая показывает, как свет отражается от поверхнос-
ти, — в зависимости от характера этой поверхности и ее ориентации по отношению к источникам света
и к глазу камеры. Физический аспект отражения света весьма сложен, поэтому программистами разра-
ботан целый ряд аппроксимаций и «трюков», которые дают приемлемый результат и в то же время до-
статочно эффективны с вычислительной точки зрения. Модель диффузного компонента отражения —
8.8. Тематические задания
547
одна из наиболее близких к реальности, и она существенно усложняется по мере того, как в ней учи-
тывается все больше и больше ингредиентов. Зеркальные отражения вообще не основываются на ка-
ких-либо физических принципах, однако могут адекватно воспроизводить возникновение бликов на
блестящих объектах. Фоновый же свет является в чистом виде абстракцией — это упрощенный метод,
избавляющий нас от построения многократных взаимных отражений объектов и одновременно делаю-
щий тени менее глубокими.
Даже простые модели затенения включают в себя несколько параметров, таких как коэффициенты
отражения, описания неровности поверхности и цвет источников света. OpenGL предоставляет возмож-
ность задавать большинство из этих параметров. Однако при выборе значений этих параметров дизай-
неру оказывается лишь минимальная помощь; часто они подбираются методом проб и ошибок — до тех
пор, пока последнее визуализированное изображение не будет «выглядеть правильно».
В данной главе мы сконцентрировали наше внимание на визуализации полигональных каркасных
моделей, вследствие чего основной задачей была визуализация полигона. Полигональные грани особен-
но просты и описываются небольшим количеством параметров, таких как координаты вершин, нормали
в вершинах, цвет поверхностей и материал поверхностей. Кроме того, существуют высокоэффектив-
ные алгоритмы для закрашивания полигональной грани вычисляемыми цветами, в особенности если
известно, что эта грань выпуклая. Эти алгоритмы могут использовать плоскостность полигона для ин-
крементальной интерполяции глубины. В этом случае алгоритм буфера глубины, применяемый для
удаления невидимых поверхностей, является простым и эффективным.
Если для аппроксимации основной гладкой поверхности используется каркасная модель, вид ребер
грани может оказаться нежелательным. В моделях закраски Гуро и Фонга предусмотрены способы ри-
сования гладких поверхностей (кроме линии их силуэта). Закраска Гуро является очень быстрой, одна-
ко недостаточно точно вопроизводит блики; при закраске Фонга получаются более реалистические ви-
зуализации, однако с вычислительной точки зрения оно обходится значительно дороже.
Реалистичность визуализированной сцены может быть значительно усилена путем текстурирова-
ния поверхностей объектов. При наличии текстуры объект может казаться сделанным из определенно-
го материала, например кирпича или дерева; кроме того, на поверхность могут быть наклеены этикетки
или другие рисунки. Текстурные отображения могут использоваться для коррекции количества света,
отраженного от объекта, а также для «отображения неровностей», что позволяет придать поверхности
изрытый вид. Отображение окружающей среды создает у наблюдателя понятие об обстановке, окружа-
ющей блестящий объект, что может придать сцене больше реалистичности, особенно при анимациях.
Отображение текстур, однако, требует тщательного выполнения с использованием необходимой интер-
поляции и сглаживания (последнее рассматривается в главе 10).
Глава заканчивается описанием нескольких простых методов для создания теней объектов. Этот
предмет достаточно сложен, для него разработано множество технологий. Два описанных алгоритма
обеспечивают простые, но неполные решения этой задачи.
Еще большей реалистичности можно достигнуть применением более сложных технологий, таких как
трассировка лучей. В главе 14 рассматриваются основные идеи этой технологии.
8.8. Тематические задания
Тематическое задание 8.1. Создание закрашенных
объектов с использованием OpenGL
Уровень сложности II, однако сложнее, чем тематическое задание 7.1.
Усложните тематическое задание 7.1, в котором камера летает по сцене, рассматривая различные
полигональные каркасные объекты: установите на сцене точечный источник света и назначьте сеткам
свойства различных материалов. Добавьте фоновый, диффузный и зеркальный компоненты освеще-
ния. Предусмотрите клавишное переключение между плоским и плавным закрашиваниями.
548
Глава 8. Визуализация граней для усиления реалистичности
Тематическое задание 8.2. Самодельный графический конвейер
Уровень сложности III.
Напишите приложение, в котором характеристики полигональной каркасной модели читаются из
файла, как это описано в главе 6, задаются камера и точечный источник света и производится визуали-
зация каркасного объекта с использованием плоского закрашивания с участием фонового и диффузно-
го света. Необходимо вычислять только интенсивности серого цвета. Не используйте в данном проекте
графический конвейер OpenGL, а создайте вместо него свой собственный. Определите матрицы моде-
лирования-вида, перспективного преобразования и преобразования в порт просмотра. Организуйте все
так, чтобы вершины проходили через две первые матрицы, после чего к ним применялась бы модель
закраски, а затем — перспективное деление (вам не потребуется делать никакого отсечения) и преобра-
зование в порт просмотра. Каждая вершина фигурирует в виде массива {х, у, z, b}, где х и у — это экран-
ные координаты, а b — градация яркости серого цвета данной вершины. Используйте в качестве теку-
щей визуализации подпрограмму для рисования заполненных полигонов; если вы применяете OpenGL,
то используйте только его компоненты для двумерного рисования (а также буфер глубины). Поэкспе-
риментируйте с различными каркасными моделями, положениями камеры и источников света, чтобы
убедиться в правильности установки освещения.
Тематическое задание 8.3. Добавление закраски полигонов
и удаления невидимых поверхностей при помощи буфера
глубины
Уровень сложности III, однако выше, чем требуется для тематического задания 8.2.
Реализуйте свой собственный буфер глубины и используйте его в приложении, которое вы уже раз-
работали в тематическом задании 8.2. Вам потребуется также разработать подпрограмму закраски по-
лигонов (см. главу 10).
Тематическое задание 8.4. Визуализация текстуры
Уровень сложности II, однако сложнее, чем тематическое задание 8.1.
Усовершенствуйте программу, которую вы написали в тематическом задании 8.1, так чтобы грани
каркасных объектов можно было раскрашивать текстурами. Скомпонуйте программу, способную чи-
тать файл ВМР-изображеиия и привязывать его к объекту текстуры OpenGL. Поэкспериментируйте с
размещением пяти различных текстурных изображений и одной процедурной текстуры на грани куба
и заставьте куб вращаться в анимации. Предусмотрите пользовательское переключение клавишей меж-
ду линейной интерполяцией и интерполяцией, более подходящей для визуализации текстур.
Тематическое задание 8.5. Применение процедурных ЗО-текстур
Уровень сложности III.
Можно достигнуть интересного эффекта, если заставить объект выглядеть изготовленным из како-
го-либо твердого материала, вроде дерева или мрамора. SD-текстуры подробно рассматриваются в гла-
ве 14 в связи с трассировкой лучей, однако для достижения убедительного эффекта на поверхность
объекта можно отображать «порции» трехмерной текстуры.
Предположим, что имеется текстурная функция В(х, у, г), придающая различным точкам трех-
мерного пространства различные интенсивности цвета. Например, с помощью функции В(х, у, г) мож-
но было бы отобразить степень «синевы» моря в точке (х, у, г). Когда вы плывете, то перед глазами
видите различную степень синевы. Если заморозить брусок воды и вырезать из этого бруска какую-
нибудь форму, то поверхность этой формы будет переливаться различными оттенками синего цвета.
Кроме того, В() может быть вектор-функцией и содержать для каждой точки (х, у, г) три значения,
представляющие собой коэффициенты диффузного отражения красного, зеленого и синего света для
8.8. Тематические задания
549
указанного материала в каждой точке пространства. Нетрудно сконструировать несколько интересных
функций В().
О Трехмерная черно-белая шахматная доска из 125 блоков формируется с помощью следующей
функции:
В(х, у, z) - ((int)(5x) + (int)(5y) + (int)(5z)) % 2 при изменении х, у, г от 0 до 1.
О В вершинах куба заданы шесть различных цветов, с непрерывно изменяющимся цветом в проме-
жуточных точках. Используйте в качестве функции В(х, у, г) = (х, у, г), где х, у, z изменяются от О
до 1. Вершина с координатами (0,0, 0) имеет черный цвет, вершина (1,0, 0) — красный и т. д.
О Все пространство может быть заполнено кубами, описанными в предыдущем пункте, поставлен-
ными друг на друга; для этого может быть использована функция В(х, у, z) = (fract(x), fract(y),
fract(z)), где fract(x) — дробная часть величины х.
Методы создания деревянной фактуры и мраморных разводов рассматриваются в главе 14, но их
можно применить и здесь.
В данном контексте мы хотим наложить на поверхности текстуру такого вида. Для того чтобы сде-
лать это, нужно с помощью функции В( ) вычислить битовую карту (bit map) для каждой грани объек-
та. Если объект, например, является кубом, то для каждой из шести граней куба вычисляется битовая
карта. Пусть определенная грань куба характеризуется плоской поверхностью Р + at + bs, где 5 и t изменя-
ются в диапазоне от 0 до 1. Затем используем в качестве текстуры функцию В(Рх + at + bs, Р + at + bts,
P + fl/ + V)- 0™етим> что если в узоре В() имеет место какая-нибудь состыковка (то есть соседние
точки обладают почти одинаковой интенсивностью или цветом), то в этом случае и соседние точки
смежных граней также будут иметь почти одинаковый цвет. Вследствие этого объект действительно
выглядит как выточенный из единого куска сплошного материала.
Расширьте тематическое задание 8.4, включив в него наложение такой текстуры на грани куба и ико-
саэдра. Используйте шахматную текстуру, текстуру цветного куба, а также древесную текстуру (они
рассматриваются в главе 14).
Сформируйте последовательность изображений для текстурированного куба, которые плавно про-
ходят через материал от кадра к кадру. Тогда будет казаться, что объект «движется сквозь» текстуру,
в которую он погружен, что весьма отличается от эффекта, который производит движущийся объект
с наклейной на него текстурой. Поэкспериментируйте с такими анимациями.
Тематическое задание 8.6. Рисование теней
Уровень сложности III.
Расширьте возможности программы, которую вы написали в тематическом задании 8.1, с целью со-
здания теней. Пусть один из объектов на сцене имеет плоскую поверхность, на которой видны тени от
других объектов. Поэкспериментируйте с методом «проецируемых граней». Если позволит время, раз-
работайте также подход с использованием буфера теней.
Тематическое задание 8.7. Расширение SDL с целью включения
текстурирования
Уровень сложности III.
Язык описания сцен (Scene Description Language — SDL) до настоящего времени не включает в себя
средства задания текстуры, которую хотелось бы наложить на каждую грань объекта. В языке имеется
ключевое слово texture, однако когда оно встречается в файле, то ничего не происходит. Тщательно изу-
чите коды классов Scene и Shape, которые доступны на web-сайте книги, после чего разработайте подход,
в котором разрешен синтаксис вида:
texture giraffe.bmp pl р2 рЗ р4
550
Глава 8. Визуализация граней для усиления реалистичности
для создания текстуры из изображения, записанного в файле (здесь это файл giraffe.bmp), и для после-
дующего наложения ее на нужные грани последовательно определяемых объектов. Определите, сколь-
ко параметров потребует метод texture и как они должны использоваться. Расширьте подпрограмму
drawOpenGLO для двух или трех форм так, чтобы она правильно отображала такую текстуру на объекты.
8.9. Дополнительная литература
В двух книгах Джима Блинна «Путешествие по графическому конвейеру» (Jim Blinn, A Trip down the
Graphics Pipeline [Blinn, 31]) и «Грязные пикселы» {Dirty Pixels [Blinn, 32]), которые входят в серию
«Уголок Джима Блинна» («Jim Blinn’s Corner»), предлагается несколько статей, содержащих четкое
объяснение проблем, возникающих при рисовании теней и гиперболической интерполяции, использу-
емой при визуализации текстуры. В работе Хекберта «Исследование наложения текстуры» (Heckbert,
«Survey of Texture Mapping» — [Heckbert, 103]) рассматривается множество интересных аспектов этой
сложной темы. Превосходное изложение темы содержится в статье Сегала «Быстрые тени и влияние
освещения при использовании текстурного отображения» (Segal, «Fast Shadows and Lighting Effects
Using Texture Mapping» — [Segal, 181]), а также в работе Хеберли и Сегала «Текстурное отображение
как фундаментальный графический примитив» (Haeberli and Segal, «Texture Mapping as a Fundamental
Drawing Primitive» — [Haeberli, 97]) (их также можно найти в Интернете на сайте http://www.sgi.com/
grafica/texmap/).
9 Приближение
к бесконечности
□ Эффективное использование повторения и рекурсии
при создании рисунков.
□ Расширение возможности визуализации сложных узоров.
□ Применение рекурсии для рисования пространственных кривых.
□ Конструирование фрактальных кривых и деревьев.
О Изучение фрактального сжатия изображений.
□ Исследование природы множеств Мандельброта и Жюлиа
и создание их изображения.
О Разработка методов «фрактализации» кривой
с использованием случайных фракталов.
Натуралисты знают: мир так плох,
Что блохи малые терзают сами блох,
А этих блохи меньшие грызут...
И нескончаем вечный этот зуд.
Джонатан Свифт (Jonathan Swift). сИз поэзии. Рапсодия*
Земляной червь, прорываясь сквозь почву, встретил другого
земляного червя и говорит ему: «О, ты прекрасна! Выйдешь
за меня замуж?». А ему в ответ: «Не будь глупцом!
Я — твой другой конец».
Роберт Хайнлайн (Robert Heinlein)
В этой главе мы «приблизимся к бесконечности» различными путями, используя мощь компьютерной
графики для демонстрации различных явлений, которые будут встречаться нам по дороге. Мы рассмот-
рим три приближения к бесконечности: к бесконечно малому — изучая как можно больше деталей или
добавляя новые уровни усложнения рисунка; к бесконечно большому — исследуя мотивы, из которых
можно соответствующим образом создавать большие узоры; наконец, к «бесконечному повтору» — ис-
следуя, что получится, если некий процесс повторяется снова и снова, теоретически бесконечно.
В разделе 9.2 «Фракталы и самоподобие» вводится понятие фракталов и самоподобия (self-similarity) —
такого свойства формы, степень шероховатости (roughness) которой не изменяется при увеличении
552
Глава 9. Приближение к бесконечности
этой формы. Представлены методы усложнения формы кривой, в которых приближение к бесконечно
малому приводит к еще большему уровню усложнения. В разделе 9.3 «Создание строк и кривые Пеано»
рассмотрен метод рисования очень сложных кривых с помощью небольшого набора правил замены од-
ной строки символов на другую. Каждое новое поколение таких кривых сложнее предыдущего.
В разделе 9.4 «Замощение плоскости» обсуждается продвижение от малого к бесконечно большому
путем заполнения всей плоскости копиями одной и той же формы, точно совмещающихся одна с дру-
гой. Рассматривается распространение этой технологии на небольшой набор форм, в их числе описы-
вается замечательный класс «рептилий» («reptile» — REPeating TILE), а также методы их рисования.
В разделе 9.5 «Создание изображений с использованием системы итерируемых функций» описывает-
ся, как рисовать сложные изображения, известные как «странные аттракторы» («strange attractors»), —
путем многократного применения совокупности аффинных преобразований к некоторому исходному
изображению. Предлагается также альтернативный метод рисования таких изображений, известный
как «Игра в Хаос» («Chaos Game»). Затем решается обратная задача: как найти совокупность аффин-
ных преобразований, если известно изображение аттрактора. Это ведет к обсуждению фрактального
сжатия изображений, в котором применяются методы, использованные для решения первой задачи.
В разделе 9.6 «Множество Мандельброта» представлено знаменитое множество Мандельброта,
рассмотрена его математическая сущность и разработаны инструменты для рисования этого множества.
В разделе 9.7 «Множества Жюлиа» описано семейство множеств Жюлиа и его связь с множеством Ман-
дельброта. Разработаны методы рисования двух видов множеств Жюлиа.
Раздел 9.8 «Случайные фракталы» посвящен «фрактализации» заданной кривой или ломаной ли-
нии, «взлохмачивания» ее с целью создания текстуры изрезанного берега или меха. Глава заканчивает-
ся восемью тематическими заданиями, углубляющими рассмотренные темы.
9.1. Введение
Компьютеры особенно хороши для повторяющихся вычислений: они будут безропотно делать все, что
угодно, снова и снова. Кроме того, высокая вычислительная точность современных компьютеров позво-
ляет алгоритму глубже заглянуть в сущность объекта, проникая во все большие уровни его усложнения.
Мы уже видели в предшествующих главах, что методы компьютерной графики позволяют создавать
изображения предметов, которых не существует в природе и, возможно, никогда не будет существовать.
Это особенно верно для объектов, изучаемых в настоящей главе, и компьютерная графика предоставля-
ет мощное средство для исследования таких объектов. Однако здесь мы пойдем еще дальше и натолк-
немся на ограниченность, присущую любому изображению, созданному на компьютере: оно обладает
ограниченным разрешением и ограниченными размерами, и оно должно создаваться в течение ограни-
ченного времени. Поэтому созданные нами изображения могут быть только приближениями к изучае-
мым явлениям, и человек, смотрящий на подобную картину, использует ее лишь как намек на то, как
выглядит истинный объект.
9.2. Фракталы и самоподобие
Кажется, что все неравнодушны к фракталам. И действительно, многие рассматривают свою первую встречу
с геометрией фракталов как абсолютно новый опыт как с эстетической, так и с научной точки зрения.
Бенуа Мандельброт (Benoit Mandelbrot). Красота фракталов
Нам нужны методы, которые позволят нам систематическим образом «приближаться к бесконеч-
ности» — или, выражаясь точнее, к бесконечно малому. Такие методы будут обладать свойством рекур-
сивное™, которая эффективно поддается управлению с помощью современных языков программиро-
вания. Иногда применение рекурсии предельно упрощает сложное геометрическое задание. Наряду с
другими обстоятельствами это позволяет раскладывать формы на меньшие части или детализировать
9.2. Фракталы и самоподобие
553
их — теоретически до бесконечности. Рекурсивные алгоритмы могут дать жизнь формам просто краси-
вым и увлекательным, а также имеющим полезные применения в науке и технике.
Многие из описываемых здесь кривых и изображений обладают одним особенно важным свойством:
они самоподобны (self-similar). Интуитивно это понятие означает, что эти формы выглядят «одинако-
во» при любом масштабировании: не имеет значения, насколько было увеличено изображение такой
кривой — она имеет одну и ту же степень сложности. Одни кривые в точности самоподобны (exactly
self-similar): какое бы сильное увеличение вы ни делали, увеличенное изображение выглядит в точнос-
ти как оригинал (за исключением, быть может, поворота и сдвига). Другие кривые являются только
статистически самоподобными (statistically self-similar): здесь неправильности и изгибы кривой при
любом увеличении картинки не изменяются только «в среднем».
В природе существуют примеры статистического самоподобия. Классическим примером такого рода
является береговая линия. При взгляде со спутника у нее имеется определенная степень изрезанности,
образуемая заливами, бухтами и полуостровами. Если пролететь над ней ниже, то можно увидеть боль-
ше подробностей. Залив приобретает свою собственную неровность, которую раньше не было видно.
При дальнейшем увеличении масштаба можно обнаружить, что отдельные валуны и изгибы пляжа прида-
ют виду аналогичную изрезанность. Если приблизиться еще больше, то мелкие камни и галька обеспечат
примерно такую же степень неровности. Этот процесс продолжается при разглядывании отдельных песчи-
нок, уже под микроскопом. Некоторые другие природные явления также являются самоподобными,
например ветви дерева, поверхность губки, трещины на тротуаре, кровеносная система животных. Обла-
ка также приблизительно подобны самим себе и являют собой любопытный пример: пролетая на самоле-
те, непросто определить размер облака. Является ли оно маленьким и близким или большим и далеким?
В 70-е годы Бенуа Мандельброт из Йельского университета (в тогдашнем Исследовательском цен-
тре фирмы IBM) обобщил и популяризовал исследования природы самоподобия (см., например,
[Mandelbrot, 136]). Он назвал различные формы самоподобных кривых фракталами (fractals)1. Прямая
линия является одномерной, а плоскость — двумерной, однако существуют «создания» и в промежутке
между ними. Например, мы можем определить кривые бесконечной длины, однако лежащие внутри
конечного прямоугольника: их размерность располагается где-то между 1 и 2.
Работа Мандельброта и других исследователей породила невероятное количество исследований
природы фракталоподобных объектов, как в области математики, так и компьютерной графики, и это
увлечение продолжается во многих научных центрах во всем мире.
9.2.1. Последовательное усложнение кривых
Очень сложные кривые можно получить рекурсивно посредством многократного «усложнения» про-
стой кривой. Вероятно, простейшим примером такого рода является кривая Коха (Koch curve), откры-
тая в 1904 году шведским математиком Хельгом фон Кохом (Helge von Koch). Эта кривая вызвала ог-
ромный интерес в математическом мире, поскольку она образует бесконечно длинную линию внутри
области конечной площади [Gardner, 76].
Последовательные поколения кривой Коха обозначаются Ко, К, , К..,.... Форма нулевого поколения
Кй — это просто горизонтальная прямая единичной длины. Кривая К, показана на рис. 9.1. Для создания
кривой разделим прямую Ко на три равные части и заменим среднюю из них треугольным «зубцом» со
сторонами длиной 1/3. Очевидно, что длина всей линии составляет 4/3. Кривая второго поколения К,, так-
же показанная на рисунке, образована путем построения зубца на каждом из четырех отрезков линии К,.
◄---------1 ----------> <---------- 1--------->
Рис. 9.1. Два поколения кривой Коха
Мандельброт образовал этот термин от латинского fractus, что означает «фрагментированный» или «нерегулярный», по также
имеет смысл «дробной размерности» («fractional dimensional»).
554
Глава 9. Приближение к бесконечности
Для создания кривой Коха Кп+1 из Кп необходимо разделить каждый отрезок кривой Кп на три рав-
ные части и заменить среднюю часть зубцом в форме равностороннего треугольника.
В течение этого процесса длина каждого отрезка увеличивается в 4/3 раза, следовательно, общая
длина кривой в 4/3 раза больше длины кривой предыдущего поколения. Тогда общая длина кривой Ki
составляет (4/3)' и увеличивается с ростом i. Когда i стремится к бесконечности, длина кривой стано-
вится бесконечной.
Снежинка Коха на рис. 9.2 образована из трех соединенных вместе кривых Коха. Периметр S. i-ro по-
коления этой формы втрое больше длины простой кривой Коха и, следовательно, равен 3-(4/3)'’, что, разу-
меется, неограниченно возрастает при увеличении i. Однако площадь, ограниченная снежинкой Коха,
растет довольно медленно и в пределе (см. упражнения 9.2.1-9.2.3) 5. составляет всего 8/5 от площади 501
Таким образом, ребро снежинки Коха становится все более извилистым и все более длинным, а ее площадь
остается ограниченной. На рис. 9.3 приведены третье, четвертое и пятое поколения снежинок Коха.
Рис. 9.2. Первые несколько поколений снежинки Коха
Рис. 9.3. Снежинки Коха s3, s4, ss
Кривая Коха Кп является самоподобной в следующем смысле: разместим маленькое окно над неко-
торым участком кривой Кп и исследуем ее зазубренную форму. Теперь выберем окно в миллиард раз
меньше и исследуем ее форму, увеличенную до видимости. Если п даже очень велико, кривая по-преж-
нему имеет ту же самую форму и извилистость. Действительно, данный участок кривой можно снова
увеличить в миллиард раз, и снова форма останется неизменной. Строго самоподобной является толь-
ко предельная кривая К~, однако эффект самоподобия может быть аппроксимирован с помощью компь-
ютерной графики: нужно сделать п настолько большим, чтобы даже при максимальном увеличении
наименьшие отрезки прямых были меньше расстояния между пикселами.
9.2.2. Рисование кривых и снежинок Коха
Можно взглянуть на кривые Коха иначе: каждое поколение состоит из четырех версий предыдущего
поколения. Например, кривая К2, показанная на рис. 9.1, состоит из четырех кривых К{, соединенных
своими концами под определенными углами между ними. Назовем п порядком (order) кривой Кп, тогда
можно говорить, что кривая Коха n-го порядка состоит из четырех кривых Коха (n-l)-ro порядка.
Здесь естественно рассуждать в терминах черепашьей графики (вспомните главу 3): для того чтобы
нарисовать кривую К2, нарисуем уменьшенную версию кривой Kv затем повернем влево на 60°, снова
нарисуем К{, повернем вправо на 120°, нарисуем К{ в третий раз и т. д. Для снежинки эта процедура
применяется трижды, с промежуточным поворотом в 120°.
9.2. Фракталы и самоподобие
555
Таким образом, мы имеем естественный рекурсивный метод для рисования кривой Коха любого
порядка; ниже приводится его псевдокод.
То draw Кп:
If (n equals 0) Draw a straight line:
else{
Draw Kn-1 ;
Turn left 60°:
Draw Kn-1 ;
Turn right 120°:
Draw Kn-1 :
Turn left 60°:
Draw Kn-1 :
}
Подпрограмма drawKochO, приведенная в листинге 9.1, рисует кривую К на базе «родительской»
прямой с длиной len, которая идет из текущей позиции в направлении dir. Можно представить под-
программу KochO как способ «усложнения» родительской прямой до кривой Коха, именно поэтому мы
и назвали эту подпрограмму именем Коха. Для отслеживания направления каждого «дочернего» поко-
ления в последовательные вызовы подпрограммы KochO передается параметр направления dir.
Листинг 9.1. Рисование кривой Коха
void drawKoch(double dir. double len. int n)
{ // "Koch" to order n the line of length len
// from CP in the direction dir
// «кохируем» до n-го порядка прямую длины len
// из точки СР в направлении dir
double dirRad = 0.0174533 * dir:
// in radians
// в радианах
if(n == 0)
lineReKlen * cos(dirRad). len * sin(dirRad)):
else{
n--;
// reduce the order
// уменьшаем порядок
len /- 3:
// and the length
// а также длину
drawKoch(dir. len. n):
dir +- 60;
drawKoch(dir. len. n):
dir -= 120:
drawKoch(dir. len. n):
dir +- 60:
drawKoch(dir. len. n):
} }
Практические упражнения
9.2.1. «Кохирование» произвольной прямой
Укажите этапы, необходимые для рисования кривой Коха п-го порядка между точками А и В.
9.2.2. Длина кривой Коха
Покажите, что если прямая длиной L «кодируется» до n-го порядка, то длина каждого наименьшего от-
резка прямой равна (£/3)л, а общая длина кривой Коха составляет (4£/3)л.
556
Глава 9. Приближение к бесконечности
9.2.3. Площадь снежинки Коха
Рассмотрим семейство снежинок Коха, представленных на рис. 9.2.
О Покажите при помощи простой геометрии, что площадь снежинки 50 равна а0 = £2-\/з/4, где L —
длина одной стороны 50. Добавление «зубцов» всегда увеличивает площадь.
О Покажите, что каждый из зубцов, добавляемых к снежинке 5Р имеет площадь а0/9, а площадь сне-
жинки 5; составляет аг = а0(1 + 1/3).
О Теперь покажите, что для каждого следующего поколения число зубцов увеличивается в четыре
раза, а площадь каждого зубца составляет одну девятую часть площади зубца, построенного в
предыдущем поколении.
О Напишите формулу для в виде суммы геометрической прогрессии и найдите ее предел при k,
стремящемся к
9.2.3. Дробная размерность
В пределе кривая Коха имеет бесконечную длину, хотя и занимает на плоскости ограниченную область.
Чему равна ее размерность? Она выглядит более сложной, чем размерность линии (одно измерение),
но все же топологически ее размерность равна единице.
Математик Феликс Хаусдорф (Felix Hausdorff) (1868-1942) ввел понятие дробных размерностей
на основе анализа простых самоподобных объектов типа прямых, квадратов и кубов. Предположим,
например, что мы разбиваем прямую линию единичной длины на N равных отрезков. Очевидно, что
отношение длины каждого из отрезков к длине исходной прямой равно г = 1/ЛГ. Пока что все хорошо.
Теперь проделаем то же с квадратом: разделим его на Af одинаковых квадратов, тогда соотношение сто-
рон каждого маленького квадрата к исходному составляет г - 1/№/2. Проделаем, наконец, ту же самую
процедуру над трехмерным объектом — кубом. Разделим его на N одинаковых частей и обнаружим, что
отношение стороны каждого «подкуба» к стороне исходного куба равно г = 1/7V1/3 раз. Просматривает-
ся закономерность: размерность объекта фигурирует в показателе степени при основании N. Можно
дать такое определение: объект обладает размерностью D, если при разделении его на N равных частей
каждая часть будет иметь сторону, меньшую, чем сторона исходного объекта, в г = 1/Nl/D раз. После
взятия логарифма (по любому основанию) обеих частей этого равенства оно упрощается следующим
образом (проверьте это!):
p = logpV) (91)
log -
И
Чему же равна дробная размерность кривой Коха? При переходе от одного поколения к следующе-
му из каждого предыдущего отрезка создается N = 4 отрезка, а их длины получаются из длин отрезков
предыдущего поколения при умножении их на множитель г = 1/3, поэтому
D = log(4)/log(3) = 1,26.
Размерность кривой Коха действительно находится между 1 и 2. Если кривая А обладает большей
размерностью D, чем кривая В, то кривая А обязательно будет более «извилистой», чем кривая В; это
означает, что она меньше похожа на линию и ей присуща большая «заполняемость плоскости». Фрак-
тальная кривая и в самом деле может «заполнить плоскость» и в силу этого приобрести размерность
два, как мы увидим позднее. Такие кривые называются кривыми Пеано1.
Усложнение каждого очередного поколения кривой для создания следующего может осуществ-
ляться и многими другими способами. На рис. 9.4 приведено три примера: квадратная кривая Коха, так
называемый «дракон» («dragon») и кривая Госпера, названная по имени Дэвида Госпера (David Gosper),
1 Названы в честь Джузеппе Пеано (Giuseppe Peano, 1858-1932), итальянского логика и математика.
9.3. Создание строк и кривые Пеано
557
американского математика, родившегося в 1943 году. В квадратной кривой Коха отрезки в каждом поко-
лении дробятся на восемь отрезков с длиной, равной одной четверти исходного отрезка, следовательно,
ее размерность D = log(8)/log(4) = 1,5. (Пунктирными линиями показано предыдущее поколение с нало-
женным на него новым поколением.) Что касается кривой дракона, то у нее каждая прямая замещается
двумя прямыми длиной 1/д/2 , тогда D = log(2)/log{41 j = 2. У кривой Госпера каждый отрезок прямой
АВ замещается семью отрезками длиной 1/41, поэтому снова размерность D = 2. Ниже рассматриваются
специальные приемы рисования таких кривых.
б
в
Рис. 9.4. Другие приемы усложнения прямых: а} квадратная кривая Коха; б) дракон (dragon); в) кривая Госпера
9.3. Создание строк и кривые Пеано
Не бывает совершенной красоты без некоторого нарушения пропорции.
Фрэнсис Бэкон (Francis Bacon)
Путем дробления отрезков прямых можно создать множество интересных кривых. При самом простом
подходе к генерации таких кривых используется так называемый метод L-систем (L-Systems) рисова-
ния сложных кривых, основанный на простом наборе инструкций [Smith, 188, Prusinkiewicz, 173].
В главе 3 мы уже видели, что можно «управлять черепахой» с помощью символьной строки. Черепа-
ха «читает» строку и интерпретирует каждый символ как команду на выполнение некоторой операции.
Зададим черепахе следующий набор команд:
’F’ forward(l, 1) переместиться вперед на расстояние 1 в текущем направлении
'+’ turn(A) повернуть направо на угол А градусов
turn(-A) повернуть налево на угол А градусов
Если, например, дана строка "F-F++F-F" и значение угла А равно 60°, то черепаха нарисует первую
генерацию К, кривой Коха, изображенную на рис. 9.1.
Но как превратить простую строку вида "F-F++F-F" в более длинную, которая создаст более сложную
кривую? Этот процесс основывается на наборе инструкций создания строк (string-production rules),
который мы включим в определяемую нами подпрограмму produceStringO. Правило для кривой Коха
имеет вид:
F' -> "F-F++F-F"
где знак означает, что каждый встреченный символ "F" замещается группой символов "F-F++F-F".
Для символов ’+' или инструкции отсутствуют, поэтому эти символы передаются без изменений.
На рис. 9.5, а представлены две стадии процесса создания строк. На первой стадии исходная строка, называ-
558
Глава 9. Приближение к бесконечности
емая атомом (atom), а в данном случае это "F", «генерирует» строку первого поколения S1-"F-F++F-F",
затем эта строка подается на вход того же самого процесса, который генерирует строку второго поколения:
S2“F-F++F-F-F-F++F-F++F-F++F-F-F-F++F-F.
Видно, что в этой строке можно выделить четыре группы, или кластера (clusters), вида "F-F++F-F",
разделенные символами '-'.затем '++' и наконец снова Если теперь черепаха интерпретирует дан-
ную строку, то она нарисует вторую генерацию кривой Коха К2\
F-F++F-F
а б
Рис. 9.5. Процедура создания строк, дважды примененная к «атому» «F» (а); IFS-машина (б)
Можно нарисовать одну из этих кривых, если заставить подпрограмму produceStringO читать стро-
ку из входного файла, а в конце записывать «сгенерированную» ею строку в выходной файл. После каж-
дого вызова produceStringO ее выходной файл становится входным файлом для следующей стадии. (Эти
файлы быстро становятся очень длинными.) В первом файле хранится только атом. Когда выполнено
нужное количество вызовов produceStringO, черепаха читает последний файл и реагирует на каждую
команду. В псевдокоде этот подход можно реализовать в виде двух подпрограмм:
Для каждой стадии produceStringO;
for(each character ch in the input file)
// для каждого символа ch во входном файле
if(ch — ’+' || ch “ write it to the output file;
// записываем его в выходной файл
else if(ch -- 'F') write "F-F++F-F" to the output file:
// записываем "F-F++F-F" в выходной файл
После этого черепаха выполняет:
for(each character ch in the input file)
// для каждого символа ch во входном файле
if(ch“ '+') turn(A):
else if(ch — '-') turn(-A):
else 1f(ch — 'F') forward(l.l);
Отметим, что данный процесс является еще одним примером системы итерируемых функций (IFS —
см. главу 2), в котором каждая строка повторно поступает в одну и ту же функцию, чтобы создать объект
более высокого порядка. (Как выглядит генерирующее правило для квадратной функции Коха на
рис. 9.5, а?) На рис. 9.5, б показана эквивалентная IFS. Позднее мы разработаем рекурсивную версию под-
программы produceStringO, после того как обогатим эту подпрограмму новыми возможностями.
Расширение языка
Если ввести в процесс генерации строк некоторые дополнительные инструкции, то можно создавать
более богатый набор кривых. Можно использовать другие символы, например "X" и "Y", и также зада-
вать им определенные инструкции. Рассмотрим, например, набор инструкций для генерации «кривых
дракона» («dragon curves»):
•F’ -> 'F'
'X' -> "X+YF+" ♦- инструкции для «дракона»
'Y' -> “-FX-Y"
atom-"FX"
9.3. Создание строк и кривые Пеано
559
Здесь символ 'F' просто воспроизводит сам себя, в то время как символ 'X' создает строку из пяти
символов, содержащую различные комбинации символов'F', ’X’. 'Y'.
Используя в качестве атома "FX", мы получим для строки 1-го порядка строку "FX+YF+”, а строка 2-го
порядка имеет вид:
S2=FX+YF++-FX-YF+
(Как выглядит строка 3-го порядка? Что будет, если в качестве атома использовать ' F' ?)
Следует указать также, как черепаха интерпретирует для рисования новые символы. Эта инструк-
ция заключается в том, что любые символы ‘X’ и 'Y' игнорируются, в то время как символы 'F’ и '+'
интерпретируются как прежде.
Что же касается инструкций для дракона, то черепаха рисует дракон 1-го порядка, игнорируя симво-
лы 'X' и 'Y' в строке "FX+YF+”, и реагирует только на строку "F+F+”, поэтому полученная кривая состоит
из двух отрезков прямой, образующих «колено» с углом А. (Чаще всего используется угол в 90°.) Для
дракона 2-го порядка черепаха реагирует на строку "F+F++-F-F+" или эквивалентную ей "F+F+F-F+", которая
образует два колена с изменением направления: "F+F", затем "F-F". На рис. 9.6, а изображен дракон 3-го по-
рядка, а дракон 2-го порядка показан на рисунке пунктиром. На рис. 9.6, б приведен дракон 12-го порядка.
а
б
Рис. 9.6. Дракон 3-го порядка (а); дракон 12-го порядка (б)
9.3.1. Рекурсивная генерация строк и рисование в программе
Математика — это единственная бесконечная человеческая деятельность. Возможно, со временем
человечество узнает все о физике и биологии. Однако ему никогда не узнать все о математике,
поскольку сам ее предмет бесконечен. Бесконечны сами числа.
Поль Эрдо (Paul Erdos)
Вместо того чтобы сохранять в файлах строки, сгенерированные подпрограммой produceStringO, мож-
но реорганизовать эту подпрограмму для рекурсивной работы — так, чтобы она создавала эти строки
на ходу и непосредственно управляла черепахой.
С этой целью мы сохраняем в переменной order количество применений этой инструкции к строке;
например, S2 — это строка 2-го порядка на базе атома ' F'.
Листинг 9.2. Подпрограмма создания строк
void produceString(char *st.int order)
for(;st; st++)
// scan through each character
// считываем каждый символ
switch(*st)
продолжение^
560
Глава 9. Приближение к бесконечности
Листинг 9.2 (продолжение)
case CD -= angle: break:
// right turn
// правый поворот
case CD +- angle: break:
// left turn
// левый поворот
case 'F': if(order > 0)
produceString(Fstr, order - 1):
else forward(length. 1): break:
case 'X': if(order > 0)
produceString(Xstr. order - 1): break;
case 'Y': if(order > 0)
produceString(Ystr. order - 1):
}
В листинге 9.2 приведена функция produceStringO, которая символ за символом сканирует входную
строку. Если символ равен '+' или то черепаха поворачивает в соответствующую сторону. Если же
символы равны 'F', 'X' или 'Y', то функция produceStringO вызывает сама себя с соответствующей стро-
кой, однако при значении порядка order, меньшем на единицу. Если переменная order равна 0, то данная
функция интерпретирует символ ' F' как команду для черепахи и рисует прямую в текущем направлении.
В функции используются глобально доступные строки Fstr, Xstr, Ystr, а также переменные angl е и 1 ength.
Отметим, что здесь черепаха использует фиксированную длину шага length. Поскольку кривые более
высоких порядков содержат больше шагов, чем кривые низших порядков, их изображения будут больше.
До начала рисования можно задать окно нужного размера и в нужном месте экрана, которое вместило
бы строящуюся кривую, однако очень трудно предсказать аналитически, какую область будет занимать
эта кривая. В тематическом задании 9.1 в конце главы описывается метод решения этой задачи: на предва-
рительной стадии черепаха проходит кривую «невидимкой», создавая при этом окно требуемого размера.
Пример 9.3.1. Кривые, построенные при генерации строк
Приведем данные для нескольких кривых, сгенерированных строками.
Кривая Коха (Koch curve):
(F. F-F++F-F. nil. nil. 60)
Квадратный остров Коха (Quadratic Koch Island):
(F+F+F+F. F+F-F-FF+F+F-F. nil. nil. 90)
Кривая Гильберта (Hilbert curve)':
(X. F. -YF+XFX+FY-. +XF-YFY-FX+. 90)
Кривая дракона (Dragon curve):
(X. F. X+YF+. -FX-Y. 90)
Шестиугольная кривая Госпера (Gosper hexagonal curve):
( XF. F. X+YF++YF-FX--FXFX-YF+. -FX+YFYF++YF+FX--FX-Y. 60)
Ковер Серпинского (Sierpinski gasket):
(FXF-FF-FF. FF. --FXF++FXF++FXF--. nil. 60)
Наконечник Серпинского (Sierpinski arrowhead):
(YF. F. YF+XF+Y, XF-YF-X. 60)
1 Эта кривая названа в честь великого математика Дэвида Гильберта (David Hilbert, 1862-1943).
9.3. Создание строк и кривые Пеано
561
Здесь приводятся данные для семи классов кривых. Для каждой кривой задаются пять ключевых
компонентов в следующем порядке: атом, F-строка, Х-строка, Y-строка, угол в градусах; словом «nil»
(нуль) здесь обозначена пустая строка. Примеры четырех из этих кривых показаны на рис. 9.7.
Некоторые кривые, показанные на рис. 9.7, фактически являются кривыми, заполняющими плос-
кость (space-filling), или кривыми Пеано (Peano curves). Как уже упоминалось ранее, дробная размер-
ность таких кривых равна 2, и они полностью заполняют определенную область плоскости. Две самые
известные из них — это кривые Гильберта и Серпинского. (Позднее была открыта «снежинка» Ман-
дельброта, рассматриваемая в тематическом задании 9.2.) На рис. 9.8 показано несколько кривых Гиль-
берта низших порядков.
Рис. 9.7. Примеры кривых, созданных с использованием инструкций генерирующих строк: а) кривая Госпера пятого
порядка; б) квадратный остров Коха третьего порядка; в) кривая Гильберта (Hilbert) шестого порядка;
г) наконечник Серпинского (Sierpinski) седьмого порядка
Гильберт доказал, что при стремлении порядка к бесконечности бесконечно тонкая непрерывная
кривая Гильберта проходит через каждую точку единичного квадрата! Кроме описанного здесь мето-
да генерации строк, существуют другие способы рисования кривых Гильберта (см. [Wirth, 213] и
[Griffith, 95]).
562
Глава 9. Приближение к бесконечности
Рис. 9.8. Несколько первых поколений кривой Гильберта
Практические упражнения
9.3.1. Как велик дракон?
Рассмотрим кривую дракона порядка п на базе отрезка прямой между точками (0, 0) и (1, 0). Дракон
лежит внутри ограничивающего прямоугольника, размеры которого увеличиваются с ростом порядка.
Какие координаты имеют углы этого прямоугольника при увеличении порядка п до бесконечности?
Чему равна длина кривой дракона n-го порядка?
9.3.2. Дракон — это сложенная полоска бумаги
Интересно отметить, что кривую дракона можно получить, последовательно складывая тонкий лист
бумаги. Разгладьте такой лист, а затем сложите его так, чтобы один конец совместился с другим. Повто-
ряйте этот процесс неограниченно, складывая лист в одном и том же направлении. (Реально можно
проделать только около семи сложений.) Когда вы развернете бумагу так, что все углы будут равны 90°,
то увидите кривую дракона. Покажите, что данный процесс действительно приводит к кривым дракона
порядков от 1 до 4.
9.3.3. Что это за кривые?
С помощью нижеприведенных инструкций определяются еще две кривые. Первая из них является вари-
антом замкнутой кривой Серпинского, а вторая — прототипом кривой Пеано [Wagon, 204]. Нарисуйте
первые три поколения каждой кривой.
О Серпинский-бис:(Г+ХГ+Г+ХГ,Г, XF-F+F-XF+F+XF-F+F-X, nil, 90);
О Прототип Пеано (кривая, заполняющая плоскость):
(X. F. XFYFX+F+YFXFY-F-XFYFX. YFXFY-F-XFYFX+F+YFXFY. 90)
9.3.4. Найдите строки для кривой Пеано—Поля
Какие инструкции генерации строк управляют созданием заполняющей плоскость кривой Поля, изоб-
раженной на рис. 9.9? На рисунке в каждом случае пунктиром показана кривая предыдущего поколе-
ния. Каждый отрезок одного поколения заменяется направленным вправо «коленом», однако направ-
ления этих колен изменяются следующим образом: L, RL, LRLR.(Это означает, что если двигаться
вдоль отрезков одного поколения, то отрезки следующего поколения будут лежать слева, затем справа,
затем слева и т. д. — по отношению к текущим отрезкам.)
Рис. 9.9. Заполняющая плоскость кривая Поля
9.3.2. Разрешение ветвления
Добавим еще одну, последнюю инструкцию генерации строк, разрешающую черепахе «снова находить
дорогу с места остановки» — с какой-либо более ранней точки рисунка. Такое свойство позволяет чере-
пахе делать ветвеподобные рисунки, наподобие ветвей дерева, когда из одной точки исходит несколько
9.3. Создание строк и кривые Пеано
563
форм. Средства для реализации этого свойства просты: нам нужен символ, который предписывает че-
репахе «запомнить текущее положение» для дальнейшего использования, и еще символ, который будет
возвращать черепаху в это положение.
Добавим к языку соответственно символы ' [' и ']придав им следующий смысл:
’ [': saveTurtl е() <- записать текущее состояние черепахи.
: restoreTurtleO <— установить состояние черепахи в ранее записанное значение.
Что входит в понятие «состояние черепахи»? У черепахи имеются координаты, и она «повернута» в
некотором направлении, поэтому ее состояние определяется текущими координатами (СР) и текущим
направлением (CD):
Состояние черепахи - {СР, CD}.
Удобно записывать последние состояния черепахи в стек, поэтому создадим черепаший стек (turtle
stack), который может выглядеть так:
(1,3,5,22), 45 <- вершина черепашьего стека
(0,7, -2,7), 30
(6,0,4,3), 180
Данный код означает, что самым последним состоянием, которое заталкивалось в стек, были текущие
координаты (1,3, 5,22) и текущее направление 45°, а до него было записано состояние СР - (0,7, -2,7),
CD = 30°. Если в строке встретится символ ' [', то текущее состояние черепахи проталкивается в стек
для дальнейшего использования. Если же встретится символ ' ]', то из стека выталкивается верхнее
значение, и состояние черепахи устанавливается равным вытолкнутому значению. Требуется добавить
всего две строки к оператору switch подпрограммы produceStringO, приведенной в листинге 9.2:
saveTurtleO: break: <- затолкнуть в стек текущее состояние черепахи
']: restoreTurtleO: break: «- вытолкнуть из стека состояние черепахи
В упражнениях, приведенных в конце раздела, предлагаются методы программной реализации это-
го вида стека.
Пример 9.3.2. Фрактальные деревья
Так называемые фрактальные деревья (fractal trees) представляют собой интересное семейство форм,
напоминающих настоящие деревья, как можно видеть па рис. 9.10. Такой кустарник можно использо-
вать для обрамления разнообразных рисунков; но фрактальные деревья сами по себе являются превос-
ходными объектами для изучения. Эти «кусты» имеют несколько «ветвей», исходящих из самых раз-
личных мест, и зачастую сама ветвь подобна уменьшенной копии целого дерева. (Если это самоподобие
сохраняется до произвольной глубины, то такой рисунок становится фракталом.)
Рис. 9.10. «Куст» четвертого порядка
564
Глава 9. Приближение к бесконечности
Куст, изображенный на рис. 9.11, создан на базе атома ’F', угла 22° и F-строки следующего вида:
F -> "FF-[-F+F+F]+[+F-F-FJ”
Начать
здесь
а б
Рис. 9.11. Первые два порядка куста
Здесь «ветвь» Т' на каждом уровне рекурсии замещается тремя элементами, как показано на
рис. 9.11, а:
О длинной прямой линией 'FF', которая является «стволом»;
О левой ветвью, состоящей из трех коротких прямых;
О правой ветвью, состоящей из трех коротких прямых.
Черепаха возвращается в точку, помеченную «вернуться сюда», каждые два раза, когда в строке
встречается команда ' ]' • При втором возврате текущее направление слегка отличается от первого. (По-
чему?) Эта точка возврата является также стартовой точкой для следующей генерации, поскольку каж-
дый символ ' F' замещается вышеуказанной строкой, заканчивающейся символом ' ]'. Очень полезно
убедиться, что куст второго порядка, изображенный на рис. 9.11, б, фактически возник в результате ге-
нерации F-строки при каждом появлении символа 'F' в предыдущей строке.
Практические упражнения
9.3.5. Другие кусты
Проанализируйте, что генерируют нижеприведенные инструкции [Prusinkiewicz, 173], и включите эти
инструкции в подпрограмму, которая нарисует то, что они сгенерировали:
О (X, F -> FF, X -> F[+X]F[-X]+X, 20°) (куст).
О (X, F -> FF. X -> F-[[X]+X]+F[+FX]-X, 22.5°) (еще один куст).
О (X, F -> F, X -> [-F+F[Y]+F][+F-F[X]-F],
Y -> [-F+F[Y]+F] [+F-F-F], 60°) (шестиугольная мозаика).
О (Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х+Х,
F —> F. X —> [F+F+F+F[--X-Y]h-h-h-F++4-h4-h-F-F-F-F],
Y -> [F+F+F+F[—YJm4-I-F+-HIunF-F-F-F], 15°) (апериодическая мозаика).
9.3.6. Реализация черепашьих стеков
О Реализуйте стек черепахи как связный список узлов типа tTurtl eStack, где каждый узел содержит
два поля, одно типа tTurtle (содержащее СР и CD), а второе — указатель на тип tTurtleStack.
О Напишите подпрограмму под названием SaveTurtleO, которая выделяет новую память для узла,
загружает в эту память состояние черепахи и проталкивает этот узел в вершину стека.
9.4. Замощение плоскости
565
О Напишите функцию RestoreTurtleO, которая выталкивает верхний узел из стека, использует по-
лученные данные для обновления текущего состояния черепахи, а затем освобождает память, за-
нимаемую узлом.
О Проверьте подпрограммы, разработанные вами в предыдущих пунктах, в программе, которая
рисует каждый из рассмотренных в этом разделе ветвящихся объектов.
9.3.3. Добавление случайности и сужения
Ветвящиеся объекты, такие как кусты, могут выглядеть более естественными, если будут сделаны ме-
нее правильными. В инструкции создания строк можно включить небольшой элемент случайности (на-
пример, путем добавления маленького случайного смещения к каждому углу поворота при каждом по-
явлении в строке символов '+' или ' -' Далее, если придать ветвям толщину, то было бы приятнее для
глаз изобразить «сужение» ветвей, становящихся более тонкими. На рис. 9.12 приведены симпатичные
примеры, построенные с помощью таких усовершенствований. Поэкспериментируйте в подпрограмме
producestring О с различными видами случайности и найдите несколько комбинаций параметров, кото-
рые приводят к наилучшим результатам.
Рис. 9.12. Добавление к деревьям случайности и сужения (с разрешения Bill McQuaid and Adam Lavine)
9.4. Замощение плоскости
Множество ярких мозаичных стен и полов в Альхамбре (Испания) доказывает нам, что мавры были великие
мастера в заполнении плоскостей одинаковыми фигурами, прилегающими друг к другу без зазоров.
Как жаль, что их религия запрещает им рисовать картины!
М. К. Эшер (М. С. Escher)
Еще один путь движения к бесконечности — повторять какую-нибудь форму снова и снова, покрывая
в конце концов всю плоскость копиями этой формы. Мы уже рассматривали некоторые способы таких
бесконечных повторений в главе 3 — при создании на обоях узоров, бесконечно повторяющихся в двух
направлениях. В случае узоров на обоях природа повторяющегося рисунка ничем не ограничивается;
любой «мотив» может быть повторен. В данном разделе1 мы исследуем интересный частный случай
обойных узоров: периодическое замощение (tiling) или мозаичное представление (tesselation) плос-
кости простой фигурой. Под этим понимается создание множества копий некоторой формы, такой как
полигон, и «укладка» их рядом на манер паззла (jig-saw puzzle), чтобы они без зазоров заполнили всю
плоскость.
1 При первом прочтении данный раздел может быть пропущен без потери целостности.
566
Глава 9. Приближение к бесконечности
Художник М. К. Эшер создал множество занимательных мозаичных представлений, два из которых
приведены на рис. 9.13. В первом примере использована фигура одинокого всадника. Повторяющиеся
всадники образуют полностью сомкнутые ряды, и более того, эти ряды смыкаются со смежными ряда-
ми повернутых всадников. В мозаике «рыбы и птицы» использованы две фигуры, и опять вся плоскость
совершенно заполнена. Когда глаз фокусируется на одной или другой детали, передний и задний пла-
ны этих фигур меняются местами.
Рис. 9.13. Две мозаики М. К. Эшера (1988 год, М. G Escher Helrs/Cordon Art-Baam-Holland)
Существует обширная теория замощений, хорошо представленная в энциклопедической работе Грюн-
баума и Шефарда (Grunbaum, Shephard (Grunbaum, 96]), хотя многие вопросы еще не получили ответа.
Здесь мы остановимся на основных идеях, обращая особое внимание на мозаики, состоящие из полигонов.
9.4.1. Моноэдрические мозаики
Вначале мы рассмотрим моноэдрические (monohedral) мозаики — на базе единственного полигона.
Если же мы вдобавок потребуем, чтобы этот полигон был правильным, то будет существовать всего три
вида правильной мозаики (regular tilings), показанных на рис. 9.14. Заполнить плоскость способны
только треугольник, квадрат и шестиугольник (гексагон).
ААЛААА
W000
Рис. 9.14. Три возможных замощения п-гонами
Отметим, что равносторонние треугольники для совмещения должны иметь разную ориентацию.
Заметим также, что треугольное замощение можно свести к гексагональному, поскольку группа из ше-
сти треугольников образует гексагон.
Гексагональные мозаичные замощения встречаются в ульях и в кристаллографии (см., например,
[Coxeter, 50]). Игра «Гекс» (Hex), изобретенная Питом Хейном (Piet Hein), также играется на поле, вы-
ложенном гексагональной мозаикой [Berlekamp, 18].
Все три вида замощения удобно обозначать в соответствии с их символом Шлефли (Schlafli symbol)
{р, q}, который указывает, что данное замощение есть заполнениер-гонами, q из которых окружают каж-
дую вершину. Тогда три замощения на рис. 9.14 будут описываться символами {3, 6}, {4, 4} и {6,3}.
Можно слегка видоизменить эти замощения: при заполнении квадратами их ряды можно сдвинуть
в горизонтальном направлении, чтобы образовать ряды «Кирпичей» или другие узоры, а полосы тре-
угольников можно сдвинуть в одном из трех направлений (в каких именно?). Для простоты мы рассмат-
9.4. Замощение плоскости
567
риваем здесь только мозаики типа «ребро к ребру» (edge-to-edge), когда два мотива соприкасаются
только вдоль всего общего ребра, в общей вершине или не касаются вовсе. Ограничение «ребро к реб-
ру» отбрасывает все варианты, оставляя только три узора, показанные на рис. 9.14.
Если же мы допускаем неправильные мозаичные мотивы, то есть протомозаики (prototiles), то воз-
можности резко возрастают. Очевидно, что произвольный параллелограмм заполняет плоскость. (По-
чему?) (Имейте в виду, что утверждение «объект X заполняет плоскость» означает, что копии объек-
тах, и только X, могут быть уложены так, чтобы они без зазоров заполнили всю бесконечную плоскость.)
Далее, каждый из следующих полигонов заполняет плоскость.
1. Произвольный треугольник.
2. Любой гексагон, имеющий центр симметрии.
3. Любой четырехугольник.
Давайте продемонстрируем эти утверждения одно за другим.
1. Чтобы показать, что любой треугольник заполняет плоскость, повернем его вокруг середины
одной из его сторон, чтобы образовать параллелограмм, который заполняет плоскость.
2. Если гексагон имеет центр симметрии (то есть если гексагон не изменяется при повороте его
вокруг центра на 180°), тогда его противоположные стороны параллельны и равны по длине.
Как показано на рис. 9.15, а, такие гексагоны всегда «прилегают» друг к другу без зазоров после
соответствующего переноса.
а б
Рис. 9.15. Любой центрально-симметричный гексагон заполняет плоскость
3. Наконец, из любого четырехугольника можно построить гексагон с точкой симметрии, просто
поворачивая четырехугольник вокруг середины одной из его сторон, как показано на рис. 9.15, б.
Поскольку такой гексагон заполняет плоскость, то и любой четырехугольник — тоже!
в б в
Рис. 9.16. Каирская мозаика
Произвольный 5-угольник не может заполнить плоскость, однако один вид неправильного равно-
стороннего Пентагона (пятиугольника) -• может, как это показано на рис. 9.16. Пентагон на рис. 9.16, а
568
Глава 9. Приближение к бесконечности
имеет равные стороны, однако его внутренние углы не равны. Четыре таких Пентагона, составленные
вместе, образуют гексагон, который заполняет плоскость. Это носит название Каирской мозаики (Cairo
tiling), поскольку многие улицы столицы Египта Каира вымощены именно таким узором.
Некоторые другие полигоны, которые могут или, напротив, не могут заполнить плоскость, показа-
ны на рис. 9.17. На рис. 9.17, а приведены некоторые из знаменитых полимино (polyominoes) Соломона
Голомба (Solomon Golomb — [Golomb, 87]), образованные соединением единичных квадратов «ребро к
ребру». Полимино являются обобщением домино, которые состоят только из двух квадратов, соединен-
ных ребром к ребру. Полиамоиды (polyiamonds) образованы посредством соединения конгруэнтных рав-
носторонних треугольников [Gardner, 78]; несколько примеров приведены на рис. 9.17, б. В упражне-
нии 9.4.1 предлагается определить, какие из изображенных на рисунке полигонов заполняют плоскость.
а б
Рис. 9.17. Полимино и полиамонды
Деформирование мозаичного мотива
Множество интересных мозаик можно создать посредством деформирования n-угольных мозаичных
мотивов, изображенных на рис. 9.14. Например, ребро квадратного мотива можно превратить в зигзаг,
если вместе с ним деформировать и противолежащее ребро, как показано на рис. 9.18. На рис. 9.19 изоб-
ражен Пегас (Pegasus), образованный именно таким способом; это было предложено МакГрегором и
Уоттом (McGregor, Watt — [McGregor, 138]). Укладывается ли в эту модель всадник Эшера с рис. 9.13?
Рис. 9.18. Деформирование ребра в зигзаг
9.4.2. Диэдральные мозаичные размещения
В диэдральных мозаиках (dihedral tilings) разрешается использовать два вида мотивов, поэтому
они предоставляют намного больше возможностей. Например, гексагональная сеть, изображенная на
рис. 9.20, основана на двух мотивах (каких именно?). Эта сеть является вариантом мозаики {6, 3} с
рис. 9.14: каждый гексагон мозаичного заполнения рисуется в той же позиции, однако уменьшен в раз-
мерах, и смежные гексагоны соединены перемычками. Эта схема размещения изучалась в столь различ-
9.4. Замощение плоскости
569
них областях знания, как компьютерные сети, сотовые системы мобильной связи и архитектура памя-
ти. Например, в компьютерных сетях роль гексагонов играют процессоры, а роль перемычек играют
линии связи, с помощью которых эти процессоры обмениваются данными.
Рис. 9.19. Создание мозаики «Пегас»
Рис. 9.20. Гексагональная сеть
Наиболее известными диэдральными мозаиками являются полурегулярные (semiregular), или Архи-
медовы (Archimedean), мозаики, которых существует всего восемь [McGregor, 138, Steinhaus, 191]. Как
показано на рис. 9.21, каждая такая мозаика состоит из двух тг-гонов и обладает следующим свойством:
каждая его вершина имеет один и тот же тип (type) — она окружена одной и той же последовательнос-
тью 72-гонов в одном и том же порядке. Например, в первой из представленных мозаик каждая вершина
окружена треугольником, затем гексагоном, затем снова треугольником, затем опять гексагоном, что
можно кратко записать в виде расширенного символа Шлефли 3.6.3.6. (Использованное ранее обозна-
чение {6, 3} означает теперь 6.6.6 — то есть каждую вершину окружают три гексагона.) Оказывается
[Martin, 137], задание вокруг каждой вершины последовательности тг-гонов является достаточным для
указания типа мозаики, поскольку мы рассматриваем только размещения ребро к ребру. В этой системе
обозначений Архимедовы мозаики выглядят так:
3.6.3.6 4.6.4.3 3.3.3.3.6 4.8.8
3.12.12 4.6.12 3.3.4.3.4 3.3.3.4.4
(Какой символ соответствует какой мозаике?)
570
Глава 9. Приближение к бесконечности
УИдавдадата
тамиИмвП-
Кдашдата_
даЯшмдаташ
датам
Рис. 9.21. Архимедовы мозаики
Практические упражнения
9.4.1. Что заполняет плоскость?
Какие полимино и какие полиамонды из изображенных на рис. 9.17 заполняют плоскость?
9.4.2. Заполняют ли плоскость эти полигоны?
Какой из полигонов, изображенных на рис. 9.22, заполняет плоскость?
Рис. 9.22. Два полигона
9.4.3. Каирская мозаика
Чему равны внутренние углы пентагонов в Каирской мозаике? Каковы относительные длины сторон
гексагонов в этой мозаике?
9.4. Замощение плоскости
571
9.4.4. Ограничения на деформации
При деформировании квадрата, изображенного на рис. 9.18, его прямые углы могут измениться. Какое
соотношение должно поддерживаться между всеми четырьмя углами?
9.4.5. Что это за группа?
Найдите группу симметрии для каждой из Архимедовых мозаик.
9.4.3. Рисование мозаик
Рисовать периодические мозаики в графической программе обычно бывает нетрудно: нужно просто
задать большое окно и затем снова и снова рисовать мотив, смещая каждую его копию на нужное коли-
чество единиц по х и по у и отсекая фигуры границами окна (см. рис. 3.11). Для некоторых мозаик про-
ще всего сначала сгруппировать несколько мотивов в одну фигуру, а затем снова и снова рисовать эту
группу. Например, при рисовании Каирской мозаики с рис. 9.16 четыре мотива следует объединить в
гексагон, который затем будет повторяться при рисовании.
Кроме того, существует много интересных непериодических мозаик (nonperiodic tilings), рисовать кото-
рые не столь просто. Ниже мы рассмотрим один класс непериодических замощений, который рисуется от
очень большого к очень малому: внутри одной большой фигуры рисуется много малых фигур. Другие типы
непериодических мозаик, таких как мозаики Пенроуза, рассматриваются в тематическом задании 9.7.
9.4.4. Рептилии
Рептилии (Reptiles — REPeate Tiles) — это класс непериодических мозаик, которые проще всего описы-
ваются с помощью рекурсии. Различные копии рептилии совмещаются друг с другом, образуя боль-
шую рептилию той же самой формы. Поэтому большой мотив можно определить рекурсивно через его
собственные уменьшенные версии.
Мотив k-й кратности (k-rep tile) — это произвольный полигон Р, который можно разбить на k кон-
груэнтных частей, каждая из которых подобна Р [McGregor, 138]. (Будем говорить также, что такой
полигон обладает «£-й кратностью».) На рис. 9.23 показано пять простых примеров. Тримино (triomino)
является полимино 4-й кратности, а сфинкс (sphinx) — полиамондом. Сфинкс — это единственный из-
вестный Пентагон 4-й кратности.
Рис. 9.23. Примеры рептилий: а) тримино; б) равносторонний треугольник; в) треугольник 30—60—90; г) трапеция; д) сфинкс
«Самовоспроизведение» рептилий возможно в двух противоположных направлениях: в сторону бес-
конечно большого и в сторону бесконечно малого. Можно составить вместе четыре сфинкса, чтобы по-
лучить сфинкса большего размера. Этот процесс можно повторять бесконечно и получить сколь угодно
большого сфинкса. Подобным же образом можно нарисовать внутри каждого сфинкса маленьких сфин-
ксов и повторять эту регрессию бесконечно для получения сколь угодно малых сфинксов. (Проверьте
эти утверждения для каждого из пяти приведенных примеров.)
572
Глава 9. Приближение к бесконечности
Отметим, что любой треугольник является рептилией 4-й кратности: нужно просто соединить сере-
дины трех его сторон. Это показывает, что любой n-угольник также является рептилией, поскольку его
всегда можно разбить на п треугольников. Кроме того, для любого заданного k существует рептилия
k-й кратности: это параллелограмм с соотношением сторон liy/k. (Как выглядит этот параллелограмм?)
Оказывается, единственная известная рептилия 7-й кратности — это такой параллелограмм.
Рисование рептилий
Представляется удобным рассуждать о рептилиях в терминах «поколений»: мотив k-й кратности можно
рассматривать как «родителя» k «потомков»; в таком случае у каждой рептилии имеется один родитель.
Для того чтобы нарисовать рептилию, мы просто рисуем ее потомков, в силу чего данный процесс есте-
ственным образом является рекурсивным. Эту рекурсию можно остановить или по достижении заданной
глубины (числа произведенных поколений), или когда размер потомков станет «достаточно малым».
Листинг 9.3. Скелет программы для рисования тримино
void doTrio(double size, int depth)
{
int i:
if(depth ~ 1) drawTrioO:
else for(i =0: i < 4: i++)
// draw four children
// рисуем четырех потомков
{
set up for the i-th child:
// подготавливаемся для i-го потомка
doTrio(size / 2. depth - 1):
// draw child
// рисуем потомка
}
}
Текущее рисование в подпрограмме doTrioO, а также выполнение операторов, обозначенных слова-
ми «set up for the i-th child», может быть выполнено несколькими способами. Для некоторых форм
более предпочтительна черепашья графика; такие формы рассматриваются ниже. Для других форм
проще изменять систему координат путем управления текущим преобразованием, как это сделано в те-
матическом задании 9.2.
На рис. 9.24 показано тримино со своими четырьмя потомками; каждый из которых для удобства
помечен. (Украшение в виде дерева сделано просто для ориентировки глаза.) На рисунке проиллюст-
рировано применение черепашьей графики: «каркас» тримино рисуется с помощью последователь-
ности инструкций forwardO и turnO, начиная с правого нижнего угла, что показано зачерненным знач-
ком, обозначающим черепаху. Если же вначале требуется нарисовать потомков, то группа операторов
«set up for the i-th child» вначале перемещает невидимую черепаху (без рисования) к одной из четы-
рех начальных точек и затем поворачивает ее в нужном направлении. В ниже приведенных упражнени-
ях будет дано задание реализовать такую подпрограмму.
Рис. 9.24. Рисование тримино
9.4. Замощение плоскости
573
а б в
Рис. 9.25. Примеры тримино: а) глубина = 3; б) глубина = 4; в) глубина = б
На рис. 9.25 показаны примеры тримино, сгенерированные посредством кода, приведенного в лис-
тинге 9.3. Для случая depth = 6 окно выбрано так, что оно целиком лежит внутри объекта, поэтому это
окно выглядит заполненным мозаикой.
Практические упражнения
9.4.6. Нахождение рептилий
Для того чтобы поближе познакомиться с рептилиями, докажите каждое из приведенных ниже утверж-
дений (позаимствовано из [Clason, 42]):
О Каждый квадрат, прямоугольник и параллелограмм являются мотивами 4-й кратности.
О Прямоугольник (или параллелограмм), основание которого вдвое больше его высоты, является
мотивом 4-й кратности в четырех направлениях.
О Прямоугольник (или параллелограмм), стороны которого относятся как 1 к 4к , является моти-
вом k-тл кратности.
О Существует две различные трапеции с двумя прямыми углами, являющиеся мотивами 4-й крат-
ности. (Подсказка. Углы каждой трапеции равны 90, 90, 60 и 120 градусов).
О Треугольник с углами 30-60-90 является мотивом 3-й кратности.
О Прямоугольный треугольник с соотношением катетов 1:2 является мотивом 5-й кратности.
9.4.7. Ковер Серпинского как рептилия
На рис. 9.26 изображен ковер Серпинского, который является рептилией на базе равностороннего треуголь-
ника. Большой треугольник нарисован посредством рисования трех внутренних треугольников меньшего
размера, при этом остаются отверстия, конгруэнтные этим треугольникам. (Какую кратность имеет этот
мотив — 3 или 4?) Применив приведенные выше идеи, покажите, как нарисовать такой треугольник.
Рис. 9.26. Ковер Серпинского — рептилия (с глубиной 5)
574
Глава 9. Приближение к бесконечности
9.4.8. Украшения из рептилий
Можно получить интересные вариации, изменяя то, что рисуется на низшем уровне (то есть изменить
способ рисования самого дальнего потомка). Для случая тримино это сам гексагон из тримино; для ковра
Серпинского это треугольник, изображенный на рис. 9.27, а. На рисунке показаны две вариации способа
рисования, предложенные Клэйсоном [Clason, 42]. Из мотива на рис. 9.27, б получается интересная сетка,
изображенная на рис. 9.28, состоящая из перекрывающихся полос. Здесь все четыре дочерних треугольных
мотива рисуются внутри каждого родителя; и, кроме того, потомки повернуты на различные углы с целью
создания полного узора. Объясните подробно, как должны быть повернуты эти дочерние мотивы.
Рис. 9.27. Вариации формы мотива
a б в
Рис. 9.28. Сетка-рептилия, полученная путем вариации
9.5. Создание изображений с использованием
системы итерируемых функций
Вот еще один способ приближения к бесконечности: многократно применять к некоторому изображе-
нию какое-либо преобразование и смотреть, что получится. Мы увидим, что это является также еще
одним хорошим способом создания фрактальных форм. Эта идея была развита Барнсли (Barnsley —
[Barnsley, 10]) для чрезвычайно высокой степени сжатия изображений, поскольку при этом все изобра-
жение может быть представлено небольшим количеством чисел.
9.5.1. Экспериментальный копир
В данном разделе снова вводятся в игру системы итерируемых функций (IFS), впервые описанные в
главе 2. Берем исходный образ 10 и помещаем его в специальный «фотокопир», создающий новое изобра-
жение /р как показано на рис. 9.29, а1. Изображение 7, является не простой копией исходного изображе-
1 Это описание основано на статье, написанной в 1990 году Юргенсом, Пайтгеном и Саулом (Jurgens, Peitgen, Saupe — [Jurgens, 119]).
9.5. Создание изображений с использованием системы итерируемых функций
575
ния /0, а, как мы скоро увидим, совмещением нескольких уменьшенных версий /0. Затем берем изобра-
жение и посылаем его обратно в копир, чтобы получить следующее изображение 12. Повторяя этот
процесс бесконечно, получим последовательность изображений /0, /(, 12.которая называется орбитой
Io (orbit of /0). (Вспомните орбиту в главе 2.) Зададимся вопросом: «сходятся» ли эти изображения к
какому-нибудь изображению и если да, то к какому?
Изображение Ik-1
Вход Копия
Исходное изображение 10
а
Рис. 9.29. Создание новых «копий» из старых
Пример 9.5.1. «Копир Серпинского»
Рассмотрим особый пример копира, который можно назвать суперкопиром, или «S-копиром». Он вкла-
дывает друг в друга три уменьшенных версии любого изображения, которое подается на его вход.
На рис. 9.29, б показано, что делает S-копир за один проход, если на вход подана буква F. Эти три умень-
шенных изображения могут быть с тем же успехом совмещены, хотя на рисунке этого не показано.
На рис. 9.30 приведено несколько первых «итераций», которые производит S-копир. Из рисунка видно,
что эти итерации сходятся к треугольнику Серпинского, который уже встречался нам ранее, и на самом
деле это так! При каждой итерации отдельный компонент Fs становится вдвое меньше, а количество
компонентов утраивается. По мере увеличения числа итераций размер букв F приближается к точке, и
эти точки выстраиваются в треугольник Серпинского. «Окончательное» изображение не зависит от
формы буквы F, а только от свойств самого суперкопира.
FFFF
F F
FF FF
F F F F
FFFFFFFF
Рис. 9.30. Начальная часть орбиты 10 для S-копира
Как же S-копир делает свои изображения? Представьте себе, что в нем имеется три линзы, каждая из
которых уменьшает подающееся на нее изображение в два раза и переносит его в новое положение. Эти
три уменьшенных и сдвинутых изображения совмещены на печатаемом выходе. Масштабирование и
смещение легко осуществляются при помощи аффинного преобразования. Следовательно, каждая лин-
за выполняет свое собственное аффинное преобразование (или «аффинное отображение») Tt(P), Т2(Р),
Т3(Р) для каждой точки Р исходного изображения, тогда на выходе S-копира будет совмещение всех
этих преобразованных точек.
576
Глава 9. Приближение к бесконечности
Допустим, что аффинное отображение Г. описывается матрицей Мг В данном S-копире использу-
ются следующие матрицы:
fl > f i fl о
- 0 0 - 0 0 - 0 -
2 2 2 4
м, = 0-0 , м2 = 0 - - , м3 = 0 - -
2 2 2 2 2
0 0 1 0 0 1 0 0 1
к > < 7 < 7
так что каждая из них осуществляет масштабирование с коэффициентом 0,5 и соответствующее сме-
щение. (Нарисуйте выходное изображение, когда на вход подается треугольник с вершинами (-1, 0),
(1,0), (0,2).)
Элементы аффинного отображения удобно записывать в виде кортежа из шести элементов (вспом-
ните уравнение (5.4)):
T={mit, mi2, m2i, т22, mt3, т23). (9.2)
Первые четыре члена этого кортежа содержат элементы, выполняющие масштабирование и пово-
рот; два последних члена осуществляют смещение. Тогда три отображения S-копира имеют следую-
щий вид:
Т1-{0.5, 0. 0. 0.5. 0. 0}
Т2={0.5. 0. 0. 0.5. 0.5. 0). (9.3)
ТЗ={0.5. 0. 0. 0.5. 0.25, 0.25).
В общем случае копир содержит N линз, каждая из которых осуществляет аффинное преобразова-
ние и затем добавляет свое изображение к выходному. Барнсли [Barnsley, 93] назвал этот набор аффин-
ных преобразований «системой итерируемых функций».
Определение. Системой итерируемых функций (iterated function system — IFS) называется набор из
N аффинных преобразований Тр где i = 1,2,..., N.
Отметим, что данное определение вступает в противоречие с использованием нами ранее аббревиа-
туры «IFS», где для осуществления итерации могла использоваться любая функция, а не только аф-
финное преобразование или набор таких преобразований.
9.5.2. Теоретические основы процесса копирования
Для того чтобы описать, как формируется изображение в S-копире, введем несколько новых терминов.
Каждая линза копира создает изображение посредством преобразования каждой точки входного изоб-
ражения и рисования ее в выходном изображении. Черно-белое изображение I можно описать просто
множеством его черных точек: I - множество всех черных точек - {(г, у) таких, что (х, у) окрашено в чер-
ный цвет}.
Пусть Z— изображение на входе копира. Тогда i-я линза, характеризуемая преобразованием ТР стро-
ит новое множество точек, которое мы обозначим Т.(/), и добавляет его к изображению, создаваемому
при текущей итерации. Каждое добавленное множество Т.(/) является множеством всех преобразован-
ных точек изображения I:
Tt(I) = {(х', у') таких, что (х', у') = Т(Р) для некоторой точки Р в /}.
При совмещении этих трех преобразованных изображений мы получим выходное изображение как
объединение выходов из всех трех линз:
выходное изображение = T^I) и Т2(Г) и Т3(Г). (9.4)
9.5. Создание изображений с использованием системы итерируемых функций
577
Обозначим через W(.) суммарное преобразование от изображения на входе до изображения на
выходе (за один проход через копир). Оно преобразует одно множество точек — одно изображение —
в другое множество точек и определяется выражением:
I7(.) = 7’1(.)u7’2(.)u7’3(.). (9.5)
Например, «копия» первого изображения 10 — это множество W(I0).
А что произойдет, если мы будем циклически итерировать копии через копир бесконечное число
раз? То есть к какому изображению сходится орбита изображений /0, /2,...? Барнсли показал, что при
мягких ограничениях, накладываемых на IFS (грубо говоря, каждое аффинное отображение должно
хотя бы слегка «уменьшать» размер своего изображения1), орбита действительно сходится к единствен-
ному изображению, именуемому аттрактором (attractor) IFS2, то есть точкой притяжения. (Аттракто-
ром IFS в примере 9.5.1 является ковер Серпинского.) Будем обозначать аттрактор как множество А;
некоторые его важнейшие свойства приведены ниже.
1. Аттрактор А является неподвижной точкой отображения 1Г(.), другими словами, 1Г(А) = А. Это зна-
чит, что при повторном помещении А в копир он вновь выдаст то же самое изображение А. Грубо
говоря, итерации уже сошлись к множеству А, поэтому дальнейшее итерирование не изменяет его.
2. Если мы начнем с любого входного изображения В и будем итерировать процесс копирования
достаточное число раз, то мы обнаружим, что орбита изображений всегда сходится к одному и
тому же изображению А. Тогда, если обозначить Ik - W1*](B) — k-ю итерацию изображения В, то
при стремлении k к бесконечности Ik становится неотличимым от аттрактора А. Примечательно,
что выбор исходного изображения В не имеет значения [Barnsley, 11].
9.5.3. Рисование k-й итерации
Можно графически изобразить каждую итерацию вдоль орбиты. Исходное изображение IQ может быть
любым множеством, однако особенно подходят к уже разработанным нами программам два следующих
варианта:
О /0 — ломаная линия (вроде буквы F с рис. 9.30). В этом случае последовательность итераций так-
же представляет собой совокупность ломаных.
О /0 — изолированная точка. Тогда последовательные итерации являются совокупностью точек.
Использование в качестве начального изображения 10 ломаной линии имеет то преимущество, что
можно наблюдать, как ломаная уменьшается в размерах при каждой последующей итерации. Однако
для рисования каждой ломаной требуется больше памяти и времени, а нам известно, что каждая лома-
ная в конце концов уменьшится настолько, что станет неотличима от точки.
При использовании в качестве 10 изолированной точки каждая итерация будет представлять собой
множество точек, поэтому естественно сохранять их в списке. Тогда если система IFS состоит из N аф-
финных отображений, то первая итерация состоит из Nточек, изображение после итерации 12 состо-
ит из N2 точек, /3 — из N3 точек и т. д.
Пример 9.5.2. Папоротник
На рис. 9.31 показан пример, основанный на хорошо известной «папоротниковой» IFS.
Для папоротника используются четыре аффинных отображения, заданных следующими уравнени-
ями [Barnsley, И]:
Т1-{0. 0. 0. .16. 0. 0}:
Т2-{.2. .23. -.26. .22. 0. 1.6}; (9.6)
ТЗ“{-.15. .26. .28. .24. 0. .44};
Т4-{.85. -.04. .04. .85. 0. 1.6}.
1 Точнее, каждое аффинное преобразование должно быть сжимающим отображением (contraction mapping). Для этого достаточно,
чтобы матрица каждого преобразования 71 имела определитель, значение которого меньше единицы.
2 Часто используют термин «странный аттрактор» (strange attractor) — в случаях, когда изображение очень сложное.
19 Ф. Хилл
578
Глава 9. Приближение к бесконечности
Рис. 9.31. Папоротник
Отметим, что в данном примере первая матрица производит масштабирование в х-направлении с
нулевым множителем, формируя вертикальный стебель папоротника. Последняя матрица осуществля-
ет малый поворот и затем лишь незначительно уменьшает обрабатываемое изображение (примерно
до 85 %), поэтому копии уменьшаются очень медленно. Для достаточно больших значений k рисунок
^-итерации будет приближаться к аттрактору А данной IFS.
Листинг 9.4. Имитация действия копира (псевдокод)
void superCopier(RealPolyArray pts. int k)
{// Draw k-th iterate of input point list pts for the IFS
// Рисуем k-ю итерацию входного списка точек pts для IFS
int i;
Real PolyArray newpts:
// reserve space for new list
// выделяем пространство для нового списка
if(k ~ 0) drawPoints(pts);
else for(i = 1,- i <= N; i++)
// apply each affine
// применяем каждое аффинное преобразование
{
newpts.num = N * pts.num:
// the list size grows fast
// размер списка быстро возрастает
for(j = 0: j < newpts.num; j++)
// transform the j-th pt
// преобразуем j-ю точку
trar.sfvrm(affines[i], pts.pttj], newpts.pt(jj):
superCopl er(newpts. k - 1);
}
Какая же подпрограмма действительно рисует аттрактор (точнее, приближение к нему)? В листин-
ге 9.4 приведена ее рекурсивная версия. Эта подпрограмма принимает список точек pts и выполняет
следующие операции:
О Если k = 0, то она рисует точки из списка.
О Если k > 0, то она поочередно применяет каждое из аффинных отображений 7\ ко всем точкам, обра-
зуя при этом новый список точек newpts, после чего осуществляет вызов superCopier(newpts, к - 1).
9.5. Создание изображений с использованием системы итерируемых функций
579
Для реализации этого алгоритма предположим, что аффинные отображения записаны в глобальном
массиве Affine affines[N],
Данный метод работоспособен, однако имеет ряд недостатков. Один из них — это неэффективность:
в нем содержится много рекурсивных вызовов, каждый из которых требует дополнительных вычисле-
ний. Еще хуже то, что требуется огромное количество памяти: при k-ii итерации нужно нарисовать Nk
точек, и каждый! вызов подпрограммы superCopierO выделяет память под новый список точек. Все ак-
тивные в данный момент рекурсивные вызовы вынуждены хранить полный список точек. (А обычно
они записывают эти списки в системный стек!) К счастью, существует и нерекурсивный метод рисова-
ния аттрактора для IFS, известный под названием «Игра в Хаос» («Chaos Game»).
9.5.4. «Игра в Хаос»
Возможно, ангел Господень обследовал бесконечное море хаоса, затем слегка прикоснулся к нему пальцем.
В этом крошечном и преходящем водовороте уравнений приобрел форму наш космос.
Мартин Гарднер (Martin Gardner)
«Игра в Хаос», известная также под названием «Алгоритм случайных итераций» («Random Iteration
Algorithm»), предлагает простой нерекурсивный метод создания изображения аттрактора IFS [Barnsley, И,
Barnsley, 12]. Пример этого мы уже видели в главе 2 (см. тематическое задание 2.2) при рисовании ков-
ра Серпинского. В листинге 9.5 приводится псевдокод, вкратце показывающий, как это было сделано.
Листинг 9.5. Краткое описание процесса рисования ковра Серпинского (псевдокод)
Set corners of triangle: p[0]=(0,0).p[l]=(1.0).p[2]=(.5.1)
И задаем углы треугольника: ...
Set Р to one of these, chosen randomly:
И Задаем в качестве точки Р один из них. выбранный случайно
do{
Draw a dot at P:
// рисуем точку P
Choose one of the 3 points at random:
// выбираем случайным образом одну из трех точек
Set newPt to the midpoint of P and the chosen point:
// Задаем в качестве newPt середину отрезка между
// точкой Р и выбранной точкой
Set Р - newPt:
}whi1е(1 bored);
// пока не надоест
Точка, обозначенная буквой Р, преобразуется в точку, лежащую посередине между самой этой точ-
кой и одной из трех фиксированных точек: р[0], р[1 ], р[2], выбранной случайно. Затем рисуется эта
новая точка, после чего данный процесс повторяется (бесконечно).
Суть метода в том, что задание точки как середины отрезка с участием точки Р на самом деле являет-
ся аффинным преобразованием. Тогда
Р = (Р + /?[..]) (нахождение точки посередине между Р и р[..])
можно записать так:
так что точка Р подвергается действию аффинного отображения и затем ее преобразованная версия
записывается снова в Р. Сдвиг этого отображения зависит от того, какая точка p[i] выбрана.
580
Глава 9. Приближение к бесконечности
Рис. 9.32. Рисование ковра Серпинского
На рис. 9.32 схематически показан этот процесс. В каждый момент случайным образом выбирается
одно из трех аффинных отображений, и с его помощью преобразуется уже имеющаяся точка Р. Новая
точка рисуется и становится следующей точкой для преобразования.
Для ковра Серпинского эти три отображения задаются следующим образом (см. также уравнение (9.3)]:
Т, = {0,5,0,0,0,5,0,5 р[0]дг, 0,5 р[0].^}, рг, = 0,33;
Т2 = {0,5,0,0,0,5,0,5р[1]дг, 0,5рг2 = 0,33; (9.7)
Т3 = {0,5,0,0, 0,5,0,5р[2]л, 0,5 р[2].у}, рг3 = 0,33.
Вместе с каждым отображением приведен список вероятностей рг., с которой данное отображение
выбирается в каждой итерации; здесь все три отображения равновероятны.
Начиная с точки PQ, последовательность итераций в этой системе функций генерирует последова-
тельность точек Ро, Pv..., которые можно назвать орбитой (orbit) системы со стартовой точкой Ро. Тем
не менее данная орбита является случайной: посещаются различные точки — в зависимости от случай-
ного выбора, производимого при каждой итерации. Возникает вопрос: как выглядит полученная сово-
купность точек на графике?
Примечательно, что эта система рисует то же самое изображение, что и суперкопир на рис. 9.30! Это
означает, что при достаточно большом числе итераций орбита покроет весь аттрактор системы IFS, за-
данной уравнением (9.3). Идея данного подхода состоит в том, что аттрактор состоит из всех точек, «до-
стижимых» при применении длинной последовательности аффинных отображений в IFS в одну из то-
чек в исходном изображении. «Игра в Хаос» рисует точки, которые на самом деле являются результатом
длинной последовательности аффинных преобразований в IFS. Случайность выбора привлечена для
того, чтобы обеспечить «полноту охвата» системы, то есть чтобы каждая комбинация аффинных ото-
бражений использовалась когда-либо на протяжении процесса.
Мы можем обобщить вышеизложенное для произвольной системы IFS и сказать, что «Игра в Хаос»
создаст то же изображение, что и суперкопир1. Это верно для любой начальной точки и для любого ра-
зумного множества вероятностей, однако при надлежащем подборе вероятностей аттрактор выполнит
свою работу быстрее. Например, папоротник на рис. 9.31 был сделан при помощи «Игры в Хаос» и пре-
образований из уравнения (9.6). Были использованы следующие вероятности:
рГ] = 0,01, рг2 = 0,07, рг3 = 0,07, рг4 = 0,85 {вероятности для папоротника}. (9.8)
Листинг 9.6. Псевдокод для «Игры в Хаос»
void chaosGameCAffine aff[], double pr[]. int N)
{
RealPoint P - {0.0.0.0}:
Этот результат известен как эргодическая теорема Элтона (Elton's ergodic theorem). Ее доказательство, требующее привлечения
серьезной математики, представлено в работе [Barnsley, 10].
9.5. Создание изображений с использованием системы итерируемых функций
581
// set some initial point
// задаем какую-нибудь начальную точку
int index;
do{
index - chooseAffine(pr. N):
// choose the next affine
// выбираем следующее аффинное преобразование
Р - transform(aff[index], Р);
drawRealDot(P):
// draw the dot
// рисуем точку
} whileC!bored):
}
В листинге 9.6 приведена схема функции chaosGame (), которая «играет в Хаос». Эта функция рисует
аттрактор системы IFS, N преобразований которой записаны в массив aff[]. Вероятности, которые над-
лежит использовать, находятся в массиве рг[]. При каждой итерации одно из Nаффинных отображений
случайно выбирается с помощью функции chooseAff ine() и используется для преобразования предыду-
щей точки в последующую. Детали реализации функции chooseAffineO рассматриваются в тематичес-
ком задании 9.3, где создается проект для рисования нескольких любопытных аттракторов.
На рис. 9.33 приводятся еще два примера. На рис. 9.33, а показан аттрактор системы IFS дракона:
Т, = {.824074, .281482, -.212346, .864198, -1.882290, -0.110607}, рг, = .787473;
Т2 = {.088272, .520988, -.463889, -.377778, 0.785360, 8.095795}, рг2 = .212527.
На рис. 9.33, б показан аттрактор системы IFS спирали:
Т, » {.787879, -.424242, .242424, .859848,1.758647,1.408065}, рг, = .895652;
Т2 = {-.121212, .257576, .151515, .053030, -6.721654,1.377236}, рг2 = .052174;
Т3 = {.181818, -.136364, .090909, .181818, 6.086107,1.568035}, рг3 - .052174
Эти и многие другие примеры можно найти в превосходной программе FRACTINT, доступной в
Интернете [Fractint, 66].
а б
Рис. 9.33. Другие примеры аттракторов: а; дракон; 5) спираль
582
Глава 9. Приближение к бесконечности
Добавление цвета
До сих пор все изображения, образуемые при помощи «Игры в Хаос», являлись двухуровневыми: чер-
ные точки на белом фоне. Нетрудно расширить этот метод так, чтобы с его помощью рисовались полу-
тоновые и цветные изображения объектов. Изображение, как всегда, можно рассматривать как сово-
купность пикселов, и при каждой итерации преобразованная точка помещается в один из этих пикселов.
Для каждого пиксела поддерживается свой счетчик, и по завершении «игры» количество «посещений»
каждого пиксела переводится в цвет в соответствии с некоторым отображением. Данное расширение
метода рассматривается в тематическом задании 9.3.
Практическое упражнение
9.5.1. Использование FRACTINT
Скачайте из Интернета копию имеющейся в свободном доступе программы FRACTINT и исследуйте
возможности этой программы. В частности, выполните различные примеры для IFS. Кроме того, по-
смотрите в Интернете группу новостей alt.fractals.
9.5.5. Нахождение системы IFS; фрактальное сжатие
изображений
С помощью «Игры в Хаос» легко генерировать изображение, заданное системой IFS. А можем ли мы
пойти другим путем: можно ли утверждать, что имеющееся изображение является аттрактором для ка-
кой-нибудь системы IFS? И если это так, то можно ли найти эту IFS и с ее помощью сгенерировать
данное изображение при помощи метода наподобие «Игры в Хаос»?
Возможность невероятных степеней сжатия изображений вызывает сильное желание попытаться
найти такую систему IFS, аттрактором которой служит заданное изображение. Обычное изображение
может содержать миллионы байт данных, однако для записи коэффициентов аффинных отображений
в системе IFS требуются только сотни или тысячи байт. Рисунок 9.34 иллюстрирует процесс фракталь-
ного сжатия изображений (fractal image compression). В процессе обработки исходного изображения
создается список аффинных преобразований, и в результате получается чрезвычайно сжатое представ-
ление этого изображения.
Изображение/
Слисок
аффинных
отображений
«Сжатое
изображение»
Изображение /'
Рис. 9.34. Фрактальное сжатие изображений и их восстановление
На этапе «декомпрессии» используется список аффинных отображений; и изображение восстанав-
ливается при помощи такого алгоритма, как «Игра в Хаос». Отметим, что такая схема компрессии дан-
ных является сжатием с потерями (lossy): изображение Г, полученное в результате работы алгоритма
«декомпрессии», не является точной копией исходного изображения I.
Нахождение списка аффинных отображений
Главная хитрость состоит в нахождении списка аффинных отображений в течение разумного машин-
ного времени. Имея некоторое изображение (будем рассматривать его как множество всех его точек),
мы хотим найти систему IFS (то есть совокупность аффинных преобразований 7^.), Т2(.).таких,
чтобы изображение 1 являлось аттрактором данной IFS. Один из способов достичь этого заключается в
том, чтобы выбрать какие-нибудь аффинные преобразования, которые «выглядят подходяще», найти
9.5. Создание изображений с использованием системы итерируемых функций 583
аттрактор при помощи «Игры в Хаос», а затем сравнить изображение I с этим аттрактором и посмот-
реть, «достаточно ли похоже». Если нет, то мы корректируем IFS и повторяем попытку. Такой подход,
однако, обречен на неудачу: «пространство поиска» возможных систем IFS слишком велико для того,
чтобы этот метод мог быть применен на практике.
В поисках более плодотворного подхода вспомним, что аттрактор системы IFS является неподвиж-
ной точкой следующего преобразования:
W(.)»T1(.)uT2(.)u...TJV(.). (9.9)
Каждой IFS соответствует функция W(.), применение которой к изображению I равносильно од-
нократному пропусканию I через специальную копировальную машину, которая была описана ранее.
Итак, мы ищем такую систему IFS, чтобы данное изображение / являлось неподвижной точкой W(.).
Другими словами, должно соблюдаться равенство:
/= IV(7) (/— неподвижная точка). (9.10)
Барнсли сформулировал теорему о коллаже (collage theorem), в которой говорится, что если функ-
ция W(I) «близка» к изображению I, то аттрактор системы IFS также является «близким» к /*. Поэтому
нам не требуется впрямую работать с аттрактором. Вместо этого мы ищем в семействе IFS такую систему,
чья функция IV(.), будучи примененной к изображению I, генерирует изображение, близкое к I. Следо-
вательно, мы стремимся выразить изображение I в форме «коллажа» (объединения) его собственных
уменьшенных, повернутых и смещенных версий. (Целое слагается из частей; части являются уменьшен-
ными копиями целого.) Для ковра Серпинского базисная система IFS может быть найдена немедленно;
однако для большинства изображений неясно даже, существует ли для них вообще базисная система IFS.
Пространство поиска по-прежнему слишком велико для полностью автоматизированного подхода.
Первые созданные алгоритмы требовали вмешательства человека для руководства этим поиском. Вна-
чале пользователь пытается разбить изображение I на сегменты, каждый из которых похож на умень-
шенную (а также, возможно, повернутую и отраженную) копию всего изображения. Преобразование,
которое превращает это целое в данный сегмент, добавляется к списку аффинных преобразований. Пос-
ле выбора начальной совокупности преобразований пользователь сопоставляет I и W(I) и подбирает
коэффициенты этих аффинных преобразований при помощи какого-нибудь устройства ввода так, что-
бы приблизить W(I) к I. Несмотря на то что нахождение IFS таким способом требует очень быстрых
компьютеров и до сих пор осуществляется слишком медленно, Барнсли удалось подвигнуть компанию
Iterated Systems, Inc. (http://www.iterated.com/) к разработке фрактального сжатия изображений. В на-
чальной стадии Барнсли удавалось достигать степеней сжатия от 10 до 100. Настоящий прорыв был
осуществлен студентом Барнсли — Жакеном (Jacquin), который разработал систему разделенных ите-
рируемых функций (Partitioned Iterated Function System — PIFS). Эта система сделала наконец воз-
можным полностью автоматизировать процесс сжатия при разумных затратах машинного времени. На
рис. 9.35 показано, как работает одна из версий этой системы. Исходное изображение I разделяется
на некоторое число неперекрывающихся блоков пикселов размерностью четыре на четыре: Ro, R,
Для каждого такого блока Rt производится поиск в пределах пиксельной зоны D. размерностью восемь
на восемь внутри самого изображения, так чтобы он при соответствующем преобразовании совпадал с
7?.. Выбранные зоны могут перекрываться. Каждое преобразование включает в себя уменьшение вдвое
по обоим направлениям (поскольку размерность зоны равна восемь на восемь, а размерность блока —
четыре на четыре), а также смещение до совпадения положений зоны и блока. Это преобразование мо-
жет также включать в себя поворот и отражение.
Пиксельный рисунок в отображенной зоне может быть в достаточной степени похож на соответ-
ствующий рисунок в блоке, если не считать большую или меньшую яркость. Поэтому алгоритм поиска
также ищет наилучшее линейное преобразование уровней яркости пикселов зоны в уровни яркости
1 В этой теореме содержится достаточно сложная математика, поскольку Барнсли для измерения похожести двух изображений ис-
пользует специальное понятие «расстояния» между двумя множествами точек.
584
Глава 9. Приближение к бесконечности
пикселов блока1. В этом случае двумерные аффинные преобразования неизбежно превращаются в
трехмерные:
(9.11)
Рис. 9.35. Нахождение аффинных преобразований в системе PIFS
Здесь точка (х, у) преобразуется в точку (х', у’) обычным способом, а яркость b преобразуется в яр-
кость Ь' с использованием коэффициентов gvih. (Значение коэффициента g следует выбрать меньше
единицы — для того, чтобы данное преобразование было сжимающим.) Тогда закодированное изобра-
жение будет состоять из списка трехмерных аффинных преобразований, а также из информации о зоне
для каждого преобразования, например о координатах ее верхнего левого угла.
Теперь на стадии реконструкции мы больше не играем в чистую «Игру в Хаос». Вместо этого мы
начинаем с произвольного изображения 10, возможно, целиком состоящего из черных пикселов. Затем
при каждой итерации каждое преобразование из списка применяется ко всем пикселам в зоне этого
отображения. Поскольку блоки не перекрываются, то каждое такое преобразование изменяет значения
пикселов в одном наборе блоков. В силу того, что преобразование является сжимающим, последова-
тельность изображений Io, It,... будет гарантированно сходиться к неподвижной точке данного преоб-
разования — на практике этот процесс требует от 8 до 10 итераций.
Подробное исследование этого метода наряду с кодом на языке С для его реализации можно найти
в книге Марка Нельсона «Сжатие данных» (Mark Nelson. Data Compression — [Nelson, 145]). На рис. 9.36
приведено исходное изображение (занимающее 64 000 байт), на котором выделены две зоны и два
блока (на рисунке они крупнее, чем четыре на четыре или восемь на восемь). Имеет место сильное
сходство между одним блоком и одной зоной и также сильное сходство между другим блоком и дру-
гой зоной. (Между какими именно?) (Фрактальное сжатие уменьшает требуемое пространство до
2849 байт!)
На рисунке 9.37 приведено то же изображение, что и на рис. 9.36, заполняемое на различных этапах
фазы декодирования. Начиная с полностью черного изображения /0, на рисунке последовательно пред-
1 В случае цветных изображений данный процесс выполняется независимо три раза, для красного, зеленого и синего компонентов.
9.5. Создание изображений с использованием системы итерируемых функций
585
ставлены изображения /(, 12,13 и 1&. Даже изображение является вполне узнаваемым, а 1& уже очень
близко к аттрактору.
Рис. 9.36. Полутоновое изображение, на котором отмечены две зоны и два блока (с разрешения Jean-Loup Gailly)
Одним из свойств фрактального сжатия изображений является его независимость от разрешения
(resolution independence). В общем случае это означает, что можно увеличить восстановленное изоб-
ражение и увидеть больше деталей. Предположим, что исходное изображение имеет размеры 256 на
256 пикселов. Обычно мы восстанавливаем его тй аффинных преобразований, начиная с полностью
черного изображения 10 размером 256 на 256 пикселов. Если же в качестве 10 взять изображение 1024 на
1024 пиксела и выполнить итерации, то восстановленное изображение станет намного больше. В вос-
становленном изображении появится в четыре раза больше деталей, при этом не будет видно никакой
«блочности», характерной при чрезмерном увеличении изображения. Разумеется, в таком изображе-
нии не появится никакой дополнительной информации: увеличенная деталь — это всего лишь деталь
«самоподобия», добавленная к изображению. Эта дополнительная деталь делает изображение более
естественным, однако следует помнить, что она является искусственной.
в г
Рис. 9.37. Восстановление изображения по его аффинным преобразованиям (с разрешения Jean-Loup Gailly)
586 Глава 9. Приближение к бесконечности
9.6. Множество Мандельброта
Там, где мир перестает быть ареной личных надежд и желаний, там, где мы, как свободные существа,
с изумлением наблюдаем его, чтобы исследовать и созерцать, там мы вступаем в царство искусства
и науки. Если мы будем выражать то, что мы видим и переживаем, на языке логики, то мы будем
создавать науку; если же мы покажем это в формах, взаимосвязи которых недоступны для здравого
рассудка, но интуитивно признаются как значимые, то мы создаем искусство. Общим для них
является приверженность тому, что находится выше личного, далеко от случайного.
Альберт Эйнштейн (Albert Einstein)
В принципе... [множество Мандельброта] могло бы быть открыто уже тогда, когда человечество научилось
считать. Однако даже если бы мы никогда не уставали и никогда не делали ошибок, то всех людей, когда-
либо живших на Земле, не хватило бы на то, чтобы выполнить элементарные арифметические вычисления,
нужные для создания множества Мандельброта довольно скромной кратности.
Артур Ф. Кларк (Arthur F. Clarke), *Дух Большого рифа»
Графика предоставляет мощный инструмент для изучения занимательной коллекции множеств, кото-
рые считаются одними из самых сложных объектов в математике. Множества Жюлиа и множество
Мандельброта основываются на нескольких удивительно простых определениях; тем не менее они об-
ладают на редкость богатой структурой и, будучи отображенными с помощью компьютерной графики,
могут являть собой впечатляющие картины удивительной красоты. Множества Жюлиа изучаются в
разделе 9.7.
Множества Жюлиа и Мандельброта возникли из направления математического анализа, известного
как теория итераций (а также как теория динамических систем), в которой задаются вопросом: что
произойдет, если итерировать функцию неограниченно? Многие ключевые результаты теории итераций
были получены в начале XX века (конечно, без помощи компьютеров) Гастоном Жюлиа (Gaston Julia)
(1893-1978) и Пьером Фату (Pierre Fatou) (1878-1929). Их идеи длительное время не были востребо-
ваны, пока их в 1970-х годах не вернул к жизни и не расширил Бенуа Мандельброт (Benoit Mandelbrot).
В части своего исследования для осуществления основных экспериментов Мандельброт использовал
компьютерную графику, которая стимулировала ряд идей по многим направлениям, что привело к даль-
нейшим исследованиям и открытиям.
В некоторых работах (см., например, [Mandelbrot, 136, Peitgen, 156, Peitgen, 157]) можно найти не-
сколько интересных сообщений об этих исследованиях, а также прекрасные изображения, созданные
при помощи технологий, которые будут описаны в последующей части этой главы.
9.6.1. Множества Мандельброта и системы итерируемых функций
Начнем с рассмотрения вопросов, относящихся к обоим множествам — и Мандельброта, и Жюлиа.
Существует всего одно множество Мандельброта и бесчисленное число множеств Жюлиа, и они тес-
но связаны между собой. Изображение множества Мандельброта (Mandelbrot set) приведено на
рис. 9.38. Оно представляет собой внутреннюю зачерненную часть рисунка, которая состоит из кар-
диоиды с кругами, приклеенными к ней, словно бородавки. В действительности граница этого множе-
ства невероятно сложна, и эту сложность можно увидеть, если увеличить участок границы и произвес-
ти вычисления для изображения крупного плана. Теоретически такое увеличение можно продолжать
до бесконечности — граница является «бесконечно сложной». (В самом деле, это же фрактальная
кривая!) Каждая точка на рисунке затенена или раскрашена в соответствии с результатом экспе-
риментального прогона в системе IFS, схема которого представлена на рис. 9.39. В ней используется
очень простая функция:
/(z)=z2 + c, (9.12)
9.6. Множество Мандельброта
587
где с — некоторая константа. Это означает, что система генерирует каждый «выход» посредством воз-
ведения «входа» в квадрат и добавления константы с. Предположим, что данный процесс начинается со
стартовой величины (starting value) s, тогда данная система генерирует следующую последовательность
значений, или орбиту (orbit) (вспомним главу 2):
d{ = (s)2 + с,
d2 = ((s)2 + с)2 + с,
d3»((($)2 + с)2 + с)2 + с, (9.13)
^4 “ ((((S)2 + С)2 + С)2 + С)2 + С>
Отметим, что эта орбита зависит от двух параметров: стартовой точки 5 и заданного значения
константы с.
Рис. 9.38. Множество Мандельброта
Орбиты s являются главными объектами изучения во множествах Жюлиа и Мандельброта. Основ-
ной вопрос состоит в следующем: если задана пара значений s и с, то как поведут себя точки dk вдоль
орбиты по мере того, как k становится все больше и больше? В частности, останется ли эта орбита
конечной (finite) (все точки на орбите останутся на конечном расстоянии от 0), или она взорвется
(explode) (то есть умчится в бесконечность)? Как мы определим более точно позднее, те орбиты, кото-
рые остаются конечными, располагаются внутри соответствующего множества Жюлиа или Мандель-
брота, в то время как «взрывающиеся» орбиты лежат вне этого множества.
s
Рис. 9.39. Система итерируемых функций для множеств Жюлиа и Мандельброта
588
Глава 9. Приближение к бесконечности
Пример 9.6.1. Орбиты при с = О
Пусть с = 0. Тогда эта машина при каждой итерации просто возводит входное значение в квадрат. Про-
верьте каждое из нижеследующих утверждений.
О При 5=1 орбита равна: 1, 1, 1, 1, 1, 1, ..., и, безусловно, является конечной. (Чему равна орбита
приз = -1?)
О Орбита при s = 1/2 равна 1/2,1/4,1/8,1/16,..., и сходится к 0.
О Если |з| < 1, то орбита конечна; если |s| > 1, то орбита взрывается.
Пример 9.6.2. Нулевые орбиты (orbits of 0) для различных значений с
Теперь рассмотрим орбиты при нулевом стартовом значении.
О Пусть с = -1. Тогда орбита для s = 0 равна 0, -1, 0, -1, 0, -1,..., и принимает одно из двух значе-
ний в бесконечном цикле. Следовательно, орбита конечна.
О Пусть с = 1. Тогда орбита для 5 = 0 равна 0,1,2,5, 26, 677, то есть происходит взрыв.
О Пусть с = -1,3. Тогда орбита для s = 0 равна 0, -1,3, j и примерно после 50 шагов зацикливает-
ся в периодическую (periodic) последовательность из четырех значений: -1,148665,0,019430,
-1,299622, 0,389018, j до бесконечности.
? ? Конечная ? Взрывается
-I-1--1-- .-.—► с
-3-2-10 1 2
Рис. 9.40. Как ведет себя нулевая орбита при различных значениях с?
Можно попытаться изобразить полученные результаты графически, чтобы посмотреть, какой диа-
пазон значений с приводит к конечным орбитам. На рис. 9.40 показана первая такая попытка. Очень
поучительно поэкспериментировать с другими значениями с. К примеру, каково будет максимальное
значение конечной орбиты при увеличении с от 0?
Основные практические упражнения
9.6.1. Чему равны нулевые орбиты?
Вычислите (вручную или на калькуляторе) нулевые орбиты для следующих значений с:
О с = 0,5;
О с = -0,8;
О с = -1;
О с =-2;
О с = -1,2.
9.6.2. Чему равны орбиты?
Пусть с = -1. Вычислите орбиты при следующих значениях s:
О 5 = 0;
О 5 = -1;
О 5=1;
0 5 = 2.
Такая система уже проявляет любопытную «динамичность». Однако она приобретает неизмеримо
более богатые возможности в случае, когда с и s являются комплексными числами и при каждом приме-
нении функции используется комплексная арифметика. При этом множества Жюлиа и Мандельброта
9.6. Множество Мандельброта
589
«живут» («live») на комплексной плоскости — плоскости комплексных чисел. Напомним, что гра-
фически комплексные числа отображаются с помощью схемы, в которой каждое комплексное чис-
ло г - х + yi изображается как точка с координатами (х, у)1.
Система, схема которой приведена на рис. 9.39, отлично работает как с комплексными, так и с веще-
ственными числами. Пусть с и s — комплексные числа, при каждой итерации мы возводим в квадрат
предыдущее число и прибавляем с. Напомним (см. приложение Б), что при возведении в квадрат комп-
лексного числа г = х + yi получается новое комплексное число:
(х + yi)2 = (х2 - у2) + (2xy)i, (9.14)
вещественная часть которого равна х? - у2, а мнимая — 2ху. Снова зададимся вопросом о «конечности»
орбиты для s: станет ли «размер» орбиты при последовательных итерациях сколь угодно велик? Под
«размером» мы подразумеваем обыкновенный модуль: |х+уг| = ^х1 +у2.
Пример 9.6.3. Чему равна нулевая орбита для с = -0,2 + 0,5i?
Рассмотрим нулевую орбиту для с = -0,2 + 0,5г. Для вычисления итераций достаточно ручного кальку-
лятора, однако различные инструменты, имеющиеся на многих компьютерах, значительно упрощают
зти расчеты2. Получаем следующую орбиту:
4 = -0,2 + 0,5г,
d2 - -0,41 + 0,3г,
г/3 =-0,1219 +0,254г,
< - -0,2497 + 0,438г,
4 '
После приблизительно 80 итераций значения dk стремятся к следующему пределу: dk = -0,249227 +
+ 0,333677г. Это называется неподвижной точкой (fixed point) данной функции, поскольку возведение
ее в квадрат и прибавление с дает в точности такое же значение. (Проверьте это!) Разумеется, любая
орбита, сходящаяся к неподвижной точке, остается конечной. Таким образом, остается конечной и
орбита -0,2+0,5г.
Некоторые замечания относительно неподвижных точек системы
При исследовании множеств Мандельброта и Жюлиа полезно рассмотреть неподвижные точки систе-
мы: /(.) - (.)2 + с. Поведение орбит сильно зависит от этих неподвижных точек — то есть от таких ком-
плексных чисел z, которые отображаются сами в себя: г2 + с = г. Это приводит к квадратному уравнению
z2-z + c = 0, и неподвижными точками этой системы будут два решения этого уравнения, то есть
Р*,Р- = | ± ~ с. (9.15)
(Отметим, что, поскольку мы работаем с комплексными числами, извлечение квадратного корня из
числа ((1/4) - с) не будет проблемой, даже если оно отрицательное или комплексное. В приложении Б
показано, как вычислять такие квадратные корни в программе.) В предыдущем примере мы получили
неподвижную точку р_ = -0,249227 + 0,333677г. Вторая неподвижная точка равна р+ = 1,249323 - 0,333677г.
Если орбита когда-либо попадет в неподвижную точку, то она останется там навсегда. Две эти непод-
вижные точки расположены симметрично на одинаковом расстоянии (на каком?) от точки 1/2 + 0г.
1 Те читатели, которые незнакомы с комплексной арифметикой, могут тем не менее создавать изображения множества Мандельбро-
та с помощью компьютерной графики. Прочтите приведенный ниже материал, не особенно углубляясь в него, и перейдите к рас-
смотрению таких алгоритмов, которые работают исключительно с точками (х, у), имеющими вещественные координаты.
2 Одним из таких инструментов является программа Mathematica. На языке Mathematica выражение Дх_] := N[x*x + с] опреде-
ляет итерационную функцию, с задается формулой с - -.2 + .5/, а при вызове программы NextList[f, 0,80] на экран выводится
список первых 80 значений орбиты. А фактически все это может быть помещено в единственную компактную команду:
NextList[N[#\2 - .2 + ,5/&], 0,80].
590
Глава 9. Приближение к бесконечности
Мы лучше поймем суть неподвижной точки, если охарактеризуем ее как точку притяжения (attracl’ng)
или отталкивания (repelling). Грубо говоря, если орбита «пролегает» вблизи от неподвижной точки р,
то следующая точка вдоль этой орбиты будет вынуждена находиться
Q ближе к точкер, если р является неподвижной точкой притяжения;
О дальше от точки р, если р является неподвижной точкой отталкивания.
Если орбита приблизится на достаточно малое расстояние к неподвижной точке притяжения, то она
будет «всасываться» в эту точку. Напротив, неподвижная точка отталкивания «отдаляет» орбиту от
себя. Нетрудно показать (см. следующее упражнение), что неподвижная точка притягивает только тог-
да, когда она отстоит от начала координат на расстояние, меньшее 1/2, — то есть внутри круга радиуса
1/2 с центром в начале координат.
Практическое упражнение
9.6.3. Неподвижные точки притяжения
Пусть, как и в случае «ручного» вычисления, точка р является неподвижной точкой функции /(), и
выберем вблизи отр точку z: z = p + £, где е — малое комплексное число. Посмотрим, насколько далеко
отстоит от р функция /( ) — то есть чему равно выражение \f(p + е) -р|. Разложим функцию f(p + е)
в ряд Тэйлора: /(р + е) = f (р') + /'(р)е + [члены более высоких порядков], тогда для малых зна-
чений Е имеем: |/(р + е) - р| = |//(/’)||е|. Но |е| = \z-р\, |/(z) -р\ приблизительно равно |/'(p)||z-p!.
Следовательно, р является точкой притяжения (то есть |/(z) - р| меньше, чем \z - р\), если |/z(p)| < 1, и
точкой отталкивания, если \f'(p)1 > 1 Для нашей функции /'(z) = 2z, поэтому р является точкой при-
тяжения при |2р| < 1. Если же /фр)! = 1, то неподвижная точка не является ни точкой притяжения, ни
точкой отталкивания и носит название «индифферентной». Орбиты вблизи индифферентных точек
также могут быть весьма сложными [Peitgen, 157].
9.6.2. Определение множества Мандельброта
Множество Мандельброта может использовать различные значения константы с, но стартовая точка s
всегда равна 0. Для каждого значения константы с это множество дает информацию о природе нулевой
орбиты, первые несколько значений которой имеют вид:
нулевая орбита 0, с, с2 + с, (с2 + с)2 + с, ((с2 + с)2 + с)2 + с,... (9.16)
Для каждого комплексного числа с его орбита либо конечная, то есть вне зависимости от удаления
орбиты ее значения остаются конечными; либо взрывная, когда ее значения становятся бесконечно
большими. Множество Мандельброта, обозначаемое буквой М, содержит только такие значения кон-
станты с, которым соответствуют конечные орбиты.
О Точка с принадлежит множеству М, если нулевая орбита конечна.
О Точка с не принадлежит множеству М, если нулевая орбита взрывается.
Определение. Множество Мандельброта М — это множество всех комплексных чисел с, которым
соответствуют конечные нулевые орбиты.
(Отметим, что для данного значения с нулевая орбита становится орбитой с после одной итерации,
поэтому поведение орбит одинаково, если начинать с 0 или с с.)
На рис. 9.41 показано несколько примеров орбит для различных значений константы с, наложенных
на схематическое изображение множества Мандельброта, приведенное для ориентации. Каждая орби-
та показана в виде ломаной линии, начинающейся в соответствующем ей значении с, показанном точ-
кой на графике. (Мы могли бы нарисовать каждую орбиту с началом в точке 0, однако это загромоздило
бы график.) Обратите особое внимание на то, что каждая точка показывает соответствующее значение с,
используемое в итерационной системе/(.) = (.)2 + с, а также стартовую точку орбиты.
Если значение с выбрано вне множества М, то полученная орбита взрывается. На рисунке показаны
четыре взрывающиеся орбиты. Если значение с выбрано вне границ множества М, то орбита обычно
9.6. Множество Мандельброта
591
дико мечется по плоскости и наконец уносится в бесконечность. Такие орбиты затруднили бы понима-
ние картины и поэтому на рисунке не показаны. В тематическом задании 9.4 в конце главы приводится
скелет программы, рисующей орбиты для произвольных значений с. Это тематическое задание являет-
ся отличной тренировкой для развития интуиции относительно итераций функции (.)2 + с.
Рис. 9.41. Примеры орбит на плоскости с
Если же значение с выбрано внутри множества М, то соответствующая орбита Может вести себя по-
разному. Для некоторых значений с она сразу втягивается в неподвижную точку, для других — движет-
ся к этой точке по спирали (очень медленно, если с находится вблизи границы М).
Для того чтобы понять возможное поведение орбиты, полезно представить, что каждое значение с
определяет две неподвижные точки в соответствии с уравнением (9.15). Если одна из них является точ-
кой притяжения (это так, если она лежит внутри круга радиуса 1/2 с центром в начале координат), то
нулевая орбита сразу втягивается в эту точку. Несколько примеров таких орбит показано на рис. 9.41.
(Отметим, что точка с не то же самое, что неподвижная точка.) С другой стороны, если ни одна не-
подвижная точка не является точкой притяжения, то орбита не будет сходиться ни к какому определен-
ному значению. Вместо этого она будет втянута в некоторую циклическую последовательность значе-
ний, которая «крутится» вокруг одной из неподвижных точек отталкивания. К примеру, орбиты
для значений с, лежащих в маленьких кругах в верхней и нижней частях множества М, имеют период,
равный трем.
Практические упражнения
9.6.4. О неподвижных точках
Чему равны неподвижные точки для следующих значений с, есть ли среди них точка притяжения и если
есть, то какая?
О с = 0;
О с = 1 + г;
О с =-2;
О с= -2 + i.
9.6.5. Когда имеется неподвижная точка притяжения?
Опишите форму области на плоскости с, для которой система (,)2 + с имеет неподвижную точку притя-
жения. Все ли значения с находятся внутри множества Мандельброта?
592
Глава 9. Приближение к бесконечности
9.6.6. Почему множество Мандельброта симметрично?
Зеркальное отражение числа с = х + yi относительно оси х представляет собой число, сопряженное
(conjugate) числу с: с* = х - yi. Как связана орбита, найденная для числа с*, с орбитой, соответствующей
числу с? (Подсказка: (z*)2 = (z2)*.) Используйте это соотношение для доказательства того, что с* при-
надлежит множеству М тогда и только тогда, когда этому множеству принадлежит с.
9.6.3. Определение того, находится ли точка с в пределах
множества Мандельброта
Нам нужна подпрограмма, которая может определить, принадлежит ли данное комплексное число с
множеству М. При стартовой точке s - 0 эта подпрограмма должна определить размер чисел dk вдоль
орбиты согласно уравнению (9.13). С ростом k значение или «взрывается» (тогда с не принадле-
жит М), или нет (тогда с принадлежит М). Одна из теорем комплексного анализа гласит о том, что если
значение какого-либо превысит 2, то орбита взорвется в некоторой точке. Число итераций, необхо-
димое для того, чтобы |rfj превысило 2, называется временем жизни (dwell) данной орбиты (возможно,
термин происходит от того, как долго орбита «живет» в области).
Если же точка с лежит внутри М, то соответствующая орбита имеет бесконечное время жизни, и мы
не можем узнать об этом без бесконечного итерирования. Лучшее, что тут можно сделать, — это задать
верхний предел Num максимального числа итераций, которое мы готовы ожидать. Типичное значение для
Num = 100. Если |JJ не превосходит числа 2 за Num итераций, то мы предполагаем, что оно и не превзойдет его
никогда, и приходим к выводу, что точка с находится внутри М. Часто случается, что орбиты для значений с,
лежащих сразу за границей М, обладают чрезвычайно большим временем жизни, и если это время жизни
превосходит Num, то мы ошибочно считаем их лежащими внутри М. (Можно ли когда-нибудь ошибиться
относительно точек с, лежащих внутри М?) Следовательно, если рисовать множество Мандельброта на
базе слишком малого значения Num, то оно получится несколько большим, чем должно быть на самом деле.
Листинг 9.7. Оценка времени жизни
int dwell(double сх. double су)
// return true dwell or Num, whichever is smaller
// возвращаем меньшую из величин:
// истинное время жизни или Num
#define Num 100
// increase this for better pictures
// увеличиваем его для улучшения изображений
double tmp. dx ° ex, dy ° cy, fsq ° сх * сх + су * су:
for(int count - 0; count <- Num && fsq <- 4: count++)
tmp - dx;
// save old real part
// сохраняем старую вещественную часть
dx - dx * dx - dy * dy + ex:
// new real part
// новая вещественная часть
dy - 2.0 * tmp * dy + cy:
// new imag. part
// новая мнимая часть
fsq - dx * dx + dy* dy:
1
return count:
// number of iterations used
// число использованных итераций
9,6. Множество Мандельброта
593
Инкапсулируем эти вычисления в подпрограмму dwell О, приведенную в листинге 9.7. Для заданно-
го значения с = сх + ci эта подпрограмма возвращает число итераций, достаточное для того, чтобы
превзошло 2, или само значение Num, если после Num итераций число 2 не было превзойдено. Для удоб-
ства сделано так, что подпрограмма dwell О сама определяет тип данных своего параметра.
При каждой итерации текущее значение dk хранится в виде пары (dx, dy), которая возводится в квад-
рат согласно равенству (9.14) и затем прибавляется к паре (сх, су), образуя тем самым следующее значе-
ние dk. Затем |JJ2 записывается в fsq и сравнивается с 4. Такое сравнение эквивалентно сравнению с 2, и
в то же время не нужно вычислять квадратный корень.
Функция dwell () играет ключевую роль при рисовании множества Мандельброта.
9.6.4. Рисование множества Мандельброта
Предположим, что мы хотим отобразить множество М на растровом дисплее. Для того чтобы сделать
это, мы задаем соответствие между каждым пикселом на дисплее и значением с и находим для этого с
время жизни. Каждому пикселу присваивается цвет в зависимости от того, конечно ли это время жизни
или оно достигло своего предела.
В простейших изображениях множества Мандельброта М точкам, находящимся внутри М (там, где
время жизни достигло своего максимума), присваивается черный цвет, а точкам, находящимся вне М
(где время жизни меньше максимального значения) — белый цвет. Однако изображения становятся
намного приятнее для глаза, если с точками вне множества М связан целый диапазон цветов. Все эти
точки обладают временем жизни меньше максимума, и им можно присвоить различные цвета в зависи-
мости от длительности времени их жизни. Можно, например, присвоить ярко-желтый цвет точкам, ко-
торые находятся сразу за границей множества М, и более темный желтый для тех, которые дальше от
границы М. Это сделает границу М очень четкой и яркой. На рис. 9.42 показано, как можно назначить
цвет точке, имеющей время жизни d. Для очень малых значений d используется только темно-синяя
составляющая. По мере достижения величиной d значения Num красного и зеленого компонентов (совме-
стно образующие желтый цвет) возрастают до максимального единичного значения. Это можно реали-
зовать в OpenGL следующим образом:
float v - d/(float)Num;
glColor3f(v * v, v*. v. 0.2):
// red & green at level v-squared
// красный и зеленый на уровне v в квадрате
Интенсивности
цветов
Рис. 9.42. Присвоение цветов в зависимости от времени жизни орбиты
Последнее, что нам нужно сделать, — это определить, как связать пиксел с определенным комплекс-
ным значением с. На рис. 9.43 предлагается простой подход: пользователь задает желаемую величину
изображения на экране, то есть:
О число строк (rows) например, rows - 80,
О число столбцов (cols) например, cols = 120.
Это задание определяет форматное соотношение экрана: R = cols/rows. Кроме того, пользователь вы-
бирает изображаемую часть комплексной плоскости: прямоугольную область с таким же форматным
соотношением, как у изображения. Для этого пользователю достаточно задать верхний левый угол этой
594
Глава 9. Приближение к бесконечности
области Р и его ширину W. (Например, можно задать Р = -1 + 0,5i [при другой форме записи Р = (-1,0,5)]
и W = 0,5.) Все остальное сделает компьютер. Высота прямоугольника определяется требуемым фор-
матным соотношением. Мы будем рисовать изображение в верхнем левом углу дисплея, как показано
на рисунке.
Рис. 9.43. Установка окна над множеством М и соответствие между точками и пикселами
Какой же комплексной величине с = сх + cj соответствует центр (i,j)-ro пиксела? После преобразо-
ваний компонентов мы видим, что оно должно быть равно:
си ~
Рх+—2.^, р-------2.^
cols cols
(9.17)
где i - 0.cols -1 и; - 0,..., rows -1. (Проверьте это!)
Выбранная область множества Мандельброта рисуется пиксел за пикселом. Для каждого пиксела
соответствующее ему значение с передается в подпрограмму dwel 10 и находится подходящий цвет, свя-
занный с временем жизни. Затем пиксел окрашивается в этот цвет. В листинге 9.8 приведен алгоритм в
форме псевдокода.
Листинг 9.8. Псевдокод для рисования части множества Мандельброта
for(j - 0: j < rows: j++)
ford - 0: 1 < cols: 1++)
{
find the corresponding c-value in Equation 9.17
// находим соответствующее значение с по уравнению 9.17
estimate the dwell of the orbit
// оцениваем время жизни орбиты
find Color determined by estimated dwell
И находим цвет, определенный заданным временем жизни
setPixeKj. k. Color);
На практике проблема заключается в том, что для изучения больших увеличений множества Ман-
дельброта числа должны храниться и обрабатываться с большой точностью. Следует использовать
арифметику двойной точности (и даже выше). Кроме того, при работе вблизи от границы множества
приходится использовать большие значения Num, что уже обсуждалось ранее. Следовательно, количе-
ство вычислений для каждого изображения будет возрастать при увеличении области границы множе-
ства М. В то же время изображения ограниченных размеров легко создавать на микрокомпьютерах за
разумное время, и результаты вполне оправдывают ожидания (см. тематическое задание 9,5).
9.7. Множества Жюлиа
595
9.6.5. Некоторые замечания по поводу множества Мандельброта
Каковы же свойства множества Мандельброта и его искрометных расширений? Это множество иссле-
довалось многими математиками, вследствие чего о нем известно много интересных фактов. В работах
[Mandelbrot, 136, Peitgen, 156, Peitgen, 157] изложены различные идеи: в этих книгах содержится мно-
жество великолепных изображений, выполненных только что рассмотренным нами способом. Вот не-
которые из содержащихся там сведений:
1. Точки с = -1 и с = -2 всегда находятся внутри множества М (почему?), и, как отмечалось ранее,
М симметрично относительно вещественной оси.
2. Самые большие «пятна» (blobs) множества Мандельброта были изучены весьма подробно [Пайт-
ген и Рихтер — Peitgen, Richter, 156]:
• граница главного пятна множества М является кардиоидой со следующим параметрическим
представлением:
с.х = 0,25 + 0,5(1 - cos(t)) cos(£); (9.18)
с.у - 0,5(1 - cos(t)) sin(t).
Орбиты внутри этой кардиоиды притягиваются к неподвижным точкам, являющимся одним
из двух решений уравнения а2 + с = z (почему?);
а круг слева от кардиоиды имеет радиус 1/4 и центр в точке св-1. Орбиты внутри этого круга
становятся периодическими с периодом 2;
• меньший круг слева от только что рассмотренного круга имеет радиус 0,0607 и центр в точке
с = -1,3107. Орбиты внутри этого круга также являются периодическими с периодом 4;
9 круги выше и ниже кардиоиды имеют радиус 0,0954 и центры в точке с = -0,1226 ± 0,7449/.
Орбиты внутри этих кругов являются периодическими с периодом 3.
3. Граница множества Мандельброта — это наиболее интересный предмет для изучения; факти-
чески она является фрактальной кривой. При сколь угодно большом увеличении какого-либо
се участка — путем использования все меньших и меньших окон, — постоянно проявляются
все новые подробности. При каждом увеличении становится видимым новый мир подроб-
ностей. Например, то, что было одиночной черной точкой при одном увеличении, становится
целой «бородавкой» («wart») при следующем увеличении («А этих блохи меньшие грызут //
II нескончаем вечный этот зуд»). Оказывается, что никакие две из этих миниатюрных борода-
вок в точности не совпадают. Другой поразительный факт, доказанный Джоном X. Хаббардом
(John Н. Hubbard) из Корнельского университета, заключается в том, что множество Ман-
дельброта является связным (connected) [Dewdney, 55]: хотя самые мелкие бородавки кажутся
свободно «плавающими» на плоскости, всегда существует тончайший усик из точек, принад-
лежащих множеству Мандельброта, который соединяет эти бородавки с родительским мно-
жеством.
9.7. Множества Жюлиа
Подобно множеству Мандельброта, множества Жюлиа являются чрезвычайно сложными множества-
ми точек на комплексной плоскости. Для каждого значения параметра с существует свое множество
Жюлиа, обозначаемоеJe Тесно связанной с ним вариацией является плотное множество Жюлиа (filled-
in Julia set); обозначаемое X. Это множество определяется проще, поэтому с него и начнем.
596
Глава 9. Приближение к бесконечности
9.7.1. Плотное множество Жюлиа Кс
Рассмотрим снова систему итерационных функций (IFS), показанную на рис. 9.39, однако теперь при-
дадим константе с некоторое фиксированное значение и посмотрим, что произойдет для различных стар-
товых точек s. Как и прежде, мы интересуемся поведением орбиты для стартовой точки з. Орбита эта
или взрывается, или нет. Если данная орбита конечна, то говорят, что точка с лежит внутри множества
Кс, а в противном случае — вне его. Тогда имеет место следующее определение.
Определение. Плотным множеством Жюлиа Кс в точке с называется множество всех стартовых то-
чек, орбиты которых конечны.
Отметим, что данное определение отличается от определения множества Мандельброта: при иссле-
довании множества М рассматриваются различные значения с и неизменно используется стартовая точ-
ка 0; при исследовании же множества Кс выбирается единственное значение с и рассматриваются раз-
личные стартовые точки. Несмотря на сходство определений, неясно, имеется ли сильная связь между
этими двумя множествами. Однако глубокая связь между ними действительно существует.
Отметим, что множество Кс всегда должно быть симметричным относительно начала координат,
поскольку орбиты для з и -з становятся идентичными уже после одной итерации. (В противополож-
ность этому, множество Мандельброта симметрично только относительно вещественной оси.)
9.7.2. Рисование плотных множеств Жюлиа
Поскольку расположение стартовой точки з внутри множества Кс зависит от того, является ли ее орби-
та конечной или взрывной, процесс рисования плотного множества Жюлиа почти идентичен аналогич-
ному процессу для множества Мандельброта. Мы снова выбираем окно в комплексной плоскости и свя-
зываем пикселы с точками этого окна. Однако теперь пикселы соответствуют различным значениям
стартовой точки з. Выбирается единственное значение параметра с, после чего для каждой позиции
пиксела исследуется орбита на предмет того, взрывается ли она и если да, то как быстро она это делает.
Поэтому в листинге 9.8 достаточно просто заменить строку псевдокода
find the corresponding c-value in Equation 9.17
// находим соответствующее значение с по уравнению 9.17
на строку
find the corresponding s-value in Equation 9.17
// находим соответствующее значение s по уравнению 9.17
Конечно, в подпрограмму dwel 10 из листинга 9.7 наряду со значением с должно теперь передаваться
также значение з, а для правильного запуска орбиты строку d = с следует заменить строкой d = з.
Иллюстрация 28 демонстрирует примеры такого рисования для с = -0,5 + 0,58г и с = -0,76 + 0,147г.
Первое значение с лежит внутри множества М, так что его множество Кс является связной областью. Вто-
рое значение с лежит вне М, поэтому для него множество Кс представляет собой так называемое «пылевое
облако Фату» («Fatou dust»). Много дополнительных изображений можно найти в работе [Peitgen, 156].
Как и в случае множества Мандельброта, создание высококачественного изображения множества Кс
требует огромных затрат машинного времени, поскольку за каждым пикселом стоят сложные вычисления.
В дальнейшем мы рассмотрим альтернативный метод ускоренного нахождения границы множества Кс.
9.7.3. Некоторые замечания относительно неподвижных
точек и бассейнов притяжения
Обратимся снова к природе неподвижных точек функции /(.) = (.)2 + с для более глубокого понимания
поведения различных орбит. Здесь легче разобраться в их поведении, чем в случае множества Мандель-
брота, поскольку активным является только одно значение с; вместо варьирования с мы рассмотрим
разворачивание орбит из различных стартовых точек.
9.7. Множества Жюлиа
597
Пример 9.7.1
В качестве разминки интересно проделать вручную несколько вычислений для множества Жюлиа, свя-
занных со значением с - -1. Вопрос стоит так: какие стартовые точки принадлежат множеству К?
Разумеется, обе неподвижные точки должны являться стартовыми точками (почему?), поэтому внача-
ле найдем именно их. Из равенства (9.15) сделаем приятный вывод: неподвижные точки связаны с золо-
тым соотношением
0 = (1+^5)/2 = 1,618...:
Неподвижные точки для с = -1:р+ = 0 = 1,618... и/?_ - -1/0 = -0,618... . (9.19)
Рассмотрим некоторые «общеупотребительные» стартовые точки:
О з = 0. Орбита равна 0, -1, 0, -1, 0.и так до бесконечности. Поэтому 0 находится внутри К г
Кстати, там же лежит и -1. (Почему?)
О з = л/0 . Орбита равна (проверьте это!) -^ф , 1/0, -1/0, -1 /0.так что попадание в неподвижную
точку происходит уже после нескольких итераций. Поэтому данное значение з, так же как и з = 1/0,
лежит внутри K_v
О з = 0,5. Вычисление вручную дает следующую орбиту: 0,5, -0,75, -0,4375, -0,809, -0,346, j, что,
в конце концов, захватывается в цикл 0, -1, 0, -l,j, который, разумеется, является конечным.
Таким образом, все числа в данной орбите также лежат внутри К г
Все это выглядит вполне «правильным», однако в дальнейшем мы увидим, что множество Кна са-
мом деле является чрезвычайно сложным!
Практическое упражнение
9.7.1. Какие из этих точек лежат внутри К -1?
Пусть с = -1. Какие из нижеперечисленных стартовых точек лежат внутри плотного множества Жюлиа?
О з = -0,5,
О з = ±1,
О з = ±2,
О з = ±1,5.
Обобщая, можно сказать, что если орбита начинается достаточно близко от неподвижной точки при-
тяжения, то орбита «всасывается» в эту точку. Если Же орбита начинается слишком далеко, то она взры-
вается. Множество тех точек, которые «всасываются», образуют так называемый бассейн притяжения
(basin of attraction) неподвижной точки р. Это множество в точности совпадает с плотным множеством
Жюлиа Кс. Нетрудно показать, что неподвижная точка, лежащая внутри круга |z| = 1/2 (с центром в нача-
ле координат и с радиусом 1/2), является точкой притяжения.
На рис. 9.44 схематически изображено множество Жюлиа при с = 0,32019 + 0,25694г. (Для простоты
на рисунке проведена только граница множества Кс.) Кроме того, на рисунке показаны заданное значе-
ние с и две неподвижные точки (0,18681 + 0,4102 И и 0,81319 - 0,41021г). Все точки, находящиеся вне К,
имеют взрывающиеся орбиты; на рисунке показан пример такой орбиты. Все точки внутри Кс имеют
орбиты, которые прямо или по спирали втягиваются неподвижной точкой притяжения; два примера
таких орбит также приведены на рисунке.
Отметим, что если стартовая точка лежит внутри множества Кс, то все точки ее орбиты также долж-
ны лежать внутри К., поскольку они сами являются полноправными стартовыми точками и все они об-
разуют конечную орбиту. Также отметим, что неподвижная точка отталкивания находится на границе
множества Кс. Это имеет место всегда.
598
Глава 9. Приближение к бесконечности
Рис. 9.44. Некоторые орбиты при с = 0,32019 + 0,25694!
Множество Кс для двух простых случаев
Оказывается, что при двух значениях с множество Кс имеет простой вид (но только для этих случаев).
1. с = 0: при старте из произвольной точки з орбита равна з, з2, з4, ..., з2*.поэтому орбита всасы-
вается по спирали в 0 при |s| < 1 и взрывается при |s| > 1. Следовательно, Ко является множеством
всех комплексных чисел, лежащих внутри единичного круга (unit circle), а именно круга с радиу-
сом 1 с центром в начале координат. (Где в этом случае находятся две неподвижные точки?)
2. с “ -2: в этом случае оказывается, что плотное множество Жюлиа состоит из всех точек, лежа-
щих на вещественной оси между -2 и 2. Доказать это отнюдь не просто [Peitgen, 156], однако
легко проиллюстрировать, вычислив вручную соответствующие орбиты (как минимум несколь-
ко первых дюжин точек) для различных стартовых значений в интервале от -2 до 2.
Для всех остальных значений с множество Ке является чрезвычайно сложным. (Фактически оно
является фракталом!) Доказано, что каждое множество Kt принадлежит к одному из двух типов
[Peitgen, 157]:
О Кс — связное множество (оно состоит из одного «куска»);
О К. — множество Кантора (Cantor set), то есть является «пылевым облаком»1.
Замечательным теоретическим результатом является то, что Кс является связным множеством в
точности для тех значений параметра с, которые лежат внутри множества Мандельброта! Поэтому
в примере 9.71, где с = -1 и лежит внутри М, множество К— связное, однако по-прежнему является
фракталом.
1 Классическое множество Кантора базируется на вещественном интервале [0,1]. Удаляем среднюю треть этого интервала, так что
остаются интервалы [0,1 /3] и [2/3,1]. Теперь удаляем среднюю треть каждого из этих интервалов, затем среднюю треть каждого
из оставшихся и т. д. В пределе остается бесконечное число точек, однако между ними нет промежутков. (Если каждую точку
представить в троичной системе счисления (например, так: 0.012100201), то в представлениях остающихся точек не будет содер-
жаться единиц.)
9.7. Множества Жюлиа
599
9.7.4. Множество Жюлиа Jc
Нетрудно декларировать, чем является множество Жюлиа для любого заданного значения с: оно явля-
ется границей множества Кс. Поскольку Кс — это множество всех стартовых точек, имеющих конечные
орбиты, то каждая точка вне Кс обладает взрывной орбитой. Можно сказать, что все точки вдоль грани-
цы Кс «занимают выжидательную позицию»: чуть-чуть внутрь границы — и все орбиты остаются ко-
нечными; чуть-чуть вне ее — и все орбиты улетают в бесконечность. Если точка з принадлежит множе-
ству^, то любое сколь угодно малое возмущение з фундаментальным образом изменяет ее орбиту. Это
очень близко к понятию хаоса, рассматриваемому в тематическом задании 3.1: бесконечно малые изме-
нения в системе приводят к кардинально различному поведению.
Прообразы и неподвижные точки
Для развития интуиции по этим вопросам следует рассмотреть орбиту точки з согласно уравне-
нию (9.13). Что будет, если процесс начнется в точке/(з) — образе (image) з? Тогда две орбиты будут
иметь вид:
s>/(s),/2(s),/3(s)> ••• (орбита з)
или
/(s)./2(s),/3(s),/\s),...
(орбита /(з)),
которые и в дальнейшем будут принимать одинаковые значения. Тогда, как упоминалось ранее, если
орбита з конечна, то конечна и орбита его образа/(з). Действительно, все точки орбиты, если рассмат-
ривать их как их собственные стартовые точки, обладают орбитами с одинаковым поведением: они или
все конечны, или все взрываются.
Поэтому можно «заранее» пойти другим путем и сказать, что любая стартовая точка, орбита кото-
рой проходит через точку з, ведет себя так же, как орбита, стартующая в самой точке з: эти две орбиты
идентичны с этого момента и навсегда. Точка, стоящая в последовательности «непосредственно перед»
точкой з, называется прообразом (preimage) точки з и равна значению функции, обратной к/(.) = (,)2 + с.
Эта обратная функция равна +yjz-c, откуда получим:
два прообраза z равны ±<Jz-c . (9.20)
Чтобы убедиться в правильности уравнения (9.20), отметим, что если любой прообраз пропустить
через функцию (,)2 + с, то результат будет равен з. Этот тест приводится на рис. 9.45, а, где черными точками
показана орбита з и отмечены оба прообраза точки з. Две орбиты этих прообразов «объединяются» в орби-
ту з. На самом деле каждый из этих прообразов тоже имеет два своих прообраза, а каждый из них —
свои два, так что существует огромное число орбит, объединяющихся в орбиту точки з, после чего они идут
по одному пути. Это «дерево» прообразов з изображено на рис. 9.45, б: точка з имеет два родительских
прообраза, 4 прародительских и т. д. Вернувшись на /г «поколений» назад, мы найдем там 2к прообразов.
Пример 9.7.2
Пусть с = -1. В предыдущем примере мы видели, что нулевая орбита равна 0, -1, 0, -1.то есть совер-
шает вечный цикл с периодом 2. Если мы рассмотрим прообразы 0 и каждый из их прообразов и т. д.,
то увидим, что существует много других значений, орбиты которых «втянуты» в этот 2-цикл:
О прообразы 0 равны ±1;
О прообразы+1 равны ±^2;
О прообразы -1 равны 0;
О прообразы +^2 равны ±-\Д/2 + 1 = ±1,553;
О прообразы -^2 равны ±(>Д/2+ 1 = ±1,6435г;
и т. д.
Чему равны прообразы ±1,553?
600
Глава 9. Приближение к бесконечности
а б
Рис. 9.45. Орбиты, совпадающие в точке s
На рис. 9.46 стрелками показано, как одни комплексные числа отображаются в другие при с = -1.
Точка 1,6435г достигает -1 после четырех шагов. (Находится ли точка 1,6435г внутри плотного множе-
ства Жюлиа К_?)
Какое значение имеют прообразы для определения множества Жюлиа? Множество Жюлиа Jc мож-
но охарактеризовать различными способами, которые более точны, чем простая декларация того, что
оно является «границей» множества К. Одна такая характеристика [Peitgen, 156], предлагающая алго-
ритм рисования Jc, имеет следующий вид:
Совокупность всех прообразов любой точки множества Jc плотна в Jc.
Это означает, что, стартуя из любой точки z в множестве Jc, мы просто вычисляем два ее родитель-
ских прообраза, четыре их прародительских прообраза, восемь пра-прародительских прообразов и т. д.
Таким образом, мы рисуем точку для каждого такого прообраза, и дисплей заполняется изображением
множества Жюлиа. То, что эти точки «плотны» в Jc, означает, что для каждой точки в Jc существует
9.7. Множества Жюлиа
601
сколь угодно близкий прообраз. Не накладывается никаких ограничений на число предыдущих «поко-
лений», которые нужно обследовать, чтобы найти нужное количество точек в множестве Jc.
Рисование множества Жюлиа Зс
Для того чтобы нарисовать Jc, необходимо только найти принадлежащую ему точку и поставить графи-
ческие точки в местах всех прообразов этой точки из множества. Тем не менее при применении этой
техники возникают две проблемы:
1. Нахождение точки, принадлежащей множеству Jc.
2. Отслеживание всех ее прообразов (их 2к для k поколений).
С обоими этими затруднениями справляется так называемый метод обратных итераций (backward-
iteration method), который обычно дает хорошие результаты. Идея этого метода проста: выберем
какую-нибудь точку z на комплексной плоскости. Эта точка может принадлежать, а может и не принад-
лежать множеству]с. Теперь начнем итерировать назад: при каждой итерации случайным образом вы-
бираем один из двух квадратных корней и получаем новое значение z. Это можно проиллюстрировать
следующим псевдокодом:
do{
if(coin flip is heads z = + -Jz-c else z = - y/z-c;
// если монета упала орлом ... если решкой ...
draw dot at z;
// рисуем точку в z
}wh11e (not bored):
// пока не надоест
И появится изумительное изображение JJ. Идея метода состоит в том, что при любой подходящей
стартовой точке уже несколько «итераций назад» приведут к точке z, принадлежащей Jc. Как будто об-
ратная орбита «всасывается» в множество Жюлиа [Peitgen, 156]. Поскольку она принадлежит множе-
ству Жюлиа, все последующие обратные итерации должны остаться там же, поэтому точка за точкой
строятся во внутренней области Jc и появляется изображение множества. Поскольку прообразы плотно
расположены в J, нам известно, что достаточно продолжительное итерирование сгенерирует мно-
жество графических точек, сколь угодно близких ко «всем» точкам множества Jc. (Неудачный выбор
стартовой точки может привести к более медленному заполнению некоторых узоров по сравнению
с другими.)
Практическое упражнение
9.7.2. Альтернативные множества Жюлиа
Множества Жюлиа базируются на функции (,)2 + с, однако с таким же успехом можно итерировать и
другие функции [Peitgen, 156, Pickover, 163]. Напишите программу, рисующую множества Жюлиа для
следующих функций:
О /(.) = ch(.) + с, где ch(z) = (ег + е~г). (Выясните, как вычислять е* от комплексного аргумента г.)
/(г) = z
z3 -1
3z2
, которая является итерационной функцией метода Ньютона для решения урав-
нения г3 - 1 = 0 [Barnsley, 10].
Другие примеры можно взять из программы FRACTINT [Fractint, 66].
602
Глава 9. Приближение к бесконечности
9.8. Случайные фракталы
Хаос и случай — именно этими словами можно описать явление, о котором мы не знаем ничего.
Свен Г. Карлсон (Sven G. Carlson)
Описанные нами до настоящего момента фрактальные формы являются полностью детерминированны-
ми: при их создании не используется никаких элементов случайности и их формы целиком предсказуемы
(хотя и очень сложны). Однако в графике термин «фрактал» получил широкое распространение в свя-
зи с кривыми и поверхностями, генерируемыми случайным образом и обладающими определенным
уровнем самоподобия. Такие кривые используются при моделировании «естественных» форм таких
объектов, как береговые линии, скалистые горы, трава и огонь.
9.8.1. Фрактал изация отрезка
Пожалуй, самый простой случайный фрактал можно сформировать при помощи рекурсивного «взлох-
мачивания», или «фрактализации», отрезка прямой. При каждом шаге каждый отрезок прямой заме-
няется «случайным коленом». Этот процесс показан на рис 9.47 применительно к отрезку прямой S
с концевыми точками А и В. Отрезок 5 заменяется двумя отрезками: от Л до С и от С до В. Для созда-
ния фрактальной кривой точка С выбирается случайным образом вдоль срединного перпендикуля-
ра L отрезка S. Колено случайным образом лежит по одну или по другую сторону «родительского»
отрезка АВ.
Рис. 9.47. Фрактализация при помощи случайного колена
На рис. 9.48 показаны три стадии фрактализации отрезка прямой. На первом этапе производится
«возмущение» средней точки отрезка АВ и создается точка С. На следующем этапе осуществляется воз-
мущение средних точек каждого из получившихся отрезков, вследствие чего получаются точки DhE.
На конечной стадии процесса добавляются новые точки: F, G, Н, I. (Сколько всего точек будет после k
шагов?)
а б в
Рис. 9.48. Шаги процесса фрактализации
9.8. Случайные фракталы
603
Как реально осуществить фрактализацию в программе? Прямая L на рис. 9.47 проходит через сере-
дину М отрезка S и перпендикулярна к этому отрезку. В главе 4 мы видели, что любая точка С на пря-
мой L имеет следующую параметрическую форму:
C(t) = М + (В - А)Ч (9.21)
для некоторого значения t, где средняя точка М = (А + В)/2. Расстояние между точками С и М равно
|5 - Л| |t|, то есть пропорционально t и длине отрезка 5. Поэтому для нахождения точки С на случайном
колене будем вычислять случайным образом именно параметр t. Если t положительно, то этот изгиб
лежит по одну сторону от отрезка АВ; если же отрицательно, то по другую.
Для большинства фрактальных кривых в качестве t используется Гауссова случайная величина с ну-
левым математическим ожиданием и некоторым среднеквадратическим отклонением. При использо-
вании нулевого среднего колено с одинаковой вероятностью лежит как выше родительского отрезка,
так и ниже его.
Листинг 9.9. Фрактализация отрезка прямой
void fract(Point2 A. Point 2 В. double stdDev)
// generate a fractal curve from A to B.
// генерируем фрактальную кривую от А до В
double xDiff = А.х - В.х, yDiff = А.у - В.у;
Point2 С:
if(xDiff * XDiff + YDiff * yDiff < minLenSq)
cvs.lintTo(B.x. B.y);
else
{
stdDev *= factor:
// scale stdDev by factor
// масштабируем stdDev с множителем factor
double t - 0:
// make a gaussian variate t lying between 0 and 12.0
// создаем Гауссову случайную величину t.
// лежащую между 0 и 12.0
for(int i - 0; 1 .12; i++)
t += rand()/3276B.O:
t - (t - 6) * stdDev:
// shift the mean to 0 and scale
// смещаем среднее в 0 и масштабируем
C.x = 0.5 * (А.х + В.х) - t * (В.у - А.у):
С.у » 0.5 * (А.у + В.у) + t * (В.х - А.х):
fract(A. С. stdDev):
fract(C. В. stdDev):
Подпрограмма fractO, представленная в листинге 9.9, генерирует кривые, приближающиеся к на-
стоящим фракталам. Эта подпрограмма рекурсивно заменяет каждый отрезок прямой на случайном
колене на еще меньшее случайное колено. Использован простой критерий выхода из цикла: когда дли-
на отрезка становится достаточно малой (а точнее, когда квадрат его длины становится меньше, чем
некоторая глобальная переменная minLenSq, задаваемая пользователем); отрезок рисуется подпрограм-
мой cvs.lineToO, где cvs — объект класса Canvas (см. главу 3). Случайная величина t имеет закон распре-
деления, близкий к Гауссовому; это достигается сложением 12 равномерно распределенных случайных
величин, лежащих между 0 и 1 [Knuth, 124]. Результат имеет математическое ожидание 6 и дисперсию 1.
Затем среднее значение смещается в 0 и случайная величина должным образом масштабируется.
Отметим, что поскольку смещение, выраженное уравнением (9.21), пропорционально длине порожда-
ющего отрезка, фрактальные кривые будут действительно самоподобными (статистически). На каждом
последовательном уровне рекурсии среднеквадратическое отклонение stdDev масштабируется с помо-
щью глобального множителя factor, который будет рассмотрен ниже.
604
Глава 9. Приближение к бесконечности
Очевидно, что глубина рекурсии в подпрограмме fractO управляется с помощью длины отрезка
прямой. Часто эта длина выбирается так, чтобы рекурсия продолжалась до предела разрешающей спо-
собности самого дисплея. Для графических приложений двигаться дальше не имеет смысла.
Практические упражнения
9.8.1. Контроль за глубиной рекурсии
Альтернативный метод прекращения рекурсивных вызовов в подпрограмме fractO заключается в пе-
редаче в нее параметра depth, задающего максимальную глубину рекурсии. Покажите, как изменить
fractO, чтобы останавливать рекурсию по достижении определенной глубины.
9.8.2. Фрактализация вплоть до разрешающей способности дисплея
Требуется фрактализовать прямые и отобразить их на дисплее размером 512 на 512 пикселов. Если вы
хотите фрактализовать эти прямые так, чтобы как горизонтальные, так и вертикальные прямые фрак-
тализовались до предела разрешающей способности дисплея, то какую максимальную глубину рекур-
сии вы будете использовать?
9.8.2. Контроль за спектральной плотностью фрактальной кривой
Пайтген [Peitgen, 88] показал, что фрактальные кривые, созданные с помощью алгоритма из листин-
га 9.9, имеют следующую «спектральную плотность» («power spectral density»):
5(/) - l/A (9-22)
где Р — показатель степени «шумового процесса» — может устанавливаться пользователем для контро-
ля за «зазубренностью» («jaggedness») фрактального шума. При Р - 2 данный процесс носит название
броуновского движения (Brownian motion), а при Р = 1 процесс называется «1//шумом»1. Этот 1//шум
является самоподобным в статистическом смысле и был признан хорошей моделью для многих физи-
ческих процессов, таких как облака, последовательности тонов в музыке самых разных культур, а также
рост некоторых кристаллов. Пайтген и его соавторы также показали, что дробная (фрактальная) раз-
мерность таких процессов равна:
D = -^₽. (9.23)
2
В подпрограмме, приведенной в листинге 9.9, масштабный множитель factor, посредством которого
масштабируется среднеквадратическое отклонение на каждом уровне, зависит от показателя степени Р
фрактальной кривой, который определяет степень зазубренности этой кривой. Коэффициент Р изме-
няется от 1 до 3: значения больше 2 приводят к гладким («устойчивым») кривым, а значения меньше 2
приводят к более зазубренным, «неустойчивым» кривым. Значение множителя factor определяется по
следующей формуле [Peitgen, 156]:
factor = 2(1'р/2). (9.24)
Таким образом, с ростом Р масштабный множитель уменьшается. Некоторые его характерные зна-
чения приведены в табл. 9.1.
Таблица 9.1. Зависимость множителя и D от р
factor ₽ D
1.4 1 2 1/Ушум
1.1 1.6 1.7
1.0 2 1.5 Броуновское движение
0.9 2.4 1.3
0.7 3 1
В некоторых работах 1 //шумом называют все семейство «шумов» со спектральной плотностью 1 /Р для всех 0 в пределах от 0,5
до 1,5 [Peitgen, 158].
9.8. Случайные фракталы
605
Отметим, что factor = 1 при 0 = 2, и в этом случае относительное среднеквадратическое отклонение не
изменяется от уровня к уровню. Это соответствует модели броуновского движения. Для устойчивых
кривых, для которых Р > 2, factor < 1, поэтому среднеквадратическое отклонение убывает от уровня к
уровню: смещения колен становятся все менее и менее статистически выраженными. С другой сторо-
ны, когда Р < 2, образуются неустойчивые кривые: для них factor больше 1, вследствие чего среднеквад-
ратическое отклонение возрастает от уровня к уровню, так что колена становятся все более и более от-
четливыми.
Листинг 9.10. Рисование фрактальной кривой (псевдокод)
double MinLenSq. factor:
// global variables
// глобальные переменные
void drawFractal (Point2 A, Point2 B)
{
double beta. StdDev;
user Inputs beta, MinLenSq. and the initial StdDev
// пользователь вводит beta. MinLenSq и начальное StdDev
factor = pow(2.0.(1.0 - beta)/2.0):
cvs.moveTo(A):
fract(A. B. StdDev):
Фрактал может быть нарисован методом, приведенным в листинге 9.10. В этой подпрограмме factor
вычисляется с помощью функции pow(...) из библиотеки C++.
На рис. 9.49 показаны примеры фрактальных кривых, построенных на базе отрезка единичной
длины при различных значениях показателя степени 0. (Для этих рисунков задано minLenSq = 0,05 и
StdDev = 0,1.) Для каждого значения 0 было сгенерировано по пять фрактальных кривых с целью показать
возможные вариации. Следует отметить четко выраженную зависимость вида фракталов от значения 0.
Рис. 9.49. Пример фрактальных кривых: <э) р = 2,4; б) р = 2; в) р = 1,6
606
Глава 9. Приближение к бесконечности
На рис. 9.50 показано, как можно фрактализовать произвольные ломаные линии. Предлагается про-
стое средство «разлохмачивания» формы, чтобы ее извивы выглядели естественно. На этом рисунке
была произведена грубая оцифровка береговой линии штата Флорида, так что этот штат аппроксими-
рован всего 20 точками (см. рис. 9.50, а). Затем каждый из отрезков береговой линии Флориды был
подвергнут фрактализации, а внутренние границы штатов, которые должны быть прямыми линиями,
были оставлены без изменения. Чрезвычайно интересно фрактализовать полигоны, представляющие
известные географические объекты: острова, страны, континенты, и увидеть, насколько естественно
могут выглядеть их границы. Можно фрактализовать и другие формы, например животных или макушку
человеческой головы, — с целью придания им естественного вида.
а б
Рис. 9.50. Создание реалистичных береговых линий
Одно из свойств фрактальных кривых, созданных с помощью генераторов псевдослучайных чисел,
состоит в том, что они полностью воспроизводимы. Все, что нужно, — это при каждой фрактализации
использовать в генераторе одно и то же начальное число (seed). В каждом из трех наборов фракталов на
рис. 9.49 использовалось то же самое начальное число, поэтому они базируются на абсолютно одинако-
вой последовательности случайных значений (за исключением масштабных множителей, соответству-
ющих различным дисперсиям). Таким образом, сложную форму вроде изрезанной береговой линии
можно полностью описать в базе данных посредством только таких записей:
О массив точек (polypoint), описывающий исходные отрезки прямых;
О значения minLenSq и StdDev;
О начальное псевдослучайное число.
По этому ограниченному количеству данных можно в любой момент воспроизвести точную копию
фрактализованной кривой.
Фрактальные поверхности
Поверхности можно фрактализовать так же, как и линии — с целью создания реалистически выглядящей
гористой местности. Методы создания подобных сцен рассматриваются в тематическом задании 9.9.
9.9. Резюме
В этой главе было рассмотрено несколько приближений к бесконечности — с использованием повторения и
рекурсии. Для ряда фигур можно двигаться к бесконечности «наружу», плотно размещая эти фигуры
без ограничения, таким образом заполняя мозаикой всю бесконечную плоскость. Можно двигаться также
«вовнутрь» к бесконечно малому, по крайней мере, в принципе. Рекурсия предоставляет нам простой
механизм для рисования все меньших и меньших «дочерних» версий фигуры внутри «родительской»
фигуры — вплоть до предела разрешения дисплея. Если выбрать подходящий класс, то изображения
9.10. Тематические задания
607
станут самоподобными (self-similar) фракталами: как бы близко мы их ни рассматривали, они продемон-
стрируют одну и ту же степень детализации. Для автоматического придания изрезанности при рисовании
береговых линий, деревьев и других природных объектов может быть использован фактор случайности.
Система итерируемых функций (IFS) — это набор аффинных преобразований, который может быть
использован при создании сложных изображений. При «Игре в Хаос» (Chaos Game) можно генериро-
вать «странный аттрактор» («strange attractor») данной IFS посредством простого процесса: многократ-
но повторяемого случайного выбора аффинных отображений и преобразования отдельной точки. Этот
процесс можно обратить: путем анализа заданного изображения может быть получена система IFS, для
которого это изображение является аттрактором. Поскольку запись представления системы IFS зани-
мает во много раз меньше места, чем сохранение всего изображения, этот подход вызвал огромный ин-
терес в области сжатия изображений.
Мы исследовали интереснейшее множество Мандельброта, граница которого сама является фрак-
тальной кривой. Если сделать увеличение области вблизи границы этого множества, то проявятся но-
вые детали изображения и будет казаться, что рисунок «бородавки» (wart) самовоспроизводится сно-
ва и снова. Поскольку этот процесс может продолжаться вечно, то множество Мандельброта является
«бесконечно сложным». Компьютерная графика предоставляет простое и мощное средство для иссле-
дования подобных явлений. Такие изображения генерируются просто, несмотря на их необычайную
сложность. Кроме того, мы узнали, как формировать множества Жюлиа и алгоритмы для их рисования,
а также то, что множество Мандельброта «преобразуется» в целое семейство множеств Жюлиа.
9.10. Тематические задания
Тематическое задание 9.1. Рисование по генерации строк
Уровень сложности II.
Создайте и протестируйте приложение, рисующее кривые на базе генерации строк (string production),
которая рассматривалась в разделе 9.3. Созданное вами приложение должно быть способно нарисовать
любую из кривых, перечисленных в примере 9.3.1, для различных порядков. После этого проверьте свою
программу на строковых инструкциях Херба Сэвиджа (Herb Savage), предназначенных для создания
набора апериодических мозаик Пенроуза (Penrose aperiodic tiles), описание которых приводится ниже
(см. тематическое задание 9.7; вышеупомянутые инструкции получены из программы FRACINT, дос-
тупной в Интернете [Fractint, 66]):
Angle - 10 degrees.
Axiom - +WF--XF--YF--ZF.
W=YF++ZF----XF[-YF----WF]++.
X=+YF-ZF[--WF--XF]+.
Y=-WF++XF[+++YF++ZF]-.
Z=--YF++++WF[+ZF++++XF]--XF,
F= empty
Для возможности автоматического изменения размеров окна, включающего каждую фигуру, приспо-
собьте подпрограмму produceStringO так, чтобы при нулевом значении переменной visible рисование не
производилось, а только вычислялись границы окна wi ndow = (w.l, w.t, w.r, w.b), полностью охватываю-
щего обрабатываемую кривую. Если же visible - 1, то подпрограмма должна рисовать эту кривую. Для
реализации этой схемы достаточно просто добавить к подпрограмме forward!) следующий тест: если
visible - 0, то программа смотрит, вышло ли последнее значение СР (Current Position — текущих коорди-
нат) за пределы окна, сформированного к этому моменту. Код для этого может выглядеть примерно так:
if(CP.x < w.l) w.l - СР.х:
if(СР.х > w.r) w.r = СР.х:
etc.
// и так далее
608
Глава 9. Приближение к бесконечности
Как инициализируется такое окно?
Необязательное дополнение. Расширьте свое приложение так, чтобы оно могло рисовать фракталь-
ные деревья, такие как «куст» на рис. 9.10.
Тематическое задание 9.2. Рисование снежинок и рептилий
Уровень сложности II.
Часть А. Снежинка Мандельброта
Мандельброт придумал замечательную самоподобную фрактальную кривую, которая в точности по-
мещается внутри снежинки Коха (Koch snowflake). На обложке апрельского (1978) выпуска журнала
Scientific American приведена кривая Мандельброта третьего порядка М3. Способ формирования кри-
вой k-ro порядка Mk основан на разбиениях равностороннего треугольника [Gardner, 78], как показано
на рис. 9.51, а. Каждая из трех сторон равностороннего треугольника АВС разделена на три равные ча-
сти точками от D до I.
а б в
Рис. 9.51. Построение снежинки Мандельброта
Далее следующие отрезки также разделяются на три равные части: отрезок EG точками К nN, отре-
зок EI— точками отрезок IG — точками L и О. Кривая Мандельброта первого порядка М( состо-
ит из 13 отрезков ломаной линии ADEFGNKMJOLIHC. Эта кривая считается «построенной на отрезке»
АС, причем она называется «левой», поскольку если смотреть из точки А на точку С, то кривая начина-
ется с поворота влево. Для формирования снежинки следующего поколения М2 следует построить кри-
вую такой же формы на каждом из 13 отрезков Л/р как показано на рис. 9.51, б. Размер каждого отрезка
определяет размер всей кривой. Некоторые из этих кривых являются левыми (£), а другие — правыми
(7?). Начиная с S, последовательность поворотов выглядит так: RLLLLRRRLLRRL. Отметим, что кривая
М2 размещается внутри снежинки Коха второго порядка. Напишите подпрограмму, которая рисует кри-
вую Мандельброта Л/; для i = 1, 2,3. (На рис. 9.51, в показана кривая М3.)
Часть Б
В разделе 9.4 был описан метод рисования рептилий — с использованием функции вроде doTrioO, ко-
торая рекурсивно вызывает сама себя и передает при этом информацию о размере, что позволяет рисо-
вать рептилии все меньшего размера внутри одной большой. Существует и альтернативный метод: ри-
совать каждого потомка посредством управления системой координат и СТ (Current Transformation —
текущим преобразованием). Как показано на рис. 9.52, для того чтобы нарисовать каждого потомка три-
мино, мы соответствующим образом изменяем систему координат и рисуем потомка в новой системе.
Назовем опорным элементом (pivot) фигуры угол, отмеченный на рисунке буквой р. Рисование каждо-
го потомка осуществляется посредством переноса системы координат в вершину его собственного опор-
9.10. Тематические задания
609
ного элемента и соответствующего поворота осей. Кроме того, система координат масштабируется мно-
жителем 0,5, поскольку потомки вдвое меньше своих родителей.
Рис. 9.52. Изменение системы координат для рисования тримино
При каждом вызове подпрограммы drawTrioO копия СТ сохраняется и восстанавливается перед вы-
ходом из подпрограммы (так что drawTrioO не оказывает глобального влияния на систему координат).
Однако следует отметить, что потомки «чувствуют» эффект от изменений системы координат — чего
мы и добиваемся, — поскольку рекурсивные вызовы drawTrioO происходят до восстановления СТ.
Листинг 9.11. Рисование тримино
void drawTriodnt depth)
{
// Draw a triomino manipulating the CT
// Рисуем тримино посредством манипуляций с СТ
if(depth >= maxDepth)
// draw the outline
// рисуем контур
moveTo(0, 0): lineToCO. 4);
lineTo(2, 4); lineTo(2. 2):
lineTo(4, 2); 11neTo(4, 0):
11neTo(0. 0):
return:
saveCTO;
// make a copy for later
// делаем копию для дальнейшего
depth++:
// update for the next generation
// обновляем для следующего поколения
scale(0.5. 0.5):
drawTrio(depth);
// Draw В
// рисуем В
translated.2):
// to pivot of C
// к опорному элементу в С
drawTrio(depth):
// Draw С
// рисуем С
translate(6.-2);
продолжение &
20 Ф. Хилл
610
Глава 9. Приближение к бесконечности
Листинг 9.11 (продолжение)
rotate(90);
drawTrio(depth):
// Draw А
И рисуем А
translated.8):
rotate(180):
drawTrio(depth):
// Draw D
// рисуем D
restored ():
// restore the original d
// восстанавливаем исходное значение d
Код подпрограммы drawTrioO приведен в листинге 9.11. Нужная максимальная глубина рекурсии
контролируется путем передачи глубины depth в drawTrioO в качестве параметра и сравнения ее с гло-
бальной переменной maxdepth; каждый потомок имеет глубину на единицу большую, чем его родитель.
Начальный вызов подпрограммы имеет вид: drawTrio(l). Что же касается эффективности, то масштаби-
рование scaled).5. 0.5) вызывается только один раз, а не для каждого потомка. Таким образом, количе-
ство вызовов масштабирования будет в два раза меньше, чем можно было ожидать. Тщательно следите
за изменениями систем координат во время различных вызовов подпрограмм.
Напишите и выполните приложение, которое рисует рептилии вышеописанным способом. Сделай-
те так, чтобы это приложение могло нарисовать все рептилии, изображенные на рис. 9.23. Кроме того,
оно должно уметь рисовать интересные рептилии из практического упражнения 9.4.6, а также ковер
Серпинского.
Необязательные дополнения.
1. Расширьте свое приложение так, чтобы оно закрашивало полигоны «потомков» самого нижнего
уровня узором [Clason, 42]. Поэкспериментируйте с каждым из узоров, приведенных на рис. 9.53,
и нарисуйте эти узоры до глубины 4 или более.
Рис. 9.53. Закрашивание областей рептилий
2. Измените программу рисования рептилий так, чтобы она могла рисовать линии, подобные изоб-
раженным на рис. 9.27, внутри полигонов самого низшего уровня, с целью получить интересные
варианты фигур, как показано на рис. 9.28. Поэкспериментируйте с различными «внутренними
линиями».
Тематическое задание 9.3. «Игра в Хаос»
Уровень сложности II.
Создайте и протестируйте приложение, которое рисует аттрактор для заданной системы итерируе-
мых функций (IFS). Это приложение могло бы выглядеть примерно так:
read the IFS from a file into arrays affine[] and prob[]
// читаем IFS из файла в массивы affine[] и prob[]
set the window and viewport
// задаем окно и порт просмотра
chaosGame(a ffine.prob,N);
9.10. Тематические задания
611
Схема подпрограммы chaosGameO приведена в листинге 9.6. Ваша программа должна прочитать
(из файла) данные для системы IFS, войти в графический режим и начать итерации в подпрограмме
chaosGameO. Для задания окна, которое вместило бы в себя аттрактор, можно воспользоваться методом,
предложенным в тематическом упражнении 9.1.
Поскольку может потребоваться несколько итераций, прежде чем точки начнут приближаться к ис-
тинному аттрактору, несколько первых итерационных точек лучше отбросить до начала рисования.
Затем при каждой итерации функция int chooseAffine (double рг[], int N) будет выбирать одно из
аффинных отображений с вероятностью рг[1] для i-ro отображения. Такие действия проще всего опи-
сать на следующем примере.
Пусть равно 4 и элементы массива рг[] составляют {0,41, 0,29, 0,04, 0,26}. Сумма этих элементов,
разумеется, равна единице. С помощью следующего кода будет осуществляться выбор чисел 0, 1, 2, 3
с соответствующими вероятностями:
val - randO % 10000:
// random value in the range 0..9999
// случайная величина в промежутке 0..9999
if(val < 4100) return 1;
else 1f(val < 4100 + 2900) return 2:
else if(val < 4100 + 2900 + 400) return 3:
else return 4:
Оператор randOXIOOOO возвращает значение, которое с равной вероятностью может быть в любой
точке интервала 0..9999. Этот интервал разбивается с помощью операторов if() так, чтобы в каждом
подынтервале находилась соответствующая часть длины интервала randOtlOOOO. Такой подход легко
обобщается на любой массив рг[].
Проверьте свою программу на каждой IFS, приведенной в разделе 9.5.4, а также возьмите другие IFS
из программы FRACTINT в Интернете [Fractint, 66].
Необязательное дополнение. Цветная «Игра в Хаос*
Дополните свое приложение так, чтобы оно рисовало цветные точки. Отображение окно — порт про-
смотра устанавливается как обычно, чтобы каждой точке (х, у) соответствовала позиция пиксела (со!,
row) (см. главу 3). Теперь при «Игре в Хаос* для каждой вычисленной новой точки счетчик соответству-
ющего пиксела увеличивается на единицу. В конце игры каждый пиксел снабжен числом, показывающим,
сколько раз этот пиксел был «посещен* точкой при ее движении по аттрактору. Для того чтобы изобра-
зить эти значения в цвете, свяжите какой-нибудь цвет с каждым значением «счетчика посещений* и
нарисуйте картинку.
Тематическое задание 9.4. Рисование орбит внутри множества
Мандельброта
Уровень сложности II.
Напишите и выполните приложение, рисующее с-орбиту системы /(.) - (.)2 + с для произвольного
значения с, вводимого пользователем. Последовательность работы этой программы следующая.
1. На экране рисуется грубый контур множества Мандельброта (см. рис. 9.41). Для этого может
пригодиться уравнение (9.18).
2. Пользователь отмечает мышью любое место на фигуре, задавая тем самым конкретное комплекс-
ное значение с. '
3. Рисуется нулевая орбита для выбранного значения с. Во избежание хаоса на рисунке начинайте
рисование орбиты с с, а не с 0. Рисуйте траекторию взрывающейся орбиты только до того мо-
мента, когда она покинет наперед заданный прямоугольник экрана.
4. Вернитесь к этапу 2.
612
Глава 9. Приближение к бесконечности
Тематическое задание 9.5. Создание изображений множества
Мандельброта
Уровень сложности II.
Напишите программу, которая рисует выбранные участки множества Мандельброта в полноцвет-
ном режиме. Ваша программа должна основываться на исследованиях раздела 9.6.4. После того как на-
рисовано очередное множество Мандельброта, пользователь должен иметь возможность увеличивать
любую прямоугольную область и выходить из программы путем нажатия любой клавиши. Для описа-
ния желаемой области увеличения пользователь отмечает мышью противоположные углы прямоуголь-
ника, после чего этот участок множества Мандельброта рисуется во весь экран.
Тематическое задание 9.6. Создание изображений
множеств Жюлиа
Уровень сложности II.
Сгенерируйте множество ЖюлиаД-0,7448185 + 0,1050935г). Поэкспериментируйте с другими зна-
чениями с (см. [Peitgen, 88]).
Тематическое задание 9.7. Непериодические мозаики;
мозаики Пенроуза
Хотя и можно создавать узоры Пенроуза с высокой степенью симметрии, но большинство узоров являются
таинственным смешением порядка и непредсказуемых отклонений от него, подобно самой Вселенной.
Мартин Гарднер (Martin Gardner)
Оценка необходимого времени: пять часов.
Периодические и непериодические мозаики были рассмотрены в разделе 9.4. Мозаика, приведенная
на рис. 9.54, является непериодической. Этот узор расширяется до бесконечности путем добавления
большего числа «колец», однако явно не является периодическим. Данный рисунок основан на так называ-
емом «многостороннике» («versatile»), предложенном Б. Грюнбаумом и Г. К. Шепардом (В. Grunbaum,
G. С. Shephard — [Grunbaum, 96]), который показан на рис. 9.55, а. (Все его девять сторон имеют одина-
ковую длину, а все смежные стороны наклонены друг к другу под углом 0 - 15°, за исключением двух
углов, которые показаны на рисунке и составляют 50 и 80.) Рисунок 9.55, б демонстрирует, что данная
форма действительно может разместиться на плоскости в виде периодической мозаики. (Почему рису-
нок доказывает это утверждение?) Таким образом, у нас имеется полигон, который образует на плоско-
сти как периодическую, так и непериодическую мозаику, — в зависимости от того, каким образом эле-
менты мозаики располагаются относительно друг друга. Получается, что таким свойством обладают
многие различные формы, подобно некоторым из рептилий, рассмотренных в разделе 9.4.4.
Рис. 9.54. Непериодическая мозаика
9.10. Тематические задания
613
Рис. 9.55. «Многосторонний» и участок мозаики
Проведенное исследование приводит нас к значительно более глубокому вопросу: существует ли
набор форм, которые создают на плоскости только непериодическую мозаику? Это означает, что ни
одна часть из этого набора не может быть размещена на плоскости периодически и в то же время все
мозаики этого набора образуют непериодическую мозаику. (При этом разрешается использовать пово-
роты и отражения элементов мозаики.) В течение многих лет считалось, что такой набор существовать
не может, однако в 1964 году Роберт Бергер (Robert Berger), аспирант из Гарварда, обнаружил набор,
состоящий из более чем 20 000 мозаичных элементов. После длительной работы число элементов со-
кратилось до 6, а в 1974 году Роджер Пенроуз (Roger Penrose) из Оксфордского университета нашел
набор всего из двух мозаичных элементов, который располагается на плоскости только непериодичес-
ким образом. (На сегодняшний день все еще неизвестно, существует ли единственный мозаичный эле-
мент некоторой формы, который выкладывается только в непериодическую мозаику.) Очень интерес-
ное изложение этой задачи и путей к ее решению можно найти в работах [Gardner, 78] и [Penrose, 160].
На рис. 9.56 приведены наиболее известные из мозаик Пенроуза, так называемые воздушный змей
(kite) и дротик (dart). Как видно из рис. 9.56, б, эти формы фундаментальным образом связаны с золо-
тым сечением! На рисунке показано, что если их соединить вместе, они образуют ромб, который, как
известно, укладывается на плоскости в периодическую мозаику (почему?); следовательно, если нам
нужны только непериодические мозаики, то такая комбинация форм должна быть запрещена. Один из
способов избежать этого — добавить к каждому элементу мозаики соответствующие «выступы» и «впа-
дины», как показано на рис. 9.56, в, после чего змей и дротик смогут соединяться только определенным
образом. Другой способ состоит в том, чтобы обозначить различные углы элементов буквами Н (head)
и Т (tail) соответственно для головных и хвостовых частей мозаики и соединять только одинаково поме-
ченные углы. Неплохой метод предложил Джон Конвей (John Conway) (рис. 9.56, г): на поверхности змея
и дротика рисуются дуги черного и серого цвета, и фрагменты могут быть соединены только так, что-
бы смежные ребра соединяли дуги одного и того же цвета (см. упражнения в конце этого тематического
задания).
Пенроуз показал, что при этих ограничениях можно укладывать змеи и дротики на плоскости бес-
конечным числом способов, однако каждая такая мозаика должна быть непериодической. (Для этого
нужно потрудиться и вырезать примерно 100 змеев и около 50 дротиков, раскрасить их, после чего мож-
но раскладывать мозаику.) Он также доказал, что соотношение змеев и дротиков в любой бесконечной
мозаике в точности равно золотому соотношению ф. Из того, что ф является иррациональным числом,
следует доказательство апериодичности любой мозаики; так как в периодической мозаике соотноше-
ние должно быть рациональным.
Пенроузу и Конвею удалось разработать ряд замечательных теорем, касающихся мозаик; все они
превосходно описаны у Мартина Гарднера (Martin Gardner [Gardner, 78]). Например, всякий раз, когда
черная или серая кривая становится замкнутой, она должна иметь пентагональную симметрию, причем
вся область внутри такой кривой должна обладать пятикратной симметрией. Более того, в большин-
стве мозаик все кривые являются замкнутыми: в узоре может быть не более двух незамкнутых кривых
каждого цвета.
614
Глава 9. Приближение к бесконечности
Рис. 9.56. Змей и дротик Пенроуза
Разработайте алгоритм для рисования мозаик Пенроуза и выполните его. {Замечание: это можно
сделать, например, при помощи генерации строк; см. тематическое задание 9.1.)
Практические упражнения
9.10.1. Форма многосторонника
Докажите, что многосторонник является замкнутым. То есть нужно показать, что многосторонник, име-
ющий углы, как на рис. 9.55, действительно является замкнутым полигоном, если все его стороны име-
ют одинаковую длину.
9.10.2. Дуги, нарисованные на змее и дротике
На рис. 9.56, г показаны черные и серые дуги, нарисованные на элементах мозаики Пенроуза. Эти дуги
только касаются друг друга. Центр каждой дуги находится на вершине и имеет такой радиус, чтобы эта
дуга «совместилась» с дугой такого же цвета на фрагменте, который уложен рядом. Покажите, что эти
дуги делят стороны змея и дротика в соотношении ф:1.
9.10.3. Из треугольников
На рис. 9.57 показано, как можно превратить равнобедренный треугольник в девятиугольник («enneagon»),
обладающий свойством без зазоров совмещаться со своей полуповернутой версией, образуя восьми-
угольник [Gardner, 78].
О Покажите, что такой восьмиугольник всегда образует на плоскости периодическую мозаику.
О Каким условиям должны удовлетворять ребра А нВ, чтобы они образовали девятиугольник?
О Докажите, что существует бесконечное множество различных форм девятиугольника.
Тематическое задание 9.8. Фрактализация кривых
Уровень сложности II.
Напишите и выполните приложение, которое рисует «фрактализованные» линии. Пользователь за-
дает ломаную линию, как обычно, с помощью мыши, после чего каждый отрезок этой ломаной рисуется
в фрактализованном виде. Предоставьте пользователю возможность вводить значения различных ис-
9.10. Тематические задания
615
пользуемых параметров (см. табл. 9.1). При выполнении своей программы поэкспериментируйте с раз-
личными величинами. Испытайте различные ломаные линии, представляющие собой острова, области
или страны, и посмотрите, придает ли им фрактализация естественный вид.
Рис. 9.57. Девятиугольник и пара фрагментов, образующих периодическую мозаику
Тематическое задание 9.9. Моделирование
фрактализованных гор
Уровень сложности III.
Для создания сложнейших «фрактальных гор* можно применить процесс фрактализации, сходный
с тем, который использовался при «взлохмачивании» прямой линии. На рис. 9.58 показана последо-
вательность этого процесса. Начинаем с треугольника АВС, лежащего в плоскости ху, затем смещаем
вертикально три средние точки а, Ь, с на случайные величины, формируя «штыри», поднимающиеся
с пола. Теперь соединяем вершины этих штырей между собой и с исходными вершинами, чтобы образо-
вать четыре треугольных микрограни а'Ь'с', а'Ь'С и т. д. Повторяем этот процесс. Тогда каждая микро-
грань будет заменяться на четыре новых микрограни тем же способом: смещаем вертикально средние
точки ее ребер на случайные величины и затем соединяем их. Этот процесс продолжается до тех пор,
пока эти микрограни не станут «достаточно малыми».
Рис. 9.58. Фрактализация поверхности
Пользователь может задавать «начальное число» для генератора псевдослучайных чисел (например,
используя стандартную функцию srandO; srand(29) устанавливает начальное число 29), после чего со-
зданная гора станет полностью воспроизводимой. Можно рисовать микрогрань или закрашивать ее ка-
ким-либо цветом в процессе создания, а можно вначале построить всю гору как большой список граней,
а затем нарисовать все микрограни сразу.
616
Глава 9. Приближение к бесконечности
Напишите приложение, которое принимает информацию о начальном треугольнике АВС и о сред-
ней высоте «смещений» и создает каркасную модель (согласно главе 6) фрактализованной горы. Затем
данное приложение устанавливает камеру, источник света и рисует фрактальную гору.
9.12. Дополнительная литература
В работе Дж. МакГрегора и А. Уатта «Искусство графики для IBM» (J. McGregor, A. Watt. The Art of
Graphics for the IBM [Mcgregor, 138]) предлагается целый ряд подробных разработок узоров и рассматри-
ваются методы их создания при помощи компьютерной графики. Несколько книг посвящены рассмотре-
нию и оценке фракталов, в их числе книги Пиковера «Компьютеры, узоры, хаос и красота» (Pickover.
Computers, Pattern, Chaos, and Beauty [Pickover, 163]) и «Лабиринты для ума» {Mazes for the Mind
[Pickover, 164]). Строгое исследование математической основы фракталов, а также несколько разносто-
ронних взглядов на фракталы в целом можно найти в работе Барнсли «Фракталы повсюду» (Barnsley.
Fractals Everywhere [Barnsley, 10]). В книгах Пайттена «Хаос и фракталы» и «Новые рубежи науки»
{Chaos and Fractals, New Frontiers of Science [Peitgen, 158]), а также в работе Барнсли «Наука о фракталь-
ных изображениях» {The Science of Fractal Images [Barnsley, И]) содержится множество прекрасных
изображений фракталов, а также четкое описание механизма, лежащего в основе их создания.
10
Средства для растровой
графики
□ Описание пиксельные карт и полезных операций над ними.
□ Разработка программных средств копирования, масштабирования
и поворота пиксельных карт.
□ Рассмотрение различных режимов рисования, таких как XOR.
□ Разработка инструментов для компоновки изображений.
□ Исследование способов определения областей и управления ими.
□ Развитие алгоритма Брезенхема для рисования прямых.
□ Создание инструментов для закрашивания зон, в частности
полигональных.
□ Исследование ступенчатости (aliasing) и разработка методов
ее устранения.
□ Разработка средств сглаживания (dithering) и рассеивания дефектов
(error diffusion) для создания большего числа оттенков серого цвета.
Создатель знает, что он достиг совершенства не тогда, когда уже
нечего добавить, а тогда, когда уже ничего нельзя удалить.
Антуан де Сент-Экзюпери (Antoine de Saint-Exupery)
В этой главе мы детально исследуем формирование изображения из графических примитивов, а также
обработку изображения для достижения ряда визуальных эффектов. В разделах 10.1 «Введение» и 10.2
«Управление пиксельными картами» вновь рассматривается пиксельная карта (pixmap) как основной
объект для хранения и обработки изображений и описывается несколько операций над пиксельными
картами. В разделе 10.3 «Объединение пиксельных карт» описываются пути комбинирования изображе-
ний и способы использования таких режимов рисования, как «исключающее ИЛИ». В разделе 10.4 «Рисо-
вание прямых своими силами: алгоритм Брезенхема» разрабатывается алгоритм Брезенхема (Bresenham)
рисования прямых, а в следующих трех разделах рассматриваются способы описания «областей» в пиксель-
ной карте, заполнение их цветом или узором и управление ими. Особое внимание уделяется заполнению
полигональных зон. Раздел 10.8 «Ступенчатость; технологии сглаживания» посвящен явлению ступен-
чатости (его иногда ласково называют «jaggies» «ступеньки»), которое является неотъемлемой частью
618
Глава 10. Средства для растровой графики
картинок, отображаемых на растровом устройстве, а также разработке технологий улучшения зритель-
ного восприятия таких картинок.
В разделе 10.9 «Увеличение количества цветов и оттенков* описывается, как различными способа-
ми заставить растровый дисплей показывать больше цветов, чем у него есть на самом деле, — с помощью
сглаживания и рассеивания дефектов. В тематических заданиях эти темы получают дальнейшее разви-
тие, а также рассматриваются важные программные проекты.
10.1. Введение
Изображения состоят из массивов пикселов и обычно отображаются на растровом дисплее. Существу-
ет два основных способа создания изображений:
1. Сканирование (и оцифровка) уже существующего фотографического или телевизионного изоб-
ражения.
2. Процедурное вычисление значений пикселов, как при визуализации сцены.
В предыдущих главах основное внимание уделялось второму пути: мы генерировали такие графи-
ческие примитивы, как прямые линии или полигоны, и рассматривали способы связать с каждым из
них цвета или текстурные кобрдййаты. С помощью OpenGL мы просто «посылали* их в порт просмот-
ра, после чего они отображались на экране. В процессе этого мы, однако, обошли молчанием ключевой
этап назначения нужного цвета каждому отдельному пикселу «внутри* прямой или полигона. Процесс
получения такой информации высокого уровня, как координаты и цвета вершин, установка цветов мно-
жества пикселов в какой-нибудь области буфера кадров, называется «преобразованием развертки»
(scan conversion) или растеризацией (rasterization). На рис. 10.1 показан участок «выходной* работы
графического конвейера, относящийся к растеризации. Когда вершины выходят из преобразования
порта просмотра, OpenGL «собирает* их в соответствующий примитив (это определяется командой
glBegin(GL_POLYGON) илй подобной ей) и затем растеризует получившийся примитив, задавая свойства
тех пикселов, которые «лежат внутри* примитива. В данной главе мы исследуем, как зто делается, по-
казывая способы рисования прямых и заполнения полигонов цветами и текстурами.
В действительности процесс растеризации не выдает отдельные пикселы; он производит фрагмен-
ты (fragments), состоящие из цвета, глубины и пары текстурных координат. С этими фрагментами про-
изводится множество различных операций и тестов (на рисунке они обозначены как «операции над
фрагментами*), прежде чем они будут записаны в буфер кадров в виде простых значений пикселов.
Мы опишем различные варианты этих операций и обсудим их смысл.
Кроме того, мы рассмотрим, как производить различные операции над изображением после его со-
здания. Они включают в себя вычисление новых значений пикселов на базе значений определенных
пикселов существующего изображения (или нескольких скомбинированных изображений). OpenGL
производит все эти манипуляции на том участке графического конвейера, который обозначен нами как
«операции над фрагментами*.
10.2. Управление пиксельными картами
619
В главе 1 введено понятие растровых изображений и описаны некоторые устройства, их отобража-
ющие. Напомним, что такое изображение хранится в памяти в форме пиксельной карты (pixmap — со-
кращение от «pixel тар») — прямоугольного массива числовых значений. Пиксельные карты могут хра-
ниться в любых областях памяти компьютера и переписываться из одного места памяти в другое. Когда
пиксельная карта копируется в буфер кадров, контроллер развертки (scan controller) производит пре-
образование значений пикселов в цветные световые «точки», в результате чего пиксельная карта стано-
вится видимой на дисплее. То, что вы видите на экране, — это «картина» того, что записано в буфере
кадров. Термин «пиксел» часто относят как к числовым значениям, записанным в пиксельной карте,
так и к самим световым точкам.
Напомним также, что ячейка каждого пиксела в пиксельной карте состоит из фиксированного
количества бит, называемых глубиной цвета (color depth) этого пиксела. Если глубина цвета пиксела
равна Ь, то он может принимать 26 различных значений и поэтому способен отобразить 2Ь различных
цветов. Если b = 1, то возможны только два цвета; двухцветные пиксельные карты часто называют
битовыми картами (bitmaps).
Таким образом, растровые изображения и дисплеи имеют дело с дискретными данными — и в про-
странственном, и в цветовом отношении. Эта дискретность наряду со способностью программы опери-
ровать в памяти непосредственно со значениями пикселов послужили основой создания специального
набора программных средств для генерирования и обработки изображений.
10.2. Управление пиксельными картами
Если два числа не равны никаким другим, то они равны между собой.
Один из компьютерных Законов Мерфи
В этом разделе мы рассмотрим некоторые программные средства, предназначенные для манипулирова-
ния с пиксельными картами как на экране (on-screen) — когда они помещаются в буфере кадров, так и
вне экрана (off-screen) — когда они находятся в обычной памяти; мы опишем также визуальные эффек-
ты этих манипуляций. Кроме того, мы увидим, какими средствами для работы с пиксельными картами
располагает OpenGL.
10.2.1. Важные операции с пиксельными картами
Обрисуем в общих чертах, какие операции можно проделывать с пиксельными картами. Затем, в после-
дующих разделах, мы рассмотрим, как выполнять каждую из этих операций и как они работают в раз-
личных ситуациях.
Рисование картинки
Операции визуализации, рисующие в буфер кадров, изменяют ту пиксельную карту, которая отобража-
ется на дисплее1. Например, когда для визуализации сцены используется OpenGL, «запись» осуществ-
ляется прямо в пиксельную карту буфера кадров.
Копирование пиксельной карты из одного места в другое
Вы можете скопировать пиксельную карту из одного раздела памяти в другой. На рис. 10.2 показано
четыре типа копирования. На рисунке приведены четыре пиксельные карты вместе с их копиями. Опера-
ция сору (копирование) копирует изображение из одного места дисплея в другое. Операция read (чтение)
копирует часть отображаемой картинки во внеэкранную (off-screen) память. Операция draw (рисование)
копирует пиксельную карту из внеэкранной памяти на дисплей. Операция, которую мы будем называть
тетСору (копирование памяти), делает резервную копию изображения во внеэкранной памяти.
1 Память буфера кадров иногда называют экранной («on-screen») памятью — по причине тесной связи между значениями пикселов
и тем, что видно на экране.
620
Глава 10. Средства для растровой графики
Рис. 10.2. Варианты операций копирования для пиксельной карты
OpenGL предлагает ряд функций для выполнения этих операций копирования (подробности отло-
жим для более позднего рассмотрения):
О glReadPixel s(); «— считывает область буфера кадров во внеэкранную память;
О glCopyPixelsO; «— копирует область буфера кадров в другую область буфера кадров;
О glDrawPixelsO; «— рисует заданную пиксельную карту в буфер кадров.
Масштабирование и поворот пиксельной карты
Часто требуется увеличить или уменьшить изображение, а также повернуть его. За этими операциями
могут стоять простые или довольно сложные процессы — в зависимости от используемых значений ко-
эффициента увеличения или угла поворота.
Сравнение двух пиксельных карт
Другой важной задачей является сравнение двух пиксельных карт для определения степени их разли-
чия. Например, можно произвести сравнение двух оцифрованных рентгенограмм и выяснить, насколь-
ко изменилась со временем опухоль. Обычно две пиксельные карты сравниваются попиксельно, при
этом над парами соответствующих пикселов производится некоторая математическая операция.
Представление и закрашивание областей в пиксельной карте
Ряд пиксельных карт содержат четко идентифицируемые объекты: круги, полигоны или просто определен-
ные области (regions) пикселов, которые являются однородными в каком-либо смысле. Нам нужны способы
описания областей пиксельной карты и их отображения на «высшем уровне», то есть в более абстрактной
или символической форме. Кроме того, мы зачастую хотим закрасить все пикселы, лежащие внутри неко-
торой области, заданным цветом или узором; такой процесс называется заполнением области (region filling).
10.2.2. Типы данных, используемые для пиксельных карт
Оценивать эффективность программ по количеству строк кода — это все равно,
что оценивать прогресс авиации путем взвешивания аэроплана.
Билл Гэйтс (Bill Gates)
Для поддержки манипуляций с пиксельными картами естественно создать несколько классов. Каждая
пиксельная карта имеет определенное количество строк и столбцов, и каждый ее пиксел содержит ин-
формацию, записанную в определенном виде:
О битовая карта (bitmap): каждый пиксел записан в одном бите, так что каждый пиксел находится
в одном из двух состояний: «включен» («оп») или «выключен» («off»);
10.2. Управление пиксельными картами
621
О пиксельная карта оттенков серого (gray-scale): каждый пиксел записан в одном байте, представ-
ляющем градации серого цвета от 0 (черный) до 255 (белый);
О LUT-индексы: каждый пиксел содержит число, представляющее собой индекс в кодовой таблице
цветов (color lookup table — LUT), как описано в главе 1. Чаще всего в LUT содержится 256 эле-
ментов, так что каждый индекс может быть записан в одном байте;
О RGB-карта (RGB-pixmap): каждый пиксел состоит из трех байт, по одному для красного, зелено-
го и синего компонентов пиксела. Считается, что такие пикселы отображают «реалистичное цве-
товоспроизведение» («true color»);
О RGBA-карта (RGBA-pixmap): каждый пиксел состоит из четырех байт: первые три байта такие
же, как и в RGB-карте, а четвертый содержит так называемый «альфа-фактор», характеризующий
непрозрачность. Мы будем рассматривать использование «альфа-канала» в разделе 10.3 «Объе-
динение пиксельных карт».
Создадим для работы с пиксельными картами класс, который содержит данные пиксельной карты и
предоставляет методы для обработки созданных в этом классе изображений. Мы разработаем детали
RGB-карт и распространим их на другие типы пиксельных карт. Для удобства использования инстру-
ментов обработки изображений OpenGL мы будем хранить данные пиксельной карты в том же виде,
в каком это делает OpenGL1.
Прежде всего определим тип под названием RGB, в котором содержится одно значение пиксела в
форме RGB-триады:
class RGB{
public: unsigned char r.g.b:
):
В листинге 10.1 приводится начало создаваемого нами класса RGBpixmap. Как принято в OpenGL, мы
представляем пиксельную карту в форме простого массива пиксельных значений pixel, который хранит-
ся строка за строкой снизу вверх и вдоль каждой строки слева направо.
Листинг 10.1. Класс RGBpixmap для обработки RGB-изображений
class RGBpixmap{
private:
int nRows, nCols:
// dimensions of the pixmap
// размеры пиксельной карты
RGB* pixel:
// array of pixels
// массив пикселов
public:
RGBpixmapO {nRows = nCols = 0: pixel = 0:}
RGBpixmapCint r. int c)
//constructor
// конструктор
nRows - r:
nCols - c;
pixel - new RGB[r*cJ;
1
void setPixel(int x. int y. RGB color)
продолжение^
1 На самом деле в OpenGL предлагается несколько способов «упаковки» пиксельной карты в памяти. Мы работаем с самым обще-
употребительным форматом.
622
Глава 10. Средства для растровой графики
Листинг 10.1 (продолжение)
if(x >= О 8J х < nCols && у >= 0 && у < nRows)
pixel[nCols * у + х] = color;
}
RGB getPixeUint x. int y)
{
return pixel[nCols * у + x];
}
//*** draw this pixmap at the current raster position
//*** рисуем эту пиксельную карту в текущей растровой
// позиции
void draw(){
glDrawPixels(nCols, nRows. GL_RGB.
GLJJNSIGNED BYTE.pixel);
}
//*** read a rectangle of pixels into this pixmap
//*** считываем прямоугольник пикселов в эту пиксельную карту
void readdnt х. int у. int wid. int ht){
nRows - ht;
nCols - w1d;
pixel = new RGB[nRows *nCols]; if(!pixel)exit(-l);
glReadPixels(x. y, nCols.
nRows.GL_RGB.GL_UNSIGNED_BYTE. pi xel);
}
//*** copy a region of the display back onto the display
//*** копируем область, взятую с дисплея, обратно на дисплей
void copyCint х. int у. int wid. int ht){
g!CopyPixels(x, y. wid. ht. GL_COLOR);
}
//*** read BMP file into this pixmap
//*** считываем BMP-файл в эту пиксельную карту
int readBmpFile(char * fname):
//*** write this pixmap to a BMP file
//*** записываем эту пиксельную карту в ВМР-файл
void writeBmpFile(char * fname);
// ...others ...
// .. .другие функции ...
}:
В листинге эскизно представлено несколько методов. Конструктор по умолчанию RGBpixmap создает
пустую пиксельную карту, а другой конструктор создает пиксельную карту с г строками и с столбцами.
Методы setPixel О и getPixel О соответственно задают и считывают определенное значение пиксела.
Методы drawO, readO, соруО реализуются непосредственно в терминах функций OpenGL:
О draw() копирует пиксельную карту в буфер кадров, помещая нижний левый угол этой карты в «те-
кущую растровую позицию» — это переменная величина, которая может быть установлена с по-
мощью подпрограммы glRasterPos2i(x, у).
О readO производит копирование в другом направлении — из прямоугольной области буфера кад-
ров в пиксельную карту. Нижний левый угол этой области находится в точке pt, а параметры wid
и ht определяют соответственно ширину и высоту области. Оператор readO выделяет память, не-
обходимую для хранения всех пикселов, а подпрограмма glReadPixelsO производит текущее ко-
пирование.
10.2. Управление пиксельными картами
623
О сору() копирует одну область буфера кадров в другую, эффективно выполняя те же операции,
что и обе функции readO и drawO, однако без создания промежуточной пиксельной карты. Ниж-
ний левый угол области лежит в точке (х, у), а его размер определяется значениями wid и ht. Эта
область копируется в новую позицию буфера кадров, нижний левый угол которой лежит в теку-
щей растровой позиции. Эта одна из форм операции «bitBLT», которую мы рассмотрим в разде-
ле 10.3.4 «Операция BitBLT».
Подпрограммы readBmpFileO и writeBmpFileO упрощают создание и сохранение пиксельных карт.
Подпрограмма readBmpFileO считывает изображение, записанное в BMP-файле, в пиксельную карту,
выделяя необходимое количество памяти. Подпрограмма writeBmpFileO создает BMP-файл, который
содержит пиксельную карту. Коды обеих этих функций приводятся в приложении В.
Класс RGBpixmap является простым и в то же время достаточно мощным. В следующем примере мы
покажем, как использовать этот класс.
Пример 10.2.1. Испытательный стенд для манипулирования с пиксельными картами
Листинг 10.2. Приложение, являющееся испытательным стендом для манипулирования с пиксельными картами
RGBpixmap pic[2];
// create two (empty) global pixmaps
// создаем две (пустые) глобальные пиксельные карты
int screenWidth = 640. screenHeight - 480:
IntPoint rasterPos(lOO.lOO):
int whichPic = 0;
// which pixmap to display
// какую карту следует отображать
//<««х««<««««««« myMouse »»»»»»»»»»»»
void myMouse(int button, int state, int mx. int my)
{
// set raster position with a left click
// задаем растровую позицию левым щелчком мыши
if (button == GLUT_LEFT_Bl)TTON)
{
rasterPos.x - mx; rasterPos.y - screenHeight - my;
glRasterPos2i(rasterPos.x. rasterPos.y);
glutPostRedisplayO;
}
else glClear(GL_COLOR_Bl)FFER_BIT);
// clear with right click
// очищаем экран правой кнопкой мыши
}
//<<<<<<<<<<<<<<<<<<<<<<<<< mouseMove »»»»»»»»>
void mouseMove(int x. int y)
// set raster position with mouse motion
// задаем растровую позицию посредством движения мыши
rasterPos.x = х; rasterPos.y = screenHeight - у:
glRasterPos2i(rasterPos.x. rasterPos.y);
glutPostRedisplayO:
}
//<<<<<<<<<<<<<<<<<<<<<<<<<< myReshape »»»»»»»»»>
void myReshape(int w. int h)
{
screenWidth - w; screenHeight - h;
}
продолжение^
624
Глава 10. Средства для растровой графики
Листинг 10.2 (продолжение)
//<<<<<<<<<<<<<<<<<<<<<<< myDisplay »»»»»»»»»»»»»
void rnyDisplay(void)
{
pic[whichPic].draw();
//draw it at the raster position
// рисуем текущую карту в растровой позиции
}
/ /<<<<<<<<<<<<<<<<<<<<<<<< myKeys >»»»»»>»»>»»>
void myKeys(unsigned char key. int x. int y)
{
switch(key)
{
case 'q‘: exit(O);
case 's': whichPic = 1 - whichPic: break:
// switch pixmaps
// переключаем пиксельные карты
case ’r’: pic[O].read(O.0.200.200): break:
// grab a piece
// захватываем фрагмент
}
gl utPostRedisplayO;
//<<<<<<<<<<<<<<<<<<<<<< main »»»»»»»»»»»»>
void main(int argc. char **argv)
{
glutlnit(&argc, argv):
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGB);
glutIni tWi ndowSi ze(screenWi dth. screenHeight):
glutInitWindowPosition(30. 30):
glutCreateWindowCExperiment with images"):
// «Экспериментируем с изображениями»
glutKeyboardFunc(myKeys):
glutMouseFunc(myMouse):
glutMotionFunc(mouseMove);
glutDisplayFunc(myDisplay):
glutReshapeFunc(myReshape):
glClearColor(0.9f, 0.9f, 0.9f, 0.0);
// background color
// цвет фона
glClear(GL_COLOR_BUFFER_BIT):
pi c[0].readBmpF11e("CokeCan2.bmp”);
// make a pixmap
// создаем пиксельную карту
pi с[1].readBmpF11e("Mandri11.bmp"):
// make another one
// создаем еще одну
glutMainLoopO;
}
В листинге 10.2 приведено приложение, в котором класс pixmap используется для управления чтением
и рисованием пиксельных карт с помощью мыши и клавиатуры. Экспериментирование с этой програм-
мой может быть весьма информативным. В начале работы подпрограммы создаются две пиксельные
10.2. Управление пиксельными картами
625
карты Р1с[0] и Рт с[1], и в них загружаются два BMP-файла. Одно из этих изображений отобража-
ется в начальной растровой позиции. После щелчка левой кнопкой мыши рисование методом drawO
осуществляется уже в позиции мыши. Если левая кнопка мыши удерживается в нажатом положении,
то данная пиксельная карта рисуется снова и снова по мере движения мыши по экранному окну. Нажа-
тие клавиши «з» осуществляет переключение между двумя рисуемыми таким способом пиксельными
картами. При нажатии клавиши «г» осуществляется чтение методом readO всего, что нарисовано в обла-
сти экрана размером 200 на 200 пикселов; эти данные помещаются.в массив ртс[О], стирая его прежнее
содержимое. По нажатию правой кнопки мыши экран очищается.
В последующих примерах будет показано, как варианты методов drawO, read() и сору() можно исполь-
зовать для решения наиболее типичных задач. Эти служебные подпрограммы используются в темати-
ческом задании 10.1.
Пример 10.2.2. Написание текста на экране
Один из простейших методов рисования текстовых символов на растровом дисплее состоит в том,
чтобы построить для каждого нужного символа отдельную пиксельную карту. На рис. 10.3 приводится
несколько примеров. В этих пиксельных картах содержатся «картинки» символов, заданные внутри
ячейки определенного размера (например, 12 на 8 пикселов). Некоторым пикселам присваивается зна-
чение 0, а остальным 1. Чем больше размер ячейки, тем больше свободы в создании формы каждого
символа, и тогда можно сделать более красивые шрифты.
Рис. 10.3. Символы, заданные как пиксельные карты
При начальном запуске рабочей станции с диска во внеэкранную память можно загрузить различ-
ные шрифты, чтобы сделать их доступными для чтения. Для того чтобы нарисовать строку симво-
лов, каждый символ рисуется с помощью функции drawO в нужном месте буфера кадров. После рисо-
вания очередного символа х-позиция увеличивается на ширину этого символа. У пропорционального
(proportionally spaced) шрифта каждый символ имеет свою ширину. (Обычно символ «i» является са-
мым узким, a «W» — самым широким.)
Пример 10.2.3. Прокрутка окна
В таких приложениях, как текстовые процессоры, экран обычно заполняется текстом — строка за стро-
кой. Для того чтобы освободить место для новой строки в нижней части экрана, весь текст выше этого
места должен быть прокручен вверх на одну строку (разумеется, с удалением верхней строки текста),
как это показано на рис. 10.4. Для того чтобы сделать это, с помощью программы копирования соруО
прямоугольная область, содержащая весь текст, кроме верхней строки, перемещается на одну строку
вверх, перезаписывая все, что было там прежде. В позицию последней строки с помощью процедуры
draw() рисуется пустая строка.
Настало время
для всех хороших людей
прийти к
Для всех хороших людей
прийти к
Пустая строка
Рис. 10.4. Прокрутка текста в окне
626
Глава 10. Средства для растровой графики
Пример 10.2.4. Всплывающие (pop-up) и спускаемые меню (pull-down menus);
диалоговые окна (dialog boxes)
В настоящее время большая часть взаимодействия с компьютером осуществляется через графический
интерфейс пользователя (graphical user interface — GUI). Наряду с другими вещами этот интерфейс
предоставляет меню и диалоговые окна, где пользователь с помощью мыши выбирает каждое нужное
ему действие.
При активизации меню оно появляется в поле зрения, временно заслоняя некоторую часть экрана.
На рис. 10.5, а показано, как спускаемое меню заслоняет часть экрана. После того как пользователь
сделает какой-нибудь выбор, это меню исчезает, а заслоненная им часть экрана показывается вновь
(рис. 10.5, б\ Эта заслоняемая часть должна быть вначале сохранена во внеэкранной памяти, чтобы впос-
ледствии она могла быть восстановлена. Управление таким меню организовано следующим образом.
1. Пользователь выбирает заголовок меню.
2. Программа определяет, какая прямоугольная область будет заслонена.
3. С помощью процедуры readO делается копия заслоняемой области во внеэкранную пиксельную
карту.
4. Процедура draw() рисует изображение меню в соответствующем месте.
5. Пользователь перемещает курсор к нужному пункту меню и отпускает кнопку мыши.
6. Приложение восстанавливает заслоненную часть экрана путем копирования внеэкранной пик-
сельной карты в ее прежнее положение.
Рис. 10.5. Спускаемое меню (а); восстановленное изображение (б)
Пример 10.2.5. Поддержка множественных окон
В настоящее время является обычной практикой одновременный запуск нескольких приложений с пере-
крывающимися окнами. На рис. 10.6 изображен дисплей с несколькими окнами. Поскольку части одного
окна перекрывают и заслоняют части другого, программа должна правильно восстанавливать эти обла-
сти экрана, когда соответствующее окно перемещено или закрыто. Пусть, например, мы хотим нарисо-
вать еще одно окно в позиции, отмеченной на рисунке. Тогда, как И прежде, мы должны:
О прочитать с помощью readO область экрана, которая будет заслонена;
О нарисовать с помощью drawl) новое окно, заслонив им данную область исходного изображения.
Позднее, если заслоняющее окно убирается, то оно вначале сохраняется для возможного дальнейше-
го использования, а исходный прямоугольник восстанавливается при помощи draw().
10.2. Управление пиксельными картами
627
Рис. 10.6. Открытие и перемещение нового окна
Эта схема работает хорошо в тех случаях, когда изображение, заслоненное окном, «заморожено» в
течение времени заслона. Но все становится значительно сложнее в том случае, когда информация в
скрытом окне изменяется. Задача заключается в том, что делать с теми частями изображений, которые
изменились в скрытом состоянии. Когда заслоненное окно впоследствии открывается, его изображение
должно быть обновлено. В литературе обсуждается несколько схем решения этой задачи [Pike, 168].
Чаще всего ответственность за отслеживание того, что происходит в таких окнах, возлагается на прило-
жение; в его задачу входит и восстановление изображения после того, как это окно становится полнос-
тью видимым.
10.2.3. Масштабирование и поворот изображений
Никогда не надевайте наушники, лежа в постели, полной гремучих змей.
Еще один компьютерный Закон Мерфи
Часто бывает нужно масштабировать или поворачивать изображения. Пусть, например, спутниковая
фотография Земли изображает Европу в пиксельной карте 1200 на 1600 пикселов, а мы хотим сравнить
эту фотографию со сделанным ранее изображением размером 1540 на 1880 пикселов. Прежде чем эти
пиксельные карты можно будет сравнить, меньшая из них должна быть увеличена так, чтобы соответ-
ствующие части изображений были «выровнены». Аналогичная задача возникает, когда мы составляем
картотеку оцифрованных отпечатков пальцев и обнаруживаем, что некоторые из изображений отпе-
чатков слегка повернуты относительно других. Для сравнения различных отпечатков их изображения
необходимо повернуть для выравнивания в едином направлении. Рассмотрим вкратце некоторые про-
стейшие типы масштабирования и поворота.
Идея состоит в том, что при масштабировании пиксельной карты с некоторым множителем $ создает-
ся пиксельная карта, которая содержит в $ раз больше пикселов как по х, так и по у. Если придерживаться
фотографической терминологии, то при $ > 1 пиксельная карта увеличивается (enlarged); в остальных
случаях она уменьшается (reduced). Сами пикселы, конечно, не изменяют размеров. Когда $ — целое
число, изображение легко может быть масштабировано при помощи повторения пикселов (pixel
replication). На рис. 10.7 показан пример повторения пикселов битовой карты символа. Каждый пиксел
меньшего символа порождает массив пикселов размерностью два на два. Для других целых значений s
каждый пиксел порождает массив размерностью s на $ пикселов.
Также нетрудно уменьшить пиксельную карту в некоторое целое число раз (тогда масштабный мно-
житель s = 1/и, где п — целое). Например, при 5 - 1/3 мы могли бы построить уменьшенную пиксельную
карту, просто оставив каждую третью строку и каждый третий столбец оригинала. Такой метод «вы-
борки» из исходной пиксельной карты обычно приводит к потере информации, поэтому уменьшенное
изображение может оказаться намного хуже оригинала. Обычно лучший результат дает вычисление
(если оно возможно) среднего значения цвета девяти пикселов и помещение его в остающийся «пред-
628
Глава 10. Средства для растровой графики
ставляющий» (representative) пиксел. Эту и другие технологии сглаживания мы будем рассматривать в
разделе «Ступенчатость; технологии сглаживания».
Рис. 10.7. Удвоение пикселов для увеличения символов
OpenGL предоставляет простой механизм масштабирования изображения, нарисованного посред-
ством пиксельной карты, с помощью подпрограмм glDrawPixelsO или glCopyPixelsO (тогда методы
drawO и сору О покажут результаты масштабирования). Функция
glPixelZoom(float sx. float sy):
задает по х и по у масштабные множители, с которыми впоследствии будут рисоваться пиксельные
карты. Сами пиксельные карты не масштабируются, масштабируются лишь изображения, задаваемые
этими пиксельными картами. Для параметров sx и sy допускаются любые, даже отрицательные веще-
ственные числа. По умолчанию их значения равны 1.0.
Масштабирование выполняется относительно текущей растровой позиции pt. Рассмотрим пиксел,
находящийся в строке г и столбце с пиксельной карты. Грубо говоря, он будет нарисован в виде прямо-
угольника шириной sx и высотой sy экранных пикселов, а нижний левый угол будет находиться в экран-
ном пикселе (ptx: + sx*r,pt.y + sy*c). Точнее, любые экранные пикселы, центры которых лежат внутри
этого прямоугольника, рисуются тем же цветом, что и пиксел пиксельной карты. Если, например, sx - 2 и
sy = 3, то пиксельная карта рисуется с правильным повторением пикселов и будет вдвое шире и втрое выше,
чем немасштабированная пиксельная карта. Если же значения sx и/или sy являются дробными, то изобра-
жение будет соответственно уменьшено и может потерять в качестве, поскольку цвет каждого экранно-
го пиксела является просто цветом того «прямоугольника», центром которого является данный пиксел.
Если sx или sy отрицательны, то изображение отражается относительно текущей растровой пози-
ции. Отражение может быть полезным при представлении пиксельной карты вверх дном (с помощью
подпрограммы glPixelZoomd.О, -1.0)), а также для создания специальных визуальных эффектов. На
рис. 10.8 показано четыре промасштабированных варианта изображения, помещенных рядом (здесь
использована последовательность масштабных множителей sx = 1, -1, 0,5, 1,5). При создании каждого
изображения задавалось новое значение sx, после чего выполнялись команды
glPixelZoom(sx. 1):
gl utPostRedisplay():
Рис. 10.8. Различные версии пиксельной карты, сформированные путем масштабирования по х
10.2. Управление пиксельными картами
629
Повороты на четверть оборота
Процесс поворота пиксельной карты на 90°, 180° или 270° очень прост: создается новая пиксельная
карта, и пикселы копируются из одной карты в другую с помощью процедур getPixelO и setPixelO
(см. упражнения в конце раздела).
Масштабирования и повороты более общего вида
Все становится сложнее, когда требуется произвольное масштабирование или поворот. Пусть, напри-
мер, мы хотим создать пиксельную карту, содержащую преобразованную версию исходной карты. На
рис. 10.9 показана пиксельная карта S (источник), которую мы хотим изменить посредством преобра-
зования Т, возможно, являющееся аффинным и состоящее из некоторого набора масштабирований и
поворотов. Результатом будет пиксельная карта D (адресат). Задача состоит в том, чтобы вычислить
правильный цвет пиксела для каждой точки р в пиксельной карте D. Простейший подход заключается
в следующем: находим для центральной точки р каждого пиксела в D цвет пиксела в S, который нахо-
дится в точке Г_,(р). Затем этот цвет используется для пиксела точки pvD. Однако использование та-
ких «выборок» может привести к плохим результатам с сильной ступенчатостью. Обычно намного луч-
ше найти усредненный цвет в той области пиксельной карты S, которая преобразуется в квадратный
пиксел в карте D, и использовать именно этот усредненный цвет. Такой подход является одной из форм
борьбы со ступенчатостью.
Рис. 10.9. Вычисление преобразованного изображения
Практические упражнения
10.2.1. Конструирование буквы R
Сконструируйте и нарисуйте двухуровневое изображение буквы R размером 8 на 16 пикселов.
Покажите сочетание единиц и нулей и картинку, которая получается, если 0 означает белый цвет,
а 1 — черный.
10.2.2. Конструирование символов
Сконструируйте красивые символы «а», «Л», «г», «/?», «?», «3» в пределах клеток из г строк и с столб-
цов. Выполните это для каждого из ниже перечисленных размеров клеток:
О (г, с)- (6,4);
О (г, с) - (10,8);
О (г, с) = (14,12).
10.2.3. Слишком малы для узнавания?
Клетка размером (5,3) состоит из 15 пикселов и поэтому допускает 215 различных двухуровневых узо-
ров из пикселов. Можно ли нарисовать в такой клетке все печатаемые ASCII-символы так, чтобы они
были различными (и узнаваемыми)?
630
Глава 10. Средства для растровой графики
10.2.4. Уменьшение символов
Один из методов уменьшения размера символа, заданного в виде прямоугольной пиксельной карты, состоит
в сокращении в два раза длины клетки в обоих измерениях. Тогда каждый пиксел уменьшенной пиксель-
ной карты должен имитировать то, что находилось в массиве пикселов размером 2 на 2 в исходной клетке.
Разработайте алгоритм, который создает пиксельный узор размером (г, с) = (6,5) из пиксельной карты раз-
мером (г, с) = (12,10). Один из возможных способов формирования нового пиксела заключается в уста-
новке его в единицу, если два или более пикселов массива 2 на 2 равны единице. Хорош ли этот способ?
10.2.5. Поворот на 90°
Рассмотрим квадратную пиксельную карту, представленную массивом А[т][j], где 1 и j изменяются от
О до N-1. Выразите величину B[col][row] этой пиксельной карты, образованную поворотом А на 90° про-
тив часовой стрелки.
10.3. Объединение пиксельных карт
В определенных обстоятельствах бывает нужно объединить две пиксельные карты для получения из них
третьей. Объединение пиксельных карт бывает полезным в таких ситуациях, как движение курсоров
по экрану, сравнение двух изображений или морфинг (morphing), то есть плавная трансформация од-
ного изображения в другое с помощью геометрических операций и цветовой интерполяции. Мы рас-
смотрим несколько примеров, имеющих практическое значение.
Пиксельные карты обычно объединяются попиксельно. Это означает, что выполняется некоторая
операция между соответствующими пикселами в старой и новой картах. В частности, две пиксельные
карты АиВ объединяются в третью карту С согласно следующей формуле:
C[i][j] = A[i][j] ® B[i][j] для каждого i,j,
где значком ® обозначена некоторая операция. Ниже приводятся несколько примеров операций.
О Усреднение двух изображений. Здесь ® означает формирование суммы из половины А и половины В:
ОДЫ = | (ОДЫ + ОДЫ)-
О Определение различий между двумя изображениями. Для этого изображения вычитаются,
и здесь операция ® означает вычитание:
ОДЫ “ОДЫ “ОДЫ-
О Поиск мест, где одно изображение ярче, чем другое. Здесь ® означает операцию «больше чем»:
ОДЫ = ОДЫ > ОДЫ-
Согласно этой формуле, каждому пикселу в карте С присваивается значение единица, если соответ-
ствующий пиксел в А ярче, чем в В; и ноль в противном случае.
Обобщение усреднения двух изображений заключается в формировании их среднего взвешенного
(weighted average). Пиксельная карта А берется с весом (1 -/), а пиксельная картаВ — с весом/, где/—
некоторая дробь:
ОДЫ = (1 -ПОДЫ +/ОДЫ- (10.1)
Например, если RGB-компоненты пиксельной карты A[i][у] равны (14, 246, 97), а карты B[i]Ы ~
(82, 12, 190), то при /- 0,2 мы получим C[i][y] - (27, 199, 115). Среднее взвешенное двух RGB-карт
можно получить с помощью подпрограмм setPixel О и getPixel О, разработанных ранее.
Пример 10.3.1. Растворение одного изображения в другом
Метод среднего взвешенного находит интересное применение в случае, когда одно изображение долж-
но быть растворено (dissolved) в другом. Вначале на дисплее видно только изображение А, однако с
течением времени оно медленно тускнеет и проступает наложенное на него изображение В, пока на
10.3. Объединение пиксельных карт
631
экране не остается только одно В. Если параметр t представляет собой время, то в момент t на экране
демонстрируется изображение
Л(1-Г) + В£,
где t плавно изменяется от 0 до 1. Данная технология напоминает «твининг», описанный в главе 4. На
рис. 10.10 показано пять стадий отображаемой картинки для значений t = 0,0,25, 0,5,0,75,1. В тема-
тическом задании 10.2 рассматривается простой способ растворения изображения — с использованием
средства OpenGL под названием «альфа-канал», которое мы опишем в разделе 10.3.2.
Рис. 10.10. Растворение одного изображения в другом
Практические упражнения
10.3.1. Формирование среднего взвешенного двух RGB-карт
Напишите код, формирующий RGB-карту С в соответствии с уравнением (10.1) и использующий мето-
ды getPixelO и setPixelO.
10.3.2. Изучение численного анализа
Блинн [Blinn, 27] говорит об ошибках округления, имеющих место при выполнении усреднения пик-
сельных карт. Прочитайте этот текст.
10.3.1. Цикл «чтение — модификация-запись»
При формировании новой пиксельной карты С как объединения двух пиксельных карт — D (адресата)
и 5 (источника) — имеет место частный случай, когда карта С — та же самая, что и D, то есть результат
операции помещается обратно в D. Этот случай можно представить следующим образом: D = D ® 5:
пикселы карты D комбинируются с пикселами карты S, а результат помещается обратно в D. Такая опера-
ция носит название цикла чтение — модификация-запись (read—modify-write cycle), поскольку внача-
ле пикселы карты D читаются из памяти, затем модифицируются путем комбинирования с пикселами
карты 5 и, наконец, получившийся результат записывается обратно в D. На рис. 10.11 в символической
форме показано, как такой цикл работает в случае, когда D является самим буфером кадров. Этот цикл
применяется поочередно к каждому пикселу карты D. В некоторых аппаратных конфигурациях эта
С ® А
Рис. 10.11. Применение цикла «чтение — модификация-запись» к буферу кадров
632
Глава 10. Средства для растровой графики
операция выполняется очень эффективно. Как мы увидим позднее, в OpenGL имеются средства для
выполнения цикла чтение — модификация-запись во всей пиксельной карте с помощью одной команды.
10.3.2. Альфа-канал и смешивание изображений
Формирование взвешенной суммы двух изображений фактически представляет собой частный случай
операции более общего вида, называемой смешиванием (blending) или компоновкой (compositing)
изображений. Операция смешивания позволяет рисовать частично прозрачное изображение поверх
другого. Суть этой операции заключается в добавлении к каждому RGB-цвету четвертого компонента,
так называемого альфа-фактора (alpha value). В терминах типов данных для хранения пикселов мы
расширяем тип RGB до типа RGBA:
class RGBA{
public: unsigned char r. g. b. a:
}:
и назначаем каждому пикселу значение альфа-фактора а от 0 до 255. Обычно альфа-фактор интер-
претируют как степень «непрозрачности» каждого пиксела: значение 0 означает полную прозрачность,
а значение 255 — полную непрозрачность. Отметим, что запись пиксельной карты в формате RGBA за-
нимает на треть больше памяти, чем ее запись в формате RGB. Совокупность альфа-факторов, находя-
щихся в пиксельной карте, часто называют альфа-каналом (alpha channel).
Как мы увидим в дальнейшем, альфа-компонент чаще всего используется в качестве масштабного
множителя в диапазоне от 0 до 1, так что фактически используется дробь а/255.
Пример 10.3.2. Наложение полупрозрачного изображения на другое изображение
На рис. 10.12 показан пример наложения изображения 5, содержащего маску и дракона, на фон D. При
создании изображения S пикселам дракона задаются альфа-факторы 255 (полная непрозрачность), аль-
фа-факторы пикселов маски устанавливаются в 128 (полупрозрачность), а для всех остальных пиксе-
лов альфа-факторы равны 0 (прозрачность). При смешивании пиксельной карты S с картой D на перед-
нем плане виден дракон поверх фона D, а часть цвета заднего плана «просвечивает» сквозь маску.
Рис. 10.12. Наложение изображения S на изображение D
Альфа-смешивание (alpha blending) может быть выполнено внутри цикла чтение — модификация-
запись путем формирования среднего взвешенного из пикселов карты источника и карты адресата и
помещения этого усредненного пиксела обратно в пиксельную карту адресата. Такая операция имеет вид
D = aS + (1 - a)D, где параметр а — это альфа-фактор источника, представляющий собой некоторую дробь
между 0 и 1. Однако альфа-фактор изменяется от пиксела к пикселу; кроме того, обе пиксельные кар-
ты — 5 и D — имеют красный, зеленый и синий компоненты, поэтому приведем более точный вид фор-
мулы для результирующего пиксела адресата в j-й строке и г-м столбце (для зеленого компонента):
D[i][j].g = + (1 - «)ОДЬМ> (Ю.2)
10.3. Объединение пиксельных карт
633
где а — дробь,
а . SHU]*
255
Обратим особое внимание на зависимость а от i nj: альфа-фактор изменяется от пиксела к пикселу.
Сходные выражения имеют место для красного и синего компонентов.
Для того чтобы осуществить такой способ смешивания в программе, нужно сначала расширить ра-
нее описанный класс RGBpixmap до класса RGBApixmap (см. упражнения в конце раздела), после чего доба-
вить метод blendO, который выполняет наложение в цикле чтение — модификация-запись. Тогда смеши-
вание пиксельных карт SiiD можно будет выполнить с помощью следующего кода:
D.drawO;
//draw D opaquely, as usual
// рисуем D непрозрачной, как обычно
S.blendO;
//use alpha values in S: form a weighted average with D
// используем альфа-факторы в S
// формируем взвешенное среднее с D
В OpenGL содержатся средства, упрощающие реализацию подпрограммы blendO: нужно просто ус-
тановить «режим наложения» («blend mode»), который определяет способ вычисления подпрограммой
blendO «масштабного множителя источника» и «масштабного множителя адресата». Для того чтобы
установить альфа-фактор источника в а, нужно просто выполнить команду
glBlendFunc(GL_SRC_ALPHA. GL_ONE_MINUS_SRC_ALPHA);
По этой команде масштабный множитель источника устанавливается равным альфа-фактору само-
го источника, а масштабный множитель адресата устанавливается равным единице минус альфа-фак-
тор источника, что нам и нужно. В листинге 10.3 приведена простая реализация подпрограммы blendO.
Листинг 10.3. Смешивание изображений источника и адресата с помощью альфа-канала
void RGBApixmap :: blendO
glBlendFunc(GL_SRC_ALPHA. GL_ONE_MINUS_SRC_ALPHA):
glEnable(GL_BLEND);
// enable blending
// смешивание разрешено
drawO:
// draw this pixmap blended with the destination
// рисуем эту пиксельную карту.
// смешанную с пиксельной картой адресата
1
Пример 10.3.3. Имитация хроматического ключа (ChromaKey):
придание прозрачности некоторым цветам
Обычно в телевизоре мы видим синоптика, стоящего перед картой, на которой отмечены различные
погодные условия. На самом деле синоптик стоит перед синим фоном (рис. 10.13, а) и одновременно
показывается отдельная метеорологическая карта. Телевизионный сигнал «на лету» переключается
между изображениями человека и карты: когда во время строковой развертки встречается синий цвет,
то показывается карта; во всех остальных случаях показывается человек.
Этот эффект можно имитировать с пиксельными картами и задать определенный цвет в карте источ-
ника прозрачным, установив его альфа-фактор в нуль. Ниже приводится подпрограмма, которая ска-
нирует пиксельную карту и устанавливает альфа-фактор каждого пиксела в нуль, если его цвет совпадает
с выбранным цветом, и в единицу в противном случае:
634
Глава 10. Средства для растровой графики
void RGBApixmap::setChromaKey(RGB с)
{
long count = 0;
for(int row = 0; row < nCols; row++)
for(int col - 0: col < nRows: col++)
RGBA p - pixel[count]:
if(p.r — c.r && p.g — c.g && p.b — c.b)
pixel[count++].a - 0:
else pixel[count++].a - 255:
}
}
Рис. 10.13. Хроматический ключ, используемый в телевидении
Пример 10.3.4. Использование рисования кистью
х программе рисования курсор мыши выступает в качестве кисти, так что можно каждому «мазку» кисти
сопоставить свой образчик цвета. Это может быть сделано в OpenGL смешиванием с помощью Ы end()
пиксельной карты кисти с изображением адресата, задавая для пикселов кисти альфа-фактор равным 10 %
или около того, эри каждом мазке кисти к изображению адресата примешивается все больше цвета
кисти, (х упражнениях приводится оценка усиления нового цвета с каждым новым мазком кисти.)
яожно придать пикселам вблизи от центра кисти больший альфа-фактор, чем по краям, и тогда цвет в
центре будет добавляться быстрее, ыа рис. 10.14 показано использование кисти в виде облака; кисть
применяется различное число раз для придания рисунку различных степеней покрытия.
Рис. 10.14. Рисование с помощью «облачной» кисти
10,3. Объединение пиксельных карт
635
Пример 10.3.5. Управление курсором
Когда пользователь перемещает мышь, курсор движется по дисплею. В каждой своей позиции курсор
делает невидимой ту часть экрана, которую он заслоняет. Когда курсор движется дальше, эта часть эк-
рана должна быть восстановлена. Этот процесс аналогичен тому, который имел место в спускаемом
меню, как видно из рис. 10.15. Прежде чем курсор рисуется на экране, делается копия прямоугольного
участка изображения, который будет закрыт курсором (на рисунке он показан как пиксельная карта
Pzxl). Затем пиксельная карта курсора смешивается в этой точке. Альфа-фактор этой карты равен еди-
нице в непрозрачной части курсора и нулю в остальных-местах, поэтому при смешивании этих двух
изображений кажется, будто стрелка парит над изображением фона. Когда курсор перемещается в но-
вую позицию, происходят следующие три события:
1. Подпрограмма draw() рисует карту Pixi с альфа-фактором 1, чтобы покрыть изображение теку-
щего курсора и восстановить исходное изображение.
2. Копия той части изображения, которая должна быть заслонена, читается с помощью read() во
внеэкранную память.
3. Курсор снова смешивается с изображением в новой позиции.
Рис. 10.15. Управление движущимся курсором
Расширения, допускаемые в OpenGL
В OpenGL имеется пара инструментов, предназначенных для установки и использования альфа-канала.
Установка альфа-факторов. При визуализации сцены можно в явном виде задать альфа-факторы
для последовательно рисуемых графических объектов при помощи подпрограммы glColor4f(r,g,b,a),
где а изменяется в диапазоне от 0,0 (полная прозрачность) до 1,0 (полная непрозрачность). По умолча-
нию альфа-фактор равен 1,0. Трехмерный объект можно также сделать полупрозрачным, задав всем
пикселам этого объекта специальные альфа-факторы. Это делается путем установки альфа-фактора в
коэффициенте диффузного отражения для каждой вершины объекта с помощью кода
glMaterialfv(GL_FRONT, GL_DIFFUSE. refl):
где refl — упорядоченная тетрада, задающая цвет диффузного компонента, например, так:
float refl[4] = (0.5. 0.3, 0.8, 0.4}.
Этот оператор присваивает альфа-фактор 0,4 всем последовательно определяемым вершинам.
Установка методов смешивания. Мы уже видели, как подпрограмма glBlendFunc(GL_SRC ALPHA,
GL_ONE_MINUS_SRC_ALPHA) используется для получения среднего взвешенного изображений источника и
адресата: D = aS + (1 - a)D. В OpenGL разрешается задавать различные значения масштабных множителей
636
Глава 10. Средства для растровой графики
источника и адресата посредством выбора параметров, входящих в подпрограмму glBlendFuncO, а имен-
но: GL_ZERO, GL_ONE, GL_DST_ALPHA, GL_SRC_COLOR ит. д. Например, команда glBlendFunc(GL_DST_ALPHA.GL_ONE_
MINUS_DST_ALPHA) устанавливает для пикселов источника и адресата веса aD и (1 - ал) соответственно, где
становится теперь альфа-фактором адресата, а не источника. А команда glBlendFunc(GL_DST_COLOR.
GL ZERO) корректирует (умножает) каждый компонент цвета пиксела источника на уровень соответству-
ющего пиксела адресата.
Практические упражнения
10.3.3. Расширение класса RGBpixmap путем включения в него альфа-компонента
Произведите изменения в классе RGBpixmap, который был определен в разделе «Типы данных, использу-
емые для пиксельных карт», так чтобы пиксельные карты поддерживали альфа-канал. Добавьте мето-
ды blendO и setChromaKeyO, после чего протестируйте их на таких операциях:
О чтение BMP-изображения в пиксельную карту (интереснее всего, если это изображение содержит
однородный фон какого-либо цвета);
О придание с помощью подпрограммы setChromaKeyO прозрачности определенному цвету;
О смешивание данной пиксельной карты с какой-нибудь другой для проверки свойства прозрачно-
сти в действии.
10.3.4. Применение нового цвета с помощью мазков кисти
Рассмотрим пиксельную карту кисти, у которой вблизи центра кисти альфа-фактор является малым,
а в остальных местах равен нулю. При каждом использовании такой кисти она смешивает цвет кисти С
с любым изображением D адресата, вследствие чего D = аС + (1 - a)D. При повторном использовании
количество цвета кисти возрастает. Докажите, что после i-ro применения кисти цвет адресата равен
£). = аС + (1 - a)Di V Определите долю цвета адресата, которая перешла от цвета источника С после
восьми мазков.
10.3.3. Логические комбинации пиксельных карт
Существуют другие способы комбинирования пиксельных карт, при которых каждый пиксел рассмат-
ривается просто как совокупность бит, причем не обращается никакого внимания на то, какое числен-
ное значение представляют эти биты. Пиксельные карты по-прежнему комбинируются пиксел за пик-
селем, однако теперь биты в пикселе комбинируются логически (logically), бит за битом. Например,
над битами могут производиться следующие операции: OR, AND, EXCLUSIVE OR.
Пусть, например, пиксел А состоит из RGB-компонентов (21,127,0). Если записать эти компоненты
в двоичной форме, то мы будем иметь А = (00010101, 01111111, 00000000). Предположим далее, что
пиксел В в двоичной форме имеет вид В = (01010101,11110000, 10000101). Если логически сложить
(OR) эти две триады, то получим следующий результирующий пиксел С:
(01010101,11111111, 10000101) <—операция OR надАиВ.
Каждый бит пиксел пиксельной карты С равен 1, если любой из соответствующих бит карт А и В
(или оба сразу) равен 1. Если же мы произведем над А и В операцию EXCLUSIVE OR (XOR — исклю-
чающее ИЛИ), то получим:
С - (01000000,10001111,10000101) «- операция XOR над А и В.
В этом случае каждый бит карты С равен единице, если ровно один из соответствующих бит карт А
и В равен 1 — это значит, что один бит, но не два, должен равняться 1. Цвет С = A XOR В зависит от
цветов А и В сложным образом (см. упражнения в конце раздела). Ответьте на вопрос, чему равно А
XOR В, если:
О В = (0, 0, 0) (черный);
О В = (255,255, 255) (белый)?
10.3. Объединение пиксельных карт
637
Интересное свойство операции XOR заключается в том, что двукратное ее применение эквивалентно
тому, как если бы ее не применяли вообще; это значит, что если С = A XOR В, то при операции С XOR В
мы имеем (A XOR В) XOR В, то есть снова Л! (См. упражнения.) Мы вернемся к этому свойству по-
зднее, при применении для формирования изображений «метода резиновой нити» («rubber banding»).
В языках типа C++ прямо поддерживаются побитовые логические операции, поэтому естественно
выполнять их внутри подпрограммы. Например, для логического сложения (OR) зеленых компонен-
тов карт А и В достаточно выполнить команду С.д=А.д|В.д. Аналогично для выполнения над красными
байтами операции исключающего ИЛИ (XOR) мы пишем: С.г=Д.гАВ.г.
Остальные операторы включают AND, NOT и их комбинации. При логическом умножении (AND)
двух величин, что для зеленого компонента на C++ имеет вид С.д=А.д&В.д, каждый бит в С.д равен 1
только тогда, когда оба соответствующих бита в картах А и В равны 1. Если над величиной произведена
операция отрицания (дополнения) NOT, то представление на C++ имеет вид: С.д=-А.д, то есть каждый
бит карты С равен 1 тогда и только тогда, когда соответствующий бит карты А равен 0.
Можно было бы использовать эти логические операторы C++ для попиксельного комбинирования
двух пиксельных карт, однако в OpenGL, к счастью, предусмотрен механизм комбинирования двух карт
целиком за одно обращение. После того как логическая операция выбрана и запущена, все последую-
щие операции рисования выполняют цикл чтение—модификация-запись пикселов источника с пиксе-
лами, находящимися в данный момент в буфере кадров.
Запуск логических операций производится с помощью команды glEnable(GL_COLOR_LOGIC_OP). Опера-
тор выбирается с помощью подпрограммы glLogicOpO, аргумент которой показан в табл. 10.1, где буквой
S обозначен пиксел источника, а буквой D — пиксел адресата. По умолчанию принято GL_COPY, в резуль-
тате чего пиксел адресата просто замещается пикселом источника.
Таблица 10.1. Допустимые логические операции в OpenGL
Значение параметра Величина, записанная в карту адресата
GL.CLEAR GL_COPY GL_NOOP GL.SET GL.COPYJNVERTED GLJNVERT GL_AND_REVERSE GL_AND GL_OR GL_NAND GL.NOR GL_XOR GL.EQUIV GL.ANDJNVERTED GLORJNVERTED 0 S D 1 NOTS NOT D S OR NOT D SANDD SORD NOT(S AND D) NOT(S OR D) SXORD NOT(S XOR D) NOT S AND D NOT S OR D
На рис. 10.16 приводятся примеры логического комбинирования двух пиксельных карт для случая
пикселов, заданных в двоичной форме. Связывание значения пиксела с цветом здесь выглядит так: 0 —
черный, 1 — белый. (Как эти пиксельные карты будут выглядеть после применения операторов GL_AND
и GL_EQUIV?)
Ниже описывается классическое применение операции XOR для рисования «резиновых прямо-
угольников»; там же показывается, как это реализуется в рамках OpenGL. При этой операции использу-
ется тот факт, что два последовательных рисования в режиме XOR стирают объект, оставляя исходное
изображение нетронутым. Еще несколько примеров рассматриваются в упражнениях.
638
Глава 10, Средства для растровой графики
Рис. 10.16. Эффекты применения различных логических операций
Пример 10.3.6. Рисование «резиновых прямоугольников»
«Резиновые прямоугольники» («rubber rectangles») и «резиновые нити» («rubber-band lines») очень
удобны для пользователя, который желает рисовать на дисплее при помощи мыши аккуратные фигуры.
На рис. 10.17 показано несколько примеров. При рисовании резинового прямоугольника (см. рис. 10.17, а)
пользователь вначале указывает мышью точку на том месте, где должен находиться один угол желаемого
прямоугольника, после чего нажимает кнопку мыши. Это действие определяет опорную точку (pivot).
Затем по мере того, как пользователь перемещает мышь от опорной точки, появляется «эластичный»
прямоугольник, один угол которого все время находится в опорной точке, а противоположный угол —
в текущей позиции мыши. При изменении этого прямоугольника он накладывается на все нарисованное
на экране, ничего там не меняя. Пользователь может корректировать этот прямоугольник взад-вперед
до тех пор, пока он в точности не охватит нужную область. При отпускании кнопки мыши последний
вариант прямоугольника остается видимым на экране, причем его координаты могут использоваться
программой для дальнейшего рисования. Резиновая нить (см. рис. 10.17, б) представляет собой элас-
тичную прямую линию, которая простирается от опорной точки до позиции мыши, увеличиваясь и
уменьшаясь в длине по мере перемещения мыши. Эта нить является вариацией резинового прямоуголь-
ника, когда рисуется только его диагональ.
Опорная точка
Рис. 10.17. Резиновый прямоугольник (а); резиновая нить (б)
10.3. Объединение пиксельных карт
639
Резиновый прямоугольник (или резиновая нить) должны непрерывно стираться и рисоваться вновь
при малейших изменениях позиции мыши. Нельзя стереть прямоугольник простым рисованием его
цветом фона, поскольку это уничтожило бы изображение, лежащее под линией. Рисование в режиме
XOR решает эту задачу. Для того чтобы стереть прямоугольник, его нужно просто нарисовать вторич-
но, тогда исходное изображение будет восстановлено.
Листинг 10.4. Подпрограммы мыши для резинового прямоугольника
IntRect гг;
// global rectangle
// глобальный прямоугольник
//««<««<««« myMouse »»»»»»»»
void myMouse(int button, int state, int mx. int my)
{
if(button == GLUT LEFT_BUTTON && state == GLUT DOWN)
{
glEnable(GL_COLOR_LOGIC_OP):
// enable logical operations
// запускаем логические операции
glLogicDp(GL_XOR):
// set it to XOR mode
// устанавливаем режим XOR
rr.left - rr.right = mx;
// set the pivot
// задаем опорную точку
rr.top - rr.bott = screenHeight - my;
}
if(button == GLUT_LEFT_BUTTON && state “ GLUT.UP)
glDisable(GL_COLOR_LOGIC_OP):
// disable logical operations
// запрещаем логические операции
}
//<«<«««<«<« mouseMove »»»»»»»»>
void mouseMove(int mx. int my)
rr.draw():
// erase the old: works only in XOR mode
// стираем старый прямоугольник: это работает только
// в режиме XOR
rr.right - mx:
// set the new opp. corner
// задаем новый противоположный угол
rr.bott - screenHeight - my;
// flip y-coord.
// зеркально отражаем координату у
rr.drawO;
// draw the new
// рисуем новый прямоугольник
}
В листинге 10.4 приведены подпрограммы для мыши, которые создают резиновый прямоугольник и уп-
равляют им. Эти процедуры обратного вызова регистрируются в программе mainO обычным способом: при
выполнении команды MouseFunc(myMouse) процедура myMouseO становится процедурой обратного вызова для
событий нажатия или отпускания кнопки мыши, а при выполнении команды gl utMouseMoti onFunc(mouseMove)
640
Глава 10. Средства для растровой графики
процедура mouseMoveO становится процедурой обратного вызова для события «перемещение мыши с
нажатой кнопкой». Глобальный объект — прямоугольник гг — используется в обеих подпрограммах и
является в них объектом ссылки. Начальный прямоугольник (нулевых размеров) устанавливается под-
программой myMouseO. Избегайте рисовать этот прямоугольник черным цветом (все нули)! (Почему?)
Отметим, что при рисовании в режиме XOR резиновый прямоугольник не имеет однородного цве-
та. Вместо этого каждый пиксел вдоль прямоугольника рисуется тем цветом, который получается пос-
ле применения операции XOR к «истинному» цвету прямоугольника и цвету фона в этой точке. Обыч-
но это отсутствие однородности цвета не слишком мешает. Более того, оно может оказаться полезным,
поскольку ясно видны объекты, находящиеся «под» этим прямоугольником.
Практические упражнения
10.3.5. Рисование различных цветов в режиме XOR
Предположим, что буфер кадров поддерживает три бита на пиксел и что цвета изображаются в соот-
ветствии со схемой с рис. 1.3. Опишите, какой цвет будет наблюдаться после выполнения операции
XOR над значением пиксела 110 и каждым из возможных значений пиксела.
10.3.6. Двукратное рисование в режиме XOR эквивалентно отсутствию рисования
Покажите для произвольных значений пикселов Ап В, что в режиме XOR двукратное рисование пик-
села В оставляет пиксел А неизменным; иначе говоря, требуется показать, что (Л XOR В) XOR В = А.
10.3.7. Симметричные операторы
Отметим, что оператор OR является симметричным: A OR В — это то же самое, что В OR А. Какие из 16
операторов А являются симметричными в том смысле, что a A b = Ь А а ?
10.3.8. Обмен данными двух изображений
Покажите, что две пиксельные карты Ап В можно поменять местами посредством выполнения следую-
щих трех операций XOR (после завершения этого процесса карта А содержит значения пикселов, кото-
рые первоначально содержала карта В, и наоборот):
О А=А XORB;
О B = AXORB;
О A=AXORB.
10.3.9. Рисование в обратном режиме
Рисование узора в обратном режиме (reverse mode) также можно использовать для стирания прямой
линии и восстановления исходных значений пикселов. Буфер кадров с глубиной b бит содержит V = 2Ь
возможных значений пикселов в диапазоне от 0 до 2b - 1. Рисование пиксела в обратном режиме означает,
что текущее значение пиксела d заменяется значением f{d) = N- d. Отметим, что эта функция рисования
является «инволюцией» (involution): повторное рисование восстанавливает оригинал, поскольку f{f{d))=
= N- f(d) = N - (N - d) = d. Опишите, как эта технология работает при рисовании резиновой нити и какие
цвета видны вдоль этой нити при ее пересечении с пикселами различных цветов. В чем состоит различие
между рисованием в обратном режиме и режиме XOR для случая однобитовой плоскости (Ь = 1)?
10.3.4. Операция BitBLT
Подпрограммы drawO, readO и соруО могут быть объединены в единую функцию с некоторыми допол-
нительными возможностями, которые значительно увеличивают их мощность и применимость. Эта
операция известна под названием BitBLT (произносится «bitblit»), что означает пересылку битовой
строки {bit boundary i/ock iransfer). Ее называют также растровой операцией (raster op) [Ingalls, 114,
Newman, 147]. Если изображение содержит больше одного бита на пиксел, то операцию BitBLT иногда
называют pixelBLT. Мы во всех случаях будем придерживаться названия BitBLT.
Иногда BitBLT выполняется программно, однако эта операция стала настолько распространенной,
что были разработаны микросхемы VLSI (СБИС — сверхбольшие интегральные схемы), специально
10.4. Рисование прямых своими силами: алгоритм Брезенхема
641
предназначенные для выполнения операций BitBLT с очень высокими скоростями (сотни миллионов
пикселов в секунду). Для микросхемы BitBLT задается всего несколько параметров, после чего она
включается и для передачи данных взаимодействует непосредственно с системной шиной.
Определение операции BitBLT
Существует несколько версий BitBLT, различающихся некоторыми деталями. В своем простейшем
виде BitBLT копирует прямоугольник пикселов источника (source rectangle) в прямоугольник пиксе-
лов адресата (destination rectangle), имеющий те же самые высоту и ширину. Как источник, так и адре-
сат могут располагаться в экранной или во внеэкранной памяти. BitBLT-процессор отслеживает эти
два прямоугольника следующим простым способом: записываются координаты х и у верхнего левого
/ угла каждого прямоугольника, а также их высота и ширина (в пикселах). Все необходимые преобразо-
вания между парой (х, у) и соответствующим адресом в памяти осуществляются самим процессором.
BitBLT копирует пикселы источника S в прямоугольник адресата D с помощью метода логической
комбинации, описанного ранее: D = D ® S. На месте символа ® могут стоять различные операции.
Некоторые версии BitBLT позволяют пользователю предварительно «смешивать» («premix») изоб-
ражение в прямоугольнике источника с какой-либо заранее выбранной пиксельной картой, которая на-
зывается полутоновым шаблоном (halftone pattern), после чего это смешанное изображение становит-
ся источником S и копируется в адресат. Полутоновый шаблон хранится в пиксельной карте некоторого
размера, например 16 на 16 пикселов. Это может быть, к примеру, шахматный шаблон из нулей и еди-
ниц, имитирующих оттенки серого цвета. Если эта маска меньше, чем изображение источника, то она
повторяется (в виде мозаики) до тех пор, пока не достигнет размеров источника. Пользователю предо-
ставляется на выбор четыре варианта для пиксельной карты источника 5:
О логическое умножение (AND) источника и полутонового шаблона;
О только источник (полутоновый шаблон игнорируется);
О только полутоновый шаблон;
О сплошной черный цвет.
Большинство BitBLT-процессоров поддерживают также отсечение прямоугольника (clipping rectangle).
Прежде чем нарисовать каждый пиксел адресата, его координаты сравниваются с границами отсекаю-
щего прямоугольника, и пиксел рисуется только в том случае, если он лежит внутри этих границ. Это
может быть проделано аппаратно, внутри процессора, и с большой скоростью. Отсекающий прямо-
угольник эффективно ограничивает ту область адресата, в которой может производиться рисование.
10.4. Рисование прямых своими силами:
алгоритм Брезенхема
В большинстве графических сред уже содержатся встроенные средства для рисования прямых линий.
Каждая среда имеет как минимум один из вариантов процедур 11пе() или 1 ineto(). Разумеется, OpenGL
идет значительно дальше. В других случаях нас не волновали подробности работы такого инструмен-
та — каким образом он решает, какие пикселы задействовать между двумя концевыми точками прямой.
Однако рисование прямой является фундаментальным для компьютерной графики, поэтому будет по-
лезно подробно рассмотреть, как работает такая подпрограмма. И на деле программистам иногда при-
ходится писать самим подпрограмму рисования прямых — в тех случаях, когда они разрабатывают или
оптимизируют новые коммерческие графические пакеты.
Начнем с простого, однако крайне неэффективного метода, чтобы разъяснить основные идеи. Затем
мы покажем значительно более быстрый метод, известный как алгоритм Брезенхема для рисования
прямых линий (Bresenham’s line-drawing algorithm).
21 Ф. Хилл
642
Глава 10. Средства для растровой графики
Предположим, что мы хотим задать значения пикселов так, что прямая появляется на экране между
целыми координатами (ах, ау) и (Ьх, Ьу). На рис. 10.18 показано, какие пикселы «включаются» вдоль
математически идеальной прямой между точками (ах, ау) и (Ьх, Ьу). Будем надеяться, что эти пикселы
можно выбрать рационально и они в совокупности создадут впечатление прямой линии (хотя и с неко-
торыми неизбежными «ступеньками»).
Рис. 10.18. Рисование отрезка прямой линии
Из элементарной алгебры известно, что прямая линия удовлетворяет уравнению
у = т(х - а ) + а ,
' у (10.3)
где х изменяется от ах до Ьх, а величина
т = (Ю.4)
Ьх -ах
является наклоном (slope) этой прямой1. Если, например, дано (ах, ау) = (23,41) и (Ьх, Ьу) = (125, 96),
то отсюда следует, что т = 55/102 - 0,5392. Наклон имеет смысл только для невертикальных прямых,
у которых ах и Ьх различны. Для горизонтальной или вертикальной прямой очевидно, какие пикселы
следует «включать», но для других прямых необходим алгоритм вычисления включаемых пикселов.
Простой, хотя и неэффективный метод заключается в том, чтобы двигаться по х от ах до Ьх с единич-
ным шагом и на каждом шаге округлять соответствующее значение т(х - ах) + ау до ближайшего целого
числа. В случае, когда ах меньше Ьх, этому методу соответствует следующий код:
float у - а.у:
// initial value
// начальное значение
for (int х - а.х: х <- Ь.х : х++. у +- т)
setPixel(х. round(y)):
где, как и ранее, процедура setPixel (х, у) записывает текущий цвет в столбец х и строку у буфера кадров.
Отметим, что значение у приходится округлять до ближайшего целого, что является довольно трудо-
емкой операцией.
10.4.1. Алгоритм Брезенхема для рисования прямых линий
Алгоритм Брезенхема имеет значительное преимущество перед только что изложенным методом, так
как в нем отсутствует арифметика с плавающей точкой и округление. Идеи, использующиеся в этом
методе, важны еще и потому, что они фигурируют также в других типах утилит, таких как алгоритмы
1 В русской математической литературе эту величину чаще называют угловым коэффициентом. — Примеч. пер.
10.4. Рисование прямых своими силами: алгоритм Брезенхема
643
рисования окружности или эллипса. Алгоритм Брезенхема является классическим примером инкре-
ментного алгоритма (incremental algorithm), в котором вычисляется положение каждого пиксела вдоль
прямой на основе информации о предыдущем пикселе*. В нем используются только целые величины,
отсутствует умножение, а также содержится компактный и эффективный внутренний цикл, генериру-
ющий искомые пикселы.
Существуют различные вариации алгоритма Брезенхема, слегка отличающиеся между собой. Мы
будем рассматривать вариант, известный под названием алгоритм средней точки (midpoint algorithm).
Этот алгоритм генерирует для прямых линий в точности такие же пикселы, что и алгоритм Брезенхема,
и такой подход можно расширить для рисования более сложных форм, например окружностей и эллипсов.
Предположим, что, как и ранее, нам даны целочисленные концевые точки прямой (ах, а,) и (bx, by).
Требуется определить наилучшую последовательность промежуточных пикселов.
Для упрощения изложения метода рассмотрим частный случай, когда ах < Ьх (то есть точка b лежит
справа от точки а) и наклон прямой находится между 0 и 1. (Позднее эти ограничения будут сняты.)
Для удобства определим границы отрезка прямой по х и у.
W= bx- ах (ширина);
Н — Ьу — ау (высота). (10.5)
В силу установленных нами ограничений, Я и ДОявляются положительными, и Н< W. Тогда по мере
возрастания х от ах до Ьх соответствующее значение у возрастает от ау до Ьу, однако у растет медленнее,
чем х. При возрастании х на единицу наилучшее целое значение у будет иногда оставаться неизменным,
а иногда увеличиваться на 1. Алгоритм средней точки быстро определяет, которая из этих двух ситуаций
имеет место. (Отметим, что у никогда не уменьшается и никогда не возрастает больше чем на 1. Почему?)
Из главы 4 мы знаем, что уравнение прямой, проходящей через точки (ах, ау) и (Ьх, Ьу), имеет вид:
-W(y-ay) + H(x-ax)-Q.
Левая часть этого уравнения равна нулю для всех точек (х, у), лежащих на этой прямой. Для удоб-
ства дальнейшего использования дадим имя этому выражению. Однако перед присвоением имени вы-
ражение нужно удвоить, поскольку это избавит нас от неудобного коэффициента 1/2 в основных форму-
лах. Таким образом, мы определяем следующую функцию:
F(x, у) - -2 W(y - ау) + 2Н(х- ах). (10.6)
Функция F(x, у) обладает следующим важным свойством: ее знак определяет, находится ли пара зна-
чений (х, у) выше или ниже прямой:
О если F(x, у) < 0, то (х, у) лежит выше прямой;
О если F(x, у) > 0, то (х, у) лежит ниже прямой.
Замечание. Дадим подсказку для размышления-, пусть точка (г, у) лежит на прямой, тогда известно,
что F(x, у) = 0. Слегка увеличим у, не изменяя х. При этом значение функции £(.,.) уменьшится. Следо-
вательно, подъем у над прямой делает F отрицательной.
Практическое упражнение
10.4.1
Уравнение отрезка прямой между точками (3,7) и (9, И) имеет вид:
Г(х, у) = (-12) (у - 7) + (8) (х-3),
причем точки на прямой, такие как (7, 29/3), удовлетворяют уравнению F(x, у) ~ 0. Какой знак имеет
функция F(x, у) для точек А = (4,4) и В = (5,9) и где по отношению к отрезку прямой лежат эти точки?
Ответ. Точка А лежит ниже прямой и для нее функция Г равна 44. Точка В лежит выше прямой и
для нее функция Г равна -8.
1 Этот алгоритм иногда называют цифровым дифференциальным анализатором (digital differential analyzer — DDA) — по назва-
нию механического устройства, предназначенного для решения дифференциальных уравнений в приращениях.
644
Глава 10. Средства для растровой графики
Как же мы решим, какие пикселы следует «включить»? На рис. 10.19 изображены некоторые пикселы
вблизи прямой. Кружок в каждой точке пересечения сетки символизирует центр пиксела. Предполо-
жим, что мы откуда-либо знаем, что для рх наилучшее значение у есть ру, и хотим определить наилучшее
значение у для следующего значения х, равного рх + 1. Мы хотим знать, находится ли прямая в точке
рх + 1 ближе к точке L = (рх + 1, ру) (от слова lower — ниже) или к точке U = (рх + 1, ру + 1) (от слова upper —
выше). На рисунке показано одно из возможных положений прямой, однако она могла бы пройти не-
сколько ниже точки L или несколько выше точки U. (Почему?)
Рис. 10.19. Схема для вывода алгоритма средней точки
Мы принимаем решение, включить пиксел U или L, в зависимости от того, лежит идеальная прямая
выше или ниже средней точки М = (рх + 1, ру + 1/2), расположенной посередине между точками U и L.
Если мы вычислим функцию Г(,) в точке М, то ее знак укажет нам, проходит ли идеальная прямая выше
или ниже точки М:
О если F(Mx, Му) < 0, то точка М лежит выше прямой, и мы выбираем точку L.
О если F(MX, Му) > 0, то точка М лежит ниже прямой, и мы выбираем точку U.
Таким образом, если F(Mx, Му) > 0, то включаемый пиксел находится выше, чем предыдущий, поэтому
мы увеличиваем у на единицу. В противном случае у остается неизменным. Остальное уже дело алгебраи-
ческой техники: найти способ быстрого вычисления F(). Суть метода заключается в том, чтобы вычислять
ее инкрементно, основываясь на том, насколько ее значение должно измениться от одного шага к следующему.
Для точки М
F(Mx,My) = -2W ру
+ 2Н(рх + 1 - ах).
(Ю.7)
Рассмотрим изменение функции Г(,) при переходе от х = рх + 1 к следующему значению х = рх + 2.
Как показано на рис. 10.19, следующей средней точкой М будет либо точка М', либо точка М". Если мы
не прибавили к у единицу на предыдущем шаге, то точкой М станет точка М' = (рх + 2,ру+ 1/2), а если
прибавили, то точкой М станет точка М" = (рх + 2,ру + 3/2).
Случай 1. Если функция Ена предыдущем шаге была отрицательна (то есть значение у не изменялось), то
лу j + 2Н(рх + 2-0,.).
( П ( 1
+ 2,ру + -J = -2W[py + - - а.
Вычтем из данного равенства равенство (10.7), чтобы определить, насколько последнее равенство
больше, чем F(Mx, Му):
( 1
F Р, + + -
= F(Mx,My) + 2Н.
10.4. Рисование прямых своими силами: алгоритм Брезенхема
645
Случай 2. Если функция Ена предыдущем шаге была положительна (то есть значение у было увели-
чено на 1), то
+ + = -2w[py + ^-ay^+2H(px+2-ax)=F(Mx,My) - 2{W-H).
В каждом из случаев к «контрольной величине», то есть к исходному значению функции, добавляет-
ся некоторая константа: 2Н — если мы не увеличивали у, и -2(VV- Н), если увеличивали.
Осталось определиться, с чего начинать этот процесс. Мы знаем, что при х = аху = а . Поэтому пер-
вый «экземпляр» средней точки М = (ах + 1, + 1/2) и тогда
Г(х,у) = -2Я^ау + + 2Я(ах + 1 “ ах) = 2Я-№. (10.8)
Замечание. Если бы мы предварительно нс умножили функцию на 2, то результат был бы Н - 0,5П(
что сделало бы невозможным использование целых значений всех участвующих величии!
Таким образом, перед началом процесса мы полагаем F= 2Н - W, х = ах,у = а . Затем на каждом шаге
делаем следующее.
1. Присваиваем пикселу (х, у) нужное значение цвета.
2. Увеличиваем х на 1; если F< 0, то добавляем к Fвеличину 2Я; в противном случае увеличиваем
у на 1 и добавляем к F величину -2( W- Н).
Листинг 10.5. Алгоритм средней точки (частный случай)
bresenham(IntPoint a. IntPoint b)
{
// restriction: а.х < b.x and 0 < H/W < 1
// ограничения: а.х < Ь.х и 0 < H/W < 1
int у = а.у. W = Ь.х - а.х. Н = Ь.у - а.у:
int F = 2 * Н - W;
// current error term
// текущая невязка
for(int х = а.х: х <= Ь.х: х+-^)
// inner loop
// внутренний цикл
setPixel (х. у):
1f(F < 0)
F+=2*H:
// set up for next pixel
// устанавливаем для следующего пиксела
else{
У++:
F += 2 * (Н - W);
J
}
Все вышеизложенное и определяет алгоритм Брезенхема для данного частного случая (см. ли-
стинг 10.5). Поскольку в этом алгоритме предусмотрена повторная инициализация для каждой новой
прямой, то он является повторяемым-, повторное рисование какой-либо прямой другим цветом полно-
стью замещает первую прямую; например, рисование цветом фона целиком удаляет ранее нарисован-
ную прямую.
646
Глава 10. Средства для растровой графики
Алгоритм Брезенхема предельно прост, в его внутреннем цикле содержатся только несколько опера-
ций сравнения и сложения. Для достижения максимальной скорости его легко реализовать на языке
ассемблера. Этот алгоритм часто реализуется аппаратно в графических устройствах специального на-
значения; где обеспечивается еще большая его скорость.
Пример 10.4.1
Полезно проследить за изменением функции Дна конкретном примере. Пусть (ах, а ) = (4,1), a (bx, bj) =
= (16,4). Тогда W= 12 иН=3. Поскольку наклон данной прямой равен 1/4, мы ожидаем, что значе-
ние у будет увеличиваться только примерно на каждом четвертом шаге по х. Начальное значение F рав-
но (-6). При каждом увеличении х мы делаем одно из двух: если значение функции F отрицательно, то
добавляем к ней 6; в противном случае вычитаем из нее 18 и увеличиваем у.
В результате получаем такую последовательность значений (после выполнения команды setPixel (х.у)):
х: 4 5 б 7 8 9 10 11 12 13 14 15 16
у: 112222333 3444
F: -6 0 -18 -12 -6 0 -18 -12 -6 0 -18 -12 -6
На рис. 10.20 показано действие алгоритма на вышеприведенном примере, причем приводится как
результирующая прямая, так и вариации функции F. На прямой ясно видны «ступеньки» в тех местах,
где короткий горизонтальный отрезок терпит разрыв при переходе к следующему горизонтальному
отрезку, на большей высоте.
Рис. 10.20. Пример действия алгоритма средней точки
Отмена ограничений на алгоритм Брезенхема
Алгоритм Брезенхема применим только в частном случае, когда ах < Ьх и наклон прямой находится в
диапазоне от нуля до единицы. Все остальные случаи также легко охватываются, если добавить код,
обрабатывающий каждый случай более общего вида.
Получение той же прямой при ах > Ьх. Алгоритм средней точки определяет нахождение пиксела по
нужную сторону от средней точки, выбирая на каждом шаге один из двух вариантов. Тогда нам нужно
изменить код из листинга 10.5 так, чтобы он выполнял алгоритм средней точки для случая ах > Ьх. В дей-
ствительности изменения требуются небольшие (см. упражнения в конце раздела). Следует отметить,
что в рассматриваемом коде различаются два случая: F< 0 и F> 0, так что случай 0 рассматривается
вместе со случаем F < 0 (где у увеличивается). Поэтому необходимо иметь в виду, что при изменении
направления прямой случай F - 0 рассматривается совместно со случаем, в котором у уменьшается.
Существует и альтернативный подход: если обнаружилось, что ах > Ьх, то ах и ^меняются местами,
после чего проделываются все шаги, предусмотренные в листинге 10.5. На деле при таком подходе не
происходит «рисования справа налево», а вместо этого конечные точки переопределяются так, что
такого рисования и не требуется. Такая технология, однако, не очень удобна в тех случаях, когда требу-
ется использовать данный алгоритм для рисования соединенных между собой отрезков прямых, как
при визуализации ломаной линии. Перестановка концевых точек нарушила бы естественный порядок,
10.4. Рисование прямых своими силами: алгоритм Брезенхема
647
в котором рисуются отрезки ломаной, а этот порядок может оказаться важным, когда эти отрезки рису-
ются штриховыми или пунктирными линиями.
Прямые с наклоном, большим единицы. В этом случае х и у просто меняются местами, делаются шаги
по у от ау до и производится такая же проверка ситуаций, когда нужно увеличивать (более медленно
изменяющееся) х.
Прямые с отрицательными наклонами. Если наклон используемой нами прямой лежит в диапазоне от
0 до -1, то Я автоматически приобретает нужный знак. Мы двигаемся по х с использованием тех же тестов,
однако вместо увеличения зависимой переменной уменьшаем ее. Если же наклон меньше -1 («более отрица-
телен»), то заменяем IV на - W и меняем местами х и у, как в том случае, когда наклон превышает единицу.
Горизонтальные и вертикальные прямые. Эти случаи встречаются в графике столь часто, что их про-
верка (например, посредством кода 1 f (а.х = Ь.х)...) и использование для них упрощенного алгорит-
ма может ускорить выполнение подпрограммы. Для вертикальной прямой изменения были бы незна-
чительными; большая часть времени, во всяком случае, тратится на выполнение процедуры setPixel О.
Что касается горизонтальной прямой, то здесь можно использовать подпрограмму, которая рисует сра-
зу много бит вдоль строки развертки, что значительно ускоряет процесс рисования. (Для изучения реа-
лизации вышеприведенных обобщений следует обратиться к упражнениям.)
Сводка свойств, которыми должна обладать рисуемая линия
Какими свойствами должна обладать линия, рисуемая с помощью нашего алгоритма? Во-первых, опа
должна быть настолько прямой, насколько возможно, и должна обязательно проходить через обе заданные
концевые точки. Во-вторых, линия должна быть «гладкой» и обладать одинаковой яркостью по всей
длине. (Прямые с различными наклонами должны иметь одну и ту же яркость.) В-третьих, при рисова-
нии линии должна быть обеспечена повторяемость: если мы позднее применим данный алгоритм к тем
же самым данным, задающим концевые точки, то он должен включать и выключать в точности те же
пикселы, что и в первый раз. Это существенно в случае стирания линии, которое выполняется посредством
перерисовки ее цветом фона или в режиме XOR-рисования. Наконец, не должно иметь значения, в каком
направлении рисуется линия: при рисовании от точки (bx, b ) к точке (ах, ау) должны быть включены те
же самые пикселы, что и при рисовании от (ах, а^) к (Ьх, Ь^). Ьсли это условие соблюдается, то приложе-
ние может стирать ранее нарисованную линию вне зависимости от того, как она была нарисована.
Рисование прямых по шаблону
Может потребоваться рисовать прямые с помощью некоторого шаблона из точек или черточек. Как
уже упоминалось в главе 2, штриховой шаблон хранится в виде последовательности битов, например
0011111100111111.
Такие шаблоны нетрудно встроить в алгоритм Брезенхема. Для этого во время каждого прираще-
ния х на единицу необходимо также увеличивать на единицу указатель в шаблоне, причем соответству-
ющее значение бита следует использовать для установки текущего цвета рисования в подпрограмме
setPixel О. Для длинных прямых шаблон используется многократно посредством циклического прира-
щения на единицу от конца шаблона к его началу.
Когда пунктиром должна быть нарисована ломаная линия, то желательно, чтобы шаблон оставался не-
прерывным от отрезка к отрезку. Для этого сам шаблон и указатель на него делаются глобально доступны-
ми для алгоритма Брезенхема, так чтобы доступ к ним мог осуществляться во время последовательных вы-
зовов алгоритма. (В упражнениях рассматриваются и другие проблемы, связанные с рисованием шаблонов.)
Практические упражнения
10.4.2. Снятие ограничений в алгоритме Брезенхема
Разработайте варианты алгоритма Брезенхема для следующих случаев:
О а > b ;
X xf
О прямые с наклонами, большими единицы;
О прямые с отрицательными наклонами,
648
Глава 10. Средства для растровой графики
и объедините свои решения для указанных частных случаев в единый алгоритм, работающий для любого
отрезка прямой. Постарайтесь сделать вашу подпрограмму возможно более эффективной. Проверьте
ее, по крайней мере, вручную.
10.4.3. Численный пример
Покажите для концевых точек (8,23) и (21,11) последовательности х, у, F, получающиеся в результате
применения алгоритма Брезенхема. Продемонстрируйте, что при начале работы алгоритма с противо-
положной концевой точки будут высвечиваться те же пикселы.
10.4.4. Алгоритм Брезенхема на ассемблере
Реализуйте полный алгоритм Брезенхема на ассемблере доступного вам графического хост-дисплея.
Сделайте код самых внутренних циклов сколь возможно эффективным. Сравните скорость версии на
ассемблере с версией на C++. Кроме того, проверьте, увеличивает ли скорость работы алгоритма специ-
альный код для горизонтальных и вертикальных прямых.
10.4.5. Рисование по шаблону
Расширьте алгоритм Брезенхема для рисования прямых с использованием 16-битового шаблона. Орга-
низуйте свою программу так, чтобы при рисовании ломаных линий шаблон непрерывно продолжался
при переходе от одного прямолинейного отрезка к другому.
10.5. Определение и заполнение областей из пикселов
На растровом дисплее области пикселов могут заполняться (fill) сплошным цветом или узором из несколь-
ких цветов. Под областью (region) мы имеем в виду совокупность пикселов, расположенных «рядом друг с
другом» заданным образом или связанных между собой каким-нибудь общим свойством. На рис. 10.21
приведено изображение, различные области которого закрашены различными оттенками серого цвета.
Рис. 10.21. Несколько областей, заполненных цветом
В настоящее время широко распространены многочисленные «программы рисования», предназна-
ченные для создания картинок в интерактивном режиме. В каждой такой программе имеется инстру-
мент, позволяющий пользователю указать мышью область и затем выбрать новый узор, после чего дан-
ная область целиком заполняется этим узором. В данном разделе мы рассмотрим, как это происходит.
10.5.1. Задание областей
Существуют различные способы задания области. Одно из главных различий состоит в том, что об-
ласть может быть определена «пиксельно» («pixel-defined») или «символически» («symbolic»).
О Пиксельно-определенная область характеризуется текущими цветами пикселов в пиксельной кар-
те. Описанием области R может служить список всех пикселов, лежащих внутри этой области R:
(34, 12), (34, 13), (34, 14) и т. д. Область R может быть также определена как совокупность
всех пикселов, значение которых равно 77 и которые каким-либо образом «связаны» с пикселом
(43,129). Понятие такой «связанности» должно быть определено очень тщательно. Для того что-
бы увидеть, что представляет собой область R, следует изучить ее пиксельную карту и выяснить,
какие именно пикселы находятся в 7? в соответствии с этим определением.
10.5. Определение и заполнение областей из пикселов
649
О При символическом определении пикселы не перечисляются, однако описывается некоторое свой-
ство, которым обладают все пикселы области R. Такие описания считаются описаниями «более
высокого уровня» или более абстрактными, чем прямое перечисление пикселов. Ниже приводят-
ся некоторые возможные способы символического описания областей:
• все пикселы, лежащие внутри окружности радиуса 8 с центром в точке (5, 23);
• все пикселы внутри полигона с вершинами (32, 56), (120, 546), (345, 129), (80, 87). Такая «по-
лигонно-определепная» (polygon-defined) область представляет собой особенно важный слу-
чай, который мы позднее рассмотрим более подробно.
Если программист хочет манипулировать с такими областями или анализировать их, он скорее все-
го выберет совсем другие структуры данных и алгоритмы, — в зависимости от того, как описаны инте-
ресующие его области.
Вначале мы исследуем методы работы с пиксельно-определенными областями. Затем рассмотрим
методы манипулирования символически-определенными областями, в особенности темп, которые оп-
ределены через полигоны.
10.5.2. Пиксельно-определенные области
Один из способов характеристики пиксельно-определенной области заключается в следующем: область R
является множеством всех пикселов цвета С, которые «связаны» с заданным пикселом S.
Такая область называется «внутренне-определенной» («interior defined»), поскольку при данном
определении задается природа всех пикселов, лежащих «внутри» R. Однако что же понимается под сло-
вом «связаны»? Будем называть два пиксела связными («connected»), если между ними существует
непрерывный путь из «смежных» пикселов. Поэтому смысл «связности» зависит от смысла «смежно-
сти», для которого в графике существует два обычных определения:
О 4-смежность (4-adjacent). Два пиксела являются 4-смежными, если они расположены рядом по
горизонтали или по вертикали. Например, пиксел (23, 35) является 4-смежпым по отношению к
пикселу (23, 36), но не по отношению к пикселу (24, 36).
О 8-смежность (8-adjacent). Два пиксела являются 8-смежными, если они расположены рядом
по горизонтали, по вертикали или по диагонали. Например, пикселы (23, 35) и (24, 36) являют-
ся 8-смежными. Очевидно, что если пикселы являются 4-смежными, то они являются также и
8-смежными.
Назовем два пиксела 4-связными (4-connected), если существует соединяющий их непрерывный
путь из 4-смежных пикселов. Аналогично, эти пикселы называются 8-связными (8-connected), если су-
ществует непрерывный путь из 8-смежных пикселов, ведущий от одного к другому.
На рис. 10.22 приведена пиксельная карта, состоящая из черных, белых и серых пикселов, один
из которых обозначен буквой S. Пусть R — область, внутренняя часть которой состоит из всех серых
пикселов, 4-связных с пикселом S. В таком случае область R на рисунке состоит из 20 пикселов.
(Отметьте их.) Пусть R' — это область, внутренняя часть которой состоит из всех серых пикселов,
8-связных с пикселом S. Тогда R' состоит из всех пикселов области R и еще восьми других пикселов.
(Каких именно?)
Кроме того, можно определять область с помощью ее границы, в этом случае область называется гра-
нично-определенной (boundary defined). Граница состоит их пикселов, имеющих определенный (гра-
ничный) цвет. Можно, например, определить область В как совокупность всех пикселов, 4-связных с
начальным пикселом S и имеющих цвет, отличный, от черного цвета границы. Таким образом, внутрен-
няя часть области В простирается до пикселов с граничным цветом, но не включает их в себя. В соответ-
ствии с этим определением область В на рис. 10.22 содержит 62 печерных пиксела, 4-связных с пиксе-
лем 5. Пять нечерных пикселов в юго-западном углу не являются 4-связными с S, вследствие чего не
принадлежат области R. Отметим, что граница в ряде мест обладает толщиной большей, чем один пиксел.
Как мы увидим позднее, одни алгоритмы хорошо воспринимают такие толстые границы, а другие в этих
случаях приходят в замешательство.
650
Глава 10. Средства для растровой графики
boo
оеовеоаоооео
оеооооооооео
оеоеоооооеео
оео@®@ооооее
оооооооооооо
Рис. 10.22. Области, определенные через цвета пикселов
Если мы определим понятие «связные» в смысле «8-связные», то область В будет содержать 67 не-
черных пикселов, 8-связных с 5, поскольку теперь 5 юго-западных пикселов будут являться частью об-
ласти.
10.5.3. Рекурсивный алгоритм заливки
Ниже мы опишем два простых алгоритма заполнения, работающих с пиксельно-определенными облас-
тями. Первый из них оперирует с внутренне-определенными, 4-связными областями. Он изменяет цвет
каждого внутреннего пиксела с i ntCol or на новый цвет newCol or. Этот алгоритм носит название алгорит-
ма заливки (flood-fill algorithm), поскольку он «заливает» область цветом newCol or, «ведя свой путь»
newCol or от «начального» пиксела с координатами (х, у) в поисках пикселов цвета 1 nt Col or, заменяя цвет
каждого из найденных пикселов на newCol or. Данный алгоритм иногда используют в интерактивных
системах рисования, поскольку пользователь может указать начальную точку внутри области и затем
запустить операцию заливки.
Идея этого алгоритма заключается в следующем: если пиксел с координатами (х, у) находится во
внутренней части области (то есть его цвет — intColor), то меняем его на newCol or и рекурсивно приме-
няем этот процесс к каждому из четырех соседних пикселов. В противном случае не делаем ничего. Из
листинга 10.6 видно, насколько прост этот алгоритм. Отметим, что для запроса цвета пиксела в точке
(х, у) используется подпрограмма get Pi xel (х.у).
Листинг 10.6. Рекурсивная заливка для внутренне-определенных областей
void floodFill(short х .short у. short intColor)
П Start at (x. y); change all pixels of intColor to newColor.
11 assume drawing color is newColor
11 4-connected version
11 Начинаем с точки (x. у): для всех пикселов цвета
// intColor изменяем цвет на newColor
// цвет рисования - newColor
// 4-связный вариант
1f(getPixel(х.у) — intColor)
setPixel(х. у);
// change its color
11 изменяем его цвет
floodFilKx - 1, у, intColor):
10.5. Определение и заполнение областей из пикселов
651
// fill left
// закрашиваем левый
floodFilKx + 1. у. intColor);
// fill right
// закрашиваем правый
floodFilKx, у + 1, intColor);
// fill down
// закрашиваем нижний
floodFilKx. у - 1. intColor)
// fill up
// закрашиваем верхний
Процесс начинается заново для адреса каждого пиксела, который появляется при вызове функции
floodFi 110. Алгоритм работает вслепую, проверяя ближайших соседей вне зависимости от того, тестиро-
вались ли они ранее. Поэтому здесь не учитывается связность области (region coherence) — вероятность
того, что пиксел, смежный с внутренним пикселом, также является внутренним пикселом. По этой при-
чине многие пикселы проверяются многократно, что требует огромного количества вызовов процедуры.
Пример 10.5.1
Рассмотрим внутренне-определенную область, состоящую всего из пяти пикселов, которая показана на
рис. 10.23. Пусть начальный пиксел, обозначенный буквой S, расположен в точке (4,2). После вызова
подпрограммы floodfill(4, 2. white) последовательность адресов пикселов, для которых происходят
дальнейшие вызовы, имеет вид:
(3,2), (2,2), (1,2), (3,2), (2, 3), (2,1), (4, 2), (3,3), (2, 3), (4,3) ....
Всего процедура вызывается 21 раз, с учетом повторных проверок одного и того же пиксела, на-
пример (2,3).
0 1 2 3 4 5 6
Рис. 10.23. Пример внутренне-определенной области для заполнения
Поскольку алгоритм заливки является в большой степени рекурсивным, стек рекурсии может стать
очень глубоким, даже для простой области. Поэтому существует вероятность переполнения стека и по-
следующего сбоя алгоритма даже для областей умеренного размера. Кроме того, для управления этой
рекурсией требуются дополнительные затраты ресурсов, которые могут значительно замедлить про-
цесс заливки. Существуют более эффективные (но и более сложные) методы, использующие связность
области; они будут рассмотрены позднее.
Для того чтобы расширить данный алгоритм до 8-связной версии, нужно просто добавить четы-
ре инструкции проверки четырех соседей по диагоналям, таких как floodFill (х+1. у-1, intColor).
Этот рекурсивный метод также может быть адаптирован для гранично-определенных областей (см. уп-
ражнения).
652
Глава 10. Средства для растровой графики
10.5.4 . Заполнение областей узорами
Алгоритм заливки закрашивает области сплошным цветом. Однако вместо этого мы можем пожелать
заполнить область некоторым узором, как показано на рис. 10.21. Пусть нужный узор хранится в массиве
RGB pattern[Width][Height]:
Рис. 10.24. Пример: мотив мозаики и результирующая мозаика
Пиксельная карта в массиве pattern[] [] может быть целым изображением, которым мы хотим «раскра-
сить» заданную область, или это может быть маленький элемент мозаики (tiling pattern), который следует
выкладывать с повторением. На рис. 10.24 приведен мотив мозаики размером восемь на восемь и результат
замощения (tiling) этого мозаичного мотива на область большего размера. Не составляет труда взять дан-
ные из массива pattern и «выложить» этот узор. Для того чтобы нарисовать пиксел в точке (х, у), нам нуж-
но задать цвет рисования элементу массива pattern[х][у], но для обеспечения повторяемости узора мы
задаем цвет рисования элементу pattern[х % Width][y % Height]. Использованная здесь функция модуля «%»
ограничивает индексы в массиве pattern до нужных пределов и копирует узор на область любого размера.
Практические упражнения
10.5.1. Гранично-определенная заливка
О Адаптируйте алгоритм из листинга 10.6 так, чтобы он производил закрашивание гранично-опре-
деленных 4-связных областей. Пусть цвет границы хранится в переменной boundaryCol or, а началь-
ная точка лежит внутри области, а не на ее границе.
О Работает ли этот метод в случае, когда значение boundaryCol or равно newCol or?
О Покажите, что если boundaryCol ог отличен от newColor, однако некоторые внутренние пикселы
имеют цвет newColor, то существует ряд геометрических узоров, при которых данный алгоритм
может зависнуть и прекратить работу до полного закрашивания области.
10.5.2. Имитация заливки вручную
Поупражняйтесь вручную с алгоритмом из листинга 10.6 — для области, внутренняя часть которой за-
дается пикселами (1, 1), (2, 1), (2, 2), (3, 2), (2, 3), (1, 3). В качестве начальной точки возьмите (2, 2).
Повторите это упражнение для случая, когда алгоритм адаптирован для 8-связных областей, где четы-
ре дополнительных проверки проводятся в следующем порядке: (х - 1, у - 1), (х + 1, у - 1), (х - 1, у + 1),
(х + 1,г/ + 1).
10.5.3. Рекурсивное закрашивание области
Для внутренне-определенной области, показанной на рис. 10.23:
О Изобразите «дерево вызовов процедуры» для случая, когда в качестве начального используется
пиксел (4, 2). Иначе говоря, нарисуйте дерево, каждый узел которого содержит адрес пиксела,
проверяемого посредством оператора if(getPixelO...), как показано в листинге 10.6. В случае
успешной проверки порождаются четыре поддерева вызовов процедуры.
10,5. Определение и заполнение областей из пикселов
653
О Чему равна «глубина» этого дерева вызовов?
□ Какое расположение четырех внутренних пикселов является для данного алгоритма наихудшим —
в том смысле, что приходится делать наибольшее количество рекурсивных вызовов процедуры?
10.5.4. Использование мозаичного мотива
Нарисуйте узоры, генерируемые следующими последовательностями бит:
11110101 1000
01101010 1100
01100101 1110
11111010 1111
при выкладывании каждого из них на большую область. Придумайте три других мозаичных мотива
четыре на четыре и создайте интересные узоры.
10.5.5. Перетаскивание области
Некоторые системы рисования позволяют пользователю сдвигать положение области с помощью мыши.
После отпускания кнопки мыши область перерисовывается заново в новой позиции. Если эта область
заполнена мозаикой, то всегда ли эта мозаика появится внутри области в том же виде? Мотивируйте
свой ответ.
10.5.5 . Использование связности: заполнение области
на основе серий пикселов
С целью увеличения производительности вышеприведенных алгоритмов и для предотвращения пере-
полнения стека рассмотрим более тонкий подход к заполнению области — не пиксел за пикселем, а це-
лыми группами пикселов, объединенных в серии. Серия (run) — это группа соседних пикселов, лежа-
щих на одной строке развертки. Если мы сможем обнаружить и закрасить за один раз целую серию
внутри области, то мы радикально ускорим процесс заполнения.
Чтобы изучить работу этого серийно-ориентированного метода, рассмотрим гранично-определен-
ную 4-связную область, изображенную на рис. 10.25, а. Буквой s на рисунке обозначен начальный пик-
сел. Первой закрашивается серия от а до Ь, содержащая пиксел s. Затем сканируется строка, лежащая
выше текущей, от а до b — с целью нахождения дополнительных серий из внутренних пикселов. Одна
такая серия обнаружена, и ее крайняя правая точка с сохраняется для дальнейшего использования (то есть
ее адрес помещается в стек). Затем сканируется строка ниже текущей, также от а до Ь\ найдена внут-
ренняя серия и ее крайний правый пиксел d записывается в стек. На рис. 10.25, б показано положение
в этот момент.
Затем данные выталкиваются из стека, образуется новая начальная точка d и процесс повторяется.
Закрашивается серия от d до е, и обнаруживаются три внутренние серии. Пикселы f,gnh проталки-
654 Глава 10, Средства для растровой графики
ваются в стек. Пиксел h затем выталкивается, его серия закрашивается, после чего обнаруживаются еще
две серии i nj. Ситуация на этой стадии показана на рис. 10.25, в. Этот процесс продолжается до тех
пор, пока стек не опустеет, к этому моменту уже будут закрашены все внутренние пикселы, достижи-
мые из начальной точки. Представляется полезным пройти этот пример вручную для лучшего понима-
ния данного алгоритма. (Как можно расширить этот метод на 8-связные области? См. упражнения в
конце раздела.)
Листинг 10.7. Скелет алгоритма серийного закрашивания
Push address of seed pixel on the stack;
// проталкиваем в стек адрес начального пиксела
while( stack not empty)
// стек не пуст
{
Pop the stack to provide the next seed;
// выталкиваем из стека очередную начальную точку
Fill in the run defined by the seed:
11 закрашиваем серию, заданную этой начальной точкой
In the row above find interior runs reachable from this run;
// на строку выше, чем текущая, находим внутренние серии.
// достижимые из данной серии
Push the addresses of the rightmost pixels of each such run;
// проталкиваем адреса крайних правых пикселов каждой
// такой серии
Do the same for the row below the current run;
// то же самое на строку ниже, чем текущая серия
}
Основные этапы алгоритма «серийного закрашивания» приведены в листинге 10.7. Алгоритм будет
работать наиболее эффективно, если область обладает связностью интервалов (span coherence), когда
много пикселов вдоль строки развертки имеют одно и то же значение, и связностью строк развертки
(scan-line coherence), когда то, что найдено на одной строке развертки, вероятно, будет найдено также
и на следующей строке. Поскольку серии горизонтальны, процесс закрашивания каждой серии яв-
ляется упорядоченным и может осуществлять эффективное закрашивание целых групп пикселов за
один прием. Левый и правый концы серии определяются посредством поиска пикселов цвета грани-
цы, и тогда целая серия закрашивается новым цветом без необходимости повторного чтения значений
ее пикселов.
Практические упражнения
10.5.6 . Имитация алгоритма серийного закрашивания
Разместите на листе миллиметровки область, представляющую букву «В» и содержащую по меньшей
мере 14 внутренних пикселов. Проделайте вручную операции алгоритма серийного закрашивания, опи-
санного в этом разделе, записывая содержимое стека перед каждым выталкиванием.
10.5.7 . Наихудшие области
Какая форма области из 20 внутренних пикселов является наихудшей для алгоритма серийного закра-
шивания — в том смысле, что потребуется наибольшее число выталкиваний из стека? Является ли ко-
личество выталкиваний разумной оценкой длительности выполнения алгоритма? Рассмотрите другие
оценки.
10.5.8 . Закрашивание 8-связных областей
Расширьте алгоритм серийного закрашивания так, чтобы он закрашивал 8-связные области.
10.6. Манипулирование символически-определенными областями
655
10.6. Манипулирование символически-определенными
областями
Алгоритмы заливки (flood-fill) и серийного закрашивания (run-fill) читают буфер кадров пиксел за пик-
селом с целью определения их цвета и таким образом «пробираются ощупью» через область. Можно
предположить, что алгоритм закраски был бы намного эффективнее, если бы он имел «высокоуровне-
вое», символическое описание области, а ему приходится перечислять пиксел за пикселом. Поэтому
давайте рассмотрим несколько способов символического описания области, каждый из которых обладает
своими достоинствами и недостатками. Чаще всего в графике используется метод описания области как
внутренней части некоторого полигона, и такой подход разработан в деталях. Упомянутые методы под-
разделяются на два класса: первый из них представляет область в виде набора прямоугольников, а вто-
рой задает область с помощью контура (path), определяющего границу этой области.
10.6.1. Области, описываемые прямоугольниками
При таком методе задания области она описывается как список прямоугольников. Размеры этих пря-
моугольников могут быть от одного пиксела вплоть до всей пиксельной карты. Область может иметь
отверстия («дыры») и даже изолированные «пятна» (blobs).
На рис. 10.26 показан простой пример, в котором каждый пиксел имеет черный или белый цвет.
Разобьем эту область на совокупность выровненных прямоугольников. Область представляется в виде
списка различных идентифицированных прямоугольников. (Быстрый просмотр фигуры обнаружива-
ет примерно И прямоугольников, но разбиение может производиться различными способами.)
Здесь описывается систематический способ разбиения области, являющийся одновременно простым
и эффективным: он обеспечивает быстрое создание формы из пиксельной карты и быстрое закрашива-
ние области, описанной с помощью этой формы. Для применения этой технологии мы начнем с верх-
ней части пиксельной карты и будем двигаться вниз вдоль каждой строки развертки, идентифицируя
прямоугольники. Как только набор серий в строке развертки становится отличным от набора серий в
предыдущей строке, начинается «новый» набор прямоугольников. Нижняя г/-координата прямоугольни-
656
Глава 10. Средства для растровой графики
ка явно не задается, поскольку она всегда на единицу меньше, чем //-координата следующего прямо-
угольника. В таком случае низ всей области должен явно задаваться как «пустой». (Почему?)
На рисунке самый верхний прямоугольник представляет собой единственный пиксел, определяе-
мый тремя значениями (17, И, 1): это означает, что этот прямоугольник начинается при у = 17 и про-
стирается отх = 11 на 1 пиксел. Следующий прямоугольник содержит всего два пиксела и задается зна-
чениями (16,11, 2). В третьей строке развертки пикселов нет вообще, так что она представлена пустым
списком. Четвертый прямоугольник задается значениями (14, И, 4) и простирается на четыре строки
развертки. Полная пиксельная карта в данном примере представляется следующей «таблицей форм»
(для некоторых строк развертки требуются списки серий, например, для прямоугольника, начинающе-
гося при у = 9; вся таблица содержит 14 прямоугольников, что несколько больше, чем мы ожидали, бла-
годаря требованию, что серии типа (19, 2) должны повторяться).
У Серия 1 Серия 2
17 11,1
16 11,2
15 Пусто
14 11,4
10 5,16
9 5,6 16,5
7 4,7 19,2
6 3,8 19,2
5 7,2
4 7,2 19,2
3 7,2
2 Пусто
Такое представление пиксельной карты иногда называют ее представлением формы (shape repre-
sentation) [Steinhart, 190; Atkinson, 6]. Иногда его еще называют «//-сортированным списком х-сорти-
рованных прямоугольников». Отметим, что посредством такого представления можно описать любую
совокупность пикселов в пиксельной карте, в том числе набор из отдельных областей. Оно может опи-
сать даже группу изолированных пикселов, хотя это было бы и неэффективным.
Области, представленные в рамках этого метода, описываются наиболее компактно, если они обла-
дают связностью интервала или связностью развертки, которые были описаны ранее. Области с высо-
кой степенью связности требуют для своей характеристики меньшего количества данных в расчете на
пиксел.
А что если пикселы могут принимать более чем два значения? Один из подходов состоит в том, что-
бы выявить все одноцветные прямоугольники и сохранить их вместе с их значением цвета. (Как и преж-
де, фон не требуется сохранять в явном виде.)
При получении указателя на структуру данных область заполняется в процессе прохода по спискам,
причем каждая серия закрашивается по мере ее вычисления. Обе эти подпрограммы рассматриваются
в дальнейшем — в тематическом задании 10.4.
Масштабирование и перемещение областей
Представление области в виде «формы» может также оказаться полезным в тех случаях, когда мы хо-
тим манипулировать этими областями другими способами. Например, для того, чтобы сдвинуть об-
ласть, представленную в виде «формы», простирающейся на 30 пикселов по х и на 55 пикселов по у, мы
просто проходим по списку и увеличиваем все значения х на 30 единиц, а все значения у на 55 единиц.
Для увеличения размера области в два раза мы вначале смещаем ее так, чтобы начальная серия находи-
лась в начале координат (0,0), а затем удваиваем все значения в структуре данных. Наконец, перемеща-
ем область в нужную позицию.
10,6. Манипулирование символически-определенными областями
657
Практические упражнения
10.6.1. Вывести списки
Выведите все списки «таблицы формы» для каждой из следующих пиксельных карт:
О стрелка курсора на рис. 1.26;
О пиксельная карта счастливой физиономии на рис. 1.20.
10.6.2. Определение структур данных
Определите подходящие типы для составляющих структуры данных, необходимых для представления
в виде «формы».
10.6.2. Области, заданные контуром
Естественно определять область посредством задания ее границы, которая обычно описывается контуром
некоторого типа. Существует несколько способов описания контура. Вот некоторые полезные способы.
О С помощью математической формулы. Формула (х - 122)2 + (у - 36)2 = 25 определяет, например,
круговой контур диаметром 10 пикселов. Язык PostScript (см. приложение Г) позволяет строить
в буфере кадров очень сложные контуры.
О С помощью множества точек. Последовательность расположения пикселов (х,,?/,), (х ,у2),...,
(хп, уп) определяет контур из ломаных линий; если эта ломаная замкнутая ((хр z/() = (хп, уп)), то опа
определяет полигон. В разделе 10.7 «Заполнение полигонально-определенных областей» рассмат-
риваются методы заполнения полигонов.
О С помощью последовательности смежных пикселов. Мы уже видели, что гранично-определен-
ная пиксельная область задается с помощью совокупности пикселов некоторого «граничного» цве-
та. Область имеет наиболее приемлемый вид, если все ее граничные пикселы образуют связный
замкнутый контур. Этот контур можно сохранить в буфере кадров как целиком, так и в виде спис-
ка расположения пикселов, например, (23,47), (24,46), (24,45),..., < много других значений >,...,
(22,46), (23,47). Если каждая пара последовательных пикселов является 4-связиой, то такой контур
называется «4-связным» («4-connected»); аналогично описывается «8-связный» контур. (Вопрос.
Определяет ли 8-связный граничный контур 4-связную область?)
Одним из наиболее эффективных способов представления контура из смежных пикселов является ме-
тод цепного кода (chain code) [Freeman, 67]. Контур задается своим стартовым пикселом, скажем, (34,57),
и последовательностью «перемещений» от пиксела к пикселу типа: «вверх, направо, вниз, налево...».
Совокупность допустимых перемещений может кодироваться различными способами. На рис. 10.27 при-
ведены два варианта. В первом из них, показанном на рис. 10.27, а, допускаются четыре направления
«по странам света», причем каждому из этих направлений поставлена в соответствие цифра от 0 до 3.
Таким образом, последовательность шагов задает 4-связный контур. На рисунке контур А задан после-
довательностью с началом в нижнем левом углу. Данный контур оказался замкнутым, однако это не
обязательно. (Какие ограничения накладываются на цифры «0», «1», «2», «3» для замкнутого контура?)
Следует отметить, что в силу использования только четырех направлений каждое из них может быть
представлено всего двумя битами.
а
Рис. 10.27. Задание контура с помощью цепных кодов
б
658
Глава 10. Средства для растровой графики
В варианте кодирования, приведенном на рис. 10.27, б, допускаются восемь направлений и поэтому
могут быть представлены 8-связные контуры. Цифра «1» означает, что следующий пиксел маршрута
находится «на единицу вверх» и «на единицу вправо»; аналогичные комбинации получаются и для ос-
тальных трех диагональных направлений. (Где находится стартовая точка для последовательности, по-
казанной на рисунке?) Цепные коды напоминают относительное рисование (черепашью графику) из
главы 3; отличие состоит в том, что здесь перемещение происходит только на один пиксел.
На рис. 10.28 приведена возможная структура данных для хранения контура. Первые два элемента
задают стартовый пиксел контура, далее идет количество шагов и список самих шагов. Цепные коды
могут обеспечивать очень компактное представление для контуров и областей определенного вида.
(Сколько бит на один шаг потребуется для кода с восемью направлениями?). Кроме того, при таком
способе легко решаются следующие стандартные задачи.
1. Перемещение контура. Это тривиально: просто поменяйте стартовый пиксел.
2. Масштабирование контура с масштабным множителем k: повторите каждый символ k раз.
3. Поворот контура на 90° против часовой стрелки: в случае цепного кода с четырьмя направлени-
ями необходимо увеличить на единицу цифру от 0 до 2 для каждого шага, а цифру 3 нужно за-
менить на 0. Точнее, следует использовать команду step=(step+l)3;3. Для кода с восемью направ-
лениями к каждому шагу следует добавлять 2 единицы.
С другой стороны, некоторые операции весьма сложны. Сложным является, например, закра-
шивание области, определенной с помощью цепного кода, поскольку серии из пикселов вдоль
строки развертки выделить достаточно трудно. Возможно, проще вначале конвертировать пред-
ставление в виде цепного кода в «таблицу форм».
10.7. Заполнение полигонально-определенных областей
Области часто определяют через полигоны, и разработано много эффективных алгоритмов для их за-
полнения сплошным цветом или узором. В некоторых графических пакетах предусмотрены свои соб-
ственные эффективные подпрограммы закрашивания. Рассмотрим, как происходит заполнение в од-
ном из таких пакетов.
Предположим, что область, подлежащая закрашиванию, представляет собой полигон Р, описанный
совокупностью адресов пикселов pi = (х, у), i = 1,..., N, которые определяют вершины полигона Р.
На рис. 10.29 приведен пример для полигона, заданного семью вершинами. Для заполнения полигона Р
мы проходим буфер кадров по строкам развертки, закрашивая необходимые участки каждой строки.
Как показано на рисунке, нужные участки определяются при нахождении пересечений каждой строки
развертки, скажем, г/ = 3, со всеми ребрами полигона Р. Те серии пикселов, которые лежат между пара-
ми ребер, должны лежать внутри Р и закрашиваются желаемым цветом.
Ниже приводится псевдокод, описывающий процесс закрашивания:
for (each scan line 1)
// для каждой строки развертки L
{
Find intersections of L with all edges of P
// находим пересечения L co всеми ребрами P
10.7. Заполнение полигонально-определенных областей
659
Sort the Intersections by increasing x-value
// сортируем пересечения по возрастанию х
Fill pixel runs between all pairs of intersections
//закрашиваем серии пикселов между всеми парами пересечений
Например, на рисунке строка развертки при у = 3 пересекает четыре ребра е2, е3, ev е5. Четыре абсциссы
точек пересечения округляются до ближайшего целого, как описывается ниже, и сортируются; в резуль-
тате получается последовательность 1, 2, 7, 9. Затем закрашиваются следующие две серии: первая от
столбца 1 до столбца 2 и вторая от столбца 7 до столбца 9.
Рис. 10.29. Закрашивание нужных участков строки развертки
Заметим, что при группировании отсортированных пересечений ребер в пары используется вари-
ант теста «внутри-снаружи» (inside-outside test). В процессе движения вдоль строки развертки мы при
каждом пересечении попадаем или внутрь полигона Р, или наружу от него, причем это состояние все
время меняется. (Иногда в данном контексте пребывание внутри называют четностью (parity), тогда
можно говорить об изменении четности при каждом пересечении.) Если мы попадаем внутрь, то эта
последовательность пикселов будет закрашиваться; если попадаем наружу, то нет. Если полигон Р цели-
ком лежит по правую сторону от начала каждой строки развертки, то начальная четность равна out (вне).
Отметим, что в данном алгоритме используется связность интервала (span coherence) — стремление
нескольких соседних пикселов вдоль строки развертки лежать рядом с внутренним пикселом. Таким
образом, целая серия может быть закрашена при минимуме вычислений.
10.7.1. Какие пикселы ребра принадлежат полигону?
Типичная сцена состоит из нескольких полигонов, причем некоторые из них (например, два) распола-
гаются рядом и в силу этого имеют общее ребро. О таких полигонах говорят, что они примыкают (abut)
друг к другу. Если мы не будем внимательны, то рассматриваемый нами алгоритм может присвоить
пикселам общего ребра сначала цвет одного полигона, а затем цвет другого. Такое повторное рисование
ребра может привести к нежелательному результату: общее ребро приобретет неестественный цвет, если
приложение производит рисование в режиме XOR, или же двойное рисование приведет к слишком
яркому цвету, если рисунок посылается на фоторегистрирующее устройство. Следовательно, алгоритм
должен решить, какой полигон «владеет» каждым ребром, тогда каждое ребро будет принадлежать толь-
ко одному из двух полигонов.
660
Глава 10. Средства для растровой графики
Хорошо работающее правило заключается в том, что полигон владеет своими левыми ребрами (в слу-
чае горизонтальных ребер — своими нижними). Тогда в случае примыкающих полигонов (рис. 10.30)
ребро принадлежит правому полигону и рисуется только один раз цветом этого полигона. Если общее
ребро горизонтально, то оно рисуется цветом верхнего полигона. На рисунке на примере простых тре-
угольников показаны четыре возможных варианта общего ребра для двух полигонов. В каждом из при-
веденных на рисунке случаев общее ребро рисуется цветом полигона В.
Рис. 10.30. Общее ребро принадлежит полигону В
Как применяется это правило при выполнении команды «закрашиваем серии пикселов между всеми па-
рами пересечений» («Fill pixel runs between all pairs of intersections»)?
На рис. 10.31 приведен пример полигона Р с девятью вершинами. Те пикселы, центры которых
лежат внутри полигона Р, закрашиваются; однако какие из пикселов, центры которых лежат на самих
ребрах, следует закрашивать? Поскольку левое и нижнее ребро принадлежат полигону Р, то пикселы,
лежащие на этих ребрах, закрашиваются, в то время как пикселы на правом и верхнем ребрах — нет.
Тогда при закрашивании интервала строки развертки между двумя пересечениями этот интервал вклю-
чает в себя крайний левый пиксел, если он лежит на ребре, но не включает такой же крайний правый
пиксел. Это правило не затрагивает ни одного пиксела, принадлежащего другим полигонам сверху и
справа от полигона Р. (Проверьте и убедитесь, что на рис. 10.31 это правило соблюдается.)
А
I
В
ООО
О
О О О О 0/0 о о
о о
о о о\о о о о о
ООО ооооооооо
о о о о о о о
о о о о о
ООО
G
D
F
о
н
с
Рис. 10.31. Закрашивание пространства внутренних пикселов
Поскольку обычно пересечения происходят при некотором значении х, лежащем между двумя це-
лыми значениями, то начало и конец каждого интервала определяются путем округления вверх или
вниз. Допустим, например, что левое пересечение серии пикселов произошло при вещественном значе-
нии xLeft, а правое пересечение при xRight. Мы хотим вычислить первый и последний пикселы в се-
рии — соответственно xFirst и xLast. Согласно вышеизложенному правилу, xFirst равно наименьшему
целому числу, которое больше или равно xLeft. Соответственно xLast — это наибольшее целое число,
строго меньшее, чем xRight. Это вычисление можно реализовать на C++ при помощи малого смещения
eps следующим образом:
#define eps 0.000001
xFirst - (short)CxLeft + 1 - eps);
// one xLeft or the next up
10.7. Заполнение полигонально-определенных областей
661
// xLeft или следующее большее число
xLast - (short)(xRight - eps):
// one smaller than xRIght
// число, меньшее чем xRight
for(x - xFirst: x <= xLast: x++) setPixeltx, y);
Обработка пересечений с использованием концевых точек
Часто случается так, что строка развертки проходит прямо через концевую точку (поскольку концевые
точки ребра — целые числа). Для обеспечения правильного изменения четности мы должны считать
такой случай за пересечение.
К примеру, строка развертки, проходящая через вершину Н (см. рис. 10.31), «видит» два пересече-
ния (одно с ребром GH, а второе с ребром Ш), так что четность по обе стороны от вершины Нкак будто
одинакова. Но эта «одинаковость» побуждает нас закрашивать справа от Н, что, очевидно, неправиль-
но. Далее, полигону принадлежит его нижнее горизонтальное ребро ВС, поэтому мы хотим учесть одно
пересечение в вершине В. (Почему?) Однако в этот полигон не входит его верхнее горизонтальное реб-
ро AI, поэтому мы хотим видеть в вершине А четное число пересечений. В действительности существу-
ет так много различных случаев, что требуется целый сложный набор правил!
Тем не менее имеется одно правило, простое и хорошо работающее во всех случаях: при подсчете
пересечений игнорировать пересечения строки развертки с верхней конечной точкой на ребре, а также
полностью игнорировать горизонтальные ребра. Поэтому на рис. 10.31 нет пересечений в точках А и I,
а есть одно пересечение в точке В и одно в точке Н, как мы и рассчитывали. Рисунок 10.32 иллюстриру-
ет другие возможные ситуации; на нем показан подсчет числа пересечений, которые «видны» при про-
хождении строк развертки через вершины нарисованного полигона. В каждом из этих случаев четность
справа от точки пересечения имеет то значение, которое необходимо для закрашивания. (Проверьте
это.) Отметим одно нелогичное следствие из этого правила: пиксел в точке Е на рис. 10.31 не рисуется,
так как он является верхним концом обоих ребер. Следовательно, необходимо переделать команду в
алгоритме закрашивания следующим образом: в команду
Find intersections of L with all edges of P
// находим пересечения L co всеми ребрами P
должно быть включено следующее уточнение:
Find the intersections of the scan line with all edges of P.
// находим пересечения строки развертки со всеми ребрами Р.
Discard intersections with horizontal edges and with the upper endpoint of any edge.
// отбрасываем пересечения с горизонтальными ребрами и
//с верхней концевой точкой любого ребра
Рис. 10.32. Число видимых пересечений с ребрами полигона
662
Глава 10. Средства для растровой графики
Практическое упражнение
10.7.1. Проверка метода
Рассмотрим образец полигона Q на рис. 10.33, содержащий следующие 16 вершин:
А: (52,30), В: (74,43), С: (60,60), D: (38,60), Е: (30,50),
F: (10,50), G: (10, 28), Н: (22,41),!: (33,10), J: (50,10),
К: (39,30), L: (40,44), М: (54,44), N: (46,34), О: (45,42),
Р: (33,34).
Заметим, что последние пять вершин образуют отверстие в полигоне/Q. Нарисуйте этот полигон на
миллиметровке и, используя метод, изложенный в данном разделе, убедитесь, что полигон закрашен
правильно.
Рис. 10.33. Пример полигона для закрашивания
10.7.2. Повышение эффективности алгоритма
Для увеличения эффективности метода, изложенного в предыдущем разделе, найдем ту его часть, кото-
рая отнимает больше всего времени. В данном случае это большое количество вычислений, связанных с
пересечениями строк развертки с ребрами. Для снижения этих затрат времени мы построим и будем
вести простой список, в результате чего сможем быстро определять точки пересечений. Этот список,
называемый списком активных ребер (active-edge list — AEL), позволяет алгоритму использовать связ-
ность ребер (edge coherence), состоящую из двух частей:
О склонность многих ребер, имеющих пересечения со строкой развертки у, пересекаться также и со
строкой развертки (у + 1);
О свойство прямой линии, заключающееся в том, что х-координата пересечения равномерно изме-
няется при переходе от одной строки развертки к другой.
В процессе закрашивания соответствующие серии пикселов вдоль каждой строки развертки закра-
шиваются просто в результате обращения к списку AEL, в котором содержатся х-координаты всех пе-
ресечений ребер для текущей (то есть закрашиваемой в данный момент) строки развертки. Эти абсцис-
сы содержатся в отсортированном виде, так что согласно правилу четности первые две абсциссы
определяют первую серию, две следующие — вторую серию и т. д.
Пусть, например, мы закрашиваем полигон, изображенный на рис. 10.34, и достигли строки развер-
тки у = 50. Эта строка развертки пересекает четыре ребра полигона. Абсциссы этих пересечений, как
легко вычислить, равны в порядке возрастания 45, 56,66, 70, 100. В таком случае закрашиваются два
интервала от 45 до 56 и от 70 до 99.
10.7. Заполнение полигонально-определенных областей
663
Форма списка AEL для такой ситуации предлагается на рис. 10.35, где показано четыре текущих
пересечения, записанных по порядку, наряду с некоторыми другими данными, которые позволяют ал-
горитму быстро обновлять AEL для использования в следующей строке развертки. Для каждого теку-
щего пересекаемого ребра в списке AEL содержатся следующие три элемента:
1. Значение абсциссы xnt пересечения ребра с текущей строкой развертки.
2. 1/ттг — обратная величина наклона ребра т.
3. Ордината yhigh верхней концевой точки ребра.
Рис. 10.35. Список AEL для строки развертки у = 50
Второй элемент используется для определения мест пересечений следующей строки развертки у = 51
с каждым ребром. Отметим, что если наклон ребра равен т, то перемещение вверх на единицу приводит
к увеличению абсциссы х пересечения на 1/ттг. (Проверьте это.) Значение 1/ти непосредственно хранит-
ся в списке AEL, как показано на рисунке. (К примеру, крайнее левое ребро простирается на 20 единиц
по х и на 40 по у, так что обратная величина наклона составляет 20/40; проверьте остальные значения,
приведенные на рисунке). Тогда при добавлении одного xnt и i/m определяется точка пересечения реб-
ра со следующей (верхней) строкой развертки, в соответствии со свойством связности ребер.
Отметим, что именно добавление \/т с последующим округлением и лежит в основе алгоритма Бре-
зенхема для перемещения от точки к точке вдоль прямой. Фактически именно метод Брезенхема (за-
ключающийся в приращении в зависимости от знака невязки с последующим обновлением этой невяз-
ки) наиболее предпочтителен в данной ситуации для достижения максимальной эффективности.
При переходе к следующей строке развертки в процессе закрашивания помимо инкрементального
перемещения по ребру могут произойти еще кое-какие вещи.
1. Новая строка развертки может теперь лежать ниже (или выше) ребра, представленного в списке
AEL. С целью упрощения проверки такой ситуации в AEL хранится ордината у верхней конце-
вой точки каждого ребра. Если новое значение у превышает это верхнее предельное значение, то
данное ребро удаляется из списка AEL.
664
Глава 10. Средства для растровой графики
2. Когда ордината у становится равной значению ординаты нижней концевой точки некоторых
ребер полигона, появляется одно или несколько новых ребер. Записи для таких ребер добавля-
ются в список AEL в форме ссылки на отдельную таблицу, которую мы рассмотрим позднее.
3. Для непростых полигонов порядок абсцисс пересечений с ребрами может измениться на обрат-
ный в случае, когда пересекаются два его ребра. Если это происходит, то список пересечений
должен быть отсортирован заново.
После закрашивания серий текущей строки развертки значение у увеличивается, абсциссы пересе-
чений обновляются, некоторые ребра удаляются из списка AEL, а другие ребра добавляются в него;
и при необходимости осуществляется пересортировка абсцисс пересечения. Закрашивание серий новой
строки развертки проводится аналогично.
Таблица ребер
Для того чтобы определить, какие ребра следует добавить при переходе к следующей строке развертки,
мы могли бы проверить каждую вершину полигона Р, чтобы узнать, какие ребра появятся после прира-
щения у, однако этот метод является неэффективным. Вместо этого информация о каждом ребре поли-
гона Рсобирается заранее и предусмотрительно помещается в специальную таблицу ребер (edge table —
ЕТ). ЕТ обеспечивает быстрый доступ к информации, необходимой для обновления списка AEL.
Таблица ЕТ оформлена в виде массива списков edgetable[], по одному списку для каждой строки
развертки. Фрагмент таблицы ЕТ для полигона Q с рис. 10.33 показан на рис. 10.36. Эта часть ЕТ фор-
мируется при начальном обходе полигона, который производится для устранения горизонтальных ре-
бер и сокращения других.
Рис. 10.36. Таблица ребер (ЕТ), характеризующая полигон Q
Список для каждой строки развертки содержит информацию о каждом ребре полигона Q, нижняя
конечная точка которого находится на данной строке развертки. (Это позволяет эффективно сортиро-
вать ребра полигона Q по их нижним ординатам у; этот процесс называют блочной сортировкой (bucket
sort) ребер полигона.) Поэтому многие из списков таблицы ЕТ являются пустыми.
Каждое ребро характеризуется записью того же типа, который используется в списке AEL. Поля yiM
и 1/ти заполняются соответствующими значениями, а в поле х помещается абсцисса х нижней конце-
вой точки рассматриваемого ребра.
Таблица ребер упрощает идентификацию тех ребер, которые подлежат включению в список AEL в
процессе его обновления. Для новой текущей строки развертки у достижимы все ребра, указанные в
строке таблицы ребер edgetabl е[у], поэтому они добавляются в список AEL. Поле xnt автоматически
содержит начальное значение абсциссы пересечения, а в прочие поля уже записаны нужные значения.
Поэтому при формировании записи для нового ребра должны быть изменены только несколько указа-
10.7. Заполнение полигонально-определенных областей
665
телей. Перед закрашиванием пиксельных серий список AEL пересортировывается по возрастанию зна-
чений xjnl с целью сохранения четности.
Листинг 10.8. Скелет алгоритма закрашивания полигона
AEL = NULL:
forty = 0; у <= maxRow; у++)
// AEL is initially empty
// вначале AEL пуст
add all edges In edgetablefy] to AEL
// добавляем в AEL все ребра из edgetablety]
iff AEL != NULL)
// any edges to process?
// есть ли какие-либо ребра для обработки?
sort AEL by xlnt value
// сортируем AEL по значениям xlnt
fill pixel values along у using AEL info
// закрашиваем пикселы по у с использованием данных AEL
delete from AEL any records for which yupper == у
// удаляем из AEL все записи, для которых yupper == у
update each xlnt value by its inverse slope
// изменяем каждое значение xlnt на величину, обратную наклону
}
}
Скелет всего рассматриваемого алгоритма приведен в листинге 10.8. Алгоритм начинает с пустого
списка AEL и успешно закрашивает каждую строку развертки, начиная с у = 0. Он быстро проходит по
основному циклу без рисования, до тех пор, пока в списке AEL не появятся первые ребра. Дополни-
тельные подробности этого алгоритма приводятся в тематическом задании 10.7.
Упрощение: заполнение «горизонтально-выпуклых» полигонов
Алгоритм в листинге 10.8 может быть значительно упрощен, если известно, что полигон, подлежащий
заполнению, в каждой строке развертки имеет только одно левое и одно правое ребро. Такие полигоны
можно назвать «горизонтально-выпуклыми» («horizontally convex»)1. Очевидно, что каждый выпуклый
полигон является также и горизонтально-выпуклым. Горизонтально-выпуклыми являются все треу-
гольники; что же касается четырехугольников, то некоторые из них являются горизонтально-выпуклы-
ми, а некоторые — нет. (Нарисуйте несколько горизонтально-выпуклых полигонов.)
Основное упрощение алгоритма заключается в том, что в случае горизонтально-выпуклых полиго-
нов список AEL всегда содержит ровно два ребра. Это обстоятельство значительно упрощает работу со
списком. Подробности рассматриваются в тематическом задании 10.7.
OpenGL способен значительно ускорить визуализацию сложных трехмерных сцен, когда в подпрограм-
му визуализации поступают только горизонтально-выпуклые прямоугольники. К счастью, большинство
программ моделирования представляют формы для визуализации только в виде выпуклых полигонов.
Практические упражнения
10.7.2. Алгоритм плоского закрашивания
Алгоритм плоского закрашивания (table-fill algorithm) очень быстро осуществляет заполнение опреде-
ленного класса полигонов. Каждое ребро такого полигона вначале подвергается, пиксел за пикселом,
сканирующему преобразованию (возможно, с помощью алгоритма Брезенхема), в результате которого
создаются пары точек (х, у), расположенные вдоль ребер полигона. При формировании каждой такой
1 Полигон является горизонтально-выпуклым, если прямая линия между двумя любыми точками внутри полигона, имеющими одну
и туже ординату у, целиком лежит внутри этого полигона.
666
Глава 10. Средства для растровой графики
пары (х, у) производится ее сравнение с двумя массивами minty] и maxfy], в которых для каждого значе-
ния у содержатся минимальное и максимальное значения абсцисс х, встретившиеся до этого момента.
Если x<mi п[у], то в массив min[y] вносится новое значение абсциссы х; аналогичные операции делаются
для массива тах[у]. Затем весь полигон закрашивается посредством рисования серий пикселов от min [у]
до тах[у] для каждой строки развертки у. Никакой сортировки не требуется, что и обеспечивает быст-
роту данного алгоритма.
Какие геометрические ограничения накладываются на полигон для гарантии его правильного за-
крашивания? Приведем несколько примеров полигонов, для которых данный метод работает, и несколь-
ко таких, с которыми он работать отказывается.
10.7.3. Алгоритм граничного закрашивания
Метод граничного закрашивания (fence-fill method) полигональных областей использует понятие «до-
полнения» или «обращения» определенных пикселов изображения. Для двухуровневого дисплея зна-
чение пиксела, равное 1 (белый цвет), превращается в 0 (черный), и наоборот. Главное свойство допол-
нения заключается в том, что при повторном его применении восстанавливается исходное значение
любого объекта, к которому эта операция была применена.
Дополнение работает следующим образом: создается вертикальная «граница» — возможно, она
пройдет через вершину подлежащего закрашиванию полигона. Все пикселы устанавливаются в 0. За-
тем для каждого ребра полигона выполняется следующее: на каждой строке развертки, проходящей че-
рез это ребро, производится обращение всех пикселов от ребра до созданной нами границы. Те пикселы
вдоль строки развертки, которые лежат вне полигона, обращаются четное число раз и поэтому остают-
ся равными 0. Пикселы же, лежащие внутри полигона, обращаются нечетное число раз и поэтому рав-
ны 1 (закрашиваются). Результат не зависит от того, где именно пролегает граница.
Нарисуйте на бумаге несколько полигонов и примените для их заполнения вручную метод гранич-
ного закрашивания. Покажите, что данный метод работает для рисунка из нескольких полигонов и для
полигонов с отверстиями. Что произойдет, если этот метод применить не к полигону, а к прямой с за-
данными понятиями «снаружи» и «внутри»?
10.8. Ступенчатость; технологии сглаживания
Ранее нам уже встречалось понятие «ступенек». Ступеньки — это одна из форм дефектов изображения
(aliasing), которые являются неотъемлемым свойством растровых дисплеев. Ступенчатость возникает из-
за дискретной природы пикселов; это означает, что пикселы появляются на дисплее в виде фиксирован-
ного прямоугольного массива. На рис. 10.37, а ступенчатость показана на примере черного прямо-
угольника. Если такой прямоугольник охватывает большое количество пикселов, то его граница будет
выглядеть относительно гладкой, хотя и останутся некоторые неровности. Однако если он занимает
лишь несколько пикселов, как на рис. 10.37, б, то «ступеньки» будут очень заметны и «режут глаз». На
этом рисунке каждый пиксел, образующий прямоугольник, окрашивается в черный цвет в том случае,
когда прямоугольник проходит через конкретную точку: центр этого пиксела. Фактически каждый пиксел
«опрашивает» прямоугольник в единственной точке — в центре пиксела, выясняя: имеется ли прямоуголь-
ник в этой точке. В зависимости от ответа вся площадь пиксела окрашивается в белый или черный цвет.
Рис. 10.37. Ступенчатость прямоугольника
10.8. Ступенчатость; технологии сглаживания
667
Такой опрос может привести к тому, что маленькие объекты (например, удаленные объекты на трех-
мерной сцене) исчезнут полностью, как показано на рис. 10.38, а. Если объект располагается между цент-
рами двух или более пикселов, то он не отображается вовсе. На рис. 10.38, б показано, как объект может
«мерцать» при анимации. На одном кадре объект может покрывать центр какого-либо пиксела, однако
Рис. 10.38. Маленькие объекты, пропущенные из-за ступенчатости
Сам термин «ступенчатость» («aliasing») пришел из теории замеров (sampling theory) при обра-
ботке сигналов [Oppenheim, 149]. Грубо говоря, если переменный сигнал замеряется чересчур редко, то
замеры будут представлять сигнал, изменяющийся с низкой частотой: частота исходного сигнала заменяет-
ся более низкой «паразитной» частотой. На рис. 10.39, а показан быстро изменяющийся прямоугольный
сигнал, замеряемый посредством равномерных опросов с интервалами, показанными точками. Если
основываться только на этих опросах, то исходный сигнал будет выглядеть как прямоугольный сигнал
с более низкой частотой, что показано на рис. 10.39, б.
Рис. 10.39. Слишком медленный опрос делает сигнал похожим на ступеньки
10.8.1. Технологии сглаживания
Как же уменьшить ступенчатость, обусловленную неэффективным опросом? Здесь поможет дисплей с
более высоким разрешением, поскольку в этом случае размеры ступенек станут меньше по отношению
к объекту. Однако на предельное разрешение дисплея накладывают свои ограничения как современная
технология, так и цена. Следовательно, мы должны искать другие способы борьбы со ступенчатостью.
Технологии сглаживания включают в себя ту или иную форму «размытия границ» («blurring»), на-
правленную на сглаживание изображения. В случае черного прямоугольника на белом фоне резкий пе-
реход от черного к белому смягчается путем применения вблизи границы прямоугольника смеси из се-
рых пикселов. Когда на изображение смотрят издали, глаз смешивает плавно изменяющиеся тени и
видит более ровное ребро.
Обычно используются три метода сглаживания: предфильтрация (prefiltering), сверхопрос (super-
sampling) и постфильтрация (postfiltering).
668
Глава 10. Средства для растровой графики
П редфил ьтра ция
В технологиях предфильтрации цвета пикселов вычисляются на основе покрытия (coverage) объектом:
вычисляется часть площади пиксела, которая покрывается объектом. Рассмотрим сканирующее преоб-
разование белого полигона на черном фоне, изображенного на рис. 10.40, а. Этот полигон размещен в
квадратной сетке, центр каждого квадрата которой соответствует центру пиксела на дисплее. Пикселу,
половина которого покрывается полигоном, присваивается интенсивность 1/2; пикселу, покрытому на
треть, — интенсивность 1/3 и т. д. Если буфер кадров использует 4 бита на пиксел, то черному цвету соот-
ветствует 0, а белому — 15; пикселу, покрытому полигоном на четверть, соответствует значение (1/4)15,
которое округляется до 4. На рис. 10.40, б приведена таблица значений, полученных после вычисления
покрытия каждого пиксела. (Какой вид имел бы этот массив значений пикселов, если бы мы просто
опросили этот полигон в центре каждого пиксела, присваивая 15 в случае покрытия прямоугольником
этого центра и 0 в противном случае?)
Рис. 10.40. Использование части площади пиксела, покрываемой объектом
0 0 0 0 1 6 0 0
0 0 0 6 13 15 8 0
0 3 11 15 15 9 7 3
3 11 14 15 12 2 0 0
0 0 1 6 5 0 0 0
б
Геометрические вычисления, необходимые для нахождения степени покрытия каждого пиксела,
могут занять, конечно, очень много времени. Было разработано несколько эффективных приемов. Мы
опишем модификацию алгоритма Брезенхема для прямых, разработанную Питтвэем и Уоткинсоном
(Pitteway, Watkinson [Pitteway, 170]). Как и в случае самого алгоритма Брезенхема, вычисления здесь
инкрементные и основываются на арифметике целых чисел.
Мы уже видели, как подпрограмма закраски полигона обрабатывает строку развертки за строкой,
используя список AEL для определения пиксельных серий, подлежащих закрашиванию. Точки пересе-
чения xint, хранящиеся в AEL, обновляются после закраски каждой строки развертки, для чего исполь-
зуется цикл, аналогичный циклу Брезенхема (увеличивать на единицу, если невязка отрицательна,
и обновлять невязку). Эти значения невязки можно также использовать для отслеживания покрытия
первого и последнего пикселов каждой серии. Затем пикселам вдоль ребер полигона задаются цвета
в соответствии с их покрытием полигоном, чем и достигается сглаживание.
На рис. 10.41 демонстрируется пример для метода Питтвэя и Уоткинсона. Наклон ребра полигона
составляет 4/10. Точками отмечены пикселы, определенные по стандартному алгоритму Брезенхема,
а затененная область в каждом из этих пикселов означает площадь внутри полигона. Для каждого пик-
села приведено числовое значение, соответствующее этой площади: 0,5, 0,9, 0,3 и т. д. Считается, что
первый пиксел покрыт на 50 %.
Из геометрических с оображений легко увидеть, что по мере движения вправо пиксел за пикселом
затененная область или увеличивается на т = 0,4, если значение у остается неизменным, или уменьша-
ется на 1 - т - 0,6, если значение у увеличивается (см. упражнения в конце раздела). Следовательно,
нетрудно инкрементно обновлять эту область в рамках алгоритма Брезенхема.
Далее, пусть максимальное значение интенсивности, поддерживаемое буфером кадров, равно
MaxLevel. Для ребра с наклоном т находим ближайшее целое 1ncl=MaxLevel * гаи или увеличиваем ин-
тенсивность каждого пиксела на 1 ncl, или уменьшаем ее на 1 nc2=MaxLevel - Incl. Основной цикл алго-
10.8. Ступенчатость; технологии сглаживания
669
ритма Брезенхема (см. листинг 10.5) требуется только слегка изменить: если F< 0, то кроме обновления
невязки на F += 2 * Н нужно обновлять также интенсивность на colval += incl. Аналогично при F > 0
невязка обновляется на 2 * (Н - W), а интенсивность — на -i пс2. В своей оригинальной работе Питтвэй
и Уоткинсон еще больше повысили эффективность своей процедуры, предусмотрев возможность заме-
ны Fна colval в качестве тестовой переменной.
Затененная
площадь
Рис. 10.41. Пример сканирующего преобразования со сглаживанием
Предфильтрация работает с детализированной геометрической формой объекта (объектов), подверг-
нутого сканирующему преобразованию, и вычисляет усредненную интенсивность для каждого пиксе-
ла, исходя из того, как этот объект размещается внутри площади каждого пиксела. Для форм, отличных
от полигонов, предфильтрация может оказаться технологией, весьма дорогостоящей с вычислительной
точки зрения; поэтому мы поищем альтернативные методы сглаживания.
Сверхопрос
Поскольку ступенчатость возникает по причине опроса объекта в слишком малом числе точек, можно
попытаться уменьшить ее эффект посредством более частого, чем один на пиксел, опроса. Такая техно-
логия носит название сверхопроса (supersampling) и означает проведение опросов сцены с большей
частотой, чем эта сцена отображается. В этом случае каждое значение пиксела дисплея формируется
как усреднение нескольких опросов.
На рис. 10.42 показан пример двойного опроса: для объекта (в данном случае это наклонная полоса)
замеры объекта делаются в два раза плотнее (как по х, так и по у), чем этот объект отображается на
дисплее. Квадраты обозначают пикселы дисплея, а по оси х отмечены те точки, в которых производи-
лись замеры сцены. Каждый результирующий пиксел дисплея может быть сформирован как среднее из
девяти «соседних» замеров: центрального пиксела и восьми окружающих его. При этом некоторые
замеры используются повторно при вычислении других пикселов. (Какие именно?) Пиксел дисплея
в точке А формируется исходя из шести замеров внутри полосы и трех замеров фона. Поэтому его цвет
состоит из двух третей цвета полосы и одной трети цвета фона. Цвет пиксела в точке В основывается на
девяти замерах, которые все лежат внутри полосы; его цвет равен цвету полосы.
На рис. 10.43, а приведена сцена, отображенная с разрешением 300 на 400 пикселов. Здесь ясно вид-
ны «ступеньки». Рисунок 10.43, б демонстрирует преимущества двойного опроса. Та же самая сцена
была опрошена с разрешением 600 на 800 пикселов, вследствие чего каждый из 300 на 400 пикселов
дисплея является усреднением девяти пикселов-соседей. При этом «ступеньки» оказались в значитель-
ной степени сглаженными.
670
Глава 10. Средства для растровой графики
Центр
пиксела дисплея
Рис. 10.42. Сглаживание с использованием сверхопроса
Рис. 10.43. Примеры сглаживания с помощью сверхопроса
Вообще говоря, при сверхопросе производится Ns замеров сцены по х и по у на один пиксел дисплея,
и при формировании значения каждого пиксела дисплея происходит усреднение соседних замеров.
Например, при N - 4 для каждого пиксела дисплея усредняются 16 замеров. (Нарисуйте картинку для
этой ситуации.)
Сглаживания можно добиться и при отсутствии сверхопроса (ЛГ = 1). На рис. 10.44 показана сце-
на, опрос которой осуществляется в углу каждого пиксела дисплея. Интенсивность каждого такого пик-
10.8. Ступенчатость; технологии сглаживания
671
села определяется усреднением четырех замеров, взятых в его углах. При этом наблюдается некоторое
смягчение «ступенек», хотя сверхопрос не проводился.
Постфильтрация
При использовании метода двойного опроса при вычислении интенсивности каждого пиксела дисплея
производится усреднение девяти соседних замеров, причем каждый из них одинаково важен. Такая
форма фильтрации, или размытия границ (blurring), может быть улучшена, если придать центрально-
му замеру больший вес, а восьми его соседям — меньший. Кроме того, может оказаться полезным вовле-
чение в процесс усреднения большего числа соседей.
При постфильтрации каждый пиксел дисплея вычисляется как среднее взвешенное (weighted average)
соответствующего набора соседних замеров сцены. На рис. 10.45 показана ситуация применительно к
двойному опросу. Каждое числовое значение описывает интенсивность опроса сцены, причем серым
цветом написаны числа, соответствующие центрам различных пикселов дисплея. На каждый серый
квадрат поочередно накладывается квадратная маска (mask), которую называют также оконной функ-
цией (window function). Затем вес каждой клеточки умножается на ее соответствующий замер, девять
произведений складываются и образуют интенсивность пиксела дисплея. К примеру, когда маска, по-
казанная на рисунке, накладывается на замер с интенсивностью 30, то среднее взвешенное равно:
30 28 + 16 + 4 + 42 + 17 + 53 + 60 + 62 _
— 4" ———................. — 32, о2Э,
2 16
что при округлении дает интенсивность 33. Эта маска придает центральному замеру вес в восемь раз
больший, чем веса остальных восьми соседей. Сумма всех весов всегда равна единице.
Оконная функция
Рис. 10.45. Постфильтрация графического изображения
Отметим, что сверхопрос, как мы его описали, представляет собой частный случай постфильтрации,
все веса которой составляют 1/9. В теории опросов и теории фильтров [Gonzalez, 88; Oppenheim, 149]
имеются аналитические методы, определяющие эффективность действия различных оконных функций
в качестве постфильтров. Иногда используются большие маски — размером пять на пять или даже семь
на семь. Такие «взгляды» в сторону дальних соседей центрального замера могут обеспечить дополни-
тельное сглаживание. На рис. 10.46 приводятся несколько примеров масок, часто используемых на
практике [Crow, 53]. Дробь, написанная перед каждой маской, определяет общий множитель, на кото-
рый умножается каждый элемент маски, так что сумма этих элементов равна единице. В первой маске
вес центрального элемента в четыре раза больше веса своих 4-связных соседей, а угловые элементы во-
обще не имеют веса. Третий пример представляет собой маску пять на пять, в которой веса присваива-
ются и соседям второго круга вокруг каждого центрального замера. Примеры с рис. 10.46, бив являют-
ся аппроксимациями так называемого «окна Барлетта» («Bartlett window»): веса линейно возрастают
по мере движения от краев маски к центру.
Постфильтрация может быть выполнена для любого значения сверхопроса Ns. При N = 4 подходят
маски размером пять на пять, семь на семь или девять на девять [Crow, 53]. Если же TV = 1, (как в случае
угловых замеров), то можно применять маску три на три, которая придает особенно большой вес цент-
672
Глава 10. Средства для растровой графики
ральному пикселу. Такое размытие границ может дать или не дать нужный эффект — в зависимости от
характера визуализируемой сцены.
Рис. 10.46. Примеры оконных функций
В главе 14 рассматриваются более современные методы сглаживания в связи с трассировкой лучей.
Большое количество дополнительной информации можно найти также в работах [Foley, 64, Blinn, 24].
Практические упражнения
10.8.1. Проверка добавочной площади
Покажите для случая ребра с наклоном т в диапазоне от 0 до 1, что площадь пиксела ребра, покрытого
полигоном, или увеличивается на т или уменьшается на 1 - т по мере движения по ребру от пиксела к
пикселу. Учитывайте при своем вычислении площадей пикселов маленькие треугольники (на рис. 10.41
они обозначены буквой Р), относящиеся к соседним верхним пикселам, как показано на рисунке для
пикселов при х = 2 и х = 7.
10.8.2. Работа алгоритма Питтуэя—Уоткинсона в других квадрантах
Мы рассматривали работу этого алгоритма, ограничиваясь диапазоном наклонов ребра полигона от О
до 1. Распространите этот метод на ребра с произвольным наклоном.
10.8.3. Сглаживание полигона
Пусть в буфере кадров хранятся значения от 0 до 15. Примените сканирующее преобразование со сгла-
живанием к каждому ребру белого полигона с вершинами (1,3), (6,7), (15,4) (И, 15), (1,8). Пусть цвет
фона — черный. Теперь закрасьте этот полигон белым цветом при помощи алгоритма граничного за-
крашивания. Возможен ли отказ данной процедуры, если на ребре полигона появится разрыв? Если да,
то как можно исправить этот недостаток?
10.8.4. Угловой опрос
Какое количество замеров сцены необходимо вычислить для растра размером R строк и С столбцов при
использовании углового опроса? Иначе говоря, сколько углов содержит данный растр? Сравните этот
тип опроса с опросом «по центру пиксела», а также с двойным опросом.
10.8.5. Другие окна
Укажите, взяв за образец окно Барлетта на рис. 10.46, б, в, какие элементы содержит окно Барлетта раз-
мером семь на семь? Чему равен общий масштабный множитель?
10.8.2. Сглаживание текстуры
В главе 8 мы рассматривали наложение текстур на поверхности для достижения большей реалистично-
сти. Накладываемые текстуры особенно подвержены явлениям ступенчатости, поскольку от текстуры
мы обычно ожидаем качественного изображения или узора. Кроме того, сама текстура обычно опреде-
ляется как пиксельная карта, причем пикселы дисплея и пикселы карты часто связаны сложными гео-
метрическими соотношениями. Мы опишем здесь специфические проблемы, возникающие при рисо-
вании текстур, и рассмотрим некоторые решения.
10.8. Ступенчатость; технологии сглаживания
673
На рис. 10.47, а показан классический пример ступенчатости: текстура, наложенная на наклонную
плоскость. Удаленные клетки шахматной доски выглядят очень неровно, что приводит к возникнове-
нию муара. На рис. 10.47, б приводится то же изображение, подвергнутое сглаживанию; в результате
оно значительно улучшилось.
Рис. 10.47. Пример ступенчатости и улучшение в результате сглаживания (с разрешения Paul Heckebert)
Напомним, что текстура определяется как функция texture(s, f) в пространстве текстуры и что преж-
де чем появиться на дисплее, она подвергается сложной последовательности преобразований. Процесс
визуализации решает другую задачу: для каждого данного пиксела дисплея с координатами (х, у) тре-
буется определить соответствующий цвет в функции texture( ).
На рис. 10.48 показан отдельный пиксел с координатами (х, у), подвергающийся визуализации, и
полученные соответствующие ему значения ($*, t*) в пространстве текстуры. Обозначим для удобства через
Т( ) все преобразование из пространства пикселов в пространство текстуры, тогда (s*, t*) = Т(х,у). (Ком-
поненты этого преобразования были рассмотрены в главе 8.)
(s*,t*)= Т(х, у)
Рис. 10.48. Причина возникновения ступенчатости при визуализации текстуры
Поскольку пикселы являются не точками, а имеют конечную площадь, нам следовало бы подумать
о том, как отображается в пространство текстуры весь квадратный пиксел с центром в точке (х, у). Этот
пиксел также изображен (см. рис. 10.48) в виде четырехугольника1. Мы будем называть такой четы-
рехугольник текстурным квадратом (texture quad), соответствующим рассматриваемому экранному
пикселу. Представим, что пространство текстуры покрывается такими квадратами, каждому из которых
соответствует экранный пиксел. Размер и форма каждого текстурного квадрата зависит от природы
преобразования Т( ) и определить их зачастую непросто. Если функция texture(,) изменяется в преде-
лах одного квадрата, то цвет экранного пиксела все равно определяется только одним значением
texture(s*, t*), вследствие чего теряется важная информация и возникает ступенчатость.
1 Если изображаемая трехмерная поверхность искр :влепа, то стороны этого четырехугольника также могут быть искривлены.
(Представьте себе это мысленно.)
22 Ф. Хилл
674
Глава 10. Средства для растровой графики
Для уменьшения эффектов ступенчатости цвет экранного пиксела следует задавать посредством
усреднения цветов внутри соответствующего текстурного квадрата. На рис. 10.49 показан текстур-
ный квадрат, наложенный на отдельные текстурные элементы, или тексели (texels) пиксельной карты
txtr[][], которая определяет функцию texture(s, t). Если бы существовал простой способ определения
площади каждого текселя, лежащего внутри данного текстурного квадрата, то усреднение не составило
бы труда: мы бы просто присвоили весовые коэффициенты этой площади каждому значению txtг[г] [с],
сложили бы результаты и разделили бы сумму на площадь квадрата. Эта процедура аналогична техно-
логии предфильтрации, которую мы уже использовали для сглаживания. К сожалению, такое вычисле-
ние очень дорогостояще, поскольку трудно найти площадь каждого текселя, покрываемого квадратом.
Хекберт исследовал различные методы, разработанные для аппроксимации данного вида предфиль-
трации [Heckbert, 102]. В частности, рекомендуется один из этих методов — фильтр с эллиптическим
средним взвешенным, или EWA-фильтр (elliptical weighted-average filter) [Greene, 93]. Как показано на
рис. 10.50, в рамках этого метода каждый экранный пиксел покрывается фильтр-функцией с круговой
симметрией (концентрические окружности изображают различные весовые уровни, как на топографи-
ческой карте), после чего эта фильтр-функция отображается в пространство текстуры, где она приобре-
тает форму эллипса, примерно соответствующего форме текстурного квадрата. Значения фильтр-функ-
ции, записанные в таблице LUT, используются для взвешивания различных точек внутри эллипса, после
чего эти взвешенные величины суммируются для получения среднего. Все это может быть осуществлено
в приращениях и с большой эффективностью (используются результаты контролируемого преобразова-
ния фильтр-функции из одного пространства в другое) и обходится всего в несколько арифметических
операций на тексель. На рис. 10.47, б показана удаляющаяся шахматная доска, визуализация которой
производилась с использованием EWA-фильтра.
Рис. 10.50. Фильтрация с эллиптическим средним взвешенным
Функция фильтрации
с центром в пикселе
10.8. Ступенчатость; технологии сглаживания
675
Другой метод, который называется стохастической выборкой (stochastic sampling) и полностью
описан в работе [Watt, 92], не требует сложных геометрических вычислений и формирует усредненный
цвет текстуры посредством замеров текселей по случайной схеме. На рис. 10.51 показан текстурный
квадрат с центром в точке (s*, /*), связанный с определенным экранным пикселом. Сам квадрат непосред-
ственно не используется; вместо этого из области в окрестности точки (s*, /*) берется определенное
число замеров, после чего цвета текселей усредняются для формирования цвета текстуры:
average = texture($* + а*, t * + Р*).
Здесь ak и Р* — малые случайные величины, которые легко создать при помощи генератора случайных
чисел, а их распределение при желании можно распространить на всю площадь текстурного квадрата.
Рис. 10.51. Сглаживание с использованием стохастической выборки
Мы снова встретимся с методом стохастической выборки в главе 14, где он будет использован в ка-
честве мощного инструмента для трассировки лучей.
10.8.3. Сглаживание с применением OpenGL
В OpenGL предусмотрен ряд средств для выполнения сглаживания. Проще всего в использовании
буфер-накопитель (accumulation buffer), являющийся дополнительной областью памяти, подобный
буферу кадров; OpenGL может его создавать и рисовать внутри него. Этот метод сглаживания напоми-
нает метод стохастической выборки. Он рисует сцену многократно со слегка различных позиций (от-
личающихся всего на доли пиксела) и добавляет результаты в буфер-накопитель. После добавления
всех этих слегка «возмущенных» рисунков в буфер-накопитель результаты копируются в буфер кад-
ров, и на дисплей выводится сглаженное изображение. Таким образом, для каждого пиксела формиру-
ется усредненное значение цвета, основанное на цветах спроектированной сцены, лежащих в непосред-
ственной близости от данного пиксела.
Ниже приводится код, который показывает, как это может быть осуществлено при съемке трехмер-
ной сцены с помощью камеры. Буфер-накопитель создается при запуске1; его содержимое при инициа-
лизации обнуляется посредством вызова подпрограммы glClear(GL_ACCUM_BUFFER_BIT). Затем сцена ри-
суется восемь раз, причем каждый раз производится малое «перемещение» камеры, данные о котором
сохраняются в векторном массиве jitterf] («дрожание»). Каждое новое изображение масштабируется
с коэффициентом одна восьмая и добавляется — пиксел за пикселом — в буфер-накопитель с помощью
подпрограммы glAccum(GL_ACCUM, 1/8.0). После того как нарисованы восемь изображений, буфер-нако-
питель копируется в буфер кадров посредством вызова glAccum(GL_RETURN, 1.0). Вот этот код:
glClear(GL_ACCUM_BUFFER_BIT):
fordnt 1=0; 1 < 8; 1++)
1 Для этого в инициализацию необходимо включить GL ACCUM: gl utInitDi spl ayModetGLUT SINGLE|GLUT_RGB|GLUT_ACCUM| GLUT_
DEPTH):.
676
Глава 10. Средства для растровой графики
{
cam.slide(f * jitter[i].x. f * jitter[i],y,0):
displayO:
// draw the scene
// рисуем сцену
glAccum(GL ACCOM. 1/8.0):
}
glAccum(GL_RETURN, 1.0):
Множитель f управляет всем смещением камеры. Вектор дрожания j 1 tter[ ] содержит восемь точек,
которые по х и по у лежат в пределах от -0,5 до 0,5. В заголовочном файле jitter.h1 используются сле-
дующие пары значений:
(-0,3348,0,4353), (0,2864, -0,3934), (0,4594,0,1415), (-0,4144, -0,1928),
(-0,1837,0,0821), (-0,0792, -0,3173), (0,1022,0,2991), (0,1642, -0,0549).
Эти точки имитируют восемь случайно выбранных смещений с центрально-симметричным распре-
делением вероятностей, что напоминает ранее описанный EWA-метод. В файле jitter.h содержатся
также другие векторы дрожания, более длинные и более короткие, которые могут быть использованы
для применения различных степеней сглаживания.
На рис. 10.52 приведена трехмерная сцена, визуализация которой производилась двумя способами: на
рис. 10.52, а показана сцена без сглаживания, а на рис. 10.52, б показано улучшение, достигнутое путем
усреднения восьми «дрожащих» вариантов визуализации в буфере-накопителе. «Ступеньки» в сцене
со сглаживанием заметно уменьшились. Этот метод является довольно медленным, поскольку для каж-
дого кадра визуализация сцены производится восемь раз.
Рис. 10.52. Визуализация сцены: а) без сглаживания; б) со сглаживанием
10.9. Увеличение количества цветов и оттенков
Часто графический дисплей поддерживает количество цветов или оттенков серого цвета, которое не-
адекватно определенному классу изображений. Например, двухуровневый дисплей выдает только чер-
ный и белый цвета, а многие дешевые терминалы допускают только четыре или восемь цветов. Как со-
здать на таких терминалах зрительное впечатление большего количества цветов или оттенков?
Одним из таких методов является метод полутонов (halftones), при котором пространственное раз-
решение выдается за цветовое [Ulichney, 203; Knuth, 124]. Типичным примером являются газеты. В них
используется только черная типографская краска, тем не менее изображение в газетах выглядит так,
как будто в нем содержится много оттенков серого цвета. Это достигается путем использования боль-
1 Этот файл является частью загружаемого пакета GLUT.
10.9. Увеличение количества цветов и оттенков
677
ших или маленьких «капелек» черной краски, расположенных вплотную друг к другу. Те области, где
больше крупных капелек, выглядят темнее для глаза, поскольку средний уровень черноты здесь выше.
Места, где капельки меньше, выглядят покрашенными в серый цвет более светлого оттенка. Глаз объ-
единяет эти капельки и воспринимает для малых областей средний уровень интенсивности. Однако у
газеты пространственная разрешающая способность намного ниже, чем у фотографии, поскольку изоб-
ражение на газете создается из отдельных капелек, размер которых не может быть сколь угодно малым.
В контексте компьютерной графики использование цифровых полутонов (digital halftones) или на-
несение шаблона (patterning) означает применение массивов из малых точек вместо точек переменного
размера. На рис. 10.53, а приводится пример, в котором массивы точек размерностью два на два (каж-
дая такая точка принимает значение 0 или 1) использованы для имитации более крупных «капелек» с
пятью возможными уровнями интенсивности. Применим для большей ясности изложения аналогию с
принтером и свяжем уровень 0 с белым цветом (краски нет), а уровень 4 — с черным. Смысл состоит в
том, что глаз видит усредненную интенсивность каждой «капельки» размером два на два, поэтому мы и
можем воспринимать пять уровней.
Рис. 10.53. Шаблоны размером два на два
Для придания нашему обсуждению конкретности предположим, что в исходном полутоновом изоб-
ражении используется массив из пикселов размерностью 100 на 100, значения интенсивности которых
изменяются в диапазоне от 0 до 4. Предположим далее, что нам доступен только двухуровневый дисп-
лей, а изображение будет отображаться в области размером 200 на 200 пикселов. Закрасим каждый блок
пикселов размером 2 на 2 таким образом, чтобы обеспечить сходство с одним из оттенков серого цвета
от 0 до 4. Мы снова выдаем пространственное разрешение за диапазон интенсивности.
Позиции черных элементов на рис. 10.53, а были выбраны сколь возможно «нестандартными», что-
бы избежать на изображении полос или других искажений. Если, например, для уровня 2 выбрать один
из узоров, приведенных на рис. 10.53, б, то в некоторых местах изображения могут возникнуть горизон-
тальные или вертикальные полосы.
На рис. 10.54, а показан пример полутонового изображения размером 872 на 599, а на рис. 10.54, б —
двухуровневое изображение размером 1744 х 1198, в котором применено структурирование размером
а б
Рис. 10.54. Пример использования структурирования размером два на два: а) полутоновое изображение;
б) структурированное на двухуровневом дисплее
678
Глава 10. Средства для растровой графики
два на два. На нем ясно видны пять четко различимых уровней серого цвета. Для обеспечения большего
количества градаций серого можно увеличить размеры клеток. На рис. 10.55 показана структура с клет-
ками три на три, что позволяет добиться 10 оттенков серого цвета. В общем случае клетки из нулей и
единиц размером п на п могут обеспечить (n2 + 1) оттенков серого. (Почему?) Структурирование чаще
всего применяется тогда, когда исходное изображение обладает меньшим разрешением, чем то, которое
способно обеспечить используемое дисплейное устройство.
Рис. 10.55. Структуры размером три на три
10.9.1. Упорядоченное размытие
Часто мы не можем позволить себе роскошь использовать несколько пикселов дисплея для имитации
одного серого пиксела большего размера. Например, нам может понадобиться отобразить картинку раз-
мером 100 на 100 пикселов, используя только 100 на 100 двухуровневых пикселов на дисплее. Как же в
таком случае нам разместить черные и белые пикселы так, чтобы это изображение воспринималось гла-
зом как многоуровневое? Иначе говоря, каков наилучший способ выбора нулевого или единичного пик-
села и насколько при этом изображение будет похоже на свой оригинал?
Наиболее простым методом выбора значения пиксела является установление порогов (thresholding).
Для каждого пиксела мы определяем пороговое значение: для пиксела с координатами (х, у} каким-либо
образом задаем пороговое значение t[x][y]. Пусть значение пиксела изображения в строке х и колонке у
равно р[х][у]. Если р[х][у] «выше порога» (то есть р[х] [у] >= t[x][y]), то мы устанавливаем значение
пиксела дисплея в 1. В противном случае оно устанавливается в 0.
Для каждого пиксела можно использовать одно и то же пороговое значение, однако это приведет
к резкому оконтуриванию (contouring) изображения, с «островками» черного и белого. (Ниже приво-
дится соответствующий пример.) Вместо этого создается массив из различных пороговых значений —
с помощью специального шаблона размытия (dither pattern); и этот массив используется для покры-
тия изображения мозаикой из переменных пороговых значений.
Рассмотрим, например, 16-уровневое изображение, истинные значения пикселов которого изменя-
ются от 0 до 15. Выберем следующий шаблон размытия размерностью два на два:
'3 9'
[12 6,
(10.9)
Эти значения выбраны как четыре равноотстоящих числа в диапазоне от 0 до 15. Представим себе,
что этот шаблон накладывается на верхнюю часть исходного изображения с повторением наподобие
шахматной доски, как показано на рис. 10.56. Если шаблон поместить в матрицу размерностью два на
два D[2][2], то процесс создания мозаики будет проходить следующим образом: t[x][y]=D[x % 2][у % 2].
Это означает, что нам не требуется создавать весь массив t[] [] целиком: каждое значение при необходи-
мости вычисляется путем индексной адресации массива В[][]. Окончательное двухуровневое изображе-
ние формируется пиксел за пикселом, как уже указывалось ранее: 0 или 1, в зависимости от относитель-
ных размеров р[х][у] и t[x][y]. При использовании шаблона размытия пороговое значение изменяется
от пиксела к пикселу, как показано на рисунке.
10.9. Увеличение количества цветов и оттенков
679
Исходное изображение
Шаблон размытия
Рис. 10.56. Установление порогов для изображения с помощью шаблона размытия
Каков эффект от переменного порогового значения? Оно порождает дополнительные видимые от-
тенки серого цвета. Чтобы представить это, рассмотрим на исходном изображении область постоянной
интенсивности, например область из восьмерок в верхнем левом углу на рис. 10.56. Поскольку 8 превы-
шает 3 и 6, но меньше, чем 9 и 12, то каждому блоку два на два в данной области соответствует матрица
Ч 04
изображения на дисплее. Эта матрица означает усредненную интенсивность 0,5, то есть посередине
между черным и белым. Это хорошо согласуется со значением пиксела 8, что также соответствует сере-
дине между черным и белым. Таким образом, шаблон из нулей и единиц в массиве два на два определя-
ет усредненную интенсивность, лучше совпадающую с усредненной интенсивностью исходного изоб-
ражения, чем при использовании простого установления порогов.
Вообще говоря, для тех областей, где исходное изображение имеет постоянную интенсивность, изоб-
ражение на дисплее будет демонстрировать один из следующих шаблонов размером два на два:
f0 0W1 0W1 OW1 С fl П
0 0’0 0’0 1’0 1’1 1’
которым соответствуют усредненные интенсивности: 0, 0,25, 0,5, 0,765,1.
На рис. 10.57 показано соответствие между усредненной наблюдаемой интенсивностью и постоян-
ными значениями пикселов исходного изображения. Следовательно, размытие предоставляет возмож-
ность изобразить на двухуровневом дисплее пять уровней яркости для областей с постоянной интен-
сивностью. Такой диапазон, конечно, значительно меньше исходных 16 уровней, однако значительно
лучше, чем всего два уровня. В областях с изменяющимися значениями пикселов эффект более сложен,
однако по-прежнему воспринимается приблизительно пять различных уровней яркости.
680
Глава 10. Средства для растровой графики
Наблюдаемая
А интенсивность
,75 -
,5 -
25 _ Значение пиксела
’ изображения
£ Й1 Й 1 1 1 '-1...l-J-l-l । ' । ►
3 6 9 12 15
Рис. 10.57. Соответствие уровней на входе и выходе
На рис. 10.58 приведены два варианта размытия изображения с рис. 10.28, а. На рис. 10.58, а показано
исходное изображение, подвергшееся размытию два на два. Все значения пикселов равны 0 или 1, но даже
в таком виде исходный рисунок все еще передается неплохо. На рис. 10.58, б показано то же исходное
изображение после размытия три на три с использованием шаблона, задаваемого формулой (10.10),
которая будет рассматриваться позднее.
Рис 10.58. Примеры размытия два на два и три на три
Для увеличения числа уровней можно использовать шаблоны размытия большего размера. Шаблон
размером я на л обеспечивает п2 + 1 уровней, поскольку число пикселов, равных 1, лежащих под таким
шаблоном, в изображении на дисплее всегда равно одному значению из ряда 0, 1,..., п2. п2 элементов
шаблона должны равномерно распределяться между 0 и максимальным значением пиксела в исходном
изображении. Если, например, значения пикселов лежат в диапазоне от 0 до 255, то шаблон размытия
размером три на три будет состоять из 10* равноотстоящих значений, каждое из которых получено ок-
руглением до ближайшего целого выражения kx 255/10, где£ = 1,2,..., 9. Вычисление этого выражения
дает ряд из девяти значений: 25, 51, 76, 102.229, которые могут быть размещены в матрице случай-
ным образом или «в порядке возрастания» [Foley, 19]. Вот одно из допустимых размещений:
'178 229
51 25
153 76
127Л
102
204
(10.10)
* Вероятно, это ошибка: число должно быть равно 9. — Примеч. пер.
10.9. Увеличение количества цветов и оттенков
681
Матрицы большей размерности — четыре на четыре, восемь на восемь и т. д. — могут быть сформи-
рованы из матрицы два на два D[][] с помощью рекурсивного соотношения (см. упражнения в конце
раздела).
Размытие увеличивает разрешение интенсивности за счет пространственного разрешения; кроме
того, создается впечатление, что к изображению добавляются некоторые «шумы». Существует много
альтернативных технологий размытия, в которых делаются попытки преодолеть эти искажения. В рабо-
те [Knuth, 124] содержится хороший обзор этих методов наряду с некоторыми усовершенствованиями.
Размытие на многоуровневых и цветных дисплеях
Размытие можно применять и в тех случаях, когда дисплей поддерживает более двух оттенков серого
цвета [Schumacher, 187] или является цветным. Возможен целый ряд вариантов, однако мы дадим основ-
ную идею метода на конкретном примере. Предположим, что исходное изображение содержит пикселы
со значениями от 0 до 255 и отображает 256 оттенков серого цвета. Предположим далее, что мы должны
представить это изображение на устройстве, поддерживающем только 8 оттенков серого: 0,1,..., 7. Один
из способов сделать это — обычное установление порогов: мы находим значение дисплейного пиксела!),
ближайшее к каждому «истинному» значению пиксела Р, затем просто делим на 32 и отбрасываем оста-
ток. Эти операции выполняются с помощью следующего кода:
0 = (int)(P/32):
// get the closest value below
// берем ближайшее меньшее значение
1f(P - 32 * 0 >- 16)
// Is error too big for this D?
// На слишком ли велика ошибка для этого D?
D++;
// yes: use the next biggest
// велика - берем следующее большее значение
Во второй строке кода производится проверка: не является ли следующее отображаемое на дисплее
значение лучшим приближением, чем текущее значение; для этого «ошибка» Р - 32 * D сравнивается с
пороговым уровнем 16. Если ошибка больше 16, то значение D увеличивается на единицу.
Другим методом улучшения воспринимаемого изображения является использование размытия.
В этом случае пороговое значение 16 заменяется совокупностью из четырех пороговых значений по-
средством индексной адресации матрицы М, которая накладывается на изображение, как было показа-
но ранее. В этом случае код имеет вид:
D - (1nt)(P/32):
1f(P - 32 * D >= M[col X 2][row X 2])
D++;
где матрица
16] (10.11)
Iм 8J
(использовано четыре равноотстоящих значения между 0 и 31). Если ошибка превышает соответству-
ющее значение из матрицы, то D увеличивается на единицу.
Рассмотрим действие размытия на области изображения, имеющие постоянную интенсивность.
Пусть для такой области Р = 178. Поскольку 178 лежит между 5 х 32 = 160 и 6 х 32 = 192, то некоторые
пикселы каждой области два на два будут равны 5, а некоторые — 6. Такие области будут отображаться
с помощью шаблонов, задаваемых матрицей
(6 6)
displayed =
I5 6)
682
Глава 10. Средства для растровой графики
Тогда усредненная интенсивность будет равна 5,75, или в трех четвертях пути от 5 до 6. Далее, три
четверти пути от 160 до 192 равны 184, поэтому усредненная интенсивность восприятия этой области
составляет 184, что не слишком далеко от «истинного» значения, равного 178. Напомним еще раз, что
размытие приводит к появлению в изображении дополнительных оттенков серого цвета.
Цветные изображения
Размытие цветных изображений осуществляется способом, аналогичным размытию черно-белых изоб-
ражений. Простейший подход заключается в независимом размытии красного, зеленого и синего компо-
нентов с использованием одной и той же матрицы размытия. Такая технология приводит к появлению
дополнительных «усредненных» оттенков в областях постоянного цвета, причем усреднения красного,
зеленого и синего цветов, сочетаясь, образуют некоторое усредненное значение цвета, которое аппрок-
симирует истинное значение цвета в данной области.
Практические упражнения
10.9.1. Размытие три на три
Пусть значения пикселов исходного изображения находятся в диапазоне от 0 до 16. Определите матри-
цу размытия размерностью три на три, аналогичную представленной формулой (10.10).
10.9.2. Матрицы размытия больших размерностей
Джарвис [Jarvis, 116] разработал рекурсивное соотношение для создания матриц размытия размерностью
2п на 2п. Альтернативный вариант предложил Хоули [Hawley, 99]. Как уже говорилось ранее, матрица
размытия размерностью п на п должна содержать в определенном порядке все элементы последователь-
ности 1,2.пг, которые масштабируются соответствующим масштабным коэффициентом, зависящим
от количества значений пикселов. Для случая два на два получим масштабированную версию матрицы
Создание из матрицы D2 матриц О4, D8 и так далее осуществляется по следующей рекуррентной
формуле:
D J Dil2 Dil2+2-2k’2'
‘ \^Dtl2+3-2tl2 Dil2+l-2tl2 '
Отсюда видно, что матрица О4 имеет размерность 4 на 4 и составлена из четырех версий матрицы Dr
О Найдите матрицу размытия D4 размерностью четыре на четыре. {Подсказка. Первая строка мат-
рицы равна 1,3,9, И.)
О Как следует масштабировать матрицу D4, чтобы она служила матрицей размытия для случая 256
уровней пикселов?
10.9.3. Операция размытия для многоуровневых дисплеев
Примените матрицу размытия размерностью три на три, заданную формулой (10.10) и должным обра-
зом масштабированную, для размытия изображения, значения пикселов которого находятся в диапазо-
не от 0 до 255. Дисплей поддерживает уровни 0...15.
10.9.2. Рассеивание ошибок
Рассеивание ошибок (error diffusion) является еще одной технологией установления порогов для ото-
бражения многоуровневых пиксельных карт на двухуровневом дисплее. Вновь предположим, что каж-
дый пиксел исходного изображения имеет интенсивности от 0 до 255 и что нам требуется разумным
образом заменить каждый такой пиксел нулем или единицей. Тогда, если интенсивность пиксела равна А,
то при простом установлении порогов нам следует заменить такой пиксел на 0, если А < 128, и на 1,
10.9. Увеличение количества цветов и оттенков
683
если А > 128. Если А не равно в точности 0 или 255, то такой метод приводит к некоторой ошибке между
«истинным» и «дисплейным» значениями. Если, к примеру, А = 42, то мы устанавливаем дисплейный
пиксел в 0, что занижено на 42 пункта. Если же Л - 167, то мы отображаем на дисплее 1 (максимальное
значение, соответствующее значению пиксела 255), что завышено на 255 - 167 = 88 пунктов. Что же
можно сделать с такой ошибкой?
В соответствии с методом рассеивания ошибок мы пытаемся скомпенсировать неизбежные ошибки
посредством их вычитания из некоторых соседних пикселов в пиксельной карте. Мы частично передаем
ошибку соседним пикселам, которые еще не были подвергнуты пороговой обработке, так что при по-
следующем установлении порогов для них используется уже новое измененное значение. Таким обра-
зом, ошибка «рассеивается» по изображению, при этом устанавливаются правильные значения усред-
ненной интенсивности.
На рис. 10.59 показан фрагмент исходной (многоуровневой) пиксельной карты, которая обрабаты-
вается в обычном порядке: сверху вниз и слева направо. Затененные пикселы на рисунке уже обработаны;
пиксел р был сопоставлен с уровнем 128, и на выходе получилось 0 или 1. Обозначим значение этого
пиксела буквой А. Если А меньше, чем 128, то дисплейный пиксел устанавливается в 0 и ошибка Е = -А.
(На дисплее отображено значение с занижением на Л.) Если А больше или равно 128, то дисплейный пик-
сел устанавливается в 1 и ошибкаЕ = 255 - А. (Теперь мы отображаем значение с превышением на 255 - А.)
Доли результирующей ошибки Е передаются теперь в пикселы a, b, с, d, как показано на рисунке.
Старые значения a, b, с, d заменяются соответственно следующими:
а = а - f Е (корректируем пиксел справа),
b = b - fbE (корректируем пиксел внизу слева), (10.12)
с = с -fcE (корректируем пиксел внизу),
(Z = d- fdE (корректируем пиксел внизу справа),
где fa,fh,fc,fd — постоянные. Обычно выбирают следующие доли ошибки: = (7/16, 3/16, 5/16,
1/16). Сумма их равна единице, так что полное значение ошибки передается соседям пикселар, что со-
храняет среднюю интенсивность в области.
Когда достигается конец строки развертки, ошибки, подлежащие передаче в пикселы а и d, не пере-
даются в начало следующей строки развертки. (Почему?) Вместо этого их можно или отбросить, или
рассеять полную ошибку в пикселах b и с. Опыт показывает, что лучшее решение — изменять направле-
ние обработки последовательных строк развертки — сначала слева направо, а затем справа налево, так
что шаблон с рис. 10.59 па следующей строке разворачивается в обратном направлении (так как теперь
пиксел а будет слева). Такую змеевидную форму сканирования иногда называют змеевидным растро-
вым шаблоном (serpentine raster pattern).
На рис. 10.60 показана пиксельная карта размером 512 на 512 после рассеивания ошибок. В методе
рассеивания ошибок был применен серпантинный растр и коэффициенты, задаваемые формулами
684
Глава 10. Средства для растровой графики
(10.12). Нетрудно распространить эту технологию на дисплеи, поддерживающие более двух уровней.
Для каждого пиксела определяется ближайший отображаемый уровень, и результирующая ошибка рас-
пределяется в точности так, как было описано выше. В случае цветных дисплеев процесс рассеивания
ошибок производится для каждого из трех компонентов цвета независимо.
Рис. 10.60. Пиксельная карта, изображенная на двухуровневом дисплее после рассеивания ошибок
Кнут [Knuth, 124] объединил технологии размытия и рассеивания ошибок в общий метод, назван-
ный им «точечным рассеиванием» («dot diffusion»); который лишь незначительно сложнее каждого из
этих методов по отдельности и способен создавать изображения лучшего качества.
Практические упражнения
10.9.4 . Сделайте это вручную
Выполните процесс рассеивания ошибок для верхней строки развертки изображения, у которого все
пикселы этой верхней строки имеют одинаковое значение 130, а все пикселы следующей строки рав-
ны 132. Объясните полученный результат.
10.9.5 . Рассеивание при других распределениях ошибки
Разъясните эффект рассеивания ошибок в случае, когда вся ошибка рассеивается на правый пиксел.
Объясните случай, когда половина ошибки рассеивается направо, а вторая половина — вниз.
10.9.6 . Добавление ошибки
Объясните, что получится, если коэффициенты в уравнении (10.12) не будут в сумме равняться едини-
це. Будет ли усредненное значение двухуровневого изображения по-прежнему соответствовать значе-
нию исходного изображения?
10.10. Резюме
В данной главе мы рассматривали задачи и возможности, возникающие при использовании для про-
смотра изображения растрового дисплея. Одним из фундаментальных свойств растрового дисплея яв-
ляется его дискретность (discreteness): рассматриваемое изображение состоит из множества светящих-
ся пикселов, расположенных в дискретных строках и столбцах, причем каждый пиксел светится одним
из нескольких дискретных цветов. Изображение является дискретным в трех «направлениях»: по гори-
зонтали, по вертикали и по значению цвета. Однако в силу того, что точки пикселов расположены очень
близко друг к другу и существует (обычно) очень много возможных значений цвета, в нашей системе
«глаз — мозг» соседние точки соединяются, и мы видим «усредненные» значения, объединяя таким обра-
зом массив светящихся точек в узнаваемые рисунки. Такое смешивание дает возможность использовать
это фундаментальное свойство растровых дисплеев: отдельные области изображения можно «запол-
нять» сплошным цветом или узором, что весьма затруднительно делать на устройствах для вычерчива-
10.11. Тематические задания
685
ния линий, таких как перьевой плоттер. Нами рассмотрен целый ряд методов заполнения областей, осо-
бое внимание уделялось областям, описываемым с помощью полигонов.
Дискретность — это одновременно и хорошо, и плохо. Дискретность в пространстве (по горизонта-
ли и по вертикали) приводит к неровностям («ступенькам»): диагональная прямая кажется резко дергаю-
щейся по своей длине, что может раздражать глаз. Поэтому были разработаны методы сглаживания, при-
званные уменьшить визуальный эффект от ступенек. Чрезмерная дискретность в цвете — например,
когда дисплей поддерживает всего два цвета — приводит к тому, что в изображении появляются неес-
тественные «полосы» или «островки» цвета и при этом теряется значительная часть информации, ко-
торую несет изображение. Были разработаны технологии размытия, в которых используется свойства
человеческого глаза смешивать близко расположенные точки, что позволяет «видеть» больше цветов,
чем их имеется в действительности.
Системы с растровыми дисплеями обладают еще одним фундаментальным свойством: пикселы мо-
гут быть представлены в виде чисел, а эти числа можно хранить в памяти. Растровый дисплей почти в
буквальном смысле является «окном» в огромный массив системной памяти и, таким образом, предо-
ставляет доступ к огромному числовому массиву — пиксельной карте (pixmap). Дисплей преобразует
числа в цвета, делает пиксельную карту наглядной. Машинные команды с легкостью манипулируют чи-
слами, что открывает дверь массе новых технологий: курсоры могут передвигаться по экрану с помощью
мыши, окна — прокручиваться, изображения — перебрасываться из экранной памяти во внеэкранную и
обратно и т. д.
Технические характеристики современных растровых дисплеев таковы, что в них содержится чрез-
вычайно много пикселов, иногда даже миллионы. Это позволяет создавать очень качественные изобра-
жения, однако одновременно увеличивает время, необходимое для выполнения определенных опера-
ций. Копирование большого числа пиксельных значений часто убыстряется при помощи специальных
аппаратных средств, таких как микросхемы bitBlit. И людям приходится разрабатывать все более эф-
фективные алгоритмы для увеличения производительности растровых операций. Во многих из этих
алгоритмов используется связность (coherence) — понятие, пронизывающее большую часть графики.
Например, связность интервала (span coherence) — это «стремление» многих смежных пикселов вдоль
строки развертки иметь один и тот же цвет. В свою очередь, связность строки развертки (scan-line
coherence) — это стремление пикселов, раположенных на соседних строках развертки, к одинаковости.
Различные технологии, рассмотренные в данной главе, направленные на формирование или улуч-
шение изображения, появляющегося на растровом дисплее, работают на уровне пикселов. Все эти тех-
нологии стараются или использовать позитивные стороны дискретности растра, или нейтрализовать
ее негативные эффекты. В силу того, что изображение содержит огромное количество пикселов, эф-
фективность каждого алгоритма играет неоценимую роль.
10.11. Тематические задания
Тематическое задание 10.1. Чтение и просмотр
BMP-файлов изображений
Напишите приложение, которое разрабатывает детали методов класса RGBpixmap: drawO, readO, сору(),
readBmpFileO, writeBmpFileO и позволяет пользователю читать изображение, записанное в ВМР-файле,
и просматривать это изображение на дисплее средствами OpenGL. Кроме того, предоставьте пользова-
телю возможность задать с помощью мыши прямоугольник па дисплее, с тем чтобы после этой опера-
ции часть пиксельной карты внутри этого прямоугольника записывалась в BMP-файл. Если же пользо-
ватель нажмет клавишу «f», то отображаемая пиксельная карта должна «отразиться» относительно
своей горизонтальной средней линии, после чего изображение должно стать перевернутым. Нажатие
клавиши «V» должно отражать изображение относительно его вертикальной средней линии.
686
Глава 10. Средства для растровой графики
Тематическое задание 10.2. Растворение одной пиксельной
карты в другой с помощью OpenGL
Уровень сложности II.
Как рассматривалось в разделе 10.2 «Управление пиксельными картами», нетрудно заставить одно
изображение раствориться в другом. На рис. 10.10 показан пример такого растворения. Если два изоб-
ражения записаны в пиксельных картах Л и В, то нам требуется только нарисовать взвешенное среднее
Л(1 -1) + Bt этих карт для последовательности значений t.
В данном тематическом задании для формирования средних взвешенных изображений использует-
ся существующая в OpenGL возможность альфа-смешивания (alpha-blending) изображений и метод
blend(), приведенный в листинге 10.3. Проделайте следующие действия:
О Прочитайте два файла изображений для образования двух пиксельных карт одинакового раз-
мера Л и В.
О Задайте нужную функцию смешивания glBlendFuncO.
О Очистите дисплей.
О Теперь для каждого значения t из совокупности 0,0,2,0,4,0,6,0,8,1,0 выполните следующее:
• Задайте альфа-фактор для пиксельной карты Л равным t.
• Нарисуйте карту В полностью непрозрачной.
• Смешайте с картой Л.
• Сделайте паузу, чтобы повосторгаться последним смешанным изображением.
В одном из изображений нам необходимо задать «глобальное» значение альфа; это означает, что для
каждого пиксела следует установить одно и то же значение альфа. Это нетрудно сделать, если добавить
метод setAlpha(float alpha) в класс RGBApixmap.
1. Напишите метод setAlpha(float alpha). Этот метод просто обходит все значения пикселов в кар-
те и устанавливает a-компонент каждого пиксела равным доле alpha от его максимального зна-
чения (равного 255).
2. Используя в качестве прототипа пример 10.3.2, напишите программу, осуществляющую раство-
рение изображения Л в В. Устройте так, чтобы нажатие клавиши «d» (dissolve) инициировало
процесс растворения Л в В, а нажатие клавиши «Ь» (баск) — обратное растворение В в Л. Вы-
полните свою программу с несколькими парами изображений.
Тематическое задание 10.3. Заполнение области на основе серий
Уровень сложности II.
Реализуйте алгоритм заполнения области из раздела «Использование связности: заполнение облас-
ти на основе серий пикселов», который ищет серии пикселов и закрашивает их, для случая 4-связной
гранично-определенной области. Проверьте свою программу для различных областей.
Дополнительное задание. Покажите, как адаптировать эту процедуру заполнения для 8-связных об-
ластей.
Тематическое задание 10.4. Работа со структурой данных
«формы»
Уровень сложности II.
В разделе «Области, описываемые прямоугольниками» была описана структура данных, пред-
ставляющая область в терминах совокупности прямоугольников. В этом тематическом задании от вас
10.11. Тематические задания
687
требуется отработать все необходимые программистские детали для фактической работы с такими
структурами:
1. Создание структуры shape (форма).
Напишите подпрограмму
void plxmap2Shape(RGBpixmap& pixmap.Shapes shape. Color3 color):
которая на основе пиксельной карты создает структуру данных shape. Структура shape должна без-
ошибочно отображать все области внутри пиксельной карты, описанные пикселами с цветом color.
2. Создание пиксельных карт из форм.
Операция, обратная вышеописанной, осуществляет создание пиксельной карты, которая «содер-
жит» все области, описанные формой. Напишите подпрограмму
void shape2P1xmap(Shape& shape. RGBpixmapS pixmap. Color3 fore, Color3 back):
создающую пиксельную карту достаточного размера, чтобы вместить области, описанные в shape.
В пиксельной карте все пикселы внутри формы закрашиваются цветом fore, а все остальные пик-
селы — цветом back.
Тематическое задание 10.5. Цепное кодирование форм
Уровень сложности II.
Цепное кодирование маршрутов было рассмотрено в разделе «Маршрутно-определенные облас-
ти». Разработайте подходящий тип данных для хранения цепного кода, подобного приведенному на
рис. 10.27, который может содержать 8-связный контур, содержащийся в пиксельной карте. Напишите
подпрограмму:
void makeCha1n(RGBpixmap& pmap. IntPoint startPt. Chain& chain):
которая создает цепной код посредством прохождения по контуру (то есть по цепочке 8-связных пикселов
одинакового цвета) внутри пиксельной карты, начиная с точки startPt. Данная подпрограмма должна
работать только на допустимых маршрутах. Напишите также процедуру void drawChainPath(Chain& chn),
которая рисует контур, описанный цепочкой chn.
Тематическое задание 10.6. Заполнение «горизонтально-
выпуклых» полигонов
Уровень сложности III.
Как говорилось в разделе «Заполнение полигонально-определенных областей», намного проще за-
крашивать горизонтально выпуклые полигоны, чем полигоны общего вида. Горизонтально выпуклые
полигоны содержат в каждой строке развертки только одно левое и одно правое ребро, так что на ней
имеется всего одна серия пикселов. AEL (active-edge list — список активных ребер) превращается в
единственную пару ребер: leftActive и rightActive. ЕТ (edge table — таблица ребер) может быть про-
стым массивом ребер, который легко сортировать в порядке убывания ординат у концевых точек. Об-
новление списка AEL также упрощается, поскольку в полигоне нет никаких локальных экстремумов,
а ребра никогда не пересекаются. Следовательно, нет необходимости заново сортировать список AEL
после каждого обновления.
Напишите программу, в которой реализуется этот способ заполнения полигона, вводимого пользо-
вателем. Ввод каждого полигона осуществляется с помощью мыши. (Нажатие на левую кнопку добав-
ляет точку к полигону; нажатие на правую кнопку замыкает полигон и запускает процесс заполнения.)
Для разнообразия заполните полигоны шахматным узором, ширина каждого квадрата которого состав-
ляет четыре пиксела.
688
Глава 10. Средства для растровой графики
Тематическое задание 10.7. Заполнение полигона общего вида
Уровень сложности III.
Напишите подпрограмму
short f111Poly(IntPolyArray& poly)
которая заполняет полигон poly. Эта подпрограмма должна возвращать -1, если полигон вырожден-
ный или неправильно сформирован или процесс закрашивания не был успешным; в остальных случаях
должен быть возвращен 0. В подпрограмме следует использовать алгоритм заполнения, описанный
в разделе «Заполнение полигонально-определенных областей», в котором для эффективности исполь-
зуются таблицы ЕТ и списки AEL.
Полигоны для тестирования нетрудно генерировать наугад: пользователь вводит желаемое число
вершин, после чего эти вершины формируются случайным образом.
Тематическое задание 10.8. Рассеивание ошибок
Уровень сложности II.
Напишите подпрограмму errorDiffuseUntRect г), выполняющую рассеивание ошибок, как это опи-
сано в уравнениях (10.12), на участке экрана внутри прямоугольника г. В подпрограмме для сканирова-
ния соседних строк развертки следует использовать серпантинный шаблон. Результаты будут наибо-
лее заметны, если дисплей поддерживает лишь небольшое число интенсивностей или цветов. Проверьте
свою подпрограмму на нескольких изображениях.
10.12. Дополнительная литература
Некоторые темы, представленные здесь, в том числе сглаживание, размытие и компоновка изобра-
жений, весьма живо обсуждаются в «Уголке Джима Блиппа» под названием «Грязные пикселы» (Jim
Blinn’s Corner: Dirty Pixels [Blinn, 32]). Книга Уличней «Цифровое полутонирование» (Ulichney, Digital
Halftoning [Ulichney, 203]) содержит скрупулезное изложение размытия, а Кнут также обрисовывает
широкие перспективы этого метода [Knuth, 124]. «Красная книга OpenGL» (OpenGL «Red Book») со-
держит множество подробностей на тему о том, как управлять в своих приложениях многими из тех
эффектов, которые рассматривались в данной главе [Woo, 215].
U Создание кривых
и поверхностей
□ Обзор областей применения компьютерной графики.
□ Разработка средств для представления и конструирования кривых.
□ Определение основных свойств кривых, таких как их «гладкость».
□ Исследование математических свойств кривых Безье и В-сплайнов.
□ Разработка инструментов для конструирования кривых Безье,
В-сплайнов и NURBS-лоскутов поверхности.
Ты сегодня в прекрасной форме, моя дорогая!
Аноним
С внешней стороны растет мех, а с внутренней стороны растет кожа;
Так что мех — это внешность, а кожа — внутренность.
Герберт Джордж Понтинг (Herbert George Ponting).
Спящий мешок (The Sleeping Bag)
До сих пор мы имели дело преимущественно с простыми геометрическими объектами, созданными из
совокупности точек или прямых линий. В этой главе мы покажем систематический способ описания и
представления значительно большего разнообразия форм, которые встречаются в программах компью-
терной графики. В разделе 11.1 «Введение» производится обзор важнейших свойств параметрического
представления кривых и разрабатываются способы оценки «гладкости» таких кривых. В разделе 11.2
«Описание кривых полиномами» мы сосредоточимся на представлении кривых в форме полиномов и
отношений полиномов, а также на описании классов форм, которые можно из них получить. В разде-
ле 11.3 «Интерактивное конструирование кривых» изложены основные идеи интерактивного построения
кривых, когда дизайнер с помощью мыши задает совокупность «контрольных точек», при помощи алго-
ритма генерирования кривой создает ее эскиз, а затем редактирует контрольные точки для улучшения
формы своей кривой. Делается акцент на различии между кривыми, проходящими через заданные точки,
и кривыми, которые только приближаются к заданным точкам. В разделе 11.4 «Применение кривых
Безье для построения кривых» вводится понятие кривых Безье в данном контексте, а в разделе 11.5
«Свойства кривых Безье» рассматриваются свойства кривых Безье, благодаря которым они стали столь
популярными в автоматизированном геометрическом дизайне (computer-aided geometric design — CAGD).
В разделе 11.6 «Нахождение лучших стыковочных функций» рассматривается ограниченность кривых
690
Глава 11. Создание кривых и поверхностей
Безье и начинается поиск лучших методов проектирования кривых, при этом особое внимание уделя-
ется кусочным полиномам. Это приводит к изучению сплайн-функций.
В разделе 11.7 «Базисные функции В-сплайнов» представлены В-сплайны, чьи полезные свойства
изучаются в разделе 11.8 «Полезные для проектирования свойства В-сплайн кривых». В разделе 11.9
«Рациональные сплайны и NURBS-кривые» описываются кривые на основе неоднородных рациональ-
ных В-сплайнов (NURBS). В разделе 11.10 «Краткое знакомство с интерполяцией» рассматриваются
некоторые методы поиска кривых, интерполирующих контрольные точки. Раздел 11.11 «Моделирова-
ние криволинейных поверхностей» посвящается проектированию сложных форм поверхностей; здесь
же понятия главы 6 распространяются на поверхности, созданные с помощью кривых Безье, В-сплайнов
и NURBS-кривых. Рассматриваются проблемы бесшовного соединения двух участков поверхности; в каче-
стве примера плавного сопряжения приводится классический чайник. Представлено несколько приме-
ров проектирования поверхностей. Тематические задания в конце главы содержат проекты для описания
и рисования различных параметрических кривых и поверхностей. В них описана игра «Эллиптипул»,
а также проекты для рисования кривых Безье, В-сплайнов и NURBS-кривых и поверхностей.
11.1. Введение
Одни формы представляют особый интерес, поскольку они способны доставить эстетическое удо-
вольствие или потому, что они отображают какой-нибудь реальный объект, существующий в природе.
Другие формы вычисляются в каких-либо аналитических программах в качестве наилучшего при-
ближения для данной задачи, как, например, изгиб крыла самолета, обеспечивающий максимальную
подъемную силу. Третьи формы, подобно кривой крыла автомобиля, спроектированы человеком на
основе сложного сочетания инженерной целесообразности, простоты изготовления и интуитивного
чувства, что это понравится клиентам.
Такие формы, как логарифмические спирали, суперэллипсы или циклоиды, имеют краткую матема-
тическую формулировку, удобную для анализа, однако это мало поможет, если мы захотим написать
подпрограмму для их рисования. Таким образом, нам необходимы методы преобразования этих форм
из одного представления в другое, более подходящее для определенных задач. Еще одним видом форм
являются «свободные формы», которые в большей степени базируются на данных, чем на математичес-
ких выражениях. Такие формы мы также хотим использовать в программе, например, чтобы найти, где
одна такая кривая пересекается с другой.
11.1.1. Параметрические кривые как траектории
Важным применением параметрического задания кривых является описание пути, который объект про-
ходит, перемещаясь во времени. Например, при проектировании анимации траекторию полета камеры
по сцене необходимо определять в каждый момент Времени. На рис. 11.1 показана камера, движущаяся
по сцене; в момент времени t она расположена в точке P(t). Дизайнер выбирает подходящую функцию
P(t) так, чтобы камера двигалась желаемым образом, например делая снимок № 1 при t - 0,1, снимок
№ 2 — при t - 0,2 и т. д. Направление взгляда камеры также должно быть определено в каждый момент
времени.
Кроме задания определенных координат камеры в определенные моменты времени дизайнер дол-
жен обеспечить плавное движение камеры в соответствии с функцией Р(0 без каких-либо резких толч-
ков, которые могут проявиться при воспроизведении анимации. Такое условие накладывает опреде-
ленные ограничения на скорость Р'(0, которые мы рассмотрим ниже.
Другие объекты также могут двигаться во время анимации: по дороге может ехать автомобиль
(см. рис. 11.1.), на пруду может изменить курс лодка, а из дома может выйти человек. Как уже обсуж-
далось в главе 5, ноги и руки человека также могут совершать свои собственные движения. Движение
каждого из этих объектов может быть описано путем задания подходящих параметрических функций
Р(Г), 6(0 и т. д.
11.1. Введение
691
Рис. 11.1. Задание пути камеры при анимации
Анимации обычно происходят в трехмерном мире, поэтому камера, разумеется, также движется
вдоль BD-траектории P(t) - (x(t), z/(t), z(t)), а каждый снимок формируется путем проецирования сцены
на пленку в камере.
11.1.2. Плавность движения
Предположим, что параметр t означает отрезок времени, а точка P(t) движется по кривой по мере роста t.
Естественно поинтересоваться скоростью функции P(t) вдоль кривой в каждый момент времени. Вектор
скорости (velocity) v(t) — это вектор, описывающий скорость и направление функции P(f) при ее про-
хождении по кривой. Скорость задается формулой:
¥(,) = £й (11.1)
v ’ dt dt dt
\ 7
Например, в любой момент времени t эллипс, определяемый уравнением P(t) = (IVcos(t), Hsin(t)),
имеет скорость v(r) - (- IVsin(t), Hcos(i)). Длину вектора v(t) часто называют величиной скорости (speed)
в момент t. На рис. 11.2 показан вектор скорости в нескольких точках вдоль эллипса. При изменении вре-
мени t меняются как величина, так и направление скорости v. (В каком месте скорость наибольшая?)
Выражение для касательной (tangent line) к кривой Р(0 в момент t = Го можно получить в параметричес-
кой форме E(w), причем параметр и означает следующее: очевидно, что касательная проходит через точку
P(t0) «при» и = 0 и «движется» в направлении v(f0). Поэтому уравнение касательной имеет следующий вид:
£(w) - P(t0) + v(f0)w. (11.2)
Рис. 11.2. Скорость функции P(t) вдоль кривой
692
Глава 11. Создание кривых и поверхностей
Эта формула дает возможность легко вычислять и строить касательные к кривым в различных при-
ложениях.
Нормальное (normal) направление к кривой также может быть найдено в каждой точке. Нормаль
определяется как направление, перпендикулярное к касательной в интересующей нас точке. Тогда, если
касательная в момент t0 имеет направление v(f0), то нормальное направление в этот же момент t0 будет
пропорционально вектору
п('о) = *1('о) =
(11.3)
Например, у эллипса, заданного функцией Р(Т), нормальный вектор равен (-Hcos(t), -ITsin(t)) или
пропорционален этой величине. В частном случае окружности нормаль n(f) пропорциональна самой
функции P(t), поэтому направление нормали совпадает с направлением радиус-вектора, соединяющего
О с точкой P(t). (Отметим, что для эллипса это не так.)
Когда кривая P(t) используется для описания движения во времени такого объекта, как камера, то
возникает следующий вопрос: движется ли этот объект по своей траектории плавно или скачкообраз-
но? Объект может двигаться по своей траектории бесконечным числом способов: стартуя, останавлива-
ясь, ускоряясь, проходя часть кривой повторно и т. д. Если мы просто рисуем кривую, то эти вады дви-
жения не имеют значения: все они дают в результате одну и ту же картину. Однако совершенно другое
дело, когда эта параметрическая функция отображает движение камеры: детали движения по траекто-
рии записываются в последовательность осуществляемых камерой снимков. Неожиданные ускорения
или прыжки приводят к выраженному визуальному эффекту, который, как правило, нежелателен.
В качестве примера рассмотрим камеру, движущуюся вдоль эллиптической траектории, однако с
видоизмененным параметрическим представлением: при t = а скорость камеры внезапно увеличивается
в три раза. Такое движение описывается следующим уравнением:
Р(г) = (х(0,у(0) =
(17cos(f),77sin(r)), 0<?<а,
, , . , .\ 2(л + а)
(iFcos (Зг - 2а), //sin (Зг - 2а)), а < t < —------
(П-4)
Такая ситуация показана на рис. 11.3. Сама траектория по-прежнему эллиптическая, однако при t = а
x(t) и y(t) одновременно начинают колебаться в три раза быстрее, вследствие чего их производные при
t = а претерпевают разрыв. Это выглядит так, как если бы временные оси с этого момента были внезапно
сжаты в три раза.
Рис. 11.3. Траектория движения с внезапным изменением скорости
11.1. Введение
693
Векторы скорости в моменты t = а- («непосредственно перед» t = а) и t = а+ («сразу после» t = а)
соответственно равны
Р'(а-) = (-ITsin(a), Hcos(a))
и (11.5)
Р'(а+) = (3IVsin(a), 3#cos(a)),
так что направление скорости до и после изменения одинаково, однако величина скорости (длина векто-
ра v(t)) внезапно скачкообразно увеличивается в три раза. На параметрическую кривую этот прыжок
не влияет, однако характер движения точки P(t) вдоль этой кривой до и после момента t = а изменяется
радикальным образом.
При изучении гладкости кривых и движения камеры полезно иметь величину, описывающую раз-
личные типы непрерывности, связанные с производными кривой. Мы будем изучать два вида гладкос-
ти, часто называемые параметрической непрерывностью (parametric continuity) и геометрической не-
прерывностью (geometric continuity).
Параметрическая непрерывность (^-непрерывность
или к-непрерывность)
Говорят, что кривая P(t) обладает параметрической непрерывностью k-ro порядка всюду в интервале
времени te [а, 6], если все производные этой кривой, до k-ii включительно, существуют и непрерывны
во всех точках внутри интервала [а, 6]. Кратко это записывается так:
Р( ) является ^-гладкой на [а, 6]1. (11.6)
Например, эллипс на рис. 11.3 является всюду 0-гладким, поскольку функция P(t) непрерывна всю-
ду. Этот эллипс, однако, не является всюду 1-гладким, поскольку Р'(£) терпит разрыв при t = а. (Эллипс
1-гладкий всюду, кроме t = а.) Для предотвращения резких движений при анимации мы обычно будем
требовать, чтобы камера двигалась по 1-гладкой кривой.
Рис. 11.4. Каким будет здесь параметрическое представление?
Кривая с непрерывной скоростью и непрерывным ускорением является 2-гладкой. Отметим, что
функция, ^-гладкая на промежутке [a, £>], непременно является и (k - 1)-гладкой. В то же время ^-гладкая
функция может быть, а может и не быть (k + 1)-гладкой.
1 Данная терминология позаимствована из [Shikin, 185]. Это эквивалентно выражению: функция принадлежит множеству С'[а, 6] —
множеству функций, все производные которых до /с-го порядка включительно существуют и непрерывны на интервале [а, 1>].
694
Глава 11. Создание кривых и поверхностей
Геометрическая непрерывность ^“-непрерывность)
Геометрическая непрерывность является менее строгой формой непрерывности и характеризует скорее
видимую гладкость самой кривой, чем гладкость движения вдоль такой кривой. Для (^'-непрерывности
в основном требуется, чтобы вектор производной имел непрерывное направление, при этом допускаются
разрывы скорости. Эллипс, фигурирующий в уравнении (11.4), является б'-непрерывным, поскольку
его скорость повсюду имеет непрерывное направление. Например, при t = а известно, что Р'(а+) = ЗР'(а-).
На примере уравнения (11.4) мы видим, что существуют странные параметрические представления,
для которых 1-гладкость отсутствует, в то время как С-непрерывность имеет место. В упражнениях мы
рассмотрим более формальное определение (^-непрерывности, основанное на существовании репара-
метризации (то есть обратной параметризации), которая устраняет нежелательные разрывы. Для це-
лей! данной книги достаточно следующего определения:
О (^-непрерывность — это то же самое, что и 0-гладкость; это просто означает, что функция P(f)
непрерывна по t на всем интересующем нас промежутке [а, 6].
О С-непрерывпость на промежутке [а, />] означает, что Р'(с-) = kP'(c+) для любого с из интервала
[а, £>]; где k — некоторая константа.
О (^-непрерывность па промежутке [а, 6] означает, что первая и вторая производные кривой име-
ют непрерывные направления: Р'(с-) = £Р'(с+) и Р"(с-) = тР"(с+) для любого с из интервала
[а, 6]; где k и т — некоторые константы.
Практические упражнения
11.1.1 . Проведение касательных к эллипсу
Напишите подпрограмму, которая рисует эллипс, изображенный на рис. 11.2, а также короткий отре-
зок касательной к этому эллипсу для любого значения параметра t, вводимого пользователем.
11.1.2 . Нахождение касательных к эллипсу
Напишите параметрические формулы касательных к эллипсу, заданному уравнениями (3.13), для следу-
ющих значений времени: t = 0, t = л/4, t = л/2, t = л. Нарисуйте на миллиметровке этот эллипс, а также
четыре касательных к нему. Кроме того, вычислите и нарисуйте в указанных точках направления нор-
малей к эллипсу.
11.1.3 . Касательные и нормали
Найдите выражение для вектора касательной и вектора нормали для суперэллипса согласно уравнени-
ям (3.18) для любого значения t.
11.1.4 . Касательные и нормали к коническим сечениям
Найдите выражения для вектора касательной и вектора нормали при любом значении t для параболы и
гиперболы.
11.1.5 . Найдите параметрическое представление
Найдите параметрическое представление Р(Г) для кривой, приведенной на рис. 11.4. Эта кривая начи-
нается в точке А при t = 0, движется на всем своем протяжении с постоянной скоростью и заканчивается
в точке В при t = 20.
11.1.6 . Другая параметрическая форма окружности
В дополнение к разнообразным представлениям, получающимся при «искривлении времени», для некото-
рых кривых существуют простые представления, сильно различающиеся по своему характеру. Покажите,
что нижеследующая форма при изменении параметра t от 0 до бесконечности образует часть окружности:
.ф) = а--;
1 + z (11.7)
1 + f
11.2. Описание кривых полиномами
695
Чему равен радиус этой окружности и где находится ее центр? Какая часть окружности генерирует-
ся при изменении t от 0 до 1?
Подсказка. Вспомните следующие соотношения для некоторого параметра Ь:
если Т - tg(Z>/2), то sin(Z>) = 2 Т/( 1 + Г2) и cos(/>) = (1 - Т2)/(1 + Г2).
11.1.7 . О Ск-непрерывности
Фарин [Farin, 60] дает следующее определение С^-непрерывности: «Кривая Р(£) является б*-непрерыв-
ной, если существует регулярная репараметризация, после которой она становится ^-гладкой». Это оз-
начает, что если можно найти монотонно возрастающую функцию g(.), такую что ее репараметризация
P(g(t)) является ^-гладкой, то исходная кривая Р(0 будет С‘-непрерывной. Для регулярности g(r) необ-
ходимо, чтобы кривая P(g(0) = (/(0, h(t)) «никогда не останавливалась». Это означает, что производ-
ные f'(t) и /г'(г) нигде не должны обращаться в нуль. Сейчас мы рассмотрим различные выводы из
данного определения.
Для примера из уравнения (11.4) найдем функцию g(t), которая устранит скачок по скорости кривой.
О Покажите, что функция
• g(t) = t при Г < а,
• g(O “ (t+ 2а)/3 при t > а
устраняет разрыв непрерывности в параметрическом представлении кривой, после чего эта кри-
вая становится 1-гладкой.
О Покажите в общем случае, что скорость С-непрерывной кривой P(t) имеет непрерывное направ-
ление. Это означает, что если дана функция g(t), такая что ее производная
d
непрерывна, то направление Р'(.) также является непрерывным. Подсказка. Может пригодиться
следующее цепное правило для производных: P'(g(t)) = (x'(g(0)g/(t), y'(g(t))g'(t)) ^g'(t)(x'(g(t)),
y'(g(t)), то есть множитель g'(t) одинаково влияет на оба компонента.
О Зададимся вопросом: зачем выдвигается требование «регулярности» репараметризации (repara-
metrization). Рассмотрим пример, в котором параметризация нерегулярна [Bartels, 14]:
(2t-t2,2t-t2), 0<f<l,
Р(0 = 2 ' • (П-8)
{2-2t + t2,2t-t2}, 1<Г<2.
Начертите эту кривую и ее скорость для каждого значения t. Обратите внимание на то, что при
t = 1 направление скорости резко изменяется, однако при этом она повсюду остается непрерывной!
Следовательно, если бы нерегулярные параметризации включались в определение С-непрерывных
кривых, то мы могли бы получить ситуацию, при которой 1-гладкая кривая не являлась бы б’-непре-
рывной. Объясните, почему это было бы нежелательно.
11.2. Описание кривых полиномами
Полиномы — это фундаментальные математические объекты; их часто используют в компьютерной
графике, поскольку они хорошо себя ведут и эффективны при вычислениях. В конце главы мы остано-
вимся на отдельных формах полиномов; здесь же мы будем рассматривать взаимодействие между неяв-
ными и параметрическими формами простых полиномов.
696
Глава 11. Создание кривых и поверхностей
Для начала напомним: полиномом £-й степени от t (L-th-degree polynomial in t) называется функ-
ция вида
ай +a{t +a2t2 + ... + aLtL, (11.9)
где константы а0, a,,..., aL — коэффициенты этого полинома, каждый из которых связан с одной из сте-
пеней t. Степенью (degree) полинома называется наибольшая степень, в которую возводится t. Для
того чтобы в данном случае это была L-я степень; необходимо, чтобы коэффициент aL не равнялся
нулю. Порядком (order) полинома называется число его коэффициентов. (Здесь порядок равен (L + 1)).
Порядок полинома всегда на единицу больше его степени.
Полиномиальные кривые степени 1
Мы уже исследовали линейные полиномы и знаем, что линейная параметрическая форма для х(Г) и y(t)
описывает прямую линию, а соответствующая неявная форма линейна по х и по у.
Полиномиальные кривые степени 2
Естественно спросить, какие формы кривых получаются при использовании квадратичных полиномов:
x(f) = at2 + 2bt + с,
y(t) = dt2 + 2et+f, (11.10)
где a, b,...,f— константы. Ответ прост (однако несколько разочаровывает): такая кривая всегда являет-
ся параболой — при любом наборе констант a, b,...,f. Таким образом, с помощью уравнений (11.10)
нельзя сформировать эллипс или гиперболу.
Неявные формы второй степени
Попробуем иной путь и рассмотрим неявные квадратичные формы, то есть полиномы степени 2 по х и по у.
Вспомним из аналитической геометрии, что общий вид неявной формы второй степени выглядит так:
Г(х, г/) “-dx2 + 2Вху + Су2 + Dx + Еу + F, (11.11)
где Л, В,..., F— константы. Кривая, описываемая уравнением F(x,y) = 0, представляет собой коническое
сечение (только если оно невырожденное; см. упражнения в конце раздела). Какое именно коническое
сечение отображается этой кривой, зависит от значения дискриминанта (discriminant) АС - В2:
Если АС - В2 > 0, то кривая является эллипсом.
Если АС - В2 = 0, то кривая является параболой. (11.12)
Если АС - В2<0, то кривая является гиперболой.
Следовательно, выражение х2 + ху + у2 - 1 является неявной функцией для эллипса (АС - В2 = 0,5),
х2 + 2ху + у2 + Зх - бу - 7 — неявная функция для параболы (АС - В2 = 0), а х2 + 4хт/ + 2у2 - 4х + у - 3 —
неявная функция для гиперболы (АС - В2 = -1).
Уравнения конических сечений с общей вершиной. Частный случай квадратичной формы общего вида,
задаваемой уравнением (11.11), является хорошей иллюстрацией взаимозависимости всех трех видов
конических сечений. Здесь используется так называемое уравнение с общей вершиной:
г/2 = 2/?х - (1 - е2)х2. (11.13)
Кривая, представленная этим уравнением, проходит через точку (0,0) и обладает общим масштабным
коэффициентом, пропорциональным константе р. Вид описываемого этим уравнением конического се-
чения зависит от значения эксцентриситета (eccentricity) е, как показано на рис. 11.5. В упражнениях
при рисовании этого множества кривых используются все возможные варианты параметризации.
Полиномиальные кривые третьей степени и выше
Кривые, параметризируемые полиномами первой и второй степеней, имеют вполне понятный вид. По-
ложение, однако, усложняется, когда степень полиномов становится выше. Седерберг [Sederberg, 180]
11.2. Описание кривых полиномами
697
показал, что для любых полиномиальных функций x(t) и y{t) всегда можно найти неявную форму, в то
время как параметрическая форма может быть найдена в общем случае, только если неявная форма
имеет первую или вторую степень.
Рис. 11.5. Уравнения конических сечений с общей вершиной
При дальнейшем рассмотрении кривых Безье и В-сплайнов нашей основной «рабочей лошадкой»
будет кубический полином; мы увидим, что он является мощным инструментом для создания кривых.
Однако все эти методы не могут работать с неявной формой и пытаются параметризировать ее. Факти-
чески они начнут с набора «контрольных точек», задаваемых дизайнером, применят определенный ал-
горитм для генерирования точек кривой и получат эту кривую вне зависимости от того, какой неявной
форме эта кривая удовлетворяет. Во многих случаях это представляется более естественным способом
создания кривых, чем чисто математический подход.
Прежде чем закончить описание аналитического подхода к созданию кривых, рассмотрим вкратце класс
функций, называемых рациональными полиномиальными функциями (rational polynomial functions),
или рациональными дробями; позднее мы исследуем его более полно. (Как мы увидим впоследствии,
именно эти функции являются основой NURBS, non-uniform rational B-spline — неоднородного рацио-
нального В-сплайна.) При первом взгляде на рациональные полиномы можно увидеть, как задание
лишь нескольких точек может определить форму всей кривой. Из этого следует важный результат: ко-
нические сечения могут быть точно представлены отношением двух квадратичных полиномов.
Рациональные параметрические формы
Рассмотрим параметризации, для которых каждая из функций х(.) и г/(.) определена как отношение
(ratio) двух полиномов. Линейный случай рассматривается в упражнениях. Рассмотрим здесь случай
квадратичных полиномов, особо выделяя параметрическую форму следующего вида:
р(0 =
P0(l-t)2 + 2®^r(l-r) + P2r2
(1 —г)2 + 2к>г(1-г) + г2
(П-14)
где PQ, и Р2 — три произвольных точки на плоскости. Эти точки в данном контексте носят название
контрольных точек (control points), поскольку именно они определяют форму кривой. Уравнение
(11.14) в действительности представляет собой два уравнения и является сокращенной записью такого
полного выражения:
(х(г),у(г)) =
x0(l-t)2+ 2x,w(l-t) + x,r2
(l-r)2+ 2®/(l-f)+z2
УоО-р2* 2ylwt(l-t) + y2t2
(1-г)2+ 2жг(1-г)+г2
(11.15)
698
Глава 11. Создание кривых и поверхностей
где х0 и уй — компоненты точки Ро, и аналогично для двух других точек. Коэффициенты квадратичных
полиномов в числителях являются компонентами контрольных точек. Полиномы в знаменателях одина-
ковы для х(.) и для у(.) и также являются квадратичными, однако не зависят от контрольных точек. В то
же время они зависят от «весового» параметра w.
Отметим, что функция P(t) является линейной комбинацией контрольных точек. Как мы уже виде-
ли в разделе «Аффинные комбинации точек» главы 4, для того чтобы P(t) приобрела смысл точки, она
должна быть аффинной комбинацией этих точек. К счастью, в нашем случае это условие выполняется;
подробнее это рассмотрено в упражнениях.
Также отметим, что если подставить в уравнение (11.15) t - 0, то его правая часть сократится до вы-
ражения (х0, уй)\ следовательно, заданная таким образом кривая проходит через точку Р№ то есть интер-
полирует (interpolates) ее. Аналогично, при t - 1 кривая проходит через точку Рг Для всех t, находя-
щихся в промежутке между t = 0 и t = 1, функция P(t) сложным образом зависит от всех трех точек.
Рисунок 11.6, а, где показаны три контрольных точки, иллюстрирует кривую, исходящую из точ-
ки Ро при нулевом значении t и заканчивающуюся в точке Р2 по достижении параметром t значения 1.
Остается открытым вопрос, какую форму эта кривая имеет в промежутке. Ответ дается на рис. 11.6, б:
кривая является одним из конических сечений, а его тип зависит от значения w:
Если w < 1, то кривая является эллипсом.
Если w - 1, то кривая является параболой. (11.16)
Если w > 1, то кривая является гиперболой.
Итак, у нас появилась возможность генерировать конические сечения параметрическим способом,
без привлечения тригонометрических функций, как мы вынуждены были делать ранее. В упражнениях
показано, как генерировать «вторую половину» каждой из этих кривых и как с помощью такой пара-
метрической формы генерировать окружность.
Рис. 11.6. Генерирование конических сечений с помощью квадратичных функций
Практические упражнения
11.2.1. Вырожденные квадратичные формы
Дайте примеры такого сочетания коэффициентов А, В,..., F в уравнении (11.11), чтобы кривая F(x, у) = О
представляла собой:
О пустое множество (то есть точек, удовлетворяющих Е(х, у) = 0, не существует);
О единственную точку;
О прямую линию;
О две параллельные прямые.
11.2. Описание кривых полиномами
699
11.2.2. Параметризация уравнения с общей вершиной
Простейшая параметризация уравнения (11.13) состоит в использовании х в качестве параметра: х = t,
тогда у = + - e2^t2, что необходимо для раздельного рисования «верхней» и «нижней» поло-
вин соответствующей кривой. Получатся ли хорошие графики этих кривых при равноотстоящих зна-
чениях t? Какой способ взятия «замеров» t дал бы лучший результат?
11.2.3. Линейные рациональные параметризации
Рассмотрим класс кривых, которые могут быть образованы с помощью следующих параметризаций:
(') =
a + bt
e + ft'
Я') =
c + dt
g + ht’
(И.17)
для постоянных a, b,..., h. Можно ли таким способом генерировать кривые, отличные от прямых линий?
Приведите несколько примеров, демонстрирующих разнообразие данного класса.
11.2.4. Прямая ли это?
Из рис. 11.6 видно, что если точки Ро, Р{ и Р2 лежат на одной прямой, то вся кривая является прямой
линией. Докажите, так ли это.
11.2.5. Применение рациональных квадратичных функций
для рисования конических сечений
На рис. 11.7, а приведена окружность, вписанная в равносторонний треугольник. Как показано на рисунке,
одну треть этой окружности можно нарисовать с помощью параметрических форм уравнений (11.4) на базе
точек PQ, Р2. Тогда окружность целиком может быть нарисована как совокупность трех дуг, причем каж-
дая из них базируется на трех точках. Можно показать [Farin, GO], что для этой окружности следует ис-
пользовать вес w = cos(a), где а — угол P2POPV Для равностороннего треугольника этот угол составляет 60°.
О Нарисуйте от руки точку P(t) из уравнения (11.14) для пяти значений t, так чтобы получившиеся
точки располагались по дуге от Ро до Р2 приблизительно равномерно.
О Является ли ваш рисунок из предыдущего пункта более эффективным способом рисования ок-
ружности, чем использование значений функций (cos(.), sin(.)) в выборочных точках? Поясните
свой ответ.
О Повторите два предыдущих пункта для одной из четырех дуг, показанных на рис. 11.7, б. Чему
в этом случае равен угол Р2Р0Р{?
Рис. 11.7. Окружность, рассматриваемая как совокупность трех или четырех дуг
11.2.6. Формирование «второй половины» конических сечений
С помощью параметрической формы уравнения (11.13) можно нарисовать только часть каждого из ко-
нических сечений при изменении t от 0 до 1.
О Можно ли нарисовать оставшуюся часть каждой кривой, если использовать значения t меньше
нуля или больше единицы — например, весь диапазон от минус бесконечности до плюс бесконечнос-
ти? Если нельзя, то какая кривая будет нарисована, если t будет пробегать значения этого диапазона?
700
Глава 11. Создание кривых и поверхностей
О Фарин [Farin, 60] показал, что каждая точка производной P'(t) на другой части конического сече-
ния, называемой «дополнительным сегментом», генерируется при изменении знака параметра да в
уравнении (11.14) и что геометрически точки Р(Г) и P'(t) являются коллинеарными (то есть лежат
на одной прямой), как показано на рис. 11.8. Для да = 0,6 (эллипс) и при соответствующем выборе
трех точек нарисуйте от руки точки P(t) и P'(t) для следующих значений t: t = 0,0,2,0,4,0,6,0,8,1,0.
Рис. 11.8. Дополнительный сегмент конического сечения
О Повторите предыдущий пункт для да = 1 (парабола).
О Повторите тот же пункт для да - 2 (гипербола).
11.2.7. Является ли это аффинной комбинацией?
Покажите, что кривая P(t), заданная уравнением (11.14), является аффинной комбинацией точекР0, Р(
и Р2. Другими словами, требуется показать, что сумма весовых коэффициентов для этих точек равна
единице для любого да и для любого значения t.
11.3. Интерактивное конструирование кривых
Я никогда не мог понять, что означают эти проклятые точки.
Лорд Рэндольф Черчилль (Lord Randolf Churchill)
Кривые, которые мы рассматривали до сих пор, имели в своей основе сравнительно простые математи-
ческие формулы. Теперь мы намерены поставить задачу шире и создавать более сложные кривые, кото-
рые будут служить определенной цели. В частности, мы хотим разработать инструменты, позволяю-
щие дизайнеру получать большое разнообразие форм путем простого задания небольшого количества
«контрольных точек».
Пусть, например, дизайнер хочет создать компьютерное представление кривой, изображенной на
рис. 11.9, а. Эта кривая может быть частью создаваемого проекта крыла автомобиля, турбинной лопат-
ки или корпуса электродрели. Или это может быть траекторией камеры, по которой она перемещается
по сцепе, делая снимки. Задача состоит в фиксации формы этой кривой в виде, который позволит при
желании воспроизводить ее, при необходимости произвольно изменять ее форму и размер, передавать
ее в машину для автоматической раскройки или литья и т. д. Как правило, не существует простой фор-
мулы для точного описания этой кривой.
Для того чтобы «ввести» кривую, дизайнер рисует эскиз кривой на графическом планшете и затем
перемещает курсор вдоль кривой, нажимая кнопку мыши в контрольных точках Ро, Pv..., располо-
женных в непосредственной близости к этой кривой, как показано на рис. 11.9, б. Последовательность
контрольных точек часто называют контрольным полигоном (control poligon)1. Дизайнер вводит конт-
рольный полигон, имея богатый опыт и ясное понимание характеристик алгоритма генерирования кри-
вых — именно такой алгоритм будет позднее использован для повторной генерирования кривой по дан-
ным точкам.
1 Термин «полигон» означает замкнутую фигуру, ограниченную прямыми линиями. Фигура еще не является полигоном, пока мы
имеем дело лишь с последовательностью точек. Тем не менее такая терминология уже стала общепринятой.
11.3. Интерактивное конструирование кривых
701
Рис. 11.9. Сценарий конструирования кривой: а) желаемая кривая; б) пользователь задает точки;
в) алгоритм генерирует множество точек вдоль «близкой» кривой
Как видно из рис. 11.10, роль алгоритма заключается в создании точки P(t) по любому введенному в него
значению t. «Данными» для этого алгоритма является набор контрольных точек, в совокупности опре-
деляющих кривую, на которую должны лечь точки P(f). Алгоритм обычно реализуется в виде функции:
Point2 curvePt(double t. RealPointArray pts),
которая возвращает точку для произвольного значения t из заданного интервала. Для того чтобы нарисо-
вать кривую, пользователь может выбрать последовательность значений t, вычислить для каждого
из них функцию curvePtO и соединить полученные точки отрезками прямой, чтобы сформировать лома-
ную линию. На рис. 11.9, в приведен набор маленьких квадратиков, указывающих точки, которые мог бы
возвратить соответствующий алгоритм после получения совокупности контрольных точек с рис. 11.9, б.
Контрольные точки:
Po.Pi...Pl
► Алгоритм генерирования кривых ►
Р(0
Любое t
Рис. 11.10. Алгоритм генерирования кривых
Надеемся, что ломаная, определяемая этими точками, будет хорошо аппроксимировать ту исходную
кривую, которую имел в виду дизайнер, вводя свои контрольные точки. Если же вновь созданная кривая
не обеспечивает адекватной аппроксимации исходной кривой, то дизайнер будет «редактировать» кон-
трольные точки — вероятно, с помощью мыши, смещая их туда-сюда и снова генерируя кривую путем
многократных вызовов функции curvePtO. Этот итерационный процесс продолжается до тех пор, пока
дизайнер не будет удовлетворен. Таким образом, интерактивный дизайн состоит из следующих этапов:
1. Отметить начальные контрольные точки.
2. Сгенерировать кривую при помощи алгоритма.
3. Если кривая удовлетворительна, то остановиться на этом.
4. Исправить некоторые контрольные точки.
5. Перейти к пункту 2.
Интерполяция в сравнении с аппроксимацией
Рисунок 11.11 демонстрирует различие между двумя основными классами алгоритмов генерирования
кривой. На рис. 11.11, а показана кривая P(t), созданная при помощи алгоритма, который интерполи-
рует контрольные точки. Этот алгоритм возвращает точки вдоль кривой P(t), которая в определенные
моменты времени t проходит точно через контрольные точки, а в промежутках между этими точками
формирует гладкую кривую. Алгоритм на рис. 11.11, б генерирует кривую R(t), которая аппроксими-
рует контрольные точки. Возвращаемые этим алгоритмом точки формируют кривую, которая прибли-
жается поочередно к каждой контрольной точке, однако фактически кривая R(t) не проходит через все
702
Глава 11, Создание кривых и поверхностей
эти точки. В процессе предстоящего нам изучения различных алгоритмов мы увидим, что каждый вид
алгоритмов имеет свои достоинства и недостатки.
Рис. 11.11. Сравнение интерполирующих и аппроксимирующих методов генерирования кривой: а) кривая интерполирует
контрольные точки; б) кривая аппроксимирует контрольные точки
Вышеприведенный сценарий итеративного создания кривых является основой автоматизированного
геометрического дизайна (computer-aided geometric design — CAGD) и часто используется при создании
изделий для производства. В следующих разделах мы постепенно создадим целый набор технологий для
проектирования как кривых, так и поверхностей. При выборе из множества возможных подходов (напри-
мер, в работах [Bartels, 14, Farm, 60, Faux, 61]) мы обратим особое внимание на интерактивное конструи-
рование кривых с использованием кривых Безье и В-сплайнов. Эти семейства кривых стали очень попу-
лярными в CAGD-приложениях. Наша «презентация» этих методов будет по необходимости краткой,
но мы приведем достаточно подробностей, чтобы позволить вам писать программы, осуществляющие
компьютерное конструирование кривых и затем создающие рисунки созданных таким образом объектов.
Рассмотрим для начала несколько технологий аппроксимации кривых (в которых кривая P(t) не обяза-
тельно интерполирует контрольные точки) и сосредоточим свое внимание на кривых Безье и В-сплайнах.
Может показаться, что у дизайнера всегда должно возникать желание интерполировать свои контрольные
точки, однако мы увидим, что и у аппроксимирующего подхода имеются свои преимущества. Затем мы по-
смотрим, как приспособить зти алгоритмы, чтобы они обеспечивали интерполяцию контрольных точек.
11.4. Применение кривых Безье для построения кривых
Начнем с простого и элегантного алгоритма де Кастельо, с помощью которого создаются кривые Безье,
ставшие фундаментальными в CAGD. Кривые Безье были разработаны Полем де Кастельо (Paul de
Casteljau) и независимо от него Пьером Безье (Pierre Bezier) примерно в 1962 году. Эти кривые были
включены в качестве составных частей в системы CAGD двух автомобильных компаний: «Ситроен» и
«Рено» — для совершенствования дизайна автомобильных кузовов.
11.4.1. Алгоритм де Кастельо
В алгоритме де Кастельо для вычисления вполне определенного значения точки Р(Г) для каждого значе-
ния Г от 0 до 1 используется последовательность точек Ро, Рр Р2>.... Таким образом, это дает возможность
сгенерировать кривую по совокупности точек. Изменение этих точек влечет за собой и изменение кривой.
Такое конструирование основывается на хорошо знакомых нам шагах «твининга» (вспомните главу 4), реа-
лизация которых достаточно проста. Поскольку твининг является столь удобной процедурой, представ-
ляется возможным вывести множество полезных свойств кривых, которые генерируются с его помощью.
Твининг трех точек для создания параболы
Начнем с трех точек: Ро, Рр Р2, как показано на рис. 11.12, а. Выберем некоторое значение параметра t в
интервале от 0 до 1, например Г = 0,3, после чего определим местонахождение точки А, находящейся
на t-й части пути вдоль прямой, соединяющей точки Ро и Pv Подобным же образом определим точку В
11,4. Применение кривых Безье для построения кривых
703
на t-й части пути между конечными точками Р1 и Р2 (при том же самом t). Мы знаем из главы 4, что эти
новые точки определяются выражениями:
A(t) = (l-t)P0 + tP,;
В(о = (1 - ОЛ + гР2- (11.18)
Рис. 11.12. Алгоритм де Кастельо для трех точек
Повторим для вновь полученных точек процесс линейной интерполяции (вновь при том же самом
значении t): найдем точку P(t), лежащую на t-й части пути между точками А и В:
P(t) = (1 - t)A + tB. (11.19)
Например, при t = 0,5 точка Р(0,5) является просто средней точкой для средних точек трех заданных
точек. Если выполнить этот процесс для каждого t в диапазоне от 0 до 1, то будет сформирована кривая
P(t), приведенная на рис. 11.12, б. Какова параметрическая форма этой кривой? После непосредствен-
ной подстановки уравнения (11.18) в уравнение (11.19) получим:
P(t) - (1 - t)2P0 + 2t( 1 - t)tP{ + t2P2. (11.20)
Уравнение (11.20) можно выразить в терминах функции TweenO из главы 4 (см. упражнения в конце
раздела).
Параметрическая форма кривой P(t) является квадратичной относительно t, а из раздела 11.2 нам
известно, что эта кривая является параболой. Она останется параболой, даже если t будет изменяться
от минус бесконечности до плюс бесконечности. Очевидно, что эта кривая проходит через точку Ро при
t = 0 и через точку Р2 при t = 1. (Почему?) Таким образом, мы имеем корректно определенный процесс
для генерирования плавной параболической кривой на базе трех заданных точек.
А что произойдет в случае, когда число контрольных точек больше трех? Чаще всего применяют
семейство кривых Безье на базе четырех контрольных точек. На рис. 11.13, а показано, как алгоритм
де Кастельо применяется к четырем точкам Ро, Рр Р2, Р3. Для фиксированного значения t точка А поме-
щается на t-й части пути между точками Ро и Р(; таким же образом размещаются точки В и С. Затем
точка D помещается на t-й части пути от точки А до точки В, и аналогично, точка Е. Наконец, искомая
точка Р ляжет на t-й части пути от точки D до точки Е. Если это проделать для каждого значения t в
пределах от 0 до 1, то будет сформирована кривая P(t), которая стартует в точке Ро, «притягивается» к
точкам Р, и Р2 и финиширует в точке Р3. Кривая P(t) и есть четырехточечная кривая Безье. На рис. 11.13, б
приведены кривые Безье, определяемые различными комбинациями четырех точек.
Нетрудно показать (см. упражнения), что четырехточечная кривая Безье имеет следующую пара-
метрическую форму:
P(t) - Ро(1 - Г)3 + Р,3(1 - t)2t + Р23(1 - t)t2 + P3t3, (11.21)
что является кубическим полиномом относительно t. Каждой контрольной точке Р в этом кубическом
полиноме придается определенный вес, после чего эти взвешенные точки складываются. Члены, входя-
щие в данный полином, носят название полиномов Бернштейна (Bernstein polynomials). Четыре куби-
ческих полинома Бернштейна имеют вид1:
1 Верхний индекс ие означает возведение в куб, а указывает на степень полинома. — Примеч. пер.
704
Глава 11. Создание кривых и поверхностей
W = H’-
в’(0=з(1-02'.
в’(0=з(1-')'2.
*33 (')='’•
(11.22)
Рис. 11.13. Кривая Безье на базе четырех точек
Кубические полиномы Бернштейна легко запомнить, поскольку они совпадают с членами разложе-
ния выражения [(1 - t) + Г]3, полученными после приведения подобных членов:
((1 - 0 + Г)3 = (1 - Г)3 + 3(1 - t)4 + 3(1 - t)t2 +
Из этого равенства непосредственно следует важное свойство этих полиномов: при любом t их сумма
равна единице. (Почему?) Математически это выглядит так:
£«,’(<)-'• <11И>
* = 0
В таком случае очевидно, что точка Р(0 является аффинной комбинацией точек, поэтому эти взве-
шенные точки можно складывать. (Вспомним задачу сложения точек в главе 4.)
На рис. 11.14 приводятся графики четырех полиномов Бернштейна третьей степени при измене-
нии t от 0 до 1. Видно, что эти полиномы плавно изгибаются по мере изменения t. Позднее мы увидим,
насколько они «плавны».
Рис. 11.14. Полиномы Бернштейна третьей степени
На рис. 11.15 приведена геометрическая иллюстрация сопряжения четырех точек Ро, Pv Р2, Р3 из урав-
нения (11.21) для формирования точки P(t). Если представить эти точки как векторы, исходящие из на-
чала координат (при этом вместо Ро мы пишем р0 и т. д.), то при t - 0,3 данное уравнение примет вид:
р(0,3) = 0,343ро + 0,441р, + 0,189р2 + 0,027р3.
На рисунке все четыре вектора умножаются на свои весовые коэффициенты и затем складываются по
правилу параллелограмма; в результате получается вектор р(0,3). Видно, что при t = 0,3 наибольшую долю
вносят векторы р0 и рг хотя эффект от вектора р2 также существенен, поскольку вектор р2 такой «большой».
11.4. Применение кривых Безье для построения кривых
705
При изменении t относительные веса этих четырех векторов тоже изменяются, вследствие чего век-
тор p(f) смещается на различные позиции. Попробуйте выяснить, какие веса будут иметь векторы при
t - 0,5 и какую долю внесет каждый из них в формирование результирующего вектора р(0,5).
Рис. 11.15. Сопряжение четырех векторов с помощью полиномов Бернштейна
Обобщение алгоритма де Кастельо на произвольное число точек
Мы уже видели, что в алгоритме де Кастельо для создания квадратичных параметрических представле-
ний используется твининг по трем точкам, а для кубических представлений — по четырем точкам. Дан-
ный алгоритм можно легко обобщить на случай использования (1 + 1) контрольной точки: Ра, .PL.
Для каждого значения t строится последовательность «поколений», для формирования каждого из ко-
торых используется твининг соседних точек, созданных в предыдущем поколении. Тогда получим:
(11.24)
где i - 0.L. Верхний индекс k в выражении /’*(/) обозначает номер поколения. Процесс начинается с
/’°(г) = ^ и заканчивается готовой кривой Безье P(t) = Pf(f}. Результирующую кривую Безье можно
записать в терминах полиномов Бернштейна следующим образом:
(11.25)
к =0
где k-i’i полином Бернштейна степени L определяется так1:
#(<) =
где биномиальный коэффициент2 функции равен:
Ш т и
= —------- для£>я.
к\(Ь-к)\
(11.26)
(11.27)
1 Читатели, знакомые с теорией вероятностей, отметят сильное сходство между этим выражением и биномиальным распределением
вероятностей.
2 В отечественной литературе для биномиальных коэффициентов чаще используется обозначение Сд. — Примеч. пер.
23 Ф. Хилл
706
Глава 11. Создание кривых и поверхностей
При L < k значение этого коэффициента равно нулю. Из равенства (11.26) видно, что каждый из
полиномов Бернштейна имеет степень L. Как и прежде, полиномы Бернштейна совпадают с членами
разложения выражения [(1 - t) + г]1;1 поэтому мы можем быть уверены, что для всех t
^BLk(t) = \ (11.28)
k =0
и что P(t) является полноправным аффинным преобразованием точек.
Практические упражнения
11.4.1. Создание кривой вручную
Используя метод де Кастельо для трех точек (0,0), (2,4), (6,1), постройте на миллиметровке кривую
P(t) для следующих значений: t = 0, 0,2, 0,4, 0,6, 0,8,1,0.
11.4.2. Квадратичные кривые должны быть плоскими
Докажите следующее утверждение: существует единственная квадратичная кривая, проходящая через
три (различные) точки. Памятуя о том, что три (неколлинеарные) точки определяют плоскость, пока-
жите, что квадратичная кривая, определяемая этими точками, никогда не выходит из этой плоскости.
Это означает, что парабола никогда не может выйти из плоскости. В качестве дополнительного задания
покажите, что кубическая кривая может быть неплоской.
11.4.3. Кривая Безье в терминах функции Tween()
Обратимся вновь к функции TweenC) из раздела «Линейная интерполяция двух точек» главы 4. Эта функ-
ция принимает в качестве своих аргументов две точки и возвращает «твин» этих точек для заданного
значения t. Покажите, что функция P(t) из уравнения (11.20) может быть записана так:
Tween(Tween(PO,Pl,t) ,Tween(Pl.P2,t) ,t).
Напишите аналогичное выражение для случая кубической функции.
11.4.4. Кубическая кривая Безье
Напишите последовательность твинов, аналогично предыдущему упражнению, и покажите правиль-
ность параметрической формы кривой Безье из уравнения (11.21).
11.4.5. Обоснование кривых Безье
С помощью уравнения (11.21) вычислите положение точки P(f) в моменты времени t- 0,2, 0,5, 0,9 для
четырех контрольных точек (2,3), (6,6), (8,1), (4, -3). Нарисуйте взвешенные векторы, как это сделано
на рис. 11.15, которые приводят к результирующему значению P(t).
11.4.6. Кривые Безье четвертого и пятого порядков
Напишите функции Бернштейна из уравнения (11.26) для случая L = 4. Покажите, что эти функции
совпадают с членами разложения выражения [(1 - Г) + £]4. Проделайте то же самое для случая L - 5.
11:4.7. Рекурсивное соотношение для полиномов Бернштейна
Покажите, что полином Бернштейна и-го порядка можно всегда получить из полиномов (и - 1)-го
порядка с помощью рекуррентной формулы
В” (/) = (1 - г)в;-' (t)+tB^ (t), (11.29)
где В„ (t) = 1, а В" (/) = 0, если j находится вне диапазона 0,..., п.
1 Бином Ньютона. — Примеч. пер.
U.S. Свойства кривых Безье 707
11.4.8. Кривые Безье интерполируют оба конца
Покажите, что кривая Безье порядка L проходит через две крайние контрольные точки Р(0) - Ро и Р( 1)- PL.
Проделайте это путем исследования значений полиномов Бернштейна при t= 0 и t = 1: покажите, что
для этих концевых точек все члены полиномов, за исключением одного, обращаются в нуль.
11.5. Свойства кривых Безье
Кривые Безье обладают несколькими важными свойствами, которые делают их весьма удобными в сис-
темах CAGD. Позднее мы увидим, что такими же свойствами обладают и В-сплайны. Исследование
различных свойств и их доказательство имеют большое значение для понимания сути кривых Безье.
Интерполяция в концевых точках
Кривая Безье P(t) на базе контрольных точек Ро, Р,.PL в общем случае не проходит через все своп
контрольные точки; иначе говоря, не интерполирует их. Однако мы уже видели, что она всегда интер-
полирует точки Ро и PL. Это очень полезное свойство, поскольку дизайнер, вводя последовательность
точек, в точности знает, где кривая Безье будет начинаться и где кончаться.
Аффинная инвариантность
Часто требуется подвергнуть кривую Безье аффинному преобразованию, чтобы масштабировать, ориен-
тировать или позиционировать ее для дальнейшего использования. Предположим, что мы хотим преобра-
зовать точку Р(Г) на кривой Безье, заданную уравнением (11.25), в новую точку <2(0, используя аффинное
преобразование Т(представленное матрицей три на три в двумерном случае и матрицей четыре на четы-
ре — в трехмерном). Тогда Q(t) = T(P(t)). На первый взгляд кажется, что для определения точки Q(t)
при любом заданном значении t необходимо вначале вычислить точку P(t) и затем преобразовать ее, начи-
ная заново при каждом новом значении t. Однако в действительности это не так: требуется преобразовать
только контрольные точки (всего один раз) и затем применить эти контрольные точки в той же самой фор-
ме Бернштейна, чтобы получить преобразованную кривую Безье для любого значения г! Это значит, что
(и.зо)
4=0
Аффинная инвариантность означает, что преобразованная кривая идентична кривой, построенной
на базе преобразованных контрольных точек.
На рис. 11.16 показана кривая Безье на базе четырех контрольных точек Ро, Pv Р2, Р3. Эти точки пос-
ле поворота, масштабирования и перемещения превращаются в новые контрольные точки Qk, после чего
рисуется кривая Безье, определяемая этими точками. Получившаяся кривая идентична — точка за точ-
кой — результату преобразования исходной кривой Безье.
Рис. 11.16. Демонстрация аффинной инвариантности
Кривые Безье обладают свойством аффинной инвариантности по очень простой причине: они сформи-
рованы как аффинная комбинация точек, а из раздела «Некоторые полезные свойства аффинных преоб-
разований» главы 5 мы знаем, что при аффинном преобразовании аффинные комбинации сохраняются.
708
Глава 11. Создание кривых и поверхностей
Инвариантность параметра при аффинных преобразованиях
До сих пор мы определяли кривые Безье в интервале параметра Те[0,1]. Однако иногда удобнее использо-
вать другой интервал. Пусть мы хотим определить кривую Безье R(u) (как и прежде, на базе контрольных
точек Ро, Pv PL), которая развертывается по мере изменения параметра и в интервале от а до Ь. Для
того чтобы сделать это, достаточно просто заменить каждое встречающееся t на следующую дробь:
и-а
Ь-а
Тогда кривая Безье будет задаваться следующим уравнением:
(11.31)
* = о yb — a J
Отметим, что при изменении и от а до b аргумент каждого полинома Бернштейна изменяется, как и
положено, от 0 до 1. Преобразование параметров от и к t, определяемое соотношением t = (и - а)/(Ь - а),
несомненно является аффинным: это масштабирование, за которым следует перемещение. Кривая Безье
инвариантна по отношению к этому преобразованию в том смысле, что 7?(w) проходит ту же траекто-
рию для интервала иг[а, Z>], что проходит P(t) для интервала fe[0,1].
Свойство выпуклой оболочки
Еще одно свойство кривой Безье, на которое часто рассчитывают дизайнеры, заключается в том, что
кривая P(t) никогда не выходит за пределы своей выпуклой оболочки. Выпуклой оболочкой для мно-
жества точек Р0,Р1.PL называется множество всех выпуклых комбинаций этих точек; то есть множе-
ство всех точек, заданных выражением
(11.32)
А = О
где все a.k неотрицательны и = 1.
Кривая P(t) из уравнения (11.25) является выпуклой комбинацией своих контрольных точек для
любого t, поскольку ни один из полиномов Бернштейна никогда не бывает отрицательным, а их сумма
равна единице. Таким образом, каждая точка на кривой Безье является выпуклой комбинацией своих
контрольных точек, поэтому она лежит внутри выпуклой оболочки своих контрольных точек.
Свойство выпуклой оболочки также непосредственно следует из того факта, что каждая точка на
кривой является результатом твининга двух точек, которые сами являются твинами, а твининг двух
точек образует их выпуклую комбинацию. На рис. 11.17 показано, как дизайнер может использовать
свойство выпуклой оболочки. Хотя восемь контрольных точек образуют самопересекающийся конт-
рольный полигон, дизайнер знает, что кривая Безье будет плавно проходить между двумя концевыми
точками, никогда не выходя за пределы выпуклой оболочки.
Линейная точность
Может ли кривая Безье быть простой прямой линией? Из свойства выпуклой оболочки следует, что
это возможно: если все контрольные точки расположены на прямой, то их выпуклая оболочка вырож-
дается в прямую линию. Следовательно, кривая Безье «захватывается» этой оболочкой и поэтому долж-
на быть также прямой линией. Такое свойство — превращение части кривой в прямую линию путем
соответствующего подбора контрольных точек — называется линейной точностью (linear precision).
Свойство уменьшения колебаний
Грубо говоря, кривые Безье не могут «колебаться» больше, чем это делает их контрольный полигон.
Точнее, ни одна прямая линия (или, в трехмерном случае, ни одна плоскость) не может иметь с кри-
вой Безье больше пересечений, чем она имеет с контрольным полигоном этой кривой. На рис. 11.18
11.5. Свойства кривых Безье
709
приведена кривая Безье на базе контрольного полигона Р. Прямая L пересекает полигон Р пять раз,
а кривую Безье только три раза. Нельзя найти ни одной прямой, которая пересекает кривую чаще, чем
она пересекает полигон Р; это свойство может быть доказано для кривой Безье в общем виде (см., напри-
мер, [Farin, 60]). Это свойство пригодится дизайнерам кривых при наметке контрольного полигона: они
могут с уверенностью предсказать, что результирующая кривая Безье не будет сильно извиваться или
демонстрировать дополнительные отклонения и извивы. (С другой стороны, некоторые альтернатив-
ные технологии конструирования кривых, например некоторые интерполяционные схемы, могут при-
водить к непредсказуемым флуктуациям.)
Рис. 11.18. Свойство уменьшения колебаний кривых Безье
Производные кривых Безье
Поскольку кривая может демонстрировать изломы и прочие неожиданные изменения, когда ее произ-
водные по t имеют разрывы, нужно исследовать производное различных порядков функции P(t) из
уравнения (11.25).
Можно показать, что первая производная кривой Безье имеет вид:
р'(г) = л£ ДР, #"(')- (И-ЗЗ)
к =0
где
ДЛ“Л+1-Л- (11-34)
(См. приведенные ниже упражнения.) Таким образом, скорость кривой Безье также является кри-
вой Безье, построенной на новой совокупности контрольных векторов ДР,. Мы просто берем разности
пар исходных контрольных точек и формируем контрольные векторы скорости. Заметим, что взятие
710
Глава И. Создание кривых и поверхностей
производной уменьшает порядок кривой на единицу (см. выражение ^’‘(t)): например, производная
кубической кривой Безье является квадратичной кривой Безье. «Гладкость» кривых Безье рассматри-
вается в упражнениях.
Создание и рисование кривых Безье
Предположим, что мы хотим создать приложение, которое рисует кривую Безье по последовательнос-
ти контрольных точек. Как может быть организовано подобное приложение? Кривая Безье P(t) из урав-
нения (11.25) будет рисоваться в виде аппроксимирующей ломаной. Замеры функции P(t) берутся для
близко расположенных значений t, например, в точках t. = i/N, где i = 0, 1,..., N, после чего точки Р(Г.)
соединяются прямыми линиями. Единственное, что требуется сделать, — это определить P(t) для каж-
дого желаемого значения t, что можно сделать, например, с помощью следующей функции:
Po1nt2 bezier(RealPolntArray poly, double t):
// compute position P(t) of the Bezier curve based on a
// control polygon
// вычисляем позицию P(t) кривой Безье на базе
И контрольного полигона
В этой подпрограмме используется массив точек, называемый контрольным полигоном (control
polygon), который хранится в poly; подпрограмма вычисляет значения правой части равенства (11.25)
для заданного t и возвращает результирующую точку. Отметим, что степень полиномов Бернштейна
хранится в poly.num. Реализацию этой подпрограммы оставим читателю в качестве полезного упражне-
ния. Большую пользу в смысле понимания проблемы может принести также экспериментирование с
приложением по генерированию кривых Безье; это позволит увидеть эффект от использования различ-
ных контрольных полигонов.
Практические упражнения
11.5.1. Матричная форма кривой Безье
В ряде случаев кривые Безье выражают в терминах матриц, что может быть полезным, когда операции
с ними производятся внутри компьютера (если, например, умножение матриц реализовано аппаратно
[Faux, 61; Foley, 64]). Развивая этот подход, удобно определить два массива уже знакомых нам вели-
чин: массив полиномов Бернштейна:
BL (г) = (во£ (/),#(/) #(')) (11-35)
и массив контрольных точек:
Р = (Р0,Р1,...,Р£). (11.36)
О P(t) в уравнении (11.25) имеет вид суммы произведений. Покажите, что формально P(t) является
скалярным произведением; другими словами, покажите, что
P(t) - В4(Г) • Р. (11.37)
О Используя приложение Б, покажите, что P(t) может быть также выражено в виде произведения
массива строки на массив столбца. Математически это выглядит так: P(t) = B£(t) • Рг, где Т озна-
чает транспонирование.
О Покажите, что поскольку каждый полином Бернштейна, в свою очередь, является полиномом в
форме (11.16), каждый такой полином можно записать в виде скалярного произведения. Напри-
мер, таким образом:
53(г) - 3(1-Г)Р = (г°, ?, I2, ?)-(0, 0,3,-3). (11.38)
О Каждому полиному 5f(f) требуется свой массив коэффициентов. Чему равен этот массив для В’(г)?
11.5. Свойства кривых Безье
711
О Массив степеней t, вида (t°, tl, t2, t3), часто называют степенным базисом (power basis). Таким об-
разом, массив Бернштейна B£(t) можно выразить путем помещения массивов коэффициентов для
различных составляющих Вк (?) один за другим в матрицу BezL. Покажите это для случая L - 3:
B3(t) = (Г°, t*. Г2, t3) Bez3, (11.39)
где
Г 1 0 0 0
-3 3 0 0
Bez3 = 3 -6 3 0
-1 к 3 -3 1
(11.40)
О Соберите вместе все вышеприведенные ингредиенты для общего случая L-ro порядка и покажи-
те, что кривая Безье может быть представлена в виде:
P(t) - Powi(r)BeziPr, (11.41)
где степенной базис равен
Pow£(r) = (l, t,t2,..., tL), (11.42)
а у-й член матрицы BezL имеет вид:
Заметим, что если вы захотите создать кривую по точкам с помощью полиномов, отличных от поли-
номов Бернштейна, то вы получите то же самое выражение (11.41), однако вместо матрицы Bez£ будет
другая матрица. (Примеры и подробности можно найти в [Faux, 61; Foley, 64].) Такое единообразие
значительно облегчает понимание процесса замены одного типа генерирования кривых на другой.
11.5.2. Нарисуйте скорость
Проставьте на миллиметровке четыре точки, нарисуйте для них кривую Безье и тщательно нарисуйте
векторы ее скорости и ускорения как функции от t.
11.5.3. Вывод скорости кривой Безье (сложное упражнение)
Докажите правильность выражения для скорости, приведенного в уравнении (11.37). Подсказка. Пока-
жите, что производная от £*(1 - Г)д~* равна ktk~ ‘(1 - t)L~k - (L - £)Р(1- t)L~k~', поэтому р'(£) можно
записать в виде разности двух кривых Безье. Поманипулируйте этими двумя кривыми (например,
изменяя индекс суммирования), так чтобы они зависели от одних и тех же полиномов Бернштейна,
а затем объедините два члена в один.
11.5.4. Ускорение кривых Безье
Поскольку взятие производной от кривой Безье сводится просто к построению кривой Безье на базе пер-
вых разностей ее контрольных точек, то вторая производная должна быть кривой Безье, построенной на
базе разностей от разностей. Покажите, что ускорение кривой Безье определяется следующей формулой:
p"(z) = l(l-i)£a2/1.b;-2(z),
*=0
(11.44)
где
Д2Р=ДР. -ДР, (11.45)
вторые разности контрольных точек. Выразите вторую разность Д2Р^ через исходные контрольные
точки. Найдите общий вид r-й разности контрольных точек и выведите выражение для r-й производ-
ной от кривой Безье.
712
Глава 11. Создание кривых и поверхностей
11.5.5. Сколько раз дифференцируемы кривые Безье L-ro порядка?
Является ли кривая Безье на базе L контрольных точек /.-гладкой кривой? Если да, то докажите это.
Если нет, то укажите наивысший порядок непрерывной производной от такой кривой.
11.5.6. Случаи второго и четвертого порядков
Найдите матрицу BezL для случаев £ = 2 и £ = 4.
11.5.7. Выведите элементы матрицы BezL
Покажите, что ij-й элемент матрицы BezL определяется уравнением (11.43).
11.6. Нахождение лучших стыковочных функций
Меня поощряли за быстрые ответы. Я ответил, что не знаю.
Марк Твен (Mark Twain)
Может показаться, что кривые Безье являются наилучшим средством проектирования кривых. При
разумном размещении контрольных точек на плоскости можно создать бесконечное разнообразие глад-
ких кривых. Однако далее мы увидим, что сами по себе кривые Безье не обеспечивают достаточной гиб-
кости при конструировании кривых. Одна из проблем состоит в том, что степень используемых поли-
номов Бернштейна связана с числом контрольных точек: кривая Безье на базе (£ + 1) контрольной
точки является комбинацией полиномов £-го порядка. Полиномы высокого порядка сложны в вычис-
лении и чувствительны к ошибкам округления. Мы хотим предоставить дизайнеру свободу выбирать
столько контрольных точек, сколько он пожелает, даже 40 и более.
11.6.1. Проблема локального контроля
Еще более серьезная проблема, чем относительная негибкость кривых Безье, заключается в том, что они
не предоставляют достаточного локального контроля (local control) над формой кривой. На рис. 11.19
показана ситуация, в которой для создания кривой Безье (сплошная линия) используется пять конт-
рольных точек, причем эта кривая несколько отходит от желаемой кривой (пунктир) в окрестности t = 1.
Для коррекции этого отклонения пользователь смещает точки Р2 и Р3 вверх, чтобы заставить кривую
Безье подойти ближе к желаемой кривой. Однако, как показано на рисунке, это также оказывает воз-
действие на первую половину кривой, уводя ее в сторону от желаемой кривой.
а б
Рис. 11.19. Редактирование участков кривой
Проблема заключается в том, что изменение любой контрольной точки изменяет всю кривую. Эта
взаимосвязь вытекает из природы полиномов Бернштейна (вспомним рис. 11.14): каждый из них «ак-
тивен» (в смысле отличен от нуля) на всем интервале [0,1]. Тот интервал, в котором функция отлична
от нуля, часто называют ее поддержкой (support). Поскольку каждый полином Бернштейна поддержи-
вается во всем интервале [0,1] и поскольку кривая Безье является объединением этих функций, то из
11.6. Нахождение лучших стыковочных функций
713
этого следует, что каждая контрольная точка оказывает влияние на кривую для всех значений t от 0 до 1.
Следовательно, изменение любой контрольной точки оказывает влияние на форму кривой повсюду, без
возможности локального контроля.
Решим эту проблему с помощью более подходящего набора стыковочных функций (blending functions),
приведенных на рис. 11.20. На рисунке показаны шесть стыковочных функций 7?0(t), R5(t), (ко-
торые должны быть найдены),1 имеющих поддержку только на части интервала [0,1]. Например, под-
держка функции R0(t) равна [0,0,25], а поддержка функции R3(t) — [0,25,1,0]. Фактически при каждом
значении t активными являются не более трех стыковочных функций.
е б
Рис. 11.20. Сопряжение функций с сосредоточенной поддержкой
Рассмотрим применение таких стыковочных функций для построения кривой V(t) на базе шести
заданных контрольных точек Ро, Р,.Р5. Используем здесь тот же тип параметрической формы, что и
для кривых Безье:
= (11.46)
к =0
На рисунке 11.20, б приведена кривая для некоторого набора контрольных точек. При каждом зна-
чении t положение кривой V(t) зависит не более чем от трех контрольных точек. В частности, для всех t
из интервала [0,75,1,0] на форму кривой влияют только точки Р3, Р4, Р5. Если только одна контрольная
точка Р4 переместится в точку Р', то изменится только та часть кривой, которая показана на рисунке
пунктиром. Таким образом, этот набор стыковочных функций предоставляет контрольным точкам оп-
ределенный локальный контроль.
11.6.2. Список пожеланий для множества стыковочных функций
Формы стыковочных функций, показанных на рис. 11.20, а, очевидно, были сфабрикованы нами лишь
для иллюстрации свойства локального контроля. Но в действительности они имеют в своей основе «реаль-
ные» функции, часто использующиеся при конструировании кривых. Их природа будет подробно опи-
сана позднее, но мы внимательно изучим их уже сейчас, чтобы выяснить, какими свойствами должен
обладать набор стыковочных функций.
Предположим, как обычно, что используемый алгоритм генерирования кривой осуществляет сопря-
жение контрольных точек в соответствии с формулой
И(/) = ^PkRk{t) дляte[а,И (11.47)
к =0
1 Как будет показано позднее, они фактически являются квадратичными В-сплайнами.
714
Глава 11. Создание кривых и поверхностей
где стыковочные функции R0(t),..., RL(t) обладают определенными свойствами, которые или обеспечи-
вают «лучшие» кривые, или делают процесс создания кривой более наглядным. Составим список таких
желательных свойств. Стыковочные функции должны:
О быть простыми в вычислении и численно устойчивыми;
О составлять в сумме единицу для любого t из [а, Ь];
О иметь поддержку лишь на небольшом участке интервала [a, 6] — для обеспечения локального конт-
роля;
О интерполировать определенные контрольные точки, выбираемые дизайнером;
О быть достаточно гладкими, чтобы образовать желаемую форму.
Рассмотрим каждое из этих свойств по отдельности.
Функции должны быть простыми в вычислении и численно устойчивыми
Для быстрого генерирования кривой мы хотим, чтобы стыковочные функции вычислялись просто.
Кроме того, желательна также минимальная чувствительность к численным ошибкам округления. Эти
рассуждения приводят нас к выбору в качестве стыковочных функций полиномов, причем степень этих
полиномов должна быть достаточно малой. Другие типы функций, такие как синусы и косинусы, ис-
пользовать было бы слишком накладно.
Функции должны составлять в сумме единицу
для любого значения t из [а, Ь]
При каждом значении t кривая V(f), согласно равенству (11.46), является взвешенной суммой точек, а это
имеет смысл, только если V(t) является аффинной суммой точек для любого t из промежутка [а, Ь].
Поэтому мы требуем, чтобы
*=о
Из рис. 11.20 можно видеть, что функции-кандидаты уже обладают этим свойством.
Функции должны иметь поддержку лишь на небольшом участке
промежутка [а, Ь]
Для обеспечения локального контроля мы хотим, чтобы поддержка каждой стыковочной функции была
сконцентрирована на небольшом участке интервала [а, 6].
Функции должны интерполировать определенные контрольные точки
Дизайнер может пожелать, чтобы кривая V(t) проходила через некоторые из контрольных точек, в то
время как к остальным она должна только приближаться (притягиваться). Для форм на рис. 11.20 ин-
терполируются первая и последняя контрольные точки. Позднее мы вкратце рассмотрим механизм из-
менения стыковочных функций с целью обеспечения интерполяции определенных точек.
Функции должны иметь достаточную гладкость
Обычно дизайнеру нужно, чтобы кривая V(t) при любом наборе контрольных точек была гладкой. Для
создания кривых желаемой формы V(t) должна обладать по крайней мере 1-гладкостью, а может быть,
даже 2-гладкостью. Гладкость V(t) зависит от гладкости стыковочных функций; в частности, если каж-
дая стыковочная функция является 1-гладкой на [а, 6], то кривая V(t) также будет 1-гладкой на [а, />].
Заметим, что стыковочные функции на рис. 11.20 внешне выглядят гладкими в своих внутренних
частях. Важно также, чтобы они плавно «начинались» и «заканчивались». На рис. 11.21 изображена
стыковочная функция вместе со своей первой производной. Производная этой функции непрерывно
изменяется от нуля в точке t = с, в которой функция начинается. Однако там, где функция заканчивается
11.6. Нахождение лучших стыковочных функций
715
(при t - d), ее производная имеет разрыв, совершая резкий скачок от А до нуля. Такая функция являет-
ся 1-гладкой всюду, кроме точки t~d. Тогда и кривая, использующая эту стыковочную функцию, не
будет 1-гладкой при t- d. Поэтому для стыковочных функций желательно, чтобы они были гладкими
внутри интервала, а также начинались и заканчивались с нулевым значением производной.
Стыковочная
функция
Первая
производная
Рис. 11.21. Предполагаемая стыковочная функция и ее производная
Некоторые из форм, изображенных на рис. 11.20, начинаются и заканчиваются там, где их произ-
водная равна нулю, а другие — нет. Те формы, которые начинаются и заканчиваются внутри интервала
[0, 1], делают это с нулевой производной, поэтому кривая V(t) будет 1-гладкой внутри интервала (0, 1).
Для производных допускается разрыв на концах интервала [0, 1], поскольку мы никогда не используем
значения t, меньшие нуля или большие единицы.
11.6.3. Кусочно-полиномиальные кривые и сплайны
Начнем с поиска хороших кандидатов на роль стыковочных функций, например, среди полиномов низкого
порядка. Существует ли, например, такой кубический полином, форма которого показана на рис. 11.22
и который удовлетворял бы всем нашим требованиям? Для изучения этого вопроса зададим функцию:
Д(Г) = at3 + bt2 + ct + d
и посмотрим, можно ли подобрать коэффициенты так, чтобы функция R(t) и ее первая производная
обращались в нуль при t = 0 и при t - 1. Это требование накладывает на коэффициенты следующие
четыре условия:
Д(0)-й?=0;
Д( 1) = а + b + с + d = 0;
Д'(0) = с = 0;
Д'(1) = За + 2Ь + с - 0.
Является ли это
кубическим полиномом?
Рис. 11.22. Можно ли подыскать такой кубический полином?
К сожалению, из этих условий следует, что а = 6 = с = б/=0, следовательно, подобной формы не
существует. У кубической формы недостаточно гибкости, чтобы «изогнуться» так, как нам это требуется.
(В упражнении 11.6.1 исследуется вопрос, подойдет ли для этой роли полином четвертого порядка.)
716
Глава 11. Создание кривых и поверхностей
С целью достижения большей гибкости попытаемся «составить» вместе несколько полиномов низ-
кого порядка. Такие кривые определяются различными полиномами на различных интервалах измене-
ния t и носят название кусочных полиномов (piecewise polynomials). Примерная форма g(t), приведен-
ная на рис. 11.23, поможет нам при введении некоторой терминологии. Видно, что кривая g(t) состоит
из трех полиномиальных сегментов (segments), определяемых следующими формулами:
з ( з У
‘W=4 Г 2.)’ <lt49)
<У) = фз-,)1.
Поддержка всей кривой g(t) равна [0, 3]; функция a(t) определена в диапазоне (span) [0, 1], b(t) —
в диапазоне [1, 2], a c(t) — в диапазоне [2,3]. Точки, в которых встречается пара отдельных сегментов,
называются стыками (joints), а те значения t, при которых эта встреча происходит, носят названия уз-
лов (knots). В нашем примере имеется четыре узла: 0,1,2,3.
Рис. 11.23. Составляющие кусочного полинома
Является ли функция g(t) непрерывной на всем диапазоне своей поддержки? Поскольку она по-
строена из полиномов, она, несомненно, непрерывна внутри каждого диапазона, и требуется проверить
только то, что сегменты нужным образом встречаются на стыках. В этом нетрудно убедиться с помо-
щью уравнения (И.49):
a(l) = Z>(l) = |,Z>(2) = c(2) = l.
Далее, производная функции g(t) непрерывна всюду, поэтому g(t) является 1-гладкой на промежут-
ке [0,3]. Для того чтобы убедиться в этом, отметим, что производная обязательно непрерывна внутри
каждого диапазона (почему?), поэтому нам требуется проверить ее непрерывность только в узлах.
В результате прямого вычисления получаем: а'(1) = />'(1) - 1 и />'(2) = с'(2) = -1. Следовательно, при
11.6. Нахождение лучших стыковочных функций
717
движении от одного полиномиального участка к другому наклон кривой не изменяется скачкооб-
разно. В противоположность этому вторая производная не является непрерывной, а резко изменяется
в узлах, совершая скачок между двумя значениями (какими?).
Форма g(t) является примером сплайн-функции (spline function) — кусочной полиномиальной функ-
ции, обладающей «достаточной» гладкостью. В частности, дадим следующее определение.
Определение сплайн-функции. Сплайн-функция М-Й степени — это кусочно-полиномиальная функ-
ция степени М, обладающая в каждом узле (А/ - 1)-гладкостью.
Нетрудно видеть, что функция g(t) из нашего примера — квадратичный сплайн, то есть кусочный
полином второго порядка с непрерывной всюду первой производной.
11.6.4. Построение из g(t) множества стыковочных функций
Как можно использовать описанную выше сплайн-функцию g(f) в качестве стыковочной функции для
представления некоторой кривой? Один способ состоит в использовании смещенных версий функции
g(0, когда каждая стыковочная функция gk(t) создается путем переноса основной формы g(t) на опре-
деленную величину. На рис. 11.24 показаны семь стыковочных функций g0(t).£>6(0> образованных
путем смещения функции g(.) на целые величины:
gt(t) = g(t ~ k), где k - 0,1. (11.50)
Рис. 11.24. Замкнутые кривые на основе сплайнов
Поскольку узлы различных версий g(.) являются целыми числами, смещение функции g(.) на целое
число равносильно такому перемещению, что узлы одной смещенной версии совпадают с узлами сле-
дующей версии. Такие смещенные версии образуют допустимый набор стыковочных функций, только
если при каждом t их сумма в точности равна единице. В действительности это выполняется для всех t
в пределах от 2 до 7! (См. упражнения в конце раздела.) Это означает, что
6
£g(z-*) = l дляГе[2,7]. (11.51)
к =0
Такое смещение может показаться магическим, однако мы увидим, что это общее свойство всех сты-
ковочных функций, которые мы в конечном счете разработаем. Чрезвычайно важно, что мы смещаем
каждую функцию на целое число единиц с целью «выровнять» их так, чтобы их сумма составляла единицу.
Итак, дизайнер выбирает семь контрольных точек и генерирует кривую с помощью следующего
алгоритма:
6
У^)=^Ркё^-к). (11.52)
к =0
Можно использовать значения г только от 2 до 7. (Почему?) Отметим, что в этом диапазоне при каж-
дом значении t активны ровно три стыковочные функции, поэтому возможен хороший локальный кон-
718
Глава И. Создание кривых и поверхностей
троль над формой кривой. Кроме того, отметим, что в моменты времени Г = 2,3,..., 7 активны только две
функции, причем обе они равны 0,5. Поэтому при этих значениях t функция V(t) будет лежать посере-
дине прямой, соединяющей две контрольные точки.
На рис. 11.25 приведен пример расположения семи контрольных точек вместе с результирующей кри-
вой. Эта кривая начинается при t - 2 в средней точке отрезка Р0Р{ и, плавно изгибаясь, проходит через
последующие средние точки ребер контрольного полигона. По мере возрастания t включаются и выклю-
чаются различные стыковочные функции, и главное влияние на кривую «передается» от точки к точке.
Рис. 11.25. Проектирование кривой с использованием смещений функций д(.)
Какими свойствами обладают кривые на базе такого набора стыковочных функций?
О Дизайнеру предоставляется некоторый локальный контроль над формой кривой, поскольку ин-
тервал поддержки каждой стыковочной функции ограничен длиной в 3 единицы.
О Дизайнер будет задавать точки, осознавая то обстоятельство, что кривая должна пройти через
середины ребер контрольного полигона. Поэтому алгоритм обладает некоторыми интуитивны-
ми геометрическими свойствами.
О Поскольку каждая стыковочная функция 1-гладкая, то вся кривая также 1-гладкая.
О Ни одна из точек на кривой не интерполируется.
О Все полиномы имеют вторую степень, поэтому их вычисление отличается быстротой и устойчи-
востью. Степень полиномов не зависит от числа контрольных точек; данная технология работает
при любом числе контрольных точек.
Вышеизложенный алгоритм генерирования кривой может быть легко реализован в подпрограмме
Po1nt2 curvePt(double t, RealPolntArray pts)
Подпрограмма возвращает точку V(t) для каждого вводимого в нее значения t. Этот алгоритм будет
более подробно рассмотрен в тематическом задании 11.4.
Пример 11.6.1. Расширение метода для рисования замкнутых кривых
Нетрудно расширить вышеизложенную технологию так, чтобы с ее помощью можно было генериро-
вать замкнутые кривые, подобные изображенной на рис. 11.26, а. На рис. 11.26, б показан замкнутый
вариант кривой, изображенной на рис. 11.25. При этом к уравнению (11.52) нужно только добавить два
слагаемых и две контрольные точки, дублирующие точки Рй и Pv (Тогда Р7 = Ро и Р8 = Рг) Мы знаем, что
при t = 7 предыдущая кривая проходила через середину участка Р5Ре. Тогда при t = 8 кривая пройдет
через середину отрезка Р6Р7, а при t - 9 через середину отрезка Р7Р8, замыкая кривую. В упражнениях
приводится также альтернативный метод.
11.6. Нахождение лучших стыковочных функций
719
Рис. 11.26. Генерирование замкнутых кривых
Практические упражнения
11.6.1. Существует ли стыковочная функция, являющаяся полиномом четвертого
порядка?
Рассмотрим полином четвертой степени г(Г) - at? + bt? + ct2 + dt + e. Существуют ли такие значения коэф-
фициентов а, Ь, с, d, е, при которых эта функция проходит через нулевую точку, а ее первая производная
равна нулю при t - 0 и при t - 1? Если да, то найдите соответствующие значения и нарисуйте кривую.
11.6.2. Покажите, что смещения д(.)дают в сумме единицу при любом t
Рассмотрим сумму смещений: g(t) + g(t - 1) + g(t - 2), где g(t) — кусочный полином, определяемый
уравнением (11.49). Покажите, что эта сумма равна единице для всех значений t в диапазоне от 2 до 3.
11.6.3. Являются ли полиномы Бернштейна сплайнами?
Покажите, что полиномы Бернштейна BLk (t) действительно являются сплайнами. Сколько кусочных
полиномов соединяются для формирования каждого из них? Где находятся узлы? Какова степень это-
го сплайна? Обладает ли он достаточной непрерывной дифференцируемостью?
11.6.4. Потренируйте интуицию на квадратичных сплайнах
Задайте в каком-нибудь сложном порядке 12 контрольных точек, после чего нарисуйте кривую, сгене-
рированную с помощью квадратичных сплайн-функций из уравнения (11.49). Используйте то обстоя-
тельство, что эта кривая проходит через середины определенных ребер контрольного полигона.
11.6.5. Построение замкнутых кривых без дополнительных контрольных точек
Покажите, что уравнение (11.52) с небольшими изменениями, а именно
6
^(0=Ep^((z-*)mod7)> (11.53)
к * О
создает замкнутую кривую на базе семи (различных) контрольных точек при изменении Г от 0 до 7. Ника-
ких дополнительных точек не требуется. Функция mod («целое число по модулю») эффективно «сверты-
вает» стыковочные функции к интервалу [0,7], активизируя их на различных участках этого интервала.
Для того чтобы увидеть, как это работает, нарисуйте для Z = 4 пять функций g((£ - k) mod (Z + 1)) для
k - 0,1,2,3,4 при изменении Г от 0 до 5.
720
Глава 11. Создание кривых и поверхностей
11.6.5. Сплайны и базисные функции
Метод, включающий в себя смещение квадратичных полиномов g(t), похоже, предоставляет в наше рас-
поряжение неплохое средство создания кривых. Поэтому стоит ли идти дальше? Проблема заключает-
ся в том, что нам требуется больший контроль над формой кривой: она должна больше «изгибаться» и
быть более гладкой, чем 1-гладкая кривая. Такое требование предполагает переход к кубическим поли-
номам. Мы также хотим, чтобы дизайнер имел возможность указывать, какие контрольные точки долж-
ны интерполироваться. И было бы хорошо иметь единый алгоритм, который осуществлял бы все вы-
шеописанные технологии дизайна, в том числе кривые Безье.
Поэтому поищем более общие семейства стыковочных функций, которые обладали бы всеми
свойствами из обсуждавшегося ранее списка пожеланий. Мы будем использовать ту же параметри-
ческую форму:
Л')=ЕРЛ(') (П-54)
к = О
на базе (L + 1) контрольных точек и (L + 1) стыковочных функций 7?0(Г),..., RL(t). Остается в силе и
требование, чтобы P(t) была аффинной суммой точек. В качестве стыковочных функций мы будем по-
прежнему использовать кусочные полиномы, однако теперь они будут определены в более общей по-
следовательности узлов, именуемой узловым вектором (knot vector):
Т-(Го, Г,, t2,...). (11.55)
Узловой вектор является просто списком узловых значений t0, tv t2.для которых предполагается,
что они не убывают, то есть t( < t.+1. Некоторые из этих узлов могут иметь одинаковые значения, однако
и в этом случае им присваивают отдельные имена. Число узлов, содержащихся в векторе Т, мы рассмот-
рим позднее.
Рисунок 11.27 иллюстрирует эту ситуацию. Каждая стыковочная функция Rk(t) является кусочным
полиномом, который равен нулю до момента времени tk, отличен от нуля на протяжении нескольких
диапазонов узлового вектора и затем снова возвращается к нулевому значению. Кроме того, мы требу-
ем, чтобы каждая функция Rk(t) была сплайн-функцией, вследствие чего она будет обладать достаточ-
ной степенью гладкости при всех поддерживающих ее значениях t.
Рис. 11.27. Обобщение понятий узлового вектора и стыковочных функций
Отметим, что и выражение для кривой Безье, и выражение, содержащее смещения g(t), удовлетво-
ряют следующей общей схеме.
О Кривая Безье. Здесь всего один диапазон — от 0 до 1, все полиномы Бернштейна имеют степень L,
имеется L + 1 узел при t = 0 и еще L + 1 узел при t- 1. Полиномы Бернштейна являются сплайна-
ми, поскольку их производные непрерывны до Z-ro порядка включительно. __
О Смещения g(t). Узловыми значениями являются целые числа 0, 1..L + 2, каждый компонент
g(t - 1г) является сплайном, состоящим из трех полиномов второй степени, активных в диапазоне
шириной 3.
11.7. Базисные функции В-сплайнов
721
Поскольку каждая функция R^t) является кусочным полиномом, то вся кривая P(t) — это сумма
кусочных полиномов с весами, определяемыми контрольными точками. Например, в каком-нибудь
диапазоне эта кривая может иметь следующий вид:
Р(Г) - P0(3t2 - 4i + 2) + P,(8f2 - 7,3t - 7,99) +... (11.56)
В соседнем диапазоне эта кривая определяется другой суммой полиномов, но мы знаем, что все ее
сегменты соединяются между собой, сохраняя непрерывность кривой. Подобная кривая носит назва-
ние сплайн кривой (spline curve) [Farin, 60]’.
Теперь можно задаться следующим вопросом: существует ли при заданном узловом векторе некото-
рое семейство стыковочных функций, которые можно использовать для генерирования всех возмож-
ных сплайн-кривых, определяемых данным узловым вектором? Такое семейство функций называют ба-
зисом (basis) сплайнов; под сплайнами здесь подразумевается любая сплайн-кривая, которую можно
задать уравнением (11.54) путем правильного выбора контрольного полигона. Ответ на этот вопрос
следующий: существует множество таких семейств, однако среди них существует один особенный базис,
для которого стыковочные функции имеют наименьшую поддержку и поэтому обеспечивают наиболь-
ший локальный контроль. Этот базис образуют так называемые В-сплайны (B-splines), или Би-сплай-
ны, где буква «В» взята из слова «базис».
11.7. Базисные функции В-сплайнов
Когда продвижение к цели становится все труднее, печаль проходит.
Роберт Бирн (Robert Bime)
Мы намерены определить стыковочные функции Rk(t) для В-сплайнов способом, который придаст им неко-
торый интуитивный смысл и помимо этого приведет к простой компьютерной реализации. Хотя в литера-
туре предлагается множество различных подходов к формулировке В-сплайнов, имеется только одна фор-
мула, определяющая В-сплайн функции каждого порядка. Это рекурсивное соотношение, легко реализуемое
программно и хорошо ведущее себя при вычислениях. (Некоторые другие методы обладают большей
вычислительной эффективностью — см. упражнения в конце раздела «Определение В-сплайн функций».)
Каждая В-сплайн функция базируется на полиномах определенного порядка т. Если т = 3, то полино-
мы будут иметь порядок 3 и, следовательно, степень 2, то есть будут являться квадратичными В-сплайна-
ми. Если т - 4, то соответствующие полиномы будут иметь степень 3, то есть будут кубическими. Эти
два случая наиболее важны, хотя обсуждаемая формула позволяет строить В-сплайны любого порядка.
11.7.1. Определение В-сплайн функций
Полезно в обозначении В-сплайн функции указывать ее порядок в явном виде, то есть вместо того, чтобы
писать просто Rk(t), мы будем обозначать стыковочную функцию В-сплайна т-го порядка символом
Л^и(0- Тогда уравнение (11.54) для В-сплайн кривой примет вид:
P(t) = £РЛм.(')- (11.57)
к-0
Систематизируем все, что мы имеем на данный момент:
О узловой вектор Т - (?0, t2,... );
О (1 + 1) контрольных точек Pk;
О порядок т В-сплайн функций.
1 Обращаем внимание на различие между сплайн-функцией, определенной в разделе «Кусочно-полиномиальные кривые и сплай-
ны», и сплайн-кривой. Сплайн-функция — это обычный кусочный полином с определенной степенью гладкости. Сплайн-кривая —
это аффинное сопряжение точек, в котором используются кусочно-полиномиальные функции сопряжения. Сплайн-кривая долж-
на быть непрерывной в своих узлах, однако производные в узлах могут терпеть разрывы.
722
Глава 11. Создание кривых и поверхностей
Основная формула, описывающая В-сплайн функцию Nt m(t), имеет следующий вид:
ч ^к у ^к+т **+1
где k - 0, 1,..., L. Такое определение является рекурсивным и описывает построение функции ти-го по-
рядка из двух В-сплайн функций (ти - 1)-го порядка. Для инициализации этой формулы мы должны
определить функцию первого порядка. Это просто постоянная единичная функция в пределах своего
диапазона:
если tk <t£tk+i,
в противном случае.
(11.59)
Отметим, что сумма такого набора функций автоматически равняется единице для всех значений i;
следовательно, при формировании комбинаций из точек использование таких функций допустимо.
Пример 11.7.1. Линейные В-сплайны
Какую форму имеет функция No 2(t), первая (k = 0) В-сплайн функция порядка т - 2, если все ее узлы —
равноотстоящие (то есть вектор Т = (Го - 0, г, - 1, t2 - 2,...))? При этих значениях параметров уравнение
(11.58) приобретает вид:
t 7 — t
^о.2(0=7^.1(0 + —^.1(0- (11.60)
Мы видим, что линейный «подъем» (up ramp) (задаваемый членом i) умножается на No ](£), а линей-
ный «спуск» (down ramp) (2 - Г) умножается на ,(Г), как показано на рис. 11.28, а. В результате сумми-
рования этих членов получается треугольный импульс (pulse, рис. 11.28, б). Отметим имеющуюся здесь
аналогию с твинингом: No 2(t) является аффинной комбинацией N0l(O и Nt ,(0. Тогда No 2(0 равно t
при 0 51 < 1, равно 2 -1 при 1 < t < 2 и равно нулю в остальных случаях.
а б
Рис. 11.28. Построение линейных В-сплайнов
Построение других линейных В-сплайнов производится аналогично. Например, Nt 2(t) — это тре-
угольный импульс, начинающийся при t - 1 и заканчивающийся при t=3: он является просто смещенной
версией предыдущего импульса. Вообще говоря, при равноотстоящих узлах любой линейный сплайн
является смещенной версией нулевого сплайна; то есть 2(t) - No 2(t - i).
Если нарисовать несколько функций Nk 2(t), то становится очевидным, что импульсы перекрывают
друг друга как раз таким образом, что их сумма при любом t равна единице. (Проделайте это!)
Отметим, что кривая, построенная на линейных В-сплайнах, совпадает с контрольной ломаной
линией. (Сохраняется ли это в случае, когда узлы не эквидистантны?) Поскольку линейные сплайны
не могут предложить ничего, кроме обычных прямых линий, то обычно их не используют для дизай-
на кривых. Однако они, разумеется, фигурируют в процессе построения В-сплайнов более высоких
порядков.
11.7. Базисные функции В-сплайнов
723
Пример 11.7.2. Квадратичные В-сплайны
Предположим, что мы хотим определить форму квадратичных (т = 3) В-сплайн функций N. 3(t) на базе
тех же равноотстоящих узлов, что и в предыдущем примере. Тогда нам нужно построить только функ-
цию No 3(t), так как остальные функции могут быть получены из этой простым смещением. Из уравне-
ния (11.58) видно, что
t 3 —/
У0.3(0 = -ЛГо.2(г) + —
Рис. 11.29. Форма первого квадратичного В-сплайна
б
(Отметим, что снова происходит твининг двух сплайн-функций более низкого порядка.) Первый
член — это произведение подъема на первый треугольный импульс, а второй член — произведение спус-
ка на второй импульс. Как показано на рис. 11.29, а, произведения подъема и спуска на треугольные
импульсы представляют собой две параболы, пересекающиеся под углом. Однако когда два соответ-
ствующих члена уравнения (11.61) складываются, углы исчезают и результирующий импульс NQ 3(t)
(рис. 11.29, б) имеет непрерывную производную.
Уравнение (11.61) можно использовать для определения алгебраического выражения квадратично-
го сплайна для каждого сегмента. В среднем сегменте содержится сумма двух квадратичных полино-
мов, а общий результат имеет вид:
-t2, 0£/<1,
2
М,.з (0 =
(11.62)
— (З-/)2, 2</<3,
0, при остальных Г.
Отметим, что No 3 зависит от четырех узлов 0, 1, 2,3, а его поддержкой является промежуток [0,3].
Сравнивая No 3(i) cg(t) из уравнения (11.49), мы видим, что они в точности совпадают. Это вызвано
тем, что в качестве g(t) была (намеренно) выбрана именно В-сплайн функция. В результате проверки
мы уже убедились, что ее первая производная непрерывна. Однако вторая производная — нет. Таким
образом, квадратичные В-сплайны (по крайней мере, при равноотстоящих узлах) действительно явля-
ются сплайнами.
724
Глава 11. Создание кривых и поверхностей
Другие формы квадратичных сплайнов, например Nk 3(i), для случая равноотстоящих узлов могут
быть легко получены. Поскольку сплайны первого порядка являются просто собственными смещенны-
ми версиями и поскольку все возрастающие члены уравнения (11.58) содержат только разности узло-
вых значений, то квадратичные сплайны также должны быть просто собственными смещенными вер-
сиями. В действительности это имеет место для В-сплайна любого порядка при равноотстоящих узлах:
Если tk - k, то Nt n(t) = N<jn(t-k'). (11.63)
Если узлы эквидистантны, то это выражение можно непосредственно подставить в уравнение (11.57).
Ранее мы утверждали, что квадратичные сплайны из уравнения (И.58) при любых значениях t в сум-
ме равны единице. В упражнениях в конце раздела будет показано, что это верно даже в случае неравно-
отстоящих узлов.
Пример 11.7.3. Кубические В-сплайны
Кубический В-сплайн — это, вероятно, наиболее часто используемый вид В-сплайна. На рис. 11.30, а
показан вид сплайна No 4(i) для равноотстоящих узлов. Его формула может быть найдена тем же спосо-
бом, что и раньше. (См. упражнения.). Сплайн No 4(t) симметричен относительно точки t - 2; его компакт-
ное выражение выглядит так:
^0.4 (0 ~
v(2-t), l<t<2,
2^t<3,
u(t-3), 3<t<4,
0
(11.64)
при остальных t.
a 6
Рис. 11.30. Кубический В-сплайн для равноотстоящих узлов
Два элемента этой формулы — функции и( ) и v{ ), изображенные на рис. 11.30, б, — имеют следую-
щий вид:
г^) = |(з?-6?+4). (11.65)
11.7. Базисные функции В-сплайнов
725
Непосредственное вычисление производных показывает, что первая и вторая производные кубичес-
кого сплайна непрерывны повсюду, поэтому кубические сплайн-кривые являются 2-гладкими, по край-
ней мере, для равноотстоящих узлов.
Основываясь на вышеприведенных рассуждениях, можно показать (см. упражнения) в общем виде,
что функция Nk m(t) начинается в точке tk и заканчивается в точке Г*+т, поэтому ее поддержка равна [tk, tk + J.
Кроме того, данная функция всюду неотрицательна.
Всегда следует предусмотреть потенциальную возможность деления на нуль: один из знаменателей
в уравнении (11.58) или оба сразу могут обратиться в нуль при определенном выборе узлов. Однако
если такое и произойдет, то соответствующая функция более низкого порядка, Nk т_ ,(t) или Nk+, „_,(£),
всегда тоже обратится в нуль. Поэтому можно ввести правило, согласно которому любой член с нуле-
вым знаменателем полагается равным нулю.
Рекурсивную формулу для функции Nk m(t) легко реализовать на компьютере и тем самым получить
возможность вычислять ее значение для любого t и для любого заданного узлового вектора. Фрагмент
этого кода, приведенный в листинге 11.1, является непосредственным переводом уравнения (11.58).
Листинг 11.1. Вычисление стыковочных функций В-сплайна
float bSpline(int k. int m, float t. float knotCJ)
{
float denoml, denom2. sum - 0.0:
if(m — 1)
return (t >- knot[k] && t < knot[k+l]);
// 1 or 0
// 1 или 0
// m exceeds 1.. use recursion
// если m больше 1. то используем рекурсию
denoml - knot[k + m -1] - knot[kj:
if(denoml !- 0.0)
sum - (t - knot[kj) * bSpline(k.m-l.t. knot) / denoml;
denom2 - knot[k + m] - knot[k+lj;
if(denom2 !- 0.0)
sum +- (knot[k+mj - t) * bSpline(k+l,m-l,t.knot) / denom2:
return sum:
}
Практические упражнения
11.7.1. Потенциальное деление на нуль
Покажите, что если два узла имеют одно и то же значение, то знаменатель в уравнении (11.58) обраща-
ется в нуль. Покажите далее, что в этом случае член с нулевым знаменателем также равен нулю.
11.7.2. Поддержка В-сплайна
Покажите, что функция Nk m(f) всегда равна нулю вне интервала [fk, tk + J, так что поддержка В-сплайна
ти-го порядка равна т диапазонов узлового вектора. Покажите также, что функция га(Г) неотрица-
тельна для всех значений t.
11.7.3. Квадратичные В-сплайн функции в сумме всегда равны единице
Мы уже показали, что линейные В-сплайн функции в сумме равны единице. Покажите, что это также
верно для квадратичных В-сплайнов.
Подсказка. При решении вам может помочь такая последовательность шагов: вы хотите показать, что
ео оо / а <” / — /
X "U')= X
* = — ‘* + 2 1 k * - — + 3 Ч +1
для всех значений t (обратите внимание, что суммирование идет от -<» до «>); в этом выражении непос-
редственно применено уравнение (11.58). Сделайте замену переменных во второй сумме (А>-> k - 1),
726
Глава 11, Создание кривых и поверхностей
затем сгруппируйте суммы в одну, учитывая, что коэффициент при Nt 2(t) всегда равен единице. Посколь-
ку к В-сплайнам второго порядка всюду прибавляется единица, то на этом доказательство закончится.
11.7.4. Вычисление кубического В-сплайна
Проверьте формулы уравнения (11.64) для кубического В-сплайна на базе равноотстоящих узлов. Кро-
ме того, вычислите первую и вторую производные кубического В-сплайна и покажите, что они непре-
рывны всюду.
11.7.5. Ручной прогон
Прогоните вручную алгоритм вычисления значения функции N3 2(2.6), приведенный в листинге 11.1,
для случая равноотстоящих узлов, где tt = i.
11.7.6. Периодические В-сплайн кривые
Покажите, что кривая
p(0=ip^o.„(G-Mmod(L+i)) (И.66)
* = 0
на базе (£ + 1) контрольной точки и В-сплайнов т-го порядка является замкнутой и, следовательно,
периодической по t.
11.7.2. Использование кратных узлов в узловом векторе
До сих пор мы использовали только В-сплайны на базе равноотстоящих узлов. Изменяя расстояние
между узлами, дизайнер получает значительно больший контроль над формой результирующей кри-
вой. Главный вопрос состоит в следующем: что произойдет с формами стыковочных функций, если два
узла окажутся очень близко друг к другу? Рисунок 11.31 показывает ситуацию, в которой узловой вектор
равен Т = (0,1,2,3,3 + Е, 4 + £,...), где е — малое положительное число. Тогда «кусок» каждого кусочного
полинома, лежащего в интервале [3,3 + е], «вжимается» в очень узкий диапазон. Очевидно, что стыковоч-
ные функции при этом больше не будут собственными смещенными версиями. Если положить Е равным
нулю, то этот диапазон полностью исчезнет, и при t - 3 будет иметь место кратный узел (multiple knot).
Рассматриваемый узел будет иметь кратность 2. На рис. 11.32 показаны результирующие стыковочные
функции. Теперь две линейные формы В-сплайнов при t = 3 имеют разрыв (рис. 11.32, б), а квадратич-
ные формы — разрывную производную (рис. 11.32, в). В общем случае в кратном узле i-гладкая кривая
превращается в (г - 1)-гладкую кривую. Кубические В-сплайн кривые (рис. 11.32, г) являются повсюду
1-гладкими, однако не 2-гладкими при t = 3. Заметим, однако, что если (см. рис. 11.32, в) использовать
квадратичные В-сплайны, то кривая будет интерполировать контрольную точку Р2, поскольку стыко-
вочная функция N2 3(t) при t = 3 равна единице, а все остальные стыковочные функции в этой точке
равны нулю. Вообще говоря, когда t приближается к узлу, имеющему кратность больше единицы, воз-
никает сильное притяжение к управляющей (governing) контрольной точке. (К какой именно?)
No,i0) N2\) ^l(t) Jj,4,l(O
О 1 2 3 \ 4+е5+б
3 + б
Рис. 11.31. Сближение узлов
Далее, квадратичные сплайны становятся разрывными вблизи узла кратности 3. Кубические сплай-
ны имеют разрывную производную вблизи узла кратности 3, причем они также интерполируют одну
из контрольных точек. Назначая кратность каждого узла, дизайнер может таким способом изменять
форму кривой. Как уравнение (11.58), так и фрагмент кода из листинга 11.1 без каких-либо изменений
могут работать с узловыми векторами, содержащими кратные узлы. Как уже упоминалось, некоторые
11.7. Базисные функции В-сплайнов
727
знаменатели в этом уравнении могут обращаться в нуль, однако в программе такая ситуация учитыва-
ется автоматически, поэтому никаких корректировок кода делать не нужно.
б
Рис. 11.32. Формы В-сплайнов вблизи узла кратности 2
11.7.3. Незамкнутые В-сплайн кривые: стандартный
узловой вектор
При дизайне кривых в качестве стандартного принят узловой вектор специального вида. При таком
выборе кривая интерполирует первую и последнюю контрольные точки, что усиливает возможности
дизайнера предсказывать поведение вычисляемой кривой.
Стандартный узловой вектор (standard knot vector) для В-сплайна порядка т начинается и за-
канчивается узлом кратности т, а между остальными узлами задается единичное расстояние. Нач-
нем с примера и увидим, как это происходит. Пусть у нас имеется восемь контрольных точек и мы
хотим использовать кубические (т = 4) В-сплайны. Тогда стандартный узловой вектор будет иметь
следующий вид:
Т-(0,0, 0,0,1,2,3,4,5,5,5,5).
Восемь стыковочных функций No 4(t),..., N7 4(0 определяются в этих узлах с помощью уравнения
(11.58) и показаны на рис. 11.33, а. Функции No 4(t) и N7 4(t) разрывны и имеют поддержку только в од-
ном диапазоне единичной длины. Только функции N3 4(t) и N4 4{t) имеют обычный диапазон в четыре
единицы. Диапазоны остальных стыковочных функций имеют ширину в две или три единицы, и форма
этих функций все больше искажается по мере их приближения к первому и последнему узлам. В упраж-
нениях исследуются специальные полиномиальные функции, из которых состоят стыковочные функ-
ции. Заметим, что совместное действие этих функций всегда обеспечивает интерполирование первой и
последней контрольных точек. Например, при t - 0 все стыковочные функции равны нулю, за исключе-
нием No 4, которая равна единице. Нетрудно также показать, что начальное направление В-сплайн кри-
вой при t = 0 совпадает с первым отрезком контрольного полигона, и аналогично для конечного направ-
ления. (См. упражнения в конце раздела.)
На рис. 11.33, б приведен пример кривой на базе восьми контрольных точек. Ясно, что первая и пос-
ледняя точки интерполируются, а направление кривой в этих точках совпадает с ожидаемым.
Отметим, что В-сплайн кривая может пересекать сама себя, в случае, если это делает контрольный
полигон.
728
Глава 11. Создание кривых и поверхностей
а
Рис 11.33. Восемь кубических стыковочных функций В-сплайна
Стандартный узловой вектор для (L + 1) контрольной точки и В-сплайнов ти-го порядка описывается
следующим образом (в скобках приводятся комментарии к соответствующим стыковочным функциям):
1. Всего в нем содержится L + т + 1 узлов, обозначаемых f0,..., tL + п.
2. Все первые т узлов t0.....tm_, имеют нулевое значение. (Первые т стыковочных функций начи-
наются при t = 0.)
3. Узлы tL возрастают с единичным шагом от 1 до L - т + 1. (Последняя стыковочная функ-
ция Nl m(t) начинается при tL=“ L - т + 1 и имеет поддержку единичной ширины.)
4. Все последние т узлов tL......tL+т равны L - т + 2.
Исходя из этих правил, нетрудно создать процедуру, генерирующую стандартный узловой вектор
для заданных значений т и L, как показано в нижеприведенном фрагменте кода.
void buildKnotsdnt m, Int L. double knotCJ)
{
// Build the standard knot vector for L + 1 control points
// and B-splines of order m
// Создаем стандартный узловой вектор для L + 1 контрольных
// точек и В-сплайнов m-ro порядка
int i;
if(L < (m - 1)) return;
// too few control points
// слишком мало контрольных точек
ford = 0; i <- L + m; i++)
if (i < m) knot[i] - 0.0;
else if (i <- L) knot[i] - i - m + 1;
// i is at least m here
// здесь i меньше или равно m
else knot[i] - I - m + 2: И
// i exceeds L here . ,
// здесь i больше m
11.7. Базисные функции В-сплайнов
729
Отметим сбойную ситуацию, которая может возникнуть из-за неправильного соотношения значе-
ний т и L. При заданном т должно быть достаточное количество контрольных точек, чтобы «хватило
места» по крайней мере для одного диапазона единичной ширины. Это приводит к следующему огра-
ничению: порядок m не может превосходить число контрольных точек L + 1.
Кривые Безье являются В-сплайн кривыми
Кривые Безье уже были введены ранее двумя способами: через алгоритм де Кастельо и через полиномы
Бернштейна. Теперь мы можем описать и третий подход: кривые Безье являются также и частным случа-
ем В-сплайнов. Дело в том, что стыковочные функции В-сплайна, определенные на стандартном узло-
вом векторе, при m - L + 1 в действительности являются полиномами Бернштейна! Это означает, что
где k = О,..., L. Отметим, что, согласно принятому соглашению, верхний индекс у В{ ) — это степень
(degree), в то время как второй параметр у N( ) — это порядок (order). Чтобы понять это, посмотрим, что
произойдет со стандартным узловым вектором, если порядок m увеличится до (Z + 1). (См. упражнения.)
Значения первых m узлов — нулевые, а последние m узлов имеют единичное значение, так что t изменяет-
ся только в промежутке [0,1]. Если, например, L - 5 и m - 6, то мы получим узловой вектор Т = (О, О, О, О,
0,0,1,1,1,1,1,1). Тогда каждый из кусочных полиномов будет иметь только один диапазон, и каждый
из этих полиномов имеет порядок m = L + 1. Это в точности совпадает с поведением полиномов Бернштей-
на. И в действительности полиномы Бернштейна можно вывести непосредственно из уравнения (11.58).
Вспомним, что основная причина перехода от кривых Безье к В-сплайн кривым состояла в желании
обеспечить локальный контроль над формой кривой. При увеличении порядка полиномов В-сплайна
на единицу поддержка каждой стыковочной функции В-сплайна расширяется на один диапазон, умень-
шая тем самым возможность локального контроля. Когда порядок m достигает своего предельного значе-
ния L + 1, то получается кривая Безье; при этом локальный контроль минимален. На рис. 11.34 показано,
как В-сплайн кривые при возрастании порядка становятся более «натянутыми», что уменьшает воз-
можность локального контроля. В этом примере имеется восемь контрольных точек, поэтому кривая
порядка m - 8 является кривой Безье. Все эти кривые были сгенерированы с помощью фрагмента кода,
представленного в листинге 11.1. (Какой вид имеет кривая при m = 2?)
m =6
Рис. 11.34. Кривые на основе сплайнов различных порядков
Практические упражнения
11.7.7. Стандартные узлы для квадратичных В-сплайн кривых
Покажите, что стандартный узловой вектор для В-сплайн кривой порядка m = 3 на базе восьми конт-
рольных точек равен Т - (0,0,0,1,2, 3,4,5,6,6,6).
730
Глава 11. Создание кривых и поверхностей
11.7.8. Узловые векторы при увеличении порядка m
Чему равен стандартный узловой вектор в случае, когда используется семь контрольных точек для
В-сплайнов следующих порядков:
О т = 3;
О z« = 4;
О т - 5;
О т = 6;
О т - 7?
11.7.9. Квадратичные В-сплайны для стандартных узловых векторов
Найдите при помощи уравнения (11.58) явные выражения для кусочных полиномов, описывающих
квадратичные стыковочные функции В-сплайна, определенного на стандартном узловом векторе.
11.7.10. Кубические В-сплайны
Найдите аналитическим способом четыре первых кубических В-сплайна, определенных на стандарт-
ном узловом векторе. Найдите также их производные при t - 0 и покажите, что начальное направление
кривой В-сплайна совпадает с направлением первого отрезка контрольного полигона.
11.7.11. Вывод полиномов Бернштейна
Покажите, что при т - L + 1 - 4 В-сплайн функции из уравнения (11.58) являются полиномами Берн-
штейна.
11.7.12, Об эффективном вычислении В-сплайнов
При рисовании В-сплайн кривой требуется задавать много точек, чтобы значения функций Nk „(0 долж-
ны были бы вычисляться при многих значениях t. При использовании рекурсивной формулы (11.58)
при каждом значении t производится большое количество избыточных вызовов В-сплайн функций бо-
лее низкого порядка. Следовательно, намного эффективнее было бы вычислять значения \„(0 всего
один раз и сохранять их в массиве, таком как i], который содержит функцию „(0, вычисленную
при t, = iAt, где At — постоянная разность между двумя нужными значениями t. Замеры функции Л^„(0
требуется делать только в области поддержки соответствующей В-сплайн функции. Более того, требу-
ется лишь несколько различных форм N[k, г], поскольку многие из них являются собственными сме-
щенными версиями и имеют такую же форму. Если у нас 55 контрольных точек, то сколько потребует-
ся различных кубических В-сплайн функций?
После сохранения каждая точка кривой может быть изменена посредством обращения к нужным
значениям функции: P(t.) формируется как векторная сумма произведений С[&] W[n,j], где С[Л] — кон-
трольная точка и выбраны правильные значения п и j. Определите правильные значения п и у для каж-
дого k и t. для случая кубических сплайнов. Заметим, что если индекс j выходит за пределы определен-
ного диапазона, то функция N[£,j] всегда равна нулю, поэтому массив не вызывается.
11.8. Полезные для дизайна свойства В-сплайн кривых
Полезно свести воедино основные свойства В-сплайнов и кривых, которые они генерируют. Мы уви-
дим также, что многие полезные свойства, характерные для кривых Безье, полностью сохраняются в
случае В-сплайн кривых.
1. В-сплайн функции ти-го порядка являются кусочными полиномами порядка т. Они являются
сплайнами, обладающими (т - 2)-гладкостью: в каждой точке своей поддержки их производные
до (т - 2)-го порядка включительно непрерывны. Они образуют базис для любого сплайна того
же порядка, заданного в тех же узлах; это означает, что любой сплайн можно представить в виде
линейной комбинации В-сплайнов. Среди всех базисов для сплайнов В-сплайны являются наи-
более сосредоточенными, поскольку обладают самой короткой поддержкой.
11.8. Полезные для дизайна свойства В-сплайн кривых
731
2. Стыковочная В-сплайн функция Nk m(t) начинается в точке tk и заканчивается в точке tk+m. Ее под-
держкой является промежуток [t4, tk + J. Поддержкой семейства функций Nk m(t) для k - 0.L
является промежуток [t0, im+£].
3. Замкнутая В-сплайн кривая на базе (Z + 1) контрольной точки может быть получена с помощью
уравнения (11.66) (в предположении, что узлы в определении No m(.) являются равноотстоящими).
4. Если используется стандартный узловой вектор, то В-сплайн кривая будет интерполировать
первую и последнюю контрольные точки. Ее начальное и конечное направления совпадают со-
ответственно с первым и последним ребрами контрольного полигона.
5. Каждая В-сплайн функция M(t) неотрицательна при любом t, а семейство таких функций
в сумме составляет единицу; это означает, что
5X„(')=1 с11-67)
i=0
для каждого te[t0, tn + J. Как мы уже видели для случаев низких порядков, это утверждение мо-
жет быть доказано методом индукции, исходя из уравнения (11.58).
6. Кривые на базе В-сплайнов аффинно инвариантны. Для преобразования В-сплайн кривой мы про-
сто преобразуем каждую контрольную точку и генерируем новую кривую на базе преобразованных
контрольных точек. Чтобы доказать это, просто заметим, что В-сплайн кривая является аффин-
ной суммой точек и что при аффинных преобразованиях аффинные комбинации сохраняются.
7. В соответствии со свойством 5, В-сплайн кривая является выпуклой комбинацией своих конт-
рольных точек и поэтому лежит внутри их выпуклой оболочки. Возможно более сильное утверж-
дение: при любом значении t только т В-сплайн функций «активны» (то есть отличны от нуля).
Таким образом, для любого t кривая должна лежать внутри выпуклой оболочки не более т после-
довательных активных контрольных точек. На рис. 11.35 показана квадратичная В-сплайн кри-
вая на базе стандартного узлового вектора. При каждом значении t активны не более трех конт-
рольных точек, поэтому соответствующие выпуклые оболочки являются треугольниками. При
возрастании t функция Р(Г) постепенно переходит из одной выпуклой оболочки в следующую
по мере того, как становится активной очередная стыковочная функция. При каких значениях t
кривая входит в закрашенную выпуклую оболочку и выходит из нее (см. рисунок)?
Рис. 11.35. Выпуклые оболочки для квадратичной В-сплайн кривой
Выпуклые оболочки т контрольных точек обычно занимают области меньшего размера, чем
оболочка всех контрольных точек. Поэтому данная кривая «захватывается» в меньшую область,
732
Глава 11. Создание кривых и поверхностей
чем кривая Безье. Узкий диапазон поддержки В-сплайнов не только предоставляет дизайнеру*
локальный контроль, но также позволяет глубже осмыслить природу кривой.
8. В-сплайн кривые обеспечивают линейную точность: если т последовательных контрольных
точек коллинеарны, то их выпуклая оболочка будет прямой линией, и кривая будет захвачена
внутрь ее.
9. В-сплайн кривые уменьшают колебание: В-сплайн кривая не пересекает никакую линию чаще,
чем это делает ее контрольный полигон [Farin, 60].
11.8.1. Использование кратных контрольных точек
Дизайнер с успехом может изменять форму В-сплайн кривой, задавая в одной и той же точке несколько
контрольных точек и создавая тем самым кратную контрольную точку (multiple control point), которая
сильнее притягивает к себе кривую.
На рис. 11.36 приведен пример, в котором используются кубические В-сплайн кривые. Кривая на
базе контрольных точек А, В, С, D, Е, F, G демонстрирует типичное для кубических сплайнов поведение.
При задании в точке D точки двойной кратности (в этом случае контрольный полигон имеет вид А, В,
С, D, D, Е, F, G) кривая сильнее притягивается к точке D. Если же в точке D помещена точка тройной
кратности, что придает контрольному полигону вид А, В, С, D, D, D, Е, F, G, то кривая фактически интер-
полирует эту точку!
Рис. 11.36. Манипулирование кривой при помощи кратных контрольных точек
Эффект интерполяции легко объясняется с помощью рис. 11.33, а. Отметим, что при таких значени-
ях t, как ts и t6, ровно три В-сплайн функции отличны от нуля и в сумме составляют единицу. Если их
вес определяется одной и той же контрольной точкой, то взвешенная сумма будет равняться самой кон-
трольной точке. Обобщая, напомним, что кубический В-сплайн всегда находится внутри некоторой
выпуклой оболочки четырех последовательных контрольных точек. При использовании в точке D точ-
ки тройной кратности выпуклые оболочки, окружающие D, состоят из ребер контрольного полигона,
поэтому кривая «захватывается» этим ребром на протяжении одного диапазона полиномов.
Отметим, что применение кратных контрольных точек — не то же самое, что использование кратт,
ных узлов, хотя эффекты от этих действий аналогичны. Дизайнеру обычно проще увеличить кратность
контрольной точки, чем узла, поскольку контрольные точки явственно видны и на них можно указы-
вать. (Для задания кратности контрольной точки дизайнеру достаточно отметить ее мышью нужное
число раз.)
11.9. Рациональные сплайны и NURBS-кривые
733
Практические упражнения
11.8.1 . Рисование выпуклой оболочки
Нарисуйте несколько различных контрольных полигонов из восьми точек. Рассмотрим квадратичные
В-сплайны на базе стандартного узлового вектора. Нарисуйте последовательные выпуклые оболочки и
определите значения t, при которых кривая входит в каждую оболочку и выходит из нее. Нарисуйте
результирующую В-сплайн кривую и отметьте на ней различные значения t. Убедитесь, что эта кривая
проходит через середины каждого внутреннего ребра контрольного полигона.
11.8.2 . Кратные контрольные точки на квадратичных В-сплайнах
Объясните эффект воздействия контрольной точки двойной кратности на квадратичную В-сплайн кри-
вую. Нарисуйте соответствующий контрольный полигон без кратных контрольных точек, покажите
последовательность выпуклых оболочек, захватывающих кривую, и нарисуйте саму кривую. Затем уве-
личьте кратность одной из контрольных точек и повторите все действия.
11.9. Рациональные сплайны и NURBS-кривые
А кто, собственно, боится NURBS?
Подслушано в автобусе на SIGGRAPH-98
В разделе «Описание кривых полиномами» мы уже вкратце упоминали о рациональных параметричес-
ких формах и отмечали, что конические сечения (эллипс, гипербола и парабола) можно полностью
сформировать из полиномов согласно равенству (11.14). В этом разделе мы более подробно остановим-
ся на рациональных полиномиальных формах на основе В-сплайнов.
Рациональная сплайн-кривая очень напоминает свой аналог среди В-сплайнов и формируется с по-
мощью уже знакомого нам сопряжения контрольных точек:
(ц-68)
к «О
однако здесь применяется слегка отличный набор стыковочных функций. Дизайнер задается набором
весов (set of weights) {и>0, wL], после чего создает следующие стыковочные функции:
Я* } = (11.69)
к =0
Эти веса, часто называемые «параметрами формы», обычно задаются неотрицательными, чтобы не
опасаться обращения знаменателя в нуль. Очевидно, что каждая функция Rk(t) является отношением
(ratio) полиномов (отсюда и произошел термин «рациональные В-сплайны»), Поскольку узловой век-
тор, используемый при определении В-сплайн функций, обычно является неравномерным (то есть узлы
в нем — неравноотстоящие), то такое семейство кривых получило название неравномерных рациональ-
ных В-сплайнов (nonuniform rational B-splines] или просто NURBS.
Заметим, что если все веса одинаковы, то знаменатель уравнения (11.69) превращается в константу
(почему?), вследствие чего эта форма сводится к уже знакомому нам В-сплайну из уравнения (11.57).
Таким образом, уравнение (11.69) является расширением уравнения (11.57) и отличается от него толь-
ко при неодинаковых весах.
Полезно понять, откуда берутся эти стыковочные функции. В соответствии с условиями упражне-
ния 11.9.3 (см. ниже), перейдем к однородным координатам и придадим k-й контрольной точке вес wk.
Возвращаясь к обычным координатам, получим NURBS-кривую. Желаемые свойства NURBS-кривых
достигаются посредством взвешивания точек в пространстве с большим числом измерений.
734
Глава 11. Создание кривых и поверхностей
Два основных преимущества NURBS-кривых
Преимущество NURBS-кривых состоит в том, что при правильном выборе контрольных точек и весов
функция P(t) является в точности коническим сечением (см. пример 11.9.2), Эта особенность каче-
ственно отличает NURBS-кривые от нерациональных В-сплайн кривых, которые способны только при-
ближаться к истинным коническим сечениям.
Второе преимущество заключается в том, что NURBS-кривые инвариантны относительно так назы-
ваемых проективных преобразований (projective transformations). Эти преобразования аналогичны
перспективным преобразованиям, рассмотренным в главе 7, которые обеспечивают перспективную про-
екцию сцены. Проективные преобразования являются обобщением аффинных преобразований. В мат-
рице аффинного преобразования четвертая строка имеет вид (0,0,0,1), в то время как четвертая строка
проективного преобразования может иметь более общий вид. Напомним, что нормальные В-сплайн
кривые являются инвариантными только относительно аффинных преобразований, поэтому NURBS-
кривые инвариантны по отношению к более широкому классу преобразований.
Среди прочего, такая инвариантность означает, что для того, чтобы нарисовать перспективную про-
екцию NURBS-кривой, достаточно просто найти перспективную проекцию каждой ее контрольной точ-
ки и затем сгенерировать на их базе кривую по тому же самому алгоритму, заданному уравнением
(11.68). (Веса также должны быть скорректированы.) Такой метод намного эффективнее, чем нахожде-
ние перспективной проекции «каждой» точки кривой в отдельности. В противоположность этому не-
рациональные В-сплайн кривые инвариантны относительно аффинных преобразований, но не относи-
тельно проективных.
Проективная инвариантность
Остановимся на некоторых деталях свойства проективной инвариантности NURBS-кривых (для 2D-
или ЗЭ-случаев). Вывод дается в тематическом задании 11.9. Основная идея заключается в том, что при
преобразовании NURBS-кривой посредством главной матрицы размерностью четыре на четыре (что
может привести к искажению перспективы) в результате получается другая NURBS-кривая, причем ее
контрольные точки являются просто преобразованными версиями исходных контрольных точек. Что-
бы эта схема работала, веса также следует скорректировать.
Рассмотрим конкретный случай ЗЭ-точек: пусть Т— преобразование, представленное главной мат-
рицей М размерностью четыре на четыре. Обозначим строки матрицы М через п)р та, т3, т4, тогда
матрицу М можно записать в блочной форме: М - (т( | т21 т31 т4)Т. (Символ Т, как всегда, означает
транспонирование.) Если последняя строка равна (0, 0, 0, 1), то данное преобразование становится
аффинным (и перспективного искажения не происходит). В результате получается [Piegl, 167], что кри-
вая T(P(t)), полученная путем применения преобразования Т( ) к NURBS-кривой из уравнения (11.68),
идентична NURBS-кривой на базе преобразованных контрольных точек Т(Рк), а именно:
Г(Р0) = , (11.70)
k = Q
со скорректированными весами
^=^(Л-т4), (11.71)
где Д = (Рх, Ру, P,,tf — обычное расширение Р на случай однородных координат. Отметим, что веса за-
висят от положения контрольных точек, а также от содержимого четвертой строки матрицы. Если пре-
образование является аффинным, то (Рк- т4) - 1, то есть веса корректировать не нужно.
11.9. Рациональные сплайны и NURBS-кривые
735
Практические упражнения
11.9.1. Создание базовых поверхностей
Обдумайте, как при помощи NURBS-кривых создать каждую из следующих поверхностей:
О круговой цилиндр;
О круговой конус;
О плоский лоскут (patch);
О сфера.
За подробностями обратитесь к тематическому заданию 11.10. Можно ли таким способом создать
произвольный лоскут Кунса?
11.9.2. Что если веса одинаковы?
Пусть все веса у NURBS-кривой <y(t) одинаковы (то есть это В-сплайн кривая). Останется ли она
NURBS-кривой после преобразования М? А В-сплайн кривой?
11.9.3. Формирование NURBS-кривых в однородных координатах
Рассмотрим формирование В-сплайн кривой на базе контрольных точек Pt, взвешенных с помощью
определенного набора весов {г^}. Такая В-сплайн кривая формируется в однородных координатах в
следующем виде:
(11.72)
4 = 0
где символом Рк обозначена контрольная точка Pk в однородных координатах (то есть для ЗВ-точки
Л = (^-л-^,1/) _ т
О Напишите выражения для отдельных KOMnoHeHTOBx(t),z/(t),2(t),®(t) для = ,
уделяя особое внимание выражению для w(t).
О Преобразуйте равенство (11.72) в обычные координаты, разделив его на w(t). Покажите, что в
результате получается равенство:
(0
р(0 = Ч------------• (Ц-73)
4 = 0
Покажите, что уравнение (11.73) имеет ту же форму, что уравнения (11.68) и (11.69).
Q
Пример 11.9.1. Получение конических сечений
Для рассмотрения частного случая уравнения (11.14) положим тп - 3 (квадратичные В-сплайны) и вы-
берем узловой вектор так, чтобы получились полиномы Бернштейна (Как именно?) Теперь, полагая
w0 = w2 = 1 и wt = w, получим уравнение (11.14).
Пример 11.9.2. Построение правильной окружности
Существует несколько способов построения правильной окружности с помощью NURBS-кривой
[Piegl, 167]. Рассмотрим основной метод, в котором применяются В-сплайны на базе семи контрольных
точек. На рис. 11.37, а показаны контрольные точки Ра.Р6, лежащие на квадрате, а также генерируемая
полная окружность. Указаны также нужные значения весов; заметим, что они равны 1 или 1/2. Узловой
вектор имеет следующий вид:
Т = |о, 0,0, -, -, -, -, -, 1,1,11.
Г 4 4 2 2 4 4 ]
736
Глава 11. Создание кривых и поверхностей
Рис. 11.37. Построение правильной окружности: а) квадрат из семи взвешенных контрольных точек;
б) семь базовых функций
Обратите внимание на узлы двойной кратности. На рис. 11.37, б приведены семь базисных функ-
ций, которыми взвешиваются контрольные точки. Форма кривой общего знаменателя для каждой фун-
кции R/t) показана на рисунке пунктиром. В упражнении 11.9.4 в конце раздела показан процесс полу-
чения формул для каждой базисной функции на каждом межузловом интервале; вы сможете убедиться,
что для всех t выполняется равенство х2^) + y\t) - 1.
Пример 11.9.3. Исследование влияния весовых множителей
На рис. 11.38, а приведена кубическая В-сплайн кривая на базе шести контрольных точек (с равноот-
стоящими узлами). Эта кривая является обычным нерациональным В-сплайном (или, что то же самое,
NURB с одинаковыми весами то.). На рис. 11.38, б показано, что получится, если веса сделать неодина-
ковыми: кривая в большей степени притягивается к точкам с большим значением веса. (Что будет, если
вес какой-нибудь точки обратится в нуль?)
NURBS приобрели популярность среди дизайнеров кривых из-за их универсальности и гибкости.
Поскольку они включают в себя как частный случай В-сплайны, с помощью одного алгоритма генери-
рования кривых можно создавать обширное семейство разнообразных форм, в том числе конические
сечения. Таким образом, дизайнеру не требуется инструментарий из многих алгоритмов для создания
кривых, а достаточно лишь одного метода.
Существует целый ряд других технологий построения кривых, причем некоторые из них предостав-
ляют пользователю даже больший контроль над формой кривой. Например, можно варьировать ряе-
стояния между узлами в узловом векторе (здесь они приняты одинаковыми) или добавлять к имШи
щимся данным дополнительные «ложные» («ghost») точки с целью управлять поведением кривой в
концевых точках. Читателю, интересующемуся различными обобщениями, следует обратиться к одно-
му из многочисленных источников по В-сплайнам, таким Лак [Bartels, 126, Farin, 60].
11.10. Краткое знакомство с интерполяцией
737
all W| = 1 Wo = w1 = w3= w5=1
W-, = w4 = 4
a 6
Рис. 11.38. Влияние неодинаковых весов на NURBS-кривую: a) = 1; б) w0 = w1 = w3 = w5 = 1, w, = w4 = 4
Практическое упражнение
11.9.4. Действительно ли это окружность?
Покажите, что NURBS-кривая, описанная в примере 11.9.2, действительно является окружностью. Для
этого найдите выражения для полиномов базисных функций в каждом межузловом интервале, вычи-
слите значение выражения x2(t) + y2(t) и покажите, что оно равно единице для всех t.
11.10. Краткое знакомство с интерполяцией
Иногда дизайнеру нужно, чтобы кривая, получающаяся в результате работы алгоритма, проходила че-
рез все контрольные точки. Такая кривая может показаться более естественной, чем кривая, получен-
ная при использовании алгоритма, который только «притягивает» ее к контрольным точкам. Однако
мы еще увидим, что если принудить кривую проходить через набор точек, то это может привести к кри-
вым с недопустимо малым локальным контролем или к нежелательным дополнительным «извивам»
между контрольными точками. Несмотря на такие ограничения, мы все же хотим обеспечить дизайне-
ра инструментальными средствами для тех случаев, когда интерполяция является предпочтительной.
У дизайнера уже есть один способ осуществить интерполяцию: использование В-сплайнов; если за-
дать контрольные точки достаточной кратности, то В-сплайн кривая будет заведомо интерполировать
эти точки. В тематическом задании 11.6 мы познакомимся с другим методом, основанным на В-сплай-
пах. Согласно этому методу, дизайнер задает точки, а алгоритм вычисляет другой набор точек, такой,
что В-сплайн кривая, сгенерированная по этим точкам, пройдет через точки, заданные дизайнером.
В данном разделе мы вкратце рассмотрим такие алгоритмы генерирования кривых, которые непо-
средственно интерполируют все контрольные точки, задаваемые пользователем. Это обширная тема с
длинной историей, поэтому мы коснемся только ограниченного класса методов. В работе Фарина
[Farin, 60] интерполяция рассматривается в более общей постановке и более подробно.
11.10.1. Интерполяция посредством кусочных
кубических полиномов
Ниже будет описана интерполяция набора контрольных точек с использованием кусочных кубических
полиномов. Мы сознательно ограничиваемся кусочными кубическими полиномами, поскольку они об-
ладают достаточными для наших нужд возможностями и гибкостью и в то же время достаточно просты
для эффективного использования.
На рис. 11.39,а приведена основная задача проектирования. Пользователь размещает последова-
тельность контрольных точек Ро, Pv..., PL (здесь L = 4) и хочет сгенерировать «достаточно гладкую»
кривую, проходящую поочередно через все эти точки. На рис. 11.39, б показана одна такая кривая R(t).
24 Ф. Хилл
738
Глава 11. Создание кривых и поверхностей
Эта кривая состоит из четырех сегментов (участков), каждый из которых является кубическим поли-
номом:
Rk(t) - Akt? + Bkt2 + Ckt + Dk, где/г = 0,1,..., L - 1; для t в промежутке [0,1]. (11.74)
A gt** + В gt* + Cjt + D j
а б
Рис. 11.39. Интерполяция кусочными кубическими полиномами
Разумеется, каждый член этого полинома содержит х- и ^-компоненты. Вопрос заключается в следу-
ющем: какими должны быть коэффициенты Ак, Вк, Ск и Dk?
Отметим, что для упрощения записи здесь используется формулировка, несколько отличная от той,
которую мы применяли ранее: каждому сегменту соответствует один и тот же интервал по t — от 0 до 1.
Поэтому, чтобы нарисовать эту кривую, нам придется рисовать четыре отдельные кривые, как это сде-
лано с помощью следующего псевдокода:
for(k - 0: k < L: к++)
{
retrieve the coefficients А[к]. В[к], С[к]. 0[к]
// вычисляем коэффициенты А[к]. В[к]. С[к]. 0[к]
Draw the curve Rk(t). using these coefficients
in short line segments, as t goes from 0 to 1
// рисуем кривую Rk(t) по этим коэффициентам
// короткими сегментами линий при изменении t от 0 до 1
}
Сегмент Rk(t) - (x(t), y(t)) является, как всегда, 2Э-кривой. Если функция R(t) интерполирует точ-
ку Р == (х, у), то функции x(t) и у(Г) должны интерполировать компоненты этой точки — соответственно х
и у. Поэтому можно рассматривать процесс интерполяции раздельно для компонентов х и у. Это упро-
щает обозначения и, кроме того, облегчает наблюдение того, что происходит.
На рис. 11.40, а показана задача интерполяции только для у-компонента. Задана последовательность
значений у. (у0, yv..., yL)’, требуется найти такой кусочный кубический полином, который проходил
бы через эти значения у и обладал 1-гладкостью. (В некоторых случаях мы сделаем этот полином даже
2-гладким, то есть сплайном). /г-й кубический сегмент кривой, показанный на рис. 11.40, б, описывается
следующей формулой:
yk(t) - akt3 + bkt2 + ckt + dk, где Л -0,1.L - 1; для t в промежутке [0,1]. (11.75)
Рис. 11.40. у-компонент интерполирующей кривой
11.10. Краткое знакомство с интерполяцией
739
Обозначим через sk значение производной этой функции в точке ук, то есть у' JO) - sk. Как мы увидим
далее, в некоторых случаях значения sk заданы (то есть введены пользователем), а иногда вычисляются,
исходя из других требуемых свойств кривой. И снова мы спрашиваем: чему равны коэффициенты?
11.10.2. Эрмитова интерполяция
Сформулируем условия, накладываемые на коэффициенты ак, bk, ск, dk, так чтобы каждый сегмент кри-
вой интерполировал заданное значение ук при t - 0 и ук+, при t - 1. Тогда для k - 0,1,..., L - 1 имеем:
при t = 0 dk = ук,
приГ=1 ak + bk + ck + dk-yk*i.
В этих двух уравнениях содержатся 2L условий. Кроме того, потребуем, чтобы производные от yk(t)
равнялись заданным значениям st при t - 0 и st t ( при t - 1 соответственно. Поскольку производная
равнаy'k(t) = 3akt2 + 2bkt + ск, то отсюда следуют дополнительные условия для k - 0,1,..., L - 1:
при t ~ 0 ск - sk,
приГ=1 Зак + 2Ьк + ск = 5Л+1.
Эти два уравнения содержат еще 2L условий, поэтому всего мы имеем 4Z условий для 4Z неизвест-
ных коэффициентов. Отметим, что из требования равенства производных заданным значениям накло-
на автоматически вытекает непрерывность наклона в узлах, поэтому кривая 1-гладкая.
Исходя из этих уравнений, нетрудно аналитически выразить искомые коэффициенты через ук и sk.
(Проверьте это.) Итак, для k - 0,1.L - 1 мы имеем:
fl* = s*+i + st"2(^+i-%):
ck “ sv
dk-yk-
Эти уравнения определяют компоненты yk(t) для каждого сегмента. Аналогично могут быть по-
лучены уравнения, определяющие коэффициенты xk(t), после чего можно нарисовать эти кубичес-
кие сегменты уже известным способом, вследствие чего будет сформирована кусочная кубическая
кривая.
Решение можно было бы считать законченным, если бы мы знали значения наклонов s* для каждого ук.
Существует несколько методов определения этих значений. Посмотрим вначале, какое влияние оказы-
вает наклон sk на форму кривой. Затем посмотрим, как сделать кривую 2-гладкой. Это приведет нас к
«естественному» кубическому сплайну.
Пример 11.10.1.0 касательных и наклонах
С целью лучшего понимания соответствия только что рассмотренных нами многочисленных коэффи-
циентов друг другу, рассмотрим кривую, состоящую из двух кубических сегментов, R0(t) и R^t), со сле-
дующими свойствами:
Сегмент 0. R0(t) проходит через точку (1, 1) при Г - 0 и через точку (4, 3) при i - 1. Кроме того, его
скорость равна (1,0) при t- 0 и (0,5) при t - 1, где S — некоторая величина, которую мы будем варьиро-
вать для выяснения зависимости от изменений наклона кривых.
Сегмент 1. R{{t) проходит через точку (4,3) при Г - 0 и через точку (0,3) при t - 1. Скорость равна (0,5)
при t - 0 и (0,1) при t - 1. Результирующая кривая для частного случая 5=1 приведена на рис. 11.41.
Параметрические сегменты показаны в плоскости ху\ кроме того, на рисунке изображены компоненты
x0(t), x^t), ya(t), y£t), образующие данную кривую.
Внимательно проследим за ходом кривой и обратим внимание, как образуется ее форма из форм
отдельных составляющих. Заметим, что кривая плавно переходит от одного сегмента к следующему,
поскольку ее скорость в этих точках непрерывна. Это обеспечивается непрерывностью на стыке функ-
740
Глава 11. Создание кривых и поверхностей
ций x(t), y(t) и их наклонов, поэтому кривая является 1-гладкой. В точке соединения наклон x(t) равня-
ется нулю для обоих сегментов, поэтому оба сегмента справа и слева от стыка горизонтальны. y(t) так-
же гладко переходит от одного сегмента к другому: его наклон равен 5=1 как слева, так и справа от места
соединения.
Рис. 11.41. Два кубических сегмента, встречающихся с заданной скоростью
Для выявления истинной природы сегментов применим уравнение (11.74) к конкретным данным.
Для составляющей у получим следующие значения:
Сегмент 0. у0 = 1, у{ = 3, s0 = 0, = 5, что приводит к кубическому уравнению у0(г) = (5 - 4)Г3 + (6 - 5)г2 + 1.
Сегмент!. = 3,у2 = 3,^ “5,s,= 1,что приводит к кубическому уравнению yt(t) = (5+ 1)Г3-(25 + 1)г2 +
+ St + 3.
Аналогично для компонента х получим следующие значения:
Сегмент 0. х0 = 1, xi = 4, s0 = 1, = 0, что приводит к кубическому уравнению х0(г) = -5г3 + 7г2 + г + 1.
Сегмент 1. х( = 4, х2 = 0, 5, = 0, s2 = 0, что приводит к кубическому уравнению х^г) = 8г3 - 12г2 + 4.
Таким образом, эти два сегмента имеют форму, определяемую следующими уравнениями:
7?0(г) “ (-5г3 + 7г2 + г + 1, (5 - 4)гз + (6 - 5)г2 + 1);
Я/г) - (8г3 - 12г2 + 4, (5 + Ог3 - (25 + 1)г2 + 5г + 3).
Полезно понаблюдать за изменением составляющей г/( ) в зависимости от изменения наклона 5 на
стыке. Меняется только величина скорости в точке соединения, но не ее направление. Из полученных
формул видно, что величина 5 влияет на коэффициенты для у0(г) и у,(г), однако не оказывает влияния
на функции х-составляющих. На рис. 11.42 показаны функции у(г) и параметрическая кривая для раз-
личных значений 5.
11.10. Краткое знакомство с интерполяцией
741
Уо(‘) У1С)
--------1--------1 1 !_>х --------t -----------L> t
12 3 4
Рис. 11.42. Эффект от изменения величины наклона
При больших значениях S кривая в месте соединения обладает большой скоростью. Для обеспече-
ния такой скорости кривая должна «выпятиться» до и после соединения, чтобы «подготовиться» к бы-
строму проходу через стык по вертикали. Это показывает, насколько «эластична» кубическая кривая:
она не может изгибаться сколь угодно быстро — для этого у нее недостаточно степеней свободы, поэтому,
чтобы приобрести требуемый наклон на одном конце, ее форма должна изменяться на всем промежутке.
При S = 0 в месте соединения образуется угол (см. нижеследующие упражнения). Скорости обеих
кривых R0(t) и Rt(t) при приближении к стыку стремятся к нулю, поэтому хотя скорость всей кривой
резко изменяет направление в точке соединения, кривая тем не менее остается 1-гладкой. (Является ли
эта кривая G1-непрерывной?)
Практические упражнения
11.10.1. Когда скорость нулевая
Пусть скорость сегмента кубической кривой равна нулю на обоих концах. Покажите, что этот сегмент
является прямой линией.
11.10.2. Исследование кривых
Напишите короткую программу, которая генерирует кривые, изображенные на рис. 11.41 и 11.42, и про-
гоните эту программу при различных значениях S. Для лучшего выполнения программы рекомендуем
определить следующую функцию для у:
Point2 y(float t. float S. int seg)
{
double t2 = t * t. t3 = t2 * t;
return (seg == 0)?
(S-4) * t3 + (6 - S) * t2 + 1:
(S+l) * t3 -(2 * $ ♦ 1) * t2 + S * t + 3:
}
и аналогичную функцию для x.
11.10.3. Создание петли
Покажите, что при 5 = -1 кривая с рис. 10.41 имеет петлю.
742
Глава 11. Создание кривых и поверхностей
11.10.3. Естественные кубические сплайны
В качестве одного из способов задания значений производных sk при формулировке Эрмита использу-
ем такие значения sk, при которых вторая производная от y(t) будет непрерывной на каждом из «внут-
ренних» стыков, где k - 1, 2,..., L - 1. (На «концах» всей кривой производным пет необходимости быть
непрерывными.) Вторая производная на каждом сегменте равна y"(t) = Qakt + 2b k, поэтому, приравни-
вая yf-iO) к У'к (0). получим:
Gak_{ + 2bk_^2bk, (11.76)
где£ = 1, 2,..., L - 1.
Используя значения коэффициентов из уравнения (11.74), после упрощений получим следующее
условие для наклонов:
+ Ч + + 1 = С11-77)
где k - 1, 2,..., L - 1. Из этого уравнения видно, как должны быть связаны соседние наклоны, чтобы
обеспечить непрерывность второй производной во внутренних точках соединения. Нам все еще остается
задать первый и последний наклоны — $0 и sL. При традиционном подходе они выбираются так, чтобы
на обоих концах кривой вторые производные равнялись нулю; то есть у" (0) = 0 и y"_t (1) = 0. Из перво-
го условия следует, что Ьа = 0, а из второго — 3aL _1 + bL _ 1 - 0. (Почему?) Снова используя уравнение
(11.74), получим два последних условия:
2s0 + s, - 3(г/, - г/0);
2sl + sl-i (11.78)
Уравнения (11.76) и (11.77) представляют в совокупности L + 1 линейное уравнение относительно
неизвестных наклонов sk. Как будет показано в упражнениях, структура этих уравнений довольно про-
ста для решения.
На рис. 11.43 приведен набор контрольных точек и интерполирующий их естественный кубический
сплайн. Отметим, что на вид эта кривая повсюду выглядит гладкой, причем на концах кривая выпрям-
ляется так, что вторая производная обращается в нуль. Пунктирной линией показан эффект от смеще-
ния одной из контрольных точек. Форма кривой изменилась везде; таким образом, естественные сплай-
ны не обеспечивают локального контроля, поскольку требование непрерывности второй производной
«связывает» производные первого порядка в узлах и изменение одной производной вызывает сквозное
возмущение всех остальных.
Рис. 11.43. Естественные кубические сплайны, интерполирующие контрольные точки
Практическое упражнение
11.10.4. Решение уравнений для наклонов естественного сплайна
Уравнения (11.76) и (11.77) более наглядны в матричной форме. Для случая L = 4 имеем:
11.10. Краткое знакомство с интерполяцией
743
(2 1 0 0 О А
4 10 0
14 10
0 14 1
(j0 > » $2 , , ^4 )
О
О
= 3(У1 -Уо, У2-Уо, Уз-К> У4~У2> У4~Уз)
0 0 0 12
к /
Эта матрица является тридиагональной (tridiagonal): ее ненулевые члены сосредоточены на трех
диагоналях. Это позволяет решать данную систему уравнений в два простых этапа, описанных ниже.
О Пройдем систему уравнений методом прямого исключения (forward-elimination) для аннулиро-
вания единиц в верхней диагонали. Для этого разделим первое уравнение на 2, вследствие чего
его первый элемент превратится в 1. Затем, начиная со второго уравнения, вычтем поочередно из
каждого уравнения соответствующую «долю» предыдущего уравнения для исключения 1, после
чего промасштабируем уравнение так, чтобы на диагонали стояла единица. Покажите, что такой
процесс преобразует систему уравнений к «нижней диагональной» форме (когда выше главной
диагонали располагаются только нули):
( 1 о
о о о А
(s0, , s2, s3, s4)
0 0
0 0 0
1 о о
v2 1 0
О v3 1,
(<7о> 9|. <72> <7з> ?<)•
(11.79)
Кроме того, покажите, как просто вычислить члены о и qt.
Листинг 11.2. Этап прямого исключения
v[0] - 0.25:
q[0] = 3.0 * (у[1] - у[0]) * v[0];
for(1 - 1; 1 < L: 1++)
{
v[1] = 1.0 / (4.0 - v[1 - 1]):
q[i] - (3.0 *(y[i]-y[i-lj) - q[i - U) * v[i]:
}
О Покажите, что код из листинга 11.2 действительно осуществляет прямое исключение на базе мас-
сивов v[] и q[].
О Для получения искомых значений s[] выполняется этап обратной подстановки (backward-
substitution). В крайнем правом столбце матрицы из уравнения (11.79) содержится единствен-
ный ненулевой элемент, поэтому $4 - g4. Покажите при помощи нижеприведенного фрагмента
кода, что, двигаясь обратно по уравнениям, можно получить любое значение s;:
s[L] - q[LJ:
ford - L - 1: 1 > 0: 1 --) s[i] - q[i] - v[i] * s[i+l]:
11.10.4. Вычисление наклонов при кубической интерполяции
Существует еще несколько методов задания наклонов кривых в местах соединения. Рассмотрим вкрат-
це наиболее популярный из них: семейство сплайнов Кэтмулла—Рома (Catmull—Rom)1 [Bartels, 126;
Farin, 60] и их вариации. Мы по-прежнему хотим, чтобы кривая была 1-гладкой во «внутренних» точ-
1 Иногда эти сплайны называют фундаментальными (cardinal), а иногда — сплайнами Оверхаузера (Overhauser). Фактически все
они являются частными случаями более общего семейства кривых Кэтмулла—Рома.
744
Глава 11. Создание кривых и поверхностей
ках соединения, однако теперь отказываемся от требования ее 2-гладкости в этих точках. Можно ожи-
дать, что отказ от дополнительной степени гладкости предоставит дизайнеру больший локальный кон-
троль над формой кривой. В противоположность заданию значений наклонов sk с целью обеспечить не-
прерывность второй производной теперь мы зададим эти наклоны исходя из координат соседних с ними
контрольных точек.
Рис. 11.44. Задание наклонов на основе значений соседних контрольных точек
Простейший метод Кэтмулла—Рома состоит в присвоении вектору скорости в точке Pk величины
P'(tk) на базе координат двух соседних точек. Как показано на рис. 11.44, этот вектор принимается просто
пропорциональным вектору, соединяющему точки Pk_, и Рмr В результате этого направление кривой в
точке Pk станет параллельным отрезку, соединяющему предыдущую и последующую точки. Таким об-
разом, потребуем, чтобы
(11.80)
где т — некоторый скаляр. (Ниже мы рассмотрим влияние коэффициента т; часто принимают т=1/2.).
В терминах предыдущих величин данное условие задает наклон ^-компонента следующим образом:
sk “ ?n(yi+! - *4-i); аналогичное выражение может быть получено и для х-компонента.
Поскольку мы задали значения наклонов sk для каждой внутренней точки соединения, теперь можно
определить коэффициенты различных кубических полиномов в уравнении (11.74) для k - 1,..., L - 2.
Нам по-прежнему требуются два дополнительных условия для задания еще не определенных наклонов
на концах $0 и sL __ r С этой целью можно использовать то же самое условие равенства нулю вторых про-
изводных на концах, что приводит нас к уравнению (11.78). В упражнениях рассматриваются и другие
возможности. На рис. 11.45 показан пример кривой, сгенерированной с помощью этого метода.
Добавление управления натяжением
С целью предоставления дизайнеру большего контроля над формой кривой в каждой точке соединения
в методе Кэтмулла—Рома вводится параметр «натяжения» Этот параметр обеспечивает дизайнеру
управление константой т в уравнении (11.80) путем изменения величины скорости P'(t) в точке соеди-
нения без изменения ее направления. Согласно этому методу, скорость в k-ii точке соединения равна
Р'(4) = |(1-^)(/’+1-/’..1), (11.81)
где k “ 1,..., L - 1. (Чему в этом случае равняется наклон sk?)
11.10. Краткое знакомство с интерполяцией
745
Рис. 11.45. Интерполирующая кривая на базе сплайна Кэтмулла—Рома (при m = 1/2)
Хотя обычно натяжение vt задается в диапазоне от -1 до 1, оно может принимать и любое другое зна-
чение. Случай vk = 0 соответствует значению т - 1/2, согласно уравнению (11.80). На рис. 11.46 показано
влияние натяжения в вершине Р.2 на форму кривой. На рис. 11.46, а натяжение v2 равно 1, поэтому скорость
в точке соединения также стала нулевой. Это выпрямляет кривую при ее приближении к стыку. (Поче-
му?) На рис. 11.46, б v2 равно -1, поэтому кривая в точке соединения выглядит более «расслабленной».
Рис. 11.46. Влияние натяжения в вершине 2: а) натяжение = 1; б) натяжение = -1
Дополнительный контроль смещенности
В классе кривых, известных как сплайны Кочанека—Бартелса (Kochanek-Bartels splines), содержатся
и другие параметры, предназначенные для лучшего манипулирования формой кривой [Kochanek, 126].
Одним из этих параметров является «смещенность» (bias). Отметим, что при т = 1/2 уравнение (11.80)
может быть записано в виде:
р'(0 = + (11.82)
что представляет собой среднее значение двух соседних векторов Рк - Рк , и +- Рк. (Посмотрите это
на рис. 11.44.) Параметр смещенности Ьк неодинаково взвешивает два вышеприведенных компонента
согласно формуле
746
Глава 11. Создание кривых и поверхностей
Р'ОО = + |(l+^)(Pt + 1-Pt), (11.83)
так что фактическая скорость, задаваемая в точке соединения, определяется одним соседним вектором
в большей степени, чем другим. При Ьк - 0 оба этих вектора взвешены одинаково. На рис. 11.47 показан
эффект от смещенности в вершине Р2 для кривой с рис. 11.45.
Рис. 11.47. Эффект от смещенности в вершине 2: а) натяжение = -0,8; б) натяжение = 0,8
Добавление управления непрерывностью
Вместо требования непрерывности скорости в точке Рк Кочанек и Бартелс (Kochanek and Bartels) вво-
дят другой параметр, призванный предоставить дизайнеру возможность сделать скорость «непосред-
ственно перед» стыком отличной от скорости «непосредственно за» ним. Рассмотрим соединение в точ-
ке Рк. (k - 1)-й сегмент Rk_ t(t) (см. уравнение (11.74)) достигает точки Рк при t = 1. Скорость на этом
сегменте при t - 1 зададим следующим образом:
Rl-.(l) = -Р4_,) + |(l+q)(Pi + I-Pt), (11.84)
где Cj— параметр непрерывности (continuity parameter). (Здесь уравнение выглядит точно так же, как и
в случае параметра смещенности: большие значения ск смещают скорость в сторону вектора Рк+1 - Рк.)
Аналогично k-ii сегмент Rk(t) выходит из точки Рк при t - 0. Его скорость в этот момент времени зада-
дим формулой
ИДО) = + + + (11.85)
где используется то же значение ск. Это снова похоже на смещенность: большие значения ск смещают
скорость в сторону Рк ~Pk_v Если ск “ 0, то обе скорости одинаковы и кривая в этой точке соединения
является 1-гладкой. Если же ск отлично от нуля, то обе скорости приобретают различные величины и
направления. На рис. 11.48 показан эффект от изменения параметра непрерывности.
На практике эти три параметра — натяжение, смещенность и непрерывность — используются совме-
стно (см. упражнения ниже); таким образом, в каждой точке соединения дизайнер может задавать их
независимо. В типичном сценарии дизайнер может выполнить следующие этапы:
1. Задать мышью начальные значения контрольных точек.
2. Изучить сгенерированную кривую. Если она подходит, то остановиться.
11.10. Краткое знакомство с интерполяцией
747
3. Отредактировать контрольные точки, откорректировать натяжение, смещенность и непрерыв-
ность для каждой точки. Дизайнер может щелкнуть мышью на контрольной точке и перетащить
ее в новую позицию. Кроме того, для коррекции различных параметров в этой точке можно вы-
полнить ряд нажатий клавиш. Например, нажатие клавиши «Ь» может уменьшать смещенность
(bias), а «В» — увеличивать ее.
4. Перейти к этапу 2.
Рис. 11.48. Влияние параметра непрерывности: а} с2 = 1; 6} с2 = -1
Практические упражнения
11.10.5. Общая формула сплайнов Кочанека-Бартелса
Напишите формулу сплайнов Кочанека-Бартелса R'_t(l) и R'(0) с одновременным учетом влияния
натяжения, смещенности и непрерывности.
11.10.6. Выбор условий на концах кривой
Напомним, что когда кубическая интерполяция выполняется по Z + 1 контрольной точке, то необходи-
мо задать 4Z коэффициентов. Поскольку 4L - 2 из них определяются условиями интерполяции и зада-
нием наклонов, то остается определить еще два коэффициента. В уравнении (11.77) они задаются из
условия равенства нулю второй производной на крайних сегментах, однако для задания этих коэффи-
циентов можно использовать и другие условия. Требуется вывести два уравнения, линейных относи-
тельно коэффициентов и независимых от остальных 4Z - 2 уравнений. Напишите уравнения для каж-
дого из следующих условий:
О Первые производные в концевых точках Ро и PL равны нулю.
О Третьи производные в точках Р{ и PL_i непрерывны. (Это называется «безузловым» условием
Бура (Boor’s «not-a-knot» constraint); в результате два первых сегмента становятся одним поли-
номом; то же относится и к последним сегментам.)
О К концам контрольного полигона добавляются две «ложные» точки (подойдут, например, Р ,
и Р;). Кривая по-прежнему рисуется от точки Рй до точки Рр однако теперь в этих двух точках
можно вывести выражения для скоростей.
11.10.7. Прохождение параболы через контрольные точки
Для нахождения наклона в точке Рк можно найти единственную параболу, проходящую через три точ-
ки Рк_,, Рк, Рк+ р и вычислить ее скорость в точке Рк (рис. 11.49). Найдите формулу для этой скорости по
любым трем контрольным точкам.
748
Глава 11. Создание кривых и поверхностей
Скорость в точке Рк
Парабола, проходящая
через заданные точки
Рис. 11.49. Задание скорости с помощью параболы, проходящей через три точки
11.10.5. Интерактивное задание касательных векторов
В некоторых программах рисования (CAGD) дизайнеру предлагаются видимые «рукоятки» для зада-
ния касательных векторов, как показано на рис. 11.50. Пользователь размещает контрольные точки,
после чего рисуется первоначальная интерполирующая кривая. Затем пользователь с помощью мыши
перемещает различные рукоятки, в результате чего соответствующие касательные векторы изменяют-
ся, а новая кривая непрерывно замещает старую. Такая видимая обратная связь позволяет пользовате-
лю быстро отредактировать кривую до желаемой формы.
Рис. 11.50. Интерактивное задание кубических сегментов
11.11. Моделирование криволинейных поверхностей
До сих пор мы занимались вопросами представления и генерирования кривых в дву- и трехмерном
пространстве. Естественно распространить эти идеи на создание криволинейных поверхностей. В гла-
ве 6 нами было рассмотрено множество поверхностей различных типов, таких как линейчатые поверх-
ности, билинейные лоскуты и лоскуты Кунса, а также поверхности вращения. Рассмотрим теперь при-
менение для создания этих поверхностей кривых Безье и В-сплайнов и таким образом разработаем
мощные инструменты для создания обширного множества криволинейных поверхностей.
11.11.1. Линейчатые поверхности на базе В-сплайнов
Особенно легко работать с линейчатыми поверхностями. Напомним из раздела «Линейчатые поверх-
ности» главы 6. что линейчатая поверхность задается двумя «концевыми кривыми» Рн(и) и Р^и), кото-
рые при каждом значении и соединяются прямой линией. Следовательно, параметрическим выражени-
11.11. Моделирование криволинейных поверхностей
749
ем для линейчатой поверхности является линейная интерполяция (или «твининг») между соответству-
ющими точками двух кривых. Для удобства повторим уравнение (6.35), согласно которому мы имеем:
Р(и, ») = (!- o)P0(w) + vPt(u). (11.86)
Рис. 11.51. Линейчатая поверхность на базе кривых Безье
Расширение здесь заключается в том, что в качестве функций P0(w) и Pt(w) выбираются В-сплайн
кривые или кривые Безье. На рис. 11.51 показана линейчатая поверхность, обе концевых кривых кото-
рой, Р (и) и P,(w), являются кубическими кривыми Безье. Кривая Р0(м) базируется на четырех конт-
рольных точках Ро°, Д°, Р2°, Р3°, а кривая P,(w) — на четырех контрольных точках Ро', Р', Р,1, Р3'. Используя
уравнение (11.25) для кривой Безье, мы можем написать выражение для такой поверхности в виде:
Р(м) = + (11.87)
к =0
Посмотрим, как ведет себя эта поверхность. Ее u-контуры являются прямыми линиями, соединяю-
щими соответствующие точки двух кривых Безье. Что касается ^-контуров, то это кривые Безье, конт-
рольные точки которых являются «твинами» (1-^)РА° + контрольных точек двух кривых Безье.
В качестве концевых кривых могут быть также использованы NURBS-кривые или В-сплайн кривые;
их даже можно задавать на других узловых векторах, если только их параметр и изменяется в том же
самом промежутке.
Столь же просто получить все частные случаи линейчатых поверхностей, такие как конусы и
цилиндры. Например, какой вид примет поверхность, если функция Р0(и) является версией функции
Р^и), перемещенной в пространстве?
11.11.2. Поверхности вращения на базе В-сплайнов
Напомним из раздела «Линейчатые поверхности» главы 6, что поверхность вращения формируется
посредством вращения с заметанием некоторого профиля (profile) C(v) = (Х(ц), Z(v)) вокруг оси г.
Результирующая кривая имеет следующую параметрическую форму:
P(w, ») - (X(»)cos(w), X(»)sin(w), Z(o)). (11.88)
Часто бывает удобно выразить профиль, используя кривые Безье или В-сплайн кривые. Выберем
L + 1 контрольных точек (Хк, Zk) и на базе их сформируем кривую:
(%(ц),г(ц))= Y(Xk,Zk)Nk,m(y). (11.89)
к = 0
На рис. 11.52, а показан профиль кубка, заданный в форме В-сплайн кривой, а также контрольный
полигон. На рис. 11.52, б приводится результирующая поверхность вращения. (Каркасный объект для
данной поверхности вращения создавался так же, как в главе 6, а сама сетка рисовалась при помощи
метода Mesh :: drawO.)
750
Глава 11. Создание кривых и поверхностей
Рис 11.52. Профиль в виде В-сплайн кривой: а) профиль: В-сплайн кривая; 6} кубкообразная поверхность вращения
Пример 11.11.1. Классический чайник
Для создания профилей можно использовать также кривые Безье. На рис. 11.53, а показан профиль кор-
пуса «чайника», впервые сконструированного Мартином Ньюэллом (Martin Newell) [Blinn, 24, Crow, 54].
Корпус чайника изображен на рис. 11.53, б. Профиль корпуса состоит из трех кривых Безье на базе
10 точек, представленных в табл. 11.1. Первая кривая Безье определяется точками 0,1,2,3; вторая —
точками 3,4,5,6, а третья — точками 6,7,8,9. Отметим, что последний сегмент каждой кривой колли-
неарен первому сегменту следующей кривой. Это условие гарантирует, что сопряжение различных
кривых Безье происходит с ^‘-непрерывностью (см. раздел «Плавность движения» данной главы)
Крышка чайника также является поверхностью вращения; она рассматривается в тематическом зада-
нии 11.8.
Таблица 11.1. Данные для профиля корпуса чайника
i X Z
0 1,4 2,25
1 1,3375 2,38125
2 1,4375 2,38125
3 1,5 2,25
4 1,75 1,725
5 2 1,2
6 2 0,75
7 2 0,3
8 1,5 0,075
9 1,5 0
11.11. Моделирование криволинейных поверхностей
751
Рис. 11.53. Профили для корпуса чайника на основе кривых Безье: а) профиль корпуса; 6) чайник
11.11.3. Лоскуты Безье
На рис. 11.51 показан фрагмент (лоскут) линейчатой поверхности на базе двух кривых Безье. Для боль-
шей гибкости проектирования можно заменить линейные u-контуры из уравнения (11.87) на кривые
Безье или В-сплайн кривые. В лоскуте Безье как для и-, так и для w-контуров применяются кривые Безье.
Если, например, u-контуры являются квадратичными кривыми Безье, а о-контуры — кубическими кри-
выми Безье, то соответствующий лоскут Безье может быть представлен в следующем виде:
3 з ( г А
Р(и,у)=^Рк(у)Вук(и) = £ 5*(м)>
(11.90)
где и и v, как обычно, изменяются от 0 до 1. Пример такого лоскута приведен на рис. 11.54. Каждый
а-контур, например при v = v0, является кривой Безье относительно и на базе четырех контрольных то-
чек Pk(v0), которые сами лежат вдоль квадратичных кривых Безье. (Как описывается каждый и-кон-
тур?) Все 12 контрольных точек Pi k образуют контрольный полиэдр (control polyhedron), определяю-
щий форму данного лоскута. Такой способ задания поверхности называется формой тензорного
произведения (tensor product).
Рис. 11.54. Пример лоскута Безье
В общем случае контрольный полиэдр является каркасом (network) из (М + 1)(Z + 1) вершин, а вы-
ражение для поверхности имеет вид:
L М
к » 0 i = 0
(11.91)
752
Глава И. Создание кривых и поверхностей
Для формирования лоскута дизайнер тщательно задает позиции этих вершин и затем при помощи
уравнения (11.91) определяет форму поверхности. В упражнениях ниже рассматривается альтернатив-
ная матричная форма поверхности Безье.
На рис. 11.55 приводится пример бикубического (bicubic) лоскута Безье (здесь L = М = 3) и его
контрольный полиэдр. За дальнейшими подробностями по поводу кривых Безье обращайтесь к работе
[Rogers, 174].
Рис. 11.55. Бикубический лоскут Безье и его контрольный полиэдр
Практические упражнения
11.11.1. Восстановление промежуточной формы
Как составить контрольный полиэдр, используемый в уравнении (11.91), чтобы осуществлялась линей-
ная интерполяция между двумя контрольными полигонами?
11.11.1. Нормали к лоскутам Безье
Используя в уравнении (6.25) параметрическую форму лоскута Безье, выведите (сложное) выражение
для нормального вектора к этому лоскуту. Упростите полученное выражение, насколько это возможно.
При всех ли значениях (и, о) нормальный вектор изменяется непрерывно?
11.11.3. Альтернативная форма лоскута Безье
Следующая форма бикубической (£ - М - 3) поверхности Безье поможет продемонстрировать совмест-
ное поведение ее частей:
(11.92)
Внешние пары векторов и матриц создают полиномы Бернштейна, а внутренняя матрица содержит
геометрию лоскута.
О Сравните уравнение (11.92) с аналогичной формой кривых Безье, определяемой уравнением (11.41).
О Покажите, что уравнение (11.92) идентично уравнению (11.91). Какое уравнение проще приме-
нить для компьютерной программы и почему?
11.11.4. Сшивание лоскутов Безье
Дизайнеру может понадобиться составить сложную форму из нескольких фрагментов поверхности
Безье так, чтобы эти лоскуты плавно стыковались на их общих границах. На рис. 11.56 показаны два
контрольных полиэдра, черный и серый, задающие два лоскута Безье. Для обоих лоскутов использует-
ся уравнение (11.91), причем при генерировании каждого лоскута значения unv изменяются от 0 до 1.
Отличаются только сами контрольные полиэдры. Какие ограничения должен наложить дизайнер
на эти два контрольных полиэдра, чтобы два лоскута соединились «без шва»? Нетрудно заставить два
11.11. Моделирование криволинейныхповерхносгей
753
таких лоскута стыковаться во всех точках вдоль их общей границы: для этого достаточно, чтобы вдоль
границы совпали их контрольные полигоны. Это так, потому что форма «границы» кривой Безье зави-
сит только от граничного полигона контрольного полиэдра. (Посмотрите, что произойдет, если в
уравнении (11.91) положить и = 0.) Поэтому дизайнер выбирает для двух лоскутов одинаковые конт-
рольные полигоны.
Рис. 11.56. Непрерывная стыковка двух лоскутов Безье
Сложнее добиться непрерывности касательной в месте соединения двух лоскутов. Однако если эта
непрерывность будет обеспечена, то будет гарантирована также непрерывность нормали к поверхности
в месте соединения. Один вариант достаточного условия [Faux, 61] приводится на рис. 11.57: каждые
два ребра полиэдров, которые встречаются на границе, например Е и Е1, должны быть коллинеарны.
Однако такое условие может оказаться неудобным для дизайнера. В работе [Faux, 61] рассматривают-
ся другие условия, несколько отличные от этого.
Рис. 11.57. Обеспечение непрерывности касательной по границе
Пример 11.11.2. Создание ручки чайника
Мы уже видели, что корпус и крышка чайника, показанные на рис. 11.53, являются поверхностями
вращения на базе кривых Безье. С другой стороны, и ручка, и носик состоят из четырех лоскутов Безье.
В этом примере мы покажем, как конструируется ручка, а носик рассматривается в тематическом зада-
нии 11.8.
На рис. 11.58, а показан трехмерный вид ручки чайника. На рис. 11.58, б дается сечение этой ручки.
Поверхность ручки симметрична относительно плоскости xz. Верхний и нижний лоскуты находятся на
^-положительной стороне плоскости xz, а зеркальные отражения верхнего и нижнего лоскутов распо-
ложены на ^-отрицательной стороне той же плоскости. Контрольный полиэдр верхнего «^-положитель-
ного» лоскута состоит из четырех прямоугольников, построенных в плоскости xz, которая отодвинута
на расстояние 0,3 внутри положительного октанта xzy. Первый такой прямоугольник использует точ-
ку Ло один раз при у = 0 и второй раз при у = 0,3; аналогично точка Во используется один раз при у = 0,3
и один раз при у - 0.
754
Глава 11. Создание кривых и поверхностей
Весь верхний ^-положительный лоскут содержит следующие 16 контрольных точек:
на базе Ад, Во: (-1,6,0,0,1,875), (-1,6, 0,3,1,875), (-1,5,0,3,2,1), (-1,5,0,0, 2,1);
на базе Л,, В,: (-2,3,0,0,1,875), (-2,3,0,3,1,875), (-2,5,0,3,2,1), (-2,5,0,0,2,1);
на базе Л2, В2: (-2,7,0,0,1,875), (-2,7,0,3,1,875), (-3,0,0,3,2,1), (-3,0,0,0,2,1);
на базе Л3, В3: (-2,7,0,0,1,65), (-2,7,0,3,1,65), (-3,0,0,3,1,65), (-3,0,0,0,1,65).
Аналогично нижний ^-положительный лоскут содержит следующие 16 контрольных точек:
на базе Л3, В3. (-2,7,0,0,1,65), (-2,7,0,3,1,65), (-3,0,0,3,1,65), (-3,0,0,0,1,65);
на базе Л4, В4: (-2,7,0,0,1,425), (-2,7,0,3,1,425), (-3,0,0,3,1,2), (-3,0,0,0,1,2);
на базе Л5, В5: (-2,5,0,0,0,975), (-2,5,0,3,0,975), (-2,65,0,3,0,7875), (-2,65, 0,0,0,7875);
на базе Л6, В6: (-2,0,0,0,0,75), (-2,0,0,3,0,75), (-1,9,0,3,0,45), (-1,9,0,0, 0,45).
В тематическом задании 11.8 вам предлагается с помощью этих данных написать программу рисо-
вания чайника с различных точек зрения.
Рис. 11.58. Конструирование ручки чайника: а) ручка чайника; 5) сечение ручки и ее контрольного полиэдра
11.11.5. В-сплайн лоскуты
Вместо полиномов Бернштейна в форме тензорного произведения можно использовать В-сплайн функ-
ции — для обеспечения большего локального контроля при проектировании поверхностей. Уравнение
имеет следующий вид:
РЕ Р>.>N>.* («К(11-93)
i=0 *=0
где N. т(и) и N^n(v) — базисные В-сплайн функции (возможно, различных порядков), задаваемые урав-
нением (11.58). Обычно для обеих В-сплайн форм берется стандартный узловой вектор, так что углы
полиэдра интерполируются точно. Замкнутые поверхности (по и и/или по v) будут образованы в том
случае, если контрольные точки дублируются или используется периодическая форма, подобная фор-
ме из уравнения (11.66). Контрольный полиэдр состоит из (L + 1)(М + 1) контрольных точек, а и и v
изменяются от нуля до максимального значения узла в соответствующих узловых векторах. Удач-
ным выбором являются кубические В-сплайны (для которых т = п = 4). В этом случае нет ограничений
на число контрольных точек, в отличие от кривых Безье, где число контрольных точек влияет на
порядок полиномов. С помощью кубических В-сплайнов можно формировать чрезвычайно сложные
поверхности. Как и прежде, для создания поверхности желаемой формы дизайнер должен выбрать
узловой полиэдр.
11.11. Моделирование криволинейных поверхностей
755
а б
Рис. 11.59. Пример В-сплайн поверхности
На рис. 11.59 приводится пример В-сплайн поверхности, периодической по одному из параметров
(см. ниже приведенные упражнения). На рисунке 11.59, а показан контрольный полиэдр, а также и- и
о-контуры на поверхности. На рисунке 11.59, б показан другой вид, откуда становится ясно, что данная
поверхность не является поверхностью вращения. Для получения поверхности вращения нужно ис-
пользовать NURBS-поверхность, которую мы рассмотрим позднее.
Практические упражнения
11.11.4. Периодические В-сплайн поверхности
Скорректируйте уравнение (11.93) для случая, когда поверхность является периодической по и. Для вы-
полнения этого задания может оказаться полезным уравнение (11.66). Какие узловые векторы подой-
дут здесь для двух видов В-сплайнов?
11.11.6. NURBS-поверхности
В разделе «Рациональные сплайны и NURBS-кривые» мы вкратце рассмотрели кривые на базе рацио-
нальных параметрических В-сплайнов. Как видно из уравнения (11.68), форма таких кривых зависит
от набора контрольных точек и от набора весов wt. Эти параметры выбираются дизайнером для получе-
ния желаемой формы искомой кривой.
Распространим понятие NURBS-кривых на NURBS-поверхности, для чего сформируем тензорное
произведение, аналогично тому, как мы делали для В-сплайнов в уравнении (11.93) [Tiller, 196, Piegl, 166]:
Р(и,г>) = ----------------. (11.94)
I=s0*a0
Для контроля над формой поверхности дизайнер задает контрольный полиэдр на базе контрольных
точек Рк к, а также веса да. k. Как и в случае В-сплайн кривых, если все веса одинаковы, то поверхность
упрощается и становится В-сплайн поверхностью из уравнения (11.93). (Проверьте это!)
Как уже рассматривалось ранее, у NURBS-поверхностей имеется два основных преимущества.
1. При правильно выбранных контрольных точках и весах контуры P(w, v) являются в точности
квадратичными поверхностями, в отличие от нерациональных В-сплайн лоскутов, контуры ко-
торых могут только приближаться к истинным квадратичным поверхностям.
756
Глава И. Создание кривых и поверхностей
2. NURBS-поверхности инвариантны относительно проективных преобразований (projective
transformations). Такая инвариантность означает, что для рисования перспективной проекции
NURBS-лоскута достаточно найти перспективную проекцию каждой из его контрольных точек,
каким-либо способом подобрать веса, а затем применить уравнение (11.94). В отличие от этого
нерациональные В-сплайн лоскуты инвариантны относительно аффинных, но не проективных
преобразований.
Благодаря их общности и гибкости NURBS-поверхности стали пользоваться популярностью у ди-
зайнеров кривых и поверхностей. Поскольку В-сплайны являются частным случаем NURBS-поверх-
ностей, можно использовать единый алгоритм для создания обширного семейства поверхностей. По-
этому дизайнеру вместо инструментария, состоящего из большого числа различных алгоритмов для
создания кривых, потребуется всего один метод.
Формирование часто используемых NURBS-поверхностей
Семейство NURBS-поверхностей включает в себя невероятное разнообразие форм, причем в него вхо-
дят как частные случаи некоторые формы, уже рассмотренные в этой главе.
Приведем примеры этого семейства.
О Линейчатые поверхности. Два ребра являются NURBS-кривыми по и; образующие также явля-
ются NURBS-кривыми первого порядка по V. На рис. 11.60, а приводится пример каркасной ли-
нейчатой поверхности.
О Экструзивные поверхности. Призматическая форма определяется NURBS-кривой по параметру и;
ее прямолинейные стороны образованы NURBS-кривыми первого порядка по V. Призма является
частным случаем линейчатой поверхности, когда обе концевые кривые имеют одинаковую форму.
О Поверхности вращения. Их профилем является NURBS-кривая, лежащая в плоскости хг, круго-
вые поперечные сечения, параллельные плоскости z = 0, используют способность NURBS-кривой
создавать истинные конические сечения. Пример такой поверхности показан на рис. 11.60, б.
О Квадратичные поверхности. В качестве профилей квадратичных поверхностей вращения ис-
пользуются конические сечения. При помощи аффинного преобразования можно деформировать
NURBS-поверхность так, чтобы она перестала обладать круговой симметрией.
Рис. 11.60. Пример NURBS-поверхностей
Обратите внимание, что единственный инструмент NURBS-дизайна оказался достаточно гибким
для того, чтобы сформировать все столь разнообразные поверхности. Тематическое задание 11.10 по-
священо подробностям проектирования и построения таких поверхностей.
Разработано множество других технологий для определения поверхностей и оперирования ими. Вот
несколько книг, в которых рассматриваются такие подходы: [Bartels, 14; Coons, 48; Farin, 60; Faux, 61;
Mortenson, 143].
11.12. Резюме
757
Практическое упражнение
11.11.5.Формирование базовых поверхностей
Объясните, как при помощи NURBS-поверхностей можно создать каждую из следующих поверхностей:
О круговой цилиндр;
О круговой конус;
О плоский лоскут;
О сфера.
За подробностями обращайтесь к тематическому заданию 11.10. Можно ли создать произвольный
лоскут Кунса?
11.12. Резюме
В данной главе мы рассмотрели несколько методов представления сложных кривых и поверхностен и
манипулирования ими. Две основных области применения таких кривых — это их визуализация в гра-
фическом приложении и моделирование движения объектов, например движение камеры при анима-
ции. Большинство наших разработок основывалось на параметрическом представлении кривой, кото-
рое впервые было описано в главе 3. Параметрическая форма является более естественной, чем неявные
уравнения, в тех случаях, когда приходится рисовать кривые, самопересекающиеся в некоторых точках
или имеющие вертикальный участок.
Среди других рассмотренных нами важных свойств — скорость кривой и нормальный вектор к
кривой в каждой ее точке. Было определено понятие «гладкости» и продемонстрированы ее топкости.
Например, 1-гладкая кривая имеет непрерывную скорость (то есть производную по параметру Z) по-
всюду вдоль своей траектории, однако если при параметризации скорость в какой-нибудь точке обра-
щается в нуль, где направление кривой меняется скачкообразно, то такая кривая по-прежнему остается
1 -гладкой, хотя в геометрическом смысле образует угол. Для описания кривых, не имеющих углов, было
введено понятие G’-непрерывности. Были исследованы различные семейства кривых. В их числе были
рассмотрены конические сечения, кривые на базе полиномов, а также на базе отношения полиномов.
В главе также рассматривался вопрос о формировании плавно изменяющихся кривых с помощью
набора контрольных точек. Этот подход является основным в задачах компьютерного геометрического
дизайна (CAGD). Дизайнер может задать небольшое количество точек, которые при различных числен-
ных сочетаниях выступают как исходные данные при создании формы кривой. Подчеркнуто различие
между кривыми, интерполирующими эти контрольные точки, и кривыми, которые только аппрокси-
мируют их. В любом случае из небольшого набора контрольных точек с помощью определенного алго-
ритма формируется бесконечное множество точек кривой, по одной для каждого значения параметра t.
Первыми были определены кривые Безье — по причине их простоты. Происхождение этих кривых
связано с итерационным процессом твикинга (процесс де Кастельо), что вносит в их свойства большую
степень интуитивности. Оказалось, что кривые Безье обладают значительным ассортиментом полез-
ных свойств, что делает их форму предсказуемой и помогает дизайнеру, когда он или она задают конт-
рольные точки.
Кривые Безье являются полезными во многих задачах конструирования, однако они не обеспечива-
ют локального контроля, поскольку входящие в них полиномы Бернштейна имеют поддержку на протя-
жении всего промежутка изменения параметра. Еще одна сложность состоит в том, что порядок базисных
полиномов возрастает по мере увеличения числа контрольных точек. Это обстоятельство приводит к
«сокращению» предполагаемых изменений и может сделать кривые более сложными и менее устойчи-
выми с вычислительной точки зрения. Поэтому нами был рассмотрен более широкий класс стыковоч-
758
Глава И. Создание кривых и поверхностей
ных функций на основе сплайнов — кусочных полиномов, соединяемых таким образом, что производ-
ные различных порядков остаются повсюду непрерывными. Базисные функции особого семейства —
В-сплайны — способны генерировать сплайн произвольного вида и имеют наименьшую поддержку в
классе таких форм. Поэтому они предоставляют дизайнеру наибольшую степень локального контроля
и в то же время обладают всеми полезными свойствами функций Безье. При увеличении порядка поли-
номов В-сплайнов до совпадения их с числом используемых контрольных точек В-сплайны превраща-
ются в полиномы Бернштейна.
Еще большая степень контроля над формой кривой обеспечивается при использовании NURBS-кри-
вых. Эти кривые сложнее, чем кривые Безье или В-сплайны, однако они включают В-сплайны как частный
случай и способны в точности представлять конические сечения. Программная среда CAGD, поддер-
живающая NURBS-алгоритм, предоставляет дизайнеру единое универсальное средство для создания
огромного разнообразия кривых различных форм.
Мы также рассмотрели алгоритмы для принудительного прохождения кривой через заданные конт-
рольные точки, вместо обычного приближения к ним. Мы уделили особое внимание кривым на основе
кусочных кубических полиномов и разработали такие условия, связывающие различные коэффициен-
ты, чтобы кривая не просто интерполировала точки, но также имела определенную скорость в каждой
точке сопряжения. Эта скорость может задаваться пользователем с целью обеспечить большую глад-
кость в точках соединения или исходя из локальной геометрической информации о соседних конт-
рольных точках. Могут вводиться дополнительные параметры, такие как натяжение и смещенность,
которые предоставляют пользователю возможность корректировать окончательную форму кривой.
В случае В-сплайнов используется другой подход к интерполяции точек: обычно кривая должна
проходить только через первую и последнюю контрольные точки. Хитрость состоит в том, чтобы
вычислить второй набор контрольных точек так, чтобы базирующаяся на них В-сплайн кривая про-
ходила через каждую из исходных контрольных точек. Этот подход рассматривается в тематическом
задании 11.6.
Мы распространили технологии дизайна кривых на создание поверхностей различных видов, вклю-
чая линейчатые поверхности, поверхности вращения и квадратичные поверхности. Мы рассмотрели
конструирование поверхностей с использованием функций Безье, В-сплайн функций, в том числе
рациональных В-сплайн функций. Лоскуты Безье можно генерировать также посредством развертки
(с заметанием) в пространстве кривой Безье переменной формы. Каждая точка перемещаемой кривой
Безье движется по траектории, которая сама является кривой Безье. Лоскуты Безье могут сопрягаться
между собой, если их контрольные полиэдры удовлетворяют определенным условиям. В-сплайн по-
верхности предоставляют дизайнеру большую гибкость: поскольку порядок входящих полиномов не
увеличивается с ростом числа контрольных точек, то с их помощью можно формировать чрезвычайно
сложные поверхности.
Наиболее обобщенным подходом являются NURBS-поверхности, которые обеспечивают дополни-
тельную степень гибкости при их конструировании, предоставляя дизайнеру возможность варьирования
набора весов с целью изменения формы лоскута. NURBS-поверхности инвариантны как к аффинному,
так и к проективному преобразованиям. Кроме того, многие другие поверхности могут быть сведены к
NURBS-поверхностям, поэтому дизайнер, вооруженный алгоритмом построения NURBS-поверхнос-
тей, может формировать и многие другие виды поверхностей.
В данной главе мы только затронули основы конструирования поверхностей. К настоящему времени
разработано множество вариаций этих технологий, и целый ассортимент таких методов часто включает-
ся в пакеты по компьютерному дизайну. Дизайнер может выбирать из множества методов и последова-
тельно настраивать создаваемые им (ею) формы — до тех пор, пока все цели дизайна не будут достигну-
ты. Некоторые формы, такие как крыло самолета или корпус парусной шлюпки, формируются исходя
из сложного сочетания теории, эстетики, интуиции и опыта.
11.13. Тематические задания
759
11.13. Тематические задания
Тематическое задание 11.1. Попурри из интересных
параметрических кривых
Уровень сложности II.
Обобщение эллипса. В параметрическом представлении эллипса фигурирует один синус и один
косинус. Можно сформировать интересное семейство кривых, если наложить несколько эллипсов, ко-
торые пробегаются с различными скоростями. Такое «суммирование гармоник» напоминает графи-
ки рядов Фурье, которые встречались нам в главе 3, однако теперь это осуществляется сразу в двух
измерениях. Начнем с двух членов, а потом обобщим. Рассмотрим семейство кривых, описываемое
уравнением:
x(f) = X,cos(2n t) + X2cos(27tfo);
y(t) = y(sin(2n£) + Y2sin(2nkt). (11.95)
Первый член в каждой формуле представляет собой эллипс, к которому добавлен второй допол-
нительный («piggyback») эллипс, пробегающий свою траекторию в k раз быстрее. При изменении t от О
до 1 первый эллипс пробегается один раз, в то время как второй — k раз. Если k — целое, то фигура
будет в точности замкнутой. Напишите программу, рисующую такие периодические фигуры по вво-
димым в нее значениям Xv Xv У(, Х2, k. Обобщите задачу, добавив в x(t) и y(t) больше членов.
Огибающая окружности. Отметим точку Р на куске нити, намотанной на ручку швабры. Держа лен-
ту натянутой, размотаем ее, поворачивая ручку швабры рукой. Траектория, которую опишет точка Р, —
это спираль, известная как «огибающая окружности». Нить, соединяющая окружность (ручку швабры)
с точкой Р, является касательной к окружности. Очевидно, что эта касательная всегда перпендикуляр-
на к спирали. Кроме того, последовательные витки спирали параллельны друг другу и отстоят друг от
друга на одно и то же расстояние. (Чему равно это расстояние?) Семейство таких спиралей формиру-
ется путем вращения фигуры (или выбором различных точек Р на нити). Каждая спираль ортогональ-
на ко всем прямым, касательным к окружности. Параметрическая форма этой кривой имеет вид:
x(t) = cos(2nt) + 2ntsin(2nt);
y(t) = sin(2nt) - 2ntcos(2nt). (11.96)
Напишите программу, которая рисует огибающие окружности.
Рис. 11.61. Взлетающий джинн
Другие синусоидальные кривые. Небольшие изменения в выражениях для x(t) и y(t) из предыду-
щего упражнения могут привести к сильно различающимся формам. Например, кривая, изображенная
на рис.-11.61 (разработанная профессором Робертом Везером (Robert Weaver) из колледжа Mount
Holyoke, South Hadley, Massachusetts), получена из следующих функций:
x(t) = cos(t) + sin(8t);
y(t) = 2sin(t) + 7sin(7t). (11.97)
760
Глава И. Создание кривых и поверхностей
Напишите подпрограмму, которая рисует эту кривую; крбме того, исследуйте различные ее вариа-
ции. При каких ограничениях па аргументы тригонометрических функций данная кривая всегда будет
замкнутой (периодической)?
Фигуры Лиссажу (Lissajous). Если частоты двух синусоид различны, то возникает новая вариация
эллипса. Пусть, например,
x(t) = cos(2nMt + angle);
y(t) = sin(2nM), (11.98)
где M и N— новые частоты, a angle — «сдвиг фазы» между двумя компонентами. Такие формы носят
название фигур Лиссажу, их часто можно увидеть в осциллографе при тестировании электрических
схем. Напишите программу, которая принимает М, N и angle в качестве параметров и отображает на
дисплее фигуры Лиссажу. Поэкспериментируйте с большими приращениями по t между выбранными
на кривых точками и понаблюдайте получающееся разнообразие форм. Если после того, как нарисова-
на каждая линия, менять местами значения переменных х и у, то можно получить интересные симмет-
ричные фигуры.
Тематическое задание 11.2. «Эллиптипул»
Уровень сложности III.
В тематическом задании 4.4 мы рассматривали отражение лучей от стенок полигональной камеры.
Интересно рассмотреть камеры другой формы. Столы эллиптической формы для игры в пул* поступили
в продажу в Соединенных Штатах в 1964 году под названием «эллиптипул» ( «Elliptipool») [Gardner, 75,
Steinhaus, 191]. Можно имитировать эллиптипул с помощью отражения лучей от внутренности эллипти-
ческой камеры, как показано на рис. 11.62. Исходный луч задается в форме S+ct, причем стартовая точка S
расположена внутри эллипса. Задается точка Р, в которой луч ударяется об эллипс, а также направление г
отраженного луча. С целью «отслеживания» этого луча от точки S к точке Р рисуется прямая. Следующий
луч задается в форме Р + rt, и весь процесс повторяется. Пусть эллипс имеет следующую неявную форму:
а луч задан в форме S + ct. Найдем точку пересечения луча с эллипсом. Если данный луч вообще когда-
либо пересекается с эллипсом, то это должно произойти при некотором значении t, когда точка 5 + ct
лежит на кривой F(P) = 0. Это приводит к условию F(5 + ct) = 0. Тогда для эллипса мы имеем следую-
щее уравнение:
I а J I b J
которое является квадратным относительно t. Квадратные уравнения легко поддаются решению и име-
ют нуль, одно или два решения, что соответствует для нас следующим событиям.
О Нет решений: луч минует эллипс.
О Одно решение: луч касается эллипса.
О Два решения: луч входит в эллипс и затем выходит из него.
Если начало луча лежит внутри камеры, то одно из решений положительное, а другое отрицатель-
ное (почему?) Возьмем положительное решение и назовем его thit. Требуется найти направление отра-
женного луча в точке соударения. Образуем из выражений уравнения (11.3) x(t) = acos(t) и y(t) = Z>sin(t)
нормальный вектор (-Z>cos(t), -asin(t)), что в терминах х и у выглядит как (-Ьх/а, -ау/b). Поскольку
нам нужно только направление нормали, то удобнее изменить масштаб и представить формулу в виде
1 Пул (pool) — род игры в бильярд. — Примеч. пер.
11.13. Тематические задания
761
(-Z>2x, -а2у). Нам требуется внутренняя нормаль, так как луч отражается от внутренней стенки эллипса.
Рассматривая рис. 11.62, можно увидеть, что х- и ^-компоненты внутренней нормали отрицательны при
положительных х и у, поэтому именно выражение
п = (~Ъ2х, -а2у) (11.99)
является направлением внутренней нормали. Направление отраженного луча г можно определить под-
становкой уравнения (11.99) в уравнение (4.27).
Рис 11.62. Имитация эллиптипула
Имитация эллиптипула демонстрирует некоторые особенности его поведения: для луча существует
только три типа возможных траекторий [Steinhaus, 191].
О Если луч проходит через один из фокусов эллипса, то после отражения он проходит через второй
фокус. Это обусловлено, конечно, свойством отражения эллипсов: луч, исходящий из одного фо-
куса, всегда отражается от эллиптической стенки и направляется к другому фокусу. Такой луч
всегда будет проходить через противоположный фокус. После нескольких прохождений его тра-
ектория будет неотличима от оси х.
О Если начальная траектория луча не проходит между фокусами, то луч не пройдет между ними
никогда. Вместо этого он будет двигаться по траекториям, касательным к эллипсу меньшего раз-
мера с теми же самыми фокусами, как показано на рис. 11.63.
Рис. 11.63. Лучи, касательные ко второму эллипсу
О Если луч при первом прохождении проходит между фокусами, он будет описывать бесконечную
траекторию, которая никогда не приблизится к фокусам больше, чем гипербола с теми же фоку-
сами, как показано на рис. 11.64.
Напишите программу, имитирующую эллиптипул, и поупражняйтесь с ней. Пользователь каким-
либо способом задает начальное положение и направление луча, после чего траектория луча прослежи-
вается на протяжении большого числа отражений. Пусть пользователь задает и способ прохождения
луча относительно фокуса. (Имейте в виду, что в этом случае ошибки округления могут привести к
непредсказуемым эффектам. Как можно нейтрализовать действие такой ошибки?) Пусть луч изменяет
762
Глава 11. Создание кривых и поверхностей
свой цвет таким образом, чтобы текущая траектория луча выделялась на фоне заполнения экрана
старыми траекториями. Поэкспериментируйте с эллипсами, имеющими различные эксцентриситеты,
включая круглые столы для пула.
Рис. 11.64. Лучи, касательные к гиперболе
Дополнительное задание. Расширьте условия эксперимента и поместите внутрь стола препятствия
круглой или другой формы (например, эллиптической). Составят ли в этом случае траектории лучей
какой-нибудь известный узор?
Дополнительное задание. Повторите эксперимент, задав в качестве формы стола суперэллипс. Поду-
майте, как вычислить соударения луча и стены, а также внутреннюю нормаль к стене в любой ее точке.
Тематическое задание 11.3. Кривые Безье
Уровень сложности II.
Напишите программу, которая принимает последовательность контрольных точек, вводимую пользо-
вателем с помощью мыши, и рисует на базе этих точек кривую Безье. Точки на кривой вычисляются
для близких значений t и соединяются прямолинейными отрезками. Выполните свою программу при
различных количествах контрольных точек. Обратите внимание на замедление вычислений при боль-
шом числе контрольных точек, поскольку в этом случае степень полиномов возрастает.
Тематическое задание 11.4. Генератор квадратичной
сплайн-кривой
Уровень сложности II.
Уравнение (11.52) задает кривую в виде взвешенной суммы стыковочных функций g(t - k), а именно:
в
^(0=
к =0
где g(t) — квадратичная сплайн-функция, определяемая уравнением (11.49). Напишите и выполните
программу, которая предоставляет пользователю возможность разместить с помощью мыши последо-
вательность контрольных точек РА, после чего рисует кривую V(t). При выполнении задания полезно
создать функцию double g(double t), которая возвращает значение v(t) и, в частности, возвращает 0,
если t лежит за пределами промежутка [0,3].
Тематическое задание 11.5. Создание редактора сплайн-кривых
Уровень сложности III.
Создайте и выполните программу, которая предоставляет пользователю возможность создать с по-
мощью мыши контрольный полигон Р. При запросе программа рисует В-сплайн кривую, определяе-
11.13. Тематические задания
763
мую полигоном Р. В программе должны быть реализованы следующие команды, выполняемые по на-
жатию соответствующих клавиш на клавиатуре (например, «Ь» для begin (начать), «с!» для delete (уда-
лить) ит.д.):
О b)egin: начать новый контрольный полигон Р;
О d)elete: удалить точку из Р, ближайшую к отмеченной;
О m)ove: переместить в новое положение отмеченную точку из Р;
О r)efresh: нарисовать Р;
О o)rder (Т..’9’): нарисовать сплайн кривую заданного порядка на базе Р;
о cHosed (‘-Г,..., ‘-9’): нарисовать замкнутую В-сплайн кривую на базе Р;
о e)rase: очистить экран;
о q)uit: выйти из программы.
Дополнительное задание 1. Поддержка нескольких контрольных полигонов. Расширьте свою про-
грамму так, чтобы в ней можно было одновременно создавать на дисплее до 10 контрольных полигонов
и по желанию редактировать каждый из них.
Дополнительное задание 2. Могут ли В-сплайны образовывать окружности? Поэкспериментируй-
те с четырьмя и с восемью контрольными точками, лежащими на окружности, и проверьте, насколько
точно аппроксимирует эту окружность замкнутая кубическая В-сплайн кривая. Подберите подходя-
щую численную оценку невязки между кривой и окружностью и попробуйте с помощью различных
конфигураций получить наилучшую кривую.
Дополнительное задание 3. Преобразования В-сплайн кривых. Расширьте свою программу так,
чтобы пользователь мог задать аффинное преобразование (возможно, из заранее составленного спис-
ка), а также контрольный полигон, после чего на базе преобразованного полигона должна рисоваться
В-сплайн кривая.
Тематическое задание 11.6. Интерполяция контрольных
точек В-сплайнами
Уровень сложности III.
Кривая на базе В-сплайн стыковочных функций и стандартного узлового вектора интерполирует
только первую и последнюю контрольные точки. Можно, однако, предварительно обработать конт-
рольные точки так, чтобы В-сплайн кривая интерполировала каждую из них. При этой предваритель-
ной обработке из заданного набора контрольных точек создается новый их набор. Особенность этого
нового набора заключается в том, что сформированная на его базе В-сплайн кривая проходит через все
точки исходного набора.
Рассмотрим основную идею этого метода на конкретном примере: совокупность из шести заданных
точек уй у5 для равноотстоящих значений t интерполируется кубическими В-сплайнами, как показа-
но на рис. 11.65, а. Вместо применения стандартного узлового вектора узлы сделаны равноотстоящи-
ми, так что функция NQi(t) начинается при t = 0 и достигает экстремума при t = 2, функция Nt 4(0 начи-
нается при t = 1 и достигает экстремума при t = 3 и т. д. Таким образом, мы пытаемся интерполироватьу0
при t = 2, у, при t = 3 и т. д.
Как показано на рис. 11.65, б, сумма
у(0 =
<=о
не проходит через заданные точки. Причина заключается в том, что поскольку В-сплайн функции
перекрываются, различные члены этой суммы взаимодействуют таким образом, что y(t) не достигает
764
Глава 11. Создание кривых и поверхностей
заданных точек. Для исправления этой ситуации вместо ух используется другой набор значений: с0,...,
с5, так что кривая базируется уже на них, а именно:
i = 0
Рис. 11.65. Попытка интерполяции шести точек кубическими В-сплайнами
Эта кривая интерполирует все точки как показано на рис. 11.65, б. Мы теперь должны найти та-
кой набор значений с., чтобы это условие действительно соблюдалось. Это может быть сделано посред-
ством решения системы линейных уравнений. Условия интерполяции шести точек следующие:
Р(2) - Уо, Р@) = yv Р(4) - у2.р(7) - уу
Поскольку В-сплайн функции при целых значениях t принимают только значения 0, 1/6 и 4/6, то
шесть указанных выше условий принимают вид:
4с0 + q - буv
с0 + 4с, + с2 - 6г/р
с, + 4с2 + с3 = 6у2, (11.101)
с. + 4с- ” бу,.
Эти уравнения почти идентичны уравнениям (11.76) и (11.77), поэтому их можно решить метода-
ми, описанными в разделе 11.10.3.
Все эти идеи легко могут быть распространены на любое число заданных точекуй, ухyL, для любо-
го нужного L. Напишите функцию
void adjust (double у[]. double с[]. int L)
которая по заданному массиву у[] создает массив с[].
Для интерполяции точек pt - (г, у) описанный процесс выполняется один раз для х-компонентов и
один раз для ^-компонентов, в результате чего создаются массивы x_new[] и y_new[]. Тогда интерполи-
рующая кривая задается формулой:
р(о =
i = o
где e (x_new[], y_new[]). Пример такой кривой приведен на рис. 11.66.
11.13. Тематические задания
765
Рис. 11.66. Пример двумерной интерполяции В-сплайнами (с разрешения Tuan Le Ngoc)
Напишите программу, которая позволяет пользователю задавать с помощью мыши последова-
тельность из (L + 1) контрольных точек, а затем рисует интерполирующую кривую на базе кубических
В-сплайнов. Поэкспериментируйте с различными значениями L.
Дополнительное задание. Расширьте свою программу так, чтобы она рисовала замкнутые кривые, ин-
терполирующие контрольные точки. Какие изменения должны быть для этого сделаны в уравнении (11.101)?
Тематическое задание 11.7. Интерполяция кубическими
полиномами
Уровень сложности III.
Напишите программу, которая позволяет пользователю задавать с помощью мыши последователь-
ность из (L +1) контрольных точек, а затем рисует интерполирующую кривую на базе кубических поли-
номов. Скорости на внутренних стыках задаются с помощью метода Кочанека—Бартелса при опреде-
ленных значениях параметров натяжения, смещенности и непрерывности. Два оставшихся условия на
кубические коэффициенты определяются исходя из требования, чтобы вторые производные на конце-
вых контрольных точках равнялись нулю.
Предоставьте пользователю возможность изменять натяжение, смещенность и непрерывность каж-
дой из внутренних контрольных точек посредством нажатия клавиш. Например, пользователь может
отметить мышью требуемую контрольную точку и нажать клавишу «V» для уменьшения значения на-
тяжения в этой точке на некоторую небольшую фиксированную величину, а клавишу «V» — для соот-
ветствующего увеличения натяжения. Пользователь может нажать клавиши <<Ь» или «В» для измене-
ния смещенности и «с» или «С» — для изменения непрерывности.
Тематическое задание 11.8. Многоуважаемый чайник
Уровень сложности II.
Напишите программу, рисующую средствами OpenGL классический чайник с различных точек зре-
ния. Не используйте GLUT-версию чайника; сформируйте свой собственный чайник из фрагментов
поверхностей.
Таблица 11.2. Данные для профиля крышки чайника
i X Z
0 0 3
1 0,8 3
2 0 2,7
3 0,2 2,55
4 0,4 2,4
5 1,3 2,4
6 1,3 2,25
Чайник состоит из четырех основных частей. Корпус (body) является поверхностью вращения, про-
филь которой состоит из трех кривых Безье в плоскости хг, как описано в разделе «Поверхности враще-
766
Глава 11. Создание кривых и поверхностей
ния на базе В-сплайнов». Ручка (handle) состоит из четырех лоскутов Безье, как описано в разделе
«Лоскуты Безье». Крышка (lid) — это поверхность вращения, профиль которой описывается двумя кри-
выми Безье (рис. 11.67), а данные для нее приведены в табл 11.2. Носик (spout), подобно ручке, состоит
из четырех лоскутов Безье. На рис. 11.68, а показан носик в разрезе, а также сечение контрольного
полиэдра для лоскутов. Как и ручка, поверхность носика симметрична относительно плоскости xz.
Весь верхний у-положительный лоскут содержит следующие 16 контрольных точек:
на базе С,,, Do: (1,7,0,0,0,45), (1,7,0,66,0,45), (1,7,0,66,1,275), (1,7,0,0,1,275);
на базе Ср £>,: (3,1,0,0,0,675), (3,1,0,66,0,675), (2,6,0,66,1,275), (2,6,0,0,1,275);
на базе С2, £>2: (2,4,0,0,1,875), (2,4,0,25,1,875), (2,3,0,25,1,95), (2,3,0,0,1,95);
на базе С3, £>3: (3,3,0,0,2,25), (3,3,0,25,2,25), (2,7,0,25,2,25), (2,7,0,0,2,25).
Нижний у-положительный лоскут содержит следующие 16 контрольных точек:
на базе С3, D3: (3,3,0,0,2,25), (3,3,0,25,2,25), (2,7,0,25,2,25), (2,7,0,0,2,25);
на базе С4, £>4: (3,525,0,0,2,34375), (3,525,0,25,2,34375), (2,8,0,25,2,325), (2,8,0,0,2,325);
на базе С5, Ds: (3,45,0,0,2,3625), (3,45,0,1,2,3625), (2,9,0,1,2,325), (2,9,0,0,2,325);
на базе С6, D6: (3,2,0,0,2,25), (3,2,0,15,2,25), (2,8,0,15,2,25), (2,8,0,0,2,25).
Рис. 11.67. Крышка чайника: а) кривая для крышки; б) визуализированная крышка
Рис. 11.68. Конструирование носика чайника: а) носик чайника; б) визуализированный носик
Тематическое задание 11.9. Инвариантность относительно
проективных преобразований
Уровень сложности I.
Данное тематическое задание содержит подробную, шаг за шагом, демонстрацию инвариантности
NURBS-кривых относительно проективного преобразования Т. Опишите каждый из шагов подробно.
11.13. Тематические задания
767
-
Пусть имеется NURBS-кривая, заданная уравнением (11.68), а преобразованию соответствует матрица М
размерностью четыре на четыре, строками которой являются векторы ш(, т2, т3, т4 в указанном порядке.
О Покажите, что после преобразования Т кривая Р(/) из уравнения (11.68), выраженная в одно-
родных координатах, превращается в кривую:
Л'тз> (11.102)
к =0
где Рк = (Рх, Ру, Pz, 1)Г — версия Рк в однородных координатах.
О Покажите, что в обычных координатах уравнение (11.102) приобретает вид:
Г(Р(/)) = —-------z------------------------. (11.103)
1=0
О Покажите, что каждая контрольная точка Рк после преобразования приобретает вид:
Г Рк ш, Рк ш2 Рк ш3 У
чЛт4’ Л т«’ Л т4,
О Покажите, что построение NURBS-кривой с весами vk на базе преобразованных контрольных
точек приводит к следующей кривой:
*=0 ^4 ' m4 'm4 ^4 ‘m4 J
к=0
О Покажите, что последнее уравнение совпадает с уравнением (11.70) в случае, когда веса vk равны
весам wt из уравнения (11.71).
Почему В-сплайны не являются проективно инвариантными? Покажите, что аналогичные выклад-
ки нельзя провести над В-сплайнами.
Распространение на поверхности. Повторите все шаги, подобные вышеприведенным, и покажите,
что NURBS-поверхности также являются инвариантными относительно проективных преобразований.
Тематическое задание 11.10. Рисование NURBS-лоскутов
Уровень сложности II.
О Напишите приложение, рисующее и- и о-контуры NURBS-поверхностей, и поэкспериментируйте
с ним. Ядром такого приложения является функция, вычисляющая точки на поверхности Р(и, v).
Прототип такой функции может выглядеть примерно так:
Point3 nurbsPoint(Points P[][],
// matrix of control points
// матрица контрольных точек
int L, int M,
// # of control pts - (L+1KM+1)
// количество контрольных точек = (L+1)(M+1)
float w[][],
// vector of weights
// вектор весов
768
Глава 11. Создание кривых и поверхностей
float knot[].
// knot vector
// узловой вектор
int m. int n,
// orders of B-splines
// порядки В-сплайнов
float u. v);
// values of parameters u and v
// значения параметров u и v
У
О
b
b
b
a
a
b
a
a
О
b
b
о --------------> X
b b О
a
Рис. 11.69. Проектирование купола
Поэкспериментируйте с контрольным полиэдром, изображенным на плоском рис. 11.69, а, где метка-
ми 0, а или Ь отмечена высота каждой точки над плоскостью ху. На рис. 11.69, б показан пример куполо-
образной (domelike) формы, созданной посредством NURBS-лоскута при определенном подборе весов
и высот а и Ь. Постройте и нарисуйте лоскуты, сформированные таким способом, при задаваемых
пользователем значениях а и Ь. Испробуйте различные способы подбора весов.
1. Все веса одинаковы.
2. Всем точкам нулевой высоты присваивается вес W, а все остальные имеют вес sIT, где значения
коэффициента з задаются пользователем.
3. Примените другие интересные соотношения весов.
Дает ли хотя бы одна из встреченных вами комбинаций купол, близкий к полусфере? Какую кор-
ректировку нужно провести для получения купола, более похожего на полусферу?
Создайте и нарисуйте различные поверхности вращения. Как мы уже видели, поверхность враще-
ния создается путем вращения профильной кривой вокруг какой-либо оси. Пусть наша профильная
кривая лежит в плоскости xz и определена как NURBS-кривая
С(м) = -----------, (11.104)
к =0
построенная на базе набора из (L + 1) контрольных точек Qk. Мы превращаем эту кривую в поверхность
вращения (ее осью вращения является ось г), объединяя ее с окружностями, перпендикулярными оси г.
Окружности также определены как NURBS-кривые, поскольку эти кривые могут формировать точные
конические сечения. Здесь используется NURBS-кривая на базе квадратичных сплайнов с семью конт-
рольными точками, описанная в примере 11.9.2.
Результирующая матрица контрольных точек формируется как внешнее произведение (outer product)
значений контрольных точек для профиля и для окружности, поэтому контрольный полиэдр является
совокупностью квадратов, расположенных параллельно оси ху на различной высоте и имеющих раз-
личные размеры в соответствии с координатами контрольных точек Qk. Попробуйте применить матри-
11.14. Дополнительная литература
769
цу весов, которая также является внешним произведением отдельных весовых векторов. Поэкспери-
ментируйте с различными профильными кривыми, чтобы создать различные поверхности вращения.
По крайней мере один раз возьмите в качестве профиля коническое сечение, вследствие чего поверх-
ность будет квадратичной.
Поэкспериментируйте с формированием экструзивных (линейно протянутых) поверхностей с по-
мощью NURBS-поверхностей. Контур C(w), описанный как NURBS-кривая, развертывается с заметани-
ем в направлении, перпендикулярном к плоскости, в которой он лежит. Прямолинейные стороны обра-
зованы NURBS-кривой первого порядка по v.
Поэкспериментируйте также с линейчатой поверхностью, две криволинейные границы которой явля-
ются NURBS-кривыми по и, а образующие — NURBS-кривыми первого порядка по v.
11.14. Дополнительная литература
В вышедшей довольно давно превосходной книге Фокса и Пратта [Faux, 61] излагаются математиче-
ские основы проектирования кривых и поверхностей. В работе Роджера и Адамса [Rogers, 174] содержит-
ся множество методов и примеров проектирования поверхностей: Фарин [Farin, 60] предлагает четкое
изложение математической теории поверхностей. В работе Бэртелса, Битти и Барски [Barties, 14] рас-
сматриваются различные варианты сплайнов, которые могут использоваться при проектировании кри-
вых и поверхностей, а также описываются их разнообразные свойства. В недавно вышедшей книге под
редакцией Блюменталя [Bloomenthal, 33] содержится несколько прекрасных глав по проектированию
поверхностей, в их числе одна написана Блинном [Blinn] и посвящена поверхностям второго порядка,
а другая принадлежит перу Баджая [Bajaj] и касается неявно определенных фрагментов поверхностей.
25 Ф. Хилл
12
Теория цвета
□ Изучение теории цвета и его цифрового описания.
□ Рассмотрение некоторых стандартов представления цвета.
□ Определение и использование различных цветовых пространств.
□ Описание различных методов уменьшения количества цветов
в изображении.
□ Разработка методов программирования кодовой таблицы цветов.
Цвета и текстуры будут важны для тебя.
Из компьютерных назиданий. Амхерст [Amherst], Массачусетс.
В этой главе рассматривается теория цвета и его представление в компьютерной графике.
В разделе 12.1 «Введение» описаны некоторые тонкости системы человеческого зрения и поставле-
на задача цифрового описания цвета надежным и воспроизводимым способом. В разделе 12.2 «Описа-
ния цветов» рассматривается процесс подбора цветов и представление любого цвета в виде линейной
комбинации трех основных цветов. Здесь же исследуется проблема выбора «хороших» основных цве-
тов. В разделе 12.3 «Международная комиссия по стандартам освещенности» развиваются основные
понятия стандартной хроматической диаграммы, разработанной Международной комиссией по освеще-
нию, и демонстрируется полезность этой диаграммы при вычислении цвета. Кроме того, обсуждается
понятие цветового охвата. В разделе 12.4 «Цветовые пространства» описываются различные цветовые
пространства и предлагаются инструменты для преобразования цвета между различными простран-
ствами. В разделе 12.5 «Квантование цвета» описываются методы, используемые при квантовании цве-
та: уменьшение числа различных цветов в изображении без видимого снижения его качества. Исследу-
ют некоторые подробности метода octree-квантования.
12.1. Введение
В моделях закрашивания, рассмотренных в одной из предыдущих глав, цвета вычисляются посредством
независимых расчетов по трем основным цветам: красному, зеленому и синему. Такой простой подход
работоспособен и совместим с большинством используемых в настоящее время графических дисплеев,
в которых цвет генерируется путем смешения в определенных количествах встроенных красного, зеле-
12.1. Введение
771
ного и синего цветов. Однако цвет как объект намного сложнее этой схемы; цвет зависит от тончайших
взаимосвязей между физикой излучения света и системой глаз — мозг. (Для более подробного озна-
комления с этой системой обращайтесь к книге [Feynman, 62].) С точки зрения написания приложений
по компьютерной графике мы должны ответить на следующие вопросы:
О Как точно описать цвет в терминах чисел?
О Насколько числовое представление цвета соответствует традиционному способу его описания?
О Как сравнивать цвета между собой?
О Какой диапазон цветов способны воспроизводить такие устройства, как дисплей с электронно-
лучевой трубкой (CRT) или цветной принтер?
О Как загружать кодовые таблицы цветов, чтобы получить требуемые цвета?
О Как передать цветовую палитру, если устройство способно отображать только, к примеру, 256 цве-
тов?
Изображения, генерируемые компьютером, должны передавать цвет. Таким образом, нам требуют-
ся инструменты для описания цвета и управления им в приложениях.
Свет — это электромагнитное явление, подобное волнам телевидения, инфракрасному излучению и
рентгеновским лучам. Под светом мы подразумеваем те волны, которые лежат в узкой полосе длин воли
в пределах так называемого видимого спектра. На рис. 12.1 показано положение видимого спектра (для
человека) на полной шкале электромагнитного спектра наряду со спектрами некоторых других обще-
известных явлений. Частота излучения f возрастает на графике слева направо, а длина волны X —
справа налево1 * *. Глаз реагирует на свет с длинами волн примерно от 400 до 700 нанометров (нм).
Ю«
_1_
Видимый свет
106 1 08 1 010 1 012 1 014/ 1018 1 018 1 020 Частота в цикл/секунду
I I I I I I I I /| I ! I I I______________________
। । । 1 I 1 I 1 Г' I 1 Г1' I 1 I 1 I
◄--------- 1018 Ю13 1011 109 107 105 10з ю .1 ю-з
Длина волны I* >К>К ►!< с ►! M-j >К
а нанометрах / \Микроволны\ ультрафиолетовый Гамма-лучи
Радио с амплитудной \ Инфракрасный
модуляцией (AM) \
Радио с частотной
модуляцией (FM), телевидение Рентгеновскиа лучи
Рис. 12.1. Электромагнитный спектр
Устройство глаза
Сетчатой оболочкой глаза является светочувствительная мембрана. Она устилает заднюю часть стенки
глаза и содержит два вида рецепторных клеток: колбочек и палочек. Колбочки (cones) являются
цветочувствительными элементами, каждая из них реагирует на определенный цвет — красный, зе-
леный или синий. В соответствии с трехцветной теорией цвет, который мы видим, является резуль-
татом совместных реакций наших колбочек на красный, зеленый и синий цвета. Каждый глаз содер-
жит от 6 до 7 миллионов колбочек, сконцентрированных в малой области сетчатки, называемой ямкой
(fovea). У каждой колбочки имеется свое нервное окончание, что позволяет глазу различать мельчай-
шие детали. Для детального рассмотрения объекта глаз смотрит прямо на него с целью спроецировать
изображение в ямку.
1 Длиной волны называется расстояние, которое свет проходит за один цикл своего колебания. Длина волны Л и частота/связаны
обратно пропорциональной зависимостью: X - v/f, где v — скорость света в интересующей нас среде. В воздухе (или в вакууме)
v - 300 000 км/с; в стекле свет распространяется со скоростью 65 % от максимальной.
Глава 12. Теория цвета
В противоположность этому палочки (rods) не способны ни различать цвета, ни видеть мелкие детали.
От 75 до 150 миллионов палочек заполняют сетчатку, окружая ямку со всех сторон. Более того, к одно-
му нервному окончанию прикреплено много палочек, что не позволяет различать детали [Gonzalez, 88].
Что же в таком случае делают палочки? Они очень чувствительны к низким уровням освещенности и
способны видеть в такой темноте, которая недоступна колбочкам. Например, ночью лучше всего смот-
реть слегка в сторону от объекта, вследствие чего изображение попадает за пределы ямки. Детали и цвет
не воспринимаются, но по крайней мере видна общая форма объекта (хищник?). И, возможно, чувстви-
тельность нашего периферийного зрения к слабому свету способствовала нашей эволюции.
Некоторые источники света, такие как лазеры, излучают свет почти исключительно с единственной
длиной волны, иначе называемый светом с «чистым спектром». Человек воспринимает свет с длиной
волны 400 нм как фиолетовый, а с длиной волны 620 нм — как красный; все другие чистые цвета нахо-
дятся между этими границами. На рис. 12.2 показано несколько примеров спектральной плотности
(spectral density) 5(Х) (мощность на единицу длины волны) для чистого света, а также общепринятые
названия соответствующих им воспринимаемых цветов.
Спектральная
площадь
Зеленый Оранжевый
\ / Красный
Фиолетовый Синий \ Желтый/ /
—---------1—И-1----“—ш----------X, нм
400 500 600 700
Рис. 12.2. Спектры для некоторых чистых цветов
Свет большинства источников не состоит из единственной длины волны; напротив, он содержит
различные количества энергии непрерывного множества длин волн, и их спектральные плотности
(или просто «спектры») охватывают некоторый диапазон длин волн. На рис. 12.3 приведено несколько
примеров спектров света. На каждом спектре указан цвет, который мы воспринимаем, когда смотрим
на такой свет. Отметим, что белый свет содержит примерно равные количества всех частот, в то время
как энергия красных цветов сосредоточена на более обширном участке длин волн. Серый цвет также
демонстрирует «плоскую» спектральную плотность, однако с меньшей интенсивностью, чем белый. Эти
примеры показывают одну из трудностей цифрового описания цвета, заключающуюся в том, что
огромное разнообразие спектральных плотностей воспринимается как один и тот же цвет. Например,
заданный образец цвета может быть «подобран» с помощью различных форм спектральной плотности
так, что цвет этого образца и любая из этих спектральных плотностей будут неотличимы, если их поме-
стить рядом.
12.2. Описания цветов
Предположим, что мы хотим точно описать цвет по телефону, например, производителю красок или
главному технологу издательской компании. Недостаточно сказать «ярко-голубой цвет яиц малинов-
ки» («а bright robin’s egg blue»); мы должны быть уверены, что слушатель воспримет точную характери-
стику именно того цвета, который мы подразумеваем. Если бы мы знали для своего цвета кривую спек-
тральной плотности, подобную изображенным на рис. 12.3, то мы могли бы попытаться описать его
уровень в примерно дюжине длин волн, однако это весьма затруднительно и выглядит слишком субъек-
тивным, поскольку один и тот же цвет может синтезироваться множеством различных спектральных
12.2. Описания цветов
773
форм. В идеале мы должны были бы произнести несколько чисел, например: «цвет объекта равен 3,24,
1,6, 85, 1,117», после чего были бы уверены, что данный цвет можно воспроизвести по данному описа-
нию в любое время.
Рис. 12.3. Примеры спектров света и воспринимаемые в них цвета
Сколько же чисел необходимо для этого и что означают эти числа? Как ни странно, ответ будет та-
ким: ровно три числа, ибо цветовое восприятие является трехмерным. Однако мы все же должны прий-
ти к соглашению о том, какую «схему кодирования» следует использовать для перевода цветов в числа
и обратно. В последующих разделах мы рассмотрим несколько таких соглашений, после чего обсудим
понятия, стоящие за существующим международным стандартом.
12.2.1. Доминантная длина волны
Один из простейших способов описания состоит в использовании самого факта разнообразия спект-
ров, которые могут воспроизводить один и тот же (воспринимаемый) цвет. При таком подходе задает-
ся спектр очень простой формы, изображенный на рис. 12.4, причем задаются три числа: доминантная
длина волны, насыщенность и яркость. Такой спектр состоит из острого «пика», расположенного на
месте доминантной длины волны (в нашем примере это 620 нм). Расположение доминантной длины
волны (dominant wavelength) определяет оттенок цвета (hue of the color), в нашем случае это красный.
774
Глава 12. Теория цвета
Кроме того, присутствует определенное количество белого цвета, представленное прямоугольным «пье-
десталом», который «разбавляет» красный свет, делая его розовым.
Рис. 12.4. Спектр цвета с использованием доминантной длины волны
Суммарная сила света, называемая его яркостью (luminance), определяется площадью под всем спект-
ром: Е = (D- А)В + AW, где D — интенсивность пика, В — его ширина, А — интенсивность спектра белого
света. (Что обозначено буквой W?) Насыщенность (saturation) света, называемая также его чистотой
(purity), задается в процентах от яркости, которая заключена в доминантном компоненте:
purity = х 100 %. (12.1)
L
Если D = А, то чистота равна нулю, в результате чего наблюдаемый свет является белым, без ма-
лейшей примеси красного. Если А = 0, то белый свет отсутствует и виден чистый красный свет. Свет-
лые (пастельные) цвета содержат большое количество белого и поэтому называются ненасыщенными
(unsaturated). Когда два цвета различаются только оттенком, то глаз способен различить около 128 раз-
личных оттенков. Если же два цвета различаются только насыщенностью, то глаз может различить при-
мерно 20 различных насыщенностей, в зависимости от оттенка.
Понятия насыщенности, яркости и доминантной длины волны полезны при описании цвета, однако
когда речь идет о конкретном цвете, то неясно, как измерять эти величины. Поэтому мы рассмотрим
несколько более эффективных способов описания цвета. Для начала нам требуется метод тестирова-
ния двух цветов на «идентичность». Это приводит нас к проблеме подбора цветов (color matching), кото-
рая является основой при задании любых цветов.
12.2.2. Подбор цветов
Цвета часто описывают, сопоставляя их со стандартным набором цветов и находя среди них наиболее
подходящий. Было составлено множество таких стандартных наборов, они широко используются в кра-
сильном деле и в индустрии печати [Munsell, 144]. Можно также попытаться получить образец цвета
путем сопоставления его с нужной комбинацией некоторых базовых цветов, как показано на рис. 12.5.
Образец цвета со спектральной плотностью 5(Х) проецируется на одну часть экрана, а на другую его
часть выводится пересечение трех основных цветов, имеющих спектральные плотности Л(Х), В(Х) и
С(Х). Наблюдатель подбирает интенсивности а, Ь, с основных цветов до тех пор, пока тестовый цвет
Т(к) - аА(к) + ЬВ(к) + сС(Х) не станет неотличимым от образца, хотя при этом два спектра, 5(Х) и Г(Х),
могут значительно различаться. В таком случае возникает соблазн сказать, что образец цвета состоит
из «суммы» «количеств» а, Ь, с трех основных цветов. Однако какой смысл имеет такая интерпретация?
Существует известная «алгебра» суперпозиции цветов [Feynman, 62]. Предположим, что две спектраль-
ные формы, 5(Х) и Р(Х), воспринимаются как один и тот же цвет; этот факт мы понимаем как равенство
S“P. Теперь добавим к двум имеющимся цветам третий цвет N, для чего наложим на оба спектра спектр
N(X). Экспериментально доказано, что получившиеся новые цвета по-прежнему будут неразличимы!
12.2. Описания цветов
775
, Образец цвета
/ S(X)
1 аА(Х) + Ьб(Х) + сС(Х)
Рис. 12.5. Подбор цветов с использованием суперпозиции базовых цветов
Вслед за символом «=», означающим неразличимость двух цветов, определим также для цветов сим-
вол «+>> так, чтобы запись S + N означала цвет, наблюдаемый при сложении спектров S(X) и N(k). Тогда
вышеупомянутый экспериментальный факт может быть записан в следующей форме:
Если (5 = Р), то (N + S = N + Р). (12.2)
То же самое имеет место и для масштабирования цветов, иначе говоря, для масштабирования их
спектральных плотностей или суммарной яркости.
Если (5 - Р), то (aS - аР) для любого скаляра а.
Имеет смысл написать линейные комбинации двух цветов Л и В:
Т - аА + ЬВ, где а и b — скаляры. (Вспомните главу 4.)
Таким образом, для цветов существует экспериментально проверенная векторная алгебра, где мы ин-
терпретируем цвета как векторы: складываем их, масштабируем, раскладываем на составляющие и т. д.
Как мы уже упоминали, другим замечательным качеством человеческого восприятия цвета является
его трехмерность1. Любой цвет С можно сконструировать в виде суперпозиции всего трех основных
цветов R, G, В по формуле:
C~rR + gG + bB, (12.3)
где r,g,b~ скаляры, описывающие количества каждого из основных цветов, содержащихся в цвете С.
Символы R, G, В наводят на мысли о красном (red), зеленом (green) и синем (blue) цветах, которые ча-
сто используются в качестве основных. (Причина предпочтения именно красного, зеленого и синего
цветов состоит в чувствительности колбочек в наших глазах именно к этим цветам.) Однако уравнение
(12.3) работает при любом другом выборе трех основных цветов, если только ни один из этих цветов не
является линейной комбинацией двух остальных.
Имея набор из трех основных цветов R, G, В, можно представить любой цвет С - rR + gG + ЬВ в виде
точки (г, g, b) в трехмерном пространстве. Например, если цвета R, G, В означают соответственно обыч-
ные красный, зеленый и синий цвета, то обозначение (0,1, 0) будет представлять чистый зеленый цвет
единичной яркости, а (0,2, 0,3, 0,5) — желтый цвет. Если удвоить каждый компонент, то мы получим
цвет вдвое более яркий, однако прежнего цвета.
Чтобы выяснить, как люди подбирают цвета, был проведен ряд экспериментов. Особенно интерес-
ным был эксперимент, в котором создавалось определенное сочетание R,G,B с целью получить цвет,
1 Иначе говоря, любые четыре цвета — линейно зависимы; это означает, что один из них может быть представлен в виде линейной
комбинации остальных трех цветов.
776
Глава 12. Теория цвета
воспринимаемый как «чистый спектральный», то есть полностью насыщенный монохромный цвет, вся
сила которого сконцентрирована на единственной длине волны. (В терминах доминантной длины вол-
ны такой цвет является 100 % насыщенным и имеет доминантную длину волны X.) На рис. 12.6 показа-
ны результаты экспериментов, проделанных большим числом участвовавших наблюдателей. В каче-
стве основных цветов были использованы чистый монохромный красный, зеленый и синий цвета с
длиной волны соответственно 700,546 и 436 нм. Функции r(X),g(X), 7>(Х) показывают, сколько требуется
красного, синего и зеленого света, чтобы цвет совпал при данном значении X с чистым спектральным
цветом. Назовем этот чистый спектральный цвет шопо(Х). Тогда
mono(X) - r(X)7? + g(X)G + 7>(Х)В. (12.4)
Рис. 12.6. Функции подбора цветов для основных RGB-цветов
Например, чистый оранжевый цвет mono(600) кажется для среднего наблюдателя идентичным
комбинации цветов 0,377? + 0,08G. Очевидно, что спектр оранжевого света не равен спектру этой сум-
мы, однако два этих света все же выглядят в точности одинаковыми.
Однако здесь есть проблема: чтобы равенство (12.4) выполнялось для данного набора значений R, G,
В, некоторые из скаляров г, g, b должны быть отрицательными! Например, при X - 520 отрицательным
будет г(Х). Какой же физический смысл имеет знак минус перед значением цвета в выражении вида
С = 0,77? + 0,5G - 0,2В? Невозможно убрать цвет, который отсутствует. К счастью, противоречие исчезает,
если мы перепишем это уравнение в виде С + 0,2В - 0,77? + 0,5G. Несмотря на то, что цвет С сам по себе
не может быть представлен как суперпозиция положительных величин основных цветов, цвет С + 0,2В
может быть составлен при положительных величинах 7? и G. Это явление имеет место в действи-
тельности при любом выборе видимых основных цветов 7?, G, В. Одни цвета могут быть созданы при
положительных коэффициентах г, g, b, а другие — нет, и тогда один из основных цветов приходится
«переносить в другую часть уравнения». Грубо говоря, проблема состоит в том, что при сложении двух
цветов получается менее насыщенный цвет, поэтому наложением двух цветов невозможно сформиро-
вать цвет с высокой насыщенностью. Это особенно очевидно в случае чистых спектральных цветов,
которые сами по себе являются насыщенными.
Полезно промасштабировать функции подбора цвета так, чтобы их сумма равнялась единице, по-
этому определим следующие величины:
_ Г(А) -(П_ я(А)
г(^)+я(^)+^(^) r(X)+g(A)+Z>(A) r(A)+g(A)+6(A)
и таким образом добьемся, чтобы г (Л) + g(A) + b(X) = 1. Эти относительные веса называются
«хроматическими значениями» для цвета шопо(Х). Они определяют те количества каждого из основ-
ных цветов, которые требуются для составления света единичной яркости при данном значении X.
12.3. Международная комиссия по стандартам освещенности
777
Устранение различий в яркости позволяет нам задавать цвета с помощью всего двух чисел, например
(^(2-). g(X)), поскольку величину третьего компонента й(Л) всегда можно определить из уравнения
й(Л) = 1-г (X)-g(A). Мы можем нарисовать положение SD-точки (г(Л), g(X), F(X)) при изменении
длины волны X вдоль всего видимого спектра, как показано на рис. 12.7. В силу примененного нами нор-
мирования все точки на этой кривой лежат в плоскости г + g + b = 1, как можно видеть на рисунке. Отме-
тим, что поскольку некоторые координаты при определенных значениях X отрицательны, то кривая не
лежит целиком внутри положительного октанта данного пространства. В стандарте, который мы будем
рассматривать позднее, предусмотрено такое изменение данной кривой, чтобы она целиком лежала
внутри положительного октанта, тогда все три координаты будут всюду положительными.
Рис. 12.7. Кривая чистых спектральных цветов при основных RGB-цветах
12.3. Международная комиссия
по стандартам освещенности
Как точно определять цвета способом, с которым согласны все? В силу того, что восприятие цвета явля-
ется трехмерным, нам требуется прийти к соглашению только по трем основным цветам, и тогда любой
другой желаемый цвет можно будет описывать с помощью триады вида (г, g, b). Однако какие именно
основные цвета следует использовать? К сожалению, все физически реализуемые основные цвета пред-
полагают наличие отрицательных коэффициентов, по крайней мере, для некоторых видимых цветов.
Для того чтобы обойти это неудобство, в 1931 году был учрежден стандарт Международной комис-
сии по освещенности (Commission International de 1’Eclairage — CIE). Комиссия CIE установила три
специальных «перенасыщенных» цвета X, Y, Z, которые не соответствуют никаким реальным цветам,
но обладают следующим свойством: все реальные цвета могут быть представлены как их положитель-
ные комбинации. Эти основные цвета определены через функции подбора цвета, аналогичные изобра-
женным на рис. 12.6.
На рис. 12.8 показаны функции подбора цвета, принятые комиссией CIE. Идея здесь та же, что и для
уравнения (12.4): монохроматический свет с длиной волны X представляется в виде линейной комби-
нации специальных основных цветов. В результате получаем следующее уравнение:
mono(X) “ х(Х)Х + г/(Х)У + z(X)Z. (12.5)
778
Глава 12. Теория цвета
Рис. 12.8. Функции подбора цвета для основных цветов X, Y, Z
Отметим, что все три функции положительны при любом значении X, следовательно, функция
mono(X) всегда является положительной линейной комбинацией основных цветов.
Как были установлены основные цвета X, Y, Z? Они определялись исходя из аффинного преобразо-
вания, примененного к функциям подбора цвета r(X), g(X), Ь(Х) из уравнения (12.4): х(Х), г/(Х) и х(к)
являются линейными комбинациями этих выражений. Для удобства функция у(Х) была взята в той же
форме, что и «функция световой отдачи», которая является измеренным откликом глаза на монохрома-
тический свет определенной силы при разных длинах волны. В результате этого количество основного
цвета У, присутствующего в цвете, равно общей интенсивности этого цвета.
Полезно вновь перейти к нормированным значениям цветности, чтобы обеспечить единичную яр-
кость, поэтому мы определяем:
у (Л)- У^
{ ’ х(Л)+у(Л)+2(Л)’ У{) х(Л)+у(Л)+2(ЛУ W’x(A)+y(A)+z(A)
и, разумеется, х(Л) = 1-х(Л)-у(Л). На рис. 12.9 приведена параметрическая форма s(A) = (x(A),y(A),z(A)),
описывающая некоторую кривую, которая теперь лежит в положительном октанте плоскости xyz. Опи-
сание специфики природы исходных основных цветов, а также подробный вывод преобразования мож-
но найти в различных работах [Billmeyer, 21, Сопгас, 44]. Возможно, однако, что для понимания и ис-
пользования CIE-стандарта вам это и не потребуется.
12.3.1. Построение С1Е-диаграммы
Спектральная кривая цвета s(X) лежит в пространстве трех измерений, но поскольку она находится в
плоскости х + у + z= 1,то эту кривую легко представить в виде двумерной диаграммы и напечатать ее
на листе бумаги для справочных целей. Для задания цвета (единичной интенсивности) нам потребуют-
ся только х и у, поскольку по заданной паре (х, у) значение z находится тривиальным образом. (Как?)
Таким образом, стандартная хроматическая CIE-диаграмма — это кривая s'(Л) = (х(Л),у(Л)),
изображенная на рис. 12.10. (Подумайте, как будет выглядеть ортографическая проекция кривой с
рис. 12.9, если смотреть вдоль оси z.) На диаграмме изображено подковообразное геометрическое место
точек для всех чистых спектральных цветов, которые отмечены на диаграмме в соответствии с их дли-
ной волны. Внутри этой подковы лежат все остальные видимые цвета. Точкам, расположенным вне под-
ковообразной области, не соответствует никакой видимый цвет.
12.3. Международная комиссия по стандартам освещенности
779
Рис. 12.9. Построение С1Е-стандарта
Рис. 12.10. Хроматическая С1Е-диаграмма
Различные области на рисунке отмечены именами, которые обычно используются для описания цве-
тов; например, точки вблизи от (0,6, 0,3) воспринимаются как красные. К сожалению, одинаковые рас-
стояния между точками на диаграмме не соответствуют одинаковым различиям в восприятии цвета.
Например, небольшие изменения положения точки внутри области G приводят только к очень малым
изменениям в воспринимаемом цвете. С другой стороны, очень малые изменения положения точки в
областях В или Y приводят к значительным изменениям воспринимаемого цвета.
780
Глава 12. Теория цвета
На хроматической CIE-диаграмме имеется несколько особенных точек. Точке с с координатами
(х, у) = (0,310, 0,316) соответствует белый цвет, называемый «иллюминент С» (Illuminant С), который и
принимается за «абсолютно ненасыщенный» цвет. Этот цвет часто берут в качестве эталона белого цвета
при настройке графических дисплеев. Иллюминенту С соответствует цвет полуденного неба, затянуто-
го облаками. Точке d с координатами (0,313, 0,329) соответствует цвет, который испускает идеально
черный излучатель при нагреве до температуры «белого каления» 6504 К. Этот цвет немного «зеленее»,
чем иллюминент С. Тщательно измерялись и другие цвета, в их числе свет, испускаемый лампой с воль-
фрамовой нитью накаливания, лунный свет, цвета раскаленной докрасна стали при различных темпе-
ратурах и т. д. [Сопгас, 44, Rogers, 174].
Важное значение хроматической CIE-диаграммы заключается в том, что она обеспечивает всемир-
ный стандарт для описания любого цвета. Разработаны инструменты для генерирования любого цвета,
имеющего координаты (х, у, г) внутри подковы, поэтому путем тщательного подбора можно измерить
«величину» любого желаемого цвета. Существуют также устройства для автоматического измерения
(х, у, z) для любого образца цвета. Кроме того, как мы увидим позднее, по этой диаграмме можно произ-
водить важные расчеты, связанные с цветами.
12.3.2. Использование хроматической С1Е-диаграммы
Хроматическая CIE-диаграмма имеет множество применений. Некоторые из них связаны с легкостью
интерпретации прямых линий на этой диаграмме (рис. 12.11).
Рис. 12.11. Использование хроматической С1Е-диаграммы
Рассмотрим прямую I между двумя цветами а и Ь. Все точки прямой I являются выпуклыми комбина-
циями а и b (см. главу 4) вида (а)а + (1 - а)6 при 0 < а < 1. Каждая точка является допустимым цветом
(для него суммах-, у- и z-компонентов равна 1; почему?), поэтому мы можем утверждать, что любые
12.3. Международная комиссия по стандартам освещенности 781
цвета на этой прямой (и только они) могут быть сгенерированы путем высвечивания на экране различ-
ных количеств цветов а и Ь.
Когда два цвета складываются и их сумма дает белый цвет, то такие цвета называются дополнитель-
ными (complementary) (по отношению к белому). Так, на рис. 12.11 цвета е (сине-зеленый) и f (оранже-
во-розовый) являются дополнительными по отношению к цвету w (белый), поскольку при сложении
этих цветов в нужной пропорции образуется белый цвет. Список некоторых известных пар дополни-
тельных цветов приведены на рис. 12.12; мы рассмотрим их позднее.
Красный Голубой
Зеленый Пурпурный
Синий о Желтый
Рис. 12.12. Дополнительные цвета
Хроматическую CIE-диаграмму можно также использовать для определения доминантной длины вол-
ны и чистоты заданного цвета, например цвета g на рис. 12.11. Действительно, цвет g должен быть линей-
ной комбинацией некоторого чистого спектрального цвета (с границы подковы) и стандартного белого
цвета w. Для того чтобы найти нужный спектральный цвет, нужно просто провести прямую от w через g
(в данном случае она пройдет вблизи от цвета h) и измерить длину волны цвета h — здесь она равна
564 нм, что соответствует желтовато-зеленому цвету. Аналогично, насыщенность (или чистота) равна
отношению расстояний gw/hw. У цвета в точке} доминантная длина волны отсутствует, поскольку продол-
жение прямой wj попадает в точку k на так называемой пурпурной прямой (purple line), которая не соответ-
ствует ни одному чистому спектральному цвету. (Цвета на этой прямой являются комбинациями красного
и фиолетового.) В этом случае доминантная длина волны определяется путем нахождения цвета, допол-
нительного к} в точке т. Длина волны, найденная таким способом, помечается нижним индексом с: 498с.
12.3.3. Цветовые охваты
CIE-диаграмма особенно полезна для определения цветовых гамм, или охватов (color gamuts), то есть
диапазона цветов, которые способно воспроизвести какое-нибудь устройство. Например, электронно-
лучевой монитор может воспроизводить комбинации только красного, зеленого и синего основных
цветов, генерируемые его тремя люминофорами. На рис. 12.13 показаны CIE-координаты этих цветов
(см. [Stone, 192]).
Основной цвет X У
Красный .628 .330
Зеленый .258 .590
Синий .1507 .060
Рис. 12.13. CIE-координаты основных цветов для типичных электронно-лучевых мониторов
Эти три точки определяют треугольную область. Любой цвет внутри этого треугольника является
выпуклой комбинацией трех основных цветов и может быть отображен1. Цвета, расположенные вне
треугольника, не входят в цветовой охват дисплея и поэтому не могут быть отображены. Белый цвет
попадает внутрь охвата, что отражает известный всем факт, что определенные количества красного,
зеленого и синего цветов образуют белый.
1 Национальный комитет по телевизионным стандартам (National Television Standards Committee — NTSC) определяет следующие
основные цвета в CIE-координатах [Rogers, 174]: красный = (0,670,0,330), зеленый - (0,210,0,710), синий = (0,140,0,80).
782
Глава 12. Теория цвета
Несколько отличается цветовой охват для процесса цветной печати. (В силу особенностей механиз-
ма цветной печати цвета на бумаге не являются в точности аддитивными, поэтому здесь гамма не
является простым треугольником.) Охват принтера немного меньше, чем охват электронно-лучевого
монитора, поэтому некоторые цвета, отображаемые монитором, не могут быть отображены принтером.
С другой стороны, некоторые точки, доступные для охвата принтера, лежат за пределами охвата мони-
тора. Поэтому некоторые цвета могут быть напечатаны, но не могут отображаться на мониторе.
Отметим, что при любом выборе основных цветов, даже если это чистые спектральные цвета на гра-
нице подковы, треугольная гамма никогда не может охватить все видимые цвета, поскольку подкова
«выступает» из-под любого треугольника, вершины которого расположены внутри нее. Естественным
выбором основных цветов являются красный, зеленый и синий, поскольку в CIE-диаграмме они лежат
на большом расстоянии друг от друга и поэтому образуемая ими гамма «покрывает» значительную
часть площади диаграммы. Если бы мы вместо них взяли в качестве основных желтый, голубой и пурпур-
ный цвета, то охват был бы намного меньше. (Можно ли в этом случае тоже получить белый цвет?)
Практическое упражнение
12.3.1. Почему красный, зеленый и синий?
Приведите физические и философские аргументы для объяснения того факта, что колбочки в наших
глазах имеют пик чувствительности для красного, синего и зеленого освещения.
12.4. Цветовые пространства
Спецификация цветов, созданная CIE, точна и стандартна, однако она не обязательно является наибо-
лее естественной. В частности, для компьютерной графики наиболее естественным является формиро-
вание нужного цвета путем комбинирования красного, зеленого и синего цветов. Некоторые, однако,
находят более удобным рассуждать о терминах цветового тона, насыщенности и яркости, а художники
при описании цвета часто обращаются к понятиям оттенков, теней и тонов. Все перечисленные спосо-
бы являются примерами цветовых моделей (color models) — выбора трех «дескрипторов» для описа-
ния цветов. Если определить три дескриптора, то можно описать любой цвет с помощью некоторой
тройки значений, например: (оттенок, тень, тон) = (0,125, 1,68, 0,045). Такое описание устанавливает
трехмерную систему координат, в которой описывается цвет. Различный выбор координат приводит к
возникновению различных цветовых пространств (color spaces), поэтому нам потребуются способы
преобразования описаний цветов из одного цветового пространства в другое.
12.4.1. Цветовые пространства RGB и CMY
Цветовая модель RGB (сокращение от «red, green, blue») описывает цвета как положительные комби-
нации трех соответствующих образом определенных основных цветов — красного, зеленого и синего,
как в уравнении (12.3). Если ограничить скаляры г, g, b значениями между 0 и 1, то все определяемые
цвета будут лежать внутри куба, изображенного на рис. 12.14 (или на его границе).
В отличие от С1Е-диаграммы RGB-модель не нормирует интенсивность цвета: точки, расположен-
ные вблизи от точки (0,0,0) — темные, а чем дальше от нее, тем светлее. Например, точке (1,1,1) соответ-
ствует чистый белый цвет. Такое цветовое пространство является наиболее естественным для компьютер-
ной графики, поскольку, например, описание цвета (0,3,0,56,0,9) можно непосредственно преобразовать
в значения, хранящиеся в кодовой таблице цветов (color lookup table — LUT). Отметим, что угол на
рисунке, обозначенный как «пурпурный», описывает тот несомненный факт, что красный и синий цве-
та образуют пурпурный; аналогично для желтого и голубого углов. Цвета, находящиеся в диагонально
противоположных углах, являются дополнительными.
12.4. Цветовые пространства
783
После приведения к единичной интенсивности все цвета, которые можно определить в рамках этой
модели, будут, разумеется, лежать внутри хроматической CIE-диаграммы в соответствии с найденны-
ми количествами красного, зеленого и синего цветов. (Какую форму имеет гамма?) Нетрудно преобра-
зовать цвет, заданный в CIE-координатах (х, у, г), в координаты цветового пространства (г, g, b) и об-
ратно. Поскольку основные цвета (R, G, В) являются линейными комбинациями основных цветов CIE
(X, Y, Z), то преобразование будет линейным. Это преобразование зависит от определения основных
цветов (/?, G, В) и от определения белого цвета. Для основных цветов, приведенных на рис. 12.13, и бе-
лого цвета, заданного точкой d на рис. 12.10, преобразование имеет следующий вид (см. подробности в
работе [Rogers, 174]):
( 2,739
(r,g,b) = (x,y,z) -1,145
-0,424
-1,110 0,138 '
2,029 -0,333
0,033 1,105
(12.6)
Естественно, для обратного преобразования RGB в XYZ используется матрица, обратная этой.
Практическое упражнение
12.4.1. Преобразование из пространства RGB в пространство CIE
Найдите матрицу, обратную к той, что приведена в равенстве (12.6), которая производит преобразова-
ние из координат RGB в пространство CIE. Важной особенностью пространства CIE является то, что
все цвета могут быть представлены в виде линейных комбинаций основных цветов X, Y, Z. Какое усло-
вие это налагает на обратную матрицу? Удовлетворяет ли этому условию вычисленная вами обратная
матрица?
12.4.2. Аддитивные и субтрактивные цветовые системы
До сих пор для формирования новых цветов мы складывали составляющие цветного света, то есть осу-
ществляли аддитивный процесс. В рамках аддитивной цветовой системы (additive color system) любой
цвет D выражается в виде суммы определенных количеств основных цветов, обычно красного, зеленого
и синего: D = (г, g, b). В аддитивной системе можно использовать любые три основных цвета, однако
поскольку в CIE-диаграмме красный, зеленый и синий цвета располагаются далеко друг от друга, они
обеспечивают большой охват.
Субтрактивные цветовые системы используются в тех случаях, когда удобнее рассуждать в терми-
нах исключения (removing) цветов. При (диффузном) отражении света от поверхности или его про-
784
Глава 12. Теория цвета
хождении сквозь частично прозрачную среду (например, при использовании фотографических фильт-
ров) определенные цвета поглощаются материалом и поэтому исключаются (вычитаются). Это и есть
субтрактивный процесс.
Субтрактивная цветовая система (subtractive color system) представляет любой цвет D в виде упо-
рядоченной тройки, так же как в аддитивной системе, однако каждая из трех величин этой тройки ука-
зывает, какое количество определенного цвета (дополнительного к соответствующему основному) под-
лежит исключению из белого света, чтобы получился цвет D. Чтобы пояснить данное утверждение,
рассмотрим наиболее общеупотребительную субтрактивную систему: CMY-систему, в которой исполь-
зуются субтрактивные основные цвета: голубой, пурпурный и желтый (CMY — сокращение от cyan,
magenta, yellow). Если мы пишем, что D = (с, тп, y)CMY, то мы имеем в виду, что цвет D образован путем
вычитания из белого цвета с единиц цвета, дополнительного к голубому (то есть красного), т единиц
цвета, дополнительного к пурпурному (зеленого), и у единиц цвета, дополнительного к желтому (сине-
го). Отсюда мы непосредственно имеем соотношение между RGB- и CMY-системами:
^)rgb = (1> 1> 1) — (с> ot’^)cmv
(12.7)
Это означает, что количество синего цвета b в данном цвете уменьшено путем увеличения цвета у,
поскольку значение у определяет то количество цвета, дополнительного к желтому, которое требуется
вычесть из белого цвета.
Рисунок 12.15 иллюстрирует этот субтрактивный процесс. Три стеклянных слайда описываются в CMY-
системе как (0,4, 0,5, 0,2)сму. Когда белый цвет, который описывается в RGB-системе как (1, 1, 1)RGB,
проходит через слайд, окрашенный в голубой цвет, то 40 % красного компонента поглощается, после
чего возникает «голубоватый» свет, описываемый как (0,6,1,1)RGB. Когда этот свет проходит через пур-
пурный слайд, то из него удаляется 50 % зеленого цвета и появляется цвет (0,6,0,5,1)RGB. (Как выглядит
этот цвет?) Наконец, этот свет проходит через желтый слайд, вследствие чего поглощается 20 % синего
компонента и получается свет (0,6,0,5,0,8)RGB.
Белый Голубой—удаляет красный
Рис. 12.15. Субтрактивный процесс
Аналогичное описание применяется к свету, рассеянному цветной поверхностью. Например, при
трехцветной печати голубая, пурпурная и желтая краски сливаются в бесцветную точку. Каждый цвет
вычитает определенную часть дополнительного компонента падающего на него света. Если, например,
пурпурные частички примешать к бесцветной краске, то эти частички отнимут от белого света зеленую
часть и отразят только красный и синий компоненты. Субтрактивная система используется для уст-
ройств цветной печати, где цвета формируются путем смешивания трех основных цветов CMY.
На рисунке 12.16 приведены аддитивные и субтрактивные основные цвета и их пересечения. (На
ил. 34 изображено то же самое в цвете.) На рис. 12.16, а лучи красного, зеленого и синего света освещают
белую поверхность. Когда два луча перекрываются, их цвета объединяются, образуя новый цвет. Напри-
мер, красный и зеленый лучи, складываясь, дают желтый. Когда же пересекаются все три луча, то обра-
зуется белый свет.
На рис. 12.16, б показана иная ситуация. Каждый кружок образован путем помещения на повер-
хность чернил указанного цвета. Если мы посмотрим при белом освещении, то один круг будет выгля-
деть желтым, поскольку его краска вычитает дополнительный (синий) цвет из падающего белого света.
12.4. Цветовые пространства
785
Когда же смешиваются желтая и голубая краски, то виден зеленый цвет, поскольку удалены синий и
красный компоненты. Центр имеет черный цвет, поскольку из него были удалены все компоненты.
а б
Рис. 12.16. Аддитивная и субтрактивная цветовые системы
12.4.3. Цветовая модель HLS
В более «интуитивной» цветовой модели для описания цветов используются следующие координаты:
Я (hue — цветовой тон), L (lightness — яркость) и S (saturation — насыщенность), поскольку человеческий
глаз с легкостью воспринимает эти величины и способен распознавать их. Эта модель возникает в ре-
зультате трансформации RGB-куба в двойной конус, как показано на рис. 12.17. Если смотреть вдоль диа-
гонали RGB-куба из точки (1,1,1) на точку (0,0,0), то шесть главных цветов (R, G,Bm. три дополнитель-
ных к ним) будут находиться в вершинах шестиугольника. Поэтому цветовой тон можно ассоциировать
с углом, изменяющимся до 0 до 360 градусов. Нулевой угол принято связывать с красным цветом. Осве-
щенность изменяется от 0, когда все RGB-компоненты равны нулю, до 1, когда все RGB-компоненты
равны единице. Такая установка хорошо согласуется с расстоянием вдоль диагонали RGB-куба от чер-
ного цвета к белому. Насыщенность, примерно соответствующая расстоянию, на которое цветовой тон
удален от диагонали RGB-куба, преобразуется в радиальное расстояние от оси яркости HLS-конуса.
Д/
Рис. 12.17. Трансформация RGB-системы в HLS-систему
786
Глава 12. Теория цвета
Цветовое HLS-пространство получается вследствие деформации RGB-пространства, что приводит
нас к поиску алгоритма, который отображает элементы одной системы в другую. Эта деформация являет-
ся весьма сложной, поэтому мы не настаиваем на точном геометрическом преобразовании. В листинге 12.1
приведен основной алгоритм преобразования координат из RGB в HLS. Отметим, что в этом алгоритме
наибольшее внимание уделяется наибольшему и наименьшему из RGB-компонентов, однако он произ-
водит полезное преобразование и к тому же является обратимым (см. упражнения в конце раздела).
После фрагмента кода приводится несколько примеров.
Листинг 12.1. Преобразование из цветовой системы RGB в HLS
class RGBColor{public: double г. g. b:}:
class HLSColorfpublic: double h. 1. s;}:
RGB to_HLS (RGBColor rgb, HLSColor& his)
{
// convert (r. g. b). each in [0. 1]. to h. 1, $
// преобразуем тройку (r. g. b). где каждый элемент
// находится в диапазоне [0. 1]. в (h. 1. s)
double mx. mn:
RGBColor tmp;
mx - MAXfrgb.r. rgb.g. rgb.b):
mn - MINtrgb.r. rgb.g. rgb.b);
hls.l =(mx + mn) / 2.0;
// compute lightness
// вычисляем яркость
if (mx =» mn)
// compute saturation
// вычисляем насыщенность
hls.s - 0.0:
// color is gray
// серый цвет
else {
// color is chromatic
// цвет хроматический
if(hls.l <= 0.5) hls.s - (mx - mn)/(mx + mn);
else hls.s « (mx - mn)/(2 - mx + mn):
// compute hue
// вычисляем цветовой тон
tmp.r =(mx - rgb.r)/(mx - mn):
tmp.g =(mx - rgb.g)/(mx - mn):
tmp.b =(mx - rgb.b)/(mx - mn);
if (rgb.r “ mx) hls.h - tmp.b - tmp.g:
else if (rgb.g -- mx) hls.h - 2 + tmp.г - tmp.b:
else if (rgb.b — mx) hls.h = 4 + tmp.g - tmp.r:
hls.h * - 60:
ifthls.h < 0.0)
hls.h += 360;
}
}
Примеры преобразования RGB-HLS
1. Найдите H, L и S для чистого зеленого цвета: (г, g, b) = (0, 1, 0). Из алгоритма листинга 12.1
видно, что mx = 1 и тп = 0, тогда яркость hls.l = 0,5. Исходя из этой яркости, мы получим насы-
щенность hls.s = 1,0, что понятно, поскольку это чистый цвет. Наконец, tmp.r = tmp.b = 1, rgb.g —
наибольший элемент, поэтому hls.h = 2, откуда hls.h = 120°, как и ожидалось. Тогда из равенства
(г, g, b) = (0,1,0) следует, что (Я, L, 5) = (120°, 0,5,1,0).
12,5. Квантование цвета
787
2. Найдите (Я, L, 5) для оттенка серого цвета: (г, g, b) - (0,4, 0,4, 0,4). Здесь тх = 0,4 и тп - 0,4,
поэтому hls.l = 0,4. Поскольку тх = тп, то свет ахроматический с насыщенностью hls.s - 0. В дан-
ном случае цветовой тон не определен.
Практические упражнения
12.4.2. Выполните несколько преобразований
Найдите (Я, L, 5) для каждого из следующих случаев и объясните смысл каждого результата:
О (г, g, Ь) -(0,2,0,8,0,1);
О (т, g, 6) = (0,0,0,8);
О (r.g,*)-(1,1,1);
О (г, g, b) -(0,0,7,0,7).
12.4.3. Преобразование из HLS в RGB
Разработайте алгоритм HLS_to_RGB(), который преобразует координаты из системы HLS в RGB. Он дол-
жен обеспечивать преобразование, обратное к уже рассмотренному преобразованию RGB_to_HLS. В ре-
зультате его применения к тройке (Я, L, S), полученной из предыдущего алгоритма, должны восстанав-
ливаться исходные значения (R, G, В),
12.4.4. Цветовая HSV-модель
А Значение
Желтый
Зеленый
п Цветовой тон
—-О Насыщенность
Красный
Голубой
1,0 белый
Пурпурный
Черный
Рис. 12.18. Цветовая HSV-модель
Еще одна цветовая модель, которая названа по первым буквам слов (Яие — цветовой тон, Saturation —
насыщенность, Value — интенсивность), также основывается на деформации RGB-куба, однако здесь
образуется не двойной конус, а одинарный, как показано на рис. 12.19. В рамках данной модели цвето-
вой тон также представляется углом (шестиугольник трансформируется в окружность, как и в HLS-
системе; насыщенность имеет тот же смысл, что и в HLS-системе). Интенсивность света описывается
величиной V, которая изменяется от 0 до 1, как показано на рисунке. Разработайте алгоритм, преобра-
зующий координаты из RGB- в HSV-систему.
12.5. Квантование цвета
При визуализации сцены создается огромное количество вещественных цветовых троек (Z, IR, Ih) — по
одной на каждый пиксел изображения. В главе 10 рассматривались методы преобразования таких цве-
товых троек в двоичные значения, которые могут посылаться на дисплей или помещаться в файл для
дальнейшего использования. Общий подход состоит в том, чтобы преобразовать каждое вещественное
значение в один байт, в результате чего изображение будет представляться «полноцветными» значения-
ми пикселов по 24 бита на пиксел, что обеспечивает реалистичное цветовоспроизведение («true-color»).
Сканеры при оцифровке фотографий обычно создают именно полноцветные файлы изображения.
788
Глава 12. Теория цвета
Однако для этого потребуется решить две серьезные проблемы.
О Некоторые дисплеи не способны поддерживать 24-битные цвета. Хотя резко падающие цены на
память и делают 24-битные дисплеи более доступными, но все же многие из них имеют более ог-
раниченные возможности. У них может быть встроенная поддержка только по пяти бит для крас-
ного, зеленого и синего цветов, или встроенная таблица LUT всего с 256 элементами, каждый из
которых допускает, например, только по шесть бит для красного, зеленого и синего цветов.
О Полноцветные изображения могут быть очень большими, что требует значительного дискового
пространства и длительного времени при передаче по сети. (Дизайнеры web-страниц хотят ис-
пользовать только маленькие, быстро скачиваемые изображения; иначе клиенты не будут посе-
щать их страницы.)
Следовательно, нам необходимы методы уменьшения размеров цветных изображений и уменьше-
ния количества цветов, содержащихся в них. Например, нам требуется способ выбора «наилучших»
256 цветов, находящихся в полноцветном изображении, и замены всех остальных цветов изображения
«хорошими» заместителями из списка 256 цветов. Такой процесс часто называют квантованием цвета
(color quantization). Задача состоит в следующем: по заданным N цветовым тройкам найти К цветов,
которые лучше всего представляют исходные цвета. (Обычно К намного меньше, чем N.) Для каждого
исходного цвета нужно найти ближайшего представителя (representative). А при желании заменить
исходную цветовую тройку индексом 0,1,..., К - 1 ее наилучшего представителя.
В процессе решения этой задачи возникает множество вопросов, например: какой смысл вкладыва-
ется в понятия «наилучший» и «ближайший»? Кроме того, поскольку Nвелико, то любой результатив-
ный алгоритм должен быть и достаточно эффективным. Мы рассмотрим четыре различных метода
уменьшения количества цветов в изображении. В каждом случае мы предполагаем, что исходное изоб-
ражение хранится в файле, состоящем из цветовых RGB-троек1, которые могут быть вещественными
или байтовыми.
Полезным предварительным этапом было бы просмотреть исходный файл, чтобы определить диа-
пазон пиксельных троек, составляющих изображение. В частности, следует найти экстремальные зна-
чения каждого из трех компонентов цвета: rmin, гтзх для r-компонента, gmin, gmax для g-компонента, Z»min, Ьтзх
для ^-компонента. Эти значения определяют параллелепипед в RGB-пространстве, как показано на
рис. 12.19. Вся совокупность цветов (color population) изображения находится внутри этого паралле-
лепипеда, который мы будем называть цветовым блоком (color block).
Рис. 12.19. Совокупность цветов, находящаяся внутри цветового блока
1 Возможно, было бы целесообразнее преобразовать RGB-цвета в какую-нибудь другую систему, например в HSV или CIE, и прово-
дить квантование уже в новой системе.
12.5. Квантование цвета
789
Подумаем о большом числе точек, представляющих цвет, которые разбросаны в различных облас-
тях цветового блока. Одни цвета могут повторяться многократно; другие могут быть сосредоточены в
компактных группах (кластерах); третьи же могут быть «одиночками» и не иметь соседей в пределах
значительной части параллелепипеда. Возникают вопросы: если много точек лежит в компактной об-
ласти, то не следует ли заменить их все цветом, близким к центру этого кластера? Если цвет повторяет-
ся много раз, но не имеет соседей, то должны ли мы стараться отображать его с высокой точностью?
12.5.1. Квантование с постоянным шагом
Простейший подход состоит в следующем: разделить цветовой блок вдоль цветовых осей на некоторое
количество непересекающихся подблоков и выбрать в качестве представителя каждого подблока зна-
чение цвета вблизи от его центра. Однако каким образом подразделять цветовой блок? Блок подразде-
ляется путем «разрезания» вдоль каждой цветовой оси, как показано на рис. 12.20. Это позволяет неза-
висимо выбирать представителей для красного, зеленого и синего компонентов. Если, например, К= 256,
то диапазон красного цвета rmin,..., rmax можно разделить на восемь слоев, зеленый — также на восемь,
а синий — на четыре, что образует как раз 256 подблоков. Или можно разбить красный и синий диапа-
зон на шесть слоев каждый, а зеленый — на семь, в результате чего получится всего 252 подобласти.
(Если загружается таблица LUT, то четыре элемента ее могут оставаться неиспользуемыми, или они
могут быть заполнены цветами для каких-либо рамок или текстового комментария.)
Столь же важно определиться, где размещать цвета-представители, являющиеся числовыми значе-
ниями, которые должны «соответствовать» элементам таблицы LUT. Предположим, например, что в
каждом элементе таблицы выделено четыре бита для зеленого цвета, что допускает изменения интен-
сивностей зеленого цвета от 0 до 15 (от 0000 до 1111 в двоичной системе). Если мы решим разбить зеле-
ный цвет на шесть слоев, то какие шесть значений от 0 до 15 следует выбрать? Отметим, что в действи-
тельности на большинстве растровых дисплеев яркость зеленого цвета, соответствующая уровню 15,
может быть установлена независимо с помощью ручки настройки на передней панели дисплея. Для та-
ких устройств нужно кодировать только относительные интенсивности. Взаимосвязь различных со-
ставляющих лучше всего пояснить с помощью примера.
Пример 12.5.1
Рассмотрим типичный случай: таблица LUT содержит К = 256 элементов, каждый из которых содержит
по четыре бита для интенсивностей красного, зеленого и синего цветов. При просмотре упорядочен-
790
Глава 12. Теория цвета
ных троек файла изображения обнаружено, что значения rmln и bmin очень близки к нулю, а - 4,0,
^шах" “ 3-0- Как преобразовать цветовые тройки в элементы таблицы LUT?
Мы принимаем решение использовать семь представителей для зеленого цвета и по шесть для сине-
го и красного. Кроме того, для простоты мы намерены распределить значения представителей возмож-
но более равномерно для 16 допустимых значений таблицы. Для красного и синего цветов лучше всего
подойдут 6 значений: 0, 3,6,9,12,15. Для зеленого цвета добиться полной равномерности невозможно,
однако достаточно хорошим выбором будут значения 0,3,5, 8, И, 13,15.
А как поместить эти значения в таблицу LUT? Для хранения шести красных значений создается
массив int г[6], аналогично создаются массивы д[] и Ь[]. Пусть, например, в массиве г[] хранятся шесть
значений 0,3,6,9,12,15. Как показано в листинге 12.2, с помощью трех вложенных циклов перебирают-
ся все комбинации значений, хранящихся в этих массивах, и для каждой такой комбинации создается
одно 12-битное число, которое помещается в массив LUT[).
Листинг 12.2. Загрузка таблицы LUT
#def1ne numRed 6
Idefine numGreen 7
#def1ne numBlue 6
Idefine pack(r.g.b) (256 * (r)+ 16 * (g) + (b))
for(rd «0: rd < numRed: rd++)
for(grn - 0: grn < numGreen; grn++)
fortblu - 0: blu < numBlue: blu++)
{
index - numRed * numGreen * rd + numBlue * grn + blu:
LUT[index] - pack(r[rd].g[grn],b[blu]):
}
Макрокоманда pack умножает значение красного цвета на 256, чтобы сдвинуть его в самые верхние
четыре бита элемента таблицы LUT. Аналогично сдвигается и значение для зеленого цвета. Если, на-
пример, rd=3, дгп=2, Ыи-5, то индекс таблицы равен 133, а величина, составленная из г[3]=9, д[2]=5,
Ь[5]=15, равна 2399, что составляет 95F в шестнадцатеричной системе, как и должно быть.
Теперь при повторном просмотре списка пиксельных троек (г, gjt b) файла изображения каждое зна-
чение г сравнивается с шестью представителями красного цвета, и определяется ближайший из них.
Ищем такой индекс j_r, для которого г является ближайшим к элементу массива г[;_г]. Если, напри-
мер, rt - 8,23, то ближайшим значением будет 9, откуда j_r = 3. Предпримем такие же шаги для опреде-
ления значений индексов j_gn j_b. После этого вычисляем значение индекса в самой таблице LUT сле-
дующим образом:; = 42 * j± г + 6 * j_g + j_b.
Метод равномерного квантования является в значительной степени неудачным: в нем не учитывает-
ся совокупность используемых цветов и не сохраняется никакой информации о просмотре исходного
файла цветов (за исключением значений rmax, g^, b^). Однако для некоторых изображений он рабо-
тает адекватно, особенно когда число бит на пиксел велико и в таблице LUT содержится большая
палитра.
Практическое упражнение
12.5.2. Проверка некоторых значений
Покажите первые 20 элементов таблицы LUT из примера 12.5.1. Выглядят ли они упорядоченно? Что
хранится в элементе LUTC29]? А в LUT[231]?
12.5.2. Алгоритм популярности
В алгоритме популярности (popularity algorithm) [Heckbert, 102] по крайней мере предпринимается по-
пытка определить, какие цвета чаще всего встречаются в файле. Алгоритм присваивает таким цветам
12.5. Квантование цвета
791
больший приоритет, даже если многие из наиболее часто встречающихся цветов очень близки друг к
другу. Основной метод заключается в формировании списка числа появлений каждого цвета в файле с
последующей сортировкой этого списка. Тогда первые К цветов в отсортированном списке и есть К наи-
более популярных цветов.
Поскольку каждый трехбайтный цвет полноцветного изображения может принимать очень много
значений (всего их 232), то вначале задача упрощается путем усечения каждого байта для красного,
зеленого и синего цветов до пяти бит, после чего остается 215 " 32 Кбайт возможных значений цветов.
Затем выделяется массив размером 32 Кбайт и все его элементы обнуляются. Файл изображения про-
сматривается, и по мере чтения каждого цвета соответствующий элемент этого массива увеличивается
на единицу. После того как прочитаны все N значений цветов, этот массив сортируется и К наиболее
часто встречающихся цветов принимаются в качестве цветов-представителей.
После этого производится повторный просмотр файла, и каждый встречающийся цвет (rd. grn, Ы u)
заменяется ближайшим цветом-представителем (г. g. Ь)[1] из списка популярности. В качестве кри-
терия «близости» часто берется наименьшее среднеквадратическое расстояние: «найягм такое значение i,
для которого (rd - г[г])2 + (gm - g[z])2 + (blu -6[г])2 наименьшее».
Эта операция может оказаться дорогостоящей.
12.5.3. Алгоритм медианного сечения
Алгоритм медианного сечения (median-cut algorithm) был впервые предложен Хекбертом [Heckbert, 102].
В нем цветовой блок разбивается на К подблоков таким образом, чтобы каждый подблок содержал при-
близительно одинаковое количество цветных точек. На рис. 12.21 показан основной процесс, для нагляд-
ности в двумерном варианте. (Предположим, что цвета содержат только красную и зеленую составляю-
щие.) Изображенный на рис. 12.21, а исходный цветовой куб вначале разделен по своему наибольшему
ребру: значение медианы (median value) г( берется таким, что в одном подблоке имеется N/2 точек,
и в другом тоже N/2. Затем каждый из этих подблоков обрабатывается тем же способом: разрезается
по среднему значению на его длинной стороне. Этот процесс продолжается до тех пор, пока не образу-
ется К подблоков. В качестве цвета-представителя каждого подблока берется центр этого подблока.
На рис. 12.21, б показано несколько примеров подблоков после того, как проделано семь сечений.
а б
Рис. 12.21. Работа алгоритма медианного сечения (для 20-цветов)
Одним из простейших способов организации такого процесса является использование списка оче-
редности подблоков. Задается соответствующая структура данных, в которой содержатся размеры бло-
ка и указатель на список цветов, содержащихся в этом блоке. На каждом этапе один блок исключается
из очереди и разделяется на два подблока по среднему значению на его длинной стороне. Затем каждый
из полученных подблоков ставится в очередь для дальнейшей обработки. Эта процедура напоминает
792
Глава 12. Теория цвета
создание дерева методом «в ширину» (breadth-first)1. Ниже приводится псевдокод, описывающий ра-
боту алгоритма медианного сечения:
numBlocks - 1;
// have one block so far
// пока имеем один блок
put original color block on the queue
// ставим исходный цветовой блок в очередь
while(numBlocks < К)
{
thisBlock » delQueueO:
// dequeue a block
// удаляем блок из очереди
if(thisBlock contains more than one color)
// если thisBlock содержит более одного цвета
{
find the median along the longest side
11 находим среднее вдоль наибольшей стороны
make two blocks Bl. В2 : split at the median
11 создаем два блока Bl. B2 : разделяем по среднему
addQueue(Bl): addQueue(B2):
// enqueue them
// включаем их в очередь
numBlocks++:
// have a net gain of one block
// инеем на один блок больше
}
else addQueue(thisBlock):
// just put it back in queue
// ставим его обратно в очередь
На данном этапе у нас имеется К подблоков, которые можно пронумеровать 0,1,...,Х - 1. Теперь
файл читается вторично, и каждый цвет проверяется на принадлежность тому или иному подблоку.
Хекберт [Heckbert, 102] предлагает ряд эффективных способов такой проверки.
12.5.4 . Octree-квантование
Гервуц и Пургатофер (Gervautz, Purgathofer [Gervautz, 180]) для уменьшения числа цветов в файле до
К штук предложили эффективный метод, основанный на октодереве (octree — древовидной структуре
данных, каждый узел которой имеет до восьми потомков). Суть этого метода состоит в следующем: чи-
тается файл цветного изображения и строится октодерево цветов, точно представляющее цвета до тех
пор, пока не встретятся К различных цветов. Затем при появлении каждого нового цвета он добавляет-
ся к октодереву, но тогда это дерево «отсекается» так, что оно вновь содержит не более К различных
цветов. Процесс отсечения вынуждает некоторые цвета «перевоплощаться» в своих представителей,
вследствие чего эти цвета заменяются на свои приближенные значения. После того как все W цветов
файла прочитаны, октодерево содержит К (или несколько меньше) цветов-представителей. Далее осу-
ществляется обход этого октодерева и каждому цвету-представителю присваивается свой индекс.
1 Это метод анализа структуры дерева, при котором каждый уровень полностью подвергается анализу до перехода к следующему
уровню. — Примеч. перво.
12.5. Квантование цвета
793
Затем файл читается еще раз, и каждый встречающийся цвет снова включается в дерево, где быстро
находит «свое место»: либо на нижнем уровне дерева, где расположено его точное представление, либо
на некотором промежуточном узле, где хранится его наилучший цвет-представитель. Индекс этого узла
затем возвращается, сообщая, какой цвет является текущим.
Таблица 12.1. Пример пути от корня дерева до листа цвета
7Z 1 о i о i о о i
G= 01101001
В= 11001110
Потомок 5360711 6
Посмотрим, как структура октодерева используется для увеличения эффективности процесса без
особых затрат памяти. На рис. 12.22 показан фрагмент октодерева: в каждом его узле содержится некоторая
информация относительно добавленных к октодереву цветов. Кроме того, каждый узел содержит восемь
указателей на своих потомков. Когда к дереву добавляется какой-либо цвет, его появление фиксируется с
помощью «увеличения» пути вниз вплоть до восьмого уровня. В табл. 12.1 приведен характерный при-
мер, в котором в двоичной системе изображены байты цветов R, G, В. Рассмотрим отдельные биты тройки
(R, G, В), начиная со старшего бита каждого из байтов R, G, В, — здесь они составляют 101. Это является
двоичным представлением числа пять, поэтому путь ведет к потомку под номером 5. Если этот потомок
до сих пор пуст, то создается и прикрепляется новый узел. Затем этот процесс повторяется со следующей
по старшинству битовой тройкой (011), вследствие чего путь ведет к потомку под номером 3. После сле-
дующих пяти итераций исследуется тройка самых младших бит (110) цвета и путь ведет к потомку номер
6. Если здесь имеется концевая вершина (leaf node — лист), то есть этот цвет уже встречался в файле ранее,
то число цветов (а это одно из полей узла) увеличивается на единицу. В противном случае создается
лист со счетчиком цвета, равным 1. Отметим, что глубина октодерева никогда не превышает восьми, а до-
бавление цвета осуществляется быстро, поскольку требует не более восьми вычислений индекса потомка.
Рис. 12.22. Октодерево, содержащее четыре цвета
794
Глава 12. Теория цвета
Каждый узел на глубине 8 представляет точный цвет (с точностью до 24 бит), в то время как внут-
ренние узлы представляют подблоки цветов. Например, узел на уровне 3 представляет все цвета, имею-
щие определенный набор трех самых старших бит R, G, В, однако следующие биты могут быть любыми.
Когда в октодереве оказывается более К цветов, оно подвергается отсечению. «Отсекаемый» узел
(имеющий как минимум двух потомков) ищется на возможно более низком уровне. (На рис. 12.22
удаляемый узел обозначен буквой А.) Для отсечения октодерева потомки отсекаемого узла удаляются
(что освобождает место для будущих узлов), после чего данный узел помечается как лист. Этот узел
уже содержит краткую информацию об уже встречавшихся цветах, которыми обладали его потомки. При
каждом отсечении число различных цветов октодерева уменьшается на величину, на единицу меньшую,
чем количество удаленных потомков. (Почему?) Теперь в октодерево можно добавлять новые цвета.
Как подробно описано в тематическом задании 12.7, каждый узел отслеживает определенную ин-
формацию, которая в закодированном виде включает в себя следующее:
long numTimes:
// # colors seen in this sub-block
// количество цветов в данном подблоке
long rSum. gSum. bSum;
// sum of color values accumulated
сумма накопленных значений цветов
int isLeaf:
// 1 if this node 1s a leaf
// 1. если данный узел - лист
По мере того как каждый цвет (R, G, В) добавляется в октодерево, каждый узел на его пути получает
обновленную информацию:
numTlmes++:
// encountered another color in this sub-block
// в данном подблоке встретился новый цвет
rSum +- R;
// total amount of red encountered
// общее количество появлений красного цвета
gSum +- G;
bSum +- В;
Таким образом, при отсечении узла (то есть при удалении его потомков) в нем уже содержится нуж-
ная информация относительно всего, что «произошло» в поддереве ниже этого узла. Позднее при про-
смотре дерева для присвоения каждому листу индекса цветом-представителем этого листа будет являть-
ся просто усредненный цвет:
( rSum gSum bSum '
цвет-представитель = ------------, ----------, ---------- .
numTimes numTimes numTimes ,
Наконец, когда W цветов читаются из файла во второй раз, каждый цвет прослеживается вниз по
своему пути со встречи с листом, и таким образом находится индекс. Поскольку никакой путь не быва-
ет длиннее восьми узлов, процесс выполняется быстро.
В тематическом задании 12.7 метод octree-квантования описывается более детально, и вас пригла-
шают поэкспериментировать с ним.
В работе Гервоца и Пургатофера [Gervautz, 80] содержатся некоторые мнения и оценки компьютер-
ных ресурсов, требуемых для каждого метода. Они утверждают, что метод octree-квантования дает ре-
зультаты, сопоставимые по качеству с результатами использования алгоритма медианного сечения, при
значительно меньших затратах процессорного времени и памяти.
12.7. Тематические задания
795
12.6. Резюме
Процесс восприятия цветов человеком через систему глаз — мозг достаточно сложен. Цвет светового
луча может быть точно определен в соответствии с его функцией спектральной плотности, однако это
неудобный формат для передачи информации о цвете; кроме того, одинаковый по восприятию цвет
может возникнуть из мириадов различных спектральных плотностей. Фактически наше восприятие
цвета является трехмерным, поэтому нам нужны методы описания цвета посредством тройки чисел.
В CIE-стандарте осуществляется точный подход к определению цветов. Произвольный цвет 5 единичной
яркости описывается всего двумя числами (х, у). Стандартом установлено, что цвет S создается путем сло-
жения нужных количеств трех специальных основных цветов X, У и Z, то есть S = хХ + уУ + (1 -х- y)Z.
Выбраны специальные основные цвета, причем они являются перенасыщенными и в действительности
не могут наблюдаться; они подобраны так, что любой чистый спектральный цвет (с единственной дли-
ной волны) может быть сформирован с использованием положительных коэффициентов х и у. Хрома-
тическая CIE-диаграмма обеспечивает всемирный стандарт описания цветов и вычисления составляю-
щих заданного цвета. Эта диаграмма также используется для изображения цветовой гаммы, которую
можно сформировать путем сложения различных количеств основных цветов.
Описаны некоторые методы перевода цветов из одной цветовой системы в другую, так что можно
преобразовывать CIE-координаты цвета в более привычные RGB-координаты. Часто применяются и
другие виды цветовых пространств, например HSV (тон, насыщенность, яркость).
При компьютерной обработке цветных изображений (например, на освещенной трехмерной сцене)
диапазон цветов, получаемых в процессе визуализации, до окончания визуализации неизвестен, поэто-
му отображать на дисплее текущий процесс визуализации сложно. Можно порекомендовать следую-
щий метод: записывать в файл все тройки пикселов по мере их вычисления и затем просматривать этот
файл с целью определить множество всех цветов, составляющих изображение. Как только это множе-
ство цветов определено, можно задать соответствующие преобразования между цветовыми тройками и
значениями цветов, которые способно поддерживать данное дисплейное устройство. Это может свес-
тись к выбору совокупности цветов для загрузки в таблицу LUT. Поскольку многие устройства могут
отображать только ограниченное число цветов, часто возникает необходимость в уменьшении количе-
ства цветов, содержащихся в изображении. Разработано несколько методов квантования цвета. Они
отличаются друг от друга сложностью их программирования, эффективностью вычислений, а также
качеством получаемых с их помощью результирующих изображений.
12.7. Тематические задания
Тематическое задание 12.1. Рисование С1Е-диаграммы
Уровень сложности II.
Напишите программу, рисующую CIE-диаграмму и высвечивающую каждую точку (х, у) диаграм-
мы посредством аппроксимации цвета, представленного координатами (х, у). Нарисуйте треугольник,
который (приблизительно) обозначает цветовой охват используемого дисплея. Те значения (х, у), ко-
торые лежат вне цветового охвата дисплея, рисуйте черным цветом.
Тематическое задание 12.2. Рисование RGB-пространства
Уровень сложности II.
Напишите программу, изображающую «разрез» цветового RGB-куба с рис. 12.14. Точки на разрезе
должны изображаться соответствующим цветом. Сделайте так, чтобы пользователь мог с помощью
мыши выбирать плоскость разреза (то есть задавать константы a, b, с, d плоскости aR + bG + сВ - d).
796
Глава 12. Теория цвета
Тематическое задание 12.3. Из HSV в RGB
Уровень сложности II.
Напишите программу, которая позволяет пользователю выбирать с помощью мыши значения Н, S, V
и показывает результирующий цвет в квадратной области экрана, а также выводит на экран соответ-
ствующие RGB-значения этого цвета.
Тематическое задание 12.4. Однородное квантование цвета
Уровень сложности III.
Напишите программу, которая позволит вам экспериментировать с однородным квантованием цве-
та. Из файла читается изображение, после чего на экране изображаются рядом две версии этого изобра-
жения: слева — полноцветная, а справа — после квантования. Пользователь выбирает допустимые ко-
личества красного, зеленого и синего цветов (например, 8, 7,4 соответственно), после чего программа
вычисляет квантованные цвета и обрабатывает изображение для показа.
Тематическое задание 12.5. Квантование цвета
по популярности
Уровень сложности III.
Напишите программу, которая позволит вам экспериментировать с методом квантования цвета по
популярности. Из файла читается полноцветное изображение. Затем пользователь задает К — допусти-
мое число различных цветов. Программа просматривает изображение, квантует RGB-триады до 15 бит,
вычисляет гистограмму значений цветов, сортирует массив и использует К наиболее популярных зна-
чений. Затем изображение просматривается повторно и для каждого пиксела отображается наилучший
набор из К цветов-представителей. На экране изображаются рядом две версии этого изображения:
слева — полноцветная, а справа — после квантования.
Тематическое задание 12.6. Квантование цвета
методом медианного сечения
Уровень сложности III.
Напишите программу, которая позволит вам экспериментировать с методом квантования цвета,
использующим медианное сечение. Скачайте код, выполняющий данный алгоритм, из Интернета
или возьмите из книг (например, [Lindley, 132]). Из файла читается полноцветное изображение. Затем
пользователь выбирает допустимое число различных цветов К. Программа просматривает изображе-
ние и с помощью метода медианного сечения находит К цветов-представителей. Затем изображе-
ние просматривается повторно и для каждого пиксела отображается наиболее подходящий цвет из К
представителей. На экране изображаются рядом две версии этого изображения: слева — полноцветная,
а справа — после квантования.
Тематическое задание 12.7. Квантование цвета
методом октодерева
Уровень сложности III.
Напишите программу, которая позволит вам экспериментировать с методом квантования цвета с
помощью октодерева. Напишите соответствующий алгоритм сами, скачайте код, выполняющий дан-
ный алгоритм, из Интернета, или возьмите из книг (например, [Lindley, 132]). Из файла читается пол-
ноцветное изображение. Затем пользователь выбирает допустимое число различных цветов К. Програм-
ма сканирует изображение, строит октодерево с К цветами-представителями, после чего просматривает
дерево для присвоения индекса каждому его листу. Затем изображение просматривается повторно, для
12.7. Тематические задания
797
каждого пиксела в дереве находится индекс и-отображается соответствующий цвет. На экране изобра-
жаются рядом две версии этого изображения: слева — полноцветная, а справа — после квантования.
Вам может понадобиться следующий тип данных для узла октодерева:
class Node{
public:
Int isLeaf;
// 1 if this node is a leaf
// 1. если данный узел является листом
int whichLevel:
// the level this node is at
// уровень, на котором находится данный узел
int index:
// its LUT index - assigned in pass 2
// его индекс в таблице LUT - присваивается
// при втором проходе
int numChildren:
// number of children this node has
// число потомков данного узла
long numTimes:
// # colors seen in this sub-block
// число цветов, представленных в данном подблоке
long Rsum. Gsum. BSum;
// sum of color values accumulated
// сумма накопленных значений цветов
Node* nextCand:
// candidate for reducing at this level
// кандидат на отсечение на данном уровне
Node* child[8J:
// the 8 children of this node
// 8 потомков данного узла
Ниже приводятся скелеты некоторых основных подпрограмм метода:
insertTree(Node& node. BYTE rgb[J)
{
// insert 24-bit color rgb into subtree
// добавляем 24-битовый цвет rgb в поддерево
if(node — NULL)
makeNewNode(node):
// make & initialize a new node
// создаем и инициализируем новый узел
i f(node.isLeaf)
{
node.numTimes++;
// inc # of pixels represented
// увеличиваем число представленных цветов
addColors(node. rgb):
// sum the color values
// суммируем значения цветов
}
else
childindex - 4 * rgb[0] + 2 * rgb[l] + rgb[2J;
insertTree(childIndex. rgb):
798
Глава 12. Теория цвета
Как найти узел для отсечения? Создадим массив reduct Ы е[] из семи стеков, по одному на каждый
уровень дерева. В элементе массива reduci Ы е[1 ] содержатся указатели на узлы дерева i-ro уровня, о кото-
рых известно, что они могут быть отсечены (у них больше одного потомка). Очередной цвет, добав-
ляемый к октодереву, следует по определенному пути и/или строит новые узлы на пути к листу. В каж-
дом посещенном узле (за исключением конечного узла — листа) количество потомков увеличивается
на единицу, после чего производится проверка: если количество потомков в точности равно двум, то
такой узел становится отсекаемым и указатель на него проталкивается в соответствующий стек.
Когда дерево должно быть отсечено, стеки проверяются в обратном порядке: от i - 7 к меньшим зна-
чениям i: первый непустой стек reduci Ые[1 ] указывает на отсекаемый узел, который затем выталкива-
ется из стека и отсекается.
void reduceTree(void)
{
thisNode - findReducibleNodeO:
thisNode.IsLeaf - 1:
numLeaves -- (thisNode.numChiIdren - 1):
freeChildren(thisNode);
12.8. Дополнительная литература
Глава лекций Фейнмана [Feynman, 62], посвященная цвету, прекрасно написана и является классическим
введением в теорию цвета. В работе Биллмейера [Billmeyer, 21] досконально рассматриваются технологии
обработки цвета. Кроме того, у Роджерса [Rogers, 105] содержится подробное введение в теорию цвета
и описывается управление цветом в компьютерной графике.
4 Удаление невидимых
виЭ поверхностей
□ Повышение реалистичности изображений посредством удаления
невидимых поверхностей сплошных объектов.
□ Изучение различных технологий удаления невидимых
поверхностей.
□ Детальная разработка некоторых фундаментальных методов
удаления невидимых поверхностей.
□ Разработка метода для удаления невидимых линий.
Доколе будешь скрывать лицо Твое от меня?
Псалом 12:2'
За хмуростью провидца скрыто сияющее лицо.
Уильям Купер (William Cowper). «Лицо, сияющее из темноты*
При визуализации трехмерных сцен во время удаления невидимых поверхностей (hidden-surface
removal — (HSR) и невидимых линий (hidden-line removal — HLR) приходится преодолевать пробле-
мы неоднозначности. В разделе 13.1 «Введение» обсуждается важность этих проблем и трудность их
разрешения. В этом разделе описывается различие между алгоритмами «точности по изображению» и
«точности по объекту» и рассматривается полезная структура данных для хранения всех полигональных
граней сцены, предварительно обрабатываемых для ускорения HSR. В разделе 13.2 «Снова об алгорит-
ме буфера глубины» мы вновь обращаемся к алгоритму буфера глубины, описанному в главе 8, чтобы
посмотреть, как он согласуется с другими HSR-методами.
В разделе 13.3 «HSR-методы со списками приоритетов» описываются три HSR-метода, основанных
на хитроумной сортировке списка граней, в рамках которых визуализатор может рисовать грани объек-
та в новом порядке, надлежащим образом скрывая те грани, которые лежат позади других граней.
Такие удачные методы, как метод двоичного разбиения пространства, требуют, чтобы некоторые грани
были разделены на две части. В разделе 13.4 «HSR-метод построчного сканирования» описывается
HSR-метод построчного сканирования, с помощью которого можно определить, какие из множества
1 В оригинале ошибочно указан Псалом 88:14. — Примеч. пер.
800
Глава 13. Удаление невидимых поверхностей
возможных граней на сцене лежат ближе к глазу в «данном пикселе», и рисовать этот пиксел только
один раз (без перерисовки).
В разделе 13.5 «Методы разбиения области» рассматриваются HSR-методы типа «разделяй и вла-
ствуй», основанные на подразделении порта просмотра на большое количество областей, внутри кото-
рых задачи HSR решаются легко. В разделе 13.6 «О методах удаления невидимых линий» предлагается
HLR-метод, рисующий все видимые ребра всех объектов на сцене. Этот метод вообще не требует ника-
кого стирания или рисования «поверх»; он полностью определяет видимость каждой части каждого
ребра до того, как начинает ее рисовать.
В разделе 13.7 «HSR-методы для криволинейных поверхностей» описываются проблемы, связан-
ные с задачей HSR для сцен, состоящих из криволинейных поверхностей, когда аппроксимировать по-
верхности полиномами нежелательно. Предлагается несколько решений этой задачи. Глава заканчи-
вается несколькими тематическими заданиями, предназначенными для закрепления различных идей
изложенных алгоритмов, а также для создания работоспособных программ визуализации, которые кор-
ректно удаляют невидимые поверхности.
13.1. Введение
Любая программа, претендующая на реалистичную визуализацию трехмерных сцен, должна справлять-
ся с задачей удаления невидимых поверхностей (hidden surface-removal — HSR). Большинство объек-
тов на сцене являются непрозрачными, вследствие чего программе не нужно рисовать никакие части
объекта, лежащие «позади» непрозрачного объекта с точки зрения камеры. Эта проблема возникает
даже в случае единственного объекта на сцене. На рис. 13.1, а показан объект, грани которого закрашены
бессистемным образом, то есть каждая грань нарисована просто поверх нарисованных ранее. Резуль-
таты неудобопонятны. На рис. 13.1, б показана корректная визуализация: закрашивались только те части
каждой грани, которые действительно видны глазу. Здесь следует применить алгоритмы, которые удаля-
ют невидимые части каждой поверхности.
Рис. 13.1. Различная последовательность рисования граней
Мы уже рассматривали два подхода к решению задачи HSR. В главе 7 описывался метод «удаления
нелицевых граней». Этот метод надежно работает только в случае, когда сцена состоит из единственного
объекта, и он может дать сбой, если этот объект невыпуклый. Несмотря на свою простоту и полезность в
некоторых ситуациях, метод удаления нелицевых граней не может считаться истинно HSR-методом.
В главе 8 нами был разработан весьма работоспособный HSR-метод, основанный на использовании
буфера глубины. Этот метод работает в широком диапазоне сцен и очень прост для программирования.
Зачем же беспокоиться о поиске каких-то других методов? Алгоритм для невидимых поверхностей
либо работает, либо нет. Это не то, что алгоритмы закрашивания и сглаживания, где один метод спосо-
13.1. Введение
801
бен давать лучший результат, чем другой. Некоторые HSR-методы «прекрасно» работают со сценами,
состоящими из объектов любого вида, в то время как другие предназначены для работы только с опре-
деленными классами объектов (такими, как полигональные сетки с выпуклыми гранями). С HSR-алго-
ритмами связана обычная проблема времени и пространства: в пределах одного класса методов один
метод отличается от другого тем, как долго он работает и сколько требует дополнительной памяти.
В случае алгоритма с буфером глубины значительное количество времени «растрачивается» на ви-
зуализацию тех поверхностей, которые позднее перекрываются другими поверхностями: алгоритм ста-
рательно визуализирует каждую поверхность и не обращает внимания на то, что позднее текущая по-
верхность может быть заслонена какой-либо другой поверхностью. Кроме того, для этого алгоритма
требуется огромное количество памяти для поддержания буфера глубины с достаточной точностью.
Однако потребность данного метода в большом количестве памяти становится теперь менее существен-
ной из-за ее удешевления. Тем не менее память всегда является конечным ресурсом, а программы визуа-
лизации испытывают все большую нужду в ней — для того, например, чтобы манипулировать большим
количеством изображений с текстурой. Алгоритм буфера глубины также должен бороться с эффекта-
ми ступенчатости, как это рассматривалось в главе 10.
Поэтому на протяжении всей истории компьютерной графики люди искали различные подходы к
решению HSR-проблем, в которых требуется меньше памяти и которые особенно эффективны для оп-
ределенных типов сцен. В компьютерной графике существует давняя традиция придумывать «еще луч-
шие» схемы HSR. Обзор большого количества таких схем дается в работе [Sutherland, 193].
Рис. 13.2. Удаление скрытых ребер
Еще одна задача, тесно связанная с HSR, — это удаление невидимых линий (hidden-line removal — HLR).
Эта задача относится к рисованию прямых линий, когда рисуются ребра каждой грани. На рис. 13.2, а
приведен каркасный вид объекта: все его ребра нарисованы полностью. На рис. 13.2, б нарисована только
та часть каждого ребра, которая на самом деле видима. Такие ребра, как Ер не нарисованы вообще, а дру-
гие, такие как Е2, нарисованы только частично: ребро Е2 отсечено в точке, в которой оно пересекается с
ребром Е3.
В этой главе мы исследуем различные HLR- и HSR-алгоритмы, объединяя их в силу схожести под
общим названием алгоритмов удаления невидимых поверхностей (hidden-surface-removal). Назначение
этих алгоритмов — эффективно определить, какие части поверхности или ребра закрываются какой-
нибудь другой поверхностью. Способы осуществления этого заключаются в сложном взаимодействии
расположения наблюдателя и различных объектов на сцене.
Основное внимание в данной главе сосредоточено на сценах, составленных из полигональных
каркасных объектов, однако рассматриваются и другие классы объектов. В главе 14 мы увидим, что
совсем другим подходом к проблеме HSR является трассировка лучей. При трассировке лучей невиди-
мые поверхности любой формы удаляются автоматически, хотя при этом требуется огромный объем
вычислений.
26 Ф. Хилл
802
Глава 13. Удаление невидимых поверхностей
13.1.1. Два подхода: «точность по объекту»
и «точность по изображению»
Алгоритмы удаления невидимых линий или поверхностей имеют различную форму в зависимости от
следующего критерия, описанного в работе [Sutherland, 193]:
О Точность по объекту1. Алгоритм с точностью данной машины вычисляет координаты каждого ви-
димого ребра каждой грани. Алгоритмы этого типа реализуются в физической системе коор-
динат, в которой описаны объекты. Этот вид точности подходит для технического черчения. При
использовании подхода точности по объекту изображение можно увеличивать во много раз, при
этом результаты будут по-прежнему точными.
О Точность по изображению. Для каждого пиксела на дисплее алгоритм определяет, какой элемент
какой грани является ближайшим к наблюдателю, и рисует этот пиксел соответствующим цве-
том. Алгоритмы точности по изображению реализуются только с точностью до оконной системы
координат экрана.
HSR-алгоритмы должны работать настолько быстро, насколько это возможно. Нас интересует, как
время вычисления зависит от сложности объектов на сцене, а также от числа объектов. Если мы обозна-
чим количество элементов на сцене — ребер или граней — буквой п, то мы можем рассчитывать, что
время работы HSR-алгоритма точности по объекту составит О(п2),2 поскольку каждый элемент должен
быть проверен относительно каждого другого элемента, чтобы выяснить, который из них заслоняет другой.
С другой стороны, алгоритм точности по изображению может происходить другим способом. Если
на дисплее имеется N пикселов, то мы можем ожидать, что скорость такого алгоритма составит 0(nN),
поскольку для каждого из N пикселов нам нужно протестировать п элементов сцены. На практике W
намного больше п.
Чтобы уменьшить количество необходимых проверок, часто используют связность; при этом HSR-
алгоритм может стать очень длинным. Цель заключается в том, чтобы уменьшить количество вычисле-
ний с О(п2) или 0(nN) до более приемлемых величин О(п log(n)), O(A4og(n)) или даже О(п). В исчер-
пывающем исследовании Сазерленда [Sutherland, 193] содержатся полезные оценки времени работы
многих популярных HSR-алгоритмов.
13.1.2. Описание данных для полигональных сеток
Для того чтобы перейти к исследованию различных HSR-методов, напомним из главы 8 процесс, кото-
рому подвергается каждая грань полигональной сетки при ее прохождении через графический конвей-
ер (рис. 13.3). Мы рассуждаем в терминах графического конвейера, наподобие конвейера OpenGL, по-
скольку это естественная схема «предварительной обработки» вершин. В то же время мы исследуем
схемы HSR, отличные от схем, предлагаемых OpenGL, поэтому непосредственно конвейер OpenGL
применяться не будет. Вершины грани подвергаются преобразованиям моделирования-вида и проек-
ции и отсечению границами канонического отображаемого объема — единичного куба с псевдоглуби-
нами в диапазоне от 0 до 1. В результате отсечения одни вершины могут исчезнуть, а другие — появить-
ся. Такие атрибуты, как псевдоглубина, текстурные координаты и нормали в вершинах, вычисляются
для этих новых вершин с помощью интерполяции. Затем для однородных координат выполняется пер-
спективное деление, и х- и ^-компоненты каждой вершины отображаются из единичного куба в теку-
щий порт просмотра на экране. Теперь значения х и у выражены в экранных координатах, однако не
округляются до целых чисел, поскольку HSR-алгоритму точности по объекту требуется высокоточная
информация о координатах объектов.
1 Для этих подходов часто используются также термины «объектное пространство» («object space») и «пространство изображения»,
или «пространство картинной плоскости» («image space»).
2 Это так называемая «нотация большого О» («big-Oh notation»), которая используется для описания того, как возрастает слож-
ность задачи в зависимости от ее «размера». Для очень больших п сложность задачи равна О(п2), если время, необходимое для ее
решения, не превышает п2 с некоторым множителем.
13.1. Введение
803
Vl.m!
производится здесь
Рис. 13.3. Графический конвейер для полигональных граней
Таким образом, на этой стадии вся совокупность координат граней содержится в «трехмерном пор-
те просмотра», показанном на рис. 13.4. Оси здесь обозначены через (х, у, z), поскольку мы привыкли к
этим обозначениям, однако мы должны помнить, что эти оси заданы не в мировых координатах, а в про-
странстве, предварительно деформированном перспективным преобразованием. По оси z измеряется
псевдоглубина, поэтому точки, находящиеся дальше от глаза, лежат дальше «в глубь экрана». Эти глу-
бины изменяются от 0 до 1.
Рис. 13.4. Трехмерный порт просмотра, содержащий всю сцену
Вышеупомянутое предварительное искажение, произведенное проекционной матрицей, весьма
полезно для HSR-алгоритмов: оно отделяет информацию о координатах (х, у) от информации о глуби-
не (z). Если у двух точек (х, у, z,) и (х, у, z2) компоненты (х, у) одинаковы, так что одна из них может
перекрывать другую, для выяснения вопроса о том, которая из точек ближе, нам достаточно сравнить z,
и z2. (В мировых же координатах глубина является сложной функцией х, у и z.)
В главе 8 мы уже видели, что для визуализации каждая грань посылается в графический конвейер.
Однако HSR-алгоритм может потребовать проверить все грани до начала любой визуализации. Пред-
положим, что все грани хранятся в массиве
Face faces[maxNumFaces];
Листинг 13.1 Возможный тип данных для хранения данных грани
class Face{
int nVerts:
// number of vertices in vert array
// количество вершин в массиве vert
Point* pt:
// array of vertices in real screen coord's
// массив вершин в вещественных экранных координатах
float* depth;
продолжение &
804
Глава 13. Удаление невидимых поверхностей
Листинг 13.1 (продолжение) ; у
// array of vertex depths
// массив глубин вершин
Plane plane;
// data for the plane of the face
// данные для плоскости грани
Cuboid extent;
// the extent of the face
// экстент грани
// other properties
// другие свойства
Тип данных Face является расширенным по сравнению с тем типом, который был использован в гла-
ве 6. В нем содержатся данные, характеризующие грань, в форме, удобной для доступа к ним подпро-
граммы HSR и визуализатора. В листинге 13.1 показано, как все это может быть организовано. У грани
имеется nVerts вершин, и данные по вершинам хранятся в массивах pt[] и depth[]. Элементы pt[ 1 ] со-
держат координаты (х, у) для i-й вершины (с точностью вещественного числа), a depth[1 ] — псевдо-
глубину этой вершины. Для повышения эффективности работы алгоритма могут добавляться и другие
поля. При работе некоторых HSR-алгоритмов грани заносятся в связный список или в двоичное дере-
во, поэтому могут быть добавлены каналы связи со следующей гранью в списке.
В поле plane содержатся данные (тпх, ту, тг, D), характеризующие уравнение плоскости для грани
(тхх + туу + mz - D); в дальнейшем будет показано, как использовать эти данные. Вектор m — это внеш-
ний нормальный вектор к данной грани. Поскольку эта информация используется для определения
того, какая из граней ближе, то нам понадобятся вектор m и псевдоглубина D для плоскости, выражен-
ной в деформированной системе координат трехмерного порта просмотра.
Поле extent описывает экстент грани. Экстент, который называют еще ограничивающим телом, кон-
тейнером и даже гизмо, — это прямоугольный параллелепипед, шесть стенок которого ориентированы
по координатным осям и плотно охватывают полигон. На рис. 13.5 показана грань, вложенная в свой
экстент. Соответствующий тип данных имеет вид:
class Cuboidffloat left. top. right, bott. near, far;}
Ни одна точка данной грани не может лежать ближе к глазу, чем near, или дальше, чем far. Обычно
экстент — это более простой геометрический объект, нежели полигон, поэтому сравнение экстентов двух
граней осуществляется быстро и может заменить собой полное сравнение самих полигонов. Кроме того,
экстент легко вычисляется (см. упражнения ниже).
Рис. 13.5. Экстент грани в трех измерениях (стереоизображение)
В остальных полях описываются нормали в вершинах, текстурные координаты, свойства поверхно-
сти, коэффициенты отражения и т. д.
13.2. Снова об алгоритме буфера глубины
805
Практические упражнения
13.1.1
Напишите код, вычисляющий экстент грани, описанной в виде объекта класса Face. (Следует просмот-
реть вершины грани и определить среди них наибольшие и наименьшие значения координат х, у, z.)
13.1.2
Напишите код, вычисляющий уравнение плоскости в поле plane для грани, описанной в виде объек-
та класса Face. Как лучше вычислять внешний нормальный вектор грани: непосредственно в виде
векторного произведения (вспомните главу 4) или посредством преобразования мировых координат
плоскости грани?
13.2. Снова об алгоритме буфера глубины
Чтобы подготовить почву для изучения различных HSR-методов, вспомним из главы 8 основные идеи
алгоритма буфера глубины (или «z-буфера»), В этом алгоритме используется буфер глубины d[x] [у],
в котором хранится ближайший предмет, видимый до настоящего момента в точке (х, у). В процессе
визуализации алгоритм обрабатывает каждую грань поочередно и не рисует пиксел, если текущая грань
обладает большей глубиной, чем та, которая встречалась до этого момента в буфере глубины (то есть
если более близкая грань закрывает текущую грань в точке (х, у)). Основные этапы этого алгоритма
приведены в листинге 13.2.
Листинг 13.2. Основной процесс алгоритма буфера глубины (псевдокод)
for (each face F)
// для каждой грани F
for (each pixel (x.y) covering the face)
//для каждого пиксела(х. у), покрывающего грань
{
depth = depth of F at (x.y):
// глубина F в точке (x. у)
if(depth < d[x][y])
// F Is closest so far
// F пока ближайшая грань
с - color of F at (x. y):
// цвет грани F в точке (x. у)
set the pixel color at (x. y) to c
// устанавливаем цвет пиксела в точке (х, у) равным с
d[x][y] = depth:
// update the depth buffer
// обновляем буфер глубины
Вдобавок к своей простоте алгоритм буфера глубины обладает еще некоторыми приятными свой-
ствами.
О Грани из списка faces[] могут быть нарисованы в произвольном порядке, то есть никакой предва-
рительной сортировки этого списка не требуется. В отличие от большинства других HSR-мето-
дов, которые зависят от той или иной сортировки, в данном алгоритме нигде не производится
никакой явной сортировки — только поиск ближайшей грани в каждом пикселе.
806
Глава 13. Удаление невидимых поверхностей
О Алгоритм удачно использует связность глубин (depth coherence), то есть тенденцию глубины
грани в одном пикселе находиться близко к глубинам в соседних пикселах, что упрощает вычисле-
ния: глубины вдоль строки развертки вычисляются инкрементно, как уже описывалось в главе 8.
Так как каждая грань рисуется отдельно, в порядке, определяемом строкой развертки, в рассмат-
риваемом алгоритме можно также использовать связность грани (face coherence) — склонность
некоторых свойств (таких, как интенсивность света и направление нормального вектора) к мед-
ленным и предсказуемым изменениям вдоль грани.
О Хотя здесь мы в основном рассматриваем визуализацию полигональных сеток, метод буфера глу-
бины так же хорошо работает при визуализации других классов объектов, таких как лоскуты
Кунса или квадратичные поверхности. В этом методе требуется только, чтобы глубину поверх-
ности в каждой точке (х, у) можно было найти, чтобы сравнить со значением df] [].
О Если буфер глубины записывается в файл вместе с изображением, то этот файл можно будет ис-
пользовать впоследствии для добавления к сцене новых объектов. Каждый новый объект визуа-
лизируется с использованием наиболее подходящей технологии, и его пикселы рисуются или не
рисуются в зависимости от глубины этого объекта в различных пикселах.
В то же время, как отмечалось в главе 8, некоторые особенности данного алгоритма ограничивают
его использование.
О Он допускает многократное рисование одного и того же пиксела. Каждый раз, когда для пиксела
(х, у) обнаруживается более близкая грань, выполняются дорогостоящие вычисления по ее за-
крашиванию. Может оказаться, что эти вычисления выполнены впустую, если впоследствии бу-
дет найдена еще более близкая грань. Некоторые визуализаторы выполняют грубую сортировку
массива facesf], чтобы грани, более близкие к глазу, рисовались первыми. Отсюда следует, что
при визуализации более удаленных граней условие проверки глубины if (depth dfx] [у]) в боль-
шинстве случаев не выполняется, поэтому повторное рисование пикселов сводится к минимуму.
О Для поддержки буфера глубины требуется большое количество памяти (по одной ячейке на каж-
дый пиксел). К тому же в каждой такой ячейке должно храниться число высокой точности — от
16 до 32 бит. (Слегка изменяя терминологию, можно сказать, что данный метод работает с «точ-
ностью по изображению» по глубине так же, как и по координатам х и у.) Какую бы точность мы
ни выбрали, она все равно может оказаться недостаточной. И когда в буфере глубины не удается
различить две очень близкие глубины, может быть нарисована не та грань1. Особенно это пробле-
матично в случае удаленных граней, имеющих псевдоглубины, близкие к своему верхнему пре-
делу. Это происходит вследствие сжатия глубины, характерного для псевдоглубины.
13.3. HSR-методы со списками приоритетов
Существует обширный класс HSR-алгоритмов, в которых массив facesf] подвергается сортировке, пос-
ле чего грани рисуются «от дальних к ближним», так что более близкие грани рисуются поверх более
далеких (и, возможно, заслоненных). Эти алгоритмы объединены в так называемые методы со списком
приоритетов (list-priority methods), поскольку список facesf] перестраивается по восходящему или ни-
сходящему приоритету, используя определение приоритета, включающее в себя глубину отдельных вер-
шин. Как мы увидим, может вообще не найтись такой перестройки массива, которая приведет к пра-
вильной результирующей картинке. Успешно работающий алгоритм должен выявлять такую ситуацию
и адекватно реагировать на нее; обычно в таких случаях грань разделяют на две части, которые по отдель-
ности никакого конфликта не вызывают.
' Предположим, что грань Л в данном пикселе имеет глубину 0,89485 и тест указывает на нее как на ближайшую грань, однако в
массиве depthf] [] эта глубина округляется до 0,895. Позднее в этом пикселе обнаруживается грань В с глубиной 0,89492 и при
сравнении этой глубины с величиной 0,895 грань В тестируется как более близкая и рисуется, что совершенно неправильно!
13.3. HSR-методы со списками приоритетов
807
В рамках данного раздела мы рассмотрим следующие три алгоритма:
О «Алгоритм беспечного художника» («heedless painter’s algorithm») — несложный, но не без изъя-
нов: в нем просто рисуются целые грани в порядке от дальних к ближним.
О «Алгоритм дерева двоичного разбиения пространства» («binary-space partition tree algorithm»)
элегантен и эффективен, однако требует предварительного этапа построения дерева граней. Одна-
ко одно и то же дерево можно использовать многократно при рисовании сцены с различных точек
зрения — например, при анимации, когда камера перемещается по неподвижной сцене.
О Алгоритм сортировки по глубине, который является классическим HSR-методом на базе сорти-
ровки массива faces[] с добавлением комплексного тестирования для устранения недостатков
алгоритма художника.
13.3.1. Алгоритм беспечного художника
Первая попытка создать альтернативу применению буфера глубины очень проста, однако часто выдает
неправильные изображения, — такие, как на рис. 13.1! Каждая грань объекта поочередно закрашивает-
ся целиком. Такой подход является одной из форм алгоритма художника (painter’s algorithm'): при рисо-
вании каждой грани в буфере кадров ее цвет перекрывает тот, который был здесь ранее; так художник
накладывает новые слои краски на старые. В этом случае цвет каждого пиксела — это самый последний
нарисованный цвет, и если две грани перекрываются по х и по у, то грань, нарисованная последней,
перекроет предыдущую грань, даже если она не находится ближе.
Для того чтобы у данного метода был хотя бы шанс нарисовать сцену правильно, мы используем
поле extent.far массива face для записи того, какая грань имеет наиболее удаленную вершину, затем
следующую по удаленности и т. д. Массив faces[] сортируется по признаку extent, far, после чего грани
рисуются в буфер кадров, начиная с самой удаленной и заканчивая самой ближней. Скелет этого алго-
ритма выглядит следующим образом:
сортируем список faces[] по значениям поля extent.far;
рисуем грани целиком в порядке от дальней к ближней.
Отметим, что в данном алгоритме присутствует процедура сортировки. Сортировка в той или иной
форме является неотъемлемой частью большинства HSR-алгоритмов, поскольку обрабатываемые ал-
горитмом объекты должны каким-либо образом упорядочиваться. (Разнообразные подпрограммы сор-
тировки можно найти в любом тексте, посвященном структурам данных и алгоритмам).
В каких случаях работает алгоритм беспечного художника? На рис. 13.6 приводятся различные ситу-
ации взаимного расположения двух граней А и В. Каждая ситуация включает в себя взаимодействие
двух ортографических проекций. На нижнем рис. 13.6, а показан трехмерный порт просмотра так, как
он виден смотрящему на экран наблюдателю, поэтому здесь показаны оси х и у. На верхнем рисунке
порт просмотра показан сверху, поэтому глубина увеличивается снизу вверх, в направлении возраста-
ния г. (Из этих двух представлений можно сформировать в уме трехмерную картину — это непросто,
зато очень полезно.)
На рис. 13.6, а крайние значения по х (назовем их х-экстентами) ХА и Хв граней А и В перекрыва-
ются, то же касается и крайних значений по у (у-экстентов) УЛ и YB, поэтому можно предположить, что
одна из граней заслоняет другую. В случае, приведенном на рисунке, одна грань действительно закры-
вает другую. Однако в силу того, что их z-экстенты не перекрываются, алгоритм беспечного художника
работает правильно. У грани A extent, far больше, поэтому она рисуется первой, а грань В позже. Здесь
не может получиться, что грань А частично перекроет грань В.
На рис. 13.6, б положения граней лишь немного отличаются от первого рисунка, но ситуация со-
вершенно другая. Грань А более удалена в соответствии с критерием extent.far, поэтому она рисуется
первой, в результате чего получается результат, помеченный на рисунке как «неправильно». Однако
в действительности — в силу своей ориентации — грань А находится ближе в том месте, где она находит
на грань В, поэтому она должна заслонять грань В, как показано на рисунке, помеченном как «правиль-
808
Глава 13. Удаление невидимых поверхностей
но». (Полезно вырезать из картона несколько образцов граней и поэкспериментировать с их различны-
ми ориентациями.) Ситуация на рис. 13.6, в еще более сложна: грани А и В проникают друг в друга.
В данном случае алгоритм беспечного художника бездумно нарисует грань В поверх грани А.
Рис. 13.6. Упорядочивание граней по глубине
Таким образом, алгоритм беспечного художника не в состоянии определить, какая часть одной грани
закрывает другую. Недопустимо просто рисовать грани целиком одну поверх другой на основе единствен-
ного критерия, такого как максимальная глубина. В разделе «Алгоритм сортировки по глубине» мы
исправим алгоритм художника путем выполнения дополнительных проверок участвующих в нем граней.
Усовершенствованный алгоритм работает правильно, однако он значительно сложнее, чем исходный.
Практические упражнения
13.3.1. Есть ли перекрывание?
Покажите, что одна грань не обязательно закрывает другую, даже если их х- иу-экстенты перекрываются.
13.3.2. Когда алгоритм беспечного художника работает?
Укажите класс сеток, для которого данный алгоритм работает для любой точки зрения на единствен-
ный объект. (Например, работает ли он в случае выпуклых объектов?) Какое условие приводит к краху
алгоритма для объектов, не принадлежащих к этому классу?
13.3.2. HSR с использованием деревьев
двоичного разбиения пространства
Элегантный метод удаления невидимых поверхностей основан на применении деревьев двоичного
разбиения пространства (binary-space partition — BSP) [Fuchs, 69, Fuchs, 70]. На предварительном эта-
пе полигоны из массива faces [] особым образом организовываются в структуру данных двоичного де-
рева, когда определенные грани разбиваются на две части, И при рисовании сцены с корректно удален-
13.3. HSR-методы со списками приоритетов
809
ными невидимыми поверхностями нужно методично «обойти» такое дерево. BSP-дерево обходится
(is traversed) путем поочередного посещения каждого его узла (в определенном порядке) и рисования
грани, обнаруженной в этом узле.
Построение BSP-дерева
Для большей наглядности мы ознакомимся с BSP-деревьями на двумерном примере, в котором фигури-
руют ребра. Поскольку структура этого дерева не зависит от размерности объектов, которые в нем содер-
жатся, то мы сразу же распространим понятие BSP-дерева на полигоны в трехмерном пространстве.
На рис. 13.7 приведены три полигона на плоскости, а также «глаз», расположенный в некоторой
точке. Вопрос заключается в следующем: что видит этот глаз? (Если вы предпочитаете иметь дело с
трехмерным пространством, то представьте, что наблюдатель стоит перед тремя большими каменными
«колоннами», поднимающимися из земли. Поперечные сечения этих колонн и изображены на рисунке.
Вопрос формулируется так: какие части стенок колонн видны, а какие заслонены? Нарисуйте резуль-
тирующую сцену для этого примера.) Все ребра на рисунке пронумерованы, так же как внешние норма-
ли к каждому ребру. Мы хотим включить все ребра в дерево так, чтобы плоскость была разделена (раз-
бита) на неперекрывающиеся полигональные области.
Рис. 13.7. Совокупность ребер, размещаемых в BSP-дереве, — двумерный случай
Начнем построение дерева для данной совокупности ребер с ребра, например номер 1. Продолжим
это ребро в обоих направлениях, вследствие чего оно разделит плоскость на два полупространства (так
для общности мы будем называть фактические полуплоскости): «внешнее» (в той стороне, куда направ-
лена внешняя нормаль к ребру) и «внутреннее». Поместим ребро 1 в корень дерева, как показано на
рис. 13.8, а. Теперь будем добавлять к дереву одно за другим все остальные ребра: те, которые лежат во
внешнем полупространстве ребра 1 (на рисунке они обозначены как внешние ребра — outsideOnes), пой-
дут в правое поддерево, а те, которые лежат во внутреннем полупространстве ребра 1 (обозначенные на
рисунке как внутренние ребра — insideOnes), пойдут в левое поддерево. При добавлении каждое ребро
«находит свое место» внизу дерева, сравнивая себя с каждым встретившимся ему узлом. Ребро направ-
ляется в поддерево outsideOnes узла, если это ребро лежит правее узла; в противном случае оно направ-
ляется в поддерево insideOnes, — до тех пор, пока оно не присоединится к дереву как новый лист.
На рис. 13.8, б показано состояние дерева после добавления к нему еще семи ребер, обозначенных
числами от двух до восьми. Ребро 2 лежит во внутреннем полупространстве ребра 1, поэтому оно встав-
ляется в поддерево insideOnes. Ребро 3 лежит во внутренних полупространствах ребер 1 и 2, поэтому
оно размещено именно так, как показано на рисунке. (Проверьте это!) Ребро 4 на рисунке не приведено;
покажите сами, куда оно должно идти.
Когда мы добавляем ребро 9, происходит нечто новое. Это ребро лежит во внешнем полупростран-
стве ребра 1, но сразу в обоих полупространствах ребра 5. Поэтому оно разбивается (split) ребром 5 на
810
Глава 13. Удаление невидимых поверхностей
два ребра — 9а и 96 (см. рис. 13.7); для каждого из этих кусков ребра 9 находится свое место вниз по
дереву. Ребро 9а лежит во внутреннем полупространстве ребра 5, поэтому оно идет налево и проверяет-
ся относительно ребер 6 и 7; ребро 9b лежит во внешнем полупространстве ребра 5, но во внутреннем —
ребра 8. Ребра 10 и 11 вставляются аналогично, но для них разбиения не требуется. (Как будет выгля-
деть результирующее дерево?)
б
Внутренние ребра Внешние ребра
а
Рис. 13.8. Построение BSP-дерева (двумерный случай)
BSP-дерево составляет список ребер специальным способом, поэтому для любого ребра можно сра-
зу сказать (по его положению на дереве), в какой «части» пространства оно расположено (например,
ребро 6 лежит во внешнем полупространстве ребра 1 и во внутреннем — ребра 5). Структура такого
дерева никоим образом не зависит от положения глаза.
Отметим, что порядок, в котором ребра добавляются к дереву, сильно влияет на «форму» этого дере-
ва. При некоторых вариантах выбора порядка ребер дерево выглядит «полным» (full) и «низкорослым»
(shallow) (число узлов от корня до самого глубокого листа невелико), а другой выбор порядка ребер
приводит к «тощему» и «глубокому» дереву. Низкорослые деревья более эффективны при обработке.
Наихудший случай формы BSP-дерева — одиночная цепочка сверху донизу.
BSP-деревья для трехмерных сцен
Нетрудно сразу же распространить все вышеизложенное на сцены, составленные из трехмерных по-
лигональных сеток. Рассмотрим блок, изображенный на рис. 13.9, а. Каждая из его восьми граней про-
нумерована и показаны их внешние нормали. На рис. 13.9, б приведена другая проекция того же самого
блока. Если грани вставляются в BSP-дерево в порядке 1,2.8, то образуется дерево, показанное на
рис. 13.9, в. Каждая из граней «находит» свой путь вниз ПО дереву точно так же, как и в двумерном слу-
чае: если она лежит во внешнем полупространстве узловой грани, то она идет в поддерево outsi deOnes
и т. д. Грань 7 разбивается на грани la и 1Ь плоскостью грани 3 (пунктирная линия на рисунке). Грань 8
также разбивается на две части. (Существует ли такой порядок добавления граней, при котором не нуж-
но ни одного разбиения граней?) В Тематическом задании 13.2 рассказывается о разбиении граней с
большими подробностями.
Рис. 13.9. Построение BSP-дерева (трехмерный случай)
13.3. HSR-методы со списками приоритетов
811
Построение самого BSP-дерева рассматривается в программе тематического задания 13.3. А мы по-
смотрим, как использовать BSP-дерево для корректного рисования сцены.
Обход дерева (для рисования всех граней)
Для рисования всех граней сцены в нужной последовательности каждый узел посещается в определен-
ном порядке и производится визуализация грани, содержащейся в этом узле. (Если это нелицевая
грань, то рисование может быть пропущено.)
Как же устанавливается порядок, в котором рисуются грани? Это зависит от положения «глаза» ка-
меры. Рассмотрим произвольную грань F дерева; предположим для определенности, что глаз камеры
лежит во внешнем полупространстве грани F. Это означает, что все грани поддерева insi deOnes грани F
лежат по другую сторону F относительно глаза, поэтому ни одна из них не может закрывать грань F в
принципе. Следовательно, мы рисуем все грани поддерева insideOnes грани F, после чего рисуем саму
грань F (она может быть нарисована поверх некоторых из этих граней). Теперь можно рисовать и все
грани поддерева outsideOnes грани F, будучи уверенными, что они не лежат позади какой-либо из уже
нарисованных граней.
Если же, напротив, глаз камеры расположен во внутреннем полупространстве грани F, то мы внача-
ле рисуем все грани поддерева outsideOnes, затем — саму грань F, а затем уже все грани из поддерева
insideOnes грани F. Заметим, однако, что в данном случае грань Fвсегда является «нелицевой гранью»
(почему?), поэтому фактически она не рисуется (за исключением случая, когда имеется необходимость
рисовать задние грани).
Вышеприведенное рассмотрение, в сущности, устанавливает правило рисования каждого поддерева
для дерева; таким образом, мы получаем следующий рекурсивный метод для рисования всей сцены: для
того чтобы нарисовать сцену целиком, нужно нарисовать одно Поддерево корня (его выбор определяет-
ся расположением глаза), затем сам корень и, наконец, второе поддерево корня. Ниже приводится псев-
докод, составленный в соответствии с этим правилом:
То draw the faces stored in the BSP tree with root F.
// Для рисования граней, находящихся в BSP-дереве с корнем F.
if (the eye is in the "outside" half-space of face F)
// глаз лежит во «внешнем» полупространстве грани F
draw all faces in the inside subtree of F:
// рисуем все грани внутреннего поддерева грани F
draw F;
// рисуем F
draw all faces in the outside subtree of F:
// рисуем все грани внешнего поддерева грани F
else
// the eye is on the "inside" of F
// глаз расположен во «внутреннем» полупространстве F
{
draw all faces in the outside subtree of F;
// рисуем все грани внешнего полупространства F
if (you want to draw back faces), draw F:
// если нужно рисовать нелицевые грани, то рисуем F:
draw all faces in the inside subtree of F;
// рисуем все грани внутреннего поддерева грани F:
)
В этом псевдокоде можно узнать «симметричный обход» («inorder traversal») двоичного дерева
[Kruse, 128], где порядок обхода каждого поддерева определяется положением глаза относительно Грани
этого поддерева.
812
Глава 13. Удаление невидимых поверхностей
Для трехмерной сцены, изображенной на рис. 13.9, а, дерево с рис. 13.9, в можно обойти по выше-
приведенной схеме, и блок будет нарисован правильно. На рис. 13.10, а стрелками показан порядок
посещения узлов BSP-дерева, изображенного на рис. 13.9, в, — для конкретного вида блока, который
приведен на рис. 13.9, а. Те грани, которые на рисунках бив подчеркнуты, являются нелицевыми и дей-
ствительно не рисуются. (Убедитесь в том, что все грани рисуются правильно.)
_1_ 7b 8b 4 3 7а 8а 6 5 2
б
J_ 4 8b 7b 3 5 8а 7а 6 2
в
а
Рис. 13.10. Порядок рисования граней, определяемый положением глаза.
Если глаз перемещается в другое положение, то для рисования сцены можно использовать то же са-
мое дерево, и алгоритм также остается неизменным. На рис. 13.10, в показан порядок рисования того
же блока при положении глаза в соответствии с рис. 13.9, б. (Ниже в упражнениях приводятся другие
примеры.) BSP-алгоритм является особенно привлекательным в тех случаях, когда предстоит форми-
ровать много изображений в режиме анимации при движении камеры вокруг неподвижной сцены.
Предварительный этап построения дерева выполняется только один раз. Однако если изменяется сама
сцена, то должно формироваться и новое BSP-дерево.
В тематическом задании 13.2 рассматривается разбиение грани плоскостью. В тематическом зада-
нии 13.3 исследуются подпрограммы для построения BSP-дерева и для рисования сцены, хранящейся
в таком BSP-дереве.
Практические упражнения
13.3.3. Построение BSP-дерева в другом порядке
Нарисуйте BSP-дерево для ребер с рис. 13.7, вставляемых в следующем порядке:
3,6,2,7,9,10,1,11,8,5,4.
13.3.4. BSP-деревья для выпуклых полигонов
Какую форму имеет BSP-дерево для выпуклого полигона?
13.3.5. Рисование колонн
Определите порядок рисования ребер с рис. 13.7, используя BSP-дерево с рис. 13.8, б (после запол-
нения всего дерева), — для случая положения глаза, показанного на рисунке. Какие ребра являются
«нелицевыми»? Правильно ли рисуется эта сцена? Повторите упражнение для случая, когда глаз пере-
местился в положение, отмеченное на рисунке как «другой глаз». Снова убедитесь, что сцена рисуется
правильно.
13.3.3. Алгоритм сортировки по глубине
Алгоритм сортировки по глубине (depth-sort algorithm) улучшает алгоритм художника, поскольку
позволяет определять, какие части одной грани находятся впереди другой грани — для тех случаев,
когда эти грани почти совпадают по глубине [Newell, 26]. Этот алгоритм выявляет неоднозначные
13.3. HSR-методы со списками приоритетов
813
ситуации и разбивает грань с целью ликвидации такой неоднозначности. Основные этапы его работы
следующие:
О Отсортировать массив faces[] по ключевому слову extent.far, как в алгоритме художника.
О Разрешить неоднозначные ситуации, перестраивая список и при необходимости разбивая грани.
О Визуализировать каждую грань обновленного списка в порядке убывания extent.far (то есть от
задней грани к передней).
Новым является второй этап, в рамках которого выполняется тщательный анализ всех полигонов,
чьи z-экстенты (то есть расстояние между extent.near и extent.far) перекрываются.
в
Рис. 13.11. Неоднозначные случаи, подлежащие разрешению с помощью алгоритма сортировки по глубине
На рис. 13.11 показаны различные неоднозначные ситуации, подлежащие разрешению. На рис. 13.11, а
грани Р и Q взаимно проникают: ни одна из них не находится полностью перед другой. То же самое
имеет место на рис. 13.11, б, где грань Q — невыпуклая; пунктиром показана прямая, по которой алго-
ритм произведет разбиение грани Р. А на рис. 13.11, в приведены два примера циклического наложения
друг на друга трех и четырех граней. Качественный HSR-алгоритм должен уметь разрешать любую из
таких ситуаций путем правильного разбиения граней до тех пор, пока для любой пары граней одна из
них не будет целиком находиться впереди другой или за ней.
Вначале список faces[] сортируется по extent.far. Пусть Р— это последний полигон в списке (самый
удаленный). Алгоритм художника нарисовал бы его целиком. Если же используется алгоритм сорти-
ровки по глубине, то вместо этого мы проверяем, не может ли данный полигон загораживать какую-
нибудь другую грань из массива faces[]. Полигон Р может заслонять другую грань только в том случае,
если его z-экстент очень близок к z-экстенту этой грани. Тогда для каждой грани Q, чей z-экстент почти
совпадает с z-экстентом грани Р, производится последовательность геометрических тестов с целью убе-
диться, можем ли мы определенно сказать, что грань Р не загораживает ни одну часть грани Q. Если
такие тесты показывают, что грань Р не может заслонить ни одну грань Q, то грань Р удаляется из спис-
ка и рисуется; затем тестируется следующая грань Р.
Если же нам встретилась такая грань Q, которую грань Р может заслонить, то мы продолжаем рабо-
тать с гранью Q. Во-первых, мы смотрим, не «маркирована» ли она как «ранее перемещенная». (Как мы
814
Глава 13. Удаление невидимых поверхностей
увидим, грани часто перемещаются по списку граней; поэтому во избежание зацикливания мы разре-
шаем переместить грань только один раз.)
Если грань Q маркирована таким образом, то мы ее дальше не тестируем: мы просто разбиваем грань Q
плоскостью грани Р и заносим образовавшиеся куски в правую часть списка (в соответствии с extent. far).
Если грань не маркирована, то мы проверяем, может ли грань Q заслонять грань Р. Если не может, то
грань Q, вероятно, находится позади грани Р и поэтому является кандидатом на рисование в следую-
щий раз. Поэтому мы помещаем ее в конец списка и, конечно, маркируем ее как перемещенную; и имен-
но с этой грани мы начнем следующую проверку. Если же этот тест не дает гарантии, что грань Q не
может заслонить грань Р, то это свидетельствует о том, что грани Р и Q безнадежно «переплетены» друг
с другом геометрически; поэтому мы разбиваем грань Q плоскостью грани Р и снова заносим образовав-
шиеся куски в список.
Листинг 13.3. Подпрограмма сортировки по глубине (псевдокод)
void depthSort(Face faces[])
{
for(P - last face in list: list not empty: P = next face in list)
// P - последняя грань в списке: список не пуст:
// Р - следующая грань в списке
{
hopeful = 1:
// have definite action to take
// действуем в определенном направлении
for((each Q overlapping P in z) && hopeful ~ 1)
// каждая грань Q. близкая с P no z
{
if( (x-extents of P and Q are disjoint)
||(y-extents of P and Q are disjoint)
||(P 1s on opposite side of Q's plane)
||(Q is on the same side of P's plane)
||(the projected faces P and Q don’t overlap))
// x-экстенты P и Q не пересекаются
// у-экстенты P и Q не пересекаются
// Р на противоположной стороне плоскости Q
// Q на той же стороне плоскости Р
// проекции граней Р и Q не перекрываются
continue:
//try next Q
// проверяем следующую грань Q
// Р might obscure this Q: see if Q is marked or behind P
// грань P может заслонять эту Q: смотрим, маркирована ли Q.
// или находится ли она позади Р
1f (Q is marked)
// Q маркирована
{
split Q by plane of P;
// разбиваем грань Q плоскостью грани P
mark and insert pieces of Q;
// маркируем куски грани Q и заносим их в список
hopeful - 0:
}
else if(Q on opposite side of P's plane ||
P on same side as Q's plane)
// грань Q на противоположной стороне плоскости грани Р
13.3. HSR-методы со списками приоритетов
815
// грань Р на той же стороне, что и плоскость грани Q
{
mark Q, pur Q at end of list:
11 маркируем грань Q. помещаем ее в конец списка
hopeful = 0:
}
else
// can't tell: They overlap too much
// невозможно ничего сказать: грани перекрываются
// слишком сильно
{
split Q by plane of P:
11 разбиваем грань Q плоскостью грани P
mark and insert pieces of Q:
// маркируем куски грани Q и заносим их в список
hopeful = 0:
}
}
// end., for each Q..
// конец цикла для каждой грани Q
If(hopeful)
drawAndRemove(P);
}
// end of for each P
// конец цикла для каждой грани Р
}
Псевдокод этого алгоритма приведен в листинге 13.3, что помогает прояснить поток используемых
тестов. Флаг hopeful остается равным 1 до тех пор, пока мы можем надеяться, что текущая грань Р не
будет заслонять какую-либо из тех граней Q, с которыми она почти совпадает по г. Эта ситуация для
нас желательна, поскольку в этом случае грань Р можно нарисовать и более ее не рассматривать. Если
же эта надежда рухнула, что может случиться в силу множества причин, то другие грани Q уже не тес-
тируются, а данная грань или разбивается, или помещается в конец списка.
Рассмотрим группу тестов, используемых для проверки того, может ли грань Р заслонять грань Q.
Эти тесты выполняются в порядке возрастания их сложности (времени обработки); и когда любой из
них выполнен успешно, то становится точно известным, что грань Р не заслоняет грань Q. Вот эти тесты.
1. Пересекаются ли х-экстенты граней Р и Q (быстрый тест)?
2. Пересекаются ли ^-экстенты граней Р и Q (быстрый)?
3. Находится ли грань Р целиком на противоположной от наблюдателя (глаза) стороне плоскости
грани Q (довольно быстрый)?
4. Находится ли грань Q целиком на той же стороне плоскости грани Р, что и глаз (довольно быстрый)?
5. Пересекаются ли проекции граней Р и Q на экране (дорогостоящий тест)?
Последний тест требует особенно больших вычислений. Вместо того чтобы просто проверить экстен-
ты или положение вершин относительно плоскости, проводится полный тест «полигон относительно по-
лигона» (в двух измерениях, то есть только с координатами х и у). Грани не пересекаются только тогда,
когда ни одно ребро грани Р не пересекается ни с одним ребром грани Q и ни одна из этих граней не
расположена внутри другой. Эти тесты более детально рассматриваются в тематическом задании 13.4.
Метод сортировки по глубине не требует ни дополнительной памяти для организации дерева, ни
предварительного этапа (за исключением начальной сортировки по extent, far). Этот алгоритм может
начинать рисовать грани, как только становится ясно, что грань Р, расположенная в конце списка, не
заслоняет ни одной грани из списка. Однако в данном алгоритме по-прежнему производится разбиение
816
Глава 13. Удаление невидимых поверхностей
граней и добавление новых граней в список, поэтому faces[] лучше реализовывать в виде связного спис-
ка (linked list), а не простого массива. Отметим, что данный метод не свободен, как и методы буфера
глубины и BSP-дерева, от проблемы повторного рисования граней поверх уже нарисованных. В сущно-
сти, работа, потраченная на визуализацию нарисованных ранее граней, пропадает впустую.
13.4. HSR-метод построчного сканирования
В этом разделе мы рассмотрим метод точности по изображению, при котором сцена визуализируется
построчно — по строкам развертки. Вдоль каждой строки развертки рассматриваются все грани сцены,
которые «попадают» на эту строку развертки, и определяется, какая грань ближе всего к глазу. Затем
пикселы закрашиваются цветом этой грани. Таким образом, данный метод производит вычисления за-
краски для каждого пиксела только один раз, повторное рисование исключается.
Листинг 13.4. Алгоритм строки развертки (псевдокод)
for (each scan line, у)
// для каждой строки развертки
for(each pixel, х. on scan line у)
// для каждого пиксела на строке развертки у
{
find the closest face that "covers" the pixel:
// находим ближайшую грань, «покрывающую» данный пиксел
с - color at (х, у) of the closest face:
// цвет ближайшей грани в точке (х. у)
set the pixel at(x, у) to color c
// устанавливаем цвет пиксела в точке (х. у) в с
}
Общая схема этого алгоритма приведена в листинге 13.4. Он аналогичен алгоритму закраски поли-
гона из главы 10, за исключением того, что для каждого пиксела рассматривается более одного полигона.
Различные варианты данного алгоритма [Bouknight, 34; Watkins, 208] отличаются друг от друга главным
образом методом определения ближайшей грани и тем порядком, в котором выполняются различные
этапы.
Серии пикселов вдоль строки развертки закрашиваются цветом того полигона, который покрывает
эту серию. Если пиксел покрывается более чем одним полигоном, то выбирается цвет полигона, обла-
дающего наименьшей глубиной. Для большей эффективности в алгоритме создаются и поддерживают-
ся различные списки, призванные в максимальной степени использовать связность вдоль строки раз-
вертки. То есть если пиксел покрывается несколькими полигонами, то вероятнее всего, что и соседний с
ним пиксел также будет покрываться этими полигонами. В алгоритме также учитывается связность
ребер — для этого ребра всех граней предварительно обрабатываются, сортируются и помещаются в спе-
циальный список.
В примере на рис. 13.12 показано, как к выполнению операции HSR приспособить алгоритм закрас-
ки из раздела 10.7.2. На рисунке приведены проекции трех перекрывающихся пространственных плос-
ких граней А, В, С. В списке активных ребер (active-edge list) хранятся те значения абсцисс х, при кото-
рых ребро какой-либо грани пересекает текущую строку развертки L. Эти точки пересечений хранятся
в списке в отсортированном виде. Каждый узел списка указывает на грань, ответственную за данное
пересечение: значение numCovered означает число граней, покрывающих данный пиксел, а в логическом
массиве covered [] покрывающим граням соответствуют значения true.
Перед началом просмотра по z поперек строки развертки всем элементам массива covered[] присваи-
ваются начальные значения false, а счетчик numCovered обнуляется. В нашем примере пикселы от х “ О
до х - х{ не покрывает ни одна грань, поэтому применяется цвет фона. В точке xt достигается грань В,
поэтому covered[B] устанавливается в true, a numCovered устанавливается в 1. Глубина каждой покрываю-
13.4. HSR-метод построчного сканирования
817
щей грани в текущем пикселе хранится в новом поле thisDepth узлов граней. Начальное значение этого
поля устанавливается в соответствии с глубиной точки первого пересечения с данной строкой разверт-
ки. При каждом последующем значении х глубина может только увеличиться на постоянную величину
depthinc, подобно тому, как это делалось в методе буфера глубины в главе 8. При этих инкрементных
вычислениях глубины используется связность глубин — возможность легко вычислить глубину точки
на грани по глубинам соседних с ней точек на той же грани.
AEL
С
Глубина
Добавочная глубина
Покрытия |т|7~|р|.'~ Число [Т]
АВС "" покрытий
Рис. 13.12. Пример списка активных ребер для строки развертки
При перемещении от х - xt до х - х2 грань В является единственной покрывающей гранью, поэтому
каждый из ее пикселов может быть закрашен в соответствии с подходящим правилом закраски. Соглас-
но этому правилу, закраска всей серии от xt до х2 может быть произведена за один прием.
В точке х2 появляется грань А, определяется ее глубина; счетчик numCovered становится равным 2;
covered[А] устанавливается в true. Продвигаясь вперед по списку активных ребер, процедура узнает, что
от х2 до х3 пикселы покрываются только двумя гранями, поэтому для каждого пиксела ближайшая грань
может быть определена простым сравнением их глубин. Если вначале ближайшей гранью является
грань А, то нет никакой гарантии, что так и будет все время; дело в том, что грани могут оказаться взаи-
мопроникающими. Это можно проверить, вычислив две глубины в точке х3. Если порядок глубин оста-
ется неизменным вдоль серии до х3, то всю серию можно закрашивать так, как если бы была только одна
покрывающая грань. В точке х3 грань В перестает быть покрывающей, поэтому цвет пиксела определя-
ется просто. (Как?) В точке х4 начинает покрывать грань С, поэтому необходимо определить соотноше-
ния глубин граней А и С.
В общем случае для каждого последующего пиксела вдоль строки развертки глубина каждой покры-
вающей грани увеличивается. При каждом пересечении с ребром элемент массива covered[] для грани
818
Глава 13. Удаление невидимых поверхностей
устанавливается в true, если эта грань начинается, и в false, если заканчивается; соответственно коррек-
тируется и счетчик numCovered. Когда пиксел покрывается более чем одной гранью, то определяется бли-
жайшая из них, после чего вычисляется цвет или оттенок этой грани. Поскольку пересечение ребер про-
исходит относительно редко, то используется связность строки развертки.
После прохода строки развертки L текущая строка развертки увеличивается на единицу, все элемен-
ты массива covered[] снова устанавливаются в false, а список активных ребер обновляется, так что он
должен точно представлять все пересечения ребер, которые встретятся вдоль новой строки развертки.
Обновление списка осуществляется так же, как в варианте закраски полигона, когда для эффективнос-
ти используется таблица ребер.
Созданы различные модификации данного алгоритма, направленные на увеличение его эффектив-
ности и на расширение класса объектов, которые можно визуализировать с его помощью (см. [Foley, 64]).
Практические упражнения
13.4.1. Объекты не являются взаимопроникающими
Часто заранее известны некоторые свойства визуализируемых объектов; в ряде случаев эта информа-
ция может позволить выбрать более простой HSR-алгоритм. Какие упрощения можно сделать в алго-
ритме построчного сканирования, если известно, что никакая пара граней не является взаимопрони-
кающей?
13.4.2. Тестирование глубины в пределах серии
Покажите, как алгоритм, рассмотренный в данном разделе, «зная» глубины всех покрывающих граней
в начале серии, может «заглянуть» в конец этой серии и определить там с помощью простого вычисле-
ния все глубины покрывающих граней. Если алгоритм обнаруживает изменение порядка глубин гра-
ней, то может ли он найти пиксел, в котором это изменение произошло? Каким образом?
13.4.3. Помогает ли выпуклость полигонов?
Рассмотрите возможные упрощения HSR-алгоритма построчного сканирования для случая, когда все
грани являются выпуклыми.
13.5. Методы разбиения области
Рассмотрим принципиально другой подход к HSR, в котором используется связность области сцены.
Мы уже употребляли этот термин: под связностью строки развертки понимается свойство многих со-
седних пикселов вдоль строки развертки покрываться или не покрываться какой-либо гранью; это связ-
ность по х при заданном у. Связность области (area coherence) — это представление о том, что многие
пикселы, соседние по х или по у, обладают одним и тем же свойством. Таким образом, имеется симмет-
рия между направлениями х и у.
Методы разбиения области основываются на разделении изображения на подобласти с последу-
ющей проверкой каждой подобласти на надичие видимых поверхностей. Если методы построчного
сканирования интересуются вопросами, относящимися к глубине каждого пиксела или, самое большее,
серии пикселов, то в методах разбиения используется принцип разобщения «разделяй и властвуй»
(«divide-and-conquer» approach). Эти методы пытаются выяснить, когда подобласть станет достаточно
«простой», чтобы ее можно было нарисовать целиком без дальнейшей проверки на глубину. Если область
проста в этом смысле, то она рисуется немедленно; в противном случае она разбивается на совокуп-
ность меньших подобластей, и тесты повторяются для каждой из этих подобластей. Если размер под-
области достигает некоего заранее определенного минимума (часто это один пиксел), то разбиение пре-
кращается и выполняются явные тесты глубины с целью определить ближайшую поверхность. Затем
эта область рисуется нужным цветом.
Существует несколько разновидностей алгоритмов разбиения области, все они носят название алго-
ритмов Варнока (Warnock algorithms), по имени Джона Варнока, который первым разработал такой под-
13.5. Методы разбиения области
819
ход [Warnock, 207]. Их различия состоят в основном в определении понятия простой области и в спо-
собе разбиения области.
13.5.1. Квадрантное разбиение
Остановимся на методе квадрантного разбиения (quadrant subdivision), который особенно прост в реа-
лизации. Другие методы рассматриваются в упражнениях в конце следующего раздела.
Правильно
Рис. 13.13. Квадрантное разбиение области
На рис. 13.13 представлен пример квадрантного разбиения прямоугольной области. На рис. 13.14, а
показаны проекции двух трехмерных граней в область R, причем не дается никакой подсказки, которая
из граней ближе к наблюдателю.
На рис. 13.13, б приводится правильное расположение граней, которое должно быть в конце концов
нарисовано: видно, что грани являются взаимопроникающими. Для того чтобы применить метод квад-
рантного разбиения, предположим, что область достаточно проста для немедленного рисования в том
случае, если в нее втянуто (involved) не более одной грани. Грань Г втянута в область R в том случае, если
какая-либо часть F перекрывает какую-либо часть R. Если втянута только одна грань, то задача HSR ре-
шается автоматически, и область легко визуализируется с помощью подпрограммы, рисующей отсе-
чение грани границами области. Если не втянуто ни одной грани, то будет рисоваться цвет фона.
Поскольку в область R на рисунке втянуты две грани, область не является достаточно простой и по-
этому должна подвергнуться разбиению. Разобьем область на четыре квадранта, которые обозначим как
страны света на карте: северо-западный (northwest — NW), северо-восточный (northeast — NE), юго-
западный (southwest — SW), юго-восточный (southeast — SE) (см. рис. 13.13, в). В квадранты NW и SW
на рисунке втянуто только по одной грани, поэтому части соответствующих граней рисуются немед-
ленно. (Предположим для удобства, что вначале весь экран закрашен цветом фона.) С другой стороны,
квадранты NE и SE имеют по две втянутых грани и поэтому должны подвергнуться разбиению, как
показано на рис. 13.13, г. Теперь все новые подобласти, кроме двух, можно визуализировать. С двумя
оставшимися подобластями продолжается процесс разбиения.
820
Глава 13. Удаление невидимых поверхностей
В процессе разбиения области могут стать чрезвычайно малыми. Как же мы решим, что область до-
статочно мала и ее дальнейшее разбиение запрещено? Области определены в порту просмотра, поэтому
применим следующий простой принцип точности по изображению: когда область уже разбита так мелко,
что она содержит только один центр пиксела, то больше ее разбивать нельзя, даже если она не является
простой. Вместо разбиения мы определим грань для рисования с помощью проверки глубин всех граней,
втянутых в эту область, из которых найдем ближайшую. Тогда пикселу присваивается цвет этой грани.
Если же область мала настолько, что не содержит ни одного центра пиксела, то она игнорируется.
Листинг 13.5. Скелет класса для поддержки алгоритма Варнока
class Region{
public:
Rect г:
// a region is a rectangle
// прямоугольная область
int getSizeO;
// how big is it?
// каковы ее размеры?
bool isSimple_Draw!t(FaceListS faces):
// if it's simple, draw it
// если она простая, то рисуем ее
void drawClosestFace(FaceListS faces):
bool is!nvolved(FaceS face):
// is the region involved with face?
// есть ли грань, втянутая в область?
int buildQuadrants(Regions nw. Regions ne. Regions sw. Regions se);
void draw(FaceListS faces)
// the main drawing method
// основной метод рисования
{
int size = getSizeO;
// how big is it?
// каковы размеры области?
if(size < Dreturn;
// nothing to draw
// рисовать нечего
if(size — 1) drawClosestFace(faces):
// covers one pixel center
// покрывает один центр пиксела
else if(isSimple_draw!t(faces))return:
// draw it and exit
// рисуем область и выходим
else
// it's not simple enough
// область недостаточно проста
{
Region NW. NE. SW. SE:
buildQuadrants(NW. NE. SW. SE):
// make subregions
// создаем подобласти
NW.draw(faces):
// draw each of them
// рисуем каждую из них
13.5. Методы разбиения области
821
NE.draw(faces);
SW.draw(faces):
SE.draw(faces):
}
}
}:
Для реализации алгоритма Варнока определим класс Region, как предлагается в листинге 13.5, и за-
дадим в нем ряд методов. Основным методом здесь является draw(FaceList&faces), который рисует обра-
батываемую область. Его параметром является список всех граней в сцене, представленный в некото-
ром подходящем типе данных Filelist. Подпрограмма drawO использует метод getSizeO для проверки
того, сколько центров пикселов содержится в области region. Если нет ни одного, то ничего не делается.
Если имеется ровно один центр пиксела, то подпрограмма drawClosestFaceO проверяет глубины всех
втянутых в центр этого пиксела граней и устанавливает в качестве цвета этого пиксела цвет ближайшей
грани. Если присутствует более одного пиксела, то метод isSimple_drawIt() проверяет, проста ли эта
область, и если да, то рисует ее. В противном случае формируются четыре подобласти и метод drawO
вызывает сам себя для каждой из этих областей.
Суть алгоритма Варнока заключается в геометрическом анализе, выполняемом с помощью метода
isSimple_drawIt(). Область следует тестировать с каждой гранью из списка граней, чтобы определить,
сколько граней втянуто в данную область. Инкапсулируем это тестирование в метод islnvol vedCFace &
face), который возвращает true, если грань face втянута в область, и false в противном случае. Чем разум-
нее составлен данный тест, тем быстрее будет работать рассматриваемый HSR-алгоритм. Какие провер-
ки могут потребоваться в этой функции? Существуют различные ситуации, в которых грань F может
быть втянута или не втянута в прямоугольную область R, как показано на рис. 13.14.
О Экстентп-непересечение {extent disjoint). Грань F называется экстентно-непересекающейся с обла-
стью R, если экстент Ене имеет пересечений с R (рис. 13.14, а). Если грань Еэкстентно не пересе-
кается с областью R, то F должна целйком лежать вне R. Эта геометрическая ситуация наиболее
проста для определения.
Рис. 13.14. Варианты втянутости грани в область: в) экстент-непересечение; б) непересечение; в) пересечение;
г) охватывание; д) заключение внутри
822
Глава 13. Удаление невидимых поверхностей
О Непересечение (disjoint). Грань /"может не пересекаться с областью R, даже когда ее экстент пере-
секается с этой областью (рис. 13.14, б). Чтобы проверить это условие, нужно произвести отсече-
ние каждого из ребер грани F областью R. Если все ребра грани отсекаются, то они должны ле-
жать целиком вне R и, следовательно, грань F не пересекается с R. Проверка данной ситуации
более сложна, чем тест на экстент-непересечение, поэтому данный тест выполняется только тог-
да, когда тест на экстент-непересечение дал отрицательный результат.
О Пересечение (intersecting). По крайней мере одно ребро грани F пересекает границу области R
(рис. 13.14, в). Позднее мы увидим, как можно объединить тесты на пересечение с тестом на непе-
ресечение. Отметим, что пересечение может иметь место даже тогда, когда нй одна из вершин гра-
ни F по существу не лежит внутри области R. (Как это может быть?)
О Охватывание (surrounding). Область R полностью охвачена гранью F (рис. 13.14, г). После боль-
шого количества разбиений подобласти исходной области R становятся очень малыми, поэтому
данное условие выполняется довольно часто,
О Заключение внутри (contained). Грань /"полностью заключена внутри области R (рис. 13.14, г).
Эта ситуация имеет место тогда и только тогда, когда все вершины F лежат внутри R.
Грань Fсчитается втянутой в область R, если имеет Место пересечение, охватывание или заключение
внутри. Поэтому наше определение «простой» области выглядит так: область R является простой, если
не более одной грани пересекается с ней, охвачено ею или заключено в ней.
Поэтому подпрограмма isinvolved(face) должна определять для грани face с областью R наличие или
отсутствие ситуаций пересечения, охватывания ИЛИ заключения внутри. Как это можно сделать наибо-
лее эффективно? Прежде всего подпрограмма выполняет простейший тест: имеет ли место экстент-не-
пересечение грани face с областью R? Если нет, то лучше всего обойти все вершины полигона face, про-
веряя каждую вершину и каждое ребро на Пересечение с областью. Поскольку область R — выпуклая, то
легко проверить, лежит ли Вершина внутри R. (Как именно?) Так же просто проверить, пересекает ли
ребро грани одно из горизонтальных или вертикальных ребер области R. (Как?)
Как только в процессе обхода грани face выясняется, что ее вершина находится внутри области R
или ее ребро пересекает R, тестирование прекращается и функция islnvol ved() возвращает true. С другой
стороны, если все вершины грани находятся вне области R и ни одно ребро с ней не пересекается, то в
таком случае грань face или не пересекается с областью R, или заключает ее внутри себя. С целью раз-
личить эти две ситуации подпрограмма проверяет, лежит ли какая-нибудь вершина области R внутри
данной грани. Это может быть сделано посредством теста на четность, который рассматривался в раз-
деле «Заполнение полигонально-определенных областей».
13.5.2. Другие определения простой области
До сих пор мы рассматривали только одно определение простоты области: область является простой,
если в нее не втянуто ни одной грани или втянута только одна грань. Однако можно использовать и
другие критерии, которые жертвуют скоростью ради простоты.
Когда «простая» означает «пустая»
Наиболее примитивное определение простой области заключается в том, что эта область должна быть
пустой — в нее втянуто ровно нуль граней. При таком критерии, разумеется, непростыми оказывается
намного больше подобластей, вследствие чего выполняется и намного больше разбиений. Фактически
для каждого пиксела, покрытого гранью, разбиения будут продолжаться вплоть до уровня одного пик-
села, так как это единственный способ их прекратить! Когда втянута только одна грань, данный метод
не может установить этот факт и продолжает разбиение. На деле данный метод выдает много «ложных
тревог», утверждая, что область является слишком сложной для решения вопроса о невидимых поверх-
ностях, тогда как в действительности эта область согласно предыдущему определению является про-
13.5. Методы разбиения области
823
стой. Преимущество же данного подхода состоит в том, что здесь не требуется никакого сканирующего
преобразования (scan conversion); единственный используемый инструмент рисования (после заливки
цветом фона) — это установка цвета пиксела.
Использование охватывающих граней
Другое широко используемое определение простой области требует более сложного тестирования, одна-
ко с его помощью очень хорошо идентифицируются простые области при значительно меньшем числе
необходимых разбиений. В данном определении отсутствует требование, чтобы в область было втяну-
то не более одной грани. Вместо этого может быть втянуто много граней, если одна из них доминирует
(dominates). Грань Fдоминирует в области R, если она является охватывающим область R многоугольни-
ком, который всюду ближе (к глазу), чем любая из остальных втянутых в область R граней. Ситуация,
при которой такое понимание простоты экономит много разбиений, показана на рис. 13.15. Область Л
(квадратик) является простой уже после двух уровней разбиения, показанных На рисунке, несмотря на
то, что в нее втянуто более одной грани, поскольку единственная охватывающая ее грань (фасад сарая)
является ближайшей и тем самым маскирует все остальные. Если бы применялось первое определение
простоты, То эту область пришлось бы разбивать вплоть до уровня пиксела, поскольку более удален-
ный сарай имеет грань, пересекающуюся с видимой гранью целиком внутри области А. (Вопрос, при
каких определениях простоты область В является простой?)
Рис. 13.15. Охватывающая грань лежит ближе
Как же проверить, что охватывающая грань является повсюду ближайшей (к глазу) внутри под-
области R? Требуется проверить ее глубину только в четырех углах R и сравнить с глубинами плоско-
стей всех остальных втянутых граней в этих же углах. Если охватывающая грань является ближайшей
во всех четырех углах, то ни одна из других втянутых граней не может перекрыть ее.
В процессе просмотра списка граней faces мы помечаем все охватывающие грани перед занесением
их в список outfaces. После того как все грани протестированы, мы проверяем глубины охватывающих
граней и выбираем ту из них, которая ближе всех остальных. (Она не всегда существует — почему?)
После этого мы тестируем «победившую» грань относительно плоскостей всех оставшихся граней из
списка faces. Если там есть «победившая» охватывающая грань, то визуализация области R произво-
дится в соответствии с цветом ее поверхности и никаких дальнейших разбиений не требуется. В про-
тивном случае рекурсивно проходится список outfaces, как и ранее. Отметим, что охватывающие грани,
помеченные в списке outfaces, не нуждаются в повторном тестировании после следующего разбиения,
так как они, несомненно, остаются охватывающими.
При использовании данного определения простоты осуществляется явный компромисс между
сложностью, состоящей в тестировании каждой грани, и необходимостью дополнительных циклов
824
Глава 13. Удаление невидимых поверхностей
разбиения. Для каждой области требуется проводить гораздо больше тестов — в надежде, что понадср
бится тестировать намного меньшее их количество (поскольку будет меньше разбиений).
Практические упражнения
13.5.1. Ручная имитация алгоритма Варнока
Пусть равнобедренный прямоугольный треугольник точно вписан в квадратную область. Проделайте
для такой ситуации ручную имитацию операции Region :: draw( ) и покажите, как составляются раз-
личные списки граней. Продолжайте имитацию до тех пор, пока не будут проверены все нужные под-
области вплоть до одной шестнадцатой части исходной области.
13.5.2. Еще одно значение простоты
При первом определении простоты требуется, чтобы в область было втянуто не более одной грани.
Но если втянуто несколько непересекающихся граней, то для решения задачи HSR не потребуется вы-
полнять никаких вычислений глубин. В этом случае подпрограмма isSimple_drawIt() построит список
граней, втянутых в данную область, и проверит их на взаимное непересечение. Если это условие соблю-
дено, то подпрограмма просто нарисует поочередно каждую из этих граней. Обдумайте сложность дан-
ного подхода. В частности, как проверить совокупность граней, втянутых в область, на непересечение?
Стоит ли такое определение простоты того, чтобы реализовывать его?
13.5.3. Альтернативные подходы к разбиению
Когда ребра граней пересекают экран дисплея по диагонали (как на рис. 13.13), то может потребо-
ваться много уровней разбиения, поскольку границы областей никогда не «выровняются» с ребрами.
На рис. 13.16 предлагается другой подход к разбиению области: по вершине А самой заметной грани
сцены. Два ребра Et и Е2 продолжены до границ области, определяя тем самым четыре подобласти
Rt,..., Re Теперь треугольник не пересекается с тремя из новых подобластей, существенно упрощая их.
Если применить к каждой из этих подобластей те же тесты, что и прежде, то простые области будут
визуализироваться, а непростые разбиваться дальше. Рассмотрите изменения, которые следует осуще-
ствить в методе квадрантного разбиения для реализации данного подхода. Нарисуйте сцену с несколь-
кими полигональными гранями и покажите, как будут выполняться разбиения с целью выявления
видимых поверхностей.
Рис. 13.16. Разбиение области вдоль ребра
13.5.4. Введение сглаживания
Как можно осуществлять сглаживание во время выполнения HSR с использованием разбиения облас-
ти? Рассмотрите разбиение ниже уровня пикселов с последующим усреднением. Обдумайте, как мож-
но это сделать и насколько эффективна будет данная технология.
13.6. О методах удаления невидимых линий
825
13.6. О методах удаления невидимых линий
Иногда нужно выполнить рисование сцены одними линиями, как это показано на рис. 8.2. Здесь рису-
ются только видимые участки каждого ребра, вследствие чего объекты выглядят объемными и непроз-
рачными. Вычерчивание линий может быть выбрано из художественных соображений, или потому, что
оно намного быстрее цветной визуализации, или из-за того, что имеющиеся устройства могут выпол-
нять только эту операцию.
Если устройство допускает «закраску поверх», так что ребра можно вначале нарисовать, а затем покрыть
сплошными областями с цветом фона, то можно применять рассмотренные нами ранее HSR-технологии.
Мы просто производим визуализацию (видимой части) каждой полигональной грани с цветом фона и
рисуем ее ребра черным цветом. При данной технологии каждая грань рисуется поверх нарисованных
ранее, при необходимости перекрывая их, так что остаются только видимые ребра. Для достижения этой
цели могут применяться список приоритетов, метод Варнока и алгоритмы буфера глубины.
Если устройство не поддерживает «рисования поверх», то нам потребуется использовать другие
методы для осуществления HLR (удаления невидимых линий). Например, после того как перьевой гра-
фопостроитель нарисовал линию, она не может быть «стерта». Кроме того, некоторые растровые уст-
ройства типа фоторегистраторов также не допускают перерисовывание линий, поскольку при повтор-
ном рисовании цвета перемешиваются, а не рисуются поверх старых.
Рис 13.17. Выполнение удаления невидимых линий
В данном разделе мы рассматриваем методы, в которых каждый элемент рисуется только после за-
вершения полной проверки на видимость, вследствие чего ни одна его часть не подлежит стиранию или
рисованию поверх нее. Сосредоточим свое внимание на рисовании видимых ребер каркасного объекта.
При прямом подходе осуществляется отсечение каждого ребра такого объекта относительно всех гра-
ней, которые его заслоняют. Как показано на рис. 13.17, некоторые ребра не изменяются вовсе (ef), дру-
гие полностью удаляются со сцены (е2), третьи отсекаются с одного конца, а четвертые разбиваются на
несколько кусков (е3).
Нужно ли тестировать каждое ребро относительно каждой грани? Нет, не нужно, поскольку о замк-
нутых объемных монолитных объектах нам известны два важных факта.
1. Если ребро закрывается нелицевой гранью, то какая-нибудь лицевая грань также обязательно
закроет это ребро. (Почему?)
2. Каждое ребро принадлежит двум граням.
Из первого факта следует, что достаточно отсекать ребра только относительно лицевых граней, так
что нелицевые грани можно исключить в самом начале, как это делалось в предшествующих алгорит-
мах. Из второго факта следует, что если ребро принадлежит двум нелицевым гранями, то оно должно
быть невидимым и может далее не рассматриваться.
826
Глава 13. Удаление невидимых поверхностей
Грань может разделить ребро на много частей. (Покажите ситуацию, в которой грань с восемью реб-
рами разделяет ребро другой грани на пять частей.) Такой алгоритм должен отслеживать все «выжив-
шие» куски ребра (то есть те, которые потенциально могут быть видимыми), и каждый из выживших
кусков должен тестироваться относительно всех оставшихся граней из списка граней.
В описываемой модели прежде всего определяются все ее потенциально видимые ребра, после чего
они помещаются в список ребер. Затем начинается выполнение цикла, в котором ребро извлекается из
списка ребер и обрабатывается. Это ребро отсекается каждой (лицевой) гранью, и если оно выжило, то
рисуется. Если же отсечение разбивает ребро на куски, то один из выживших кусков тестируется отно-
сительно всех оставшихся граней, а остальные куски помещаются обратно в список ребер. Если в ка-
кой-нибудь точке ребро отсекается целиком, то цикл начинается вновь — с извлечения из списка следу-
ющего ребра. Этот цикл продолжается до тех пор, пока список ребер не опустеет.
Рис 13.18. Эффект разделения ребра на видимые части
На рис. 13.18 приведен пример, в котором ребро Е, простирающееся от вершины А до вершины В,
тестируется относительно грани F и разделяется на четыре видимых части. Первое выжившее ребро
становится ребром Е, а остальные выжившие заносятся в список ребер.
Тип данных для ребер
Листинг 13.6. Скелет типа данных для класса Edge
class Edge{
Point3 first, second:
// end points of the edge
// концевые точки каждого ребра
Face *facel. *face2;
// pointers to its two faces
// указатели на две грани ребра
Cuboid extent:
//3D extent of edge
// трехмерный экстент ребра
Face *nextFace:
// next face for testing
// следующее ребро для тестирования
}:
В листинге 13.6 приведен скелет класса Edge, представляющего каждое ребро, подлежащее тестирова-
нию. Помимо очевидной необходимости сохранять концевые точки ребра (или индексы списка вершин,
если такой список используется), о каждом ребре хранится дополнительная информация — с целью
обеспечить максимальную эффективность. Эта информация состоит из следующих элементов:
1. extent: экстент ребра — параллелепипед, выровненный по осям координат, который точно охва-
тывает ребро.
2. facel, face2: указатели на две грани, связанные с данным ребром. Поскольку ни одна из этих
граней не может заслонять ребро, то их не нужно тестировать, и поэтому они пропускаются.
13.6. О методах удаления невидимых линий
827
3. nextFace: указатель на следующую грань в списке граней, подлежащую тестированию. Когда ребро
разделяется на части и одна его часть заносится обратно в список ребер, то она уже была проте-
стирована относительно каких-либо граней. Следовательно, когда она позднее будет извлечена
из списка, то ее нужно будет протестировать только относительно граней, оставшихся в списке.
Для построения исходного списка ребер просматривается список граней, и ребра каждой лицевой
грани заносятся в список ребер. Ребра-дубликаты удаляются из списка, после чего заполняются поля
каждого объекта класса Edge.
Отметим, что имеются некоторые преимущества упорядочивания списка граней таким образом, чтобы
самые «заметные» грани (грани большого размера вблизи от глаза камеры) находились в начале списка.
В этом случае ребра будут тестироваться прежде всего относительно таких граней, которые вероятнее
всего устранят их.
Удобно выделить геометрическое тестирование ребра относительно грани в подпрограмму:
bool edgeTest(Edge& Е. Face& F):
которая проверяет ребро Еотносительно грани Ей возвращает true тогда и только тогда, когда есть «вы-
жившие» ребра. Эта подпрограмма устанавливает Е равным первому выжившему ребру, а остальные
выжившие ребра помещает в список ребер.
Эти соображения приводят нас к алгоритму, скелет которого приведен в листинге 13.7.
Листинг 13.7. Скелет HLR-алгоритма
void drawVisibleEdges(FaceL1st faces)
{
EdgeList edges;
// the edge list
// список ребер
build the edge list of all potentially visible edges
11 создаем список ребер из всех потенциально видимых ребер
whileiedges is not empty)
// edges не пустой список
{
Edge E - getNext(edges);
// remove the next edge
// удаляем следующее ребро
bool IsVis - true;
// suppose it's visible
// предполагаем его видимым
for(F - E.nextFace: 1sV1s && F !» NULL; F is next face)
11 следующая грань F
{
if(F belongs to F) continue;
// E принадлежит F
// no need to test this face
// эту грань тестировать не нужно
isVis - edgeTest(E.F);
// put survivors on edge list
// заносим выжившие ребра в список ребер
}
if (isVis) Е.drawO;
// Е is visible: draw it
// E - видимое ребро; рисуем его
}
}
828
Глава 13. Удаление невидимых поверхностей
Практические упражнения
13 .6.1. Ручная имитация HLR
Для объектов, изображенных на рис. 13.17, пометьте каждую лицевую грань и каждое ребро, которое
принадлежит хотя бы одной лицевой грани. Составьте список лицевых граней, которые закрывают каж-
дую нелицевую грань. Покажите, что произойдет с каждым ребром при его отсечении всеми лицевыми
гранями.
13 .6.2. Ситуация сортировки списка граней
Для какого типа сцен особенно полезно предварительно отсортировать список граней? Состоит ли та-
кая сцена из многих граней или из немногих? Что можно сказать о гранях, имеющих много сторон?
Нарисуйте несколько примеров, для которых предварительная сортировка оправдывает себя, и несколь-
ко таких, для которых — нет.
13 .6.3. Ручная имитация
Для объектов с рис. 13.17 проделайте вручную алгоритм из листинга 13.7. Нарисуйте соответствующие
списки граней и ребер и покажите состояние этих списков в момент, когда ребро е3 только что отсечено
ближайшей к глазу гранью.
13.6.1 . Геометрическое тестирование в подпрограмме edgeTestQ
Основная работа HLR-алгоритма, скелет которой приводится в листинге 13.7, возлагается на функцию
edgeTest(E.F). Простейшие тесты должны выполняться первыми, чтобы сколь возможно быстро опре-
делиться с ребром Е. Если одного теста недостаточно, то должен выполняться следующий. Хотя воз-
можно много вариантов, разумной последовательностью тестов является такая:
О Тестирование экстента. Экстент по х ребра Е тестируется относительно экстента грани F. Если
они не пересекаются, то грань Ене может заслонять ребро Е. Если же пересечение имеет место, то
тестируются соответствующие экстенты по у, и ребро Е по-прежнему «выживет», если и эти эк-
стенты не пересекаются. Оба этих теста — очень быстрые.
О Ребро на ближней стороне. Если обе концевые точки V} и У2 ребра Е находятся ближе, чем плос-
кость грани F, то такое ребро не может заслоняться гранью F и потому выживает. Если уравнение
плоскости грани F имеет вид m Р = D, где m — внешняя нормаль, то можно сформировать две ве-
личины s, = (m • Vt - D) и s2 = (m • V2 - D). Если обе эти величины положительны, то ребро Е
лежит на ближней стороне плоскости (с той же стороны, что и глаз). (Почему?) Мы уже видели
подобный тест относительно плоскости грани в методе сортировки глубины в листинге 13.3.
О Ребро проходит сквозь плоскость. Если величины s, и s2 имеют различные знаки, то ребро должно
«протыкать» плоскость грани. В этом случае удобно разделить его на два куска, один из которых
находится на ближней стороне плоскости грани, а второй — на дальней. Ближний кусок несом-
ненно переживет процесс тестирования и поэтому отправится в список выживших ребер, возвра-
щаемых подпрограммой edgeTestO. Судьба дальнего отрезка ребра по-прежнему остается невы-
ясненной. Аналогично, если обе величины s, и s2 отрицательны, то все ребро Е лежит на дальней
плоскости и для него требуется дальнейшее тестирование.
Для того чтобы найти, где ребро Е с концевыми точками Vt и И, протыкает плоскость, напишем для
этого ребра обычную параметрическую форму V/l -1) + V2t и подставим ее в уравнение плоскости гра-
ни. Как обычно, решим полученное уравнение для времени соударения thjt. Значение ihit мы будем использо-
вать в параметрической форме плоскости для вычисления точки пересечения ребра Е с плоскостью грани.
Этой стадии тестирования достигнет только такое ребро, которое целиком лежит на дальней стороне
плоскости грани F. Грань может закрывать ребро, а может не закрывать его. Если ребро на предыдущих
этапах было разделено, то полезно произвести повторное тестирование х- и г/-экстентов оставшегося
куска в надежде, что теперь перекрывание отсутствует. Если предположить, что экстенты перекрыва-
13.7. HSR-методы для криволинейных поверхностей
829
ются, то остается только вычислить точки пересечения ребра (мы будем обозначать его по-прежнему Е)
с каждым из ребер грани F. Используем для ребра Е параметрическую форму (как в предыдущем пара-
графе) и вычислим время каждого пересечения ребра Е с каким-нибудь из ребер грани. В результате
получаем список значений t. Для случая, приведенного в листинге 13.7, этот список содержит величи-
ны: t,, t2, t3, t4, t5, t6 (предполагается, что список начинает формироваться, когда ребро находится между
вершинами v{ и п2). Значения времени t сортируются, и список анализируется на предмет выяснения,
где находятся участки ребра, лежащие вне грани (см. ниже приведенные упражнения). В конце кон-
цов эти отрезки ребер, лежащие вне грани, помещаются в список выживших элементов для возвраще-
ния в подпрограмму edgeTestO.
Рис. 13.19. Нахождение точек пересечения ребра Е с ребрами грани F
Практическое упражнение
13 .6.4. Анализ списка значений t
Как только что обсуждалось, при тестировании ребра Е на пересечения со сторонами грани F создается
список значений t. Пусть этот список состоит из следующих значений: 0,6, 0,4, 0,1, -0,3, -0,8, 1,4. Что
еще должно быть известно, чтобы можно было сказать, какие из интервалов t соответствуют кускам реб-
ра Е, лежащим вне грани? Разработайте общий метод для анализа такого списка и построения нужных
интервалов t.
13.7. HSR-методы для криволинейных поверхностей
В главе 6, раздел «Формирование полигональной сетки для криволинейной поверхности», мы имели
дело со следующим подходом: криволинейные поверхности перед визуализацией обычно «полигони-
зируются». Поверхность, заданная в параметрической форме Р(и, v), разделяется на плоские полигоны
вдоль линий постоянства параметров и и v. Однако это может привести к образованию очень большого
количества полигонов и крупным затратам памяти. Кроме того, на окончательной картинке могут наблю-
даться некоторые дефекты изображения, такие как контуры, выглядящие неприятно полигональными.
Иногда бывает предпочтительнее визуализировать криволинейные поверхности непосредственно.
Был разработан целый ряд методов [Catmull, 40; Blinn, 27, Lane, 129; Clark, 41; Blinn, 28] решения задач
HSR и визуализации параметрически заданных фрагментов поверхностей (лоскутов). Здесь мы рас-
смотрим эти проблемы и опишем один из методов, признанный очень удачным.
На рис. 13.20 изображена совокупность лоскутов, сопряженных друг с другом и образующих еди-
ную криволинейную поверхность. Видно, что строка развертки у = у} пересекает один из лоскутов в неко-
торой точке ее контура.
Кэтмулл [Catmull, 40] разработал метод, в котором каждый лоскут рекурсивно разбивается на четыре
лоскута — до тех пор, пока проекция лоскута не станет покрывать не более одного пиксела. С помощью
буфера глубины определяется, является ли данный лоскут ближайшей к глазу поверхностью, видимой
в текущий момент в этом пикселе, и если это так, то пиксел рисуется. Псевдокод этого метода приведен
в листинге 13.8.
830
Глава 13. Удаление невидимых поверхностей
Рис. 13.20. Визуализация нескольких фрагментов поверхности
Листинг 13.8. Метод Кэтмулла разбиения лоскутов (псевдокод)
push all patches onto a stack;
// проталкиваем все лоскуты в стек.
initialize the depth buffer;
// инициализируем буфер глубины
whileCstack not empty)
{
pop patch from stack:
11 выталкиваем лоскут из стека
if (patch covers at most one pixel)
11 лоскут покрывает не больше одного пиксела
{
iflpatch is the closest yet in z)
// лоскут является ближайшим no z на данный момент
get its color, draw it. and update the depth buffer:
11 берем цвет лоскута, рисуем им и обновляем буфер глубины
)
else
{
subdivide patch into 4 subpatches:
// разбиваем лоскут на 4 лодлоскута
push subpatches onto stack:
// проталкиваем подлоскуты в стек
}
}
Все лоскуты сцены (за исключением тех, чьи экстенты лежат целиком вне отображаемого объема
камеры) загружаются в стек. Затем эти лоскуты один за другим извлекаются из стека и определяется
размер их проекций. Если этот размер больше пиксела, то лоскут разбивается снова (в пространстве
параметров и и г) и четыре новых лоскута проталкиваются обратно в стек для последующей обработки.
Если же этот размер достаточно мал, то находится глубина поверхности в этом пикселе и сравнивается
с соответствующей глубиной в буфере глубины. Если данный лоскут является ближайшей на данный
момент поверхностью, то определяется его цвет и пиксел рисуется этим цветом.
Кэтмулл предлагает несколько путей повышения эффективности этого метода. Определение разме-
ра проекции лоскута является дорогостоящей операцией, поэтому вместо лоскута проецируется поли-
гон, сформированный из четырех угловых точек лоскута, и определяется размер этого полигона. Кроме
того, перед тем как проталкивать каждый лоскут в стек, его можно пометить как находящийся целиком
внутри отображаемого объема или нет. Когда впоследствии этот лоскут выталкивается из стека, его не
нужно отсекать, а если он будет разбиваться дальше, то будет известно, что все четыре его куска также
целиком находятся внутри.
Блинн и Уиттед (Whitted) [Blinn, 28] независимо друг от друга разработали похожие алгоритмы
построчного сканирования, в которых видимые куски лоскутов отслеживаются от одной строки раз-
13.7. HSR-методы для криволинейных поверхностей
831
вертки к другой. Оба метода требуют сложных численных расчетов для нахождения значений парамет-
ров (и, v), при которых координата у лоскута Р(и, v) принимает заданное значение строки развертки.
Существует и другой достаточно успешный подход, в котором лоскуты разбиваются до тех пор, пока
они не станут «достаточно плоскими», чтобы рассматривать их как плоскостные четырехугольники,
после чего они визуализируются с помощью HSR-алгоритма построчного сканирования. Если лоску-
ты, вовлеченные в процесс, являются лоскутами Безье или В-сплайн лоскутами, то существуют эффек-
тивные методы их разбиения посредством формирования нового контрольного полиэдра (эти методы
описаны в работе [Foley, 65]). Похожие методы для строк развертки были разработаны Лэйном и Кар-
пентером, а также Кларком ([Clark, 41; Lane, 129]). При подходе Лэйна—Карпентера лоскут разбивает-
ся только тогда, когда строка развертки начинает пересекать его; в методе Кларка все лоскуты разбива-
ются заранее, до начала процесса. В первом методе требуется большее число разбиений, но последний
метод требует больше памяти.
Листинг 13.9. Метод построчного сканирования Лэйна-Карпентера (псевдокод)
void LaneCarpenterC..)
{
add all patches to the patch table;
// добавляем все лоскуты в таблицу лоскутов
initialize the active patch list (APL);
// инициализируем список активных лоскутов (APL)
for(eac7j scan line y)
11 для каждой строки развертки у
{
update the APL:
И обновляем список APL
for(each patch P in the APL)
// для каждого лоскута P в APL
{
if(P is " planar enough'")
// P - «достаточно плоский»
add P to the polygon list;
// добавляем P к списку полигонов
else
{
split the patch into subpatches:
// разбиваем лоскут на подлоскуты
forieach new subpatch S)
11 для каждого нового подлоскута S
if(S sti11 intersects the scan line)
// если S по-прежнему пересекает строку развертки
add S to the APL:
// добавляем S к списку APL
else
add S to the patch table:
11 добавляем S в таблицу лоскутов
1
1
do scan line HSR process for this scan line for
the polygons in the polygon list:
// выполняем HSR-процесс для данной строки развертки
// для полигонов, входящих в список полигонов
832
Глава 13. Удаление невидимых поверхностей
В листинге 13.9 представлен псевдокод метода Лэйна—Карпентера. При работе подпрограммы)^
лоскуты прежде всего помещаются в таблицу лоскутов (patch table), напоминающую таблицу ребер,
которая применялась для хранения ребер в главе 10. Кроме того, имеется список активных лоскутов
(active-patch list), в котором содержатся все лоскуты, пересекающие текущую строку развертки, а так-
же список полигонов (polygon list), содержащий «достаточно плоские» четырехугольники, готовые для
визуализации.
Каждый лоскут из списка активных лоскутов тестируется поочередно; если он является достаточно
плоским, то аппроксимирующий его плоский четырехугольник помещается в список полигонов для
визуализации (поскольку данный лоскут пересекает текущую строку развертки). Если же лоскут недо-
статочно плоский, то он разбивается на четыре лоскута, и те из них, которые пересекают текущую стро-
ку развертки, добавляются в список активных лоскутов. Что касается тех лоскутов, которые не пересе-
кают текущую строку развертки (потому что лежат выше ее), то они отправляются обратно в список
лоскутов, чтобы стать активными позднее. Когда все лоскуты из списка для текущей строки развертки
обработаны должным образом, по полученному списку полигонов вызывается HSR-процесс построч-
ного сканирования, рисующий вдоль строки развертки нужные полигоны.
13.8. Резюме
Удаление невидимых поверхностей и линий — фундаментальная проблема компьютерной графики,
поэтому для качественного выполнения этой работы разработано много различных технологий. Алго-
ритмы удаления невидимых поверхностей (hidden-surface-removal — HSR) имеют обыкновение быть
сложными, с большим временем исполнения, поэтому было затрачено много усилий для увеличения их
эффективности. Полезно разделить различные методы на две категории. Одни алгоритмы оперируют
на уровне «точности по объекту»: это означает, что все геометрические вычисления, осуществляемые в
этих методах для определения относительных положений точек, ребер и плоскостей, делаются с макси-
мально возможным для данной машины уровнем точности. Другие методы работают на уровне «точно-
сти по изображению»: это означает, что все операции там происходят «пиксел за пикселом», а расстоя-
ния сравниваются при помощи индикатора, обладающего конечной точностью.
В данной главе мы рассмотрели различные подходы к проблеме HSR для важного класса объектов,
моделируемых полигональными сетками. Для повышения эффективности HSR все грани на сцене под-
вергаются предварительной обработке: их нелицевые грани удаляются, а лицевые отсекаются отображае-
мым объемом. Выжившие после этой процедуры грани отображаются в трехмерный порт просмотра с
использованием перспективного преобразования и перспективного деления, так что каждая вершина в
порте просмотра имеет результирующее положение (х, у) и значение псевдоглубины. Такая же предва-
рительная обработка производилась и на подготовительном этапе алгоритма с буфером глубины, кото-
рый описывался в главе 8. В целях сравнения мы в этой главе снова напомнили об алгоритме буфера
глубины. Это весьма эффективный HSR-метод с точностью по изображению, особенно простой в реали-
зации. Однако скорость этого метода ограничена большим количеством повторных рисований пикселов,
которое в нем приходится делать. Кроме того, большое количество дополнительной памяти, необходи-
мое для буфера глубины, может серьезно ограничить память, доступную для других задач программы,
а фиксированная точность буфера глубины может привести к ошибкам в определении малых различий
глубин удаленных объектов.
Поскольку HSR-методы основаны на принятии решения, какой из двух элементов «ближе» к глазу,
чем другой, или какой элемент из группы является «ближайшим», то ядром каждого HSR-алгоритма
являются сортировка и переупорядочивание. (Это обстоятельство становится особенно ясным после чте-
ния превосходного обзора HSR-методов, сделанного Сазерлендом и другими авторами [Sutherland, 19$],)
Поскольку сортировка может оказаться дорогостоящей, ключ к эффективности алгоритма — не делать
эту сортировку больше, чем это абсолютно необходимо. В таких методах, как алгоритм буфера глуби.;
ны, используется огромное количество памяти только для уменьшения расходов на сортировку (обыч-
но она сводится просто к поиску ближайшего элемента).
13.8. Резюме
833
Сортировка по х, у, z производится различными алгоритмами в различном порядке, в соответствии с
порядком обработки данных, как это сделано в следующем псевдокоде:
forCeach pixel){
// каждый пиксел
for(each face){...} }
// каждая грань
в сравнении с таким порядком:
forCeach face){
forCeach pixel){...}
Во всех этих алгоритмах сделан различный компромиссный выбор между скоростью, пространством
памяти и простотой.
Для уменьшения вычислительных затрат при работе HSR-метода были разработаны хитроумные
способы использования связности. Связность — это тенденция какого-нибудь аспекта сцены к плавно-
му изменению в некотором направлении движения, так что свойство, имеющееся в одной точке, очень
похоже на то же свойство в близлежащих точках. В рассмотренных здесь методах использовались раз-
личные типы связности, такие как связность области, связность глубин, связность строки развертки,
а также связность ребра.
Мы рассмотрели три HSR-алгоритма со «списками приоритетов» — это технологии, основанные на
хитроумной сортировке списка граней, так чтобы визуализатор мог рисовать грани в новом порядке,
удаляя те из них, которые находятся позади других граней. В успешно действующих методах, таких как
метод дерева двоичного разбиения пространства, определенные грани разделяются на две части. По-
добно подходу с буфером глубины, методы со списками приоритетов несвободны от большого количе-
ства повторного рисования пикселов.
Был рассмотрен также HSR-метод построчного сканирования, в котором повторное рисование пик-
селов отсутствует. Вместо этого в данном методе для каждого пиксела из всех граней сцены определя-
ется ближайшая к наблюдателю «в этом пикселе», и эта грань рисуется только один раз. В этом методе
используются также связность граней и связность строк развертки (поскольку ближайшая грань стре-
мится остаться таковой на целом участке строки развертки), что позволяет за одни раз закрашивать
целые «серии» пикселов; это обстоятельство существенно ускоряет процесс рисования.
В методе разбиения области (алгоритм Варнока) вышеприведенная идея развивается сразу в двух
направлениях — посредством поиска областей, в которых одна и та же грань легко определяется как
ближайшая. Если область содержит грани, которые еще нуждаются в сортировке по глубине, то алго-
ритм просто разбивает такую область на меньшие, с тем чтобы для каждой из малых областей найти
более простой ответ. В этом методе повторное рисование пикселов также не требуется.
Мы познакомились с методом удаления невидимых линий (HSL), который особенно подходит для
устройств, не допускающих стирание линий или рисование поверх старых линий. Этот алгоритм прове-
ряет видимость каждого ребра относительно всех лицевых граней модели. Поскольку геометрическое тес-
тирование ребра относительно грани может оказаться сложным, выполняются серии тестов возрастающей
сложности — до тех пор, пока не будет найден ответ. Ребро, лежащее частично позади грани, можно разде-
лить на несколько кусков, каждый из которых должен обрабатываться поочередно. Для организации это-
го процесса используется знакомая технология сохранения в стеке «всего, что еще будет обрабатываться».
Наконец, мы бегло ознакомились с задачей рисования трехмерных сцен, состоящих из криволиней-
ных поверхностей, — для случая, когда нежелательно аппроксимировать эти поверхности полигонами.
Ряд решений этой проблемы включает алгоритмы построчного сканирования, которые определяют для
каждого пиксела вдоль строки развертки тот элемент поверхности, который ближе всего к глазу наблю-
дателя. Другие методы обрабатывают лоскут за лоскутом, разбивая их на все меньшие и меньшие под-
лоскуты, которые поэтому становятся все более и более плоскими — до тех пор, пока не удастся одно-
значно решить, которая из них ближе всего к глазу и какого она цвета.
Кроме этих методов, придумано и исследовано много других HSR- и HLR-методов. В некоторых из
них (например, [Foley, 17; Rogers, 105]) за счет простоты применяются дополнительные приемы увели-
27 Ф. Хилл
834
Глава 13. Удаление невидимых поверхностей
чения эффективности. Другие методы [Butland, 38; Rogers, 175] работают с математическими функци-
ями или с обширными классами форм поверхностей.
13.9. Тематические задания
Тематическое задание 13.1. Проверка алгоритма художника
Уровень сложности II.
Напишите подпрограмму HeedlessPainterO, реализующую алгоритм беспечного художника. Грани в
массиве faces[] сортируются по псевдоглубине их наиболее удаленных вершин, затем полученный список
просматривается и каждая грань рисуется целиком, поверх любых ранее нарисованных граней. Для упро-
щения тестирования этого и прочих HSR-алгоритмов напишите подпрограмму, которая генерирует
списки граней для набора из ЛГ кубов со случайно выбираемыми размерами, положениями и ориентацией
в пространстве. Проверьте подпрограмму HeedlessPainterO на сценах, составленных из Nслучайных кубов.
Тематическое задание 13.2. Тест и разбиение
Уровень сложности I.
Напишите и протестируйте подпрограмму FaceWithPlaneO, которая проверяет, находится ли задан-
ная выпуклая полигональная грань целиком по одну или по другую сторону от плоскости. Если это не
так, то подпрограмма разбивает эту грань на два полигона, один из которых лежит целиком с внутрен-
ней стороны плоскости, а другой — целиком с внешней ее стороны. Вам может оказаться полезным сле-
дующий прототип (или придумайте свой собственный):
int FaceWith Plane(Face& face.
// face to be tested
// грань, подлежащая проверке
Face& node.
// with the plane of this face
// с плоскостью этой грани
Face& inFace.
// the inside piece when split
// внутренний кусок при разбиении
Face& outFace);
// the outside piece when split
// внешний кусок при разбиении
Данная процедура возвращает следующие значения:
О -1, если face лежит с внутренней стороны плоскости node.
О +1, если face лежит с внешней стороны плоскости node.
О 0, если face разбивается на две грани — inFace и outFace.
Как может работать такая подпрограмма? На рис. 13.21 показан пример разбиения выпуклой грани
плоскостью. Предположим, что грань F имеет вершины Vo, Vv ..., ,, а уравнение плоскости имеет
вид m • Р - D, где ш — нормальный вектор к плоскости, указывающий на ее внешнюю сторону. Под-
программа обходит вершины грани F, занося каждую из них, V[i], во внешний или во внутренний список
вершин, в зависимости от результатов следующего теста:
О V[i] лежит с внешней стороны плоскости, если ш • V[i] > D {заносим вершину во внешний список};
О V[i] лежит с внутренней стороны плоскости, если ш • Г[г] < D {заносим вершину во внутренний список}.
Если при переходе от одной вершины к другой знак выражения m • V[i] - D изменяется, то соответ-
ствующее ребро продолжается по обе стороны плоскости. Таким образом, процедура находит пересече-
13.9. Тематические задания
835
ние ребра с плоскостью и заносит это ребро в оба списка. (Почему?) В примере на рис. 13.21 Пентагон
(пятиугольник) разбивается на Пентагон и четырехугольник. Создаются два куска, и любая информа-
ция, содержавшаяся в исходной грани, копируется в оба этих куска. (Если имелись нормали в верши-
нах и текстурные координаты, то для вновь созданных вершин они определяются интерполяцией.)
Рис. 13.21. Разбиение выпуклой грани плоскостью
Обдумайте те обобщения, которые должны быть сделаны в данной подпрограмме, если полигон будет
невыпуклым.
Тематическое задание 13.3. Удаление невидимых поверхностей
с использованием BSP-деревьев
Уровень сложности III.
Предположим, что подпрограмма визуализации трехмерной сцены (без HSR) уже доступна. Напи-
шите приложение, которое визуализирует грани из массива faces[] и для решения задачи удаления не-
видимых граней (HSR) использует BSP-дерево. Проверьте полученную программу на интересных сце-
нах, состоящих из нескольких объектов, например из набора случайных кубов.
Обобщенный тип данных Face включает два указателя Face *1nsideOnes и Face *outs1 deOnes, которые
в момент построения массива faces[] устанавливаются в NULL. Перед началом визуализации грани по-
мещаются в BSP-дерево с помощью примерно такой подпрограммы:
Face *tree - NULL;
// create an empty BSP tree
// создаем пустое BSP-дерево
ford - 0: i < NumFaces: i++)
tree - insertBSP(&faces[1]. &tree);
Когда в дерево вставляется грань faces[i] (без разбиения), то устанавливаются только указатели ее
потомков; при этом грань faces[i] находится одновременно в массиве faces[] и в дереве. Если грань
faces[i ] подлежит разбиению, то создаются две новые грани (как обсуждалось в тематическом зада-
нии 13.2), которые добавляются в дерево.
Листинг 13.10. Подпрограмма добавления грани в BSP-дерево
void insertBSP(Face& *Root. Face* face)
{
// insert face into subtree whose root is *Root.
// добавляем грань в поддерево с корнем *Root
ifdface) return;
// nothing to insert
// добавлять нечего
Face inFace. outFace:
// hold the two pieces of the face
// удерживаем два куска грани
if(tree is empty so far) , .
продолжение#
836
Глава 13. Удаление невидимых поверхностей
Листинг 13.10 (продолжение)
// дерево до сих пор пусто
{
attach the face to the tree
// присоединяем грань к дереву
return:
}
switch(FaceWithPlane(face. Rott. inFace. outFace)
{
case -1:
// face lies inside plane
// грань лежит с внутренней стороны плоскости
insertBSP(face into insideOnes subtree): break:
// грань в поддерево insideOnes
case 1:
// face lies outside plane
// грань лежит с внешней стороны плоскости
insertBSP(face into outsideOnes subree): break:
// грань в поддерево outsideOnes
case 0:
// face was split
// произошло разбиение грани
insertBSPCinFace into the insideOnes subtree):
// inFace в поддерево insideOnes
insertBSPCoutface into the outsideOnes subtree):break:
// outFace в поддерево outsideOnes
}
}
В листинге 13.10 приведена подпрограмма, предназначенная для добавления грани в BSP-дерево;
при необходимости эту подпрограмму можно скорректировать с целью исправления каких-либо дефек-
тов. Функция FaceWithPlane()(cM. тематическое задание 13.2) используется для определения того, с ка-
кой стороны плоскости лежит грань; при необходимости эта функция разбивает грань на две части, до-
бавляя их к нижней части дерева.
Сцена, хранящаяся в BSP-дереве, впоследствии рисуется с помощью подпрограммы, подобной той,
псевдокод которой приводится в тематическом задании 13.2.
Тематическое задание 13.4. HSR с использованием
сортировки по глубине
Уровень сложности III.
Предположим, что подпрограмма визуализации трехмерной сцены (без HSR) уже доступна. Напи-
шите приложение, которое осуществляет визуализацию сцены с использованием метода сортировки по
глубине из раздела «Алгоритм сортировки по глубине» для удаления невидимых граней. Проверьте
полученную программу на интересных сценах, состоящих из нескольких объектов, например из набо-
ра N случайных кубов, как это рассматривалось в тематическом задании 13.1.
Тематическое задание 13.5. Использование HSR-метода
построчного сканирования
Уровень сложности III.
Предположим, что подпрограмма визуализации трехмерной сцены (без HSR) уже доступна. Напи-
шите приложение, которое осуществляет визуализацию сцены с использованием алгоритма построч-
ного сканирования из раздела «HSR-метод построчного сканирования» для удаления невидимых гра-
ней. Проверьте полученную программу на интересных сценах, состоящих из нескольких объектов.
13.10. Дополнительная литература
837
Тематическое задание 13.6. Рисование при помощи
алгоритма Варнока
Уровень сложности III.
Предположим, что подпрограмма визуализации трехмерной сцены (без HSR) уже доступна. Напишите
приложение, которое осуществляет визуализацию сцены с использованием алгоритма Варнока для удале-
ния невидимых граней. При этом используйте первое определение простой области: не более одной грани
втянуто в область (то есть пересекается с ней, охватывает ер или содержит в себе). Затем разработайте
необходимые подпрограммы, рассмотренные в разделе «Методы разбиения области»: isSimple_drawIt(),
drawFaceO, isInvolvedO, regionSizeO, buildQuadrantsO, drawClosestFaceO. Проверьте полученную програм-
му на интересных сценах, состоящих из нескольких объектов, таких как набор случайных кубов.
Обратите внимание, что после разбиения необходимо произвести тестирование подобластей-«по-
томков», чтобы в дальнейшем рассматривать только те грани, которые втянуты в «родительскую» об-
ласть. Любые грани, которые не пересекаются с родительской областью, заведомо не будут пересекать-
ся и с ее подобластями. В дальнейшем мы обсудим, как исключить из дальнейшего рассмотрения те
грани, которые не пересекаются с областью.
В результате такого усовершенствования подпрограмма isSimpleRegionO работает следующим обра-
зом: при инициализации ей присваивается значение false, а массив faces устанавливается в NULL. Каждая
грань в faces тестируется на втянутость в область. (Поскольку тестирование этого списка осуществля-
ется четырьмя экземплярами функции drawRegion, то он должен сохраняться до окончания всех четырех
просмотров.) Втянутость определяется с помощью функции int IsInvolvedCRect region. Face * f), которая
возвращает true, если грань f втянута в область region, и fal se в противном случае. Копия указателя на каж-
дую втянутую грань проталкивается в стек outpaces, и число таких проталкиваний хранится в специаль-
ном счетчике. Когда массив faces пройден, просматривается значение этого счетчика: если оно равно 0
или 1, то подпрограмма возвращает true. Отметим, что данная версия подпрограммы i sSimpl eRegionC )
должна тестировать каждую грань из входного списка, независимо от ее втянутости: подпрограмма не
прерывает работу после обнаружения двух втянутых граней.
Тематическое задание 13.7. HLR с помощью алгоритма
стека ребер
Уровень сложности II.
Напишите приложение, выполняющее рисование на трехмерной сцене прямых линий с использованием
алгоритма drawVisibleEdges, описанного в разделе «О методах удаления невидимых линий», где ребра
рисуются только тогда, когда их видимость полностью установлена. Проверьте полученную программу
на интересных сценах, состоящих из нескольких объектов, таких как набор случайных кубов, о которых
говорилось в тематическом задании 13.1.
Для загрузки начального состояния стека ребер напишите подпрограмму makeEdgeStackO, которая
просматривает каждую грань в массиве faces[], анализирует каждое ее ребро и загружает в запись типа
Edge данные по ребрам для всех потенциально видимых ребер (без дубликатов). Определитесь, что де-
лать с теми ребрами, которые принадлежат только одной невидимой грани.
13.10. Дополнительная литература
В классической работе Сазерленда и других авторов [Sutherland, 193] содержится превосходный обзор
проблемы удаления невидимых поверхностей, а также блестящие описания численных HSR-алгоритмов
и их ожидаемой производительности. В работе Роджерса [Rogers, 105] подробно рассматривается боль-
шое число HSR-алгоритмов, а также приводится множество полезных примеров. Фоли и его соавторы
[Foley, 17] также представляют ценный обзор HSR-проблемы и предлагают множество ее решений.
fl Л Введение в трассировку
ЛПг лучей
□ Разработка фундаментальной концепции трассировки лучей.
□ Подготовка математического аппарата и алгоритмов
для выполнения трассировки лучей.
□ Построение и визуализация сцен из сфер, конусов, цилиндров,
выпуклых многогранников и других объемных тел.
□ Создание высокореалистичных изображений с эффектами
прозрачности и преломления света.
□ Разработка средств для работы с ЗО-текстурами объемных
объектов и растровыми изображениями.
Мы пытаемся абстрагироваться от сложности явления с помощью простых систем,
свойства которых могут быть описаны математически. Мощь этой абстракции
обеспечивает поразительно точное математическое описание природы.
Морис Клайн (Morris Kline)
Для первобытного человека непостижимой тайной было пространство.
Для человека технологической эпохи эту же роль играет время.
Маршалл Мак-Лухан (Marshall McLuhan)
Полны бриллиантов чистейшей воды
Пещеры бездонного темного моря.
Томас Грей (Thomas Gray), Элегия, строфа 14
Вы, звезды малые, гасите
и без того чуть видные лучи!
Александр Поуп (Alexander Pope)
По причине своей эффективности трассировка лучей является широко применяемой технологией
рисования. В разделе 14.1 «Введение» дается введение в эту технологию, а в разделе 14.2 «Построение
геометрии трассировки лучей» вводятся камера и геометрические понятия, необходимые для трассиров-
ки лучей. В разделе 14.3 «Обзор процесса трассировки лучей» демонстрируется выполнение трассировки
лучей в приложении. В разделе 14.4 «Пересечение луча с объектом» описаны различные примитивные
формы, удобные для трассировки, и разрабатывается ядро технологии пересечения объекта лучом.
14.1. Введение
83d
Обсуждаются преимущества, достигаемые вследствие преобразования луча в базовую систему коорди-
нат объекта.
В разделе 14.5 «Организация трассировщика луча в приложении» разрабатываются различные клас-
сы и подпрограммы, составляющие трассировщиюлучей (ray tracer) с использованием объектно-ори-
ентированного подхода, а также рассматривается взаимодействие различных компонентов. Создается
полный, хотя и примитивный, трассировщик лучей. В разделе 14.6 «Пересечение лучей с другими при-
митивами» обсуждаются вопросы пересечения лучей с множеством различных форм, включая кони-
ческие цилиндры и выпуклые многогранники.
В разделе 14.7 «Рисование закрашенных изображений сцен» с помощью модели закрашивания из
главы 8 разрабатывается полноцветный трассировщик лучей, который оперирует с фоновым, диф-
фузным и зеркальным типами отражения света от поверхностей. Также рассматриваются физически
обоснованные модели отражения света, например модель отражения Кука—Торренса. В разделе 14.8
«Наложение текстуры на поверхности» исследуются технологии «наложения» на поверхности тексту-
ры во время визуализации. При этом уделяется внимание как 2В-текстурам, получаемых из изображе-
ний, так и ЗО-текстурам, таким как раскраска под мрамор или дерево. Рассматриваются также вопросы
сглаживания при трассировке лучей. В разделе 14.9 «Использование экстентов» исследуются способы
радикального ускорения трассировки лучей с помощью разумного использования ограничивающих па-
раллелепипедов (боксов) и других видов экстентов, позволяющих сэкономить на многих дорогостоя-
щих пересечениях лучей.
В разделе 14.10 «Добавление теней для большей реалистичности» рассматривается «порождение»
вторичных лучей с целью увеличения реалистичности трассировщика лучей. Описывается метод прав-
доподобного формирования теней. Раздел 14.11 «Отражения и прозрачность» посвящен исследованию
подробностей генерирования вторичных лучей с целью имитации отражения света от блестящей по-
верхности, а также преломления света при прохождении его через прозрачный объект.
В разделе 14.12 «Составные объекты: логические операции с объектами» класс объектов, с которыми
возможна трассировка лучей, расширяется до сложных объектов, определяемых посредством конструк-
тивной стереометрии. Разрабатываются методы трассировки лучей для объектов сколь угодно слож-
ной формы. Глава заканчивается тематическими заданиями, которые помогут вам создавать и тестиро-
вать работающие трассировщики лучей.
14.1. Введение
В главах с 6 по 8 мы описали методы визуализации сцен, составленных из полигональных сеток, кото-
рые включали в себя модели закраски, отображающие (по крайней мере, приблизительно) отражение
света от поверхности полигона. Кроме того, с целью уменьшить «многогранную» природу каркасной
модели были использованы интерполяционные схемы Гуро и Фонга. Изображения, сформированные
таким способом, представляют собой гладкую поверхность (за исключением ребер силуэта), несмотря
на то, что сама модель состоит из дискретных граней.
Трассировка лучей (ray tracing), иногда называемая также испусканием лучей (ray casting), представ-
ляет собой похожий, но более мощный подход к визуализации сцен. На рис. 14.1 показана его основная
идея. Будем рассматривать буфер кадров как простой массив из пикселов, расположенных в простран-
стве, и пусть глаз смотрит на сцену через этот буфер. Для каждого пиксела из буфера кадров задается
вопрос: «Что именно „видит" глаз через этот пиксел?» Можно представить себе также луч света, иду-
щий до глаза из некоторой точки Р на сцене через пиксел.
В действительности данный процесс происходит в обратном порядке. Луч исходит из глаза, проходит
через центр пиксела и движется далее на сцену. Его путь прослеживается, чтобы увидеть, с каким объектом
он соударяется первым и в какой точке. Отметим, что при таком процессе проблема невидимых поверхнос-
тей решается автоматически, поскольку первая поверхность, с которой соударяется луч, и есть ближайшая
к глазу; более удаленных поверхностей он никогда не достигнет. Имея описания источников света на
сцене, к точке первого соударения можно применить уже известную модель закрашивания, для чего
840
Глава 14. Введение в трассировку лучей
нужно вычислить все компоненты света — фоновый, диффузный и зеркальный. Результирующий цвет
затем отображается в данном пикселе. Поскольку траектория луча прослеживается по всей сцене, не-
трудно добавить интересные визуальные эффекты, такие как затенение, отражение и преломление, что
приводит к изображениям поразительной реалистичности, которые трудно получить другим способом.
кадров
Рис. 14.1. Просмотр точки на сцене через пиксел
Еще одна особенность трассировки лучей — возможность работы с более обширным классом гео-
метрических объектов, чем полигональные сетки. Объемные тела конструируются из разнообразных
геометрических примитивов, таких как сферы, конусы и цилиндры. Каждая такая форма не аппрокси-
мируется многогранником, а описывается точным математическим выражением. Для упрощения работы
со сложными сценами эти формы также могут быть подвергнуты различным преобразованиям. Напри-
мер, их размер и ориентация до добавления в сцену могут быть изменены.
В данной главе будет описана «тяжелая артиллерия» алгоритмов, необходимых для создания высо-
кокачественных изображений сложных сцен с помощью трассировки лучей. Наши разработки будут
вестись по нарастающей, так что мы сможем создавать простые изображения с помощью небольших
программ уже через несколько разделов главы. Для создания набора более современных развитых тех-
нологий попутно будут разрабатываться дополнительные инструменты.
14.2. Построение геометрии трассировки лучей
О, жизнь! Как прекрасно твое утро,
Холмы расцвечены лучами юной Фантазии!
Пренебрегая уроками Осторожности,
Мы мчимся прочь,
Как школяры, от разных поучений,
Играть и радоваться всласть.
Роберт Бернс (Robert Bums)
Для того чтобы производить трассировку лучей, нам необходимо удобное представление луча, прохо-
дящего через определенный пиксел. Чтобы использовать уже знакомые понятия, соберем вместе необ-
ходимые ингредиенты процесса визуализации из глав 6 и 7. Применим ту же камеру, что и в главе 7:
глаз камеры находится в точке eye, оси камеры выровнены по векторам u, v, w, как показано на рис. 14.2.
Ближняя плоскость лежит на расстоянии N перед глазом, и в ней расположен буфер кадров. Модель
камеры принята такой же, как в главе 7 (рис. 14.3): угол зрения обозначен через 0, а окно на ближней
плоскости имеет форматное соотношение aspect. Тогда камера простирается в v-направлении от -Н до
Нив u-направлении от -17 до W, где
// = Wtg
(14.1)
и
W-H-aspect.
14.2. Построение геометрии трассировки лучей
841
Рис 14.2. Установка камеры для трассировки лучей
Напомним из главы 7, что преобразование порта просмотра устанавливает соответствие между точ-
ками ближней плоскости и пикселами порта просмотра. Здесь используется то же самое соответствие,
однако без явного преобразования порта просмотра. Действительно, проще всего представлять порт
просмотра «вставленным» в окно ближней плоскости, так что глаз смотрит на сцену «сквозь» отдельные
пикселы. Допустим, что порт просмотра содержит nCols столбцов и nRows строк пикселов, и рассмот-
рим пиксел на пересечении строки г и столбца с, причем г изменяется от 0 до nRows - 1, а с изменяется
от 0 до nCols - 1. Будем называть такой пиксел гс-пикселом; он показан на рис. 14.3, б. Где же находится
этот пиксел на ближней плоскости?
Рис. 14.3. Модель камеры
Нижний левый угол пиксела лежит в точке с координатами (ис, vr), которые определяются следую-
щими соотношениями (см. упражнения в конце раздела):
2с
u=-W+W——,с = 0,1,...,nCols- 1;
nCols
Jr
vr = -Н + Н-----, г = 0,1,..., nRows - 1. (14.2)
nRows
Для того чтобы получить выражение для луча, проходящего через эту точку, нам нужно выразить ее
положение в трехмерном пространстве: это текущая точка на ближней плоскости. Сделать это нетрудно:
мы просто найдем, на каком расстоянии от глаза находится эта точка. Начнем с точки eye и определим,
какое расстояние мы должны пройти в каждом из направлений u, v, w, чтобы достичь угла пиксела.
При этом выясняется, что нам следует пройти расстояние N в отрицательном п-направлении, ис вдоль
вектора и и г вдоль вектора V. Тогда трехмерная точка будет иметь вид:
eye - Ml + ми + vy (расположение угла пиксела в пространстве).
Основная операция при трассировке луча — зто вычисление траектории луча, который выходит из
глаза и проходит через данный пиксел на ближней плоскости; в частности, нам нужно определить,
с какими объектами соударяется этот луч. Пусть при t = 0 луч лежит в точке eye, а при t = 1 проходит
через угол гс-пиксела. Тогда для этого луча имеем следующую параметрическую форму;
r(t) = еуе(1 - t) + {eye - Nn + ии + г v)t.
842
Глава 14. Введение в трассировку лучей
(Внимательно проверьте это выражение!) Полезно выделить начальную точку и начальное направ-
ление этого луча: r(t) = eye + dirret. После простых преобразований вышеприведенного выражения по-
лучим уравнение луча, проходящего через гс-пиксел в виде:
г(Г) = eye + dirret;
dirre
= -Nn + fF
(2c A
-------1 u + Z7
nCols I
2r i I
-------1 V .
nRows I
(14.3)
Назовем этот луч rc-лучом (rcth ray). Отметим важное свойство каждого луча из этого семейства: по
мере возрастания t от 0 «точка луча» удаляется все дальше и дальше от глаза. Если луч на своем пути
сталкивается с двумя объектами в моменты времени ta и tb, то более близкому объекту соударения соот-
ветствует меньшее значение t. Таким образом, сортировка объектов по глубине (по расстоянию от гла-
за) соответствует сортировке моментов соударений, при которых эти объекты пересекаются с лучом.
Кроме того, любые объекты с отрицательными значениями времени соударения t должны находиться
позади глаза и поэтому должны игнорироваться.
Практические упражнения
14.2.1. Отработайте детали
Детально проработайте уравнения (14.1)-(14.3) и докажите, что тс-луч действительно имеет указанное
направление. Где находится этот луч в моменты времени Г “ 2 и -1?
14.2.2. Численное определение местонахождения луча
Пусть для камеры заданы eye - (0,0, -5), и - ( 1,0,0), v - (0,1,0). Пусть также ее угол зрения состав-
ляет 30°, a aspect - 1,5. Найдите для nRows - 480 и nCols - 640 параметрическое выражение rc-луча при
г = 100 и с - 200.
14.2.3. Где находятся углы пиксела?
Найдите формулы для координат (и, v) центра гс-пиксела, а не его нижнего левого угла.
14.2.4. Инкрементное вычисление лучей
Заметим из уравнения (14.3), что вдоль строки развертки луч можно вычислить инкрементно, по его преды-
дущему значению, с помощью простого (векторного) сложения. Выразите направление dirr с+, через dirr с.
14.3. Обзор процесса трассировки луча
Следя Божественного света...
И. Ф. фон Шиллер (J. С. F. von Schiller)
Вначале мы сделаем обзор трассировщика луча, чтобы описать основные операции, которые нам потре-
буются. Позднее мы опишем, как применять эти операции в программе.
Листинг 14.1. Скелет трассировщика луча (псевдокод)
define the objects and light sources in the scene
11 определяем объекты и источники света на сцене
set up the camera
И устанавливаем камеру
for(int г - 0: г < nRows: г++)
fordnt с - 0: с < nCols; C++)
{
1. Build the rc-th ray
И Строим rc-луч
14.3. Обзор процесса трассировки луча
843
2. Find all Intersections of the rc-th ray with objects in the scene
// находим все пересечения rc-луча с объектами на сцене
3. Identify the intersection that lies closest to. and in front of. the eye
11 идентифицируем пересечение, лежащее ближе
// всего к глазу и перед ним
4. Compute the "hit point" where the ray hits this object, and the normal vector at that point
11 вычисляем «точку соударения» луча с данным объектом
// и нормальный вектор в этой точке
5. Find the color of the light returning to the eye along the ray from the point of intersection
11 находим цвет луча света, возвращающегося к глазу вдоль
// данного луча от точки пересечения
6. Place the color in the rc-th pixel.
// помещаем этот цвет в rc-й пиксел
В листинге 14.1 приводятся основные этапы работы трассировщика луча. Сцена, подлежащая трас-
сировке, заполнена различными геометрическими объектами и источниками света. Типичная сцена
может содержать сферы, конусы, параллелепипеды, цилиндры и тому подобные тела, каждое из кото-
рых имеет определенную форму, размер и положение. Все эти объекты определенным образом описы-
ваются и помещаются в список объектов. Кроме этого, уже описанным образом создается камера. Затем
поочередно для каждого пиксела мы конструируем луч, начинающийся в точке глаза и проходящий
через нижний левый угол пиксела. Это делается простым вычислением направления dir^ для гс-луча.
Шаги 3-5 псевдокода являются новыми и подробно описываются в следующих разделах. Вначале
найдем, пересекается ли rc-луч с каждым объектом из списка, и если да, то запишем «время соударе-
ния» — значение t, при котором луч r(t) совпадает с поверхностью объекта. После проверки всех объек-
тов ближайшим к глазу будет объект с наименьшим временем соударения. Затем находим положение
«точки соударения» с этим объектом, а также нормальный вектор к поверхности объекта в этой точке.
Далее вычисляется и записывается в пиксел цвет света, отраженного от объекта в направлении глаза.
На рис. 14.4 показана простая сцена, состоящая из нескольких цилиндров и сфер, а также трех кону-
сов. Снеговик состоит преимущественно из сфер. (Из каких примитивов состоит его шляпа?) Показаны
также два источника света. Отметим, что объекты сцены могут быть взаимопроникающими. Что каса-
ется данной картины, то нас интересуют, конечно, ближайшие внешние поверхности.
Рис. 14.4. Трассировка луча на сцене
Описания всех объектов хранятся в списке объектов (object list), который на рисунке представлен
в виде связного списка дескриптивных записей. Показанный на рисунке луч пересекает сферу, цилиндр
и два конуса. Все остальные объекты лучом пропускаются. Определяется объект с наименьшим временем
соударения — в данной сцене это цилиндр. Точка соударения Phit легко определяется из самого луча —
подстановкой в уравнение луча (14.3) момента времени thjt:
Phit - eye + dirr /hjt (точка соударения). (14.4)
844
л
Глава 14. Введение в трассировку лучей
14.4. Пересечение луча с объектом
С помощью времени природа не дает произойти всему сразу.
Неизвестный
Ничто не озадачивает меня больше, чем время и пространство; и ничто
не беспокоит меня меньше, ибо я никогда не думаю о них.
Чарльз Лэм (Charles Lamb)
В главе 5 мы ввели класс Scene, который может читать файл на языке SDL и строить список объектов
сцены. Мы будем использовать этот инструмент и при трассировке лучей, строя сцену с помощью сле-
дующего кода:
Scene sen:
// create a scene
// создаем сцену
scn.readCniyScene.dat");
// read the SDL scene file
// читаем SDL-файл сцены
Объекты сцены создаются и помещаются в список. Каждый объект является экземпляром «базовой»
формы типа сферы или конуса вместе со своим аффинным преобразованием, которое определяет, как
данный объект масштабирован, ориентирован в пространстве и где помещен на сцене. Некоторые из
таких базовых форм мы ввели в главе 6. На рис. 14.5 приведены некоторые базовые формы, для кото-
рых мы будем строить ход луча.
Рис. 14.5. Некоторые основные базовые формы, используемые при трассировке луча
В то время как в главе 5 для рисования объектов мы использовали OpenGL (посредством метода
drawOpenGLO, разработанного нами для каждого типа формы), здесь мы будем рисовать их с помощью
трассировки луча. Это означает, что мы ищем точку пересечения луча с каждым объектом сцены. Как
мы увидим в дальнейшем, проще всего это сделать, используя неявную форму каждой из фигур, рас-
смотренную в разделе «Представления поверхностей» главы 6. Например, неявная форма для базовой
сферы имеет вид:
F(x, у, z) = х? + у2 + z2 - 1 (базовая сфера). (14.5)
Если мы для удобства используем форму записи F(P), где аргументом неявной функции является
точка, то неявная форма для базовой сферы примет вид:
F(P) - |Р|2 - 1 (базовая сфера).
Аналогично, неявная форма для базового цилиндра имеет вид:
F(x, у, г) = х? + у2 - 1, где 0 < z < 1 (базовый цилиндр). (14.7)
В реальной сцене каждая базовая форма при помощи аффинного преобразования переходит в фор-
му со значительно отличающейся неявной формой записи. Однако в действительности, как будет пока-
(14.6)
14.4. Пересечение луча с объектом
845
зано ниже, нам достаточно вычислить пересечения лучей только с базовой формой! Поэтому неявная
форма записи каждой базовой формы приобретает в трассировке лучей фундаментальное значение.
Как же найти пересечение луча с формой, неявная форма записи которой имеет вид F(P)? Предпо-
ложим, что луч исходит из точки S в направлении с. (Это более простая форма записи по сравнению с
той, в которой используется стартовая точка eye и направление dirrc.) Тогда уравнение луча имеет вид:
г(£) = 5 + сГ. (14.8)
Нетрудно сформулировать общую теорию. Все точки на поверхности формы удовлетворяют урав-
нению F(P) - 0, а луч соударяется с поверхностью в каждый момент времени, когда точка r(t) совпадает
с поверхностью. Поэтому условие совпадения луча с точкой на поверхности имеет вид p(r(z)) = 0. Это
произойдет в «момент соударения» thjt, который можно определить, решив уравнение:
Р(5 + сГЫ[) = 0. (14.9)
Основная часть работы при трассировке лучей состоит в попытках эффективного решения этого
уравнения для интересующих нас объектов. Ниже мы увидим, что для простых форм, таких как плос-
кость или сфера, это уравнение решается просто.
14.4.1. Пересечение луча с базовой плоскостью
В сцену часто включают полы и стены какой-нибудь комнаты. Их легко моделировать плоскостями.
Иногда они имеют один и тот же цвет, а иногда могут покрываться «текстурой», например шахматным
узором или оцифрованным изображением.
Базовая плоскость — это плоскость ху, или z = 0, поэтому ее неявная форма имеет вид: F{x, у, z) = г.
Луч S + ct пересекает базовую плоскость, когда 52 + cth = 0. Это простое линейное уравнение, его реше-
ние имеет вид:
(14.10)
сг
Если сг = 0, то луч движется параллельно плоскости и пересечения нет (за исключением, разумеется,
случая, когда 52 также равно нулю; тогда луч ударяется в конец плоскости и не может быть виден).
В остальных случаях луч пересекается с плоскостью в точке Phjt = S- с(5г/сг). (Почему?)
Пример 14.4.1. Где заданный луч соударяется с заданной плоскостью?
В каком месте луч r(t) = (4,1, 3) + (-3, -5, -3) t соударяется с базовой плоскостью?
Решение
Результат решения уравнения (14.10): tA=-3/-3 = 1.
Точка соударения S + с = (1, -4,0). Отметим, что данная точка действительно лежит в плоскости г = 0.
14.4.2. Пересечение с базовой сферой
В какой точке луч S + ct пересекается со сферой, неявная форма которой задается уравнением (14.6)?
Подставляя S + ct в уравнение F(P) = 0, получаем |5 + сг|2 -1 = 0 или (используя уравнение (4.13))':
|с|2Г2 + 2(5 с) t + (|5|2 - 1)т0. (14.11)
Это квадратное уравнение относительно t вида At2 + 2Bt + С = 0, где
А = |с|2,
В = 5- с, (14.12)
С = |5|2- 1.
1 Отметим некоторую вольность с обозначениями, предпринятую для компактности. S является точкой, а не вектором, поэтому
технически ее нельзя использовать в скалярном произведении. Считайте обозначение |5|2 просто сокращенной записью выра-
жения + S2 + S2.
846
Глава 14. Введение в трассировку лучей
Это уравнение решается с помощью формулы:
t = -£ + ^д2~Л£. (14.13)
* А А
Если дискриминант В2-АС отрицателен, то решений нет и луч проходит мимо (misses) сферы. Если
дискриминант равен нулю, то луч касается (grazes) сферы в единственной точке, и время соударения
равно -В/А. Если же дискриминант положителен, то существуют два времени соударения tt и tv соот-
ветствующие знакам плюс и минус в уравнении (14.13).
Приятным обстоятельством при пересечении луча с плоскостью или со сферой является то, что по-
лучающееся линейное или квадратное уравнение легко решается относительно t. Для некоторых дру-
гих простых форм тоже получаются приемлемые уравнения относительно t, но для многих форм это не
так. Мы исследуем некоторые из этих форм в разделе «Пересечение лучей с другими примитивами»
данной главы.
Пример 14.4.2. Где луч пересекает базовую сферу?
В каком месте луч r(t) - (3,2,3) + (-3, -2, -3) t пересекает базовую сферу?
Решение
Из уравнения (14.12) получаем Л - 22, В = -22, С- 21. Уравнение (14.13) имеет решение tt = 0,7868
и t2 - 1,2132. Двумя точками соударения являются следующие:
5 + ct, - (3,2,3) (1 - 0,7868) - (0,6393, 0,4264,0,6396);
S + ct2- (3,2,3) (1 - 1,2132) - (-0,6393, -0,4264, -0,6396).
Легко заметить, что обе эти точки находятся на единичном расстоянии от начала координат, как и
следовало ожидать. Обратите внимание на красивую симметричность точек соударения; она возникает
здесь в силу того, что луч проходит через начало координат и центр базовой сферы тоже располагается
в начале координат.
14.4.3. Пересечение луча с преобразованными объектами
Если я пытаюсь объяснить спрашивающему меня, что это означает, то я не знаю.
Св. Августин о природе времени
С каждым объектом сцены связано преобразование Т, придающее ему желаемые размер, ориентацию и
положение на сцене. А что это преобразование делает с уравнениями и результатами, полученными
нами в предыдущем разделе?
Эта задача иллюстрируется рис. 14.6: преобразование Т отображает базовую сферу W' в эллип-
соид W. Спрашивается: когда луч S + ct пересечется с W? Допустим, что может быть найдена неявная
форма G( ) для преобразованного объекта W. Тогда для определения времени соударения требуется
решить уравнение G(S + ct) - 0.
Рис. 14.6. Пересечение луча с эллипсоидом
14.4. Пересечение луча с объектом 847
Таким образом, задача сводится к нахождению неявной формы преобразованного объекта. Однако
из раздела «Влияние аффинного преобразования» главы 6 мы знаем, что если неявная функция ис-
ходного базового объекта равна F(P), то для преобразованного объекта она приобретает вид Р(Т~*(Р)),
где Т-1 - преобразование, обратное Т (то есть матрица преобразования Т'1 равна Л/"1, если преобразова-
нию Т соответствует матрица М). Таким образом, нам нужно решить следующее уравнение:
F(T-\S + ct)) = О
(14.14)
относительно времени соударения t. Это уравнение может оказаться весьма неприятным. Однако в
действительности оно просто означает решение для времени, при котором обратно преобразованный
луч (inverse transformed ray) T'*(S + ct) соударяется с исходным базовым объектом! Поскольку преобра-
зование Т линейно, обратно преобразованный луч можно представить в виде:
T-l(S + ct) = (T-'S) + (T-lc)t.
На рис. 14.6 этот луч обозначен S' + c't. Неудивительно, что обратно преобразованный луч является
по-прежнему лучом, то есть прямой линией, выходящей из точки S' в направлении с'. Предположим,
что преобразованию Т соответствует матрица М. Тогда, используя однородные координаты, получим
следующее уравнение для обратно преобразованного луча:
r(f) = M~'
+м-'
t =S'+ct (обратно преобразованный луч).
(14.15)
Отметим, что матрица М~1 в одном случае умножается на точку, а в другом случае — на вектор. S' фор-
мируется из S' путем отбрасывания 1; а с' формируется из с' отбрасыванием 0.
Таким образом, вместо попыток определить пересечение луча с преобразованным объектом, мы ис-
следуем пересечение «обратно преобразованного» луча с базовым объектом. Применяется описанная
ниже технология.
Каждый объект в списке объектов обладает своим собственным аффинным преобразованием.
Для пересечения луча 5 + ct с преобразованным объектом мы:
О Обратно преобразуем луч (получаем S' + c't).
О Находим время соударения th этого луча с базовым объектом.
О Используем это же время th в луче 5 + ct для нахождения фактической точки соударения.
Изящество данного подхода заключается в том, что нам требуется разработать код, относящийся
только к пересечению луча с базовым объектом. Это вдвойне выигрышная ситуация (выигрывает про-
граммист и выигрывает компьютер): мы можем применять к объектам аффинные преобразования для
целей моделирования (чтобы получить нужные нам сцены) и не платим за это усложнением кода под-
программ, вычисляющих пересечение. «Расходы на аффинное преобразование» просто перекладыва-
ются на преобразование самого луча.
Пример 14.4.3. Где заданный луч соударяется с преобразованной сферой?
Предположим, что эллипсоид Wформируется из базовой сферы при помощи следующих SDL-команд:
translate 2 4 9
scale 14 4
sphere
То есть базовая сфера вначале масштабируется и затем сдвигается. Прямое и обратное преобразова-
ния этой сферы соответственно имеют следующие матрицы:
848
Глава 14. Введение в трассировку лучей
(Проверьте их!) Определите, где луч (10,20,5) + (-8, -12,4) t пересекается с W.
Решение
Уравнение обратного преобразованного луча имеет вид: (8,4, -1) + (-8, -3,1) Г. (Проверьте это тоже!)
Подставим это в уравнение (14.12) и получим (Л, В, С) = (74, -77,80), откуда дискриминант равен 9. Таким
образом, происходит два пересечения. Из уравнения (14.13) находим моменты пересечения: 1,1621 и
0,9189. Точку соударения находим, подставляя меньшее время соударения в представление луча: (10,
20,5) + (-8, -12,4)0,9189 = (2,649,8,97,8,67). (Как убедиться в том, что эта точка лежит на сфере?)
Практические упражнения
14.4.1. Найти точки пересечения
Найдите моменты и точки пересечения луча (3, 5, 8) + (-4, -2, -6) t со сферой радиуса 5 с центром в
точке (1,2,1).
Решение
t “0,41751 или? = 1,58248, две точки пересечения равны (1,33,4,165,5,495) и (-3,33,1,835, -1,495).
14.4.2. Соударение с плоскостью
Когда и где луч (10 - t, 8 - 2t, 3 + t) соударяется с плоскостью, созданной на языке SDL посредством
следующих команд:
translate 4 5 6 rotate 90 1 0 0 plane?
14.5. Организация трассировщика луча в приложении
Теперь, вооружившись теорией, мы можем сконструировать настоящий трассировщик луча, основанный
на скелете кода из листинга 14.1. Мы будем использовать класс Scene и язык SDL, впервые введенный в
главе 5, поскольку они предоставляют удобные средства для описания сложной сцены. Начнем с уже по-
строенного списка объектов сцены, в котором с каждым объектом связано его аффинное преобразование.
Трассировщик луча должен иметь дело с несколькими различными взаимодействующими объекта-
ми: с камерой, осматривающей сцену, экраном, на котором создается изображение, с лучами, исходя-
щими из камеры и проходящими через сцену, а также с самой сценой, содержащей множество геомет-
рических объектов и источников света. При объектно-ориентированном подходе следует тщательно
определять типы участвующих объектов и решать, какие действия должен выполнять каждый тип дан-
ных, а также какой информацией должен обладать каждый объект для осуществления нужных дей-
ствий. Здесь определен один из методов «сверху вниз», однако вы можете выбрать иной способ разде-
ления задач.
При выбранном нами подходе камере дается задание провести трассировку луча, для чего необходи-
мо добавить к существующему классу Camera следующий метод:
void Camera :: raytrace(Scene& sen, int blockSize):
Для трассировки луча в камеру передается сцена. В переменной blockSize следует описать раз-
мер блока пикселов. Из глаза камеры испускается луч, проходящий через каждый угол пиксела на
сцену, и определяется цвет света, возвращающегося обратно вдоль этого луча. Затем пиксел рисуется
этим цветом.
14.5. Организация трассировщика луча в приложении
849
Для текущего рисования пиксела мы будем использовать OpenGL; ниже показано, как функция
raytraceO задает матрицу моделирования-вида и проекционную матрицу так, чтобы рисовать непо-
средственно на экране. Поэтому функция displayO в главном цикле имеет очень простой вид: требует-
ся только очистить экран и дать команду объекту cam класса Camera провести трассировку луча. Можно
использовать следующий псевдокод:
void display(void)
{
glClear(GL_COLOR_BUFFER_BIT);
// clear the screen
// очищаем экран
cam.raytrace(scn. blockSize);
// ray trace the scene
// производим трассировку луча на сцене
Даже небольшое изменение данного подхода может привести к большим отличиям при разработке
вашего трассировщика луча. В нашем распоряжении уже имеется инструмент, рисующий SDL-сцену с
помощью функций OpenGL, поэтому полезно непосредственно перед каждой трассировкой луча делать
«эскиз» («preview») сцены. Такой эскиз позволит нам быстро убедиться в том, что камера нацелена пра-
вильно, а объекты находятся в нужных местах. В процессе трассировки эскиз сцены закрашивается,
пиксел за пикселом, «истинными» цветами, которые эти пикселы получают в соответствии с трасси-
ровкой луча. Если все сделано правильно, то объекты после трассировки в точности совпадут с этими
же объектами на эскизе. Любые ошибки трассировщика луча становятся очевидными.
Для рисования эскиза сцены достаточно дополнить функцию displayO следующим кодом:
void display(void)
{
H clear the screen and reset the depth buffer
// очищаем экран и обнуляем буфер глубины
glClear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT):
cam.drawOpenGL(sen);
H draw the preview
// рисуем эскиз
cam.raytrace(scn, blockSize):
// ray trace over the preview
// трассируем луч по эскизу
}
На рис. 14.7 показан пример процесса трассировки луча: эскиз уже нарисован, и нижняя половина
экрана уже обработана трассировщиком луча. Здесь важно то, что трассировка луча точно накладыва-
ется на эскиз сцены.
Рис. 14.7. Процесс трассировки луча по эскизно нарисованной сцене
850 Глава 14. Введение в трассировку лучей
Составные части метода raytraceO
Метод raytraceO класса Camera реализует этапы, приведенные в листинге 14.1. Для каждой строки г и каж-
дого столбца с создается объект-луч, исходящий из глаза и проходящий через нижний левый угол гс-пик-
села на сцену. Для этого требуется класс Ray, начальные элементы которого показаны в листинге 14.2.
В данном классе имеются поля для хранения начальной точки луча и его направления. Позже мы добавим
другие поля. Для установки начальной точки и направления заданного луча предназначены два метода.
Листинг 14.2. Начальные элементы класса Ray
class Ray{
public:
Point3 start:
Vectors dir;
void setStart(point3& p){start.x - p.x; etc..}
void setDir(Vector3& v){dir.x - v.x: etc..}
// other fields and methods
// другие поля и методы
};
Листинг 14.3. Скелет метода raytraceO
void Camera :: raytrace(Scene& sen. int blockSize)
{
Ray theRay:
Colors clr;
theRay.setStart(eye):
// set up OpenGL for simple 2D drawing
// производим установки OpenGL для простого 20-рисования
glMatrixMode(GL_MODELVIEW):
glLoadldentityO:
glMatrixMode(GL_PROJECTION):
glLoadldentityO:
glu0rtho20(0.nCols.0.nRows);
// whole screen is the window
// окном является весь экран
glDisable(GL_LIGHTING);
// so glColorSfO works properly
// поэтому glColorSfO работает правильно
// begin ray tracing
// начинаем трассировку луча
forGnt row - 0; row < nRows: row +- blockSize)
for(int col - 0: col < nCols: col +- blockSize)
{
confute the ray's direction
// вычисляем направление луча
theRay.setDIr(<direction>):
// set the ray’s direction
// устанавливаем направление луча
clr.ser(scn.shade(theRay));
// find the color
// находим цвет
glColor3f(clr.red. clr.green. clr.blue):
glRecti(col.row.col + blockSize. row + blockSize);
}
}
14.5. Организация трассировщика луча в приложении
851
В листинге 14.3 приведен скелет метода raytraceC). В нем начальная точка луча theRay устанавливает-
ся один раз для глаза, а затем для каждого пиксела вычисляется и устанавливается направление гс-луча
в соответствии с уравнением (14.3). Затем объекту sen класса Scene предписывается определить цвет,
возвращающийся по данному лучу:
clr - scn.shade(theRay).
В методе shadeO выполняется сложная работа: он «испускает» («casts») луч на сцену, определяет
пересечения, вычисляет цвет света, идущего обратно по лучу, и возвращает значение этого цвета. Мы раз-
работаем этот метод в конце главы.
Рисование «пиксельных блоков»
Параметр blockSize определяет размер блока из пикселов, которые рисуются на каждом шаге. Отобра-
жение пиксельных блоков просто экономит время программы-просмотрщика (viewer) во время работы
трассировщика луча: сформированные изображения являются черновыми, однако появляются быстро;
вместо трассировки луча через каждый пиксел, при котором изображение появляется медленно, пиксел
за пикселом, трассировка осуществляется только для нижнего левого угла каждого пиксельного блока.
На рис. 14.8, а показано, как работает данная процедура для простого дисплея с 16 строками и 32 столб-
цами истинных пикселов, когда blocksize задан равным 4. Каждый блок состоит из 16 пикселов. Опре-
деляется цвет луча, проходящего через угол блока, и этот цвет присваивается всему блоку (всем его
16 пикселам). Изображение будет выглядеть как растровое 4 на 8 блоков, что дает только очень грубое
приближение к трассировке с полным разрешением. Зато такое изображение может рисоваться очень
быстро. Если это грубое изображение показывает, что все делается правильно, то программа просмот-
ра может сделать повторную трассировку сцены с полным разрешением, задав blocksize равным 1.
На рис. 14.8, б показана простая сцена, для которой трассировка луча производилась с размерами
блоков 4, 2 и 1. Визуализация первого варианта происходит в 16 быстрее, чем последнего.
б
Рис. 14.8. Трассировка луча с пиксельными блоками (а); трассировка луча при разных размерах блоков {б)
Отметим, что метод raytraceO для рисования пиксельных блоков вызывает матрицы OpenGL. Мат-
рица моделирования-вида устанавливается равной единичной матрице, а проекционная матрица
осуществляет простое масштабирование окна в порт просмотра — без проецирования. На этих этапах^
852
Глава 14. Введение в трассировку лучей
графический конвейер.OpenGL является полностью «прозрачным», так что квадрат можно рисо-
вать прямо в порт просмотра с помощью функции glRecti О. (Мы предполагаем, что при первом запус-
ке программы порт просмотра уже установлен равным полноэкранному окну при помощи команды
glViewport(0, 0, nCols. nRows).)
Чтобы функция gTCol or3f () работала правильно, освещение OpenGL также должно быть отключено.
Основы shade(ray)
Листинг 14.4. Скелет shade (ray)
Color3 Scene :: shade(Ray& ray)
{
// return the color of this ray
// возвращаем цвет данного луча
Color3 color;
// total color to be returned
// суммарный возвращаемый цвет
Intersection best;
// data for the best hit so far
// данные для «наилучшего» на данный момент соударения
getFirstHitCray. best):
// fill the 'best' record
// закрашиваем «наилучшую запись»
if(best.numHits == 0)
// did the ray miss every object?
//не прошел ли луч мимо всех объектов?
return background:
col or. set (the emissive color of the object)-.
11 эмиссионный цвет объекта
color.aMiambient. diffuse and specular components')-.
// фоновый, диффузный и зеркальный компоненты
// add more contributions
// добавляем другие составляющие
col or. add( reflected and refracted components'):
// отраженный и преломленный компоненты
return color;
}
Ядро трассировщика лучей помещается в подпрограмме shadeO, скелет которой приведен в листин-
ге 14.4. Первая задача трассировщика — определить, соударяется ли луч с каким-нибудь объектом,
и если да, то с каким. Для этого используется подпрограмма getFirstHitCray, best), которая помещает
данные, соответствующие первому соударению, в запись пересечений (intersection record) под именем
best. Как только становится известной информация о первом соударении, подпрограмма shadeC) начи-
нает определять «цвет луча». Если нет соударения ни с одним объектом, то это просто цвет фона, кото-
рый и возвращается подпрограммой shadeO. Если же соударение луча с объектом произошло, то shadeO
накапливает различные составляющие цвета в переменной color. В ней содержится цвет, испускаемый
объектом, если он светится; фоновый, диффузный и зеркальный компоненты, являющиеся частью клас-
сической модели закрашивания, которая описана в главе 8; а также свет, отраженный от блестящей по-
верхности и преломленный прозрачной поверхностью.
Подпрограмма getFirstHitO находит объект, с которым луч соударяется первым, и возвращает ин-
формацию об этом в запись пересечений best. Мы реализуем записи пересечений с применением класса
Intersection:
class Intersection!
public:
int numHits:
14.5. Организация трассировщика луча в приложении
853
// # of hits at positive hit times
// число соударений для положительных значений времени
Hitinfo hit[8]:
// list of hits - may need more than 8 later
// список соударений - позднее их понадобится больше 8
... various methods ...
// различные методы
}:
Этот класс имеет два поля: число соударений луча с объектом и массив, содержащий данные о каж-
дом соударении. Мы будем считать легитимными только такие соударения, которые происходят при
положительных значениях времени соударения (перед исходной точкой луча); соударения «позади гла-
за» не представляют для нас интереса. Особенно нас интересует первое соударение луча с объектом.
Если inter — запись пересечений, a inter.numHits больше нуля, то информация о первом соударении
хранится в inter.hit[0].
Зачем же хранить информацию обо всех соударениях луча с объектами (в положительные моменты
времени), а не только о первом из них? Одним из главных преимуществ метода трассировки луча явля-
ется его способность визуализации логических (Boolean) объектов (см. раздел «Пересечения лучей с
Булевыми объектами» данной главы). Для обработки таких объектов нам необходимо хранить запись
данных обо всех соударениях луча с объектом, поэтому мы предпринимаем усилия для этого уже сей-
час. Обычно глаз находится позади всех объектов и луч соударяется с объектом дважды — один раз при
входе в объект, и один раз при выходе из него. Для таких случаев inter.numHits равно 2, a inter.hit[0]
описывает, где луч входит в объект, а в inter.hit[l] — где луч выходит из него. Однако некоторые объек-
ты, например тор или логические объекты, показанные на рис. 14.9, могут иметь более двух соударений.
На рис. 14.9, а имеется четыре соударения с положительными значениями времени соударения, поэто-
му inter.numHits равно 4, а информация об этих соударениях хранится в inter.hit[0],..., inter.hit[3].
На рис. 14.9, б луч соударяется с объектом восемь раз, однако глаз находится внутри этого объекта
(который предполагается прозрачным), поэтому всего трем соударениям соответствуют положитель-
ные значения времени (inter.numHits равно3).
Рис. 14.9. Множественные соударения с объектом, некоторые из них происходят при отрицательных значениях времени
Информация о каждом соударении хранится в записи типа Hitinfo:
class Hitinfo {
// data for each hit with a surface
// данные о каждом соударении с поверхностью
public:
double hitTime;
// the hit time
// время соударения
GeomObj* hitobject;
// the object hit
// обьект соударения
bool isEntering:
854
Глава 14. Введение в трассировку лучей
// is the ray entering or exiting?
// луч входит в объект или выходит из него?
int surface:
// which surface is hit?
// с какой поверхностью происходит соударение?
Points hitPoint:
// hit point
// точка соударения
Vector3 hitNormal:
// normal at hit point
// нормаль в точке соударения
... other fields and methods ...
// другие поля и методы
};
Запись соударений содержит несколько полей, описывающих соударение: время соударения, указа-
тель на объект, с которым происходит соударение, информация о том, входит луч в объект при соударе-
нии или выходит из него, расположение точки соударения и нормальный вектор к поверхности в этой
точке. Все эти поля будут важны для нас на различных этапах процесса трассировки луча.
Листинг 14.5. Метод getFirstHit()
void Scene:: getFirstHit(Ray& ray. Intersections best)
{
Intersection inter;
// make intersection record
// создаем запись пересечений
best.numHits » 0:
//no hits yet
// пока соударений нет
for(GeomObj* pObj - obj: pObj !- NULL: pObj - pObj->next)
{
// test each object in the scene
// проверяем каждый объект на сцене
if(!pObj->hit(ray. inter))
// does the ray hit pObj?
// соударяется ли луч с объектом pObj?
continue:
// miss: test the next object
// соударения нет: проверяем следующий объект
If(best.numHits — 0 ||
// best has no hits yet
// в best пока нет соударений
inter.hit[0].hitTime < best.hit[O].hitTime)
best.set(inter);
// copy inter into best
// копируем inter в best
}
}
В листинге 14.5 приведена подпрограмма getFi rstHitO. Она просматривает весь список объектов
(начиная с obj, указателя на первый объект в этом списке — см. класс Scene в приложении В) и проверя-
ет, происходит ли соударение луча с каждым объектом. Для этого используется собственный метод hit()
каждого из объектов, который мы рассмотрим в следующем разделе. Каждый метод hit() возвращает
14.5. Организация трассировщика луча в приложении
855
true, если происходит легитимное соударение, и fal se в противном случае. Если соударение имеет мес-
то, то метод строит полную запись пересечений, в которой описываются все соударения с рассматрива-
емым объектом, и помещает эту запись в inter. Затем метод getFirstHitO сравнивает (первое положи-
тельное) время соударения в inter со временем в best, записи с «наилучшим соударением на данный
момент». Если обнаружилось более раннее время соударения, то данные из inter копируются в best.
Начальное значение best.numHits равно нулю, так что первое реальное соударение будет учтено при про-
смотре pObj списка объектов.
Отметим, что метод getFirstHitO перекладывает тяжесть вычисления пересечений лучей на подпро-
грамму hit(), имеющуюся для каждого объекта. Для каждого типа объектов мы разработаем свой метод
hit О. В целях эффективности следует использовать знание о форме базового объекта. Это является
прекрасным примером использования полиморфизма для упрощения кода и увеличения его устойчи-
вости и эффективности. Подпрограмма hit() является виртуальным методом класса GeomObj, порожда-
ющего все имеющиеся классы Shape.
Работа метода hit() данного класса состоит в том, чтобы принять луч, построить запись пересече-
ний и загрузить в эту запись все детали пересечений луча с объектом. Ниже мы разработаем метод hit()
для сферы и посмотрим, что в него входит.
14.5.1. Подпрограмма для вычисления пересечений
луча со сферой
Листинг 14.6. Метод hit() для класса Sphere
bool Sphere:: hit (Ray &r. Intersections, inter)
{
Ray genRay:
// need to make the generic ray
// необходимо создать базовый луч
xfrmRayCgenRay.invTransf.г):
double А, В. С;
А = dot3D(genRay.dir. genRay.dir):
В - dot3D(genRay.start. genRay.dir):
C - dot3D(genRay.start, genRay.start) - 1.0;
double discrim = В * В - A * C:
ifCdiscrim < 0.0)
// ray misses
// луч проходит мимо
return false:
int num = 0:
// the # of hits so far
// число соударений на данный момент
double discRoot = sqrtCdiscrim);
double tl - (-B - discRoot)/A:
// the earlier hit
// более раннее соударение
if(tl > 0.00001)
// is hit in front of the eye?
// находится ли данное соударение впереди глаза?
{
inter.hit[0],hitTime - tl;
inter.hit[0].hitobject = this;
inter.hitCOJ.isEntering = true;
inter.hit[0].surface - 0;
Point3 P(rayPos(genRay. tl));
продолжение &
856
Глава 14. Введение в трассировку лучей
Листинг 14.6 (продолжение)
// hit spot
// точка соударения
inter.hit[0].hitPoint.set(P):
inter.hit[0].hitNormal,set(P):
num = 1:
// have a hit
// имеем соударение
}
double t2 = (-B + discRoot)/A;
// the later hit
// более позднее соударение
if( t2 > 0.00001)
{
inter.hit[num].hitTime = t2:
inter.hit[num].hitobject - this:
inter.hit[num].isEntering = false:
inter.hit[num].surface - 0:
Point3 P(rayPos(genRay. t2)):
// hit spot
// точка соударения
i nter.hi t[num].hi tPoi nt.set(P):
inter.hit[num].hitNormal.set(P);
num++:
// have another hit
// имеем еще одно соударение
}
inter.numHits = num:
return (num >0):
// true or false
// true или false
}
В листинге 14.6 приведен метод hit() для класса Sphere. Сначала он преобразует луч г в базовые коор-
динаты данной сферы, используя при этом обратное преобразование для именно этой сферы. Подпро-
грамма xfrmRayO преобразует луч в соответствии с уравнением (14.15) (см. упражнения в конце раздела).
Далее определяются коэффициенты А, В, С квадратного уравнения (14.12) и исследуется дискрими-
нант В2 - АС. Если он меньше нуля, то данное уравнение не имеет вещественных решений, и мы делаем
вывод, что данный луч должен пройти мимо сферы. Тогда метод hit() возвращает false и запись inter
не используется.
При t2
Рис. 14.10. Какие точки соударения находятся впереди глаза?
Если же дискриминант положителен, то из уравнения (14.13) определяются два момента соударения.
Обозначим более раннее из этих времен через tv а более позднее — через t2. Как показано на рис. 14.10,
имеются три возможности: сфера может находиться впереди глаза, и в этом случае оба времени соударе-
ния положительны; глаз может находиться внутри сферы, и в этом случае отрицательно, a t2 — положи-
тельно; кроме того, сфера может находиться позади глаза, и тогда оба времени соударения отрицатель-
ны. Если время tj строго положительно, то данные о первом соударении помещаются в inter.hit[0],
14.5. Организация трассировщика луча в приложении
857
а переменной num присваивается значение единица, что означает, что соударение имело место. Если t2
положительно, то данные о следующем соударении помещаются в inter.hit[num], (Если первое время
соударения отрицательно, то данные о втором времени соударения автоматически помещаются в hi t[0].)
Данные помещаются в каждую запись соударения с учетом информации о сфере. Например, по-
скольку сфера является выпуклым объектом, луч должен войти в нее в более раннее время соударения,
а выйти — в более позднее. Значение переменной surface устанавливается в нуль, поскольку у сферы
только одна поверхность. (Мы разберем это понятие позднее.) Точки (в базовых координатах), в кото-
рых луч соударяется со сферой, также записываются в поле hitPoint. Точка соударения всегда (по опре-
делению) совпадает с положением луча в данный момент соударения, который находится с помощью
следующей функции (см. упражнения):
Points rayPos(Ray& г. float t):
// returns the ray’s location at time t
// возвращает положение луча в момент времени t
Вычислить нормальный вектор в точке соударения для сферы также нетрудно: поскольку нормаль
является радиус-вектором из центра сферы, ее координаты совпадают с координатами самих точек со-
ударения.
Практические упражнения
14.5.1. Преобразуйте луч из координат сцены в базовые координаты
Напишите подпрограмму xfrmRayO, в которой метод hit() используется для преобразования луча в базовые
координаты сферы. Особое внимание обратите на различие между преобразованием точки и вектора.
14.5.2. Функция rayPosQ
Реализуйте описанную ранее функцию rayPosO. Эта функция принимает луч и время, а возвращает
положение луча в этот момент времени.
14.5.3. Когда луч касается сферы
Посмотрите, какие значения будут вычисляться и записываться для случая, когда луч только касается
сферы.
14.5.4. О сложности вычислений
Насколько дорого обходится пересечение луча со сферой? Сколько умножений, делений и извлечений
квадратного корня необходимо произвести для вычисления соударения луча со сферой?
14.5.2. Полный трассировщик лучей для сцен
с излучающей сферой
Вон совершенно круглая луна
Кружит божественно сквозь синие глубины,
И под ее немеркнущим лучом
Пустынный круг раскинулся, как будто
Круг океана опоясан небом.
Прекрасна ночь!
Роберт Саути (Robert Southey)
Мы располагаем достаточными средствами, чтобы создать простой трассировщик лучей для сцен, состав-
ленных из сфер (и, конечно, эллипсоидов). Очень полезно выполнить эту довольно значительную работу
до усложнения ситуации, чтобы увидеть, как собрать вместе все уже рассмотренные нами ингредиенты.
Главное — ничего не упустить, поскольку все эти инструменты понадобятся нам в дальнейшем.
На данный момент мы можем создавать объект, светящийся некоторым светом, только путем присво-
ения его эмиссионному компоненту в SDL-файле некоторого ненулевого значения, например командой
emissive 0.3 0.6 0.2. Нетрудно скорректировать метод Scene::shadeO из листинга 14.4 так, чтобы в нем
858
Глава 14. Введение в трассировку лучей
поддерживался только излучаемый (эмиссионный) свет: нужно просто удалить те строки color.addO,
в которых определяются другие составляющие света. Результат будет следующим:
Со1огЗ Scene :: shade(Ray& ray)
{
Color3 color:
Intersection best:
getFirstHitCray. best):
IfCbest.numHits -- 0) return background:
Shape* myObj = (Shape*)best.hit[O].hitobject:
// the hit object
// объект соударения
color.set(myObj->mtrl.emissive):
return color:
}
Направление луча в каждом пиксельном блоке вычисляется только в тех частях метода
Camera :: raytraceO из листинга 14.3, которые требуют конкретизации1:
forCint row - 0: row < nRows: row += blocksize)
for(int col - 0; col < nCols: col +- blockSize)
{
float x - -W + col * 2 * W / (float)nCols;
float у - -H + row * 2 * H / (float)nRows;
theRay.setDirC -nearDist * n.x + x * u.x + у * v.x.
-nearDist * n.y + x * u.y + у * v.y.
-nearDist * n.z + x * u.z + у * v.z):
Color3 clr - sen. shade!theRay):
// color of this ray
// цвет данного луча
glColor3f(clr.red. clr.green, clr.blue):
glRecti(col. row. col + blockSize. row + blockSize):
}
В тематическом задании 14.1 реализация простого трассировщика лучей для сцен со сферами рас-
сматривается более детально.
14.6. Пересечение лучей с другими примитивами
Разработаем метод hit() для других классов форм. Все эти методы hit() похожи друг на друга: вначале
луч преобразуется в базовые координаты рассматриваемого объекта, затем вычисляются различные
пересечения луча с базовым объектом. Нам остается только разработать специфические детали пересе-
чения для каждой базовой формы.
14.6.1. Пересечение с квадратом
Квадрат является полезной базовой формой. Базовый квадрат лежит в плоскости г = 0 и простирается
от -1 до 1 по х и по у. (Неявная форма уравнения квадрата имеет вид: F(P) = Рг, где |PJ < 1 и |Ру| < 1.)
Квадрат может быть преобразован в параллелограмм произвольного вида, расположенный в простран-
1 Отметим, что вычисление некоторых из этих переменных для эффективности может быть выведено за пределы внутреннего
цикла. (Каких именно?)
14.6. Пересечение лучей с другими примитивами
859
стве, так что его часто используют в сценах для получения тонких плоских поверхностей, таких как
стены и окна. Функция hit() вначале определяет, где луч соударяется с базовой плоскостью, а затем
проверяет, находится ли эта точка соударения внутри квадрата, как показано в листинге 14.7.
Листинг 14.7. Метод hit() для класса Square
// ««««««««< hit for Square »»»»»»»».
//«««<««<««« соударение с квадратом »»»».
bool Square:: hit(Ray Sr. Intersections inter)
{
Ray genRay:
// need to make the generic ray
// требуется создать базовый луч
inter.numHits “ 0:
// initial assumption
// начальное предположение
xfrmRay(genRay. invTransf. r):
double denom = genRay.dir.z:
// denominator
// знаменатель
if(fabs(denom) < 0.0001) return false:
// ray parallel to plane: miss
// луч параллелен плоскости: пропускаем
double time - -genRay.start.z/denom:
// hit time
// время соударения
ifCtime <- 0.0) return false:
// it lies behind the eye
// квадрат лежит позади глаза
double hx - genRay.start.x + genRay.dir.x * time:
// x at hit
// x в точке соударения
double hy - genRay.start.у + genRay.dir.у * time;
// у at hit
// у в точке соударения
if((hx > 1.0) || (hx < -1.0)) return false:
// misses in x-direction
// проходит мимо в направлении х
1f((hy > 1.0) || (hy < -1.0)) return false:
// misses in y-direction
// проходит мимо в направлении у
inter.numHits ” 1:
// have a hit
// имеем соударение
inter.hitCOD.hitobject - this:
inter.hit[0].hitTime * time:
inter.hit[0].1sEntering - true;
inter.hit[0].surface - 0:
inter.hit[0].hitPoint.set(hx.hy.0):
inter.hit[OJ.hitNormal.set(O.O.l):
return true:
860
Глава 14. Введение в трассировку лучей
14.6.2. Пересечение с коническим цилиндром
На рис. 14.11 показаны базовый конический цилиндр и несколько лучей. Боковая сторона цилиндра
является частью бесконечно длинной «стенки» с радиусом 1 при z = 0 и «малым радиусом» s при z = 1.
Из уравнения (6.30) нам известно, что неявная форма для этой стенки имеет вид:
F(x, у, г) = х2 + у2 - (1 + ($ - 1) г)2, где 0 < z < 1.
Если s = 1, то данная форма становится базовым цилиндром; если s = 0, то она превращается в базо-
вый конус. Мы разработаем метод hit() для конического цилиндра, который одновременно предостав-
ляет методы hit() для цилиндра и конуса.
Рис. 14.11. Базовый конический цилиндр
На рисунке показано также несколько лучей, иллюстрирующих разнообразие вариантов, при кото-
рых луч может соударяться с данным объектом или пройти мимо него. Луч А соударяется со стенкой
дважды в пределах боковой поверхности цилиндра (для краткости мы часто будем называть коничес-
кий цилиндр просто «цилиндром»). Луч В пересекает бесконечную стенку, затем входит в цилиндр через
его крышку, после чего выходит через боковую поверхность цилиндра. Луч С соударяется вначале со
стенкой цилиндра и затем выходит через его основание. Луч D входит через основание и выходит через
крышку. Луч Е соударяется с бесконечной стенкой, однако вне пределов экстента цилиндра, и поэтому
проходит мимо объекта. Непоказанным остался луч, который проходит вообще мимо цилиндрической
стенки. (Какие еще случаи не показаны на рисунке?)
При таких многочисленных возможностях нам требуется организованный подход, в котором не будет
большого количества тестов вида if О. .else. Решение состоит в идентификации соударений в каком-
либо удобном порядке и помещении их в список inter.hit[J вне зависимости от порядка. В конце кон-
цов, если два соударения в списке inter.hit[] не соответствуют установленному порядку, то эти эле-
менты списка переставляются местами. Хорошо бы, чтобы к этому моменту уже был список, в который
можно поместить эти соударения.
Отдельные тесты вполне очевидны. Для того чтобы определить, попадает ли луч в бесконечную стен-
ку, мы просто подставляем 5 + ct в неявную форму конического цилиндра и получаем квадратное урав-
нение At2 + 2Bt + С - 0. Нетрудно показать, что
А = сх +су-d2,
В = Sxcx+Sycy-Fd, (14.16)
C = S2x+S2-F2.
где d = (s - 1) c2 и F= 1 + (s - 1) Sx. (Какой вид принимают эти уравнения для цилиндра и для конуса?)
Используем полученные коэффициенты так же, как в случае сферы. Если дискриминант В2 - АС отри-
цателен, то луч проходит мимо стенки конического цилиндра. Если же дискриминант не отрицателен,
то луч соударяется со стенкой, и тогда моменты соударения могут быть найдены путем решения данно-
го квадратного уравнения. Для проверки того, происходит ли каждое соударение на стенке заданного
конечного цилиндра, следует найти z-компонент точки соударения. Луч соударяется с цилиндром толь-
ко в том случае, если этот z-компонент находится в пределах от 0 до 1.
14.6. Пересечение лучей с другими примитивами
861
Для проверки пересечения с основанием рассмотрим пересечение данного луча с плоскостью z = 0.
Пусть соударение происходит в точке (х, у, 0). Точка соударения лежит в пределах основания, если
х1 + у2 < 1. (Почему?) Аналогично для проверки пересечения с крышкой рассмотрим пересечение дан-
ного луча с плоскостью z = 1. Предположим, что соударение происходит в точке (х, у, 1). Точка соударе-
ния лежит в пределах крышки, если х2 + у2 < $2.
Цилиндр имеет более одной поверхности, и впоследствии нам захочется знать, с какой именно по-
верхностью происходит соударение. (Например, нам захочется наложить на стенку и на крышку раз-
личные текстуры.) Поэтому мы принимаем следующую нумерацию: стенка является поверхностью 0,
основание — поверхностью 1, а крышка — поверхностью 2. Соответствующее значение помещается в
поле surface каждой записи соударения.
Листинг 14.8. Скелет метода hit() для класса TaperedCylinder
bool TaperedCylinder::hit(Ray &r. Intersection Sinter)
{
Ray genRay:
// generic ray
// базовый луч
xfrmRay(genRay.1nvTransf,r):
double А. В. C. discrim. disc_root. tl.t2.tb.tc:
double sm - small Radi us - 1:
double fDir = sm * genRay.dir.z:
// handy short names
// удобные сокращенные имена
double fStart = sm * genRay.start.z + 1;
get A, B. and C as in Equation 14.16
// вычисляем А. В. С. как в уравнении 14.16
discrim - B*B - A*C;
int num - 0:
// no hits yet
// пока соударений нет
ifCdiscrim > 0.0)
// can take square root
// можно извлечь квадратный корень
{
disc_root = (double)sqrt(double(discrim));
tl - (-B - disc_root)/A;
// earlier hit
// более раннее соударение
float zHit - genRay.start.z + genRay.dir.z * tl:
// z component of ray
// z-компонент луча
IfCtl > 0.00001 && zHit <= 1.0 && zHit >= 0)
{
inter.hit[num].hitTime = tl:
inter.hit[num++],surface = 0:
// hit Is with wall
// соударение co стенкой
t2 = (-B + disc_root)/A:
// second hit
// второе соударение
продолжение &
862
Глава 14. Введение в трассировку лучей
Листинг 14.8 (продолжение)
zHit - genRay.start.г + genRay.dir.z * t2: i
if(t2 > 0.00001 && zHit <- 1.0 && zHit >-0)
{
inter.hit[num].hitTime - t2:
inter.hit[nunH+J.surface - 0:
// hit is with wall
// соударение co стенкой
)
)
// end 1f(discrim > 0)
// конец блока if(discrim > 0)
// test the base at z - 0
// проверяем основание при z - 0
tb - -genRay.start.z/genRay.dir.z:
// hit time at z - 0 plane
// время соударения с плоскостью z - 0
if(tb > 0.00001 && SQRCgenRay.start.x + genRay.dir.x * tb)
+ SQR(genRay.start.у + genRay.dir.y * tb) < 1)
// within disc of base
// внутри диска основания
{
inter.hit[num].hitTime - tb:
inter.hit[num++],surface - 1:
// 1 for the base
// 1 для основания
}
// test the cap at z - 1
// проверяем крышку при z - 1
tc - (1 - genRay.start.z)/genRay.dir.z:
// hit time at z - 1 plane
// время соударения с плоскостью z - 1
ifCtc > 0.00001 && SQR(genRay.start.x + genRay.dir.x * tc)
+ SQRCgenRay.start.y + genRay.dir.y * tc) <
SQR(smallRadius))
// within disc
// внутри диска
{
inter.hit[num].hitTime - tc:
inter.hit[num++].surface - 2:
// 2 for the cap
// 2 для крышки
}
if(num — 0) return false:
// missed everything, or behind the eye
// луч проходит мимо всего или находится позади глаза
inter.numHits - num:
if(num — 1)
// eye inside cylinder, only have the exiting hit
// глаз внутри цилиндра, имеется только соударение выхода
{
inter.hit[0].isEntering » false:
inter.hit[0].hitObject - this:
)
14.6. Пересечение лучей с другими примитивами
863
else
// have two hits - first must be entering
// имеется два соударения - первое должно быть вхождением
{
// now sort the two hits
// теперь сортируем два соударения
if(inter.hit[O].hitTime > inter.hit[l].hitTime)
// must reverse them
// следует поменять их местами
{
И need only swap the hitTime and surface fields
// требуется только переставить hitTime и поля поверхностей
double tmpT » inter.hit[0],hitTime:
// swap times
// переставляем значения времени
inter.hit[0],hitTime - inter.hit[lj.hitTime;
inter.hit[l],hitTime - tmpT:
int tmpS » inter.hit[0].surface:
// swap surfaces
U переставляем поверхности
inter.hit[0],surface - inter.hit[l].surface:
inter.hit[lj.surface - tmpS:
}
inter.hit[O].isEntering - true;
inter.hit[l].isEntering » false:
inter.hit[0],hitobject - inter.hit[lJ.hitobject » this:
}
// now set the hit point and normal for the hit or hits
// теперь устанавливаем точку соударения и нормаль
// для одного или нескольких соударений
forfint i » 0: i < num: i++)
Point3 PO(rayPos(genRay. inter.hit[ij.hitTime)):
// position of first hit
// положение первого соударения
inter.hit[i].hitPoint.set(PO):
int surf » inter.hit[i].surface;
if(surf ~ 0)
// wall
// стенка
inter.hit[i],hitNormal.set(P0.x. PO.y, -sm * (1 + sm * PO.z));
else if(surf — 1)
// base
// основание
inter.hit[i].hitNormal.set(0.0.-1):
else inter.hit[i].hitNormal.set(0,0,l):
// cap
// крышка
}
return true;
}
В листинге 14.8 все эти идеи собраны вместе в скелет кода, соответствующий базовому коническому
цилиндру. (Как и раньше, выражения, выделенные жирным шрифтом, означают псевдокод.) Отметим,
864
Глава 14. Введение в трассировку лучей
что каждая поверхность цилиндра проверяется поочередно и допустимые соударения добавляются
в «список соударений», включая данные о том, какая поверхность участвует в соударении.
Отметим, что в двух точках соударения необходимо найти нормальный вектор. Как уже говорилось
в главе 6, нормаль к стенке цилиндра в точке (х, у, г) имеет вид: (х, у, (s - 1) (1 + (s - 1)г)). Нормали к
крышке и к основанию равны соответственно (0,0,1) и (0,0, -1). Поля hitNormal заполняются соответ-
ствующими значениями с помощью метода hit().
Практические упражнения
14.6.1. Реализация метода hit() для конического цилиндра
Проверьте уравнение (14.16) и убедитесь, что коэффициенты квадратного уравнения для коничес-
кого цилиндра написаны правильно. Конкретизируйте код метода TaperedCylinder :: hit(Ray& г.
Intersections inter).
14.6.2. Реализация метода hit() для пересечения с конусом
Если бы вы захотели иметь подпрограмму hit(), специально предназначенную для класса Cone, то чем
бы она отличалась от той, что написана для класса TaperedCyl i nder? Покажите, какие строки кода долж-
ны быть изменены для увеличения эффективности подпрограммы.
14.6.3. О сложности вычислений
Сколько сложений/вычитаний и умножений/делений требуется для пересечения луча с квадратом и
с коническим цилиндром?
14.6.4. Другие квадратичные поверхности
В главе 6 мы рассмотрели представления различных квадратичных поверхностей, таких как гипербо-
лоид и эллиптический конус.
О Как разумно определить базовую версию для каждого типа квадратичной поверхности?
О Для каждой базовой квадратичной поверхности покажите, что поиск пересечения ее с лучом при-
водит к квадратному уравнению; приведите это уравнение.
14.6.3. Пересечение с кубом (или с любым другим
выпуклым полиэдром)
Выпуклые полиэдры доказали свою полезность во многих ситуациях машинной графики и уже рассматри-
вались в некоторых разделах данной книги (см., например, обсуждение Платоновых тел в главе 6). Посколь-
ку выпуклые полиэдры определены в терминах ограничивающих плоскостей, нетрудно разработать под-
программу пересечения луча с любым выпуклым полиэдром. Мы сделаем это позднее в данном разделе.
Частный случай выпуклого полиэдра, базовый куб (generic cube), заслуживает особого внимания. Центр
его расположен в начале координат, а углы лежат в точках (±1, ±1, ±1), где использованы все восемь
комбинаций +1 и -1. Ребра базового куба направлены вдоль координатных осей, а шесть его граней лежат
в плоскостях, которые показаны в табл. 14.1. Для упрощения визуализации базового куба каждой плоско-
сти присвоено название согласно тому, как она видна из точки вида (0,0,10). В таблице приводится внеш-
няя нормаль к каждой из плоскостей, а также характерная точка — пятно, лежащее на этой плоскости.
Таблица 14.1. Шесть плоскостей, определяющих базовый куб
Плоскость Название Уравнение Внешняя нормаль Пятно
0 Верхняя (top) у=1 (0, 1, 0) (0,1, 0)
1 Нижняя (bottom) у=-1 (0,-1,0) (0,-1,0)
2 Правая (right) х= 1 (1,0,0) (1, 0, 0)
3 Левая (left) х=-1 (-1,0,0) (-1,0,0)
4 Передняя (front) z= 1 (0, 0, 1) (0, 0, 1)
5 Задняя (back) z=-l (0, 0,-1) (0, 0,-1)
14.6. Пересечение лучей с другими примитивами
865
Базовый куб важен по следующим двум причинам:
О С помощью аффинного преобразования базового куба может быть смоделировано и помещено
на сцену большое количество разнообразных и интересных «блоков». Затем при трассировке лу-
чей каждый луч может быть подвергнут обратному преобразованию в системе координат базово-
го куба, поэтому мы можем использовать подпрограмму пересечения луча с базовым кубом (ко-
торую можно сделать весьма эффективной).
О Базовый куб можно использовать как экстент (extent) для других базовых примитивов в каче-
стве ограничивающего параллелепипеда (bounding box): каждый базовый примитив, например
цилиндр, прекрасно вписывается в такой куб. Как мы увидим позднее, часто весьма эффективно
проверять пересечение луча с экстентом объекта перед тем, как выяснять соударение луча с самим
объектом, особенно если подпрограмма пересечения луча с объектом является дорогостоящей с
вычислительной точки зрения. Если луч проходит мимо экстента, то он обязательно пройдет и
мимо объекта. Поэтому получить в свое распоряжение высокоэффективный алгоритм пересече-
ния луча с базовым кубом — большое достижение.
Алгоритм пересечения для базового куба
Процесс пересечения луча с кубом по своей сути является алгоритмом Сайруса-Бека, описанным в разделе
«Алгоритм Сайруса—Бека» главы 4, где прямая линия отсекается границами выпуклого окна в двумерном
пространстве. Данный алгоритм был также использован для отсечения прямой линии отображаемым
объемом камеры в главе 8. Основная идея заключается в том, что каждая плоскость куба определяет
«внутреннее» и «внешнее» полупространства и что точка на луче лежит внутри этого куба тогда и толь-
ко тогда, когда она лежит «внутри» каждого полупространства куба. Тогда пересечение луча с кубом
сводится к определению интервала времени, в течение которого луч лежит внутри всех плоскостей куба.
Обозначим куб буквой Р. Протестируем луч поочередно с каждой плоскостью куба Р, вычисляя мо-
менты времени, в которые луч или входит во внутреннее полупространство данной плоскости, или вы-
ходит из него. Мы будем отслеживать этот «возможный интервал» («candidate interval» — CI) — такой
интервал времени, в который, на основе выполненных до данного момента тестов, луч может находить-
ся внутри данного объекта. Этот интервал ограничен значениями времени tjn и tout то есть CI = [tin, iout].
По мере проверки каждой плоскости куба Р мы «усекаем» этот интервал, либо увеличивая t.n, либо
уменьшая tout. Если для какой-нибудь точки CI становится пустым, то луч должен пройти мимо данного
объекта, определяя «досрочный выход». Если после проверки всех плоскостей куба Р мы обнаружим,
что оставшийся интервал CI не пуст, то луч входит в объект в момент tir) и выходит из него в момент tout.
а б
Рис. 14.12. Луч протыкает базовый куб (а); двумерный случай (5)
Для иллюстрации этого процесса на рис. 14.12, а показан пример, в котором луч входит в базовый
куб при t = 3,6 и выходит из него при t = 4,1. Тогда при завершении тестирования остается интервал
CI = [3,6, 4,1]. На рис. 14.12, б для простоты показан двумерный вариант того же процесса; здесь мы
хотим найти пересечение луча с квадратом. С нашей «всевидящей» обзорной точки мы видим, что луч
вначале соударяется с верхней плоскостью квадрата при t = 1,6 и входит во внутреннее полупростран-
28 Ф. Хилл
866
Глава 14. Введение в трассировку лучей
ство квадрата. Затем он соударяется с правой плоскостью при t - 1,8, также входя во внутреннее полу-
пространство. Луч соударяется с левой плоскостью при t = 2,7 и выходит из внутреннего полупростран-
ства; наконец, он выходит из нижней плоскости при t = 2,9. '
Предположим, что мы проверяем плоскости (стороны) квадрата в указанном порядке, начиная с плос-
кости 1 и заканчивая плоскостью 4. Вначале устанавливаем интервал CI - (-«>, оо). Соударение с плоско-
стью 1 дает время выхода 2,9, поэтому нам понятно, что луч после этого момента времени должен быть
вне квадрата, следовательно, CI = (-«=, 2,9). Тестирование с плоскостью 2 показывает, что фактически
луч выходит еще раньше, в момент времени 2,7, поэтому полагаем tout равным 2,7. Тест с плоскостью 3
показывает, что луч не может войти раньше, чем при t - 1,6, поэтому присваиваем tin это значение. Нако-
нец, тестирование с плоскостью 4 показывает, что фактически tjn составляет 1,8. Тогда окончательный
CI - [1,8, 2,7]. На каждом этапе tjn и tout вычисляются с помощью следующего кода:
if (the ray is entering at thit)
tin = max(tln. thit)
else if(the ray is exiting at thit)
tout min(tout. thit)
Переходя к деталям, предположим, что луч имеет уравнение 5 + ct и что рассматриваемая плоскость
имеет внешнюю нормаль m и содержит в себе точку В. Неявная форма уравнения этой плоскости имеет
вид F(P) - m • (Р - В), поэтому луч соударяется с ней, когда m • (5 + ct - В) - 0, или в момент соударения
numer /П СХ J л/пч
/ =-------, где числитель numer - m • (В - 5), а знаменатель denom -тс. (14.17)
denom
Таблица 14.2. Пересечение луча с внутренним полупространством плоскости
Ситуация Условие
Проходит вовнутрь Выходит наружу Целиком внутри Целиком снаружи denom < 0 denom > 0 denom = 0, numer > 0 denom = 0, numer < 0
Луч переходит во внешнее полупространство плоскости, если denom > 0 (поскольку векторы тис
в этом случае образуют угол, меньший 90°), и переходит во внутреннее полупространство, если denom < 0.
Если же denom - 0, то луч параллелен плоскости и значением числителя numer определяется, лежит он
целиком с внутренней или с внешней стороны плоскости, как было показано в разделе «Алгоритм Сай-
руса-Бека» главы 4. Четыре имеющиеся возможности приведены в табл. 14.2. Все это работает как в
двух, так и в трех измерениях. Для базового куба значения numer и denom могут быть вычислены очень
быстро: скалярные произведения вычисляются тривиально, поскольку каждый вектор m имеет по два
нулевых компонента. Для плоскостей из табл. 14.1 получаются следующие значения (проверьте их).
Плоскость Numer Denom
0 1-S, S
1 1 + S, "Cy
2 1-SM C,
3 1 + s. -4
4 i-s. C.
5 l+S, -4
Листинг 14.9. Метод hit() для класса Cube
bool Cube:: hit(Ray& r. Intersections inter)
double tHit. numer. denom:
14.6. Пересечение лучей с другими примитивами
867
double tin = -100000.0. tOut = 100000.0;
// plus-minus infinity
// плюс-минус бесконечность
Ray genRay:
int inSurf. outSurf;
// which of the six surfaces
// которая из шести плоскостей
xfrmRay(genRay. invTransf. r);
for (int i = 0: i < 6: i++)
switch(i)
// which plane of cube to test
// какую плоскость куба проверять
case 0: numer = 1.0 - genRay.start.у:
denom - genRay.dir.y: break:
case 1. case 2. case 3. case 4 similarly
// аналогично
case 5: numer = 1.0 + genRay.start.z:
denom - -genRay.dir.z: break:
}
if(fabs(denom) < 0.00001)
// ray is parallel
// луч параллелен
if(numer < 0) return false:
// ray is out;
// луч снаружи
else:
// ray inside, no change to tln.tOut
// луч внутри, никаких изменений в tln.tOut
}
else
// ray is not parallel
// луч не параллелен
{
tHit = numer / denom;
if(denom > 0){
// exiting
// выход луча
if(tH1t < tOut){
// a new earlier exit
// новый, более ранний выход
tOut = tHit: outSurf = i:
}
}
else {
// denom is negative: entering
// denom отрицателен: вход луча
if(tHit > tln){
// a new later entrance
// новый, более поздний вход
tin = tHit: inSurf = i:
продолжение £>
868
Глава 14. Введение в трассировку лучей
Листинг 14.9 (продолжение)
}
}
}
if(tln >= tOut) return false:
// it's a miss - early out
// луч проходит мимо - досрочный выход
}
// end of the for loop
// конец цикла for
int num = 0:
// no positive hits yet
// до сих пор нет положительных соударений
if(tln > 0.00001)
// is first hit in front of the eye?
// находится ли первое соударение перед глазом?
{
inter.hit[0].hitTime = tin:
inter.hit[OJ.surface = inSurf:
inter.hit[0].isEntering = 1:
// is entering
// луч входит
inter.hit[0],hitobject = this;
inter.hit[0).hitPoint.set!rayPos(genRay.start.
genRay.dir.tin)):
i nter.hi t[0].hi tNorma1.set(cubeNorma1(i nSurf)):
num++;
// have a hit
// имеется соударение
}
if(t0ut > 0.00001)
inter.hit[num].hitTime = tOut;
inter.hit[num],surface = outSurf:
inter.hit[num].isEntering = 0:
// is exiting
// выход луча
inter.hit[num],hitObject = this:
inter.hit[num],hitPoint.set(rayPos(genRay.start.
genRay.dir.tOut)):
inter.hit[num].hitNormal.set(cubeNorma1(outSurf));
num++:
}
inter.numHits = num:
// number of hits in front of eye
// количество соударений перед глазом
return (num > 0);
}
В листинге 14.9 приведена подпрограмма hit() для класса Cube, в которой реализованы все необхо-
димые тесты. Как и в случае других подпрограмм hit(), луч преобразуется в базовые координаты объек-
та и все тестирование производится с базовым лучом. Затем шесть плоскостей тестируются в цикле,
причем используются соответствующие значения numer и denom. Первоначально бесконечный интер-
14.6. Пересечение лучей с другими примитивами
869
вал CI «усекается» до его окончательного значения (tin, tOut), если только интервал не становится пус-
тым после какого-нибудь из тестов, что указывает на то, что луч проходит мимо куба. Поскольку важно
отслеживать, какая плоскость связана с текущими значениями tin и tOut, эта информация сохраняется
в переменных surln и surOut.
Когда протестированы все шесть плоскостей, мы знаем моменты времени соударения tin и tOut. Если
tin положительно, то данные о соударении в момент tin записываются в inter.hit[O], данные о соударе-
нии в момент tOut записываются в inter. hit[l]. Если положительным является только tOut, то данные о
его соударении загружаются в inter.hit[OJ.
Нормальный вектор к каждой плоскости соударения определяется с использованием вспомогатель-
ной функции cubeNormal (i), которая возвращает внешнюю нормаль, показанную в табл. 14.1. Например,
cubeNormal (0) возвращает вектор (0,1, 0), a cubeNormal (3) возвращает (-1, 0, 0) (см. упражнения в конце
раздела).
Алгоритм пересечения для произвольного выпуклого полиэдра
Нетрудно распространить метод hit() на любой выпуклый полиэдр. Предположим, что существует
N ограничивающих плоскостей и в i-й плоскости содержится точка В. и имеется (указывающий наружу)
нормальный вектор пт. Все в методе hit() для куба остается неизменным, за исключением того, что для
вычисления numer и denom теперь используется уравнение (14.17). Теперь следует вычислить два трудо-
емких скалярных произведения, после чего цикл for приобретет следующий вид:
for (int i = 0; i < N; 1++)
// for each plane of the polyhedron
// для каждой плоскости полиэдра
{
numer = dot3 (mi. Bi - S):
denom - dot3 (mi. c):
if(fabs(denom) < eps) ... as before
// как и прежде
... same as before ...
// все как прежде
}
Алгоритм пересечения для каркасного объекта
Поскольку у нас имеется богатый ассортимент каркасных объектов из главы 6, а также метод drawOpenGLC)
для любой сетки (mesh), то естественно рассмотреть трассировку луча для сеток. Для разработки метода
hit() для сеток используем прежний подход. Напомним, что объекты класса Mesh описываются посред-
ством списка граней, а каждая грань представляет собой список вершин вместе с нормальным вектором
в каждой вершине. Мы будем брать поочередно каждую грань сетки и рассматривать ее как ограничиваю-
щую плоскость. Назовем плоскость, связанную с каждой гранью, ее «плоскостью грани» («face plane»).
Объект, для которого производится трассировка луча, представляет собой пересечение внутренних по-
лупространств каждой из плоскостей граней объекта.
На рис. 14.13 показаны две формы (для простоты взяты двумерные) с отмеченными плоскостями
граней. Объект на рис. 14.13, а — выпуклый, поэтому его плоскости граней совпадают с соответствую-
щими ограничивающими плоскостями. Трассировка луча для такой формы будет осуществлена кор-
ректно. На рис. 14.13, б показан невыпуклый объект, причем та его часть, которая находится внутри
плоскостей граней, закрашена. Именно это отобразит на дисплее трассировщик лучей! (Нарисуйте
такой невыпуклый объект, который при трассировке лучей вообще будет невидимым.) Итак, данный
метод для сеток будет работать только в том случае, когда сетка представляет строго выпуклый объект.
Чтобы построить метод hit() для сетки, мы формируем для каждой грани поочередно переменные numer
и denom. В качестве репрезентативной точки на каждой плоскости грани выбираем нулевую вершину
870
Глава 14. Введение в трассировку лучей
этой грани, а именно pt[face[f] ,vert[O]. vert Index], а в качестве нормали к плоскости грани принимаем
нормаль, связанную с этой вершиной: norm[face[f]. vert[0]. normindex]. Тогда код примет следующий вид:
fordnt f = 0: f < numFaces: f++){
Vector3 diff:
Vectors normal(norm[ face[ f].vert[ 0].normindex] );
// use constructors
// используем конструкторы
Points point(pt[ face! f] ,vert[ 0] .vertlndex] ):
form diff = point - genRay. start
// формируем разность...
numer = dot3D(normal.diff):
denom = dot3D(normal.genRay.dir):
if(fabs(denom) < eps) ... as before
// как раньше
... same as before ... .
// так же. как и раньше
}
а б
Рис. 14.13. Двумерные объекты и их плоскости граней: а) выпуклый; б) невыпуклый
Практические упражнения
14.6.5. Задание нормального вектора для пересечения куба
Напишите функцию Vectors cubeNormal (int which), которая возвращает внешнюю нормаль к грани which
куба, в соответствии с листингом 14.1. Возможно, что наиболее читабельный код получится при исполь-
зовании одного оператора переключателя на шесть положений, который присваивает вектору одно из
шести аппаратно заданных значений. При слегка сокращенном подходе осуществляется распознавание
структуры нормалей и их вычисление для помощи следующих команд:
int го - which/2.n - (whichW? -1:1;
if(m ” 0)v.set( 0. n. 0):
else if(m ~ 1) v.set( n. 0. 0):
else v.set( 0. 0. n):
Разберитесь, как работает данный метод, и перепишите функцию cubeNormal так, чтобы она исполь-
зовала этот метод.
14.6.6. Плоскости тетраэдра
Используя для руководства табл. 6.7, покажите элементы списка плоскостей для правильного тетраэдра.
14.6.7. Усовершенствование метода hit() для выпуклого полиэдра
Напишите с подробностями метод ConvexPolyhedron :: hit() для пересечения луча с выпуклым полиэд-
ром. (За деталями класса ConvexPolyhedron обращайтесь к классу Shapes в приложении В.)
14.6.8. Ручное вычисление моментов «протыкания» базового куба
Найдите для луча (4, 5, 6) + (-8, -8, -10) t шесть моментов протыкания, начертите их так, как на
рис. 14.12, а, и определите интервал времени t, для которого луч находится внутри куба. Повторите все
это для луча (4,5,6) + (-12, -8, -10) t. Пересекается ли с кубом этот луч?
14.6. Пересечение лучей с другими примитивами
871
14.6.9. Пересечение с тетраэдром
Найдите интервал времени t, для которого луч (0,0,0) + (1,2,3) t находится внутри тетраэдра с верши-
нами (1,0,0), (-1,0, -1), (-1,0,1), (0,1,0).
14.6.10. О сложности вычислений
Сколько умножений/делений требуется для тестирования каждой плоскости выпуклого полиэдра?
Иногда время tin превышает tOut уже после тестирования всего нескольких плоскостей. Какова будет
эвристическая оценка среднего числа тестов, выполняемых для выпуклого полиэдра из N плоскостей,
если тестируется случайно выбранный луч? Сравните получившийся уровень сложности с тем, кото-
рый использовался при пересечении луча со сферой.
14.6.4. Добавление новых примитивов
Можно выйти за пределы рассмотренных до сих пор примитивов и добавить другие типы форм. Требует-
ся только знать для этой формы неявную запись уравнения F(P). Тогда, как и прежде, для нахождения
места пересечения луча S + etc поверхностью подставляем S + ct вместо Рв уравнение F(P), в результа-
те чего получается следующая функция от времени t
d(t) = F(S + ct). (14.18)
Эта функция:
О положительна при тех значениях времени t, для которых луч (точнее, точка на луче) лежит вне
объекта;
О равна нулю, когда луч совпадает с поверхностью объекта;
О отрицательна, когда луч находится внутри объекта.
При поиске пересечений мы ищем такие значения Г, при которых d(t) = 0, поэтому пересечение луча
эквивалентно решению данного уравнения. Мы уже видели, что для сферы и других квадратичных по-
верхностей d(t) является обычным квадратным уравнением.
Иная ситуация возникает в случае тора. Неявная функция для базового тора имеет следующий вид
(см. табл. 6.11):
F(P) = (A/PI2 +Ру2 -dJ+P? -1, (14.19)
вследствие чего получается уравнение четвертого порядка. Решение такого уравнения значительно слож-
нее, хотя его решения в аналитическом виде можно найти в математических справочниках.
Рассмотрим вид функции d(t) при возрастающих значениях t. Если луч направлен на рассматривае-
мый объект и стартовая точка S лежит вне объекта, то мы получаем кривые, аналогичные изображен-
ным на рис. 14.14. Значение d(0) положительно, поскольку луч стартует вне объекта. По мере прибли-
жения луча к объекту d(t) уменьшается, достигая нуля, если луч пересекает поверхность объекта (на
рисунке это tj). В тот период времени, когда луч находится внутри объекта, d(t) < 0. Когда луч появля-
ется вновь, то d(t) проходит через нуль и продолжает возрастать. (При работе с такими объектами, как
тор, луч может повторно войти в объект, так что нарисуйте типичную форму кривой d(t) для этого слу-
чая.) Если же луч проходит мимо объекта (этот случай показан на рисунке пунктиром), то хотя значе-
ние d(t) в течение какого-то времени уменьшается, однако затем все время возрастает, не достигая нуля.
Для квадратичных поверхностей, таких как сфера, функция d(t) имеет параболическую форму, а для
тора — форму полинома четвертого порядка. Для других поверхностей d(t) может быть настолько слож-
ной, что нам придется определять те значения t, при которых функция d{.) обращается в нуль, числен-
ными методами. Рассмотрим, например, суперэллипсоид из табл. 6.11. Этой поверхности соответству-
ет функция
d{t)^Sx +cxt)n + (Sy + cyt}n\’ + (Sy+cyt)m -1, (14.20)
872
Глава 14. Введение в трассировку лучей
где т и п — константы, определяющие форму поверхности. Для того чтобы найти наименьшее поло-
жительное значение t, обращающее функцию d(t) в нуль, мы вычисляем d(t) для последовательности
значений t и определяем среди них такое, при котором d(t) очень мала. При использовании таких алго-
ритмов, как метод Ньютона [Conte, deBoor, 45], возможно получать все лучшие и лучшие приближения
t, но, как правило, численные методы требуют большого числа итераций, что, несомненно, существенно
замедляет процесс трассировки луча.
Луч Луч
входит в объект выходит из объекта
Рис. 14.14. Зависимость функции d(t) от времени t для заданного луча и заданного объекта
Были разработаны методы трассировки луча для множества прочих объектов, среди которых важ-
но выделить фрактальные поверхности, поверхности вращения, а также призматические цилиндры
[Kajiya, 120]. (См. тематическое задание 14.7, где рассматриваются подходы к трассировке луча для таких
объектов.) Поиск эффективных алгоритмов трассировки луча для все большего набора форм является
постоянным предметом исследования в графике.
Практические упражнения
14.6.11. Пересечения с тором
Посмотрите в математическом справочнике, как находить решение уравнения четвертого порядка,
и укажите шаги, которые необходимо выполнить для нахождения одного или нескольких пересечений
луча 5 + ct с тором, заданным уравнением (14.19).
14.6.12. Трассировка луча для седла (гиперболического параболоида)
Укажите шаги, которые требуются для нахождения пересечений луча 5 + ct с гиперболическим парабо-
лоидом из табл. 6.10.
14.7. Рисование закрашенных изображений сцен
Трассировщик луча, рисующий светящиеся объекты, — это неплохо для начала, однако его несостоя-
тельность обнаруживается сразу после того, как нам понадобятся картины с высокой степенью реалис-
тичности. Для рисования таких картин нам следует определить природу света, который отражается от
точки соударения по направлению к глазу. В своих вычислениях мы будем вначале руководствоваться
моделью закраски OpenGL, которую рассматривали в главе 8. Затем мы посмотрим, как можно усовер-
шенствовать эту модель с целью достижения еще большего реализма.
В OpenGL сцены рисуются путем комбинирования фоновой, диффузной и зеркальной составляю-
щих света, освещающего вершину объекта. Для вычисления зеркальной составляющей света исполь-
зуется модель Фонга. На рис. 14.15 показаны основные составляющие. Из рисунка видно, что гс-луч
пересекает сфероид в точке соударения Рк. Источник света расположен в точке L. Мы хотим вычислить
количество света, возвращающееся из точки Ph обратно к глазу. Основные интересующие нас векторы —
s, v, т. Вектор s указывает на источник света и поэтому определяется равенством s = L - Ph; вектор v
указывает на наблюдателя и поэтому противоположен вектору направления луча dir; вектор m являет-
ся нормалью к поверхности в точке Ph.
14.7. Рисование закрашенных изображений сцен
873
Рис. 14.15. Применение модели закрашивания
Как было впервые указано в главе 8, суммарная интенсивность света, видимого глазом, состоит из
фоновой, диффузной и зеркальной составляющих:
I= / Ро + IdPd х lambert + Ispps х phong/, (14.21)
где / — интенсивность фонового света, / — интенсивность источника света, а также по определению
lambert = max О, ,S |m.
, L h'in
phong = max 0, т-г—:
(14.22)
Величины pa, Pj, ps — это коэффициенты отражения, а/— степень зеркального отражения. Вектор h —
«промежуточный вектор», задаваемый равенством h = s + v.
Если на сцене присутствует несколько источников света, то суммарная интенсивность I складывает-
ся из составляющих диффузного и зеркального света каждого из источников. Напомним, что фоновая
составляющая включает в себя свет, составленный из различных видов многочисленных отражений от
соседних предметов всей сцены. Позже мы увидим, что нам придется отдельно отслеживать все много-
кратные отражения некоторых лучей — в том случае, если объект достаточно блестящий. Составляю-
щая фонового света по-прежнему помогает приближенно учесть эффект от всех менее заметных лучей,
циркулирующих по сцене, слишком многочисленных для индивидуального учета.
Так же как в главе 8, мы распространим эти понятия на цветные лучи света и объекты. Тогда свет,
достигающий глаза, будет иметь красный, зеленый и синий компоненты, задаваемые формулами:
К “ Lfiar+ hfidrх lambert + Isptpsr х phong/,
4 = + х lambert + 4Л х Phong< (14.23)
4 = LPab+ АЛ. х lambert + Ispbpsb х phong/,
где различные I и р — соответственно интенсивности и коэффициенты отражения для отдельных со-
ставляющих цвета. Отметим в частности, что во всех трех составляющих цвета используются одни и те
же коэффициенты lambert и phong, а также векторы m, s, h, поэтому трассировку луча достаточно произ-
вести только один раз, и коэффициенты lambert и phong также требуется вычислять лишь однократно.
При вычислениях закрашивания необходимо знать точку соударения Рь, а также векторы h, s, m.
Позднее мы рассмотрим проблему вычисления вектора т, для чего нам понадобится некоторая инфор-
мация, целиком содержащаяся в записи пересечений.
14.7.1. Нахождение нормали в точке соударения
Вектор m — это вектор, нормальный к поверхности соударения в точке, где это соударение произошло.
Вначале мы находим вектор m наиболее простым способом — в базовых координатах — и затем преоб-
разуем его в мировые координаты. В разделе «Влияние аффинного преобразования» главы 6 мы пока-
874
Глава 14. Введение в трассировку лучей
зали, что если один объект преобразуется в другой посредством матрицы М, то нормальный вектор т'
преобразуется в нормальный вектор
(14.24)
где М~т означает транспонированную обратную к М матрицу. Поэтому искомая нормаль m может быть
найдена путем вычисления нормали к поверхности базового объекта в точке соударения с последую-
щим умножением этого вектора на матрицу М~т.
К счастью, мы уже вычислили и сохранили нормаль в точке соударения в базовых координатах; она
размещается в поле hitNormal записи пересечений рассматриваемого соударения. Таким образом, ее
можно преобразовать в мировые координаты (см. упражнение в конце следующего раздела).
14.7.2. Раскраска объектов в соответствии
с материалами поверхностей
Цвет, видимый в точке соударения, зависит от сочетания фоновой, диффузной и зеркальной составля-
ющих света. Коэффициенты отражения par, pdg и остальные хранятся вместе с объектом соударения и
доступ к ним возможен через поля mtrl .ambient, mtrl .diffuse, mtrl .specular. Загрузка в эти поля проис-
ходит при первом чтении SDL-файла.
На практике зеркальный цвет по Фонгу обычно принимают равным цвету источника света. Для это-
го коэффициенту отражения присваивают одинаковые красный, зеленый и синий компоненты: (0,9,0,9,
0,9), поэтому при умножении на этот коэффициент цвет источника света дает тот же цвет, хотя и слегка
ослабленный. В результате этого эффекта материал выглядит как блестящая пластмасса.
Если коэффициент mtrl. specul аг выбирать более тщательно, то можно несколько увеличить реалис-
тичность бликов Фонга. Коэффициенты, приведенные в табл. 8.1 согласно работе Мак-Рейнольдса и
Блайта (McReynolds, Blythe), обеспечивают более реалистичный вид различных материалов.
Коэффициенты отражения легко могут быть добавлены в SDL-файл сцены. Различные материалы
вначале определяются посредством следующего кода:
def Copper{ antient 0.19125 0.0735 0.0225
diffuse 0.7038 0.27048 0.0828
specular 0.256777 0.137622 0.086014 exponent 12.8}
def Gold{ antient 0.24725 0.1995 0.0745
diffuse 0.75164 0.60648 0.22648
specular 0.628281 0.555802 0.366065 exponent 51.2}
и затем используются для задания свойств различных объектов сцены, что делается примерно так:
use Gold
sphere ! make the sphere out of gold
! создаем сферу из золота
translate 12 1
use Copper cube ! and the cube out of copper
! и куб из меди
Листинг 14.10. Добавление вычислений закрашивания в подпрограмму shaded (псевдокод)1
Со1огЗ Scene :: shade(Ray& г)
{
Get the first hit using getFirstHit(r, best):
// Получаем первое соударение с помощью
Make handy copy h - best.hit[0]:
14.7. Рисование закрашенных изображений сцен
875
// создаем удобную копию
// data about the first hit
// данные по первому соударению
Form hitPoint based on h.hitTime
// Формируем hitPoint на базе h.hitTime
Form v - - ray.dir:
// direction to viewer
// направление на наблюдателя
v. normalized:
Shape* myObj = (Shape*)h.hitobject;
// point to the hit object
// указатель на объект соударения
Color3 color(myObj->mtrl.emissive)* :
//start with emissive part
// начинаем с эмиссионной части
color.addtambient contribution):
// compute ambient color
// вычисляем фоновый цвет
Vector3 normal;
// transform the generic normal to the world normal
// преобразуем нормаль из базовых координат в мировые
xfrmNormal(normal. myObj->invTransf. h.hitNormal);
normal, norma lizeO:
// normalize it
// нормируем ее
forCeach light source. L)
// sum over all sources
// суммируем все источники
{
1f(islnShadowC...)) continue:
// skip L if it's in shadow
// пропускаем точку L. если она в тени
Form s - L.pos - hitPoint;
// vector from hit point to source
// вектор от точки соударения до источника
s.normalized:
float mDotS - s.dot(normal):
// the Lambert term
// член Ламберта
if(mDotS > 0.0)
// hit point is turned toward the light
// точка соударения повернута к свету
Form diffuseColor = mDotS * myObj->mtrl.diffuse * L.color;
color.add(diffuseColor):
// add the diffuse part
продолжение#
1 Предполагается, что к классам Vector3 и Col огЗ добавлены некоторые удобные конструкторы: Vectors s(A, В) вычисляет вектор
как разность двух точек А и В, а СоТогЗ col or (с) создает цвет, имеющий те же компоненты, что и цвет с.
876
Глава 14. Введение в трассировку лучей
Листинг 14.10 (продолжение)
// добавляем диффузную часть
Form h - v + s:
// the halfway vector
// промежуточный вектор
h.normalizeO:
float mDotH - h.dot(normal):
// part of phong term
// часть члена Фонга
if(mDotH <= 0) continue;
// no specular contribution
// зеркального отражения нет
float phong = pow (mDotH. myObj->mtrl.specularExponent);
specColor - phong * myObj->mtrl.specular * L.col or;
color.add(specColor):
return color;
}
Нетрудно добавить в трассировщик луча вычисления фоновой, диффузной и зеркальной составляю-
щих света. В листинге 14.10 показан скелет кода, который требуется добавить в метод shadeO из листин-
га 14.4. Запись наилучшего пересечения best, формируемая в подпрограмме getFirstHitO, исследуется
с целью сбора данных о первом соударении луча с объектом. Копию best. hit[O] удобно помещать в Hitinfo,
запись h. Положение точки соударения hitPoint вычисляется при помощи луча и h.hitTime. Нормаль в
точке соударения, хранящаяся в h.hitNormal в базовых координатах, преобразуется с помощью уравнения
(14.24) в мировые координаты. Различные составляющие суммарного цвета, возвращающиеся обратно
по лучу, вычисляются и помещаются в color. Определяются эмиссионная и фоновая составляющие света
и для каждого источника света исходящие из него диффузная и зеркальная составляющие; все они вычис-
ляются и добавляются ко все растущему color. Если в точке соударения на данный источник света па-
дает тень от другого объекта, то от такого источника не добавляется ничего. (Мы будем рассматривать
тени в разделе «Добавление теней для большей реалистичности»; пока же просто опустим строку кода
if(is!nShadow(...)) continue:
чтобы убрать любое тестирование на отбрасывание теней.) Зеркальная составляющая определяется в
соответствии с уравнением (14.21), для чего требуется вычислить вектор h и использовать коэффици-
ент зеркального отражения (и показатель степени/), хранящийся в myObj->mtrl .specular.
На рис. 14.16 показана сцена, визуализация объектов которой производилась с учетом фонового,
диффузного и зеркального света, однако без вычисления теней. Из-за зеркальных бликов объекты ка-
жутся изготовленными из блестящей пластмассы.
Практическое упражнение
14.7.1. Преобразование нормального вектора
Напишите подпрограмму
void xfrmNormal(Vector3& res. Affine4& aff.-Vector3& v).
в которой вектор v умножается на транспонированную матрицу, в исходном виде хранящуюся в aff, в
результате чего получается вектор res. Данная подпрограмма используется в трассировщике луча по-
средством вызова
xfrmNormal(normal. myObj->invTransf. h.hitNormal).
14.7. Рисование закрашенных изображений сцен
877
Рис. 14.16. Объекты, освещенные фоновым, диффузным и зеркальным светом
Это означает, что нормальный вектор h.hitNormal в базовых координатах преобразуется посредством
матрицы, обратной матрице myObj-> InvTransf, которая записана в объекте соударения, после чего полу-
чается нормальный вектор normal в мировых координатах.
14.7.3. Физически обоснованные модели закраски:
закрашивание Кука—Торренса
Блики Фонга легко генерируются, но с ними объекты выглядят как блестящая пластмасса. Если для
закрашивания используется OpenGL, то приходится рисовать блики Фонга, однако если визуализация
объекта осуществляется посредством трассировки'лучей, то в нашем распоряжении больше опций и
можем выбирать для вычисления зеркальных бликов различные алгоритмы.
В поисках большего реализма многими исследователями разрабатывались все более замысловатые
модели закраски. Эти модели исходят из физических принципов, характеризующих отражение света
от истинной поверхности, и используют математические выражения для интенсивности и цвета отра-
женного света, достигающего наблюдателя. В этих моделях обращается внимание на «баланс» световой
энергии на поверхности: энергия падающего света разделяется на части: одна из них поглощается матери-
алом в форме тепла, другая взаимодействует с поверхностью и рассеивается в виде диффузного света,
а третья часть отражается от поверхности как зеркальный свет. Для различных материалов разделение
падающего света происходит по-разному; например, шероховатая поверхность дает больше рассеянно-
го (диффузного) света и меньше зеркального, чем гладкая блестящая поверхность.
В ранних работах Торренса и Спэрроу (Sparrow) [Torrance, 198], а также Троубриджа и Рейца (Reitz)
[Trowbridge, 201] шероховатая поверхность концептуально моделировалась в виде совокупности блес-
тящих «микрограней», ориентированных в различных направлениях, как показано на рис. 14.17. Свет
падает под углом ф к направлению усредненной нормали m и отражается в различных направлени-
ях, зависящих от микрограней, с которыми он соударяется. Часть этого света отражается в направ-
лении наблюдателя. Блинн использовал такую модель при разработке алгоритма для компьютерной
графики и показал, что получающиеся в результате зеркальные блики существенно отличаются от
бликов Фонга [Blinn, 25]. Кук и Торренс [Cook, 46] расширили и уточнили модель Блинна, показав
наличие в зеркальных бликах «смещения света», что лучше согласуется с отражением света от реаль-
ных материалов.
Мы опишем главные моменты модели Кука—Торренса и покажем, как она может быть включена в
трассировщик лучей. Мы рассмотрим три основных аспекта этой модели и их влияние на количество
отраженного зеркального света. Каждый из этих аспектов претендует на точное описание физического
явления, участвующего в отражении света, в форме, пригодной для включения в алгоритм.
878
Глава 14. Введение в трассировку лучей
свет
Усредненная
нормаль m
Рис. 14.17. Моделирование шероховатой поверхности как совокупности
микрограней, ориентированным случайным образом
Распределение ориентации микрограней
В модели Кука—Торренса принимается, что каждая микрогрань выступает как совершенное маленькое
зеркальце, и только те из них, которые ориентированы правильно, вносят свой вклад в свет, отражаемый
в определенном направлении. Как показано на рис. 14.18, а, только те из микрограней, чьи нормали на-
правлены вдоль вектора h - s + v, вносят свой вклад в свет, видимый в направлении V. Следовательно,
необходимо знать, какая доля микрограней имеет такую ориентацию. Были проведены статистические
исследования того, как в действительности распределены на поверхности, сделанной из определенного
материала, случайно ориентированные микрограни. В результате этих исследований была получена
функция распределения D(8), определяющая долю микрограней, нормали которых составляют угол 5 с
нормалью поверхности ш. На рис. 14.18, б показано, что если угол падения равен ф, а наблюдатель нахо-
дится под углом 0, то только грани, лежащие под углом 8 - (0 - ф)/2, обладают нужной ориентацией и
способны отражать свет по направлению к наблюдателю. (См. упражнения в конце раздела.) Доля мик-
рограней, имеющих нужную ориентацию, составляет D(8).
Рис. 14.18. Определение доли микрограней, ориентированных под углом 8
Были разработаны различные виды функций распределения. Кук и Торренс использовали распре-
деление Бекмана [Beckmann, 16], описываемое формулой для плотности:
1 4—Т
D(5) = 7^-47^^ ” (14.25)
4т cos (8)
которое дает хорошее математическое приближение для многих имеющихся шероховатых поверхнос-
тей. Это распределение имеет максимум при 5 - 0 и быстро уменьшается при возрастании 5. Параметр
т определяет степень шероховатости поверхности. (Он является среднеквадратическим наклоном
микрограней.) Величина этого параметра варьируется от значения 0,2 для почти гладких поверхнос-
тей до 0,6 для шероховатых. При малых значениях т плотность распределения D(8) быстрее убывает
с ростом 8.
Кук и Торренс включили распределение Z>(8) в качестве масштабного множителя зеркальной
составляющей отражения в различных направлениях, а за 8 приняли угол между векторами h и т.
На рис. 14.18, в показано изменение интенсивности зеркального отражения для различных направле-
ний наблюдения при т - 0,3. Этот рисунок похож на «диаграмму излучения» с рис. 8.12. Относитель-
ной величине зеркальной составляющей в каждом направлении соответствует длина стрелки. Она яв-
ляется наибольшей в направлении полного отражения (под углом ф), поскольку нормали микрограней
чаще всего параллельны вектору т. При отклонении от направления полного отражения, скажем на
14.7. Рисование закрашенных изображений сцен
879
угол е, эта величина уменьшается, так как при этом микрогрань должна иметь нормаль, направленную
на е/2 в сторону от ш, а из плотности распределения следует, что таких граней меньше (см. упражнения
в конце раздела).
Затенение и экранирование
Торренс и Спэрроу учитывали также эффекты «экранирования» («masking») и «затенения», которые
могут иметь место на поверхности, состоящей из микрограней. Это привело к появлению «геометри-
ческого члена» G, масштабирующего интенсивность зеркальной составляющей. На рис. 14.19 показана
зависимость этого эффекта от геометрии типичной грани. На рис. 14.19, а луч падает на грань под
таким углом, что вся грань освещена и весь свет «уходит» с грани. В этом случае коэффициент G будет
равен единице. На рис. 14.19, б направление отражения относительно вектора h таково, что часть света,
покидающего грань, экранируется ребром соседней грани. Для учета этого эффекта значение G соот-
ветственно уменьшается. На рис. 14.19, в освещена только часть грани, а остальная ее часть затенена
ребром соседней грани. В этом случае коэффициент G меньше единицы.
Рис. 14.19. Экранирование и затенение света на уровне граней
Блинн выразил эти геометрические эффекты простыми членами, содержащими только скалярные
произведения. В геометрическом множителе используется наименьшее из трех значений: 1, Gs, Gm. Мате-
матически это описывается так:
G-min(l, Gm, Gs), (14.26)
где величины
„ 2(m-h)(m-s) 2(m-h)(m-v)
Gm= k Gs = -А,- .Л----L (14.27)
hs h-s
определяют соответственно часть неэкранированного и незатененного света.
Коэффициент Френеля
Третий множитель в модели Торренса—Спэрроу также регулирует количество зеркального света. Блес-
тящие микрограни не являются совершенными зеркалами, а, подобно реальным материалам, отражают
только часть падающего на них света, в то время как оставшаяся часть передается внутрь поверхности.
Доля отраженного света определяется коэффициентом Френеля1 Д(0, Т|), где ф — угол падения, как на
рис. 14.18 (угол между векторами m и s), а Т| — показатель преломления материала. Позднее, при трас-
сировке лучей для случая прозрачных материалов2 (в разделе «Отражения и прозрачность») мы будем
работать с показателем преломления, однако он играет роль и в случае непрозрачных материалов,
таких как металлы.
Коэффициент Френеля Р(ф, Т|) может быть выведен из главных законов отражения электромагнит-
ных волн, если применить их к поверхности с коэффициентом преломления т]. Математическое выра-
жение этого коэффициента выглядит так:
1 Огюстен Жан Френель (Augustin Jean Fresnel, 1788-1827), французский физик, разработавший основополагающие принципы от-
ражения, преломления и поляризации света.
2 Показатель преломления материала — это отношение скорости света в воздухе к скорости света в этом материале. Взаимосвязь
между длиной волны и цветом света была описана в главе 12.
880
Глава 14. Введение в трассировку лучей
= 1 (g-Q2
2(g + c)2
c(g + c)-l
c(g-c)+l
(14.28)
1 +
где с - cos(0) = m • s ng2 = 1]! + с2 - 1. Отметим, что промежуточный членgзависит от показателя пре-
ломления материала. Для многих материалов показатель преломления непростым образом зависит от
длины волны света, что делает зависимость коэффициента F от длины волны действительно сложной.
На рис. 14.20 приведена основная форма зависимости коэффициента Гот угла 0 для различных зна-
чений показателя Г|. Видно, что коэффициент Френеля зависит от материала при «нормальном паде-
нии» (0 = 0) и плавно возрастает до 1,0 при «касательном угле» (ф - л/2). К тому же
О при нормальном падении Г(0, г|) < 1;
О при касательном падении Г(л/2, г|) = 1.
Рис. 14.20. Зависимость коэффициента Френеля от угла падения
В своей модели мнкрограней Торренс и Спэрроу [Torrance, 198] объединили эти факторы и тем са-
мым создали физически обоснованную модель зеркального отражения. Они показали, что относитель-
ное количество отраженного света является произведением трех членов F, D, G, деленным на скалярное
произведение m • v, то есть
spec , (14.29)
(mv)
Знаменатель m • v (он равен cos(6), см. рис. 14.18, б) появляется по следующей причине: при наблю-
дении поверхности под углом скольжения (grazing angle) 6, то есть углом между падающим лучом и
поверхностью, который велик и поэтому имеет маленький косинус, внутри пространственного угла вид-
но больше микрограней, чем в случае, когда наблюдение осуществляется при малом угле 6. Видимость
большего числа микрограней приводит к увеличению количества света, поэтому меньшее значение m • v
приводит к большей интенсивности.
Блинн адаптировал данную модель для компьютерной графики и сравнил ее с зеркальными блика-
ми Фонга [Blinn, 25]. Особый интерес представляет различное поведение этих моделей при различных
углах падения 6. При закрашивании Фонга зеркальный блик всегда наибольший в направлении «пол-
ного отражения» и резко падает при углах, даже слегка отличных от этого направления. На рис. 14.21, а
приведена «диаграмма излучения», описывающая убывание интенсивности бликов Фонга с ростом угла.
На рисунке показаны диаграммы излучения для двух значений углов падения. Форма диаграммы из-
лучения не зависит от угла падения ф. Диаграммы излучения для модели микрограней приведены на
рис. 14.21, б. (Упражнения в конце раздела развивают представление об этих диаграммах излучения.)
Когда угол ф мал (пунктирные линии), то форма диаграммы похожа на диаграмму бликов Фонга. Однако
14.7.Рисование закрашенных изображений сцен
881
для углов скольжения (сплошные линии) данная диаграмма не только имеет другую форму, но и на-
правление наибольшей интенсивности теперь не совпадает с направлением зеркального отражения! Это
вызывает «ореол» («halo») света вокруг зеркального отраженного света, что значительно отличается от
вида отраженного света Фонга, и такое явление действительно наблюдается при отражении света от
реальных поверхностей.
Рис. 14.21. Различие в изменении зеркальной интенсивности от угла падения:
а) диаграммы излучения Фонга; 6) диаграммы излучения Кука—Торренса
Кук и Торренс [Cook, 46] усовершенствовали эту модель в двух направлениях. Во-первых, они учли,
как энергия падающего света разделяется на фоновую, диффузную и зеркальную составляющие света.
Во-вторых, они приняли во внимание зависимость показателя преломления падающего света от длины
волны в реальных материалах. В силу этой зависимости коэффициент Френеля также зависит от дли-
ны волны, что, в свою очередь, приводит к изменению зеркальной составляющей цвета при различных
углах падения. Это изменение цвета в зависимости от угла падения, называемое «смещением цвета»,
также наблюдается в реальных материалах.
После объединения в единое целое выражений для каждого из рассмотренных явлений модель по-
лучает следующую общую форму:
Л =/ог^о^’(0,т]г) + 15rd<nkdF (0,т]г) х lambert + —-у—
(14.30)
В данном уравнении дается интенсивность только красной составляющей цвета; зеленая и синяя
составляющие имеют такой же вид, за исключением того, что используются соответственно показатели
Г| и Т|4. Интенсивности фонового света и источника для красного цвета равны соответственно Iar и 1^,
поэтому могут быть определены три составляющие — от фонового, диффузного и зеркального света.
Обычно интенсивность Iar составляет лишь малую часть от Isr. (Если имеется более одного источника
света, то подобным же образом определяются диффузная и зеркальная составляющие для каждого ис-
точника, после чего все вклады суммируются.)
Коэффициенты отражения фонового и диффузного света базируются на коэффициентах Френеля
F(0, Т|г) при нормальном падении. Это всего лишь приближение, которое Кук и Торренс используют
для простоты, поскольку отмечено лишь малое изменение значений коэффициента Р(ф, Г|г) при значе-
ниях угла падения ф вблизи нуля, поэтому разумно использовать в качестве приближения значение ко-
эффициента именно при 0 = 0. Отметим, что данный коэффициент имеет различные значения для раз-
личных длин волн (то есть «обладает цветом»): зеленая и синяя составляющие зависят соответственно
от F(Q, T]g) и от F(0, ц6) и их значения различны, поскольку показатели преломления различаются для
разных цветов.
882
Глава 14. Введение в трассировку лучей
Член, соответствующий диффузному свету, содержит уже знакомый нам коэффициент Ламберта
(см. уравнение (14.22)), а также два других множителя. Член — это пространственный угол, образу-
емый источником света в точке соударения (рис. 14.22). Для простоты предполагается, что данный член
одинаков для всех точек сцены; он обычно выбирается в виде малой константы, например 0,0001. (Солн-
це образует пространственный угол, равный 0,000068 стерадиан.) Множитель kd (и соответствующий
ему коэффициент ks в члене зеркального отражения) характеризует разделение падающего света на диф-
фузную и зеркальную составляющие. Эти два множителя являются свойствами материала и в сумме
составляют единицу: kd + ks= 1. Зеркальный член совпадает с таким же членом из уравнения (14.29),
выказывая явную зависимость коэффициента Френеля от длины волны.
7777777777777777
Р
Рис. 14.22. Источник образует пространственный угол dw
Для того чтобы использовать эти формулы, нам необходимо знать коэффициент преломления рас-
сматриваемого материала для различных длин волн. Обычно такая информация недоступна. Однако
доступны измеренные значения «нормальной отражательной способности» различных материалов;
иными словами, значения коэффициентов F(0, Т]) при различных длинах волн. Кук и Торренс вывели
показатель преломления из этих экспериментальных значений посредством следующих рассуждений:
если мы вычислим значение Р(ф, Т]) из уравнения (14.28) при ф - 0, то получим с -1 ng - т]. (Проверьте
это!) Следовательно, все выражение упрощается до
где Fo означает величину нормальной отражательной способности F(0, Т]). Из данного уравнения не-
трудно выразить Т|:
(14.31)
Таким образом, по заданным значениям Fo мы можем определить соответствующий коэффициент
преломления. В табл. 14.3 приводятся некоторые измеренные значения Fo для четырех полированных
металлических поверхностей [Touloukian, 200].
Таблица 14.3. Измеренная нормальная отражательная способность при различных длинах волн
Материал Fo (красный) Fo (зеленый) Fo (синий)
Золото 0,989 0,876 0,399
Серебро 0,95 0,93 0,88
Медь 0,755 0,49 0,095
Железо 0,53 0,505 0,480
Иллюстрация 40 сопоставляет методы закрашивания Кука—Торренса и Фонга для сфер, сделанных
из четырех металлов согласно списку из табл. 14.3. Каждая сфера освещается двумя источникам света.
Эти источники расположены так, чтобы один зеркальный блик получился при угле скольжения. Левые
сферы отображают блики Фонга, а правые — Кука—Торренса. Обратите внимание на изменение ярко-
14.8. Наложение текстуры на поверхности
883
сти и цвета блика по мере удаления точек от центра сферы, а также на различную форму блика в случае
угла скольжения.
Модель Кука—Торренса является более дорогой с вычислительной точки зрения, чем модель Фонга,
однако многие предпочитают платить такую цену за предоставляемую этой моделью большую реалис-
тичность. С целью еще большей реалистичности визуализацию сцен нужно производить для числа длин
волн, гораздо большего трех, после чего объединить эти цвета. Использование только красного, зелено-
го и синего цветов, более или менее соответствующих таким же цветам CRT-дисплеев, накладывает не-
устранимое ограничение на реалистичность компьютерных изображений.
Практические упражнения
14.7.2. Какой угол соответствует зеркальному отражению?
Покажите, что угол 8 на рис. 14.18, б должен быть равен 6 = (9 - 0)/2, чтобы свет от источника под углом ф
отражался к наблюдателю под углом 6.
14.7.3. Диаграммы излучения для модели микрограней
Поскольку падающий и отраженный лучи света лежат в одной и той же плоскости, коэффициенты G,
D, Fht. д., используемые в уравнении (14.29), могут быть выражены через угол падения 6 и угол на
наблюдателя ф.
О Покажите, что коэффициент G из уравнения (14.26) может быть записан в виде
G(0,0) = min 1,
О Покажите, что величина spec из уравнения (14.29) имеет в таком случае вид
F(M)£p^W,0)
___ \ 7___
cos(0)
О Постройте графики зависимости spec от угла 0 для различных значений угла ф, шероховатости т,
а также показателя преломления.
14.8. Наложение текстуры на поверхности
Как мы видели в главе 8, компьютерные изображения могут быть сделаны намного более живыми и
реалистичными, если на их поверхности накладывать текстуры. На рис. 14.23 приведена сцена с не-
сколькими примерами текстур после трассировки лучей. В главе 8 поверхности являлись полигонами,
и для визуализации каждой грани был использован OpenGL. Для каждой грани F к каждой вершине
этой грани была прикреплена пара текстурных координат, и OpenGL «закрашивал» каждый пиксел
внутри грани тем же цветом, что и соответствующая точка внутри изображения текстуры.
Теперь мы хотим посмотреть, как включить текстурирование в трассировщик лучей. В основном
используют два вида текстур:
О Текстура с изображением (image texture) — двумерное изображение «наклеивается» на каждую
поверхность объекта.
О Текстура твердого тела (solid texture) — объект считается вырезанным из блока некоторого мате-
риала, который сам обладает текстурой. Трассировщик лучей показывает цвет текстуры в каж-
дой точке на поверхности объекта.
884
Глава 14. Введение в трассировку лучей
Рис. 14.23. Сцена с несколькими текстурированными поверхностями
Начнем с текстуры твердого тела, работать с которой проще. В тематическом задании 8.5 мы уже
рассматривали метод применения текстуры твердого тела с помощью OpenGL при рисовании полиго-
нальных граней, однако такой метод слишком сложен. К счастью, он естественным образом встраивает-
ся в структуру метода трассировки лучей.
14.8.1. Текстура твердого тела
Иногда текстуру твердого тела называют «SD-текстурой». Впервые она была представлена одновремен-
но Перлином [Perlin, 161] и Пичи [Peachey, 153]. Объект рассматривается как вырезанный из некото-
рого обладающего текстурой материала, такого как мрамор или дерево. Эта текстура представлена
текстурной функцией texture(x, у, z), которая генерирует значение цвета (г, g, Ь) для каждой точки
пространства. Можно думать о такой текстуре как о цвете или об «окраске», которые изменяются с коор-
динатами точки. Если вы посмотрите (с помощью рентгена) на различные точки (х, у, z), то увидите
различные цвета. Когда в таком пространстве определен объект некоторой формы, а весь материал вне
этой формы отсекается, чтобы обнажить поверхность объекта, то точка (х, у, z) на поверхности стано-
вится видна и обладает указанной текстурой.
Рассмотрим сначала несколько интересных примеров, упомянутых в тематическом задании 8.5,
а затем покажем, как включить такую текстуру в трассировщик лучей. Затем мы разработаем другие
типы материалов, такие как древесина и мрамор.
Пример 14.8.1. Трехмерная шахматная доска, заполняющая пространство
Представьте себе трехмерную шахматную доску, сделанную из чередующихся красных и черных кубов,
которые вплотную составлены вместе и заполняют все пространство. Поместим один из таких «куби-
ков» вершиной в точку (0,0,0) и придадим ему такой размер, чтобы его вершина на другом конце диа-
гонали лежала в точке S - (S.x, S.y, S.z). Все остальные кубы имеют такой же размер (ширина S.x, высо-
та S.y, глубина S.z) и плотно прилегают один к другому во всех трех измерениях. Нетрудно написать
выражение для такой шахматной текстуры: нужно сложить целые части x/S.x, у/S.y, z/S.z и вычислить
остаток их суммы при делении на 2:
jump(x, у, z) = (int(A + x/Sx) + int(X + y/S.y) + intfA + z/5.z))%2. (14.32)
Сделаем так, чтобы функция texture(x, у, z) возвращала черный цвет, если jump( ) - 0, и красный, если
jump( ) = 1. Поскольку округление с помощью функции int в окрестности нуля работает специфически,
все ее аргументы для отдаления от нуля смещаются на некоторую константу А (например, на 100).
На рис. 14.24 приведены базовая сфера и базовый куб, «вырезанные» из материала с такой сплош-
ной текстурой. Цвет материала и есть цвет текстуры. Отметим, что сфера и куб действительно выгля-
дят сделанными из сплошных «кубиков». Сопоставьте для контраста вид этих объектов, если бы на них
было «наклеено» двумерное изображение шахматной доски.
14.8. Наложение текстуры на поверхности
885
Рис. 14.24. Трассировка лучей для некоторых объектов со сплошной шахматной текстурой
Пример 14.8.2. Набор кубов с плавно изменяющимися цветами
Вы также имеете возможность составлять вместе копии одного и того же куба. Один куб демонстриру-
ет плавно изменяющуюся в пределах всего спектра окраску по мере того, как вы перемещаетесь внутри
него. Все его восемь углов имеют черный цвет, а центральная точка куба (0,5,0,5, 0,5) белая. В проме-
жутках цвет изменяется плавно. Для того чтобы красный компонент цвета возрастал до единицы и затем
снова убывал до нуля вдоль оси х, следует задать red = 1 - |2х - 1|. Аналогично зеленый компонент управ-
ляется координатой у, а синий — координатой 2. Для образования бесконечного числа копий такого
куба, граничащих без зазоров в пространстве, следует использовать дробные части координат х, у, z.
texture(x, у, z) = (1 - |2fract(x) - 1|, 1 - |2fract(y) - 1|,1 - |2fract(z) - 1|), (14.33)
где fract(x) в 1 - int(x). (Представьте себе, как будет выглядеть сфера радиуса 100, сделанная из такого
материала.)
Трассировка лучей для объектов с текстурой твердого тела
Если у нас имеется текстурная функция texture( ), то для включения сплошной текстуры в трассиров-
щик луча почти больше ничего не нужно. Имеется два способа, с помощью которых текстура может
изменить свет, приходящий из некоторой точки поверхности.
1. Свет можно задать равным самому значению функции texture( ), как если бы объект «светился»
таким цветом.
2. Текстура может модулировать коэффициенты отражения фонового и диффузного света, так что
/ = texture(x, у, z)(Iapa + /р/м • “»» + Шиь' итУ< (14.34)
где texture(x, у, z) вычисляется в точке соударения луча (х, у, z). Последний способ используется
для текстуры чаще всего: поверхность выглядит так, как будто присущий ей цвет в различных
точках становится светлее или темнее, в соответствии с изменениями значений функции texture( ).
Здесь зеркальный блик имеет цвет источника света и не зависит от текстуры. Вследствие этого
текстурированный объект выглядит блестящим, словно сделанным из пластмассы.
Точка соударения (х, у, z), фигурирующая в уравнении (14.34), может выражаться как в базовых, так
и в мировых координатах. Обычно используются базовые координаты, и в этом случае объект «несет» с
собой эту текстуру, когда он поворачивается или перемещается в свое конечное положение на сцене.
При анимации, когда объект от кадра к кадру поворачивается или движется, текстура будет прочно при-
креплена к объекту.
Если же, с другой стороны, точка (х, y,z) задана в мировых координатах, то текстура фиксируется
относительно пространства. Теперь, когда объект при анимации поворачивается или перемещается, тексту-
886
Глава 14. Введение в трассировку лучей
ра будет «окружать» его, и в каждой новой позиции объект будет казаться вырезанным из нового матери-
ала. Это может дать интересный визуальный эффект, хотя и не соответствует физической реальности.
Нетрудно создать богатую и разнообразную коллекцию сплошных текстур, некоторые из них точ-
но моделируют существующие материалы. Двумя классическими примерами являются древесина
и мрамор.
Древесная текстура
Текстура деревянного бревна состоит из концентрических цилиндров различного цвета, которым соот-
ветствуют «кольца» на срезе бревна. Поскольку расстояние точек до некоторых осей меняется, функ-
ция скачет взад-вперед между двумя значениями. Этот эффект можно смоделировать с помощью функ-
ции остатка:
rings(r) - (dnt)r) % 2
где радиус колец, разбегающихся от оси z, г = ^х2 + у2. Функция rings( ) принимает значения нуль и
единица по мере возрастания радиуса г от нуля. С помощью следующей функции можно сделать так,
чтобы текстура принимала два заранее заданных значения D и D + А:
simple_wood(x. у. z) = D + А * rings(r/M)):
где, как и раньше, г = jx2 + у2. В результате получаются кольца шириной М, концентрические относи-
тельно оси z.
Будет еще интереснее, если мы сможем поворачивать кольца, сделаем их «дрожащими» (wobble) и
«несимметричными» (skew) [Watt, 138]. Для получения дрожащих колец в функцию добавляется ком-
понент, изменяющийся вместе с азимутом 0 относительно оси z:
rings
г
— + ATsin
(м
о \
n J
Теперь даже при постоянном радиусе наблюдаются колебания колец при изменении угла 0, что за-
ставляет кольца «дрожать» туда и обратно Wраз за один оборот вокруг оси. Отметим, что для достиже-
ния большего эффекта мы используем вложенные функции: аргументом для rings( ) служит не сам
радиус г, а сумма r/М и синусоиды, которая сама зависит от угла и от N. Перлин [Perlin, 153] плодотворно
использовал мощь такого сочетания функций для получения множества интересных визуальных эффек-
тов. Мы можем пойти еще дальше и добавить к колеблющемуся древесному волокну «кручение»:
rings
( г „ . (Q п
— + ЛГзш —\-Bz
М
(14.35)
Теперь фаза синусоиды зависит от z, поэтому по мере изменения z колебание еще и закручивается.
А если мы хотим «наклонить» это волокно так, чтобы оно было концентрическим относительно не z,
а другой оси, то можно применить вращение до вычисления г и 0. Например, можно задавать радиус г в
форме ^х'2 + у'2 , где (х\ у', г') = Т(х, у, z), а Т( ) — некоторое преобразование вращения. На рис. 14.25
показано несколько объектов, «вырезанных» из древесины, структура которой была задана рассмотрен-
ными выше способами.
Трехмерный шум и мраморная текстура
Зернистость в таких материалах, как мрамор, имеет весьма хаотический характер, как показано на
рис. 14.26. Через камень проходят «турбулентные» прожилки из более темного материала со случайно
расположенными завихрениями и пятнами, как если бы этот камень образовался из сильно перемешан-
ного расплава. Эту турбулентность можно имитировать, построив «шумовую функцию», возвращаю-
щую в каждой точке (х, у, z) пространства истинно случайную величину. Затем это «шумовое поле»
контролируемым образом «перемешивается» для получения эффекта турбулентности.
14.8. Наложение текстуры на поверхности
887
Рис. 14.25. Объекты, «вырезанные» из дерева
Рис. 14.26. Объекты, «вырезанные» из мрамора
Само по себе шумовое поле запрограммировать нетрудно. Представим себе случайную величину,
определенную для каждой целочисленной точки в пространстве, то есть в точках (х, у, z) = (г,у, k) для любой
комбинации целых чисел i,j, k. Такое размещение точек называется целочисленной решеткой (integer
lattice). На рис. 14.27, а приведен двумерный вариант, где для различных точек двумерной целочислен-
ной решетки помечены значения шума в пределах от нуля до единицы. Например, точке (1,2) соответ-
ствует значение шума 0,653, а в точке (3,1) шум равен 0,129. На рис. 14.29, б показана трехмерная цело-
численная решетка. Представьте себе, что каждой целочисленной точке соответствует фиксированное
значение шума, как, например, 0,7341 для точки (2,2,1).
а б
Рис. 14.27. Определение шумовых значений в каждой точке трехмерной целочисленной решетки
888
Глава 14. Введение в трассировку лучей
Совокупность значений шума можно было бы хранить в массиве огромных размеров: float
N[10000][10000][10000], однако для этого понадобилось бы непозволительно большое количество памя-
ти. Гораздо проще генерировать значение шума каждый раз, когда потребуется. С этой целью нам нуж-
на функция, например float 1atticeNoise(int i.int j.int k), которая возвращает истинно случайную
величину по заданным целым значениям i,j, k, определяющим положение данного значения шума в ре-
шетке. Такая функция должна быть эффективной и полностью воспроизводимой, то есть всегда воз-
вращать одно и то же значение шума для данных (г, j, k). В превосходной работе нескольких авторов
«Текстурирование и моделирование» («Texturing and Modeling») [Ebert, 59] описываются соответствующие
методы. Мы сосредоточимся на одном из них, предложенном Перлином и усовершенствованном Пичи.
Генерирование псевдослучайных значений шума
При данном подходе на этапе инициализации нужно задать постоянный массив noiseTablе[], состоя-
щий из псевдослучайных значений шума. Длина массива, равная 256, оказалась вполне достаточной,
поэтому мы примем именно такую длину.
Теперь основная функция latticeNoised, j, к) просто указывает на массив noiseTablе[], что являет-
ся воспроизводимым. Для того чтобы добиться отсутствия или, по крайней мере, незначительности
повторяющихся значений шума при изменении i, j, k, в индексирующей функции производится эффек-
тивное «перемешивание» значений комбинации (г, j, k) в пределах от 0 до 255. Это легко сделать с по-
мощью введения второго массива index[], который содержит случайным образом переставленные зна-
чения от 0 до 255. (Если бы мы работали, скажем, с массивами длиной 8, то массив i ndex[] содержал бы
что-нибудь вроде {3,7,0,1, 6,5,4,2}.) Пичи определил следующие два макроса:
#define PERM(x) indexC (х) & 255]
#define INDEXdx. iy. iz) PERM( (ix) + PERM((iy) + PERM(iz)) )
Макрос PERM принимает целое значение x и выполняет над ним операцию «поразрядное AND», ос-
тавляя только восемь младших бит, в результате чего значение х попадает в пределы от 0 до 255. Тогда
значение PERM становится равным одному из значений массива индексов. Макрос INDEX трижды исполь-
зует макрос PERM, чтобы трижды просмотреть массив индексов и в каждом случае выбрать элемент мас-
сива index[] на базе одного из трех значений ix, iy, iz. Отметим, что это эффективная и воспроизводи-
мая операция, обеспечивающая достаточную степень перемешивания. Тогда функция latticeNoised
приобретает следующий простой вид:
float latticeNoisednt i. int j. int k)
{
return noiseTable[ INDEXd.j.k)];
Разработка класса Noise
Представляется удобным инкапсулировать все вышеописанные действия в класс Noise, который мы
будем использовать при генерировании мраморной текстуры, а также других текстур, содержащих шум.
На рис. 14.41 приведено объявление этого класса (см. также приложение В).
Листинг 14.11. Генерирование воспроизводимых значений шума
class Noise{
public:
Noised
// a constructor
// конструктор
{
int i;
index = new unsigned char[256]:
ford = 0: i < 256: i++) index[i] = i;
// fill array with indices
// заполняем массив индексами
14.8. Наложение текстуры на поверхности
889
ford = 0: 1 < 256: 1++)
// shuffle It
// перемешиваем его
{
int which = randO % 256:
// choose random place in array
// выбираем случайное место в массиве
unsigned char tmp = index[which];
// swap them
// переставляем их
indexfwhich] = indexfi];
indexfi] = tmp:
}
noiseTable = new float[256];
ford = 0: i < 256: i++)
noiseTable[i] - rand0 /32767.99:
}
// end of constructor
// конец конструктора
float noise(float x. float y, float z);
float noise(float scale. Point3& p):
float turbulence(float s. Point3& p):
float marble(float x, float y. float z);
float marble(float strength,Point3& p):
private:
float* noiseTable:
// array of noise values
// массив значений шума
unsigned char * index;
// pseudo random indices
// псевдослучайные индексы
float mySpline(float x):
// used for marble
// используется для мрамора
float 1atticeNoise(int i. int j. int k)
{
// return noise value on an integer lattice
// возвращаем значение шума на целочисленной решетке
#define PERM(x) index[(x) & 255]
#define INDEX(ix, iy. iz) PERM( (ix) + PERM((iy) + PERM(iz)) )
return noiseTable[INDEX(i
}
}:
Наибольший интерес представляет метод данного класса тагЫеО, возвращающий координатно-за-
висимое значение яркости в пределах от нуля до единицы, которое имитирует прожилки темного и свет-
лого камня в мраморе. Позднее мы детально разработаем этот метод. Он будет использован на началь-
ной стадии трассировки лучей для создания зеленоватого мрамора путем конструирования объекта
noise с помощью команды
Noise п;
// create and construct a noise objecc
// создаем и конструируем объект класса noise
890
Глава 14. Введение в трассировку лучей
и последующего вычисления значения функции texture(.r, у, г) в любой точке (х, у, г) простым вызовом
оператора
n.marble(x, у. z):
В свою очередь метод шагЫеО использует методы noiseO и turbulenceO, которые мы вкратце опишем,
а также «вспомогательную» функцию latticeNoiseO. Конструктор класса создает и заполняет массивы
noiseTable[] и index[J. Случайные значения, помещаемые в массив noiseTable[], создаются с помощью
стандартной С-функции randO, которая масштабирует эти значения в диапазон от 0,0 до 1,0. Массив
index[] вначале загружается числами от 0 до 255 в порядке возрастания, а затем «перемешивается» посред-
ством поочередной перестановки каждого элемента с каким-либо другим случайно выбранным элементом.
Имея в своем распоряжении функцию latticeNoiseO, которая выдает случайные значения для точек
целочисленной решетки, мы хотим получить функцию noise(.r, у, г), которая выдает псевдослучайные
значения в промежуточных точках, фактически в любой точке пространства. Кроме того, желательно,
чтобы шум изменялся плавно при изменении значений х, у, z.
У
2
X
0,6 1
2
Рис. 14.28. Линейная интерполяция значений шума (двумерный случай)
Приемлемые результаты дает простая линейная интерполяция между значениями решетки1. На
рис. 14.28 показана двумерная интерполяция: случай трех измерений выглядит аналогично. Здесь мы
хотим вычислить шум в точке (х, у) = (0,6,1,4) по заданным значениям шума в четырех углах решетки,
окружающих данную точку. Вначале интерполируем по х при значениях у-1иу=-2, в результате чего
получаем значения2
n(0,6,1) - 1егр(0,6, n01, пи);
п(0,6,2) = 1егр(0,6, п02, п12),
затем производим интерполяцию по у.
п(0,6,1,4) - 1егр(0,4, n(0,6,1), п(0,6,2)).
Листинг 14.12. Функция для генерирования шума в произвольной точке р
float Noise:: noise(float scale. Point3& p)
{
// linearly interpolated lattice noise
// шум с линейной интерполяцией по решетке
#define lerp(f. А. В) A + f * (В - A)
float d[2][2][2]:
Point3 pp;
pp.x - p.x * scale + 10000:
// offset avoids negative values
// смещаем во избежание отрицательных значений
1 Перлин н Пичи показали, что кубическая интерполяция приводит к более реалистичным результатам [Ebert, 59].
2 Напомним, что функция 1 егр () была впервые введена в главе 4:1егр(/, А, В) = А + (В - Л)/—значение, лежащее на части/рассто-
яния от А до В.
14.8. Наложение текстуры на поверхности
891
рр.у “ РУ * scale + 10000:
pp.z = p.z * scale + 10000:
long ix = (long)pp.x: long iy = (long)pp.y:
long iz = (long)pp.z:
float tx.ty.tz. x0,xl,x2.x3. yO.yl:
tx - pp.x - ix; ty = pp.y - iy: tz = pp.z - iz:
// fractional parts
// дробные части
float mtx = 1.0 - tx. mty = 1.0 - ty. mtz = 1.0 - tz:
for(int k = 0; k <= 1; k++)
// get noise at В lattice points
// получаем шум в 8 точках решетки
for(int j “ 0; j <= 1: j++)
for(int 1=0: i <= 1; i++)
d[k][j][i] = latticeNoise(ix + i. iy + j.iz + k):
xO = lerp(tx. d[0][0][0],d[0][0][l]):
xl = lerp(tx. d[0][l][0],d[0][l][l]):
x2 = lerp(tx. d[l][0][0].d[l][0][l]):
x3 = lerp(tx. d[l][l][0].d[l][l][l]):
yO = lerp(ty, xO, xl):
yl = lerpCty, x2. x3):
return lerp(tz. y0. yl):
В листинге 14.12 представлена возможная реализация функции noi se() для трехмерного случая. У нее
имеется дополнительный параметр scale, который масштабирует заданную трехмерную точку (х, у, z);
он пригодится нам при создании турбулентности. Вначале масштабированная точка смещается на 1000 по
х, у, z, чтобы все составляющие были положительны. (Поскольку значения на решетке все равно оста-
ются случайными, то это смещение не изменяет статистической природы генерируемого шума.) Затем
генерируются значения шума в восьми вершинах решетки, окружающих данную точку. В конечном счете
для определения интерполированного значения шума используется семь вызовов функции lerp.
На рис. 14.29, а приводится график функции noise(20. х. у, 0), где черный цвет соответствует зна-
чению 0,0, а белый — 1,0. На рисунке диапазоны изменения х и у составляют от -1 до 1. В шумовом поле
просматривается определенная упорядоченность, обусловленная причудами процесса генерирования
случайных чисел, однако она не является чрезмерной.
Рис. 14.29. Примеры графиков функций: a) noise() (шум); б) turb() (турбулентность)
892
Глава 14. Введение в трассировку лучей
Турбулентность
Перлином [Perlin, 161; Ebert, 59] был разработан метод генерирования шума более интересного вида,
чем вышеописанный. Его идея состоит в том, чтобы смешать несколько составляющих шума: одну —
медленно изменяющуюся при плавном перемещении в пространстве, вторую — изменяющуюся вдвое
быстрее, третью — изменяющуюся в четыре раза быстрее и т. д. Интенсивности более быстро изменяю-
щихся компонентов уменьшаются в геометрической прогрессии. Функция
turb(s,x,y,z) = — noise(s,x,y,z) + — noise (2s,х,у,z) + -noise(4s,x,y,z) (14.36)
2 4 8
складывает три таких компонента, каждый из которых вдвое слабее и вдвое быстрее предыдущего.
Параметр $ масштабирует расстояния, как это делалось в функции noise(). Рисунок 14.30 демонстриру-
ет колебания функции turbo (для двумерного случая). Представьте себе плоскость ху, заполнен-
ную фиксированными значениями функции noise(l, х, у, 0). На рисунке показано, как для каждой
точки Р = (г, у) в теле функции turb(l, х, у, 0) смешиваются три значения шума: в точках (х, у), (2х, 2г/),
(4х, 4г/). В соседней точке Р' значение шума noise(l, х', у', 0) очень близко к значению noise(l, х, у, 0),
однако noise(2, х’, у', 0) будет существенно отличаться от noise(2, х, у, 0), а отличие noise(4, х', у', 0) от
своего аналога будет еще сильнее. Свойства первого компонента шума в следующем компоненте будут
проявляться в половинном размере, в следующем за ним через один — в размере одной четверти. Мож-
но добавить в функцию turb( ) больше членов, в результате чего получим для некоторого М:
I Л/ I
turb(s,x,y,z) = — X “noise(2*5,x)y,z). (14.37)
2 * = о 2
Рис. 14.30.0 поведении функции turb()
Размер каждого компонента вдвое меньше предыдущего на каждом уровне детализации, однако его
частота (скорость колебаний) вдвое превышает частоту предыдущего компонента. Такая совокупность
условий приводит к своего рода самоподобию (self-similarity), с которым мы уже встречались в главе 9.
Действительно, при определенных условиях функция turb( ) дает хорошую аппроксимацию к так назы-
ваемому 1//-шуму (см. раздел «Контроль за спектральной плотностью фрактальной кривой» главы 9),
который обнаруживается в различных естественных образованиях. На рис. 14.29, б приведен график
функции turb( ), сформированной из шумового поля функции noise( ) с рис. 14.29, а при М = 3. Отчет-
ливо видно увеличение уровня детализации, а сами колебания выглядят мягкими и более похожими на
облака. Турбулентность, обеспечиваемая функциями типа turb( ), может использоваться для внесения
возмущения в некоторые атрибуты формы или текстуры, чтобы придать им более реалистичный вид,
как мы вскоре увидим на примере мрамора.
Мраморная текстура
На мраморе видны прожилки из темного и светлого материала, имеющие определенную регулярность,
в то же время в узоре видны сильно хаотичные нерегулярности. Вслед за Уаттом и Уаттом [Watt, 209]
14.8. Наложение текстуры на поверхности
89:
мы можем построить похожую на мрамор трехмерную текстуру, придав прожилкам, например, в г-на
правлении плавные колебания, а затем хаотические возмущения при помощи функции turb( ). Начнем
с текстуры, которая постоянна в направлениях х и у и слегка изменяется по г:
marble (х, у, г) = undulate(sin(z)).
Здесь undulate( ) — это функция, имеющая форму сплайна (рис. 14.31, [Watt, 209]), изменяющаяся
от некоторого темного до некоторого светлого значения при изменении ее аргумента от -1 до 1. (Эта
сплайн-функция рассматривается в упражнениях в конце раздела.) При использовании sin(z) в каче-
стве аргумента функция undulate( ) производит некоторую «рябь» по г, пробегающую взад и вперед по
сплайн-кривой, что приводит к колебанию интенсивности, показанному на рис. 14.31, б. Конечно, вер-
тикальные цветные прожилки в мраморе выглядят слишком регулярными, поэтому аргумент функции
sin( ) модулируется некоторой турбулентностью:
marble (х, у, z) = undulate(sin(z + A turb(s, х, у, z))).
Рис. 14.31. Конструирование мраморной текстуры: а) сплайн-кривая; б) невозмущенная мраморная текстура
Фаза функции sin( ) смещена в различных местах мрамора на различные величины, что значитель-
но увеличивает реалистичность прожилок. Параметр s ускоряет или замедляет турбулентность в раз-
личных точках, а параметр А определяет величину возмущения. Уатт продемонстрировал, что если
функцию undulate( ) заменить обычной прямой линией, то результат будет значительно менее удов-
летворительным.
а
в
Рис. 14.32. Мраморная текстура: а) А = 1; б) А = 3; в) А = б
На рис. 14.32 приведена мраморная текстура, изображенная на грани куба. Она является графиком
функции:
g = undulate(sin(2nz + А х turb(5, х, у, z))),
где z изменяется от 0 справа до единицы слева, а ось у направлена вверх. На рис. 14.32, а амплитуда А = 1,
в результате чего имеет место лишь малая турбулентность. На рис. 14.32, бив амплитуда А равна
соответственно 3 и 6, и турбулентность там намного более значительна.
Значение функции marble( ) можно использовать в качестве коэффициента отражения в уравне-
нии (14.34), чтобы модулировать количество света, возвращаемого из различных точек объекта, кото-
894
Глава 14. Введение в трассировку лучей
рые посещаются различными лучами. Нетрудно расширить функцию marble( ) так, чтобы она возвра-
щала красный, зеленый и синий компоненты полноцветных трассировщиков лучей. На рис. 14.33 пока-
зана сцена, состоящая из нескольких мраморных объектов. Эффект весьма убедителен.
Рис. 14.33. Сцена с мраморными объектами
Практические упражнения
14.8.1. Сплайн-функция, подходящая для создания мраморной текстуры
Функция
float Noise:: undulate(float х)
{
if(x <-0.4) return 0.15 + 2.857 * SQR(x + 0.75):
else if(x < 0.4) return 0.95 - 2.8125 * SQR(x):
else return 0.26 + 2.666 * SQR(x - 0.7):
}
описывает гладкую кривую по у при изменении х и от -1 до 1. Эта функция составлена из трех полино-
мов, определенных в различных частях этой области. Аккуратно нарисуйте график этой функции, чтобы
увидеть ее форму (здесь через SQR(x) обозначен квадрат х), а затем измените значения коэффициентов,
чтобы придать кривой другую волнистость.
14.8.2. Эксперименты с генераторами случайного шума
Приведенный в листинге 14.11 конструктор noise основан на свойствах стандартной С-функции randO,
которую неправильно называют генератором случайных чисел (random-number generator — RNG), хотя
она не выдерживает некоторых статистических тестов. (Поиск RNG в Интернете быстро приводит нас
к странице http://stat.fsu.edu/~geo/, поддерживаемой Джорджем Марсалья (George Marsaglia), где про-
изводится тестирование RNG.) Разрабатываются более совершенные RNG, однако они становятся зна-
чительно сложнее. Поищите в Сети исходники улучшенных RNG и обсуждение их свойств.
14.8.2. Наложение изображений на поверхности
В главе 8 мы уже рассматривали вопрос о том, как накладывать (paste) изображения на полигональные
поверхности при помощи OpenGL В данном разделе мы рассмотрим, как накладывать изображения на
произвольные криволинейные поверхности в рамках трассировщика лучей. Подпрограммы для этой
операции просты, а результаты могут получиться превосходными, однако для их работы обычно требу-
ется больше компьютерного времени, чем при работе с OpenGL. Каждый пиксел вычисляется индиви-
дуально, причем нельзя использовать никакой связности строк развертки.
14.8. Наложение текстуры на поверхности
895
Как в главе 8, предположим, что определена двумерная текстурная функция texture(u, о), каждый из
аргументов которой и и р изменяется от 0 до 1, определяющая интенсивность или цвет в каждой точке
(и, v). Функция texture(u, v) может быть процедурной текстурой, такой как шахматная доска или мно-
жество Мандельброта, а может быть текстурой изображения, хранящегося в пиксельной карте. Пусть
такая пиксельная карта организована как массив пиксельных значений Уна М, обозначенный txtr[][].
Тогда, задавая значения и и v в пределах от нуля до единицы, мы можем указывать на соответствующий
пиксел массива txtr простым вызовом
txtr[ (int) (u*N)J [ (int) (V*M)L
Проще наложить текстуру на базовый объект, чем на объект, преобразованный в координаты сцены.
Дизайнер связывает текстурные координаты с координатами базового объекта таким образом, что при
преобразовании объекта в координаты сцены текстура корректно (и с нужными пропорциями) отобра-
жалась на преобразованном объекте.
Обертывание текстур вокруг поверхностей
Нам нужен способ связывания точек (х, у, z) на поверхности базового объекта с текстурными коор-
динатами (и, о). Как показано на рис. 14.34, дизайнер просто выбирает на плоскости «окно» (со своими
четырьмя границами: left, top, right, bottom), и если луч соударяется с плоскостью в пределах этого окна,
то легко вычислить, какую точку (и, v) текстуры следует использовать. В частности, если точка соуда-
рения (х, у, 0) задана в базовых координатах, то соответствующие текстурные координаты имеют вид:
./-bottom
right-left top-bottom
Кроме этого, дизайнеру следует решить, как обрабатывать те точки соударения, которые находятся
вне заданного окна. В таких случаях обычно задают некоторое постоянное значение, которое использу-
ют для текстуры.
Рис. 14.34. Отображение текстуры на квадрат или плоскость
Пример 14.8.3. Текстуры для цилиндра
Обертывать текстуры вокруг цилиндра почти так же легко, как наклеивать их на квадрат или на плос-
кость. (Вспомните обсуждение этой задачи в разделе «Обертывание текстуры вокруг криволинейных
поверхностей» главы 8.) На рис. 14.35 изображен базовый конический цилиндр с выделенным на его
поверхности «окном». Это окно простирается по азимуту от а( до а2 и по z от z( до z2. Когда луч соударя-
ется с цилиндром в точке (х, у, z), мы просто вычисляем ее азимут:
0 - arctg(z/, х),
а затем текстурные координаты (w, v) по формулам:
0 - a, z-z,
и =------ и v =---L
а2 ~а1 Z2~ Z\
Если же точка соударения лежит вне назначенного окна, то дизайнер должен выбрать цвет для исполь-
зования в качестве текстуры. Отметим, что если цилиндр сильно сужается, то отображенный текстурный
(14.39)
896
Глава 14. Введение в трассировку лучей
образ будет искаженным. Наклеивание текстуры на крышку или основание цилиндра рассматривается
далее в упражнениях. Туда же отнесена и задача обертывания текстуры вокруг сферы или конуса.
Рис. 14.35. Обертывание текстуры вокруг цилиндра
Практические упражнения
14.8.3. Наложение текстуры на крышку и основание цилиндра
Рассмотрите в подробностях наложение текстуры на крышку и основание конического цилиндра. Часть
битовой карты должна быть наклеена так, чтобы она полностью покрывала крышку или основание.
14.8.4. Обертывание текстуры вокруг сферы
Рассмотрите в подробностях, как обертывать текстуру вокруг участка базовой сферы. «Окно» для тек-
стуры простирается по азимуту от а, до а, и по широте от /, до /2. Оцените серьезность искажения, кото-
рое претерпит битовая карта, если или 12 принять слишком близким к ±90°. Если вместо битовой кар-
ты использовать текстурную функцию, то можно ли ее определить так, чтобы даже вблизи от полюсов
сферы искажения отсутствовали?
14.8.5. Обертывание карты мира вокруг сферы
Предположим, что у вас имеется географическая база данных о границах всех стран мира. Такой файл
содержит большое число ломаных линий, концевые точки которых заданы в форме (долгота, широта).
Можно ли применить эту базу данных для обертывания географически точной карты мира вокруг ба-
зовой сферы? Если да, то опишите, как это сделать.
14.8.6. Обертывание текстуры вокруг конуса
Объясните в подробностях, как обернуть текстуру вокруг стенки базового конуса. Какова естественная
интерпретация параметров «окна»? Обдумайте природу искажения, которое будет претерпевать бито-
вая карта в различных ситуациях. Опишите, как отобразить текстуру на основание конуса.
14.8.3. Сглаживающая трассировка лучей
Трассировка лучей является изначально точечным процессом: производятся дискретные «взгляды» на
сцену вдоль отдельных лучей. Поэтому неудивительно, что качество изображений, полученных при
трассировке лучей, часто страдает от эффектов ступенчатости. Как мы видели в главе 10, влияние сту-
пенчатости может быть уменьшено посредством тестирования сцены в большем числе точек; этот ме-
тод часто называют сверхопросом (supersampling). Это можно применить и при трассировке лучей:
через каждый пиксел производится трассировка нескольких лучей, и интенсивности возвращающихся
лучей усредняются. Разумеется, ценой этого является значительное увеличение времени выполнения.
На рис. 14.36, а приведена схема опроса, при которой лучи пропускаются через углы группы пиксе-
лов. Окончательный цвет каждого пиксела является средним для цветов, определенных в этих четырех
углах. Такая степень сглаживания осуществляется просто (что нужно изменить в коде из листин-
га 14.3?) и требует лишь незначительного времени (сколько лучей требуется трассировать для изоб-
ражения, состоящего из R строк и С столбцов?). Сверхопрос может задействовать намного большее чис-
ло лучей на пиксел. На рис. 14.36, б приведен пример с пропусканием девяти лучей через различные
14.9. Использование экстентов
897
части пиксела. Для формирования окончательного значения пиксела усредняется свет, возвращающий-
ся вдоль всех этих девяти лучей.
Рис. 14.36. Методы сверхопроса для сглаживания
Кроме вышеописанного метода, было разработано несколько более сложных и более совершенных
технологий. Уайтед [Whitted, 212] предложил скорректированную процедуру, в которой в области, тре-
бующие дополнительного сглаживания, испускается большее число лучей. Согласно методу Уайтеда,
лучи испускаются через четыре угла пиксела и вычисляется средняя интенсивность, однако затем эта
средняя интенсивность сравнивается со всеми четырьмя отдельными интенсивностями. Если интен-
сивность в одном из углов слишком сильно отличается от средней, то пиксел подразделяется на квад-
ранты (как в HSR-алгоритме Варнока), и через углы этих квадрантов испускаются дополнительные
лучи. Рисунок 14.36, в иллюстрирует этот подход. Четыре луча пиксела Р возвращают примерно оди-
наковую интенсивность, поскольку в этой области сцена не изменяется, в то время как один из лучей
пиксела Q возвращает интенсивность, значительно отличающуюся от остальных. Следовательно, через
углы нижнего левого квадранта пикселя Q будет пропущено три новых луча, и интенсивность каждого
из них будет опять сравниваться со средней интенсивностью. Разбиение производится рекурсивно, до
тех пор, пока не будет достигнут заранее установленный уровень рекурсии или пока все четыре интен-
сивности не станут «достаточно близки» к усредненной. После того как эта процедура проведена для
всех четырех квадрантов пиксела, окончательное значение пиксела формируется как среднее взвешен-
ное средних интенсивностей квадрантов.
В другом методе, основанном на распределенной выборке (distributed sampling) [Cook, 47], исполь-
зуется разновидность стохастической выборки, с которой мы уже имели дело в главе 10 в связи со сгла-
живанием текстуры. Через каждый пиксел на сцену испускается случайная совокупность лучей, после
чего полученные интенсивности усредняются. Например, пиксел может быть разбит на правильную
сетку размером четыре на четыре. Однако вместо испускания лучей точно через узлы сетки лучи испус-
каются через смещенные («дрожащие») узлы. Это дрожание точек отсчета добавляет в изображение
некоторое количество «шума» (наблюдаемые интенсивности берутся со слегка смещенных точек изоб-
ражения), однако этот шум меньше раздражает глаз, чем ступенчатость изображения. Применяя дро-
жание, можно использовать меньшие сетки, чем без него.
14.9. Использование экстентов
При трассировке лучей один и тот же набор функций выполняется снова и снова для очень большого
числа лучей. Приходится производить пересечение каждого луча с каждым объектом, что достигается
огромным числом вычислений этих пересечений. (Ситуация еще больше ухудшается, когда мы добав-
ляем тени, отражения и преломления света.) Поэтому мы приветствуем любую технологию, позволяю-
щую уменьшить число объектов, которые приходится тщательно исследовать и обрабатывать. Значи-
тельно ускорить процесс трассировки лучей позволяет использование экстентов.
Экстентом (extent) объекта называется форма, охватывающая этот объект. Использование экстен-
тов убыстряет процесс трассировки лучей, поскольку с их помощью можно быстро определить, когда
текущий луч заведомо не может пересечь определенный объект. Смысл состоит в том, что если луч про-
ходит мимо экстента, то он заведомо пройдет и мимо самого объекта. Если экстент имеет простую фор-
29 Ф. Хилл
898
Глава 14. Введение в трассировку лучей
му, то обработка пересечения луча с ним обходится недорого, в то время как пересечение луча с вложен-
ным объектом может оказаться очень дорогостоящим.
На рисунке 14.37 показан пример окружения тора, пересечение с которым обходится дорого, экстен-
том в форме параллелепипеда (боксом), пересечение с которым считается быстро. При тестировании
луча относительно этого экстента возможны следующие три ситуации:
О Луч проходит мимо экстента. Следовательно, тестирование с тором пропускается.
О Луч соударяется с параллелепипедом, поэтому выполняется полное тестирование с тором, в ре-
зультате которого выясняется, что луч проходит мимо тора. (Это можно назвать «ложной трево-
гой»: первоначальный тест показал, что луч соударяется с тором, однако на самом деле это не так.)
О Луч соударяется с параллелепипедом, поэтому выполняется полное тестирование с тором, в ре-
зультате которого выясняется, что луч соударяется также и с тором.
Если стоимость полного теста на соударение значительно превышает стоимость теста с экстентом, то
имеет смысл делать дополнительный тест в тех достаточно частых случаях, когда луч пересекает экстент.
Рис. 14.37. Вложение тора в прямоугольный экстент
Краткий анализ сэкономленных ресурсов
Предположим, что тестирование луча относительно экстента стоит Т единиц времени, а тестирование
его относительно тора — тТ единиц. Предположим далее, что для создания изображения выпускается
N лучей и что только их /-я доля соударяется с боксом. Отсюда следует, что выполняется N тестов
относительно экстента общей стоимостью NT, а также JN тестов относительно тора общей стоимостью
fNniT. Суммарная стоимость составляет NT(1 + fm). С другой стороны, если не использовать экстенты,
то все N лучей придется тестировать относительно тора, и общая стоимость этих тестов составит mNT.
В результате такого анализа мы приходим к следующему соотношению:
цена без экстентов m
компьютерное время =-------------=-------. (14.40)
цена с экстентами 1 + f • m
Например, если m = 20 1/40 (каждый объект на типичной сцене занимает лишь незначитель-
ную часть площади изображения), то соотношение скоростей равно примерно 13, то есть для трасси-
ровки такой сцены без использования экстентов потребовалось бы в 13 раз больше времени.
Отметим, что желательно сделать f как можно меньше. То есть мы хотим сделать каждый эк-
стент таким, чтобы с ним соударялось как можно меньше лучей. Это согласуется с нашим интуитив-
ным желанием сделать так, чтобы экстент как можно более «плотно» прилегал к соответствующему ему
объекту.
В какой момент процесса трассировки лучей следует вставить тестирование экстента? Арво и Кирк
(Arvo, Kirk) провели в своей работе [Arvo, 5] превосходный обзор возможных подходов, включая
использование иерархических экстентов, охватывающих целые группы объектов. Сосредоточим свое
внимание на усовершенствовании базового метода hit(), которым обладает каждый объект сцены.
14.9. Использование экстентов
899
Вспомним подпрограмму getFirstHitO из листинга 14.5, которая тестирует текущий луч относительно
каждого объекта, используя для каждого объекта его собственный метод hit():
for(each object, obj)
// для каждого объекта
{
i f(!obj->hi t(ray,1nter)) conti nue:
compare this hit time with the best so far, etc.
// сравниваем это время соударения с наилучшим на данный
// момент и т. д.
}
Для убыстрения каждого индивидуального теста мы будем использовать тестирование относитель-
но экстента внутри метода hit(). Если мы можем до начала полного вычисления пересечений быстро
определить, что данный луч не соударяется с объектом, то общая скорость трассировщика луча значи-
тельно возрастет. Еще одно преимущество заключения тестирования экстента внутрь каждого метода
hit() заключается в том, что тогда это тестирование может быть лучше приспособлено к особенностям
исследуемой геометрической формы.
Существует несколько способов создания и использования экстентов при трассировке лучей. Неко-
торые из них реализуются просто, а другие требуют больше программного кода, однако обеспечивают
лучшую производительность. Мы рассмотрим несколько различных простых методов и покажем, как
они вписываются в логическую схему трассировщика лучей. Другие методы описываются в упражне-
ниях в конце следующего раздела.
14.9.1. Боксы и сферические экстенты
Для экстентов чаще всего используются две формы: сфера и «выровненный бокс».
О Сферический экстент (sphere extent). Сфера, полностью охватывающая данный объект, опреде-
ляется парой чисел (С, г) — точкой центра С и радиусом г.
О Бокс (box extent). Прямоугольный параллелепипед, стороны которого выровнены по коорди-
натным осям, определяется шестью числами: (left, top, right, bottom, front, back).
Мы уже видели, что пересечение каждой из этих форм с лучом осуществляется достаточно быстро.
Что касается сферы, то нам нужно составить квадратное уравнение и проверить, положителен ли его
дискриминант (см. листинг 14.6). В случае выровненного бокса нам следует произвести пересече-
ние луча с шестью плоскостями и проверить, вырождаются ли в нуль «возможные интервалы» (tin,
(см. листинг 14.9.) Каждое из пересечений с плоскостью осуществляется очень быстро, поскольку не
требуется вычислять ни одного скалярного произведения. Кроме того, часто происходит «досрочный
выход», когда возможный интервал обращается в нуль уже после проверки нескольких плоскостей.
Существует два пространства, в которых мы можем производить тестирование относительно экстен-
тов: мировые и базовые координаты. Напомним, что каждый объект трансформируется для сцены из
некоторой базовой формы посредством аффинного преобразования. Чтобы пересечь луч с объектом,
мы вначале преобразовываем луч в базовые координаты и пересекаем базовый луч с базовым объектом.
Однако можно поместить на сцену экстент, охватывающий объект, и тестировать текущий луч относи-
тельно него. Если луч проходит мимо этого экстента, то базовый луч вычислять не нужно, что экономит
нам одно преобразование. Можно также разместить экстент вокруг базового объекта и тестировать от-
носительно него обратно преобразованный луч. Если луч проходит мимо этого экстента, то снимается
необходимость теста на полное пересечение.
В мировых координатах экстенты могут не очень плотно охватывать свои объекты. На рис. 14.38, а
показаны два конических цилиндра, окруженных сферическим и прямоугольным экстентами, на сцене,
для которой производится трассировка лучей. На рис. 14.38, б приведен цилиндр (для простоты он
принят двумерным). Если этот цилиндр длинный и тонкий, то сферический экстент не охватывает его
достаточно плотно, поэтому его использование может привести к многочисленным «ложным тревогам».
900
Глава 14. Введение в трассировку лучей
Прямоугольный экстент прилегает к цилиндру плотно даже в том случае, если он длинный и тонкий,
если только цилиндр не повернут в сторону относительно координатных осей. (В упражнениях в конце
раздела вам предлагается оценить вероятность ложных тревог для различных случаев.)
Рис. 14.38. Экстенты, сформированные в мировых и базовых координатах
Экстенты в базовых координатах обычно охватывают объекты более плотно. На рис. 14.53, в приве-
ден базовый конический цилиндр, окруженный сферическим и прямоугольным экстентами. Сферичес-
кий экстент прилегает к цилиндру достаточно плотно, а прямоугольный — очень плотно.
При выборе тестирования экстента в мировых или в базовых координатах имеется определенный
компромисс. Тестирование в мировых координатах происходит быстро, поскольку нет необходимости
вычислять обратно преобразованный луч. Однако экстенты могут не охватывать свои объекты доста-
точно плотно. Тестирование в базовых координатах требует нахождения базового луча, зато экстенты
прилегают к объектам более тесно. Трудно сказать в общем случае, какой тип тестирования лучше.
Столь же трудно говорить в общем случае о преимуществах сферических экстентов перед прямоуголь-
ными. Применяя один или несколько методов, дизайнеры выполняют тщательные временные тесты для
шаблонных сцен и выбирают наилучшее сочетание для использования в своих трассировщиках лучей.
Один неформальный тест сцены из ста случайным образом масштабированных и ориентированных
конических цилиндров показал, что использование сферических экстентов в мировых координатах
уменьшает время трассировки лучей на 27 %, в то время как применение любой другой комбинации
экстентов увеличивает это время. Однако, как мы увидим позднее, при включении в трассировщик лучей
больших возможностей результаты могут радикально измениться.
Листинг 14.13. Тестирование относительно сферических экстентов внутри метода hit() для цилиндра
bool TaperedCylinder::hit(Ray &r. Intersection Sinter)
{
if(IrayHitsSphereExtent(r.worldSphereExtent)) return false:
Ray genRay;
// make the generic ray
// создаем базовый луч
xfrmRay(genRay.i nvTransf,r);
// expensive
// стоит дорого
if(IrayHitsSphereExtent(genRay.genSphereExtent)) return false:
...Do expensive full testing with the generic cylinder...
II выполняем дорогостоящее полное тестирование
// относительно базового цилиндра
}
В листинге 14.13 показано, как тестирование экстента вводится внутрь метода hitO для случая ко-
нического цилиндра. Здесь приводится тестирование сферического экстента, причем тест выполняется
как в мировых, так и в базовых координатах, чтобы показать, где появляется код тестирования. (Возмож-
14.9. Использование экстентов
901
но, в реальном трассировщике луча будет применен только один из этих тестов.) Для того чтобы посмот-
реть, соударяется ли луч со сферическим экстентом, вызывается подпрограмма rayHitsSphereExtentO,
и если соударения нет, то происходит «досрочный выход» из метода hit О. В первый раз эта подпрограмма
вызывается с лучом в мировых координатах и тестирование производится с экстентом worl dSphereExtent.
Если луч соударяется с этим экстентом, то луч подвергается обратному преобразованию. Затем под-
программа вызывается вторично, чтобы посмотреть, соударяется ли базовый луч с базовым сферичес-
ким экстентом. Как и прежде, если луч проходит мимо, то осуществляется досрочный выход и тест пе-
ресечения с базовым цилиндром пропускается. Если мы почувствуем, что для конического цилиндра
прямоугольные экстенты будут эффективнее, чем сферические, то мы можем заменить подпрограмму
rayHitsSphereExtentO на rayHitsBoxExtentO. Мы могли бы даже поместить внутрь метода hit() оба теста
экстентов, хотя это вероятнее всего привело бы к ненужным потерям в скорости.
Мы должны выбирать, какие тесты включать в каждый метод hit() для различных классов форм.
В ряде случаев выбор очевиден: для объектов класса Sphere нет смысла выполнять тест со сферическим
экстентом в базовых координатах. (Почему?) Вы никогда не будете выполнять также тест относитель-
но прямоугольного экстента в базовых координатах для объектов класса Cube. Для класса Plane экстен-
тов не существует, поэтому в метод Plane :: hit О не включается никаких тестов. Для класса Square по-
строение экстента имеет смысл, однако здесь тест на пересечение настолько прост, что тест относительно
экстента не принесет никакой выгоды. Напротив, объект класса Mesh содержит большое число ограни-
чивающих плоскостей, и тест на пересечение с ним стоит дорого, поэтому тест относительно экстента
может принести значительные выгоды.
Реализация тестирования относительно экстентов
Как же формировать экстенты для каждой геометрической формы и как осуществлять тестирование
относительно каждого экстента? Естественно хранить информацию об экстенте объекта внутри самого
объекта, поэтому добавим несколько новых полей в класс GeomObj (см. приложение В). Нам может понадо-
биться любой из четырех типов тестирования экстентов, поэтому мы добавим поля для каждого из них:
Sphereinfo genSphereExtent. worldSphereExtent;
Cuboid genBoxExtent. worldBoxExtent:
В классе Sphereinfo (см. приложение В) описание сферы хранится в двух полях: поле center содер-
жит координаты центра сферического экстента, а в поле radSq хранится квадрат радиуса этой сферы.
(Там мог бы храниться сам радиус, однако в тесте относительно экстента используется только квадрат
радиуса.) Класс Cuboid содержит шесть полей: left, top, right, bottom, front, back. Под этим понима-
ется, что прямоугольный экстент простирается по оси х от left до right, по оси у от bottom до top, а по
оси z от back до front.
После построения списка объектов, но до начала трассировки лучей данные для каждого объекта из
списка объектов помещаются в эти поля. Затем, во время трассировки лучей, внутри каждого метода
hit() вызывается некоторая комбинация подпрограмм rayHitsSphereExtentO и rayHitsBoxExtentO. Осо-
бенно прост тест луча относительно сферического экстента (см. упражнения в конце раздела); он реа-
лизуется с помощью следующей функции:
bool rayHitsSphereExtent(Ray & ray. Spherelnfo& sph)
{
double A » dot3D(ray.dir. ray.dir):
Vector3 diff - ray.start - sph.center;
double В » dot3D(diff. ray.dir):
double C » dot3D(diff.diff) - sph.radSq:
return(B * В >“ A * C):
В этой функции проверяется положительность дискриминанта соответствующего квадратного урав-
нения. Для вычисления этого дискриминанта требуется одиннадцать умножений, поэтому тест не со-
всем «бесплатный».
902
Глава 14. Введение в трассировку лучей
Тест rayHitsBoxExtent() является адаптацией метода hit() из класса Cube к работе с прямоугольным
экстентом, описанным в структуре данных класса Cuboi d. Его следует хорошо отладить для обеспечения
максимальной скорости (см. упражнения).
Построение сферических и прямоугольных экстентов
Для каждого заданного объекта нам необходимо построить сферический и прямоугольный экстенты.
Базовые экстенты нужно создавать всего один раз для каждого типа формы, однако мировые экстенты
должны делаться заново для каждого экземпляра объекта — с учетом аффинного преобразования, свя-
занного с этим экземпляром. Как, например, найти сферический экстент для цилиндра, который был
сложным образом масштабирован и повернут?
Один совсем простой метод заключается в том, что с каждой формой ассоциируется кластер точек
(point cluster). Это множество точек, выпуклая оболочка которых заключает в себе данный объект.
Напомним простой интуитивный способ представить себе выпуклую оболочку некоторой совокупнос-
ти точек: окружите эти точки воздушным шаром и позвольте этому шару постепенно сдуваться, стяги-
ваясь вокруг них. Получившийся полиэдр и будет выпуклой оболочкой. Имея кластер точек, нетрудно
создать сферу, охватывающую этот кластер. Разумеется, такая сфера будет охватывать и исходный объект.
(В силу транзитивности, если форма Л охватывает форму BviB охватывает форму С, то А охватыва-
ет С.) Мы можем также получить выпуклую оболочку для преобразованного объекта: для этого нужно
просто преобразовать каждую точку из кластера, в результате чего получим новые точки, которые и
составят преобразованный кластер. Поскольку при аффинных преобразованиях сохраняется «нахожде-
ние внутри» («inside-ness»), то если объект А лежит внутри выпуклой оболочки В, то преобразованный
объект Г(А) должен лежать внутри выпуклой оболочки Г(В), построенной на преобразованных точках.
Следовательно, нам нужно построить для каждого типа формы кластер точек. Для классов Cube
и Square это просто: их собственные вершины и являются этими точками. Просто это и для класса Mesh:
в качестве кластера точек здесь используется сам список вершин.
Рис. 14.39. Определение кластеров точек для цилиндра и для сферы
С классами Sphere и TaperedCy 11 nder проблем больше, поскольку они определяются скорее через свой-
ства симметрии, чем с помощью точек. Один из приемлемых подходов заключается в том, чтобы заклю-
чить каждую форму в плотно охватывающий ее полиэдр и в качестве кластера точек использовать вер-
шины этого полиэдра. На рис. 14.39, а показан базовый конический цилиндр, заключенный в призму, оба
основания которой являются гексагонами. Для плотного охвата круглого основания цилиндра радиус гек-
сагона основания должен равняться 4/3 (см. упражнения). Отметим, что такой кластер точек формируется
индивидуально для каждого экземпляра конического цилиндра и строится отдельно для каждой специ-
фической формы цилиндра. На рис. 14.39, б приведена базовая сфера, заключенная в икосаэдр, 12 вершин
которого составляют кластер точек для этой сферы. Для плотного охвата единичной сферы вершины
икосаэдра должны находиться на расстоянии примерно 1,26 от центра сферы (см. упражнения).
Кластеры точек для каждого типа формы можно хранить в простой структуре данных Pointcluster,
содержащей поле num для числа точек в кластере и массив р[г] (см. приложение В). Для каждого класса
форм разработан метод makeExtentPoints(PointCluster& clust), он вызывается только один раз на этапе
предварительной обработки для каждого объекта на сцене (см. упражнения).
14.9. Использование экстентов
903
После того как мы построили кластер точек для базового объекта, нетрудно найти прямоугольный и
сферический экстенты. Каждое поле прямоугольного экстента содержит самую большую или самую
маленькую координату, обнаруженную в массиве точек кластерар[г]: left - minp[z] jc , top - maxp[i].y
и t. д., так что все поля можно найти по точкам кластера внутри одного цикла. Для этой цели предназ-
начена подпрограмма
void makeBoxExtent(PointCluster& clust.Cuboid& cub)
принимающая кластер точек и генерирующая структуру данных класса Cuboid, которая затем записы-
вается в объект (см. упражнения).
Создание сферического экстента лишь немного сложнее. За центр экстента принимается центроид
кластера точек, поскольку это удобная центральная точка (центр тяжести кластера, см. раздел «Аффинные
комбинации точек» главы 4). Для того чтобы найти центроид, нужно покомпонентно сложить все точки
и разделить полученную сумму на число точек. Затем определяется радиус охватывающей сферы — как наи-
большее расстояние от центра экстента до любой из точек кластера. На основе такого подхода нетрудно
написать подпрограмму void makeSphereExtent (PointCluster& clust, Spherelnfo& sph) (см. упражнения).
Наконец, легко сформировать прямоугольный и сферический экстенты в мировых координатах: просто
преобразуем каждую точку из кластера точек базового объекта, в результате чего получим кластер точек в
мировых координатах, а затем для получения желаемых экстентов используем те же подпрограммы.
Практические упражнения
14.9.1. Оценка уровня ложных тревог
На рис. 14.38, б показан силуэт конического цилиндра, заключенный в круг. Вычислите «степень пус-
тоты» для различных удлинений и поворотов этого цилиндра внутри круга. Степень пустоты опреде-
ляется по следующей формуле:
степень пустоты =
(площадь круга)
и дает грубую оценку вероятности ложной тревоги: это такая ситуация, когда тест относительно экстен-
та указывает на соударение с лучом, в то время как полный тест обнаруживает прохождение луча мимо
объекта. Повторите это упражнение для тестирования прямоугольного экстента.
14.9.2. Разработка теста для сферического экстента
Адаптируйте алгоритм пересечения луча со сферой (листинг 14.6) для случая сферы радиуса г с цент-
ром в точке center.
14.9.3. Тестирование луча со сферическим экстентом
О Покажите, что наименьшая сфера, охватывающая базовый цилиндр с единичным радиусом крыш-
ки, имеет центр в точке (0,0,05) и радиус ^/1,25
О Покажите, что уравнение этой сферы в неявной форме имеет вид:
( 1V
F(x,y,z) = x2+ у2+ Z" “1,25.
О Покажите, что решение уравнения F(S + ct) = 0 обычно приводит к квадратному уравнению At2 +
+ 2Bt + С = 0, где А - |с|2, В - с • S', С -15'|2 - 1,25, a S' определено как S' = (5., Sy, 5 - 0,5).
14.9.4. Реализация теста для базового прямоугольного экстента
Усовершенствуем метод Cube :: hi t () путем разработки подпрограммы
bool rayHitsBoxExtent(Ray& ray, Cuboid& cub)
которая проверяет пересечение заданного луча с экстентом, описанном в cub. Это приводит к упрощению
метода hit() без изменения его логики. Покажите, что значения переменных numer и denom, необходимых
(площадь круга)-(площадь цилиндра)
904
Глава 14. Введение в трассировку лучей
для каждой плоскости бокса, зависят отданных, содержащихся в cub. (Например, для верхней плоскости
top используются numer = cub.top-ray.start.у: denom = ray.di г.у.) При пересечении каждой плоскости
бокса с лучом возможный интервал (tin, tout) обновляется; если этот интервал становится пустым, то про-
исходит «досрочный выход» и тест возвращает значение false.
14.9.5. Кластер точек для конического цилиндра
Покажите, что гексагон, описанный около круга единичного радиуса, должен иметь радиус 4/3. Выве-
дите формулы 12 вершин кластера точек для цилиндра. Напишите метод makeExtentPoi nts (Poi ntCl uster&
clust) для класса TaperedCylinder.
14.9.6. Кластер точек для сферы
При помощи списка вершин икосаэдра, приведенного в табл. 6.8, определите, как следует масштабиро-
вать этот икосаэдр, чтобы он плотно охватывал базовую сферу. (Достаточно ли для этого масштабного
множителя f = 1,071?) Напишите для класса Sphere метод makeExtentPoints(PointCluster& clust). Задача
решается при помощи трех двойных циклов for. Например, четыре вершины икосаэдра лежат в точках
(0, ±/, ±/т), где т - 0,618034.
14.9.7. Подпрограммы для создания сферического и прямоугольного экстентов
Напишите подпрограммы, которые по заданному кластеру точек строят соответственно сферический и
прямоугольный экстенты:
void makeSphereExtent(PointCluster& clust.Sphere!nfo& sph)
void makeBoxExtent(PointCluster& clust.Cuboid& cub),
14.9.2. Использование проекционных экстентов
Существует другой тип экстентов, использование которого радикально увеличивает скорость трасси-
ровщика лучей. В отличие от прямоугольного и сферического экстентов, оперирующих в трехмерном
пространстве, этот экстент представляет собой прямоугольную область на экране.
Проекционный экстент (projection extent) объекта — это выровненный прямоугольник на экране,
который заключает в себе проекцию этого объекта, как показано на рис. 14.40, а. Более подробно проек-
ционный экстент изображен на рис. 14.40, б. Проекционный экстент описывается четырьмя числами:
{left, top, right, bottom}.
244 296
a 6
Рис. 14.40. Проекционный экстент объекта
Проекционные экстенты очень легко использовать в процессе трассировки лучей. Каждый луч про-
ходит через экран в месте пересечения некоторых строки и столбца; назовем эту точку (г, с). Если точка
(г, с) лежит вне проекционного экстента объекта, то у луча нет возможности пересечься с таким объек-
том. Если в примере на рис. 14.40, б столбец с меньше 244 или больше 296 или если строка г меньше 237
или больше 319, то луч определенно пройдет мимо объекта.
Поскольку проекционные экстенты в конечном счете связаны с геометрией камеры и положени-
ем глаза, то их можно использовать только для «лучей глаза» — то есть лучей, испускаемых из глаза.
14.9. Использование экстентов
905
В следующих разделах мы будем генерировать лучи для затенения, отражения и преломления; а посколь-
ку эти лучи испускаются из произвольных точек сцены, то не существует такого экрана, на котором
можно было бы поместить проекцию. Однако данная технология прекрасно работает для лучей глаза и
способна многократно ускорить процесс трассировки лучей!.
Проекционные экстенты для каждого объекта сцены создаются на этапе предварительной подготовки
и записываются вместе со своими объектами так же, как это делалось для прямоугольного и сферическо-
го экстентов. Для того чтобы обеспечить эту запись, добавим к классу GeomObj поле IntRect screenExtent.
Кроме того, расширим класс Ray так, чтобы луч «знал», через какие строку и столбец на экране он про-
ходит. Придадим лучу дополнительную информацию: его так называемый «рекурсивный уровень»
(«recursion level»), который будет играть важную роль в нашей дальнейшей работе с отражением и пре-
ломлением лучей. Здесь же этот уровень просто фиксирует, является или нет данный луч лучом глаза.
Для лучей глаза рекурсивный уровень задается равным нулю.
Листинг 14.14. Тестирование относительно сферических экстентов внутри метода hit() для цилиндра
bool TaperedCylinder::h:t(Ray &r. Intersection Sinter)
Iffr.recurseLevel == 0 &&
r.col < projExtnt.left ||
r.col > projExtnt.right11
r.row < projExtnt.bottom ||
r.row > projExtnt.top ) return false;
// misses screen extent
// проходит мимо экранного экстента
1 f(!rayHitsSphereExtent(r.worldSphereExtent)) return false;
make, and inverse transform, the generic ray
// создаем луч с его обратным преобразованием в базог
// системе координат
1f(!rayHitsSphercExtentfgenRay.genSphereExtent)) return false:
...do expensive full testing with the generic cylinder...
11 делаем дорогое полное тестирование относительно
// базового цилиндра
1
В процессе трассировки лучей в начале метода hit() для каждого типа объекта выполняется новый!
тест — перед тестами относительно сферических или прямоугольных экстентов. В листинге 14.14 показано,
где расположен этот тест для класса TaperedCylinder. (Такой же тест используется для всех типов объек-
тов, за исключением сферы.) Сравните этот листинге листингом 14.13. В этом тесте проверяется, явля-
ется ли данный луч лучом глаза, и если да, то строка и столбец этого луча сравниваются с соответству-
ющими элементами проекционного экстента, хранящимися вместе с объектом. Если строка или столбец
луча лежат вне проекционного экстента, то такой луч должен пройти мимо данного объекта; следова-
тельно, метод hit немедленно возвращает false. Этот тест действительно выполняется очень быстро.
Вычисление проекционных экстентов
Па этапе предварительной подготовки для каждого объекта сцены необходимо вычислить проекцион-
ный экстент. Этот экстент легко вычисляется по заданному кластеру точек объекта. Кластер точек ба-
зового объекта переводится в мировые координаты с помощью преобразования, соответствующего это-
му объекту, — так же, как это делалось для сферического и прямоугольного экстентов, в результате чего
этот кластер становится «облаком» точекр[0],/?[!],..., размещенных на сцепе. На рис. 14.41 показано
12 точек кластера для преобразованного цилиндра.
Теперь каждая из точек p[ij проецируется на ближнюю плоскость камеры. Для любой точки р на
сцене можно найти ее проекцию р' с помощью вычислений, основанных на положении точки р и гео-
906
Глава 14. Введение в трассировку лучей
метрии камеры. Спроецированная точка р' связана с определенными строкой г и столбцом с. (Выраже-
ние для этой связи выводится в упражнениях в конце раздела.) В результате точка р проецируется в
пиксел с координатами (г, с), где
nRows ( NP„
2 НР„
и (14.41)
r_nCols( NPU\
2 WP„
k "J
(Перед записью выражений в правой части соответственно в г и с их необходимо округлить до цело-
го.) Здесь Ри, Pv, Рп являются скалярными произведениями с осями камеры u, V, п:
Ри “ (Р - eye) • и;
рв “ (Р “ eye) • v; (14.42)
Р„ “ (Р ~ eye) п.
Таким способом проецируется каждая точка массива _р[г], и для нее вычисляется пара чисел (г, cf).
Затем по списку (г, с.) определяются наименьшие и наибольшие значения г и с, которые после нахожде-
ния записываются в структуру данных проекционного экстента {left, top, right, bottom}.
Рис. 14.41. Построение проекционного экстента
На рис. 14.42 показана сцена, полученная трассировкой лучей, причем на каждый объект наложен
его проекционный экстент. (Некоторым программистам нравится в целях отладки рисовать проекци-
онные экстенты каждого объекта перед тем, как начать трассировку лучей. Во время закраски пикселов
окончательными цветами при трассировке лучей эти прямоугольники исчезают.)
Рис. 14.42. Сцена, полученная трассировкой лучей, с видимыми проекционными экстентами
14.10. Добавление теней для большей реалистичности
907
Практические упражнения
14.9.8 . Нахождение проекции точки
Докажите правильность равенств (14.41) и (14.42). Для этого «инвертируйте» уравнение (14.3), которое
задает направление луча, проходящего через лг-пиксел: по заданному направлению выведите значения г и с.
Луч, идущий из глаза через точку р, имеет направление К(р - eye), где К — некоторый масштабный коэф-
фициент. Это направление должно совпадать с вектором dir из уравнения (14.3). Для выделения неко-
торых членов умножим скалярно обе части выражений на вектор и:
I 1с А
K(p-eye)U = W —— -1 .
I nCols I
При последующем скалярном умножении на векторы v и п можно получить еще два уравнения, одно из
которых определяет значение К через известные величины. Покажите, что из этого равенства следует, что
АУИ = ! _ 2с
WP„ nCols'
откуда можно выразить с и получить один из результатов уравнения (14.41). Аналогично выведите
второй результат.
14.9.9 . Объединенные экстенты для дальнейшей экономии времени
Некоторые сцены содержаг-оольшие области, на которых виден только фон и отсутствуют какие-либо
объекты. С целью дополнительной экономии времени во время трассировки лучей можно создать объ-
единенный экстент (union extent), то есть наименьший выровненный прямоугольник, охватывающий
все индивидуальные экстенты объектов на сцене. Каждый луч в первую очередь тестируется с этим эк-
стентом. Если луч лежит вне экстента, то ему незамедлительно присваивается цвет фона. В противном
случае, как обычно, будет просматриваться весь список объектов. Покажите, как сформировать объеди-
ненный экстент и как применять его в вашем трассировщике лучей.
14.9.10 . Списки для кластеров объектов
Значительно сократить вычисления может еще одно усовершенствование — в тех случаях, когда оно
применимо. Когда объекты на сцене образуют в достаточной степени изолированные группы — «клас-
теры», то каждый такой кластер объектов можно поместить в отдельный список объектов — назовем
его кластерным списком (cluster list). Для каждого кластера вычисляется объединенный экстент. В этом
случае список объектов превращается в список кластерных списков. Во время трассировки лучей каждый
луч тестируется относительно объединенного экстента каждого кластерного списка, и только в случае про-
хождения этоТо теста луч тестируется относительно отдельных объектов кластера. Покажите, как сле-
дует организовать типы данных и сам алгоритм трассировки лучей, чтобы реализовать этот подход.
14.10. Добавление теней для большей реалистичности
Морочит нас летучая звезда
И страсти бес.
Но для заблудших душ всегда
Был свет с небес.
Роберт Бернс (Robert Bums)
Присутствие теней нужной формы и яркости значительно увеличивает реалистичность компьютерных
изображений. Мы уже видели в главе 8, что в OpenGL имеются кое-какие элементарные механизмы
для создания теней, однако использовать эти средства затруднительно, и они образуют тени только в
ограниченном числе ситуаций. В то же время добавление теней при трассировке лучей требует лишь
908
Глава 14. Введение в трассировку лучей
незначительных программистских усилий. (К сожалению, рисование теней чрезвычайно замедляет про-
цесс трассировки.) На рис. 14.43 приведена сцена, визуализированная с тенями и без них.
Рис. 14.43. Визуализация стенами и без теней
Интенсивности света, которые мы исследовали до сих пор, вычислялись в предположении, что
точка соударения луча с первым объектом соударения Ph освещена различными источниками света.
Однако может случиться так, что между точкой Ph и источником света расположен какой-либо другой
объект. В этом случае точка Ph по отношению к этому источнику света находится в тени, вследствие
чего диффузный и зеркальный компоненты света отсутствуют. Остается лишь один компонент фоно-
вого света.
На рис. 14.44 изображены различные ситуации затенения. Между точкой Р и источником света Z,
нет никаких объектов, поэтому точка Р не находится в тени по отношению к источнику Lv Однако эта
же точка Р находится в тени куба от источника L2. Далее, источник L3 расположен так, что от точки Р его
закрывает сам объект соударения; это носит название «самозатенения» («self-shadowing»). Таким обра-
зом, в изображенной на рисунке конфигурации единственным светом, ничем.не заслоненным от точки
Р, является свет от источника Z(.
Рис. 14.44. Различные случаи закраски точки соударения
Испускание дополнительных лучей. «Щупы теней»
Для правильного вычисления теней нам необходимо знать, когда точка соударения находится в тени
относительно источника света. Итак, нам нужна подпрограмма slnShadowO, которая возвращает true,
если хоть какая-нибудь часть какого-нибудь объекта лежит между точкой соударения и данным источ-
ником света; в противном случае возвращается fal se. Для разработки такой подпрограммы мы «испус-
тим» новый луч, часто называемый щупом теней (shadow feeler), который выходит из точки соударе-
ния Ph в момент времени t = 0 и достигает источника L при t = 1. Тогда параметрическое представление
щупа теней будет иметь вид Ph + (L - Ph)t. Для того чтобы проверить, соударяется ли этот луч с чем-
нибудь, просматривается весь список объектов, и каждый объект из этого списка тестируется на пересе-
чение со щупом теней. Если в интервале времени от t = 0 до t - 1 обнаружено хотя бы одно пересече-
ние, то isInShadowO возвращает true.
14.10. Добавление теней для большей реалистичности
909
Однако при наивном использовании этого подхода нас подстерегает трудная проблема: это пробле-
ма «самозатенения». Если щуп теней действительно выходит из точки Ph, то пересечение щупа теней и
самого объекта будет иметь место всегда: при t - 0! В этом случае подпрограмма 1 sInShadow() всегда бу-
дет возвращать true, что очевидно неправильно. Некоторые пытаются обойти эту проблему, учитывая
только такие пересечения, которые происходят при t, строго больших нуля. Однако, как показано на
рис. 14.45, а, при таком подходе будет пропущено истинное пересечение с квадратом или плоскостью,
если источник света находится на противоположной стороне этого квадрата относительно глаза. Щуп
из точки Р к источнику правильно сообщит об отсутствии пересечений, однако щуп от точки Р к ис-
точнику Z2 также сообщит об отсутствии пересечений (почему?), хотя сам квадрат затеняет точку Р.
(Почему эта аномалия не возникает для других форм, таких как сферы и конусы?)
Рис. 14.45. Стратегии использования щупа теней
Надежно работающая стратегия заключается в том, что слегка преобразованный щуп теней посыла-
ется в подпрограмму isInShadowO, как показано на рис. 14.45, б. Стартовая точка щупа теней смещена
на малую величину по направлению к глазу. Если направление луча равно dir, а точка соударения Ph, то
стартовая точка щупа теней смещена в точку Ph - е dir, где е — малое положительное число. Это поме-
щает стартовую точку немного «впереди» объекта соударения («со стороны глаза»). Если мы примем
для щупа теней такую стартовую точку, то убедимся, что при t = 0 пересечение с объектом отсутствует,
так что проблема самозатенения решена.
Щуп теней включается в метод Scene :: shade(ray) следующим образом: после того как подпрограм-
ма getFi rstHit() возвратила запись наилучшего пересечения, определяется точка соударения и нормаль-
ный вектор в этой точке соударения. Определяется цвет фонового света для связанного с этой точкой
луча. Далее формируется щуп теней, в качестве его стартовой точки принимается точка Ph - Е dir. Его
рекурсивный уровень recurseLevel устанавливается в единицу, что выключает проекционные экстенты
в различных методах hit(). Затем для каждого источника L вычисляется направление щупа по формуле
L.pos - feeler.start и вызывается подпрограмма IsInShadow(feeler), которая проверяет наличие соуда-
рения щупа с любым объектом. Если соударение имеет место, то вычисление диффузной и зеркальной
составляющих света для данного источника пропускается. Псевдокод для той части процесса, которая
связана с затенением, выглядит так:
feeler.start - hitPoint-e ray.dir:
feeler.recurselevel - 1;
color » ambient part:
for(each light source. L)
// для каждого источника света L
{
feel er.di г = L.pos-hitPoint:
if(is!nShadow(feeler))continue:
color.add(diffuse light);
color.add(specular light);
}
910
Глава 14. Введение в трассировку лучей
Код возможной реализации самой подпрограммы isInShadowO выглядит следующим образом:
bool Scene :: 1sInShadow(Ray& f)
{
for(GeomObj* p - obj: p: p - p->next)
if(p->hit(f))return true:
return false:
Отметим, что в этой подпрограмме просто просматривается список объектов в поисках соударения;
если соударение найдено, то возвращается false. Если ни одного соударения не обнаружено, то возвращает-
ся true. В этой подпрограмме используется упрощенный вариант метода hit() для каждого типа объекта,
который принимает только один аргумент — для него не нужно создавать запись пересечения. Этот ва-
риант метода hi t() отличается от того, с которым мы работали до сих пор, по следующим трем пунктам:
1. Он учитывает только те соударения, для которых время соударения лежит между нулем и еди-
ницей, поскольку объект, находящийся за источником света, не отбрасывает тени.
2. Если такое соударение обнаружено, то метод закрывается немедленно, без вычисления каких-
либо данных о самом соударении.
3. Метод не может использовать проекционные экстенты, поскольку щупы теней могут начинать-
ся с любой точки сцены. Поэтому он проделает некоторую тщательно выбранную комбинацию
тестов со сферическим и/или прямоугольным экстентами для каждого типа объекта.
14.11. Отражения и прозрачность
Одним из наиболее сильных сторон метода трассировки лучей является та простота, с которой в нем
имитируется как отражение, так и преломление света. Это позволяет создавать высокореалистичные
сцены1, включающие зеркала, аквариумы, линзы и т. п. Могут изображаться множественные отражения,
когда свет, перед тем как дойти до наблюдателя, отражается от нескольких блестящих поверхностей,
а также сложные сочетания преломления и отражения. В каждом из таких процессов требуется созда-
ние и трассировка вспомогательных лучей.
Рис. 14.46. Добавление отраженного и преломленного света
На рис. 14.46 показан луч, исходящий из глаза в направлении dir, который соударяется с поверхностью
в точке Ph. На рисунке основные компоненты представлены двумерными, что допустимо, поскольку
основное свойство отражения и преломления заключается в том, что все векторы лежат в одной и той же
плоскости. Но все формулы мы выведем для трех измерений. Если поверхность зеркальная или прозрач-
ная (или и то и другое), то свет I, достигающий глаза, может содержать следующие пять составляющих:
I Arab Aiff Арес Aefl Aran'
(14.43)
* Некоторые называют такие сцены «суперреалистичными».
14.11. Отражения и прозрачность
911
Первые три из них — это уже знакомые нам фоновый, диффузный и зеркальный компоненты света.
Диффузный и зеркальный компоненты происходят от тех источников света в окружающей среде, кото-
рые видны в точке Ph. Составляющая отраженного света /гсП возникает из света IR, который падает в точ-
ку Ph в направлении -г. Это направление определяется равенством углов падения и отражения, поэто-
му из уравнения (4.27) получаем:
г = dir - 2(dir • m) m, (14.44)
где нормальный вектор m в точке Ph имеет единичную длину.
Подобным же образом составляющая света Ztran является долей света 1Т, прошедшей через прозрач-
ный материал к точке Ph в направлении -t. Часть этого света проходит сквозь поверхность, преломляет-
ся внутри нее и продолжает свой путь в направлении -dir. Направление преломленного света t зависит
от нескольких факторов, которые будут подробно рассмотрены в следующем разделе.
Так же как свет / является суммой различных компонентов света, так и каждая составляющая света
IR и IL, в свою очередь, состоит из своих пяти компонентов — фонового, диффузного и т. д. Как пока-
зано на рис. 14.46, IR — это свет, видимый глазом в точке Ph вдоль луча от точки Р' до точки Ph. Для того
чтобы определить свет IR, мы фактически испускаем вспомогательный луч из точки Ph в направлении г,
находим первый объект, с которым этот луч соударяется, и затем повторяем вычисление компонентов
света согласно уравнению (14.43). Это, в свою очередь, может потребовать испускания вспомогательных
лучей. Свет 1Т определяется путем испускания луча в направлении t с последующим нахождением первой
поверхности соударения, после чего в этой точке вычисляются составляющие света и т. д.
Рис. 14.47. Световое дерево
На рис. 14.47, а показано, как возрастает число составляющих света в каждой точке контакта. Свет I
является суммой трех компонентов: компонента отражения 7?(, компонента преломленного света Т
и «локального» компонента Z.r Локальный компонент — это просто сумма обычных составляющих
фонового, диффузного и зеркального отражений в точке Ph. Локальные компоненты зависят только от
имеющихся источников света, и для их вычисления испускание вспомогательных лучей не используется.
Напомним, что роль фоновой составляющей заключается в приближенном учете эффекта диффузного и
зеркального отражений от других поверхностей. В свою очередь, складывается из Ry Т3 и локальной
составляющей L. Сам компонент Т3 является суммой трех других компонентов. (Каких именно?) Итак,
каждая составляющая представляет собой сумму трех других, возможно, до бесконечности. Все это на-
водит на мысль о рекурсивном подходе к вычислению интенсивности света.
На рис. 14.47, б различные источники света обобщенно представлены в виде «дерева» составляю-
щих света, причем компоненты преломленного света находятся на левых ветвях дерева, а отраженно-
го — на правых ветвях [Whitted, 212]. В каждом узле должен быть добавлен еще локальный компонент,
однако для простоты он на рисунке не показан.
912
Глава 14. Введение в трассировку лучей
Листинг 14.15. Скелет рекурсивного метода shade()
Со1огЗ Scene :: shade(Ray& г)
{
Get the first hit, and build hitinfo h
// Получаем первое соударение и строим запись соударения h
Shape* myObj = (Shape*)h.hitObject;
// pointer to the hit object
// указатель на объект соударения
Color3 color.setCtte emissive component):
// эмиссионный компонент
color.add(ambient contribution):
// фоновый компонент
get the normalized normal vector m at the hit point
// получаем нормированный нормальный вектор го в точке
// соударения
forCeach light source)
И для каждого источника света
add the diffuse and specular components
11 добавляем диффузный и зеркальный компоненты
// now add the reflected and transmitted components
// теперь добавляем компоненты отраженного и
// преломленного света
if(r.recurseLevel “= maxRecursionLevel)
return color:
// don't recurse further
// дальше рекурсию не производим
if(hit object is shiny enough)
11 объект соударения достаточно блестящ
// add any reflected light
// добавляем любой отраженный свет
{
get reflection direction
// определяем направление отражения
build reflected ray. refl
// строим отраженный луч refl
refl.recurseLevel = r.recurseLevel + 1:
color.addCshininess * shade(refl)):
}
if(hit object is transparent enough)
11 если объект соударения достаточно прозрачен
{
get transmited direction
И определяем направление преломленного света
build transmitted ray. trans
И строим преломленный луч trans
trans.recurseLevel = r.recurseLevel + 1:
color.add(transparency * shade(trans));
}
return color:
}
14.11. Отражения и прозрачность
913
Для включения этих визуальных эффектов произведено усовершенствование метода Scene ::
shadeO, допускающее его рекурсивный самовызов. В листинге 14.15 приведен скелет метода shadeO;
следует обратить внимание, что он добавляется к версии этого же метода shadeO из листинга 14.4. При
корректных условиях метод shade О вызывает себя дважды: для учета компонентов отраженного и пре-
ломленного света. Если объект соударения «достаточно блестящ», чтобы оправдать затрату усилий на
«углубленную» трассировку лучей, то испускается отраженный луч и метод shade() определяет, сколь-
ко света возвращается обратно в направлении отражения. Количество света, найденное методом shadeO,
умножается на коэффициент отражения reflectivity объекта соударения. Этот коэффициент отраже-
ния хранится в одном из полей самого объекта. Пользователь задает этот коэффициент в SDL-файле,
например, так: reflectivity 0.8 (см. приложение Д). Э же коэффициент используется для тестиро-
вания «if shiny enough» («если достаточно блестящ»), например:
1f(reflect!vity > 0.6)...
Если объект соударения «достаточно прозрачен», чтобы оправдать дальнейшую трассировку лучей, то
испускается преломленный луч, после чего метод shaded вычисляет, сколько света возвращается назад в
направлении преломления. Найденное количество света умножается на коэффициент преломления
transparency объекта соударения. Этот коэффициент также хранится вместе с объектом, и он же использует-
ся для тестирования объекта соударения «if transparent enough» («если достаточно прозрачен»), например:
if(transparency > 0.5)...
В силу того, что при определенных условиях лучи могут бесконечно порождать новые отраженные и
преломленные лучи (рассмотрим, например, сцену, состоящую из четырех абсолютных зеркал, установ-
ленных под такими углами, что луч отражается от них бесконечно), необходимо наложить некоторые
ограничения на глубину рекурсии. Это нетрудно сделать путем контроля каждым лучом своей «глуби-
ны»: поле recurseLevel (уровень рекурсии), уже упоминавшееся в связи с затенением, является частью
записи каждого луча. Для лучей, исходящих из глаза, значение recurseLevel устанавливается в нуль.
Каждый раз, когда формируется отраженный или преломленный луч, этот уровень увеличивается па
единицу. Если уровень луча достигает предельного значения maxRecursionDepth (которое хранится в поле
объекта Scene и задается в SDL-файле, например, так: maxRecursionDepth 5), то больше никаких отражен-
ных или преломленных лучей не испускается. Обычно при максимальном уровне рекурсии 4 или 5 по-
лучаются достаточно реалистичные изображения.
14.11.1. Преломление света
Будь радугой для жизненных невзгод,
Лучом вечерним, что окрасит тучи
И нам предскажет завтрашний восход!
Лорд Байрон (Lord Byron)
Когда луч света соударяется с прозрачным объектом, то часть этого луча проходит сквозь этот объект,
как показано на рис. 14.48. Если скорость света в среде № 1 и в среде № 2 различна, то луч изменит свое
направление с dir на t. (Вектор t продолжает лежать в той же плоскости, что и направление dir, и нор-
маль ш.) Если угол падения луча обозначить через 0р то согласно закону Снелла (Snell’s law) угол пре-
ломления 02 определяется следующим уравнением [Halliday, 98]:
sin(e2) = sin(e,) (1445)
с2 С1 ’
где с( — скорость света в среде 1, а с2 — скорость света в среде 2, как показано на рисунке. Важно
только отношение этих скоростей с2/ср Его часто называют коэффициентом преломления (index of
refraction) среды 2 относительно среды I1. Отметим, что если угол падения 0! равен нулю, то это же
1 Поскольку под коэффициентом преломления одни понимают с{/с2, а другие с2/с(, то мы будем избегать в формулах его обозначе-
ния, а будем писать прямо: с2/с(.
914
Глава 14. Введение в трассировку лучей
происходит с углом преломления 02: свет, падающий на граничную поверхность под прямым углом, не
отклоняется.
Рис. 14.48. Преломление света в прозрачной среде
Пример 14.11.1. Найдите угол
Пусть среда 2 представляет собой такой сорт стекла, в котором свет движется со скоростью лишь 54 %
от его скорости в вакууме. Предположим далее, что угол падения внедряющегося света составляет 60°
от вертикали. Чему равен угол преломленного света?
Решение
Вычислим sin(02) в уравнении (14.45), подставляя в него c2/ct - 0,54 и 810(0!) - 0,866, тогда получим:
sin(02) = (0,54) (0,866) = 0,4676, а угол 02 = 27,88°. Таким образом, луч отклоняется ближе к нормали,
если он движется из среды с большей скоростью света в среду с меньшей скоростью света.
Таблица 14.4. Относительная скорость света в различных средах
Воздух
Стекло
Вода
30%-й раствор сахара
Ацетон и этиловый спирт
Хлорид натрия
Бензол
Сапфир
Алмаз
99,97 %
От 52,2 % до 59%
75,19%
72,46 %
73,5 %
64,93 %
55,5 %
56,50 %
41,33 %
В табл. 14.4 приведена скорость света в различных средах относительно скорости света в вакууме.
Скорости, перечисленные в таблице, даны несколько упрощенно, поскольку скорость света обычно
зависит от длины его волны. Например, относительная скорость света в плавленом кварце состав-
ляет 0,680 при Л - 400 нм (красный цвет), 0,685 при Л = 520 нм (зеленый), 0,687 при Л = 680 нм (синий)
[Halliday, 98]. Этот разброс служит причиной известного эффекта, при котором луч белого света при
прохождении через стеклянную призму расщепляется на «радугу» спектральных цветов (см. упражне-
ния в конце раздела).
Критический угол
В примере 14.11.1 отмечалось, что если свет входит в среду, в которой он движется медленней, чем в той
среде, откуда он пришел (то есть c2/cl < 1), то лучи света отклоняются в сторону нормали. Это с очевидно-
стью следует из уравнения (14.45), поскольку sin(02), равный (c2/Cj) sin(0j), меньше, чем sin(0(), поэтому
угол 02 должен быть меньше угла 0)t
Верно и обратное утверждение: когда луч при переходе из одной среды в другую увеличивает ско-
рость, он отклоняется дальше от нормали. Закон Снелла полностью симметричен относительно пере-
становки индексов 1 и 2. На рис. 14.49, а показан свет, движущийся из среды с большей скоростью
в среду с меньшей скоростью; на рис. 14.49, б приведен случай обратного движения. Пары углов в обоих
случаях одинаковы: нужно только поменять обозначения. На рис. 14.49, виг показаны аналогичные
ситуации, однако больший угол близок к 90°. При этом меньший угол приближается к так называе-
14.11. Отражения и прозрачность
915
мому критическому углу (critical angle). Когда меньший угол (соответствующий среде с меньшей ско-
ростью света) становится достаточно большим, он «приближает» больший угол к 90°. Большее значе-
ние угла невозможно, поэтому во вторую среду свет вообще не проходит. Такое явление называется пол-
ным внутренним отражением (total internal reflect^). На рис. 14.49, г, где при переходе от одной среды
к другой скорость света возрастает, из равенства sin(0t) - (с,/с2) sin(02) следует, что 0, - arcsin(c1/c2)
достигает максимально возможного значения при 02- 90°. Например, при переходе света из воды в воз-
дух с(/с2 = 0,7519, поэтому критический угол для воды равен 48,75°.
Быстрее
VZVZ'ZWZ'Z
Медленнее/
е,» 90’
ГГУ777777777777}
С2
62
в г
Рис. 14.49. Симметрия прохождения света и критический угол
Критический угол проявляется в некоторых обыденных ситуациях. Когда вы из-под воды водоема
смотрите вверх на поверхность, вы можете наблюдать мир вокруг водоема только внутри ограниченно-
го пространственного угла от вертикали. Если смотреть под углом примерно 48°, то видна кромка водо-
ема. (Начертите это.) С другой стороны, если вы плывете на лодке и смотрите вниз в воду, то каков
будет диапазон углов зрения? Существует ли ограниченный конус зрения, вне которого вы не можете
видеть объекты? (См. упражнения в конце раздела.)
Пример 14.11.2. Какова форма радуги?
Скорость света в воде изменяется с его длиной волны, именно это является причиной появления радуги.
На рис. 14.50, а показано несколько сферических капелек, висящих в воздухе. Солнечный луч, идущий
слева, слегка преломляется при входе в капельку и, прежде чем выйти из нее, претерпевает полное внут-
реннее отражение. Угол между входящим и выходящим лучами составляет около 42°. Красный свет
преломляется несколько меньше, чем синий, поэтому направления выходящих лучей слегка различны.
Таким образом, красные лучи исходят из мириадов дождевых капель в одном направлении, а синие —
в другом, немного отличном от него направлении.
Синий
Красный
Дождевые
Рис. 14.50. Происхождение радуги
916
Глава 14. Введение в трассировку лучей
В 1637 году Декарт (Descartes) объяснил форму радуги с помощью простых аргументов, основан-
ных на прослеживании лучей. На рис. 14.50, б показан наблюдатель, стоящий спиной к солнцу и смот-
рящий на туман из дождевых капель. Когда наблюдатель смотрит примерно под 42° в сторону от солн-
ца, то он видит кольца света. Капельки, расположенные вдоль конуса с определенным углом, отражают
назад свет одного цвета; при небольшом изменении угла этот цвет плавно изменяется. Таким образом,
радуга представляет собой совокупность круговых колец, и при этом каждый наблюдатель имеет свою
личную радугу.
Определение направления преломленного луча t
Для трассировки лучей нам понадобится направление t (см. рис. 14.48) между нормалью к поверхнос-
ти ш и направлением луча dir. Определим его при помощи не зависящих от системы координат скаляр-
ных произведений, тогда полученный результат будет применим для любых направлений dir и ш. Как
мы увидим в упражнениях, искомый вектор t является линейной комбинацией векторов m и dir (в пред-
положении, что оба этих вектора нормированы к единичной длине). В частности,
t = — dir +
ct
—(m-dir)-cos(02) m,
(14.46)
где cos(02) найден по закону Снелла, а именно:
cos(02) = ,ll-
(14.47)
Можете проверить правильность значения полученного вектора t для случаев, когда скорость света
одинакова в обеих средах или когда угол падения равен 0°.
Полное внутреннее отражение будет иметь место тогда, когда подкоренное выражение в уравнении
(14.47) становится отрицательным; при этом вектор t перестает существовать. Это происходит при зна-
чениях угла, равных или превышающих критическое. В упражнениях вам предлагается написать реа-
лизацию подпрограммы transmitDirectiоп(), в которой вычисляется вектор t. Отметим, что, поскольку
при выводе t были использованы только скалярные произведения, он в равной степени применим и к
двумерному случаю. В тематическом задании 14.8 вам предлагается написать программу, демонстри-
рующую преломление в двух направлениях.
При разработке трассировщика лучей проще всего моделировать прозрачные объекты таким об-
разом, чтобы их коэффициент преломления не зависел от длины волны света. Тогда для трассировки
красных, зеленых и синих компонентов можно будет использовать одни и те же лучи. В противном
случае потребуется раздельная трассировка лучей для каждого компонента цвета, так как они пре-
ломляются в слегка различающихся направлениях. Такая раздельная трассировка будет дорогостоя-
щей с вычислительной точки зрения и все равно даст вам лишь приближение к реальности, поскольку
точная модель преломления света потребовала бы учета большего количества цветов, а не только трех
основных.
Практические упражнения
14.11.1. Эффекты, связанные с преломлением
На рис. 14.51, а изображен глаз на высоте Н, смотрящий из воздуха на пруд с водой. Рыбка находится
на расстоянии L от глаза по горизонтали и на глубине D. В каком месте глаз видит рыбку, если свет в
воздухе распространяется вдвое быстрее, чем в воде?
14.11.2. Создание радуги
На рис. 14.51, б показан луч белого света, входящий в призму с внутренним углом 60°. Призма изго-
товлена из плавленого кварца. Вычислите и нарисуйте траектории красного, зеленого и синего ком-
понентов света при их прохождении внутри призмы и при выходе из нее. Будет ли видна радуга
14.11. Отражения и прозрачность
917
при выходе луча, если белый луч пропускается через пластину из плавленого кварца с параллельны-
ми стенками?
Рис. 14.51. Некоторые эксперименты с преломлением
14.11.3. Вывод направления преломленного луча
На рис. 14.52 предлагается разумный способ вывода направления t преломленного луча света, который
также пригодится для создания эффективного алгоритма (предложено Хекбертом [Heckbert, 104]).
Единичные векторы dir и m определяют плоскость, в которой лежат как отраженный, так и преломлен-
ный лучи. На рисунке показан также единичный круг, нарисованный в этой плоскости. Поскольку все
векторы единичные, длины их различных компонентов вдоль вектора m и перпендикулярно к нему чис-
ленно совпадают с синусами и косинусами углов 0, и 02.
О Покажите, что вектор, обозначенный на рисунке буквой п, равен
n = cos(0t) m + dir,
что его длина равна sin(01), так что нормированный вектор ия = n/sin^). Докажите при помощи
скалярных произведений, что вектор п лежит в плоскости векторов m и dir и перпендикулярен
вектору ш.
О Докажите, что
t = sin(02)u„- cos(02)m = —dir + — cos(0!)-cos(02) m
c* \j
и что это уравнение совпадает с уравнением (14.46).
О При помощи закона Снелла покажите, что
Рис. 14.52. Вывод направления t преломленного луча
918
Глава 14. Введение в трассировку лучей
14.11.4. Подпрограмма для вычисления направления преломленного луча
Напишите подпрограмму
Vector3transm1tD1rection(Vector3 m, Vector3 dlr, float cl, float c2)
которая вычисляет направление вектора t по заданным единичным нормальным векторам ш и dir и
скоростям света в двух средах.
14.11.2. Обработка преломления методом shade()
При трассировке лучей для сцен, содержащих прозрачные объекты, нам необходимо отслеживать сре-
ду, через которую проходит луч, поэтому мы можем определить значение с2/с{ для очередного пересече-
ния, где луч или выходит из текущего объекта, или входит в другой объект. Такое отслеживание проще
всего осуществить путем добавления к записи луча поля, содержащего указатель на объект, внутри ко-
торого движется луч.
Как метод shade() работает с лучами, находящимися внутри объектов? Ответ зависит от того, сколь-
ко свободы дается разработчику модели при описании сцен. Рассмотрим несколько «конструкторских
установок», которых должен придерживаться разработчик.
1-я конструкторская установка: не допускается взаимопроникновение
двух прозрачных объектов
Предположим для начала, что разработчик обещает никогда не допускать взаимопроникновения двух
прозрачных объектов. Так, нельзя помещать один стеклянный шарик внутрь другого или водяной куб
внутрь стеклянной коробки. В таком случае каждый луч или находится только в воздухе, или внутри
только одного объекта.
1. Пусть текущий луч в методе shadeO находится вне всех объектов и при соударении этого луча,
скажем, с объектом А мы находим этот объект А «достаточно прозрачным». Тогда метод shadeO
вычисляет направление t преломленного луча согласно уравнению (14.46), причем принимается
= 1 (для воздуха), а значение с2 берется из свойств объекта А. Соответственно создается новый
луч, его уровень рекурсии recurseLevel должным образом увеличивается на единицу, причем этот
луч содержит указатель на объект А. Затем подпрограмма shadeO вызывается рекурсивно и
в конечном счете возвращает цвет, который затем умножается на прозрачность объекта А
transparency и добавляется к цветам, накопленным до этого момента.
2. Предположим, с другой стороны, что текущий луч находится внутри некоторого объекта А и
соударяется с другой поверхностью. Поскольку это обязательно должна быть поверхность
объекта А (почему?), то луч выходит на воздух. (Подпрограмма может проверить, что луч
соударяется с тем же объектом, внутри которого он находится в текущий момент.) В силу того,
что луч находится внутри объекта, нормаль в точке соударения должна изменить знак: мы
хотим, чтобы она указывала внутрь той среды, куда движется луч. Когда луч находится внутри
объекта, обычно считается, что там объект не освещен и поэтому нет необходимости вычислять
локальные интенсивности фонового, диффузного и зеркального света. (Достаточно ли обосно-
ванно такое приближение?) Внутренняя стенка объекта Л может считаться «достаточно блестя-
щей», чтобы обеспечить путь отраженного луча обратно в объект А. (Будет ли разумно исполь-
зовать одно и то же значение «блеска» как для наружной, так и для внутренней поверхности
объекта?) В таком случае отраженный луч создается и испускается обычным способом. Что ка-
сается преломленного луча, то очевидно, что объект А является достаточно прозрачным (поче-
му?), поэтому значение скорости с( берется из свойств объекта А, а скорости с2 присваивается
единица (для воздуха). Если угол падения меньше критического, то испускается новый луч (его
указатель устанавливается в NULL, поскольку он теперь не находится внутри какого-либо объек-
та) и посылается по своему маршруту накапливать другие компоненты света.
14.11. Отражения и прозрачность
919
2-я конструкторская установка: взаимопроникновение прозрачных
объектов разрешается
Задача несколько усложнится, если мы разрешим разработчику модели размещать прозрачные объекты
на сцене так, чтобы они проникали друг в друга. На рис. 14.53, а показан стеклянный куб, в который вложе-
но несколько объектов: сферический кварцевый шарик, цилиндрическая «воздушная полость», запол-
ненный водой куб и частично вставленный стеклянный конус. В каждом из объектов свет распространяется
с различной скоростью. На рис. 14.53, б изображен в разрезе луч, проходящий через совокупность прозрач-
ных объектов. Этот луч входит в объекты и выходит из них в сложной последовательности. Рядом с
каждым отрезком луча показан список объектов, через которые проходит луч. Читая этот список вдоль
траектории луча, можно отметить сложную последовательность включений объектов в этот список и
исключений из него. Разумеется, это запутанная сцена, однако стоит посмотреть, во что нам обойдется
гарантия того, что подпрограмма shadeO всегда будет обрабатывать такие сцены корректно. (Тогда это
дополнительное свойство можно будет включать в трассировщик лучей или исключать из него).
шарик полость
Рис. 14.53. Несколько взаимопроникающих прозрачных объектов
Что же означает быть одновременно внутри двух прозрачных объектов, так что определенные точки
пространства «принадлежат» двум объектам? На стадии моделирования вы должны решить, какова
природа материала внутри каждой области стыка. Если зеленый мрамор полностью содержится в си-
нем мраморе, то имеет смысл сказать, что такая область стыка принадлежит зеленому мрамору, и задать
ее зеленой. Если же, однако, объекты проникают друг в друга частично, как на рис. 14.53, б, то отнюдь
не очевидно, свойства какого из них следует использовать в стыковочных областях. Дизайнер должен
задать каждому объекту приоритет, тогда в каждой области стыка будет доминировать объект с наи-
высшим приоритетом.
Один из способов обработки такой ситуации заключается в следующем: можно добавить к каждому
экземпляру объекта еще одно поле, содержащее приоритет этого объекта, а также дополнить указатель в
структуре данных Ray до списка указателей. Тогда для любого экземпляра луч находится внутри множества
объектов, определяемого списком указателей. Если этот список пуст, то луч находится вне всех объектов.
Тогда мы можем усовершенствовать тип Ray, как показано в листинге 14.16. (Список реализуется как мас-
сив, а не как связный список, для обеспечения копирования целого объекта при создании нового луча.)
Листинг 14.16. Усовершенствование типа Ray
class Ray{
public:
Point3 start:
Vectors dir;
int recurseLevel:
int row, col:
// to assist with screen extents
// для облегчения работы с экранными экстентами
int numlnside;
продолжение^
920
Глава 14. Введение в трассировку лучей
Листинг 14.16 (продолжение)
// number of objects on the list
// число объектов в списке
GeomObj* inside[8]:
// array of object pointers
// массив указателей объекта
RayO {recurseLevel = numinside = 0;}
// constructor
// конструктор
... other methods ...
// другие методы
Как такой «внутренний список» используется в методе shadeO? В любой момент времени луч нахо-
дится внутри некоторой совокупности объектов, определяемой этим списком. Когда луч соударяется с
поверхностью очередного объекта В, мы предпринимаем различные действия — в зависимости от того,
входит луч в объект В или выходит из него (это определяется состоянием поля i sEnteri ng в записи со-
ударений).
1. Предположим, что луч входит в объект В. Если В не является достаточно прозрачным, то мЬт
прекращаем испускание преломленных лучей, зато испускаем отраженный луч, если объект В
достаточно блестящ. Если же объект В достаточно прозрачен, то в качестве скорости мы при-
нимаем скорость света в объекте, обладающем наивысшим приоритетом в текущем списке. Если
высший приоритет имеет объект В, то в качестве с2 принимается его скорость света; в против-
ном случае с2 принимается равной сг После этого объект В добавляется в список. Затем создает-
ся новый проходящий луч, причем в него копируется текущий список (с добавленным в него
объектом В). Наконец, производится рекурсивный вызов метода shadeO.
2. Предположим теперь, что луч покидает объект В. Тогда в качестве скорости (\ принимается ско-
рость света того объекта из списка, который обладает наивысшим приоритетом. Далее объект В
удаляется из списка и в качестве скорости с2 принимается скорость света объекта с наивысшим
приоритетом из оставшихся в списке. Затем создается новый проходящий луч и в него копиру-
ется текущий «внутренний список». Наконец, производится рекурсивный вызов метода shade().
На рис. 14.54 приведена сцена, содержащая несколько прозрачных объектов. Хорошо видно откло-
нение луча света при его преломлении внутри прозрачного объекта.
Рис. 14.54. Сцены с преломлением света и без него
14.12. Составные объекты: логические операции с объектами
921
Практические упражнения
14 .11.5. Еще одна возможная конструкторская установка: если два прозрачных
объекта взаимопроникающие, то один из них должен содержать в себе другой
Предположим, что дизайнер обещает не располагать два прозрачных объекта так, чтобы они пере-
крывались частично: они либо не пересекаются, либо один из них полностью содержит в себе другой.
(В терминах теории множеств их пересечение или пусто, или совпадает с одним из этих объектов.) Рас-
смотрите изменения, к которым это приведет в логике метода shadeO. В частности, покажите, что обра-
ботка списков упростится: не понадобится никаких приоритетов, и список можно будет рассматривать
как стек. Опишите, как это делается.
14 .11.6. Прохождение света через цветное стекло
Рассмотрите добавление эффекта преломления света, проходящего через сферу из оранжевого стекла.
14.12. Составные объекты: логические операции
с объектами
До настоящего времени мы могли производить трассировку лучей только для ограниченного набора
форм: преобразованных сфер, плоскостей, конусов и т. д. Однако если бы нашелся способ объединить
эти простейшие формы в более сложные и разработать для них метод трассировки лучей, то с помощью
такого метода можно было бы обрабатывать намного более богатые и более интересные сцены. Такой
метод предлагается в рамках технологии, известной как конструктивная стереометрия (constructive
solid geometry — CSG). В соответствии с CSG произвольно сложные формы задаются с помощью
теоретико-множественных операций (они называются также логическими операциями) над простыми
формами [Ballard, 9, Mortenson, 143]. Такие объекты, как линзы, пустые аквариумы, а также объекты с
отверстиями, могут быть легко сформированы посредством объединения базовых форм, которые уже
рассматривались нами ранее. В разных работах такие объекты называют составными (compound),
логическими, или Булевыми (Boolean), или CSG-объектами. На составные объекты очень естественно
распространяются методы трассировки лучей: одной из наиболее сильных сторон метода трассировки
лучей считается именно то, что он естественным образом «подходит» для составных объектов.
Рассмотрим на примерах использование трех логических операторов: объединение (union), пересе-
чение (intersection), разность (difference). На рис. 14.55 показаны два составных объекта, построенных из
сфер. На рис. 14.55, а изображена линза, построенная как пересечение двух сфер. Это означает, что точ-
ка лежит внутри линзы тогда и только тогда, когда она лежит внутри обеих сфер. Событие «Линза L
является пересечением сфер и 52» символически записывается так:
L~S^S2. (14.48)
На рис. 14.55, б изображен сферический аквариум, образованный при помощи операции разно-
сти. Точка является разностью множеств Ап В (это обозначается как А - В), если она лежит в Л и не
лежит в В.
a
Рис. 14.55. Линза и аквариум
922
Глава 14. Введение в трассировку лучей
Применение операции разности аналогично удалению материала — вырезанию или отсечению. Наш
сферический аквариум определяется так:
Б = (51-52)-С. (14.49)
Сплошной шар Sj «опустошается» посредством удаления всех точек внутренней сферы S2, в резуль-
тате чего образуется сферическая пустотелая оболочка. Затем ее верхушка открывается путем удале-
ния всех точек конуса С.
Точка находится в объединении двух множеств А и В (обозначается ЛиВ), если она лежит или в А,
или в В, или в обоих вместе. Формирование объединения двух объектов аналогично их склеиванию. На
рис. 14.56 изображена ракета, созданная как объединение двух конусов и двух цилиндров:
R = (14.50)
Рис. 14.56. Объединение четырех примитивов
Конус Сх лежит на цилиндре С2. Конус С3, частично внедренный в С2, лежит на более толстом
цилиндре С4.
Практическое упражнение
14.12.1. Декомпозиция составных форм
Напишите уравнение, описывающее каждый из объектов, показанных на рис. 14.57, в терминах опера-
ций над множествами, приложенных к сферам, конусам, цилиндрам и прямоугольным параллелепипе-
дам. Обратите внимание, что для некоторых из объектов возможны различные выражения.
а б г
Рис. 14.57. Различные формы, сделанные из примитивов
14.12.1. Трассировка лучей для CSG-объектов
Как осуществляется трассировка лучей для объектов, являющихся логическими комбинациями более
простых объектов? Для начала рассмотрим вышеприведенные примеры. На рис. 14.58 показан луч, вхо-
дящий в сферы S] и S2 и выходящий из них в указанные на рисунке моменты времени. Таким образом,
луч находится внутри линзы L в промежуток времени от t3 до t2, момент соударения равен t3. Если линза
матовая, то для определения цвета линзы в точке соударения применяются знакомые нам правила зак-
рашивания. Если же линза зеркальная или прозрачная, то в нужных направлениях генерируются вспо-
могательные лучи, для которых и производится дальнейшая трассировка.
Аналогичная ситуация имеет место для аквариума на рис. 14.58, б. Луч 1 вначале соударяется с ак-
вариумом в момент tp наименьший из моментов времени, в которые он находится в 5(, но ни в 52, ни в С.
С другой стороны, луч 2 впервые соударяется с аквариумом в момент t5. Опять же, это наименьшее
значение времени, для которого луч находится в но ни в другой сфере, ни в конусе. Соударения
в более ранние моменты времени являются соударениями с компонентами аквариума, однако не с самим
аквариумом.
14.12. Составные объекты: логические операции с объектами
923
а 6
Рис. 14.58. Трассировка лучей для линзы и аквариума
Сведем эти идеи в алгоритм трассировки лучей для любого составного объекта [Roth, 177]. Рассмот-
рим два объекта Ли В совместно с лучом. Построим список моментов времени, в которые данный луч
входит в объект А и выходит из него, и упорядочим этот список по возрастанию моментов. Поскольку
объект трехмерный, моменты входа и выхода различны. Построим аналогичный список времени входа
и выхода для объекта В. Оба эти списка приведены на рис. 14.59. Более темным цветом на рисунке показан
каждый интервал времени между входом и выходом: на протяжении каждого темного интервала луч нахо-
дится внутри соответствующего объекта. Назовем множество значений t, при которых луч находится
внутри объекта, его внутренним множеством (inside set). Внутреннее множество определяется упорядо-
ченным списком перемежающихся моментов времени входа и выхода луча: (t); t.2,...), где t( — время входа,
t2 — время выхода, t3 — время входа, t4 — время выхода и т. д. Иногда такой список называют t-списком.
А л В ..............
А-В ...............х
В-А k
Рис. 14.59. Списки значений t взаимодействия луча с двумя объектами
Располагая внутренними множествами для луча с объектами А и В, найдем внутреннее множество
для этого же луча с составным объектом, построенным из А и В. При помощи операций АиВ, АпВ, А-В,
В-A можно образовать четыре новых объекта. Рассмотрим АиВ. Луч находится внутри объединения
объектов, если он находится внутри хотя бы одного из них. Поэтому внутреннее множество для объекта
АиВ является просто объединением индивидуальных внутренних множеств. Те же соображения при-
менимы и к остальным трем объектам: внутреннее множество для объекта АпВ является пересечением
индивидуальных внутренних множеств, внутреннее множество для объекта A-В является разностью
внутренних множеств объекта А и объекта В, аналогичный результат получается и для объекта В-А
(с перестановкой А и В). Вообще говоря, если обозначить через Т(А) и Т(В) внутренние множества двух
объектов Л и В, то
Т(А ор В) - Т(А) ор Г(В), (14.51)
где ор — один из Булевых операторов и, п, -. Таким образом, нахождение внутренних множеств состав-
ных объектов эквивалентно выполнению логических операций над списками интервалов.
924
Гла а -4. Введение в трассировку лучей
Отметим, что, хотя нас в конечном счете интересует только первый элемент внутреннего множе-
ства — время первого соударения, в процессе построения списков нам необходимо сохранять полные
списки, поскольку результирующее время первого соударения может располагаться глубоко внутри
одного из промежуточных списков. К счастью, в нашем распоряжении уже имеется «артиллерия» для
создания внутренних множеств внутри трассировщика лучей: в методе hit() для каждого типа фор-
мы в массиве inter.hit[] аккуратно сохраняются все случившиеся соударения луча с объектом, причем
уже отсортированные по времени. До сих пор мы использовали из этого списка только время первого
соударения. Однако поскольку мы начали трассировку лучей для Булевых объектов, нам понадобится
весь список.
Пример 14.12.1. Формирование внутренних множеств
Рассмотрим следующие два списка, представляющие собой внутренние множества:
А_список: 1.2 1.5 2.1 2.5 3.1 3.8
В_список: 0.6 1.1 1.8 2.6 3.4 4.0
Для построения четырех новых внутренних множеств применим приведенные выше правила (про-
верьте их правильность):
ЛиВ - 0.6,1.1,1.2,1.5,1.8,2.6,3.1,4.0;
ЛпВ = 2.1,2.5,3.4,3.8;
Л-В -1.2,1.5,3.1,3.4;
В-А - 0.6,1.1,1.8,2.1,2.5,2.6,3.8,4.0.
Для формирования новых внутренних множеств нам потребуется функция combineListsO, которая
принимает в качестве аргументов оператор и два t-списка и создает новый список t-значений в соответ-
ствии с одним из четырех Булевых операторов. Работу этой подпрограммы мы рассмотрим позднее.
Процесс трассировки лучей для составного объекта сводится к трассировке каждого из компонен-
тов такого объекта, созданию для каждого из них внутренних множеств с последующей компоновкой
этих множеств. Первое положительное время соударения из составного списка определяет точку пер-
вого соударения луча с составным объектом. Затем производится обычное закрашивание, включающее
испускание вспомогательных лучей, если поверхность блестящая или прозрачная.
Практическое упражнение
14.12.2. Найдите внутренние множества
Предположим, что для заданного луча объекты CuD имеют следующие t-списки:
С_список: 1.7 2.2 2.9 4.7 5.55
.О_список: 1.2 1.5 2.1 2.5 3.1 3.8 4.7 8.3
Найдите t-список для каждой из четырех возможных Булевых комбинаций объектов С и D.
14.12.2. Структура данных для Булевых объектов
Натуралисты знают: мир так плох,
Что блохи малые терзают сами блох,
А этих блохи меньшие грызут...
И нескончаем вечный этот зуд.
Джонатан Свифт (Jonathan Swift). *Из поэзии. Рапсодия*
Как следует представлять в программе составные объекты вида ((ЛпВ)-С)-В ? Поскольку состав-
ной объект всегда является комбинацией двух других объектов (возможно, тоже составных), напри-
мер, ObjjOp Obj2, то естественным описанием будет структура двоичного дерева. На рис. 14.60 приведе-
но дерево, соответствующее объекту (((В, uB2)uC2)u((S, -S2)-B3))-C,. Каждый внутренний узел
14.12. Составные объекты: логические операции с объектами
925
(кружок) представляет оператор, а каждый лист (квадратик)1 — элементарную форму. Дерево строит-
ся путем комбинирования поддеревьев, которые, в свою очередь, являются элементарными объектами
или поддеревьями («И нескончаем вечный этот зуд»). Когда узел содержит оператор разности, то он
понимается как «левое поддерево минус правое поддерево», а не наоборот.
Рис. 14.60. Составной объект и его CSG-дерево
Выражение для составного объекта может быть до некоторой степени перегруппировано без изме-
нения окончательной формы представляемого им объекта. Каждая перегруппировка приводит к отли-
чающемуся дереву (см. упражнения в конце раздела). Таким образом, для заданного составного объек-
та дерево не является единственным.
На данный момент все уже рассмотренные нами типы объектов, такие как Sphere и Cube, порождены
от класса Shape, который, в свою очередь, порожден от базового класса GeomObj. (Иерархия наследования
приводится в приложении В.) Естественно породить от класса GeomObj еще один новый класс Boolean
так, чтобы список объектов, являющийся списком класса GeomObj, мог «содержать в себе» объект типа
Boolean. В свою очередь, в объекте Boolean должно храниться двоичное дерево, поэтому мы включаем в
Boolеап указатели left и right на его дочерние поддеревья. Эти указатели должны указывать на объекты
GeomObj, поскольку в одних случаях они указывают на геометрические формы, а в других — на деревья
Boolean. Таким образом, первая часть класса Boolean выглядит так:
class Boolean: public GeomObj{
public:
GeomObj *left. *right:
// pointers to the children
// указатели на потомков
Boolean!) {left = right = NULL:}
// constructor
// конструктор
virtual bool hit(Ray Sr. Intersection Sinter):
...other methods...
// другие методы
}:
Поскольку объекты класса GeomObj имеют сферический и прямоугольный экстенты, то их имеют и
Booleans, что весьма полезно, так как объекты Booleans при трассировке лучей требуют много ресурсов и
хорошо все, что убыстряет эту трассировку. Мы разработаем специальную подпрограмму hit() для
класса Booleans, которая «знает», как искать пересечения луча с объектами этого класса; таким обра-
зом, мы вновь используем полиморфизм для упрощения кода. Действительно, поскольку подпрограм-
ма hit О должна оперировать с объединениями, пересечениями и разностями различным образом, то
1 Согласно тексту, на рис. 14.60, б буквы с индексами следует заключить в квадратики, что не сделано в оригинале (замечание для
художника).
926
Глава 14. Введение в трассировку лучей
полезно для трех видов Booleans образовать отдельные классы. В соответствии с этим сформируем классы
UnionBool, Intersect! onBool, DifferenceBool. Определение класса UnionBool имеет следующий простой вид:
class UnionBool : public Boolean{
public:
UnionBooK) {BooleanO:}
// constructor
// конструктор
virtual bool hitCRay Sr. Intersection Sinter):
...other methods...
};
Остальные определения почти идентичны. Каждому типу будет соответствовать своя подпрограм-
ма hit(), которая наилучшим образом приспособлена к его специфической природе.
Отметим, что класс Booleans не содержит собственного аффинного преобразования; оно имеется
только в классе Shapes. Вследствие этого преобразования Булева дерева могут производиться только в
его листьях. Такое конструкторское решение имеет как преимущества, так и недостатки, и в действи-
тельности некоторые системы моделирования и трассировщики лучей функционируют по-разному.
Для того чтобы понять это различие, рассмотрим рис. 14.61, а, на котором показано дерево для Булева
объекта, который имеет преобразование в каждом внутреннем узле, а также и в каждом листе. Влияние
каждого преобразования «ощущается» всеми узлами «ниже его» в его поддеревьях. Как разъясняется в
упражнениях, такое дерево геометрически эквивалентно дереву, изображенному на рис. 14.61, б (в том
смысле, что оба дерева представляют одну и ту же форму), где преобразования «стекли» к листовым
узлам и скомпоновались так, что каждый лист стал обладателем всего одного преобразования.
Одно из преимуществ сохранения во внутренних узлах явного вида преобразований заключается в
том, что дизайнер может независимо изменять отдельное преобразование глубоко внутри дерева, что-
бы корректировать форму CSG-объекта уже после его создания. При этом предоставляется больший
контроль за «плотностью прилегания» различных экстентов к Булевым объектам. С другой стороны,
заметным недостатком является низкая скорость трассировки лучей, поскольку при таком подходе луч
подлежит обратному преобразованию на каждом узле дерева, а не только на его листьях.
Рис. 14.61. Включение преобразований во внутренние узлы составных объектов
Задание Булевых объектов в SDL-файлах осуществляется путем использования одного из клю-
чевых слов union, intersection, difference, за которыми следует вначале спецификации «левого» гео-
метрического объекта, а затем — спецификации «правого» (эти объекты сами могут быть Булевыми).
В качестве примера приведем аквариум с рис. 14.55, б, форма которого задана выражением (St-S2)-C и
может быть описана посредством следующего кода:
! make a fish bowl
! создаем аквариум
14.12. Составные объекты: логические операции с объектами 927
rotate -90 1 О О
difference
difference
sphere
! outer sphere
! внешняя сфера
push scale 0.9 0.9 0.9 sphere pop
! inner sphere
! внутренняя сфера
push translate 0 0 1.3 rotate 180 1 0 0 cone pop
При первом преобразовании весь аквариум поворачивается вокруг оси х. Затем формируется раз-
ность между левым объектом (который сам является разностью двух сфер) и конусом. Поскольку пре-
образования, передаваемые в SDL, умножаются на текущее преобразование справа, и текущее преоб-
разование помещается в объект формы в момент своего создания, то преобразования автоматически
«стекают вниз по дереву».
Практические упражнения
14.12.3. Перегруппировка выражений для Булевых объектов
Поскольку при записи выражений составных объектов допускается некоторая гибкость, каждый такой
объект может быть представлен более чем одним деревом. Например, операции п и и коммутативны,
поэтому, в частности, АиВ = ВиА. Проверьте правильность следующих утверждений:
О (А - В) - С = А - (ВиС).
О (АиВ) - (AuQ = Аи(В - Q.
О (ЛиВ)п(ЛиС) = Лп(Ви0.
14.12.4. Как преобразования стекают вниз по Булевому дереву
Рассмотрите дерево на рис. 14.61, а, в котором преобразования поддерживаются в каждом внутреннем
узле.
О Докажите или опровергните утверждение, что геометрическая форма, представленная этим де-
ревом, является той же самой, что и для дерева на рис. 14.61, б. Используется ли в этом доказа-
тельстве то, что преобразования являются аффинными?
О Если преобразование Г. с рис. 14.61 представлено в однородных координатах матрицей Л£, то будет
ли результирующая матрица для куба с рис. 14.61, б равняться МаМ2М3М3 или М5М3М2М0?
Подсказка. Докажите, что в общем случае Т(А орг В) = Т(А) орг Т(В), где Т( ) — однозначное пре-
образование, А и В — множества точек, а орг — один из операторов п, и, -.
14.12.5. Почему трассировка лучей автоматически обрабатывает объединения?
Объясните, почему трассировка лучей для объединения ЛиВ двух объектов А и В (вне зависимости от
их взаимопроникновения) эквивалентна их индивидуальной трассировке в сцене?
14.12.6. Сцена как единый CSG-объект
Рассмотрите аргументы «за» и «против» моделирования всей сцены как единого составного объекта в
сравнении с использованием списка более простых (но, возможно, также составных) объектов.
14.12.3. Пересечения лучей с Булевыми объектами
Нам необходимо разработать метод hit О, работающий с каждым типом Булевых объектов. Этот метод
должен формировать внутреннее множество для луча с левым поддеревом, затем с правым поддеревом,
после чего корректно объединять эти множества. Скелет такого метода hit() приведен в листинге 14.17
для случая операции пересечения. Прежде всего производятся тесты с экстентами на предмет наличия
досрочного выхода (это рассматривается в следующем разделе). Затем вызывается соответствующая
928
Глава 14. Введение в трассировку лучей
подпрограмма hi t ()для левого поддерева (которое также может быть Булевым), и если луч не проходит
мимо этого поддерева, то формируется список соударений 1 ftlnter. В случае прохождения луча мимо
подпрограмма hit() немедленно возвращает false («досрочный выход»), поскольку для соударения с
пересечением объектов луч должен соударяться с обоими поддеревьями. После этого формируется вто-
рой список соударений nt Inter.
Листинг 14.17. Скелет метода hit() для пересечения с Булевым объектом
bool IntersectionBool:: hitCRay &r. Intersection Sinter)
{
Intersection 1ftlnter. rtlnter:
if(ray misses the extents') return false:
// луч проходит мимо экстентов
i fС(!1eft->hit С г.1ftlnter))11(!right->hit(r,rtlnter)))
return false;
// early out
// досрочный выход
таке the combined list: place it in inter
11 создаем составной список и помещаем его в inter
return(inter.numHits > 0);
// true if inter is not empty
// true, если inter не пуст
}
Для классов Uni onBool и DifferenceBool код аналогичен данному. В методе Uni onBool :: hit() дваспис-
ка соударений формируются с использованием оператора
i f(С!left->hit(г.1ftlnter))&&(!right->hit Cr.rtlnter)))
return false:
в котором предусмотрен досрочный выход только в случае, если пусты оба списка соударений. Для мето-
да DifferenceBool :: hit() используется код:
if((!left->hit(r.1ftlnter)) return false;
// a miss
// прохождение мимо
if(!right->hit(r.rtlnter))
{
inter = Iftlnter:
return true;
}
В этом коде досрочный выход происходит в случае, если луч проходит мимо левого поддерева, по-
скольку тогда он проходит и мимо всего объекта. Если же имеются соударения с левым поддеревом, но
не имеются с правым, то окончательный список будет таким же, как и для левого поддерева. (Почему?)
Компоновка t-списков
Компоновка t-списков является сложной, но логичной операцией. Рассмотрим приведенные на рис. 14.62, a
два примера списков соударений L и R (соответственно для левого и правого поддеревьев). Назовем для
краткости левый список L[] вместо leftInter.theHit[]; аналогично для правого списка. С этой же целью
не показаны поля hitObject и surface. Список L фиксирует для своего объекта восемь соударений, а спи-
сок R — пять. В каждом списке содержатся положительные моменты соударения, упорядоченные по вре-
мени, причем входное поле нулевого элемента показывает, что делает луч при первом соударении: вхо-
дит в объект или выходит из него (его время положительно, то есть объект находится «перед глазом»).
Поскольку все объекты объемные, значения entering после нулевого элемента чередуются.
14.12. Составные объекты: логические операции с объектами
929
.1 .3 .4 .5 .7 .8 .9 1.1
LQ -Ч--------<--Ъ—I------->—4----> -----I
RQ
.2 .35 .6 .75 .84
4---» <---Н—<—
.3,35 .6 .7 .84 .9 1,1
Объединение > <—< > <
.2 .3 .7 .75 .9 1,1
Разность ------->—<-------------HP----> I
.1 .2 .4 .5 .75 .8
Объединение —+—4---------н—4--------ы-------------
б
Рис. 14.62. Пример пересекающихся записей
Компоновка этих списков осуществляется посредством их просмотра, в процессе которого на каждом
шаге отмечается, которому из «очередных» элементов из двух списков соответствует меньшее время со-
ударения, а также определяется, находится ли луч перед этим очередным соударением внутри данного
объекта или вне его. Эти фрагменты информации компонуются способом, соответствующим используе-
мому оператору: объединение {union), пересечение {intersection), разность (difference). На рис. 14.62, б при-
веден результирующий t-список после компоновки — для каждого из Булевых операторов.
Рассмотрим специфический пример логики, используемой при компоновке списков. Предположим,
что оператор — difference, а момент времени — непосредственно перед следующим временем соударе-
ния, причем луч находится внутри левого объекта и вне правого, вследствие чего он должен быть внут-
ри разности этих объектов. Следующее время соударения исследуется в каждом из списков; предполо-
жим, что время из правого списка оказалось меньшим. Это означает, что сразу после этого следующего
времени соударения луч будет находиться внутри правого объекта, поэтому сейчас он должен быть вне
разности объектов. В данном примере состояние луча в составном объекте изменяется из «внутреннос-
ти» во «внешность».
Состояние луча (внутри или вне объекта он находится в текущий момент времени) при прохожде-
нии его через поддеревья мы отслеживаем с помощью следующих переменных:
bool Iftlnside:
// true if ray is inside left object:
// true, если луч внутри левого объекта
bool rtlnside:
// true if ray is inside right object;
// true, если луч внутри правого объекта
bool comblnside:
// true if ray is inside combined object:
// true, если луч внутри составного объекта
Существуют и состояния луча между соударениями — то есть до рассмотрения следующего соуда-
рения. Начальное значение переменной Iftlnside задается в соответствии с тем, входит ли луч в левый
объект или выходит из него, то есть в соответствии со значением L[0]. 1 sEnteri ng. Говоря более конкретно,
величина Iftlnside равна false, если при первом соударении имеет место вхождение луча (поскольку до
этого соударения луч должен быть снаружи), и равна true, если первое соударение — выход. Поэтому
можно инициализировать величину 1 ftInside как !L[0]. isEntering. Аналогично осуществляется инициа-
лизация rtlnside. Затем величина comblnside находится как логическая комбинация 1 ftInside и rtlnside:
если оператор — union, то comblnside равна true в том случае, если равны true 1 ftInside, rtlnside или оба
вместе. Это может быть описано при помощи логических операторов
comblnside « Iftlnside || rtlnside
Зи Ф. Хилл
930
Глава 14. Введение в трассировку лучей
Если оператором является intersection, то используется формула
comblnside = Iftlnside && rtlnside.
Для оператора difference формула имеет вид
comblnside - Iftlnside && Irtlnside.
Далее алгоритм движется по обоим спискам L[] и R[], на каждом шаге фиксируется наименьшее из
времен соударения, используемое для обновления значений 1 ft Inside, rtlnside, comblnside. Если в какой-либо
точке значение comblnside изменяется, то более позднее событие соударения добавляется в список С[].
Когда список L[] или R[] окажется исчерпанным (то есть когда в нем просмотрено последнее время
соударения), то с оставшимся неисчерпанным списком можно проделать следующее:
О В случае пересечения неисчерпанный список игнорируется.
О В случае объединения неисчерпанный список просматривается и его события соударения добав-
ляются как обычно.
О В случае разности: если неисчерпанным оказался левый список, то он просматривается, и его со-
бытия соударения добавляются как обычно. Если же неисчерпанным является правый список, то
он игнорируется.
В листинге 14.18 приведен псевдокод для метода DifferenceBool :: hit(), чтобы проиллюстрировать
процесс компоновки списков.
Листинг 14.18. Метод hit() для класса DifferenceBool
bool DifferenceBool:: hitCRay Sr. Intersection Sinter)
{
Intersection Iftlnter. rtlnter:
1ftInter.numHits - rtlnter.numHits - 0:
// initially
// начальные значения
if(ray misses extents) return false:
// луч проходит мимо экстентов
// early out?
// досрочный выход?
if(!left->hit(г.1ftInter))return false:
GeomObj* leftobject - Iftlnter.hit[OJ.hitObject:
// may need this later
// это может понадобиться позднее
if(!right->hit(г.rtlnter))
{
inter - Iftlnter:
// right tree has no effect
// правое дерево не дает эффекта
return true:
// early out
// досрочный выход
}
// combine the lists. Initial states:
// компонуем списки. Начальные состояния:
bool Iftlnside = '(Iftlnter.hit£O].isEntering):
// initial insideness
// начальная «внутренность»
bool rtlnside = !(rtlnter.hit[O].isEntering):
bool comblnside = Iftlnside SS 'rtlnside
// for the difference
14.12. Составные объекты: логические операции с объектами
931
// для разности
// go through lists until one has been consumed
// просматриваем списки, пока один из них не исчерпается
int iL - 0. iR - 0. iC - -1:
Hitinfo nextHit:
while((iL < Iftlnter.numHits) && (iR < rtlnter.numHits))
{
// while both lists are nonempty
// пока оба списка не пусты
bool newlnside:
// the new result state
// новое результирующее состояние
if(lftInter.hit[iL],hitTime <- rtInter.hit[iR].hitTime)
{
nextHit - Iftlnter.hit[iL++];
// grab left item;
// берем левый элемент
Iftlnside - !Iftlnside;
// state is reversed by hit
// при соударении состояние изменяется на противоположное
newlnside - Iftlnside && irtlnside;
// state after the hit
// состояние после соударения
leftobject - nextHit.hitObject;
// needed when exiting right tree
// понадобится при выходе из правого дерева
if(newlnside !- comblnside)
// has result state changed?
// изменилось ли результирующее состояние?
{
inter,hit[++iC] - nextHit:
// put hit data on combined list
// помещаем данные о соударении в объединенный список
comblnside - newlnside:
inter.hit[iС].isEntering - comblnside;
}
else
// smaller hit time is on right list
// меньшее время соударения находится в правом списке
{
nextHit - rtInter.hit[iR++]:
// grab right item; inc to next
// берем правый элемент; переходим к следующему
rtlnside - irtlnside;
// reverse the inside-ness
// изменяем внутреннее состояние на противоположное
newlnside - Iftlnside && irtlnside:
// new combined state
// новое состояние составного объекта
if(newlnside !- comblnside)
продолжение#
932
Глава 14. Введение в трассировку лучей
Листинг 14.18 (продолжение)
// has result state changed?
// изменилось ли результирующее состояние?
{
inter.hit[++iC] - nextHit:
combinside - newlnside:
inter.hittiC].isEntering - combinside:
if(comblnside)
{
nextHit. hitNormal .flipO:
// reverse normal on right object
// инвертируем нормаль на правом объекте
inter.hit[iС].hitObject - leftobject:
// point to left object
// указываем на левый объект
} Z
}
}
// end else
// конец случая else
}
// end of for - while both lists nonempty
// конец цикла for - пока оба списка не пусты
whiledL < 1 ftlnter.numHits)
// gobble rest of left list
// «расправляемся» с остатком левого списка
{
nextHit - 1 ftlnter.hit[iL++]:
Iftlnside - !Iftlnside;
inter.hit[++iC] - nextHit:
inter.hittiC].isEntering - Iftlnside:
}
inter.numHits - iC + 1:
return (inter.numHits > 0);
}
Отметим, что при компоновке списков необходимо следить за тем, чтобы в каждую новую запись
hit[] была помещена вся необходимая информация. В частности, должны быть правильно заполнены
поля isEntering и hitObject, поскольку если соударение является первым соударением луча, то мы будем
искать свойства соударения с поверхностью в самом hitObject. Когда соударение при выходе из правого
объекта вызывает вхождение луча в сам объект, мы должны быть уверены, что информация об этом
соударении указывает на левый объект, поэтому то, что мы видим в «дыре», является свойствами левого
объекта.
Кроме того, необходимо убедиться в том, что логика метода hit() для CSG-объектов правильно ра-
ботает в тех случаях, когда объект является прозрачным и луч проходит внутри Булева объекта (когда
луч, например, проходит через бокал мартини). Проверьте, что для вышеупомянутого объекта разно-
сти в список соударений помещается правильная информация о соударении, даже когда лучи начина-
ются внутри объекта.
На рис. 14.63 показаны черно-белые примеры различных составных объектов, для которых трасси-
ровка лучей была произведена в соответствии с вышеприведенной технологией. Попытайтесь выделить
отдельные формы, из которых был сформирован каждый Булев объект.
14.12. Составные объекты: логические операции с объектами
933
Рис. 14.63. Черно-белые примеры трассировки лучей для составных объектов
Практические упражнения
14.12.7. Имитация алгоритма вручную
Сымитируйте вручную алгоритм компоновки списков из листинга 14.17 — для списков из примера 14.12.1.
14.12.8. Написание методов hit()
Реализуйте методы hit() для классов UnionBool и Intersect!onBool. Каждый из них следует наилучшим
образом приспособить к требованиям соответствующего Булева оператора.
14.12. 4. Построение и использование экстентов
для CGG-объектов
Нам осталось рассмотреть проблему создания проекционных, сферических и прямоугольных экстентов
для CSG-объектов. На этапе предварительной обработки производится просмотр дерева CSG-объекта,
для каждого его узла строятся экстенты и записываются внутри этого узла. Позднее, в процессе трасси-
ровки лучей, луч может тестироваться относительно каждого встречающегося экстента, при этом воз-
можен потенциальный выигрыш в виде «досрочного выхода» из процесса пересечения, если становит-
ся ясно, что соударение луча с объектом невозможно. Эта процедура может уменьшить расход ресурсов
при компоновке списков далее вверх по CSG-дереву.
Тестирование экстентов производится, как обычно, внутри метода hi t () класса данного объекта, как
показано в листинге 14.17. Если же луч соударяется с экстентом для заданного узла дерева, то его пере-
сечение с левым и правым поддеревьями осуществляется обычным способом.
Построение прямоугольных экстентов
Как целесообразно определить прямоугольный экстент для CSG-узла? (Мы имеем в виду, конечно, пря-
моугольные экстенты в мировых координатах, поскольку у Булева объекта версия в базовых координатах
отсутствует.) Предположим, что узел представляет объект А орг В, где А и В — формы, а орг — один из
Булевых операторов. Прямоугольный экстент (бокс) для этого объекта должен охватывать весь объект,
так что мы должны быть уверены, что луч проходит мимо объекта, если он проходит мимо экстента.
Форма объекта может быть достаточно сложной (например, пересечение кругового тора с деформиро-
ванным кубом), так что будет очень трудно найти самый прилегающий выровненный параллелепипед
автоматически, без большого объема вычислений.
Рассмотрим простейший подход и создадим прямоугольный экстент объекта L орг R из прямоуголь-
ного экстента £(L) объекта L и прямоугольного экстента £(7?) объекта R. Для различных операторов
прямоугольный экстент определяется различно:
934
Глава 14. Введение в трассировку лучей
1. Union (объединение). В качестве прямоугольного экстента берем выровненный параллелепи-
пед, охватывающий одновременно объекты Е(Е) и E(R). Это эквивалентно E(E(L)uE(R)). (Во-
просы. Всегда ли данное выражение равно E(LuR)? Не будет ли эффективнее тестировать объек-
ты E(L) и E(R) раздельно? Если луч проходит мимо обоих раздельных экстентов, то обязательно
ли он проходит мимо объекта IajR?)
2. Intersection (пересечение). Возьмем в качестве прямоугольного экстента пересечение объектов
Е(Е) и E(R). Пересечение двух выровненных параллелепипедов всегда является также выровнен-
ным параллелепипедом, причем его компоненты (left, top, right, bottom, front, back) вычисляются
просто. (Как?) (Вопрос. Вы уверены, что луч пройдет мимо объекта L(\R, если он проходит мимо
объекта E(Z)n£(7?)?) Экстент вида E(L)rE(R) вероятнее всего будет достаточно плотно приле-
гать к объекту, если экстенты объектов £ и R являются плотными. (Почему?)
3. Difference (разность). В качестве прямоугольного экстейта возьмем просто Е(Е). Это подход с
большим запасом, поскольку мы отказываемся от использования преимуществ для того случая,
когда разность L-R значительно меньше, чем объект L: может быть, объект R отсекает у L очень
много пространства. Однако выполнять более подробный анализ было бы слишком дорого.
Формирование прямоугольных экстентов осуществляется рекурсивно, потому что прямоугольный
экстент Булева дерева может быть образован из прямоугольных экстентов его дочерних узлов. Как рас-
сматривалось ранее, для форм прямоугольный экстент может быть сформирован без рекурсии, посред-
ством нахождения «облака точек» для объекта в мировых координатах и построения вокруг этого обла-
ка выровненного параллелепипеда. Для каждого типа формы существует свой метод makeBoxExtentO.
Каждый такой метод строит прямоугольный экстент, сохраняет его вместе с объектом и возвращает этот
экстент для использования другими объектами. Например, для класса UnionBool можно использовать
следующую подпрограмму:
Cuboid UnionBool :: makeBoxExtentO
{
Cuboid 1ft - left->makeBoxExtent():
Cuboid rt - right->makeBoxExtent():
Cuboid tmp:
tmp.left - min(lft.left.rt.left):
// form the union
// формируем объединение
tmp.top - max(lft.top.rt.top);
etc. for the other four values
// и так далее для остальных четырех значений
worldBoxExtent - tmp:
// store it in the object
// сохраняем его в объекте
return tmp;
На предварительном этапе можно было бы вызывать метод makeBoxExtentO для каждого объекта из
списка объектов. Когда же этот метод вызывается для Булева объекта, то он создает и сохраняет прямо-
угольные экстенты как для корневого узла дерева, так и для каждого внутреннего узла.
Создание сферических экстентов
Сферические экстенты в мировых координатах строятся примерно таким же способом, как и прямо-
угольные. Как уже обсуждалось ранее, для форм определяется облако точек в мировых координатах,
а сферический экстент — это сфера, наиболее плотно охватывающая это облако. Что касается Булевых
объектов, то нам необходимо определиться, как формировать сферический экстент для объединения,
разности и пересечения двух объектов.
14.13. Резюме
935
Для случая разности все просто: используется сферический экстент самого левого объекта. Такой
экстент не будет очень плотным, но он подойдет. Можно было бы принять такой же выбор для пересе-
чений, поскольку в случае пересечения очень трудно вычислить истинный сферический экстент. Для
объединений, возможно, проще всего объединить облака точек для левого и правого объектов, после
чего образовать вокруг получившегося облака одну сферу.
Создание проекционных экстентов
Есть сильное искушение использовать для CSG-объектов проекционные экстенты ввиду низкой стои-
мости трассировки лучей для таких экстентов. Проекционный экстент можно было бы построить для
каждого узла CSG-объекта тем же способом, как мы строили прямоугольные экстенты: проекционный
экстент узла формируется как комбинация проекционных экстентов левого и правого подобъектов.
Обозначим через P(pbject) проекционный экстент объекта object, после чего, в соответствии с вышеиз-
ложенными правилами, получим:
P(IxjR) - P(P(L)vP(R)),
P(Lr\R) - P(L)nP(R),
P(L-R) - P(L).
Как и прежде, у каждого класса имеется свой метод makeProjectionExtentO.
14.13. Резюме
Трассировка лучей представляет собой концептуально простой и единообразный метод создания в выс-
шей степени реалистичных изображений. Осуществляется трассировка (отслеживание) большого коли-
чества нужных лучей света для сцены, составленной из различных объектов, каждый из которых анали-
зируется на предмет того, сколько света он возвращает в глаз наблюдателя. В результате использования
этого механизма становятся возможными многие визуальные эффекты. В дополнение к обычной имита-
ции фонового, диффузного и зеркального компонентов света трассировка лучей позволяет относительно
легко имитировать тени, отражения от зеркальных поверхностей, а также прохождение преломленного
света сквозь прозрачные объекты. Трассировка лучей предоставляет также естественный способ нало-
жения на объекты как дву-, так и трехмерных текстур.
Ядром применения метода трассировки лучей является подпрограмма, определяющая пересечения
между лучом и объектом. Для создания изображения с высоким разрешением испускается огромное
количество лучей, причем многие из этих лучей порождают вторичные лучи, вследствие чего на нахож-
дение пересечений тратится много компьютерного времени. Поскольку каждый луч тестируется отно-
сительно каждого объекта сцены, время, необходимое для трассировки лучей, возрастает приблизитель-
но пропорционально сложности этой сцены. При разумном использовании экстентов удается добиться
множества «досрочных выходов», что освобождает от необходимости проводить для многих объектов
более полный тест на пересечение и значительно убыстряет процесс трассировки лучей.
Трассировка лучей автоматически решает задачу удаления невидимых поверхностей, поскольку
моменты соударения различных объектов с лучом являются прямой мерой их расстояния от наблюда-
теля. Таким образом, объект с наименьшим временем соударения является ближайшим и не может быть
заслонен никаким другим объектом.
Тот же самый принцип может быть с легкостью применен для вычисления теней: если между инте-
ресующей нас точкой и источником света расположен какой-нибудь объект, то такая точка находится в
тени этого объекта по отношению к данному источнику света. Следовательно, определение такого зате-
нения эквивалентно решению следующего вопроса: существует ли какой-нибудь объект, имеющий с
«щупом теней» время соударения в диапазоне от нуля до единицы.
Некоторые формы легко поддаются трассировке лучей, поскольку определение их пересечения с
лучом эквивалентно решению линейного или квадратного уравнения. Типичными примерами таких
форм являются плоскости, сферы, цилиндры и конусы. Разработчик сцены начинает с базовых версий
936
Глава 14. Введение в трассировку лучей
каждой из этих фигур и приводит их с помощью аффинного преобразования к нужным размерам, ори-
ентации и расположению. В результате сферы могут превратиться в эллипсоиды, кубы — в параллеле-
пипеды и т. д., что расширяет класс объектов, фигурирующих в сцене. Также нетрудно смоделировать
любой выпуклый полиэдр и произвести с ним трассировку лучей, поскольку его внутренняя часть яв-
ляется просто пересечением некоторого числа полупространств.
Лучи — вещь простая и работать с ними легко, поэтому не составляет труда произвести испускание
новых лучей из заданной стартовой точки в некотором новом направлении и затем проверить, с какими
объектами сцены они соударяются. Это обеспечивает прямую возможность накапливать составляющие
света, возникающие при его отражении от блестящих поверхностей и при его прохождении сквозь про-
зрачные предметы. Реализация этих технологий требует незначительных программистских усилий.
Применение методов трассировки лучей для CSG-объектов радикально увеличивает разнообразие
сцен, для которых возможна визуализация. Можно моделировать и производить трассировку в высшей
степени сложных форм. Внутренняя логика алгоритма трассировки лучей для CSG-объектов проста и
легко реализуема в программах.
Трассировка лучей на сегодня является одним из наиболее мощных методов компьютерного синте-
за изображений. Хотя в силу огромного объема необходимых вычислений этот метод является одним
из наиболее медленных методов генерирования изображений, получающиеся картинки обладают сте-
пенью реалистичности, трудно достижимой при применении других технологий.
14.14. Тематические задания
Тематическое задание 14.1. Эмиссионный трассировщик
Уровень сложности II.
Напишите и выполните приложение, осуществляющее трассировку лучей для сцены, описанной на
языке SDL. Данный трассировщик лучей должен быть способен обрабатывать излучающие объекты,
испускающие свой собственный свет. (Тогда при трассировке лучей нет необходимости оперировать с
фоновым, диффузным и зеркальным компонентами света.) Ваша подпрограмма должна корректно про-
изводить трассировку лучей по крайней мере для сферы, конического цилиндра, куба, квадрата и плос-
кости. Другие формы, описанные в файле SDL-сценария, просто игнорируются. До начала выполнения
трассировки рисуется эскиз сцены с помощью метода Scene::drawOpenGLO.
Для управления работой программы используются нажатия клавиш. Клавиши «1», «2», «4», «8» за-
дают размер пиксельных блоков, рассмотренных в разделе «Организация трассировщика луча в прило-
жении» данной главы, которые позволяют экспериментировать с различными разрешениями. С помо-
щью других клавиш изменяется положение и ориентация камеры.
Кроме того, создайте сцену, содержащую несколько «переключателей» («jacks») и «восьмерок»
(«octos»), причем организуйте все так, чтобы для этой сцены была возможна трассировка лучей. Пере-
ключатель состоит из трех взаимно перпендикулярных «стержней», причем стержень является удли-
ненной сферой с маленькой сферой на конце. Восьмерка состоит из маленьких сфер, расположенных в
шести вершинах октаэдра, а 12 ребер между этими вершинами сделаны из удлиненных сфер.
Тематическое задание 14.2. Усовершенствованный
трассировщик лучей
Уровень сложности II — на основе эмиссионного трассировщика из тематического задания 14.1.
Усовершенствуйте трассировщик лучей из тематического задания 14.1 так, чтобы он мог правильно
обрабатывать фоновый, диффузный и зеркальный (по Фонгу) компоненты. Не нужно обрабатывать
отражение, преломление света, а также затенение. Должна корректно производиться трассировка лучей
для базовых примитивов, а также для сеток, представляющих выпуклые полиэдры. Как и в предыду-
щем случае, перед началом трассировки лучей рисуется эскиз сцены.
14.14. Тематические задания
937
В порядке дополнительного контроля напишите код так, чтобы пользователь мог с помощью мыши
указывать прямоугольную область на дисплее, после чего производилась, бы трассировка лучей для ука-
занной области с полным разрешением (размер блока =1). Это удобно для пользователя, которому нуж-
на быстрая трассировка лучей, а полное разрешение требуется лишь для ограниченных областей сцены.
Тематическое задание 14.3. Реализация теней
при трассировке лучей
Уровень сложности I — на основе трассировщика лучей из тематического задания 14.2.
Усовершенствуйте трассировщик лучей из тематического задания 14.2 так, чтобы он правильно ото-
бражал тени.
Тематическое задание 14.4. Использование экстентов
для ускорения трассировки лучей
Уровень сложности II — на основе трассировщика лучей из тематического задания 14.3.
Реализуйте применение сферических, прямоугольных и проекционных экстентов в рамках трасси-
ровщика лучей из тематического задания 14.3 и определите относительное ускорение, которое обеспе-
чивается использованием каждого из этих типов экстентов. Предоставьте пользователю возможность
включать и выключать каждый тип экстентов посредством нажатия назначенных клавиш и видеть вре-
мя, необходимое для каждой трассировки лучей.
Тематическое задание 14.5. Трассировка лучей с ЗО-текстурами
Уровень сложности II — на основе трассировщика лучей из тематического задания 14.2.
Скорректируйте усовершенствованный трассировщик лучей из тематического задания 14.2 так, чтобы
он поддерживал отображение некоторых 313-текстур, в том числе шахматный узор, древесную текстуру
и мрамор. Пользователь должен иметь возможность выбирать тип текстуры посредством нажатия раз-
личных клавиш, причем все объекты сцены должны визуализироваться с выбранной текстурой.
Укажите способ расширения SDL и метода Scene :readO так, чтобы в SDL-файле можно было задавать
параметры и прикреплять их к последовательно определяемым объектам. Используйте эти параметры
для выбора текстуры, из которой создается каждый из объектов, и для спецификации нескольких чис-
ленных параметров, присутствующих в определении этой текстуры. Например, строки на языке SDL
parameter 3 12.6 -91
cube
прикрепляют к кубу три указанных параметра и приписывают этому объекту текстуру номер 3.
Тематическое задание 14.6. Сглаживание
Уровень сложности II — на основе трассировщика лучей из тематического задания 14.2.
Скорректируйте усовершенствованный трассировщик лучей из тематического задания 14.2 так, что-
бы он при трассировке лучей производил сглаживание сцены. Для каждого основного луча он должен
испускать N лучей в слегка различных направлениях и усреднять цвета, возвращающиеся вдоль этих
лучей. Поэкспериментируйте с различными величинами «дрожания» направлений этих лучей, а также
с различными значениями N.
Тематическое задание 14.7. Трассировка лучей
для других примитивов
Уровень сложности III — на основе трассировщика лучей из тематического задания 14.2.
Изучите статью Джима Каджийа [Kajiya, 120] о трассировке лучей для различных форм, таких как
призмы, фрактальные горы и поверхности вращения. Реализуйте технологию по меньшей мере для
938
Глава 14. Введение в трассировку лучей
фрактальных гор и расширьте язык SDL так, чтобы он воспринимал ключевое слово mountain и следую-
щие за ним несколько параметров, определяющих природу трассируемой горы.
Тематическое задание 14.8. Двумерный трассировщик
лучей для работы с преломлением
Уровень сложности II.
Поскольку в формуле (14.46) для направления преломленного света t используются только скаляр-
ные произведения, она справедлива как для двумерных, так и для трехмерных векторов. Напишите и
выполните программу, генерирующую изображения, подобные представленным на рис. 14.50. Пользо-
ватель задает показатель преломления и угол падения, после чего программа рисует падающий и пре-
ломленный лучи.
Тематическое задание 14.9. Отраженный и преломленный свет
Уровень сложности III — на основе трассировщика лучей из тематического задания 14.2.
Усовершенствуйте трассировщик лучей из тематического задания 14.2 так, чтобы он правильно об-
рабатывал как отражение света от блестящих поверхностей, так и преломление света, проходящего че-
рез прозрачные объекты. Для исследования основных свойств преломления света поэкспериментируй-
те с различными прозрачными формами и различными показателями преломления.
Тематическое задание 14.10. Трассировка
Булевых комбинаций объектов
Уровень сложности III — на основе трассировщика лучей из тематического задания 14.2.
Скорректируйте усовершенствованный трассировщик лучей из тематического задания 14.2 так, что-
бы он правильно производил трассировку лучей для Булевых объектов любой сложности. Создайте
интересную сцену из объектов, состоящих из:
О объекта с цилиндрическим отверстием;
О сферической линзы Аг\(В - С) (сформированной как пересечение двух сфер),
О объекта, заданного формулой Аг>(В - С), где А, В, С — формы.
Сделайте так, чтобы сквозь отверстие и через линзу можно было видеть другие объекты.
14.15. Дополнительная литература
В книге «Введение в трассировку лучей» («Ап Introduction to Ray Tracing») под редакцией Эндрю
Гласснера [Glassner, 5] содержится превосходная коллекция обзорных работ, в которых используются
важнейшие алгоритмы трассировки лучей, а также методы убыстрения процесса трассировки. В работе
Уатта и Уатта [Watt, 209] нарисована широкая перспектива трассировки лучей и применяемых в ней
методов. На дискете, прилагаемой к книге Линдлея [Lindley, 132], приводится множество примеров про-
граммного кода.
А Графический инструментарий:
получение OpenGL
Большая часть программного кода, рассматриваемого в этой книге, основана на использовании OpenGL
в качестве интерфейса прикладного программирования (Application Programming Interface — API).
В данном приложении мы опишем, как получить те средства OpenGL, которые вам потребуются при
построении собственных приложений, использующих OpenGL.
Al. Получение и инсталляция OpenGL
Не требуется никаких затрат — ни времени, ни денег — для получения необходимого программного обеспе-
чения OpenGL для почти всех используемых в настоящее время компьютерных платформ. Давайте посмот-
рим, как получить доступ к этому программному обеспечению для каждой из основных платформ. Кроме
того, огромное количество дополнительной информации относительно OpenGL доступно через Интернет1.
Информационные архивы для OpenGL
Интернет-сайт http://www.opengl.org/ является богатейшим источником информации общего характера
по OpenGL, а также отправной точкой при загрузке программного обеспечения. Множество информа-
ции доступно на сайте фирмы Silicon Graphics: http://www.sgi.com/software/opengl/manual.html. Интер-
нет-сайт этой книги (см. введение) содержит дополнительную информацию и ссылки на тему OpenGL.
Превосходная книга Мейсона By, Джеки Нейдер и Тома Дэвиса «OpenGL: Руководство пользователя»
{OpenGL Programming Guide, by Mason Woo, Jackie Neider, and Tom Davis (1999)), вышедшая в настоя-
щее время третьим изданием, является основным источником информации по использованию OpenGL
и содержит ряд указаний по получению и инсталляции необходимого математического обеспечения.
Что вам потребуется
Для любой системы следует начать с хорошего компилятора C/C++ и установить соответствующие
заголовочные файлы и библиотеки OpenGL. Для использования OpenGL в том виде, как он описан в дан-
ной книге, требуются следующие три библиотеки и связанные с ними файлы:
О OpenGL (основной инструментарий API);
О GLU (OpenGL Utility Library — библиотека утилит);
О GLUT (OpenGL Utility Toolkit — инструментарий утилит OpenGL, оконный инструмент, под-
держивающий системные операции).
1 WWW-адреса являются правильными на момент написания книги, но, разумеется, они могут измениться.
940
Приложение А. Графический инструментарий: получение OpenGL
Обычно с каждой библиотекой связано несколько файлов: заголовочный файл (.h), библиотечный
файл (.11b) и, для некоторых систем, файл динамически подключаемой библиотеки (.dll).
Добавление заголовочных файлов. Поместите три файла Gl .h, Glu.h, Glut.h в поддиректорию gl дирек-
тории include своего компилятора. В каждом приложении вам необходимо написать следующие опера-
торы включения:
include <gl/Gl.h>
#include <gl/Glu.h>
#include <gl/glut.h>
Компоновка (linking) файлов библиотеки. Каждое приложение будет являться частью проекта, кото-
рый подлежит компиляции и компоновке. Кроме написанных вами файлов (с расширением . с или . срр),
добавьте к своему проекту соответствующие библиотечные файлы OpenGL (.lib) так, чтобы компо-
новщик мог их найти.
Теперь рассмотрим индивидуальные требования для каждой из основных типов систем.
Microsoft Windows 95/98/NT
Большая часть OpenGL уже инсталлирована на машинах с Windows NT. (В момент написания книги
OpenGL, кроме того, уже установлен на машинах с системами Windows 95 OSR 2 и Windows 98 Second
Edition.) Для перечисленных систем часть этапов, описываемых ниже, не потребуется.
Подходящей программной средой для использования OpenGL для Windows является Microsoft
Visual C++ 5.0 или более поздних версий. (Если вы объявляете свое приложение как «Win32 console
application» (консольное приложение Win32), то нет необходимости создавать графический интерфейс
пользователя: ввод с клавиатуры и вывод текста осуществляются через отдельное консольное окно.)
Последняя информация относительно OpenGL для Windows находится на странице «Downloads» по
адресу http://www.opengl.org/Downloads/Downloads.htmL Кроме того, библиотеки в форме самораскрываю-
щихся архивных файлов доступны на ftp-сайте фирмы Microsoft ftp://ftp.microsoft.com/softlib/mslfiles/
opengl95.exe. Добавлены файлы gl.h, glu.h, glu32.1ib, opengl32.1 ib, glu32.dll, opengl32.dll. (He следует
использовать более старые файлы с расширением .aux.)
Библиотека glut доступна по адресу http://reality.sgi.com/opengl/glut3/glutdlls.zip. Добавлены файлы
glut.h, glut32.1 ib, glut32.dll. (He используйте файлы glut.lib и glut.dll.)
После того как эти файлы загружены и разархивированы, поместите файлы .lib в какую-нибудь
подходящую директорию, из которой вы будете добавлять их к каждому своему проекту. Файлы .dll
следует поместить в директорию Windows\System (если их там пока нет).
Для включения указанных файлов в свои приложения напишите следующие операторы:
#include «windows.h>
#include <gl/Gl.h>
#include <gl/Glu.h>
#include <gl/glut.h>
Macintosh
Основным источником no OpenGL для систем Macintosh является адрес http://www.apple.com/opengl/.
Следуйте инструкциям, сопровождающим это математическое обеспечение.
Системы UNIX и Linux
Мезаструктура (mesa) OpenGL, внешне похожая на библиотеку, доступна для свободного использова-
ния. В настоящее время лучшее место для ее получения — это http://www.mesa3d.org/. Следуйте инст-
рукциям, сопровождающим каждую загружаемую версию. Другие источники этой мезаструктуры мож-
но найти на странице linux3d по адресу http://www.linux3d.org software.html.
Поскольку эти библиотеки работают под X windows, то необходимо написать следующий оператор
включения:
#include <X11/Xll.h>
Немного математики
для компьютерной графики
Кто понимает математику, тот видит в ней не только истину, но и совершенную красоту —
красоту холодную и строгую, подобную красоте скульптуры.
Бертран Рассел (Bertrand Russell)
В этом приложении приводятся и обобщаются различные математические результаты, на которые име-
ются ссылки во всем тексте книги. В ряде случаев дается краткий вывод результата, однако в основном
этот материал носит справочный характер.
Б1. Некоторые основные определения, относящиеся
к матрицам и операциям над ними
В данном приложении делается обзор некоторых фундаментальных понятий, относящихся к матри-
цам, а также действия с матрицами. Другие операции над матрицами можно найти в посвященных им
книгах (например, [Birkhoff, 22, Faux, 61]).
Матрица (matrix) — это прямоугольный массив элементов, чаще всего чисел. Матрицу, имеющую
т строк и п столбцов, называют матрицей размерностью m на п (обозначается т х п). Например,
f 3 2 -5Л
I1 21 2J
это матрица целых чисел размерностью 4 на 3, а матрица
В = (1,34, -6,275, 0,0, 81,6)
это матрица один на четыре, также называемая «четверкой» («quadruple») или вектором. Обычно матри-
цу размерностью один на п называют «вектором-строкой» (row vector), а матрицу размерностью п на
один — «вектором-столбцом» (column vector).
Отдельные элементы матрицы обычно обозначаются строчными буквами с различными нижними
индексами: ij-й элемент матрицы В обозначается btj. Это элемент z-й строки и j'-ro столбца. Например,
для матрицы А из уравнения (А2.1) элемент а32 = 3.
942
Приложение Б. Немного математики для компьютерной графики
Матрица называется квадратной (square), если число ее строк и столбцов одинаково. В графике мы
часто имеем дело с матрицами размерностью два на два, три на три и четыре на четыре. Часто использу-
ются следующие два типа квадратных матриц: нулевая матрица (zero matrix) и единичная матрица
(identity matrix). Все элементы нулевой матрицы равны нулю. У единичной матрицы равны нулю все
элементы, за исключением элементов главной диагонали (main diagonal) cl. (у которых i = j), которые
равны единице. Следовательно, единичная матрица три на три имеет вид:
О 0>
1= 0 1
О О
О
1
7
Б1.1. Действия с матрицами
Числовая матрица В может быть масштабирована (scaled) числом s (умножена на число s). При этом
каждый элемент матрицы В умножается на s. Полученная матрица обозначается sB. К примеру, для
матрицы А из уравнения (А2.1) получим:
18 12 -30
6А = -6 48 0
36 18 54
I6 126 12
Две матрицы С и D, имеющие одинаковое число строк и столбцов, называются матрицами одинако-
вой размерности (shape)1, и их можно складывать. Элемент ij этой суммы Е = С + D является просто
суммой соответствующих элементов: etj - с;> + dif Например,
1 (S со '0 5 -Г '3 7 -6'
-18 0 9 8-3 8 16 -3
+ =5
6 3 9 2 6 18 8 9 27
J 21 2, Л 2 7, <5 23 9?
Поскольку матрицы можно масштабировать и складывать, имеет смысл определить линейные ком-
бинации (linear combinations) матриц (одинаковой размерности), например, 2А - 4В. Из определений
сложения и масштабирования непосредственно следуют свойства коммутативности, ассоциативности
и дистрибутивности для трех матриц А, В, С одинаковой размерности:
А+В-В + А;
А + (В + С) - (А + В) + С;
(f+g)(A + B)-fA+fB + gA+ gB.
Результат транспонирования (transpose) матрицы М, обозначаемый Мт, образуется посредством
перестановки (взаимной замены) строк и столбцов матрицы М: ij-й элемент матрицы Мт равен jz-му
элементу матрицы М. Например, транспонирование матрицы А из уравнения (А2.1) дает:
'3 -16 Г
Аг = 2 8 3 21
-5 0 9 2
\ 7
Результатом транспонирования вектора-строки является вектор-столбец. Например,
1 В некоторых источниках размерность называют структурой матрицы. — Примеч. пер.
Б1. Некоторые основные определения, относящиеся к матрицам и операциям над ними
943
(3, 2, -5)г =
Матрица называется симметричной (symmetric), если она не изменяется при транспонировании.
Симметричными могут быть только квадратные матрицы. Таким образом, матрица М размерностью
п х п является симметричной, если тп^ = тп.; для всех i и j от 1 до п.
Б1.2. Умножение двух матриц
Преобразования, впервые рассматриваемые в главе 5, включают в себя умножение вектора на матрицу
и умножение двух матриц друг на друга. Первое понятие является частным случаем второго.
Произведение (product) АВ двух матриц А и В определено только в том случае, если эти две матри-
цы являются согласованными (conform). Это означает, что число столбцов первой матрицы А равно
числу строк второй матрицы В. Таким образом, если матрица А имеет размерность 3 х 5, а матрица В —
5 х 2, то произведение АВ определено, а произведение ВА — нет. Каждый элемент произведения С мат-
риц А и В С - АВ является скалярным произведением некоторой строки матрицы А на некоторый стол-
бец матрицы В. А именно, ij-й элемент с{. этого произведения является скалярным произведением г-й
строки матрицы А на j-й столбец матрицы В. Тогда произведение матрицы размерностью п х тп на мат-
рицу т х г будет матрицей п х г. Пример:
'2 0 6
8 1 -4
0 5 7
-3"
о
2'
1
1
8J
'45
35
11
V
-14ч
13
20
Здесь, например, элемент с12 = -14, поскольку (2, 0, 6, -3)(2, 1, 1, 8) = -14. Подпрограмма умноже-
ния квадратных матриц приведена в приложении В; ее легко расширить для нахождения произведения
двух любых согласованных матриц.
Перечислим некоторые полезные свойства умножения матриц. Пусть матрицы А, В, С согласуются
должным образом. Тогда
(АВ) С ~ А (ВС),
А (В + С) •= АВ + АС,
(А + В) С = АС + ВС,
(АВ)Т = ВТАТ,
A (sB) = sAB,
где $ — число.
При формировании произведения двух матриц А и В имеет значение порядок следования этих мат-
риц. О выражении АВ мы говорим: «А умножается слева (premultiplies) на В» или «В умножается
справа (postmultiplied) на А». Если обе матрицы А и В — квадратные матрицы одной и той же размер-
ности, то оба произведения — АВ и ВА — определены, однако эти два произведения могут содержать
различные элементы. Если для двух матриц АВ = ВА, то эти две матрицы называются коммутативными
(commute). (Всегда ли коммутативны две симметричные матрицы?)
Умножение вектора на матрицу
Частным случаем умножения матриц является случай, когда одна из матриц является вектором-стро-
кой или вектором-столбцом. В графике часто встречается случай, когда матрица М умножается слева
на вектор-столбец w, что обозначается Mw. Пусть, например
944
Приложение Б. Немного математики для компьютерной графики
Г 2 Л
вектор w = 5
(2 О
= (2, 5, - 3)Г, а матрица М = 8 1
О 5
6 '
-4
7
В данном случае вектор w согласуется с матрицей М, следовательно, можно сформировать произведение
(2
Мы = 8
О
'-14'
33
4
Согласно вышеприведенным правилам, каждый компонент матрицы Мы является скалярным про-
изведением соответствующей строки матрицы М на вектор w. Можно также умножить матрицу слева
на вектор-строку v:
(2 0 6 А
уМ = (3, -1, 7) 8 1
= (-2, 34, 71).
О 5
Снова скалярные и векторные произведения
В ряде аналитических преобразований полезно записывать скалярное произведение а • Ь двух корте-
жей (tuples) n-го порядка в форме произведения вектора на матрицу. Для этого рассмотрим вектор Ь
как матрицу-строку и транспонируем ее в матрицу-столбец Ьг размерностью п на 1. Тогда
а • b - аЬг.
Из тех же самых соображений а • Ь - Ьаг.
Аналогично векторное произведение двух триад а х Ь (см. раздел «Векторное произведение двух век-
торов» главы 4) можно записать в виде произведения
( О
axb = (fl(
а2 аз) ^3
-Ьз Ь2
О -bt
bt о
Векторное произведение также является матрицей (какой именно?), умноженной справа на вектор-
столбец аг. Для еще одного вида произведения: внешнего, или тензорного произведения (outer or tensor
product), существует полезная форма записи:
' atb2 «А'
а®Ь = а7Ь = а2 (&,, Ь2, Ь3) = а2^1 а2^2 «2*3
а. ^3Ь, а3Ь2 «3*3у
откуда следует, что Ь ® а - (а ® Ь)г. (Почему?) Легко доказывается также свойство
а (Ь ® с) = (а • Ь) с.
Б1.3. Разбиение матрицы на блоки
Иногда полезно разбить матрицу на блоки из элементов и дать различным блокам свои имена. Например,
Б1. Некоторые основные определения, относящиеся к матрицам и операциям над ними
945
где входящие блоки равны соответственно:
(2 (Л
Ч =
1 8 1
. М2 = | J, М3 = (3, 2),
а Л/, состоит из единственного элемента 7.
Это называется разбиением (partition) матрицы М на четыре указанных блока. Отметим, что когда
один блок находится над другим, то эти блоки должны иметь одинаковое число столбцов. Когда же два
блока располагаются рядом, то они должны иметь одинаковое число строк. Две блочные (partitioned)
матрицы, разбиение которых было произведено одинаково (соответствующие блоки имеют одинаковую
размерность), можно складывать поблочно. Для транспонирования блочных матриц следует транспони-
ровать каждый блок по отдельности и затем транспонировать расположение блоков. Таким образом,
ГЛ7, М2 У Г
М3 М4
k J к 2
л/1
Две блочные матрицы можно также умножать посредством обычного матричного умножения их
подматриц, если эти подматрицы являются согласованными:
(М1 МЛ Гм5 м6> 'м,м3 +М2М7 М3М6+МгМ^
*4 М3М5+М4М2 М3М6+М4М3
Б1.4. Определитель матрицы
С каждой квадратной матрицей М связано некоторое число, которое называется ее определителем
(determinant) и обозначается |Л/| или det М. Определитель характеризует объем соответствующих гео-
метрических форм и содержит информацию о влиянии линейного преобразования на площади и объемы
объектов.
Определитель матрицы два на два является просто разностью двух произведений:
"’ll
/и2.
/и,2
?и22
= /инт22-/п12т21.
Если М — матрица три на три, то ее определитель имеет следующий вид:
|Л/| =
"’ll
"'21
'"з1
?и12
"’22
"’зг
"»13
'"23
"»зз
= 772,!
"»22
"»32
7И,3 /7721
- "’12
"’зз 77231
/7123 "’21
+ /72|3
77133 /7731
'"22
"»32
Например,
2 О
8 1
О 5
6
-4 = 294.
Отметим, что здесь определитель |Л4| равен сумме следующих трех членов: тиМп + ml2Mi2 + mi3Mi3,
в силу чего он имеет форму скалярного произведения: ]ЛУ| = (тп,,, 7/?12,7П|3) • (Mlt, Mt2, Mi3). Что означают
элементы MtJ называется алгебраическим дополнением (cofactor) элемента тп,] матрицы М. Посколь-
ку мы еще будем сталкиваться с алгебраическими дополнениями при обращении матриц, то дадим им
формальное определение.
Определение. Каждому элементу mt] квадратной матрицы М соответствует алгебраическое дополнение
Mijt равное произведению (-l)i+' на определитель матрицы, полученной при удалении из матрицы М i-w
строки и j-ro столбца.
946
Приложение Б. Немного математики для компьютерной графики
Отметим, что при удалении строки или столбца множитель (-1)'*-' принимает значения 1 и -1. Это
можно изобразить как наложенный на элементы матрицы шаблон из чисел 1 и -1, расположенных в
шахматном порядке.
Существует общее правило нахождения определителя \М| произвольной матрицы п на п: выберите
любую строку матрицы М, найдите алгебраическое дополнение для каждого элемента этой строки и
вычислите скалярное произведение этого ряда на n-кортеж, составленный из этих алгебраических до-
полнений. Можно также взять любой столбец матрицы М и произвести такую же операцию. (Действу-
ет ли это правило для матрицы два на два?)
Ниже приведены некоторые полезные свойства определителей:
О |Л/|-|М|г.
О Если два строки (или два столбца) матрицы М одинаковы, то |Л/1 - 0.
О Для двух квадратных матриц Ми В \МВ\ = |Л/| |В|.
О Если матрица В образована из матрицы М перестановкой двух строк (или двух столбцов) матри-
цы М, то |В| “ -|М|.
О Если матрица В образована из матрицы М умножением одной строки (или столбца) матрицы М
на число k, то |В| = k |Л/|.
О Если матрица В образована из матрицы М прибавлением произведения одной строки (или столб-
ца) матрицы М на какое-либо число к другой ее строке, то |В| - |М|.
Б1.5. Обращение матрицы
Матрица М размерностью п на п называется невырожденной (nonsingular), если ее определитель |М|
отличен от нуля. В этом случае матрица М имеет обратную (inverse) матрицу М~', обладающую следу-
ющим свойством:
М М~' “ Л/-1 М “ I,
где I— единичная матрица размерностью п на п. Кроме того, матрица, обратная к произведению квад-
ратных матриц, имеет вид:
(АВ)-'- В-'А'1.
Нетрудно выразить элементы обратной матрицы М~' через алгебраические дополнения матрицы М.
Пусть А — матрица, обратная к матрице М. Тогда ij-м элементом матрицы А будет число:
а =
v И’
Это означает, что мы находим алгебраическое дополнение элемента ттг. и делим его на определитель
всей матрицы. Обратите внимание на индексы: при вычислении элемента используется алгебраическое
дополнение т~. Для нахождения обратной матрицы нужно проделать следующую последовательность
операций.
1. Создайте промежуточную матрицу С из алгебраических дополнений = Mif
2. Найдите определитель \М| как скалярное произведение любой строки матрицы С на соответству-
ющую строку матрицы М.
3. Транспонируйте матрицу С и получите Ст.
4. Умножьте каждый элемент матрицы Ст на 1/|Л/|, чтобы получить М~'.
Б1. Некоторые основные определения, относящиеся к матрицам и операциям над ними
947
Пример
Обратите матрицу
'2 0 6'
М= 8 1 -4
0 5 7
к
Решение
Построим матрицу С из алгебраических дополнений матрицы М:
'27 -56 40 '
30 14 -10 .
-6 56 2
к 7
Далее найдем определитель |Л/| “ (2,0,6) • (27, -56,40) - 294. Теперь транспонируем матрицу С и умно-
жим каждый ее элемент на l/[Af|, тогда получим:
( 27 30 -бА
Проверьте получившийся результат посредством умножения ММ~1 и М~'М. В обоих случаях долж-
на получиться единичная матрица I.
Обращение матриц часто используется при решении систем линейных уравнений (set of linear
equations) вида
где заданы матрица N размерностью п на п и вектор-столбец Ь, а требуется найти вектор х такой, чтобы
все эти п уравнений удовлетворялись одновременно. Если N— невырожденная матрица (ее определи-
тель не равен нулю), то решение может быть найдено как произведение
х - УЪ.
Тем не менее существует целый ряд методов решения такой системы уравнений, которые работают
быстрее и более устойчивы к вычислениям, чем прямое вычисление матричного произведения ЛЛЪ.
Отметим, что хотя в компьютерной графике превалирует применение векторов-столбцов, вышепри-
веденная система уравнений иногда записывается с использованием векторов-строк:
(*р*2...хя)М~(Ь1,Ь2,...,Ья).
Нетрудно показать, что данная система уравнений совпадает с предыдущей, когда М - NT, а ее реше-
ние имеет вид х - ЬЛ/Н.
Ортогональные матрицы
Для некоторых преобразований, например для поворотов (см. главу 5), для соответствующих матриц
найти обратную матрицу особенно просто. Матрица М называется ортогональной (orthogonal), если к
ее обращению приводит ее простое транспонирование, то есть если Мт - 1И-1. Следовательно, ММТ= I.
Если матрица М ортогональна, то из равенства ММТ=: / следует, что каждая строка матрицы Мпредстав-
948
Приложение Б. Немного математики для компьютерной графики
ляет собой вектор единичной длины и что строки взаимно ортогональны. То же верно и для столбцов
матрицы М. (Почему?)
Например, если матрица М имеет размерность три на три, разобьем ее на три строки:
Тогда каждая триада а, Ь, с имеет единичную длину иа-Ь = а- с = Ь- с = 0.
Б2. Некоторые свойства векторов и операции над ними
Рассмотрим три операции над векторами: перп-скалярное произведение, смешанное произведение и
двойное векторное произведение.
Б2.1. Перп вектора; перп-скалярное произведение
Понятие перпа и перп-скалярного произведения применимо только к двумерным векторам.
Перп вектора
Пусть имеется вектор а = (ах, а^). Тогда перпендикуляр к этому вектору, полученный поворотом ис-
ходного вектора на 90° против часовой стрелки, сокращенно именуемый «перп» («регр») и обозначае-
мый aS определяется как а1 = (-а , ах). Перп имеет следующие свойства:
1. Векторы а и а1 имеют одинаковую длину: |а| = |ах|.
2. Линейность: (а + Ь)1 = а1 + Ь1 и (Аа)х = Аа1 для любого скаляра А.
3. Применение перпа дважды образует противоположный к а вектор: а11 = (а1)1 = -а.
Перп-скалярное произведение а1* b
1. Перп скалярного произведения а1- b = ab - abx.
2. ах - а = 0. (Перп а1 перпердикулярен вектору а.)
3. |ах|2 = |а|2. (Вектор а и его перп а1 имеют одинаковую длину.)
4. а1- Ь = -Ьх- а. (Перп-скалярное произведение антисимметрично.)
5. а1- b можно записать в форме определителя
а а
ахЬ = х у.
Ъх ьу
6. (а1-Ь)2 + (а • Ь)2 = |а|2|Ь|2.
7. Если а + Ь + с = 0, то а1- Ь = Ь1- с = с1- а.
8. ах - b > 0 тогда и только тогда, когда поворот от вектора а к вектору b производится против часо-
вой стрелки (CCW).
9. а1- Ь = 0, если вектор Ь параллелен или антипараллелен вектору а.
10. |ах- Ь| равен площади параллелограмма, построенного на векторах а и Ь.
Б2. Некоторые свойства векторов и операции над ними
949
Б2.2. Смешанное произведение
Для трех пространственных векторов а, Ь, с существует очень полезная комбинация векторного и ска-
лярного произведений. Чтобы определить эту величину для трех заданных векторов а, b и с, сформиру-
ем следующий скаляр:
5 = а • (Ь х с) = ах(Ьсг - Ьгсу) + ау(Ьсх - Ьхсг) + аг(Ьсу - bcj.
Это удобно записать в форме определителя:
Перестановка строк в определителе приводит только к изменению его знака, поэтому двойная пере-
становка не приводит ни к каким изменениям. Следовательно, циклическая перестановка векторов не
влияет на величину 5, которая поэтому имеет три эквивалентных формы:
5 = а • (Ь х с) = b • (с х а) = с • (а х Ь).
Смешанное произведение (scalar triple product) имеет простую геометрическую интерпретацию (оно
играет в трехмерном пространстве ту же роль, что и перп-скалярное произведение Ь1- с в двумерном):
О Его модуль |5] равен объему параллелепипеда, образованного векторами а, Ь, с, исходящими из
одной точки.
О Знак смешанного произведения такой же, как у cos(0): последний положителен, если \ф\ < 90°, и
отрицателен, если |0| > 90°. (Вопрос: изменится ли значение 5, если выразить векторы а, Ь, с в ле-
восторонней системе координат?)
Отметим, что если все три вектора лежат в одной и той же плоскости, то смешанное произведение
будет равно нулю, так как объем соответствующего параллелепипеда в этом случае вырождается в нуль.
Предположим, что ни один из векторов а, Ь, с не равен нулю. В этом случае смешанное произведение
а • (Ь х с) = 0 тогда и только тогда, когда все три вектора компланарны (coplanar). (Вывод: три вектора
являются компланарными, если два из них параллельны.) Это свойство можно использовать при опре-
делении того, насколько плоским является полигон.
Пересечение трех плоскостей
Пусть две плоскости пересекаются по прямой линии, а третья плоскость пересекает эту прямую в единствен-
ной точке. С помощью смешанного произведения векторов можно написать аналитическое выражение для
этой точки. Если плоскости заданы уравнениями п(. • г = Dt, где i = 1,2,3, то их точка пересечения имеет вид:
г = Д|(п2ХПз) + А(ПзХП1) + Дз(П|ХП2)
iv(n2xn3)
при условии, что знаменатель отличен от нуля.
Выражение для вектора г можно проверить, убедившись, что он лежит в каждой из трех плоскостей:
для этого нужно просто подставить выражение каждой плоскости в формулу для г и для доказательства
равенства использовать свойства смешанного произведения.
Полезное тождество для векторных произведений
При исследовании векторов, нормальных к поверхностям, приходится иметь дело с векторным про-
изведением двух преобразованных трехмерных векторов, то есть (Ma) х (Mb), где а и b — трехмер-
ные векторы, а М — матрица размерностью три на три. Вопрос заключается в том, как выразить это
950
Приложение Б. Немного математики для компьютерной графики
векторное произведение через векторное произведение а х Ь исходных векторов а и Ь. Это выражение
имеет вид:
(Л/а) х (Mb) - (detM) М~т (а х Ь),
так что а х b масштабируется определителем матрицы М и умножается на обратную транспонирован-
ную матрицу от М. Для вывода этого результата можно проделать следующие шаги (может быть, вам
удастся найти более быстрый вывод?).
Обозначьте строки матрицы М векторами гр г2, г3. Сначала покажите, что
г2хг3
(Л/а) х (Л/b) = r3xr, (axb).
Г1хг2
Затем покажите, что
Наконец, покажите, что произведение первых двух матриц в правой части является диагональной
матрицей, каждый диагональный элемент которой равен определителю матрицы М. (Подсказка-, исполь-
зуйте свойства смешанного произведения а • с х а - 0.)
Б2.3. Двойное векторное произведение
Двойное векторное произведение (triple vector product — TVP) трех векторов а, Ь, с равно TVP - а х (Ь х с).
Оно часто встречается при ручных вычислениях с применением векторных произведений. Двойное век-
торное произведение можно записать в виде разности двух масштабированных векторов:
TVP = (а • с) Ь - (а-Ь) с.‘
Скалярно-векторное произведение четырех векторов
Для любых четырех трехмерных векторов а, b, с, d справедливо равенство:
(а х Ь) • (с х d) “ (а • с) (Ь • d) - (а • d) (Ь • с).2
БЗ. Арифметика комплексных чисел
Вообще говоря, в геометрических методах компьютерной графики комплексные числа использовать не
обязательно. Однако в силу того, что комплексные числа и операции с ними предоставляют возмож-
ность по-новому взглянуть на некоторые факты, их все-таки стоит изучить. В данном приложении со-
браны в одном месте элементарные сведения об арифметике комплексных чисел, чтобы освежить па-
мять у тех читателей, которые когда-либо встречались с ней.
Комплексное число, например г = 3 + 4г, состоит из двух частей. Его вещественная (real) часть, обо-
значаемая Re(z), равна 3, а его так называемая мнимая (imaginary) часть, обозначаемая Im(z), равна 4.
Число г, определяемое равенством г2 ~ -1, обычно записывается в виде i = -7-1. На самом деле в этих
объектах нет ничего комплексного или мнимого; они просто определяются набором правил, в соответ-
1 Если двойное векторное произведение раскрыть в виде: а х (Ь х с) “ Ь (а • с) - с (а • Ь), то можно использовать мнемоническое
правило «бац минус цаб». — Примеч. пер.
2 Тождество Лагранжа. — Примеч. пер.
БЗ. Арифметика комплексных чисел
951
ствии с которыми над ними производятся операции. При выполнении арифметики применяются сле-
дующие операции:
О сложение: (а + Ы) + (с + di) = (а + с)+ (b + d) i;
О умножение: (а + Ы) * (с + di) - (ас - bd) + (ас + cd) i,
причем здесь член bdi2 заменен на -bd в соответствии с правилом i2 = -1. Например, (3 + 2i) + (1 + г) =
= 4 + 3i, а (3 + 2i) (1 + i) = 1 + 5i.
Благодаря соответствию комплексных чисел точкам на плоскости эти числа и операции с ними имеют
глубокий геометрический смысл. Комплексное число х + yi связывается с точкой (х, у) в обычной прямо-
угольной системе координат. Координата х соответствует вещественной части этого числа, а координа-
та у — его мнимой части. Например, числу 3 + 4i соответствует точка (3,4). Любое комплексное число мо-
жет быть «отмечено» на плоскости. Такое представление называется диаграммой Аргана (Argand diagram)1.
На рис. 15.1, а показано комплексное число 3 + 4i, нарисованное в виде точки (3,4). Для усиления связи
с комплексными числами обычная ось х часто называется вещественной осью, а ось у — мнимой осью.
А ,гп
3 + 41
/•—-3 + 4i
5/
> Re
Рис. Б.1. Диаграмма Аргана
Поскольку точка (3,4) находится на расстоянии V32 +42 = 5 от начала координат, говорят, что комп
лексное число с - а + Ы имеет величину (magnitude), или модуль (modulus), равный
Неудивительно, что угол (angle), или аргумент (argument), числа с = а + bi — это угол ф на рис. 15.1, б.
Аргумент числа z часто обозначают Arg(z), тогда Arg(z) - ф. Следовательно, вещественная часть числа с
равна |с| cos(0), а его мнимая часть равна |с| sin(0), поэтому можно записать число с в тригонометричес-
кой («полярной») форме:
с = |с| cos0 + i |с| sin0.
Предположим, что комплексное число z имеет тригонометрическую форму z - |z| (cos0 + i sin0)
(то есть обладает модулем |z| и аргументом 0). Умножим с на z и упростим результат:
cz = |с| (cos0 + i sin0) |z| (cos0 + i sin0) = |c| |z| (cos(0 + 0) + isin(0 + 0)). (Б.2)
Можно сделать следующие выводы:
О модуль произведения двух комплексных чисел равен произведению их модулей;
О аргумент произведения двух комплексных чисел равен сумме их аргументов.
Рисунок Б.2 иллюстрирует геометрический смысл сложения и умножения комплексных чисел. Сложе-
ние комплексных чисел (рис. Б.2, а) подчиняется тем же правилам, что и сложение векторов. Умноже-
ние комплексных чисел показано на рис. Б.2, б. Отметим, что треугольник, образованный точками 0,1
и с, подобен треугольнику, образованному точками 0, z и cz, поэтому умножение на комплексное число
преобразует треугольник в подобный ему треугольник.
1 Названа по имени Жана Робера Аргана (Jean Robert Argand), швейцарского счетовода, который описал такую диаграмму в 1806 году.
В действительности норвежский топограф Каспер Бессель (Casper Wessel) описал такую же диаграмму девятью годами ранее, и
примерно в это же время ее применял Гаусс.
952
Приложение Б. Немного математики для компьютерной графики
Полагая в уравнении (Б.2) z = с, получим z2 = |z|2 (cos20 + zsin2ф), что можно обобщить в выраже-
ние для z". (Какое?) Полагая |z| = 1, получаем знаменитую формулу Муавра (DeMoivre)1:
(cos0 + zsin0)n = cos(n0) + zsin(n0).
Рис. Б.2. Сложение и умножение комплексных чисел
Исследуем более подробно функцию cos0 + zsin0. Назовем ее/(0). Из формулы Муавра следует, что
/п(ф) =Дпф)\ возведение функции в n-ю степень эквивалентно умножению ее аргумента на п. Функция
/( ) очень напоминает экспоненту и, как может быть строго доказано, действительно является ею. Это
приводит нас к формуле Эйлера (Euler’s formula):
е* = cos0 + zsin0.
(Доказательство. Обе части разлагаются в бесконечные ряды с одинаковыми коэффициентами.)
Отметим несколько частных случаев: ei0 = 1, е'"/2 = г, е’л = 1. (Последнее равенство устанавливает замеча-
тельное соотношение между четырьмя фундаментальными математическими величинами: е, i, п, 1.).
Формула Эйлера предоставляет нам альтернативную и очень компактную полярную, а именно показа-
тельную форму для комплексного числа с с амплитудой |с| и углом ф:
с -
Например, все п вершин n-гона радиуса R задаются п комплексными числами:
pk= Rei2nl,/n, где k - 1,2,.... п.
Каждое комплексное число z имеет сопряженное (conjugate) число, обозначаемое z*. Если z = х + iy,
то по определению, z* = х - iy. Тогда |z*| = |z| и Arg(z*) = -Arg(z). Вычисление сопряженного числа гео-
метрически эквивалентно отражению относительно оси х. (Чему равны модуль и аргумент числа (z*)"?)
Квадратный корень Vz из комплексного числа z
Если комплексное число z имеет полярную форму z = |z| то, очевидно, что
Таким образом, квадратный корень из комплексного числа z извлекает квадратный корень из моду-
ля этого числа и делит пополам его аргумент. Это соотношение можно написать и не пользуясь поляр-
ной формой. Если z = х + iy, то
Jz = a + ib, если у > О
Jz = -а + ib, если у < О, (Б.З)
1 При |z| * 1 формула Муавра имеет вид: [|z|(cos0 + isinф)]"- |z|” [cos(n0) + isin(n0)]. — Примеч. nep.
64. Сферические координаты и направляющие косинусы
953
/Н + Х , /|z| -х
где а = л—-- и о = . —--.
V 2 Y 2
Проверка. Возведите в квадрат а + ib и -а + ib и после алгебраических преобразований увидите, что
результат равен z.
Практические упражнения
Б3.1. Операция деления
Покажите, что если г и ж - комплексные числа, то
z _ Н '(M0-M»)) _ _ zW*
W |®| WW* |®|2
Б3.2. Отношение, модуль которого всегда равен единице
Покажите, что модуль отношения двух комплексно-сопряженных чисел (а + ib)/(a - ib) для любых а и
b равен единице.
БЗ.З. В каком случае четыре комплексных числа лежат на одной окружности?
Покажите, что Arg((z3 - zt)/(z2 - z,)) - Arg((z4 - z,)/(z4 - z2)) тогда и только тогда, когда z,,..., z4 лежат на
одной окружности, а на прямой линии тогда и только тогда, когда отношение [(z3 - z^)/{z2 - zt)]/
[(z4 — zt)/(z4 - z2)] вещественно.
Б4. Сферические координаты и направляющие косинусы
В данном разделе излагается понятие сферических координат, а также преобразование из сферических
координат в декартовы и обратно.
Рис. Б.З. Сферические координаты
На рис. Б.З показано, как определяется точка U в сферических координатах. Расстояние от точки U
от начала координат равно Л,аф означает угол, образуемый радиус-вектором точки U с плоскостью xz;
этот угол носит название широты (latitude) точки U. Угол 0 называется долготой, или азимутом (azimuth),
точки U, это угол между плоскостью ху и плоскостью, проходящей через точку U и ось у. Угол ф лежит
в интервале -л/2 < ф < л/2, а угол 0 — в интервале 0 < 0 < 2л.
При помощи простых тригонометрических преобразований можно вывести соотношения между этими
величинами и декартовыми координатами точки U (их, иу, иг). Эти соотношения имеют следующий вид:
их - /?cos(0) cos(0),
иу = /?sin(0), (Б.4)
иг - 7?sin(0) sin(0).
954
Приложение Б. Немного математики для компьютерной графики
Можно обратить эти соотношения и выразить (R, ф, 0) через (их, иу, иг):
R = ^u2+u2y+u2 ;
ф =arcsin
(Б.5)
0 - arctg(u2, их).
Приведенная здесь функция arctg(,) является двухаргументной формой арктангенса и определя-
ется так:
х>0,
arctg(y,x) =
I V 1
л+arctg — х<0,
(Б.6)
л
2
л
’2
х = 0, у > О,
х = 0, у < 0.
Эта функция может отличать случай, когда х и у положительны, от случая, когда они оба отрицатель-
ны, в отличие от обычной функции arctg(z//x), которая всегда выдает углы в диапазоне от -л/2 до л/2.
Пример Б4.1
Пусть точка U находится на расстоянии 2 от начала координат, расположена в 60° вверх от плоскос-
ти xz и на отрицательной части оси х. Следовательно, точка U лежит в плоскости ху. Тогда точка U имеет
сферические координаты (2,60°, 180°). Используя уравнение (Б.4) для пересчета точки U в декартовы
координаты, получим: U- (-1, 1,732,0).
Направляющие косинусы
Направление точки U из предыдущего примера задается с помощью двух углов: широты и долготы.
Часто направления задаются другим удобным способом — через направляющие косинусы. Направляю-
щие косинусы прямой линии, проходящей через начало координат, равны косинусам трех углов, кото-
рые зта прямая составляет соответственно с осями х, у, г.
Напомним, что косинус угла между двумя единичными векторами равен их скалярному произведению.
Сформируем для заданной точки U радиус-вектор (их, иу, иг). Длина этого вектора равна R, поэтому его сле-
дует нормировать и получить вектор единичной длины m = (ux/R, uy/R, u2/R). Тогда косинус угла, который
этот вектор составляет с осью х, задается скалярным произведением m • i = ux/R, что совпадает с первым
компонентом вектора т. Аналогично второй и третий компоненты вектора m являются соответственно
вторым и третьим направляющим косинусом. Обозначив а, Р, у углы с осями х, у, z соответственно, полу-
чим следующие выражения для трех направляющих косинусов прямой, соединяющей 0 с точкой U:
cos(a) = —,
k ' R
C0S(P) = ^>
К
(Б.7)
cos(Y) = b-.
Отметим, что три направляющих косинуса связаны друг с другом, поскольку сумма их квадратов
всегда равна единице.
Б4. Сферические координаты и направляющие косинусы
955
Практические упражнения
Б4.1
Преобразуйте точку (х, у, z) - (2,4, -3) в сферические координаты.
Б4.2
Преобразуйте точку (г, ф, 0) - (5,35°, -67°) в декартовы координаты.
Б4.3
Найдите направляющие косинусы вектора п, если
О n = (1,1,1);
О п = (2,3,4).
В Некоторые полезные классы
и служебные подпрограммы
В данном приложении описываются некоторые типы данных и алгоритмы, которые могут оказаться
полезными при разработке графических приложений. Основные типы данных помещены далее в раз-
личные классы, для некоторых из этих классов даны полные описания, в то время как для других клас-
сов некоторые методы определены, но не описаны. Заполнить тела этих методов предоставляется чита-
телю. Некоторые классы представлены только своим «скелетом», для того чтобы подсказать, как их
можно было бы развить в конкретном приложении.
В большинстве классов принцип инкапсуляции принят в ослабленном виде: большинство полей дан-
ных определены как publ iс, а не private, — для краткости, а также чтобы избежать необходимости опре-
деления большого числа функций аксессоров (accessor) и мутаторов (mutator).
Еще один прекрасный источник классов и утилит можно найти в серии «Жемчужины графики»
(«Graphics Gems»), онлайновое представление которого расположено в Интернете по адресу http://
www.acm.org/tog/GraphicsGems/index.html.
Классы, определенные в данном приложении, собраны в заголовочных файлах (. h) и в файлах ис-
ходного кода (.срр), которые также доступны на Интернет-сайте книги (см. введение). Совокупности
описанных ниже классов.
1. Классы для двумерной графики. Эти классы обеспечивают определенную поддержку рисова-
ния двумерных рисунков и включают в себя IntPoint, Point2, Polyline, IntRect, Vector2, Canvas.
2. RGBpixmap. Классы (то есть mRGB и RGBpixmap) обеспечивают поддержку создания и рисования
пиксельных карт (pix map), в том числе чтение изображения, записанного в формате BMP.
3. SDL. Классы поддерживают управление и рисование трехмерных сцен, в том числе сцен,
описанных на языке SDL (см. приложение Д). Сюда включены следующие классы: Point3,
Vector3, Color3, Light, Affine4, AffineStack, Material, GeomObj, Boolean, UnionBool, IntersectionBool,
DifferenceBool, Shape, Cube, Sphere, TaperedCylinder, Square, Plane, Face, Mesh, Torus, Teapot, Scene.
4. Шум (Noise). В эту группу классов входит класс Noi se, предназначенный для создания трехмер-
ного шума и турбулентности для текстуры твердого тела.
5. Классы трассировки луча (ray-tracing). Включают в себя: Pointcluster, Sphereinfo, Cuboid, Ray,
Hitinfo, Intersection.
Bl. Классы для двумерной графики
957
В1. Классы для двумерной графики
// graphics2d.h
// A collection of classes to support 2D graphics
// Набор классов для поддержки двумерной графики
#ifndef _GRAPHICS2D
#define _GRAPHICS2D
#include <string>
#include <iostream>
#include <fstream*
#include <strstream>
using namespace std:
#include <windows.h>
//change if using xWindows or other platform
// изменяем, если используется xWindows или другая
// платформа
#include <assert.h>
#include <math.h>
#include <stdlib.h>
#include <gl/Gl.h>
#include <gl/Glu.h>
#include <gl/glut.h>
//@@@@@@@@@@@@@@@@@0 IntPoint class @@@@@@@@@@@0@@@@
class IntPoint{
// for 2D points with integer coordinates
// для двумерных точек с целыми координатами
public:
int х.у:
void set(int dx. int dy){x = dx: у = dy:}
void set(IntPoint& p){ x - p.x; у = p.y:}
IntPoint(int xx. int yy){x - xx: у = yy:}
IntPoint(){ x = у - 0;}
}:
//00@00@0000@@000000 Point2 class 0000000000000000
class Point2{
// for 2D points with real coordinates
// для двумерных точек с вещественными координатами
public:
float х.у:
void set(float dx. float dy){x = dx; у = dy:}
void set(Point2& p){ x = p.x: у = p.y:}
Point2(float xx. float yy){x = xx; у = yy:}
Point2(){x - у = 0:}
}:
//««<«<«««««<«< PolyLine »»»»»»»»»»»»>
class PolyLine{
// a polyline is a num plus an array of points
// ломаная - это число плюс массив точек
public:
int num:
Point2 pt[80]:
958
Приложение В. Некоторые полезные классы и служебные подпрограммы
//may need larger arrays in some circumstances
// в некоторых случаях могут понадобиться большие массивы
PolyLine(){num =0:}
}:
// IntRect class
class IntRect{
// a rectangle with integer border values
// прямоугольник с целыми значениями границ
public:
int left. top. right, bott:
IntRect(){left = top = right = bott = 0:}
IntRect(int 1. int t. int r. int b)
{left - 1: top = t: right = r: bott = b:}
void set(int 1. int t. int r. int b)
{left - 1: top - t: right = r: bott = b;}
void set(IntRect& r)
{left - r.left: top = r.top: right - r.right: bott - r.bott:}
}:
//@@@@@@@@@@@@@@@@@0 Vector2 class
class Vector2{
public:
float x.y:
void set(float dx. float dy){ x = dx: у = dy: }
void set(Vector2& v){ x = v.x: у = v.y;}
void setDiff(Point2& a. Point2& b)//set to difference a - b
{x - a.x - b.x: у - a.у - b.y;}
void normalize()//adjust this vector to unit length
{ double sizeSq - x * x + у * у;
1f(sizeSq < 0.0000001)
{
cerr « "\nnormalizeO sees vector (0.0)!”:
return:
// does nothing to zero vectors:
// не делает ничего для обнуления векторов
}
float scaleFactor = 1.0/(float)sqrt(sizeSq):
х *= scaleFactor: у *• scaleFactor:
}
Vector2(float xx, float yy){x = xx; у - yy: }
Vector2(Vector2& v){x - v.x; у = v.y: }
Vector2(){x - у - 0:} //default constructor
float dot(Vector2 b) // return this dotted with b
{return x * b.x + у * b.y:}
void perpO // perp this vector
{float tmp - x: x - -у: у - tmp:}
float perpDot(Vector2& v) // return perp of this dotted with v
{return x *v.x - у * v.y:}
}:
//«««««<<«««« Canvas class »»»»»>
// a global Canvas object (described in Chapter 3) knows how to draw lines in world coordinates and to perform
turtlegraphics
// глобальный объект класса Canvas (описан в главе 3).
// Он знает, как рисовать прямые в мировых координатах
Bl. Классы для двумерной графики
959
// и как работать с черепашьей графикой
class Canvas {
private:
Point2 СР;
// current position in world
// текущее положение в мировых координатах
float CD:
// current direction in degrees
// текущее направление в градусах
public:
float windowAspect;
Canvasdnt width, int height, char* title):
void setWindow(float 1. float r. float b. float t):
void setviewport(int 1. int r. int b. int t):
float getWindowAspect(void) { return windowAspect:}
void lineTo(float x. float y);
void moveTo(float x, float y){CP.x - x: СР.у - y:j
void turn(float ang) {CD +- ang:}
void turnTo(float ang) {CD - ang:}
void forward(float dist, int vis);
void initCTO
// initialize the CT (model view matrix)
// инициализируем СТ (матрицу моделирования-просмотра)
{
glMatrixMode(GL MODELVIEW); glLoadldentityO:
}
void rotate2D(double angle)
{
glMatrixMode(GL_MODELVIEW); glRotated(angle. 0.0. 0.0. 1.0):
}
void translate2D(double dx. double dy)
{
glMatrixMode(GL MODELVIEW): glTranslated(dx. dy. 0.0);
}
void scale2D(double sx. double sy)
{
glMatrixMode(GL MODELVIEW): glScaled(sx. sy. 1.0);
}
void pushCT(void)
{
glMatrixMode(GL_MODELVIEW): glPushMatrix();
}
void popCT(void)
{
glMatrixMode(GL MODELVIEW); glPopMatrixO;
}
void ngon(int n. float ex. float cy, float radius);
#endif
// end of graphics2d.h
// конец файла graphics2d.h
// graphics2d.cpp - use #include ”graphics2d.h"
// graphics2d.cpp - используется #include "graphics2d.h“
960
Приложение В. Некоторые полезные классы и служебные подпрограммы
// Some methods for the classes defined in graphics2d.h
// Некоторые методы для классов.
// определенных в graph!cs2d.h
#include ”graphics2d.h"
Canvas :: Canvas(int width, int height, char* title)
{
char* list:
// dummy list for glutlnit
// пустой список для glutlnit
int numArgs - 1:
// dummy value for glutlnit
// пустая величина для glutlnit
glutlnitC&numArgs, &list):
glut!nitDisplayMode(GLUT_SINGLE | GLUT_RGB):
glutInitWindowSize(width. height);
glutlnitWindowPositiondOO. 100);
glutCreateWindow(title):
CP.x - СР.у = 0.0:
windowAspect = 1.0:
}
void Canvas :: setWindowffloat 1. float r. float b. float t)
{
g1 Mat ri xMode(GL_PROJ ЕСТION):
glLoadldentityO:
glu0rtho2D((GLdouble)l. (GLdouble)r. (GLdouble)b. (GLdouble)t):
if(t == b) return;
windowAspect = (r - 1 )/(t - b):
}
void Canvas :: setViewportfint 1, int r. int b, int t)
{glViewportC(GLint) 1. (GLint)b. (GLint)(r-1), (GLint)(t-b)):}
void Canvas :: lineTo(float x. float y)
{
glBegin(GL_LINES):
glVertex2f((GLfloat)CP.x. (GLfloat)CP.y);
CP.x - x: СР.у = у:
glVertex2f((GLf1 oat)CP.x, (GLf1 oat)CP.y):
glEndO: glFlushO:
}
void Canvas :: forward(float dist. int vis)
{
#define RadPerDeg 0.017453393
// radians per degree
// радиан на градус
float x - CP.x + dist * cos(RadPerDeg * CD):
float у - СР.у + dist * sin(RadPerDeg * CD):
if(vis) lineTo(x, y):
else moveTofx, y):
CP.x = x: СР.у = у:
}
void Canvas::ngon(int n.float ex. float cy, float radius)
{
#define RadPerDeg 0.017453393 //radians per degree
if(n < 3) return; // bad number of sides
В2. RGBPixmap CLASS
961
double angle = 0. angleinc » 2 * 3.14159265 /n: //angle
increment
moveTo(cx + radius, cy):
forCint к » 1: к <- n: k++)
angle +- angleinc:
lineToCradius * cos(angle) + ex. radius * sin(angle) + cy):
}
}
// end of graphics2d.cpp
// конец файла graph!cs2d.cpp
B2. RGBPixmap CLASS
// RGBpixmap.h: a class to support working
// with RGB pix maps.
// RGBpixmap.h: класс для поддержки работы с RGB
// пиксельными картами.
#ifndef _RGBPIXMAP
#define _RGBPIXMAP
#include <fstream»
// Needs the IntPoint and IntRect classes to be defined
// Требуется определить классы IntPoint и IntRect
typedef unsigned char uchar:
class mRGB{
// the name RGB is already used by Windows
// имя RGB уже используется в Windows
public: uchar r.g.b:
mRGB(){r - g » b - 0:}
mRGB(mRGB& p){r » p.r; g • p.g: b - p.b:}
mRGB(uchar rr. uchar gg. uchar bb){r - rr; g - gg; b - bb;}
void set(uchar rr. uchar gg. uchar bb){r - rr; g - gg: b - bb:}
}:
//$$$$$$$$$$$$$$$$$ RGBPixmap class
class RGBpixmap{
private:
mRGB* pixel;
// array of pixels
// массив из пикселов
public:
int nRows, nCols:
// dimensions of the pix map
// размеры пиксельной карты
RGBpixmapO {nRows - nCols - 0: pixel - 0:}
RGBpixmapdnt rows, int cols) //constructor
{
nRows - rows:
nCols = cols:
pixel - new mRGB[rows*cols];
31 Ф. Хилл
Приложение В. Некоторые полезные классы и служебное подпрограммы
int readBMPFile(string fname):
// read BMP file into this pix map
// читаем BMP-файл в эту пиксельную карту
void freeltO
// give back memory for this pix map
// возвращаем память для этой пиксельной карты
{
delete []pixel: nRows - nCols - 0:
}
//<«««««««<« copy »»»»»»»»»>
void copydntPoint from. IntPoint to. int x. int y. int width, int height)
{
// copy a region of the display back onto the display
// копируем область дисплея обратно на дисплей
if(nRows — 0 || nCols “ 0) return;
glCopyPixels(x, у. width. height,GL_COLOR):
}
//<««««<«<««« draw »»»»»»»»>
void drawO
{
// draw this pix map at current raster position
// рисуем эту пиксельную карту в текущей растровой позиции
if(nRows “ 0 || nCols “ 0) return:
// tell OpenGL: don’t align pixels with 4-byte
// boundaries in memory
// указываем OpenGL не выравнивать пикселы
// по 4-битовым границам в памяти
glPixelStorei(GL_UNPACK_ALIGNMENT. 1):
glDrawPixels(nCols. nRows,GL_RGB. GL_UNSIGNEO_BYTE.pixel);
}
//«<«««<<««« read »»»»»»»»
int readdnt x. int y. int wid. int ht)
{
// read a rectangle of pixels into this pixmap
// читаем прямоугольник из пикселов в данную пиксельную карту
nRows - ht:
nCols - wid:
pixel - new mRGB[nRows *nCols]: 1f(Ipixel) return -1;
// tell OpenGL: don’t align pixels with
// 4-byte boundaries in memory
// указываем OpenGL не выравнивать пикселы
// по 4-битовым границам в памяти
glPixelStorei(GL_PACK_ALIGNMENT.l);
glReadPixels(x. у. nCols, nRows.
GL_RGB,GL_UNSIGNED_BYTE.pixel):
return 0;
//<«««<«««<« read from IntRect »»»»»»»»
int read(IntRect r)
{
// read a rectangle of pixels into this pix map
// читаем прямоугольник пикселов в эту пиксельную карту
nRows - г.top - r.bott:
B?, RGBPixmap CLASS
963
nCols - r.right - r.left:
pixel - new mRGB[nRows *nCols]: if( ’pixel) return -1:
// tell OpenGL: don’t align pixels with
// 4-byte boundaries in memory
// указываем OpenGL не выравнивать пикселы
// no 4-битовым границам в памяти
glPixelstorei(GL_PACK_ALIGNMENT.1);
glReadPixels(r.left.r.bott. nCols. nRows. GL_RGB,
GL_UNSIGNED_BYTE, pixel):
return 0:
}
//««««««« setPixel »»»»»»>
void setPixel(int x. int y. mRGB color)
{
if(x>-0 && x <nCols && у >-0 && у < nRows)
pixel[nCols * у + x] - color:
}
//<<<<<<<<<<<<<<<< getPixel »»»»»>
mRGB getPixel(int x. int y)
{
mRGB bad(255.255.255):
assert(x >- 0 && x < nCols):
assert(y >- 0 && у < nRows);
return pixel[nCols * у + x]:
}
}:
// end of class RGBpixmap
// конец класса RGBpixmap
#endi f
// RGBpixmap.cpp - routines to read a BMP file
// RGBpixmap.cpp - подпрограммы для чтения BMP-файла
#include "RGBpixmap.h"
typedef unsigned short ushort:
typedef unsigned long ulong:
fstream inf:
// global in this file for convenience
// глобальная в этом файле - для удобства
//<<<<<<<<<<<<<<<<<<<<< getShort »»»»»»»»»»
ushort getShortО
// helper function
// вспомогательная функция
{
// BMP format uses little-endian integer types
// в BMP-формате используются целые типы little-endian
// get and construct in memory a 2-byte integer
// stored in little-endian form
// получаем и конструируем в памяти двубайтовое целое,
// записанное в форме little-endian
char ic:
ushort ip:
inf.get(ic): ip - ic;
// first byte is little one
// первый байт младший
964
Приложение В. Некоторые полезные классы и служебные подпрограммы
inf.get(ic): ip |- ((ushort)ic « 8):
// or in high order byte
// или в старшем no порядку байте
return ip:
}
//<<<<<<<<<<<<<<<<<<<< getLong >»»»»»»»»»
ulong getLongO
// helper function
// вспомогательная функция
{
// BMP format uses little-endian integer types
// в BMP-формате используются целые типы little-endian
// get and construct in memory a 4-byte integer stored in
// little-endian form
// получаем и конструируем в памяти четырехбайтовое целое.
// записанное в форме little-endian
ulong ip - 0:
char ic - 0:
unsigned char uc - ic:
inf.get(ic): uc - ic: ip - uc:
inf.get(ic): uc - ic: ip |-((ulong)uc « 8):
inf.get(ic): uc - ic: ip |-((ulong)uc « 16):
inf.get(ic): uc - ic: ip |-((ulong)uc « 24):
return ip;
}
//««««<«<««« RGBPixmap:: readBmpFile»»»»»»>
int RGBpixmap:: readBMPFileCstring fname)
{
// Read into memory an mRGB image
// from an uncompressed BMP file.
// читаем в память mRGB изображение
// из неупакованного ВМР-файла
// return 0 on failure. 1 on success
// возвращаем 0 при ошибке. 1 при успехе
inf.open(fname.c_str(). ios::in|ios::binary);
// read binary char's
// читаем двоичные символы
if(!inf){ cout «" can’t open file: " « fname « endl:
return 0;}
int k. row. col. numPadBytes. nBytesInRow:
// read the file header information
// читаем информацию заголовочного файла
char chi. ch2:
inf.get(chl): inf.get(ch2):
// type: always ’BM‘
// тип: всегда ’BM’
ulong fileSize - getLongO:
ushort reservedl - getShortO:
// always 0
// всегда 0
ushort reserved2- getShortO:
// always 0
// всегда 0
В2. RGBPixmap CLASS
965
ulong off Bits - getLongO:
// offset to image - unreliable
// смещение изображения - ненадежно
ulong headerSize - getLongO;
// always 40
// всегда 40
ulong numCols - getLongO;
// number of columns in image
// число столбцов в изображении
ulong numRows - getLongO;
// number of rows in image
// число строк в изображении
ushort planes - getShortO:
// always 1
// всегда 1
ushort bitsPerPixel-getShortO:
// В or 24; allow only 24 here
// 8 или 24; здесь разрешается только 24
ulong compression - getLongO:
// must be 0 for uncompressed
// должно быть 0 для несжатых
ulong imageSize - getLongO;
// total bytes in image
// всего байт в изображении
ulong xPels - getLongO;
// always 0
// всегда 0
ulong yPels - getLongO;
// always 0
// всегда 0
ulong numLUTentries «getLongO:
// 256 for В bit. otherwise 0
// 256 для В бит. в противном случае 0
ulong impcolors - getLongO;
// always 0
// всегда 0
if(bitsPerPixel !- 24)
{
// error - must be a 24-bit uncompressed image
// ошибка - должно быть 24-битовое несжатое изображение
cout « "not a 24-bit pixel image, or is compressed!\n";
inf.closeO; return 0;
}
// add bytes at end of each row so total # is a multiple of 4
// round up 3*numCols to next mult, of 4
// добавляем байты в конец каждой строки так, чтобы
// общее количество было кратно 4
// округляем в большую сторону 3*numCols до следующей
// степени 4
nBytesInRow - ((3 * numCols + 3)/4) * 4:
numPadBytes - nBytesInRow - 3 * numCols:
// need this many
// необходимо такое количество
966
Приложение В. Некоторые полезные классы и служебные подпрограммы
nRows - numRows:
// set class's data members
// устанавливаем элементы данных класса
nCols - numCols:
pixel - new mRGB[nRows * nCols]:
// make space for array
// выделяем пространство для массива
if(lpixel) return 0;
// out of memory!
// нехватка памяти!
long count - 0:
char dum;
for(row - 0; row < nRows: row++)
// read pixel values
// читаем значения пикселов
for(col - 0: col < nCols: col++)
{
char r.g.b:
inf.get(b); inf.get(g): inf.get(r);
// читаем байты/Zread bytes
pixel[count].r - r:
// place them in colors
// отправляем их в цвета
pixel[count].g - g:
pixel[count++].b - b:
}
for(k - 0; k < numPadBytes : k++)
// skip pad bytes at row's end
// пропускаем незначащие байты в конце строки
inf » dum:
}
inf.closed: return 1:
// success
// успешно
}
ВЗ. Класс SCENE и сопутствующие классы
// SDL.h
// definition of simple support classes:
// определение простых сопутствующих классов:
♦ifndef _SDL
♦define _SDL
♦include <string>
♦include <iostream>
#include <fstream*
♦include <strstream>
using namespace std:
♦include <windows.h>
♦include <assert.h>
ВЗ. Класс SCENE и сопутствующие классы
967
#include <math.h>
#include <gl/Gl.h>
#include <gl/Glu.h>
#include <gl/glut.h>
// include RGBpixmap if you wish to add a pix map field to
Scene:
// включаем RGBpixmap. если хотим добавить поле пиксельной
// карты к Scene:
//#include "RGBpixmap.h"
//000000000000000000 Points class
class Point3{
public:
float x.y.z;
void set(float dx. float dy. float dz){x - dx; у - dy: z - dz;}
void set(Point3& p){x - p.x; у - p.y; z - p.z:}
Point3(float xx. float yy. float zz){x - xx; у - yy; z - zz:}
Point3(){x - у - z - 0:}
void build4tuple(float v[])
{
// load 4-tuple with this color: v[3] - 1 for homogeneous
// загружаем тетрады этим цветом: v[3] - 1 для однородных
v[0] - х; v[l] - у; v[2] - z; v[3] - l.Of:
}
}:
//000000000000000000 Vectors class 0000000000000000
class Vector3{
public:
float x.y.z:
void set(float dx. float dy. float dz){ x - dx: у - dy: z - dz:}
void set(Vector3& v){ x - v.x: у - v.y: z - v.z:}
void flip(){x - -x: у - -y; z - -z;}
// reverse this vector
// обращаем этот вектор
void setDiff(Point3& a. Point3& b)
// set to difference a - b
// устанавливаем его в разность а - b
{ х - а.х - b.x: у - а.у - b.y: z - a.z - b.z:}
void normalizeO:
// adjust this vector to unit length
// приводим этот вектор к единичной длине
Vector3(float xx. float yy. float zz){x - xx: у - yy: z - zz:}
Vector3(Vector3& v){x - v.x: у - v.y; z - v.z:}
Vector3(){x - у - z - 0:}
// default constructor
// конструктор по умолчанию
Vector3 cross(Vector3 b):
// return this cross b
// возвращаем это векторное произведение на b
float dot(Vector3 b):
// return this dotted with b
// возвращаем это скалярное произведение на b
}:
968
Приложение В. Некоторые полезные классы и служебные подпрограммы
// меееееоюммеемюе colors class
class Со1огЗ {
// holds a red. green, blue 3-tuple
// содержит триаду красного, зеленого и синего цветов
public:
float red. green, blue:
Color3(){red - green - blue - 0:}
Color3(float r. float g. float b){red - r; green - g: blue - b;}
Color3(Color3& c){red - c.red: green - c.green: blue - c.blue:}
void set(float r. float g. float b){red - r: green - g: blue - b:}
void set(Color3& c)
{red - c.red: green - c.green: blue - c.blue:}
void add(float r. float g. float b)
{red +- r; green +- g: blue +- b:}
void add(Color3i src. ColorSi refl):
void add(Color3& coir):
void build4tuple(float v[]):
}:
light class
class Light{
// for a linked list of light sources' color and position
// для связанного списка цвета и положения источников света
public:
Point3 pos:
Color3 color:
Light* next:
void setPosition(Point3 p){pos.set(p):}
void setColor(Colors c){color.set(c);}
Light(){next - NULL:}
}:
// Affine4 class
class Affine4{
// manages homogeneous affine transformations
// including inverse transformations
// and a stack to put them on
// used by Scene class to read SDL files
// управляет однородными аффинными преобразованиями.
// в том числе обратными преобразованиями, а также стеком.
// используемым в классе Scene для чтения SDL-файлов
public:
float m[16J:
// hold a 4-by-4 matrix
*/ содержат матрицу 4 на 4
Affine4();
void setldentityMatrixO:
void set(Affine4 a):
void preMult(Affine4 n):
void postMuit(Affine4 n);
}:
// end of Affine4 class
// конец класса Affine4
ВЗ. Класс SCENE и сопутствующие классы
969
//0000000000 AffineNode class
class AffineNode{
// used by Scene class to read SDL files
// используется классом Scene для чтения SDL-файлов
public:
Affine4 * affn:
Affine4 * invAffn:
AffineNode * next:
AffineNodeO
{
next - NULL:
affn - new Affine4;
// new affine with identity in it
// новое аффинное с единичной матрицей внутри
invAffn - new Affine4;
// and for the inverse
// а также для обратного
}
-AffineNodeO
// destructor
// деструктор
{
delete affn:
delete invAffn:
}
}:
//0000000000000000 AffineStack class 000000000000
class AffineStack{
// used by Scene class to read SDL files
// используется классом Scene для чтения SDL-файлов
public:
AffineNode * tos;
AffineStack0
// default constructor;puts identity on top
// конструктор по умолчанию; посылает единичную
// матрицу на вершину стека
{
tos - new AffineNode:
// node with identity in it
// узел, содержащий единичную матрицу
tos->next - NULL:
}
void dup():
void setldentityO:
// make top item the identity matrix
// записываем в верхний элемент единичную матрицу
void popAndDropO:
void releaseAffinesO:
// pop and drop all remaining items
// выталкиваем и бросаем оставшиеся элементы
void rotate(float angle. Vector3 u):
void scale(float sx. float sy. float sz):
void translate(Vector3 d):
970
Приложение В. Некоторые полезные классы и служебные подпрограммы
// end of AffineStack class
// конец класса AffineStack
//this was Shapes.h
// это был файл Shapes.h
// Shapes class and Supporting classes
// класс Shapes и сопутствующие классы
Material class
class Material{
public:
Color3 ambient, diffuse, specular, emissive:
int numParams:
// for textures
// для текстур
float params[10]:
// for textures
// для текстур
int textureType:
// 0 for none, neg for solids, pos for images
// 0. если нет. отрицательное для объемных.
// положительное для изображений
float specularExponent. reflectivity, transparency. speedOfLight:
float specularFraction. surfaceRoughness:
void setDefaultO;
void set(Material& m);
// end of Material
// конец класса Material
GeomObj class
class GeomObj{
public:
//IntRect scrnExtnt:
GeomObj * next:
GeomObjO: next(NULL){}
virtual void ToadStuff(){}
virtual void drawOpenGL(){}
virtual void telIMaterialsGL(){}
}:
Boolean
class Boolean: public GeomObj{
public:
GeomObj *left. *right:
Bool ean 0:1 eft (NULL). ri ght (NULL){}
virtual void drawOpenGLO
{
// just draw its children
// теперь рисуем его потомков
i f(1eft)1 eft-[greaterIdrawOpenGL();
i f(ri ght)ri ght-[greater]drawOpenGL():
ВЗ. Класс SCENE и сопутствующие классы
971
//00000000000000000000 UnionBool
class UnionBool : public Boolean{
public:
UnionBool(){Boolean();}
// constructor
// конструктор
}:
IntersectionBool 0000000000000000
class IntersectionBool : public Boolean{
public:
IntersectionBool(){Boolean();}
}:
DifferenceBool 0000000000000000
class DifferenceBool : public Boolean{
public:
Di fferenceBoolО {Bool ean0:}
}:
shape 000000000000000000000
class Shape: public GeomObj{
public:
Material mtrl;
Affine4 transf.invTransf;
// virtual Color3 textureCHitlnfoS h. int whichTexture):
Shape!){mtrl.textureType • 0; mtrl.numParams - 0:}
void setMaterial(Materials mt){mtrl.set(mt):}
void tellMaterialsGLO:
virtual void drawOpenGLO{}
}:
// end: Shape class
// конец класса Shape
//0$0$0$0$0$0$0$0$0 Cube class $0$0$0$0$0$0$0$0$0$0
class Cube: public Shape{
public:
Cube!){}
void drawOpenGLO
{
tel 1Materi alsGL О; glPushMatri x();
glMultMatrixf(transf.m):
// load affine
// загружаем аффинное
glEnable(GL_NORMALIZE):
glutSolidCube!2.0);
// a cube with vertices -1 to +1
// куб с вершинами от -1 до 1
glPopMatrixO;
}
//0$0$0$0$0$0$0$0$ Sphere class 0$0$0$0$0$0$0$0$0$0$0$0
class Sphere: public Shape{
public:
void drawOpenGLO
{
972
Приложение В. Некоторые полезные классы и служебные подпрограммы
tel 1MaterialsGL(): glPushMatrixC);
glMultMatrixf(transf.m):
glutSoli dSphere(1.0,20.20);
glPopMatrixO;
}
SphereO { }
}:
//@$@$$$@$@$@$@$@$@$0 TaperedCylinder class
class TaperedCylinder: public Shape{
public:
float small Radi us:
TaperedCylinder(){}
void drawOpenGL(){ /* to be implemented */}
// подлежит реализации
}:
//@$@$@$@$@$@$@$@$@ Square class
class Square: public Shape{
public:
SquareO{}
void drawOpenGLO{ /* to be implemented */}
// подлежит реализации
//@$@$@$$$@$@$@$@$@$0 Plane class
class Plane: public Shape{
public:
PlaneO {}
void drawOpenGLO{ /* to be implemented */}
// подлежит реализации
}:
//ттшшшш Class VertexID йййййййййййййййй
H used to define a Mesh
// использован для определения Mesh
class VertexID{public: int vertlndex. normlndex;};
//ШШШШ class FACE ЙЙЙЙЙЙЙЙЙЙЙЙЙЙ
11 used to define a Mesh
// использован для определения Mesh
class Face{
public:
int nVerts;
VertexID * vert;
// array of vertex and normal indices
// массив индексов вершин и нормалей
FaceO{ nVerts - 0: vert - NULL;}
~Face(){delete[] vert: nVerts - 0:}
}:
//@$@$@$@$@$@$@$@$@$0 Mesh class
class Mesh : public Shape{
private:
int numVerts, numNorms. numFaces;
Point3 *pt:
// array of points
// массив указателей
Vectors *norm;
ВЗ. Класс SCENE и сопутствующие классы
973
// array of normals
// массив нормалей
Face *face:
// array of faces
// массив граней
int lastVertUsed:
int lastNormUsed:
int lastFaceUsed:
public:
void readMeshCstring fname):
void writeMeshCchar* fname):
void printMeshO:
void drawMeshO:
void drawEdgesO:
void freeMeshO;
int isEmptyO;
void makeEmptyO:
Mesh О:
virtual void drawOpenGLO:
Mesh(string fname):
Vector3 newel 140 nt 1ndx[J):
string meshFileName:
// holds file name for this Mesh
// хранит имя файла для данного Mesh
}:
// end of Mesh class
// конец класса Mesh
Torus class
class Torus: public Shape{
public:
void drawOpenGLO{
telIMaterialsGLО: glPushMatrix():
glMultMatrixf(transf.m):
glutSolidTorus(0.2,1.0,10,12):
//1f(doEdges) glutWireTorus(0.2.1.0.10.12):
glPopMatrixO:}
}:
//@$@$@$@$@$@$@$@$@$@ Teapot class @$@$@$@$@$@$@$@$0$
class Teapot: public Shape{
public:
void drawOpenGLO{ tellMaterialsGLO: glPushMatrixO:
glMultMatrixf(transf.m):
glutSoli dTeapot(1.0): glPopMatrixC):}
}:
DefUnit & DefUnitStack classes
// used in Scene to read SDL files
// используется классом Scene для чтения SDL-файлов
class DefUnit{
// developed by Steve Morin
// разработан Стивом Морином
public:
string name, stuff:
DefUnit(string n. string s) {stuff - s:name - n:}
974
Приложение В. Некоторые полезные классы и служебные подпрограммы
}:
class DefUnitStack {
public:
DefUnitStackO {stack - NULL;}
void push(string n. string s);
void printO;
int search(string s):
string contents(string s):
void released;
private:
struct D4S {
DefUnit *current:
struct D4S *next;
} d4s:
D4S *stack:
}:
// end of DefUnitStack class
// конец класса DefUnitStack
//++444Ч-НЧ-Н-Н- TokenType +++++++++++++
enum mTokenType {IDENT. LIGHT. ROTATE. TRANSLATE.
SCALE. PUSH. POP. IDENTITYAFFINE.
GLOBALAMBIENT. BACKGROUND. MINREFLECTIVITY.
MINTRANSPARENCY, MAXRECURSIONDEPTH. CUBE. SPHERE. TORUS. PLANE.
SQUARE. CYLINDER. CONE. TAPEREDCYLINDER,TETRAHEDRON. OCTAHEDRON.
DODECAHEDRON. ICOSAHEDRON.BUCKYBALL. TEAPOT.
DIAMOND.UNION.INTERSECTION. DIFFERENCEa. MAKEPIXMAP.
MESH. DEFAULTMATERIALS. AMBIENT. DIFFUSE.SPECULAR.
SPECULARFRACTION. SURFACEROUGHNESS.EMISSIVE. SPECULAREXPONENT.
SPEEDOFLIGHT. TRANSPARENCY.REFLECTIVITY. PARAMETERS. TEXTURE.
FTCURLY, RGHTCURLY. DEF. USE. T_NULL. F_EOF, UNKNOWN }:
//0000000000000 Scene class 00000000000000000000
class Scene{
public:
Light *light:
// attach linked list of lights here
// здесь прикрепляем связанный список источников света
GeomObj * obj:
// attach the object list here
// здесь прикрепляем список объектов
Color3 background, ambient;
int maxRecursionDepth:
// must #include RGBpixmap.h to have following texture fields
// должна быть команда finclude RGBpixmap.h для
// следующих полей текстуры
//RGBpixmap pixmap[8J:
// list of attached pixmaps
// список прикрепленных пиксельных карт
float minReflectivity. minTransparency;
// bool isInShadow(Ray& f):
// for ray tracing: implementation left to the reader
// для трассировки лучей: реализация оставлена читателю
Scene():11ght(NULL).obj(NULL).tail(NULL)
ВЗ. класс SCENE и сопутствующие классы
975
// default constructor
// конструктор по умолчанию
{
currMtrl .setDefaultO:
background.set(0.О.О.6f);
ambient.set(O.lf.O.lf.O.lf);
minReflectivity - 0.5:
minTransparency - 0.5:
maxRecursionDepth - 3:
}
Scene(string fname){Scene(): read(fname):}
void freeSceneO:
void makeLightsOpenGL(){/* to be Implemented */}
// подлежит реализации
void drawSceneOpenGLO;
bool read(string fname);
GeomObj* getObjectO:
private:
// private stuff used only for reading a scene
11 private материал, используется только для чтения сцены
int line;
int nextline:
ifstream *file_in;
strstream *f_in:
strstream temp_fin:
DefUni tStack *def_stack;
GeomObj * tail:
// tail of object list
// остаток списка объектов
AffineStack affStk;
// affine stack
// аффинный стек
Material currMtrl;
string nexttoken(void):
float getFloatO:
bool isidentifierCstring keyword):
void cleanUpO:
mTokenType whichtoken(string keyword):
}:
// end of Scene.h
// конец файла Scene.h
#endif
//SDL.cpp
// support code for the classes in SDL.h
// вспомогательный код для классов в файле SDL.h
include "SDL.h''
// Vector3 methods
11 методы Vector3
Vectors Vectors :: cross(Vector3 b)
//return this cross b
//возвращаем зто векторное произведение на b
{
976
Приложение В. Некоторые полезные классы и служебные подпрограммы
Vector3 c(y*b.z - z*b.y. z*b.x - x*b.z. x*b.y - y*b.x);
return c:
}
float Vectors dot(Vector3 b)
// return this dotted with b
// возвращаем это скалярное произведение с b
{return х * Ь.х + у * b.y + z * b.z:}
void Vectors :: normalize()
// adjust this vector to unit length
// приводим данный вектор к единичной длине
{
double sizeSq -x*x + y*y + z*z:
1f(sizeSq < 0.0000001)
{
cerr « "\nnormalizeO sees vector (0.0,0)!":
return:
// does nothing to zero vectors:
// для нулевых векторов не делается ничего
}
float scaleFactor - 1.0/(float)sqrt(sizeSq):
х *- scaleFactor: у *- scaleFactor: z *- scaleFactor:
}
// Colors methods
// методы Color3
void Colors ::add(Color3& src. Color3& refl)
{
// add the product of source color and reflection coefficient
// добавляем произведение цвета источника и коэффициента
// отражения
red +- src.red * refl.red:
green +- src.green * refl.green:
blue +- src.blue * refl.blue:
}
void Color3:: add(Color3* coir)
{
// add coir to this color
// добавляем coir к данному цвету
red +“ coir.red : green +- coir.green: blue +- coir.blue:}
void Colors :: build4tuple(float v[J)
{
// load 4-tuple with this color: v[3] - 1 for homogeneous
// загружаем тетраду с этим цветом: v[3] - 1 для однородных
v[0] “ red: v[l] - green; v[2] - blue: v[3] - l.Of:
}
// Affine4 methods
// методы Affine4
Affine4::Affine4(){
// make identity transform
// создаем тождественное преобразование
m[0] - m[5] - m[10] - m[15] - 1.0:
m[l] - m[2] - m[3] - m[4] - 0.0;
ВЗ. Класс SCENE и сопутствующие классы
977
т[6] - т[7] - т[В] - т[9] - 0.0:
т[11]- т[12] - т[13] - т[14] - 0.0:
}
void Affine4 :: set!dentityMatrix(){
// make identity transform
// создаем тождественное преобразование
m[0] - m[5] - m[10] - m[15] - 1.0:
m[l] - m[2] - m[3] - m[4] - 0.0:
m[6] - m[7] - m[8] - m[9] - 0.0:
m[ll]- m[12] - m[13] - m[14] - 0.0:
}
void Affine4 ::set(Affine4 a)
// set this matrix to a
// устанавливаем эту матрицу в а
{
fordnt i - 0: i < 16: i++)
m[i]-a.m[i]:
}
I/««««««« preMult »»»>»»>
void Affine4 ::preMult(Affine4 n)
{
// postmultiplies this with n
// умножает this справа на n
float sum:
Affine4 tmp:
tmp,set(*this):
// tmp copy
// копия tmp
// following mult’s : this - tmp * n
// следующие умножения: this - tmp * n
fordnt c - 0: c < 4: C++)
fordnt r “ 0: r <4 : r++)
{
sum - 0:
fordnt k - 0: k < 4: k++)
sum +- n.m[4 * k + r]* tmp.m[4 * c + kJ;
m[4 * c + r] - sum:
}
H end of for loops
// конец циклов for
}
// end of preMultO
// конец preMultO
11«««««« postMult »»»»»>
void Affine4 ::postMult(Affine4 n){
// postmultiplies this with n
11 this умножается справа на n
float sum;
Affine4 tmp:
tmp.set(*this):
// tmp copy
// копия tmp
fordnt c • 0: c < 4: C++)
Приложение В. Некоторые полезные классы и служебные подпрограммы
m
// form this - tmp * n
// формируем this - tmp * n
for(1nt r - 0; r <4 : r++)
{
sum - 0:
for(int k - 0: k < 4: k++)
sum +- tmp.m[4 * k + r]* n.m[4 * c + kJ:
m[4 * c + r] - sum:
}
// end of for loops
// конец циклов for
}
// AffineStack methods
// методы AffineStack
void AffineStack :: dup()
{
AffineNode* tmp - new AffineNode:
tmp->affn - new Affine4(*(tos->affn)):
tmp->invAffn - new Affine4(*(tos->1nvAffn)):
tmp-[greater]next - tos:
tos - tmp;
}
void AffineStack :: setldentityO
// make top item the identity matrix
// делаем верхний элемент единичной матрицей
{
assert(tos !- NULL):
tos->affn->setIdentityMatrix():
tos->invAffn->set!dentityMatrix():
}
void AffineStack :: popAndDropO
{
if(tos ~ NULL) return:
// do nothing
// не делаем ничего
AffineNode *tnp - tos:
tos - tos-[greater]next:
delete tmp;
// should call destructor, which deletes matrices
// нужно вызвать деструктор, удаляющий матрицы
}
void AffineStack :: releaseAffinesO
{
// pop and drop all remaining items
// выталкиваем и отбрасываем все оставшиеся элементы
while(tos) popAndDropO:
}
void AffineStack :: rotate(float angle. Vectors u)
{
Affine4 rm:
// make identity matrix
// создаем единичную матрицу
Affine4 invRm:
В3< Класс SCENE и сопутствующие классы
979
u.normalized:
// make the rotation axis unit length
// создаем ось поворота единичной длины
float ang - angle * 3.14159265/ 180:
// deg to
// градусы в радианы
float с - cos(ang). s - sin(ang);
float me - 1.0 - c:
// fill the 3x3 upper left matrix -
11 заполняем 3x3 верхних левых элемента матрицы
rm.m[0] с + me * u.x * u.x;
rm.m[l] - me * u.x * u.y + s * u.z:
rm.m[2] - me * u.x * u.z - s * u.y:
rm.m[4] inc * u.y * u.x - s * u.z:
rm.m[5] - c + me * u.y * u.y;
rm.m[6] - me * u.y * u.z + s * u.x:
rm.m[8] - me * u.z * u.x + s * u.y;
rm.m[9] - me * u.z * u.y - s * u.x;
rm.m[10] - c + me * u.z * u.z:
// same for inverse: just sign of s is changed
// то же для обратной: только знак s меняется
1nvRm.m[0] - с + me * u.x * u.x:
1nvRm.m[l] - me * u.x * u.y - s * u.z:
1nvRm.m[2] - me * u.x * u.z + s * u.y;
invRm.m[4] - me * u.y * u.x + s * u.z:
invRm.m[5] - c + me * u.y * u.y:
1nvRm.m[6] - me * u.y * u.z - s * u.x:
invRm.m[8] - me * u.z * u.x - s * u.y:
invRm.m[9] - me * u.z * u.y + s * u.x:
invRm.m[10] - c + me * u.z * u.z;
tos->affn->postMult(rm);
tos->invAffn->preMult(invRm);
void AffineStack :: scale(float sx. float sy. float sz)
{
// post multiply top item by scaling
// умножаем справа верхний элемент на матрицу
// масштабирования
#define sEps 0.00001
Affine4 scl:
// make an identity
// создаем единичную матрицу
Affine4 InvScl:
scl,m[0] - sx:
scl.m[5] - sy:
scl.m[10] - sz;
// adjust it to a scaling matrix
// приспосабливаем к матрице масштабирования
if(fabs(sx) < sEps || fabs(sy) < sEps || fabs(sz) < sEps)
cerr « "degenerate scaling transformation!\n":
// вырожденное преобразование масштабирования!
980
Приложение В. Некоторые полезные классы и служебные подпрограммы
invScl,m[0] - 1/sx: invScl.m[5] - 1/sy: invScl.m[10] - 1/sz:
tos->affn->postMult(scl): //
tos->invAffn->preMultdnvScl);
}
void AffineStack :: translate(Vector3 d)
{
Affine4 tn:
// make identity matrix
// создаем единичную матрицу
Affine4 invTr:
tr.m[12] - d.x: tr.m[13] - d.y: tr.m[14] - d.z:
invTr.m[12] - -d.x: invTr.m[13] - -d.y; invTr.m[14] - -d.z;
tos->affn->postMult(tr);
tos->invAffn->preMult(i nvTr):
}
// Material methods
// методы Material
void Material :: setDefault(){
textureType - 0;
// for none
// для отсутствия материала
numParams - 0:
reflectivity - transparency - 0.0:
speedOfLight - specularExponent - 1.0;
specularFraction - 0.0:
surfaceRoughness - 1.0:
ambient.set(O.lf.O.lf.O.lf):
diffuse.set(0.8f.0.8f.0.8f):
specular,set(0.0.0):
emissive.set(O.O.O):
}
void Material :: set(Material& m)
{
textureType - m.textureType:
numParams “ m.numParams;
fordnt 1 - 0: i < numParams: i++) params[i] - m.params[i];
transparency - m.transparency:
speedOfLight - m.speedOfLight:
reflectivity - m.reflectivity:
specularExponent - m.specularExponent:
specularFraction - m.specularFraction:
surfaceRoughness • m.surfaceRoughness:
ambient.set(m.ambient):
di ffuse.set(m.di ffuse):
specular.set(m.specular):
emissive.set(m.emissive):
}
// Shape methods
// методы Shape
void Shape :: tellMaterialsGLO
{
float amb[4].diff[4].spec[4], emiss[4J:
float zero[] - {0.0.0.1}:
ВЗ. Класс SCENE и сопутствующие классы
981
mtrl.ambient.bui1d4tuple(amb):
// fill the array
// заполняем массив
mtrl.diffuse.build4tuple(diff);
mtrl.specular.build4tuple(spec):
mtrl.emissive.build4tuple(emiss);
glMateri alfv(GL_FRONT/*_AND_BACK*/.GL_AMBIENT.amb);
glMaterialfv(GL_FRONT/*_AND_BACK*/.GL_DIFFUSE.diff);
glMaterial fv(GL_FRONT/*_AND_BACK*/,GL_SPECULAR.spec);
gl Materi a 1 f v (GL_FRONT/*_AND_BACK*/. GLJMISS ION .emiss):
glMaterialf(GL_FRONT/*_AND BACK*/.GL SHININESS.mtrl.specularExponent);
}
// Mesh methods
// методы Mesh
Mesh :: MeshO{
numVerts “ numFaces - numNorms • 0:
pt “ NULL: norm - NULL: face “ NULL:
lastVertUsed - lastNormUsed - lastFaceUsed - -1:
}
void Mesh :: freeMeshO
{
// free up memory used by this mesh.
// освобождаем память, используемую этой сеткой
delete [] pt;
// release whole vertex list
// освобождаем весь список вершин
delete [] norm;
for(int f - 0: f < numFaces; f++)
delete[] face[f].vert:
// delete the vert[] array of this face
// удаляем массив vert[] этой грани
delete [] face;
}
int Mesh :: isEmptyO
{
return (numVerts == 0) || (numFaces “ 0) || (numNorms — 0);
}
void Mesh :: makeEmptyO
{
numVerts » numFaces - numNorms - 0;
}
void Mesh :: drawOpenGLO
{
tel 1 Materi al sGLO: gl PushMatrix():
glMultMatrixf(transf.m):
drawMeshO;
// if(doEdges) drawEdgesO:
glPopMatrixO;
}
Mesh :: Mesh(string fname){
// read this file to build mesh
// читаем этот файл для построения сетки
numVerts » numFaces - numNorms - 0;
982
Приложение В. Некоторые полезные классы и служебные подпрограммы
pt - NULL; norm - NULL: face “ NULL:
lastVertUsed - lastNormUsed - lastFaceUsed - -1:
readMesh(fname):
}
Vectors Mesh :: newel14(1 nt indx[])
{
/* return the normalized normal to face with vertices
pt[indx[0]J............pt[indx[3]]. i.e. indx[] contains the four indices
into the vertex list to be used in the Newell calculation */
/* возвращаем нормированную нормаль на грань с вершинами
pt[indx[0]]............pt[1ndx[3]]. то есть indx[]
содержит четыре индекса в списке вершин
для использования в вычислениях по Ньюэллу
*/
Vectors m:
fordnt i - 0: i < 4 ; 1++)
{
int next - (i— 3) ? 0 : i + 1:
// which index is next?
// какой индекс следующий?
int f - indx[i], n - indx[next]:
// names for the indices in the pair
II имена для индексов в nape
m.x +- (pt[f].y - pt[n].y) * (pt[f].z + pt[n].z):
m.y +- (pt[f].z - pt[n].z) * (pt[f].x + pt[n].x):
m.z +- (pt[f].x - pt[n].x) * (pt[f].y + pt[n].y):
}
m. normalized:
return m;
}
//<<<<<<<<<<<<<<<<<<<<<<<<<<<< readMesh »»»»»»»»»»»»
void Mesh:: readMesh(string fname)
{
fstream inStream:
inStream.open(fname.c_str(). ios ::in):
// open needs a c-like string
// для открытия требуется тип строки как в С
ifdnStream.faiK) || InStream.eofd)
{
cout « "can't open file or eof: “ « fname « endl:
makeEmptyd; return;
}
inStream » numVerts » numNorms » numFaces;
// make arrays for vertices, normals, and faces
// создает массивы для вершин, нормалей и граней
pt - new Point3[numVertsJ: assert(pt !- NULL):
norm - new Vector3[numNorms]: assert(norm !» NULL):
face - new Face[numFacesJ: assert(face !- NULL):
fordnt i - 0; i < numVerts: i++)
// read in the vertices
// читаем в вершинах
InStream » pt[1].x » pt[i].y » pt[i].z:
fordnt 11 - 0: ii < numNorms; 11++)
ВЗ. Класс SCENE и сопутствующие классы
983
// read in the normals
// читаем в нормалях
inStream » norm[ii].x » norm[ii].y » norm[ii].z;
forlint f - 0: f < numFaces: f++)
// read in face data
// читаем данные no грани
{
inStream » face[f].nVerts:
int n - face[f],nVerts;
face[f].vert - new VertexID[n]; assert(face[f].vert !-
NULL):
for(int k = 0: k < n; k++)
// read vertex indices for this face
// читаем индексы вершин для данной грани
inStream » face[f].vert[k].vertlndex:
for(int kk - 0; kk < n: kk++)
// read normal indices for this face
// читаем индексы нормали для данной грани
inStream » face[f].vert[kk],normindex;
}
inStream.closeO:
)
// end of readMesh
// конец readMesh
//<<<<<<<<<<<<<<<<<<<<<< drawMesh »»»»»»»»»»
void Mesh :: drawMeshO
{
// draw each face of this mesh using OpenGL: draw each polygon.
// рисуем каждую грань данной сетки при помощи OpenGL
// рисуем каждый полигон
if(isEmptyO) return;
// mesh is empty
// сетка пуста
forlint f - 0: f < numFaces; f++)
{
int n - face[f].nVerts:
glBegin(GL_POLYGON);
for(int v - 0; v < n; v++)
{
int in - face[f].vert[v],normindex;
assertdn >- 0 && in < numNorms):
glNormal3f(norm[in].x. norm[in].y. norm[in].z):
int iv - face[f].vert[v].vertlndex; assertliv >- 0 && iv < numVerts):
glVertex3f(pt[iv].x. pt[iv].y. pt[iv].z);
}
glEndO;
)
glFlushO:
}
//<<<<<<<<<<<<<<<<<<<<<<<<<<<< wri te mesh*»»»»»»»»»»»»»»»»
void Mesh:: writeMesh(char * fname)
{
// write this mesh object into a new Chapter 6 format file.
984
Приложение В. Некоторые полезные классы и служебные подпрограммы
// записываем данный объект mesh в файл нового формата
// из главы б
1 f(numVerts — 0 || numNorms — 0 || numFaces ~ 0) return:
// empty
И пусто
fstream outStream(fname. ios ::out):
H open the output stream
// открываем поток вывода
If(outStream.failO) {cout « "can't make new file: " « fname « endl:
// не могу открыть новый файл
return:}
outStream « numVerts « " " « numNorms « ’ " « numFaces <<"\n";
// write the vertex and vertex normal list
// записываем список вершин и нормалей в вершинах
fordnt i - 0; i < numVerts; i++)
outStream « pt[i].x « " " « pt[i].y « " " « pt[i].z « “\n”:
fordnt ii - 0; ii < numNorms; 11++)
outStream « norm[ii].x « • " « norm[ii].y « " " « norm[ii].z « "\n":
// write the face data
И записываем данные по грани
fordnt f - 0; f < nwnFaces: f++)
{
int n - face[f].nVerts:
outStream « n « "\n";
fordnt v - 0: v < n; v++)
// write vertex indices for this face
И записываем индексы вершин для данной грани
outStream « face[f].vert[v].vertlndex « " ": outStream « "\n":
fordnt k - 0: k < n: k++)
// write normal indices for this face
// записываем индексы нормалей для данной грани
outStream « face[f].vert[k].normindex « " ": outStream « "\n":
}
outStream.closeO:
}
// Scene methods
// методы Scene
//«««« methods »»»»»>
string Scene : nexttoken(void) //HMfffflf nexttokenO
{
char c:
string token;
int lastchar - 1:
if (!f_in) {return(token); }
if (f_in->eof()) {return(token):}
while (f in->get(c))
{
if (f_in->eof()) {
return(token):
}
switch (c) {
case '\n': nextline +» 1:
case ' ' :
ВЗ. Класс SCENE и сопутствующие классы
985
case *\t‘:
case Ла':
case ЛЬ*:
case '\v':
case '\f:
case Лг': {
if ( lastchar — 0 ) {return(token);}break; }
case '{': {
token - c: return(token); break:}
case '}': {
token - c:
return(token);
break; }
case ’!’: {
while ( c !• Лп' && f in->get(c)) {
}
nextline++: break;}
default: {
token - token + c:
lastchar - 0:
if ((f_in->peek() — '{') ||
(f_in->peek() — '}') ) {
if ( lastchar — 0 ) {
return(token);
} else {
f_in->get(c):
token - c:
return(token);
}
}
line - nextline:
}
}
}
returnC ");
}
//««««««« getFi oat »»»»»»»»
float Scene :: getFloatO //ШШШ getFloatO
{
strstream tmp:
float number;
string str - nexttokenO;
tmp « str;
if(!(tmp » number))
{
cerr « "Line " « line « ": error getting float" « endl:
// ошибка получения вещественного числа
exit(-l);
}
else
{
char t:
if ( (tmp » t ) )
986
Приложение В. Некоторые полезные классы и служебные подпрограммы
{
cerr « “Line " « line « bum chars in number” « endl:
// неверные символы в числе
exit(-l):
}
}
return number;
}
//<<<<<<<<<<<<<<<<< isidentifier »»»»»»»»
bool Scene :: isidentifier(string keyword) { //fflOffl
isidentifier
string temp - keyword:
if (! 1sa1pha(temp[0])) return(false):
for (int count - 1; count < temp.lengthO: count++) {
if ((!isalnum(temp[count]))&& (temp[count]!-'.'))
return(false):
}
return(true):
}
//<<<<<<<<<<<<<<<< cleanllp »»»»»»»»
void Scene :: cleanUpO //ШШШ cleanup
{ // release stuff after parsing file
// освобождаем место после анализа файла
affStk.releaseAffi nes():
// delete affine stack
// удаляем аффинный стек
def_stack->release():
delete def_stack;
// release the DefUnitStack memory
}
//<<<<<<<<<<<<<<<<< freeScene »»»»»»»
void Scene :: freeSceneO
{ // release the object and light lists
// освобождаем списки объектов и источников света
GeomObj *р - obj:
while(p)
{
GeomObj* q - p:
p - p->next:
delete q:
}
Light * q - light:
while(q)
{
Light* r - q:
q - q->next:
delete r:
}
}
//<<«<«««««« whichToken »»»»»»»>
mTokenType Scene :: whichtoken(string keyword)
{
string temp - keyword;
ВЗ. Класс SCENE и сопутствующие классы
987
if ( temp ~ "light” ) return LIGHT:
if ( temp -- "rotate" ) return ROTATE;
if ( temp — "translate” ) return TRANSLATE:
if ( temp -» “scale") return (SCALE):
if ( temp “ “push") return (PUSH):
if ( temp = "pop") return (POP):
if ( temp = “identityAffine") return (IDENTITYAFFINE):
if ( temp — "cube") return (CUBE);
if ( temp “ "sphere") return (SPHERE):
if ( temp — "torus") return (TORUS):
if ( temp = "plane") return (PLANE):
if ( temp "square") return (SQUARE):
if ( temp — “cylinder") return (CYLINDER);
if ( temp — "taperedCylinder") return (TAPEREDCYLINDER):
if ( temp “ "cone") return (CONE):
if ( temp — "tetrahedron") return (TETRAHEDRON):
if ( temp — "octahedron”) return (OCTAHEDRON):
if ( temp — "dodecahedron") return (DODECAHEDRON);
if ( temp “ "icosahedron") return (ICOSAHEDRON):
if ( temp — "buckyball") return (BUCKYBALL):
if ( temp ~ "diamond") return (DIAMOND):
if ( temp — "teapot") return (TEAPOT);
if ( temp — "union") return (UNION):
if ( temp = "intersection") return (INTERSECTION):
if ( temp = "difference") return (DIFFERENCEa):
if ( temp = "mesh") return (MESH):
if ( temp ~ "makePixmap") return (MAKEPIXMAP);
if ( temp — "defaultMaterials") return (DEFAULTMATERIALS);
if ( temp — "ambient") return (AMBIENT);
if ( temp “ "diffuse") return (DIFFUSE):
if ( temp = "specular” return (SPECULAR):
if ( temp ~ "specularFraction") return (SPECULARFRACTION):
if ( temp — "surfaceRoughness") return (SURFACEROUGHNESS);
if ( temp — "emissive") return (EMISSIVE):
if ( temp “ "specularExponent") return (.SPECULAREXPONENT):
if ( temp — "speedOfLight") return (SPEEDOFLIGHT):
if ( temp “ "transparency") return (TRANSPARENCY);
if ( temp ” "reflectivity") return (REFLECTIVITY);
if ( temp = "parameters") return (PARAMETERS);
if ( temp “ "texture”) return (TEXTURE);
if ( temp — "globalAmbient") return (GLOBALAMBIENT):
if ( temp “ “minReflectivity") return (MINREFLECTIVITY):
if ( temp ~ "minTransparency") return (MINTRANSPARENCY):
if ( temp ~ "maxRecursionDepth") return (MAXRECURSIONDEPTH)
if ( temp = “background") return (BACKGROUND):
if ( temp — "{") return (LFTCURLY):
if ( temp ~ "}") return (RGHTCURLY):
if ( temp — "def") return (DEF);
if ( temp ~ "use") return (USE):
if ( temp ” “ “ ) return (T-NULL):
if ( isidentifier(temp) ) return (IDENT):
cout « temp « “:" « temp.lengthO « endl:
return(UNKNOWN);
988
Приложение В. Некоторые полезные классы и служебные подпрограммы
} // end of whichtoken
// конец whichtoken
//««««« drawSceneOpenGL »»»»»»»».
void Scene :: drawSceneOpenGL0
{ //draw each object on object list
// рисуем каждый объект из списка объектов
for(GeomObj* р - obj: р : р - p->next)
p->drawOpenGL(): //draw it
}
//<<<<<<<<<<<<<<< Scene :: read »»»»»»»»
bool Scene:: read(string fname)
// return true if ok: else false
// возвращаем true, если все ok: иначе false
{
file_1n - new ifstream(fname.c_str()):
1f(!(*file in))
{
cout « "I can’t find or open file: " « fname « endl;
//не могу найти или открыть файл
return false;
}
f_in - new strstreamO:
line - nextline - 1:
def_stack - new DefUnitStackO:
char ch:
freeSceneO: //delete any previous scene
// удаляем любую предшествующую сцену
// initialize all for reading:
// инициализируем все для чтения
obj - tail - NULL:
light - NULL:
affStk.tos - new AffineNode;
affStk.tos->next - NULL:
while (fi1e_in->get(ch)) {*f_in « ch:}
// read whole file
// читаем весь файл
whiled)
//read file, collecting objects, until EOF or an error
// читаем файл, собирая объекты, до конца файла или ошибки
{
GeomObj * shp - getObjectO:
// get the next shape
// получаем следующую форму
if(ishp) break;
// no object: either error or EOF
// нет объекта: ошибка или конец файла
shp->next - NULL: // to be safe
if(obj “ NULL){ obj - tail - shp:}
// empty list so far
// список пока пуст
else{tail->next - shp; tail - shp:}
// add new object to queue
// добавляем новый объект в очередь
ВЗ. Класс SCENE и сопутствующие классы
989
}
file_in->close();
cleanUpO:
И delete temp lists, etc.
// удаляем временные списки и т. д.
return true:
}
// end of readO
// конец readO
//««««««« Scene :: getObject »»»»»»»>
GeomObj* Scene :: getObjectO
{ //reads tokens from stream f_in (a data member of Scene).
// building lights, getting materials, doing transformations, until it finds a new object
// returns NULL if any error occurs, or end of file
// читает метки из потока f_1n (элементы данных Scene).
//создает источники света, получает материалы.
// производит преобразования.
// пока не находит новый объект
// возвращает NULL, если обнаружена любая ошибка или
// конец файла
string s;
GeomObj * newShape:
mTokenType typ;
while ((typ - (whichtoken( s “ nexttoken() ))) !- T NULL)
{
if(typ ~ UNION || typ — INTERSECTION || typ — DIFFERENCEa)
{
switch(typ)
{
case UNION: newShape - new UnionBool(); break:
case INTERSECTION: newShape - new IntersectionBool 0: break:
case DIFFERENCEa: newShape - new DifferenceBool():break:
}
// end of little switch
// конец малого переключателя
GeomObj* p - newShape:
p - getObjectO: // get left child
// получаем левого потомка
if(!p) return NULL;
// Error! should always get an object
// Ошибка! всегда должен получить объект
((Boolean*)newShape)->left - р:
// hook it up
// подключаем его
р - getObjectO:
// get right child
// получаем правого потомка
if(!p) return NULL:
((Boo1ean*)newShape)->right - p:
// hook it up
// подключаем его
return newShape:
}
Приложение В. Некоторые полезные классы и служебные подпрограммы
// end of if(typ “ UNION etc....
// конец if(typ “ UNION etc....
switch(typ)
{
case LIGHT: {
Point3 p;
Color3 c:
p.x - getFloatO: p.y - getFloatO: p.z - getFloatO;
c.red - getFloatO: c.green - getFloatO: c.blue - getFloatO:
Light *1 - new Light:
l->setPosition(p):
l->setColor(c):
l->next - light:
// put it on the list
// помещаем его в список
light - 1: break;}
case ROTATE: {
float angle:
Vectors u:
angle • getFloatO: u.x - getFloatO;
u.y - getFloatO: u.z - getFloatO:
affStk.rotate(angle.u):break:}
case TRANSLATE: {
Vectors d:
d.x - getFloatO: d.y - getFloatO: d.z - getFloatO:
affStk.translate(d):break:}
case SCALE: {
float sx. sy. sz:
sx - getFloatO: sy - getFloatO: sz - getFloatO:
affStk.scale(sx. sy. szkbreak:}
case PUSH: affStk.dupO: break:
case POP: affStk.popAndDropO; break;
case IDENTITYAFFINE: affStk.setIdentity0;break:
case AMBIENT: {
float dr. dg. db:
dr - getFloatO: dg - getFloatO: db.- getFloatO;
currMtrl.ambi ent.set(dr,dg.db): break:}
case DIFFUSE: {
float dr.dg.db:
dr - getFloatO: dg - getFloatO: db - getFloatO:
currMtrl.diffuse.set(dr.dg.db); break;} r
case SPECULAR:{
float dr.dg.db;
dr - getFloatO: dg - getFloatO: db - getFloatO:
currMtrl.specular.set(dr.dg.db): break;}
case EMISSIVE: {
float dr.dg.db:
dr - getFloatO; dg - getFloatO: db - getFloatO:
currMtrl.emi ssi ve.set(dr.dg,db): break;}
case PARAMETERS: {
// get a list of numParams parameters
И получаем список из numParams параметров
currMtrl .numParams - (int)getFloatO:
Bj, Клэд; SCENE и сопутствующие классы
991
for(int 1 - 0: 1 < currMtrl.numParams: i*+)
currMtrl,params[i] - getFloatO:
break;}
case SPECULARFRACTION: currMtrl.specularFraction -getFloatO; break:
case SURFACEROUGHNESS: currMtrl.surfaceRoughness -
getFloatO: break:
case TEXTURE: {
// get type. 0 for none
// получаем тип. 0 если нет
currMtrl.textureType - getFloatO;}
break:
case DEFAULTMATERIALS: currMtrl.setDefaultO:break:
case SPEEDOFLIGHT:
currMtrl.speedOfLight - getFloatO: break:
case SPECULAREXPONENT:
currMtrl.specularExponent - getFloatO: break;
case TRANSPARENCY:
currMtrl.transparency - getFloatO: break:
case REFLECTIVITY:
currMtrl.reflectivity - getFloatO: break:
case GLOBALAMBIENT:
ambient.red - getFloatO: ambient.green - getFloatO;
ambient.blue - getFloatO; break:
case BACKGROUND:
background.red - getFloatO:
background.green - getFloatO:
background.blue - getFloatO:break:
case MINREFLECTIVITY:
minReflectivity - getFloatO; break;
case MINTRANSPARENCY:
minTransparency - getFloatO: break;
case MAXRECURSIONDEPTH:
maxRecursionDepth - getFloatO: break;
case MAKEPIXMAP: {
// get BMP file name for a pix map
// получаем имя BMP-файла для пиксельной карты
/* to be implemented, along the lines:
/ * для построчной реализации
int which - getFloatO:
// index of this pix map in pix map array
// индекс этой пиксельной карты в массиве пиксельной карты
if(which < 0 || which > 7){cout « "\nbad index'of RGBpixmap!\n":}
// неверный индекс пиксельной карты RGB
string fname - nexttokenO:
// get file name for mesh
// получаем имя файла для сетки
cout « "I got fname - " « fname « endl:
// Я получил имя файла - ...
i f(!pi xmapLwhi ch].readBMPF i1e(fname))
{
// read BMP file into this pix map
// читаем BMP-файл в данную пиксельную карту
cout « " \ncan’t read that RGBpixmap f11e!\n";
992
Приложение В. Некоторые полезные классы и служебные подпрограммы
// не смог прочитать указанный RGB-файл для пиксельной карты
return NULL: } */
break:}
// end of case: MAKEPIXMAP
// конец случая MAKEPIXMAP
case T_NULL: break;
// The null token represents end-of-file
// метка null представляет конец файла
case DEF: {
string name. temp. lb. rb:
int 1 - line:
string inp:
name - nexttokenO:
if ( whichtoken(name) !- IDENT ) {
cout « "Error: Identifier expected.” « endl:
// Ошибка: должен быть идентификатор
return NULL:
}
if ( def_stack->search(name) ) {
cout « line « ": " « name:
cout « ": attempt to redefine. " « endl:
// пытаемся переопределить
return NULL:
}
lb - nexttokenO:
if ( whichtoken(lb) !- LFTCURLY ) {
cout « "Error: { expected." « endl:
// Ошибка: ожидалась {
return NULL:
}
while ( whichtoken( temp - nexttokenO) !- RGHTCURLY ) {
cout « temp « endl:
inp - inp + temp + " ";
if (!f_in) {
cout « "Error: end of file detected." « endl:
// Ошибка: обнаружен конец файла
return NULL:
}
}
// Push the contents of the string onto the stack.
// проталкиваем в стек содержимое строки
def_stack->push(name, inpl.-
break:}
// end of case: DEF
// конец случая DEF
case USE: {
string name:
name - nexttokenO:
if ( whichtoken(name) !- IDENT ) {
cout « line « ": “ « name:
cout « ": identifier expected.";
// ожидался идентификатор
return NULL;
ВЗ. Класс SCENE и сопутствующие классы
993
}
if (! def_stack->search(name) ) {
cout « line « " « name:
cout « ": not defined.":
// не определено
return NULL:
}
cout « def_stack->contents(name) « endl:
strstream *temp_fin = new strstream:
*temp_fin « def_stack-contents(name) « "
*temp_fin « f_in->rdbuf():
delete (f_in):
f_in = temp_fin:
break: }
// end of case: USE
// конец случая USE
default: {
// inner switch for Shapes
// внутренний переключатель для Shapes
switch(typ)
{
case CUBE: newShape = new Cube:break:
case SPHERE: newShape = new Sphere:break;
case TETRAHEDRON:
newShape = new Mesh("tetra.3vn"):break;
case TORUS: newShape = new Torus:break:
case PLANE: newShape = new Plane;break:
case SQUARE: newShape - new Square;break:
case TAPEREDCYLINDER: newShape = new TaperedCylinder:
((TaperedCylinder*)newShape)->smallRadius - getFloatO: break;
case CONE: newShape - new TaperedCylinder;
((TaperedCylinder*)newShape)->smallRadius = 0: break:
case CYLINDER: newShape = new TaperedCylinder:
((TaperedCylinder*)newShape)->smallRadius = 1: break:
case OCTAHEDRON:
newShape = new Mesh("octa.3vn");break:
case DODECAHEDRON:newShape = new Mesh("dodeca.3vn"):
break:
case ICOSAHEDRON:newShape = new Mesh("icosa.3vn"): break:
case BUCKYBALL: newShape = new Mesh("bucky.3vn"): break;
case DIAMOND: newShape = new Mesh("diamond.3vn"): break:
case TEAPOT: newShape = new Teapot; break:
case MESH: {
// get a filename (with extension) for this mesh
// получаем имя файла (с расширением) для данной сетки
string fname = nexttokenO:
// get file name for mesh
// получаем имя файла для сетки
newShape = new Mesh(fname): break:
}
// end of case: MESH
// конец случая MESH
default: {
32 Ф. Хилл
994
Приложение В. Некоторые полезные классы и служебные подпрограммы
сегг « "Line ” « nextline « unknown keyword “ « s « endl;
// неизвестное ключевое слово в строке...
return NULL;
}
}
// end of inner switch
// конец внутреннего переключателя
// common things to do to all Shape’s
// общие вещи для всех Shapes
((Shape*)newShape)->mtrl.set(currMtrl);
// load transform and its inverse
// загружаем преобразование и обратное ему
((Shape*)newShape)->transf,set(*(affStk.tos->affn));
((Shape*)newShape)->invTransf.set(*(affStk.tos->invAffn));
return newShape;
}
// end of default: block
// конец блока default
}
// end of outer switch
// конец внешнего переключателя
}
// end of while
// конец while
return NULL:
}
// end of getObject
// конец getObject
// DefUnitStack methods
void DefUnitStack :: push(string n. string s) {
D4S *temp_d4s = new D4S:
temp_d4s->current = new DefUnitCn, s):
temp_d4s->next = stack:
stack = temp_d4s;
)
void DefUnitStack :: printO {
D4S Hemp = stack;
string t:
while (temp) {
cout « temp->current->name « :
cout « temp->current->stuff « endl:
temp - temp->next:
}
}
int DefUnitStack :: search(string s) {
D4S *temp = stack:
while (temp) {
if ( temp->current->name ~ s ) {
return(l):
}
temp - temp->next:
В4. Класс NOISE
995
return(O):
}
string DefUnitStack :: contents(string s) {
D4S *temp - stack:
while (temp) {
if (temp->current->name == s ) {
return(temp->current->stuff):
}
temp = temp->next;
}
return(NULL);
}
void DefUnitStack :: releaseO
{
whlle(stack)
D4S* tmp = stack:
// grab it
// захватываем его
//cerr « "releasing def_stack item: "« tmp->current->name« endl:
// освобождение элемента def_stack
stack - stack->next:
// advance p
// продвигаем p
delete tmp->current:
// release 2 strings
// освобождаем две строки
delete tmp;
// release node
// освобождаем узел
}
stack - NULL:
)
// end of SDL.cpp
// конец SDL.cpp
B4. Класс NOISE
//Noise.h
// Noise class for generating pseudorandom noise fields
// based on noise lattice a la Peachey/Perlin
// Класс Noise для генерирования полей псевдослучайного
// шума на основе решетки Печи-Перлина
#include <assert.h>
class Noise{
public:
NoiseO
// construct a noise object
// конструируем объект класса noise
{
996
Приложение В. Некоторые полезные классы и служебные подпрограммы
int i:
index - new unsigned char[256]; assert(index);
ford - 0: i < 256: i++) index[i] - i;
// fill array with indices
// заполняем массив индексами
ford— 0: 1 < 256: 1++)
// shuffle it
// перемешиваем его
{
int which - randO t 256;
// choose random place in array
// выбираем случайное место в массиве
unsigned char tmp - index[which]:
// swap them
// меняем их местами
index[which] - index[i];
index[1] - tmp:
}
noiseTable - new float[256]: assert(noiseTable):
ford - 0: i < 256: i++) noiseTable[i] - randO/32767.99:
}
// end of constructor
// конец конструктора
float noise(float scale. Point3& p)
{ // linearly interpolated lattice noise
// линейно интерполированный шум решетки
#define lerp(f. А. В) A + f * (В - A)
float d[2][2][2];
Point3 pp:
pp.x - p.x * scale + 10000:
// offset avoids negative values
// смещение позволяет избежать отрицательных значений
рр.у Р-У * scale + 10000:
pp.z - p.z * scale + 10000:
long ix - (long)pp.x; long iy - (long)pp.y:
long iz - (long)pp.z:
float tx.ty.tz. x0.xl.x2.x3. yO.yl:
tx - pp.x - ix: ty - pp.y - iy: tz - pp.z - iz:
// fractional parts
// дробные части
float mtx - 1.0 - tx. mty - 1.0 - ty. mtz - 1.0 - tz:
fordnt k - 0: k <- 1; k++)
// get noise at 8 lattice points
// получаем шум в В точках решетки
fordnt j - 0: j <- 1: j++)
fordnt i - 0: i <“ 1: i++)
d[k][j][i] - latticeNoisedx + i. iy + j.iz + k):
xO “ lerp(tx. d[0][0][0],d[0][0][l]):
xl “ lerp(tx. d[0][l][0].d[0][l][l]);
x2 “ lerp(tx. d[l][0][0].d[l][0][l]);
x3 - lerp(tx. d[l][l][0].d[l][l][l]):
yO - lerp(ty. xO. xl):
В4. Класс NOISE
997
yl = lerpCty. x2, x3):
return lerp(tz. yO. yl):
)
float turbulence(float s. Point3& p)
{
float val = noiseCs . p) / 2 +
noiseCs * 2. p) / 4 +
noise(s * 4. p) / 8 +
noiseCs * 8. p) / 16;
return val;
}
float marbleCfloat strength.Point3S p)
float turbul = turbulenceClO. p):
float val » sin(6 * p.z + strength * turbul);
return mySplineCval);
}
float gaussO
{ // Add up 12 independent noise samples. Sum is Gaussian
// with mean zero and variance 1.0.
// добавляем 12 независимых отсчетов шума. Сумма является
// Гауссианой с нулевым средним и дисперсией 1.0
float sum = 0:
forCint 1 - 0; i < 12; i++)
sum += noiseO:
return sum - 6.0;
}
private:
float* noiseTable;
// array of noise values
// массив значений шума
unsigned char * index:
// Pseudorandom indices
// псевдослучайные индексы
float mySpline(float x)
// used for marble
// используется для мрамора
{
if(x <-0.4) return 0.15 + 2.857 * SQRCx + 0.75):
else if(x < 0.4) return 0.95 - 2.8125 * SQRCx);
else return 0.26 + 2.666 * SQRCx - 0.7):
}
float latticeNoiseCint i. int j. int k)
{ // return PR noise value on an integer lattice
// возвращаем значение псевдослучайного шума
// на целочисленную решетку
#define PERM(x) index[(x) & 255]
#define INDEXCix. iy. iz) PERMC (ix) + PERM(Ciy) + PERM(iz)))
return noisefable[INDEX(i.j.k)];
}
}:
// end of Noise class
// конец класса Noise
998
Приложение В, Некоторые полезные классы и служебные подпрограммы
В5. Некоторые классы, полезные при трассировке лучей
Pointcluster class
class PointCluster{
public:
// holds array of points for the bounding hull of a shape
// содержит массив точек для граничной оболочки формы
int num:
Point3* pt:
PointClusterO {num - 0: pt - NULL:}
PointCluster(int n)
// make a cluster of n points
// создаем кластер из n точек
{
pt - new Point3[nJ; assert(pt):
num - n;
}
}:
Sphereinfo
class Spherelnfo{
// holds the center and radius of a sphere
// содержит центр и радиус сферы
public:
Points center:
float radSq:
void set(float x. float у. float z. float rsq)
{
center.set(x.y.z);
radSq - rsq:
}
}:
Cuboid
class Cuboid{
// holds six border values of a cuboid
// содержит шесть граничных значений кубоида
public:
float left. top. right, bott. front, back:
void set(float 1. float t. float r. float b. float f. float bk)
{
left - I: top - t; right - r: bott - b: front - f: back - bk:}
void set(Cuboid& c)
{
left - c.left: top - c.top: right - c.right:
bott - c.bott: front - c.front: back - c.back:
}
}:
Ray
class Ray{
public:
Points start;
Vectors dir:
int recurseLevel:
В5. Некоторые классы, полезные при трассировке лучей
999
int row. col;
// for screen extents
// для экстентов экрана
int numinside:
// number of objects on list
// число объектов на список
GeomObj* inside[10J:
// array of object pointers
// массив указателей на объекты
Ray(){start.set(0.0.0): dir.set(O.O.O); numinside - 0:}
Ray(Point3 origin):
// constructor: set start point of ray
// конструктор: устанавливаем начальную точку луча
Ray(Point3& origin. Vector3& direction)
{ start.set(origin): dir.set(direction); numinside - 0;}
void setstart(Point3& p){start.set(p);}
void setDirCfloat x. float y. float z)
{dir.x - x; dir.у - у; dir.z - z:}
void setRayDirection(Light *L):
// for shadow feelers
// для щупов теней
void setRayDirection(Vector3& dir):
// for spawned rays
// для порожденных лучей
int isInShadowO:
void makeGenericRay(GeomObj* p. Ray& gr):
Hitinfo
class Hitinfo {
// data for each hit with a surface
// данные для каждого соударения с поверхностью
public:
double hitTime:
// the hit time
// момент соударения
GeomObj* hitObject:
// the object hit
// объект соударения
int surface:
// which surface is hit?
// с какой поверхностью соударение?
int isEntering:
// is ray entering the object?
// входит ли луч в объект?
Point3 hitPoint:
// hit point
// точка соударения
Vector3 hitNormal:
// normal at hit point
// нормаль в точке соударения
HitlnfoO
{
1000
Приложение В. Некоторые полезные классы и служебные подпрограммы
hitobject - NULL: hitTime - -1000:
surface - 0: isEntering - 0:
} void set(Hit!nfo& h) ।
{
hitTime - h.hitTime: hitobject - h.hitobject:
surface - h.surface: isEntering - h.isEntering:
hi tPoi nt.set(h.hi tPoi nt): hi tNormal.set(h.hi tNormal):
}
}:
Intersection
class Intersection
// hold the hit list
// содержит список соударений
public:
#define maxNumHits 8
int numHits:
// the number of hits
// число соударений
Hitinfo hit[maxNumHits]:
// list of hits:
// список соударений
Intersection!){numHits - 0;}
// default constructor
// конструктор no умолчанию
void set(Intersections intr)
{
// copy intersection info
// копируем информацию no пересечению
numHits - intr.numHits;
fordnt 1 - 0: 1 < maxNumHits: i++)
hi t[i ]. setd ntr. hi t[i ]):
1° Введение в PostScript®
PostScript® — это язык программирования, известный как «язык разметки страниц», поскольку его обычно
используют для описания того, как должна быть напечатана страница. Сценарий (script) на PostScript —
это последовательность команд на языке PostScript. Многие популярные текстовые процессоры посы-
лают на принтер отформатированный документ именно в форме такого сценария. Сценарий посылает-
ся на принтер, где встроенный интерпретатор языка PostScript выполняет каждую команду поочеред-
но. Интерпретатор в точности определяет, как установить цвет каждой точки страницы (обычно это
черный и оттенки серого цвета), чтобы получить нужное изображение, а затем принтер в соответствии
с этим рисунком (pattern) точек «кладет чернила» на страницу. Интерпретатор PostScript — это очень
мощная программа, она может рисовать большое разнообразие форм. Например, получив команду на-
рисовать букву «G», интерпретатор с помощью математических формул определяет форму контура
буквы «G» для текущего шрифта и затем закрашивает этот контур черным цветом.
Важным свойством языка PostScript является его аппаратная независимость. Это означает, что за-
данный сценарий может быть послан на множество различных устройств отображения, по на них будет
визуализирована одна и та же картинка, причем всегда с наивысшим разрешением, которое доступно
для данного устройства.
В этом приложении мы представим язык PostScript и покажем, как можно его использовать для созда-
ния высококачественных рисунков. Изучение языка PostScript и экспериментирование с ним легко может
занять целый курс по графике1: интерфейс прикладного программирования (Application Programming
Interface — API) PostScript предлагает свой подход к программированию графики, весьма отличающийся
от OpenGL, однако между этими подходами имеются важные параллели, особенно в вопросах преобра-
зования координат. А студент получает в свое распоряжение простое программное средство для созда-
ния сложных и детализированных рисунков очень высокого качества.
Обычный метод работы с PostScript заключается в том, чтобы настроить текстовый процессор на
создание сценария PostScript, а затем передать файл принтеру PostScript. Такой принтер может быть
установлен в режим интерпретации сценария и создания изображения, а не просто печати этого сцена-
рия как текста.
Удобный альтернативный подход предлагают такие программы, как Ghostscript. Программа Ghostscript,
доступная свободно, работает с различными персональными компьютерами и платформами рабочих
1 На интернет-сайте книга можно найти различные примеры и целые проекты. Кроме того, по адресу http://partners.adobe.com/asn/
developer/technotes.htmI доступно руководство «PostScript Language Reference manual», а по адресу http://www.cs.indiana.edu/
docproject/programming/postsscript/postscript/html находится учебное пособие no PostScript.
1002
Приложение Г. Введение в PostScript®
станций1. Ghostscript интерпретирует сценарий PostScript и отображает картинку на мониторе компью-
тера. Это намного упрощает отладку сценария, поскольку вы сразу можете увидеть результаты на эк-
ране без печати.
Приводимый ниже пример сценария PostScript рисует прямоугольник со стороной в один дюйм в
центре страницы размером 8S на 11 дюймов (все, что в сценарии написано после символа «%» и до
конца строки, является комментарием и игнорируется интерпретатором):
300 300 moveto % move to the center of the page
% движемся к центру страницы
372 300 lineto X draw across to the bottom right corner
X проводим линию поперек до нижнего правого угла
372 372 lineto X draw upwards to the top right corner
X проводим линию вверх до верхнего правого угла
300 372 lineto X draw to the top left corner
X проводим линию до верхнего левого угла
closepath % draw to the starting point
% проводим линию до начальной точки
stroke X lay “ink" on the path just described
X "кладем чернила" по всему вышеописанному пути
showpage X print the page and eject 1t from the printer
X печатаем страницу и выталкиваем ее из принтера
Использованные здесь численные значения могут показаться непонятными, однако некоторые опе-
раторы, вроде moveto и 11 net о, нам уже знакомы. Отметим, что каждая команда появляется после своих
параметров. Такой способ записи называется «постфиксной нотацией (записью)» («postfix notation»);
иногда ее называют «обратной польской (бесскобочной) записью» в честь его создателя, польского ма-
тематика Яна Лукашевича (Jan Lukasiewicz). Это означает запись 3 4 * вместо 3 * 4или 5.0 sqrt вместо
sqrt(5.0). Само название PostScript является намеком на использование постфиксной нотации.
Как мы увидим, постфиксная нотация имеет некоторые преимущества. Одно из них состоит в том,
что для группирования частей математического выражения никогда не требуются скобки. (Поэтому
PostScript может вкладывать в использование скобок смысл, отличный от привычного.) Другое преи-
мущество заключается в том, что выражения при постфиксной записи обычно короче. Кроме того,
PostScript побуждает думать в терминах объектов, располагаемых в «стеке». Многим такая ментальная
модель выполнения основных математических операций представляется более удобной; так как при
таком подходе им намного проще отслеживать подробности вычислений.
Г1. О языке PostScript
Сценарии на PostScript являются удобочитаемыми; это означает, что в них содержатся только «печата-
емые» символы и не придается смысла другим символам, вроде escape или control-G. Вследствие этого
сценарии легко печатать и редактировать. Это обстоятельство также способствует передаче файлов
PostScript по сети, где в других случаях некоторые служебные символы могли бы нарушить передачу.
Г1.1. Некоторые предварительные замечания
Символы, появляющиеся в сценарии, могут употребляться в различных смыслах. Начнем с некоторых
простых правил.
Комментарии. Все символы, начиная с «%» и до конца текущей строки, являются комментариями и
игнорируются интерпретатором. Комментарии воспринимаются как ровно один пробел.
1 Ghostscript доступен по адресу http://www.cs.wisc.edu./-ghost/. См. также web-сайт данной книги.
Г1. О языке PostScript
1003
Регистр. Регистр имеет значение, так что cos, COS и Cos — не одно и то же.
Пустое пространство (white space). Такие символы, как пробелы (spaces), символы табуляции (tabs),
перевод строки (то есть возврат каретки), оставляют свободные места на странице сценария; для таких
символов употребляется общее название «пустое пространство» («white space»). Пустое пространство
используется для разделения объектов. Один или более стоящих подряд символов пустого простран-
ства эквивалентны одному пробелу. Таким образом, выражение
24 16 moveto
эквивалентно следующему:
24
16 moveto
Символ «\» вместе со следующим сразу за ним переводом строки (то есть печатается символ «\» и
затем сразу переводится каретка) игнорируется интерпретатором, так что выражение
24 16 moveto
идентично следующему:
24 16 mov\
eto
Это свойство дает возможность продолжать длинную строку PostScript на следующей физической
строке сценария.
Числа в PostScript
Числа записываются обычным способом, как с десятичной точкой, так и без нее. Например, 123 и -98 явля-
ются целыми (десятичными) числами, в то время как числа -002, -3.62 и 123.65е12 — это веществен-
ные числа (с плавающей точкой). Запись е!2 означает 10, возведенное в 12-ю степень.
Г1.2. PostScript основан на стеке
Язык PostScript аналогичен языку Forth1 в том смысле, что он поддерживает стек объектов, именуемый
стеком операндов (operand stack). Напомним, что стек — это список объектов, который разрешается
изменять только с одного конца, называемого «вершиной» этого стека. Разрешается только проталки-
вать (push) новый объект в вершину стека или выталкивать (pop) объект из вершины стека. Классичес-
кой метафорой для иллюстрации проталкивания/выталкивания (push-down, up-up) является штабель
подносов в кафетерии: вы можете поставить поднос на верхнюю часть штабеля или снять верхний под-
нос. Стек часто называют структурой данных «последним пришел — первым обслужен» («last-in, first-
out»)-. любой объект, который протолкнули в стек последним (позже по времени) всегда является пер-
вым объектом, который впоследствии выталкивается из стека.
В своей внутренней памяти интерпретатор PostScript поддерживает несколько структур данных.
Большинство команд сценария выполняются в стеке операндов, в котором могут содержаться числа,
процедуры, массивы и другие типы объектов. Для того чтобы протолкнуть число в стек операндов,
в сценарии просто пишется это число. В следующем фрагменте сценария
34 -5.2 % push 34 then -5.2 onto the stack
% в стек проталкивается сначала 34. а затем -5.2
12 S push 12 on top
% в вершину проталкивается 12
вначале в стек проталкивается число 34, затем -5,2 проталкивается выше 34, и наконец в вершину
проталкивается 12. На рис. Г.1 показан стек в виде классического штабеля подносов в кафетерии:
1 См., например, http://www.engin.umd.umich.edu/CIS/course.des/cis400/forth/forth.html, а также книгу Лео Броди «Основы FORTH»
[Brodie, Leo/Forth, INC., StartingFORTH, 2d ed. (Engleuood Cliffs, NJ: Prentice-Hall, 1987)].
1004
Приложение Г. Введение в PostScript®
по мере того как каждый элемент (item) помещается на вершину, он проталкивает все остальные эле-
менты дальше вниз. ,
Мы используем более простую форму записи для иллюстрации того, что содержится в стеке после
данной операции: стек показан «сбоку», причем его вершина находится справа. Тогда последователь-
ность проталкиваний, показанная на рис. Г.1, выглядит следующим образом:
<empty> (meaning the stack is empty)
(подразумевается, что стек пуст)
34
34 -5.2
34 -5.2 12
Пустой После 34
34
После -5,2 После 12
-5,2 12
34 -5,2
34
Рис. Г.1. Стек операндов после каждого введенного числа
Г1.3. Некоторые операции со стеком: pop, dup, exch, clear
Существует несколько операторов языка PostScript, называемых «командами», с помощью которых
можно легко управлять стеком. Например, команда pop удаляет верхний элемент (и отбрасывает его),
поэтому последовательность команд:
34 -5.2 12 pop
оставляет стек в состоянии 34 -5.2.
Мы будем использовать стрелку вправо (-») в качестве стенографического символа вместо слов «ос-
тавляет стек в состоянии», тогда команда pop может быть описана так:
34 -5.2 12 pop -> 34 -5.2
Запись будет выглядеть еще короче, если пропускать те элементы, которые находятся глубже в стеке
и не влияют на рассматриваемый оператор (то есть числа 34 и -5.2), тогда команда pop будет выглядеть
следующим образом:
12 pop -> —
где символ «—» означает не то, что в данный момент стек обязательно пуст, а что просто убран тот эле-
мент, который был в его вершине.
Оператор dup копирует верхний элемент:
12 dup -> 12 12
оператор exch меняет местами два верхних элемента:
-5.2 12 exch -> 12 -5.2
Оператор clear очищает весь стек:
34 -5.2 12 clear -> <empty>
Можно с полным основанием утверждать, что операторы dup, exch и cl ear нарушают смысл истинно-
го стека, поскольку в них делается больше, чем просто проталкивание или выталкивание. (Например,
dup должен «посмотреть» на элемент в вершине стека, чтобы скопировать его.) Это действительно так,
однако эти операторы настольно удобны, что PostScript позволяет себе некоторую поэтическую воль-
ность и поддерживает их.
Г1. О языке PostScript
1005
Г1.4. Более сложные операторы работы со стеком
Кроме простейших операторов push или pop, часто используется целый ряд дополнительных операто-
ров. При первом прочтении их можно пропустить.
Оператор n index выталкивает число п, отсчитывает сверху вниз п элементов в стеке (при этом верх-
ний элемент считается нулевым) и проталкивает в стек копию n-го элемента:
34 12 94 2 index -> 34 12 94 34
6 0 index -> 6 6 X same as dup
% то же самое, что dup
Оператор п сору выталкивает п элементов и затем проталкивает в стек копию верхних п элементов:
12 6 2 сору -> 12 6 12 б
12 95 23 3 сору -> 12 95 23 12 95 23
Оператор num shifts roll проталкивает shifts и num, а затем производит циклический сдвиг верхних
num элементов shift раз (положительные значения shift означают движение вверх по стеку, а отрица-
тельные значения shift означают движение вниз):
-3 144 78 3 1 roll -> 78 -3 144
-3 144 78 3 -1 roll -> 144 78 -3
23 12 -3 144 78 4 -2 roll -> 23 144 78 12 -3
Оператор count подсчитывает количество элементов в стеке и проталкивает это значение в стек:
12 35 121 count -> 12 35 121 3
Практические упражнения
Г1. Развлечения со стеком
Исходное состояние стека операнда: 345 129 -24 366 89. Покажите состояние стека после каждого из
нижеприведенных операторов (в применении к исходному стеку):
dup dup pop 23 exch
pop pop 34 23 2 copy
count dup 3 index
3 copy 6 copy
Г2. Инвертор
Какая последовательность операторов стека PostScript изменяет порядок верхних К элементов, если
О К-3;
О К-4.
ГЗ. Копирование?
Если бы команды сору уже не было в языке PostScript, смогли бы вы создать ее из других операторов PostScript?
Г1.5. Некоторые арифметические операторы
Два верхних элемента стека могут быть скомбинированы с помощью одного из нескольких арифмети-
ческих операторов, таких как add, sub, mul. В случае любого из операторов два верхних элемента вытал-
киваются и комбинируются в соответствии с оператором, а результат проталкивается обратно в стек.
Если оба оператора целые, то результат также целый. В противном случае результат вещественный.
Ниже приведены примеры работы этих операторов:
Add: -5.2 12 add -+ 6.8
Subtract: -5.2 12 sub -> -17.2
Multiply: -5.2 12 mul -> -62.4
1006
Приложение Г. Введение в PostScript*
Для деления существует два оператора: div и idiv. Оператор div Выполняет обычное деление с це-
лыми и вещественными числами и в результате выдает вещественное число. Оператор idiv работает
только с целыми и возвращает Целую часть результата деления:
-27 8 div -> -3.375
-27 8 idiv -+ -3
Оператор модуля mod возвращает остаток от деления второго от вершины стека целого числа на верх-
нее целое число:
178 34 25 7 mod -> 178 34 4
178 18 2547 10 mod 178 18 7
С помощью последовательности операторов проталкивания и арифметических операторов можно
использовать PostScript для вычисления значений более сложных выражений, сохраняя результат в
стеке.
Пример
Вычислите выражение 1 + 3- 5- б- 8- 9и оставьте результат в вершине стека.
Решение
1 3 5 mul add 6 8 9 mul mul sub
Пример
Вычислите 8 - 242 - 3 - 24 + 8.
Решение
24 dup mul 8 mul 3 24 mul sub 8 add
Кроме того, PostScript предлагает «побитовые» операторы, работающие с отдельными битами цело-
го числа. Если пит — целые числа, то
п m and -ч (п & m) (.% the bitwise and of n and m)
X побитовое умножение пит
n in or ч (n | m)(J the bitwise or of n and m)
X побитовое сложение пит
птхогч (п ж т) (Я the bitwise exclusive or of n and m)
X побитовое исключающее n или m
n not -ч (!n) (% the bitwise complement of n
X побитовое дополнение n
где в правой части использованы операторы языка С (&, |, л, !), чтобы показать результат применения
данного оператора к числам. Позднее эти операторы снова встретятся нам в различном контексте.
Пример
Что делают следующие фрагменты, помещенные в стек?
12 5 and
34 15 or
56 not
12 45 xor
Решение
О В двоичной системе 12 равно 1100, а 5 равно 0101, Тогда 12 & 5 равняется 0100, что в десятичной
системе составляет 4.
О В двоичной системе 34 равно 100010, а 15 равно 001111, тогда 34115 равняется 101111, что в деся-
тичной системе составляет 47.
Г1. О языке PostScript
1007
О В двоичной системе 56 равно 111000, тогда 156 равняется 000111, что в десятичной системе со-
ставляет 7.
О В двоичной системе 12 равно 001100, а 45 равно 101101, тогда 12 Л 45 равняется 100001, что в деся-
тичной системе составляет 33.
Кроме этого, в языке PostScript предусмотрен целый ряд операторов, принимающих только один
аргумент. В каждом таком случае элемент выталкивается из вершины стека, с ним производится опера-
ция, а результат проталкивается обратно в стек. Тип результата (целый или вещественный) совпадает с
типом аргумента. Ниже приводятся унарные операторы PostScript:
-23.3 abs -> 23.3 X absolute value
Я абсолютная величина
45.6 neg -> -45.6 % negate
% отрицание
34.5 floor -> 34.0 t largest integer less than or equal to
X наибольшее целое, меньшее или равное аргументу
-34.5 floor -> -35.0
34.6 ceiling -> 35.0 t smallest integer greater than or equal to
% наименьшее целое, большее или равное аргументу
-34.6 ceiling -» -34.0
34.6 truncate -> 34.0 t truncate towards zero
Я округление в сторону нуля
-34.6 truncate -> -34.0
34.6 round -> 35 X round to nearest integer (round up if a tie)
% округление до ближайшего целого (если одинаково, то вверх)
В PostScript содержатся известные математические функции. Их аргумент может быть целым или
вещественным. Тип результата всегда вещественный. Ниже приведены некоторые из таких функций:
2.0 sqrt -> 1.41421356 % square root
% квадратный корень
2.0 In -> 0.69314718 % natural logarithm
% натуральный логарифм
2.0 log -> 0.301029996 t logarithm to the base 10
% десятичный логарифм
45.0 cos -> 0.707106781 t cosine (note: the angle is in degrees)
% косинус (отметим: угол в градусах)
45.0 sin -> 0.707106781 % sine (note: the angle is in degrees)
X синус (отметим: угол в градусах)
Функция для тангенса отсутствует.
Две математические функции выталкивают из стека два верхних элемента и оперируют с ними:
1. ехр. Экспоненциальная функция а Ь ехр возводит число а в степень Ь:
3.0 5.0 ехр -> 243.0
2. atari. Арктангенс принимает два аргумента а и b и возвращает угол (в градусах, в диапазоне от 0
до 360), тангенс которого равен а/b. Одно из чисел, а или Ь, может равняться нулю (но не оба
сразу). Ниже приводится несколько примеров:
0 1 atan -» 0.0
1 0 atan —» 90.0
-100 0 atan -» 270.0
4 4 atan -> 45.0
1008
Приложение Г. Введение в PostScript®
Генерирование случайных чисел
Функция rand проталкивает в стек целое число в диапазоне от 0 до 23' - 1. Это число создается с помо-
щью генератора псевдослучайных чисел. «Начальное число» для функции rand может быть установле-
но при помощи функции seed srand. (Посредством функции rrand в стек проталкивается внутреннее
начальное число.) Ниже приводятся примеры:
rand -» 28394 X your results may vary
X ваши результаты могут различаться
rand -> 910293 S successive calls return different numbers
% успешные вызовы возвращают различные числа
rand -> 21
56 23 srand —> 6 S set the seed to 23
% устанавливаем начальное число 23
rand -» 38475 X get some random value
% получаем некоторое случайное число
56 23 srand -» 56 % set it again
% устанавливаем его ( 23) снова
rand -> 38475 X get the same sequence
% получаем ту же самую последовательность
Г2. Графические операторы в PostScript
В языке PostScript имеются операторы, облегчающие рисование прямых линий, окружностей, кривых
Безье и многих других фигур. В этом разделе мы рассматриваем методы создания изображений любой
сложности с использованием комбинаций операторов (команд) PostScript. Полезно запомнить, что при
работе операторы рисования «кладут чернила» на страницу, вследствие чего каждый прорисовывае-
мый объект полностью закрывает любые объекты, которые были нарисованы в этом месте ранее.
Г2.1. Системы координат и преобразования
Все рисование происходит в какой-нибудь системе координат. Система координат, принятая по умол-
чанию, показана на рис. Г.2, а. Начало координат расположено в нижнем левом углу поверхности дисп-
лея (которая обычно называется страницей), направление осей х и у показано на рисунке. Единицей
измерения по умолчанию принята 1/72 часть дюйма1, так что точка в один дюйм находится прямо над
началом координат и имеет координаты (0,72).
Рис. Г.2. Система координат PostScript по умолчанию
1 Это очень близко к классической «принтерной точке», которая равна 1/72,27 дюйма.
Г2. Графические операторы в PostScript
1009
В PostScript не предполагается какого-нибудь стандартного размера страницы; все фигуры, рисуемые
по сценарию, могут быть масштабированы так, чтобы заполнить страницу любого размера. Рассмот-
рим, например, лист бумаги размером 8S на 11 дюймов, с книжной ориентацией (portrait orientation) —
то есть его длинная сторона расположена вертикально. Эта ориентация показана на рис. Г.2, б. Правый
верхний угол рабочей поверхности имеет координаты (8,5 х 72, 11 х 72) = (612,792).
Фигуры рисуются на PostScript посредством задания контура (path), образуемого в результате вы-
полнения последовательности операторов построения контура (path construction operators). Как толь-
ко контур построен, его можно нарисовать с помощью оператора stroke. Это аналогично передаче перу
инструкции: провести чернилами черту вдоль указанного контура. В качестве альтернативы использу-
ется команда: fill. По этой команде область, определяемая контуром, заполняется каким-либо цветом
или оттенком серого цвета.
Существует несколько операторов создания контура, причем наиболее известными из них являются
moveto и 1 ineto. В языке PostScript поддерживаются такие же текущие координаты (current position — СР),
какие рассматривалась в главе 2. Например, команда 1 ineto для формирования точки (х, у) выталкивает
два верхних аргумента (это означает, что первым выталкиваемым значением является у, а вторым — х), за-
тем добавляет к текущему контуру отрезок прямой линии от СР до точки (х, у) и обновляет СР на (х, у).
Г2.2. Команды создания контура
Команда moveto выталкивает из стека два элемента и в соответствии с ними устанавливает СР:
х у moveto —
Пример
Для установки СР в позицию (34,56.1) следует использовать команду:
34 56.1 moveto.
Команда 1 ineto выталкивает из стека два верхних элемента, образуя точку (х, у), добавляет к теку-
щему контуру отрезок прямой линии от СР до (х, у) и устанавливает СР в (х, у):
х у 11neto -> —
Пример
Для добавления к текущему контуру отрезка от СР до точки (1,7, -34) и установки СР в точку (1,7, -34)
используйте команду:
1.7 -34 1ineto
Команда newpath очищает текущий контур.
Команда closepath добавляет к текущему контуру отрезок от СР до начальной точки пути. Значение
СР можно получить с помощью команды currentpoint, которая проталкивает в стек значение (х, у) теку-
щих координат:
— currentpoint -> х у
Пример
Ниже приводится сценарий, который рисует два квадрата, изображенные на рис. Г.З.
newpath 1 1 moveto % draw the outline of the top square
S рисуем контур верхнего квадрата
1 3 1ineto 3 3 1ineto
3 1 1ineto closepath stroke
2 2 moveto 4 2 1ineto 4 0 1ineto % fill the bottom square
% закрашиваем нижний квадрат
2 0 1ineto closepath fill
showpage
1010
Приложение Г. Введение в PostScript*
(3,3)
(4,2)
(1.1)
Рис. Г.З. Рисунок на базе двух квадратов
Две команды осуществляют относительное рисование (relative drawing), которое было описано
в главе 3, причем величина изменения СР берется из стека:
О rmoveto выталкивает из стека два верхних элемента (dx, dy) и перемещает СР на величину (dx, dy):
dx dy rmoveto -> —
О rl ineto выталкивает из стека два верхних элемента (dx, dy), добавляет к текущему контуру Отре-
зок прямой от СР до точки (CP.x + dx, СР.у + dy), а затем присваивает СР новое значение:
dx dy rlineto —
Пример
Приведенный ниже код рисует верхний квадрат, показанный на рис. Г.З:
newpath 1 1 moveto
О 2 rlineto 2 0 rlineto
О -2 rlineto closepath stroke
showpage
Г2.3. Дуги окружностей
Дуги окружностей в языке PostScript рисуются посредством одной из двух команд: аге и агсп. Обе эти
команды выталкивают из стека пять элементов и интерпретируют их так, как это показано на рис. Г.4.
Ниже приводится пример каждой из этих команд:
center.х center.у rad start_angle end_angle arc -> —
center.x center.y rad start_angle end_angle aren -» —
Рис Г.4. Рисование дуг окружностей
Г2. Графические операторы в PostScript
1011
Команды аге и агсп добавляют к текущему контуру дугу окружности с центром (center.х, center .у) и
радиусом rad, причем эта дуга начинается с угла start_angle, отсчитываемого от положительного на-
правления оси х, и простирается до угла end_angle. Команда аге добавляет контур дуги против часовой
стрелки, в то время как агсп добавляет контур дуги по часовой стрелке (см. рис. Г.4).
До начала построения дуги оба этих оператора добавляют отрезок прямой линии от СР до первой
концевой точки дуги. Если же текущий контур пуст, то никакого отрезка не добавляется.
Пример
Следующий сценарий рисует форму, изображенную на рис. Г.5, а, которая состоит из двух дуг и двух
отрезков:
newpath 3 2 1 90 180 arc Ж add first arc
% добавляем первую дугу
3 2 2 180 90 агсп Ж add line and second arc
Ж добавляем прямую и вторую дугу
closepath stroke It add line and draw it
Ж добавляем прямую и рисуем все это
Первая дуга с радиусом 1 добавляется к контуру, а СР остается в точке (2,2). Затем (поскольку кон-
тур не пуст) добавляется прямая от СР до начала второй дуги в точке (1,2). Добавляется вторая дуга,
и контур замыкается в точку (3,3). Если бы заключительный оператор был fill, а не stroke, то фигура
была бы закрашена текущим оттенком серого цвета.
б
Рис. Г.5. Фигура, созданная с использованием средств для рисования дуг
Практическое упражнение
Г4. Круговые диаграммы
О Напишите и протестируйте сценарий PostScript pieChart, который рисует круговую диаграмму
с вырезанным сектором, как показано на рис. Г.5, б.
О Расширьте сценарий pieChart так, чтобы он получал значение из вершины стека в качестве той
доли целого круга, которую должен составлять вырезанный сектор. Например, команда 35 pieChart
рисует круговую диаграмму с сектором, равным 35 % от целого круга.
Г2.4. Использование операторов закрашивания
Мы уже видели команды stroke и fil 1. С помощью этих и немногих других команд обеспечивается хоро-
шее управление рисованием.
stroke «Закрашивает» линию текущего контура текущими толщиной и цветом этой линии. Стыки между соединяющимися отрезками прямой рисуются цветом текущей линии (см. команду setl inejoin). Концы открытых контуров закрашиваются цветом текущего контура (см. команду setl i necap). По завершении работы stroke выполняет команду newpath
fill Заполняет текущим цветом область, ограниченную текущим контуром. Новый цвет покрывает все расположенные под ним рисунки. Оператор f i 11 выполняет команду cl osepath перед началом закрашивания и команду newpath после закраски
1012
Приложение Г. Введение в PostScript*
setlinewidth setgray Выталкивает из стека верхний элемент и присваивает его значение текущей толщине линии Выталкивает верхний элемент, который должен представлять собой число от 0 до 1, и присваивает его значение текущему оттенку серого цвета. Здесь 0 означает черный цвет, а 1 — белый
setrgbcolor Устанавливает текущий цвет равным (red, green, blue), где каждое число лежит в диапазоне от 0 до 1. Его форма: red green blue setrgbcolor S — (Этот оператор годится только ^ля устройств цветного изображения, таких как цветные лазерные принтеры)
dip Устанавливает текущий контур в режим линии отсечения. Последующее рисование отсекается на этой границе
setlinecap Устанавливает форму окантовки на концах открытых отрезков контура. На рис. Г.б показан эффект различных возможных значений параметра этого оператора. Отрезок прямой показан в виде тонкой внутренней линии. В зависимости от толщины этой линии окантовка может иметь форму выпуклой полуокружности или квадрата
setlinejoin Устанавливает форму соединения двух отрезков линий. На рис. Г.7 показаны возможные значения параметра. Если параметр равен 1, то диаметр дуги равен толщине линии
Рис. Г.б. Способы окантовки контура
Рис. Г.7. Варианты соединения двух толстых отрезков
Г2.5. Преобразования координат
В PostScript предусмотрен мощный механизм изменения рисунков. Система координат, в которой на-
ходится рисунок (ее называют пользовательской системой координат), может быть изменена с помо-
щью команд translate, rotate, scale. Начнем с команды.
translate Выталкивает из стека два верхних элемента в качестве (z, у)1 и смещает систему координат на величину
{dx, dy) относительно старой системы координат. Его форма такова: dx dy translate —
На рис. Г.8 показан пример для страницы размером 8S на И дюймов, где вначале действует система
координат с началом отсчета в нижнем левом углу. Серая окружность может быть нарисована с помо-
щью следующего сценария:
0.5 setgray
50 50 50 0 360 arc fill
Черную окружность можно нарисовать, сместив вначале систему координат в центр страницы:
306 396 translate
0 setgray
50 50 50 0 360 arc fill
Отметим, что обе эти окружности рисуются с помощью одного и того же кода; но с переносом систе-
мы координат.
Если выполняется последовательность операторов translate, то каждый из них «добавляется» к ос-
тальным (см. главу 5 о композиции преобразований). Например, если в данный момент выполняется
Это означает, что верхний элемент берется в качестве у, а следующий — в качестве х.
Г2. Графические операторы в PostScript
1013
команда 80 80 translate, то пользовательская система координат смещается на (80,80) добавочных еди-
ниц от ее последнего положения (в центре страницы).
rotate Выталкивает верхний элемент из стека, воспринимает его как некоторый угол (в градусах) и поворачивает
пользовательскую систему координат против часовой стрелки на этот угол. Его форма такова:
angle rotate -»—
Рис. Г.8. Смещение пользовательской системы координат
На рис. Г.9 показано влияние, которое оказывает на исходную систему координат оператор 30 rotate:
исходные оси поворачиваются по отношению к странице. Предположим, что команда myRectangle рисует
серый выровненный прямоугольник, показанный на рисунке (позднее мы увидим, как писать на PostScript
новые команды типа myRectangle). Тогда приведенная ниже комбинация операторов нарисует два пря-
моугольника, один из которых выровнен по отношению к странице, а второй выровнен относительно
повернутых осей:
myRectangle Ж draw the rectangle aligned with the sides of the page
Ж рисуем прямоугольник, выровненный по сторонам страницы
30 rotate Ж rotate the axes
% поворачиваем оси
myRectangle Ж draw the rotated rectangle
Ж рисуем повернутый прямоугольник
Рис. Г.9. Поворот пользовательской системы координат
Пример. Рисование на странице с альбомной (landscape) ориентацией
В некоторых ситуациях более естественно рисовать на странице так, чтобы рисунок располагался пря-
мо, в то время как страница повернута набок. На рис. Г. 10, а показан ряд звезд, которые не помещаются
на странице с книжной ориентацией, но хорошо смотрятся на странице с альбомной ориентацией.
Нетрудно подготовить пользовательскую систему координат для рисования с альбомной ориента-
цией: мы просто смещаем начало координат в нижний правый угол страницы (если ширина страницы
составляет 8!4 дюйма, то такое смещение производится оператором 612 0 translate) и затем поворачива-
ем оси на 90°. (В конце мысленно поверните «страницу» на 90° по часовой стрелке так, чтобы вы видели
1014
Приложение Г. Введение в PostScript151
систему координат справа сверху.) Результат этой операции показан на рис. Г.10, б. Ось х теперь направ-
лена горизонтально вправо вдоль нижнего края страницы ее длинной стороны. Если предположить, что
у нас имеется команда drawStars, рисующая четыре звезды в ряд, то вся картина будет нарисована с помо-
щью следующего кода:
612 0 translate % shift the origin to the right corner ~
X смещаем начало координат в правый угол
90 rotate % rotate the axes for landscape orientation
% поворачиваем оси для альбомной ориентации
drawStars X draw the picture
% рисуем картину
Рис. Г.1О. Изменение ориентации на альбомную: а) книжная ориентация;
d) альбомная ориентация
Пример
С помощью команды rotate легко создавать фигуры, обладающие круговой симметрией. Пусть команда
drawOval рисует овал, изображенный на рис. Г. 11, а относительно начала заданной системы координат
(оно показано точкой левее овала). Тогда последовательность команд
300 400 translate % set origin near center of page
% устанавливаем начало координат в центре страницы
drawOval
60 rotate
drawOval
60 rotate
drawOval
60 rotate
drawOval
60 rotate
drawOval
60 rotate
drawOval
60 rotate % restore original orientation
% восстанавливаем исходную ориентацию
нарисует узор, изображенный на рис. Г.11, б в центре страницы размером 8S на 11 дюймов. Каждая
команда 60 rotate добавляет по 60° к повороту системы координат. В последней команде 60 rotate нет
необходимости, однако это является хорошим стилем: исходную ориентацию системы координат по
завершении всего фрагмента кода следует оставлять неизменной.
Кстати, позднее мы увидим, что приведенный код можно сократить следующим образом:
300 400 translate
6 {drawOval 60 rotate } repeat
Команда
scale
Выталкивает два верхних элемента из стека в качестве (sx, sy) и масштабирует координатные оси этими
множителями. Команда имеет следующую форму: sx sy scale -»—
Г2. Графические операторы в PostScript
1015
а б
Рис. Г.11. Рисование фигур с круговой симметрией
Например, если вначале каждая единица равняется 1/72 дюйма, то команда 3 3 scale сделает каж-
дую единицу равной 3/72 дюйма.
Предположим, что команда star рисует звезду А на рис. Г. 12. Тогда следующий фрагмент сценария
star % draw original star
Ж рисуем исходную звезду
2 2 scale Ж magnify by 2
Ж увеличиваем в 2 раза
star И, draw star В
t рисуем звезду Б
0.5 0.5 scale Ж back to the original system
t возвращаемся к исходной системе
1 2 scale Ж differential scaling
Ж неравномерное масштабирование
star % draw star С
t рисуем звезду В
нарисует три звезды: А, Б, В. Звезда Б вдвое больше звезды А и расположена вдвое дальше от начала
координат. Команда 0.5 0.5 scale аннулирует первое масштабирование (позднее мы увидим лучший
способ «восстановления исходной фигуры»), а команда 1 2 scale выполняет неравномерное масшта-
бирование (differential scaling), когда два масштабных множителя не равны друг другу. Теперь выпол-
нение команды star нарисует звезду В, которая растянута в два раза по вертикали, а также расположена
по оси х вдвое дальше, чем звезда А. Неравномерное масштабирование обычно искажает фигуры. Если
один или оба масштабных множителя отрицательны, то можно производить отражения.
Рис. Г.12. Масштабирование системы координат
Пример. Отражения
Команду scale можно использовать для отражения объектов относительно оси х или у; для этого нужно
принять масштабный множитель равным -1.
Предположим, что команда drawBox рисует кубическую коробку, изображенную на рис. Г. 13, а, после
смещения начала координат в точку (300,200). Тогда команда 1 -1 scale зеркально отразит (flip) систему
координат в вертикальном направлении относительно точки (300,200). Теперь при рисовании коробка
будет изображена «вверх ногами», то есть отраженной относительно оси х. Рисунок Г.13, а получен
при выполнении последовательности команд:
1016
Приложение Г. Введение в PostScript®
300 200 translate Ж move the origin up to (300, 200)
Ж перемещаем начало координат в точку (300. 200)
drawBox
1 -1 scale % reflect the у-direction about the x-axis
Ж отражаем направление у относительно оси х
drawBox It draws the reflected box
Ж рисуем отраженную коробку
Рис. Г.13. Использование команды scale для отражения объектов
Практические упражнения
Г5. Рисование четырехсторонней симметрии
Пусть команда drawFish рисует левую верхнюю рыбу, показанную на рис. Г. 13, б. С помощью каких ко-
манд будут нарисованы все четыре рыбы?
Гб. «Экранная» система координат
Задайте команды, которые изменят систему координат PostScript по умолчанию на ту, которая показа-
на на рис. Г. 13, в.
Г2.6. Операторы графического состояния
Два оператора PostScript — gsave и grestore — упрощают многие графические задания. В основном опе-
ратор gsave выполняет «снимок» множества текущих графических параметров, которые в совокупнос-
ти называются графическим состоянием (graphics state), и сохраняет их, пока программа выполняет
следующие операторы сценария. В дальнейшем оператор grestore извлекает этот снимок и делает все
содержащиеся в этом снимке графические операторы текущими. Если быть более точным, оператор
gsave делает копию «графического состояния» интерпретатора и проталкивает их в особый стек, име-
нуемый стеком графического состояния (graphics state stack); а оператор grestore выталкивает верх-
ний элемент из этого стека и записывает его обратно в графическое состояние. Таким образом, каждый
оператор grestore восстанавливает то графическое состояние, которое было текущим в тот момент, ког-
да выполнялся последний по времени оператор gsave.
Графическое состояние складывается из следующих пунктов (а также из некоторых других, менее
важных):
О текущее преобразование: композиция результатов воздействия всех предшествующих вызовов
translate, rotate, scale;
О текущий контур: контур, составленный из различных команд, создающих контур, начиная с мо-
мента выполнения последней команды newpath, stroke, fill;
О текущие координаты СР: последние по времени обращения координаты текущего контура;
О текущий шрифт: шрифт, который был выбран последним;
О цвет или оттенок серого: текущее значение цвета или оттенка серого;
О толщина линии, форма перекрытия и соединения линий: текущие значения толщины, перекры-
тия и соединения.
Г2. Графические операторы в PostScript
1017
Пример
Напомним, что оператор stroke неявно выполняет команду newpath. Для закрашивания домика с рис. Г. 14,
а также для рисования его контура пришлось бы создавать его контур дважды — используя следующий
код:
< lots of lines to make the path of the house>
% много строк для построения контура домика
fill % fill the object: destroys the current path
X закрашиваем объект; уничтожаем текущий контур
< repeat the lines to make the path of the house>
% повторно пишем строки, создающие контур домика
stroke % draw the outline
X рисуем контур
Рис. Г.14. Закрашивание объекта и рисование его контура
Здесь за словами «много строк» может скрываться сложная последовательность команд. Однако
поскольку оператор gsave делает копию текущего контура, проще и эффективнее использовать следу-
ющий код:
< lots of lines to make the path of the house>
% много строк для построения контура домика
gsave X save current path in the graphics state
% записываем текущий контур в графическое состояние
fill
grestore % restore the current path
% восстанавливаем текущий контур
stroke
Особенно удобно, что оператор gsave сохраняет текущее преобразование. Допустим, что в некото-
ром сценарии вы выполнили несколько преобразований и намерены выполнить несколько дополни-
тельных преобразований, однако знаете, что позднее вам понадобится вернуться «сюда». В этом случае
нужно просто выполнить оператор gsave, сохранив тем самым запись всех преобразований, выпол-
ненных на данный момент. Позднее, для того чтобы вернуться сюда, достаточно выполнить команду
grestore. Например, в том фрагменте кода, который был использован для создания рис. Г. 12, требуется
«аннулировать» операцию 2 2 scale посредством операции 0.5 0.5 scale. Лучше, однако, написать этот
фрагмент так:
star X draw star
% рисуем звезду
gsave X save current transformation
% сохраняем текущее преобразование
2 2 scale % magnify by 2
% увеличиваем в 2 раза
star % draw star В
% рисуем звезду Б
grestore % return to initial state
X возвращаемся в исходное состояние
1 2 scale % differential scaling
1018
Приложение Г. Введение в PostScript81
Ж неравномерное масштабирование
star % draw star С
Я рисуем звезду В _
Еще один пример: пусть нам нужно нарисовать правильный узор из окружностей — такой, как пока-
зано на рис. Г. 15.
Рис. Г.15. Использование операторов gsave и grestore
Допустим, что команда circ рисует закрашенный круг в начале координат. Начнем с нижнего
левого круга и нарисуем круги первого ряда, перемещая с помощью команды translate начало коор-
динат поперек страницы. Затем вернемся к самому левому кругу и «поднимем» его к началу следую-
щего ряда. Такой «возврат» можно легко выполнить командой grestore, как показано в следующем
фрагменте кода:
gsave Ж save current state until the end
Ж записываем текущее состояние до самого конца
30 25 translate circ Ж set origin for the first circle in
Ж bottom row: draw circle
Ж устанавливаем начало координат для первого круга
% в нижнем ряду; рисуем круг
gsave Ж remember where we are
% запоминаем, где мы находимся
30 0 translate circ
30 0 translate circ
grestore Ж back to lower left circle
% возвращаемся к нижнему левому кругу
0 25 translate circ % go up to second row and draw left circle
2 поднимаемся во второй ряд и рисуем левый круг
gsave % push this graphics state, too;
X remember where we are
% проталкиваем в стек это графическое состояние;
% запоминаем, где мы находимся
30 0 translate circ
30 0 translate circ
grestore % back to left side of second row
Ж назад к левой стороне второго ряда
0 25 translate circ Ж up to third row. draw left circle
X наверх к третьему ряду, рисуем левый круг
30 0 translate circ
30 0 translate circ
grestore % restore state from the beginning
% восстанавливаем начальное состояние
Возможность «вернуться» к предыдущей системе координат упрощает структуру сценария и его от-
слеживание. Позднее мы приведем несколько других примеров.
Г4. Определение новых переменных и процедур
1019
ГЗ. Рисование текста в PostScript
Наибольший интерес для нас представляет графика, но в большинстве сценариев Postscript на страни-
цу кладется тщательно подобранный текст, что подразумевает последовательность символьных строк.
В PostScript существует много команд, способствующих выполнению этой задачи; важнейшие из них
осуществляют следующее:
1. Выбор шрифта для строки и его масштабирование до желаемого размера.
2. Позиционирование строки на странице.
3. Рисование этой строки как графического объекта.
Это можно сделать, например, так:
/Helvetica findfont Ж request a particular font
Ж запрашиваем конкретный шрифт
15 scalefont Ж scale it to the desired size
% масштабируем его до желаемого размера
setfont It make this font the current font
Ж устанавливаем этот шрифт в качестве текущего
100 200 moveto Ж set the position of the first character
Ж устанавливаем положение первого символа
(Hi. Jess, how are you?) It specify the string to be printed
Ж “Привет. Джесс, как ты?" - задание строки для печати
show % draw the string at the CP
% рисуем данную строку в текущем положении
Обратите внимание на символ «/» (слэш — slash), который предшествует названию шрифта. Этот
символ создает из слова Helvetica «литерал» (literal) и очень важен, как мы увидим в следующем разде-
ле. Кроме того, следует иметь в виду, что команда 15 scalefont запрашивает шрифт в 15 единиц в про-
странстве пользователя. Если по умолчанию задействован единичный размер, составляющий 1/72 дюй-
ма (точка принтера), то данная команда выдаст шрифт размером в 15 точек. С другой стороны, если вы
ранее выполнили, допустим, команду 3 3 scale, то в результате получите 45-точечный шрифт. Отметим,
наконец, что строки всегда заключаются в скобки.
Кроме уже приведенного шрифта Helvetica, наиболее часто используются следующие шрифты:
/Hel vet i са - Во 1 d /Нel veti са -0Ы i que
/Times-Roman /Times-Bold
/Times-Italic /Times-Boldltalic
/Courier
Г4. Определение новых переменных и процедур
PostScript является открытым языком — это означает, что вы можете добавлять в ассортимент его ко-
манд новые операторы и другие объекты. Эти новые объекты становятся действенной частью языка на
все время работы с вашим сценарием. Такая возможность упрощает создание сценариев и делает более
эффективной их интерпретацию на PostScript.
Для создания нового объекта нужно пометить в стек следующие три элемента:
1. Слэш («/»), за которым следует новое имя для объекта.
2. Определение самого объекта.
3. Ключевое слово def.
В этом разделе мы покажем, как определять два типа объектов: переменные и процедуры.
1020
Приложение Г. Введение в PostScript®
Г4.1. Определение переменных
При помощи ключевого слова def легко определить переменную или изменить ее значение. Пусть, на-
пример, нам требуется определить переменную num с начальным значением 251 и поместить ее в сцена-
рий. Оператор def выполняет весьма специализированные действия: он выталкивает из стека два верх-
них элемента и добавляет в словарь языка новый компонент к уже имеющимся в нем словам. В нашем
примере слово num добавляется в словарь и ассоциируется со значением 251. Более поздние ссылки на
слово num (уже без слэша), например, 34 num add, предписывают PostScript отыскать значение перемен-
ной num и протолкнуть его в стек. Если в момент выполнения этого оператора значение переменной num
по-прежнему равно 251, то в стек проталкивается значение 285.
/num 251 def
Символ слэш («/») указывает, что /num является литералом (literal), так что в стек фактически про-
талкивается имя num, а не его значение.
Какие имена допустимы для новых элементов? Это может быть любая последовательность сим-
волов, которую нельзя интерпретировать как число. Вот примеры допустимых имен: Merilee, meriLee,
somethingl23, 2$abe. (В то же время для упрощения работы со сценариями следует выбирать осмыслен-
ные и удобочитаемые имена.)
Изменение значения переменной производится посредством ее переопределения. Если переменная
num была определена со значением 251, то переопределение
/num 7 def
изменяет ее значение на 7. Для того чтобы добавить к переменной 1, нужно получить ее текущее значе-
ние, добавить к нему 1 и переопределить переменную:
//num num 1 add def % increment num
X прибавляем 1 к num
Для того чтобы добавить к num 4 и возвести результат в квадрат, необходимо выполнить следующее:
/num num 4 add dup mul def % add 4 to num and square it
% добавляем 4 к num и возводим в квадрат
Тщательно проследите за состоянием стека по мере выполнения каждой части этого оператора. Следует
отметить, что добавление 4 и возведение в квадрат происходит до интерпретации части def, поэтому в
момент выполнения def двумя верхними элементами в стеке являются /num и 121 (то есть 11 в квадрате).
Бывает, что в процессе некоторого вычисления вам нужно сохранить для дальнейшего использова-
ния то значение, которое записано в какой-нибудь переменной (например, fred), находящейся в верши-
не стека. Это можно сделать так:
/fred exch def % put the value on top of the stack into the variable fred
% помещаем значение верхнего элемента стека в переменную fred
Для правильной работы оператора def чрезвычайно важно поменять местами два верхних элемента
стека, чтобы числовое значение было наверху, а литерал — под ним.
Г4.2. Определение процедур
Как и во всех других языках программирования, представляется очень удобным группировать несколь-
ко команд в одну процедуру (называемую также подпрограммой или функцией). Обычно такой проце-
дуре присваивается какое-нибудь имя. Когда это имя используется в дальнейшем, выполняется соот-
ветствующая последовательность команд. В языке PostScript команды заключаются в фигурные
(французские) скобки: {dup add}. Например, приводимая ниже процедура smal 1 ег масштабирует едини-
цу текущей системы координат коэффициентами (0,8,0,8):
/smaller {.8 .8 scale} def X scale the system by 0.8
% масштабируем систему коэффициентом O.B
Г4. Определение новых переменных и процедур
1021
В результате создается новый элемент словаря с именем smaller и ассоциируется с единственным
«объектом», который является процедурой {. 8 .8 scale}. Когда эта процедура в дальнейшем появляется в
сценарии в виде простого выражения smaller, то система координат соответствующим образом масш-
табируется.
Пример
Мы определяем процедуру box (прямоугольник), которая рисует закрашенный квадрат со стороной две
единицы и с центром в начале координат, как показано на рис. Г. 16, а.
/box {11 moveto 1-1 lineto
-1 -1 lineto -1 1 lineto
closepath fill } def
При совместном использовании процедур box и smaller можно нарисовать совокупность вложенных
прямоугольников с рис. Г.16, б:
200 200 translate 60 60 scale 1 set the initial coordinate system
X устанавливаем начальную систему координат
.8 setgray box X draw the largest box
X рисуем наибольший прямоугольник
.6 setgray smaller box
.4 setgray smaller box
.2 setgray smaller box % draw the innermost box
X рисуем наиболее глубоко вложенный прямоугольник
(Почему прямоугольники приходится рисовать именно в таком порядке?)
Часто бывает удобно передавать в процедуры параметры, определенные пользователем. Это делает-
ся посредством проталкивания этих параметров в стек перед вызовом процедуры. Процедура выталки-
вает значения этих параметров из стека и использует их.
а
б
Рис. Г.16. Примитив box: а) прямоугольник; б) несколько прямоугольников
Мы можем, например, изменить процедуру smaller так, чтобы она принимала в качестве параметра
масштабный множитель. Дадим этой процедуре более осмысленное имя scalelt:
/scalelt {dup scale} def % scale the system by the value on the stack
X масштабируем систему множителем из стека
Теперь мы можем увеличивать или уменьшать систему координат посредством примерно такого
вызова:
.5 scalelt % cut the size of a unit in half
% уменьшаем единицу измерения вдвое
или так:
3 scalelt % triple the size of a unit
1 утраиваем единицу измерения
1022 Приложение Г. Введение в PostScript18
Пример. Нарисуем «точку»
Единственную точку с координатами (х, у) можно нарисовать с помощью процедуры:
/drawDot {newpath 2 copy moveto 1ineto stroke} def
В данной процедуре предполагается, что величины х и у находятся в стеке. Копии х и у проталкива-
ются в стек командой 2 сору, причем обе эти копии удаляются из стека при использовании команд moveto
и 1 ineto. В большинстве принтеров, воспринимающих язык PostScript, перемещение к точке и рисова-
ние прямой линии до той же точки приводит к рисованию точки. Можно выразить эффект воздействия
процедуры drawDot на стек следующим образом:
х у drawDot -» —
а типичный вызов этой процедуры имеет вид:
240 367 drawDot
Пример. Используя большее число параметров, нарисовать прямоугольник
произвольного размера
Можно расширить возможности процедуры box, если задавать масштаб и положение рисуемого ею пря-
моугольника. Тогда ее влияние на стек задается следующим образом:
size х у drawBox } - t draw box of size units on a side centered at (x.y)
t рисуем прямоугольник co стороной side и с центром в точке (х.у)
а соответствующее определение имеет вид:
/drawBox { gsave t avoid any global effects on system
t избегаем любых глобальных влияний на систему
translate t set the center of the box
t задаем центр прямоугольника
2 div dup scale t adjust the size
t корректируем размер
box % draw the box
t рисуем прямоугольник
grestore % restore the previous system
X восстанавливаем предыдущее состояние системы
} def
Первым оператором, использующим значения х и у, является transl ate. Затем, поскольку процедура
box рисует квадрат со стороной две единицы, мы делим параметр size на 2 и помещаем в стек size/2.
После этого прямоугольник рисуется. Все эти операторы окаймляются парой команд gsave grestore,
чтобы предотвратить изменение системы координат.
Пример. Написание текста «на следующей строке»
При написании строк текста вы в конце концов достигаете правого поля страницы, и вам требуется пе-
рейти на «новую строку»; это означает, что вы перемещаетесь вниз на следующую строку и начинаете
писать с левого поля. Предположим, что определены следующие переменные:
/LM 72 def X left margin 1 inch from left edge of page
X левое поле - 1 дюйм от левого края страницы
//RM 540 def X right margin 1 inch from right edge of page
X правое поле - 1 дюйм от правого края страницы
/HneHeight 12 def X vertical distance between adjacent lines of text
X расстояние по вертикали между двумя соседними строками текста
Кроме того, переменная ypos содержит текущую позицию у, в которой на данной странице пишется
текст. Тогда следующая процедура:
/doNewl1пе
{/ypos ypos HneHeight sub def X decrease ypos and save it
Г4. Определение новых переменных и процедур
1023
% уменьшаем значение ypos и сохраняем его
LM ypos moveto{ def % move to next line
% перемещаемся на следующую строку
вначале уменьшает ypos на величину lineHeight, а затем переходит к левому полю новой строки.
Практические упражнения
Г7. Изменение процедуры drawBox
Рассмотрим формулировку процедуры drawBox, порядок следования параметров в которой отличается
от того, который использовался раньше:
х у size drawBox —> — % draw box centered at (x.y) with size units on a side
% рисуем прямоугольник с центром (x.y) и стороной size
При такой формулировке процедуры нельзя просто произвести сначала масштабирование, а затем
перемещение. (Почему нельзя?) Напишите два варианта такой процедуры drawBox, применяя следую-
щие подходы:
О Определите локальную переменную /S, в которой верхний параметр стека сохраняется и исполь-
зуется позднее в процедуре, например, так:
/drawBox{/S exch def ...} def.
О Внутри процедуры drawBox измените порядок параметров в стеке, чтобы он стал таким: size х у,
после чего примените исходную формулировку данной процедуры.
Г8. Рисование больших точек
Напишите процедуру bigDot, которая работает со стеком следующим образом:
х у size bigDot -» —
и рисует круг радиуса radi us с центром в х, у.
Г9. Нарисуйте Большую Медведицу
Напишите сценарий для языка PostScript, который рисует созвездие Большой Медведицы с рис. 2.5,
используя в качестве звезд точки.
Г10. Рисование форм посредством процедур
Определите процедуры для рисования каждого из объектов, показанных на рис. Г. 17. В каждой из этих
процедур должны задаваться размер и расположение рисуемой формы. Выполните эти процедуры и
скомпонуйте из всех этих примитивов интересную сцену.
в г
Рис. Г.17. Примитивы для рисования некоторых форм: а) круг; б) пентаграмма (звезда); в) домик; г) овал
1024
Приложение Г. Введение в PostScript®
Пример. Определение центра страницы
Удобно иметь процедуры, которые возвращают местоположение центра страницы. Пусть имеется стра-
ница размером 8S на 11 дюймов в книжной ориентации (система координат — принятая по умолча-
нию), тогда эти процедуры имеют следующие определения:
/halfwayAcross 8.5 72 mul def 1 define the variables
X определяем переменные
/halfwayUp 11 72 mul def
/pageCenter {halfwayAcross halfwayUp} def
Теперь фрагмент кода pageCenter moveto перемещает СР в середину страницы.
В чем разница?
Отметим, что hal fwayAcross лучше было бы определить как процедуру, а не как переменную:
/halfwayAcross { 8.5 72 mul} def X define it as a procedure
t определяем ее как процедуру
В чем же разница? Когда halfwayAcross определяется как переменная, то оператор 8.5 72 mul выпол-
няется раньше, чем def, и полученное значение связано с hal fwayAcross. Если же hal fwayAcross определе-
на как процедура, то код 8.5 72 mul выполняется всякий раз, когда интерпретатор встречает hal fwayAcross
в дальнейшем тексте сценария. Таким образом, оба варианта — с переменной и с процедурой — делают
в конце концов одно и то же, хотя и различными способами: оба они проталкивают в стек значение 612.
Однако в других случаях результат может быть ошибочным. Допустим, например, что мы попытаемся
написать pageCenter как переменную:
/pageCenter halfwayAcross halfwayUp def
Данный код проталкивает первые три элемента в стек, а затем def выталкивает два верхних элемента
и пытается осмыслить их, что приводит к ошибке.
Связывание процедур
После определения процедуры можно поместить оператор bind:
/bigCirc { 2 2 scale circ .5 .5 scale} bind def
Оператор bind не влияет на стек; в то же время он предписывает PostScript компилировать связан-
ное с ним определение. Фактически bind «отыскивает» определение каждого слова внутри скобок, таких
как scale и circ, и заменяет их соответствующим машинным кодом. Такой подход обладает следующи-
ми двумя преимуществами:
1. Когда процедура bigCirc вызывается в следующий раз, она будет выполняться быстрее, посколь-
ку ее определение не нужно будет интерпретировать повторно.
2. Если какие-либо слова в определении, например drawDot, между вызовами были переопределе-
ны, то такое изменение никак не повлияет на bigCirc; с процедурой bigCirc связан исходный
смысл слова circ.
Г4.3. Простейшая форма итерации с использованием
оператора repeat
Мы будем рассматривать различные способы управляемого повтора процедур в разделе Г.5.3, однако
один такой оператор настолько удобен, что мы решили представить его уже теперь. Оператор repeat
заставляет процедуру выполняться заданное число раз. Он выталкивает из стека два верхних аргумен-
та, чтобы получить: (1) — требуемое число итераций, (2) — процедуру, подлежащую повторению.
num proc repeat -» —
Г4. Определение новых переменных и процедур
1025
Например, код
б }5 0 translate box{ repeat % draw б boxes in a row
% рисуем б прямоугольников в ряд
выполняет указанную процедуру (box) шесть раз и рисует в ряд шесть закрашенных прямоугольников.
Пример. Рисуем пентаграмму
Звезду, изображенную на рис. Г. 18, можно нарисовать посредством пяти повторений рисования гори-
зонтальной прямой, обозначенной на рисунке как «theLine», перемежаемых последовательными пово-
ротами системы координат на 72°. То есть если процедура drawStarEdge рисует «theLine», то код
5 { drawStarEdge 72 rotate} repeat % draw the star
% рисуем звезду
нарисует звезду целиком. Использование оператора repeat облегчает понимание этой процедуры.
(Чему равен полный поворот системы координат когда процесс полностью завершен?) Теперь ко-
нечные точки «theLine» равны (7?cos(a), 7?sin(a)), где а = 18°. (Почему?) Пусть радиус R хранится в
переменной starRad. Создадим внутри процедуры drawStarEdge переменные tmpX и tmpY для хранения
соответственно 7?cos(18°) и 7?sin(18°), после чего нарисуем желаемую прямую. (Напомним, что аргу-
менты функций cos и sin измеряются в градусах.) Собирая все эти идеи вместе, получим следующую
процедуру:
/drawStarEdge {
/tmpX starRad 18 cos mul def % tmpX~Rcos(18°)
/tmpY starRad 18 sin mul def % tmpY=Rsin(18°)
tmpX tmpY moveto % draw “theLine"
% рисуем "theLine"
tmpX neg tmpY 1ineto stroke
}def
Рис. Г.18. Рисование звезды как пяти повернутых прямых линий
Практическое упражнение
Г11. Альтернативная звезда
Приводимая ниже процедура также рисует звезду, но без всякой сложной тригонометрии:
/drawStarf X stack: х у
% в стеке находятся х у
moveto currentpoint translate
4{ 72 0 1ineto
currentpoint translate
33 Ф. Хилл
1026
Приложение Г. Введение в PostScript*
-144 rotate
} repeat closepath fill
} def
Объясните, как работает этот алгоритм на примере вызова 300 400 drawStar. Где расположен центр
этой звезды? Где находится начало координат системы, после того как звезда нарисована?
Г5. Команды решений и итераций
Во всех языках программирования предусмотрены способы проверки величин, хранящихся в памяти,
и выполнения различных операций в зависимости от результатов этой проверки. Кроме того, поддержи-
ваются также команды управления повторением некоторого действия определенное число раз. Разуме-
ется, язык PostScript также обладает такими свойствами.
В PostScript определены две логические, или булевы (Boolean), величины: true (истина) и false
(ложь), причем имеется возможность проталкивать в стек любую из этих величин и выталкивать
ее. Логические величины генерируются командами, список которых приводится ниже. Каждая из
приводимых там команд выталкивает из стека два верхних аргумента и сравнивает их. Каждая
команда проталкивает обратно в стек логическую величину true, если поставленное условие верно;
в противном случае она проталкивает false. Таким образом, каждый из них воздействует на стек сле-
дующим образом:
numl num2 operator —> bool
где numl и num2 — числа, operator — один из операторов из списка, a bool — это true или false.
Пусть а и b являются числовыми величинами. Тогда, если обозначить словом «iff» понятие «if and
only if» («тогда и только тогда»), мы имеем:
a b eq выдает true iff а - b;
а b пе выдает true iff а * b;
а b де выдает true iff а > b:
а b 1е выдает true iff a s b;
a b gt выдает true iff a > b:
a b It выдает true iff a < b;
(Эти команды соответственно эквиваленты следующим операторам языка С: ==, !=, >=, <=, >, <,.)
Приведенные выше команды работают и в том случае, когда а и b являются символьными строками.
Например, команда a eq b выдает true тогда и только тогда, когда строка а совпадает со строкой b. С другой
стороны, команда a gt b равна true тогда и только тогда, когда строка а «лексически больше» строки Ь. Лек-
сическое расположение строк иногда называют «лексикографическим порядком» («dictionary order»).
Предположим, что строки а и b совпадают вплоть до n-го символа. В этом случае a b gt равно true тогда
и только тогда, когда следующий символ строки а имеет большее ASCII-значение, чем следующий сим-
вол строки b (или если в строке b следующий символ отсутствует, а в строке а он есть). Например, каждое
из следующих выражений равно true'.
(rug)(rag) gt X 'u' is "bigger" than 'a'
% ‘u‘ «больше», чем 'a'
(lionize) (lion) gt % the longer string is “bigger”
% более длинная строка «больше»
(bobHBob) gt % lowercase letters are "bigger" than uppercase letters
% строчные буквы «больше», чем прописные
Г5. Команды решений и итераций 1027
Г5.1. Команды, принимающие логические
величины в качестве аргументов
Логические величины можно комбинировать, чтобы получить другие логические величины. Если Ы и
Ь2 — логические величины {true или fake), то, по-прежнему используя слово «iff» в смысле «тогда и толь-
ко тогда», получим:
Ы Ь2 and выдает zraeiff bl и Ь2 обе равны true:
Ы Ь2 or выдает true iff Ы или Ь2 (или обе) равны true:
Ы Ь2 хог выдает true iff Ы или Ь2 (но не обе) равны true:
Ы not выдает true iff Ы равна false.
Кроме того, сами величины true и false можно проталкивать в стек с помощью команд:
true проталкивает true в стек;
false проталкивает false в стек.
Практическое упражнение
Г12. Что помещают в стек следующие операторы: true или false?
34 12 gt 5 7 eq or
23 2 add 5 mul 6 It
56 67 exch ge 12 14 2 sub ge xor
Г5.2. Принятие решений
Логические величины используются двумя командами, 1 f и i fel se, предназначенными для управления
последовательностью операций, выполняемых в сценарии.
1. Оператор i f выталкивает из стека два верхних элемента, воспринимаемые как логическая вели-
чина и процедура, и выполняет эту процедуру, если логическая величина равна true:
bool proc if-» —
2. Оператор el sei f выталкивает из стека три верхних элемента как параметры bool 1 procl proc2;
оператор выполняет процедуру procl, если bool равно true: в противном случае выполняется про-
цедура ргос2:
bool procl proc2 el seif —> —
Пример. Проверка достижения правого поля
При написании текстовых строк нам приходится проверять, достигнуто ли правое поле страницы. Про-
цедура atEndOfLi ne производит проверку того, не вышла ли СР за пределы правого поля RM, и если да, то
она вызывает определенную ранее процедуру doNewline:
/atEndOfLine{
currentpoint pop Я get x position
% получаем позицию x
RM g X beyond right margin?
% за пределами правого поля?
{doNewLine} if % if so. go to next line
X если да. то переходим на следующую строку
} def
1028
Приложение Г. Введение в PostScript81
Пример. Мозаики Труше
На рис. Г.19 показан красивый орнамент, называемый «мозаикой Труше» («Truchet tiles») в честь
Себастьяна Труше (Sebastien Truchet), который занимался такими орнаментами в 1704 году. Орнамент
составлен посредством сочетания двух мотивов, приведенных на рис. Г.20, а и Г.20, б; они размещаются
вплотную друг к другу и заполняют плоскость. Оба мотива идентичны, однако один из них повернут
на 90°; орнамент составляется посредством случайного выбора этих мотивов. В результате получается
совокупность непрерывных кривых (см. рис. Г.20, в), причем некоторые из них образуют «острова»,
а другие составляют непрерывные формы, извивающиеся по всей плоскости.
Рис. Г.19. Мозаики Труше
На языке PostScript основной мозаичный мотив с рис. Г.20, в образуется как четверть окружности
вместе с ее отражением относительно осей х и у. Процедура tile рисует эти две дуги радиуса rad в нача-
ле координат:
/width 10 def % width of tile
% ширина мотива
/rad width 2 div def % radius-width/2
/Arc {newpath rad rad rad 180 270 arc stroke} def
/tile { Arc gsave -1 -1 scale Arc grestore} def
а б в
Рис. Г.20. Построение мозаик Труше: а) мозаичный мотив; б) повернутый мозаичный мотив; в) орнамент
Количество рядов и столбцов записывается в num. Орнамент рисуется внутри двух циклов repeat: во
внешнем цикле рисуются num рядов, для каждого из которых вложенный цикл рисует ряд из num моти-
вов. После рисования каждого ряда начало отсчета системы координат переносится обратно на левую
Г5. Команды решений и итераций
1029
сторону с помощью оператора grestore, а затем начало поднимается на ширину мотива для подготовки
к рисованию следующего ряда:
/пит 20 def % number of rows and columns
X количество рядов и столбцов
72 72 translate X set Initial origin
X устанавливаем исходное начало отсчета
num{ gsave
num{ rand 2 mod 0 eq X true or false with equal likelihood
X zz-иеили falser равной вероятностью
{tile}
{gsave 90 rotate tile grestore}ifelse
width 0 translate % move to the right
X перемещаемся вправо
} repeat
grestore
0 width translate 1 move up a row
% перемещаемся вверх на один ряд
}repeat
showpage
Каждый элемент выбирается посредством «бросания монеты»: оператор rand 2 mod генерирует слу-
чайную величину 0 или 1 с одинаковой вероятностью, а оператор 0 eq помещает в стек соответственно
true или false. Если в вершине стека находится true, то команда ifelse выполняет процедуру {tile};
в противном случае этот оператор вначале поворачивает элемент на 90° и только затем рисует его.
Г5.3. Итерация
Мы уже видели простейшую форму итерации, использующей команду repeat:
repeat выталкивает из стека два верхних элемента в качестве числа N и процедуры, после чего вы-
полняет эту процедуру N раз.
Пример
При создании снежинки, изображенной на рис. Г.21, оператор repeat используется для рисования шес-
ти повернутых версий простой формы, которая, в свою очередь, нарисована некоторой процедурой
moti f. Код имеет следующий вид:
6 {motif 60 rotate} repeat
Рис. Г.21. Использование операторов repeat и rotate
В PostScript предусмотрено два других способа управления итерациями. В одном из них оператор
1 оор выталкивает из стека верхний элемент в качестве процедуры и затем неоднократно выполняет ее.
Для предотвращения бесконечной итерации должен быть способ выхода из нее. Команда exit выводит
процесс за пределы самого внутреннего активного цикла, никак не влияя на состояние стека. Опе-
раторы loop совместно с exit обычно используются тогда, когда число итераций, которое необходимо
1030
Приложение Г. Введение в PostScript*
выполнить, не может быть подсчитано заранее. Процесс итерации заканчивается, когда какое-нибудь
условие вызывает выполнение оператора exl t.
Пример
Допустим, мы хотим нарисовать на странице последовательность прямоугольников со случайным рас-
стоянием между ними, как показано на рис. Г.22. После того как каждая полоска нарисована, к коорди-
нате х добавляется случайная величина. Этот процесс продолжается неизвестное число раз — до тех
пор, пока координата х не достигнет правого края страницы.
Ниже приведен фрагмент кода, рисующий такой ряд полосок, причем для выхода из цикла исполь-
зуется оператор exl t:
/xpos 10 def % Initial x position
% начальная позиция x
/drawBar
{ 0 90 rlineto X assumes CP is at lower left corner
предполагается, что СР в нижнем левом углу
13 0 rlineto
О -90 rlineto
closepath fill} def % the main loop to draw the row of bars
% главный цикл для рисования ряда полосок
} /xpos xpos 16 add % make increment at least 16
% задаем шаг не менее 16
rand 30 mod add def X plus a random amount; set xpos
X добавляем случайную величину и устанавливаем xpos
xpos 600 gt {exit} if X escape if xpos > 600
К, выходим, если xpos > 600
xpos 500 moveto drawBar % draw next bar
% рисуем следующую полоску
}loop
showpage
Рис. Г.22. Случайная строка из полосок
Третий путь контроля числа повторений состоит в использовании цикла for. Когда число итераций
известно заранее, цикл for предоставляет некоторый дополнительный контроль над итерациями. Опе-
ратор for поддерживает «переменную-счетчик*, контролирующую итерации. Эта переменная не имеет
настоящего имени; как мы увидим, она просто проталкивается в стек при каждой итерации данного
цикла. Для удобства здесь мы будем называть ее CV (counting variable). Для работы с циклом for в сте-
ке предполагается наличие четырех параметров:
О начальное значение CV (здесь будем называть его init);
О приращение, которое претерпевает CV при каждой итерации (назовем его iпег);
О предельное значение CV, при котором итерация прекращается (назовем его limit);
О процедура, выполняемая при каждой итерации (назовем ее proc).
Команда для for имеет следующий вид:
init incr limit proc for -» —
В зависимости от знака приращения работа оператора for слегка различается.
Г5, Команды решений и итераций
1031
Когда приращение incr положительное
Когда 1 пег положительно, начальное значение CV устанавливается в i ni t. Если CV не превосходит 11 ml t,
то значение CV проталкивается в стек операндов (для возможного использования внутри процедуры),
и выполняется процедура proc. Ватем к CV прибавляется приращение i ncr. CV снова сравнивается с
limit, и если она не превосходит limit, то процедура выполняется. Работу цикла проще понять, если
сравнить ее с тем, как работает цикл for на языке С:
forCCV * 1nit; CV <» Hm1t; CV +- incr)
< push CV >: /* pseudo-code: push the value of CV */
/* псевдокод: проталкиваем значение CV */
< execute proc >;
}
Примеры
Тщательно проследите содержимое стека при каждой итерации на примерах следующих фрагментов кода:
О Проталкиваем в стек значения 12 3 4 5:
1 1 5 { } for % note the empty procedure
% отметим, что процедура пустая
Поскольку значения CV были протолкнуты в стек командой for, но не были вытолкнуты оттуда
внутри процедуры, они остаются в стеке.
О Помещаем в стек первые десять степеней двойки (то есть 1,2,4,8,..., 1024):
1 0 1 10 {pop dup 2 mul} for
При старте в стек помещается 1. Вдесь значение CV не используется, поэтому его необходимо
выталкивать при каждой итерации.
О Просуммируем числа от 1 до 10 и оставим результат в стеке:
0 1 1 10 {add} for
Первый 0 перед параметрами for требуется для того, чтобы поместить в стек начальное значение
суммы (0).
О Нарисуем шахматную доску с рис. Г.23, используя уровни серого цвета 0,3 и 0,7 и задав начало
координат в левом нижнем углу.
Рис Г.23. Рисование шахматной доски
Ниже приводится сценарий, содержащий два вложенных цикла, которые выполняют итерации по
восьми рядам и восьми столбцам шахматной доски. При вычислении нужного уровня серого цвета
берется сумма счетчиков рядов и столбцов и проверяется на четность. Данному сценарию эквивален-
тен следующий код на С:
1f( (row + col) % 2 — 0) /* is row + col even? */
/* четна ли сумма row + col? */
setgrayC.3); /* yes. use dark color */
1032
Приложение Г. Введение в PostScript®
/* да, используем темный цвет */
else setgray(.7): /* по. use light color */
/* нет. используем светлый цвет */
Для реализации этого кода на языке PostScript CV для внешнего цикла сохраняется в row при каж-
дой итерации, поскольку это значение должно использоваться восемь раз во внутреннем цикле, у кото-
рого есть своя CV, а именно счетчик столбцов. Код row add 2 mod возвращает 0, когда сумма счетчиков
рядов и колонок четная. Позиция следующего подлежащего рисованию квадрата изменяется с по-
мощью известного метода перемещения системы координат при каждой итерации. Реализация может
иметь следующий вид:
/W 40 def Я width of each square
% ширина каждого квадрата
/box {0 0 moveto О W lineto
W W lineto W 0 lineto closepath fill} def
72 72 translate S initial lower left corner
% начальный нижний левый угол
1 1 8{ /row exch def S draw next row of squares
% рисуем очередной ряд квадратов
gsave
1 1 8{ row add 2 mod Я 0 if row + col is even
0 eq
{0.3 setgray}
{0.7 setgray} ifelse
box
W 0 translate S move to right
% перемещаемся вправо
}for
grestore S back to left side
% назад на левый край
О W translate Я up to next row
2 вверх к следующему ряду
{for
showpage
Когда приращение incr отрицательно
Смысл использования отрицательного приращения для оператора for состоит в «обратном отсчете» до
некоторого нижнего предела. Этот процесс похож на случай положительных приращений, за исключе-
нием того, что CV по-другому сравнивается с limit. Эквивалентный код на С выглядит так:
for(CV - init: CV >- limit: CV +- incr)
< push CV >: /* pseudocode: push CV */
/* псевдокод: проталкиваем CV */
< execute proc >:
}
Приращение (отрицательное значение) по-прежнему добавляется к CV в конце каждой итерации,
однако вместо проверки CV < limit теперь производится проверка CV >- limit. Иначе говоря, итерация
продолжается, пока CV строго меньше, чем limit.
Примеры
О Просуммируем первые 10 целых чисел 1 + 2 +...+ 10:
О 10 -1 1 {add} for
Г5. Команды решений и итераций
1033
О Протолкнем в стек значения 3,0,2,5,2,0,1,5,1,0:
3 -.5 1 {} for
О Нарисуем строку «размытых» («smeared») символов, показанную на рис. Г.24.
Рис. Г.24. «Размытие» текста для визуального эффекта
Такую строку можно нарисовать при помощи простого цикла for, который последовательно рисует
ее в слегка смещенных позициях (здесь справа налево) при уменьшающемся значении параметра setgray
от 0,95 до 0, так что строка становится все темнее в последующих позициях. Этот процесс завершается
рисованием поверх всего этой же строки ярко-белого цвета. Код выглядит так:
/Times-Italic findfont 60 scalefont setfont
/Showlt { 0 0 moveto (Gee Whiz) show} def % to draw it once
% для однократного рисования
320 400 translate % set placement
% задаем расположение
.95 -.05 0 X init. incr. limit
of the for loop
{setgray Showlt -1 .5 translate}for % draw many versions
% рисуем много вариантов
1 setgray Showlt S the final one
Я заключительная строка
showpage
Практические упражнения
Г.13
Поместите в стек первые 20 квадратов чисел (то есть 1,4,9,16, 25,..., 400).
Г.14
Поместите в стек первые 20 чисел Фибоначчи (1, 1, 2,3, 5, 8,...). Здесь каждое последующее число яв-
ляется суммой двух предыдущих. (Разумеется, используйте алгоритмическое вычисление последова-
тельности чисел на языке PostScript.)
Г.15
Напишите сценарии для рисования каждой из фигур, изображенных на рис. Г.25. Эти фигуры напоми-
нают объемные освещенные сферы.
ос
а б
Рис. Г.25. Освещенные сферы
1034
Приложение Г. Введение в PostScript*
Г.16
Напишите сценарий для рисования семи «целующихся» окружностей, показанных на рис. Г.26.
Рис Г.26. Семь плотно примыкающих окружностей
Гб. Печать численных значений
Иногда требуется напечатать на странице PostScript какие-либо численные значения. Например, вы
можете запросить значения некоторых внутренних переменных при отладке сценария или разметить
оси графика, который вы хотите напечатать. Все это может быть сделано посредством преобразования
численного значения в строку с последующим выводом этой строки символов на печать. Строка
/str 15 string def % create a string of 15 characters
X создаем строку из 15 символов
выделяет память для строки из 15 символов и связывает с этой строкой переменную str. Команда cvs преоб-
разует численное значение в нужную строку символов. Он также выталкивает из стека два верхних элемен-
та в качестве числа и имени строки, после чего проталкивает в стек строковое представление этого числа:
12 6 mul str cvs -> (72)
% i.e., the string holding the characters 7' and ’2’
X то есть строка, содержащая символы 7’ и '2'
Пример
Начиная с позиции (20, 20), напечатайте 12 случайных чисел в диапазоне 0...35:
/Times-Bold findfont 16 scalefont setfont
20 20 moveto X set the starting point
1 устанавливаем начальную позицию
/str 30 string def X space for a string
X выделяем память для строки
12{rand 36 mod str cvs show X print a random value
X печатаем случайное число
( ) show}
repeat X print a space (to separate values)
X печатаем пробел (для разделения чисел)
showpage
Печать стека (без разрушения информации)
При отладке часто бывает полезно в процессе выполнения сценария исследовать стек в некоторых клю-
чевых местах. Команда pstack выводит на печать все элементы стека операндов без какого-либо измене-
ния этого стека:
pstack X nondestructive stack printout
X неразрушающая печать стека
Г7. Рисование полутоновых изображений
1035
Значения элементов стека не печатаются на странице; вместо этого они отправляются в ту програм-
му, которая послала данный сценарий в интерпретатор PostScript. Например, в случае программы
GhostScript элементы стека посылаются в диалоговое окно GhostScript.
Г7. Рисование полутоновых изображений
В PostScript можно также печатать полутоновые изображения, основанные на битовых картах (bit
maps). (См. главу 10.) Главным средством для этого является команда image. Здесь мы не станем описы-
вать каждый нюанс этого оператора, а покажем только его самое обычное использование (см. «Спра-
вочное руководство по языку PostScript» — PostScript Language Reference Manual).
Начнем с примера, а затем увидим, как легко этот пример обобщается. Изображение, приведенное
на рис. Г.27, содержит 100 строк и 116 столбцов, причем каждый пиксел может принимать 256 возмож-
ных уровней яркости. Мы хотим напечатать его в прямоугольной области шириной 3 дюйма с тем же
форматным соотношением, что и в исходном изображении. Пусть нижний левый угол рисунка находит-
ся в двух дюймах от левого края страницы и в трех дюймах от ее нижнего края. Сценарий для печати
этой картинки выглядит так1:
/nRows 362 def % number of rows in the image
% число строк в изображении
/nCols 282 def % number of columns in the image
% число столбцов в изображении
/nBits 8 def % number of bits per pixel in the image
% число бит на пиксел в изображении
/inch {72 mul} def Я handy conversion from units to inches
% удобный перевод единиц в дюймы
2 inch 3 inch translate % location of lower left corner of
% image on page
% положение нижнего левого угла изображения на странице
3 inch 1.28 3 mul inch scale % set up the picture size;
% preserve aspect ratio
% задаем размер картины с сохранением форматного
% соотношения
/picstr hCols string def % make space for a string of
S characters
% выделяем место для строки символов
nCols nRows nBits S size of image and 8 bits/pixel
% размер изображения при 8 битах на пиксел
[nCols 0 0 nRows 0 nRows neg]
% mapping from unit square to the image
% отображаем с единичного квадрата на изображение
{currentfile % starts just after the image command
% начинается прямо после команды image
picstr readhexstring pop} % read the data as hex digits
% читаем данные как шестнадцатеричные числа
image % print the image
% печатаем изображение
A4A4A4A4A4A4A4A4A4A4A4A4A4A4A4A5A5A5A4A4A4A4A4A4A4A4A4A4A4A4A4A4
A4A4A4A4A5A5A5A4A4A4A4A4A4A4A4A4A4A4A4A4A4A4A4A4A4A5A5A5A4A4A4A6
A6A6A6A6A6A6A6A6A6A6A6A5ASA5A5A5
Целиком файл данных для этого изображения, а также несколько других можно найти па web-сайте книги (см. введение)
1036
Приложение Г. Введение в PostScript®
about 7960 lines of hex data in here
2 здесь находится примерно 7960 шестнадцатеричных чесел
989C9C9C9F9F9F9F9F9FA2A2A2A4A4A4A2A2A2A2A2A2A2A2A2A1A1A19E9E9E9B
9В9В989898949494929292929292
Рис. Г.27. Тестовое изображение PostScript
В данном сценарии содержится несколько новых идей. Одна из них является простым фокусом
с командой i nch, которая упрощает задание длин в дюймах.
Оператор image предполагает наличие в стеке пяти элементов:
1. Число столбцов в изображении.
2. Число строк в изображении.
3. «Глубина» градаций серого цвета (бит на пиксел) в изображении (см. главу 4). Могут быть ис-
пользованы значения 1,2,4 и 8, это соответственно означает, что каждый пиксел имеет 2,4,16 и
256 уровней яркости.
4. Массив из шести величин, составляющих преобразование, что мы вкратце объясним позднее.
5. Процедура для чтения значений пикселов, что также будет объяснено позднее.
Кажется, что приходится предпринимать слишком много шагов, однако большинство изображений
сделаны таким же способом. Картина на рис. Г.27 содержит nRows строк и nCols столбцов, а каждый ее
пиксел занимает nBits бит.
Как же используется в PostScript массив из шести величин? PostScript рассматривает изображение
как прямоугольный массив из квадратов (пикселов) с единичной стороной. Противоположные углы
нижнего левого квадрата равны (0, 0) и (1, 1). Противоположные углы верхнего правого квадрата со-
ставляют (nCols -1, nRows - 1) и (nCols, nRows). Рисунок Г.28 показывает изображение, расположенное в
этом «пространстве изображений»; оно занимает в этом пространстве прямоугольную область.
Упомянутый массив из шести чисел — [nCols 0 0 nRows 0 nRows neg] — описывает аффинное преоб-
разование, заданное некоторой матрицей, примерно такой, как в уравнении (5.4). Первые четыре числа
определяют верхнюю левую подматрицу размерностью два на два, а два последние — это пг13 и пг23. На
рисунке это преобразование обозначено буквой I. Тогда точка (х, у) пространства пользователя отобра-
жается в точку (ix, iy) пространства образа следующим образом:
'ix' ' nCols 0 0 ' fx'
iy = 0 nRows -nRows У
i \ J 0 0 1 7 i \ 7
или просто ix - nColsx, iy - nRowsy — nRows. Допускаются и более сложные преобразования, однако
для обработки большинства изображений достаточно и этих.
PostScript читает значения пикселов слева направо и снизу вверх и использует преобразование /для
рисования пикселов в единичном квадрате пространства пользователя. Такое маленькое выражение,
конечно, не может быть использовано, поэтому вначале приходится перемещать и масштабировать этот
Г7. Рисование полутоновых изображений
1037
единичный квадрат до получения нужного положения, размера и формы посредством комбинации пре-
образований translate и scale (а при желании и rotate). Комбинация таких преобразований обозначена
на рисунке буквой Р. Тогда полное преобразование из гипотетического прямоугольника в пространстве
изображения в результирующее изображение будет задаваться формулой I~'P. PostScript автоматичес-
ки обрабатывает это преобразование.
Единичный квадрат
Рис. Г.28. Преобразования, используемые оператором image
Последний аргумент, запрашиваемый оператором image, — это процедура. Обычно для чтения дан-
ных по изображению используется
{currentfile picstr readhexstring pop}
Оператор image выполняет эту процедуру многократно, до тех пор пока не получит необходимое число
значений пикселов. Ожидается, что данные находятся в том же файле, что и сам оператор image, непосред-
ственно после слова image (и возврата каретки). Каждый вызов такой процедуры посылает оператору
image последовательность шестнадцатеричных цифр, которые image должным образом интерпретирует.
Оператор readhexstring читает последовательность шестнадцатеричных цифр ‘О’..’9’ и 'А’..’Г
(или ‘а’.. ’Г). Он игнорирует нешестнадцатеричные символы и ему не мешают промежуточные про-
белы, переходы на новую строку и другие символы в файле. Данная подпрограмма проталкивает в стек
строку, состоящую из полученных символов, а также логическую величину: true для нормальной ситуа-
ции и false, если конец файла был обнаружен раньше, чем были получены все требуемые данные.
Если, например, nBits равно 8, то каждая пара шестнадцатеричных цифр конвертируется в число в
диапазоне от 0 до 255. Для конкретного потока данных 73А42406... эти значения равны 115,168,36,6.
С другой стороны, если nBits равно 1, то каждая шестнадцатеричная цифра отображает четыре отдель-
ных значения пикселов. Для потока данных 73А8... эти значения равны 0111 0011 1010 1000....
1
Введение в SDL
I
Язык описания сцен (Scene Description Language — SDL) — это очень простой язык для описания гео-
метрических объектов и источников света в ясной и понятной манере. Этот язык воспринимается мето-
дом геасЮкласса Scene (см. определение этого класса в приложении В). Вначале мы в общих чертах рас-
смотрим основы класса Scene, а затем опишем сам язык SDL и рассмотрим, как он используется.
Для того чтобы прочитать файл myScene.dat, написанный на SDL, определим глобальный объект
класса Scene под названием sen и вызовем для него метод readO, задав ему для обработки имя какого-
нибудь SDL-файла:
Scene sen;
// create a Scene object
// создаем объект класса Scene
sen. read ("myScene. dat ”):
// read the SDL file: make the scene
// читаем SDL-файл: создаем сцену
В процессе чтения и интерпретации файла myScene.dat создается список объектов. Кроме того, со-
ставляется список источников света. Эти списки доступны через поля sen.obj и sen.light соответствен-
но. Списки используются в методе drawOpenGLO, который был описан в главе 5, где он применялся для
визуализации сцен с использованием возможностей OpenGL, а также подпрограммой shadeO, описан-
ной в главе 14 и использованной там для визуализации сцен посредством трассировки лучей.
Класс Scene
Объект класса Scene имеет несколько полей, описывающих свойства сцены. Главным ингредиентом яв-
ляется список геометрических форм, присутствующих на сцене. Поле obj является указателем на пер-
вую форму списка. Для того чтобы нарисовать все объекты из списка, достаточно пройтись по нему,
предписывая каждому из объектов нарисовать самого себя:
for(GeomObj* р - sen.obj: р !- NULL; р - p->next)
p->drawOpenGL():
Все объекты в списке принадлежат к одному из типов Shape (например, Sphere, Cube, Icosahedron и т. д.),
а каждый из них знает, как нарисовать самого себя. Здесь используется полиморфизм: все типы Shape
Д1. Синтаксис SDL
1039
порождены от базового типа GeomObj (сокращение от «геометрический объект»), в силу чего тип Shape
может находиться в списке, указывающем на GeomObj.
В классе Scene имеются следующие четыре поля:
Light* light:
// the light-source list
// список источников света
GeomObj* obj:
// the object list
// список объектов
Color3 background:
// the background color
// цвет фона
Color3 ambient;
// the global ambient color
// глобальный фоновый цвет
В дополнение к этим полям имеется еще три поля, используемые для трассировки лучей (см. главу 14):
maxRecursionDepth, minShinyness, minTransparency.
Д1. Синтаксис SDL
Язык SDL чувствителен к регистру, однако обладает свободным форматом: все разделители (пробел,
знак табуляции, перевод строки, подача страницы и т. д.) эквивалентны одному пробелу. Комментарии
начинаются с восклицательного знака «!» и продолжаются до конца текущей строки. Ключевые слова в
SDL используются для задания различных аффинных преобразований, геометрических объектов, ис-
точников света, а также атрибутов сцены, таких как цвет фона.
Создание геометрических объектов
Для создания объекта и помещения его в список объектов достаточно просто объявить его тип. Напри-
мер, так:
cube добавляет кубический объект в список объектов, а
sphere добавляет сферический объект.
Прочие геометрические объекты включают в себя (полный список содержится в файле Sdl. h) torus
(тор), plane (плоскость), square (квадрат), cylinder (цилиндр), cone (конус), tetrahedron (тетраэдр),
octahedron (октаэдр), dodecahedron (додекаэдр), icosahedron (икосаэдр), buckyball (бакибол), diamond
(ромб), teapot (чайник). Когда любой из этих объектов указан в файле, то соответствующий объект до-
бавляется к списку объектов (в его конец).
Существуют дополнительные типы геометрических объектов, требующие параметр, который явля-
ется или вещественным числом, или именем файла. Этот параметр помещается сразу за именем объекта:
taperedCylinder .312
! make a tapered cylinder with small radius .312
! создаем конический цилиндр с меньшим радиусом 0.312
mesh pawn.3vn
! make a mesh
! создаем сетку
В первом примере создается объект «конический цилиндр», параметр которого используется для
задания его точной формы; во втором примере создается объект «сетка», списки вершин и граней кото-
рого описаны в файле pawn.3vn. (На Интернет-сайте книги доступно много файлов в формате 3vn с при-
мерами, в числе которых икосаэдр, ромб и бакибол.)
1040
Приложение Д. Введение в SDL
Управление аффинными преобразованиями
Аффинное преобразование хранится вместе с каждым вновь создаваемым объектом. (Кроме того, хранится
и обратное преобразование; оно используется при трассировке лучей.) Преобразование, которое инсталли-
руется вместе с объектом, — это текущее преобразование (current transformation — СТ), которое активно
в данный момент. В SDL-файле следом за СТ указываются различные ключевые слова. Например, слово
identityAffine
помещает в СТ единичное преобразование (задаваемое единичной матрицей размерностью четыре на
четыре), которое является таковым в момент, когда метод readO начинает интерпретировать SDL-файл.
Для изменения СТ в SDL используются ключевые слова scale, rotate, translate, за каждым из кото-
рых следуют соответствующие параметры; это напоминает способ использования в OpenGL подпро-
грамм glScalefO, glRotatefO, glTranslatefО для изменения матриц моделирования-вида и проекции.
В частности, каждое слово умножает СТ справа на соответствующее преобразование, а произведение
помещается обратно в СТ, например:
CT-CT*Trans
где Trans — матрица четыре на четыре, представляющая новое преобразование.
В следующих трех командах
scale <sx> <sy> <sz>
rotate <ang> <ux> <uy> <uz>
translate <dx> <dy> <dz>
О scale принимает три вещественных параметра, которые являются масштабными множителями
в направлениях осей х, у, г соответственно;
О rotate принимает четыре параметра: угол (в градусах) поворота, а также компоненты осей х, у, z, во-
круг которых осуществляется этот поворот (положительные значения угла ang приводят к повороту
против часовой стрелки вокруг м-оси, если смотреть из точки и по направлению к началу координат);
О translate принимает три параметра: компоненты х, у, z вектора, посредством которого осуществ-
ляется данное смещение.
Например, в результате выполнения команд
scale 2 1.3 -5.33
translate 4-5 6
rotate 45 0 1 О
будут соответственно созданы следующие матрицы:
Sc = '2 0 0 0 1,3 0 0 0 -5,33 О' 0 0 , Тг = '10 0 4' 0 10-5 0 0 16 , Rot = ' 0,707 0 0,707 0 1 0 -0,707 0 -0,707 О' 0 0 •
Кажд< 1° ° ° d 1я из этих команд умножг .0 0° U 1ет СТ справа на ее ма- 1 ° ° ° 1J грицу и помещает резу. пьтат обратно в СТ.
Стек аффинных преобразований
Матрица текущего преобразования СТ находится на самом верху стека матриц. Этот стек управляется
с помощью слов push и pop:
О push делает копию СТ и проталкивает ее в стек (после чего в нем находятся два идентичных элемента);
О pop выталкивает СТ из стека и отбрасывает его. Та матрица, которая находилась в стеке сразу за
верхней, становится СТ. Если же за верхним элементом нет никаких элементов, то команда pop не
делает ничего.
Д1. Синтаксис SDL
1041
Управление свойствами материалов
При создании каждого объекта в нем создается запись свойств его материала, именуемая текущими
материалами (current materials — СМ). Эта запись состоит из следующих полей:
О четыре поля цвета, каждый в форме RGB-триады: ambient, diffuse, specular, emissive;
О шесть скалярных полей: specularExponent, specularFraction, surfaceRoughness, speedOfLight, transparency,
reflectivity (последние пять из них используются при трассировке лучей);
О три поля для описания текстурных свойств объекта: textureType определяет, какая текстура при-
меняется к объекту, numParams — число параметров, задаваемых для объекта, а массив param[] со-
держит 10 значений параметров.
Изменения текущих материалов СМ осуществляются с помощью следующих ключевых слов SDL,
причем за каждым из них может следовать одно или несколько чисел в формате float:
ambient <r> <g> <b>
diffuse <r> <g> <b>
specular <r> <g> <b>
emissive <r> <g> <b>
specularExponent <value>
specularFraction <value>
surfaceRoughness <value>
speedOfLight <value>
transparency <value>
reflectivity <value>
textureType <value>
parameters <value> <value> <value> ...
За ключевым словом parameters следует число задаваемых параметров и список значений этих пара-
метров. Например, для того чтобы поместить в массив param[] последовательно определяемых объектов
три значения 4,5, 6, —12, используется следующая команда:
parameters 3 4.5 6 -12
Изначально СМ содержит следующие значения по умолчанию:
ambient = ( 0.1. 0.1. 0.1)
diffuse = (0.8. 0.8. 0.8)
specular = (0. 0. 0)
emissive = (0. 0. 0)
specularExponent 1
specularFraction 0
surfaceRoughness 1.0
speedOfLight - 1
transparency = 0
reflectivity = 0
textureType 0
Для возвращения CM к этим значениям по умолчанию можно использовать ключевое слово
defaultMaterials.
Приводимые ниже ключевые слова относятся к источникам света, глобальным атрибутам, логичес-
ким объектам и пиксельным картам:
Источники света
light <х> <у> <z> <r> <д> <Ь>
! place a light at (x.y.z) having color (r.g.b)
! помещаем в точку (x.y.z) источник с цветом (r.g.b)
1042
Приложение Д. Введение в SDL
Задание глобальных атрибутов сцены
globalAmbient <г> <д> <Ь>
! give the global ambient source the color (r.g.b)
! задаем глобальный источник фонового света с цветом (r.g.b)
minReflectivity <value>
minTransparency <va1ue>
maxRecursionDepth <value>
background <r> <g> <b>
Ниже приводится пример SDL-файла:
! myScenel.dat - f.s.hill
! has several simple glowing objects
! содержит несколько простых светящихся объектов
globalAmbient .4 .2 .3
light 0 10 О 1 1 1
! white light at (0.10.0)
! белый свет в точке (0,10,0)
background 0 0 .5
ambient .2 .2 .2
diffuse .8 .7 .6
emissive .800
! objects emit red
! объекты излучают красный цвет
cube
! put a generic cube at the origin
! помещаем базовый куб в начало координат
emissive 010
! put a glowing ellpsoid at (2. 0. 0)
! помещаем светящийся эллипсоид в точку (2. 0. 0)
push translate 200 rotate 45 0 0 1 scale .5 .5 2 sphere pop
push translate -2 0 0 cone pop
land a cone at (-2. 0. 0)
! помещаем конус в точку (-2. 0. 0)
Логические (Булевы) объекты
SDL также поддерживает спецификацию логических объектов с помощью следующих ключевых слов:
union
! объединение
intersection
! пересечение
difference
! разность
Каждая из этих команд создает логический объект специального типа и помещает его в список объек-
тов. В SDL-файле за каждым таким объектом должно следовать два объекта (каждый из которых мо-
жет быть геометрическим либо логическим объектом), которые становятся левым и правым потомками
созданного вначале логического объекта.
Ниже приводится SDL-код, описывающий сцену, в которой содержится два логических объекта.
Первый из них является пересечением (intersection) куба с объединением (union) тетраэдра и бакибо-
ла. Второй объект является разностью (difference) тетраэдра и пересечения плоскости с объединением
тора и додекаэдра.
Д2. Макросы в SDL
1043
light 1 2 3 0.2 0.3 0.4
intersection
cube
! left child of intersection
! левый потомок пересечения
union
! right child of intersection
! правый потомок пересечения
. diffuse .2 .5 .7 tetrahedron
! left child of union
! левый потомок обьединения
rotate 180 3 4 5 buckyball
! right child of union
! правый потомок обьединения
difference
! another boolean
! другой логический объект
tetrahedron intersection
plane union
torus dodecahedron
Команда
makePixmap <value> <fname>
определяет пиксельную карту, которая будет использоваться для нанесения текстуры. Первый ее аргу-
мент является целым и используется для идентификации пиксельной карты; второй параметр — это
имя BMP-файла, содержащего текстурное изображение. К примеру, следующий SDL-код
makePixmap 5 clouds.bmp
makePixmap 2 stone.bmp
texture 5
parameters 40110
push scale 3 4 2 cube pop
texture 2
parameters 3 .2 .82
sphere
создает две текстуры. Данный код связывает число 5 (вместе с четырьмя параметрами) с масштабиро-
ванным кубом, а число 2 (вместе с тремя параметрами) со сферой. (Вопрос о том, как в действительно-
сти эта текстура накладывается на объект, оставляется, конечно, на усмотрение программиста.)
Д2. Макросы в SDL
Для удобства вводится ключевое слово def, которое позволяет объединять любое количество команд
SDL в макрос и присваивать им единое имя. Команды SDL, образующие тело макроса, заключаются в
скобки. Например, команда
def red {ambient 100 diffuse 100}
связывает макрос под именем red с заключенными в скобки словами. Если в SDL-файле позднее встре-
тится команда
use red
1044
Приложение Д. Введение в SDL
то в данном месте будет помещена фраза ambient 10 0 diffuse 1 0 0 , как если бы вы ее набрали в этом
месте файла. Макросы позволяют сократить набор и допускают повторное использование определе-
ний. Например, стек в форме символа «L» из четырех кубов можно определить посредством следующе-
го кода:
def Lstack {push cube translate 2 0 0 cube
translate -220 cube
translate 020 cube pop}
Этот макрос можно позднее использовать для помещения на сцене символов L различной формы.
Код для этого может выглядеть, например, так:
use Lstack
push translate 3 2 4 scale .5 .5 .5 use Lstack pop
push translate -3 -2 -4 scale .5 .5 .5 use Lstack pop
ДЗ. Расширение SDL
К SDL нетрудно добавлять новые ключевые слова. С помощью двух примеров мы опишем, как это де-
лается.
Пример Д3.1. Добавление атрибута к сценам
Допустим, что вы хотите добавить к классу Scene новое поле fogThickness, которое описывает плотность
(thickness) тумана (fog) на сцене. Для управления этой величиной, помещаемой в данном поле, можно
добавить к языку SDL ключевое слово с именем fogginess (туманность). Фраза
fogginess 0.5
в SDL-файле будет выставлять в 0,5 значение fogThickness. Чтобы довести это до конца, проделайте сле-
дующие изменения.
О Изменения в SDL-файле с расширением . h.
1. Добавьте в класс Scene поле float fogThickness.
2. Добавьте элемент FOGTHICKNESS всюду в списке перечислений TokenType.
О Изменения в SDL-файле с расширением .срр.
1. В функции whichtokenO добавьте следующую строку:
if (temp — "fogginess") return (FOGTHICKNESS):
2. В функции getObject О добавьте следующую строку:
case FOGTHICKNESS: fogThickness - getFloatO: break:
Вопрос о том, как использовать это новое поле, разумеется, остается за программистом. Так, при раз-
работке трассировщика лучей программист может добавить к методу Scene::shadeO некоторый код,
например:
i f (fogThi ckness > 0) do something..-,
Пример Д3.2. Определение нового типа объекта
Допустим, что вы хотите добавить pie slice {ломтик пирога) к набору возможных объектов, появляю-
щихся в сценах. Это будет часть тонкого кругового диска, лежащего в плоскости ху. Ломтик начинается
с угла 0 (вдоль оси х) и продолжается против часовой стрелки (если смотреть из точки (0,0,1) в сторо-
ну начала координат) до угла sweep {развертка), измеряемого в градусах. Таким образом, если sweep
равен 180, то круговой сектор равен половине круга в положительном полупространстве у, а если sweep
ДЗ. Расширение SDL
1045
равен 360, то круговой сектор составит полный круг. Расширим язык SDL так, чтобы распознавалось
ключевое слово pieSlice с последующим параметром для угла sweep, например, так:
pieSlice 90
О Изменения в SDL-файле с расширением .h.
1. Определите класс PieSlice вместе с полем для хранения угла sweep с помощью следующего
кода:
class PieSlice : public Shape {
public:
float sweep:
// и т. д.
}:
2. Напишите код для соответствующих методов данного класса, таких как drawOpenGLO.
О Изменения в SDL-файле с расширением .срр.
1. Добавьте следующую строку к функции whichtokenO:
if (temp == "pieSlice") return (PIESLICE):
2. В функции getObjectO добавьте следующие строки:
case PIESLICE:
newShape = new PieSlice:
((PieSlice*)newShape) ->angle = getFloatO: break:
Литература
На некоторые журналы и тексты так много ссылок, что в данной библиографии они приводятся в со-
кращенной форме.
SIGGRAPH. Это ссылка на журнал «Компьютерная графика: Труды Конференции специальной
группы интересов по компьютерной графике Ассоциации компьютерной техники в Нью-Йорке»
(«Computer Graphics, the Conference Proceeding of the Special Interest Group on Computer Graphics of
the Association of Computing Machinery in New York»), издаваемый ежегодно. К примеру, ссылка
SIGGRAPH92 означает ссылку на выпуск 1992 года.
GEMS. Это ссылка на серию из пяти книг «Жемчужины графики» («Graphics Gems»), изданную
Academic Press in Boston, MA. Ниже приведены все пять книг, их редакторы и даты публикации:
Graphics Gems
Graphics
Graphics
Graphics
Graphics
Gems II
Gems III
Gems IV
Gems V
Andrew Glassner, Ed., 1990
James Arvo, Ed., 1991
David Kirk, Ed., 1992
Paul Heckbert, Ed., 1994
Alan Paeth, Ed. 1995
1. Эбелсон X, де Cecca А. А. «Черепашья геометрия».
• Abelson, H., and A. A. di Sessa. 1981. Turtle Geometry. Cambridge, MA.: MIT Press.
2. Эктон Ф. С. «Работающие численные методы».
• Acton, F. S. 1970. Numerical Methods That Work. New York: Harper & Row.
3. Энджел Эдвард. «Интерактивная компьютерная графика».
• Angel, Edward. 1970. Interactive Computer Graphics, a Top-Down Approach with OpenGL. Reading, MA:
Addison-Wesley.
4. Апостол T. M. «Вычисления».
• Apostol, T. M. 1961. Calculus. New York: Blaisdell.
5. Эрво Дж., Кирк Д. «Обзор методов ускорения трассировки лучей», в предисловии к «Введению в трасси-
ровку лучей» Эндрю Гласснера.
• Arvo, J., and D. Kirk. 1989. «А Survey of Ray Tracing Acceleration Techniques,» in An Introduction To Ray
Tracing. Andrew Glassner, ed. New York: Academic Press.
6. Эткинсон Уильям Д. «Методы и аппаратные средства для сжатия и обработки изображений».
• William D. Atkinson. Method and Apparatus for Image Compression and Manipulation. U.S. patent number
4,622,545, Nov. 11,1986.
7. Эйерс Ф. «Проективная геометрия».
• Ayers, F. 1967. Projective Geometry. New York: McGraw-Hill.
Литература
1047
8. Болл У. У. Р„ Коксетер X. М. С. «Математические развлечения и этюды».
• Ball, W. W. R., and Н. М. S. Coxeter. 1974. Mathematical Recreations and Essays. Toronto: University of
Toronto Press.
9. Бэллард Д. X„ Браун К. M. «Машинное зрение».
• Ballard, D. Н., and С. М. Brown. 1982. Computer Vision. Englewood Cliffs, NJ: Prentice-Hall.
10. Бэнсли M. Ф. «Фракталы повсюду».
• Barnsley, M. F. 1993. Fractals Everywhere, 2d ed. Boston: Academic Press.
И. Бэнсли M. Ф., Девани P. Л., Мандельброт Б. Б., Пейтджен X. О., Сэйп Д., Восс Р. Ф. «Наука фрактальных
изображений».
• Barnsley, М. F., R. L. Devaney, В. В. Mandelbrot, Н. О. Peitgen, D. Saupe, and R. F. Voss. 1999. The Science
of Fractal Images. New York: Springer-Verlag.
12. Бэрр Э. «Суперквадрики и Преобразования с сохранением углов».
• Barr, А. 1981. «Superquadrics and Angle-preserving Transformations». IEEE Computer Graphics 1 (January):
11-25.
13. Бэрр Аллан. «Глобальные и локальные деформации объемных примитивов».
• Barr, Alan. «Global and Local Deformations of Solid Primitives». Siggraph 84, pp. 21-30.
14. Бэртелс P. X., Битти Дж. К., Бэрски Б. А. «Введение в сплайны для использования в компьютерной гра-
фике и геометрическом моделировании».
• Bartels, R. Н„ J. С. Beatty, and В. A. Barsky. 1987. An Introduction to Splines for Use in Computer Graphics
and Geometric Modeling. Los AltOs, CA.: Morgan Kaufman Publishers, Inc.
15. Бекман IL, Спиззичино А. «Рассеивание электромагнитных волн неровными поверхностями».
• Beckmann, Р., and A. Spizzichino. 1963. The Scattering of Electromagnetic Waves From Rough Surfaces.
New York: Pergamon Press.
16. Бехренс Уве. «Закрашивание границ».
• Behrens, Uwe. 1994 «Fence Shading». Graphics Gems IV.
17. Берджерон P. Д., Боно П. P., Фолей Дж. Д. «Программирование графики с использованием системы CORE».
• Bergeron R. D., P. R. Bono, and J. D. Foley. 1978. «Graphics Programming Using the CORE System». ACM
Computing Surveys 10: 389-443.
18. Берлекэмп E. P., Конвей Дж. X„ Гай P. К. «Пути к успеху».
• Berlekamp, Е. R., J. Н. Conway, and R. К. Guy. 1982. Winning Ways. New York: Academic Press.
19. Биджлоу К. «Разработка шрифтов для персональных рабочих станций».
• Bigelow, С. 1985. «Font Design for Personal Workstations.» Byte (January): 225-270.
20. Бир E. А., Слоэн К. P. «Отображения текстур в два этапа».
• Bier, Е. A., and К. R. Sloan, Jr. 1986. «Two-part Texture Mappings». IEEE CG&A (September), pp. 40-53.
21. Биллмейер Ф. У., Сальтцман M. «Основы технологии цвета».
• Billmeyer, F. W., and М. Saltzman. 1981. Principles of Color Technology. New York: Wiley.
22. Биркхофф Г., Маклейн С. «Обзор современной алгебры».
• Birkhoff, G., and S. MacLane. 1967. A Survey of Modem Algebra. New York: Macmillan.
23. Бишоп Г., Уеймер Д. М. «Быстрое закрашивание Фонга».
• Bishop, G., and D. М. Weimer. 1986. «Fast Phong Shading». SIGGRAPH 86. Computer Graphics 20 (August):
103-106.
24. Блинн Дж. Ф., Ньюэлл М. Е. «Текстура и отражение в компьютерной графике».
• Blinn, J. F., and М. Е. Newell. 1976. «Texture and Reflection in Computer Graphics». Comm ACM19(10),
542-7.
25. Блинн Дж. Ф. «Модели отражения света для изображений, синтезируемых на компьютере».
• Blinn, J. F. 1977. «Models of Light Reflection for Computer Synthesized Pictures». Computer Graphics 11(2)
(Proc. SIGGRAPH, 77).
26. Блинн Дж. Ф., Ньюэлл М. Е. «Отсечение с использованием однородных координат».
• Blinn, J. F., and М. Е. Newell. 1978 «Clipping Using Homogeneous Coordinates». Computer Graphics 12
(August): 245-251.
1048
Литература
27. Блинн Дж. Ф. «Алгоритм строк развертки для компьютерного изображения параметрически заданных
поверхностей».
• Blinn, J. F. «А Scan Line Algorithm for the Computer Display of Parametrically Defined Surfaces».
SIGGRAPH 78.
28. Блинн Дж. Ф. «Имитация складчатых поверхностей».
• Blinn, J. F. «Simulation of Wrinkled Surfaces». SIGGRAPH 78, 12(3), 286-92.
29. Блинн Дж. Ф., Карпентер Л., Лэйн Дж., Уиттед Т. «Методы строк развертки для изображения параметри-
чески заданных поверхностей».
• Blinn, J. Е., L. Carpenter, J. Lane, and Т. Whitted. 1980. «Scan-line Methods for Displaying Parametrically
Defined Surfaces». Communications of the ACM 23 (January): 23-34.
30. Блинн Дж. Ф. «Платоновы тела».
• Blinn, J. F. 1987 «Platonic Solids». IEEE CG&A (November), pp. 62-66.
31. Блинн Дж. «Уголок Джима Блинна. Вниз по графическому конвейеру».
• Blinn, J. 1996. Jim Blinn’s Corner: A Trip Down the Graphics Pipeline. San Francisco: Morgan Kaufman.
32. Блинн Дж. «Уголок Джима Блинна. Грязные пикселы».
• Blinn, J. Jim Blinn’s Comer: Dirty Pixels. 1998. San Francisco: Morgan Kaufman.
33. Блументаль Дж. «Введение в неявные поверхности».
• Bloomenthal, J., ed. 1997. Introduction to Implicit Surfaces. San Francisco: Morgan Kaufman.
34. Боунайт У. Дж. «Процедура для генерирования трехмерных полутоновых компьютерных графических
презентаций».
• Bouknight, W. J. 1970. «А Procedure for Generation of Three-Dimensional Half-Tone Computer Graphics
Presentations». CACM, 13(9) (September): 527-536.
35. Брезенхэм Дж. E. «Алгоритм для компьютерного управления цифровым плоттером».
• Bresenham, J. Е. 1965. «Algorithm for Computer Control of Digital Plotter». IBM Systems Journal 4: 25-30.
36. Броуни M. У. «Новый причудливый класс молекул порождает новую ветвь химии».
• Browne, М. W. 1990. «Bizarre New Class of Molecules Spawns Its Own Branch of Chemistry» New York
Times, Dec. 25, p. 13.
37. Верден Ричард Л., Дуглас Фэйрес Дж. «Численный анализ».
• Burden, Richard L, and J. Douglas Faires. 1985. Numerical Analysis. Boston: Prindle, Weber, and Schmidt.
38. Бутлэнд Дж. «Упрощенное рисование поверхностей».
• Butland.J. 1979. «Surface Drawing Made Simple». Computer-aided Design 11 (January): 19-22.
39. Карлбом И., Пасиорек Дж. «Плоские геометрические проекции и преобразования просмотра».
• Carlbom, I. and Paciorek, J. 1978. «Planar Geometric Projections and Viewing Transformations». ACM
Computing Surveys 10 (4), pp. 465-502.
40. Кэтмулл E. «Компьютерное изображение криволинейных поверхностей».
• Catmull, Е. 1975. «Computer Display of Curved Surfaces». Proc. IEEE Conf. Computer Graphics Pattern
Recognition Data Structures (May), p. 11.
41. Кларк Дж. X. «Быстрый алгоритм строк развертки для рендеринга параметрически заданных поверхностей».
• Clark, J. Н. «А Fast Scan-line Algorithm for Rendering Parametric Surfaces». 1979. Computer Graphics 13
(supplement to SIGGRAPH 79).
42. Клэйсон P. Г. «Мозаичные изображения на Logo».
• Clason, R. G. 1990,1991. «Tile Patterns with Logo» .Journal of Computers in Mathematics and Science Teaching.
10 (1), Fall 1990, pp. 11-23; 10 (2),Winter 1990/91, pp. 59-69; 10 (3), Spring 1991, pp. 59-71.
43. Клауссен Уте. «Об упрощении метода закрашивания Фонга».
• Claussen, Ute. 1990. «On Reducing the Phong Shading Method». Computers and Graphics 14(1): 73-81.
44. Корпорация Конрэк. «Руководство по растровой графике».
• Conrac Corporation. 1985. Raster Graphics Handbook, 2d ed. New York:Van Nostrand Reinhold.
45. Конте С. Д., де Бур К. «Элементарный численный анализ».
• Conte, S. D., and С. deBoor. 1980. Elementary Numerical Analysis. New York: McGraw-Hill.
Литература
1049
46. Кук Р. Л., Торрэнс К. Е. «Модель отражательной способности для компьютерной графики».
• Cook, R. L, and К. Е. Torrance. 1981. «А Reflectance Model for Computer Graphics». Computer Graphics 15
(August): 307-316.
47. Кук P. Л., Портер T., Карпентер Л. «Распределенная трассировка лучей».
• Cook, R. L., T. Porter, and L. Carpenter. «Distributed Ray Tracing». SIGGRAPH84, pp. 137-145.
48. Кунс С. А. «Поверхности для автоматизированного проектирования пространственных форм».
• Coons, S. А. 1967. Surfaces for Computer-aided Design of Space Forms. Report MAC-TR-41, Project MAC,
Massachusetts Institute of Technology, Cambridge, MA.
49. Курант P., Роббинс X. «Что такое математика?»
• Courant, R., and H. Robbins. 1961. What is Mathematics? New York: Oxford University Press.
50. Коксетер X. M. С. «Правильные многогранники».
• Coxeter, H. M. S. Regular Polytopes. 1963. New York: Macmillan.
51. Коксетер X. С. M. «Введение в геометрию».
• Coxeter, H. S. M. Introduction to Geometry. 1969. New York: J. Wiley and Sons.
52. Кроу Ф. К. «Алгоритмы затенения в компьютерной графике».
• Crow, F. С. «Shadow Algorithms for Computer Graphics». Computer Graphics 11(3), 242-8 (SIGGRAPH 77).
53. Кроу Ф. К. «Сравнение технологий сглаживания».
• Crow, F. C. 1981. «А Comparison of Antialiasing Techniques». IEEE Computer Graphics and Applications 1
(January): 40-49.
54. Кроу Ф. К. «Возникновение чайника».
• Crow, F. C. 1987. «The Origins of the Teapot». IEEE Computer Graphics and Applications (January): 8-19.
55. Сайрус M., Бек Дж. «Обобщенное дву- и трехмерное отсечение».
• Cyrus, М. and J. Beck. 1987. «Generalized Two- and Three-dimensional Clipping». Computers and Graphics
3:23-28.
56. де Бур. «Практическое руководство по сплайнам».
• DeBoor, С. 1978. Practical Guide to Splines. New York: Springer-Verlag.
57. Демко С., Ходжес Л., Нэйлор Б. «Построение фрактальных объектов с помощью систем итерируемых функ-
ций».
• Demko, S., L Hodges, and В. Naylor. 1985. «Construction of Fractal Objects with Iterated Function Systems».
SIGGRAPH 1985, Computer Graphics 19 (July): 271-278.
58. Дьюдней А. К. «Вселенная кресел».
• A. К. Dewdney. 1988.The Armchair Universe. New York:W. H. Freeman and Co.
59. Еберт Д., Масгрэйв Ф. К., Пичи Д., Перлин К., Уорли С. «Тестурирование и моделирование».
• Ebert, D., F. К. Musgrave, D. Peachey, К. Perlin, and S. Worley. 1998.Texturing and Modeling, 2d ed. San
Diego: Academic Press.
60. Ферин Г. «Кривые и поверхности для автоматизированного геометрического проектирования».
• Farin, G. 1990. Curves and Surfaces for Computer-aided Geometric Design, 2d ed. Boston:Academic Press.
61. Фокс И. Д., Прэтт М. Дж. «Вычислительная геометрия для проектирования и производства».
• Faux, I. D., and М. J. Pratt. New York: 1979. Computational Geometry for Design and Manufacture. J .Wiley
and Sons.
62. Фейнман P. «Цветовое видение. Из Фейнмановских лекций по физике».
• Feynman, R. 1963. «Color Vision», in The Feynman Lectures on Physics. Reading, MA: Addison-Wesley.
63. Фишер Ф., By А. «Сравнение двух видов зеркальных бликов (R. Е и N. Н.)».
• Fisher, F., and A. Woo. 1994. «R. Е. versus N. H Specular Highlights». Graphics GemsIV.
64. Фолей Дж. Д., Ван Дам А., Фейнер С. К., Хаггес Дж. Ф. «Компьютерная графика: теория и практика».
• Foley, J. D„ A. Van Dam, S. К. Feiner, and J. F. Hughes 1990. Computer Graphics, Principles and Practice.
Reading: MA: Addison-Wesley.
1050
Литература
65. Фолей Дж. Д., Ван Дам А., Фейнер С. К., Хаггес Дж. Ф., Филлипе Р. Л. «Введение в компьютерную гра-
фику».
• Foley, J. D., A. Van Dam, S. К Feiner, J. F. Hughes, and R. L Phillips. 1994. Introduction to Computer Graphics.
Reading, MA: Addison-Wesley. 1994.
66. FRACTINT — свободно распространяемая программа, доступная в целом ряде мест в Интернете.
• FRACTINT, a freeware program available in several places on the Internet,
67. Фримен X- «Компьютерная обработка рисованных изображений»,
• Freeman, Н. 1974. «Computer Processing of Line Drawing Images». Computer Surveys 6(1): 57-98
68. Фримен X. «Обучение и избранные тексты по интерактивной компьютерной графике*.
• Freeman, Н. Tutorial and Selected Readings in Interactive Computer Graphics. 1980. Silver Spring, MD:
IEEE Comp. Soc. Press.
69. Фаче X., Кедем 3. M., Нэйлор Б. Г, «О генерировании ВИДИМЫХ поверхностей посредством априорных дре-
вовидных структур».
• Fuchs, Н., Z. М. Kedem, and В. G. Naylor. «On Visibile Surface Generation by A Priori Tree Structures».
SIGGRAPH 80, pp. 124-133.
70. Фаче X., Эйбрам Г. Д., Грант Е. Е. «Изображение жестких объектов с тенями близко к реальному времени».
• Fuchs, Н., G. D. Abram, and Е. Е. Grant. «Near Real-Time Shaded Display of Rigid Objects». SIGGRAPH 83,
pp. 65-72.
71. Фуллер P. Б., Маркс P. <Dymaxion-Mup Бакминстера Фуллера».
• Fuller, R. B„ and R. Marks. The Dymaxion World of Buckminster Fuller. 1973. New York: Doubleday/Anchor
Books.
72. Фуллер P. Б. «Синергетика»,
• Fuller, R. B. 1975. Sinergetics. New York: Macmillan.
73. Гарднер M. «Суперэллипс Пита Хейна».
• Gardner, M. 1975. «Piet Hein’s Superellipse», in Mathematical Carnival. New York: Knopf,
74. Гарднер M. «Вторая книга „Scientific American" по математическим развлечениям и головоломкам»,
• Gardner, М. 1961. Second Scientific American book of Mathematical Puzzles and Diversions. New York:
Simon & Schuster.
75. Гарднер M. «Новые математические развлечения из „Scientific American"».
• Gardner, M. 1971. New Mathematical Diversions from Scientific American, New York; Simon & Schuster.
76. Гарднер M. «Белая и коричневая музыка. Фрактальные кривые и флуктуации вида один к/».
• Gardner, М. 1978. «White and Brown Music, Fractal Curves and One-over-/ Fluctuations». Scientific
American (April): 16-32.
77. Гарднер M. «Путешествие во времени».
• Gardner, M. Time Travel. 1988. New York;W. H. Freeman and Co.
78. Гарднер M. «Мозаики Пенроуза для дверных шифров».
• Gardner, М. Penrose Tiles to Trapdoor Ciphers. 1989. New York;W. H. Freeman and Co.
79. Графические жемчужины. Серия из пяти книг. Graphics Gems I-V, a series of five books:
О Гласснер Эндрю.
• Andrew Glassner, ed., Graphics Gems, 1990. Boston: Academic Press.
О Эрво Джеймс.
• James Arvo, ed., Graphics Gems II. 1991. Boston: Academic Press.
О Кирк Дэвид.
• David Kirk, ed., Graphics Gems HI. 1992, Boston: Academic Press.
О Хекберт Поль.
• Paul Heckbert, ed., Graphics Gems IV. 1994. Boston: AP Professional.
О Пэф Алан.
• Alan Paeth, ed., Graphics Gems V. 1995. Boston: AP Professional.
Литература
1051
80. Гервиц М., Пургахофер У. «Простой метод квантования цвета: квантование с помощью октодеревьев*.
• Gervautz, М., and W. Purgathofer. 1990. «А Simple Method for Color Quantization: Octree Quantization»
Graphics Gems I, pp. 287-293.
81. Глэсснер А. С. «Введение в трассировку лучей».
• Glassner, A. S., ed. 1989. An Introduction to Ray Tracing, New York: Academic Press.
82. Голдман P. H. «Запрещенные выражения в векторной алгебре».
• Goldman, R. N. 1985. «Illicit Expressions in Vector Algebra» ACM Transactions on Graphics 4 (July): 223-243.
83. Голдман P. «Матрицы и преобразования».
• Goldman, R. «Matrices and Transformations», in GEMS, pp. 472-475.
84. Голдман Рональд, «Еще о матрицах и преобразованиях. Сдвиг и псевдопсрспектива».
• Ronald Goldman. «More Matrices and Transformations: Shear and Pseudo-Perspective» in GEMSII, p. 338.
85. Голдман Рональд. «Разложение перспективных преобразований».
• Ronald Goldman. «Decomposing Projective Transformations» in GEMS III, p. 98.
86. Голдман Рональд. «Разложение линейных и аффинных преобразований».
• Ronald Goldman. «Decomposing Linear and Affine Transformations» in GEMS III, p. 108.
87. Голон P. К. «Полимино».
• Golomb, S. 1965. POLYOMINOES. New York. Scribner’s.
88. Гонзалес P. К., Уинц П. «Цифровая обработка изображений».
• Gonzalez, R. C„ and P. Wintz. 1987. Digital Image Processing. Reading, MA: Addison-Wesley.
89. Гордон У. Дж., Ризенфельд Р. Ф. «В-сплайн кривые и поверхности».
• Gordon, W. J., and R. F. Riesenfeld. 1974. «В-spline Curves and Surfaces» in Computer-aided Geometric Design,
edited by R. E. Barnhill and R. F. Riesenfeld. New York: Academic Press.
90. Гуро X. «Непрерывное закрашивание криволинейных поверхностей».
• Gouraud Н. 1971. «Continuous Shading of Curved Surfaces». IEEE Transactions on Computers (June): 623-629.
91. Грэй, Альфред. «Современная дифференциальная геометрия кривых и поверхностей с пакетом Mathematica».
• Gray, Alfred. 1993. Modem Differential Geometry of Curves and Surfaces with Mathematica. BostomCRC Press.
92. Грин H. «Отображение среды и другие приложения мировых проекций».
• Greene, N. «Environment Mapping and Other Applications of World Projections» 1986. IEEE CG&A 6(11),
21-9.
93. Грин H„ Хекберт П. С. «Создание из многовидовых перспективных проекций растровых Omnimax изоб-
ражений с использованием фильтра с эллиптически взвешенным усреднением».
• Greene, N., & Р. S. Heckbert. «Creating Raster Omnimax Images from Multiple Perspective Views Using
the Elliptical Weighted Average Filter». 1986. IEEE CG&A 6(6), 21-27.
94. Грин H. «Особенности преобразований».
• Greene, N. «Transformation Identities» in GEMS I, p. 485.
95. Гриффитс Дж. Г. «Таблично-управляемые алгоритмы для генерирования заполняющих пространство кри-
вых».
• Griffiths, J. G. 1983. «Table-driven Algorithms for Generating Space-filling Curves». Computer-aided Design
17 (January): 37.
96. Грюнбаум Б„ Шепард Г. К. «Мозаичное замощение и мотивы».
• Grunbaum, В., and G. С. Shephard. Tiling and Patterns. 1986. New York: W. H Freeman.
97. Хеберли П„ Сегал M. «Текстурное отображение как фундаментальный графический примитив».
• Haeberli, Р„ and М. Segal (http://www.sgi.com/grafica/texmap/). 1993. «Texture Mapping as a Fundamental
Drawing Primitive». Fourth Eurographics Workshop on Rendering, M- F. Cohen, C. Peuch, and F. Sillion,
eds. pp. 259-266.
98. Холлидэй Д., Ресник P. «Основы физики».
• Halliday, D., and R. Resnick. 1970. Fundamentals of Physics. New York: John Wiley.
99. Хоулей С. «Упорядоченное размытие».
• Hawley, S. 1990. «Ordered Dithering», in GEMS 1,1990, p. 176.
1052
Литература
100. Хэйес Б. «О взлетах и падениях числа градип».
• Hayes, В. 1984. «On the Ups and Downs of Hailstone Numbers». Scientific American 250 (January): 10-13.
101. Херн Д., Бэйкер M. П. «Компьютерная графика».
• Hearn, D„ and М. Р. Baker. 1994. Computer Graphics, 2d ed. Englewood Cliffs, NJ.: Prentice Hall.
102. Хекберт П. «Квантование цветного изображения для буфера кадров дисплея».
• Heckbert, Р. 1982. «Color Image Quantization for Frame Buffer Display». Computer Graphics 16: 297-307.
103. Хекберт П. «Обзор текстурного отображения».
• Heckbert, Р. «Survey of Texture Mapping». 1986. IEEE CG&A (November): 56-61.
104. Хекберт П. «Написание трассировщика лучей».
• Heckbert, Р. S. «Writing a Ray Tracer», in An Introduction to Ray Tracing 1989. Edited by Glassner, A. S.
New York: Academic Press.
105. Хекберт П., Мортон X. П. «Интерполяция при наложении текстуры и закрашивании полигонов».
• Heckbert, Р., and Moreton, Н. Р. 1991. «Interpolation for Polygon Texture Mapping and Shading» in State
of the Art in Computer Graphics:Visualization and Modeling, edited by David F. Rogers and Rae A. Earnshaw.
New York: Springer-Verlag, pp. 101-111.
106. Хекберт П. С. «Деформирование изображений билинейными лоскутами Кунса».
• Heckbert, Р. S. 1994. «Bilinear Coons Patch Image Warping» in Graphics Gems IV, pp. 438-446.
107. Хилберт Д„ Кон-Воссен С. «Геометрия и воображение».
• Hilbert, D., and S. Cohn-Vossen. 1952. Geometry and the Imagination. New York: Chelsea.
108. Хилл-мл. Ф. С. «Фи — драгоценный камень».
• Hill, F. S., Jr. 1978. «Phi — Precious Jewel». IEEE Communications Society Magazine (September: 35-37).
109. Хилл-мл. Ф. С. «Что нового в эллипсах».
• Hill, F. S., Jr. 1979. «What’s New in Ellipses». IEEE Communications Magazine (July): 23-27.
110. Хилл-мл. Ф. С. «Радости перп-скалярного произведения».
• Hill, F. S. Jr. «The Pleasures of the Perp-Dot Product», in GEMSIV, p. 138.
111. Хофстадтер Д. P. «Метамагические темы».
• Hofstadter, D. R. 1985, Metamagical Themas. New York: Basic Books.
112. Хоггар С. Г. «Математика для компьютерной графики».
• Hoggar, S. G. Mathematics for Computer Graphics. 1992. New York: Cambridge University Press.
ИЗ. Хантли X. E. «Божественная пропорция. Этюд о математической красоте».
• Huntley, Н. Е. 1970. The Divine Proportion: A Study in Mathematical Beauty. New York: Dover.
114. Ингаллс Д. X. «Проектирование и реализация системы программирования Smalltalk-76».
• Ingalls, D. Н. 1978. «The Smalltalk-76 Programming System Design and Implementation». Fifth ACM
Symposium on Principles of Programming Languages (January).
115. Джэнсон X. У. «История искусств. Т. 1».
• Н. W. Janson. 1986. History of Art, vol. 1. Englewood Cliffs, NJ: Prentice Hall.
116. Джарвис Дж. Ф., Джудис К. Н., Нинке У. X. «Обзор техники отображения непрерывных тоновых картин
на двухуровневых дисплеях».
117. Jarvis, J. F., С. N. Judice, and W. Н. Ninke. 1976. «А Survey of Techniques for the Display of Continuous Tone
Pictures on Bilevel Displays». CGIP5, pp. 13-40.
118. Журнал графических программных средств.
• Journal of Graphics Tools. Natick, M.A., A. K. Peters, Ltd., http://www.akpeters.com.
119. Джурденс X., Пайтген X. О, Сауп Д. «Язык фракталов».
• Jurgens Н., Н. О. Peitgen, and D. Saupe. 1990. «The Language of Fractals». Scientific American (August):
pp. 60-67.
120. Каджийа T. «Новые методы трассировки лучей процедурно задаваемых объектов».
• Kajiya, Т. 1983. «New Techniques for Ray Tracing Procedurally Defined Objects». ACM Transactions on
Graphics 2 (July): 161-181.
Литература
1053
121. Капрафф Дж. «Связи: геометрический мост между искусством и наукой*.
• Kappraff, J. «Connections:The Geometric Bridge between Art and Science*. 1991. New York: McGraw Hill.
122. Керрод Б. «Звезды и планеты».
• Kerrod, В. 1979. Stars and Planets. New York: Arco Publ., Inc.
123. Кнут Д. E. «Искусство программирования на компьютере. Т. 1».
• Knuth, D. Е. 1973. The Art of Computer Programming. Vol. 1: Fundamental Algorithms. Reading,MA: Addison-
Wesley.
124. Кнут Д. E. «Цифровые полутона с помощью точечной диффузии».
• Knuth, D. Е. 1987. «Digital Halftones by Dot Diffusion». ACM Transactions on Graphics 6 (October): 245-273.
125. Кнут Д. E. «Искусство программирования на компьютере. Т. 2».
• Knuth, D. Е. 1998. The Art of Computer Programming. Vol 2: Seminumerical Algorithms, 3d ed. Reading,
MA: Addison-Wesley.
126. Кочанек Д. X. У., Бэртелс P. X. «Интерполирующие сплайны с локальным натяжением».
• Kochanek, D. Н. U., and R. Н. Bartels, «Interpolating Splines with Local Tension, Continuity, and Bias Control».
SIGGRAPH 84, Computer Graphics 18(3), pp. 33-41.
127. Копек T. E. «Адаптивное квантование цветных изображений».
• Kopec, Т. Е. 1985. Adaptive Quantization of Color Images. Master’s thesis, University of Massachusetts.
128. Крус P. Л. «Структуры данных и разработка программ».
• Kruse, R. L. 1984. Data Structures and Program Design. Englewood Cliffs, NJ: Prentice-Hall.
129. Лэйн Дж. M., Карпен1ер Л. К. «Обобщенный алгоритм строк развертки для компьютерного изображения
параметрически заданных поверхностей».
• Lane, J. М., and L. С. Carpenter. 1979. «А Generalized Scan Line Algorithm for the Computer Display of
Parametrically Defined Surfaces». Computer Graphics Image Processing 11, pp. 290-297.
130. Лэйн Дж. M., Карпентер Л. К., Уиттед Т., Блинн Дж. Ф. «Методы строк развертки для изображения пара-
метрически заданных поверхностей».
• Lane J. М., L С. Carpenter, Т. Whitted, and J. F. Blinn. 1980. «Scan Line Methods for Displaying Parametrically
Defined Surfaces». CACM 23, pp. 23-34.
131. Лианг Дж., Бэрски Б. «Новая концепция и метод отсечения прямых линий».
• Liang, Y, and В. Barsky. 1984. «А New Concept and Method for Line Clipping». ACM Trans, on Graphics 3(1):
1-22.
132. Линдлей К. «Практическая трассировка лучей на языке С».
• Lindley, С. 1992. Practical Ray Tracing in C. New York: J. Wiley and Sons.
133. Лопец-Лопец Ф. Дж. «Снова о треугольниках».
• Lopez-Lopez, F. J. «Triangles Revisited», in Graphics GemsIII, p. 215.
134. Лаки P. У. «Силиконовые мечты».
• Lucky, R. W. 1989. Silicon Dreams. New York: St. Martin’s Press.
135. Мэйлот, Пэтрик-Гилле. «Применение кватернионов для кодирования трехмерных преобразований».
• Maillot, Patrick-Gilles. «Using Quartemions for Coding 3D Transformations», in GEMS I, pp. 498-515.
136. Манделброт Б. «Фрактальная геометрия природы».
• Mandelbrot, В. 1983. The Fractal Geometry of Nature. New York: Freeman.
137. Мартин Г. «Геометрия преобразований».
• Martin, G. 1982. Transformation Geometry. New York: Springer-Verlag.
138. Мак-Грегор Дж., Уатт А. «Искусство графики для IBM PC».
• McGregor, J., and A. Watt. 1986. The Art Of Graphics for the IBM PC. Reading, MA: Addison-Wesley
Publishing Co.
139. Мак-Рейнолдс Том, Блиф Дэвид. «Программирование на OpenGL: улучшенный рендеринг».
• McReynolds, Tom, and David Blythe. «Programming with OpenGL: Advanced Rendering» (course notes)
SIG GRAPH 97.
1054
Литература
140. Мейер Г., Гринберг Д. «Перцепционные цветные пространства для компьютерной графики».
• Meyer, G., and D. Greenberg. 1980. «Perceptual Color Spaces for Computer Graphics». Computer Graphics 14:
254-261
141. Миллер, Гэвин, Холстед Марк, Клифтон Майкл. «Оперативное вычисление текстуры для закрашивания
поверхностей в реальном времени».
• Miller, Gavin, Mark Halstead, and Michael Clifton, 1980. «Оп-the-Fly Texture Computation for Real-Time
Surface Shading». CG&A 18(3), pp. 44-58.
142. Морет Б. M. E., Шапиро X. Д. «Алгоритмы от и до NP. Т. 1».
• Moret, В. М. Е., and Н. D. Shapiro. 1991. Algorithms from to NP, Vol. 1. Reading MA: Benjamin Cummings.
143. Мортенсон M. «Геометрическое моделирование».
• Mortenson, M. 1985. Geometric Modelling. New York: Wiley.
144. Мансел A. X. «Представление цвета».
• Munsel, A. H. 1941. A Color Notation, 9th ed. Baltimore: Munsell Color Co.
145. Нелсон Марк. «Книга по сжатию данных».
• Nelson, Mark. The Data Compression Book, 2d ed. 1996. New York: M&T Books.
146. Ньюэлл M. E., Ньюэлл P. Г., Санча T. Л. «Решение задачи о невидимых поверхностях».
• Newell, М. Е., R. G. Newell, and Т. L. Sancha. «А Solution to the Hidden Surface Problem». Proceedings of the
ACM National Conference 1972, pp. 443-450. Also in H. Freeman, Tutorial and Selected Readings in Interactive
Computer Graphics, pp. 236-243.
147. Ньюман У. M., Спроул Р. Ф. «Основы интерактивной компьютерной графики».
• Newman, W. М., and R. F. Sproull. 1979. Principles of Interactive Computer Graphics. New York: McGraw-Hill.
148. Огилви С. «Экскурсии в геометрию».
• Ogilvy, S. Excursions in Geometry. 1969. New York: Oxford University Press.
149. Опперхейм А. В., Уиллски А. С. «Сигналы и системы».
• Oppenheim, A. V., and A. S. Willsky. 1983. Signals and Systems, Englewood Cliffs, NJ: Prentice-Hall.
150. О'Рейли T., Куерси В., Лэмб Л. «Руководство по системам X Windows».
• O’Reilly, T., V. Quercia, and L Lamb. 1988, The X Windows System User's Guide, Vol. 3. Newton, MA: O’Reilly
and Assoc.
151. Паеф А. У. «Быстрый алгоритм растрового поворота общего вида».
• Paeth, A. W. «А Fast Algorithm for General Raster Rotation», in GEMS I, p. 197.
152. Паеф Алан У. «Тождество половинного угла для численных вычислений. Прелести тангенса половинно-
го угла».
• Alan W. Paeth. 1991. «А Half-Angle Identity for Digital Computation:The Joys of the Half Tangent», in
Graphics Gems II, edited by James Arvo. New York: Academic Press, p. 381.
153. Пичи Д. P. «Объемное текстурирование сложных поверхностей».
• Peachey, D. R. «Solid Texturing of Complex Surfaces». SIGGRAPH 85, pp. 279-86.
154. Педу Дэн. «Полный курс геометрии».
• Pedoe, Dan. 1970. Geometry, a Comprehensive Course. New York: Dover Publications.
155. Педу Д. «Геометрия и изобразительное искусство».
• Pedoe, D. 1976. Geometry and the Visual Arts. New York: Dover Publications.
156. Пайтген X. О., Рихтер П. X. «Красота фракталов».
• Peitgen, H. О., and Р. Н. Richter. 1986. Die Beauty of Fractals. New York: Springer-Verlag.
157. Пайтген X. О., Сауп Д. «Наука о фрактальных изображениях».
• Peitgen, Н. О., and D. Saupe. 1988. The Science of Fractal Images. New York: Springer-Verlag.
158. Пайтген X. О., Джурденс X., Сауп Д. «Хаос и фракталы. Новые границы науки».
• Peitgen Н. О., Н. Jurgens, and D. Saupe. 1992. Chaos and Fractals, New Frontiers of Science. New York:
Springer-Verlag.
159. Пенна M„ Пэттерсон P. «Проективная геометрия и ее приложения к компьютерной графике».
• Penna, М„ and R. Patterson. 1986. Projective Geometry and Its Applications to Computer Graphics.
Englewood Cliffs, NJ: Prentice-Hall.
Литература 1055
160. Пенроуз Р. «Новый разум императора».
• Penrose, R. 1989. The Emperor’s New Mind. New York: Oxford University Press.
161. Перлин К. «Синтезатор изображений».
• Perlin К. «Ап Image Synthesizer». SIGGRAPH ‘85, pp. 287-296.
162. Фонг Б-Т. «Осевещение изображений, создаваемых на компьютере».
• Phong, В-Т. 1975. «Illumination for Computer Generated Images». Communications of the ACM 18: 311-317.
163. Пиковер Клиффорд А. «Компьютеры, узоры, хаос и красота».
• Pickover, Clifford А. 1990. Computers, Patterns, Chaos, and Beauty. New York: St. Martin’s Press.
164. Пиковер К. «Лабиринты для ума».
• Pickover, С. 1992. Mazes for the Mind. New York: St. Martin's Press.
165. Пигл Л., Тиллер У. «Зверинец рациональных В-сплайн окружностей».
• Piegl, L., and W. Tiller. «А Menagerie of Rational В-Spline Circles». IEEE CG&A, Sept. 1989, pp. 48-56.
166. Пигл Л. «Обзор неравномерных рациональных В-сплайнов (NURBS)».
• Piegl, L. «On NURBS: A Survey». 1991. IEEE Computer Graphics and Applications (January), pp. 55-71.
167. Пигл Л., Тиллер У. «Книга о NURBS (монографии о видеосвязи)».
• Piegl, L, and W. Tiller. 1997. The NURBS Book (Monographs in Visual Communications). New York: Springer-
Verlag.
168. Пайк P. «Графика перекрывающихся растровых слоев».
• Pike, R. 1983. «Graphics in Overlapping Bitmap Layers». Computer Graphics (July): 331-356.
169. Пайпс Л. А. «Прикладная математика для инженеров и физиков».
• Pipes, L. А. 1985. Applied Mathematics for Engineers and Physicists. New York: McGraw-Hill.
170. Питтуэй M. Л. В., Уоткинсон Д. Дж. «Алгоритм Брезенхэма для оттенков серого цвета».
• Pitteway, М. L. V., and D. J. Watkinson. 1980. «Bresenham’s Algorithm with Gray Scale». Communications
of the ACM 23'. 625-626.
171. Плаугер П. Дж. «Стандартная библиотека С»,
• Plaugher, P.J. 1992. The Standard C Library. Englewood Cliffs, NJ: Prentice Hall.
172. Преперата Ф., Шеймос M. И. «Введение в вычислительную геометрию».
• Preparata, F., and М. I. Shamos. Computational Geometry, an Introduction. 1985. New York: Springer-Verlag.
173. Прасинкивиц П. «Системы Линденмайера. Фракталы и записи лекций о биологии растений».
• Prusinkiewicz, Р. 1980. Lindenmayer Systems, Fractals, and Plants Lecture Notes in Biology, № 79. New
York: Springer-Verlag.
174. Роджерс Д. E., Адамс Дж. А. «Математические основы компьютерной графики».
• Rogers, D. Е„ and J. A. Adams 1990. Mathematical Elements for Computer Graphics. New York: McGraw-Hill.
175. Роджерс Д. «Процедурные основы компьютерной графики».
• Rogers, D. 1998. Procedural Elements for Computer Graphics. New York: McGraw-Hill.
176. Труды конференции SIGGRAPH.
• SIGGRAPH.Conference proceedings, the Association for Computing Machinery’s Special Interest Group in
Computer Graphics.
177. Рот Скотт Д. «Испускание лучей для моделирования объемных тел».
• Roth, Scott D. 1982. «Ray Casting for Modeling Solids». Computer Graphics and Image Processing 18:109-144.
178. Шлик К. «Быстрая альтернатива модели отражения Фонга».
• Schlick, С. 1994. «А Fast Alternative to Phong's Specular Model», Graphics Gems IV.
179. Шредер Манфред. «Фракталы, хаос, степенные зависимости».
• Schroeder, Manfred. 1991. Fractals, Chaos, Power Laws. New York. W. B. Freeman.
180. СедербергТ. У., Голдман P. H., Андерсон Д. К. «Неявность, инверсия и пересечение рациональных куби-
ческих кривых: компьютерный аспект».
• Sederberg, Т. W., R. N. Goldman, and D. С. Anderson. 1985. «Implicitization, Inversion and Intersection of
Rational Cubic Curves: Computer Vision», Graphics and Image Processing 31:89-102.
1056 Литература
181. Сегал М., Коробкин К., ван Уиденфельт Р., Дж. Форэн, Хэйберли П. «Быстрые эффекты света и тени с ис-
пользованием наложения текстуры».
• Segal, М., С. Korobkin, R. van Widenfelt, J. Foran, and P. Haeberli. «Fast Shadows and Lighting Effects
Using Texture Mapping». SIGGRAPH 92, pp. 249-252.
182. фон Сеггерн Дэвид X. «Макет справочника по математическим кривым и поверхностям».
• Von Seggem, David Н. 1990. CRC Handbook of Mathematical Curves and Surfaces. New York: CRC Press.
183. Семпл Дж. Г., Нибон Г. Т. «Алгебраическая проективная геометрия».
• Semple, J. G., and G. Т. Kneebone. 1952. Algebraic Projective Geometry. Oxford: Oxford Univ. Press.
184. Шеперд P. «Взгляды разума».
• . Sheperd R. Mind Sights. 1990. New York: W. H. Freeman and Co.
185. Шикин E. В. «Справочник и атлас кривых».
• Shikin, Е. V. 1995. Handbook and Atlas of Curves. New York: CRC Press.
186. Шумейке Кен. «Полярное разбиение матриц».
• Shoemake, Ken. «Polar Matrix Decomposition», in GEMSIV, p. 207.
187. Шумахер Д. «Сравнительный анализ цифровых полутоновых технологий».
• Schumacher, D. 1991. «А Comparison of Digital Halftoning Techiniqucs», in GEMS II. p. 57.
188. Смит A. P. «Растения, фракталы и формальные языки».
• Smith, A. R. «Plants, Fractals, and Formal Languages». SIGGRAPH84, pp. 1-10.
189. Соренсон П. «Фракталы».
• Sorenson, P. 1984. «Fractals». Byte (September): 157.
190. Стейнхарт Джонатан E. «Алгебра форм связности строк развертки».
• Steinhart, Jonathan Е. «Scanline Coherent Shape Algebra», GEMSII, pp. 31-45.
191. СтейнхаусХ. «Математические кадры».
• Steinhaus, H. 1969. Mathematical Snapshots. New York: Oxford University Press.
192. Стоун M. К., Коэн У. Б., Битту Дж. К. «Отображение цветной гаммы и печать цветных цифровых изобра-
жений».
• Stone, М. С., W. В. Cowan, and J. С. Beatty. 1988. «Color Gamut Mapping and the Printing of Digital Color
Images». ACM Transactions on Graphics 7: 249-292.
193. Саферлэнд И. E., Спроул P. Ф., Шумахер P. «Характеристика десяти алгоритмов для невидимых поверх-
ностей».
• Sutherland, I. Е., R. F. Sproull, and Schumacker, R. 1974. «А Characterization of Ten Hidden Surface
Algorithms». ACM Computing Surveys 6(1), pp. 1-55.
194. Томас Г. «Вычисления и аналитическая геометрия».
• Thomas, G. В. 1953. Calculus and Analytic Geometry. Reading, MA: Addison-Wesley.
195. Томас С. E. «Разложение матрицы на простые преобразования».
• Thomas, S. Е. «Decomposing a Matrix into Simple Transformations», in GEMSII, p. 320.
196. Тиллер У. «Рациональные В-сплайны для представления кривых и поверхностей».
• Tiller, W. «Rational В-Splines for Curve and Surface Representation». 1983. IEEE Computer Graphics and
Applications 3(6), pp. 61-69.
197. Труды Ассоциации по вычислительной технике (АСМ), публикуются ежеквартально.
• ACM Transactions on Graphics, published quarterly.
198. Торрэнс К. E., Спэрроу E. M. «Теория незеркалыгого отражения от шероховатых поверхностей».
• Torrance, К. Е., and Е. М. Sparrow. 1967. «Theory of Off-specular Reflection from Roughened Surfaces».
199. Журнал Американского оптического общества.
• Journal of Optical Society of America 57:1105-1114.
200. Тулукиан Й. С., де Уитт Д. П. и др. «Термофизические свойства вещества».
• Touloukian, Y. S., D. Р. DeWitt, eds. 1970. «Thermophysical Properties of Matter, the TPRC Data Series»,
Metallic Elements and Alloys, Vol. 7. New York: Plenum.
Литература
1057
201. Троубридж Т. С., Рейц К. П. «Усредненная неравномерность шероховатой поверхности для отражения
луча».
• Trowbridge, Т. S., and К. Р. Reitz. 1975. «Average Irregularity of a Roughened Surface for Ray Reflection».
202. Журнал Американского оптического общества.
• Journal of Optical Society of America 65(5): 531-536.
203. Уличней P. «Цифровое тонирование».
• Ulichney, R. 1987. Digital Halftoning. Cambridge, MA: MIT Press.
204. Уэгон С. «Математика в действии».
• Wagon, S. 1991. Mathematica in Action. New York: W. H. Freeman and Co.
205. Уокер Дж. «О калейдоскопах».
• Walker, J. 1985. «On Kaleidoscopes». Scientific American (September): 134-145.
206. УонгУ., Бэрри Джо. «Устойчивое вычисление минимизирующего поворот фрейма для моделирования
заметающей поверхности».
• Wang, W., and Barry Joe. 1997. «Robust Computation of the Rotation Minimizing Frame for Sweep Surface
Modeling». Computer-aided Design 29(5): 379-391.
207. Уорнок Дж. «Алгоритм невидимых поверхностей для генерируемых компьютером полутоновых изобра-
жений».
• Warnock, J. 1969. «А Hidden-surface Algorithm for Computer Generated Half-Tone Pictures». Technical
Report TR 4-15, NTIS AD-753 671, Computer Science Department, University of Utah, Salt Lake City,
UT (June).
208. Уоткинс Г. «Алгоритм видимых поверхностей в реальном времени».
• Watkins, G. S. 1970. A Real Time Visible Surface Algorithm.Ph.D. thesis, Thech. Report UTEC-CSs-70-101,
NTIS A 762 004, Computer Science Department, University of Utah, Salt Lake City, UT (June).
209. Уатт А., Уатт M. «Передовые технологии анимации и рендеринга».
• Watt, A. and М. Watt. 1992. Advanced Animation and Rendering Techniques. Reading, MA: Addison-Wesley
Publ. Co.
210. Уэйлер К., Афертон П. «Удаление невидимых поверхностей с использованием сортировки площадей по-
лигонов».
• Weiler, К., and Р. Atherton. 1977. «Hidden Surface Removal Using Polygon Area Sorting». Computer
Graphics 11(2): 214.
211. Веннинджер Магнус Дж. «Модели многогранников».
• Wenninger, Magnus J., 1971. New York: Polyhedron Models Cambridge Univ. Press.
212. Уиттед T. «Улучшенный метод освещения для закрашенного изображения».
• Whitted, Т. 1980. «Ап Improved Illumination Method for Shaded Display». Communications of the ACM 23
(June): 343-349.
213. Уирф H. «Алгоритмы + структуры данных - программы».
• Wirth, N. 1976. Algorithms+data structures=programs. Englewood Cliffs, NJ: Prentice-Hall.
214. By А., Полуин П., Фурни А. «Обзор алгоритмов затенения».
• Woo, А., Р. Poluin, and A. Fournier. 1990. «А Survey of Shadow Algorithms». IEEE CG&A 10(6): 13-32.
215. By M., Нейдер Дж., Дэвис T. «OpenGL: руководство по программированию».
• Woo, М., J. Neider, and Т. Davis. 1997. «OpenGL Programming Guide*, 3d ed. Reading, MA: Addison-Wesley
Developer’s Press.
216. Яглом И. M. «Геометрические преобразования».
• Yaglom, I. М. 1962. Geometric Transformations.Toronto. Random House.
217. Ятс P. К. «Кривые».
• Yates, R. C. 1946. Curves Dept, of Mathematics, U. S. Military Academy .West Point, NY.
34 Ф. Хилл
Список терминов
А
acquire — запрашивать.
adjust — корректировать.
aliasing — ступенчатость, зубцеобразные дефекты изображения.
ambient — фоновая освещенность.
amounting to — в сумме.
antialiasing — сглаживание, устранение контурных неровностей (в растровой графике).
area coherence — связность области (стремление пикселов, соседних по х и по у, лежать в той же области).
array — совокупность.
aspect ratio — форматное соотношение.
attenuation factor — коэффициент ослабления.
В
back face — нелицевая (задняя) грань.
back plane — дальняя плоскость.
band — ломтик (часть шара в форме диска; шаровой пояс).
beam pattern — форма пучка, диаграмма излучения.
bias — смещенность (характеристика кривой).
binary-space partition — двоичное разбиение пространства.
binary-space partition trees — деревья двоичного разбиения пространства.
bitBlt [bit block transfer] — пересылка битовой строки, перенос фрагментов растрового изображения.
blending function — стыковочная функция (в компьютерной графике).
blob — пятно, клякса.
block size — размер (длина) блока (например, данных).
blow up — увеличенный (о фотографии).
blowup — увеличение.
box — бокс (экстент в форме параллелепипеда), прямоугольный экстент.
breadth first search — поиск в ширину (метод анализа структуры дерева, при котором каждый уровень
полностью анализируется до перехода к следующему уровню).
brightness — яркость.
С
candidate interval — возможный интервал.
capture — сохранять.
Список терминов
1059
cardinal spline — фундаментальный сплайн.
cavalier — косоаксонометрическая (проекция).
chop — усекать, отсекать.
chroma key — хроматический ключ (средство объявления некоторого цвета видеоизображения «про-
зрачным»),
closed form solution — решение в аналитическом виде.
close-up photography — фотосъемка крупным планом.
color depth — глубина цвета, цветовая насыщенность.
color look-up table (LUT) — кодовая таблица цветов.
color matching — подбор, соответствие цветов.
color value — код цвета.
component function — координатная функция.
computer science — вычислительная техника.
computer-aided — автоматизированный.
concave — невыпуклый.
conceptual view — концептуальное представление, концептуальный разрез.
contraction mapping — сжимающее отображение.
cross product — векторное произведение.
culling — отбор; отбраковка.
current position — текущие координаты.
cutoff angle — угол пропускания, угол прямого выхода (излучения).
D
demanding — ответственный.
depth buffer — буфер глубины.
depth-sort algorithm — алгоритм сортировки по глубине.
dialog box — диалоговое окно.
diamond — ромб (символ логической блок-схемы), бриллиант.
differential scaling — дифференцированное масштабирование.
diffuse — диффузная (освещенность), диффузная составляющая цвета.
display — устройство отображения.
display surface — поверхность отображения.
dithering — сглаживание, размытие.
down ramp — спуск (на графике).
Е
emissive color — эмиссионный цвет.
error condition — сбойная ситуация; состояние ошибки.
error diffusion — рассеивание ошибок (дефектов).
exclusive OR — исключающее ИЛИ.
extent — экстент, ограничивающий прямоугольник (параллелепипед), бокс, гизмо.
extruding — выдавливание, продавливание, экструзия.
F
far plane — дальняя плоскость.
feature-length — полнометражный.
fill, filling — закрашивание.
flat shading — плоское (постоянное) закрашивание.
flesh out — расширять (текст), конкретизировать.
foreshortening factor — коэффициент укорачивания (ракурса).
form feed — подача страницы.
1060
Список терминов
fortune cookie — афоризм; назидание; изречение (обычно выводимые на экран в процессе регистрации
пользователя или загрузки).
forward-elimination method — метод прямого исключения (решения системы линейных уравнений).
frame — оконная коробка, кадр.
frame buffer — буфер кадров, кадровый буфер.
front face — лицевая (передняя) грань (вершины которой занесены в список или появляются на экране
против часовой стрелки).
front plane — ближняя плоскость.
full tree — в математике полное дерево.
G
game engine — игровая машина.
gate — вентиль.
generic — базовый, порождающий, системный.
ghost — ложный, мнимый.
glint — отраженный свет, луч рассеянного света.
gray levels — оттенки серого (уровни интенсивности серого цвета).
grazing angle — угол скольжения (угол между падающим лучом и поверхностью).
GUI (graphical user interface) — графический интерфейс пользователя.
н
halfway vector — промежуточный вектор.
head of vector — конец вектора.
heedless painter's algorithm — алгоритм беспечного художника.
hidden surface — невидимые (нелицевые) поверхности.
hidden-line-removal method — метод удаления невидимых линий.
hidden-surface removal — удаление невидимых поверхностей.
highlights — блики, (наиболее) яркие участки изображения.
hit point — точка соударения, точка попадания.
hue — тон, цвет, оттенок.
identity transformation — тождественное преобразование.
I
image precision — точность по изображению.
in-between — промежуток, интервал.
infinitesimal — бесконечно малый.
inherent — неотъемлемый, присущий, свойственный.
inorder traversal — симметричный обход (дерева).
integer lattice — целочисленная решетка.
interconnection — схема соединения.
interpenetrate —проникать друг в друга, взаимопроникать.
iterated function systems — системы итерируемых функций (IFS).
J
jack — переключатель.
joint — стык.
Julia — Жюлиа.
К
keystroke, combination keystr. — нажатие клавиши или кнопки; нажатие комбинации клавиш.
knob — рукоятка.
Список терминов
1061
knot — узел.
knot vector — узловой вектор.
L
last-in, first-out — последним вошел, первым вышел; последним пришел, первым обслужен.
leaf node — концевая вершина, лист (дерева).
level of effort — уровень сложности.
lightness — яркость, светлота.
list-priority methods — методы со списком приоритетов.
lookup table LUT — кодовая таблица цветов.
м
Mach band — полоса Маха.
masking — экранирование, маскирование.
master coordinate system — эталонная система координат.
mean square value — среднеквадратическое значение.
median-cut algorithm — алгоритм деления по среднему.
medium — носитель.
memory location — ячейка памяти.
mesh file — сеточный файл.
modelview matrix — матрица моделирования-вида (макетная матрица).
morphing — морфинг (плавное преобразование одного изображения в другое с помощью геометричес-
ких операций и цветовой интерполяции).
N
near plane — передняя плоскость.
nine-point circle — девятиточечная окружность.
noise function — функция шума.
nonsingular — неособенный.
normalize — нормировать.
О
object precision — точность по объекту.
oblique projection — косоугольная проекция.
occlude — закрывать, скрывать.
OpenGL — библиотека графических инструментов; аппаратно-независимый интерфейс прикладного
программирования.
orthographical projection — ортографическая проекция.
outlined text — контурный текст.
overlap — 1) частично покрывать; заходить один задругой; перекрывать; 2) частично совпадать, почти
совпадать.
Р
patch — лоскут, фрагмент (поверхности).
perpendicular bisector — срединный перпендикуляр.
persistent — устойчивый, постоянный.
perspective — перспектива (аксонометрического представления объемных объектов на плоскости), про-
екция.
perspective transformation — перспективное преобразование.
perspective view — перспектива.
perturbation — возмущение.
1062
Список терминов
pick-and-place — выбор и размещение; манипулятор для захвата, транспортировки и установки деталей,
pinhole camera — камера-обскура.
pitch — тангаж (наклон самолета или судна относительно поперечной оси).
pivot — опорный элемент.
pixel center — центр пиксела.
pixel replication — повторение пикселов.
pointing — нацеливание (камеры).
polygon — полигон, многоугольник.
polygonalize — полигонизировать.
population — заполнение, совокупность.
pop-up menu — «всплывающее» меню; меню, отображаемое во временном окне.
position — положение (точки на прямой), координаты.
position vector — координатный вектор, радиус-вектор.
PostScript — язык разметки страниц.
preimage of set — прообраз множества.
processing time — время обработки (данных).
projection matrix — проекционная матрица.
projector — проецирующий луч.
prototiles — мотивы (элементы) протомозаики.
pull-down menu — ниспадающее меню.
push-pop pair — стековые скобки «втолкнуть — вытолкнуть».
R
ramp — (быстрое) изменение по линейному закону.
ray tracing — трассировка луча (лучей), трассирующий луч.
recursion level — уровень рекурсии.
redraw — перерисовка, обновление.
refining — детализация, уточнение, усложнение, «взлохмачивание» (кривых).
region — область.
rendering — воспроизведение изображения, визуализация, рендеринг.
right — прямой (цилиндр, конус).
roll — крен (наклон самолета или судна относительно продольной оси).
rotational sweep — развертка вращения (с заметанием).
rough (up) — лохматить, всклокочивать, возмущать, изрезать.
row — строка, ряд.
rubber band method — метод резиновой нити (для формирования изображений на дисплее).
ruling — образующая.
S
samples — замеры, результаты опроса.
scale factor — масштабный множитель.
scan line — строка развертки.
scan-line HSR method — метод построчного сканирования.
shade — оттенок.
shading — закрашивание, закраска.
shallow tree — в математике низкорослое дерево (с небольшим числом уровней).
shape — размерность (матрицы), форма (объекта).
shrink-wrapping — обертывание (текстурой) со сжатием.
singular — особенный.
slice — долька.
slide — скользить.
sliding — скольжение (камеры).
Список терминов
1063
smooth shading — плавное (гладкое) закрашивание, тонирование (поверхностей) с плавными цветовы-
ми переходами.
solid geometry — стереометрия.
solid graphics — графика монолитных (сплошных) тел (в отличие от каркасных конструкций).
solid model — объемная (монолитная) модель (трехмерного объекта в машинной графике).
solid texture — текстура объемного объекта; текстура твердого тела, 30-текстура.
solidity — монолитность, цельность.
span — диапазон, полоса.
span coherence — связность интервалов.
specular — бликовая освещенность, зеркальная, отражающая составляющая цвета.
spot — место.
spotlight — прожектор (тип источника света в трехмерной компьютерной графике).
stack — стек, стопка.
storage cell — ячейка памяти.
string-production rules — инструкции создания (генерации) строк.
stroke — нажатие (клавиши).
subtle — неуловимый, тончайший.
supersaturated — перенасыщенный, пересыщенный.
surrounder — охватывающий многоугольник.
survive — выдержать, выжить, уцелеть.
sweep — 1) развертка, развертывать; 2) развертка с заметанием (процесс сложной пространственной эк-
струзии по нелинейным путям).
sweep over — проноситься, пробегать, охватывать.
sweeping — заметание, протаскивание.
т
tail of vector — начало вектора.
taper — изменить поперечное сечение (сузить).
tapered cylinder — конический цилиндр, усеченный конус.
terrain — ландшафт, местность.
tesselate — мозаично представить, разбить на ячейки.
tesselation — мозаичное представление.
test — проверка.
tiler — плиточник.
tiling — мозаика, мозаичное покрытие (выкладывание, размещение).
times — произведение.
top of stack — вершина (верхушка) стека.
trace — след (матрицы — сумма элементов главной диагонали).
translation — перенос, смещение, сдвиг.
traverse — обходить (по кругу).
trivial accept — тривиальный прием.
trivial reject — тривиальное отклонение.
true color — реалистичное цветовоспроизведение.
и
underlying — базисный, основной.
undulation — волнистость.
uniform quantization — равномерное квантование (с постоянным шагом)
uniform scaling — равномерное масштабирование.
unwieldy — большой, громоздкий, объемистый.
up ramp — подъем (на графике).
1064
Список терминов
V
vanishing-point — точка схода (параллельных линий).
vantage point — точка наблюдения, точка расположения камеры.
verb — команда.
view — вид.
view volume — отображаемый объем.
viewing process — процесс наблюдения.
viewport — порт просмотра, окно проекции.
W
waist — перетяжка.
wart — бородавка (множества Мандельброта).
wire-frame model — каркасная (сеточная) модель.
world coordinates — мировые (общие, глобальные) координаты.
wrap — обертывать, нанизывать.
Y
yaw — рыскание (поворот самолета или судна относительно вертикальной оси).
Z
zooming in — приближение, увеличение масштаба, зуминг.
zooming out — отдаление, уменьшение масштаба, зуминг.
Алфавитный указатель
4-связные пикселы, 649
8-связные пикселы, 649
А
Add, 1005
ASCII-значения, 102
Atan(Arctg), 1007
В
В-сплайн, базисные функции, 721
использование кратных узлов
в узловом векторе, 726
квадратичные В-сплайны, 723
кубические В-сплайны, 724
линейные В-сплайны, 722
незамкнутые В-сплайн
кривые, 727
определение, 721
стандартный узловой вектор, 727
В-сплайн кривые
кратные контрольные точки, 732
кривые Безье как, 729
свойства проектирования, 730
В-сплайн лоскуты, 754
BitBLT-операция, 623,640
исходные пикселы, 641
определение, 641
Blend(), 633
BMP-файлы изображений, чтение/
отображение, 685
BSP-деревья для ЗО-сцен, 810
для удаления невидимых
поверхностей, 835
обход дерева, 811
BuildQuadrants(), 837
С
Canvas.h — заголовочный файл, 142
ChaosGame(), 581
ChooseAffine(), 581
ChopCI(), 245
CIE хроматическая диаграмма, 778
использование, 780
рисование, 795
Clear, 1004
clip, 1012
clipSegment(), 135,138
CMY-система, 782
CombineLists(), 924
Copy(), 622,685
CSG-объекты, 921
CyrusBeckClipO, 243
D
d isplay(), 533,849
Div, 1006
dot(), 489
doTrio(), 572
Draw(), 622,685
drawArc(), 160
drawCircle(), 160,235
drawClosestFace(), 837
drawDino(), 310
drawDot(), 79
drawEdges(), 483
drawEllipse(), 169
drawFace(), 837
drawLine(), 69
drawMesh(), 483
drawOpenGLO, 336,349,869,
1038,1045
drawPoint(), 68
drawPolyLineFile(), 88
drawRealDot(), 581
drawRoundRect(), 162
drawSceneOpenGL(), 335
drawTrio(), 609
drawTween(), 220
dup, 1004
E
Exch, 1004
Exp, 1007
F
fill, ion
floodFillO, 651
Forward(), 572
Forward (float dist, int isVisible), 149
fract(), 603
FRACTINT программа, 581
G
getFirstHit(), 899,909
getpixel(), 622,650
Ghostscript, 1001
GL_LINE_LOOP, 86
GL.LINES, 74,83
GL_POINTS, 74
GL_POLYGON, 74
GL_QUAb_STRIP, 98
GL_QUADS, 97
GL_TRIANGLE_FAN, 97
GL_TRIANGLE_STRIP, 97
GL.TRIANGLES, 97
glAccum(), 675
glBegin(), 74,83,501
glBegin(GL_POLYGON), 86,96,618
1066
Алфавитный указатель
glBindTexturef), 533 glutlnitWindowPositionf), 73
glBlendFuncf), 633,635 glutlnitWindowSizef), 73
glClear(GL_COLOR_BUFFER_ gl utKey board Func( my Keyboard),
BIT), 76 71,98
glClearColorfred,green, blue, glutMainLoop(), 71
alpha), 76 glutMotionFunc(myMovedMouse), 98
glColorf), 635 glutMouseFunc(myMouse), 71,98
glColor3f(), 85,852 glutReshapeFuncfmyReshape), 71
glCopyPixelsf), 620 glutSolidCubef), 324
glCullFacef), 501 glutSolidSpheref), 324,329
glDrawPixelsf), 620 glutSwapBuffersO, 131,439,534
glEnablef), 501,533,637 glVertex2i(), 74
glEnd(), 74 glVertex3d(), 317
gLfloat, 75 glVertex3f(), 517
glFlushO, 77 glViewportf), 461,852
glFrontFacef), 501 glFrustumf), 456 H
glGenTexturesf), 533 hexSwirlf), 128
glHintf), 533 hit(), 856,868,898,905,910,927
gLint, 75 HLS цветовая модель, 785
gl Light f(), 500 HSV в RGB преобразование, 796
glLightfvf), 502 т
glLightModeli(), 500
glLineWidth(4.0), 85 image, 1035
glLoadldentityO, 306,436 incr, 1030
glLoadMatrixf), 436 IntColor, 650
glLogicOpO, 637 isInShadowf), 909
glMaterialfv(), 503,635 islnvolvedf), 837
glMatrixModef), 436 isSimpleRegionf), 837
glMatrixMode(MODELVIEW), 306 glOrthoO, 320,475 Iterated Systems Inc, 583
glPointSizef), 76 glPopMatrixO, 312,328,329 glPushMatrixO, 312,328,329 К К-я итерация, 107
glReadPixelsf), 620 L
glRectif), 852 glRotatedf), 306,317,502 glRotateff), 1040 glScaledf), 306,317 glTexCoord2f(), 517 glTexImage2D(), 533 glTexParameteri(), 533 glTranslatedf), 306,317,502 glTranslateff), 1040 gluLookAtO, 321,328,431 L-системы, 557 latticeNoisef), 888 Lengthf), 489 lerp(), 219 line(), 69 Iine(xl,yl,x2,y2), 68 lineRelf), разработка, 146 lineto, 1009 lineTof), 69
gluOrtho2D(), 77 использование для рисования
gluPerspectivef), 456 прямых, 304,316
GLUT_SINGLE, 131 Linux и OpenGL, 940
glutCreateWindowf), 73,144 LUT-индексы, 621
glutDisplayFunc(myDisplay), 71 М
glutlnit(&argc, argv), 73,144
glutInitDisplayMode(GLUT_ М на п матрица, 941
SINGLE |GLUT_RGB), 73 Macintosh и OpenGL, 940
makeBoxExtentO, 934
makeEdgeStackf), 837
Marblef), 889
Microsoft Windows 95/98/NT
и OpenGL, 940
moveRelf), разработка, 146
moveto, 1009
moveToQ, 69,304,316
использование для рисования
прямых, 91
Mul, 1005
myDisplayO функция, 77
mylnitf) функция, 76
N
п-угольник, 153
вариации, 155
определение, 153
порождающая окружность, 153
черепашья графика, 154
NURBS-кривые, преимущества, 734
NURBS-лоскуты, рисование, 767
NURBS-поверхности, 755
квадратичные поверхности, 756
линейчатые поверхности, 756
поверхности вращения, 756
формирование, 756
экструзивные поверхности, 756
О
octree-квантование, 792,796
OpenGL, 67,263
GL.LINES, 74,83
GL_POINTS, 74
GL_POLYGON, 74
GL_QUAD_STRIP, 98
GL_QUADS, 97
GL_TRIANGLE_FAN, 97
GL_TRIANGLE_STRIP, 97
GLTRIANGLES, 97
glBeginf), 74,83
glClear(GL_COLOR_BUFFER_
BIT), 76
glClearColorfred,green,blue,
alpha), 76
glColor3f(), 85
glEnd(), 74
GLfloat, 75
glFlushf), 77
GLint, 75
glLineWidth(4.0), 85
glPointSizef), 76
gluOrtho2D(), 77
Алфавитный указатель
1067
OpenGL
glutCreateWindow(), 144
glutlnitO, 144
glutInitWindowSize(), 144
glutKeyboardFunc
(myKeyboard), 98
glutMotionFunc
(myMovedMouse), 98
glutMouseFunc(myMouse), 98
glutReshapeFunc(), 134
glutSwapBuffersO, 131
glVertex2i(), 74
mylnitf) функция, 76
альфа-каналы, инструменты, 635
готовая программа в OpenGL, 77
двойная буферизация, 131
инструментарий утилит (GLUT),
70,98
информационные архивы, 939
использование
для преобразований, 267
для примера
текстурирования, 528
источники света
использование, 497
перемещение, 502
создание, 498
модель освещения, 500
определение префикса gl, 75
ослабление света
с расстоянием, 500
отображение среды, 539
отсечение прямых, 76
переменные состояния 45, 76
получение, 939
преобразование окно — порт
просмотра, 124
прожекторы, 499
работа со свойствами
материалов, 503
рисование элементарных форм
с помощью, 323
система координат, установка, 76
создание закрашенных
объектов, 547
типы данных, 75
OpenGL — руководство
программиста, 939
PixelBLT, 640
рорСТ(), 311
PostScript, 60,1001
арифметические операторы, 1005
PostScript (продолжение)
графические операторы, 1008
графического состояния, 1016
дуги окружностей, 1010
закрашивания, 1011
печать значений, 1034
полутоновые изображения,
рисование, 1035
преобразования координат, 1012
пустой пробел, 1003
системы координат и
преобразования, 1008
стека, 1004
стековая природа, 1003
комментарии, 1002
определение
переменных, 1020
процедур, 1020
регистр, 1003
решения/итерации, 1026
рисование текста, 1019
produceStringO, 558,565
pushCT(), 312
putPixel(), 68
R
Rand(), 894
rayHitsBoxExtent(), 901
rayHitsSphereExtentO, 901
rayPos(), 857
raytrace(), 849
гс-луч, 842
Read(), 622
read(), 685
readBMPFile(), 531
regionSize(), 837
repeat, 1024
Resize событие, 134
RGB, 782
RGB-пространство, рисование, 795
RGB А пиксельная карта, 621
rotate, 1013
rotate 2D(), 311
s
scale, 1012,1016,1037
Screen Width, 119
setChromaKeyO, 633
Setgray, 1012
setlinecap, 1012
Setlinejoin, 1012
Setlinewidth, 1012
setModelviewMatrix(), 436
setPixel(), 68,622,647
SetPixel(x,y,color), 68
Setrgbcolor, 1012
setShape(), 436
shade(), 852,876,913,918,921
Shape — структура данных, работа
с ней, 687
spinner(), 534
StdDev, 603,606
Stroke, 1011
Sub, 1005
T
translate, 1012,1037
turb(), 893
turn(float angle), 149
turnTo(float angle), 148
Txtr[][], 674,895
u
и-контур, 387
undulate(), 893
Unix и OpenGL, 940
V
v-контур, 387
w
writeBMPFile(), 623,685
www.siggraph.org, 29
X
xfrmRayO, 857
z
Z-буфер, 511
Z-буфера алгоритм, 805
A
абсолютно черное тело, 486
автоматизированное
проектирование, 34
автоматизированный
архитектурный дизайн, 35
геометрический дизайн (CAGD),
689,702
аддитивная цветовая система, 783
азимут, 430
аксонометрические проекции, 472
1068
Алфавитный указатель
алгебраическое дополнение
(кофактор), 945
алгоритм
буфера глубины, 805
граничного закрашивания, 666
заливки, 650
сортировки по глубине, 812,836
альбомная ориентация, 95
альфа-значения, 632
установка, задание, 635
альфа-канал, 631
амплитуда, комплексные числа, 951
аналогия с Волшебным экраном, 165
анимация
достижение плавности, 130
ствинингом, 250
твининг, 219
увеличение масштаба рисунка,
приближение к рисунку, 129
аппаратно-независимое графическое
программирование, 69
аппаратно-независимый язык, 60
аппроксимация, 702
Аргана диаграмма, 951
аргумент, комплексные числа, 951
арки, рисование, 182
Архимедова спираль, 171
Архимедовы
мозаики, 569
тела, 371
атом, 558
аффинная инвариантность, 707
аффинные
комбинации векторов, 198
преобразования, 82,264,270,389
3D, 284,289,291,293,299,303
аффинные комбинации точек,
сохранение, 284
и площади фигур, 288
параллельность прямых/
плоскостей, 285
системы координат,
изменение, 300
элементарные 20-
преобразования, 271,279
элементарные операции, 289
ахроматический свет, 486
Б
базис, 721
базовая сфера, 391,844
базовый
конус, 393
базовый (продолжение)
куб, 864
цилиндр, 392,844
бакибол, 372
барабанные графопостроители, 51
Барр, Алан, 408
бассейны притяжения, 597
Безье
кривые, 689,702,762
алгоритм де Кастельо, 702
аффинная инвариантность, 707
инвариантность, 708
интерполяция концевой
точки, 707
как В-сплайн кривые, 729
линейная точность, 708
производные, 709
свойство, 707,708
создание/рисование, 710
лоскуты
поверхности, 751
сшивание, 752
Безье, Пьер, 702
Бернштейна полиномы, 704
бесконечность, стремление к, 551
беспечного художника алгоритм, 807
тестирование, 834
библиотечные файлы,
компоновка, 940
бикубический лоскут Безье, 752
билинейно сопряженные
поверхности, 399
билинейные лоскуты, 397
битовые карты, 44,619
ближняя плоскость, 316,427
блочная сортировка, 664
блуждание, 129
боковое торможение, 506
боксы, 899
Большая Медведица
движение звезд во времени, 195
пример, 78
Брезенхема алгоритм, 44,641,668
как инкрементный алгоритм, 643
как рисование прямых своими
силами, 641
снятие ограничений, 646
Бреннан, Сьюзен Е., 220
броуновское движение, 604
буфер
глубины, 511
псевдоглубина, вычисление
для каждого пиксела, 5И'*>-
буфер (продолжение)
сокращение глубины
на больших расстояниях, 513
кадров, 53
теней, 544
визуализация сцены, 545
загрузка, 545
буфер-накопитель, 675
В
в порт просмотра преобразование,
317,462
валюатор, 62
Варнок,Джон, 818
Варнока алгоритм, 818,837
ввод, 30
ввода примитивы, 61
валюатор, 62
выбор, 62
движение, захват, 65
локатор, 62
строка, 61
типы, 61
трехмерные объекты,
оцифровка, 65
физические, типы, 62
физические устройства ввода, 62
джойстик, 63
клавиатура, 62
кнопки, 62
мышь, 62
планшет, 62
рукоятки, 63
трекбол, 63
шар и перчатки данных, 64
вектор скорости
(velocity), 691
вектор(ы)
2D перп-векторы, 204
аффинные комбинации, 198
важность, 194
векторное произведение двух
векторов, 209
выпуклые комбинации, 198
вычитание, 197
длина, 200
единичные векторы, 200
запись в форме
матрицы-столбца, 196
матрицы-строки, 196
касательный, 748
квадрат длины, 202
координатный орт, 203
Алфавитный указатель
1069
вектор (ы) (продолжение)
линейные комбинации, 198,216
масштабирование, 197
нормаль, 352
нормирование, 200,203,355,
389,407
обзор, 195
однородное представление, 215
операции, 197
определение нормалей, 352
ортогональный, 203
основы, 194
представления основных
геометрических объектов, 212
системы координат/
координатные фреймы, 213
проецирование, 206
промежуточный, 491
разложение, 206
расстояние от точки
до прямой, 207
ребра, 246
системы координат, 194
левые, 194
начало отсчета, 194
системы координат правые, 194
скалярное произведение, 201
знак, 203
коммутативность, 201
линейность, 201
определение, 201
перпендикулярность, 203
свойства, 201
угол между двумя
векторами, 202
сложение, 197
стандартный узловой, 727
сумма точки и вектора, 196
угол между двумя векторами, 202
узловой, 726
умножение, 197
векторное произведение двух
векторов, 209
геометрическая
интерпретация, 210
нахождение нормали
к плоскости, 211
векторные
дисплеи, 51
инструменты, 192
произведения, полезные
тождества, 949
векторный анализ, 193
векторы ребра, 246
величина скорости
(speed), 691
вершин список, 353
ветвление, 562
видеомонитор, 52
визуализация, 482
внешнее отсечение, 248
внешняя нормаль, 241
внутренне определенные
области, 649
внутренне-внешняя функция,
164,387
внутреннее отсечение, 248
внутренние множества, 923
формирование, 924
внутри-снаружи тест, 659
воздушный змей (мозаики
Пенроуза), 613
возможный интервал (CI), 242,458
вписанная окружность, 235
вращательная развертка с
заметанием, 402
выбор, 62
выпуклость, 169
выпуклые
комбинации векторов, 198
объекты, 357
полигоны, 96,239
пересечения лучей
и отсечение, 240
выровненные прямоугольники
рисование, 92
форматное соотношение, 94
выталкивать, 1003
выходной код, 460
Г
гексагональные мозаики, 315
генератор квадратичной В-сплайн
кривой, 762
геодезические купола, 373
геометрическая
информация, список вершин, 353
непрерывность, 693
Гилберта кривые, 560
гипербола, 696
гиперболический параболоид, 407
гиперболоид
двуполостный, 406
однополостный, 406
гипотрохоида, 189
главные
оси, 466
плоскости, 466
главные (продолжение)
следы, 406
гладкие объекты, каркасные
аппроксимации, 386
глаз, 771
камера, 427
колбочки, 771
линии, проходящие позади, 446
глаза координаты, 319,440
глобальный фоновый свет, цвет, 500
Голомб, Соломон, 568
горизонтально-выпуклые
полигоны, 665
заполнение, 687
Госпер, Дэвид, 556
Госпера кривая, 556,560
готовая программа в OpenGL, 77
граней список, 353
грани
визуализация текстуры, 519
добавление
текстурных координат
к каркасным объектам, 518
текстуры, 514
мозаичное размещение
текстуры, 516
наложение текстуры на плоскую
поверхность, 517
раскрашивание, 505
текстурное пространство, 514
гранично-определенный, 649
графические
дисплеи, 51
примитивы, 37
заполненные области, 42
ломаные линии, 37
растровые изображения, 43
текст, 40
трехмерные объекты, 65
устройства отображения, 50
графические дисплеи, 51
кодовая таблица цветов
(LUT), 56
палитра, 57
растровые устройства
отображения, 52
графический
конвейер, 267,548
добавление, 449
и закрашивание, 496
однородные координаты,
451,460
отсечение граней границами
отображаемого объема, 456
1070
Алфавитный указатель
графический (продолжение)
преобразование, 454,461
природа перспективного
преобразования, 453
курсор, 62
режим, 40
графического состояния стек, 1016
графическое состояние, 1016
Гуро закрашивание, 507
Гуро и Фонга интерполяционные
схемы, 839
д
дальняя плоскость, 316,427
движение, запись, 65
двойная буферизация, 131,439
двойное векторное
произведение, 950
двойственный полиэдр, 367
двумерная
графика, классы, 956
трассировка лучей, 253
двумерные
аффинные преобразования
аффинные комбинации точек,
сохранение, 284
геометрические эффекты, 271
относительные размеры,
сохранение, 287
параллельность прямых/
плоскостей, сохранение, 285
площади фигур, 288
полезные свойства, 284
примеры композиции, 279
разложение, 340
элементарные операции, 288
перп-векторы, 204
двухточечная перспективная, 467
двухуровневые растровые
изображения, 47
де Кастельо алгоритм, 702
распространение на любое число
точек, 705
твининг трех точек для создания
параболы, 703
девятиточечная окружность, 235,250
деревья двоичного разбиения
пространства
использование HSR, 808
джойстик, 63
диапазон, 716
дизайн кривых и поверхностей
В-сплайн кривые
кратные контрольные точки, 732
свойства проектирования, 730
интерполяция
естественный кубический
сплайн, 742
моделирование криволинейных
поверхностей
криволинейные лоскуты
Безье, 751
управление
натяжением, добавление, 744
непрерывностью,
добавление, 746
смещенностью, добавление, 745
диметрические проекции, 473
дискретность, 684
дискретные данные, 619
дискриминант, 696
дисплеи
с плазменными панелями, 59
случайной развертки, 51
диффуз! 1ая составляющая,
вычисление, 488
диффузного отражения
коэффициент, 488
диффузное рассеяние, 486
диэдральные мозаики, 568
додекаэдр, 324,371
долгота, 953
доминантная длина волны, 773
дополнительные цвета, 781
досрочный выход, 242
драконы, кривые, 558
древесная текстура, добавление, 886
дробные размерности, 556
дротик (мозаики Пенроуза), 613
дуги
окружностей, в PostScript, 1010
рисование, 159
сопряжение, 161
Е
единичная матрица, 942
единичные векторы, 200
единичный круг, 598
естественный кубический
сплайн, 742
Ж
жидкокристаллический дисплей
(LCD), 59
Жюлиа, Гастон, 586
Жюлиа множества, 595
бассейны притяжения, 597
заполненные, 595
множсствоДс, 599
неподвижные точки, 596
определение, 596
рисование, 596
создание изображений, 612
3
заголовочные файлы,
добавление, 940
задание альфа-значений, 635
закрашивание полигона общего
вида, 688
закрашивания модели, 482,486,487
OpenGL, использование
источников света, 497
абсолютно черное тело, 486
ахроматический свет, 486
графический конвейер, 496
диффузное рассеяние, 486
зеркальные отражения, 486,489
источники, 491
комбинирование составляющих
света, 493
коэффициент зеркального
отражения, 490
рассеянная составляющая,
вычисление, 488
роль фонового света, 493
Фонга модель, 490
фоновый свет, 486
цвет, сложение, 494
заметание, 365,375
замощение, 652
заполнение полигонов, 96
заполненные области, 42
атрибуты, 43
определение, 648
затенение, 879
звездчатая форма, 155
зеркального отражения
коэффициент, 490,495
зеркальные отражения, 486,489
зеркальный свет, 484
змеевидный растровый шаблон, 683
значение определителя, 288
золотое отношение, 111
золотые прямоугольники, 95,369
Алфавитный указатель
1071
И
Игра в Хаос, 552,579,607
добавление цвета, 582,611
изменение масштаба
изображения, 129
изображение, 29
обработка, 31
главная задача, 31
один бит на пиксел, 47
элементы, 37
изометрические проекции, 473
икосаэдр, 324,369
имитации, изображение, 33
индикатор состояния, 32
индикаторная панель, 52
инкрементный алгоритм, 643
инструменты для рисования, 119
интерполяция, 698,701,737
вычисление наклона в кубической
интерполяции, 743
естественный кубический
сплайн,742
контрольных точек с В-
сплайнами, 763
кубическая, вычисление
наклона, 743
посредством кусочных кубических
полиномов, 737
с кубическими полиномами, 765
сравнение с аппроксимацией, 701
эрмитова интерполяция, 739
информация об ориентации, список
нормалей, 353
инфракрасное излучение, 771
исходный прямоугольник, 641
итерируемых функций система
(IFS), 79,106,558,586
k-я итерация, 107
рисование, 577
аттрактор, 577
нахождение, 582
определение, 576
орбита, 107
проект пряничный человечек, 108
процесс копирования, основная
теория, 576
рисование последовательности
градин, 107
создание изображения
с ее помощью, 574
третья итерация, 107
экспериментальный копир, 574
К
кабинетная проекция, 474
кадры,129
Каирские мозаики, 568
каллиграфические дисплеи, 51
камера, 427
gluLookAt(), 431
setModelviewMatrix(), 436
без крена, 431
встраивание в программу, 434
глаз, 427
использование при рисовании
SDL, 440
матрица моделирования-вида, 429
отображаемый объем, 427
установка, 428
перспективные проекции
ЗЭ-объектов, 440
пилотирование, 436,477
плоскость просмотра, 427
поворот, 437
позиционирование/
нацеливание, 321
позиционирование/
ориентирование, 429
проекционная матрица, 428
произвольная ориентация/
позиция, 429
скольжение, 437
угол зрения, 427
установка в OpenGL, 320
форматное соотношение, 427
канонический отображаемый
объем,455
капли, 163
рисование узоров, 163
кардиоида, 171
каркасная визуализация, 482
каркасные аппроксимации гладких
объектов, 386
касательная прямая, 691
касательные векторы, задаваемые
интерактивно, 748
Кастельо, Поль де, 702
квадрантное разбиение, 819
квадратичные
В-сплайны, 723
поверхности, 404
гиперболический
параболоид, 407
гиперболоид, 406
нормальные векторы, 407
квадратичные (продолжение)
эллипсоид, 404
эллиптический параболоид, 406
квадратная матрица, 942
квадратный остров Коха, 560
клавиатура, 62
взаимодействие, 102
кладка кирпича, 376
класс
Canvas, 307
forward(float dist, int
isVisible), 149
turn(float angle), 149
turnTo(float angle), 148
заголовочный файл
Canvas.h, 142
класс, 141,142
объявление, 142
разработка, 140
реализация, 144,179
Noise, 995
Noise, разработка, 888
RGBpixmap, 531,622,633,636,961
Scene, 966
Sphere, 856
Sphereinfo, 901
UnionBool, 934
кластерный список, 907
ключевые кадры, 221
книжная ориентация, 95,1009
кнопки, 62
кодовая таблица цветов (LUT),
56,782
колбочки
глаза, 771
коммутативное скалярное
произведение, 201
комплексные числа
амплитуда, 951
аргумент, 951
арифметика, 950
вещественная часть, 950
диаграмма Аргана, 951
мнимая часть, 950
модуль, 951
сопряженные, 952
угол, 951
формула Эйлера, 952
компоновка, 632
компьютерная графика
автоматизированное
проектирование, 34
анимации, 30
главная задача, 31
1072
Алфавитный указатель
компьютерная графика
(продолжение)
графические дисплейные
устройства, 50
и обработка изображений, 31
издательское дело, 30
имитации, изображение, 33
искусство, 30
как инструменты, 29
как картинки, 28
как предмет изучения, 29
компьютерные игры, 31
мониторинг процесса, 32
необходимость изучения, 30
определение, 28
оформление
журналов, 31
книг, 31
слайдов, 31
презентационная графика, 31
приложения, 29
просмотр в Интернете, 31
создание фильмов, 30
специальные эффекты, 30
конечная точка схода, 466
конические сечения, 166
конический цилиндр, 324,392
конструктивная стереометрия, 921
контрольные точки, 697
контрольный
полигон, 700,710
полиэдр, 751
контур, 1009
конус, 397
рисование, 324
концевой точки интерполяция, 707
координат преобразование, 268
координатные
пары, 62
фреймы, 265
последовательные
изменения, 301
координаты материальной
точки, 165
корпус чайника, 765
косоаксонометрическая
проекция, 474
косоугольные проекции, 474
Коха
кривая, 553
порядок, 554
рисование, 554
усложнение порождающей
прямой, 555
Коха (продолжение)
снежинка, 554
рисование, 554
Кохена—Сазерленда
алгоритм, 135
clipSegment(), 138
разделение на границе каждого
окна, 137
реализация на C/C++, 177
тестирование на тривиальные
прием/отклонение, 136
отсечения алгоритм, 248
Кочанека-Бартелса сплайны, 745
коэффициент, 696
отражения фонового света, 493
Крамера правило, 207
кратные
контрольные точки, 732
узлы, 726
крен, 430
криволинейные поверхности
HSR-методы, 829
моделирование, 748
линейчатые поверхности на базе
В-сплайнов, 748
лоскуты Безье, 751
формирование полигональных
сеток, 394
кривые
ЗП-крнвые, 172
второго порядка, уравнения с
общей вершиной, 696
однозначные, 164
параметрические формы, 165
последовательное
усложнение, 553
представленные параметрически,
рисование, 167
суперэллипсы, 169
формы в полярных
координатах, 171
фрактализация, 614
критический угол, 915
круговой цилиндр, 398
круговые диаграммы, 163
крышка, 392
чайника, 766
куб, рисование, 324
кубическая интерполяция,
вычисление наклона, 743
кубические
В-сплайны, 724
полиномы, интерполяция, 765
Кука—Торренса закрашивание, 877
затенение/экранирование, 879
Френеля коэффициент, 879
Кунс, Стивен, 399
курс, 430
кусочные полиномы, 716
Кэтмулл—Рома семейство
сплайнов, 743
Л
лабиринты,115
правильные, 116
лазерный принтер, 52,60
Ламберта закон, 488
Ламе, Габриэль, 169
левые системы координат, 194
Лианга—Барски алгоритм, 458
линейная
интерполяция, 219
комбинация векторов, 198
точность, кривые Безье, 708
линейное скалярное
произведение, 201
линейные
В-сплайны, 722
графики, рисование, 86
полиномы, 696
линейчатые поверхности, 396
билинейно сопряженные
поверхности, 399
билинейные лоскуты, 397,398
конусы, 397
Кунса лоскуты, 399
линейчатый лоскут, 397
образующая, 398
определение, 396
цилиндры, 398
линейчатый лоскут, 397
линий рисование, 83
выровненные прямоугольники, 92
форматное соотношение, 94
использование moveto()
nlineto(), 91
ломаные/полигоны, 86
Лиссажу фигуры, 760
лицевая грань, 501
логарифмическая спираль, 172
логистическое преобразование
исследование, 175
определение, 175
логические
(булевы) объекты, 921
структура данных, 924
вентили, 185
Алфавитный указатель
1073
логические (продолжение)
значения, 1026
команды, принимающие их
в качестве аргументов, 1027
комбинации пиксельных карт, 637
операции с полигонами, 260
локальная система координат, 314
локатор, 62
ломаные линии, 38,86
drawPolyLineFile(), 88
атрибуты, 39
определение, 38,86
параметризация рисунков, 89
рисовальщик ломаных, создание,
86,126
лоскут, 386
бикубический лоскут Безье, 752
билинейный, 397
Кунса, 399
линейчатый, 397
поверхности Безье, 751
луч, 222
лучей
испускание, 839
трассировка, 838
2П-трассировщик лучей, 938
3D-inyM и мраморная текстура,
886
CSG-объектов, 922
raytrace(), 850
shadeO, 918
shade(ray), 852
t-списки, компоновка, 928
воспроизводимые случайные
величины, генерирование, 888
древесная текстура,
добавление, 886
задание геометрии, 840
изображения закрашенных сцен,
рисование, 872
каркасный объект, алгоритм
пересечения, 869
класс Noise, 888
критический угол, 915
Кука—Торренса закрашивание,
877,878,879
логические операции
с объектами, 921
мраморная текстура,
добавление, 892
наложение изображений
на поверхности, 894
наложение текстуры
на поверхности, 883
лучей (продолжение)
нормальный вектор, нахождение
в точке соударения, 872,873
обертывание текстуры вокруг
поверхности, 895
обзор процесса, 842
определение, 839
отражения/прозрачность, 910
отраженный свет, 938
пересечение луча, 844—846,856,
858,860,864,865,869,927
пиксельные блоки,
рисование, 851
полезные классы, 998
полная, для сцен с излучающими
сферами, 857
преломление света, 913,938
приложение, организация, 848
проекционные экстенты,
построение, 935
прохождение лучей,
определение направления, 916
прямоугольные экстенты,
построение, 933
раскрашивание объекта, 874
с ЗЭ-текстурами, 937
сглаживание, 896,937
составные объекты, 921
структура данных для
логических объектов, 924
текстура твердого тела,
наложение, 884
тени, 907,937
турбулентность, 892
усовершенствованный
трассировщик лучей, 936
щупы теней, 908
экстенты, 897,933,937
эмиссионный
трассировщик, 936
Мандельброт, Бенуа, 553,586
Мандельброта
множества, 553,586
время жизни орбиты, 592
замечания, 595
и системы итерируемых
функций, 586
определение, 590
рисование, 593,611
создание изображений, 37
снежинка, 561,608
Марсалья, Джордж, 894
маска, 671
масштабированная матрица, 942
математика, 941
матрица
главная диагональ, 942
действия с матрицами, 942
единичная, 942
квадратная, 942
коммутативные, 943
линейная комбинация, 942
масштабированная, 942
невырожденная, 946
нулевая, 942
обратная, 946
определение, 941
определитель, 945
разбиение, 945
размерность, 942
размерностью
тнап, 941
один на четыре, 941
симметричная, 943
скалярное/векторное
произведение, 944
транспонированная, 942
умножение, 943
умножение вектора
на матрицу, 943
умножение слева, 943
умножение справа, 943
четверка, 941
матричный принтер, 52
Маха полоса, 506
машиностроение, использование
рисунков, 183
меандр, 152
медианного сечения алгоритм,
791,796
медианы, 217
меридианы, 391,402
мерцание, 55
мировые
координаты, 119
окна, 119
многовидовые ортографические
проекции, 472
модели для Платоновых тел, 367
моделирование
криволинейных поверхностей, 748
линейчатые поверхности на базе
В-сплайнов, 748
лоскуты Безье, 751
1074
Алфавитный указатель
моделирование (продолжение)
поверхности вращения
на базе В-сплайнов, 749
объемных тел полигональными
сетками, 350
моделирования преобразование, 314
моделирования-вида матрица, 305,
318,429,461
модуль, комплексные числа, 951
мозаики, 186,312,565
к-рептилия, 571
Архимедова, 569
гексагональная, 315
деформирование, 568
диэдральная, 568
Каирская, 568
моноэдрическая, 566
непериодическая, 571
основные, 186
полимино, 568
полурегулярные, 569
правильные, 566
протомозаики, 567
ребро к ребру, 567
рептилии, 571
рисование, 571
тримино, 571
Труше мозаики, 186
элемент, 652
мозаичное выкладывание окна, 127
монолитная сетка, 357
монохромные дисплеи, 55
моноэдрические мозаики, 566
мотив, 127,186
создание узоров, 310
мотив крючка, создание из него
фигуры, 149
мраморная текстура, добавление, 892
мышь, 62
взаимодействие, 98
движение, 35
задание прямоугольника, 99
размещение точек, 98
создание ломаной линии, 100
управление ковром
Серпинского, 100
черчение «от руки» толстой
кистью, 101
н
направляющие косинусы, 954
насыщенность, 774
натяжением управление,
добавление, 744
наутилус, 172
научный анализ и визуализация, 36
нацеливание камеры, 321
начало отсчета координатных
фреймов, 214
начертание шрифта, 41
невидимые грани, 479
невидимых
линий удаление (HLR), 801
алгоритм со стеком ребер, 837
методы, 825
поверхностей удаление (HSR),
задача
HSR-методы для
криволинейных
поверхностей, 829
алгоритм сортировки по
глубине, 812,836
беспечного художника
алгоритм, 807
использование деревьев
разбиения пространства,
810-812,835
квадрантное разбиение, 819
методы разбиения области, 818
простая область, 822
список приоритетов HSR-
методов, 816,833
строки развертки HSR-метод,
816,833,836
удаления невидимых
поверхностей методы, 829
поверхностей удаление (HSR),
проблема, 800
независимость от разрешения, 585
незамкнутые В-сплайн кривые, 727
нелицевые грани, 501
Нельсон, Марк, 584
ненасыщенные цвета, 774
неоднородные рациональные
В-сплайны (NURBS), 690,733
непериодические мозаики, 571,612
неподвижная точка, 577
неравномерное
масштабирование, 1015
неявная форма, 164
поверхности, 387
неявное уравнение, 387
нормалей список, 353
нормали в вершинах в сравнении
с нормалями граней, 352
нормальные векторы, 203,352
к квадратичным
поверхностям, 407
нормальные векторы (продолжение)
к платоновым телам, 369
к поверхности, 388
нахождение, 355
нормирование векторов, 200
носнк чайника, 766
нулевая матрица, 942
Ньюэлл, Мартин, 355
Ньюэлла метод, вывод, 414
О
о коллаже теорема, 583
области, 620
заданные контуром, 657
заполнение, 620
сериями, 686
узорами, 652
описываемые
прямоугольниками, 655
определение, 648
пикселов, определение/
заполнение, 648
полигонально-определенные,
заполнение, 658
обобщенные ЗП-сдвиги, 344
образ, 268
обрамление объекта, 132
обратной подстановки этап, 743
обратных итераций метод, 601
обход BSP-деревьев, 811
объединение, 921,929,934
полигоны, 258
объединенные экстенты, 907
объекта преобразование, 268
объектов список, 843
Оверхаузера сплайны, 743
ограничивающие прямые, 239
нахождение, 239
ограничивающий прямоугольник
или параллелепипед, 132,865
один
бит на пиксел, изображение, 47
на четыре, матрица, 941
однозначные кривые, 164
однородное
квантование цвета, 789
представление точек
и векторов, 215
однородные координаты, 451
одноточечная перспектива, 466
окна, автоматическая установка, 132
окно — порт просмотра
отображение, 120
Алфавитный указатель
1075
окно — портпросмотра
(продолжение)
преобразование, 123
построение, 124
окопная функция, 671
оконное программирование, 70
оконтуривание, 678
округление, 642
окружности
вписанные, 235,250
вращение вокруг
окружностей, 189
девятиточечные, 235,250
дуги в PostScript, 1010
огибающая, 759
рисование, 159
<жтаэд$>, 324
операндов стек, 1003
операторы построения контура, 1009
орбита, 175,580
ориентация символов, 41
ортогональные
векторы, 203
проекции, 206
ортографические проекции, 471
осевая симметрия, 308
оси
отражения, 280
поворот вокруг, 346
основание, 392
относительное рисование, 146,1010
moveRel() и lineRel( ),
разработка, 146
черепашья графика, 148
относительные размеры,
сохранение, 287
отображаемый объем, 316,427
канонический, 455
отсечение граней границами, 456
преобразование, 455
установка, 428
отображение
из окна в порт просмотра, 120
между мировым окном и портом
просмотра, 119
неровностей, 527
отражение, 539
построение, 124
со сжатием, 577
среда, 539
точек в новые точки, 268
хромированное, 539
отражение, 208
в комнате, 253
оси, 280
отражения
карта
отображение
хромированное, 539
коэффициенты, 490,495
выбор, 495
наложение текстуры
с модулированием, 527
отраженный свет, 938
геометрические составляющие
для нахождения, 487
отрезки прямой, 222
нахождение пересечения, 231
отсекмощийпрямоутолътмк, 641
отсечение
границами произвольных
полигонов, 246
процесс, 128,236
для выпуклых полигонов, 240
прямых, 135
clipSegment(), 135
алгоритм Кохена—Сазерленда,
135,136,137
оттенок цвета, 773
п
палитра, 57
палочки, 772
панели с активной матрицей, 59
панорамирование, 129
парабола, 696
параллели, 391,402
параллельность прямых/
плоскостей, 285
сохранение, 285
параллельные
проекции, 470,478
косоугольные проекции, 474
ортографические проекции, 471,
472,473
теория, 470
прямые
длинные, аномалия
при рассматривании, 448
проецирование, 445
параметризация рисунков, 89
параметрическая
непрерывность, 693
параметрические формы
кривых, 165
нахождение неявной
формы из, 166
параметрическое представление
прямых, 223
параметров пространство, 230
параметры, 1021
Пеано кривые, 556
и генерация строк, 557
пеленг, 430
Пенроуза мозаики, 613
пересечение, 921,929,934
луча со сферой, вычисление, 856
лучом, для выпуклых
полигонов, 240
полигонов, 258,260
69
перп вектора, 948
перп-скалярное произведение,
206,948
перпендикулярность, 203
перспективное
деление, 452,460
преобразование, 452
укорачивание, 442
перспективные проекции
ЗЭ-объектов, 440
и графический конвейер, 449
прямой линии, 444
точки, 441
перьевые графопостроители, 51
пиксела глубина, 47
пиксельно-определенные
области, 648
пиксельные карты, 531,619,685
Брезенхема алгоритм, 641
важные операции, 619
комбинирование, 630
копирования из одного места
в другое, 619
логические комбинации, 637
масштабирование/поворот, 620
изображений, 627
полезные типы данных, 620
представление/раскрашивание
областей, 620
растворение одной пиксельной
карты в другой в OpenGL, 686
сравнение, 620
управление, 619
пикселы, 43
пиксельная карта, 43
плавная анимация, достижение, 130
1076
Алфавитный указатель
плавное закрашивание, 507
Гуро закрашивание, 507
Фонга закрашивание, 509
плавность движения, 691
планшет, 62
планшетные графопостроители, 51
Платоновы тела, 366
додекаэдр, 371
икосаэдр, 369
модели, 367
нормальные векторы, 369
тетраэдр, 369
плиточник, 505
плоские
дисплеи, 58
лоскуты, 229
плоский полигон, 357
плоского закрашивания
алгоритм, 665
плоское закрашивание, 483,504
плоскости
в ЗП-пространстве, 226
параметрическое
представление, 226
плоские лоскуты, 229
представление, 222
точечная нормальная форма, 227
плоскость просмотра, 427
плотные множества Жюлиа, 595
поверхности
аффинные преобразования,
влияние, 389
вращения, 402,768
с дискретным шагом, 419
на базе явных функций двух
переменных, 410
неявная форма, 387
нормаль к поверхности, заданной
неявно, 388,389
параметрически, 388
нормальный вектор, 388
отображения, 52
представления, 386
повороты
SD-аффинные
преобразования, 291
поверхностей, 402
повторяющиеся узоры, 186
позиционирование камеры, 321,429
показатель спектральной
плотности, 604
полиамонды, 568
полигон, 39
плоский, 357
полигонально-определенные
области, 649
горизонтально-выпуклые
полигоны, заполнение, 665
заполнение, 658
концевые точки ребер, обработка
пересечений, 661
таблица ребер, 664
эффективность алгоритма,
повышение, 662
полигональные
грани, стороны, 501
сетки, 350
базовая сфера, 391
выпуклость, 357
данные, 802
использование SDL, 362
каркасные модели для
немонолитных объектов, 358
квадратичные поверхности,
404,406
линейчатые поверхности,
396-399
монолитность, 357
нормали в вершинах
в сравнении с нормалями
к граням, 352
нормальные векторы, 352,355
Ньюэлла метод, вывод, 414
определение, 353
плоскостность, 357
поверхности вращения, 402
поверхности на базе явных
функций двух
переменных, 410
полиэдр, 363
полнота, 359
призмы, 416
простота, 357
работа в программах, 359
свойства, 357
связность, 357
супергиперболоид, 408
суперквадрики, 408
супертороид, нормальные
векторы, 409
суперэллипсоид, нормальные
векторы, 409
трубы на базе ЗВ-кривых, 409
формирование
для криволинейной
поверхности, 394
экструзивные полосы
из четырехугольников, 417
полигонизация, 386 (
полигонов заполнение, 688
добавление, 548
полигоны, 86
GL_LINE_LOOP, 86
glBegin(GL_POLYGON), 86,96
выпуклые, 96,239
горизонтально-выпуклые,
заполнение, 665,687
заполнение, 96
контрольные, 700
Кохена-Сазерленда алгоритм
отсечения, 248
логические операции, 260
пересечение, 258,260
правильные, 153
рисунки на их основе, 153
проблемы, 238
произвольные, отсечение, 246
работа, 239
разность, 258
Сазерленда—Ходгмана отсекатель,
248,254
Сайруса— Бека алгоритм
отсечения, 243,248,254
Уейлера—Азертона алгоритм
отсечения, 248,257
штриховка, ИЗ
полимино, 568
полиномы
L-ro порядка от t, 696
Бернштейна, 704
кусочные, 716
описание кривых, 695
полиномиальные кривые
1 порядка, 696
2 порядка, 696
рациональные параметрические
формы, 697
полиспирали, 150
полиэдры, 238,363
Архимедовы тела, 371
бакибол, 372
геодезические купола, 373
частота, 373
двойственные полиэдры, 367
каркасные аппроксимации гладких
объектов, 386
представления
поверхностей, 386
определение, 363
Платоновы тела, 366
правильные, 366
Алфавитный указатель
1077
полиэдры (продолжение)
призмы/антипризмы, 365
экструзивные формы, 375
полная тень, 546
полное внутреннее отражение, 915
полноцветные изображения, 50
полосы из четырехугольников, 417
экструзивные, 377
полуправильныетела, 371
полурегулярные мозаики, 569
полутень, 546
полутона, 676
полутоновая пиксельная карта, 621
полутоновые
изображения, рисование
на PostScript, 1035
растровые
изображения, 47,48
растровые изображения, 47
сегментация, 48
полутоновый шаблон, 641
популярности алгоритм, 791,796
порождающая прямая, 222,231
порта просмотра матрица, 318
порты просмотра, 119
автоматическая установка, 133
согласованные, 134
порядок, 729
полиномов, 696
постфиксная нотация, 1002
постфильтрация, 667,671
параллельные
проекции
косоугольные проекции, 474
ортографические проекции, 471
полигональные
сетки
квадратичные поверхности,
406,407
массивы призм, 417
хранение в файлах, 412
правильные
многоугольники
п-угольник, 153
простые, 153
мозаики, 566
полигоны
п-угольник, 154,155
определение, 153
рисунки на их основе, 153
призмы, 365
правые системы координат, 194
предфнльтрация, 667
преломление света, 938
преобразования, 122,193,263
glRotated(), 317
glScaled(), 317
glTranslated(), 317
аффинное, 264,270
в порт просмотра, 317
из окна в порт просмотра, 124
использование с OpenGL, 267
камера
позиционирование/
нацеливание, 321
установка в OpenGL, 320
координат, 268
матрица
моделирования-вида, 318
порта просмотра, 318
моделирование, 314
объектов, 268
основные, 265
процесс просмотра/графический
конвейер, 316
разработка, 315
рисование ЗО-сцен с помощью
OpenGL, 316
стек, 311
текущее преобразование, 305
точек, 268
призмы, 365,416
массивы призм, 417
правильные, 365
прямые, 365
создание, 375
экструзивные, массивы, 376
программа компоновки страницы, 31
программирование, управляемое
событиями, 70
программный интерфейс
приложения (API), 67
проективная инвариантность, 734
проективные преобразования,
734,756
инвариантность, 766
проектирование кривых
и поверхностей, 690
В-сплайн лоскуты, 754
В-сплайны, базисные
функции, 721
использование кратных
узлов, 726
квадратичные В-сплайны, 723
кубические В-сплайны, 724
линейные В-сплайны, 722
незамкнутые В-сплайн
кривые, 727
проектирование кривых
и поверхностей (продолжение)
определение, 721
стандартный узловой
вектор, 727
NURBS-поверхности, 755
геометрическая непрерывность, 693
интерполяция, 737
вычисление наклона при
кубической интерполяции, 743
посредством кусочных
кубических полиномов, 737
касательные векторы, задаваемые
интерактивно, 748
кривые Безье
алгоритм де Кастельо, 702
аффинная инвариантность, 707
инвариантность, 708
интерполяция концевой
точки, 707
линейная точность, 708
производные, 709
свойство, 707,708
создание/рисование, 710
кусочные полиномиальные кривые
и сплайны, 715
лоскуты Безье, сшивание, 752
моделирование криволинейных
поверхностей, 748
поверхности вращения на базе
В-сплайнов, 749
набор стыковочных функций
создание из g(t), 717
список пожеланий, 713
параметрическая
непрерывность, 693
параметрические кривые как
траектории, 690
плавность движения, 691
полиномы, описание кривых
посредством их, 695
рациональные сплайны
и NURBS-кривые, 733
сплайн кривые и базисные
функции, 720
проекции
классификация, 465
ортогональные, 206
приложения, 208
проекционная матрица, 319,428,
456,461
проекционные экстенты,
построение, 935
1078
Алфавитный указатель
проецирование параллельных
прямых, 445
произвольная ориентация/позиция
камеры, 429
произвольные полигоны, отсечение
границами, 246
промежуточный вектор, 491
простая сетка, 357
простой полигон, 39,153
проталкивать, 1003
протомозаики, 567
деформирование, 568
профиль, 749
проход с прямым исключением, 743
прохождение лучей, нахождение
направления, 916
процедурные ЗП-текстуры, 548
прямая
перспективная проекция, 444
призма, 365
прямой
круговой цилиндр, 324
цилиндр, 398
прямоугольник-адресат, 641
прямоугольники
адресат, 641
выровненные
рисование, 92
форматное соотношение, 94
золотые, 95,369
отсечение, 641
резиновые, 99
рисование, 638
прямоугольные экстенты
построение, 933
прямые линии
атрибуты, 39
в 2D- и ЗП-пространствах, 222
отрезки, 222,231
параметрическое
представление, 223
пересечение прямых,
приложение, 234
пересечения с плоскостями, 236
переход от одного представления
к другому, 225
порождающая прямая, 222,231
представление, 222
точечная нормальная форма
уравнения, 224
псевдоглубина, 449
псевдослучайные облака из точек
графики рассеяния, 104
тематическое задание, 104
разбиение
единицы, 199
на ячейки, 386
области, способы, 818
простая область, 819
разбиение на квадранты, 819
развертки
HSR-метод, 816
контроллер, 54
преобразование, 618
строка, 55
размытие переходов, 678
для многоуровневых и цветных
дисплеев, 681
упорядоченное размытие, 678
цветных изображений, 682
разность, 921,929,934
полигонов, 258
рассеивание ошибок, 682
рассеяния графики, 104
растеризация, 618
растровая операция (ор), 640
растровые
изображения, 43
битовая карта, 44
вычисленные изображения, 44
двухуровневые, 47
изображения, созданные
вручную, 44
основные источники, 44
пикселы, 43
пиксельная карта, 43
полутоновые, 47
сканированные изображения, 45
ступеньки, 45
цвет, 49
устройства
для производства твердых
копий, 59
отображения, 52,53—59
рациональные
полиномиальные функции, 697
сплайны и NURBS-кривые, 733
реалистичность, 527
OpenGL, пример использования
текстур, 528
закрашивание грани, 505
и трассировка лучей, 839
отображение
неровностей, 527
отражения, 539
реалистичность (продолжение)
плавное закрашивание
Гуро закрашивание, 507
Фонга закрашивание, 509
плоское закрашивание, 504
светящиеся объекты, создание, 527
текстура, 485
обертывание вокруг
криволинейных
поверхностей, 534
тени
добавление, 542
как текстура, 543
создание с использованием
буфера теней, 544
удаление невидимых
поверхностей, 511
язык описания сцен (SDL),
закрашивание сцен, 503
редактор CM.AppBrowser
редактор ломаных линий, 114
резиновые прямоугольники, 99
рисование, 638
рекурсивный алгоритм, 552
заливки, 650
рентгеновские лучи, 771
рептилии, 571,608
к-рептилия, 571
тримино, 571
рисовальщик ломаных линий,
создание, 86
рисование
прямой пунктиром, ИЗ
фигур, 67
OpenGL, 69
аппаратно-независимая графика,
программирование, 69
взаимодействие посредством
мыши/клавиатуры, 98
оконное программирование, 70,
71, 72,73
основные графические
примитивы, 73
основы, 67
программирование на базе
Windows, 71,73
рисование прямых, 83
экранное окно, 68
розетка, 155
розы (кривые), 171
растровые
устройства
отображения, 55
рисование фигур OpenGL, 74
Алфавитный указатель
1079
рукоятки, 63
ручка чайника, 766
рыскание, 430
С
Сазерленда—Ходгмана отсекатель,
248,254
Сайруса—Бека алгоритм отсечения,
193,243,254
самодельный графический конвейер,
479,548
самозатенение, 908
самоподобие, 553,604,892
самоподобный в точности, 553
сверхопрос, 667,669,896
свет, 771
преломление, 913
света компоненты,
комбинирование, 493
светящиеся объекты, создание, 527
свойство выпуклой оболочки,
кривые Безье, 708
связная сетка, 357
связность, 653,685
глубин, 806
грани, 806
интервала, 659,685
области, 651,818
по интервалу, 654
ребер, 662
строки развертки, 654,685
связные пикселы, 649
сгенерированные строки, 607
сглаживание, 666
текстуры, 672
сдвиг, 474
сегментация, 48
сегментированные экструзии,
создание, 379
сегменты, 62,222,716
фрактализация, 602
серия, 653
Серпинского
ковер, пример, 79
кривые, 560
сетки, 352
Сжатие данных (Нелсон), 584
символически определенные области
манипулирование, 655
масштабирование и смещение
областей, 656
области, заданные контуром, 657
области, описываемые
прямоугольниками, 655
символические области, 648
символы, ориентация, 41
симметричная матрица, 943
системы
координат
и OpenGL, 302
и координатные фреймы, 213
изменение, 300
локальная, 314
поворот, 301
пользовательская, 1012
установка, 76
линейных уравнений, 947
рисования, 31
скалярно-векторное произведение
четырех векторов, 950
скалярное произведение, 201
знак, 203
коммутативность, 201
линейность, 201
определение, 201
перпендикулярность, 203
свойства, 201
угол между двумя векторами, 202
скаляры, 197
след, 406
случайные фракталы, 602
случайных
итераций алгоритм, 552
чисел генерирование, 1008
смешанное произведение, 949
смещенности
параметр, 745
смещенностью
управление, добавление, 745
Смита графики, 185
снежинки, 608
рисование, 308
шквал, рисование, 310
событий очередь, 73
согласованные порты просмотра,
создание, 134
сопряжение, 632
методы, определение, 635
сопряженные комплексные
числа, 952
составные объекты, 921
спектральные плотности, 772
спираль, 172
Архимеда, 171
список
у-сортированный
из х-сортированных
прямоугольников, 656
список (продолжение)
активных ребер, 662
приоритетов, HSR-методы, 806
ребер, 419
сплайн-кривые, 721
генератор, 762
редактор, создание, 762
сплайн-функция, 717
сплайны
естественный кубический, 742
Кочанека—Бартелса, 745
Оверхаузера, 743
фундаментальный, 743
среднее взвешенное, 630,671
средняя точка, 80,224
стандартные единичные
векторы, 203
стандартный узловой вектор, 727
статистически самоподобный, 553
стек преобразований, 311
стенка, 392
степени, 729
полиномов, 696
стереоизображения, создание, 463
стохастическая выборка, 675
странные аттракторы, 552
строка, 61
ориентация, 41
струйные графопостроители, 52,60
ступенчатость, 617,666
использование
OpenGL, 675
термина, 667
ступеньки, 45
субтрактивная цветовая система, 784
супергипербола, 170
супергиперболоид
однополостный, 408
суперквадрики, 408
суперокружности, 169
супертороид, нормальные
векторы, 409
суперэллипсоид, нормальные
векторы, 409
суперэллипсы, 169,190
сфера, рисование, 324
сферические координаты, 953
сферический экстент, 899
схема сжатия с потерями, 582
сцены
описание, чтение из файла, 333
описания язык (SDL), 264,
334,1038
аффинные преобразования, 1040
1080
Алфавитный указатель
сцены (продолжение)
закрашивание сцен, 503
класс Scene, 1038
макросы, 1043
расширение, 1044
расширение для включения
текстурирования, 549
свойства материалов,
управление, 1041
синтаксис, 1039
таблица ребер (ЕТ), 664
тангаж, 430
твердая копия, 52
Твин, определение, 219
твининг и анимация, 250
текст, 40
текстовый режим, 40
текстура
визуализация, 548
добавление, 485
наложение на грани, 514
обертывание вокруг
криволинейных
поверхностей, 534
сглаживание, 672
твердого тела, наложение, 884
текстурное пространство, 514
текстурный квадрат, 673
текущее
направление, 148
преобразование, 305
тела Архимедовы, 371
телевизионные волны, 771
тензорного произведения форма, 751
тени
как текстура, 543
реализация в трассировщике
лучей, 937
рисование, 549
тетрада, 47
тетраэдр, 324,369
типы данных, OpenGL, 75
топологическая информация,
список граней, 353
тор, 402
рисование, 324
тороидальная спираль, 173
точек
кластер, 902
созвездия, рисование, 79
точки
аффинные комбинации, 216
точки (продолжение)
контрольные, 697,700
кратная контрольная, 732
линейная интерполяция по двум
точкам, 219
неподвижные, множества
Жюлиа, 596
однородное представление, 215
перспективная проекция, 441
преобразование, 268
в новые точки, 268
схода, 445
конечная, 445
твининг, для рисования/
анимации, 219
точность по объекту, 802
транспонированная матрица, 300
трекбол, 63
третья итерация, 107
треугольник, центроид, 217
трехмерное проектирование
проекции, 466—468
трехмерные
аффинные преобразования, 289
компонование, 293
повороты, 291
разложение, 347
свойства, 299
элементарные, 289
кривые, 172
спираль, 172
тороидальная спираль, 173
объекты
перспективные проекции, 440
текстуры, процедурные,
приложение, 548
трехмерный
просмотр
графический конвейер,
добавление перспективы, 449
камера, 427
перспективные проекции
ЗВ-объектов, 440
проекции, 463,465
шум и мраморная текстура, 886
трехточечная перспективная, 468
трехцветная теория, 771
тридиагональная матрица, 743
триметрические проекции, 473
тримино, 571
трохоиды, 189
трубы, 418
на базе ЗО-кривых, 409
Труше мозаики, 186
турбулентность, 892
у чФ
угол
зрения, 427
комплексные числа, 951
У ейлера—Азертона алгоритм
отсечения, 248,257
узловой вектор, 720
узлы, 716
укороченная прямая, 472
упорядоченная тройка, 50
упорядоченное размытие, 678
управление непрерывностью,
добавление, 746
усовершенствованный трассировщик
лучей, 936
установление порогов, 678
устройство записи на пленку, 52,59
Ф
файлы ломаных линий, создание/
использование, 112
Фату облако, 596
Фату, Пьер, 586
фигуры, рисование, 67
физика, используемые рисунки, 183
фильтр с эллиптическим средним
взвешенным (EWA), 674
ФонгБуи-туонг, 509
Фонга
закрашивание, 509
модель, 490
фоновый свет, 486
источники, 493
отражения, 493
роль, 492
форматное соотношение, 94,427
автоматическая установка порта
просмотра, 133
камера, 427
формы
в полярных координатах, 171
представление, 656
цепное кодирование, 687
фрагменты, 618
фрактализованные горы,
моделирование, 615
фракталы
поверхности, 606
случайные, 602
фрактальное
дерево, 563
сжатие изображений, 582
аффинные карты, нахождение
списка, 582
Алфавитный указатель
1081
фреймы
ключевые, 221
координатные, 214
Френе базис, формирование, 380
Френеля коэффициент, 879
Фуллер, Бакминстер, 372
Фуллерин, 373
фундаментальные сплайны, 743
функции обратного вызова, 73
X
Хайн.Пнт, 169
хаос, имитация, 175
Хаусдорф, Феликс, 556
хромированное отображение, 539
ц
цвет, 68
добавление, 494
зеркального света, 495
эмиссионный, 503
цвета, 772
CIE хроматическая
диаграмма, 778
использование, 780
глубина, пикселы, 50
доминантная длина волны, 773
дополнительные цвета, 781
квантование, 787
octree-квантование, 792
алгоритм, 791,796
однородное квантование, 789
цветов совокупность, 788
квантование цвета, 788
подбор цветов, 774
теория, 770
цветовая модель HLS, 785
цветовые
охваты, 781
пространства, 782
цветные растровые изображения, 49
полноцветные изображения, 50
цветов
кодовая таблица (LUT), 56
подбор, 774
совокупность, 788
цветовые
модели, 782
охваты, 781
пространства, 782
RGBhCMY, 782
цветовые (продолжение)
аддитивная цветовая
система, 783
субтрактивная цветовая
система, 784
целочисленная решетка, 887
центр тяжести треугольника, 217
цепное кодирование форм, 687
цепной код, 657
цикл чтение-модификация-
запись, 631
циклоиды, 190
цилиндры,398
цифро-аналоговые преобразователи
(ЦАП), 54
цифровые полутона, 677
ч
частота, 373
регенерации, 55
черепашьи стеки, 563
черепашья графика, 148
для п-угольника, 154
четверка, 941
четность, 659
ш
шаблон размытия, 678
широта, 953
Шлефли символ, 367,566
шрифты, 41
штриховка, 51
щ
щупы теней, 908
э
Эйлер, Леонард, 294
Эйлера
теорема, 294
углы, 294
формула, 952
экземпляр объекта, 314
экранирование, 879
экранное окно, 68
изменение размеров, 134
экстенты, 865,937
боксы, 899
объединенные, 907
построение/использование
для CSG-объектов, 933
экстенты (продолжение)
применение, 937
проекционные
вычисление, 905
построение, 937
прямоугольные, построение,
902,933
сферические
построение, 902
сферический, 899
тестирование экстента,
реализация, 901
экономия ресурсов, 898
экстраполяция, 220
экструзивные
полосы из четырехугольников, 377
призмы, массивы, 376
формы
дискретно заметаемые
поверхности вращения, 385
сегментированная экструзия,
построение, 379
трубы на базе SD-кривых,
проектирование, 380
Френе базис, формирование, 380
экструзивные, 376,377
экструзии с поворотом, 377
экструзия, 365,375
эксцентриситет, 696
электронные схемы
проектирование, 35
электростатические поля, 184
элементарные 2В-преобразования
геометрические эффекты, 271
примеры композиции, 279
эллипс, 696
обобщение, 696
эллипсоид, 404
эллиптипул, 760
эллиптический параболоид, 406
эмиссионный
трассировщик, 936
цвет, 503
эпитрохоида, 189
Эрмита интерполяция, 739
Эшер, М. К., 468,566
Я
язык описания страниц, 60
ямка, 771
яркость, 774
I I г 1
)грХмкшрование
ДЛЯ ПРОФЕССИОНАЛОВ
И/Л
Информация, которую вы найдете в книге:
♦ трехмерное преобразование объектов;
♦ язык описания сцен SDL;
♦ средства моделирования каркасных объектов;
♦ управление камерой просмотра трехмерных сцен;
♦ построение перспективных проекций;
♦ создание фрактальных трехмерных изображений;
♦ пиксельные карты изображений;
♦ кривые Безье, В-сплайны и NURBS-кривые;
♦ хроматическая диаграмма стандарта CIE и квантование цвета;
♦ HSR-методы быстрой визуализации.
Если вы хотите глубже проникнуть в восхитительный
мир компьютерной графики, научиться разрабатывать
и создавать сложные графические объекты, освоить
разнообразнейшие методы и приемы, повышающие
эффективность отображения и управления трехмерными
изображениями, то эта книга для вас!
ШШШ Широта охвата
и Глубина изложения
ЖЖ Профессиональный подход
, Л'-Л
Посетите наш web-магазин: http://www.piter.com
ISBN 5-318-00219-6
785318
002199
O.
Уровень пользователя: Серия:
Опытный/эксперт Для профессионалов