НАЧАЛА
ιιιι=Μΐ=ιιι=ιιι=ιη=ιιιί:::::::::::::::::::::
i=in=iii=iii=in=iiis£:::::::::::::::::::::
ιιι=ιιι=ιιι=ι»ι=»ι=ιιιί::::::::::::::.::':::
1=1111=111=111=111=111»;:::::::::::::::::::::
ni=iii=iii=ni=in=ni£::::::::::: ::::::::::
i=iii=ui=mi=ui=Mi=::::::::::::::::::::::
mm 111=in=in=his ιιιέ= ήί= ι'ιί = im «= № Μ Ы i'
Ml = III = III = Ml = III = III = llT= III = III = III S Ml ?
Ι = ΙΙΙ = № = Ι»Ι = ΙΙΙ = ΙΙΙ = ΜΙ = ΙΜ = ΜΙ = ΙΙΙ = ΙΙΙ =
III = III Ш III = III = III = III = III = III = Ml = III = III ?
Ill = III = III = III = III = III = III = Ml = Ml = III = III ?
I = Ml = III = III 3 III = III = III = Ml = III = III = III =
till = Ml = III = Ml S III = Ml = III = III = III = Ml = III ·
ιηί=ιη=ηϊ=ills iiis iii=ηϊ=ιιΤ=μϊ=" ι
111 = 111 = 111 = 111 = 111 = 111 = 111 = 111 = 111 ι >'
ini = IH = MISMI = lll = in = lll = »l= Л ...-■,
■HI 39 i|fi μ i|i bk |M| ■» ||l жм iii ж l|| am mi а _ ί ■ l
mis hi=mi=ιιί= ιιΓ= in=ni= , .. . = in i j
41 = 111 = 111 = № = 111 = 111,= III .Si Л SHIS;
111 = 111 = 111 = 111 = 111= I =. ..-=111 = 1111;
HsihisuI9MI = IM= .! 'I insiiiiam»
ГРАФИКИ
шшшшт
::::::};:::::::::::::
J
Q шюшт

Ε. Β. Шикин, А. В. Боресков, А. А. Зайцев
НАЧАЛА
КОМПЬЮТЕРНОЙ
ГРАФИКИ
под общей редакцией
профессора МГУ Шикина Е. В.
щ
"ДИАЛОГ-МИФИ"
Москва 1993

ПРЕДИСЛОВИЕ
D
.1 J настоящее время в связи с широким внедрением персональных компьютеров
во все сферы жизни, резкой интенсификацией процесса научных исследований,
революционным совершенствованием его технологии, значительным повышением
возможностей аппаратуры все больший интерес вызывают идеи, алгоритмы и
средства компьютерной графики. Спектр использования компьютерной графики
чрезвычайно широк: от создания рекламных роликов, компьютерных
мультфильмов и игр, кроя одежды, малых и монументальных форм дизайна, компьютерной
живописи до визуализации результатов научных изысканий и конструирования
фактически нового инструментария в процессе получения знаний.
В Европе, США и Японии ежегодно проводятся представительные
международные конференции по компьютерной графике, издаются десятки журналов и
выпускается множество книг, посвященных различным аспектам компьютерной
графики и ее применениям. Наши успехи в этом направлении выглядят
значительно скромнее. Правда, в самое последнее время наметились определенные
тенденции к изменению ситуации: проведены две международные конференции
Трафикон-9Г и мГрафикон-92м и начал выходить журнал "Компьютерная
графика". Что же касается литературы, то отечественных пособий и руководств
по компьютерной графике практически нет.
Вместе с тем, как показало оживленное обсуждение проблем преподавания
компьютерной графики на конференции Трафикон-92", проходившей в октябре
1992 года в Москве, интерес к машинной графике в нашей стране и разнообразен,
и очень велик. Поэтому во многих российских учебных центрах появилось
намерение организовать на базе университетов и крупных инженерных вузов чтение
курсов по компьютерной графике. Одним из серьезных препятствий на этом пути
является практическая невозможность обеспечить слушателей подобных курсов
доступной учебной литературой. Отчасти это можно объяснить быстрым
развитием новых методов компьютерной графики, многие из которых описаны только
в журнальных публикациях.
Изучение книжного рынка показало наличие значительной потребности
в книгах по компьютерной графике. Подобный интерес обусловлен в первую
очередь красотой и эффективностью самой компьютерной графики, знакомство
с которой необходимо разработчику аппаратуры и инженеру-конструктору,
дизайнеру и кинооператору, художнику-модельеру и специалисту по рекламе.
Существующая литература (фактически только переводная) издана довольно
давно, далеко не всегда удовлетворяет отечественным (традиционно высоким)
требованиям, предъявляемым к учебной литературе и, наконец, практически
недоступна.

Последние несколько лет на факультете вычислительной математики и
кибернетики Московского государственного университета им. М. В. Ломоносова
читается курс "Начала компьютерной графики", вызывающий чрезвычайно
большой интерес у студентов разных курсов и факультетов, а также у слушателей
инженерного потока. Опыт чтения этого курса показывает, что даже сравнительно
небольшого, просто и доступно изложенного набора сведений по компьютерной
графике оказывается достаточно для самостоятельного выполнения весьма
содержательных геометрических и графических задач без привлечения дополнительной
литературы.
Название предлагаемой книги - "Начала компьютерной графики" - довольно
верно отражает и ее содержание, и цели, которые ставили перед собой авторы
при ее написании. Предпринимая попытку познакомить читателя с одним из
бурно развивающихся направлений использования персональных компьютеров, мы
сознательно ограничились изложением только самых основных понятий, приемов
и фактов, связывая это не столько с допустимым объемом издания (он
сравнительно невелик), сколько с тем обстоятельством, что практически каждый
новый выпуск любого из журналов, посвященных работе на персональных
компьютерах, приносит многие интересные результаты, раскрывающие направления
развития возможностей и вглубь, и вширь. Частью этих материалов авторы
пользовались при подготовке книги. На отбор материала повлияло также желание дать
в руки читателю инструмент пусть и не слишком изощренный, но достаточно
совершенный для того, чтобы решать содержательные задачи.
Среди многообразия возможностей, предоставляемых современными
вычислительными средствами, те, что основаны на пространственно-образном
мышлении человека, занимают особое место. Современные
программно-оперативные средства компьютерной графики представляют собой весьма эффективный
инструмент поддержки такого мышления при выполнении работ самых разных
видов, и проектно-конструкторских, и научно-исследовательских, и производственно-
оформительских. С другой стороны, именно пространственно-образное мышление
является неформальной творческой основой для расширения изобразительных
возможностей компьютеров. Это важное обстоятельство предполагает взаимно
обогащающее, органическое сотрудничество все более совершенной техники и
человека со всем богатством знания, накопленного предшествующими
поколениями. Глаз и раньше был эффективным средством познания человеком мира и себя.
Поэтому столь привлекательной оказывается компьютерная визуализация,
особенно визуализация динамическая, которую следует рассматривать как важнейший
инструмент для обучения наукам.
По мнению авторов, во вводном курсе основное внимание следует уделить
алгоритмам и методам компьютерной графики, не оставляя в стороне, разумеется,
ее программного и технического обеспечения. Алгоритмы и методы, используемые
при первом знакомстве, должны быть достаточно простыми.
Читатель познакомится с ключевыми понятиями компьютерной графики,
получит рабочее представление об основных ее направлениях, включая методы
построения реалистических изображений, освоит основные программистские

приемы реализации алгоритмов компьютерной графики на персональном
компьютере, включая принципы организации работы с современными графическими
интерфейсами.
Книга содержит материал, отобранный на основе опыта чтения указанного
выше курса и "визуализированного" приема экзаменов, заключавшегося в
демонстрации выполненного задания (динамической картинки) на экране персонального
компьютера.
Книгу можно рассматривать как практическое руководство: в ней приводятся
примеры графических задач, которые способен самостоятельно выполнить
на персональном компьютере пользователь, прочитавший книгу.
По желанию можно приобрести дискету содержащую тексты всех программ,
приведенных в книге, а также обучающую программу "Геометрические
преобразования", иллюстрирующую в динамике один из разделов книги. За дискетой
нужно обращаться в издательский отдел АО "ДИАЛОГ-МИФИ".
На пути от замысла этой книги до ее выхода произошло значительное число
событий, прямо или косвенно повлиявших на ее судьбу. Среди случившихся
обстоятельств наряду с объективными было много трудностей, носивших вполне
субъективный характер.
В наше непростое время неожиданной и весьма приятной оказалась
поддержка издательского отдела "ДИАЛОГ-МИФИ" и его сотрудников. Без нее, а также
нетривиального участия в самый критический момент Александра Ивановича
Плиса и Андрея Фазыловича Мубаракшина книга вряд ли дошла бы до читателя.
Выражением благодарности к ним я и хочу завершить предисловие.
19 июля 1993 года
Е. В. Шикин

ГРАФИЧЕСКИЕ ПРИМИТИВЫ В ЯЗЫКАХ ПРОГРАММИРОВАНИЯ
LJ
X Ха большинстве ЭВМ (в том числе на всех основных типах ПЭВМ) принят
растровый способ изображения графической информации - изображение
представлено прямоугольной матрицей точек (пикселов), и каждый пиксел имеет свой
цвет, выбираемый из заданного набора цветов - палитры. Для реализации этого
подхода компьютер содержит в своем составе видеоадаптер, который, с одной
стороны, хранит в своей памяти (ее принято называть видеопамятью) изображение
(при этом на каждый пиксел изображения отводится фиксированное количество
бит памяти), а с другой - обеспечивает регулярное (около 50 раз в секунду)
отображение видеопамяти на экране монитора. Размер палитры определяется объемом
видеопамяти, отводимой под один пиксел, и зависит от типа видеоадаптера.
Для ПЭВМ типа IBM PC/AT и PS/2 существует несколько различных
типов видеоадаптеров, различающихся как своими возможностями, так и
аппаратным устройством и принципами работы с ними. Основными видеоадаптерами для
этих машин являются CGA, EGA, VGA и Hercules. Существует также большое
количество адаптеров, совместимых с EGA/VGA, но предоставляющих по
сравнению с ними ряд дополнительных возможностей.
Практически каждый видеоадаптер поддерживает несколько режимов работы,
отличающихся друг от друга размерами матрицы пикселов (разрешением) и
размером палитры (количеством цветов, которые можно одновременно отобразить на
экране). Зачастую даже разные режимы одного адаптера имеют разную
организацию видеопамяти и способы работы с ней.
Однако большинство адаптеров строится по принципу совместимости с
предыдущими. Так, адаптер EGA поддерживает все режимы адаптера CGA.
Поэтому программа, рассчитанная на работу с адаптером CGA, будет
работать и с адаптером EGA, даже не замечая этого. При этом адаптер EGA
поддерживает, конечно, еще ряд своих собственных режимов. Аналогично адаптер
VGA поддерживает все режимы адаптера EGA.
Фактически любая графическая операция сводится к работе с отдельными
пикселами. Однако большинство графических библиотек поддерживают работу и с
более сложными объектами, поскольку работа только на уровне отдельно взятых
пикселов была бы очень затруднительной для программиста и неэффективной
(отличалась бы невысоким быстродействием).
Среди подобных объектов, представляющих собой объединения пикселов,
можно выделить следующие основные группы:
• линейные изображения (растровые образы кривых);
• сплошные объекты (растровые образы двумерных областей);
• шрифты;
• картинки (прямоугольные матрицы пикселов).

Как правило, каждый язык программирования имеет свою графическую
библиотеку, обеспечивающую работу с основными группами графических объектов.
При этом требуется, чтобы подобная библиотека поддерживала работу с
основными типами видеоадаптеров.
Существует несколько путей обеспечения этого.
Например, можно написать версии библиотеки для всех основных типов
адаптеров. Однако программист должен изначально знать, для какого конкретно
видеоадаптера он пишет свою программу, и использовать соответствующую
библиотеку. Полученная при этом программа уже не будет работать на других
адаптерах, несовместимых с тем, для которого писалась программа. Поэтому вместо
одной программы получается целый набор программ для разных видеоадаптеров.
Принцип совместимости адаптеров выручает здесь не сильно: хотя программа,
рассчитанная на адаптер CGA, и будет работать на VGA, но она не сможет
использовать его возможности и будет работать с ним только как с CGA.
Можно включить в библиотеку версии процедур для всех основных типов
адаптеров. Это обеспечит некоторую степень машинной независимости. Однако нельзя
исключать случай наличия у пользователя программы какого-либо типа адаптера, не
поддерживаемого библиотекой (например, XGA). Но самым существенным
недостатком такого подхода является слишком большой размер получаемого выполняемого
файла, что уменьшает объем оперативной памяти, доступный пользователю.
Наконец, можно использовать драйверы устройств. При этом выделяется
некоторый основной набор графических операций так, что все остальные операции
можно реализовать, используя графические операции основного набора. Привязка к
видеоадаптеру заключается именно в реализации этих основных (базисных) операций.
Для каждого адаптера пишется так называемый драйвер - небольшая программа со
стандартным интерфейсом, реализующая все эти операции для данного адаптера и
помещаемая в отдельный файл. Библиотека в начале своей работы определяет тип
имеющегося видеоадаптера и загружает соответствующий драйвер в память. Таким
образом достигается почти полная машинная независимость написанных программ.
Рассмотрим работу одной из наиболее популярных графических библиотек -
модуля Graph системы Turbo Pascal 6.0. Все дальнейшее изложение будет вестись
применительно к языку Turbo Pascal, однако следует иметь в виду, что
реализация этой библиотеки в других продуктах фирмы Borland практически не
отличается от этой версии. Для подключения графической библиотеки пользователь
должен использовать оператор uses Graph в своей программе.
Рассмотрим основные группы операций.
Инициализация и завершение работы с библиотекой
Для инициализации библиотеки служит процедура InitGraph
procedure InitGraph (var Driver, Mode: Integer;
DriverPath: String)
Первый параметр задает библиотеке тип адаптера, с которым будет вестись
работа. В соответствии с этим параметром будет загружен драйвер указанного видео-

адаптера и произведена инициализация всей библиотеки. Определен ряд констант,
задающих набор стандартных драйверов: CGA, EGA, VGA, HercMono и Detect.
Значение Detect сообщает библиотеке о том, что тип имеющегося
видеоадаптера надо определить ей самой и выбрать для него режим наибольшего
разрешения.
Второй параметр Mode определяет режим.
Параметр Режим
CGACO, CGAC1, CGAC2, CGAC3 320 на 200 точек на 4 цвета
CGAHi 640 на 200 точек на 2 цвета
EGALo 640 на 200 точек на 16 цветов
EGAHi 640 на 350 точек на 16 цветов
VGALo 640 на 200 точек на 16 цветов
VGAMed 640 на 350 точек на 16 цветов
VGAHi 640 на 480 точек на 16 цветов
HercMono 720 на 348 точек на 2 цвета
Если в качестве первого параметра было взято значение Detect, то параметр
Mode не используется.
В качестве третьего параметра выступает имя каталога, где находится
драйвер адаптера - файл типа BGI (Borlands Graphics Interface):
• CGA.BGI - драйвер адаптера CGA;
• EGAVGA.BGI - драйвер адаптеров EGA и VGA;
• HERC.BGI - драйвер адаптера Hercules.
Функция GraphResult возвращает код завершения предыдущей графической
операции
function GraphResult: Integer;
Успешному выполнению соответствует значение grOk.
Для окончания работы с библиотекой необходимо вызвать процедуру
CloseGraph
procedure CloseGraph;
Η program GraphTest;
uses
Graph;
var
Drv, Mode : Integer;
begin
Drv := Detect;
InitGraph (Drv, Mode, '');
if GraphResult <> grOk then

begin
WriteLn ('Ошибка при инициализации графики');
Halt (1);
end;
Line (О, О, О, GetMaxY);
Line (О, GetMaxY, GetMaxX, GetMaxY);
Line (GetMaxX, GetMaxY, GetMaxX, 0);
Line (GetMaxX, 0, 0, 0);
CloseGraph;
end.
Программа переходит в графический режим и ( 'J- А*
рисует на экране прямоугольник наибольшего
размера. В случае ошибки выдает диагностическое
сообщение. После инициализации библиотеки адаптер
переходит в соответствующий режим, экран очищается и
на нем устанавливается следующая координатная си- '
стема (рис. 1.1). Начальная точка с координатами (0, Yt
0) располагается в левом верхнем углу экрана. рис / /
Узнать максимальные значения X и Υ координат
пиксела можно, используя функции GetMaxX и GetMaxY
function GetMaxX i Integer;
function GetMaxY : Integer;
Для определения текущего режима можно воспользоваться функцией
GetGraphMode
function GetGraphMode : Integer;
Работа с отдельными точками
Процедура PutPixel ставит пиксел заданного цвета Color в точке с
координатами (х, у)
procedure PutPixel (χ, у : Integer; Color : Word);
Функция GetPixel возвращает цвет пиксела с координатами (х, у)
function GetPixel (χ, у : Integer) : Word;
Рисование линейных объектов
При рисовании линейных объектов основным инструментом является перо
(то, чем эти объекты как бы рисуются). Перо имеет следующие характеристики
(параметры):
• цвет (по умолчанию белый);
• толщина (по умолчанию 1);
• шаблон (по умолчанию сплошной).

Шаблон служит для рисования пунктирных и штрихпунктирных линий.
Для установки параметров пера используются следующие процедуры выбора.
Процедура SetColor устанавливает цвет пера
procedure SetColor (Color : Word);
Процедура SetLineStyle определяет остальные параметры пера
procedure SetLineStyle (Style, Pattern, Width : Word);
Первый параметр задает шаблон линии. Обычно в качестве этого параметра
выступает один из предопределенных шаблонов: SolidLn, DottedLn, DashedLn
Значение UserBitLn означает, что шаблон задается (пользователем) вторым
параметром. Шаблон определяется 8 битами, где значение бита 1 означает, что в
соответствующем месте будет поставлена точка, а значение 0, что точка ставиться
не будет.
Третий параметр задает толщину линии в пикселах. Возможными
значениями этого параметра являются только 1 и 3.
При помощи пера можно рисовать ряд линейных объектов - прямолинейные
отрезки, дуги окружностей и эллипсов, ломаные.
Рисование прямолинейных отрезков
Процедура Line рисует отрезок, соединяющий точки (xj, yj) и (*£, у2).
procedure Line (xl, yl, x2, y2 : Integer);
Рисование окружностей
Процедура Circle рисует окружность радиуса г
с центром в точке (х, у).
procedure Circle (χ, у, г : Integer);
Рисование дуг
Процедуры Arc и Ellipse рисуют дуги
окружности (с центром в точке (х, у) и радиусом г) и эллипса
(с центром (х, у), полуосями гх и гу, параллельными
координатным осям), начиная с угла StartAngle и заканчивая углом EndAngle.
Углы задаются в градусах в направлении против часовой стрелки (рис. 1.2)
procedure Arc (χ, у, StartAngle, EndAngle, r : Integer);
procedure Ellipse (x, y, StartAngle, EndAngle, rx,ry: Integer);
Рисование сплошных объектов
Закрашивание объектов
С понятием закрашивания тесно связано понятие кисти. Кисть определяется
цветом и шаблоном - матрицей 8 на 8 точек (бит), где бит, равный 1, означает, что
нужно ставить точку цвета кисти, а 0 - что нужно ставить черную точку (цвета 0).
Для задания кисти используются следующие процедуры:
procedure SetFillStyle (Pattern, Color : Word);
procedure SetFillPattern (Pattern : FillPatternType;
Color : Word);

Тип FillPatternType определен следующим образом:
type
FillPatternType = array [1..8] of Byte;
Процедура SetFillStyle служит для задания кисти. Параметр Style определяет
шаблон кисти либо как один из стандартных (EmptyFill, SolidFill, LineFill, SlashFill
и т. д.), либо как шаблон, задаваемый пользователем (UserFill). Пользовательский
шаблон устанавливает процедура SetFillPattern, первый параметр в которой
и задает шаблон - матрицу 8 на 8 битов, собранных по горизонтали в байты.
По умолчанию используется сплошная кисть белого цвета.
Процедура Ваг закрашивает выбранной кистью прямоугольник с левым
верхним углом (xj, yj) и правым нижним углом (х2, у2)
procedure Bar (xl, yl, x2, y2 ι Integer);
Процедура FillEllipse закрашивает сектор эллипса
procedure FillEllipse (x, у, StartAngle, EndAngle, rx, ry:
Integer);
Процедура FloodFill служит для закраски связной области, ограниченной
линией цвета BorderColor и содержащей точку (х, у) внутри себя:
procedure FloodFill (χ, у : Integer; BorderColor : Word);
Работа с изображениями
Библиотека поддерживает также возможность запоминания прямоугольного
фрагмента изображения в обычной (оперативной) памяти и выводе его на экран.
Это может использоваться для запоминания изображения в файл, создания
мультипликации и т. п.
Объем памяти, требуемый для запоминания фрагмента изображения, в
байтах можно получить при помощи функции ImageSize
function ImageSize (xl, yl, x2, y2 : Integer) : Word;
Рекомендуется получать требуемую память динамическим путем, используя
процедуры GetMem и FreeMem (см. пример, приведенный ниже).
Для запоминания изображания служит процедура Getlmage
procedure Getlmage (xl, yl, x2, y2 : Integer; var Image);
При этом записывается прямоугольный фрагмент, определяемый точками
(х/, yj) и (х2, у2), в область памяти, задаваемую последним параметром Image.
Проверок на то, что памяти хватит, не производится.
Для вывода изображения служит процедура Putlmage
procedure Putlmage (χ, у : Integer; var Image; Method : Word);
Хранящееся в памяти изображение, которое задается параметром Image,
выводится на экран так, чтобы точка (х, у) была верхним левым углом
изображения. Последний параметр определяет способ наложения выводимого
изображения на уже имеющееся на экране (см. процедуру SetWriteMode).

uses
Graph;
var
Size : Word;
Image : Pointer;
begin
Size := ImageSize (xl, yl, x2, y2);
GetMem (Image, Size);
Getlmage (xl, yl, x2, y2, Image*);
Putlmage (x, y, Image*, NormalPut);
FreeMem (Image, Size);
end.
В этой программе происходит динамическое выделение под заданный
фрагмент изображения на экране требуемого объема памяти. Этот фрагмент
запоминается в отведенную память. Далее сохраненное изображение выводится на
новое место (в вершину левого верхнего угла - (х, у)) и отведенная под
изображение память освобождается.
Работа со шрифтами
Под шрифтом обычно понимается набор изображений символов. Шрифты
могут различаться по организации (растровые и векторные), по размеру, по
направлению вывода и др. Шрифт может быть фиксированным (размеры всех
символов совпадают) или пропорциональным (высоты символов совпадают, но они
могут иметь разную ширину).
Для выбора шрифта и его параметров служит процедура SetTextStyle
procedure SetTextStyle (Font, Direction, Size : Word);
Здесь параметр Font задает идентификатор одного из шрифтов:
• DefaultFont - стандартный растровый шрифт размером 8 на 8 точек,
находящийся в ПЗУ видеоадаптера;
• TriplexFont, GothicFont, SansSerifFont, SmallFont - стандартные
пропорциональные векторные шрифты, входящие в комплект Turbo Pascal
(каждый шрифт хранится в файле типа CHR и по этой команде
подгружается в оперативную память; эти файлы должны находиться в том
же каталоге, где находятся драйверы устройств).
Параметр Direction задает направление вывода:
• HorizDir - вывод по горизонтали;
• VertDir - вывод по вертикали.

Параметр Size задает, во сколько раз нужно увеличить шрифт перед выводом
на экран. Допустимые значения 1, 2, .... 10.
При желании в формате CHR можно использовать любые шрифты (а не
только стандартные). Для этого в качестве первого параметра следует взять
значение, возвращаемое функцией InstallUserFont
function InstallUserFont (FontFileName : String) : Integer;
g| Font ;= InstallUserFont ('C:\TP\FONTS\GREEK.CHR');
SetTextStyle (Font, HorizDir, 1);
Для вывода текста служит процедура OutTextXY
procedure OutTextXY (x, у : Integer; text : String);
При этом строка text выводится так, что точка (х, у) оказывается вершиной
левого верхнего угла первого символа.
Для определения размера, который займет на экране строка текста при
выводе текущим шрифтом, используются функции, возвращающие ширину и высоту
в пикселах строки текста
function TextWidth (text : String) : Integer;
function TextHeight (text : String) : Integer;
Понятие режима (способа) вывода
При выводе изображения на экран обычно происходит замещение пиксела,
ранее находившегося на этом месте, на новый. Можно, однако, установить такой
режим, что в видеопамять будет записываться результат наложения ранее
имевшегося значения на выводимое. Поскольку каждый пиксел представлен
фиксированным количеством битов, то естественно, что в качестве такого
наложения выступают побитовые операции. Для установки используемой
операции служит процедура SetWriteMode
procedure SetWriteMode (Mode : Integer);
Параметр Mode задает способ наложения и может принимать одно из
следующих значений:
• NormalPut- происходит простой вывод (замещение);
• NotPut - происходит вывод инверсного изображения;
• OrPut - используется побитовая операция ИЛИ;
• XorPut - используется побитовая операция ИСКЛЮЧАЮЩЕЕ ИЛИ;
• AndPut - используется побитовая операция И.
Чаще всего используются значения NormalPut и XorPut. Режим XorPut
удобен тем, что повторный вывод одного и того же изображения на то же место
уничтожает результат первого вывода, восстанавливая изображение, которое было
на экране до этого.
Процедуры закраски игнорируют установленный режим наложения (вывода).

Понятие окна (порта вывода)
При желании пользователь может создать на экране окно - своего рода
маленький экран со своей локальной системой координат. Для этого служит
процедура SetViewPort
procedure SetViewPort (xl, yl, x2, y2: Integer; Clip: Boolean);
Эта процедура устанавливает окно с глобальными координатами (xj, yj) -
(χ2> У2^· При этом локальная система координат вводится так, что точке
с координатами (0, 0) соответствует точка с глобальными координатами (xj, yj).
Фактически это означает, что локальные координаты отличаются от глобальных
координат лишь сдвигом на (xj, yj). При этом все процедуры рисования (кроме
SetViewPort) работают всегда с локальными координатами. Параметр Clip
определяет, нужно ли проводить отсечение изображения, не помещающегося
внутрь окна, или нет.
Понятие палитры
Адаптер EGA и все совместимые с ним адаптеры предоставляют
дополнительные возможности по управлению цветом. Как уже отмечалось, максимально
возможное число цветов, которые можно одновременно отобразить на экране
монитора, определяется количеством бит видеопамяти, отводимой адаптером под
пиксел. Для адаптера EGA максимально возможное количество цветов равно 16.
Однако монитор, подключаемый к адаптеру EGA, чисто физически способен
отобразить 64 цвета, так как имеет 6-битовый видеосигнал. Тем самым видеоадаптер
переводит 4-битовый цвет пиксела в 6-битовый видеосигнал. Для перевода
используется аналог таблицы (фактически адаптер имеет 16 специальных внутренних
регистров, где для каждого логического цвета хранится его 6-битовое значение
видеосигнала), называемый палитрой. Существует возможность изменять эту
таблицу, устанавливая для любого логического цвета его видеосигнал, т. е. выбирая
его из возможных 64 цветов адаптера. Для этого служит процедура SetPalette
procedure SetPalette (Color : Word, ColorValue : Shortlnt);
Эта процедура устанавливает для логического цвета Color физический цвет
ColorValue, который формируется следующим образом. Поскольку любой цветной
монитор получает цвета путем наложения трех базовых цветов - красного,
зеленого и синего - разных интенсивностей, то видеосигнал задает интенсивность
этих трех компонент (по 2 бита на каждую компоненту), причем эти биты идут
следующим образом:
rgbRGBOO,
где rR - интенсивность красной компоненты, gG - интенсивность зеленой и
ЬВ - синей: набор заканчивается двумя нулевыми битами.
Адаптер VGA предоставляет еще более широкие возможности по управлению
цветами: для каждого цвета можно задать его 18-битную раскладку по
компонентам (по 6 бит на каждую компоненту). Для этого служит процедура
SetRGBPalette

procedure SetRGBPalette (Color, RedValue, GreenValue,
BlueValue : Integer)?
где Color - логический номер цвета, a RedValue, GreenValue и BlueValue - его
RGB-интенсивности.
Понятие видеостраниц и работа с ними
Для большинства режимов (например, для EGAHi) объем видеопамяти,
необходимый для хранения всего изображения (экрана), составляет менее половины
имеющейся видеопамяти (256 Кбайт для EGA). В этом случае вся видеопамять
делится на равные части (их количество обычно является степенью двойки),
называемые страницами, так, что для хранения всего изображения достаточно
каждой страницы. Для режима EGAHi видеопамять делится на 2 страницы - 0-ю
(адрес $А000:0) и 1-ю (адрес $А000:$8000).
Видеоадаптер отображает на экран только одну из имеющихся у него
страниц. Эта страница называется видимой и устанавливается следующей
процедурой SetVisualPage
procedure SetVisualPage (Page : Word);
где Page - номер той страницы, которая станет видимой на экране после
вызова этой процедуры.
Графическая библиотека также может осуществлять работу с любой из
имеющихся страниц. Страница, с которой работает библиотека, называется активной.
Активная страница устанавливается процедурой SetActivePage
procedure SetActivePage (Page : Word);
где Page - номер страницы, с которой работает библиотека и на которую
происходит весь вывод.
Использование видеостраниц играет очень большую роль при
мультипликации. Реализация мультипликации на ПЭВМ заключается в
последовательном рисовании на экране очередного кадра. При традиционном
способе работы (кадр рисуется, экран очищается, рисуется следующий кадр)
постоянные очистки экрана и построение нового изображения на чистом экране
создают крайне нежелательный эффект мерцания изображения.
Для устранения этого эффекта очень удобно использовать страницы
видеопамяти. При этом, пока на видимой странице пользователь видит один кадр,
активная, но невидимая страница, очищается и на ней рисуется новый кадр.
Как только кадр готов, активная и видимая страницы меняются местами
и пользователь вместо старого кадра сразу видит новый.

Д| DrawFrame (0); { нарисовать 0-й кадр }
SetActivePage (1); { установить активную страницу }
for Frame := 1 to MaxFrames do { цикл по кадрам }
begin
ClearViewPort; { очистить страницу }
DrawFrame (i); { нарисовать следующий кадр }
{ поменять страницы местами }
SetVisualPage (i mod 2);
SetActivePage (1 - (i mod 2));
end;
Подключение нестандартных драйверов устройств
Иногда возникает необходимость использовать нестандартные драйвера
устройств. Это может возникнуть, например, в случае, если вы хотите работать с режимом
адаптера VGA разрешением 320 на 200 точек при количестве цветов 256. Такой
режим не поддерживается стандартными драйверами, и следует воспользоваться
драйвером VGA256.BGI, не входящим в стандартный комплект Turbo Pascal, Turbo С.
Ниже приводится пример программы подключающей этот драйвер.
Д uses
Graph;
var
Drv, Mode : Integer;
{$F+}
function AdapterPresent : Integer;
begin
AdapterPresent ;= I;
end;
{$F->
begin
if InstallUserDriverf 'VGA256.BGI', ^AdapterPresent) <> grOk
then Halt (1);
Drv := Detect;
InitGraph (Drv, Mode, '');
CloseGraph;
end;
В этом примере функция AdapterPresent используется библиотекой для
проверки наличия соответствующего адаптера. Для простоты изложения она не
проверяет наличие соответствующего видеоадаптера, возвращая 1 в любом случае.
Для корректной работы программы во всех случаях следует производить проверку
наличия адаптера. Для этого можно использовать функцию VGAPresent,
описанную в главе, посвященной прямой работе с графическими устройствами.

<f Формулы (*) можно рассматривать двояко:
а) сохраняется /почка и изменяется
координатная система (рис. 2.2) - произвольная
точка Μ остается той же, изменяются
лишь ее координаты
б) изменяется точка, и сохраняется
координатная система (рис. 2.3) - формулы (*)
задают отображение, переводящее
произвольную точку М(х,у) в точку М(х ,у ),
координаты которой определены в той
же координатной системе.
В дальнейшем нам удобно рассматривать
формулы (*) в смысле б.
Начнем рассмотрение с нескольких частных
случаев, считая для простоты, что заданная система
координат является прямоугольной декартовой.
А. Поворот (вокруг начальной точки на угол φ)
(рис. 2.4) описывается формулами
х* = *cos(cp) - >>sin((p),
У = xsin(cp) + >>cos((p)
Б. Растяжение (сжатие)
осей можно задать так
χ = сое,
У* = Ф.
а>0,£>0
Растяжение (сжатие) вдоль оси абсцисс
обеспечивается при условии, что α > 1 (α < 1
соответственно). На рис. 2.5 а- 6> 1.
В. Отражение (относительно оси абсцисс)
(рис. 2.6) задается при помощи формул
X = Ху
Υ
0
Υ*\^
Μ
•
/(гЧ
/**
X
Рис. 2.2
γ
Рис. 2.3
вдоль координатных р „,
Υ
0
/Ί*
/м*
X
Рис. 2.5
Г. На рис. 2.7 вектор переноса
обеспечивают соотношения
χ = χ + Л,
/ = У + М-
ММ* имеет координаты λ и μ. Перенос

ПРЕОБРАЗОВАНИЯ НА ПЛОСКОСТИ И В ОРОСТРАНСТВЕ
В.
"ывод изображения на экран дисплея и разнообразные действия с ним, в том
числе и визуальный анализ, требуют от пользователя известной геометрической
грамотности. Геометрические понятия, формулы и факты, относящиеся прежде
всего к плоскому и трехмерному случаям, играют в задачах компьютерной
графики особую роль. Геометрические соображения, подходы и идеи в соединении с
постоянно расширяющимися возможностями вычислительной техники являются
неиссякаемым источником существенных продвижений на пути развития
компьютерной графики, ее эффективного использования в научных и иных
исследованиях. Порой даже самые простые геометрические методики обеспечивают
заметные продвижения на отдельных этапах решения большой графической
задачи. С простых геометрических рассмотрений мы и начнем наш рассказ.
Заметим прежде всего, что особенности использования геометрических
понятий, формул и фактов, как простых и хорошо известных, так и новых, более
сложных, требуют особого взгляда на них и иного осмысления.
Μ (χ, у)
Аффинные преобразования на плоскости
В компьютерной графике все, что относится к двумерному случаю, принято
обозначать символом (2D) (2-dimension).
Предположим, что на плоскости введена
прямолинейная координатная система. Тогда каждой точке
Μ ставится в соответствие упорядоченная пара
чисел (х,у)ее координат (рис. 2.1). Вводя на
плоскости еще одну прямолинейную систему координат, мы
ставим в соответствие той же точке Μ другую пару
чисел [х ,у ).
Переход от одной прямолинейной координатной системы на плоскости к
другой описывается следующими соотношениями
х" = ах + $у + λ,
/=γ* + δ)> + μ, (*)
где α,β,γ,λ,μ произвольные числа, но
Ια β|
Рис. 2.1
γ δ
*0

Выбор этих частных случаев определяется
двумя обстоятельствами:
1) каждое из приведенных выше преобразований
имеет простой и наглядный геометрический смысл и
2) как доказывается в курсе аналитической
геометрии, любое преобразование (*) всегда можно
представить как последовательное исполнение
(суперпозицию) простейших преобразований вида А,
Б, В и Г (или части этих преобразований).
Значит, и любое отображение вида (*) можно
описать при помощи отображений, задаваемых
формулами А, Б, В и Г.
Для эффективного использования этих
известных формул в задачах компьютерной графики более
удобной является их матричная запись. Матрицы,
соответствующие случаям А, Б и В, строятся легко.
Они имеют соответственно следующий вид:
Рис. 2.6
/М*
'М
Рис. 2.7
cos φ
sin φ
-sin φ
cos φ
1 О
О 1
Желая, однако, охватить матричным подходом все четыре простейших
преобразования (в том числе и перенос), мы должны перейти к описанию произвольной
точки плоскости уже не парой чисел, как это было сделано выше, а тройкой.
Введем для этого однородные координаты произвольной точки. Широко
используемые в проективной геометрии однородные координаты позволяют
эффективно описывать так называемые несобственные элементы (по существу, те,
которыми проективная плоскость отличается от привычной нам евклидовой
плоскости).
Пусть Μ - произвольная точка плоскости с координатами χ и у.
Однородными координатами точки называется тройка одновременно неравных нулю
чисел *1,*2,*3, если выполнены следующие соотношения
х\ х2
— = *,— = у.
х3 х3
В компьютерной графике однородные координаты
обычно вводятся так: точке М(х, у) ставится в
соответствие точка М'(хууу\) в пространстве (рис. 2.8).
Заметим, что произвольная точка на прямой,
соединяющей начало координат, точку 0(0, 0, 0),
с точкой M'(x,yJ), может быть задана тройкой
(hx, hy, h)
Исключая точку О из рассмотрения, будем
считать, что h * 0.
Рис. 2.8

Вектор, определяемый тройкой hx, hy, h, является направляющим вектором
прямой, соединяющей точки О и Л/'. Эта прямая пересекает плоскость z=/
в точке (х, у, I), которая однозначно определяет точку (х, у) координатной
плоскости хОу. Тем самым между точкой (х, у) и множеством троек (hx, hy, h),
h * 0 устанавливается взаимно однозначное соответствие. Это позволяет считать
числа hx, hy, h ее координатами.
Как уже говорилось выше, такие координаты называются однородными.
В проективной геометрии для них принято следующее обозначение
х:у:\
или, более общо,
х\:х2'Хз
(напомним, что здесь непременно требуется, чтобы числа *ι,*2»*3 одновременно
в нуль не обращались).
Применение однородных координат оказывается удобным уже при решении
простейших задач.
Рассмотрим, например, вопросы, связанные с изменением масштаба. Если
устройство отображения работает только с целыми числами (или необходимо
работать только с целыми числами), то для произвольного значения h (например,
Л=1) точку с однородными координатами
(0.5; 0.1; 2.5)
представить нельзя. Однако при разумном выборе можно добиться того, чтобы
координаты этой точки были целыми числами. В частности, при Л=10 для
рассматриваемого примера имеем
(5;1;2.5).
Результаты преобразования, разумеется, не должны приводить к
арифметическому переполнению. Поэтому для преобразования точки с координатами
(80000, 40000, 1000)
можно взять, например, Л=0,01. В результате получим
(800, 400, 10).
Последние два примера показывают полезность использования однородных
координат при проведении расчетов. Однако основной целью введения однородных
координат в компьютерной графике является их несомненное удобство.
Считая Л=1, сравним две записи: помеченную символом (*) и
нижеследующую, матричную:
(*\/.1) = (*.у.1)|
α
β
_λ
γ 0"
δ 0
» 1.
Нетрудно заметить, что после перемножения выражений, стоящих в правой
части последнего соотношения, мы получим две формулы (*) и верное числовое
равенство 1 = 1.
Тем самым эти две сравниваемые записи можно считать равносильными.

S Иногда в литературе используется другая запись - запись по столбцам
ία ρ λΐ
1
γ δ
о о
Эта запись эквивалентна приведенной выше записи по строкам.
Чтобы реализовать то или иное отображение по заданным геометрическим
характеристикам, надо найти элементы соответствующей матрицы. Обычно ее
построение разбивают на этапы. На каждом этапе строится матрица для одного
из выделенных выше случаев А, Б, В или Г. Выпишем эти матрицы.
А. Матрица вращения (rotation)
cos φ sin φ θ!
Μ-
- sin φ cos φ О
О 0 1
α
0
0
0
δ
0
0"
0
1_
Б. Матрица растяжения(сжатия) (dilatation)
[D] =
В. Матрица отражения (reflection)
Γι о о]
[Λί]= О -1 0|
[о о ι
Г. Матрица переноса (translation)
[Т} =
Ί
0
_х
0
1
μ
о"
0
1_
Рассмотрим несколько примеров.
Пример /. Построить матрицу поворота вокруг
точки А(а, Ь) на угол φ (рис. 2.9).
1-й шаг. Перенос на вектор -А(-а,-Ь) для
совмещения центра поворота с началом координат;
Г cos φ sin φ θ]
[/?φ J = - sin φ cos φ 0 -
[ О О 1J
матрица соответствующего преобразования.
Υ
0
•
..,.Κίί?....
•
•
Χ
Рис. 2.9

2-й шаг. Поворот на угол φ; матрица соответствующего преобразования
имеет вид
"1 0 01
[Т-а]"
0
1 0
-Ь 1
Ί о
0 1
а Ь
о"
0
Г
3-й шаг. Перенос на вектор А(а, Ь) для возвращения центра поворота
в прежнее положение;
Ш-
матрица соответствующего преобразования.
Перемножим матрицы в том же порядке, в котором они выписаны
[Г-аКЫ
В результате получим, что искомое преобразование выглядит следующим
образом
(х*Ул) = {х,уЛ)х
COS0J
-sin^>
-acos<p + bsin<p + a
sin φ 0
cos φ 0
-a sin φ- bcos<p + b 1
Элементы полученной матрицы (особенно в последней строке) не так легко
запомнить. Да и надо ли?
Пример 2. Построить матрицу растяжения с коэффициентами растяжения
α вдоль оси абсцисс и β вдоль оси ординат и с центром в точке
А(а, Ъ) {рис. 2.10).
1-й шаг. Перенос на вектор -А(-а, -Ь) для
совмещения центра растяжения с началом координат;
1 0 Ol
Ы =
0
-а
1 0
-Ъ 1
матрица соответствующего преобразования.
2-й шаг. Растяжение вдоль координатных осей
с коэффициентами α и δ соответственно; матрица
преобразования имеет вид
[D].
Рис. 2.10
"а 0
0 δ
0 0
о"
0
1_

Γι
0
[a
0
1
b
0"
0
1
3-й шаг. Перенос на вектор А(а, Ь) для возвращения центра растяжения
в прежнее положение; матрица соответствующего преобразования -
[7*] =
Перемножив матрицы в том же порядке
[T-a][D][Ta],
получим окончательно
а 0 0
0 £ 0
(Ι-α)ίΐ (\-S)b l
(/./.l) = U*l)
Аффинные преобразования в пространстве
Обратимся теперь к трехмерному случаю (3D) и начнем с введения
однородных координат.
Поступая аналогично тому, как это было сделано в размерности два, заменим
тройку (х, у, ζ), задающую точку в пространстве, на четверку
(jc.y.z.l)
или, более общо, на
(hxthy,hzth),h * 0.
Тем самым каждая точка пространства (кроме начальной точки О) может
быть задана четверкой одновременно не равных нулю чисел; эта четверка
определена однозначно с точностью до общего множителя.
Предложенный переход дает возможность воспользоваться матричной
записью и в более сложных, трехмерных задачах.
Как известно, любое аффинное преобразование в трехмерном пространстве
может быть представлено в виде суперпозиции вращений, растяжений, отражений
и переносов. Поэтому достаточно подробно описать матрицы только этих
последних преобразований.
А. Матрицы вращения в пространстве.
Матрица вращения вокруг оси абсцисс на угол φ:
Ίο о ol
0
0
0
cos φ
-sin φ
0
sin φ
cos φ
0
0
0
1

Матрица вращения вокруг оси ординат на угол ψ:
[cosψ 0 -sinψ θ1
Kl·
0
sin ψ
0
1
0
0
0
cos ψ
0
0
0
1
Матрица вращения вокруг оси аппликат на угол χ:
cos χ sin χ 0 θ]
W=
I - sin χ cos χ 0 0
0 0 10
0 0 0 1
Б. Матрица растяжения (сжатия):
|α О О О]
|0 β О О
| 0 0 γ О Г
10 0 0 1
[D] =
здесь α > 0 - коэффициент растяжения (сжатия) вдоль оси абсцисс,
β > 0 - коэффициент растяжения (сжатия) вдоль оси ординат,
γ > 0 - коэффициент растяжения (сжатия) вдоль оси аппликат.
В. Матрицы отражения.
Матрица отражения относительно плоскости хОу:
"1 0 0 Ol
0
0
0
1
0
0
0
-1
0
0
0
1
Матрица отражения относительно плоскости yOz:
-1 О О О]
[",]■
Матрица отражения относительно плоскости ζΟχ:
Ί 0 0 01
0
0
0
1
0
0
0
1
0
0
0
1
Kl·
0
0
0
-1
0
0
0
1
0
0
0
1

Г. Матрица переноса:
"10 0 0
0 10 0
0 0 10
λ μ ν 1
[г] =
здесь (λ,μ,ν) - вектор переноса.
Заметим, что, как и в двумерном случае, все выписанные матрицы
невырождены.
Приведем важный пример построения матрицы сложного преобразования.
Пример. Построить матрицу вращения на угол φ вокруг прямой L,
проходящей через точку А(а, Ъ, с) и имеющую направляющий
вектор (I, т, п). Можно считать, что направляющий вектор
прямой является единичным:
I2 +т2 +п2 =1.
1-й шаг. Перенос на вектор -А(-а, -Ь, -с) при помощи матрицы
1 0 0 01
[Т] =
0
0
-а
1
0
-ь
0 0
1 0
-с 1
ζ
0
ч
'Л
ψ/
ι //
ι //
\У
/L у
чу
χ
В результате этого переноса мы добиваемся того, чтобы прямая L проходила
через начало координат.
2-й шаг. Совмещение оси аппликат с прямой L
двумя поворотами вокруг оси абсцисс и оси ординат
(рис. 2.11).
1-й поворот - вокруг оси абсцисс на угол ψ
(подлежащий определению). Чтобы найти этот угол,
заметим прежде всего, что прямая L' является
ортогональной проекцией на плоскость Х-0 исходной
прямой L с направляющим вектором (I, m, п).
Поэтому направляющий вектор прямой V
определяется просто. Он равен
(0,т,л.)
Отсюда вытекает, что
η т
cos ψ = — ,sini{/ = —,
d d
где d = Vm2 +л2.
Рис. 2. Π

Соответствующая матрица вращения имеет следующий вид
"10 О (Л
0
0
0
nld
-mid
0
mid
nld
0
0
0
1
[*.]'
Под действием преобразования, описываемого этой матрицей, крординаты
вектора (I, т, п) изменятся. Пересчитаем их и получим
{l,m,n,\)[Rx] = {l9o,d,l).
2-й поворот - вокруг оси ординат на угол Θ, определяемый соотношениями
cosG = /,sin0 = -d.
Соответствующая матрица вращения имеет следующий вид
/ 0 d Ol
К]=
0
-d
0
1
0
0
0
/
0
0
0
1
3-й шаг. Вращение вокруг прямой L на заданный угол φ. Так как теперь
прямая L совпадает с осью аппликат, то соответствующая матрица имеет вид
О 01
[*<l·
cos φ sin φ
-sin φ cos φ 0 О
О 0 10
О 0 0 1
4-й шаг. Поворот вокруг оси ординат на угол -Θ и затем вокруг оси
абсцисс на угол -ψ .
S Вращение в пространстве некоммутативно. Поэтому порядок, в
котором проводятся вращения, является весьма существенным.
5-й шаг. Перенос на вектор А(а, Ъ, с) .
Перемножая найденные матрицы в порядке их построения, окончательно
получим следующую матрицу
[тЫФЛфк.ПП1-
Рассматривая другие подобные примеры, будем получать в результате
невырожденные матрицы вида
«1
β.
Υι
λ
α2
β2
Ϊ2
μ
α3
Рз
Уз
ν
0
0
0
1

При помощи этих матриц можно подвергать
простейшим преобразованиям любые плоские и
пространственные фигуры. Возьмем, к примеру, выпуклый
многогранник. Он однозначно задается массивом своих
вершин. Подействовав на этот массив найденной
матрицей, мы получаем новый массив, задающий
выпуклый многогранник - образ исходного (рис. 2.12).
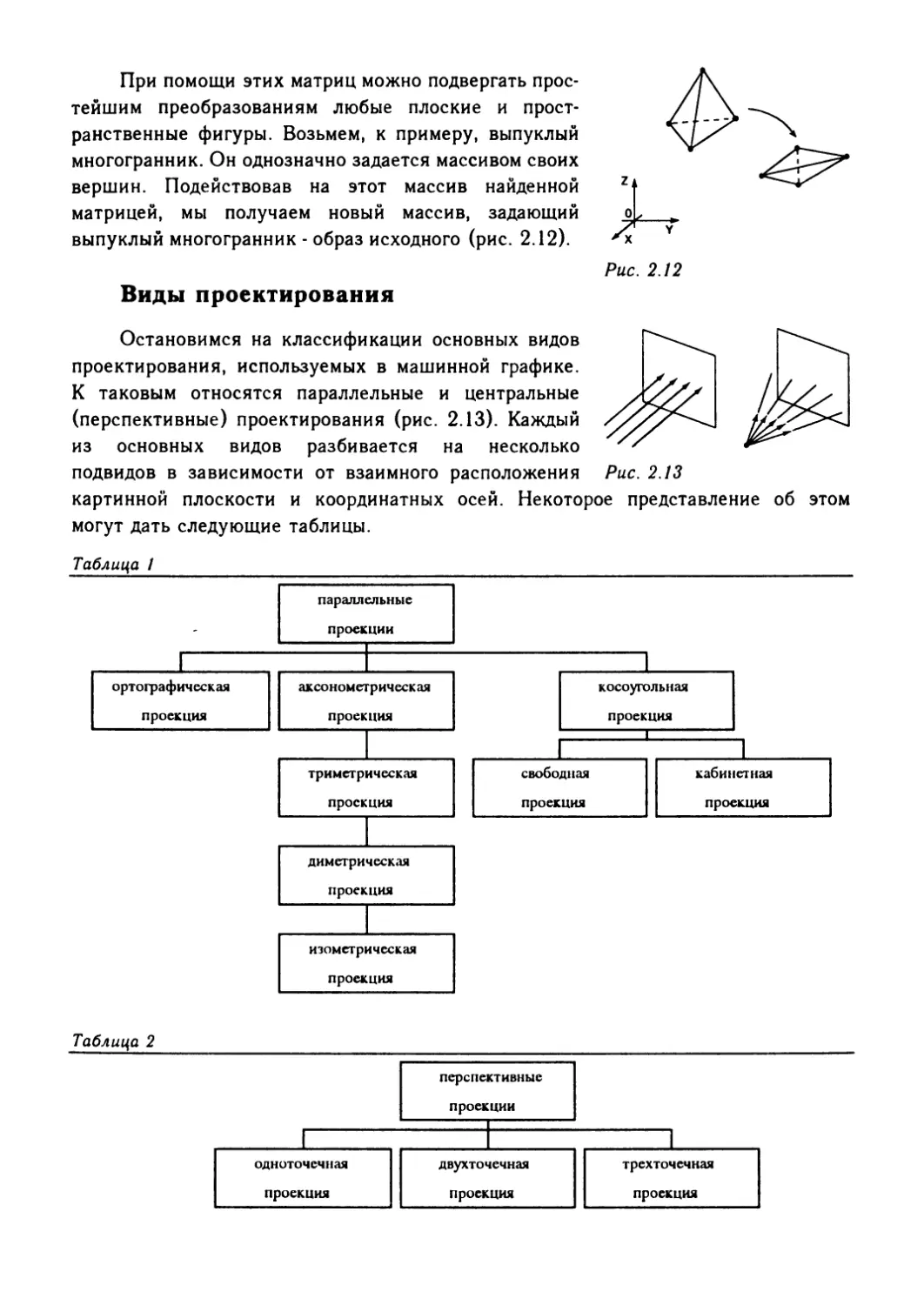
Виды проектирования
Остановимся на классификации основных видов
проектирования, используемых в машинной графике.
К таковым относятся параллельные и центральные
(перспективные) проектирования (рис. 2.13). Каждый
из основных видов разбивается на несколько
подвидов в зависимости от взаимного расположения
Рис. 2.12
«&-
Рис. 2.13
картинной плоскости и координатных осей,
могут дать следующие таблицы.
Таблица I
Некоторое представление об этом
ортографическая
проекция
параллельные
проекции
аксонометрическая
проекция
триметрическая
проекция
косоугольная
проекция
1
ι
свободная
проекция
кабинетная
проекция
диметрическая
проекция
изометрическая
проекция
Таблица 2
перспективные
проекции
1
одноточечная 1
проекция
1
двухточечная 1
проекция
трехточечная
проекция

Рис. 2.14
Пояснения к таблицам.
Для описания преобразований проектирования
будем использовать матрицы и однородные
координаты, что позволит упростить изложение и
зримо облегчит решение задач геометрического
моделирования.
Ортографическая проекция - картинная плоскость совпадает с одной из
координатных плоскостей или параллельна ей (рис. 2.14). Матрица проектирования
вдоль оси X на плоскость YOZ имеет вид
W-
В случае, если плоскость проектирования параллельна координатной
плоскости, необходимо умножить матрицу [Рх] кз матрицу сдвига. Имеем
0 0 0 0]
0 10 0
0 0 10'
[р 0 0 1J
Аналогично записываются матрицы проектирования вдоль
двух других координатных осей:
0
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
['.]■
1
0
0
Ρ
0
1
0
0
0
0
1
0
0"
0
0
0
1
0
0
0
0
0
0
я
0
0
1
0
о]
0
о Г
lj
10 0 0
0 10 0
0 0 0 0
О 0 г 1
Аксонометрическая проекция - проектирующие прямые
перпендикулярны картинной плоскости.
Различают три вида проекций в зависимости от взаимного
расположения плоскости проектирования и координатных осей:
• триметрия - нормальный вектор картинной плоскости
образует с ортами координатных осей попарно различные
углы (рис. 2.15);
• диметрия - два угла между нормалью картинной
плоскости и координатными осями равны (рис. 2.16);
• изометрия - все три угла между нормалью картинной
плоскости и координатными осями равны (рис. 2.17).
Каждый из трех видов указанных проекций получается
комбинацией поворотов, за которой следует параллельное
проектирование.
Рис. 2.15
Рис. 2 6
Рис. 2.17

Из курса аналитической геометрии известно, что любые две одинаково
ориентированные тройки координатных осей (обе правые или обе левые) можно
совместить двумя поворотами, при каждом из которых остается неизменной одна
координатная ось. При повороте на угол ψ относительно оси Υ, на угол φ вокруг
оси X и последующего проектирования на плоскость Ζ=0 возникает матрица
]=
cos ψ
0
sin ψ
0
cos ψ 0
0 1
sin ψ 0
0
0
sin φ cos
ψ
cos φ
-sinφ -cosψ
0
-sin ψ θ]
0 0
cos ψ 0
0 1
Γι
0
0
ο
0 0
0 0
0 0
0 1
0
cos φ
-sin φ
0
_
0
sin φ
cos φ
0
°1
0
0
1
Γι ο ο ο
0 10 0
0 0 0 0
0 0 0 1
При этом преобразуются и единичные орты координатных осей Χ, Υ, Ζ:
(10 0 1)[Л/] = (cosvj/ sincpsini|/ 0 1),
(0 1 0 1)[Л/] = (0 coscp 0 1),
(0 О 1 l)[A/] = (sini|/ -sincpcosij/ 0 1).
При триметрии длины полученных в результате проекций различны.
Диметрия характеризуется тем, что длины двух проекций совпадают:
cos y + sin ?>sin ψ -
cos φ
В случае изометрии дополнительно имеем
• 2 -2 2 2
sin ψ + sin 0>cos ψ = cos φ.
Из последних двух соотношений легко получаем, что
. 2 1
sin V=2>
. 2 1
sin*^ -.
проекция (пучок прямых не перпендикулярен
Наконец, косоугольная
плоскости экрана).
Выделяют два вида косоугольных проекций: свободную
проекцию (угол наклона проектирующих прямых к
плоскости экрана равен половине прямого) и кабинетную проекцию
(частный случай свободной проекции; масштаб по третьей
оси вдвое меньше).
При косоугольном проектировании орта оси Ζ на
плоскость ΧΟΥ (рис. 2.18) имеем
(0 0 1 1)ь*(<х β 0 1).
Рис 2.18

Матрица соответствующего преобразования имеет следующий вид
1 0 0 01
0 10 0
α β 0 0
0 0 0 1
В случае свободной проекции
α = В = cos — ,
4
в случае кабинетной
α = β = —cos — .
2 4
Перспективные (центральные) проекции строятся YT (x,y,z)
более сложно. Предположим, что центр проектирования
лежит на оси Z,
С(0,0,с)
а плоскость проектирования совпадает с координатной рцс £ \д
плоскостью XOY (рис. 2.19). Возьмем в пространстве
произвольную точку М(хУу,г), проведем через нее и точку С прямую и запишем
ее параметрические уравнения. Имеем
X* = Jtr, Y* =yt, Z* =c + {z-c)(.
Найдем координаты точки пересечения этой прямой с плоскостью XOY.
Из того, что Z* = 0, получаем
1
1
и, далее,
1
-χ, Υ =
1
-у-
Тот же самый результат мы получим, привлекая матрицу
10 0 0
0 1 0
0 0 0
0 0 0
0
-1/с
1

В самом деле,
(х У ζ \)
или, что то же,
"1
0
0
0
0
1
0
0
0
0
0
0
0
0
-\/с
1
-(* у о i-f)
!_ί ,_ί
О 1
1 0
0 1
0 0
0 0
0
0
1
0
0
0
-Μ с
1
Матрица проектирования, конечно, вырождена; матрица же
соответствующего перспективного преобразования (без проектирования) имеет следующий вид
[е] =
Рассмотрим пучок прямых, параллельных оси Ζ, и попробуем выяснить, что
с ним происходит под действием матрицы [Q].
Каждая прямая пучка однозначно определяется точкой своего пересечения
с плоскостью ΧΟΥ и описывается уравнениями
X = xit Y = yit Z = t.
Переходя к однородным координатам и используя матрицу [Q], получаем
{х у г \) [Q] = (x у t \--λ
ИЛИ, '
λΐο то же,
( \
x У C_L· ι
ι-ί ι-ί l~c
V с с )
Устремим t в бесконечность
Точка
{х У Ζ 1)
преобразуется в
(0 0 10)
достаточно разделить все на t ,
ί£ > ι 1Ϊ
\t t t)

и перейти к пределу. Соответствующая ей точка
(О О -с 1)
получается подобным же образом из
( \
χ у t
1
t-c
1
с с
Тем самым бесконечно удаленный центр (θ 0 1 θ) пучка параллельных
оси Ζ прямых переходит в точку (θ 0 -с l) оси Z. Полученная точка
называется точкой схода.
И вообще, каждый несобственный пучок прямых (совокупность прямых,
параллельных заданному направлению), не параллельный картинной плоскости,
под действием преобразования, задаваемого матрицей [β], переходит в
собственный пучок.
Центр получаемого при этом пучка называют точкой схода. Принято
выделять так называемые главные точки схода, соответствующие пучкам прямых,
параллельных координатным осям.
Для преобразования с матрицей [β]
существует лишь одна главная точка схода
(рис. 2.20). В общем случае (когда оси
координатной системы не параллельны плоскости
экрана) таких точек три. Матрица
соответствующего преобразования выглядит так:
10 0 -XI а
0 1 0 -Mb
0 0 1 -Мс
0 0 0 1
Пучок прямых, параллельных оси
OX OY
(10 0 0) (0 10 0),
переходит в пучок прямых с центром
Υ
г^^^
Υ
^L<C
-Х-
:~7
а^^^^^ X
Рис. 2.20
(,..-!) (...-I)
или, что то же,
{-а 0 0 1)
(главные точки схода).
{-Ь 0 0 1)
Рис. 2.21
На рис. 2.21 изображены проекции куба со сторонами, параллельными
координатным осям, с одной и с двумя главными точками схода.

Особенности проекций гладких отображений
Изображение объектов на картинной плоскости
связано с еще одной геометрической операцией -
проектированием при помощи пучка прямых. Наиболее
употребимые на практике виды проектирования суть
параллельное и центральное (рис. 2.22).
Для получения проекции объекта на картинную Рис 2 22
плоскость необходимо провести через каждую его точку прямую из заданного
проектирующего пучка (собственного или несобственного) и затем найти
координаты точки пересечения этой прямой с плоскостью изображения. В случае
центрального проектирования все прямые исходят из одной точки - центра
собственного пучка; при параллельном же проектировании центр (несобственного)
пучка считается лежащим в бесконечности.
Прежде чем переходить к более подробной классификации указанных видов
проектирования, остановимся на некоторых эффектах, неизбежно возникающих
при проектировании искривленных объектов (главным образом поверхностей) на
картинную плоскость. При этом важно отметить, что описываемые ниже эффекты
возникают вне зависимости от того, является ли проектирование параллельным
или центральным.
Будем считать для простоты, что проектирование проводится при помощи
пучка параллельных прямых, идущих перпендикулярно картинной плоскости, а
система координат (X, У, Z) в пространстве выбрана так, что картинная плоскость
совпадает с координатной плоскостью X = 0.
Укажем три принципиально различных случая.
1-й случай
Спроектируем заданную поверхность - плоскость,
описываемую уравнением Ζ = X, на плоскость X = О
(рис. 2.23). Записав ее уравнение в неявном виде
X - Ζ = 0,
вычислим координаты нормального вектора. Имеем
# = (1, 0, -1).
Вектор L, вдоль которого осуществляется
проектирование, имеет координаты
£ = (1, 0, 0). Рис 2 23
Легко видеть, что скалярное произведение
(//,£) = 1>0
Тем самым, вектор проектирования и нормальный вектор рассматриваемой
поверхности не перпендикулярны ни в одной точке.
Отметим, что полученная проекция особенностей не имеет.

2-й случай
Заданная поверхность - параболический цилиндр с уравнением Ζ = X или,
что то же,
X2 - Ζ = 0.
Нормальный вектор
Ν = {2Χ9 0, -1)
ортогонален вектору проектирования L в точках оси Υ. Это вытекает из того, что
(#,£) = 2Х.
Здесь в отличие от первого случая точки плоскости
Х = 0 разбиваются на три класса: к 1-му относятся точки
(Ζ>θ), у которых два прообраза (на рис. 2.24 этот класс
заштрихован), ко 2-му - те, у которых прообраз один
(Ζ = θ). Что же касается точек 3-го класса, то у них
прообразов на цилиндре нет вовсе.
Прямая X = О, Ζ = 0 является особой. Вдоль нее
векторы N и L ортогональны. Особенность этого типа
называется складкой.
3-й случай
Рассмотрим поверхность, заданную уравнением
Ζ = Χ3 +ΧΥ
или, что то же,
X3 + ΧΥ - Ζ = 0.
Рис. 2 24
Вычислим нормальный вектор этой поверхности
Рис. 2.25
N = (ЗХ2 + Υ, ХУ -\)
и построим ее, применив метод сечений. Пусть Υ = 1.
Тогда
ζ = χ3 +х
(рис. 2.25). При Υ = 0 имеем
ζ = χ3
(рис. 2.26). Наконец, при Υ = -1 получаем
Ζ = X3 - X
(рис. 2.27).
Построенные сечения дают представление обо
всей поверхности. Поэтому нарисовать ее теперь уже
несложно (рис. 2.28).
Τ
λ
Рис. 2.26
Рис 2.27

Из условия
(N,L) = 3X2 + Y = 0
и уравнения поверхности получаем, что вдоль лежащей на
ней кривой с уравнениями
Υ = -ЗХ2, Ζ = -2Χ3
вектор проектирования L и нормальный вектор N
рассматриваемой поверхности ортогональны. Исключая X,
получаем, что
(-К/3)3 =(-Ζ/2)2
Рис. 2.28
Рис. 2.29
21ZL = -4Y\
Последнее равенство задает на координатной
плоскости X = О полукубическую параболу (рис. 2.29),
которая делит точки этой плоскости на три класса: к 1-му
относятся точки, лежащие на острие (у каждой из них на
заданной поверхности ровно два прообраза), внутри острия
каждая точка имеет по три прообраза, а вне его по одному.
Особенность этого типа называется сборкой.
S Возникающая в 3 случае полу кубическая парабола имеет точку
заострения. Однако ее прообраз
X = Χ, Υ = -ЗХ2, Ζ = -2Х3
является регулярной кривой, лежащей на заданной поверхности.
В теории особенностей (или катастроф)
доказывается, что при проектировании на плоскость
произвольного гладкого объекта - поверхности возможны (с
точностью до малого шевеления, рассыпающего более
сложные проекции) только три указанных типа
проекций - обыкновенная проекция, складка и сборка.
Сказанное следует понимать так: при
проектировании гладких поверхностей на плоскость могут
возникать и другие, более сложные особенности. Однако
в отличие от трех перечисленных выше все они
оказываются неустойчивыми - при малых изменениях
либо направления проектирования, либо взаимного
расположения плоскости и проектируемой
поверхности эти особенности не сохраняются и
переходят в более простые.
<f По существу, в приведенных примерах рассмотрены три типа
отображения 2-плоскости в 2-плоскость (рис. 2.30).
ιυ2
^
1
Υ,
ΓΥι=Χ?+ΧιΧ
I У2=х2
Рис. 2 30

ГЕОМЕТРИЧЕСКИЕ СШШЫ
И
X Хсторию сплайнов принято отсчитывать от момента появления первой работы
Шенберга в 1946 году. Сначала сплайны рассматривались как удобный инструмент
в теории и практике приближения функций. Однако довольно скоро область их
применения начала быстро расширяться и обнаружилось, что сущестует очень
много сплайнов самых разных типов. Сплайны стали активно использоваться в
численных методах, в системах автоматического проектирования и автоматизации
научных исследований, во многих других областях человеческой деятельности
и, конечно, в компьютерной графике.
Сам термин "сплайн" происходит от английского spline. Именно так
называется гибкая полоска стали, при помощи которой чертежники проводили
через заданные точки плавные кривые. В былые времена подобный способ
построения плавных обводов различного рода тел, например таких, как корпус
корабля, фюзеляж или крыло самолета, кузов автомобиля и т. п., был довольно
широко распространен в практике машиностроения. В результате форма тела
задавалась при помощи набора очень точно изготовленных сечений - плазов.
Появление компьютеров позволило перейти от этого, плазово-шаблонного, метода
к более эффективному способу задания поверхности обтекаемого тела. В основе
этого подхода к описанию поверхностей лежит использование сравнительно
несложных формул, позволяющих восстанавливать облик изделия с необходимой
точностью. Ясно, что для большинства тел, встречающихся на практике, вряд ли
возможно отыскание простых универсальных формул, которые описывали бы
соответствующую поверхность глобально, т. е. в целом. Это означает, что при
решении задачи построения достаточно произвольной поверхности небольшим
количеством формул, как правило, обойтись не удается. Вместе с тем
аналитическое описание (описание посредством формул) внешних обводов изделия, т. е.
задание двухмерной поверхности в трехмерном пространстве) должно быть
достаточно экономным. Это особенно важно, когда речь, идет об обработке
изделия на станках с числовым программным управлением. Обычно поступают
следующим образом: задают координаты сравнительно небольшого числа опорных
точек, лежащих на искомой поверхности, и через эти точки проводят плавные
поверхности. Именно так поступает конструктор при проектированиии кузова
автомобиля (ясно, что на этой стадии процесс проектирования сложного объекта
явно содержит неформальную составляющую). На следующем шаге конструктор
должен получить аналитическое представление для придуманных кривых или
поверхностей. Вот для таких задач и используются сплайны.
Средства компьютерной графики, особенно визуализация, существенно
помогают при проектировании, показывая конструктору, что может получаться в

результате, и давая ему многовариантную возможность сравнить это с тем, что
есть у него в голове.
Мы не ставим перед собой и читателем задачи рассказать обо всех сплайнах,
в частности, потому, что это отдельная большая тема, требующая и большего
внимания и большего объема. Во вводном курсе нам кажется более уместным
показать в сравнении некоторые из преимуществ использования сплайнов
в задачах геометрического моделирования при проектировании кривых и
поверхностей. Такое представление полезно начинающему пользователю для его
ориентации в стремительно расширяющемся мире сплайнов.
Достаточно типичной является следующая задача: по заданному массиву
точек на плоскости (2D) или в пространстве (3D) построить кривую либо
проходящую через все эти точки (задача интерполяции), либо проходящую вблизи
этих точек (задача сглаживания).
Совершенно естественно возникают вопросы:
1) в каком классе кривых искать решение поставленной задачи и
2) как искать.
Начнем с обсуждения правил выбора класса кривых, обратившись для
определенности к задаче интерполяции.
Ясно, что допустимый класс кривых должен быть таким, чтобы решение
задачи было единственным (это обстоятельство сильно помогает в преодолении
многих трудностей поиска). Кроме того, хорошо бы, чтобы построенная кривая
изменялась плавно.
Пусть на плоскости задан набор точек
(*„X),i = 0,l m
причем х0 < χγ <...< xm_i < хт (рис. 3.1). Будем ν
искать кривую в классе многочленов.
Как известно из курса математического анализа, ° °'
существует интерполяционный многочлен Лагранжа
ω„(*)
Μ*) = Σ"0*
(*-*,)ω ;,(*,)
о (Хщ,Ут)
. (х.,У.)
где ω«,(*)=ΓΤ"= (x-Xj), график которого проходит Рис. 3.1
через все заданные точки. Это обстоятельство и простота описания (заметим, что
многочлен однозначно определяется набором своих коэффициентов; в данном
случае их число совпадает с количеством точек в массиве) являются несомненными
достоинствами построенного интерполяционного многочлена (есть и другие).
Остановимся на некоторых недостатках предложенного подхода.
1. Степень многочлена Лагранжа на единицу меньше числа заданных точек.
Поэтому чем больше точек задано, тем выше степень такого многочлена. И, хотя
он всегда будет проходить через все точки массива, его уклонение (от
ожидаемого) может оказаться довольно значительным (рис. 3.2).

Рис. 3.2
2. Изменение одной точки (ситуация, довольно
часто встречаемая на практике) требует полного
пересчета и к тому же может существенно повлиять
на вид многочлена.
С другой стороны, можно поступить совсем
просто: последовательно соединив точки заданного
массива, мы получим ломаную (рис. 3.3). При такой,
кусочно-линейной, интерполяции требуется найти
всего 2т чисел (коэффициентов Jfc, и bt отрезков
прямых), но, к сожалению, построенная таким образом
аппроксимирующая функция не обладает никакой
гладкостью: уже первая производная этой функции
терпит разрывы в узлах интерполяции.
Рассмотрев эти две крайние ситуации,
попробуем найти класс функций, которые в основном
сохранили бы перечисленные выше достоинства
обоих подходов и одновременно были бы в известном
смысле свободны от их недостатков.
Для этого поступим следующим образом. Будем использовать многочлены
(как и в первом случае) и строить их последовательно, звено за звеном (как во
втором случае). При таком подходе очень важно правильно выбрать степень этих
многочленов. А чтобы результирующая кривая изменялась плавно, необходимо
еще найти подходящие коэффициенты (для гладкого сопряжения соседних
звеньев).
То, что получится в результате, называют сплайн-функциями или просто
сплайнами.
Для того, чтобы понять, какое отношение имеют
сплайн-функции к чертежным сплайнам, возьмем
гибкую стальную линейку, поставим ее на ребро и,
закрепив один из концов в заданной точке, поместим
между опорами, которые располагаются в плоскости
Оху в точках
y=kixx+bi
Рис. 3.3
Рис. 3.4
(*,·, у,·), ι = 0, 1, ..., т,
где х0 < х{ < ...< хт_х < хт (рис. 3.4).
Интересно отметить, что функция S(x), описывающая профиль линейки,
между любыми двумя соседними опорами является многочленом третьей степени
и дважды непрерывно дифференцируема на всем промежутке [д:0, хт].
Построенная функция S(x) относится к так называемым интерполяционным
кубическим сплайнам. Этот класс в полной мере удовлетворяет высказанным
выше требованиям и обладает еще целым рядом замечательных свойств.
Перейдем, однако, к точным формулировкам.

Интерполяционным кубическим сплайном называется функция S(x),
обладающая следующими свойствами:
1) S(Xj) = yh 1 = 0, 1 m;
2) на каждом из отрезке [*,·, *;+i], i = 0, 1, ..., m-1, функция
3) на всем отрезке задания [*о,*т] функция S(x) имеет непрерывную
вторую производную.
Так как на каждом из отрезков [*,·, *ί+|] сплайн S(x) определяется четырьмя
коэффициентами, то для его полного построения на всем отрезке задания
необходимо найти всего 4т чисел.
Для выполнения третьего условия достаточно потребовать непрерывности
сплайна во всех внутренних узлах χ.J = 1 m-1 (это дает m-1 условий на
коэффициенты), а также его первой (т - 1 условий) и второй (еще т - 1 условий)
производных в этих узлах. Вместе с требованием 1) получаем
m-l + m-l+m-l+m + 1 = 4m-2
равенств. Недостающие два условия для полного определения коэффициентов
можно получить, задав, к примеру, знфчения первых производных на концах
отрезка [*о»*т] (граничные условия):
S'(xQ) = l0,S'(xm) = lm.
Похожим образом решается более сложная задача построения по заданному
массиву точек в пространстве (3D) интерполяционной функции двух переменных.
Покажем, например, как можно построить интерполяционный бикубический сплайн.
Пусть на плоскости задан набор из (т + 1)(л + 1)
точек (рис. 3.5)
(*/,)';). ί = 0, 1, ..., т; у = 0, 1, ..., л,
где
Х0 <х{ < ...<*m_i <Хт, Уо<У\<
Добавим к каждой паре
координату цу. (*/, yjy ц).
Тем самым мы получаем массив
-<Уп-\ <Уп-
(дг,,у7) третью
Уп
о
Уо
Υ
' 0
Х(
т
)
Хп
и X
Рис. 3.5.
(*ι, У], Zij\ / = 0, 1 m; у = 0, 1 п.
Прежде чем строить поверхность, проходящую через все точки заданного
массива, определим функцию, графиком которой будет эта поверхность.

Интерполяционным бикубическим S(xyy) сплайном называется функция двух
переменных, обладающая следующими свойствами:
1) S(xt,yj) = г„„1 = 0,1 m;j = ΟΧ.,.η;
2) на каждом частичном прямоугольнике
[■*/. *i+i]x[ty· yj+\\ i = 0> l m_1» J = 0> l n~l
функция
3) на всем прямоугольнике задания [*п,д:т] х [уо»Уя] Функция S(xty) имеет
непрерывную вторую производную.
Для того, чтобы построить по заданному массиву {(*,·, yj, z,y)}
интерполяционный бикубический сплайн, достаточно определить все \6тп коэффициентов.
Как и в одномерном случае, отыскание коэффициентов сплайн-функции сводится к
построению решения системы линейных уравнений, связывающих искомые
коэффициенты alf.. Последняя возникает из первого и третьего условий, после
добавления к ним недостающих соотношений путем задания значений производной
искомой функции в граничных узлах прямоугольника [*o»*m] х [уо»У«] (или иных
соображений).
Прежде чем переходить к рассмотрению задачи сглаживания, подведем
некоторые итоги.
Достоинства предложенного способа несомненны: для решения линейных
систем, возникающих в ходе построения сплайн-функций, существует много
эффективных методов, к тому же эти системы достаточно просты; графики
построенных сплайн-функций проходят через все заданные точки, полностью
сохраняя первоначально заданную информацию.
Вместе с тем изменение лишь одной точки (случай на практике довольно
типичный) требует пересчета практически всех коэффициентов. Часто исходный
набор точек задается приближенно, и, значит, неукоснительное прохождение
графика построенной функции через все точки оказывается излишним.
От этих недостатков свободны некоторые из методов сглаживания, к
описанию которых мы и переходим, расширив класс объектов, в котором будет
вестись поиск соответствующих кривых и поверхностей. Более точно, мы
откажемся от требования однозначного проектирования искомой кривой или
поверхности на координатную плоскость. Такой подход позволяет ослабить и
требования к заданному массиву. Правда, при этом оказывается необходимым
небольшое геометрическое введение.
Начнем, как и прежде, с кривых.
Нам будет удобно пользоваться параметрическими уравнениями кривой.
Напомним необходимые понятия.

Параметрически заданной кривой называется множество γ точек M(x,y,z),
координаты ху уу ζ которых определяются соотношениями
χ = дг(г), у = y(t), z = z(t), a<t<by (1)
где x(t), y(t), z(t) - функции, непрерывные на
отрезке [α, b] (рис. 3.6).
Соотношения (1) называются параметрическими
уравнениями кривой γ.
Без ограничения общности можно считать, что
а = 0 и Ъ = \\ этого всегда можно добиться при
помощи замены вида
t- a
и = .
Ъ-а
Рис. 3 6
Весьма полезна векторная форма записи параметрических уравнений
г = r(t)y 0< t < 1,
где г(0 = (дг(0, y(f), z(O).
Параметр t задает ориентацию
параметризованной кривой γ (порядок прохождения точек при
монотонном изменении параметра). Кривая γ
называется регулярной кривой, если r'(t) * 0 в каждой ее
точке. Это означает, что в каждой точке кривой
существует касательная к ней и эта касательная
меняется непрерывно вслед за перемещением вдоль
кривой ее текущей точки (рис. 3.7) Единичный
вектор касательной к кривой γ равен
Рис 3 7
7V(f) =
\rV)\'
Если дополнительно потребовать, чтобы
задающая кривую векторная функция имела вторую
производную, то определен вектор кривизны кривой
[rV)*r"(t)]xr'(t)
K(t)-
\r'(t)
модуль которого характеризует степень ее
отклонения от прямой (рис. 3.8). В частности, К = 0, Рис 3S
если γ - отрезок прямой.

Υ При дальнейшем изложении мы имеем в виду расположение
рассматриваемых объектов в трехмерном пространстве. Тем не менее,
практически все сказанное будет верно и для плоского случая (более
общего, чем рассмотренный выше). Дело в том, что параметрическое
описание плоской кривой не накладывает никаких ограничений на ее
расположение относительно координатных осей: кривая не обязана
однозначно проектироваться на координатную ось, как это имеет
место в случае ее явного задания у = у(х).
В частности, она вполне может быть замкнутой,
самопересекающейся и т. д. Все последующие
построения будут законны и в этих достаточно
сложных случаях. Рассмотрим некоторые из
возможных подходов к построению сглаживающей
кривой. Пусть на плоскости или в пространстве задан
упорядоченный набор точек, определяемых векторами
V0> Vx Vm (рис. 3.9). Ломаная V0Vx...Vm Рис 3.9
называется контрольной ломаной, порожденной
массивом V = {ν0,ν{ Vm] (рис. 3.10).
Кривой Безье, определяемой массивом V,
называется кривая, определяемая векторным уравнением
'(') = 2Г=0Ст'''(1-')т"'^· 0S,S1-
(2)
ζ
0
ν°-
л2
•~/v3
Υ
Vm-1
коэффициенты в разложении Рис- 3.10
где CL = 4} ^7
т il(m-i)\
бинома Ньютона (число сочетаний из т элементов по / ).
Кривая Безье обладает замечательными свойствами:
• она является гладкой;
• начинается в точке V0 и заканчивается в точке Vm
отрезков VqVi и Vm~\Vm контрольной ломаной;
• функциональные коэффициенты Cltl(\-t)m~l
касаясь при этом
при
Vit i = 0, 1,
суть универсальные многочлены
вершинах
(многочлены
Бернштейна); они неотрицательны, и их сумма
(r + (l-r))w=l.
Σ^'α "Ο*"'
Поэтому кривая Безье целиком лежит в выпуклой оболочке, порождаемой
массивом (рис. 3.11).
Порядок точек в массиве существенно влияет на вид кривой Безье. На рис. 3.12
показан вид кривых Безье для массива из четырех точек. Нетрудно заметить, что,

Рис. 3.11
'^t
Рис. 3 12
находясь в одной и той же выпуклой оболочке, эти
кривые сильно разнятся, пытаясь повторить
контрольную ломаную в гладком варианте.
Основных недостатков у кривых Безье два:
• степень функциональных коэффициентов
напрямую связана с количеством точек в
массиве (на единицу меньше);
• при добавлении хотя бы одной точки
необходимо произвести полный пересчет
параметрических уравнений;
• изменение хотя бы одной точки приводит ~
к заметному изменению всей кривой.
И вновь, как и прежде, попытаемся найти класс
кривых, сохраняющих достоинства кривых Безье и
лишенных их недостатков.
Так как в векторном уравнении, задающем
кривую Безье, векторные составляющие постоянны
(это просто вершины массива), то мы уделим
основное внимание выбору функциональных коэффициентов, стараясь сохранить
при этом их замечательные свойства.
Заменим в векторном уравнении (2) многочлены Бернштейна на В-сплайны
(базовые (base) сплайны).
Новые функциональные коэффициенты введем при помощи рекуррентных
формул.
Пусть 0 = г0 < ({ < ...< rm_! <tm=\
#1.1(0 = 1. rG[r/' 'ι+ll
tfM(0 = 0, t€[th /,+,]
и далее (рис. 3.13)
t-t; жт ,.ч . Ч+q ~ *
i+q-\ ~ Ч Ч+q
Заметим, что с увеличением индекса q степень
многочленов, определяющих вводимые функции, растет: для
функций на отрезке [г,·, ti+q] она равна q - 1.
Отметим еще некоторые очевидные свойства этих
функций:
• Niq(t)>0 на интервале (f/, ti+q);
• N/(?(r) = 0 вне интервала (г,·, ti+q)\
разбиение отрезка [0,1]- Положим
*/.*(') = ■: ^,„-1(0+ '** , *,41tg-l(0-
Ч+а-\ ~ Ч Ч Ч+q ~ Ч+\
ti t,+1 tj+2
N,,3
ti+3 .
ti ti+1 ti+2
Puc 3.13

• на всей области задания функция Nt-^(r), </>3, имеет непрерывные
производные до порядка q - 2 включительно.
* Для построения кубического сплайна Ν,·4(ί) требуется пять узлов
разбиения г,·, г/+1, г/+2, Г/+3» '/+4 отрезка /О, //. Поэтому если узлов не
хватает, то их набор определенным образом расширяют, например
полагая г_3 = r_2 = t_{ = О, tm+l = tm+2 = tm+3 = 1.
Дополнительно введенные отрезки имеют
нулевую длину и первоначальные первый
Го = 0 и последний tm = 1 узлы становятся
кратными. На рис. 3.14 показан полный набор
кубических В-сплайнов, построенных на
расширенном множестве узлов
Г_3 = Г_2 = Г_! = г0 = 0;
fj = 0,2; Г2 = 0,4; г3 = 0,6; г4 = 0,8;
'5 = '6 = '7 = '8 = 1·
Интересно, что для введенных функций
сохраняется равенство
0,4 0,6
Рис. 3.14
Это означает, что кривая, заданная векторным уравнением
(3)
всегда принадлежит выпуклой оболочке вершин массива. Кроме того, она выходит
из вершины Vq и входит в вершину Vm, касаясь конечных отрезков контрольной
ломаной.
В силу третьего свойства сохраняется достаточная гладкость кривой: если
взять </>4, то все функциональные коэффициенты будут иметь непрерывные
вторые производные. Для практических задач большей гладкости, как правило,
не требуется. Поэтому далее мы ограничимся рассмотрением случая, когда q = 4.
Построенная кривая обладает важным
локальным свойством: изменение одной вершины в массиве
уже не ведет, как прежде, к полному изменению всей
кривой. В силу свойств функциональных
коэффициентов пересчета требуют только пять слагаемых.
Коэффициенты при четырех последовательных
вершинах в формуле (3) положительны, и их сумма
равна единице. Это означает, что определяемый ими
отрезок кривой должен лежать внутри их выпуклой
оболочки - четырехугольника в плоском случае и тетраэдра - в пространственном
(рис. 3.15).
Рис 3.15

В-сплайны обладают многими другими замечательными свойствами. В
частности, их можно использовать и для построения замкнутых кривых.
Рассмотрим следующую достаточно типичную ситуацию. По заданному
массиву точек мы построили В-сплайн, вывели результат на экран и, внимательно
изучив то, что получилось, захотели в одном или нескольких местах немного
подправить кривую, не изменяя первоначального массива.
Наиболее подходящим инструментом для подобной процедуры являются
параметры, введенные в уравнение кривой. Такую возможность предоставляют
бета-сплайны, к которым мы и обратимся, описав при этом для большей полноты
картины несколько иной подход, отличный от приведенного выше, а именно
использующий составные кривые.
В построении составной регулярной кривой важную роль играют условия
сопряжения в точках контакта слагающих ее отрезков регулярных кривых.
Пусть Yj и γ2 - регулярные кривые, заданные параметрическими
уравнениями
r = r{(t), 0<r<l; r = r2(t), 0<t<\
соответственно и имеющие общую точку
П(\) = г2(0. (4)
Для того, чтобы кривая γ, составленная из кривых γ, и γ2, была регулярной,
потребуем совпадения в общей точке единичных касательных векторов
г'О) _ г'(0)
(5)
|*"(1)| |г'(0)|
и векторов кривизны
[ηΌ)χη'(1)]χη'(1) = [rj(0) x rj'(O)] x rj(0)
|η'(ΐ)|4 ki(0)|4
(6)
сопрягаемых кривых γ, и γ2.
Нетрудно проверить, что если радиусы-векторы кривых γ, и γ2 связаны
условиями геометрической непрерывности
»i(0) = »i(l),
г2'(0) = Р,гД1),
r2'tO) = pfr,'(l) + p2r1'(l)> (7)
где /?ι > 0, /?2 ^ 0 - числовые параметры, то каждое
из условий (4) - (6) будет выполнено.
Рассмотрим набор из m +1 точек
Vn, V,.
Vm_j, Vm, заданных своими радиусами-
векторами (рис. 3.16).

Будем искать сглаживающую составную регулярную кривую γ при помощи
частичных кривых уп описываемых уравнениями вида
>?('> = Zl=-2VW>· o<t<i (8)
ΤΆβ bja) = J^Mckjifll9fl2)gk. j = -2, -1. 0. 1 - (9)
не зависящие от i весовые функциональные коэффициенты.
Для того, чтобы найти эти весовые коэффициенты, потребуем, чтобы
векторы /)(г) и /;Ч1(0 в точке сопряжения удовлетворяли условиям геометрической
непрерывности (7). С учетом формул (8) эти условия можно записать так:
Σΐ-AW...., = β? ς;,-Α"( w./+ ^K^(\wUi (10)
Это позволяет найти все функциональные коэффициенты
bj{t\ j = -2, -l, 0, 1.
Расписав, например, первое из равенств (10) подробнее
Ь_2{т~\ +*-i(0)V{ +M0)V/+1 +bl(0)Vu2=b.2(\)Vi.2+b.l(\)Vi.x+b0(\)Vi+bl(\)Vi+l
и приравняв коэффициенты при одинаковых векторах, получим
0 = *_2(1),*_2(0) = b.^Wb.^O) = b0(\),b0{0) = ^(1)^,(0) = 0.
Подобным же образом из двух других векторных равенств (9) получаются
соотношения, связывающие значения в точках 0 и 1 первых и вторых
производных весовых коэффициентов.
Привлекая формулы (9), получаем в итоге линейную систему для искомых
чисел ckjt определитель которой
δ=2/ή + 4/?,2 + 4/?! +β2 + 2 > 0.
Вычислим коэффициенты и подставим их в формулы (9).
Найденные выражения для весовых функций
*2(0 = ^0-0\
о
b_.it) = |[2р?г(г2 - Зг + 3) + 2β?(ί3 - Зг2 + 2) + 2β,(Γ3 - Зг + 2) + β2(2Γ3 - Зг2 + 1)1,
δ
W = |(2pif2(-r + 3) + 2β,ί(-'2 + 3) + β/(-2ί + 3) + 2(-r5 + I)],
Ο
о,з

годятся для всей конструкции. Подставляя их в формулу (8), получаем значения
векторных функций
'2(0 'ϋΐ-ΐΟ-
Заметим, что кривая, определяемая векторной
функцией r((f) и, значит, вершинами VJ_j» Vj, VJ+|, V^,
лежит в их выпуклой оболочке (рис. 3 17).
Для того, чтобы составная кривая γ проходила
через вершины V0 и Vm, касаясь отрезков VqVi и
Vm-\Vm контрольной ломаной (рис. 3.18), следует
добавить к полученному набору вектор-функций еще
четыре:
2 з 2 з
r0{0 = (\-—)V0+ — Vl9
г,(0 = [МО + * i(')]V0 + bQ{t)Vx + /7,(r)V2,
^(0 = ΜθνΜ_2 + МОК,, + [Ь0(0 + МЖ>
Я«с J 18
^,ω^^α-04-,+π
о
2β?
(1-ΟΊ.
Тем самым искомая составная - кривая γ -
найдена.
На рис. 3.19 показано, что изменение
параметров β, и β2 влечет изменение формы
результирующей кривой.
В заключение немного поговорим о
сглаживающих поверхностях. И здесь целесообразно
начать с необходимого напоминания.
Регулярной поверхностью называется множество
точек М{ху уу ζ) пространства, координаты ху уу ζ
которых определяются из соотношений
χ = jt(m,v), у = y(u,v), ζ = z(uyv), (м,ν) e D (11)
(здесь D · некоторая область на плоскости
параметров и и ν), где x(utv)y y(utv)y z(uyv) - гладкие
функции своих аргументов, причем выполнено
соотношение
Beta1 = 1,0E+00
Beta2=0,0E+00
Beta1 = 1.0E+00
Beta2=2,OE+01
Рис 3 19
xu(u>v) Уи(и^) zm{u,vY\
*v(M>v) yv(u>v) zv{uyv)j
Рис. 3.20
Приведенное неравенство означает, что в каждой точке регулярной
поверхности существует касательная плоскость и она изменяется непрерывно при
непрерывном перемещении по повехности текущей точки Μ (рис. 3.20).

Уравнения (11) называются параметрическими уравнениями поверхности
Их часто записывают также в векторной форме:
г = r(w,v), (w,v) e D,
где r(w,v) = (x(w,v), )>(w,v), z(w,v)).
В дальнейшем будем считать для простоты, что
область на плоскости параметров представляет собой
квадрат со стороной 1 (рис. 3.21).
Предположим заданным набор точек
ш
Шл
zt \п /г
λ /'ν
0
^^γ
Ν Υ
n=ruxrv
rv
ί = 0, 1,
m; у = 0, 1,
Соединяя Рис. 3.21
Рис. 3.22
соответствующие вершины прямолинейными отрезками,
получаем контрольный многогранник заданного массива V
(рис. 3.22).
Сглаживающая поверхность строится относительно
просто, в виде так называемого тензорного произведения.
Например, уравнение бикубической поверхности Безье
имеет вид
*«.*>=ς;=0ς %0с^о - «)m-v(i - vr' n,.
0<м<1, 0<ν<1.
Это -
0<м<1, 0 < ν < 1 -
уравнение бикубической В-сплайновой поверхности, а это -
0 < и < 1, 0<ν<1 -
уравнение (i,k) -вырезка бикубического бета-сплайна.
Ясно, что так построенные поверхности "наследуют" некоторые свойства
одноименных кривых. Это вытекает из способа их задания.
Мы остановились в этой главе лишь на некоторых простых способах
построения плавно изменяющихся кривых и поверхностей Вводный характер
книги и жесткие ограничения на ее объем не позволяют говорить об этом более
подробно. Тем не менее мы стремились к тому, чтобы у читателя сложилось
правильное начальное представление о геометрических сплайнах и том месте,
которое они занимают в компьютерной графике. По нашему мнению, даже
небольшая самостоятельная попытка компьютерной реализации высказанных здесь
простых геометрических соображений будет, несомненно, полезна в освоении
практически неисчерпаемых возможностей компьютерной графики.

РАСТРОВЫЕ АЛГОРИТМЫ
В
этой главе под дискретной плоскостью будем понимать множество всех
точек с целочисленными координатами на обычной двухмерной плоскости
Дискретную плоскость называют также целочисленной решеткой, растровой
плоскостью или растром.
Рис. 4 1
Простейшие свойства множеств на целочисленной решетке
Для удобства дальнейшего изложения будем
считать, что на плоскости имеется квадратная сетка с
шагом 1, причем узлы нашей целочисленной решетки
являются центрами соответствующих квадратных
ячеек сетки. Другими словами, узлы растра
окружены "единичными" квадратными окрестностями
"радиуса" 1/2. Инициализации точки растра с
координатами (i, j) соответствует закраска каким-
либо цветом ее квадратной окрестности (рис. 4.1).
Точки на плоскости называются 4-соседями (или "непосредственными"
соседями), если у них отличаются только х-координаты или только {/-координаты,
причем только на 1.
Точки на плоскости называются 8-соседями (или "косвенными"соседями),
если у них отличаются х-координаты или {/-координаты, но не более чем на 1.
Заметим, что в соответствии с этими соглашениями всякий
непосредственный сосед является в то же время и косвенным соседом.
Всякая точка на плоскости имеет четырех непосредственных
соседей и восемь косвенных соседей, откуда и второе название для
таких точек. Если точки являются непосредственными соседями,
то их квадратные окрестности имеют общую сторону; квадратные
окрестности косвенных соседей имеют общую сторону или общую
вершину (рис. 4.2).
Введем понятие пути на целочисленной решетке.
4-путем (или сильносвязным путем) на плоскости называется рис 4.2
множество точек, А\, Л2, ..., Ап, для которых точки Ait Ai+i
являются косвенными соседями для / = 1,2, ..., п-\.
8-путем (или слабосвязным путем) на плоскости называется множество точек
А\% Л2,..., Ап, для которых точки А{, At+\ являются слабыми соседями для i = 1,
2, .... /i-l.
Путь называется замкнутым, если Αι = Ап.
• · ·
VN'
• · ·

Множество на целочисленной решетке называется сильносвязным (четырех-
связным), если любые две точки его можно соединить сильносвязным путем.
Множество на целочисленной решетке называется слабосвязным (восьми-
связным), если любые две точки его можно соединить слабосвязным путем.
Попробуем определить кривую на дискретной плоскости, т. е. "одномерное"
множество на целочисленной решетке.
Простой кривой на плоскости называется множество, у которого все точки,
за исключением двух, имеют ровно двух соседей (слабых или сильных, в
зависимости от вида кривой). Эти две исключительные точки имеют ровно по одному
соседу.
Простой замкнутой кривой на плоскости называется множество, у которого
все точки имеют ровно двух соседей (слабых или сильных, в зависимости от вида
кривой).
Простая замкнутая слабосвязная кривая разбивает плоскость на два
сильносвязных множества. Простая замкнутая сильносвязная кривая разбивает
плоскость на два слабосвязных множества.
Растровое представление геометрических объектов
Понятие растрового представления геометрического объекта
В дальнейшем целочисленную решетку будем называть растром.
Предположим, что на обычной двухмерной плоскости имеется некоторый
геометрический объект и нужно получить дискретное представление объекта на
целочисленной решетке, или, как говорят, растровое представление объекта.
Это означает, что заданной геометрической фигуре (линии или области)
следует поставить в соответствие множество на целочисленной плоскости, которое
в некотором смысле является приближением исходной фигуры.
Такое представление неоднозначно, так как, что такое приближение, можно
понимать по-разному и существуют разные способы приближения непрерывного
объекта.
Для "заполненной" геометрической фигуры растровым приближением можно
считать множество точек дискретной плоскости, принадлежащих этой фигуре.
Однако такое определение теряет смысл, если мы хотим получить растровое
представление отрезков прямых или дуг кривых.
Например, растровым приближением круга на плоскости может служить
множество точек, попавших внутрь этого круга, а растровым приближением
прямой - множеств'о точек, являющихся центрами ячеек решетки, с которыми
прямая пересекается.
Можно предложить и другие способы растрового представления этих
объектов.
Важным является вопрос реализации того или иного представления, т. е.
об алгоритмах растровой развертки и об их эффективности.
Уточним задачу. Будем считать, что в нашем распоряжении имеется
элементарная операция - инициализация точки с целочисленными координатами.

В каждом конкретном случае нужно указать алгоритм выбора последовательности
точек, которые нужно инициировать на растре, чтобы получить соответсвующее
растровое представление объекта в целом
Возникает естественный вопрос· зачем нужно знать, как работают алгоритмы
генерации отрезка прямой, окружности или эллипса, алгоритмы закраски
многоугольника или, в более общем случае, области плоскости, если все они
реализованы в виде стандартных процедур в любом пакете типа Turbo Pascal или Turbo С
Дело в том, что монитор не единственное растровое устройство, а при работе с
такими устройствами, как принтер, плоттер, мышь, необходимо уметь программно
реализовывать растровую генерацию соответствующих геометрических объектов
Необходимость "залезть внутрь" алгоритма генерации возникает и тогда,
когда атрибуты инициируемого пиксела (цвет, наличие или отсутствие) зависят от
каких-либо условий. Например, от положения пиксела на прямой или внутри
закрашиваемого многоугольника. Умение построить соответствующий алгоритм
часто позволяет изменить структуру существующего алгоритма с целью ускорения
его работы. Такие ситуации типичны при разработке алгоритмов удаления
невидимых линий и поверхностей (например, для растровой реализации одной из
версий метода плавающего горизонта или метода буфера глубины).
Растровая развертка отрезка. Алгоритм Брезенхема
Процесс последовательной инициализации множества пикселов экрана,
изображающего отрезок прямой линии, называется растровой разверткой отрезка,
а само это множество - растровым представлением отрезка. Из сказанного ясно,
что важно знать не только, как устроено это множество, но и владеть способом
его генерации, т. е. располагать алгоритмом, позволяющим последовательно
строить точки этого множества.
Более точно, если нам известны целочисленные координаты концов отрезка,
мы должны знать, какие точки надлежит последовательно инициировать на
растре, чтобы получить полное растровое представление отрезка Эта задача решается
неоднозначно. Ее решение зависит от того, какого типа растровый образ мы хотим
получить. Даже если ограничить класс растровых представлений отрезка
простыми растровыми кривыми в смысле определений предыдущего пункта, то таких
представлений может быть два - восьмисвязное и четырехсвязное. Возможны и
другие растровые модели отрезка в зависимости от того, какими свойствами мы
хотели бы наделить полученный образ Не углубляясь в обсуждение этого
вопроса, предложим сначала простое, "наивное", решение
задачи.
Чтобы выбрать промежуточные пикселы (точки
растра), которые являются в некотором смысле наименее
удаленными от идеального отрезка, можно, например,
инициализировать последовательно все точки растра, окрестности
которых пересекаются с этим отрезком (рис. 4.3).

Задача. Убедитесь, что в результате получится четырехсвязная
растровая развертка отрезка. Предложите алгоритм последовательной
генерации точек этой кривой.
Пусть концы Λί/ и М2 отрезка имеют координаты (xj, y{) и (х^, l/^)· Тогда
отрезок определяется уравнением у = У\ + к(х - Х\),
где к =у*~у* ,χχ <χ<1χ2.
х2 - хх
Для простоты предположим, что угловой коэффициент к неотрицателен
и не превосходит 1: к < 1.
Ниже представлена процедура генерации растровой развертки отрезка.
QI Dx := 1; Dy ;= abs(y2-yl )/(x2-xl) ;
x:=xl; y:=yl;
for i:=0 to L-l do
begin
PutPixel (x, round(y)) ;
χ := χ + Dx; у ;= у + Dy;
end.
Схема работы этого алгоритма проста: получаем очередную точку на отрезке
и инициируем пиксел, ближайший к этой точке.
Условие к < 1 нужно, чтобы в процессе построения растровой развертки не
было пропущено ни одной точки; шаг по оси χ единичный, а по оси у - меньше 1. Если
угловой коэффицент прямой больше 1, нужно поменять ролями переменные χ и у.
Заметим, что целочисленная абсцисса точки изменяется на каждом шаге на 1, в
то время как целочисленная ордината претерпевает изменение лишь в случае, когда
в результате накопления приращений Dy вещественная ордината точки окажется в
окрестности радиуса 0.5 соседнего уровня по оси ординат. Учтем эти наблюдения и
несколько изменим алгоритм по форме, оставляя основную схему без изменения.
Η χ := xl; у := yl; η := х2 - xl;
т := у2 - yl; d := т/п; е := 0;
for i:=l to n do
begin
{ шаг по оси абсцисс и вычисление отклонения }
χ := х+1; e:=e-hd;
{ если отклонение по оси ординат от текущего
значения у превосходит 1/2, то нужно увеличить у на 1
и скорректировать отклонение е от нового значения у }
if e > 0.5 then
begin
у:=у+1; е:=е-1
end
PutPixel (χ,у)
end

Нетрудно заметить, что в результате работы алгоритма получится
восьмисвязное представление отрезка, так как переход к следующей точке
развертки осуществляется на одну из восьми соседних клеток.
Попытаемся теперь сформулировать соображения, которые позволяют
описать как восьмисвязное, так и четырехсвязное растровые представления
отрезка на плоскости.
Проанализировав расположение отрезка относительно квадратных
окрестностей узлов решетки, можно предложить следующие правила генерации
четырехсвязной и восьмисвязной развертки отрезка:
1) четырехсвязная развертка отрезка включает те и только те точки
решетки, квадратные окрестности которых пересекаются с отрезком;
2) восьмисвязная развертка отрезка включает те и
только те точки решетки, боковые стороны
квадратных окрестностей которых пересекаются
с отрезком (рис. 4.4)
Пользуясь правилом 1), выпишем алгоритм для
генерации четырехсвязной развертки. Имеем
Щ χ := xl; у := yl/
л : = х2 - xl; т := у2 - yl ;
d ;= (т/п); е := d/2;
for i:=l to n+m do
begin
{ шаг по оси абсцисс и вычисление отклонения }
χ := х+1; e:=e-hd;
{ если отклонение по оси ординат от текущего
значения у превосходит 0.5, то надо увеличить у на 1
и скорректировать отклонение е от нового значения у }
if e > 0.5 then
Рис 4 4
begin
end
else
begin
у:=У+1; е:=е-1
=x+l; e:=e-f-d
end
PutPixel(x,y)
end
В этой схеме переменная е выражает разницу между ординатой текущей
точки на прямой и ординатой точки пересечения прямой с правой границей
квадратной окрестности текущей точки растровой развертки.
Если е < 0.5, то отрезок пересекается с боковой стороной квадратной
окрестности точки, лежащей справа от текущей точки, и нужно сместиться вправо на 1.

i-г·
"f-
Если е>0.5, то отрезок пересекается с нижней
границей квадратной окрестности, лежащей выше точки,
и нужно сместиться на 1 вверх. Эти соображения
показывают также, что в результате работы последнего
алгоритма получится четырехсвязная развертка (рис. 4.5).
Известно, что операции с вещественными числами
осуществляются гораздо медленнее соответствующих δι < 0.5; δ2> 0.5
операций с целыми числами. Поэтому для повышения Рис. 4.5
эффективности работы алгоритма желательно освободиться от операций,
использующих вещественную арифметику. С этой целью в алгоритме для получения восьми-
связной развертки отрезка, умножая переменные е и d на целое число 2л, мы
избавляемся от дробных чисел. Изменив "масштаб" переменных и внеся корректировки в
неравенства, используемые в операциях сравнения, получим "целочисленную"
версию алгоритма:
|] х := xl; у := yl ;
л := х2 - xl; т := у 2 - yl;
dx := 2*m; dy := 2*п; е ;= 0; { 1 —> dy = 2*п }
for i:=l to n do
begin
{ шаг по оси абсцисс и вычисление отклонения }
χ := х+1; e:=e-hd;
{ если отклонение по оси ординат от текущего
значения у превосходит 1/2, то нужно увеличить у на 1
и скорректировать отклонение е от нового значения у }
if е > η then
begin
у:=у+1; е:=e-dy
end
PutPixel(x,y)
end
Полученный алгоритм носит название целочисленного алгоритма Брезенхема
для восьмисвязной развертки отрезка в первом квадранте.
Используя аналогичные преобразования, запишем процедуру генерации
четырехсвязной развертки. Имеем:
Η χ := xl; у := yl;
η := х2 - xl; m := у2 - yl;
dx := 2*m; dy := 2*n: e := m;
for i:=l to n+m do
begin
{ шаг по оси абсцисс и вычисление отклонения }
χ := х+1; e:=e-hd;
{ если отклонение по оси ординат от текущего

значения у превосходит 1/2, то нужно увеличить у на 1
и скорректировать отклонение е от нового значения у }
if е > η then
begin
end
else
begin
у:=y+l; e;=e-dy
x:=x+l; e:=e+dx
end
PutPixel(x,y)
end
Полученный алгоритм называется целочисленным алгоритмом Брезенхема
для четырехсвязной развертки отрезка в первом квадранте.
Общий алгоритм Брезенхема
для восьмисвязной развертки отрезка
Для получения общего алгоритма растровой развертки нужно избавиться
от ограничений, которые мы до сих пор накладывали на расположение отрезка
на плоскости, а именно от требования 0 < к < 1 на угловой коэффициент k.
Учитывая ориентацию отрезка относительно положительных направлений
осей координат и меняя ролями переменные χ и у в случае \k\ > 1, получим
окончательные общие версии алгоритма.
Общий алгоритм Брезенхема для восьмисвязной развертки отрезка:
Η PROCEDURE line_8(xl,yl,x2,y2: integer);
VAR
x,y,sl,s2,dx,dy,e,z: integer;
change: boolean;
BEGIN
χ: =xl ; у: =yl; dx: =abs (x2-xl) ; dy: =abs (y2-yl) ;
si:=sign(x2-xl); s2:=sign(y2-yl);
if dy>dx then
begin z:=dx; dx:=dy; dy:=z;
change:=true
end
else change:=false;
e:= 2*dy-dx;
for i:=l to dx do
begin
putPixel(x,y,color);
while e>=0 do
begin

if change then x:=x+sl
else y:=y+s2; e:=e-2*dx;
end;
if change then y:=y+s2
else x:=x+sl;
e:=e-h2*dy
end;
putPixel(x,y,color)
END;
Общий алгоритм Брезенхема для четырехсвязной развертки отрезка:
Д PROCEDURE line_4(xl,yl,x2,у2: integer);
VAR
х,у,sl,s2,dx,dy,e,z: integer;
change: boolean;
BEGIN
x: =xl ; у: =yl ; dx : =abs (χ2-xl ) ; dy: =abs (y2-yl ) ;
sx:=sign(x2-xl); sy:=sign(y2-yl); e:= 2*dy-dx;
if dy<dx then change:=false
else
begin z:=dx; dx:=dy; dy:=z;
change:=true
end
for i:=l to dx-f-dy do
begin
if e < dx then
begin
if change then y:=y-hsy
else x:=x-f-sx;
e:=e-h2*dy;
end
else
if change then x:=x+sx
else y:=y+sy;
e:=e-2*dx
end;
putPixel(x,y,color)
END;

Заполнение сплошных областей
Вопрос о заполнении внутренности сплошной области занимает важное место
среди задач растровой графики. Большинство задач о заполнении двухмерной
фигуры может быть отнесено к одному из двух типов: заполнение внутренности
многоугольника, заданного своими вершинами или ребрами, и заполнение
внутренности области, ограниченной замкнутым контуром, представленным своей
растровой разверткой.
Тест принадлежности точки многоугольнику
Будем понимать под многоугольником фигуру, ограниченную на плоскости
простой (несамопересекающейся) замкнутой ломаной. Сама ломаная задается
набором своих вершин Л(-(дс,·, у{), i = 1, 2, .... я, причем соседние точки в этом
списке являются смежными вершинами ломаной. Задача состоит в том, чтобы
получить растровую развертку многоугольника, т. е. инициировать его внутренние
точки.
Начнем с обсуждения задачи о локализации точки относительно
многоугольника. Решение этой задачи даст возможность эффективно определять, является ли
точка внутренней или внешней по отношению к нему.
Знаменитая теорема Жордана утверждает, в частности, что простая (т е.
не имеющая самопересечений) замкнутая плоская ломаная разбивает плоскость
на две связные компоненты - ограниченную, которая является внутренностью
многоугольника, и неограниченную, которая является ся внешней по отношению
к многоугольнику.
Алгоритм должен уметь различать внутренние и внешние точки плоскости.
Обозначим ребра многоугольника через £,·:
Е- \AitAi+Il i = 1, 2, .... п.
Пусть Р(х, у) - некоторая точка плоскости, не лежащая на ломаной, и
нужно определить, принадлежит она этому многоугольнику или нет.
Проведем через точку Ρ горизонтальную полупрямую с правым концом в
точке Р. Так как ломаная ограничена, то всегда легко найти на этой полупрямой
достаточно удаленную точку Q, которая заведомо не принадлежит
многоугольнику. Если отрезок QP не имеет пересечений с границей многоугольника, то точки
Q и Ρ лежат в одной компоненте связности и, следовательно, точка Ρ · внешняя.
Рассмотрим случай, когда отрезок QP _/\
пересекает ломаную (рис. 4.6). Будем двигаться от /\ ~/^ \
точки Q в направлении к точке Р. Миновав первое —/- V -т- · \
пересечение отрезка и границы, мы попадем внутрь ^ \
многоугольника. Миновав следующее пересечение ~~Х~ * у
отрезка и границы, мы окажемся снаружи ^ч /
многоугольника, и так далее. Легко видеть, что если ———^/
мы встретим на своем пути четное число рис 4.6
пересечений, то точка Ρ будет внешней точкой
многоугольника. Если же число пересечений окажется нечетным, то точка Ρ будет
внутренней точкой многоугольника. Важно только удостовериться, что

пересечения отрезка с границей были существенными, т. е. отрезок действительно
пересек ломаную, а не просто касался ее в одной из вершин.
Для выявления существенных пересечений можно воспользоваться
следующим правилом. Пересечения отрезка с горизонтальными ребрами игнорируются.
При подсчете числа пересечений негоризонтальных ребер ломаной с отрезком PQ
пересечение игнорируется, если точкой пересечения является верхняя вершина
ребра, и засчитывается в любом другом случае. С учетом этого соглашения
касание отрезка PQ с ломаной в точках максимума игнорируется, а в точках
минимума считается дважды. Тем самым несущественные пересечения не
изменяют четности общего числа пересечений. Если же существенное пересечение
имеет место в вершине ломаной (верхнее ребро пересекает отрезок PQ в нижней
вершине, а нижнее ребро - в верхней вершине, и по нашему соглашению
принимается во внимание лишь первое пересечение), то число подсчитанных
пересечений увеличивается на единицу.
Высказанные выше соображения приводят к следующему алгоритму:
Η begin
s:=0;
for i:=l to η do
if { ребро не горизонтально } then
if { ребро пересекает PQ не в верхнем конце }
then s := s+1;
if { s четно } then {Ρ снаружи }
else { Ρ внутри }
end.
Заполнение многоугольников
Для заполнения внутренности многоугольника можно было бы
воспользоваться описанным выше тестом принадлежности, перебирая последовательно точки
растра и инициируя те из них, которые лежат внутри многоугольника. Такой
алгоритм прост и понятен, однако в смысле временных затрат очень
неэффективен. Его можно несколько улучшить, поместив многоугольник внутрь
минимального объемлющего прямоугольника со сторонами, параллельными осям координат,
и анализировать лишь те точки, которые попали внутрь прямоугольника.
Ломаная, ограничивающая многоугольник, разбивает всякую горизонтальную
прямую на чередующиеся интервалы, лежащие внутри или снаружи
многоугольника. Для определения концов этих интервалов можно поступить следующим образом.
Зафиксируем горизонтальную прямую L, на которой предполагается
определить местоположение интервалов, находящихся внутри многоугольника,
ищем точки пересечения с этой прямой, если они есть, каждого ребра
многоугольника. Для проверки наличия пересечения предварительно убедимся
в том, что концы ребра расположены по разные стороны от прямой.
При поиске точек пересечения будем пользоваться правилами,
примененными в тесте принадлежности. Тогда кратные пересечения с контуром
многоугольника в его вершинах будут правильно учтены. Далее упорядочим

Рис 4 7
Рис. 4.8
полученные точки слева направо и сгруппируем их
попарно. Эти пары и будут являться концами
интервалов, лежащих внутри многоугольника и
подлежащих закраске (рис. 4.7).
Изложенная схема заполнения многоугольника
носит название заполнения в порядке сканирования
строк, а сам алгоритм относится к типу алгоритмов
построчного сканирования.
Для ускорения работы алгоритма можно
предварительно упорядочить ребра в порядке возрастания
наибольшей из ординат концов. При перемещении
сканирующей прямой сверху вниз проверке на пересечение
подвергаются лишь те ребра, у которых значение
максимальной ординаты больше ординаты сканирующей
прямой. При этом из списка исключаются ребра,
значение минимальной ординаты которых больше
ординаты сканирующей прямой. Таким образом
поддерживается информация о множестве "активных" ребер,
пересекающихся со сканирующей прямой (рис. 4 8).
Приведенный алгоритм пригоден для заполнения
произвольных многоугольников. Если же
многоугольник является выпуклым, то алгоритм можно
упростить и повысить его эффективность. Заметим, что
границу выпуклого многоугольника можно разбить на
две ломаные - "левую" и "правую" и, возможно, два
ребра - "верхнее" и "нижнее" так что каждая из
боковых ломаных имеет ровно одно пересечение с
каждой сканирующей прямой (рис. 4 9) Используя
алгоритм Брезенхема и одновременно генерируя
растровое представление для ребер левой и правой ломаных
границы, получим левый и правый пикселы границы многоугольника на каждой
сканирующей горизонтальной прямой. Последовательно заполняя интервалы
между этими пикселами для каждого значения ординаты от верхней строки
развертки к нижней, получим растровую развертку выпуклого многоугольника
Алгоритмы заполнения области с затравкой
В алгоритмах заполнения области с затравкой используется иной подход
В них предполагается, что граница области задана на растровой плоскости и
указана одна из внутренних точек области, которая называется затравочной
Требуется заполнить определенным цветом связную компоненту области, содержащую
затравочный пиксел Под связностью понимается 4- или 8-связность на дискретной
плоскости (в зависимости от постановки задачи) Можно представить, что в
затравочной точке находится источник, заливающий всю область определенным
цветом. Поэтому этот процесс иногда называют заливкой области
Рис 4 9

Опишем алгоритм заполнения области с затравкой, использующий стек Под
стеком понимается линейный массив (список) элементов, причем вставки и удаления
элементов можно производить лишь с одного конца, т. е. если элемент был вставлен
в список последним, он должен быть обработан и удален из списка первым
Будем предполагать, что нужно получить заполнения 4-компоненты,
ограниченной заданным контуром
Начнем с того, что поместим затравочной пиксел в стек Далее, пока стек не
пуст, будем извлекать из него очередной пиксел и, закрасив его, анализировать
пикселы, соседние с ним Если среди них есть пикселы, не принадлежащие
границе и не окрашенные нужным цветом, то поместим их в стек. После этого
вернемся к операции извлечения пиксела из стека. По окончании работы
алгоритма все внутренние пикселы области будут закрашены.
Формально алгоритм можно описать так*
Η {erf x, у; - цвет пиксела с координатами (х,у)
Сь - цвет границы, С± - цвет внутренности области.
(хо'Уо) ~ координаты затравочного пиксела.}
{ Помеща ем (хо, у о ) в стек. }
while { стек не пуст } do
begin
{ извлекаем пиксел (х,у) из стека }
if (с(χ,у) о Ci) then с(χ,у) := Ci;
for { каждого соседнего пиксела (х,у) } do
if (с(х,у) о СЪ) and (с(х,у) <> Ci) then
{ поместить пиксел (х,у) в стек }
end
Приведенный выше алгоритм заполнения области весьма неэффективен, так
как предполагает неоднократную обработку одних и тех же пикселов и
неконтролируемый рост величины стека Ниже приводится более эффективный
алгоритм заполнения области
Построчный алгоритм заполнения с затравкой
Применим идею построчного сканирования для
решения задачи заполнения Заметим, что на каждой
строке множество пикселов, подлежащих закраске,
состоит из интервалов, принадлежащих внутренности
области. Эти интервалы отделены друг от друга
интервалами из пикселов, принадлежащих границе Рис 4 10
или внешности области Кроме того, если набор пикселов образует связный
интервал, принадлежащий внутренней части области, то пикселы на и под этим
интервалом либо являются граничными, либо принадлежат внутренней части
области (рис 4 10) Последние могут служить в качестве затравочных пикселов
для строк, лежащих выше и ниже рассматриваемой строки. Принимая
во внимание сказанное, можно предложить следующую схему заполнения области

Инициализируем стек, помещая в него затравочный пиксел. Пока стек не пуст:
Φ извлекаем пиксел (х,у) из стека;
Φ заполняем максимально возможный интервал, в котором
находится пиксел, вправо и влево вплоть до достижения
граничных пикселов;
G) запоминаем крайнюю левую Lx и крайнюю правую Rx
абсциссы заполненного интервала;
® в соседних строках над и под интервалом (Lx,Rx)
находим незаполненные к настоящему моменту внутренние
пикселы области, которые, как мы уже заметили,
объединены в интервалы, а в каждом из этих интервалов
находим крайние правые пикселы. Каждый из этих
пикселов вносим в стек в качестве затравочного.
Алгоритм правильно заполняет любую область,
в том числе и такую, в которой присутствуют
отверстия (рис. 4.11).
Рис 4 Π
{Рор(х,у) - процедура, которая
извлекает из стека координаты очередного пиксела,
Push(х,у) - процедура, которая помещает в стек координаты
пиксела
С(Х*У) - цвет пиксела с координатами (х,у)
С£ - цвет границы, С± - цвет внутренности области.
(х0,у0) - координаты затравочного пиксела.}
Push(xo,yo);
while { стек не пуст } do
begin
{извлекаем пиксел из стека и инициализируем его}
Рор(х,у); с(х,у) := Ci;
xm:=x; {запоминаем абсциссу пиксела затравки}
while c(x,y)<>Cb do {заполняем интервал справа}
5 6/

begin
с(χ,у):=Ci; χ:=x+l
end;
Rx:=x-1; {запоминаем крайний справа пиксел интервала}
x:=xm; {восстанавливаем абсциссу пиксела затравки}
while с(χ,у)<>Cb do {заполняем интервал слева}
begin
с(х,у):=Ci; x:=x-l
end;
Lx:=x+1; {запоминаем крайний справа пиксел интервала}
х:=хш; {восстанавливаем абсциссу пиксела затравки}
{находим затравочные пикселы на нижней строке
начиная с левого края интервала (Lx,Rx), затем ту же
операцию проделываем на верхней строке }
for j:=-l step 2 to 1 do
begin
y:=y+l; x:=Lx;
while χ <= Rx do
begin
Emp ty: =fa lse;
while (c(x/y)<>Cb)and(c(x/y)<>Ci)and(x<Rx) do
{точка внутри не заполнена}
begin
if not Empty then Empty:=true; x:=x-hl
end;
{крайний справа пиксел помещаем в стек}
if Empty then
begin
if(x=Rx)and(c(x,y)<>Cb)and(c(x,y)<>Ci) then
Push(x,y)
else Push(x-1 ,y) ;
Empty:=false
end;
{ищем другие незаполненные интервалы на строке}
xb:=x;
while (c(x,y)=Cb)or(c(x,y)=Ci)and(x<Rx) x:=x+l;
if x=xb then x:=x+l
end
end {for}

УДАЛЕНИЕ НЕВИДИМЫХ ЛИНИЙ И ПОВЕРХНОСТЕЙ
С.
'оздание реалистических изображений трехмерных тел является одной из
важнейших задач машинной графики. Основная трудность, возникающая при
разработке эффективных методов визуализации, состоит в необходимости создания
достаточно качественного изображения за ограниченное время. Проблема
удаления невидимых линий и частей поверхностей является одной из наиболее
сложных составляющих общей задачи визуализации трехмерных объектов. Способы
достижения эффектов прозрачности, отражения и т. п., строго говоря, не входят в
задачу удаления невидимых частей трехмерных объектов и, тем не менее,
некоторые из них, такие, например, как построение теней, тесно связаны с настоящей
проблемой и могут быть естественно встроены в рассматриваемые алгоритмы.
Постановка проблемы и терминология
Рассмотрим общую постановку задачи удаления невидимых частей
поверхности, подлежащей визуализации.
Предположим, что в пространстве расположен некоторый объект, заданный
ограничивающей его поверхностью (не обязательно связной); изобразим, что
видит наблюдатель, находящийся на некотором расстоянии от этого объекта.
Формализация приводит к такой постановке
задачи. Выделим в пространстве R3 некоторую
плоскость R2. Пространство R3 в дальнейшем будем
называть объектным пространством, а плоскость R2 -
картинной плоскостью. Пусть в объектном пространстве
находится некоторая поверхность S, расположеннная
по одну сторону от картинной плоскости. Будем
считать, что наблюдатель расположен по другую сторону
от картинной плоскости в центре проектирования (в
случае ортогональной проекции центр
проектирования бесконечно удален) (рис. 5.1).
Будем говорить, что точка р\ поверхности S
загораживает точку р2 этои поверхности, если
проекции этих точек на картинную плоскость
совпадают и при этом точка р\ оказывается
расположенной между р2 и их общей проекцией на
картинную плоскость. Точка ρ поверхности
называется видимой, если эта точка не загорожена
никакой другой точкой поверхности (рис. 5.2).
ABC
Рис. 5.2

Задача удаления невидимых частей поверхности состоит в выявлении всех ее
видимых участков и изображении их на картинной плоскости.
Несмотря на кажущуюся простоту постановки задачи, на сегодняшний день
не известен универсальный высокопроизводительный алгоритм удаления
невидимых линий и поверхностей. Ниже мы рассмотрим некоторые подходы к решению
этой задачи, которую часто называют также задачей загораживания.
Начнем с некоторых простых эвристических соображений, которые могут
служить отправной точкой для решения задачи загораживания.
A. Пусть сцена разбита на два фрагмента - А и В. Если
самые дальние точки фрагмента А лежат ближе к
наблюдателю, чем самые ближние точки фрагмента
В, то части Б, очевидно, никак не могут загородить
фрагмента А. Поэтому, если мы сначала построим
изображение фрагмента В, а затем изображение
фрагмента А, то в результате получим правильное
изображение всей сцены. Тем самым мы
устанавливаем приоритет, в соответствии с которым нужно
производить обработку исходных данных для получения целостного
изображения (рис. 5.3).
Б. Предложим несколько иной способ вычисления приоритетов отдельных
фрагментов сцены. Пусть в объектном пространстве нам удалось найти
плоскость, которая разделяет все пространство на такие два
полупространства, в одном из которых находятся фрагмент А и наблюдатель, а в
другом - фрагмент В. Ясно, что при этих условиях фрагмент В не может
загораживать фрагмент А.
В качестве примера рассмотрим сцену, состоящую
из двух непересекающихся шаров. В данном случае
разделяющая плоскость строится легко: она проходит через
точку отрезка, соединяющую центры шаров перпендикулярно
ему (рис. 5.4). Остается лишь узнать, в какое
полупространство попал набюдатель.
Если непересекающиеся фрагменты А и В выпуклы,
то, как известно, разделяющая плоскость обязательно
имеется. Если же фрагменты А и В невыпуклы, то можно попытаться поместить
их в непересекающиеся выпуклые тела (например, в шары возможно меньших
радиусов), что в случае успеха позволит свести задачу к предыдущему более
простому случаю. Так же можно поступить и при вычислении расстояний до
наблюдателя (см. А)
B. Предыдущие примеры показывают, что полезно установить, при каких
условиях обработка одного из фрагментов сцены, скажем А, может
производиться позже, чем обработка другого фрагмента, и при этом изображение
в целом ^останется правильным. Полезно также знать, когда два фрагмента
могут обрабатываться независимо друг от друга. Даже если у нас нет
^

Рис 5 5
средств для параллельных вычислении, решение задачи загораживания
в подобных случаях все равно заметно упрощается. Например, если
проекции фрагментов А и В на картинную плоскость не пересекаются,
то обработка каждого из них может производиться независимо.
Общая задача о пересечении проекций произвольных объектов весьма
сложна, однако использование простых достаточных условий непересечения часто
оказывается полезным. Например, описав вокруг проекций прямоугольники со
сторонами, параллельными осям координат, и убедившись, что они не пересекаются
(это сведется к проверке нескольких неравенств), мы можем быть уверены, что
исходные фигуры также не пересекаются. Правила вычисления приоритета или
установления факта независимости фрагментов должны быть достаточно
простыми, иначе "средство" не оправдает "цель"
Г. Заметим, что высказанные выше соображения
можно применить для построения каждого из
фрагментов А и В: нужно только разбить фрагмент
А на подфрагменты А' и А\ а фрагмент В - на В* и
В" и снова применить описанную выше процедуру.
Идея этого метода состоит в применении общего
принципа, известного под названием "разделяй и
властвуй". Вместо решения одной сложной задачи
рекурсивно решается серия простых задач. Задача
дробится до тех пор, пока ситуация не упростится настолько, что ее
можно будет разрешить на основе простых правил (рис 5.5)
Д. Вместо того, чтобы расчленять сцену, можно попытаться разбивать
картинную плоскость и обрабатывать независимо те части изображения,
которые попадают в соответствующие фрагменты картинной плоскости.
Принцип тот же, что и выше (см. Г), только анализ производится не в
объектном пространстве, а на плоскости изображения.
Е. Нетрудно заметить, что свойства сцены связаны со свойствами
изображения на картинной плоскости, и поэтому их стоит учитывать при выборе
метода решения задачи загораживания.
Например, такие "хорошо организованные" объекты, как выпуклые
многогранники или гладкие несамопересекающиеся поверхности, существенно
отличаются по своим свойствам от большого количества произвольных многоугольников,
нагроможденных случайным образом в пространстве. Первая и вторая сцены в
отличие от третьей обладают свойством так называемой когерентности по
видимости. Это свойство выражается в том, что в силу определенной упорядоченности
видимость каждого элемента сцены зависит от видимости близлежащих
элементов, а характер видимости меняется некоторым регулярным образом. Например, в
случае выпуклого многогранника всякая грань либо полностью видима, либо
полностью невидима. Это свойство будет использовано несколько позже при
обсуждении способов визуализации выпуклых тел.

Невыпуклые многогранные поверхности подобным
свойством не обладают, однако и в этом случае изменение
видимости при переходе от одних элементов к соседним
также носит регулярный характер. А именно, либо элемент
полностью невидим, либо полностью видим, либо если он
частично видим, а частично нет, то его проекция на
картинную плоскость обязательно пересекается с проекцией
другого ребра многогранника, через которое проходит
складка проектирования поверхности многогранника на
картинную плоскость, т. е. такая последовательность ребер Рис 5.6.
многогранника, каждое из которых является смежным к двум граням, различным
образом ориентированным по отношению к наблюдателю (нормали к этим граням
направлены в разные стороны относительно луча проектирования) (рис 5 6). Это
свойство характера видимости граней многогранной поверхности и аналогичное
свойство, имеющее место в случае гладких поверхностей, является основанием
для применения в задачах загораживания так называемых методов
количественной невидимости.
Известные методы решения задачи загораживания различаются между собой
по четырем основным характеристикам:
• выбору структуры данных для представления поверхности;
• пространству, в котором происходит анализ видимости;
• способу визуализации поверхности;
• использованию специфических геометрических свойств изображаемых
объектов.
Важной характеристикой метода является "асимптотическое" время работы
соответствующего алгоритма в зависимости от разрешения изображаемого
объекта и разрешения картинной плоскости. Это время может быть связано со
свойствами изображаемой поверхности, внутренней структурой используемого
алгоритма, а также некоторыми другими факторами.
Рассмотрим эти характеристики подробнее.
Представление поверхности может быть:
• аналитическим - поверхность представлена неявно при помощи
аналитического выражения; такое представление обычно используется для
задания простых объектов - сфер, конусов, цилиндров и т. π ;
• полиэдральным - поверхность представлена совокупностью многоугольных
граней;
• параметрическим - в виде набора частей, каждая из которых представляет
собой параметрически заданную поверхность; нередко при помощи
триангуляции такие поверхности заменяют их представлением в виде
многогранника.
Под разрешением полиэдральной поверхности понимается количество ее
граней. Под разрешением картинной плоскости понимается количество точек растра
(пикселов) на экране монитора.

Ребра многогранника и линии сетки параметрического
представления называют каркасными линиями, а соответствующее
изображение - каркасным. Если же поверхность изображается с
использованием полутоновой закраски ее элементов, то такое
изображение называется полутоновым, а сам процесс закраски - Рис. 5.7
полутоновым заполнением (граней) (рис. 5.7). Процесс полутонового заполнения
часто сам представляет собой нетривиальную задачу компьютерной графики.
По типу пространства, в котором происходит анализ видимости, алгоритмы
делятся на три группы:
• объектные - анализирующие взаимное расположение частей поверхности
в объектном пространстве (временные характеристики таких алгоритмов
обычно обладают квадратичной зависимостью от числа объектов сцены
и их разрешения);
• картинные - определяющие видимость каждого элемента картинной
плоскости (пиксела) в плоскости изображения (временные характеристики
таких алгоритмов оцениваются как линейные функции от произведения
числа объектов на число точек растра);
• смешанные - использующие для анализа как первый, так и второй подход.
По способу визуализации алгоритмы загораживания разделяются на две
группы, в одну из которых входят алгоритмы, ориентированные на получение
каркасного, а в другую - полутонового изображения.
Под глубиной элемента поверхности понимается расстояние от этого
элемента до картинной плоскости. В алгоритмах загораживания широко используются
две специфические процедуры: тест глубины и тест принадлежности, смысл
которых будет ясен из дальнейшего изложения.
Некоторые подходы к решению задач загораживания
Методы переборного типа
Алгоритмы переборного типа были исторически
первыми алгоритмами, решающими задачу загораживания. Часто
их относят к методам "грубой силы", так как при анализе
видимости предполагается прямой перебор элементов сцены.
При их создании стремились точно решить задачу о том,
какие именно части элементов сцены должны быть удалены
Поэтому эти алгоритмы лучше разработаны для получения ^х^! ^
каркасных изображений. В алгоритмах переборного типа, как
правило, рассматривается каждое ребро, принадлежащее
каждому из объектов сцены, и анализируется его взаимное
., Рис. 5.8
расположение со всеми гранями каждого из объектов,
составляющих сцену (рис. 5.8). При этом возможны следующие ситуации.
А. Ребро находится в том же полупространстве относительно грани, что и
наблюдатель.
В этом случае ребро полностью видимо относительно этой грани.

Б. Ребро полностью расположено в полупространстве, не содержащем
наблюдателя.
Сначала нужно выяснить, не закрыто ли оно гранью. При анализе
взаимного расположения проекции ребра и проекции контура грани на
картинную плоскость достаточно проверить, расположена ли первая проекция
вне второй или пересекается с ней. В первом случае ребро видимо
относительно грани. Во втором случае проверяем, лежит ли первая проекция
полностью внутри проекции грани. Если да, то ребро полностью закрыто
гранью и его нужно исключить из дальнейших рассмотрений. Если же оно
частично закрыто гранью, то нужно выявить видимые части проекции и
перейти к анализу взаимного расположения ребра с очередной гранью.
В. Ребро пересекается с плоскостью, несущей рассматриваемую грань
В этом случае следует разбить ребро на две части точкой пересечения
и применить описанные выше процедуры для каждой из частей
После завершения процесса будут известны все видимые части ребра
Временная сложность алгоритмов такого типа пропорциональна
произведению количества ребер и количества граней в сцене, τ е является квадратичной
от числа элементов сцены (или разрешения объекта). Никакие дополнительные
свойства изображаемых объектов не учитываются
Метод Z-буфера
Другим методом "грубой силы" является метод z-буфера, который весьма
удобен для аппаратной реализации ввиду простоты алгоритма и используемого в
нем набора операций Временные характеристики этого метода линейно зависят
от количества точек растра и "глубинной сложности сцены", τ е усредненного
числа граней, взаимно закрывающих друг друга
Подчеркнем, что время работы алгоритма не зависит от разрешения объекта
(числа граней поверхности многогранника).
Как правило, метод привлекается для изображения
сложных сцен с применением ортогонального
проектирования на картинную плоскость. Для его реализации
используются две области памяти: буфер глубины (z-буфер) и
буфер кадра (хранящий информацию о состоянии пикселов
экрана компьютера) Буфер глубины используется для
хранения координаты ζ (глубины) каждого видимого на
данной стадии анализа изображения пиксела картинной рис 5 9
плоскости В буфере кадра запоминаются атрибуты
(интенсивность и цвет) соответствующего пиксела (рис. 5 9).
В начальный момент буфер глубины инициализируется значением глубины
фона, а буфер кадра - атрибутами фона В процессе работы проекция очередной
грани объекта разлагается в растр После этого анализируется глубина (значение ζ)
каждого нового пиксела изображения путем сравнения ее с глубиной того

пиксела, который имеет ту же проекцию на картинную плоскость и уже занесен в
буфер глубины.
Если значение ζ нового пиксела проекции меньше значения глубины
соответствующего пиксела в z-буфере, то рассматриваемый элемент изображения
находится ближе к картинной плоскости, чем часть уже построенной сцены. В этом
случае атрибуты нового пиксела заносятся в буфер кадра и, кроме того,
производится корректировка координаты ζ соответствующего элемента буфера глубины
Если же сравнение дает противоположный результат, то никаких действий
не производится и, следовательно, буфер глубины и буфер кадра сохраняются
без изменений. Таким образом, на каждом шаге мы имеем "правильное
изображение" той части сцены, которая уже подверглась анализу.
Формальное описание метода таково. Предположим, что сцена представлена
в виде объединения многоугольников (возможно, пересекающихся) Построим
ортогональную проекцию сцены на картинную плоскость ζ = 0.
Предлагается следующая последовательность шагов:
Φ Инициализировать буфер кадра фоновыми значениями
интенсивности или цвета,
(2) Инициализировать буфер глубины значениями глубины фона.
G) Для каждой грани сцены последовательно:
® преобразовать проекцию грани в растровую форму;
(3) для каждого пиксела проекции вычислить его глубину
z=z(x,y);
© сравнить значение z(x,y) с соответствующим значением
буфера глубины Z(x,y).
Φ Если z(x,y) < Z(x,y), то:
Φ записать атрибуты этого пиксела в буфер кадра;
(2) записать значение z(x,y) в соответствующую позицию
буфера глубины Z(x,y).
® Иначе никаких действий не производить.
Алгоритм, использующий метод z-буфера, легко модифицировать для
получения сечений поверхности параллельными плоскостями Пусть нас интересует
изображение части сцены, расположенной между параллельными плоскостями,
Z\ < Ζ < Ζ2·
Требуемое изображение можно получить, если
выводить на экран проекции только тех точек поверхности,
значение глубины которых в сцене лежит в интервале
между ζ\ и Ζ2 (рис. 5.10). Для этого оператор сравнения в
предыдущем описании нужно заменить на следующий:
(ζ(χ, у) < Ζ(χ, у)) и (ζ! < ζ(χ, у) < ζ2).

В результате на картинной плоскости останутся только те части сцены,
которые заключены между секущими плоскостями, параллельными картинной
плоскости и расположенными в пространстве по отношению к картинной плоскости
соответственно "на глубине" Z\ и ζ2·
Удаление нелицевых граней многогранника
Пусть в пространстве задан многогранник (не обязательно выпуклый). Задача
состоит в построении его изображения на картинной плоскости либо с
использованием центральной проекции с центром проектирования Р, либо ортогонального
проектирования с направляющим вектором /.
Пусть F - некоторая грань многогранника. Плоскость,
несущая эту грань, разделяет пространство на два
полупространства. Назовем полупространство, в которое "смотрит"
внешняя нормаль к грани F, положительным (рис. 5.11).
В случае центральной проекции назовем грань F
многогранника лицевой, если центр проектирования Ρ лежит в
положительном по отношению к грани F полупространстве,
и нелицевой, если Ρ лежит в отрицательном полупрост- рис 5//
ранстве. В случае ортогональной проекции назовем грань F
лицевой, если вектор проектирования / и вектор η внешней нормали к грани F
образуют острый угол, и нелицевой - в противном случае
Если многогранник является выпуклым, то удаление
всех нелицевых граней полностью решает задачу
визуализации с удалением невидимых граней. В случае
произвольного многогранника нелицевые грани заведомо
невидимы, поэтому нужно проанализировать на предмет
видимости лишь лицевые грани многогранника Хотя в этом ?ис 5 12
случае метод не дает окончательного решения, тем не менее количество граней,
подлежащих анализу, можно сократить примерно вдвое, так как нелицевые грани
заведомо невидимы (рис. 5 12). Подчеркнем, что эти соображения применимы
лишь к поверхности, являющейся границей некоторого трехмерного тела
Формальное описание метода
Пусть F\, F2, .., /*n - грани многогранника. Рассмотрим одну из граней
Например, F,
Обозначим вершины, инцидентные грани Fv через V\, V2, , Vy
Найдем вектор нормали к грани Fj, вычислив векторное произведение любых
двух смежных ребер этой грани. Имеем*
nrWi V2. Vr2 V3\
Пусть л{ = (Av Bv С,·), тогда опорная функция грани Fj имеет вид:
Цр) = Atx + В& + Ctz + Dif Di = - (nifV,)f
где ρ = ρ(χ, у, ζ)

Тогда уравнение плоскости, несущей грань Fx, можно записать так:
Ljix, у, ζ) = 0.
В случае, если многогранник является выпуклым, коэффициенты Ах, Вх и С,·
легко выбрать так, чтобы вектор пх = (А\, Bv Сх) был вектором внешней нормали.
Для этого найдем какую-либо внутреннюю точку многогранника W, например его
барицентр:
W = (Р! + Р2 +...+ Pm)/m,
где Р\, Ρ<ι, ·-, Рт ■ множество всех вершин многогранника;
и положим kx = - sign(Lj(W))
и, далее,
At:= к{А{, Bt:= kfiit Ct:= kfiit Dt:= £Д·.
Положительное R+ и отрицательное R. по отношению к грани Fx
полупространства определяются соответственно неравенствами
Ц() > 0 и L{(p) < 0.
Сформулируем условия, определяющие, является ли грань лицевой
В случае центрального проектирования грань Fx является лицевой, если
Lx(p) > 0, и нелицевой, если Lx(p) < 0.
В случае ортогонального проектирования грань Fx - лицевая, если (пх, I) > 0,
и нелицевая,если (пх, I) < 0.
Методы количественной невидимости
Методы количественной невидимости основаны на подсчете числа точек,
закрывающих данную точку поверхности.
Рассмотрим на поверхности целочисленную функцию, значение которой в
точке поверхности определяется как количество закрывающих ее точек. Эта
функция называется функцией количественной невидимости точки и обозначается
через v(x).
Обозначим через f(x) отображение проектирования гладкой поверхности S
на картинную плоскость R2.
Точка поверхности называется регулярной точкой
отображения /, если она вместе с некоторой своей малой
окрестностью проектируется взаимно однозначно на
картинную плоскость, и нерегулярной, если это условие не
выполнено (рис. 5.13)
Множество всех нерегулярных точек отображения /
естественным образом распадается на связные компоненты,
каждая из которых, как правило, имеет структуру гладкой Рис- 5 13
кривой, лежащей на поверхности. Эти кривые часто называют контурными
линиями. Видимые части контурных линий составляют очертания любого
предмета (рис. 5.14).

Рис 5.15
Если поверхность находится "в общем положении", то
отображение проектирования имеет лишь "типичные особенности" - линии
складки (представляющие собой регулярные кривые на
поверхности, взаимно однозначно проектирующиеся на картинную
плоскость) и изолированные точки сборки, которые лежат на линиях
складки и являются особыми точками проектирования линии
складки на картинную плоскость. Подчеркнем, что в точках сборки
сама линия складки не имеет особенностей. Особенность имеет
отображение проектирования (рис. 5.15).
Возникает вопрос: насколько "типичным" является
случай общего положения поверхности по отношению к
проектированию на картинную плоскость? В теории
особенностей гладких отображений доказывается, что
всякую поверхность можно привести в общее положение
сколь угодно малым "шевелением", если же поверхность
находится в общем положении, то никакое достаточно
малое шевеление поверхности не может испортить этого
свойства.
Понаблюдав за изменением видимости при
движении точки по поверхности, можно выявить
следующие свойства функции υ(χ) (рис. 5.16).
А.Функция ν(χ) является локально постоянной
во всех точках поверхности, на которых
отображение проектирования / принимает
регулярные значения, т. е. в прообразе значения ν(χ)
нет нерегулярных точек отображения /.
Б. Функция ν(χ) меняет скачком свое значение Рис 5'6
только в окрестности точек поверхности, проектирующихся на проекции
контурных линий (состоящих из точек складок проектирования)
Эти наблюдения позволяют свести задачу
загораживания на гладкой поверхности к анализу взаимного
расположения элемента поверхности и ее контурных линий.
Впрочем, дальнейшие рассмотрения показывают, что и этот
анализ избыточен и достаточно изучить функцию υ(χ) лишь
на контурных линиях поверхности. Для этого, в свою
очередь, нужно исследовать взаимное расположение линий,
состоящих из точек складок проектирования на поверхности
при отображении проектирования (рис. 5.17).
Какими свойствами обладает функция υ(χ) на линиях
складки проектирования (или контурных линиях) в случае Рис & ^
поверхности общего положения? Можно показать, что функция υ(χ) может
менять свое значение на линиях складки лишь в двух типах точек (рис. 5.18):

Α. Β точках, проекции которых являются
пересечением, или самопересечением, проекций линий складки
на картинную плоскость (в этих точках функция
υ(χ) имеет скачок, кратный 2).
Б. В точках сборки отображения проектирования
(в этих точках υ(χ) меняется на 1).
Первый случай достаточно очевиден: участок
поверхности загораживается складкой другого участка
поверхности.
Второй случай менее прост (и потому более
интересен). В окрестности точек сборки проектирования
поверхность загораживает сама себя и потому изменение
значения функции ν(χ) происходит, казалось бы, без
видимой причины (рис. 5.19). рис 5.19
S При решении задачи загораживания для многогранных поверхностей
геометрические соображения, связанные с функцией видимости, также
можно использовать. Функция видимости на многогранниках обладает
свойствами, аналогичными рассмотренным выше, правда, анализ
несколько усложняется.
Алгоритмы, использующие понятие количественной невидимости, в отличие
от алгоритмов "грубой силы" имеют линейные характеристики временной
сложности от разрешения поверхности, что является неулучшаемым по порядку
результатом для алгоритмов, работающих в объектном пространстве. Однако
в результате работы такого алгоритма получается контурное изображение, что
предполагает в дальнейшем его наполнение видимыми каркасными линиями или
полутоновой закраской. Это составляет отдельную задачу машинной графики.
Для ее решения используются свойства функции υ(χ) в точках, являющихся
прообразами регулярных значений отображения проектирования.
Такие точки образуют на поверхности открытое множество. Так как функция
ν(χ) локально постоянна на этом множестве, то на всякой его связной
компоненте она постоянна. Вычисляя значение функции ν(χ) в некоторой точке
х0 и выявляя все точки, лежащие в той же компоненте связности, мы
последовательно определим видимость всех участков поверхности
В случае использования этого подхода для многогранных поверхностей
возникает известная задача о перечислении всех ребер (или вершин) связной
компоненты некоторого графа, а также перечисления всех компонент связности
графа. Здесь в качестве графа выступает одномерный остов многогранника.

Разбиение картинной плоскости. Алгоритм Варнака
Рассмотрим область картинной плоскости
(прямоугольник в простейшем случае), которую назовем активным окном
(рис. 5 20). Логически возможны следующие случаи:
А. Окно пусто (в него не попала проекция ни одного
элемента сцены).
мм
ш
Окно закрашивается цветом фона.
Б. Окно охватывается проекцией ближайшего к нему Рис 5 20
по глубине многоугольника
Окно закрашивается цветом этого прямоугольника.
В. Размеры окна меньше пиксела картинной плоскости
Принимается специальное решение о его закраске (например, цветом
любого из прямоугольников, пересекающихся с окном)
Г. Не выполнено ни одно из предыдущих условий.
Окно разбивается на четыре части и анализ повторяется для каждой
из частей
О ° Я
О
Рис 5 21
В результате мы получаем тетрарное дерево изображения,
терминальными узлами которого являются атрибуты цвета
соответствующего окна (рис. 5 21).
Возможны и другие правила анализа активного окна,
позволяющие сократить число разбиений. Для реализации метода
необходимо выбрать эффективный способ анализа взаимного
расположения прямоугольника (окна) и многоугольника (проекции
грани на картинную плоскость). Известна модификация алгоритма,
при которой разбиение картинной плоскости осуществляется с использованием
граней изображаемого многогранника Метод позволяет применить для анализа
изображения параллельные вычисления.
Кеширование по равномерной сетке
При анализе взаимного расположения ребер и граней
многогранника с целью выявления видимых частей ребер
большая часть временных затрат приходится на поиск тех пар
ребро · грань, проекции которых имеют на картинной
плоскости фактическое пересечение. Ребро и грань,
составляющие такую пару, назовем инцидентными (рис 5 22)
Рассмотрим некоторые простые необходимые условия
инцидентности ребра и грани
А. Оболочечный тест Если ребро и грань инцидентны,
то прямоугольные оболочки проекций ребра и грани на картинную
плоскость со сторонами, параллельными координатным осям,
Рис 5 22

пересекаются. Если для пары ребро - грань это условие не выполнено,
т. е прямоугольные оболочки не пересекаются, то из дальнейшего анализа
такую пару можно исключить.
Б. Разобьем картинную плоскость при помощи
равномерной сетки на прямоугольные ячейки Назовем
ребро и ячейку инцидентными, если ячейка пересекается
с проекцией ребра на картинную плоскость Грань и
ячейка называются инцидентными, если проекция
грани пересекается с ячейкой. Вычислив
предварительно для каждой ячейки сетки все инцидентные с
ней грани, перейдем к анализу взаимного
расположения ребер и граней С этой целью для каждого ребра многогранника
найдем все ячейки, инцидентные с ним Далее анализу подлежат лишь те
грани, которые имеют с ребром общие инцидентные ячейки (рис 5 23)
Список таких граней для каждой ячейки у нас уже имеется
Оценим грубо временную сложность алгоритмов без кеширования и с кеши-
рованием. При прямом переборе для полного анализа необходимо порядка 0(№)
операций. В алгоритме с кешированием количество операций, необходимых для
полного анализа видимости ребер, имеет порядок O(N). Однако в последнем
случае для хранения информации об инцидентности граней с ячейками сетки
требуется дополнительная память
Рис 5 23
Рис 5 24
Методы приоритетов
Общая схема методов приоритетов состоит в попытке
предварительно упорядочить элементы сцены по какому-
либо признаку. Обычно в качестве параметра упорядочения
выбирается глубина элемента в сцене. В качестве простого
примера рассмотрим способ изображения поверхности,
представляющей собой график функции двух переменных,
которая задана на прямоугольной сетке (рис 5.24)
Простейший вариант метода художника.
Полутоновое изображение поверхности
Предположим, что нужно изобразить поверхность в ортогональной проекции.
Используя стандартную триангуляцию области задания
функции и кусочно линейное приближение, получим
приближение поверхности в виде многогранной
поверхности, гранями которой являются треугольники (рис.
5 25) Выберем такую нумерацию узлов сетки
Ajj = A(xj, yj), 0 <= i <= Ν, 0 <= j <= Μ,
чтобы точка (х0, у0) была ближайшей к наблюдателю.
Закрашивая грани соответствующим цветом, сбросим
проекции граней на картинную плоскость:
Рис 5 25

Д for i:=N-l down to 0 do
for j:=M-l down to 0 do
for k:=2 downto 1 do DrawFace(F[i,j,k])
При таком упорядочении граней многогранника проекции граней, лежащих
ближе к наблюдателю, сбрасываются на картинную плоскость позже граней,
лежащих дальше от точки наблюдения. Более точно, если грань F\ предшествует
грани F% в смысле такого упорядочения, то найдется разделяющая их
гиперплоскость, такая, что F\ принадлежит одному полупространству, a F<± и точка
наблюдения - дополнительному полупространству.
Метод плавающего горизонта
Предположим теперь, что мы хотим получить
каркасное изображение поверхности (рис. 5.26). Введем
нумерацию ребер Eli, j, fc/, где (i, j) - номер
соответствующей прямоугольной ячейки, a k = 1 для
"горизонтального" катета, k = 2 для "вертикального" катета,
k = 3 для гипотенузы. На этот раз будем сбрасывать ребра
в обратном порядке:
Рис. 5.26
Ц| for i:=0 to N-l do
for j:=0 to M-l do
for k:=l to 3 do DrawEdge(E[i,j,k])
Относительно процедуры DrowEdge необходимо
сделать пояснения. Для изображения проекции ребра на
картинную плоскость используем какой-либо способ растрового
представления отрезка, например алгоритм Брезенхема.
При выводе очередной точки проекции на картинную
плоскость будем анализировать видимость текущей точки ребра
при помощи нижней и верхней границ уже полученной к
этому моменту части изображения (рис. 5.27). Эти границы рис 5 27
носят название соответственно нижнего и верхнего
плавающих горизонтов; "плавающих" потому, что в процессе работы алгоритма их
положение корректируется с учетом видимости (или невидимости) очередной
сбрасываемой на экран точки проекции ребра. В нашем случае верхний и нижний
горизонты можно реализовать как два целочисленных массива min(/] и тах[/], где
/ = 0, 1, .... L (L - количество точек растра по горизонтали).
При выполнении процедуры DrawEdge для текущего ребра нужно проделать
следующие операции:
Φ Получить растровые координаты текущей точки
ребра (х,у).

(2) Если у > тах[х], το
изобразить точку (х,у); тах[х]:= у;
иначе
если у < min[x], to
изобразить точку (х,у); min[x]:= у;
В процессе работы алгоритма изображение достраивается вне "запрещенной"
области, определяемой верхним и нижним горизонтами. Так как внутри этой
области находится часть изображения, расположенная к наблюдателю заведомо
ближе, чем еще не обработанные к этому времени элементы сцены, то эти
элементы не могут загораживать той части сцены, изображение которой уже
получено на экране.
Метод плавающего горизонта. Растровая версия
Приведем текст основной процедуры, используемой
в растровой версии метода, а именно процедуры обработки
проекций ребер изображаемой многоранной поверхности
По существу, это версия алгоритма Брезенхема растровой
развертки для проекции ребра многогранника на картинную |_|
плоскость. Функции плавающих горизонтов выполняют
массивы Hmax(jt) и Hmin(jc) (рис 5 28).
g| PROCEDURE Line_Hidden(xl ,yl fx2,y2)
BEGIN
η:=abs(x2-xl); m:=abs(y2-yl);
sx:=sign(x2-xl); sy:=s±gn(y2-yl);
x:=xl; y:=yl; s:=0; e:=0;
n2:=2*n; m2:=2*m;
while s < (n-1) do
begin
s:=s+l; x:=x+sx; e:=e+m2;
if e>n then
begin y:=y+sy; e:=e-n2 end;
PutPoint(x,y)
if у < Hmin(x) then
begin
PutPixel(x,y,UpColor)/ Hmin(x):= у
end
else
if у > Hmax(x) then
begin
PutPixel(x,y,DownColor)/ Hmax(x):= у
end
end
END;

ш
Рис. 5.29
Рис. 5.30
Буквальная реализация приведенного выше описания
алгоритма плавающего горизонта дает корректное
изображение лишь в том случае, когда изображения ребер
многогранника на картинной плоскости представляют
собой отрезки с угловым коэффициентом k, по абсолютной
величине не превосходящим единицы. Лишь в этом случае
растровая развертка отрезка устроена таким образом, что
при переходе от одной ее точки к другой обязательно изменяется
абсцисса точки. Последнее гарантирует сравнение ординаты
соответствующей точки с другой компонентой массивов max(jt)
и minU) (рис. 5.29).
Если же угловой коэффициент k проекции ребра на
картинную плоскость больше единицы, то растровая развертка
проекции может иметь "вертикальные" участки, и тогда часть
изображения этого участка, а именно все те точки участка, которые
лежат ниже его самой верхней точки, может быть утеряна. Это
произойдет, например, в случае, если часть проекции ребра находится выше
верхнего горизонта и движение по растровой развертке ребра происходит с
уменьшением ординаты у, т. е. в направлении верхнего горизонта. Тогда первое
сравнение у>тах(х) даст положительный результат, будет инициирована точка
(х, у) и произойдет присвоение тах(х):=у. Далее, при движении по развертке
координата χ останется без изменений, а координата у уменьшится на единицу.
При очередном сравнении у>тах(х) (= у+\) результат будет отрицательным и
очередная точка изображена не будет, хотя она и лежит выше запрещенной
области (рис. 5.30). Эту неприятность можно преодолеть разными способами.
Один из них реализован в приведенном ниже тексте программы.
Η PROCEDURE line_Hidden(xl,yl,х2,у2: integer);
VAR
n,m,n2,m2,sx,sy,s,e,z,
u,v,x,y,xo,yo: integer;
flag: boolean;
PROCEDURE pathl;{случай, когда к не превосходит 1}
BEGIN
n2:=2*n; m2:=2*m;
while s < (n-1) do
begin
s:=s+l; x:=x+sx; e:=e+m2;
if e>n then
begin y:=y+sy; e:=e-n2 end;
PutPoint(x,y)
if у < Hmin(x) then

begin
PutPixel(x,y,UpColor); Hmin(χ):= у
end
else
if у > Hmax(x) then
begin
PutPixel(x,y,DownColor); Hmax(x):= у
end
end
END;
PROCEDURE path2; {случай, когда к превосходит 1}
BEGIN
z:=m; m:=n; n:=z;
n2:=2*n; m2:=2*m;
u:=x; v:=y; xo:=x; yo:=y;
while s < (n-1) do
begin
s:=s+l; v:=y+sy; e:=e+m2;
if e>n then
begin u:=x+sx; e:=e-n2 end;
if y<Hmin[x] then
begin
PutPixel(x,y,UpColor);
if u<>x then
begin
if sy>0 then
Hmin[xo]:=yo else Hmin[x]:=y;
xo:=u; yo:=v
end
end
else
if y>Hmax[x] then
begin
PutPixel(χ,у,DownColor);
if u<>x then
begin
if sy<0 then
Hmax[xo]:=yo else Hmax[χ]:=y;
xo:=u; yo:=v
end;
end
else
if u<>x then begin xo:=u; yo:=v end;

x:=u; y:=v
end;
END;
BEGIN
η: =abs (x2-xl) ; m: =abs (y2-yl) ;
sx:=sign (x2-xl) ; sy:=sign (y2-yl) ;
x:=xl; y:=yl; s:=0; e:=0;
if m < η then Pathl else begin Path2;
END;
Метод двоичного разбиения пространства
Этот метод использует идеи, заложенные в
алгоритме художника, когда после предварительной
обработки (сортировки граней по глубине) на картинную
плоскость сбрасываются грани, начиная с самых
дальних, а проекции граней, расположенных к рис 5 j/
наблюдателю ближе, накладываются на проекции
граней, сброшенных ранее. При завершении этого процесса получится правильное
изображение сцены (рис 5.31).
Для упорядочения граней используется правило,
согласно которому грань F\ предшествует грани F<i, если
грань Z7! и центр проектирования лежат по одну сторону от
плоскости, несущей грань /72 В противном случае
считается, что грань F\ следует за гранью F2 Заметим, что
грани могут одновременно предшествовать и следовать друг
за другом! Иными словами, определение порядка Г2< ^ι
следования граней зависит не только от их взаимного рис 5 32
расположения в пространстве, но и от априорного порядка,
в котором эти грани рассматриваются (рис. 5.32)
Если несущая плоскость пересекает тестируемую грань, то мы разрезаем ее
вдоль этой плоскости и включаем в рассмотрение взамен разрезанной две новые
грани.
Выберем произвольным образом некоторую грань. На этом шаге будем
называть ее активной. Разделим все оставшиеся грани на две группы в одну из
них отнесем те, которые лежат относительно активной грани в одном
полупространстве с наблюдателем, а в другую те, которые лежат в
дополнительном полупространстве. Грани первой группы не могут загораживаться
активной гранью, и активная грань не может быть загорожена никакой гранью
второй группы Поэтому если бы мы сначала получили правильное изображение
части сцены, состоящей из граней второй группы, затем изобразили бы активную
грань и, наконец, построили правильное изображение части сцены, состоящей из
\

Рис. 5.33
граней первой группы, то в результате имели бы верное
изображение сцены в целом (рис. 5.33).
Таким образом, разбиение сцены на две части с
использованием активной грани позволяет свести задачу
загораживания для исходного множества граней к решению
двух независимых задач загораживания внутри каждой
группы граней. Это наблюдение приводит к построению
рекурсивного алгоритма изображения сцены.
Для этого в каждой группе снова произвольным образом
выделяем активную грань и производим дальнейшее деление. Процесс рекурсивно
повторяется, пока не будут отсортированы все грани. Эта процедура напоминает
известный алгоритм быстрой сортировки Хоара. Результат
разбиения множества всех граней может быть представлен
в виде двоичного дерева, устроенного следующим образом.
В каждом узле дерева помещается грань, в левой
ветви дерева - "лицевые" грани по отношению к корневой, в
правой ветви - "нелицевые" (рис. 5.34). Для получения
изображения с использованием этого дерева достаточно
рекурсивно сбросить на плоскость изображения проекций
граней по следующему правилу:
Φ Процедура "Изобразить дерево",
Φ Изобразить правое поддерево (если оно не пусто).
G) Изобразить корневую грань,
® Изобразить левое поддерево (если оно не пусто).
Описанный алгоритм анализирует сцену исключительно в объектном
пространстве. При этом совершенно неважно, пересекаются грани или нет и какой они
формы. Однако в этом и слабая сторона метода: он никак не учитывает
когерентности по видимости частей сцены, если она в изображаемой сцене присутствует.
/
г*
Рис.
г,
/\
г5 г2
/\
Гз Г4
/\
г7 г8
5.34
Алгоритмы построчного сканирования
Алгоритмы построчного сканирования используют
последовательный вывод изображения части сцены,
полученной в результате пересечения всей сцены семейством
горизонтальных плоскостей, соответствующих горизонтальным
строкам развертки экрана. Каждая такая плоскость
(называемая плоскостью развертки) определяет совокупность
отрезков прямых, возникающих в результате пересечения с ней
граней (рис. 5.35).
Для формирования изображения требуется решить в
каждой плоскости двухмерную задачу загораживания, проанализировав взаимное
расположение отрезков относительно наблюдателя на плоскости сканирования.
Рис. 5.35

Анализ во всех плоскостях сканирования позволяет сформировать множество
всех строк развертки изображения и, таким образом, синтезировать изображение
в целом. Этот подход позволяет также формировать каркасные изображения
Настоящий метод использует последовательно работу в
объектном пространстве и в плоскости изображения, сводя
трехмерную задачу загораживания к последовательности
двухмерных задач загораживания (для отрезков на
плоскости)(рис 5.36)
Метод допускает растровую версию, и поэтому его
часто используют для аппаратной реализации Учет
когерентности по видимости позволяет произвести ряд
существенных улучшений за счет использования более
сложных структур данных Например, при анализе содержимого плоскости
развертки формируется список точек, в которых изменяется состояние видимости
какого-либо из ребер
Пусть некоторое ребро видимо в своей концевой точке До тех пор, пока
состояние видимости ребра не меняется, продолжается вывод на картинную
плоскость отрезка пересечения секущей плоскости с гранью, содержащей это
ребро. Если же состояние видимости ребра внутри текущей сканирующей
плоскости изменилось, τ е ребро стало невидимым, то, очевидно, мы окажемся в
одной из точек указанного выше списка И теперь границей выводимого на экран
отрезка будет пересечение сканирующей плоскости с текущим видимым ребром.
Метод построчного сканирования позволяет использовать известный в
вычислительной геометрии принцип "заметающей плоскости" и соответствующую
структуру данных, приспособленную для работы с динамически меняющейся
информацией о расположении отрезков пересечения сканирующей плоскости
с гранями многогранника

ТРИАНГУЛЯЦИЯ. ПОСТРОЕНИЕ ЛИНИИ УРОВНЯ
Приближение функции на нерегулярной сетке.
Триангуляция с вершинами в произвольном множестве точек
Задача аппроксимации функции от двух переменных состоит в следующем:
значения функции заданы в N произвольным образом расположенных точках и
требуется аппроксимировать ее в некоторой новой точке.
Один из возможных подходов к решению этой задачи
основывается на кусочно-линейной аппроксимации, при
которой поверхность, определяемая функцией, приближается
кусочно-линейной поверхностью, состоящей из
треугольников. Для этого на плоскости (х, у) создается сеть из
непересекающихся треугольников. Проекция каждой точки
пространства на плоскость (х, у) принадлежит лишь одной
из треугольных граней, и значение функции f(x, у)
аппроксимируется кусочно-линейной функцией, принимающей
заданные значения в точках опорного множества. Процесс триангуляции состоит в
создании сети непересекающихся треугольников с вершинами в заданных точках
(рис. 6.1).
По сравнению с прямоугольной сеткой триангуляция исходных данных имеет
ряд преимуществ. Во-первых, это отсутствие единого, произвольно выбранного
масштаба для всех данных, тогда как размер ячейки прямоугольной сетки
автоматически устанавливает предел подробности карты и все сгущения точек будут
усредняться до размера ячейки решетки. Триангуляция же точек естественным
образом подстраивается под данные. Там, где исходные точки разрежены,
треугольники крупнее, там, где есть сгущения, - мельче. Количество треугольников
определяется количеством исходных точек (по теореме Эйлера, оно не превышает
удвоенного числа исходных точек).
Во-вторых, у прямоугольной сетки есть два выделенных направления, никак
не согласованных с начальными данными. Поэтому при ее построении естественно
требовать такой точности аппроксимации, чтобы при повороте решетки на любой
угол результирующая поверхность практически не менялась. Для адекватного
отображения сильно меняющихся поверхностей приходится значительно
измельчать сетку, что требует больших вычислительных мощностей и ведет к
образованию неустойчивостей. При триангуляции этого нет.
В то же время за преимущества триангуляции приходится платить
сложностью программирования.
Для определения "качества" триангуляции известно несколько критериев,
которые выбираются, исходя из требований для ошибки интерполяции.
ш

На практике, к примеру, может возникнуть необходимость минимизировать
суммарную длину ребер триангуляции (минимальная взвешенная триангуляция)
Известен метод "жадной триангуляции", при котором никогда не отменяется то,
что уже было сделано ранее. Этот метод последовательно порождает ребра, и
процесс завершается после того, как порождено необходимое число ребер (оно
полностью определяется размером множества точек и его выпуклой оболочки)
Если цель состоит в минимизации суммарной длины ребер, то все, что можно
сделать, используя "жадный" метод, - это применить локальный критерий, добавляя
на каждом шаге кратчайшее из возможных ребер, совместимое с ранее
порожденными ребрами, т. е. не пересекающее ни одно из них.
В настоящее время в большинстве приложений
используется триангуляция Делоне Она строится
однозначно и соединяет исходные точки в сеть наиболее
правильных треугольников, что удобно в расчетах.
Триангуляции Делоне исходных данных естественным
образом соответствует непрерывная кусочно-линейная
поверхность в пространстве, состоящая из треугольников
(рис. 6.2) При обработке больших наборов данных этим
можно и удовлетвориться
Алгоритм построения триангуляции
Как уже говорилось, задача триангуляции состоит в соединении заданных N
точек на плоскости непересекающимися отрезками так, чтобы каждая область
внутри выпуклой оболочки этого множества точек являлась треугольником.
Результатом решения этой задачи должен быть список ребер, образующих
триангуляцию.
Рассмотрим алгоритм построения триангуляции Делоне. Ее построению
предшествует разбиение плоскости на так называемые области Вороного.
Обозначим исходное множество из N точек плоскости
через S. Будем считать, что никакие 4 точки исходного
множества не лежат на одной окружности Областью
Вороного V для точки ρ множества S называется множество
таких точек плоскости, расстояние от которых до точки ρ
меньше, чем до любой другой точки этого множества.
Получаемые таким образом /V обляотрй образуют разбиение
плоскости. Объединенная граница этих областей
представляет собой некоторую сеть - диаграмму Вороного (рис 6 3)
Если множество S состоит из двух точек, то срединный перпендикуляр к
соединяющему их отрезку делит плоскость на две соответствующие области
Вороного В общем случае область Вороного точки ρ - это пересечение всех
полуплоскостей, содержащих эту точку и ограниченных срединными перпендикулярами
к отрезкам, соединяющим ρ с остальными точками множества S. Поэтому каждая
область Вороного V будет ограничена выпуклой ломанной - либо замкнутой, либо

незамкнутой: области Вороного внутренних точек выпуклой
оболочки опорных точек будут многоугольниками, внешних
- уходить на бесконечность. Ребрами получившейся
решетки являются отрезки срединных перпендикуляров
(рис 6.4). Если некоторая вершина О области V получена
пересечением срединных перпендикуляров к отрезкам АВ и
ВС, то она равноудалена от точек А и В и от точек В и С,
т. е. О - центр окружности, описанной вокруг треугольника рис β 4
ABC и срединный перпендикуляр к отрезку АС также
проходит через точку О.
Оказывается, каждая вершина диаграммы Вороного является точкой
пересечения в точности трех ребер диаграммы.
Рассмотрим теперь граф, двойственный диаграмме Вороного, т. е планарный
граф, получаемый в результате соединения отрезками каждой пары точек
множества S, многоугольники Вороного которых имеют общее ребро. В результате
получится граф с вершинами в исходных точках
Имеет место следующий факт. Граф, двойственный диаграмме Вороного,
является триангуляцией множества S (рис. 6 4). Эту триангуляцию называют
триангуляцией Делоне.
Сформулируем два важных свойтва триангуляции Делоне
А. Триангуляция является триангуляцией Делоне, если
в любой паре треугольников с общим ребром, в
которой это ребро можно перебросить, не нарушая
планарности триангуляции ("сделать флип"), от
такой переброски минимальный из шести углов в паре
треугольников не увеличится (рис. 6 5) Иными
словами, от любой локальной перестройки
триангуляции Делоне треугольники становятся более
неправильными.
Б. Для того чтобы некоторая триангуляция была
триангуляцией Делоне, необходимо и достаточно,
чтобы внутри окружности, описанной вокруг любого
из ее треугольников, не лежало больше ни одной
вершины триангуляции Делоне (круговой критерий)
(рис. 6.6).
Построение триангуляции осуществляется индуктивно.
Пусть для некоторого шага триангуляция Делоне уже по- Рис 6 6
строена. На следующем шаге в нее включается новая точка, после чего
производится локальная перестройка триангуляции Для каждой новой точки ищется либо
треугольник, в который она попала, если она лежит внутри выпуклой оболочки
триангуляции (рис 6.7), построенной на предыдущем шаге, или вершины, с
которыми ее необходимо соединить, если точка не принадлежит выпуклой
оболочке (рис. 6 8). Затем проверяется выполнимость кругового критерия и при
ж
Φ

Рис. 6.7
необходимости делаются флипы (рис. 6.9). Как правило,
при каждой перестройке будет производиться лишь
несколько перебросок ребер. Но, вообще говоря, возможны
ситуации, когда серия флипов приведет к изменению всей
решетки.
Выбор приведенного алгоритма обусловлен временем
его работы, которое пропорционально числу точек.
В случае, если бы мы строили триангуляцию при
помощи областей Вороного, то для каждой точки необходимо
было бы провести срединные перпендикуляры к отрезкам,
соединяющим ее со всеми остальными вершинами.
Следовательно, время работы такого алгоритма квадратично
зависит от числа точек.
Для того чтобы найти треугольник, в который попала
очередная точка (NewV), соединим ее отрезком с
предыдущей обработанной вершиной (Last) и посмотрим, какие
ребра и треугольники он пересекает. Если треугольник,
которому принадлежит очередная точка, найден, то остается
соединить ее с вершинами этого треугольника и, при
необходимости, сделать флипы. Если точка лежит вне выпуклой
оболочки, то необходимо соединить ее с последним ребром,
которое пересек отрезок с вершинами Last и NewV. Однако
это еще не все. Для того чтобы сохранить свойство
выпуклости триангуляции, нужно соединить ребрами с NewV
все вершины, которые лежат между опорными прямыми.
Структура данных для представления
планарного графа
Для представления планарного графа часто используется реберный список
с двойными связями (РСДС). Аналогичное представление допустимо и для графа,
соответствующего поверхности многогранника, τ е. графа, уложенного на гладкой
поверхности.
Рис. 6.8
Рис. 6 9
Пусть V = {Vj, ..., Vn) - вершины графа и Ε = {eJt
η)
множество его ребер. Главная компонента РСДС для планарного
графа (V,E) - реберный узел. Каждое ребро представляется одним
реберным узлом, который содержит шесть полей* V/ - начало
ребра, Vq · его конец, // - номер грани, лежащей справа от ребра, f2 -
номер грани, лежащей слева от ребра, Pj (Р2) - номер первого
ребра, встречаемого вслед за ребром (V/,^) при повороте от него
против часовой стрелки вокруг Vj (соответственно V2) (рис. 6.10)
Фрагменту графа, изображенного на рисунке, соответствует
следующий фрагмент РСДС (рис 6.11).

Для того чтобы можно было легко вычислить у, v2 f! f2 Pi P2
ребра, инцидентные заданной вершине, или ребра,
ограничивающие заданную грань, введем два массива
- HV[1:N] и HF[l:/l, где / - количество граней (оно не
больше, чем количество ребер), ί-й элемент массива
HV содержит номер одного из ребер, инцидентных ί-й Рис 6 И
вершине; ί-й элемент массива HF содержит номер одного из ребер,
принадлежащих ί-й грани.
Type Arr=Array[1. .Max] of Integer;
Номера инцидентных ребер запишем в массив В:Агг, их количество - в
переменную /. Тогда процедура нахождения инцидентных ребер выглядит следующим
образом:
Η procedure Incident(i:Integer;var A:Arr; var к:Integer);
var a,aO:Integer;
begin
a:=HF[j]; aOz=a; B[l]:=a; i:=l;
if vl[a]=j then a:=pl[a] else a:=p2[a];
while a<>aO do
begin
B[i]:=a; i:=i+l;
if vl[a]=j then a:=pl[a] else a:=p2[a]
end
end {Incident};
Аналогичным образом мы можем написать процедуру
Face(i:Integer;A:Arr),
определяющую три ребра /-го треугольника (элементы массива А).
Построение линий уровня функции двух переменных
Карты линий уровня, или изолиний, функций двух
переменных широко применяются как в теоретических
исследованиях, так и в прикладных областях. Достаточно
вспомнить всем знакомые топографические карты, которые
являются по существу картами изолиний функции высоты
рельефа местности (рис. 6.12).
На практике значения функций часто доступны лишь
в точках некоторого конечного нерегулярного множества
(например, на множестве случайно распределенных точек
в некоторой области плоскости).
Если сетка, на которой заданы значения функции, является достаточно
редкой для вычисления приближенных значений на более частой сетке, то
предварительно используют интерполяцию, что не представляет труда в случае
прямоугольной сетки. Затем, разбивая каждую прямоугольную ячейку на два
треугольника, получаем стандартную триангуляцию области задания функции.
1
4
2
1
1
1
2
-

График функции можно заменить многогранной поверхностью при помощи
кусочно-линейной интерполяции с вершинами, проектирующимися вдоль оси ζ
в узлы сетки.
Таким образом, мы сводим исходную задачу к задаче построения линий
уровня получившейся кусочно линейной функции, определенной на объединении
треугольников. Гранями этой поверхности служат треугольники с вершинами
в точках Рц (хц, уц, /,·;), где (хц, уц) - узлы прямоугольной сетки, fij -
соответствующие значения функции f(x, у).
Линией уровня этой функции, соответствующей значению уровня /ζ,
является объединение проекций на плоскость (х, у) отрезков, получающихся в
результате пересечения горизонтальной плоскости ζ = h с треугольными гранями
поверхности многогранника.
Итак, для решения задачи нужно иметь в своем
распоряжении процедуру нахождения пересечения треугольной
грани с горизонтальной плоскостью. Применив процедуру
последовательно к каждой грани, получим
кусочно-линейную аппроксимацию линий уровня функции / (рис. 6.13).
Заметим: возможны следующие случаи взаимного
расположения треугольника и плоскости (рис. 6.14):
A. Треугольник и плоскость не пересекаются - все рис 6.13
вершины лежат по одну сторону от плоскости.
Б. Треугольник касается плоскости одной вершиной -
все вершины лежат по одну сторону от плоскости.
B. Треугольник пересекается с плоскостью по ребру -
все вершины лежат по одну сторону от плоскости,
причем две вершины - в плоскости.
Г. Треугольник пересекается с плоскостью - найдется
пара вершин, лежащих по разные стороны от
плоскости.
Д. Треугольник лежит в плоскости - все вершины
лежат в плоскости.
Ниже приводится текст процедуры нахождения проекции пересечения
плоскости и треугольной грани, заданной своими вершинами.

PROCEDURE isoline;
VAR i,j,κ,ηΐ,p,q,s : integer;
zmin,zmax,zfmin,zfmax,z,r,hh,eps : real;
RainBow : array [0..15] of integer;
PROCEDURE exeF(i,j,k: integer);
VAR
s,p,q,sn,pn,qn : integer;
t,z : real;
χ : array [0..2] of vector;
PROCEDURE Fsection(ζ: real);
VAR l,s,nz,i: integer;
sg: array [0..2] of integer;
a: array [1..3,1..2] of real;
BEGIN
nz:=0; s:=0;
for i:=0 to 2 do
if x[i,3]<z then sg[i]:=-l else
if x[i,3]>z then sg[i]:=] else
begin sg[i]:=0; nz:=nz+l end;
Case nz of
0: begin
for i:=0 to 2 do
begin
p:=i; q:=(i+l) mod 3 ;
if sg[p]*sg[q]<0 then
begin
t: = (z-x[p,3])/(x[q,3]-x[p, 3]);
if (0<=t) and (t<=l) then
begin
s:=s+l;
a[s,l]:=x[p,l]+t*(x[q,l]-
x[p,l]);
a[s,2]:=x[p,2]+t*(x[q,2]~
x[p,2]);
end
end;
end;
lines(a[l,l], a[l,2), a[2,l], a[2,2J)
end;

1: begin
for i:=0 to 2 do if sg[i]=0 then
begin p:=(i+l) mod 3; q:=(i+2) mod 3 end;
if sg[p]*sg[q]<0 then
begin
a[l,l]:=x[i,l]; a[1,2]:=x[i,2];
t:=(z-x[p,3])/(x[q,3]-x[p,3]);
a[2,l]:=x[p,l]+t*(x[q,l]-x[p,l]);
a[2,2]:=x[p,2]+t*(x[q,2]-x[p,2]);
lines(a[l,l], a[l,2], a[2,l], a[2r2])
end;
end;
2: begin
for i:=0 to 2 do
if sg[i]=0 then
begin
s:=s+l;
a[s,l]:=x[i,l]; a[s,2]:=x[i,2]
end;
lines(a[l,l], a[l,2], a[2,l], a[2,2))
end;
3: for i:=0 to 2 do
lines(x[i,l], x[i,2],
x[(i+l) mod 3,1],x[(i+l) mod 3,2]);
end;
END;
BEGIN
case к of
1: begin
x[0]:=v[i,j]*.vec;
χ[1]:=v[i+1,j]*.vec;
x[2]:=v[i,j+1]A.vec;
end;
2: begin
x[0]:=v[i+l,j]*.vec;
x[l]:=v[i+l,j+1]л.vec;

x[2]:=v[i,j+l]~.vec;
end;
end;
min3(x[0,3],x[l ,3],x[2,3],zfmin,zfmax) ;
pn:=trunc((zfmin-zmin)/hh)+1; qn:=trunc((zfmax-
zmin)/hh) ;
for sn:=pn to qn do
begin
SetColor(RainBow[ sn*16 div nl MOD 15+1 ]);
ζ:=zmin+sn*hh;
Fsection(z);
end;
END;
В случае, когда значения функции заданы в точках нерегулярного
множества, можно поступить следующим образом. Одним из известных методов
получить триангуляцию с вершинами в точках этого множества. После разбиения
области определения функции на треугольники построить кусочно-линейную
интерполяция функции с вершинами в точках исходного множества (через три
различные точки в пространстве, не лежащие на одной прямой, можно провести
единственную плоскость - для этого и нужна была триангуляция)
Применяя теперь описанную выше процедуру нахождения проекции
пересечения плоскости и треугольника к треугольникам, образующим график
кусочно-линейной функции, получим линии уровня функции для различных
значений уровня h. Затем воспользуемся описанной выше процедурой для
генерации линий уровня соответствующей кусочно-линейной поверхности

РАБОТА С ОСНОВНЫМИ ГРАФИЧЕСКИМИ УСТРОЙСТВАМИ
LJ
X Аесмотря на наличие различных графических библиотек (например, таких,
как модуль Graph в Turbo Pascal), часто возникает необходимость прямой работы
с тем или иным графическим устройством. Это может быть связано как с тем, что
библиотека не поддерживает соответствующее устройство (например, мышь или
принтер), так и с тем, что работа с данным устройством организована не
достаточно эффективно или не использует всех возможностей устройства.
Рассматрим основные приемы работы с некоторыми устройствами.
Мышь
Наиболее распространенным устройством ввода графической информации
в ПЭВМ является мышь. Мышь представляет собой "коробочку" с двумя или
тремя кнопками, соединенную с компьютером. При перемещении мыши и/или
нажатии/отпускании кнопок мышь передает информацию в компьютер о своих
параметрах (величине перемещения и статусе кнопок). Существует много
различных типов устройства типа мышь, отличающхся как по принципу работы
(механическая, оптомеханическая и оптическая), так и по способу общения
(протоколу) с ПЭВМ. Для достижения некоторой унификации каждая мышь
поставляется обычно вместе со своим драйвером - специальной программой,
понимающей данный конкретный тип мыши и предоставляющей некоторый почти
универсальный интерфейс прикладным программам. При этом вся работа с мышью
происходит через драйвер, который отслеживает перемещения мыши, нажатие и
отпускание кнопок мыши и обеспечивает работу с курсором мыши - специальным
маркером на экране (обычно в виде стрелки), дублирующим все передвижения
мыши и позволяющим пользователю указывать мышью на те или иные объекту на
экране.
Работа с мышью реализуется через механизм прерываний. Прикладная
программа осуществляет прерывание ЗЗА ($33), передает в регистрах необходимые
параметры и в регистрах получает значения, выданные драйвером мыши.
Для использования механизма прерываний в языке Turbo Pascal в модуле
Dos введена процедура Intr
procedure IntrflntNo: Byte; var Regs: Registers)
Параметр IntNo задает номер прерывания, которое необходимо осуществить,
a Regs - структура, моделирующая регистры процессора. При вызове данной
процедуры в регистры процессора помещаются соответствующие значения
из полей Regs, вызывается прерывание, а по окончании прерывания значения
регистров записываются в поля структуры Regs.

Ниже будут приведены примеры работы с мышью на языке Turbo Pascal,
иллюстрирующие основные функции драйвера мыши. Во всех этих примерах
для работы требуется модуль DOS.
Инициализация и проверка наличия мыши
Функция ResetMouse производит инициализацию мыши и возвращает
значение True, если мышь обнаружена.
Д function ResetMouse : Boolean;
var
г : Registers;
begin
r.ax := 0;
intr ($33, r);
ResetMouse : = r.ax = $FFFF;
end;
Высветить на экране курсор мыши
Процедура ShowMouseCursor выводит на экран курсор мыши. При этом
курсор перемещается синхронно с перемещениями самой мыши.
Д procedure ShowMouseCursor;
var
г : Registers;
begin
r.ax := 1;
intr ($33, r);
end;
Убрать (сделать невидимым) курсор мыши
Процедура HideMouseCursor убирает курсор мыши с экрана. Однако при
этом драйвер мыши продолжает отслеживать ее перемещения.
Д procedure HideMouseCursor;
var
г : Registers;
begin
r.ax := 2;
intr ($33, r);
end;
Прочесть состояние мыши (ее координаты и состояние кнопок)
True, если кнопка нажата. Координаты возвращают
ся в пикселах даже для текстового режима (при работе в текстовом режиме
эти координаты необходимо разделить на 8 для получения текстовых координат).
Процедура ReadMouseState возвращает состояние мыши в своих аргументах.

Д procedure ReadMousestate (var x, у : Integer; var
LeftButton, MiddleButton, RightButton : Boolean)
var
r : Registers;
begin
r.ax := 3;
intr ($33, r);
χ ;= r.cx;
у := r.dx;
LeftButton ;= (r.bx And 1) <> 0;
RightButton :- (r.bx And 2) <> 0;
MiddleButton ;= (r.bx And 4) <> 0;
end;
Передвинуть курсор мыши в точку с заданными координатами
Для этого используется процедура MoveMouseCursor.
Η procedure MoveMouseCursor (x, у : Integer);
var
г : Registers;
begin
r.ax ;= 4;
r.cx := x;
r.dx := y;
intr ($33, r);
end;
При работе с мышью следует иметь в виду, что выводить изображение
поверх курсора мыши нельзя. Поэтому, если нужно произвести вывод на экран
в том месте, где может находиться курсор мыши, следует убрать его с экрана,
выполнить требуемый вывод и затем снова вывести курсор мыши на экран.
Принтер
В качестве устройства для получения "твердой" копии изображения
на экране обычно выступает матричный принтер. Практически любой матричный
принтер позволяет осуществить построение изображения, так как сам выводит
символы, построенные из точек (каждый символ представляется матрицей точек;
для большинства принтеров - матрицей размера 8 на 11).
Дли осуществления управления принтером существует специальный набор
команд (обычно называемых Esc-последовательностями), позволяющий управлять
режимом работы принтера, прогонки бумаги на заданное расстояние и печати
графической информации. Каждая команда представляет собой некоторый набор
символов (кодов), просто посылаемых (печатаемых) на принтер. Чтобы принтер

мог отличить эти команды от обычного печатаемого текста, они обычно
начинаются с символа с кодом меньше 32, т. е. кода, которому не соответствует
ни одного ASCII символа. Для большинства команд в качестве такого символа
выступает символ Escape (код 27).
Как правило, каждый принтер имеет свои особенности, которые, естественно,
находят отражение в наборе команд. Однако можно выделить некоторый набор
команд, реализованных на достаточно широком классе принтеров.
Рассмотрим класс 9-игольчатых принтеров типа EPSON, STAR и совместимы
с ними. Ниже приводится краткая сводка основных команд для этого класса
принтеров.
Мнемоника Десятичный код Комментарий
LF 10 Переход на следующую строку, каретка
не возвращаеся к началу строки
CR 13 Возврат каретки к началу строки
FF 12 Прогон бумаги до начала следующей
страницы
ESC Ά'η 27, 65, η Установить расстояние между строками
(величину прогона бумаги по команде
LF) в п/72 дюйма
ESC'J'n 27, 74, η Передвинуть бумагу на п/216 дюйма
ESCK'nj n2 data 27, 75, r\\, n2, data Печать блока графики высотой
8 пикселов и шириной n2*256 + nj
пикселов с нормальной плотностью
(80 точек/дюйм)
ESC'L'nj n2 data 27, 76, nj, n2, data Печать блока графики высотой
8 пикселов и шириной п2*256 + п\
пикселов с двойной плотностью
(120 точек/дюйм)
ESC'3'n 27, 51, η Установка расстояния между строками
для последующих команд перевода
строки. Расстояние устанавливается
равным п/216 дюйма
Например, для возврата каретки в начальное положение и сдвиг бумаги
на 5/216 дюйма нужно послать на принтер следующие байты: 13, 27, 74, 5.
Первый байт обеспечивает возврат каретки, а три следующих - сдвиг бумаги.
При печати графического изображения, головка принтера за один проход
рисует блок (изображение) шириной nj + 256л2 точек и высотой 8 точек. После
П2 идут байты, задающие изображение, - по 1 байту на каждые 8 вертикально
стоящих пикселов. Если нужно ставить точку в i-м снизу пикселе, то в байте /-Й
бит равен 1.

Например.
Value
128 -- О- О- О-
64-0 -- - - -0--
32 О- __0-
16-0 - - - - _ о - -
8 -- О- О- о - - -
4 __ О- ____
2 О- О- О- 0-0-
1 __ о-
34 80 138 0 143 0 138 80 34 О
Рассмотрим, как формируются байты для этой команды. Так как ширина
изображения равна 10, то отсюда Я/=10 div 256, «2=10 mod 256. Для
формирования первого байта, описывающего изображение, возьмем первый столбец из 8
пикселов и закодируем его битами: точке поставим в соответствие 1, а пустому
месту - 0. Получившиеся биты запишем сверху вниз. При этом получается
двоичное число 00100010, десятичное значение которого равно 34. Второй столбец
кодируется набором бит 01010000 с десятичным значением 80. Проведя
аналогичные расчеты, получим, что для печати этого изображения на принтер
необходимо послать следующие коды:
27 75 10 0 34 80 138 0 143 0 138 80 34 0.
Для вывода на принтер изображения высотой больше 8 пикселов оно
разбивается на полосы высотой по 8 пикселов.
Пример. Копирование прямоугольной области экрана (xj,yi)-(x2>y2) на при*"
тер с заданием множество цветов, которые следует считать фоном.
Η type
ColorSert = set of [Black..White];
procedure HardCopy (xl, yl, x2, у2 : Integer;
BackGround : ColorSet);
const
Esc = 27;
LPTPort = I;
var
ScanLine : Integer; { The current scan line }
nl, n2 : Byte; { 2 byte printer control code }
Mask : Byte;
height : Integer;
{ Send one byte to the printer }
procedure SendByte(B : byte);

var
Regs : Registers;
begin
repeat
Regs.AH := 0;
Regs.AL := B;
Regs.DX := Pred(LPTPort);
Intr($17, Regs);
if (Regs.AH and $01 <> 0) then
{ time-out error }
if (Regs.AH and $40) <> 0 then
Error ('Printer not ready') { Printer not
turned on }
else
if Regs.AH = $A1 then
Error ('Printer busy') { Used by PRINT }
else
if (Regs.AH and $20) <> 0 then
Error ('Printer out of paper')
else
Error ('Printer OFF-LINE') { some other error }
else
exi t;
until False;
end; { SendByte }
{$B+} { Turn off short circuit boolean evaluation }
function ConstructByte(X, Υ : integer) : byte;
{ Construct a print byte by reading bits from the graphics
screen buffer }
const
Bits : array[0..7] of byte = (128,64,32,16,8,4,2,1);
var
CByte, Bit, CPix : byte;
begin
CByte := 0;
for Bit := 0 to 7 do
begin
CPix := GetPixel (X,Y + Bit);
if not (CPix in BackGround) then
CByte := CByte + Bits [Bit];
end;

ConstructByte := CByte;
end; { ConstructByte }
{$B-} { Turn on short circuit boolean evaluation }
procedure DoLine; { Dumps one print line to the printer }
var
XPixel : integer;
PrintByte : byte;
begin
SendByte (Esc);
SendByte(Ord('K')); { Select double-density graphics print
mode }
SendByte(nl); { Send 2 byte control code }
SendByte(n2);
for XPixel := xl to x2 do
begin
PrintByte := ConstructByte (XPixel, yl + ScanLine*8)
and Mask;
SendByte(PrintByte) ;
end;
SendByte(10); { Send line feed }
SendByte(13); { send carriage return }
end; { DoLine }
begin { HardCopy }
Mode := Mode mod 5; { Modes 0 through 4 supported }
SendByte (Esc); { Select 23/216-inch line spacing }
SendByte (Ord(f3'));
SendByte (23)
nl := Lo (x2 - xl +1); { Determine 2 byte control code
for }
n2 := Hi (x2 - xl -f-1); { the number of dots per print
line }
StartX := xl;
EndX := x2;
Mask := $FF;
height := у 2 - yl -hi;
for ScanLine := 0 to (height div 8) - 1 do
DoLine;
if (height mod 8) <> 0 then

begin
Mask ;= Byte (not ($FF shr (height mod 8)));
ScanLine := height div 8;
DoLine;
end;
SendByte(Esc) ;
SendByte(ord( Ά')) ;
SendByte(12);
SendByte(lO);
SendByte(13);
end; { HardCopy }
Видеокарты EGA и VGA
Основным графическим устройством, с которым чаще всего приходится
работать, является видеосистема компьютера. Обычно она состоит из видеокарты
(адаптера) и подключенного к ней монитора. Изображение хранится в растровом
виде в памяти видеокарты: аппаратура карты обеспечивает регулярное
("50 раз/сек) чтение этой памяти и ее отображание на экране монитора. Поэтому
вся работа с изображением сводится к тем или иным операциям с видеопамятью.
Приведем список основных режимов для этих карт. Каждый режим
определяется номером, разрешением экрана и количеством цветов.
Количество цветов
Номер режима
$0D
$0Е
$10
$12
$13
Разрешение
320x200
640x200
640x350
640x480
320x200
экрана
Кол
16
16
16
16
256
Для установки нужного режима можно воспользоваться процедурой
SetVMode:
Η procedure SetVMode (Mode : Word)
var
r : Registers;
begin
r.ax := Mode;
intr ($10, r);
end;

Функции EGAPresent и VGAPresent позволяют определить наличие EGA-
или VGA-совместимой видеокарты.
Д function EGAPresent : Boolean;
var
г : Registers;
begin
r.ax := $1200;
r.bx := $0010;
intr ($10, r);
EGAPresent := (r.bx And $00FF) <> $0010
end;
function VGAPresent: Boolean;
var
r : Registers;
begin
r.ax := $1A00;
intr ($10, r);
VGAPresent := (r.ax And $00FF) = $001A;
end;
Ниже будет рассмотрена работа с видеопамятью на карте EGA (Enhanced
Graphics Adapter) и VGA (Video Graphics Array).
16-цветные режимы адаптеров EGA и VGA
Для 16-цветных режимов под каждый пиксел изображения необходимо
выделить 4 бита видеопамяти. Однако эти 4 бита выделяются не последовательно
в одном байте, а разнесены в 4 разных блока (цветовые плоскости) видеопамяти.
Вся видеопамять карты (обычно 256 Кбайт)
делится на 4 равные части, называемые цветовыми
плоскостями. При этом каждому пикселу ставится в
соответствие по одному биту в каждой плоскости,
причем все эти биты одинаково расположены
относительно ее начала. Обычно эти плоскости
представляют параллельно расположенными одна над другой,
так что каждому пикселу соответствует 4
расположенных друг под другом бита. Все эти плоскости
проектируются на один и тот же участок адресного пространства процессора,
начиная с адреса $А000:0. При этом все операции чтения и записи видеопамяти
опосредуются видеокартой! Поэтому если вы записали байт по адресу $А000:0, то
это вовсе не означает, что в действительности посланный байт запишется хотя бы
в одну плоскость и что при операции чтения прочитанный байт будет совпадать с
одним и 4 байтов в соответствующих плоскостях. Механизм этого опосредования
Рис 7 1

определяется логикой карты, но для программиста существует возможность
известного управления этой логикой, при работе одновременно с 8 пикселами.
Для работы с пикселом необходимо определить адрес байта в видеопамяти,
содержащего данный пиксел, и битовую маску, определяющую позицию пиксела
внутри байта (поскольку один пиксел отображается на один бит в каждой
плоскости, то байт соответствует сразу 8 пикселам). Для режимов с горизонтальным
разрешением в 640 пикселов эти величины определяются следующим образом:
PixelAddr := у * 80 + (х div В);
PixelMask := $80 Shr (x mod В);
где (х, у) - координаты пиксела; PixelAddr - адрес байта видеопамяти по сегменту
$А000; PixelMask - битовая маска для данного пиксела.
На видеокарте находится набор специальных 8-битовых регистров. Часть из
них доступна только для чтения, часть - только для записи, а некоторые вообще
недоступны программисту. Доступ к регистрам осуществляется через порты
ввода/вывода процессора.
Регистры видеокарты делятся на несколько групп. При этом каждой группе
соответствует пара последовательных портов (порт адреса и порт значения).
Для записи значения в регистр видеокарты необходимо сначала записать номер
регистра в первый порт (порт адреса), а затем записать значение в следующий
порт (порт значения).
Ниже мы рассмотрим две основные группы регистров, принадлежащих двум
частям видеокарты, - Graphics Controller и Sequencer.
Каждой группе соответствует своя пара портов.
Graphics Controller (порты $ЗСЕ- $3CF)
Номер
0
1
2
3
4
5
6
7
8
Регистр
Set/Reset
Enable Set/Reset
Color Compare
Data rotate
Read Map Select
Mode
Miscellaneous
Color Don't Care
Bit Mask
Стандс
$00
$00
$00
$00
$00
$10
$05
$0F
$FF
Для записи в регистр необходимо сначала послать номер регистра в порт
$ЗСЕ, а затем записать соответствующее значение в порт $3CF.
Проиллюстрируем это на процессе установки регистра битовой маски (Bit
Mask) (установка остальных регистров осуществляется аналогично).

Процедура SetBitMask устанавливает значение регистра битовой маски.
Д procedure SetBitMask (Mask : Byte);
begin
Port [$3CE] := 8;
Port [$3CF] ;= Mask;
end;
Sequencer (порты $ЗС4-$ЗС5)
Из всех регистров этой группы мы рассмотрим только регистр маски
плоскости (Map Mask) и номер 2.
Процедура SetMapMask устанавливает значение регистра маски плоскости.
Д procedure SetMapMask (Mask : Byte)
begin
Port [$3C4] := 2;
Port [$3C5] ;= Mask;
end;
Рассмотрим теперь, как происходит работа с видеопамятью.
При операции чтения байта из видеопамяти читаются сразу 4 байта - по одному
из каждой плоскости. При этом прочитанные значения записываются в специальные
регистры - "защелки" (latch-регистры), недоступные для прямого доступа. Байт,
прочитанный процессором, является комбинацией значений latch-регистров.
При операции записи посланный процессором байт накладывается на
значения latch-регистров по правилам, определяемым значениями других регистров,
а результирующие 4 байта будут записаны в соответствующие плоскости.
Так как при записи используются значения latch-регистров, то часто
необходимо, чтобы перед записью в них были известны исходные значения тех байтов,
которые затем изменяются. Это часто приводит к необходимости осуществить
чтение байта по адресу перед записью по этому адресу нового значения.
Правила, определяющие наложение при записи посланных процессором
данных на значения latch-регистров, определяются установленным режимом записи,
и, соответственно, режим чтения задает способ, которым определяется значение,
прочитанное процессором.
Видеокарта EGA поддерживает 2 режима чтения и 3 режима записи, у карты
VGA есть еще один дополнительный режим записи.
Установка режимов чтения и записи осуществляется записью
соответствующих значений в регистр Mode. Бит 3 отвечает за режим чтения, биты 0 и 1
за режим записи.
Процедура SetRWMode иллюстрирует установку режимов чтения и записи.
Д procedure SetRWMode (ReadMode, WriteMode : Byte);
begin
Port [$3CE] := 5;
Port [§3CF] := (WriteMode And 3) Or ((ReadMode And 1) Shi 3);
end;

Режимы чтения
Режим чтения О
В этом режиме возвращается байт из latch-регистра (плоскости) с номером
из регистра Read Map Select.
Η function ReadPixel (χ, у : Integer) : Integer;
var
PixelMask : Byte;
PixelAddr : Word;
Plane : Integer;
Color : Integer;
Latch : Byte;
begin
Color := 0;
PixelAddr := у * 80 + (x div 8);
PixelMask := $80 shr (x mod 8);
for Plane := 3 downto 0 do
begin
Part [$3CE] := 4;
Port [$3CF] := Plane;
Latch := (Mem[$A000:PixelAddr] And PixelMask) shr (xmod8);
Color := (Color shl 1) Or Latch;
end;
ReadPixel := Color;
end;
В приведенном примере возвращается значение (цвет) пиксела с
координатами (х, у) Для этого с каждой из плоскостей по очереди читаются
соответствующие биты и из них собирается цветовое значение пиксела
Режим чтения 1
В возвращаемом значении ί-й бит равен 1, если
GetPixel And ColorDon'tCare = Color Compare And Col orDon'tCare
В случае, если ColorDon'tCare = $0F, в прочитанном байте в тех позициях,
где цвет пиксела совпадает со значением в регистре ColorCompare, будет стоять 1.
Этот режим очень удобен для поиска точек заданного цвета.
В procedure FindPixel (Color : Integer; var χ, у : Integer;
var Res : Boolean);
var
PixelAddr : Word;
PixelMask : Word;
Mask : Word;
begin
Res := False;

PixelAddr := y*80 + (χ div 8);
Mask := Not ($FF Shr (x mod 8));
SetRWMode (1, 0);
SetColorCompare (Color);
while χ < 640 do
begin
PixelMask := Mem [ $A000:PixelAddr ] And Mask;
inc (PixelAddr) ;
Mask := $FF;
if PixelMask <> 0 then
begin
while (PixelMask And $80) = 0) do
begin
PixelMask := PixelMask Shi 1;
inc (x);
end;
exit;
end;
inc (x, 8);
end;
end;
Приведенная процедура осуществляет поиск пиксела цвета Color в строке у,
начиная с позиции х. При этом используется режим чтения 1. Все байты,
соответствующие данной строке, читаются по очереди и, как только будет получено
ненулевое значение (найден, по крайней мере, один пиксел данного цвета в
байте), определяется пиксел с наименьшим номером, имеющий данный цвет.
Переменная Mask служит для отсеивания из байта, соответствующего начальной
точке (х, у), тех пикселов, у которых абсцисса χ меньше стартового значения.
Режимы записи
Режим записи О
Это, пожалуй, самый сложный из всех рассматриваемых режимов, дающий
однако самые большие возможности.
В рассматриваемом режиме регистр BitMask позволяет защищать от
изменения определенные пикселы. В тех позициях, где соответствующий бит из
регистра BitMask равен 0, пиксел не изменит своего значения. Регистр MapMask
позволяет защищать от изменения определенные плоскости.
Биты 3 и 4 регистра DataRotate определяют способ наложения выводимого
изображения на существующее (аналогично процедуре SetWriteMode в языке
Turbo Pascal).

Значение битов Операция Эквивалент в Turbo Pascal
О О
0 1
1 О
1 1
Замена
Ог
And
Хог
NormalPut
OrPut
AndPut
XorPut
Процедура SetWriteMode устанавливает соответствующий режим наложения.
3 procedure SetWriteMode (Mode : Byte);
begin
Port [$3CE] := 3;
Port [$3CF] := (Byte And 3) Shi 3;
end;
Посланный процессором байт циклически сдвигается ("прокручивается")
вправо указанное в битах 0 - 2 регистра Data Rotate количество раз.
Результирующее значение определяется следующим образом:
На плоскость, соответствующий бит которой в регистре Enable Set /Reset
равен 0, накладывается посланный процессором байт, "прокрученный" заданное
количество раз с учетом регистров BitMask и MapMask. Если соответствующий
бит равен 1, то во все позиции, разрешенные регистром BitMask, записывается
бит из регистра Set/Reset, соответствующий плоскости.
На практике наиболее часто встречаются следующие два случая:
A. Enable Set/Reset = 0
(байт, посланный процессором, циклически сдвигается в соответствии со
значением битов 0 - 2 регистра Data Rotate; после этого получившийся
байт накладывается заданным способом (см. биты 3 - 4 регистра Data
Rotate) на те плоскости, которые разрешены регистром Map Mask, причем
изменяются лишь разрешенные регистром BitMask биты).
Б. Enable Set/Reset = $0F
(в позиции, разрешенные регистром BitMask, ставятся точки цвета,
заданного в регистре Set/Reset; байт, посланный процессором, никакой
роли не играет).
Пример. Построение точки заданного цвета.
Для того, чтобы нарисовать только нужный пиксел, необходимо поставить
регистр BitMask так, чтобы защитить остальные 7 пикселов, соответствующих
этому байту, от изменения. Это достигается установкой всех битов регистра в О,
кроме бита с номером χ mod 8.
В
procedure SetPixel (χ, у : Integer; Color : Byte);
var
Addr : Word;
Mask : Byte;

begin
Addr := (χ div 8) + у * 80;
Mask := $80 shr (x mod 8);
SetEnableSetReset ($0F);
SetSetReset (Color);
SetBitMask (Mask);
inc (Mem [$AOOO:Addr]);
SetEnableSetReset (0); { восстановить исходное значение
регистра }
SetBitMask ($FF); { восстановить исходное значение регистра
}
end;
Режим записи 1
В чтом режиме значения latch-регистров непосредственно копируются в
соответствующие плоскости Регистры масок и режима не действуют. Посланное
процессором значение не играет никакой роли. Этот режим позволяет
осуществлять быстрое копирование фрагментов видеопамяти. При чтении байта по
исходному адресу прочитанные 4 байта с плоскостей загружаются в latch-регистры,
а при записи значения latch-регистров записываются в плоскости по адресу,
по которому шла запись Таким образом, за одну операцию перезаписи
копируется сразу 4 байта (8 пикселов).
{Процедура копирования прямоугольной области экрана}
procedure Copy (xl, yl, х2, у2, xn, yn : Integer);
var
SrcAddr : Word;
DstAddr : Word;
Cols : Integer;
NextRow : Integer;
x, у : Integer;
begin
SrcAddr := yl * 80 +
DstAddr := yn * 80 +
Cols := (x2 shr 3) -
NextRow := 80 - Cols;
(xl
(xn
(xl
shr 3);
shr 3);
shr 3);
SetRWMode (0, 1); { Set read mode 0, write mode 1 }
for у := yl to у2 do

begin
for χ := 1 to Cols do
begin
Mem [$AOOO:DstAddr] := Mem [$AOOO:ScrAddr];
inc (DstAddr);
inc (SrcAddr);
end;
inc (SrcAddr, NextRow);
inc (DstAddr, NextRow);
end;
SetRWMode (0, 0);
end;
В силу ограничений режима записи 1 эта процедура может копировать только
области, где х\ кратно 8 и ширина кратна 8, так как копирование осуществляется
блоками по 8 пикселов сразу. Кроме того, этот пример не учитывает возможности
того, что область, куда производится копирование, имеет непустое пересечение с
исходной областью. В этом случае возможна некорректная работа процедуры. Чтобы
подобного не возникало, необходимо проверять области на пересечение и в случае
непустого пересечения осуществлять копирование в обратном порядке.
Режим записи 2
В этом режиме младшие 4 бита байта, посланного процессором, определяют
цвет, которым будут построены не защищенные битовой маской пикселы. Регистр
битовой маски защищает от изменения определенные пикселы. Регистр маски
плоскости защищает от изменения определенные плоскости. Регистр DataRotate
устанавливает способ наложения построенных пикселов на существующее
изображение.
Η {Процедура закраски прямоугольника}
procedure Rect (xl, yl, x2, y2 : Integer; Color : Byte);
var
PixelAddr : Word;
Rows : Integer;
Cols : Integer;
NextRow : Integer;
LeftMask : Byte;
RightMask : Byte;
x, у : Integer;
Latch : Byte;
begin
Rows := у2 - yl;
Cols := (x2 div 8) - (xl div 8) - 1;
LeftMask := $FF Shr (xl mod 8);

RightMask := $FF Shi (7 - x2 Mod 8);
NextRow := 79 - Cols;
PixelAddr := yl * 80 + (xl div 8);
if Cols < 0 then
begin
LeftMask := LeftMask And RightMask;
RightMask := 0;
Cols := 0;
end;
SetRWMode (0, 2);
for у := yl to у2 do
begi η
SetBitMask (LeftMask);
Latch := Mem [$AO00:PixelAddr];
Mem [$A000:PixelAddr] := Color;
inc (PixelAddr);
SetBitMask ($FF);
for χ := 1 to Cols do
begin
Latch := Mem [$A000:PixelAddr];
Mem [$АО00:PixelAddr] := Color;
inc (PixelAddr);
end;
SetBitMask (RightMask);
Latch := Mem [$A000:PixelAddr];
Mem [$AOOO:PixelAddr] := Color;
inc (PixelAddr, NextRow);
end;
SetBitMask ($FF);
SetRWMode (0, 0);
end;

256-цветный режим адаптера VGA
Из всех видеорежимов этот режим является самым простым При
разрешении экрана 320*200 точек он позволяет одновременно использовать все 256
цветов. Для отображения 256 цветов одновременно необходимо под каждую точку
на экране отвести по 8 бит. В рассматриваемом режиме эти 8 бит идут
последовательно один за другим, образуя 1 байт. Тем самым в этом режиме
плоскости не используются. Видеопамять начинается с адреса $А000:0 При этом
точке с координатами (х, у) соответствует байт памяти по адресу 320*/ + χ
3 procedure SetPixel (χ, у, : Integer; Color : Byte);
begin
Mem [$A000:320*y+x] := Color;
end;
function GetPixel (x, у : Integer) : Byte;
begin
GetPixel := Mem [$A000:320*y+x];
end;

ГРАМШИ! ШЬЗОВШЬСШ ИНТЕРФЕЙС
И
X Антерфейс - некоторый способ (стандарт) взаимодействия (обмена
информацией, данными) между программой и человеком, другой программой и т. п.
Под графическим пользовательским интерфейсом (GUI - Graphical User
Interface) понимается некоторая система (среда), служащая для организации
интерфейса прикладных программ с пользователем на основе графического
многооконного представления данных.
Если посмотреть на любую хорошо сделанную прикладную программу, то
придется признать, что не менее половины всего кода программы служит именно
для организации интерфейса - ввод/вывод информации, работа с мышью,
организация меню, реакция на ошибки и т. п.
В среде GUI организацию всего взаимодействия с пользователем берет на себя
именно сама среда, оставляя прикладной программе делать только свою работу.
Считается, что основы GUI были заложены работами в исследовательском
центре PARC фирмы Rank Xerox. В значительной степени под влиянием этих
разработок в начале 1984 года возник компьютер Macintosh фирмы Apple (a
вместе с ним и встроенный графический интерфейс). Macintosh был фактически
первым компьютером, специально спроектированным для работы с GUI и
имевшим для этого все необходимое аппаратное и программное обеспечение
(основная часть последнего находится в ПЗУ компьютера). Использование GUI в
компьютере Macintosh сделало работу с ним чрезвычайно наглядной и понятной
даже для начинающих пользователей.
Укажем некоторые преимущества этой среды. Все основные объекты (диски,
каталоги, программы и пр.) представляются пиктограммами. Каждой программе
отводится одно или несколько окон на экране, которые пользователь по своему
усмотрению может передвигать, изменять размеры, уничтожать. Для
манипулирования объектами активно используется мышь. Все программы имеют общие
принципы построения, одинаковый дизайн, состоящий из одних и тех же
элементов, причем все эти элементы просты и наглядны.
Вслед за этой средой появились другие графические среды - GEM фирмы
Digital Research и Microsoft Windows (первая версия - ноябрь 1985 года) - для
персонального компьютера фирмы IBM.
К числу других графических сред можно также отнести:
• Presentation Manager (OS/2);
• OpenXook, Motif (Unix - станции);
• NextStep (Next).
Укажем несколько общих принципов, лежащих в основе перечисленных
выше систем. К числу таковых относятся:
• графический режим работы;

• представление ряда объектов пиктограммами;
• многооконность;
• использование указующего устройства - мыши;
• адекватность изображения на экране изображаемому объекту (принцип
WYSIWYG - What You See Is What You Get);
• наглядность;
• стандартизация всех основных действий и элементов (все программы для
данной графической среды выглядят и ведут себя совершенно одинаково,
используют одинаковые принципы функционирования, так что если
пользователь освоил работу с одной из программ, то он может легко
освоить и остальные программы для данной среды);
• наличие большого числа стандартных элементов (кнопок, переключателей,
полей редактирования), которые могут использоваться при
конструировании прикладных программ, делая их похожими в обращении
и облегчая процесс их написания.
Рассмотрим теперь концепции, лежащие в основе многих GUI.
Одной из концепций, характерной для большинства существующих систем
и программ для них, является понятие программы, управляемой данными Как
правило, эта концепция практически реализуется через механизм сообщений.
Внешние устройства (клавиатура, мышь, таймер) посылают сообщения модулям
программы о наступлении тех или иных событий (например, при нажатии
клавиши или передвижении мыши). Поступающие сообщения попадают в очередь
сообщений, откуда извлекаются прикладной программой.
Таким образом, программа не должна все время опрашивать мышь,
клавиатуру и другие устройства в ожидании, не произошло ли чего-нибудь,
заслуживающего внимания. Когда событие произойдет, программа получит
извещение об этом с тем, чтобы надлежащим образом его обработать Поэтому
программы для таких сред обычно представляют собой цикл обработки
сообщений: извлечь очередное сообщение, обработать его, если оно интересно, либо
передать стандартному обработчику сообщений, обычно входящему в систему и
представляющему собой стандартные действия системы в ответ на то или иное
событие.
Сообщения могут посылаться не только устройствами, но и отдельными
частями программы (в частности, возможна посылка сообщения себе). Так один
модуль может послать сообщение другому модулю, так меню посылает сообщение
о выборе определенного пункта. При этом существует еще способ прямой
посылки сообщения, минуя очередь, когда непосредственно вызывается
обработчик сообщений адресата.
Второй основополагающей концепцией является понятие окна, окна как
объекта. Окно - это не просто прямоугольная область на экране, это и программа
(процедура, функция), способная выполнять различные действия, присущие окну.
Одним из основных таких действий является реагирование на поступающие
сообщения и посылка сообщений другим объектам.

Д type Window = object
χ, у : Integer; { координаты окна }
Width : Integer; { ширина окна }
Height : Integer; { высота окна }
{ процедура реакции на сообщения }
procedure Handle (var m : Message); virtual;
end;
В данном примере окно введено как объект языка Turbo Pascal и содержит
координаты вершины верхнего левого угла (х, у), размеры (Width, Height) и
процедуру реагирования на сообщения (Handle), которая сделана виртуальной,
предоставляя объектам, происходящим из Windows, возможность переопределения
этой процедуры.
В среде Windows окно - это запись (record), одним из полей которой
является адрес функции, выполняющей обработку сообщений.
Одной из основных функций окна является перерисовка содержания окна.
Любое окно должно уметь при получении соответствующего запроса перерисовать
себя (или свою часть) на экране. Перерисовка может реализовываться или как
реакция на специальное сообщение, или как виртуальная функция
(при использовании объектно-ориентированных языков). В состав любой GUI
обязательно входит достаточно мощный графический модуль (GDI в Windows,
QuickDraw в Mac), обеспечивающий выполнение всех основных графических
операций и поддерживающий отсечение изображения по заданной (в том числе и
довольно сложной) области отсечения. За счет этого реализуется возможность
перерисовки фрагмента окна - устанавливается область отсечения, совпадающая
с требуемым фрагментом, а затем выполняется запрос
на перерисовку. При отработке запроса на
перерисовку окно может определить размер текущей
области отсечения и не пытаться рисовать то, что
заведомо будет отсечено.
Следует заметить, что стандартная графическая
библиотека, входящая в состав Turbo Pascal
(Turbo С), производит отсечение некоторых объектов
(таких, как текст) некорректно.
Среди окон вводятся отношения принадлежности
и следования, т. е. любое окно может иметь окно-
родителя, которому оно принадлежит, и,
следовательно, задается во внутренних координатах
родительского окна, отсекается в размерах родительским
окном и уничтожается при уничтожении
родительского окна. Любое окно может иметь и
принадлежащие ему окна (подокна), причем последние некоторым образом упорядочиваются.
Тем самым окна образуют древовидные структуры подчинения (рис. 8.1).
На приведенном дереве узлы соответствуют окнам, а отрезки - отношениям
принадлежности. Так, окно w не имеет родителя, но зато имеет два подокна - wl
W
w,
N
ν
W2
w.
wd
Puc. S.t

и w2. В свою очередь, окно w2 является родительским окном для окна w3,
которое является родителем окна w4.
Q type
PWindow = лWindow;
Window = object
Parent : PWindow; { ссылка на родительское окно,
или NIL}
Child : PWindow; { ссылка на первое подокно }
Next : PWindow; { ссылка на следующее окно
с тем же родителем }
Prev : PWindow; { ссылка на предыдущее окно
с тем же родителем }
end;
Родительское окно и принадлежащие ему подокна могут обмениваться
сообщениями друг с другом. Эти сообщения обычно разделяются на два класса -
запрос на выполнение окном некоторого действия и сообщение, оповещающее
окно о том, что в другом окне (обычно подокне) произошли некоторые изменения.
Любая система обычно предоставляет для работы некоторый стандартный
набор типов окон. Это своеобразные кирпичики, из которых пользователь может
строить свои программы.
Основные типы окон
Нормальное ("классическое") окно
Состоит из заголовка
(Caption), кнопки уничтожения
(или системного меню) и рабочей
области. Кроме этого могут
присутствовать кнопки минимизации
(кнопка минимизации
превращает окно в пиктограмму),
максимизации (кнопка
максимизации делает окно наибольшего
возможного размера) и скрол-
леры (Scroll Bar), служащие для
управления отображением в окне объекта, слишком большого, чтобы целиком
уместиться в нем (рис. 8.2).
[Н Notepad (Untitled)
[Же Edit Search belp
ш
■El
Ι*
Τ]
J
♦Ι
Τι

Кнопка (нажимаемая кнопка - Pushbutton)
Может быть с текстом или картинкой. При нажатии кнопка
посылает уведомляющее сообщение родительскому окну (рис. 8.3).
ок
Рис 8.3
Check Box (переключатель)
Переключатель может находиться в одном из двух И Т*Ь1« Gridlines
состояний; при переключении посылает уведомляющее сооб- D T£xt Boundaries
щение родителю (рис. 8.4). Рис 8 4
Radio Button
Radio Buttons действуют аналогично Check
Box, но, как правило, объединяются в группы
так, что всякий раз включен только один
переключатель из группы. При включении
посылает уведомляющее сообщение родителю
переключатели из той же группы (рис. 8.5).
Редактор
Однострочный или многострочный редактор текста,
предоставляющий все стандартные средства для
редактирования текста (рис. 8.6).
Статический текст
Прямоугольная область с текстом или картинкой (рис. 8.7).
О £lobal {Available to All Documents)
О With Document Template
<§> Erompt foi Each New
Рас. 8 5
и выключает остальные
[chapter 8. docj
Рис. 8 6
Save File as Jype:
Рис. 8 7
Скроллер (Scroll Bar)
Предназначен для графического выбора
непрерывного значения из некоторого диапазона.
Имеет кнопки для плавного изменения величины и
"движок", который можно перемещать мышью до
нужного значения. Скроллер бывает или
горизонтальным, или вертикальным (рис. 8.8)
trzn
Fuc. 8.8
Список (List Box)
Содержит список объектов, позволяет их добавлять,
удалять и выбирать. В качестве объектов могут выступать как
строки текста, так и совершенно абстрактные объекты,
умеющие сообщить свой размер и нарисовать себя. Список
может поддерживать сортировку и множественное выделение,
позволяющее просто отметить ряд элементов. Все действия,
связанные с выбором элементов, приводят к посылке
chaptei1.doc
chaptef3.doc
chapter4.doc
chapter 5. doc
chapter6.doc
contents.doc
oxers doc
ofossary.doc
intro.doc
♦Ι
Τ]
Рис. 8 9

уведомляющего сообщения родительскому окну (рис. 8.9).
Как видно из последних примеров, в состав окна могут входить другие окна
и действовать при этом как единое целое. Например, в состав окна-списка входит
скроллер.
Среди окон обычно выделяются так называемые диалоговые окна,
предназначенные для ведения диалога с пользователем, ввода данных и т. п. Обычно в
их основе лежит стандартное окно с большим набором подокон, играющих роль
управляющих элементов. Как правило, диалоговое окно (или процедура, ведущая
диалог) снабжается специальной функцией для координации работы управляющих
элементов. Например, диалог для выбора файла (рис 8.10).
FJejja
или
Ichapter1.doc
chapter3.doc
Ichapter4.doc
Ichapter5.doc
1 chapters doc
chapter7.doc
chapier8.doc
1 chapters doc
{contents.doc
exert, doc
glossary, doc
1 intro.doc
jj
T]
directories:
с All!
OK
Caned |
find Fie . ]
Priyes:
Ε
cidiskl
List Fees of J>pe:
[Word Documents C.docT
Ш
a
G Bead Only
Рис. 8.10
Кроме стандартных окон пользователь может создавать свои собственные
типы окон, либо добавляя какие-то новые свойства, либо переопределяя часть
старых и наследующих все остальное.
Ц type MyWindow = object (Window)
procedure Handle (var m : Message); virtual;
{ переопределили }
end;
procedure MyWindow.Handle (var m : Message)
begin
case m.Code of
else { все, что мы хотим оставить по-старому }
Window,Handle (m);
end;

В приведенном примере создается новый тип объекта - MyWindow,
происходящий от базового типа Window, но отличающийся от него иной
обработкой некоторых сообщений.
Рассмотрим механизм передачи окну сообщений от мыши и клавиатуры.
Обычно все сообщения от мыши посылаются тому окну, над которым
находится курсор мыши (произошло событие). Однако существует путь обхода
этого. Окно может "поймать" мышь, после чего все сообщения от мыши, где бы
они ни происходили, будут поступать только этому окну до тех пор, пока окно,
"поймавшее" мышь, не "отпустит" ее.
Рассмотрим следующую ситуацию: пользователь нажал кнопку мыши в тот
момент, когда курсор мыши находился над нажимаемой кнопкой. В этом случае
нужно "нажать" ее (перерисовать ее изображение) и удерживать нажатой, пока
нажата кнопка мыши и курсор мыши по-прежнему находится над нажимаемой
кнопкой. Однако если пользователь резко сдвинет мышь, удерживая кнопку мыши
нажатой, то нажимаемая кнопка не получит сообщения о том, что мышь покинула
пределы нажимаемой кнопки, вследствие того, что, как только мышь покинет эти
пределы, сообщения от нее будут поступать уже другому окну. При этом кнопка
все время будет оставаться нажатой. Поэтому нажимаемая кнопка должна
"захватить" мышь и удерживать ее, пока кнопка мыши нажата и курсор мыши
находится над нажимаемой кнопкой. Когда хотя бы одно из этих условий
нарушится, кнопка "отжимается" и мышь "освобождается".
При работе с клавиатурой важную роль играет понятие фокуса ввода.
Фокус ввода - это то окно, которому поступают все сообщения от
клавиатуры. Существует несколько способов перемещения фокуса ввода:
• при нажатии кнопки мыши фокус передается тому окну, над которым это
произошло;
• окна диалога обычно переключают фокус между управляющими
элементами диалога при нажатии определенных клавиш (стандартно это
Tab и Shift-Tab);
• посредством явного вызова функции установки фокуса ввода.
Окну, теряющему фокус ввода, обычно посылается уведомление об этом,
и оно может предотвратить переход фокуса от себя. Окну, получающему фокус,
передается сообщение о том, что оно получило фокус ввода.
Рассмотрим теперь механизм реализации основных оконных функций.
Изображание окна
Устанавливается область
отсечения, равная пересечению окна с
родительским окном, и выполняется
операция перерисовки.
Удаление окна с экрана
Для того, чтобы убрать окно с эк- рис β.11
рана, необходимо восстановить то, что
оно ранее закрывало. Для этого перебираются все окна, лежащие под убираемым,
г
1
W2 '
w3
J
w,

и определяется, какие области каких окон станут видимыми. После чего для всех
таких окон происходит перерисовка открывшихся фрагментов (рис. 8.11).
Передвижение окна
Старое изображение окна, как правило, просто копируется на новое место,
при этом появляются области, требующие перерисовки. Это открывшиеся
фрагменты других окон и часть текущего окна, невидимая ранее, но ставшая
видимой теперь.
Изменение размеров окна
Окно перерисовывается целиком. Если при этом открываются фрагменты
других окон, то они перерисовываются так, как описано выше.

СОЗДАНИЕ РЕАЛИСТИЧЕСКИХ ИЗОБРАЖЕНИЙ
IJ
JL Ааиболее распространенными методами построения реалистических
изображений являются трассировка лучей (Ray Tracing) и излучательность
(Radiosity). Ниже будет дано краткое описание обоих методов.
Трассировка лучей
Считается, что метод трассировки лучей дает наивысшую возможную
степень реализма. Кроме того, он предоставляет возможность для простого
решения широкого круга задач.
При построении изображения луч посылается в заданном направлении
для оценки приходящей оттуда световой энергии. Эта энергия определяется
освещенностью первой поверхности, встретившейся на пути луча.
Рассмотрим механизм
возникновения этой освещенности более
детально. Каждый источник света
испускает лучи во всех направлениях.
Попадая на поверхность, луч частично
преломляется, частично отражается и
частично рассеивается (рис. 9.1).
Проходя через прозрачный
материал, луч претерпевает естественное
ослабление с коэффициентом k = ехр (β
/), где / - длина пути внутри материала, Рис. 9.1
а β - коэффициент его прозрачности.
Отражение может быть зеркальным и диффузным. При зеркальном
отражении угол, составляемый отраженным лучом с нормалью к гладкой поверхности,
равен углу между падающим лучом и этой нормалью
и лежит с ним в той же плоскости. При диффузном
отражении (рассеянии) световая энергия, согласно
закону Ламберта, с одинаковой интенсивностью
рассеивается во все стороны.
Возьмем на поверхности точку Ρ с единичным
вектором внешней нормали η (рис. 9.2).
Пусть точка Ρ освещается точечным источником
света в направлении, определяемом единичным
вектором /. Тогда энергия Lr, отражаемая в
направлении вектора υ, задается формулой
к

F _ RLj(nJ)
Чг ~ 2 '
Г
где R - коэффициент отражения; L, - интенсивность источника; г - расстояние от
точки Ρ до источника света.
С учетом диффузного отражения можно записать:
R = sRs + dRd ,
ί + ί/ = 1 ,
где Rs - коэффициент для зеркального отражения (при чисто зеркальном
отражении вся энергия отражается в направлении v-2(l, n)n-l ); Rd - диффузная
составляющая (от направления не зависит).
Пусть падающий луч составляет угол θ с нормалью п. Определим угол #'
следующим образом:
sin#'= —sin# ,
где ns - коэффициент преломления материала.
Тогда
Rd =k2F(Q,ns)
cosg- nscos&\
COS Θ+ /Jf COS &\
Коэффициенты кх и к2 зависят от материала.
Преломленный луч будет лежать в плоскости исходного луча и нормали
к поверхности и составлять с нею угол Θ', введенный выше. Интенсивность
преломленного луча задается формулой
L, = s[\-F(9,n)]Li .
Поступая таким образом, можно определить освещенность каждой
поверхности сцены и построить требуемое изображение
Из каждого источника выпускаются лучи во все стороны. При пересечении
луча с поверхностью получаются отраженный и преломленный лучи, а если
моделировать диффузное освещение, то и пучок лучей, равномерно
распространяющихся во все стороны. Прослеживая все лучи, мы обнаружим, что часть из
них, пересекая картинную плоскость, в конце концов попадет в глаз наблюдателя.
Однако полный просчет лучей, называемый прямой трассировкой, из-за
огромного количества вычислений, которые необходимо произвести, как правило,
не применяется. Кроме того, большая часть работы окажется проведенной
впустую, так как значительное число усилий уйдет на определение освещенности
поверхностей, невидимых наблюдателю.
F(Otns).
KjCOSfl- COSff
/Jj COS 0 + COS #

Поэтому такой подход применяется редко. Обычно используется так
называемая обратная трассировка, при которой отслеживаются только лучи,
попадающие в глаз наблюдателя.
Это происходит так. Из глаза наблюдателя через каждый пиксел картинной
плоскости в сцену пропускается луч, и затем он отслеживается в обратном
направлении. Когда луч наталкивается на поверхность, интенсивность
соответствующего пиксела картинной плоскости определяется освещенностью
ближайшей точки пересечения луча и поверхности. Освещенность этой точки
складывается из отраженной и преломленной энергий, непосредственно
полученных от источников света, и отраженной и преломленной энергий, идущих
от других объектов сцены.
Для определения освещенности, порождаемой непосредственным
освещением, из точки пересечения выпускаются лучи ко всем источникам света
и определяется вклад тех источников, которые не заслонены другими объектами.
Для определения остальных величин из точки Ρ выпускаются вторичные
лучи (отраженный и преломленный) и определяется приносимая ими энергия.
Для моделирования диффузных поверхностей из точки Ρ выпускается пучок
лучей, равномерно распределенных по всем направлениям.
При трассировке луча может возникнуть ситуация, когда луч имеет
бесконечную длину, т. е. на пути луча не возникает никакого объекта В этом
случае энергия, приносимая лучом, приходит из окружающего пространства.
Окружающее пространство может быть однородным, т. е. не зависящим
от направления (например, небо). Однако в ряде случаев однородная модель
не подходит (например, когда окружающим пространством служит вид из окна).
В таких случаях сцена окружается некоторой достаточно большой поверхностью,
на которую проектируется окружающее пространство. В худшем случае луч
попадает на эту поверхность, и его интенсивность легко определяется путем
интерполяции картины на ней.
Таким образом, метод трассировки лучей заключается в моделировании
прохождения лучей в рамках геометрической оптики. Лучше всего он подходит
для сцен, не содержащих диффузных поверхностей, ибо обмен энергией между
ними моделируется сложно.
Случай точечных источников света и идеально зеркальных или прозрачных
тел является наиболее простым: для каждого луча мы можем построить дерево,
узлам которого будут соответствовать точки пересечения луча с поверхностью, а
ветвям - отрезки луча между точками пересечения. При этом в каждой точке луч
или отражается, или разделяется на отраженный и преломленный. Тем самым
разделение луча на несколько лучей может произойти в каждом узле. При этом один
луч, выпущенный из глаза наблюдателя, может породить дерево, содержащее
сотни или даже тысячи лучей. Таким образом, даже в простейшем случае объем
вычислений может оказаться очень большим. Чтобы его как-то уменьшить, обычно
вводят ограничения на глубину дерева. Так как не все лучи вносят одинаковый
вклад в итоговую освещенность, то, оценивая вклад конкретного луча в итоговую

интенсивность пиксела картинной плоскости, можно прекратить дальнейшую его
трассировку, как только результат окажется ниже требуемой точности.
Цвет каждого пиксела определяется интенсивностями трех составляющих
цветов - красного, зеленого и синего.
Тем самым при трассировке луча необходимо вычислить сразу три
интенсивности, определяющие итоговый цвет. Коэффициенты отражения и
преломления для трех составляющих цветов различны и определяются цветом
поверхности (обычно зависимостью коэффициента преломления от цвета
пренебрегают).
Излучательность
Основными недостатками метода трассировки лучей являются
неэффективность работы с диффузными поверхностями и то, что определение
освещенности поверхностей проводится параллельно с построением изображения
и зависит от положения наблюдателя.
Метод излучательности устраняет эти недостатки, обеспечивая высокую
точность при работе с диффузными объектами и отдельное вычисление
глобальной освещенности независимо от положения наблюдателя.
В основе метода излучательности лежит закон сохранения энергии
в замкнутой системе. Все объекты разбиваются на фрагменты, и для этих
фрагментов составляются уравнения баланса энергии.
Пусть
В, - энергия, отбрасываемая i-м фрагментом сцены;
Et - собственная излучательность фрагмента;
Fi} - доля энергии /-го фрагмента, попадающая на i-и фрагмент (коэффициенты
формы);
р, - коэффициент отражения.
Уравнения баланса энергии имеют вид
η
Bi = Ei+PiTFijBj> i = l ".
Эти соотношения можно переписать в следующей форме:
η
В результате получаем систему линейных алгебраических уравнений. То, что
это система с сильным диагональным преобладанием, позволяет использовать для
ее решения итерационные методы (типа Гаусса-Зейделя), дающие за небольшое
число итераций вполне удовлетворительное решение.
Для определения цвета фрагмента соответствующие системы записываются
для каждой из трех основных цветовых составляющих, причем коэффициенты
формы от цвета не зависят и определяются только геометрией сцены.

Обычно после определения освещенности каждого фрагмента производится
билинейная интерполяция освещенности по всем объектам, дающая плавное
естественное освещение.
После выбора точки наблюдения объекты сцены проектируются на
картинную плоскость и строится изображение.
Наиболее трудоемким шагом метода излучательности является вычисление
коэффициентов формы. Рассмотрим этот процесс подробнее.
Выберем фрагменты А( и А; и
элементарные участки dA[ и dA; на них с нормалями
соответственно п£* и п; (рис. 9.3). Тогда доля
энергии элемента dA;, попадающей на элемент
dA-b равна
cos с?,· cos с?,
F(dAi,dAj) = Yl Y}
Рис. 9.3
F(dAhAj) = jA
-dAj .
где г - расстояние между элементами dAt и
dAj-, φ,, и φj - углы между нормалями к ним и
соединяющим их отрезком.
Интегрируя по фрагменту А;, получим
cos φ·χ cos (pj
Повторное интегрирование приводит к формуле
1 r r COS Φ; COS Ф\
Fy = FiAi.Aj) = -J 4-J-dtyM, .
л, "л, *л; яг^
Последнее соотношение не учитывает объектов, закрывающих часть одного
фрагмента от другого. Для их учета в подынтегральное выражение нужно
добавить еще один член - функцию HID/;, принимающую значения из отрезка
[0,1] и характеризующую степень видимости фрагмента Л/ с фрагмента Ар
FV ~ aJaJa;
cos (pi cos φ j
HIDijdAjdAi .
Точное вычисление этого интеграла, как правило, представляет значительные
трудности. Поэтому для отыскания коэффициентов формы используется ряд
достаточно эффективных приближенных методов. Наиболее распространенным
является метод полукуба.
Будем считать, что расстояние между фрагментами велико по сравнению
с их размерами. Тогда, выбрав в качестве точки на фрагменте Л/ его центр,
можно записать приближенно, что
г cose?,· cos©,

Построим воображаемый куб таким
образом, чтобы его центр совпал с центром
фрагмента, а за направление оси Oz (в системе
координат куба) возьмем нормаль к фрагменту
в его центре (рис. 9.4).
Разобьем часть поверхности куба,
лежащую в плоскости ζ > О, на квадратные
пикселы, и спроектируем все пространство на пять
граней получившегося полукуба. Для каждого
пиксела полукуба определяется ближайший
проектируемый на него фрагмент, после чего
вычисляется вклад каждого пиксела
коэффициентов формы.
О
\
\
л\
А
\>1*^^
г
/
У
[/
V
X
■Ъ
Рис 9.4
полукуба в /-ю строку матрицы
Если пиксел лежит на верхней грани, то его вклад в коэффициент формы
равен
ΔΑ
π{χ2 + у2 +1)2
где ΔΛ- площадь соответствующего пиксела, а для пиксела на боковой стороне
ζΔΑ
7Г(Х2+у2+\)2
Таким образом, коэффициенты формы от А{ определяются сразу ко всем
остальным фрагментам.
Для сокращения объема вычислений иногда используется метод
прогрессивной излучательности. В этом методе каждый раз ищется поверхность с
наибольшей излучательностью (сначала это источники света) и определяются
коэффициенты формы от нее ко всем остальным поверхностям. После этого
излучательности всех остальных фрагментов корректируются, находится фрагмент
с наибольшей излучательностью и так далее. Процесс продолжается до
достижения нужной степени точности.

ГРАФИЧЕСКИЙ ПРАКТИКУМ
Контрольные вопросы и задания
1. Перечислите типы графических устройств. Сформулируйте принципы
работы и основные различия между векторными и растровыми устройствами.
2. Назовите основные области применения компьютерной графики
и сформулируйте требования, предъявляемые в этих областях к соответствующим
аппаратным и программным средствам.
3. Сформулируйте концепцию машинной независимости программных средств
и назовите пути ее реализации.
4. Перечислите основные функции и предоставляемые возможности
библиотеки языка Turbo Pascal.
5. Напишите и отладьте на компьютере программу, которая бы
последовательно иллюстрировала применение основных графических процедур
библиотеки среды Turbo Pascal.
6. Дайте общие сведения о форматах BMP и PCX.
7. Сформулируйте основные задачи, возникающие при обработке растровых
изображений.
8. Напишите и отладьте программу для сжатия и растяжения произвольного
растрового изображения ( черно-белый вариант).
9. Опишите основные приемы работы с мышью и принтером.
10. В чем состоят способы организации видеопамяти для режимов EGA
и VGA?
11. Напишите и отладьте программы построения точки с заданными
атрибутами и заполнения прямоугольника с заданными вершинами.
12. Опишите основные типы и свойства множеств на целочисленной решетке.
Что такое растровое представление геометрического объекта?
13. Реализуйте на компьютере алгоритмы Брезенхема четырех- и восьми-
связной развертки отрезка.
14. Опишите возможные подходы к генерации растрового представления
непараметрических кривых.
15. Перечислите различные постановки задачи заполнения многоугольника.
16. Реализуйте на компьютере алгоритм заполнения выпуклого
многоугольника, заданного своими вершинами.
17. Опишите схему алгоритма заполнения многосвязной области с затравкой.
18. Реализуйте алгоритм заполнения многосвязной области с затравкой
с использованием стека.
19. Напишите матрицу общего преобразования на плоскости.
20. Что такое однородные координаты и в каких задачах они применяются?

21. Напишите программу нахождения точки пересечения двух произвольных
отрезков на плоскости.
22. Напишите матрицу общего преобразования в пространстве.
23. Напишите матрицы перспективного преобразования с использованием
однородных координат.
24. Получите каркасное изображение одного из пяти Платоновых тел
(тетраэдра, куба, октаэдра, икосаэдра, додекаэдра) в центральной или
ортогональной проекции.
25. Напишите программу, которая бы строила изображения ортогональной
и центральной проекций каркаса куба на картинную плоскость. Положения куба и
картинной плоскости считаются заданными.
26. Реализуйте в виде программы тест принадлежности точки относительно
произвольному многоугольнику, заданному последовательностью вершин.
27. Опишите схему триангуляции области с вершинами в заданном
множестве точек.
28. Опишите различные подходы к решению задачи построения линий уровня
функции двух переменных.
29. Реализуйте алгоритм построения линий уровня функции, заданной
в узлах прямоугольной сетки. Линии уровней различной высоты должны
различаться по цвету.
30. Дайте формулировку задачи загораживания и сформулируйте простейшие
эвристические принципы, используемые при ее решении.
31. Приведите классификацию алгоритмов загораживания.
32. Реализуйте алгоритм буфера глубины для изображения сцены, состоящей
из случайно расположенных в пространстве многоугольников.
33. Реализуйте алгоритм удаления нелицевых граней Платоновых тел - куба,
тетраэдра, октаэдра, икосаэдра и додекаэдра.
34. Перечислите основные подходы к решению общей задачи загораживания
и выясните, какие эвристические принципы используются в каждом из подходов.
35. Реализуйте растровую версию алгоритма плавающего горизонта.
36. Сформулируйте, в чем состоят методы Фонга и Гуро закраски
поверхности. Реализуйте алгоритм закраски поверхности методами Фонга и Гуро
и сравните результаты. В качестве поверхности возьмите сферу
37. Приведите примеры различных моделей освещения поверхности. Какие
физические принципы используются при создании моделей освещенности.
38. Опишите метод одношаговой трассировки.
39. Опишите метод трассировки лучей. Какие имеются пути повышения
эффективности метода?
40. Опишите общую схему и основные математические задачи, возникающие
при использовании метода излучательности.
41. Сравните условия применимости методов трассировки и излучательности.
42. Дайте общее представление о графическом пользовательском интерфейсе
и требованиях к нему.

43. В чем состоят основные способы построения графического
пользовательского интерфейса?
44. Что такое ресурс на примере среды Windows?
Приводимые ниже задания разбиты условно по степени сложности на пять
уровней.
Задания первого уровня
1. Вращение ЗО-твердых тел относительно заданного неподвижного центра
(центр вращения может находиться как внутри тела, так и снаружи, набор
вращаемых тел ограничить Платоновыми телами).
2. Вращение ЗО-твердых тел относительно заданной прямой линии,
произвольно расположенной относительно вращаемого тела (вращаемые тела -
Платоновы).
3. "Облет" ЗО-твердого (платонова) тела заданной траектории (например,
траектория - винтовая линия, твердое тело - тетраэдр).
4. Интерполяция и сплайны (кривые). Создание пакета программ,
включающего в себя следующие составные части: интерполяционный многочлен
Ньютона и/или Лагранжа, кубические сплайны, кривые Безье, В-сплайны, beta-
сплайны.
5. Интерполяция и сплайны (поверхности). Для случая прямоугольной
области построить приближение функции двух переменных поверхностью Безье,
бикубическим В-сплайном, бикубическим beta-сплайном.
Задания второго уровня
1. Двухмерная графика. Создание пакета программ по построению линий
уровня и изображению поверхностей для функций двух переменных на
прямоугольной декартовой сетке.
2. Изобразить поверхность Кэли, описываемую функцией
у = ζ3 - ху (-2 < χ < 2, -2 < у <2).
3. Изобразить коноид Плюккера, описываемый уравнением
wx2 -y2z = О (-2 < χ < 2, -2 <у <2, w - параметр).
4. Изобразить вращение ЗО-твердого тела (например, полнотория)
относительно неподвижной точки и/или произвольной прямой линий.
Задания третьего уровня
1. Вращение нескольких сцепленных между собой торов.
2. Построение трехмерных проекций четырехмерных тел (например, 4D-Ky6a
и/или 40-полнотория).

Задания четвертого уровня
1. Компьютерная визуализация пространственно-временной динамики
ансамбля, состоящего из нескольких ЗО-твердых тел (например, Платоновых),
каждое из которых перемещается по фиксированной траектории.
2. Разработка и реализация системы трехмерного компьютерного
проектирования, которая включала бы в себя набор простейших логических операций над
ЗО-объектами (например, Платоновыми телами): объединение и пересечение тел,
логическое вычитание, дополнение.
Задания пятого уровня
1. Создание реалистического изображения ЗО-сцены, состоящей из
нескольких (платоновых) тел, при их произвольном взаимном расположении.
2. Создание реалистического изображения четверки "целующихся" сфер.
Точечный источник света считается помещенным в заданную точку.

ГЛОССАРИЙ
Аппаратные средства обработки объемных данных
(three-dimensional hardware)
аппаратура дисплейного процессора изображений.
Буфер кадров (frame buffer)
специально выделенная область памяти компьютера, в которой целое
изображение или кадр хранится в виде, готовом для вывода на экран.
Векторная графика (vector graphics)
раздел компьютерной графики, предусматривающий построение изображения
из отдельных прямолинейных отрезков, а не из полутонов.
Векторный шрифт (vector font)
шрифт, в котором каждый символ задан как набор прямолинейных отрезков;
векторные шрифты легко масштабируются, поворачиваются.
Видеопамять (bit map)
область памяти, автоматически отображаемая на экран.
Визуализация (visualization)
процесс, помогающий пользователю наблюдать результаты моделирования
и вычислений и широко применяемый при решении многомерных научных
и инженерных задач.
Визуальные вычисления (visual computing)
программная вычислительная техника для создания и работы с цифровыми
изображениями и графикой.
Визуальный атрибут (visual attribute)
визуальная характеристика воспроизводимых объектов, таких, как материал,
текстура, показатель преломления, блеск, цвет.
Воксел (voxel)
(объемный пиксел) элемент массива параллелепипедов равного объема,
задающих равномерное разбиение трехмерного пространства.
Воспроизведение (rendering)
создание изображения по тому или иному представлению объекта.
Воспроизведение объекта при помощи поверхности
(surface rendering)
метод представления внешнего вида трехмерного объекта, но без его
внутреннего строения.

Геометрический примитив (geometric primitive)
элементарный фрагмент изображения, при помощи которого описывается
объемный объект.
Дисплейный файл (display list)
последовательность команд, при помощи которых формируется, обновляется
и регенерируется воспроизводимое графическое изображение
Диффузное отражение (diffuse)
отражение, при котором падающий на поверхность луч рассеивается
одинаково по всем направлениям.
Закраска методом Гуро (Gouraud shading)
закраска треугольника, основанная на линейной интерполяции освещенности,
заданной в его вершинах.
Закраска методом Фонга (Phong shading)
более реалистическая закраска, при которой интерполируются не только
освещенность в опорных вершинах, но и векторы нормали к поверхности.
Затенение граней или плоскостей (facet or flat shading)
закрашивание многогранника, при котором каждая видимая грань
закрашивается одним цветом с учетом ее ориентации в пространстве
по отношению к источнику света и наблюдателю.
Затенение со сглаживанием (smooth shading)
метод закрашивания с переходом через ребра граней, благодаря которому
поверхность объекта выглядит более гладкой.
Излучательность (radiosity)
метод построения изображений фотореалистического качества, основанный
на расчете глобальной освещенности сцены, возникающей в результате
многократного диффузного отражения света.
Конструктивная геометрия (Constructive Solid Geometry, CSG)
представление сложных трехмерных объектов путем комбинирования
простых тел. Над телами производятся операции пересечения, объединения
и вычитания.
Карты отражений (reflection maps)
представление среды, при помощи которой строятся отражения для
блестящих объектов в процессе визуализации.
Курсор мыши (mouse cursor)
пиктограмма (обычно в виде стрелки), синхронно перемещающаяся при
передвижении мыши; в отличие от курсора текстового режима реализуется
программно через драйвер мыши.
Лестничный эффект (aliasing)
ступенчатый характер прямых линий и зазубренность границ, возникающие
при изображении объектов на растровом дисплее.

Масштабирование (scaling, zoom)
увеличение или уменьшение объекта на экране.
Матирование (matting)
процесс затемнения частей фона изображения, когда на переднем плане
появляется какой-либо объект.
Метаморфоза (metamorphosis)
постепенное преобразование одного объекта в другой путем изменения таких
параметров, как цвет, ориентация, размер, прозрачность и т. п.
Моделирование поверхностей (surface modeling)
покрытие проволочного каркаса многоугольниками и заплатами для
образования цельной поверхности.
Мозаичное представление изображения (tesselation)
разбиение гладких поверхностей на многоугольники, соединенные в
мозаичной структуре.
Нелицевая грань (back face)
грань многогранника, внешняя нормаль которой направлена в сторону,
противоположную той, где находится наблюдатель.
Непрозрачность (opacity)
способность материала закрывать объекты, лежащие на заднем плане.
Объем памяти кадров (frame volume)
число графических кадров, ограничиваемое разрешением, набором цветов
и способом хранения изображений.
Объемная визуализация (volume visualization)
представление данных в виде трехмерного объекта с поверхностными
и внутренними элементами.
Объемное восприятие (volume rendering)
метод создания изображения, при котором представляется не только
поверхность, ограничивающая трехмерный объект, но и его внутреннее
содержание.
Объемное моделирование (solid modeling)
создание трехмерного представления объекта на экране дисплея с
использованием математических моделей, описывающих объекты в природной
среде.
Октарные деревья (octree)
древовидная структура организации трехмерного пространства, в которой куб
рекурсивно разбивается на восемь равных подкубов.
Отбрасывание тени (shadow casting)
отражение на экране дисплея зависимости взаимной ориентации объектов
и источников света.

Отображение прозрачности (transparency mapping)
метод визуализации, позволяющий делать объекты прозрачными,
полупрозрачными или матовыми.
Отсечение (clipping)
процесс отбрасывания частей изображения, выходящих за границы окна.
Палитра (palette)
набор возможных цветов.
Перспективная проекция (perspective projection)
отображение трехмерного пространства на плоскость экрана, учитывающее
перспективу.
Пиксел (pixel)
минимальный дискретный элемент, изображаемый на экране растрового
дисплея.
Пиктограмма (icon)
маленькая картинка, служащая для обозначения объекта или операции.
Полигональная модель (poligon mash)
представление объекта набором соединенных между собой многоугольников.
Пороговая обработка (thresholding)
метод, используемый для классификации материалов при воспроизведении
изображений.
Построение промежуточных кадров (tweening)
термин, обозначающий процесс создания промежуточных кадров с
незначительными отличиями друг от друга и используемый в мультипликации.
Примитив (primitive)
простейший геометрический объект, используемый для построения более
сложных объектов.
Проволочный каркас (wire-frame)
совокупность ребер многоугольников, составляющих полигональную модель
объекта.
Прогрессивная развертка (non-interlaced)
способ развертки, уменьшающий мерцание.
Прозрачность (transparency)
степень пропускания света изображаемым объектом.
Процессор памяти кадров (frame store precessor)
процессор памяти изображений, специализированный для обработки
изображений.
Псевдоокраска (pseudocolor)
способ назначения ложных цветов элементам изображения для выделения
какого-либо свойства.

Развертка-"заметание" (sweep)
процесс сложной пространственной экстузии по нелинейным путям.
Разложение в растр
представление объекта набором светящихся точек (пикселов).
Разрешение (resolution)
количество пикселов экрана по каждой из координат.
Рассеянный свет (ambient)
освещенность сцены, не зависящая от расположения объектов и источников
света.
Растр (raster)
двухмерный массив точек, упорядоченных в строки и столбцы на экране
электронно-лучевой трубки.
Растровая развертка (raster scan)
способ воспроизведения изображений, при котором электронный луч
пробегает по экрану определенным путем, а элементы люминофора
"включаются" согласно данным, содержащимся в буфере кадра.
Растровые данные (raster data)
представление изображения в виде двухмерной матрицы дискретных ячеек
(пикселов), каждая из которых имеет свою яркость и цвет.
Растровый шрифт (raster font)
шрифт, в котором каждый символ задан прямоугольной матрицей точек.
Сглаживание (antialiasing)
устранение или подавление лестничного эффекта и других искажений
изображения, вызванных дискретизацией.
Сканирование (scanning)
процесс считывания данных по регулярным горизонтальным линиям
развертки при обработке целого изображения или экрана.
Совмещение (registration)
совпадение характерных элементов двух изображений.
Составление (compositing)
процесс собирания различных изображений в единое целое.
Способ вывода (положения) (write mode)
способ, определяющий, как выводимый пиксел взаимодействует с пикселом,
на место которого он выводится; обычно в качестве способа вывода
выступает или простое замещение (новый пиксел ложится на место старого),
или используется одна из побитовых операций над битовыми (двоичными)
записями цветов пикселов.

Сплайн (spline)
кривая или поверхность специальной конструкции, используемая для
представления сложных гладких кривых или поверхностей.
Ступеньки (jaggies)
дефекты пилообразного типа, появляющиеся на линиях, границах и световых
бликах в растровом дисплее.
Сцена (scene)
термин, используемый для обозначения совокупности изображаемых
объектов.
Текстура (texture)
детализация строения поверхности, состоящая в нанесении на гладкую
поверхность заранее заданного узора.
Текстурное отображение (texture mapping)
усовершенствованный метод затенения; на базе каркасного представления
для объекта вычисляется "карта" и строятся поверхности с заданными
характеристиками.
Текстурные карты (texture maps)
графический эквивалент фотообоев.
Топология (topology)
математическое понятие для описания таких свойств геометрических
объектов, как связность, наличие полостей, отверстий и т. п.
Трансформация изображения (warping)
преобразование изображения, в результате которого оно в одних местах
может увеличиться, а в других уменьшиться.
Трассировка лучей (ray tracing)
метод реалистической визуализации, моделирующий движение светового
луча в изображаемой сцене; яркость точки экрана (пиксела) определяется
интенсивностью проходящего через нее луча.
Триангуляция (triangulation)
представление плоской области или поверхности в виде объединения
треугольников, пересекающихся только по целым ребрам и вершинам.
Файл изображения (picture file)
файл компьютера, в котором содержатся все данные, необходимые
для создания изображений.
Фильмоцикл (film-loop)
представление последовательности изображений на экране дисплея,
создающей эффект движения в реальном времени.
Фотореалистичность (photorealism)
создание цифровых изображений, сравнимых по качеству с фотографиями.

Экранизация (rendering)
вычисление изображения для представления на экране массивом пикселов.
Экструзия (extrusion)
способ построения трехмерной модели путем выталкивания двухмерной
фигуры в определенном направлении.
Элемент изображения (pixel picture element)
минимальная область двухмерного изображения, которую можно
воспроизвести на экране.
Элемент объемного изображения (объема) (voxel volume,
picture element)
наименьший трехмерный элемент объема, несущий в себе содержательную
информацию.
CGA (Color Graphics Adapter)
цветной графический адаптер, одна из первых видеокарт для IBM PC.
EGA (Enhanced Graphics Adapter)
улучшенный графический адаптер; более совершенная видеокарта,
поддерживающая организацию видеопамяти в виде параллельных плоскостей
и режима с 16 цветами.
Hercules Graphics Card
графическая карта Hercules; монохромная карта, несовместима с EGA и
VGA.
RGB (red, green, blue)
модель цветовосприятия, представляющая любой цвет как сумму трех
основных цветов (красного, зеленого, синего), взятых в определенной
пропорции.
VGA (Video Graphics Array)
графический видеомассив; видеокарта с большим разрешением, чет EGA,
поддерживает режим 256 цветов, имеет аналоговый видеосигнал.
Windows, Microsoft Windows
графическая среда для IBM PC/AT; отличается машинной независимостью,
многозадачностью, полным использованием всех резервов компьютера.
2=буфер (Z-bu?fer)
алгоритм удаления невидимых поверхностей, основанный на запоминании
координаты или глубины для каждого видимого пиксела в пространстве
изображения.

ББК 32.973
Ш57
УДК 681.327.1
Ε. В. Шикни, А. В. Боресков, А. А. Зайцев
Ш57 Начала компьютерной графики. — М.: "ДИАЛОГ-
МИФИ", 1993. — 138 с.
ISBN 5-86404-035-5
Книга знакомит с такими понятиями компьютерной графики, как
растровые алгоритмы, геометрические сплайны, преобразования на
плоскости и в пространстве и проектирование. Она дает рабочее
представление об основных направлениях и методах компьютерной
графики, включая способы построения реалистических изображений и
удаления невидимых линий, позволит освоить базовые приемы
реализации ее алгоритмов на персональных компьютерах. Книгу можно
рассматривать как практическое руководство. Она рассчитана на
читателей, знакомых с элементами аналитической геометрии, линейной
алгебры и языком программирования Pascal.
2404000000-008
Ш Г70ОШ-93 Бе3 объявл· ББК 32·973
Учебно-справочное издание
Евгений Викторович Шикин
Алексей Викторович Боресков
Андрей Александрович Зайцев
Начала компьютерной графики.
Редактор О. А. Голубев
Макет и обложка О. А. Кузьминовой
Корректор В. С. Кустов
Лицензия ЛР N 070109 от 29.08.91. Подписано в печать 23.12.93.
Формат 60x84/16. Бум. офс. Печать офс. Гарнитура Тайме.
Усл. печ. л. 8.37. Уч.-изд. л. 6.45. Тираж 15 000 экз. Заказ 12^1
Акционерное общество "ДИАЛОГ-МИФИ"
115409, Москва, ул. Москворечье, 31, корп. 2
Подольская типография
142100, г. Подольск, Московская обл., ул. Кирова, 25
© Е. В. Шикин, А. В. Боресков,
А. А. Зайцев 1993
ISBN 5-86404-035-5 ©Оригинал-макет, оформление обложки.
АО "ДИАЛОГ-МИФИ", 1993