Author: Ирьянова Н.Я.
Tags: программирование олимпиады издательство москва математические олимпиады
ISBN: 5-7038-2900-3
Year: 2011
Similar
Text
И
Московский государственный техническим
университет имени Н.Э.Баумана
2011
ФИЗИКА, МАТЕМАТИКА
демонстрационные варианты
и задания для тренировки
тематический сборник информационно-методических
и образовательных материалов
Министерство образования и науки Российской Федерации
Московский государственный технический университет имени Н. Э. Баумана
Олимпиада школьников “Шаг в будущее”
Демонстрационные варианты и задания для тренировки
по физике и математике
Под ред. канд. техн, наук, доцента Н.Я.Ирьянова
Тематический сборник
информационно-методических и образовательных материалов
Москва
2011
Составители: Власова Елена Александровна,
Ирьянов Николаи Яковлевич,
Паршев Леонид Петрович,
Струков Юрий Алексеевич,
Шишкина Светлана Ивановна
Рецензент: д.т.н., проф. каф. ФН-2 Зарубин Владимир Степанович
Олимпиада школьников “Шаг в будущее”. Демонстрационные варианты и
задания для тренировки по физике и математике. Тематический сборник ин-
формационно-методических и образовательных материалов / Под ред.
Н.Я.Ирьянова.- М.: МГТУ им. Н.Э.Баумана, 2011.- 150 с.
В сборнике представлены сведения о правилах организации и проведения, мето-
дическом и технологическом обеспечении академического соревнования по физике и
математике Олимпиады школьников «Шаг в будущее», дана информация о правилах
участия, определении победителей и призеров олимпиады и их правах.
Демонстрируются варианты олимпиадных заданий по физике и математике с
включением решенных в них задач, что дает представление об уровне требований к
подготовленности конкурсантов, предложен набор тренировочных задач и вариантов
заданий.
Назначение этого сборника - помочь школьникам и их наставникам подгото-
виться к участию в Олимпиаде.
Для школьников, абитуриентов и слушателей подготовительных курсов МГТУ
им. Н.Э. Баумана, преподавателей и организаторов.
© МГТУ им. Н.Э. Баумана, 2011
Предисловие
Московский государственный технический университет имени Н.Э. Баумана
проводит целенаправленную работу как научно-методического, так и организационно-
технического характера по созданию кадровой базы контингента абитуриентов для
формирования состава студентов университета из учащихся, нацеленных на получение
образования по инженерно-техническому направлению, проявляющих интерес к науч-
но-исследовательской деятельности и наиболее подготовленных и способных к освое-
нию учебных программ ВУЗа. Главная цель организационной работы - вовлечение воз-
можно большего количества учащейся молодежи в сферу научно-технической деятель-
ности путем научного просвещения, выявления и развития у обучающихся творческих
способностей и интереса к физико-математическим наукам, создания положительной
мотивации овладения инженерной специальностью и профориентация.
В последние годы в сложных социально-экономических условиях и демографи-
ческом спаде, в условиях непрерывного реформирования системы образования, когда
осложнилась задача обеспечения и повышения качества набора, в МГТУ им.
Н.Э.Баумана на базе накопленного опыта усилиями ректората и всего коллектива уни-
верситета при государственной поддержке была построена комплексная, динамично
развивающаяся, адаптированная к современным условиям система профориентации и
приема на первый курс. Основой ее функционирования является тесное взаимодействие
ученых и преподавателей университета с педагогическими коллективами
III
кол, уча-
щимися и их родителями. Эта совместная деятельность в рамках широкомасштабной
программы «Шаг в будущее», Молодежного космического центра, Специализирован-
ного учебно-научного центра, Физико-математической
III
колы, лицеев
№1580, №1581,
около двухсот профильных школ, подготовительных курсов и др. направляется Ректо-
ратом и Приемной комиссией и координируется недавно созданным Центром довузов-
ской подготовки университета.
Охватывая широкие круги школьников во многих регионах России, разработан-
ная система обеспечивает достаточно эффективное вовлечение молодых людей в сферу
инженерного творчества и исследовательской работы, поиск, воспитание и научно-
образовательную подготовку абитуриентов, желающих учиться в МГТУ им.
Н.Э.Баумана. Задача формирования состава студентов первого курса - набор абитури-
ентов, способных осваивать непростые образовательные программы, решается путем
конкурсного отбора по результатам ЕГЭ, вступительных испытаний, проводимых
МГТУ самостоятельно для установленного Министерством образования круга абиту-
риентов, а также по результатам участия
in
сольников в системе предметных олимпиад
по физике и математике разного уровня, олимпиады школьников «Шаг в будущее»,
проводимых МГТУ им. Н.Э.Баумана и Российским советом олимпиад школьников
(РСОШ).
Хотя элементы процедуры проведения, значимость олимпиад, количество при-
зеров из года в год корректируется, победители и призеры олимпиад, включаемых в ут-
верждаемый РСОШ перечень, получают существенные льготы при поступлении в ВУЗ.
Так в 2010 году победители и призеры олимпиады «Шаг в будущее» по комплексу
предметов «Техника и технологии», предметных олимпиад по физике и математике, по
решению Ученого совета в зависимости от статуса дипломанта и выбранной специаль-
ности могли быть либо зачислены на специальность без вступительных испытаг
ли-
бо им засчитывалось 100 баллов вместо их оценки за ЕГЭ по соответствующему пред-
мету. Этим правом воспользовалось около 1500 человек. Таким образом участие в этих
олимпиадах является для школьников своеобразным способом поступления в универ-
ситет, а для ВУЗа проведение таких мероприятий является приоритетным, поскольку
их результаты - важный источник набора на первый курс мотивированных, осознанно
выбравших специальность молодых людей.
Итоги набора 2009 - 2010 года, анализ успеваемости студентов, зачисленных по
результатам олимпиад, беседы с победителями свидетельствуют о том, что участие
школьников в разного формата интеллектуальных соревнованиях, олимпиадах и других
контрольно-диагностических мероприятиях, поэтапно проводимых университетом в
рамках функционирования системы «ВУЗ - средняя школа» играет важную образова-
тельно-воспитательную роль в развитии школьников. Оно способствует формированию
базовой грамотности школьников и ее совершенствованию, стимулирует их творче-
скую активность, дает возможность освоения приемов научно-исследовательской дея-
тельности и приобретения соревновательного опыта, позволяет им тщательно и плано-
мерно подготовиться и реализовать свое стремление поступить туда, куда хотел, а за-
тем успешно использовать приобретенные навыки самообразования в своем образова-
тельном маршруте.
В свете этого развитие и повышение эффективности созданной в МГТУ им.
Н.Э.Баумана системы довузовской подготовки и набора на первый курс является акту-
альной задачей. Решение ее связано с расширением олимпиадного движения, с совер-
шенствованием методического сопровождения.
4
Основное назначение предлагаемых материалов - предоставить информацию
участникам олимпиады, родителям и педагогам об орган
ационно-технологическом и
контрольно-диагностическом обеспечении многопредметной олимпиады «Шаг в буду-
щее» МГТУ им. Н.Э. Баумана, продемонстрировать уровень требований, предъявляе-
мых к подготовленности абитуриента для поступления и дальнейшего обучения, пока-
зать образцы вариантов заданий олимпиад по физике и математике с решением вклю-
ченных в них задач, предложить набор тренировочных задач и вариантов.
Надеемся, что учебные материалы сборника и работа с ними позволят школьни-
кам не только хорошо подготовиться к участию в олимпиаде, но и увереннее чувство-
вать себя на ЕГЭ или при сдаче вступительных экзаменов по физике и по математике.
Раздел 1. Общие сведения и методические материалы
по проведению Олимпиады школьников «Шаг в будущее»
(физика, математика)
1.1. Алгоритм и технология проведения мероприятия
В системе набора МГТУ им. Н.Э. Баумана при организации различных творче-
ских и научно-образовательных конкурсов, олимпиад школьников и других контроль-
но-диагностических мероприятий используется корректируемая применительно к кон-
кретным мероприятиям следующая технология и схема их организации:
- Принятие решения и разработка регламентирующих и организационно-
методических материалов по проведению мероприятия.
- Формирование круга участников и информирование образовательных учреж-
дений (ОУ) о мероприятии. Разработка системы информационного обеспечения (со-
провождения).
- Проведение конференции: обмен мнениями представителей ОУ и организато-
ров мероприятия.
- Прием документов и регистрация участников в базе данных.
- Формирование потоков учасников и оперативного расписания «технологии»
проведения конкретной Олимпиады.
- Формирование системы обеспечения: кадрового (организаторы, эксперты,
операторы), материально-технического (аудиторный фонд, комплекты бумаги и др.) и
контрольно-диагностического (варианты заданий, правила оценивания и определения
рейтинга).
- Проведение мероприятия (олимпиады) в соответствии с утвержденным поряд-
ком и регламентом.
- Предварительная обработка аудиторных материалов в пункте приема в соот-
ветствие с инструкцией по информационной безопасности. Формирование папок с вы-
полненными работами для экспертной оценки заданий.
- Экспертиза и выставление баллов за выполненные задания в соответствии с
установленными правилами оценивания.
- Сбор и обработка проверенных материалов Олимпиады. Фиксация поименных
результатов на бумажных носителях и в электронном виде.
6
- Информирование участников о личных достигнутых результатах, организация
показа работ, разбор задач и консультация участников.
- Работа апелляционной комиссии.
- Статистическая обработка результатов и формирование рейтинг-листа участ-
ников Олимпиады.
- Информирование участников о результатах Олимпиады, личных достижениях
каждого и возможности использования этих результатов для продолжения образования
(в качестве одной из форм участия в конкурсе).
1.2. Основополагающие документы и регламент проведения
Олимпиады «Шаг в будущее»
Согласно Порядку' проведения Олимпиад
III
кольников («Порядок»), утвержден-
ному Приказом №285 Министерства образования и науки РФ «Порядок проведения
Олимпиад школьников» от 22 октября 2007 года (в редакции Приказов Министерства
образования и науки Российской Федерации от 4 сентября 2008 г. №255, от 22 марта
2009 г. №92, от 6 октября 2009 г. №371, от I октября 2010 г. №1006) Олимпиада состо-
ит из двух этапов - отборочного и заключительного (очного). К участию в заключи-
тельном (очном) этапе Олимпиады школьников допускаются только победители и при-
зеры отборочного этапа Олимпиады. Победители и призеры Олимпиады определяются
по результатам заключительного этапа. При этом общее количество победителей и при-
зеров не должно превышать 35 процентов от общего числа участников заключительно-
го этапа Олимпиады.
При поступлении в государственные и муниципальные образовательные учреж-
дения среднего профессионального образования, а также в государственные и муници-
пальные образовательные учреждения высшего профессионального образования по
решению образовательного учреждения, в зависимости от общеобразовательного
предмета, соответствующего профилю Олимпиады, и уровня Олимпиады, победителям
и призерам Олимпиады в течение одного года с момента утверждения списков победи-
телей и призеров Олимпиады, в соответствии с законом Российской Федерации «Об
образовании», представляется одна из следующих льгот первого или второго порядков:
- льгота первого порядка - быть зачисленным в образовательное учреждение без
вступительных испытаний на направления подготовки (специальности), соответствую-
щие профилю Олимпиады; соответствие реализуемых образовательным учреждением
7
направлений подготовки (специальностей) профилю Олимпиады определяется образо-
вательным учреждением самостоятельно;
- льгота второго порядка - быть приравненным к лицам, набрав
1IIS
м максималь-
ное количество баллов по единому государственному экзамену по общеобразователь-
ному предмету, соответствующему профилю Олимпиады.
Основным организационно-методическим документом, регламентирующим под-
готовку и проведение предметных Олимпиад по физике и математике Олимпиады
школьников «Шаг в будущее» (академическое соревнование), является «Положение об
«Олимпиаде школьников «Шаг в будущее» (Олимпиаде), которое составляется в соот-
ветствии с «Порядком» и утверждается приказом Ректора МГТУ им. Н.Э. Баумана. Со-
гласно этому приказу Центром довузовской подготовки, на который возлагается ответ-
ственность за организацию и проведение Олимпиады, создается и разрабатывается
«Регламент проведения Олимпиады», создаются и утверждаются состав Оргкомитета,
Методическая комиссия и Жюри Олимпиады.
Ректор МГТУ им. Н.Э. Баумана ежегодно утверждает список базовых организа-
ций, участвующих в подготовке и проведении Олимпиады и согласовывает его с
РСОШ. Список базовых организаций Олимпиады формируется Центром довузовской
подготовки МГТУ им. Н.Э. Баумана из числа координационных центров, ассоцииро-
ванных участников, организаций и ВУЗов-партнеров Олимпиады школьников «Шаг в
будущее», зарегистрированных в установленном порядке.
1.3. Методика проведения Академического соревнования
Первый этап академического соревнования организуется в очной и заочной
форме и (или) с применением дистанционных образовательных технологий в период с
1 сентября по 31 января.
Второй (заключительный этап) академического соревнования организуется
только в очной форме в виде выполнения заданий по общеобразовательным предметам
физике и математике и/или комплексам предметов с 1 февраля по 31 марта в городе
Москве, а также в других городах Российской Федерации с участием базовых органи-
зации и ВУЗов-партнеров Олимпиады.
Конкретные сроки и периоды проведения мероприятий академического сорев-
нования, правила участия, и форма регистрации ежегодно утверждаются председателем
оргкомитета Олимпиады и размещаются на сайте МГТУ им. Н.Э. Баумана
8
www//bmstu.ru и официальном портале Олимпиады школьников «Шаг в будущее»
http://priem.bmstu.ru/olinipiada/.
Для участия в первом этапе академического соревнования обучающиеся в обра-
зовательных учреждениях регистрируются в оргкомитетах соответствующих Олимпиад
по общеобразовательным предметам в определенные Оргкомитетом Олимпиады сроки,
выполняют олимпиадные испытания по заданиям, утвержденным Методической ко-
миссией Олимпиады.
По результатам первого этапа академического соревнования оргкомитеты
Олимпиад по общеобразовательным предметам определяют победителей и призеров
первого этапа Олимпиады. Общее количество победителей и призеров первого этапа
академического соревнования Олимпиады не должно превышать 35 процентов от об-
щего числа участников первого этапа академического соревнования Олимпиады. Побе-
дители и призеры первого этапа академического соревнования Олимпиады допускают-
ся к участию во втором (заключительном) этапе академического соревнования Олим-
пиады.
Для участия во втором этапе академического соревнования, обучающиеся обра-
зовательных учреждений, подают заявку на регистрацию по установленному образцу в
Центр довузовской подготовки МГТУ им. Н.Э. Баумана.
При регистрации участники в личном заявлении указывают специальности (с
указанием вуза и факультета), при поступлении на которые они хотели бы реализовать
право получения льгот, в том случае, если станут победителями (призерами) Олимпиа-
ды. Максимальное количество специальностей, которое может указать в проиоритет-
ном порядке участник, устанавливается ежегодно регламентом Олимпиады.
Победители и призеры Олимпиады определяются по результатам заключитель-
ных этапов каждого вида конкурсных испытаний Олимпиады, проводимых в МГТУ им.
11.9. Баумана, базовых организациях и ВУЗах-партнерах Олимпиады «Шаг в будущее».
Победителям и призерам Олимпиады выдаются дипломы, подписанные предсе-
дателем Оргкомитета Олимпиады, утвержденные Министерством образования и науки
Российской Федерации.
Победителями Олимпиады считаются участники Олимпиады, награжденные ди-
пломами 1-ой степени. Призерами Олимпиады считаются участники Олимпиады, на-
гражденные дипломами 2-ой и 3-ей степени. Участники Олимпиады могут награждать-
ся свидетельствами участника, грамотами, памятными подарками.
9
Количество победителей и призеров Олимпиады не должно превышать 35 про-
центов от общего числа участников заключительного этапа Олимпиады. Количество
победителей Олимпиады не должно превь
III
ать 10 процентов от общего числа участни-
ков заключительного этапа Олимпиады по соответствующему общеобразовательному
предмету (комплексу предметов).
1.4. Порядок проведения Олимпиады
Для непосредственного проведения Олимпиады распоряжением председателя
методической комиссии создаются предметные экспертные комиссии, бригада органи-
заторов, группа обработки выполненных олимпиадных работ. В соответствии с количе-
ством участников готовятся комплекты бланков бумаги, аудиторный фонд и комплекты
вариантов заданий. Олимпиад
>ie задания разрабатываются и формируются методиче-
ской комиссией. Вся ответственность за обеспечение информационной безопасности на
этапе подготовки этих заданий возлагается на разработчика и одного из назначаемых
членов методической комиссии. Задания разрабатываются комплектами, содержание
каждого из которых соответствует профилю Олимпиады.
Подготовленные комплекты вариантов тиражируются их разработчиком в спе-
IB
ально отведенном для этих целей помещег
151
я в количестве, соответствующем числу
участников по каждому профилю Олимпиады.
Растиражированные комплекты вариантов раскладываются разработчиком по
отдельным конвертам, количество которых соответствует числу аудиторий, выделен-
ных для проведения Олимпиады по соответствующему профилю. После чего конверты
опечатываются и передаются лицу, ответственному за хранение и выдачу олимпиадных
заданий. Член методической комиссии, ответственный за хранение и выдачу заданий,
помещает опечатанные конверты вместе с журналом учета в специальный сейф, ключ
от которого хранится у председателя методической комиссии - первого проректора-
проректора по учебной работе Университета.
Процедура выдачи комплектов заданий начинается в день проведения Олимпиа-
ды по соответствующему профилю за 30 минут до её начала. Распределение участников
Олимпиады по аудиториям проводится накануне её проведения системой «Электрон-
ный университет». Плакаты с регистрационными номерами школьников и номерами
аудиторий, где проводится Олимпиада, вывешиваются в помещениях оргкомитета в
день её проведения. Перед началом Олимпиады комплект опечатанных заданий в при-
сутствии руководителя бригады организаторов Олимпиады извлекается из сейфа пер-
10
кого проректора лицом, ответственным за их хранение и выдачу, и конверты с зада-
ниями передаются руководителю бригады организаторов. Руководитель бригады орга-
низаторов сообщает старшим oprat
аторам номера аудиторий для работы и раздаёт
конверты с вариантами заданий и комплекты бланков бумаги для участников.
аудитории организаторы проверяют количество явг
Тиш
«хся участников Олим-
пиады, о чем старший oprat
UK
атор делает соответствующую запись в посадочной ве-
домости. Участники, опоздав
IIIS
е на Ох
UIJJIU
аду и явившиеся после вскрытия конверта
В
с заданиями Олимпиады, в аудиторию не допускаются. Размещение участников по мес-
гам в аудитор
su
осуществляется в соответствии с установленным правилом.
Организаторы проводят краткий инструктаж по порядку проведения Олимпиады
v изложением следующей информации:
— продолжительность выполнения заданий Олимпиады 240 минут;
после посадки в аудиторию участник до сдачи выполненной работы имеет право
не более одного раза выйти в туалет в сопровождении одного из организаторов, поря-
док выхода определяется старшим организатором;
— на рабочем месте участника при выполнении задания могут находиться только
। депорт, материалы, выданные организатором, а так же удостоверение и авторучки;
при заполнен
титульного листа и на
сании выполненной работы участники
могут использовать только ручки с пастой черного или синего цвета;
— запрещается вставать с мест, пересаживаться, разговаривать с другими участни-
ками и решать задачи других вариантов, а так же запрещается использовать источники
информации,
UU
средства оперативной связи и вычислительной техники;
- за нарушение правил поведения на Олимпиаде, в частности за пользование шпар-
галками или электронной техникой, участник удаляется независимо от числа правильно
решенных заданий без проверки работы;
— сообщают участникам, что на титульном листе запрещено записывать результаты
решений и ответы по заданию. Все чистовые решения необходимо представить на по-
лученном от организатора чистовом бланке, на этом бланке категорически запрещено
писать Ф.И.О. и номер удостоверения; на чистовике все остав
ins
еся пустые места, не-
заполненные ответами на вопросы, участники обязаны прочеркнуть латинской буквой
— сообщают участникам, что работы проверяются в зашифрованном виде, на про-
верку поступают только чистовики, черновики сдаются отдельно.
11
После проведения инструктажа участникам Олимпиады раздают комплекты эк-
заменационных бланков, объясняют, как заполнять титульный лист, каждому участни-
ку выдают олимпиадное задание, сообщают о необходимости записи № задания на ти-
тульном листе и в чистовике. Объявляют устно и записывают на доске время начала и
окончания работы, а также дату и время объявления результатов проверки выполнен-
ных заданий.
Во время проведения Олимпиады организаторы следят за порядком, не коммен-
тируют выполняемые задания и не занимаются их решением. При необходимости вы-
дают участникам дополнительные чистовые бланки с обязательной последующей от-
меткой их количества на титульном листе участника. Организаторам запрещается во
время проведения Олимпиады посещение других аудиторий, а также использование
средств мобильной связи.
По окончании Олимпиады, после завершения сбора работ старший организатор
пересчитывает их, сопоставляет число сданных работ с количеством участников Олим-
пиады, присутствующих в аудитории, вносит число сданных работ в соответствующую
графу посадочной ведомости. Затем он доставляет работы в пункт приема и обработки
письменных работ, где сдаёт их представителю оргкомитета, под руководством которо-
го, производится шифровка работ.
За
in
лфрованные работы обезличиваются путем удаления титульных листов с
информацией об участниках Олимпиады, вновь пересчитываются и передаются пред-
седателю предметной экспертной группы для оценки их содержания. Факт передачи
оформляется соответствующим образом в журнале учета.
Титульные листы с информацией об участниках Олимпиады пересчитываются
представителем оргкомитета и помещаются им в сейф до завершения процедуры про-
верки и оцеь
и
аания зашифрованных письменных работ.
Проверка анонимных письменных работ производится в специально отведенной
для этих целей аудитории, оборудованной системой сигнализации. Вынос работ из ау-
дитории и доступ в нее посторонних лиц запрещен. Выход члена экспертной группы из
аудитории допускается только после сдачи всех проверяемых им работ председателю
экспертной группы или его заместителю. Работы, не находящиеся на проверке, хранят-
ся в сейфе, которым оборудована аудитория. Ответственность за соблюдения режима
проверки возлагается на руководителя экспертной группы и двух его заместителей.
В процессе проверки работы член экспертной группы проводит оценку ее со-
держания согласно правилам оценивания, разработанным методической комиссией по
12
проведению Олимпиады и утвержденным Ректором университета. Результаты оцени-
вания каждой задачи в баллах и общая сумма баллов вносятся в специальную таблицу,
содержащуюся на бланке чистовика письменной работы. По завершении проверки всех
письменных работ каждый член экспертной комиссии заполняет специальную ведо-
мость с указанием шифра работы и суммы баллов, в которых оценено ее содержание.
Проверенные в зашифрованном виде работы передаются на дешифровку пред-
ставителю оргкомитета по проведению Олимпиады.
Дешифровка работ производится группой
III
афроваль
IIISI
сов под руководством
представителя оргкомитета в пункте приема и учета письменных работ. Де
III
яфрован-
ные работы обрабатываются, а результаты оценивания их содержания заносятся в про-
токол результатов и в электронную базу данных участников Олимпиады. Протокол ре-
зультатов заверяется представителем оргкомитета и членами предметной экспертной
комиссии.
После обработки письменные работы передаются на ответственное хранение в
оргкомитет Олимпиады.
1.5. Структура, содержание и правила оценивания
олимпиадных заданий
Успешность освоения образовательных программ университета зависит, как по-
казывает опыт, не только от интеллектуального потенциала абитуриента, но и от степе-
ни его интереса к овладению избранной профессией, его эмоционально-волевой устой-
чивости, психофизической мобильности. Олимпиада, как интеллектуальное соревнова-
ние школьников, мотивированных на деятельность в определенной предметной облас-
ти, проводимая в ограниченных временных рамках, является как раз тем мероприятием,
когда есть возможность оценить общий уровень подготовленности абитуриента к обу-
чению в университете. Средством же или инструментом, который позволяет распреде-
лить (дифференцировать) абитуриентов по степени подготовленности их к обучению в
университете является олимпиадное задание. Содержание задания, его объём и состав
задач, должны быть структурированы таким образом, чтобы по результатам выполне-
ния такого задания можно было с приемлемой достоверностью судить о степени сфор-
мированное™ предметно-значимых качеств абитуриента и его умении творчески их
применять в жёстких соревновательных и временных условиях.
Опыт проведения в МГТУ им. Н.Э. Баумана различных четырёхчасовых кон-
трольно-диагностических мероприятий (КДМ) - вступительных экзаменов, тестирова-
13
ний, Олимпиад - показал, что десять разных и по трудности, и по тематике, и по назна-
чению задач - объём задания, достаточный, чтобы уверенно судить о «профессиональ-
ном» портрете конкурсанта и установить его рейтинг.
В процессе подготовки Олимпиад задачи разрабатываются и подбираются мето-
дической комиссией, а её ответственные сотрудники формируют задания и комплекты
заданий, содержание каждого из которых соответствует профилю Олимпиады. Ком-
плект формируется из шести параллельных вариантов заданий, что минимизирует воз-
можность контактов участников Олимпиады с одинаковыми номерами вариантов зада-
ний в ходе Олимпиады. Варианты заданий каждого комплекта по своей структуре и
сложности параллельны, т.е. содержат одинаковое как общее количество, так и количе-
ство задач одинаковой сложности. Формирование вариантов заданий осуществляется
на основе, разработанной в университете модели оценивания трудности задач и вари-
антов заданий, а так же опыта специалистов-предметников. Демонстрационные (типо-
вые) варианты обсуждаются методической комиссией и утверждаются ректором -
председателем оргкомитета Олимпиады.
Методика составления олимпиадных заданий содержательно базируется на ос-
новных положениях образовательных программ по математике и физике федерального
компонента Государственного образовательного стандарта среднего (полного) общего
образования. В соответствии с целями Олимпиады каждый вариант задания делится на
три части по уровню сложности задач (например: с соотношением сложности 1,0; 1,25;
1,5). Задачам каждой из частей назначается определённый максимальный балл (напри-
мер: 8, 10, 12) таким образом, чтобы сумма баллов, за полностью безупречно выпол-
ненное задание составляла 100. Такое деление предполагает наличие задач, одни из ко-
торых нацелены на выявление базовых теоретических знаний, навыков владения тер-
минологией, понятийным аппаратом и стандартными алгоритмами; другие - на выяв-
ление комплексных предметных интеллектуальных умений применять для решения
конкретных задач знания нескольких разделов школьной программы, а третий - на вы-
явление общей эрудиции, степени ориентированности в теоретическом материале, ло-
гики мышления, способности анализировать ситуацию и находить подходы и верный
путь решения в нестандартных случаях. Варианты олисмпиадных заданий по своему
содержанию носят комплексный, сбалансированный характер, охватывая все ключи-
вые, наиболее важные элементы программного учебного материала. Отличительной
особенностью заданий по математике является относительно высокий «вес» в них гео-
метрических задач, вкючая задачу по стериометрии. Поэтому для успеха на Олимпиаде
14
oi конкурсанта требуется, как свободное владение теоретическим материалом школь-
ного курсов планиметрии и стериометрии, так и практические навыки определения в
задачах элементов плоских фигур и пространственных тел, умение строить различные
сечения, анализировать их конфигурацию и выполнять теоретические обоснования
ключевых шагов решения. Примеры и конкретные характеристики задач и вариантов
< а даний предметных Олимпиад приведены ниже.
Проверка работ участников Олимпиады осуществляется предметными эксперт-
ными комиссиями университетского жюри Олимпиады в состав которых входят веду-
щие преподаватели и профессора факультета «Фундаментальные науки». С целью ис-
ключенния влияния субъективизма и его последствий каждый вариант задания прове-
ряется двумя экспертами. При проверке применяется алгоритм пошагового оценивания
решения каждой задачи, когда эксперт положительно оценивает всякое верное дейст-
вие, каждый аргументированный «шаг» конкурсанта на пути продвижения его к ответу.
Для оценки степени решенности задачи используется пятиразрядный ряд: -1;
0,75; 0,5; 0,25; 0 - отметки, зависящие от количества ошибок при решении задач. Диаг-
ноз «1» ставится при полностью безупречном решении и наличии ответа, а «О» - если
конкурсант либо не приступал к решению задачи или в решении отсутствуют положи-
тельные признаки. Промежуточные отметки (диагнозы) устанавливаются председате-
лем предметной экспертной комиссии после коллегиального обсуждения экспертами
задач варианта при проверке. Оценка за выполненную задачу фиксируется как колли-
чество баллов, определяемое произведением отметки (диагноза) на максимальное кол-
личество баллов, назначенное за задачу. Так, если за задачу назначено 12 баллов, то в
зависимости от степени её решенности , конкурсант может получить 12, 9, 6, 3 или О
баллов. Конечный результат определяется суммированием «заработанных» баллов за
решенные им задачи.
Такая схема оценивания обеспечивает широкую балльную вариативность (от О
до 100 уровней), надёжную дифференциацию в определении рейтинга участников.
Правила оценивания устанавливаются при формировании вариантов заданий и утвер-
ждаются ректором.
15
Раздел 2. Математика
2.1. Содержание варианта задания Олимпиады
по математике в МГТУ им. Н.Э. Баумана
Задания Олимпиады разработаны на основе Федерального компонента государ-
ственного образовательного стандарта среднего (полного) общего образования. Тексты
задав
в целом соответствуют формулировкам, принятым в учебниках и учебных по-
собиях, включенных в Федеральный перечень.
Контрольно - диагностические материалы (КДМ) позволяют установить уровень
усвоения выпускниками федерального компонента государственного образовательного
стандарта среднего (полного) общего образования, а также позволяют проявить творче-
ский потенциал, способность к самостоятельному мышлению, необходимые для ус-
пешного освоения вузовской программы технического профиля.
Каждый вариант по математике состоит из 10 заданий: четырех заданий первого
уровня сложности, двух заданий второго уровня и четырех задач третьего уровня
сложности.
Все задания требуют от участников развернутого ответа, т.е. должно быть запи-
сано полное обоснованное решение задачи. Задачи одного билета охватывают все ос-
новные разделы школьного курса математики.
ЗАДАЧИ ПЕРВОГО УРОВНЯ СЛОЖНОСТИ требуют знания алгоритмов ре-
шения задач из одного или двух разделов математики. Для их решения требуются про-
стые математические преобразования и вычисления. Это могут быть текстовые задачи:
задачи на движение, производительность, на пропорции и процентные отношения, на
прогрессии; тригонометрические уравнения или системы уравнений, примеры на тож-
дественные преобразования тригонометрических выражений; рациональные, иррацио-
нальные, показательные, логарифмические уравнения, и их системы; задачи, связанные
со свойствами геометрических фигур, в том числе, задачи по планиметрии и простей-
шие стереометрические задачи.
2.2. Примеры задач первого уровня сложности:
Текстовые задачи
1. Два экскаватора, работая одновременно, могут вырыть котлован за 4 часа. Один пер-
16
пый экскаватор затратит на эту работу на 6 ч больше, чем один второй. За какое время
может вырыть котлован каждый экскаватор, работая отдельно? Ответ: 12 и 6 ч.
2. Расстояние между станциями А и В равно 103 км. Из А в В вышел поезд и, пройдя
некоторое расстояние, был задержан, а потому оставшийся путь до В проходил со ско-
ростью, на 4 км/ч больше прежней. Найти первоначальную скорость поезда, если из-
вестно, что оставшийся путь до В был на 23 км длиннее пути, пройденного до задерж-
ки, и на прохождение пути после задержки было затрачено на 15 мин больше. Чем на
прохождение пути до задержки. Ответ: 80 км/ч.
3. Два лыжника стартовали друг за другом с интервалом в 6 минут. Второй лыжник
догнал первого в двух километрах от точки старта. Дойдя до отметки 5 км, второй
лыжник повернул обратно и встретил первого на расстоянии 1 км от точки поворота.
11айдите скорости лыжников. Ответ: 10 и 20 км/ч.
4. Турист проехал на автомобиле 5/8 всего пути, а остальную часть - на катере. Ско-
рость катера на 20 км/ч меньше скорости автомобиля. На автомобиле турист ехал на 15
мин дольше, чем на катере. Чему равны скорость автомобиля и скорость катера, если
весь путь туриста равен 60 км? Ответ: 100 км/ч и 90 км/ч, или 80 км/ч и 60 км/ч.
5. Если сначала половину заказа выполнит один рабочий, а потом другую половину -
второй рабочий, то весь заказ будет выполнен за 2 часа. Если же первый рабочий вы-
полнит одну треть заказа, а потом оставшуюся часть выполнит второй, то весь заказ
будет сделан за 2 ч 10 мин. За сколько времени каждый рабочий отдельно может вы-
полнить весь заказ? Ответ: 1.5 и 2.5 ч.
6. Поезд вышел из пункта А в пункт В, расстояние между которыми 230 км. Через час
навстречу ему вышел из пункта В торой поезд, скорость которого на 15 км/ч больше,
чем у первого. Определите скорости поездов, если известно, что они встретились на
расстоянии 120 км от пункта А. Ответ:40 и 55 км/ч.
7. Рабочий должен был по плану изготовить за несколько дней 72 детали. Так как рабо-
чий каждый день изготавливал на 2 детали меньше плана, то закончил работу через 3
дня после срока. Сколько деталей в день должен был изготовлять рабочий по плану?
Ответ: 8 деталей.
8. Вкладчик взял из банка сначала 1/4 своих денег, а потом 4/9 оставшихся и еще 64
тыс. руб. После этого у него осталось на вкладе 3/20 всех его денег. Какова сумма
вклада? Ответ:240 тыс. руб.
9. Найти сумму трех чисел, зная, что третье относится к первому как 4,5: 15\4 и состав-
ляет 40 % второго, а сумма первого и второго равна 400. Ответ: 500.
17
10. Кусок сплава меди и цинка массой 36 кг содержит 45% меди. Какую массу меди
нужно добавить к этому куску, чтобы полученный новый сплав содержал 60% меди?
Ответ: 13,5 кг.
Прогрессии
1. Сумма первых девяти членов арифметической прогрессии равна 117, а сумма после-
довательных членов этой прогрессии, начиная с десятого номера и до пятнадцатого
включительно, равна 213. Найдите четвертый член прогрессии. Ответ: 10.
2. Сколько членов содержится в возрастающей арифметической прогрессии с положи-
тельными членами, у которой сумма членов с нечетными номерами составляет 52%
суммы членов всей прогрессии? Ответ: 51.
3. Укажите все значения п, при которых сумма п последовательных членов арифмети-
ческой прогрессии 25, 22, 19,..., начиная с первого, не меньше 66. Ответ: 3<п< 14, hgN.
4. Сколько последовательных членов арифметической прогрессии 36, 33, 30, ..., начи-
ная с первого, надо сложить, чтобы получить сумму, большую 201? Ответ:
8< п< 17, пе N.
5. Какое наибольшее значение может принять сумма первых п членов арифметической
прогрессии 68, 65, 62...? Ответ: 805.
6. В арифметической прогрессии 10 членов, их сумма равна 245. Сумма членов с чет-
ными номерами относится к сумме членов с нечетными номерами, как 27: 22. Опреде-
лите первый член и разность прогрессии. Ответ: д, = 2, d = 5.
7. Найти три числа, которые образуют возрастающую арифметическую прогрессию ес-
ли известно, что сумма их равна 30, и что если к ним прибавить соответственно 1, 2, 9.
то новые три числа образуют геометрическую прогрессию. Ответ: 5,10, 15.
8. Три числа образуют арифметическую прогрессию. Если вместо третьего числа по-
ставить сумму трех чисел, а остальные числа оставить без изменения, то получится
геометрическая прогрессия. Найдите эти числа, если второе число равно 12. Ответ: 4;
12; 20.
Логарифмические и показательные уравнения
1. Решите уравнение
2,+Л + 4 = 9^2^. Ответ: 16.
1 3Л±3
2. Решите уравнение 8• 64* - 3- 2 * 4-16 = 0. Ответ: 3.
18
3.r+2 l-.x
I Решите уравнение 22л ь-' — 22л+3 =1. Ответ: 1.
•I Решите уравнение 64 • 9 х + 12*+l — 27 16х = 0. Ответ: 2.
S Решите уравнение 9^ -4х'+1 — 81^"4' = 12 • З'х "4х* — 4 • Q'*"4'. Ответ: 1-272, 3-72, 4.
ь, Решите уравнение 2х2 • 2>^2 4- х • 2Х+1 = 2х2 2х + х • 2i^x^’. Ответ: 0; 1; 2.
7 Решите уравнение х,ов29 — 8 • 31°82* = 9. Ответ: 4.
~ 3
К Решите уравнение 2 -9х 1 = —. Ответ: -1; l-log23.
1
•> Решите уравнение х1о8б4<3*) — 31083 2 . Ответ: 9;
10. Решите уравнение 31~2,х' +91+|х| =28. Ответ:х=+-.
^2»
11. Решите уравнение (log2 х + logx 2 + 2)(log2 х - log2x х) = 6. Ответ: 4; -.
х2 11
12. Решите уравнение 2log; 2516х + log2 — + 8 = 0. Ответ: -, —
64 1024 4
1.1. Решите уравнение Jlog() 5 (х2 - 5х + 6) +1 = х - 4 + д/log 3 (х -1) -1. Ответ: 4.
। । г» 1 1
II. Решите уравнение log2 Зх---------
к 6
IS Решите уравнение
• logx — = 1. Ответ: х = 1/2.
^2»
2
16. Решите уравнение logv/9x2 +51og9x х3 -121og3v 7х = 0. Ответ: 1; 3; 3 11
ЗАДАЧИ ВТОРОГО УРОВНЯ СЛОЖНОСТИ содержат рациональные, ирра-
циональные, показательные, логарифмические неравенства, смешанные неравенства и
их системы; задачи, связанные с исследованием функций, проверяющие умение выпол-
нясь действия с функциями, строить их графики, использовать основные свойства эле-
ментарных функций, а именно: находить области определения и множества значеь
151
учитывать непрерывность, монотонность.
19
2.3. Примеры задач второго уровня сложности:
Неравенства
1. Решите неравенство
>0. Ответ:
х е [-1;-0,5) о (0; 0,5).
2. Найдите область определения функции f (х) =
Ответ: х е [0; 9) и (16; 25].
4. Решите неравенство
т/х + з 2>/х + 11
2-4х x-7-Jx + IO
Ответ: х е [0; 4) и (4; 16]
5. Найдите область определения функции f(x) = log
Ответ: хе (0; 1]и[3; 4).
6. Решите неравенство
. Ответ: х е [0; 4) и (4; 16].
Ill
1тенеравенство (cosх-1)(1 - Vx + 5) < 0. Ответ:
х е [-5;—4] и {2ли, п = 0,1,2,...}.
log, (2х +4Х — 2)
8. Найдите область определения функции у=—=-------------. Ответ: хе (0;3)и(3;+°°).
х-3
9. Решите неравенство (lg(x +1) - 1)л/х2 -Зх + 2 £ 0. Ответ: х е (-1; 1] о [2; 9].
6 — х
10. Решите неравенство --------— < 1. Ответ: х е [1; 2) о [5; °°).
vx-1-1
11. Решите неравенство
(4х -12-2х + 32)(*-1)
л/х-1
> 0. Ответ: хе [0; 1) u(1; 2)и(3; + «»).
13. Ре
11Г| и
12. Решите неравенство
> 0. Ответ: х е [1; 2] и {О}.
De неравенство
<0. Ответ:
хе[3;4)и(4;7]и(12;оо).
14. Решите неравенство
Ответ: х 6 [0; 1) и (1; 9).
20
15. Решите неравенство
л/20-х2 4-х \llO-x2
2х-3 х—6
Ответ: х 6 {—4; 5} о [-3; 1,5).
. Q /„2_3 Y — 1 Я
16. Решите неравенство у/х2 -Зх-18 £--------------
Ответ: х е {-3} и [6; 11].
17. Решите неравенство
18. Решите неравенство
1(). Решите неравенство
?0. Решите неравенство
(3’ - 1)7х2-4х+3 > 0. Ответ: х е {1} и [2; + ~).
(х -1)71-х2 й (Зх - 2)71-х2. Ответ: х е {1} и [-1; 0,5].
72-Jx + l -2 > Vl + x - 5. Ответ: х€ [0; 80).
(log, 4XlogSx 0,25x10g, 32х) £ log,
(Ивет: xg (О,
Т ригонометрия
I. Решите уравнение V2 cos2 х 4- 2V2 sin2 х = 3sin х. Укажите его корни, лежащие в
7я 5я
л » Х2 ~~ а ’ =
4 4
। |ромежутке [-2я; я / 2]. Ответ: х = (-1)" —
4
ге уравнение cos2х4-5sin | х |= 3. Ответ: х=± (-1)" — 4-яг
neZ. n^Q.
1. Решите уравнение 3 4- 2 sin 2х = tgx 4- ctgx. Ответ: х = (-1)" — 4- —, п 6 Z.
I. Решите уравнение cos(3x4-#)-cos5x4-V2sin 4x4- —
= 0. Укажите его корни, ле-
житие в промежутке [я/2;я].
< я ли . Зя л «у,
Ответ: х=—+—, х=±—4-2ли, we Z;
8 4 4
5я
7я
Зя
4
»f >___ __________ • л /ч /ч л XX_________ ft 1 ft
V Решите уравнение sin 9х - 2 sin Зх = 0. Ответ: х = —, х = ±—4-—
3 18 3
fy о *5
6, Решите уравнение sin 4х - sin х = sin Зх. Ответ: х, = —
5
’ 7. Решите уравнение | cos Зх 14-sin 6х = 0. Ответ: х =—4-—-
я яи
8+”Г
я яи
18+Т
[ sinx4-cosy = l,
8. Решите систему уравнений < 2 . 2
21
Ответ: (лп,2лк),
— + 2#и; —+ лк
2 2
не Z, к g Z .
9. Решите уравнение Зд/1-cosx + л/б sinх = 0. Ответ: х = —+2лп, х = 2л п, neZ.
10. Решите уравнение sin(4Vx) + 2 cos2 4х = 1. Ответ:
,/?б Z,w > 1; х =
ке Z,A >0.
о Л"
11. Решите уравнение (1 + tg"x)(l + cos 2x)ctgx+4 cosx = 0. Ответ: x = (-1) —+л n, n g Z
6
12. Решите уравнение 2cos2x + 2V2 cosx cos2 4x + cos24x = 0. Ответ: x=±
Г» „ „ _ . ~ ЯП ЛЯ
13. Решите уравнение cos 2x = 2 cos x cos 5x -1. Ответ: x = —x = у,
14. Решите уравнение sin4 9л + cos715xcos2 9x = I. Ответ: x = —x -
л лп
—+—. ne Z .
18 9
15. Решите уравнение cosx^/16(tgA+l)| tgr-l|-+9=4sinx+cosx. Ответ: x=arctg-+^w, wg Z .
Множества значений функций
1. Найдите множество значений функции /(х) = log0 5(3 + sin х). Ответ: Е = [-2;-1].
2. Найдите множество значений функции /(x) = 2cos
—sin(x2+2х+2) .Ответ: [V2;2].
4 )
3. Найдите множество значений функции f (х) = log0 25 (5 - log3 х) + log0J5 (log3 х -1).
. „ . х л л c(2"log^)logTr
4. Найдите множество значений функции ] (х) = 4 • 0,5 J J
5. Найдите множество значений функции /(х) = log0 5
sinx
cosx
6. Найдите множество значений функции /(х) = arccos----
I cosx + 2
.Ответ: [arccosl/З; л].
7. Найдите множество значений функции /(х) = arcsin
8. Найдите множество значений функции /(х) = 4 sin-
^(77^7
12
3л ~
—+2^w, wg Z.
4
9
22
< Инет: [- 2л/2; 2 Д .
•>, Найдите множество значений функции f(x) = 15 -х2 -4v9-x2 . Ответ: Е/ = [2; 6].
10. Найдите множество значений функции
/(х) = 2“(2arccos Jt)/'r, если X > - 1/V2 .
• hiier: [1/V8; 1].
Ill la идите множество значении функции /(jc)=log)2
80
13+1о^(125+х4)
.Ответ: [-1;+°°).
ЗАДАЧИ ТРЕТЬЕГО УРОВНЯ СЛОЖНОСТИ включают задания по планимет-
рии на нахождение геометрических величин (длин, углов, площадей), проверяющие
ишния основных свойств и соотношений в треугольниках, четырехугольниках, много-
угольниках, свойств окружностей и их касательных, умение выполнять геометрические
построения. Так же предлагается задача на использование производной, которая прове-
рнет умение выполнять действия с функциями, вычислять произвол
11:1
ле, использовать
। еометрический смысл производной, составлять уравнения касательных к графикам
функций, находить экстремумы функций, наибольшие и наименьшие значения на от-
резке и владеть основами аналитической геометрии (выполнять действия с координа-
ции и векторами на плоскости). К этой группе относится и задача, которая требует
умения решать алгебраические уравнения, неравенства или системы уравнений с пара-
метрами при наличии ограничений на неизвестные. Умение решать подобные задачи
показывает уровень логического мышления участника, его способность находить вы-
ход из нестандартной ситуации. Последней задачей является задача по стереометрии.
Дня ее решения необходимо владеть методикой построения стереометрических черте-
жей и навыками применения теорем планиметрии и стереометрии для вычисления тре-
буемых элементов. Успе
111
-юе решение данной задачи показывает уровень пространст-
венного воображения школьника, которое необходимо будущему инженеру.
2.4. Примеры задач третьего уровня сложности:
Планиметрии
I. Площадь треугольника АВС равна 16д/3, сторона АВ = 8, угол = 60°. На сторо-
нах АВ, ВС и АС выбраны точки К, L и М так, что АК : КВ = 3 :5, BL .LC = 1:7,
.1Л/: МС=3:1. Найдите площадь круга, описанного около треугольника KLM.
23
Ответ: —л.
9
2. В равностороннем треугольнике АВС на сторонах АВ, ВС и АС выбраны точки
К, L и Л/ так, что АК : КВ = 3:5, BL : LC = 1:7, AM : МС =3:1. Площадь круга,
91
описанного около треугольника KLM равна —л. Найдите длину стороны треугольни-
9
ка АВС. Ответ: 8.
3. В прямоугольном треугольнике АВС из вершины прямого угла С проведена высота
СК. Медиана СМ треугольника АСК равна 3, а медиана CN треугольника ВС К
равна 2л/3. Найдите площадь треугольника АВС. Ответ: 6 V2.
4. Окружность с центром О касается сторон угла В в точках А и С. Лучи АО и ВС
пересекаются в точке М, ОМ = 5, ZCA М = 0,5 arccos 0,6. Найдите площадь треуголь-
ника ВОМ. Ответ: 15.
5. На стороне ВС треугольника АВС отмечена точка К. Известно, что
ZB + ZC = Z-AKB, АК = 5, ВК = 16, КС = 2. Найдите площадь круга, вписанного в тре-
угольник АВС. Ответ:
243
6. Площадь прямоугольного треугольника равна 12, а его гипотенуза равна 2л/13. Най-
дите косинус острого угла между медианами данного треугольника, проведенными к
его катетам. Ответ:
1зУГо
50
7. Один из углов трапеции ABCD равен 30°, а прямые, содержащие боковые стороны
АВ и CD, пересекаются в точке М под прямым углом. Радиус вписанной в греуголь-
15л/з
ник AMD окружности равен 2(Тз -1), а площадь трапеции ABCD равна-----. Най-
дате длины оснований трапеции. Ответ: 2,8.
8. Около окружности радиуса 2 описана равнобокая трапеция ABCD с углом А. рав-
ным 60с. Точки К и N - точки касания окружности с боковыми сторонами АВ и CD,
5л/3
соответственно. Найдите площадь четырехугольника KBCN . Ответ: ——.
9. Периметр параллелограмма ABCD равен 28. угол А составляет 120 , ВК и BN -
высоты параллелограмма, проведенные к прямым, содержащим стороны AD и CD со-
24
н । нс гственно. Найдите площадь параллелограмма ABCD , если длина отрезка KN рав-
HII x/l 11 . Ответ: 5 = 24л/3 .
10. Четырехугольник ABCD вписан в окружность, его диагонали АС и Z?D пересека-
нием в точке F, причем AF : FC =3:1, BF : FD = 4:3, угол Z. AFD=arccos—. Найдите
4
6
ри щус описанной около треугольника AFD окружности, если АС = 4. Ответ:
1 ^5
II. В равнобедренном треугольнике АВС вписанная окружность касается основания
К в точке D, а боковой стороны АВ в точке Е . Отрезок FD, где F - середина сто-
роны АВ , пересекает вписанную окружность в точке G, причем G не совпадает с D.
• 1ерсз точку G проведена касательная к окружности, пересекающая сторону АВ в точ-
3
иг //. Найдите величину угла ВС А , если FH : НЕ = 2:3. Ответ: arccos —.
4
IЛ В трапеции ABCD основания AD = 9, ВС = 2. углы А и D при основании равны
2
i»K (g4 и arctg— . соответственно. Найдите радиус окружности, вписанной в треуголь-
2
ник С BE , где Е - точка пересечения диагоналей трапеции. Ответ:-7=.
4+V5
13. В треугольнике АВС со сторонами АВ = -713 и ВС = Тб проведена медиана BD.
< дружности, вписанные в треугольники ABD и DBC , касаются отрезка BD в точках
Л -Лз-л/б
Л/ и N. Найдите длину отрезка MN. Ответ:--------.
I I. На стороне АС треугольника АВС как на диаметре построена окружность, пересе-
кающая стороны АВ и ВС в точках D и Е соответственно. Угол ZLEDC равен 30°,
ниощадь треугольника ЛЕС равна л/з/2, а площадь треугольника DBE относится к
и пощади треугольника АВС как 1:2. Найдите стороны треугольника АВС .
I Чист: 2; >/б; л/З +1.
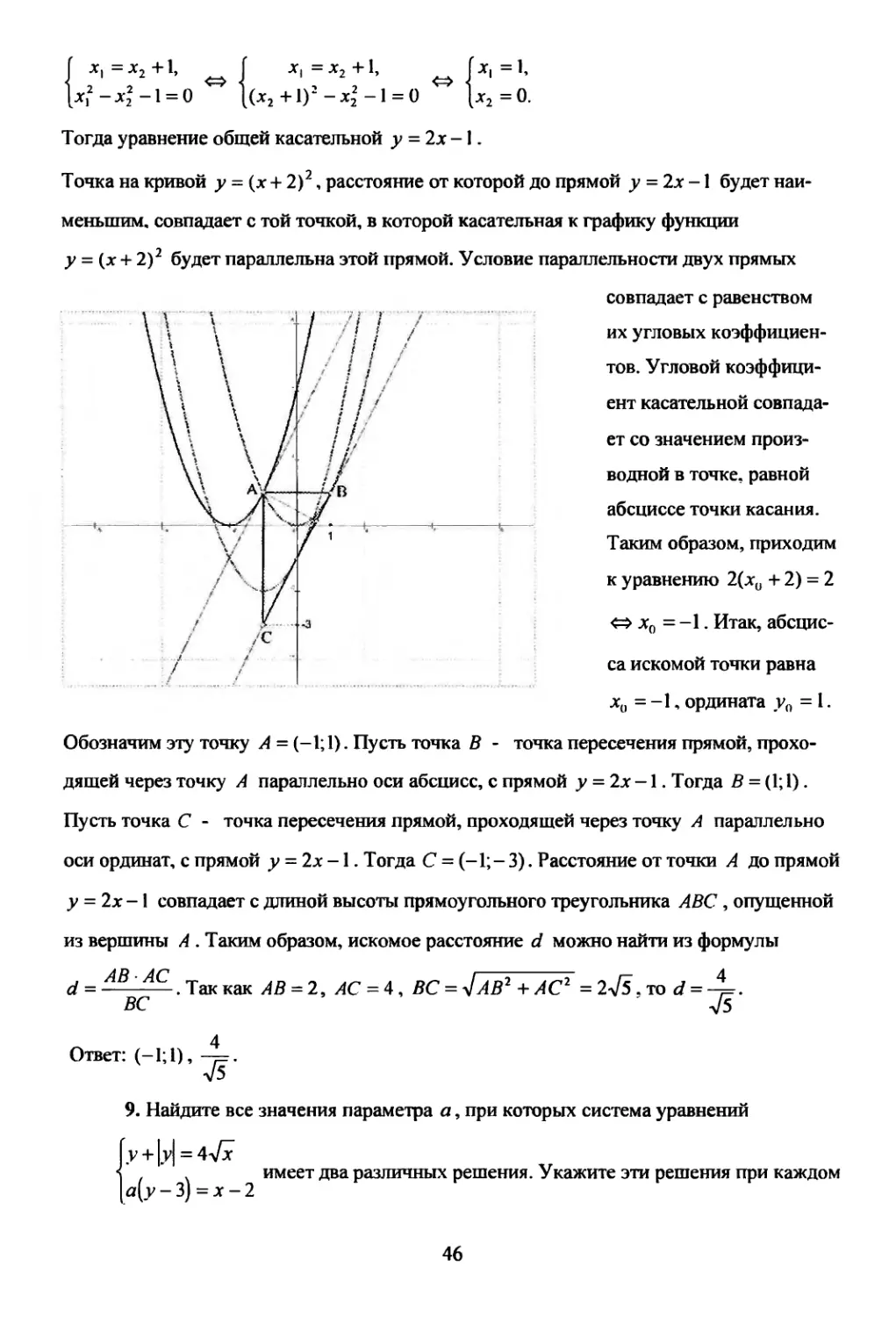
Задачи на производную
I 11айдите площадь треугольника, одна сторона которого лежит на касательной к гра-
фику функции у = 0,25х -х + 4 в точке с абсциссой = 4. а две стороны - на каса-
гспьпых к этому графику, проходящих через точку Л(5; 3). Ответ: 3.
?. Разность одной стороны треугольника и половины второй равна 3, а угол между ни-
25
ми равен arccos—. Какую наименьшую длину может иметь третья сторона этого тре-
угольника? Ответ: —г=.
3. На кривой у = х2 + х найдите точку, расстояние от которой до точки М(-1; 1) явля-
ется наименьшим. Найдите это расстояние. Ответ: точка А(-1,5; 0,75), наименьшее
75
расстояние —-.
4. Какую наименьшую площадь может иметь прямоугольный треугольник, на гипоте-
нузе которого лежит точка Л/ (0; 3), а его катеты лежат на прямых х = -1 и у = 0.
Ответ: 6.
5. Какую наибольшую площадь может иметь плоский треугольник, ограниченный осью
3
Ох прямой х = — и касательной к графику функции у = 2х2 в точке с абсциссой х(),
2^
если 0 < х~ < 3 ? Ответ: 2.
6. Найдите наибольший и наименьший периметры, которые могут быть у прямоуголь-
ника, две вершины которого лежат на оси х, а две другие — на графике функции
у = 2л/2(1 + sinx), - тг/2 < х < Зя/2.
7. Какую наибольшую площадь может иметь треугольник, две вершины которого лежат
на графике функции у = V4x-x2 -3 , хе (1; 3), одна вершина находится в начале ко-
ординат, а сторона параллельна оси х ? Ответ: 0,5.
32
8. Составьте уравнения общих касательных к графикам функций у = — х3 и
8 8
у = (х + 1)2. Ответ: у = 0; у = 6х-3; у = -х+—.
3 9
9. Какое наибольшее значение может принимать площадь прямоугольного треугольни-
ка, одна вершина которого совпадает с началом координат, другая лежит на кривой
(х -1)2 + (у-1)2 = 2, а вершина прямого угла расположена на прямой у = х.
Ответ: —.
4
26
х2
10 11айдите угол между касательными к графику функции у = —, проходящими через
1 2
н»чку Л/(2л/3;-3). Ответ: 90*.
Задачи с параметрами
I 11пйдите все значения параметра р„ при которых система уравнений
28>>+195 = 3—,
X
1р = 4(х-1)2,
имеет ровно два различных решения, и решите ее при каждом р.
111нс।: /?б (~°°;2] х, = 1+^4-/?, х2 = 1+^/З-р,
/•< (3.4) x,2=\±yl^p.
1> 1 г|=1,х2=2.
11пйдите все значения а, при которых уравнение (х—а)2 + а -12 =
гцннственное решение, и решите его при каждом а.
(11 нет: а6 (—4;3)[J{8; 12} х=а+>/12—а.
I 11пйдите все значения а, при которых уравнение (х+а)2 + 2а =
имеет
имеет един-
। iценное решение, и решите его при каждом а.
< I»нет: а 6 (-4; 2] (J [41 х = —а—>/8—2а.
I 11ийдите все значения а, при которых уравнение (х+2)2 + (а+---)2 = 25 имеет два
х—1
I hi ишчных решения, и решите его при каждом а.
Hi нет: а=-4
Xj =-2, х2 =2
</. |-3:3) х, =—2—^25—(а—I)2 =-2+^25-(а+1)г,
ч> (5;6) х,,2 = -2±725-(а-1)2.
« I (айдите все значения а, при которых уравнение х2 + х|х| = 4(3 + 2ах - 5а) имеет два
|ы шинных решения, и решите его при каждом а.
27
Стереометрия
1. Найдите площадь сечения правильной треугольной призмы ABCA]B]Ci плоскостью,
проходящей через центр описанной около призмы сферы и вершину основания А и
пересекающей сторону основания ВС в точке F так, что CF =2BF, если стороны ос-
нования призмы равны 6, а расстояние от центра основания призмы до секущей плос-
кости равно л/з /з. Ответ: 5 V6.
2. Цилиндр с высотой h и радиусом основания V2A вписан в конус так, что одно из
оснований лежит в плоскости основания конуса, а окружность другого основания — на
боковой поверхности. В свою очередь, конус должен быть вписан в сферу возможно
меньшего радиуса. При какой высоте конуса радиус описанной около него сферы будет
9
наименьшим? Найдите значение радиуса. Ответ: ЗЛ, = —h.
4
3. В сферу радиуса R вписана правильная треугольная пирамида, у которой высота от-
носится к боковому ребру, как <2 : >/3 . Какую наименьшую площадь может иметь се-
чение пирамиды плоскостью, проходящей через высоту основания? Найдите отноше-
ния объемов частей, на которые секущая плоскость разбивает пирамиду в этом случае.
Ответ: Smul = Л2
3:19.
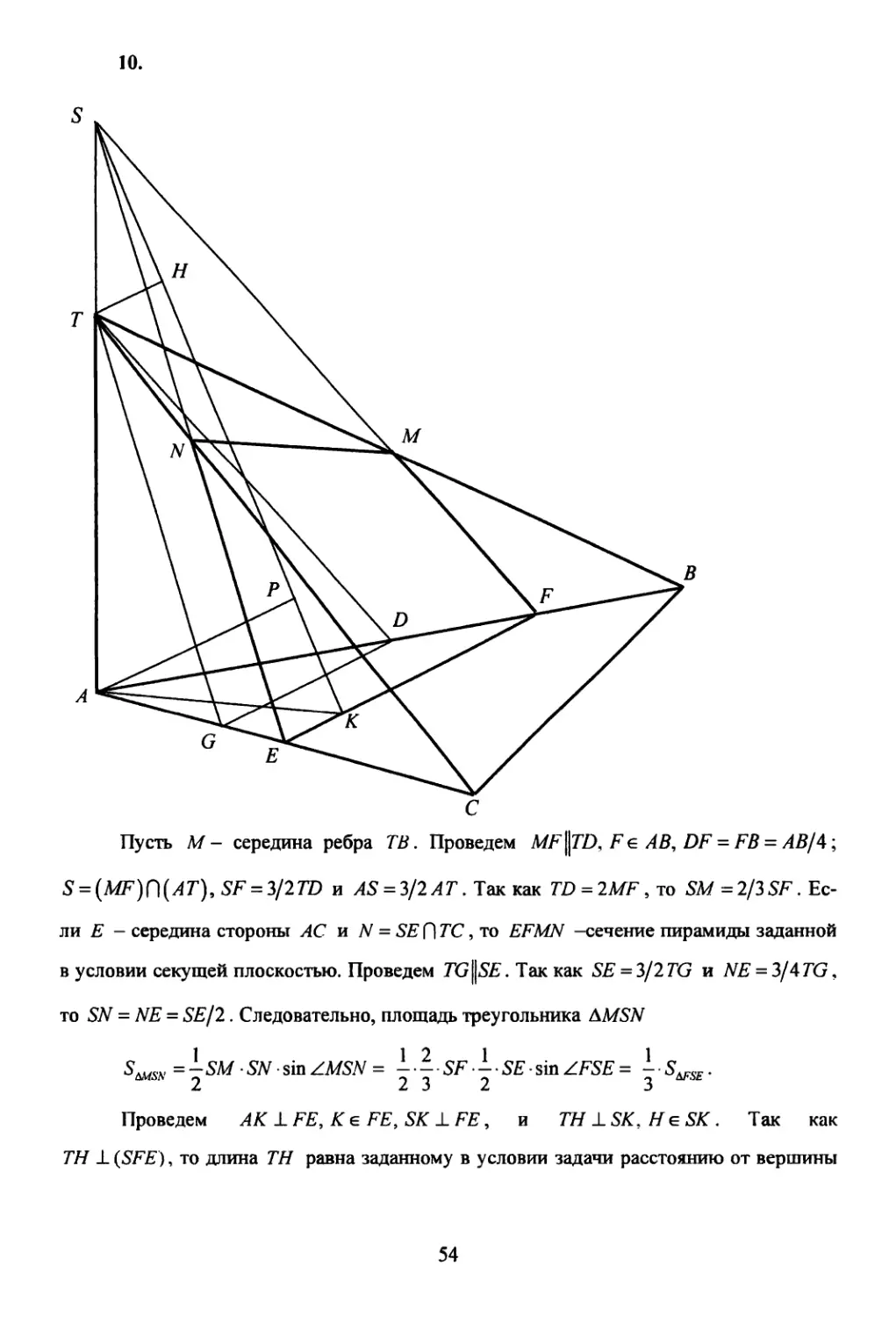
4. Основанием пирамиды ТАВС служит треугольник АВС , все стороны которого равны
V3, а высота пирамиды совпадает с боковым ребром ТА . Найдите площадь сечения
пирамиды плоскостью, параллельной медиане основания AD, пересекающей ребро
АВ в точке М 9 так что МВ = 2 AM , и проходящее через центр сферы, описанной око-
ло пирамиды, если радиус сферы равен 5/2. Ответ: 22V3/15 .
5. Основанием пирамиды ТАВС служит прямоугольный треугольник АВС . Все боко-
вые ребра пирамиды наклонены к плоскости основания под углом 45°, а угол между
боковым ребром ТВ и гипотенузой основания АС равен 60°. Какую наименьшую
площадь может иметь сечение пирамиды плоскостью, проходящей через ребро ТВ и
28
Hi’iuy Л / на стороне АС, если высота пирамиды равна h ? Найдите расстояние от се-
1<* uiiiii.i гипотенузы АС до точки М, когда площадь сечения наименьшая?
• Мнит:
hL
4(>' з
h I h кованием пирамиды TABC служит треугольник ABC, все стороны которого рав-
ны J\4 , а высота пирамиды совпадает с боковым ребром ТА. Найдите площадь сече-
н1 hi плоскостью, проходящей через середины стороны основания АС и бокового ребра
I II и параллельной медиане TD боковой грани ВТС , если расстояние от вершины А
г 21л/3
•hi секущей плоскости равно V3 . Ответ:---.
4
/ I Основанием пирамиды ТАВС служит треугольник АВС, все стороны которого рав-
ны
1ч/7
, а высота г
амиды совпадает с боковым ребром ТА. Найдите площадь сече-
нии пирамиды плоскостью, проходящей через середины стороны основания АС и боко-
|ни о ребра ТВ и параллельной медиане BD боковой грани ВТС , если расстояние от
in ршины пирамиды Т до секущей плоскости равно V2 . Ответ: 21.
II Шар радиуса 6 с центром в точке О вписан в правильную треугольную пирамиду со
м пропой основания, равной 36. Через точку О проходит плоскость, параллельная сто-
роне основания пирамиды и апофеме, проведенной к другой стороне основания. Най-
ihic площадь сечения пирамиды указанной плоскостью. Ответ: 35V39.
I In высоте ТО правильной треугольной пирамиды ТАВС выбрана точка М, так что
ТМ =3-ОМ . Через точку М проходит плоскость, параллельная стороне основания пи-
рпмиды и апофеме, проведенной к другой стороне основания. Найдите объемы частей,
пн которые делит пирамиду указанная плоскость, если сторона основания пирамиды
121 135
I nun hi 8, а высота пирамиды равна 2 V3 . Ответ: , И2 = —
8 8
10, h правильной четырехугольной пирамиде TABCD с высотой, равной 9, и стороной
нгпонания, равной 4, проведена плоскость, проходящая через апофему ТК боковой гра-
ни ГАВ и параллельная медиане СМ боковой грани TCD. На каком расстояь
от этой
п hi ivkoctk находится центр основания
IHI*
амиды? Ответ:
18
11
29
2.5. ПРИМЕРЫ ВАРИАНТОВ ЗАДАНИЙ ОЛИМПИАДЫ
I ЭТАП ОЛИМПИАДЫ ШКОЛЬНИКОВ
ВАРИАНТ № 1
1. Каждый из двух рабочих должен был изготовить по 45 деталей. Второй рабо-
чий приступил к выполнению задания на 25лп/н позднее первого, по трети задания они
выполнили к одному времени, а к моменту окончания работы второй рабочий ещё по-
мог первому, изготовив за него 6 деталей. Сколько деталей в час изготавливал каждый
рабочий? (8 баллов)
2. Укажите все значения и, при которых сумма п последовательных членов
арифметической прогрессии 31, 28, 25...., начиная с первого, не меньше 84.(8 баллов)
3. Решите уравнение 2Л+1 = 7 + 22"г. (8 баллов)
4. Ре
Ills
гге уравнение cos 2х + 5 sin х = 3 . Укажите корни, принадлежащие проме-
жутку [-Зл/2;л/2]. (8 баллов)
5. Решите неравенство
(10 баллов)
6. Найдите множество значений функции f (х) = 11 - х2 - 2д/9 - х2 .(10 баллов)
7. Периметр параллелограмма ABCD равен 28, угол А составляет 60“, ВК и
BN - высоты параллелограмма, проведенные к прямым, содержащим стороны AD и
CD соответственно. Найдите площадь параллелограмма ABCD , если длина отрезка
KN равна V39 .(12 баллов)
8. Найдите угол между касательными к графику функции у = х2/3, проходящи-
ми через точку М (>/3; 3/41 .(12 баллов)
9. Укажите все значения а, при которых система уравнений
(х-а)2 =у + а
имеет хотя бы одно решение, и решите ее при каждом а. (12 баллов)
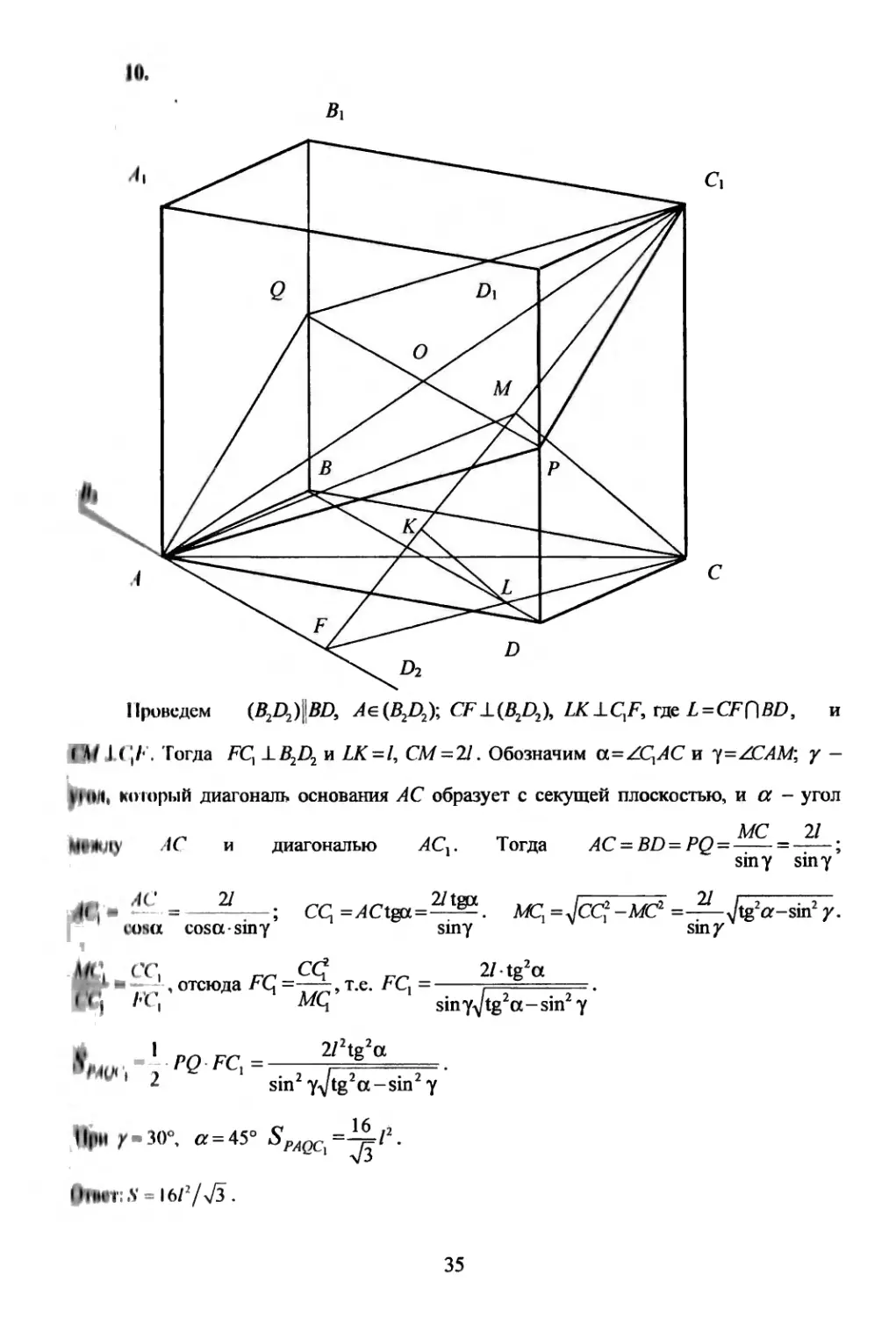
10. Найдите площадь сечения прямоугольного параллелепипеда ABCDA{B{CXD}
плоскостью, проходящей через диагональ ACt и параллельной диагонали основания
BD, если расстояние от BD до секущей плоскости равно /, а другая диагональ основа-
ния АС образует с секущей плоскостью угол 30° и с диагональю АС{ - угол 45°. (12
баллов)
30
2.6. Решения варианта №1
1. Каждый из двух рабочих должен был изготовить по 45 деталей. Второй рабо-
чий приступил к выполнению задания на 25лн/н позднее первого, по трети задания они
>и и к hi пили к одному времени, а к моменту окончания работы второй рабочий ещё по-
пнг первому, изготовив за него 6 деталей. Сколько деталей в час изготавливал кажцый
рпОпчий?
Решение.
Пусть первый рабочий изготавливал х - деталей в час, второй рабочий у - дета-
15 15 25 24 36
и II и час, тогда----=—; — = —
2 111
— =—; — = —; х = 12, у = 18.
Зх 12 х 12
Ответ: 12 и 18 деталей.
2. Укажите все значения л, при которых сумма п последовательных членов
н||||фмстической прогрессии 31, 28, 25,...,
на1?
зая с первого, не меньше
84.
1Я
Решение.
3 I + 31 — 3(/? — 1) о . _ 2 ге 1/ОХЛ 65 ±47 о 1О5/
-----------и >84; Зп -65л + 168<0; и12 =-----, ^=3, и2=18%.
2 ~ 6
Ответ: 3 < п < 18, пе N.
3. Решите уравнение 2х+| = 7 + 22
Решение.
2х+| = 7+22-х; 2(2х)2-7-2х-4 = 0; 2(2х-4)(2х + 1/г)=0; 2х =4, х = 2.
Ответ: х = 2 .
тш
4. Решите уравнение cos 2х + 5 sin х = 3 . Укажите корни, принадлежащие проме-
i‘V 1ку [-Зп/2;я/2].
Решение.
cos2x + 5sinx = 3 <=> 2sin2x-5sinx + 2 = 0; sinx = (5±3)/4.
1) sin x = 2 - решений нет. 2) sin х = —, х = (-1)” — + mt, п е Z . В заданный про-
2 6
минуток входят корни
7л. л|
T’6j
Ответ: х = (-1) — + ил, не Z ;
v 6
31
2
5. Решите неравенство
Решение.
Замена: = t > 0, х = /2.
3^ 2
Г2-3/4-2 ~ г2-2/4-1
(Г-1)(Г-2) (?-1)2<°
(/-2)«-1)2 "
+ 1 120
——г<0 <=>
-2)0-I)2
t е [0; 1) и (1; 2) <=> х е [0; 1) и (1; 4).
Ответ: х g [0; 1) о (1; 4).
6. Найдите множество значений функции f(x) = 11 - х2 - 2>/9-х2 .
Решение.
Функция / = л/9-л2 принимает значения /е[0;3]. Рассмотрим функцию
у = 11 - (9 -1 )-2t, определенную на отрезке [0; 3]. Графиком функции у = t - 2t + 2
является парабола с вершиной в точке с абсциссой t = 1 и ветвями, направленными
вверх. Таким образом, минимальное значение у равно 1, оно достигается в точке t = 1,
максимальное значение равно 5, оно достигается в точке t = 3. Функция у = /(х) при-
нимает значения из отрезка [1; 5J.
Ответ: Ef = [1; 5].
7. Периметр параллелограмма ABCD равен 28, угол А составляет 60", ВК и
BN - высоты параллелограмма, проведенные к прямым, содержащим стороны AD и
CD соответственно. Найдите площадь параллелограмма ABCD , если длина отрезка
KN равна V39.
Решение.
Пусть стороны параллело-
грамма а и b . Найдем высоты ВК и
BN:
£K = asin60
BN = bsin60'
2
В треугольнике KBN угол
Z? равен 60°. По теореме косинусов
32
I.N' -BK' + BN1 -2BK-BNcos60 = - + — = 39 => cr+b2-ab = 52.
4 4 4
Тогда <
a2 + b2 - ab = 52,
a + b = 14,
f ab = 48,
b = 14-a
Решая уравнение a2 -14a + 48 = 0, получаем: a = 8 или a = 6. Тогда 6 = 6 и
a = X или 6 = 8 и a = 6. Площадь параллелограмма S = 24V3 .
Ответ: 5 = 24-Уз .
8. Найдите угол между касательными к графику функции у = х2 /3, проходящи-
ми через точку М (>/3;3/4).
Решение.
Уравнение касательной к графику заданной функции имеет вид
I*
где хп - абсцисса точки
касания. Так как касательная проходит
через точку Л/, ~(V3 - х( J; х,;-2\/Зх(,+9/4 = 0; х0=\/3±>/з/2;
(ч,|)1 = 3>/з/2. (х0) =>/з/2. Угловые коэффициенты касательных:
iMgo, =>/з, ^=60°; 2)tga2 =—U, а2=30°. Угол между касательны-
ми: <р = 60° - 30° = 30°.
Ответ: 30°.
9. Укажите все значения а, при
которых система уравнений
; (х-а)2 = у + а имеет хотя бы одно решение, и решите ее при каждом а.
1115
Решение.
I. При х > 0 у = 2, х2 -2ах + а2 - а-2 = 0 (*).
Уравнение (*) имеет два различных положительных корня х, 2 = а±\/а + 2, если:
/)/4 = а + 2>0,
а> 0,
а2 -а-2 > 0
а > -2,
а>0, <=> а >2.
а<-1,
а > 2
Уравнение (*) имеет один положительный корень х12 =a + Va + 2, если:
33
П. При х<0, у=Оч х2-2ах+а2 —а = 0 (**).
Уравнение (**) не может иметь двух отрицательных корней, так как система не-
Т)/4 = а>0,
равенств <
а <0,
а2 —а>0.
решений не имеет.
Уравнение (**) имеет о,
а отрицательный корень х = а-
если
D/4=a = 0,
а < 0,
а2-д<0, <=>0<а<1
х>0
х<0
Ответ: при об (-l;0]U[l;2] x = o+Va + 2, у = 2;
при ое (0;1) х, =а+у/а+2, yi =2; х2 =а-у/а', у2 =0,
при ае (2;-н») х12 =а±\/а+2} у}2 = 2.
34
10.
Вх
Проведем (B2D2) BD, Ae(B2D2\, CF-L(B2D2), LK±CtF, где L=CFC\BD, и
I M I Тогда FC, CB.D, и LK-l, CM=21. Обозначим a=AC.AC и У=АСАМ: у —
I 1 м X» i » ж
11 Hit, который диагональ основания AC образует с секущей плоскостью, и а - угол
АС и диагональю АС 2/ И • —- = - ; CQ=^Ctga= Г* сона cosasiny 1* * z V» Г’/”2 4С,. Тогда AC = BD=PQ=^- = —; siny siny . MCX =jcc? -MC2 =—Jtg2a~sin2 y. siny sin /
PQFCl= Ъ sin y^/l 1I|IH y»30°, a = 45° SPAQC} - limit; .S'= 16/773. , t.c. FCi , smy^/tg a-sm у r2tg2a :g2a-sin2 у =1Lp r— € • V3
35
2.7. Вариант № 2
1. Один велосипедист проходит за час на 6 км больше, чем другой, так как один
километр он проходит на 20 секунд быстрее. Найдите скорости велосипедистов.(8 бал-
лов)
2. Решите уравнение Vi + sinx + ^2 sin х = 0. (8 баллов)
3. Решите уравнение (log2 (7 - 6х)) logг (1/2) = 1. (8 баллов)
5. Решите неравенство
5х + 4^ [
х4 —5х2 + 4 < 0. (10 баллов)
6. Найдите множество значений функции f (х) = log0 5 (3 + cos х). (10 баллов)
7. В прямоугольном треугольнике АВС из вершины прямого угла С проведена
высота СК. Медиана СМ треугольника АСК равна V13. а медиана CN треугольника
ВСК равна -/21. Найдите площадь треугольника АВС. (12 баллов)
8. Траектории, по которым двигаются снаряды зенитного орудия, задаются
уравнением у = рх-0,5(1 + р2)х2,х> 0,у > 0, где параметр р (0< р< +<») определя-
ется наклоном траектории в начальной точке. Может ли снаряд попасть в точку
Л/(3/4;1/4) ? Укажите на плоскости хувсе точки, через которые проходят траектории.
(12 баллов)
9. Укажите все значения а, при которых уравнение 64а(х-10) + 384 = (х+|х|)2
имеет хотя бы одно решение, и решите его при каждом а. (12 баллов)
10. Правильная треугольная призма с высотой h и стороной основания y[6h
вписана в конус так, что одно из оснований лежит в плоскости основания конуса, а
вершины другого основания - на боковой поверхности. В свою очередь, конус должен
быть вписан в сферу возможно меньшего радиуса. При какой высоте конуса радиус
описанной около него сферы будет наименьшим? Найдите это значение радиуса. (12
баллов)
2.8. Решения варианта №2
1. - = —------
V К-6 180
; 180К-1080 = 180К-К2 +6К; К2-6V-1080 = 0;
36
F- 3 1 71089 = 3±33; Г =36.
Ответ: 36 и 30 км/ч.
2. Vi +sinx + V2sinx = 0, 2sirrx-sinx-1 = 0; sinx = (l±3)/4. 1) sinx = l>0,
iiih юронний корень. 2) sinx = -1/2, x = (-I)”+ л/6+ил, «6 Z .
Ответ: sinx = (—1) л/6 + ил, пе Z .
3. (log2(7-6x))log,(l/2) = l; log2(7-6x)-
log2 (1/2)
log2x
= 1; log2(7-6x) + log2x = 0;
« 7x +1 = 0, x = (7 ±5)/l2, x, = 1 - посторонний корень, x2 = 1/6.
Ответ: x = l/6.
x2-9 1
x3 — 27 x + 2
x2+5x + 6—x2-3x-9 _
(x2 + 3x + 9)(x + 2)
Ответ: xe (-
oo;-2)U(1,5;3)U(3;+oo).
5x+4 —e 2 t л
-----Vx -5x + 4 < 0
4X ;
x e (-oo;—) о
0<5л+4<1
4x
(x2-l)(x2-4)>0
(x - l)(x+l)(x -2)(x+2)>0
Ответ:
6. Найдите множество значений функции f (х) = log0 5 (3 + cos х)
NuhHue. 2£3 + cosx<4 <=> log0 5 4 < log0 5 (3 + cos х) < Iog0 5 2 <=> /(х) g [-2;-1].
Ответ: Е = [-2;-1].
7. В прямоугольном треугольнике АВС из вершины прямого угла С проведена
НЫ1ЧГН1 ('К. Медиана СМ треугольника АСК равна V13, а медиана CN треугольника
//( Л равна у/2Т. Найдите площадь треугольника АВС.
37
Решение.
ДВСК « ЛАСК
ВК _ СК
СК~ АК
СК2 = АК • ВК
CK=h, АК = 2у, ВК = 2х, h2 =4ху
Применяем теорему Пифагора для треугольников
ЛСКМ и ЛСКМ.
х2 + 4ху = 21
у2 -ь4ху = 13
f X2 -у2 =8
[у2 +4ху = 13
х2 -у2 =8
13х2-32ху-21/ =0
13х2-32ху-21у2
13^--32--21 = 0, - = 3, х = 3у, х = 3, у = 1, й = л/12, S^c = (х + y)h = 8V
У У У
Ответ: 8д/3.
8. Пере
IHIII
ем уравнение относительно неизвестной р : х2р2 - 2хр 4- х2
+ 2у = 0;
D/4 = x2-х4-2х2у>0; область достижимости х>0, 0<у<(1-х2)/2. В точке М
7 1
— < —. Точка М лежит над границей области достижимости, снаряд не
32 4
может попасть в нее ни при каком значеь
КН
р-
9.1.Прих>0 х2-16ох-ь160о-96 = 0 (*).
Уравнение (*) имеет два
различных
неотрицательных корня
X) 2 = 8а ± 4>/4а2 -10а + 6 , если:
'©/4 = 16(4а2-10а + 6)>0,
а > О,
160а - 96 > О
а<1,
а > 3/2,
<=> < а > О,
3/5 S а < 1,
а >3/2.
2. Уравнение (*) имеет один неотрицательный корень x = 8a + 4V4a2-10a + 6 ,
если:
160a-96<0
a = 3/2,
а < 3/5.
38
П. При х < 0 х = ———- < 0 => 0 < а < 3/5. Сравнивая с I, 2, замечаем, что при
а
0 < а < 3/5, также будет два различных корня уравнения.
Ответ: при а е [3/5 ;1) U (3 / 2;+©®) х, 2 = 8я ± 4>/4л2 - Юл+ 6 ;
при 0<л<3/5 х = —=8а+4^4л2-10я+6;
при ае (-“>;0]U{l}U{3/2} х = 8а+4л/4а2-10а+6 .
10. MN = h - боковое ребро
отсюда 2R = Н
В ДТЯ5 О2А2 =TO2 O2S, или г2 = Я(2Я-Я)
2Hh2
(H-h)1'
(2Л)'=1 + 2Л
2(H-h)2-2(H-h)H 2h
4 = 0.
(H-h)
39
(H-h)3 =2h2(H+h); H3-3hH2 + h2H-3h3=0- H2(H-3h) + h2(H-ЗЛ) = О;
(Я2+й2)(Я-ЗЛ) = 0; H = 3h. R = 1[зЛ + ^Д] = -й.
v л ' 2^ 4/? J 4
9
Ответ: 7?min =—h.
ПИП Л
4
2.9. ЗАКЛЮЧИТЕЛЬНЫЙ ЭТАП ОЛИМПИАДЫ ШКОЛЬНИКОВ
МАТЕМАТИКА ВАРИАНТ № 3
1. Два спортсмена бегают по одной замкнутой круговой трассе. Скорость каждо-
го постоянна, а на пробег круга один тратит на 9 секунд меньше другого. Если они бе-
гут в одном направлении, то один обгоняет другого ровно на круг за 3 минуты. Через
какое время они будут встречаться, если побегут в противоположных направлениях? (8
баллов)
2. Количество членов геометрической прогрессии является четным числом.
Сумма всех членов прогрессии в 5 раз больше суммы членов, стоящих на нечетных
местах. Найдите знаменатель прогрессии. (8 баллов)
2
3. Решите уравнение logo 5 4* + log2
= 7(log49 4X+3-log72 \(8баллов)
4. Решите уравнение ctg6хV2sin 2х + 1 = c(gl0xV2sin 2х + 1. (8 баллов)
5. Ре
III
srre неравенство х
-tfy -^х2 + у[у - 3. (Ю баллов)
6. Найдите множество значений функции
/(х) = log0 2 (4 - log 6 х) + log 0 2 (6 + log 6 х). (10 баллов)
7. Около окружности радиуса 5 описана равнобокая трапеция ABCD с углом А,
равным arccos 0,6. Точки £ и N - точки касания окружности с боковыми сторонами
АВ и CD, соответственно. Найдите площади четырехугольников AKND и KBCN . (12
баллов)
8. На кривой у = (х + 2)2 найдите точку, расстояние от которой до общей каса-
тельной к графикам функций у = х2 и у = х2 + 2х -1 будет наименьшим. Найдите это
расстояние. (12 баллов)
40
9. Найдите все значения параметра а, при которых система уравне-
дом из найдет
ISI
имеет два различных решения. Укажите эти решения при каж-
ьгх значений а. (12 баллов)
10. Шар радиуса 1 с центром в точке О вписан в правильную треугольную пи-
рамиду. Через точку О проходит плоскость, параллельная стороне основания пирами-
ды и апофеме, проведенной к другой стороне основания. Найдите площадь сечения пи-
рамиды указанной плоскостью, если расстояние от центра описанной около основания
пирамиды окружности до этой плоскости равно 1/V1J (12 баллов).
2.10. Решения варианта №3
1. Два спортсмена бегают по одной замкнутой круговой трассе. Скорость каждо-
го постоянна, а на пробег круга один тратит на 9 секунд меньше другого. Если они бе-
гут в одном направлении, то один обгоняет другого ровно на круг за 3 минуты. Через
какое время они будут встречаться, если побегут в противоположных направлениях? (8
баллов).
Решение. За единицу измерения расстояния примем длину трассы. Пусть
л(тр/сек) - скорость первого спортсмена, а у (тр/сек) - скорость второго. В таблице
отметим пробег спортсменами всей трассы, движение с общей линии старта в одном
направлении, а также в противоположных направлениях. Если они начинают бег с об-
щего старта одновременно и в одном направлег
то через 3 минуты или 180 секунд
1Ш
более быстрый спортсмен пробежит расстояние на одну трассу большее, чем второй
спортсмен. Если они побегут одновременно с общей линии старта в противоположных
направлениях, то к моменту встречи пробегут расстояние в сумме равное длине одной
трассы. В итоге, имеем таблицу:
р(тр/сек) t (сек) 5(тр)
t 1
У t+9 1
X 180 S+l
У 180 5
X ti s.
V В* ti 1-й
41
Необходимо найти tj. Согласно таблице, получаем систему из шести уравнений
с шестью неизвестными:
xt = 1
180jc- 1 (1
180х = 5 + 1
180^ = 5,
<180лг = 180^4-1
180 V* )
= 180х-1
У~ 180 ’
(180х-1)(1 + 9х) = 180х
180jc-1
У~ 180 ’
1620х -9х-1 = 0,
180х-1
У~ 180 ’
36’
45
9
Ответ: 20 секунд.
2. Количество членов геометрической прогрессии является четным числом.
Сумма всех членов прогрессии в 5 раз больше суммы членов, стоящих на нечетных
местах. Найдите знаменатель прогрессии. (8 баллов)
Решение.
Пусть количество членов геометрической прогрессии равно 2и. Тогда сумма
, „ W'-i)
всех членов прогрессии определяется по формуле S2„ =——------, а сумма членов,
0-1
стоящих на нечетных местах &нечеп1 =-;--
2л ^^нечет 9
довательно, q = 4.
Ответ: 4.
2
3. Решите уравнение log0 5 4х -I- 10g2
Y X
= 7(l°g‘”4 -log, 2 ) (8баллов)
Решение.
Преобразуем правую часть данного уравнения:
y(log49 4x+3-log72X) _^(0,5log74x+3-log72x) =^log72x+3 х
= 7log78=8. Тогда ис-
ходное уравнение равносильно следующему log^ 5 4x4- Iog2
= 8. Используя свойства
логарифмов, имеем
42
(log,>.5 4 + logn, x)2 + log2 x2 - log2 8 = 8
log2 x = -7 или log2 x = 1
---или x = 2.
128
Ответ:-----, 2.
128
4. Решите уравнение c/g6x72sin 2x + l = c/gl0xv2sin 2x + l. (8 баллов)
Решение.
Данное уравнение равносильно следующему (c/g6x-c/gl0x)V2sin2x+T = О
rcos6x cosIOx
< sin 6x sin 1 Ox
V2sin2x+1 =0
cos 6x sin 1 Ox - cos 1 Ox sin 6x м . -г _
V2sin2x + 1 =0
sin 6х sin 1 Ox
sin 4x i
---------------V2 sm 2x +1 = 0
sin 6x sin 1 Ox
sin 4x = 0,
sin 2x = -0,5,
sin 1 Ox * 0,
sin 2x > -0,5
x = —, wg Z
4
. Зли
sin-
2
. 5 ли
sm —
2
. ли
sm—>
2
3
2
4 2
12 2
12 2
/eZ, (m = 2Z)
ke Z.
Ответ: — + 7d, I e Z, (-1)*+1 — + —, к e Z.
4 12 2
5. Pe
1115
те неравенство x
> 3. (10 баллов)
Решение.
Имеем равносильное неравенство x-iJy>Jx2 +у[у-9+3.
Так как правая часть неравенства неотрицательная, то левая часть удовлетворяет
неравенству х-\[у>0. Тогда х>\[у>0, и (х-\[у)2 > (Jx2 +у[у -9 +3)2, или
-xtfy >3Jx2 +Jy -9. Так как
левая часть последнего неравенства неположительная, а правая неотрицательная, то это
43
неравенство выполняется только при условии
*77 = 0,
+77-9=о.
Первое уравнение сис-
темы распадается на два уравнения: х = 0 или у = 0. Если х = 0, то из условия
х > 77 0 следует у = 0, но точка (0; 0) не удовлетворяет второму уравнению систе-
мы. Если у = 0. То из второго уравнения системы имеем х2 =9, с учетом условия
х > 77 - 0 приходим к выводу, что х = 3. Итак, решением исходного неравенства яв-
ляется единственная точка (3; 0).
Ответ: (3;0).
6. Найдите множество значений функции
f(x) = logo 2(4 - 1о8б *) + logо,2(6 + log6 *)• ПО баллов)
Решение.
Пусть у = /(х). Сделаем замену t = log6 х. Тогда получим
у = log 0 2 (4 - /) + log 0 2 (I + 6), t е (-6; 4). Используя свойства логарифмов и выделяя
полный квадрат, приходим к функции у = log0 2 ((4 - t)(t + 6)) = log0 2 (25 - (t +1) ), оп-
ределенной при 16 (-6; 4). Пусть z = 25 - (t +1)2. Тогда
«та
и t е (-6; 4) имеем
z 6 (0; 25]. Так как логарифмическая функция с основанием 0,2 < 1 убывает, и
у = log0 2 Z, ZE (0; 25], то ye [logOj2 25; + «>) = [-2; + «>).
Ответ: E(y) = [-2; + <»).
7. Около окружности радиуса 5 описана равнобокая трапеция ABCD с углом А,
равным arccos 0,6. Точки К и N - точки касания
окружности с боковыми сторонами АВ и CD, со-
ответственно. Найдите площади четырехугольни-
ков AKND и KBCN .(12 баллов)
Решение. По условию имеем
Z-A = а = arccos 0,6, г = 5, ABCD - равнобокая
трапеция, где г - радиус вписанной в трапецию окружности. Точки К и N - точки ка-
сания окружности с боковыми сторонами АВ и CD, соответственно. Пусть точки М и
L - точки касания окружности с основаниями AD и ВС, соответственно. Тогда име-
ем KN || AD || ВС, AKND и KBCN - трапеции. Пусть h\ - высота AKND , /?2 - высота
KBCN . Из свойств касательных к окружности имеем АК = AM = х, ВК = BL = у.
44
Тогда Z.KML = —,
LM = Н = 2r, &KLM - прямоугольный, Z.K =90°,
А'Л/=2rcos—, AZ=2rsin—, x = ——
2 2 a
tg2
а , . ,
—, "2 =ysina, hx = xsina.
Ar
Основания трапеций AKND и KBCN определяем по формулам KN = 2{у + у cos а)
или KN = 2(х — xcos а), AD = 2х, ВС = 2у.
AKND ~
+ KN , . r2(2-cosa)sin a r2(2-cosa)(14-cosa)sina
-----/?, = tlx - x cos a)x sin a = — -------= — -----------------------
2 . 2 a (1-cosa)
2 a
's г
„ BC + KN, . 2,- . . 2 a
kbcn =---------"2 = (2y + vcos a)y sin a = r (2 + cos a) sin a tg — =
^2 2
_ r2(2 + cosa)(l-cosa)sina
(14-cos a)
_ r2(2 - cosa)(l 4- cos a) sin a _ 25(2 - 0,6)(l + 0,6)0,8 1O
AKND ~ 7. 7 “ , —112.
(1-cosa) 1-0,6
c _ r (2 4-cos a)(l-cos a) sin a 25(24-0,6)(l-0,6)0,8 1<5
-----------7Г.------\---------=---------1 ',' ЛГ------= 1J-
(14- cos a) 14- 0,6
Ответ: 112, 13.
8. На кривой у = (х 4- 2)2 найдите точку, расстояние от которой до общей каса-
тельной к графикам функций у = х2 и у = х2 + 2х -1 будет наименьшим. Найдите это
рассто!
е. (12 баллов)
Решение.
Найдем уравнения общей касательной к графикам функций у = х1 и
у = х2 + 2х -1. Уравнение касательной к графику функции у = х2,
сса точки ка-
сания которой равна jq имеет вид у = 2хх (х - Xj) 4- х2. Уравнение касательной к графи-
ку функции у = х2 + 2х -1, абсцисса точки касания которой равна х2 имеет вид
у = (2х2 + 2)(х - х2) 4- х2 4- 2х2 -1. Так как две прямые у = к}х 4- д, и у = к2х 4- Ь2 совпа-
дают тогда и только тогда, когда кх = к2 и Ьх = Ь2, имеем следующую систему уравне-
ний с неизвестными xt и х2 для уравнений совпадающих касательных:
45
Тогда уравнение общей касательной у = 2х -1.
Точка на кривой у = (х + 2)2, расстояние от которой до прямой у = 2х -1 будет наи-
меньшим, совпадает с той точкой, в которой касательная к графику функции
у = (х + 2)2 будет параллельна этой прямой. Условие параллельности двух прямых
совпадает с равенством
их угловых коэффициен-
тов. Угловой коэффици-
ент касательной совпада-
ет со значением произ-
водной в точке, равной
абсциссе точки касания.
Таким образом, приходим
к уравнению 2(х0 + 2) = 2
<=> х0 = -1. Итак, абсцис-
са искомой точки равна
х0 = -1, ордината у0 = 1.
Обозначим эту точку А = (-1; 1). Пусть точка В - точка пересечения прямой, прохо-
дящей через точку А параллельно оси абсцисс, с прямой у = 2х — 1. Тогда В = (1; 1).
Пусть точка С - точка пересечения прямой, проходящей через точку А параллельно
оси ординат, с прямой у = 2х -1. Тогда С = (-1;- 3). Расстояние от точки А до прямой
у = 2х -1 совпадает с длиной высоты прямоугольного треугольника АВС, опущенной
из вершины А . Таким образом, искомое расстояние d можно найти из формулы
d _ АВ АС Так как АВ = 2 АС = 4 вс _ ^АВ2+АСг = 2^_ то d _ ±
ВС V5
4
V5 ’
Ответ: (-1;1)
те все значения параметра а, при которых система уравнев
151
9. Пай;
115
имеет два различных решения. Укажите эти решения при каждом
46
tn найденных значений а. (12 баллов)
Решение.
Рассмотрим два случая раскрытия модуля в первом уравнении системы.
I. Если у > 0, то у = 1у[х, а(14х - 3) = х - 2. Сделаем замену переменного у[х = t > 0.
11олучим следующее квадратное уравнение г - 2at + За - 2 = 0, для которого
= (а-1)(а-2); г, +г2 = 2я;
z,/2 = За - 2. Таким образом,
два
Ха - 1)(а - 2) > О
различных решения: *
За-2 > О
V.
При ае
имеем решения:
()дно решение:
При ае
и {1; 2} имеем решение:
(а-1)(а-2) = 0
а>0
За-2 < О
f3a-2 = 0
а<0
<=> ае
х = (а + д/а2 -За+ 2)
у = 2а + 2у/а2 -За + 2
II. Если у < 0, то х = О,
а(у-3) = -2, у = 3~ — <0,
а
при ае
Ответ: при а е
имеем 2 решения:
и (2; + оо) имеем 2 решение:
а > О
10. Шар радиуса 1 с центром в точке О вписан в правильную треугольную пи-
рамиду. Через точку О проходит плоскость, параллельная стороне основания пирами-
ды и апофеме, проведенной к другой стороне основания. Найдите площадь сечения пи-
рамиды указанной плоскостью, если расстояние от центра описанной около основания
пирамиды окружности до этой плоскости равно 1/V13 (12 баллов)
47
Решение.
Обозначим расстояние от центра описанной около основания пирамиды окруж-
ности до плоскости, содержащей сечение, d = -jLr, радиус вписанного шара г = 1.
ем построение сечения. Центр О вписанного шара лежит на высоте ТС\ пра-
вильной треугольной пирамиды ТАВС . Пусть
TD апофема пирамиды, поведенная к
стороне АС. В плоскости TBD через точку О проведем прямую параллельную
TD, S = DB П SL, L = ТВ П SL. Через точку S в плоскости основания проведем пря-
мую NK, параллельную стороне
основания СВ, N = АС A NK ,
K = ABQNK .
Соед
тит
зяем точки
К и L. Через точку L в плоско-
сти ТВС проводим прямую ML,
параллельную стороне основания
СВ, М = ТС A ML. Соединяем
точки N и М. Трапеция KLMN
искомое сечение пирамиды. Най-
дем его площадь. Пусть а - длина
стороны основания пирамиды.
1) Z.ODO{ = а, ATDO} = 2а,
г _ 6г _ 6
O[D yfoa 43а
ОО1 = г , tga=
2) TD || SL, AOSOl = ZTD(\ = 2а, SO4
г _r(\-tg2a) _Л(а2-12)
tg2a 2tga 12а
3) АР и BD - медианы основания пирамиды, О, - точка их пересечения, R - точка пе-
48
•сечения АР и NK , ZDBC = Z.RSO. =30°, O.R = ^=—{a——
1 1 2 24а
/>Ц =-BD = — .
1 3 6
•I) Длина высоты прямоугольного треугольника OO}R, проведенной из вершины пря-
мого угла Ot, совпадает с расстоянием от центра описанной около основания пирами-
цы окружности до плоскости, содержащей сечение. Пусть Z.OO{R = у. Тогда
d OfR
•'"’Г = - = -Г==Т’
r Jr'+O,R2
1 = 7з(а2-12)
^576а2+3(а2-12)2
7
= дТ -12, а = 6
5) DS =OyD-SO\ ---12) _2л/3
1 6 12а 3
US = ЗО| D - DS = — - LU = 1LL.
В треугольнике TBD имеем TD || SL
DS _ TL
BS ~ LB
DS_2 TL _ 2
BS ~ 7 ’ LB~ 7
В треугольнике TBD имеем ML || СВ
ML _TL
СВ ' ТВ
2
2а 4
ML = — = -
(>) О, R =
Гак как NK || СВ, то
2 2 1 1 3 6 6
NK AR 2AR И „„ 11
--=----= _ - = — => NK = —.
СВ АР Ла 18 3
7) ОЛ = >/г2+О1/?2 = —.
К) /.MNK = Z.OSR = !5,tgP =
OR
SR
49
9) Н = NK MLtgfi = —j№.
2 18
10) Sce4 = NK±MLH = — >/39.
сеч 2 36
2.11. Вариант № 4
1. Двое рабочих одновременно приступили к изготовлению одинаковых партий
деталей. Когда первый рабоч
сделал половину деталей, второму оставалось изгото-
вить 24 детали, а когда второй выполнил половину работы, первому оставалось сделать
15 деталей. Сколько деталей осталось изготовить второму рабочему, когда первый вы-
полнил свою работу? (8 баллов)
2. Решите уравнение vl + cosx + v2 sinх = 0. (8 баллов)
3. Ре:
III
яте уравнение log4(1 Ох + 46) = 1 + log2 (2 — х). (8 баллов)
4. Ре
III
аге неравенство logx (4х - 3) > 2. (8 баллов)
5. Решите неравенство (х-2)\/б-х-х2 > (2-Зх)\/б-х-х2. (10 баллов)
6. Найдите множество значений функции /(х) = sin
JV । z - _ _ .
—— I. (10 баллов)
7. Какой наибольший угол может быть между гипотенузой прямоугольного тре-
угольника и медианой, проведенной из острого угла? (12 баллов)
8. Какую наименьшую площадь может иметь прямоугольный треугольник, на
гипотенузе которого лежит точка Л/(0;1), а его катеты лежат на прямых х=-2 и у=0.
(12 баллов)
9. Укажите все значения а, при которых система уравнений
(х-д)2 =80>-х+а-2),
l-log2x
имеет хотя бы одно решение, и решите ее при
каждом а. (12 баллов)
10. Основанием пирамиды ТАВС служит треугольник АВС все стороны кото-
рого равны 2>/14, а высота пирамиды совпадает с боковым ребром ТА . Найдите объе-
мы частей, на которые делит пирамиду плоскость, проходящая через середины стороны
50
основания ЛСи бокового ребра ТВ и параллельная медиане TD боковой грани АТВ,
|‘гии расстояние от вершины пирамиды Т до секущей плоскости равно 1. (12 баллов)
2.12. Решения варианта №4
1. Если п — количество деталей в партии, р\ и р2 — производительности рабочих,
п п — 24 п л-15 п п — х
го ----=------;----=-------; — =-----. Из первых двух уравнении получаем:
Р2 2Pi Pi Pi Pi
п /4 = п2 -39л+ 360, или п2 -52л + 480 = 0; л = 26 ±14, л1 = 12 - пост, корень, л2 = 40.
.. 20 16 40 40-лг
1юдставляя л = 40 в первое и третье уравнения, получаем — = — и — =-----, отку-
Pi Pi Pi Pi
да 40 — x = 32, .x = 8.
Ответ: 8 деталей.
2. Vl + cosx + у/2sinх = 0; 2sin2x = l + cosx; 2cos2x+cosx-1 = 0; cosx = ———.
4
1) cosx = -1, A] = л+2лл; 2) <
cosx = 1/2, д
x. =-----\-2kit.
sin x < 0, 3
Ответ: = л + 2лл, x2 = —+2kn, n, ke Z.
3. log4(10x + 46) = l + log2(2-x); 0,51og2(10x + 46) = log2(2(2-x));
IOx + 46 = 4(2-x)2, -4,6<x<2; 4x2 -26x-30 = 0, x12 = (13±17)/4; x( =7,5 >2 - не
входит в ОДЗ, х2 = -1.
Ответ: х = -1.
4.
logx(4x-3)>2. ОДЗ: ле (3/4;l)U(l;+°°)- logT-^-<0.
4х-3
5
2
4х-3
Ответ: xg (3/4;l)U (1;3).
5. (х — 2) \1б — х — х2 > (2 — Зх) л/б —х —х2 .
51
«хе {-3}U[1;2].
х = 2
Ответ: х е {-3} U [ 1; 2].
Пусть
z(x) = 1 л/л2 -х2
при
—л < х < л — л/3 < z <, 2 л/3. На этом промежутке функция sin(z) принимает наимень-
шее значение f (-л/3) = -л/З/2 и наибольшее значение f (л/2) = 1.
Ответ: -Тз/2;1 .
7. Построим окружность с диаметром, совпадающим с гипотенузой А В тре-
угольника АВС . Соединим D (середи-
ну катета ВС) с центром окружности
(9; очевидно, РО||ЯС и ZBDO = 90°.
Следовательно, точка D лежит на ок-
ружности с диаметром О В. Угол меж-
ду гипотенузой АВ и медианой AD
будет наибольшим, если медиана каса-
ется этой окружности (положение AD}). В AAD{O2 D}O2 = 1/4 АВ и АО2 = 3/4 АВ, от-
сюда sin ZD{AO2 = D\O2/AO2 = 1/3.
Ответ: arcsin(l/3).
8. у = 1 + кх, x.j = --, ув = 1 - 2к.
к
к. = —-пост.
1 2
корень, к 2
5ПШ1 = 0,5 • 4 • 2 = 4 ед2. Ответ: 4 ед2.
52
9. Второе уравнение равносильно системе: х > О, у = х. Подставляя у - х
в первое уравнение, получаем; (х-а)2 = 8(а-2), или х2-2ах + а2-8а + 16 = 0 (*), у
которого D/4 = а2 - а2 + 8а -16 = За -16. Количество решений заданной системы урав-
нений зависит от числа корней этого квадратного уравнения.
Очевидно, при а < 2 уравнение решений не имеет.
Рассмотрим случаи, когда система будет иметь два различных решения. Квад-
ратное уравнение (*) будет иметь два различных положительных корня
хк2 = а ± \/8а-16 , если
За-16 > О,
а >0,
а2-8а + 16>0,
4-4а + а2 - За + 16^0
V
а > 2,
а2 -12а+ 20* 0
2<а<4,
4<а<10,
10<а<+«
Рассмотрим уравнение в оставшихся отдельных точках.
При а = 2 уравнение принимает вид (х-2)2 = 0, его корень х = 2 не удовлетво-
ряет ограничениям, наложенным на неизвестное х во втором уравнении системы.
При а = 4 уравнение принимает вид х2 - 8х = 0, его корень х = 0 — посторон-
ний, другой корень х = 8 входит в область допустимых значений уравнений системы;
при а = 4 система уравнений имеет одно решение х = 8. у = 8.
При а = 10 получаем (х-10)2 =8 8, откуда х12=10±8; корень х = 2 - посто-
ронний, второй корень х = 18 входит в область допустимых значений системы. При
а = 10 система уравнений имеет одно решение х = 18, у = 18. Объединяя найденные
значения а. получим ответ.
Ответ: при ае (2;4)U(4; 10)U(10;+°°), х = у = а±у/3а-\6 ;
а = 4, х = 8, у = 8;
а = 10, х = 18, у = 18 .
53
10.
Пусть М- середина ребра ТВ. Проведем MF\TD, Fе АВ, DF = FB = АВ/Ь\
S = (MF)C\{AT),SF = 3I2TD и AS = 3/2 АТ. Так как TD = ?MF, то SM = 2/3SF. Ес-
ли Е - середина стороны АС и N = SE А ТС, то EFMN -сечение пирамиды заданной
в условии секущей плоскостью. Проведем TG |S£. Так как SE = 3/2TG и NE = 3/4TG,
то SN = NE = SE/2. Следовательно, площадь треугольника AMSN
S.uw =-SM SNsmZMSN = SF-SEsm^FSE = -S^.
лил» 2 2 3 2 3
Проведем AK ± FE, К e FE, SK ± FE, и TH ±SK, He SK . Так как
TH _L (SFE), то длина TH равна заданному в условии задачи расстоянию от вершины
54
пирамиды Т до секущей плоскости. Введем обозначения а = АВ
d = TH, тогда
AP = 3d.
и
Сравним объемы пирамид TMSN и AFSE. Так
как TH = — АР
ДЛ/SV
&FSE’
PMSK ъ r AFSE ’
и
Сравним
объемы
пирамид
SAFE
ТАВС.
Очевидно,
ч IVF =-------Ут = — Утаяг • Следовательно, объем
Sjirc л л л 1 х /Я/Я ’
2 4 2 16
одной
части пирамиды, пяти-
8
8 9
гранника AFETMN , ViFEnm=--V&tltE =
9 9 16
Г.1ЛС
2 к ТАВС •
То есть, секущая плос-
кость разбивает пирамиду на две равновеликие части.
В bAFE
EF2 = АЕ2 4- AF2 - 2АЕ • AF • cos ABAC =
а За 1
2 Т 2
7а2
16
EF =
9
„ 1 1 z-on • AF • sm 60 а За
Iак как — • АК EF АЕ AF sin60 , АК =------—--------= — • —-
2 2 EF 2 4
ч/З 4 _3-73а
2 а J7 ~ 4у/7 ’
В &ASK
РК=\1аК2-АР2 = J— -9d2 = 3^3д2 l12rfZ.
V16-7 4^7
2
и AS =
АРАК
РК
3d 3>/3 а 4л/7 _ 2>E>ad
4>/7 Зч/За2-112d2 ч/За2 -1Ш2
;AT=-AS=
3
2ч/3а</
V3a2-112d2
Объем пирамиды
- -1 2ч/ЗадГ = a2d = a2d
ГАВС~3 4 V3a2 -112d2 2ч/3а2 -112d2 2^3-112(d/a)2
Объемы частей пирамиды V = VX=V2 =
a2d
4^3-112(d/a)2
При а = 2J14, d = 1 V= . 414 , =14.
4^/3—112 1/56
Ответ: 14.
55
2.13. Типовые задания для самостоятельного решения
Вариант № 5
1. По плану одной бригаде нужно изготовить на 900 изделий больше, чем другой
за то же время. Чтобы каждая бригада выполнила свой план на 2 дня раньше, в первую
бригаду добавили 3 человека, а во вторую 2. Сколько рабочих было в каждой бригаде
во время работы, если каждый из них изготовлял в среднем по 15 изделий в день? (8
баллов). Ответ: 18 и 12 рабочих.
2. Сколько членов содержится в возрастающей арифметической прогрессии, у
которой сумма членов с четными номерами составляет 90% суммы членов с нечетными
номерами? (8 баллов). Ответ: 19.
3. Решите уравнение (х10^13”'1 -4-)~ +^/(2v -6х-2)(2* -х-1) = 0. (8 баллов)
Ответ: 5.
4. Решите уравнение 3cosx + cos y/64tgx | /gx -114-9 = 8 sin х. (8 баллов)
Ответ: arctg — + ли, п g Z.
5. Решите неравенство
10(< -27)Л2 +10х + 25
(х2 +3х + 9)(х2 +2х-15)
> х-3 . (10 баллов)
Ответ: - 7] и (-5; 3) и (3; 13].
6. Найдите множество значений функции f(x) = log0 5
лМ-х2
(10 баллов) Ответ: Е(у) = [3; + °°).
7. Окружность радиуса = V3 касается сторон АВ и ВС треугольника АВС ,
а окружность радиуса R2 = 3v3
вне
in
зим образом касается первой окружности и сто-
рон АС и ВС треугольника АВС . Общая касательная к этим окружностям, не содер-
жащая сторону ВС , пересекает отрезки АВ и АС в точках М и N соответственно.
Найдите длины сторон треугольника АВС, если Z.AMN =30°, ZANM =90°.(12 бал-
лов). Ответ: 7>/3+15, 5>/3 + 7, 107з+14.
8. Какую наименьшую длину может иметь отрезок А В , если точка А принад-
лежит кривой х2 4- 4х 4- у2 - 20у 4-103 = 0, а точка В - графику функции у = 31 х | ? (12
баллов). Ответ: (4/VTo) -1.
56
9. При каких значениях параметра а система уравнений
ш+а = 2х-х2
[ у + х2 = 2х + а2
име-
•ч ровно 4 различных решения. Найдите эти решения при каждом из полученных а. (12
Ни илов). Ответ:
ас (-1;-0,5)и(-0,5; 0),
^1/2 =а2 -а;
у,/4 =а2 +а + 1.
10. Основанием пирамиды TABCD является трапеция ABCD , стороны ВС и
I/) которой лежат на параллельных прямых, ВС = 4, ВС < AD , а радиус вписанной в
i|шпецию ABCD окружности равен -Уб. Боковые грани пирамиды наклонены к плос-
кости основания пирамиды под одним и тем же углом. Расстояние между медианой
Ш боковой грани TAB и высотой ТК боковой грани ТВС равно -73/2. Найдите объ-
ем пирамиды TABCD , если известно, что вокруг нее можно описать сферу (12 баллов).
< Ивет: 20.
2.14. Вариант № 6
1. Один рабочий за два часа делает на 5 деталей больше, чем другой, соответст-
венно на изготовление 100 деталей он затрачивает на 2 ч меньше. Какое время тратит
каждый рабочий на изготовление 100 деталей? (8 баллов)
2. Сколько последовательных членов арифметической прогрессии 32, 28, 24, ...,
начиная с первого, надо сложить, чтобы получить сумму, равную 132? (8 баллов)
3. Решите уравнение 91+2л^ - 28 • 9^ + 3 = 0. (8 баллов)
4. Найдите все корни уравнения cos3x = -73sin4x + cos5x, принадлежащие про-
межутку [я/2; л]. (8 баллов)
5. Решите неравенство
х-зУГЛ+1
4д/х--Т - 2 - х
< 0. (10 баллов)
6. Найдите множество значений функции /(x) = 2sin
-|(>/4-х2 -I)2 I (10
баллов)
7. Периметр параллелограмма ABCD равен 28, его площадь равна 24-73, угол
А составляет 60 , ВК и BN - высоты параллелограмма, проведенные к прямым, со-
держащим стороны AD и CD соответственно. Найдите длину отрезка KN . (12 баллов)
57
8. Найдите угол между касательными к графику функции у = х2 V3/24 , прохо-
дящими через точку
Л/(4;-2-Уз). (12 баллов)
9. Укажите все значения а, при которых уравнение (х - а)2 = т—+а+1
имеет хотя бы одно решение, и ре
и
ите его при каждом а. (12 баллов)
10. Расстояние между диагональю прямоугольного параллелепипеда и не пере-
секающей ее диагональю основания равно /, а диагональ параллелепипеда наклонена к
плоскости основания под углом 30°. Плоскость, проходящая через диагональ паралле-
ли
llil
сюда и параллельная диагонали основания, образует с плоскостью основания угол
45°. Найдите площадь сечения параллелепипеда этой плоскостью. (12 баллов)
Ответы. 1. 8 и 10 ч. 2. 6 или 11. 3. х = 1/4.4. хе {я/2;3л/4;я;2л:/3} .
5. хе [1; 2)о(2; 5]и(10; оо). 6. ^=[-1;л/з]. 7. V39. 8. 90°. 9. Ответ: при
ае (-l;0]U[l;2] x = a+Va + 2 ; при (0;1) Х| = а + \М + 2, х2 =a-Ja ; при аб(2;-к»)
х, 2 = а ± л/я + 2.10. S = 4>/б/:.
2.15. Вариант Xs 7
1. Партию обуви, купленную за 180 тыс. рублей, в первую неделю продавали по
цене, большей закупочной на 25%, затем наценка была снижена до 16% от закупочной
цены; а вся партия обуви была продана на 20% дороже, чем куплена. На какую сумму
продали обуви в первую неделю? (8 баллов)
2. Решите уравнение cosx + sin 2х = 0. (8 баллов)
3. Какое наибольшее значение может принять сумма первых п членов арифмети-
ческой прогрессии 100,97, 94,...? (8 баллов)
4. Ре
III
ате уравнение (log3 х) • log4 (х/3) = log2 3. (8 баллов)
5. Решите неравенство
277+13
X-W7+4
. (10 баллов)
6. Функция /(х) = с/(х-с) определена на отрезке [1;3]. Найдите все значения
с, при которых наименьшее значение функции на этом отрезке меньше -0,25. (10 бал-
лов)
58
7. Площадь треугольника АВС равна 49>/з/4, сторона АВ = 7, угол ZB = 60°.
Ин сторонах АВ, ВС и АС выбраны точки K,L и М так, что АК: КВ = 2:5,
///.: LC = 1: 6, AM : МС =4:3. Найдите площадь круга, описанного около треугольни-
ки KLM. (12 баллов)
8. Какую наибольшую площадь может иметь фигура на плоскости ху, располо-
женная между прямыми х = -3 и х = 1 и ограниченная снизу осью х, а сверху — каса-
тельной к графику функции у = х2 +16 с абсциссой х0 тог
касания, лежащей в про-
М5
межутке -3 < х0 <17(12 баллов)
9. Укажите все значения параметра р, при которых система уравнений
* I / 2
г -бу+ 10 = 5|х/х, у + 1 -р = (х-р) имеет ровно два различных решения. Найдите
п и решения. (12 баллов)
10. В сферу радиуса R вписана правильная треугольная пирамида, у которой вы-
сота равна 4Л/3. Какую наименьшую площадь может иметь сечение пирамиды плоско-
стью, проходящей через медиану основания? Найдите отношение объёмов частей, на
которые секущая плоскость разбивает пирамиду в этом случае. (12 баллов)
Ответы. 1. 100 тыс. рублей. 2.
5. хе [0; 1)^(1; 16). 6. 7. се (-~;-1/3)11 (3;+~). 8. 68. 9. -2<р<1,
.г, =р + у1б-р9 у, = 5; х2 =р + ^2-р, у2 = 1; р = 2, х} =4, у} =5; х2 =2, у2 =1;
2<р<6,
= Р±у/6-р, У1Л =5.10.
3:19.
2.16. Вариант № 8
1. Два тела движутся равномерно по окружности в одну сторону. Первое тело
проходит окружность на 3 с быстрее второго и догоняет второе тело каждые полторы
минуты. За какое время каждое тело проходит окружность? (8 баллов)
2. Решите уравнение 71-cos х = 72 cosx. (8 баллов)
3. Решите уравнение (log2 х)- log81 (8х)= log3 2. (8 баллов)
4. Решите неравенство
6
Зх-1
> 3х . (8 баллов)
59
5. Решите неравенство
Vx2 + Зх -18 <
6л/х2 + 3х —18
х + 2
.(10 баллов)
5sinx-3
6. Найдите множество значений функции f (х) =
sinx+l
.(10 баллов)
7. Четырехугольник ABCD вписан в окружность, его диагонали АС и BD пе-
ресекаются в точке F, причем AF: FC = 3:1, BF: FD = 4:3, угол
Z/4FD = arcsin( V15/4). Найдите радиус вписанной в треугольник CFD окружности,
если BD = 3,5. (12 баллов)
8. На плоскости хОу прямые ^ = Зх-2 и х = -1 пересекаются в точке В, а
прямая, проходящая через начало координат, пересекает заданные прямые соответст-
венно в точках А и С. При каком положительном значении абсциссы точки А пло-
щадь треугольника АВС будет наименьшей? Найдите эту площадь. (12 баллов)
9. Найдите все значения а, при которых система уравнений
(х-а)2 =9(у-х+а-2), 1~log^=1
V ’ l-log2jc
имеет хотя бы одно решение, и решите ее при каждом а .(12 баллов)
10. Найдите площадь сечения правильной треугольной призмы АВСА}В}С} плос-
костью, параллельной диагонали ВС} боковой грани ВССХВ} и прохо;
[ей через центр
1шп
описанного около призмы шара и вершину основания А, если стороны основания
призмы равны 3, а высота призмы равна 10/3. (12 баллов)
Ответы. 1. 15 с и 18 с. 2. х = ±— + 2ил, п е
Z.3. {1/16;2}.4. 0<х<1.
5. хе{-6}и[3;4].б. Е(у) = [0,1;+«). 7. 5/15/12.8.1; Smin=4.
9. ае (2;3)U(6;ll)U(lU+®o), х = y = a+3>Ja—2 ; ае [3;6](J{11}, х = у = а + Зу/а—2 .
10. 19>/з/5
60
Раздел 3. Физика
3.1. Содержание варианта задания олимпиады по физике
в МГТУ им. Н.Э. Баумана
Специфика системы подготовки специалистов в МГТУ им. Н.Э.Баумана, боль-
шой объем контрольных заданий по каждому предмету, включенному в образователь-
ный курс, интенсивность проверок выполнения этих заданий, налагают определенные
требования к формированию контингента будущих первокурсников. Существует необ-
ходимость отбора из числа абитуриентов школьников, не только обладающих знаниями
по школьному курсу физики, но глубоко понимающих сущность физических процессов
(из числа рассматриваемых в школьном курсе), логически мыслящих, творчески ищу-
щих пути решения сложных задач, умеющих самостоятельно работать с литературой.
Структура и содержание задания по физике при проведении олимпиады направ-
лены на проверку глубины усвоения абитуриентом школьного курса физики, прочности
выработанных им навыков применения знаний основных законов физики к решению
задач и практически являются инструментальным средством оценки подготовленности
абитуриентов к последующему обучению в МГТУ им. Н.Э. Баумана.
Каждый вариант контрольного задания олимпиады содержит системный набор
задач различного направления, упорядоченных по возрастанию сложности, и состоит
из 10 заданий: двух задач первого уровня сложности, либо одного вопроса качествен-
ного характера и одной задачи первого уровня сложности; шести задач второго уровня
сложности и двух задач третьего уровня сложности. Задачи одного варианта задания
охватывают все основные разделы школьного курса физики. При этом в нём могут
быть, например, задачи первого уровня сложности из раздела «Механика», второго
уровня сложности из разделов «Термодинамика», «Электростатика», «Оптика», тогда
задачи третьего уровня сложности будут представлять собой сочетание разделов
«Электричество», «Колебания» и «Механика». Уровень сложности задач соответствует
Программе вступительных экзаменов для поступаю!
II!
[х в высшие учебные заведения
России. Специальные экспериментально-теоретические исследования и накопленный
опыт предлагаемых вариантов заданий олимпиад позволяют утверждать, что, несмотря
на множество вариантов сочетаний задач различной трудоёмкости из разных разделов
61
физики, варианты заданий в целом по трудоемкости и уровню сложности являются
одинаковыми.
ВОПРОС КАЧЕСТВЕННОГО ХАРАКТЕРА. Термин «качественного» подчер-
кивает главную особенность всех вопросов такого типа - внимание в них акцентирует-
ся на качественной стороне рассматриваемого физического явления. Этот вопрос при-
зван выявить глубину понимания абитуриентом сущности физических явлений и зако-
нов, умение объяснить смысл физических величин и понятий. Он служит средством
проверки практических навыков абитуриента, умения применить теоретические знания
для объяснения явлений природы, быта, техники. Ответ на этот вопрос позволяет также
оценить технический кругозор абитуриента, проверить его способность к логическим
умозаключениям, базирующимся на знании основных законов физики.
3.2. Примеры вопросов качественного характера:
1. Что называют инертностью тела?
2. Напишите формулу для вычисления ускорения свободного падения на по-
верхности Земли. Поясните смысл входящих в неё физических величин и укажите еди-
ницы их измерения.
3. Напишите формулу закона Ома для участка цепи, изображен-
ной на рисунке. Укажите единицы измерения входящих в неё физиче-
ских величин.
4. Приведите примеры, когда сила трения является «движущей» силой.
5. В чем состоит особенность теплового расширения воды?
6. Какова физическая сущность удельной теплоты плавления у кристаллических
твердых тел?
7. Какова физическая причина наличия удельной теплоты парообразования у
жидкостей?
8. Действует ли сила Архимеда на тела, находящиеся в жидкости в космическом
корабле, движущемся по круговой орбите вокруг Земли?
9. Объясните, почему теплоёмкость двухатомных
газов больше теплоёмкости одноатомных газов.
10. На рисунке представлена схема энергетических
уровней атома. Какой цифрой обозначен переход с погло-
щением фотона наибольшей частоты? Ответ обосновать.
62
11. По двум прямолинейным длинным проводникам, расположенным во взаимно
перпендикулярных плоскостях, текут равные токи.
Какое из показанных на рисунке направлений имеет
вектор В индукции магнитного поля, созданного
этими токами, в точке О? Ответ обосновать.
12. Изменения состояния газа при некотором круговом процессе 1-2-3-1 пока-
заны на графике зависимости объема газа от абсолютной тем-
пературы. Изобразите этот цикл на графике зависимости дав-
ления газа от объема. Укажите, на каких участках графика газ
получает теплоту извне.
13. На каком явлении основан принцип действия трансформатора?
14. Алюминиевое кольцо подвешено на двух нитях.
Северный полюс магнита приближается с некоторой скоро-
стью к кольцу, двигаясь вдоль его оси перпендикулярно
плоскости кольца. Будет ли при этом кольцо притягиваться к
магниту или отклоняться от него? Ответ поясните
15. Почему белый свет, проходя сквозь призму, разла-
гается в цветной спектр?
16. Чем вызвана необходимость замедления нейтронов, испускаемых при деле-
нии ядер в ядерных реакторах?
17. Как изменится период колебаний в колебательном контуре, состоящем из
воздушного конденсатора и катушки индуктивности, если про-
странство между обкладками конденсатора заполнить диэлектри-
ком? Ответ поясните.
18. Два одинаковых шарика начали одновременно и с одинаковой скоростью
двигаться по абсолютно гладким сферическим поверхностям. Бу-
дет ли отличаться время движения каждого шарика к моменту их
прибытия в точку В? Ответ поясните.
19. Тело соскальзывает из точки А в точку В один раз по
дуге АМВ, другой раз по дуге АКВ. Коэффициент трения остается
постоянным. В каком случае скорость тела в точке В больше? По-
чему?
63
20. Какие силы создают центростремительное ускорение самолёту при повороте
в горизонтальной плоскости?
21. Какие силы создают центростремительное ускорение велосипедисту при по-
вороте на горизонтальной дороге?
Ответ: Силы трения и силы реакции со стороны дороги.
ЗАДАЧИ ПЕРВОГО УРОВНЯ СЛОЖНОСТИ — задачи, в которых рассматри-
ваются явления, относящиеся к одному разделу физики. Алгоритм решения этих задач
обычно виден из условия задачи и для их решения необходимо, используя основные
законы физики и их аналитические выражения, провести несложные математические
преобразования и вычисления. Задачи этого уровня, как правило, позволяют выявить не
только сам факт знания абитуриентом основных законов физики, но и умения приме-
нить аналитические выражения этих законов к решению задач. Кроме того, выявляется
умение абитуриента пользоваться системой измерения физических величин СИ и пере-
водить внесистемные единицы измерения в СИ.
Несмотря на кажущуюся простоту задач первого уровня сложности, у абитури-
ентов встречаются затруднения при их решении, не позволяющие абитуриенту полу-
чить максимальные баллы, например:
• При знании формулировок законов Ньютона не учитывается векторный ха-
рактер этих законов.
• Путают формулы для нахождения емкости батареи конденсаторов при их па-
раллельном и последовательном соединении с формулами для определения сопротив-
ления участка цепи постоянного тока при последовательном и параллельном соедине-
нии проводников.
• Часто путают основное уравнение молекулярно-кинетической теории иде-
ального газа с уравнением состояния идеального газа.
• Встречаются затруднения в записи аналитических выражений изопроцессов,
адиабатного процесса и применении первого закона термодинамики для этих процес-
сов.
• При использовании законов сохранения импульса и механической энергии,
забывают про векторный характер закона сохранения импульса.
• К сожалению, многие абитуриенты не знают правильного определения таких
понятий, как напряженность и потенциал электростатического поля, забывают о век-
64
горлом характере напряженности, не могут использовать принцип суперпозиции полей,
ле имеют четкого представления о физическом смысле этих характеристик поля. Не
пользуются графическим представлением электрического и магнитного полей.
• При описании колебательного движения не учитывается зависимость ампли-
туда и фазы колебаний тела от внешних условий, вызвавших эти колебания.
3.3. Примеры задач первого уровня сложности:
1. Две частицы движутся с ускорением g в однородном поле тяжести. В началь-
ный момент частицы находились в одной точке и имели скорости Vi = 3,0 м/с и vi = 5,0
м/с, направленные горизонтально и в противоположные стороны. Найдите расстояние
между частицами в момент, когда векторы их скоростей окажутся взаимно перпенди-
кулярными.
Решение.
Падая, обе частицы, находятся в одной
горизонтальной плоскости, на одной вы-
соте, определяемой составляющей
vу = gt . Расстояние между частицами L
определяется горизонтальными состав-
ляющими скоростей, т.е. начальными скоростями v01 и v02, и временем падения час-
тиц t до момента, когда скорость ц станет перпендикулярной скорости v2. Время па-
дения частиц находим из треугольников скоростей. Треугольник АВС - прямоуголь-
ный v01 ц>2 = (gt) , отсюда t = V()l V°2 (1), L = (w0| + w02)/ (2).
g
Подставив (1) в (2), получим L =
(Vpi + Uo2
g
(3 + 5)V3~5
9,8
M .
Ответ:
Ответ: F= 10 H
3. С вершины башни, высотой 125 м, броси-
ли мяч в горизонтальном направлении со скоро-
стью Do = 20 м/с. Пренебрегая сопротивлением воз-
духа, найдите модуль вектора перемещения мяча за четвертую секунду полёта.
65
Ответ:
Ar = ^Arv2 4-Ar.2 = 40,3 м
4. Два тела, находящиеся на одной и той же высоте, брошены одновременно с
одинаковыми скоростями \)0 = 10 м/с, одно вертикально вверх, а другое вертикально
вниз. Определите т - разницу во времени движения тел о момента падения их на зем-
лю.
Ответ:
5. Четвёртая часть однородной линейки, имеющей массу m и длину L , выступа-
ет за край стола. Найдите минимальную величину силы F, которую необходимо прило-
жить, чтобы сдвинуть линейку с места. Коэффициент тре-
ния между линейкой и столом равен ц .
Ответ: F = jUmg .
6. При падении тела с большой высоты в воздухе через некоторый промежуток
времени его скорость становится постоянной. Учитывая, что сила лобового сопротив-
ления прямо пропорциональна площади поперечного сечения тела и квадрату его ско-
рости, определите отношение установившихся скоростей vRlv,. двух шаров радиусами
R и г. Шары изготовлены из одного и того же материала.
Ответ:
7. Тело движется по прямой. Под действием по-
стоянной силы F = 4 Н за время At = 2с импульс тела увеличился с
р} до р2 = 20 К- --. Определите величину импульса р}.
Ответ:
_. __ . _ , _ К2 ’ М
р{= р2— FAt = 20 - 4•2 = 12---
с
8. Тело движется по прямой. Начальный импульс тела р} = 50 е . Определи-
с
те импульс тела р2 через At = 2с , если в течение этого времени на
его действует постоянная сила трения F =1 ОН.
F
66
Ответ: р2 = р{~ F& = 50-10 2 = 30
кг • м
9. Движение материальной точки вдоль оси х описывается уравнением
v = 0,06 cos 0,5тй м. Масса точки m = 10 г. Найдите изменение импульса Дрх матери-
ппьной точки за интервал времени от tj = 1 с до t2 = 3 с.
z х . . Л-3 кгм
fn(v2x ~v\x) = 1,88 10 -------
v
Ответ: Др
£2
О х
10. В вершинах квадрата расположены равные точечные положительные заряды.
(Птределите напряженность электрического поля в центре квадрата.
Ответ: Е = 0 .
11. Диэлектрическая проницаемость воды £ = 81. Как нужно изменить расстоя-
ние между двумя точечными зарядами, чтобы при погружении их в воду, сила взаимо-
действия между ними была такой же, как первоначально в вакууме?
Ответ:
Я - q—
2 2
П £ ' r2
Уменьшить в 9 раз.
12. Два пружинных маятника имеют одинаковые массы гру-
зов. На графике показана зависимость сил упругости пружин Fynp.
этих маятников от растяжения ДЬ. Период колебаний какого маят-
ника будет больше? Объясните, почему.
Решение,
Из закона Гука следует, что Fynp
= k ДЬ , из графика следует, что к, > к 2, а
так как период колебаний Т = ?то ^2
L/4
13. Однородный стержень длины L и массы m
шарнирно закреплён в точке О, отстоящей на L/4 от
конца стержня. Середина стержня точка С прикреп-
лена к пружине. На концах стержня закреплены два маленьких груза массами 2m и т,
как показано на рисунке. Найдите силу упругости, возникающую в пружине в положе-
нии равновесия стержня, когда он неподвижен и расположен горизонтально. Массой
пружины и силами трения пренебречь.
Ответ: Г = 2mg .
67
14. В процессе поступательного движения тела вдоль оси х на него действует
сила F, зависимость проекции которой от коорди-
наты х представлена на графике. Определите ра-
боту, совершаемую силой при перемещении тела
от координаты х = 0 до х = 5 м.
Решение.
Работа численно равна площади фигуры,
образованной графиком и осью х.. При этом площадь фигуры над осью х берётся со
знаком плюс (она соответствует положительной работе), а площадь фигуры под осью
х- со знаком минус (она соответствует отрицательной работе).
Ответ: А = - 2,5 Дж .
15.. Конденсатор емкости Ci зарядили до напряжения Ui = 500 В. При парал-
лельном подключении этого конденсатора к незаряженному конденсатору емкости Сг =
4 мкФ вольтметр, подключенный к батарее конденсаторов показал напряжение U2 = 100
В. Найдите ёмкость С]
Ответ:
С. =_^2—^2_ = i мкф
и.-и2
16. Найдите работу А, которую необходимо совершить
над одним молем идеального газа для его изобарного сжатия,
при котором концентрация молекул в конечном состоянии в
а = 2 раз больше, чем в начальном? Первоначальная темпера-
тура газа Т| = 300 К.
Ответ:
А = vRT. а - = 1246 Дж
а
V
17. Внутренняя энергия U некоторой массы одноатомного газа при температуре t
= 27°С равна 1,0 Дж. Сколько молекул N содержит эта масса газа?
Ответ:
18. Сосуд объема V = 40 дм3 разделен тонкой подвижной перегородкой на две
части. В левую часть помещены 36 граммов воды, а в правую - 28 граммов азота (N2).
Температура поддерживается равной t = 100°С. Определите объём правой части сосуда.
Ответ:
68
19. На рисунке показаны предмет АВ и его
изображение AiBi, полученное с помощью линзы.
Определите построением положение линзы и её главной
оптической оси.
Ответ: Луч, выходящий из любой точки предмета, после преломления в линзе,
проходит через соответствующую точку действительного изображения этого предмета.
JLIIII
По, так как лучи, проходящие через оптический центр линзы, не меняют своего
направления, то для нахождения положения оптического центра линзы, соединим
прямыми линиями точки А , А| и В, Bi Полученная на их пересечении точка О является
оптическим центром линзы. Для определения положения линзы кроме положения
оптического центра, необходима ещё одна точка, принадлежащая линзе. Для её
нахождения воспользуемся тем, что луч, идущий
вдоль прямой АВ, преломляясь в линзе, проходит
вдоль прямой Ai В|. Таким образом, точка С, в
которой происходит преломление луча, является
второй точкой, принадлежащей линзе.
20. Максимальная кинетическая энергия материальной точки массы m = 10 г, со-
вершающей гармонические колебания с периодом Т = 2 с, равна W = 1 • 10-4 Дж. Опре-
делите амплитуду А колебаний этой точки.
21. Предмет расположен на расстоянии 0,15 м от рассеивающей линзы с фокус-
ным расстоянием 0,3 м. На каком расстоянии от линзы получается изображение данно-
го предмета?
Ответ:
22. Постройте изображение
предмета АВ в собирающей линзе,
верхняя половина которой закрыта не-
прозрачным экраном. Для построения
используйте только те лучи, которые
непосредственно попадают на линзу.
69
Ответ:
23. Определите изменение внутренней энергии 2 г водорода при нагревании его
при постоянном давлении на ДТ = 10 К, если газу сообщено количество теплоты Q =
291 Дж. Молярная масса водорода у. = 0,002 кг/моль.
Ответ:
ди =Q-—RAT = 207,9 Дж
И
24. На рисунке показан цикл тепловой машины, состоя-
щий из изотермического расширения 1-2, изохорического про-
цесса 2-3 и адиабатного сжатия 3-1. Напишите уравнение пер-
вого начала термодинамики для процесса
1-2.
Ответ: Q = А .
25. По струне слева направо бежит поперечная
гармоническая волна со скоростью v = 40 м/с. Длина
волны X = 60 см, амплитуда А = 2 мм. Найдите ско-
рость vo точки О струны в момент времени, соответст-
вующий рисунку.
Ответ:
, 2лАч
vfl =Аа) =--= 0,94 м/с
26. В идеальном электрическом колебательном
контуре емкость конденсатора
равна 1 мкФ, а индуктивность катушки 1 Гн. Чему равна амплитуда напряжения на
конденсаторе для незатухающих свободных колебаний, если амплитуда тока в контуре
составляет 100 мА
Ответ:
2 2
CU LI
2 ~ 2
откуда
27. Два маленьких одинаковых металлических шарика, заряженных разноимен-
ными зарядами +5q и -q, расположены на расстоянии L друг от друга. Шарики привели
70
в соприкосновение и раздвинули на прежнее расстояние. Найдите отношение модулей
сил взаимодействия между шариками до соприкосновения и после того, как их раздви-
нули.
Ответ: F, ~ 5<?2; F2 = 4q2 ; откуда
28. При фотоэффекте максимальный импульс, передаваемый поверхности
вольфрамовой пластинки при вылете каждого электрона р = 3,45 10"25 кгм/с. Найдите
энергию е квантов применяемого облучения. Работа выхода вольфрама А = 4,5 эВ.
Ответ:
2
П -19
£ = hv = = 7,85 10 Дж
2т
29. Допишите ядерную реакцию 4 В е + ? —> 6 С + 0 П .
Ответ:
30. Определите энергию у - кванта, если соответствующая ему длина волны
А. = 1,610“|2м.
he -и
Ответ: £ = Ьи = —= 12,4-10 Дж,
ЗАДАЧИ ВТОРОГО УРОВНЯ СЛОЖНОСТИ — задачи, в которых рассматри-
ваются явления, обычно также относящиеся к одному разделу физики. Но для их реше-
ния кроме знаний основных законов физики требуется отыскать алгоритм решения за-
дачи: выявить физическое явление, присутствующее в задаче, адекватное определен-
ному закону физики, математически описать рассматриваемое в задаче явление, т.е. со-
ставить уравнение или систему уравнег
а и решить их. При этом особое внимание об-
ращается на понимание абитуриентом векторного характера ряда величин, входящих в
формулы, когда для полного определения этих величин необходимо учитывать не
только их числовое значение, но и направление.
При этом при решении задач на кинематику оцениваются:
• умение абитуриента графически представить зависимость кинематических
параметров движения от времени;
71
• способность найти все силы, вызывающие движение тел в конкретных
условиях, умение заменить действие нескольких сил их равнодействующей;
• рациональность выбора системы координат, обеспечивающей наиболее
простой вид системы уравнений, приводящей к решению задачи.
При решении задач на динамику обращается внимание
• на влияние начальных условий на характер движения тел,
• на различное воздействие на характер движения тел сил трения покоя и сил
трения скольжения,
• на определение направления полного ускорения и равнодействующей силы при
неравномерном движении тела по окружности и т. д.
При решении задач второго уровня сложности встречаются случаи, когда
абитуриенты допускают непонимание и неточности, приводящие к снижению балла,
получаемого за эту задачу, например:
• При решении задач из раздела «статика» многие абитуриенты забывают второе
условие равновесия твердого тела - условие равенства нулю суммарного момента
внешних сил.
• Незнание выражения теплоемкости одноатомного идеального газа при
постоянном объеме и постоянном давлении вызывает трудности при решеь
термодинамических задач.
• Недостаточно глубокое понимание физического содержания закона
электромагнитной индукции Фарадея вызывает большие трудности при решении задач
на его практическое применение.
• При расчете цепей, содержащих электродвигатель, не учитывается ЭДС
индукции, возникающей при вращении якоря электромотора.
• Много ошибок встречается при решении задач на применение формулы
рассеивающей линзы и при построении изображений в таких линзах.
• Особую сложность вызывают задачи на построение изображений в оптических
системах, состоящих из нескольких линз и зеркал.
Задачи второго уровня сложности позволяют выявить способность абитуриента
осознанно применять физические законы к описываемому в задаче явлению, а также
умение использовать для решения физических задач математический аппарат: состав-
72
пять алгебраические уравнения, связывающие физические величины, которые характе-
ризуют рассматриваемое явление с количественной стороны.
3.4. Примеры задач второго уровня сложности:
1. В сплошной однородной тонкой пластине, имеющей фор-
му круга радиуса R и первоначальную массу М, вырезали отверстие
вдвое меньшего радиуса, касающееся края пластины. Пластину
подвесили на двух невесомых нитях 1 и 2, как показано на рисунке.
() пре де лите силу натяжения нити 2 .
Ответ: Т2 = — Mg .
о
2. Однородная палочка массы m наполовину погружена в воду,
как показано на рисунке. Угол наклона палочки к горизонту а. С какой
силой давит на стенку цилиндрического сосуда верхний конец палочки?
Трением пренебречь.
Ответ:
N = — mgctga.
4
3. В вертикально располо-
женном сосуде с сечениями S i и S2
находятся два невесомых поршня. Поршни соединены тонкой
Найдите силу натяжения проволоки Т, если пространство ме-
жду поршнями заполнено водой. Трением пренебречь. Концы
сосуда открыты в атмосферу. Плотность воды равна р.
Ответ:
проволокой длины L.
4. Через блок, подвешенный к динамометру, перекинут не-
весомый нерастяжимый шнур, на концах которого укреплены
грузы массы т| = 2кгигп2=8кг. Чему равно показание динамо-
метра при движении грузов? Массой блока и силами трения пре-
небречь.
Ответ:
4/и1/и2
т,
I 4-
m2
g = 62,7 И
73
5. На гладком горизонтальном столе покоятся два ма-
леньких шарика массами 3m и 2m, скрепленных невесомым
жестким стержнем длины L. На шарик массой 3m налетает и
93m
прилипает к нему кусочек пластилина массы т, двигав
1Ш1
лея
О 2m
вдоль стола со скоростью перпендикулярно стержню. ро
Определите силу упругости, возникающую в стержне, при дальнейшем движении ша-
риков.
Ответ:
mvo
V2L
6. Бетонная однородная свая массы m лежит на дне водоема глубиной h, боль-
шей, чем длина сваи L. Привязав трос к одному концу сваи, её медленно вытаскивают
из воды так, что центр тяжести сваи поднимается на высоту Н над поверхностью воды
(Н > L). Какую работу нужно совершить при подъеме сваи? Плотность бетона в п раз
больше плотности воды. Силами сопротивления пренебречь.
Ответ:
7. Санки съезжают с горы, имеющей высоту Н и угол наклона а, и движутся да-
лее по горизонтальному участку. Коэффициент трения на всем пути одинаков и равен
к. Определите расстояние S, которое пройдут санки,
двигаясь по горизонтальному участку, до полной
остановки.
Ответ:
Н(1 -petga)
О —
ц
8. Какую работу надо совершить, чтобы втащить
сани с грузом (общей массы m = 30 кг ) на гору высоты Н
10 м? Угол наклона горы a = 30°. Коэфф
ЯШ
сиент трения
между санями и горой линейно убывает вдоль пути от
kj= 0,5 у подножия до к 2 = 0,1 у верг
1151
зы. Скорость тела в конце подъема равна нулю.
74
Ответ:
А = mgH 1 + к1 +к2 ctga = 4,5-103 Дж
9. Два груза, массы которых 2m и гл, связаны невесомой не-
растяжимой нитью, переброшенной через неподвижный блок. В
начальный момент груз массы 2m удерживают на высоте h над
столом. Затем его без толчка отпускают. Какое количество тепло-
ты выделится при ударе этого груза о стол? Удар абсолютно неуп-
ругий. Массой блока и силами трения в блоке пренебречь.
2 Г
Ответ: Q = nigh .
10. В сосуде имеются две несмешивающиеся жидкости с плотностями р| и рг;
толщины слоев этих жидкостей равны d| и di соответственно. С поверхности жидкости
в сосуд опускают маленькое обтекаемое тело, которое достигает дна как раз в тот мо-
мент, когда его скорость становится равной нулю. Найдите плотность материала, из ко-
торого сделано тело. Силами вязкого трения пренебречь.
Ответ:
_ Pidj + Pz^2
d| + d2
11. На гладком горизонтальном столе покоится «горка», угол наклона которой
плавно изменяется от некоторого значения до нуля. С вершины «горки» соскальзывает
без трения небольшое тело массы т. Найдите ско-
рость тела относительно горки после соскальзыва-
ния, если высота «горки» h, масса М? Трением
между горкой и столом пренебречь.
Ответ:
12. Тонкостенный цилиндр массы m и радиуса R раскрутили во-
круг его оси до угловой скорости со и поместили затем в угол. Коэффи-
циент трения между стенками угла и ци-
линдром равен ц. Сколько оборотов сделает
цилиндр до остановки.
Ответ:
(D2R (1 + |12)
п =----------------—
4ng |1(1 + |1)
75
13. Горизонтальная платформа совершает гармонические колебания в верти-
кальном направлении вместе с лежащим на ней грузом. Силы, с которыми груз давит
на платформу в крайних нижнем и верхнем положениях, отличаются в п = 2 раза. Най-
дите частоту колебаний, если их амплитуда составляет А = 6,8 см. Принять g =10 м/с2.
Ответ:
14. Два одинаковых пластилиновых шара, движущихся с равными по величине
скоростями, совершают неупругий удар, после которого слипаются в одно целое. Какой
угол а составляли друг с другом векторы скоростей ша-
ров до удара, если при ударе половина начальной кине-
тической энерг
шаров перешла в тепло?
Ответ:
15. Человек, находящийся в лодке, переходит с носа на корму. На какое расстоя-
ние S переместится лодка длиной L = 3 м, если масса человека m = 60 кг, а масса лодки
М =120 кг ? Сопротивление воды не учитывать.
Ответ:
16. Определите максимальную амплитуду
4k
гармонических колебаний системы, состоящей из
двух брусков и двух невесомых пружин, при которой бруски будут совершать
колебания по горизонтальной плоскости без проскальзывания относительно друг друга.
Жесткость пружин 2k и 4k. Масса нижнего бруска т, верхнего — 2т, коэффициент тре-
ния между брусками равен р.. В положении равновесия пружины не деформированы.
Трение между нижним бруском и плоскостью отсутствует.
Ответ:
д = gmg
2k
17. На горизонтальной плоскости лежат два бруска массы m и 2m, соединенные
ненапряженной пружиной. Какую наименьшую постоянную силу F, направленную го-
ризонтально, нужно приложить к бруску массы 2m, чтобы
сдвинулся и второй брусок? Коэффициент трения брусков
о плоскость равен Ц.
76
Решение.
Если брусок массы m остается неподвижным при смещении на х бруска массы
?т, то сила F совершает работу по растяжению пружины и против сил трения (при ус-
иовии, что в конечный момент скорость бруска массы 2m обращается в нуль):
Ь Y “ L Y
1‘х =--+p-2mgx . (1) т.е. F = — + |1 2mg . (2)
Условие начала скольжения бруска массы m: kx = |img . (3)
Таким образом, подставив (3) в (2), найдем Fmin
Pm g 5
——+ |i2mg = -|img .
18. В точках А, В, C, D расположены не-
подвижные точечные заряды +q, +q, +2q, -6q,
как показано на рисунке. Определите работу,
которую необходимо совершить для перемещения заряда +q из точки В в бесконеч-
ность, где потенциал электрического поля принимается равным нулю.
Ответ: А = 0.
1^—. -
19. Три положительных точечных заряда +q, +2q и +q,
связанных между собой нитями, расположены в вершинах пра-
вильного треугольника со стороной а. После разрыва одной из
нитей заряды расположились вдоль одной прямой, как показано
па рисунке. Найдите работу сил электрического поля, необходимую для перестройки
системы расположения зарядов.
Ответ:
Я___
$ЯЕаа
20. Две бусинки, имеющие заряды +2q и
q, m
2ч,
о
О
t-q, удерживаются на длинном горизонтальном
изолирующем стержне на расстоянии Lo друг
от друга. Бусинку, имеющую заряд +q и массу m отпускают, и она начинает скользить
по стержню. Коэффициент трения скольжения равен ц. Найдите максимальное рас-
стояние L между бусинками.
Ответ:
2
Я
mgL о
77
21. В электрической цепи, схема которой показана на
рисунке, ЭДС источника тока Е = 42 В. Считая параметры
элементов схемы известными, найдите установившееся на-
пряжение U между обкладками конденсатора. Внутренним
сопротивлением источника тока пренебречь.
Ответ:
Е 3R 42 3R3
-----=--------= 27 В
R^ 147?
22. Определите массу меди, выделившейся из раствора Си SO4 за время t = 100 с,
если ток, протекавший через электролит, менялся по закону I = ( 5 - 0,02 t) А, где t -
время в секундах. Валентность меди п = 2.
Ответ:
и 0,064 Л1_ -з
m=-------q =---------—q = 0,13 10 кг
Fn 9,65 10 2
23. Электромотор питается от батареи с ЭДС Е = 12 В. Какую мощность Р раз-
вивает мотор при протекании по его обмотке тока 1 = 2 А, если при полном затормажи-
вании якоря по цепи течет ток 10 = 3 А?
Ответ:
Р = IE
Вт
24. Найдите количество теплоты, которое выделится в
цепи при переключении ключа К из положения 1 в положе-
ние 2. Параметры элементов цепи, изображённых на рисун-
ке, считать известными.
Решение.
При переключении ключа через источник тока Е протечет некоторый заряд q.
Работа батареи равна E q. Эта работа может частично пойти на увеличение энергии,
запасенной в батарее конденсаторов, частично на выделение тепла в цепи. Как видно из
рисунка, заряд и, следовательно, энергия, запасенная в батарее конденсаторов, не изме-
няются при переключении ключа. Меняются лишь знаки зарядов на обкладках. Следо-
вательно, при переключении ключа К через источник тока протекает заряд
q — 2СбатЕ, где СБАТ — С, т.е. q — СЕ
4 2
и в цепи выделилось количество теплоты Q = qE = — СЕ .
78
Ответ: Q — qE — — СЕ2
25. Электрон, ускоренный разностью потенциалов U = 1000 В, влетает в одно-
родное магнитное поле, перпендикулярное направлению его движения. Индукция маг-
нитного поля В = 1,19 10 Тл . Найдите: 1) радиус окружности, по которой движется
>лектрон, 2) период обращения его по окружности.
Решение.
/и v
В соответствии с законом сохранения энергии-------= eU, откуда скорость элек-
2
трона v =
2eU mv
. В соответствии со вторым законом Ньютона
m----------------------------------------------R
eUB, откуда ра-
диус
окружности,
по
которой
движется
электрон
2m U
mv _ 1
еВ Bl е 1,19 10
2-9,1-10 31 • 10
19
1,6 10
Период обращения электрона по окружности
2 л/? m _
----— 2л— = 310 с, т.е. период
v еВ
-8
не зависит от скорости электрона.
mv
Ответ: R ----- 9,0 10 м Т =
еВ
2лР
m ~8
= 2тг—= 3-10 с.
еВ
26. Источник света расположен на двойном фокусном расстоянии от собираю-
щей линзы на её главной оптической оси. За линзой перпендикулярно оптической оси
расположено плоское зеркало. На каком расстоянии от линзы нужно поместить зерка-
ло, чтобы лучи, отраженные от зеркала, пройдя вторично через линзу, стали параллель-
ными? Фокусное расстояние линзы F = 10см.
Решение
В отсутствие плоского зеркала
изображение S i источника располагается
на двойном фокусном расстоянии от
линзы. Для того чтобы лучи, отражен-
ные от зеркала, пройдя вторично через
линзу, стали параллельными, необходи-
~ 9,0 10 м.
V
79
мо, чтобы они пересекались в заднем фокусе линзы. Это произойдет в том случае, ко-
гда расстояние L между линзой и зеркалом будет равно 3F/2 т. е. L = 3F/2 = 15 см
Ответ: L = 3F/2 = 0,15 м
27. На дне сосуда, наполненного жидкостью до высоты h,
находится точечный источник света S. На поверхности жидко-
сти плавает круглый диск радиуса R так, что центр диска нахо-
дится над источником света. Определите показатель преломле-
ния жидкости п, при котором ни один луч не выйдет через по-
верхность жидкости.
Ответ:
28. На V-T диаграмме изображен цикл 1-2-3-4,
совершаемый двумя молями азота, и состоящий из двух
изохор и двух изобар. Известно, что точки 2 и 4 лежат на
одной изотерме, а средние квадратичные скорости моле-
кул азота в точке 1 ц = 300 м/с, а в точке 3 - = 700 м/с. Определите работу, совер-
шаемую газом за цикл. Молярная масса азота ц = 0,028 кг/м о ль.
Ответ:
V|1
29. Два моля кислорода, имеющих температуру Т] =
100 К в состоянии 1, последовательно переводят в состояние
3. Считая кислород идеальным газом, определите среднюю
квадратичную скорость его молекул в состоянии 3.
Ответ:
|3RT, м
^ср кв ~ J ~~ ~ 684
V V С
30. Идеальный одноатомный газ в количестве 10 моль сна-
чала охладили, умень
III!
в при этом давление в 3 раза, а затем на-
грели до первоначальной температуры 300 К. Найдите количество
теплоты, сообщённое газу на участке 2-3.
Ответ: 02з = ~ 4 1,6к^ж.
80
31. Какой максимальный заряд q может накопиться на удаленном от других тел
медном шарике радиуса г = 3 см при облучении его электромагнитным излучением с
длиной волны Л, = 0,14 мкм? Работа выхода для меди А = 4,47 эВ.
Ответ:
h - А
q = Атте „г —-------= 1,45 10 Кл
е
ЗАДАЧИ ТРЕТЬЕГО УРОВНЯ СЛОЖНОСТИ — это комбинированные задачи,
требующие углубленного понимания физических явлений, творческого мышления,
комплексного использования знаний по различным разделам физики, позволяющего
путем логических рассуждении связать происходящие физические явления или процес-
сы, оценить их с качественной и количественной сторон.
В комбинированных задачах оценивается способность абитуриента осмыслить
физическое содержание задачи, понять, какие физические процессы и явления включе-
ны в её условие, его умение отыскать в динамике процессов момент, который можно
описать, используя математический аппарат в рамках школьной программы. Комб
рованные задачи являются лучшим критерием оценки глубины усвоения программного
материала. Метод подхода к решению этих задач позволяет оценить способность аби-
туриента творчески мыслить и логически рассуждать, т.е. качества, которые в конечном
счете являются необходимыми для формирования исследовательского стиля умствен-
ной деятельности студентов Университета.
3.5. Примеры задач третьего уровня сложности:
1. На концах и в сере,
IISI
те невесомого жесткого вертикального стержня длины
укреплены маленькие шарики 1, 2, 3 равного объема, массы которых равны m, 2m и 3m,
а заряды +3q, +2q, +q соответственно. В пространстве, где нахо-
дятся шарики, создано однородное электрическое поле напря-
женности Е, силовые линии которого направлены вертикально
вниз. Какую скорость будут иметь шарики в момент падения их
на горизонтальную поверхность? Силами трения и влиянием
индуцированных на горизонтальной поверхности зарядов пре-
небречь.
3
q О 3m
Е
12
2qQ 2m
81
Ответ:
у, =2
2L(2mg+qE)
Im
2. Небольшое тело начинает соскальзывать без начальной
скорости из верхней точки неподвижной полусферы радиуса R.
На какую высоту h оно подскочит после удара о горизонтальную
поверхность, на которой находится полусфера? Удар считать аб-
солютно упругим, полусфера жестко закреплена на плоскости.
Решение.
1) Используя закон сохранения энергии, запишем выражения для полной энергии
i;iii
в начальной точке траектории и в точке максимального подъема:
_ mvr2 , w
mgR = —— + mgh, отсюда найдем h = R —— (1), где vx = v cosa.
2
2) Скорость V и cos а найдем, используя закон сохранения энергии и исходя из усло-
вия отрыва тела от сферы (Сила реакции N об-
ратится в ноль при значении а, при котором
cosa = 2/3. Далее тело будет свободно двигать-
ся в поле тяжести):
2
mv
2
mv
= mgR(l -cosa)
*. Отсюда
2]
cosa = —
= mg cos a
Подставим эти выражения в (1), найдем
Ответ:
3. В системе, показанной на рисунке, масса каждого бруска m = 1 кг , жесткость
пружины к = 20 Н/м , коэффициент трения между бруском и плоскостью ц = 0,4. Массы
блока и пружины пренебрежимо малы. Система пришла в движение с нулевой началь-
ной скоростью при недеформ
ованной пружине.
Найдите максимальную скорость брусков. При
вычислениях принять ускорение свободного паде-
ния g = 10 м/с2.
82
Ответ.
H=g(l-/z)J^ = 0,95^.
V 2k c
4. Три одинаковых одноименно заряженных шарика, заряд
каждого из которых равен q, а масса т, соединены невесомыми,
нерастяжимыми и непроводящими нитями длины L каждая так,
что нити образуют равносторонний треугольник. Нить между
шариками 1 и 3 пережигают. Найдите максимальную скорость
шарика 2.
Ответ:
5. Коэффициент жёсткости резинового жгута, длина которого L и масса ш, равен
к. Кольцо, изготовленное из этого жгута, вращается с угловой скоростью со в горизон-
тальной плоскости вокруг вертикальной оси, проходящей
через центр кольца. Определите радиус вращающегося
кольца.
Решение.
Обозначим через Lbp. длину вращающегося кольца
(LBP = 2xR). Рассмотрим небольшой участок кольца дли-
ной AL и массой Д/и =---
AL . На выделенный участок с
двух сторон действуют силы Т , и Тг, направленные по касательным к кольцу и оди-
наковые по модулю (Т/ = Т2). Их равнодействующая F направлена по радиусу к цен-
тру кольца и сообщает рассматриваемому участку центростремительное ускорение
ШТ
2 । * ^2/
а = G) л . Из рисунка видно, что г = 2Т • sin — . Запишем уравнение движения выде-
г 2 л д (X 2
ленного участка: г — СО К-ООП или 2Тsin —» = cd R
(1)
(X (X Л/,
Поскольку Т = k{LBP — L) , Lep — 2/cR 9 а при малых углах sin - = — = — , то из ра-
2 2 2R
венства (1) получаем k(2nR — L)
2R
й)2ш
2п
&L. Отсюда
2я££
4л? к - й?т
83
Ответ:
2ftkL
^тг2к - со2т
6. Маленький шарик массы m подвешен на пружине жесткости к и несет заряд q.
В начальный момент шарик удерживают так, что пружина не дефор-
мирована. Под шариком на расстоянии h лежит такой же шарик с за-
рядом -q. Верхний шарик отпускают. При каком минимальном значе-
нии q нижний
Ответ:
7. По двум параллельным металлическим направляющим, на-
шарик подпрыгнет?
гл----------- . kh - 2mg
Я mm = yftnwig h
kh + 2mg ’
клоненным под углом а к горизонту и расположенным на расстоянии
b друг от друга, скользит без трения ме-
таллическая перемычка массы т. Направляющие замкну-
ты снизу на батарею конденсаторов, емкость каждого из
которых равна С. Вся конструкция находится в магнит-
ном поле, индукция которого В направлена перпендику-
лярно плоскости, в которой перемещается перемычка. Определите ускорение перемыч-
ки. Сопротивлением направляющих, перемычки и индуктивностью контура пренеб-
речь.
Ответ:
8. Тонкая, запаянная с одного конца трубка заполнена
водой и закреплена на горизонтальной платформе, вращаю-
щейся с угловой скоростью со вокруг вертикальной оси. От-
крытое и запаянное колена трубки вертикальны. Геометриче-
ские размеры установки указаны на рисунке. Атмосферное
давление Ро плотность воды р. Найдите давление воды у запаянного конца трубки. Си-
лами поверхностного натяжения пренебречь.
Ответ: р3 = р0 + pg(H - h)
рсо L
2
9. Массы двух звезд равны mi и шг, расстояние между ними равно £. Найдите
период Т обращения этих звезд по круговым орбитам вокруг их общего центра масс.
84
Ответ:
10. По металлической ленте, толщина которой равна h, течет ток 1. Лента поме-
щена в однородное магнитное поле, индукция которого
равна В и направлена перпендикулярно поверхности
ленты. Определите разность потенциалов между точка-
ми А и С ленты, если концентрация свободных электро-
нов в металле равна п.
Решение.
Поле Е, возникающее из-за разделения зарядов
под действием силы Лоренца, равно E = vB.
Скорость электронов в ленте V = = —-—, тогда
еп dhen
Bl
dhne
. Разность потенциалов между точками А и С (рА — <рс = Ed =
BI
neh
Ответ:
1. Два шарика массы 2m и m соединены
невесомой пружиной жесткости к и длины L и
лежат неподвижно на гладком горизонтальном
столе. Третий шарик массы m движется со скоростью по v линии, соединяющей
центры первых двух, и упруго соударяется с шариком массы 2m. Пренебре-
гая временем соударения шариков по сравнению с временем деформации пружины, оп-
ределите максимальное расстояние между шариками, связанными пружиной, при их
дальнейшем движении.
m 2m____m
о—- 0-^335065^0
u. 1,1
12. На подставке лежит тело массы т, подвешенное на пру-
жине жесткости к. В начальный момент пружина не растянута. Под-
ставку начинают опускать вниз с ускорением а. Найдите время, че-
рез которое подставка оторвётся от тела. Каким будет максимальное
растяжение пружины?
85
Ответ:
l2m(g-a)
V Ка
л, mg mja(2g - а)
AL = —— н-1-------
13. Горизонтальный контур образован двумя замкнутыми на катушку индуктив-
ности L параллельными проводниками, находящимися
на расстоянии h друг от друга. По проводникам без
трения может скользить перемычка массы ш. Контур
помещен в вертикальное однородное магнитное поле. В начальный момент времени
неподвижной перемычке сообщают скорость ь»0. Определите индукцию магнитного по-
ля В, если известно расстояние S, которое пройдет перемычка до первой остановки, а
также найдите время ti, за которое перемычка пройдёт половину этого расстояния. Со-
противлением всех элементов контура пренебречь.
пана К. Найдите, через какое время t после открытия клапана, вся жидкость вытечет из
горизонтальной части трубки, длина которой равна 2L. Силами трения и поверхностно-
го натяжения пренебречь. При течении жидкость заполняет всё сечение трубки.
Ответ:
15. В схеме, показанной на рисунке, перед замыканием ключа К батарея, со-
стоящая из двух одинаковых конденсаторов емкости С ка-
ждый, не была заряжена. Ключ замыкают на некоторое
время, в течение которого конденсаторы зарядились до на-
пряжения U. Определите, какое количество теплоты Q 2
выделится за это время на резисторе сопротивления R 2*
ЭДС источника тока равна Е, его внутренним сопротивле-
нием пренебречь.
Ответ:
86
16. В системе, состоящей из двух концентрических про-
водящих сфер радиусами R и 3R, внутренняя сфера соединена с
землей через источник ЭДС, равной Е. Заряд внешней сферы
равен +2q. На расстоянии 2R от центра системы находится то-
чечный заряд -q. Зная величины q, Е, R, определите заряд
внутренней сферы. Потенциал земли принять равным нулю.
Решение.
Согласно
приг
IHSII
суперпозиции, потенциал внутренней
сферы равен
„ Q q 2q
(р = -Е = ------------+-----—,
4ke„R 4keo-2R 4tceo3R
откудд находим искомый заряд внутренней сфе-
Ответ:
17. Стержень ОА сопротивлением R и длиной L скользит
по полукольцу, сопротивление которого ничтожно мало. Кон-
тур находится в однородном магнитном поле с индукцией В,
линии которой перпендикулярны плоскости контура. В контур
включен источник тока с ЭДС Е и внутренним сопротивлением г. Угловая скорость
вращения стержня со. Найдите разность потенциалов между точками О и А стержня.
2eR - BL сиг
Ответ: <ро - (рА -----------
18. Четыре одинаковых шарика массы 2m каждый,
соединенные одинаковыми пружинами жесткости к, обра-
зуют квадрат. Одновременно все четыре шарика толкнули,
сообщив им одинаковые по модулю скорости, направлен-
ные к центру квадрата. Через какое минимальное время
после этого пружины будут сильнее всего сжаты? Массами
пружин пренебречь.
87
Ответ:
19. Проводник AOK, согнутый под углом а = 90°, расположен в плоскости ху,
как показано на рисунке, в постоянном однородном магнитном поле индукции В, пер-
пендикулярной плоскости ху. По проводнику из начала координат О перемещают по-
ступательно вдоль оси у с постоянной скоростью V перемычку MN, параллельную оси
х. Сопротивление единицы длины перемычки равно р. Пренебрегая сопротивлением
проводника и скользящих контактов, а также ин-
дуктивностью контура, найдите полное количе-
ство теплоты Q, выделившейся в перемычке, за
время её движения до точки С. Длина отрезка ОС
равна L.
Ответ:
20. К оси колеса, масса m которого равномерно распределена по ободу, присое-
динена пружина жесткости к. Второй конец пружины прикреплен к стене. С
помощью нити, перекинутой через блок, к оси колеса подвешены два груза: mi = т, и
m2 = Зт. Система пришла в движение с нулевой начальной скоростью при недеформи-
рованной пружине. Считая, что колесо катится по
горизонтальной поверхности без проскальзыва-
ния, определите максимальную силу натяжения
тш
нити, соед
яяющей грузы mi и m2, при их даль-
нейшем движении. Массами пружины, нити и
блока пренебречь.
Решение.
1) Квадрат круговой частоты аг
к = к =
+ т2 + 2т т + 3т + 2т 6т
88
. (m,+m,)g 4mg
2) Амплитуда колебании грузов А = —-2— =
к к
4WJ? к *”)
3) Максимальное ускорение а = Ай)2 = -- — =
к 6т 3
w max
4) Уравнение 2-го закона Ньютона для момента времени, когда груз на,ходится в ниж-
нем положении; при этом сила натяжения нити максимальная: т2а = Т - m2g, откуда
Ответ: Т = 5mg
ЗАДАЧА СЧИТАЕТСЯ ПОЛНОСТЬЮ РЕШЁННОЙ, ЕСЛИ:
• приведены ссылки на законы, используемые для решения данной задачи, с
учетом, если необходимо, их векторного характера; указаны физические явления, рас-
сматриваемые в задаче;
• даны текстовые пояснения по ходу решения задачи;
• записаны необходимые для решения задачи уравнения, правильно проведены
все алгебраические преобразования и получен ответ в буквенном виде;
• если необходимо по условию задачи, выполнены числовые расчеты и записан
окончательный ответ в системе СИ с указанием единиц измерения полученных вели-
чин.
3.6. ПРИМЕРЫ ВАРИАНТОВ ЗАДАНИИ ОЛИМПИАДЫ
1 ЭТАП ОЛИМПИАДЫ ШКОЛЬНИКОВ
ВАРИАНТ № 1
ЗАДАЧAt
С помощью системы из подвижного и неподвижного блоков
поднимают с поверхности земли груз массой m = 15 кг. За какое
время груз достигнет высоты Н = 1,1 м, если верёвку тянуть с по-
стоянной силой Q = 90 Н ? Массами верёвки, блоков и трением в
осях блоков пренебречь.
ЗАДАЧА!.
Какие силы создают центростремительное ускорение конькобежцу при повороте
на ледовой дорожке?
89
3 А Д А Ч A 3.
: Шарик массы m падает под углом а к нормали со скоростью
у. а/ v v • ^осле упругого соударения с горизонтальной плоскостью он от-
скакивает под таким же углом и движется с такой же по модулю
z/zzz7//zzz
скоростью. Найдите модуль изменения импульса шарика за время
соударения и работу силы упругости со стороны горизонтальной плоскости, действие
которой испытал шарик.
ЗАДАЧ А4.
График изменения состояния идеального газа в координатах
V - Т представляет собой прямую 1—2. Как изменялось давление
газа в этом процессе? Ответ обосновать.
ЗАДАЧ А5.
На Р - V диаграмме изображен цикл 1-2-3-1, прово-
димый с одноатомным идеальным газом. Определите коэф-
фициент полезного действия этого цикла.
ЗАДАЧ А6.
Как изменится ёмкость плоского воздушного конденсатора, если площадь об-
кладок и расстояние между ними уменьшить в два раза и заполнить всё пространство
между обкладками диэлектриком с диэлектрической проницаемостью £ = 4 ?
3 А Д А Ч А 7.
В электрической цепи, схема которой показана на ри-
сунке, установившееся напряжение на конденсаторе U = 28 В.
Считая параметры элементов схемы известными, определите
величину ЭДС источника тока.
3 А Д А Ч А 8.
Чему равен коэффициент преломления стекла, из которого изготовлена симмет-
ричная собирающая линза, если фокусное расстояние этой линзы равно половине ра-
диуса кривизны ее поверхностей?
90
I А ДАЧ А 9.
Тонкое проволочное кольцо площади S = 100 см 2,
имеющее сопротивление R = 0,01 Ом, помещено в
однородное магнитное поле. Изменение проекции
вектора магнитной индукции этого поля (Вх) на ось
х, перпендикулярную плоскости кольца, от време-
ни представлено на графике. Найдите заряд q, про-
шедший через поперечное сечение кольца за интервал времени от t = 2с до t = 4с. Ин-
дуктивностью кольца пренебречь.
ЗА ДАЧА 10.
Два маленьких шарика массы m каждый соединены жест-
ким невесомым изолирующим стержнем длины L и размещены
вертикально в углу, образованном гладкими плоскостями.
Верхний шарик имеет заряд равный +7q, а нижний заряд +3q. В
пространстве, где находятся шарики, создано однородное элек-
трическое поле напряженности Е, силовые линии которого направлены вертикально
вниз. Нижний шарик смещают вдоль нормали к вертикальной плоскости на очень ма-
ленькое расстояние, и гантель начинает двигаться. Найдите скорость нижнего шарика и
в тот момент, когда верхний шарик оторвется от вертикальной плоскости.
3.7. РЕШЕНИЕ ВАРИАНТА № 1
ЗАДАЧА 1. (8 баллов)
2
(20 — mg) at
Ускорение груза а =---------. Высота поднятия груза Н =----.
т 2
Из записанных уравнений находим время
Ответ: t = 1 с
ЗАДАЧА 2. (8 баллов)
Ответ: Силы реакции, действующие на конькобежца со стороны льда.
ЗАДАЧА 3. (10 баллов)
Ответ: &р = т vj3
91
ЗАДАЧА 4.(10 баллов)
Ответ: Давление уменьшалось.
ЗАДАЧА 5. (10 баллов)
Полезная работа газа в прямом цикле пропорциональна площади цикла на графике P-V.
А = —ДР-ДУ = —(4Р -P.)(2V -Vo) = -p Vo =-— RT
полезн 2 ° ° ° 7 2 ° 2 |1 °
6,2 = Д(У12 + Л|2 =с„-Д7’12+|(Л+4Р0)(2К„-Г„) =
= -Я —(8Г„-TJ+-PX = — — RT+- — RT„ =13 — я:
// 2 2 // 2 р р
А 3 13
Следовательно, п = = -• — = — = 0,115 = 11,5% •
' Ql2 2 13 26
Ответ:
ЗАДАЧА 6.(10 баллов)
Ответ: Ёмкость конденсатора увеличится в четыре раза.
ЗАДАЧА 7. (10 баллов)
1) Полное сопротивление цепи
Я^ = Я + 2Я + —Я = 15 Я.
X 4 4
2) Ток в источнике ЭДС равен току в сопротивлении, под-
ключенном параллельно конденсатору
Е U U ^У 15 15
- = ,откуда Е =------^ = —U = — 28 = 105 В.
Ry R У R 4
15
Ответ: £’ = 105 В
ЗАДАЧА 8. (10 баллов)
Положим в равенстве — = (п -1)(— + —) R|= Rz= R; F = 0,5R, получим
F Rx R2
1
0,5 R
Откуда n = 2.
= —RT
A
4
Ответ: n = 2
92
ЗАДАЧА 9. (12 баллов)
И в,=2
R R
S _ 0,2 1 (Г
10
= 0,2
Кл
Ответ:
Вс,Тла
ЗАДАЧА 10. (12 баллов)
Пусть в момент отрыва верхнего шарика от вертикальной плоскости гантелька состав-
ляет у гол а с вертикалью, скорость верхнего шарика равна W, скорость нижнего - и.
Согласно закону сохранения энергии
2 2
—V 4- = mg&h + IqE&h = (mg + lqE)L(\ - cos а), или
2 2 2(mg + 7qE) z v
v + и =----2 *—-— L(1 - cosa)
m
(1)
(m-масса каждого шарика; Vq-заряд верхнего шарика,
v, и, g, Е- модули соответствующих векторов).
Поскольку стержень жесткий, vcosa = usina. Следова-
sin а
тельно, и = и--------- (2)
cos а
Подставляя (2) в (1) получим
> sin2 а , 2(mg + lqE) ( ч
и~ —-—+w -------2-----—Z(l-cosa).
cos а т
m
2 2(mg + lqE) / 2 3
После преобразований получим и =-----------Ljcos a-cos а
т
До момента отрыва центр масс гантельки двигался с горизонтальным ускорени-
ем ( это ускорение сообщалось силой реакции вертикальной стенки). Поэтому к момен-
ту' отрыва верхнего шарика от вертикальной стенки скорость и ( а, следовательно, и го-
ризонтальная составляющая скорости) максимальна. Найдем значение cos а, при кото-
ром выражение cos2 a - cos4 а (смотри формулу (3)) максимально. Обозначим х = cos
a.
2
2х—Зх = 0 при х - 2/3, т.е. cos a = 2/3.
93
Подставив это значение cos а в (3). найдем: и = —
2 (wg + 7qE)L
т
Ответ:
2 12 (mg + 7qE)L
U~3V3 m
3.8. Заключительный этап олимпиады
и
кольников
ВАРИАНТ № 2
ЗАДАЧ А 1.
Тело массы m = 1 кг движется по оси .т по закону х = 5 + 4/ - 2г м. Определите
величину импульса тела в момент времени t = 1 с.
3 А Д А Ч А 2.
Пятая часть однородной линейки, имеющей массу m [
и длину L, выступает за край стола. Найдите минимальную
величину работы А, которую необходимо совершить, чтобы
переместить всю линейку на стол, сдвигая её силой, направленной вдоль длинной сто-
роны. Коэффициент трения между линейкой и столом равен р.
3 А Д А Ч А 3.
Однородный стержень массы m закреплён в точке А с по-
мощью шарнира и удерживается за второй конец стержня под
углом а = 30° к горизонту с помощью невесомой нерастяжимой
нити, расположенной под таким же углом а к вертикали, как по-
казано на рисунке. Найдите силу натяжения нити.
3 А Д А Ч А 4.
m -<W5^-2m
На горизонтальной плоскости лежат два бруска, массы
которых m и 2m, соединенных ненапряженной пру-
жиной. Какую наименьшую постоянную силу F, на-
правленную горизонтально, нужно приложить к бруску массы 2m, чтобы сдвинулся и
второй брусок? Коэффициент трения брусков о плоскость равен ц.
3 А Д А Ч А 5.
Идеальный одноатомный газ в количестве 1 моль сначала
охладили, а затем нагрели до первоначальной температуры 300 К,
увеличив при этом объём газа в 3 раза. Найдите количество тепло-
ты, отданное газом на участке 1-2.
94
3 А Д А Ч A 6.
А +2q ' к В +q с D э с L >-6q
В точках А, С, D расположены неподвижные то-
чечные заряды +2q, +q, - 6q, как показано на ри-
сунке. Определите работу сил поля при перемеще-
нии заряда +q из бесконечности, где потенциал электрического поля принимается рав-
ным нулю, в точку В.
ЗАДАЧА7.
В электрической цепи, схема которой показана на ри-
сунке, установившееся напряжение на конденсаторе
U = 20 В. Считая параметры элементов схемы известными,
определите величину ЭДС источника тока. Внутренним со-
противлением источника тока пренебречь.
ЗАДАЧА8.
Постройте изображение предмета АВ в
собирающей линзе.
ЗАДАЧА9.
При фотоэффекте максимальный импульс, передаваемый поверхности вольфра-
мовой пластинки при вылете каждого электрона р = 3,45 Ю"25 кгм/с. Найдите энергию
£ квантов применяемого облучения. Работа выхода вольфрама А = 4,5 эВ.
ЗАДАЧА10.
Из проволоки, общим сопротивлением R, сделан пло-
ский замкнутый контур, состоящий из двух квадратов со сто-
ронами а и 2а. Контур находится в однородном магнитном по-
ле с индукцией В, направленной перпендикулярно плоскости
контура. Найдите заряд, который протечёт через поперечное
сечение провода при равномерном уменьшении индукции поля до нуля. Между пересе-
кающимися на рисунке проводами электрический контакт отсутствует.
3.9. РЕШЕНИЕ ВАРИАНТА № 2
ЗАДАЧА 1.(10 баллов)
Ответ: р = mv = тх = m(4-4t). При t=lc. р = 1 (4-4 1) = 0
95
ЗАДАЧА 2. (8 баллов)
Ответ: A = pngL
п* = gmg
ЗАДАЧА 3.(10 баллов)
Условие равновесия стержня: mg—cos а = TL
mg cos a
где L - длина стержня. Откуда 1 =---------
п ~ ™о Т Mgcosa mgjl
При а = 30 Т =-----=-----
2 4
Ответ: Т =
ЗАД АЧА 4. (10 баллов)
Если брусок массы m остается неподвижным при
смещении на х бруска массы 2m, то сила F совершает ра-
боту по растяжению пружины и против сил трения (при условии, что в конечный мо-
„ кх2 «
мент скорость бруска массы 2m обращается в нуль): гх =-----l-|j,-2mgx , (1) т.е.
Т5Т
m 2m
Уравнение движения второго бруска массы m ma = kx—jjmg (3)
Брусок массы m сдвинется при условии а > 0, т.е. при условии кх > ц • mg (4)
Минимальное значение Fmin. получим, если положим кх = |lmg (5)
Таким образом, подставив (5) в (2), найдем
Цгп g 5
F„„„ =—;—+Ji2mg =-pmg .
2 2
Ответ: F •
5
= —Mmg
ж
4
F
2
ЗАДАЧА 5. (10 баллов)
В соответствии с первым законом термодинамики А (7 = Q + Авн с .
Учитывая, что на участке 1-2 : А12 = 0. получим Ql2 = — Л(712 • (1)
96
Формула расчёта изменения внутренней энергии: ДЦ2 =— vR(T2 -7j) (2)
И V
Применив закон Гей - Люссака для состояний 2 и 3, запишем—= — , откуда
* з Аа
у
Т2 =—Т3. Учитывая, что объём газа в состоянии 3 Уз увеличился в три раза, а темпе-
*3
у т т
ратура в состоянии 3 равна первоначальной, т.е. Тз = Т|, Т2 = (3). Тогда
подставив (3) в (2), а затем в (1), получим формулу для расчёта количества теплоты,
отданного газом на участке 1-2:
\ J у
3 2
= — у5—7] = vRT{. Подставив теперь числовые значе-
2 3
ния, найдём 012 = vR7\ = 1 • 8,31 • 300 ~ 2,5 кДж
Ответ: Ql2 = vR7\ ~ 2,5кДж.
ЗАДАЧА 6. (8 баллов)
Используя принцип суперпозиции, найдём
tpR = k — +k — -k— = 0,тогда Л = 0.
L L 2L
Ответ: А = 0
ЗАДАЧА 7. (10 баллов)
1) Полное сопротивление цепи
R = R + 4R+—R= — R.
L 5 5
2) Ток в источнике ЭДС равен току в сопротивлении,
подключенном параллельно конденсатору
р т т и * 31
— = — ,откуда Е =---------— = ——£/ =—20 = 315.
5у 45 45 4-5 20
Ответ: Е = 31 В
97
ЗАДАЧА 8. (10 баллов)
Ответ:
ЗАДАЧА 9. (12 баллов)
р Л 49
Ответ: £ = hV = А +— = 7,85• 10 Дж.
2т
ЗАДАЧА 10. (12 баллов)
Е = - Е2. По закону электромагнитной индукции Фарадея
ДФ, ДФ2
----+-----, где ДФ, и &Ф2- изменения магнитных
потоков через поверхность большого и малого квадратов.
ДФ, ДФ, _ ДВ ~ ДВ _ _ . ДВ
„ ~ г Е „ w ZA,
По закону Ома I = . Искомый заряд q = /Аг =
R
R-<2a) ~Я
то а =----В =-------
R R
За
•В = —
R
В.
п
Ответ: q =-----В
R
3.10. ВАРИАНТ №3
ЗАДАЧА1.
Южный полюс магнита приближается с некоторой скоро-
стью к металлическому кольцу, двигаясь вдоль его оси перпенди-
кулярно плоскости кольца. На рисунке покажите направление ин-
дукционного тока в кольце.
98
ЗАДА Ч А 2.
На столе лежат стопкой 10 одинаковых книг. В каком случае нужно приложить
меньшую силу: чтобы сдвинуть четыре верхние книги или вытянуть из стопки третью
книгу сверху? Ответ обосновать.
3 А Д А Ч А 3.
Открытый бак, состоящий из двух соосных цилиндров
диаметрами d и 2d, заполнен жидкостью плотности р, как пока*
зано на рисунке. Бак стоит на полу лифта, который поднимает-
ся вверх с ускорением а = 0,25 g. Определите силу давления
жидкости на горизонтальную поверхность АВ, соединяющую ба цилиндра. Атмосфер-
ное давление равно р0.
3 А Д А Ч А 4.
Груз массы m подвешен через пружину жёсткости к на
нерастяжимой нити, перекинутой через блок, соединённой с
бруском 2, лежащим на горизонтальной плоскости. В
начальный момент груз m удерживается так, что пружина
находится в ненапряжённом состоянии, затем его отпускают
без начальной скорости. Найдите минимальную массу бруска 2, при которой он ещё
будет оставаться неподвижным. Коэффициент трения между бруском 2 плоскостью
равен р. Массой пруж
м, нити, блока и трением в нём пренебречь.
3 А ДАЧ А5.
Один моль одноатомного идеального газа переходит из
состояния 1 в состояние 3 по изохоре 1-2 и изотерме 2-3, как
показано на графике зависимости объёма V от температуры Т
(Т 0 =100 К). На участке 2-3 к газу подводят 2,5 кДж теплоты.
Найдите отношение полной работы газа А123 ко всему количеству подведённой к газу
теплоты Q12з •
ЗАДАЧА6
лч По кольцу радиуса R равномерно распределён заряд q. Опреде-
R । А лите потенциал ф в точке А, находящейся на оси, перпендикулярной
н—я---
f о 5 r плоскости кольца, и отстоящей от центра кольца на расстоянии п = 0, 5
V R.
99
3 А Д А Ч A 7.
Предмет располагается перед собирающей линзой, как показано на рис. 1. Линзу
разрезали по оси 001. Нижнюю половину линзы удалили, а верхнюю половину сдвину-
ли вверх по отношению к предмету, как показано на рис. 2. Постройте изображение
предмета в оставшейся верхней половине линзы (рис. 2).
3 А Д А Ч А 8.
Найдите максимальный потенциал ф, до которого может зарядиться удаленный
от других тел медный шарик при облучении его электромагнитным излучением с дли-
ной волны X = 0.14 мкм. Работа выхода для меди А = 4.47 эВ.
3 А Д А Ч А 9.
В электрической цепи, представленной на рисунке, ключ К в начальный момент
замкнут, и по цепи идет постоянный ток. Какое количество теплоты
выделится в резисторе Ri после размыкания ключа. Параметры эле-
ментов цепи: индуктивность кату
III
<и равна L, R| = R, R 2 = 2R, R 3 =
R, ЭДС исто1?
i:ui
<а тока равна Е. Активным сопротивлением катуш-
ки и сопротивлением источника тока пренебречь.
ЗАДАЧА 10.
На гладкой горизонтальной поверхности массивной плиты
покоится клин массы М с углом наклона а = 30°. Клин плотно прилегает к поверхности
плиты. Летящий по параболической траектории шар массы
m ударяется о гладкую наклонную поверхность клина, при-
чём в момент удара его скорость направлена горизонтально
(удар абсолютно упругий). В результате клин начинает двигаться по плите. Найдите
отношение т/М, если через некоторое время шар попадает в ту же самую точку на
клине, от которой он отскочил.
3.11. РЕ
[ЕНИЕ ВАРИАНТА № 3
ЗАДАЧА 1. (8 баллов)
Ответ:
100
ЗАДАЧА 2. (8 баллов)
I) Сила F11 необходимая для того, чтобы сдвинуть верхние четыре книги Г, = 4 pmg .
2) Сила Fz. необходимая для того, чтобы вытянуть из стопки третью книгу:
F2 = 2 pmg 4- 3 pmg = 5 pmg . F( < F2 . Таким образом, меньшую силу
F} = 4pmg нужно приложить, чтобы сдвинуть верхние четыре книги.
Ответ: Меньшую силу Fx — A pmg нужно приложить, чтобы сдвинуть верх-
ние четыре книги.
ЗАДАЧА 3.(10 баллов)
Г = [Ро + ph(g + a)]S , где
/Г / 2 2 \ 3 2
5 = — (2d) -d = — nd
4 \ 7 4
F = [р„ + Ph(g + 0,25 g)]^-Kd' = ^-Tcd (ро + 1,25 pgh )
4 4
F=—xd (pa +1,25 pgh).
4
О
Ответ: F - —nd (p0 + 1,25 pgh ) .
4
ЗАДАЧА 4. (10 баллов)
Брусок массы М на плоскости остается неподвижным до тех
пор, пока сила упругости, действующая на него со стороны нити, не
достигнет максимального значения силы трения покоя, т.е.
FTP = Т , где Frp = pN = pMg . Тогда pMg = Т (1).
Величина силы упругости нити Т зависит от амплитуды колебании груза т. Амплитуда
А равна начальному отклонению груза от положения равновесия, которое определяется
равенством mg = кх 0 — кА , откуда хо = А = —-—. Следовательно, максимальное
к
растяжение пружины равно
= 2 А =
max
2 mg
------. Соответственно, сила упругости
к
Т = ^шах = (2)-
Подставляя (2) в (1), получим pMg = 2 mg
. . 2 mg 2 т
откуда М =-----------
Pg Р
101
2 т
Ответ: М =------
A
ЗАДАЧА 5. (Ю баллов)
Согласно первому закону термодинамики
0123 — "1" ^123 ’ ГДе ^123 ^12 "1" ^23
Д£/123 = Д(/12 + Д(/23. В изохорном процессе Л12=0, и
Л|23 = Л23; а в изотермическом процессе Д(/23=0 и
Д(/|23 = Д(712. Поэтому 0123 = Д£/12 + Я,,. При переходе 2 —» 3 : 023 = ДСД, + Л,3 = А23.
Следовательно, 0Ш = Д£/)2+023. Изменение внутренней энергии газа при переходе
1—>2: Д(/12 =—у/?ДТ12. Поскольку ДТ|2=2ТП, то Д(/|2 = 3vRT{}. Поэтому:
0123 ~ +023
^123 _ 023
0123 3v/?7^+023
Ответ:
^- = 0,5
0123
ЗАДАЧА 6. (10 баллов)
. q R 2q q /5
(D = к - , г = /5 ; (о =------~ = - — .
г 2 4яе„Я 5 10^,/?
Ответ:
ЗАДАЧА 7. (10 баллов)
Ответ:
ЗАДАЧА 8. (10 баллов)
В результате фотоэффекта на шарике накапливается положительный заряд, поле
которого тормозит фотоэлектроны. Величина заряда определяется электрической ёмко-
стью шарика и его потенциалом, т.е. q = 4л£ог • ср. Максимальный потенциал ^тах ша-
рика зависит от начальной кинетической энергии электронов. Так как приращение ки-
нетической энергии электронов равно работе сил поля шарика, то, принимая потенциал
102
поля шарика и скорость электронов в бесконечности равными нулю, а также то, что за-
ряд электрона отрицательный, можно записать
mv max mv max
= откуда =— ------
(1)
/WV max . .
Используя формулу Эйнштейна для фотоэффекта, получим--------= п V — А (2),
2
1 А -------
hv-A 2
и подставив (2) в (1), получим ^гаах =-----=--------
-34 8
6,625 10 -3 10 A A A_ A A n
Ux =----------------— -4,47=8,87-4,47=4,4 B.
1,6 10 0,14 10
Ответ:
max
h----А
----= 4,4 В
е
ЗАДАЧА 9. (12 баллов)
1) . До размыкания ключа установившаяся сила тока равна / = — ( через рези-
Л»
сторы R| и R-2 ток не течет, так как. разность потенциалов на катушке индуктивности
равна нулю).
2) . После размыкания ключа электрическая энергия катушки выделит-
ся в виде тепла на резисторах Ri и Ra (через резистор R3 ток течь не
LI2 LE2
будет):в- 2 "2«=,-
Ri
R2
3) . Так как резисторы Ri и Иг соединены параллельно, разности потен-
циалов на них равны: 1}R} = I2R2 = U.
Rj
По закону Джоуля Ленца количества
теплоты, выделяющиеся в рези-
сторах за небольшой интервал
времени zv, равны
Л,
ЛЩаш — e^max,
2
е
е
Е
к
9
Д02 =/,2Л2д/ = —Az.
103
Из этих уравнений следует, что 0, /?,= Q2 R2. Вместе с тем, Ql + Q2 = О. Окончатель-
но находим 01 =
R
1 LE2
Подставляя Ri = R, R2 = 2R, R3 = R, получим Q} =--
Ответ:
ЗАДАЧА 10. (12 баллов)
Пусть vo - скорость шара в момент удара.
Так как трение между клином и плитой отсутствует, то вдоль оси х выполняется закон
сохранения е
1ЛП
ульса: mvo = (m + M)vx (1), где vx-горизонтальная составляющая ско-
рости шара после столкновения, равная скорости клина ( в противоположном случае
шар не упадёт в ту же точку).
Закон сохранения энергии:
mvn (т + М) 2 т 2
-—=--------------vx +-vy (2), где vy вертикальная
jfa* jfa* jfa*
X
составляющая скорости шара после столкновения с клином. Пусть за время удара Дг
шарика о клин между ними действовала сила, среднее значение которой равно F. Тогда
в проекциях на координатные оси уравнение второго закона Ньютона для обоих тел
будет иметь вид:
mvy = ГД/cos а, (3)
Mvx = F&t sin а (4).
Из-за отсутствия трения сила F направлена перпендикуляр-
но поверхности клина. Исключив ГД/ из (3) и (4), получим выражение
т vy cos а
—— = “ ’
м v sin а
М cos#
откуда vv =—vx ——. (5)
т sin#
Подставим иу в (2) и преобразуем полученное выражение:
2 2 2 2 2
2 2 т sin # + mA/sin а + М cos а 2
т vo =--------------------------------их2 (6).
sin а
104
Возведя (1) в квадрат и поделив его на (6), найдём искомое соотношение:
2 2
т cos a-sin а
2
sin а
Ответ:
3.12. ВАРИАНТ № 4
ЗАДАЧ А 1.
Из верхней точки окружности А одновременно начинают
двигаться две одинаковые бусинки. Одна бусинка падает вдоль
диаметра AD, другая скользит по абсолютно гладкой спице АВ,
вписанной в окружность, составляющей угол а = 60° с вертика-
лью AD, как показано на рисунке. Найдите отношение времени,
за которое одна бусинка достигнет точки D, ко времени, за которое другая бусинка дос-
тигнет точки В.
ЗАДАЧА!.
Однородный стержень длины L и массы m
шарнирно закреплён в точке О. Середина стержня
опирается на пружину. На стержне закреплены
о
m
два маленьких груза массы 2m и т, положения которых показаны на рисунке. Найдите
силу упругости, возникающую в пружине в положении равновесия стержня, если в
этом положении стержень расположен горизонтально. Массой пружины и силами тре-
ния пренебречь.
ЗАДАЧ АЗ.
Начальная скорость снаряда, выпущенного из пушки вертикально вверх, равна
vo = 200 м/с. В точке максимального подъёма снаряд разорвался на два одинаковых
осколка. Первый осколок упал на землю вблизи точки выстрела, имея скорость в два
раза больше начальной скорости снаряда. На какую максимальную высоту поднялся
второй осколок? Сопротивлением воздуха пренебречь.
105
ЗАДАЧ А 4.
Вокруг горизонтальной оси О может свободно вращаться
легкий рычаг, плечи которого равны 2L и L. На концах рычага
укреплены грузы, массы которых 2m и ш. Первоначально рычаг
удерживается в горизонтальном положении, как показано на ри-
сунке. Затем рычаг отпускают без начальной скорости. Опреде-
лите линейные скорости грузов в момент прохождения стержнем положения равнове-
сия.
ЗАДАЧ А5.
Теплоизолированный сосуд разделён пористой неподвижной перегородкой на
две части. Атомы гелия могут свободно проникать через поры в перегородке, а атомы
аргона - нет. В начальный момент в одной части сосуда находится vHe = 2 моль гелия,
а в другой - v ,k = 1 моль аргона. Температура гелия тИг =300 к , а температура аргона
ТАг =600 К. Считая аргон и гелий идеальными газами, определите температуру гелия
после установления равновесия в системе.
3 А Д А Ч А 6.
Три положительных точечных заряда +q, +q и +2q, свя-
занных между собой нитями, расположены в вершинах пра-
вильного треугольника со стороной а. После разрыва одной из
нитей заряды расположились вдоль одной прямой, как показано
на рисунке. Найдите работу сил электрического поля, необходимую для перестройки
системы расположения зарядов.
ЗАДАЧ А7.
Оптическая система состоит из рассеивающей
Л] и собирающей Ла линз с общей главной оптической
осью. Главные фокусы рассеивающей линзы обозначе-
ны Fi, а собирающей линзы - Fa. Постройте дальней-
ший ход луча АВ через оптическую систему.
106
3 А Д А Ч A 8.
Найдите максимальный заряд q. который может накопиться на удаленном от
других тел медном шарике радиуса г = 3 см при облучении его электромагнитным из-
лучением с длиной волны X = 0,14 мкм. Работа выхода для меди А = 4,47 эВ.
3 АД АЧ А9.
В схеме, показанной на рисунке, перед замыканием
ключа К батарея, состоящая из двух одинаковых конденсато-
ров ёмкости С каждый, не была заряжена. Ключ замыкают на
некоторое время, в течение которого конденсаторы заряди-
лись до напряжения U. Определите, какое количество теплоты
Qi выделится за это время на резисторе сопротивления R|.
ЭДС источника тока равна Е, его внутренним сопротивлением пренебречь.
ЗА ДАЧ А 10.
Горизонтальный контур образован двумя замк-
нутыми на катушку индуктивности L параллельными
проводниками, находящимися на расстоянии h друг от
друга. По проводникам без трения может скользить перемычка. Контур помещен в вер-
тикальное однородное магнитное поле с индукцией В. В начальный момент времени
неподвижной перемычке сообщают скорость и0. Определите массу перемычки и время
11, за которое скорость перемычки уменьшится в два раза, если известно расстояние S,
которое пройдет перемычка до первой остановки. Сопротивлением всех элементов кон-
тура пренебречь.
3.13. РЕШЕНИЕ ВАРИАНТА № 4
ЗАДАЧА 1. (8 баллов)
Пусть диаметр окружности равен d, т.е. путь, пройденный первой бусинкой
. gt \ld „
а =---, тогда время свободного падения бусинки до точки D tx = — . Перемещение
2 V g
второй бусинки АВ = d coscr, а её ускорение а = g cos а, следовательно, время её дви-
жения до точки В t2
2d cos а
geos а
2d
Вывод: Бусинки одновременно достигают точек В и D, т.е.
107
ЗАДАЧА 2. (8 баллов)
Условие равновесия стержня: Xmo(F,) = 0
-2тg mg----------mgL + T — = 0, отсюда
4 2^
2 = 4 mg
Ответ: Т — 4mg
ЗАДАЧА 3. (10 баллов)
Согласно закону сохранения энергии высоту подъёма снаряда и второго осколка
Ж 1 mVo L Vo2 ; Г . m2V22
можно рассчитать по формулам: mgn = ——, откуда h =-----, m2gnma)i = m2gh 4- - - .
2 2g 2
Из закона сохранения энергии определяем начальную скорость первого осколка:
»ii(2v„)2 . , mxv2
— ------= m} gn + —, откуда
= ^4vo2 -2gh = -vo2 = V3v„.
Согласно закону сохранения импульса m}= m2v2,
т.п,
откуда начальная скорость второго осколка после разрыва снаряда и2 = ——
m7
£
2v 2
Максимальная высота подъёма второго осколка = —— = 8000л/.
Ответ:
=^ = 8000л.
g
ЗАДАЧА 4. (10 баллов)
Пусть скорости грузов в момент прохождения поло-
жения равновесия равны ц и v2. Тогда, пренебрегая тре-
нием, в соответствии с законом сохранения механической
энергии запишем:
2m ц2 mv2
2^2
= 2mg2L-mgL ,(1)
108
Поскольку угловая скорость со вращения грузов одинакова, то
ц = 6w2L , v2 = , ц = 2v2 (2).
v 2 2
Подставив (2) в (1), получим 4v221 +—2— = 3gL, 9v22 = 6gL.
Следовательно, искомые скорости равны: v2 =
ЗАДАЧА 5. (Ю баллов)
Не
^Не =
ГЯе=300
Аг
^,=1
7\ = 600
лг
1) После установления равновесия в системе, температура
обеих частей сосуда станет одинаковой и равной Т, а ге-
лий равномерно распределится по всему сосуду.
2) Температура в сосуде определяется из закона сохране-
ния энергии и = -vHeRTHe +-vArRTAr = -(и;/е
+ vAr)RT.
Отсюда Т = Уне^Ие +улг^аг
VНе + * Аг
2 300 + 1 -600 600 + 600
-------------------------= 400/f .
Ответ: Т = 400А?
ЗАДАЧА 6. (10 баллов)
Работа сил электрического поля, необходимая для пере-
стройки системы, равна убыли потев
Ills
действующих зарядов при изменении конфигурации расположе-
ния зарядов А = - W2.
альной энергии взаимо-
2
Начальная энергия системы FF, = к + к q %q + к %q q = 5к—.
а а а а
Конечная энергия системы W2 =
kq q I kq 2q I kq 2q
a la a
2 2 2 2
A=W,-W2 =5k——4k — = k — = ——.
а а а Ая£оа
Ответ:
Ья£оа
= 4kl-
““ i rv .
109
ЗАДАЧА 7. (10 баллов)
ЗАДАЧА 8. (10 баллов)
В результате фотоэффекта на шарике накапливается положительный заряд, поле
которого тормозит фотоэлектроны. Величина заряда определяется электрической ёмко-
стью шарика и его потенциалом, т.е. q = Aft£or (р. Максимальный потенциал $0П1ах, а
следовательно, и максимальный заряд шарика, зависит от начальной кинетической
энергии электронов. Так как приращение кинетической энергии электронов равно ра-
боте сил поля шарика, то принимая потенциал поля шарика и скорость электронов в
бесконечности равными нулю, а также то, что заряд электрона отрицательный, можно
записать:
mv max т V max
д^лин = ~е(Рт!^ т.е.-------— = откуда ^raax
(1)
2е
2
2
mV max , .
Используя формулу Эйнштейна для фотоэффекта, получим-----------= nV — А (2)
е
hv-A
Из (1) и (2) получим ^тах =-, и
е
1 h---А
hv-A я
9гав=4яе<(г--- -
е
е
Подставим числовые значения для работы выхода для меди, получим
h-----А
q = 4ЯЕ,/----------- 4# • Ео • 3 • 10
е
-4,47
= 1,45 10 ‘ кл
0,14 10
Ответ:
h С - А
q = 4fi£or-^ = 1,45 10 "и Кл
е
ЗАДАЧА 9.(12 баллов)
1) На обоих резисторах выделяется количество теплоты
Q = А - AIT , где
2) А=ДЧЕ = (СВЛТи2-СиА1и,)Е.
НО
Т.к. U । = О, U2= U; СВдт= 2С, то А = 2CUE.
2CU2
3) ДИг = И/2-Иг1 = —'-= CU2-приращение энергии батареи конденсаторов
4) Q = 2CUE-CU2.
5) Так как резисторы соединены параллельно, то Q = Q{ +Q2.
6) По закону Джоуля-Ленца =----Az, Q2 =---А/, тогда
Л. Л,
Л,
7) Из 4), 5) и 6) находим Qj = Q = CU(2E - U) —-2р
К| + К2 К| + к
Ответ: Q, =CU(2E-U)
R1
л,+/?2 •
ЗАДАЧА 10. (12 баллов)
Так как сопротивление контура R = 0, то суммарная ЭДС в контуре должна быть
равна нулю. Значит, суммарный магнитный поток через контур не должен изменяться.
Если перемычка сдвинулась на величину х, и в ней поя-
вился ток 1, то изменение суммарного магнитного пото-
r Bh
ка ДФ = Bhx + LI =0. Отсюда I —----, - х .
v
о
h
В2 h2
По закону Ампера сила, действующая на перемычку с током Лг = ~--г
2 2
, Лг В h
Ускорение перемычки ах = — =--------х. Из последнего уравнения следует, что пе-
т mL
ремычка совершает колебательное движение с круговой частотой СО — т= .
J mL
Для колебательного движения максимальная скорость Vraax = Асо. В нашем случае
t>max = Vo - максимальная скорость перемычки, А = S - амплитуда колебаний, равная
расстоянию, которое проходит перемычка до первой остановки. Поэтому
о SBh S1B1h1
vo =S(O=—==. Отсюда найдем т =----------—. Скорость перемычки описывается
VLm Lvo
уравнением V = ио cos (би); В момент времени t—скорость У — ~~
о
111
Тогда
V 1
— = vo COS O)ti, COS CDt} = -~', CDt
откуда /| =-—, где CD—
Зев
О rr
-. Тогда
3v
О
Ответ:
IVo ’
112
Раздел 4.
ФИЗИКО-МАТЕМАТИЧЕСКАЯ ОЛИМПИАДА ШКОЛЬНИКОВ
8-10 КЛАССОВ
Ежегодно в марте-апреле в МГТУ им. Н.Э. Баумана силами преподавательского
состава лицея №1581 при МГТУ им. Н.Э. Баумана проводятся олимпиады по физике и
математике для школьников 8-10 классов. Результаты этих олим
II!
ад учитываются
при поступлении школьников в лицеи и профильные школы при МГТУ им. Н.Э. Бау-
мана. Ниже приводятся варианты олимпиадных работ по физике и математике разных
лет.
4.1. Математика
10 класс вариант 2009г
1. (16 баллов) Сорок участников школьной олимпиады по легкой атлетике соревнова-
лись в беге на 60 м, в прыжках в длину и в прыжках в высоту. Результаты соревнований
выявили 25 призеров по бегу, а также по 22 призера - в прыжках в длину и в высоту.
Кроме того, по бегу и/или по прыжкам в длину выявлено 33 призера, по бегу и/или по
прыжкам в высоту - 32 призера, по прыжкам в длину и/или в высоту - 31 призер. Во
всех трех видах призерами стали 10 участников. - Сколько участников стали призерами
по каждому, но только одному, виду соревновании? - Сколько всего призеров только
по одному виду соревнований?
2. (12 баллов) Центр окружности, проходящей через середины сторон неравнобед-
ренного треугольника АВС, лежит на биссектрисе угла А. Найдите угол А.
3. (12 баллов) Докажите неравенство
Illi 11 w(n + 3)
(__!—+ _!_). ( 1 + - ..... (_!_+_*—) > 2’ 2“•
sin 2 a cos 2 а7 vsin4a cos 4 а vsin2wa cos 2" a
4. (12 баллов) Натуральное число N записано в виде цифровой строки, состоящей из
121 цифры, среди которых встречаются только единица, тройка и пятерка, причем
число единиц на 11 больше числа пятерок. Найдите остаток при делении числа N на 9.
5. (10 баллов) Найдите действительные корни уравнения (2х2 +4)2 = 25 • (х3 + 1) •
6. (10 баллов) При каких значениях t больший корень уравнения
5х2-4(/ + 3)х + 4 = /2 больше 103 и меньше 104, а меньший корень больше (—104) и
меньше (—103)?
113
7. (10 баллов) При каких значениях а четыре различных действительных корня уравне-
ния х4-(3-я)х2 + (я + 100)2 =0 являются последовательными членами арифме-
тической прогрессии? Для каждого такого а найдите подходящую прогрессию.
8. (6 баллов) Правильный октаэдр составлен из двух четырехугольных пирамид:
EABCD и Е’ABCD, имеющих общее основание ABCD. Все ребра имеют длину 1. Най-
дите угол:
1) между боковыми ребрами АЕ и ЕС; 2) между ребрами BE и DC;3) между боковыми
гранями ВЕС и DEC.
9. (12 баллов) Правильный октаэдр составлен из двух четырехугольных пирамид:
EABCD и E’ABCD, имеющих общее основание ABCD. Все ребра имеют длину 1.
Пусть точки F, Н, К — середины соответственно ребер АЕ, ЕС и AD. Постройте сечение
данного октаэдра плоскостью (FHK) и найдите: 1) площадь сечения; 2) угол между
плоскостями (FHK) и (АВС); 3) площадь проекции сечения на плоскость (АВС).
4.2. Решение и ответы варианта 2009г
1. Сорок участников школьной олимпиады по легкой атлетике соревновались в
беге на 60 м, в прыжках в длину и в прыжках в высоту. Результаты соревнований вы-
явили 25 призеров по бегу, а также 22 призера — по прыжкам в длину и в высоту. Кроме
того, по бегу и/или по прыжкам в длину выявлено 33 призера, по бегу и/или по прыж-
кам в высоту - 32 призера, по прыжкам в длину и/или в высоту - 31 призер. Во всех
трех видах призерами стали 10 участников. Сколько участников стали призерами по
каждому, но только одному, виду соревнований? Сколько призеров только по одному
виду соревнований?
Решение.
1. Обозначим Б множество призеров по бегу, В — множество призеров по прыж-
кам в высоту, Д — множество призеров по прыжкам в
длину. Отметим, что среди перечисленных содержатся
призеры и по другим видам соревнований. Воспользуем-
ся обозначениями рис. 1 и найдем:
— количество призеров по бегу и прыжкам в длину
\Бг\Д |=| Б | + | Д |-| Би Д 1= 25 + 22-33 = 14,
— количество призеров по бегу и прыжкам в высоту
| Б п В |=| Б | + | В | - | Б и В |= 25 + 22 - 32 = 15, Рис. 1
114
- количество призеров по прыжкам в высоту и в длину
| В п Д |=| В | + | Д | - | Д и В |= 22 + 22 - 31 = 13
2. Среди перечисленных содержатся победители по всем трем видам. Действи-
тельно, все луночки на рис. 2 имеют общую часть, обозначающую 10 призеров во всех
трех видах соревновании. С учетом предыдущих вычислений, найдем число призеров в
двух видах соревнований, множество которых заполняет дополнения их общей части в
каждой луночке на рис. 1. - это соответственно 4, 5, 3. Затем установим, что:
только по бегу призерами стали 25-( 10+4+5)= 6 школьников;
только по прыжкам в длину - 22-( 10+4+3)= 5 школьников;
только по прыжкам в высоту - 22-( 10+5+3)= 4 школьника.
Следовательно, только по одному виду соревнований призерами стали 6+5+4= 15
школьников — они образуют затененное множество на рис. 1.
Ответ: Только по бегу - 6 призеров; только по прыжкам в длину - 5 призеров;
только по прыжкам в высоту - 4 призера. Только по одному виду соревнований призе-
рами стали 15 участников.
2. Центр окружности, проходящей через середины сторон неравнобедренного
треугольника АВС, лежит на биссектрисе угла А. Найдите угол А.
Решение.
1. Точки А', В’, С ’ - середины сторон треугольника АВС, АО
- биссектриса угла А. Обозначим: ZBAC = Л, ZAB'O = /3, ZAC7O = (X (рис.2).
Из треугольников АОС и АОВ' по теореме синусов, находим равенства
|ОС'| \ОА\ lOB’l IОАI
----- — ---L 9 --- = -----
sin 4 sina Sin- sin£
2 2
из которых, с учетом | ОС’|=|ОВ’ |= R, вытекает
равенство sin (X — sin /3, откуда следует, что либо (X = Д, либо (X = я-ft.
115
2. Из равенства ОС = р следует равенство углов С'ОА и В’ОА , а также - по
второму признаку - равенство треугольников С'ОА И В'О А , влекущее равенство
соответственных сторон АС и АВ', противоречащее условию о неравенстве сторон
треугольника АВС.
3. Рассмотрим равенство ОС = ТГ-/7. Запишем выражение для суммы внутренних
углов четырехугольника АВ’ОС’
ZC'OB'+a + /7 + А = или ZC'OB' = ^~/4
Вписанный угол SCATS' = — ZCOB' — —— острый. Отрезки А'С' и А’В’ -
средние линии А АВС, поэтому (А'С)||(АС) И (А'В')Ц(АВ). Отсюда вытекает ра-
венство А = ZC'A’B’ = {я — /4)/2, равносильное равенству ЗА = Я, откуда А = - .
Ответ:
7Г
3
3. Докажите неравенство
sin2 а
cos 2 а 4 sin 4 а
—) •... • (--------Z— +-------5,--) > 2 2
cos4 a sin2" a cos2" а
Решение.
Воспользуемся неравенством Коши для доказательства вспомогательного нера-
венства
из которого вытекает следующее неравенство
1о§2(-^4^+- 4*-)*A+1
sm a cos 2Л а
Сложим почленно левые и правые части этого неравенства и получим
к = п z 1
I 'Z.
к = \ sin 2/с а
1 \ к = п
--------S (£ + 1) = 2 + 3 + ... + /? +
cos 2 К а к = \
п(п + 3)
2
116
Преобразуем левую часть полученного неравенства и найдем
sin 2 а
cos
sin 4 а
cos4 а7 vsin2”a
1 А > п(п+3)
cos2wa 2
а после потенцирования - получим требуемое неравенство.
4. Натуральное число N за
II!
сано в виде цифровой строки, состоящей из 121
цифры, среди которых встречаются только единица, тройка и пятерка, причем число
единиц на 11 больше числа пятерок. Чему равен остаток при делении числа N на 9?
Решение.
1. Докажем утверждение: остаток от деления натурального числа
N — ап aw_j.. Лл на 9 равен остатку от деления суммы всех значащих цифр чис-
ла У на 9.
Доказательство. Произвольное натуральное число N = апап_\...а\а§ в десятичной
системе счисления обозначает следующую запись
N = а„10" +аи_110”-1 +... + О]101 +ао1О° =
= аи(10” -l)+...+oi(101 -1)+(аи +<V-1 +...+«[ +«о)
Поскольку каждая из скобок кратна 9, то остаток при делении числа N на 9 равен ос-
татку при делении на 9 суммы ст = а + a -i +... + ал + всех его значащих цифр.
Отсюда вытекает также признак делимости на 9: если сумма (У всех значащих цифр
натурального числа N делится на 9, то и число У делится на 9. Утверждение доказано.
2. Введем обозначения: У] — количество единиц, У3 — количество троек,
У5 — количество пятерок, (У — сумма всех значащих цифр данного числа. По усло-
вию задачи, выполнена система условий
а = 1 • Vj + 3 • v3 + 5 • v5.
Выразим у} = 1 2 1 - и, - v 5 =121-v1-(v1-11)=132-2vi и вычислим
<t = 1v, +3 v3+5 v5 =1и + 3(132-2vi) + 5(v1 -11) = 396-55 = 341.
3. Остаток при делении числа 341 на 9 равен остатку при делении суммы цифр
числа 341 на 9, то есть 8. Ответ: {8}.
117
2 2 3
5. Найти действительные корни уравнения (2х +4) = 25•(х +1).
(Указание. Возведем обе части данного уравнения в квадрат и после приведения по-
добных получим алгебраическое уравнение четвертой степени
4х^ - 25х^ +16х -9 = 0, решение которого методом неопределенных коэффициен-
тов позволяет получить два квадратных уравнения с целочисленными коэффициента-
ми, из которых одно не имеет корней, а другое имеет корни
Решение.
Преобразуем данное уравнение
(2х2 + 4)2 = 2 5 • (х3 +1) <=> 4х4 - 25х3 +16х2 - 9 = 0-
Воспользуемся методом неопределенных коэффициентов
4х4 — 25х3 + 16х2 -9 = 0 <=> (х2 + ах + 6)(4х2 + сх + d) = 0
4х4 — 25х3 + 16х2 -9 = (х2 + ах + 6)(4х2 +cx + d) = 0 «
4а + с = -25,
4Ь + ас + d = 16,
ad + be = 0,
bd = -9.
Система 4-го, 3-го и 1-го уравнений имеет решение b = -3, d = 3; а = с = -5;
при этом второе уравнение дает истинное равенство: —12 + 25 + 3 = 16.
Таким образом, данное уравнение преобразуется к виду:
(х2 - 5х - 3)(4х2 - 5х + 3) = О
х2 - 5х - 3 = О,
4х2 - 5х + 3 = 0.
Второе уравнение действительных корней не имеет, а первое - имеет корни
5±V37
оба больше -1.
Ответ: ----
2
6. При каких значениях параметра t больший корень уравнения
5 х 2 - 4 (/ + 3 )л- + 4 = / 2
118
больше 103 и меньше I О4, а меньший корень больше (-104) и меньше (-103)?
Решение.
Дискриминант данного квадратного уравнения равен
1 2 2 2
- D = 4(t + 3) — 5(4 — t ) = (3t 4- 4) . Запишем корни данного уравнения - это
7—/
X] = t 4- 2, ху =--На рис. 3 линии 1 соответствует график функции х = t 4- 2, а
линии 2
4 4 _ л
, их точка пересечения А(—,—)• При /<— корень
4
х2 =тах(Х1,х2), а при t>-~ корень jq = тах(х19х2). Ограничения на корни за-
ем в виде совокупности систем
Рис. 3
-2-104 < Z < 2-5 103,
2 + 5 Ю3 <Г<104-2,
t е (-2-1О4,2-5 • 103 ) и (2 + 5 • 103,104 -2).
Ответ: (-2-104,2-5Ю3)и(2 + 5Ю3,104-2).
7. При каких значениях а четыре различных действительных корня уравнения
_(3_а)Х2 + (л + 1 о)2 = о являются последовательными членами арифме-
тической прогрессии? Для каждого такого а найдите подходящую прогрессию.
Решение.
По условию, данное биквадратное уравнение имеет четыре действительных кор-
ня. Расположенные в порядке возрастания, они имеют вид:
119
d
2
3d
•э /У
d > 0 (соответствующие точки числовой
прямой симметричны относительно начала отсчета, рис. 4)
___________ о ____________________,
*1 Л2 х3 jt4 -V
Рис. 4
2 d2
Обозначим х = t > 0, очевидно, = —
9^2
----. По теореме Виета, корни квад-
4
2 2
ратного уравнения t — (3 — a)t + (а + 10) =0 удовлетворяют соотношениям:
5d2
~Т
9rf4
'1
Эквивалентные преобразования позволяют получить систему уравнений
—=|а+10|
4
5d2 7
— =3—а,
2
109
. При этом значению
d
2
109
а~—1 отвечает прогрессия {—3,—1,1,3}, а значению а =--------- прогрессия
Ответ: Значению а = —7 отвечает прогрессия {-3,-1,1,3};
109 ( „
значению а =--------- прогрессия 3 •
8. Правильный октаэдр составлен из двух четырехугольных пирамид, EABCD и
E’ABCD с равными ребрами единичной длины, имеющих общее основание ABCD.
Найти угол: 1) между боковыми ребрами АЕ и ЕС;
2) между ребрами BE и DC;
3) между боковыми гранями ВЕС и DEC.
Ответы: 1) 90°; 2) 60°; 3) arccos^A).
9. Правильный октаэдр составлен из двух четырехугольных пирамид, EABCD и
E’ABCD с равными ребрами единичной длины, имеющих общее основание ABCD.
Пусть точки F, Н, К - середины соответственно ребер АЕ
120
ЕС и AD. Построить сечение данного октаэдра плоскостью (FHK) и найти:
1) площадь сечения;
2) угол между плоскостями (FHK) и (АВС);
3) площадь проекции сечения на плоскость (АВС).
Ответы: 1) 3>/2/8; 2) 45°; 3)3/8.
4.3. Вариант 2010г
1. (10 баллов) Имеются два одинаковых стакана, заполненных до одного и того же
уровня соответственно чистой водой и подкрашенной водой. Сначала берут одну чай-
ную ложку подкрашенной воды и вливают в стакан с чистой водой и перемешивают;
затем чайную ложку смеси вливают в стакан с подкрашенной водой. Чего больше: под-
крашенной воды в стакане с чистой водой или чистой воды в стакане с подкрашен-
ной водой? - Что будет, если число переливаний не ограничено?
2. (15 баллов) При каких значенияхх числа ^1-х39 у/х — 7, -ух2 —63 образуют гео-
Д/ 8 2
метрическую прогрессию?
3. (15 баллов) Найдите наибольшее и наименьшее значения выражения х2 + 2 у2, если
х2 - ху + 2у2 = 1.
4. (15 баллов) Три окружности радиусом 1, 2, 3 соответственно, лежат в одной плоско-
сти и попарно касаются друг друга. Найти площадь круга, ограниченного окружно-
стью, проходящей через точки касания данных окружностей.
IIIS
4sin2 Зх - 2 со s2 (х - я) - sin cos = sin(2x - ^).
ах-ау — Ъ9
6. (10 баллов) Решить систему уравнений
\V(^-o2+o-i>2+7и-з)2+/ = Vs.
7. (15 баллов) Три шара, имеющих центры А, В, С и радиусы l5/g, 6/s, °/з соответствен-
но, попарно касаются друг друга. Найти площадь треугольника, вершины которого ле-
жат в точках касания данных шаров с общей опорной плоскостью.
121
8. (10 баллов) При каких значениях параметра t больший корень уравнения
/2 + 4(/ + 3)х - 5х2 -4 = 0 больше 103 и меньше 104, а меньший корень больше (-104)
и меньше (-103)?
4.4. Решения варианта 2010г
Составление, подготовка, ответы В.Е. Епихин
1. При перемешивании, независимо от числа переливании, во втором стакане подкра-
шенной воды будет не меньше, чем чистой воды. Также и для чистой воды в первом
стакане.
Без
перемешивания, во втором стакане умень
1115
тся содержание подкрашенной воды
ровно настолько, насколько прибавилось чистой воды. Следовательно, из второго ста-
кана в первый перелито столько же подкрашенной воды, сколько - из первого стакана
во второй перелито чистой воды. Поэтому подкрашенной воды в стакане с чистой во-
дой окажется столько же, сколько чистой в стакане с подкрашенной водой.
Ответ: Количество инородной жидкости в каждом стакане одно и тоже.
2. Решение.
□ /7
ОДЗ: а& [~,+°°). Признак ГП:
>/х-7 -JjX |Vx2 -63 <=> х3 -71х + 56 = 0
хе {8,-(4+ >/23),-4+ >/23}.
С учётом ОДЗ заг
тип
ем Ответ:
{8}
3. Решение.
Преобразуем дополнительное условие и сделаем замену неизвестных
£ = sin/, 77 = cos/, 0 < / < 2/г;
x = sin/+ ' cos/,>>= 2 cos/.
Представим целевую функцию в виде:
/(/) = X2 (/) + 2у2 (/) = ; + (Icos 2/ + -^ • cos 2/),
или /(/) = | + -^ sin(2/ + 0),откуда 8 </(/)<^|^-.
122
_ 8-2 х/2 8+2>/2
Ответ: —=— и —?—.
4. Теорема. Если три окружности с центрами в точках А, В, С попарно касаются друг
друга, то окружность, вписанная в А АВС касается сторон А АВС в точках их каса-
ния.
Решение.
зами в центрах данных ок-
Искомая окружность bi
IK
сана в треугольник с вер:
III5I
Ответ: г = 1, S = Л.
5. Решение.
Применим формулу двойного аргумента и данное уравнение преобразуем к ви-
ду: 2(1 - cos 6х) - 2 cos2 х + cos 2х = 0 <=>,
<=> 2(1 - cos 6х) - (1 + cos 2х) + cos 2х = 0 <=> 2 cos 6х = 1,
К frk
имеющему корни: ±--1- —
18 3
IО 3
6. Решение.
Второе уравнение системы равносильно уравнению <у = у(3 —х); при этом
точка С(х,у)е [АВ], где А(1;1), В(3;0) (рис.2).
Первое уравнение преобразуем к виду Зах = За + 10, имеюще-
му решение: а = 0 —> 0, а 0 —> (3^° , • В виду ог-
Рис. 2
раничения: 1 < х < 3, или
О < у < 1 - находим, что при
а< 7, ->0,
5 ___ /За+10 За-5\
гч Л 5 / . /О< 5 / . /За+10 За—5\
Ответ: а < Д —> 0, а > Д —> (——, -т=—).
з ’ з v За За 7
7. Решение.
Расстояние между точками касания шаров с радиусами г и R вычисляется по
формуле 2y[rR . Поэтому длины сторон треугольника будут 3, 4, 5, а его площадь рав-
на 6. Ответ: {6}
123
8. Решение.
Дискриминант данного
квадратного уравнения равен
= 4(f + З)2 - 5(4 - /2) = (3t + 4)2, и его корни рав-
2-t
ны:х|=/ + 2, Х2=—-• На рис. 3 график функции
х = t + 2 соответствует линии 1, а график функции
Х = —- - линии 2; точка их пересечения 1). При
5 v З’З7
t < - у корень х2 = тах(х! ,х2)» а ПРИ t>
корень X] = тах(х|,х2)- Следователь-
но,
ограничения на корни имеют
вид
совокупности
4 2-5Ю4 </ < 2-5 103,
-2-Ю4 < t < -2-103;
4
3
-2-10 </<2-510 , 2-] о4,2-5 -1()3) и (2 + 5 103,104-2).
2 + 5103 </<104-2,
Ответ: (-2 - 104,2 - 5 1 О3 ) и (2 + 5 1 О3,104 - 2).
4.5.8 класс вариант 2006г
1. (10 баллов) Мальчик сбежал вниз по движущемуся эскалатору и насчитал 30 ступе-
нек. Сколько ступенек насчитает он, если побежит по этому же эскалатору вверх, если
при спуске по неподвижному эскалатору он насчитал 50 ступеней?
2.(15 баллов) Вычислить:
11 15
91 95 95-99
3.(10 баллов) Делится ли на 9 сумма цифр числа о=254+319?
4. (10 баллов) Решить уравнение при всех допустимых значениях параметра Ь:
Vx2 +14х + 49 =
ч/ГЛ 6-1
Jb+i+y/b^i у1ь2-\-ь+],
124
5. (10 баллов) Участнику игры «Поле чудес» выносят две шкатулки, в одной из которых
находится приз, и дают право задать ведущему только один вопрос, на который тот
сможет ответить «да» или «нет». Известно, что ведущий один день говорит правду, а
другой врёт (и так через день). Какой вопрос должен задать игрок ведущему, чтобы
верно выбрать шкатулку с призом?
6. (15 баллов) В прямоугольной системе координат построить множество точек, удов-
летворяющих условию: у(х - 2) - у2
x2-8x + 15
х-5
7. (15 баллов) Диагонали трапеции ABCD с основаниями AD и ВС пересекаются в точ-
ке О. Найти площадь трапеции, если Saboc=Si, Saaod=S2.
8 .(15 баллов) Разрезать прямоугольный неравнобедренный треугольник на три тре-
угольника так, чтобы из них можно было составить ромб с диагоналями, которые рав-
ны катетам данного треугольника.
4.6. Решение варианта 2006г
30/, =(50-30)/2
xt{ = (х-50)/2
30(х - 50) = х • 20
Юл-= 50-30
л- = 150cm
t|- время, которое тратит мальчик на проход 1-ой ступени.
t2 - эскалатор, х - число ступеней.
2‘ 4^3 7 7 11 11 15
1 _ 1 11 Ъ1Г1_ 1
+ 91 95 95 99у"”4<3 99;
96 32
4-3-99
8
99
3. (n-1 )3+п3+(п+1 )3=Зп3+6п=Зп(п2+2)
Докажем, что п(п2+2):3. Рассмотрим три случая:
1).л = ЗЛ’=> и:3.
2л = ЗК + 1=>л2 +2=9К2 + 6К + 3=>(л2 +2):3.
> => (Зи(п2 + 2)):9
3)л = ЗК + 2 => п2 + 2 = 9К2 + 6К + 6 => (и2 + 2);3.
125
4.
r y/b-i | i
+ y/b^i(4b+\-V*-i) I 7(5-i)(*+i)
= yJb2-}-(b-l) + yJb2-l + (b-l) = 2 =
((6+i)-(z>-i))Vz>2-i z>+i-z>+i
x=-6 b-i>Q b>l
x = -8 6 + l>0 b>-l
Ответ: {- 6; - 8}при b> 1
5. Что бы Вы ответили вчера, если бы я Вас спросил: «Приз находится в правой
шкатулке?»
Пусть приз в правой шкатулке, тогда ответ будет «нет».
6. 2) у2^(х-5)(х-3)^ [Мх-2)-(х-3)-у2=0^ [(лг-2)(у-1)-(у-1) = 0
(х-5) |х*5 [х^5
^-1)((х-2)-(у + 1)) = 0
|х Ф 5
7. Найдем S:
5
s'.
тр =51+2Тзд +S, =ф^у^)2
4.7. Вариант 2010г
1. (5 баллов) Сколькими способами можно разменять 2010 рублей 5- и 10-рублевыми
монетами?
2. (5 баллов) Температуру можно измерять в градусах Цельсия (°C) и Фаренгейта (°F).
Зависимость линейная. Вода замерзает при 0°С или при 32°F, а кипит при 100°С или
126
при 2I2°F. Термометр показывает температуру +5°С. Сколько это градусов по Фарен-
гейту?
3. (10 баллов) Имеются два сосуда, объемы которых равны V| и V2 соответственно. Ка-
ждый сосуд заполнен (т.е. раствор занимает весь объем сосуда) водным раствором од-
ной и той же соли, но концентрация этой соли в растворах различна для сосудов V i и
V2. Также есть пара стаканов од
такового объема. В первый стакан налили раствор из
первого сосуда, во второй - раствор из второго. Затем раствор из второго стакана пере-
лили в первый сосуд, а из первого стакана - во второй сосуд. После выполнения этих
действий концентрации солей в растворах в первом и втором сосуде стали равны меж-
ду собой. Каков объем стакана?
4. (10 баллов) Из трех данных фи-
гур сложите 2 разные, одна из ко-
торых имеет ось симметрии, а дру-
I : Г I ?
гая центр симметрии.
Каждую фигуру нужно использовать ровно один раз, прикладывая их без наложений.
Изобразите ось (центр) симметрии.
5. (15 баллов) Определите сумму всех натуральных чисел п, для которых числа 3920 и
4320 делятся без остатка на п и п+7 соответственно.
6.(15 баллов) Около остроугольного треуголы
151
<а АВС описана окружность с центром
О и радиусом R. Угол АВС равен а. AM и CN-высоты треугольника АВС. Сторона АС
равна а. Найдите площадь четырехугольника BMON.
7. (15 баллов) Найдите значение выражения без помощи калькулятора. Если точное
значение найти невозможно, округлите значение до сотых.
8. (25 баллов)
Г-14 + >/з17-68У7
, V3 + V2V7
2х2 + 15х + 25
—;---------< -5
х2 + 9х +10
f(x) =
Зх4 — 91 х31 +6х2 . _
---;----!--!------, X G [-5
3(х2-| 2х|)(| х| -1)
Постройте график функции f(x). Нацди-
2х2 - 15x4- 25 _
—;---------> 5;
х2 -9х + 20
те область определения и область значений. Найдите количество корней уравнения f(x) = а в
зависимости от значений параметра а.
127
4.8. Решения варианта 2010г
1.В числе 2010-201 десяток. Следовательно, способов размена 202. Первый -
только из пятерок, а каждый следующий способ-с заменой двух пятерок на десятку. А
так как их 201,следовательно, кроме первого способа можно воспользоваться еще 201.
Т.е. кол-во способов = 201+1=202.
2. Нужно установить зависимость градусов Цельсия и Фаренгейта: Если (х)-
температура в Цельсиях, то (1,8х+32)-температура в Фаренгейтах. Т.е. если х=5, то
температура в Фаренгейтах = 1,8 к 5+32=9+32=41.
Ответ:41.
3. Пусть концентрация соли в 1-ом растворе равна (х) моль/л., а во 2-ом - (у)
моль/л. А объем стакана примем за (z) л., тогда z л. из первого сосуда будут содержать
(zx) молей соли, а из второго- zy моль.
йся в первом сосуде раствор (после того, как забрали z л.) будет со-
держать (Vj-z)x моль, а второй-(V2-z)y моль. Концентрация после доливания в 1-ый со-
суд стакана с раствором из второго будет равна ((Vj-z)x+zy).V/,
во втором - ((V2-z)y+zx):V2. По условию эти концентрации равны, поэтому со-
II!
ставим уравнение:
((Vi-z)x+zy):Vi=((V2-z)y+zx):V2 => V 1V2X-V2Zx+V2?y=ViV2y-Vizy+V/zx =
К; Vtf- Vi V2y= V]ZX+ K2ZX- Vizy- V2Zy => zVl(x-y)+zV2(x-y)= V/ V2(x-y) ->
z=V1V2/(Vl^V2).
Ответ: объем стакана равен Vj Vj)-
4.Ось симметрии обозначена
красным. У 2-ой фигуры - централь-
ная ось симметрии.
5. По основной теореме
алгебры любое число можно представить в виде произведения простых чисел
возведенных в определенную степень.
3920=1-72 24 5.
4320=1-33-25-5.
128
Среди делителей числа 4320 нет кратных 7, поэтому если взять «:7, то и («+5)
:7. Значит, возьмем п= каждому делителю числа 3920, который не кратен 7.
1,2,4,5,8,10,16,20,40,80. При этом «4-7=8,9,11,12,15,17,23,27,47,87. Поэтому нам подхо-
дят «=1,2,5,8,20. Сумма «=36.
Ответ: 36.
6. В данном треугольнике проведем радиусы описанной окружности и введем
некоторые обозначения: Z\=АОАВ=АОВА (углы при основании равнобедренного
треугольника с боковыми сторонами равными радиусу описанной окружности). Соот-
ветственно Z 2= Z ОВС= А ОС В, АЪ=А ОСА= Z ОА С. Сумма углов треугольника равна
ZОАВ+ ZОВА4- ZОВС+ ZОСВ+ ZОСА4- АОАС=2(Z14- Z 24- Z 3)= 180°. Треугольники
BMN и АВС подобны с коэффициентом подобия £=соза.Следовательно, угол BMN ра-
вен углу ВАС,который в свою очередь равен Z14-Z3. BO(\MN=K. В треугольнике
ВКМ АКВМ= Z2, АВМК=А 14-Z3. Т.е. сумма этих двух углов равна 90°, откуда дела-
ем вывод, что ВО A MN. Площадь четырехугольника BNOM равна сумме площадей тре-
угольников BNO и BOM=\H(NM) хВО=\И(а cosa)R=0,5/ta cosa
Ответ: Искомая площадь равна 1/2&? cosa.
-14+7з17-68>/7
2) = 3 4 - 3 - = -2VS
3)= 7-2V6 4 2V6-7
4) (-2у 5) X 7 s -42
Ответ:-42.
8. 1) Строим график функции yi=
Зх4 —91 х314-6х2 * 4
3(х2-| 2х|)(|х|-1)
,хе [0;5];
После упрощения =>Строим график yi=x. D(yi)=(0;5]\{ 1;2};
2х2-15x4-25
2) Строим график функции уз=—-------
После упрощения =>Строим график уз=--------4- 2. П(уз)=(5;4-оо);
х-4
График этой функции представляет собой гиперболу с асимптотами: х=4 и =2
3
(т.е. для пос1роения смещаем график функции ,у=— на 4 единицы вправо и 2 вверх).
129
3) После выполнения пунктов 1-2 отображаем график функции относительно
оси ОУ.
4)Р(у)=Л\{-2;-1;0;1;2}.£(у)=(0;5]\{1;2}.
5) -оо<д<0 => нет корней, 0<о<1 => 2 корня, о=1 => нет корней, 1<а<2 => 2 кор-
ня,
а =2 => нет корней, 2< а <5 -> 4 корня, а =5 => 2 корня, а >5 => нет корней.
Ответ: Df= [-4;4] \{±3; ±1; ±1/2; 0} Е/= (0;6]\{3/2;3}
ае (-оо; 0] и {3/2;3 } и (6 ;-+-«>) - нет решений, а е (0;3/2) и (3/2;2) и (3;6] - два решения
а = 2 - четыре решения, а е (2;3) - шесть решений
4.9. Варианты для самостоятельного решения
Вариант 2008г
1. (6 баллов) Разложить на множители: х4+1.
2. (8 баллов) Сравнить: 72008 + V2005 и V2006 + 72007
3. (10 баллов) Эстафета длинной 2008 км состоит из нескольких этапов одинаковой
длины, выраженной целым числом километров. Участники команды города Энск пре-
одолевали её несколько дней, проходя каждый этап ровно за 1 час. Сколько времени
длилась эстафета, если известно, что они прошли её менее чем за 2 недели?
а
4. (12 баллов) Даны отрезки —_
. Построить с помощью циркуля
и линейки отрезок с, такой что c=yj2b* + 2ab+a*. Сколько решений имеет задача?
Всегда ли возможно построение?
130
5. (8 баллов) В прямоугольнике, разбитом на квадраты, вырезан цен-
тральный квадрат. Укажите различные способы разрезания данной
фигуры на 2 равные части, чтобы линия разреза шла по сторонам
клеток. (Способы считаются различными, если части, получаемые
при одном способе разрезания, не равны частям, полученным при другом способе).
6. (10 баллов) В квадрате, состоящем из 9 клеток, расставить числа 1, 2, 3, 4, 5, 6,7, 8, 9
так, чтобы суммы чисел, стоящих в каждом вертикальном ряду, в каждом горизонталь-
ном ряду, а также на любой диагонали были равны.
7. (8 баллов) На плоскости хОу построить множество точек, таких что: у + = 2.
х + у
8. (12 баллов) В лесу 99% сосен и 1 % берёз. Вырубили часть сосен так, что сосны те-
перь составляют 98% всего леса. Какую часть леса вырубили?
9. (12 баллов) Г рафик функции у = ах2 + Ьх + с при всех значениях х расположен ниже
прямой у = 2. Определить знак выражения: а - b + с -3.
10. (14 баллов) В параллелограмме ABCD точки М и К - сере,
а сторон CD и AD со-
1ICISI
ответственно, Р - точка пересечения отрезков AM и ВК. Найти отношение площади
треугольника АРК к площади параллелограмма.
9 класс вариант 2010г
1. Докажите, что при всех действительных значениях переменных х и у выполняется
неравенство: я* 4 2яу 4 4 4 ©у 4- 3 > О.
2. Решите неравенство:
£r 4 5)х2 4 10(5л: 4 4) 4 Юзе2 > 7(5% 4 4^x4 5 — (х 4- S)(S^ 4 4) 4-7k2 * \&?4 S.
3. Функция у = Дх) - чётная, её областью определения является множество действи-
тельных чисел. Известно, что уравнение — S в О имеет 2011 различных корней.
Найдите /(($. Ответ обоснуйте.
4. При каких значениях параметра а уравнение
Й 4 2)(х2 4 41$2 - 2(а - 1)(х2 4* 4- Ю) - а- 2 = 0 имеет ровно два различных
решения?
5. Три пловца должны проплыть из А в В и обратно. Сначала стартует первый, через 5
секунд - второй, ещё через 5 секунд - третий. Некоторую точку С, находящуюся между
131
пунктами А и В, все пловцы миновали одновременно (до этого ни один из них в В не
побывал). Третий пловец, доплыв до В и повернув назад, встречает второго в 9 метрах
от В, а первого — в 15 метрах от В. Найдите скорость третьего пловца, если расстояние
АВ равно 55 метров.
6. Правильный десятиугольник со стороной равной 2 см вписан в окружность. Не поль-
зуясь калькулятором и таблицами, найдите точное значение выражения -1) й, где R
- радиус описанной вокруг десятиугольника окружности.
7. На прямой, проходящей через центр О окружности радиуса 12 см, взяты точки А и В
так, что ОА=15 см, АВ=5 см (точки А и В лежат с одной стороны от точки О). Из точек
А и В проведены касательные к окружности, точки касания которых лежат по одну
сторону от прямой АВ. Найдите площадь треугольника АВС, если С - точка пересече-
ния этих касательных.
4.10. Физика
10 класс вариант 2009г
1. Траектория. Камень бросили с поверхности земли под некоторым углом к горизон-
ту. Выберем начало координат в точке броска, ось х направим горизонтально вдоль по-
верхности земли, а ось у - вертикально. Тогда уравнение траектории камня описывает-
ся функцией у(х) = — кх2 + х ч где ^ = 0,2м_|. Пренебрегая сопротивлением воздуха,
посчитайте время движения камня.
2. Полет самолета. Самолет летит по прямой горизонтально со скоростью Ко = 720
км/ч. Чтобы сделать разворот в горизонтальной плоскости, ему необходимо увеличить
скорость. Какой будет эта скорость К, и под каким углом а к вертикали, самолет дол-
жен наклонить плоскость крыльев, чтобы разворот произошел по окружности радиуса
R = 8 км? Подъемная сила направлена перпендикулярно плоскости крыльев и пропор-
циональна квадрату скорости самолета (коэффициент пропорциональности в обоих
случаях, в прямолинейном и наклонном полете, считайте одинаковым).
3. Давление шариков. Два шарика из одинакового материала радиусами г и 2г помес-
тили в цилиндрический сосуд диаметром 4,5г, как показано на ри-
сунке. В сосуд наливают жидкость плотности р. Когда жидкость до-
ходит до середины верхнего шарика, нижний шарик перестает да-
вить на дно. С какой силой в этот момент верхний шарик давит на
132
нижний? Чему равна плотность материала шариков?
Примечание. Объём шара радиуса г вычисляется по формуле'. V — —71Г .
4. Пятерка превращается.... На рисунке изображен график
изменения объема V идеального газа от его абсолютной темпе-
ратуры Т в процессе 1-2-3-4-5-6. Считая массу газа постоян-
ной, изобразите, соблюдая правильный масштаб, как будет вы-
глядеть зависимость давления Р от абсолютной температуры Т
для этого процесса.
5. КПД. Коэфф
аент полезного действия цикла 1-2-3-4-1
ни
цикла 1-3-4-1.
представленного на рисунке, равен т). Определите КПД
9
4.11. Решение варианта 2009г
Задача 1. Уравнение траектории у =
—, —-х—х2 +tgax.
2Г02 cos2 а
О
По условию Xх)= — *х + х. => tga = 1, => Of = 45".
g -k
2К02 cos2 а
Ио =—!— = ^J,9’8 = х/49 = 7 м/с.
cosa\2fc уХ’0,2
Время движения камня
2К0 sin а
Задача 2. При движении по прямой: mg = AF0 .
При движении по окружности:
133
k = ^
„ mV
x: Fcosa =---
R
« у: F sin a = Mg,
F = kV2.
ky cos а -
И02
cosa=— ,
gR 9,8 8 10
2002
~ 0,5, => (X — 60
kV2 sina = wg.
V = Л" = 215 м/с =774 км/ч.
x/sina
Ответ, a = arccos
\gR)
= 60 \ V =
v„
Vsina
215 м/с ==774 км/ч.
Задача 3
FM -/Vcoscr-z^g = 0,
FA2 + Fcosa-M2g = 0.
p^r(2r)’g- TVcosa-д„ ±x(2r)3g = 0,
2 4
p—xr3g + N cos а- рш— nF g - 0.
34 з 36 з л 17
p-nrg-p—nr g = 0,=> Pw = —P-
J J lo
T.k. диаметр цилиндра D = r + rsinaf+2r + 2rsina = 3r(14-sincif) = 4,5r, тс
sin(X = 0,5, => a = 30u. Подставляя это значение угла в любое уравнение системы
32
получим /V = 1ф%Г •
134
Состояние Параметры Вычисления
1 Ра,У0,тй
2 Л) ’^0 ’ ^0 Р Р — = — => Р2 =2Р0 2Г0 То 2 °
3 />3,2^0,27; Р3-2Уо = Р2Уо^Р3^Ро
4 Л,2Г0,Г0 ^4 _ ^3 р ^0 т; 2Т0 4 2
5 />4-2Ко=Р5-ЗИо^Р5=^
6 р6,зк0,2т0 N) II и II Lk) | bJ
Задача 5. Обозначим работу за цикл 1-2-3-4-1 Яо. Тогда в цикле 1-2-3-4-1 полученное
тепло 0„ол = 012 + 023, а отданное 0omd = Q34 + 04| . Тогда 4, = Q„o„ - Qomd.
В цикле 1-3-4-1 работа за цикл равна Aq/2, Q^=Q13’
Qomd
пол Qomd Qno.i Qomd *
Кпд циклов 1-2-3-4-1 т] и 1-3-4-1 rf вычисляются по формулам:
= Л/2 = __V2_
Qnon -A® 1'2' +Qomd
Тогда кпд цикла 1-3-4-1 выражается через кпд цикла 1-2-3-4-1.
7
^0 + Qomd 1 _L ^Qomd
. Ответ: п' = ———
2-Т] 2-Т]
Л
135
4.12. Вариант 2010г
1. Мальчик бросил мяч в заднюю вертикальную стенку отъезжающего автобуса. Мяч
подлетает к стенке под углом а < 45°, а отлетает от нее под углом 2а. Углы отсчиты-
ваются от нормали к стенке. Определите скорость мяча в момент удара, если скорость
автобуса в этот момент равна и. Время удара считайте очень малым, а сам удар абсо-
лютно упругим.
2. Представьте себе, что на полюсе Земли пробурили шахту, направленную к центру
Земли. Какую скорость разовьет маленький камушек, упавший в эту шахту, пролетев
расстояние равное одной четвертой радиуса Земли. Для сравнения, первая космическая
скорость равна V] = 8 км/с. Силами сопротивления пренебречь.
3. N комочков пластилина достали из холодильника, поэтому все комочки имеют тем-
пературу 0°С. Массы комочков равны т, 2т, 3m,..., Nm. Их положили на лед в ряд
один за другим в произвольном порядке, причем первым оказался самый легкий кусо-
чек пластилина. Этот кусочек толкнули вдоль линии, на которой лежат остальные ко-
мочки, сообщив ему кинетическую энергию Ж. При каждом столкновении комочки
CI
151
лаются, так что после всех столкновений образуется одно большое тело. Какую
максимальную температуру может иметь это тело, если удельная теплоемкость пласти-
151
ла равна с?
4. Воздушный шар с массой оболочки т имеет внизу отверстие, через которое воздух в
шаре нагревается горелкой до температуры t = 77°С. Если к оболочке прикрепить груз
массой 4m, то шар сможет подняться в воздух и плавать вблизи поверхности Земли. На
какую максимальную высоту способен подняться этот воздушный шар, если с него
сбросить половину массы груза? Температура окружающего воздуха на этой высоте
равна t\ = -23°С, а вблизи поверхности Земли /о = 27°С. Как известно, атмосферное
давление уменьшается в два раза через каждые пять километров высоты. Оболочку ша-
ра считайте нерастяжимой.
5. С
некоторым количеством идеального одноатомного газа совершают цикличес>
процесс, состоящий из двух изобар и двух изохор. Середина изобары 2-3 и середина
изохоры 3-4 лежат на одной изотерме, соответствующей температуре Т.
136
> v
а) Докажите, что точки 2 и 4 цикла также лежат на одной
изотерме.
б) Считая известными температуру Т и температуру Тз газа
в состоянии 3, найдите коэффициент полезного действия
этого цикла.
4.13. Решение варианта 2010г
Задача 1. Для решения задачи рассмотрим движение мяча в двух системах от-
счета: в неподвижной системе отсчета ху, связанной с землей, в ней скорость мяча в
момент удара обозначим V, скорость мяча после удара - V , скорость автобуса — й
(рис а) и в движущейся системе отсчета, связанной с автобусом (рис. б).
а) в неподвижной С.0 б) в движущейся С.0 в) в неподвижной С.0
В движущейся системе отсчета относительная скорость мяча И, = V — и (рис. б),
fx': Klx = V cos а — и,
[/:Kv = Ksina.
После упругого отражения от стенки скорость мяча К2 сохраняет свой модуль и
угол падения равен углу отражения.
[Х : C0S# +
1У: У2у = f'u- =l'sin а-
137
Перейдем снова в неподвижную систему отсчета (рис в). И = V2 + и.
х: Vx = V2x + и = -Kcosa + 2w,
j:P' = K = Г sin a.
Т.к. из рисунка к задаче следует, что мяч отлетает влево под углом 2а, то Vx < О
V
V
tg2a =
И sin а
К sin a
|И'| —V cos а + 2а| V cos а-2и
2и
Ответ: V —--------—----------= 4wcostz.
cos ос—sin а • ctg 2а
Задача 2. Сила гравитационного взаимодействия однородного шара радиуса R с
материальной точкой массы т, находящейся внутри шара на расстоянии г < R от цен-
тра шара равна силе, с которой взаимодействует материальная точка с однородным ша-
ром радиуса г и массы ЛГ (см. рис) г (х) = G—г—.
w - *
Это утверждение можно доказать, пользуясь, например, теоремой Гаусса для гра-
витационного поля. Школьники могут использовать его без доказательства.
Пусть х - расстояние, отсчитанное от полюса Р, которое пролетел камушек, тогда
сила его притяжения к Земле равна
Р
тМ т 4 з
Г(х) = G—--у = G—--7 р-n{R - хУ =
(R-x) (R-x) 3
т
R
к
К
*
Gmp—ft(R — x), где р — средняя плотность Земли:
*5
М
-г---, М - масса Земли, R - радиус
-ЛЁ*
>-z ч „тМ ч R-x
Земли. F(x) = G ——(R ~х) = mg-------.
R R
Работа силы тяготения, вычисляемая по графику F(x), равна изме-
R
нению кинетической энергии камушка.
mV2
~2”
2
138
Ответ: V =
Vj =5,3 км/с.
mV*
Задача 3. Обозначим через V - скорость комочка массой т, тогда W =—-—,
лх V N(N+1)
через и - скорость большого тела массы м = т + 2w +... + г/т =---
т.
При всех столкновениях сохраняется импульс: тК — Ми,
mV
и =-
М
а о/ т^2 Ми1 mV2 ( т
Изменение энергии Дгг =--------=----- 1----
2 2 2 I М
Пренебрегая потерями энергии,
W
Ответ: t =-
сМ
= W 1-
N(N +1)
_2W ТУ2 + ТУ - 2 _ 20%У - !)(# + 2)
~ cm N\N + \}2~ emN2 (N +1)2
Задача 4. Условие плавания вблизи поверхности Земли:
(т + 4/и + тг в )g = pegK , где т? 9 - масса горячего воздуха в шаре, V- объем шара,
рв - плотность воздуха снаружи шара.
Обозначим Ро - давление вблизи поверхности Земли, тогда
О’
рои
RT0'
Р - 5mRT°T
RT RT0 ’ 0 Vp(T-T0)'
Найдем теперь давление Р на высоте, куда поднялся шар с грузом 2т.
Условие плавания на этой высоте: (т + 2т + т'гв )g = p'gV ,
, PVu , Ри , PVu PVu n ImRT.T
" RT RT{ RT RTi Vp(T-Tx)
Po 5T0(T-T) 5-300 100
Отношение давлений равно — =------=----------
P ЗТЛТ-Т) 3 250-50
0 р
9
Ответ: Н = 10 км.
139
Задача 5.
а) у, ±*3.) = + Р2) рл = vRT , е)
=> P2VX = PXV3, => Т2 = Т4, точки 2 и 4 лежат на одной изо-
;4 терме.
£—б) Из (*) => vRT2 + vRT3 = 2vRT, |Г2 =Г4 = 2Г^
Температуру Т\ можно найти, записав уравнения изохорных процессов 1-2 и 3-4.
Работа за цикл равна площади цикла 1-2-3-4-1.
А = (Л -Р2)(К3 -V,) = vR(T3 -Т>-Т1 + Т{)=vR^P-
Л
Г аз получает тепло на участках 1-2 и 2-3: Qnon = 012 + 023 •
02 = ^v{T2 - Г,) = |(2Т - Т3) - (2ГгГз)2>
3vR
(2Т-Т3)(Т3-Т).
& = ^V(T3 - Т2) = (Т3 - (2Г - Т3)) = 5vR(T3 - Т).
3vR 2vR
L. = ^(2Г - Т3 )(Г3 - Г) + 5vR(Т3 - Т) = — (Т3 - Т)(ЗТ + Т3).
Ответ: КПД цикла Т] =
2(Г3 - Т)
4.14. Варианты для самостоятельного решения
8 класс вариант 2008г
1. В какой воде и почему легче плавать: морской или речной?
2. Пользуясь системой подвижных и неподвижных блоков, необходимо поднять груз
весом 600 Н. Из скольких подвижных и неподвижных блоков должна состоять система.
140
чтобы этот груз мог поднять один человек, прикладывая силу в 65 Н.
3. Сколько времени мимо мотоциклиста, едущего со скоростью 63 км/ч, будет проез-
жать встречная колонна автомобилей длиной 300 м, имеющая скорость 45 км/ч?
4. В калориметр, где находиться 1кг льда при температуре 0 °C. В воду помещают ку-
сок льда массой 400 г, температура которого - 30 °C. Какая температура установиться в
калориметре? Какой станет масса льда?
5. Алюминиевый кубик ставят на лед, имею
[ий температуру 0 °C. До какой температу-
ры должен быть нагрет кубик, чтобы он погрузился в лед наполовину? Полностью?
6. Каково сопротивление цепи, если сопротивление каждого из резисторов 1 Ом?
31
9 класс вариант 2009г
1. (32 балла) Два заряженных шарика массами m и Зш и зарядами q и 2q одного знака
были отпущены в одной точке и разлетелись с горизонтальными начальными скоро-
стями. Первый из них упал на расстоянии г = 0,75 м от эпицентра разлета, второй ока-
зался в тот же момент на той же горизонтальной плоскости, что и первый. Найти силу
Кулоновского взаимодействия шариков в момент падения на плоскость, q = 1 нКл. Ео =
9 »-i 1 <71<72
1/4л.9.10 Ф/м. Сила Кулона рассчитывается как г =------г—
4лг0 г
2. (32 балла) Деревянный кубик заглубили с помощью спицы в воду так, что его верх-
няя грань стала параллельной поверхности воды на глубине, равной одной трети ребра
кубика. Найти работу силы Архимеда по перемещению кубика из этого положения в
положение равновесия после всплытия. Колебаниями и изменением высоты уровня во-
ды пренебречь. Плотность дерева принять равной 2/3 от плотности воды. Длина ребра
18 см. g = 10 м/с2. Увеличится или уменьшится эта величина, если верхний слой воды
толщиной 6 см заменить слоем масла с плотностью 0,8 от плотности воды?
141
3. (12 баллов) Как объяснить образование облачка при открывании охлажденной бу-
тылки с газированной водой?
4. (12 баллов) На концах последовательного соединения пяти одинаковых резисторов
большого сопротивления напряжение 120 В. Концы второго из цепочки резисторов со-
единены проводником. Оценить напряжение на первом из них?
5. (12 баллов) Как надо перенастроить оптику микроскопа (телескопа), чтобы можно
было фотографировать наблюдаемый объект?
Вариант 2010г
1. Тренируясь, спортсмен взбегает вверх по лестнице эскалатора. Поднимаясь по не-
подвижному эскалатору, он преодолевает No ступенек, а по движущемуся вверх - в 1,5
раза меньше. Сколько ступенек придётся преодолеть спортсмену, поднимаясь по эска-
латору, который движется вниз?
1151
таковых шарика связаны невесомой нерастяжимой ни-
тью, перекинутой через невесомый блок, причем один из шариков
погружен в сосуд с жидкостью. С какой установившейся скоростью
и будут двигаться шарики, если известно, что установившаяся ско-
рость падения одиночного шарика в той же жидкости равна Vo? Си-
ла сопротивления жидкости пропорциональна скорости. Плотность
жидкости равна рж, плотность материала шариков равна р.
3.Одновременно из одной то*
135
брошены два тела с одинаковыми по модулю скоро-
стями vo = Ю м/с: первое вертикально вверх, второе под углом а = 30° к горизонту. Оп-
ределите модуль скорости первого тела относительно второго V12 в момент времени,
когда второе тело достигнет % своей максимальной высоты подъёма. Сопротивлением
воздуха пренебречь.
4. Три одинаковых шарика бросают вертикально вверх из одной точки на земле с
наковыми начальными скоростями, равными vo = 30 м/с. Второй шарик бросают, когда
первый достигает наибольшей высоты, а трет
515
шарик бросают, когда первый сталки-
вается со вторым. Сколько времени будут находиться в полете первый и второй шари-
ки? Считать, что при ударах шарики обмениваются скоростями, не отклоняясь от вер-
тикали. Сопротивлением воздуха пренебречь.
142
5. Сопротивления, из которых собран участок цепи, равны Ri = 4 Ом, Ra=8 Ом, R3 = 10
Ом и R4 = 2 Ом, сопротивление перемычки АВ пренебрежимо мало. Найти ток I во
внешней цепи, если через перемычку АВ протекает ток 1П — 3 А.
Ri R3
R2
10 класс вариант 2008г
1. Тонкую пластинку, имеющую форму равностороннего треугольника АВС
раскрутили и бросили на гладкую горизонтальную плоскость так, что пластинка в мо-
мент падения на плоскость была горизонтальной. В некото-
рый момент времени скорость точки А пластинки оказалась
направленной вдоль стороны АВ, а скорость точки В - парал-
лельной стороне АС (см. рисунок).
Как направлена в этот момент скорость точки С? Чему
при этом равны модули скоростей точек В и С, если скорость
точки А равна v?
2. Оцените, как изменилась бы продолжительность земного года, если бы масса
Земли сравнялась с массой Солнца, а расстояние между ними осталось бы прежним?
3. Гантель, состоя
III
,ая из жесткого невесомого стержня с маленькими шариками
массами Зт и т на концах, находится внутри гладкой полусферической чаши, как по-
казано на рисунке.
Длина стержня равна радиусу ча
in
я. Будучи отпущенной, ган-
тель движется в вертикальной плоскости так, что шарики все
время касаются поверхности чаши.
С какой силой шарики действуют на стержень в момент, когда он горизонтален?
4. По гладкому горизонтальному проволочному кольцу могут скользить без трения две
маленькие бусинки массами т и 2т. Вначале бусинки находились в точке А кольца, как
показано на рисунке. Бусинкам сообщают начальные скорости: бусинке массой т —
143
скорость 2v, а бус*
CI
т А 2т
се массой 2т — скорость v, направленные в
противоположные стороны. В процессе своего движения бусин-
ки многократно сталкиваются друг с другом.
Считая столкновения бусинок абсолютно упругими, опре-
делите угол АОС, если С — точка, в которой оказываются бусин-
ки в момент их 101-го столкновения.
5. На гладком горизонтальном столе находится
цилиндрический сосуд длиной £, разделённый пере-
городкой на две равные части (см. рисунок). В одной
части сосуда находится кислород, а в другой - азот.
Давление кислорода вдвое больше давления азота, а
температуры од
JI5I
таковы. В перегородке открывается шторка, в результате чего газы в
сосуде перемешиваются. На какое расстояние при этом сдвинется сосуд? Массой сосу-
да и перегородки пренебречь. Процесс считать изотермическим.
144
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА ПО ПОДГОТОВКЕ К ОЛИМПИАДАМ
по математике
1. Конкурсные задачи по математике и физике: Пособие для поступающих в МГТУ им.
Н.Э.Баумана / Л.П.Паршев, А.Г. Андреев, Н.А. Гладков и Ю.А. Струков; Под ред С.В.
Белова.- М.: Ма
IIISI
построение, 1993.- 192с.
2. Справочное пособие для абитуриентов. Программы и содержание вступительных
экзаменов по физике, математике, русскому языку и литературе литература / Сост.: Бе-
лов С.В., Камалова Р.А., Паршев Л.П., Струков Ю.А.; Под ред. С.В. Белова. М.: Изд-во
МГТУ им. Н.Э. Баумана, 2001.-144с.
3. Типовые варианты заданий вступительных испыта
5 в 2003 г. математика, физика,
русский язык и литература / Сост.: Камалова Р.А., Паршев Л.П., Струков Ю.А.; Под
ред. Н.Я. Ирьянова / МГТУ им. Н.Э. Баумана. - М., 2003.-45с.
4. Власова Е.А. Показательные и логарифмические уравнения и неравенства. М.:
МГТУ им. Н.Э. Баумана, ISBN 5-7038-2900-3, 2006.-115с.
5. Краткое изложение стандартных и нестандартных методов решения задач по эле-
ментарной математике: Учеб, пособие / И.А. Соловьев, Г.В. Арутюнян, Е.В. Марчев-
ская и др. - М.: ГУЗ, 2005.-216с.
6. Ляпин А.А, Родионов Е.М, Синякова С.Л. Математика. Сборник задач. 4-е изд., пе-
рераб. и доп. - М.: Ориентир, 2006. - 392с.
7. Родионов Е.М. Справочник по математике для поступающих в вузы. Решение задач
с параметрами. - М.: МЦ "Аспект”, 1992. - 144с.
8. Элементарная геометрия. Методы решения задач : учеб, пособие / Г.В. Арутюнян,
Е.В. Марчевская, И.К. Марчевский. - М.: Изд-во МГТУ им. Н.Э. Баумана. 2010.- 222с.
зил
9. Будак А.Б., Щедрин Б.М. Элементарная математика. Руководство для постулат
в вузы. Изд. 3-е. перераб. и доп. — М. Издат. отдел УНЦ ДО, 2001 - 690 с. ISBN 5-
88800-132-5
10. Голубев В.И. Решение сложных и нестандартных задач по математике.— М:
ИЛЕКСА, 2007. - 252 с: ил.
11. Горнштейн ГЕИ., Полонский В.Б., Якир М.С. Задачи с параметрами. — К.: РИА
"Текст”; МП "ОКО”, 1992. -290 с.
12. Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для поступающих
в вузы (Избранные вопросы элементарной математики) - Изд. 5-е, перераб., 1976 - 638с.
145
13. Козко А.И., Чирский В.Г. Задачи с параметром и другие сложные задачи. - М.,
МЦНМО, 2007. - 296с.
14. Математика. Сборник задач по базовому курсу (ЕГЭ, олимпиады, экзамены в вуз).
Учебно-методическое пособие / Золотарёва Н. Д., Попов Ю. А., Семендяева Н. Л., Фе-
дотов М. В. - М.: Фойлис, 2010. - 236 с: ил. Под редакцией М. В. Федотова ISBN 978-5-
91860-009-2
15. Мельников И.И., Сергеев И.Н. Как решать задачи по математике на вступительных
экзаменах.- М.: Изд-во Моск, ун-та, 1990. - 304с.
16. Моденов В.П. Математика. Пособие для поступающих в вузы. - М., Новая волна,
2002. - 796 с.
17. Олехник С.Н. , Потапов М.К, Пасиченко П.И. Уравнения и неравенства. Нестан-
дартные методы решения: справочник. М.: Изд-во Факториал, 1997. - 219с.
18. Панферов В.С., Сергеев И.Н. Отличник ЕГЭ. Математика. Решение сложных задач;
ФИЛИ - М.: Интеллект-Центр, 2010. - 80 с. ISBN 978-5-89790-612-3
19. Потапов М. К., Олехник С. Н., Нестеренко Ю. В. Конкурсные задачи по математи-
ке: Справочное пособие.— Изд. 3-е, стер. — М.: ФИЗМАТЛИТ, 2003. — 416 с.
20. Цыпкин А. Г. Справочное пособие по математике с методами решения задач для
поступающих в вузы / А. Г. Цыпкин, А. И. Пинский. — 3-е изд., испр. — М.: ООО «Из-
дательство Оникс»: ООО «Издательство «Мир и Образование», 2007. — 640 с: ил.
ISBN 5-94666-341-0(000 «Издательство«Мир и Образование»)
21. Черкасов О. Ю., Якушев А. Г. Математика: интенсивный курс подготовки к экза-
мену. — 7-е изд. — М.: Айрис-пресс, 2003. — 432 с: ил. — (Домашний репетитор).
ISBN 5-8112-0256-3
22. Шарыгин, И. Ф. Математика для поступающих в вузы : учеб, пособие / И. Ф. Ша-
рыгин. — 6-е изд., стереотип. — М.: Дрофа, 2006. — 479, [1] с.: ил. ISBN 5-358-01163-3
23. Алгебра. Базовый курс с решениями и указаниями (ЕГЭ, олимпиады, экзамены в
вуз). Учебно-методическое пособие / Золотарёва Н. Д., Попов Ю.А., Семендяева Н. Л.,
Федотов М. В. - М.: Фойлис, 2010. - 568 с: ил. (Под редакцией М. В. Федотова ISBN
978-5-91860-008-5)
24. Геометрия. Базовый курс с решениями и указаниями. (ЕГЭ, олимпиады, экзамены в
вуз).: Учебно-методическое пособие / Золотарёва Н. Д., Семендяева Н. Л., Федотов М.
В. - М: Изд-во Фойлис, 2010. - 296 стр. : ил. (Под редакцией М. В. Федотова ISBN 978-
5-91860-004-7)
146
25. Сборник задач по математике для поступающих во втузы (с решениями). В 2-х
книгах. Кн. 1. Алгебра. /Егерев В.К., Кордемский Б.А., Зайцев В.В. и др. Под ред. М.И.
Сканави . - 7-е изд., перераб. и доп. - М., Высш.шк., 1994. _ 528 с.
26. Сборник задач по математике для поступающих во втузы (с решениями). В 2-х
книгах. Кн. 2. Геометрия /Егерев В.К., Кордемский Б.А., Зайцев В.В. и др. Под ред.
М.И. Сканави . - 7-е изд., перераб. и доп. - М., Высш.шк., 1995. _ 368 с.
27. Олимпиада «Ломоносов» по математике (2005—2008). — М.: Издательство ЦПИ
при механико-математическом факультете МГУ, 2008. — 48 с, илл.
28. Всероссийская олимпиада школьников по математике 1993-2006; Окружной и фи-
нальный этапы / Под ред. Н.Х. Агаханова - М.: МЦНМО, 2007. - 472с.
по физике
29. Сборник тем научных работ для участников научно-образовательного соренования
«Шаг в будущее, Москва». - М.: Ml ТУ им. Н.Э.Баумана, 2010. - 104 с.
30. Сборник организационных и методических материалов для профильных школ и
поступающих в МГТУ им. Н.Э.Баумана. - М.: МГТУ им. Н.Э.Баумана, 2010. - 20 с.
31. Сборник лу^
ш
их работ Одиннадцатой научной конференции «Шаг в буду-
щее,Москва» - М.: МГТУ им. Н-Э.Баумана, 2008. - 256 с.
32. Бендриков Г.А., Буховцев Б.Б., Керженцев В.В., Мякишев Г.Я. Задачи по физике
для поступающих в вузы. - М.: Наука, 1987. - 384 с.
33. Буховцев Б.Б., Кривченко В.Д., Мякишев Г.Я., Сараева И.М. Сборник задач по
элементарной физике. -М.: Наука, 1987. -415 с.
34. Бутиков Е.И., Быков А.А., Кондратьев А.С. Физика для поступающих в вузы. - М.:
Наука, 1979. - 608 с.
35. Дмитриев С.Н., Васюков В.И., Струков Ю.А. Физика: сборник задач для посту-
пающих в вузы. Изд. 5. - М.: Ориентир, 2003. - 208 с.
36. Задачи вступительных экзаменов. / Сост.: А.А.Егоров, В.А.Тихомирова. - М.: Бюро
Квантум, 2008. - 176 с.
37. Яворский Б.М., Селезнев Ю.А. Справочное руководство по физике для поступаю-
щих в вузы и самообразования. - М., 1979. - 512 с.
147
Оглавление
Предисловие..............................................................3
Раздел 1. Общие сведения и методические материалы по проведению Олимпиады
школьников «Шаг в будущее» (физика, математика)..........................6
1.1. Алгоритм и технология проведения соревнования (мероприятия)..6
1.2. Основополагающие документы и регламент проведения Олимпиады «Шаг
в будущее»........................................................7
1.3. Методика проведения Академического соревнования..............8
1.4. Порядок проведения олимпиады................................10
1.5. Структура, содержание и правила оценивания олимпиадных заданий.13
Раздел 2. Математика....................................................16
2.1. Содержание варианта задания олимпиады по математике в МГТУ
им. Н.Э. Баумана.................................................16
2.2. Примеры задач первого уровня сложности.....................16
Текстовые задачи.............................................16
Прогрессии...................................................18
Логарифмические и показательные уравнения....................18
2.3. Примеры задач второго уровня сложности.................... 20
Неравенства..................................................20
Тригонометрия................................................21
Множества значений функций...................................22
2.4. Примеры задач третьего уровня сложности:...................23
Планиметрия..................................................23
Задачи на производную........................................25
Задачи с параметрами.........................................27
Стереометрия.................................................28
2.5. Примеры вариантов заданий олимпиады. I этап олимпиады школьников.
Вариант № 1......................................................30
2.6. Решения варианта №1........................................30
2.7. Вариант № 2................................................36
2.8. Решения варианта №2........................................36
2.9. Заключительный этап олимпиады. Математика. Вариант № 3.....40
2.10. Решения варианта №3........................................41
148
2.11. Вариант № 4..........................................
2.12. Решения варианта №4..................................
2.13. Типовые задания для самостоятельного решения Вариант № 5
2.14. Вариант № 6..........................................
2.15. Вариант № 7..........................................
2.16. Вариант № 8..........................................
Раздел 3. Физика..................................................
50
51
56
57
58
59
61
3.1. Содержание варианта задания олимпиады по физике в МГТУ им. Н.Э.
Баумана...........................................................61
3.2. Примеры вопросов качественного характера.....................62
3.3. Примеры задач первого уровня сложности.......................65
3.4. Примеры задач второго уровня сложности.......................73
3.5. Примеры задач третьего уровня сложности......................81
3.6. Примеры вариантов задании олимпиады. I этап олимпиады школьников.
Вариант № 1.......................................................89
3.7. Решения варианта №1..........................................91
3.8. Заключительный этап олимпиады. Вариант № 2...................94
3.9. Решения варианта №2..........................................95
3.10. Вариант № 3.................................................98
3.11. Решения варианта №3........................................100
3.12. Вариант № 4................................................105
3.13. Решения варианта №4........................................107
Раздел 4. Физико — математическая олимпиада школьников 8-10 классов......113
4.1. Математика 10 класс вариант 2009г...........................113
4.2. Решение и ответы варианта 2009г.............................114
4.3. Вариант 2010г...............................................121
4.4. Решения варианта 2010г......................................122
4.5. 8 класс вариант 2006г.......................................124
4.6. Решение варианта 2006г......................................125
4.7. Вариант 2010г...............................................126
4.8. Решения варианта 2010г......................................128
4.9. Варианты для самостоятельного решения Вариант 2008г.........130
9 класс вариант 2010г.......................................131
4.10. Физика 10 класс вариант 2009г..............................132
149
4.11. Решение варианта 2009г......................................133
4.12. Вариант 2010г...............................................136
4.13. Решение варианта 2010г......................................137
4.14. Варианты для самостоятельного решения 8 класс вариант 2008г.140
9 класс вариант 2009г........................................141
Вариант 2010г................................................142
10 класс вариант 2008г.......................................143
Рекомендуемая литература по подготовке к Олимпиадам......................145
по математике.....................................................145
по физике.........................................................147
150
МОСКОВСКИМ ГОСУДАРСТВЕННЫМ ТЕХНИЧЕСКИМ
УНИВЕРСИТЕТ ИМЕНИ Н.Э.БАУМАНА
105005, г. Москва, 2-я Бауманская ул., д. 5
Главный корпус, 3 этаж, ком. 374
Телефоны: +7(499)263-68-12
E-mail: cdp@bmstu.ru
Сайт: http://cendop.bmstu.ru/
Центр довузовской подготовки
подготовка и профессиональное обучение довузовской молодежи
МГТУ им. Н.Э.Баумана
В
пгт» !.•••,
Основная цель деятельности Центра заключается
в научно-методическом обеспечении и координации
работы Университета, связанной с планированием,
подготовкой и проведением мероприятий, направленных
на обеспечение и формирование нового набора студентов в
Университет. z
Довузовская работа строится как
образовательная система «школа—вуз»
в различных организационных формах.
непрерывная
и проводится
ПРОФИЛЬНЫЕ УЧЕБНЫЕ ЗАВЕДЕНИЯ
(всего более 200)
Между МГТУ им. Н.Э.Баумана и профильными
школами осуществляется тесное учебно-
методическое, научно-методическое и
организационное взаимодействие; ведется активная
профориентационная работа с учащимися,
предлагаются контрольно-диагностические работы,
участие в олимпиадах и научно-образовательных
мероприятиях (начиная с 8 класса), проводимых
Университетом.
*/ ‘ д Z
НАУЧНО-ОБРАЗОВАТЕЛЬНЫЕ
ШКОЛЫ-ЛАБОРАТОРИИ
Организуются в целях расширения
профессиональной ориентации школьников,,
повышения заинтересованности молодежи в
получении инженерного образования. В программе
школ-лабораторий:
• знакомство с кафедрами;
• мастер-классы ведущих исследователей и
ученых;
• экскурсии на предприятия с демонстрацией
инновационных технологий и продуктов.
НАУЧНО-ОБРАЗОВАТЕЛЬНЫЕ
И АКАДЕМИЧЕСКИЕ СОРЕВНОВАНИЯ
Управление ежегодно ведет работу по
выявлению, привлечению и отбору наиболее
способных к дальнейшему обучению в МГТУ им
Н.Э.Баумана школьников, проводит научно-
образовательное соревнование «Шаг в будущее,
Москва» и академическое соревнование
«Профессор Жуковский» (по направлению «техниы
и технологии»), осуществляет организационную,
методическую и научную подготовку к проведению
научных и образовательных мероприятий.
ЦЕЛЕВОЙ НАБОР
Целевой набор осуществляется в рамках системы
непрерывного профессионального образовании
«школавузпредприятие» в интересах Оборонно
промышленного комплекса. В осуществлении
целевой подготовки в МГТУ им. Н.Э.Баумана
участвуют предприятия Государственной
корпорации по атомной энергии «Росатом»
Федерального космического агентства «Роскосмос»
и Министерства промышленности и торговли
Российской Федерации.