ИЗДАТЕЛЬСТВО
«МИР»

SUPERCONDUCTIVITY
OF METALS
AND ALLOYS
P. G. DE GENNES
Faculte des Sciences,
Orsay, France
W. A. BENJAMIN, INC.
NEW YORK-AMSTERDAM
1966

П. ДЕ ЖЕН ¦
Сверхпроводимость
металлов
и сплавов
Перевод с английского
А. И. РУСИНОВА
Под редакцией
Л. П. ГОРЬКОВА
Издательство „МИР*
Москва 1968

УДК 539.2
Явление сверхпроводимости, открытое свыше 50 лет и на-
нашедшее объяснение около 10 лет назад, получает все более
широкое применение. Расширяются также экспериментальные и
теоретические исследования сверхпроводящих материалов.
Предлагаемая читателям книга французского физика Де Жена
в живой и физически ясной форме освещает важнейшие свой-
свойства сверхпроводников и современные теоретические предста-
представления, лежащие в основе интерпретации наблюдаемых эффектов
и расчетов устройств для практических применений.
Кинга рассчитана на физиков и инженеров, занимающихся
экспериментальными исследованиями сверхпроводников, и сту-
студентов, приступающих к изучению сверхпроводимости.
ИНДЕКС 2-3-6
Редакция литературы по физике

ОТ РЕДАКТОРА ПЕРЕВОДА
Книга известного французского физика-теоретика П. Де Жена
представляет собой очень интересное явление. В ее основе лежит
курс лекций по теории сверхпроводимости, рассчитанный на физиков,
достаточно образованных, но с физикой сверхпроводников не знако-
знакомых. Нам кажется, что сейчас это лучшая книга, по которой можно
действительно разобраться в самом явлении сверхпроводимости, по-
почувствовать ее реальные проблемы — экспериментальные и теоретиче-
теоретические. Книга живо написана, насыщена содержанием, хотя изложение
местами отрывочно, а иногда небрежно.
Книга очень конкретна. Сейчас, когда прошло около десятка лет
после создания микроскопической теории сверхпроводимости, для мно-
многих физиков достаточно знать основные идеи теории и быть уверен-
уверенными, что с этой теорией все в порядке. С другой стороны, различные
физические приложения сверхпроводимости становятся все более и более
существенными. Для этих приложений совершенно необязательно пускать
в ход весь громоздкий механизм микроскопической теории. Боль-
Большинство явлений может быть описано на весьма простой основе.
По моему мнению, этот момент является самой сильной стороной
книги Де Жена. Излагая очень сжато, но в то же время очень по-
понятно и просто основные идеи современной теории сверхпроводимо-
сверхпроводимости, автор сумел вместить в небольшую по объему книгу решение
Огромного количества физических задач.
Отметим, что автор, ссылаясь на те или иные оригинальные ра-
работы, часто не приводит библиографических данных. В большинстве
случаев это сделано переводчиком. Кроме того, в русском издании до-
добавлен ряд новых ссылок и дано несколько редакционных примечаний.
Для русского издания автор любезно прислал краткое предисловие
и ряд уточнений и дополнений к тексту. Считаю своим приятным
долгом поблагодарить его за это.
Член-корреспоидент АН СССР
Л. П. Горькое

ПРЕДИСЛОВИЕ
В основе этой книги лежат записи лекций, прочитанных автором в Орсэ
в период 1962—1963 гг. Этот курс лекций носил вводный характер, и глаз-
иая цель его состояла в том, чтобы ознакомить экспериментаторов и теоре-
теоретиков нашей небольшой группы (включая лектора) с основными сведениями
о сверхпроводимости и, исходя из этого, качать планирование новых экспе-
экспериментов.
Вполне возможно (и такой путь нам казался заманчивым) подойти
к явлению сверхпроводимости как к новому случаю дальнего порядка и за-
затем из рассмотрения фазы параметра упорядочения вывести сверхтекучиз
свойства, квантование потока и эффект Джозефсона. Несколько позднее
можно было бы получить уравнения Гинзбурга—Ландау и обсудить магнит-
магнитные свойства сверхпроводников. Наконец, сделав целый ряд конкргтных
допущений, можно было бы прийти к теории Бардина — Купера — Шриф-
фера и ее применениям.
Однако нам в Орсэ хотелось как можно скорее приступить к экспе-
экспериментам по сверхпроводимости, поэтому мы даже не пытались осуще-
осуществить вышеуказанный подход. Изложение начинается с элементарного
обсуждения магнитных свойств сверхпроводников первого и второго рода.
Потом строится микроскопическая теория на основе боголюбовского пред-
представления самосогласованного поля; такой подход оказывается достаточно
общим, чтобы при рассмотрении охватить интересные ситуации, в которых
параметр порядка модулирован в пространстве. Кроме того, этот метод по-
позволяет в какой-то мере сохранить интуитивные представления, основанные
на одночастичных волновых функциях. На этой стадии параллельно со свой-
свойствами чистых металлов систематически обсуждаются свойства сплавов, и
в частности так называемых .грязных" сплавов. (Последние, несмотря на на-
название, являются зачастую наиболее чистыми системами, с которыми нам уда-
удается экспериментировать.)
Ряду вопросов мы сознательно уделили мало внимания. Так, до мини-
минимума сведено обсуждение электрон-электронных взаимодействий, поскольку
для большинства металлических сверхпроводников (как и для случая ферро-
ферромагнитных металлов) до настоящего момента не удается строго вычислить
значения фундаментальных констант связи. Мы не касаемся такжз моделей,
которые в прошлом оказались весьма полезными, но редко применяются в но-
новых работах; примерами такого рода могут служить теория Гортера — Кази-
Казимира, ламинарная модель смешанного состояния сверхпроводников второго

8 Предисловие
рода. Некоторые другие вопросы ие обсуждаются потому, что для их рас-
рассмотрения требуется более высокий теоретический уровень, чем принятый
в наших лекциях; к ним относятся, в частности, эффекты так называемой
„сильной связи", вопрос о возбужденных состояииях куперовских пар и эф-
эффекты, связанные с разрушением анизотропии параметра порядка в А-про-
страистве при внесении примесей.
Книга в ее иастоящем виде представляет результат усилий многих лиц(
прямо или косвенно участвовавших в ее создании. Обсуждение обобщенного
метода самосогласованного поля примен ительно к ядрам, проводившееся на
семинаре, руководимом К. Блохом, явилось исходной точкой при написа-
написании гл. V. Короткая заметка П. Андерсон а о спин-орбитальных эффектах по-
послужила основой для используемого нами подхода к проблемам, касающимся
•грязных' сверхпроводников. Группа в Орсэ в составе Ж. Бурже, Г. Дей-
чера, Е. Гийона, К. Кароли, А. Мартинэ, Ж. Матрикона совместно с нашими
друзьями Д. Сент-Джеймсом, Г. Сарма, М. Тинкхамо.и и П. Пинкусом уча-
участвовала в обсуждении и уточнении разделов, в которых затрагиваются по-
последние достижения. Автор хотел бы выразить каждому из них свою глубо-
глубокую благодарность и особо упомянуть П. Пинкуса, взявшего на себя труд
по подготовке американского издания, а также М. Тинкхама, критически
прочитавшего окончательный вариант рукописи.. Автор надеется, что вооду-
воодушевление, которое мы испытывали в тот период догадок и споров, в какой-то
мере передастся читателю и найдет в нем отклик.
В конце каждой главы приведено очень ограниченное число ссылок
на дополнительную литературу. Они ие претендуют иа полноту и ие учиты-
учитывают вопросов приоритета: например, я всегда рекомендовал студентам
не оригинальную статью Бардина, Купера и Шриффера, а лекции Тиикхама,
прочитанные в летней школе физики в Лезуш, в которых материал изла-
излагается в более доступной форме.
П. Де Жен
Орсэ,
октябрь 1965
К РУССКОМУ ИЗДАНИЮ
Я хотел бы выразить глубокую благодарность А. Русинову,
выполнившему перевод книги на русский язык, и редактору русского
издания проф. Л. Горькову. Мне кажется, что такие объединенные уси-
усилия физиков разных стран являются типичным примером между-
международной солидарности ученых, которую мы должны стремиться вся-
всячески развивать и поддерживать.
П. Де Жен

Глава I
ФУНДАМЕНТАЛЬНЫЕ СВОЙСТВА
§ 1. НОВЫЙ ТИП КОНДЕНСИРОВАННОГО СОСТОЯНИЯ
Возьмем кусок олова и охладим его; при определенной темпера-
температуре ГС = 3,7°К мы обнаружим скачок его теплоемкости (фиг. \,а).
Очевидно, что при более низких температурах (Т < Тс) олово нахо-
находится в новом термодинамическом состоянии. Что же произошло?
Этот переход не связан с изменением кристаллической структуры.
Об этом мы знаем из данных рентгеновского анализа. Он также
не имеет ничего общего с ферро- или антиферромагнитным пере-
переходом. (С помощью магнитного рассеяния нейтронов можно убедиться
в том, что атомы олова не приобретают магнитного момента.) По-
Поразительной особенностью этого перехода является то обстоятельство,
что в новом состоянии электрическое сопротивление олова равно
нулю. (Например, наблюдалось, что ток, наведенный в кольце из олова,
циркулировал в нем свыше года без затухания.) Таким образом, олово
в этой новой особой фазе становится, как говорят, сверхпроводни-
сверхпроводником, а незатухающий ток в нем называют сверхпроводящим током.
Сверхпроводниками может быть большое число металлов и сплавов,
причем критическая температура Тс меняется в пределах 0,1° К ^Гс<
< 18° К1'• Недавно было обнаружено, что некоторые сильно легиро-
легированные полупроводники также являются сверхпроводниками2*. Исто-
Исторически первый сверхпроводник (ртуть) был открыт Камерлинг-Онне-
сом [1] в 1911 г.
На основе опытных данных по теплоемкости можно вычислить
плотность свободной энергии Fs сверхпроводящей фазы; на фиг. 1, б
она представлена сплошной линией. Пунктирная линия изобра-
изображает соответствующую кривую Fn нормального металла. Разность
(Fn—Fs)t=o носит название энергии конденсации; в расчете на один
электрон она равна по порядку величины (&bTcJ/?>. что сущест-
существенно меньше энергии Ь,вТс (Ер — фермиевская энергия электронов
проводимости в нормальном металле). Используя типичные значе-
значения Ер~\эв и АвГс~10~3эв, находим, что доля проводящих элект-
электронов, заметно изменяющих свою энергию в процессе конденсации,
весьма мала и составляет величину ~ квТс1Ер <~10~3.
[) В соединениях Nb3Al -f- Nb3Oe получена наиболее высокая в настоя-
настоящее время температура перехода, равная 20,4° К [2]. — Прим. ред.
2)См. [3,4].-/Грим. ред. ' ¦

(KeTcI
T
Фиг. 1. Поведение термодинамических величин при сверхпроводящем пе«
реходе.
с — температурная зависимость электронной теплоемкости сверхпроводника С (в расчете на
один атом) в отсутствие магнитного поля. Выше Т? (нормальная фаза) теплоемкость линейна,
С ~ ft2 Т/Ер. При ннзкнх температурах Т <g Tc теплоемкость меняется по экспоненциальному
закону С ~ ехр (-1,767^/Г); в точке перехода Т = Т? имеется скачок теплоемкости,
б—температурная зависимость плотности свободной энергии (в расчете на один атом) сверх-
сверхпроводящейi if ) и нормальной (Fn) фаз. Кривые касаются в точке перехода Г = 'с- ПриГ^О
разность Fn~Fs имеет порядок (ЬвтсJ1ЕР-

Фундаментальные свойства П
§ 2. ДИАМАГНЕТИЗМ
Уравнение Ф. и Г. Лондонов
Распространим теперь начатое выше энергетическое рассмотрение
на тот случай, когда в образце имеются сверхпроводящие токи с плот-
плотностью ls(r) и связанные с ними магнитные поля h(rIJ. Мы увидим,
что в пределе, когда все поля, токи и т. д. являются слабыми и
медленно изменяются в пространстве, условие минимума свободной
энергии приводит к простому соотношению между полями и токами
(Ф. Лондон и Г. Лондон [5, 6J, 1935 г.).
Для этого рассмотрим чистый металл с параболической зоной про-
проводимости; эффективная масса электронов равна т. Свободная энер-
энергия имеет теперь следующей вид:
A.1)
где Fs — отнесенная к единице объема энергия электронов в конден-
конденсированном состоянии в системе покоя, а Екка — кинетическая энер-
энергия, связанная с незатухающими токами. Обозначим через v(r) ско-
скорость дрейфа электронов в точке г. Она связана с плотностью
тока ]s соотношением
A.2)
где е — заряд электрона, ns — число „сверхпроводящих" электро-
электронов в 1 см3 вещества. Кинетическую энергию можно записать в сле-
следующем простом виде:
1 Г
A.3)
где интеграл берется по объему образца. Выражение A.3) было бы
точным в случае однородного течения (v = const); в рассматриваемой
задаче оно остается справедливым приближенно при условии, что ско-
скорость v (г) — медленно меняющаяся функция г (позже мы вернемся
к этому ограничению).
Наконец, энергия Еы!а.н, связанная с магнитным полем h(r), опре-
определяется соотношением
?магн =J-?tfr. A.4)
Поле h связано с плотностью тока js уравнением Максвелла
A.5)
') Мы используем h для обозначения локального поля; символ Н сохра-
сохранен для обозначения термодинамического поля.

У2 Глава 1
Используя A.3)—A.5), представим свободную энергию &" в виде
<Г=<^0+т?г [ (h2 + ^|roth|2)firr.
<^0= ) Fsdr,
где величина kL, имеющая размерность длины, определяется следую-
следующим образом:
тс2 У12 п 7л
) A7)
(при JT=O имеем ns=n, где п — полное числе электронов прово-
проводимости в 1 см3). С помощью этого выражения мы можем оценить
значение ki. Для простых металлов, например Al, Sn и т. п., в ко-
которых масса т близка к массе свободного электрона, нахо-
находим ki —500 А. В переходных металлах и соединениях с узкой d-зо-
ной масса т больше, соответственно больше длина A,t (до 2000 А).
Будем теперь минимизировать свободную энергию A.6) относи-
относительно распределения поля h (г). При изменении поля h (г) на вели-
величину 6h(r) энергия $~ меняется на "
== ^ J (h -+- kl rot rot h) • 6h dx. A.8)
(Второй член мы проинтегрировали по частям.) Следовательно, кон-
конфигурация поля внутри образца, приводящая к минимуму свободной
энергии, должна удовлетворять уравнению
h-|-*lrotroth = 0. A.9)
Уравнение A.9) впервые было предложено (в несколько иных обо-
обозначениях) Ф. Лондоном и Г. Лондоном. Совместно с уравнением
Максвелла A.5) оно позволяет находить распределение полей и
токов.
Эффект Мейсснера
Применим теперь уравнение Лондонов A.9) к задаче о проникно-
проникновении магнитного поля h в сверхпроводник. Выберем простейшую
геометрию: поверхность образца совпадает с плоскостью ху, область
г < 0 является пустой (фиг. 2). Тогда поле h и ток \s зависят лишь
от z. Помимо уравнения A.9), имеют место, как обычно, уравнения
Максвелла
Возможны два случая:
-^j* A.10)
С
divh = 0. A.11)

Фундаментальные свойства
13
1. Поле h параллельно оси г. Тогда уравнение A.11) дает
просто dhjdz = 0, т. е. поле h постоянно в пространстве. Поэтому,
как следует из уравнения A.10), roth = 0 и js = 0. Подставляя этот
результат в уравнение A.9), находим, что h=0, т. е. поле не мо-
может быть нормально к поверхности образца.
Вануум ¦
Сверхпроводник -
Фиг. 2. Проникновение слабого магнитного поля в сверхпроводник (А. —
глубина проникновения поля).
На расстояниях, в несколько раз превышающих глубину проникновения К, поле становится
пренебрежимо малым. В тех случаях, когда справедливо лондоновское уравнение A.9), поле
изменяется экспоненциально [Л=Лоехр(—*/?¦?)]•
2. Поле h тангенциально (и направлено вдоль оси лг). В этом
случае уравнение A.11) удовлетворяется автоматически, а из уравне-
уравнения A.10) следует, что ток js направлен вдоль оси у
¦? = ^7, A-12)
Наконец, уравнение A.9) дает
~dz
d2h ±_
тс
me
A.13)
A.14)
Решение, конечное внутри сверхпроводника, является экспоненциально
убывающим:
h(z) = h(fi)e-zlhL, A.15)
т. е. внутрь образца поле проникает лишь на глубину Xl- Этот
результат, полученный для полупространства, легко обобщить на слу-
случай макроскопического образца произвольной формы. Как мы уже

J4 Глава I
видели, „глубина проникновения" kL мала, поэтому для любой геомет-
геометрии слабое магнитное поле практически совсем не проникает
в макроскопический образец1' (т. е. образец, размеры которого велики
по сравнению с глубиной проникновения). Силовые линии вытесняются
образцом, как это показано на фиг. 3.
Фиг. 3. Выталкивание магнитных силовых линий макроскопическим сверх-
сверхпроводником (т. е. сверхпроводником, размеры которого значительно пре-
превышают глубину проникновения).
В не слишком сильных полях сверхпроводник выталкивает силовые линии полностью (эффект
Мейсснера).
В равновесии сверхпроводник находится в состоянии, в кото-
котором сумма кинетической и магнитной энергий минимальна; для ма-
макроскопических образцов это состояние отвечает полному вы-
выталкиванию наружу магнитного потока.
Выталкивание силовых линий было обнаружено в 1933 г. в опытах
Мейсснера и Оксенфельда [7]. Эти результаты особенно важны тем,
что была доказана истинная равновесность достигнутого состояния.
Относительно приведенного вывода необходимо сделать три за-
замечания:
1. Предположив существование незатухающих токов в термоди-
термодинамически равновесном состоянии, мы пришли к заключению о на-
наличии у сверхпроводников диамагнитных свойств. Более привычным,
однако, является обратный ход рассуждений, когда в качестве от-
') В более сильном поле этот результат можег оказаться полностью
или частично неверным.

Фундаментальные свойства 15
правного момента берется эффект Мейсснера, а затем делается вывод
о существовании незатухающих токов. Я предпочел первый способ,
поскольку хотел на этом примере показать, из каких частей соста-
составляется полная энергия сверхпроводника [см. A.6)], что будет по-
полезно в дальнейшем (гл. III).
2. Уравнение A.9) мы получили из условия минимума свободной
энергии <^". являющейся правильным термодинамическим потенциалом
для случая, когда внешнее поле создается постоянными магнитами.
В том случае когда источником поля служит катушка с заданным то-
током /, правильным термодинамическим потенциалом является не 4?',
а так называемый термодинамический потенциал Гиббса ??1). К счастью,
можно показать, что оба потенциала приводят к одинаковому условию
локального равновесия в образце (обсуждение этого вопроса см. в гл. II).
3. Отметим, что вышеприведенный расчет справедлив лишь при
условии, что приложенное поле является достаточно слабым. В более
сильных полях энергетически выгодным может оказаться разрушение
сверхпроводимости в некоторых областях образца и связанное с ним
проникновение в сверхпроводник силовых линий магнитного поля-
Детально этот вопрос будет рассмотрен в гл. II и III.
§ 3. ОТСУТСТВИЕ ВОЗБУЖДЕНИЙ МАЛЫХ ЭНЕРГИЙ
Рассмотрим сначала газ свободных невзаимодействующих электро-
электронов. Состояние индивидуального электрона характеризуется импуль-
импульсом р и энергией p2j2m. Основное состояние всей системы можно по-
получить, помещая в соответствии с принципом Паули электроны в каж-
каждое состояние р так, чтобы все состояния, лежащие ниже энергии
Ферми, оказались заполненными, а выше — пустыми. (Условие р == рр
определяет в пространстве импульсов сферу Ферми.) Чтобы получить
возбужденное состояние газа, достаточно переместить электрон из
первоначально занятого состояния р (р ^ рЛ в пустое р' (р' > рр)
1) В дальнейшем читатель все время будет сталкиваться с терминами
.потенциал Гиббса", „термодинамический потенциал Гиббга". Следует помнит-.,
что в книге при этом имеется в виду потенциал свободной энергии во вне-
внешнем поле, причем в каждой конкретной задаче используются в качестве
независимой переменной либо Н, либо В. Это разные потенциалы, и их точ-
точное термодинамическое определение читатель найдет в книге Ландау и Лиф-
шица [8]. Чтобы не употреблять слишком громоздких названий, при переводе
чаще всего использовалось в соответствии с оригиналом название .потен-
.потенциал Гиббса". При чтении книги это не вызывает никаких недоразумений.
Стоит еще, может быть, заметить, что в качестве „обычных" независимых
переменных автор берет V и Т, тогда как в экспериментальной практике
сверхпроводящий переход происходит при постоянном давлении. Как известно,
изменением объема при переходе металл — сверхпроводник также можно пре-
пренебречь. Поэтому все дальнейшее изложение ведется достаточно корректно,
если иметь в виду практические приложения. — Прим. ред.

16
Глава I
(фиг. 4). Энергия, необходимая для возбуждения такой электрон-
дырочной пары, равна
т Е*=Р'22~т~Р2>°- A16>
Если оба импульса р и р' лежат близко к поверхности Ферми, то
энергия Ерр/ мала. Иными словами, в газе свободных электронов име-
имеется огромное число возбуждений с малыми энергиями. В нормаль-
нормальном металле картина свободного газа электронов качественно не ме-
меняется. Наличие возбуждений малых энергий проявляется в следующих
экспериментальных результатах:
Дырка
Электрон
Фиг. 4. Возбужденное состояние электронного газа в нормальном металле,
возникающее в результате перемещения электрона из состояния с импуль-
импульсом р внутри ферми-сферы в состояние р' снаружи от иее.
Если импульсы р и р' близки по величине к фермиевскому импульсу pp=hhp, то энергия
возбуждения (р'2 —р')/2/л мала.
а) Теплоемкость нормального металла пропорциональна темпера-
температуре Т и сравнительно велика [порядка /гвСквТ/Ер) на один электрон].
б) При воздействии на систему электронов внешних возмущений
малой частоты (электромагнитных волн, ультразвука, прецессии ядер-
ядерного спина и т. д.) в ней возникают сильные диссипативные процессы.
Для большинства сверхпроводников дело обстоит совершенно
иначе. В этом случае выражение A.16) более непригодно для опре-
определения энергии Ерр, необходимой для рождения пары возбуждений; по-
последняя, во всяком случае, должна превышать вполне определенную
величину, равную „энергии спаривания" 2Д:
?РР,>2Д. A.17)
Эта „щель" 2Д связана с температурой перехода приближенным со-
соотношением 2k — 3,5kBTc. Типичное значение 2Д имеет порядок 10° К
(как видно из табл. 1).

Фундаментальные свойства
17
Таблица I
Величина энергетической щели при абсолютном
нуле*
Металл
Zn
Cd
Hg
Al
In
Oa
Sn
Pb
V
Nb
Та
2A, °K
I
1,8
18,4
6,01
13,6
13,0
28,7
18,0
27,4
II
3,17
4,4
11,9
4,03
18,5
37,4
15,7
Ш
18,0
4,2
11,9
12,9
30,9
18,0
35,0
16,1
• Данные взяты из работы [9|. Величина 2Д определялась
следующими методами: I—поглощение фотонов микроволновой
или далекой инфракрасной области; И —затухание ультразвука
(ультразвуковые эксперименты часто проводятся иа монокристал-
монокристаллах, поэтому величина щели в этом случае может несколько за-
зависеть от направления распространения звуковой волны); III —
туннельные эксперименты-
Заметим, что 2Д—минимальная энергия, требуемая для рождения
пары возбуждений; энергия, приходящаяся на одно возбуждение,
равна Д.
Величина Д измеряется на опыте с помощью целого ряда различ-
различных методов. Здесь мы укажем на некоторые из них:
1. Измерения теплоемкости при низких температурах. Теплоем-
Теплоемкость изменяется экспоненциально как ~ ехр (— Д//гвТ).
2. Измерение поглощения электромагнитного излучения. Фотон
с частотой to может создать электронно-дырочную пару лишь при
условии, что М>]> 2Д (фиг. 5, а). (Это соответствует фотонам далекой
инфракрасной области; типичные длины волн лежат в миллиметровом
диапазоне.)
3. Затухание ультразвука. В этом случае фотон имеет низкую
частоту, поэтому его распад с образованием пары возбуждений невоз-
невозможен. Однако фотон может поглотиться при столкновении с уже
существующим возбуждением (фиг. 5, б); вероятность такого процесса
пропорциональна числу имеющихся возбуждений и при низких темпе-
температурах мала, — ехр (— A/kBT).
4. Туннельный эффект. Сверхпроводник 5 и нормальный металл
N разделены тонким непроводящим слоем (толщина обычно около
2 Зак. 1020

18 Глава I
25 А), который создает энергетический барьер между ними (фиг.
6, а). Однако существует конечная вероятность прохождения элек-
электронов через этот барьер (туннельный эффект). При этом электрон
должен быть возбужден из конденсированной фазы, что требует
затраты энергии, равной Д. Следовательно, при низких температурах
Возбуждение
Фотон
Возбуждение
» Возбуждение
Возбуждение
Фиг. 5. Типичные процессы, приводящие к диссипации энергии в сверх-
сверхпроводнике.
о —порождение фотоном пары возбуждений (процесс вэзмэжеи лишь прн йи > 2Д). б —погло-
—поглощение фотонов имеющимися возбуждениями. Этот процесс может произойти даже в том слу-
случае, когда йи < 2Д. При низких температурах число тепловых возбуждений мало и такой про-
процесс идет медленно. Аналогичные процессы имеюг место при замене^фотона иа фонон.
( Тс) ток практически отсутствует до тех пор, пока величина
eV, т. е. энергия, которую приобретает электрон за счет приложен-
приложенной к барьеру разности потенциалов V, не станет больше Д. Типич-
Типичная вольтамперная характеристика показана на фиг. 6, б (сопротив-
(сопротивление V// контакта размером 1X1 мм2 в нормальном состоянии
лежит в пределах от 10~2 до 104 ом).
Возникает вопрос: является ли наличие энергетической щели необходи-
необходимым условием для существования незатухающего тока („сверхтекучести"
электронного тока)? На этот вопрос следует ответить отрицательно — извес-
известен ряд примеров, когда эта „сверхтекучесть" имеет место, даже если нет
щели в спектре элементарных возбуждений. Простейшим примером может
служить так называемая „поверхностная сверхпроводимость". Явление со-
состоит в том, что некоторые металлы или сплавы в определенной области

Фундаментальные свойства
19
значений магнитного поля являются сверхпроводящими лишь в узком слое
(толщиной ~> 1000А) вблизи поверхности образца. В этом случае отсутствует
щель в энергетическом спектре всей системы. Возбуждения могут „проса-
„просачиваться" из внутренних (нормальных) областей на поверхность образца.
Приповерхностный слой остается тем не менее в сверхпроводящем состоя-
состоянии. (Это заключение было проверено недавно в экспериментах по туннель-
туннельному эффекту.) Имеются также и другие примеры; некоторые из них мы
обсудим позже.
е
О-
Сверхпроводник
Нормальный
металл
"Z5A
а
Нормальное
состояние
Оксидный слой
Сверхпроводящее
состояние
Фиг. 6. Туннельный контакт между нормальным металлом и сверхпровод-
сверхпроводником.
о —геометрия системы; б —вольтамперные характеристики для случаев, когда S-стороиа явля-
является сверхпроводящей (Г <^ Г^) или нормальной (Т > Т?у Если оба металла находятся в нор-
нормальном состоянии, сопротивление перехода размером 1X1 -М- лежит обычно в пределах
от 10 ом до 104 ом. При низких температурах Т <^Т? для извлечения одного электрона из
сверхпроводящего конденсата требуется минимальная энергия Д» поэтому при eV < Д ток
практически отсутствует.
§ 4. ДВА ТИПА СВЕРХПРОВОДНИКОВ
При выводе уравнения Лондонов A.9) мы предположили, что
скорость v(r), или, то же самое, плотность сверхпроводящего тока
медленно изменяется в пространстве. Здесь мы хотели бы

20 Глава 1
уточнить, что надо понимать под словами „медленно изменяется".
В конденсированной системе скорости двух электронов 1 и 2 кор-
релированы, если расстояние между ними Rl2 меньше определенной
величины; для чистых металлов эта корреляционная длина обознача-
обозначается через |0. Наш вывод справедлив, когда скорость v(r) мало
меняется на расстояниях порядка |0. Для оценки ?0 заметим, что
область существенных значений импульсов электронов задается не-
неравенством
где ЕР — энергия Ферми. Толщина соответствующего слоя в р-про-
странстве равна 6р =& 2Ajvp, где vF = рр\т — фермиевская скорость
электронов. (Здесь мы учли тот факт, что всегда А <^ Ер.) Мини-
Минимальная протяженность в пространстве волнового пакета, образован-
образованного плоскими волнами с разбросом по импульсам Ьр, равна Ьх —
~hjbp. Это приводит к следующему выражению:
Eo = -^f- 0-19)
Множитель 1/я введен из соображений удобства для дальнейшего.)
Длина |0, определяемая выражением A.19), носит название длины
когерентности сверхпроводника.
Из A.15) и A.13) следует, что величины h, js и v меняются на
расстояниях порядка KL. Поэтому приведенный вывод уравнения
Лондонов справедлив лишь при условии KL ^> ?0.
1. В простых (непереходных) металлах, как мы видели, глубина
%L мала ('—' 300А). Вместе с тем фермиевская скорость vF велика
0>Л08 см\сек) и в соответствии с A.19) велик и параметр |0 (для
алюминия !0=%;104А). Поэтому уравнение Лондонов непригодно
для описания эффекта Мейсснера в этих металлах. Для того чтобы
произвести расчет глубины проникновения в этом случае, необходимо
заменить уравнение A.9) несколько более сложным, форма кото-
которого была предложена Пиппардом. В дальнейшем мы будем называть
такие сверхпроводники сверхпроводниками первого рода, или типа I
(а также пиппардовскими); более подробно о них говорится в гл. II.
2. В переходных металлах и интерметаллических соединениях
типа Nb3Sn и V3Ga эффективная масса электрона очень велика,
глубина проникновения KL также велика (— 2000 А), а фермиевская
скорость мала (~ 106 см\сек). Кроме того, температура перехода
Тс, выше которой сверхпроводимость исчезает, оказывается высокой
(ТС=18°К Для Nb3Sn). Как мы увидим позже, параметр Л примерно
пропорционален Те и поэтому тоже велик. По всем указанным при-
причинам в таких материалах длина когерентности |0 весьма мала

Фундаментальные свойства 21
(.— 5оА), и уравнение A.9) хорошо описывает их поведение в слабых
полях. Мы будем называть их сверхпроводниками второго рода,
или типа II (а также лондоновскими сверхпроводниками).
Для полноты необходимо упомянуть о случае сверхпроводящих
сплавов, в которых длина когерентности и глубина проникновения
становятся зависящими от длины свободного пробега электронов.
Подробно этот вопрос мы обсудим в дальнейшем; качественно ре-
результат состоит в том, что если длина свободного пробега вслед-
вследствие неупорядоченности структуры мала, то длина когерентности
становится меньше значения |0 = Йг»/г/яА для чистого металла, а глу-
глубина проникновения KL, наоборот, возрастает по сравнению со зна-
значением A.7). Поэтому часто оказывается, что добавление примесей
в пиппардовский сверхпроводник переводит его в лондоновский.
Отмеченное здесь различие между двумя типами сверхпроводников
имеет принципиальное значение при постановке любых экспериментов
в присутствии внешних магнитных полей. Исторически сложилось
так, что в течение 20 лет после открытия эффекта Мейсснера эк-
эксперименты проводились главным образом на сверхпроводниках пер-
первого рода. Детальное изучение сверхпроводников второго рода
началось совсем недавно. Парадоксально, что теория развивалась
в обратном порядке: уравнение A.9) было введено братьями Лондо-
нами в 1935 г., а необходимые видоизменения для сверхпроводников
первого рода были предложены Пиппардом лишь в 1953 г. Перей-
Перейдем теперь к подробному рассмотрению магнитных свойств сверх-
сверхпроводников обоих типов.
ЛИТЕРАТУРА
Уравнения Лондонов
London P., Superfluids, 2d ed., vol. I, New York, 1961.
Обсуждение экспериментальных данных о сверхпроводниках
Lynton E. A., Superconductivity, 2d ed., London, 1965. (Имеется перевод
1-го издания: Э. А. Л и н т о н, Сверхпроводимость, изд-во „Мир", 1964.)
Развитие представлений о сверхпроводимости
Bardeen J., Schrleffer J. R., в книге Progress in Low Temperature
Physics, ed. C. G. Gorter, vol. Ill, Amsterdam, 1961. (Имеется перевод:
Дж. Бардин, Дж. Шриффер, Новое в изучении сверхпроводи-
сверхпроводимости, М., 1962.)
В1 a 11 J. M., Theory ol Superconductivity, New York, 1964.
Quantum Fluids, ed. D. F. Brewer, Amsterdam, 1966.

Глава II
МАГНИТНЫЕ СВОЙСТВА СВЕРХПРОВОДНИКОВ
ПЕРВОГО РОДА
§ 1. КРИТИЧЕСКОЕ ПОЛЕ ДЛИННОГО ЦИЛИНДРА
Поместим длинный сверхпроводящий цилиндр радиусом г0 в со-
соленоид радиусом г, > г0 (фиг. 7). По обмотке соленоида течет
слабый ток /. Возникающее распределение поля h(r) показано на
фиг. 8. Вне образца поле постоянно и
равно Н, а внутри оно быстро спадает
до нуля (глубина проникновения поля
К "-' 500 А). Ограничимся рассмотрением
макроскопических образцов (го^>7С);
в этом случае можно считать, что поле
всюду в образце равно нулю.
Такое полное вытеснение потока на-
наблюдается в слабом внешнем поле Н;
однако когда поле Н достигает некоторой
критической величины Нс, ситуация корен-
коренным образом изменяется: во-первых, поле
становится однородным во всем объеме
образца, во-вторых, образец перестает
быть сверхпроводящим (в принципе в этом
можно убедиться, измеряя сопротивление
между концами цилиндра). Можно пока-
показать, что для достаточно совершенных
образцов этот переход является обратимым:
при уменьшении тока соленоида / сверх-
сверхпроводящее состояние восстанавливается и
магнитный поток опять полностью вытес-
вытесняется из образца. Типичные значения Нс
приведены в табл. 2. С возрастанием
температуры критическое поле убывает, что
приближенно описывается соотношением
Фиг. 1. Схема опыта по из-
измерению критического поля.
Образец в форме длинного ци-
цилиндра (длиной L и радиусом г0)
помещен в катушку радиусом г,.
Нс (Г) = Нс @)(l—
B.1)
(При Т >ТС материал находится в нормальном состоянии даже в ну-
нулевом поле, Тс — температура перехода в отсутствие поля.) Зная
Нс, можно вычислить разность свободных энергий образца в нор-
нормальном и сверхпроводящем состояниях.

Магнитные свойства сверхпроводников первого рода
23
Таблица 2
Значения Тс
/МО), гс
Тс, °К
Zn
53
0,88
Cd
30
0,56
и Нс для некоторых металлов
aHg
4,15
AI
99
1,19
Оа
51
1,09
In
283
3,41
Т1
162
1,37
Sn
306
3,72
Pb
803
7,18
а) Когда цилиндр находится в нормальном состоянии, поле в со-
соленоиде однородно и равно
*=^-. B-2)
где TV — число витков соленоида, L — его длина, совпадающая с дли-
длиной образца. Свободная энергия системы равна
= nr20LFn-\-nrU h2
8я '
B.3)
где Fn — плотность свободной энергии образца в нормальном состо-
состоянии. Второй член в этой формуле представляет собой магнитную
энергию, запасенную в катушке.
Фиг. 8. Распределение поля в цилиндре и катушке для случая, когда ци-
цилиндр является сверхпроводящим.
Поле проникает в цилиндр на расстояние, приблизительно равное глубине проникновения.
В масштабе рисунка можно считать, что поле скачком обращается в нуль внутри образца.
б) Предположим теперь, что цилиндр переходит в сверхпроводя-
сверхпроводящее состояние, причем ток в катушке поддерживается неизменным.
Тогда поле в образце становится равным нулю, однако в области

24 Глава II
r0 < г < гх оно остается равным значению B.2I'. Свободная энергия
теперь принимает следующий вид:
^-6 = nr^Fs + n(rj— r^L-^-, B.4)
где Fs — плотность свободной энергии образца в сверхпроводящем
состоянии. При записи соотношения B.4) мы пренебрегли проникно-
проникновением поля в образец, а также кинетической энергией экранирующих
токов — оба эффекта носят поверхностный характер и в случае макро-
макроскопического цилиндра (г0 ^> К) их вклад мал.
Отметим, что <^ < <^а, поскольку, во-первых, Fs < Fn и, во-
вторых, магнитная энергия в состоянии "б" меньше, чем в состоянии
"а". Разность Fn — Fs находится путем следующего рассмотрения.
При переходе из состояния "а" в состояние "б" заключенный в кату-
катушке поток ф уменьшается, вследствие чего в ней индуцируется на-
напряжение V. Работа, совершаемая этим напряжением во внешней цепи,
равна
/
В процессе перехода ток / поддерживается постоянным, поэтому
яг2^-. B.6)
Если состояния "а" и "б" находятся в равновесии (Л = Нс), то
Должно выполняться равенство
Используя B.3) и B.4), окончательно находим
B7)
Полученное соотношение позволяет вывести ряд термодинамических
свойств. Зафиксируем ток / и будем изменять температуру. Энтропия
(на 1 си*3) каждой из фаз определяется формулами
B-8)
') Чтобы продемонстрировать это свойство, запишем уравнение rot h =
¦¦ 4л; j/с в интегральной форме
а в качестве контура интегрирования возьмем силовую линию, проходящую
через катушку в области ro< r < Г\. Для достаточно длинного соленоида
можно пренебречь вкладом, вносимым в ф h - d\ той частью силовой линии,
которая проходит вне катушки. В результате получим h iNIl

Магнитные свойства сверхпроводников первого рода 25
Следовательно, для фаз, находящихся в равновесии, разность зна-
значений энтропии равна
Отсюда находим скрытую теплоту перехода
-Sj = —L.He^. B.10)
Величина L положительна, т. е. при переходе из сверхпроводящего
состояния в нормальное должно поглощаться тепло1).
Если переход происходит в отсутствие внешнего поля, то теплота
L обращается в нуль. Действительно, при Т = ТС критическое поле
Нс равно нулю. С другой стороны, опыт показывает, что для всех
до сих пор изученных сверхпроводников производная dHJdT остается
конечной. Таким образом, Шн_0 = 0, т. е. в нулевом поле сверх- J
проводящий переход является фазовым переходом второго рода. 1
В соответствии с этим теплоемкость в точке перехода испытывает
скачок, равный 2)
с
Экспериментально установлено, что для ряда металлов соотношения
B.10) и B.11) выполняются с точностью выше 1% (исключительно
хорошее согласие найдено для Sn, In и Та). При постановке таких
экспериментов должна соблюдаться некоторая осторожность; в особен-
особенности необходимо быть уверенным в том, что достигнутое состояние
является равновесным, т. е., например, отсутствуют "замороженные"
потоки. Соотношения B.10) и B.11) представляют большой практи-
практический интерес, так как они связывают термодинамические величины
(скрытую теплоту перехода и теплоемкость) с температурной зависи-
зависимостью критического поля, которую часто легче измерить.
§ 2. ГЛУБИНА ПРОНИКНОВЕНИЯ
Связь между током и полем в сверхпроводниках
первого рода
При макроскопическом подходе можно считать, что слабое поле
(h < Нс) совсем не проникает в сверхпроводник первого рода.
В микромасштабе, однако, поле на поверхности не может испытывать
') Если при переходе из сверхпроводящего состояния в нормальное об-
образец теплоизолирован, то его температура понижается.
2) Это соотношение часто называют формулой Рутгерса. — Прим. ред.

26 Глава II
разрыва. Поэтому оно неизбежно проникает в металл на некоторую
глубину "к. Вычислим эту величину.
В гл. I мы получили выражение для "к с помощью уравнения
Лондонов
rotJ = —7^-Ь. B.12)
которое, однако, неприменимо в рассматриваемом случае сверхпро-
сверхпроводников первого рода (?0 ^> К). Необходимо найти более общую
зависимость между полем и током, справедливую даже в случае быст-
быстрых изменений j и h в пространстве.
Как мы увидим, значительно более удобно использовать в каче-
качестве переменной вместо поля h(r) вектор-потенциал А (г), связанный
с полем соотношением
rotA = h. B.13)
Соотношение B.13) определяет вектор-потенциал А (г) неоднозначно,
поэтому часто оказывается удобным выбрать его так, чтобы выпол-
выполнялись следующие дополнительные условия:
divA = 0,
А„ = 0 на поверхности образца,
где А„ — нормальная к поверхности образца компонента вектора А.
При выполнении условий B.14) говорят, что вектор-потенциал А
выбран в лондоновской калибровке. В этой калибровке уравнение
B.12) можно записать в виде
J = — ^1 А. B.15)
1 тс v '
Действительно, подстановка соотношения B.15) в B.13) приводит
к уравнению B.12), а подстановка в B.14) дает
dlv j = 0 (уравнение непрерывности),
\п = 0 на поверхности образца.
Последнее условие выполняется, если к образцу не подводится внеш-
внешних токов.
Соотношение B.15) применимо лишь в том случае, когда j и А
медленно изменяются в пространстве на расстояниях ~ \^. В общем
случае можно предположить, что ток j(r) в определенной точке г
зависит от вектора-потенциала А (г') во всех соседних точках г',
удовлетворяющих условию | г — г' | < |„. Феноменологическое соот-
соотношение для описания этого эффекта было предложено Пиппардом
[10, 11]. В лондоновской калибровке оно имеет вид
R=r — r'. B.16)

Магнитные свойства сверхпроводников первого рода 27
Коэффициент С легко определить, заметив, что при медленном из-
изменении вектора-потенциала А (на расстояниях '—'?0) его можно вы-
вынести из-под знака интеграла, а ток приравнять лондоновскому зна-
значению B.15). В результате получаем
?! B.17)
Такая простая форма соотношения B.16) между током и вектором-
потенциалом была предложена Пиппардом на чисто феноменологиче-
феноменологической основе. Конечно, это была просто догадка. Позже в связи
с развитием микроскопической теории было показано, что точная
связь тока с полем очень напоминает соотношение B.16), если вы-
выбрать
Точное соотношение между j и А будет обсуждаться в гл. IV. Оно
гораздо сложнее математически, чем приближенный результат Пип-
парда B.16), и поэтому последний до сих пор не утратил своего
значения. Мы используем его сейчас для изучения глубины проникно-
проникновения поля в сверхпроводник.
Глубина проникновения
Выражение B.16) справедливо лишь для массивного сверхпровод-
сверхпроводника. Однако теперь нас интересует проникновение. поля в образец,
т. е. процессы, происходящие вблизи его поверхности. Вообще го-
говоря, в этом случае соотношение между j и А видоизменяется. Для
расчетов можно воспользоваться следующим правилом: сохраним вы-
выражение B.16), но будем проводить интегрирование лишь по точ-
точкам г' сверхпроводника, из которых электрон, двигаясь по прямой
линии, может попасть в точку г. Так, если в металле имеется не-
небольшая полость, то при интегрировании следует исключить область
„тени", как показано на фиг. 9. (Это правило справедливо в обычном
случае, когда отражение отдельных электронов от поверхности
является диффузным. Ниже мы получим этот результат с помощью
микроскопической теории.)
Рассмотрим образец, занимающий полупространство z > 0; пусть
его поверхность совпадает с плоскостью ху. Векторы А и j напра-
направлены вдоль оси х. Глубину проникновения можно оценить с по-
помощью следующих интуитивных соображений, принадлежащих Пип-
. парду. Если бы вектор A (z) был постоянен на расстояниях ~?0
вблизи поверхности, то из B.16) мы получили бы в этой области
лондоновский результат
j=_^?lA.
J me

28
Глава II
На самом же деле вектор-потенциал A (z) отличен от нуля в более
узкой области толщиной К, поэтому интеграл B.16) следует умень-
уменьшить приблизительно в \J"k раз, т. е.
ш?2 Я .
Используя это соотношение вместе с уравнением rot h = Dл/с) j, мы
получаем приближенный закон проникновения поля в виде h{z) =
Область
тени
Сверхпроводник
S
Фиг. 9. «Эффект теш», возникающий при расчете тока j(r) при наличии
вектора-потенциала А (г').
Полость или диэлектрическое включение занимает область С внутри сверхпроводника S; отра-
отражение электронов на 5С-границе носит диффузный характер. Значения вектора-потенциала А (г')
в области Сив области тени не дают вклада в ток J (г).
= /z@)exp(— z/K), где величина К определяется следующим самосо-
самосогласованным образом:
.-2 Аяпе2 Я
Строгий, но значительно более сложный расчет дает
Существенный вывод, который можно сделать, состоит в том, что
в пиппардовском пределе глубина проникновения К становится больше!
лондоновского значения KL, а именно A/^-z.'—' у ioAx, ^5> 1. н0 тем не
менее она значительно меньше длины когерентности

Магнитные Свойства сверхпроводников первого рода
29
Методы измерения глубины проникновения
Исторически первые оценки величины X были сделаны путем из-
измерения магнитной восприимчивости очень малых образцов (коллои-
(коллоидальных частиц или тонких пленок)'). При использовании этого
метода сначала убеждаются опытным путем, что температура пере-
перехода коллоидальных частиц (размером порядка 100 А) не очень сильно
отличается от температуры перехода массивного образца. Исходя из
Стеклянная
^, трубка
*^. Ппенка
Передающая
катушка A)
Приемная
катушка (Z)
Соленоид-
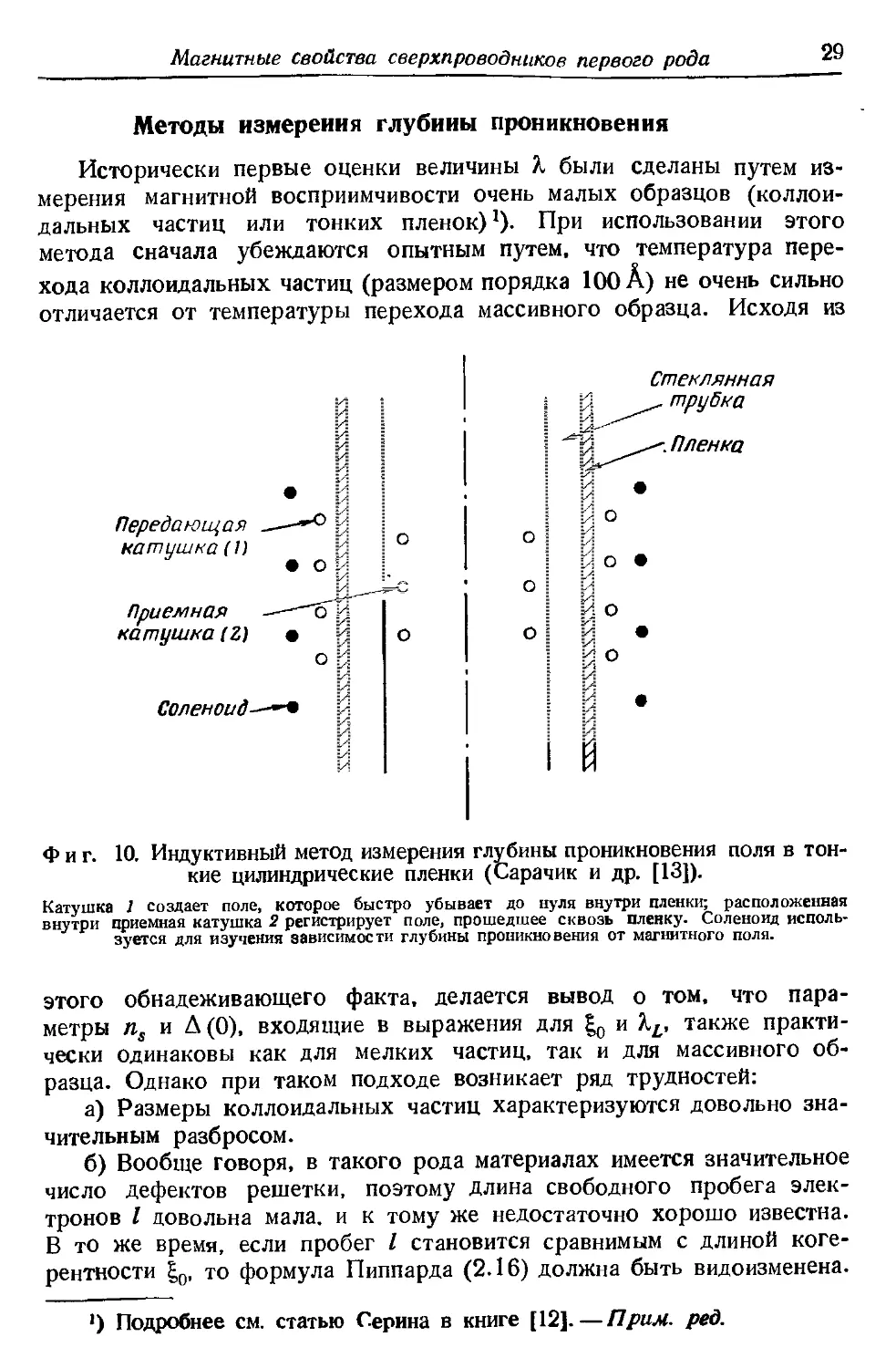
Фиг. 10. Индуктивный метод измерения глубины проникновения поля в тон-
тонкие цилиндрические пленки (Сарачик и др. [13]).
Катушка 1 создает поле, которое быстро убывает до нуля внутри пленки; расположенная
внутри приемная катушка 2 регистрирует поле, прошедшее сквозь пленку. Соленоид исполь-
используется для изучения зависимости глубины проникновения от магнитного поля.
этого обнадеживающего факта, делается вывод о том, что пара-
параметры ns и А@), входящие в выражения для |0 и %L, также практи-
практически одинаковы как для мелких частиц, так и для массивного об-
образца. Однако при таком подходе возникает ряд трудностей:
а) Размеры коллоидальных частиц характеризуются довольно зна-
значительным разбросом.
б) Вообще говоря, в такого рода материалах имеется значительное
число дефектов решетки, поэтому длина свободного пробега элек-
электронов / довольна мала, и к тому же недостаточно хорошо известна.
В то же время, если пробег / становится сравнимым с длиной коге-
когерентности |0, то формула Пиппарда B.16) должна быть видоизменена.
') Подробнее см. статью Герина в книге [12].—Прим. ред.

30
Глава II
Другие методы определения глубины проникновения "к сводятся
к измерению величины само- или взаимоиндукции в присутствии
сверхпроводника. Схема расположения катушек при измерении взаим-
взаимной индукции представлена на фиг. 10.
Катушка / создает поле he на внешней поверхности пленки и
поле ht—phe<^ihe во внутренней области, измеряемое с помощью
катушки 2. Зная р, с помощью соответствующего теоретического
анализа можно определить Я,. Практически можно измерить значение
р^>, 10~ . Это позволяет работать с относительно толстыми пленками
(толщиной ~ 10Я,), у которых можно надежно определить кристалло-
кристаллографическую структуру. (Благодаря этому частично снимаются труд-
трудности, отмеченные выше в пункте „б".)
Сверх проводник
катушка
Фиг. 11. Метод определения глубины проникновения поля в сверхпроводя-
сверхпроводящий цилиндр радиусом R.
Цилиндр окружен катушкой радиусом ft + e. Магнитный поток заключен в кольце толщиной
е + К. На практике величина е точно неизвестна, поэтому удается измерить лишь изменение
"К с температурой-
Можно также измерить самоиндукцию катушки, охватывающей
сверхпроводящий цилиндр (метод Казимира [14]1)). Магнитный поток
заключен в области с площадью сечения — nR (е -\- К), где е — рас-
расстояние между катушкой и образцом (фиг. 11). Так как Л,'-~103А.
зазор е следует делать по возможности малым (обычно е=г»0,2 мм,
а ^==5=4 мм). На практике величина е известна недостаточно точно,
так что описанный метод в основном служит для определения тем-
температурной зависимости глубины проникновения ^G). Другая, но
в принципе аналогичная методика состоит в использовании микро-
микроволнового резонатора со сверхпроводящими стенками2).
') См. также [15]. — Прим. ред.
2) Этот последний метод, видимо, является наилучшим. Здесь уместно
будет также заметить, что величина % выше всюду появлялась в экспонен-
экспоненциальном законе убывания поля в толщу сверхпроводника. Между тем этот

Магнитные свойства сверхпроводников первого рода
31
Обсуждение
Проникновение поля
ЧвЛЛ
Возникает вопрос: можно ли с помощью
экспериментально найденных значений X
при ЧабсолютномЛЛнуле проверить феноменологическое соотношение
Пиппарда? Для чистых металлов при абсо-
абсолютном нуле мы можем независимо вычислить
bv I me2 V/j
^° = лД @) И L~ \ Алпе2') '
Определив значения vF и п/т из измерений удельной теплоемкости,
аномального скин-эффекта и т. д. на образце в нормальном состоя-
состоянии, а значения А@) из измерений тех же величин на образце
в сверхпроводящем состоянии, мы можем теоретически предсказать
величину Я, (напомним, что Я,3 = 0,62Я|?э для XL<^l,u; при kL —13
формула несколько усложняется). В табл. 3 сравниваются теорети-
теоретические и экспериментальные значения к (экстраполированные к 0°К).
Налицо качественное согласие, хотя без дополнительной информации
довольно трудно определить |0, исходя из значений X. Подобные
измерения не дают возможности уточнить вид соотношения B.1 бI).
Таблица 3
Значения к и lfl для некоторых металлов *
Металл
А!
Sn
Pb
KL, A
157
355
370
lo. А
16000
2300
830
Чеор' А
530
560
480
*эксп- А
490—515
510
390
* Данные взяты из работы [161.
В настоящее время разработаны и применяются более тонкие ме-
методы проверки теории; важнейшим из них является измерение про-
проникновения магнитного поля сквозь пленки. В частности, полное
закон не всегда верен. Физическое же определение А как эффективной
длины, на которую проникает магнитный поток, всегда однозначно:
— \
= ХН0, где fi0 — поле на поверхности, а поток отнесен к еди-
единице длины периметра образца. — Прим. ред.
') Количественное сопоставление данных, полученных из экспериментов
с нормальным металлом и сверхпроводником, оказывается очень затрудни-
затруднительным, так как, например, такая величина, как эффективная масса элек-
электрона, очень анизотропна для нормального металла. — Прим. ред.

82
Глава И
решение, полученное с помощью B.16) для тонких пленок, указывает
на то, что в случае |0 ^> Я. поле может изменить знак, а отноше-
отношение р может стать отрицательным. Экспериментально это явление
наблюдалось Дрангайдом и Зоммерхальдером [17, 18].
Можно ожидать, что в том случае, ког-
когда длина свободного пробега электронов I
уменьшается вследствие присутствия приме-
примесей, в выражении, связывающем ток в точке г и вектор-потенЦиал
в точке г', появится затухающий множитель типа ехр(—|г — г' |//).
Таким образом, можно предположить, следуя Пиппарду [10, 11], что
[A(r')-R]R
Обобщение на случай
сплавов
Нормировочный множитель С предполагается не зависящим от / и
равным своему значению —Ъпе2/4лтсЬ,0 в чистом металле. Другими
Ю
го
40
60
10'* см
80
Фиг. 12. Зависимость глубины проникновения Л от длины свободного про-
пробега для сплавов Snin (Пиппард [10]).
Результаты находятся в полном согласии с теорией того же автора |см. B.21)|.
словами, предполагается, что вклад в ток j (г), вносимый точками г',
соседними с точкой г (|г' — г|^/), не меняется при наличии при-
примесей. С помощью этой гипотезы Пиппарду удалось объяснить ре-
результаты ряда опытов с разбавленными сплавами Snin. Из фиг. 12
видно, что глубина проникновения % растет с увеличением концент-
концентрации примесей — вывод, который удается разумно истолковать на
основе выражения B.19). Особый интерес представляет предельный
случай А.^>/, когда можно пренебречь изменениями А (г') в B.19).
Выполняя интегрирование, получаем
B.20)

Магнитные свойства сверхпроводников первого рода 33
Это — уравнение лондоновского типа, но коэффициент отличается от
его значения в чистом металле. Если, кроме того, I <^ ?0, то
j(r) = ——-i-A(r),
JV me la к '
откуда получаем следующее выражение для глубины проникновения:
*=ЦтГ при
В этой области глубина проникновения X пропорциональна I ,
т. е. квадратному корню из концентрации примесей.
Согласие между теорией и экспериментом для системы Snln
является блестящим подтверждением правильности предположений,
сделанных Пиппардом. В гл. IV мы увидим, что эти результаты
следуют из микроскопической теории.
До сих пор мы ограничивались рассмотре-
Изменение глубины случая Т = 0. Для конечных температур
проникновения J r Jr
с температурой ситуацию качественна можно описать сле-
следующим образом. Пиппардовское выражение
B.16) остается в силе, причем величина ?0 почти не зависит от тем-
температуры. Нормировочный коэффициент С является функцией темпе-
температуры и обращается в нуль в точке перехода Тс. Непосредственно
вблизи Тс коэффициент С является линейной функцией разности
Тс — Т. Универсальная теоретическая кривая для С, полученная
с помощью микроскопической теории, приведена в гл. IV, § 5.
Зная С, можно, пользуясь соотношением B.20), вычислить X').
Чтобы избежать громоздких математических выкладок, эксперимен-
экспериментаторы часто прибегают к следующей эмпирической зависимости:
з^Чз- B-22)
Соотношение B.22) хорошо согласуется с экспериментальными дан-
данными для олова и приводит к правильной температурной зависимости
Х~(ТС — Т)~I* при Т—>Тс. Следует, однако, подчеркнуть, что
универсальный закон вида B.22) нельзя безоговорочно применять
ко всем сверхпроводникам из-за того, что в расчете X используются
два независимых параметра (например, ?0 и лондоновская глубина
проникновения XL).
') Это законно для сверхпроводников лондоновского типа. Для пиппар-
довских сверхпроводников см. B.16). В этом случае вблизи Тс есть область,
где Л ~ (Тс — Т)~\ — Прим. ред.
3 Зак. 1020

34 Глава II
§ 3. МАГНИТНЫЕ СВОЙСТВА ОБРАЗЦОВ ПРОИЗВОЛЬНОЙ
ФОРМЫ. ПРОМЕЖУТОЧНОЕ СОСТОЯНИЕ
Происхождение промежуточного состояния
Для определения критического поля Нс мы выше помещали
цилиндрический образец в магнитное поле, параллельное оси цилиндра.
Если пренебречь влиянием концов, то такая геометрия обеспечивает
постоянство значения поля h на всей поверхности цилиндра.
Фиг. 13. Распределение магнитного поля вблизи сверхпроводящей сферы
радиусом а.
При Н- < ЪН^Ъ (где Но — приложенное поле) эффект Мейсснера является полным: поле на
экваторе (в любой точке на окружности С) равно ЗЯ0/2, а на полюсах Q и Q' равно нулю.
При Нс > Яо > 2//суз сфера находится в промежуточном состоянии.
Рассмотрим теперь менее тривиальный случай, например сверх-
сверхпроводящую сферу радиусом а, помещенную в однородное внешнее
магнитное поле Ио. Если поле Но мало, а именно меньше '2HJZ, то
силовые линии вытесняются из образца, как изображено на фиг. 13.
Распределение поля вне сферы определяется уравнениями
div h = rot h = 0 n h->H0 при г —> хэ,
B.23)
где г—расстояние, отсчитываемое от центра сферы. Наконец, необ-
необходимо учесть эффект Мейсснера, т. е. то обстоятельство, что силовые
линии не могут проникать внутрь сверхпроводящей сферы. Отсюда

Магнитные свойства сверхпроводников первого рода 35
следует, что нормальная компонента поля hn должна исчезать на
поверхности сферы
(Ая),-« = 0. B.24)
Соответствующее решение для внешней по отношению к образцу
области имеет вид
4(^). B-25)
Компонента поля h, параллельная поверхности образца, равна
В точках Q и Q' поле h равно нулю; на экваторе сферы @ = л/2)
тангенциальная составляющая максимальна и равна 3HJ2. Величина
поля в остальных точках поверхности лежит между этими предель-
предельными значениями. Когда поле Ио достигает величины 2HJ3, поле
на экваторе становится равным Нс. Следовательно, для полей
Но > 2Нс/2> некоторые области сферы переходят в нормальное состоя-
состояние. Однако, поскольку в остальных местах Но < Нс, сверхпрово-
сверхпроводимость должна сохраниться. (Если бы сфера перешла в нормальное
состояние полностью, то поле в любой точке сферы стало бы рав-
равным Ио. В силу условия Но < Нс это состояние будет неустойчивым,
сверхпроводимость должна вновь появиться.) Таким образом, для
значений поля, лежащих в интервале
!•#,</*„<//«. B.27)
нормальные и сверхпроводящие области должны сосуществовать. Такое
состояние называется промежуточным.
Отметим, что область полей Но, при которых будет наблюдаться
равновесие между двумя фазами, определяется неравенством B.27)
лишь для образцов сферической формы. Если вместо сферы в поле
поместить вытянутый (сплюснутый) эллипсоид с осью вращения,
параллельной направлению поля Но, то на экваторе поле будет меньше
(больше) отличаться от Ио и область существования промежуточного
состояния будет иной. В частности, если мы рассмотрим тонкую
металлическую пластину в поле, перпендикулярном ее плоскости, то
промежуточное состояние будет существовать во всей области полей
О < Но < Нс. (Если бы в отличном от нуля поле Но пластина оста-
оставалась полностью сверхпроводящей, то поле на краю пластины было бы
очень большим, т. е. больше Нс, что неизбежно привело бы к по-
появлению нормальных областей.)
Рассмотрим подробнее случай пластины толщиной е. Распределе-
Распределение нормальных (N) и сверхпроводящих {S) областей представлено

36
Глава II
на фиг. 14: области N и S образуют слои, перпендикулярные пло-
плоскости чертежа. Силовые линии проходят только через области N.
Чтобы обеспечить равновесие, поле h на плоскостях раздела областей
N к S должно быть равно Нс. В областях Л/ поле h параллельно оси z,
т. е. divh = roth = 0. Следовательно, в областях Л/ поле h по-
постоянно и равно Нс, а в S-областях h = 0. Доля объема, занятая
S-областями p = dj(ds~\- dn), для этой простой конфигурации опре-
определяется непосредственно из условия сохранения потока. Вдали от
Фиг. 14. Распределение силовых линий в пластине в поле, перпендику-
перпендикулярном ее плоскости.
При любом значении поля Н < Н образец находится в промежуточном состоянии, т. е. обла-
обладает ламинарной структурой из чередующихся нормальных и сверхпроводящих областей
(не учитываются небольшие искажения общей картины вблизи краев пластины).
пленки поле однородно, h = H0, и поток равен SH0 (где S — пло-
площадь поверхности пленки); в самой пленке поток проходит через
площадь S(l —р), а поле равно Нс. Следовательно,
0 = S(l—p)Hc.
— 1 — Н°
~Н~с'
B.28)
В результате наблюдений установлено, что толщины слоев ds и dn
для макроскопических образцов (е~^>Ь,0) существенно меньше раз-
размеров образца. (Эксперименты, на основании которых сделан этот
важный вывод, описаны ниже.) Поэтому при решении многих задач
можно полностью игнорировать микроскопическую структуру чере-
чередующихся слоев и оперировать лишь относительным объемом
5-областей р.
Для пластины вычисление коэффициента р представляет собой
довольно простую задачу. Для образцов более сложной формы опре-

Магнитные свойства сверхпроводников первого рода 37
деление р и макроскопического среднего значения поля в любой
точке требует более общего анализа. Эта задача была решена
Пайерлсом. Ниже мы приведем этот анализ, а затем применим резуль-
результаты к решению некоторых типичных задач.
Некоторые термодинамические соотношения
Дадим теперь определение некоторых макроскопических величин
(например, индукции В, напряженности магнитного поля Н и т. д.),
удобных при описании тех случаев, когда имеется частичное про-
проникновение силовых линий в образец (например, промежуточного
состояния). Другие приложения рассматриваются в гл. III в связи
со специальными задачами для сверхпроводников второго рода.
Рассмотрим систему, состоящую из образца
Определение свободной и внешних объектов (катушек, генераторов
и т. д.). Определим свободную энергию сле-
следующим образом. Во-первых, запишем энергию электронов в образце
где А — вектор-потенциал, связанный с полем h (r) соотношением
rotA = h, V-t, — энергия электрон-электронного взаимодействия, Vi-—¦
одноэлектронный потенциал. Во-вторых, добавим к этой энергии
энтропийный член —TS. Оба вклада можно представить в виде
интеграла по объему образца
U-TS= J Fsdr. B.30)
Образец
В-третьих, включим в рассмотрение энергию магнитного поля
j (Л2/8я)йг. Сумма этих трех вкладов носит название свободной
энергии
^Г= J F&dr+ j 4dr" B'31)
Образец Все пространство
Мы часто будем сталкиваться с ситуациями,
Определение индукции в которых микроскопическое поле h (r)
в образце сильно меняется в пространстве
на расстояниях Ал:, гораздо меньших, чем размеры образца. (При-
(Примером может служить промежуточное состояние, изображенное на
фиг. 14.) В этих случаях удобно ввести вектор В (г), определяющий
среднее значение поля h в окрестности точки г в области, размеры
которой малы по сравнению с размерами образца, но велики в срав-
сравнении с Длг. По определению,
B = h B.32)

38 . Глава II
внутри образца и В = h снаружи. Микроскопическое поле h удо-
удовлетворяет уравнениям
,, 4л .
rolh = —-j,
с B.33)
divh = 0,
где j — локальная плотность тока. Отсюда находим уравнения для В:
rotB^i^jT
с B.34)
div В = 0.
где j — макроскопическая плотность тока.
Предположим, что при изменении тока в ка-
Определение тушках распределение поля h(r) несколько
магнитного поля Н изменилось. В соответствии с этим величина
В (г) в каждой точке г изменится на неболь-
небольшую величину 6В(г). В первом порядке по 6В наиболее общее вы-
выражение для изменения свободной энергии 6<^~ имеет вид
B.35)
где коэффициент 1/4я введен для удобства; Н(г) — некоторая функ-
функция координат, которую мы будем называть магнитным полем
в точке г ')• Вне образца должны выполняться соотношения
B.36,
Поэтому вне образца h —Н = В. Соотношение B.35) определяет
величину Н довольно формально. Чтобы почувствовать ее физический
смысл, рассмотрим случай, когда отсутствуют внешние токи, вте-
втекающие в образец. Тогда плотность тока можно записать в виде
Г=Г,+ Ь B.37)
гДе j«(r) —средняя плотность сверхпроводящего тока в точке г об-
образца (вне образца, по определению, js= 0); je —ток в катушках, гене-
генераторах и т. д. Поскольку токи не втекают в образец, ясно видно
различие между je и j^ (в образце je = 0). Тогда имеем просто
rotH = -?-!,. B.38)
') Отметим, что в случае полного эффекта Мейсснера (?s=0) поле Н
не определено.

Магнитные свойства сверхпроводников первого рода 39
Доказательство уравнения B.38). Если индукция В (г) испы-
испытывает изменение 6В (г) за время Ы, то возникает электрическое поле Е
в соответствии с уравнением
Работа, совершенная электрическим полем Е над внешними токами, равна
6/ Г \е ¦ Е их, тогда как работа, совершаемая внешними токами, равна
B.39)
Из термодинамики известно, что для обратимого процесса при постоянной
температуре должно выполняться равенство бН7 = бс5г. Сравним выражения
B.39) и B.35). Для этой цели преобразуем последнее следующим образом:
Ъ&=Ы±- Гн-4?-Л = — Ы± Гн-го(ЕЛ =
= _б*-?- jE-rotHrfr — ?±- Г(ЕХН)-Лг. B.40)
Последний из написанных интегралов берется по поверхности, охватываю-
охватывающей всю систему. Он равен излучаемой системой энергии, которой для
медленных, т. е. обратимых, процессов можно пренебречь. Сравнивая B.40)
и B.39), мы убеждаемся в справедливости B.38).
ЗАКЛЮЧЕНИЕ
В rot В дают вклад все токи [см. B.34)]; напротив, в rotH
[см. B.38)] вносит вклад лишь ток ]е. Поэтому появляется искуше-
искушение считать, что Н представляет собой поле, которое существовало бы
в отсутствие образца (при условии, что ток в катушках поддержи-
поддерживается постоянным). Это правильно для цилиндрической геометрии,
показанной на фиг. 7, но в общем случае неверно. Рассмотрим,
например, сферический образец (см. фиг. 13). Здесь силовые линии
искажаются из-за присутствия образца, что приводит к изменению
Н(г) (но не rotH).
ЗАМЕЧАНИЕ ПО ПОВОДУ ГРАНИЧНЫХ УСЛОВИЙ
Уравнение div В = 0 означает, как обычно, что нормальная компонента
В„ непрерывна на поверхности образца. Наоборот, тангенциальная компо-
компонента В/, вообще говоря, терпит разрыв, поскольку в rot В дает вклад
сверхпроводящий ток. Обычно он локализован на поверхности образца
(точнее, в слое толщиной А вблизи поверхности). Если обозначить через \s
ток, приходящийся на I см длины поверхности, то, интегрируя уравнение
B.34), находим
^ B.4!)
где п — единичный вектор, нормальный к поверхности и направленный на-
Ружу.

40 Глава II
Термодинамический потенциал для фиксированных
значений Т и \е
Если изменяется как поле, так и температура, то вариация сво-
свободной энергии B.35) запишется в виде
6c§r=-^- J H-6Bdr — SbT, B.42)
где 5 — энтропия. При фиксированных значениях индукции В (г)
(в каждой точке г) и температуры Т состоянию равновесия соответ-
соответствует минимум функции й?". Однако довольно часто этот случай
интереса не представляет. Во время эксперимента обычно поддержи-
поддерживаются постоянными температура Т и токи в катушках \е. Построим
термодинамический потенциал, пригодный в такой ситуации. Введем
определение
& = 3~ — -± JB-Hdr. ¦ B.43)
Тогда
Ъ& = — -^ J B-6Hdr — S67. B.44)
Так как divB = 0, можно положить В = rot А (где А — „макроско-
„макроскопический" вектор-потенциал), после чего, интегрируя по частям,
получим
567 + 6^= — -L J rot А • 6Н tfr =
= -^ J A-rot6Hdr=-|J A-6jedr. B.45)
Таким образом, при заданных Т и je имеем Ь?? = О, т. е. состояние
равновесия соответствует минимуму потенциала <??. На практике обычно
сначала находят & и В для микроскопической модели, а затем строят
потенциал В, минимизируя который получают условие равновесия.
Это условие играет такую же роль, как соотношение В = (хН в случае
магнитной среды.
Связь между В и Н в промежуточном состоянии [19, 20]
Чтобы получить связь между В и Н, вычислим потенциал
Гиббса G их для элемента объема образца, находящегося в проме-
промежуточном состоянии [доля р объема dx находится в сверхпрово-
сверхпроводящем (S) состоянии, а A —р) — в нормальном (N)]. В нормальном
состоянии микроскопическое поле h имеет определенное значение hn,
а в сверхпроводящем оно равно нулю. Мы покажем, что условие
минимума потенциала & приводит к равенству hn = Нс. В силу опре-
определения коэффициента р имеем
B.46)

Магнитные свойства сверхпроводников первого рода 41
Плотность свободной энергии равна
F==Fn~ Ifcf + C1 ~P)-8S": B-47)
здесь второй член представляет собой энергию конденсации в сверх-
сверхпроводящих областях, а третий — магнитную энергию. Мы пренебрегли
энергией поверхности раздела нормальных и сверхпроводящих обла-
областей, а также членами, учитывающими искажение силовых линий
вблизи поверхности образца (для макроскопических тел эти поверх-
поверхностные члены пренебрежимо малы). В переменных р и В свободная
энергия F принимает вид
В2
B-48)
Обратимся теперь к термодинамическому потенциалу G
ВН рН2 В2 ВН
G(B, p) = F -г- =Fn— -L-L-f_— B.49)
v v> 4я " 8я ' 8яA — p) 4я v
и будем его минимизировать по переменным р и В.
1. Минимизация по р дает
\В\ = Не{\— р). B.50)
Из сравнения соотношений B.50) и B.46) следует, что поле в нор-
нормальной области равно hn = Нс. (Это свойство мы использовали ранее
в связи с примером на стр. 35.)
2. В результате минимизации по В получаем
дв B.51)
—р).
Отсюда можно заключить, что, во-первых В и Н параллельны и,
во-вторых, величина поля Н постоянна и равна Нс во всем объеме
образца. Это условие эквивалентно соотношению В = \лН для пара-
парамагнитной среды. Единственное отличие состоит в том, что получен-$
ная зависимость В(Н) носит нелинейный характер. Распределение •
поля в образце можно найти, решив систему уравнений
divB = 0, B.52)
rotH = 0, B.53)
Н = В^- " B.54)
при обычном условии непрерывности Вп и Ht на поверхности образца.
Уравнение B.53) отражает сделанное раньше предположение об отсут-
отсутствии токов, втекающих в образец [см. B.38)].

42
Глава II
Применения
Как и прежде, ограничимся рассмотрением наиболее распростра-
распространенного случая, когда образец не связан непосредственно с генера-
генератором тока. Тогда внутри образца силовые линии будут прямыми.
Приведем принадлежащее Лон-
Лондону доказательство этого ут-
утверждения:
Ф и г. 15. Поле на экваторе и полюсах
сверхпроводящей сферы.
Для 0 < И < 2И J3 имеет место полный эффект
Мейсснера: поле на полюсах равно нулю. Для
2НС/3 < Не < Н? сфера находится в промежу-
промежуточном состоянии; при увеличении И поле на
экваторе остается неизменным и равным Н?, тогда
как поле на полюсах линейно растет от нуля
до Н„.
= 2(H-V)H+2HXrotH.
B.55)
В самом образце rotH = 0,
так что (Н • V) Н = 0. Вектор Н
не меняется вдоль силовой ли-
линии, следовательно, последняя
представляет собой прямую.
Пример. Вернемся к рассмо-
рассмотрению сферического образца, по-
помещенного во внешнее поле Но,
причем 2HJ3 <На<Нс. Реше-
Решение системы уравнений B.52) —
B.54) в этом случае строится сле-
следующим образом.
Будем считать, что внутри
сферы (г < а) векторы В и Н па-
пау
ры (г < а) в
= Нс, а В —
раллельны оси г и постоянны по величине (Н = Нс, а В — неизвестная пока
величина, которую мы обозначим через Ве). С другой стороны, во внеш-
внешней области
B.56)
где Я, — вторая константа, которую нам предстоит определить. Ив условия
непрерывности на поверхности тангенциальной составляющей Н, получаем
¦% (jH0+^-)sine = Hc sin 6. B.57)
* Аналогично из условия непрерывности нормальной составляющей Вп имеем
(#0 — Я,) cos в = Во cos 6.
Сравнивая эти два уравнения, находим
В0 = ЗН0~2Нс,
Hi=2(Hc-Ha).
B.58)
B.59)
выводы
1. Всегда можно построить решение, отвечающее постоянному значению
индукции В, а следовательно, и доли сверхпроводящих областей р = 1—Ва/Н с
везде внутри сферы.

Магнитные свойства сверхпроводников первого рода
43
Критический ток
в сверхпроводящей
проволоке
2. Индукция Во является линейной функцией приложенного поля Но.
На опыте индукцию Во можно измерить, помещая магнитные пробники вблизи <
полюсов Q и Q' сферы. Из условия непрерывности Вп следует, что поле '
вне сферы непосредственно у ее полюсов Q и Q' равно Во. Аналогично °
измерение поля Нс, как ясно из условия непрерывности для Ht, должно
производиться с помощью пробника, расположенного на экваторе сферы.
Форма полученных таким путем экспериментальных диаграмм для чистых
образцов весьма близка к теоретической (фиг. 15). «
Проволока радиусом а присоединена к полю-
полюсам генератора, который создает в ней
ток/. Поле-на поверхности проволоки равно
И (а) = 21lea. Если Н(а) < Нс, то прово-
проволока может находиться полностью в сверхпроводящем состоянии.
Это условие определяет критический ток
1с=-Щ-"с- B-60)
Когда ток / становится больше, чем 1С,
то Н (а) > Нс и проволока вблизи поверх-
поверхности должна перейти в нормальное со-
состояние. Однако полностью она не может
стать нормальной, поскольку- в этом слу-
случае ток / распределился бы равномерно
по всему сечению проволоки и поле h
стало бы чрезвычайно малым в централь-
центральной ее части. Следовательно, проволока
должна (по крайней мере частично) оста-
остаться сверхпроводящей. Таким образом,
можно прийти к выводу, что внешняя
область проволоки (/? < г < а) является
нормальной, а внутренняя @ < г < /?)
находится в сверхпроводящем или про-
промежуточном состоянии. Во внешней обла-
области В = Н, а на границе H{R) = HC. От-
Отсюда находим выражение для тока /v
текущего по внутреннему сечению,
cRHc
2
B.61)
B.62)
т. е. /] < 1С < /. Остающийся ток / — 1Х
должен течь по внешней части сечения.
Так как эта область является нормальной,
должно возникать электрическое поле Е,
проволоки и имеющее постоянное значение
условия rot Е = 0.
Ф и г. 16. Картина доменной
структуры в сверхпроводя-
сверхпроводящей проволоке радиусом а.
несущей ток / > /^
Поверхностный слой находится в
нормальном состоянии, а сердце-
сердцевина радиусом /?— в промежуточ-
промежуточном состоянии. Радиус поверхно-
поверхности раздела R определяется урав-
уравнением H(R) — H
с'
направленное вдоль оси
по всей ее длине в силу

44
Глава I!
Приведенное рассуждение показывает, что внутренняя область
| проволоки не может быть полностью сверхпроводящей, поскольку в
| противном случае она накоротко замкнула бы полюсы генератора. Таким
1 образом, внутренняя область должна находиться в промежуточном
1 состоянии с N- и S-слоями, расположенными перпендикулярно оси
1цилиндра (фиг. 16). Детальное обсуждение возникающей картины
"можно найти в книге Лондона [21], § 20.
Криотрон —это управляющее устройство,
Принцип криотроиа изобретенное Бак0'м [22] в 1956 г.; принцип
действия криотрона поясняется схемой на фиг. 17. Управляющий ток /'
создает поле Н' = AnNI'jcL в соленоиде (М—число витков, a L—длина
катушки). Сверхпроводящая проволока АВ
диаметром 2а помещена в соленоид, создаю-
создающий критическое поле Нс. При Н' < Нс со-
сопротивление проволоки равно нулю; при
Н' > Нс сопротивление проволоки конечно.
Следовательно, током /, проходящим по про-
проволоке АВ, можно управлять с помощью
тока /'. Минимальный ток /', необходимый I
для того чтобы перевести проволоку АВ
в нормальное состояние, равен
' Н <263>
В
Ф и г. 17. Принципиаль-
Принципиальная схема криотрона.
Током в сверхпроводящей про-
проволочке АВ можно управлять
с помощью тока соленоида /'.
Когда поле соленоида стано-
становится равным И' , проволочка
переходит в нормальное сос-
состояние.
Вместе с тем ток / не может быть слишком
большим, так как в противном случае про-
проволока АВ перейдет в промежуточное со-
состояние. Как мы только что видели,
Усиление криотрона по току равно
B.64)
B.65)
В первом эксперименте Бака управляющая катушка была сделана
из ниобиевой проволоки диаметром —^0,1 мм (ниобий —сверхпровод-
—сверхпроводник с высоким значением критического поля ~ 2000 гс). Танталовая
проволока АВ диаметром 2а = 0,2 мм имела критическое поле
Нс—100 гс при 4,2° К- Для катушки, состоящей всего из одного
витка, это соответствует значениям NalL^X и G~6. Обычно
нецелесообразно увеличивать число витков N, поскольку это приводит
к возрастанию индуктивности катушки и в конечном счете к увели-

Магнитные свойства сверхпроводников первого рода 45
чению постоянной времени т криотрона. (У одновитковой катушки
т^>,10~5 сек.) На практике постоянная времени может быть значи-
значительно снижена путем замены устройства, показанного на фиг. 17,
двумя тонкими скрещенными металлическими пленками (фиг. 18),
Фиг. 18. Криотрон с малой постоянной времени.
Две скрещенные металлические пленки разделены тонким слоем диэлечтрнка.
разделенными изолирующим слоем толщиной приблизительно 1000 А
Так как коэффициент самоиндукции пропорционален толщине этого
слоя, то его величина оказывается чрезвычайно малой, в соответствии
с чем постоянная времени снижается до — 10~"8—10~9 сек.
Микроскопическая структура промежуточного
состояния [23]
Пусть пластина толщиной е с поперечными размерами Lx, Ly
(большими по сравнению с толщиной) помещена в перпендикулярное .
ее плоскости поле Но, в результате чего в ней образуются нормаль-
нормальные и сверхпроводящие области. Предположим, что эти области |
имеют форму слоев, как показано на фиг. 19. Такая конфигурация .
довольно часто наблюдается на опыте. Мы хотим определить тол-
толщины dn и ds нормальных и сверхпроводящих областей, а также
период доменной структуры dn -\- ds = d.
Чтобы решить эту задачу, запишем выражение для свободной
энергии $~ и будем минимизировать его относительно dn и ds (или
эквивалентных параметров) при заданном значении поля Но. Зада-
Задание Но означает, что фиксирован поток через пластину, т. е. под-
подходящим термодинамическим потенциалом является &Г, а не &?.
В нулевом приближении мы полностью пренебрежем поверхност-
поверхностной энергией и будем считать области S и N идеально плоскими
слоями. Тогда свободная энергия просто равна

46
Глава II
Здесь первое слагаемое представляет собой энергию конденсации
в областях S, а второе — энергию магнитного поля Л2/8л в областях /V,
где h = H0(dldn), как следует из условия сохранения потока.
S
d
N
ап
S
Фиг. 19. Микроскопическая структура из нормальных и сверхпроводящих
областей в пластине в промежуточном состоянии.
Домены образуют ламинарную структуру с периодом а ~ Veh (е —толщина пластины, б —тол-
—толщина границы раздела).
Чтобы перейти к приближению первого порядка, необходимо
учесть три типа вкладов в свободную энергию.
1 Создание границы между областями S и N сопряжено с зат-
затратой некоторой поверхностной энергии у (отнесенной на 1 см2 пло-
площади). Из соображений размерности величину y удобно записать
в виде
Y = W6, B.67)
где длина 6 порядка 103— 10" А. Соответствующий вклад в энер-
энергию <?Г равен
Н2 2L
yeLy X (Число границ) = -g^- beLy -~. B.68)
2. Силовые линии „расходятся" вблизи поверхности образца; соот-
соответственно сверхпроводящие домены становятся тоньше на концах.
На этом в объеме -~dsLy для каждой области S проигрывается опре-
определенная энергия. Это дает вклад
-2±d2sLy-?U0(pJ. B.69)
где ps = djd, a Uo (ps) — безразмерная функция, которую можно вы-
вычислить, зная точную форму „тонких" областей.

Магнитные свойства сверхпроводников первого рода 47
3. Энергия магнитного поля | (Л2/8я) dr также изменяется вблизи
поверхности, что дает член вида
Н1 L
-~ d2sLy -f- Vo (ps), B.70)
где V0(ps) — другая безразмерная функция. (Расчет Uo и VQ описан
в книге Ландау и Лифшица [8]'), § 44.)
Выберем в качестве независимых переменных р^ и d. Если сна-
сначала произвести минимизацию свободной энергии по переменной ps,
то для макроскопического образца (е ~^> |0) найдем
Это уравнение, как мы уже знаем, выражает тот факт, что поле
в нормальной области равно Нс. Теперь минимизируем функцию &F
по d. Зависящий от d вклад в функцию ?Г дают три только что
выписанных дополнительных члена
У]] B.72)
Значение d, приводящее к минимуму &Г• равно
где ф = 0,5 rp2f/o-f-p2n—Р5J^о]- ^ типичном случае, когда
HJHc-^0,7, ф~10~2, имеем d~ 10 Убё. Взяв е= 1 см, 6=3000 А,
получаем, что d«4s0,6 мм. Вблизи краев (р5-»-0 илир5^»1) ф->0,
а величина d соответственно становится больше. Для наблюдения
доменной структуры используется ряд различных методов2).
1. Метод, примененный Мешковским и Шальниковым [25] в 1947 г.,
состоит в измерении сопротивления тонкой висмутовой проволочки
при передвижении ее вдоль поверхности исследуемого образца. Со-
Сопротивление проволочки сильно зависит от величины магнитного поля
и поэтому изменяется от больших значений вблизи областей Af до
малых в окрестности областей 5.
2. Порошковый метод [26—29]. На поверхность образца нако-
накосится слой порошка ниобия. Вследствие большой величины критиче-
критического поля ниобия (~ 2000 гс) зерна порошка всегда остаются
•) Подробный расчет дан в работе [24]. — Прим. ред.
*) См. примечание на стр. 29. — Прим. ред.

48 Глава II
в сверхпроводящем (т. е. диамагнитном) состоянии, поэтому они,
стремясь избежать силовых линий, собираются вблизи областей S.
3. Оптический метод [30]. Образеи покрывают тонким слоем це-
риевого стекла (толщиной ^ 0,1 мм), в котором наблюдается сильно
выраженный эффект Фарадея. Через стекло в направлении магнитного
поля Но, перпендикулярного поверхности образца, пропускают поля-
поляризованный свет. При прохождении света через стекло плоскость
поляризации поворачивается на угол 0. Затем свет отражается от
поверхности образца, в результате полный угол поворота равен 2В.
Так как, вообще говоря, угол 6 пропорционален величине поля
@sfeO,O2° мм • гс~1), то при наблюдении образца сквозь скрещен-
скрещенную систему анализатора и поляризатора области N, где h фО, ока-
оказываются светлыми. В конечном счете эти измерения позволяют опре-
определить энергию границы, т. е. длину 6.
Задача. Найти поправки к величине критического поля пластины, обу-
обусловленные конечностью ее толщины е.
Решение. Минимизируя выражение для свободной энергии относи-
относительно d при заданных значениях приведенного поля hr = H0IHc и ps = dsjd,
находим
В интересующей нас области hr близко к 1, a ps —к нулю, тогда для
можно написать
где б2 = 0,51 Uo @) + vo @) | = In 2/я = 0,22. (Это численное значение полу-
получено в вышеупомянутом расчете Ландау и Лифшица.) Далее, минимизируя ?Г
относительно р5, получаем условие
Поле достигает критического значения для пластины в том случае, когда
величина ff~ становится равной свободной энергии нормального состояния
(H^l8л) eLxLy. Отсюда получаем еще одно условие
Ps
Оба условия выполняются одновременно, если
-26 (А)*].

Магнитные свойства сверхпроводников первого рода 49
При е = \ мм и 6 = 104 А уменьшение критического поля составляет 3?6.
Подобные отклонения от макроскопической теории имеют место для любой
геометрии. Это обстоятельство весьма часто играет важную роль при обсу-
обсуждении экспериментальных данных для сверхпроводников первого рода.
Если внимательно посмотреть на доменную
арадокс структуру, изображенную на фиг. 20, а, то
легко заметить, что в определенных точках области N, как, скажем,
в точке А, силовые линии „раздвигаются". Поэтому в таких точках
величина поля h значительно меньше, чем, например, поле h(P),
в точке Р (находящейся на границе), т. е. ниже величины Нс- На
первый взгляд, это может вызвать беспокойство, поскольку, каза-
казалось бы, область вблизи точки А должна вновь перейти в сверх-
сверхпроводящее состояние. Это осложнение было проанализировано Лан-
Ландау [31], который пришел к выводу, что нормальные области должны
испытывать „ветвление" (фиг. 20, б), возможно, до столь мелкого
масштаба, что доменная структура становится ненаблюдаемой. Факти-
Фактически, однако, довольно часто наблюдается простая доменная струк-
структура. В чистых образцах с размерами ~1 ел „ветвления" вообще
не происходит. Это связано с уменьшением величины критического
поля в точке А до величины, меньшей Нс, вследствие эффекта, ана-
аналогичного рассмотренному в предыдущей задаче. Отличие состоит
лишь в величине эффекта. Теперь роль характерного размера вместо е
играет d и поэтому эффект велик. Следовательно, окрестность
точки А становится нормальной уже в довольно слабых полях.
Если бы мы располагали сверхпроводником с толщиной f~l о
(d ~~> 1 см), то можно было бы применить к нему макроскопическое
рассмотрение вблизи точки Р. В этом случае можно было бы обна-
обнаружить ветвление. Отсюда видно, что разветвленная модель не является
ошибочной; она просто непригодна для описания образцов обычных
размеров. (Другой способ создать условия, благоприятные для воз-
возникновения ветвления, состоит не в увеличении е, а в уменьшении 6;
этого можно добиться путем выбора подходящего сплава.)
Обсудим качественно два предельных случая.
поверхностной L ^'^>%- B предыдущем макроскопическом
энергии рассмотрении предполагалось наличие резкой
границы между нормальной и сверхпроводя-
сверхпроводящей областями (для определенности будем считать, что эта граница
лежит в плоскости yz, причем поле направлено вдоль оси z, а об-
области N соответствуют значения х < 0). В области /V термодинамиче-
термодинамический потенциал уменьшается за счет „магнитного" члена нЦЪп—Нс/^я
[см. B.49)], тогда как в области 5 значение $¦ понижается за счет
энергии конденсации — H2cjSn. Что же происходит при микроскопи-
микроскопическом рассмотрении? Если величина Я, мала, то предположение о том,
что поле скачком изменяется на плоскости х = 0, остается в силе.
4 Зак. 1020

Вакуум -
• /V —
- Поверхность
- Сверхпроводник-
а
Фиг. 20. Картина доменной структуры вблизи поверхности образца.
а — неразветвленная модель. Отметим, что ft (Л) < h(P) = Hc; это показано с помощью различ-
различной кривизны силовых линий. Имеется также несколько небольших нормальных областей вблизи
краев, где ft < Н^
б—равветвленная модель Ландау. Ветвление необходимо, чтобы условие ft > Ис выполнялось
всюду в нормальных областях. Фактически, однако, ветвления не происходит, так как условие
ft > He применимо к нормальным областям макроскопических размеров. Для малых областей
вблизи поверхности критические поля значительно меньше ffg, так что справедлива простая
неразветвленная модель.

Магнитные свойства сверхпроводников первого рода
51
Новым здесь является то обстоятельство, что в 5-области (л: > 0)
сверхпроводимость „портится" на расстояниях порядка |0 вблизи гра-
границы; это сопровождается соответствующим проигрышем в энергии
конденсации. Отсюда находим энергию границы y ~ (#с/вя) |а
(т. е. 6~|0).
2. io<d^- Только что рассмотренный вклад в этом случае прене-
пренебрежимо мал. Распределение поля мы можем рассчитать с помощью
уравнения Лондонов; оно представлено на фиг. 21. В прежних обо-
обозначениях в N-области h~Hc, в 5-области h = Hc ехр(—xfk).
Термодинамический потенциал Гиббса принимает вид
h2 Hh Л2 / dh
M
лг>0
Здесь первый член — свободная энергия нормальной фазы в нулевом
поле; второй — энергия конденсации (р = 0 для х < 0 и р = 1 для
h
N
Фиг. 21. Микроскопическая картина распределения поля вблизи границы
раздела между нормальной и сверхпроводящей областями.
В нормальной области А=Я?, при удалении внутрь сверхпроводника поле h спадает на рас-
расстояниях порядка глубины проникновения К
х > 0); третий член — энергия магнитного поля и четвертый — микро-
микроскопический аналог величины — Б///4я. Наконец, последний член
представляет кинетическую энергию токов.
Легко убедиться в том, что вдали от границы плотность термо-
термодинамического потенциала Гиббса одинакова в обеих фазах (условие
равновесия) и что величину & можно записать в виде
где 5 — площадь границы, а V — поверхностное натяжение
СО <»
J 4 (?)IJ
= Т5Г J
л.*

52 Глава II
В этом предельном случае поверхностное натяжение отрица-
отрицательно, т. е. система может понизить свою энергию путем образо-
образования новых границ. Таким образом, возникает тенденция максимально
увеличить число границ, и, очевидно, магнитные свойства будут сильно
отличаться от рассмотренных выше. Именно по этой причине мате-\
риалы с ?q < Я, носят название сверхпроводников второго рода. Мы ]
изучим их в следующей главе.
ЛИТЕРАТУРА
Макроскопическое описание сверхпроводников первого рода
London F., Superfluids, vol. I, New York, 1950.
Ландау Л. Д., Л и ф ш и ц Е. М.. Электродинамика сплошных сред, М.,
1959, гл. 6.
Нелокальная связь между током и вектором-потенциалом
Р i р р а г d А. В., Proc. Roy. Soc., A216, 547 A953).
Измерение глубины проникновения
Schawlow A. L., Devlin G., Phys. Rev., 113, 120 A959).
Р i р р а г d А. В., Ргос. 7 th Internet. Conf. Low Temp. Phys., Toronto,
1960, p. 320.
Промежуточное состояние
Оптическое наблюдение доменов
De Sorbo W., Phys. Rev. Lett., 4, 406 A960).
D e S о r b о W., Proc. 7 th Internat. Conf. Low Temp. Phys., Toronto. 1960,
p. 370.
Измерение поверхностной энергии
S chaw low A. L.. Phys. Rev-. 101, 573 A956).
Кинетика перехода из нормального в сверхпроводящее состояние
F a b е г Т. Е., Р i p p а г d А. В., в книге Progress in Low Temperature Phy-
Physics, ed. С. О. Oorter, vol. I, Amsterdam, 1955, ch. 9.

Глава III
МАГНИТНЫЕ СВОЙСТВА СВЕРХПРОВОДНИКОВ
ВТОРОГО РОДА
§ 1. КРИВЫЕ НАМАГНИЧИВАНИЯ ДЛИННОГО ЦИЛИНДРА
Сверхпроводники второго рода характеризуются следующими
макроскопическими свойствами.
1. Цилиндр, помещенный в продольное поле Н, не обладает
свойством полностью вытеснять магнитный поток (эффект Мейсснера),
за исключением области слабых полей Н < Нп '). Если вычислить
критическое поле Нс, определяемое разностью свободных энергий
в нормальном и сверхпроводящем состояниях в нулевом поле
то можно обнаружить, что поле НЛ заметно меньше, чем Нс. На-
Например, для соединения V3Ga калориметрические измерения разности
Fn — Fs в нулевом поле дают (Нс)т^0 «s» 6000 гс, в то время как из
магнитных измерений следует, что (//с1O-=0 =*s 200 гс.
2. При Н >• Нсх силовые линии проникают в цилиндр, однако
даже при установлении теплового равновесия это проникновение не
является полным. Поток <f>, проходящий через цилиндр, имеет мень-
меньшую величину, чем в том случае, когда образец находится в нор-
нормальном состоянии. Это указывает на существование незатухающих
токов в образце, который, следовательно находится все еще в сверх-
сверхпроводящем состоянии. Такая ситуация имеет место для полей Нс1 -^
-^ Н <; Н&- Поле На превышает Нс и в некоторых случаях очень
велико; для V3Ga, например, (Нс^)т=0«» 300 000 гс.
3. При Н > НЛ макроскопический образец вообще не выте-
вытесняет потока (В = //). Однако даже в этом случае сверхпроводи-
сверхпроводимость разрушается не полностью: в области полей Н^ < И < Н&
на поверхности цилиндра сохраняется сверхпроводящая прослойка
(толщиной ~ 103А). В большинстве случаев Н^я^ 1,69/У^. Существо-
Существование такой прослойки можно обнаружить, например, путем измере-
измерения сопротивления между двумя контактами на поверхности образца.
1 Оказывается, что при малых измерительных токах сопротивление
1 отсутствует. Физическая причина наличия прослойки состоит в сле-
следующем: небольшой сверхпроводящей области легче образоваться
') Обозначение Нс1 для нижнего поля было рекомендовано участниками
конференции по сверхпроводимости в Колгвйте в 1963 г.

54
Глава III
вблчзи поверхности образца точно так же, как пузырьку воздуха
легче образоваться на дне кружки пива, чем в любой точке внутри ее.
(Несколько более сложное доказательство этого утверждения мы
обсудим в гл. V').)
Изменение полей Hcv НЛ и НсЪ с температурой показано на
фиг. 22. Мы сосредоточим теперь наше внимание на области полей
НЛ < И < Н^ в которой проникновение потока является частичным.
Впервые существование этой области на плоскости (Н, Т) было ясно
сз
Поверхностная
сверхпроводимость
Полный эффект
Мейсснера
в=0
Фиг. 22. Фазовая диаграмма для сверхпроводника второго рода в форме
длинного цилиндра.
продемонстрировано Шубниковым [32] в его ранних опытах со спла-
сплавами в 1937 г. Мы будем называть эту область фазой Шубни-
кова или иногда вихревым состоянием2). (Последнее название свя-
связано с микроскопической картиной, описанной в § 2 этой главы).
Частичное проникновение потока в фазе Шубникова можно опи-
описать с помощью диаграммы В (Н). Такая диаграмма показана,
') Принято называть сверхпроводниками второго рода только те ве-
вещества, для которых Hci > Ис. Что же касается упомянутой выше поверх-
поверхностной прослойки, то возможен случай, когда Hci < Нс, но Нсз > Нс. —
Прим. ред.
*) Следуя Абрикосову [33], это состояние чаще называю! смешанным
состоянием. — Прим. ред.'

Сверхпроводник
1-го рода
Сверхпроводник
Z-го рода
W,
Н.
'сг
Н
Фиг. 23. Зависимость индукции В от величины приложенного поля Н для
сверхпроводников первого и второго рода.
-4лМ
Сверхпроводник
Z-го рода А
У
/
/
к
Сверхпроводник
/ 1-го рода
-
и и и и и
Фиг. 24. Обратимые кривые намагничивания сверхпроводников первого
и второго рода в форме длинного цилиндра.
Если значения поля //^.одинаковы для обоих материалов, то площади ОАВ и ОА'В' равны.

56 Глава III
например, на фиг. 23. Иногда вместо индукции экспериментаторы
предпочитают изображать намагниченность М, определяемую соот-
соотношением
Кривая М(Н) показана на фиг. 24. (На практике наблюдение этих
кривых часто усложняется из-за трудности, связанной с достиже-
достижением равновесного состояния; например, наличие структурных де-
дефектов препятствует перемещению силовых линий.) Пунктиром на
фиг. 24 изображена кривая намагничивания для сверхпроводника
• первого рода с тем же значением Нс. Эти две кривые обладают ин-
интересным свойством: охватываемые ими площади равны.
Доказательство. Обозначим через Gs плотность потенциала Гиббса
для образца в сверхпроводящем состоянии
GS = FS (В)--??-. C.3)
В равновесии при заданном поле Н функция Gs обладает минимумом
Рассмотрим теперь плотность термодинамического потенциала Гиббса для
образца в нормальном состоянии
Gn = Fn + -^--^L. C.5)
Из условия термодинамического равновесия в нормальной фазе (<3Gn/dB) = О
следует, что В= И. Отсюда
G =У=- — —
Дадим теперь полю Н приращение W, тогда из C.3) и C.4) следует
dos в
дН
Из C.6) аналогично находим
6О„ И
-б# = -^Г- <3-8)
т. е.
Проинтегрируем теперь обе части последнего соотношения в пределах от
Н = 0 до Н = Ис2. При Н = Нс2 обе фазы находятся в термодинамическом
равновесии (О„ = Gs). При Н = О (В — 0) имеем Gn — Fn и Gs — /> Учи-
Учитывая, кроме того, определение
_ii

Магнитные свойства сверхпроводников второго рода 57
в результате получаем
----ьГ- (ЗЛО)
С
Отсюда видно, что площадь, охватываемая кривой на фиг. 24, зависит лишь
от величины Нс. Таким образом, путем измерения равновесных кривых на-
намагничивания мы можем определить Нс, а значит, и энергию конденсации.
Обсудим теперь переход, происходящий во внешнем поле И, рав-
равном одному из предельных значений Нл или Н^. Сначала рассмотрим
переход при Н = И^. Опыт показывает, что для всех изученных до
сих пор случаев этот переход является фазовым переходом второго
рода.
1. Из магнитных измерений следует, что кривая В(Н) непре-
непрерывна при Н = Ис2.
2. В том небольшом числе случаев (например, для V3Ga), когда
производились тепловые измерения, оказалось, что скрытая теплота
перехода отсутствует, а теплоемкость терпит разрыв.
Величину скачка теплоемкости удается связать с ходом кривых
намагничивания на основе чисто термодинамического рассмотрения
(Гудман [34, 35]). Пусть / и j обозначают рассматриваемые фазы
(в частности, индекс i будет относиться к фазе Шубникова, а у —
к фазе с В^Н, в которой основная часть образца находится в нор-
нормальном состоянии). Запишем потенциал Гиббса для единицы объема
Z-й фазы
Ol==Ft(T.BJ-M-. C.11)
Связь между Полем И и индукцией В в этой фазе следует из ус-
условия минимума G при заданных И и Т
ж, рл-**>=-&• <ЗЛ2>
Энтропия St определяется из соотношений
Фазы /и у находятся в равновесии, когда поле удовлетворяет опре-
определенному условию Н = Н* (Т) (в данном случае Н* = Н^; вдоль
этой кривой
Q^Qj. C.14)
Предположим теперь, что скрытая теплота перехода отсутствует.
Тогда на кривой Н = Н*(Т) энтропия обеих фаз также имеет оди-
одинаковое значение
S^Sj. C.15)

58 Глава III
Отсюда следует, что индукция В в точке перехода не может иметь
разрыва. Чтобы убедиться в этом, вычислим производную
взятую вдоль кривой равновесия [dH = {dH*ldT)dT\. Отсюда с по-
помощью C.11)—C.13) находим производную от G (также вдоль
кривой равновесия)
dT — ~ ^ ~Щ ~W
Поскольку вдоль равновесной кривой (Gt =
dT'
из C.17) неизбежно следует, что Bt = Bj, т. е. при переходе ин-
индукция В остается непрерывной.
Вычислим теперь теплоемкость в постоянном поле И
Удобно, как и раньше, выразить фигурирующую здесь частную про-
производную через полную производную от энтропии, взятую вдоль
кривой равновесия,
dSi /dSi\ ,(dSt\ Ш*
)^\~дн) <6Л
(
Чт —\-дт)и^~\~дн)т ат
Согласно C.15), вдоль кривой равновесия
следовательно,
Образуем теперь с помощью C.12) и C.13) производную (dSJdH)?
следующим образом:
idSi\ ldS,\ (дВЛ __ d*Fi (дВЛ 1 дН (Ви Т) I dBt \
\'Ш)т=\'Щ)т\дН~)т-~'ШЖ\днI- 4л дТ \дН)т
C.21)
Наконец, изменение поля Н* с температурой Т запишем в виде
dH* ,дН\ . I dH \ dB C 22)
_
Г = [-дГ)В + {-ЩO dT •

Магнитные свойства сверхпроводников второго рода 69
где производная
йВ dBt
If =~dT~~~dT
представляет собой изменение индукции В вдоль равновесной кривой.
Подставляя (дН,'дТ)в из C.22) в C.21), получаем
Ё1\ — ^!» _j__Li
дН)Г— 4S" dT \дН)т~Г4я dT
аН*\*\(дВЛ (dBl
Следовательно, если известна зависимость Н* (Т) и магнитная
проницаемость (pBtldH)T каждой из фаз, можно предсказать величину
скачка теплоемкости при переходе. Для интересующего нас перехода
i->j (см. фазовую диаграмму на фиг. 23) из вихревого состояния I
(восприимчивость конечна и больше единицы) в нормальное состоя-
состояние ] (восприимчивость равна единице) имеем Ct > Cj. Существую-
Существующих в настоящее время экспериментальных данных недостаточно для
количественной проверки соотношения C.24). Тем не менее для слу-
случая V3Ga значения Ct — С;- и dH^dt известны. Делая разумную
экстраполяцию производной dBjdH, чтобы оценить ее значение при
Н — Нл, мы получаем согласие магнитных и калориметрических из-
измерений в пределах 10%. Аналогичное рассмотрение можно произ-
произвести в принципе также для перехода при Н = На. В этом случае,
однако, проницаемость (дВ1дН)И_И в фазе Шубникова, по всей
вероятности, обращается в бесконечность, как следует из теорети-
теоретического анализа § 2 настоящей главы. Согласно C.24), это должно
привести к бесконечному пику на кривой теплоемкости в точке пере-
перехода. На самом деле эта особенность является слабой и легко мо-
может быть замаскирована различными гистерезисными эффектами. Не-
Недавно она наблюдалась на ниобии группой экспериментаторов из
университета Рутгерса в США [36. 37]').
§ 2. МИКРОСКОПИЧЕСКОЕ ОПИСАНИЕ ВИХРЕВОГО
СОСТОЯНИЯ
Отрицательная поверхностная энергия
Выше мы видели, что в лондоновском сверхпроводнике (? < К)
поверхностное натяжение на границе раздела между нормальной и
сверхпроводящей областями является отрицательным. При таких
условиях естественно считать, что при .наличии поля возникает со-
состояние, в котором области N и S подразделены очень мелко, т. е.
сильно перемешаны, а энергия границ вносит важный вклад в термо-
1) См. также [38]. — Прим. ред.

60
Глава 111
динамический потенциал Гиббса. Эта ситуация сильно отличается от
той, с которой мы сталкивались в случае пиппардовского сверхпро-
сверхпроводника, когда число границ мало и их энергией можно пренебречь
при макроскопическом подходе.
2?
Фиг. 25. Структура изолированной вихревой нити в сверхпроводнике
второго рода.
л —конфигурация полей и токов, создаваемых вихревой нитью; б—зависимость магнитного
поля от расстояния до центра нити; в — изменение плотности сверхпроводящих электронов п
в области остова нити (г <С Ъ).
Магнитное поле максимально в центре нити и убывает по мере удаления от него, т. е. заклю-
заключено в области порядка глубины проникновения >.; наоборот, плотность электронов уменьша-
уменьшается лишь в небольшой области остова, имеющего радиус ?.
Рассмотрим предельный случай, когда индукция В мала (т. е.
мало число силовых линий, проникающих в образец и, следовательно,
лишь незначительная часть объема находится в нормальном состоя-
состоянии). Наиболее вероятными представляются два типа областей N.

Магнитные свойства сверхпроводников второго рода 61
для которых можно ожидать наибольшей величины отношения по-
поверхностных эффектов к объемным: слои очень малой толщины (^-|)
и нити малого диаметра (~ |). В случае % ~^§> | теоретический расчет
(см. задачу на стр. 75) показывает, что меньшей энергией обладает
нитевидная структура, изучением которой мы сейчас и займемся.
Структура изолированной вихревой нити показана на фиг. 25, а.
Нить обладает жестким остовом радиусом |, в котором плотность
сверхпроводящих электронов ns при приближении к центру убывает
до нуля, как показано на фиг.25, в. Силовые линии магнитного поля
имеются не только в области остова. Поле имеет максимальное зна-
значение в центре нити и простирается на расстояния г ~ А,; круговые
токи j, связанные с полем, приводят к экранированию последнего
при г ~>^ А. (фиг. 25, б). При г > |, т. е. в большей части области,
представляющей для нас интерес, распределение полей и токов можно
просто рассчитать с помощью уравнений Лондонов. Забегая вперед,
заметим, что радиус и точная форма остова входят в соответствующие
величины лишь под знаком логарифма, т. е. нам не нужно знать их
точно. Действительно, мы увидим, что в пределе |<^[А, свойства
изолированной вихревой нити могут быть сравнительно легко рас-
рассчитаны до конца.
Найдем величину магнитного потока
связанного с одной нитью. Эксперимент и теория показывают, что
если через отверстие в массивном сверхпроводнике проходит неко-
некоторое число силовых линий магнитного поля, то связанный с ними
магнитный поток может принимать лишь дискретные значения
. C.25)
S7 2
где k — целое число. Объяснение этого эффекта будет дано в конце
гл. IV. Результат C.25) определяет также величину потока, связан-
связанного с отдельной нитью. Иначе говоря, требование, чтобы с вихревой
нитью был связан один квант потока <f>0, как раз и соответствует
максимальному расслоению системы на фазы. Это условие определяет
масштаб картины распределения поля вблизи нити на фиг. 25, б и
полностью задает структуру отдельной нити.
Такая квантовая нить, состоящая из очень тонкого и жесткого
остова, окруженного круговыми токами, весьма напоминает вихревые
нити, которые образуются в сверхтекучем Не4 при вращении содер-
содержащего его сосуда. Единственное отличие состоит в том, что атомы
Не4 не заряжены, т. е. в уравнении A.13) нужно положить е = 0.
Таким образом, мы видим, что глубина проникновения А, в случае Не4

62 Глава HI
бесконечна и что на больших расстояниях от нити поток j, связан-
связанный с движением частиц, не убывает экспоненциально, а медленно
спадает (как 1/г). Впервые вихревые нити обсуждались Онсагером [39]
и Фейнманом [40] в связи с явлением сверхтекучести Не4; обобщение
на случай сверхпроводимости произвел Абрикосов [33] в 1956 г.
Если в сверхпроводящем металле плотность вихревых нитей конечна,
то мы будем часто впоследствии говорить, что он находится в вих-
вихревом состоянии.
Свойства изолированной вихревой нити
Перейдем теперь к детальному изучению структуры отдельной
вихревой нити в пределе А, ^> Ъ,- Поскольку „жесткий остов" (радиус
которого |) в этом случае мал, при вычислении энергии мы на не-
некоторое время пренебрежем его вкладомг). Выражение для энергии
отдельной нити можно представить в виде
9= \
C.26)
Выражение C.26) было выведено в гл. I (в предположении, что
). Глубина проникновения "к для чистого сверхпроводника дается
выражением Лондонов
Для сверхпроводящих сплавов с Я,^>| выражение C.26) по-преж-
по-прежнему применимо, однако вместо X нужно подставить несколько боль-
большее значение [см. обсуждение формулы B.20) в гл. И]. Интегриро-
Интегрирование в C.26) ведется по всему пространству, за исключением остова,
т. е. по области г > |. Вычислим энергию 0, отнесенную к единице
длины нити, и назовем ее линейным натяжением.
Из условия минимальности значения 0 мы приходим обычным
образом к уравнению Лондонов
h + *,2rotroth = 0, \r\>\. C.28)
Внутри остова вместо C.28) следует применить несколько более
сложное уравнение, однако, поскольку радиус остова весьма мал,
можно заменить имеющуюся особенность двумерной б-функцией ^(г)
и написать
h + A,2rotroth = ?062(r). C.29)
где ф0— некоторый вектор вдоль направления линии.
') То есть пренебрежем изменением энергии конденсации сверхпрово-
сверхпроводящей фазы. — Прим. ред.

Магнитные свойства сверхпроводников второго рода 63
Покажем сейчас, что сила источника ф0 в уравнении C.29) пред-
представляет собой полный поток, переносимый нитью. Проинтегрируем
для этого обе стороны уравнения по площади кругового контура С
радиусом г, центр которого лежит на оси нити. Воспользовавшись
формулой Стокеа, получим
dl = f0. C.30)
Будем считать, что г ^> X. тогда токами
а следовательно, и контурным интегралом можно пренебречь. Таким
образом, полный поток, связанный с нитью, равен ф0.
Перейдем к решению уравнения C.29) совместно с уравнением
Максвелла
divh = 0. C.31)
Поле h направлено вдоль оси г, линии тока являются окружностями
в плоскости ху. Нетрудно вычислить величину roth (т. е. ток) в об-
области \<^.r<^%. Действительно, вернемся к уравнению C.30),
в котором круговой контур С лежит в рассматриваемой области.
В этом случае можно пренебречь первым членом, поскольку через
контур С проходит относительно малая доля (~ г2/Я2) полного по-
потока ф0. Таким образом,
I22nr\ roth | = ^о- C-32)
или
lrothl = W7' Z<r<il. C.33)
Полагая
dh
и интегрируя, находим
( ) C-34)
Для определения постоянной интегрирования в выражении C.34)
необходимо воспользоваться точным решением уравнений C.30) и
C.31):
* = -52пг*о(-Й. C-35)
где Ко— функция Бесселя нулевого порядка от мнимого аргумента [41].
Нам понадобится лишь асимптотический вид C.34) этого решения
для г<^К где постоянная, как можно показать, равна нулю. Что же

64 Глава III
касается поведения на больших расстояниях, то оно следует из C.35):
Зная выражение для поля, легко вычислить энергию ?f. Инте-
Интегрируя по частям второй член в C.26), находим
a. C.37)
где интеграл по а берется по поверхности остова, в качестве кото-
которого мы выберем цилиндр радиусом порядка \. Соответственно ли-
линейное натяжение 0 запишем в виде
g_E. C.38)
Подставив сюда выражения C.33) и C.34), окончательно получим
В связи с выражением C.39) обратим вни-
Обсуждение мание на следующие важные моменты.
формулы C.39) j Линейное натяжение д лишь лога.
рифмически зависит от |.
2. Величина if пропорциональна квадрату полного потока нити.
Это означает, например, что в том случае, когда поток равен 2ф0,
образование двух нитей, каждая из которых несет квант потока ^>0
(полная энергия равна 2^), более предпочтительно, нежели образо-
образование одной нити с удвоенным потоком (с энергией Ад). Таким об-
образом, фигурирующий здесь поток ф0 должен иметь наименьшее зна-
значение, равное кванту потока [см. C.25)].
3. Запишем выражение для д (при Т = 0) в несколько ином
виде, используя формулы
™~~2ег> ® ~ ^о — яд (гл C.40)
и соотношение (которое будет доказано при изложении микроскопи-
микроскопической теории) между энергией конденсации и энергетической
щелью А@)
-^-=1^@)Д2@), C.41)
где N @) = m2vFj2n2t)z—плотность состояний (с данным направле-
направлением спина) на фермиевской поверхности в нормальном металле.

Магнитные свойства сверхпроводников второго рода 65
Комбинируя эти формулы, получаем
я3 Hi К
я=-зш%21пт (Г=0)- C-42)
Такая форма • записи представляет интерес по следующей причине.
До сих пор мы пренебрегали вкладом остова в энергию нити. Так как
в области остова сверхпроводимость более или менее разрушена,
этот вклад составляет ~~(нЦ8я)Ъ?. По своей структуре это выра-
выражение имеет много общего с выражением C.42) для 0', но численно
дает гораздо меньшие значения. Детальный расчет приводит к сле-
следующему выражению для линейного натяжения:
где числовая постоянная е учитывает вклад остова нити и прибли-
приближенно равна 0,1.
Задача. Обсудить структуру вихря, образующегося в тонкой пластинке
в магнитном поле, перпендикулярном ее плоскости (Пирл [42]).
Решение. Здесь, как и в случае вихревой иити, имеется „жесткий
остов" малого радиуса I, окруженный кольцевыми токами. Однако, поскольку
эти токи могут располагаться теперь лишь в пределах толщины пластинки rf,
их экранирующее действие является слабым и поле может проникать на
значительно большие расстояния, чем в предыдущем случае.
Внутри пластинки применимо уравнение C.29)
где j — плотность тока, а п2— единичный вектор нормали к поверхности
пластинки. Удобно перейти от поля h к вектору-потенциалу А, воспользо-
воспользовавшись соотношением
h = rot A.
В лондоновской калибровке имеем
в цилиндрической системе координат: Фг = Фг — 0, Фе = фо/2пг.
Произведем теперь усреднение по толщине пластинки, учитывая, что
при d <^ К величины j и А почти не зависят от г. Обозначив полный ток
через J, находим
Заменим теперь задачу о пластинке конечной толщины задачей о плоскости
(г = 0), по которой течет ток с плотностью J6 (г). Такая процедура законна
до тех пор, пока толщина пластинки d мала по сравнению с глубиной про-
проникновения поля.
С помощью найденного выражения для плоского тока напишем теперь
уравнение, справедливое во всем пространстве,
rot rot A = rot h = ^-j — Л^фф(Ф — АN(г),
5 Зак. 1020

66 Глава III
или, считая калибровку лондоновской (rot rot А = — V2A),
^ {г).
Этот результат мы получили, основываясь на уравнении Лондонов C.29).
К сожалению, для реальных пластинок столь простое уравнение применимо
далеко не всегда. Тем не менее можно считать, что отклик системы имеет
по-прежнему линейный характер
где Лэфф — некоторая неизвестная константа, которую можно найти из не-
независимых измерений. В сущности ЛЭфф есть глубина проникновения для
пластинки в поле, параллельном ее плоскости; проще всего ее определить
из опытов на полых цилиндрах (изготовленных из того же материала).
Чтобы решить уравнение относительно А, введем трех- и двумерные
фурье-компоненты:
kqk = J А (х, у, г) е1 (V+V+**) dx dy л>
Ач = -к J V dk = J Аб B> е' (V+^y) dx dy dz,
Тогда
Выразив отсюда kqk и интегрируя затем по к, находим
А9 = Ф„
Эти формулы позволяют получить все интересующие нас сведения.
а) Фурье-компонента тока равна
При q ^> Л^ф компонента iq пропорциональна Ф?, поэтому на малых рас-
расстояниях г от центра вихря
Сф
При q <^ К-^ф имеем
сфп

Магнитные свойства сверхпроводников второго рода 67
Радиус области экранирования составляет ~> Я.Эфф, однако даже при г > ЛЭфф
ток У медленно спадает с расстоянием.
б) Нормальная составляющая поля hz дается выражением
При
Для больших расстояний г поле hz наиболее просто найти, исходя непосред-
непосредственно из выражения для тока J (г):
в) Собственную энергию вихря можно получить с помощью выраже-
выражения C.26); необходимые для такого расчета компоненты h и rot h на поверх-
поверхности остова (? <^ ХЭфф) приведены выше. В результате находим
СМ
* * 1г/эфф_137 Не
111 Г "тс \ 111
¦эфф ^ 16 Хэфф
Типичное значение Аэфф~>Ю0ОА и ?-^30 зв.
г) Сила взаимодействия между двумя вихрями равна
и соответствует отталкиванию. Поэтому на больших расстояниях, где J~R~2,
энергия взаимодействия убывает лишь как R~~l. Такое медленное спадание
связано с тем, что взаимодействие в основном происходит не через сверх-
сверхпроводник, а через пустое пространство снаружи от иего.
Взаимодействие вихревых нитей
г Рассмотрим две нити, параллельные оси z
луча д ух нит и ПрОХОдящие ПрИ г—о через точки rI—(xv уг)
и г2 = (л;2, у2). Результирующее распределение магнитного поля
описывается уравнением
h +1? rot rot h = ?0 [6 (г — rj) + б (г — г2)], C.44)
которое является просто обобщением уравнения C.29). Решение h
представляет собой суперпозицию двух полей hj и h2, создаваемых
соответственно нитями 1 и 2
h + h
C>45)
5,*

68 Глава III
Выражение для энергии системы сохраняет свой прежний вид
C.46)
где интеграл по а берется на этот раз по поверхности остовов
(|г — rf| = ?) обеих нитей. Выписывая в явной форме вклад от
каждой нити, имеем
В =" Ш J <Л1 + ^ • (Ь> + ^ X (fOt hl + fOt ^ Cl47)
Фигурирующие здесь 8 членов разобьем на следующие три группы:
1. Сумма собственных энергий изолированных нитей
2g = Ш U d°l ' (hi Xroth,)+ J d<j2 ¦ (h2Xroth2)].
2. Члены вида
J (h, 4- h2) ¦ (rot hj X da2 + rot h2 X d^).
стремящиеся к нулю в пределе |<С!^. поскольку величины hx —f— li2
и rothj остаются конечными в области интегрирования по ст2.
3. Остающиеся члены вида
Un = -?" [ J (hi X rot h2) • d<72 +- J (h2 X rot h,) • daj C.48)
описывают вклад в энергию за счет взаимодействия нитей.
Рассмотрим первый член в C.48). Согласно C.33),
|roth2|~ |Г1__Г2| ПРИ 1<|Г! —г
поэтому входящий в C.48) интеграл отличен от нуля даже в пределе
|—>0. То же самое относится и ко второму члену. Полагая в C.48)
^
C.49)
и используя C.33), находим энергию взаимодействия, отнесенную
к единице длины одной из нитей
Очевидно, энергия Ul2 отвечает отталкиванию нитей. На больших
расстояниях она убывает
?/12~ е~г'2/ при г,2->со
и логарифмически расходится как In | Vri21 на малых расстояниях
между нитями.

Магнитные свойства сверхпроводников второго рода 69
Замечание по поводу сил. Воспользуемся найденным выражением C-50)
для энергии взаимодействия ?/12 и вычислим силу f2, действующую на нить 2,
f _
/2Х—
Введем теперь плотность тока ]=nsev, который существовал бы в точке (лг2, У2)
при наличии лишь одной нити 1. Из уравнения Максвелла следует
, l_^iL
JV~ 4л tix2 *
Сравнивая это выражение с C.51), находим
/гх*=~г]у=ъ^у. C.52)
Полученный результат C.52) остается в силе и в том случае, когда нить 2
взаимодействует с произвольным числом других нитей; при этом v следует
понимать как суммарную скорость „сверхтекучего" движения в точке (х2, у2)
в отсутствие нити 2. В частности, если „сверхтекучая" скорость в любой
точке на оси иити равна нулю, последняя находится в статическом равновесии.
Построим теперь термодинамический потен-
Кривые циал Гиббса для системы большого числа
намагничивания
нитей, а затем из условия его минимума
найдем равновесную плотность нитей в образце. В предыдущих
обозначениях
и
Первый член в этом выражении представляет сумму энергий невзаимо-
невзаимодействующих нитей (пL—число нитей на единицу площади). Поскольку
каждая нить переносит один квант потока ф0, индукцию В можно
записать в виде
B = nLf0. C.54)
Второй член в C.53) описывает энергию отталкивателыюго взаимо-
взаимодействия между нитями; явное выражение для U-tj было приведено
выше [см. C.49) и C.50I- Наконец, последний член учитывает
влияние внешнего магнитного поля Н; благодаря ему энергетически
выгодны большие значения индукции В. Иными словами, поле Н
играет роль внешнего давления, которое стремится увеличить плот-
плотность нитей.
Чтобы произвести количественную оценку роли взаимодействия,
удобно выделить несколько областей.
1. Область малых значений индукций (nL№ <^C 1), в которой
существенную роль играет лишь взаимодействие ближайших соседей.
В результате сумма по / и j быстро сходится и может быть легко
вычислена.
2. Область больших значений индукции (nLl2^> 1), где радиус
взаимодействия ~ X велик по сравнению с пространственным периодом

70 Глава 111
решетки, образованной нитями. Для вычисления суммы по / и ] не-
необходим другой подход.
3. Наконец, область, где плотность нитей nL сравнима с ?~2
и остовы нитей начинают перекрываться. В этом случае исполь-
используемые здесь элементарные способы расчета неприменимы. Каче-
Качественно, однако, ясно, что перекрытие остовов означает почти полное
разрушение сверхпроводимости в толще образца при В—<j>Jl2.
• При малой плотности вихревых нитей (ма-
пиишее поле пл лых ^ их взаиыОдействие мало, поэтому
в первом приближении им можно пренебречь. Тогда получаем,
согласно C.53),
Отсюда видно, что при И < 4Лс?[ф0 плотность потенциала Гиббса
является возрастающей функцией В, т. е. наименьшему значению G
отвечает 5 = 0 (полный эффект Мейсснера).
Напротив, при Н > 4п??/ф0 значение О может быть меньше при
В Ф0. Это соответствует частичному проникновению силовых линий
в сверхпроводник.
Таким образом, нижнее поле определяется соотношением
_ Фв . К _
Величина этого поля часто может быть значительно меньше поля Нс,
определяемого соотношением C.1). Например, при 7' = 0, исполь-
используя C.40) и C.41), находим
¦^- = -^=-lln^-, C.57)
т. е. отношение HclJHc-^-yk, и поэтому может принимать довольно
малые значения.
Измерение значений НсХ и Нс позволяет в принципе определить \
и к. Например, для V3Ga при Т = 0 имеем Нс ~ 6000 гс и Нс1 — 200 гс,
и, согласно C.57), Х/|~80. С помощью C.56) находим %—2000 А
и | — 25 А. Эти оценки верны лишь по порядку величины, поскольку
существующие в настоящее время значения Нс и Hci известны
недостаточно точно. Однако есть основания надеяться, что в бли-
ближайшем будущем положение улучшится.
Поле е н го Если плотность нитей конечна (конечные зна-
превышающее Нс% чения 5)- то необходимо учитывать в C.53)
член, описывающий взаимодействие нитей.
При этом естественно ожидать, что минимуму отталкивательного
взаимодействия будет отвечать вполне определенное периодическое
расположение нитей. Детальный расчет на основе соотношения C.53)

Магнитные свойства сверхпроводников второго рода
71
показывает [43, 44], что для всех значений индукции В энергети-
энергетически наиболее выгодной является треугольная решетка нитей (фиг. 26).
Очевидно, когда поле Н лишь ненамного превышает значение Hcv
равновесная плотность нитей nL мала, а расстояние d между бли-
ближайшими нитями велико (й > К), Поэтому в члене взаимодействия
Остовы
вихревых
нитей
Фиг. 26. Треугольная решетка вихревых нитей (Клейнер и др. [44]).
Плоскость фигуры перпендикулярна направлению поля. Замкнутые контуры являются линиями
" " ~ :я к случаю а " ' "
крываются).
Постоянных значений ns. Схема относится к случаю сильных полей (остовы нитей почти пере-
мы можем учитывать вклад только от ближайших пар соседей; тогда
выражение C.53) принимает вид
()] <38>
где z — число ближайших соседей данной нити (для треугольной
решетки z = 6), а расстояние d связано с индукцией В соотношением
' fS d2 '
C.59)
Вид функции О {В) показан на фиг. 27. При Н > На начальный
наклон (dG/dB)B=0 отрицателен. При увеличении индукции В член
взаимодействия начинает расти, однако довольно медленно. Это свя-
связано с тем, что он содержит множитель /C0(rf/l), который при rf>l,
согласно C.36), имеет вид
/ f "
*0D)~«р(-4)=ехр(_1.07-
C.60)
Таким образом, при малых значениях В взаимодействие мало. Однако
при больших значениях В вклад этого члена является преобладающим,
что приводит к росту функции G(B). Следовательно, при некотором
значении В — В(Н) функция G достигает минимума [В {И)—рав-
{И)—равновесное значение индукции в поле Н].

Фиг. 27. Зависимость термодинамического потенциала & от индукции В.
Величина В = щ<Р§ характеризует число вихревых нитей, проходящих через I см* поверхности.
Минимуму if соответствует равновесное значение индукции Вк (Я).
Z00
400 600
Н, гс
800
1000
Фиг. 28. Экспериментальная кривая намагничивания сплава молибден — ре-
рений при Т = 0,522Тс (Джойнер и Блоер [45]).
Для сравнения по.саэаны две теоретические кривые намагничивания, рассчитанные Гудманом
C4]; пунктирная кривая относится к лами тртй модели, сплошная —к модели с вихревыми
нитями.

Магнитные свойства сверхпроводников второго рода 73
Теоретическая кривая В (Я) = Н -\- 4лЖ (Н) была рассчитана
Гудманом [34, 35]*). Результат показан на фиг. 28, где для сравне-
сравнения приведены также экспериментальные данные для особо хорошо
приготовленного сплава MoRe. По поводу имеющихся расхождений
необходимо сделать ряд оговорок. Теоретическая кривая имеет бес-
бесконечный наклон при нижнем поле: (<Ш/дЯ)я=// =оо. Физически это
отражает тот факт, что отталкивание нитей носит экспоненциальный
характер <~e~d/\ т. е., грубо говоря, имеет конечный радиус дейст-
действия порядка X. Поэтому при полях, немного превышающих Нс1,
в образце может возникнуть сравнительно много вихревых нитей,
ибо это почти не вызовет увеличения энергии взаимодействия. Наобо-
Наоборот, наклон экспериментальных кривых (dMjdff)H=H не очень велик.
Это также не удивительно, так как в рассматриваемой области
взаимодействие между нитями является слабым, в результате чего
они легко могут „зацепляться" за всевозможные структурные дефекты.
Тем не менее уже при полях, превосходящих Нс1 на 10% или более,
имеется хорошее согласие между теорией и экспериментом.
Аналогичная теоретическая кривая может быть построена для
другой модели, в которой принимается, что поток переносится не
вихревыми нитями, а слоями (см. задачу на стр. 75). Для больших
расстояний d между слоями мы снова получим для энергии отталки-
отталкивания экспоненциальную зависимость ~ e~dl^. Однако в этом случае
индукция В пропорциональна не d~2, как имеет место для решетки
из нитей [см. C.59)], а всего лишь d~l. По этой причине намагни-
намагниченность М (Н) при Н > Нс1 в ламинарной модели убывает быстрее,
чем в модели вихревых нитей. Теоретическая кривая для ламинарной
модели также приведена на фиг. 28. Ясно, что модель вихревых
нитей приводит к лучшему согласию с экспериментом. Впервые на
этот факт обратил внимание Гудман [34].
В этой области вихревые нити образуют
Область решетку с довольно малым периодом, по-
1А2<С!Я? <d l'!2 этому во взаимодействии участвуют и дале-
далекие соседи. Опишем способ вычисления энер-
энергии взаимодействия в таких случаях. Поле h (r), направленное вдоль
оси z, является решением уравнений
r/),
div h = 0,
где rl=(xl, yj) — координаты i-tt вихревой нити. Точки rt обра-
образуют двумерную периодическую решетку. Введем фурье-компоненту hj
') См. аналогичный расчет для квадратной решетки в работе Абрико-
Абрикосова [33].— Прим. ред.

74 Глава III
посредством преобразования
h3 = nL \ h(xr y^e^
Я'ейкэ
где интегрирование производится по основной ячейке. Вследствие
периодичности функции h (xt, yt) фурье-компонента hj отлична от
нуля лишь для векторов J, кратных вектору обратной решетки.
С помощью C.61) находим
Ш- C-62)
Наконец, свободную энергию <&" можно представить в виде
~~~ 8я Ы 1-f W2 "" 8я ^ 8я Li 1
i
В последней сумме минимальная величина вектора J составляет
— \jd — YnL* т- е- в интересующей нас области, очевидно, (XJJ~
— nLk2'^> 1. Следовательно, мы можем заменить \/(l-\-k2J2) на
1/ЯА/2 и вычислить 2j \fP. Последняя сумма определяется исклю-
чительно свойствами конкретной выбранной решетки. Чтобы упро-
упростить дальнейший расчет, перейдем от суммы к интегралу
11 1 A I A I 1
lip dJxdJy 1 r
2j T2" ""*" 12яУ21п J У2^ *" 2яи. J
•'макс ... ,
•» «•» • , -/макс
= -n 1П
У2
•*MH
где Jum~l[d и Умакс~< 1/|. (Фурье-компоненты с J>JMaKC должны
быть исключены, поскольку они соответствуют пространственным
изменениям поля на расстояниях, меньших толщины остова нити.)
В итоге находим
t ~ . —\— . j~[ ..
Г — F ML v«-«^
4я~"
Фигурирующий здесь коэффициент р имеет порядок единицы; для
треугольной решетки точный расчет [43] дает р = 0,381.
Зависимость В {И) обычным образом получается из условия
dG=0.

Магнитные свойства сверхпроводников второго рода
75
Для треугольной решетки получим
In Ф'
C.65)
где p'=pe~I/!, a d и В связаны соотношением C.59). Логарифмическая
зависимость C.65) находится в хорошем согласии с обратимыми кри-
кривыми намагничивания, получаемыми на опыте для материалов с ^
Здесь, как уже указывалось, используемая
Область nL~%~2 простая модель становится непригодной. Более
строгий подход, в основе которого лежат
уравнения Гинзбурга — Ландау, будет развит в гл. VI. Мы покажем,
что верхнее поле Нс2 имеет порядок ФОЦ,2- Физически это соответст-
соответствует перекрытию остовов вихревых нитей («L~|-2).
Задача. Вычислить потенциал Гиббса для ламинарной структуры. Резуль-
Результаты сравнить с ранее полученными для вихревого состояния.
Фиг. 29. Структура фазы Шубникова в ламинарной модели.
Тонкие (толщиной 2?) нормальные слои чередуются со сверхпроводящими. Нормальные слои
отталкиваются друг от друга; радиус действия сил отталкивания равеи глубине проникнове-
проникновения ?..
Решение. Ограничимся, как и прежде, предельным случаем ^
Ламинарная структура представляет собой систему тонких эквидистантно
расположенных N-слоев. Обозначим через d период структуры и будем счи-
считать, что плоскости слоев перпендикулярны оси х (фиг. 29). Внутри N-слоев
сверхпроводимость сильно подавлена, а в остальной части (области S) она

76 Глава III
характеризуется обычным значением плотности сверхпроводящих электронов,
равным ns. Впервые такая модель была детально изучена Гудманом в 1961 г.
Поле h (x) параллельно оси г и удовлетворяет уравнению Лондонов
везде, за исключением очень узких N-слоев. Решение имеет вид
где Р = d/2X, а Нт — магнитное поле внутри N-слоев.
Плотность свободной энергии в областях S, согласно C.26), равна
_ 2 г -
' (dhidxJ H2 th P
8л 8я Р '
К этому выражению необходимо добавить энергию (на 1 смъ) образования
.TV-слоев
F
с
2 ~ 8л d 8я Ра '
где и = Я/|. Наконец, для получения плотности потенциала Гиббса мы
должны учесть член
ви нт th р
4л~ —-Н л Р~-
Таким образом,
Q = ' f^ th р , ^ 9WW ^.)
иламин "8л" \ га Р ' Рк ^ппт р ]•
Минимизируя выражение для G относительно Нт, находим, что при
Для Н < Нс1У~п минимуму G соответствует бесконечно большое значение Р
(полный эффект Мейсснера); при И > hJVy. минимум достигается при
конечных значениях Р. Следовательно, нижнее поле в ламинарной модели
равно Ис/У'уГ. Для сравнения приведем результат, получающийся в модели
вихревых нитей [см. C.56)]
я In и
н И при
При v. ~^> 1 имеем Нс1 < Нс/х. Из сказанного следует, что в интервале
^ламин == ^мейссн»
т. е.
^вихр ^ ^ламнн-
В области малых значений индукции энергетически более выгодным является
вихревое состояние.

Магнитные свойства сверхпроводников второго рода 77
Аналогичное сравнение можно также провести для больших значений
поля Н. Рассмотрим, например, область Н^Н^ Для ламинарной модели
в этой области величина Р мала (Р<С10- Полагая ШРяР — Р3/^, легко
определить минимальное значение G
я2
С другой стороны, в модели вихревых нитей величина G, согласно C.64) и
(&65), равна
где v — константа порядка единицы. При Т = О
В интересующей нас области (//'
Следовательно,
н2 ннс
При Н < кЯс (величина кЯс, грубо говоря, совпадает со значением верх-
верхнего критического поля Пс2) имеем Оламин > ОВихр. Таким образом, в обла-
области промежуточных и больших значений поля вихревое состояние по-преж-
по-прежнему является наиболее устойчивым ').
Задача. Обсудить равновесную кривую намагничивания для образца
(сверхпроводник второго рода) в форме эллипсоида вращения в поле Но,
параллельном его продольной оси.
Решение. Исходными являются уравнения
divB = 0,
rot H = 0.
Они допускают решение с постоянными значениями В и Н внутри эллип-
эллипсоида
здесь Ве (И) — равновесное значение индукции для длинного цилиндра в про-
продольном поле И, а N — размагничивающий фактор для эллипсоида. Отсюда
находим связь между индукцией В н приложенным полем Но
В = 1
1-СЛГ/4Я) J •
') Если поле И близко к НС2, использованный выше элементарный под-
подход недостаточен. Позднее мы вернемся к изучению этой области полей
с помощью уравнений Гинзбурга — Ландау.

78 Глава III
Очевидно, индукция В отлична от нуля лишь для полей Нв > Нс1 A /)
величина наклона (,dB/dHB)B=0 конечна и равна AnfN. Верхнее критическое
поле остается равным Ис2, поскольку при фазовом переходе второго рода
В (Нс2) = Нс2.
Задача. Обсудить рассеяние медленных нейтронов на периодической
решетке вихревых нитей в сверхпроводнике [46, 47].
Решение. Взаимодействие нейтрона с вихревой ннтью имеет вид
\inh (г), где ц„ = l,91efi/Afc — магнитный момент нейтрона, а М — его масса.
Рассмотрим акт рассеяния, при котором нмпульс нейтрона изменяется от Йк0
до fi(ko-J-q) Соответствующая амплитуда рассеяния в борновском прибли-
приближении равна
Это выражение отлично от нуля лишь при q = J, где J — любой вектор
обратной решетки для (двумерной) „решетки нитей". Согласно C.62),
где V — объем образца, nL — плотность нитей. Следовательно,
Для треугольной решетки нитей nL = 2/^3 d2, т. е. первому брэгговскому
отражению отвечает J = 4л/У~3 d (d — расстояние между ближайшими сосе-
соседями). Полагая В = 2000 гс (п. ~~> 10'% находим d ~ 103А, J ~ 6,7 • 105 см~1;
для Л=1000А это соответствует (Я,/J и 45 ^>1. Оценим значение ампли-
амплитуды рассеяния в расчете на один атом (величина, с которой обычно имеет
дело экспериментатор). Подставляя вместо V атомный объем (~»ЗОА3), полу-
получаем а и 0,7 • 10~13 см; соответствующее „сечение когерентного рассеяния"
имеет малую (но измеримую) величину 4ял2 ж 5 • 10~28 см2 = 0,5 мбарн.
Для первого отражения угол рассеяния 6 очень мал:
где Хп = 2я/&0 — длина волны нейтрона. При использовании тепловых нейт-
нейтронов Лп может достигать в лучшем случае ~ бА. Для приведенного при-
примера это дает угол 6~6- 10~3 рад (=20')- Измерения на металлическом Nb
были проведены Крибье и др. [46] '). Из-за наличия множителя [1 + (Я,/J] ~'
в выражении для амплитуды рассеяния а им удалось наблюдать лишь первое
отражение (с наименьшим значением У). Результаты показаны на фиг. 30.
Задача. Рассчитать уширение линии ядерного магнитного резонанса,
вызванное неоднородностью поля в случае вихревого состояния [48] 2).
') Недавно решетку вихревых нитей удалось наблюдать непосредственно
с помощью порошкового метода; см. [136]. — Прим. ред.
2) Независимо аналогичный расчет был выполнен Шмидтом [49]
Прим. ред.

Магнитные свойства сверхпроводников второго рода
79
Решение. В области промежуточиых значений поля НС1 ^^С2
вихревые нити образуют плотную решетку, распределение поля в которой
можно описывать с помощью компонент Фурье [см. C.62)]. Форма линии
ядерного резонанса определяется, вообще говоря, всеми моментами распре-
распределения поля (при условии, конечно, что неоднородность поля является
единственным источником уширения). Однако, часто на опыте „аномальные"
(о
I
Л - >г (увеличено)
10
15
в; углов, мин
Фиг. 30. Угловая диаграмма для рассеяния иейтронов решеткой вихревых
нитей в металлическом ниобии при Т =4,2° К. (По данным Крибье.)
Кривая / получена при //=1640 гс, кривая 2—при //=4103 гс (> Нс2)-
боковые максимумы не наблюдаются [50]. В этом случае для определе-
определения ширины центрального пика достаточно зиать второй момент (см., на-
например, [51]). Именно, ширина линии равна
АН = ((Л*) \
где (...) означает усреднение по пространству. Член (Л) просто равен
В = и^.Ф0; член (Л2) легко рассчитать с помощью C.62)
<л2>=4- J
2 hJh-j=*\*i
где S — площадь сечения образца плоскостью, перпендикулярной полю. За-
Заменяя, как раньше [см. обсуждение формулы C.63)], сумму по векторам
обратной решетки интегралом, находим
['+(")]"*•
где для простоты мы предположили, что решетка нитей является квад-
квадратной. Полученный результат справедлив при условии, что й ^> |.

80 Глава III
В области промежуточных полей (d<^Jk) эта формула дает
АЯ
~ V-2 BлK/2/,2
Отметим, что ширина линии по порядку величины равна Ис1 (для V3Oar
например, X—2000А, Д//« 20 гс) и почти не зависит от поля вплоть до
полей —Нс2; при Н = Hci уширение, вызванное неоднородностью поля, ис-
исчезает совсем. Для полей, близких к Hcl (d ~>, А), уширение становится
сильнее. Более детальный расчет формы линии, основанный на C.62), вы-
выполнен Матриконом.
Задача. Вихревая нить расположена параллельно плоской границе об-
образца. Вычислить ее энергию во внешнем поле Н.
Решение. Выберем систему декартовых координат так. чтобы ось г
совпадала с направлением нити (и поля), а плоскость уг — с поверхностью
образца (сверхпроводник занимает полупространство д:>0). Распределение
поля h (r) описывается уравнением
h + X2 rot rot h = Фо 62 (г — rL),
где ri = (xL, 0) — точка пересечения нити с плоскостью г = 0 („коорди-
(„координата" нити); вектор ф0 направлен вдоль оси г. Граничные условия на по-
поверхности образца имеют вид
h = H
и
(rot Ь)х = 0 при х = 0;
второе условие, очевидно, следует из равенства нулю нормальной к поверх-
поверхности компоненты тока.
Решение h (г) будем искать в виде
Член h1 = Hexp(—X/^L) определяет проникновение в образец внешнего
поля в отсутствие вихревой нити. Напротив, поле h2 всецело связано с на-
наличием нити и может быть найдено методом изображений. Суть метода со-
состоит в добавлении в точке (— х,, 0) фиктивной вихревой нити, которая
является зеркальным изображением исходной нити (х,, 0) и в которой
кольцевые токи текут в противоположном направлении; поле h2 равно ал-
алгебраической сумме полей, вызванных каждой нитью в отдельности. Легко
проверить, что найденное таким образом поле h2 автоматически обращается
в нуль на границе х = 0. Следовательно, мы нашли поле, удовлетворяющее
исходному уравнению и обоим граничным условиям.
Зная h (г), мы вычислим теперь термодинамический потенциал
J I
+А2(ГС*11J h-H
Написанный здесь интеграл берется по всему объему образца (х>0). за
исключением области, занимаемой „остовом* нити. Последний член в по-
подынтегральном выражении представляет собой микроскопический аналог
обычного слагаемого — В - Н/4я, фигурирующего при феноменологическом
описании. Преобразуя выражение для & в поверхностный интеграл и ис-
используя уравнение Лондонов для h, находим
S'+S"
где поверхность интегрирования S' -\-S" состоит из поверхности остова (S')
и поверхности образца (S"). Соответствующие вклады в & обозначим че-

Магнитные свойства сверхпроводников второго рода 81
рез &' и &." Как обычно, в пределе |->0 основной вклад в интеграл по S'
дает расходящийся член в rot h [см. C.33)]; в результате получаем
? [44
Вклад &" можно записать в виде
&"=-tL. Г rfa-(h,Xroth),
поскольку на поверхности образца поле равно h = h, = H. Произведем раз-
разбиение rot h = rot l^-f-rot h2 и выделим в &" вклад от выражения
h, Xroth,. Он представляет собой энергию в отсутствие нити, т. е. адди-
аддитивную постоянную, которой мы в дальнейшем будем пренебрегать. Остаю-
Остающийся член дает
J
S"
Перепишем этот интеграл в виде
;;
S" S' +S" S'
тогда, используя для поля h (вне остова нити) уравнение Лондонов, легко
видеть, что
J do ¦ (h, X rot h2) = J rfa • (h2 X rot h,).
S'+S" S'+S"
Поскольку на поверхности S' поле h, не имеет особенности, вклад этой
области в написанный интеграл пренебрежимо мал при |-»0. Аналогично
равен нулю интеграл по поверхности S" в силу граничного условия
(Ь2)х 0 = 0. С учетом сказанного находим
S'
Заметим попутно, что & = 0, когда нить находится на самой поверхности
(xL = 0), поскольку h2 (х — 0) = 0.
Как вначале было установлено, поле h„(г^.) является суммой двух по-
полей, первое из которых создается непосредственно самой нитью, а второе —
ее зеркальным изображением. Первое слагаемое при подстановке в выра-
выражение для & дает собственную энергию изолированной нити
?_ фона
а второе описывает притяжение между нитью и изображением
где h(r)—величина поля на расстоянии г от нити [см. C.35)]. Оконча-
Окончательно
6 Зак. 1020

82
Глава III
Обсуждение
1. Член (<t>0Hj4n) exp ( — xJty описывает взаимодействие вихревой нити
с внешним полем и связанными с ним экранирующими токами. По своему
виду этот член вполне аналогичен выражению C50) и соответствует оттал-
отталкиванию.
а
Н < н
Вакуум
CI
6
4S> H >
н - и
а Н > Hs
Фиг. 31. Поверхностный барьер, препятствующий вхождению вихревых
нитей в сверхпроводник второго рода.
а — поле И меньше Н t; на вихревую нить действует сила, направленная наружу; внутри
(идеального) образца вихревых нитей нет.
б—поле лежит в интервале между И и Н ', проникновение нити в глубь образца сопро-
сопровождается выигрышем энергии ($J1n\(H — Hc,\. Однако из-за наличия барьера вблизи по-
поверхности образца (которая предпочагается достаточно чистой) проникновения не происходит,
в о Н б Н бр осет
рдоааес д ) р
в —поле Н больше Н ] барьер отсутствует.
2. Член —Ф0кBх,)[8л описывает притяжение между вихревой нитью
и ее изображением. Этот член отличается от C.50) множителем, равным '/2-
Тем не менее выражение для силы притяжения сохраняет прежний вид Фй][с
[см. C.52)], поскольку производная от Л B-v?) no x дает недостающий мно-
множитель 2.

Магнитные свойства сверхпроводников второго рода
83
3. Вид функции &(xL) для различных значений приложенного поля Н
показан на фиг. 31, а — в. Отсюда ясно, что при полях Н~НС1 имеется вы-
высокий барьер, препятствующий вхождению нитей в образец. Происхождение
барьера легко понять. Пусть Н = Нси при этом & (xL — 0) = S' (x. = оо)=0.
На больших расстояниях х энергия отталкивания [-^ехр(—Х/АI. оче-
очевидно, превышает энергию притяжения [~ ехр (— 2xLffc)\t поэтому & > 0
и возникает барьер. Однако в сильных полях Н > //s = Ф0/4я>-| барьер ис-
исчезает (фиг. 31, в); при этом, как можно видеть из выражения для &, на-
наклон (dSr\dXjy становится отрицательным ')•
Из сказанного следует важный вывод, что в полях Н < Hs нити не
могут входить в образец с идеальной поверхностью (хотя при Н > Нс1 это
термодинамически выгодно). Впервые на существование поверхностного
барьера независимо указали Бин и Ливингстон [53] и группа авторов, ра-
работающих в Орсэ (см. [54]). Экспериментально наличие барьера на по-
поверхности сверхпроводника наблюдалось в сплавах свинец — таллий [55]
и в металлическом ниобии [56]. Главное требование к образцам состоит
в том, чтобы поверхность была достаточно хорошей (на расстояниях
порядка Л).
Фиг. 32. Взаимное движение двух «антипараллельных» вихревых нитей
в чистом сверхпроводнике второго рода.
Через v (v Л обозначена сверхтекучая скорость, обусловленная наличием нити 1 B). При
показанной геометрии обе ннтн движутся с одной и той же скоростью v^, направленной пер-
перпендикулярно плоскости ABCD.
Движение вихревых нитей
Рассмотрим две „антипараллельные" вихревые нити, показанные
на фиг. 32. Согласно C.50), -между ними действует сила притяже-
притяжения. Будут ли нити двигаться под действием этой силы или оста-
') Позже с помощью микроскопического рассмотрения мы покажем, что
введенное здесь поле Hs совпадает по порядку величины с термодинами-
термодинамическим критическим полем Нс.

84
Глава III
ваться неподвижными? Этот вопрос широко обсуждался в последнее
время. Мое личное мнение состоит в том, что в чистом металле
кажаая из нитей должна дрейфовать в поле скоростей, созда-
создаваемых другой нитью. Точнее говоря, обе нити будут двигаться
под прямым углом к соединяющей их пло-
плоскости, причем
va = v№ C.66)
^
W
» г
Фиг. 33. Движение
двух «антипараллель-
«антипараллельных» вихревых нитей
в «.грязном» сверх-
сверхпроводнике второго
рода.
Нити движутся навстречу
друг другу со скоростью.
определяющейся трением
о решетку.
ность которых (на
где vl2 — „сверхтекучая" скорость, создаваемая
нитью 1 в точках расположения нити 2. Такой
дрейф должен привести к любопытной картине
коллективных колебаний в системе вихревых ни-
нитей для очень чистых сверхпроводников второго
рода [57].
Наоборот, в грязных сверхпроводниках ха-
характер движения нитей в основном опреде-
определяется их трением о решетку, так что две анти-
параллельные нити 1 и 2 будут перемещаться
навстречу друг другу (фиг. 33) со скоростями
vdB) = — vd0.) = — . C.67)
Здесь / — сила притяжения между нитями, опи-
описываемая выражением C.52); г\ — коэффициент
вязкости. Чтобы оценить величину г), предпо-
предположим, что остов нити 2 не меняет распреде-
распределения токов, созданное нитью 1. Иными сло-
словами, мы предполагаем, что в обла:ти нормаль-
нормального остова нитей плотность тока дается
прежним выражением j = nevl2. Это приво-
приводит к возникновению тепловых потерь, мощ-
единицу длины нити 2) равна
где a = ne2x/m — проводимость в нормальном состоянии, | — радиус
остова нити. Эта диссипируемая мощность должна быть приравнена
совершенной за единицу времени работе
Вспоминая, что, согласно C.52),
1

Магнитные свойства сверхпроводников второго рода 85
в результате находим
4 C-68)
Этот механизм потерь позволяет разумно описать наблюдавшееся
в опытах Кима и др. [58] вязкое движение вихревых нитей в гряз-
грязных сверхпроводниках.
§ 3. НЕРАВНОВЕСНЫЕ СВОЙСТВА
До настоящего момента мы изучали обратимое поведение сверх-
сверхпроводников второго рода. В частности, мы пришли к важному за-
заключению, что для материалов с малой длиной когерентности | сверх-
сверхпроводимость сохраняется вплоть до очень больших значений поля
С точки зрения технических применений наибольший интерес пред-
представляет получение сверхпроводящей проволоки, способной нести
большой ток. Однако состояние с большим током не является термо-
термодинамически равновесным, как видно из следующего. В самом деле,
рассмотрим провод кругового сечения радиусом а, по которому течет
ток /. (Когда ток / мал, он почти весь течет в слое толщиной %
вблизи поверхности провода.) Поле на поверхности провода равно
2/
Н = — . C.69)
са v '
Токовое состояние является устойчивым, если Н < Нс1. Напротив,
при Н > Нс1 в сверхпроводнике начинают образовываться замкнутые
вихревые нити в виде колец (в соответствии с формой силовых линий
магнитного поля). В момент зарождения на поверхности провода вих-
вихревое кольцо имеет радиус а, но в последующие моменты времени
оно стремится сжаться (уменьшая тем самым линейную энергию), пока,
наконец, не исчезнет на оси провода. Очевидно, этот процесс сопро-
сопровождается диссипацией энергии. Иными словами, в идеальном образце
сопротивление отсутствует лишь при полях Н < HcV т. е. для токов
/ < саНсХ\2. Чтобы иметь возможность пропускать по проводу токи
большей величины, необходимо каким-то способом приостановить
движение вихревых колец. Такое „закрепление" вихревых нитей на
практике осуществляется путем создания подходящих для этой цели
дефектов решетки, т. е. осуществления неравновесных ситуаций.
В то время как поле Нс2 является характерным свойством, присущим
данному металлу или сплаву, измеряемый на проволоке критический
ток сильно зависит от способа металлургической обработки данного
образца. На различную природу Нл и /кр впервые обратил внимание
Гортер.

86 Глава III
На практике благоприятные дефекты структуры получают сле-
следующими способами:
1. Неполным спеканием образца (например, Nb3Sn).
2. Пугем холодной обработки (например, сплавы MoRe).
3. С помощью быстрой кристаллизации раствора (например,
сплавы на основе свинца).
Получаемые таким образом материалы обладают высокими значе-
значениями критического тока и носят название жестких сверхпровод-
сверхпроводников.
В настоящее время имеются лишь смутные догадки относительно
механизмов взаимодействия вихревых нитей с дефектами структуры.
Сравнительно прост случай, когда в сверхпроводящем материале
имеются только большие полости, образовавшиеся, например, в про-
процессе спекания. Естественно думать, что вихревые нити в этом слу-
случае будут прилипать к границам полостей, поскольку это отвечает
меньшей длине нитей в сверхпроводящем материале и, следовательно,
меньшему значению энергии. Что касается механических напряжений,
получающихся при холодной обработке, то они могут привести к не-
некоторым (по всей вероятности, малым) локальным изменениям энергии
конденсации и плотности сверхпроводящих электронов ns. Это в свою
очередь должно вызывать локальные изменения параметров А, и | и
соответственно собственной энергии 0 вихревых нитей и их взаимо-
взаимодействий U. В целом вся картина носит очень сложный характер,
и в последующем мы ограничимся только феноменологическим опи-
описанием возникающих эффектов.
Критическое состояние при абсолютном нуле
Рассмотрим жесткий сверхпроводник, находящийся во внешнем
магнитном поле Н, направленном вдоль оси z. В состоянии термо-
термодинамического равновесия плотность вихревых нитей одинакова во
всех точках образца и равна В(Н)/ф0. Обратимся теперь к метаста-
бильному слу чаю, когда индукция В ф В (И) меняется от точки
к точке, скажем, вдоль оси х. Тогда 1) плотность нитей непостоянна
в пространстве и 2) вдоль оси у течет макроскопический ток с плот-
плотностью
с дВ
J~~ 4я дх '
Силы, действующие в системе нитей, можно разбить на две группы.
Прежде всего силы отталкивания между нитями; под их влиянием
области с повышенной плотностью нитей (большие значения индук-
индукции В) имеют тенденцию расширяться за счет областей с меньшей
плотностью нитей. Этот эффект можно описать путем введения давле-

Магнитные свойства сверхпроводников второго рода 87
ния р в рассматриваемой двумерной системе нитей'). Тогда сила,
действующая на единицу объема, равна — др/дх. С другой стороны,
движению нитей препятствует „зацепление" последних за структурные
дефекты. Величина сил зацепления не может принимать сколь угодно
большие значения, а ограничена определенным пороговым значе-
значением ат. Необходимым условием механического равновесия является
выполнение неравенства
I dp
дх
C.70)
Если в некоторой точке образца | др/дх | > ат, то начнется переме-
перемещение вихревых нитей, сопровождающееся диссипацией энергии; оно
будет продолжаться до тех пор, пока снова не будет выполнено
условие C.70). В реальных ситуациях автоматически устанавливается
такая плотность нитей B(x)/<j>0, чтобы пороговое условие [знак ра-
равенства в формуле C.70)] выполнялось во всех точках образца. Такое
состояние сверхпроводника впервые было рассмотрено Бином [59, 60]
и получило название критического состояния. Наглядное представле-
представление о критическом состоянии дает аналогия с песчаным холмом. Если
крутизна спуска холма превышает некоторое критическое значение,
песок начнет скатываться вниз — возникает лавина. Эта картина очень
близка к той, которая имеет место в жестких сверхпроводниках;
в тщательных опытах (с использованием регистрирующих катушек)
было показано, что в закритическом режиме вихревые нити начи-
начинают двигаться не поодиночке, а в форме лавин, включающих до 50
и более нитей.
Чтобы воспользоваться условием C.70), перейдем теперь к явному
вычислению давления р в системе нитей. Рассмотрим группу из
N нитей, пересекающих плоскость ху на участке площадью 5. Энер-
Энергия нитей (на единицу длины вдоль оси z) равна
где О для одной нити определяется выражением C.64). Давление р
представляет собой частную производную от потенциала ?? по пло-
площади 5 (т. е. по „объему") при заданном значении N
п с да
Вместе с тем при фиксированном значениии /V, очевидно,
dS _ dB
S ~ В '
!) Вообще говоря, при таком подходе нужно исходить из тензора энер-
энергии — импульса Р1К Здесь мы ограничимся изотропным приближением и пре-
пренебрежем тензорными свойствами величины р.

88 Глава 111
поэтому
Таким образом, зная G, мы можем найти зависимость р (В), т. е.
связь давления с плотностью нитей. Интересующий нас градиент да-
давления др/дх можно представить в довольно простом виде. Положим
для этого
где функция F(В) определяет собственную энергию нитей и энер-
энергию их взаимодействия. Равновесные значения В(Н) и Н (В) нахо-
находятся из условия (dG/dB) — Q. Например,
С учетом сказанного получим
др _ р дЮ дВ _ В дН(В) дВ
дх~~ дВ2 дх ~~ An дВ дх '
др _ В дН(В) C*72)
дх 4я дх
Если функция И (В) известна, то мы можем сразу же вычислить гра-
градиент давления как функцию В и дВ/дх.
Для сверхпроводников второго рода {Нс1<^Н^ функция Н(В)
при Н^$>Нс1 приближенно равна В, как ясно из вида кривой на-
намагничивания (см. фиг. 23). В этой области имеем просто
др В дВ BJV
— JL = — — -j- = —L. C.72')
дх An дх с v '
Соответственно условие критического состояния запишется в виде
В дВ
4я дх
BJ
= ат при Я (fl) ;>//„. C.73)
Для вычисления В(х) в критическом состоянии необходимо знать
зависимость максимальной силы „зацепления" <хт от величины индук-
индукции В (т. е. от плотности нитей). Первоначально Бин предположил,
что зависимость ат от В является линейной. Это приводит к постоян-
постоянной величине плотности тока Уу (обычно ~ 10s ajcM2) в критическом
состоянии. В дальнейшем Ким и др. [61] с помощью серии экспери-
экспериментов показали, что для сплавов NbZr и Nb3Sn (подвергнутых спе-
специальной металлургической обработке) в области полей ^ 104 гс
достаточно хорошим является предположение о независимости ат
от В. К сожалению, этот простой результат до сих пор не получил
полного теоретического объяснения. Напротив, казалось бы, влияние

Магнитные свойства сверхпроводников второго рода
89
центров зацепления должно быть наиболее сильным в том случае,
когда их размеры сравнимы с расстоянием между нитями, а это по-
последнее зависит от В (как В~ ).
Форма профиля В(х) в критическом состоянии для моделей Бина
и Кима показана на фиг. 34. Для типичных жестких сверхпровод-
сверхпроводников в приложенном поле порядка 104 гс полная толщина Ал; об-
области проникновения силовых линий составляет <¦—• 1 мм. Простейший
— Сверхпроводник
Вакуум
Фиг. 34. Необратимое проникновение магнитного потока в жесткий сверх-
сверхпроводник.
в —модель Бина; б —модель Кима — Андерсона (параболический профиль).
метод экспериментального определения зависимости В(х) [или ат(В)]
состоит в измерении потока <j>. заключенного в цилиндрическом
образце радиусом R (фиг. 35), во внешнем поле Н, растущем со
временем.
1. Если R<^&x, то индукция почти однородна по всему образцу;
(НI)
') Мы предполагаем, что поверхностный барьер, препятствующий вхо-
вхождению вихревых нитей в цилиндр, отсутствует. Поверхностный барьер
иногда играет роль, однако его влияние можно легко отделить.

90
Глава III
2. Если R~^>^x, мы практически имеем одномерный случай.
Обозначим через х расстояние, отсчитываемое от центра по радиусу
цилиндра; тогда
л
fr=2nR j B(x)dx. C.74)
Л-Д*
На границе области проникновения потока (х — R — Да;) индукция В
обращается в нуль [,8 = 0, Н(В) = Нс1]; на поверхности цилиндра
Фиг. 35. Проникновение магнитного поля //„, растущего со временем,
в цилиндрический образец
Силовые линии проиикают только в заштрихованную область.
x = R (снова считаем, что поверхностный барьер отсутствует) равно-
равновесное значение индукции В определяется приложенным полем:
В = В(Н). Переходя в C.74) к интегрированию по Н и используя
равенства C.72) и C.70), находим
и
В2(Н)
4ла
'тН
dH, атН==ат[В(Н)].
Особый интерес представляет производная
йФ _ R В2(Н)
dH ~ 2 а_„ *
C.75)

Фиг. 36. Принципиальная схема опытов на полых цилиндрах, изготовлен-
изготовленных из жестких сверхпроводников.
Приложенное поле равно Н; измеряется поле Н' в полой части цилиндра.
Сверхпроводник
-Вакуум
Фиг. 37. Распределение индукции В внутри жесткого сверхпроводника,
находящегося в переменном во времени внешнем магнитном поле Н.
Пунктирная н сплошная кривые дают соответственно распределение индукции при начальном,
возрастании поля до значения Н и последующем его уменьшении до Н^.

92 Глава III
Таким образом, измерив намагниченность в возрастающем поле, мы
можем вычислить значения атН и ат(В).
Другой метод, использованный Кимом и сотрудниками, состоит
в измерении поля Н' внутри полого цилиндра в продольном внеш-
внешнем поле И (фиг. 36). При начальном увеличении поля Н (от нуле-
нулевого значения) поле И! остается строго равным нулю. Затем, когда
фронт потока достигает внутренней поверхности цилиндра, поле Н'
также начинает возрастать (в идеальном случае поле И' должно скач-
скачком увеличиться до значения Не1, а потом расти непрерывно). С по-
помощью этого метода можно непосредственно измерить величину Ал;
(равную толщине стенки цилиндра), фиксируя значение Н, при кото-
котором поле Н' начинает возрастать.
Более сложная картина возникает, когда поле Н циклически то
увеличивается, то уменьшается со временем (фиг. 37). При этом
в различные циклы производная дВ'дх может быть как положитель-
положительной, так и отрицательной, но абсолютная величина | dpjdx | всегда
остается равной ат. Детальный расчет гистерезисных циклов можно
произвести, если известна зависимость ат(В).
Движение вихревых нитей при Т Ф О
При конечных температурах вихревая нить с некоторой вероят-
вероятностью может скачком преодолеть барьер, создаваемый центром „за-
„зацепления". Если при этом градиент давления отличен от нуля
(др[дх Ф 0), то вихревые линии будут перемещаться в области
с меньшим значением В. Обозначим среднюю скорость перемещения
нитей вдоль оси х через vx. Для регистрации такого движения (или
„крипа") можно использовать следующие методы:
1. Магнитные измерения на сплошных или полых цилиндрах.
Например, в последнем случае, если поле И увеличивается от нуля
до определенной величины, то поле И', измеряемое внутри цилиндра,
будет медленно возрастать со временем.
2. Электрические измерения. При перемещении вихревых нитей
возникает электродвижущая сила, которую можно непосредственно
измерить. Простейший случай показан на фиг. 38; по проволоке,
помещенной в магнитном поле Н (вдоль оси z), пропускают ток
с плотностью J (вдоль оси у). Вихревые нити направлены вдоль оси z.
Поскольку производная дВ/дх = AnJjc отлична от нуля, то нити нач-
начнут перемещаться вдоль оси х. В результате возникает электрическое
поле ?у, направленное вдоль проволоки (ось у). В предельном случае
Н^>Нс1 это поле равно
Еу = -^. C.76)
Для доказательства соотношения C.76) достаточно приравнять мощ-
мощность EyJ, диссипируемую в единице объема образца, работе (dpjdx)vx,

Магнитные свойства сверхпроводников второго рода
93
совершаемой над нитями при наличии градиента давления, и восполь-
воспользоваться выражением C.72')- Следовательно, чтобы поддерживать ток J
постоянным, в образце должно существовать постоянное электриче-
электрическое поле Еу. Как показали Ким и Андерсон [61], этот диссипатив-
ный механизм позволяет описать многие особенности сопротивления
жестких сверхпроводников.
Существенно заметить, что скорости движения нитей, получаемые
при магнитном A) и электрическом B) способах измерений, имеют
Вихревые нити
Фиг. 38. Схема электрических измерений на проволоке из жзсткого сверх-
сверхпроводника.
При протекании вдоль проволоки тока У=— (с/4я) (dBldx) плотность вихревых нитей выше
на левой стороне проволоки (dB/dx < 0). Это приводит к дрейфу нитей со скоростью v вдоль
положительного направления оси х.
совершенно разный порядок величин. В случае 1 „крип" обычно изме-
измеряется в течение часов или дней, а скорость vx составляет ~ 1 мм
за 1 день, или vx—10~6 см/сек; в случае 2, полагая в C.76) В=№4 гс.
-2
Ey—10 ejcM, получаем vx—10 см\сек. Основная трудность,
встречающаяся при электрических измерениях, связана с возможной
неоднородностью проволоки вдоль ее длины. Экспериментально най-
найдено, что в различных кусках одной и той же проволоки поле Еу
часто имеет разную величину.
Полученные результаты позволяют сделать следующие выводы:
а) Скорость „крипа" носит активационный характер
C.77)
Величина vQ точно не известна, но обычно находится в области
— 103 см/сек. Энергия активации Е может достигать 100° К-
б) Энергия активации Е зависит от градиента давления др/дх по

94 Глава 111
где величина р имеет размерность длины и обычно составляет ~ 500 А.
Величины Ео и р можно связать с критическим градиентом давле-
давления ат, если заметить, что при Т—>0 скорость vx отлична от нуля
лишь при ? = 0. Согласно C.78),
о» = |?- G = 0). C.79)
Укажем также на некоторые важные следствия из этих результа-
результатов (которые в основном были получены Андерсоном, Кимом и их
сотрудниками). Прежде всего из-за наличия сильной зависимости
C.77) скорости vx от энергии Е представление о критическом со-
состоянии можно распространить на конечные температуры. Введем
минимальную (с точки зрения возможности экспериментального наблю-
наблюдения) скорость движения нитей vuim. Тогда при
квт
можно считать, что структура нитей „заморожена". Следовательно,
критическое состояние при температуре Т формально отвечает вы-
выполнению условия
Е,
¦о
dx
или C.80)
dp
1х~
Вообще говоря, величина ат изменяется с температурой (поскольку
в ее определение входят зависящие от температуры величины К, | и
энергия конденсации). Однако, если температура Т значительно ниже
температуры перехода Тс, этим изменением можно пренебречь. Тогда
результирующая температурная зависимость определяется лишь множи-
множителем kBT. Линейное изменение градиента | dpjdx | с температурой
было экспериментально подтверждено Кимом на различных сплавах и
соединениях (критический ток жестких сверхпроводников оказался
при этом сильно зависящим от температуры даже в области Т <^ Тс),
Другим важным следствием соотношения C.77), как было отме-
отмечено Андерсоном, является возможность появления сильной тепловой
неустойчивости. Действительно, предположим, что в некоторой малой
области образца энергия активации Ео несколько меньше, чем
в остальной части; тогда вихревые нити в этой области будут рас-
рассеивать большую мощность —(dp[dx)vx (на 1 см3). Это приведет
к быстрому возрастанию локальной температуры (если теплопровод-
теплопроводность материала достаточно низка) и, согласно C.77), к увеличению
скорости vx, что означает появление неустойчивости. Этот тепловой
эффект всегда следует иметь в виду при проектировании сверх-
сверхпроводящих магнитов.

Магнитные свойства сверхпроводников второго рода 95
Наше обсуждение эффектов „зацепления"
Заключительные вихревых нитей и явления „крипа" носило
замечания чисто феноменологический характер. Без-
Безусловно, хотелось бы попытаться вычислить величины ?0, р ицд
на основе микроскопической теории. Имеются, однако, две трудности:
1. Не вполне ясно, каков механизм взаимодействия между вихре-
вихревыми нитями и дефектами решетки. Ранее уже отмечалось, что важ-
важный вклад в это взаимодействие дают локальные изменения глубины
проникновения X из-за упругих напряжений и дефектов. Другой, более
очевидный вклад связан с изменением энергии конденсации. Суще-
Существуют, по-видимому, и другие механизмы.
2. Отсутствует математический аппарат для описания состояния
метастабильного равновесия и необратимого движения сильно взаимо-
взаимодействующих нитей в присутствии случайных возмущений. Возвращаясь
к вышеуказанной аналогии, можно сказать, что теория, с одной сто-
стороны, должна давать возможность определить равновесную форму
склона холма, с другой — описывать процесс образования лавин. Обе
задачи достаточно сложны. Имеется одно интересное предложение,
сделанное Франком: описывать явление „крипа" как результат дви-
движения дислокаций в двумерной решетке вихревых нитей.
ЛИТЕРАТУРА
Структура вихревого состояния
Абрикосов А. А., ЖЭТФ, 32, 1442 A957).
Ooodman В. В., Rev. Mod. Phys., 36, 12 A964).
Обратимые кривые намагничивания
Livingston J. D., Phys. Rev., 129, 1943 A963).
К i n s el Т., L у п t о n E. A., Serin В., Phys. Lett., 3, 30 A962).
Дифракция нейтронов на вихревых нитях
С г 1 b 1 е г D., J а с г о t В., Rao L. M., F а г п о u x В., Phys. Lett, 9,
106 A964).
С г IЫ е г D. et al., в книге Progress In Low Temperature Physics, ed.
C. O. Oorter, vol. V. Amsterdam. 1967.
Наблюдение нитей методом электронной микроскопии
Т г a u b е Н„ Essmann U., Phys. Stat. Sol., 20, 95 A967).
Зацепление вихревых нитей и явление „крипа"
Bean C.P. Phys. Rev. Lett., 8, 250 A962).
Bean СР.. Rev. Mod. Phys., 36, 31 A964).
Anderson P. W., Phys. Rev. Lett., 9, 309 A962).
Kim Y. В., Н e m p s t e a d C.F, S t г п a d A. R., Phys. Rev., 129, 528 A963).
F г 1 e d e 1 J., D e Q e n n e s P. Q., M a t г 1 с о n J., Appl. Phys. Lett., 2.
199 A963).
Вязкое движение вихревых нитей
Kim Y. В., Hempstead С F., Strnad A. R., Phys. Rev., A139, 1163
A965).

Глава IV
ОПИСАНИЕ КОНДЕНСИРОВАННОГО СОСТОЯНИЯ
§ 1. НЕУСТОЙЧИВОСТЬ НОРМАЛЬНОГО СОСТОЯНИЯ
ПРИ НАЛИЧИИ ПРИТЯЖЕНИЯ МЕЖДУ ЧАСТИЦАМИ
Основное состояние свободного газа электронов соответствует
заполнению всех одноэлектронных уровней энергии fi2A>2/2m (k —
волновой вектор) вплоть до некоторой энергии EF = h2kfj2m —
энергии Ферми. Однако такое состояние является неустойчивым при
наличии сколь угодно слабого притяжения между частицами, как
было показано Купером [62]. Происхождение неустойчивости можно
понять, изучая поведение двух выделенных электронов (с координа-
координатами г, и г2) в присутствии остальных электронов, рассматриваемых
по-прежнему как свободный электронный газ. Роль этого электрон-
электронного газа сводится к тому, что в соответствии с принципом Паули
выделенные электроны не могут занимать состояния с k < kF. Введем
волновую функцию двух электронов i|5(rlt r2) и будем рассматривать
только такие состояния, для которых центр инерции пары (г,, г2)
покоится. Тогда функция ф зависит лишь от разности г, — г2; раз-
разлагая ее в ряд по плоским волнам, получаем
Ф (fi — r2>= S g-(k)ci4<r>-^, D.1)
где g(k) — амплитуда вероятности обнаружить один из электронов
в состоянии с импульсом йк, а другой в состоянии — йк. Поскольку
все состояния с k < kp уже заняты, то, согласно принципу Паули,
g (k) = 0 для k < kF. D.2)
Уравнение Шредингера для рассматриваемых двух электронов имеет
вид
?(!) (^). D.3)
Здесь Е — энергия пары, отсчитываемая от состояния, в котором оба
электрона находятся на уровне Ферми. Подставив D.1) в D.3), по-
получим уравнение для §"(к)
к'
где

Описание конденсированного состояния 97
— матричный элемент взаимодействия между состояниями к и к',
a L? — объем системы. Уравнение D.4) совместно с принципом
Паули D.2) иногда называют уравнением Бете — Голдстоуна для за-
задачи двух электронов. При Е > 2Ер оно имеет непрерывный спектр
и описывает процесс рассеяния двух электронов из начального со-
СЮ1НИЯ (к, —к) в конечное (к', —к') (с той же энергией). Однако
если взаимодействие V отвечает притяжению, то возможны также
решения, соответствующие некоторым связанным состояниям
с энергиями Е < 2Ер. Чтобы убедиться в этом, рассмотрим упро-
упрощенное взаимодействие вида
V 2
= 0 в противном случае.
(Это взаимодействие соответствует притяжению и постоянно по вели-
величине в области энергий шириной fi<o0, расположенной выше уровня
Ферми.) Тогда уравнение D.4) принимает вид
[-~-+Е+ 2Ef) S 00 = С, D.6)
где правая часть С не зависит от к;
" D-7)
о
Из сравнения D.6) и D.7) находим условие самосогласованности //
V v 1 ' - Ь-'е
1==tj2j ^р • ?~ v
Ь + ~^Г ^г D.8)
Если положить
и ввести плотность числа состояний в единичном интервале энергий
^ ; BпK (%' '
то условие D.8) примет вид
ЙСОд
j N(Z'J/l_E. D.10)
7 Зак. 1020

98 Глава IV
Если предположить, кроме того, что haD<^Ep, то величину /V(|')
можно рассматривать как постоянную и заменить ее значением /V @)
на уровне Ферми. Взяв интеграл D.10), получим
1 Е — 2/2Ш,,
i ?—Д, - D.11)
или, в пределе слабого взаимодействия N (fS)V <^\,
. D.12)
Таким образом, в рассмотренном случае существует связанное со-
состояние двух электронов с энергией Е < 0. Если мы имеем сначала
свободный электронный г'азГа затём^включаем взаимодействие V, то
можно ожидать, что электроны будут группироваться в пары, отда-
отдавая энергию внешней среде. Следовательно, нормальное состояние
является неустойчивым.
НЕСКОЛЬКО ВАЖНЫХ ЗАМЕЧАНИЙ
1. Неустойчивость сохраняется даже в том случае, когда взаимодей-
взаимодействие V является весьма Слабым, при условии, что оно отвечает притяже-
притяжению. В этом состоит существенное отличие найденного результата от обыч-
обычной задачи двух тел. Если мы имеем всего две частицы, потенциал взаимо-
взаимодействия (притяжения) которых характеризуется конечным радиусом действия,
1то они образуют связанное состояние только в том случае, если величина
j притяжения превышает некоторое пороговое значение.
Для задачи двух тел (?^ = 0) плотность состояний N (с,) при ?->0 из-
изменяется по закону |''2 и выражение
Jk- D.13)
остается конечным даже для Е — 0. Поэтому, если величина V мала, то
/ (?) < / @) < 1 для Е < 0, и условие / (?) = 1 не будет выполняться в об-
области связанных состояний. Напротив, в нашей задаче ./V (?) « const, / @) =
= оо, следовательно, всегда найдется значение Е < 0, такое, что / (?) = 1.
2. Энергия связи пропорциональна ехр(—2/NV). Очевидно, такую за-
зависимость нельзя разложить в ряд по степеням V при V -> 0. Эта алгебраи-
алгебраическая трудность явилась значительной помехой для развития теории сверх-
сверхпроводимости.
3. В предыдущем расчете мы учли принцип Паули для системы, состоя-
состоящей из электрона 1 (или 2) и электронов внутри сферы Ферми. Кроме этого,
необходимо обеспечить условие антисимметрии волновой функции относи-
относительно перестановки электронов 1 и 2. Для упрощенного взаимодействия V,
описываемого формулой D.5), амплитуда g (k) зависит лишь от ?, т. е. от
величины вектора к. Поэтому, как следует из D.1), координатная часть вол-
волновой функции i|)(r,, г2) симметрична, а спиновая часть должна быть анти-
антисимметричной, т. е. иметь внд
(Мы следуем обозначениям, принятым в книге Шиффа [63].)

Описание конденсированного состояния 99
Эта функция описывает состояние с равным нулю полным спином пары,
т. е. антипараллельное спаривание. Если бы взаимодействие Vw не имело
простой формы D.5), а сильно зависело от угла между к и к', то можно
было бы обнаружить а) несколько связанных состояний, б) пространственно
анизотропные решения и, следовательно, более сложную спиновую зависи-
зависимость. Практически оказывается, что угловая зависимость Vw в сверхпро-
сверхпроводящих металлах не является достаточно сильной, чтобы привести к не-
неожиданным эффектам.
Задача. Вычислить средний квадрат радиуса р куперовской пары.
Решение. По определению.
Г|Ф<,,)|Р
р2 = - ? , R = г, — г2,
||ф|»Л1
2 I V(k) P N@) (^/c)ft)i-o J
k °
й
В приближении D.5) g=C/(E — 2|). Кроме того, (dk/dl)^n= l/hv^ где
vF — фермиевская скорость. Выполняя интегрирование, находим
р=7г ~Г'
§ 2. ПРИРОДА ПРИТЯЖЕНИЯ
В обычном электронном газе единственным взаимодействием между
частицами является кулоновское отталкивание, так что эффект
Купера возникнуть не может. Для получения матричных элемен-
элементов Vkv, отвечающих притяжению, необходимо, чтобы электроны
были связаны с другой системой частиц (или возбуждений) твердого
тела. (Такими возбуждениями могут быть, например, фононы, элек-
электроны из других зон, спиновые волны в магнитной среде и т. д.)
В настоящее время установлено, что важную роль играет лишь один
механизм, а именно электрон-фононное взаимодействие, на что впер-
впервые указал Фрёлих [64]. К обсуждению этого вопроса мы и перейдем.
Квантовомеханическое описание
Найдем матричный элемент Vw электрон-электронного взаимо-
взаимодействия, отвечающий переходу двух электронов из начального со-
состояния (к, —к) в конечное (к', —к'). Обозначим эти состояния
соответственно через I и П. В общем случае матричный элемент VW
состоит из двух членов:

100
Глава IV
а) Член, отвечающий прямому кулоновскому отталкиванию элек-
электронов Uc(r1 — г2). Соответствующий матричный элемент имеет вид
II) = J
rtdr2, D.14)
, = k'-k D.15)
(волновые функции нормированы на единичный объем).
-k-q k + q
-k-q
-к
Фиг. 39. Взаимодействие электронов, обусловленное фононами.
а —электрон в состоянии к испускает фонон с волновым вектором —q, который затем погло-
поглощается вторым электроном; б—электрон в состоянии —к испускает фонон с волновым веВтО-
ром q, который поглощается первым электроном.
б) Член, отвечающий такому процессу, когда один из электронов
испускает фонон, который затем поглощается другим электроном.
Этот процесс показан на фиг. 39. Энергия начального состояния I
равна
где |к определяется соотношением D.9) (для удобства мы всюду
будем отсчитывать одноэлектронные энергии |к от уровня Ферми).
Аналогично энергия конечного состояния II равна
Условию сохранения импульса удовлетворяют два промежуточных
состояния:
1. Электрон 1 находится в состоянии k' = k-|-q, электрон
2 — в состоянии — к; испущен фонон с волновым вектором — q и
энергией й
(отметим, что ^ и ©к являются четными функциями ft).

Описание конденсированного состояния 101
2. Электрон 1 находится в состоянии к, электрон 2 — в состоя-
состоянии — к' = — (k-f-q), фонон имеет волновой вектор q и энергию /м»ч
Во втором порядке теории возмущений матричный элемент, связы-
связывающий состояния I и II, равен
„ I 0 ( ?„!-?, + ?,-?,) (/ I ^--Фо« I ">• D-16)
Здесь сумма берется по всем допустимым промежуточным состояниям;
&^?эл.-фон — гамильтониан электрон-фононного взаимодействия. Обо-
Обозначим через Wq матричный элемент, соответствующий испусканию
или поглощению одного фонона с волновым вектором q. Тогда
12 1 1
(^ D.17)
где мы определили частоту со как разность
&o = |v—|ч. D.18)
Таким образом, йю и Aq равны соответственно изменению энергии и
импульса электрона 1 при переходе 1->П. Полный матричный эле-
элемент равен
(I|^|H)^t/q+2|^qp 2Mq 2. DЛ9)
Й со —со„
Для to < cdq член, соответствующий косвенному обмену, отрицателен,
т. е. отвечает притяжению. Таким образом, мы приходим к выводу,
что результирующее взаимодействие представляет собой притяжение,
если член Uq не слишком велик.
Описание с помощью диэлектрической проницаемости
Эффективное электрон-электронное взаимодействие можно описы-
описывать также следующим образом. „Голое" кулоновское отталкивание
между двумя электронами е2/г приводит к матричному элементу
4зте2/<72. Однако это взаимодействие экранируется другими электро-
электронами, а также положительными ионами решетки. Если интересующие
нас частоты близки к собственным частотам юч движения ионов, то
может возникнуть явление резонанса. Ионы могут „переэкранировать"
отрицательный заряд электрона 1, в результате возникает положи-
положительно заряженное облако, которое будет притягиваться электроном 2.
На практике эффекты экранирования можно описывать с помощью
диэлектрической проницаемости e(q, и), являющейся функцией

102 Глава IV
волнового вектора и частоты. Эффективное взаимодействие тогда равно
взаимодействию „голых" частиц, уменьшенному в е раз:
Задача заключается в вычислении е. Мы произведем этот расчет для
очень простой модели и покажем, что выражения D.19) и D.20)
согласуются между собой.
ы р е« Рассмотрим систему электронов, имеющих
одель „ж л массу т и заряд —е, и ионов с массой М и
зарядом -f- Ze. В целом система нейтральна, если число ионов в 1 см3
равно «/Z. где п — плотность электронов. Учтем электростатическое
взаимодействие между частицами и отвлечемся от того факта, что
ионы образуют решетку, т. е. будем трактовать их как жидкость.
Эта простая модель металла носит название модели „желе" J). Она
не учитывает в основном следующих обстоятельств:
1. Наличия короткодействующего отталкивания между ионами,
обусловленного перекрытием их глубоко расположенных электронных
оболочек.
2. Того факта, что электронные волновые функции должны быть
ортогональны к волновым функциям глубоко лежащих уровней каждого
иона. (Это привело бы к отталкивательному электрон-ионному взаимо-
взаимодействию.)
3. Возможности распространения поперечных колебаний (попереч-
(поперечных фононов) в ионной системе. Такие колебания существуют в реаль-
реальном теле, но не описываются нашей жидкостной моделью.
Хотя введенные упрощения носят довольно произвольный характер,
результаты, полученные с помощью столь простой модели, оказы-
оказываются полезными для качественного понимания взаимодействий. Ди-
Диэлектрическая проницаемость e(q, а) определяется следующим обра-
образом. Предположим, что к системе добавляется извне небольшой заряд
с плотностью
6р(г) = 6рcos(q • г)еш-f- Компл. сопр. D.21)
Это приводит к возникновению в системе экранирующего заряда
р (г) = р cos (q • г) еш -f- Компл. сопр. D.22)
1) Впервые модель „желе* была применена к теории сверхпроводимости
Пайнсом [65]; индуцированная фононами часть взаимодействия была полу-
получена несколько ранее Бардином и Пайнсом [66]. Описание электрон-ионных
систем с помощью единой диэлектрической проницаемости было разработано
Нозьером (неопубликованная работа) и обобщено Пайнсом в лекциях, про-
прочитанных в летней школе физики в Лезуш [67].

Описание конденсированного состояния 103
Диэлектрическая проницаемость, по определению, равна отношению
внесенного заряда к полному
HV с4-23)
Таким образом, задача заключается в вычислении „зарядового" от-
отклика р. В нашем случае заряд р складывается из электронной и
ионной компонент
Р = Ре + Pi-
ИсхОДНЫМИ уравнениями служат:
а) уравнение Пуассона, связывающее электростатический потен-
потенциал V с плотностью зарядов 6р, р(-, ре,
У21/ = -4лFр + Р/ + ре); D.24)
б) уравнение движения ионов в электрическом поле Е = — VV
M-^-=nZe2E, D.25)
где jt — переносимый ионами ток, который связан с pf уравнением
непрерывности
^-+divj, = O. D.26)
Предполагая смещение ионов слабым, мы можем заменить полную
производную djjjdt в уравнении D.25) частной d'ljdt. Исключая затем j(-
из D.25) и D.26), получаем
_nZe^
dt* M
Наконец, лелая замену djdt = la и используя D.24), приходим к урав-
уравнению
а2Р(. (q. ю) = to2 [p. (q, ю) + ре(q, ю) + 6р (q, «>)], D.28)
где
Ю/ = 1/4™^. D.29)
Позже мы увидим, что частота to,- определяет в основном ширину
фопонного спектра в рассматриваемой простой модели. Типичное
значение со,-—1013 сек~х;
в) нам потребуется, кроме того, уравнение, описывающее отклик
электронного газа (т. е. ре) на приложенный электростатический
потенциал V. При составлении этого уравнения необходимо принять
во внимание одно упрошающее обстоятельство. Электронный газ обла-
обладает двумя характерными частотами: EFjh и плазменной частотой
4лпе2 I M\'h

104 Глава IV
Обе эти частоты чрезвычайно велики. Наоборот, частота to мала
(о — o)t). Следовательно, в этой части расчета мы можем полностью
пренебречь частотой со и вычислять ре просто для статического
возмущения V.
Мы сделаем еще одно приближение и найдем ре, используя метод
Томаса — Ферми (что строго справедливо только для длинных волн
q<^ikF). В этом приближении электронная плотность в точке г про-
пропорциональна \EF -f- eV (r)] '2. Следовательно, относительное изменение
этой величины для малых V составляет
-¦?¦-!?• D-30)
е г
Соответствующую фурье-компоненту pe(q) можно, используя D.24),
записать в виде
где
,2 блпе2
Объединяя D.28) и D.31), находим
Исходя из этого выражения, найдем сначала фононную частоту toq
в зависимости от q. Поскольку речь идет о нахождении собственных
колебаний в системе, внешний заряд необходимо положить равным
нулю [6р=0, e(q, ю) = 0]. Для данного вектора q частота щ равна
Для длинных волн частота щ — (ojk^q линейно зависит от
величины q и скорости звука (Ot/ks. При практических применениях
эта формула дает довольно разумное значение скорости звука для
всех непереходных металлов, если в качестве Z в D.29) выбрать
валентность металла. С помощью D.33) выражение D.32) можно
представить в виде

Описание конденсированного состояния 105
Тогда матричный элемент взаимодействия запишется следующим
образом:
2 2
Это выражение совпадает по форме с D.19), однако численные коэф-
коэффициенты теперь найдены в явном виде. Первый член представляет
собой экранированное кулоновское отталкивание, а второй — взаимо-
взаимодействие, обусловленное фононами, отвечающее притяжению для ю < юч.
Средняя частота фонона юч — a>D (u>D — дебаевская частота мате-
материала). Поэтому средний интервал энергий, в котором имеется при-
притяжение, составляет по порядку й©о = kB®D, где kB — постоянная
Больцмана, а дебаевская температура GD имеет порядок 300° К
(&BGD~0,03 эв). Отметим, что частота foq (или wD) зависит от массы
ионов М. Из выражений D.29) и D.33) следует, что ©ч — М~'1г. По-
Поэтому два изотопа одного и того же сверхпроводника имеют разные
ширины областей притяжения и их температуры перехода несколько
отличаются. Этот изотопический эффект был впервые предсказан
Фрёлихом и вскоре обнаружен экспериментально Максвеллом [68] и
Рейнольдсом и др. [69]. Существование изотопического эффекта
указывает на то, что колебания решетки вносят важный вклад в элек-
электрон-электронное взаимодействие.
Численные значения констант взаимодействия
В настоящее время не существует надежного способа вычисле-
вычисления матричных элементов VW. так как мы слишком мало знаем
о зонной структуре рассматриваемых систем, о взаимодействиях элек-
электронов с фононами и т. п. Особенно затрудняет расчеты то обстоя-
обстоятельство, что при низких частотах ю кулоновское отталкивание и
косвенное взаимодействие в значительной степени компенсируют друг
друга. В частности, легко видеть, что в модели „желе" e(q, ю) —voo,
когда ©->0. В этой модели статическое возмущение 6р полностью
экранируется, поскольку ничто не мешает положительным, ионам
образовать „облако" любой плотности, чтобы нейтрализовать заряд
бр1). Если же учесть короткодействующие силы между ионами, этот
эффект исчезает—экранирование делается неполным и величина e(q, 0)
становится конечной. Это замечание показывает, что энергетическая
') Единственным представляющим физический интерес примером столь
полного экранирования является, по-видимому, случай палладия, в котором
растворены атомы водорода. Если к гидрогенизированному таким способом
палладию добавляется металлическая примесь, то экранирующий заряд вокруг
примеси обязан главным образом наличию обладающих высокой подвиж-
подвижностью протонов, а не электронов.

106 Глава IV
ширина зоны притяжения и сама величина силы притяжения довольно
чувствительны к деталям физической модели. Поэтому очень важно
делать одинаковые приближения при вычислении прямого и косвен-
косвенного взаимодействия, чтобы избежать большой ошибки при нахожде-
нахождении их суммы.
Задача. Оценить в модели .желе" величину N @) Vр для простых ме-
металлов.
Решение. Определим Vp как притягательную часть взаимодействия
при ш = 0. Тогда
v = ^fi_
р K+f
В качестве д возьмем корень из среднего значения величины q2 ~Zq%l&,
где дп находится из условия дебаевского обрезания
<2яK Т 9Г>
(v0 — атомный объем). Наконец,
D-36)
mkp
2те2 ft
Величина $s определена выше [см. D.31)] как функция плотности электро-
электронов п
n=^=i- <438)
Комбинируя полученные результаты и учитывая, что h2/me2 — а0 = 0.529А
(а0 — боровский радиус), находим ')
N @) Vp = ! л-. D.39)
Задача. Определить для низких частот знак взаимодействия между
электронами в магнитной среде.
Решение. Предположим, что взаимодействие электрона, расположен-
расположенного в точке г и имеющего спин S/, с локальной намагниченностью среды
М (г) в той же точке имеет скалярную форму
Ht = — TS/ • М (г).
') Результат D.39) отличается от полученного Андерсоном и Морелом
[70]. Различие объясняется тем, что указанные авторы пользовались соот-
соотношением со„ = ra^k^ q вместо самосогласованной формы
q
Обсуждение эффективного взаимодействия в форме, позволяющей учесть
периодичность структуры, более точное рассмотрение явлений экранирова-
экранирования и т. д. можно найти в книге Пайнса [71], гл. 5.

Описание конденсированного состояния 107
Поскольку нас интересует предельный случай нулевой частоты, мы вы-
вычислим лишь статический отклик магнитной среды на возмущение Нх.
В первом порядке по Г отклик имеет вид
2
Р
где Хар — тензор обобщенной восприимчивости; а, р = лг, у, г. Напишем
теперь выражение для взаимодействия V между 6М и некоторым другим
электроном (со спином Sy) в точке г'
V (г - г') = -rs,- • 6М (г') = -Г* 2 SyaXap (г - О %
ар
Здесь снова удобно рассматривать фурье-компоненту
2
ap
Тензор статической восприимчивости Хар (q) симметричен, и поэтому его
можно диагонализовать соответствующим выбором осей. Три главных зна-
значения восприимчивости Xaa (Ч) всегда положительны. (В противном случае
магнитный материал обладал бы неустойчивостью относительно синусои-
синусоидальных с волновым вектором q искажений намагниченности.)
Если спины S/ и S/ антипараллельны (синглет), то статическое взаимо-
взаимодействие имеет знак плюс (отталкивание). Из соображений непрерывности
можно заключить, что этот результат справедлив также и при конечных
частотах, малых по сравнению с частотами, соответствующими обменному
взаимодействию в магнитной среде. (В упорядоченной системе знак взаимо-
взаимодействия меняется при ео=со где со_ — наименьшая при заданном волновом
векторе q частота спиновой волны.) Таким образом, в магнитной среде
. низкочастотная часть взаимодействия электронои г янтипаоаллельными спи-
спинами (т ё. куперопской папки носит отталкивательный характер. Напротив.
[для пар электронов с параллельными спинами (триплет) можно в принципу
получить притяжение на низких частотах.
§ 3. ОСНОВНОЕ СОСТОЯНИЕ И ЭЛЕМЕНТАРНЫЕ
ВОЗБУЖДЕНИЯ
Выбор пробной волновой функции
Согласно соображениям Купера (см. § 1), нормальное основное
состояние газа свободных электронов оказывается неустойчивым
при наличии притяжения между частицами. Конечно, эти соображения
носят лишь предположительный характер; в частности, в них не
учитывается возможность рассеяния электронов, расположенных над
фермиевской поверхностью, на электронах внутри нее. Теперь мы
более детально остановимся на расчете структуры конденсированного
состояния, рассматривая все электроны как равноправные.
В § 1 мы описывали пару электронов с помощью волновой функ-
функции \j)(r, - r2). Чтобы рассмотреть все N электронов на равных
основаниях, естественно попытаться написать волновую функцию

108 Глава IV
в следующем более общем виде:
Г2 rN) = 4>(rl— Г2)ф(Г3 — Г4) ... ф^д,.,— Гд,). D.40)
В состоянии, описываемом функцией q>N, электроны сгруппированы
попарно;" при этом волновая функция любой пары равна ф. Вид этой
функции мы можем определить, отыскав минимум энергии в состоя-
состоянии фдг.
ТРИ ВСПОМОГАТЕЛЬНЫХ ЗАМЕЧАНИЯ
а) Функцию фд, можно построить лишь для четного числа электронов.
Для нечетного числа N понадобилось бы поместить последний электрон
в отдельное состояние. Для электронного газа (N~ 1023) наличие этого
электрона привело бы к совершенно несущественным поправкам порядка 1/N
для энергии в расчете на одну частицу и для других свойств конденсиро-
конденсированного состояния. Наоборот, в случае сверхтекучести фермионных систем
с небольшим числом N (атомные ядра) четность или нечетность числа N
имеет большое значение, в особенности для формы спектра возбуждений.
б) В определении функции фд, мы не учли спиновых индексов. Руко-
Руководствуясь аналогией с рассмотренным в § 1 случаем, будем считать на-
направления спинов электронов пары противоположными, т. е. рассматривать
состояния (f^). Такой выбор функции фд, является наиболее подходящим
для взаимодействия V^i, слабо зависящего от угла между к и к'.
в) Функция фд, должна быть антисимметричной. Это свойство мы будем
записывать с помощью оператора А
)- D.41)
Алгебраические преобразования
Хотя формула D.41) представляет собой явное выражение для фд,'
(что, конечно, является ее достоинством), при конкретных расчетах
ее применение приводит к значительным трудностям. Для дальнейшего
удобно ввести фурье-компоненту gk функции пары ф(г):
<p(r) = Zgkeik-r: D-42)
к
тогда
ФЛГ "~ к, ' ' ' кд,/2 к. " ' " "Л72
Функция A exp [/kj • (г,—г2)] ... exp [/kw2 • (rN_x—rN)] (Ц)(Ц) - (Щ)
имеет простой физический смысл. Она описывает состояние, в кото-
котором один из электронов находится в состоянии (k,f), другой —
в состоянии (—kjj), третий — в состоянии (k2f) и т. д. Наличие опе-
оператора А обеспечивает должную антисимметрию волновой функции. Эта
антисимметричная функция в литературе обычно носит название детер-

Описание конденсированного состояния 109
минанта Слейтера, образованного из состояний
В обозначениях Вигнера—Иордана детерминант Слейтера можно
представить в иной, более удобной форме
Оператор рождения а+а, действуя на вакуумное состояние ф0, создает
электрон в состоянии (ка). Мы также будем пользоваться оператором
уничтожения ак , сопряженным оператору с+а и обладающим свойством
Вигнер и Иордан показали, что все свойства слейтеровского детер-
детерминанта в точности передаются формой D.44), если операторы а и с+
подчиняются следующим соотношениям антикоммутации'):
D.45)
В этих обозначениях функция фд, принимает вид
Выражение D.46) по-прежнему не вполне удобно для вычислений.
Рассмотрим вместо фд, производящую функцию
ГЛ*)Фо> D-47)
где произведение JJ берется по всем плоским волнам ^ аС — нор-
k
мировочная постоянная. Из сравнения D.46) и D.47) легко видеть,
что с точностью до множителя С функция фд, представляет собой
часть функции ф, содержащую N операторов рождения (действую-
(действующих на ф0), т. е. компоненту ф, которая описывает yV-частичное
состояние. Запишем выражение для ф в несколько ином виде, введя
множитель С под знак произведения:
Ч^к*)Фо. D-48)
') См. книгу Ландау и Лифшица [72].
2) Заметим что все множители под знаком J~[ коммутируют между
собой, в чем можно убедиться с помощью соотношений D.45).

по
Глава IV
где
D.49)
Последнее условие обеспечивает нормировку ф. Мы предполагаем,
что gk, uu и vk являются вещественными функциями. (В дальнейшем
мы увидим, что это ограничение можно снять.) Функция ф, которая
была введена Бардином, Купером и Шриффером в их фундаменталь-
фундаментальной работе [73] в 1957 г., имеет значительно более простую струк-
структуру, чем фдг- Оказывается, что для больших значений N все рас-
расчеты можно выполнять, используя функцию ф, а не ф^. Чтобы уяснить
это обстоятельство, напишем разложение
ф = 2 М>л
D.50)
при условии
N
обеспечивающем нормировку. (Отметим, что сделанный ранее выбор
фазы в ик и vk автоматически приводит к вещественности коэф-
коэффициентов Ядг.) На фиг. 40 показан вид кривой %N для больших
Фиг. 40. Амплитуда вероятности kN нахождения системы, описываемой
волновой функцией <р [см. D.48)], в состоянии с заданным числом частиц N.
При N=N* имеется очень узкий пик.
значений Л/; он не зависит от структуры коэффициентов gk. Кривая
имеет острый максимум, положение которого можно найти, вычислив
среднее значение числа частиц в рассматриваемом состоянии
D.51)

Описание конденсированного состояния Ш
где Q — объем образца. Подобно этому, мы можем вычислить средне-
среднеквадратичное отклонение для распределения |^|2- С помощью D.48)
находим
m - w=S кк=w J к<<*• D.52)
к
Поскольку разность (N2) — (NJ пропорциональна объему Q, а сле-
следовательно, и N*, то полуширина кривой составляет примерно У N*.
Таким образом, относительные флуктуации числа частиц N очень
малы, порядка l/УлГ*. Напротив, величина у/V* по-прежнему велика
по сравнению с единицей; отсюда вытекает, что при увеличении или
уменьшении N на небольшое число р изменение коэффициентов KN
пренебрежимо мало,
V D-53)
Изучим теперь вопрос о соответствии матричных элементов про-
произвольного оператора F, вычисленных с помощью q>N или ф:
(ФIF IФ) = ^S, V-лг <«PwI FI <Рлг'>- D-54)
Сначала предположим, что оператор F сохраняет число частиц; тогда
(Ф|'?|Ф> = 2|^12(Ч'^|/?|Ч>^>. D-55)
N
Матричный элемент (ф^ | F \ yN) является медленно меняющейся функ-
функцией N, поэтому мы можем заменить его значением в точке максимума
GV = /V*). Из условия 2l^vl2== ! находим
N
D.56)
Аналогично, если действие оператора F на ф^ дает состояние
с (N -\- р) частицами, то
(ФIF | ф) = | V+A <^+pl F I %> ^
•|Фл,*). D.57)
Следовательно, использование функций ф и фдг приводит на практике
к одинаковым результатам.
Определение энергии основного состояния
Пусть $№ — гамильтониан системы взаимодействующих электронов.
Если бы мы работали с волновой функцией ф^, то могли непосред-
непосредственно применить вариационный принцип и искать минимум среднего

112 Глава IV
значения (фд-| $в I Фту)- Если же используется волновая функция ф,
то здесь имеется небольшое отличие: число частиц в системе более
не фиксировано, поэтому мы должны минимизировать выражение
где N —оператор числа частиц, a EF — лагранжев множитель, который
мы назовем энергией Ферми. Перечислим теперь члены, дающие вклад
в $№—EFN. Член, соответствующий кинетической энергии, равен
D.59)
Член, соответствующий потенциальной энергии $въъ, содержит матрич-
матричные элементы, описывающие рассеяние двух электронов:
(ка) (к'Р) -^ (к + q, а) (к' - q, P).
п. Ц, hi
kk'q
а, В
При написании выражения D.60) учтены законы сохранения импульса
и полного спина.
Вероятность того, что в состоянии с волновой функцией <р со-
состояние к окажется занятым, равна v\. Поэтому кинетическая энер-
энергия имеет вид
(ф|^о1Ф) = 2 2|к^. D.61)
ка
В 3@ва дают вклад следующие члены:
1. Диагональные члены V (к, к'; к, к?).
2. Обменные члены V(k, k'; к', к).
3. Члены V (I, — 1; к, — k) = Vk|, описывающие переход пары
из состояния (kf, — к|) в состояние (If, —1|).
Члены 1 и 2 дают вклад в S^ea Уже в нормальном металле.
Вскоре мы увидим, что их можно просто включить в ?к, поэтому
забудем о них на время. Интересующий нас вклад дают члены типа 3.
Для нахождения этого вклада разложим сначала волновую функ-
функцию ф на два слагаемых фк1 и фк0, в которых парное состояние
(kf, —k|) соответственно занято или не занято. Согласно D.48),
Ф = «кФко + ^кФкг D-62)
Подобно этому мы можем разложить ф на четыре компоненты, опи-
описывающие заполнение двух различных парных состояний (kf, —k|)

Описание конденсированного состояния 113
и (If, -lj):
Ф = vk«,<pMi „ + «^кФк1> 10+ «к^,Фк0, „ 4- «к«,Фк0,10. D.63)
При вычислении вклада VkI в энергию взаимодействия (ф |
мы должны использовать компоненты
Матричный элемент, входящий в это выражение, равен просто Vk!.
Таким образом,
(Ф | &€ - ЕpN | ф) = 2 2 %kvlЧ- g VklukvkulVl. D.64)
Для учета условия uk-{-vk=l при нахождении минимума выра-
выражения (ф|е%?—EFN\qi) удобно положить
¦ нк = sin 6к, vk = cos 6k. D.65)
Тогда
(Ф | &в — EFN | Ф> = 2 2 |к cos2 вк + i J) sin 26k sin 2e,V^kl. D.66)
4
к к, I
Минимизация дает
О = -щ- (ф I Ш — EPN I ф) = — 2 У, ?к sin 26к 4- /. cos 26k sin
к к, I
ИЛИ
=-i S VkI sin 2e«-
I
Определим
2 D.68)
D-69)
Тогда
—|-, D.70)
sin2ek=-^, D.71)
— 4 + ^k = cos2ek = — &-. D.72)
(Знак в последнем уравнении выбран таким образом, что для больших
положительных значений |к имеем ик—1, г/к=0; тогда сумма ^j 2^k,
к
дающая полное число электронов, сходится.)
X Зак. 1020

114 Глава IV
Подставляя выражение для и^ в D.68), получаем, наконец,
уравнение для Дк
Сразу заметим, что это уравнение всегда имеет тривиальное реше-
решение Дк = 0. отвечающее выбору
1 для Ък < 0,
0 для |к > 0.
Соответствующая функция ф равна просто
ТТ а+а+ ф . D.75)
Это волновая функция газа невзаимодействующих электронов. Она
представляет собой слейтеровский детерминант, составленный из всех
состояний с энергиями, меньшими EF = h2k^l2m. Чтобы показать
в явном виде, что могут быть также другие решения, используем
упрощенное взаимодействие вида
r_v. «л» |M,|i,|<fcv D76)
I 0 в противном случае.
Постоянная V считается положительной. Мы будем называть взаимо-
взаимодействие такого простого вида взаимодействием БКШ. Для этого
случая легко показать, что
ДЛЯ | !fc | > tl(i>n,
D.77)
причем величина Д не зависит от к. Задача состоит в вычислении Д.
Перепишем уравнение D.73), просуммировав по всем направле-
направлениям 1 при фиксированном значении |,. Это приводит к множи-
множителю N(?|). равному плотности состояний (по энергии) для данной
ориентации спина в нормальном состоянии. Поскольку нас интересуют
энергии, заключенные в интервале шириной ha>D<^^EF, мы можем
вместо функции Af(|() подставить ее значение /V@) на уровне Ферми:
-hoD
A=N^V J Awmw- <4-78>
i 1D «
N@)V
= J -=^=-=1«

Описание конденсированного состояния 115
Решение этого уравнения существует лишь при положительных зна-
значениях V (т. е. лишь в случае притяжения) и имеет вид
sh [\jN{4)V] " D.80)
В дальнейшем мы будем интересоваться исключительно пределом
слабой связи [Af@)V<^ 1], в котором
&. = 2haDe-l'N(°)v. D.81)
Возникает вопрос: в какой мере оправдано использование этого пре-
предельного случая. Несколько позднее мы увидим, что температура пере-
перехода в этой простой модели определяется соотношением Д= \,75kBTc,
т. е. ехр[—1/N@)V\ = 0,88Tcl@D (@D — дебаевская температура,
h(?>D-=kB@D). Для большинства сверхпроводящих металлов бд*— 300°К.
Гс~'10оК. Следовательно, из эмпирических соображений можно за-
заключить, что Л/@I/Г<0,3. (Свинец и ртуть составляют исклю-
исключение. Температура Дебая GD у этих металлов очень низка, так
что значения N @)V равны соответственно 0,39 и 0,35.)
Зная Д, можно явно вычислить кинетическую и потенциальную
энергии. В пределе слабой связи получаем из D.64)
- D-82)
Здесь первый член равен кинетической энергии электронов в нормаль-
нормальном состоянии (Д = 0). Тем же путем находим
(ф|<яи $> = -¦?• D-83>
Разность энергий для состояния ф и нормального состояния <р„ равна
(ф | &в | Ф) - <ф„ | W | ф"„)(Д=0) = - Щ^-. D.84)
т. е. энергия конденсированного состояния ниже, чем нормального.
Однако этот выигрыш оказывается чрезвычайно малым, порядка
&21ЕР на одну частицу. Для Д=10°К и ?'/г=104°К это дает
Д2/?'/г== 10~2оК. Энергию нормального состояния мы не можем
вычислить с такой точностью. К счастью, члены, которыми мы пре-
пренебрегли при расчете, имеют почти одинаковую величину для нор-
нормального и для конденсированного состояний. Каждый из членов,
входящих в D.82), взятый по отдельности, не точен, но разность
очень близка к точному значению, причем именно эта разность изме-
измеряется на опыте.
Исходя из вида ф, можно установить некоторые простые свойства
конденсированного состояния.

116
Глава IV
а) Рассмотрим вероятность нахождения электрона в состоянии | ка)
для конденсированной фазы. Согласно D.70) и D.55). эта вероят-
вероятность равна
Функция г? в зависимости от k показана на фиг. 41. Она дает
распределение электронов по импульсам в основном состоянии. В прин-
принципе распределение v^ можно было бы получить на основе измере-
измерений, например, эффекта Комптона, аннигиляции позитронов в сверх-
сверхпроводнике и т. д. Однако в действительности такие измерения
Фиг. 41. Функция распределения электронов по импульсам | vk |2 в сверх-
сверхпроводнике при Т = 0 а амплитуда конденсации Fw
В нормальном металле функция распределения скачком обращается в нуль при ft = Ьр; в сверх-
сверхпроводнике этот спад происходит в интервале 6ft ~ 1Ц0
в наиболее интересной области значений k потребовали бы очень
высокой точности. В самом деле, vk = 1 при k <^ kp и vk = 0 при
k"^$>kF. В отличие от нормального металла, где функция распре-
распределения имеет разрыв при k = kp, в сверхпроводнике ч% меняется
непрерывно. Область изменения v^ от нуля до единицы имеет ши-
ширину — Д по энергии, а ее ширина по импульсу bk определяется из
соотношения
т. е.
D.86)
6»,
б) Добавим к системе, описываемой волновой функцией фд,, два
электрона, которые первоначально находились в состояниях к\ и —к|.
Спрашивается, чему равна амплитуда вероятности найти систему

Описание конденсированного состояния П7
в состоянии с волновой функцией Флг+2? Обозначим эту амплитуду
через Fk. По определению,
Fk = <Ф^+21 SVlk J 4W> = <Ф | <А 11Ф). D.87)
Используя также определение ф, отсюда находим
D.88)
Мы назовем Fk амплитудой конденсации в состоянии к. Из D.88)
видно, что она отлична от нуля лишь в переходной области и имеет
наибольшее значение при k = kF (см. фиг. 41).
Низшие возбужденные состояния
Мы построили волновую функцию фуу, описывающую основное
состояние, в котором все Л/ частиц спарены. Добавим теперь к си-
системе еще одну частицу в состоянии, описываемом плоской волной
(т, а). Тогда мы придем к волновой функции
4W+1. т„ (Г1 TN+l) = АФ (Г1 - Г2) • • • Ф (Г„_! - Г„) X
X е""'*"*1 (If) ... (Щ) (ЛГ+ 1, а). D.89)
Введем соответствующую ей производящую функцию
„- D-90)
Повторяя для фта рассуждения, проведенные выше для ф, находим
Фт„ =
Очевидно, что функция фта ортогональна к ф.
Вычислим энергию для состояния фта. Для кинетической энергии
можно написать
(Фта1^о|Фта) = (ф|^о|ф) + 0-2^Iт. D.92)
Это следует из того, что волновая функция фта соответствует случаю
занятого состояния та, тогда как волновая функция ф описывает
состояние, в котором суммарная вероятность нахождения электрона
в состояниях (щ|) и (— ш|) равна 2г^. Для нахождения потенциаль-
потенциальной энергии заметим, что вклад в ее величину дают лишь члены,
отвечающие переходам (к, а)(—к, —а)->(к', а)(— к', —а) для
к, к'^ш, поскольку при спаривании состояние (та) не может быть

118 Глава IV
использовано. Таким образом,
Полная энергия равна
(Фиш I да I Фп,«) = ^0 + 0 -
- 2 S
Е2 А2
-f=-+-J»==E0-|_em. D.94)
Поскольку f0—энергия основного состояния ф, величина ет =
— у Д^ -f-1^, представляет собой энергию, необходшгую для того,
чтобы поместить новую частицу в состояние (та). Отметим, что даже
при ^ = 0 энергия ет остается конечной и равной Aft = Д.
Таким же путем мы могли бы попытаться построить состояния
с 2, 3 п возбуждениями. Например, для состояния с двумя
возбуждениями напрашивается мысль взять волновую функцию в виде
Д п («к
D.95)
К сожалению, функции такого вида, вообще говоря, не ортогональны
исходной функции ф. Так
(ф|2т4_т*) = г;т=гь0. D.96)
Эту трудность можно обойти двумя способами.
а) Добавим к S слагаемое fop, в котором параметр К выбирается
с таким расчетом, чтобы результирующая функция стала ортого-
ортогональной к ф. Этот метод использовали Бардин, Купер и Шриффер
в своей оригинальной работе, однако на практике он неудобен.
б) Вернемся к волновой функции фта для состояния с одним
возбуждением и попытаемся представить ее в виде
ш =v+ ф, D.97)
где у+а играет роль оператора рождения для элементарного возбуж-
возбуждения. Если бы нам удалось подобрать операторы -у4 и сопряжен-
сопряженные им операторы у таким образом, чтобы они 1) подчинялись фер-
мионным правилам коммутации, 2) удовлетворяли соотношению
•утаф = 0 (т. е. функция ф соответствовала состоянию -без воз-
возбуждений), тогда можно было бы легко показать с помощью соот-
соотношений коммутации, что все состояния, полученные путем воздей-
воздействия произвольного числа операторов у* на ф, нормированы, орто-
ортогональны друг к другу и к исходному основному состоянию ф*

Описание конденсированного состояния П9
С кинематической точки зрения удобство таких функций состоит
в возможности описывать состояния с большим числом возбуждений.
Задача заключается, таким образом, в нахождении у+. В каче-
качестве первой попытки заметим, что
Это соотношение легко проверить с помощью D.91) и соотношений
коммутации типа Gmaama = ® и Т" л' Однако операторы (l/«m)^a
не подчиняются упомянутым правилам антикоммутации. В качестве
второй попытки воспользуемся тем, что
При использовании операторов (.^/vm)ama мы опять сталкиваемся
с той же трудностью, связанной с правилами коммутации. Попыта-
Попытаемся теперь определить у+ как линейную комбинацию предыдущих
операторов. Если положить
тогда легко показать, что D.97) и условия 1 и 2 будут выполнены.
Например, справедливость условия 2 можно проверить следующим
образом:
К+vfr0^) (в«°«*-v«fli«*) (и«-Н'«0^0^
«к + ^Й^н)«т%(^т,-^т,)Фо = О, D.101)
где мы использовали соотношения #_шаФо—0, йта^таФо==Фо и
соотношения антикоммутации. Таким образом, мы нашли операторы
у + , с помощью которых можно построить набор взаимно ортогональ-
ортогональных возбужденных состояний, ортогональных также к основному
состоянию. Операторы у и \+ были введены независимо Боголю-
Боголюбовым [74, 75] и Валатином [76] в 1958 г. Использование этих
операторов существенно упрощает все расчеты, так или иначе свя-
связанные с возбужденными состояниями. Возбуждения, порождаемые
операторами у+, будем называть квазичастицами.
НЕСКОЛЬКО ФИЗИЧЕСКИХ ЗАМЕЧАНИЙ
а) Из того факта, что оператор у^а представляет собой линейную ком-
комбинацию операторов а^а и а_т _а, следует, что состояние <p^+i, ka можно
б б k я
а +
создать либо добавлением одного электрона (ka) к основному состоя-
состоянию «Рд,, либо удалением электрона (—к —а) из состояния

120 Глава IV
б) Предположим, что исходным является основное состояние ф^.. Как
мы уже видели, заполнение состояния к связано с затратой энергии не
меньшей, чем Ер -\- А. Такие опыты по „инжекции* электронов не являются
чисто теоретическим построением. Их можно реально поставить, вводя
электроны в сверхпроводник через тонкий оксидный слой. Впервые это
было сделано Жавером [77] в 1959 г. Открытое им явление носит название
туннельного эффекта (о чем уже упоминалось выше). С его помощью удается
произвести измерение щели А.
в) Если не рассматривать туннельных экспериментов, то обычно при
изучении возбужденных состояний число частиц TV остается неизменным.
Примером могут служить опыты по инфракрасному поглощению. Если
число Л^ четно, то первое возбужденное состояние рассматриваемого типа
соответствует разрыву пары и описывается волновой функцией вида
¦у^а\'|"|ф (ка=?ИР). Энергия возбуждения легко вычисляется и равна ек -f- е,.
Минимальное значение этой энергии (отвечающее порогу инфракрасного
поглощения) равно 2Д. Если число N нечетно (N=2K-{-1), то основное
состояние содержит, помимо К пар, один неспаренный электрон. В этом
случае в принципе возможны два сорта возбуждений; либо, как и раньше,
происходит расщепление куперовской пары (щель равна 2Д), либо изменяется
состояние неспаренного электрона (щель отсутствует). Однако интенсивность
поглощения для первого процесса по порядку в TV раз больше, чем второго.
На практике N <~ 1023, поэтому всегда наблюдают порог поглощения, рав-
равный 2Д.
г) Минимальная энергия возбуждения равна 2Д, но энергия, приходя-
приходящаяся на одну возбужденную частицу, составляет величину Д. По этой
причине при низких температурах вероятность нахождения частицы в воз-
возбужденном состоянии к (к « kp) изменяется по закону ~ ехр (— Д^Л^Г).
Случай двух связанных сверхпроводников
Рассмотрим два сверхпроводника S и S', разделенных изолирую-
изолирующим слоем. Если толщина слоя велика, электроны не могут про-
проходить через него и сверхпроводники S и S' полностью независимы.
Однако если слой становится достаточно тонким (толщина менее 30 А).
то электроны могут проходить через него за счет туннельного
эффекта. Это приводит к появлению связи между областями 5 и S',
которую мы сейчас и рассмотрим. С формальной точки зрения про-
прохождение электронов можно описать путем добавления к гамильто-
гамильтониану электронов Stfss' (для несвязанных между собой областей 5
и S') малого члена Щ1Т, вызывающего туннельные переходы элек-
электронов из 5 в S' и наоборот:
2 К^Л,+«JW^fi). -102)
к,
где оператор fl?s создает электрон в состоянии к в области 5,
а оператор «is- уничтожает электрон в состоянии 1 в области S'.
Матричные элементы Тк1 можно найти в явном виде, решив уравне-

Описание конденсированного состояния 121
ние Шредингера для одного электрона при наличии барьера. (От-
(Отметим, что полный гамильтониан ?f6ssi для областей S к S' вклю-
включает взаимодействие V электронов между собой.) Собственные функ-
функции гамильтониана e/tfss' будем искать в виде произведения двух
функций типа D.43), относящихся соответственно к областям 5 и S':
*v = 4^-v)^ ^ss-% = EvK D-ЮЗ)
Функция i])v описывает состояние всей системы, в котором в областях
S к S' находятся соответственно 2v и 2(N — v) спаренных элеро-
элеронов. Полное число электронов 2Л/ предполагается фиксированным;
число v, напротив, заранее неизвестно.
Определим зависимость энергии Ev от числа v. Если увеличить v
на единицу, переместив два электрона из области S' в область 5,
то, согласно термодинамике,
[&p — &P], D.104)
где ЕУр — химический потенциал (уровень Ферми) в области 5. Пред-
Предположим на время, что разность потенциалов между S и Sf отсут-
отсутствует, тогда ?>==?> и, следовательно, совокупность функ-
функций i])v образует вырожденную систему (EV = E независимо от v).
Возмущение <~}6Т приводит к снятию этого вырождения. Матричный
элемент, связывающий состояния tyv и *1\,+ 1, во втором порядке по
Цвт равен
k, I k', Г '
где |/) обозначает промежуточное состояние, в котором Bv-f- 1)
электронов находятся в области 5 и 2 (N — v) — 1 электронов —
в области S'. Гамильтониан ef6T действует сначала на состояние,
содержащее v пар в области 5, что приводит к появлению в этой
области лишнего неспаренного электрона с волновым вектором к'
(состояние | /)). При последующем действии S@t на I ¦О в области 5
возникает второй неспаренный электрон в состоянии к. Поскольку
конечное состояние, на которое проецируется полученное состояние,
содержит (v —(— 1) пар, то должно быть выполнено условие к = — к'.
Аналогичным образом легко показать, что 1=—1'. Воспользовавшись
также соотношением симметрии Т_у_1 = Т+1 и полученными ранее
результатами для возбужденных состояний, находим
Jo = — 4 У Гм|2 , • D.106)
Г! к+ '
Во втором порядке по возмущению <§?вт можно написать
i)- D-107)

122 Глава IV
Правильная волновая функция представляет собой линейную комби-
комбинацию функций \KV. Рассматриваемая задача формально эквивалентна
задаче о движении электрона в линейной цепочке атомов; функ-
функция i])v есть аналог волновой функции электрона, локализованного
на v-ом атоме. В приближении сильно связанных электронов примем,
что искомая волновая функция \J)A в соответствии с теоремой Блоха
имеет вид
2"*. DЛ08>
где k—аналог волнового вектора. Соответствующая энергия E(k)
равна
D.109)
Построим теперь волновой пакет с помощью состояний tyk, вол-
волновой вектор которых заключен в интервале от k до k-\-&k. Со-
Согласно используемой аналогии с линейной цепочкой, этот волновой
пакет имеет пространственную протяженность Av~ 1/Д&. Так как
число v очень велико (v~ 1022), величину Av также можно считать
весьма большой (например, Av^ }/"v~ 1011). В этом случае значе-
значения ДА и Av/v будут малыми (— 10"п). Таким образом оказывается
возможным одновременно задать с хорошей точностью значения А и V.
Групповая скорость движения пакета равна
Движению волнового пакета соответствует изменение со временем
величины v, т. е. между S и S' должен течь ток
l ^ D.111)
Другими словами, если систему SS' включить в замкнутую цепь, то
по ней может протекать ток (< 4еУ0/й) при нулевой разности по-
потенциалов. Уравнение D.111) позволяет понять на простом примере
возникновение сверхтекучих свойств в конденсированном состоянии.
Отметим, что для нормальной системы (иьРу^О), согласно D.106),
У0 = 0. Рассмотренный эффект был предсказан Джозефсоном [78]
в 1961 г. и впервые наблюдался Андерсоном и Роуэллом [79]. (Ти-
(Типичное значение плотности тока составляет '— Ю~2 а/с .и2.) Приве-
Приведенный здесь вывод принадлежит Феррелу [80].
Как изменятся эти результаты при наличии разности потенциа-
потенциалов V между S к Sf? В этом случае Evtl— Ev = 2eV, и мы имеем
полную аналогию с задачей об атомной цепочке в однородном
электрическом поле. Движение волнового пакета описывается „урав-

Описание конденсированного состояния 123
нением Ньютона"
D.112)
Уравнения D.111) и D.112) полностью определяют поведение тун-
туннельного контакта. В частности, если напряжение V поддерживается
постоянным, то k линейно растет со временем, а ток / изменяется
синусоидально с частотой 1eV\h.
Задача. Джозефсоновский контакт SS' последовательно включается
В цепь, состоящую из сопротивления R и генератора напряжения U. Вы-
Вычислить ток.
Решение. Напряжение на контакте равно
V = U — RI = U-\-^-sink.
Согласно D.112),
dk Че
~df~~h
где
J.R \
SL- sink) = w0 A-Я sin k).
2eU
hV
a Jm—максимальный сверхпроводящий ток, который может течь через
контакт.
Интегрирование уравнения движения легко выполнить. В результате
имеем
Рассмотрим два случая.
а) Если Л > 1, то знаменатель подынтегрального выражения имеет по-
полюс при k = k0 (sin k0 = 1 'Я). В этом случае k->k0 при *->со, т. е. ток
стремится к своему предельному значению U/R. При достижении током этого
значения напряжение на контакте, равное U—R1, падает до нуля. Таким об-
образом, возможен режим, в котором ток остается постоянным во времени.
б) Если Я < 1, то знаменатель не может обратиться в нуль. Интеграл
берется в явном виде. Положив
в результате интегрирования найдем
m = Я + VT=X* tg [I W=T* «0 (t — to)\ ,
т. е. /я, а следовательно, и k являются периодическими функциями времени
с периодом, равным 2л/<в0 jA — Я2. Отметим, что при этих условиях ток не.
синусоидален, за исключением случая, когда Я = 0.

124 ' Глава IV
§ 4. ВЫЧИСЛЕНИЯ ПРИ КОНЕЧНЫХ ТЕМПЕРАТУРАХ
Определение свободной энергии
При Т Ф 0 происходит тепловое возбуждение состояний \+<р,
^к^1+(Р и Т- •"¦• ^РИ низких температурах (kBT<^A) возбуждений
мало и их можно считать независимыми. Однако, когда величина kBT
становится сравнимой с Д, число возбуждений велико. Мы изучим
теперь усредненный эффект взаимодействия между возбуждениями и
покажем, что его просто можно описать, допустив изменение энер-
энергетической щели Д с температурой.
Фермионные операторы у? будем задавать по-прежнему с по-
помощью преобразования D.100), параметры которого и^ и v% пока
не определены. Возбуждения системы будем трактовать как газ не-
независимых квазичастиц; вероятность найти квазичастицу в состоянии
с волновым вектором к и спином а1) при температуре Т равна
/ка = 0№а> = ! - (VkaYk+a). D.113)
Символ ( ) означает усреднение по Гиббсу. Мы построим сначала
выражение для свободной энергии, пригодное при произвольной
функции распределения fu, а затем будем отыскивать ее минимум
по ии, vk и /к.
1. Вычисление средней кинетической энергии с помощью D.92)
дает
> = 2 h К
к
2. В потенциальную энергию в рамках рассматриваемого прибли-
приближения по-прежнему дают вклад лишь члены, описывающие рассея-
рассеяние
(kf, — k|)->(lf, —1|),
В этом выражении операторы а+, а являются линейными комбина-
комбинациями операторов Y+ и у, описывающих систему независимых фер-
мионов. Имеет место следующее простое свойство:
04) + @,04) @203) - {0,03) @204>. D-116)
') В большинстве случаев функция /ки не зависит от а, поэтому обычно
мы будем писать просто /к.

Описание конденсированного состояния 125
где под символом 0 подразумевается оператор а или а4. Это свой-
свойство (частный случай теоремы Вика) можно проверить, явно выра-
выражая операторы а через Y и производя усреднение. Применение тож-
тождества D.116) позволяет сильно упростить последующие вычисления.
В данном случае взаимодействие содержит три члена. Два из них
включают средние вида (а+ак} и приводят к поправкам типа Хартри
и поправкам, имеющим обменное происхождение. Обе поправки в ос-
основном не зависят от температуры. Поэтому, как и раньше, мы их
всюду будем опускать. Остающийся член вида {а+а+) (аа) дает
<^вз>= S^Ww.O -я/Ж1 -2/.)- DЛ1?)
k, I
3. Энтропия 5 системы невзаимодействующих фермионов описы-
описывается выражением
S = -^2[/kln/k + (l-/k)ln(l-/k)]. D.118)
ка
4. Свободная энергия имеет вид
F={$eo-\-$ew)—TS. D.П9)
Потребуем сначала стационарности выражения для Р относительно
и\ и vu- Снова полагая ик = sin 0k и i>u = tos0k, получаем условие
2^ О - 2/к) ^п 26k = 2J Vu cos 26k sin 26, A - 2/к) A - 2/,).
D.120)
Если ввести определение
\ = —5%Уы5[а2Ч1-Щ D-121)
i
то опять приходим к системе уравнений D.69) — D.72). Единствен-
Единственное видоизменение связано с тем, что выражение D.121) для Дк
в отличие от D.68) содержит числа заполнения для возбуждений.
Минимизируя выражение для F по отношению к Д, получаем
=0.
D.122)
Отсюда с помощью D.69) — D.72) находим
Это обычный вид функции распределения свободных фермионов по
энергиям еи. Однако зависимость Д от температуры не является
столь простой, потому что eh и Д^ теперь зависят от температуры.

126 Глава IV
¦к
Изменение щели с температурой и точка перехода
Условие самосогласованности, аналогичное уравнению D.73),
имеет вид
5X^ D-124)
Возьмем сначала в качестве Vu\ простое по форме взаимодействие
БКШ [см. D.76)]. Тогда уравнение D.124) примет вид
1 =N@)V f ^^ [l -VWW+Щ- DЛ25)
jj V I2 + A2
Это уравнение определяет в неявной форме зависимость Д от Т.
При 7"= 0, полагая фермиевскую функцию /(е) равной нулю (е > 0),
мы снова возвращаемся к уравнению D.79). Для общего случая
вид Д G) приведен на фиг. 42, откуда видно, что величина щели А (Т)
уменьшается при повышении температуры Т и, наконец, щель исче-
исчезает при определенной температуре Тс. Выше Тс единственным ре-
решением уравнения D.124) является Дь = 0 (нормальное состояние).
Таким образом, Тс представляет собой температуру перехода между
5- и Л/-состояниями (в нулевом магнитном поле). Величину Тс можно
найти, положив в D.125) Д = 0:
йюд
l=N@)V f x-th-^yr-. D.126)
В случае h(aD'^>kBTc ясно, что интеграл имеет асимптотический
вид
f
Rb'c
поскольку в большей части области интегрирования гиперболический
тангенс можно положить равным единице. Более точный расчет по-
показывает, что С = 1п1,14. Следовательно,
l,14/ton
1 =N@)^111-^-^
Rb' с
или
kBTc=\A 4/j(oDe - vw (О v. D.127)
Полагая в D.127) hcoD = kB@D и беря значения дебаевской темпе-
температуры 6D из измерений теплоемкости в нормальном состоянии, можно
связать величину ./V @) V с критической температурой Тс. Соответ-

Описание конденсированного состояния
127
ствующие значения для непереходных металлов приведены в табл. 4.
В большинстве случаев TC<^@D, т. е. константа связи N@)V очень
мала; исключение составляют лишь свинец и ртуть (по-видимому,
метод самосогласованного поля в случае этих металлов дает не очень
.й@)*),Ш8Тс
&*>32кеТсП-(Г/Тс)]'?г
I т/тс
Фиг. 42. Зависимость параметра порядка А от температуры Т, следую-
следующая из теории БКШ.
Таблица 4
Экспериментальные значения 0D, Тс и коне гаи гы
связи W@) V
Металл
Zn
Cd
Hg
Al
In
Tl
Sn
Pb
235
164
70
375
109
100
195
96
тс, "К
0,9
0,56
4,16
1,2
3,4
2,4
3,75
7,22
1ЛГ@)К|9КСП
0,18
0,18
0,35
0,18
0,29
0,27
0,25
0,39
большую точность). Как видно из экспоненциальной формы D.127),
для N@)V <0,1 ивд«=200°К температура Те попадает в область
значений —Ю~3сК- При столь низких значениях Тс сверхпроводи-
сверхпроводимость может быть подавлена за счет различных посторонних явле-
явлений (таких, как магнитное поле Земли, влияние ядерных спинов
и т. п.). Поэтому вполне возможно, что в некоторых металлах,
сверхпроводимость которых до сих пор ясно не установлена, взаи-
взаимодействие носит характер притяжения. Наконец, отметим, что ка-
качественные предсказания, сделанные на основе модели .желе".

128 Глава IV
оправдываются на опыте в том отношении, что для больших значений
валентности Z и больших атомных объемов v0 наблюдаются большие
значения константы связи N @) V ').
„ „ . . Для взаимодействия БКШ [см. D.761) темпе-
Изотопический эффект -г
ратура перехода /с пропорциональна частоте
обрезания <oD. Как уже упоминалось ранее, два изотопа с одинако-
одинаковыми электронными свойствами, но различными массами ионов обла-
.,-1/,
дают различными значениями частоты <bd, изменяющимися как /И ,
(Этот результат является общим. Он следует из того факта, что
сила F, входящая в уравнение движения иона М (tfxjdt2) = F,
не зависит от массы иона.) Таким образом, из выражения D.127)
следует изотопический эффект Тс~М~ . Такая зависимость наблю-
наблюдается на опыте для целого ряда непереходных металлов (Hg, Pb,
Mg, Sn, Tl). Однако во многих других сверхпроводниках (переходные
металлы и соединения) изотопический эффект менее выражен и даже
отсутствует совсем (Ru, Os). Предложены различные механизмы для
объяснения этих отклонений, которые в основном можно свести
к следующим двум:
1. Предполагается, что взаимодействие по-прежнему обусловлено
фононами, однако использованная в теории БКШ форма для Vw
является чересчур упрощенной.
2. Принимается, что взаимодействие обусловливается другими
(т. е. не связанными с движением решетки) низкочастотными возбу-
возбуждениями.
Второе объяснение можно с определенным успехом приме-
применить в ряде случаев, но его правильность очень трудно
доказать (или опровергнуть) экспериментально. Здесь мы
обсудим только первое объяснение.
При обсуждении электрон-электронных вза-
Учет кулоновского имодействий в начале этой главы мы полу-
полуотталкивания _ J
чили два члена. Первый член описывает
кулоновское отталкивание (в основном не зависящее от частоты),
а второй — притяжение, обусловленное фононами. (Этот член суще-
существен при частотах <о < <bd, но становится пренебрежимо малым для
больших частот @^>o)D.)
Пренебрежем, как и раньше, зависимостью матричного элемента VM
от угла между к и I и запишем его в виде
*Ve-Vp{e>).
D.128)
') Однако при количественном сравнении обнаруживается, что модель
„желе" приводит к завышенным значениям для N @) V даже при учете
кулоновского отталкивания.

Описание конденсированного состояния 129
Уравнение D.126), определяющее температуру перехода, тогда заме-
заменится следующим:
Д(Е) = -ЛГ(О) J d&V(i^)A(fc')-^=|p!. D.129)
К сожалению, это интегральное уравнение очень трудно решить даже
для простого взаимодействия D.128), поэтому наше дальнейшее рас-
рассмотрение будет весьма приближенным. Выделим в D.129) вклад
от кулоновского члена и обозначим его через А
dl'Vc Д (Г) ^Щ^- • D-130)
Очевидно, что величина А не зависит от g. Уравнение для Д при-
примет вид
J (l^il) 1Ц®) +A D.131)
При | ? | ^. й<Од интеграл не может быть большим, так как множи-
множители V р{Ъ,— |') и 1/|' не могут одновременно принимать больших
значений. Поэтому в этой области весьма приближенно можно поло-
положить Д(?)=А Наоборот, в области малых значений |?| интеграл
становится существенным. Обозначим через В среднее значение Д
в области ha>D > | ? |. Тогда имеем
/}<B
^N{O)VpB\n-r-^--+A, D.132)
В с
где Vр — некоторым образом усредненное значение Vр (<о) на интер-
интервале — юо < ю < (DD. Наконец, уравнение D.130), определяющее А,
можно представить в виде
В J +А J +А J +Л J
^-). D.133)
где (?>с—частота обрезания (практически порядка Ер'Щ для куло-
кулоновского взаимодействия. Из условия совместности выражений
9 Зак. 1020

130
Глава IV
D.133) и D.132) получаем
квТс
D.134)
Уравнение вида D.134) для температуры перехода впервые было
получено Толмачевым (см. [75]) в 1958 г. Из него можно вывести
ряд интересных следствий.
In
|
I
15
10
5
1
f
Gq,
¦
,t H9
. . oo
Zn.Cd
• Al
\
\
\oSn
\ о РЬ
%°l о T OS
\ \* Mo
Ч о
о 44 °
Ru <^ V^t
Ti ф Th'^s
о _ /
• -Z
• -3
fl -4
i -5
Q -6
• - 7
•-8
V "~"
NbjSn
VjSi
VjGq
i
о i г з
6 7 8 9 10 И
у, I0'3dm ¦ град~г- моль'1
IZ
Фиг. 43. Соотношение между константой связи Кр электрон-электронного
взаимодействия, обусловленного фононами, и параметром \ для электронной
теплоемкости в нормальном состоянии, полученное на основании опытных
данных для ряда элементов и соединений (Бюхер и др. [137]).
1) Nb—Mo, Nb—Zr; 2) Nb—Ru; 3) Mo—Re, 4) Nb—Re, Mo—Re (o-Mn); 5) о-фазы (элементы
второй и третьей переходных групп); 6) Mo—Ru, Mo—Pd, Mo—Tc; 7) переходные элементы;
S) В-металлы.
1. Кулоновское отталкивание, описываемое с помощью Кс, не
очень эффективно препятствует появлению сверхпроводимости из-за
наличия множителя
1

Описание конденсированного состояния 131
В частности, может оказаться, что даже при Кр < Кс (т. е. в том
случае, когда во всей области константа взаимодействия соответствует
отталкиванию) сверхпроводимость тем не менее сохраняется, если
выполнено условие
2. Изотопический эффект претерпевает изменения. При относи-
относительном изменении массы иона на bMjM дебаевская частота получает
соответствующее приращение 6<oD/©D = — 6Ж/2Ж и температура
перехода смещается по закону
т
с
т. е. величина изотопического эффекта уменьшается. Особенно силь-
сильным это уменьшение должно быть для металлов с узкими зонами
(частота сос мала). Возможно, по этой причине изотопический эффект
слабо выражен в переходных металлах и их соединениях [81].
Наоборот, используя экспериментальные значения критической
температуры Тс и величины изотопического эффекта, а также пред-
предполагая справедливость описанной модели, можно оценить величины
Кр и Кс. Результаты, полученные для самых различных металлов,
показывают сильную корреляцию между величиной Кр и коэффи-
коэффициентом V. который входит в выражение для электронной тепло-
теплоемкости нормальной фазы •) (фиг. 43).
Вычисление термодинамических величин
Объединяя выражения для кинетической и потенциальной энергий
D.114) и D.115) и используя выражения D.69) — D.72) для ии и vu,
находим полную энергию
D.135)
В частности, при абсолютном нуле (/ = 0) мы возвращаемся к выра-
выражению Для энергии, полученному в § 3. Для энтропии D.118) найдем
ts = 2 2 к/ og+fte7- in A + Л/**7)]- D.i 36)
h
') Коэффициент у пропорционален плотности состояний на уровне Ферми-
Однако между у и N @) имеется различие: коэффициент у обычно берется
в расчете на один атом, тогда как плотность состояний N{0) — на единицу
объема.
9*

132 , Глава IV
Теплоемкость, по определению, равна
С=Т-~. D.137)
Имея в виду, что энергия ек зависит от Т, получаем, используя D.136),
| / (ек) [ 1 - /(ек)] (eg + Pek ^) D.138)
(где $=\jkBT). В приближении БКШ (dEu!dT)ek = (dAidT)A (неза-
(независимо от к). Тогда
= 2p»VV@) f dg/(e) [1 -/(е)] (е» - Г Д-^-) ,
D.139)
Ход теплоемкости показан на фиг. 1.
При очень низких температурах ((?А^> 1) членом (dAjdT)A можно
пренебречь
Р2А:ВЛ/(О)Д2| die » Д^ _
о
СО
— 2p2A?W@) Д2е-Рд» f ф-№*\ D.140)
6
где Д0г=ДG' = 0). Фигурирующий здесь интеграл равен
Температурная зависимость теплоемкости Cs в основном определяется
множителем ^^ехр(—рД0), как и предполагалось ранее. Из изме-
измерений теплоемкости при низких температурах можно определить
величину Др.
Наличие члена {dAjdT)A в выражении D.139) приводит к скачку
теплоемкости в точке перехода и сверхпроводящее состояние
Численный расчет с помощью D.125) дает (d&z/dfi)T = 10,2р|, т. е.
с
D.142)

Описание конденсированного состояния 133
Согласно D.119), плотность свободной энергии Fs представляет
собой разность выражений D.135) и D.136):
[( ^) ]. D.143)
Это выражение можно несколько упростить, заметив, что
к
2Ек
ZJ 2е "Г
к
где первый член в правой части в приближении БКШ, согласно
условию D.124), равен —Д2/1Л Таким образом,
F* = - 'у + 2 [~ 2е^ ^ + & - У " D-] 44>
Зная Fs, мы можем найти термодинамическое критическое поле Нс
из соотношения (см. гл. II)
/7»-F*==w- DЛ45)
В частности, при Т — 0 (Hc — i
Детальный расчет с помощью D.144) показывает, что при конечных
температурах Т кривая НС(Т) весьма близка к эмпирической зави-
зависимости
%^ ffJ D.146)
Однако оказывается, что для сверхпроводников со слабой связью
[параметр Л^ @) V не слишком велик] получающаяся из теории БКШ
зависимость Нс от Т находится в лучшем количественном согласии
с опытными данными, чем упрощенная формула D.146).
Формулы для вероятностей переходов
Предположим, что на электроны сверхпроводника действует внеш-
внешнее зависящее от времени возмущение, например ультразвук или
микроволновое поле. Рассмотрим эти два случая.
/. Ультразвук. Продольная акустическая волна изменяет потен-
потенциальную энергию каждого электрона на UQ (r, t), где 0 — локальное

134
Глава IV
искажение решетки, U — постоянная (так называемый „деформацион-
„деформационный потенциал"). По порядку величина U равна нескольким
электронвольтам. Матричный элемент этого возмущения для пере-
переходов электрона из состояния к в к' равен ?/0к_к/ (где 0Ч — фурье-
действующее на всю систему элек-
элеккомпонента 0(г)).
тронов, запишется
Возмущение,
в виде
к, к ,
D-147)
2. Микроволновое поле. При наличии электромагнитного возму-
возмущения, описываемого вектором-потенциалом А (г, t), энергия элек-
электрона становится равной (р — еА/сJ/2/к. В первом приближении по А
возмущение имеет вид (—?/2/яс)(рА-|- Ар), или, записывая его через
операторы а и а+,
* = - 2
D-148>
U, иш а
В общем случае, таким образом, возмущение можно записать
в виде
Set= S ^(ka|kV)a+A,a.. D.149)
к, dj к , Ct
Под влиянием ?№х возникают следующие два эффекта:
1. Возмущение $вх индуцирует переходы между различными возбу-
возбужденными состояниями, описываемыми с помощью операторов у+. Для
классификации этих переходов выразим ??6Х через операторы у и у+.
Обращая выражение D.100), получаем
Таким образом,
/о -\\
=(i oj-
ukvk.
2
Члены Y/+Y,- и Y/Vt описывают переходы, при которых квазичастица
рассеивается из состояния / в состояние j (и наоборот). Член Yj"Yt
приводит к рождению двух квазичастиц в состояниях / и J, а член
V/Y/ — к уничтожению их.

Описание конденсированного состояния 135
2. Возмущение §ЬХ может модулировать параметры системы (на-
(например, параметр Д), описывающие структуру конденсированного со-
состояния. Такая модуляция также приводит к поглощению энергии.
Во многих случаях, однако, этим эффектом можно пренебречь. Рас-
Рассмотрим, например, задачу о поглощении ультразвука. Исходное воз-
возмущение имеет вид ?/0(г). При модуляции потенциал спаривания
изменяется на величину 6Д = С Д0 (г), где С — постоянная порядка
единицы. Это в свою очередь приводит к изменениям самосогласо-
самосогласованного поля. Поскольку U имеет порядок 1 —10 эв, а СД—поря-
СД—порядок 10~3 эв, ясно, что модуляция Д в этом случае несущественна1).
Забудем поэтому на некоторое время об этом эффекте (позже в связи
с рассмотрением эффекта Мейсснера мы вернемся еще раз к затро-
затронутому здесь вопросу).
Обратимся теперь к выражению D.151) для е%?\ и рассмотрим
процессы, при которых квазичастица переходит из состояния (к'а')
в состояние (ка). Соответствующий матричный элемент М (ка | к'а')
равен коэффициенту при YhaYh-o.' ^ УчеТ0м соотношения Yi^Y^. ==
== — ^k'a'^ba (для k' a=^=k'1 a') впишем суммарный вклад от пер-
первых двух членов выражения D.151) в виде
М (ka | kV) = В (ka | k'a') ukuk- —
-»Л 2, PavPaa^C-b'a'l-ka). D-152)
Of О
Сумма 2В(—k'a'|—ka)PO'a'Paa ФакТиЧески представляет собой
сто'
матричный элемент fi(ka|k'a'), в котором направления спинов и им-
импульсов изменены на обратные. Для взаимодействия S$t рассматри-
рассматриваемого вида эти два матричных элемента отличаются самое большее
знаком
S В (- k'a' | - ka) paapaV = цВ (ka | k'a'), D.153)
аа'
где
f -|-1 для случая 1,
4 = 1
[ —1 для случая 2.
Таким образом*
М (ka | k'a') = В (ka | k'a') («kuk. — rfiw). D.154)
Величина (uuitw — VPu^k1) носит название фактора когерентности пере-
перехода. Отнесенное к единице времени число переходов (k'a') —> (ka)
') Рассуждение нестрогое, поэтому не всегда верное. Для задач, связан-
связанных с поглощением ультразвука, имеющих сейчас экспериментальный смысл,
тем ие менее можно пренебречь изменением Д. — Прим. ред.

136 Глава IV
за вычетом обратных переходов равно
v = ~ | М (ка | к'а') Р {/ (екО [ 1 - / Ы1 —
—/Ы[1 —/(ек')]}6(Ек —Ек'—й©), D.155)
где мы предположили, что возмущение S@\ зависит от времени синусо-
синусоидально с частотой со.
Поглощаемая мощность равна
1Г1== 2 vfico. D.156)
к, к'
Чтобы вычислить Wv произведем сначала усреднение квадрата мат-
матричного элемента В по всем возможным направлениям волновых век-
векторов к и к' и спинов частиц
В* = \В(ка\к'а')\2.
Поскольку | Ъ,и | и | |k' j малы по сравнению с Ер [это обеспечивается
множителями / в D.155)], величину В2 можно считать постоянной;
тогда
W1 = 2люВ2 J Ns (e) Ns (е') (аи' — rpv'f X
X I/ (/> — /(е)] 6 (е — е' — fico) rfe rfe'. D.157)
Здесь Ns (e) = /V @) | d|/^e | — плотность состояний для возбуждений
в сверхпроводнике
rJ__ (е>Д). D.158)
Используя определения D.71) и D.72) для и к v, можно написать
D.159)
При подстановке D.159) в D.157) и при переходе к интегрированию
по ? необходимо иметь в виду, что каждому значению е соответ-
соответствуют два значения | с противоположными знаками. Поэтому член
??'/ее' исчезает при суммировании по этим значениям. В результате
получаем
W. = 4nco?W2 @) f de f dz'
— e'— йсо). D.160)
Аналогичный расчет можно выполнить для нахождения мощ-
мощности W2, поглощаемой за счет процессов рождения и аннигиляции

Описание конденсированного состояния 137
двух квазичастиц. Она Отлична от нуля лишь при ha > 2Д. Окон-
Окончательная формула для суммарной мощности Ws=W1-\-W2 отли-
отличается от D.160) только пределами интегрирования
dede'
Х[/(«0— /(е)]б(е— е'— ha), D.161)
где e и е' имеют произвольный знак, но | е | > Д и | е' | > Д. На
опыте мощность Ws всегда сравнивают с мощностью Wn, поглощае-
поглощаемой в нормальном состоянии [ее просто получить из D.161), поло-
положив Д = 0],
оо со
w; = ik J \dedE> 2_ *'ZT_ i% х
-со -со (Е А ) (.? — Л )
Х1/(е') — /(е)]6(е — г1— ha). D.162)
Применения L Поглош>ение звУка- В ЭТОм случае Т]=1
и фактор когерентности мал, когда е и е'
одновременно близки к Д или —Д. В случае когда Лох^Д или
tia<^ikBTc, соотношение D.162) принимает вид
^- = — ( de е2~'А2 М. = 2 . D.163)
W. J е2 — Д2 де I 4-ерА
" |е1>Д '
Отсюда видно, что поглощение очень мало при низких температурах
и быстро возрастает при Т-+Тс. Это дае^г один из способов измере-
измерения Д (Т), который широко используется на практике1). На фиг. 44
приведена кривая поглощения ультразвука в олове, полученная Мор-
зом [82].
2. Ядерная релаксация. Взаимодействие ?№х между ядерными
спинами и электронами проводимости имеет довольно сложный вид.
Можно показать, однако, что оно относится к случаю г\ — — 1.
На опыте измеряется время Тх, необходимое для установления
теплового равновесия ядерных спинов с электронами в нулевом поле.
Отношение скоростей релаксации TlnjTx в сверхпроводящем и нор-
нормальном состояниях по-прежнему дается формулой D.162), в которой
частота со теперь равна частоте прецессии ядерного спина в локаль-
локальном поле соседних ядер. Эта частота мала (<в~104 сек'1), поэтому
мы можем устремить а к нулю. Таким образом,
|Е|> А
Подробнее см. обзор Дугласа [9]. —Прим. ред.

Г "К
Фиг. 44. Результаты измерения коэффициента поглощения ультразвука
в олове (Морз и др. [82]).
Для сравнения приведена кривая, полученная на основе теории БКШ-
Фиг. 45. Зависимость вр'емени ядерной релаксации Г, в алюминии от тем-
температуры (Масуда и Редфилд [84]).
При температурах, немного меньших критической, наблюдается резкое уменьшение времени 7",.
Сплошная кривая вычислена на основе теории БКЩ в предположении, что пик плотности
состояний размазан в энергетическом интервале шириной ~ А/5.

Описание конденсированного состояния 139
В данном случае фактор когерентности не обращается в нуль при
| е | = Д одновременно со знаменателем. В результате интеграл лога-
логарифмически расходится. Однако в реальных металлах параметр Дк
анизотропен. Учет этого обстоятельства приводит к „размазыванию"
плотности состояний Ns(e) вблизи особенности, так что интеграл
становится сходящимся. Результат зависит от конкретного вида Дк.
Фактически параметр Дк проявляет довольно слабую анизотропию;
изменение Г, с температурой для этого случая показано на фиг. 45.
Для температур Т, весьма близких к Тс, скорость релаксации
в сверхпроводящем состоянии оказывается больше, чем в нормаль-
нормальном состоянии. Этот характерный результат связан с возрастанием
плотности состояний Ns(z) ниже Тс. При низких температурах Т<^ТС,
напротив, релаксация становится очень медленной из-за фактора „на-
„населенности" dfjdt. Такой тип зависимости 1/7^ от Т впервые наблю-
наблюдался Гебелем и Слихтером [83] в 1957 г. Предсказание того, что
факторы когерентности и соответственно характер ультразвукового
поглощения и ядерной релаксации могут быть совершенно различными,
явилось одним из больших успехов теории БКЦ].
ЛИТЕРАТУРА
Т i n k h a m M., Superconductivity, New York, 1965.
Lynton E. A., Superconductivity, 2d ed., London, 1965, ch. 8—11. (Имеется
перевод 1-го издания: Э. Л и н т о н, Сверхпроводимость, изд-во .Мир"
IS""

Глава V
МЕТОД САМОСОГЛАСОВАННОГО ПОЛЯ
§ 1. УРАВНЕНИЯ БОГОЛЮБОВА
В гл. IV мы изучали однородный электронный газ при наличии
притяжения между частицами. Рассмотрим теперь более общую задачу,
когда электроны, помимо этого, испытывают также воздействие со
стороны произвольного внешнего поля с потенциалом U0(r) (что
важно для описания влияния примесей и поверхности образца) и маг-
магнитного поля Н = rot A.
На первый взгляд, наиболее естественный метод учета потен-
потенциала U0(r) состоит в следующем:
1. Найдем одноэлектронные волновые функции wn, являющиеся
решениями уравнения
(^)a. E.1)
2. Заметим, что каждому значению энергии %п отвечают по край-
крайней мере два решения
и
где символ | а) обозначает спиновое состояние.
3. Построим по методу БКШ пробную волновую функцию, опи-
описывающую спаривание электронов в вырожденных по энергии со-
состояниях wn и w~,
где а^ — оператор рождения электрона в состоянии W-. Последую-
Последующий анализ проводится так же, как и в гл. IV, § 3.
Однако такой подход обладает рядом недостатков: а) он неприме-
неприменим при наличии магнитного поля, б) свобода в выборе пробной
функции сильно ограничена. На самом деле энергия системы часто
может быть меньше, если спаривание электронов производится в со-
состояниях, более удачно выбранных, чем wn.
Перейдем теперь к описанию более мощного метода, развитого
Боголюбовым [85] в 1959 г. По существу он является обобщением
метода Хартри — Фока на случай сверхпроводимости. Сначала перей-
перейдем в гамильтониане ?№ системы электроновот операторов ака (удоб-
(удобных только в случае ?/0 = 0) к их пространственным фурье-компо-

Метод самосогласованного поля 141
ментам
к E.4)
S е-'к'го+а.
Для простоты мы считаем объем системы равным единице; a — спи-
спиновый индекс, принимающий значения | и |. Операторы W подчи-
подчиняются следующим правилам аптикоммутации:
XY (ra) Чг (r'p) -t- 4F (r'p) 4F (ra) = О,
lF! (ra) »F+ (r'p) + W + (r'p) ?+ (ra) = 0, E.5)
«F+ (ra) 4' (r'p) + *F (r'p) ?+ (ra) = 6ap6 (r - r')-
Оператор числа частиц имеет вид
ka a
Гамильтониан ©$? тоже весьма просто записать через W и Ч/+ (см.
книгу Ландау и Лифшица [72], гл. 9)
Ро = S J
Потенциал t/0(r) мы считаем здесь не зависящим от спина.
(В дальнейшем при описании обменного взаимодействия электронов
в магнитной среде нам понадобится ввести член, явно зависящий от
спина.) Мы также использовали простейшую форму электрон-элек-
электрон-электронного взаимодействия <§ЪХ, а именно предположили, что а) взаимо-
взаимодействие не зависит от спина (это справедливо для немагнитных
материалов), б) взаимодействие имеет точечный характер и, следова-
следовательно, описывается всего лишь одним коэффициентом V (приближе-
(приближение БКШ).
Отметим также, что при написании е%?0 мы пренебрегли взаимо-
взаимодействием спина электрона проводимости с магнитным полем (это
законно, если еШ//ис<^Д).
Как и прежде, при рассмотрении оказывается удобным пользо-
пользоваться вместо гамильтониана &>6'0 оператором
- EPN = 21 J <*гЧ'+ (ra) Же^ (ra), E.10)
U.

142 Глава V
Определение эффективных потенциалов
Заменим теперь взаимодействие VyV+yV+xVxV средним потенциалом,
содержащим только два оператора х?+ или ЧЛ Будем исходить из
следующего эффективного гамильтониана:
ёГэфф = J dr Г ^ V+ (га) &ве (г) ХУ (га) + ?/ (г) Ч'+ (га) W (га) +
1
+ Л(г) Ч'4 (г f ) Ч'+ (г |) +Д*(г) Ч (г | )? (г f ) I - E.12)
Член, содержащий U, уничтожает и рождает один электрон, оставляя,
таким образом, полное число частиц неизменным. С другой стороны,
члены с А увеличивают или уменьшают число частиц на два. Это не
должно вызывать беспокойства, поскольку оператор е^эфф действует
на волновые функции (такие, как ф), не являющиеся собственными
функциями оператора числа частиц. В гл. IV рассматривался простой
случай, когда средние типа /ф I а+^г+ь | ф^ не обращались в нуль.
Здесь по тем же причинам произведение типа Ч^Ч7* отлично от
нуля; этот член в дальнейшем будет играть важную роль. Мы назо-
назовем А (г) потенциалом спаривания. [Заметим, что члены типа
4J'(rt)^r(rt) обращаются в нуль тождественно в силу коммутацион-
коммутационных соотношений E.5).]
Уровни энергии эффективного гамильтониана
Предположим на время, что гамильтониан ё%?Эфф нам известен и
попытаемся определить его собственные функции и соответствующие
значения энергии. Оператор ё%?эфф квадратичен по W и W+, поэтому
его можно привести к диагональному виду с помощью унитарного
преобразования, которое по аналогии с D.100) мы запишем в сле-
следующем виде:
где Чпа и Чпа—система новых операторов, подчиняющихся по-преж-
по-прежнему фермиевским коммутационным соотношениям
^па^т|3 ' YmpYna = °ш„°ар>
V V +V V =0 EЛ4)

Метод самосогласованного поля 143
Преобразование E.13) должно приводить ©%?Эфф к диагональному
виду, т. е. •
^эФФ~? ~+ SenY+Yn. E.15)
эфф g па па а
где Eg—энергия основного состояния, а е„ — энергия возбуждения
с квантовым числом п. Это условие можно записать иначе, вычислив
коммутаторы ё%?Эфф с vna и y^
Условия E.16) определяют выбор функций ип и vn, фигурирую-
фигурирующих в преобразовании E.13). Чтобы найти уравнения для и и v,
вычислим коммутатор [ё%?Эфф' ^- Используя определение E.12) для
^?эфф и антикоммутационные свойства операторов W и W+, получаем
(г|),
E.17)
Выразим теперь в этих уравнениях W и W+ через Y и Y+ c помощью
E.13) и используем найденные значения коммутаторов E.16). Сравни-
Сравнивая затем коэффициенты при уп (и у+) с обеих сторон получающихся
равенств, приходим к уравнениям Боголюбова
ей (г) = [&e.-\-U (г)] и (г) + А (г) v (r), ^
ew (Г) = _ \&е\ + U (г)] «(г) + Л* (г) и (г).
Матрицы I I являются собственными функциями линейной системы
уравнений E.18) с собственными значениями е„
ЗАМЕЧАНИЯ
1. В присутствии магнитного поля оператор &Ве отличен от оператора
0 Г
1 / •> E.1 У)
= 2ST (/fiv ~ 7 А) + ^ « ? ^
Оба оператора &ef и ^"* эрмитовы-

144 Глава V
2. Оператор Q эрмитов, следовательно, различные собственные функции
I " ) ортогональны между собой.
3. Если | I — решение, соответствующее собственному значению е, то
(v* \
ж I — решение, соответствующее — е1). В согласии с E.15) мы удерживаем
только решения, отвечающие положительным значениям е.
Выбор потенциалов U и А
Определим теперь оператор 3$э1ьф, исходя из условия минималь-
минимальности плотности свободной энергии г, вычисленной на основе состоя-
состояний, диагонализующих е%'Эфф. По определению,
F = {SV)—TS, E.20)
•где ?76 — исходный гамильтониан ??С ~ е№0-\- S№v среднее от кото-
которого описывается выражением
Матричные элементы берутся по собственным функциям | <р) гамиль-
гамильтониана ^эфф
^!Ф>- E-22)
Дальнейший расчет ($@) заключается в замене Чт в E.7) — E.9)
на V s соответствии с E.13) и последующем использовании правил
вычисления средних значений:
E.23)
е " -]- 1
Нет необходимости, однако, производить этот расчет полностью.
Запишем (е#?) в виде
г+ (га) Ш^ (га)) —
r(xF+(raLJ'^(rPLJ1(i
') Последние два свойства доказываю! унитарность преобразования E.13).

Метод самосогласованного поля 145
Произведение (Ч/"|~Чг1~Ч/1Ч'1) можно упростить, обращаясь к теореме
Вика, в формулировке которой используется лишь тот факт, что
операторы Ч/+ и W являются линейными комбинациями операторов у+
и у. Согласно этой теореме.
'+ A) W+ B) W C) W D)) = (W+ A) W D)) (Ч'+ B)
- <Ч'+ A) W C)) (Ч'+ B) Ч' D)> +
+ <Ч'+ A) ?+ B)) <?C) Ч'D)>. E.25)
Дадим теперь амплитуде I I и числам заполнения /п прираще-
ния I и 6/„. Тогда свободная энергия F, согласно E.20), полу-
получит приращение
6F = J dx j J] б (Ч'+ (га) ^?е Ч' (га)) —
— V
(га) W (га)>6 <?+ (га) W (га))
conp.j} - TbS.
E.26)
Имея в виду „немагнитный случай", мы положили (^(rf ^(r j)) = 0.
Величина
Л = (^эфф)-Г5 E-27)
стационарна по отношению к вариациям Ьип, bvn и б/„, поскольку
оператор е%?эфф диагоналей относительно состояний, описываемых
в терминах возбуждений. С помощью E.12) запишем это условие
в следующем явном виде:
+ [Д (гN<4'+ (г |) Ч^+ (г|)>+ Компл. сопр.] }— T6S. E.28)
Из сравнения выражений E.26) и E.28) видно, что свободная
энергия F минимальна, если в качестве эффективных потенциалов
10 Зак. 1020

146 Глава V
взять
t/(r) = -K(T+(rt)^(rt)> = -^<^+(r|)^(r|)> E.29)
(обычный результат Хартри — Фока для точечного взаимодействия) и
A(r) = -K(V(r|)T(rt)> = K(T(rt)lff(r|)>. E.30)
Заменяя Ч? и *F4 через у и Y+ c помощью E.13) и используя пра-
правила вычисления средних значений E.23), полученные результаты
можно представить в явной форме
-^2[|Мг)Р/п + К(г)РA-/„)], E.31)
А (г) = + V 2 иа(г) <(г)A - 2/„). E.32)
п
Эти условия обеспечивают самосогласованность потенциалов U и А.
Фактически между U (г) и А (г) имеется важное различие, которое
состоит в следующем. Потенциал Хартри — Фока U (г) получается
в результате суммирования по всем состояниям ниже уровня Ферми.
Следовательно, он почти не зависит от температуры и приближенно
его можно считать равным потенциалу Хартри — Фока нормального
состояния. Это значительно упрощает его расчет. Наоборот, потен-
потенциал спаривания А (г) определяется суммой членов типа unv*n. Такие
члены, как мы уже видели в случае однородного газа, отличны от
нуля лишь вблизи поверхности Ферми, поэтому потенциал А (г) сильно
зависит от температуры.
В случае однородного газа потенциал А (г) не зависел от коорди-
координат, а уравнение самосогласованности E.31) сводилось к определению
постоянной А. В общем случае изменяющегося в пространстве потен-
потенциала А (г) условию самосогласованности удовлетворить значительно
труднее. К этому вопросу мы еще неоднократно вернемся в даль-
дальнейшем.
Задача. Рассмотреть спектр квазичастиц в чистом сверхпроводнике, в ко-
котором течет однородный ток. Токовое состояние описывается потенциалом
спаривания вида
Д = | Д | enq-r,
где q — вектор в направлении тока (средний импульс на электрон в этом
состоянии равен fiq).
Решение. Решение системы E.18) ищем в виде
с (г) = IV'<"-«¦',
что приводит к следующей системе уравнений для собственных значений:

Метод самосогласованного поля 147
Положительные собственные значения ек определяются выражением
Как мы увидим далее, основной интерес представляют значения
^кр. В приближении, линейном по q, имеем
_, h .
~ m K
где ek = у |2 -j- | Д |2 — спектр возбуждений в отсутствие тока (q = 0),
а величину fiq/m = v,s обычно называют сверхтекучей скоростью. Отметим,
что щель в энергетическом спектре обращается в нуль при г^=|Д|/ЙА_ =
= |Д|'/> . (При применении написанных формул необходимо иметь в виду,
что самосогласованное значение | Д |, вообще говоря, зависит от vs.)
Принципиально этот спектр можно было бы изучать на тонких пленках
чистых металлов. Практически это невозможно по следующим причинам.
Ток в пленке будет однородным в том случае, если ее толщина d меньше
глубины проникновения X. Однако толщина d должна оставаться большой
по сравнению с ?„, иначе диффузное рассеяние на границах пленки приведет
к существенным изменениям в спектре системы. Таким образом, пленка
должна быть изготовлена из чистого сверхпроводника второго рода (А, ^> !•„).
Но в этом случае появляется другая трудность: при vs~> \&\1рр плотность
тока ensvs велика, а поле на поверхности пленки, составляющее по порядку
величины
«W ,. V (Т_0)
о ЬЧо ( ~U)l
становится больше значения нижнего поля Нс1 на фактор ~> rf/|0 > 1. В итоге
в пленке начнут образовываться вихревые нити и ситуация не будет иметь
ничего общего с рассматриваемой.
Тем не менее приведенный расчет можно использовать для обсуждения
спектра квазичастиц в шубниковской фазе массивных (чистых) сверхпро-
сверхпроводников второго рода (Сиро [86]). Предположим, что а) параметр Гин-
Гинзбурга — Ландау х, = Я,/?„ значительно больше единицы, б) поле Н значи-
значительно меньше верхнего поля Нс2- Тогда расстояние d между вихревыми
нитями превышает |0 и большинство возбуждений имеет энергию е ~ Д^,
где Д^ — амплитуда потенциала спаривания вдали от нитей. Для определения
величины е вычислим сверхтекучую скорость \s (г) в точке г и предположим,
что спектр возбуждений в этой точке .смещен" относительно спектра
в отсутствие нитей:
е(к, г) = (Д
где
2/я
Минимальный размер волнового пакета, построенного из таких возбуждений|
имеет порядок !•„, в то время как поле и скорэгть v, изменяются на рас-
расстояниях ~>А,>?0, поэтому в большинства случаев такой подход является
10*

148 Глава V
законным. Однако он становится неприменим при нахождении низколе-
жащих возбужденных состояний (е <^ Д о), локализованных в непосред-
непосредственной близости от нити, где скорость \s и параметр порядка Д изме-
изменяются очень быстро. Этот особый тип возбуждений мы обсудим в задаче
на стр. 154.
§ 2. НЕКОТОРЫЕ ТЕОРЕМЫ О ПОТЕНЦИАЛЕ СПАРИВАНИЯ
И СПЕКТРЕ ВОЗБУЖДЕНИЙ
Градиентная инвариантность
Одиоэлектронный гамильтониан
и соответствующее ему комплексно сопряженное выражение
&Ve (А) = -^ (р + ~ А)' + U - Ер
зависят от выбора вектора-потенциала А. Выбор А не однозначен;
при замене А на
А' = А + ?5с(г), E.33)
где х (г) — произвольная функция, имеем
rot A' = rot A = h,
т. е. А и А' равным образом пригодны для описания конфигурации
поля h (r). При этом все физические величины не должны зависеть
от выбора вектора-потенциала А или А'. Это свойство мы докажем
на примере энергии квазичастичных возбуждений [т. е. для собствен-
собственных значений уравнения E.18)].
Предположим, что мы знаем собственные функции I и" ) уравне-
\vn/
ния E.18) с вектором-потенциалом А. Рассмотрим теперь уравнение
E.18) с вектором-потенциалом А'. При этом происходят изменения
двоякого рода.
а) Собственные функции | ". ) отличаются от [ ):
v' (r) = v (r) e
б) Потенциал спаривания также изменяется; если вектору-потен-
вектору-потенциалу А соответствует значение А (г), то
E.35)

Метод самосогласованного поля 149
Доказательство. Для функции ип, определяемой соотношением
E.34), можно написать
(р - ±. А') а'п (г) = (- /fiV - -f A') e«xW*'«B (r) =
= в1еХ/Ас (- «V —f А' + т **) «„ (г) = ^^ (Р - f А) «„. E.36)
[Здесь мы использовали преобразование E.35).] Повторим эту операцию
(Р— — А) ы„ = е (р —ТА) ил,
, , E-37а)
<Я?г (А ) и„ = d^p (А) ыл.
Аналогично
<S?/e (A') w', = ^?* (A) vn. E.376)
Поскольку I " ) есть собственная функция системы E.18), мы имеем
&ее (А) ип+л» я = е„ы№
Умножим это уравнение на exp (iex/fic) и воспользуемся равенством E.37а).
В результате получим
Же(Л')и'п + Д'» „ = е„и„ E.38а)
и аналогично
- Ов\ (A') v'n + д'«; = Еи^ E.386)
/ ' \
Таким образом, I , ! — система собственных функций, соответствующая
вектору-потенциалу А' и потенциалу спаривания Д'. Более того, если потен-
потенциал Д удовлетворяет условию самосогласованности E.32) при соответ-
соответствующем выборе функций и и v, то штрихованные величины и', v' и Д'
также удовлетворяют этому условию.
вывод
Мы приходим, таким образом, к заключению, что волновые функции,
а также потенциал спаривания изменяются при градиентном преобразовании
А -> А'. Можно сказать, что потенциал А, например, является градиентно
ковариантной величиной. Что касается собственных значений е„, то они не
меняются при этом градиентном преобразовании, т. е. градиентно инвариантны.
Тем же способом можно показать, что все физически измеримые величины
(скажем, плотность тока в данной точке) являются градиентно инвари-
инвариантными.
ЗАМЕЧАНИЕ
Ограничения, налагаемые на функцию %. Потенциал спаривания Д (г)
должен быть однозначной функцией г при любом выборе калибровки. Рас-
Рассмотрим, например, образец в форме полого цилиндра, ось которого совпа-
совпадает с осью г. Угол поворота вокруг оси z обозначим через <р. Возьмем
функцию преобразования в виде
Х = ?«Ф. E-39)

150 Глава V
где т — произвольная постоянная. Тогда
Д' (г) = Д (г) elm<f. E.40)
Обе функции Д и Д' должны быть однозначными. Отсюда следует, что
т — целое число. В общем случае для кольца произвольной формы прира-
приращение % при совершении полного обхода вокруг отверстия равно
2з1/гс {cbfte) = mch/2s (m — по-прежнему целое число).
Должным выбором функции преобразова-
Специальные выборы ния иногда удается перейти от А к век-
калибровки ,., ,г
н тору-потенциалу А , обладающему рядом
преимуществ по сравнению с исходным. Здесь мы остановимся на
двух примерах.
Пример 1. Для односвязного образца положим
divA' = 0 E.41а)
внутри образца и
А' • п = 0 E.416)
на его поверхности (п — единичный вектор нормали к поверхности). Функция
преобразования % внутри образца удовлетворяет уравнению
V2x = — d«vA E.42a)
со следующим граничным условием на поверхности:
n-Vx = —п-А. E.426)
Из общих теорем электростатики следует, что решение % уравнения E.42а)
при условии E.426) для односвязного образца единственно. Поэтому вектор-
потенциал А' также определен однозначно. Условия E.41а) и E.416) задают
так называемую лондоновскую калибровку вектора-потенциала А'.
Пример 2. Для данного вектора-потенциала А потенциал спаривания Д (г)
также определен. Выделим амплитуду и фазу Д
Д(г) = |Д(г)|е*Р'. E.43)
Совершим теперь градиентное преобразование А -> А' с помощью функции
Х = —?ф- E-44)
Поскольку Д — однозначная функция, такой выбор % всегда допустим ')•
Новый потенциал спаривания равен просто
Д' (г) = | Д (г) |.
Таким образом, надлежащим выбором калибровки всегда можно сделать
потенциал спаривания вещественным. Для односвязного сверхпроводника
в отсутствие внешних токов эта калибровка фактически совпадает с лон-
доновской, но она применима н в более общих случаях.
Квантование потока
Рассмотрим сверхпроводящее кольцо, изображенное на фиг. 46
(диаметр и толщина кольца предполагаются большими по сравнению
') На это свойство внимание автора обратил д-р П. Маркус.

Метод самосогласованного поля 151
с глубиной проникновения). Эксперименты Долла и Небауэра [87],
а также Дивера и Фербанкса [88] показали, что поток 0, проходящий
через кольцо, может принимать только определенные дискретные
значения
ф = пф0,
фо=?^2. 10~7гс- см2.
где п — произвольное целое число.
(Измерения столь малых потоков производились на металлических
пленках, осажденных на поверхность капилляров (диаметром ~ 10 мк).
Квант потока ^>0 в этом случае соответствует вполне разумному зна-
значению поля ~0,1 гс.)
Экранирующие тони
Область без поля
контур С
Фиг. 46. Сверхпроводящее кольцо с замороженным магнитным моментом.
Толщина кольца предполагается большой по сравнению с глубиной проникновения поля, так
что всегда можно выбрать целиком лежащий внутри сверхпроводника контур С, во всех точ-
точках которого поле и ток равны нулю.
В теоретическом плане „квантование потока" следует из условия
однозначности функции А (г).
Доказательство. Введем вектор
а — ЬЩ — ~К E.46)
где ф — определенная выше фаза потенциала спаривания Д. Отметим сразу,
что величина и является градиентно инвариантной, в чем легко убедиться
с помощью законов преобразований E.34) и E.35). В физических ситуациях,
в которых величина | Д | постоянна в пространстве, вектор и пропорционален
локальному значению плотности сверхпроводящего тока (примером может
служить случай, рассмотренный в задаче на стр. 146, когда А = 0, а плот-
плотность тока постоянна во всем образце). В произвольной точке, находящейся
в глубине кольца, поле, а следовательно, и ток отсутствуют; таким образом1
и = 0. Проинтегрируем теперь обе части соотношения E.46) по контуру Ct

152 Глава V
который нигде не подходит близко к поверхности образца, как показано на
фиг. 46. Тогда
|(?)Д = 0, E.47)
поскольку u = 0 вдоль контура С. Интеграл
& А • й\ = Ф
с
равен потоку, заключенному в кольце. Второй интеграл
V ¦ d\ = [ф]
представляет собой изменение фазы ф потенциала Д(г) при полном обходе
контура С; из требования однозначности Д (г) следует, что [ф] = 2згп
(и — целое число). Подставляя полученные результаты в E.47), приходим
к соотношению E.45).
Впервые явление квантования потока рассмотрел Ф. Лондон, который
получил для кванта потока величину ch/e, вдвое превышающую эксперимен-
экспериментальное значение. Здесь мы повторим ход рассуждений Ф. Лондона (для
чистого металла при Г = 0), а затем постараемся внести нужные исправления.
Обозначим через Ф0(г,, .... Гд,) волновую функцию электронов в основ-
основном состоянии сверхпроводника (в отсутствие тока). Состояние с однород-
однородным током получается путем замены Фо функцией
соответствующей плотности тока netiq/m. Более общий случай макроскопи-
макроскопического движения можно описать с помощью функции вида
Ф = ФвеЧЧ*>)+~+Ч'„)\ E.49)
где S (г) — медленно меняющаяся функция координат. Учитывая также на-
наличие вектора-потенциала А; окончательно запишем плотность тока в виде
Предположим, что в сверхпроводнике реализуются лишь состояния, опи-
описываемые волновыми функциями типа E.49). Тогда, беря ротор от обеих
сторон выражения E.50), можно легко получить уравнение Лондонов, т. е.
прийти к эффекту Мейсснера. ЧтЬбы изучить квантование потока, рассмо-
рассмотрим снова образец в виде кольца. Внутри кольца (вдали от его поверх-
поверхности) j = 0, а вектор-потенциал описывается соотношением
A = -^VS. E.51)
Если через отверстие кольца проходит некоторый поток ф, то функция S
становится неоднозначной. Действительно, рассмотрим снова контур С, ко-
который нигде не подходит к поверхности (см. фиг. 46). Тогда соотношение
E.51) определяет вектор-потенциал в любой точке контура С. Таким обра-
образом, поток, заключенный внутри контура С, равен
Ch-da = &\.dl=^-&VS-dl = — ^, E.52)

Метод самосогласованного поля 153
где символ &" обозначает приращение функции S после полного обхода
вдоль контура С. Чтобы найти &", заметим, что волновая функция Ф должна
быть однозначной функцией координат rY rN. Например, если г, изме-
изменяется вдоль контура С, то после полного обхода мы должны вернуться
к исходному значению функции. Учитывая, кроме того, что функция Фо
также однозначна, приходим к условию & = 2пп, где п — целое число. Сле-
Следовательно, величина кванта потока, согласно E.52), равна chje.
Приведенный вывод, однако, неудовлетворителен в одном отношении [89].
Дело в том, что в действительности состояния Фоехр {/ [S (r,)-f- ... -\- 5(Гд,)]}
не являются единственными состояниями макроскопического движения, осу-
осуществимыми в сверхпроводнике. Чтобы убедиться в этом, необходимо более
детально знать вид истинной волновой функции Ф. Здесь мы проведем до-
доказательство на простом примере волновой функции электронов сверхпро-
сверхпроводника, удовлетворяющей периодическим граничным условиям
Ф(ж, ... xt ... xN) = O(xt ...xt + L...xN), E.53)
где индекс i пробегает все значения от 1 до N. Построим состояние посту-
поступательного движения всей системы, при котором на каждый электрон при-
приходится импульс fiq. Спаривая состояния (k-}-4> f) и (—k + q, ф), можно
получить волновые функции, вполне аналогичные использованным в тео-
теории БКШ.
1. Если qL = <5" = 2лл, мы используем одноэлектронные состояния с вол-
волновыми векторами к. удовлетворяющими обычному условию периодичности.
kxL = 2лпх E.54)
(я и пх— целые числа).
2. Если qL = & = я Bл -f-1), то значения к должны удовлетворять иному
граничному условию вида
kxL = nBnx+l). E.55)
В обоих случаях условие E.53) выполняется.
Функции типа 1 аналогичны использованным Лондоном. Они отличаются
от волновой функции БКШ (для покоящейся системы) лишь множителем
ех.р [iq (х х-\- ... +•%)]¦ Это не относится, однако, к функциям типа 2. Оба
типа функций в равной мере пригодны для описания макроскопических
движений в сверхпроводнике. В обоих случаях полная энергия системы
описывается выражением
?=?0 + ^-^. E-56)
которое получено в предположении, что
k L >> 1 и -L >> 1. E.57)
г *о
Действительно, при выполнении условий E.57) все суммы по допустимым
значениям к могут быть заменены интегралами, величина которых не за-
зависит от того, каким условием мы пользуемся — E.54) или E.55).
Найденные результаты легко перенести на случай отверстия. Теперь мы
получаем, что ?Р = ял и, следовательно, квант потока равен hc/2e.
Задача. Найти закон изменения коэффициентов и и v преобразования
Боголюбова при полном обходе кольца.
Решение. Ответ, конечно, зависит от выбора калибровки. Возьмем
калибровку, в которой параметр Д веществен; тогда после полного обхода
кольца коэффициенты и и v приобретут по одинаковому множителю (—1)"
(л — число квантов потока в кольце).

154
Глава V
Для доказательства вернемся опять к простому случаю однородной
трансляции, удовлетворяющей граничным условиям E.53). Для калибровки,
в которой Д = | Д | exp Biqx), мы нашли, что (см. задачу на стр. 146)
E.58)
/и\ /C/kexp[Z(k + q).r]\
Из предыдущего ясно, что в случае <5" = лп одноэлектронные состояния
exp (/к • г) должны выбираться с таким расчетом, чтобы
Отсюда следует, что коэффициенты и iiv в выбранной калибровке являются
периодическими функциями координат.
В калибровке, в которой параметр Д веществен, получаем для искомых
коэффициентов и' и v'
lu'\ /f/kexp№.r)\
U'ГUexp (/к-г) J- (ЫВ>
т. е. они действительно умножаются на (—1)" при замене х на x-\-L.
Задача. Рассмотреть низколежащие возбуждения сверхпроводника, лока-
локализованные вблизи центра вихревой нити [52, 90].
Решение. Ограничимся случаем чистого сверхпроводника второго
рода и будем исходить из системы уравнений E.18). Рассмотрение будем
\й(г)\ 1
Фиг. 47. Изменение амплитуды параметра порядка | Д (г) | вблизи изоли-
изолированной вихревой нити в чистом сверхпроводнике второго рода.
При г=0 параметр порядка обращается в нуль, наклон кривой | А (г) I при этом остается ко-
конечным. РаДИуС ООЛаСТИ, Ц, КОТОРОЙ пппътЧППиТ аяиатигчя иоиниашл I А I~\ I п~ .. ~ .
вытекающим нз теории БКШ
происходит заметное изменение | Д (/•) | по сравнению с
значением Д (показано пунктиром), составляет ~ |0.
вести в цилиндрических координатах г, в, z (ось z направлена вдоль нити)
в калибровке, в которой Д (г) = | Д (г)| е~ю. Вектор-потенциал в этой спе-
специальной калибровке по-прежнему обозначим через А. Амплитуда | Д (г) |
равна нулю при г = 0; при удалении от центра нити она растет (линейно
при малых г) и, наконец, достигает значения Дот на расстояниях г > \
(фиг. 47).
Введем спинор
И:)

Метод самосогласованного поля 155
и исключим фазу потенциала Д, положив
-0,6/2 ~
Ф = е г ij).
Тогда систему E.18) можно записать в следующем компактном виде:
°« [ 2^Г (Р ~°гТ А - Ь-Т- VQf - Ef] У + °х ДФ = Е*
где ах, аг — матрицы Паули. Заметим, что А -^ Иг и
(где 0О = ch/2e — квант потока). Для возбуждений рассматриваемого типа
r^l и
еА Hj2
сйуе ~ Фо ~
т. е. всеми магнитными эффектами можно полностью пренебречь.
Решение будем искать в виде
т ikpz cos a lvS-2
где kp — фермиевский волновой вектор, а — произвольный угол, а 2ц — не-
нечетное целое число. Последнее условие обеспечивает изменение знака функ-
функции ф при полном обходе вокруг нити, как и требуется в случае калибровки
с вещественным значением Д и при наличии одного кванта потока. Опуская
член с А в уравнении для ф, получаем
Это уравнение удается решить до конца в важной области 0 < \х
Рассмотрим радиус гс, удовлетворяющий условию
Для г <гс членом с Д можно пренебречь, и решение
/ =
имеет вид
¦(;:)
/± (/-) = А ±Уц т ,/г [(kp sin a±q)r],
где У(х) — функция Бесселя, q = e/ftf р sin а; Л±—произвольные коэффи-
коэффициенты.
Для г > гс решение f ищем в виде
/ = ?(r) Hm (kpT sin а) + Компл. сопр. f т = у м-2 + -fj •
где Л/т — функция Ханкеля, а ^ — медленно меняющаяся амплитуда. Урав-
Уравнение для g можно свести к следующему:
dg л / цй2 \ - hkp
sin а r&org =1еЧ rlfi'. ^в = —*-•
йт \ 2mr J r m

156 Глава V
Для е <^ Д^ и kpr ^> [X правая часть мала. Учитывая ее в первом при-
приближении, находим
4
где
V — / ехр (—-g-яр)
(/-) = (fWf sin а)""' Г Д (/") Л",
* {гс) « - , (Ve sin «)- + 2,„- 2
Произведем теперь сшивку решений при г = гс, воспользовавшись асимпто-
асимптотическим разложением
Jm (г) = const • г-'А sin [г + -^- - -? (ях - |)
и т. д. При |я =^ 0 это дает
Сравнивая этот результат с предыдущим выражением для -ф (гс), мы видим,
что все члены, зависящие от гс, выпадают, так что для собственных значе-
значений получаем
Еца = й^ Sin а = V (*/-' sin a)~' •
= u (kp sin a)" • (~\=в g (a) (^ =^ 0,
Введенная здесь безразмерная функция g-(a) зависит от точного вида по-
потенциала Д (г), но по порядку величины она всегда близка к единице.
В частности, g @) = g (я) = 1. Таким образом, собственные значения соста-
составляют по порядку nA^Jkjg ~ цД2^? причем наименьшее значение соответ-
соответствует [J. == '/2-
Плотность состояний Nh связанная с этими возбуждениями, описывается
выражением
[/d&\ -\~1 /,'р г sin2 a aL
¦ _ -if ——-rfa при — <:e<cд^
0
(для одного направления спина и на единицу длины нити). Отметим, что
Ni (e) ~ yV @) g2, т. е. каждая нить эквивалентна нормальной области радиу-
радиусом — g. В совокупности области, дающие вклад в плотность состояний при
малых энергиях, занимают лишь долю порядка |2/rf2 — В/Нс2 от всего объема
образца. Они играют важную роль главным образом при низких темпера-
температурах Т [грубо говоря, когда (|/dJ exp (Д^/7) > 1]. В этих условиях тепло-

Метод самосогласованного поля
157
емкость линейно зависит от Т, теплопроводность анизотропна (с максималь-
максимальным значением вдоль направления нити), а скорость ядерной релаксации
может в некоторых случаях определяться скоростью спиновой диффузии.
Край спектра возбуждений в неоднородных системах
Рассмотрим чистый металл в отсутствие полей и токов. Обычно
потенциал спаривания А постоянен в пределах образца, а функции и
и v представляют собой плоские волны. Легко проверить, что в этом
случае энергетическая щель равна А. Однако в достаточно тонких
образцах оказывается возможным создать пространственное изменение
параметра А(г) (например, осаждая металл с другими свойствами
на сверхпроводник).
Здесь мы рассмотрим особенно простой случай, показанный
на фиг. 48. Потенциал спаривания изменяется только в направлении х
fix) й 1х)
Сольная Слабая Сильная
сверхпроводимость сверхпроводимость сверхпроводимость
Фиг. 48. Вид потенциала спаривания Д(х) для системы из трех метал-
металлических слоев.
Центральный слой является слабыч сверхпроводником с минимальным значением параметров Д,
равным Дт« Амплитуда / (х) описывает вэлнэвой пакет с малой пространственной протяжен-
протяженностью с центром в точке дг=О; соответствующая энергия возбуждения очень близка к Дт.
и при х = 0 имеет минимальное значение Дш. При х ф 0 параметр А
возрастает; расстояние, на котором происходит его заметное изме-
изменение, обычно довольно велико (по меньшей мере порядка ?0).
Покажем, что пороговая энергия е0 квазичастиц, т. е. минимальное
положительное собственное значение системы уравнений E.18), при-
приближенно равна Аш. В введенных ранее спинорных обозначениях
система E.18) имеет вид
Е'ф = (&6eoz -\~ Аол) ¦$ — Qty, E.60)
где
и
V

158 Глава V
а ах и ог — матрицы Паули
ОП /10
1 0/' °*~\0 —1
Для доказательства высказанного утверждения о близости е0 к Ат
воспользуемся вариационным принципом. К сожалению, оператор Q
не является положительно определенным (е и —е одновременно пред-
представляют собой его собственные значения), поэтому необходимо обра-
обратиться к рассмотрению оператора
?2 = ©^ + Л2+<[©^, Л]оу E.61)
[при выводе E.61) мы воспользовались тождествами oxaz-{-GzGx — 0
и axaz—агах =— 2/Oj,]. Возьмем пробную функцию вида
«'?/W?r E.62)
где Z — любое направление в плоскости, перпендикулярной оси х,
а (ру — постоянный спинор, такой, что оу<ру = ± <ру. Поскольку энер-
энергия &ве отсчитывается от уровня Ферми, мы имеем просто
(Функция / при сделанном выборе волнового вектора не имеет нулей
в основном состоянии, что способствует понижению кинетической
энергии.) Вычисляя среднее значение оператора Q2, получаем
± i J Г (*) [~ ^ ^. А (*)] / (*) dx. E.64)
Для вегцественной функции /(х) последний интеграл обращается
в нуль. Если, помимо этого, функция f(x) не имеет особенностей
и меняется на расстояниях порядка L, то член кинетической энергии
дает вклад в е2, равный a (S2/2mL2J (где а — численный коэффициент
порядка единицы). Относительно потенциала спаривания А(х) сделаем
предположение, что он меняется по параболическому закону вблизи Дт
E.65)
где 6^§>?. Тогда член, соответствующий потенциальной энергии,
примет вид Ад [l -|-13(Z,/6J], где р —другой численный коэффициент.
Таким образом,

Метод самосогласованного поля 159
Минимизируя это выражение относительно L, находим
E-67)
где ц~Ь2/2т62Лт. Для 6—|—tivFjkm имеем ц—1/^Е0—1(Г2— 1(Г3,
т. е. значение е0 на практике весьма близко к Лш.
Немагнитные сплавы. Теорема Андерсона
Изучим теперь спектр возбуждений сверхпроводящего сплава
в нулевом магнитном поле. Мы должны решить систему урав-
уравнений E.18)
ги=(- ¦?у2+и (г) -Е? )и+Av-
I W г E-68)
ew=(ж у2 - и )д*
здесь ?/ (r) — полный потенциал Хартри, действующий на электрон
в нормальном металле. При выводе уравнений E.68) предполагалось,
как обычно, что электрон-электронное взаимодействие носит примерно
точечный характер, т. е. имеет вид [—^(г,—г2)], а потенциал U (г)
не зависит от спиновых индексов (т. е. сплав немагнитен). Потенциал
примесей включен в U (г), т. е. система уравнений E.68) в принципе
позволяет учесть и всевозможные эффекты многократного рассеяния
электронов на примесях, поэтому она очень сложна. Положение
заметно улучшается, если предположить, что А (г) не зависит от г
даже при наличии примесей. Строго говоря, это не так1), однако,
если примеси в химическом отношении не слишком сильно отличаются
от исходного чистого материала, такое предположение допустимо [92]2).
Уравнения значительно упрощаются, если с самого начала исходить
из одноэлектронных волновых функций <wn (r) для нормального ме-
металла. По определению,
!Л (г) = ("? V2+t/(r)-?f) <*,„(,•)• E.69)
Для чистого металла wn (r) представляют собой блоховские функции;
Для сплава они имеют значительно более сложный вид, так как
описывают последовательные соударения электрона с различными
примесями. К счастью, для приводимого ниже расчета нет необходи-
необходимости знать детальный вид этих функций.
Заменим потенциал спаривания А (г) константой А; тогда, оче-
очевидно, решения системы E.68) будут зависеть от координат так же,
¦) Точнее, область, где происходит изменение Д (г) вблизи атома примеси,
имеет атомные размеры, благодаря чему вклад от этих областей мал при
малых концентрациях примеси. — Прим. ред.
2) См. также [91]. — Прим. ред.

160 Глава V
как wn(r). Положим
ия (г) = «»„№«„.
«я(г) = «'я(г)»|1.
Тогда, как легко видеть, система E.68) сводится к следующей:
Л*Ии-(ев + и«я = 0. ( '
Отсюда, как обычно, находим
^=^+|А|2- E-72)
Коэффициенты й„ и vn зависят лишь от \п и удовлетворяют условию
нормировки
1«ЯР + |«ЯР=1- E-73)
С помощью E.71) их можно записать в явной форме
E'74)
Функции ип, vn и дап будем считать вещественными; это допустимо,
поскольку wn (г) представляют собой собственные функции веще-
вещественного оператора. Использование стоячих волн вместо бегущих
окажется полезным и в дальнейшем при обсуждении свойств сплавов.
Условие самосогласованности E.32) запишется в виде
)]. E-75)
Полезно ввести также плотность состояний N (г) в данной точке_г
в нормальном металле для энергий вблизи уровня Ферми
Ц). E.76)
п
Используя это определение, запишем условие E.75) в виде
f AA~2/) d\. E.77)
2+|A|
Отсюда ясно, что условие самосогласованности E.77) не является
точным, так как, по предположению, А — константа, в то время как
здесь параметр А (г) пропорционален N (г) и потому может меняться
в пространстве за счет примесей. Однако, если примеси химически

Метод самосогласованного поля 161
близки к основному материалу, то плотность состояний N (г) мало
отличается от своего среднего значения N и условие самосогласован-
самосогласованности принимает вид
По виду это уравнение совпадает с аналогичным уравнением для
случая чистого металла, поэтому в первом приближении спектр воз-
возбуждений и остальные термодинамические свойства у сплава и у чистого
металла одинаковы. Впервые на это обстоятельство указал Андер-
Андерсон [93]. На опыте оно проявляется в отсутствии заметного влияния не-
немагнитных примесей на критическую температуру сверхпроводников *).
§ 3. ЭФФЕКТ МЕЙССНЕРА В МЕТАЛЛАХ И СПЛАВАХ
Учет магнитного поля как возмущения
Теперь рассмотрим токи j, индуцируемые слабым магнитным полем
H = rotA в газе сверхпроводящих электронов. Математический
аппарат, необходимый для такого расчета, содержится в § 2. Будем
исходить из условия самосогласованности, записанного с помощью
собственных состояний одноэлектронного гамильтониана:
+ у(г)_Ер E 79)
Мы не будем требовать постоянства потенциала U (г) в пространстве
и даже его периодичности. Это позволит нам вести рассмотрение
одновременно для чистых металлов и сплавов.
В первом порядке по Н (или А) положим-
E-80)
где «{J" и ift) — собственные функции системы E.18) для случая
А = 0 [см. E.70)]. Кроме того, примем
') Существуют определенные эффекты, которые не удается описать
с помощью грубого приближения для взаимодействия вида —V6 (г, — г2).
Однако малость этих эффектов указывает на то, что сделанное приближе-
приближение является достаточно хорошим, по крайней мере при предварительном
рассмотрении.
11

162 Глава V
В общем случае добавочный член Д, отличен от нуля. Другими сло-
словами, самосогласованное поле А может измениться в результате
наложения магнитного поля Это замечание, принадлежащее Бого-
Боголюбову, необходимо иметь в виду, чтобы не нарушить градиентной
инвариантности.
Рассмотрим типичный случай, когда добавка Д, может быть отлична
от нуля. Положим А = ?х (•") (гДе X — произвольная функция), тогда
H = rotA —0. Легко проверить, что система уравнений E.18) со-
совместно с уравнением самосогласованности E.32) имеет решение
V =:^0)e(-/e/te)x(r) E.81)
Д (г) = A^'2'*/**» * <r).
Как и следовало ожидать, j = 0. Разлагая найденное решение в ряд,
имеем в первом порядке по х (иЛИ А):
Таким образом, в этом частном случае Ах Ф 0 Вообще в линейном
приближении связь между Дх и А имеет вид
E-83)
где а=д;, у, z, a интеграл берется по объему образца. Для одно-
однородного и изотропного металла ядро Р(г, г') зависит лишь от раз-
разности R = г — г' и представляет собой вектор, направленный вдоль R.
Вид функции Р (R) легко определить для только что рассмотренного
частного случая, для которого
¦^АоХ(г) = j P(r- г') • VX(rVr'. E.84)
Ограничимся рассм^,рением частного класса функций /(г), убы-
убывающих на бесконечности (г—>оо). Интегрируя по частям, пере-
перепишем E.84) в следующем виде:
-^ А0Х (г) = - J ЗС (г') div Р (г - г') rfr\
Отсюда
lip
div Р ^г - г') = - —- Д06 (г - г').

Метод самосогласованного поля 163
Поскольку вектор Р направлен по радиусу R, написанное уравнение
имеет единственное решение
_
R
Это выражение применимо также и для сплавов, если нас интере-
интересует усредненное по всем конфигурациям примесей значение А2 (после
усреднения система снова становится однородной и изотропной).
Зная P(R), можно доказать следующую теорему: если вектор-
потенциал А выбран в лондоновской калибровке (т. е. divA — О и
равна нулю нормальная к поверхности образца компонента А), то
Aj = O. В самом деле,
0: E-86>
здесь п—-единичный вектор нормали к поверхности образца. Важно
подчеркнуть, что эта теорема верна лишь при выполнении следующих
условий: 1) металл изотропен; 2) взаимодействие между электронами
носит точечный характер. Действительно, при учете нелокальности
взаимодействия потенциал спаривания А (г, г') зависит от двух аргу-
аргументов. Изменение величины А в этом случае имеет вид
А, (г, г') = J Ка (г. г', г") Аа (г") dx". E.87)
Соображения, основанные на симметрии задачи, не позволяют теперь
свести Aj к градиенту некоторой функции !).
Найдем теперь в явном виде поправки ф) и Ф~> в лондоновской
калибровке (Aj = 0), в которой вычисления имеют наиболее простой
вид. Выпишем сначала уравнения E.18) и E.19), сохранив в них
лишь члены, линейные по А,
E
«-??Ч-^ (г)] «?> (г) - AV'> (г) = Ц (А- V + V• A)tf (r).
Далее, разложим «W и v<?> в ряд по ортонормированной системе
функций wn:
йй)(г) = 2вят«'т(г),
" E.89)
¦) Детальное KOflnqecTBeHHoe рассмотрение показывает, что поправки,
возникающие за счет размазанности взаимодействия, малы и мало влияют
на диамагнетизм [94J.

164 Глава V
Напомним, что функции wn мы считаем вещественными. Умножим
каждое из уравнений E.88) на wm и проинтегрируем обе стороны
по г. Используя значения E.74) для и<Р> и v@\ находим
— U — Abnm =
где
^j ~Fmn. E.91)
Решение системы E.90) имеет вид
E-92)
Ьпт = /™2 Ке» - U »„ + Д« J-
Находя «W и ©W с помощью этих выражений и используя уравнения
самосогласованности E.32), прямым вычислением можно убедиться,
что в лондоновской калибровке А! = 0, как и предполагалось с самого
начала.
Связь диамагнитного отклика с проводимостью системы
в нормальном состоянии
Зная волновую функцию в первом порядке по А, можно вычис-
вычислить ток
При дальнейшем обсуждении мы ограничимся случаем абсолютного
нуля (Г = 0). В нулевом порядке по А. очевидно, у = 0. В первом
порядке, выражая W через у, производя усреднение и разлагая
и = и@>-\-иA> и т.д., находим
S «'*W»+ Ч0*^ - Компл. сопр.) =
КК и], E.93)
п, т
I. E.94)
» - - --• --г Л
п, т

Метод самосогласованного поля 165
Согласно E.92), имеют место следующие свойства:
Опт = — "пт'
где
Выпишем симметричную часть коэффициента Rn
_ / /е е \ "я/я "I" "пи Ц inim ~t~ е/геш
Связь тока с вектором-потении алом имеет вид
/ii(r) = S JXv (г. О Av (О Л' Qi. v = *. у. *); E.95)
V
здесь
E.96)
где через p(tnm мы обозначили величину
Рцпт (г) = [wn (г) У„тт (г) — дат (г) V>1wn (г)].
Для чистого металла, имеющего неограниченные размеры, функции wn
являются плоскими волнами, и величины рпт можно найти сразу.
Однако на практике необходимо учитывать наличие примесей и влия-
влияние поверхности образца; построить wn в явном виде в этих слу-
случаях не удается.
Тем не менее вид 5^v нетрудно получить, замечая, что электро-
электропроводность о^ нормального металла содержит те же матричные
элементы. Этим обстоятельством объясняется также успех феномено-
феноменологического описания Пиппарда, которое приводит для сверхпровод-
сверхпроводника к соотношению между j и А, совершенно аналогичному соот-
соотношению между j и Е в случае нормального металла.
Точнее говоря, проводимость otlV(r, г'; Q) на частоте Й опреде-
определяется следующим образом. Приложенное к образцу электрическое
поле
Е (г') е ~lQt -f Компл. сотр.
индуцирует в каждой его точке г ток с плотностью
J(r) <-'°Ч-Компл. сопр.,

166 Глава V
который связан с полем линейным соотношением
h @ = | о^ (г. г'; О) Ev (г') dx'.
Мы можем найти величину о^ в явном виде, воспользовавшись соот-
соотношением Чемберса между током и полем (см. [95]) *)
^« = ^5^2 J -^^^1/AЧ(гУг'. E.97)
V
где R=r — г', /—транспортная длина свободного пробега. Инте-
Интегрирование производится только по объему образца. При выводе
соотношения E.97) используются три предположения.
1. Отражение электронов от поверхности считают диффузным,
как это имеет место в большинстве случаев.
2. Предполагается, что поле Е и ток j носят поперечный харак-
характер (divE=0, div j = 0.) и не имеют составляющих, нормальных
к поверхности. Это ограничение не должно служить поводом для
беспокойства, поскольку в сверхпроводящем состоянии возмущение
(вектор-потенциал А) в лондоновской калибровке также является
поперечным.
3. Принимается, что частота Q меньше, чем kBTjh. Из E.97)
находим, что тензор электропроводности для точек г и г', находя-
находящихся внутри образца, описывается выражением
v(r, о_?«^^Л.«•„-«: E.98)
если же хотя бы одна из точек г или г' лежит вне образца, то
о = 0. Фактически нам потребуется лишь вещественная часть о^,
определяющая диссипируемую мощность
jRs[ailv(r, r'; Q)]}drdr'.
Ц, V
E.99)
Выразим теперь о^ через одноэлектронные волновые функции
нормального металла «'„(г) и покажем, что величину Re о можно
представить в виде, аналогичном выражению E.96) для 5 v. Будем
исходить из одноэлектронного гамильтониана для нормального металла
') Вывод соотношения Чемберса имеется также в статье Бардина
в книге [12].—Прим. ред.

Метод самосогласованного поля 167
где U0(r)—потенциал решетки с учетом примесей и поверхности
образца. Переменное электрическое поле не содержится в ?/0,
а выражается через вектор-потенциал
В силу того что поле Е представляет собой малое возмущение,
можно написать
где
E.102)
Собственными функциями гамильтониана ?№й являются wn(r). Воз-
Возмущение $%?) осциллирует во времени и вызывает переходы и —>т.
для которых \т — ?„ = ± Ш. Вероятность перехода в единицу вре-
времени описывается выражением
*я»=-т-п -/e™)i/a»)K»i«^ii«>Px
Х[6(!п-|от + лй)-Ь-6(!п-|т-Ш)], E.ЮЗ;
где
S J ^ С) P (г) rfr- E. Ю4)
V
Зная g"n/n, найдем диссипируемую мощность
W = Ъ gnmilm-ln)- EЛ05)
я, /я
Из сравнения E.105) и E.99) следует
п, т
X Ртт(г) Pvnm(г')бA„ ~%т- АО). E.106)
Чтобы сравнить это выражение с формулой Чемберса, рассмотрим
область Ш <С[ &b7"; здесь

168 Глава V
Таким образом, выражение E.106) принимает вид
Re V = ^ [-^-JN@) %р»пт(г)р^т(г')Ьап -%m-hQ), E.107)
где символ ( ) означает усреднение по одноэлектронным состояниям
на поверхности Ферми нормального металла').
Расчет диамагнитных токов2)
Выражения E.107) и E.96) показывают, что выражение для
электропроводности о^ в нормальном состоянии содержит те же
матричные элементы, что и ядро S^, описывающее диамагнитный
отклик сверхпроводника. Произведя в E.96) замену
Запишем это фундаментальное соотношение в виде
S^(r. r') = ^JL(l, |')Re[o,,v(r. r'; 1=1^
—-^-6^6A- —r'). E.108)
Подставляя сюда выражение Чемберса для о^, находим
где
—оо —оо
и введены обозначения %% = Лг^/зт А @), R = r — г'. Из вида ?(?, I')
легко заключить, что в написанный интеграл важный вклад вносит
область \ — |' *~ Д. Поэтому область пространства, где ядро /(/?)
отлично от нуля, имеет размер порядка hvFjn А @) = |0 (численный
коэффициент в определении ?0 нам понадобится позже). Переходя
к явному вычислению /(/?), сделаем замену переменных | = Ash0,
') Заметим, что при [l^l^;^ результат усреднения в E.107) сильно
зависит от йй и слабо от |„.
2) Более строгое рассмотрение читатель может найти в работе Маттиса
и Бардина [96].— Прим. ред.

Метод самосогласованного поля 169
|'=Ash0' и положим а = F —0')/2, Р = @+0')/2. Тогда
Г ^
-¦* Г
—со —со
где u = sha. Выполняя интегрирование по и, окончательно находим
-2Д (Q) KchR/hv
'• EЛ12>
Здесь первый член отличен от нуля лишь в начале координат.
Выполняя в E.95) интегрирование по г', мы обнаруживаем, что он
в точности компенсирует член (—ne2jmc)biivb(f() выражения E.109).
Таким образом, можно написать
где
со
Формулы E.95), E.113) и E.114) дают полное решение задачи
о нахождении токов, индуцированных в сверхпроводнике слабым
статическим магнитным полем.
выводы
1. При А ф 0 в сверхпроводнике существуют незатухающие токи.
К сожалению, этот решающий результат был получен после длин-
длинных вычислений и его физический смысл не вполне ясен. Мы поста-
постараемся разобраться в этом вопросе в гл. VI.
2. В чистом металле (/ = оо) радиус действия ядра S^ (r, г')
определяется функцией /(/?) и имеет порядок g0. В теории Пиппарда
предполагается, что /(/?) = *-я/|о; точная зависимость E.114) не
является экспоненциальной, но различие мало. В частности, отметим,
что при Т = 0

170
Глава V
т. е. в этом пункте точный результат и формула Пиппарда совпа-
совпадают.
3. Если вектор-потенциал А (г') в бесконечном чистом металле
медленно меняется на расстояниях порядка ?<,, его можно вынести за
знак интеграла E.95). Интегрируя остающееся выражение, получаем
соотношение Лондонов
rotj = —
пе'
cm
Н.
E.115)
4. При наличии примесей ядро S^v(r, r') уменьшается из-за
появления множителя e~RI1, где /—транспортная длина свободного
пробега электронов в нормальном металле. Этот результат также был
предсказан Пиппардом до создания микроскопической теории.
Фиг. 49. Температурвая зависимость относительной величины диамагнит-
диамагнитного отклика для лондоновского сверхпроводника.
5. Если вектор-потенциал А в случае загрязненного металла
медленно меняется на расстояниях порядка (l/go-f-1//), его, как и
прежде, можно вынести из-под знака интеграла; тогда мы получим
новое соотношение лондоновского типа, обычно записываемое в форме
— сЛ01(г)=А(г).
или
— cA0rotj(r) = H, E.116)
где
при Г=0. В частности, при /<С1о Функцию /(/?) можно поло-
положить равной единице; тогда
^Ш E-118)

Метод самосогласованного поля
6. Наше рассмотрение относится к случаю T = Q. Тем же спосо-
способом можно рассмотреть случай Т Ф 0. Оказывается, что при этом
соотношение E.95) по-прежнему применимо, но определение ядра
L (?, ?') необходимо обобщить. Интегрирование должно выполняться
численно. При этом оказывается, что вид координатной зависимости
ядра ^(г, г') почти не меняется с температурой. В частности,
радиус действия ядра в чистом металле по-прежнему составляет при-
примерно ?о даже при Т->ТС. Наоборот, нормировка ядра изменяется,
поскольку сверхпроводящие токи убывают с ростом температуры,
пока не исчезнут совсем при Т = Тс. Нормировка обычно задается
с помощью зависящего от температуры коэффициента Ат, опреде-
определяемого соотношением
= -^-. E.119)
Температурная зависимость, отношения Л0/Лг приведена на фиг. 49.
Позже мы вернемся к обсуждению параметров, определяющих Лг
при Т^=ТС, в связи с теорией Гинзбурга — Ландау.
ЛИТЕРАТУРА
Метод самосогласованного поля и теорема Андерсона
Anderson P. W., Ргос. 8 th Internet. Conf. Low Temp. Phys., London, 1963-
Квантование потока и дальний порядок в сверхпроводниках
Y a n g С. N.. Rev. Mod. Phys., 34, 694 A962).
Эффект Мейсснера и его связь с энергетической щелью в теории БКШ
Tinkham M., Superconductivity, New York, 1965.

Глава VI
ФЕНОМЕНОЛОГИЧЕСКИЕ УРАВНЕНИЯ
ГИНЗБУРГА — ЛАНДАУ
§ 1. ВВЕДЕНИЕ
Прежде всего повторим еще раз все, что нам известно о микро-
микроскопических свойствах сверхпроводника в присутствии статического
магнитного поля Н. Первоначально для определения незатухающих
токов j, индуцированных полем, мы использовали уравнение Лондонов
)-H- FЛ)
Однако уравнение F.1) применимо лишь при выполнении следующих
условий:
1. Глубина проникновения X (Т) должна быть больше, чем
0/1о+ W» где io==o>I8(fiwf/^B^<;I a l—длина свободного про-
пробега.
2. Поле Н должно быть слабым, чтобы его можно было рассмат-
рассматривать как возмущение.
3. Плотность сверхпроводящих электронов ns(r) должна быть
примерно постоянной в пространстве.
Затем мы ослабили первое условие, заменив уравнение F.1) нело-
нелокальным соотношением Пиппарда. Однако условия 2 и 3 остаются
в силе, что не позволяет нам решить, например, задачу о границе,
отделяющей нормальную область (Н = НС, ns=0) от сверхпрово-
сверхпроводящей (Н = О, ns ф 0) для сверхпроводника первого рода.
В принципе мы могли бы вернуться к общему методу и попытаться
а) написать уравнения движения возбуждений
m (г)=-L [(р - тАJ—
е^ (г) =- - -—¦ [(р + у АJ - Ef] v (г) + Д* (г) и (г);
б) задаться конкретным видом пространственной зависимости по-
потенциала спаривания А (г);
в) вычислить и и v (что позволит нам найти плотность тока и
другие физические величины);
г) проверить с помощью уравнения самосогласованности, что
выбранная форма для А (г) является правильной, т. е.

Феноменологические уравнения Гинзбурга — Ландау 173
Однако на практике такая программа является чрезвычайно трудной
и громоздкой.
Расчеты значительно упрощаются, если ограничиться окрестностью
температуры перехода Тс. Действительно, при Т->ТС
1) глубина проникновения к(Т) становится большой (в лондоно-
вском предельном случае А,(Т)— nj'k, а число сверхпроводящих
электронов ns стремится к нулю, как Тс — Т;
2) толщина границы, разделяющей области N и S, также стано-
становится большой. Из эмпирических данных для чистых сверхпроводников
первого рода следует, что ее толщина меняется как |0A —TjTc)~'12.
Вообще во многих физических ситуациях можно считать ток j(r)
и потенциал спаривания Д(г) медленно меняющимися функциями
координат при условии, что температура достаточно близка к тем-
температуре перехода. В этих условиях оказывается, что физические
свойства можно изучать с помощью довольно простых уравнений,
выводом которых мы сейчас и займемся.
§ 2. ПОСТРОЕНИЕ СВОБОДНОЙ ЭНЕРГИИ
Рассмотрим однородный сверхпроводящий металл или сплав. По-
Построим сначала выражение для свободной энергии для случая, когда
потенциал спаривания А (г) и вектор-потенциал А (г) являются про-
иввольными медленно меняющимися функциями координат. Миними-
Минимизируя затем полученную энергию, мы придем к уравнению для А (г)
и к выражению для тока j(r).
а) Вернемся сначала к тривиальному случаю, когда, во-первых,
параметр А одинаков во всех точках пространства и, во-вторых,
магнитное поле отсутствует. Для произвольного фиксированного зна-
значения А мы можем определить значения и и v, а затем вычислить
с помощью метода, изложенного в гл. IV, плотность свободной
энергии F как функцию А. В частности, для малых значений А (что
соответствует температуре Т, близкой к Тс) получим
где Fп — свободная энергия нормальной фазы; коэффициенты А и В,
согласно теории БКШ, при Т->ТС имеют следующий вид:
ы\ъ F-3)
В (Т) = 0,098^
Существенно, что в разложении F.2) содержатся только четные по А
члены.

174 Глава VI
В более общем случае можно предположить, что точное выраже-
выражение для свободной энергии дается разложением типа F.2), коэф-
коэффициенты А и В которого обладают следующими свойствами: коэф-
коэффициент А отрицателен при Т < Тс и обращается в нуль при Т = ТС,
наклон (dAjdT)T остается конечным; коэффициент В положителен
с
и конечен при Т=ТС, так что его можно заменить значением при
Т = ТС.
Для Т < Гс минимуму F соответствует отличное от нуля значе-
значение Д
^ = -4 = 10.2*!^ <ТС-Т). F'4)
которое является равновесным в отсутствие магнитного поля. В соот-
соответствии с этим свободная энергия равна
F = Fs = Fn--§. F.5)
При наших предположениях относительно А и В разность Fn—Fs —
= н1/8п пропорциональна (Тс — ТJ, что характерно для любых
фазовых переходов второго рода.
б) Будем теперь считать, что параметр Д медленно изменяется
от точки к точке, однако по-прежнему Н = А —0. Найдем, какие
изменения нужно при этом внести в выражение F.2) для свободной
энергии. Так как в отсутствие магнитного поля равновесию соот-
соответствует Д — const, последующие члены разложения должны иметь
вид (дА/дхJ, (dAjdx)(dh!dy) и т. д. Для простоты в дальнейшем мы
изучим только случай кубической симметрии. Тогда
Будем считать, что коэффициент С отличен от нуля и положителен
при Т = ТС. Позднее с помощью микроскопического расчета мы по-
покажем, что для чистого металла С-~ N@)^, т. е.. энергия неодно-
родностей, которой соответствует последний член в разложении F.6),
составляет
— N @) Д2|^ (-1 -А\ .
Выражение F.6), связывающее плотность свободной энергии F
с параметром порядка Д в окрестности температуры перехода, было
предложено Ландау в качестве исходного пункта при построении
общей феноменологической теории фазовых переходов второго рода

Феноменологические уравнения Гинзбурга — Пандау 175
(см. [97]). Например, в ферромагнетике роль параметра порялк;
играет намагниченность').
Задача. Рассмотреть флуктуации потенциала спаривания Д в нормаль-
нормальной фазе G" > Тс) в отсутствие поля.
Решение. Вероятность найти конфигурацию с определенной прост-
пространственной зависимостью потенциала спаривания Д (г) пропорциональна
ехр (— (?r/kBTy где ff~ — свободная энергия всего образца [вычисляемая
с помошью выражения F.6) ]. Для Т > Тс в разложении F.6) достаточно
удержать лишь члены порядка Д2. В калибровке, в которой А = 0, а пара-
параметр Д веществен, имеем
<F = J rfr [^41 Л (г)
где
Дь = ?~3 f A (r) elk'r dr.
а I? — объем образца. (Как мы увидим из дальнейшего, это уравнение
справедливо для чистого сверхпроводника при условии Щ,ц<^. !•) Термоди-
Термодинамическое усреднение дает
(|k|)
А+СЬ'
Среднее (|Ah p) можно связать с пространственной корреляционной функ-
функцией параметра Д
|2) = L~6 J (Д (г) Д (r')> elk-ir-r') rfr rfr' =
= i~3 Г (Д @) Д (R)) elkR dR
[среднее (Д(г)Д(г')) зависит лишь от разности R = r — г']. Совершив
обратное преобразование Фурье, находи*! выражение для корреляционной
функции
(Д @) Д (R)> = — f ^ ^L
V V " BлK J
где g2 = — AlC > 0. Для чистого металла С ~>N @) g?, поэтому отношение
(А(Р)А(В)) W_J_ -QR
') Как показывают недавно выполненные эксперименты и теоретические
расчеты, выражение вида F.6) для F имеет ограниченную применимость
в случае магнитных материалов, для которых реальная зависимость носит
более сложный характер. Однако для сверхпроводников выражение F.6)
превосходно оправдывается. Усложнения, возникающие в магнитном случае
связаны главным образом с так называемыми эффектами ближнего порядка
В случае сверхпроводников эти эффекты очень малы (см. задачу).

176 Глаяа VI
т. е. очень мало. Этим доказывается сделанное утверждение о малости эф-
эффектов ближнего порядка в большинстве сверхпроводников.
в) Для описания эффектов, связанных с магнитным полем h,
введем в выражение F.6) вектор-потении ал A(h = rotA). При этом
свободная энергия не должна зависеть от выбора калибровки А.
(Действительно, поскольку замена А' = л + v% не приводит к изме-
изменению магнитного поля h, должна оставаться неизменной и свободная
энергия F.) В гл. V мы нашли, что потенциал спаривания при
градиентном преобразовании изменяется по закону
Поэтому для обеспечения инвариантности F мы должны заменить
разложение F.6) следующим:
i / о _ \ о 1,2
±ш- F-7)
Последний член Л2/8я представляет энергию магнитного поля в пустоте.
Имеется формальная аналогия между членами порядка | Д |2 в разло-
разложении F.7) и выражением для плотности энергии частицы с зарядом 2е,
описывающейся волновой функцией г]з (г). Действительно, положим
„__,.__ Р(-У- --1-1
2т С ' ' \2т) С2 ' 20 ~ 8я
тогда
-^. F-9)
Выражение F.9) для свободной энергии было предложено Гинз-
Гинзбургом и Ландау [98] в 1958 г., т. е. значительно раньше, чем
началось развитие микроскопической теории. В то время физический
смысл волновой функции г|з (г) был далеко не ясен; более того, вели-
величина заряда е*, входящего в комбинацию —/AV — (е*/с)А, оставалась
неизвестной (первоначально Гинзбург и Ландау взяли е* = е). По-
Построение выражения F.9), не зависящего от выбора конкретной
модели сверхпроводящего состояния, явилось настоящим триумфом
физической интуиции.
Отметим, что выбор массы свободного электрона т в качестве
множителя в выражениях F.8) и F.9) сделан совершенно произ-
произвольно — с равным успехом мы могли бы взять массу Солнца ')¦
') В работах некоторых авторов вместо массы т используется удвоен-
удвоенная масса 2т. Наша нормировка отвечает оригинальной работе Гинзбурга
и Ландау [98J.

Феноменологические уравнения Гинзбурга — Ландау 177
Напротив, наличие заряда 2е в слагаемом Bе/с)А не является услов-
условным, но выражает тот фундаментальный факт, что потенциал спа-
спаривания представляет собой результат усреднения произведения двух
операторов уничтожения Д = V (W (r f) Ч*1 (гj)).
§ 3. УРАВНЕНИЯ РАВНОВЕСИЯ
Теперь наша задача состоит в минимизации свободной энергии,
во-первых, относительно параметра порядка Л (г) и, во-вторых, от-
относительно распределения магнитного поля, т. е. А (г). Положим
где интеграл берется по объему образца. При изменении функций
ф (г) и А (г) соответственно на бгр (г) и бА (г) приращение свободной
энергии после интегрирования по частям примет вид
-г-Компл. сопр.|+ Jdr6A -< — -^roth —
— -^ [V (- ibV —Ц- А) ф + Компл. сопр. ] }. F.10)
Заметим, что слагаемое A/4л)roth под знаком второго интеграла,
согласно уравнениям Максвелла, равно j/c, где j — плотность тока-
Положив б^" = 0, находим
i(^)Ч F.11)
^^ F.12)
Система уравнений F.11) и F.12) (совместно с уравнениями Макс-
Максвелла. — Ред.) представляет собой фундаментальную систему урав-
уравнений Гинзбурга — Ландау, позволяющую определить, во-первых,
параметр порядка и, во-вторых, токи, т. е. диамагнитный отклик
сверхпроводника.
ЗАМЕЧАНИЯ
1. Выражение F.12) формально совпадает с выражением для плотности
тока, создаваемого частицей с зарядом 2е, массой т в состоянии с волновой
функцией -ф (г).
2. При выводе выражения F.10) мы опустили поверхностный интеграл
~Ш J б** (~~ibv ~ ^Г А) *"da + Компл- СОпР-
Ю 9.., 1ПОП

178 Глава VI
Сохранив этот член и потребовав, чтобы он был равен нулю, получим сле-
следующее граничное условие:
(— itfl —Ц- А)я ф = 0 F.13)
где индекс п обозначает компоненту вектора, нормальную к поверхности об-
образца. Гинзбург и Ландау в их оригинальной работе шли именно этим путем.
При этом неявно предполагалось, что выражение F.9) для плотности свобод-
свободной энергии справедливо даже в непосредственной близости к поверхности
В дальнейшем, исходя из микроскопической теории, мы увидим, что для гра-
границы сверхпроводник — изолятор условие F.13) выполняется; наоборот, для
границы сверхпроводник — нормальный металл в это граничное условие не-
необходимо внести принципиальные изменения.
При подстановке условия F.13) в выражение для плотности тока F.12)
легко видеть, что )„ = 0, т. е. втекающие или вытекающие из сверхпровод-
сверхпроводника токи отсутствуют. Если же, наоборот, потребовать выполнения условия
jn = 0, то вместо F.13) мы получим более слабое условие
Bе \
с /П
где Я. — произвольная вещественная постоянная. На практике такого типа
граничное условие встречается при рассмотрении контакта сверхпроводника
с нормальным металлом.
§ 4. ДВЕ ХАРАКТЕРНЫЕ ДЛИНЫ
Уравнения Гинзбурга—Ландау F.11) и F.12) содержат две ха-
характерные длины, к обсуждению которых мы сейчас и перейдем.
а) Сначала рассмотрим случай, когда магнитные поля и токи от-
отсутствуют. Выберем калибровку, в которой функция ф вещественна,
и для простоты ограничимся одномерным случаем. Тогда уравне-
уравнение F.11) заметно упрощается
Это уравнение имеет два очевидных решения: 1) решение ф =
относящееся к нормальному состоянию, и 2) решение i1j=i]H, где
описывающее обычное сверхпроводящее состояние. Второе решение
существует и отвечает более низкой энергии, когда а < О, т. е.
когда Т < Тс. Однако мы хотели бы рассмотреть также решения
более общего вида, например, для случаев, когда под действием ка-
какого-либо внешнего фактора параметр порядка ty(x) в некоторой
точке имеет значение, отличное от ф0. Возникает вопрос, как ведет
себя ф(х) в окрестности этой точки?

Феноменологические уравнения Гинзбурга — Ландау 179
Чтобы найти характерную длину в уравнении F.14), целесооб-
целесообразно перейти к приведенным переменным
Ф = Фо/. F.16)
2^Ы=?(П F-17)
где параметр |(Т) имеет размерность длины. В этих переменных
уравнение F.14) принимает вид
0. F.18)
Отсюда следует, что параметр" |(Г) является естественной единицей
для измерения расстояний, на которых может меняться функция /.
Мы будем называть его длиной когерентности при данной темпе-
температуре Т. Чтобы оценить порядок величины 1G"), заметим, что,
согласно F-8),
Ранее уже отмечалось, что для чистого металла
Используя числовые значения коэффициентов, получаем
\. F.19)
Характерная длина для изменений ф есть 1G"), поэтому очевидно, что
для температур 7\ близких к Тс, параметр порядка мало меняется
на расстояниях порядка Ь^.
Задача. Вычислить энергию NS-границы для сверхпроводника первого
рода (фиг. 50) в предельном случае, когда глубиной проникновения поля
можно полностью пренебречь.
Решение. По предположению, поле не проникает в область, в кото-
которой параметр порядка t|) отличен от нуля. Следовательно, для нахождения i|)
можно использовать уравнение F.18) со следующими граничными условиями:
/=0 при х = 0,
/ -> 1 при х -> со.
Умножая обе части уравнения F.18) на dfjdx и интегрируя, находим пер-
первый интеграл
-1ЧТ) (%J - Г + j Г = const.
12»

180
Глава VI
Чтобы удовлетворить граничному условию на бесконечности, константу не-
необходимо положить равной — lj2- Это дает
Это уравнение имеет решение
которое удовлетворяет нашим граничным условиям при х = 0.
Энергия, отнесенная к единице площади границы, равна
Поверхностная энергия (//^8л)б представляет собой разность между Fp и
анергией конденсации, которую мы получили бы, если все полупространство
Нормальная „ .
область Сверхпроводящая оБпасть
Фиг. 50. Пространственное изменение магнитного поля и параметра по-
порядка вблизи Лга-границы для сверхпроводника первого рода [|(Г)^>А(Г)].
Эффективная глубина проникновения *-эфф нмеет порядок Уц^ (см. задачу на стр. 233).
х !> 0 было заполнено однородным (г|) — %) сверхпроводником. Таким об-
образом,
Подставляя сюда найденное выражение для приведенного параметра / и
используя соотношения F.8) и F.17), находим

Феноменологические уравнения Гинзбурга — Ландау 181
С помощью первого интеграла для dfjdx величину б можно представить
в следующем виде:
со 1
б = 2 J dx (I -PY = 2 J A -f*y |? df~
о о
= 2/21G-) f A ~Р) df= ^~%(Т) = 1,89|(Г).
о
б) Вторая характерная длина появляется, когда мы переходим
к рассмотрению электромагнитных эффектов, например при вычисле-
вычислении глубины проникновения слабого магнитного поля. Предположим,
что сверхпроводник занимает полупространство z^-0, а область
z •< 0 или пуста, или заполнена диэлектриком; в обоих случаях
применимо граничное условие F.13).
В 'случае слабого поля в первом порядке по h параметр \ty\2
в области z^-Q можно заменить его равновесным вначением |ty012
в отсутствие поля [см. F.15)]. Возьмем ротор от обеих сторон ура-
уравнения F.12); тогда мы придем к уравнению лондоновского типа
F.20)
поскольку величина ty0 не зависит от координат. Решая F.20) вместе
с уравнениями Максвелла, мы получаем, как и в гл. II, решение лишь
в том случае, когда вектор h лежит в плоскости ху. Выберем ось х
в направлении h; тогда
F.21)
^ F.22а)
или
^(Л=^-СА?, F.226)
где Ао — равновесное значение потенциала спаривания. С помощью
F.226) можно связать коэффициент С с величинами, непосредственно
измеряемыми на опыте1). Отметим, что глубина Я, G) пропорцио-
пропорциональна tyjj, т. е. A — Т/Т^Г^. Для чистого металла в приближении
свободных электронов микроскопическая теория БКШ дает
4,@) (Т->ТХ F.23)
') В кристаллах, не обладающих кубической симметрией, необходимо
учитывать тензорный характер коэффициента С.

182 Глава VI
где %L @) — лондоновская глубина проникновения при абсолютном
нуле
тс'
(п — число электронов в 1 ел3). Выражение F.23) с точностью до
численного коэффициента можно получить также с помощью F.22),
если принять
ЗАМЕЧАНИЕ
Исходя из предположений Гинзбурга и Ландау, в частности используя
выражение F.7) для свободной энергии при наличии поля, мы нашли ло-
локальную связь F.12) между током и вектором-потенциалом. С другой сто-
стороны, из микроскопического рассмотрения, приведенного в гл. V, следует,
что в частном случае, когда параметр | Д | постоянен и поле h мало, точная
связь носит нелокальный характер, т. е. для чистого металла плотность
тока j (г) в данной точке г зависит от значений вектора-потенциала А (г'),
где г' лежит в области | г — г' |^|0. Для выполнимости локального прибли-
приближения необходимо потребовать, чтобы плотность тока или вектор-потен-
вектор-потенциал А медленно изменялись на расстояниях порядка |0. т- е-
<64>
Для чистого металла это соответствует температурам, достаточно близким
к Тс. Однако для некоторых непереходных металлов, в особенности для А1,
лондоновская глубина kL @) настолько мала по сравнению с ?0, что темпе-
температурный интервал, необходимый для выполнения условия F.24), оказы-
оказывается очень узким.
в) Выше мы нашли две характерные длины |G) и h(T), опре-
определяющие поведение сверхпроводника вблизи критической темпера-
температуры. Обе величины расходятся как (Тс — Т)~'!г при Т —>ТС, поэтому
представляет особый интерес их отношение
F.25)
Используя определения F.17) и F.22а) величин |G) и h(T), полу-
получаем
_ ш_ /_р_\'А __ he I В \'/а 6 26

Феноменологические уравнения Гинзбурга — Ландау 183
Отношение и носит название параметра Гинзбурга—Пандау для
данного вещества. В зависимости от величины параметра к сверх-
сверхпроводники делятся на два типа: значения и .< 1 (% < |) отвечают
сверхпроводникам первого рода; значения к ^ 1 (к > \) соответствуют
сверхпроводникам второго рода. Позже мы уяидим. что точно граница
соответствует значению и = 1/У^- Мы покажем также, что для
чистого вещества
АЛО)
х = 0.96-^-. F.27)
50
Обратим внимание на тот интересный факт, что параметр и можно
определить непосредственно из экспериментальных данных о глубине
проникновения и величине поля Нс, полученных в области примени-
применимости уравнений Гинзбурга — Ландау. Действительно, с помощью
F.22а), F.15) и F-8) выражение F.26) легко преобразовать к виду
F.28)
Выражение F.28) иногда записывают в другой форме, которая часто
бывает полезна при численных расчетах
ИС(Т) = =-*2 ., F.29)
где ф0 = chl2e — квант потока.
В настоящей главе мы обсудим также другие методы определения
величины и.
§ 5. ЗАДАЧИ С ПОСТОЯННЫМ ЗНАЧЕНИЕМ АМПЛИТУДЫ
ПАРАМЕТРА ПОРЯДКА |ф|
Применим теперь уравнения Гинзбурга — Ландау для решения
некоторых конкретных задач. Сначала рассмотрим особенно простой
случай, когда амплитуда | ty| параметра порядка постоянна во всех
точках образца. С такой ситуацией мы уже однажды сталкивались
при вычислении глубины проникновения слабого магнитного поля
в массивный образец. Рассмотрим сейчас случаи совершенно иного
рода. Речь пойдет о тонких образцах (пленки, проволочки и т. п.),
в которых всякое изменение функции ф по толщине энергетически
невыгодно, поскольку оно привело бы к резкому вырастанию члена
| Vty p в выражении для свободной энергии. При этом поле h или
ток j не предполагаются слабыми, поэтому амплитуда | гр | (оставаясь
постоянной) не обязательно должна быть равна своему невозмущен-
невозмущенному значению i|>0.

184 Глава VI
Критический ток в тонкой пленке [99]
Пусть по пленке толщиной d течет ток с плотностью j, напра-
направленной вдоль оси х, как показано на фиг. 51. Предположим, что
выполняются следующие неравенства: ^<С[?(Г) и d<^K(T). Первое
из них обеспечивает постоянство по толщине пленки амплитуды | о|) |,
а второе — постоянство плотности тока j *). При выполнении напи-
написанных условий исходные уравнения значительно упрощаются. Дей-
Действительно, положим
где амплитуда | г|)) не зависит от г. Тогда выражение для плотности
тока можно написать в виде
|^ — Ax\ = 2e\ty\2v, F.30)
где
F.31)
т \ дх с
величина v представляет собой скорость „частиц" в состоянии с вол-
волновой функцией г|). Плотность свободной энергии F.9) также при-
принимает простой вид
Имея в виду упомянутую аналогию, мы записали третий член выра-
выражения, стоящего в скобках, в форме кинетической энергии для ча-
частицы. Условие минимума F относительно | г|) | дает
а+р|г|>р-]_ 1,^ = 0. F.33)
Полагая, как прежде, | ф | = i]H/, где г|;^ = —- сх/р, и исключая из
F.30) и F.33) скорость v, находим
f - Г)''- F-34)
Связь между J и / показана на фиг. 51, б. Отсюда видно, что при
возрастании j от нуля функция / убывает от начального значения
/ = 1. Когда плотность тока J становится больше определенного
') Легко убедиться, что условие постоянства амплитуды | ty | совместимо
с граничным условием F.13).

Феноменологические уравнения Гинзбурга — Ландау
185
значения
т$(Т)
F.36)
решения с /=?0 отсутствуют вовсе. Таким образом, при j > jc пленка
находится в нормальном состоянии. Легко видеть, что в самой точке
перехода при j = jc параметр / скачком изменяется от значения,
равного 0,8, до 0. Величина jc но-
носит название критической плотности
тока для пленки. Выражение F-36)
определяет ее как функцию от г|^
и %(Т), т. е. фактически через па-
параметры аир теории Гинзбурга —
Ландау. Для оценок порядка вели-
величин иногда бывает удобным ввести
в рассмотрение критическую ско-
скорость vc, которая, по определению,
отвечает критической плотности тока
(J — jc). Из F.30) и F.35) видно,
что при j = j'c скорость v =
= vc — b\m\ (T). Для чистого ме-
металла
fivL
-Vi
поэтому
tnv.
V7")'
F.37)
F.38)
Фиг. 51. Определение критиче-
критического тока тонкой пленки тол-
толщиной d.
о —геометрия системы; б—соотношение
между параметром порядка / и плотно-
плотностью протекающего тока j /величины нор-
нормированы соответственно на значение па-
параметра порядка в отсутствие гока и на
величину критической плотности тока j?y
При j > jc параметр порядка скачком
обращается в нуль.
Интересно сравнить значение F.38) с максимальной величиной
скорости, связанной с мейсснеровскими токами в массивных сверх-
сверхпроводниках. Во внешнем поле И ток вблизи поверхности составляет
H'k соответственно скорость v равна
сН
F.39)
где К— глубина проникновения. Последняя дается выражением F.22а),
если температура достаточно близка к критической. Подставляя сюда
максимальное значение поля Яе = Dл/РI/:1|а| и используя определения

186 Глава VI
F.25) и F.26) параметра к, находим, что для сверхпроводников
первого рода наибольшая скорость равна
По порядку величины этот результат совпадает со значением F.38).
Для сверхпроводников второго рода максимальное поле, вплоть до
которого эффект Мейсснера остается полным, равно Нс1 ~~ Нс/я и,
следовательно, v~hlmk{T)<^hlm%(T), т. е. в массивных образцах
сверхпроводящие токи менее устойчивы, чем в пленках, вследствие
возможности образования вихревых нитей.
Поскольку критическая скорость пропорциональна (Тс — ТI*,
а критический ток меняется как tyfyvc, последний пропорционален
(Тс-Т)\
Измерение величины jc представляет собой очень тонкую экспери-
экспериментальную процедуру. Особое внимание нужно обратить на сле-
следующие моменты.¦
а) Необходимо обеспечить неизменность распределения магнитного
поля вблизи пленки. Обычно это осуществляется с помощью системы
экранов, сделанных из другой сверхпроводящей пленки.
б) Переход происходит сначала в каком-то „горячем участке*,
после чего остальная часть пленки переходит в нормальное состояние
за счет чисто тепловых эффектов. Положение вещей можно несколько
улучшить, если изготовить подложку пленки из материала с большой
теплопроводностью или работать в импульсном режиме.
в) Переход, определяемый по вольтамперным характеристикам,
оказывается „размазанным", а не скачкообразным.
Несмотря на эти трудности, результаты ряда тщательно поставлен-
поставленных опытов находятся, по всей видимости, в неплохом согласии
; теорией. В качестве примера сошлемся на работу Ньюхауза и Бре-
мера {100], в которой изучались тонкие пленки олова [|0^2300А,
rf^3000A, Тс^д>. 1(Г2оК, %L(T)~d и UT)^>d].
При указанных условиях измеренная плотность тока ]с составляла
— 104 ajcM2. Зависимость величины | ip | (или |А|) от тока можно
в принципе найти с помощью туннельных измерений величины щели.
(Детальный расчет показывает, что для данной геометрии щель
в спектре возбуждений примерно равна | А |.)
Сравнение опытных данных по критическим токам с теорией
следует проводить тоже с известной осторожностью. Во-первых, при
к (Т) — й становится существенным изменение плотности тока по
толщине пленки. Соответствующий расчет j легко выполнить, по-
поскольку при |г|)| = const в области применимости уравнений Гилз-
бурга—Ландау распределение плотности тока описывается простым

Феноменологические уравнения Гинзбурга — Ландау
187
лондоновским уравнением. Во-вторых, если, помимо условия
выполняется также более сильное неравенство d < ^G'=0), то урав-
уравнения Гинзбурга — Ландау вообще становятся неприменимыми (см. за-
задачу на стр. 225).
Эффект Литтла и Паркса [101, 102]
Рассмотрим сверхпроводящую пленку, нанесенную на изолирующую
подложку в форме цилиндра радиусом R, как показано на фиг. 52;
толщина пленки d<^R(d^300— ЮООА). Вдоль оси цилиндра при-
приложено однородное магнитное поле Н (составляющее обычно по
порядку величины несколько десятков гаусс).
Вычислим температуру сверхпроводящего перехода как функцию
приложенного магнитного поля. Излагаемый ниже метод расчета, осно-
основанный на уравнениях Гинзбурга — Ландау,
принадлежит Тинкхаму [103, 104]J). По-
прежнему будем считать, что d<^\(T),
d"^lh(T), а амплитуда |гр | постоянна внутри
пленки. Как обычно, положим
J
И
свободная энергия дается прежним выраже-
выражением F.32).
Если составляющая тока вдоль оси ци-
цилиндра равна нулю, то скорость v — тан-
тангенциальный вектор постоянной длины.
В предыдущем случае, когда ток в пленке
был фиксирован, скорость v была связана
с плотностью тока равенством
v=-
| -ф |
Фиг. 52. Схема опыта
Литтла и Паркса.
Измерялась температура сверх-
сверхпроводящего перехода тонкой
ной d, нанесенной на цилиндр
радиусом R ^> й, в аксиальном
поле Н.
В рассматриваемом случае задано внешнее цилиндрической пленки толщи-
магнитное поле Н. Чтобы связать его с ве-
величиной скорости v, рассмотрим циркуляцию
ф v • d\, где интегрирование ведется по окружности цилиндра ра-
радиусом R. Имеем
F.40)
ГДе [0] — изменение фазы при полном обходе вокруг цилиндра.
Функция г|) (г), будучи пропорциональной самосогласованному полю
') Теоретически этот вопрос в рамках уравнения Гинзбурга — Ландау
рассматривался Гинзбургом [105] в 1962 т. —Прим. ред.

188 Глава VI
А (г), должна быть однозначной (см. гл. V), т. е. [6] = 2т, где
п — любое целое число. Второй член в выражении F.40) пропор-
пропорционален интегралу
[ F.41)
т. е. магнитному потоку, заключенному внутри цилиндра. Следова-
Следовательно,
где ф0 = hcj2e — квант потока.
При фиксированном поле И поток ф также фиксирован, а ско-
скорость v, согласно F.42), может иметь бесконечный ряд дискретных
значений. Однако из F.32) следует, что свободная энергия имеет
минимум лишь при таком значении п, при котором величина ско-
скорости | v | минимальна. Таким образом,
^|) F-43>
т. е. v является периодической функцией поля Н с периодом ^0/
(значению R = 7 • 103А соответствует <j>(JnR2^il4 гс). Зная скорость v,
мы можем найти минимум свободной энергии относительно | ib |.
Это дает
(^i) F.44)
Очевидно, решение существует лишь при выполнений условия
— a > m'u2j2. Температура перехода Тн определяется условием
— а(Тн) = т1р12, т. е. Тн—периодическая функция поля Н. По-
Поскольку а~G"—Тс), окончательно можно заключить, что теорети-
теоретическая кривая Тн состоит из ряда параболических дуг. Наибольшее
смещение температуры перехода имеет место при
2m|» (?¦„)
Для пленки чистого вещества (толщиной d > l^), используя ранее
найденную зависимость ?G1) = 0,74|0A —TjT^~lh, получаем
= 0,55Ге (^J. F.46)

Феноменологические уравнения Гинзбурга — Ландау
189
ЗАМЕЧАНИЯ
1. Из F.45) следует, что условия d <^ ЦТ) я d
выполняются, если d <^ 2R, d <^_ 2Ян.
А (Т) фактически
а
Фиг. 53. Результаты опыта Литтла и Паркса [102].
в—температурная зависимость сопротивления R в нулевом поле при Г* ss Тс~ б —«кван-
—«квантовый гребешок» (осцилляции сопротивления как функции поля) при заданной температуре
Г* и Т?. Период осцилляции соответствует проникновению в цилиндр одного кванта потока
и равен ДЯ=ф„/я/?2 (Я —радиус пленки). Параболический «фон», по-видимому, объясняется
неточной ориентацией поля.
2. Практически часто используются пленки, для которых d < g0. В этом
случае F.46) заменяется следующим выражением:
Доказательство этого результата будет дано позднее (см. задачу на стр. 225).
3. Описываемые явления были обнаружены в опыте Литтла и Паркса
[101, 102] на тонких пленках. Очевидно, что для получения измеримой
величины смещения Те — Т радиус R должен быть по возможности малым.

190 Глава VI
Выше уже отмечалось, что значение R обычно составляет приблизительно
0,7 мк (пленка наносится на тонкую синтетическую нить), a d ~ 350A Со-
Сопротивление измеряется путем пропускания тока вдоль оси цилиндра. Же-
Желательно, чтобы ток был как можно слабее.
В отсутствие поля зависимость сопротивления /?(// = 0, Т) от темпера-
температуры имеет вид, показанный на фиг. 53; ширина области, в которой осу-
осуществляется переход, составляет примерно 0,0о° К.
В экспериментах выбиралась температура 7"*, лежащая в области пере-
перехода. Затем измерялась зависимость сопротивления R(H, T*) от поля.
Результирующая кривая (фиг. 53, б) для цилиндра радиусом /? = 0,7 мк
осциллирует с периодом, равным 14 гс. Из этих данных можно непосред-
непосредственно определить величину кванта потока Фо. Наоборот, вопрос относи-
относительно амплитуды осцилляции R (Н) до конца не выяснен, поскольку не-
недостаточно изучены механизмы диссипативных процессов, происходящих
в области перехода. (Установлено, в частности, что при наложении поля И
кривая R(T) не только сдвигается вдоль температурной оси, но и дефор-
деформируется.]
Как видно из фиг. 53, б, на осцилляции накладывается монотонное уве-
личеше сопротивления, квадратичное по Н, которое связано с диамагне-
диамагнетизмом образца. Выше предполагалось, что поле Н строго параллельнэ оси
цилиндра и d <^ К (Т). В этих условиях поле h не меняется по толщине
пленки и силовые 'линии почти не смещаются при переходе образца из нор-
нормального в сверхпроводящее состояние, т. е. диамагнетизмом последнего
можно пренебречь. Сказанное несправедливо в случае, когда поле направлено
под углом к оси цилиндра. Это обстоятельство приводит к заметному иска-
искажению силовых линий при сверхпроводящем переходе и к появлению в вы-
выражении для энергии члена, пропорционального Н2, ответственного за на-
наблюдаемое поведение сопротивления. (Экспериментально установлено, что
этот эффект очень чувствителен к ориентации цилиндра.)
Пластина в параллельном поле
Рассмотрим пластину толщиной d <|(T) в параллельном ее пло-
плоскости поле И, имеющем равные значения на обеих границах, т. е.
при z = ± d/2. Таким образом, в отличие от предыдущего случая
здесь мы с самого начала предполагаем, что результирующий ток
в пластине отсутствует. Чтобы убедиться в этом, рассмотрим случай,
когда поле h направлено вдоль оси у, а ток j — вдоль оси х. Тогда
из уравнения Максвелла
dh{z) __ 4я
dz с
следует, что
-d/2
т. е. в среднем токи в пластине взаимно компенсируются.
Рассмотрим подробнее распределение токов. Сначала обсудим
частный случай | ty | = const. Тогда, как мы уже видели, уравнение
Гинзбурга—Ландау сводится к уравнению Лондонов. Запишем по-

Феноменологические уравнения Гинзбурга — Ландау
следнее в виде
Отсюда
F9)
(как обычно, у = | л]? !/"ф0)- Решая это уравнение с граничным условием
/z(±d/2) = /y, находим
Ь=Н*№<ГI. F.50)
Ch (Е//2)
где z = dfk(T). Подставляя выражение для h в F.47) или F.48),
можно найти плотность тока ]. Для дальнейших вычислений удобно
ввести, как обычно, дрейфовую скорость электронов
г._ j = 2еК(Т)Н shlzf/ЦТ)]
mcf ch(e//2)
Зная скорость v, мы можем с помощью соотношения F.32) вы-
вычислить свободную энергию. Найдем усредненное (по толщине пла-
пластины) значение кинетической энергии
П« ]2/iH/) F.52)
* _\п 2 L mcf ch(E//2)
Минимизируя выражение F.32) относительно /, находим
/21 +
F-53>
С помощью основных соотношений F.8), F.15) и F.22) полученный
результат представим в виде
Ш2 =4/2A- Я ГA//2) - F.54,
Согласно F.54), величина / убывает с ростом И. В области с/
зависимость имеет вид
\нс) &
(I-/2). <*<С-^г-- F-55)
При е^^ 1 (позже мы увидим, что в интересующей нас области /
близко к единице)соотношениеF.54'записывается следующим образом:
F-56)
Найдем теперь критическое поле пленки, т. е. максимальное до-
допустимое значение Н. В том случае, когда переход в нормальное

192 Глава VI
состояние осуществляется путем фазового перехода первого рода, мы
должны для этого вычислить и сравнить значения потенциала Гиббса G
(при фиксированных значениях Н и Г) в сверхпроводящей и нормаль-
нормальной фазах! Вычислим сначала с помощью F.32) и F.52) плотность
свободной энергии Fs в сверхпроводящей фазе. Используя затем усло-
условие равновесия F.53) и соотношения F.8) и F.15), представим ее в виде
Hi ft*
EfтЕ F.57)
где
A* = l [tfdz = hPj-f+sbzl , F.58)
dJ/2 E/(l+che/) ;
а величина / дается выражением F.54). Нам также понадобится вы-
выражение для индукции В, которое легко получить, усредняя выра-
выражение F.50) для поля h:
B=H2th?fl2K F.59a)
е/
Читатель может легко проверить, что dF/dB = Н/4п. Поэтому поле Н
является равновесным полем — результат, который можно предсказать
сразу, исходя из приведенного в гл. II общего рассмотрения. По-
Построим, наконец, потенциал Гиббса
s s in " 8я [ e/(l+ che/) If \ 8я
4я " 8я [ E/(l+chE/) If J
F.596)
В нормальной фазе Gn = Fn — //2/8л. Чтобы найти критическое поле Н^
положим Gn == Gs, или, в явном виде,
4th(e/i/2)
Решая совместно уравнения F.54) и F.60), мы сможем определить
поле Ht и соответствующее ему значение параметра порядка ^ =
Исключая Н[ из этих уравнений, находим
n^:. F.61)
6 l-fj 3 Sh(E/,)-E/,
На фиг. 54, а отложены обе стороны уравнения F.61) в зависимости
от /|. При /j—>-0 левая часть изменяется как l-|-/j?/6, а правая —
как 1 4- (е/г/30J, т. е. для е > у^5 правая часть растет быстрее
левой. При /i = 1 левая часть расходится. Поэтому для е > |/

0,1 0,1 0,3 Ofi 0,5 0,6 0,7 0,8 0,3 7,0
Фиг. 54. Поведение пленки в параллельном магнитном поле.
а—график левой (пунктир) н правой (сплошная кривая) сторон уравнения F.61) в зависимо-
зависимости от нормированного параметра порядка fj. Показан случай, когда имеет место пересечение
кривых [d > YskjTJl. „
б —зависимость параметра порядка /^ от отношения ?=<*/?. (Г) при "е> Vs (переход первого
рода); прн е < V5 имеет место фазовый переход второго рода (/,=5 0).
в — зависимость энергетической щели в алюминии от магнитного поля, полученная Дугласом
|109| на основе туннельных измерений на двух образцах: d Я 3000 А, Г = 0,745Гс, d/K=l,9
(образец 1) и dpi 4000 А, Г=О,774 Т^ d/K=3,5 (образец 2). Для более тонкой пленки скачок
практически не заметен.
13 Зак. 1020

194 Глава VI
в области между fl = 0 и /^=1 должна существовать точка пересе-
пересечения. Напротив, при е < У^5 такое пересечение отсутствует (см. также
фиг. 54, б).
Таким образом, при d > |/5 К (Т) имеет место фазовый переход
первого рода при критическом поле Hv определяемом соотношениями
F.60) и F.61). При d < \^5 К (Г) во всей области существования
решения /; ф 0 потенциал Gs лежит ниже, чем Ол; параметр г]э при
увеличении поля И убывает по закону F.54), пока не обращается
в нуль при поле
;?р F.62)
Переход, происходящий в поле Ht, является фазовым переходом вто-
второго рода. Возможность существования двух типов поведения в за-
зависимости от величины отношения djK(T) была предсказана Гинзбур-
Гинзбургом [106] в 1952 г. (см. также [107]). В дальнейшем его выводы
получили качественное подтверждение в экспериментах Дугласа [108]
по туннельному эффекту на алюминии (|0 = 16 000 А). Дуглас пока-
показал, что
1) энергетическая щель е0 в спектре возбуждений убывает с уве-
увеличением поля; о
2) при Г =& 0,757^ в пленках толщиной d~> 3500 А щель скачком
падает от конечного значения до нуля при достижении полем крити-
критического значения; о
3) при той же температуре в пленках толщиной d < 3500 А щель е0
плавно уменьшается до нуля при возрастании поля вплоть до крити-
критического значения.
Эти результаты представлены на фиг. 54, в. Отчетливо видна
разница в поведении, характерном для фазового перехода первого
и второго рода. К сожалению, дальше этих качественных суждений
продвинуться трудно по следующей причине. Для всех изученных
пленок выполнялось неравенство Я (Г), d < Iq, поэтому плотность
тока j сильно менялась на расстояниях порядка |0 (вспомним, что при
переходе с одной стороны пленки на другую плотность тока j меняет
знак). Очевидно, что в этих условиях уравнения Гинзбурга — Ландау
становятся неприменимыми').
') На первый взгляд, кажется заманчивой возможность сохранить в рас-
рассматриваемом случае уравнения Гинзбурга — Ландау, введя некоторый
„эффективный" параметр и, меняющийся по толщине пленки. Однако, по-
поскольку распределение плотности тока j зависит одновременно от d и К (Г),
ясно, что при данной толщине пленки параметр и также будет зависеть
от X (Т) и, таким образом, потеряет свою универсальность. Более того, даже
в пределе Л G") ^> d численные значения параметра и, полученные из изме-
измерений критического поля и критического тока (для той же пленки), будут
различными.

Феноменологические уравнения Гинзбурга — Ландау 195
Отметим, что в сильных полях энергетическая щель е0 для тонких
пленок не совпадает со значением параметра | Д |. В частности, имеется
конечная область в плоскости (И, Г), в которой е„ = 0, но Д Ф О
(бесщелевая сверхпроводимость). Это обстоятельство также несколько
усложняет анализ результатов эксперимента.
Задача. Сверхпроводящая пленка в форме тонкостенного цилиндра ра-
радиусом R (большим по сравнению с толщиной пленки 2rf) находится в маг-
магнитном поле Ло, параллельном оси цилиндра. Определить поле Лг в полости
цилиндра для следующих двух случаев:
а) так называемый „флюксоид" Ф/ (см. определение ниже) поддерживается
постоянным;
б) величина Фу может меняться и принимает наиболее выгодное значение.
Решение По определению, „флюксоид" Фу пропорционален измене-
изменению фазы [<р] параметра порядка при полном обходе вокруг цилиндра:
Сразу отметим, что изменение [<р], допустимое пунктом „б" условия задачи,
на практике непременно должно сопровождаться образованием в пленке ви-
вихревых нитей либо макроскопических „пучков" нитей.
а) Полагая в F.12)
запишем плотность тока в виде
Для слабых полей h0 амплитуду параметра порядка [ ij? | можно считать равной
ее значению i]50 в отсутствие поля. Интегрируя затем обе стороны написан-
написанного выражения по окружности, проходящей по внутренней поверхности
цилиндра, находим
где Ф[ — поток, заключенный в полости, а К — глубина проникновения [см.
F.22а)]. Можно считать, что поле h внутри пленки удовлетворяет уравнению
(ось х направлена перпендикулярно пленке) и граничным условиям (при
х= ±d)
h(d)^h0, h{—d) = hl.
Решение, очевидно, имеет вид
l,_K-hi 8"<*'*-> i hc+h
" — 2 ШЩЦ "I ~
Вычисляя теперь в явном виде циркуляцию ф j • rfl и сравнивая ее с преды-
предыдущим выражением, легко найти искомое поле
Ф/ 2ft0
^4+
1 2 ctB{2dA)+ /?//, nlf 2shBd/k)
13*

196 Глава VI
В частности, при (Еу = 0 имеем
Вообще говоря, поле hi очень мало по сравнению с внешним полем Ло, за
исключением случая чрезвычайно тонких пленок (d ^ Л2//?).
б) Предположим теперь, что Of может меняться; в заданном поле Ао его
величина определяется из условия минимума потенциала Гиббса &. Запишем
выражение для & в виде
* = W J (?)* * + Т5Г J (Л - ^J rfr + const-
Подставляя сюда ранее полученное решение для поля, можно показать, что
минимуму потенциала & соответствует /гг=й0.
Таким образом, в состоянии термодинамического равновесия поле внутри
полого цилиндра равно приложенному. Однако в экспериментах, в которых
поле меняется во времени, часто случается, что равновесие не успевает уста-
установиться за время наблюдения. Тогда мы встречаемся со случаем, когда поле
внутри цилиндра мало.
§ 6. ИЗМЕНЕНИЕ АМПЛИТУДЫ |ф| В ПРОСТРАНСТВЕ
Образование зародышей внутри массивного образца
Рассмотрим сверхпроводящий металл, находящийся в сильном маг-
магнитном поле. Если сделать величину поля достаточно большой, сверх-
сверхпроводимость разрушится и поле становится однородным во всем объеме
образца. Будем теперь плавно уменьшать величину поля. Тогда при
достижении полем определенного значения Н = НС2 в образце спон-
спонтанно начнут образовываться сверхпроводящие области. Дальше мы
увидим, что поле НЛ не совпадает с полем Нс; в зависимости от
условий оно может быть как больше, так и меньше.
В той области, где начинают возникать сверхпроводящие зародыши,
параметр | if | мал, что позволяет произвести линеаризацию уравнения
Гинзбурга — Ландау
(^)Ч = -сяр. F.63)
Кроме TorOj в уравнении F.63) можно считать, что го1А = Н, где
Н — однородное внешнее поле. Это допустимо потому, что сверхпро-
сверхпроводящие токи пропорциональны | я|> р, следовательно, вызванные ими
поправки к полю в линейном приближении пренебрежимо малы. Таким
образом, уравнение F.63) формально совпадает с уравнением Шре-
дингера для частицы с зарядом 2е и массой т в однородном маг-
магнитном поле.
Рассмотрим сначала случай неограниченной среды, в которой ча-
частица движется вдоль поля с постоянной скоростью vz и одновременно

Феноменологические уравнения Гинзбурга — Ландау 197
совершает движение по окружности в плоскости ху с частотой
Уровни энергии, соответствующие собственным функциям уравнения
F.63), имеют вид
^!D) F.64а)
где п—положительное целое число. В частности, наинизшему уровню
энергии отвечает vz = О и п = О, так что
-a = 2*L. F.646)
тс v '
Полученное таким образом поле Н представляет собой поле Н^.
(Другим уровням с vzф0 и пфО соответствуют при том же значе-
значении а меньшие поля.) Используя соотношение а2/2р = Щ\%п и выра-
выражение F.26) для параметра и теории Гинзбурга — Ландау, оконча-
окончательно получаем
или
ОБСУЖДЕНИЕ ФОРМУЛЫ F.65)
1. Для и> 1/У, т. е. Ис < Яй, конденсированная фаза A|)?=0)
образуется в толще образца при полях Н < Яй. Эта фаза не может
приводить к полному вытеснению магнитного потока из образца, по-
поскольку при полях Н > Нс полный эффект Мейсснера энергетически
невыгоден, и мы можем считать, что Нс < И < Нл. Фактически со-
состояние, получающееся при полях, меньших Ил, представляет собой
смешанное состояние, которое мы обсуждали в гл. III. Как там и
предсказывалось, верхнее поле имеет порядок фу%,2(Т). Это значение
поля соответствует плотной упаковке вихревых нитей, каждая из
которых несет квант потока $0 и имеет остов радиусом порядка |(^).
2. Для v. < 1/У^2, т. е. Нл < //с, при уменьшении поля сначала
достигается поле Нс, при котором возникает полный эффект Мейсснера,
иначе говоря, мы имеем сверхпроводник первого рода. Таким обра-
образом, деление сверхпроводников на два типа можно произвести в за-
зависимости от величины параметра и. Для сверхпроводников первого
рода и < 1/У^2, для сверхпроводников второго рода и> ^
Образование зародышей вблизи поверхности образца
Соотношение F.65) справедливо лишь для безграничной среды,
поскольку при его выводе мы полностью пренебрегли эффектами на
границах образца. В действительности в идеальных материалах, как

198 Глава VI
впервые было показано в работе Сент-Джеймса и автора [ПО], об-
образование сверхпроводящих зародышей всегда в первую очередь
происходит на поверхности образца. Рассмотрим теперь подробнее
влияние поверхности образца в простейшем случае, когда эту по-
поверхность можно считать плоской [радиус кривизны намного пре-
превышает 1G")]. Кроме того, будем предполагать, что сверхпроводник
находится в контакте с диэлектриком или вакуумом, следовательно,
применимо граничное условие F.13). Рассмотрим два случая.
1. Поле (направленное вдоль оси г) перпендикулярно поверхно-
поверхности (плоскость ху). Очевидно, функция я]), соответствующая наиниз-
наинизшему уровню F.646), является также собственной функцией опера-
оператора Пг — — thipjdz) — leAJc с собственным значением 0. Поэтому
условие F.13) автоматически удовлетворяется и поверхность не влияет
на величину поля, при котором впервые образуются зародыши.
2. Поле, по-прежнему направленное вдоль оси z, параллельно
поверхности образца (плоскость у г), а сверхпроводник занимает по-
полупространство х>-0. Возьмем калибровку, в которой Ах — Az — G,
А И и будем искать решение в виде
F.66)
Тогда уравнение F.63) принимает вид
h* d»f , 1 / 2еНх \а t
ш[Г)F.67)
с граничным условием
(SL F-68)
Уравнение F.67) совершенно аналогично уравнению Шредингера
для гармонического осциллятора с частотой сос [см. F.63а)] и поло-
положением равновесия в точке
Х F-69)
Несколько усложняет анализ наличие граничного условия F.68).
Пусть л:0^^> ^(У); тогда волновая функция локализована вблизи х0
и близка к нулю на поверхности, т. е. условие F.68) автоматически
выполняется. Эта волновая функция имеет вид
Собственное значение по-прежнему определяется уравнением F.63).
Если же л;0>=0, то функция вида F.70) тоже удовлетворяет гра-
граничному условию F.68) и соответствует прежнему собственному зна-
значению F.63). Покажем теперь, что в промежутке между этими край»

Феноменологические уравнения Гинзбурга —Ландау 199
ними случаями, а именно при лго~|(Г) существует решение, кото-
которое отвечает наинизшему собственному значению [меньшему F.646)].
Для доказательства заменим уравнение F.67), справедливое лишь
при х > О, уравнением
которое справедливо во всем интервале —: оо < х < оо. Потен-
Потенциал V (х) при х > 0 совпадает с потенциалом, входящим в исход-
исходное уравнение F.67), а при х •< 0 является его симметричным про-
продолжением, как показано на фиг. 55, а:
г- (х — хЛ2, х > О,
V(x)= mc* * F.72)
V(~x), x<0.
Волновая функция основного состояния [соответствующая наимень-
наименьшему собственному значению уравнения F.71)] не имеет нулей
и является четной, т. е. автоматически удовлетворяет условию F.68).
В области х < 0 потенциал V(x) удовлетворяет неравенству
(см. фиг. 55, а), поэтому, очевидно, наинизший уровень энергии при
наличии потенциала V (х) лежит ниже значения, определяемого урав-
уравнением F.646). Следовательно, наличие поверхности способствует
образованию зародышей.
Численный расчет показывает, что оптимальное значение х0 равно
0,59|(Г); тогда для собственного значения получаем
-0 = 0.59-^-. F.73)
Соответствующая собственная функция представляет собой функцию
Вебера, имеющую довольно сложный вид. Однако, как впервые от-
отметил Киттель (не опубликовано), хорошее приближение к точному
решению можно получить более простым путем, применяя вариацион-
вариационный метод к уравнению Шредингера F.67)г). Беря в качестве проб-
пробной функции гауссову функцию
f(x) = e-™<
и минимизируя | а | по отношению к г и х0, получаем
N^F 1-«-^г==0-60-^г-
Обозначим через Нс3 поле, при котором начинается образование
зародышей. Используя F.65), запишем основной результат F.73)
в виде
Яс3 = 2,4иЯс = 1,7ЯЙ. F.74)
') Расчет поверхностной сверхпроводимости с помощью вариационного
метода см. в работе [139]. — Прим. ред.

Фиг. 55. Поверхностная сверхпроводимость в сильных магнитных полях,
о—потенциал гармонического осциллятора V м=соп8* (¦*—¦*„)'. симметричный потенциал
V (jc) и собственная функцня / (Jf) основного состояння. Так как V < ^гарм. низший уровень,
отвечающий потенциалу V, лежит ниже, чем для потенциала Vra_M.
б—поверхностная сверхпроводимость в случае сферы. Если Н немного меньше 7/^, вдоль
экватора образуется узкий сверхпроводящий пояс. При уменьшении // этот пояс расши-
расширяется и при ff—ff^ достигает полюсов.
в —принципиальная схема определения полей Нс2 и Нсз для полого цилиндра (Бурже и др.
[lllj). Поле Н> И перпендикулярно оси цилиндра. На его поверхности образуются две нор-
нормальные области в виде продольных полос (показаны штриховкой). Их возникновение сопровож-
сопровождается резким увеличением самоиндукции, что регистрируется с помощью катушки, навитой
на цилиндр. Ширину полос можно определить, измеряя сопротивление между точками А ч В.
Ток течет от А к А', далее по сверхпроводящей области от А' к В', затем от В' к В, Со-
Сопротивление пропорционально расстоянию А А'.

Феноменологические уравнения Гинзбурга — Ландау
201
ОБСУЖДЕНИЕ СООТНОШЕНИЯ F.74)
1. Сверхпроводники второго рода. Приведенное рассмотрение пока-
показывает, что при полях, больших Нсъ в интервале НС2 < Н < Исъ сверхпро-
сверхпроводимость разрушается не полностью; основная часть материала находится
в нормальном состоянии, однако в определенных областях поверхности со-
сохраняется сверхпроводящий слой. В цилиндре, находящемся в продольном
поле, этот слой занимает всю боковую поверхность. В случае сферы поло-
положение иное. Когда поле Н лишь незначительно меньше, чем Нс3, сверхпро-
сверхпроводящий слой представляет собой узкий пояс вдоль экватора (фиг. 55, б).
При уменьшении величины Н пояс расширяется и, наконец, достигает по-
полюсов при Н = Нс2.
i.o - _
0.5-
<i
HCZ
i
Snln
i
,-x-x
!
/7
10
300
400
Н, гс
а
500
30 60
в, град
6
90
Фиг. 56. Экспериментальные данные относительно критических полей для
сверхпроводников второго рода
й —результаты измерений самоиндукции на полых цилиндрах нз сплава Snln (см. фиг. 55, в).
Если поле Н перпендикулярно оси цилиндра, то разность потенциалов V, пропорциональная
самоиндукции катушки, резко возрастает при //=//. Еслн же поле // параллельно оси, воз-
возрастание потенциала происходит при Н—Н3 (Бурже и др. [111]).
б —угловая зависимость величины ^C3(W^C2 для сплава РЬ + 5 ат. % В1 при температурах
4,2° К G) н 1.6° К B) (Бурже и др. |112]).
Для наблюдения сверхпроводящего слоя на поверхности используются
различные методы, например: а) измерение сопротивления (при слабых
измерительных токах сопротивление слоя равно нулю); б) индукционные
измерения на низких частотах. Пока на поверхности цилиндра имеется
сверхпроводящий слой, силовые линии не могут пересекать его и самоин-
самоиндукция катушки мала; при достижении полем значения Н = Нсз сверхпро-
сверхпроводящий слой исчезает и восстанавливается полная величина самоиндук-
самоиндукции (фиг. 56, а). Аналогичные, но более трудные эксперименты можно

202 Глава VI
в принципе выполнить с помощью измерений импеданса в микроволновом
диапазоне.
При работе с пленками, толщина которых велика по сравнению с ? (Г),
можно использовать различные чувствительные методы, например измерение
плотности состояний с помощью туннельных экспериментов. При наличии
сверхпроводящего слоя эта величина сильно отличается от ее значения для
нормальной пленки. Другой метод состоит в измерении крутильного мо-
момента, который может возникнуть при появлении в образце небольших
диамагнитных областей.
В результате подобных опытов было установлено, что в образцах с до-
достаточно чистой поверхностью и с радиусом кривизны, значительно пре-
превышающим величину ? G), сверхпроводящий слой действительно существует
в полях, лежащих в интервале НС2 < Н < Нсз (9), где 9 — угол между по-
полем Н и нормалью к поверхности. При 9 = 0 экспериментальная величина
Нсз @) весьма близка к теоретическому значению F.74). Зависимость Нсг (9)
от угла в для сплавов PbBl показана на фиг. 56, б; при 9 -> я/2 поле Нсз (9)
стремится к значению Нс2. _
2. Сверхпроводники первого рода с 0,42 <¦/,</ Y2. В данном случае
Нсз < Нс, но Нсз > Не поэтому в области полей Нс < И < На по-преж-
по-прежнему должен существовать сверхпроводящий слой (если поле Н параллельно
или почти параллельно поверхности образца). Такой слой действительно
наблюдался на некоторых сверхпроводниках первого рода, а именно на
чистом свинце, а также его разбавленных сплавах.
3. Сверхпроводники первого рода с у. < 0,42. Здесь Нс3 < Нс, поэтому
в состоянии термодинамического равновесия сверхпроводящий слой наблю-
наблюдать невозможно. Тем не менее величину поля Нсз удается измерить. Дело
в том, что хорошие образцы могут оставаться в нормальном (метастабиль-
ном) состоянии при понижении поля до значений, меньших Нс. Например,
для А1 поле можно понизить, не вызывая перехода, до значений, мень-
меньших Нс/10. Однако метастабильная нормальная фаза никогда не сохраняется
вплоть до нулевого значения поля, поскольку при достижении поля Исз
вблизи поверхности образца могут образоваться сверхпроводящие слои,
причем этот процесс происходит без затраты энергии. При полях Н ¦<//«
нормальная фаза абсолютно неустойчива. Процессы образования зародышей
были тщательно изучены в опытах Фабера [ИЗ] на различных сверхпровод-
сверхпроводниках первого рода. Он показал, что зародыши возникают прежде всего
вблизи поверхности образца (в то время не было ясно, что это является
фундаментальным свойством), и измерил соответствующее значение поля,
которое мы теперь называем полем Нсз. Используя его результаты, можно
попытаться оценить с помощью уравнения F.74) значения параметра к для
изученных им материалов. Грубая оценка дает следующие значения к
0,015 для А1; 0,07 для In; 0,10 для Sn.
Такой способ нельзя считать вполне корректным для рассматриваемых
чистых металлов, поскольку для них уравнения Гинзбурга — Ландау при-
применимы лишь при температурах, очень близких к Тс, в то время как поля
переохлаждения измерялись обычно при более низких температурах. Для
полноты мы приведем также „теоретические" значения и, полученные с по-
помощью соотношения F.27) [параметры ^@) и ? находятся с помощью
данных по измерению поверхности Ферми в нормальном состоянии и экспе-
экспериментальных значений Тс]. Эти значения к таковы:
0,010 для А1; 0,05 для In; 0,15 для Sn.

Феноменологические уравнения Гинзбурга — Ландау 203
§ 7. СТРУКТУРА СМЕШАННОГО СОСТОЯНИЯ В СИЛЬНЫХ
ПОЛЯХ Н ~Н а
Рассмотрим цилиндрический образец, изготовленный из сверх-
сверхпроводника второго рода (и>1Д^2), во внешнем поле И, парал-
параллельном оси цилиндра. Если уменьшать поле Н, то при Н = Н(Л
в объеме образца начнут образовываться сверхпроводящие зародыши.
При этом амплитуда параметра порядка | ty | мала, так что вид функ-
функции т|з можно определить, исходя из линеаризованного уравнения
Гинзбурга — Ландау F.63). При дальнейшем уменьшении поля Н
число зародышей увеличивается, амплитуда | ty | также возрастает
и для определения характера образующейся периодической струк-
структуры необходимо решать систему сложных нелинейных уравнений
Гинзбурга — Ландау. Такая задача может быть решена только чис-
численным образом.
Однако, если поле Н лишь незначительно меньше Нс2, возникают
значительные упрощения [33]. Из соображений непрерывности сле-
следует ожидать, что решение ty полной системы уравнений Гинзбурга —
Ландау должно быть во многих отношениях близко к решению 1р?
линеаризованного уравнения
\ I . 2е
где
rotA0= @, 0, Нс2). F.756)
Собственные функции т|з? уравнения F.75а) сильно вырождены; фи-
физически это связано с тем, что зародыши могут независимо возни-
возникать в любой части образца. Например, для рассматриваемой калиб-
калибровки А0=@, хНл, 0) мы уже нашли решения вида
Ф* = exp (iky) ехр [- I {х 7±J1.
А* F-76>
где k — произвольный параметр. Такие решения описывают зародыши
в форме полосы [шириной —|СО]. перпендикулярной оси х; поло-
положение ее середины (х = х0) зависит от выбранного значения k.
Функция !])?, как мы знаем, должна представлять собой линейную
комбинацию функций tyk- Из упрощенного анализа, проведенного
в гл. III, следует, что амплитуда 11|) | является периодической функ-
функцией хну. Следовательно, если период по у равен 2n/q, функция tyL

204 Глава VI
должна иметь вид
F.77)
Чтобы амплитуда | igL | также являлась периодической функцией по х,
необходимо на коэффициенты Сп наложить условие периодичности.
Следуя Абрикосову, положим
где v — фиксированное целое число; тогда
Независимо от конкретного вида функции 1|э? [см. F.77)] удается
установить ряд общих теорем.
/. Нормировка функции %. Исходные уравнения F.11) и F.12)
являются нелинейными относительно ф, поэтому вопрос о нормировке
функции tyL не является тривиальным. Предположим, что пробная
функция !])? дает значение свободной энергии, остающееся стацио-
стационарным при замене 1р?->A +е)ф?, где е — малое число, не зави-
зависящее от г. В линейном по е приближении вариацию свободной
энергии можно написать в виде
. F.78)
Для простоты интегралы типа 11|^ р dr, взятые по объему V образца,
будем обозначать через V^i^l2. Тогда, используя F.78), условию
стационарности Ь^ = 0 можно придать вид
= 0. F.79)
Это уравнение можно несколько упростить, приняв во внимание, что
функция "фЛ удовлетворяет уравнению F.75а). Для этого положим
A = A0-f-Aj, где Aq—соответствующий полю НЛ вектор-потенциал,
определяемый соотношением F.756). Добавка Aj появляется вслед-
вследствие того, что, во-первых, приложенное поле несколько меньше,
чем НЛ, и, во-вторых, в образце возникают сверхпроводящие токи,
также дающие вклад в величину поля. Выделяя в уравнении F.79)
члены первого порядка по Aj и используя F.75а), находим
РИМ- Т VH = 0. F.80)

где
Феноменологические уравнения Гинзбурга — Ландау 205
= ir [*I (- т - Ч Ао) *i + Компл- СОПР-]
— плотность тока, соответствующая невозмущенному решению. Инте-
Интегрируя в F-80) второй член по частям и полагая rotA1 = h1, roths =
= Dл/с) \L, окончательно получаем
Р|~Ф1Г—-^«4^ = 0. F.82)
2. Связь между полем и параметром порядка. Чтобы записать
условие F.82) в явном виде, необходимо знать поля hx и hs. (Осно-
(Основываясь на результатах гл. III, можно думать, что поля hj и hs всюду
параллельны оси Z.) Положим
А1(г) = //-//Й + А,(г). F.83)
где поле hs описывает вклад сверхпроводящих токов 1).
Для вычисления поля hs предварительно докажем следующее
свойство. Если tyL отвечает наинизшему собственному значению
— а = h(oJ2 уравнения F.75а), то линии тока \L совпадают с линиями
\§L | = const.
Доказательство. Введем вектор
П = Bт/гсвс)-1/2 (- ihV — Ц- Ао)
и П± = П^ ± Шу; коммутатор [П+, П_| равен единице. В этих обозначе-
обозначениях уравнение F.75а) можно записать в виде
П^П_ф? = 0. F.84)
Собственные функции уравнения F.84) удовлетворяют условию
Положим
Тогда, приравнивая действительную и мнимую части выражения П_ф? нулю
и используя F.85), находим
, . F-86)
i =?*_?_!* IS
JLy m Ox I ^LI'
l) Ток )L = (с/4я) rot h^ не является, строго говоря, сверхпроводящим,
поскольку в выражение F.81) вместо А, входит Ао. Однако мы скоро уви-
увидим, что величины Яс2 — И и | ф \2 одного порядка и, следовательно, член
(Ао — А) | ф |2 того же порядка, что и | Ир |4, т. е. в рассматриваемом прибли-
приближении им можно полностью пренебречь.

206 Глава VI
Отсюда видно, что линии тока являются одновременно линиями постоянных
значений | Ф^ |.
Сравнивая F.86) и определение rot hs — Dя/с) \L, легко получить
явное выражение для поля hs, возникающего из-за наличия сверх-
сверхпроводящих токов
Постоянная интегрирования выбрана равной нулю из условия, что
рф7Р = 0 при Й5 = О. Подставляя F.83) и F.87) в F.82), оконча-
окончательно находим
F.88а)
Полезно переписать это уравнение в несколько ином виде, положив
|il>?| = il>o/ и вводя величины и и И^ с помощью соотношений
F.26) и F.64):
ОИМ^-0- F-88б)
В такой форме уравнение F.886) играет особо важную роль, по-
поскольку оно не зависит от конкретного вида функции ^L, т. е. не
зависит от характера структуры, образуемой вихревыми нитями.
Выбирая определенную решетку, т. е. считая известными значение q
и период коэффициентов Сп, можно явно вычислить величину отно-
отношения
й ^А. F.89)
(/2J ГА
соответствующего данной решетке. В свою очередь, зная рЛ, легко
найти с помощью F.886) и F.89) средние /4 и /2. Этих сведений
вполне достаточно для вычисления индукции и свободной энергии.
1. Индукция В, по определению, представляет собой результат
усреднения поля Н + п5. С помощью F.87) ее можно представить
в виде
в=н + К=н—
в=н
тс
н -
f2
2. Плотность свободной энергии F можно вычислить, исходя
из F.9) и F.11):
Hi
F-91>

Феноменологические уравнения Гинзбурга —Ландау 207
Возвращаясь к F.87), выразим h2 через Н, f2 и /4. Исключая затем И,
/2, /4 с помощью F.886), F.89) и F.90), получаем выражение для
плотности свободной энергии, содержащее только индукцию В:
Д» (Яс2-ДJ
Г ^ЬУ2)
1. При заданном значении индукции В свободная энергия F является
возрастающей функцией §А, если к > 1/|^2. Наиболее выгодная „решетка"
соответствует наименьшему значению РЛ. [Заметим, что, согласно F.89),
РА>Ч
Формально выбор решетки осуществляется путем наложения опреде-
определенных условий периодичности на коэффициенты Сп в разложении F.77).
Практически подробно исследованы два вида решеток вихревых нитей,
а именно квадратная и треугольная. Квадратная решетка получается,
если положить все коэффициенты Сп равными между собой, а треугольная
при условии, что
с, = /с0.
В обоих случаях параметр <? выбирается из требования, чтобы величина рл
для данной конфигурации имела минимальное значение. Найдено, что для
квадратной решетки РЛ=1,18; для треугольной рд=1,16, т. е. последняя
обладает несколько большей устойчивостью [43, 44]. Линии | -ф |2 = const
для треугольной решетки показаны на фиг. 26.
2. Зная Рл, с помощью выражения F.92) для свободной энергии можно
произвести расчеты интересующих нас термодинамических величин. Прежде
всего легко убедиться, что
как и следовало ожидать. Затем можно вычислить намагниченность
М = = f , -^ <^ 1. F.93)
4Я 4ярBх21) Н ^
Как мы и предполагали, М имеет порядок [ ф |2; при Н — Нс2 намагничен-
намагниченность обращается в нуль. В этой точке имеет место фазовый переход вто-
второго рода. (Однако, если параметр к лишь незначительно превышает 1/У~2,
то величина наклона | dM/dH \ становится очень большой.) Детальная про-
проверка выражения F.93) была проведена в опыте Кинсела и др. [114] на
сплаве InBi, содержащем 2,5% Bi. Этот сплав представляет собой сверхпро-
сверхпроводник второго рода с почти обратимой кривой намагничивания. Получен-
Полученная из измерений намагниченности фазовая диаграмма для этого сплава
показана на фиг. 57. По экспериментальным значениям поля Нс2 вблизи Тс
можно определить параметр
4
х4=».8О-
Y 2 Нс
С другой стороны, полагая рл=1,16 в выражении F.93) и сравнивая его
с экспериментальной кривой намагничивания, найдем
и =1,81.

208
Глава VI
Полученное прекрасное согласие подтверждается также теоретическим рас-
расчетом параметра к описанным ниже ').
Задача. Показать, что поверхностная энергия для сверхпроводников
первого рода обращается в нуль при к = 1/)/2~.
300
Z00
100
'cl
г. "к
Фиг. 57. Фазовая диаграмма для сверхпроводника второго рода — сплава
inBi (Кинсел и др. [114]).
Решение. Используемый ниже метод расчета принадлежит Сарма (не
опубликовано). Пусть поле h направлено вдоль оси z; тогда уравнение
Гинзбурга — Ландау становится двумерным:
где П= р — B<?А/с). Полагая II ± = Нх ± 1Иу, имеем
Будем рассматривать решения ф, удовлетворяющие условию
Для этого частного класса решений значения поля h и параметра порядка ф
в произвольной точке сверхпроводника связаны между собой простым со-
') Столь хорошее согласие представляется даже несколько удивитель-
удивительным, поскольку экспериментальные кривые намагничивания не вполне обра-
обратимы, что в свою очередь должно приводить к погрешностям при опреде-
определении наклона (dM/dH)H .

Феноменологические уравнения Гинзбурга — Ландау 209
отношением
Естественно, поля и токи, вычисленные с помощью этих частных реше-
решений, не должны противоречить уравнению Максвелла
rot h = ^-} = ^
Используя полученную ранее зависимость h (т])), преобразуем левую часть
последнего уравнения следующим образом. Выполнив дифференцирование,
имеем
Воспользуемся снова условием П+ф = 0, представив его в виде
Окончательно получаем
ду дх eh2 ТУ Т'
Это уравнение согласуется с уравнением Максвелла, если
4ле Рте
тс eh2
т. е. х = 1/у1Г в соответствии с условием задачи.
Обратимся теперь к рассмотрению границы, разделяющей нормальную
и сверхпроводящую области. Пусть она лежит в плоскости yz. Тогда при
х -> — со, т. е. в нормальной области h = Н^ ф = 0, тогда как при
дг->-|-оо, т. е. в сверхпроводящей области h = 0, I ijj I2 = — а/р. Оба усло-
условия согласуются с полученным выше выражением для h (ф), поэтому его
можно использовать для решения поставленной задачи. Запишем термодина-
термодинамический потенциал (на единицу площади в плоскости yz)
Т
(Здесь последний -член представляет собой микроскопический аналог члена
— В///4я, в котором следует положить Н = Нс.) Интегрируя по частям тре-
третий член этого выражения и учитывая, что функция ij) удовлетворяет урав-
уравнению Гинзбурга — Ландау, запишем & в виде
а? =
Для получения поверхностной энергии \ из написанного выражения нужно
вычесть интеграл Г(Я^/8я)йл:, равный термодинамическому потенциалу
в нормальной (или сверхпроводящей) фазе:

210 Глава VI
Представим зависимость h (i])) в виде
1
при Х-7Г
/ тс \2 1
Отсюда следует, что у = 0, если и = l/j/.
Аналогичным образом тем же методом удается вычислить до конца энер-
энергию изолированной вихревой нити для и = l/j/ ¦ В результате оказывается,
что для этого частного значения параметра у. все три поля Нси //с2 и Нс
равны по величине.
ЛИТЕРАТУРА
Дальнейшие применения уравнений Гинзбурга — Ландау
Saint-James D., Sarma G., Thomas E. J., II Type Superconductivity,
London, 1968.

Глава VII
МИКРОСКОПИЧЕСКИЙ АНАЛИЗ УРАВНЕНИЙ
ГИНЗБУРГА —ЛАНДАУ
§ 1. ЛИНЕАРИЗАЦИЯ УРАВНЕНИЯ САМОСОГЛАСОВАННОСТИ
В гл. VI мы вывели уравнения Гинзбурга — Ландау, постулировав
выражение для свободной энергии F, содержащее неизвестный коэф-
коэффициент [например, коэффициент С в выражении F.7)]. Этот коэф-
коэффициент учитывает энергию, связанную с пространственными измене-
изменениями параметра порядка. Горьков [115] показал, что уравнения
Гинзбурга — Ландау можно получить из микроскопической теории, и
вычислил, в частности, коэффициент С. Здесь мы приведем эти рас-
расчеты в несколько упрощенном виде.
Учет А по теории возмущений
Будем исходить из уравнения самосогласованности
Д (г) = V 2 «„ (г) v* (г) [1 — 2/(е VI, G.1)
где коэффициенты преобразования Боголюбова ип, vn являются соб-
собственными функциями системы уравнений
6 А = I"ЯГ (Р ~ Т А) + U - Ef\ "" + Avn'
G.2)
для положительных собственных значений е„. Как обычно, влияние
примесей и тому подобные эффекты включены в U. Представим пра-
правую часть уравнения G.1) в виде ряда по степеням Д, положив
*» = *+<+-• G-3)
В нулевом приближении, согласно G.2), функции и°п и v°n про-
пропорциональны одноэлектронным волновым функциям ф„ для нормаль-
нормального металла
Ьл>«=[ ш (р - т АГ+и - ер] *»• G-4)
14*

212
Глава VII
Именно
= о. ^ =
G-5)
и е°=|?я1- Поскольку везде m^J = O, в нулевом приближении пра-
правая часть уравнения G.1) равна нулю.
Чтобы найти поправки первого порядка и1п и vxn, разложим их
в ряд по полной системе функций ф„
G'6)
Подставим G.6) в G.2), умножим первое уравнение на ф^, а второе
на фт и проинтегрируем по г. Тогда система примет вид
Как обычно, диагональные члены типа епп следует приравнять нулю
для сохранения условия нормировки \и \2-\-\v\2= 1.
Выделим в уравнении самосогласованности G.1) члены первого
порядка по А. Используя затем уравнения G.6) и G.7) для и' и «Л,
получаем
A(s)= jtf(s. r)A(r)dr, G.8)
где
/C(s, г) = ^
/z, m
Входящие сюда функции и^ (или г»^), согласно G.5), отличны от нуля
лишь для ?„>0 (или Ея<0). Функция 1 — 2/(ел) = th(Р|я/2) не-
нечетна по ?„. Это позволяет нам объединить члены типа ии и w.
Симметризуя, кроме того, выражение под знаком суммы по индек-
индексам пит, окончательно напишем
W-

Микроскопический анализ уравнений Гинзбурга — Ландау 213
Иногда бывает удобно несколько преобразовать этот результат, вос-
воспользовавшись разложением
где h(n = '2.nkBT(у-\-xli), а суммирование производится по всем це-
целым (положительным и отрицательным) числам v. Тождество G.10)
легко проверить, сравнивая с обеих сторон положение полюсов
в комплексной плоскости \ и вычетов в них. [Заметим, что вместо
минуса перед / в знаменателе в G.10) можно поставить и плюс, по-
поскольку величина <о при суммировании принимает оба знака.] Таким
образом,
th(P?/2) + tb(P?'/2) _ т у 1 / 1 ¦ 1 \ __
F—/to)
@
о л, яг
Уравнение G.8) вместе с явным выражением G.11) для ядра пред-
представляет собой линеаризованное условие самосогласованности G.1).
Огромное преимущество уравнения G.8) по сравнению с G.1) состоит
в том, что в него не входят функции и, v, а входит лишь един-
единственная неизвестная функция А (г). Конечно, необходимо всегда пом-
помнить, что линеаризованная форма применима лишь при малых значе-
значениях А, т. е. в непосредственной близости к точке фазового пере-
перехода.
Выделение магнитных эффектов
Предположим, что вектор-потенциал А мало меняется в простран-
пространстве. Тогда собственные функции фя в нормальном металле при нали-
наличии вектора-потенциала А отличаются от собственных функций wn
(в отсутствие А) лишь фазовым множителем
G.12)
Функции wn мы выбрали вещественными. Легко убедиться, что за-
замена G.12) совместима с уравнением G.4) и с определением wn, если
полностью пренебречь пространственными изменениями вектора-потен-
вектора-потенциала А. Остановимся подробнее на вопросе об области примени-
применимости сделанного приближения.

214 Глава VII
1. Позже мы увидим, что радиус действия ядра /C(s, r) в чистом
металле имеет порядок %0 = 0,l8(tivplkBTc). Следовательно, вектор-
потенциал должен мало меняться на таких расстояниях. Это означает,
что поле h должно изменяться медленно; иными словами, глубина
проникновения kL(T) должна быть большой по сравнению с ?„:
G-13)
2. Наоборот, если поле h = rotA изменяется медленно, то отсюда
не следует автоматически, что вектор-потенциал А также будет
меняться медленно, поскольку на расстояниях | s — г j — ?0 последний
может измениться на величину порядка ?0А. Это дает следующую
неопределенность в фазе:
последняя величина должна быть мала по сравнению с единицей.
Таким образом, мы приходим к еще одному условию
где ас = еЩтс —¦ циклотронная частота электронов в нормальном
металле в поле А. Для массивных сверхпроводников первого рода
поле А самое большее может быть равно полю ИС(Т). Согласно
F.29), F.25) и F.19), для чистого металла
T
J с
где и — параметр Гинзбурга — Ландау, a <j>0 = hcjie — квант потока.
Тогда условие G.14) можно записать в простом виде A —Т/Тс) < и.
Это условие менее жесткое, чем неравенство G.13), которое можно
записать в виде A—T/tJ1' < и. Для сверхпроводников второго
рода поле А имеет самое большее порядок поля Нс2 — (Фо1Щ(^—^/^с)-
Условие G.14) в этом случае принимает вид A —TjT^)<^ 1.
3. Совершенно ясно, что замена G.12) возможна только в тех
случаях, когда радиус электронной орбиты R = mcVp/eh в поле А
велик по сравнению с радиусом действия ядра К (s, r). Это условие
позволяет пренебречь всеми эффектами, связанными с диамагнетизмом
Ландау. Запишем требование R^>lo в виде
c; G.15;
последнее условие является менее жестким, чем G.14).
Таким образом, мы приходим к выводу, что для чистых металлов
замена G.12) законна, если температура Т достаточно близка к кри-
критической температуре Тс. Дальше мы увидим, как с помощью этой

Микроскопический анализ уравнений Гинзбурга — Ландау 215
замены можно непосредственно перейти к уравнениям Гинзбурга —
Ландау. В „грязных" сплавах ситуация оказывается даже более благо-
благоприятной. Именно, линейное интегральное уравнение G.8) при всех
температурах можно заменить дифференциальным уравнением вто-
второго порядка, формально напоминающим линеаризованное уравнение
Гинзбурга — Ландау.
Окончательно имеем
Д (s) = J drK0 (s, г) ехр [2| А • (s - г)] Д (г), G.16)
к (ti r\ — Vk Г V V Wn(r)wm(r)w
A0(S, r) — VHBi ^j 2л (tmtt
Бесконечная однородная среда
Чаще всего приходится рассматривать ядро /Со для бесконечной
однородной среды. Если эта среда представляет собой чистый металл,
то ядро K0(s, г), очевидно, будет зависеть лишь от разности s — г.
Напротив, в сплавах трансляционная инвариантность отсутствует
и, чтобы обеспечить ее, необходимо сделать дополнительные пред-
предположения. Усредним уравнение G.16) по всевозможным конфигура-
конфигурациям примесей; тогда в его правой части появится среднее типа
/C0(s, г)Д(г). Аппроксимируем его следующим образом:
Ко (s, г) Д (г) -> Ко (s, г) Д (г). G.18)
Замена G.18) не является вполне строгой, поскольку при этом мы
пренебрегаем эффектами изменения потенциала спаривания Д непосред-
непосредственно вблизи каждой примеси. Подробные вычисления [92] показы-
показывают, однако, что такое приближение во всяком случае разумно,
если потенциал примесей можно рассматривать как. малое возмущение.
Имея в виду это обстоятельство, мы будем считать, что компоненты
сплава не слишком сильно отличаются в химическом отношении1).
Тогда замена G.18) законна, и интегральное уравнение для А (г)
можно записать через усредненное ядро /Со(«, г), зависящее лишь
от разности s — г.
Связь ядра Л",, с функцией корреляции
На первый взгляд может показаться, что наличие произведения
Четырех функций wn в выражении G.17) сильно затрудняет даль-
дальнейший анализ. Однако, как мы сейчас увидим, это произведение
имеет довольно простой физический смысл. Рассмотрим для простоты
') См. примечание 1 на стр. 159. — Прим. ред.

216 Глава VII
однородную бесконечную среду и перейдем к фурье-компонентам
Ко (q) = ZT3 J dx dsK0 (s — г) «*И»-г) _
-VL~\ Т У W*I"О U I'"**!") r7 1
~KL *?/ л (i«-/fi»)(im4-^) ' GЛ
(i4
со, п, m
где Z,3 — объем образца, а вектор q направлен вдоль оси л\ Входящие
сюда матричные элементы определяются следующим образом:
(п | в»* | m) = J ^я (г) e'4"wm (r)rfr.
Полезно обсудить сначала вещественную функцию
g (<?• О) = 2 (п|е'**|т)(лф-«*|в) 6 (^ -1„ — Ш), G.20)
которую иногда называют спектральной плотностью одноэлектрон-
ного оператора eiqx. Черта означает усреднение по всем состояниям
с заданной энергией Ь,п (уровню Ферми отвечает |я = 0). Функция
g(q, Q) сильно зависит от Q и слабо—от |„, так что фактически
усреднение производится при энергии, равной фермиевской. Зная g,
можно сразу написать выражение для ядра
Функция g(q, Q) имеет простой физический смысл. Введем гейзен-
гейзенберговский оператор
описывающий изменение во времени оператора eiqx для электрона
в нормальном металле в отсутствие примесей; ?}6
одного электрона:
В терминах оператора e'W) спектральная плотность принимает сле-
следующий простой вид:
g(q, Q) = -~ J d/e'O^nle-'e'We'e'WIn). G.23)
Соотношения G.23) легко проверить, если выписать в явном виде
матричные элементы оператора в'?* О между состояниями num.
Таким образом, для вычисления спектральной плотности g не-
необходимо знать функцию корреляции оператора е^х, т. е. функцию
? (\\) G.24)
для электрона, находящегося на уровне Ферми в нормальном металле.

Микроскопический анализ уравнений Гинзбурга — Ландау 217
1. Чистый металл. Предположим, что при ? = 0 электрон
находится в точке х0 на оси х и имеет вдоль этой оси компоненту
скорости t>Fcos0 @ — угол между q и направлением скорости элек-
электрона). Тогда
giqx (О _ Qiq (xo+vpt cos в)
Следовательно,
=i. ( smQdQeiQVFtcose G.25)
E
о
gig, Q)=iFsinerfe6(Q№cose) f
I 0. IQI > qvF.
G.26)
2. „Грязный" металл. Для „грязного" металла, в котором длина
свободного пробега / мала по сравнению с характерной длиной
волны q~x, изменение оператора eW) со временем происходит по
закону случайных блужданий. В этом случае при l^\
=zze-Dq2\t\%
РЯ2 G-27>
где D = lvp[3 — коэффициент диффузии.
Явное выражение для ядра Ко
Исходя из G.21) и используя выражения G.26) и G.27) для g(q, Q),
легко найти явный вид ядра K0(q). Выберем в качестве переменных
интегрирования ? и ftQ = |'—|; интегрирование по ? легко выпол-
выполняется с помощью теории вычетов. В результате для чистого металла
получаем
qvp
г dQ
arctg Г
2ТЙ7 *

218 Глава VII
Аналогично в случае „грязного" металла
W@) VkJ
при
ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
1. Обрезание взаимодействия V по частоте. До сих пор мы пре-
пренебрегали тем обстоятельством, что взаимодействие V в приближении БКШ
связывает лишь состояния с энергиями 111 < 6юд. Это приводит к тому,
что суммы G.28) расходятся. Последнее, однако, легко исправить, записав
/Co<tf) = *o(O) + [Ko@-Ko<O)]. G.29)
Здесь расходящимся является лишь первый член Ко @), который легко
вычисляется с помощью G.17)
J -Jth(f) = A4O)V4ni^L. G.30)
При выводе этой формулы мы выполнили интегрирование по s, воспользо-
воспользовавшись ортогональностью функций wn (s) ')•
2. Пространственная зависимость ядра Ко- Совершая обратное пре-
преобразование Фурье, находим из G.28)
1 -2\a\R/vB
G-31а)
G-316)
где R ==¦ s — г. При ЯфО суммы сходятся.
Особый интерес представляет асимптотическое поведение ядра Ко (R)
на больших расстояниях. Для таких расстояний важный вклад в сумму по «
') С результатом G.30) мы уже сталкивались при рассмотрении более
простого случая, а именно бесконечного однородного сверхпроводника
в отсутствие полей и токов, когда параметр Д (г) можно считать постоянным
во всем пространстве. Тогда линеаризованное уравнение самосогласованности
принимает особенно простой вид Д = ^0 @) Д. Его нетривиальное решение
Д ф 0 существует лишь при выполнении условия ^0 @) = 1, определяющего
критическую температуру Тс сверхпроводника

Микроскопический анализ уравнений Гинзбурга — Ландау 219
дают только члены с fc=± лквт (,~±лквТсУ Таким образом, при Т —Тс
4R) kBTc 1 -Чяк Т mhv " Т
G.32а)
ь
G.326)
вь/вол
Для чистого металла при Т^аТс радиус действия ядра K0(R)
составляет.— 40 = 0,18 (hvPjkBTc), как уже упоминалось выше. Если же
пробег / мал, то соотношение G.326) дает для радиуса действия
величину —УЫ- Применимость соотношения G.326) ограничена
условием R^>1, откуда следует (IqZ) ~^>l, или
По терминологии, введенной Андерсоном, сплавы, для которых вы-
выполняется неравенство G.33), называются „грязными". Если матрица
сплава является непереходным металлом с большой величиной ?0 (на-
о
пример, для алюминия ?0=1,6- 104А), то небольшой доли примесей
(— 10~3) достаточно, чтобы сделать металл „грязным" *).
Представляет также интерес сравнить Ко с ядром S^ (см. гл. V),
определяющим ток, который возникает в сверхпроводнике при нали-
наличии вектора-потенциала А. Мы знаем, что радиус действия ядра S^
в „грязном" сплаве имеет порядок /, в то время как для Ко эта ве-
величина составляет "
Чтобы понять причину такого отлнчия, выразим оба ядра S^v и ^0 че-
через усредненные одноэлектронные функции корреляции в нормальном ме-
металле в отсутствие полей
f))Bp. G.34)
= | ^v @) v } di di> [th <w/a+g( к'/ЗД ] x
L el «"б') '/* F [r @) - r,l 6 [r @ - r2])Ep, G.35)
где (/ц/v) — функция корреляции поперечного тока, а F6) — функция кор-
корреляции плотности.
Соотношения G.34) и G.35) легко проверить, явно вычисляя матричные
элементы, появляющиеся в произведениях типа jajv Из-за интегрирований
¦) В обычных сплавах физические явления (такие, например, как пере-
переход чистого сверхпроводника первого рода в категорию сплавов второго
рода) разыгрываются при /~6, где 6 — глубина проникновения. Напомним,
что обычно 6 <^ |0 у большинства металлов. — прим. ред.

220 Глава VII
по | и I' в G.34) и G.35) при Т к Тс в окончательный результат суще-
существенный вклад дает интервал t ~> Ъ\к^Гс. В отсутствие соударений за время t
электрон проходит расстояние v^^^, поэтому оба ядра S^v и Ка имеют
радиус действия порядка ?0- Если же сплав является .грязным", то функция
корреляции скорости быстро спадает до нуля при прохождении электроном
расстояния ~ /, т. е. характерный радиус ядра S(IV ~> /. На таких расстоя-
расстояниях функция корреляции плотности еще отлична от нуля. Согласно ура-
уравнению диффузии, средний путь, проходимый электронами за время t, равен
~> YDt (D = lvpJZ — коэффициент диффузии), поэтому радиус действия
ядра/Со составляет ~>У~Ш~УШ'
§ 2. УРАВНЕНИЯ ГИНЗБУРГА—ЛАНДАУ
Введение нелинейных членов в уравнение
самосогласованности
Линеаризованное уравнение самосогласованности G.8) для потен-
потенциала спаривания применимо лишь для бесконечно малых значений
параметра А, т. е. в самой точке перехода (при условии, что изучае-
изучаемый переход является фазовым переходом второго рода, т. е. пара-
параметр Д непрерывно уменьшается до нуля при повышении температуры).
Обозначим через Т* наивысшую температуру, при которой уравне-
уравнение G.8) впервые обладает нетривиальным решением А (г), т. е. имеет
место фазовый переход. Температура Т* определяется условиями
опыта. Например, для массивного сверхпроводника второго рода,
помещенного во внешнее поле Н, температура Т* определяется ура-
уравнением НЛ (Т*) = И. В дальнейшем мы обсудим этот вопрос более
подробно. Сейчас перед нами стоит несколько иная задача. Мы хотим
обобщить предыдущий анализ на случай температур, близких к кри-
критической (Т < Т*). Для этого нужно учесть нелинейные члены в раз-
разложении правой части уравнения G.1) в ряд по Л. Вычисляя и и v
с точностью до членов более высокого порядка по А, аналогично
предыдущему получаем
Л (s) = J Ko (s, г) е2'? IA'(S -r>I/*c A (r) dr +
R(s, r, 1, m)b*(r)A(l)b(m)drdldm. G.36)
Следует отметить, что в написанном разложении отсутствуют члены
порядка А2. Явный вид ядра /?(s, г, 1, ш) можно вычислить; здесь
необходимо помнить лишь одно его важное свойство: в чистом ме-
металле область действия ядра R имеет размеры ^^ Иными словами,
при интегрировании по г, 1 и m в последнем члене основной вклад
дают такие точки г, 1 и гп, которые одновременно близки к точке S.
В сплавах область интегрирования еще больше сокращается. Это
позволяет нам избежать подробных вычислений ядра R.

Микроскопический анализ уравнений Гинзбурга — Ландау 221
Гипотеза о медленности изменений
Предположим, что величины типа Д(г)ехр[—2/еА • (г—s)/fic]
медленно меняются на расстояниях порядка радиуса действия ядер Ко
и R; это определяет область применимости уравнений Гинзбурга —
Ландау. Разложим функцию Д(г)ехр[—2ieA - (г — s)//»cl в ряд Тей-
Тейлора вблизи точки s:
о. Р
где введен фазовый параметр
Выполняя дифференцирование, получаем
\ 2(r - s)°(r -
д (Г) е- 2/ф (г) = е- 2/ф (» J д (S) _|_ 2J (г — s)a6аД +
I а
„)рД], G.37)
а, Р
Подставим разложение G.37) в линейный член уравнения G.36); для
члена, кубического по Д, с хорошей точностью можно полностью
пренебречь пространственной зависимостью Д и положить Д (г) =
= Д A) = Д (щ) = Д (s). Наконец, для бесконечного однородного ме-
металла члены типа [ K0(r—s)(r—s)dr обращаются в нуль в силу
симметрии. Таким образом, приходим к уравнению
Д (s) = Q Д (s) +12 Iap6a6p Д (s) + RI A (s) P Д (s), G.38)
а,Р
где
Q=JK0(s-r)dr,
L4 - J Ко (s - г) (sa - rj (sp - rp) dr. G.39)
R = J R (s, r, 1, m) dr d\ dm.
Для кубического кристалла ?„„ = Lba^, в этом случае уравнение G.38)
совпадает с уравнением Гинзбурга—Ландау F.11). Введенные здесь
коэффициенты Q, L и R связаны с коэффициентами А, В и С

222
Глава VII
выражения F.7) следующим соотношением:
^Atl = Tf = Y-Z:' <7-40>
Обсуждение коэффициентов
Коэффициенты А и В для случая, когда А = 0 и Д = const, были
определены ранее [см. F.3)]. Аналогичным образом можно найти
численные значения коэффициентов Q и R. Мы знаем, что Д= const
при А = 0; в этом случае уравнение самосогласованности G.1) при-
принимает ВИД
haD
Согласно теореме Андерсона (см. гл. V), уравнение G.41) применимо
как к чистым металлам, так и к сплавам. Разлагая правую часть
этого уравнения в ряд по Д и выполняя интегрирование, получаем
G.42)
Наибольший интерес представляет коэффициент L, описывающий
влияние пространственных изменений параметра Д. С помощью явного
выражения G.31) для ядра Ко находим, что для чистого металла
. G.43а)
В с
Для „грязного" металла
В С
G.436)
[Суммирование по ю в G.43а) должно выполняться численно; для
вычисления суммы в G.436) достаточно продифференцировать тожде-
тождество G.10) по ? и затем положить ?=0.]
Эти результаты позволяют получить ряд полезных соотношений.
1. Коэффициент С в выражении F.7) для свободной энергии
имеет вид
Г L A l L П АЛ^

Микроскопический анализ уравнений Гинзбурга — Ландау 223
2. Характерную длину ?G), входящую в уравнение Гинзбурга —
Ландау F.18) в отсутствие поля, можно получить, сравнивая F 17)
и F.8):
В согласии с F.19) она расходится как A—T/Tc)~'/s при Т^Т .
3. Параметр Гинзбурга — Ландау и, по определению [см. F.26)],
равен
1 ( В V/. he
тс- G-46>
Для чистого металла отсюда следует вышеприведенный результат:
% = 0,96^? @)/^,. Для „грязного" металла
X, @)
х = 0.75-til. /<Cio. G-47)
где
— лондоновская глубина проникновения для чистого металла при Т = 0.
Результат G.47) можно представить в другом виде, введя вместо /
и ^@) величины, непосредственно измеримые на опыте с нормаль-
нормальными металлами. Длина свободного пробега / связана с удельным
сопротивлением р соотношением1)
\ N@)e2vl. G.48)
Далее, лондоновская глубина проникновения равна2)
^Vf. G.49)
8nN @) v2Fe*) '
') Плотность тока j в нормальном металле дается выражением
j = — eDVn+ Е/р, где п — число электронов в 1 см3. В состоянии равно-
равновесия « = «0 — 2N @) еV, где V — потенциал электрического поля Е = — VV.
Отсюда, полагая j = 0. получаем соотношение G.48).
2) При наличии статического вектора-потенциала А сфера Ферми в им-
импульсном пространстве испытывает смещение как целое иа величииу 6р = ehjc,
что приводит к появлению тока с плотностью
где / — функция распределения электронов. После несложных вычислений
находим
Отсюда непосредственно следует выражение G.49) для %L @).

224 Глава VII
Наконец, выразив плотность состояний N @) через электронную часть
теплоемкости Сеп при низких температурах (отнесенную к единице
объема)
окончательно получим
X, @) 1 се
Выражая р в ом~1 • см~1 вместо единиц CGS, получаем
G-51)
НЕСКОЛЬКО ЗАМЕЧАНИЙ ОТНОСИТЕЛЬНО „ГРЯЗНЫХ- СПЛАВОВ
1. Согласно G.47), параметр у. для сплава зависит только от /, т. е.
определяется транспортными свойствами системы в нормальном состоянии.
2. Если исходный чистый металл является сверхпроводником первого
рода (я<^1 1), то сплав представляет собой сверхпроводник второго рода
(и > I/I'?), когда длина свободного пробега I меньше критического значе-
значения lc= l,06Az @). Этот закон был проверен в опытах Серафима и др. [116]
на индии [X @) ~ 400А] с различным содержанием примесей. Критическая
концентрация сильно зависит от рода используемой примеси (например,
для Т1 она равна 7%, а для Bi всего лишь 0,8%), однако значение 1С при
этом остается почти неизменным (/с= 440 ± ЮоА для Bi, Pb, Sn, Cd, Tl и Hg).
3. Для сплава InBi B,5% Bi) из магнитных измерений Кинсела и др.
[114] следует, что у. = 1,79. Теоретическая оценка по формуле G.51) дает
v. к 1,7. Основные параметры чистых и «грязных" металлов сопоставляются
в табл. 5.
ЗАКЛЮЧИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
Все предыдущее рассмотрение касалось только первого уравнения
Гинзбурга — Ландау, т. е. уравнения самосогласованности F.11) для Д(г)
[или tj) (г)]. Чтобы завершить микроскопический анализ, нужно было бы
вычислить также плотность тока j (г) в произвольной точке г и показать,
что она описывается выражением типа F.12). Это можно проделать совер-
совершенно аналогично предыдущему, выражая j(r) через пики разлагая по-
полученное выражение в ряд до членов второго порядка по Д. Мы не при-
привели здесь этого расчета, поскольку он ие дает ничего нового; все три
коэффициента А, В и С в выражении для свободной энергии F.7) уже из-
известны и мы могли бы изучать непосредственно выражение для свободной
энергии. В принципе оба подхода совершенно эквивалентны. Мы предпочли,
имея в виду дальнейшие применения, обсудить уравнение самосогласован-
самосогласованности для Д.

Микроскопический анализ уравнений Гинзбурга — Ландау
225
Таблица О
Основные параметры чистого и -«грязного» металлов
Радиус дейст-
действия ядра
5(lv, связы-
связывающего
ток с векто-
ром-потен-
ром-потенциалом
Радиус дейст-
действия ядра Ко,
входящего
в уравнение
самосогла-
самосогласованности
для А (г)
Масштаб про-
странствен-
странственных измене-
изменений | А | в
области при-
применимости
уравнений
Гинзбурга —
Ландау
Глубина про-
проникновения
в области
применимо-
применимости уравне-
уравнений Гинз-
Гинзбурга —
Ландау
Чис гый металл
hv „
t — О IS F
so iU»
Be
/ T \~l/2
| (?) = 0,74g0 1 — — -
\ * с 1
\ IT\ 1 /n\ M I
Ь\')= .лг^ @I 1 ~-\
v 2 L \ i с 1
«Грязный» металл
/
~(WI/2
t m_ 0 851/77/4 T \~1/2
s w; — u.eoj' go' 11 1
Л(Г) = 0,64Х @)i/IX
r t
/ r \-l/2
Задача. Вывести уравнение Гинзбурга — Ландау для тонкой пленки
^ go) B случае диффузного отражения электронов от границ.
ешение. Вообще говоря, ответа на поставленный вопрос не суще-
существует — уравнения Гинзбурга — Ландау применимы не всегда ').- Например,
эффективный параметр % может зависеть от угла между магнитным полем
и плоскостью пленки. Хуже того, он мог бы зависеть от отношения d/K (Г),
которое в свою очередь сильно изменяется с температурой.
') См. примечание на стр. 194. —Прим. ред.
15 Зак. 1020

226 Глава VII
Существует, тем не менее, один случай, когда можно построить дву-
двумерное уравнение Гинзбурга — Ландау, имеющее вполне определенный смысл.
Для этого должны выполняться два условия. 1) Амплитуда параметра Д по-
постоянна по толщине пленки. Это условие выполняется, если d < g0, т. е.
(где z — направление нормали к пленке). 2) Изменение вектора-потенциала А
по толщине пленки пренебрежимо мало. Это означает, что поле должно быть
перпендикулярно пленке и что толщина пленки должна быть меньше неко-
некоторой эффективной глубины проникновения (см. ниже). Вместе с тем вели-
величины А и А могут медленно изменяться лишь в плоскости пленки (пло-
(плоскость ху). Тогда свободная энергия имеет вид
Чтобы найти коэффициент С, будем исходить из линеаризованного уравне-
уравнения самосогласованности G.16). Рассмотрим фурье-компоненту ядра Ка (q),
где q — вектор в плоскости ху. Для малых толщин (rf<§^ lo) большая часть
электронов испытывает несколько соударений со стенками за время ti/k T .
Поэтому функция g (q, Q) описывается уравнением диффузии, как и в случае
„грязного" сверхпроводника ')• Вычисления вполне аналогичны приведенным
при выводе G.43) и G.44). В результате получаем
Здесь коэффициент диффузии D составляет ~ vpd вместо прежнего значе-
значения vFl/3. Удобно выразить его через электропроводность а пленки, которую-
можно найти из измерений в нормальном состоянии. Согласно G.48).
Д
16e2 kBTc '
Теоретический расчет а можно найти, например, в книге Олсена [117].
На практике, безусловно, предпочтительнее брать экспериментальные значе-
значения а для той же самой пленки в нормальном состоянии.
') Имеется небольшая доля электронов, которые не испытывают соуда-
соударений с границами, так как их скорости лежат в плоскости пленки. Оказы-
Оказывается, что их можно включить в рассмотрение строго. Однако для про-
простоты мы будем здесь считать, что в объеме пленки также присутствуют
примеси, следовательно, /-^s0. H0 l> d (I — длина свободного пробега
в массивном материале). При таких условиях вкладом от этих .аномальных"
электронов можно пренебречь.

Микроскопический анализ уравнений Гинзбурга — Ландау
227
ОБСУЖДЕНИЕ
1. По порядку величины электропроводность а равна ne2d/mvp, поэтому
2. Зная коэффициент С, мы можем написать выражение для плотности
тока (в направлении оси х)
~ 1Ь \ дх ~а дх )
Ы
Подчеркнем, что даже для малых толщин d истинное распределение плот-
плотности тока ]х (г) по толщине пленки неоднородно (фиг. 58). Написанное вы-
выражение для тока представляет собой результат усреднения функции jx (г)
по толщине пленки.
Фиг. 58. Распределение тока по сечению тонкой пленки (d < *„) для
случая диффузного отражения электронов от поверхности.
3. Хотя плотность тока jx (z) меняется по толщине, вектор-потенциал А
с хорошей точностью можно считать не зависящим от г. Действительно-
с помощью уравнения Максвелла
легко показать, что
относительное изменение
в том случае, когда Ах является четной функцией zy
иие величины Ах по толщине составляет ~ d3/le№<^\.
§ 3. ПОВЕРХНОСТНЫЕ ЗАДАЧИ И УРАВНЕНИЯ
ГИНЗБУРГА — ЛАНДАУ
Граничные условия нз поверхности раздела
В § 2, исходя из микроскопической теории, мы получили урав-
уравнения Гинзбурга — Ландау для бесконечной однородной среды. Рас-
Рассмотрим теперь сверхпроводящий образец, занимающий полупро-
полупространство х ^> 0; область х < 0 занята либо диэлектриком, либо*
15*

228
Глава VII
нормальным металлом. В обоих случаях будем предполагать отсут-
отсутствие токов через границу раздела!).
Очевидно, в пределах расстояния *,, от границы раздела выраже-
выражения для ядер Л(г, г') и S^sr, r') должны быть видоизменены2).
й
Ь
Ф и г. 59. Поведение параметра порядка А вблизи границы раздела сверх-
сверхпроводника (S) и нормального металла (N).
а — результат микроскопического рассмэтрения; б —макроскопическое описание той же ситуации
при температурах, близких к критической, когда \ (Г) >> Ь.
Наша задача состоит в том, чтобы с помощью микроскопической
теории найти эти видоизменения, а затем рассчитать пространствен-
пространственное распределение плотности тока j и параметра порядка Д в воз-
') В том случае, когда в образце одновременно существуют нормальные
и сверхпроводящие токи, возникают процессы диссипации, которые должны
вычисляться с помощью более общих уравнений, чем уравнения Гинзбурга —
Ландау.
2) Приведенная оценка относится к чистому металлу. В „грязных" спла-
сплавах ширина „области перзхода", очевидно, уменьшится до величины по-
порядка Viol-

Микроскопический анализ уравнений Гинзбурга — Ландау 229
мущенном слое вблизи границы. Поведение Д качественно показано
на фиг. 59, а. С другой стороны, на расстояниях порядка |(Г) или
Я (Г), на которых применима теория Гинзбурга — Ландау 11G"), Я(Г)^>
^§>|0], влияние поверхности образца легко учесть, введя новый тип
граничного условия при х — О (фиг. 59, б). В случае к^гда А = О,
а параметр Д веществен, это граничное условие можно записать
в виде следующего ряда:
НЕСКОЛЬКО ЗА МЕЧ АЛИЙ ОТНОСИТЕЛЬНО ФОРМУЛЫ G.52)').
1. Из общего вида уравнения самосогласованности следует, что
разложение G.52) может содержать только нечетные степени Д.
Кроме того, длины Ь, с и т. д. должны быть вещественными.
2. Производные более высокого порядка в разложении G.52)
можно не рассматривать, поскольку с помощью уравнений Гинзбурга —
Ландау их можно выразить через первую производную и саму функ-
функцию.
3. Можно ожидать, что нелинейные эффекты становятся сущест-
существенными при h~kBTc (коэффициенты \[b, \jc и т. д., вообще го-
говоря, имеют одинаковый порядок величины .<С 1/?о). Вблизи Тс отно-
отношение члена порядка Д3 к члену порядка Д составляет ~(klkBTcJ<^ 1.
Таким образом, в области применимости теории Гинзбурга — Ландау
вторым членом в G.52) можно пренебречь и граничное условие ста-
становится линейным. Для определения коэффициента b нужно решить
уравнение самосогласованности G.8) вблизи поверхности (при Т=ТС
и А = 0). При наличии магнитного поля вместо G.52) можно написать
М_2Ь Л =Ь-1. G.53)
\ их Ьс х 1Х=О Ъ '
Граничное условие вида G.53) обеспечивает градиентную инва-
инвариантность, которая должна иметь место в соответствии с общими
соображениями, приведенными в гл. V. В условии G.53) параметр Д
можно заменить пропорциональной ему функцией 1|з. С помощью G.53)
легко также убедиться в том, что при вещественном значении коэф-
коэффициента Ь ток F.12), текущий через границу раздела, равен нулю,
как и предполагалось с самого начала.
') Микроскопический вывод граничных условий для контакта нормаль-
нормального металла со сверхпроводником содержится в работах Зайцева [118]. —
Прим. ред.
16 Зак. 1020

230 Глава VII
Контакт сверхпроводника с диэлектриком
(или вакуумом)
Покажем, что в том случае, когда сверхпроводник граничит с ди-
диэлектриком, коэффициент 1/й мал. Задача состоит в решении урав-
уравнения
A(s)= J/C0(s. r)A(r)rfr G.54)
при А —0, Т=ТС. Из выражения G.17) для ядра K0(s, г) следует,
что параметр A(s) содержит произведение двух функций [wn(s) и
«>m(s)], которые убывают экспоненциально при удалении от границы
внутрь диэлектрика. Следовательно, величина A (s) мала при sx < 0.
Напротив, в области sx > ^ функция Д (s) линейно возрастает
при удалении от границы')
A(s)=,A0(H-^). G.55)
Действительно, для расстояний sx, гх > ?0 ядро K0(s, г) переходит
в ядро Кр (s — г) для массивного металла. При Г — 7"с любая ли-
линейная функция вида G.55) представляет собой решение уравнения
A (s) =JMS — О А (r)dr-
поскольку
а интеграл
Jp(s — r)[A(r)-A(s)]dr
обращается в нуль в силу симметрии.
Чтобы определить интересующую нас длину Ь, перепишем урав-
уравнение G.54) в виде
K0(s, r)— Kp(r-s)]A(r)dr = ~H(s). G.56)
Функция H (s) обращается в нуль при sx > |0, поскольку Ко -> /^„,
и также при $„. < —10, поскольку А (г) = 0 для гх < 0, а радиус
действия ядра Кр составляет ~'|0. Уравнение G.56) обладает тем
') На первый взгляд может показаться, что линейная зависимость G.55)
не имеет физического смысла, поскольку она приводит к очень большим
значениям А иа больших расстояниях от границы. На самом же деле при
температурах, лежащих немного ниже 7"с, правильное решение Д (х) имеет
отрицательную кривизну и внутри сверхпроводника [х > g (T)] достигает
значения Д,,. Здесь мы интересуемся областью л:~|(><^|G'), в которой
влиянием кривизны можно пренебречь.

Микроскопический анализ уравнений Гинзбурга — Ландау 231
преимуществом, что его правая часть содержит возмущение, локали-
вованное в точке. Считая пока H(s). известной функцией, будем
искать решение Д с помощью преобразования Лапласа
G.57)
где
Явный вид L дается выражениями G.43). Применяя преобразование
Лапласа к уравнению G.56), получаем
Отсюда в пределе р -> 0 с помощью G.57) находим
>—Л @) =-///(*,) rfs. G.58)
С другой стороны, при р—>-0 зависимость А от координат в основном
линейна [см. G.55)]:
А(/»—? J 8У*ав = $. G.59)
о
где 2—площадь поверхности. Сравнивая G.58) и G.59), получаем
I = Л- J H(sx)ds = -J^ { (/fp(s-r)-K0 (s, r)J Д (r) dt ds. G.60)
Чтобы упрсстить это выражение, предположим, что взаимодействие V
постоянно. Воспользовавшись ортогональностью функций wn (s), можно
написать
где
л
— плотность состояний на поверхности Ферми в данной точке г,
N @) — ее обычное вначение для массивного металла. Окончательно
имеем
4^
16*

232 Глава VII
Входящее сюда отношение А(х)/А0 обращается в нуль при переходе
в диэлектрик и имеет порядок единицы в металле. Отношение N (x)/N@)
изменяется от нуля до единицы на нескольких межатомных расстоя-
расстояниях; следовательно, подынтегральное выражение отлично от нуля
лишь в слое шириной порядка межатомного расстояния а. Таким обра-
образом, эффективная длина b равна
Ь~~, G.63)
т. е., вообще говоря, очень велика (для чистого металла L —12,
?0=к10~4 см, что дает й«ьЛ см). Это позволяет нам при рассмо-
рассмотрении задач, в которых сверхпроводник находится в контакте с диэлек-
диэлектриком, положить 1/Ь = 0 и пользоваться граничным условием F.13).
Более точный критерий применимости условия F.13) выражается не-
неравенством Ь^§>?,(Т), которое эквивалентно условию1)
Контакт между сверхпроводником
и нормальным металлом
Обсудил теперь кратко случай контакта между нормальным ме-
металлом и сверхпроводником. Если контакт между областями N и S
является достаточно хорошим в электрическом отношении, то купе-
ровские пары могут диффундировать из сверхпроводника в нормаль-
нормальный металл. Математически это означает, что функция A(s) прости-
простирается в область N (х < 0) на довольно большое расстояние: t,N *—-
— ^vfn\^bT (если N представляет собой чистый металл).
Для рассматриваемого случая выражение G.60) остается в силе.
Однако теперь нам необходимо знать точную форму Д(х)/Д0, т. е.
точное решение интегрального уравнения G.54). Разумную аппрокси-
аппроксимацию дает выражение вида
Д~Д0-^7\Л При х<0, G.64)
s
rRtNNINs— отношение плотностей состояний [см. G.61)], a Tj—коэф-
Tj—коэффициент прохождения через границу электрона с энергией, равной
') Уравнения Гинзбурга — Ландау приближенно применимы также для
описания сверхтекучего Не4 в окрестности температуры фазового пере-
перехода 7\. Однако в отличие от сверхпроводников для Не4 параметр |0 равен
а \ъ ~ о. <С! ? С)], поэтому условие на границе выглядит совершенно иначе
и довольно близко к условию ф =0.

Микроскопический анализ уравнений Гинзбурга — Ландау
233
фермиевской. Подставляя G.64) в G.62), находим
Л/„ 1 L
G.65)
Если {NNjNs)Tj—1, то длина Ъ—\N [т. е. мала по сравнению
с \ (Т)] и граничное условие имеет совершенно другой вид, чем в слу-
случае контакта сверхпроводника с диэлектриком.
Задача. Определить изменение глубины проникновения поля в сверхпро-
сверхпроводник, возникающее в результате покрытия его слоем нормального металла
(фиг. 60) [119].
металл
Фиг. 60. Распределение магнитного поля вблизи границы нормальный ме-
металл — сверхпроводник.
Решение. Будем вести вычисления с помощью уравнений Гинзбурга —
Ландау. Поле на //S-границе можно считать равным приложенному, по-
поскольку естественно принять (как имеет место в действительности), что N-мь-
талл не дает вклада в экранирование магнитного поля. Что касается пара-
параметра порядка, то наличие //-металла приводит к граничному условию типа
G.53) на поверхности (х = 0) сверхпроводника.
1. В отсутствие поля решение ty(x) запишем в виде
параметр, который определяется, согласно G.53), из
где х0— неизвестный
условия
Предположим, что электрический контакт на MS-границе является хорошим
(тогда плотность состояний в yV-металле сравнима с аналогичной величиной
в S-металле) и что толщина слоя N велика по сравнению с ?0 « ^р/^в^е'
в этом случае Ь имеет порядок ?0. Поэтому можно считать Ь <^ \ (Т), что
соответствует очень малому значению / @) параметра порядка на поверхности
сверхпроводника [/ @) ~ blVT I (Т) <^ Ц.

234 Глава VII
2. Наложим теперь вдоль оси г слабое магнитное поле hz (x) =
дАу (х)/дх. Тогда уравнение для вектора-потенциала принимает вид
дх2 me2 * >| (Г) у
Для слабых полей функцию / можно заменить приведенным выше значением
в отсутствие поля. Получающееся в результате уравнение для Ау удается
решить точно с помощью гипергеометрических функций (см. аналогичную
задачу в книге Ландау и Лифшица [72], § 23). Приведем здесь результат
для предельного случая ЬЦ (Т) ->¦ О [х0 -> О, /@)-»()]:
?¦ 1 Г(— 5/2+ l/У.УГ) Г A/2 + S/2+ 1/и VT)
" Y.YT
Для малых значений v.
Последний результат легко получить на основании следующих простых сообра-
соображений. Когда глубина проникновения мала, мы можем заменить (в области
проникновения поля) точное выражение для / (при х0 = 0) приближенным
Уравнение для Ау тогда принимает вид
Ьх2 2%\(Т) I2 (П
Следовательно, глубина проникновения по порядку величины равна
L
В противоположном предельном случае, когда и->со, имеем [А/А^. (Т)] -> 1.
Этот результат также не удивителен, поскольку при | G1) <^ KL (T) наличие
Af-слоя приводит к искажению функции ty(x) лишь вблизи границы на рас-
расстояниях, малых по сравнению с л^ (Т).
3. В сильных полях глубина проникновения быстро растет с увеличе-
увеличением поля, если y. « l/|/2" и Ь <^ \ (Т). Этот вывод следует из рассмотрения
полной системы-нелинейных уравнений Гинзбурга — Ландау; недавно он был
подтвержден в опытах Бурже и др. [138] на системе Си — РЬ.
Контакт S—N—S'
Рассмотрим теперь систему из трех слоев S — N—S', показан-
показанную на фиг. 61; два сверхпроводника S н S' разделены либо слоем
диэлектрика N (толщиной d^s20 — 50 А), либо слоем нормального
металла (rf^fc 103 А). При не слишком больших толщинах d куперов-
ские пары могут переходить из 5 в S' и обратно за счет туннель-

Микроскопический анализ уравнений Гинзбурга — Ландау
235
ного эффекта. Мы проведем анализ этого эффекта, делая следующие
предположения:
1) в металлах S к S' выполнены условия применимости уравнений
Гинзбурга — Ландау;
2) толщина й мала по сравнению с ^L(T) и |(Г).
В этом случае роль пленки N сводится к наложению определен-
определенных граничных условий, связывающих значения Д и йЩйх на обеих
Фиг. 61. Контакт S—N—S'.
JV—либо диэлектрик (d ~ 50 А), либо нормальный металл (й ~ 10»А).
сторонах TV-области. Как и раньше, граничные условия можно запи-
записать в линейной форме. Выпишем их сначала для случая, когда вектор-
потенциал А равен нулю:
G.66)
Направление оси х совпадает с нормалью к плоскости пленки. Ве-
Величина Д+ представляет собой значение А (х, у, z), полученное в ре-
вультате экстраполяции решения уравнения Гинзбурга — Ландау из
области S' на плоскость х = 0 и т. д. (см. фиг. 61). Коэффициенты Ltj
можно определить, находя точный вид решения линеаризованного
уравнения самосогласованности G.8) (при Т = Тс и А = 0) в области N,
а также в областях 5 и S' вблизи границ. Поскольку при А = 0 ядро
K0(s, r) этого уравнения вещественно, коэффициенты L
Lti также

236 Глава VII
вещественны. Иногда бывает удобно пользоваться вместо А функцией ф,
для которой граничные условия G.66) при А = 0 можно представить
в виде
Если металлы S и S' не одинаковы, то отношение гр/Д, согласно опре-
определению F.8), имеет разные значения в областях S и Sr. Отсюда сле-
следует, что коэффициенты Мц, вообще говоря, отличны от коэффициен-
коэффициентов Ltj, но по-прежнему вещественны. Они не являются совершенно
независимыми, но связаны между собой соотношением, вытекающим
из условия непрерывности тока на границе. Сверхпроводящий ток
через единицу площади поверхности описывается выражением (при
А = 0)
1еЪ I, * dty \
К сопр.1 =
-S— Компл- со«р-) • G-67>
Сравнивая G.67) и G.66'), получаем
^11^22 — ^12^21 = L G-68)
что позволяет записать плотность тока Ix в виде
{*te* U*)K™m-сопр" f =
(*-*+ -Компл- сопр-)- G-69>
Ив G.69) видно, что через контакт может протекать сверх-
сверхпроводящий ток — результат, полученный Джозефсоном в 1962 г.
Для больших толщин d коэффициент МХ2 становится большим, а ток
соответственно малым. Явление протекания сверхпроводящего тока
через контакт впервые наблюдалось в опыте Андерсона и Роуэлла
в 1963 г.
Полученные ревультаты легко обобщить на случай А Ф 0. Как
всегда, будем предполагать выполненным условие непрерывности
вектора-потенциала А в области применимости уравнений Гинзбурга —
Ландау1). Полагая АХ = АХ(О, у, z), заменим систему G.66') сле-
•) Если калибровка выбрана различной по обе стороны от фаницы, то
вектор-потенциал А, очевидно, может иметь разрыв.

Микроскопический анализ уравнений Гинзбурга — Ландау 237
дующей:
Выражение для тока G.69) остается неизменным 1).
С точки зрения практических применений выражение G.69) при-
принимает наиболее простой вид в том случае, когда область N мало-
прозрачна для куперовских пар, т. е. ток 1Х мал по сравнению
с критическими токами для сверхпроводников 5 и S' (в виде мас-
массивных образцов).
В этом случае мы можем положить амплитуды |'Ф+| и Ity I
(в силу их слабой зависимости от тока) равными значениям -ф9, и ty&
в отсутствие последнего. Тогда
(величины i]>s и ij>s, вещественны). Напротив, фазы ф5 и ф5,, вообще
говоря, весьма чувствительны к присутствию токов или магнитных
полей, поэтому заранее ничего нельзя сказать относительно их вида.
Производя соответствующую замену в G.69), окончательно приходим
к следующему выражению для тока:
Максимальная величина тока, очевидно, равна
Для определения величин tys и -ф5, нам осталось лишь решить уравне-
уравнение Гинзбурга — Ландау в областях S и S' для простого случая А — О
в предположении вещественности функции i]>. Одномерные решения
такого типа нам уже известны:
IK*):
х>0,
G.73>
') Особенно прост случай симметричного контакта (Ми = М22). Принимая
во внимание условие G.68), мы видим, что в этом случае коэффициенты Л%
можно задать всего с помощью двух независимых параметров.

238 Глава VII
где фр5 и ?s (T) — соответственно параметр порядка и длина коге-
когерентности при температуре Т для массивного металла S. Длины xs
и xs, связаны с величинами tys и tys, соотношениями
G-74)
с, = ib„„, th
Явный вид их можно найти, потребовав, чтобы решения G.73) удо-
удовлетворяли граничным условиям G.66'). Это дает
G.75)
Чтобы определить -ф5 и гр^,, систему уравнений G.75) следует решать
численно.
Здесь мы укажем два предельных случая, когда эта система
уравнений упрощается.
1. Если слой N представляет собой диэлектрик, то его наличие
почти не сказывается на поведении функции ф(->с) (ф5 =ь ф05); коэф-
коэффициенты Мп и M%\ малы, а Жп ^ 1 (см. микроскопический расчет,
•следующий ниже). Выражение для максимального тока приобретает
вид
Так как коэффициент М12 при Т->ТС конечен, а величины ф05
и -ф^,, согласно F.15), меняются как (Тс—Tjh, максимальный ток
линеен относительно Тс — Т.
2. Если слой N представляет собой нормальный металл, толщина
которого достаточно велика, чтобы ток Im оставался малым, но мала
по сравнению с Я,^G) и |G"), то на основании предыдущего анализа
для .MS-границы мы можем теперь заключить, что
Следовательно, система G.75) допускает линеаризацию. Максималь-
Максимальный ток равен
т eh Г ъ I2
1\ *

Микроскопический анализ уравнений Гинзбурга — Ландау 239
т. е. меняется как (Тс — ТJ. Такая зависимость наблюдалась недавно
в серии весьма изящных экспериментов, выполненных Кларке.
Рассмотрим симметричный контакт с диэлек-
Микроскопический триком толщиной d<CSo и бУдем исходить
расчет Му для из линеарИЗОванного уравнения самосогла-
диэлектрического слоя СОванности G<8) при А:=о и Т = ТС.
Согласно G.35), ядро К0(г, г') существенным образом опреде-
определяется видом функции F [г — г(О)]6[г' — r(f)])? . которая с физи-
физической точки зрения представляет собой вероятность того, что элек-
электрон с энергией, равной фермиевской, в момент t находится в точке г'
(в нормальном металле), если в момент времени /==0 он находился
в точке г. Отсюда мы можем непосредственно выразить ядро К0(г, г')
через ядро /СЧНСт («" —г') для неограниченного чистого металла S.
Проделав это, эапишем уравнение G.8) в виде
А (Г) = J
чнсх
Кчнсх (Г - Г') Д (Г')
- г') [^А(г') + *УЬ(Р) dr% G.76)
J
и
где первый интеграл (I) соответствует прямому переходу электрона
из г в г', а область интегрирования определяется условием, что обе
точки гиг' находятся по одну сторону от границы. Второй инте-
интеграл (II) учитывает эффекты отражения электронов от контакта и
прохождения через него; коэффициент Т} = 1 — Rj представляет собой
коэффициент прохождения через барьер для электронов с энергией Ер
в нормальном металле. Точка г' — (— х'. у', z') является зеркальным
изображением точки г' относительно границы. Для простоты будем
считать, что отражение носит зеркальный характер, а коэффициент
отражения не зависит от угла падения электрона на границу.
Уравнение G.76) имеет четное решение A(jc) = A(—х), постоян-
постоянное в пространстве, в силу условия
,„ (г — s) dr = 1 при T = Tc
Чтобы определить М12, необходимо знать второе независимое реше-
решение, например нечетное решение Д(л;) = —А(—х).
Положим Д+ (х) = A(x)S (x), где
S(X)==\O. x<0.
Тогда уравнение G.76) можно записать в форме
Д1 C*) = S(jc) J Д+ (*') l*o (r, r') + (l -2Tj)K0{r, r')] dr.

240- Глава VII
или
AUx)-JK0(r, r')A+{r')dr' = J Л'А+(г0[-5(-*)^о(г. 0 +
4-5 (x) A — 27,) Л-о(г, г')) = — И (х). <7.77>
Функция Н(х) соответствует источнику, локализованному в области
| х | < |„. Полученное уравнение аналогично уравнению G.56) и может
быть решено тем же способом
о о
27, J rfx J их' j dy'dz'b+{x')K0(r, r')- G.78)
со со
Поскольку на поверхности сверхпроводник граничит со слоем диэлек-
диэлектрика, функция Д+(лг) мало меняется в области интегрирования
(*'~1о)-
Сделав замену Д+(л:)—>-Д+, остающийся интеграл можно легко
вычислить, используя определение Кчисг:
О со
jdx J йх1 \ d/ dz'K4KCT (r - г') = 10. G.79)
-со О
Окончательно получаем
Сравнивая этот результат и граничное условие G.66), находим
J G.80)
Поскольку L — Щ. мы видим, что ^12~!о/^У На практике коэф-
коэффициент прохождения Tj через слой изолятора толщиной d, превы-
превышающей несколько ангстрем, чрезвычайно мал. Это означает, что
весьма мал и максимальный сверхпроводящий ток, который может
протекать через контакт,
'«-^ЧЧ'оРТУ G.81)

Микроскопический анализ уравнений Гинзбурга — Ландау
241
Распределение полей и
токов в области
контакта
Типичное распределение токов показано на
фиг. 62. Поле Н лежит в плоскости кон-
контакта; вдоль внешних границ областей 5
и S' текут поверхностные токи, экранирую-
экранирующие приложенное поле. Рассмотрим, каким образом эти токи проходят
через контакт. Поскольку максимальная плотность тока /т мала, линии
тока в области контакта должны прохо-
проходить глубоко внутри сверхпроводников 5
и S'. В случае контакта, содержащего ^s s'
тонкий слой диэлектрика, типичное зна- г*т*^ г*—Н
чение глубины проникновения линий тока
составляет 6— 1 мм. При несколько
больших значениях поля ситуация еще s
больше усложняется и существенную роль
начинает играть образование вихревых ни-
нитей в плоскости контакта (фиг. 63).
Феррел и Пранге [80] предложили
простое уравнение, описывающее распре-
QH
W
S'
/9\
Фиг. 62. Характерный вид линий тока вблизи
контакта S — ./V — S' в слабом приложен-
приложенном поле.
Фиг. 63. Распределение токов
в области контакта в умерен-
умеренных магнитных полях.
Так как ток через переход мал, поле проникает на Характерной особенностью является
большую глубину 6. наличие линейной цепочки вихревых
нитей с осями, расположенными в пло-
плоскости контакта.
деление поля и тока в области контакта в такого рода ситуациях.
Чтобы получить это уравнение, рассмотрим контакт, целиком зани-
занимающий плоскость л: = 0; магнитное поле направим вдоль оси z и

242 Глава VII
будем описывать с помощью вектора-потенциала, направленного вдоль
оси у:
h(x, у) = -^-Ау(х, у).
Решение уравнений Гинзбурга — Ландау будем искать в виде
( »ч> (у)
\ ^(х)е s при л: > О,
Ф(*. У)=Н гф,у) G-82)
( ф (х) е s при х < 0.
Дальше мы увидим, что изменение фазы <р5 (или <ps,) происходит на
расстояниях 6, значительно превышающих % (Т). Следовательно, функ-'
ция ф(лг) фактически совпадает с решением G.73).
Рассмотрим сначала область х > 0 вдали от контакта Лх: ~^> Я^Л,
в которой эффект Мейсснера является полным и токи равны нулю.
Тогда из F.12) следует
2е dqv, (у)
и аналогично
ЖАу=^дГ при x<^-%s- G-83б>
Таким образом, функция Ау(х, у) имеет вполне определенные зна-
значения по обе стороны вдали от контакта. Обозначим их через As(y}
и As' (у). На самом переходе (л: = 0) мы для удобства положим
Ау@, у) = 0. Магнитное поле й@, у) = Л0(у) на самом контакте
(х — 0) легко найти следующим образом.
Обозначим через ks и ksf глубину проникновения поля соответ-
соответственно в областях S и S' вблизи контакта1). По определению,
G-84)
As = J h dx = Я,5й0.
Отсюда и из G.83) следует
he I dfps, he I d(ps
G85)
') Если область N является нормальным металлом, то вблизи контакта
значение ф(лс) мало, что необходимо учитывать при расчете глубины про-
проникновения, подобно тому как мы это делали в случае //S-граниды.

Микроскопический анализ уравнений Гинзбурга — Ландау 243
Далее, используя уравнение Максвелла
roth= — j,
запишем связь между значениями поля и тока в плоскости контакта
в виде
^ = ^ I* = ^ L ^n «Ps - Ф*0- G.86)
При переходе к последнему равенству мы воспользовались выражением
G.71). Подставляя G.85) в G.86), приходим к уравнению Феррела —
Пранге
J ^ G.87)
где Ф = ф5 —ф5-.
2 Дс . G.88)
Оценим характерную длину б для контакта, содержащего слой
диэлектрика. Используя оценку G.81) для /т, находим
тс2 |- 1 Я, (Г) ?
16яв»|фо|» Я?(Г) 7\ Гу • w<o^
Для диэлектрика толщиной й <-~- 20 А коэффициент прохождения Г у
обычно имеет порядок 10~ . Если положить, кроме того, Я,?(Г)~
— 1о—103А, то получим Ь~\ мм.
Уравнение G.87) формально совпадает с уравнением движения
математического маятника, поэтому его решения хорошо известны.
Особый интерес представляют два предельных случая.
/. Очень слабые поля. В этом случае уравнение G.87) линеа-
линеаризуется и имеет решения вида
ф = фое-у№, йо = Яе-У'й, G.90)
где у = 0 есть линия пересечения плоскости контакта с поверхностью
образца; Н — поле вне образца. Таким образом, глубина проникно-
проникновения слабого поля в окрестности контакта равна 6. Эта картина имеет
место, пока ф <^ ф0, или, что то же самое, при Н <^ ^/о (ks -\- Я,5-)-
т. е. пока проникающий в область контакта поток остается меньше
величины кванта потока ф0.
2. Область полного проникновения поля. Если #^>&/6 (Я,5+Я-5')>
то поле становится почти однородным на всей плоскости контакта
[й0(у) ->•//]. Величину ф легко найти из уравнения G.85)
SL + const. ^ Фо GЛИ)
L (Л5 + Л5')"

•244 Глава VII
¦Следовательно, распределение тока имеет периодический характер
с периодом L
Im sin [2я (у ~ Ур) ]. G.92)
Подставляя G.91) в правую часть G.87), легко проверить, что про-
производные d2q>[dy2 и dhjdy действительно пренебрежимо малы при
условии ZL<^6.
Распределение токов показано на фиг. 63. Оно напоминает линей-
линейную структуру из вихревых нитей, расположенных в плоскости
контакта. В частности, в обоих случаях периоду структуры отвечает
один квант потока. Поскольку глубина проникновения 6 очень велика
{о^>Ео)' рассматриваемая ситуация аналогична наблюдающейся в сверх-
сверхпроводниках второго рода (XL ^> Iq). С помощью прямого расчета
термодинамического потенциала можно также показать, что в пределе
L <^ 6 поле h0 весьма близко к величине приложенного поля.
Наконец, вычислим полный ток, текущий из 5 в S', для контакта
в виде прямоугольной полосы шириной D @ < у < D). Ток, при-
приходящийся на единицу длины вдоль оси z. равен
D
¦ полн '
Учитывая, что L <^ б, находим
/полн^^^/ Лр81Пф = н|?-{сО8ф@) — COS^@)-t--^_—]}•
Максимальное значение тока /полн достигается при ф@) = я/2 —nDjL
и равно
/макс lmL nD
'полн — —к— Sin-
2it
при ?<С&. G.93)
Входящий сюда множитель DjL равен полному числу квантов потока
в контакте. Очевидно, полный ток обращается в нуль, когда отно-
отношение D/L равно целому числу, и максимален при полуцелых значе-
значениях D/L. Весьма подробное сравнение формулы G.93) с опытом
можно найти в работах Фиске [120] и Роуэлла [121].
Задача. Получить зависимость максимального сверхпроводящего тока /
от величины приложенного магнитного поля И для системы, состоящей
из двух параллельно включенных контактов S—N—S' (.квантовый интер-
интерферометр'). Схема устройства и обозначения приведены на фиг. 64. Задан
магнитный поток Ф в кольце, которое образуется при параллельном вклю-
включении контактов в цепь. Для простоты будем считать, что а) толщина кон-
контактов А и В и область проникновения поля около каждого из них малы,
т. е. мал заключенный в них суммарный поток 2dkH<^ ф0; б) толщина
сверхпроводящих соединений 1 и 2 велика по сравнению с глубиной про-
проникновения.

Микроскопический анализ уравнений Гинзбурга — Ландау
245
Решение. Полный ток, текущий из 1 в 2, равен
/ = 1тй [sin (Фм - Фм) + sin (ф2В - ф1в)].
Входящие сюда четыре значения фазы <р^Д, ф2Л и т. д. связаны между собой
Фиг. 64. Принципиальная схема «квантового интерферометра».
Сечения А а В представляют собой контакты джозефсоновского типа. Измеряется зависимость
максимального тока / от поля Н внутри кольца.
Одним соотношением, содержащим поток Ф. Чтобы получить это соотноше-
соотношение, будем исходить из выражения для плотности тока в произвольной
точке сверхпроводника 1
гдз ф — значение фазы потенциала спаривания в выбранной точке. Рассмот-
Рассмотрим контур Си целиком лежащий внутри сверхпроводника и достаточно
удаленный от его поверхности. Тогда j = 0 вдоль С\, т. е.
= Ц. А.
Отсюда, интегрируя, получаем
Аналогично
Складывая эти равенства, приходим к искомому соотношению
где Ф — заключенный в кольце полный ноток.

•246 Глава VII
Кроме полученного соотношения, иа фазы ц>1А, ц>2А и т. д. не налагается
никаких других ограничений. Ток / будет максимальным, если мы выбираем
тогда
¦т. е. максимальное значение сверхпроводящего тока периодически зависит
or Ф (или Н). Чтобы наблюдать на опыте такую периодичность по полю,
площадь кольца S необходимо сделать по возможности малой; роль джозеф-
соновских контактов А и В при этом могут выполнять просто два механи-
механических контакта между концами сверхпроводящих проволочек. Эксперимен-
Экспериментально рассмотренный эффект впервые изучили Жаклевич, Мерсеро и др. [ 122].
ЛИТЕРАТУРА
Микроскопический вывод уравнений Гинзбурга — Ландау
Горькое Л. П., ЖЭТФ, 36, 1918; 37, 1407A959).
Сравнение экспериментальных данных для х в „грязных" сплавах
с формулой Горькова
Goodman В. В., IBM Journ., 6, 63 A962).
К i n s e 1 Т., L у п t о п Е. A., Serin В., Phys. Lett., 3, 30 A962).
Эффект Джозефсона и условия на границе сверхпроводника
с нормальным металлом
J о s e p h s о п В. D., Rev. Mod. Phys., 36, 216 A964).
De Oennes P. О., Rev. Mod. Phys., 36, 225 A964).

Глава VIII
ЭФФЕКТЫ В СИЛЬНЫХ МАГНИТНЫХ ПОЛЯХ И
РОЛЬ МАГНИТНЫХ ПРИМЕСЕЙ
Обсудим теперь два на первый взгляд совершенно разных физи-
физических явления.
1. Поведение "грязных' сверхпроводников и образцов малых раз-
размеров в сильных магнитных полях.
2. Влияние парамагнитных примесей на свойства сверхпроводников.
Однако оказывается, что явления 1 и 2 имеют много важных об-
общих черт.
а) В обоих случаях возмущение действует с противоположным зна-
знаком на электроны куперовской пары. В случае 1 возмущением явля-
является член
меняющий знак при замене р -> — р. В случае 2 взаимодействие маг-
магнитной примеси i, имеющей спин Sf, с электроном проводимости
(с координатой ге и спином Se), обычно берется в виде
(Г называют константой обменного взаимодействия, хотя фактически
его происхождение имеет более сложный характер). Знак Г может
быть любым, а типичное значение составляет ~0,1 эв=Ю3°К1).
Поскольку электроны, образующие куперовскую пару, обладают
противоположными спинами, это взаимодействие имеет противополож-
противоположный знак для электронов одной пары.
б) На опыте такая "антисимметрия" возмущения приводит в обоих
случаях к сильному понижению критической температуры сверхпро-
сверхпроводника, как изображено на фиг. 65 и 66. Подчеркнем, что решаю-
решающим фактором является "антисимметрия"; немагнитные примеси (даю-
(дающие "симметричное" возмущение) оказывают очень слабое влияние на
критическую температуру (теорема Андерсона).
') Отметим, что энергия Г не имеет никакого отношения к магнитному
дипольному взаимодействию между парамагнитной примесью и электроном
проводимости. Действительно, константа связи дипольного взаимодействия
равна ~~> \n2Bja3-^ Г К (\ив —магнетон Бора, а — атомный радиус), т. е. значи-
значительно меньше, чем Г.

113 4 5 6
Концентрация Gu, am. %
Фиг. 65. Температура перехода сплава LaOd в сверхпроводящее (Тс) и
ферромагнитное (Г^.) состояния (Маттиас [123]).
Следует отметить сильное понижение сверхпроводящей темтературы перехода при добавлении
к La небольшого количества магнитных атомов Gd.
500
0,5
IО
Фиг. 66. Зависимость верхнего поля ДЛ,2 от температуры для «грязного»
сверхпроводника второго рода (Sn-f-5 ат. % In) (Гийон и др. [124]).
Сплошной линией показана теоретическая кривая.

Эффекты в сильных магнитных полях и роль примесей 249
в) В силу хаотичности рассеяния электронов на разного рода
примесях и границах образца в обоих случаях куперовская пара в раз-
различные моменты времени должна испытывать со стороны "антисим-
"антисимметричного" возмущения воздействие разного знака. Это приводит,
как мы увидим, к ряду удивительных свойств, и в частности к явле-
явлению бесщелевой сверхпроводимости [125].
§ 1. ТЕМПЕРАТУРА ПЕРЕХОДА И СВОЙСТВА СИСТЕМЫ ПРИ
ОБРАЩЕНИИ ВРЕМЕНИ
Попытаемся теперь более точно математически сформулировать
приведенные, выше качественные соображения относительно антисим-
антисимметричных свойств возмущения. Проделаем это на примере вычисле-
вычислений температуры перехода сверхпроводника в заданном магнитном поле
(случай 1) или при заданной концентрации магнитных примесей (слу-
(случай 2). Опыт показывает, что в обоих случаях мы имеем фазовый
переход второго рода. Это означает, что в окрестности точки пере-
перехода параметр Л (г) можно считать малым и пользоваться линеари-
линеаризованным уравнением самосогласованности вида G.8).
Обратимся сначала к случаю 1, когда спин не играет роли и
уравнение G.8) применимо непосредственно. Перепишем ядро K(rv r2)
уравнения G.8) в форме, эквивалентной G.11):
*}™ (8.1)
/(г,. г2; о)=SФ;(Г1)Ф;(г,)Фт"о^ФДГ2N(im-in-so); (8.2)
здесь У — объем образца; N @) — плотность состояний на единицу
объема в нормальном металле, так что 7°N @) — полная плотность
состояний для образца в нормальном состоянии. При написании выра-
выражения (8.1) мы произвели замену V-^- \ J°N @)dl,n. Суммирование
п
по со, как обычно, происходит по всем значениям со = {kBTfh) к X
XBv-f-l). Среднее в выражении (8.2) берется по всем состояниям
п при заданной энергии |„ (фактически при энергии, равной ферми-
евской, ?„ = 0). Постараемся выразить произведение двух функций
Ф и ф* через матричные элементы, образованные с помощью одно-
электронных состояний кит. Однако сразу это сделать не удается
вследствие очевидной трудности, связанной с операцией комплексного
сопряжения. Обойдем эту трудность, введя специально для этой цели
оператор К, который, действуя на произвольную функцию, дает, по
определению, комплексно сопряженную величину
^Ф/« ^ Фт для случая 1. (8.3)
17 Зак. 1020

250 Глава VIII
Оператор К мы будем называть оператором обращения времени.
Используя определение К, можно написать
Ф« (га) Фт (га) = < /и , /Г 6 (г — га) | в }, (8.4)
/(г,. r2; Q) =
= S ( « [ б(г — гг) /С | т >< т | /С+ 6(г — г2) | п > б (?,„ — Sm — ftQ).
На этой стадии, как обычно, удобно перейти с помощью обрат-
обратного фурье-преобразования к функции
/(IV r2; O=JdQe-«'/(ri. r2; Q) =
= ( б [г (/) — Г1] К (ёуК+{0) 6 [г @) — г2] >. (8.5)
Здесь К (f) и г(/) являются гейзенберговскими операторами, описы-
описывающими изменение во времени операторов /Сиг для электрона,
гамильтониан которого имеет вид (в случае 1)
i(f)+f/<r)-/f'" (8i6a)
например
К@ = ете'1*Ке1^1\ (8.6б)
Непривычный знак (плюс) во второй экспоненте связан с тем, что
Ki =— IK- Ураннение движения оператора K(t) имеет вид
dK (Q / .-,,
для случая 1. (8.7)
Отсюда следует, что изменение /С (/) со временем происходит лишь
из-за наличия в гамильтониане §?е „антисимметричных" членов, свя-
связанных с магнитным полем, т. е. членов, изменяющих знак при обра-
обращении времени.
Подведем итог полученным результатам. Для определения темпе-
температуры перехода нам необходимо знать ядро K{rv r2), которое
в свою очередь мы выразили через функцию корреляции /(гр r2; t)
[см. (8.4)]. Удобство последней состоит в том, что она, как мы уже
видели ранее, тесно связана с транспортными свойствами системы
в нормальном состоянии. Дальнейшие усложнения, связанные с „анти-
„антисимметричным" характером возмущений, можно просто описать с по-
помощью оператора обращения времени K(t).
Предыдущие результаты можно непосредственно обобщить на
случай, когда в металле имеются магнитные примеси, т. е. при

Эффекты в сильных магнитных полях и роль примесей 251
вычислениях необходимо учитывать спиновые индексы. Здесь мы
вкратце остановимся на таком обобщении. Полный гамильтониан
системы имеет вид
О, V
~" *F+(r, g)W^ (r, vLr(r, vL'(r. o)l, (8.8)
a, v J
где Ч?+ (г, о) — оператор рождения электрона со спином а в точке г
и т. д. Действующий на электроны потенциал Uav в рассматривае-
рассматриваемом случае магнитного сплава зависит от спиновых переменных.
Для простоты записи мы считаем здесь, что U представляет собой
локальный оператор, связывающий значения Ч* и W в одной точке.
Наиболее важным моментом является сделанное нами предположение,
что потенциал U является статическим; тем самым мы с самого
начала пренебрегаем движением спинов примесей. Позже мы увидим,
что такое предположение выполняется лишь для очень разбавлен-
разбавленных сплавов. В сплавах с большей концентрацией примесей суще-
существенную роль начинает играть взаимодейстпие спинов примесей друг
с другом, что приводит к прецессии спина каждой примеси в обмен-
обменном поле ближайших соседей.
Потенциал спаривания Д (г) определяется прежним выражением
которое можно записать в следующей форме:'
(W (г гЛ Ч*" i г п1\ ffi ОЛ
о, ц
где
О 1
— 1 О,
Подобно тому как делалось в гл. V, напишем теперь уравнения
движения для операторов Ч*" и Чг+, а затем, считая параметр Д от-
отличным от нуля, линеаризуем их. Для Чг линеаризованное уравнение
движения имеет вид
А
If, w ГО (г гг\ Г-ЯО? \Т/ (г гт\1
tiJ - у I ( Г, UJ \QjV » 1 (Г, U II
01
.оL
17*

252 Глава VIII
(Как обычно, мы вычли химический потенциал EF.) Чтобы перейти
к описанию с помощью элементарных возбуждений, совершим пре-
преобразование
Чг(г, о) = 2.[«я(г. °)Yn4-<(r, о)у+]
и наложим обычное условие
Коэффициенты преобразования и и v представляют собой собствен-
собственные функции следующей системы уравнений:
Г(р--АГ 1
ш (г, а) = | У g^— /:rJ и (г, а)
-EP\v(r.
-м»(г. о)=
Нас интересует предельный случай А—>-0. В нулевом порядке
по Д система уравнений для и и v сводится к уравнению Шредин-
гера для волновой функции ф„ электрона в нормальном металле
|ф(г, о) =
Ф(г, оL-У t/ (г)ф(г. ц) = ^вф(г. а).
Поэтому
«о = / ф«'
" [0.
В первом приближении по Д напишем
ип = «04- S аптч>, •
тфп
1) = if> 4~ ^j Ь (Г * .

Эффекты в сильных магнитных полях и роль примесей 253
Коэффициенты апт и Ьпт можно получить обычным образом по тео-
теории возмущений,
0. 1Л > 0,
а"т=i тп 21dr^*» (Г2> °) р^ф« (**•ц)Л (Г2)* Е« < °-
о, \х
1
'«(г2. о) р^0Ф„ (r2, fx) Д (га). |я > 0.
О, |Л
0. 6„ < 0.
Подставим теперь найденные выражения для и и v в уравнение
самосогласованности для Д. С учетом спиновых индексов оно при-
принимает вид
о, ц га
Сохраняя лишь члены, линейные по Д, мы возвращаемся к знакомому
уравнению
A(r,)=J^(r1. r2)A(r2)rfr2, (8.11)
в котором ядро К(г1, г2) по-прежнему связано с функцией корре-
корреляции соотношениями (8.1) и (8.5). Единственное отличие состоит
в том, что оператор обращения времени, входящий в выражение (8.5),
теперь зависит от спиновых индексов. В явном виде имеем
что часто записывают с помощью матриц Паули следующим об-
образом:
где Сф = ср*. а матрица iay=p [см. (8.9)]. Таким образом, во всех
случаях, представляющих для нас интерес, задача сводится к изуче-
изучению зависимости от времени одноэлектронного оператора К в нор-
нормальном металле.
На первый взгляд смысл оператора К кажется не совсем ясным.
Однако ему можно дать вполне определенную физическую интерпре-
интерпретацию. Рассмотрим, например, случай, когда имеется магнитное поле,
действующее лишь на орбитальное движение электрона; зависимость
от времени оператора К описывается уравнением (8.7). В выраже-
выражении (8.1) существенны значения |? — \'\ — kBT, следовательно,
в функции корреляции /{гг; r2; f) следует рассматривать интер-
интервалы времени t~bjkBT. За такое время электрон проходит путь.

254 Глава VIII
значительно превышающий фермневскую длину волны. Следовательно,
движение оператора K{t) мы можем рассматривать кллссически и
записать (8.7) в виде
dt ~ l dt
Отсюда
(8-12)
Стоящий здесь интеграл берется по классической траектории дан-
данного электрона в нормальном металле. Заменив р на т\ (раз-
(разностью eh\c между р и т\ можно пренебречь по сравнению
с величиной фермиевского импульса) в выражении для фазы ф,
получим
„ = .* JA.v«ff = i?jA.dl. (8.13)
Расчет функции корреляции /(г,, r2; t) для случая 1 состоит
в следующем. Рассмотрим псе возможные траектории, двигаясь по
которым электрон за интервал времени t попадает из точки г, в г2.
(В чистом металле имеется только одна такая траектория, а именно
прямая линия, поскольку циклотронный радиус электрона очень велик
по сравнению с расстоянием vFt. В более „грязных'1 системах имеется
множество допустимых траекторий в виде ломаных линий.) Вь.члсли.ч
затем для каждой траектории фазовый множитель ещ. Искомая функ-
функция представляет собой сумму вкладов от отдельных траекторий,
каждый из которых берется со статистическим весом, равным веро-
вероятности попадания электрона на соответствующую траекторию в ре-
результате последовательных актов рассеяния. Таким образом, как и
утверждалось ранее, нахождение функции / сводится к рассмотрению
транспортных свойств.
Нам осталось получить уравнение движения для оператора К (t)
в случае 2 (магнитный сплав). Представим одноэлектронный гамиль-
гамильтониан в виде
#?e = i4 + B-Se. (8.14)
где член А включает кинетическую энергию электрона и не завися-
зависящую от спинов энергию взаимодействия; коэффициент В определяет
суммарную энергию обменного взаимодействия электрона с магнит-
магнитными примесями. Используя определение (8.3') для К и аналогичные
выражения для сопряженного оператора К\ легко показать, что
К+теК=А — B-Se. (8.15)

Эффекты в сильных магнитных полях и роль примесей 255
Ицыми словами, оператор KY^teK можно получить из &се, заме-
заменив А на А* (это эквивалентно замене р —> — р) и Se на — Se. Этот
результат можно получить иначе, изменяя знак времени на противо-
противоположный во всех величинах, относящихся к электронам проводи-
проводимости, чем и объясняется название „оператор обращения времени".
Замечая, что К+К = КК+ = 1, можно написать
\&ие. К] ------ ЖеК - К3?е = К {К+&СеК — ??'е). (8.16)
Рассмотрим, например, магнитный сплав (случай 2) в отсутствие
внешнего поля, т. е. при А = А*. Подстановка (8.14) и (8.15) в (8.16)
дает
^^ l^tf(Ql 4*WB'S«- (8Л7)
Подчеркнем, что зависимость К(t) от времени определяется исклю-
исключительно обменным взаимодействием Г. Как и прежде, мы могли бы
попытаться описать ее с помощью зависящей от времени фазы опе-
оператора К (t). Однако на практике такой подход не дает желаемых
результатов, поскольку теперь мы не можем рассматривать фазу клас-
классически; это связано с тем, что потенциал В (г) сильно меняется
на атомных расстояниях (т. е. на расстояниях порядка фермиевской
длины волны электрона проводимости). Позже мы покажем, как можно
описать изменение K(t) в подобного рода ситуациях. Прежде чем
вдаваться в детали таких рзечетоа, сначала мы качественно обсудим
ряд общих свойств оператора КA), связанных с характером одно-
электронных траекторий и присущих одновременно случаям 1 и 2.
§ 2. ЭРГОДИЧЕСКОЕ И НЕЭРГОДИЧЕСКОЕ ПОВЕДЕНИЕ.
БЕСЩЕЛЕВАЯ СВЕРХПРОВОДИМОСТЬ
Ограничимся пока рассмотрением систем, в которых амплитуда|Д |
потенциала спаривания А (г) не зависит от пространственных коор-
координат. Благодаря этому предположению обсуждение линеаризованного
уравнения (8.11) значительно упрощается и позволяет сразу устано-
установить наиболее важные черты явления. Более того, такая постановка
задачи имеет не только академический интерес, но и находит приме-
применение в ряде конкретных ситуаций. Примером могут служить
1) коллоидные растворы мелких сверхпроводящих частиц;
2) тонкие сверхпроводящие пленки в магнитном поле, параллель-
параллельном их плоскости;
3) сверхпроводящие сплавы, содержащие магнитные примеси (в от-
отсутствие магнитного поля).
В случае коллоидного раствора амплитуда |А | не будет сильно
меняться от точки к точке, если все размеры зерен малы по сравне-
сравнению с | (У). Что касается тонких пленок, то здесь необходимо проявить

256 Глава VIII
некоторую осторожность, поскольку у пленки лишь один размер
является малым. В частности, в магнитном поле, перпендикулярном
плоскости пленки, в последней могут возникать вихревые нити (как
это имеет место в сверхпроводниках второго рода), что приводит
к сильным изменениям амплитуды |Д| в пространстве [103]. Чтобы
избежать этой трудности, будем рассматривать исключительно случай
поля, параллельного плоскости пленки. На пленки и на коллоидные
частицы налагается также другое ограничение, связанное с тем, что
мы с самого начала считаем происходящий переход фазовым перехо-
переходом второго рода. В сверхпроводниках первого рода это предполо-
предположение подтверждается на опыте, если размеры образца (толщина
в случае пленки) меньше глубины проникновения поля.
Наконец, для магнитного сплава (в отсутствие поля) также разумно
принять в качестве исходного предположение о постоянстве j Д |
(при этом мы не учитываем только малых изменений Д (г) вблизи
каждой примеси).
Получим теперь уравнение для температуры перехода. Выберем
калибровку вектора-потенциала А так, чтобы параметр Д(г) в каж-
каждой точке принимал вещественное значение (для односвязного об-
образца это всегда можно сделать), т. е. Д (г) = | Д | = const. Тогда
мы можем проинтегрировать обе стороны уравнения самосогласован-
самосогласованности (8.11) по гх по объему 7°; это дает
A?e=|dr1drj^(rI.
Сокращая в этом уравнении множитель ДУ и используя (8.1), (8.5),
приходим к условию
g
АЛ (g — ilia) E' -(- //to)
-'в/; (8.18)
здесь g(Q)— спектральная плотность оператора К. Можно также
записать уравнение (8.18) с помощью фермиевской функции распре-
распределения /(§):
1 = N @) V J d\ d% l ~/|(l|.~ ЛГ) g (^jr-) ¦ (8-18')
[Ряд свойств легче усмотреть из выражения (8.18'), однако при кон-
конкретных расчетах более удобным оказывается выражение (8.18).]
Обсуждение уравнения (8.18). В частном случае, когда одно-
электронный гамильтониан е%?е инвариантен относительно обращения
времени ([К(f), 3@e] = 0, K(f)^K@)), имеем

Эффекты в сильных магнитных полях и роль примесей 257
т. е. спектральная плотность оператора К отлична от нуля лишь
при Q = 0. Уравнение (8.18') в этом случае, очевидно, сводится к из-
известному уравнению теории БКШ
определяющему температуру перехода чистых (или содержащих не-
немагнитные примеси) сверхпроводников.
При [К (t), e%?e] ф 0 нам придется более детально изучить структуру
функции #@- Мы уже указывали, что нас интересуют значения
Q—kBTjh и t.— hjkBT, т. е. главный интерес представляет асимпто-
асимптотическое поведение функции (К+ @)К(t)) для больших времен t.
Асимптотическое поведение этой функции может быть самым разно-
разнообразным. Наиболее важны для нас следующие два случая:
I) lim (К+@)К@) = цФ0, (8.19)
II) lim (K+@)K(t)) = e~titK. (8.20)
Фигурирующие здесь параметры г\ и хк определенным образом зави-
зависят от величины возмущения (т. е. магнитного поля или концентрации
магнитных примесей). Системы, характеризующиеся асимптотическим
поведением типа I или II, мы будем называть соответственно неэр-
годическими или эргодическими в смысле Маркова.
Неэргодические системы
Положим
(8.21)
где функция R(t) быстро убывает со временем. Например, для ма-
малых образцов с поведением типа I характерное время убывания
функции R @ составляет ~ d\vF (d — размер образца, d <C[ J^,
т. е. dfvF<^hlkBT). Поэтому в интересующей нас области времен
в нулевом приближении членом R(t) можно пренебречь. Тогда урав-
уравнение (8.18') снова принимает вид, подобный уравнению БКШ,
\=N(O)Vr\ f db, ^f(?l. (8.22)
Отсюда температура перехода Т* равна
kB T* == 1,14 ha ив-1'" <°) *Ч (8.23)

258
Глава VIII
Это выражение имеет стандартную форму, характерную для сверх-
сверхпроводников в отсутствие поля, но в отличие от последних константа
связи N@)Vr\ зависит теперь (посредством г)) от величины возмуще-
возмущения. В нижеследующей задаче мы обсудим пример конкретной физи-
физической системы, поведение которой относится к типу I.
Задача. Найти поведение функции (Д+ @) f( (t) ) при больших временах
для тонкой пленки (толщиной d), находящейся в продольном магнитном поле //
(Де Жен и Тинкхам [126, I27]1)). Считать, что объемные дефгкты отсутствуют,
а отражение электронов иа границах пленки является диффузным.
Решение. Рассмотрим траекторию электрона, который из начальной
точки г0 (для t — 0) в результате ряда последовательных соударений с гра-
границами пленки при t = t\,t2, . . ., tn попадает в конечную точку tt в момент
Фиг. 67. Траектория электрона в топкой пленке в случаг диффузного
характера отражения на границах.
времени t (фиг. 67). Согласно (8.13), результирующая фаза ф равна сумме
приращений на отдельных прямолинейных участках пути:
Ф =
¦ + Лфя-1, я f
В калибровке, в которой параметр Л веществен, вектор-потенциал А имеет
лишь одну отличную от нуля компоненту Ау=Нх. Тогда легко видеть,
что в этой калибровке все приращения, за исключзпнем Л'р01 и Дф„, с равны
пулю. Именно
Х- d:l
J
x--d:2
поскольку траектория между двумя последовательными соударениями пред-
стазляет собой прямую линию (координата у является линейной функцией х),
а интегрирование вгдегся в симметричных пределах (d\i- фиг. 67). Таким
образом,
ф = Афо, -|- Лф„, /.
Далее, для интересующих нас времен t^>djvp число соударений п велико
поэтому можно считать, что корреляция между временными интервалами
') См. также работу Шаповала [128]. — Прим. ред.

Эффекты в сильных магнитных полях и роль примесей 2Ь9
()->/, и tn->t отсутствует. Пмылы словами
при t ->• со.
Значение г), вообще говоря, не равно нулю; несмотря на бесчисленные хаоти-
хаотические столкновения электронов с поверхностью, система является неэр-
годической в определенном выше смысле. В полученном выражении для г) не-
необходимо теперь произвести усреднение по всевозможным начальным положе-
положениям г0, а также по всевозможным направлениям (при заданной величине i> )
начальной скорости электрона, для чего удобно ввести угол ф между
направлением проекции скорости на плоскость ху и направлением оси х.
Приведем эти вычисления
dn я/2
Ч—5Г fdx fd*J
-dn -л/2
dp
— Г
О
где Ф0 = сЛ/2е—квант потока. Приведем результат для двух предельных
случаев:
I _ ЛИ я
при
Эргодические (марковские) системы
Если для больших времен t выполняется экспоненциальный за-
закон (8.20), мы можем написать
g(Q)=- T« . (8-24)
Подставляя это выражение в (8.18) и интегрируя по | и |', прихо-
приходим к уравнению
2пкцТ* -л 1
4l (8'25)
со
Здесь сумма по о) расходится. Это объясняется тем, что мы не учли
обрезания взаимодействия на дебаевской частоте <0д [см. обсуждение
уравнения G.28) на стр. 218] С учетом обрезания выражение (8.25)
принимает вид

260
Глава VIII
Эта сумма теперь сходится. Результат удобно выразить через табу-
табулированную функцию
где Г (z) — гамма-функция. Тогда
2лквТ*
2 ) со | + 1/Тд-
Окончательно связь между 1/т^- и Г* в неявной форме дается вы-
выражением
Соотношение такого вида весьма часто встречается в теории сверх-
сверхпроводимости, поэтому мы введем для него специальное обозначение
JL = kBTc\Jn(^\. (8.26')
К \ с /
„Универсальная" функция Un(x) показана на фиг. 68. При х—>0
имеем ип(л;)—>• 1,76 и bjxK—> 1,7 6kBTc = AQ (где Ао — значение
Нормальный металл (N)
Бесщелевой
сверхпроводник IS,)
Сверхпроводник
со щелью (S,)
Фиг. 68. Фазовая диаграмма сверхпроводника при наличии «асимметрич-
«асимметричного» возмущения для эргодической системы.
Величина возмущения пропорциональна ft/T/f. Температура Т* (верхняя кривая) обращается
в нуль при h/Tf(=l,7b kT
энергетической щели в теории БКШ для чистого сверхпроводника
в отсутствие поля при Т = 0). При х —> 1 имеем
11п(л;)->-^-A — л:), (8.27)
А. ^-^кв (Тс -Г*) при J- _> 0 (Г* _> Тс).
1к к

Эффекты в сильных магнитных полях и роль примесей 261
Приведем ряд примеров систем, которые
,,эргоди"ескиТ систем ™тся эргодическими:
а) мелкие коллоидальные частицы в поле Н;
б) тонкие „грязные" пленки в поле Н, параллельном поверхности
(как было показано выше, для пленок со строго постоянной тол-
толщиной одного рассеяния на поверхности недостаточно для выполне-
выполнения условия эргодичности);
в) тонкие пленки с нерегулярной толщиной в поле Н\
г) сплавы, содержащие магнитные примеси.
В следующих двух задачах мы подробно остановимся на вычис-
вычислениях параметра хк для конкретных марковских систем. В частности,
полученная в первой задаче зависимость хк от магнитного поля
позволяет найти с помощью (8.26) критическое поле образцов малых
размеров как функцию температуры.
Задача. Определить т^. для „грязных" образцов малых размеров и
произвольной формы, находящихся во внешнем магнитном поле Н (Маки
[129]).
Решение. Рассмотрим образец, размеры а которого велики по срав-
сравнению с длиной свободного пробега электронов I. Кроме того, на величину d
налагается (сверху) другое важное ограничение, связанное с требованием
постоянства амплитуды параметра порядка (| А | = const) во всем объеме
образца. Действительно, при больших значениях d, как мы знаем, при //,
близком к полю образования зародышей Нс2 (или Hcs), сверхпроводящая
фаза существенно неоднородна, т. е. параметр Д сильно зависит от про-
пространственных координат. Размер неоднородностей по порядку величины
равен
где |0 = 0,18 (TmJkgTj. Условие |Л|= const приводит к неравенству
Окончательное условие
накладывает довольно жесткие ограничения на допустимые значения d.
Тем не менее этот случай представляет принципиальный интерес, поскольку
он является простейшим примером эргодического поведения.
Если исходить из представления об одноэлектронных траекториях, то
условие d < J^g0/ означает, что средний путь YDt (D = vpl/3 — коэффи-
коэффициент диффузии), проходимый электроном за время t <~ ti/k T?, велик по
сравнению с размерами образца. Следовательно, за время t электрон успеет
побывать во всех точках образца. В соответствии с этим мы будем считать
приращение фазы на отдельных участках пути случайной величиной и поль-
пользоваться для вычисления результирующей фазы q> (t) распределением Гаусса.
Тогда получаем

2C2 Глава VIII
Используя (8.13), запишем ф (t) в виде
ф (О =• f » (О dC
где ы — 2е\-к1Ьс. Для времен t. больших по сравнению со средним вре-
временем между последовательными соударениями т = l',vp, имеем
->2t\ (ю @) a ((')} dt' для
6
[ющихся в точке г, можно
(« @) о (У)) =(~УУ К (г) Лр (г') (г/а @) г/р (t')) =
6
Для траекторий, начинающихся в точке г, можно написать
= Iтг) А2 (г) "з~ е~'/т (а- Р = *. у. *)¦
поскольку за время порядка т изменение координаты г вдоль траектории
пренебрежимо мало (~ /) по сравнению с характерным расстоянием (~ d),
на котором меняется вектор-потенциал А (г). В результате имеем
1 i
ХК з
(среднее от А2 берется по объему образца). Подчеркнем, что выбор калиб-
калибровки для А фиксирован условием Д = const. Для некоторых простейших
геометрий калибровку можно найти непосредственно.
1. Тонкая пленка толщиной d (вдоль оси х) находится в однородном
поле Н, направленном по оси г. В отсутствие суммарного тока в пленке
Лу = Их
(расстояние х измеряется от середины пленки). Отсюда находим
12
2. Для сферического образца малого радиуса R в однородном ноле Н
имеем
Задача. Вычислить хк для сплава, содержащего парамагнитные примеси
(Абрикосов и Горьков [125]).
Решение. Здесь мы приведем довольно нестрогий расчет. Будем
исходить из выражений
...

Эффекты в сильных магнитных полях и роль примесей 2СЗ
где усреднение производится по одноэлекгронным состояниям при заданной
энергии |„ (фактически по поверхности Ферми). Возьмем Q ~^§> 1/т^. (однако
Q <^C Ep/h), тогда g (fi) ~> 1/jiQ2tк и можно написать
т
Т 2 Г<" I Г*?*- *11 m' I26 (En - U - №).
m
Коммутатор [сЯ?е, Т] мы уже вычислили раньше [см. (8.17)]:
где
I
С точностью до членов второго порядка по взаимодействию электрона
с примесями можно заменить точные одноэлектронные состояния [ п) и [ т)
плоскими волнами вида
4>n->?-Vk-r.
Следовательно,
V [ ¦'ok | 2В ¦ S e [ |xk') |26 (?к — |к, — i
о, ц Is'
Суммирование по спиновым индексам о и ц выполняется следующим об-
образом:
4" У! (ст I (Se)x I'1 ) (V I (S<?)jc I °; = 4" У! (° I (Se)x \°J = "Г-
О, ]Х а
и т. л. Используя выражение для В, представим орбитальную часть мат-
матричных элементов в виде
(к | В | к') = L~3 V Sie1 ^--'1-riY (к —к'),
где
.:) = J eifirT(r)dr.
Далее, возводя в квадрат и удерживая лишь члены вида SiSi (принимаем,
что корреляция между спинами различных примесей отсутствует), получаем
1 л п S, (S. + 1) V1
— i \ i i у I Г (к — к') |2б ^Ёь Е MX)
V ' h'
где п — число атомов примеси в единице объема. Фигурирующая здесь
сумма по к' слабо зависит от Ш (при Ш <^ Е ), и поэтому мы можем

264 Глава VIII
перейти к пределу /??!-> О, а также положить |к = 0, т. е. вычислить
на поверхности Ферми1). В результата получаем
1 tins, (S,+i)N (С)
к
где dQkr — элемент телесного угла в направлении к', a k = k' = kp. Обозначая
через х атомную концентрацию примеси и вводя атомный объем в3 (так что
п = х[аг), находим
^(°>~W-- Г fo) ~ Га».
Р
Следовательно,
х ~* ? ¦
/С У
Несколько замечаний по поводу этой формулы.
1. При малых х величина 1/т^. также мала. Это позволяет использовать
разложение (8.27) для нахождения температуры перехода 7"*. Качественно
имеем
x
т. е. температура Т* очень быстро убывает при добавлении магнитных
примесей. Действительно, беря типичные значения Г ~»0,2 эв, Ер~2 эв
(Т2/Е ~ 2 ¦ 102°К), мы видим, что уже при л:~10~2 уменьшение темпера-
температуры Т* составляет ~»2°К. Такое быстрое понижение температуры пере-
перехода наблюдалось на опыте. Оно используется на практике в качестве наи-
наиболее чувствительного метода для проверки того, является ли данная
примесь в той или иной матрице магнитной или нет.
2. Проведенные вычисления справедливы лишь при условии х (Г2/Ер) <§^
<^ kBTc. Рассмотрим этот вопрос несколько подробнее. Наличие обмен-
обменного взаимодействия Г между электронами проводимости и магнитными при-
примесями приводит к появлению косвенного взаимодействия самих примесей,
имеющего вид
Р
где Ер = h2kp/2m — анергия Ферми для электронов проводимости, а
безразмерная функция, которая иа больших расстояниях ведет себя как
(kpR)~s cos Bk /?) (Рудерман и Киттель [130]). Взаимодействие Н.. приводит
к тому, что при низких температурах происходит магнитное упорядочение
(ферро- или антиферромагнитное) спинов примесей. Температура этого пере-
перехода (температура Кюри) Т к = х (Т*1квЕр), очевидно, должна быть мала
по сравнению с температурой сверхпроводящего перехода (Тк <^ Тсу
При этих условиях
а) спии дайной примеси слабо связан со всеми остальными и его на-
направление почти не меняется со временем (статическая модель);
') В связи с предельным переходом fi-»0 в окончательном выражении
отметим, что первоначальное ограничение на величину Й(]]^> VTK) является
в действительности несущественным и понадобилось нам лишь при замене
точных состояний на невозмущенные (| п) -»| к)).

Эффекты в сильных магнитных полях и роль примесей 265
б) эффект корреляции спинов соседних примесей имеет порядок
ТК/Тс, т. е. пренебрежимо мал (спины независимы).
3. Добавление к одноэлектронному гамильтониану Фве члена, описываю-
описывающего спин-орбитальное взаимодействие, не меняет величины 1/т„. Это
ясно без вычислений, поскольку спин-орбитальное взаимодействие инвари-
инвариантно относительно обращения времени. Укажем в этой связи на сущест-
существенное отличие времени т„ от времени релаксации ядерного спина Ту в ко-
которое эффекты спин-орбитальной связи вносят соответствующий вклад.
4. Весь расчет справедлив с точностью до членов ~ Г2. В более высо-
высоких приближениях картина усложняется из-за так называемого „эффекта
Кондо" [131].
Бесщелевая сверхпроводимость
При температурах, несколько меньших температуры перехода
Т* [см. (8.26)], параметр А отличен от нуля, но все еще мал. Тогда
мы можем рассматривать его как возмущение и вычислить спектр
возбуждений е„ квазичастиц в сверхпроводящей фазе. Как обычно,
для нахождения энергии е с точностью до членов-—А2 достаточно
знать коэффициенты и и v в первом порядке по А. Используя зна-
значения и и v, полученные при выводе соотношения (8.11), находим
(штрих у знака суммы означает, что при переходе к интегрированию
по | надлежит взять главную часть при |„ = — ?т).
Если одноэлектронный гамильтониан е%?е инвариантен относи-
относительно обращения времени [Ше, К] = 0, то матричный элемент
(п | К | т) отличен от нуля лишь при %п = \т и равен нулю во всех
остальных случаях. Тогда при малых значениях ?п энергетический
знаменатель, равный 2|„, тоже мал и поправка к энергии расходится,
что говорит о непригодности теории возмущений. Причина этой
расходимости, очевидно, связана с наличием у сверхпроводников
энергетической щели. Сказанное относится к любой неэргодической
системе.
Напротив, для эргодических систем матричный элемент (п | К | т)
не имеет особенности при Ъ,п = \т и отличен от нуля во всей полосе
шириной 11„ — ?т | ~ fi/Тд-, так что точки |„ = \т ничем не выде-
выделены. По этой причине обращение в нуль величины \п или Ъ,т в зна-
знаменателе выражения (8.28) не играет роли и применение теории
возмущений оправдано. Параметром разложения служит величина
Ат^/А вместо отношения А/1 \п | в предыдущем случае. Чтобы найти
энергию е„ в явном виде, воспользуемся выражением (8.24) для
спектральной плотности оператора К и перейдем в (8.28) от суммы
18 Зак. 1020

266
Глава VIII
к интегралу
2|Л|2Ш
Дт
при
(8.29)
(Символ Р означает, что интеграл берется в смысле главного зна-
значения.) Для Е, ~^> hjxK формула дает результат БКШ для обычных
сверхпроводников (ея&=|-|-А2/2|^55угА2+|2). В пределе |—>0 энер-
энергия возбуждений линейно стремится к нулю
Следовательно, щель в спектре возбуждений отсутствует. Ре-
Результат (8.29) можно выразить также с помощью плотности состоя-
состояний Ns(e). С точностью до членов порядка А2 имеем
Ь
(8.30)
Отсюда видно, что при z<hl2xK плотность состояний Ns(e) меньше
значения N @) в нормальном металле и всюду остается конечной
(фиг. 69).
п/гтк
е.эв
Фиг. 69. Плотность состояний для возбуждений фгрмиевского типа как
функция их энергии в случае бесщелевой сверхпроводимости.
Такая зависимость имеет место, если потенциал спаривания А мал но сравнению с ftAt/f- Отме-
Отметим, что роль характерной энергии играет величииа А/т/( (а не 4
Тем не менее, несмотря на отсутствие энергетической щели,
материал остается сверхпроводящим. Например, путем непосред-
непосредственного вычисления можно показать, что экранирующие токи в об-
образце, вызванные приложенным полем Н, отличны от нуля и имеют
обычную величину порядка ~ Л2.

Эффекты в сильных магнитных полях и роль примесей 267
Это замечательное явление „бесщелевой сверхпроводимости" имеет
место, однако, лишь в узкой области значений А, в которой ряд
теории возмущений сходится (а именно при Лт^/й < 1). При воз-
возрастании А щель появляется снова. Сказанное можно пояснить с по-
помощью диаграммы, на которой по оси абсцисс отложена величина hjxK
(т. е. величина взаимодействия), а по оси ординат—температура
(см. фиг. 68). На этой диаграмме имеются три области: нормальная
область (N), область бесщелевой сверхпроводимости (Sj) и область
обычной сверхпроводимости со щелью (S2). Граница между N и Sl
описывается универсальной функцией (8.26'). Граница между Sx и S2
находится гораздо сложнее (на нашем языке для этого надо сумми-
суммировать весь ряд теории возмущений по А).
В настоящее время имеется ряд Опытных данных, свидетельствую-
свидетельствующих в пользу существования области 5, в магнитных сплавах (см.,
например, работы Райфа и Вулфа [132, 133], в которых с помощью
туннельной методики изучался подвергнутый зэкалке твердый раствор
InFe). К сожалению, в области х (T^JEp) ~ kBTc, представляющей
наибольший интерес, спины примесей быстро прецессируют в резуль-
результирующем обменном поле, что сильно усложняет анализ любых
опытных данных, полученных на магнитных сплавах. Область S1
должна также проявляться при измерениях на сверхпроводящих кол-
коллоидальных частицах и тонких пленках в магнитном поле, парал-
параллельном их плоскости. Однако здесь также имеются трудности, вы-
вызванные значительными погрешностями при определении размеров
малых образцов, от которых зависит величина т^-1). Чтобы иметь
возможность наблюдать область S,, величина хк должна фиксиро-
фиксироваться с точностью до нескольких процентов, что выходит за пре-
пределы современных возможностей. Более реальные примеры бесщеле-
бесщелевой сверхпроводимости приводятся в § 3, где рассматривается случай,
когда величина | А | может зависеть от пространственных координат.
§ 3. „ГРЯЗНЫЙ" СВЕРХПРОВОДНИК В СИЛЬНОМ
МАГНИТНОаМ ПОЛЕ
Рассмотрим теперь „грязный* сплав, в котором имеются только
немагнитные примесные атомы. Точнее говоря, будем считать, что
длина свободного пробега / меньше длины когерентности Е^ =
= G,\%(pVp4iBTc) и, кроме того, меньше любого размера образца d.
Предположим также, что образец (произвольной формы) вдоль всей
поверхности покрыт изолятором, так что ни в одной точке он не
'). Обычно к указываемым в эксперименгальных работах размерам ма-
малых образцов нужно относиться с известной осторожностью. Например,
„пленка толщиной 500 А* обычно представляет собой весьма неравномерный
слой с шероховатостями порядка 100 А или более.
18*

268 Глава VIII
находится в контакте с нормальным металлом. Относительно зави-
зависимости амплитуды | А | от координат мы не будем делать никаких
конкретных допущений.
Покажем сейчас, что при сделанных предположениях интеграль-
интегральное уравнение G.8) можно заменить дифференциальным уравнением
второго порядка, которое является обобщением линеаризованного
уравнения Гинзбурга — Ландау на любые температуры. Такое
упрощение возможно главным образом потому, что транспортные
свойства нормального металла описываются дифференциальным урав-
уравнением второго порядка типа диффузионного уравнения.
Согласно (8.1) — (8.5), ядро К (г,, г2) уравнения G.8) связано
простым образом с функцией корреляции /(г,, г2; С), Нетрудно
получить дифференциальное уравнение, которым описывается функция /
в предельном случае очень „грязного" сплава. Рассмотрим для этого
два близких момента времени ^>0 и t~\-z (разность е мала). За
время е частица в процессе диффузии перемещается из точки г' (где
она находилась в момент времени t) в точку г,. Поскольку расстоя-
расстояние между г, и г' мало, для приращения фазы Аф оператора K(t)
можно написать
По определению,
/(IV г2; г-М)= j cPr'f(rr, r2; fJl(Tv г'|е)е'Дф, (8.31)
где 3 (rj, г' | е) — функция источника. Она описывает распределение
частиц, находившихся первоначально в точке rv по прошествии вре-
времени е и удовлетворяет диффузионному уравнению
с начальным условием
Нш^(г1, г/|е) = б(г1 — г')
р.->о
и условием (S/'3>)n = 0 на поверхности образца. Например, в случае
неограниченной среды эта функция имеет вид
,, , 1 -In-!-' |2/4?>е
Разложив функцию /(г', г2; 0 в ряд Тейлора вблизи точки г,,
выделив обычным образом в уравнении (8.31) члены первого порядка
по е (напомним, что I гж — г' р — е) и приравняв соответстующие коэф-
коэффициенты с обеих сторон, получим искомое дифференциальное урав-
уравнение
^ (^J г2; 0 при *>0. (8.32)

Эффекты в сильных магнитных полях и роль примесей 269
Соответственно граничное условие на поверхности образца прини-
принимает вид
^^)/ = 0. (8.33)
где п — единичный вектор нормали к поверхности. Наконец, при t->0
функция / должна переходить в б-функцию от координат (с соответ-
соответствующим нормировочным множителем). Исходя из определения (8.2),
легко видеть, что
/(г,. г2; 0) = 7--16(r2-r1), (8.34)
где 7"—объем образца.
Предположим теперь, что нам известна система нормированных
собственных функций gp(r) линейного оператора в правой части (8.32)
/ 2le Y еР
— D\V —Aj gp(r)=-f gp{r) (8.35)
с граничным условием (8.33). Разложим б-функцию в (8.34) в ряд
по функциям g; тогда для t > О получим
/(гг r2; ^) = ^-1S<(r2)^(r1)e-V/ft. (8.36)
Подставляя (8.36) в (8.1) и интегрируя по t, находим
со р
С помощью (8.37) исходному уравнению (8.8) можно придать вид
Собственными функциями этого линейного интегрального уравнения
относительно Д, очевидно, служат функции g. Действительно, положим
в уравнении (8.38) Л-(г) = g"? (г); тогда вследствие условия ортого-
ортогональности функций g в сумме по р отличен от нуля единственный
член с p — q и уравнение (8.38) удовлетворяется, если выполнено
условие
^ (8-39)
Используя определение универсальной функции Un (л:) [см. (8.26) и
(8.26')]. решение уравнения (8.39) запишем в уже знакомом нам виде

270 Глава VIII
При фиксированном значении поля И и заданной форме образца ве-
величины Eq также фиксированы [в принципе их можно вычислить, ре-
решив уравнения (8.35), хотя этот расчет довольно трудоемок]. Обычно
интерес представляет наиболее высокая температура Т (для заданной
величины поля И), при которой уравнение (8.38) имеет нетривиальное
решение. Поскольку функция Un(x) является монотонно убывающей,
ясно, что это решение должно отвечать наименьшему собственному
значению еи.
Расчет поля, при котором в „грязном" образце произвольной формы
впервые образуется сверхпроводящий зародыш, производится следую-
следующим образом. В первую очередь необходимо решить уравнения (8.35)
и (8.33) и найти наименьшее собственное значение е0 как функ-
функцию поля И. Тогда интересующая нас величина поля образования за-
зародыша И* при заданной температуре Т может быть легко получена
из соотношения
(8.40)
Задача. Вывести формулу для критического поля Нс2 „грязного" сверх-
сверхпроводника, пригодную при любых температурах [127, 129, 134, 135].
Решение. Уравнение (8.35) имеет вид уравнения Шредингера для ча-
частицы с массой h/2D и зарядом 2е в магнитном поле И. Циклотронная ча-
частота движения такой частицы определяется соотношением
™С ск Фо
где 0о — квант потока. Наинизшее собственное значение равно
Полагая в (8.40) П* = НС2 и используя соотношение f0 — Un(T'Tc), придем
к следующему уравнению:
1п-^=-фD-)- /! ш''~
Чтобы решить это уравнение, рассмотрим сначала температуры Т, близ-
близкие к Тс. В этом случае поле И'с2 мало и для LJn (x) можно использовать
разложение (8.27). При этом получаем
н _ кв{Тст)Фа
Л^ЛБ ->'?•
Легко проверить, что это согласуется с выражением Гинзбурга — Ландау
Нс2 = у. YiHc, если в него подставить значение к G.47), полученное Горь-
ковым [115] для предельного случая „грязного" сверхпроводника,
?./ @)
к = 0,75 —f— при /
С другой стороны, при Т = 0
Ч-xhDH
^—-2. = *вГси„@)=1,7

Эффекты в си 1ьных магнитных полях ч роль примесей 271
Напишем также выражение для критического поля Нс0 массивного сверх-
сверхпроводника (H*vJ8n = N @) AJo/^) в виде
Сравнивая эти два выражения, находим
Ь/^га 2 / /
Таким образом, отношение Hci'\r2Hc возрастает всего лишь на 2096
при изменении температуры от Т = Тс до Т = 0. Аналогичные вычисления
показывают, что для плоской границы отношение ИсЪ\НЛ остается равным 1,69
при всех температурах. Кроме того, если поле И составляет угол 8 с поверх-
поверхностью образца, форма угловой зависимости Нсз (9)/Яс2 @) тоже не зависит
от температуры. Все эти выводы подтверждаются экспериментально. Заметим,
что факт применимости линеаризованной теории Гинзбурга — Ландау к опи-
описанию .грязных" сплавов при низких температурах является довольно не-
неожиданным.
Дальнейший анализ для температур, лежащих
Теорема о локальной немного ниже температуры перехода Г*, мо-
плотности состоянии ' J' v
жно провести совершенно аналогично тому,
как это делалось в § 2. В частности, мы можем вычислить плотность
состояний Ns(r, е) для возбуждений с энергией е. Прежде всего, по-
поскольку параметр А (г) теперь меняется в пространстве, плотность со-
состояний, очевидно, зависит от положения точки наблюдения г'). Кон-
Конкретный расчет [127] показывает, что во втором порядке по | А | функ-
функция Ns(r, е) обладает следующими простыми свойствами.
1. Плотность состояний Ns(r, e) в точке г зависит лишь от зна-
значения А (г) в той же точке. Такая локальная связь на первый взгляд
представляется удивительной, поскольку в исходном выражении вели-
величина Ns(r, е) в точке г зависит от значений А(г'). где точка г' на-
находится от г на расстоянии порядка 1G/). Это объясняется следующим
образом. Вблизи температуры перехода функция А (г) имеет простой
вид, а именно пропорциональна собственной функции go(r) уравне-
уравнения (8.35). Благодаря этому мы можем выполнить интегрирование в вы-
выражении для Ns(r, е), так что окончательный результат оказывается
зависящим лишь от А (г).
2. Явный вид N4(r, е) дается выражением (8.30), в котором под
величиной А нужно понимать локальное значение параметра А(г).
Кроме того, фигурирующий в этой формуле параметр hjxK в данном
случае равен е0; его зависимость от температуры описывается фор-
формулой (8.40). Следовательно, в рассматриваемой области [Атк-//г<^1,
т. е. (//* — H)jH* <С[ 1], „грязный" сплав всегда является бесще-
бесщелевым сверхпроводником. Это предсказание теории было подтверждено
') Зависимость Ns (г) непосредственно может быть измерена на опыта
с помощью туннельной методики.

272 Глава VIII
в недавних туннельных экспериментах Гийона и др. [124] на различных
сплавах в области полей от W^//с2 До Нс3. В частности, было пока-
показано, что интервал энергий (в единицах h/xK = eQ), в пределах кото-
которого плотность состояний отличается от ее величины Л/ @) в нормаль-
нормальном состоянии, имеет конечную ширину даже при очень малых значениях
параметра порядка А (г) (т. е. при полях //, весьма близких к полю//*).
Фактически такие измерения позволяют довольно точно определить па-
параметр хк. В заключение отметим, что частые сверхпроводники вто-
второго рода также, строго говоря, являются бесщелевыми в поле Н >//с]
(см. задачу на стр. 156).
ЛИТЕРАТУРА
Роль магнитных примесей и бесщелевая сверхпроводимость
Теория
А б р и к о с о в А. А., Г о р ь к о в Л. П., ЖЭТФ, 39, 1781 A960).
Эксперимент
Woolf M. A., Reif F., Phys. Rev., A137, 557 A965).
Явления в сильном магнитном поле
Теория
Maki К., Physics, 1, 21, 127 A964).
D e G e n n e s P. G., T i n k h a m M., Physics, 1, 107 A964).
De Gennes P. G., Phys. Kond. Materie, 3, 79 A964).
Эксперимент
Guy on E., Adv. Phys., 15, 417 A966).

БИБЛИОГРАФИЯ ')
Обзоры и монографии
London F., Superfluids, vol. I, New York, 1950.
Шенберг Д., Сверхпроводимость, ИЛ, 1955.
Боголюбов Н. Н., Толмачев В. В., Ширков Д. В., Новый метод в
теории сверхпроводимости, изд-во АН СССР, 1958.
Физика низких температур, сб. статей, ИЛ, 1959.
Бардин Дж., Ш р и ф ф е р Дж., Новое в изучении сверхпроводимости, М.,
1962.
Л и н т о и Э., Сверхпроводимость, изд-во «Мир», 1964.
Lynton E. A., Superconductivity, 2d ed., London, 1965.
В 1 a 11 J. M., Theory of Superconductivity, New York, 1964.
Schrieffer J., Theory of Superconductivity, New York, 1964. (Готовится
русский перевод.)
T i n k h a m M., Superconductivity, New York, 1965.
Quantum Fluids, ed. D. F. Brewer, Amsterdam, 1966.
Дуглас Д., Ф а л и к о в Л., Энергетическая щель в сверхпроводниках, в сб.
«Сверхпроводимость», М., 1967.
Жарков Г. Ф., Туннельный эффект Джозефсона в сверхпроводниках, в сб.
«Сверхпроводимость», М., 1967.
Goodman В. В., Туре II Superconductors, Report on Progress in Physics,
vol. 29, London, 1966, Pt. 2.
Saint-James D., Sarma Q., Thomas E. J., II Type Superconductivity,
London, 1968.
Цитированная литература
1. Kammerlingh Onnes H., Commun. Phys. Lab. Univ. Leiden.,
No. 119b, 120b, 122b, 124c A911).
2*. M a 11 h i a s В. Т. et al., Science,' 156, 645 A967).
3*.Schooley J. F, Hosier W. R., Cohen M. L., Phys. Rev. Lett., 12,
474 A964).
4*. School ey J. F., Hosier W. R., Ambler E., Becker J. H., Co-
hen M. L., Koonce С S., Phys. Rev. Lett., 14, 305 A965).
5. London H., London F., Proc. Roy. Soc, A149, 71 A935).
6. London H., London F., Physica, 2, 341 A935).
7. Meissner W., Ochsenfeld R., Naturwiss., 21, 787 A933).
8. Ландау Л. Д., Лифшиц Е. М., Электродинамика сплошных сред,
М., 1959.
9. Douglass D. Н., Jr., F а 1 i с о v L. М., в книге Low Temperature
Physics, ed. C. J. Gorter, vol. IV, Amsterdam, 1964. (Имеется перевод
в сб. «Сверхпроводимость», М., 1967.)
') Составлена переводчиком. Библиография содержит: а) работы, цити-
цитируемые автором в тексте книги, б) работы, упомянутые автором без указа-
указания точных библиографических данных, в) работы, цитированные в приме-
примечаниях редактора перевода (отмечены звездочкой), — Прим, ред%

274 Библиография
10 Р i р р а г d А. В., Proc. Roy. Soc, A2I6, 547 A953).
11. Pippard А. В., Physica, 19, 765 A953).
12*. Физика низких температур, сб. статей, ИЛ, 1959.
13. Sarachik M. P., Qarvin R. L., Erlbach E., Phys. Rev. Lett., 4,
52 A960).
14. Casimir H. В. Q., Physica, 7, 887 A940).
15. Шальников А. И., Шарвин Ю. В., ЖЭТФ. 18, 102 A948).
16. В а г d e e n J., Schricffer J. R., в книге Low Temperature Physics,
ed. C. J. Gorter, vol. Ill, Amsterdam, 1961. (Имеется перевод: Дж. Бар-
Бардин, Дж. Ill рифф ер, Новое в изучении сверхпроводимости, М., 1962.)
17. D range id К. Е., SommerhalderR., Phys. Rev. Lett., 8, 467 A962).
18. Drangeid К. Е., Sommerhalder R., IBM Journ., 8, 13 A964).
19. Peierls R., Proc. Roy. Soc, A155, 613 A936).
20. London F., Physica. 3, 450 A936).
21. London F., Superfluids, vol. I, New York, 1950.
22. В u с k D. A., Proc. IRE, 44, 482 A956).
23. Ланд а у Л. Д., ЖЭТФ, 7, 371 A937).
24*.Лифшиц Е. М., Шарвин Ю. В., ДАН СССР, 79, 783 A951).
25. Мешков с кий А. Г., Шальников А. И., ЖЭТФ, 17, 851 A947).
26. S с h a w 1 о w A. L., Matthias В. Т., Lewis H. W., Devlin Q. Е.,
Phys.'Rev., 95, 1344 A954).
27*. Б а л а ш о в а В. М., Ш а р в и н Ю. В., ЖЭТФ, 31, 40 A956).
28. Faber Т. Е., Proc. Roy. Soc, A248, 460 A958).
29*. Sarma N. V., Moon J. R., Phys. Lett., A24, 580 A967).
30. De Sorb о W., Phys. Rev. Lett., 4, 406 A960).
31. Ландау Л. Д., ЖЭТФ, 13, 377 A943).
32. Шубников Л. В., X о т к е в и ч В. И., Шепелев Ю. Д., Р я б и-
нин Ю. Н., ЖЭТФ, 7, 221 A937).
33. Абрикосов А. А., ЖЭТФ, 32, 1442 A957).
34. Goodman В. В., IBM Journ., 6, 63 A962).
35. Goodman В. В., Rev. Mod. Phys., 36, 12 A964).
36. McConville Т., Serin В., Phys. Rev. Lett., 13, 365 A964).
37. McConville T, Serin В., Rev. Mod. Phys., 36, 112 A964).
38*. F e r r e i r a da S i I v a J., В u r g e m e i s t e r E. A., D о к о р о u 1 Z.,
Phys. Lett., A25, 354 A967).
39. О n s a g e r L-, Nuovo Cim., 6, 249 A949).
40. F e у n m a n R. P., в книге Progress in Low Temperature Physics ed.
С J. Gorter, vol. I, Amsterdam, 1955, ch. II.
41. Morse P., Feshbach H., Methods of Theoretical Physics, New York,
1953, ch. 10. (Имеется перевод: Ф. Морс, Г. Ф е ш б а х, Методы тео-
теоретической физики, ИЛ, 1960, гл. 10.)
42. Pearl J., Appl. Phys. Lett., 5, 65 A964).
43. Matricon J., Phys. Lett., 9, 289 A964).
44. Kleiner W. H., R о t h L. M., A u 11 er S. H., Phys. Rev., A133,1226 A964).
45. Joiner W. С. Н., Blaugher R. D., Rev. Mod. Phys., 36, 67 A964).
46. С r i b i e r D., J а с г о t В., Rao L. M., F а г п о u x В., Phys. Lett., 9,
106 A964).
47. С r i b i e r D., J а с г о t В., F а г п о u x В., Rao L. M., Joura Appl.
Phys., 37, 952 A966).
48. Pincus P., Gossard A. C, Jaccarino V., Wernick J H.,
Phys. Lett., 13, 21 A964).
49*. Шмидт В. В., ЖЭТФ, 46, 649 A964).
50. Gossard А. С, Jaccarino V., Wernick J. H., Journ. Appl Phys.,
36, 1190 A965).
51. Abraham A., Principles of Nuclear Magnetism, London, 1961. (Имеет-
(Имеется перевод: А. Абрагам, Ядерный магнетизм, ИЛ, 1963.)

Библиография 275
52. Caroli С, Ma trie on J., Phys Kond. Materie, 3, 380 A965).
53. Bean C. P., Livingston J. D., Phys. Rev. Lett., 12, 14 A964).
54. De Qennes P. G., Solid State Comm., 3, 127 A965).
55. Joseph A. S., Tomasch W. J., Phys. Rev. Lett., 12, 219 A964).
.56. De Blois R. W., De Sorbo W., Phys. Rev. Lett., 12, 499 A964).
J57. De Qennes P. Q., Matricon J., Rev. Mod Phys., 36, 45 A964).
58. Kim J. В., H e m p s t e a d С R, S t г п a d A. R.. Phys. Rev., A139,
1163 A965).
59. Bean С. Р., Phys. Rev. Lett., 8, 250 A962).
60. BeanC. P., Rev. Mod. Phys., 36. 31 A964).
61. Anderson P. W., Kim V. В., Rev. Mod. Phys.. 36, 39 A964).
62. Cooper L. N.. Phys. Rev., 104, 1189 A956).
63. Schiff L. I., Quantum Mechanics, 2d ed., New York. 1955, ch. 9.
(Имеется перевод: Л. Ill и ф ф. Квантовая механика, ИЛ. 1958, гл. 9.)
64 Frolich H., Phys. Rev., 79, 845 A950). (Имеется перепоя в сб. «Тео-
«Теория сверхпроводимости», ИЛ, 1960, г.тр. 11.)
65. Pines D., Phys. Rev., 109, 280 A958). (Имеется перевод в сб. «Теория
сверхпроводимости», ИЛ, 1960, стр. 186.)
66 В а г d e e n J., P i n e s D., Phys. Rev., 99, 1140 A955)
67. Pines. D., The Many Body Problems, New York, 1961. (Имеется пере-
перевод: Д. Пайнс, Проблема многих тел, ИЛ, 1963.)
68. Maxwell E., Phys. Rev., 78, 477 A950).
69. Reynolds С. A., Serin В., Wright W. П., Nesbitt L В.,
Phys. Rev., 78, 487 A950).
70 Morel P., Anderson P. W., Phys. Rev., 125, 1263 A962)
71. Pines D., Elementary Excitations in Solids, New York, 1963. (Имеется
перевод: Д. Пайнс, Элементарные возбуждения в твердых телах,
изд-во «Мир», 1965.)
72. Ландау Л. Д., Лифшиц Е. М.. Квантовая механика, М., 1963.
73. Bardee'n J., Cooper L. N.. Schrieffer J. R.. Phys. Rev., 108,
1175 A957). (Имеется перевод в сб. «Теория сверхпроводимости», ИЛ,
1960, стр. 103.)
74 Б о г о л ю б о в Н. Н., ЖЭТФ. 34, 58 A958).
75* Боголюбов Н. Н., Толмачев В. В., Ширков Д. В., Новый ме-
метод в теории сверхпроводимости, изд-во АН СССР, 1958.
76 V а 1 a t i n J. G., Nuovo Cim, 7, 843 A958).
77. Giaever I., Phys. Rev. Lett., 5, 147; 6, 464 A960).
78. JosephsonB., Phys. Lett., 1, 251 A962).
79. Anderson P. W., Rowel 1 J., Phys. Rev. Lett, 10, 230 A963).
80. Ferrel R. A., Prange R., Phys. Rev. Lett., 10, 479 A963).
81. Garland J. W., Phys. Rev. Lett., 11, 111, 114 A963).
82. Morse R. W., IBM Journ., 6, 58 A962).
83 Hebel L. C, Slichter С. Р., Phys. Rev.. 107, 401 A957).
84. M a s u d a Y., R e d f i e I d A. G., Phys. Rev., 125. 159 A962).
85. Боголюбова H,»H, 67, 549 "A959).
86. Cyrot M., Phys. Kond. Materie. 3, 374 A965).
87. Doll R., Nabauer M.. Phys. Rev. Lett, 7, 51 A961)
88. Deaver B. S., Fair bank W. M., Jr., Phys. Rev. Lett, 7, 43 A961).
89. Bronig W., Phys. Rev. Lett., 7, 337 A961).
90. Caroli C, De Gen nes P. G., Matricon J., Phys. Lett., 9,307 A964).
91*. Абр и к ос о в А. А., Горько в Л. П., Дзялошинский И. Е., Ме-
Методы квантовой теории поля в статистической физике, М., 1962.
92 Caroli С, De Gennes Р. С, Matricon J, Journ. Phys. Rad.. 23.
707 A962). (Имеется перевод в книге «Строение металлических твердых
растворов», М., 1966.)
93 Anderson P. W., Journ, Phys. Chem. Solids, 11, 26 A959).

276 Библиография
94. Rickaysen Q., Phys. Rev., 115, 795 A959).
95. P i p p a r d А. В., Adv. Electronics, ed. L. Morton, vol. 6, New York, 1954.
96*.Mattis D. C, Bardeen J., Phys. Rev., Ill, 412 A958). (Имеется
перевод в сб. «Теория сверхпроводимости», ИЛ, 1960, стр. 172.)
97. Ландау Л. Д., Лифшиц Е. М., Статистическая физика, М., 1964.
98. Г и н з б у р г В. Л., Ландау Л. Д., ЖЭТФ, 20, 1064 A950).
99. Гинзбург В. Л.. ДАН СССР, 118, 464 A958).
100. Bremer J. W., Newhouse V. L., Phys. Rev., 116, 309 A959).
101. L i 111 e W. A., P a r k s R, D., Phys. Rev. Lett, 9, 9 A962).
102. P a r k s R. D., L i 111 e W. A., Phys. Rev., A133, 97 A964).
103. Tinkham M., Phys. Rev., 129, 2413 A963).
104. Ti nkh am M., Rev. Mod. Phys., 36, 268 A964).
105*. Гинзбург В. Л., ЖЭТФ, 42, 299 A962).
106. Гизбург В. Л., ДАН СССР, 83, 385 A952).
107. Г и н з б у р г В. Л., ЖЭТФ, 34, 113 A958).
108. Douglass D. H., Jr., Phys. Rev. Lett, 6, 346; 7, 14 A961).
109. DouglassD. H., Jr., IBM Joura, 6, 44 A962).
110. Saint-James D., De Qennes P. G., Phys. Lett, 7, 306 A963).
111. Burger J. P., Detscher Q., Guyon E., Martinet A., Solid
State Comm., 2, 101 A964).
112. Burger J. P., Deutscher Q., Guyon E., Martinet A., Phys.
Rev., A137, 853 A965).
113. Faber T. E., Proc. Roy. Soc, A214, 392 A952); A241, 531 A957).
114. К ins el Т., Lynton E. A., Serin В., Phys. Lett, 3, 30 A962).
115. Горькое Л. П., ЖЭТФ, 36, 1918; 37, 1407 A959).
116. Chiou С, Connell R. A., Seraphim D. P., Phys. Rev., 129, 1070
A963).
117. Olsen J. L, Electron Transport Properties in Metals, New York, 1962,
p. 80.
118*.3айцев Р. О., ЖЭТФ, 48, 644, 1759 A965); 50, 1055 A966).
119. De Gennes P. G., Matricon J., Solid State Comm., 3, 151 A965).
120. FiskeM, Rev. Mod. Phys., 36, 221 A964).
121. R о well J., Phys. Rev. Lett, 11, 200 A963).
122. Jackie vie R., Lambe J., Silver A., Mercer eau J., Phys. Rev.
Lett., 12, 159 A964).
123. Matthias В. Т., IBM Journ., 6,250 A962).
124. G u у о n E., Martinet A., Matricon J., P i n с u s P., Phys Rev.,
A138, 746 A965).
125. Абрикосов А. А., Гор ь ков Л. П., ЖЭТФ, 39, 1781 A960).
126. De Gennes P. G., Tinkham M., Physics, 1, 107 A964).
127. De Gennes P. G., Phys. Kond. Materie, 3, 79 A964).
128*. Шаповал Е. А., ЖЭТФ, 47, 1007; 49, 930 A965).
129. Maki K.. Physics, 1, 21, 127 A964). Erratum: Carol i C, Cyrot M.,
De Gennes P. G., Solid State Comm., 4, 17, A966).
130. R u d e r m a n M. А., К i 11 e 1 C, Phys. Rev., 96, 99 A954).
131. Kondo J., Progr. Theor. Phys., 33, 575 A965).
132. Reif F., Woo If M. A., Phys. Rev. Lett, 9, 315 A962).
133. Woo If M. A., Reif F., Phys. Rev., A137, 557 A965).
134. Helfand E., Werthamer N. R., Phys. Rev. Lett, 13, 686 A964).
135*.Helfand E., Werthamer N. R., Phys. Rev., 147, 288 A966).
136*. S arm a N. V., Phys. Lett, A25, 315 A967).
137. В u cher E., Heiniger F., MOller J., Phys. Kond. Materie, 2, 210
A964).
138. Труды X Международной конференции по физике низких температур, М.,
1967.
139*. А б р и к о с о в А. А., ЖЭТФ. 47, 720 A964).

ОГЛАВЛЕНИЕ
От редактора перевода 5
Предисловие 7
Глава 1. фундаментальные свойства 9
§ 1. Новый тип конденсированного состояния 9
§ 2. Диамагнетизм 11
Уравнение Ф. и Г. Лондонов 11
Эффект Мейсснера 12
§ 3. Отсутствие возбуждений малых энергий 15
§ 4. Два типа сверхпроводников 19
Литература , 21
Глава II. Магнитные свойства сверхпроводников первого рода ... 22
§ 1. Критическое поле длинного цилиндра 22
§ 2. Глубина проникновения 25
Связь между током и полем в сверхпроводниках первого рода 25
•Глубина проникновения 27
Методы измерения глубины проникновения 29
Обсуждение 31
Проникновение поля в чистые металлы при абсолютном
нуле C1). Обобщение на случай сплавов C2). Изменение
глубины проникновения с температурой C3).
§ 3. Магнитные свойства образцов произвольной формы. Проме-
Промежуточное состояние 34
Происхождение промежуточного состояния 34
Некоторые термодинамические соотношения 37
Определение свободной энергии C7). Определение индук-
индукции C7). Определение напряженности магнитного поля
Н C8).
Термодинамический потенциал для фиксированных значений
Т и % 40
Связь между В и Н в промежуточном состоянии 40
Применения 42
Критический ток в сверхпроводящей проволоке D3).
Принцип криотрона D4).
Микроскопическая структура промежуточного состояния ... 45
Парадокс D9). Природа поверхностной энергии D9).
Литература 52

278 Оглавление
Глава III. Магнитные свойства сверхпроводников второго рода ... 53
§ 1. Кривые намагничивания длинного цилиндра 53
§ 2. Микроскопическое описание вихревого состояния . . . . ¦ 59
Отрицательная позерхностная энергия 59
Свойства изолированной вихревой нити 62
Обсуждение формулы C.39) F4).
Взаимодействие вихревых нитей 67
Случай двух нитей F7). Кривые намагничивания F9).
Нижнее поле Hci G0). Поле, немного превышающее
НсХ G0). Область \/l?<€inL<€^/l2 <73)- Область
лА~Г2 G5).
Движение вихревых нитей 83
§ 3. Неравновесные свойства 85
Критическое состояние при абсолютном нуле 86
Движение вихревых нитей при Т Ф 0 92
Заключительные замечания (95).
Литература 95
Глава IV. Описание конденсированного состоянии 95
§ 1. Неустойчивость нормального состояния при нашччи протя-
протяжения между частицами Ьб
§ 2. Природа притяжения 99
Квантовомеханическое описание 99
Описание с помощью диэлектрической проницаемости .... 101
Модель «желе» A02).
Численные значения констант взаимодействия 105
§ 3. Основное состояние и элементарные возбуждения 107
Выбор .фобной волновой функции 107
Алгебраические преобразования 108
Определение энергии основного состояния 111
Низшие возбужденные состояния 117
Случай двух связанных сверхпроводников 120
§ 4. Вычисления при конечных температурах 124
Определение свободной энергии 124
Изменение щели с температурой и точка перехода 126
Изотопический эффект A28). Учет кулоновского оттал-
отталкивания A28).
Вычисление термодинамических величин 131
Формулы для вероятностей переходов 133
Применения A37).
Литература 139
Глава V. Метод самосогласованного пола 140
§ 1. Уравнения Боголюбова 140
Определение эффективных потенциалов 142
Уровни энергии эффективного гамильтониана 142
Выбор потенциалов t/иД 144

Оглавление 279
§ 2. Некоторые теоремы о потенциале спаривания и спектре воз-
возбуждений 148
Градиентная инвариантность .'.'.' 148
Специальные выборы калибровки A50).
Квантование потока 15Q
Край спектра возбуждений в неоднородных системах . . . 157
Немагнитные сплавы. Теорема Андерсона 159
§ 3. Эффект Мейсснера в металлах и сплавах 161
Учет магнитного поля как возмущения _ igi
Связь диамагнитного отклика с проводимостью системы
в нормальном состоянии 164
Расчет диамагнитных токов 168
Литература 171
Глава VI. Феноменологические уравнения Гинзбурга — Ландау . . . 172
§ 1. Введение 172
§ 2. Построение свободной энергии . ' 173
§ 3. Уравнения равновесия 177
§ 4. Две характерные длины 178
§ 5. Задачи с постоянным значением амплитуды параметра по-
порядка |*| 183
Критический ток в тонкой пленке 181
Эффект Литтла и Паркса 187
Пластина в параллельном поле 190
§ 6. Изменение амплитуды | * | в пространстве 196
Образование зародышей внутри массивного образца . . . • . 196
Образование зародышей вблизи поверхности образца .... 197
§ 7. Структура смешанного состояния в сильных полях Н -~>//с2 203
Литература 210
Глава VII. Микроскопический анализ уравнений Гинзбурга—Ландау 211
§ 1. Линеаризация уравнения самосогласованности 211
Учет А по теории возмущений 211
Выделение магнитных эффектов 213
Бесконечная однородная среда 215
Связь ядра Ко с функцией корреляции 215
Явное выражение для ядра Ко ¦ ¦ ¦ 217
§ 2. Уравнения Гинзбурга — Ландау 220
Введение нелинейных членов в уравнение самосогласованности 220
Гипотеза о медленности изменений 221
Обсуждение коэффициентов 222
§ 3. Поверхностные задачи и уравнения Гинзбурга — Ландау . . 227
Граничные условия на поверхности раздела 227
Контакт сверхпроводника с диэлектриком (или вакуумом) 230
Контакт между сверхпроводником и нормальным металлом 232
Контакт S — N—S' 234
Микроскопический ра.чет Мц для диэлектрического слоя
B39). Распределение полей и токов в области контактаB41).
Литература 246

280 Оглавление
Глава VIII. Эффекты в сильных магнитных полях и роль магнит-
магнитных примесей 247
§ 1. Температура перехода и свойства системы при обращении
времени 249
§ 2. Эргодическое и неэргодическое поведение. Бесщелевая сверх-
сверхпроводимость 255
Неэргодические системы 257
Эргодические (марковские) системы 259
Примеры «эргодических» систем B61).
Бесщелевая сверхпроводимость 265
§ 3. «Грязный» сверхпроводник в сильном магнитном поле . . . 267
Теорема о локальной плотности состоянии B71).
Литература 272
Библиография • ... 273
/7. ДЕ ЖЕН
Сверхпроводимость металлов и сплавов
Редактор И. Г. Нахимсон Художник Л. М. Муратова
Художественный редактор П. Ф- Иекупдэ Технический редактор Т. В. Чечик
Корректор К. Г. Кривда
Сдано в производство 22/ХП 1967 г. Подписано к печати 12/VI 1968 г. Бумага № i бОхЭО'/щ-
-8,75 бум. л. Печ. л. 17,50. Уч.-изд. л. 16,29. Изд. № 2/4505. Цена 1 р. 35 к. Зак. 1020.
ИЗДАТЕЛЬСТВО «МИР»
Москва, 1-й Рижский пер., 2
Ленинградская типография № 2 имени Евгении Соколовой Главполиграфпрома
Комитета по печати прн Совете Министров СССР. Измайловский проспект. 29,